code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/FeatureCollection/column_statistics_by_group.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/FeatureCollection/column_statistics_by_group.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=FeatureCollection/column_statistics_by_group.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/FeatureCollection/column_statistics_by_group.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The following script checks if the geehydro package has been installed. If not, it will install geehydro, which automatically install its dependencies, including earthengine-api and folium.
```
import subprocess
try:
import geehydro
except ImportError:
print('geehydro package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geehydro'])
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once.
```
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
# Load a collection of US census blocks.
blocks = ee.FeatureCollection('TIGER/2010/Blocks')
# Compute sums of the specified properties, grouped by state code.
sums = blocks \
.filter(ee.Filter.And(
ee.Filter.neq('pop10', {}),
ee.Filter.neq('housing10', {}))) \
.reduceColumns(**{
'selectors': ['pop10', 'housing10', 'statefp10'],
'reducer': ee.Reducer.sum().repeat(2).group(**{
'groupField': 2,
'groupName': 'state-code',
})
})
# Print the resultant Dictionary.
print(sums.getInfo())
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
# Making journal-quality figures using Matplotlib
```
import numpy as np
import pandas as pd
import seaborn as sns
sns.set(font_scale=1.4)
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.patches import ConnectionPatch
import matplotlib.gridspec as gridspec
from matplotlib import text
```
Let's begin by loading some data. We have two data frames that I've saved previously. They're columns are the exact same, except for those labeled ```r2``` -- the values of these columns depend on whether a previously fit linear transformation was univariate (1d) or multivariate (2d).
We'll start by loading the data, dropping unnecessary columns, renaming the columns of interest, and merging the two DataFrames.
```
data_dir = '/Users/kristianeschenburg/Desktop/Data/'
dim1_file = '%sConnectopy/Templated/FieldModeling/L.1D.ConnectopyMaps.Merged.csv' % (data_dir)
dim2_file = '%sConnectopy/Templated/FieldModeling/L.2D.ConnectopyMaps.Merged.csv' % (data_dir)
dim1_data = pd.read_csv(dim1_file, index_col=0)
dim1_data = dim1_data.rename(columns={'r2': 'r2_1d'})
dim1_data = dim1_data.drop(columns={'w_signal', 'signal', 'w_corr', 'distance', 'diameter'})
dim2_data = pd.read_csv(dim2_file, index_col=0)
dim2_data = dim2_data.rename(columns={'r2': 'r2_2d'})
dim2_data = dim2_data.drop(columns={'w_signal', 'signal', 'w_corr', 'distance', 'diameter'})
df = pd.merge(dim1_data, dim2_data, on=['source', 'target', 'subject', 'scale', 'sigma', 'cost', 'corr', 'dnorm'])
df = df[df['source'] != df['target']]
merged_GA = df.groupby(['source', 'target'], as_index=False).mean()
from scipy.stats import ttest_ind
ttest_map = {treg: {'tstat': None, 'pval': None} for treg in df.source.unique()}
tstats = []
pvals = []
for treg in df.source.unique():
T = T = ttest_ind(merged_GA[merged_GA['source'] == treg]['r2_2d'],
merged_GA[merged_GA['source'] == treg]['r2_1d'])
ttest_map[treg]['tstat'] = T[0]
ttest_map[treg]['pval'] = T[1]
tstats.append(T[0])
pvals.append(T[1])
d = pd.DataFrame({'region': df.source.unique(),
't': tstats,
'p': pvals})
df.head()
r2_diff = df.groupby(['source', 'target']).mean()[['r2_1d', 'r2_2d']].unstack()
```
Let's define the space over which we want to plot out data.
```
fig = plt.figure(constrained_layout=False, figsize=(18, 12))
gs = fig.add_gridspec(nrows=3, ncols=3, hspace=0.3)
ax1 = fig.add_subplot(gs[0, :-1]);
ax1.set_title('[0, :-1]', fontsize=20)
ax2 = fig.add_subplot(gs[1:, :-1]);
ax2.set_title('[1:, :-1]', fontsize=20);
ax3 = fig.add_subplot(gs[0, 2]);
ax3.set_title('[0, 2]', fontsize=20);
ax4 = fig.add_subplot(gs[1, 2]);
ax4.set_title('[1, 2]', fontsize=20);
ax5 = fig.add_subplot(gs[2, 2]);
ax5.set_title('[2, 2]', fontsize=20);
df
fig = plt.figure(figsize=(20, 20))
gs = fig.add_gridspec(nrows=3, ncols=3, hspace=1, wspace=0.15)
ax1 = fig.add_subplot(gs[0, :-1]);
g = sns.barplot('region', 't', data=d, alpha=0.75, );
ax1.tick_params(rotation=90, labelsize=10)
ax1.axhline(y=2.035, c='k', linestyle='--');
ax1.axhline(y=-2.035, c='k', linestyle='--');
ax1.axhline(y=0, c='k');
ax1.grid(True)
ax1.set_ylabel('t', fontsize=20)
ax1.set_xlabel('Source Region', fontsize=20)
ax1.set_title('Linearity as function of dimension\n2D > 1D', fontsize=20)
ax2 = fig.add_subplot(gs[1:, :-1]);
g = sns.heatmap(r2_diff['r2_2d'] - r2_diff['r2_1d'], cmap='seismic')
ax2.set_xlabel('Target Region', fontsize=15)
ax2.set_ylabel('Source Region', fontsize=15)
ax2.tick_params(labelsize=12)
ax2.set_title(r'2d-$R^{2}$ > 1d-$R^{2}$', fontsize=20);
ax3 = fig.add_subplot(gs[0, 2]);
ax3.set_title('[0, 2]', fontsize=20);
ax3.scatter(df['dnorm'], np.log(df['r2_1d']), marker='.');
ax4 = fig.add_subplot(gs[1, 2]);
ax4.set_title('[1, 2]', fontsize=20);
ax4.scatter(df['dnorm'], np.log(df['r2_2d']), marker='.');
ax5 = fig.add_subplot(gs[2, 2]);
ax5.set_title('[2, 2]', fontsize=20);
ax5.scatter(np.log(df['corr']), np.log(df['r2_2d']), c='k', marker='.', alpha=0.5);
ax5.scatter(np.log(df['corr'])+10, np.log(df['r2_1d']), c='r', marker='.', alpha=0.5);
```
|
github_jupyter
|
# <div align="center">BERT (Bidirectional Encoder Representations from Transformers) Explained: State of the art language model for NLP</div>
---------------------------------------------------------------------
<img src='asset/9_6/main.png'>
you can Find me on Github:
> ###### [ GitHub](https://github.com/lev1khachatryan)
BERT (Bidirectional Encoder Representations from Transformers) is a recent paper published by researchers at Google AI Language. It has caused a stir in the Machine Learning community by presenting state-of-the-art results in a wide variety of NLP tasks, including Question Answering (SQuAD v1.1), Natural Language Inference (MNLI), and others.
BERT’s key technical innovation is applying the bidirectional training of Transformer, a popular attention model, to language modelling. This is in contrast to previous efforts which looked at a text sequence either from left to right or combined left-to-right and right-to-left training. The paper’s results show that a language model which is bidirectionally trained can have a deeper sense of language context and flow than single-direction language models. In the paper, the researchers detail a novel technique named ***Masked LM (MLM)*** which allows bidirectional training in models in which it was previously impossible.
# <div align="center">Background</div>
---------------------------------------------------------------------
In the field of computer vision, researchers have repeatedly shown the value of transfer learning — pre-training a neural network model on a known task, for instance ImageNet, and then performing fine-tuning — using the trained neural network as the basis of a new purpose-specific model. In recent years, researchers have been showing that a similar technique can be useful in many natural language tasks.
A different approach, which is also popular in NLP tasks and exemplified in the recent ELMo paper, is feature-based training. In this approach, a pre-trained neural network produces word embeddings which are then used as features in NLP models.
# <div align="center">How BERT works</div>
---------------------------------------------------------------------
BERT makes use of ***Transformer***, an attention mechanism that learns contextual relations between words (or sub-words) in a text. In its vanilla form, ***Transformer includes two separate mechanisms*** — an ***encoder*** that reads the text input and a ***decoder*** that produces a prediction for the task. Since BERT’s goal is to generate a language model, only the encoder mechanism is necessary. The detailed workings of Transformer are described in a paper by Google.
***As opposed to directional models, which read the text input sequentially (left-to-right or right-to-left), the Transformer encoder reads the entire sequence of words at once. Therefore it is considered bidirectional, though it would be more accurate to say that it’s non-directional. This characteristic allows the model to learn the context of a word based on all of its surroundings (left and right of the word).***
The chart below is a high-level description of the Transformer encoder. The input is a sequence of tokens, which are first embedded into vectors and then processed in the neural network. The output is a sequence of vectors of size H, in which each vector corresponds to an input token with the same index.
When training language models, there is a challenge of defining a prediction goal. Many models predict the next word in a sequence (e.g. “The child came home from ... ”), a directional approach which inherently limits context learning. To overcome this challenge, BERT uses two training strategies:
# <div align="center">Masked LM (MLM)</div>
---------------------------------------------------------------------
Before feeding word sequences into BERT, 15% of the words in each sequence are replaced with a ***MASK*** token. The model then attempts to predict the original value of the masked words, based on the context provided by the other, non-masked, words in the sequence. In technical terms, the prediction of the output words requires:
* Adding a classification layer on top of the encoder output.
* Multiplying the output vectors by the embedding matrix, transforming them into the vocabulary dimension.
* Calculating the probability of each word in the vocabulary with softmax.
<img src='asset/9_6/1.png'>
The BERT loss function takes into consideration only the prediction of the masked values and ignores the prediction of the non-masked words. As a consequence, the model converges slower than directional models, a characteristic which is offset by its increased context awareness.
***Note:*** In practice, the BERT implementation is slightly more elaborate and doesn’t replace all of the 15% masked words:
Training the language model in BERT is done by predicting 15% of the tokens in the input, that were randomly picked. These tokens are pre-processed as follows – 80% are replaced with a **MASK** token, 10% with a random word, and 10% use the original word. The intuition that led the authors to pick this approach is as follows:
* If we used [MASK] 100% of the time the model wouldn’t necessarily produce good token representations for non-masked words. The non-masked tokens were still used for context, but the model was optimized for predicting masked words.
* If we used [MASK] 90% of the time and random words 10% of the time, this would teach the model that the observed word is never correct.
* If we used [MASK] 90% of the time and kept the same word 10% of the time, then the model could just trivially copy the non-contextual embedding
# <div align="center">Next Sentence Prediction (NSP)</div>
---------------------------------------------------------------------
In the BERT training process, the model receives pairs of sentences as input and learns to predict if the second sentence in the pair is the subsequent sentence in the original document. During training, 50% of the inputs are a pair in which the second sentence is the subsequent sentence in the original document, while in the other 50% a random sentence from the corpus is chosen as the second sentence. The assumption is that the random sentence will be disconnected from the first sentence.
To help the model distinguish between the two sentences in training, the input is processed in the following way before entering the model:
* A [CLS] token is inserted at the beginning of the first sentence and a [SEP] token is inserted at the end of each sentence.
* A sentence embedding indicating Sentence A or Sentence B is added to each token. Sentence embeddings are similar in concept to token embeddings with a vocabulary of 2.
* A positional embedding is added to each token to indicate its position in the sequence. The concept and implementation of positional embedding are presented in the Transformer paper.
<img src='asset/9_6/2.png'>
To predict if the second sentence is indeed connected to the first, the following steps are performed:
* The entire input sequence goes through the Transformer model.
* The output of the [CLS] token is transformed into a 2×1 shaped vector, using a simple classification layer (learned matrices of weights and biases).
* Calculating the probability of IsNextSequence with softmax.
When training the BERT model, Masked LM and Next Sentence Prediction are trained together, with the goal of minimizing the combined loss function of the two strategies.
# <div align="center">How to use BERT (Fine-tuning)</div>
---------------------------------------------------------------------
Using BERT for a specific task is relatively straightforward:
BERT can be used for a wide variety of language tasks, while only adding a small layer to the core model:
* Classification tasks such as sentiment analysis are done similarly to Next Sentence classification, by adding a classification layer on top of the Transformer output for the [CLS] token.
* In Question Answering tasks (e.g. SQuAD v1.1), the software receives a question regarding a text sequence and is required to mark the answer in the sequence. Using BERT, a Q&A model can be trained by learning two extra vectors that mark the beginning and the end of the answer.
* In Named Entity Recognition (NER), the software receives a text sequence and is required to mark the various types of entities (Person, Organization, Date, etc) that appear in the text. Using BERT, a NER model can be trained by feeding the output vector of each token into a classification layer that predicts the NER label.
In the fine-tuning training, most hyper-parameters stay the same as in BERT training, and the paper gives specific guidance (Section 3.5) on the hyper-parameters that require tuning. The BERT team has used this technique to achieve state-of-the-art results on a wide variety of challenging natural language tasks, detailed in Section 4 of the paper.
# <div align="center">Takeaways</div>
---------------------------------------------------------------------
* Model size matters, even at huge scale. BERT_large, with 345 million parameters, is the largest model of its kind. It is demonstrably superior on small-scale tasks to BERT_base, which uses the same architecture with “only” 110 million parameters.
* With enough training data, more training steps == higher accuracy. For instance, on the MNLI task, the BERT_base accuracy improves by 1.0% when trained on 1M steps (128,000 words batch size) compared to 500K steps with the same batch size.
* BERT’s bidirectional approach (MLM) converges slower than left-to-right approaches (because only 15% of words are predicted in each batch) but bidirectional training still outperforms left-to-right training after a small number of pre-training steps.
<img src='asset/9_6/3.png'>
# <div align="center">Conclusion</div>
---------------------------------------------------------------------
BERT is undoubtedly a breakthrough in the use of Machine Learning for Natural Language Processing. The fact that it’s approachable and allows fast fine-tuning will likely allow a wide range of practical applications in the future. In this summary, we attempted to describe the main ideas of the paper while not drowning in excessive technical details. For those wishing for a deeper dive, we highly recommend reading the full article and ancillary articles referenced in it. Another useful reference is the BERT source code and models, which cover 103 languages and were generously released as open source by the research team.
|
github_jupyter
|
# Customised Kernel of the ACBC (only trained with the score tensor generated from Integrated model.ipynb)
```
from sklearn.metrics import classification_report
class MyModel:
def __init__(self, w, lr):
self.w = w
self.size = w.shape[0]
self.lr = lr
def predict(self, x):
length = x.shape[0]
y_hat = np.zeros((length))
for i in range(length):
xi = x[i]
w_masked = np.array([0 if np.isnan(xi[j]) else self.w[j] for j in range(self.size)])
x_masked = np.array([0 if np.isnan(xij) else xij for xij in xi])
w_sum = np.sum(w_masked)
y_hat[i] = 0 if np.sum(x_masked * w_masked) / w_sum < 0.5 else 1
return y_hat
def GD_kernel(self, x,y):
x_checking = x[np.isnan(x)]
if x_checking.shape[0] == x.shape[0]:
return 0, np.repeat(0, 36)
W = self.w
w_masked = np.array([0 if np.isnan(x[i]) else W[i] for i in range(self.size)])
x_masked = np.array([0 if np.isnan(xi) else xi for xi in x])
wx = w_masked * x_masked
mask = np.array([0 if np.isnan(xi) else 1 for xi in x])
sum_w = np.sum(w_masked)
sum_wx = np.sum(wx)
p = sum_wx / sum_w
d_p = (x_masked*sum_w - sum_wx)/(sum_w**2) * mask
loss = (y*(1-p) + (1-y)*p)
gradients = -2*y*d_p + d_p
gradients = gradients * mask
label = 0.0 if p <0.5 else 1.0
label = 1 if label == y else 0
return label, gradients
def train(self,x,y,epochs):
length = x.shape[0]
prev_w = self.w
for i in range(epochs):
avg_loss = 0
gradients = np.zeros((length, self.size))
for j in range(length):
loss, g = self.GD_kernel(x[j], y[j])
if loss == 0:
gradients[i] = g
avg_loss += loss
gradient = np.sum(gradients, axis = 0)
self.w = self.w - gradient*self.lr
print(self.w)
print('acc in epoch',i,':',float(avg_loss)/float(length))
from sklearn import metrics
from sklearn.metrics import accuracy_score
import pandas as pd
vehicle_types = ['ZVe44', 'ZV573', 'ZV63d', 'ZVfd4', 'ZVa9c', 'ZVa78', 'ZV252']
def test_report(vehicle_type, train, test):
print(train.shape)
print('summary of test accuracy for vehicle type:', vehicle_type)
model = MyModel(np.ones((36)),0.0002)
model.train(train[:, 0:36], train[:,36],10)
scores = model.predict(test[:,0:36])
print(scores.shape[0])
print(scores[scores==1].shape[0])
#scores = np.mean(test[:,0:36],axis=1)
print(scores.shape)
#scores = np.array([1 if s >= 0.5 else 0 for s in scores])
acc = accuracy_score(test[:,36], scores)
print(classification_report(test[:,36], scores, digits=4))
print('acc:', acc)
fpr, tpr, thresholds = metrics.roc_curve(test[:,36], scores, pos_label=1)
print('AUC:',metrics.auc(fpr, tpr))
correct = int(acc * test.shape[0])
print(correct,'/',test.shape[0])
return correct
avg_acc = 0
for i in range(1):
path = '../data/final/feature_tensors/'
print(path)
train_tensor = dict()
test_tensor = dict()
for vehicle_type in vehicle_types:
train_tensor[vehicle_type] =pd.read_csv(path+vehicle_type+'_train.csv',sep=',',header=None).to_numpy()
test_tensor[vehicle_type] = pd.read_csv(path+vehicle_type+'_test.csv', sep=',',header=None).to_numpy()
correct = 0
nums = 0
for vehicle_type in vehicle_types:
nums += test_tensor[vehicle_type].shape[0]
correct += test_report(vehicle_type, train_tensor[vehicle_type], test_tensor[vehicle_type])
avg_acc += (correct / nums)
print('Test acc:', correct / nums)
print('average accuracy:', avg_acc)
```
|
github_jupyter
|
```
"""
Main application and routing logic
"""
# Standard imports
import os
# Database + Heroku + Postgres
from dotenv import load_dotenv
from flask import Flask, jsonify, request
from flask_sqlalchemy import SQLAlchemy
import psycopg2
from .models import DB, Strain
from flask_cors import CORS
# import model
#from nearest_neighbors_model import predict
####################################################
import pickle
import pandas as pd
from sklearn.neighbors import NearestNeighbors
from sklearn.feature_extraction.text import TfidfVectorizer
# changed from relative to to full path
strains = pd.read_csv("https://github.com/Build-Week-Med-Cabinet-Two/Data-Science/blob/master/cannabis.csv")
transformer = TfidfVectorizer(stop_words="english", min_df=0.025, max_df=0.98, ngram_range=(1,3))
dtm = transformer.fit_transform(canabis['spaCy_tokens'])
dtm = pd.DataFrame(dtm.todense(), columns=transformer.get_feature_names())
model = NearestNeighbors(n_neighbors=10, algorithm='kd_tree')
model.fit(dtm)
def predict(request_text):
transformed = transformer.transform([request_text])
dense = transformed.todense()
recommendations = model.kneighbors(dense)[1][0]
output_array = []
for recommendation in recommendations:
strain = strains.iloc[recommendation]
output = strain.drop(['total_text', 'spaCy_tokens']).to_dict()
output_array.append(output)
return output_array
##################################################
def create_app():
"""Create and configure an instance of the Flask application"""
app = Flask(__name__)
CORS(app)
# consider using config
app.config['SQLALCHEMY_DATABASE_URI'] = os.getenv("DB_URL")
app.config['SQLALCHEMY_TRACK_MODIFICATIONS'] = False
# load file from .env file
load_dotenv()
db_name = os.getenv("DB_NAME")
db_user = os.getenv("DB_USER")
db_password = os.getenv("DB_PASSWORD")
db_host = os.getenv("DB_HOST")
# establish cursor and connection
connection = psycopg2.connect(dbname=db_name, user=db_user, password=db_password, host=db_host)
print("CONNECTION:", connection)
cursor = connection.cursor()
print("CURSOR:", cursor)
# binding the instance to a very specific Flask app
# initialize app for use with this database setup
db = SQLAlchemy(app)
db.init_app(app)
# root route
@app.route('/')
def root():
DB.create_all()
return "Welcome to Med Cab"
@app.route("/test", methods=['POST', 'GET'])
def predict_strain():
text = request.get_json(force=True)
predictions = predict(text)
return jsonify(predictions)
return app
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mahfuz978/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/module1-join-and-reshape-data/Mahfuzur_Join_and_Reshape_Data_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science_
# Join and Reshape datasets
Objectives
- concatenate data with pandas
- merge data with pandas
- understand tidy data formatting
- melt and pivot data with pandas
Links
- [Pandas Cheat Sheet](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf)
- [Tidy Data](https://en.wikipedia.org/wiki/Tidy_data)
- Combine Data Sets: Standard Joins
- Tidy Data
- Reshaping Data
- Python Data Science Handbook
- [Chapter 3.6](https://jakevdp.github.io/PythonDataScienceHandbook/03.06-concat-and-append.html), Combining Datasets: Concat and Append
- [Chapter 3.7](https://jakevdp.github.io/PythonDataScienceHandbook/03.07-merge-and-join.html), Combining Datasets: Merge and Join
- [Chapter 3.8](https://jakevdp.github.io/PythonDataScienceHandbook/03.08-aggregation-and-grouping.html), Aggregation and Grouping
- [Chapter 3.9](https://jakevdp.github.io/PythonDataScienceHandbook/03.09-pivot-tables.html), Pivot Tables
Reference
- Pandas Documentation: [Reshaping and Pivot Tables](https://pandas.pydata.org/pandas-docs/stable/reshaping.html)
- Modern Pandas, Part 5: [Tidy Data](https://tomaugspurger.github.io/modern-5-tidy.html)
```
!wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
!tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
%cd instacart_2017_05_01
!ls -lh *.csv
```
# Assignment
## Join Data Practice
These are the top 10 most frequently ordered products. How many times was each ordered?
1. Banana
2. Bag of Organic Bananas
3. Organic Strawberries
4. Organic Baby Spinach
5. Organic Hass Avocado
6. Organic Avocado
7. Large Lemon
8. Strawberries
9. Limes
10. Organic Whole Milk
First, write down which columns you need and which dataframes have them.
Next, merge these into a single dataframe.
Then, use pandas functions from the previous lesson to get the counts of the top 10 most frequently ordered products.
```
import pandas as pd
order_products__prior = pd.read_csv('order_products__prior.csv')
order_products__prior.head()
order_products__prior.shape
# we need order id and product id
order_products__train = pd.read_csv('order_products__train.csv')
order_products__train.head()
order_products__train.shape
# we need order id and product id
products = pd.read_csv('products.csv')
products.head()
# we need product_name & product_id
products.shape
# we dont need aisles csv
aisles = pd.read_csv('aisles.csv')
aisles.head()
# we dont need department csv
departments = pd.read_csv('departments.csv')
departments.head()
orders = pd.read_csv('orders.csv')
orders.shape
orders.head()
# i need order id and order number
order_products = pd.concat([order_products__train,order_products__prior])
order_products.head()
#we need order_id amd product_id so,
concat_1 = order_products.loc[:,['order_id','product_id']]
concat_1.head()
data_1 = products.loc[:,['product_name','product_id']]
data_1.head()
data_2 = orders.loc[:,['order_id','order_number']]
data_2.head()
merge_1 = pd.merge(concat_1,data_1,on='product_id')
merge_1.head()
Final_merge = pd.merge(merge_1,data_2, on='order_id')
Final_merge.head()
final = Final_merge['product_name'].value_counts()
final.head(10)
```
## Reshape Data Section
- Replicate the lesson code
- Complete the code cells we skipped near the beginning of the notebook
- Table 2 --> Tidy
- Tidy --> Table 2
- Load seaborn's `flights` dataset by running the cell below. Then create a pivot table showing the number of passengers by month and year. Use year for the index and month for the columns. You've done it right if you get 112 passengers for January 1949 and 432 passengers for December 1960.
```
%matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
table1 = pd.DataFrame(
[[np.nan, 2],
[16, 11],
[3, 1]],
index=['John Smith', 'Jane Doe', 'Mary Johnson'],
columns=['treatmenta', 'treatmentb'])
table2 = table1.T
table1
table2
table1 = table1.reset_index()
table1
tidy = table1.melt(id_vars='index')
tidy
tidy = tidy.rename(columns={
'index': 'name',
'variable': 'trt',
'value': 'result'
})
tidy
tidy.trt=tidy.trt.str.replace('treatment', '')
tidy
tidy.pivot_table(index='name', columns='trt',values='result')
```
# Tidy ----------> 2
```
table2
table2 = table2.reset_index()
table2
tidy1 = table2.T.reset_index().melt(id_vars='index').rename(columns= {
'index': 'name',
'variable': 'trt',
'value': 'result'
})
tidy1
tidy1['trt']= tidy1['trt'].str.replace('treatment','')
tidy1 = tidy1.set_index('name')
tidy1
tidy1.pivot_table(index = 'name', columns= 'trt', values = 'result' ).T
flights = sns.load_dataset('flights')
flights.head()
wide = flights.pivot_table(index= 'year', columns = 'month', values = 'passengers')
wide
```
## Join Data Stretch Challenge
The [Instacart blog post](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2) has a visualization of "**Popular products** purchased earliest in the day (green) and latest in the day (red)."
The post says,
> "We can also see the time of day that users purchase specific products.
> Healthier snacks and staples tend to be purchased earlier in the day, whereas ice cream (especially Half Baked and The Tonight Dough) are far more popular when customers are ordering in the evening.
> **In fact, of the top 25 latest ordered products, the first 24 are ice cream! The last one, of course, is a frozen pizza.**"
Your challenge is to reproduce the list of the top 25 latest ordered popular products.
We'll define "popular products" as products with more than 2,900 orders.
```
##### YOUR CODE HERE #####
```
## Reshape Data Stretch Challenge
_Try whatever sounds most interesting to you!_
- Replicate more of Instacart's visualization showing "Hour of Day Ordered" vs "Percent of Orders by Product"
- Replicate parts of the other visualization from [Instacart's blog post](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2), showing "Number of Purchases" vs "Percent Reorder Purchases"
- Get the most recent order for each user in Instacart's dataset. This is a useful baseline when [predicting a user's next order](https://www.kaggle.com/c/instacart-market-basket-analysis)
- Replicate parts of the blog post linked at the top of this notebook: [Modern Pandas, Part 5: Tidy Data](https://tomaugspurger.github.io/modern-5-tidy.html)
```
##### YOUR CODE HERE #####
```
|
github_jupyter
|
# Real World Example:
### AI, Machine Learning & Data Science
---
# What is the Value for your Business?
- By seeing acutal examples you'll be empowered to ask the right questions (and get fair help from consultants, startups, or data analytics companies)
- This will help you make the correct decisions for your business
# Demystify
This is a real world example of how you'd solve a Machine Learning prediciton problem.
**Common Machine Learning Use Cases in Companies:**
- Discover churn risk of customers
- Predict optimal price levels (investments / retail)
- Predict future revenues
- Build recommendation systems
- Customer value scoring
- Fraud detection
- Customer insights (characteristics)
- Predict sentiment of text / client feedback
- Object detecton in images
- etc etc...
## Why Python?
Python is general purpose and can do Software development, Web development, AI. Python has experienced incredible growth over the last couple of years.
<img src='https://zgab33vy595fw5zq-zippykid.netdna-ssl.com/wp-content/uploads/2017/09/growth_major_languages-1-1400x1200.png' width=400px></img>
Source: https://stackoverflow.blog/2017/09/06/incredible-growth-python/
# Everything is free!
The best software today is open source and it's also enterprise-ready. Anyone can download and use them for free (even for business purposes).
**Examples of great, free AI libraries:**
* Anaconda
* Google's TensorFlow
* Scikit-learn
* Pandas
* Keras
* Matplotlib
* SQL
* Spark
* Numpy
## State-of-the-Art algorithms
No matter what algorithm you want to use (Linear Regression, Random Forests, Neural Networks, or Deep Learning), **all of the latest methods are implemented optimized for Python**.
## Big Data
Python code can run on any computer. Therefore, you can scale your computations and utilize for example cloud resources to run big data jobs.
**Great tools for Big Data:**
- Spark
- Databricks
- Hadoop / MapReduce
- Kafka
- Amazon EC2
- Amazon S3
# Note on data collection
- Collect all the data you can! (storage is cheap)
---
----
# Real world example of AI: Titanic Analysis
Titanic notebook is open source. All of our material is online. Anyone can developt sophisticated AI programs and solutions.
___
## The difficult part is never to implement the algorithm
The hard part of a machine learning problem is to get data into the right format so you can solve the problem. We'll illustrate this below.
___

# __Titanic Survivor Analysis__
**Sources:**
* **Training + explanations**: https://www.kaggle.com/c/titanic
___
___
# Understanding the connections between passanger information and survival rate
The sinking of the RMS Titanic is one of the most infamous shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. This sensational tragedy shocked the international community and led to better safety regulations for ships.
One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others.
### **Our task is to train a machine learning model on a data set consisting of 891 samples of people who were onboard of the Titanic. And then, be able to predict if the passengers survived or not.**
# Import packages
```
# No warnings
import warnings
warnings.filterwarnings('ignore') # Filter out warnings
# data analysis and wrangling
import pandas as pd
import numpy as np
# visualization
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# machine learning
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB # Gaussian Naive Bays
from sklearn.linear_model import Perceptron
from sklearn.tree import DecisionTreeClassifier
import xgboost as xgb
from plot_distribution import plot_distribution
plt.rcParams['figure.figsize'] = (9, 5)
```
### Load Data
```
df = pd.read_csv('data/train.csv')
```
<a id='sec3'></a>
___
## Part 2: Exploring the Data
**Data descriptions**
<img src="data/Titanic_Variable.png">
```
# preview the data
df.head(3)
# General data statistics
df.describe()
```
### Histograms
```
df.hist(figsize=(13,10));
# Balanced data set?
y_numbers = df['Survived'].map({0:'Deceased',1:'Survived'}).value_counts()
y_numbers
# Imbalanced data set, our classifiers have to outperform 62 % accuracy
y_numbers[1] / y_numbers[0]
```
> #### __Interesting Fact:__
> Third Class passengers were the first to board, with First and Second Class passengers following up to an hour before departure.
> Third Class passengers were inspected for ailments and physical impairments that might lead to their being refused entry to the United States, while First Class passengers were personally greeted by Captain Smith.
```
# Analysis of survival rate for the socioeconmic classes?
df[['Pclass', 'Survived']].groupby(['Pclass'], as_index=True) \
.mean().sort_values(by='Survived', ascending=False)
```
___
> #### __Brief Remarks Regarding the Data__
> * `PassengerId` is a random number (incrementing index) and thus does not contain any valuable information.
> * `Survived, Passenger Class, Age, Siblings Spouses, Parents Children` and `Fare` are numerical values (no need to transform them) -- but, we might want to group them (i.e. create categorical variables).
> * `Sex, Embarked` are categorical features that we need to map to integer values. `Name, Ticket` and `Cabin` might also contain valuable information.
___
```
df.head(1)
```
### Dropping Unnecessary data
__Note:__ It is important to remove variables that convey information already captured by some other variable. Doing so removes the correlation, while also diminishing potential overfit.
```
# Drop columns 'Ticket', 'Cabin', 'Fare' need to do it
# for both test and training
df = df.drop(['PassengerId','Ticket', 'Cabin','Fare'], axis=1)
```
<a id='sec4'></a>
____
## Part 3: Transforming the data
### 3.1 _The Title of the person can be used to predict survival_
```
# List example titles in Name column
df.Name
# Create column called Title
df['Title'] = df['Name'].str.extract(' ([A-Za-z]+)\.', expand=False)
# Double check that our titles makes sense (by comparing to sex)
pd.crosstab(df['Title'], df['Sex'])
# Map rare titles to one group
df['Title'] = df['Title'].\
replace(['Lady', 'Countess','Capt', 'Col', 'Don', 'Dr',\
'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
df['Title'] = df['Title'].replace('Mlle', 'Miss') #Mademoiselle
df['Title'] = df['Title'].replace('Ms', 'Miss')
df['Title'] = df['Title'].replace('Mme', 'Mrs') #Madame
# We now have more logical (contemporary) titles, and fewer groups
# See if we can get some insights
df[['Title', 'Survived']].groupby(['Title']).mean()
# We can plot the survival chance for each title
sns.countplot(x='Survived', hue="Title", data=df, order=[1,0])
plt.xticks(range(2),['Survived','Deceased']);
# Title dummy mapping: Map titles to binary dummy columns
binary_encoded = pd.get_dummies(df.Title)
df[binary_encoded.columns] = binary_encoded
# Remove unique variables for analysis (Title is generally bound to Name, so it's also dropped)
df = df.drop(['Name', 'Title'], axis=1)
df.head()
```
### Map Gender column to binary (male = 0, female = 1) categories
```
# convert categorical variable to numeric
df['Sex'] = df['Sex']. \
map( {'female': 1, 'male': 0} ).astype(int)
df.head()
```
### Handle missing values for age
```
df.Age = df.Age.fillna(df.Age.median())
```
### Split age into bands and look at survival rates
```
# Age bands
df['AgeBand'] = pd.cut(df['Age'], 5)
df[['AgeBand', 'Survived']].groupby(['AgeBand'], as_index=False)\
.mean().sort_values(by='AgeBand', ascending=True)
```
### Suvival probability against age
```
# Plot the relative survival rate distributions against Age of passangers
# subsetted by the gender
plot_distribution( df , var = 'Age' , target = 'Survived' ,\
row = 'Sex' )
# Recall: {'male': 0, 'female': 1}
# Change Age column to
# map Age ranges (AgeBands) to ordinal integer numbers
df.loc[ df['Age'] <= 16, 'Age'] = 0
df.loc[(df['Age'] > 16) & (df['Age'] <= 32), 'Age'] = 1
df.loc[(df['Age'] > 32) & (df['Age'] <= 48), 'Age'] = 2
df.loc[(df['Age'] > 48) & (df['Age'] <= 64), 'Age'] = 3
df.loc[ df['Age'] > 64, 'Age']=4
df = df.drop(['AgeBand'], axis=1)
df.head()
# Note we could just run
# df['Age'] = pd.cut(df['Age'], 5,labels=[0,1,2,3,4])
```
### Travel Party Size
How did the number of people the person traveled with impact the chance of survival?
```
# SibSp = Number of Sibling / Spouses
# Parch = Parents / Children
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
# Survival chance against FamilySize
df[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=True) \
.mean().sort_values(by='Survived', ascending=False)
# Plot it, 1 is survived
sns.countplot(x='Survived', hue="FamilySize", data=df, order=[1,0]);
# Create binary variable if the person was alone or not
df['IsAlone'] = 0
df.loc[df['FamilySize'] == 1, 'IsAlone'] = 1
df[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=True).mean()
# We will only use the binary IsAlone feature for further analysis
df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1, inplace=True)
df.head()
```
# Feature construction
```
# We can also create new features based on intuitive combinations
# Here is an example when we say that the age times socioclass is a determinant factor
df['Age*Class'] = df.Age.values * df.Pclass.values
df.loc[:, ['Age*Class', 'Age', 'Pclass']].head()
```
## Port the person embarked from
Let's see how that influences chance of survival
<img src= "data/images/titanic_voyage_map.png">
>___
```
# Fill NaN 'Embarked' Values in the dfs
freq_port = df['Embarked'].dropna().mode()[0]
df['Embarked'] = df['Embarked'].fillna(freq_port)
# Plot it, 1 is survived
sns.countplot(x='Survived', hue="Embarked", data=df, order=[1,0]);
df[['Embarked', 'Survived']].groupby(['Embarked'], as_index=True) \
.mean().sort_values(by='Survived', ascending=False)
# Create categorical dummy variables for Embarked values
binary_encoded = pd.get_dummies(df.Embarked)
df[binary_encoded.columns] = binary_encoded
df.drop('Embarked', axis=1, inplace=True)
df.head()
```
### Finished -- Preprocessing Complete!
```
# All features are approximately on the same scale
# no need for feature engineering / normalization
df.head(7)
```
### Sanity Check: View the correlation between features
```
# Uncorrelated features are generally more powerful predictors
colormap = plt.cm.viridis
plt.figure(figsize=(12,12))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(df.corr().round(2)\
,linewidths=0.1,vmax=1.0, square=True, cmap=colormap, \
linecolor='white', annot=True);
```
<a id='sec5'></a>
___
### Machine Learning, Prediction and Artifical Intelligence
Now we will use Machine Learning algorithms in order to predict if the person survived.
**We will choose the best model from:**
1. Logistic Regression
2. K-Nearest Neighbors (KNN)
3. Support Vector Machines (SVM)
4. Perceptron
5. XGBoost
6. Random Forest
7. Neural Network (Deep Learning)
### Setup Training and Validation Sets
```
X = df.drop("Survived", axis=1) # Training & Validation data
Y = df["Survived"] # Response / Target Variable
print(X.shape, Y.shape)
# Split training set so that we validate on 20% of the data
# Note that our algorithms will never have seen the validation
np.random.seed(1337) # set random seed for reproducibility
from sklearn.model_selection import train_test_split
X_train, X_val, Y_train, Y_val = \
train_test_split(X, Y, test_size=0.2)
print('Training Samples:', X_train.shape, Y_train.shape)
print('Validation Samples:', X_val.shape, Y_val.shape)
```
___
> ## General ML workflow
> 1. Create Model Object
> 2. Train the Model
> 3. Predict on _unseen_ data
> 4. Evaluate accuracy.
___
## Compare Different Prediciton Models
### 1. Logistic Regression
```
logreg = LogisticRegression() # create
logreg.fit(X_train, Y_train) # train
acc_log_2 = logreg.score(X_val, Y_val) # predict & evaluate
print('Logistic Regression accuracy:',\
str(round(acc_log_2*100,2)),'%')
```
### 2. K-Nearest Neighbour
```
knn = KNeighborsClassifier(n_neighbors = 5) # instantiate
knn.fit(X_train, Y_train) # fit
acc_knn = knn.score(X_val, Y_val) # predict + evaluate
print('K-Nearest Neighbors labeling accuracy:', str(round(acc_knn*100,2)),'%')
```
### 3. Support Vector Machine
```
# Support Vector Machines Classifier (non-linear kernel)
svc = SVC() # instantiate
svc.fit(X_train, Y_train) # fit
acc_svc = svc.score(X_val, Y_val) # predict + evaluate
print('Support Vector Machines labeling accuracy:', str(round(acc_svc*100,2)),'%')
```
### 4. Perceptron
```
perceptron = Perceptron() # instantiate
perceptron.fit(X_train, Y_train) # fit
acc_perceptron = perceptron.score(X_val, Y_val) # predict + evalaute
print('Perceptron labeling accuracy:', str(round(acc_perceptron*100,2)),'%')
```
### 5. Gradient Boosting
```
# XGBoost, same API as scikit-learn
gradboost = xgb.XGBClassifier(n_estimators=1000) # instantiate
gradboost.fit(X_train, Y_train) # fit
acc_xgboost = gradboost.score(X_val, Y_val) # predict + evalute
print('XGBoost labeling accuracy:', str(round(acc_xgboost*100,2)),'%')
```
### 6. Random Forest
```
# Random Forest
random_forest = RandomForestClassifier(n_estimators=500) # instantiate
random_forest.fit(X_train, Y_train) # fit
acc_rf = random_forest.score(X_val, Y_val) # predict + evaluate
print('Random Forest labeling accuracy:', str(round(acc_rf*100,2)),'%')
```
### 7. Neural Networks (Deep Learning)
```
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add( Dense(units=300, activation='relu', input_shape=(13,) ))
model.add( Dense(units=100, activation='relu'))
model.add( Dense(units=50, activation='relu'))
model.add( Dense(units=1, activation='sigmoid') )
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
model.fit(X_train, Y_train, epochs = 50, batch_size= 50)
# # Evaluate the model Accuracy on test set
print('Neural Network accuracy:',str(round(model.evaluate(X_val, Y_val, batch_size=50,verbose=False)[1]*100,2)),'%')
```
### Importance scores in the random forest model
```
# Look at importnace of features for random forest
def plot_model_var_imp( model , X , y ):
imp = pd.DataFrame(
model.feature_importances_ ,
columns = [ 'Importance' ] ,
index = X.columns
)
imp = imp.sort_values( [ 'Importance' ] , ascending = True )
imp[ : 10 ].plot( kind = 'barh' )
print ('Training accuracy Random Forest:',model.score( X , y ))
plot_model_var_imp(random_forest, X_train, Y_train)
```
<a id='sec6'></a>
___
## Appendix I:
#### Why are our models maxing out at around 80%?
#### __John Jacob Astor__
<img src= "data/images/john-jacob-astor.jpg">
John Jacob Astor perished in the disaster even though our model predicted he would survive. Astor was the wealthiest person on the Titanic -- his ticket fare was valued at over 35,000 USD in 2016 -- it seems likely that he would have been among of the approximatelly 35 percent of men in first class to survive. However, this was not the case: although his pregnant wife survived, John Jacob Astor’s body was recovered a week later, along with a gold watch, a diamond ring with three stones, and no less than 92,481 USD (2016 value) in cash.
<br >
#### __Olaus Jorgensen Abelseth__
<img src= "data/images/olaus-jorgensen-abelseth.jpg">
Avelseth was a 25-year-old Norwegian sailor, a man in 3rd class, and not expected to survive by classifier. However, once the ship sank, he survived by swimming for 20 minutes in the frigid North Atlantic water before joining other survivors on a waterlogged collapsible boat.
Abelseth got married three years later, settled down as a farmer in North Dakota, had 4 kids, and died in 1980 at the age of 94.
<br >
### __Key Takeaway__
As engineers and business professionals we are trained to answer the question 'what could we do to improve on an 80 percent average'. These data points represent real people. Each time our model was wrong we should be glad -- in such misclasifications we will likely find incredible stories of human nature and courage triumphing over extremely difficult odds.
__It is important to never lose sight of the human element when analyzing data that deals with people.__
<a id='sec7'></a>
___
## Appendix II: Resources and references to material we won't cover in detail
> * **Gradient Boosting:** http://blog.kaggle.com/2017/01/23/a-kaggle-master-explains-gradient-boosting/
> * **Jupyter Notebook (tutorial):** https://www.datacamp.com/community/tutorials/tutorial-jupyter-notebook
> * **K-Nearest Neighbors (KNN):** https://towardsdatascience.com/introduction-to-k-nearest-neighbors-3b534bb11d26
> * **Logistic Regression:** https://towardsdatascience.com/5-reasons-logistic-regression-should-be-the-first-thing-you-learn-when-become-a-data-scientist-fcaae46605c4
> * **Naive Bayes:** http://scikit-learn.org/stable/modules/naive_bayes.html
> * **Perceptron:** http://aass.oru.se/~lilien/ml/seminars/2007_02_01b-Janecek-Perceptron.pdf
> * **Random Forest:** https://medium.com/@williamkoehrsen/random-forest-simple-explanation-377895a60d2d
> * **Support Vector Machines (SVM):** https://towardsdatascience.com/https-medium-com-pupalerushikesh-svm-f4b42800e989
<br>
___
___

|
github_jupyter
|
# CW10: Ordinary Differential Equations
Notes:
- solution to a differential equation is a function or set of functions
- Euler's Method serves as the basis for all others
- The names of each method gives insight to how the functions look/behave graphically
Solving a differential equation with initial condition:
$dy/dx = cos(x)$ $y(0) = -1$
multiply both sides by $dx$
$$1dy = cos(x)dx$$
find the antiderivative of both sides
$$\int 1dy = \int cos(x)dx$$
$$y = sin(x)+C; y(0) = -1$$
plug $y(0) = -1$ into any $y$ values
$$-1 = sin(0) + C$$
$$-1 = 0 + C$$
$$-1 = C$$
plug $C$ in to achieve particular solution
$$y = sin(x) - 1$$
Euler Method:
- Euler method is used to obtain solutions numerically. From any point on a curve, you can find an approximate of a nearby point on the curve by moving a short distance along a line tangent to the curve
- Looking at the taylor expansion, Euler Method solves to an error squared/of order 2.
- $f(t+\Delta t)=f(t)+f'(t)\Delta t+\mathcal{O}(\Delta t)^2$
- IDEA: the curve is initially unknown but the starting point is known. From a differential equation the slope to the curve at the starting point can be computed and the tangent line
Leapfrog (Midpoint) Method:
- The Leapfrog Method takes the initial starting point (similar to Euler) then takes a "step" back on the graph ($\Delta t$) and finds the point along that slope instead
- Euler's Method finds the next point when the tangent intersectsthe vertical line ($\Delta t$) which veers away from the curve/larger error. Leapfrog Method uses the tangent at the midpoint which yeilds a more accurate approximation of the curve
- Looking at the taylor expansion, Leapfrog Method solves to an error cubed/of order 3 which is a smaller error/more accurate compared to Euler Method
- $f(t+\Delta t)-f(t-\Delta t)=2f'(t)\Delta t+\mathcal{O}(\Delta t)^3$
Heun's (Trapezoid) Method:
- Euler Method improves linearly when the step size is decreased. Heun Method improves accuracy quadratically
- The point estimated by Heun's Method takes both tangent lines provided by the points determined by Euler's Method, then takes the average between the two intersections of the tangent lines to $\Delta t$ (In the equation below (x-y coordinates), h is equivalent to $\Delta t$)
- $y_{n+1} = y_n + (h/2)(f(x_n,y_n)+f(x_n+h, y_n+hf(x_n,y_n)))$
2nd-order Runge-Kutta Method:
- Slope $K_1$ is halved to obtain a midpoint. This midpoint yeilds another slope, approximating point $K_2$. This differs from Heun's method because slopes of points are used rather than tangent lines.
4th-order Runge-Kutta Method:
- $K_1$ is the linear approximation of the difference between $u_{k+1}$ and $u_{k}$. $K_2$ is the linear approximation using $\Delta t/2$ between $K_1$. $K_3$ uses the slope of $K_2$ stopping at $\Delta t/2$. $K_4$ is found similarly to $K_3$, using the slope of $K_3$ instead of $K_2$. A more detailed description of the graph is given by the two midpoints versus endpoints. The midpoints allow us to determine any nonlinearity in the function.
|
github_jupyter
|
```
from sklearn.base import clone
from itertools import combinations
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
class SBS():
def __init__(self, estimator, k_features, scoring=accuracy_score,
test_size=0.25, random_state=1):
self.scoring = scoring
self.estimator = clone(estimator)
self.k_features = k_features
self.test_size = test_size
self.random_state = random_state
def fit(self, X, y):
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=self.test_size,
random_state=self.random_state)
dim = X_train.shape[1]
self.indices_ = tuple(range(dim))
self.subsets_ = [self.indices_]
score = self._calc_score(X_train, y_train,
X_test, y_test, self.indices_)
self.scores_ = [score]
while dim > self.k_features:
scores = []
subsets = []
for p in combinations(self.indices_, r=dim - 1):
score = self._calc_score(X_train, y_train,
X_test, y_test, p)
scores.append(score)
subsets.append(p)
best = np.argmax(scores)
self.indices_ = subsets[best]
self.subsets_.append(self.indices_)
dim -= 1
self.scores_.append(scores[best])
self.k_score_ = self.scores_[-1]
return self
def transform(self, X):
return X[:, self.indices_]
def _calc_score(self, X_train, y_train, X_test, y_test, indices):
self.estimator.fit(X_train[:, indices], y_train)
y_pred = self.estimator.predict(X_test[:, indices])
score = self.scoring(y_test, y_pred)
return score
import pandas as pd
import os
df_wine = pd.read_csv(os.path.join('..', '..', 'data', 'input', 'wine.data'), header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
print('Class labels', np.unique(df_wine['Class label']))
df_wine.head()
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, stratify=y)
from sklearn.preprocessing import StandardScaler
stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)
sbs = SBS(knn, k_features=1)
sbs.fit(X_train_std, y_train)
k_feat = [len(k) for k in sbs.subsets_]
plt.plot(k_feat, sbs.scores_, marker='o')
plt.ylim([0.7, 1.02])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.tight_layout()
plt.show()
k3 = list(sbs.subsets_[10])
print(df_wine.columns[1:][k3])
df_wine.columns
k3
knn.fit(X_train_std, y_train)
print('Training accuracy: ', knn.score(X_train_std, y_train))
print('Test accuracy: ', knn.score(X_test_std, y_test))
knn.fit(X_train_std[:, k3], y_train)
print('Training accuracy: ', knn.score(X_train_std[:, k3], y_train))
print('Test accuracy: ', knn.score(X_test_std[:, k3], y_test))
from sklearn.ensemble import RandomForestClassifier
feat_labels = df_wine.columns[1:]
forest = RandomForestClassifier(n_estimators=500, random_state=1)
forest.fit(X_train, y_train)
importances = forest.feature_importances_
indices = np.argsort(importances)[::-1]
for f in range(X_train.shape[1]):
print("%2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]]))
plt.title('Feature Importance')
plt.bar(range(X_train.shape[1]), importances[indices], align='center')
plt.xticks(range(X_train.shape[1]), feat_labels[indices], rotation=90)
plt.xlim([-1, X_train.shape[1]])
plt.tight_layout()
plt.show()
from sklearn.feature_selection import SelectFromModel
sfm = SelectFromModel(forest, threshold=0.1, prefit=True)
X_selected = sfm.transform(X_train)
print('Number of features that meet this threshold', 'criterion:', X_selected.shape[1])
for f in range(X_selected.shape[1]):
print("%2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]]))
```
|
github_jupyter
|
## Importing Libraries
```
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from matplotlib.offsetbox import (AnchoredOffsetbox, TextArea)
import statsmodels.formula.api as smf
import requests
import sklearn as skl
from sklearn import datasets
import scipy.stats as spstats
from scipy.special import inv_boxcox
```
<br><br>
## Functions
```
def df_index_slice(df, indices, include=True, sort=False, sort_col=None, desc=True):
"""
====================================================================================================
PURPOSE:
| Given a DataFrame and a list of indices, either exclude or include the rows of thos indices.
| Then sort the DataFrame on a specific column if desired.
|
==========
PARAMETERS:
| df : pandas DataFrame to slice.
|
| indices : List of indices to slice the DataFrame by.
|
| include : If set to True (default), will include the rows based on the indices provided and will
| will exclude others. If set to False, will exclude the rows based on the indices provided
| and will include others.
|
| sort : If False (default), no sorting will be done on the sliced DataFrame. If True, will sort.
|
| sort_col : If sorting enabled, the column name on which sorting will be determined.
|
| desc : If True (default), sliced DataFrame will be sorted descending based on the column specified,
| else, if False, will be sorted ascending based on the column specified.
|
==========
OUTPUT:
| - A sliced DataFrame
|
====================================================================================================
"""
if include:
df = df.iloc[df.index.isin(indices)]
else:
df = df.iloc[~df.index.isin(indices)]
if sort:
sort_switch = False if desc else True
try:
df = df.sort_values(by=[sort_col], ascending=sort_switch)
except:
print(f"Unable to sort!")
else:
pass
return df
def invert_transform(value, reversed_transformation=None, pre_xfrm='N', lamb=None, mean=None, std=None, min_val=None, col_sum=None, shift=None):
"""
====================================================================================================
PURPOSE:
| Given a value and the transformation that was used to transform that value, get the inverse
| transformation of the value.
|
==========
PARAMETERS:
| value : Value to inverse transform.
|
| reversed_transformation : Select the transformation that you want to inverse.
| - boxcox
| - log
| - recip (aka reciprocal)
| - reflect
| - x2
| - normalize
| - zscore
| - exp
|
| pre_xfrm:
| - N : Values were not shifted prior to transformation.
| - Y : Values were shifted prior to transformation. In this case you'll need to enter the
| parameters used to shift the values.
|
| lamb : Required to inverse boxcox transformation.
|
| mean : Required to inverse zscore transformation.
|
| std : Required to inverse zscore transformation.
|
| min_val : Required to inverse reflect transformation.
|
| col_sum : Required to inverse normalization transformation.
|
| shift : Amount that values were shifted prior to transformation. Required if pre_xfrm parameter
| set to 'Y' and transformation utilizes shift.
|
==========
OUTPUT:
| - The inverse representation of a value that was transformed.
|
====================================================================================================
"""
if reversed_transformation == 'boxcox':
if lamb is None:
print('Must specify lambda!')
else:
rev_val = inv_boxcox(value, lamb)
return rev_val
elif reversed_transformation == 'log':
if pre_xfrm.upper()=='N':
rev_val = math.exp(value)
else:
if shift is None:
print(f"Enter amount to shift values or set pre_xfrm='N'")
else:
rev_val = math.exp(value) - shift
return rev_val
elif reversed_transformation == 'recip':
if pre_xfrm.upper()=='N':
rev_val = (1 / value)
else:
if shift is None:
print(f"Enter amount to shift values or set pre_xfrm='N'")
else:
rev_val = (1 / value) - shift
return rev_val
elif reversed_transformation == 'reflect':
if min_val is None:
print(f"Must enter minimum value used to reflect original data!")
else:
rev_val = min_val + value
return rev_val
elif reversed_transformation == 'x2':
if pre_xfrm.upper()=='N':
rev_val = math.sqrt(value)
else:
if shift is None:
print(f"Enter amount to shift values or set pre_xfrm='N'")
else:
rev_val = (math.sqrt(value)) - shift
elif reversed_transformation == 'normalize':
if pre_xfrm.upper()=='N':
if col_sum is None:
print(f"Must enter the sum used to normalize the original data!")
else:
rev_val = col_sum * value
else:
if col_sum is None or shift is None:
print(f"Must enter the sum used to normalize and the amount of shift done prior to normalization!")
else:
rev_val = (col_sum * value) - shift
elif reversed_transformation == 'zscore':
if mean is None or std is None:
print(f"Must enter mean and standard deviation used to obtain zscore for the data!")
else:
rev_val = (value * std) + mean
elif reversed_transformation == 'exp':
rev_val = np.exp(value)
```
<br><br>
## Classes
```
class SwissDF(object):
"""
====================================================================================================
DEVELOPER: Patrick Weatherford
CLASS OVERVIEW:
This is the Data Science swiss army knife for a pandas DataFrames!!
"""
def __init__(self, df):
"""
====================================================================================================
PURPOSE:
| Instantiate SwissDF object.
|
==========
PARAMETERS:
| df : A pandas DataFrame or something that can be converted into a pandas DataFrame. Will first try
| to convert the variable into a DataFrame and if unsuccessful, will output an error message.
|
==========
OUTPUT:
| SwissDF object created that has an attribute .df for the DataFrame instantiated with the object.
|
====================================================================================================
"""
try:
self.df = pd.DataFrame(df) # try to convert to pandas DataFrame
except:
print('Is not or cannot convert to pandas.DataFrame!')
def df_dist_plot(self, graph_type='histplot', hist_color="grey", kde_color="black"):
"""
====================================================================================================
PURPOSE:
| Take a DataFrame and plot a histogram/kde plot for each variable in the DataFrame.
|
==========
PARAMETERS:
| graph_type : Type of graph to disply.
| - histplot (default) - histogram w/KDE
| - cdf - Cumulative Distribution Function
|
| hist_color : Color of histogram bars.
|
| kde_color : Color of kernel density estimation (kde) line.
|
==========
OUTPUT:
| Multiple plot figures with a shape of rows=1, cols=3. The number of plots depends on the number of
| variables (aka columns) in the DataFrame.
|
====================================================================================================
"""
iterations = math.ceil(len(self.df.columns) / 3)
num_vars = len(self.df.columns)
var_cnt = 0
for row in range(iterations):
fig = plt.figure()
fig.set_figwidth(fig.get_figwidth() * 3)
for col in range(3):
plt_loc = int('13' + str(col+1))
plt.subplot(plt_loc)
if var_cnt >= num_vars:
pass
else:
if graph_type == 'histplot':
sns.histplot(self.df.iloc[:,[var_cnt]]
, kde=True
, alpha=.5
, line_kws={"lw":4}
, facecolor=hist_color
, edgecolor=None
).lines[0].set_color(kde_color)
elif graph_type == 'cdf':
sns.ecdfplot(self.df.iloc[:,[var_cnt]])
var_cnt+=1
plt.show()
def get_outlier_info(self, outlier_method='iqr', exclude_cols=None):
"""
====================================================================================================
PURPOSE:
| Take the object DataFrame attribute and flag outliers for each variable recording the index for
| each of them in a list. The outlier list will then be instantiated as an attribute and will also
| be used to instantiate an outlier DataFrame which can be used to review the outliers before taking
| action on them.
|
==========
PARAMETERS:
| outlier_method : Calculation method to define outliers.
| - iqr (default) : x < q1 - iqr * 1.5 OR x > q3 + iqr * 1.5
| - zscore : If zscore for the variable is > 3
|
| exclude_cols : List of column names to exclude from outlier analysis.
|
==========
OUTPUT:
| - object attribute .outlier_indices : list of row indices where any variable has an outlier.
| - object attribute .outlier_dict : dictionary of all columns and the outlier row indices for the variable.
| - object attribute .outlier_df : DataFrame of all rows where any variable has an outlier.
|
|
====================================================================================================
"""
df_copy = self.df
if exclude_cols is None:
pass
else:
df_copy = df_copy.drop([exclude_cols])
indices = []
outlier_indices = []
outlier_dict = {}
if outlier_method == 'zscore':
for col in df_copy.columns:
index = df_copy.index[((df_copy[col] - df_copy[col].mean()) / df_copy[col].std()) > 3].tolist()
indices.extend(index)
outlier_dict[col] = index
elif outlier_method == 'iqr':
for col in df.columns:
q1 = df_copy[col].quantile(0.25)
q3 = df_copy[col].quantile(0.75)
iqr = q3-q1
lower_bound = q1 - (iqr * 1.5)
upper_bound = q3 + (iqr * 1.5)
index = df_copy.index[(df[col] < lower_bound) | (df_copy[col] > upper_bound)].tolist()
indices.extend(index)
outlier_dict[col] = index
for i in indices:
if i in outlier_indices or i is None or i == '':
pass
else:
outlier_indices.append(i)
if len(outlier_indices) > 0:
self.outlier_indices = outlier_indices
self.outlier_dict = outlier_dict
self.outlier_df = self.df.iloc[self.df.index.isin(self.outlier_indices)]
else:
print(f"No outliers found in DataFrame.")
def remove_outliers(self, outlier_method='iqr', for_vars='All'):
"""
====================================================================================================
PURPOSE:
| Remove all variable outlier rows or only outlier rows for specified variables.
|
==========
PARAMETERS:
| outlier_method : Calculation method to define outliers.
| - iqr (default) : x < q1 - iqr * 1.5 OR x > q3 + iqr * 1.5
| - zscore : If zscore for the variable is > 3
|
| for_vars : specifiy the rows to remove for specified variables
|
==========
OUTPUT:
| Will modify the object DataFrame attribute and remove all variable outlier rows or only outlier
| rows for specified variables.
|
====================================================================================================
"""
df_start_len = len(self.df)
try:
self.outlier_dict # check to see if object attribute exists and outlier analysis ran
pass
except:
self.get_outlier_info(outlier_method=outlier_method)
if for_vars=='All':
self.df = self.df.iloc[~self.df.index.isin(self.outlier_indices)]
df_end_len = len(self.df)
print(f'{df_start_len-df_end_len} rows removed!')
else:
index_holder = []
index_filter_list = []
for col in for_vars:
index_holder.extend(self.outlier_dict[col])
for i in index_holder:
if i in index_filter_list:
pass
else:
index_filter_list.append(i)
self.df = self.df.iloc[~self.df.index.isin(index_filter_list)]
df_end_len = len(self.df)
print(f'{df_start_len-df_end_len} rows removed!')
def col_transform(self, transform_type='log', transform_cols=None):
"""
====================================================================================================
PURPOSE
| Can be used to transform specific columns into other representations and then add the columns onto
| the existing DataFrame associated with the object.
|
| Right (positve) skew (from lowest to strongest skew):
| - log
| - recip
|
| Left (negative) skew (from lowest to strongest skew):
| - reflect (*then must do appropriate right-skew transformation)
| - x2
| - exp
|
==========
PARAMETERS
| transform_type : specify the transformation for the new column
| - log : Takes the log of each of the values. Will first check to see if the minimum value for the
| column is <= 0. If so, will add the absolute value of the minimum + 1 to ensure no log of
| of 0 or negative number.
|
| - recip : (reciprocal) = 1 / value. Will first check to see if the minimum value for the
| column is <= 0. If so, will add the absolute value of the minimum + 1 to ensure no
| log of of 0 or negative number.
|
| - normalize : The data value divided by the sum of the entire column.
|
| - zscore : (data value - mean) / standard deviation
|
| - reflect : Subtract every value from the minimum value. Then perform
|
| - x2 : Square each value of x
|
| - exp : e**x
|
| - boxcox : scipy.stats.boxcox(x)
|
| transform_cols : specify the column names to transform in a list format
|
==========
OUTPUT:
| - Modified object DataFrame attribute with new columns that are transformations of existing columns
| specified in the object's DataFrame.
|
| - Object attribute for parameters used for transformation
|
====================================================================================================
"""
transform_cols = transform_cols
self.xfrm_params = {}
if transform_cols is None:
print(f"No columns selected!")
else:
if transform_type == 'log':
for col in transform_cols:
new_col_name = col + '_LOG'
if self.df[col].min() > 0:
self.df[new_col_name] = np.log(self.df[col]) # log(value)
self.xfrm_params[new_col_name] = {
"PRE_XFRM":'N'
,"SHIFT":0
,"X_FORM":"log(x)"
}
elif self.df[col].min() <= 0:
self.df[new_col_name]=np.log(self.df[col] + abs(self.df[col].min()) + 1) # log(value accounting for negative & 0)
self.xfrm_params[new_col_name] = { # parameters needed to inverse column values
"PRE_XFRM":'Y'
,"SHIFT":abs(self.df[col].min())+1
,"X_FORM":"log(x + abs(min(x)) + 1)"
}
print(f"{transform_type} of {transform_cols} successfully added to object DataFrame!")
elif transform_type == "recip":
for col in transorm_cols:
new_col_name = col + '_RECIP'
if self.df[col].min() > 1:
self.df[new_col_name] = 1 / (self.df[col]) # 1 / value
self.xfrm_params[new_col_name] = {
"PRE_XFRM":"N"
,"X_FORM":"1 / x"
}
elif self.df[col].min() <= 1:
self.df[new_col_name] = 1 / (self.df[col] + abs(self.df[col].min()) + 2) # 1 / value accounting for negative, 1, and 0
self.xfrm_params[new_col_name] = { # parameters needed to inverse column values
"PRE_XFRM":"Y"
,"SHIFT":abs(self.df[col].min())+2
,"X_FORM":"1 / (x + abs(min(x)) + 2)"
}
print(f"{transform_type} of {transform_cols} successfully added to object DataFrame!")
elif transform_type == 'normalize':
for col in transform_cols:
new_col_name = col + '_NORMLZ'
if self.df[col].min() > 0:
self.df[new_col_name] = self.df[col] / sum(self.df[col]) # value / sum of column values
self.xfrm_params[new_col_name] = {
"PRE_XFRM":"N"
,"SHIFT":0
,"COL_SUM":sum(self.df[col])
,"X_FORM":"x / (sum(x))"
}
elif self.df[col].min() <= 0:
self.df[new_col_name] = (self.df[col] + abs(self.df[col].min()) + 1) / (sum((self.df[col] + abs(self.df[col].min()) + 1)))
self.xfrm_params[new_col_name] = {
"PRE_XFM":"Y"
,"SHIFT":self.df[col].min()+1
,"COL_SUM":sum(self.df[col])
,"X_FORM":"(x + abs(min(x)) + 1) / (sum( (x + abs(min(x)) + 1) ))"
}
print(f"{transform_type} of {transform_cols} successfully added to object DataFrame!")
elif transform_type == 'zscore':
for col in transform_cols:
new_col_name = col + '_Z'
self.df[new_col_name] = (self.df[col] - self.df[col].mean()) / self.df[col].std()
self.xfrm_params[new_col_name] = {
"MEAN":self.df[col].mean()
,"STD":self.df[col].std()
,"X_FORM":"(x - mean(x)) / std(x)"
}
print(f"{transform_type} of {transform_cols} successfully added to object DataFrame!")
elif transform_type == 'reflect':
for col in transform_cols:
new_col_name = col + '_REFLECT'
self.df[new_col_name] = self.df[col].min() - self.df[col] # min - value
self.xfrm_params[new_col_name] = {
"ABS_MIN":abs(self.df[col].min())
,"X_FORM":"min(x) - x"
}
print(f"{transform_type} of {transform_cols} successfully added to object DataFrame!")
elif transform_type == 'x2':
for col in transform_cols:
new_col_name = col + '_X2'
if self.df[col].min() > 0:
self.df[new_col_name] = self.df[col]**2
self.xfrm_params[new_col_name] = {
"PRE_XFRM":"N"
,"SHIFT":0
,"X_FORM":"x**2"
}
elif self.df[col].min() <= 0:
self.df[new_col_name] = self.df[col] + abs(self.df[col].min())
self.xfrm_params[new_col_name] = {
"PRE_XFRM":"Y"
,"SHIFT":abs(self.df[col].min())
,"X_FORM":"( x + abs(min(x)) )**2"
}
elif transform_type == 'exp':
for col in transform_cols:
new_col_name = col + '_EXP'
self.df[new_col_name] = (match.e)**self.df[col] # exponentiating values
self.xfrm_params[new_col_name] = {
"PRE_XFRM":"N"
,"X_FORM":"e**x"
}
elif transform_type == 'boxcox':
for col in transform_cols:
new_col_name = col + '_BOXCOX'
self.df[new_col_name], lamb = spstats.boxcox(self.df[col])
self.xfrm_params[new_col_name] = {
"PRE_XFRM":"N"
,"LAMBDA":lamb
,"X_FORM":"scipy.stats.boxcox(x)"
}
def corr_hm(self, method='pearson', cmap='bwr'):
fig, ax = plt.subplots(figsize=(6,1))
fig.subplots_adjust(bottom=0.6)
ax.set_facecolor('black')
cm = eval(f"mpl.cm.{cmap}")
norm = mpl.colors.Normalize(vmin=-1, vmax=1)
cbar = mpl.colorbar.ColorbarBase(ax
, cmap=cm
, norm=norm
, orientation='horizontal')
ax.set_facecolor('yellow')
plt.title("Correlation")
plt.show()
corr_hm = self.df.corr(method='pearson').style.background_gradient(cmap=cm, vmin=-1, vmax=1)
return corr_hm
```
<br><br>
## Testing
```
## regression data set
cal_housing_df = datasets.fetch_california_housing(as_frame=True).data
cal_housing_df['MEDIAN_PRICE'] = datasets.fetch_california_housing(as_frame=True).target
## classification data set
iris_df = datasets.load_iris(as_frame=True)
new_col_names = [
"MEDIAN_INCOME"
,"MEDIAN_HOUSE_AGE"
,"AVG_ROOMS"
,"AVG_BEDROOMS"
,"BLOCK_POP"
,"AVG_HOUSE_OCC"
,"LAT"
,"LON"
,"MEDIAN_PRICE"
]
cal_housing_df.columns = new_col_names
df = cal_housing_df
df1 = SwissDF(df)
df1.df
df1.df_dist_plot() # takes forever to run due to crazy outliers
df1.df.describe()
```
<br>
What in the world is going on with **[AVG_HOUSE_OCC]**, **[AVG_ROOMS]**, and **[AVG_BEDROOMS]**??
```
df1.get_outlier_info(outlier_method='iqr')
df_index_slice(df1.df
, df1.outlier_dict['AVG_HOUSE_OCC']
, sort=True, sort_col='AVG_HOUSE_OCC'
, desc=True).head(30)
df_index_slice(df1.df
, df1.outlier_dict['AVG_ROOMS']
, sort=True, sort_col='AVG_ROOMS'
, desc=True).head(30)
df_index_slice(df1.df
, df1.outlier_dict['AVG_BEDROOMS']
, sort=True, sort_col='AVG_BEDROOMS'
, desc=True).head(30)
```
<br><br>
After searching the Latitude/Longitude on Google, it looks like a lot of places where the AVG_HOUSE_OCC, AVG_BEDROOMS, and AVG_ROOOMS is high are places like colleges, prisons, communities, resorts, etc. If we are looking specifically at house prices, I think it would be safe to remove these.
```
df1.remove_outliers(for_vars=['AVG_ROOMS','AVG_BEDROOMS','AVG_HOUSE_OCC'])
```
<br><br>
Now lets see what the distributions look like.
```
df1.df_dist_plot()
```
<br><br>
Now I'm curious about the outliers for **[MEDIAN_HOUSE_AGE]** and **[MEDIAN_PRICE]**
```
df_index_slice(df1.df
, df1.outlier_dict['MEDIAN_HOUSE_AGE']
, sort=True, sort_col='MEDIAN_HOUSE_AGE'
, desc=True).head(30)
```
No outliers detected for **[MEDIAN_HOUSE_AGE]**
<br><br>
```
df_index_slice(df1.df
, df1.outlier_dict['MEDIAN_PRICE']
, sort=True, sort_col='MEDIAN_PRICE'
, desc=True).head(30)
```
After review, the high price homes seem to located in fancy-pants-ville so I think those outliers should stay.
<br><br>
I still think we can clean the data a little further. For the next step, I'll attempt to make some the right-skewed data more normal by taking the boxcox transformation of those columns.
```
transform_cols = [
'MEDIAN_INCOME'
,'BLOCK_POP'
,'MEDIAN_PRICE'
]
df1.col_transform(transform_type='boxcox', transform_cols=transform_cols)
df1.df_dist_plot()
```
I'm liking that **[BLOCK_POP_LOG]**, **[MEDIAN_INCOME_LOG]**, now taking on a more normal distribution. I think I'll use that moving forward.
Ok final data set.
```
df1.df = df1.df.drop(columns=['MEDIAN_INCOME','BLOCK_POP','MEDIAN_PRICE'])
df1.df_dist_plot()
```
<br><br>
Example of how to revert value in transformed distribution back to a meaningful value
```
## first find the parameters used in the transformation for each transformed column
df1.xfrm_params
```
<br><br>
After parameters found, use those to transform to a meaningful representation
```
boxcox_mean = df1.df['BLOCK_POP_BOXCOX'].mean()
reg_mean = invert_transform(boxcox_mean, reversed_transformation='boxcox', lamb=df1.xfrm_params['BLOCK_POP_BOXCOX']['LAMBDA'])
boxcox_mean, reg_mean
```
<br><br>
Correlation heatmap
```
df1.corr_hm()
```
|
github_jupyter
|
## Neural Networks in PyMC3 estimated with Variational Inference
(c) 2016 by Thomas Wiecki
## Current trends in Machine Learning
There are currently three big trends in machine learning: **Probabilistic Programming**, **Deep Learning** and "**Big Data**". Inside of PP, a lot of innovation is in making things scale using **Variational Inference**. In this blog post, I will show how to use **Variational Inference** in [PyMC3](http://pymc-devs.github.io/pymc3/) to fit a simple Bayesian Neural Network. I will also discuss how bridging Probabilistic Programming and Deep Learning can open up very interesting avenues to explore in future research.
### Probabilistic Programming at scale
**Probabilistic Programming** allows very flexible creation of custom probabilistic models and is mainly concerned with **insight** and learning from your data. The approach is inherently **Bayesian** so we can specify **priors** to inform and constrain our models and get uncertainty estimation in form of a **posterior** distribution. Using [MCMC sampling algorithms](http://twiecki.github.io/blog/2015/11/10/mcmc-sampling/) we can draw samples from this posterior to very flexibly estimate these models. [PyMC3](http://pymc-devs.github.io/pymc3/) and [Stan](http://mc-stan.org/) are the current state-of-the-art tools to consruct and estimate these models. One major drawback of sampling, however, is that it's often very slow, especially for high-dimensional models. That's why more recently, **variational inference** algorithms have been developed that are almost as flexible as MCMC but much faster. Instead of drawing samples from the posterior, these algorithms instead fit a distribution (e.g. normal) to the posterior turning a sampling problem into and optimization problem. [ADVI](http://arxiv.org/abs/1506.03431) -- Automatic Differentation Variational Inference -- is implemented in [PyMC3](http://pymc-devs.github.io/pymc3/) and [Stan](http://mc-stan.org/), as well as a new package called [Edward](https://github.com/blei-lab/edward/) which is mainly concerned with Variational Inference.
Unfortunately, when it comes traditional ML problems like classification or (non-linear) regression, Probabilistic Programming often plays second fiddle (in terms of accuracy and scalability) to more algorithmic approaches like [ensemble learning](https://en.wikipedia.org/wiki/Ensemble_learning) (e.g. [random forests](https://en.wikipedia.org/wiki/Random_forest) or [gradient boosted regression trees](https://en.wikipedia.org/wiki/Boosting_(machine_learning)).
### Deep Learning
Now in its third renaissance, deep learning has been making headlines repeatadly by dominating almost any object recognition benchmark, [kicking ass at Atari games](https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf), and [beating the world-champion Lee Sedol at Go](http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html). From a statistical point, Neural Networks are extremely good non-linear function approximators and representation learners. While mostly known for classification, they have been extended to unsupervised learning with [AutoEncoders](https://arxiv.org/abs/1312.6114) and in all sorts of other interesting ways (e.g. [Recurrent Networks](https://en.wikipedia.org/wiki/Recurrent_neural_network), or [MDNs](http://cbonnett.github.io/MDN_EDWARD_KERAS_TF.html) to estimate multimodal distributions). Why do they work so well? No one really knows as the statistical properties are still not fully understood.
A large part of the innoviation in deep learning is the ability to train these extremely complex models. This rests on several pillars:
* Speed: facilitating the GPU allowed for much faster processing.
* Software: frameworks like [Theano](http://deeplearning.net/software/theano/) and [TensorFlow](https://www.tensorflow.org/) allow flexible creation of abstract models that can then be optimized and compiled to CPU or GPU.
* Learning algorithms: training on sub-sets of the data -- stochastic gradient descent -- allows us to train these models on massive amounts of data. Techniques like drop-out avoid overfitting.
* Architectural: A lot of innovation comes from changing the input layers, like for convolutional neural nets, or the output layers, like for [MDNs](http://cbonnett.github.io/MDN_EDWARD_KERAS_TF.html).
### Bridging Deep Learning and Probabilistic Programming
On one hand we Probabilistic Programming which allows us to build rather small and focused models in a very principled and well-understood way to gain insight into our data; on the other hand we have deep learning which uses many heuristics to train huge and highly complex models that are amazing at prediction. Recent innovations in variational inference allow probabilistic programming to scale model complexity as well as data size. We are thus at the cusp of being able to combine these two approaches to hopefully unlock new innovations in Machine Learning. For more motivation, see also [Dustin Tran's](https://twitter.com/dustinvtran) recent [blog post](http://dustintran.com/blog/a-quick-update-edward-and-some-motivations/).
While this would allow Probabilistic Programming to be applied to a much wider set of interesting problems, I believe this bridging also holds great promise for innovations in Deep Learning. Some ideas are:
* **Uncertainty in predictions**: As we will see below, the Bayesian Neural Network informs us about the uncertainty in its predictions. I think uncertainty is an underappreciated concept in Machine Learning as it's clearly important for real-world applications. But it could also be useful in training. For example, we could train the model specifically on samples it is most uncertain about.
* **Uncertainty in representations**: We also get uncertainty estimates of our weights which could inform us about the stability of the learned representations of the network.
* **Regularization with priors**: Weights are often L2-regularized to avoid overfitting, this very naturally becomes a Gaussian prior for the weight coefficients. We could, however, imagine all kinds of other priors, like spike-and-slab to enforce sparsity (this would be more like using the L1-norm).
* **Transfer learning with informed priors**: If we wanted to train a network on a new object recognition data set, we could bootstrap the learning by placing informed priors centered around weights retrieved from other pre-trained networks, like [GoogLeNet](https://arxiv.org/abs/1409.4842).
* **Hierarchical Neural Networks**: A very powerful approach in Probabilistic Programming is hierarchical modeling that allows pooling of things that were learned on sub-groups to the overall population (see my tutorial on [Hierarchical Linear Regression in PyMC3](http://twiecki.github.io/blog/2014/03/17/bayesian-glms-3/)). Applied to Neural Networks, in hierarchical data sets, we could train individual neural nets to specialize on sub-groups while still being informed about representations of the overall population. For example, imagine a network trained to classify car models from pictures of cars. We could train a hierarchical neural network where a sub-neural network is trained to tell apart models from only a single manufacturer. The intuition being that all cars from a certain manufactures share certain similarities so it would make sense to train individual networks that specialize on brands. However, due to the individual networks being connected at a higher layer, they would still share information with the other specialized sub-networks about features that are useful to all brands. Interestingly, different layers of the network could be informed by various levels of the hierarchy -- e.g. early layers that extract visual lines could be identical in all sub-networks while the higher-order representations would be different. The hierarchical model would learn all that from the data.
* **Other hybrid architectures**: We can more freely build all kinds of neural networks. For example, Bayesian non-parametrics could be used to flexibly adjust the size and shape of the hidden layers to optimally scale the network architecture to the problem at hand during training. Currently, this requires costly hyper-parameter optimization and a lot of tribal knowledge.
## Bayesian Neural Networks in PyMC3
### Generating data
First, lets generate some toy data -- a simple binary classification problem that's not linearly separable.
```
%matplotlib inline
import pymc3 as pm
import theano.tensor as T
import theano
import sklearn
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('white')
from sklearn import datasets
from sklearn.preprocessing import scale
from sklearn.cross_validation import train_test_split
from sklearn.datasets import make_moons
X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000)
X = scale(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5)
fig, ax = plt.subplots()
ax.scatter(X[Y==0, 0], X[Y==0, 1], label='Class 0')
ax.scatter(X[Y==1, 0], X[Y==1, 1], color='r', label='Class 1')
sns.despine(); ax.legend()
ax.set(xlabel='X', ylabel='Y', title='Toy binary classification data set');
```
### Model specification
A neural network is quite simple. The basic unit is a [perceptron](https://en.wikipedia.org/wiki/Perceptron) which is nothing more than [logistic regression](http://pymc-devs.github.io/pymc3/notebooks/posterior_predictive.html#Prediction). We use many of these in parallel and then stack them up to get hidden layers. Here we will use 2 hidden layers with 5 neurons each which is sufficient for such a simple problem.
```
# Trick: Turn inputs and outputs into shared variables.
# It's still the same thing, but we can later change the values of the shared variable
# (to switch in the test-data later) and pymc3 will just use the new data.
# Kind-of like a pointer we can redirect.
# For more info, see: http://deeplearning.net/software/theano/library/compile/shared.html
ann_input = theano.shared(X_train)
ann_output = theano.shared(Y_train)
n_hidden = 5
# Initialize random weights between each layer
init_1 = np.random.randn(X.shape[1], n_hidden)
init_2 = np.random.randn(n_hidden, n_hidden)
init_out = np.random.randn(n_hidden)
with pm.Model() as neural_network:
# Weights from input to hidden layer
weights_in_1 = pm.Normal('w_in_1', 0, sd=1,
shape=(X.shape[1], n_hidden),
testval=init_1)
# Weights from 1st to 2nd layer
weights_1_2 = pm.Normal('w_1_2', 0, sd=1,
shape=(n_hidden, n_hidden),
testval=init_2)
# Weights from hidden layer to output
weights_2_out = pm.Normal('w_2_out', 0, sd=1,
shape=(n_hidden,),
testval=init_out)
# Build neural-network using tanh activation function
act_1 = T.tanh(T.dot(ann_input,
weights_in_1))
act_2 = T.tanh(T.dot(act_1,
weights_1_2))
act_out = T.nnet.sigmoid(T.dot(act_2,
weights_2_out))
# Binary classification -> Bernoulli likelihood
out = pm.Bernoulli('out',
act_out,
observed=ann_output)
```
That's not so bad. The `Normal` priors help regularize the weights. Usually we would add a constant `b` to the inputs but I omitted it here to keep the code cleaner.
### Variational Inference: Scaling model complexity
We could now just run a MCMC sampler like [`NUTS`](http://pymc-devs.github.io/pymc3/api.html#nuts) which works pretty well in this case but as I already mentioned, this will become very slow as we scale our model up to deeper architectures with more layers.
Instead, we will use the brand-new [ADVI](http://pymc-devs.github.io/pymc3/api.html#advi) variational inference algorithm which was recently added to `PyMC3`. This is much faster and will scale better. Note, that this is a mean-field approximation so we ignore correlations in the posterior.
```
%%time
with neural_network:
# Run ADVI which returns posterior means, standard deviations, and the evidence lower bound (ELBO)
v_params = pm.variational.advi(n=50000)
```
< 40 seconds on my older laptop. That's pretty good considering that NUTS is having a really hard time. Further below we make this even faster. To make it really fly, we probably want to run the Neural Network on the GPU.
As samples are more convenient to work with, we can very quickly draw samples from the variational posterior using `sample_vp()` (this is just sampling from Normal distributions, so not at all the same like MCMC):
```
with neural_network:
trace = pm.variational.sample_vp(v_params, draws=5000)
```
Plotting the objective function (ELBO) we can see that the optimization slowly improves the fit over time.
```
plt.plot(v_params.elbo_vals)
plt.ylabel('ELBO')
plt.xlabel('iteration')
```
Now that we trained our model, lets predict on the hold-out set using a posterior predictive check (PPC). We use [`sample_ppc()`](http://pymc-devs.github.io/pymc3/api.html#pymc3.sampling.sample_ppc) to generate new data (in this case class predictions) from the posterior (sampled from the variational estimation).
```
# Replace shared variables with testing set
ann_input.set_value(X_test)
ann_output.set_value(Y_test)
# Creater posterior predictive samples
ppc = pm.sample_ppc(trace, model=neural_network, samples=500)
# Use probability of > 0.5 to assume prediction of class 1
pred = ppc['out'].mean(axis=0) > 0.5
fig, ax = plt.subplots()
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1])
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
sns.despine()
ax.set(title='Predicted labels in testing set', xlabel='X', ylabel='Y');
plt.savefig("nn-0.png",dpi=400)
print('Accuracy = {}%'.format((Y_test == pred).mean() * 100))
```
Hey, our neural network did all right!
## Lets look at what the classifier has learned
For this, we evaluate the class probability predictions on a grid over the whole input space.
```
grid = np.mgrid[-3:3:100j,-3:3:100j]
grid_2d = grid.reshape(2, -1).T
X, Y = grid
dummy_out = np.ones(grid.shape[1], dtype=np.int8)
ann_input.set_value(grid_2d)
ann_output.set_value(dummy_out)
# Creater posterior predictive samples
ppc = pm.sample_ppc(trace, model=neural_network, samples=500)
```
### Probability surface
```
cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True)
fig, ax = plt.subplots(figsize=(10, 6))
contour = ax.contourf(X, Y, ppc['out'].mean(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1])
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Posterior predictive mean probability of class label = 0');
plt.savefig("nn-1.png",dpi=400)
```
### Uncertainty in predicted value
So far, everything I showed we could have done with a non-Bayesian Neural Network. The mean of the posterior predictive for each class-label should be identical to maximum likelihood predicted values. However, we can also look at the standard deviation of the posterior predictive to get a sense for the uncertainty in our predictions. Here is what that looks like:
```
cmap = sns.cubehelix_palette(light=1, as_cmap=True)
fig, ax = plt.subplots(figsize=(10, 6))
contour = ax.contourf(X, Y, ppc['out'].std(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1])
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Uncertainty (posterior predictive standard deviation)');
plt.savefig("nn-2.png",dpi=400)
```
We can see that very close to the decision boundary, our uncertainty as to which label to predict is highest. You can imagine that associating predictions with uncertainty is a critical property for many applications like health care. To further maximize accuracy, we might want to train the model primarily on samples from that high-uncertainty region.
## Mini-batch ADVI: Scaling data size
So far, we have trained our model on all data at once. Obviously this won't scale to something like ImageNet. Moreover, training on mini-batches of data (stochastic gradient descent) avoids local minima and can lead to faster convergence.
Fortunately, ADVI can be run on mini-batches as well. It just requires some setting up:
```
from six.moves import zip
# Set back to original data to retrain
ann_input.set_value(X_train)
ann_output.set_value(Y_train)
# Tensors and RV that will be using mini-batches
minibatch_tensors = [ann_input, ann_output]
minibatch_RVs = [out]
# Generator that returns mini-batches in each iteration
def create_minibatch(data):
rng = np.random.RandomState(0)
while True:
# Return random data samples of set size 100 each iteration
ixs = rng.randint(len(data), size=50)
yield data[ixs]
minibatches = zip(
create_minibatch(X_train),
create_minibatch(Y_train),
)
total_size = len(Y_train)
```
While the above might look a bit daunting, I really like the design. Especially the fact that you define a generator allows for great flexibility. In principle, we could just pool from a database there and not have to keep all the data in RAM.
Lets pass those to `advi_minibatch()`:
```
%%time
with neural_network:
# Run advi_minibatch
v_params = pm.variational.advi_minibatch(
n=50000, minibatch_tensors=minibatch_tensors,
minibatch_RVs=minibatch_RVs, minibatches=minibatches,
total_size=total_size, learning_rate=1e-2, epsilon=1.0
)
with neural_network:
trace = pm.variational.sample_vp(v_params, draws=5000)
plt.plot(v_params.elbo_vals)
plt.ylabel('ELBO')
plt.xlabel('iteration')
sns.despine()
```
As you can see, mini-batch ADVI's running time is much lower. It also seems to converge faster.
For fun, we can also look at the trace. The point is that we also get uncertainty of our Neural Network weights.
```
pm.traceplot(trace);
```
## Summary
Hopefully this blog post demonstrated a very powerful new inference algorithm available in [PyMC3](http://pymc-devs.github.io/pymc3/): [ADVI](http://pymc-devs.github.io/pymc3/api.html#advi). I also think bridging the gap between Probabilistic Programming and Deep Learning can open up many new avenues for innovation in this space, as discussed above. Specifically, a hierarchical neural network sounds pretty bad-ass. These are really exciting times.
## Next steps
[`Theano`](http://deeplearning.net/software/theano/), which is used by `PyMC3` as its computational backend, was mainly developed for estimating neural networks and there are great libraries like [`Lasagne`](https://github.com/Lasagne/Lasagne) that build on top of `Theano` to make construction of the most common neural network architectures easy. Ideally, we wouldn't have to build the models by hand as I did above, but use the convenient syntax of `Lasagne` to construct the architecture, define our priors, and run ADVI.
While we haven't successfully run `PyMC3` on the GPU yet, it should be fairly straight forward (this is what `Theano` does after all) and further reduce the running time significantly. If you know some `Theano`, this would be a great area for contributions!
You might also argue that the above network isn't really deep, but note that we could easily extend it to have more layers, including convolutional ones to train on more challenging data sets.
I also presented some of this work at PyData London, view the video below:
<iframe width="560" height="315" src="https://www.youtube.com/embed/LlzVlqVzeD8" frameborder="0" allowfullscreen></iframe>
Finally, you can download this NB [here](https://github.com/twiecki/WhileMyMCMCGentlySamples/blob/master/content/downloads/notebooks/bayesian_neural_network.ipynb). Leave a comment below, and [follow me on twitter](https://twitter.com/twiecki).
## Acknowledgements
[Taku Yoshioka](https://github.com/taku-y) did a lot of work on ADVI in PyMC3, including the mini-batch implementation as well as the sampling from the variational posterior. I'd also like to the thank the Stan guys (specifically Alp Kucukelbir and Daniel Lee) for deriving ADVI and teaching us about it. Thanks also to Chris Fonnesbeck, Andrew Campbell, Taku Yoshioka, and Peadar Coyle for useful comments on an earlier draft.
|
github_jupyter
|
This notebook is broken into two sections, firstly an introduction to the NumPy package and secondly a breakdown of the NumPy random package.
# The NumPy Package
## What is it?
NumPy is a Python package used for scientific computing. Often cited as a fundamental package in this area, this is for good reason. It provides a high performance multidimensional array object, and a variety of routines for operations on arrays. NumPy is not part of a basic Python installation. It has to be installed after the Python installation.
The implemented multi-dimensional arrays are very efficient as NumPy was mostly written in C; the precompiled mathematical and numerical functions and functionalities of NumPy guarantee excellent execution speed.
At its core NumPy provides the ndarray (multidimensional/n-dimensional array) object. This is a grid of values of the same type indexed by a tuple of non-negative integers. This is explained in further detail in the basics section below.
## The Basics
In Numpy, axes are called dimensions, lets take a hypothetical set of coordinates and see what exactly this means.
The coordinates of a point in 3D space [1, 4, 5] has one axis that contains 3 elements ie. has a length of 3.
Let's take another example to reinforce this idea.
Using the illustrated graph below we can see that the set of coordinates has 2 axes. Axis 1 has a length (shown in colour) of 2, and axis 2 has a length of 3.
<mark>FIGURE 1</mark>

One of NumPy's most powerful features is it's array class: ```ndarray``` This is not to be confused with the Python's array class ```array.array``` which has less functionality and only handles one-dimensional arrays.
##### Let's use some of ndarray's functions to prove and reinforce what we learnt above.
#### A Simple Example
Before we use NumPy we have to import it.
It is very common to see NumPy renamed to "np".
```
import numpy as np
```
From here let's create an array of values that represent distances eg. in metres
```
mvalues = [45.26, 10.9, 26.3, 80.5, 24.1, 66.1, 19.8, 3.0, 8.8, 132.5]
```
Great, now let's do some NumPy stuff on that. We're going to turn our array of values into a one-dimensional NumPy array and print it to the screen.
```
M = np.array(mvalues)
print(M)
```
Now let's say that we wanted to convert all of our values in metres to centimetres. This is easily achieved using a NumPy array and scalar multiplication.
```
print(M*100)
```
If we print out M again you can see that the values have not been changed.
```
print(M)
```
Now if you wanted to do the same thing using standard Python, as shown below, then hopefully you can clearly see the advantage in using NumPy instead.
```
mvalues = [ i*100 for i in mvalues]
print(mvalues)
```
The values for mvalues have also all been permanently changed now, whereas we didn't need to alter them when using NumPy
Earlier I explained that NumPy provides the ndarray object. "M" is an instance of the class ```numpy.ndarray```, proven below:
```
type(M)
```
# The NumPy Random Package
The NumPy random package is used for sampling and generating random data. Across this section I've split the descriptions and examples into 4 sections:
Simple Random Data
Permutations
Distributions
Random Generator
In order to use the random package the name of package must be specified, followed by the function.
eg. ```np.random.rand(3,3)``` (It's implied that NumPy has been imported as np)
As a precursor, you will notation that looks like this **[num, num]** across this notebook.
This is known as interval notation. This brief explanation from Wikipedia nicely describes the notations found in this notebook.
"In mathematics, a (real) interval is a set of real numbers with the property that any number that lies
between two numbers in the set is also included in the set."
"For example, (0,1) means greater than 0 and less than 1. A closed interval is an interval which includes all
its limit points, and is denoted with square brackets. For example, [0,1] means greater than or equal to 0 and
less than or equal to 1. A half-open interval includes only one of its endpoints, and is denoted by mixing the
notations for open and closed intervals. (0,1] means greater than 0 and less than or equal to 1, while [0,1)
means greater than or equal to 0 and less than 1."
## Simple Random Data
Let's go over some of the functions that NumPy provides to help us deal with simple random data.
### rand
`numpy.random.rand`
Used to generate random values in a given shape. The dimensions of the input should be positive and if they are not or they're empty a float will be returned. The example below creates an array of specified shape and populates it with random samples from a uniform distribution over [0, 1).
Let's use that example and construct a 2D array of random values. If you wanted a 3D array or greater you would simply add an additional parameter to the function.
```
import numpy as np
np.random.rand(3,3)
```
### randn
`numpy.random.randn`
Returns a sample (or samples) from the “standard normal” distribution.
A standard normal distribution is a normal distribution where the average value is 0, and the variance is 1.
When the function is provided a positive "int_like or int-convertible arguments", randn generates an array of specified shape (d0, d1, ..., dn), filled with random floats sampled from this distribution. Like ```rand```, a single float is returned if no argument is provided.
```
import numpy as np
np.random.randn(3,2)
```
Additional computations can be added for greater specificity
```
np.random.randn(3,2) + 8
```
### randint
`numpy.random.randint`
Returns random integers from low (inclusive) to high (exclusive).
the parameters for ```randint``` are **(low, high=None, size=None, dtype='l')**
* **low and high** simply refer to the lowest and highest numbers that can be drawn from the distribution,
* **size** refers to the output shape,
* **dtype** is optional but if you have a desired output type you may specifiy it here.
The example below generates a 4 x 4 array of ints between 0 and 4, inclusive:
```
import numpy as np
np.random.randint(5, size=(4, 4))
```
`randint` is often used for more simple operations eg. generate a random number between 1-10
```
np.random.randint(1,10)
```
### random_integers
`numpy.random.random_integers`
Returns random integers of type np.int from the “discrete uniform” distribution in the closed interval [low, high].
`random_integers` is similar to ```randint```, only for the closed interval [low, high].
0 is the lowest value if high is omitted when using `random_integers`, whereas it is 1 in the case that high is omitted when using `randint`. This function however has been deprecated so it is advised you use ```randint``` instead ie. `np.random.random_integers(10) --> randint(1, 10 + 1)`
### random_sample
`numpy.random.random_sample`
Returns random floats in the half-open interval [0.0, 1.0).
The inputs may be an int or a tuple of ints denoting the shape of the array.
This example shows how to draw a random sample from 0-5.
```
import numpy as np
x = 5 * np.random.random_sample((250, 250)) + 0
x
```
Below is a plot of the interval above which shows the continuous uniform distribution produced by `random_sample`, in the form of a histogram
```
# Import matplot in order to generate a histogram
import matplotlib.pyplot as plt
# Define the amount of bins (series of intervals) for the histogram
num_bins = [0,1,2,3,4,5]
# Plot and display the histogram
n, bins, patches = plt.hist(x, num_bins, facecolor = 'green', alpha = 0.8)
plt.show()
```
### random, ranf and sample
An interesting point to note is the homogeniety between the `random_sample`, `random`, `ranf` and `sample` functions. As noted in the official NumPy documentation, all of these functions,
"Return random floats in the half-open interval [0.0, 1.0)."
To prove that the functions are the same and can be used interchangeably we can use the `is` keyword to compare object identity ie. "Do I have two names for the same object?"
```
np.random.random_sample is np.random.random
np.random.random_sample is np.random.ranf
np.random.random_sample is np.random.sample
```
### choice
`numpy.random.choice`
Generates a random sample from a given 1-D array. If you use a ndarray as the input then a random number will be selected from the elements provided. This may be useful for situations where you have a large pool of numbers to choose from and need a random selection eg.
```
import numpy as np
j = [2,4,9,125,3,19,8,62,1004,203]
# Convert array to a NumPy array
o = np.array(j)
# Output a random choice
np.random.choice(o)
```
The sample assumes a uniform distribution over all entries, however, if we wanted to change this and account for different probabilities we can use a parameter to set the probability for each individual entry. Remember that probability must add up to 1.
```
import numpy as np
# Apply probabilities for each individual entry
np.random.choice(o, p = [0.1, 0.025, 0.025, 0.025, 0.025, 0.1, 0.1, 0.3, 0.2, 0.1])
```
### bytes
`numpy.random.bytes`
This a useful function that simply return a string of bytes of given length eg.
```
import numpy as np
# Output a string of 15 random bytes
np.random.bytes(15)
```
## Permutations
This definition from Wikipedia explains nicely what a permutation is:
In mathematics, the notion of permutation relates to the act of arranging all the members of a set into some
sequence or order, or if the set is already ordered, rearranging its elements, a process called permuting.
The number of permutations on a set of n elements is given by n! (factorial)
For example:
3! = 3x2x1 = 6
the six possible rearrangements would be (1x2x3), (2x3x1), (3x1x2), (1x3x2), (2x1x3), (3x2x1)
### shuffle
`numpy.random.shuffle`
`shuffle` as the name implies, shuffles an array or list. This function only shuffles the array along the first axis of a multi-dimensional array. The order of sub-arrays is changed but their contents remains the same.
Shown below is an example of creating a 1D array, reshaping it and shuffling the contents.
```
import numpy as np
# Create an array of values between 0-15, reshape to 4x4 array
arr = np.arange(16).reshape((4,4))
# Shuffle the array
np.random.shuffle(arr)
arr
```
But what if I want to shuffle a 2D array? If this is the case then you can use the `ravel` function to flatten a multi-dimensional array like so:
```
# Create the NumPy array
e = np.array([[20,30,40],[50,60,70],[80,90,100]])
e
# Flatten the array, shuffle and output result
np.random.shuffle(e.ravel())
e
```
### permutation
`numpy.random.permutation`
Randomly permutes a sequence or returns a permuted range of values. In the case the the value is an array, `permutation` will copy and shuffle the elements randomly. If x is an integer, np.arange(x) is called and randomly permuted.
```
import numpy as np
# Return a random permutation from an array of values in the range of 0-5
# (np.arange uses the half-open interval of [0,1))
np.random.permutation(6)
# Return a shuffled copy of the permutation of the array
np.random.permutation([1, 4, 9, 12, 15])
# Permute
arr = np.arange(4).reshape((2, 2))
np.random.permutation(arr)
```
## Distributions
The distribution of a statistical data set (or a population) is a listing or function showing all the possible values (or intervals) of the data and how often they occur. When a distribution of categorical data is organized, you see the number or percentage of individuals in each group. When a distribution of numerical data is organized, they’re often ordered from smallest to largest, broken into reasonably sized groups (if appropriate), and then put into graphs and charts to examine the shape, center, and amount of variability in the data.
The world of statistics includes dozens of different distributions for categorical and numerical data; the most common ones have their own names. One of the most well-known distributions is called the normal distribution, also known as the bell-shaped curve. The normal distribution is based on numerical data that is continuous; its possible values lie on the entire real number line. Its overall shape, when the data are organized in graph form, is a symmetric bell-shape. In other words, most (around 68%) of the data are centered around the mean (giving you the middle part of the bell), and as you move farther out on either side of the mean, you find fewer and fewer values (representing the downward sloping sides on either side of the bell).
Due to symmetry, the mean and the median lie at the same point, directly in the center of the normal distribution. The standard deviation is measured by the distance from the mean to the inflection point (where the curvature of the bell changes from concave up to concave down).
### Normal Distribution
`np.random.normal`
The probability density function of the normal distribution, is often called the bell curve because of its characteristic shape.
What this example does is it creates the data for a normal distribution plot centered around a mean of 100, showing 3 standard deviations of the data, and creates 30,000 random data points that are of normal distribution. Remember this is the normal() function, which means that the data will be normalized. 68% of the data values will generated will be (or very close to) ±1 standard deviations of the mean. 95% of the data values generated will be within ±2 standard deviations of the mean. 99.7% of the data values generated will be within ±3 standard deviations of the mean.
```
# Import required packages
import matplotlib.pyplot as plt
import numpy as np
# Set the mean and standard deviation
mu, sigma = 100, 3
#
s = np.random.normal(mu, sigma, 30000)
#
count, bins, ignored = plt.hist(s, 25, density=True, color='blue')
# Plot a line that shows the probability density function for the normal distribution
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
linewidth=2, color='r')
plt.show()
```
## The Binomial Distribution
`np.random.binomial`
It can be used to obtain the number of successes from N Bernoulli trials.
Samples are drawn from a binomial distribution with specified parameters, n trials and p probability of
success where n an integer >= 0 and p is in the interval [0,1]. (n may be input as a float, but it is
truncated to an integer in use)
Here we're going to use Seaborn, a Python data visualization library based on matplotlib, to graph the distribution.
```
import numpy as np
import matplotlib.pyplot as plt
# Import the Seaborn package for graphing
import seaborn as sb
# Number of trials, probability of each trial
n, p = 100, .1
# Generate binomial distribution
s = np.random.binomial(n, p, 30000)
# Plot the graph with Seaborn
ax = sb.distplot(s,
kde=False,
color='blue',
hist_kws={"linewidth": 30,'alpha':0.8})
ax.set(xlabel='Binomial', ylabel='Frequency')
p = 4/15 = 27%. 0.27*15 = 4,
```
What I've shown here is that a binomial distribution is very different from a normal distribution, and yet if the sample size is large enough, the shapes will be quite similar as can be seen here. I used 30,000 as the size of both distributions and both produced a bell shaped curve.
The main difference between the two is that the binomial distribution is discrete, whereas the normal distribution is continuous. Continuous simply means that (in theory) it's possible to find a data value between any two data values. Things like the heights of people vary continuously, there are lots of random influences, generally their overall distribution is close to normal.
A discrete probability distribution on the other hand is one where the possible outcomes are distinct and non-overlapping. eg. rolling a dice, you can roll a 5 or a 6 but not 5.5. As a result the graphed distribution looks "stepped".
## Pareto Distribution
`numpy.random.pareto`
This draw samples from a Pareto II or Lomax distribution with specified shape.
The original Pareto distribution, is a power-law probability distribution that was originally applied to describing the distribution of wealth in a society, showing the trend that a large portion of the wealth is held by a small percentage of the population and that this is observable across a number of natural phenomena ie. that a few items account for a lot of subject and a lot of items account for a little of it.
The Lomax or Pareto II distribution is a shifted Pareto distribution. We can obtain the original Pareto distribution from the Lomax distribution by adding 1 and multiplying by the scale parameter 2.0
```
import matplotlib.pyplot as plt
import numpy as np
# shape and mode
a, m = 3., 2.
# Calculate original pareto
s = (np.random.pareto(a, 1000) + 1) * m
count, bins, _ = plt.hist(s, 100, density=True, color="blue")
fit = a*m**a / bins**(a+1)
plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='red')
plt.show()
```
## Random Generators
### RandomState
`numpy.random.RandomState`
The container for the Mersenne Twister pseudo-random number generator.
This class is what is primarily used in NumPy to generate random numbers. If no seed is provided, the generator will try to use the system clock as a seed.
### seed
`numpy.random.seed`
We can use `seed` to seed the RandomState generator. The only requirement is that it must be convertible to 32 bit unsigned integers.
One of the main uses a seed is when testing a program you've written and you want to make sure you generate the same pseudo-random numbers. This works as a seed is actually the starting point in the sequence. If we use same seed every time, it will yield same sequence of random numbers.
```
import numpy as np
# Set seed
np.random.seed(25)
# Generate random numbers
a = np.random.rand(5)
# Change seed
np.random.seed(55)
# Generate random numbers again
b = np.random.rand(5)
# Output results
print("a: ", a)
print("b: ", b)
```
## References:
https://docs.scipy.org/doc/numpy-1.15.1/reference/routines.random.html
https://www.quora.com/What-is-seed-in-random-number-generation
https://www.dummies.com/education/math/statistics/what-the-distribution-tells-you-about-a-statistical-data-set/
https://magoosh.com/statistics/understanding-binomial-distribution/
http://wiki.stat.ucla.edu/socr/index.php/AP_Statistics_Curriculum_2007_Pareto
|
github_jupyter
|
# 1.1 Getting started
## Prerequisites
### Installation
This tutorial requires **signac**, so make sure to install the package before starting.
The easiest way to do so is using conda:
```$ conda config --add channels conda-forge```
```$ conda install signac```
or pip:
```pip install signac --user```
Please refer to the [documentation](https://docs.signac.io/en/latest/installation.html#installation) for detailed instructions on how to install signac.
After successful installation, the following cell should execute without error:
```
import signac
```
We start by removing all data which might be left-over from previous executions of this tutorial.
```
%rm -rf projects/tutorial/workspace
```
## A minimal example
For this tutorial we want to compute the volume of an ideal gas as a function of its pressure and thermal energy using the ideal gas equation
$p V = N kT$, where
$N$ refers to the system size, $p$ to the pressure, $kT$ to the thermal energy and $V$ is the volume of the system.
```
def V_idg(N, kT, p):
return N * kT / p
```
We can execute the complete study in just a few lines of code.
First, we initialize the project directory and get a project handle:
```
import signac
project = signac.init_project(name="TutorialProject", root="projects/tutorial")
```
We iterate over the variable of interest *p* and construct a complete state point *sp* which contains all the meta data associated with our data.
In this simple example the meta data is very compact, but in principle the state point may be highly complex.
Next, we obtain a *job* handle and store the result of the calculation within the *job document*.
The *job document* is a persistent dictionary for storage of simple key-value pairs.
Here, we exploit that the state point dictionary *sp* can easily be passed into the `V_idg()` function using the [keyword expansion syntax](https://docs.python.org/dev/tutorial/controlflow.html#keyword-arguments) (`**sp`).
```
for p in 0.1, 1.0, 10.0:
sp = {"p": p, "kT": 1.0, "N": 1000}
job = project.open_job(sp)
job.document["V"] = V_idg(**sp)
```
We can then examine our results by iterating over the data space:
```
for job in project:
print(job.sp.p, job.document["V"])
```
That's it.
...
Ok, there's more...
Let's have a closer look at the individual components.
## The Basics
The **signac** data management framework assists the user in managing the data space of individual *projects*.
All data related to one or multiple projects is stored in a *workspace*, which by default is a directory called `workspace` within the project's root directory.
```
print(project.root_directory())
print(project.workspace())
```
The core idea is to tightly couple state points, unique sets of parameters, with their associated data.
In general, the parameter space needs to contain all parameters that will affect our data.
For the ideal gas that is a 3-dimensional space spanned by the thermal energy *kT*, the pressure *p* and the system size *N*.
These are the **input parameters** for our calculations, while the calculated volume *V* is the **output data**.
In terms of **signac** this relationship is represented by an instance of `Job`.
We use the `open_job()` method to get a *job handle* for a specific set of input parameters.
```
job = project.open_job({"p": 1.0, "kT": 1.0, "N": 1000})
```
The *job* handle tightly couples our input parameters (*p*, *kT*, *N*) with the storage location of the output data.
You can inspect both the input parameters and the storage location explicitly:
```
print(job.statepoint())
print(job.workspace())
```
For convenience, a job's *state point* may also be accessed via the short-hand `sp` attribute.
For example, to access the pressure value `p` we can use either of the two following expressions:
```
print(job.statepoint()["p"])
print(job.sp.p)
```
Each *job* has a **unique id** representing the state point.
This means opening a job with the exact same input parameters is guaranteed to have the **exact same id**.
```
job2 = project.open_job({"kT": 1.0, "N": 1000, "p": 1.0})
print(job.id, job2.id)
```
The *job id* is used to uniquely identify data associated with a specific state point.
Think of the *job* as a container that is used to store all data associated with the state point.
For example, it should be safe to assume that all files that are stored within the job's workspace directory are tightly coupled to the job's statepoint.
```
print(job.workspace())
```
Let's store the volume calculated for each state point in a file called `V.txt` within the job's workspace.
```
import os
fn_out = os.path.join(job.workspace(), "V.txt")
with open(fn_out, "w") as file:
V = V_idg(**job.statepoint())
file.write(str(V) + "\n")
```
Because this is such a common pattern, **signac** signac allows you to short-cut this with the `job.fn()` method.
```
with open(job.fn("V.txt"), "w") as file:
V = V_idg(**job.statepoint())
file.write(str(V) + "\n")
```
Sometimes it is easier to temporarily switch the *current working directory* while storing data for a specific job.
For this purpose, we can use the `Job` object as [context manager](https://docs.python.org/3/reference/compound_stmts.html#with).
This means that we switch into the workspace directory associated with the job after entering, and switch back into the original working directory after exiting.
```
with job:
with open("V.txt", "w") as file:
file.write(str(V) + "\n")
```
Another alternative to store light-weight data is the *job document* as shown in the minimal example.
The *job document* is a persistent JSON storage file for simple key-value pairs.
```
job.document["V"] = V_idg(**job.statepoint())
print(job.statepoint(), job.document)
```
Since we are usually interested in more than one state point, the standard operation is to iterate over all variable(s) of interest, construct the full state point, get the associated job handle, and then either just initialize the job or perform the full operation.
```
for pressure in 0.1, 1.0, 10.0:
statepoint = {"p": pressure, "kT": 1.0, "N": 1000}
job = project.open_job(statepoint)
job.document["V"] = V_idg(**job.statepoint())
```
Let's verify our result by inspecting the data.
```
for job in project:
print(job.statepoint(), job.document)
```
Those are the basics for using **signac** for data management.
The [next section](signac_102_Exploring_Data.ipynb) demonstrates how to explore an existing data space.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/DJCordhose/ml-workshop/blob/master/notebooks/tf-intro/2020-01-rnn-basics.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Sequences Basics
Example, some code and a lot of inspiration taken from: https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/
```
import matplotlib.pyplot as plt
%matplotlib inline
import matplotlib as mpl
mpl.rcParams['figure.figsize'] = (20, 8)
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
print(tf.__version__)
```
## Univariate Sequences
just one variable per time step
### Challenge
We have a known series of events, possibly in time and you want to know what is the next event. Like this
[10, 20, 30, 40, 50, 60, 70, 80, 90]
```
# univariate data preparation
import numpy as np
# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
X, y = list(), list()
for i in range(len(sequence)):
# find the end of this pattern
end_ix = i + n_steps
# check if we are beyond the sequence
if end_ix > len(sequence)-1:
break
# gather input and output parts of the pattern
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
#@title Prediction from n past steps
# https://colab.research.google.com/notebooks/forms.ipynb
n_steps = 3 #@param {type:"slider", min:1, max:10, step:1}
# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# summarize the data
list(zip(X, y))
X
```
### Converting shapes
* one of the most frequent, yet most tedious steps
* match between what you have and what an interface needs
* expected input of RNN: 3D tensor with shape (samples, timesteps, input_dim)
* we have: (samples, timesteps)
* reshape on np arrays can do all that
```
# reshape from [samples, timesteps] into [samples, timesteps, features]
n_features = 1
X = X.reshape((X.shape[0], X.shape[1], n_features))
X
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.layers import Dense, LSTM, GRU, SimpleRNN, Bidirectional
from tensorflow.keras.models import Sequential, Model
model = Sequential()
model.add(SimpleRNN(units=50, activation='relu', input_shape=(n_steps, n_features), name="RNN_Input"))
model.add(Dense(units=1, name="Linear_Output"))
model.compile(optimizer='adam', loss='mse')
model.summary()
EPOCHS = 1000
%time history = model.fit(X, y, epochs=EPOCHS, verbose=0)
loss = model.evaluate(X, y, verbose=0)
loss
import matplotlib.pyplot as plt
plt.yscale('log')
plt.ylabel("loss")
plt.xlabel("epochs")
plt.plot(history.history['loss']);
```
### Let's try this on a few examples
```
# this does not look too bad
X_sample = np.array([[10, 20, 30], [70, 80, 90]]).astype(np.float32)
X_sample = X_sample.reshape((X_sample.shape[0], X_sample.shape[1], n_features))
X_sample
y_pred = model.predict(X_sample)
y_pred
def predict(model, samples, n_features=1):
input = np.array(samples).astype(np.float32)
input = input.reshape((input.shape[0], input.shape[1], n_features))
y_pred = model.predict(input)
return y_pred
# do not look too close, though
predict(model, [[100, 110, 120], [200, 210, 220], [200, 300, 400]])
```
## Exercise
* go through the notebook as it is
* Try to improve the model
* Change the number of values used as input
* Change activation function
* More nodes? less nodes?
* What else might help improving the results?
# STOP HERE
### Input and output of an RNN layer
```
# https://keras.io/layers/recurrent/
# input: (samples, timesteps, input_dim)
# output: (samples, units)
# let's have a look at the actual output for an example
rnn_layer = model.get_layer("RNN_Input")
model_stub = Model(inputs = model.input, outputs = rnn_layer.output)
hidden = predict(model_stub, [[10, 20, 30]])
hidden.shape, hidden
```
#### What do we see?
* each unit (50) has a single output
* as a sidenote you nicely see the RELU nature of the output
* so the timesteps of the input are lost
* we are only looking at the final output
* still with each timestep, the layer does produce a unique output we could potentially use
### We need to look into RNNs a bit more deeply now
#### RNNs - Networks with Loops
<img src='https://djcordhose.github.io/ai/img/nlp/colah/RNN-rolled.png' height=200>
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
#### Unrolling the loop
<img src='https://djcordhose.github.io/ai/img/nlp/colah/RNN-unrolled.png'>
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
#### Simple RNN internals
<img src='https://djcordhose.github.io/ai/img/nlp/fchollet_rnn.png'>
## $output_t = \tanh(W input_t + U output_{t-1} + b)$
From Deep Learning with Python, Chapter 6, François Chollet, Manning: https://livebook.manning.com/#!/book/deep-learning-with-python/chapter-6/129
#### Activation functions
<img src='https://djcordhose.github.io/ai/img/sigmoid-activation.png' height=200>
Sigmoid compressing between 0 and 1
<img src='https://djcordhose.github.io/ai/img/tanh-activation.png' height=200>
Hyperbolic tangent, like sigmoind, but compressing between -1 and 1, thus allowing for negative values as well
```
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
!nvidia-smi
from argparse import Namespace
import sys
import os
home = os.environ['HOME']
os.environ['CUDA_VISIBLE_DEVICES'] = '0,1'
print(os.environ['CUDA_VISIBLE_DEVICES'])
os.chdir(f'{home}/pycharm/automl')
# os.chdir(f'{home}/pycharm/automl/search_policies/rnn')
sys.path.append(f'{home}/pycharm/nasbench')
sys.path.append(f'{home}/pycharm/automl')
import torch
import torch.nn as nn
import utils
from image_dataloader import load_dataset
from search_policies.cnn.search_space.nasbench101.nasbench_api_v2 import NASBench_v2
from search_policies.cnn.search_space.nasbench101.util import load_nasbench_checkpoint, transfer_model_key_to_search_key, nasbench_zero_padding_load_state_dict_pre_hook
from search_policies.cnn.procedures.train_search_procedure import darts_model_validation
from search_policies.cnn.search_space.nasbench101.model_search import NasBenchNetSearch
utils.torch_random_seed(10)
print('loading cifar ...')
train_queue, valid_queue, test_queue = load_dataset()
print("loading Nasbench dataset...")
nasbench = NASBench_v2('data/nasbench/nasbench_only108.tfrecord', only_hash=True)
sanity_check = True
# load one model and
MODEL_FOLDER='/home/yukaiche/pycharm/automl/experiments/reproduce-nasbench/rank_100002-arch_97a390a2cb02fdfbc505f6ac44a37228-eval-runid-0'
CKPT_PATH=MODEL_FOLDER + '/checkpoint.pt'
model_folder = MODEL_FOLDER
ckpt_path = CKPT_PATH
print("load model and test ...")
hash = model_folder.split('arch_')[1].split('-eval')[0]
print('model_hash ', hash)
spec = nasbench.hash_to_model_spec(hash)
print('model spec', spec)
# model, ckpt = load_nasbench_checkpoint(ckpt_path, spec, legacy=True)
from search_policies.cnn.cnn_search_configs import build_default_args
# def project the weights
default_args = build_default_args()
default_args.model_spec = spec
spec = nasbench.hash_to_model_spec(hash)
model, ckpt = load_nasbench_checkpoint(ckpt_path, spec, legacy=True)
model = model.cuda()
model.eval()
model_search = NasBenchNetSearch(args=default_args)
model_search.eval()
model_search = model_search.cuda()
source_dict = model.state_dict()
target_dict = model_search.state_dict()
# Checking the loaded model state dict.
if sanity_check:
for ind, k in enumerate(source_dict.keys()):
if ind > 5:
break
print(k, ((source_dict[k] - target_dict[k]).sum()))
trans_dict = dict()
for k in model.state_dict().keys():
kk = transfer_model_key_to_search_key(k, spec)
if kk not in model_search.state_dict().keys():
print('not found ', kk)
continue
# if sanity_check:
# print(f'map {k}', source_dict[k].size())
# print(f'to {kk}' ,target_dict[kk].size())
trans_dict[kk] = source_dict[k]
padded_dict = nasbench_zero_padding_load_state_dict_pre_hook(trans_dict, model_search.state_dict())
if sanity_check:
target_dict = model_search.state_dict()
for ind, k in enumerate(padded_dict.keys()):
if ind > 5:
break
print(k)
print((padded_dict[k] - target_dict[k]).sum().item())
print((ckpt['model_state'][k] - target_dict[k]).sum().item())
# print((padded_dict[k][trans_dict[k].size()[0]] - trans_dict[k]).sum())
# loaded the padded dict and test the results.
model_search.load_state_dict(padded_dict)
model_search = model_search.change_model_spec(spec)
model_search = model_search.eval()
res = darts_model_validation(test_queue, model, nn.CrossEntropyLoss(),Namespace(debug=False, report_freq=50))
print('original model evaluation on test split', res)
search_res = darts_model_validation(test_queue, model_search, nn.CrossEntropyLoss(),Namespace(debug=False, report_freq=50))
print('Reload to NasBenchSearch, evaluation results ' ,search_res)
# results get worse after padding to original node. Somethings goes wrong.
# Further sanity checking, by loading part of the model and continue.
# print(model.stacks['stack0']['module0'].vertex_ops.keys())
# print(spec.ops)
# m0 = model.stacks['stack0']['module0']
# print([k for k in m0.state_dict().keys() if 'vertex_1' not in k and 'proj' not in k ])
# # print([k for k in m0.state_dict().keys() if 'vertex_1' not in k and 'proj' not in k ])
# load_keys = sorted([transfer_model_key_to_search_key(k, spec) for k in k1])
# train_param_keys = sorted(train_param_keys)
# # for a1, a2 in zip(load_keys, train_param_keys):
# # print(a1)
# # print(a2)
# for a1 in load_keys:
# if a1 not in train_param_keys:
# print(a1)
# print(len(load_keys), len(train_param_keys))
model.eval()
model_search.load_state_dict(padded_dict)
model_search.eval()
# This debugs the entire network's output.
img, lab = iter(test_queue).__next__()
img = img.cuda()
lab = lab.cuda()
bz = 32
with torch.no_grad():
m1 = model.forward_debug(img[:bz, :, : ,:])
m2 = model_search.forward_debug(img[:bz, :, :, :])
for ind,(a,b) in enumerate(zip(m1, m2)):
print(ind, (a - b).sum().item())
# model_search.stem[1].eval()
# model.stem[1].eval()
# m1stem_out = model.stem(img)
# model_search.stem.load_state_dict(model.stem.state_dict())
# m2stem_out = model_search.stem(img)
# for k, v in model.stem.state_dict().items():
# print(k, (v - model_search.stem.state_dict()[k]).sum().item())
# print((m1stem_out - m2stem_out).sum().item())
s1input = m1[0].cuda()
m1stack = model.stacks['stack0']['module0']
m2stack = model_search.stacks['stack0']['module0']
print(m1stack.__class__.__name__)
print(m2stack.__class__.__name__)
print((m1stack(s1input) - m2stack(s1input)).sum().item())
m1out = m1stack.forward_debug(s1input)
m2out = m2stack.forward_debug(s1input)
# Cell level, not true after 1 iters
for k, v in m1out.items():
print(k, (v - m2out[k]).sum().item())
print(m1stack.execution_order.items())
# vertex level
m1vertex = m1stack.vertex_ops['vertex_1']
m2vertex = m2stack.vertex_ops['vertex_1']
print('vertex_1 difference', (m1vertex([s1input,]) - m2vertex([s1input,])).sum().item())
print(m1vertex)
print(m2vertex)
# inside vertex level, proj_ops and vertex_op
m1_proj = m1vertex.proj_ops[0](s1input)
m1_out = m1vertex.op(m1_proj)
m2_proj = m2vertex.current_proj_ops[0](s1input)
m2_out = m2vertex.current_op(m2_proj)
print('after v1 proj diff',(m1_proj - m2_proj).sum().item())
print('after v1 diff',(m1_out - m2_out).sum().item())
# proj level
m1projop = m1vertex.proj_ops[0]
m2projop = m2vertex.current_proj_ops[0]
print(m1projop)
print(m2projop)
print(m1projop[1].training)
print(m2projop.bn.training)
# m2vertex.train()
model_search.eval()
print(m1projop[1].training)
print(m2projop.bn.training)
import glob
model_lists = glob.glob('/home/yukaiche/pycharm/automl/experiments/reproduce-nasbench/*')
print(model_lists)
for model_folder in model_lists:
if len(glob.glob(model_folder + '/checkpoint.pt')) > 0:
hash = model_folder.split('arch_')[1].split('-eval')[0]
rank = model_folder.split('rank_')[1].split('-arch')[0]
print(rank, hash)
```
|
github_jupyter
|
SOP036 - Install kubectl command line interface
===============================================
Steps
-----
### Common functions
Define helper functions used in this notebook.
```
# Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import json
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {} # Output in stderr known to be transient, therefore automatically retry
error_hints = {} # Output in stderr where a known SOP/TSG exists which will be HINTed for further help
install_hint = {} # The SOP to help install the executable if it cannot be found
first_run = True
rules = None
debug_logging = False
def run(cmd, return_output=False, no_output=False, retry_count=0, base64_decode=False, return_as_json=False):
"""Run shell command, stream stdout, print stderr and optionally return output
NOTES:
1. Commands that need this kind of ' quoting on Windows e.g.:
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='data-pool')].metadata.name}
Need to actually pass in as '"':
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='"'data-pool'"')].metadata.name}
The ' quote approach, although correct when pasting into Windows cmd, will hang at the line:
`iter(p.stdout.readline, b'')`
The shlex.split call does the right thing for each platform, just use the '"' pattern for a '
"""
MAX_RETRIES = 5
output = ""
retry = False
global first_run
global rules
if first_run:
first_run = False
rules = load_rules()
# When running `azdata sql query` on Windows, replace any \n in """ strings, with " ", otherwise we see:
#
# ('HY090', '[HY090] [Microsoft][ODBC Driver Manager] Invalid string or buffer length (0) (SQLExecDirectW)')
#
if platform.system() == "Windows" and cmd.startswith("azdata sql query"):
cmd = cmd.replace("\n", " ")
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# When running `kubectl`, if AZDATA_OPENSHIFT is set, use `oc`
#
if cmd.startswith("kubectl ") and "AZDATA_OPENSHIFT" in os.environ:
cmd_actual[0] = cmd_actual[0].replace("kubectl", "oc")
# To aid supportability, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
# Display an install HINT, so the user can click on a SOP to install the missing binary
#
if which_binary == None:
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
print(f"START: {cmd} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if rules is not None:
apply_expert_rules(line)
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
try:
line_decoded = line.decode()
except UnicodeDecodeError:
# NOTE: Sometimes we get characters back that cannot be decoded(), e.g.
#
# \xa0
#
# For example see this in the response from `az group create`:
#
# ERROR: Get Token request returned http error: 400 and server
# response: {"error":"invalid_grant",# "error_description":"AADSTS700082:
# The refresh token has expired due to inactivity.\xa0The token was
# issued on 2018-10-25T23:35:11.9832872Z
#
# which generates the exception:
#
# UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa0 in position 179: invalid start byte
#
print("WARNING: Unable to decode stderr line, printing raw bytes:")
print(line)
line_decoded = ""
pass
else:
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
# inject HINTs to next TSG/SOP based on output in stderr
#
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
# apply expert rules (to run follow-on notebooks), based on output
#
if rules is not None:
apply_expert_rules(line_decoded)
# Verify if a transient error, if so automatically retry (recursive)
#
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
def load_json(filename):
"""Load a json file from disk and return the contents"""
with open(filename, encoding="utf8") as json_file:
return json.load(json_file)
def load_rules():
"""Load any 'expert rules' from the metadata of this notebook (.ipynb) that should be applied to the stderr of the running executable"""
# Load this notebook as json to get access to the expert rules in the notebook metadata.
#
try:
j = load_json("sop036-install-kubectl.ipynb")
except:
pass # If the user has renamed the book, we can't load ourself. NOTE: Is there a way in Jupyter, to know your own filename?
else:
if "metadata" in j and \
"azdata" in j["metadata"] and \
"expert" in j["metadata"]["azdata"] and \
"expanded_rules" in j["metadata"]["azdata"]["expert"]:
rules = j["metadata"]["azdata"]["expert"]["expanded_rules"]
rules.sort() # Sort rules, so they run in priority order (the [0] element). Lowest value first.
# print (f"EXPERT: There are {len(rules)} rules to evaluate.")
return rules
def apply_expert_rules(line):
"""Determine if the stderr line passed in, matches the regular expressions for any of the 'expert rules', if so
inject a 'HINT' to the follow-on SOP/TSG to run"""
global rules
for rule in rules:
notebook = rule[1]
cell_type = rule[2]
output_type = rule[3] # i.e. stream or error
output_type_name = rule[4] # i.e. ename or name
output_type_value = rule[5] # i.e. SystemExit or stdout
details_name = rule[6] # i.e. evalue or text
expression = rule[7].replace("\\*", "*") # Something escaped *, and put a \ in front of it!
if debug_logging:
print(f"EXPERT: If rule '{expression}' satisfied', run '{notebook}'.")
if re.match(expression, line, re.DOTALL):
if debug_logging:
print("EXPERT: MATCH: name = value: '{0}' = '{1}' matched expression '{2}', therefore HINT '{4}'".format(output_type_name, output_type_value, expression, notebook))
match_found = True
display(Markdown(f'HINT: Use [{notebook}]({notebook}) to resolve this issue.'))
```
### Install Kubernetes CLI
To get the latest version number for `kubectl` for Windows, open this
file:
- https://storage.googleapis.com/kubernetes-release/release/stable.txt
NOTE: For Windows, `kubectl.exe` is installed in the folder containing
the `python.exe` (`sys.executable`), which will be in the path for
notebooks run in ADS.
```
import os
import sys
import platform
from pathlib import Path
if platform.system() == "Darwin":
run('brew update')
run('brew install kubernetes-cli')
elif platform.system() == "Windows":
path = Path(sys.executable)
cwd = os.getcwd()
os.chdir(path.parent)
run('curl -L https://storage.googleapis.com/kubernetes-release/release/v1.17.0/bin/windows/amd64/kubectl.exe -o kubectl.exe')
os.chdir(cwd)
elif platform.system() == "Linux":
run('sudo apt-get update')
run('sudo apt-get install -y kubectl')
else:
raise SystemExit(f"Platform '{platform.system()}' is not recognized, must be 'Darwin', 'Windows' or 'Linux'")
print('Notebook execution complete.')
```
|
github_jupyter
|
<img align="left" src="https://lever-client-logos.s3.amazonaws.com/864372b1-534c-480e-acd5-9711f850815c-1524247202159.png" width=200>
<br></br>
<br></br>
## *Data Science Unit 4 Sprint 3 Assignment 1*
# Recurrent Neural Networks and Long Short Term Memory (LSTM)

It is said that [infinite monkeys typing for an infinite amount of time](https://en.wikipedia.org/wiki/Infinite_monkey_theorem) will eventually type, among other things, the complete works of Wiliam Shakespeare. Let's see if we can get there a bit faster, with the power of Recurrent Neural Networks and LSTM.
This text file contains the complete works of Shakespeare: https://www.gutenberg.org/files/100/100-0.txt
Use it as training data for an RNN - you can keep it simple and train character level, and that is suggested as an initial approach.
Then, use that trained RNN to generate Shakespearean-ish text. Your goal - a function that can take, as an argument, the size of text (e.g. number of characters or lines) to generate, and returns generated text of that size.
Note - Shakespeare wrote an awful lot. It's OK, especially initially, to sample/use smaller data and parameters, so you can have a tighter feedback loop when you're trying to get things running. Then, once you've got a proof of concept - start pushing it more!
```
import sys
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import LSTM
from keras.callbacks import ModelCheckpoint
from keras.utils import np_utils
# load ascii text and covert to lowercase
filename = "content/shakespeare.txt"
raw_text = open(filename, 'r', encoding='utf-8').read()
raw_text = raw_text.lower()
bad_chars = ['#', '*', '@', '_', '\ufeff']
for i in range(len(bad_chars)):
raw_text = raw_text.replace(bad_chars[i],"")
# create mapping of unique chars to integers, and a reverse mapping
chars = sorted(list(set(raw_text)))
char_to_int = dict((c, i) for i, c in enumerate(chars))
int_to_char = dict((i, c) for i, c in enumerate(chars))
# summarize the loaded data
n_chars = len(raw_text)
n_vocab = len(chars)
print("Total Characters: ", n_chars)
print("Total Vocab: ", n_vocab)
# prepare the dataset of input to output pairs encoded as integers
seq_length = 100
dataX = []
dataY = []
for i in range(0, n_chars - seq_length, 1):
seq_in = raw_text[i:i + seq_length]
seq_out = raw_text[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
n_patterns = len(dataX)
# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (n_patterns, seq_length, 1))
# normalize
X = X / float(n_vocab)
# one hot encode the output variable
y = np_utils.to_categorical(dataY)
# define the LSTM model
model = Sequential()
model.add(LSTM(256, input_shape=(X.shape[1], X.shape[2]), return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(256))
model.add(Dropout(0.2))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
# define the checkpoint
filepath="weights-improvement-{epoch:02d}-{loss:.4f}-bigger.hdf5"
checkpoint = ModelCheckpoint(filepath, monitor='loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
# fit the model
model.fit(X, y, epochs=50, batch_size=64, callbacks=callbacks_list)
import numpy as np
import random
import sys
filename = "content/shakespeare.txt"
text = open(filename, 'r', encoding='utf-8').read()
text = text.lower()
bad_chars = ['#', '*', '@', '_', '\ufeff']
for i in range(len(bad_chars)):
text = text.replace(bad_chars[i],"")
characters = sorted(list(set(text)))
char2indices = dict((c, i) for i, c in enumerate(characters))
indices2char = dict((i, c) for i, c in enumerate(characters))
maxlen = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
# Converting indices into vectorized format
X = np.zeros((len(sentences), maxlen, len(characters)), dtype=np.bool)
y = np.zeros((len(sentences), len(characters)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char2indices[char]] = 1
y[i, char2indices[next_chars[i]]] = 1
from keras.models import Sequential
from keras.layers import Dense, LSTM,Activation,Dropout
from keras.optimizers import RMSprop
#Model Building
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(characters))))
model.add(Dense(len(characters)))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer=RMSprop(lr=0.01))
print (model.summary())
def pred_indices(preds, metric=1.0):
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / metric
exp_preds = np.exp(preds)
preds = exp_preds/np.sum(exp_preds)
probs = np.random.multinomial(1, preds, 1)
return np.argmax(probs)
# Train and Evaluate the Model
for iteration in range(1, 10):
print('-' * 40)
print('Iteration', iteration)
model.fit(X, y,batch_size=128,epochs=1)
start_index = random.randint(0, len(text) - maxlen - 1)
for diversity in [0.2, 0.7,1.2]:
print('\n----- diversity:', diversity)
generated = ''
sentence = text[start_index: start_index + maxlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(400):
x = np.zeros((1, maxlen, len(characters)))
for t, char in enumerate(sentence):
x[0, t, char2indices[char]] = 1.
preds = model.predict(x, verbose=0)[0]
next_index = pred_indices(preds, diversity)
pred_char = indices2char[next_index]
generated += pred_char
sentence = sentence[1:] + pred_char
sys.stdout.write(pred_char)
sys.stdout.flush()
print("\nOne combination completed \n")
```
## Stretch goals:
- Refine the training and generation of text to be able to ask for different genres/styles of Shakespearean text (e.g. plays versus sonnets)
- Train a classification model that takes text and returns which work of Shakespeare it is most likely to be from
- Make it more performant! Many possible routes here - lean on Keras, optimize the code, and/or use more resources (AWS, etc.)
- Revisit the news example from class, and improve it - use categories or tags to refine the model/generation, or train a news classifier
- Run on bigger, better data
## Resources:
- [The Unreasonable Effectiveness of Recurrent Neural Networks](https://karpathy.github.io/2015/05/21/rnn-effectiveness/) - a seminal writeup demonstrating a simple but effective character-level NLP RNN
- [Simple NumPy implementation of RNN](https://github.com/JY-Yoon/RNN-Implementation-using-NumPy/blob/master/RNN%20Implementation%20using%20NumPy.ipynb) - Python 3 version of the code from "Unreasonable Effectiveness"
- [TensorFlow RNN Tutorial](https://github.com/tensorflow/models/tree/master/tutorials/rnn) - code for training a RNN on the Penn Tree Bank language dataset
- [4 part tutorial on RNN](http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/) - relates RNN to the vanishing gradient problem, and provides example implementation
- [RNN training tips and tricks](https://github.com/karpathy/char-rnn#tips-and-tricks) - some rules of thumb for parameterizing and training your RNN
|
github_jupyter
|
```
"""
A randomly connected network learning a sequence
This example contains a reservoir network of 500 neurons.
400 neurons are excitatory and 100 neurons are inhibitory.
The weights are initialized randomly, based on a log-normal distribution.
The network activity is stimulated with three different inputs (A, B, C).
The inputs are given in i a row (A -> B -> C -> A -> ...)
The experiment is defined in 'pelenet/experiments/sequence.py' file.
A log file, parameters, and plot figures are stored in the 'log' folder for every run of the simulation.
NOTE: The main README file contains some more information about the structure of pelenet
"""
# Load pelenet modules
from pelenet.utils import Utils
from pelenet.experiments.sequence import SequenceExperiment
# Official modules
import numpy as np
import matplotlib.pyplot as plt
# Overwrite default parameters (pelenet/parameters/ and pelenet/experiments/sequence.py)
parameters = {
# Experiment
'seed': 1, # Random seed
'trials': 10, # Number of trials
'stepsPerTrial': 60, # Number of simulation steps for every trial
# Neurons
'refractoryDelay': 2, # Refactory period
'voltageTau': 100, # Voltage time constant
'currentTau': 5, # Current time constant
'thresholdMant': 1200, # Spiking threshold for membrane potential
# Network
'reservoirExSize': 400, # Number of excitatory neurons
'reservoirConnPerNeuron': 35, # Number of connections per neuron
'isLearningRule': True, # Apply a learning rule
'learningRule': '2^-2*x1*y0 - 2^-2*y1*x0 + 2^-4*x1*y1*y0 - 2^-3*y0*w*w', # Defines the learning rule
# Input
'inputIsSequence': True, # Activates sequence input
'inputSequenceSize': 3, # Number of input clusters in sequence
'inputSteps': 20, # Number of steps the trace input should drive the network
'inputGenSpikeProb': 0.8, # Probability of spike for the generator
'inputNumTargetNeurons': 40, # Number of neurons activated by the input
# Probes
'isExSpikeProbe': True, # Probe excitatory spikes
'isInSpikeProbe': True, # Probe inhibitory spikes
'isWeightProbe': True # Probe weight matrix at the end of the simulation
}
# Initilizes the experiment, also initializes the log
# Creating a new object results in a new log entry in the 'log' folder
# The name is optional, it is extended to the folder in the log directory
exp = SequenceExperiment(name='random-network-sequence-learning', parameters=parameters)
# Instantiate the utils singleton
utils = Utils.instance()
# Build the network, in this function the weight matrix, inputs, probes, etc. are defined and created
exp.build()
# Run the network simulation, afterwards the probes are postprocessed to nice arrays
exp.run()
# Weight matrix before learning (randomly initialized)
exp.net.plot.initialExWeightMatrix()
# Plot distribution of weights
exp.net.plot.initialExWeightDistribution(figsize=(12,3))
# Plot spike trains of the excitatory (red) and inhibitory (blue) neurons
exp.net.plot.reservoirSpikeTrain(figsize=(12,6), to=600)
# Weight matrix after learning
exp.net.plot.trainedExWeightMatrix()
# Sorted weight matrix after learning
supportMask = utils.getSupportWeightsMask(exp.net.trainedWeightsExex)
exp.net.plot.weightsSortedBySupport(supportMask)
```
|
github_jupyter
|
## shuffle
### 计算机如何生成素数
只简单介绍一种方法,**线性同余法**
$$N_{j+1} = (A*N_j + B) mod M $$
其中A,B,M是设定的常数。$N_0$被叫做随机种子,是计算机主板的计数器在内存中的记数值。
从公式中可以看出$N_{j+1}$ 与 $N_j$ 存在线性。
线性同余法生成的是均匀分布,如果需要生成其他分布则是据此进行采样。
### 那么如何随机打乱一个数组
1. 考虑一种方法:对于一个长度为n的数组,每次随机选取两个index,交换这两个index对应的数字。并将他们标记。循环直到数组中所有元素被处理
```
import random
def shuffle_1(array):
N = len(array)
swaped = [False]*N
while not all(swaped):
a = random.randrange(N)
b = random.randrange(N)
array[a],array[b] = array[b],array[a]
swaped[b] = True
swaped[a] = True
test_case = [1,2,3]
shuffle_1(test_case)
print(test_case)
```
这个打乱算法是**有问题**的。
- 不一定能退出循环
- 时间复杂度为$O(n)$
- 各种组合的概率不均匀
时间复杂度为什么为$O(n)$
这个问题实际上可以抽象为在袋子里有n个球的情况下,每次抽2个球,放回抽样,需要抽多少次才能全部抽过一遍。求这个次数的期望
而这个随机变量的期望值与 $n^2$ 有关
```
def shuffle_2(array):
"Knuth's algorithm P"
N = len(array)
for i in range(N-1): # 这里N 或者N-1都没有问题。N只是多做一次计算
j = random.randrange(i,N)
array[i],array[j] = array[j],array[i]
shuffle_2(test_case)
```
显然,这个算法的时间复杂度为$O(n)$
```
from collections import defaultdict
def test_shuffler(shuffler,case="abc",n=100000):
counter = defaultdict(int)
for i in range(n):
case_array = list(case)
shuffler(case_array)
counter["".join(case_array)] += 1
e = n*1.0/factorial(len(case))
test_ok = all(0.9 <= e/counter[j] <= 1.1 for j in counter)
name = shuffler.__name__
if test_ok:
print("%s ok" %name)
else:
print("%s failed" %name)
for k,v in sorted(counter.items()):
print(k,v/n)
def factorial(n):
if n<= 1: return 1
else:
return n*factorial(n-1)
test_shuffler(shuffle_1)
test_shuffler(shuffle_2)
def shuffle_3(array):
N = len(array)
swaped = [False]*N
while not all(swaped):
a = random.randrange(N)
b = random.randrange(N)
array[a],array[b] = array[b],array[a]
swaped[a] = True
def shuffle_4(array):
N = len(array)
for i in range(N):
j = random.randrange(N)
array[i],array[j] = array[j],array[i]
test_shuffler(shuffle_3)
test_shuffler(shuffle_4)
```
## 纸牌游戏
```
def hand_rank(hand):
ranks = card_ranks(hand)
if straight(ranks) and flush(hand):
return (8,max(ranks))
elif kind(4,ranks):
return (7,kind(4,ranks),kind(1,ranks))
elif kind(3,ranks) and kind(2,ranks):
return (6,kind(3,ranks),kind(2,ranks))
elif flush(hand):
return (5,ranks)
elif straight(ranks):
return (4,max(ranks))
elif kind(3,ranks):
return(3,kind(3,ranks),ranks)
elif two_pair(ranks):
return(2,two_pair(ranks),ranks)
elif kind(2,ranks):
return(1,kind(2,ranks),ranks)
else:
return(0,ranks)
def card_ranks(hand):
ranks = ['--23456789TJQKA'.index(r) for r, s in hand]
ranks.sort(reverse=True)
return [5,4,3,2,1] if (ranks==[14,5,4,3,2]) else ranks
def flush(hand):
suits = [s for r,s in hand]
return len(set(suits))==1
def straight(ranks):
return (max(ranks)-min(ranks)==4) and len(set(ranks))==5
def kind(n,ranks):
for r in ranks:
if ranks.count(r) == n: return r
def two_pair(ranks):
pair = kind(2,ranks)
lowpair = kind(2,list(reversed(ranks)))
if pair and lowpair!= pair:
return (pair,lowpair)
else:
return None
```
### homework
1. Seven Card Stud
Write a function best_hand(hand) that takes a seven
card hand as input and returns the best possible 5
card hand. The itertools library has some functions
that may help you solve this problem.
```
def test_best_hand():
assert (sorted(best_hand("6C 7C 8C 9C TC 5C JS".split()))==["6C","7C","8C","9C","TC"])
assert (sorted(best_hand("TD TC TH 7C 7D 8C 8S".split()))
== ['8C', '8S', 'TC', 'TD', 'TH'])
assert (sorted(best_hand("JD TC TH 7C 7D 7S 7H".split()))
== ['7C', '7D', '7H', '7S', 'JD'])
return 'test_best_hand passes'
import itertools
help(itertools)
a = itertools.combinations("6C 7C 8C 9C TC 5C JS".split(),5)
list(a)
def best_hand(hand):
combs = itertools.combinations(hand,5)
comb_rank = [(comb,hand_rank(comb)) for comb in combs]
comb_rank.sort(reverse=True,key=lambda x : x[1])
return comb_rank[0][0]
test_best_hand()
## answer
def best_hand(hand):
return max(itertools.combinations(hand,5), key=hand_rank)
```
2. wild jokers
Write a function best_wild_hand(hand) that takes as
input a 7-card hand and returns the best 5 card hand.
In this problem, it is possible for a hand to include
jokers. Jokers will be treated as 'wild cards' which
can take any rank or suit of the same color.
The
black joker, '?B', can be used as any spade or club
and the red joker, '?R', can be used as any heart
or diamond.
```
def best_wild_hand(hand):
car_res = [hand.copy()]
if "?R" in hand:
car_res[0].remove("?R")
variation = [i+j for i in "23456789TJQKA" for j in "HD"]
car_res = [j+[i] for i in variation for j in car_res]
if "?B" in hand:
for i in car_res:
if "?B" in i:
i.remove("?B")
variation = [i+j for i in "23456789TJQKA" for j in "SC"]
car_res = [j+[i] for i in variation for j in car_res]
results = [max(itertools.combinations(x,5),key= hand_rank) for x in car_res]
return max(results,key= hand_rank)
def test_best_wild_hand():
assert (sorted(best_wild_hand("6C 7C 8C 9C TC 5C ?B".split()))
== ['7C', '8C', '9C', 'JC', 'TC'])
assert (sorted(best_wild_hand("TD TC 5H 5C 7C ?R ?B".split()))
== ['7C', 'TC', 'TD', 'TH', 'TS'])
assert (sorted(best_wild_hand("JD TC TH 7C 7D 7S 7H".split()))
== ['7C', '7D', '7H', '7S', 'JD'])
return 'test_best_wild_hand passes'
test_best_wild_hand()
```
## answer
```
def best_wild_card(hand):
hands = set(best_hand(h) for h in itertools.product(*map(replacements,hand)))
return max(hands,key=hand_rank)
def replacements(card):
if card == "?B": return blackcards
elif card == "?R": return readcards
else: return [card]
```
|
github_jupyter
|
# Basics
```
print("Hello World!")
# This is comment!
bread=10
print(bread)
bread=input()
bread
43+5
'43'+5
```
**Find out the reason behind the above error.**
**Tip**: Copy the error and search in [Google](https://www.google.com/).
```
8
8+3
```
### Data Types
Integers: -2, -1, 0, 1, 2, 3, 4, 5
Floating-point numbers: -1.25, -1.0, --0.5, 0.0, 0.5, 1.0, 1.25
Strings: 'a', 'aa', 'aaa', 'Hello!', '11 cats'
**Math Operations**
```
#Addition
2+3
#Subtraction
8-3
#Multiplication
2*4
#Division
42/10
# Exponent
2**4
#Modulus/Remainder
42%10
#Floored Quotient
42//10
```
**Note**: The precedence rule is BODMAS.
The ** operator is evaluated first; the *, /, //, and % operators are evaluated next, from left to right; and the + and - operators are evaluated last (also from left to right). You can use parentheses to override the usual precedence if you need to.
```
2 + 3 * 6
(2 + 3) * 6
48565878 * 578453
2 ** 8
23 / 7
23 // 7
23 % 7
#extra spaces? no problem
#python is chill :P
2 + 2
(5 - 1) * ((7 + 1) / (3 - 1))
```
#### Explanation
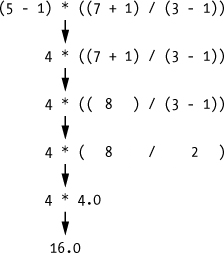
```
5 +
42 + 5 + * 2
```
The operations applicable for integers are also applicable for floating numbers too.
```
bread=10
bread
print(bread)
butter=3
bread+butter
print(bread+butter)
bread=bread+2
bread
bread++
```
**Note**: Coding in python is entirely different from c/cpp.
### Strings
```
msg='Hello'
msg
print(msg)
msg='Goodbye'
print(msg)
len(msg)
print(len(msg))
msg+1
msg+'1'
msg+str(1)
```
### Variable Names
**Valid** ✔️
balance
currentBalance
current_balance
_spam
SPAM
account4
----
**Invalid** ❌
'hello' (special characters like ' are not allowed)
current-balance (hyphens are not allowed)
4account (can’t begin with a number)
42 (can’t begin with a number)
current balance (spaces are not allowed)
total_$um (special characters like $ are not allowed)
```
#INPUT: Hi! :)
msg=input()
print(msg)
print(type(msg))
#INPUT: 12
msg=input()
print(msg)
print(type(msg))
#integer input
#INPUT : 12
msg=int(input())
print(msg)
print(type(msg))
#change the datatype
msg=str(msg)
print(msg)
print(type(msg))
print(int(msg)+1)
print(float(msg)+1)
print(int(7.7))
print(int(7.7) + 1)
```
Please understand this small program
```
print('Hello world!')
print('What is your name?') # ask for their name
myName = input()
print('It is good to meet you, ' + myName)
print('The length of your name is:')
print(len(myName))
print('What is your age?') # ask for their age
myAge = input()
print('You will be ' + str(int(myAge) + 1) + ' in a year.')
```
## Task 1
Write a program for polling booth. It should ask a name, his age and ask for vote (NDA/UPA).
# Flow Control
```
print(True, False)
print(1,0)
```
### Operators
```
#equal to
2==3
#not equal to
2!=3
#greater than
2>3
#less than
2<3
#less/greater than equal to
print(2>=3)
print(2<=3)
1==True
print('hello' == 'hello')
print('hello' == 'Hello')
True!=False
42==42.0
42=='42'
bread=21
bread>10
```
### Binary and Boolean Operations
```
True and True
False or False
not False
```
### Conditional Statements
```
if(4<5):
print("Yo!")
bread=int(input())
if(bread>10):
print("I have 10+ bread")
elif(bread==10):
print("I have exactly 10 bread")
else:
print("I have less than 10 bread")
if(True):
print("This is how you overide a conditional statement.")
if(False):
print("This will not print anything.")
if(input()):
print("This will print anything.")
```
You may be wondering why the above code worked. It worked because `input()` always take the input as *string* format not *boolen* format.
You can convert it into *boolean* by modifying it as `bool(input())`
```
bread=12
if(bread):
print("Every value other than 0 is considered as True")
bread=0
if(bread):
print("I told you already. :P")
```
## Taks 2
Implement this following flowchart
Take the initial values as
```python
name='Dracula'
age=4000
```
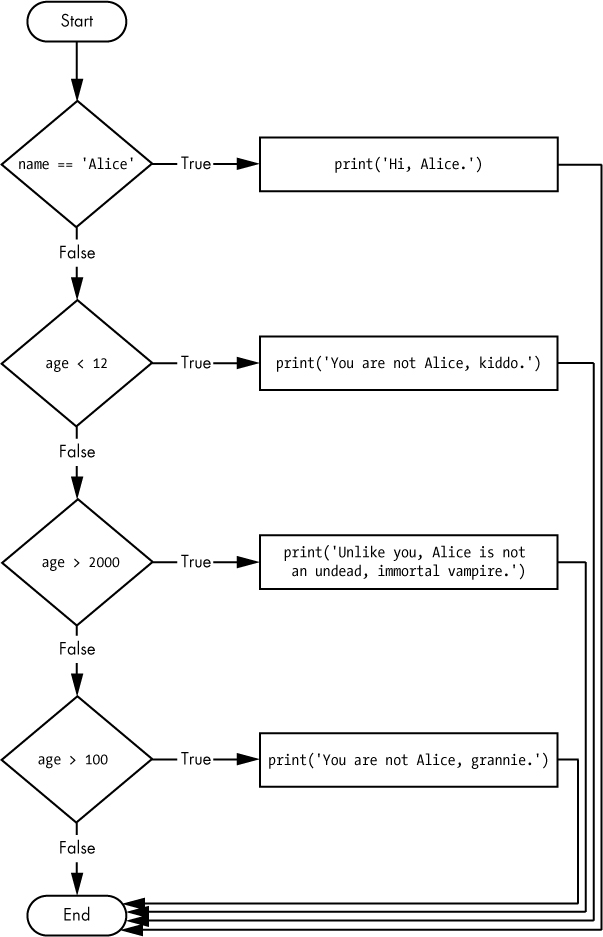
### Loops
### `while`
```
bread=0
while(bread<5):
print("need more bread")
bread=bread+1
"""
while True:
print("This is an infinite loop!!")
"""
```
Please have a look at the below code and understand it.
```
name = ''
while name != 'your name':
print('Please type your name.')
name = input()
print('Thank you!')
```
The above code will ask your input again and again until you give `your name` as input. You can build infinite loops accordingly.
The below code is a re-written version of the above. You can control infinite loops with valid `break` statements.
```
while True:
print('Please type your name.')
name = input()
if name == 'your name':
break
print('Thank you!')
```
The keyword `continue` skips all the statements which are below itself. Look at the following
```
bread=0
while(bread<5):
print("bread added")
bread=bread+1
if(bread<3):
print("I am hungry.")
continue
print("I need more bread.")
```
### `for`
```
for i in range(3):
print("I need "+str(i)+" bread.")
#sum of n natural numbers program
total=0
n=int(input("Enter the n: "))
for i in range(n+1):
total=total+i
print(total)
```
**Note**: You can actually use a `while` loop to do the same thing as a `for` loop; `for` loops are just more concise.
`starting`, `stopping` and `stepping` arguments in `for` loop
```
for i in range(0,10):
print(i)
for i in range(0,10,3):
print(i)
```
## Task 3
Write a program for polling booth. It should ask a name, his age and ask for vote (NDA/UPA/Others). It should verify your age too. You need to ask for vote untill you see no voters left. Have seperate counters for the parties and increase the counter accordingly.
# Importing Modules
Python comes with many set of modules which can be used. Each module is a Python program that contains a related group of functions that can be embedded in your programs. For example, the math module has mathematics-related functions, the random module has random number–related functions, and so on.
Before you can use the functions in a module, you must import the module with an import statement.
```
#importing a module normally
import random
for i in range(5):
print(random.randint(1, 10))
#importing a module using an object
import random as rd
for i in range(5):
print(rd.randint(1, 10))
#importing one function from that module
#here, other functions of that module doesn't work
from random import randint
for i in range(5):
print(randint(1, 10))
#importing one function using an object
from random import randint as ri
for i in range(5):
print(ri(1, 10))
#importing all functions from that module
from random import *
for i in range(5):
print(randint(1, 10))
```
# Functions
```
def getBread():
print("bread!")
print("bread!!!")
getBread()
getBread()
getBread()
def getBread(number):
print("I want "+str(number)+" bread.")
getBread(3)
getBread(5)
getBread(8)
getBread()
```
**Error**: python is not like C/C++. You can define only one funtion with one name. You cannot differentiate with arguments.
```
def makeItEven(n):
return n*2
result=makeItEven(3)
print(result)
result=makeItEven(2)
print(result)
def makeItEven(n):
return n*2
print(makeItEven(3))
print(makeItEven(2))
```
`None` represents absence of any value.
```
def getNothing():
return
getNothing()
print(getNothing())
def getNone():
return None
getNone()
print(getNone())
```
**Fact**: Behind the scenes, Python adds return `None` to the end of any function definition with no return statement. This is similar to how a `while` or `for` loop implicitly ends with a continue statement.
### Scope (Global and Local)
```
def getDosa():
dosa=8
getDosa()
print(dosa)
```
**Error**: The above error is because the variable `dosa` is defined only fro the `getDosa` function and out of the defined scope, a variable cannot be used.
```
dosa=3
def getDosa():
print("dosa=",dosa)
getDosa()
print(dosa)
dosa=3
def getDosa():
dosa=8
print("dosa=",dosa)
getDosa()
print("dosa=",dosa)
def getDosa():
global dosa
dosa=8
print("dosa=",dosa)
getDosa()
print("dosa=",dosa)
def getDosa():
print("dosa=",dosa)
dosa=8 #1
dosa=3 #2
getDosa()
print("dosa=",dosa)
```
**Error**: This error happens because Python sees that there is an assignment statement for `dosa` in the `getDosa` function #1 and therefore considers `dosa` to be local. But because `print("dosa=",dosa)` is executed before `dosa` is assigned anything, the local variable `dosa` doesn’t exist. Python will not fall back to using the global `dosa` variable #2.
### Error Handling
```
def divideBy(n):
return 4/n
print(divideBy(4))
print(divideBy(1))
print(divideBy(0))
```
**Note**: The division by zero is not possible, so it raised error. Instead of stopping the program abruptly, we can handle the error (using `try-except`) such that an error message is displayed and the program finished the execution without any interruption.
```
def divideBy(n):
try:
return 4/n
except ZeroDivisionError:
print("Invalid argument.")
print(divideBy(4))
print(divideBy(1))
print(divideBy(0))
def divideBy(n):
return 4/n
try:
print(divideBy(4))
print(divideBy(1))
print(divideBy(0))
except ZeroDivisionError:
print("Invalid argument.")
```
## Task-4
Implement the following scenario. It is *Guess the number* game. (need to be be the exact similar)
```
I am thinking of a number between 1 and 20.
Take a guess.
10
Your guess is too low.
Take a guess.
15
Your guess is too low.
Take a guess.
17
Your guess is too high.
Take a guess.
16
Good job! You guessed my number in 4 guesses!
```
## Task-5
### The Collatz Sequence
Write a function named `collatz()` that has one parameter named number. If number is even, then collatz() should print `number // 2` and return this value. If number is odd, then collatz() should print and `return 3 * number + 1`.
*Hint*: An integer number is even if `number % 2 == 0`, and it’s odd if `number % 2 == 1`.
## Task-6
### The Input Sequence
Add `try-except` statements to the previous project to detect whether the user types in a noninteger string. Normally, the `int()` function will raise a `ValueError` error if it is passed a noninteger string, as in `int('puppy')`. In the `except` clause, print a message to the user saying they must enter an integer.
|
github_jupyter
|
# Google form analysis visualizations
## Table of Contents
['Google form analysis' functions checks](#funcchecks)
['Google form analysis' functions tinkering](#functinkering)
```
%run "../Functions/1. Google form analysis.ipynb"
```
## 'Google form analysis' functions checks
<a id=funcchecks />
## 'Google form analysis' functions tinkering
<a id=functinkering />
```
binarizedAnswers = plotBasicStats(getSurveysOfBiologists(gform), 'non biologists', includeUndefined = True)
gform.loc[:, [localplayerguidkey, 'Temporality']].groupby('Temporality').count()
#sample = gform.copy()
samples = [
[gform.copy(), 'complete set'],
[gform[gform['Language'] == 'en'], 'English'],
[gform[gform['Language'] == 'fr'], 'French'],
[gform[gform['What is your gender?'] == 'Female'], 'female'],
[gform[gform['What is your gender?'] == 'Male'], 'male'],
[getSurveysOfUsersWhoAnsweredBoth(gform), 'answered both'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'en']), 'answered both, en'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'fr']), 'answered both, fr'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['What is your gender?'] == 'Female']), 'answered both, female'],
[getSurveysOfUsersWhoAnsweredBoth(gform[gform['What is your gender?'] == 'Male']), 'answered both, male'],
]
_progress = FloatProgress(min=0, max=len(samples))
display(_progress)
includeAll = False
includeBefore = True
includeAfter = True
includeUndefined = False
includeProgress = True
includeRelativeProgress = False
for sample, title in samples:
## basic stats:
### mean score
### median score
### std
## sample can be: all, those who answered both before and after,
## those who played between date1 and date2, ...
#def plotBasicStats(sample, title, includeAll, includeBefore, includeAfter, includeUndefined, includeProgress, includeRelativeProgress):
stepsPerInclude = 2
includeCount = np.sum([includeAll, includeBefore, includeAfter, includeUndefined, includeProgress])
stepsCount = stepsPerInclude*includeCount + 3
#print("stepsPerInclude=" + str(stepsPerInclude))
#print("includeCount=" + str(includeCount))
#print("stepsCount=" + str(stepsCount))
__progress = FloatProgress(min=0, max=stepsCount)
display(__progress)
sampleBefore = sample[sample['Temporality'] == 'before']
sampleAfter = sample[sample['Temporality'] == 'after']
sampleUndefined = sample[sample['Temporality'] == 'undefined']
#uniqueBefore = sampleBefore[localplayerguidkey]
#uniqueAfter =
#uniqueUndefined =
scientificQuestions = correctAnswers.copy()
allQuestions = correctAnswers + demographicAnswers
categories = ['all', 'before', 'after', 'undefined', 'progress', 'rel. progress']
data = {}
sciBinarized = pd.DataFrame()
allBinarized = pd.DataFrame()
scoresAll = pd.DataFrame()
sciBinarizedBefore = pd.DataFrame()
allBinarizedBefore = pd.DataFrame()
scoresBefore = pd.DataFrame()
sciBinarizedAfter = pd.DataFrame()
allBinarizedAfter = pd.DataFrame()
scoresAfter = pd.DataFrame()
sciBinarizedUndefined = pd.DataFrame()
allBinarizedUndefined = pd.DataFrame()
scoresUndefined = pd.DataFrame()
scoresProgress = pd.DataFrame()
## basic stats:
### mean score
### median score
### std
if includeAll:
sciBinarized = getAllBinarized( _source = scientificQuestions, _form = sample)
__progress.value += 1
allBinarized = getAllBinarized( _source = allQuestions, _form = sample)
__progress.value += 1
scoresAll = pd.Series(np.dot(sciBinarized, np.ones(sciBinarized.shape[1])))
data[categories[0]] = createStatSet(scoresAll, sample[localplayerguidkey])
if includeBefore or includeProgress:
sciBinarizedBefore = getAllBinarized( _source = scientificQuestions, _form = sampleBefore)
__progress.value += 1
allBinarizedBefore = getAllBinarized( _source = allQuestions, _form = sampleBefore)
__progress.value += 1
scoresBefore = pd.Series(np.dot(sciBinarizedBefore, np.ones(sciBinarizedBefore.shape[1])))
temporaryStatSetBefore = createStatSet(scoresBefore, sampleBefore[localplayerguidkey])
if includeBefore:
data[categories[1]] = temporaryStatSetBefore
if includeAfter or includeProgress:
sciBinarizedAfter = getAllBinarized( _source = scientificQuestions, _form = sampleAfter)
__progress.value += 1
allBinarizedAfter = getAllBinarized( _source = allQuestions, _form = sampleAfter)
__progress.value += 1
scoresAfter = pd.Series(np.dot(sciBinarizedAfter, np.ones(sciBinarizedAfter.shape[1])))
temporaryStatSetAfter = createStatSet(scoresAfter, sampleAfter[localplayerguidkey])
if includeAfter:
data[categories[2]] = temporaryStatSetAfter
if includeUndefined:
sciBinarizedUndefined = getAllBinarized( _source = scientificQuestions, _form = sampleUndefined)
__progress.value += 1
allBinarizedUndefined = getAllBinarized( _source = allQuestions, _form = sampleUndefined)
__progress.value += 1
scoresUndefined = pd.Series(np.dot(sciBinarizedUndefined, np.ones(sciBinarizedUndefined.shape[1])))
data[categories[3]] = createStatSet(scoresUndefined, sampleUndefined[localplayerguidkey])
if includeProgress:
data[categories[4]] = {
'count' : min(temporaryStatSetAfter['count'], temporaryStatSetBefore['count']),
'unique' : min(temporaryStatSetAfter['unique'], temporaryStatSetBefore['unique']),
'median' : temporaryStatSetAfter['median']-temporaryStatSetBefore['median'],
'mean' : temporaryStatSetAfter['mean']-temporaryStatSetBefore['mean'],
'std' : temporaryStatSetAfter['std']-temporaryStatSetBefore['std'],
}
__progress.value += 2
result = pd.DataFrame(data)
__progress.value += 1
print(title)
print(result)
if (includeBefore and includeAfter) or includeProgress:
if (len(scoresBefore) > 2 and len(scoresAfter) > 2):
ttest = ttest_ind(scoresBefore, scoresAfter)
print("t test: statistic=" + repr(ttest.statistic) + " pvalue=" + repr(ttest.pvalue))
print()
## percentage correct
### percentage correct - max 5 columns
percentagePerQuestionAll = pd.DataFrame()
percentagePerQuestionBefore = pd.DataFrame()
percentagePerQuestionAfter = pd.DataFrame()
percentagePerQuestionUndefined = pd.DataFrame()
percentagePerQuestionProgress = pd.DataFrame()
tables = []
if includeAll:
percentagePerQuestionAll = getPercentagePerQuestion(allBinarized)
tables.append([percentagePerQuestionAll, categories[0]])
if includeBefore or includeProgress:
percentagePerQuestionBefore = getPercentagePerQuestion(allBinarizedBefore)
if includeBefore:
tables.append([percentagePerQuestionBefore, categories[1]])
if includeAfter or includeProgress:
percentagePerQuestionAfter = getPercentagePerQuestion(allBinarizedAfter)
if includeAfter:
tables.append([percentagePerQuestionAfter, categories[2]])
if includeUndefined:
percentagePerQuestionUndefined = getPercentagePerQuestion(allBinarizedUndefined)
tables.append([percentagePerQuestionUndefined, categories[3]])
if includeProgress or includeRelativeProgress:
percentagePerQuestionProgress = percentagePerQuestionAfter - percentagePerQuestionBefore
if includeProgress:
tables.append([percentagePerQuestionProgress, categories[4]])
if includeRelativeProgress:
# use temporaryStatSetAfter['count'], temporaryStatSetBefore['count']?
percentagePerQuestionProgress2 = percentagePerQuestionProgress.copy()
for index in range(0,len(percentagePerQuestionProgress.index)):
if (0 == percentagePerQuestionBefore.iloc[index,0]):
percentagePerQuestionProgress2.iloc[index,0] = 0
else:
percentagePerQuestionProgress2.iloc[index,0] = \
percentagePerQuestionProgress.iloc[index,0]/percentagePerQuestionBefore.iloc[index,0]
tables.append([percentagePerQuestionProgress2, categories[5]])
__progress.value += 1
graphTitle = '% correct: '
toConcat = []
for table,category in tables:
concat = (len(table.values) > 0)
for elt in table.iloc[:,0].values:
if np.isnan(elt):
concat = False
break
if(concat):
graphTitle = graphTitle + category + ' '
toConcat.append(table)
if (len(toConcat) > 0):
percentagePerQuestionConcatenated = pd.concat(
toConcat
, axis=1)
if(len(title) > 0):
graphTitle = graphTitle + ' - ' + title
_fig = plt.figure(figsize=(20,20))
_ax1 = plt.subplot(111)
_ax1.set_title(graphTitle)
sns.heatmap(percentagePerQuestionConcatenated.round().astype(int),ax=_ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d')
__progress.value += 1
### percentage cross correct
### percentage cross correct, conditionnally
if(__progress.value != stepsCount):
print("__progress.value=" + str(__progress.value) + " != stepsCount=" + str(stepsCount))
_progress.value += 1
if(_progress.value != len(samples)):
print("__progress.value=" + str(__progress.value) + " != len(samples)=" + str(len(samples)))
# sciBinarized, sciBinarizedBefore, sciBinarizedAfter, sciBinarizedUndefined, \
# allBinarized, allBinarizedBefore, allBinarizedAfter, allBinarizedUndefined
ttest = ttest_ind(scoresBefore, scoresAfter)
type(scoresBefore), len(scoresBefore),\
type(scoresAfter), len(scoresAfter),\
ttest
type(tables)
sciBinarized = getAllBinarized( _source = scientificQuestions, _form = sample)
series = pd.Series(np.dot(sciBinarized, np.ones(sciBinarized.shape[1])))
#ids = pd.Series()
ids = sample[localplayerguidkey]
#def createStatSet(series, ids):
if(0 == len(ids)):
ids = series.index
result = {
'count' : len(ids),
'unique' : len(ids.unique()),
'median' : series.median(),
'mean' : series.mean(),
'std' : series.std()}
result
## percentage correct
### percentage correct - 3 columns
### percentage cross correct
### percentage cross correct, conditionnally
#_binarized = allBinarized
#_binarized = allBinarizedUndefined
_binarized = allBinarizedBefore
#def getPercentagePerQuestion(_binarized):
totalPerQuestionDF = pd.DataFrame(data=np.dot(np.ones(_binarized.shape[0]), _binarized), index=_binarized.columns)
percentagePerQuestion = totalPerQuestionDF*100 / _binarized.shape[0]
percentagePerQuestion
#totalPerQuestion = np.dot(np.ones(allSciBinarized.shape[0]), allSciBinarized)
#totalPerQuestion.shape
totalPerQuestionSci = np.dot(np.ones(sciBinarized.shape[0]), sciBinarized)
totalPerQuestionAll = np.dot(np.ones(allBinarized.shape[0]), allBinarized)
percentagePerQuestionAll = getPercentagePerQuestion(allBinarized)
percentagePerQuestionBefore = getPercentagePerQuestion(allBinarizedBefore)
percentagePerQuestionAfter = getPercentagePerQuestion(allBinarizedAfter)
percentagePerQuestionUndefined = getPercentagePerQuestion(allBinarizedUndefined)
percentagePerQuestionConcatenated = pd.concat(
[
percentagePerQuestionAll,
percentagePerQuestionBefore,
percentagePerQuestionAfter,
percentagePerQuestionUndefined,
]
, axis=1)
_fig = plt.figure(figsize=(20,20))
_ax1 = plt.subplot(111)
_ax1.set_title('percentage correct per question: all, before, after, undefined')
sns.heatmap(percentagePerQuestionConcatenated.round().astype(int),ax=_ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d')
samples = [gform, gform[gform['Language'] == 'en'], gform[gform['Language'] == 'fr'],
getSurveysOfUsersWhoAnsweredBoth(gform),
getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'en']),
getSurveysOfUsersWhoAnsweredBoth(gform[gform['Language'] == 'fr'])]
for sample in samples:
sciBinarized, sciBinarizedBefore, sciBinarizedAfter, sciBinarizedUndefined, \
allBinarized, allBinarizedBefore, allBinarizedAfter, allBinarizedUndefined = plotBasicStats(sample)
```
### abandoned algorithms
```
#totalPerQuestion = np.dot(np.ones(sciBinarized.shape[0]), sciBinarized)
#totalPerQuestion.shape
totalPerQuestionSci = np.dot(np.ones(sciBinarized.shape[0]), sciBinarized)
totalPerQuestionAll = np.dot(np.ones(allBinarized.shape[0]), allBinarized)
totalPerQuestionDFAll = pd.DataFrame(data=np.dot(np.ones(allBinarized.shape[0]), allBinarized), index=allBinarized.columns)
percentagePerQuestionAll = totalPerQuestionDFAll*100 / allBinarized.shape[0]
#totalPerQuestionDF
#percentagePerQuestion
#before
totalPerQuestionDFBefore = pd.DataFrame(
data=np.dot(np.ones(allBinarizedBefore.shape[0]), allBinarizedBefore), index=allBinarizedBefore.columns
)
percentagePerQuestionBefore = totalPerQuestionDFBefore*100 / allBinarizedBefore.shape[0]
#after
totalPerQuestionDFAfter = pd.DataFrame(
data=np.dot(np.ones(allBinarizedAfter.shape[0]), allBinarizedAfter), index=allBinarizedAfter.columns
)
percentagePerQuestionAfter = totalPerQuestionDFAfter*100 / allBinarizedAfter.shape[0]
_fig = plt.figure(figsize=(20,20))
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax2.get_yaxis().set_visible(False)
ax3.get_yaxis().set_visible(False)
sns.heatmap(percentagePerQuestionAll.round().astype(int),ax=ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionBefore.round().astype(int),ax=ax2,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionAfter.round().astype(int),ax=ax3,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=True)
ax1.set_title('percentage correct per question - all')
ax2.set_title('percentage correct per question - before')
ax3.set_title('percentage correct per question - after')
# Fine-tune figure; make subplots close to each other and hide x ticks for
# all but bottom plot.
_fig.tight_layout()
_fig = plt.figure(figsize=(20,20))
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax2.get_yaxis().set_visible(False)
ax3.get_yaxis().set_visible(False)
sns.heatmap(percentagePerQuestionAll.round().astype(int),ax=ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionBefore.round().astype(int),ax=ax2,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionAfter.round().astype(int),ax=ax3,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=True)
ax1.set_title('percentage correct per question - all')
ax2.set_title('percentage correct per question - before')
ax3.set_title('percentage correct per question - after')
# Fine-tune figure; make subplots close to each other and hide x ticks for
# all but bottom plot.
_fig.tight_layout()
_fig = plt.figure(figsize=(20,20))
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax2.get_yaxis().set_visible(False)
ax3.get_yaxis().set_visible(False)
sns.heatmap(percentagePerQuestionAll.round().astype(int),ax=ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionBefore.round().astype(int),ax=ax2,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=False)
sns.heatmap(percentagePerQuestionAfter.round().astype(int),ax=ax3,cmap=plt.cm.jet,square=True,annot=True,fmt='d', cbar=True)
ax1.set_title('percentage correct per question - all')
ax2.set_title('percentage correct per question - before')
ax3.set_title('percentage correct per question - after')
# Fine-tune figure; make subplots close to each other and hide x ticks for
# all but bottom plot.
_fig.tight_layout()
percentagePerQuestionConcatenated = pd.concat([
percentagePerQuestionAll,
percentagePerQuestionBefore,
percentagePerQuestionAfter]
, axis=1)
_fig = plt.figure(figsize=(20,20))
_ax1 = plt.subplot(111)
_ax1.set_title('percentage correct per question: all, before, after')
sns.heatmap(percentagePerQuestionConcatenated.round().astype(int),ax=_ax1,cmap=plt.cm.jet,square=True,annot=True,fmt='d')
```
### sample getters tinkering
```
##### getRMAfter / Before tinkering
#def getRMAfters(sample):
afters = sample[sample['Temporality'] == 'after']
#def getRMBefores(sample):
befores = sample[sample['Temporality'] == 'before']
QPlayed1 = 'Have you ever played an older version of Hero.Coli before?'
QPlayed2 = 'Have you played the current version of Hero.Coli?'
QPlayed3 = 'Have you played the arcade cabinet version of Hero.Coli?'
QPlayed4 = 'Have you played the Android version of Hero.Coli?'
```
#### set operators
```
# equality tests
#(sample1.columns == sample2.columns).all()
#sample1.columns.duplicated().any() or sample2.columns.duplicated().any()
#pd.concat([sample1, sample2], axis=1).columns.duplicated().any()
```
##### getUnionQuestionnaires tinkering
```
sample1 = befores
sample2 = afters
#def getUnionQuestionnaires(sample1, sample2):
if (not (sample1.columns == sample2.columns).all()):
print("warning: parameter columns are not the same")
result = pd.concat([sample1, sample2]).drop_duplicates()
```
##### getIntersectionQuestionnaires tinkering
```
sample1 = befores[:15]
sample2 = befores[10:]
#def getIntersectionQuestionnaires(sample1, sample2):
if (not (sample1.columns == sample2.columns).all()):
print("warning: parameter columns are not the same")
result = pd.merge(sample1, sample2, how = 'inner').drop_duplicates()
```
##### getIntersectionUsersSurveys tinkering
```
sample1 = befores
sample2 = afters
# get sample1 and sample2 rows where users are common to sample1 and sample2
#def getIntersectionUsersSurveys(sample1, sample2):
result1 = sample1[sample1[localplayerguidkey].isin(sample2[localplayerguidkey])]
result2 = sample2[sample2[localplayerguidkey].isin(sample1[localplayerguidkey])]
result = getUnionQuestionnaires(result1,result2)
len(sample1), len(sample2), len(result)
```
##### getGFormBefores tinkering
```
sample = gform
# returns users who declared that they have never played the game, whatever platform
# previousPlayPositives is defined in '../Static data/English localization.ipynb'
#def getGFormBefores(sample):
befores = sample[
~sample[QPlayed1].isin(previousPlayPositives)
& ~sample[QPlayed2].isin(previousPlayPositives)
& ~sample[QPlayed3].isin(previousPlayPositives)
& ~sample[QPlayed4].isin(previousPlayPositives)
]
len(befores)
```
##### getGFormAfters tinkering
```
sample = gform
# returns users who declared that they have already played the game, whatever platform
# previousPlayPositives is defined in '../Static data/English localization.ipynb'
#def getGFormAfters(sample):
afters = sample[
sample[QPlayed1].isin(previousPlayPositives)
| sample[QPlayed2].isin(previousPlayPositives)
| sample[QPlayed3].isin(previousPlayPositives)
| sample[QPlayed4].isin(previousPlayPositives)
]
len(afters)
```
##### getGFormTemporality tinkering
```
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[3]
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
sample = gform
answerTemporalities[1]
#while result != 'after':
_GFUserId = getRandomGFormGUID()
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
# returns an element of answerTemporalities
# previousPlayPositives is defined in '../Static data/English localization.ipynb'
#def getGFormRowGFormTemporality(_gformRow):
result = answerTemporalities[2]
if (_gformRow[QPlayed1] in previousPlayPositives)\
or (_gformRow[QPlayed2] in previousPlayPositives)\
or (_gformRow[QPlayed3] in previousPlayPositives)\
or (_gformRow[QPlayed4] in previousPlayPositives):
result = answerTemporalities[1]
else:
result = answerTemporalities[0]
result
```
#### getSurveysOfUsersWhoAnsweredBoth tinkering
```
sample = gform
gfMode = True
rmMode = False
#def getSurveysOfUsersWhoAnsweredBoth(sample, gfMode = True, rmMode = False):
befores = sample
afters = sample
if gfMode:
befores = getGFormBefores(befores)
afters = getGFormAfters(afters)
if rmMode:
befores = getRMBefores(befores)
afters = getRMAfters(afters)
result = getIntersectionUsersSurveys(befores, afters)
((len(getGFormBefores(sample)),\
len(getRMBefores(sample)),\
len(befores)),\
(len(getGFormAfters(sample)),\
len(getRMAfters(sample)),\
len(afters)),\
len(result)),\
\
((getUniqueUserCount(getGFormBefores(sample)),\
getUniqueUserCount(getRMBefores(sample)),\
getUniqueUserCount(befores)),\
(getUniqueUserCount(getGFormAfters(sample)),\
getUniqueUserCount(getRMAfters(sample)),\
getUniqueUserCount(afters)),\
getUniqueUserCount(result))
len(getSurveysOfUsersWhoAnsweredBoth(gform, gfMode = True, rmMode = True)[localplayerguidkey])
```
#### getSurveysThatAnswered tinkering
```
sample = gform
#_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[1]
#sample = gform[gform[localplayerguidkey] == _GFUserId]
hardPolicy = True
questionsAndPositiveAnswers = [[Q6BioEdu, biologyStudyPositives],
[Q8SynBio, yesNoIdontknowPositives],
[Q9BioBricks, yesNoIdontknowPositives]]
#def getSurveysThatAnswered(sample, questionsAndPositiveAnswers, hardPolicy = True):
filterSeries = []
if hardPolicy:
filterSeries = pd.Series(True, sample.index)
for question, positiveAnswers in questionsAndPositiveAnswers:
filterSeries = filterSeries & (sample[question].isin(positiveAnswers))
else:
filterSeries = pd.Series(False, sample.index)
for question, positiveAnswers in questionsAndPositiveAnswers:
filterSeries = filterSeries | (sample[question].isin(positiveAnswers))
result = sample[filterSeries]
```
#### getSurveysOfBiologists tinkering
```
sample = gform
hardPolicy = True
#def getSurveysOfBiologists(sample, hardPolicy = True):
Q6BioEdu = 'How long have you studied biology?' #biologyStudyPositives
#irrelevant QInterest 'Are you interested in biology?' #biologyInterestPositives
Q8SynBio = 'Before playing Hero.Coli, had you ever heard about synthetic biology?' #yesNoIdontknowPositives
Q9BioBricks = 'Before playing Hero.Coli, had you ever heard about BioBricks?' #yesNoIdontknowPositives
questionsAndPositiveAnswers = [[Q6BioEdu, biologyStudyPositives],
[Q8SynBio, yesNoIdontknowPositives],
[Q9BioBricks, yesNoIdontknowPositives]]
result = getSurveysThatAnswered(sample, questionsAndPositiveAnswers, hardPolicy)
print(len(result) > 0)
gform.index
len(result)
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[0]
sample = gform[gform[localplayerguidkey] == _GFUserId]
len(getSurveysOfBiologists(sample)) > 0
```
#### getSurveysOfGamers tinkering
```
sample = gform
hardPolicy = True
#def getSurveysOfGamers(sample, hardPolicy = True):
Q2Interest = 'Are you interested in video games?' #interestPositives
Q3Play = 'Do you play video games?' #frequencyPositives
questionsAndPositiveAnswers = [[Q2Interest, interestPositives], [Q3Play, frequencyPositives]]
result = getSurveysThatAnswered(sample, questionsAndPositiveAnswers, hardPolicy)
len(result)
type(filterSeries)
len(afters[afters[QPlayed1].isin(previousPlayPositives)
| afters[QPlayed2].isin(previousPlayPositives)
| afters[QPlayed3].isin(previousPlayPositives)
| afters[QPlayed4].isin(previousPlayPositives)
]),\
len(afters[afters[QPlayed1].isin(previousPlayPositives)]),\
len(afters[afters[QPlayed2].isin(previousPlayPositives)]),\
len(afters[afters[QPlayed3].isin(previousPlayPositives)]),\
len(afters[afters[QPlayed4].isin(previousPlayPositives)])
```
#### getSurveysWithMatchingAnswers tinkering
```
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[2]
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
sample = gform
sample = gform
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
hardPolicy = False
Q4 = 'How old are you?'
Q5 = 'What is your gender?'
Q2Interest = 'Are you interested in video games?'
Q3Play = 'Do you play video games?'
Q6BioEdu = 'How long have you studied biology?'
Q7BioInterest = 'Are you interested in biology?'
Q8SynBio = 'Before playing Hero.Coli, had you ever heard about synthetic biology?'
Q9BioBricks = 'Before playing Hero.Coli, had you ever heard about BioBricks?'
Q42 = 'Language'
strictList = [Q4, Q5]
extendedList = [Q2Interest, Q3Play, Q6BioEdu, Q8SynBio, Q9BioBricks, Q42]
#def getSurveysWithMatchingAnswers(sample, _gformRow, strictList, extendedList = [], hardPolicy = False):
questions = strictList
if (hardPolicy):
questions += extendedList
questionsAndPositiveAnswers = []
for q in questions:
questionsAndPositiveAnswers.append([q, [_gformRow[q]]])
getSurveysThatAnswered(sample, questionsAndPositiveAnswers, True)
```
#### getMatchingDemographics tinkering
```
sample = gform
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
hardPolicy = True
#def getMatchingDemographics(sample, _gformRow, hardPolicy = False):
# age and gender
Q4 = 'How old are you?'
Q5 = 'What is your gender?'
# interests, hobbies, and knowledge - evaluation may vary after playing
Q2Interest = 'Are you interested in video games?'
Q3Play = 'Do you play video games?'
Q6BioEdu = 'How long have you studied biology?'
Q7BioInterest = 'Are you interested in biology?'
Q8SynBio = 'Before playing Hero.Coli, had you ever heard about synthetic biology?'
Q9BioBricks = 'Before playing Hero.Coli, had you ever heard about BioBricks?'
# language may vary: players may have missed the opportunity to set it, or may want to try and change it
Q42 = 'Language'
getSurveysWithMatchingAnswers(
sample,
_gformRow, [Q4, Q5],
extendedList = [Q2Interest, Q3Play, Q6BioEdu, Q8SynBio, Q9BioBricks, Q42],
hardPolicy = hardPolicy
)
questionsAndPositiveAnswers
```
#### getGFormRowCorrection tinkering
```
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
_source = correctAnswers
#def getGFormRowCorrection( _gformRow, _source = correctAnswers):
result = _gformRow.copy()
if(len(_gformRow) == 0):
print("this gform row is empty")
else:
result = pd.Series(index = _gformRow.index, data = np.full(len(_gformRow), np.nan))
for question in result.index:
_correctAnswers = _source.loc[question]
if(len(_correctAnswers) > 0):
result.loc[question] = False
for _correctAnswer in _correctAnswers:
if str(_gformRow.loc[question]).startswith(str(_correctAnswer)):
result.loc[question] = True
break
result
```
#### getGFormRowScore tinkering
```
_gformRow = gform[gform[localplayerguidkey] == _GFUserId].iloc[0]
_source = correctAnswers
#def getGFormRowScore( _gformRow, _source = correctAnswers):
correction = getGFormRowCorrection( _gformRow, _source = _source)
_counts = correction.value_counts()
_thisScore = 0
if(True in _counts):
_thisScore = _counts[True]
_thisScore
```
#### getGFormDataPreview tinkering
```
_GFUserId = getSurveysOfBiologists(gform)[localplayerguidkey].iloc[2]
sample = gform
# for per-gform, manual analysis
#def getGFormDataPreview(_GFUserId, sample):
gforms = gform[gform[localplayerguidkey] == _GFUserId]
result = {}
for _ilocIndex in range(0, len(gforms)):
gformsIndex = gforms.index[_ilocIndex]
currentGForm = gforms.iloc[_ilocIndex]
subresult = {}
subresult['date'] = currentGForm['Timestamp']
subresult['temporality RM'] = currentGForm['Temporality']
subresult['temporality GF'] = getGFormRowGFormTemporality(currentGForm)
subresult['score'] = getGFormRowScore(currentGForm)
subresult['genderAge'] = [currentGForm['What is your gender?'], currentGForm['How old are you?']]
# search for other users with similar demographics
matchingDemographics = getMatchingDemographics(sample, currentGForm)
matchingDemographicsIds = []
#print(type(matchingDemographics))
#print(matchingDemographics.index)
for matchesIndex in matchingDemographics.index:
matchingDemographicsIds.append([matchesIndex, matchingDemographics.loc[matchesIndex, localplayerguidkey]])
subresult['demographic matches'] = matchingDemographicsIds
result['survey' + str(_ilocIndex)] = subresult
print(result)
for match in result['survey0']['demographic matches']:
print(match[0])
```
|
github_jupyter
|
```
from xml.etree import ElementTree
from xml.dom import minidom
from xml.etree.ElementTree import Element, SubElement, Comment, indent
def prettify(elem):
"""Return a pretty-printed XML string for the Element.
"""
rough_string = ElementTree.tostring(elem, encoding="ISO-8859-1")
reparsed = minidom.parseString(rough_string)
return reparsed.toprettyxml(indent="\t")
import numpy as np
import os
valve_start = 1
hyb_start = 51
reg_start = 1
num_rounds = 14
data_type = 'U'
valve_ids = np.arange(valve_start, valve_start + num_rounds)
hyb_ids = np.arange(hyb_start, hyb_start + num_rounds)
reg_names = [f'{data_type}{_i}' for _i in np.arange(reg_start, reg_start + num_rounds)]
source_folder = r'D:\Pu\20220102-CTP11-1000_CTP12-DNA_from_1229'
#target_drive = r'\\KOLMOGOROV\Chromatin_NAS_4'
target_drive = r'\\10.245.74.158\Chromatin_NAS_1'
# imaging protocol
imaging_protocol = r'Zscan_750_647_561_s50_n250_10Hz'
# reference imaging protocol
add_ref_hyb = False
ref_imaging_protocol = r'Zscan_750_647_561_405_s50_n250_10Hz'
ref_hyb = 0
# bleach protocol
bleach = True
bleach_protocol = r'Bleach_750_647_s5'
cmd_seq = Element('command_sequence')
if add_ref_hyb:
# add hyb 0
# comments
comment = Comment(f"Hyb 0")
cmd_seq.append(comment)
# flow imaging buffer
imaging = SubElement(cmd_seq, 'valve_protocol')
imaging.text = f"Flow Imaging Buffer"
# change directory
change_dir = SubElement(cmd_seq, 'change_directory')
change_dir.text = os.path.join(source_folder, f"H0C1")
# wakeup
wakeup = SubElement(cmd_seq, 'wakeup')
wakeup.text = "5000"
# imaging loop
_im_p = ref_imaging_protocol
loop = SubElement(cmd_seq, 'loop', name='Position Loop Zscan', increment="name")
loop_item = SubElement(loop, 'item', name=_im_p)
loop_item.text = " "
# delay time
delay = SubElement(cmd_seq, 'delay')
delay.text = "2000"
# copy folder
copy_dir = SubElement(cmd_seq, 'copy_directory')
source_dir = SubElement(copy_dir, 'source_path')
source_dir.text = change_dir.text
target_dir = SubElement(copy_dir, 'target_path')
target_dir.text = os.path.join(target_drive,
os.path.basename(os.path.dirname(source_dir.text)),
os.path.basename(source_dir.text))
del_source = SubElement(copy_dir, 'delete_source')
del_source.text = "True"
for _i, (_vid, _hid, _rname) in enumerate(zip(valve_ids, hyb_ids, reg_names)):
# select protocol
_im_p = imaging_protocol
# TCEP
tcep = SubElement(cmd_seq, 'valve_protocol')
tcep.text = "Flow TCEP"
# wash tcep
tcep_wash = SubElement(cmd_seq, 'valve_protocol')
tcep_wash.text = "Flow Wash Buffer"
# comments
comment = Comment(f"Hyb {_hid} with {_vid} for {_rname}")
cmd_seq.append(comment)
# flow adaptor
adt = SubElement(cmd_seq, 'valve_protocol')
adt.text = f"Hybridize {_vid}"
if bleach:
# delay time
delay = SubElement(cmd_seq, 'delay')
delay.text = "3000"
# change directory
bleach_change_dir = SubElement(cmd_seq, 'change_directory')
bleach_change_dir.text = os.path.join(source_folder, f"Bleach")
# wakeup
bleach_wakeup = SubElement(cmd_seq, 'wakeup')
bleach_wakeup.text = "5000"
# imaging loop
bleach_loop = SubElement(cmd_seq, 'loop', name='Position Loop Zscan', increment="name")
bleach_loop_item = SubElement(bleach_loop, 'item', name=bleach_protocol)
bleach_loop_item.text = " "
# delay time
delay = SubElement(cmd_seq, 'delay')
delay.text = "3000"
else:
# delay time
adt_incubation = SubElement(cmd_seq, 'valve_protocol')
adt_incubation.text = f"Incubate 10min"
# wash
wash = SubElement(cmd_seq, 'valve_protocol')
wash.text = "Flow Wash Buffer"
# readouts
readouts = SubElement(cmd_seq, 'valve_protocol')
readouts.text = "Flow RNA common readouts"
# incubate readouts
readout_incubation = SubElement(cmd_seq, 'valve_protocol')
readout_incubation.text = f"Incubate 10min"
# wash readouts
readout_wash = SubElement(cmd_seq, 'valve_protocol')
readout_wash.text = f"Flow Wash Buffer"
# flow imaging buffer
imaging = SubElement(cmd_seq, 'valve_protocol')
imaging.text = f"Flow Imaging Buffer"
# change directory
change_dir = SubElement(cmd_seq, 'change_directory')
change_dir.text = os.path.join(source_folder, f"H{_hid}{_rname.upper()}")
# wakeup
wakeup = SubElement(cmd_seq, 'wakeup')
wakeup.text = "5000"
# imaging loop
loop = SubElement(cmd_seq, 'loop', name='Position Loop Zscan', increment="name")
loop_item = SubElement(loop, 'item', name=_im_p)
loop_item.text = " "
# delay time
delay = SubElement(cmd_seq, 'delay')
delay.text = "2000"
# copy folder
copy_dir = SubElement(cmd_seq, 'copy_directory')
source_dir = SubElement(copy_dir, 'source_path')
source_dir.text = change_dir.text#cmd_seq.findall('change_directory')[-1].text
target_dir = SubElement(copy_dir, 'target_path')
target_dir.text = os.path.join(target_drive,
os.path.basename(os.path.dirname(source_dir.text)),
os.path.basename(source_dir.text))
del_source = SubElement(copy_dir, 'delete_source')
del_source.text = "True"
# empty line
indent(target_dir)
final_str = prettify(cmd_seq)
print( final_str )
```
# save this xml
```
save_filename = os.path.join(source_folder, f"generated_dave_H{hyb_start}-{hyb_start+num_rounds-1}.txt")
with open(save_filename, 'w') as _output_handle:
print(save_filename)
_output_handle.write(final_str)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W3D2_DynamicNetworks/W3D2_Tutorial1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Neuromatch Academy: Week 3, Day 2, Tutorial 1
# Neuronal Network Dynamics: Neural Rate Models
__Content creators:__ Qinglong Gu, Songtin Li, Arvind Kumar, John Murray, Julijana Gjorgjieva
__Content reviewers:__ Spiros Chavlis, Lorenzo Fontolan, Richard Gao, Maryam Vaziri-Pashkam,Michael Waskom
---
# Tutorial Objectives
The brain is a complex system, not because it is composed of a large number of diverse types of neurons, but mainly because of how neurons are connected to each other. The brain is indeed a network of highly specialized neuronal networks.
The activity of a neural network constantly evolves in time. For this reason, neurons can be modeled as dynamical systems. The dynamical system approach is only one of the many modeling approaches that computational neuroscientists have developed (other points of view include information processing, statistical models, etc.).
How the dynamics of neuronal networks affect the representation and processing of information in the brain is an open question. However, signatures of altered brain dynamics present in many brain diseases (e.g., in epilepsy or Parkinson's disease) tell us that it is crucial to study network activity dynamics if we want to understand the brain.
In this tutorial, we will simulate and study one of the simplest models of biological neuronal networks. Instead of modeling and simulating individual excitatory neurons (e.g., LIF models that you implemented yesterday), we will treat them as a single homogeneous population and approximate their dynamics using a single one-dimensional equation describing the evolution of their average spiking rate in time.
In this tutorial, we will learn how to build a firing rate model of a single population of excitatory neurons.
**Steps:**
- Write the equation for the firing rate dynamics of a 1D excitatory population.
- Visualize the response of the population as a function of parameters such as threshold level and gain, using the frequency-current (F-I) curve.
- Numerically simulate the dynamics of the excitatory population and find the fixed points of the system.
- Investigate the stability of the fixed points by linearizing the dynamics around them.
---
# Setup
```
# Imports
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize as opt # root-finding algorithm
# @title Figure Settings
import ipywidgets as widgets # interactive display
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# @title Helper functions
def plot_fI(x, f):
plt.figure(figsize=(6, 4)) # plot the figure
plt.plot(x, f, 'k')
plt.xlabel('x (a.u.)', fontsize=14)
plt.ylabel('F(x)', fontsize=14)
plt.show()
def plot_dr_r(r, drdt):
plt.figure()
plt.plot(r, drdt, 'k')
plt.plot(r, 0. * r, 'k--')
plt.xlabel(r'$r$')
plt.ylabel(r'$\frac{dr}{dt}$', fontsize=20)
plt.ylim(-0.1, 0.1)
def plot_dFdt(x, dFdt):
plt.figure()
plt.plot(x, dFdt, 'r')
plt.xlabel('x (a.u.)', fontsize=14)
plt.ylabel('dF(x)', fontsize=14)
plt.show()
```
# Section 1: Neuronal network dynamics
```
# @title Video 1: Dynamic networks
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="p848349hPyw", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
```
## Section 1.1: Dynamics of a single excitatory population
Individual neurons respond by spiking. When we average the spikes of neurons in a population, we can define the average firing activity of the population. In this model, we are interested in how the population-averaged firing varies as a function of time and network parameters. Mathematically, we can describe the firing rate dynamic as:
\begin{align}
\tau \frac{dr}{dt} &= -r + F(w\cdot r + I_{\text{ext}}) \quad\qquad (1)
\end{align}
$r(t)$ represents the average firing rate of the excitatory population at time $t$, $\tau$ controls the timescale of the evolution of the average firing rate, $w$ denotes the strength (synaptic weight) of the recurrent input to the population, $I_{\text{ext}}$ represents the external input, and the transfer function $F(\cdot)$ (which can be related to f-I curve of individual neurons described in the next sections) represents the population activation function in response to all received inputs.
To start building the model, please execute the cell below to initialize the simulation parameters.
```
# @title Default parameters for a single excitatory population model
def default_pars_single(**kwargs):
pars = {}
# Excitatory parameters
pars['tau'] = 1. # Timescale of the E population [ms]
pars['a'] = 1.2 # Gain of the E population
pars['theta'] = 2.8 # Threshold of the E population
# Connection strength
pars['w'] = 0. # E to E, we first set it to 0
# External input
pars['I_ext'] = 0.
# simulation parameters
pars['T'] = 20. # Total duration of simulation [ms]
pars['dt'] = .1 # Simulation time step [ms]
pars['r_init'] = 0.2 # Initial value of E
# External parameters if any
for k in kwargs:
pars[k] = kwargs[k]
# Vector of discretized time points [ms]
pars['range_t'] = np.arange(0, pars['T'], pars['dt'])
return pars
```
You can use:
- `pars = default_pars_single()` to get all the parameters, and then you can execute `print(pars)` to check these parameters.
- `pars = default_pars_single(T=T_sim, dt=time_step)` to set new simulation time and time step
- After `pars = default_pars_single()`, use `pars['New_para'] = value` to add an new parameter with its value
## Section 1.2: F-I curves
In electrophysiology, a neuron is often characterized by its spike rate output in response to input currents. This is often called the **F-I** curve, denoting the output spike frequency (**F**) in response to different injected currents (**I**). We estimated this for an LIF neuron in yesterday's tutorial.
The transfer function $F(\cdot)$ in Equation $1$ represents the gain of the population as a function of the total input. The gain is often modeled as a sigmoidal function, i.e., more input drive leads to a nonlinear increase in the population firing rate. The output firing rate will eventually saturate for high input values.
A sigmoidal $F(\cdot)$ is parameterized by its gain $a$ and threshold $\theta$.
$$ F(x;a,\theta) = \frac{1}{1+\text{e}^{-a(x-\theta)}} - \frac{1}{1+\text{e}^{a\theta}} \quad(2)$$
The argument $x$ represents the input to the population. Note that the second term is chosen so that $F(0;a,\theta)=0$.
Many other transfer functions (generally monotonic) can be also used. Examples are the rectified linear function $ReLU(x)$ or the hyperbolic tangent $tanh(x)$.
### Exercise 1: Implement F-I curve
Let's first investigate the activation functions before simulating the dynamics of the entire population.
In this exercise, you will implement a sigmoidal **F-I** curve or transfer function $F(x)$, with gain $a$ and threshold level $\theta$ as parameters.
```
def F(x, a, theta):
"""
Population activation function.
Args:
x (float): the population input
a (float): the gain of the function
theta (float): the threshold of the function
Returns:
float: the population activation response F(x) for input x
"""
#################################################
## TODO for students: compute f = F(x) ##
# Fill out function and remove
raise NotImplementedError("Student excercise: implement the f-I function")
#################################################
# add the expression of f = F(x)
f = ...
return f
pars = default_pars_single() # get default parameters
x = np.arange(0, 10, .1) # set the range of input
# Uncomment below to test your function
# f = F(x, pars['a'], pars['theta'])
# plot_fI(x, f)
# to_remove solution
def F(x, a, theta):
"""
Population activation function.
Args:
x (float): the population input
a (float): the gain of the function
theta (float): the threshold of the function
Returns:
float: the population activation response F(x) for input x
"""
# add the expression of f = F(x)
f = (1 + np.exp(-a * (x - theta)))**-1 - (1 + np.exp(a * theta))**-1
return f
pars = default_pars_single() # get default parameters
x = np.arange(0, 10, .1) # set the range of input
# Uncomment below to test your function
f = F(x, pars['a'], pars['theta'])
with plt.xkcd():
plot_fI(x, f)
```
### Interactive Demo: Parameter exploration of F-I curve
Here's an interactive demo that shows how the F-I curve is changing for different values of the gain and threshold parameters.
**Remember to enable the demo by running the cell.**
```
# @title
# @markdown Make sure you execute this cell to enable the widget!
def interactive_plot_FI(a, theta):
"""
Population activation function.
Expecxts:
a : the gain of the function
theta : the threshold of the function
Returns:
plot the F-I curve with give parameters
"""
# set the range of input
x = np.arange(0, 10, .1)
plt.figure()
plt.plot(x, F(x, a, theta), 'k')
plt.xlabel('x (a.u.)', fontsize=14)
plt.ylabel('F(x)', fontsize=14)
plt.show()
_ = widgets.interact(interactive_plot_FI, a=(0.3, 3, 0.3), theta=(2, 4, 0.2))
```
## Section 1.3: Simulation scheme of E dynamics
Because $F(\cdot)$ is a nonlinear function, the exact solution of Equation $1$ can not be determined via analytical methods. Therefore, numerical methods must be used to find the solution. In practice, the derivative on the left-hand side of Equation $1$ can be approximated using the Euler method on a time-grid of stepsize $\Delta t$:
\begin{align}
&\frac{dr}{dt} \approx \frac{r[k+1]-r[k]}{\Delta t}
\end{align}
where $r[k] = r(k\Delta t)$.
Thus,
$$\Delta r[k] = \frac{\Delta t}{\tau}[-r[k] + F(w\cdot r[k] + I_{\text{ext}}(k;a,\theta))]$$
Hence, Equation (1) is updated at each time step by:
$$r[k+1] = r[k] + \Delta r[k]$$
**_Please execute the following cell to enable the WC simulator_**
```
# @title Single population rate model simulator: `simulate_single`
def simulate_single(pars):
"""
Simulate an excitatory population of neurons
Args:
pars : Parameter dictionary
Returns:
rE : Activity of excitatory population (array)
Example:
pars = default_pars_single()
r = simulate_single(pars)
"""
# Set parameters
tau, a, theta = pars['tau'], pars['a'], pars['theta']
w = pars['w']
I_ext = pars['I_ext']
r_init = pars['r_init']
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
# Initialize activity
r = np.zeros(Lt)
r[0] = r_init
I_ext = I_ext * np.ones(Lt)
# Update the E activity
for k in range(Lt - 1):
dr = dt / tau * (-r[k] + F(w * r[k] + I_ext[k], a, theta))
r[k+1] = r[k] + dr
return r
print(help(simulate_single))
```
### Interactive Demo: Parameter Exploration of single population dynamics
Note that $w=0$, as in the default setting, means no recurrent input to the neuron population in Equation (1). Hence, the dynamics is entirely determined by the external input $I_{\text{ext}}$. Try to explore how $r_{\text{sim}}(t)$ changes with different $I_{\text{ext}}$ and $\tau$ parameter values, and investigate the relationship between $F(I_{\text{ext}}; a, \theta)$ and the steady value of $r(t)$. Note that, $r_{\rm ana}(t)$ denotes the analytical solution.
```
# @title
# @markdown Make sure you execute this cell to enable the widget!
# get default parameters
pars = default_pars_single(T=20.)
def Myplot_E_diffI_difftau(I_ext, tau):
# set external input and time constant
pars['I_ext'] = I_ext
pars['tau'] = tau
# simulation
r = simulate_single(pars)
# Analytical Solution
r_ana = (pars['r_init']
+ (F(I_ext, pars['a'], pars['theta'])
- pars['r_init']) * (1. - np.exp(-pars['range_t'] / pars['tau'])))
# plot
plt.figure()
plt.plot(pars['range_t'], r, 'b', label=r'$r_{\mathrm{sim}}$(t)', alpha=0.5,
zorder=1)
plt.plot(pars['range_t'], r_ana, 'b--', lw=5, dashes=(2, 2),
label=r'$r_{\mathrm{ana}}$(t)', zorder=2)
plt.plot(pars['range_t'],
F(I_ext, pars['a'], pars['theta']) * np.ones(pars['range_t'].size),
'k--', label=r'$F(I_{\mathrm{ext}})$')
plt.xlabel('t (ms)', fontsize=16.)
plt.ylabel('Activity r(t)', fontsize=16.)
plt.legend(loc='best', fontsize=14.)
plt.show()
_ = widgets.interact(Myplot_E_diffI_difftau, I_ext=(0.0, 10., 1.),
tau=(1., 5., 0.2))
```
## Think!
Above, we have numerically solved a system driven by a positive input and that, if $w_{EE} \neq 0$, receives an excitatory recurrent input (**try changing the value of $w_{EE}$ to a positive number**). Yet, $r_E(t)$ either decays to zero or reaches a fixed non-zero value.
- Why doesn't the solution of the system "explode" in a finite time? In other words, what guarantees that $r_E$(t) stays finite?
- Which parameter would you change in order to increase the maximum value of the response?
# Section 2: Fixed points of the single population system
```
# @title Video 2: Fixed point
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="Ox3ELd1UFyo", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
```
As you varied the two parameters in the last Interactive Demo, you noticed that, while at first the system output quickly changes, with time, it reaches its maximum/minimum value and does not change anymore. The value eventually reached by the system is called the **steady state** of the system, or the **fixed point**. Essentially, in the steady states the derivative with respect to time of the activity ($r$) is zero, i.e. $\displaystyle \frac{dr}{dt}=0$.
We can find that the steady state of the Equation. (1) by setting $\displaystyle{\frac{dr}{dt}=0}$ and solve for $r$:
$$-r_{\text{steady}} + F(w\cdot r_{\text{steady}} + I_{\text{ext}};a,\theta) = 0, \qquad (3)$$
When it exists, the solution of Equation. (3) defines a **fixed point** of the dynamical system Equation. (1). Note that if $F(x)$ is nonlinear, it is not always possible to find an analytical solution, but the solution can be found via numerical simulations, as we will do later.
From the Interactive Demo, one could also notice that the value of $\tau$ influences how quickly the activity will converge to the steady state from its initial value.
In the specific case of $w=0$, we can also analytically compute the solution of Equation (1) (i.e., the thick blue dashed line) and deduce the role of $\tau$ in determining the convergence to the fixed point:
$$\displaystyle{r(t) = \big{[}F(I_{\text{ext}};a,\theta) -r(t=0)\big{]} (1-\text{e}^{-\frac{t}{\tau}})} + r(t=0)$$ \\
We can now numerically calculate the fixed point with the `scipy.optimize.root` function.
<font size=3><font color='gray'>_(Recall that at the very beginning, we `import scipy.optimize as opt` )_</font></font>.
\\
Please execute the cell below to define the functions `my_fp_single` and `check_fp_single`
```
# @title Function of calculating the fixed point
# @markdown Make sure you execute this cell to enable the function!
def my_fp_single(pars, r_init):
"""
Calculate the fixed point through drE/dt=0
Args:
pars : Parameter dictionary
r_init : Initial value used for scipy.optimize function
Returns:
x_fp : value of fixed point
"""
# get the parameters
a, theta = pars['a'], pars['theta']
w = pars['w']
I_ext = pars['I_ext']
# define the right hand of E dynamics
def my_WCr(x):
r = x
drdt = (-r + F(w * r + I_ext, a, theta))
y = np.array(drdt)
return y
x0 = np.array(r_init)
x_fp = opt.root(my_WCr, x0).x
return x_fp
print(help(my_fp_single))
def check_fp_single(pars, x_fp, mytol=1e-4):
"""
Verify |dr/dt| < mytol
Args:
pars : Parameter dictionary
fp : value of fixed point
mytol : tolerance, default as 10^{-4}
Returns :
Whether it is a correct fixed point: True/False
"""
a, theta = pars['a'], pars['theta']
w = pars['w']
I_ext = pars['I_ext']
# calculate Equation(3)
y = x_fp - F(w * x_fp + I_ext, a, theta)
# Here we set tolerance as 10^{-4}
return np.abs(y) < mytol
print(help(check_fp_single))
```
## Exercise 2: Visualization of the fixed point
When it is not possible to find the solution for Equation (3) analytically, a graphical approach can be taken. To that end, it is useful to plot $\displaystyle{\frac{dr}{dt}=0}$ as a function of $r$. The values of $r$ for which the plotted function crosses zero on the y axis correspond to fixed points.
Here, let us, for example, set $w=5.0$ and $I^{\text{ext}}=0.5$. From Equation (1), you can obtain
$$\frac{dr}{dt} = [-r + F(w\cdot r + I^{\text{ext}})]/\tau $$
Then, plot the $dr/dt$ as a function of $r$, and check for the presence of fixed points.
Finally, try to find the fixed points using the previously defined function `my_fp_single(pars, r_init)` with proper initial values ($r_{\text{init}}$). You can use the previously defined function `check_fp_single(pars, x_fp)` to verify that the values of $r{\rm fp}$ for which $\displaystyle{\frac{dr}{dt}} = 0$ are the true fixed points. From the line $\displaystyle{\frac{dr}{dt}}$ plotted above, the proper initial values can be chosen as the values close to where the line crosses zero on the y axis (real fixed point).
```
pars = default_pars_single() # get default parameters
# set your external input and wEE
pars['I_ext'] = 0.5
pars['w'] = 5.0
r = np.linspace(0, 1, 1000) # give the values of r
# Calculate drEdt
# drdt = ...
# Uncomment this to plot the drdt across r
# plot_dr_r(r, drdt)
################################################################
# TODO for students:
# Find the values close to the intersections of drdt and y=0
# as your initial values
# Calculate the fixed point with your initial value, verify them,
# and plot the corret ones
# check if x_fp is the intersection of the lines with the given function
# check_fpE(pars, x_fp)
# vary different initial values to find the correct fixed point (Should be 3)
# Use blue, red and yellow colors, respectively ('b', 'r', 'y' codenames)
################################################################
# Calculate the first fixed point with your initial value
# x_fp_1 = my_fp_single(pars, ...)
# if check_fp_single(pars, x_fp_1):
# plt.plot(x_fp_1, 0, 'bo', ms=8)
# Calculate the second fixed point with your initial value
# x_fp_2 = my_fp_single(pars, ...)
# if check_fp_single(pars, x_fp_2):
# plt.plot(x_fp_2, 0, 'ro', ms=8)
# Calculate the third fixed point with your initial value
# x_fp_3 = my_fp_single(pars, ...)
# if check_fp_single(pars, x_fp_3):
# plt.plot(x_fp_3, 0, 'yo', ms=8)
# to_remove solution
pars = default_pars_single() # get default parameters
# set your external input and wEE
pars['I_ext'] = 0.5
pars['w'] = 5.0
r = np.linspace(0, 1, 1000) # give the values of r
# Calculate drEdt
drdt = (-r + F(pars['w'] * r + pars['I_ext'],
pars['a'], pars['theta'])) / pars['tau']
with plt.xkcd():
plot_dr_r(r, drdt)
# Calculate the first fixed point with your initial value
x_fp_1 = my_fp_single(pars, 0.)
if check_fp_single(pars, x_fp_1):
plt.plot(x_fp_1, 0, 'bo', ms=8)
# Calculate the second fixed point with your initial value
x_fp_2 = my_fp_single(pars, 0.4)
if check_fp_single(pars, x_fp_2):
plt.plot(x_fp_2, 0, 'ro', ms=8)
# Calculate the third fixed point with your initial value
x_fp_3 = my_fp_single(pars, 0.9)
if check_fp_single(pars, x_fp_3):
plt.plot(x_fp_3, 0, 'yo', ms=8)
plt.show()
```
## Interactive Demo: fixed points as a function of recurrent and external inputs.
You can now explore how the previous plot changes when the recurrent coupling $w$ and the external input $I_{\text{ext}}$ take different values.
```
# @title
# @markdown Make sure you execute this cell to enable the widget!
def plot_intersection_single(w, I_ext):
# set your parameters
pars['w'] = w
pars['I_ext'] = I_ext
# note that wEE!=0
if w > 0:
# find fixed point
x_fp_1 = my_fp_single(pars, 0.)
x_fp_2 = my_fp_single(pars, 0.4)
x_fp_3 = my_fp_single(pars, 0.9)
plt.figure()
r = np.linspace(0, 1., 1000)
drdt = (-r + F(w * r + I_ext, pars['a'], pars['theta'])) / pars['tau']
plt.plot(r, drdt, 'k')
plt.plot(r, 0. * r, 'k--')
if check_fp_single(pars, x_fp_1):
plt.plot(x_fp_1, 0, 'bo', ms=8)
if check_fp_single(pars, x_fp_2):
plt.plot(x_fp_2, 0, 'ro', ms=8)
if check_fp_single(pars, x_fp_3):
plt.plot(x_fp_3, 0, 'yo', ms=8)
plt.xlabel(r'$r$', fontsize=14.)
plt.ylabel(r'$\frac{dr}{dt}$', fontsize=20.)
plt.show()
_ = widgets.interact(plot_intersection_single, w=(1, 7, 0.2),
I_ext=(0, 3, 0.1))
```
---
# Summary
In this tutorial, we have investigated the dynamics of a rate-based single population of neurons.
We learned about:
- The effect of the input parameters and the time constant of the network on the dynamics of the population.
- How to find the fixed point(s) of the system.
Next, we have two Bonus, but important concepts in dynamical system analysis and simulation. If you have time left, watch the next video and proceed to solve the exercises. You will learn:
- How to determine the stability of a fixed point by linearizing the system.
- How to add realistic inputs to our model.
---
# Bonus 1: Stability of a fixed point
```
# @title Video 3: Stability of fixed points
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="KKMlWWU83Jg", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
```
#### Initial values and trajectories
Here, let us first set $w=5.0$ and $I_{\text{ext}}=0.5$, and investigate the dynamics of $r(t)$ starting with different initial values $r(0) \equiv r_{\text{init}}$. We will plot the trajectories of $r(t)$ with $r_{\text{init}} = 0.0, 0.1, 0.2,..., 0.9$.
```
# @title Initial values
# @markdown Make sure you execute this cell to see the trajectories!
pars = default_pars_single()
pars['w'] = 5.0
pars['I_ext'] = 0.5
plt.figure(figsize=(8, 5))
for ie in range(10):
pars['r_init'] = 0.1 * ie # set the initial value
r = simulate_single(pars) # run the simulation
# plot the activity with given initial
plt.plot(pars['range_t'], r, 'b', alpha=0.1 + 0.1 * ie,
label=r'r$_{\mathrm{init}}$=%.1f' % (0.1 * ie))
plt.xlabel('t (ms)')
plt.title('Two steady states?')
plt.ylabel(r'$r$(t)')
plt.legend(loc=[1.01, -0.06], fontsize=14)
plt.show()
```
## Interactive Demo: dynamics as a function of the initial value
Let's now set $r_{\rm init}$ to a value of your choice in this demo. How does the solution change? What do you observe?
```
# @title
# @markdown Make sure you execute this cell to enable the widget!
pars = default_pars_single()
pars['w'] = 5.0
pars['I_ext'] = 0.5
def plot_single_diffEinit(r_init):
pars['r_init'] = r_init
r = simulate_single(pars)
plt.figure()
plt.plot(pars['range_t'], r, 'b', zorder=1)
plt.plot(0, r[0], 'bo', alpha=0.7, zorder=2)
plt.xlabel('t (ms)', fontsize=16)
plt.ylabel(r'$r(t)$', fontsize=16)
plt.ylim(0, 1.0)
plt.show()
_ = widgets.interact(plot_single_diffEinit, r_init=(0, 1, 0.02))
```
### Stability analysis via linearization of the dynamics
Just like Equation $1$ in the case ($w=0$) discussed above, a generic linear system
$$\frac{dx}{dt} = \lambda (x - b),$$
has a fixed point for $x=b$. The analytical solution of such a system can be found to be:
$$x(t) = b + \big{(} x(0) - b \big{)} \text{e}^{\lambda t}.$$
Now consider a small perturbation of the activity around the fixed point: $x(0) = b+ \epsilon$, where $|\epsilon| \ll 1$. Will the perturbation $\epsilon(t)$ grow with time or will it decay to the fixed point? The evolution of the perturbation with time can be written, using the analytical solution for $x(t)$, as:
$$\epsilon (t) = x(t) - b = \epsilon \text{e}^{\lambda t}$$
- if $\lambda < 0$, $\epsilon(t)$ decays to zero, $x(t)$ will still converge to $b$ and the fixed point is "**stable**".
- if $\lambda > 0$, $\epsilon(t)$ grows with time, $x(t)$ will leave the fixed point $b$ exponentially, and the fixed point is, therefore, "**unstable**" .
### Compute the stability of Equation $1$
Similar to what we did in the linear system above, in order to determine the stability of a fixed point $r^{*}$ of the excitatory population dynamics, we perturb Equation (1) around $r^{*}$ by $\epsilon$, i.e. $r = r^{*} + \epsilon$. We can plug in Equation (1) and obtain the equation determining the time evolution of the perturbation $\epsilon(t)$:
\begin{align}
\tau \frac{d\epsilon}{dt} \approx -\epsilon + w F'(w\cdot r^{*} + I_{\text{ext}};a,\theta) \epsilon
\end{align}
where $F'(\cdot)$ is the derivative of the transfer function $F(\cdot)$. We can rewrite the above equation as:
\begin{align}
\frac{d\epsilon}{dt} \approx \frac{\epsilon}{\tau }[-1 + w F'(w\cdot r^* + I_{\text{ext}};a,\theta)]
\end{align}
That is, as in the linear system above, the value of
$$\lambda = [-1+ wF'(w\cdot r^* + I_{\text{ext}};a,\theta)]/\tau \qquad (4)$$
determines whether the perturbation will grow or decay to zero, i.e., $\lambda$ defines the stability of the fixed point. This value is called the **eigenvalue** of the dynamical system.
## Exercise 3: Compute $dF$ and Eigenvalue
The derivative of the sigmoid transfer function is:
\begin{align}
\frac{dF}{dx} & = \frac{d}{dx} (1+\exp\{-a(x-\theta)\})^{-1} \\
& = a\exp\{-a(x-\theta)\} (1+\exp\{-a(x-\theta)\})^{-2}. \qquad (5)
\end{align}
Let's now find the expression for the derivative $\displaystyle{\frac{dF}{dx}}$ in the following cell and plot it.
```
def dF(x, a, theta):
"""
Population activation function.
Args:
x : the population input
a : the gain of the function
theta : the threshold of the function
Returns:
dFdx : the population activation response F(x) for input x
"""
#################################################
# TODO for students: compute dFdx ##
raise NotImplementedError("Student excercise: compute the deravitive of F")
#################################################
# Calculate the population activation
dFdx = ...
return dFdx
pars = default_pars_single() # get default parameters
x = np.arange(0, 10, .1) # set the range of input
# Uncomment below to test your function
# df = dF(x, pars['a'], pars['theta'])
# plot_dFdt(x, df)
# to_remove solution
def dF(x, a, theta):
"""
Population activation function.
Args:
x : the population input
a : the gain of the function
theta : the threshold of the function
Returns:
dFdx : the population activation response F(x) for input x
"""
# Calculate the population activation
dFdx = a * np.exp(-a * (x - theta)) * (1 + np.exp(-a * (x - theta)))**-2
return dFdx
pars = default_pars_single() # get default parameters
x = np.arange(0, 10, .1) # set the range of input
df = dF(x, pars['a'], pars['theta'])
with plt.xkcd():
plot_dFdt(x, df)
```
## Exercise 4: Compute eigenvalues
As discussed above, for the case with $w=5.0$ and $I_{\text{ext}}=0.5$, the system displays **three** fixed points. However, when we simulated the dynamics and varied the initial conditions $r_{\rm init}$, we could only obtain **two** steady states. In this exercise, we will now check the stability of each of the three fixed points by calculating the corresponding eigenvalues with the function `eig_single`. Check the sign of each eigenvalue (i.e., stability of each fixed point). How many of the fixed points are stable?
Note that the expression of the eigenvalue at fixed point $r^*$
$$\lambda = [-1+ wF'(w\cdot r^* + I_{\text{ext}};a,\theta)]/\tau$$
```
def eig_single(pars, fp):
"""
Args:
pars : Parameter dictionary
fp : fixed point r_fp
Returns:
eig : eigevalue of the linearized system
"""
# get the parameters
tau, a, theta = pars['tau'], pars['a'], pars['theta']
w, I_ext = pars['w'], pars['I_ext']
print(tau, a, theta, w, I_ext)
#################################################
## TODO for students: compute eigenvalue ##
raise NotImplementedError("Student excercise: compute the eigenvalue")
#################################################
# Compute the eigenvalue
eig = ...
return eig
pars = default_pars_single()
pars['w'] = 5.0
pars['I_ext'] = 0.5
# Uncomment below lines after completing the eig_single function.
# Find the eigenvalues for all fixed points of Exercise 2
# x_fp_1 = my_fp_single(pars, 0.).item()
# eig_fp_1 = eig_single(pars, x_fp_1).item()
# print(f'Fixed point1 at {x_fp_1:.3f} with Eigenvalue={eig_fp_1:.3f}')
# x_fp_2 = my_fp_single(pars, 0.4).item()
# eig_fp_2 = eig_single(pars, x_fp_2).item()
# print(f'Fixed point2 at {x_fp_2:.3f} with Eigenvalue={eig_fp_2:.3f}')
# x_fp_3 = my_fp_single(pars, 0.9).item()
# eig_fp_3 = eig_single(pars, x_fp_3).item()
# print(f'Fixed point3 at {x_fp_3:.3f} with Eigenvalue={eig_fp_3:.3f}')
```
**SAMPLE OUTPUT**
```
Fixed point1 at 0.042 with Eigenvalue=-0.583
Fixed point2 at 0.447 with Eigenvalue=0.498
Fixed point3 at 0.900 with Eigenvalue=-0.626
```
```
# to_remove solution
def eig_single(pars, fp):
"""
Args:
pars : Parameter dictionary
fp : fixed point r_fp
Returns:
eig : eigevalue of the linearized system
"""
# get the parameters
tau, a, theta = pars['tau'], pars['a'], pars['theta']
w, I_ext = pars['w'], pars['I_ext']
print(tau, a, theta, w, I_ext)
# Compute the eigenvalue
eig = (-1. + w * dF(w * fp + I_ext, a, theta)) / tau
return eig
pars = default_pars_single()
pars['w'] = 5.0
pars['I_ext'] = 0.5
# Find the eigenvalues for all fixed points of Exercise 2
x_fp_1 = my_fp_single(pars, 0.).item()
eig_fp_1 = eig_single(pars, x_fp_1).item()
print(f'Fixed point1 at {x_fp_1:.3f} with Eigenvalue={eig_fp_1:.3f}')
x_fp_2 = my_fp_single(pars, 0.4).item()
eig_fp_2 = eig_single(pars, x_fp_2).item()
print(f'Fixed point2 at {x_fp_2:.3f} with Eigenvalue={eig_fp_2:.3f}')
x_fp_3 = my_fp_single(pars, 0.9).item()
eig_fp_3 = eig_single(pars, x_fp_3).item()
print(f'Fixed point3 at {x_fp_3:.3f} with Eigenvalue={eig_fp_3:.3f}')
```
## Think!
Throughout the tutorial, we have assumed $w> 0 $, i.e., we considered a single population of **excitatory** neurons. What do you think will be the behavior of a population of inhibitory neurons, i.e., where $w> 0$ is replaced by $w< 0$?
---
# Bonus 2: Noisy input drives the transition between two stable states
## Ornstein-Uhlenbeck (OU) process
As discussed in several previous tutorials, the OU process is usually used to generate a noisy input into the neuron. The OU input $\eta(t)$ follows:
$$\tau_\eta \frac{d}{dt}\eta(t) = -\eta (t) + \sigma_\eta\sqrt{2\tau_\eta}\xi(t)$$
Execute the following function `my_OU(pars, sig, myseed=False)` to generate an OU process.
```
# @title OU process `my_OU(pars, sig, myseed=False)`
# @markdown Make sure you execute this cell to visualize the noise!
def my_OU(pars, sig, myseed=False):
"""
A functions that generates Ornstein-Uhlenback process
Args:
pars : parameter dictionary
sig : noise amplitute
myseed : random seed. int or boolean
Returns:
I : Ornstein-Uhlenbeck input current
"""
# Retrieve simulation parameters
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
tau_ou = pars['tau_ou'] # [ms]
# set random seed
if myseed:
np.random.seed(seed=myseed)
else:
np.random.seed()
# Initialize
noise = np.random.randn(Lt)
I_ou = np.zeros(Lt)
I_ou[0] = noise[0] * sig
# generate OU
for it in range(Lt - 1):
I_ou[it + 1] = (I_ou[it]
+ dt / tau_ou * (0. - I_ou[it])
+ np.sqrt(2 * dt / tau_ou) * sig * noise[it + 1])
return I_ou
pars = default_pars_single(T=100)
pars['tau_ou'] = 1. # [ms]
sig_ou = 0.1
I_ou = my_OU(pars, sig=sig_ou, myseed=2020)
plt.figure(figsize=(10, 4))
plt.plot(pars['range_t'], I_ou, 'r')
plt.xlabel('t (ms)')
plt.ylabel(r'$I_{\mathrm{OU}}$')
plt.show()
```
## Example: Up-Down transition
In the presence of two or more fixed points, noisy inputs can drive a transition between the fixed points! Here, we stimulate an E population for 1,000 ms applying OU inputs.
```
# @title Simulation of an E population with OU inputs
# @markdown Make sure you execute this cell to spot the Up-Down states!
pars = default_pars_single(T=1000)
pars['w'] = 5.0
sig_ou = 0.7
pars['tau_ou'] = 1. # [ms]
pars['I_ext'] = 0.56 + my_OU(pars, sig=sig_ou, myseed=2020)
r = simulate_single(pars)
plt.figure(figsize=(10, 4))
plt.plot(pars['range_t'], r, 'b', alpha=0.8)
plt.xlabel('t (ms)')
plt.ylabel(r'$r(t)$')
plt.show()
```
|
github_jupyter
|
```
import xarray as xr
import pandas as pd
from joblib import load
import os
import math
from datetime import datetime,timedelta
from sklearn import preprocessing
def redondeo(coordenadas, base=1/12):
"""
Devuelve las coordenadas pasadas redondeadas
Parametros:
coordenadas -- lista de latitud y longitud
base -- base del redondeo
"""
return base * round(coordenadas/base)
fecha = '2018-11-16'
coordenadas = '[-26.99053888888889, -70.78993333333334]'
salto = 1/12
var = ['mlotst','zos','bottomT','thetao','so','uo','vo']
separacion = coordenadas.index(', ')
final = coordenadas.index(']')
coordenadas = [float(coordenadas[1:separacion]),float(coordenadas[separacion+2:final])]
coordenadas = [redondeo(coordenadas[0]),redondeo(coordenadas[1])]
coordenadas
def genera_resultados(fecha, coordenadas):
# se cogerian los datos de copernicus
# generar dataframe
#normalizarlo
# meterlo al modelo
modelo = load('C:\\Users\pablo\Desktop\medusas\static\modelo.joblib')
df,fechas = genera_estructura(fecha,coordenadas)
df = normaliza_min_max(df)
salida = modelo.predict(df)
print(salida,fechas)
# lista = [{'y': '2020-1-1', 'v': 1},
# {'y': '2020-2-1', 'v': 10},
# {'y': '2020-1-5', 'v': 5},
# {'y': '2020-3-5', 'v': 2}]
# return lista
return df
def genera_estructura(f,c):
dataframe = pd.DataFrame(columns=list(range(231)))
fechas = genera_fechas(f)
for index,dia in enumerate(fechas):
listado_variables = []
# cargo el dataset
ds =busca_archivo(dia) # cambiar para cada dia
c = comprueba_datos(c[0],c[1],ds)
coord = dame_coordenadas(c)
for j in coord:
variables1 = ds.sel({'latitude':coord[0][0],'longitude': coord[0][1], 'depth' : 0 },method='nearest').to_dataframe()
l1 = dame_lista(variables1)[0]
variables2 = ds.sel({'latitude':coord[1][0],'longitude': coord[1][1], 'depth' : 5 },method='nearest').to_dataframe()
l2 = dame_lista(variables2)[0]
variables3 = ds.sel({'latitude':coord[2][0],'longitude': coord[2][1], 'depth' : 10},method='nearest').to_dataframe()
l3 = dame_lista(variables3)[0]
l1+=l2
l1+=l3
listado_variables+=(l1)
dataframe.loc[index] = listado_variables
return dataframe,fechas
def normaliza_min_max(df_atributos):
"""
Normaliza los datos del dataframe pasado
"""
X = df_atributos.values.tolist()
n = load('normalizador.pkl')
x_normalizado_2 = n.transform(X)
df_norm = pd.DataFrame(x_normalizado_2,columns=list(range(231)))
return df_norm
def genera_fechas(f):
lista_fechas = []
for i in range(5):
fecha= datetime.strptime(f, '%Y-%m-%d')
fecha += timedelta(days=i)
lista_fechas.append(str(fecha))
return lista_fechas
def dame_lista(df):
Row_list = []
for index, rows in df.iterrows():
my_list =[rows.mlotst, rows.zos, rows.bottomT, rows.thetao, rows.so,
rows.uo, rows.vo]
Row_list.append(my_list)
# Print the list
return Row_list
def busca_archivo(fecha):
"""
Devuelve el archivo .nc de la fecha pasada por parametro
Parametros:
fecha -- fecha en formato AñoMesDia (20140105)
"""
listado_archivos = os.listdir('C:\\Users\pablo\Desktop\medusas\documentos\copernicus') # Listo todos los archivos de Copernicus
texto ='_{}_'.format(str(fecha).split()[0].replace('-',''))
archivo = [x for x in listado_archivos if str(texto) in x]
data = xr.open_dataset('C:\\Users\pablo\Desktop\medusas\documentos\copernicus\{}'.format(archivo[0])) # cargo el archivo
return data # devuelvo dataset
def dame_coordenadas(c):
paso = 1/12
return [[c[0],c[1]],
[c[0],c[1]-paso],[c[0]+paso,c[1]-paso],[c[0]+(paso*2),c[1]-paso],[c[0]-paso,c[1]-paso],[c[0]-(paso*2),c[1]-paso],
[c[0],c[1]-(2*paso)],[c[0]+paso,c[1]-(2*paso)],[c[0]+(paso*2),c[1]-(2*paso)],[c[0]-paso,c[1]-(2*paso)],[c[0]-(paso*2),c[1]-(2*paso)]]
def comprueba_datos(latitud,longitud,ds):
"""
Comprueba si el dataset contiene valores en las coordenadas pasadas
Devuelve las coordenadas mas cercanas con datos
Parametros:
latitud -- latitud
longitud -- longitud
ds -- dataset del que extraer los valores
"""
valor = dame_datos(latitud,longitud,ds)
while math.isnan(valor.mlotst[0]):
longitud = longitud - salto
valor = dame_datos(latitud,longitud,ds)
return latitud,longitud # devuelvo las coordenadas con datos
def dame_datos(latitud,longitud,ds):
"""
Devuelve los datos del dataset en las coordenadas pasadas
Parametros:
latitud -- latitud
longitud -- longitud
ds -- dataset del que extraer los valores
"""
return ds.sel({'latitude':latitud,'longitude': longitud})
d = genera_resultados(fecha,coordenadas)
d
```
|
github_jupyter
|
# `sourmash tax` submodule
### for integrating taxonomic information
The sourmash tax (alias `taxonomy`) commands integrate taxonomic information into the results of sourmash gather. tax commands require a properly formatted taxonomy csv file that corresponds to the database used for gather. For supported databases (e.g. GTDB), we provide these files, but they can also be generated for user-generated databases. For more information, see the [databases documentation](https://sourmash.readthedocs.io/en/latest/databases.html).
These commands rely upon the fact that gather results are non-overlapping: the fraction match for gather on each query will be between 0 (no database matches) and 1 (100% of query matched). We use this property to aggregate gather matches at the desired taxonomic rank. For example, if the gather results for a metagenome include results for 30 different strains of a given species, we can sum the fraction match to each strain to obtain the fraction match to this species.
As with all reference-based analysis, results can be affected by the completeness of the reference database. However, summarizing taxonomic results from gather minimizes the impact of reference database issues that can derail standard k-mer LCA approaches. See the [blog post]() for a full explanation, and the [`sourmash tax` documentation](https://sourmash.readthedocs.io/en/latest/command-line.html#sourmash-tax-prepare-prepare-and-or-combine-taxonomy-files) for additional usage details.
## Download example inputs for `sourmash tax`
In this example, we'll be using a small test dataset run against both the `GTDB-rs202` database
and our legacy `Genbank` database. (New genbank databases coming soon, please bear with us :).
#### download and look at the gtdb-rs202 lineage file
This is the taxonomy file in `csv` format.
The column headers for `GTDB` are the accession (`ident`), and the taxonomic ranks `superkingdom` --> `species`.
```
%%bash
mkdir -p lineages
curl -L https://osf.io/p6z3w/download -o lineages/gtdb-rs202.taxonomy.csv
%%bash
head lineages/gtdb-rs202.taxonomy.csv
```
#### download NCBI lineage files
Now let's go ahead and grab the Genbank taxonomy files as well.
```
%%bash
curl -L https://osf.io/cbhgd/download -o lineages/bacteria_genbank_lineages.csv
curl -L https://osf.io/urtfx/download -o lineages/protozoa_genbank_lineages.csv
```
If you do a `head` on these files, you'll notice they have an extra `taxid` column, but otherwise follow the same format.
```
%%bash
head lineages/protozoa_genbank_lineages.csv
```
## Combining taxonomies with `sourmash tax prepare`
All sourmash tax commands must be given one or more taxonomy files as parameters to the `--taxonomy` argument.
`sourmash tax prepare` is a utility function that can ingest and validate multiple CSV files or sqlite3
databases, and output a CSV file or a sqlite3 database. It can be used to combine multiple taxonomies
into a single file, as well as change formats between CSV and sqlite3.
> Note: `--taxonomy` files can be either CSV files or (as of sourmash 4.2.1) sqlite3 databases.
> sqlite3 databases are much faster for large taxonomies, while CSV files are easier to view
> and modify using spreadsheet software.
Let's use `tax prepare` to combine the downloaded taxonomies and output into a sqlite3 database:
```
# to see the arguments, run the `--help` like so:
! sourmash tax prepare --help
%%bash
sourmash tax prepare --taxonomy lineages/bacteria_genbank_lineages.csv \
lineages/protozoa_genbank_lineages.csv \
lineages/gtdb-rs202.taxonomy.csv \
-o lineages/gtdb-rs202_genbank.taxonomy.db
```
> Note that the **order is important if the databases contain overlapping
accession identifiers**. In this case, GTDB contains only a subset of all identifiers
in the NCBI taxonomy. Putting GTDB last here will allow the GTDB lineage information
to override the lineage information provided in the NCBI file, thus utilizing GTDB
taxonomy when available, and NCBI lienages for all other accessions.
```
%%bash
ls -lsrht lineages/
```
We'll use this prepared database in each of the commands below.
## `sourmash tax metagenome`
```
# to see the arguments, run the `--help` like so:
! sourmash tax metagenome --help
```
#### Download a small demo `sourmash gather` output file from metagenome `HSMA33MX`.
This `gather` was run at a DNA ksize of 31 against both GTDB and our legacy Genbank database.
```
%%bash
mkdir -p gather
curl -L https://osf.io/xb8jg/download -o gather/HSMA33MX_gather_x_gtdbrs202_genbank_k31.csv
```
Take a look at this gather file:
```
%%bash
head gather/HSMA33MX_gather_x_gtdbrs202_genbank_k31.csv
```
### summarize this metagenome and produce `krona` output at the `species` level:
```
%%bash
sourmash tax metagenome --gather-csv gather/HSMA33MX_gather_x_gtdbrs202_genbank_k31.csv \
--taxonomy lineages/gtdb-rs202_genbank.taxonomy.db \
--output-format csv_summary krona --rank species \
--output-base HSMA33MX.gather-tax
# build krona plot
!ktImportText HSMA33MX.gather-tax.krona.tsv
```
#### This will produce both `csv_summary` and `krona` output files, with the basename `HSMA33MX.gather-tax`:
```
%%bash
ls HSMA33MX.gather-tax*
%%bash
head HSMA33MX.gather-tax.summarized.csv
%%bash
head HSMA33MX.gather-tax.krona.tsv
# generate krona html
!ktImportText HSMA33MX.gather-tax.krona.tsv
```
### comparing metagenomes with `sourmash tax metagenome`:
We can also download a second metagenome `gather` csv and use `metagenome` to generate a
`lineage_summary` output to compare these samples.
> The lineage summary format is most useful when comparing across metagenome queries.
> Each row is a lineage at the desired reporting rank. The columns are each query used for
> gather, with the fraction match reported for each lineage. This format is commonly used
> as input for many external multi-sample visualization tools.
```
%%bash
curl -L https://osf.io/nqtgs/download -o gather/PSM7J4EF_gather_x_gtdbrs202_genbank_k31.csv
%%bash
sourmash tax metagenome --gather-csv gather/HSMA33MX_gather_x_gtdbrs202_genbank_k31.csv \
gather/PSM7J4EF_gather_x_gtdbrs202_genbank_k31.csv \
--taxonomy lineages/gtdb-rs202_genbank.taxonomy.db \
--output-format lineage_summary --rank species \
--output-base HSMA33MX-PSM7J4EF.gather-tax
%%bash
head HSMA33MX-PSM7J4EF.gather-tax.lineage_summary.tsv
```
Note, these are mini gather results, so your unclassified fraction will hopefully be much smaller!
## Classifying genomes with `sourmash tax genome`
To illustrate the utility of genome, let’s consider a signature consisting of two different
Shewanella strains, Shewanella baltica OS185 strain=OS185 and Shewanella baltica OS223 strain=OS223.
For simplicity, we gave this query the name “Sb47+63”.
When we gather this signature against the gtdb-rs202 representatives database, we see 66% matches to one strain, and 33% to the other:
abbreviated `gather_csv`:
```
f_match,f_unique_to_query,name,query_name
0.664,0.664,"GCF_000021665.1 Shewanella baltica OS223 strain=OS223, ASM2166v1",Sb47+63
0.656,0.335,"GCF_000017325.1 Shewanella baltica OS185 strain=OS185, ASM1732v1",Sb47+63
```
> Here, f_match shows that independently, both strains match ~65% percent of this mixed query.
> The f_unique_to_query column has the results of gather-style decomposition. As the OS223 strain
> had a slightly higher f_match (66%), it was the first match. The remaining 33% of the query
> matched to strain OS185.
#### download the gather results
```
%%bash
curl -L https://osf.io/pgsc2/download -o gather/Sb47+63_x_gtdb-rs202.gather.csv
%%bash
head gather/Sb47+63_x_gtdb-rs202.gather.csv
```
#### Now, let's run `tax genome` classification:
```
%%bash
# to see the arguments, run the `--help` like so:
sourmash tax genome --help
%%bash
sourmash tax genome --gather-csv gather/Sb47+63_x_gtdb-rs202.gather.csv \
--taxonomy lineages/gtdb-rs202_genbank.taxonomy.db \
--output-base Sb47+63.gather-tax
```
The default output format is `csv_summary`.
This outputs a csv with taxonomic classification for each query genome. This output currently consists of six columns:
`query_name`,`rank`,`fraction`,`lineage`,`query_md5`,`query_filename`, where `fraction` is the fraction of the query matched to
the reported rank and lineage. The `status` column provides additional information on the classification:
- `match` - this query was classified
- `nomatch` - this query could not be classified
- `below_threshold` - this query was classified at the specified rank,
but the query fraction matched was below the containment threshold
```
!ls Sb47+63.gather-tax*
!head Sb47+63.gather-tax.classifications.csv
```
> Here, we see that the match percentages to both strains have been aggregated, and we have 100% species-level
> Shewanella baltica annotation (fraction = 1.0).
## `sourmash tax annotate`
`sourmash tax annotate` adds a column with taxonomic lineage information for each database match to gather output.
It does not do any LCA summarization or classification. The results from `annotate` are not required for any other
`tax` command, but may be useful if you're doing your own exploration of `gather` results.
Let's annotate a previously downloaded `gather` file
```
%%bash
sourmash tax annotate --gather-csv gather/Sb47+63_x_gtdb-rs202.gather.csv \
--taxonomy lineages/gtdb-rs202_genbank.taxonomy.db
!head Sb47+63_x_gtdb-rs202.gather.with-lineages.csv
```
|
github_jupyter
|
```
def preprocess_string(s):
plaintext = ''
for i in s:
temp = ord(i)
if ((temp < 123 and temp > 96) or (temp < 91 and temp > 64)
or (temp < 58 and temp > 47) or temp == 32):
plaintext += i
return plaintext
def char_to_bits(s, char_size = 4):
if (char_size == 4):
ans = bin(int(s, 2 ** char_size))[2:]
ans = '0' * (char_size - len(ans)) + ans
return ans
elif (char_size == 8):
ans = hex_to_bits(hex(ord(s)))
ans = '0' * (char_size - len(ans)) + ans
return ans
def char_chunk_to_bits(s, char_size = 4):
ans = ''
for i in s:
ans += char_to_bits(i, char_size)
return ans
def create_chunks(s, chunk_size, char_size = 4, bogus = 'F'):
char_count = chunk_size // char_size
increment = len(s) % char_count
if increment:
s += ((len(s) // char_count + 1) * char_count - len(s)) * bogus
chunks = [s[i:i + char_count] for i in range(0, len(s), char_count)]
return chunks
def get_bit_chunks(s, chunk_size, char_size = 4, bogus = 'F'):
s = preprocess_string(s)
chunks = create_chunks(s, chunk_size, char_size, bogus)
bit_chunks = [char_chunk_to_bits(i, char_size) for i in chunks]
return bit_chunks
```
## 1. DES
```
def shift_left(s, n):
for i in range(n):
s = s[1:] + s[0]
return s
def permute(s, key):
ans = []
for i in key:
ans.append(s[i - 1])
return ''.join(ans)
def create_keys(key_with_parity_bits):
parity_bit_drop_table = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
number_of_bits_shifts = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
key_compression_table = [14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32]
cipher_key = permute(key_with_parity_bits, parity_bit_drop_table)
left_key = cipher_key[0:28]
right_key = cipher_key[28:56]
keys = []
for i in range(16):
left_key = shift_left(left_key, number_of_bits_shifts[i])
right_key = shift_left(right_key, number_of_bits_shifts[i])
keys.append(permute(left_key + right_key, key_compression_table))
return keys
def permute(s, key):
ans = []
for i in key:
ans.append(s[i - 1])
return ''.join(ans)
def substitute(s, key):
answer = ''
for i in range(0, 48, 6):
vertical_entry = s[i] + s[i + 5]
horizontal_entry = s[i + 1:i + 5]
temp = key[i // 6][int(vertical_entry, 2)][int(horizontal_entry, 2)]
temp = bin(temp)[2:]
temp = '0' * (4 - len(temp)) + temp
answer += temp
return answer
def round_normal_without_swapping(P, key):
left_plaintext = P[0:32]
right_plaintext = P[32:64]
right_expansion_p_box_table = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
right_expanded_plaintext = permute(right_plaintext, right_expansion_p_box_table)
xored_right_text = ''
for i, j in zip(right_expanded_plaintext, key):
xored_right_text += str(int(i) ^ int(j))
substitution_table = [
[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
],
[[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
],
[[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
],
[[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
],
[[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
],
[[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
],
[[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
],
[[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
]
]
straight_permutation_table = [16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25]
substituted_right_text = substitute(xored_right_text, substitution_table)
des_function_out = permute(substituted_right_text, straight_permutation_table)
xored_left_text = ''
for i, j in zip(left_plaintext, des_function_out):
xored_left_text += str(int(i) ^ int(j))
return xored_left_text + right_plaintext
def round_normal(P, key):
ciphertext = round_normal_without_swapping(P, key)
return ciphertext[32:] + ciphertext[0:32]
def round_last(P, key):
return round_normal_without_swapping(P, key)
def DES(plaintext, K):
keys = create_keys(K)
initial_permutation_table = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
final_permutation_table = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
blocks = get_bit_chunks(P, 64)
encrypted_blocks = []
for i in blocks:
permuted_text = permute(i, initial_permutation_table)
cipher_text = permuted_text
for i in range(15):
cipher_text = round_normal(cipher_text, keys[i])
cipher_text = round_last(cipher_text, keys[15])
cipher_text_final = permute(cipher_text, final_permutation_table)
encrypted_blocks.append(cipher_text_final)
return ''.join(encrypted_blocks)
# P = input("Enter Plaintext: ")
# K = input("Enter DES Key: ")
P = "0123456789ABCDEF"
K = "0001001100110100010101110111100110011011101111001101111111110001"
ciphertext = DES(P, K)
print(ciphertext)
P = "123456ABCD132536"
K = get_bit_chunks("AABB09182736CCDD", 64)[0]
ciphertext = DES(P, K)
print(ciphertext)
```
## 2. AES : 10 Round, 128 bit input, 128 bit key
```
def hex_to_bits(a):
x = bin(int(a, 16))[2:]
x = '0' * (8 - len(x)) + x
return x
def left_shift(s):
return s[1:] + s[0]
def sub_word(s):
subbytes_table = [['0x63', '0x7c', '0x77', '0x7b', '0xf2', '0x6b', '0x6f', '0xc5', '0x30', '0x1', '0x67', '0x2b', '0xfe', '0xd7', '0xab', '0x76'],
['0xca', '0x82', '0xc9', '0x7d', '0xfa', '0x59', '0x47', '0xf0', '0xad', '0xd4', '0xa2', '0xaf', '0x9c', '0xa4', '0x72', '0xc0'],
['0xb7', '0xfd', '0x93', '0x26', '0x36', '0x3f', '0xf7', '0xcc', '0x34', '0xa5', '0xe5', '0xf1', '0x71', '0xd8', '0x31', '0x15'],
['0x4', '0xc7', '0x23', '0xc3', '0x18', '0x96', '0x5', '0x9a', '0x7', '0x12', '0x80', '0xe2', '0xeb', '0x27', '0xb2', '0x75'],
['0x9', '0x83', '0x2c', '0x1a', '0x1b', '0x6e', '0x5a', '0xa0', '0x52', '0x3b', '0xd6', '0xb3', '0x29', '0xe3', '0x2f', '0x84'],
['0x53', '0xd1', '0x0', '0xed', '0x20', '0xfc', '0xb1', '0x5b', '0x6a', '0xcb', '0xbe', '0x39', '0x4a', '0x4c', '0x58', '0xcf'],
['0xd0', '0xef', '0xaa', '0xfb', '0x43', '0x4d', '0x33', '0x85', '0x45', '0xf9', '0x2', '0x7f', '0x50', '0x3c', '0x9f', '0xa8'],
['0x51', '0xa3', '0x40', '0x8f', '0x92', '0x9d', '0x38', '0xf5', '0xbc', '0xb6', '0xda', '0x21', '0x10', '0xff', '0xf3', '0xd2'],
['0xcd', '0xc', '0x13', '0xec', '0x5f', '0x97', '0x44', '0x17', '0xc4', '0xa7', '0x7e', '0x3d', '0x64', '0x5d', '0x19', '0x73'],
['0x60', '0x81', '0x4f', '0xdc', '0x22', '0x2a', '0x90', '0x88', '0x46', '0xee', '0xb8', '0x14', '0xde', '0x5e', '0xb', '0xdb'],
['0xe0', '0x32', '0x3a', '0xa', '0x49', '0x6', '0x24', '0x5c', '0xc2', '0xd3', '0xac', '0x62', '0x91', '0x95', '0xe4', '0x79'],
['0xe7', '0xc8', '0x37', '0x6d', '0x8d', '0xd5', '0x4e', '0xa9', '0x6c', '0x56', '0xf4', '0xea', '0x65', '0x7a', '0xae', '0x8'],
['0xba', '0x78', '0x25', '0x2e', '0x1c', '0xa6', '0xb4', '0xc6', '0xe8', '0xdd', '0x74', '0x1f', '0x4b', '0xbd', '0x8b', '0x8a'],
['0x70', '0x3e', '0xb5', '0x66', '0x48', '0x3', '0xf6', '0xe', '0x61', '0x35', '0x57', '0xb9', '0x86', '0xc1', '0x1d', '0x9e'],
['0xe1', '0xf8', '0x98', '0x11', '0x69', '0xd9', '0x8e', '0x94', '0x9b', '0x1e', '0x87', '0xe9', '0xce', '0x55', '0x28', '0xdf'],
['0x8c', '0xa1', '0x89', '0xd', '0xbf', '0xe6', '0x42', '0x68', '0x41', '0x99', '0x2d', '0xf', '0xb0', '0x54', '0xbb', '0x16']]
ans = ''
for i in range(0, 32, 8):
s_i = s[i:i+8]
ans += hex_to_bits(subbytes_table[int(s_i[0:4], 2)][int(s_i[4:8], 2)])
return ans
def rot_word(s):
return s[8:] + s[:8]
def add_bit_array(a, b):
ans = ''
for i, j in zip(a, b):
ans += str(int(i) ^ int(j))
return ans
def create_keys(key):
Rcons = ['01', '02', '04', '08', '10', '20', '40', '80', '1B', '36']
words = [key[0:32], key[32:64], key[64:96], key[96:128]]
for i in range(4, 44):
if i % 4:
words.append(add_bit_array(words[i - 1], words[i - 4]))
else:
Rcon = Rcons[(i - 4) // 4] + '000000'
bit_rcon = ''
for j in range(4):
bit_rcon += hex_to_bits('0x' + Rcon[2*j : 2*(j + 1)])
t = add_bit_array(sub_word(rot_word(words[i - 1])), bit_rcon)
words.append(add_bit_array(t, words[i - 4]))
return words
def plaintext_to_matrix_state(plaintext):
ans = [['', '', '', ''], ['', '', '', ''], ['', '', '', ''], ['', '', '', '']]
for i in range(16):
ans[i % 4][i // 4] = plaintext[8 * i : 8 * (i + 1)]
return ans
def add_matrix(A, B, n = 4):
ans = [['', '', '', ''], ['', '', '', ''], ['', '', '', ''], ['', '', '', '']]
for i in range(n):
for j in range(n):
ans[i][j] = add_bit_array(A[i][j], B[i][j])
return ans
def bit_matrix_to_hex(A):
B = [['', '', '', ''], ['', '', '', ''], ['', '', '', ''], ['', '', '', '']]
for i in range(len(A)):
for j in range(len(A)):
B[i][j] = hex(int(A[i][j], 2))
return B
def sub_bytes(state):
sub_bytes_table = [['0x63', '0x7c', '0x77', '0x7b', '0xf2', '0x6b', '0x6f', '0xc5', '0x30', '0x1', '0x67', '0x2b', '0xfe', '0xd7', '0xab', '0x76'],
['0xca', '0x82', '0xc9', '0x7d', '0xfa', '0x59', '0x47', '0xf0', '0xad', '0xd4', '0xa2', '0xaf', '0x9c', '0xa4', '0x72', '0xc0'],
['0xb7', '0xfd', '0x93', '0x26', '0x36', '0x3f', '0xf7', '0xcc', '0x34', '0xa5', '0xe5', '0xf1', '0x71', '0xd8', '0x31', '0x15'],
['0x4', '0xc7', '0x23', '0xc3', '0x18', '0x96', '0x5', '0x9a', '0x7', '0x12', '0x80', '0xe2', '0xeb', '0x27', '0xb2', '0x75'],
['0x9', '0x83', '0x2c', '0x1a', '0x1b', '0x6e', '0x5a', '0xa0', '0x52', '0x3b', '0xd6', '0xb3', '0x29', '0xe3', '0x2f', '0x84'],
['0x53', '0xd1', '0x0', '0xed', '0x20', '0xfc', '0xb1', '0x5b', '0x6a', '0xcb', '0xbe', '0x39', '0x4a', '0x4c', '0x58', '0xcf'],
['0xd0', '0xef', '0xaa', '0xfb', '0x43', '0x4d', '0x33', '0x85', '0x45', '0xf9', '0x2', '0x7f', '0x50', '0x3c', '0x9f', '0xa8'],
['0x51', '0xa3', '0x40', '0x8f', '0x92', '0x9d', '0x38', '0xf5', '0xbc', '0xb6', '0xda', '0x21', '0x10', '0xff', '0xf3', '0xd2'],
['0xcd', '0xc', '0x13', '0xec', '0x5f', '0x97', '0x44', '0x17', '0xc4', '0xa7', '0x7e', '0x3d', '0x64', '0x5d', '0x19', '0x73'],
['0x60', '0x81', '0x4f', '0xdc', '0x22', '0x2a', '0x90', '0x88', '0x46', '0xee', '0xb8', '0x14', '0xde', '0x5e', '0xb', '0xdb'],
['0xe0', '0x32', '0x3a', '0xa', '0x49', '0x6', '0x24', '0x5c', '0xc2', '0xd3', '0xac', '0x62', '0x91', '0x95', '0xe4', '0x79'],
['0xe7', '0xc8', '0x37', '0x6d', '0x8d', '0xd5', '0x4e', '0xa9', '0x6c', '0x56', '0xf4', '0xea', '0x65', '0x7a', '0xae', '0x8'],
['0xba', '0x78', '0x25', '0x2e', '0x1c', '0xa6', '0xb4', '0xc6', '0xe8', '0xdd', '0x74', '0x1f', '0x4b', '0xbd', '0x8b', '0x8a'],
['0x70', '0x3e', '0xb5', '0x66', '0x48', '0x3', '0xf6', '0xe', '0x61', '0x35', '0x57', '0xb9', '0x86', '0xc1', '0x1d', '0x9e'],
['0xe1', '0xf8', '0x98', '0x11', '0x69', '0xd9', '0x8e', '0x94', '0x9b', '0x1e', '0x87', '0xe9', '0xce', '0x55', '0x28', '0xdf'],
['0x8c', '0xa1', '0x89', '0xd', '0xbf', '0xe6', '0x42', '0x68', '0x41', '0x99', '0x2d', '0xf', '0xb0', '0x54', '0xbb', '0x16']]
ans = [['', '', '', ''], ['', '', '', ''], ['', '', '', ''], ['', '', '', '']]
n = len(state)
for i in range(n):
for j in range(n):
ans[i][j] = hex_to_bits(sub_bytes_table[int(state[i][j][0:4], 2)][int(state[i][j][4:8], 2)])
return ans
def rot_word_for_shift_rows(s):
return s[1:] + s[:1]
def shift_rows(state):
for i in range(4):
for j in range(i):
state[i] = rot_word_for_shift_rows(state[i])
return state
def shift_and_reduce(s):
irreducible = '100011011'
if (s[0] == '1'):
return add_bit_array(s + '0', irreducible)[1:]
else:
return s[1:] + '0'
def one_term_multiply(s, n):
for i in range(n):
s = shift_and_reduce(s)
return s
def multiply(a, b):
a = '0' * (8 - len(a)) + a
temp = '0' * 8
n = len(b)
for i in range(n):
if (b[-(i + 1)] == '1'):
temp = add_bit_array(temp, one_term_multiply(a, i))
return temp
def multiply_for_mix_columns(a, b):
return multiply(a, bin(b)[2:])
def mix_columns(state):
mix_columns_constant_matrix = [[2, 3, 1, 1],
[1, 2, 3, 1],
[1, 1, 2, 3],
[3, 1, 1, 2]]
ans = [['', '', '', ''], ['', '', '', ''], ['', '', '', ''], ['', '', '', '']]
for i in range(4):
temp = []
for j in range(4):
temp.append(state[j][i])
for j in range(4):
temp_2 = '00000000'
for k in range(4):
x = multiply_for_mix_columns(temp[k], mix_columns_constant_matrix[j][k])
temp_2 = add_bit_array(temp_2, x)
ans[j][i] = temp_2
return ans
def add_round_key(A, key):
return add_matrix(A, plaintext_to_matrix_state(key))
def round_normal(plaintext, key):
x = add_round_key(mix_columns(shift_rows(sub_bytes(plaintext))), key)
return x
def round_final(plaintext, key):
x = add_round_key(shift_rows(sub_bytes(plaintext)), key)
return x
def AES(plaintext, key):
blocks = create_keys(key)
keys = [blocks[4 * i] + blocks[4 * i + 1] + blocks[4 * i + 2] + blocks[4 * i + 3] for i in range(11)]
plaintext_blocks = get_bit_chunks(plaintext, 128, 8)
cipher_text_blocks = []
for block in plaintext_blocks:
initial_state = plaintext_to_matrix_state(block)
pre_round_transformed_state = add_matrix(initial_state, plaintext_to_matrix_state(keys[0]))
cipher_text_state = pre_round_transformed_state
for i in range(1, 10):
cipher_text_state = round_normal(cipher_text_state, keys[i])
cipher_text_state = round_final(cipher_text_state, keys[10])
cipher_text = ''
for j in range(4):
for i in range(4):
cipher_text += cipher_text_state[i][j]
cipher_text_blocks.append(cipher_text)
hex_ciphertext = bit_matrix_to_hex(cipher_text_state)
for i in hex_ciphertext:
print(i)
return ''.join(cipher_text_blocks)
plaintext = "Two One Nine Two"
key = get_bit_chunks("5468617473206D79204B756E67204675", 128)[0] # please keep only necessary chars in key, no space
ciphertext = AES(plaintext, key)
print(ciphertext)
```
|
github_jupyter
|
# Import Libraries
```
import sys
import pandas as pd
import numpy as np
from sklearn import preprocessing
from sklearn.decomposition import PCA
from sklearn import random_projection
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import fbeta_score, roc_curve, auc
from sklearn import svm
import pprint
sys.path.insert(0, '../../scripts/modeling_toolbox/')
# load the autoreload extension
%load_ext autoreload
# Set extension to reload modules every time before executing code
%autoreload 2
from metric_processor import MetricProcessor
import evaluation
%matplotlib inline
```
# Data preparation
```
features = ['dimension',
'size',
'temporal_dct-mean',
'temporal_gaussian_mse-mean',
'temporal_gaussian_difference-mean',
'temporal_threshold_gaussian_difference-mean'
]
path = '../../machine_learning/cloud_functions/data-large.csv'
metric_processor = MetricProcessor(features,'UL', path, reduced=False, bins=0)
df = metric_processor.read_and_process_data()
df.shape
display(df.head())
# We remove the low bitrates since we are only focused on tampering attacks. The rotation attacks are also
# removed since they will be detected by the pre-verifier just by checking output dimensions
df = df[~(df['attack'].str.contains('low_bitrate')) & ~(df['attack'].str.contains('rotate'))]
df.head()
(X_train, X_test, X_attacks), (df_train, df_test, df_attacks) = metric_processor.split_test_and_train(df)
print('Shape of train: {}'.format(X_train.shape))
print('Shape of test: {}'.format(X_test.shape))
print('Shape of attacks: {}'.format(X_attacks.shape))
```
The train and test are **only** composed by legit assets
```
# Scaling the data
ss = StandardScaler()
x_train = ss.fit_transform(X_train)
x_test = ss.transform(X_test)
x_attacks = ss.transform(X_attacks)
```
# One Class SVM
```
# Train the model
OCSVM = svm.OneClassSVM(kernel='rbf',gamma='auto', nu=0.01, cache_size=5000)
OCSVM.fit(x_train)
fb, area, tnr, tpr_train, tpr_test = evaluation.unsupervised_evaluation(OCSVM, x_train, x_test, x_attacks)
# Show global results of classification
print('TNR: {}\nTPR_test: {}\nTPR_train: {}\n'.format(tnr, tpr_test, tpr_train))
print('F20: {}\nAUC: {}'.format(fb, area))
# Show mean distances to the decision function. A negative distance means that the data is classified as
# an attack
train_scores = OCSVM.decision_function(x_train)
test_scores = OCSVM.decision_function(x_test)
attack_scores = OCSVM.decision_function(x_attacks)
print('Mean score values:\n-Train: {}\n-Test: {}\n-Attacks: {}'.format(np.mean(train_scores),
np.mean(test_scores),
np.mean(attack_scores)))
train_preds = OCSVM.predict(x_train)
test_preds = OCSVM.predict(x_test)
attack_preds = OCSVM.predict(x_attacks)
df_train['dist_to_dec_funct'] = train_scores
df_test['dist_to_dec_funct'] = test_scores
df_attacks['dist_to_dec_funct'] = attack_scores
df_train['prediction'] = train_preds
df_test['prediction'] = test_preds
df_attacks['prediction'] = attack_preds
```
# Report
```
# Zoom in in the mean distances of the test set to the decision function by resolution. Percentiles, standard
# deviation, min and max values are shown too.
display(df_test[['dist_to_dec_funct', 'dimension']].groupby('dimension').describe())
# Zoom in in the mean distances of the attack set to the decision function by resolution. Percentiles, standard
# deviation, min and max values are shown too.
display(df_attacks[['dist_to_dec_funct', 'dimension']].groupby('dimension').describe())
# Zoom in in the mean distances of the test set to the decision function by attack type. Percentiles, standard
# deviation, min and max values are shown too.
df_attacks['attack_'] = df_attacks['attack'].apply(lambda x: x[x.find('p') + 2:])
display(df_attacks[['dist_to_dec_funct', 'attack_']].groupby(['attack_']).describe())
resolutions = sorted(df_attacks['dimension'].unique())
pp = pprint.PrettyPrinter()
# Accuracy of the test set by resolution
results = {}
for res in resolutions:
selection = df_test[df_test['dimension'] == res]
count = sum(selection['prediction'] == 1)
results[res] = count/len(selection)
pp.pprint(results)
# Accuracy on the attack set by resolution
results = {}
for res in resolutions:
selection = df_attacks[df_attacks['dimension'] == res]
count = sum(selection['prediction'] == -1)
results[res] = count/len(selection)
pp.pprint(results)
attacks = df_attacks['attack_'].unique()
# Accuracy on the attack set by attack type
results = {}
for attk in attacks:
selection = df_attacks[df_attacks['attack_'] == attk]
count = sum(selection['prediction'] == -1)
results[attk] = count/len(selection)
pp.pprint(results)
# Accuracy on the attack set by attack type
results = {}
for res in resolutions:
results[res] = {}
for attk in attacks:
selection = df_attacks[(df_attacks['attack_'] == attk) & (df_attacks['dimension'] == res)]
count = sum(selection['prediction'] == -1)
results[res][attk] = count/len(selection)
pp.pprint(results)
```
|
github_jupyter
|
# AMPL Model Colaboratory Template
[](https://github.com/ampl/amplcolab/blob/master/template/colab.ipynb) [](https://colab.research.google.com/github/ampl/amplcolab/blob/master/template/colab.ipynb) [](https://kaggle.com/kernels/welcome?src=https://github.com/ampl/amplcolab/blob/master/template/colab.ipynb) [](https://console.paperspace.com/github/ampl/amplcolab/blob/master/template/colab.ipynb) [](https://studiolab.sagemaker.aws/import/github/ampl/amplcolab/blob/master/template/colab.ipynb)
Description: Basic notebook templace for the AMPL Colab repository
Tags: ampl-only, template, industry
Notebook author: Filipe Brandão
Model author: Gilmore, P. and Gomory, R.
References:
1. Gilmore, P. and Gomory, R. (1963). A linear programming approach to the cutting stock
problem–part II.
```
# Install dependencies
!pip install -q amplpy ampltools
# Google Colab & Kaggle interagration
MODULES=['ampl', 'coin']
from ampltools import cloud_platform_name, ampl_notebook
from amplpy import AMPL, register_magics
if cloud_platform_name() is None:
ampl = AMPL() # Use local installation of AMPL
else:
ampl = ampl_notebook(modules=MODULES) # Install AMPL and use it
register_magics(ampl_object=ampl) # Evaluate %%ampl_eval cells with ampl.eval()
```
### Use `%%ampl_eval` to evaluate AMPL commands
```
%%ampl_eval
option version;
```
### Use %%writeifile to create files
```
%%writefile cut2.mod
problem Cutting_Opt;
# ----------------------------------------
param nPAT integer >= 0, default 0;
param roll_width;
set PATTERNS = 1..nPAT;
set WIDTHS;
param orders {WIDTHS} > 0;
param nbr {WIDTHS,PATTERNS} integer >= 0;
check {j in PATTERNS}: sum {i in WIDTHS} i * nbr[i,j] <= roll_width;
var Cut {PATTERNS} integer >= 0;
minimize Number: sum {j in PATTERNS} Cut[j];
subject to Fill {i in WIDTHS}:
sum {j in PATTERNS} nbr[i,j] * Cut[j] >= orders[i];
problem Pattern_Gen;
# ----------------------------------------
param price {WIDTHS} default 0;
var Use {WIDTHS} integer >= 0;
minimize Reduced_Cost:
1 - sum {i in WIDTHS} price[i] * Use[i];
subject to Width_Limit:
sum {i in WIDTHS} i * Use[i] <= roll_width;
%%writefile cut.dat
data;
param roll_width := 110 ;
param: WIDTHS: orders :=
20 48
45 35
50 24
55 10
75 8 ;
%%writefile cut2.run
# ----------------------------------------
# GILMORE-GOMORY METHOD FOR
# CUTTING STOCK PROBLEM
# ----------------------------------------
option solver cbc;
option solution_round 6;
model cut2.mod;
data cut.dat;
problem Cutting_Opt;
option relax_integrality 1;
option presolve 0;
problem Pattern_Gen;
option relax_integrality 0;
option presolve 1;
let nPAT := 0;
for {i in WIDTHS} {
let nPAT := nPAT + 1;
let nbr[i,nPAT] := floor (roll_width/i);
let {i2 in WIDTHS: i2 <> i} nbr[i2,nPAT] := 0;
};
repeat {
solve Cutting_Opt;
let {i in WIDTHS} price[i] := Fill[i].dual;
solve Pattern_Gen;
if Reduced_Cost < -0.00001 then {
let nPAT := nPAT + 1;
let {i in WIDTHS} nbr[i,nPAT] := Use[i];
}
else break;
};
display nbr;
display Cut;
option Cutting_Opt.relax_integrality 0;
option Cutting_Opt.presolve 10;
solve Cutting_Opt;
display Cut;
```
### Use `%%ampl_eval` to run the script cut2.run
```
%%ampl_eval
commands cut2.run;
```
|
github_jupyter
|
# TV Script Generation
In this project, you'll generate your own [Simpsons](https://en.wikipedia.org/wiki/The_Simpsons) TV scripts using RNNs. You'll be using part of the [Simpsons dataset](https://www.kaggle.com/wcukierski/the-simpsons-by-the-data) of scripts from 27 seasons. The Neural Network you'll build will generate a new TV script for a scene at [Moe's Tavern](https://simpsonswiki.com/wiki/Moe's_Tavern).
## Get the Data
The data is already provided for you. You'll be using a subset of the original dataset. It consists of only the scenes in Moe's Tavern. This doesn't include other versions of the tavern, like "Moe's Cavern", "Flaming Moe's", "Uncle Moe's Family Feed-Bag", etc..
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
data_dir = './data/simpsons/moes_tavern_lines.txt'
text = helper.load_data(data_dir)
# Ignore notice, since we don't use it for analysing the data
text = text[81:]
```
## Explore the Data
Play around with `view_sentence_range` to view different parts of the data.
```
view_sentence_range = (20, 30)
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import numpy as np
print('Dataset Stats')
print('Roughly the number of unique words: {}'.format(len({word: None for word in text.split()})))
scenes = text.split('\n\n')
print('Number of scenes: {}'.format(len(scenes)))
sentence_count_scene = [scene.count('\n') for scene in scenes]
print('Average number of sentences in each scene: {}'.format(np.average(sentence_count_scene)))
sentences = [sentence for scene in scenes for sentence in scene.split('\n')]
print('Number of lines: {}'.format(len(sentences)))
word_count_sentence = [len(sentence.split()) for sentence in sentences]
print('Average number of words in each line: {}'.format(np.average(word_count_sentence)))
print()
print('The sentences {} to {}:'.format(*view_sentence_range))
print('\n'.join(text.split('\n')[view_sentence_range[0]:view_sentence_range[1]]))
```
## Implement Preprocessing Functions
The first thing to do to any dataset is preprocessing. Implement the following preprocessing functions below:
- Lookup Table
- Tokenize Punctuation
### Lookup Table
To create a word embedding, you first need to transform the words to ids. In this function, create two dictionaries:
- Dictionary to go from the words to an id, we'll call `vocab_to_int`
- Dictionary to go from the id to word, we'll call `int_to_vocab`
Return these dictionaries in the following tuple `(vocab_to_int, int_to_vocab)`
```
import numpy as np
import problem_unittests as tests
def create_lookup_tables(text):
"""
Create lookup tables for vocabulary
:param text: The text of tv scripts split into words
:return: A tuple of dicts (vocab_to_int, int_to_vocab)
"""
filtered_out = ['']
tokenized_text = set([t.lower() for t in text if t not in filtered_out])
vocab_to_int = {t: i for i, t in enumerate(tokenized_text)}
int_to_vocab = {i: t for i, t in enumerate(tokenized_text)}
return vocab_to_int, int_to_vocab
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_create_lookup_tables(create_lookup_tables)
```
### Tokenize Punctuation
We'll be splitting the script into a word array using spaces as delimiters. However, punctuations like periods and exclamation marks make it hard for the neural network to distinguish between the word "bye" and "bye!".
Implement the function `token_lookup` to return a dict that will be used to tokenize symbols like "!" into "||Exclamation_Mark||". Create a dictionary for the following symbols where the symbol is the key and value is the token:
- Period ( . )
- Comma ( , )
- Quotation Mark ( " )
- Semicolon ( ; )
- Exclamation mark ( ! )
- Question mark ( ? )
- Left Parentheses ( ( )
- Right Parentheses ( ) )
- Dash ( -- )
- Return ( \n )
This dictionary will be used to token the symbols and add the delimiter (space) around it. This separates the symbols as it's own word, making it easier for the neural network to predict on the next word. Make sure you don't use a token that could be confused as a word. Instead of using the token "dash", try using something like "||dash||".
```
def token_lookup():
"""
Generate a dict to turn punctuation into a token.
:return: Tokenize dictionary where the key is the punctuation and the value is the token
"""
return {
'.': '||period||',
',': '||comma||',
'"': '||quotation_mark||',
';': '||semicolon||',
'!': '||exclamation_mark||',
'?': '||question_mark||',
'(': '||left_parentheses||',
')': '||right_parentheses||',
'--': '||dash||',
'\n': '||line_break||',
}
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_tokenize(token_lookup)
```
## Preprocess all the data and save it
Running the code cell below will preprocess all the data and save it to file.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# Preprocess Training, Validation, and Testing Data
helper.preprocess_and_save_data(data_dir, token_lookup, create_lookup_tables)
```
# Check Point
This is your first checkpoint. If you ever decide to come back to this notebook or have to restart the notebook, you can start from here. The preprocessed data has been saved to disk.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
import numpy as np
import problem_unittests as tests
int_text, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
```
## Build the Neural Network
You'll build the components necessary to build a RNN by implementing the following functions below:
- get_inputs
- get_init_cell
- get_embed
- build_rnn
- build_nn
- get_batches
### Check the Version of TensorFlow and Access to GPU
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
from distutils.version import LooseVersion
import warnings
import tensorflow as tf
# Check TensorFlow Version
assert LooseVersion(tf.__version__) >= LooseVersion('1.0'), 'Please use TensorFlow version 1.0 or newer'
print('TensorFlow Version: {}'.format(tf.__version__))
# Check for a GPU
if not tf.test.gpu_device_name():
warnings.warn('No GPU found. Please use a GPU to train your neural network.')
else:
print('Default GPU Device: {}'.format(tf.test.gpu_device_name()))
```
### Input
Implement the `get_inputs()` function to create TF Placeholders for the Neural Network. It should create the following placeholders:
- Input text placeholder named "input" using the [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder) `name` parameter.
- Targets placeholder
- Learning Rate placeholder
Return the placeholders in the following the tuple `(Input, Targets, LearingRate)`
```
def get_inputs():
"""
Create TF Placeholders for input, targets, and learning rate.
:return: Tuple (input, targets, learning rate)
"""
inputs = tf.placeholder(tf.int32,
shape=[None, None],
name="input")
targets = tf.placeholder(tf.int32,
shape=[None, None],
name="target")
learning_rate = tf.placeholder(tf.float32,
name="learning_rate")
return inputs, targets, learning_rate
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_inputs(get_inputs)
```
### Build RNN Cell and Initialize
Stack one or more [`BasicLSTMCells`](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn/BasicLSTMCell) in a [`MultiRNNCell`](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn/MultiRNNCell).
- The Rnn size should be set using `rnn_size`
- Initalize Cell State using the MultiRNNCell's [`zero_state()`](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn/MultiRNNCell#zero_state) function
- Apply the name "initial_state" to the initial state using [`tf.identity()`](https://www.tensorflow.org/api_docs/python/tf/identity)
Return the cell and initial state in the following tuple `(Cell, InitialState)`
```
keep_prob = 0.8
lstm_layers = 16
def get_init_cell(batch_size, rnn_size):
"""
Create an RNN Cell and initialize it.
:param batch_size: Size of batches
:param rnn_size: Size of RNNs
:return: Tuple (cell, initialize state)
"""
lstm = tf.contrib.rnn.BasicLSTMCell(rnn_size)
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
cell = tf.contrib.rnn.MultiRNNCell([drop], lstm_layers)
initial_state = tf.identity(cell.zero_state(batch_size, tf.float32), "initial_state")
return cell, initial_state
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_init_cell(get_init_cell)
```
### Word Embedding
Apply embedding to `input_data` using TensorFlow. Return the embedded sequence.
```
def get_embed(input_data, vocab_size, embed_dim):
"""
Create embedding for <input_data>.
:param input_data: TF placeholder for text input.
:param vocab_size: Number of words in vocabulary.
:param embed_dim: Number of embedding dimensions
:return: Embedded input.
"""
embedding = tf.Variable(tf.random_uniform((vocab_size, embed_dim), -1, 1))
embedding_lookup = tf.nn.embedding_lookup(embedding, input_data)
return embedding_lookup
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_embed(get_embed)
```
### Build RNN
You created a RNN Cell in the `get_init_cell()` function. Time to use the cell to create a RNN.
- Build the RNN using the [`tf.nn.dynamic_rnn()`](https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn)
- Apply the name "final_state" to the final state using [`tf.identity()`](https://www.tensorflow.org/api_docs/python/tf/identity)
Return the outputs and final_state state in the following tuple `(Outputs, FinalState)`
```
def build_rnn(cell, inputs):
"""
Create a RNN using a RNN Cell
:param cell: RNN Cell
:param inputs: Input text data
:return: Tuple (Outputs, Final State)
"""
outputs, final_state = tf.nn.dynamic_rnn(cell, inputs, dtype=tf.float32)
final_state = tf.identity(final_state, "final_state")
return outputs, final_state
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_build_rnn(build_rnn)
```
### Build the Neural Network
Apply the functions you implemented above to:
- Apply embedding to `input_data` using your `get_embed(input_data, vocab_size, embed_dim)` function.
- Build RNN using `cell` and your `build_rnn(cell, inputs)` function.
- Apply a fully connected layer with a linear activation and `vocab_size` as the number of outputs.
Return the logits and final state in the following tuple (Logits, FinalState)
```
def build_nn(cell, rnn_size, input_data, vocab_size):
"""
Build part of the neural network
:param cell: RNN cell
:param rnn_size: Size of rnns
:param input_data: Input data
:param vocab_size: Vocabulary size
:return: Tuple (Logits, FinalState)
"""
embeds = get_embed(input_data, vocab_size, rnn_size)
outputs, final_state = build_rnn(cell, embeds)
w_initializer = tf.truncated_normal_initializer(stddev= 0.1)
b_initializer = tf.zeros_initializer()
logits = tf.contrib.layers.fully_connected(outputs,
vocab_size,
activation_fn=None,
weights_initializer=w_initializer,
biases_initializer=b_initializer)
return logits, final_state
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_build_nn(build_nn)
```
### Batches
Implement `get_batches` to create batches of input and targets using `int_text`. The batches should be a Numpy array with the shape `(number of batches, 2, batch size, sequence length)`. Each batch contains two elements:
- The first element is a single batch of **input** with the shape `[batch size, sequence length]`
- The second element is a single batch of **targets** with the shape `[batch size, sequence length]`
If you can't fill the last batch with enough data, drop the last batch.
For exmple, `get_batches([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], 2, 3)` would return a Numpy array of the following:
```
[
# First Batch
[
# Batch of Input
[[ 1 2 3], [ 7 8 9]],
# Batch of targets
[[ 2 3 4], [ 8 9 10]]
],
# Second Batch
[
# Batch of Input
[[ 4 5 6], [10 11 12]],
# Batch of targets
[[ 5 6 7], [11 12 13]]
]
]
```
```
def shuffle(arr, seq_length, n_batches):
reshape = arr.reshape(-1, seq_length)
splits = [[] for _ in range(n_batches)]
for i, a in enumerate(reshape):
splits[i % n_batches].append(a)
return splits
def get_batches(int_text, batch_size, seq_length):
"""
Return batches of input and target
:param int_text: Text with the words replaced by their ids
:param batch_size: The size of batch
:param seq_length: The length of sequence
:return: Batches as a Numpy array
"""
n_batches = len(int_text) // (batch_size * seq_length)
max_length = n_batches * batch_size * seq_length
inputs = np.array(int_text[:max_length]) # drop last batch
targets = np.array(int_text[1:max_length+1]) # shift
s_inputs = shuffle(inputs, seq_length, n_batches)
s_targets = shuffle(targets, seq_length, n_batches)
return np.array(list(zip(s_inputs, s_targets)))
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_batches(get_batches)
```
## Neural Network Training
### Hyperparameters
Tune the following parameters:
- Set `num_epochs` to the number of epochs.
- Set `batch_size` to the batch size.
- Set `rnn_size` to the size of the RNNs.
- Set `seq_length` to the length of sequence.
- Set `learning_rate` to the learning rate.
- Set `show_every_n_batches` to the number of batches the neural network should print progress.
```
# Number of Epochs
num_epochs = 200
# Batch Size
batch_size = 64
# RNN Size
rnn_size = 256
# Sequence Length
seq_length = 256
# Learning Rate
learning_rate = 0.01
# Show stats for every n number of batches
show_every_n_batches = 10
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
save_dir = './save'
```
### Build the Graph
Build the graph using the neural network you implemented.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
from tensorflow.contrib import seq2seq
train_graph = tf.Graph()
with train_graph.as_default():
vocab_size = len(int_to_vocab)
input_text, targets, lr = get_inputs()
input_data_shape = tf.shape(input_text)
cell, initial_state = get_init_cell(input_data_shape[0], rnn_size)
logits, final_state = build_nn(cell, rnn_size, input_text, vocab_size)
# Probabilities for generating words
probs = tf.nn.softmax(logits, name='probs')
# Loss function
cost = seq2seq.sequence_loss(
logits,
targets,
tf.ones([input_data_shape[0], input_data_shape[1]]))
# Optimizer
optimizer = tf.train.AdamOptimizer(lr)
# Gradient Clipping
gradients = optimizer.compute_gradients(cost)
capped_gradients = [(tf.clip_by_value(grad, -1., 1.), var) for grad, var in gradients]
train_op = optimizer.apply_gradients(capped_gradients)
```
## Train
Train the neural network on the preprocessed data. If you have a hard time getting a good loss, check the [forms](https://discussions.udacity.com/) to see if anyone is having the same problem.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
batches = get_batches(int_text, batch_size, seq_length)
with tf.Session(graph=train_graph) as sess:
sess.run(tf.global_variables_initializer())
for epoch_i in range(num_epochs):
state = sess.run(initial_state, {input_text: batches[0][0]})
for batch_i, (x, y) in enumerate(batches):
feed = {
input_text: x,
targets: y,
initial_state: state,
lr: learning_rate}
train_loss, state, _ = sess.run([cost, final_state, train_op], feed)
# Show every <show_every_n_batches> batches
if (epoch_i * len(batches) + batch_i) % show_every_n_batches == 0:
print('Epoch {:>3} Batch {:>4}/{} train_loss = {:.3f}'.format(
epoch_i,
batch_i,
len(batches),
train_loss))
# Save Model
saver = tf.train.Saver()
saver.save(sess, save_dir)
print('Model Trained and Saved')
```
## Save Parameters
Save `seq_length` and `save_dir` for generating a new TV script.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# Save parameters for checkpoint
helper.save_params((seq_length, save_dir))
```
# Checkpoint
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import tensorflow as tf
import numpy as np
import helper
import problem_unittests as tests
_, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
seq_length, load_dir = helper.load_params()
```
## Implement Generate Functions
### Get Tensors
Get tensors from `loaded_graph` using the function [`get_tensor_by_name()`](https://www.tensorflow.org/api_docs/python/tf/Graph#get_tensor_by_name). Get the tensors using the following names:
- "input:0"
- "initial_state:0"
- "final_state:0"
- "probs:0"
Return the tensors in the following tuple `(InputTensor, InitialStateTensor, FinalStateTensor, ProbsTensor)`
```
def get_tensors(loaded_graph):
"""
Get input, initial state, final state, and probabilities tensor from <loaded_graph>
:param loaded_graph: TensorFlow graph loaded from file
:return: Tuple (InputTensor, InitialStateTensor, FinalStateTensor, ProbsTensor)
"""
# TODO: Implement Function
input_tensor = loaded_graph.get_tensor_by_name("input:0")
initial_state_tensor = loaded_graph.get_tensor_by_name("initial_state:0")
final_state_tensor = loaded_graph.get_tensor_by_name("final_state:0")
probs_tensor = loaded_graph.get_tensor_by_name("probs:0")
return input_tensor, initial_state_tensor, final_state_tensor, probs_tensor
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_tensors(get_tensors)
```
### Choose Word
Implement the `pick_word()` function to select the next word using `probabilities`.
```
def pick_word(probabilities, int_to_vocab):
"""
Pick the next word in the generated text
:param probabilities: Probabilites of the next word
:param int_to_vocab: Dictionary of word ids as the keys and words as the values
:return: String of the predicted word
"""
word = np.random.choice(list(int_to_vocab.values()), p=probabilities)
return word
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_pick_word(pick_word)
```
## Generate TV Script
This will generate the TV script for you. Set `gen_length` to the length of TV script you want to generate.
```
gen_length = 200
# homer_simpson, moe_szyslak, or Barney_Gumble
prime_word = 'moe_szyslak'
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
loaded_graph = tf.Graph()
with tf.Session(graph=loaded_graph) as sess:
# Load saved model
loader = tf.train.import_meta_graph(load_dir + '.meta')
loader.restore(sess, load_dir)
# Get Tensors from loaded model
input_text, initial_state, final_state, probs = get_tensors(loaded_graph)
# Sentences generation setup
gen_sentences = [prime_word + ':']
prev_state = sess.run(initial_state, {input_text: np.array([[1]])})
# Generate sentences
for n in range(gen_length):
# Dynamic Input
dyn_input = [[vocab_to_int[word] for word in gen_sentences[-seq_length:]]]
dyn_seq_length = len(dyn_input[0])
# Get Prediction
probabilities, prev_state = sess.run(
[probs, final_state],
{input_text: dyn_input, initial_state: prev_state})
pred_word = pick_word(probabilities[dyn_seq_length-1], int_to_vocab)
gen_sentences.append(pred_word)
# Remove tokens
tv_script = ' '.join(gen_sentences)
for key, token in token_dict.items():
ending = ' ' if key in ['\n', '(', '"'] else ''
tv_script = tv_script.replace(' ' + token.lower(), key)
tv_script = tv_script.replace('\n ', '\n')
tv_script = tv_script.replace('( ', '(')
print(tv_script)
```
# The TV Script is Nonsensical
It's ok if the TV script doesn't make any sense. We trained on less than a megabyte of text. In order to get good results, you'll have to use a smaller vocabulary or get more data. Luckly there's more data! As we mentioned in the begging of this project, this is a subset of [another dataset](https://www.kaggle.com/wcukierski/the-simpsons-by-the-data). We didn't have you train on all the data, because that would take too long. However, you are free to train your neural network on all the data. After you complete the project, of course.
# Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_tv_script_generation.ipynb" and save it as a HTML file under "File" -> "Download as". Include the "helper.py" and "problem_unittests.py" files in your submission.
|
github_jupyter
|
# Random Signals and LTI-Systems
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*
## Measurement of Acoustic Impulse Responses
The propagation of sound from one position (e.g. transmitter) to another (e.g. receiver) conforms reasonable well to the properties of a linear time-invariant (LTI) system. Consequently, the impulse response $h[k]$ characterizes the propagation of sound between theses two positions. Impulse responses have various applications in acoustics. For instance as [head-related impulse responses](https://en.wikipedia.org/wiki/Head-related_transfer_function) (HRIRs) or room impulse responses (RIRs) for the characterization of room acoustics.
The following example demonstrates how an acoustic impulse response can be estimated with [correlation-based system identification techniques](correlation_functions.ipynb#System-Identification) using the soundcard of a computer. The module [`sounddevice`](http://python-sounddevice.readthedocs.org/) provides access to the soundcard via [`portaudio`](http://www.portaudio.com/).
```
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sig
import sounddevice as sd
```
### Generation of the Measurement Signal
We generate white noise with a uniform distribution between $\pm 0.5$ as the excitation signal $x[k]$
```
fs = 44100 # sampling rate
T = 5 # length of the measurement signal in sec
Tr = 2 # length of the expected system response in sec
x = np.random.uniform(-.5, .5, size=T*fs)
```
### Playback of Measurement Signal and Recording of Room Response
The measurement signal $x[k]$ is played through the output of the soundcard and the response $y[k]$ is captured synchronously by the input of the soundcard. The length of the played/captured signal has to be of equal length when using the soundcard. The measurement signal $x[k]$ is zero-padded so that the captured signal $y[k]$ includes the complete system response.
Be sure not to overdrive the speaker and the microphone by keeping the input level well below 0 dB.
```
x = np.concatenate((x, np.zeros(Tr*fs)))
y = sd.playrec(x, fs, channels=1)
sd.wait()
y = np.squeeze(y)
print('Playback level: ', 20*np.log10(max(x)), ' dB')
print('Input level: ', 20*np.log10(max(y)), ' dB')
```
### Estimation of the Acoustic Impulse Response
The acoustic impulse response is estimated by cross-correlation $\varphi_{yx}[\kappa]$ of the output with the input signal. Since the cross-correlation function (CCF) for finite-length signals is given as $\varphi_{yx}[\kappa] = \frac{1}{K} \cdot y[\kappa] * x[-\kappa]$, the computation of the CCF can be speeded up with the fast convolution method.
```
h = 1/len(y) * sig.fftconvolve(y, x[::-1], mode='full')
h = h[fs*(T+Tr):fs*(T+2*Tr)]
plt.figure(figsize=(10, 5))
t = 1/fs * np.arange(len(h))
plt.plot(t, h)
plt.axis([0.0, 1.0, -1.1*np.max(np.abs(h)), 1.1*np.max(np.abs(h))])
plt.xlabel(r'$t$ in s')
plt.ylabel(r'$\hat{h}[k]$')
```
**Copyright**
This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples*.
|
github_jupyter
|
```
import json
import os
import re
import tqdm
import random
from PIL import Image
%matplotlib inline
from pycocotools.coco import COCO
from pycocotools import mask as cocomask
import numpy as np
import skimage.io as io
import matplotlib.pyplot as plt
import pylab
import random
import os
pylab.rcParams['figure.figsize'] = (8.0, 10.0)
IMAGES_FOLDER_PATH="/mount/SDB/myfoodrepo-seth/myfoodrepo-images/images"
ANNOTATIONS_PATH="/mount/SDB/myfoodrepo-seth/prepared_annotations/coco_annotations_assignments_2018_08_02_14-29-36.json"
OUTPUT_DIRECCTORY = "/mount/SDE/myfoodrepo/mohanty/myfoodrepo-mask-rcnn/data"
TRAIN_PERCENT = 0.8
VAL_PERCENT = 0.1
TEST_PERCENT = 1 - (TRAIN_PERCENT + VAL_PERCENT)
# Build index of image_id to filepath
image_path_map = {}
rootDir = IMAGES_FOLDER_PATH
for dirName, subdirList, fileList in tqdm.tqdm(os.walk(rootDir, topdown=False)):
for fname in fileList:
if len(re.findall("^\d+.jpg$", fname))>0:
#print('.', end='', flush=True)
image_path_map[fname.replace(".jpg", "")] = os.path.join(dirName, fname)
annotations = json.loads(open(ANNOTATIONS_PATH).read())
# Index annotations by image_id
annotations_by_image_id = {}
for item in annotations:
try:
annotations_by_image_id[item["image_id"]].append(item)
except:
annotations_by_image_id[item["image_id"]] = [item]
images_in_annotations = list(annotations_by_image_id.keys())
random.shuffle(images_in_annotations)
TRAIN_IDX = int(len(images_in_annotations) * TRAIN_PERCENT)
VAL_IDX = TRAIN_IDX + int(len(images_in_annotations) * VAL_PERCENT)
TEST_IDX = len(images_in_annotations)
TRAIN_IMAGES = images_in_annotations[0:TRAIN_IDX]
VAL_IMAGES = images_in_annotations[TRAIN_IDX:VAL_IDX]
TEST_IMAGES = images_in_annotations[VAL_IDX:TEST_IDX]
def generate_image_object(_image, IMAGES_DIR):
image_path = image_path_map[_image]
target_filename = "{}.jpg".format(_image.zfill(12))
_image_object = {}
_image_object["id"] = int(_image)
_image_object["file_name"] = target_filename
im = Image.open(image_path)
width, height = im.size
_image_object["width"] = width
_image_object["height"] = height
im.save(os.path.join(IMAGES_DIR, target_filename))
im.close()
return _image_object
def generate_annotations_file(IMAGES, OUTPUT_DIRECTORY):
d = {}
d["info"] = {'contributor': 'spMohanty', 'about': 'My Food Repo dataset', 'date_created': '04/08/2018', 'description': 'Annotations on myfoodrepo dataset', 'version': '1.0', 'year': 2018}
d["categories"] = [{'id': 100, 'name': 'food', 'supercategory': 'food'}]
d["images"] = []
d["annotations"] = []
IMAGES_DIR = os.path.join(OUTPUT_DIRECTORY, "images")
if not os.path.exists(IMAGES_DIR):
os.makedirs(IMAGES_DIR)
annotation_count = 0
for _image in tqdm.tqdm(IMAGES):
try:
image_path = image_path_map[_image]
except:
print("Errorr Processing : ", _image)
continue
_image_object = generate_image_object(_image, IMAGES_DIR)
assert _image_object != None
d["images"].append(_image_object)
for _annotation in annotations_by_image_id[_image]:
_annotation["id"] = annotation_count
annotation_count += 1
_annotation["image_id"] = int(_image)
d["annotations"].append(_annotation)
fp = open(os.path.join(OUTPUT_DIRECTORY, "annotations.json"), "w")
fp.write(json.dumps(d))
fp.close()
print(len(d["images"]))
print(d["images"][0])
generate_annotations_file(TRAIN_IMAGES, os.path.join(OUTPUT_DIRECCTORY, "myfoodrepo-train"))
generate_annotations_file(VAL_IMAGES, os.path.join(OUTPUT_DIRECCTORY, "myfoodrepo-val"))
generate_annotations_file(TEST_IMAGES, os.path.join(OUTPUT_DIRECCTORY, "myfoodrepo-test"))
"""
Test if the annotations work properly
!pip install git+https://github.com/crowdai/coco.git#subdirectory=PythonAPI
"""
def test_annotations(subdir_name):
IMAGES_DIRECTORY = "../data/{subdir_name}/images".format(subdir_name=subdir_name)
ANNOTATIONS_PATH = "../data/{subdir_name}/annotations.json".format(subdir_name=subdir_name)
coco = COCO(ANNOTATIONS_PATH)
category_ids = coco.loadCats(coco.getCatIds())
print(category_ids)
image_ids = coco.getImgIds(catIds=coco.getCatIds())
random_image_id = random.choice(image_ids)
img = coco.loadImgs(random_image_id)[0]
print(img)
image_path = os.path.join(IMAGES_DIRECTORY, img["file_name"])
I = io.imread(image_path)
annotation_ids = coco.getAnnIds(imgIds=img['id'])
annotations = coco.loadAnns(annotation_ids)
plt.imshow(I); plt.axis('off')
coco.showAnns(annotations)
#test_annotations("myfoodrepo-train")
#test_annotations("myfoodrepo-val")
test_annotations("myfoodrepo-test")
```
|
github_jupyter
|
# Lab 01 - Modelling and Systems Dynamics
```
import math, pandas
from matplotlib import pyplot
```
## Section 01 - Starting Jupyter Notebook
```
print(math.sin(4))
```
## Section 02 - Number and Arithmetic
```
print(5 / 8)
print(5 / 8.0) # or print(5 / float(8))
print(5 * 8)
print((1 / 2.0) ** 2)
```
### Review Question
```
print(math.exp(10))
```
## Section 03 - Variables and Assignments
```
ans = 5 * math.pi
ans += 1
print(ans + 2)
```
### Review Question
```
vel = 5
print((7 + (vel / 3)) ** 2)
```
## Section 04 - User Defined Functions
```
def f(x):
return x ** 2 + 1
print(f(4))
print(f(2.5))
def sum_squares(x, y):
return x ** 2 + y ** 2
print(sum_squares(3, 4))
```
### Review Question
#### Part A
```
def p(t):
return 100 * math.exp(0.1 * t)
print(p(12))
```
#### Part B
```
def pop(init_pop, r, t):
return init_pop * math.exp(r * t)
print(pop(1000, 0.15, 12))
```
## Section 05 - Printing
```
x = 3.0
print("x =", x, "and its square is", x ** 2)
```
## Section 06 - Loops and Lists
```
list_1 = [1, 3, 5.0]
list_2 = [1, "one", 2, "two"]
list_3 = []
print(list_1, list_2, list_3)
list_4 = list(range(15))
list_5 = list(range(5, 15))
list_6 = list(range(4, 15, 3))
print(list_4, list_5, list_6)
```
### Review Question 01
```
print(list(range(3, 16, 4)))
dist = 0
for i in range(7):
dist += 0.25
print(dist)
for i in range(10):
print(i, " ", i ** 2)
```
### Review Question 02
```
dist = 1
for i in range(20):
dist *= 2
print(dist)
```
## Section 07 - Supplementary Python Programming Exercises
### Exercise 01
```
def sim(initial_pop, growth_rate_unit, sim_len, time_step):
pops = []
times = []
pop = initial_pop
time = 0
pops.append(pop)
times.append(time)
GROWTH_RATE = growth_rate_unit * time_step
while (time <= sim_len):
time += time_step
pop += pop * GROWTH_RATE
pops.append(pop)
times.append(time)
ACTUAL_POP = initial_pop * ((1 + growth_rate_unit) ** sim_len)
END_POP = pops[len(pops) - 1]
RELATIVE_ERR = abs((ACTUAL_POP - END_POP) / END_POP)
return pops, times, ACTUAL_POP, RELATIVE_ERR
```
#### Part A
```
INITAL_POP = 100
GROWTH_RATE_PER_HOUR = 0.1
SIM_LEN = 200
pops_0_0001, times_0_0001, actual_pop, relative_err = sim(INITAL_POP, GROWTH_RATE_PER_HOUR, SIM_LEN, 0.0001)
pops_0_025, times_0_025, actual_pop, relative_err = sim(INITAL_POP, GROWTH_RATE_PER_HOUR, SIM_LEN, 0.025)
pops_0_5, times_0_5, actual_pop, relative_err = sim(INITAL_POP, GROWTH_RATE_PER_HOUR, SIM_LEN, 0.5)
print("The number of bacteria at the end of one week =", pops_0_5[168 * 2])
INITAL_POP_DOUBLE = INITAL_POP * 2
index = -1
```
#### Part B
```
for i in range(len(pops_0_0001)):
if pops_0_0001[i] < INITAL_POP_DOUBLE:
continue
index = i
break
if index != -1:
print("The time taken for the population to double lies between", round(times_0_0001[index - 1], 4), "hrs and", round(times_0_0001[index], 4), "hrs")
```
#### Part C
```
pyplot.title("Population growth simulation")
pyplot.ylabel("Population")
pyplot.xlabel("Time (hrs)")
pyplot.plot(times_0_0001, pops_0_0001, label="0.0001hrs")
pyplot.plot(times_0_025, pops_0_025, label="0.025hrs")
pyplot.plot(times_0_5, pops_0_5, label="0.5hrs")
pyplot.legend()
pyplot.show()
```
### Exercise 02
#### Part A
```
INITAL_POP = 15000
INITAL_POP_DOUBLE = INITAL_POP * 2
GROWTH_RATE_PER_YEAR = 0.02
TIME_STEP = 0.25
SIM_LEN = 20
ACTUAL_POP_20_YRS = INITAL_POP * (GROWTH_RATE_PER_YEAR ** SIM_LEN)
pops, times, actual_pop, relative_err = sim(INITAL_POP, GROWTH_RATE_PER_YEAR, SIM_LEN, TIME_STEP)
print("Actual population after", SIM_LEN, "yrs is", actual_pop)
```
#### Part B
```
pyplot.title("Animal population growth simulation")
pyplot.ylabel("Population")
pyplot.xlabel("Time (yrs)")
pyplot.plot(times, pops)
pyplot.show()
```
#### Part C
```
TIME_PAD = 10
POP_PAD = 20
print("Time (yrs)".ljust(TIME_PAD), "Population".ljust(POP_PAD), "Growth")
print("0".ljust(TIME_PAD), str(INITAL_POP).ljust(POP_PAD), "INTERVAL")
for i in range(1, len(pops)):
GROWTH = str(100 * round((pops[i] - pops[i - 1]) / pops[i - 1], 8)) + "%"
print(str(times[i]).ljust(TIME_PAD), str(pops[i]).ljust(POP_PAD), GROWTH)
```
#### Part D
```
INDEX = int(1 / TIME_STEP)
pop = pops[INDEX]
print("Population at end of 1 year:", pop, "growth of", pop - INITAL_POP, "(" + str(100 * round((pop - INITAL_POP) / INITAL_POP, 8)) + "%)")
pop = pops[2 * INDEX]
print("Population at end of 2 years:", pop, "growth of", pop - INITAL_POP, "(" + str(100 * round((pop - INITAL_POP) / INITAL_POP, 8)) + "%)")
pop = pops[3 * INDEX]
print("Population at end of 3 years:", pop, "growth of", pop - INITAL_POP, "(" + str(100 * round((pop - INITAL_POP) / INITAL_POP, 8)) + "%)")
```
### Exercise 03
#### Part A
```
INITIAL_SAMPLE = 20
GROWTH_RATE = -0.000120968
SIM_LEN = 25000
def carbon_date(sample, proportion, sim_len, time_step):
carbons = []
times = []
carbon = sample
time = 0
carbons.append(carbon)
times.append(time)
while (time <= sim_len):
time += time_step
carbon = 20 * math.exp(proportion * time)
carbons.append(carbon)
times.append(time)
return carbons, times
carbons, carbon_times = carbon_date(INITIAL_SAMPLE, GROWTH_RATE, SIM_LEN, 0.25)
pyplot.title("Carbon dating simulation")
pyplot.ylabel("Carbon")
pyplot.xlabel("Time (yrs)")
pyplot.plot(carbon_times, carbons)
pyplot.show()
```
#### Part B
```
print("Estimation of carbon-14 remaining after 25,000yrs =", str(carbons[25000 * 4]) + "g")
```
### Exercise 04
#### Part A
dT / dt is directly proportional to T - 25. Therefore, dT / dt = k(T - 25).
#### Part B
dT / dt = k(T - 25)
du / dt = ku, where u = T - 25
(1 / u) du = k dt
ln(u) = kt + c
u = e ^ (kt + c)
u = Ae ^ kt
T - 25 = Ae ^ kt
T = Ae ^ kt + 25
#### Part C
T(0) = A + 25
A = -19
T(1) = -19e ^ k + 25
20 = -19e ^ k + 25
5 = 19e ^ k
k = ln(5 / 19)
#### Part D
T(0.25) = -19e ^ (0.25 * ln(5 / 19)) + 25
T(0.25) = 25 - 19 * (5 / 19)^0.25
T(0.25) = 11.4
|
github_jupyter
|
# Visualize real data
Get to know the real data
```
import pandas as pd
import os
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
savefolder = 'figures_real_data'
folder = 'data'
df = pd.read_excel(os.path.join(folder, '20211128 - Full DART Data (Model & Test).xlsx'), header=2)
df.head()
import pylab
labeled_df = df[df['Sample Types'] == 'Model']
recol = [(float('.'.join(col.split('.')[:2])) if isinstance(col, str) else col) for col in df.columns[4:]]
unique_classes = labeled_df['Class'].unique()
NUM_COLORS = len(unique_classes)
cm = pylab.get_cmap('gist_rainbow')
cgen = (cm(1.*i/NUM_COLORS) for i in range(NUM_COLORS))
for label in unique_classes:
plt.figure(figsize=(12,8))
mask = labeled_df['Class'] == label
color = next(cgen)
for ind, row in labeled_df.loc[mask, :].iterrows():
data = row[df.columns[4:]].values
data[data<25] = 0
plt.plot(recol, data, color=color)
plt.ylabel('%')
plt.xlabel('Mass')
plt.savefig(os.path.join(savefolder, f'sample_class_{label}_ind_{ind}.png'))
#plt.show()
plt.close()
# Rename numerical columns
recol = [(float('.'.join(col.split('.')[:2])) if isinstance(col, str) else col) for col in df.columns[4:]]
plt.plot(recol)
recol
```
It appears there are more than 3 measurement iterations? Why?
```
Xcols = [f'Col{i}' for i in range(len(recol))]
df.columns = list(df.columns[:4]) + Xcols
df.head(n=10)
df[df.columns[4:]].iloc[0:3]
```
## Data formatting
```
def build_data_structure(df, labels, column_name_mass_locations):
"""
Convert dataframe which has columns of the mass locations and values of the intensities
to array format where the sample is a list of peaks and the samples are grouped by the number of peaks.
Input:
df: dataframe with columns of the mass locations and values of the intensities
Col0 Col1 Col2 ...
0 0.0 0.0 0.0
column_name_mass_locations: column names of the mass locations
[59.00498,
72.00792,
74.00967,
...
]
We split it up just in case duplicate mass locations are present since multiple scans can be represented.
Output:
[ [samples with smallest number of peaks],
[samples with 2nd smallest number peaks],
...,
[samples with largest number of peaks]
]
where each sample is an array of lists (mass, intensity):
array([[peak_location1, peak_intensity1], [peak_location2, peak_intensity2], ...])
"""
df = df.copy()
# Get nonzero values (aka "peaks")
data = df.apply(lambda x: np.asarray([[column_name_mass_locations[i], val] for i, (val, b) in enumerate(zip(x, x.gt(0))) if b]), axis=1)
X = []
Y = []
# Group so we have groups of the same number of peaks
lengths = np.array([len(x) for x in data])
unique_lengths = np.unique(lengths)
for length in unique_lengths:
mask_length = lengths == length
mask_idx = np.where(mask_length)
y = labels[mask_idx]
x = np.stack(data.loc[mask_length].values.tolist())
X.append(x)
Y.append(y)
return X, Y
labeled_df = df[df['Sample Types'] == 'Model']
from sklearn import preprocessing
lb = preprocessing.LabelBinarizer()
lb.fit(labeled_df['Class'].unique())
X, Y = build_data_structure(labeled_df[labeled_df.columns[4:]], labeled_df['Class'].values, recol)
y = [lb.transform(y) for y in Y]
len(X), X[0].shape, len(y), y[0].shape
```
## Investigate test-train partition
```
df['Sample Types'].value_counts()
df['Class'].value_counts()
df[df['Sample Types'] == 'Model']['Class'].value_counts()
df[df['Sample Types'] == 'Test']['Class'].value_counts()
```
## Seeing no labels in the Test split, we must split the train for a supervised evaluation
```
labeled_df = df[df['Sample Types'] == 'Model']
X = build_data_structure(df[df.columns[4:]])
from sklearn import model_selection
from sklearn import preprocessing
lb = preprocessing.LabelBinarizer()
lb.fit(labeled_df['Class'])
train_labeled_df, test_labeled_df = model_selection.train_test_split(labeled_df, train_size=None, shuffle=True, stratify=labeled_df['Class'])
X_train = build_data_structure(train_labeled_df[train_labeled_df.columns[4:]])
X_test = build_data_structure(test_labeled_df[test_labeled_df.columns[4:]])
y_train = lb.transform(train_labeled_df['Class'])
y_test = lb.transform(test_labeled_df['Class'])
print(len(X_train), len(X_test))
print(X_train[12][0].shape, y_train[0].shape, X_test[12][0].shape, y_test[0].shape)
from core import RealDataGenerator
gen = RealDataGenerator(
X_train, y_train,
X_test, y_test,
X_test, y_test
)
```
|
github_jupyter
|
```
import pandas as pd
import matplotlib.pyplot as plt
ppd_df = pd.read_csv("policedata/ppd_complaints.csv")
display(ppd_df.head())
# Add date of complaint
date_pattern = r"(\d{1,2}-\d{1,2}-\d{2,4})" #parentheses is to treat all characters as a "group", making extract work
complaint_str_series = ppd_df['summary'].str.extract(date_pattern, expand=False) #expand=False to get series
complaint_str_series.replace("2-29-18","03-01-18",inplace=True) #replace faulty leap year day
ppd_df['date_of_complaint'] = pd.to_datetime(complaint_str_series)
# Basic information and visualizations
print("Number of complaints: {}\n".format(ppd_df.shape[0]))
print("Complaints over time")
# optionally, exclude the first few years
complaints_over_time_series = ppd_df[ppd_df['date_of_complaint']>"01-01-2014"].groupby('date_of_complaint').size()
#complaints_over_time_series = ppd_df.groupby('date_of_complaint').size().asfreq(freq="d",fill_value=0)
display(complaints_over_time_series.groupby(pd.Grouper(freq="M")).sum().plot(figsize=(20,10)))
plt.show()
print("Complaints by district")
display(ppd_df['district_occurrence'].value_counts())
print("Complaints by classification")
print(ppd_df['general_cap_classification'].value_counts())
disciplines_df = pd.read_csv("policedata/ppd_complaint_disciplines.csv")
disciplines_df.head()
# Basic counts
for col in ['po_race','po_sex','allegations_investigated','investigative_findings','disciplinary_findings']:
print(col)
display(disciplines_df[col].value_counts())
# Merge the datasets, keeping rows with a complaint id a
complaint_key = ['complaint_id','officer_id','allegations_investigated']
merged_df = ppd_df.merge(disciplines_df,on='complaint_id',how='inner').drop_duplicates()
# Add column for # of rws that appeared for each complaint key
num_complaints_df = disciplines_df.drop_duplicates()\
.groupby(complaint_key).size()
print("Number of unique allegations made (specific complaint, officer and allegation): ",str(num_complaints_df.shape[0]))
multiple_complaints_df = num_complaints_df.rename("num_complaint_rows")
# Make dataframe which will contain final investigative outcome for each complaint key
outcome_df = merged_df.merge(multiple_complaints_df,
how='inner',
left_on=complaint_key,
right_index=True)
assert(all(~outcome_df.duplicated()))
# display(outcome_df)
# Find all complaints where at least one row had a Sustained Finding, and store those keys into a set
sustained_findings_df = outcome_df[outcome_df['investigative_findings']=='Sustained Finding']
print('Number of unique allegations made with investigative outcome "Sustained Findings":',
str(sustained_findings_df.shape[0]))
#display(sustained_findings_df)
assert(all(~sustained_findings_df.duplicated()))
assert(all(~sustained_findings_df[complaint_key].duplicated()))
sustained_findings_keys = {",".join(str(x) for x in arr) for arr in sustained_findings_df[complaint_key].values}
# Find all complaints where at least one row had a Guilty Finding disciplinary finding
guilty_df = outcome_df[outcome_df['disciplinary_findings'] == 'Guilty Finding']
print('Number of unique allegations made with disciplinary outcome "Guilty Finding":',
str(guilty_df.shape[0]))
guilty_finding_keys = {",".join(str(x) for x in arr) for arr in guilty_df[complaint_key].values}
# Find all complaints where at least one row was Guilty Finding or Training/Counseling
some_punishment_df = outcome_df[(outcome_df['disciplinary_findings'] == 'Guilty Finding') |
(outcome_df['disciplinary_findings'] == 'Training/Counseling')]
print('Number of unique allegations made with disciplinary outcome "Guilty Finding" or "Training/Counseling":',
str(some_punishment_df.shape[0]))
some_punishment_keys = {",".join(str(x) for x in arr) for arr in some_punishment_df[complaint_key].values}
# Remove duplicate rows for each complaint in the outcome dataframe, then add column with
# True if the investigation had sustained findings
outcome_df = outcome_df.drop_duplicates(subset=complaint_key)\
.drop(['investigative_findings','disciplinary_findings'],axis=1)
key_column = [",".join(str(x) for x in arr) for arr in outcome_df[complaint_key].values]
outcome_df['complaint_key'] = key_column
outcome_df['sustained_investigative_finding'] = outcome_df['complaint_key'].isin(sustained_findings_keys)
outcome_df['guilty_disciplinary_finding'] = outcome_df['complaint_key'].isin(guilty_finding_keys)
outcome_df['training_counseling_or_guilty_disciplinary_finding'] = outcome_df['complaint_key'].isin(some_punishment_keys)
display(outcome_df)
# Add complainant demographics columns
complainant_demographics_df = pd.read_csv('policedata/ppd_complainant_demographics.csv').set_index('complaint_id')
display(complainant_demographics_df.head())
outcome_df = outcome_df.merge(complainant_demographics_df, left_on='complaint_id',right_index=True)
outcome_df
outcome_df.to_csv("outputdata/outcome_df.csv")
#outcome_to_test = "guilty_disciplinary_finding"
outcome_to_test = 'training_counseling_or_guilty_disciplinary_finding'
print('Outcome to test: {}'.format(outcome_to_test))
print("Total number of complaints: {0}\nTotal number of successful complaints: {1}\nPercent of complaints which succeeded: {2:.2f}% "\
.format(outcome_df.shape[0],outcome_df[outcome_to_test].sum(),
100*outcome_df[outcome_to_test].sum()/outcome_df.shape[0]))
for column in ['complainant_sex','complainant_race','po_race','po_sex','allegations_investigated']:
print("Fraction of complaints with true outcome by {}".format(column))
print(outcome_df[outcome_df[outcome_to_test]==True][column].value_counts(normalize=True))
print("Fraction of complaints with false outcome by {}".format(column))
print(outcome_df[outcome_df[outcome_to_test]==False][column].value_counts(normalize=True))
for column in ['complainant_sex','complainant_race','po_race','po_sex','allegations_investigated']:
print("% of successful complaints by {}".format(column))
for column_possibility in outcome_df[column].unique():
print("When {} = {}".format(column,column_possibility))
if pd.isna(column_possibility):
print(outcome_df[outcome_df[column].isna()][outcome_to_test].value_counts())
print(outcome_df[outcome_df[column].isna()][outcome_to_test].value_counts(normalize=True))
else:
print(outcome_df[outcome_df[column]==column_possibility][outcome_to_test].value_counts())
print(outcome_df[outcome_df[column]==column_possibility][outcome_to_test].value_counts(normalize=True))
outcome_df['officer_id'].value_counts()
outcome_df
print("\n".join(outcome_df[outcome_df['officer_id']==29180642.0]['summary']))
print(outcome_df[outcome_df['officer_id']==29180642.0]['sustained_investigative_finding'].sum())
print(outcome_df[outcome_df['officer_id']==29180642.0]['guilty_disciplinary_finding'].sum())
```
|
github_jupyter
|
```
# Dependencies and Setup
import pandas as pd
import numpy as np
# Load the file and set up the path for it
purchase_data = "Resources/purchase_data.csv"
# Read Purchasing File, store it in Panda frame, read the head of the file (first 5 items)
purchase_data_df = pd.read_csv(purchase_data)
purchase_data_df.head()
purchase_data_df.describe()
###PLAYER COUNT
TotalNrPlayer = len(purchase_data_df["SN"].value_counts())
TotalNrPlayer
#create a data frame to show the total players
TotalNrPlayer = pd.DataFrame({"Total Number of Players" : [TotalNrPlayer]})
TotalNrPlayer
###PURCHASING ANALYSIS (TOTAL)
#number of unique items
NrUniqueItems = len((purchase_data_df["Item ID"]).unique())
NrUniqueItems
#calculate average price
AveragePrice = float((purchase_data_df["Price"]).mean())
AveragePrice
#calculate total number of purchases
TotalPurchases = len((purchase_data_df["Purchase ID"]).value_counts())
TotalPurchases
#calculate total revenue
TotalRevenue = float((purchase_data_df["Price"]).sum())
TotalRevenue
#create data frame with the values we just calculated
total_purchasing_analysis_df = pd.DataFrame ({
"Number of Unique Items" : [NrUniqueItems],
"Average Purchase Price" : [AveragePrice],
"Total Number of Purchases" : [TotalPurchases],
"Total Revenue" : [TotalRevenue]
})
total_purchasing_analysis_df
#format for $ sign and 2 decimals
total_purchasing_analysis_df["Average Purchase Price"] = total_purchasing_analysis_df["Average Purchase Price"].map("${:.2f}".format)
total_purchasing_analysis_df["ATotal Revenue"] = total_purchasing_analysis_df["Total Revenue"].map("${:.2f}".format)
total_purchasing_analysis_df
### GENDER DEMOGRAPHICS
#group by gender status, using groupby function
GenderStatus_df = purchase_data_df.groupby("Gender")
GenderStatus_df.head()
#calculate the total number of gender type
GenderCount_df = GenderStatus_df["SN"].nunique()
GenderCount_df
#calculate percentage of gender type
GenderPercentage_df = purchase_data_df["Gender"].value_counts(normalize=True) * 100
GenderPercentage_df
#create data frame for the Gender Demographics table
Gender_Demographics_df = pd.DataFrame({
"percentage of players" : GenderPercentage_df,
"count of players" : GenderCount_df
})
Gender_Demographics_df
#format table for % sign and 2 decimals
Gender_Demographics_df["percentage of players"] = Gender_Demographics_df["percentage of players"].map("{:.2f} %".format)
Gender_Demographics_df
### PURCHASING ANALYSIS (GENDER)
#Calculate Purchase Count by Gender
PurchaseCount_df = GenderStatus_df["Purchase ID"].count()
PurchaseCount_df
#Calculate Average Purchase Price by Gender
AveragePurchase_df = GenderStatus_df["Price"].mean()
AveragePurchase_df
#Calculate Total Purchase Value by Gender
TotalValue_df = GenderStatus_df["Price"].sum()
TotalValue_df
#Calculate Average Purchase Total per Person by Gender
Average_Person_Gender_df = TotalValue_df/GenderCount_df
Average_Person_Gender_df
#Create Data Frame based on the calculations we just made
Gender_Demographics_df = pd.DataFrame({
"Purchase Count": PurchaseCount_df,
"Average Purchase Price": AveragePurchase_df,
"Average Purchase Value":TotalValue_df,
"Avg Purchase Total per Person": Average_Person_Gender_df
})
Gender_Demographics_df
#Format the table to $ sign and 2 decimals
Gender_Demographics_df["Average Purchase Price"] = Gender_Demographics_df["Average Purchase Price"].map("${:.2f}".format)
Gender_Demographics_df["Average Purchase Value"] = Gender_Demographics_df["Average Purchase Value"].map("${:.2f}".format)
Gender_Demographics_df["Avg Purchase Total per Person"] = Gender_Demographics_df["Avg Purchase Total per Person"].map("${:.2f}".format)
Gender_Demographics_df
### AGE DEMOGRAPHICS
# Create bins for ages
BinsAge = [0, 9, 14, 19, 24, 29, 34, 39, 99]
BinsAge
# Create the names for the bins
BinNames = ["<10", "10-14", "15-19", "20-24", "25-29", "30-34", "35-39", "40+"]
BinNames
# Segment and sort age values into bins established above
purchase_data_df["Age Group"] = pd.cut(purchase_data_df["Age"], BinsAge, labels = BinNames)
purchase_data_df
# Group by "Age Group"
GroupedAge = purchase_data_df.groupby("Age Group")
GroupedAge
# Calculate total players by age category
TotalCount_age = GroupedAge ["SN"].nunique()
TotalCount_age
# Calculate percentages by age category
Percentage_age = (TotalCount_age/576) * 100
Percentage_age
# Create data frame with the values we just calculated
Age_Demographics_df = pd.DataFrame ({
"Total Count" : TotalCount_age,
"Percentage of Players" : Percentage_age,
})
Age_Demographics_df
#Format the table to % sign and 2 decimals
Age_Demographics_df["Percentage of Players"] = Age_Demographics_df["Percentage of Players"].map("{:.2f} %".format)
Age_Demographics_df
#Calculate purchases count by age group
PurchaseCountAge = GroupedAge["Purchase ID"].count()
PurchaseCountAge
# Calculate average purchase count by age
AveragePriceAge = GroupedAge["Price"].mean()
AveragePriceAge
# Calculate total purchase value by age
TotalPurchases_age = GroupedAge["Price"].sum()
TotalPurchases_age
# Calculate Average Purchase Total per Person by Age Group
AverageTotal_person_age = TotalPurchases_age/TotalCount_age
AverageTotal_person_age
#create data frame with the values we just calculated
Age_Demographics_Analysis_df = pd.DataFrame ({
"Purchase Count" : PurchaseCountAge,
"Average Purchase Price" : AveragePriceAge,
"Total Purchase Value" : TotalPurchases_age,
"Average Purchase Total per Person by Age Group" : AverageTotal_person_age
})
Age_Demographics_Analysis_df
#Format the table for $ sign and 2 decimals
Age_Demographics_Analysis_df["Average Purchase Price"] = Age_Demographics_Analysis_df["Average Purchase Price"].map("${:.2f}".format)
Age_Demographics_Analysis_df["Total Purchase Value"] = Age_Demographics_Analysis_df["Total Purchase Value"].map("${:.2f}".format)
Age_Demographics_Analysis_df["Average Purchase Total per Person by Age Group"] = Age_Demographics_Analysis_df["Average Purchase Total per Person by Age Group"].map("${:.2f}".format)
Age_Demographics_Analysis_df
###Top Spenders
#Create a new group by SN
spender_group = purchase_data_df.groupby("SN")
spender_group
# Calculate purchases count by spender group
PurchaseCountSpender = spender_group["Purchase ID"].count()
PurchaseCountSpender
# Calculate average purchase price by spender
AveragePriceSpender = spender_group["Price"].mean()
AveragePriceSpender
# Calculate total purchase value by spender
TotalPurchases_spender = spender_group["Price"].sum()
TotalPurchases_spender
# Create data frame with obtained values
top_spender_group_df = pd.DataFrame({
"Purchase Count": PurchaseCountSpender,
"Average Purchase Price": AveragePriceSpender,
"Total Purchase Value":TotalPurchases_spender
})
top_spender_group_df
#Format table by "Total Purchase Value" Descending order
spender_gropu_formatted_df = top_spender_group_df.sort_values(["Total Purchase Value"], ascending=False).head()
spender_gropu_formatted_df
#format the table for $ sign and 2 decimals
spender_gropu_formatted_df["Average Purchase Price"] = spender_gropu_formatted_df["Average Purchase Price"].map("${:.2f}".format)
spender_gropu_formatted_df["Total Purchase Value"] = spender_gropu_formatted_df["Total Purchase Value"].map("${:.2f}".format)
spender_gropu_formatted_df
###MOST POPULAR ITEMS
# Create new data for most popular items
PopularItems = purchase_data_df.set_index(["Item ID", "Item Name"])
PopularItems
# Group by Item ID, Item Name
Grouped_PopularItems = PopularItems.groupby(["Item ID","Item Name"])
Grouped_PopularItems
# Calculate the number of times an item has been purchased
Item_purchase_count = Grouped_PopularItems["Price"].count()
Item_purchase_count
# Calcualte the average value per item
Item_average_value = Grouped_PopularItems["Price"].mean()
Item_average_value
# Calcualte the total purchase value per item
Item_purchase_value = Grouped_PopularItems["Price"].sum()
Item_purchase_value
# Create data frame with obtained values
MostPopularItem_df = pd.DataFrame({
"Purchase Count": Item_purchase_count,
"Item Price": Item_average_value,
"Total Purchase Value":Item_purchase_value
})
MostPopularItem_df
#Format table by " Purchase Count" Descending order
MostPopularItem_formatted_df = MostPopularItem_df.sort_values(["Purchase Count"], ascending=False).head()
MostPopularItem_formatted_df
# Format the table for $ sign and 2 decimals
MostPopularItem_formatted_df["Item Price"] = MostPopularItem_formatted_df["Item Price"].map("${:.2f}".format)
MostPopularItem_formatted_df["Total Purchase Value"] = MostPopularItem_formatted_df["Total Purchase Value"].map("${:.2f}".format)
MostPopularItem_formatted_df
###MOST PROFITABLE ITEMS
#Format table by " Total Purchase Value" Descending order
MostProfitableItem_formatted_df = MostPopularItem_df.sort_values(["Total Purchase Value"], ascending=False).head()
MostProfitableItem_formatted_df
#Format the table for $ sign and 2 decimals
MostProfitableItem_formatted_df["Item Price"] = MostProfitableItem_formatted_df["Item Price"].map("${:.2f}".format)
MostProfitableItem_formatted_df["Total Purchase Value"] = MostProfitableItem_formatted_df["Total Purchase Value"].map("${:.2f}".format)
MostProfitableItem_formatted_df
### WRITTEN DESCRIPTION OF 3 OBSERVABLE TRENDS BASED ON THE DATA
#1. If we look at the Age Group we observe that 46% of the total values were purchased by people in between 20 and 24 years old.
#2. If we look at the Gender Group, the Male population is taking the lead. They purchased 83% of the entire purcahses
#3. Final Critic and Oathbreaker, Last Hope of the Breaking Storm were the Most Popular and the Most Profitable games
```
|
github_jupyter
|
## TCLab Function Help

#### Connect/Disconnect
```lab = tclab.TCLab()``` Connect and create new lab object, ```lab.close()``` disconnects lab.
#### LED
```lab.LED()``` Percentage of output light for __Hot__ Light.
#### Heaters
```lab.Q1()``` and ```lab.Q2()``` Percentage of power to heaters.
#### Temperatures
```lab.T1``` and ```lab.T2``` Value of current heater tempertures in Celsius.
| **TCLab Function** | **Example** | **Description** |
| ----------- | ----------- | ----------- |
| `TCLab()` | `tclab.TCLab()` | Create new lab object and connect |
| `LED` | `lab.LED(45)` | Turn on the LED to 45%. Valid range is 0-100% |
| `Q1` | `lab.Q1(63)` | Turn on heater 1 (`Q1`) to 63%. Valid range is 0-100% |
| `Q2` | `lab.Q2(28)` | Turn on heater 2 (`Q2`) to 28%. Valid range is 0-100% |
| `T1` | `print(lab.T1)` | Read temperature 1 (`T1`) in °C. valid range is -40 to 150°C (TMP36 sensor) |
| `T2` | `print(lab.T2)` | Read temperature 2 (`T2`) in °C. with +/- 1°C accuracy (TMP36 sensor) |
| `close()` | `lab.close()` | Close serial USB connection to TCLab - not needed if using `with` to open |
### Errors

Submit an error to us at support@apmonitor.com so we can fix the problem and add it to this list. There is also a list of [troubleshooting items with frequently asked questions](https://apmonitor.com/pdc/index.php/Main/ArduinoSetup). If you get the error about already having an open connection to the TCLab, try restarting the **kernel**. Go to the top of the page to the **Kernel** tab, click it, then click restart.
### How to Run a Cell
Use the symbol to run the needed cell, left of the program. If you don't see a symbol, try selecting the cell and holding `Ctrl`, then pressing `Enter`. Another option is clicking the "Run" button at the top of the page when the cell is selected.
### Install Temperature Control Lab

This code trys to import `tclab`. If it if it fails to find the package, it installs the program with `pip`. The `pip` installation is required once to let you use the Temperature Control Lab for all of the exercises. It does not need to be installed again, even if the IPython session is restarted.
```
# install tclab
try:
import tclab
except:
# Needed to communicate through usb port
!pip install --user pyserial
# The --user is put in for accounts without admin privileges
!pip install --user tclab
# restart kernel if this doesn't import
import tclab
```
### Update Temperature Control Lab
Updates package to latest version.
```
!pip install tclab --upgrade --user
```
### Connection Check

The following code connects, reads temperatures 1 and 2, sets heaters 1 and 2, turns on the LED to 45%, and then disconnects from the TCLab. If an error is shown, try unplugging your lab and/or restarting Jupyter's kernel from the Jupyter notebook menu.
```
import tclab
lab = tclab.TCLab()
print(lab.T1,lab.T2)
lab.Q1(50); lab.Q2(40)
lab.LED(45)
lab.close()
```

Another way to connect to the TCLab is the `with` statement. The advantage of the `with` statement is that the connection automatically closes if there is a fatal error (bug) in the code and the program never reaches the `lab.close()` statement. This prevents a kernel restart to reset the USB connection to the TCLab Arduino.
```
import tclab
import time
with tclab.TCLab() as lab:
print(lab.T1,lab.T2)
lab.Q1(50); lab.Q2(40)
lab.LED(45)
```
|
github_jupyter
|
# Face Generation
In this project, you'll use generative adversarial networks to generate new images of faces.
### Get the Data
You'll be using two datasets in this project:
- MNIST
- CelebA
Since the celebA dataset is complex and you're doing GANs in a project for the first time, we want you to test your neural network on MNIST before CelebA. Running the GANs on MNIST will allow you to see how well your model trains sooner.
If you're using [FloydHub](https://www.floydhub.com/), set `data_dir` to "/input" and use the [FloydHub data ID](http://docs.floydhub.com/home/using_datasets/) "R5KrjnANiKVhLWAkpXhNBe".
```
data_dir = './data'
# FloydHub - Use with data ID "R5KrjnANiKVhLWAkpXhNBe"
data_dir = '/input'
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
helper.download_extract('mnist', data_dir)
helper.download_extract('celeba', data_dir)
```
## Explore the Data
### MNIST
As you're aware, the [MNIST](http://yann.lecun.com/exdb/mnist/) dataset contains images of handwritten digits. You can view the first number of examples by changing `show_n_images`.
```
show_n_images = 25
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
%matplotlib inline
import os
from glob import glob
from matplotlib import pyplot
mnist_images = helper.get_batch(glob(os.path.join(data_dir, 'mnist/*.jpg'))[:show_n_images], 28, 28, 'L')
pyplot.imshow(helper.images_square_grid(mnist_images, 'L'), cmap='gray')
```
### CelebA
The [CelebFaces Attributes Dataset (CelebA)](http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html) dataset contains over 200,000 celebrity images with annotations. Since you're going to be generating faces, you won't need the annotations. You can view the first number of examples by changing `show_n_images`.
```
show_n_images = 25
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
mnist_images = helper.get_batch(glob(os.path.join(data_dir, 'img_align_celeba/*.jpg'))[:show_n_images], 28, 28, 'RGB')
pyplot.imshow(helper.images_square_grid(mnist_images, 'RGB'))
```
## Preprocess the Data
Since the project's main focus is on building the GANs, we'll preprocess the data for you. The values of the MNIST and CelebA dataset will be in the range of -0.5 to 0.5 of 28x28 dimensional images. The CelebA images will be cropped to remove parts of the image that don't include a face, then resized down to 28x28.
The MNIST images are black and white images with a single [color channel](https://en.wikipedia.org/wiki/Channel_(digital_image%29) while the CelebA images have [3 color channels (RGB color channel)](https://en.wikipedia.org/wiki/Channel_(digital_image%29#RGB_Images).
## Build the Neural Network
You'll build the components necessary to build a GANs by implementing the following functions below:
- `model_inputs`
- `discriminator`
- `generator`
- `model_loss`
- `model_opt`
- `train`
### Check the Version of TensorFlow and Access to GPU
This will check to make sure you have the correct version of TensorFlow and access to a GPU
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
from distutils.version import LooseVersion
import warnings
import tensorflow as tf
# Check TensorFlow Version
assert LooseVersion(tf.__version__) >= LooseVersion('1.0'), 'Please use TensorFlow version 1.0 or newer. You are using {}'.format(tf.__version__)
print('TensorFlow Version: {}'.format(tf.__version__))
# Check for a GPU
if not tf.test.gpu_device_name():
warnings.warn('No GPU found. Please use a GPU to train your neural network.')
else:
print('Default GPU Device: {}'.format(tf.test.gpu_device_name()))
```
### Input
Implement the `model_inputs` function to create TF Placeholders for the Neural Network. It should create the following placeholders:
- Real input images placeholder with rank 4 using `image_width`, `image_height`, and `image_channels`.
- Z input placeholder with rank 2 using `z_dim`.
- Learning rate placeholder with rank 0.
Return the placeholders in the following the tuple (tensor of real input images, tensor of z data)
```
import problem_unittests as tests
def model_inputs(image_width, image_height, image_channels, z_dim):
"""
Create the model inputs
:param image_width: The input image width
:param image_height: The input image height
:param image_channels: The number of image channels
:param z_dim: The dimension of Z
:return: Tuple of (tensor of real input images, tensor of z data, learning rate)
"""
# TODO: Implement Function
input_real = tf.placeholder(tf.float32, (None, image_width, image_height, image_channels), name="input_real")
input_z = tf.placeholder(tf.float32, (None, z_dim), name="input_z")
l_rate = tf.placeholder(tf.float32, name='l_rate')
return input_real, input_z, l_rate
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_model_inputs(model_inputs)
```
### Discriminator
Implement `discriminator` to create a discriminator neural network that discriminates on `images`. This function should be able to reuse the variabes in the neural network. Use [`tf.variable_scope`](https://www.tensorflow.org/api_docs/python/tf/variable_scope) with a scope name of "discriminator" to allow the variables to be reused. The function should return a tuple of (tensor output of the generator, tensor logits of the generator).
```
def discriminator(images, reuse=False):
"""
Create the discriminator network
:param image: Tensor of input image(s)
:param reuse: Boolean if the weights should be reused
:return: Tuple of (tensor output of the discriminator, tensor logits of the discriminator)
"""
# TODO: Implement Function
alpha = 0.2
with tf.variable_scope('discriminator', reuse=reuse):
# Input layer is 28x28x3
x1 = tf.layers.conv2d(images, 64, 5, strides=2, padding='same')
relu1 = tf.maximum(alpha * x1, x1)
# 14x14x64
x2 = tf.layers.conv2d(relu1, 128, 5, strides=1, padding='same')
bn2= tf.layers.batch_normalization(x2, training=True)
relu2 = tf.maximum(alpha * bn2, bn2)
# 14x14x128
x3 = tf.layers.conv2d(relu2, 128, 5, strides=2, padding='same')
bn3= tf.layers.batch_normalization(x3, training=True)
relu3 = tf.maximum(alpha * bn3, bn3)
# 7x7x256
# Flatten it
flat = tf.reshape(relu2, (-1, 7*7*256))
logits = tf.layers.dense(flat, 1)
output = tf.sigmoid(logits)
return output, logits
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_discriminator(discriminator, tf)
```
### Generator
Implement `generator` to generate an image using `z`. This function should be able to reuse the variabes in the neural network. Use [`tf.variable_scope`](https://www.tensorflow.org/api_docs/python/tf/variable_scope) with a scope name of "generator" to allow the variables to be reused. The function should return the generated 28 x 28 x `out_channel_dim` images.
```
def generator(z, out_channel_dim, is_train=True):
"""
Create the generator network
:param z: Input z
:param out_channel_dim: The number of channels in the output image
:param is_train: Boolean if generator is being used for training
:return: The tensor output of the generator
"""
# TODO: Implement Function
alpha = 0.2
with tf.variable_scope('generator', reuse=not is_train):
# First fully connected layer
x1 = tf.layers.dense(z, 7*7*256)
# Reshape it to start the convolutional stack
x1 = tf.reshape(x1, (-1, 7, 7, 256))
x1 = tf.layers.batch_normalization(x1, training=is_train)
x1 = tf.maximum(alpha * x1, x1)
# 7x7x256 now
x2 = tf.layers.conv2d_transpose(x1, 128, 5, strides=2, padding='same')
x2 = tf.layers.batch_normalization(x2, training=is_train)
x2 = tf.maximum(alpha * x2, x2)
# 14x14x128 now
x3 = tf.layers.conv2d_transpose(x2, 64, 5, strides=2, padding='same')
x3 = tf.layers.batch_normalization(x3, training=is_train)
x3 = tf.maximum(alpha * x3, x3)
# 28x28x64 now
# Output layer
logits = tf.layers.conv2d_transpose(x3, out_channel_dim, 5, strides=1, padding='same')
# 28 x 28 x out_channel_dim
output = tf.tanh(logits)
return output
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_generator(generator, tf)
```
### Loss
Implement `model_loss` to build the GANs for training and calculate the loss. The function should return a tuple of (discriminator loss, generator loss). Use the following functions you implemented:
- `discriminator(images, reuse=False)`
- `generator(z, out_channel_dim, is_train=True)`
```
def model_loss(input_real, input_z, out_channel_dim):
"""
Get the loss for the discriminator and generator
:param input_real: Images from the real dataset
:param input_z: Z input
:param out_channel_dim: The number of channels in the output image
:return: A tuple of (discriminator loss, generator loss)
"""
# TODO: Implement Function
smooth = 0.1
g_model = generator(input_z, out_channel_dim, is_train=True)
d_model_real, d_logits_real = discriminator(input_real)
d_model_fake, d_logits_fake = discriminator(g_model, reuse=True)
d_loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real,
labels=tf.ones_like(d_model_real) * (1 - smooth)))
d_loss_fake = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, labels=tf.zeros_like(d_model_fake)))
g_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, labels=tf.ones_like(d_model_fake)))
d_loss = d_loss_real + d_loss_fake
return d_loss, g_loss
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_model_loss(model_loss)
```
### Optimization
Implement `model_opt` to create the optimization operations for the GANs. Use [`tf.trainable_variables`](https://www.tensorflow.org/api_docs/python/tf/trainable_variables) to get all the trainable variables. Filter the variables with names that are in the discriminator and generator scope names. The function should return a tuple of (discriminator training operation, generator training operation).
```
def model_opt(d_loss, g_loss, learning_rate, beta1):
"""
Get optimization operations
:param d_loss: Discriminator loss Tensor
:param g_loss: Generator loss Tensor
:param learning_rate: Learning Rate Placeholder
:param beta1: The exponential decay rate for the 1st moment in the optimizer
:return: A tuple of (discriminator training operation, generator training operation)
"""
# TODO: Implement Function
t_vars = tf.trainable_variables()
d_vars = [var for var in t_vars if var.name.startswith('discriminator')]
g_vars = [var for var in t_vars if var.name.startswith('generator')]
# Optimize
d_train_opt = tf.train.AdamOptimizer(learning_rate, beta1=beta1).minimize(d_loss, var_list=d_vars)
g_train_opt = tf.train.AdamOptimizer(learning_rate, beta1=beta1).minimize(g_loss, var_list=g_vars)
return d_train_opt, g_train_opt
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_model_opt(model_opt, tf)
```
## Neural Network Training
### Show Output
Use this function to show the current output of the generator during training. It will help you determine how well the GANs is training.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import numpy as np
def show_generator_output(sess, n_images, input_z, out_channel_dim, image_mode):
"""
Show example output for the generator
:param sess: TensorFlow session
:param n_images: Number of Images to display
:param input_z: Input Z Tensor
:param out_channel_dim: The number of channels in the output image
:param image_mode: The mode to use for images ("RGB" or "L")
"""
cmap = None if image_mode == 'RGB' else 'gray'
z_dim = input_z.get_shape().as_list()[-1]
example_z = np.random.uniform(-1, 1, size=[n_images, z_dim])
samples = sess.run(
generator(input_z, out_channel_dim, False),
feed_dict={input_z: example_z})
images_grid = helper.images_square_grid(samples, image_mode)
pyplot.imshow(images_grid, cmap=cmap)
pyplot.show()
```
### Train
Implement `train` to build and train the GANs. Use the following functions you implemented:
- `model_inputs(image_width, image_height, image_channels, z_dim)`
- `model_loss(input_real, input_z, out_channel_dim)`
- `model_opt(d_loss, g_loss, learning_rate, beta1)`
Use the `show_generator_output` to show `generator` output while you train. Running `show_generator_output` for every batch will drastically increase training time and increase the size of the notebook. It's recommended to print the `generator` output every 100 batches.
```
def train(epoch_count, batch_size, z_dim, learning_rate, beta1, get_batches, data_shape, data_image_mode):
"""
Train the GAN
:param epoch_count: Number of epochs
:param batch_size: Batch Size
:param z_dim: Z dimension
:param learning_rate: Learning Rate
:param beta1: The exponential decay rate for the 1st moment in the optimizer
:param get_batches: Function to get batches
:param data_shape: Shape of the data
:param data_image_mode: The image mode to use for images ("RGB" or "L")
"""
# TODO: Build Model
class GAN:
def __init__(self, data_shape, z_size, learning_rate, alpha=0.2, beta1=0.5):
#tf.reset_default_graph()
_, image_width, image_height, image_channels = data_shape
self.input_real, self.input_z, self.learning_rate = model_inputs(image_width, image_height,
image_channels,
z_size)
self.d_loss, self.g_loss = model_loss(self.input_real, self.input_z, image_channels)
self.d_opt, self.g_opt = model_opt(self.d_loss, self.g_loss, learning_rate, 0.5)
net = GAN(data_shape, z_dim, learning_rate, alpha=0.2, beta1=beta1)
saver = tf.train.Saver()
#sample_z = np.random.uniform(-1, 1, size=(50, z_dim))
samples, losses = [], []
batches = 0
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(epoch_count):
for batch_images in get_batches(batch_size):
batches += 1
#dataset range from -0.5 to 0.5
#batch_images = batch_images.reshape((batch_size, 784 * data_shape[3]))
batch_images = batch_images * 2
# Sample random noise for G
batch_z = np.random.uniform(-1, 1, size=(batch_size, z_dim))
# Run optimizers
_ = sess.run(net.d_opt, feed_dict={net.input_real: batch_images, net.input_z: batch_z})
_ = sess.run(net.g_opt, feed_dict={net.input_z: batch_z})
if batches % 10 == 0:
# At the end of each epoch, get the losses and print them out
train_loss_d = net.d_loss.eval({net.input_z: batch_z, net.input_real: batch_images})
train_loss_g = net.g_loss.eval({net.input_z: batch_z})
print("Epoch {}/{}...".format(e+1, epoch_count),
"Discriminator Loss: {:.4f}...".format(train_loss_d),
"Generator Loss: {:.4f}".format(train_loss_g))
# Save losses to view after training
losses.append((train_loss_d, train_loss_g))
if batches % 100 == 0:
_ = show_generator_output(sess, 16, net.input_z, data_shape[3], data_image_mode)
saver.save(sess, './checkpoints/generator.ckpt')
with open('samples.pkl', 'wb') as f:
pkl.dump(samples, f)
return losses, samples
```
### MNIST
Test your GANs architecture on MNIST. After 2 epochs, the GANs should be able to generate images that look like handwritten digits. Make sure the loss of the generator is lower than the loss of the discriminator or close to 0.
```
batch_size = 128
z_dim = 100
learning_rate = 0.0001
beta1 = 0.5
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
epochs = 2
mnist_dataset = helper.Dataset('mnist', glob(os.path.join(data_dir, 'mnist/*.jpg')))
with tf.Graph().as_default():
train(epochs, batch_size, z_dim, learning_rate, beta1, mnist_dataset.get_batches,
mnist_dataset.shape, mnist_dataset.image_mode)
```
### CelebA
Run your GANs on CelebA. It will take around 20 minutes on the average GPU to run one epoch. You can run the whole epoch or stop when it starts to generate realistic faces.
```
batch_size = 128
z_dim = 100
learning_rate = 0.0001
beta1 = 0.5
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
epochs = 1
celeba_dataset = helper.Dataset('celeba', glob(os.path.join(data_dir, 'img_align_celeba/*.jpg')))
with tf.Graph().as_default():
train(epochs, batch_size, z_dim, learning_rate, beta1, celeba_dataset.get_batches,
celeba_dataset.shape, celeba_dataset.image_mode)
```
### Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_face_generation.ipynb" and save it as a HTML file under "File" -> "Download as". Include the "helper.py" and "problem_unittests.py" files in your submission.
|
github_jupyter
|
# Modeling and Simulation in Python
Chapter 21
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
```
### With air resistance
Next we'll add air resistance using the [drag equation](https://en.wikipedia.org/wiki/Drag_equation)
I'll start by getting the units we'll need from Pint.
```
m = UNITS.meter
s = UNITS.second
kg = UNITS.kilogram
```
Now I'll create a `Params` object to contain the quantities we need. Using a Params object is convenient for grouping the system parameters in a way that's easy to read (and double-check).
```
params = Params(height = 381 * m,
v_init = 0 * m / s,
g = 9.8 * m/s**2,
mass = 2.5e-3 * kg,
diameter = 19e-3 * m,
rho = 1.2 * kg/m**3,
v_term = 18 * m / s)
```
Now we can pass the `Params` object `make_system` which computes some additional parameters and defines `init`.
`make_system` uses the given radius to compute `area` and the given `v_term` to compute the drag coefficient `C_d`.
```
def make_system(params):
"""Makes a System object for the given conditions.
params: Params object
returns: System object
"""
unpack(params)
area = np.pi * (diameter/2)**2
C_d = 2 * mass * g / (rho * area * v_term**2)
init = State(y=height, v=v_init)
t_end = 30 * s
return System(params, area=area, C_d=C_d,
init=init, t_end=t_end)
```
Let's make a `System`
```
system = make_system(params)
```
Here's the slope function, including acceleration due to gravity and drag.
```
def slope_func(state, t, system):
"""Compute derivatives of the state.
state: position, velocity
t: time
system: System object
returns: derivatives of y and v
"""
y, v = state
unpack(system)
f_drag = rho * v**2 * C_d * area / 2
a_drag = f_drag / mass
dydt = v
dvdt = -g + a_drag
return dydt, dvdt
```
As always, let's test the slope function with the initial conditions.
```
slope_func(system.init, 0, system)
```
We can use the same event function as last time.
```
def event_func(state, t, system):
"""Return the height of the penny above the sidewalk.
"""
y, v = state
return y
```
And then run the simulation.
```
results, details = run_ode_solver(system, slope_func, events=event_func)
details.message
```
Here are the results.
```
results
```
The final height is close to 0, as expected.
Interestingly, the final velocity is not exactly terminal velocity, which suggests that there are some numerical errors.
We can get the flight time from `results`.
```
t_sidewalk = get_last_label(results)
```
Here's the plot of position as a function of time.
```
def plot_position(results):
plot(results.y)
decorate(xlabel='Time (s)',
ylabel='Position (m)')
plot_position(results)
savefig('figs/chap09-fig02.pdf')
```
And velocity as a function of time:
```
def plot_velocity(results):
plot(results.v, color='C1', label='v')
decorate(xlabel='Time (s)',
ylabel='Velocity (m/s)')
plot_velocity(results)
```
From an initial velocity of 0, the penny accelerates downward until it reaches terminal velocity; after that, velocity is constant.
**Exercise:** Run the simulation with an initial velocity, downward, that exceeds the penny's terminal velocity. Hint: You can create a new `Params` object based on an existing one, like this:
`params = Params(params, v_init = -30 * m / s)`
What do you expect to happen? Plot velocity and position as a function of time, and see if they are consistent with your prediction.
```
# Solution
params = Params(params, v_init = -30 * m / s)
system = make_system(params)
results, details = run_ode_solver(system, slope_func, events=event_func)
details.message
plot_position(results)
# Solution
plot_velocity(results)
```
**Exercise:** Suppose we drop a quarter from the Empire State Building and find that its flight time is 19.1 seconds. Use this measurement to estimate the terminal velocity.
1. You can get the relevant dimensions of a quarter from https://en.wikipedia.org/wiki/Quarter_(United_States_coin).
2. Create a `Params` object with the system parameters. We don't know `v_term`, so we'll start with the inital guess `v_term = 18 * m / s`.
3. Use `make_system` to create a `System` object.
4. Call `run_ode_solver` to simulate the system. How does the flight time of the simulation compare to the measurement?
5. Try a few different values of `t_term` and see if you can get the simulated flight time close to 19.1 seconds.
6. Optionally, write an error function and use `fsolve` to improve your estimate.
7. Use your best estimate of `v_term` to compute `C_d`.
Note: I fabricated the observed flight time, so don't take the results of this exercise too seriously.
```
# Solution
# Here's a `Params` object with the dimensions of a quarter,
# the observed flight time and our initial guess for `v_term`
params = Params(params,
mass = 5.67e-3 * kg,
diameter = 24.26e-3 * m,
v_term = 18 * m / s,
flight_time = 19.1 * s)
# Solution
# Now we can make a `System` object
system = make_system(params)
# Solution
# And run the simulation
results, details = run_ode_solver(system, slope_func, events=event_func)
details
# Solution
# And get the flight time
flight_time = get_last_label(results) * s
# Solution
# The flight time is a little long, so we could increase `v_term` and try again.
# Or we could write an error function
def error_func(v_term, params):
"""Final height as a function of C_d.
C_d: drag coefficient
params: Params object
returns: height in m
"""
params = Params(params, v_term=v_term)
system = make_system(params)
results, details = run_ode_solver(system, slope_func, events=event_func)
flight_time = get_last_label(results) * s
return flight_time - params.flight_time
# Solution
# We can test the error function like this
guess = 18 * m / s
error_func(guess, params)
# Solution
# Now we can use `fsolve` to find the value of `v_term` that yields the measured flight time.
solution = fsolve(error_func, guess, params)
v_term_solution = solution[0] * m/s
# Solution
# Plugging in the estimated value, we can use `make_system` to compute `C_d`
params = Params(params, v_term=v_term_solution)
system = make_system(params)
system.C_d
```
### Bungee jumping
Suppose you want to set the world record for the highest "bungee dunk", [as shown in this video](https://www.youtube.com/watch?v=UBf7WC19lpw). Since the record is 70 m, let's design a jump for 80 m.
We'll make the following modeling assumptions:
1. Initially the bungee cord hangs from a crane with the attachment point 80 m above a cup of tea.
2. Until the cord is fully extended, it applies no force to the jumper. It turns out this might not be a good assumption; we will revisit it.
3. After the cord is fully extended, it obeys [Hooke's Law](https://en.wikipedia.org/wiki/Hooke%27s_law); that is, it applies a force to the jumper proportional to the extension of the cord beyond its resting length.
4. The jumper is subject to drag force proportional to the square of their velocity, in the opposite of their direction of motion.
Our objective is to choose the length of the cord, `L`, and its spring constant, `k`, so that the jumper falls all the way to the tea cup, but no farther!
First I'll create a `Param` object to contain the quantities we'll need:
1. Let's assume that the jumper's mass is 75 kg.
2. With a terminal velocity of 60 m/s.
3. The length of the bungee cord is `L = 40 m`.
4. The spring constant of the cord is `k = 20 N / m` when the cord is stretched, and 0 when it's compressed.
```
m = UNITS.meter
s = UNITS.second
kg = UNITS.kilogram
N = UNITS.newton
params = Params(y_attach = 80 * m,
v_init = 0 * m / s,
g = 9.8 * m/s**2,
mass = 75 * kg,
area = 1 * m**2,
rho = 1.2 * kg/m**3,
v_term = 60 * m / s,
L = 25 * m,
k = 40 * N / m)
```
Now here's a version of `make_system` that takes a `Params` object as a parameter.
`make_system` uses the given value of `v_term` to compute the drag coefficient `C_d`.
```
def make_system(params):
"""Makes a System object for the given params.
params: Params object
returns: System object
"""
unpack(params)
C_d = 2 * mass * g / (rho * area * v_term**2)
init = State(y=y_attach, v=v_init)
t_end = 30 * s
return System(params, C_d=C_d,
init=init, t_end=t_end)
```
Let's make a `System`
```
system = make_system(params)
system
```
`spring_force` computes the force of the cord on the jumper:
```
def spring_force(y, system):
"""Computes the force of the bungee cord on the jumper:
y: height of the jumper
Uses these variables from system|
y_attach: height of the attachment point
L: resting length of the cord
k: spring constant of the cord
returns: force in N
"""
unpack(system)
distance_fallen = y_attach - y
if distance_fallen <= L:
return 0 * N
extension = distance_fallen - L
f_spring = k * extension
return f_spring
```
The spring force is 0 until the cord is fully extended. When it is extended 1 m, the spring force is 40 N.
```
spring_force(80*m, system)
spring_force(55*m, system)
spring_force(54*m, system)
```
`drag_force` computes drag as a function of velocity:
```
def drag_force(v, system):
"""Computes drag force in the opposite direction of `v`.
v: velocity
returns: drag force
"""
unpack(system)
f_drag = -np.sign(v) * rho * v**2 * C_d * area / 2
return f_drag
```
Now here's the slope function:
```
def slope_func(state, t, system):
"""Compute derivatives of the state.
state: position, velocity
t: time
system: System object containing g, rho,
C_d, area, and mass
returns: derivatives of y and v
"""
y, v = state
unpack(system)
a_drag = drag_force(v, system) / mass
a_spring = spring_force(y, system) / mass
dvdt = -g + a_drag + a_spring
return v, dvdt
```
As always, let's test the slope function with the initial params.
```
slope_func(system.init, 0, system)
```
And then run the simulation.
```
ts = linspace(0, system.t_end, 301)
results, details = run_ode_solver(system, slope_func, t_eval=ts)
details
```
Here's the plot of position as a function of time.
```
plot_position(results)
```
After reaching the lowest point, the jumper springs back almost to almost 70 m, and oscillates several times. That looks like more osciallation that we expect from an actual jump, which suggests that there some dissipation of energy in the real world that is not captured in our model. To improve the model, that might be a good thing to investigate.
But since we are primarily interested in the initial descent, the model might be good enough for now.
We can use `min` to find the lowest point:
```
min(results.y)
```
At the lowest point, the jumper is still too high, so we'll need to increase `L` or decrease `k`.
Here's velocity as a function of time:
```
plot_velocity(results)
subplot(1, 2, 1)
plot_position(results)
subplot(1, 2, 2)
plot_velocity(results)
savefig('figs/chap09-fig03.pdf')
```
Although we compute acceleration inside the slope function, we don't get acceleration as a result from `run_ode_solver`.
We can approximate it by computing the numerical derivative of `ys`:
```
a = gradient(results.v)
plot(a)
decorate(xlabel='Time (s)',
ylabel='Acceleration (m/$s^2$)')
```
And we can compute the maximum acceleration the jumper experiences:
```
max_acceleration = max(a) * m/s**2
```
Relative to the acceleration of gravity, the jumper "pulls" about "1.7 g's".
```
max_acceleration / g
```
### Solving for length
Assuming that `k` is fixed, let's find the length `L` that makes the minimum altitude of the jumper exactly 0.
Here's the error function:
```
def error_func(L, params):
"""Minimum height as a function of length.
length: length in m
params: Params object
returns: height in m
"""
params = Params(params, L=L)
system = make_system(params)
ts = linspace(0, system.t_end, 201)
results, details = run_ode_solver(system, slope_func, t_eval=ts)
min_height = min(results.y)
return min_height
```
Let's test it with the same initial guess, `L = 100 m`:
```
guess = 150 * m
error_func(guess, params)
```
And find the value of `L` we need for the world record jump:
```
solution = fsolve(error_func, guess, params)
```
**Optional:** Search for the combination of length and spring constant that yields minimum height 0 while minimizing peak acceleration.
```
# Solution
ks = np.linspace(1, 31, 11) * N / m
for k in ks:
guess = 250 * m
params = Params(params, k=k)
solution = fsolve(error_func, guess, params)
L = solution[0] * m
params = Params(params, L=L)
system = make_system(params)
results, details = run_ode_solver(system, slope_func, t_eval=ts)
a = gradient(results.v)
g_max = max(a) * m/s**2 / g
print(k, L, g_max)
```
**Optional exercise:** This model neglects the weight of the bungee cord, which might be non-negligible. Implement the [model described here](http://iopscience.iop.org/article/10.1088/0031-9120/45/1/007) and see how different it is from our simplified model.
### Under the hood
The gradient function in `modsim.py` adapts the NumPy function of the same name so it works with `Series` objects.
```
%psource gradient
```
|
github_jupyter
|
**Important**: This notebook is different from the other as it directly calls **ImageJ Kappa plugin** using the [`scyjava` ImageJ brige](https://github.com/scijava/scyjava).
Since Kappa uses ImageJ1 features, you might not be able to run this notebook on an headless machine (need to be tested).
```
from pathlib import Path
import pandas as pd
import numpy as np
from tqdm.auto import tqdm
import sys; sys.path.append("../../")
import pykappa
# Init ImageJ with Fiji plugins
# It can take a while if Java artifacts are not yet cached.
import imagej
java_deps = []
java_deps.append('org.scijava:Kappa:1.7.1')
ij = imagej.init("+".join(java_deps), headless=False)
import jnius
# Load Java classes
KappaFrame = jnius.autoclass('sc.fiji.kappa.gui.KappaFrame')
CurvesExporter = jnius.autoclass('sc.fiji.kappa.gui.CurvesExporter')
# Load ImageJ services
dsio = ij.context.getService(jnius.autoclass('io.scif.services.DatasetIOService'))
dsio = jnius.cast('io.scif.services.DatasetIOService', dsio)
# Set data path
data_dir = Path("/home/hadim/.data/Postdoc/Kappa/spiral_curve_SDM/")
# Pixel size used when fixed
fixed_pixel_size = 0.16
# Used to select pixels around the initialization curves
base_radius_um = 1.6
enable_control_points_adjustment = True
# "Point Distance Minimization" or "Squared Distance Minimization"
if '_SDM' in data_dir.name:
fitting_algorithm = "Squared Distance Minimization"
else:
fitting_algorithm = "Point Distance Minimization"
fitting_algorithm
experiment_names = ['variable_snr', 'variable_initial_position', 'variable_pixel_size', 'variable_psf_size']
experiment_names = ['variable_psf_size']
for experiment_name in tqdm(experiment_names, total=len(experiment_names)):
experiment_path = data_dir / experiment_name
fnames = sorted(list(experiment_path.glob("*.tif")))
n = len(fnames)
for fname in tqdm(fnames, total=n, leave=False):
tqdm.write(str(fname))
kappa_path = fname.with_suffix(".kapp")
assert kappa_path.exists(), f'{kappa_path} does not exist.'
curvatures_path = fname.with_suffix(".csv")
if not curvatures_path.is_file():
frame = KappaFrame(ij.context)
frame.getKappaMenubar().openImageFile(str(fname))
frame.resetCurves()
frame.getKappaMenubar().loadCurveFile(str(kappa_path))
frame.getCurves().setAllSelected()
# Compute threshold according to the image
dataset = dsio.open(str(fname))
mean = ij.op().stats().mean(dataset).getRealDouble()
std = ij.op().stats().stdDev(dataset).getRealDouble()
threshold = int(mean + std * 2)
# Used fixed pixel size or the one in the filename
if fname.stem.startswith('pixel_size'):
pixel_size = float(fname.stem.split("_")[-2])
if experiment_name == 'variable_psf_size':
pixel_size = 0.01
else:
pixel_size = fixed_pixel_size
base_radius = int(np.round(base_radius_um / pixel_size))
# Set curve fitting parameters
frame.setEnableCtrlPtAdjustment(enable_control_points_adjustment)
frame.setFittingAlgorithm(fitting_algorithm)
frame.getInfoPanel().thresholdRadiusSpinner.setValue(ij.py.to_java(base_radius))
frame.getInfoPanel().thresholdSlider.setValue(threshold)
frame.getInfoPanel().updateConversionField(str(pixel_size))
# Fit the curves
frame.fitCurves()
# Save fitted curves
frame.getKappaMenubar().saveCurveFile(str(fname.with_suffix(".FITTED.kapp")))
# Export results
exporter = CurvesExporter(frame)
exporter.exportToFile(str(curvatures_path), False)
# Remove duplicate rows during CSV export.
# See https://github.com/brouhardlab/Kappa/issues/12
df = pd.read_csv(curvatures_path)
df = df.drop_duplicates()
df.to_csv(curvatures_path)
0.13**2
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content-dl/blob/main/tutorials/W1D1_BasicsAndPytorch/student/W1D1_Tutorial1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Tutorial 1: PyTorch
**Week 1, Day 1: Basics and PyTorch**
**By Neuromatch Academy**
__Content creators:__ Shubh Pachchigar, Vladimir Haltakov, Matthew Sargent, Konrad Kording
__Content reviewers:__ Deepak Raya, Siwei Bai, Kelson Shilling-Scrivo
__Content editors:__ Anoop Kulkarni, Spiros Chavlis
__Production editors:__ Arush Tagade, Spiros Chavlis
**Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs**
<p align='center'><img src='https://github.com/NeuromatchAcademy/widgets/blob/master/sponsors.png?raw=True'/></p>
---
# Tutorial Objectives
Then have a few specific objectives for this tutorial:
* Learn about PyTorch and tensors
* Tensor Manipulations
* Data Loading
* GPUs and Cuda Tensors
* Train NaiveNet
* Get to know your pod
* Start thinking about the course as a whole
```
# @title Tutorial slides
# @markdown These are the slides for the videos in this tutorial today
from IPython.display import IFrame
IFrame(src=f"https://mfr.ca-1.osf.io/render?url=https://osf.io/wcjrv/?direct%26mode=render%26action=download%26mode=render", width=854, height=480)
```
---
# Setup
Throughout your Neuromatch tutorials, most (probably all!) notebooks contain setup cells. These cells will import the required Python packages (e.g., PyTorch, NumPy); set global or environment variables, and load in helper functions for things like plotting. In some tutorials, you will notice that we install some dependencies even if they are preinstalled on google colab or kaggle. This happens because we have added automation to our repository through [GitHub Actions](https://docs.github.com/en/actions/learn-github-actions/introduction-to-github-actions).
Be sure to run all of the cells in the setup section. Feel free to expand them and have a look at what you are loading in, but you should be able to fulfill the learning objectives of every tutorial without having to look at these cells.
If you start building your own projects built on this code base we highly recommend looking at them in more detail.
```
# @title Install dependencies
!pip install pandas --quiet
!pip install git+https://github.com/NeuromatchAcademy/evaltools --quiet
from evaltools.airtable import AirtableForm
# Imports
import time
import torch
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from torch import nn
from torchvision import datasets
from torchvision.transforms import ToTensor
from torch.utils.data import DataLoader
# @title Figure Settings
import ipywidgets as widgets
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/content-creation/main/nma.mplstyle")
# @title Helper Functions
atform = AirtableForm('appn7VdPRseSoMXEG','W1D1_T1','https://portal.neuromatchacademy.org/api/redirect/to/97e94a29-0b3a-4e16-9a8d-f6838a5bd83d')
def checkExercise1(A, B, C, D):
"""
Helper function for checking exercise.
Args:
A: torch.Tensor
B: torch.Tensor
C: torch.Tensor
D: torch.Tensor
Returns:
Nothing.
"""
errors = []
# TODO better errors and error handling
if not torch.equal(A.to(int),torch.ones(20, 21).to(int)):
errors.append(f"Got: {A} \n Expected: {torch.ones(20, 21)} (shape: {torch.ones(20, 21).shape})")
if not np.array_equal( B.numpy(),np.vander([1, 2, 3], 4)):
errors.append("B is not a tensor containing the elements of Z ")
if C.shape != (20, 21):
errors.append("C is not the correct shape ")
if not torch.equal(D, torch.arange(4, 41, step=2)):
errors.append("D does not contain the correct elements")
if errors == []:
print("All correct!")
else:
[print(e) for e in errors]
def timeFun(f, dim, iterations, device='cpu'):
iterations = iterations
t_total = 0
for _ in range(iterations):
start = time.time()
f(dim, device)
end = time.time()
t_total += end - start
if device == 'cpu':
print(f"time taken for {iterations} iterations of {f.__name__}({dim}, {device}): {t_total:.5f}")
else:
print(f"time taken for {iterations} iterations of {f.__name__}({dim}, {device}): {t_total:.5f}")
```
**Important note: Google Colab users**
*Scratch Code Cells*
If you want to quickly try out something or take a look at the data you can use scratch code cells. They allow you to run Python code, but will not mess up the structure of your notebook.
To open a new scratch cell go to *Insert* → *Scratch code cell*.
# Section 1: Welcome to Neuromatch Deep learning course
*Time estimate: ~25mins*
```
# @title Video 1: Welcome and History
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Av411n7oL", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"ca21SNqt78I", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing
atform.add_event('Video 1: Welcome and History')
display(out)
```
*This will be an intensive 3 week adventure. We will all learn Deep Learning. In a group. Groups need standards. Read our
[Code of Conduct](https://docs.google.com/document/d/1eHKIkaNbAlbx_92tLQelXnicKXEcvFzlyzzeWjEtifM/edit?usp=sharing).
```
# @title Video 2: Why DL is cool
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1gf4y1j7UZ", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"l-K6495BN-4", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 2: Why DL is cool')
display(out)
```
**Describe what you hope to get out of this course in about 100 words.**
---
# Section 2: The Basics of PyTorch
*Time estimate: ~2 hours 05 mins*
PyTorch is a Python-based scientific computing package targeted at two sets of
audiences:
- A replacement for NumPy to use the power of GPUs
- A deep learning platform that provides significant flexibility
and speed
At its core, PyTorch provides a few key features:
- A multidimensional [Tensor](https://pytorch.org/docs/stable/tensors.html) object, similar to [NumPy Array](https://numpy.org/doc/stable/reference/generated/numpy.ndarray.html) but with GPU acceleration.
- An optimized **autograd** engine for automatically computing derivatives.
- A clean, modular API for building and deploying **deep learning models**.
You can find more information about PyTorch in the appendix.
## Section 2.1: Creating Tensors
```
# @title Video 3: Making Tensors
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Rw411d7Uy", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"jGKd_4tPGrw", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 3: Making Tensors')
display(out)
```
There are various ways of creating tensors, and when doing any real deep learning project we will usually have to do so.
**Construct tensors directly:**
---
```
# we can construct a tensor directly from some common python iterables,
# such as list and tuple nested iterables can also be handled as long as the
# dimensions make sense
# tensor from a list
a = torch.tensor([0, 1, 2])
#tensor from a tuple of tuples
b = ((1.0, 1.1), (1.2, 1.3))
b = torch.tensor(b)
# tensor from a numpy array
c = np.ones([2, 3])
c = torch.tensor(c)
print(f"Tensor a: {a}")
print(f"Tensor b: {b}")
print(f"Tensor c: {c}")
```
**Some common tensor constructors:**
---
```
# the numerical arguments we pass to these constructors
# determine the shape of the output tensor
x = torch.ones(5, 3)
y = torch.zeros(2)
z = torch.empty(1, 1, 5)
print(f"Tensor x: {x}")
print(f"Tensor y: {y}")
print(f"Tensor z: {z}")
```
Notice that ```.empty()``` does not return zeros, but seemingly random small numbers. Unlike ```.zeros()```, which initialises the elements of the tensor with zeros, ```.empty()``` just allocates the memory. It is hence a bit faster if you are looking to just create a tensor.
**Creating random tensors and tensors like other tensors:**
---
```
# there are also constructors for random numbers
# uniform distribution
a = torch.rand(1, 3)
# normal distribution
b = torch.randn(3, 4)
# there are also constructors that allow us to construct
# a tensor according to the above constructors, but with
# dimensions equal to another tensor
c = torch.zeros_like(a)
d = torch.rand_like(c)
print(f"Tensor a: {a}")
print(f"Tensor b: {b}")
print(f"Tensor c: {c}")
print(f"Tensor d: {d}")
```
*Reproducibility*:
- PyTorch random number generator: You can use `torch.manual_seed()` to seed the RNG for all devices (both CPU and CUDA)
```python
import torch
torch.manual_seed(0)
```
- For custom operators, you might need to set python seed as well:
```python
import random
random.seed(0)
```
- Random number generators in other libraries
```python
import numpy as np
np.random.seed(0)
```
Here, we define for you a function called `set_seed` that does the job for you!
```
def set_seed(seed=None, seed_torch=True):
"""
Function that controls randomness. NumPy and random modules must be imported.
Args:
seed : Integer
A non-negative integer that defines the random state. Default is `None`.
seed_torch : Boolean
If `True` sets the random seed for pytorch tensors, so pytorch module
must be imported. Default is `True`.
Returns:
Nothing.
"""
if seed is None:
seed = np.random.choice(2 ** 32)
random.seed(seed)
np.random.seed(seed)
if seed_torch:
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
print(f'Random seed {seed} has been set.')
```
Now, let's use the `set_seed` function in the previous example. Execute the cell multiple times to verify that the numbers printed are always the same.
```
def simplefun(seed=True, my_seed=None):
if seed:
set_seed(seed=my_seed)
# uniform distribution
a = torch.rand(1, 3)
# normal distribution
b = torch.randn(3, 4)
print("Tensor a: ", a)
print("Tensor b: ", b)
simplefun(seed=True, my_seed=0) # Turn `seed` to `False` or change `my_seed`
```
**Numpy-like number ranges:**
---
The ```.arange()``` and ```.linspace()``` behave how you would expect them to if you are familar with numpy.
```
a = torch.arange(0, 10, step=1)
b = np.arange(0, 10, step=1)
c = torch.linspace(0, 5, steps=11)
d = np.linspace(0, 5, num=11)
print(f"Tensor a: {a}\n")
print(f"Numpy array b: {b}\n")
print(f"Tensor c: {c}\n")
print(f"Numpy array d: {d}\n")
```
### Coding Exercise 2.1: Creating Tensors
Below you will find some incomplete code. Fill in the missing code to construct the specified tensors.
We want the tensors:
$A:$ 20 by 21 tensor consisting of ones
$B:$ a tensor with elements equal to the elements of numpy array $Z$
$C:$ a tensor with the same number of elements as $A$ but with values $
\sim U(0,1)$
$D:$ a 1D tensor containing the even numbers between 4 and 40 inclusive.
```
def tensor_creation(Z):
"""A function that creates various tensors.
Args:
Z (numpy.ndarray): An array of shape
Returns:
A : 20 by 21 tensor consisting of ones
B : a tensor with elements equal to the elements of numpy array Z
C : a tensor with the same number of elements as A but with values ∼U(0,1)
D : a 1D tensor containing the even numbers between 4 and 40 inclusive.
"""
#################################################
## TODO for students: fill in the missing code
## from the first expression
raise NotImplementedError("Student exercise: say what they should have done")
#################################################
A = ...
B = ...
C = ...
D = ...
return A, B, C, D
# add timing to airtable
atform.add_event('Coding Exercise 2.1: Creating Tensors')
# numpy array to copy later
Z = np.vander([1, 2, 3], 4)
# Uncomment below to check your function!
# A, B, C, D = tensor_creation(Z)
# checkExercise1(A, B, C, D)
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_ad4f6c0f.py)
```
All correct!
```
## Section 2.2: Operations in PyTorch
**Tensor-Tensor operations**
We can perform operations on tensors using methods under ```torch.```
```
# @title Video 4: Tensor Operators
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1G44y127As", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"R1R8VoYXBVA", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 4: Tensor Operators')
display(out)
```
**Tensor-Tensor operations**
We can perform operations on tensors using methods under ```torch.```
```
a = torch.ones(5, 3)
b = torch.rand(5, 3)
c = torch.empty(5, 3)
d = torch.empty(5, 3)
# this only works if c and d already exist
torch.add(a, b, out=c)
#Pointwise Multiplication of a and b
torch.multiply(a, b, out=d)
print(c)
print(d)
```
However, in PyTorch most common Python operators are overridden.
The common standard arithmetic operators (+, -, *, /, and **) have all been lifted to elementwise operations
```
x = torch.tensor([1, 2, 4, 8])
y = torch.tensor([1, 2, 3, 4])
x + y, x - y, x * y, x / y, x**y # The ** operator is exponentiation
```
**Tensor Methods**
Tensors also have a number of common arithmetic operations built in. A full list of **all** methods can be found in the appendix (there are a lot!)
All of these operations should have similar syntax to their numpy equivalents.(Feel free to skip if you already know this!)
```
x = torch.rand(3, 3)
print(x)
print("\n")
# sum() - note the axis is the axis you move across when summing
print(f"Sum of every element of x: {x.sum()}")
print(f"Sum of the columns of x: {x.sum(axis=0)}")
print(f"Sum of the rows of x: {x.sum(axis=1)}")
print("\n")
print(f"Mean value of all elements of x {x.mean()}")
print(f"Mean values of the columns of x {x.mean(axis=0)}")
print(f"Mean values of the rows of x {x.mean(axis=1)}")
```
**Matrix Operations**
The ```@``` symbol is overridden to represent matrix multiplication. You can also use ```torch.matmul()``` to multiply tensors. For dot multiplication, you can use ```torch.dot()```, or manipulate the axes of your tensors and do matrix multiplication (we will cover that in the next section).
Transposes of 2D tensors are obtained using ```torch.t()``` or ```Tensor.T```. Note the lack of brackets for ```Tensor.T``` - it is an attribute, not a method.
### Coding Exercise 2.2 : Simple tensor operations
Below are two expressions involving operations on matrices.
$$ \textbf{A} =
\begin{bmatrix}2 &4 \\5 & 7
\end{bmatrix}
\begin{bmatrix} 1 &1 \\2 & 3
\end{bmatrix}
+
\begin{bmatrix}10 & 10 \\ 12 & 1
\end{bmatrix}
$$
and
$$ b =
\begin{bmatrix} 3 \\ 5 \\ 7
\end{bmatrix} \cdot
\begin{bmatrix} 2 \\ 4 \\ 8
\end{bmatrix}
$$
The code block below that computes these expressions using PyTorch is incomplete - fill in the missing lines.
```
def simple_operations(a1: torch.Tensor, a2: torch.Tensor, a3: torch.Tensor):
################################################
## TODO for students: complete the first computation using the argument matricies
raise NotImplementedError("Student exercise: fill in the missing code to complete the operation")
################################################
# multiplication of tensor a1 with tensor a2 and then add it with tensor a3
answer = ...
return answer
# add timing to airtable
atform.add_event('Coding Exercise 2.2 : Simple tensor operations-simple_operations')
# Computing expression 1:
# init our tensors
a1 = torch.tensor([[2, 4], [5, 7]])
a2 = torch.tensor([[1, 1], [2, 3]])
a3 = torch.tensor([[10, 10], [12, 1]])
## uncomment to test your function
# A = simple_operations(a1, a2, a3)
# print(A)
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_5562ea1d.py)
```
tensor([[20, 24],
[31, 27]])
```
```
def dot_product(b1: torch.Tensor, b2: torch.Tensor):
###############################################
## TODO for students: complete the first computation using the argument matricies
raise NotImplementedError("Student exercise: fill in the missing code to complete the operation")
###############################################
# Use torch.dot() to compute the dot product of two tensors
product = ...
return product
# add timing to airtable
atform.add_event('Coding Exercise 2.2 : Simple tensor operations-dot_product')
# Computing expression 2:
b1 = torch.tensor([3, 5, 7])
b2 = torch.tensor([2, 4, 8])
## Uncomment to test your function
# b = dot_product(b1, b2)
# print(b)
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_00491ea4.py)
```
tensor(82)
```
## Section 2.3 Manipulating Tensors in Pytorch
```
# @title Video 5: Tensor Indexing
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1BM4y1K7pD", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"0d0KSJ3lJbg", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 5: Tensor Indexing')
display(out)
```
**Indexing**
Just as in numpy, elements in a tensor can be accessed by index. As in any numpy array, the first element has index 0 and ranges are specified to include the first but before the last element. We can access elements according to their relative position to the end of the list by using negative indices. Indexing is also referred to as slicing.
For example, [-1] selects the last element; [1:3] selects the second and the third elements, and [:-2] will select all elements excluding the last and second-to-last elements.
```
x = torch.arange(0, 10)
print(x)
print(x[-1])
print(x[1:3])
print(x[:-2])
```
When we have multidimensional tensors, indexing rules work the same way as numpy.
```
# make a 5D tensor
x = torch.rand(1, 2, 3, 4, 5)
print(f" shape of x[0]:{x[0].shape}")
print(f" shape of x[0][0]:{x[0][0].shape}")
print(f" shape of x[0][0][0]:{x[0][0][0].shape}")
```
**Flatten and reshape**
There are various methods for reshaping tensors. It is common to have to express 2D data in 1D format. Similarly, it is also common to have to reshape a 1D tensor into a 2D tensor. We can achieve this with the ```.flatten()``` and ```.reshape()``` methods.
```
z = torch.arange(12).reshape(6, 2)
print(f"Original z: \n {z}")
# 2D -> 1D
z = z.flatten()
print(f"Flattened z: \n {z}")
# and back to 2D
z = z.reshape(3, 4)
print(f"Reshaped (3x4) z: \n {z}")
```
You will also see the ```.view()``` methods used a lot to reshape tensors. There is a subtle difference between ```.view()``` and ```.reshape()```, though for now we will just use ```.reshape()```. The documentation can be found in the appendix.
**Squeezing tensors**
When processing batches of data, you will quite often be left with singleton dimensions. e.g. [1,10] or [256, 1, 3]. This dimension can quite easily mess up your matrix operations if you don't plan on it being there...
In order to compress tensors along their singleton dimensions we can use the ```.squeeze()``` method. We can use the ```.unsqueeze()``` method to do the opposite.
```
x = torch.randn(1, 10)
# printing the zeroth element of the tensor will not give us the first number!
print(x.shape)
print(f"x[0]: {x[0]}")
```
Because of that pesky singleton dimension, x[0] gave us the first row instead!
```
# lets get rid of that singleton dimension and see what happens now
x = x.squeeze(0)
print(x.shape)
print(f"x[0]: {x[0]}")
# adding singleton dimensions works a similar way, and is often used when tensors
# being added need same number of dimensions
y = torch.randn(5, 5)
print(f"shape of y: {y.shape}")
# lets insert a singleton dimension
y = y.unsqueeze(1)
print(f"shape of y: {y.shape}")
```
**Permutation**
Sometimes our dimensions will be in the wrong order! For example, we may be dealing with RGB images with dim [3x48x64], but our pipeline expects the colour dimension to be the last dimension i.e. [48x64x3]. To get around this we can use ```.permute()```
```
# `x` has dimensions [color,image_height,image_width]
x = torch.rand(3, 48, 64)
# we want to permute our tensor to be [ image_height , image_width , color ]
x = x.permute(1, 2, 0)
# permute(1,2,0) means:
# the 0th dim of my new tensor = the 1st dim of my old tensor
# the 1st dim of my new tensor = the 2nd
# the 2nd dim of my new tensor = the 0th
print(x.shape)
```
You may also see ```.transpose()``` used. This works in a similar way as permute, but can only swap two dimensions at once.
**Concatenation**
In this example, we concatenate two matrices along rows (axis 0, the first element of the shape) vs. columns (axis 1, the second element of the shape). We can see that the first output tensor’s axis-0 length ( 6 ) is the sum of the two input tensors’ axis-0 lengths ( 3+3 ); while the second output tensor’s axis-1 length ( 8 ) is the sum of the two input tensors’ axis-1 lengths ( 4+4 ).
```
# Create two tensors of the same shape
x = torch.arange(12, dtype=torch.float32).reshape((3, 4))
y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
#concatenate them along rows
cat_rows = torch.cat((x, y), dim=0)
# concatenate along columns
cat_cols = torch.cat((x, y), dim=1)
# printing outputs
print('Concatenated by rows: shape{} \n {}'.format(list(cat_rows.shape), cat_rows))
print('\n Concatenated by colums: shape{} \n {}'.format(list(cat_cols.shape), cat_cols))
```
**Conversion to Other Python Objects**
Converting to a NumPy tensor, or vice versa, is easy. The converted result does not share memory. This minor inconvenience is actually quite important: when you perform operations on the CPU or on GPUs, you do not want to halt computation, waiting to see whether the NumPy package of Python might want to be doing something else with the same chunk of memory.
When converting to a numpy array, the information being tracked by the tensor will be lost i.e. the computational graph. This will be covered in detail when you are introduced to autograd tomorrow!
```
x = torch.randn(5)
print(f"x: {x} | x type: {x.type()}")
y = x.numpy()
print(f"y: {y} | y type: {type(y)}")
z = torch.tensor(y)
print(f"z: {z} | z type: {z.type()}")
```
To convert a size-1 tensor to a Python scalar, we can invoke the item function or Python’s built-in functions.
```
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
```
### Coding Exercise 2.3: Manipulating Tensors
Using a combination of the methods discussed above, complete the functions below.
**Function A**
This function takes in two 2D tensors $A$ and $B$ and returns the column sum of A multiplied by the sum of all the elmements of $B$ i.e. a scalar, e.g.,:
$ A = \begin{bmatrix}
1 & 1 \\
1 & 1
\end{bmatrix} \,$
and
$ B = \begin{bmatrix}
1 & 2 & 3\\
1 & 2 & 3
\end{bmatrix} \,$
so
$ \, Out = \begin{bmatrix} 2 & 2 \\
\end{bmatrix} \cdot 12 = \begin{bmatrix}
24 & 24\\
\end{bmatrix}$
**Function B**
This function takes in a square matrix $C$ and returns a 2D tensor consisting of a flattened $C$ with the index of each element appended to this tensor in the row dimension, e.g.,:
$ C = \begin{bmatrix}
2 & 3 \\
-1 & 10
\end{bmatrix} \,$
so
$ \, Out = \begin{bmatrix}
0 & 2 \\
1 & 3 \\
2 & -1 \\
3 & 10
\end{bmatrix}$
**Hint:** pay close attention to singleton dimensions
**Function C**
This function takes in two 2D tensors $D$ and $E$. If the dimensions allow it, this function returns the elementwise sum of $D$-shaped $E$, and $D$; else this function returns a 1D tensor that is the concatenation of the two tensors, e.g.,:
$ D = \begin{bmatrix}
1 & -1 \\
-1 & 3
\end{bmatrix} \,$
and
$ E = \begin{bmatrix}
2 & 3 & 0 & 2 \\
\end{bmatrix} \, $
so
$ \, Out = \begin{bmatrix}
3 & 2 \\
-1 & 5
\end{bmatrix}$
$ D = \begin{bmatrix}
1 & -1 \\
-1 & 3
\end{bmatrix}$
and
$ \, E = \begin{bmatrix}
2 & 3 & 0 \\
\end{bmatrix} \,$
so
$ \, Out = \begin{bmatrix}
1 & -1 & -1 & 3 & 2 & 3 & 0
\end{bmatrix}$
**Hint:** `torch.numel()` is an easy way of finding the number of elements in a tensor
```
def functionA(my_tensor1, my_tensor2):
"""
This function takes in two 2D tensors `my_tensor1` and `my_tensor2`
and returns the column sum of
`my_tensor1` multiplied by the sum of all the elmements of `my_tensor2`,
i.e., a scalar.
Args:
my_tensor1: torch.Tensor
my_tensor2: torch.Tensor
Retuns:
output: torch.Tensor
The multiplication of the column sum of `my_tensor1` by the sum of
`my_tensor2`.
"""
################################################
## TODO for students: complete functionA
raise NotImplementedError("Student exercise: complete function A")
################################################
# TODO multiplication the sum of the tensors
output = ...
return output
def functionB(my_tensor):
"""
This function takes in a square matrix `my_tensor` and returns a 2D tensor
consisting of a flattened `my_tensor` with the index of each element
appended to this tensor in the row dimension.
Args:
my_tensor: torch.Tensor
Retuns:
output: torch.Tensor
Concatenated tensor.
"""
################################################
## TODO for students: complete functionB
raise NotImplementedError("Student exercise: complete function B")
################################################
# TODO flatten the tensor `my_tensor`
my_tensor = ...
# TODO create the idx tensor to be concatenated to `my_tensor`
idx_tensor = ...
# TODO concatenate the two tensors
output = ...
return output
def functionC(my_tensor1, my_tensor2):
"""
This function takes in two 2D tensors `my_tensor1` and `my_tensor2`.
If the dimensions allow it, it returns the
elementwise sum of `my_tensor1`-shaped `my_tensor2`, and `my_tensor2`;
else this function returns a 1D tensor that is the concatenation of the
two tensors.
Args:
my_tensor1: torch.Tensor
my_tensor2: torch.Tensor
Retuns:
output: torch.Tensor
Concatenated tensor.
"""
################################################
## TODO for students: complete functionB
raise NotImplementedError("Student exercise: complete function C")
################################################
# TODO check we can reshape `my_tensor2` into the shape of `my_tensor1`
if ...:
# TODO reshape `my_tensor2` into the shape of `my_tensor1`
my_tensor2 = ...
# TODO sum the two tensors
output = ...
else:
# TODO flatten both tensors
my_tensor1 = ...
my_tensor2 = ...
# TODO concatenate the two tensors in the correct dimension
output = ...
return output
# add timing to airtable
atform.add_event('Coding Exercise 2.3: Manipulating Tensors')
## Implement the functions above and then uncomment the following lines to test your code
# print(functionA(torch.tensor([[1, 1], [1, 1]]), torch.tensor([[1, 2, 3], [1, 2, 3]])))
# print(functionB(torch.tensor([[2, 3], [-1, 10]])))
# print(functionC(torch.tensor([[1, -1], [-1, 3]]), torch.tensor([[2, 3, 0, 2]])))
# print(functionC(torch.tensor([[1, -1], [-1, 3]]), torch.tensor([[2, 3, 0]])))
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_ea1718cb.py)
```
tensor([24, 24])
tensor([[ 0, 2],
[ 1, 3],
[ 2, -1],
[ 3, 10]])
tensor([[ 3, 2],
[-1, 5]])
tensor([ 1, -1, -1, 3, 2, 3, 0])
```
## Section 2.4: GPUs
```
# @title Video 6: GPU vs CPU
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1nM4y1K7qx", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"9Mc9GFUtILY", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 6: GPU vs CPU')
display(out)
```
By default, when we create a tensor it will *not* live on the GPU!
```
x = torch.randn(10)
print(x.device)
```
When using Colab notebooks by default will not have access to a GPU. In order to start using GPUs we need to request one. We can do this by going to the runtime tab at the top of the page.
By following Runtime -> Change runtime type and selecting "GPU" from the Hardware Accelerator dropdown list, we can start playing with sending tensors to GPUs.
Once you have done this your runtime will restart and you will need to rerun the first setup cell to reimport PyTorch. Then proceed to the next cell.
(For more information on the GPU usage policy you can view in the appendix)
**Now we have a GPU**
The cell below should return True.
```
print(torch.cuda.is_available())
```
CUDA is an API developed by Nvidia for interfacing with GPUs. PyTorch provides us with a layer of abstraction, and allows us to launch CUDA kernels using pure Python. *NOTE I am assuming that GPU stuff might be covered in more detail on another day but there could be a bit more detail here.*
In short, we get the power of parallising our tensor computations on GPUs, whilst only writing (relatively) simple Python!
Here, we define the function `set_device`, which returns the device use in the notebook, i.e., `cpu` or `cuda`. Unless otherwise specified, we use this function on top of every tutorial, and we store the device variable such as
```python
DEVICE = set_device()
```
Let's define the function using the PyTorch package `torch.cuda`, which is lazily initialized, so we can always import it, and use `is_available()` to determine if our system supports CUDA.
```
def set_device():
device = "cuda" if torch.cuda.is_available() else "cpu"
if device != "cuda":
print("GPU is not enabled in this notebook. \n"
"If you want to enable it, in the menu under `Runtime` -> \n"
"`Hardware accelerator.` and select `GPU` from the dropdown menu")
else:
print("GPU is enabled in this notebook. \n"
"If you want to disable it, in the menu under `Runtime` -> \n"
"`Hardware accelerator.` and select `None` from the dropdown menu")
return device
```
Let's make some CUDA tensors!
```
# common device agnostic way of writing code that can run on cpu OR gpu
# that we provide for you in each of the tutorials
DEVICE = set_device()
# we can specify a device when we first create our tensor
x = torch.randn(2, 2, device=DEVICE)
print(x.dtype)
print(x.device)
# we can also use the .to() method to change the device a tensor lives on
y = torch.randn(2, 2)
print(f"y before calling to() | device: {y.device} | dtype: {y.type()}")
y = y.to(DEVICE)
print(f"y after calling to() | device: {y.device} | dtype: {y.type()}")
```
**Operations between cpu tensors and cuda tensors**
Note that the type of the tensor changed after calling ```.to()```. What happens if we try and perform operations on tensors on devices?
```
x = torch.tensor([0, 1, 2], device=DEVICE)
y = torch.tensor([3, 4, 5], device="cpu")
# Uncomment the following line and run this cell
# z = x + y
```
We cannot combine cuda tensors and cpu tensors in this fashion. If we want to compute an operation that combines tensors on different devices, we need to move them first! We can use the `.to()` method as before, or the `.cpu()` and `.cuda()` methods. Note that using the `.cuda()` will throw an error if CUDA is not enabled in your machine.
Genrally in this course all Deep learning is done on the GPU and any computation is done on the CPU, so sometimes we have to pass things back and forth so you'll see us call.
```
x = torch.tensor([0, 1, 2], device=DEVICE)
y = torch.tensor([3, 4, 5], device="cpu")
z = torch.tensor([6, 7, 8], device=DEVICE)
# moving to cpu
x = x.to("cpu") # alternatively, you can use x = x.cpu()
print(x + y)
# moving to gpu
y = y.to(DEVICE) # alternatively, you can use y = y.cuda()
print(y + z)
```
### Coding Exercise 2.4: Just how much faster are GPUs?
Below is a simple function `simpleFun`. Complete this function, such that it performs the operations:
- elementwise multiplication
- matrix multiplication
The operations should be able to perfomed on either the CPU or GPU specified by the parameter `device`. We will use the helper function `timeFun(f, dim, iterations, device)`.
```
dim = 10000
iterations = 1
def simpleFun(dim, device):
"""
Args:
dim: integer
device: "cpu" or "cuda"
Returns:
Nothing.
"""
###############################################
## TODO for students: recreate the function, but
## ensure all computations happens on the `device`
raise NotImplementedError("Student exercise: fill in the missing code to create the tensors")
###############################################
# 2D tensor filled with uniform random numbers in [0,1), dim x dim
x = ...
# 2D tensor filled with uniform random numbers in [0,1), dim x dim
y = ...
# 2D tensor filled with the scalar value 2, dim x dim
z = ...
# elementwise multiplication of x and y
a = ...
# matrix multiplication of x and y
b = ...
del x
del y
del z
del a
del b
## TODO: Implement the function above and uncomment the following lines to test your code
# timeFun(f=simpleFun, dim=dim, iterations=iterations)
# timeFun(f=simpleFun, dim=dim, iterations=iterations, device=DEVICE)
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_232a94a4.py)
Sample output (depends on your hardware)
```
time taken for 1 iterations of simpleFun(10000, cpu): 23.74070
time taken for 1 iterations of simpleFun(10000, cuda): 0.87535
```
**Discuss!**
Try and reduce the dimensions of the tensors and increase the iterations. You can get to a point where the cpu only function is faster than the GPU function. Why might this be?
## Section 2.5: Datasets and Dataloaders
```
# @title Video 7: Getting Data
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1744y127SQ", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"LSkjPM1gFu0", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 7: Getting Data')
display(out)
```
When training neural network models you will be working with large amounts of data. Fortunately, PyTorch offers some great tools that help you organize and manipulate your data samples.
```
# Import dataset and dataloaders related packages
from torchvision import datasets
from torchvision.transforms import ToTensor
from torch.utils.data import DataLoader
from torchvision.transforms import Compose, Grayscale
```
**Datasets**
The `torchvision` package gives you easy access to many of the publicly available datasets. Let's load the [CIFAR10](https://www.cs.toronto.edu/~kriz/cifar.html) dataset, which contains color images of 10 different classes, like vehicles and animals.
Creating an object of type `datasets.CIFAR10` will automatically download and load all images from the dataset. The resulting data structure can be treated as a list containing data samples and their corresponding labels.
```
# Download and load the images from the CIFAR10 dataset
cifar10_data = datasets.CIFAR10(
root="data", # path where the images will be stored
download=True, # all images should be downloaded
transform=ToTensor() # transform the images to tensors
)
# Print the number of samples in the loaded dataset
print(f"Number of samples: {len(cifar10_data)}")
print(f"Class names: {cifar10_data.classes}")
```
We have 50000 samples loaded. Now let's take a look at one of them in detail. Each sample consists of an image and its corresponding label.
```
# Choose a random sample
random.seed(2021)
image, label = cifar10_data[random.randint(0, len(cifar10_data))]
print(f"Label: {cifar10_data.classes[label]}")
print(f"Image size: {image.shape}")
```
Color images are modeled as 3 dimensional tensors. The first dimension corresponds to the channels (C) of the image (in this case we have RGB images). The second dimensions is the height (H) of the image and the third is the width (W). We can denote this image format as C × H × W.
### Coding Exercise 2.5: Display an image from the dataset
Let's try to display the image using `matplotlib`. The code below will not work, because `imshow` expects to have the image in a different format - $H \times W \times C$.
You need to reorder the dimensions of the tensor using the `permute` method of the tensor. PyTorch `torch.permute(*dims)` rearranges the original tensor according to the desired ordering and returns a new multidimensional rotated tensor. The size of the returned tensor remains the same as that of the original.
**Code hint:**
```python
# create a tensor of size 2 x 4
input_var = torch.randn(2, 4)
# print its size and the tensor
print(input_var.size())
print(input_var)
# dimensions permuted
input_var = input_var.permute(1, 0)
# print its size and the permuted tensor
print(input_var.size())
print(input_var)
```
```
# TODO: Uncomment the following line to see the error that arises from the current image format
# plt.imshow(image)
# TODO: Comment the above line and fix this code by reordering the tensor dimensions
# plt.imshow(image.permute(...))
# plt.show()
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_b04bd357.py)
*Example output:*
<img alt='Solution hint' align='left' width=835.0 height=827.0 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/W1D1_BasicsAndPytorch/static/W1D1_Tutorial1_Solution_b04bd357_0.png>
```
#@title Video 8: Train and Test
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1rV411H7s5", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"JokSIuPs-ys", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 8: Train and Test')
display(out)
```
**Training and Test Datasets**
When loading a dataset, you can specify if you want to load the training or the test samples using the `train` argument. We can load the training and test datasets separately. For simplicity, today we will not use both datasets separately, but this topic will be adressed in the next days.
```
# Load the training samples
training_data = datasets.CIFAR10(
root="data",
train=True,
download=True,
transform=ToTensor()
)
# Load the test samples
test_data = datasets.CIFAR10(
root="data",
train=False,
download=True,
transform=ToTensor()
)
# @title Video 9: Data Augmentation - Transformations
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV19B4y1N77t", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"sjegA9OBUPw", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 9: Data Augmentation - Transformations')
display(out)
```
**Dataloader**
Another important concept is the `Dataloader`. It is a wrapper around the `Dataset` that splits it into minibatches (important for training the neural network) and makes the data iterable. The `shuffle` argument is used to shuffle the order of the samples across the minibatches.
```
# Create dataloaders with
train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=True)
```
*Reproducibility:* DataLoader will reseed workers following Randomness in multi-process data loading algorithm. Use `worker_init_fn()` and a `generator` to preserve reproducibility:
```python
def seed_worker(worker_id):
worker_seed = torch.initial_seed() % 2**32
numpy.random.seed(worker_seed)
random.seed(worker_seed)
g_seed = torch.Generator()
g_seed.manual_seed(my_seed)
DataLoader(
train_dataset,
batch_size=batch_size,
num_workers=num_workers,
worker_init_fn=seed_worker,
generator=g_seed
)
```
**Note:** For the `seed_worker` to have an effect, `num_workers` should be 2 or more.
We can now query the next batch from the data loader and inspect it. For this we need to convert the dataloader object to a Python iterator using the function `iter` and then we can query the next batch using the function `next`.
We can now see that we have a 4D tensor. This is because we have a 64 images in the batch ($B$) and each image has 3 dimensions: channels ($C$), height ($H$) and width ($W$). So, the size of the 4D tensor is $B \times C \times H \times W$.
```
# Load the next batch
batch_images, batch_labels = next(iter(train_dataloader))
print('Batch size:', batch_images.shape)
# Display the first image from the batch
plt.imshow(batch_images[0].permute(1, 2, 0))
plt.show()
```
**Transformations**
Another useful feature when loading a dataset is applying transformations on the data - color conversions, normalization, cropping, rotation etc. There are many predefined transformations in the `torchvision.transforms` package and you can also combine them using the `Compose` transform. Checkout the [pytorch documentation](https://pytorch.org/vision/stable/transforms.html) for details.
### Coding Exercise 2.6: Load the CIFAR10 dataset as grayscale images
The goal of this excercise is to load the images from the CIFAR10 dataset as grayscale images. Note that we rerun the `set_seed` function to ensure reproducibility.
```
def my_data_load():
###############################################
## TODO for students: load the CIFAR10 data,
## but as grayscale images and not as RGB colored.
raise NotImplementedError("Student exercise: fill in the missing code to load the data")
###############################################
## TODO Load the CIFAR10 data using a transform that converts the images to grayscale tensors
data = datasets.CIFAR10(...,
transform=...)
# Display a random grayscale image
image, label = data[random.randint(0, len(data))]
plt.imshow(image.squeeze(), cmap="gray")
plt.show()
return data
set_seed(seed=2021)
## After implementing the above code, uncomment the following lines to test your code
# data = my_data_load()
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_6052d728.py)
*Example output:*
<img alt='Solution hint' align='left' width=835.0 height=827.0 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/W1D1_BasicsAndPytorch/static/W1D1_Tutorial1_Solution_6052d728_1.png>
---
# Section 3: Neural Networks
*Time estimate: ~1 hour 30 mins (excluding video)*
Now it's time for you to create your first neural network using PyTorch. This section will walk you through the process of:
- Creating a simple neural network model
- Training the network
- Visualizing the results of the network
- Tweeking the network
```
# @title Video 10: CSV Files
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1xy4y1T7kv", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"JrC_UAJWYKU", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 10: CSV Files')
display(out)
```
## Section 3.1: Data Loading
First we need some sample data to train our network on. You can use the function below to generate an example dataset consisting of 2D points along two interleaving half circles. The data will be stored in a file called `sample_data.csv`. You can inspect the file directly in Colab by going to Files on the left side and opening the CSV file.
```
# @title Generate sample data
# @markdown we used `scikit-learn` module
from sklearn.datasets import make_moons
# Create a dataset of 256 points with a little noise
X, y = make_moons(256, noise=0.1)
# Store the data as a Pandas data frame and save it to a CSV file
df = pd.DataFrame(dict(x0=X[:,0], x1=X[:,1], y=y))
df.to_csv('sample_data.csv')
```
Now we can load the data from the CSV file using the Pandas library. Pandas provides many functions for reading files in various formats. When loading data from a CSV file, we can reference the columns directly by their names.
```
# Load the data from the CSV file in a Pandas DataFrame
data = pd.read_csv("sample_data.csv")
# Create a 2D numpy array from the x0 and x1 columns
X_orig = data[["x0", "x1"]].to_numpy()
# Create a 1D numpy array from the y column
y_orig = data["y"].to_numpy()
# Print the sizes of the generated 2D points X and the corresponding labels Y
print(f"Size X:{X_orig.shape}")
print(f"Size y:{y_orig.shape}")
# Visualize the dataset. The color of the points is determined by the labels `y_orig`.
plt.scatter(X_orig[:, 0], X_orig[:, 1], s=40, c=y_orig)
plt.show()
```
**Prepare Data for PyTorch**
Now let's prepare the data in a format suitable for PyTorch - convert everything into tensors.
```
# Initialize the device variable
DEVICE = set_device()
# Convert the 2D points to a float32 tensor
X = torch.tensor(X_orig, dtype=torch.float32)
# Upload the tensor to the device
X = X.to(DEVICE)
print(f"Size X:{X.shape}")
# Convert the labels to a long interger tensor
y = torch.from_numpy(y_orig).type(torch.LongTensor)
# Upload the tensor to the device
y = y.to(DEVICE)
print(f"Size y:{y.shape}")
```
## Section 3.2: Create a Simple Neural Network
```
# @title Video 11: Generating the Neural Network
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1fK4y1M74a", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"PwSzRohUvck", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 11: Generating the Neural Network')
display(out)
```
For this example we want to have a simple neural network consisting of 3 layers:
- 1 input layer of size 2 (our points have 2 coordinates)
- 1 hidden layer of size 16 (you can play with different numbers here)
- 1 output layer of size 2 (we want the have the scores for the two classes)
During the course you will deal with differend kinds of neural networks. On Day 2 we will focus on linear networks, but you will work with some more complicated architectures in the next days. The example here is meant to demonstrate the process of creating and training a neural network end-to-end.
**Programing the Network**
PyTorch provides a base class for all neural network modules called [`nn.Module`](https://pytorch.org/docs/stable/generated/torch.nn.Module.html). You need to inherit from `nn.Module` and implement some important methods:
`__init__`
In the `__init__` method you need to define the structure of your network. Here you will specify what layers will the network consist of, what activation functions will be used etc.
`forward`
All neural network modules need to implement the `forward` method. It specifies the computations the network needs to do when data is passed through it.
`predict`
This is not an obligatory method of a neural network module, but it is a good practice if you want to quickly get the most likely label from the network. It calls the `forward` method and chooses the label with the highest score.
`train`
This is also not an obligatory method, but it is a good practice to have. The method will be used to train the network parameters and will be implemented later in the notebook.
> Note that you can use the `__call__` method of a module directly and it will invoke the `forward` method: `net()` does the same as `net.forward()`.
```
# Inherit from nn.Module - the base class for neural network modules provided by Pytorch
class NaiveNet(nn.Module):
# Define the structure of your network
def __init__(self):
super(NaiveNet, self).__init__()
# The network is defined as a sequence of operations
self.layers = nn.Sequential(
nn.Linear(2, 16), # Transformation from the input to the hidden layer
nn.ReLU(), # Activation function (ReLU) is a non-linearity which is widely used because it reduces computation. The function returns 0 if it receives any
# negative input, but for any positive value x, it returns that value back.
nn.Linear(16, 2), # Transformation from the hidden to the output layer
)
# Specify the computations performed on the data
def forward(self, x):
# Pass the data through the layers
return self.layers(x)
# Choose the most likely label predicted by the network
def predict(self, x):
# Pass the data through the networks
output = self.forward(x)
# Choose the label with the highest score
return torch.argmax(output, 1)
# Train the neural network (will be implemented later)
def train(self, X, y):
pass
```
**Check that your network works**
Create an instance of your model and visualize it
```
# Create new NaiveNet and transfer it to the device
model = NaiveNet().to(DEVICE)
# Print the structure of the network
print(model)
```
### Coding Exercise 3.2: Classify some samples
Now let's pass some of the points of our dataset through the network and see if it works. You should not expect the network to actually classify the points correctly, because it has not been trained yet.
The goal here is just to get some experience with the data structures that are passed to the forward and predict methods and their results.
```
## Get the samples
# X_samples = ...
# print("Sample input:\n", X_samples)
## Do a forward pass of the network
# output = ...
# print("\nNetwork output:\n", output)
## Predict the label of each point
# y_predicted = ...
# print("\nPredicted labels:\n", y_predicted)
```
[*Click for solution*](https://github.com/NeuromatchAcademy/course-content-dl/tree/main//tutorials/W1D1_BasicsAndPytorch/solutions/W1D1_Tutorial1_Solution_af8ae0ff.py)
```
Sample input:
tensor([[ 0.9066, 0.5052],
[-0.2024, 1.1226],
[ 1.0685, 0.2809],
[ 0.6720, 0.5097],
[ 0.8548, 0.5122]], device='cuda:0')
Network output:
tensor([[ 0.1543, -0.8018],
[ 2.2077, -2.9859],
[-0.5745, -0.0195],
[ 0.1924, -0.8367],
[ 0.1818, -0.8301]], device='cuda:0', grad_fn=<AddmmBackward>)
Predicted labels:
tensor([0, 0, 1, 0, 0], device='cuda:0')
```
## Section 3.3: Train Your Neural Network
```
# @title Video 12: Train the Network
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1v54y1n7CS", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"4MIqnE4XPaA", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 12: Train the Network')
display(out)
```
Now it is time to train your network on your dataset. Don't worry if you don't fully understand everything yet - we will cover training in much more details in the next days. For now, the goal is just to see your network in action!
You will usually implement the `train` method directly when implementing your class `NaiveNet`. Here, we will implement it as a function outside of the class in order to have it in a ceparate cell.
```
# @title Helper function to plot the decision boundary
# Code adapted from this notebook: https://jonchar.net/notebooks/Artificial-Neural-Network-with-Keras/
from pathlib import Path
def plot_decision_boundary(model, X, y, device):
# Transfer the data to the CPU
X = X.cpu().numpy()
y = y.cpu().numpy()
# Check if the frames folder exists and create it if needed
frames_path = Path("frames")
if not frames_path.exists():
frames_path.mkdir()
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
grid_points = np.c_[xx.ravel(), yy.ravel()]
grid_points = torch.from_numpy(grid_points).type(torch.FloatTensor)
Z = model.predict(grid_points.to(device)).cpu().numpy()
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.binary)
# Implement the train function given a training dataset X and correcsponding labels y
def train(model, X, y):
# The Cross Entropy Loss is suitable for classification problems
loss_function = nn.CrossEntropyLoss()
# Create an optimizer (Stochastic Gradient Descent) that will be used to train the network
learning_rate = 1e-2
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
# Number of epochs
epochs = 15000
# List of losses for visualization
losses = []
for i in range(epochs):
# Pass the data through the network and compute the loss
# We'll use the whole dataset during the training instead of using batches
# in to order to keep the code simple for now.
y_logits = model.forward(X)
loss = loss_function(y_logits, y)
# Clear the previous gradients and compute the new ones
optimizer.zero_grad()
loss.backward()
# Adapt the weights of the network
optimizer.step()
# Store the loss
losses.append(loss.item())
# Print the results at every 1000th epoch
if i % 1000 == 0:
print(f"Epoch {i} loss is {loss.item()}")
plot_decision_boundary(model, X, y, DEVICE)
plt.savefig('frames/{:05d}.png'.format(i))
return losses
# Create a new network instance a train it
model = NaiveNet().to(DEVICE)
losses = train(model, X, y)
```
**Plot the loss during training**
Plot the loss during the training to see how it reduces and converges.
```
plt.plot(np.linspace(1, len(losses), len(losses)), losses)
plt.xlabel("Epoch")
plt.ylabel("Loss")
# @title Visualize the training process
# @markdown ### Execute this cell!
!pip install imageio --quiet
!pip install pathlib --quiet
import imageio
from IPython.core.interactiveshell import InteractiveShell
from IPython.display import Image, display
from pathlib import Path
InteractiveShell.ast_node_interactivity = "all"
# Make a list with all images
images = []
for i in range(10):
filename = "frames/0"+str(i)+"000.png"
images.append(imageio.imread(filename))
# Save the gif
imageio.mimsave('frames/movie.gif', images)
gifPath = Path("frames/movie.gif")
with open(gifPath,'rb') as f:
display(Image(data=f.read(), format='png'))
# @title Video 13: Play with it
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Cq4y1W7BH", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"_GGkapdOdSY", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 13: Play with it')
display(out)
```
### Exercise 3.3: Tweak your Network
You can now play around with the network a little bit to get a feeling of what different parameters are doing. Here are some ideas what you could try:
- Increase or decrease the number of epochs for training
- Increase or decrease the size of the hidden layer
- Add one additional hidden layer
Can you get the network to better fit the data?
```
# @title Video 14: XOR Widget
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1mB4y1N7QS", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"oTr1nE2rCWg", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
# add timing to airtable
atform.add_event('Video 14: XOR Widget')
display(out)
```
Exclusive OR (XOR) logical operation gives a true (`1`) output when the number of true inputs is odd. That is, a true output result if one, and only one, of the inputs to the gate is true. If both inputs are false (`0`) or both are true or false output results. Mathematically speaking, XOR represents the inequality function, i.e., the output is true if the inputs are not alike; otherwise, the output is false.
In case of two inputs ($X$ and $Y$) the following truth table is applied:
\begin{array}{ccc}
X & Y & \text{XOR} \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
Here, with `0`, we denote `False`, and with `1` we denote `True` in boolean terms.
### Interactive Demo 3.3: Solving XOR
Here we use an open source and famous visualization widget developed by Tensorflow team available [here](https://github.com/tensorflow/playground).
* Play with the widget and observe that you can not solve the continuous XOR dataset.
* Now add one hidden layer with three units, play with the widget, and set weights by hand to solve this dataset perfectly.
For the second part, you should set the weights by clicking on the connections and either type the value or use the up and down keys to change it by one increment. You could also do the same for the biases by clicking on the tiny square to each neuron's bottom left.
Even though there are infinitely many solutions, a neat solution when $f(x)$ is ReLU is:
\begin{equation}
y = f(x_1)+f(x_2)-f(x_1+x_2)
\end{equation}
Try to set the weights and biases to implement this function after you played enough :)
```
# @markdown ###Play with the parameters to solve XOR
from IPython.display import HTML
HTML('<iframe width="1020" height="660" src="https://playground.arashash.com/#activation=relu&batchSize=10&dataset=xor®Dataset=reg-plane&learningRate=0.03®ularizationRate=0&noise=0&networkShape=&seed=0.91390&showTestData=false&discretize=false&percTrainData=90&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false" allowfullscreen></iframe>')
# @markdown Do you think we can solve the discrete XOR (only 4 possibilities) with only 2 hidden units?
w1_min_xor = 'Select' #@param ['Select', 'Yes', 'No']
if w1_min_xor == 'No':
print("Correct!")
else:
print("How about giving it another try?")
```
---
# Section 4: Ethics And Course Info
```
# @title Video 15: Ethics
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Hw41197oB", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"Kt6JLi3rUFU", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
# @title Video 16: Be a group
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1j44y1272h", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"Sfp6--d_H1A", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
# @title Video 17: Syllabus
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1iB4y1N7uQ", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"cDvAqG_hAvQ", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
Meet our lecturers:
Week 1: the building blocks
* [Konrad Kording](https://kordinglab.com)
* [Andrew Saxe](https://www.saxelab.org/)
* [Surya Ganguli](https://ganguli-gang.stanford.edu/)
* [Ioannis Mitliagkas](http://mitliagkas.github.io/)
* [Lyle Ungar](https://www.cis.upenn.edu/~ungar/)
Week 2: making things work
* [Alona Fyshe](https://webdocs.cs.ualberta.ca/~alona/)
* [Alexander Ecker](https://eckerlab.org/)
* [James Evans](https://sociology.uchicago.edu/directory/james-evans)
* [He He](https://hhexiy.github.io/)
* [Vikash Gilja](https://tnel.ucsd.edu/bio) and [Akash Srivastava](https://akashgit.github.io/)
Week 3: more magic
* [Tim Lillicrap](https://contrastiveconvergence.net/~timothylillicrap/index.php) and [Blake Richards](https://www.mcgill.ca/neuro/blake-richards-phd)
* [Jane Wang](http://www.janexwang.com/) and [Feryal Behbahani](https://feryal.github.io/)
* [Tim Lillicrap](https://contrastiveconvergence.net/~timothylillicrap/index.php) and [Blake Richards](https://www.mcgill.ca/neuro/blake-richards-phd)
* [Josh Vogelstein](https://jovo.me/) and [Vincenzo Lamonaco](https://www.vincenzolomonaco.com/)
Now, go to the [visualization of ICLR papers](https://iclr.cc/virtual/2021/paper_vis.html). Read a few abstracts. Look at the various clusters. Where do you see yourself in this map?
---
# Submit to Airtable
```
# @title Video 18: Submission info
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1e44y127ti", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"JwTn7ej2dq8", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
```
This is Darryl, the Deep Learning Dapper Lion, and he's here to teach you about content submission to airtable.
<br>
<img src="https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/static/DapperLion.png" alt="Darryl">
<br><br>
At the end of each tutorial there will be an <b>Airtable Submission Cell</b>. Run the cell to generate the airtable submission button and click on it to submit your information to airtable.
<br><br>
if it is the last tutorial of the day your button will look like this and take you to the end of day survey:
<br>
<img src="https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/static/SurveyButton.png?raw=1" alt="Survey Button">
otherwise it look like this:
<br>
<img src="https://raw.githubusercontent.com/NeuromatchAcademy/course-content-dl/main/tutorials/static/AirtableSubmissionButton.png?raw=1" alt="Submission Button">
<br><br>
It is critical that you push the submit button for every tutorial you run. <b> even if you don't finish the tutorial, still submit!</b>
Submitting is the only way we can verify that you attempted each tutorial, which is critical for us to be able to track your progress.
### TL;DR: Basic tutorial workflow
1. work through the tutorial, answering Think! questions and code exercises
2. at end each tutorial, (even if tutorial incomplete) run the airtable submission code cell
3. Push the submission button
4. if the last tutorial of the day, Submission button will also take you to the end of the day survey on a new page. complete that and submit it.
### Submission FAQs:
1. What if I want to change my answers to previous discussion questions?
> you are free to change and resubmit any of the answers and Think! questions as many times as you like. However, <b> please only run the airtable submission code and click on the link once you are ready to submit</b>.
2. Okay, but what if I submitted my airtable anyway and reallly want to resubmit?
> After making changes, you can re-run the airtable submission cell code cell. This will result in a second submission from you for the data. This will make Darryl sad as it will be more work for him to clean up the data later.
3. HELP! I accidentally ran the code to generate the airtable submission button before I was ready to submit! what do I do?
> If you run the code to generate the link, anything that happens afterwards will not be captured. Complete the tutorial and make sure to re-run the airtable submission again when you are finished before pressing the submission button.
4. What if I want to work on this on my own later, should I wait to submit until I'm finished?
> Please submit wherever you are at the end of the day. It's graet that you want to keep working on this, but it's important to see the places where we tried things that didn't quite work out, so we can fix them for next year.
Finally, we try to keep the airtable code as hidden as possible, but if you ever see any calls to `atform` such as `atform.add_event()` in the coding exercises, just know that is for saving airtable information only.<b> It will not affect the code that is being run around it in any way</b> , so please do not modify, comment out, or worry about any of those lines of code.
<br><br><br>
Now, lets try submitting today's course to Airtable by running the next cell and clicking the button when it appears.
```
# @title Airtable Submission Link
from IPython import display as IPyDisplay
IPyDisplay.HTML(
f"""
<div>
<a href= "{atform.url()}" target="_blank">
<img src="https://github.com/NeuromatchAcademy/course-content-dl/blob/main/tutorials/static/SurveyButton.png?raw=1"
alt="button link to survey" style="width:410px"></a>
</div>""" )
```
---
# Bonus - 60 years of Machine Learning Research in one Plot
by [Hendrik Strobelt](http://hendrik.strobelt.com) (MIT-IBM Watson AI Lab) with support from Benjamin Hoover.
In this notebook we visualize a subset* of 3,300 articles retreived from the AllenAI [S2ORC dataset](https://github.com/allenai/s2orc). We represent each paper by a position that is output of a dimensionality reduction method applied to a vector representation of each paper. The vector representation is output of a neural network.
*The selection is very biased on the keywords and methodology we used to filter. Please see the details section to learn about what we did.
```
# @title Import `altair` and load the data
!pip install altair vega_datasets --quiet
import requests
import altair as alt # altair is defining data visualizations
# Source data files
# Position data file maps ID to x,y positions
# original link: http://gltr.io/temp/ml_regexv1_cs_ma_citation+_99perc.pos_umap_cosine_100_d0.1.json
POS_FILE = 'https://osf.io/qyrfn/download'
# original link: http://gltr.io/temp/ml_regexv1_cs_ma_citation+_99perc_clean.csv
# Metadata file maps ID to title, abstract, author,....
META_FILE = 'https://osf.io/vfdu6/download'
# data loading and wrangling
def load_data():
positions = pd.read_json(POS_FILE)
positions[['x', 'y']] = positions['pos'].to_list()
meta = pd.read_csv(META_FILE)
return positions.merge(meta, left_on='id', right_on='paper_id')
# load data
data = load_data()
# @title Define Visualization using ALtair
YEAR_PERIOD = "quinquennial" # @param
selection = alt.selection_multi(fields=[YEAR_PERIOD], bind='legend')
data[YEAR_PERIOD] = (data["year"] / 5.0).apply(np.floor) * 5
chart = alt.Chart(data[["x", "y", "authors", "title", YEAR_PERIOD, "citation_count"]], width=800,
height=800).mark_circle(radius=2, opacity=0.2).encode(
alt.Color(YEAR_PERIOD+':O',
scale=alt.Scale(scheme='viridis', reverse=False, clamp=True, domain=list(range(1955,2020,5))),
# legend=alt.Legend(title='Total Records')
),
alt.Size('citation_count',
scale=alt.Scale(type="pow", exponent=1, range=[15, 300])
),
alt.X('x:Q',
scale=alt.Scale(zero=False), axis=alt.Axis(labels=False)
),
alt.Y('y:Q',
scale=alt.Scale(zero=False), axis=alt.Axis(labels=False)
),
tooltip=['title', 'authors'],
# size='citation_count',
# color="decade:O",
opacity=alt.condition(selection, alt.value(.8), alt.value(0.2)),
).add_selection(
selection
).interactive()
```
Lets look at the Visualization. Each dot represents one paper. Close dots mean that the respective papers are closer related than distant ones. The color indicates the 5-year period of when the paper was published. The dot size indicates the citation count (within S2ORC corpus) as of July 2020.
The view is **interactive** and allows for three main interactions. Try them and play around.
1. hover over a dot to see a tooltip (title, author)
2. select a year in the legend (right) to filter dots
2. zoom in/out with scroll -- double click resets view
```
chart
```
## Questions
By playing around, can you find some answers to the follwing questions?
1. Can you find topical clusters? What cluster might occur because of a filtering error?
2. Can you see a temporal trend in the data and clusters?
2. Can you determine when deep learning methods started booming ?
3. Can you find the key papers that where written before the DL "winter" that define milestones for a cluster? (tipp: look for large dots of different color)
## Methods
Here is what we did:
1. Filtering of all papers who fullfilled the criterria:
- are categorized as `Computer Science` or `Mathematics`
- one of the following keywords appearing in title or abstract: `"machine learning|artificial intelligence|neural network|(machine|computer) vision|perceptron|network architecture| RNN | CNN | LSTM | BLEU | MNIST | CIFAR |reinforcement learning|gradient descent| Imagenet "`
2. per year, remove all papers that are below the 99 percentile of citation count in that year
3. embed each paper by using abstract+title in SPECTER model
4. project based on embedding using UMAP
5. visualize using Altair
### Find Authors
```
# @title Edit the `AUTHOR_FILTER` variable to full text search for authors.
AUTHOR_FILTER = "Rush " # @param space at the end means "word border"
### Don't ignore case when searching...
FLAGS = 0
### uncomment do ignore case
# FLAGS = re.IGNORECASE
## --- FILTER CODE.. make it your own ---
import re
data['issel'] = data['authors'].str.contains(AUTHOR_FILTER, na=False, flags=FLAGS, )
if data['issel'].mean()<0.0000000001:
print('No match found')
## --- FROM HERE ON VIS CODE ---
alt.Chart(data[["x", "y", "authors", "title", YEAR_PERIOD, "citation_count", "issel"]], width=800,
height=800) \
.mark_circle(stroke="black", strokeOpacity=1).encode(
alt.Color(YEAR_PERIOD+':O',
scale=alt.Scale(scheme='viridis', reverse=False),
# legend=alt.Legend(title='Total Records')
),
alt.Size('citation_count',
scale=alt.Scale(type="pow", exponent=1, range=[15, 300])
),
alt.StrokeWidth('issel:Q', scale=alt.Scale(type="linear", domain=[0,1], range=[0, 2]), legend=None),
alt.Opacity('issel:Q', scale=alt.Scale(type="linear", domain=[0,1], range=[.2, 1]), legend=None),
alt.X('x:Q',
scale=alt.Scale(zero=False), axis=alt.Axis(labels=False)
),
alt.Y('y:Q',
scale=alt.Scale(zero=False), axis=alt.Axis(labels=False)
),
tooltip=['title', 'authors'],
).interactive()
```
---
# Appendix
## Official PyTorch resources:
### Tutorials
https://pytorch.org/tutorials/
### Documentation
https://pytorch.org/docs/stable/tensors.html (tensor methods)
https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view (The view method in particular)
https://pytorch.org/vision/stable/datasets.html (pre-loaded image datasets)
## Google Colab Resources:
https://research.google.com/colaboratory/faq.html (FAQ including guidance on GPU usage)
## Books for reference:
https://www.deeplearningbook.org/ (Deep Learning by Ian Goodfellow, Yoshua Bengio and Aaron Courville)
|
github_jupyter
|
### 1 - e-posta baten histograma
Ahalik eta funtzio gehien sortuko ditugu, azpiproblema bakoitza funtzio beten bidez adierazteko. Adibidez:
* e-posta batetako testua, ilara zerrenda moduan (goiburua deskartatu)
* hitz batetako ertzetatik puntuazio zeinuak kendu
* hitz bat soilik karaktere alfabetikoez osotua ote dagoen
```
def eposta(bideizena,kodifikazioa="utf-8"):
with open(bideizena,encoding=kodifikazioa) as f:
for ilara in f:
if ilara == "\n" :
break
return list(f)
```
`string` modulua erabil dezakegu puntuazio zeinu guztiak lortzeko (seguruenik batenbat ahaztuko genuke...):
```
import string
string.punctuation
def hitza_garbitu(w):
return ...
```
Prozesatzera goazen testuak ingelesez daudenez, `string.ascii_letters` erabil dezakegu:
```
string.ascii_letters
def soilik_alfa(w):
return True/False
```
Aurreko funtzioak erabiliz, `histograma` funtzioa askozaz errazagoa izango da:
```
def histograma(bideizena):
h = {}
for ilara in eposta(bideizena):
for w in ilara.split():
w = hitza_garbitu(w)
if soilik_alfa(w) :
w = w.lower()
h[w] ...
return h
```
### 2 - histogramen *batura*
Bi histograma ditugularik, beraien batura histograma bat izango da. Histograma horretan, batutako bi histogrametako hitz guztiak agertuko dira eta balioak hi histogrametako balioen batura izango da.
```
def hist_batura(h1,h2):
# h1 = h1 + h2
# return h1 + h2
```
### 3 - histogramen normalizazioa
Agerpen kopuruetatik maiztasunetara
```
def hist_norm(h):
...
return hnorm
h = ...
h_norm = hist_norm(h)
sum(h_norm.values()) == 1
```
### 4 - Gai baten eredua sortu
Gai batetako eredua (histograma normalizatua) lortzeko, gai horretako korreo guztien histogramen batura kalkulatuko dugu eta azkenik histograma hori normalizatu:
$$h_{gaia} = norm \left( \sum_{posta \in gaia}{h_{posta}} \right)$$
Hau lortzeko ondoko pausuak emango ditugu:
* Gai batetako entrenamenduko fitxategi bideizenen zerrenda lortu
* Bideizen zerrenda batetako korrreoen histogramen batura lortu
* Histogramen baturaren normalizazioa egin
#### Entrenamenduko fitxategiak
Gai bat dugularik, adibidez `alt.atheism`, bere entrenamenduko fitxategien bideizen zerrenda `20news-bydate/listas_train/alt.atheism.txt` fitxategian egongo da. Gure kasuan:
```
karpeta = '/home/data/'
gaia = 'alt.atheism'
bideizena = karpeta + '20news-bydate/listas_train/' + gaia + '.txt'
```
Fitxategi horretan, ilara bakoitzean entrenamenduko korreo baten bideizen **erlatiboa** agertzen da:
```
20news-bydate-train/alt.atheism/49960
20news-bydate-train/alt.atheism/51060
20news-bydate-train/alt.atheism/51119
20news-bydate-train/alt.atheism/51120
20news-bydate-train/alt.atheism/51121
...
```
Ondoko kodeak, esaterako, bideizen guzti horiek dituen zerrenda lortuko du:
```
karpeta = '/home/data/'
gaia = 'alt.atheism'
bideizena = karpeta + '20news-bydate/listas_train/' + gaia + '.txt'
with open(bideizena,encoding="utf8") as f:
izenak = f.readlines()
```
Baina bideizen horiek ez dira absolutuak (aurretik '/home/data/20news-bydate/') gehitu behar zaie eta amaieran duten `"\n"`-a kendu behar zaie. Sortu gai baten entrenamenduko bideizen absolutuen zerrenda bueltatuko duen funtzioa:
```
def gaiko_entrenamendu_bideizenak(gaia):
z = []
...
return z
```
Sortu gai batetako eredua, hau da, histogramen batura normalizatua lortuko duen funtzioa:
```
def eredua(gaia):
H = {}
for bideizena in gaiko_entrenamendu_bideizenak(gaia):
# h = histograma(...)
# joan H-n h guztiak batzen
# H normalizatu
# emaitza buetatu
```
### 5 - Gai guztien ereduak sortu
`20news-bydate/gaiak.txt` fitxategian gai guztiak ditugu. Sortu gai guztien izen zerrenda bueltatuko duen funtzioa:
```
def gai_zerrenda():
...
```
Azkenik sortu gai bakoitzaren eredua.
```
def Ereduak():
# Eredu guztiak gordetzen dituen (hiztegien) hiztegia sortu
# E[gaia] = eredua(gaia)
return E
```
### 6 - Histograma normalizatuen arteko distantzia
#### Gainjartze distantzia
$$d(h_{a},h_{b}) = 1 - \sum_{w \in a}{\min(h_{a}(w),h_{b}(w))}$$
#### Euklidesen distantzia
$$d(h_{a},h_{b}) = \sqrt{ \sum_{w \in a,b}{(h_{a}(w)-h_{b}(w))^2} }$$
#### korrelazio distantzia
$$d(h_{a},h_{b}) = 1 - \sum_{w \in a}{h_{a}(w) \cdot h_{b}(w)}$$
```
def dist_gainjartze(ha,hb):
def dist_euklides(ha,hb):
def dist_korrelazio(ha,hb):
```
### 7 - Histograma normalizatua sailkatu
```
def sailkatu(h,E,dist=dist_gainjartze):
#dist()
z = [ (d,gaia) , (d,gaia) , (d,gaia), ... ]
z.sort()
return z
```
### 8 - Errore tasa neurtu
Test-eko posta elektroniko bat sailkatzen dugunean lehenengo posizioan postari dagokion gaia ez badago, sailkapen errore bat dugu. Errore tasa, $k$ errore kopurua eta $N$ posta kopuru arteko zatidura izango da:
$$errore\_tasa = \frac{k}{N}$$
#### test-eko fitxategiak
Gai bat dugularik, adibidez `alt.atheism`, bere test-eko fitxategien bideizen zerrenda `20news-bydate/listas_test/alt.atheism.txt` fitxategian egongo da. Gure kasuan:
```
karpeta = '/home/data/'
gaia = 'alt.atheism'
#frogak egiteko
#bideizena = karpeta + '20news-bydate/listas_minitest/' + gaia + '.txt'
bideizena = karpeta + '20news-bydate/listas_test/' + gaia + '.txt'
def gaiko_test_bideizenak(gaia):
z = []
...
return z
```
#### Errore tasa lortu
```
def errore_tasa(E,dist=dist_gainjartze):
#gai bakoitza zeharkatu
for gaia in ... :
#gaiko test-eko bideizenak zeharkatu
for bideizena in ...
#histograma normalizatua lortu
#sailkatu
#lehenengo gaia zuzena ez bada, errorea kontabilizatu
return k/N
```
|
github_jupyter
|
# Classification metrics
Author: Geraldine Klarenberg
Based on the Google Machine Learning Crash Course
## Tresholds
In previous lessons, we have talked about using regression models to predict values. But sometimes we are interested in **classifying** things: "spam" vs "not spam", "bark" vs "not barking", etc.
Logistic regression is a great tool to use in ML classification models. We can use the outputs from these models by defining **classification thresholds**. For instance, if our model tells us there's a probability of 0.8 that an email is spam (based on some characteristics), the model classifies it as such. If the probability estimate is less than 0.8, the model classifies it as "not spam". The threshold allows us to map a logistic regression value to a binary category (the prediction).
Tresholds are problem-dependent, so they will have to be tuned for the specific problem you are dealing with.
In this lesson we will look at metrics you can use to evaluate a classification model's predictions, and what changing the threshold does to your model and predictions.
## True, false, positive, negative...
Now, we could simply look at "accuracy": the ratio of all correct predictions to all predictions. This is simple, intuitive and straightfoward.
But there are some problems with this approach:
* This approach does not work well if there is (class) imbalance; situations where certain negative or positive values or outcomes are rare;
* and, most importantly: different kind of mistakes can have different costs...
### The boy who cried wolf...
We all know the story!

For this example, we define "there actually is a wolf" as a positive class, and "there is no wolf" as a negative class. The predictions that a model makes can be true or false for both classes, generating 4 outcomes:

This table is also called a *confusion matrix*.
There are 2 metrics we can derive from these outcomes: precision and recall.
## Precision
Precision asks the question what proportion of the positive predictions was actually correct?
To calculate the precision of your model, take all true positives divided by *all* positive predictions:
$$\text{Precision} = \frac{TP}{TP+FP}$$
Basically: **did the model cry 'wolf' too often or too little?**
**NB** If your model produces no negative positives, the value of the precision is 1.0. Too many negative positives gives values greater than 1, too few gives values less than 1.
### Exercise
Calculate the precision of a model with the following outcomes
true positives (TP): 1 | false positives (FP): 1
-------|--------
**false negatives (FN): 8** | **true negatives (TN): 90**
## Recall
Recall tries to answer the question what proportion of actual positives was answered correctly?
To calculate recall, divide all true positives by the true positives plus the false negatives:
$$\text{Recall} = \frac{TP}{TP+FN}$$
Basically: **how many wolves that tried to get into the village did the model actually get?**
**NB** If the model produces no false negative, recall equals 1.0
### Exercise
For the same confusion matrix as above, calculate the recall.
## Balancing precision and recall
To evaluate your model, should look at **both** precision and recall. They are often in tension though: improving one reduces the other.
Lowering the classification treshold improves recall (your model will call wolf at every little sound it hears) but will negatively affect precision (it will call wolf too often).
### Exercise
#### Part 1
Look at the outputs of a model that classifies incoming emails as "spam" or "not spam".

The confusion matrix looks as follows
true positives (TP): 8 | false positives (FP): 2
-------|--------
**false negatives (FN): 3** | **true negatives (TN): 17**
Calculate the precision and recall for this model.
#### Part 2
Now see what happens to the outcomes (below) if we increase the threshold

The confusion matrix looks as follows
true positives (TP): 7 | false positives (FP): 4
-------|--------
**false negatives (FN): 1** | **true negatives (TN): 18**
Calculate the precision and recall again.
**Compare the precision and recall from the first and second model. What do you notice?**
## Evaluate model performance
We can evaluate the performance of a classification model at all classification thresholds. For all different thresholds, calculate the *true positive rate* and the *false positive rate*. The true positive rate is synonymous with recall (and sometimes called *sensitivity*) and is thus calculated as
$ TPR = \frac{TP} {TP + FN} $
False positive rate (sometimes called *specificity*) is:
$ FPR = \frac{FP} {FP + TN} $
When you plot the pairs of TPR and FPR for all the different thresholds, you get a Receiver Operating Characteristics (ROC) curve. Below is a typical ROC curve.

To evaluate the model, we look at the area under the curve (AUC). The AUC has a probabilistic interpretation: it represents the probability that a random positive (green) example is positioned to the right of a random negative (red) example.

So if that AUC is 0.9, that's the probability the pair-wise prediction is correct. Below are a few visualizations of AUC results. On top are the distributions of the outcomes of the negative and positive outcomes at various thresholds. Below is the corresponding ROC.


**This AUC suggests a perfect model** (which is suspicious!)


**This is what most AUCs look like**. In this case, AUC = 0.7 means that there is 70% chance the model will be able to distinguish between positive and negative classes.


**This is actually the worst case scenario.** This model has no discrimination capacity at all...
## Prediction bias
Logistic regression should be unbiased, meaning that the average of the predictions should be more or less equal to the average of the observations. **Prediction bias** is the difference between the average of the predictions and the average of the labels in a data set.
This approach is not perfect, e.g. if your model almost always predicts the average there will not be much bias. However, if there **is** bias ("significant nonzero bias"), that means there is something something going on that needs to be checked, specifically that the model is wrong about the frequency of positive labels.
Possible root causes of prediction bias are:
* Incomplete feature set
* Noisy data set
* Buggy pipeline
* Biased training sample
* Overly strong regularization
### Buckets and prediction bias
For logistic regression, this process is a bit more involved, as the labels assigned to an examples are either 0 or 1. So you cannot accurately predict the prediction bias based on one example. You need to group data in "buckets" and examine the prediction bias on that. Prediction bias for logistic regression only makes sense when grouping enough examples together to be able to compare a predicted value (for example, 0.392) to observed values (for example, 0.394).
You can create buckets by linearly breaking up the target predictions, or create quantiles.
The plot below is a calibration plot. Each dot represents a bucket with 1000 values. On the x-axis we have the average value of the predictions for that bucket and on the y-axis the average of the actual observations. Note that the axes are on logarithmic scales.

## Coding
Recall the logistic regression model we made in the previous lesson. That was a perfect fit, so not that useful when we look at the metrics we just discussed.
In the cloud plot with the sepal length and petal width plotted against each other, it is clear that the other two iris species are less separated. Let's use one of these as an example. We'll rework the example so we're classifying irises for being "virginica" or "not virginica".
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
X = iris.data
y = iris.target
df = pd.DataFrame(X,
columns = ['sepal_length(cm)',
'sepal_width(cm)',
'petal_length(cm)',
'petal_width(cm)'])
df['species_id'] = y
species_map = {0: 'setosa', 1: 'versicolor', 2: 'virginica'}
df['species_name'] = df['species_id'].map(species_map)
df.head()
```
Now extract the data we need and create the necessary dataframes again.
```
X = np.c_[X[:,0], X[:,3]]
y = []
for i in range(len(X)):
if i > 99:
y.append(1)
else:
y.append(0)
y = np.array(y)
plt.scatter(X[:,0], X[:,1], c = y)
```
Create our test and train data, and run a model. The default classification threshold is 0.5. If the predicted probability is > 0.5, the predicted result is 'virgnica'. If it is < 0.5, the predicted result is 'not virginica'.
```
random = np.random.permutation(len(X))
x_train = X[random][30:]
x_test = X[random][:30]
y_train= y[random][30:]
y_test = y[random][:30]
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(x_train,y_train)
```
Instead of looking at the probabilities and the plot, like in the last lesson, let's run some classification metrics on the training dataset.
If you use ".score", you get the mean accuracy.
```
log_reg.score(x_train, y_train)
```
Let's predict values and see what this ouput means and how we can look at other metrics.
```
predictions = log_reg.predict(x_train)
predictions, y_train
```
There is a way to look at the confusion matrix. The output that is generated has the same structure as the confusion matrices we showed earlier:
true positives (TP) | false positives (FP)
-------|--------
**false negatives (FN)** | **true negatives (TN)**
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train, predictions)
```
Indeed, for the accuracy calculation: we predicted 81 + 33 = 114 correct (true positives and true negatives), and 114/120 (remember, our training data had 120 points) = 0.95.
There is also a function to calculate recall and precision:
Since we also have a testing data set, let's see what the metrics look like for that.
```
from sklearn.metrics import recall_score
recall_score(y_train, predictions)
from sklearn.metrics import precision_score
precision_score(y_train, predictions)
```
And, of course, there are also built-in functions to check the ROC curve and AUC! For these functions, the inputs are the labels of the original dataset and the predicted probabilities (- not the predicted labels -> **why?**). Remember what the two columns mean?
```
proba_virginica = log_reg.predict_proba(x_train)
proba_virginica[0:10]
from sklearn.metrics import roc_curve
fpr_model, tpr_model, thresholds_model = roc_curve(y_train, proba_virginica[:,1])
fpr_model
tpr_model
thresholds_model
```
Plot the ROC curve as follows
```
plt.plot(fpr_model, tpr_model,label='our model')
plt.plot([0,1],[0,1],label='random')
plt.plot([0,0,1,1],[0,1,1,1],label='perfect')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend()
plt.show()
```
The AUC:
```
from sklearn.metrics import roc_auc_score
auc_model = roc_auc_score(y_train, proba_virginica[:,1])
auc_model
```
You can use the ROC and AUC metric to evaluate competing models. Many people prefer to use these metrics to analyze each model’s performance because it does not require selecting a threshold and helps balance true positive rate and false positive rate.
Now let's do the same thing for our test data (but again, this dataset is fairly small, and K-fold cross-validation is recommended).
```
log_reg.score(x_test, y_test)
predictions = log_reg.predict(x_test)
predictions, y_test
confusion_matrix(y_test, predictions)
recall_score(y_test, predictions)
precision_score(y_test, predictions)
proba_virginica = log_reg.predict_proba(x_test)
fpr_model, tpr_model, thresholds_model = roc_curve(y_test, proba_virginica[:,1])
plt.plot(fpr_model, tpr_model,label='our model')
plt.plot([0,1],[0,1],label='random')
plt.plot([0,0,1,1],[0,1,1,1],label='perfect')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend()
plt.show()
auc_model = roc_auc_score(y_test, proba_virginica[:,1])
auc_model
```
Learn more about the logistic regression function and options at https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
|
github_jupyter
|
```
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
from matplotlib import animation
from IPython.display import HTML
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
%matplotlib inline
# Set up colors:
color_map = ListedColormap(['#1b9e77', '#d95f02', '#7570b3'])
# Make raw data using blobs
X, y = make_blobs(
n_samples=200,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0
)
# Plot the raw data:
plt.scatter(X[:,0], X[:, 1], c=y, cmap=color_map)
# Define some initial centers, these are designed to be "bad":
initial = np.array(
[
[-3.0, 0.0],
[-2.0, 0.0],
[-1.0, 0.0],
]
)
y_c = [0, 1, 2]
# Plot the initial situation:
fig0, ax0 = plt.subplots(constrained_layout=True)
ax0.scatter(X[:,0], X[:, 1], c=y, cmap=color_map)
ax0.scatter(initial[:,0], initial[:, 1],
c=y_c, cmap=color_map, marker='X', edgecolors='black', s=150)
ax0.text(-3, 5, 'Iteration: 0', fontsize='xx-large')
xlim = ax0.get_xlim()
ylim = ax0.get_ylim()
results = [(np.full_like(y, 0), initial)]
# Run clustering for different number of maximum iterations:
max_clusters = 15
for iterations in range(1, 15):
km = KMeans(n_clusters=3, init=initial, n_init=1, max_iter=iterations,
random_state=0)
y_km = km.fit_predict(X)
results.append((y_km, km.cluster_centers_))
figi, axi = plt.subplots(constrained_layout=True)
axi.scatter(X[:, 0], X[:, 1], c=y_km, cmap=color_map)
axi.set_xlim(xlim)
axi.set_ylim(ylim)
axi.text(-3, 5, 'Iteration: {}'.format(iterations), fontsize='xx-large')
axi.scatter(km.cluster_centers_[:, 0],
km.cluster_centers_[:, 1],
c=y_c, cmap=color_map,
marker='X', edgecolors='black', s=150)
%%capture
# Create an animation:
fig2, ax2 = plt.subplots(constrained_layout=True)
ax2.set_xlim(xlim)
ax2.set_ylim(ylim)
yi, centers = results[0]
scat = ax2.scatter(X[:, 0], X[:, 1])
cent = ax2.scatter(centers[:, 0], centers[:, 1], c=y_c, cmap=color_map,
marker='X', edgecolors='black', s=250)
text = ax2.text(-3, 5, 'Iteration: 0', fontsize='xx-large')
def animate(i):
"""Update the animation."""
yi, centers = results[i]
cent.set_offsets(centers)
text.set_text('Iteration: {}'.format(i))
if i == 0:
colors = ['#377eb8' for _ in yi]
else:
colors = [color_map.colors[j] for j in yi]
scat.set_facecolors(colors)
return (cent, scat, text)
anim = animation.FuncAnimation(fig2, animate,
frames=max_clusters,
interval=300, blit=True, repeat=True)
HTML(anim.to_jshtml())
```
|
github_jupyter
|
```
# Name: example_analysis_data_creation.ipynb
# uthors: Stephan Meighen-Berger
# Example how to construct a data set to use for later analyses
# General imports
import numpy as np
import matplotlib.pyplot as plt
import sys
from tqdm import tqdm
import pickle
# Adding path to module
sys.path.append("../")
# picture path
PICS = '../pics/'
# Module imports
from fourth_day import Fourth_Day, config
# Scenario Settings
# These are general settings pertaining to the simulation run
config['scenario']['population size'] = 10 # The starting population size
config['scenario']['duration'] = 600 * 5 # Total simulation time in seconds
config['scenario']['exclusion'] = True # If an exclusion zone should be used (the detector)
config['scenario']['injection']['rate'] = 1e-2 # Injection rate in per second, a distribution is constructed from this value
config['scenario']['injection']['y range'] = [5., 10.] # The y-range of injection
config['scenario']['light prop'] = { # Where the emitted light should be propagated to (typically the detector location)
"switch": True, # If light should be propagated
"x_pos": 3., # The x-coordinates
"y_pos": 0.5 * 15. - 0.15, # The y-coordinates
}
config['scenario']['detector'] = { # detector specific properties, positions are defined as offsets from the light prop values
"switch": True, # If the detector should be modelled
"type": "PMTSpec", # Detector name, implemented types are given in the config
"response": True, # If a detector response should be used
"acceptance": "Flat", # Flat acceptance
"mean detection prob": 0.5 # Used for the acceptance calculation
}
# ---------------------------------------------
# Organisms
# Organisms properties are defined here
config['organisms']['emission fraction'] = 0.2 # Amount of energy an organism uses per pulse
config['organisms']['alpha'] = 1e1 # Proportionality factor for the emission probability
config['organisms']["minimal shear stress"] = 0.05 # The minimal amount of shear stress needed to emit (generic units)
config["organisms"]["filter"] = 'depth' # Method of filtering organisms (here depth)
config["organisms"]["depth filter"] = 1000. # Organisms need to exist below this depth
# ---------------------------------------------
# Geometry
# These settings define the geometry of the system
# Typically a box (simulation volume) with a spherical exclusion zone (detector)
config['geometry']['volume'] = {
'function': 'rectangle',
'x_length': 30.,
'y_length': 15.,
'offset': None,
}
# Reduce the observation size to reduce the computational load
config['geometry']['observation'] = {
'function': 'rectangle',
'x_length': 30.,
'y_length': 15.,
"offset": np.array([0., 0.]),
}
# The detector volume
config['geometry']["exclusion"] = {
"function": "sphere",
"radius": 0.15,
"x_pos": 3.,
"y_pos": 0.5 * 15. - 0.15,
}
# ---------------------------------------------
# Water
# Properties of the current model
config['water']['model']['name'] = 'custom' # Use a custom (non analytic) model
config['water']['model']['off set'] = np.array([0., 0.]) # Offset of the custom model
config['water']['model']['directory'] = "../data/current/Parabola_5mm/run_2cm_npy/" # The files used by the custom model
config['water']['model']['time step'] = 5. # in Seconds
# Which detectors we want to use
wavelengths = {
"Detector 1": ["1", "#4575b4"],
"Detector 5": ["2", "#91bfdb"],
"Detector 8": ["3", "#e0f3f8"],
"Detector 3": ["4", "#fee090"],
"Detector 10": ["5", "#fc8d59"],
}
# Launching multiple simulations to use in the analysis
seeds = np.arange(100)[1:]
print(seeds)
counter = 0
for seed in tqdm(seeds):
# General
config["general"]["random state seed"] = seed
# Creating a fourth_day object
fd = Fourth_Day()
# Launching solver
fd.sim()
# Fetching relevant data
# Totals
total = fd.measured["Detector 1"].values
for detector in wavelengths.keys():
if detector == "Detector 1":
continue
fd.measured[detector].values
total += fd.measured[detector].values
storage_dic = {
"time": fd.t,
"data": total
}
pickle.dump(storage_dic, open("../data/storage/vort_run_%d.p" % counter, "wb"))
counter += 1
```
|
github_jupyter
|
# Case: Impact of p_negative
Situation:
- 70% agent availability on weekdays and weekends
Task:
- Evaluate Shift Coverage over p_negative: [.001, .0025, .005, .0075, .01, .02, .03, .05, .1, .2]
- Evaluate Agent Satisfaction over p_negative: [.001, .0025, .005, .0075, .01, .02, .03, .05, .1, .2]
```
import abm_scheduling
from abm_scheduling import Schedule as Schedule
from abm_scheduling import Nurse as Nurse
import time
from datetime import datetime
import abm_scheduling.Log
from abm_scheduling.Log import Log as Log
import matplotlib.pylab as plt
%matplotlib inline
log = Log()
```
## Define situation
```
num_nurses_per_shift = 5
num_nurses = 25
degree_of_agent_availability = 0.7
works_weekends = True
p_negatives = [.001, .0025, .005, .0075, .01, .02, .03, .05, .1, .2]
schedule = Schedule(num_nurses_needed=num_nurses_per_shift, is_random=True)
model = abm_scheduling.NSP_AB_Model()
nurses = model.generate_nurses(num_nurses=num_nurses,
degree_of_agent_availability=degree_of_agent_availability,
works_weekends=works_weekends)
schedule.print_schedule(schedule_name="Intial Situation")
p_neg_reg_util_results = []
for p_neg in p_negatives:
p_neg_reg_util_result = model.run(schedule_org=schedule,
nurses_org=nurses,
p_to_accept_negative_change=p_neg,
utility_function_parameters=None,
print_stats=False)
p_neg_reg_util_results.append(p_neg_reg_util_result)
plt.figure()
plt.plot(p_negatives, [r.shift_coverage for r in p_neg_reg_util_results], label="Shift Coverage")
plt.title(f'Shift coverage as a function of p_negative')
plt.xlabel("p_negative")
plt.ylabel("Shift Coverage")
plt.legend()
plt.show()
p_neg_as_util_results = []
for p_neg in p_negatives:
p_neg_as_util_result = model.run(schedule_org=schedule,
nurses_org=nurses,
p_to_accept_negative_change=p_neg,
utility_function_parameters=None,
print_stats=False)
p_neg_as_util_results.append(p_neg_as_util_result)
plt.figure()
plt.plot(p_negatives, [r.total_agent_satisfaction for r in p_neg_as_util_results], label="Agent Satisfaction")
plt.title(f'Agent satisfaction as a function of p_negative')
plt.xlabel("p_negative")
plt.ylabel("Agent Satisfaction")
plt.legend()
plt.show()
```
|
github_jupyter
|
# First Attempt
batch size 256 lr 1e-3
### Import modules
```
%matplotlib inline
from __future__ import division
import sys
import os
os.environ['MKL_THREADING_LAYER']='GNU'
sys.path.append('../')
from Modules.Basics import *
from Modules.Class_Basics import *
```
## Options
```
classTrainFeatures = basic_features
classModel = 'modelSwish'
varSet = "basic_features"
nSplits = 10
ensembleSize = 10
ensembleMode = 'loss'
maxEpochs = 200
compileArgs = {'loss':'binary_crossentropy', 'optimizer':'adam'}
trainParams = {'epochs' : 1, 'batch_size' : 256, 'verbose' : 0}
modelParams = {'version':classModel, 'nIn':len(classTrainFeatures), 'compileArgs':compileArgs}
print "\nTraining on", len(classTrainFeatures), "features:", [var for var in classTrainFeatures]
```
## Import data
```
trainData = h5py.File(dirLoc + 'train.hdf5', "r+")
valData = h5py.File(dirLoc + 'val.hdf5', "r+")
```
## Determine LR
```
lrFinder = batchLRFindClassifier(trainData, nSplits, getClassifier, modelParams, trainParams, lrBounds=[1e-5,0.1], trainOnWeights=False, verbose=0)
compileArgs['lr'] = 1e-2
```
## Train classifier
```
results, histories = batchTrainClassifier(trainData, nSplits, getClassifier, modelParams, trainParams, cosAnnealMult=2, trainOnWeights=False, patience=200, maxEpochs=maxEpochs, verbose=1)
```
## Construct ensemble
```
with open('train_weights/resultsFile.pkl', 'r') as fin:
results = pickle.load(fin)
ensemble, weights = assembleEnsemble(results, ensembleSize, ensembleMode, compileArgs)
```
## Response on development data
```
batchEnsemblePredict(ensemble, weights, trainData, ensembleSize=10, verbose=1)
print 'Training ROC AUC: unweighted {}, weighted {}'.format(roc_auc_score(getFeature('targets', trainData), getFeature('pred', trainData)),
roc_auc_score(getFeature('targets', trainData), getFeature('pred', trainData), sample_weight=getFeature('weights', trainData)))
```
## Response on val data
```
batchEnsemblePredict(ensemble, weights, valData, ensembleSize=10, verbose=1)
print 'Testing ROC AUC: unweighted {}, weighted {}'.format(roc_auc_score(getFeature('targets', valData), getFeature('pred', valData)),
roc_auc_score(getFeature('targets', valData), getFeature('pred', valData), sample_weight=getFeature('weights', valData)))
```
## Evaluation
### Import in dataframe
```
def convertToDF(datafile, columns={'gen_target', 'gen_weight', 'pred_class'}, nLoad=-1):
data = pandas.DataFrame()
data['gen_target'] = getFeature('targets', datafile, nLoad)
data['gen_weight'] = getFeature('weights', datafile, nLoad)
data['pred_class'] = getFeature('pred', datafile, nLoad)
print len(data), "candidates loaded"
return data
devData = convertToDF(trainData)
valData = convertToDF(valData)
sigVal = (valData.gen_target == 1)
bkgVal = (valData.gen_target == 0)
```
### MVA distributions
```
getClassPredPlot([valData[bkgVal], valData[sigVal]], weightName='gen_weight')
def AMS(s, b):
""" Approximate Median Significance defined as:
AMS = sqrt(
2 { (s + b + b_r) log[1 + (s/(b+b_r))] - s}
)
where b_r = 10, b = background, s = signal, log is natural logarithm """
br = 10.0
radicand = 2 *( (s+b+br) * math.log (1.0 + s/(b+br)) -s)
if radicand < 0:
print 'radicand is negative. Exiting'
exit()
else:
return math.sqrt(radicand)
def amsScan(inData, res=0.0001):
best = [0,-1]
for i in np.linspace(0.,1.,1./res):
ams = AMS(np.sum(inData.loc[(inData['pred_class'] >= i) & sigVal, 'gen_weight']),
np.sum(inData.loc[(inData['pred_class'] >= i) & bkgVal, 'gen_weight']))
if ams > best[1]:
best = [i, ams]
print best
amsScan(valData)
def scoreTest(ensemble, weights, features, cut, name):
testData = pandas.read_csv('../Data/test.csv')
with open(dirLoc + 'inputPipe.pkl', 'r') as fin:
inputPipe = pickle.load(fin)
testData['pred_class'] = ensemblePredict(inputPipe.transform(testData[features].values.astype('float32')), ensemble, weights)
testData['Class'] = 'b'
testData.loc[testData.pred_class >= cut, 'Class'] = 's'
testData.sort_values(by=['pred_class'], inplace=True)
testData['RankOrder']=range(1, len(testData)+1)
testData.sort_values(by=['EventId'], inplace=True)
testData.to_csv(dirLoc + name + '_test.csv', columns=['EventId', 'RankOrder', 'Class'], index=False)
scoreTest(ensemble, weights, classTrainFeatures, 0.83498349834983498, 'Model_0_Basic_Features_256_1e-2_swish_mult2_200E')
```
## Save classified data
```
name = dirLoc + signal + "_" + channel + "_" + varSet + '_' + classModel + '_classifiedData.csv'
print "Saving data to", name
valData.to_csv(name, columns=['gen_target', 'gen_weight', 'gen_sample', 'pred_class'])
```
## Save/load
```
name = "weights/DNN_" + signal + "_" + channel + "_" + varSet + '_' + classModel
print name
```
### Save
```
saveEnsemble(name, ensemble, weights, compileArgs, overwrite=1)
```
### Load
```
ensemble, weights, compileArgs, inputPipe, outputPipe = loadEnsemble(name)
```
|
github_jupyter
|
# Programming Assignment
## Готовим LDA по рецептам
Как вы уже знаете, в тематическом моделировании делается предположение о том, что для определения тематики порядок слов в документе не важен; об этом гласит гипотеза <<мешка слов>>. Сегодня мы будем работать с несколько нестандартной для тематического моделирования коллекцией, которую можно назвать <<мешком ингредиентов>>, потому что на состоит из рецептов блюд разных кухонь. Тематические модели ищут слова, которые часто вместе встречаются в документах, и составляют из них темы. Мы попробуем применить эту идею к рецептам и найти кулинарные <<темы>>. Эта коллекция хороша тем, что не требует предобработки. Кроме того, эта задача достаточно наглядно иллюстрирует принцип работы тематических моделей.
Для выполнения заданий, помимо часто используемых в курсе библиотек, потребуются модули json и gensim. Первый входит в дистрибутив Anaconda, второй можно поставить командой
pip install gensim
или
conda install gensim
Построение модели занимает некоторое время. На ноутбуке с процессором Intel Core i7 и тактовой частотой 2400 МГц на построение одной модели уходит менее 10 минут.
### Загрузка данных
Коллекция дана в json-формате: для каждого рецепта известны его id, кухня ("cuisine") и список ингредиентов, в него входящих. Загрузить данные можно с помощью модуля json (он входит в дистрибутив Anaconda):
```
import json
with open("recipes.json") as f:
recipes = json.load(f)
print recipes[1]
```
### Составление корпуса
```
from gensim import corpora, models
import numpy as np
```
Наша коллекция небольшая и влезает в оперативную память. Gensim может работать с такими данными и не требует их сохранения на диск в специальном формате. Для этого коллекция должна быть представлена в виде списка списков, каждый внутренний список соответствует отдельному документу и состоит из его слов. Пример коллекции из двух документов:
[["hello", "world"], ["programming", "in", "python"]]
Преобразуем наши данные в такой формат, а затем создадим объекты corpus и dictionary, с которыми будет работать модель.
```
texts = [recipe["ingredients"] for recipe in recipes]
dictionary = corpora.Dictionary(texts) # составляем словарь
corpus = [dictionary.doc2bow(text) for text in texts] # составляем корпус документов
corpus[0]
print texts[0]
print corpus[0]
```
У объекта dictionary есть две полезных переменных: dictionary.id2token и dictionary.token2id; эти словари позволяют находить соответствие между ингредиентами и их индексами.
### Обучение модели
Вам может понадобиться [документация](https://radimrehurek.com/gensim/models/ldamodel.html) LDA в gensim.
__Задание 1.__ Обучите модель LDA с 40 темами, установив количество проходов по коллекции 5 и оставив остальные параметры по умолчанию. Затем вызовите метод модели show_topics, указав количество тем 40 и количество токенов 10, и сохраните результат (топы ингредиентов в темах) в отдельную переменную. Если при вызове метода show_topics указать параметр formatted=True, то топы ингредиентов будет удобно выводить на печать, если formatted=False, будет удобно работать со списком программно. Выведите топы на печать, рассмотрите темы, а затем ответьте на вопрос:
Сколько раз ингредиенты "salt", "sugar", "water", "mushrooms", "chicken", "eggs" встретились среди топов-10 всех 40 тем? При ответе __не нужно__ учитывать составные ингредиенты, например, "hot water".
Передайте 6 чисел в функцию save_answers1 и загрузите сгенерированный файл в форму.
У gensim нет возможности фиксировать случайное приближение через параметры метода, но библиотека использует numpy для инициализации матриц. Поэтому, по утверждению автора библиотеки, фиксировать случайное приближение нужно командой, которая написана в следующей ячейке. __Перед строкой кода с построением модели обязательно вставляйте указанную строку фиксации random.seed.__
```
np.random.seed(76543)
# здесь код для построения модели:
ldamodel = models.ldamodel.LdaModel(corpus, id2word=dictionary, num_topics=40, passes=5)
topics = ldamodel.show_topics(num_topics=40, num_words=10, formatted=False)
c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs = 0, 0, 0, 0, 0, 0
for topic in topics:
for word2prob in topic[1]:
word = word2prob[0]
if word == 'salt':
c_salt += 1
elif word == 'sugar':
c_sugar += 1
elif word == 'water':
c_water += 1
elif word == 'mushrooms':
c_mushrooms += 1
elif word == 'chicken':
c_chicken += 1
elif word == 'eggs':
c_eggs += 1
def save_answers1(c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs):
with open("cooking_LDA_pa_task1.txt", "w") as fout:
fout.write(" ".join([str(el) for el in [c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs]]))
save_answers1(c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs)
print c_salt, c_sugar, c_water, c_mushrooms, c_chicken, c_eggs
```
### Фильтрация словаря
В топах тем гораздо чаще встречаются первые три рассмотренных ингредиента, чем последние три. При этом наличие в рецепте курицы, яиц и грибов яснее дает понять, что мы будем готовить, чем наличие соли, сахара и воды. Таким образом, даже в рецептах есть слова, часто встречающиеся в текстах и не несущие смысловой нагрузки, и поэтому их не желательно видеть в темах. Наиболее простой прием борьбы с такими фоновыми элементами - фильтрация словаря по частоте. Обычно словарь фильтруют с двух сторон: убирают очень редкие слова (в целях экономии памяти) и очень частые слова (в целях повышения интерпретируемости тем). Мы уберем только частые слова.
```
import copy
dictionary2 = copy.deepcopy(dictionary)
```
__Задание 2.__ У объекта dictionary2 есть переменная dfs - это словарь, ключами которого являются id токена, а элементами - число раз, сколько слово встретилось во всей коллекции. Сохраните в отдельный список ингредиенты, которые встретились в коллекции больше 4000 раз. Вызовите метод словаря filter_tokens, подав в качестве первого аргумента полученный список популярных ингредиентов. Вычислите две величины: dict_size_before и dict_size_after - размер словаря до и после фильтрации.
Затем, используя новый словарь, создайте новый корпус документов, corpus2, по аналогии с тем, как это сделано в начале ноутбука. Вычислите две величины: corpus_size_before и corpus_size_after - суммарное количество ингредиентов в корпусе (иными словами, сумма длин всех документов коллекции) до и после фильтрации.
Передайте величины dict_size_before, dict_size_after, corpus_size_before, corpus_size_after в функцию save_answers2 и загрузите сгенерированный файл в форму.
```
more4000 = [w for w, count in dictionary2.dfs.iteritems() if count > 4000]
dict_size_before = len(dictionary2.items())
dictionary2.filter_tokens(bad_ids=more4000)
dict_size_after = len(dictionary2.items())
def get_corpus_size(corp):
res = 0
for doc in corp:
res += len(doc)
#for w in doc:
# res += w[1]
return res
corpus_size_before = get_corpus_size(corpus)
corpus2 = [dictionary2.doc2bow(text) for text in texts] # составляем корпус документов
corpus_size_after = get_corpus_size(corpus2)
def save_answers2(dict_size_before, dict_size_after, corpus_size_before, corpus_size_after):
with open("cooking_LDA_pa_task2.txt", "w") as fout:
fout.write(" ".join([str(el) for el in [dict_size_before, dict_size_after, corpus_size_before, corpus_size_after]]))
save_answers2(dict_size_before, dict_size_after, corpus_size_before, corpus_size_after)
```
### Сравнение когерентностей
__Задание 3.__ Постройте еще одну модель по корпусу corpus2 и словарю dictioanary2, остальные параметры оставьте такими же, как при первом построении модели. Сохраните новую модель в другую переменную (не перезаписывайте предыдущую модель). Не забудьте про фиксирование seed!
Затем воспользуйтесь методом top_topics модели, чтобы вычислить ее когерентность. Передайте в качестве аргумента соответствующий модели корпус. Метод вернет список кортежей (топ токенов, когерентность), отсортированных по убыванию последней. Вычислите среднюю по всем темам когерентность для каждой из двух моделей и передайте в функцию save_answers3.
```
np.random.seed(76543)
# здесь код для построения модели:
ldamodel2 = models.ldamodel.LdaModel(corpus2, id2word=dictionary2, num_topics=40, passes=5)
coherences = ldamodel.top_topics(corpus)
coherences2 = ldamodel2.top_topics(corpus2)
import numpy as np
list1 = np.array([])
for coh in coherences:
list1 = np.append(list1, coh[1])
list2 = np.array([])
for coh in coherences2:
list2 = np.append(list2, coh[1])
coherence = list1.mean()
coherence2 = list2.mean()
def save_answers3(coherence, coherence2):
with open("cooking_LDA_pa_task3.txt", "w") as fout:
fout.write(" ".join(["%3f"%el for el in [coherence, coherence2]]))
save_answers3(coherence, coherence2)
```
Считается, что когерентность хорошо соотносится с человеческими оценками интерпретируемости тем. Поэтому на больших текстовых коллекциях когерентность обычно повышается, если убрать фоновую лексику. Однако в нашем случае этого не произошло.
### Изучение влияния гиперпараметра alpha
В этом разделе мы будем работать со второй моделью, то есть той, которая построена по сокращенному корпусу.
Пока что мы посмотрели только на матрицу темы-слова, теперь давайте посмотрим на матрицу темы-документы. Выведите темы для нулевого (или любого другого) документа из корпуса, воспользовавшись методом get_document_topics второй модели:
Также выведите содержимое переменной .alpha второй модели:
У вас должно получиться, что документ характеризуется небольшим числом тем. Попробуем поменять гиперпараметр alpha, задающий априорное распределение Дирихле для распределений тем в документах.
__Задание 4.__ Обучите третью модель: используйте сокращенный корпус (corpus2 и dictionary2) и установите параметр __alpha=1__, passes=5. Не забудьте задать количество тем и зафиксировать seed! Выведите темы новой модели для нулевого документа; должно получиться, что распределение над множеством тем практически равномерное. Чтобы убедиться в том, что во второй модели документы описываются гораздо более разреженными распределениями, чем в третьей, посчитайте суммарное количество элементов, __превосходящих 0.01__, в матрицах темы-документы обеих моделей. Другими словами, запросите темы модели для каждого документа с параметром minimum_probability=0.01 и просуммируйте число элементов в получаемых массивах. Передайте две суммы (сначала для модели с alpha по умолчанию, затем для модели в alpha=1) в функцию save_answers4.
```
def save_answers4(count_model2, count_model3):
with open("cooking_LDA_pa_task4.txt", "w") as fout:
fout.write(" ".join([str(el) for el in [count_model2, count_model3]]))
```
Таким образом, гиперпараметр alpha влияет на разреженность распределений тем в документах. Аналогично гиперпараметр eta влияет на разреженность распределений слов в темах.
### LDA как способ понижения размерности
Иногда распределения над темами, найденные с помощью LDA, добавляют в матрицу объекты-признаки как дополнительные, семантические, признаки, и это может улучшить качество решения задачи. Для простоты давайте просто обучим классификатор рецептов на кухни на признаках, полученных из LDA, и измерим точность (accuracy).
__Задание 5.__ Используйте модель, построенную по сокращенной выборке с alpha по умолчанию (вторую модель). Составьте матрицу $\Theta = p(t|d)$ вероятностей тем в документах; вы можете использовать тот же метод get_document_topics, а также вектор правильных ответов y (в том же порядке, в котором рецепты идут в переменной recipes). Создайте объект RandomForestClassifier со 100 деревьями, с помощью функции cross_val_score вычислите среднюю accuracy по трем фолдам (перемешивать данные не нужно) и передайте в функцию save_answers5.
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import cross_val_score
def save_answers5(accuracy):
with open("cooking_LDA_pa_task5.txt", "w") as fout:
fout.write(str(accuracy))
```
Для такого большого количества классов это неплохая точность. Вы можете попроовать обучать RandomForest на исходной матрице частот слов, имеющей значительно большую размерность, и увидеть, что accuracy увеличивается на 10-15%. Таким образом, LDA собрал не всю, но достаточно большую часть информации из выборки, в матрице низкого ранга.
### LDA --- вероятностная модель
Матричное разложение, использующееся в LDA, интерпретируется как следующий процесс генерации документов.
Для документа $d$ длины $n_d$:
1. Из априорного распределения Дирихле с параметром alpha сгенерировать распределение над множеством тем: $\theta_d \sim Dirichlet(\alpha)$
1. Для каждого слова $w = 1, \dots, n_d$:
1. Сгенерировать тему из дискретного распределения $t \sim \theta_{d}$
1. Сгенерировать слово из дискретного распределения $w \sim \phi_{t}$.
Подробнее об этом в [Википедии](https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation).
В контексте нашей задачи получается, что, используя данный генеративный процесс, можно создавать новые рецепты. Вы можете передать в функцию модель и число ингредиентов и сгенерировать рецепт :)
```
def generate_recipe(model, num_ingredients):
theta = np.random.dirichlet(model.alpha)
for i in range(num_ingredients):
t = np.random.choice(np.arange(model.num_topics), p=theta)
topic = model.show_topic(0, topn=model.num_terms)
topic_distr = [x[1] for x in topic]
terms = [x[0] for x in topic]
w = np.random.choice(terms, p=topic_distr)
print w
```
### Интерпретация построенной модели
Вы можете рассмотреть топы ингредиентов каждой темы. Большиснтво тем сами по себе похожи на рецепты; в некоторых собираются продукты одного вида, например, свежие фрукты или разные виды сыра.
Попробуем эмпирически соотнести наши темы с национальными кухнями (cuisine). Построим матрицу A размера темы x кухни, ее элементы $a_{tc}$ - суммы p(t|d) по всем документам d, которые отнесены к кухне c. Нормируем матрицу на частоты рецептов по разным кухням, чтобы избежать дисбаланса между кухнями. Следующая функция получает на вход объект модели, объект корпуса и исходные данные и возвращает нормированную матрицу A. Ее удобно визуализировать с помощью seaborn.
```
import pandas
import seaborn
from matplotlib import pyplot as plt
%matplotlib inline
def compute_topic_cuisine_matrix(model, corpus, recipes):
# составляем вектор целевых признаков
targets = list(set([recipe["cuisine"] for recipe in recipes]))
# составляем матрицу
tc_matrix = pandas.DataFrame(data=np.zeros((model.num_topics, len(targets))), columns=targets)
for recipe, bow in zip(recipes, corpus):
recipe_topic = model.get_document_topics(bow)
for t, prob in recipe_topic:
tc_matrix[recipe["cuisine"]][t] += prob
# нормируем матрицу
target_sums = pandas.DataFrame(data=np.zeros((1, len(targets))), columns=targets)
for recipe in recipes:
target_sums[recipe["cuisine"]] += 1
return pandas.DataFrame(tc_matrix.values/target_sums.values, columns=tc_matrix.columns)
def plot_matrix(tc_matrix):
plt.figure(figsize=(10, 10))
seaborn.heatmap(tc_matrix, square=True)
# Визуализируйте матрицу
```
Чем темнее квадрат в матрице, тем больше связь этой темы с данной кухней. Мы видим, что у нас есть темы, которые связаны с несколькими кухнями. Такие темы показывают набор ингредиентов, которые популярны в кухнях нескольких народов, то есть указывают на схожесть кухонь этих народов. Некоторые темы распределены по всем кухням равномерно, они показывают наборы продуктов, которые часто используются в кулинарии всех стран.
Жаль, что в датасете нет названий рецептов, иначе темы было бы проще интерпретировать...
### Заключение
В этом задании вы построили несколько моделей LDA, посмотрели, на что влияют гиперпараметры модели и как можно использовать построенную модель.
|
github_jupyter
|
# Reading Notebooks
* https://nbformat.readthedocs.io/en/latest/api.html
## Read a .ipynb file
A notebook consists of metadata, format info, and a list of cells. Very simple.
```
import nbformat
from nbformat.v4.nbbase import new_code_cell, new_markdown_cell, new_notebook
# read notebook file
filename = "02.01-Tagging.ipynb"
with open(filename, "r") as fp:
nb = nbformat.read(fp, as_version=4)
# display file metadata
print(f"nbformat = {nb.nbformat}.{nb.nbformat_minor}")
display(nb.metadata)
```
## Loop over cells
The heavy lifting is in the list of cells.
Here's how to loop over cells. The cell metadata is editable in JupyterLab, and has a 'tags' key where you manage a list of your own tags. If you wanted to remove cells, this would be the place to tag them.
```
for n, cell in enumerate(nb.cells):
print(f"\nCell {n}")
print(" metadata:", cell.metadata)
print(" cell_type:", cell.cell_type)
print(" keys():", cell.keys())
```
## Remove Code Elements
Remove code segments with specific tags. This uses regular expressions to identify code segments in code cells. This is actually a bit more general and would allow substitution as well.
```
import re
SOLUTION_CODE = "### BEGIN SOLUTION(.*)### END SOLUTION"
HIDDEN_TESTS = "### BEGIN HIDDEN TESTS(.*)### END HIDDEN TESTS"
def replace_code(pattern, replacement):
regex = re.compile(pattern, re.DOTALL)
for cell in nb.cells:
if cell.cell_type == "code" and regex.findall(cell.source):
cell.source = regex.sub(replacement, cell.source)
print(f" - {pattern} removed")
replace_code(SOLUTION_CODE, "")
replace_code(HIDDEN_TESTS, "")
```
## Remove cells with a specified tag
Note the use of a generator. This keeps things fast, but does need an explicit `list` if you need a list of tagged cells.
```
# a example of an iterator that returns all cells satisfying certain conditions.
def get_cells(nb, tag):
for cell in nb.cells:
if cell.cell_type == "markdown":
if "tags" in cell.metadata.keys():
if tag in cell.metadata["tags"]:
yield cell
tagged_cells = list(get_cells(nb, "exercise"))
tagged_cells
# remove all cells with a specified tag
def remove_cells(nb, tag):
tagged_cells = list(get_cells(nb, tag))
if tagged_cells:
print(f" - removing cells with tag {tag}")
nb.cells = list(filter(lambda cell: cell not in tagged_cells, nb.cells))
remove_cells(nb, "exercise")
```
## Write file out
```
with open("out.ipynb", "w") as fp:
nbformat.write(nb, fp)
```
## Execute notebooks
https://nbconvert.readthedocs.io/en/latest/execute_api.html
```
import nbformat
from nbconvert.preprocessors import CellExecutionError, ExecutePreprocessor
nb_filename = "out.ipynb"
nb_filename_out = "executed_" + nb_filename
# read file
with open("out.ipynb", "r") as fp:
nb = nbformat.read(fp, as_version=4)
# instantiate an execution processor allowing errors
ep = ExecutePreprocessor(timeout=600, kernel_name="python3", allow_errors=True)
ep.preprocess(nb, {"metadata": {"path": "./"}})
with open(nb_filename_out, mode="w", encoding="utf-8") as f:
nbformat.write(nb, f)
```
|
github_jupyter
|
# Paginación
El objetivo es crear una lista de páginas a mostrar. Se mostrará la página actual y las 3 siguientes y las 3 anteriores, y además la primera y la última. El algoritmo debe calcular qué numeros se muestran, y crear una lista con ellos. Además se pondrán espacios en blanco en el lugar donde irán los puntos suspensivos.
Si el número total de páginas es inferior a 10, se mostrarán todas las páginas.
```
def lista_paginas(paginas, actual):
if paginas < 10:
pagination = list(range(paginas))
else:
if actual <= 4:
pagination = (actual + 6)*['']
pagination[-1] = paginas - 1
pages = range(0, actual+4)
for i, p in enumerate(pages):
pagination[i] = p
elif actual >= paginas - 5:
pagination = (paginas - actual + 5)*['']
pagination[0] = 0
pages = range(actual-3, paginas)
for i, p in enumerate(pages):
pagination[i+2] = p
else:
pagination = 11*['']
pagination[0] = 0
pagination[-1] = paginas -1
pages = range(actual-3, actual+4)
for i, p in enumerate(pages):
pagination[i+2] = p
return pagination
# comprobación de que funciona
for pags, act in [
(8, 4), (9, 4), (10, 2), (10, 3), (10, 4), (10, 5), (10, 6), (10, 7), (10, 8), (10, 9), (10, 10),
(20, 3), (20, 4), (20, 5), (20, 6), (20, 7), (20, 13), (20, 14), (20, 15), (20, 16), (20, 17), (20, 18),
]:
print(pags, act, lista_paginas(pags, act))
```
Ahora personalizo, puedo escoger el número de páginas anteriores y posteriores a mostrar.
```
def lista_paginas_custom(paginas, actual, num=3):
"""Calcula la lista de páginas a mostrar. Las cadenas
nulas corresponden a puntos suspensivos.
Argumentos
----------
paginas: int
Total de páginas que hay.
actual: int
página actual.
num: int
número de paginas anteriores y posteriores que queremos
mostrar.
Devuelve
--------
paginacion: list
lista de páginas calculada.
"""
if paginas < 10:
pagination = list(range(paginas))
else:
if actual <= num + 1:
pagination = (actual + num + 3)*['']
pagination[-1] = paginas - 1
pages = range(0, actual+num+1)
for i, p in enumerate(pages):
pagination[i] = p
elif actual >= paginas - num - 2:
pagination = (paginas - actual + num + 2)*['']
pagination[0] = 0
pages = range(actual-num, paginas)
for i, p in enumerate(pages):
pagination[i+2] = p
else:
pagination = (num*2 + 5)*['']
pagination[0] = 0
pagination[-1] = paginas -1
pages = range(actual-num, actual+num+1)
for i, p in enumerate(pages):
pagination[i+2] = p
return pagination
# comprobación de que funciona
for pags, act in [
(8, 4), (9, 4), (10, 2), (10, 3), (10, 4), (10, 5), (10, 6), (10, 7), (10, 8), (10, 9), (10, 10),
(20, 3), (20, 4), (20, 5), (20, 6), (20, 7), (20, 13), (20, 14), (20, 15), (20, 16), (20, 17), (20, 18),
]:
print(lista_paginas_custom(pags, act) == lista_paginas(pags, act))
# comprobación de que funciona
for pags, act in [
(8, 4), (9, 4), (10, 2), (10, 3), (10, 4), (10, 5), (10, 6), (10, 7), (10, 8), (10, 9), (10, 10),
(20, 3), (20, 4), (20, 5), (20, 6), (20, 7), (20, 13), (20, 14), (20, 15), (20, 16), (20, 17), (20, 18),
]:
print(f'pags={pags} act={act} num=1: {lista_paginas_custom(pags, act, 1)}')
print(f'pags={pags} act={act} num=2: {lista_paginas_custom(pags, act, 2)}')
print(f'pags={pags} act={act} num=3: {lista_paginas_custom(pags, act, 3)}')
print(f'pags={pags} act={act} num=4: {lista_paginas_custom(pags, act, 4)}')
print(f'pags={pags} act={act} num=5: {lista_paginas_custom(pags, act, 5)}')
a=3.8
int(a)
# misma función, pero añadiendo 1 (e.g. las páginas van de 1 al número total de páginas)
def lista_paginas_más_uno(paginas, actual, num=3):
"""Calcula la lista de páginas a mostrar. Las cadenas
nulas corresponden a puntos suspensivos.
Argumentos
----------
paginas: int
Total de páginas que hay.
actual: int
página actual.
num: int
número de paginas anteriores y posteriores que queremos
mostrar.
Devuelve
--------
paginacion: list
lista de páginas calculada.
"""
if paginas < 10 or (actual <= num + 1 and actual >= paginas - num - 1):
pagination = list(range(1, paginas+1))
else:
if actual <= num + 2:
pagination = (actual + num + 2)*['']
pagination[-1] = paginas
pages = range(1, actual+num+1)
for i, p in enumerate(pages):
pagination[i] = p
elif actual >= paginas - num - 1:
pagination = (paginas - actual + num + 3)*['']
pagination[0] = 1
pages = range(actual-num, paginas+1)
for i, p in enumerate(pages):
pagination[i+2] = p
else:
pagination = (num*2 + 5)*['']
pagination[0] = 1
pagination[-1] = paginas
pages = range(actual-num, actual+num+1)
for i, p in enumerate(pages):
pagination[i+2] = p
return pagination
for pags, act in [
(8, 4), (9, 4), (10, 2), (10, 3), (10, 4), (10, 5), (10, 6), (10, 7), (10, 8), (10, 9), (10, 10),
(20, 3), (20, 4), (20, 5), (20, 6), (20, 7), (20, 13), (20, 14), (20, 15), (20, 16), (20, 17), (20, 18),
(11, 6),
]:
for n in range(1, 6):
print(f'pags={pags} act={act} num={n}: {lista_paginas_custom(pags, act, n)} {lista_paginas_más_uno(pags, act, n)}')
```
|
github_jupyter
|
```
#Author: Eren Ali Aslangiray, Meryem Şahin
import pandas as pd
import os
import time
import sys
path1 = "/Users/erenmac/Desktop/NEW_DATA/Text/text_emotion.csv"
path2 = "/Users/erenmac/Desktop/NEW_DATA/Text/primary-plutchik-wheel-DFE.csv"
path3 = "/Users/erenmac/Desktop/NEW_DATA/Text/ssec-aggregated/train-combined-0.66.csv"
path4 = "/Users/erenmac/Desktop/NEW_DATA/Text/twitter_emotion_SocialCom_Wang/dev.txt"
path5 = "/Users/erenmac/Desktop/NEW_DATA/Text/twitter_emotion_SocialCom_Wang/train_2_10.txt"
path6 = "/Users/erenmac/Desktop/NEW_DATA/Text/twitter_emotion_SocialCom_Wang/test.txt"
path7 = "/Users/erenmac/Desktop/NEW_DATA/Text/GroundedEmotions/collected_data/collected_news_data.txt"
path8 = "/Users/erenmac/Desktop/NEW_DATA/Text/GroundedEmotions/collected_data/collected_tweets.txt"
path9 = "/Users/erenmac/Desktop/NEW_DATA/Text/GroundedEmotions/collected_data/collected_user_history_data.txt"
path10 = "/Users/erenmac/Desktop/NEW_DATA/Text/GroundedEmotions/collected_data/collected_weather_dataset.txt"
path11 = "/Users/erenmac/Desktop/NEW_DATA/Text/ssec-aggregated/test-combined-0.66.csv"
path12 = "/Users/erenmac/Desktop/NEW_DATA/Text/twitter-emotion/train.csv"
path13 = "/Users/erenmac/Desktop/NEW_DATA/Text/emotion.data"
path14 = "/Users/erenmac/Desktop/NEW_DATA/Text/xmltext.txt"
path15 = "/Users/erenmac/Desktop/NEW_DATA/Text/SentiWords_1.1.txt"
path16 = "Users/erenmac/Desktop/NEW_DATA/Text/NRC-Emotion-Lexicon-Wordlevel-v0.92.txt"
pathjson1 = "/Users/erenmac/Desktop/NEW_DATA/Text/cybertroll.json"
#mytask = [2,4,7,8,9,11,13,14,json]
#df1 = pd.read_csv(path1)
#df2 = pd.read_csv(path2)
#df3 = pd.read_csv(path3, error_bad_lines=False, header = None )
#df4 = pd.read_csv(path4, sep="\t", header = None) #twitter
df5 = pd.read_csv(path5, sep="\t", header = None)
df6 = pd.read_csv(path6, sep="\t", header = None)
#df7 = pd.read_csv(path7, sep="|", header = None)
#df8 = pd.read_csv(path8, sep="|", header = None) #twitter
#df9 = pd.read_csv(path9, sep="|", header = None) #twitter
#df10 = pd.read_csv(path10, sep="|", header = None)
#df11 = pd.read_csv(path11, error_bad_lines=False, header = None )
#df12 = pd.read_csv(path12,encoding = 'ISO-8859-1')
#df13 = pd.read_csv (path13)
#dfjson1 = pd.read_json(pathjson1, lines = True)
dfx = df5.append(df6, ignore_index=True)
dfx.to_json("/Users/erenmac/Desktop/NEW_DATA/tweets.json")
template_dict = {"anger":[],"disgust":[],"sad":[],"happy":[],"suprise":[],"fear":[],"neutral":[]}
```
# DF2
```
df2 = df2.drop(columns = ["emotion_gold","emotion:confidence","_unit_id", "_golden","_unit_state","_trusted_judgments","_last_judgment_at","id","idiom_id"])
unique_emoniotns = df2.emotion.unique()
unique_emoniotns
reverse_dict = {"Anger":"anger", "Aggression":"anger","Disgust":"disgust","Contempt":"disgust","Sadness":"sad","Disapproval":"sad","Remorse":"sad","Optimism":"happy","Love":"happy","Joy":"happy","Trust":"happy","Surprise":"surprise","Fear":"fear","Awe":"fear","Neutral":"neutral","Ambiguous":"neutral"}
dropemo = ["Anticipation","Submission"]
df2 = df2[df2.emotion != "Anticipation"]
df2 = df2[df2.emotion != "Submission"]
df2["emotion"] = df2["emotion"].map(reverse_dict)
df2 = df2.reset_index(drop=True)
for i in range (2270):
k = df2["sentence"][i]
if "." in k:
k = k.replace(".","")
if "," in k:
k = k.replace(",","")
if "?" in k:
k = k.replace("?","")
if "!" in k:
k = k.replace("!","")
df2["sentence"][i] = k
df2final = df2
df2final.to_csv("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/DF2.csv")
```
# DF4
```
import tweepy
auth = tweepy.OAuthHandler("wso6hl1mmqx5YlLuuiJ7apQci", "QQ1mGejEs70qBmpzODBGhMc2FLzVo30hctpaZjSVlBtlmsTiSZ")
auth.set_access_token("1055878812-fI40KKPy7zNOK8N18WROQ02AgnH820WFeOhTIDS", "q5WJXcqCWFRoU7KxR797fz4Ku3C6a876xdECJchupsnfY")
try:
redirect_url = auth.get_authorization_url()
except tweepy.TweepError:
print('Error! Failed to get request token.')
api = tweepy.API(auth)
tweets = []
code8errorlist = []
def tweetminer(id):
tweet = api.get_status(id)
return tweet.text
#loaddf.to_json("/Users/erenmac/Desktop/NEW_DATA/semi_cleaned_data/loaddf.json")
loaddf = pd.read_json("/Users/erenmac/Desktop/NEW_DATA/semi_cleaned_data/loaddf.json")
for i in range (len(loaddf)):
if i%100 == 0:
print(i)
if loaddf[2][i] == "aslangiray":
try:
x = (tweetminer(loaddf[0][i]))
loaddf[2][i] = x
except tweepy.TweepError as e:
e1 = "'code': 88" in str(e)
e2 = "'code': 144" in str(e)
e3 = "'code': 179" in str(e)
e4 = "'code': 34" in str(e)
e5 = "'code': 63" in str(e)
if e1 == True:
print ("Have code 88 error, waiting 5 min.")
time.sleep((60*5)+5)
elif e2 == True:
loaddf[2][i] = "delet dis pls"
elif e3 == True:
loaddf[2][i] = "delet dis pls"
elif e4 == True:
loaddf[2][i] = "delet dis pls"
elif e5 == True:
loaddf[2][i] = "delet dis pls"
else:
errorlist.append(i)
errorlist.append(e)
len(errorlist)
loaddf = loaddf.drop(columns = [0])
loaddf = loaddf[loaddf[2] != "delet dis pls"]
loaddf = loaddf.reset_index(drop = True)
loaddf.to_json("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/DF4.json")
```
# DF7
```
None
```
# DF8
```
df8[3] = "aslangiray"
df8
tweets8 = []
errorlist8 = []
code88errorlist = []
for i in range (len(df8)):
if i%100 == 0:
print(i)
if df8[3][i] == "aslangiray":
try:
x = (tweetminer(df8[0][i]))
df8[3][i] = x
except tweepy.TweepError as e:
e1 = "'code': 88" in str(e)
e2 = "'code': 144" in str(e)
e3 = "'code': 179" in str(e)
e4 = "'code': 34" in str(e)
e5 = "'code': 63" in str(e)
if e1 == True:
print ("Have code 88 error, waiting 5 min.")
time.sleep((60*5)+5)
elif e2 == True:
df8[3][i] = "delet dis pls"
elif e3 == True:
df8[3][i] = "delet dis pls"
elif e4 == True:
df8[3][i] = "delet dis pls"
elif e5 == True:
df8[3][i] = "delet dis pls"
else:
errorlist.append(i)
errorlist.append(e)
df8 = df8.drop(columns = [0,1])
df8 = df8[df8[3] != "delet dis pls"]
df8 = df8.reset_index(drop = True)
df8.to_csv("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/DF8.csv")
```
# DF9
```
None
```
# DF11
```
for i in range (1431):
k = df11[0][i]
if "---" in k:
k = k.replace("---","")
if "\t" in k:
k = k.replace("\t", " ")
if "." in k:
k = k.replace(".","")
if "," in k:
k = k.replace(",","")
if "?" in k:
k = k.replace("?","")
if "!" in k:
k = k.replace("!","")
if "#" in k:
k = k.replace("#"," ")
df11[0][i] = k
import re
def remove_mentions(input_text):
return re.sub(r'@\w+', '', input_text)
for i in range (1431):
k = df11[0][i]
k = remove_mentions(k)
k = k.replace("SemST","")
df11[0][i] = k
emotions_list = ["Anger","Anticipation","Disgust","Joy","Fear","Sadness","Trust","Surprise"]
rowlist = []
for i in range (len(df11)):
k = df11[0][i]
k = k.split()
rowlist.append(k)
dellist = []
for i in range (len(rowlist)):
if len(rowlist[i]) < 5:
dellist.append(i)
dellist.remove(911)
i = 0
for item in dellist:
rowlist.pop(item-i)
i = i +1
dfdict = {}
for i in range (len(rowlist)):
for k in range (3):
if k == 0:
if rowlist[i][k] in emotions_list:
dfdict[i] = [rowlist[i][k]]
else:
dfdict[i] = []
else:
if rowlist[i][k] in emotions_list:
dfdict[i] += [rowlist[i][k]]
for q in range (len(dfdict[i])):
rowlist[i].pop(0)
df11s = pd.DataFrame.from_dict(dfdict, orient='index')
df11s[3] = "sad"
for i in range (len(rowlist)):
k = ' '.join(rowlist[i])
df11s[3][i] = k
df11s = df11s.dropna(subset=[0])
df11final = df11s.reset_index(drop = True)
unique_emoniotns = df11final[1].unique()
unique_emoniotns
reverse_dict = {"Trust":"happy", "Joy":"happy","Anticipation":"neutral","Anger":"anger","fear":"Fear","Sadness":"sad","Disgust":"disgust","Surprise":"surprise"}
df11final[0] = df11final[0].map(reverse_dict)
df11final[1] = df11final[1].map(reverse_dict)
df11final[2] = df11final[2].map(reverse_dict)
df11final.to_csv("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/DF11.csv")
```
# DF13
```
df13 = df13.drop(columns = ["Unnamed: 0"])
unique_emoniotns = df13.emotions.unique()
unique_emoniotns
reverse_dict = {"sadness":"sad", "joy":"happy","love":"happy","anger":"anger","fear":"fear","surprise":"surprise"}
df13["emotions"] = df13["emotions"].map(reverse_dict)
df13final = df13
df13final.to_csv("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/DF13.csv")
```
# DFJSON1
```
dfjson1 = dfjson1.drop(columns = ["extras","metadata"])
labellist = []
for i in range (len(dfjson1)):
if dfjson1["annotation"][i]["label"] == ['1']:
labellist.append("negative")
else:
labellist.append("del")
for i in range (len(labellist)):
k = labellist[i]
dfjson1["annotation"][i] = k
dfjson1 = dfjson1[dfjson1.annotation != "del"]
dfjson1final = dfjson1
dfjson1final.to_csv("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/DF17.csv")
```
# Finalize DB
```
meryem1 = pd.read_json("/Users/erenmac/Downloads/df12f.json")
meryem2 = pd.read_json("/Users/erenmac/Downloads/result2.json")
meryem1
erenfin = pd.read_json("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/final_multilabel.json")
erenfin2[0] = erenfin2.annotation
erenfin2[1] = erenfin2.content
erenfin2 = erenfin2.drop(columns= ["annotation","content"])
erenfin2 = pd.read_csv("/Users/erenmac/Desktop/NEW_DATA/Cleaned_Data/df17.csv")
erenfin2 = erenfin2.drop(columns = ["Unnamed: 0"])
frames = [erenfin2,meryem1]
result = pd.concat(frames)
result = result.reset_index(drop = True)
result.to_json("/Users/erenmac/Desktop/NEW_DATA/Finalized_Data/pos_neg_emotion_data.json")
result
test1 = pd.read_json("/Users/erenmac/Desktop/NEW_DATA/Finalized_Data/pos_neg_emotion_data.json")
test2 = pd.read_json("/Users/erenmac/Desktop/NEW_DATA/Finalized_Data/multilabel_emotion_data.json")
test1
```
|
github_jupyter
|
```
%matplotlib inline
import matplotlib
from matplotlib import pyplot as plt
import seaborn as sns
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('retina')
sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.set_palette(sns.color_palette())
import pandas as pd
import pickle
from mcmcjoint.samplers import *
from mcmcjoint.tests import *
seed = 10000
m_dim = 1
num_trials = 5
nthreads = 5
num_samples = 5e5
burn_in_samples = 0
geweke_thinning_samples = 50
mmd_thinning_samples = 500
tau = 1
alpha = 0.05
for exper in range(1):
if exper == 0:
print(f'Experiment {exper}: no error')
model = t_mixture_sampler
else:
print(f'Experiment {exper}: error')
exec('model = t_mixture_sampler_error_'+str(exper))
t_mix = model(D=m_dim, M=2, N=2, v=5,
m_mu=[-1. * np.ones(m_dim), 1. * np.ones(m_dim)],
S_mu=[10. * np.identity(m_dim), 10. * np.identity(m_dim)],
v_Sigma=2.*np.array([3., 3.]),
Psi_Sigma=2.*np.array([1. * np.identity(m_dim), 1. * np.identity(m_dim)]),
alpha_p=np.array([2., 2.]))
t_mix.set_nthreads(1)
theta_indices = t_mix.theta_indices
t_mix_exper = sample_experiment(num_trials=num_trials, nthreads=nthreads, seed=seed,
sampler=t_mix,
num_samples=num_samples,
burn_in_samples=burn_in_samples,
geweke_thinning_samples=geweke_thinning_samples,
mmd_thinning_samples=mmd_thinning_samples,
tau=tau, alpha=alpha, savedir = './results/t_mixture', experiment_name=exper_name)
lst_saved = t_mix_exper.run()
df_results = pd.DataFrame(index=np.arange(0, num_trials*3), columns=('experiment', 'test_type', 'result'))
i=0
for exper in range(2):
for thread in range(9):
for trial in range(1):
with open('./results/t_mixture/error_'+str(exper)+'_results_'+str(thread)+'_'+str(trial)+'.pkl', 'rb') as f:
result = pickle.load(f)[0][0]
df_results.loc[i] = [str(exper), 'geweke', onp.array(result['geweke'][0]).max()] # reject null if at least one test rejects
df_results.loc[i+1] = [str(exper), 'backward', float(result['backward'][0])]
df_results.loc[i+2] = [str(exper), 'wild', float(result['wild'][0])]
i+=3
df_results['result'] = pd.to_numeric(df_results['result'])
df_results=df_results.groupby(['experiment', 'test_type']).mean()
df_results
```
|
github_jupyter
|
```
import os, re
import pandas as pd
import numpy as np
import requests
from bs4 import BeautifulSoup
import time
import json
URL_LIST_BASE = "https://www.dogbreedslist.info/all-dog-breeds/list_1_{}.html" # {} in [1, 19]
def get_dog_list_page(n):
r = requests.get(URL_LIST_BASE.format(n))
soup = BeautifulSoup(r.content, 'html.parser')
divs = soup.find_all('div', {'class': 'left'})
dog_urls = [div.find_all('a')[0]["href"] for div in divs]
return [(re.findall("/all-dog-breeds/(.*)?\.html", url)[0], url) for url in dog_urls]
def load_dog_list_page():
return json.load(open("./dog_url_list.json", "rb"))
# URL_LIST_ALL_DOGS = []
# for i in range(1, 20):
# URL_LIST_ALL_DOGS.extend(get_dog_list_page(i))
# time.sleep(2)
# json.dump(URL_LIST_ALL_DOGS, open("./dog_url_list.json", "w+"))
URL_LIST_ALL_DOGS_loaded = load_dog_list_page()
def get_dog_info(n):
"""Gets breed-specific info. Unfortunately, numbered by index."""
dog = URL_LIST_ALL_DOGS_loaded[n]
r = requests.get(dog[1])
soup = BeautifulSoup(r.content, 'html.parser')
info_table = soup.find_all('table', {'class': 'table-01'})
characteristics_table = soup.find_all('table', {'class': 'table-02'})
dog_classes = [[i for i in tr.contents if i != '\n'] for tr in characteristics_table[0].find_all("tr")][1:]
characteristics = {dog_class[0].string: dog_class[1].p.contents[0][0] for dog_class in dog_classes}
info = dict([[i.string for i in info_table[0].find_all("tr")[2:][i].contents if i != '\n'] for i in [0, 4]])
dog_info = [info["Name"], {**characteristics, **{'Size': info["Size"]}}]
return dog_info
# ALL_DOG_INFO = {}
# for i in range(len(URL_LIST_ALL_DOGS_loaded)):
# try:
# time.sleep(1)
# gdi = get_dog_info(i)
# ALL_DOG_INFO[gdi[0]] = gdi[1]
# except Exception as e:
# print(i, e)
## SPECIAL CASES DUE TO BAD HTML.
# dog = URL_LIST_ALL_DOGS_loaded[332]
# r = requests.get(dog[1])
# soup = BeautifulSoup(r.content, 'html.parser')
# info_table = soup.find_all('table', {'class': 'table-01'})
# characteristics_table = soup.find_all('table', {'class': 'table-02'})
# dog_classes = [[i for i in tr.contents if i != '\n'] for tr in characteristics_table[0].find_all("tr")][1:]
# characteristics = {dog_class[0].string: dog_class[1].p.contents[0][0] for dog_class in dog_classes}
# # info = dict([[i.string for i in info_table[0].find_all("tr")[2:][i].contents if i != '\n'] for i in [0, 4]])
# dog_info = {**characteristics, **{"Size": "Medium"}}
# ALL_DOG_INFO["American Husky"] = dog_info
# dog = URL_LIST_ALL_DOGS_loaded[369]
# r = requests.get(dog[1])
# soup = BeautifulSoup(r.content, 'html.parser')
# info_table = soup.find_all('table', {'class': 'table-01'})
# characteristics_table = soup.find_all('table', {'class': 'table-02'})
# dog_classes = [[i for i in tr.contents if i != '\n'] for tr in characteristics_table[0].find_all("tr")][1:]
# characteristics = {dog_class[0].string: dog_class[1].p.contents[0][0] for dog_class in dog_classes}
# # info = dict([[i.string for i in info_table[0].find_all("tr")[2:][i].contents if i != '\n'] for i in [0, 4]])
# dog_info = {**characteristics, **{"Size": "Medium"}}
# ALL_DOG_INFO["Mountain Cur"] = dog_info
json.dump(ALL_DOG_INFO, open("./dog_metadata.json", "w+"))
```
|
github_jupyter
|
## Dependencies
```
import json, glob
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts_aux import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras import layers
from tensorflow.keras.models import Model
```
# Load data
```
test = pd.read_csv('/kaggle/input/tweet-sentiment-extraction/test.csv')
print('Test samples: %s' % len(test))
display(test.head())
```
# Model parameters
```
input_base_path = '/kaggle/input/239-robertabase/'
with open(input_base_path + 'config.json') as json_file:
config = json.load(json_file)
config
# vocab_path = input_base_path + 'vocab.json'
# merges_path = input_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
vocab_path = base_path + 'roberta-base-vocab.json'
merges_path = base_path + 'roberta-base-merges.txt'
config['base_model_path'] = base_path + 'roberta-base-tf_model.h5'
config['config_path'] = base_path + 'roberta-base-config.json'
model_path_list = glob.glob(input_base_path + '*.h5')
model_path_list.sort()
print('Models to predict:')
print(*model_path_list, sep = '\n')
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
```
# Pre process
```
test['text'].fillna('', inplace=True)
test['text'] = test['text'].apply(lambda x: x.lower())
test['text'] = test['text'].apply(lambda x: x.strip())
x_test, x_test_aux, x_test_aux_2 = get_data_test(test, tokenizer, config['MAX_LEN'], preprocess_fn=preprocess_roberta_test)
```
# Model
```
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
logits = layers.Dense(2, name="qa_outputs", use_bias=False)(last_hidden_state)
start_logits, end_logits = tf.split(logits, 2, axis=-1)
start_logits = tf.squeeze(start_logits, axis=-1)
end_logits = tf.squeeze(end_logits, axis=-1)
model = Model(inputs=[input_ids, attention_mask], outputs=[start_logits, end_logits])
return model
```
# Make predictions
```
NUM_TEST_IMAGES = len(test)
test_start_preds = np.zeros((NUM_TEST_IMAGES, config['MAX_LEN']))
test_end_preds = np.zeros((NUM_TEST_IMAGES, config['MAX_LEN']))
for model_path in model_path_list:
print(model_path)
model = model_fn(config['MAX_LEN'])
model.load_weights(model_path)
test_preds = model.predict(get_test_dataset(x_test, config['BATCH_SIZE']))
test_start_preds += test_preds[0]
test_end_preds += test_preds[1]
```
# Post process
```
test['start'] = test_start_preds.argmax(axis=-1)
test['end'] = test_end_preds.argmax(axis=-1)
test['selected_text'] = test.apply(lambda x: decode(x['start'], x['end'], x['text'], config['question_size'], tokenizer), axis=1)
# Post-process
test["selected_text"] = test.apply(lambda x: ' '.join([word for word in x['selected_text'].split() if word in x['text'].split()]), axis=1)
test['selected_text'] = test.apply(lambda x: x['text'] if (x['selected_text'] == '') else x['selected_text'], axis=1)
test['selected_text'].fillna(test['text'], inplace=True)
```
# Visualize predictions
```
test['text_len'] = test['text'].apply(lambda x : len(x))
test['label_len'] = test['selected_text'].apply(lambda x : len(x))
test['text_wordCnt'] = test['text'].apply(lambda x : len(x.split(' ')))
test['label_wordCnt'] = test['selected_text'].apply(lambda x : len(x.split(' ')))
test['text_tokenCnt'] = test['text'].apply(lambda x : len(tokenizer.encode(x).ids))
test['label_tokenCnt'] = test['selected_text'].apply(lambda x : len(tokenizer.encode(x).ids))
test['jaccard'] = test.apply(lambda x: jaccard(x['text'], x['selected_text']), axis=1)
display(test.head(10))
display(test.describe())
```
# Test set predictions
```
submission = pd.read_csv('/kaggle/input/tweet-sentiment-extraction/sample_submission.csv')
submission['selected_text'] = test['selected_text']
submission.to_csv('submission.csv', index=False)
submission.head(10)
```
|
github_jupyter
|
```
%matplotlib inline
from refer import REFER
import numpy as np
import skimage.io as io
import matplotlib.pyplot as plt
```
# Load Refer Dataset
```
data_root = '../../data' # contains refclef, refcoco, refcoco+, refcocog and images
dataset = 'refcoco'
splitBy = 'unc'
refer = REFER(data_root, dataset, splitBy)
```
# Stats about the Dataset
```
# print stats about the given dataset
print ('dataset [%s_%s] contains: ' % (dataset, splitBy))
ref_ids = refer.getRefIds()
image_ids = refer.getImgIds()
print ('%s expressions for %s refs in %s images.' % (len(refer.Sents), len(ref_ids), len(image_ids)))
print ('\nAmong them:')
if dataset == 'refclef':
if splitBy == 'unc':
splits = ['train', 'val', 'testA', 'testB', 'testC']
else:
splits = ['train', 'val', 'test']
elif dataset == 'refcoco':
splits = ['train', 'val', 'test']
elif dataset == 'refcoco+':
splits = ['train', 'val', 'test']
elif dataset == 'refcocog':
splits = ['train', 'val'] # we don't have test split for refcocog right now.
for split in splits:
ref_ids = refer.getRefIds(split=split)
print ('%s refs are in split [%s].' % (len(ref_ids), split))
# randomly sample one ref
ref_ids = refer.getRefIds(split='test')
ref_id = ref_ids[np.random.randint(0, len(ref_ids))]
print(ref_id)
print(ref_ids[0])
print(refer.Refs[0])
ref = refer.Refs[ref_ids]
ref_ids = refer.getRefIds(split='test')
ref_id = ref_ids[0]
print('REF ID: ,' , ref_id)
ref = refer.Refs[ref_id]
print()
print(ref)
print()
img_id = refer.getImgIds(ref_id)
img = refer.loadImgs(img_id)[0]
print('IMG INFOS: ',img)
print('IMG ID: ',img_id)
ann_ids = refer.getAnnIds(img['id'])
print('ANN IDS: ',ann_ids)
for i in range(len(ann_ids)):
ann = refer.loadAnns(ann_ids[i])[0]
print('IMAGE ID ',ann['image_id'])
print('ANN '+str(i+1)+': ', ann)
print('#################')
print(refer.loadAnns(ann_ids))
```
# Show Refered Object and its Expressions
```
# randomly sample one ref
ref_ids = refer.getRefIds()
ref_id = ref_ids[np.random.randint(0, len(ref_ids))]
ref = refer.Refs[ref_id]
print ('ref_id [%s] (ann_id [%s])' % (ref_id, refer.refToAnn[ref_id]['id']))
# show the segmentation of the referred object
plt.figure()
refer.showRef(ref, seg_box='seg')
plt.show()
# or show the bounding box of the referred object
refer.showRef(ref, seg_box='box')
plt.show()
# let's look at the details of each ref
for sent in ref['sentences']:
print ('sent_id[%s]: %s' % (sent['sent_id'], sent['sent']))
```
|
github_jupyter
|
# Binary trees
```
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
from dtreeviz.trees import *
from lolviz import *
import numpy as np
import pandas as pd
%config InlineBackend.figure_format = 'retina'
```
## Setup
Make sure to install stuff:
```
pip install -U dtreeviz
pip install -U lolviz
brew install graphviz
```
## Binary tree class definition
A binary tree has a payload (a value) and references to left and right children. One or both of the children references can be `None`. A reference to a node is the same thing as a reference to a tree as the tree is a self similar data structure. We don't distinguish between the two kinds of references. A reference to the root node is a reference to the entire tree.
Here is a basic tree node class in Python. The constructor requires at least a value to store in the node.
```
class TreeNode:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
def __repr__(self):
return str(self.value)
def __str__(self):
return str(self.value)
```
## Manual tree construction
Here's how to create and visualize a single node:
```
root = TreeNode(1)
treeviz(root)
```
**Given `left` and `right` nodes, create node `root` with those nodes as children.**
```
left = TreeNode(2)
right = TreeNode(3)
root = ...
treeviz(root)
```
<details>
<summary>Solution</summary>
<pre>
left = TreeNode(2)
right = TreeNode(3)
root = TreeNode(1,left,right)
treeviz(root)
</pre>
</details>
**Write code to create the following tree structure**
<img src="3-level-tree.png" width="30%">
```
left = ...
right = ...
root = ...
treeviz(root)
```
<details>
<summary>Solution</summary>
<pre>
left = TreeNode(2,TreeNode(4))
right = TreeNode(3,TreeNode(5),TreeNode(6))
root = TreeNode(1,left,right)
treeviz(root)
</pre>
</details>
## Walking trees manually
To walk a tree, we simply follow the left and right children references, avoiding any `None` references.
**Q.** Given tree `r` shown here, what Python expressions refer to the nodes with 443 and 17 in them?
```
left = TreeNode(443,TreeNode(-34))
right = TreeNode(17,TreeNode(99))
r = TreeNode(10,left,right)
treeviz(r)
```
<details>
<summary>Solution</summary>
<pre>
r.left, r.right
</pre>
</details>
**Q.** Given the same tree `r`, what Python expressions refer to the nodes with -34 and 99 in them?
<details>
<summary>Solution</summary>
<pre>
r.left.left, r.right.left
</pre>
</details>
## Walking all nodes
Now let's create a function to walk all nodes in a tree. Remember that our template for creating any recursive function looks like this:
```
def f(input):
1. check termination condition
2. process the active input region / current node, etc…
3. invoke f on subregion(s)
4. combine and return results
```
```
def walk(p:TreeNode):
if p is None: return # step 1
print(p.value) # step 2
walk(p.left) # step 3
walk(p.right) # step 3 (there is no step 4 for this problem)
```
Let's create the simple 3-level tree we had before:
```
left = TreeNode(2,TreeNode(4))
right = TreeNode(3,TreeNode(5),TreeNode(6))
root = TreeNode(1,left,right)
treeviz(root)
```
**Q.** What is the output of running `walk(root)`?
<details>
<summary>Solution</summary>
We walk the tree depth first, from left to right<p>
<pre>
1
2
4
3
5
6
</pre>
</details>
## Searching through nodes
Here's how to search for an element as you walk, terminating as soon as the node with `x` is found:
```
def search(p:TreeNode, x:object):
print("enter ",p)
if p is None: return None
print(p)
if x==p.value:
return p
q = search(p.left, x)
if q is not None:
return q
q = search(p.right, x)
return q
```
**Q.** What is the output of running `search(root, 5)`?
<details>
<summary>Solution</summary>
We walk the tree depth first as before, but now we stop when we reach the node with 5:<p>
<pre>
1
2
4
3
5
</pre>
</details>
To see the recursion entering and exiting (or discovering and finishing) nodes, here is a variation that prints out its progress through the tree:
```
def search(p:TreeNode, x:object):
if p is None: return None
print("enter ",p)
if x==p.value:
print("exit ",p)
return p
q = search(p.left, x)
if q is not None:
print("exit ",p)
return q
q = search(p.right, x)
print("exit ",p)
return q
search(root, 5)
```
## Creating (random) decision tree "stumps"
A regression tree stump is a tree with a decision node at the root and two predictor leaves. These are used by gradient boosting machines as the "weak learners."
```
class TreeNode: # acts as decision node and leaf. it's a leaf if split is None
def __init__(self, split=None, prediction=None, left=None, right=None):
self.split = split
self.prediction = prediction
self.left = left
self.right = right
def __repr__(self):
return str(self.value)
def __str__(self):
return str(self.value)
df = pd.DataFrame()
df["sqfeet"] = [750, 800, 850, 900,950]
df["rent"] = [1160, 1200, 1280, 1450,1300]
df
```
The following code shows where sklearn would do a split with a normal decision tree.
```
X, y = df.sqfeet.values.reshape(-1,1), df.rent.values
t = DecisionTreeRegressor(max_depth=1)
t.fit(X,y)
fig, ax = plt.subplots(1, 1, figsize=(3,1.5))
t = rtreeviz_univar(t,
X, y,
feature_names='sqfeet',
target_name='rent',
fontsize=9,
colors={'scatter_edge': 'black'},
ax=ax)
```
Instead of picking the optimal split point, we can choose a random value in between the minimum and maximum x value, like extremely random forests do:
```
def stumpfit(x, y):
if len(x)==1 or len(np.unique(x))==1: # if one x value, make leaf
return TreeNode(prediction=y[0])
split = np.round(np.random.uniform(min(x),max(x)))
t = TreeNode(split)
t.left = TreeNode(prediction=np.mean(y[x<split]))
t.right = TreeNode(prediction=np.mean(y[x>=split]))
return t
```
**Run the following code multiple times to see how it creates different y lists in the nodes, according to the split value.**
```
root = stumpfit(X.reshape(-1),y)
treeviz(root)
```
## Creating random decision trees (single variable)
And now to demonstrate the magic of recursion. If we replace
```
t.left = TreeNode(prediction=np.mean(y[x<split]))
```
with
```
t.left = treefit(x[x<split], y[x<split])
```
(and same for `t.right`) then all of the sudden we get a full decision tree, rather than just a stump!
```
def treefit(x, y):
if len(x)==1 or len(np.unique(x))==1: # if one x value, make leaf
return TreeNode(prediction=y[0])
split = np.round(np.random.uniform(min(x),max(x)))
t = TreeNode(split)
t.left = treefit(x[x<split], y[x<split])
t.right = treefit(x[x>=split], y[x>=split])
return t
root = treefit(X.reshape(-1),y)
treeviz(root)
```
You can run that multiple times to see different tree layouts according to randomness.
**Q.** How would you modify `treefit()` so that it creates a typical decision tree rather than a randomized decision tree?
<details>
<summary>Solution</summary>
Instead of choosing a random split, we would pick the split value in $x$ that got the best average child $y$ purity/similarity. In other words, exhaustively test each $x$ value as candidate split point by computing the MSE for left and right $y$ subregions. The split point that gets the best weighted average for left and right MSE, is the optimal split point.
</details>
|
github_jupyter
|
```
# reload packages
%load_ext autoreload
%autoreload 2
```
### Choose GPU (this may not be needed on your computer)
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=''
```
### load packages
```
from tfumap.umap import tfUMAP
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
import umap
import pandas as pd
```
### Load dataset
```
from sklearn.datasets import make_moons
X_train, Y_train = make_moons(1000, random_state=0, noise=0.1)
X_train_flat = X_train
X_test, Y_test = make_moons(1000, random_state=1, noise=0.1)
X_test_flat = X_test
X_valid, Y_valid = make_moons(1000, random_state=2, noise=0.1)
plt.scatter(X_test[:,0], X_test[:,1], c=Y_test)
```
### Create model and train
```
embedder = tfUMAP(direct_embedding=True, verbose=True, negative_sample_rate=5, training_epochs=100)
z = embedder.fit_transform(X_train_flat)
```
### Plot model output
```
fig, ax = plt.subplots( figsize=(8, 8))
sc = ax.scatter(
z[:, 0],
z[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow embedding", fontsize=20)
plt.colorbar(sc, ax=ax);
```
### View loss
```
from tfumap.umap import retrieve_tensors
import seaborn as sns
loss_df = retrieve_tensors(embedder.tensorboard_logdir)
loss_df[:3]
ax = sns.lineplot(x="step", y="val", hue="group", data=loss_df[loss_df.variable=='umap_loss'])
ax.set_xscale('log')
```
### Save output
```
from tfumap.paths import ensure_dir, MODEL_DIR
output_dir = MODEL_DIR/'projections'/ 'moons' / 'direct'
ensure_dir(output_dir)
embedder.save(output_dir)
loss_df.to_pickle(output_dir / 'loss_df.pickle')
np.save(output_dir / 'z.npy', z)
```
### Compare to direct embedding with base UMAP
```
from umap import UMAP
z_umap = UMAP(verbose=True).fit_transform(X_train_flat)
### realign using procrustes
from scipy.spatial import procrustes
z_align, z_umap_align, disparity = procrustes(z, z_umap)
print(disparity)
fig, axs = plt.subplots(ncols=2, figsize=(20, 8))
ax = axs[0]
sc = ax.scatter(
z_align[:, 0],
z_align[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow", fontsize=20)
#plt.colorbar(sc, ax=ax);
ax = axs[1]
sc = ax.scatter(
z_umap_align[:, 0],
z_umap_align[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP with UMAP-learn", fontsize=20)
#plt.colorbar(sc, ax=ax);
```
|
github_jupyter
|
# Train and hyperparameter tune with RAPIDS
## Prerequisites
- Create an Azure ML Workspace and setup environmnet on local computer following the steps in [Azure README.md](https://gitlab-master.nvidia.com/drobison/aws-sagemaker-gtc-2020/tree/master/azure/README.md )
```
# verify installation and check Azure ML SDK version
import azureml.core
print('SDK version:', azureml.core.VERSION)
```
- Install [AzCopy](https://docs.microsoft.com/en-us/azure/storage/common/storage-use-azcopy-v10) to download dataset from [Azure Blob storage](https://docs.microsoft.com/en-us/azure/storage/blobs/storage-blobs-overview) to your local computer (or another storage account).
In this example, we will use 20 million rows (samples) of the [airline dataset](http://kt.ijs.si/elena_ikonomovska/data.html):
```
!./azcopy cp 'https://airlinedataset.blob.core.windows.net/airline-20m/airline_20m.parquet' '/home/jzedlewski/code/drobinson/aws-sagemaker-gtc-2020/azure/notebooks
'
```
## Initialize workspace
Load and initialize a [Workspace](https://docs.microsoft.com/azure/machine-learning/service/concept-azure-machine-learning-architecture#workspace) object from the existing workspace you created in the prerequisites step. `Workspace.from_config()` creates a workspace object from the details stored in `config.json`
```
from azureml.core.workspace import Workspace
# if a locally-saved configuration file for the workspace is not available, use the following to load workspace
# ws = Workspace(subscription_id=subscription_id, resource_group=resource_group, workspace_name=workspace_name)
ws = Workspace.from_config()
print('Workspace name: ' + ws.name,
'Azure region: ' + ws.location,
'Subscription id: ' + ws.subscription_id,
'Resource group: ' + ws.resource_group, sep = '\n')
datastore = ws.get_default_datastore()
print("Default datastore's name: {}".format(datastore.name))
```
## Upload data
Upload the dataset to the workspace's default datastore:
```
path_on_datastore = 'data_airline'
datastore.upload(src_dir='/add/local/path', target_path=path_on_datastore, overwrite=False, show_progress=True)
ds_data = datastore.path(path_on_datastore)
print(ds_data)
```
## Create AML compute
You will need to create a [compute target](https://docs.microsoft.com/azure/machine-learning/service/concept-azure-machine-learning-architecture#compute-target) for training your model. In this notebook, we will use Azure ML managed compute ([AmlCompute](https://docs.microsoft.com/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute)) for our remote training using a dynamically scalable pool of compute resources.
This notebook will use 10 nodes for hyperparameter optimization, you can modify `max_node` based on available quota in the desired region. Similar to other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. [This article](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-manage-quotas) includes details on the default limits and how to request more quota.
`vm_size` describes the virtual machine type and size that will be used in the cluster. RAPIDS requires NVIDIA Pascal or newer architecture, you will need to specify compute targets from one of `NC_v2`, `NC_v3`, `ND` or `ND_v2` [GPU virtual machines in Azure](https://docs.microsoft.com/en-us/azure/virtual-machines/sizes-gpu); these are VMs that are provisioned with P40 and V100 GPUs. Let's create an `AmlCompute` cluster of `Standard_NC6s_v3` GPU VMs:
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# choose a name for your cluster
gpu_cluster_name = 'gpu-cluster'
if gpu_cluster_name in ws.compute_targets:
gpu_cluster = ws.compute_targets[gpu_cluster_name]
if gpu_cluster and type(gpu_cluster) is AmlCompute:
print('Found compute target. Will use {0} '.format(gpu_cluster_name))
else:
print('creating new cluster')
# m_size parameter below could be modified to one of the RAPIDS-supported VM types
provisioning_config = AmlCompute.provisioning_configuration(vm_size = 'Standard_NC6s_v3', max_nodes = 10, idle_seconds_before_scaledown = 300)
# create the cluster
gpu_cluster = ComputeTarget.create(ws, gpu_cluster_name, provisioning_config)
# can poll for a minimum number of nodes and for a specific timeout
# if no min node count is provided it uses the scale settings for the cluster
gpu_cluster.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
# use get_status() to get a detailed status for the current cluster
print(gpu_cluster.get_status().serialize())
```
## Prepare training script
Create a project directory that will contain code from your local machine that you will need access to on the remote resource. This includes the training script and additional files your training script depends on. In this example, the training script is provided:
<br>
`train_rapids_RF.py` - entry script for RAPIDS Estimator that includes loading dataset into cuDF data frame, training with Random Forest and inference using cuML.
```
import os
project_folder = './train_rapids'
os.makedirs(project_folder, exist_ok=True)
```
We will log some metrics by using the `Run` object within the training script:
```python
from azureml.core.run import Run
run = Run.get_context()
```
We will also log the parameters and highest accuracy the model achieves:
```python
run.log('Accuracy', np.float(accuracy))
```
These run metrics will become particularly important when we begin hyperparameter tuning our model in the 'Tune model hyperparameters' section.
Copy the training script `train_rapids_RF.py` into your project directory:
```
import shutil
shutil.copy('../code/train_rapids_RF.py', project_folder)
```
## Train model on the remote compute
Now that you have your data and training script prepared, you are ready to train on your remote compute.
### Create experiment
Create an [Experiment](https://docs.microsoft.com/azure/machine-learning/service/concept-azure-machine-learning-architecture#experiment) to track all the runs in your workspace.
```
from azureml.core import Experiment
experiment_name = 'train_rapids'
experiment = Experiment(ws, name=experiment_name)
```
### Create environment
The [Environment class](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.environment.environment?view=azure-ml-py) allows you to build a Docker image and customize the system that you will use for training. We will build a container image using a RAPIDS container as base image and install necessary packages. This build is necessary only the first time and will take about 15 minutes. The image will be added to your Azure Container Registry and the environment will be cached after the first run, as long as the environment definition remains the same.
```
from azureml.core import Environment
# create the environment
rapids_env = Environment('rapids_env')
# create the environment inside a Docker container
rapids_env.docker.enabled = True
# specify docker steps as a string. Alternatively, load the string from a file
dockerfile = """
FROM rapidsai/rapidsai-nightly:0.13-cuda10.0-runtime-ubuntu18.04-py3.7
RUN source activate rapids && \
pip install azureml-sdk && \
pip install azureml-widgets
"""
#FROM nvcr.io/nvidia/rapidsai/rapidsai:0.12-cuda10.0-runtime-ubuntu18.04
# set base image to None since the image is defined by dockerfile
rapids_env.docker.base_image = None
rapids_env.docker.base_dockerfile = dockerfile
# use rapids environment in the container
rapids_env.python.user_managed_dependencies = True
# from azureml.core.container_registry import ContainerRegistry
# # this is an image available on Docker Hub
# image_name = 'zronaghi/rapidsai-nightly:0.13-cuda10.0-runtime-ubuntu18.04-py3.7-azuresdk-030920'
# # use rapids environment, don't build a new conda environment
# user_managed_dependencies = True
```
### Create a RAPIDS Estimator
The [Estimator](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.estimator.estimator?view=azure-ml-py) class can be used with machine learning frameworks that do not have a pre-configure estimator.
`script_params` is a dictionary of command-line arguments to pass to the training script.
```
from azureml.train.estimator import Estimator
script_params = {
'--data_dir': ds_data.as_mount(),
'--n_bins': 32,
}
estimator = Estimator(source_directory=project_folder,
script_params=script_params,
compute_target=gpu_cluster,
entry_script='train_rapids_RF.py',
environment_definition=rapids_env)
# custom_docker_image=image_name,
# user_managed=user_managed_dependencies
```
## Tune model hyperparameters
We can optimize our model's hyperparameters and improve the accuracy using Azure Machine Learning's hyperparameter tuning capabilities.
### Start a hyperparameter sweep
Let's define the hyperparameter space to sweep over. We will tune `n_estimators`, `max_depth` and `max_features` parameters. In this example we will use random sampling to try different configuration sets of hyperparameters and maximize `Accuracy`.
```
from azureml.train.hyperdrive.runconfig import HyperDriveConfig
from azureml.train.hyperdrive.sampling import RandomParameterSampling
from azureml.train.hyperdrive.run import PrimaryMetricGoal
from azureml.train.hyperdrive.parameter_expressions import choice, loguniform, uniform
param_sampling = RandomParameterSampling( {
'--n_estimators': choice(range(50, 500)),
'--max_depth': choice(range(5, 19)),
'--max_features': uniform(0.2, 1.0)
}
)
hyperdrive_run_config = HyperDriveConfig(estimator=estimator,
hyperparameter_sampling=param_sampling,
primary_metric_name='Accuracy',
primary_metric_goal=PrimaryMetricGoal.MAXIMIZE,
max_total_runs=100,
max_concurrent_runs=10)
```
This will launch the RAPIDS training script with parameters that were specified in the cell above.
```
# start the HyperDrive run
hyperdrive_run = experiment.submit(hyperdrive_run_config)
```
## Monitor HyperDrive runs
Monitor and view the progress of the machine learning training run with a [Jupyter widget](https://docs.microsoft.com/en-us/python/api/azureml-widgets/azureml.widgets?view=azure-ml-py).The widget is asynchronous and provides live updates every 10-15 seconds until the job completes.
```
from azureml.widgets import RunDetails
RunDetails(hyperdrive_run).show()
# hyperdrive_run.wait_for_completion(show_output=True)
# hyperdrive_run.cancel()
```
### Find and register best model
```
best_run = hyperdrive_run.get_best_run_by_primary_metric()
print(best_run.get_details()['runDefinition']['arguments'])
```
List the model files uploaded during the run:
```
print(best_run.get_file_names())
```
Register the folder (and all files in it) as a model named `train-rapids` under the workspace for deployment
```
# model = best_run.register_model(model_name='train-rapids', model_path='outputs/model-rapids.joblib')
```
## Delete cluster
```
# delete the cluster
# gpu_cluster.delete()
```
|
github_jupyter
|
```
import sys
sys.executable
```
[Optional]: If you're using a Mac/Linux, you can check your environment with these commands:
```
!which pip3
!which python3
!ls -lah /usr/local/bin/python3
```
```
!pip3 install -U pip
!pip3 install torch==1.3.0
!pip3 install seaborn
import torch
torch.cuda.is_available()
# IPython candies...
from IPython.display import Image
from IPython.core.display import HTML
from IPython.display import clear_output
%%html
<style> table {float:left} </style>
```
Perceptron
=====
**Perceptron** algorithm is a:
> "*system that depends on **probabilistic** rather than deterministic principles for its operation, gains its reliability from the **properties of statistical measurements obtain from a large population of elements***"
> \- Frank Rosenblatt (1957)
Then the news:
> "*[Perceptron is an] **embryo of an electronic computer** that [the Navy] expects will be **able to walk, talk, see, write, reproduce itself and be conscious of its existence.***"
> \- The New York Times (1958)
News quote cite from Olazaran (1996)
Perceptron in Bullets
----
- Perceptron learns to classify any linearly separable set of inputs.
- Some nice graphics for perceptron with Go https://appliedgo.net/perceptron/
If you've got some spare time:
- There's a whole book just on perceptron: https://mitpress.mit.edu/books/perceptrons
- For watercooler gossips on perceptron in the early days, read [Olazaran (1996)](https://pdfs.semanticscholar.org/f3b6/e5ef511b471ff508959f660c94036b434277.pdf?_ga=2.57343906.929185581.1517539221-1505787125.1517539221)
Perceptron in Math
----
Given a set of inputs $x$, the perceptron
- learns $w$ vector to map the inputs to a real-value output between $[0,1]$
- through the summation of the dot product of the $w·x$ with a transformation function
Perceptron in Picture
----
```
##Image(url="perceptron.png", width=500)
Image(url="https://ibin.co/4TyMU8AdpV4J.png", width=500)
```
(**Note:** Usually, we use $x_1$ as the bias and fix the input to 1)
Perceptron as a Workflow Diagram
----
If you're familiar with [mermaid flowchart](https://mermaidjs.github.io)
```
.. mermaid::
graph LR
subgraph Input
x_1
x_i
x_n
end
subgraph Perceptron
n1((s)) --> n2(("f(s)"))
end
x_1 --> |w_1| n1
x_i --> |w_i| n1
x_n --> |w_n| n1
n2 --> y["[0,1]"]
```
```
##Image(url="perceptron-mermaid.svg", width=500)
Image(url="https://svgshare.com/i/AbJ.svg", width=500)
```
Optimization Process
====
To learn the weights, $w$, we use an **optimizer** to find the best-fit (optimal) values for $w$ such that the inputs correct maps to the outputs.
Typically, process performs the following 4 steps iteratively.
### **Initialization**
- **Step 1**: Initialize weights vector
### **Forward Propagation**
- **Step 2a**: Multiply the weights vector with the inputs, sum the products, i.e. `s`
- **Step 2b**: Put the sum through the sigmoid, i.e. `f()`
### **Back Propagation**
- **Step 3a**: Compute the errors, i.e. difference between expected output and predictions
- **Step 3b**: Multiply the error with the **derivatives** to get the delta
- **Step 3c**: Multiply the delta vector with the inputs, sum the product
### **Optimizer takes a step**
- **Step 4**: Multiply the learning rate with the output of Step 3c.
```
import math
import numpy as np
np.random.seed(0)
def sigmoid(x): # Returns values that sums to one.
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(sx):
# See https://math.stackexchange.com/a/1225116
# Hint: let sx = sigmoid(x)
return sx * (1 - sx)
sigmoid(np.array([2.5, 0.32, -1.42])) # [out]: array([0.92414182, 0.57932425, 0.19466158])
sigmoid_derivative(np.array([2.5, 0.32, -1.42])) # [out]: array([0.07010372, 0.24370766, 0.15676845])
def cost(predicted, truth):
return np.abs(truth - predicted)
gold = np.array([0.5, 1.2, 9.8])
pred = np.array([0.6, 1.0, 10.0])
cost(pred, gold)
gold = np.array([0.5, 1.2, 9.8])
pred = np.array([9.3, 4.0, 99.0])
cost(pred, gold)
```
Representing OR Boolean
---
Lets consider the problem of the OR boolean and apply the perceptron with simple gradient descent.
| x2 | x3 | y |
|:--:|:--:|:--:|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
```
X = or_input = np.array([[0,0], [0,1], [1,0], [1,1]])
Y = or_output = np.array([[0,1,1,1]]).T
or_input
or_output
# Define the shape of the weight vector.
num_data, input_dim = or_input.shape
# Define the shape of the output vector.
output_dim = len(or_output.T)
print('Inputs\n======')
print('no. of rows =', num_data)
print('no. of cols =', input_dim)
print('\n')
print('Outputs\n=======')
print('no. of cols =', output_dim)
# Initialize weights between the input layers and the perceptron
W = np.random.random((input_dim, output_dim))
W
```
Step 2a: Multiply the weights vector with the inputs, sum the products
====
To get the output of step 2a,
- Itrate through each row of the data, `X`
- For each column in each row, find the product of the value and the respective weights
- For each row, compute the sum of the products
```
# If we write it imperatively:
summation = []
for row in X:
sum_wx = 0
for feature, weight in zip(row, W):
sum_wx += feature * weight
summation.append(sum_wx)
print(np.array(summation))
# If we vectorize the process and use numpy.
np.dot(X, W)
```
Train the Single-Layer Model
====
```
num_epochs = 10000 # No. of times to iterate.
learning_rate = 0.03 # How large a step to take per iteration.
# Lets standardize and call our inputs X and outputs Y
X = or_input
Y = or_output
for _ in range(num_epochs):
layer0 = X
# Step 2a: Multiply the weights vector with the inputs, sum the products, i.e. s
# Step 2b: Put the sum through the sigmoid, i.e. f()
# Inside the perceptron, Step 2.
layer1 = sigmoid(np.dot(X, W))
# Back propagation.
# Step 3a: Compute the errors, i.e. difference between expected output and predictions
# How much did we miss?
layer1_error = cost(layer1, Y)
# Step 3b: Multiply the error with the derivatives to get the delta
# multiply how much we missed by the slope of the sigmoid at the values in layer1
layer1_delta = layer1_error * sigmoid_derivative(layer1)
# Step 3c: Multiply the delta vector with the inputs, sum the product (use np.dot)
# Step 4: Multiply the learning rate with the output of Step 3c.
W += learning_rate * np.dot(layer0.T, layer1_delta)
layer1
# Expected output.
Y
# On the training data
[[int(prediction > 0.5)] for prediction in layer1]
```
Lets try the XOR Boolean
---
Lets consider the problem of the OR boolean and apply the perceptron with simple gradient descent.
| x2 | x3 | y |
|:--:|:--:|:--:|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
```
X = xor_input = np.array([[0,0], [0,1], [1,0], [1,1]])
Y = xor_output = np.array([[0,1,1,0]]).T
xor_input
xor_output
num_epochs = 10000 # No. of times to iterate.
learning_rate = 0.003 # How large a step to take per iteration.
# Lets drop the last row of data and use that as unseen test.
X = xor_input
Y = xor_output
# Define the shape of the weight vector.
num_data, input_dim = X.shape
# Define the shape of the output vector.
output_dim = len(Y.T)
# Initialize weights between the input layers and the perceptron
W = np.random.random((input_dim, output_dim))
for _ in range(num_epochs):
layer0 = X
# Forward propagation.
# Inside the perceptron, Step 2.
layer1 = sigmoid(np.dot(X, W))
# How much did we miss?
layer1_error = cost(layer1, Y)
# Back propagation.
# multiply how much we missed by the slope of the sigmoid at the values in layer1
layer1_delta = sigmoid_derivative(layer1) * layer1_error
# update weights
W += learning_rate * np.dot(layer0.T, layer1_delta)
# Expected output.
Y
# On the training data
[int(prediction > 0.5) for prediction in layer1] # All correct.
```
You can't represent XOR with simple perceptron !!!
====
No matter how you change the hyperparameters or data, the XOR function can't be represented by a single perceptron layer.
There's no way you can get all four data points to get the correct outputs for the XOR boolean operation.
Solving XOR (Add more layers)
====
```
from itertools import chain
import numpy as np
np.random.seed(0)
def sigmoid(x): # Returns values that sums to one.
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(sx):
# See https://math.stackexchange.com/a/1225116
return sx * (1 - sx)
# Cost functions.
def cost(predicted, truth):
return truth - predicted
xor_input = np.array([[0,0], [0,1], [1,0], [1,1]])
xor_output = np.array([[0,1,1,0]]).T
# Define the shape of the weight vector.
num_data, input_dim = X.shape
# Lets set the dimensions for the intermediate layer.
hidden_dim = 5
# Initialize weights between the input layers and the hidden layer.
W1 = np.random.random((input_dim, hidden_dim))
# Define the shape of the output vector.
output_dim = len(Y.T)
# Initialize weights between the hidden layers and the output layer.
W2 = np.random.random((hidden_dim, output_dim))
# Initialize weigh
num_epochs = 10000
learning_rate = 0.03
for epoch_n in range(num_epochs):
layer0 = X
# Forward propagation.
# Inside the perceptron, Step 2.
layer1 = sigmoid(np.dot(layer0, W1))
layer2 = sigmoid(np.dot(layer1, W2))
# Back propagation (Y -> layer2)
# How much did we miss in the predictions?
layer2_error = cost(layer2, Y)
# In what direction is the target value?
# Were we really close? If so, don't change too much.
layer2_delta = layer2_error * sigmoid_derivative(layer2)
# Back propagation (layer2 -> layer1)
# How much did each layer1 value contribute to the layer2 error (according to the weights)?
layer1_error = np.dot(layer2_delta, W2.T)
layer1_delta = layer1_error * sigmoid_derivative(layer1)
# update weights
W2 += learning_rate * np.dot(layer1.T, layer2_delta)
W1 += learning_rate * np.dot(layer0.T, layer1_delta)
##print(epoch_n, list((layer2)))
# Training input.
X
# Expected output.
Y
layer2 # Our output layer
# On the training data
[int(prediction > 0.5) for prediction in layer2]
```
Now try adding another layer
====
Use the same process:
1. Initialize
2. Forward Propagate
3. Back Propagate
4. Update (aka step)
```
from itertools import chain
import numpy as np
np.random.seed(0)
def sigmoid(x): # Returns values that sums to one.
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(sx):
# See https://math.stackexchange.com/a/1225116
return sx * (1 - sx)
# Cost functions.
def cost(predicted, truth):
return truth - predicted
xor_input = np.array([[0,0], [0,1], [1,0], [1,1]])
xor_output = np.array([[0,1,1,0]]).T
X
Y
# Define the shape of the weight vector.
num_data, input_dim = X.shape
# Lets set the dimensions for the intermediate layer.
layer0to1_hidden_dim = 5
layer1to2_hidden_dim = 5
# Initialize weights between the input layers 0 -> layer 1
W1 = np.random.random((input_dim, layer0to1_hidden_dim))
# Initialize weights between the layer 1 -> layer 2
W2 = np.random.random((layer0to1_hidden_dim, layer1to2_hidden_dim))
# Define the shape of the output vector.
output_dim = len(Y.T)
# Initialize weights between the layer 2 -> layer 3
W3 = np.random.random((layer1to2_hidden_dim, output_dim))
# Initialize weigh
num_epochs = 10000
learning_rate = 1.0
for epoch_n in range(num_epochs):
layer0 = X
# Forward propagation.
# Inside the perceptron, Step 2.
layer1 = sigmoid(np.dot(layer0, W1))
layer2 = sigmoid(np.dot(layer1, W2))
layer3 = sigmoid(np.dot(layer2, W3))
# Back propagation (Y -> layer2)
# How much did we miss in the predictions?
layer3_error = cost(layer3, Y)
# In what direction is the target value?
# Were we really close? If so, don't change too much.
layer3_delta = layer3_error * sigmoid_derivative(layer3)
# Back propagation (layer2 -> layer1)
# How much did each layer1 value contribute to the layer3 error (according to the weights)?
layer2_error = np.dot(layer3_delta, W3.T)
layer2_delta = layer3_error * sigmoid_derivative(layer2)
# Back propagation (layer2 -> layer1)
# How much did each layer1 value contribute to the layer2 error (according to the weights)?
layer1_error = np.dot(layer2_delta, W2.T)
layer1_delta = layer1_error * sigmoid_derivative(layer1)
# update weights
W3 += learning_rate * np.dot(layer2.T, layer3_delta)
W2 += learning_rate * np.dot(layer1.T, layer2_delta)
W1 += learning_rate * np.dot(layer0.T, layer1_delta)
Y
layer3
# On the training data
[int(prediction > 0.5) for prediction in layer3]
```
# Now, lets do it with PyTorch
First lets try a single perceptron and see that we can't train a model that can represent XOR.
```
from tqdm import tqdm
import torch
from torch import nn
from torch.autograd import Variable
from torch import FloatTensor
from torch import optim
use_cuda = torch.cuda.is_available()
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
sns.set_style("darkgrid")
sns.set(rc={'figure.figsize':(15, 10)})
X # Original XOR X input in numpy array data structure.
Y # Original XOR Y output in numpy array data structure.
device = 'gpu' if torch.cuda.is_available() else 'cpu'
# Converting the X to PyTorch-able data structure.
X_pt = torch.tensor(X).float()
X_pt = X_pt.to(device)
# Converting the Y to PyTorch-able data structure.
Y_pt = torch.tensor(Y, requires_grad=False).float()
Y_pt = Y_pt.to(device)
print(X_pt)
print(Y_pt)
# Use tensor.shape to get the shape of the matrix/tensor.
num_data, input_dim = X_pt.shape
print('Inputs Dim:', input_dim)
num_data, output_dim = Y_pt.shape
print('Output Dim:', output_dim)
# Use Sequential to define a simple feed-forward network.
model = nn.Sequential(
nn.Linear(input_dim, output_dim), # Use nn.Linear to get our simple perceptron
nn.Sigmoid() # Use nn.Sigmoid to get our sigmoid non-linearity
)
model
# Remember we define as: cost = truth - predicted
# If we take the absolute of cost, i.e.: cost = |truth - predicted|
# we get the L1 loss function.
criterion = nn.L1Loss()
learning_rate = 0.03
# The simple weights/parameters update processes we did before
# is call the gradient descent. SGD is the sochastic variant of
# gradient descent.
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
```
(**Note**: Personally, I strongely encourage you to go through the [University of Washington course of machine learning regression](https://www.coursera.org/learn/ml-regression) to better understand the fundamentals of (i) ***gradient***, (ii) ***loss*** and (iii) ***optimizer***. But given that you know how to code it, the process of more complex variants of gradient/loss computation and optimizer's step is easy to grasp)
# Training a PyTorch model
To train a model using PyTorch, we simply iterate through the no. of epochs and imperatively state the computations we want to perform.
## Remember the steps?
1. Initialize
2. Forward Propagation
3. Backward Propagation
4. Update Optimizer
```
num_epochs = 1000
# Step 1: Initialization.
# Note: When using PyTorch a lot of the manual weights
# initialization is done automatically when we define
# the model (aka architecture)
model = nn.Sequential(
nn.Linear(input_dim, output_dim),
nn.Sigmoid())
criterion = nn.MSELoss()
learning_rate = 1.0
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
num_epochs = 10000
losses = []
for i in tqdm(range(num_epochs)):
# Reset the gradient after every epoch.
optimizer.zero_grad()
# Step 2: Foward Propagation
predictions = model(X_pt)
# Step 3: Back Propagation
# Calculate the cost between the predictions and the truth.
loss_this_epoch = criterion(predictions, Y_pt)
# Note: The neat thing about PyTorch is it does the
# auto-gradient computation, no more manually defining
# derivative of functions and manually propagating
# the errors layer by layer.
loss_this_epoch.backward()
# Step 4: Optimizer take a step.
# Note: Previously, we have to manually update the
# weights of each layer individually according to the
# learning rate and the layer delta.
# PyTorch does that automatically =)
optimizer.step()
# Log the loss value as we proceed through the epochs.
losses.append(loss_this_epoch.data.item())
# Visualize the losses
plt.plot(losses)
plt.show()
for _x, _y in zip(X_pt, Y_pt):
prediction = model(_x)
print('Input:\t', list(map(int, _x)))
print('Pred:\t', int(prediction))
print('Ouput:\t', int(_y))
print('######')
```
Now, try again with 2 layers using PyTorch
====
```
%%time
hidden_dim = 5
num_data, input_dim = X_pt.shape
num_data, output_dim = Y_pt.shape
model = nn.Sequential(nn.Linear(input_dim, hidden_dim),
nn.Sigmoid(),
nn.Linear(hidden_dim, output_dim),
nn.Sigmoid())
criterion = nn.MSELoss()
learning_rate = 0.3
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
num_epochs = 5000
losses = []
for _ in tqdm(range(num_epochs)):
optimizer.zero_grad()
predictions = model(X_pt)
loss_this_epoch = criterion(predictions, Y_pt)
loss_this_epoch.backward()
optimizer.step()
losses.append(loss_this_epoch.data.item())
##print([float(_pred) for _pred in predictions], list(map(int, Y_pt)), loss_this_epoch.data[0])
# Visualize the losses
plt.plot(losses)
plt.show()
for _x, _y in zip(X_pt, Y_pt):
prediction = model(_x)
print('Input:\t', list(map(int, _x)))
print('Pred:\t', int(prediction > 0.5))
print('Ouput:\t', int(_y))
print('######')
```
MNIST: The "Hello World" of Neural Nets
====
Like any deep learning class, we ***must*** do the MNIST.
The MNIST dataset is
- is made up of handwritten digits
- 60,000 examples training set
- 10,000 examples test set
```
# We're going to install tensorflow here because their dataset access is simpler =)
!pip3 install torchvision
from torchvision import datasets, transforms
mnist_train = datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
mnist_test = datasets.MNIST('../data', train=False, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
# Visualization Candies
import matplotlib.pyplot as plt
def show_image(mnist_x_vector, mnist_y_vector):
pixels = mnist_x_vector.reshape((28, 28))
label = np.where(mnist_y_vector == 1)[0]
plt.title('Label is {}'.format(label))
plt.imshow(pixels, cmap='gray')
plt.show()
# Fifth image and label.
show_image(mnist_train.data[5], mnist_train.targets[5])
```
# Lets apply what we learn about multi-layered perceptron with PyTorch and apply it to the MNIST data.
```
X_mnist = mnist_train.data.float()
Y_mnist = mnist_train.targets.float()
X_mnist_test = mnist_test.data.float()
Y_mnist_test = mnist_test.targets.float()
Y_mnist.shape
# Use FloatTensor.shape to get the shape of the matrix/tensor.
num_data, *input_dim = X_mnist.shape
print('No. of images:', num_data)
print('Inputs Dim:', input_dim)
num_data, *output_dim = Y_mnist.shape
num_test_data, *output_dim = Y_mnist_test.shape
print('Output Dim:', output_dim)
# Flatten the dimensions of the images.
X_mnist = mnist_train.data.float().view(num_data, -1)
Y_mnist = mnist_train.targets.float().unsqueeze(1)
X_mnist_test = mnist_test.data.float().view(num_test_data, -1)
Y_mnist_test = mnist_test.targets.float().unsqueeze(1)
# Use FloatTensor.shape to get the shape of the matrix/tensor.
num_data, *input_dim = X_mnist.shape
print('No. of images:', num_data)
print('Inputs Dim:', input_dim)
num_data, *output_dim = Y_mnist.shape
num_test_data, *output_dim = Y_mnist_test.shape
print('Output Dim:', output_dim)
hidden_dim = 500
model = nn.Sequential(nn.Linear(784, 1),
nn.Sigmoid())
criterion = nn.MSELoss()
learning_rate = 1.0
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
num_epochs = 10
losses = []
plt.ion()
for _e in tqdm(range(num_epochs)):
optimizer.zero_grad()
predictions = model(X_mnist)
loss_this_epoch = criterion(predictions, Y_mnist)
loss_this_epoch.backward()
optimizer.step()
##print([float(_pred) for _pred in predictions], list(map(int, Y_pt)), loss_this_epoch.data[0])
losses.append(loss_this_epoch.data.item())
clear_output(wait=True)
plt.plot(losses)
plt.pause(0.05)
predictions = model(X_mnist_test)
predictions
pred = np.array([np.argmax(_p) for _p in predictions.data.numpy()])
pred
truth = np.array([np.argmax(_p) for _p in Y_mnist_test.data.numpy()])
truth
(pred == truth).sum() / len(pred)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
from math import sqrt
from numpy import concatenate
from matplotlib import pyplot
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
```
### Interpolation
```
df = pd.DataFrame(
{
'name': ['A','A', 'B','B','B','B', 'C','C','C'],
'value': [1, np.nan, np.nan, 2, 3, 1, 3, np.nan, 3],
}
)
df
df.fillna(method="pad")
df['value'].interpolate()
df['value'].interpolate(method="quadratic")
# For cumsums
df['value'].interpolate(method="pchip")
```
### LSTM
```
from pandas import read_csv
from datetime import datetime
# load data
def parse(x):
return datetime.strptime(x, '%Y %m %d %H')
dataset = read_csv('data/raw_pollution.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse)
dataset.drop('No', axis=1, inplace=True)
# manually specify column names
dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain']
dataset.index.name = 'date'
# mark all NA values with 0
dataset['pollution'] = dataset['pollution'].interpolate()
# drop the first 24 hours
dataset = dataset[24:]
# summarize first 5 rows
print(dataset.head(5))
# save to file
dataset.to_csv('data/pollution.csv')
from pandas import read_csv
from matplotlib import pyplot
# load dataset
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# specify columns to plot
groups = [0, 1, 2, 3, 5, 6, 7]
i = 1
# plot each column
pyplot.figure(figsize=(20, 13))
for group in groups:
pyplot.subplot(len(groups), 1, i)
pyplot.plot(values[:, group])
pyplot.title(dataset.columns[group], y=0.5, loc='right')
pyplot.grid()
i += 1
pyplot.show()
# convert series to supervised learning
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
# load dataset
dataset = read_csv('data/pollution.csv', header=0, index_col=0)
values = dataset.values
dataset
values
# integer encode wind_direction
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
# ensure all data is float
values = values.astype('float32')
# normalize features
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# frame as supervised learning
reframed = series_to_supervised(scaled, 1, 1)
# drop columns we don't want to predict
reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)
print(reframed.head())
# split into train and test sets
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# split into input and outputs
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]
# reshape input to be 3D [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
```
We will define the LSTM with 50 neurons in the first hidden layer and 1 neuron in the output layer for predicting pollution. The input shape will be 1 time step with 8 features.
We will use the Mean Absolute Error (MAE) loss function and the efficient Adam version of stochastic gradient descent.
```
# design network
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# fit network
history = model.fit(train_X, train_y, epochs=50, batch_size=64,
validation_data=(test_X, test_y), verbose=2, shuffle=False)
# plot history
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
# make a prediction
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
# invert scaling for forecast
inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1)
inv_yhat = scaler.inverse_transform(inv_yhat)
inv_yhat = inv_yhat[:,0]
# invert scaling for actual
test_y = test_y.reshape((len(test_y), 1))
inv_y = concatenate((test_y, test_X[:, 1:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:, 0]
# calculate RMSE
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse)
pyplot.plot(range(len(inv_yhat)), inv_yhat, alpha=0.5, label="Predicted")
pyplot.show()
pyplot.plot(range(len(inv_y)), inv_y, alpha=0.5, label="Expected")
pyplot.show()
```
### N previous lags
```
# load dataset
dataset = read_csv('data/pollution.csv', header=0, index_col=0)
values = dataset.values
# integer encode direction
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
# ensure all data is float
values = values.astype('float32')
# normalize features
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# specify the number of lag hours
n_hours = 3
n_features = 8
# frame as supervised learning
reframed = series_to_supervised(scaled, n_hours, 1)
print(reframed.shape)
```
Next, we need to be more careful in specifying the column for input and output.
We have 3 * 8 + 8 columns in our framed dataset. We will take 3 * 8 or 24 columns as input for the obs of all features across the previous 3 hours. We will take just the pollution variable as output at the following hour, as follows:
```
# split into train and test sets
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours]
test = values[n_train_hours:]
# split into input and outputs
n_obs = n_hours * n_features
train_X, train_y = train[:, :n_obs], train[:, -n_features]
test_X, test_y = test[:, :n_obs], test[:, -n_features]
print(train_X.shape, len(train_X), train_y.shape)
# reshape input to be 3D [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], n_hours, n_features))
test_X = test_X.reshape((test_X.shape[0], n_hours, n_features))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# design network
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# fit network
history = model.fit(train_X, train_y, epochs=50,
batch_size=64, validation_data=(test_X, test_y),
verbose=2, shuffle=False)
# plot history
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
# make a prediction
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], n_hours*n_features))
# invert scaling for forecast
inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1)
inv_yhat = scaler.inverse_transform(inv_yhat)
inv_yhat = inv_yhat[:,0]
# invert scaling for actual
test_y = test_y.reshape((len(test_y), 1))
inv_y = concatenate((test_y, test_X[:, -7:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:,0]
# calculate RMSE
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse)
```
|
github_jupyter
|
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import xarray as xr
import scipy
import os
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
import glob
```
Notebook for creating complete HRDPS file for 2007 from 2007 data, for every variable, all at once. For a more polished notebook, see generalPredictions4c. This notebook has been superceded by that notebook.
## Importing Training Data
| Description | HRDPS | CANRCM |
| ----------- | ----------- | ----------- |
| Near-Surface Air Temperature | tair | tas |
| Precipitation | precip | pr |
| Sea Level Pressure | atmpres | psl |
| Near Surface Specific Humidity | qair | huss |
| Shortwave radiation | solar | rsds |
| Longwave radiation | therm_rad | rlds |
```
variables = [['tair', 'tas', 'Near-Surface Air Temperature'],
['precip', 'pr', 'Precipitation'],
['atmpres', 'psl', 'Sea Level Pressure'],
['qair', 'huss', 'Near Surface Specific Humidity'],
['solar', 'rsds', 'Shortwave radiation'],
['therm_rad', 'rlds', 'Longwave radiation']]
def import_data(variable):
global name
name = variable[2]
global data_name_hr
data_name_hr = variable[0]
global data_name_can
data_name_can = variable[1]
##2007 HRDPS import
files = glob.glob('/results/forcing/atmospheric/GEM2.5/gemlam/gemlam_y2007m??d??.nc')
files.sort()
## 3-hour averaged matrix
global hr07
hr07 = np.zeros( (8*len(files), 266, 256))
for i in range(len(files)):
dayX = xr.open_dataset(files[i])
##adding 1 day of 3-hour averages to new data array
hr07[8*i:8*i + 8,:,:] = np.array( dayX[ data_name_hr ] ).reshape(8, 3, 266, 256).mean(axis = 1)
p_can07 = '/home/arandhawa/canrcm_' + data_name_can + '_2007.nc'
##CANRCM 2007 import
global can07
d1 = xr.open_dataset(p_can07)
can07 = d1[data_name_can][16:,140:165,60:85] ##the first two days are removed to be consistent with 2007 HRDPS
def import_wind_data():
##2007 HRDPS import
files = glob.glob('/results/forcing/atmospheric/GEM2.5/gemlam/gemlam_y2007m??d??.nc')
files.sort()
## 3-hour averaged matrix
global hr07_u
global hr07_v
## 3-hour averaged matrix
hr07_u = np.zeros( (8*len(files), 266, 256))
hr07_v = np.zeros( (8*len(files), 266, 256))
for i in range(len(files)):
dayX = xr.open_dataset(files[i])
u = np.array( dayX['u_wind'] ).reshape(8, 3, 266, 256)
v = np.array( dayX['v_wind'] ).reshape(8, 3, 266, 256)
avg_spd = np.mean(np.sqrt(u**2 + v**2), axis = 1)
avg_th = np.arctan2(v.mean(axis = 1), u.mean(axis = 1))
avg_u = avg_spd*np.cos(avg_th)
avg_v = avg_spd*np.sin(avg_th)
hr07_u[8*i:8*i + 8, : , : ] = avg_u ##adding 3-hour average to new data array
hr07_v[8*i:8*i + 8, : , : ] = avg_v
del avg_u
del avg_v
del dayX
del u
del v
del avg_spd
del avg_th
p_can07u = '/home/arandhawa/canrcm_uas_2007.nc'
p_can07v = '/home/arandhawa/canrcm_vas_2007.nc'
##CANRCM 2007 import
global can07_u
global can07_v
d1 = xr.open_dataset(p_can07u)
can07_u = d1['uas'][16:,140:165,60:85] ##the first two days are removed to be consistent with 2007 HRDPS
d2 = xr.open_dataset(p_can07v)
can07_v = d2['vas'][16:,140:165,60:85] ##the first two days are removed to be consistent with 2007 HRDPS
```
## PCA Functions
```
##transforms and concatenates two data sets
def transform2(data1, data2):
A_mat = transform(data1)
B_mat = transform(data2)
return np.concatenate((A_mat, B_mat), axis=0)
##inverse function of transform2 - splits data matrix and returns two data sets
def reverse2(matrix, orig_shape):
split4 = int( matrix.shape[0]/2 )
u_data = reverse(matrix[:split4,:], orig_shape) ##reconstructing u_winds from n PCs
v_data = reverse(matrix[split4:,:], orig_shape) ##reconstructing v_winds from n PCs
return (u_data, v_data)
##performs PCA analysis using sklearn.pca
def doPCA(comp, matrix):
pca = PCA(n_components = comp) ##adjust the number of principle conponents to be calculated
PCs = pca.fit_transform(matrix)
eigvecs = pca.components_
mean = pca.mean_
return (PCs, eigvecs, mean)
##data must be converted into a 2D matrix for pca analysis
##transform takes a 3D data array (time, a, b) -> (a*b, time)
##(the data grid is flattened a column using numpy.flatten)
def transform(xarr):
arr = np.array(xarr) ##converting to numpy array
arr = arr.reshape(arr.shape[0], arr.shape[1]*arr.shape[2]) ##reshaping from size (a, b, c) to (a, b*c)
arr = arr.transpose()
return arr
def reverse(mat, orig_shape):
arr = np.copy(mat)
arr = arr.transpose()
arr = arr.reshape(-1, orig_shape[1], orig_shape[2]) ##reshaping back to original array shape
return arr
##graphing percentage of original data represented by the first n principle conponents
def graph_variance(matrix, n):
pcaG = PCA(n_components = n) ##Number of principle conponents to show
PCsG = pcaG.fit_transform(matrix)
plt.plot(np.cumsum(pcaG.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
plt.show()
del pcaG
del PCsG
##can be used to visualize principle conponents for u/v winds
def graph_nPCs(PCs, eigvecs, n, orig_shape):
fig, ax = plt.subplots(n, 3, figsize=(10, 3*n))
ax[0, 0].set_title("u-conponent")
ax[0, 1].set_title("v-component")
ax[0, 2].set_title("time-loadings")
for i in range(n):
mode_u, mode_v = get_mode(PCs, i, orig_shape)
colors = ax[i, 0].pcolormesh(mode_u, cmap = 'bwr')
fig.colorbar(colors, ax = ax[i,0])
colors = ax[i, 1].pcolormesh(mode_v, cmap = 'bwr')
fig.colorbar(colors, ax = ax[i,1])
ax[i, 2].plot(eigvecs[i])
plt.tight_layout()
plt.show()
##converts PCs (column vectors) to 2d conpoents for u and v wind
def get_mode(PCs, n, orig_shape):
split = int(PCs.shape[0]/2)
mode_u = PCs[:split, n].reshape(orig_shape[1], orig_shape[2])
mode_v = PCs[split:, n].reshape(orig_shape[1], orig_shape[2])
return (mode_u, mode_v)
```
## Multiple Linear Regression Functions
```
##functions that use multiple linear regression to fit eigenvectors
##takes CANRCM eigenvectors (x1, x2, x3, x4...) and HRDPS eigenvectors (y1, y2, y3...)
##For each y from 0:result_size, approximates yn = a0 + a1*x1 + a2*x2 + a3*x3 ... using num_vec x's
##getCoefs returns (coeficients, intercept)
##fit_modes returns each approximation and the R^2 value of each fit as (results, scores)
def getCoefs(vectors, num_vec, data, num_modes, type = 'LS'):
X = vectors[0:num_vec,:].T
coefs = np.zeros((num_modes, X.shape[1]))
intercept = np.zeros(num_modes)
if type == 'LS':
for i in range(num_modes):
y = data[i,:]
reg = LinearRegression().fit(X, y)
coefs[i] = reg.coef_[0:num_vec]
intercept[i] = reg.intercept_
elif type == 'MAE':
for i in range(num_modes):
y = data[i,:]
reg = QuantileRegressor(quantile = 0.5, alpha = 0, solver = 'highs').fit(X, y)
coefs[i] = reg.coef_[0:num_vec]
intercept[i] = reg.intercept_
return (coefs, intercept)
def fit_modes(vectors, num_vec, data, result_size, type = 'LS'):
X = vectors[0:num_vec,:].T
result = np.zeros((result_size, X.shape[0]))
scores = np.zeros(result_size)
if type == 'LS':
for i in range(result_size):
y = data[i,:]
reg = LinearRegression().fit(X, y)
result[i] = reg.predict(X)
scores[i] = reg.score(X, y)
elif type == 'MAE':
for i in range(result_size):
y = data[i,:]
reg = QuantileRegressor(quantile = 0.5, alpha = 0, solver = 'highs').fit(X, y)
result[i] = reg.predict(X)
scores[i] = reg.score(X, y)
return (result, scores)
##returns the ratio of the average energy between two sets of eigenvectors (element-wise)
##"energy" is defined as value^2 - two sets of eigenvectors with the same "energy" would
##recreate data with approximately the same kinetic energy (v^2)
def getEnergyCoefs(eigs, old_eigs):
coefs = np.sqrt( (old_eigs[0:eigs.shape[0]]**2).mean(axis = 1)/(eigs**2).mean(axis = 1))
return coefs
```
## Projection Function
```
##scalar projection of u onto v - with extra 1/norm factor (for math reasons)
##projectData projects the data onto each principle conponent, at each time
##output is a set of eigenvectors
def project(u, v):
v_norm = np.sqrt(np.sum(v**2))
return np.dot(u, v)/v_norm**2
def projectData(data_mat, new_PCs, n):
time = data_mat.shape[1]
proj = np.empty((n, time))
for j in range(n):
for i in range(time):
proj[j, i] = project(data_mat[:,i], new_PCs[:,j])
return proj
```
## Overall Function
```
def reconstruct(downscale_mat, mean, can_PCs, can_me, hr_PCs, hr_me, n, r, method = 'LS', EB = 'False'):
coefs = getCoefs(can_me, n + 1, hr_me, r + 1, type = method)
proj = np.concatenate((mean.reshape(1, -1), projectData(downscale_mat - mean, can_PCs, n)), axis = 0)
pred_eigs = np.matmul(coefs[0], proj) + coefs[1].reshape(-1, 1) ##multiple linear regression output
if (EB == 'true'):
energyCoefs = getEnergyCoefs( fit_modes(can_me, n + 1, hr_me, r + 1, type = method)[0], hr_me)
energyCoefs = energyCoefs.reshape(-1, 1)
pred_eigs = pred_eigs*energyCoefs ##energy balancing
if (EB == 'function'):
energyCoefs = getEnergyCoefs( fit_modes(can_me, n + 1, hr_me, r + 1, type = method)[0] , hr_me)
def f(x):
return np.exp(-x/50)
for x in range(r + 1):
energyCoefs = (energyCoefs - 1)*f(x) + 1
energyCoefs = energyCoefs.reshape(-1, 1)
pred_eigs = pred_eigs*energyCoefs ##energy balancing
recon = np.matmul(hr_PCs[:,0:r], pred_eigs[1:r+1]) + pred_eigs[0]
data_rec = reverse(recon, (-1, 266, 256))
if (EB == 'constant'):
data_rec *= 1.3
return data_rec
def reconstruct2(downscale_mat, mean, can_PCs, can_me, hr_PCs, hr_me, n, r, method = 'LS', EB = 'f2alse'):
coefs = getCoefs(can_me, n + 1, hr_me, r + 1, type = method)
proj = np.concatenate((mean.reshape(1, -1), projectData(downscale_mat - mean, can_PCs, n)), axis = 0)
pred_eigs = np.matmul(coefs[0], proj) + coefs[1].reshape(-1, 1) ##multiple linear regression output
if (EB == 'true'):
energyCoefs = getEnergyCoefs( fit_modes(can_me, n + 1, hr_me, r + 1, type = method)[0], hr_me)
energyCoefs = energyCoefs.reshape(-1, 1)
pred_eigs = pred_eigs*energyCoefs ##energy balancing
if (EB == 'function'):
energyCoefs = getEnergyCoefs( fit_modes(can_me, n + 1, hr_me, r + 1, type = method)[0] , hr_me)
def f(x):
return np.exp(-x/50)
for x in range(r + 1):
energyCoefs = (energyCoefs - 1)*f(x) + 1
energyCoefs = energyCoefs.reshape(-1, 1)
pred_eigs = pred_eigs*energyCoefs ##energy balancing
recon = np.matmul(hr_PCs[:,0:r], pred_eigs[1:r+1]) + pred_eigs[0]
u_data_rec, v_data_rec = reverse2(recon, (-1, 266, 256))
if (EB == 'constant'):
u_data_rec *= 1.3
v_data_rec *= 1.3
return (u_data_rec, v_data_rec)
```
## Reconstructing Data
```
data = ()
##reconstructing u and v winds
import_wind_data()
##PCA on CANRCM 2007
can07_mat = transform2(can07_u, can07_v)
can07_PCs, can07_eigs, can07_mean = doPCA(100, can07_mat)
##PCA on HRDPS 2007
hr07_mat = transform2(hr07_u, hr07_v)
hr07_PCs, hr07_eigs, hr07_mean = doPCA(100, hr07_mat)
## combining the eigenvectors and mean together in one array for analysis
can07_me = np.concatenate((can07_mean.reshape(1, -1), can07_eigs))
hr07_me = np.concatenate((hr07_mean.reshape(1, -1), hr07_eigs))
##calculating average of rows
mean_2007 = can07_mat.mean(axis = 0)
u_data_rec, v_data_rec = reconstruct2(can07_mat, mean_2007, can07_PCs, can07_me, hr07_PCs, hr07_me, 65, 65, method = 'LS')
u_data_rec *= 1.25
v_data_rec *= 1.25
data += (('u_wind', u_data_rec),)
data += (('v_wind', v_data_rec),)
print("u and v winds done")
del can07_u
del can07_v
del hr07_u
del hr07_v
del can07_mat
del can07_PCs
del can07_eigs
del can07_me
del can07_mean
del u_data_rec
del v_data_rec
del hr07_mat
del hr07_PCs
del hr07_eigs
del hr07_me
del hr07_mean
##reconstructing other variables
for i in variables:
import_data(i)
##PCA on CANRCM 2007
can07_mat = transform(can07)
can07_PCs, can07_eigs, can07_mean = doPCA(100, can07_mat)
##PCA on HRDPS 2007
hr07_mat = transform(hr07)
hr07_PCs, hr07_eigs, hr07_mean = doPCA(100, hr07_mat)
## combining the eigenvectors and mean together in one array for analysis
can07_me = np.concatenate((can07_mean.reshape(1, -1), can07_eigs))
hr07_me = np.concatenate((hr07_mean.reshape(1, -1), hr07_eigs))
##calculating average of rows
mean_2007 = can07_mat.mean(axis = 0)
data_rec = reconstruct(can07_mat, mean_2007, can07_PCs, can07_me, hr07_PCs, hr07_me, 65, 65, method = 'LS')
if data_name_hr == 'precip' or data_name_hr == 'qair' or data_name_hr == 'solar' or data_name_hr == 'therm_rad':
avg = np.mean(data_rec, axis = 0)
data_rec[data_rec < 0] = 0
avg2 = np.mean(data_rec, axis = 0)
data_rec *= avg/avg2
data += ((data_name_hr, data_rec),)
print(data_name_hr, "done")
del can07
del hr07
del can07_mat
del can07_PCs
del can07_eigs
del hr07_mat
del hr07_PCs
del hr07_eigs
del can07_me
del hr07_me
del data_rec
for j in data:
print(j[0])
data_var = {}
dims = ('time_counter', 'y', 'x')
times = np.arange('2007-01-03T00:00', '2008-01-01T00:00', np.timedelta64(3, 'h'), dtype='datetime64[ns]')
for i in range(363):
for j in data:
data_var[ j[0] ] = (dims, j[1][8*i:8*i + 8], {})
coords = {'time_counter': times[8*i:8*i + 8], 'y': range(266), 'x': range(256)}
ds = xr.Dataset(data_var, coords)
d = pd.to_datetime(times[8*i])
if d.month < 10:
month = '0' + str(d.month)
else:
month = str(d.month)
if d.day < 10:
day = '0' + str(d.day)
else:
day = str(d.day)
path = '/ocean/arandhawa/reconstructed_data_2007_p2/recon_y2007m' + month + 'd' + day + '.nc'
encoding = {var: {'zlib': True} for var in ds.data_vars}
ds.to_netcdf(path, unlimited_dims=('time_counter'), encoding=encoding)
files = glob.glob('/ocean/arandhawa/reconstructed_data_2007/recon_*')
len(files)
```
|
github_jupyter
|
# DBSCAN without Libraries
```
import time
import warnings
import queue
import numpy as np
import pandas as pd
from sklearn import cluster, datasets, mixture
from sklearn.neighbors import kneighbors_graph
from sklearn import datasets
# from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
from scipy.stats import norm
from matplotlib import pyplot
import matplotlib.cm as cm
import matplotlib.pyplot as plt
from random import sample
from itertools import cycle, islice
np.random.seed(0)
# ============
# Generate datasets. We choose the size big enough to see the scalability
# of the algorithms, but not too big to avoid too long running times
# ============
n_samples = 1500
n_components = 2 # the number of clusters
X1, y1 = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
X2, y2 = datasets.make_moons(n_samples=n_samples, noise=0.05)
X3, y3 = datasets.make_blobs(n_samples=n_samples, random_state=8)
X4, y4 = np.random.rand(n_samples, 2), None
# Anisotropicly distributed data
random_state = 170
# scatter plot, data points annotated by different colors
df = pd.DataFrame(dict(feature_1=X1[:,0], feature_2=X1[:,1], label=y1))
cluster_name = set(y1)
colors = dict(zip(cluster_name, cm.rainbow(np.linspace(0, 1, len(cluster_name)))))
fig, ax = pyplot.subplots()
grouped = df.groupby('label')
for key, group in grouped:
# group.plot(ax=ax, kind='scatter', x='feature_1', y='feature_2', color=colors[key].reshape(1,-1))
group.plot(ax=ax, kind='scatter', x='feature_1', y='feature_2')
# pyplot.title('Original 2D Data from {} Clusters'.format(n_components))
pyplot.show()
# Based on Implementation of
# https://github.com/kiat/Machine-Learning-Algorithms-from-Scratch/blob/master/DBSCAN.py
class CustomDBSCAN():
def __init__(self):
self.core = -1
self.border = -2
# Find all neighbour points at epsilon distance
def neighbour_points(self, data, pointId, epsilon):
points = []
for i in range(len(data)):
# Euclidian distance
if np.linalg.norm([a_i - b_i for a_i, b_i in zip(data[i], data[pointId])]) <= epsilon:
points.append(i)
return points
# Fit the data into the DBSCAN model
def fit(self, data, Eps, MinPt):
# initialize all points as outliers
point_label = [0] * len(data)
point_count = []
# initilize list for core/border points
core = []
border = []
# Find the neighbours of each individual point
for i in range(len(data)):
point_count.append(self.neighbour_points(data, i, Eps))
# Find all the core points, border points and outliers
for i in range(len(point_count)):
if (len(point_count[i]) >= MinPt):
point_label[i] = self.core
core.append(i)
else:
border.append(i)
for i in border:
for j in point_count[i]:
if j in core:
point_label[i] = self.border
break
# Assign points to a cluster
cluster = 1
# Here we use a queue to find all the neighbourhood points of a core point and
# find the indirectly reachable points
# We are essentially performing Breadth First search of all points
# which are within Epsilon distance for each other
for i in range(len(point_label)):
q = queue.Queue()
if (point_label[i] == self.core):
point_label[i] = cluster
for x in point_count[i]:
if(point_label[x] == self.core):
q.put(x)
point_label[x] = cluster
elif(point_label[x] == self.border):
point_label[x] = cluster
while not q.empty():
neighbors = point_count[q.get()]
for y in neighbors:
if (point_label[y] == self.core):
point_label[y] = cluster
q.put(y)
if (point_label[y] == self.border):
point_label[y] = cluster
cluster += 1 # Move on to the next cluster
return point_label, cluster
# Visualize the clusters
def visualize(self, data, cluster, numberOfClusters):
N = len(data)
colors = np.array(list(islice(cycle(['#FE4A49', '#2AB7CA']), 3)))
for i in range(numberOfClusters):
if (i == 0):
# Plot all outliers point as black
color = '#000000'
else:
color = colors[i % len(colors)]
x, y = [], []
for j in range(N):
if cluster[j] == i:
x.append(data[j, 0])
y.append(data[j, 1])
plt.scatter(x, y, c=color, alpha=1, marker='.')
plt.show()
dataset = df.astype(float).values.tolist()
# normalize dataset
X = StandardScaler().fit_transform(dataset)
custom_DBSCAN = CustomDBSCAN()
point_labels, clusters = custom_DBSCAN.fit(X, 0.25, 4)
# print(point_labels, clusters)
custom_DBSCAN.visualize(X, point_labels, clusters)
# Let us change the data and see the results
df = pd.DataFrame(dict(feature_1=X2[:,0], feature_2=X2[:,1], label=y2))
dataset = df.astype(float).values.tolist()
# normalize dataset
X = StandardScaler().fit_transform(dataset)
custom_DBSCAN = CustomDBSCAN()
point_labels, clusters = custom_DBSCAN.fit(X, 0.25, 4)
# print(point_labels, clusters)
custom_DBSCAN.visualize(X, point_labels, clusters)
# Let us change the data and see the results
df = pd.DataFrame(dict(feature_1=X3[:,0], feature_2=X3[:,1], label=y3))
dataset = df.astype(float).values.tolist()
# normalize dataset
X = StandardScaler().fit_transform(dataset)
custom_DBSCAN = CustomDBSCAN()
point_labels, clusters = custom_DBSCAN.fit(X, 0.25, 4)
# print(point_labels, clusters)
custom_DBSCAN.visualize(X, point_labels, clusters)
# Let us change the data and see the results
df = pd.DataFrame(dict(feature_1=X4[:,0], feature_2=X4[:,1], label=y4))
dataset = df.astype(float).values.tolist()
# normalize dataset
X = StandardScaler().fit_transform(dataset)
custom_DBSCAN = CustomDBSCAN()
point_labels, clusters = custom_DBSCAN.fit(X, 0.25, 4)
# print(point_labels, clusters)
custom_DBSCAN.visualize(X, point_labels, clusters)
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet # IGNORE_COPYRIGHT: cleared by OSS licensing
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Transfer Learning Using Pretrained ConvNets
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/examples/community/en/tensorflow_for_poets_reboot.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/examples/community/en/tensorflow_for_poets_reboot.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
```
from __future__ import absolute_import, division, print_function
import tensorflow.compat.v2 as tf #nightly-gpu
tf.enable_v2_behavior()
import os
import numpy as np
import matplotlib.pyplot as plt
from functools import partial
tf.__version__
```
## Data preprocessing
### Data download
```
_URL = "https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz"
zip_file = tf.keras.utils.get_file(origin=_URL,
fname="flower_photos.tgz",
extract=True)
base_dir = os.path.join(os.path.dirname(zip_file), 'flower_photos')
IMAGE_SIZE = 224
BATCH_SIZE = 64
datagen = tf.keras.preprocessing.image.ImageDataGenerator(
rescale=1./255,
validation_split=0.2)
train_generator = datagen.flow_from_directory(
base_dir,
target_size=(IMAGE_SIZE, IMAGE_SIZE),
batch_size=BATCH_SIZE,
subset='training')
val_generator = datagen.flow_from_directory(
base_dir,
target_size=(IMAGE_SIZE, IMAGE_SIZE),
batch_size=BATCH_SIZE,
subset='validation')
for image_batch, label_batch in train_generator:
break
image_batch.shape, label_batch.shape
train_generator.class_indices
```
## Create the base model from the pre-trained convnets
```
IMG_SHAPE = (IMAGE_SIZE, IMAGE_SIZE, 3)
# Create the base model from the pre-trained model MobileNet V2
base_model = tf.keras.applications.MobileNetV2(input_shape=IMG_SHAPE,
include_top=False,
weights='imagenet')
```
## Feature extraction
You will freeze the convolutional base created from the previous step and use that as a feature extractor, add a classifier on top of it and train the top-level classifier.
```
base_model.trainable = False
```
### Add a classification head
```
model = tf.keras.Sequential([
base_model,
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(5, activation='softmax')
])
```
### Compile the model
You must compile the model before training it. Since there are two classes, use a binary cross-entropy loss.
```
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss='categorical_crossentropy',
metrics=['accuracy'])
model.summary()
```
The 2.5M parameters in MobileNet are frozen, but there are 1.2K _trainable_ parameters in the Dense layer. These are divided between two `tf.Variable` objects, the weights and biases.
```
len(model.trainable_variables)
train_generator.labels
```
### Train the model
<!-- TODO(markdaoust): delete steps_per_epoch in TensorFlow r1.14/r2.0 -->
```
epochs = 10
history = model.fit(train_generator,
epochs=epochs,
validation_data=val_generator)
```
### Learning curves
Let's take a look at the learning curves of the training and validation accuracy/loss when using the MobileNet V2 base model as a fixed feature extractor.
```
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.legend(loc='lower right')
plt.ylabel('Accuracy')
plt.ylim([min(plt.ylim()),1])
plt.title('Training and Validation Accuracy')
plt.subplot(2, 1, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.legend(loc='upper right')
plt.ylabel('Cross Entropy')
plt.ylim([0,1.0])
plt.title('Training and Validation Loss')
plt.xlabel('epoch')
plt.show()
```
Note: If you are wondering why the validation metrics are clearly better than the training metrics, the main factor is because layers like `tf.keras.layers.BatchNormalization` and `tf.keras.layers.Dropout` affect accuracy during training. They are turned off when calculating validation loss.
To a lesser extent, it is also because training metrics report the average for an epoch, while validation metrics are evaluated after the epoch, so validation metrics see a model that has trained slightly longer.
## Fine tuning
In our feature extraction experiment, you were only training a few layers on top of an MobileNet V2 base model. The weights of the pre-trained network were **not** updated during training.
One way to increase performance even further is to train (or "fine-tune") the weights of the top layers of the pre-trained model alongside the training of the classifier you added. The training process will force the weights to be tuned from generic features maps to features associated specifically to our dataset.
Note: This should only be attempted after you have trained the top-level classifier with the pre-trained model set to non-trainable. If you add a randomly initialized classifier on top of a pre-trained model and attempt to train all layers jointly, the magnitude of the gradient updates will be too large (due to the random weights from the classifier) and your pre-trained model will forget what it has learned.
Also, you should try to fine-tune a small number of top layers rather than the whole MobileNet model. In most convolutional networks, the higher up a layer is, the more specialized it is. The first few layers learn very simple and generic features which generalize to almost all types of images. As you go higher up, the features are increasingly more specific to the dataset on which the model was trained. The goal of fine-tuning is to adapt these specialized features to work with the new dataset, rather than overwrite the generic learning.
### Un-freeze the top layers of the model
All you need to do is unfreeze the `base_model` and set the bottom layers be un-trainable. Then, you should recompile the model (necessary for these changes to take effect), and resume training.
```
base_model.trainable = True
# Let's take a look to see how many layers are in the base model
print("Number of layers in the base model: ", len(base_model.layers))
# Fine tune from this layer onwards
fine_tune_at = 100
# Freeze all the layers before the `fine_tune_at` layer
for layer in base_model.layers[:fine_tune_at]:
layer.trainable = False
```
### Compile the model
Compile the model using a much lower training rate.
```
model.compile(loss='categorical_crossentropy',
optimizer = tf.keras.optimizers.Adam(1e-5),
metrics=['accuracy'])
model.summary()
len(model.trainable_variables)
```
### Continue Train the model
If you trained to convergence earlier, this will get you a few percent more accuracy.
```
history_fine = model.fit(train_generator,
epochs=5,
validation_data=val_generator)
```
Let's take a look at the learning curves of the training and validation accuracy/loss, when fine tuning the last few layers of the MobileNet V2 base model and training the classifier on top of it. The validation loss is much higher than the training loss, so you may get some overfitting.
You may also get some overfitting as the new training set is relatively small and similar to the original MobileNet V2 datasets.
## Convert to TFLite
```
saved_model_dir = 'save/fine_tuning'
tf.saved_model.save(model, saved_model_dir)
model = tf.saved_model.load(saved_model_dir)
concrete_func = model.signatures[
tf.saved_model.DEFAULT_SERVING_SIGNATURE_DEF_KEY]
concrete_func.inputs[0].set_shape([1, 224, 224, 3])
converter = tf.lite.TFLiteConverter.from_concrete_function(concrete_func)
tflite_model = converter.convert()
with open('model.tflite', 'wb') as f:
f.write(tflite_model)
```
Download the converted model
```
from google.colab import files
files.download('model.tflite')
acc += history_fine.history['accuracy']
val_acc += history_fine.history['val_accuracy']
loss += history_fine.history['loss']
val_loss += history_fine.history['val_loss']
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.ylim([0.8, 1])
plt.plot([initial_epochs-1,initial_epochs-1],
plt.ylim(), label='Start Fine Tuning')
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.subplot(2, 1, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.ylim([0, 1.0])
plt.plot([initial_epochs-1,initial_epochs-1],
plt.ylim(), label='Start Fine Tuning')
plt.legend(loc='upper right')
plt.title('Training and Validation Loss')
plt.xlabel('epoch')
plt.show()
```
## Summary:
* **Using a pre-trained model for feature extraction**: When working with a small dataset, it is common to take advantage of features learned by a model trained on a larger dataset in the same domain. This is done by instantiating the pre-trained model and adding a fully-connected classifier on top. The pre-trained model is "frozen" and only the weights of the classifier get updated during training.
In this case, the convolutional base extracted all the features associated with each image and you just trained a classifier that determines the image class given that set of extracted features.
* **Fine-tuning a pre-trained model**: To further improve performance, one might want to repurpose the top-level layers of the pre-trained models to the new dataset via fine-tuning.
In this case, you tuned your weights such that your model learned high-level features specific to the dataset. This technique is usually recommended when the training dataset is large and very similar to the orginial dataset that the pre-trained model was trained on.
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Preamble" data-toc-modified-id="Preamble-1"><span class="toc-item-num">1 </span>Preamble</a></span><ul class="toc-item"><li><span><a href="#Some-general-parameters" data-toc-modified-id="Some-general-parameters-1.1"><span class="toc-item-num">1.1 </span>Some general parameters</a></span></li><li><span><a href="#Functions" data-toc-modified-id="Functions-1.2"><span class="toc-item-num">1.2 </span>Functions</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Create-overlap" data-toc-modified-id="Create-overlap-1.2.0.1"><span class="toc-item-num">1.2.0.1 </span>Create overlap</a></span></li><li><span><a href="#Activity-representation" data-toc-modified-id="Activity-representation-1.2.0.2"><span class="toc-item-num">1.2.0.2 </span>Activity representation</a></span></li></ul></li></ul></li></ul></li><li><span><a href="#The-example" data-toc-modified-id="The-example-2"><span class="toc-item-num">2 </span>The example</a></span></li></ul></div>
# Preamble
```
import pprint
import subprocess
import sys
sys.path.append('../')
import numpy as np
import scipy as sp
import statsmodels.api as sm
import matplotlib.pyplot as plt
import matplotlib
import matplotlib.gridspec as gridspec
from mpl_toolkits.axes_grid1 import make_axes_locatable
import seaborn as sns
%matplotlib inline
np.set_printoptions(suppress=True, precision=5)
from network import Protocol, NetworkManager, Network
from patterns_representation import PatternsRepresentation
from analysis_functions import calculate_persistence_time, calculate_recall_quantities, calculate_triad_connectivity
from plotting_functions import plot_weight_matrix, plot_network_activity_angle, plot_persistent_matrix
```
## Some general parameters
```
epsilon = 10e-80
vmin = -3.0
remove = 0.010
strict_maximum = True
dt = 0.001
tau_s = 0.010
tau_a = 0.250
g_I = 2.0
g_a = 2.0
G = 50.0
sns.set(font_scale=3.5)
sns.set_style("whitegrid", {'axes.grid': False})
plt.rcParams['figure.figsize'] = (12, 8)
lw = 10
ms = 22
alpha_graph = 0.3
colors = sns.color_palette()
```
## Functions
#### Create overlap
```
from copy import deepcopy
def create_overalaped_representation(manager, representation_overlap, sequence_overlap):
x = deepcopy(manager.canonical_activity_representation)
to_modify = int(representation_overlap * len(x[0]))
sequence_size = int(0.5 * len(x))
sequence_overlap_size = int(sequence_overlap * sequence_size)
start_point = int(0.5 * sequence_size + sequence_size - np.floor(sequence_overlap_size/ 2.0))
end_point = start_point + sequence_overlap_size
for sequence_index in range(start_point, end_point):
pattern = x[sequence_index]
pattern[:to_modify] = manager.canonical_activity_representation[sequence_index - sequence_size][:to_modify]
return x
```
#### Activity representation
```
activity_representation = np.array([[0, 0, 0], [1, 1, 1], [2, 2, 2], [3, 3, 3], [4, 4, 4], [5, 5, 5],
[10, 10, 10], [11, 11, 11], [2, 2, 12], [3, 3, 13], [14, 14, 14], [15, 15, 15]])
```
# The example
```
sigma_out = 0.0
tau_z_pre = 0.025
tau_z_post = 0.020
hypercolumns = 3
minicolumns = 20
n_patterns = 12
patterns_per_sequence = 6
representation_overlap = 0.75
sequence_overlap = 0.5
# Training protocol
training_times_base = 0.100
training_times = [training_times_base for i in range(n_patterns)]
ipi_base = 0.0
inter_pulse_intervals = [ipi_base for i in range(n_patterns)]
inter_sequence_interval = 1.0
resting_time = 1.0
epochs = 1
T_persistence = 1.0 / patterns_per_sequence
# Manager properties
values_to_save = ['o']
# Neural Network
nn = Network(hypercolumns, minicolumns, G=G, tau_s=tau_s, tau_z_pre=tau_z_pre, tau_z_post=tau_z_post,
tau_a=tau_a, g_a=g_a, g_I=g_I, sigma_out=sigma_out, epsilon=epsilon, prng=np.random,
strict_maximum=strict_maximum, perfect=False, normalized_currents=True)
# Build the manager
manager = NetworkManager(nn=nn, dt=dt, values_to_save=values_to_save)
# Build the representation
representation = PatternsRepresentation(activity_representation, minicolumns=minicolumns)
inter_pulse_intervals[patterns_per_sequence - 1] = inter_sequence_interval
# Build the protocol
protocol = Protocol()
protocol.simple_protocol(representation, training_times=training_times, inter_pulse_intervals=inter_pulse_intervals,
inter_sequence_interval=inter_sequence_interval, epochs=epochs, resting_time=resting_time)
# Run the protocol
timed_input = manager.run_network_protocol_offline(protocol=protocol)
# Set the persistent time
manager.set_persistent_time_with_adaptation_gain(T_persistence=T_persistence, from_state=1, to_state=2)
patterns_per_sequence = 6
T_cue = 2.0 * manager.nn.tau_s
T_recall = T_persistence * 6 + T_cue
nr1 = representation.network_representation[:patterns_per_sequence]
nr2 = representation.network_representation[patterns_per_sequence:]
# Success 1
aux1 = calculate_recall_quantities(manager, nr1, T_recall, T_cue, remove=remove, reset=True, empty_history=True)
success1, pattern_sequence1, persistent_times1, timings1 = aux1
# Success 2
aux2 = calculate_recall_quantities(manager, nr2, T_recall, T_cue, remove=remove, reset=False, empty_history=False)
success2, pattern_sequence2, persistent_times2, timings2 = aux2
total_success = 0.5 * success1 + 0.5 * success2
cmap = matplotlib.cm.binary
ax1, ax2 = plot_network_activity_angle(manager, cmap=cmap, time_y=False)
ax1.axvline(T_recall - tau_s, ls='--', color='red')
nr1 = representation.network_representation[:patterns_per_sequence]
nr2 = representation.network_representation[patterns_per_sequence:]
# Success 1
aux1 = calculate_recall_quantities(manager, nr1, T_recall, T_cue, remove=remove, reset=True, empty_history=True)
success1, pattern_sequence1, persistent_times1, timings1 = aux1
o1 = manager.history['o']
# Success 2
aux2 = calculate_recall_quantities(manager, nr2, T_recall, T_cue, remove=remove, reset=True, empty_history=True)
success2, pattern_sequence2, persistent_times2, timings2 = aux2
o2 = manager.history['o']
rect = plt.Rectangle((0.29, 0.2), 0.2, 0.72, linewidth=1, edgecolor='black',facecolor='gray', alpha=0.2)
rect2 = plt.Rectangle((0.29, 0.2), 0.2, 0.72, linewidth=1, edgecolor='black',facecolor='gray', alpha=0.2)
rect3 = plt.Rectangle((0.29, 0.2), 0.2, 0.72, linewidth=1, edgecolor='black',facecolor='gray', alpha=0.2)
factor_scale = 1.5
s1 = int(16 * factor_scale)
s2 = int(12 * factor_scale)
gs = gridspec.GridSpec(2, 2)
fig = plt.figure(figsize=(s1, s2))
ax = fig.add_subplot(gs[:, 0])
ax.set_ylim([0, minicolumns * hypercolumns])
start = T_persistence * 0.25
dx = T_persistence
dy = minicolumns * 0.4
y1 = 28
y2 = 2
sequence1 = activity_representation[:patterns_per_sequence]
sequence2 = activity_representation[patterns_per_sequence:]
x = start
for pattern in sequence1:
for index, unit in enumerate(pattern):
ax.text(x, y1 + index*dy, str(pattern[index]))
x += dx
x = start
for pattern in sequence2:
for index, unit in enumerate(pattern):
ax.text(x, y2 + index*dy, str(pattern[hypercolumns - 1- index]))
x += dx
ax.add_patch(rect)
#ax.axis('off')
ax2 = fig.add_subplot(gs[0, 1])
cmap = matplotlib.cm.binary
extent = [0, manager.T_recall_total, 0, minicolumns * hypercolumns]
ax2.imshow(o1.T, origin='lower', cmap=cmap, aspect='auto', extent=extent)
ax2.add_patch(rect2)
ax3 = fig.add_subplot(gs[1, 1])
cmap = matplotlib.cm.binary
extent = [0, manager.T_recall_total, 0, minicolumns * hypercolumns]
ax3.imshow(o2.T, origin='lower', cmap=cmap, aspect='auto', extent=extent)
ax3.add_patch(rect3)
rect = plt.Rectangle((2*T_persistence, 0.2), 2*T_persistence, 55,
linewidth=1, edgecolor='black',facecolor='gray', alpha=0.2)
rect2 = plt.Rectangle((2*T_persistence, 0.2), 2*T_persistence, minicolumns * hypercolumns,
linewidth=1, edgecolor='black',facecolor='gray', alpha=0.2)
intersection = {2, 3}
save = True
frame_recall = False
sns.set(font_scale=3.5)
sns.set_style("whitegrid", {'axes.grid': False})
factor_scale = 1.6
s1 = int(16 * factor_scale)
s2 = int(12 * factor_scale)
gs = gridspec.GridSpec(2, 2)
fig = plt.figure(figsize=(s1, s2))
ax = fig.add_subplot(gs[:, 0])
ax.set_ylim([0, minicolumns * hypercolumns])
start = T_persistence * 0.25
dx = T_persistence
dy = minicolumns * 0.4
y1 = 32
y2 = 4
sequence1 = activity_representation[:patterns_per_sequence]
sequence2 = activity_representation[patterns_per_sequence:]
x = start
for pattern in sequence2:
for index, unit in enumerate(pattern):
if pattern[index] in intersection:
color = 'black'
else:
color = 'blue'
ax.text(x, y1 + index*dy, str(pattern[index]), color=color)
x += dx
x = start
for pattern in sequence1:
for index, unit in enumerate(pattern):
if pattern[index] in intersection:
color = 'black'
else:
color = 'red'
ax.text(x, y2 + index*dy, str(pattern[index] + 1), color=color)
x += dx
ax.add_patch(rect)
ax.axis('off')
#ax.text(0.3, 25, r'{', rotation=270, fontsize=150)
################
# The sequence recall
###############
ax2 = fig.add_subplot(gs[:, 1])
cmap.set_under(color='red')
cmap.set_over(color='blue')
cmap = matplotlib.cm.binary
extent = [0, manager.T_recall_total, 0, minicolumns * hypercolumns]
ax2.imshow((-1 * o1 + 2 * o2).T, origin='lower', cmap=cmap, aspect='auto', extent=extent, vmin=0.0, vmax=1.0)
ax2.axhline(minicolumns, ls='--', color='gray')
ax2.axhline(2 * minicolumns, ls='--', color='gray')
ax2.set_xlabel('Time (s)')
ax2.set_ylabel('Unit Id')
ax2.add_patch(rect2);
if not frame_recall:
ax2.spines['top'].set_visible(False)
ax2.spines['right'].set_visible(False)
ax2.spines['bottom'].set_visible(False)
ax2.spines['left'].set_visible(False)
fig.tight_layout()
if save:
directory = '../plot_producers/'
file_name = 'rep_diagram'
format_string = '.svg'
string_to_save = directory + file_name + format_string
fig.savefig(string_to_save, frameon=False, dpi=110, bbox_inches='tight', transparent=True)
2 in {2, 3}
```
|
github_jupyter
|
# BiDirectional LSTM classifier in keras
#### Load dependencies
```
import keras
from keras.datasets import imdb
from keras.preprocessing.sequence import pad_sequences
from keras.models import Sequential
from keras.layers import Embedding, SpatialDropout1D, Dense, Flatten, Dropout, LSTM
from keras.layers.wrappers import Bidirectional
from keras.callbacks import ModelCheckpoint # new!
import os # new!
from sklearn.metrics import roc_auc_score, roc_curve # new!
import matplotlib.pyplot as plt # new!
%matplotlib inline
# output directory name:
output_dir = 'model_output/bilstm'
# training:
epochs = 6
batch_size = 128
# vector-space embedding:
n_dim = 64
n_unique_words = 10000
max_review_length = 200
pad_type = trunc_type = 'pre'
drop_embed = 0.2
# neural network architecture:
n_lstm = 256
droput_lstm = 0.2
```
#### Load data
For a given data set:
* the Keras text utilities [here](https://keras.io/preprocessing/text/) quickly preprocess natural language and convert it into an index
* the `keras.preprocessing.text.Tokenizer` class may do everything you need in one line:
* tokenize into words or characters
* `num_words`: maximum unique tokens
* filter out punctuation
* lower case
* convert words to an integer index
```
(x_train, y_train), (x_valid, y_valid) = imdb.load_data(num_words=n_unique_words)
```
#### Preprocess data
```
x_train = pad_sequences(x_train, maxlen=max_review_length, padding=pad_type, truncating=trunc_type, value=0)
x_valid = pad_sequences(x_valid, maxlen=max_review_length, padding=pad_type, truncating=trunc_type, value=0)
x_train[:6]
for i in range(6):
print len(x_train[i])
```
#### Design neural network architecture
```
model = Sequential()
model.add(Embedding(n_unique_words, n_dim, input_length=max_review_length))
model.add(SpatialDropout1D(drop_embed))
# model.add(Conv1D(n_conv, k_conv, activation='relu'))
# model.add(Conv1D(n_conv, k_conv, activation='relu'))
# model.add(GlobalMaxPooling1D())
# model.add(Dense(n_dense, activation='relu'))
# model.add(Dropout(dropout))
model.add(Bidirectional(LSTM(n_lstm, dropout=droput_lstm)))
model.add(Dense(1, activation='sigmoid'))
model.summary()
n_dim, n_unique_words, n_dim * n_unique_words
max_review_length, n_dim, n_dim * max_review_length
```
#### Configure Model
```
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
modelcheckpoint = ModelCheckpoint(filepath=output_dir+"/weights.{epoch:02d}.hdf5")
if not os.path.exists(output_dir):
os.makedirs(output_dir)
model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs,
verbose=1, validation_data=(x_valid, y_valid), callbacks=[modelcheckpoint])
```
#### Evaluate
```
model.load_weights(output_dir+"/weights.01.hdf5") # zero-indexed
y_hat = model.predict_proba(x_valid)
len(y_hat)
y_hat[0]
plt.hist(y_hat)
_ = plt.axvline(x=0.5, color='orange')
pct_auc = roc_auc_score(y_valid, y_hat)*100.0
"{:0.2f}".format(pct_auc)
```
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
from skimage.color import rgb2gray
from skimage.filters import gaussian
import scipy
import cv2
from scipy import ndimage
import Image_preperation as prep
import FitFunction as fit
import FileManager as fm
import Image_preperation as prep
def calc_mean(points):
size = len(points)
p1 = points[-1]
p2 = points[0]
mean_sum = scipy.spatial.distance.euclidean(p1,p2)
for i in range(size-1):
p1 = points[i]
p2 = points[i+1]
mean_sum += scipy.spatial.distance.euclidean(p1,p2)
return mean_sum / size
def calc_internal2(p1,p2,mean_points):
return np.sum( (p2 - p1)**2 ) / mean_points
def calc_internal(p1,p2,mean_points):
return scipy.spatial.distance.euclidean(p1,p2) / mean_points
def calc_external_img2(img):
median = prep.median_filter(img)
edges = prep.edge_detection_low(median)
return -edges
def calc_external_img(img):
img = np.array(img, dtype=np.int16)
kx = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
Gx = cv2.filter2D(img,-1,kx)
ky = np.array([[-1,-2,-1],[0,0,0],[1,2,1]])
Gy = cv2.filter2D(img,-1,ky)
G = np.sqrt(Gx**2 + Gy**2)
return G
def calc_external(p, external_img):
p = p.astype(int)
max_value = np.abs(np.min(external_img))
return external_img[p[1],p[0]] / max_value
def calc_energy(p1, p2, external_img, mean_points,alpha):
internal = calc_internal(p1,p2, mean_points)
external = calc_external(p1, external_img)
return internal + alpha * external
def get_point_state(point, rad, number, pixel_width):
positive = number // 2
if(positive == 1):
state = (number + 1) / 2
else:
state = -(number / 2)
return fit.get_point_at_distance(point, state, rad)
def unpack(number, back_pointers, angles, points, pixel_width):
size = len(points)
new_points = np.empty((size,2))
new_points[-1] = get_point_state(points[-1],angles[-1], number, pixel_width)
pointer = back_pointers[-1,number]
for i in range(size-2, -1, -1):
new_points[i] = get_point_state(points[i],angles[i], pointer, pixel_width)
pointer = back_pointers[i,pointer]
return new_points
#https://courses.engr.illinois.edu/cs447/fa2017/Slides/Lecture07.pdf
#viterbi algo
def active_contour(points, edge_img, pixel_width, alpha):
size = len(points)
num_states = (2*pixel_width +1)
trellis = np.zeros((size, num_states), dtype=np.float16)
back_pointers = np.zeros((size, num_states), dtype=int)
#external_img = calc_external_img(img)
if(np.dtype('bool') == edge_img.dtype):
external_img = -np.array(edge_img,dtype=np.int8)
else:
external_img = -edge_img
mean_points = calc_mean(points)
#init
trellis[0,:] = np.zeros((num_states))
back_pointers[0,:] = np.zeros((num_states))
angles = get_angles_of(points)
#recursion
for i in range(1, size):
for t in range(num_states):
trellis[i,t] = np.inf
for d in range(num_states):
p1 = get_point_state(points[i-1], angles[i-1], d, pixel_width)
p2 = get_point_state(points[i],angles[i], t, pixel_width)
energy_trans = calc_energy(p1, p2, external_img,mean_points, alpha)
tmp = trellis[i-1,d] + energy_trans
if(tmp < trellis[i,t]):
trellis[i,t] = tmp
back_pointers[i,t] = d
#find best
t_best, vit_min = 0, np.inf
for t in range(num_states):
if(trellis[size-1, t] < vit_min):
t_best = t
vit_min = trellis[size-1, t]
new_points = unpack(t_best, back_pointers,angles, points, pixel_width)
return new_points
def active_contour_loop(points, img, max_loop, pixel_width, alpha):
old_points = points
for i in range(max_loop):
new_points = active_contour(old_points, img, pixel_width, alpha)
if np.array_equal(new_points, old_points):
print(i)
break
#old_points = new_points
head, tail = np.split(new_points, [6])
old_points = np.append(tail, head).reshape(new_points.shape)
return new_points
def resolution_scale(img, points, scale):
new_points = resolution_scale_points(points, scale)
new_img = resolution_downscale_img(img, scale)
return new_img, new_points
def resolution_scale_points(points, scale):
return np.around(points*scale)
def resolution_downscale_img(img, scale):
x, y = img.shape
xn = int(x*scale)
yn = int(y*scale)
return cv2.resize(img, (yn ,xn))
def get_angles_of(points):
size = len(points)
angles = np.zeros(size)
for i in range(size):
if(i==size-1):
p1, p2, p3 = points[i-1], points[i], points[0]
else:
p1, p2, p3 = points[i-1], points[i], points[i+1]
angles[i] = fit.get_normal_angle(p1, p2, p3)
return angles
def show_results():
piece = fm.load_img_piece()
edge_img = prep.canny(piece)
tooth = fm.load_tooth_of_piece(2)
fm.show_with_points(edge_img, tooth)
new_tooth = active_contour(tooth, edge_img, 25, 1)
fm.show_with_points(edge_img, new_tooth)
def show_influence_ext_int():
new_piece, new_tooth = piece, tooth
mean = calc_mean(new_tooth)
ext = calc_external_img(new_piece)
fm.show_with_points(ext, new_tooth[0:2])
print(calc_external(new_tooth[0],ext))
print(calc_internal(new_tooth[0], new_tooth[1], mean))
print(calc_energy(new_tooth[0],new_tooth[1],ext,mean,10))
if __name__ == "__main__":
piece = fm.load_img_piece()
tooth = fm.load_tooth_of_piece()
ext = prep.calc_external_img_active_contour(piece)
fm.show_with_points(ext, tooth)
ext2, stooth = fm.resolution_scale(ext, tooth, 1/6)
fm.show_with_points(ext2, stooth)
```
|
github_jupyter
|
# Homework (15 pts) - Classification
```
# Questions are based on the mouse cortex protein expression level dataset used in lecture.
# The Data_Cortex_Nuclear.csv file is available in the same folder as this notebook
# or at https://www.kaggle.com/ruslankl/mice-protein-expression
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.metrics import classification_report
from sklearn.metrics import roc_curve, auc
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['axes.titlesize'] = 14
plt.rcParams['legend.fontsize'] = 12
plt.rcParams['figure.figsize'] = (8, 5)
%config InlineBackend.figure_format = 'retina'
mice = pd.read_csv('Data_Cortex_Nuclear.csv')
mice
```
---
1. (3 pts) Remove mice/samples with missing measurements from the dataframe. Store the result in the mice variable for use with subsequent questions.
```
mice.isnull().sum()
mice = mice.dropna()
```
---
2. (3 pts) Use both logistic regression and a random forest to classify the mice as either memantine or saline treated based on their protein expression profiles. Contrast the overall accuracy of the two classifiers on a withheld test set. You can ignore any warnings similar to those seen in the lecture for the purposes of this assignment, not that you should ignore these for a real analysis.
```
X = mice.loc[:,'DYRK1A_N':'CaNA_N'] # just protein expression levels
y = mice['Treatment']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state = 1)
model = LogisticRegression()
model.fit(X_train, y_train)
LogisticRegression()
y_test_pred = model.predict(X_test)
lr_treatment_accuracy = model.score(X_test, y_test)
lr_treatment_accuracy
X = mice.loc[:,'DYRK1A_N':'CaNA_N'] # just protein expression levels
y = mice['Treatment']
X_train2, X_test2, y_train2, y_test2 = train_test_split(X, y, test_size = 0.4, random_state = 1)
model2 = RandomForestClassifier(n_estimators = 100, random_state = 1)
model2.fit(X_train2, y_train2)
y_test_pred2 = model.predict(X_test2)
rf_treatment_accuracy2 = accuracy_score(y_test2, y_test_pred2)
rf_treatment_accuracy2
print("Random forests are a better predictor")
```
---
3. (3 pts) For the two classifiers trained in #2 above, contrast their confusion matrices based on predictions for a withheld test set.
```
cm = confusion_matrix(y_test, y_test_pred)
lr_treatment_cmd = ConfusionMatrixDisplay(confusion_matrix = cm, display_labels = model.classes_)
lr_treatment_cmd.plot();
cm = confusion_matrix(y_test, y_test_pred2)
rf_treatment_cmd = ConfusionMatrixDisplay(confusion_matrix = cm, display_labels = model.classes_)
rf_treatment_cmd.plot();
```
---
4. (3 pts) For the two classifiers trained in #2 above, contrast their ROC curves based on predictions for Memantine treatment in withheld test set.
```
y_test_proba = model.predict_proba(X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_test_proba[:,1], pos_label = model.classes_[1])
plt.plot(fpr, tpr, color = 'r', label = model.classes_[0])
plt.plot([0, 1], [0, 1], color = 'k', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend();
y_test_proba2 = model2.predict_proba(X_test2)
fpr2, tpr2, thresholds2 = roc_curve(y_test2, y_test_proba2[:,1], pos_label = model2.classes_[1])
plt.plot(fpr2, tpr2, color = 'b', label = model2.classes_[0])
plt.plot([0, 1], [0, 1], color = 'k', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend();
```
---
5. (3 pts) Use a random forest to classify the mice into each of the 8 classes defined by genotype, fear conditioning and treatment based on their protein expression profiles. Repeat this classification 77 separate times, where on the ith time you will use only the first i proteins. For example, the 1st time you will only use expression of DYRK1A_N, the 2nd time you will use both DYRK1A_N and ITSN1_N as predictive features, the 3rd time DYRK1A_N, ITSN1_N and BDNF_N, etc. until the 77th time you will use all 77 proteins from DYRK1A_N to CaNA_N. Plot the accuracy of the classifier on a withheld test set as a function of the number of protein features used as predictors.
```
proteins = X_train.shape[1]
accuracies = np.zeros((proteins,))
rFor = RandomForestClassifier(n_estimators = 100, random_state = 1)
for i in np.arange(proteins) + 1:
pTrain = X_train.iloc[:, 0:i]
pTest = X_test.iloc[:, 0:i]
rFor.fit(pTrain, y_train)
rForPred = rFor.predict(pTest)
rForAcc = accuracy_score(y_test, rForPred)
accuracies[i-1] = rForAcc
plt.plot(np.arange(proteins) + 1, accuracies)
plt.xlabel("Number of Features")
plt.ylabel("Accuracy")
plt.title("Accuracy vs Number of Features")
```
|
github_jupyter
|
# Assignment 2: Parts-of-Speech Tagging (POS)
Welcome to the second assignment of Course 2 in the Natural Language Processing specialization. This assignment will develop skills in part-of-speech (POS) tagging, the process of assigning a part-of-speech tag (Noun, Verb, Adjective...) to each word in an input text. Tagging is difficult because some words can represent more than one part of speech at different times. They are **Ambiguous**. Let's look at the following example:
- The whole team played **well**. [adverb]
- You are doing **well** for yourself. [adjective]
- **Well**, this assignment took me forever to complete. [interjection]
- The **well** is dry. [noun]
- Tears were beginning to **well** in her eyes. [verb]
Distinguishing the parts-of-speech of a word in a sentence will help you better understand the meaning of a sentence. This would be critically important in search queries. Identifying the proper noun, the organization, the stock symbol, or anything similar would greatly improve everything ranging from speech recognition to search. By completing this assignment, you will:
- Learn how parts-of-speech tagging works
- Compute the transition matrix A in a Hidden Markov Model
- Compute the emission matrix B in a Hidden Markov Model
- Compute the Viterbi algorithm
- Compute the accuracy of your own model
## Outline
- [0 Data Sources](#0)
- [1 POS Tagging](#1)
- [1.1 Training](#1.1)
- [Exercise 01](#ex-01)
- [1.2 Testing](#1.2)
- [Exercise 02](#ex-02)
- [2 Hidden Markov Models](#2)
- [2.1 Generating Matrices](#2.1)
- [Exercise 03](#ex-03)
- [Exercise 04](#ex-04)
- [3 Viterbi Algorithm](#3)
- [3.1 Initialization](#3.1)
- [Exercise 05](#ex-05)
- [3.2 Viterbi Forward](#3.2)
- [Exercise 06](#ex-06)
- [3.3 Viterbi Backward](#3.3)
- [Exercise 07](#ex-07)
- [4 Predicting on a data set](#4)
- [Exercise 08](#ex-08)
```
# Importing packages and loading in the data set
from utils_pos import get_word_tag, preprocess
import pandas as pd
from collections import defaultdict
import math
import numpy as np
```
<a name='0'></a>
## Part 0: Data Sources
This assignment will use two tagged data sets collected from the **Wall Street Journal (WSJ)**.
[Here](http://relearn.be/2015/training-common-sense/sources/software/pattern-2.6-critical-fork/docs/html/mbsp-tags.html) is an example 'tag-set' or Part of Speech designation describing the two or three letter tag and their meaning.
- One data set (**WSJ-2_21.pos**) will be used for **training**.
- The other (**WSJ-24.pos**) for **testing**.
- The tagged training data has been preprocessed to form a vocabulary (**hmm_vocab.txt**).
- The words in the vocabulary are words from the training set that were used two or more times.
- The vocabulary is augmented with a set of 'unknown word tokens', described below.
The training set will be used to create the emission, transmission and tag counts.
The test set (WSJ-24.pos) is read in to create `y`.
- This contains both the test text and the true tag.
- The test set has also been preprocessed to remove the tags to form **test_words.txt**.
- This is read in and further processed to identify the end of sentences and handle words not in the vocabulary using functions provided in **utils_pos.py**.
- This forms the list `prep`, the preprocessed text used to test our POS taggers.
A POS tagger will necessarily encounter words that are not in its datasets.
- To improve accuracy, these words are further analyzed during preprocessing to extract available hints as to their appropriate tag.
- For example, the suffix 'ize' is a hint that the word is a verb, as in 'final-ize' or 'character-ize'.
- A set of unknown-tokens, such as '--unk-verb--' or '--unk-noun--' will replace the unknown words in both the training and test corpus and will appear in the emission, transmission and tag data structures.
<img src = "DataSources1.PNG" />
Implementation note:
- For python 3.6 and beyond, dictionaries retain the insertion order.
- Furthermore, their hash-based lookup makes them suitable for rapid membership tests.
- If _di_ is a dictionary, `key in di` will return `True` if _di_ has a key _key_, else `False`.
The dictionary `vocab` will utilize these features.
```
# load in the training corpus
with open("WSJ_02-21.pos", 'r') as f:
training_corpus = f.readlines()
print(f"A few items of the training corpus list")
print(training_corpus[0:5])
# read the vocabulary data, split by each line of text, and save the list
with open("hmm_vocab.txt", 'r') as f:
voc_l = f.read().split('\n')
print("A few items of the vocabulary list")
print(voc_l[0:50])
print()
print("A few items at the end of the vocabulary list")
print(voc_l[-50:])
# vocab: dictionary that has the index of the corresponding words
vocab = {}
# Get the index of the corresponding words.
for i, word in enumerate(sorted(voc_l)):
vocab[word] = i
print("Vocabulary dictionary, key is the word, value is a unique integer")
cnt = 0
for k,v in vocab.items():
print(f"{k}:{v}")
cnt += 1
if cnt > 20:
break
# load in the test corpus
with open("WSJ_24.pos", 'r') as f:
y = f.readlines()
print("A sample of the test corpus")
print(y[0:10])
#corpus without tags, preprocessed
_, prep = preprocess(vocab, "test.words")
print('The length of the preprocessed test corpus: ', len(prep))
print('This is a sample of the test_corpus: ')
print(prep[0:10])
```
<a name='1'></a>
# Part 1: Parts-of-speech tagging
<a name='1.1'></a>
## Part 1.1 - Training
You will start with the simplest possible parts-of-speech tagger and we will build up to the state of the art.
In this section, you will find the words that are not ambiguous.
- For example, the word `is` is a verb and it is not ambiguous.
- In the `WSJ` corpus, $86$% of the token are unambiguous (meaning they have only one tag)
- About $14\%$ are ambiguous (meaning that they have more than one tag)
<img src = "pos.png" style="width:400px;height:250px;"/>
Before you start predicting the tags of each word, you will need to compute a few dictionaries that will help you to generate the tables.
#### Transition counts
- The first dictionary is the `transition_counts` dictionary which computes the number of times each tag happened next to another tag.
This dictionary will be used to compute:
$$P(t_i |t_{i-1}) \tag{1}$$
This is the probability of a tag at position $i$ given the tag at position $i-1$.
In order for you to compute equation 1, you will create a `transition_counts` dictionary where
- The keys are `(prev_tag, tag)`
- The values are the number of times those two tags appeared in that order.
#### Emission counts
The second dictionary you will compute is the `emission_counts` dictionary. This dictionary will be used to compute:
$$P(w_i|t_i)\tag{2}$$
In other words, you will use it to compute the probability of a word given its tag.
In order for you to compute equation 2, you will create an `emission_counts` dictionary where
- The keys are `(tag, word)`
- The values are the number of times that pair showed up in your training set.
#### Tag counts
The last dictionary you will compute is the `tag_counts` dictionary.
- The key is the tag
- The value is the number of times each tag appeared.
<a name='ex-01'></a>
### Exercise 01
**Instructions:** Write a program that takes in the `training_corpus` and returns the three dictionaries mentioned above `transition_counts`, `emission_counts`, and `tag_counts`.
- `emission_counts`: maps (tag, word) to the number of times it happened.
- `transition_counts`: maps (prev_tag, tag) to the number of times it has appeared.
- `tag_counts`: maps (tag) to the number of times it has occured.
Implementation note: This routine utilises *defaultdict*, which is a subclass of *dict*.
- A standard Python dictionary throws a *KeyError* if you try to access an item with a key that is not currently in the dictionary.
- In contrast, the *defaultdict* will create an item of the type of the argument, in this case an integer with the default value of 0.
- See [defaultdict](https://docs.python.org/3.3/library/collections.html#defaultdict-objects).
```
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_dictionaries
def create_dictionaries(training_corpus, vocab):
"""
Input:
training_corpus: a corpus where each line has a word followed by its tag.
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
emission_counts: a dictionary where the keys are (tag, word) and the values are the counts
transition_counts: a dictionary where the keys are (prev_tag, tag) and the values are the counts
tag_counts: a dictionary where the keys are the tags and the values are the counts
"""
# initialize the dictionaries using defaultdict
emission_counts = defaultdict(int)
transition_counts = defaultdict(int)
tag_counts = defaultdict(int)
# Initialize "prev_tag" (previous tag) with the start state, denoted by '--s--'
prev_tag = '--s--'
# use 'i' to track the line number in the corpus
i = 0
# Each item in the training corpus contains a word and its POS tag
# Go through each word and its tag in the training corpus
for word_tag in training_corpus:
# Increment the word_tag count
i += 1
# Every 50,000 words, print the word count
if i % 50000 == 0:
print(f"word count = {i}")
### START CODE HERE (Replace instances of 'None' with your code) ###
# get the word and tag using the get_word_tag helper function (imported from utils_pos.py)
word, tag = get_word_tag(line=word_tag, vocab=vocab)
# Increment the transition count for the previous word and tag
transition_counts[(prev_tag, tag)] += 1
# Increment the emission count for the tag and word
emission_counts[(tag, word)] += 1
# Increment the tag count
tag_counts[tag] += 1
# Set the previous tag to this tag (for the next iteration of the loop)
prev_tag = tag
### END CODE HERE ###
return emission_counts, transition_counts, tag_counts
emission_counts, transition_counts, tag_counts = create_dictionaries(training_corpus, vocab)
# get all the POS states
states = sorted(tag_counts.keys())
print(f"Number of POS tags (number of 'states'): {len(states)}")
print("View these POS tags (states)")
print(states)
```
##### Expected Output
```CPP
Number of POS tags (number of 'states'46
View these states
['#', '$', "''", '(', ')', ',', '--s--', '.', ':', 'CC', 'CD', 'DT', 'EX', 'FW', 'IN', 'JJ', 'JJR', 'JJS', 'LS', 'MD', 'NN', 'NNP', 'NNPS', 'NNS', 'PDT', 'POS', 'PRP', 'PRP$', 'RB', 'RBR', 'RBS', 'RP', 'SYM', 'TO', 'UH', 'VB', 'VBD', 'VBG', 'VBN', 'VBP', 'VBZ', 'WDT', 'WP', 'WP$', 'WRB', '``']
```
The 'states' are the Parts-of-speech designations found in the training data. They will also be referred to as 'tags' or POS in this assignment.
- "NN" is noun, singular,
- 'NNS' is noun, plural.
- In addition, there are helpful tags like '--s--' which indicate a start of a sentence.
- You can get a more complete description at [Penn Treebank II tag set](https://www.clips.uantwerpen.be/pages/mbsp-tags).
```
print("transition examples: ")
for ex in list(transition_counts.items())[:3]:
print(ex)
print()
print("emission examples: ")
for ex in list(emission_counts.items())[200:203]:
print (ex)
print()
print("ambiguous word example: ")
for tup,cnt in emission_counts.items():
if tup[1] == 'back': print (tup, cnt)
```
##### Expected Output
```CPP
transition examples:
(('--s--', 'IN'), 5050)
(('IN', 'DT'), 32364)
(('DT', 'NNP'), 9044)
emission examples:
(('DT', 'any'), 721)
(('NN', 'decrease'), 7)
(('NN', 'insider-trading'), 5)
ambiguous word example:
('RB', 'back') 304
('VB', 'back') 20
('RP', 'back') 84
('JJ', 'back') 25
('NN', 'back') 29
('VBP', 'back') 4
```
<a name='1.2'></a>
### Part 1.2 - Testing
Now you will test the accuracy of your parts-of-speech tagger using your `emission_counts` dictionary.
- Given your preprocessed test corpus `prep`, you will assign a parts-of-speech tag to every word in that corpus.
- Using the original tagged test corpus `y`, you will then compute what percent of the tags you got correct.
<a name='ex-02'></a>
### Exercise 02
**Instructions:** Implement `predict_pos` that computes the accuracy of your model.
- This is a warm up exercise.
- To assign a part of speech to a word, assign the most frequent POS for that word in the training set.
- Then evaluate how well this approach works. Each time you predict based on the most frequent POS for the given word, check whether the actual POS of that word is the same. If so, the prediction was correct!
- Calculate the accuracy as the number of correct predictions divided by the total number of words for which you predicted the POS tag.
```
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: predict_pos
def predict_pos(prep, y, emission_counts, vocab, states):
'''
Input:
prep: a preprocessed version of 'y'. A list with the 'word' component of the tuples.
y: a corpus composed of a list of tuples where each tuple consists of (word, POS)
emission_counts: a dictionary where the keys are (tag,word) tuples and the value is the count
vocab: a dictionary where keys are words in vocabulary and value is an index
states: a sorted list of all possible tags for this assignment
Output:
accuracy: Number of times you classified a word correctly
'''
# Initialize the number of correct predictions to zero
num_correct = 0
# Get the (tag, word) tuples, stored as a set
all_words = set(emission_counts.keys())
# Get the number of (word, POS) tuples in the corpus 'y'
total = len(y)
for word, y_tup in zip(prep, y):
# Split the (word, POS) string into a list of two items
y_tup_l = y_tup.split()
# Verify that y_tup contain both word and POS
if len(y_tup_l) == 2:
# Set the true POS label for this word
true_label = y_tup_l[1]
else:
# If the y_tup didn't contain word and POS, go to next word
continue
count_final = 0
pos_final = ''
# If the word is in the vocabulary...
if word in vocab:
for pos in states:
### START CODE HERE (Replace instances of 'None' with your code) ###
# define the key as the tuple containing the POS and word
key = (pos, word)
# check if the (pos, word) key exists in the emission_counts dictionary
if key in emission_counts: # complete this line
# get the emission count of the (pos,word) tuple
count = emission_counts[key]
# keep track of the POS with the largest count
if count > count_final: # complete this line
# update the final count (largest count)
count_final = count
# update the final POS
pos_final = pos
# If the final POS (with the largest count) matches the true POS:
if pos_final == true_label: # complete this line
# Update the number of correct predictions
num_correct += 1
### END CODE HERE ###
accuracy = num_correct / total
return accuracy
accuracy_predict_pos = predict_pos(prep, y, emission_counts, vocab, states)
print(f"Accuracy of prediction using predict_pos is {accuracy_predict_pos:.4f}")
```
##### Expected Output
```CPP
Accuracy of prediction using predict_pos is 0.8889
```
88.9% is really good for this warm up exercise. With hidden markov models, you should be able to get **95% accuracy.**
<a name='2'></a>
# Part 2: Hidden Markov Models for POS
Now you will build something more context specific. Concretely, you will be implementing a Hidden Markov Model (HMM) with a Viterbi decoder
- The HMM is one of the most commonly used algorithms in Natural Language Processing, and is a foundation to many deep learning techniques you will see in this specialization.
- In addition to parts-of-speech tagging, HMM is used in speech recognition, speech synthesis, etc.
- By completing this part of the assignment you will get a 95% accuracy on the same dataset you used in Part 1.
The Markov Model contains a number of states and the probability of transition between those states.
- In this case, the states are the parts-of-speech.
- A Markov Model utilizes a transition matrix, `A`.
- A Hidden Markov Model adds an observation or emission matrix `B` which describes the probability of a visible observation when we are in a particular state.
- In this case, the emissions are the words in the corpus
- The state, which is hidden, is the POS tag of that word.
<a name='2.1'></a>
## Part 2.1 Generating Matrices
### Creating the 'A' transition probabilities matrix
Now that you have your `emission_counts`, `transition_counts`, and `tag_counts`, you will start implementing the Hidden Markov Model.
This will allow you to quickly construct the
- `A` transition probabilities matrix.
- and the `B` emission probabilities matrix.
You will also use some smoothing when computing these matrices.
Here is an example of what the `A` transition matrix would look like (it is simplified to 5 tags for viewing. It is 46x46 in this assignment.):
|**A** |...| RBS | RP | SYM | TO | UH|...
| --- ||---:-------------| ------------ | ------------ | -------- | ---------- |----
|**RBS** |...|2.217069e-06 |2.217069e-06 |2.217069e-06 |0.008870 |2.217069e-06|...
|**RP** |...|3.756509e-07 |7.516775e-04 |3.756509e-07 |0.051089 |3.756509e-07|...
|**SYM** |...|1.722772e-05 |1.722772e-05 |1.722772e-05 |0.000017 |1.722772e-05|...
|**TO** |...|4.477336e-05 |4.472863e-08 |4.472863e-08 |0.000090 |4.477336e-05|...
|**UH** |...|1.030439e-05 |1.030439e-05 |1.030439e-05 |0.061837 |3.092348e-02|...
| ... |...| ... | ... | ... | ... | ... | ...
Note that the matrix above was computed with smoothing.
Each cell gives you the probability to go from one part of speech to another.
- In other words, there is a 4.47e-8 chance of going from parts-of-speech `TO` to `RP`.
- The sum of each row has to equal 1, because we assume that the next POS tag must be one of the available columns in the table.
The smoothing was done as follows:
$$ P(t_i | t_{i-1}) = \frac{C(t_{i-1}, t_{i}) + \alpha }{C(t_{i-1}) +\alpha * N}\tag{3}$$
- $N$ is the total number of tags
- $C(t_{i-1}, t_{i})$ is the count of the tuple (previous POS, current POS) in `transition_counts` dictionary.
- $C(t_{i-1})$ is the count of the previous POS in the `tag_counts` dictionary.
- $\alpha$ is a smoothing parameter.
<a name='ex-03'></a>
### Exercise 03
**Instructions:** Implement the `create_transition_matrix` below for all tags. Your task is to output a matrix that computes equation 3 for each cell in matrix `A`.
```
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_transition_matrix
def create_transition_matrix(alpha, tag_counts, transition_counts):
'''
Input:
alpha: number used for smoothing
tag_counts: a dictionary mapping each tag to its respective count
transition_counts: transition count for the previous word and tag
Output:
A: matrix of dimension (num_tags,num_tags)
'''
# Get a sorted list of unique POS tags
all_tags = sorted(tag_counts.keys())
# Count the number of unique POS tags
num_tags = len(all_tags)
# Initialize the transition matrix 'A'
A = np.zeros((num_tags,num_tags))
# Get the unique transition tuples (previous POS, current POS)
trans_keys = set(transition_counts.keys())
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each row of the transition matrix A
for i in range(num_tags):
# Go through each column of the transition matrix A
for j in range(num_tags):
# Initialize the count of the (prev POS, current POS) to zero
count = 0
# Define the tuple (prev POS, current POS)
# Get the tag at position i and tag at position j (from the all_tags list)
key = (all_tags[i], all_tags[j])
# Check if the (prev POS, current POS) tuple
# exists in the transition counts dictionary
if key in transition_counts: #complete this line
# Get count from the transition_counts dictionary
# for the (prev POS, current POS) tuple
count = transition_counts[key]
# Get the count of the previous tag (index position i) from tag_counts
count_prev_tag = tag_counts[key[0]]
# Apply smoothing using count of the tuple, alpha,
# count of previous tag, alpha, and total number of tags
A[i,j] = (count + alpha) / (count_prev_tag + (alpha * num_tags))
### END CODE HERE ###
return A
alpha = 0.001
A = create_transition_matrix(alpha, tag_counts, transition_counts)
# Testing your function
print(f"A at row 0, col 0: {A[0,0]:.9f}")
print(f"A at row 3, col 1: {A[3,1]:.4f}")
print("View a subset of transition matrix A")
A_sub = pd.DataFrame(A[30:35,30:35], index=states[30:35], columns = states[30:35] )
print(A_sub)
```
##### Expected Output
```CPP
A at row 0, col 0: 0.000007040
A at row 3, col 1: 0.1691
View a subset of transition matrix A
RBS RP SYM TO UH
RBS 2.217069e-06 2.217069e-06 2.217069e-06 0.008870 2.217069e-06
RP 3.756509e-07 7.516775e-04 3.756509e-07 0.051089 3.756509e-07
SYM 1.722772e-05 1.722772e-05 1.722772e-05 0.000017 1.722772e-05
TO 4.477336e-05 4.472863e-08 4.472863e-08 0.000090 4.477336e-05
UH 1.030439e-05 1.030439e-05 1.030439e-05 0.061837 3.092348e-02
```
### Create the 'B' emission probabilities matrix
Now you will create the `B` transition matrix which computes the emission probability.
You will use smoothing as defined below:
$$P(w_i | t_i) = \frac{C(t_i, word_i)+ \alpha}{C(t_{i}) +\alpha * N}\tag{4}$$
- $C(t_i, word_i)$ is the number of times $word_i$ was associated with $tag_i$ in the training data (stored in `emission_counts` dictionary).
- $C(t_i)$ is the number of times $tag_i$ was in the training data (stored in `tag_counts` dictionary).
- $N$ is the number of words in the vocabulary
- $\alpha$ is a smoothing parameter.
The matrix `B` is of dimension (num_tags, N), where num_tags is the number of possible parts-of-speech tags.
Here is an example of the matrix, only a subset of tags and words are shown:
<p style='text-align: center;'> <b>B Emissions Probability Matrix (subset)</b> </p>
|**B**| ...| 725 | adroitly | engineers | promoted | synergy| ...|
|----|----|--------------|--------------|--------------|--------------|-------------|----|
|**CD** | ...| **8.201296e-05** | 2.732854e-08 | 2.732854e-08 | 2.732854e-08 | 2.732854e-08| ...|
|**NN** | ...| 7.521128e-09 | 7.521128e-09 | 7.521128e-09 | 7.521128e-09 | **2.257091e-05**| ...|
|**NNS** | ...| 1.670013e-08 | 1.670013e-08 |**4.676203e-04** | 1.670013e-08 | 1.670013e-08| ...|
|**VB** | ...| 3.779036e-08 | 3.779036e-08 | 3.779036e-08 | 3.779036e-08 | 3.779036e-08| ...|
|**RB** | ...| 3.226454e-08 | **6.456135e-05** | 3.226454e-08 | 3.226454e-08 | 3.226454e-08| ...|
|**RP** | ...| 3.723317e-07 | 3.723317e-07 | 3.723317e-07 | **3.723317e-07** | 3.723317e-07| ...|
| ... | ...| ... | ... | ... | ... | ... | ...|
<a name='ex-04'></a>
### Exercise 04
**Instructions:** Implement the `create_emission_matrix` below that computes the `B` emission probabilities matrix. Your function takes in $\alpha$, the smoothing parameter, `tag_counts`, which is a dictionary mapping each tag to its respective count, the `emission_counts` dictionary where the keys are (tag, word) and the values are the counts. Your task is to output a matrix that computes equation 4 for each cell in matrix `B`.
```
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_emission_matrix
def create_emission_matrix(alpha, tag_counts, emission_counts, vocab):
'''
Input:
alpha: tuning parameter used in smoothing
tag_counts: a dictionary mapping each tag to its respective count
emission_counts: a dictionary where the keys are (tag, word) and the values are the counts
vocab: a dictionary where keys are words in vocabulary and value is an index.
within the function it'll be treated as a list
Output:
B: a matrix of dimension (num_tags, len(vocab))
'''
# get the number of POS tag
num_tags = len(tag_counts)
# Get a list of all POS tags
all_tags = sorted(tag_counts.keys())
# Get the total number of unique words in the vocabulary
num_words = len(vocab)
# Initialize the emission matrix B with places for
# tags in the rows and words in the columns
B = np.zeros((num_tags, num_words))
# Get a set of all (POS, word) tuples
# from the keys of the emission_counts dictionary
emis_keys = set(list(emission_counts.keys()))
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each row (POS tags)
for i in range(num_tags): # complete this line
# Go through each column (words)
for j in range(num_words): # complete this line
# Initialize the emission count for the (POS tag, word) to zero
count = 0
# Define the (POS tag, word) tuple for this row and column
key = (all_tags[i], vocab[j])
# check if the (POS tag, word) tuple exists as a key in emission counts
if key in emission_counts: # complete this line
# Get the count of (POS tag, word) from the emission_counts d
count = emission_counts[key]
# Get the count of the POS tag
count_tag = tag_counts[key[0]]
# Apply smoothing and store the smoothed value
# into the emission matrix B for this row and column
B[i,j] = (count + alpha) / (count_tag + (alpha * num_words))
### END CODE HERE ###
return B
# creating your emission probability matrix. this takes a few minutes to run.
B = create_emission_matrix(alpha, tag_counts, emission_counts, list(vocab))
print(f"View Matrix position at row 0, column 0: {B[0,0]:.9f}")
print(f"View Matrix position at row 3, column 1: {B[3,1]:.9f}")
# Try viewing emissions for a few words in a sample dataframe
cidx = ['725','adroitly','engineers', 'promoted', 'synergy']
# Get the integer ID for each word
cols = [vocab[a] for a in cidx]
# Choose POS tags to show in a sample dataframe
rvals =['CD','NN','NNS', 'VB','RB','RP']
# For each POS tag, get the row number from the 'states' list
rows = [states.index(a) for a in rvals]
# Get the emissions for the sample of words, and the sample of POS tags
B_sub = pd.DataFrame(B[np.ix_(rows,cols)], index=rvals, columns = cidx )
print(B_sub)
```
##### Expected Output
```CPP
View Matrix position at row 0, column 0: 0.000006032
View Matrix position at row 3, column 1: 0.000000720
725 adroitly engineers promoted synergy
CD 8.201296e-05 2.732854e-08 2.732854e-08 2.732854e-08 2.732854e-08
NN 7.521128e-09 7.521128e-09 7.521128e-09 7.521128e-09 2.257091e-05
NNS 1.670013e-08 1.670013e-08 4.676203e-04 1.670013e-08 1.670013e-08
VB 3.779036e-08 3.779036e-08 3.779036e-08 3.779036e-08 3.779036e-08
RB 3.226454e-08 6.456135e-05 3.226454e-08 3.226454e-08 3.226454e-08
RP 3.723317e-07 3.723317e-07 3.723317e-07 3.723317e-07 3.723317e-07
```
<a name='3'></a>
# Part 3: Viterbi Algorithm and Dynamic Programming
In this part of the assignment you will implement the Viterbi algorithm which makes use of dynamic programming. Specifically, you will use your two matrices, `A` and `B` to compute the Viterbi algorithm. We have decomposed this process into three main steps for you.
* **Initialization** - In this part you initialize the `best_paths` and `best_probabilities` matrices that you will be populating in `feed_forward`.
* **Feed forward** - At each step, you calculate the probability of each path happening and the best paths up to that point.
* **Feed backward**: This allows you to find the best path with the highest probabilities.
<a name='3.1'></a>
## Part 3.1: Initialization
You will start by initializing two matrices of the same dimension.
- best_probs: Each cell contains the probability of going from one POS tag to a word in the corpus.
- best_paths: A matrix that helps you trace through the best possible path in the corpus.
<a name='ex-05'></a>
### Exercise 05
**Instructions**:
Write a program below that initializes the `best_probs` and the `best_paths` matrix.
Both matrices will be initialized to zero except for column zero of `best_probs`.
- Column zero of `best_probs` is initialized with the assumption that the first word of the corpus was preceded by a start token ("--s--").
- This allows you to reference the **A** matrix for the transition probability
Here is how to initialize column 0 of `best_probs`:
- The probability of the best path going from the start index to a given POS tag indexed by integer $i$ is denoted by $\textrm{best_probs}[s_{idx}, i]$.
- This is estimated as the probability that the start tag transitions to the POS denoted by index $i$: $\mathbf{A}[s_{idx}, i]$ AND that the POS tag denoted by $i$ emits the first word of the given corpus, which is $\mathbf{B}[i, vocab[corpus[0]]]$.
- Note that vocab[corpus[0]] refers to the first word of the corpus (the word at position 0 of the corpus).
- **vocab** is a dictionary that returns the unique integer that refers to that particular word.
Conceptually, it looks like this:
$\textrm{best_probs}[s_{idx}, i] = \mathbf{A}[s_{idx}, i] \times \mathbf{B}[i, corpus[0] ]$
In order to avoid multiplying and storing small values on the computer, we'll take the log of the product, which becomes the sum of two logs:
$best\_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]$
Also, to avoid taking the log of 0 (which is defined as negative infinity), the code itself will just set $best\_probs[i,0] = float('-inf')$ when $A[s_{idx}, i] == 0$
So the implementation to initialize $best\_probs$ looks like this:
$ if A[s_{idx}, i] <> 0 : best\_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]])$
$ if A[s_{idx}, i] == 0 : best\_probs[i,0] = float('-inf')$
Please use [math.log](https://docs.python.org/3/library/math.html) to compute the natural logarithm.
The example below shows the initialization assuming the corpus starts with the phrase "Loss tracks upward".
<img src = "Initialize4.PNG"/>
Represent infinity and negative infinity like this:
```CPP
float('inf')
float('-inf')
```
```
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: initialize
def initialize(states, tag_counts, A, B, corpus, vocab):
'''
Input:
states: a list of all possible parts-of-speech
tag_counts: a dictionary mapping each tag to its respective count
A: Transition Matrix of dimension (num_tags, num_tags)
B: Emission Matrix of dimension (num_tags, len(vocab))
corpus: a sequence of words whose POS is to be identified in a list
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
best_probs: matrix of dimension (num_tags, len(corpus)) of floats
best_paths: matrix of dimension (num_tags, len(corpus)) of integers
'''
# Get the total number of unique POS tags
num_tags = len(tag_counts)
# Initialize best_probs matrix
# POS tags in the rows, number of words in the corpus as the columns
best_probs = np.zeros((num_tags, len(corpus)))
# Initialize best_paths matrix
# POS tags in the rows, number of words in the corpus as columns
best_paths = np.zeros((num_tags, len(corpus)), dtype=int)
# Define the start token
s_idx = states.index("--s--")
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each of the POS tags
for i in range(num_tags): # complete this line
# Handle the special case when the transition from start token to POS tag i is zero
if A[s_idx][i] == 0: # complete this line
# Initialize best_probs at POS tag 'i', column 0, to negative infinity
best_probs[i,0] = np.NINF
# For all other cases when transition from start token to POS tag i is non-zero:
else:
# Initialize best_probs at POS tag 'i', column 0
# Check the formula in the instructions above
best_probs[i,0] = np.log(A[s_idx, i]) + np.log(B[i, vocab[corpus[0]]])
### END CODE HERE ###
return best_probs, best_paths
best_probs, best_paths = initialize(states, tag_counts, A, B, prep, vocab)
# Test the function
print(f"best_probs[0,0]: {best_probs[0,0]:.4f}")
print(f"best_paths[2,3]: {best_paths[2,3]:.4f}")
```
##### Expected Output
```CPP
best_probs[0,0]: -22.6098
best_paths[2,3]: 0.0000
```
<a name='3.2'></a>
## Part 3.2 Viterbi Forward
In this part of the assignment, you will implement the `viterbi_forward` segment. In other words, you will populate your `best_probs` and `best_paths` matrices.
- Walk forward through the corpus.
- For each word, compute a probability for each possible tag.
- Unlike the previous algorithm `predict_pos` (the 'warm-up' exercise), this will include the path up to that (word,tag) combination.
Here is an example with a three-word corpus "Loss tracks upward":
- Note, in this example, only a subset of states (POS tags) are shown in the diagram below, for easier reading.
- In the diagram below, the first word "Loss" is already initialized.
- The algorithm will compute a probability for each of the potential tags in the second and future words.
Compute the probability that the tag of the second work ('tracks') is a verb, 3rd person singular present (VBZ).
- In the `best_probs` matrix, go to the column of the second word ('tracks'), and row 40 (VBZ), this cell is highlighted in light orange in the diagram below.
- Examine each of the paths from the tags of the first word ('Loss') and choose the most likely path.
- An example of the calculation for **one** of those paths is the path from ('Loss', NN) to ('tracks', VBZ).
- The log of the probability of the path up to and including the first word 'Loss' having POS tag NN is $-14.32$. The `best_probs` matrix contains this value -14.32 in the column for 'Loss' and row for 'NN'.
- Find the probability that NN transitions to VBZ. To find this probability, go to the `A` transition matrix, and go to the row for 'NN' and the column for 'VBZ'. The value is $4.37e-02$, which is circled in the diagram, so add $-14.32 + log(4.37e-02)$.
- Find the log of the probability that the tag VBS would 'emit' the word 'tracks'. To find this, look at the 'B' emission matrix in row 'VBZ' and the column for the word 'tracks'. The value $4.61e-04$ is circled in the diagram below. So add $-14.32 + log(4.37e-02) + log(4.61e-04)$.
- The sum of $-14.32 + log(4.37e-02) + log(4.61e-04)$ is $-25.13$. Store $-25.13$ in the `best_probs` matrix at row 'VBZ' and column 'tracks' (as seen in the cell that is highlighted in light orange in the diagram).
- All other paths in best_probs are calculated. Notice that $-25.13$ is greater than all of the other values in column 'tracks' of matrix `best_probs`, and so the most likely path to 'VBZ' is from 'NN'. 'NN' is in row 20 of the `best_probs` matrix, so $20$ is the most likely path.
- Store the most likely path $20$ in the `best_paths` table. This is highlighted in light orange in the diagram below.
The formula to compute the probability and path for the $i^{th}$ word in the $corpus$, the prior word $i-1$ in the corpus, current POS tag $j$, and previous POS tag $k$ is:
$\mathrm{prob} = \mathbf{best\_prob}_{k, i-1} + \mathrm{log}(\mathbf{A}_{k, j}) + \mathrm{log}(\mathbf{B}_{j, vocab(corpus_{i})})$
where $corpus_{i}$ is the word in the corpus at index $i$, and $vocab$ is the dictionary that gets the unique integer that represents a given word.
$\mathrm{path} = k$
where $k$ is the integer representing the previous POS tag.
<a name='ex-06'></a>
### Exercise 06
Instructions: Implement the `viterbi_forward` algorithm and store the best_path and best_prob for every possible tag for each word in the matrices `best_probs` and `best_tags` using the pseudo code below.
`for each word in the corpus
for each POS tag type that this word may be
for POS tag type that the previous word could be
compute the probability that the previous word had a given POS tag, that the current word has a given POS tag, and that the POS tag would emit this current word.
retain the highest probability computed for the current word
set best_probs to this highest probability
set best_paths to the index 'k', representing the POS tag of the previous word which produced the highest probability `
Please use [math.log](https://docs.python.org/3/library/math.html) to compute the natural logarithm.
<img src = "Forward4.PNG"/>
<details>
<summary>
<font size="3" color="darkgreen"><b>Hints</b></font>
</summary>
<p>
<ul>
<li>Remember that when accessing emission matrix B, the column index is the unique integer ID associated with the word. It can be accessed by using the 'vocab' dictionary, where the key is the word, and the value is the unique integer ID for that word.</li>
</ul>
</p>
```
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: viterbi_forward
def viterbi_forward(A, B, test_corpus, best_probs, best_paths, vocab):
'''
Input:
A, B: The transition and emission matrices respectively
test_corpus: a list containing a preprocessed corpus
best_probs: an initilized matrix of dimension (num_tags, len(corpus))
best_paths: an initilized matrix of dimension (num_tags, len(corpus))
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
best_probs: a completed matrix of dimension (num_tags, len(corpus))
best_paths: a completed matrix of dimension (num_tags, len(corpus))
'''
# Get the number of unique POS tags (which is the num of rows in best_probs)
num_tags = best_probs.shape[0]
# Go through every word in the corpus starting from word 1
# Recall that word 0 was initialized in `initialize()`
for i in range(1, len(test_corpus)):
# Print number of words processed, every 5000 words
if i % 5000 == 0:
print("Words processed: {:>8}".format(i))
### START CODE HERE (Replace instances of 'None' with your code EXCEPT the first 'best_path_i = None') ###
# For each unique POS tag that the current word can be
for j in range(num_tags): # complete this line
# Initialize best_prob for word i to negative infinity
best_prob_i = np.NINF
# Initialize best_path for current word i to None
best_path_i = None
# For each POS tag that the previous word can be:
for k in range(num_tags): # complete this line
# Calculate the probability =
# best probs of POS tag k, previous word i-1 +
# log(prob of transition from POS k to POS j) +
# log(prob that emission of POS j is word i)
prob = best_probs[k, i-1] + np.log(A[k, j]) + math.log(B[j, vocab[prep[i]]])
# check if this path's probability is greater than
# the best probability up to and before this point
if prob > best_prob_i: # complete this line
# Keep track of the best probability
best_prob_i = prob
# keep track of the POS tag of the previous word
# that is part of the best path.
# Save the index (integer) associated with
# that previous word's POS tag
best_path_i = k
# Save the best probability for the
# given current word's POS tag
# and the position of the current word inside the corpus
best_probs[j,i] = best_prob_i
# Save the unique integer ID of the previous POS tag
# into best_paths matrix, for the POS tag of the current word
# and the position of the current word inside the corpus.
best_paths[j,i] = best_path_i
### END CODE HERE ###
return best_probs, best_paths
```
Run the `viterbi_forward` function to fill in the `best_probs` and `best_paths` matrices.
**Note** that this will take a few minutes to run. There are about 30,000 words to process.
```
# this will take a few minutes to run => processes ~ 30,000 words
best_probs, best_paths = viterbi_forward(A, B, prep, best_probs, best_paths, vocab)
# Test this function
print(f"best_probs[0,1]: {best_probs[0,1]:.4f}")
print(f"best_probs[0,4]: {best_probs[0,4]:.4f}")
```
##### Expected Output
```CPP
best_probs[0,1]: -24.7822
best_probs[0,4]: -49.5601
```
<a name='3.3'></a>
## Part 3.3 Viterbi backward
Now you will implement the Viterbi backward algorithm.
- The Viterbi backward algorithm gets the predictions of the POS tags for each word in the corpus using the `best_paths` and the `best_probs` matrices.
The example below shows how to walk backwards through the best_paths matrix to get the POS tags of each word in the corpus. Recall that this example corpus has three words: "Loss tracks upward".
POS tag for 'upward' is `RB`
- Select the the most likely POS tag for the last word in the corpus, 'upward' in the `best_prob` table.
- Look for the row in the column for 'upward' that has the largest probability.
- Notice that in row 28 of `best_probs`, the estimated probability is -34.99, which is larger than the other values in the column. So the most likely POS tag for 'upward' is `RB` an adverb, at row 28 of `best_prob`.
- The variable `z` is an array that stores the unique integer ID of the predicted POS tags for each word in the corpus. In array z, at position 2, store the value 28 to indicate that the word 'upward' (at index 2 in the corpus), most likely has the POS tag associated with unique ID 28 (which is `RB`).
- The variable `pred` contains the POS tags in string form. So `pred` at index 2 stores the string `RB`.
POS tag for 'tracks' is `VBZ`
- The next step is to go backward one word in the corpus ('tracks'). Since the most likely POS tag for 'upward' is `RB`, which is uniquely identified by integer ID 28, go to the `best_paths` matrix in column 2, row 28. The value stored in `best_paths`, column 2, row 28 indicates the unique ID of the POS tag of the previous word. In this case, the value stored here is 40, which is the unique ID for POS tag `VBZ` (verb, 3rd person singular present).
- So the previous word at index 1 of the corpus ('tracks'), most likely has the POS tag with unique ID 40, which is `VBZ`.
- In array `z`, store the value 40 at position 1, and for array `pred`, store the string `VBZ` to indicate that the word 'tracks' most likely has POS tag `VBZ`.
POS tag for 'Loss' is `NN`
- In `best_paths` at column 1, the unique ID stored at row 40 is 20. 20 is the unique ID for POS tag `NN`.
- In array `z` at position 0, store 20. In array `pred` at position 0, store `NN`.
<img src = "Backwards5.PNG"/>
<a name='ex-07'></a>
### Exercise 07
Implement the `viterbi_backward` algorithm, which returns a list of predicted POS tags for each word in the corpus.
- Note that the numbering of the index positions starts at 0 and not 1.
- `m` is the number of words in the corpus.
- So the indexing into the corpus goes from `0` to `m - 1`.
- Also, the columns in `best_probs` and `best_paths` are indexed from `0` to `m - 1`
**In Step 1:**
Loop through all the rows (POS tags) in the last entry of `best_probs` and find the row (POS tag) with the maximum value.
Convert the unique integer ID to a tag (a string representation) using the list `states`.
Referring to the three-word corpus described above:
- `z[2] = 28`: For the word 'upward' at position 2 in the corpus, the POS tag ID is 28. Store 28 in `z` at position 2.
- `states[28]` is 'RB': The POS tag ID 28 refers to the POS tag 'RB'.
- `pred[2] = 'RB'`: In array `pred`, store the POS tag for the word 'upward'.
**In Step 2:**
- Starting at the last column of best_paths, use `best_probs` to find the most likely POS tag for the last word in the corpus.
- Then use `best_paths` to find the most likely POS tag for the previous word.
- Update the POS tag for each word in `z` and in `preds`.
Referring to the three-word example from above, read best_paths at column 2 and fill in z at position 1.
`z[1] = best_paths[z[2],2]`
The small test following the routine prints the last few words of the corpus and their states to aid in debug.
```
# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: viterbi_backward
def viterbi_backward(best_probs, best_paths, corpus, states):
'''
This function returns the best path.
'''
# Get the number of words in the corpus
# which is also the number of columns in best_probs, best_paths
m = best_paths.shape[1]
# Initialize array z, same length as the corpus
z = [None] * m
# Get the number of unique POS tags
num_tags = best_probs.shape[0]
# Initialize the best probability for the last word
best_prob_for_last_word = float('-inf')
# Initialize pred array, same length as corpus
pred = [None] * m
### START CODE HERE (Replace instances of 'None' with your code) ###
## Step 1 ##
# Go through each POS tag for the last word (last column of best_probs)
# in order to find the row (POS tag integer ID)
# with highest probability for the last word
for k in range(num_tags): # complete this line
# If the probability of POS tag at row k
# is better than the previously best probability for the last word:
if best_probs[k, m-1] > best_prob_for_last_word: # complete this line
# Store the new best probability for the lsat word
best_prob_for_last_word = best_probs[k, m-1]
# Store the unique integer ID of the POS tag
# which is also the row number in best_probs
z[m - 1] = k
# Convert the last word's predicted POS tag
# from its unique integer ID into the string representation
# using the 'states' dictionary
# store this in the 'pred' array for the last word
pred[m - 1] = states[z[m-1]]
## Step 2 ##
# Find the best POS tags by walking backward through the best_paths
# From the last word in the corpus to the 0th word in the corpus
for i in range(len(corpus)-1, -1, -1): # complete this line
# Retrieve the unique integer ID of
# the POS tag for the word at position 'i' in the corpus
pos_tag_for_word_i = z[i]
# In best_paths, go to the row representing the POS tag of word i
# and the column representing the word's position in the corpus
# to retrieve the predicted POS for the word at position i-1 in the corpus
z[i - 1] = best_paths[pos_tag_for_word_i, i]
# Get the previous word's POS tag in string form
# Use the 'states' dictionary,
# where the key is the unique integer ID of the POS tag,
# and the value is the string representation of that POS tag
pred[i - 1] = states[z[i-1]]
### END CODE HERE ###
return pred
# Run and test your function
pred = viterbi_backward(best_probs, best_paths, prep, states)
m=len(pred)
print('The prediction for pred[-7:m-1] is: \n', prep[-7:m-1], "\n", pred[-7:m-1], "\n")
print('The prediction for pred[0:8] is: \n', pred[0:7], "\n", prep[0:7])
```
**Expected Output:**
```CPP
The prediction for pred[-7:m-1] is:
['see', 'them', 'here', 'with', 'us', '.']
['VB', 'PRP', 'RB', 'IN', 'PRP', '.']
The prediction for pred[0:8] is:
['DT', 'NN', 'POS', 'NN', 'MD', 'VB', 'VBN']
['The', 'economy', "'s", 'temperature', 'will', 'be', 'taken']
```
Now you just have to compare the predicted labels to the true labels to evaluate your model on the accuracy metric!
<a name='4'></a>
# Part 4: Predicting on a data set
Compute the accuracy of your prediction by comparing it with the true `y` labels.
- `pred` is a list of predicted POS tags corresponding to the words of the `test_corpus`.
```
print('The third word is:', prep[3])
print('Your prediction is:', pred[3])
print('Your corresponding label y is: ', y[3])
```
<a name='ex-08'></a>
### Exercise 08
Implement a function to compute the accuracy of the viterbi algorithm's POS tag predictions.
- To split y into the word and its tag you can use `y.split()`.
```
# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: compute_accuracy
def compute_accuracy(pred, y):
'''
Input:
pred: a list of the predicted parts-of-speech
y: a list of lines where each word is separated by a '\t' (i.e. word \t tag)
Output:
'''
num_correct = 0
total = 0
# Zip together the prediction and the labels
for prediction, y in zip(pred, y):
### START CODE HERE (Replace instances of 'None' with your code) ###
# Split the label into the word and the POS tag
word_tag_tuple = tuple(y.rstrip().split('\t'))
# Check that there is actually a word and a tag
# no more and no less than 2 items
if len(word_tag_tuple) != 2: # complete this line
continue
# store the word and tag separately
word, tag = word_tag_tuple
# Check if the POS tag label matches the prediction
if prediction == tag: # complete this line
# count the number of times that the prediction
# and label match
num_correct += 1
# keep track of the total number of examples (that have valid labels)
total += 1
### END CODE HERE ###
return num_correct/total
print(f"Accuracy of the Viterbi algorithm is {compute_accuracy(pred, y):.4f}")
```
##### Expected Output
```CPP
Accuracy of the Viterbi algorithm is 0.9531
```
Congratulations you were able to classify the parts-of-speech with 95% accuracy.
### Key Points and overview
In this assignment you learned about parts-of-speech tagging.
- In this assignment, you predicted POS tags by walking forward through a corpus and knowing the previous word.
- There are other implementations that use bidirectional POS tagging.
- Bidirectional POS tagging requires knowing the previous word and the next word in the corpus when predicting the current word's POS tag.
- Bidirectional POS tagging would tell you more about the POS instead of just knowing the previous word.
- Since you have learned to implement the unidirectional approach, you have the foundation to implement other POS taggers used in industry.
### References
- ["Speech and Language Processing", Dan Jurafsky and James H. Martin](https://web.stanford.edu/~jurafsky/slp3/)
- We would like to thank Melanie Tosik for her help and inspiration
|
github_jupyter
|
### Dependencies for this notebook:
* pip install spacy, pandas, matplotlib
* python -m spacy.en.download
```
from IPython.display import SVG, display
import spacy
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime
%matplotlib inline
#encode some text as uncode
text = u"I'm executing this code on an Apple Computer."
#instantiate a language model
#to download language model: python -m spacy.en.download
nlp = spacy.load('en') # or spacy.en.English()
#create a document
document = nlp(text)
for function in nlp.pipeline:
print(function)
### Modifying the Language Model
def identify_starwars(doc):
for token in doc:
if token.text == u'starwars':
token.tag_ = u'NNP'
def return_pipeline(nlp):
return [nlp.tagger, nlp.parser, nlp.matcher, nlp.entity, identify_starwars]
text = u"I loved all of the starwars movies"
custom_nlp = spacy.load('en', create_pipeline=return_pipeline)
new_document = custom_nlp(text)
for function in custom_nlp.pipeline:
print(function)
texts = [u'You have brains in your head.'] * 10000
for doc in nlp.pipe(texts,n_threads=4):
doc.is_parsed
### Deploying Model on Many Texts with .pipe
runtimes = {}
for thread_count in [1,2,3,4,8]:
t0 = datetime.now()
#Create generator of processed documents
processed_documents = nlp.pipe(texts,n_threads=thread_count)
#Iterate over generator
for doc in processed_documents:
#pipeline is only run once we access the generator
doc.is_parsed
t1 = datetime.now()
runtimes[thread_count] = (t1 - t0).total_seconds()
ax = pd.Series(runtimes).plot(kind = 'bar')
ax.set_ylabel("Runtime (Seconds) with N Threads")
plt.show()
```
### Accessing Tokens and Spans
```
import pandas as pd
def info(obj):
return {'type':type(obj),'__str__': str(obj)}
text = u"""spaCy excels at large-scale information extraction tasks.
It's written from the ground up in carefully memory-managed Cython. """
document = nlp(text)
token = document[0]
span = document[0:3]
pd.DataFrame(list(map(info, [token,span,document])))
```
### Sentence boundary detection
```
print(list(document.sents))
print()
for i, sent in enumerate(document.sents):
print('%2d: "%s"' % (i, sent))
```
### Tokenization
```
for i, token in enumerate(document):
print('%2d: "%s"' % (i, token))
```
### Morphological decomposition
```
token = document[13]
print("text: %s" % token.text)
print("suffix: %s" % token.suffix_)
print("lemma: %s" % token.lemma_)
```
### Part of Speech Tagging
```
#Part of speech and Dependency tagging
attrs = list(map(lambda token: {
"token":token,
"part of speech":token.pos_,
"Dependency" : token.dep_},
document))
pd.DataFrame(attrs)
```
### Noun Chunking
```
print("noun chunks: %s" % list(document.noun_chunks))
```
### Named Entity Recognition
```
ents = [(ent, ent.root.ent_type_) for ent in document.ents]
print("entities: %s" % ents)
```
### Text Similarity (Using Word Vectors)
```
#document, span, and token similarity
def plot_similarities(similarities, target):
import matplotlib.pyplot as plt
%matplotlib inline
f, ax = plt.subplots(1)
index = range(len(similarities))
ax.barh(index, similarities)
ax.set_yticks([i + 0. for i in index])
ax.set_yticklabels(document2)
ax.grid(axis='x')
ax.set_title("Similarity to '{}'".format(target))
plt.show()
return ax
computer = nlp(u'computer')
document2 = nlp(u'You might be using a machine running Windows')
similarities = list(map(lambda token: token.similarity(computer), document2))
ax = plot_similarities(similarities, computer)
```
|
github_jupyter
|
```
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
```
# Unpacking the paper - CATEGORICAL REPARAMETERIZATION WITH GUMBEL-SOFTMAX
* https://arxiv.org/pdf/1611.01144.pdf
## Introduction
* Not much to get here
## THE GUMBEL-SOFTMAX Distribution
* Gumbel-Softmax distribution, a continuous distribution over the simplex that can approximate samples from a categorical distribution: Simplex means that it consist of variables that are all between 0 .. 1, and the sum of all these variables is 1. Example: [0.2,0.2,0.2,0.4]
* z is a categorical variable with class probabilities π1, π2, ...πk
* k is the number of classes
* samples (e.g., z's) are encoded as k-dimensional 1-hot vector. So if you have five classes, an examples is: [0,0,0,1,0]
### you can draw samples z efficiently by:
* drawing k samples from a gumbel distribution $g_1...g_k$. The samples are independent and identically distributed drawn from a Gumbel Distribution $(\mu=0,\beta=1)^1$
* calculating $argmax(g_i + log(\pi_i))$ for all $k$ samples, with $\pi_i$ being the class probability.
* create a one hot encoded of that argmax.
### if you use softmax as approximation of argmax, you'll get gumbel-softmax
* additionally, they add $\tau$ as a temperature parameter to their softmax
* $y_i = exp(x_i) / sum of all exp(x_n) $ for $n = 1..k$
https://en.wikipedia.org/wiki/Gumbel_distribution
$$c = \sqrt{a^2 + b^2}$$
## Sampling from a gumbel distribution
* GIST: https://gist.github.com/ericjang/1001afd374c2c3b7752545ce6d9ed349
Footnote 1 on page 2
```
def sample_gumbel(shape, eps=1e-20):
U = tf.random_uniform(shape,minval=0,maxval=1)
return -tf.log(-tf.log(U + eps) + eps)
def gumbel_softmax_sample(logits, temperature):
y = logits + sample_gumbel(tf.shape(logits))
return tf.nn.softmax( y / temperature)
def gumbel_softmax(logits, temperature, hard=False):
"""Sample from the Gumbel-Softmax distribution and optionally discretize.
Args:
logits: [batch_size, n_class] unnormalized log-probs
temperature: non-negative scalar
hard: if True, take argmax, but differentiate w.r.t. soft sample y
Returns:
[batch_size, n_class] sample from the Gumbel-Softmax distribution.
If hard=True, then the returned sample will be one-hot, otherwise it will
be a probabilitiy distribution that sums to 1 across classes
"""
y = gumbel_softmax_sample(logits, temperature)
if hard:
k = tf.shape(logits)[-1]
#y_hard = tf.cast(tf.one_hot(tf.argmax(y,1),k), y.dtype)
y_hard = tf.cast(tf.equal(y,tf.reduce_max(y,1,keep_dims=True)),y.dtype)
y = tf.stop_gradient(y_hard - y) + y
return y
```
|
github_jupyter
|
# Sentiment Analysis
## Using XGBoost in SageMaker
_Deep Learning Nanodegree Program | Deployment_
---
As our first example of using Amazon's SageMaker service we will construct a random tree model to predict the sentiment of a movie review. You may have seen a version of this example in a pervious lesson although it would have been done using the sklearn package. Instead, we will be using the XGBoost package as it is provided to us by Amazon.
## Instructions
Some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this notebook. You will not need to modify the included code beyond what is requested. Sections that begin with '**TODO**' in the header indicate that you need to complete or implement some portion within them. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a `# TODO: ...` comment. Please be sure to read the instructions carefully!
In addition to implementing code, there may be questions for you to answer which relate to the task and your implementation. Each section where you will answer a question is preceded by a '**Question:**' header. Carefully read each question and provide your answer below the '**Answer:**' header by editing the Markdown cell.
> **Note**: Code and Markdown cells can be executed using the **Shift+Enter** keyboard shortcut. In addition, a cell can be edited by typically clicking it (double-click for Markdown cells) or by pressing **Enter** while it is highlighted.
## Step 1: Downloading the data
The dataset we are going to use is very popular among researchers in Natural Language Processing, usually referred to as the [IMDb dataset](http://ai.stanford.edu/~amaas/data/sentiment/). It consists of movie reviews from the website [imdb.com](http://www.imdb.com/), each labeled as either '**pos**itive', if the reviewer enjoyed the film, or '**neg**ative' otherwise.
> Maas, Andrew L., et al. [Learning Word Vectors for Sentiment Analysis](http://ai.stanford.edu/~amaas/data/sentiment/). In _Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies_. Association for Computational Linguistics, 2011.
We begin by using some Jupyter Notebook magic to download and extract the dataset.
```
# %mkdir ../data
# !wget -O ../data/aclImdb_v1.tar.gz http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
# !tar -zxf ../data/aclImdb_v1.tar.gz -C ../data
```
## Step 2: Preparing the data
The data we have downloaded is split into various files, each of which contains a single review. It will be much easier going forward if we combine these individual files into two large files, one for training and one for testing.
```
import os
import glob
def read_imdb_data(data_dir='../data/aclImdb'):
data = {}
labels = {}
for data_type in ['train', 'test']:
data[data_type] = {}
labels[data_type] = {}
for sentiment in ['pos', 'neg']:
data[data_type][sentiment] = []
labels[data_type][sentiment] = []
path = os.path.join(data_dir, data_type, sentiment, '*.txt')
files = glob.glob(path)
for f in files:
with open(f) as review:
data[data_type][sentiment].append(review.read())
# Here we represent a positive review by '1' and a negative review by '0'
labels[data_type][sentiment].append(1 if sentiment == 'pos' else 0)
assert len(data[data_type][sentiment]) == len(labels[data_type][sentiment]), \
"{}/{} data size does not match labels size".format(data_type, sentiment)
return data, labels
data, labels = read_imdb_data()
print("IMDB reviews: train = {} pos / {} neg, test = {} pos / {} neg".format(
len(data['train']['pos']), len(data['train']['neg']),
len(data['test']['pos']), len(data['test']['neg'])))
from sklearn.utils import shuffle
def prepare_imdb_data(data, labels):
"""Prepare training and test sets from IMDb movie reviews."""
#Combine positive and negative reviews and labels
data_train = data['train']['pos'] + data['train']['neg']
data_test = data['test']['pos'] + data['test']['neg']
labels_train = labels['train']['pos'] + labels['train']['neg']
labels_test = labels['test']['pos'] + labels['test']['neg']
#Shuffle reviews and corresponding labels within training and test sets
data_train, labels_train = shuffle(data_train, labels_train)
data_test, labels_test = shuffle(data_test, labels_test)
# Return a unified training data, test data, training labels, test labets
return data_train, data_test, labels_train, labels_test
train_X, test_X, train_y, test_y = prepare_imdb_data(data, labels)
print("IMDb reviews (combined): train = {}, test = {}".format(len(train_X), len(test_X)))
train_X[100]
```
## Step 3: Processing the data
Now that we have our training and testing datasets merged and ready to use, we need to start processing the raw data into something that will be useable by our machine learning algorithm. To begin with, we remove any html formatting that may appear in the reviews and perform some standard natural language processing in order to homogenize the data.
```
import nltk
nltk.download("stopwords")
from nltk.corpus import stopwords
from nltk.stem.porter import *
stemmer = PorterStemmer()
import re
from bs4 import BeautifulSoup
def review_to_words(review):
text = BeautifulSoup(review, "html.parser").get_text() # Remove HTML tags
text = re.sub(r"[^a-zA-Z0-9]", " ", text.lower()) # Convert to lower case
words = text.split() # Split string into words
words = [w for w in words if w not in stopwords.words("english")] # Remove stopwords
words = [PorterStemmer().stem(w) for w in words] # stem
return words
import pickle
cache_dir = os.path.join("../cache", "sentiment_analysis") # where to store cache files
os.makedirs(cache_dir, exist_ok=True) # ensure cache directory exists
def preprocess_data(data_train, data_test, labels_train, labels_test,
cache_dir=cache_dir, cache_file="preprocessed_data.pkl"):
"""Convert each review to words; read from cache if available."""
# If cache_file is not None, try to read from it first
cache_data = None
if cache_file is not None:
try:
with open(os.path.join(cache_dir, cache_file), "rb") as f:
cache_data = pickle.load(f)
print("Read preprocessed data from cache file:", cache_file)
except:
pass # unable to read from cache, but that's okay
# If cache is missing, then do the heavy lifting
if cache_data is None:
# Preprocess training and test data to obtain words for each review
#words_train = list(map(review_to_words, data_train))
#words_test = list(map(review_to_words, data_test))
words_train = [review_to_words(review) for review in data_train]
words_test = [review_to_words(review) for review in data_test]
# Write to cache file for future runs
if cache_file is not None:
cache_data = dict(words_train=words_train, words_test=words_test,
labels_train=labels_train, labels_test=labels_test)
with open(os.path.join(cache_dir, cache_file), "wb") as f:
pickle.dump(cache_data, f)
print("Wrote preprocessed data to cache file:", cache_file)
else:
# Unpack data loaded from cache file
words_train, words_test, labels_train, labels_test = (cache_data['words_train'],
cache_data['words_test'], cache_data['labels_train'], cache_data['labels_test'])
return words_train, words_test, labels_train, labels_test
# Preprocess data
train_X, test_X, train_y, test_y = preprocess_data(train_X, test_X, train_y, test_y)
```
### Extract Bag-of-Words features
For the model we will be implementing, rather than using the reviews directly, we are going to transform each review into a Bag-of-Words feature representation. Keep in mind that 'in the wild' we will only have access to the training set so our transformer can only use the training set to construct a representation.
```
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.externals import joblib
# joblib is an enhanced version of pickle that is more efficient for storing NumPy arrays
def extract_BoW_features(words_train, words_test, vocabulary_size=5000,
cache_dir=cache_dir, cache_file="bow_features.pkl"):
"""Extract Bag-of-Words for a given set of documents, already preprocessed into words."""
# If cache_file is not None, try to read from it first
cache_data = None
if cache_file is not None:
try:
with open(os.path.join(cache_dir, cache_file), "rb") as f:
cache_data = joblib.load(f)
print("Read features from cache file:", cache_file)
except:
pass # unable to read from cache, but that's okay
# If cache is missing, then do the heavy lifting
if cache_data is None:
# Fit a vectorizer to training documents and use it to transform them
# NOTE: Training documents have already been preprocessed and tokenized into words;
# pass in dummy functions to skip those steps, e.g. preprocessor=lambda x: x
vectorizer = CountVectorizer(max_features=vocabulary_size,
preprocessor=lambda x: x, tokenizer=lambda x: x) # already preprocessed
features_train = vectorizer.fit_transform(words_train).toarray()
# Apply the same vectorizer to transform the test documents (ignore unknown words)
features_test = vectorizer.transform(words_test).toarray()
# NOTE: Remember to convert the features using .toarray() for a compact representation
# Write to cache file for future runs (store vocabulary as well)
if cache_file is not None:
vocabulary = vectorizer.vocabulary_
cache_data = dict(features_train=features_train, features_test=features_test,
vocabulary=vocabulary)
with open(os.path.join(cache_dir, cache_file), "wb") as f:
joblib.dump(cache_data, f)
print("Wrote features to cache file:", cache_file)
else:
# Unpack data loaded from cache file
features_train, features_test, vocabulary = (cache_data['features_train'],
cache_data['features_test'], cache_data['vocabulary'])
# Return both the extracted features as well as the vocabulary
return features_train, features_test, vocabulary
# Extract Bag of Words features for both training and test datasets
train_X, test_X, vocabulary = extract_BoW_features(train_X, test_X)
```
## Step 4: Classification using XGBoost
Now that we have created the feature representation of our training (and testing) data, it is time to start setting up and using the XGBoost classifier provided by SageMaker.
### (TODO) Writing the dataset
The XGBoost classifier that we will be using requires the dataset to be written to a file and stored using Amazon S3. To do this, we will start by splitting the training dataset into two parts, the data we will train the model with and a validation set. Then, we will write those datasets to a file and upload the files to S3. In addition, we will write the test set input to a file and upload the file to S3. This is so that we can use SageMakers Batch Transform functionality to test our model once we've fit it.
```
print(len(train_y))
import pandas as pd
from sklearn.model_selection import train_test_split
# TODO: Split the train_X and train_y arrays into the DataFrames val_X, train_X and val_y, train_y. Make sure that
# val_X and val_y contain 10 000 entires while train_X and train_y contain the remaining 15 000 entries.
train_X, val_X, train_y, val_y = train_test_split(train_X, train_y, test_size=0.4)
train_X = pd.DataFrame(train_X)
train_y = pd.DataFrame(train_y)
val_X = pd.DataFrame(val_X)
val_y = pd.DataFrame(val_y)
print(train_X.shape)
print(val_X.shape)
```
The documentation for the XGBoost algorithm in SageMaker requires that the saved datasets should contain no headers or index and that for the training and validation data, the label should occur first for each sample.
For more information about this and other algorithms, the SageMaker developer documentation can be found on __[Amazon's website.](https://docs.aws.amazon.com/sagemaker/latest/dg/)__
```
# First we make sure that the local directory in which we'd like to store the training and validation csv files exists.
data_dir = '../data/xgboost'
if not os.path.exists(data_dir):
os.makedirs(data_dir)
# First, save the test data to test.csv in the data_dir directory. Note that we do not save the associated ground truth
# labels, instead we will use them later to compare with our model output.
pd.DataFrame(test_X).to_csv(os.path.join(data_dir, 'test.csv'), header=False, index=False)
# TODO: Save the training and validation data to train.csv and validation.csv in the data_dir directory.
# Make sure that the files you create are in the correct format.
pd.concat([train_y, train_X], axis=1).to_csv(os.path.join(data_dir, 'train.csv'), header=False, index=False)
pd.concat([val_y, val_X], axis=1).to_csv(os.path.join(data_dir, 'validation.csv'), header=False, index=False)
# To save a bit of memory we can set text_X, train_X, val_X, train_y and val_y to None.
test_X = train_X = val_X = train_y = val_y = None
```
### (TODO) Uploading Training / Validation files to S3
Amazon's S3 service allows us to store files that can be access by both the built-in training models such as the XGBoost model we will be using as well as custom models such as the one we will see a little later.
For this, and most other tasks we will be doing using SageMaker, there are two methods we could use. The first is to use the low level functionality of SageMaker which requires knowing each of the objects involved in the SageMaker environment. The second is to use the high level functionality in which certain choices have been made on the user's behalf. The low level approach benefits from allowing the user a great deal of flexibility while the high level approach makes development much quicker. For our purposes we will opt to use the high level approach although using the low-level approach is certainly an option.
Recall the method `upload_data()` which is a member of object representing our current SageMaker session. What this method does is upload the data to the default bucket (which is created if it does not exist) into the path described by the key_prefix variable. To see this for yourself, once you have uploaded the data files, go to the S3 console and look to see where the files have been uploaded.
For additional resources, see the __[SageMaker API documentation](http://sagemaker.readthedocs.io/en/latest/)__ and in addition the __[SageMaker Developer Guide.](https://docs.aws.amazon.com/sagemaker/latest/dg/)__
```
import sagemaker
session = sagemaker.Session() # Store the current SageMaker session
# S3 prefix (which folder will we use)
prefix = 'sentiment-xgboost'
# TODO: Upload the test.csv, train.csv and validation.csv files which are contained in data_dir to S3 using sess.upload_data().
test_location = session.upload_data(os.path.join(data_dir, 'test.csv'), key_prefix=prefix)
val_location = session.upload_data(os.path.join(data_dir, 'train.csv'), key_prefix=prefix)
train_location = session.upload_data(os.path.join(data_dir, 'validation.csv'), key_prefix=prefix)
```
### (TODO) Creating the XGBoost model
Now that the data has been uploaded it is time to create the XGBoost model. To begin with, we need to do some setup. At this point it is worth discussing what a model is in SageMaker. It is easiest to think of a model of comprising three different objects in the SageMaker ecosystem, which interact with one another.
- Model Artifacts
- Training Code (Container)
- Inference Code (Container)
The Model Artifacts are what you might think of as the actual model itself. For example, if you were building a neural network, the model artifacts would be the weights of the various layers. In our case, for an XGBoost model, the artifacts are the actual trees that are created during training.
The other two objects, the training code and the inference code are then used the manipulate the training artifacts. More precisely, the training code uses the training data that is provided and creates the model artifacts, while the inference code uses the model artifacts to make predictions on new data.
The way that SageMaker runs the training and inference code is by making use of Docker containers. For now, think of a container as being a way of packaging code up so that dependencies aren't an issue.
```
from sagemaker import get_execution_role
# Our current execution role is require when creating the model as the training
# and inference code will need to access the model artifacts.
role = get_execution_role()
# We need to retrieve the location of the container which is provided by Amazon for using XGBoost.
# As a matter of convenience, the training and inference code both use the same container.
from sagemaker.amazon.amazon_estimator import get_image_uri
container = get_image_uri(session.boto_region_name, 'xgboost')
# TODO: Create a SageMaker estimator using the container location determined in the previous cell.
# It is recommended that you use a single training instance of type ml.m4.xlarge. It is also
# recommended that you use 's3://{}/{}/output'.format(session.default_bucket(), prefix) as the
# output path.
xgb = sagemaker.estimator.Estimator(container, # The image name of the training container
role, # The IAM role to use (our current role in this case)
train_instance_count=1, # The number of instances to use for training
train_instance_type='ml.m4.xlarge', # The type of instance to use for training
output_path='s3://{}/{}/output'.format(session.default_bucket(), prefix),
# Where to save the output (the model artifacts)
sagemaker_session=session) # The current SageMaker session
# TODO: Set the XGBoost hyperparameters in the xgb object. Don't forget that in this case we have a binary
# label so we should be using the 'binary:logistic' objective.
xgb.set_hyperparameters(max_depth=6,
eta=0.2,
gamma=0,
min_child_weight=1,
subsample=0.8,
objective='binary:logistic',
early_stopping_rounds=10,
num_round=200)
```
### Fit the XGBoost model
Now that our model has been set up we simply need to attach the training and validation datasets and then ask SageMaker to set up the computation.
```
s3_input_train = sagemaker.s3_input(s3_data=train_location, content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data=val_location, content_type='csv')
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
### (TODO) Testing the model
Now that we've fit our XGBoost model, it's time to see how well it performs. To do this we will use SageMakers Batch Transform functionality. Batch Transform is a convenient way to perform inference on a large dataset in a way that is not realtime. That is, we don't necessarily need to use our model's results immediately and instead we can peform inference on a large number of samples. An example of this in industry might be peforming an end of month report. This method of inference can also be useful to us as it means to can perform inference on our entire test set.
To perform a Batch Transformation we need to first create a transformer objects from our trained estimator object.
```
# TODO: Create a transformer object from the trained model. Using an instance count of 1 and an instance type of ml.m4.xlarge
# should be more than enough.
xgb_transformer = xgb.transformer(instance_count = 1, instance_type = 'ml.m4.xlarge')
```
Next we actually perform the transform job. When doing so we need to make sure to specify the type of data we are sending so that it is serialized correctly in the background. In our case we are providing our model with csv data so we specify `text/csv`. Also, if the test data that we have provided is too large to process all at once then we need to specify how the data file should be split up. Since each line is a single entry in our data set we tell SageMaker that it can split the input on each line.
```
# TODO: Start the transform job. Make sure to specify the content type and the split type of the test data.
xgb_transformer.transform(test_location, content_type='text/csv', split_type='Line')
```
Currently the transform job is running but it is doing so in the background. Since we wish to wait until the transform job is done and we would like a bit of feedback we can run the `wait()` method.
```
xgb_transformer.wait()
```
Now the transform job has executed and the result, the estimated sentiment of each review, has been saved on S3. Since we would rather work on this file locally we can perform a bit of notebook magic to copy the file to the `data_dir`.
```
!aws s3 cp --recursive $xgb_transformer.output_path $data_dir
```
The last step is now to read in the output from our model, convert the output to something a little more usable, in this case we want the sentiment to be either `1` (positive) or `0` (negative), and then compare to the ground truth labels.
```
predictions = pd.read_csv(os.path.join(data_dir, 'test.csv.out'), header=None)
predictions = [round(num) for num in predictions.squeeze().values]
from sklearn.metrics import accuracy_score
accuracy_score(test_y, predictions)
```
## Optional: Clean up
The default notebook instance on SageMaker doesn't have a lot of excess disk space available. As you continue to complete and execute notebooks you will eventually fill up this disk space, leading to errors which can be difficult to diagnose. Once you are completely finished using a notebook it is a good idea to remove the files that you created along the way. Of course, you can do this from the terminal or from the notebook hub if you would like. The cell below contains some commands to clean up the created files from within the notebook.
```
# First we will remove all of the files contained in the data_dir directory
!rm $data_dir/*
# And then we delete the directory itself
!rmdir $data_dir
# Similarly we will remove the files in the cache_dir directory and the directory itself
!rm $cache_dir/*
!rmdir $cache_dir
```
|
github_jupyter
|
```
__name__ = "k1lib.callbacks"
#export
from .callbacks import Callback, Callbacks, Cbs
import k1lib, os, torch
__all__ = ["Autosave", "DontTrainValid", "InspectLoss", "ModifyLoss", "Cpu", "Cuda",
"DType", "InspectBatch", "ModifyBatch", "InspectOutput", "ModifyOutput",
"Beep"]
#export
@k1lib.patch(Cbs)
class Autosave(Callback):
"""Autosaves 3 versions of the network to disk"""
def __init__(self): super().__init__(); self.order = 23
def endRun(self):
os.system("mv autosave-1.pth autosave-0.pth")
os.system("mv autosave-2.pth autosave-1.pth")
self.l.save("autosave-2.pth")
#export
@k1lib.patch(Cbs)
class DontTrainValid(Callback):
"""If is not training, then don't run m.backward() and opt.step().
The core training loop in k1lib.Learner don't specifically do this,
cause there may be some weird cases where you want to also train valid."""
def _common(self):
if not self.l.model.training: return True
def startBackward(self): return self._common()
def startStep(self): return self._common()
#export
@k1lib.patch(Cbs)
class InspectLoss(Callback):
"""Expected `f` to take in 1 float."""
def __init__(self, f): super().__init__(); self.f = f; self.order = 15
def endLoss(self): self.f(self.loss.detach())
#export
@k1lib.patch(Cbs)
class ModifyLoss(Callback):
"""Expected `f` to take in 1 float and return 1 float."""
def __init__(self, f): super().__init__(); self.f = f; self.order = 13
def endLoss(self): self.l.loss = self.f(self.loss)
#export
@k1lib.patch(Cbs)
class Cuda(Callback):
"""Moves batch and model to the default GPU"""
def startRun(self): self.l.model.cuda()
def startBatch(self):
self.l.xb = self.l.xb.cuda()
self.l.yb = self.l.yb.cuda()
#export
@k1lib.patch(Cbs)
class Cpu(Callback):
"""Moves batch and model to CPU"""
def startRun(self): self.l.model.cpu()
def startBatch(self):
self.l.xb = self.l.xb.cpu()
self.l.yb = self.l.yb.cpu()
#export
@k1lib.patch(Cbs)
class DType(Callback):
"""Moves batch and model to a specified data type"""
def __init__(self, dtype): super().__init__(); self.dtype = dtype
def startRun(self): self.l.model = self.l.model.to(self.dtype)
def startBatch(self):
self.l.xb = self.l.xb.to(self.dtype)
self.l.yb = self.l.yb.to(self.dtype)
#export
@k1lib.patch(Cbs)
class InspectBatch(Callback):
"""Expected `f` to take in 2 tensors."""
def __init__(self, f:callable): super().__init__(); self.f = f; self.order = 15
def startBatch(self): self.f(self.l.xb, self.l.yb)
#export
@k1lib.patch(Cbs)
class ModifyBatch(Callback):
"""Modifies xb and yb on the fly. Expected `f`
to take in 2 tensors and return 2 tensors."""
def __init__(self, f): super().__init__(); self.f = f; self.order = 13
def startBatch(self): self.l.xb, self.l.yb = self.f(self.l.xb, self.l.yb)
#export
@k1lib.patch(Cbs)
class InspectOutput(Callback):
"""Expected `f` to take in 1 tensor."""
def __init__(self, f): super().__init__(); self.f = f; self.order = 15
def endPass(self): self.f(self.y)
#export
@k1lib.patch(Cbs)
class ModifyOutput(Callback):
"""Modifies output on the fly. Expected `f` to take
in 1 tensor and return 1 tensor"""
def __init__(self, f): super().__init__(); self.f = f; self.order = 13
def endPass(self): self.l.y = self.f(self.y)
#export
@k1lib.patch(Cbs)
class Beep(Callback):
"""Plays a beep sound when the run is over"""
def endRun(self): k1lib.beep()
!../../export.py callbacks/shorts
```
|
github_jupyter
|
# DataFrame & Series
Di Pandas terdapat 2 kelas data baru yang digunakan sebagai struktur dari spreadsheet:
1. Series:
satu kolom bagian dari tabel dataframe yang merupakan 1 dimensional numpy array sebagai basis datanya, terdiri dari 1 tipe data (integer, string, float, dll).
2. DataFrame:
gabungan dari Series, berbentuk rectangular data yang merupakan tabel spreadsheet itu sendiri (karena dibentuk dari banyak Series, tiap Series biasanya punya 1 tipe data, yang artinya 1 dataframe bisa memiliki banyak tipe data).
```
import pandas as pd
# Series
number_list = pd.Series([1,2,3,4,5,6])
print("Series:")
print(number_list)
# DataFrame
matrix = [[1,2,3],
['a','b','c'],
[3,4,5],
['d',4,6]]
matrix_list = pd.DataFrame(matrix)
print("DataFrame:")
print(matrix_list)
```
# Atribut DataFrame & Series - Part 1
Dataframe dan Series memiliki sangat banyak atribut yang digunakan untuk transformasi data, tetapi ada beberapa attribute yang sering dipakai. Di sini series number_list dan dataframe matrix_list pada subbab sebelumnya digunakan kembali.
```
import pandas as pd
# Series
number_list = pd.Series([1,2,3,4,5,6])
# DataFrame
matrix_list = pd.DataFrame([[1,2,3],
['a','b','c'],
[3,4,5],
['d',4,6]])
# [1] attribute .info()
print("[1] attribute .info()")
print(matrix_list.info())
# [2] attribute .shape
print("\n[2] attribute .shape")
print(" Shape dari number_list:", number_list.shape)
print(" Shape dari matrix_list:", matrix_list.shape)
# [3] attribute .dtypes
print("\n[3] attribute .dtypes")
print(" Tipe data number_list:", number_list.dtypes)
print(" Tipe data matrix_list:", matrix_list.dtypes)
# [4] attribute .astype()
print("\n[4] attribute .astype()")
print(" Konversi number_list ke str:", number_list.astype("str"))
print(" Konversi matrix_list ke str:", matrix_list.astype("str"))
```
# Atribut DataFrame & Series - Part 2
```
import pandas as pd
# Series
number_list = pd.Series([1,2,3,4,5,6])
# DataFrame
matrix_list = pd.DataFrame([[1,2,3],
['a','b','c'],
[3,4,5],
['d',4,6]])
# [5] attribute .copy()
print("[5] attribute .copy()")
num_list = number_list.copy()
print(" Copy number_list ke num_list:", num_list)
mtr_list = matrix_list.copy()
print(" Copy matrix_list ke mtr_list:", mtr_list)
# [6] attribute .to_list()
print("[6] attribute .to_list()")
print(number_list.to_list())
# [7] attribute .unique()
print("[7] attribute .unique()")
print(number_list.unique())
```
# Atribut DataFrame & Series - Part 3
```
import pandas as pd
# Series
number_list = pd.Series([1,2,3,4,5,6])
# DataFrame
matrix_list = pd.DataFrame([[1,2,3],
['a','b','c'],
[3,4,5],
['d',4,6]])
# [8] attribute .index
print("[8] attribute .index")
print(" Index number_list:", number_list.index)
print(" Index matrix_list:", matrix_list.index)
# [9] attribute .columns
print("[9] attribute .columns")
print(" Column matrix_list:", matrix_list.columns)
# [10] attribute .loc
print("[10] attribute .loc")
print(" .loc[0:1] pada number_list:", number_list.loc[0:1])
print(" .loc[0:1] pada matrix_list:", matrix_list.loc[0:1])
# [11] attribute .iloc
print("[11] attribute .iloc")
print(" iloc[0:1] pada number_list:", number_list.iloc[0:1])
print(" iloc[0:1] pada matrix_list:", matrix_list.iloc[0:1])
matrix = [[1,2,3],
['a','b','c'],
[3,4,5],
['d',4,6]]
matrix_list = pd.DataFrame(matrix)
matrix_list.iloc[0:2,2].to_list()
```
# Creating Series & Dataframe from List
Untuk membuat Series atau Dataframe bisa dari berbagai macam tipe data container/mapping di python, seperti list dan dictionary, maupun dari numpy array.
Pada sub bagian ini, membuat Series dan Dataframe yang bersumber dari list. Sekadar meninjau bahwa list merupakan sebuah kumpulan data berbagai macam tipe data yang mutable (dapat diganti).
```
import pandas as pd
# Creating series from list
ex_list = ['a',1,3,5,'c','d']
ex_series = pd.Series(ex_list)
print(ex_series)
# Creating dataframe from list of list
ex_list_of_list = [[1 , 'a', 'b' , 'c'],
[2.5, 'd', 'e' , 'f'],
[5 , 'g', 'h' , 'i'],
[7.5, 'j', 10.5, 'l']]
index = ['dq', 'lab', 'kar', 'lan']
cols = ['float', 'char', 'obj', 'char']
ex_df = pd.DataFrame(ex_list_of_list, index=index, columns=cols)
print(ex_df)
```
# Creating Series & Dataframe from Dictionary
Untuk membuat Series atau Dataframe bisa dari berbagai macam tipe data container/mapping di python, seperti list dan dictionary, maupun dari numpy array.
Pada sub bagian ini, akan membuat Series dan Dataframe yang bersumber dari dictionary. Sekadar meninjau bahwa, dictionary merupakan kumpulan data yang strukturnya terdiri dari key dan value.
```
import pandas as pd
# Creating series from dictionary
dict_series = {'1':'a',
'2':'b',
'3':'c'}
ex_series = pd.Series(dict_series)
print(ex_series)
# Creating dataframe from dictionary
df_series = {'1':['a','b','c'],
'2':['b','c','d'],
'4':[2,3,'z']}
ex_df = pd.DataFrame(df_series)
print(ex_df)
```
# reating Series & Dataframe from Numpy Array
Untuk membuat Series atau Dataframe bisa dari berbagai macam tipe data container/mapping di python, seperti list dan dictionary, maupun dari numpy array.
Pada sub bagian ini, akan membuat Series dan Dataframe yang bersumber dari numpy array. Sekadar meninjau bahwa, numpy array kumpulan data yang terdiri atas berbagai macam tipe data, mutable, tapi dibungkus dalam array oleh library Numpy.
```
import pandas as pd
import numpy as np
# Creating series from numpy array (1D)
arr_series = np.array([1,2,3,4,5,6,6,7])
ex_series = pd.Series(arr_series)
print(ex_series)
# Creating dataframe from numpy array (2D)
arr_df = np.array([[1 ,2 ,3 ,5],
[5 ,6 ,7 ,8],
['a','b','c',10]])
ex_df = pd.DataFrame(arr_df)
print(ex_df)
```
# Read Dataset - CSV dan TSV
CSV dan TSV pada hakikatnya adalah tipe data text dengan perbedaan terletak pada pemisah antar data dalam satu baris. Pada file CSV, antar data dalam satu baris dipisahkan oleh comma, ",". Namun, pada file TSV antar data dalam satu baris dipisahkan oleh "Tab".
Fungsi .read_csv() digunakan untuk membaca file yang value-nya dipisahkan oleh comma (default), terkadang pemisah value-nya bisa di set ‘\t’ untuk file tsv (tab separated values).
```
import pandas as pd
# File CSV
df_csv = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
print(df_csv.head(3)) # Menampilkan 3 data teratas
# File TSV
df_tsv = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_tsv.tsv", sep='\t')
print(df_tsv.head(3)) # Menampilkan 3 data teratas
```
# Read Dataset - Excel
File Excel dengan ekstensi *.xls atau *.xlsx cukup banyak digunakan dalam menyimpan data. Pandas juga memiliki fitur untuk membaca file excel.
```
import pandas as pd
# File xlsx dengan data di sheet "test"
df_excel = pd.read_excel("https://storage.googleapis.com/dqlab-dataset/sample_excel.xlsx", sheet_name="test")
print(df_excel.head(4)) # Menampilkan 4 data teratas
```
# Read Dataset - JSON
Method .read_json() digunakan untuk membaca URL API yang formatnya JSON dan mengubahnya menjadi dataframe pandas.
```
import pandas as pd
# File JSON
url = "https://storage.googleapis.com/dqlab-dataset/covid2019-api-herokuapp-v2.json"
df_json = pd.read_json(url)
print(df_json.head(10)) # Menampilkan 10 data teratas
```
# Read Dataset - SQL
Fungsi .read_sql() atau .read_sql_query() digunakan untuk membaca query dari database dan translate menjadi pandas dataframe, contoh case ini database sqlite.
# Read Dataset - Google BigQuery
Untuk data yang besar (big data), umumnya digunakan Google BigQuery. Layanan ini dapat digunakan jika telah memiliki Google BigQuery account.
Fungsi .read_gbq() digunakan untuk membaca Google BigQuery table menjadi dataframe pandas.
# Write Dataset
Dalam bekerja sebagai data scientist/analis setelah dilakukan data cleaning dataset yang sudah rapi tentunya disimpan terlebih dahulu ke dalam media penyimpanan.
Pandas menyediakan fitur demikian secara ringkas melalui penerapan method pada dataframe/series yang ditabelkan berikut ini:
- .to_csv()
→ digunakan untuk export dataframe kembali ke csv atau tsv
CSV
df.to_csv("csv1.csv", index=False)
TSV
df.to_csv("tsv1.tsv", index=False, sep='\t')
- .to_clipboard()
→ export dataframe menjadi bahan copy jadi nanti bisa tinggal klik paste di excel atau google sheets
df.to_clipboard()
- .to_excel()
→ export dataframe menjadi file excel
df_excel.to_excel("xlsx1.xlsx", index=False)
- .to_gbq()
→ export dataframe menjadi table di Google BigQuery
df.to_gbq("temp.test", project_id="XXXXXX", if_exists="fail")
temp: nama dataset,
test: nama table
if_exists: ketika tabel dengan dataset.table_name yang sama sudah ada, apa action yang ingin dilakukan
("fail": tidak melakukan apa-apa,
"replace': membuang tabel yang sudah ada dan mengganti yang baru,
"append": menambah baris di tabel tersebut dengan data yang baru
)
# Head & Tail
Seperti yang telah dipelajari sebelumnya bahwa ada method .head yang diterapkan pada suatu variabel bertipe pandas dataframe/series.
Method .head ditujukan untuk membatasi tampilan jumlah baris teratas dari dataset. Sementara itu, method .tail ditujukan untuk membatasi jumlah baris terbawah dari dataset.
```
import pandas as pd
# Baca file sample_csv.csv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
# Tampilkan 3 data teratas
print("Tiga data teratas:\n", df.head(3))
# Tampilkan 3 data terbawah
print("Tiga data terbawah:\n", df.tail(3))
```
# Indexing - Part 1
Index merupakan key identifier dari tiap row/column untuk Series atau Dataframe (sifatnya tidak mutable untuk masing-masing value tapi bisa diganti untuk semua value sekaligus).
Jika tidak disediakan, pandas akan membuat kolom index default secara otomatis sebagai bilangan bulat (integer) dari 0 sampai range jumlah baris data tersebut.
Kolom index dapat terdiri dari:
1. satu kolom (single index), atau
2. multiple kolom (disebut dengan hierarchical indexing).
Index dengan multiple kolom ini terjadi karena unique identifier tidak dapat dicapai hanya dengan set index di 1 kolom saja sehingga membutuhkan beberapa kolom yang menjadikan tiap row menjadi unique.
# Indexing - Part 2
Secara default setelah suatu dataframe dibaca dari file dengan format tertentu, index-nya merupakan single index.
Pada sub bab ini akan mencetak index dan kolom yang dimiliki oleh file "https://storage.googleapis.com/dqlab-dataset/sample_csv.csv". Untuk menentukan index dan kolom yang dimiliki oleh dataset yang telah dinyatakan sebagai sebuah dataframe pandas dapat dilakukan dengan menggunakan atribut .index dan .columns.
```
import pandas as pd
# Baca file TSV sample_tsv.tsv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_tsv.tsv", sep="\t")
# Index dari df
print("Index:", df.index)
# Column dari df
print("Columns:", df.columns)
```
# Indexing - Part 3
Di sub bab sebelumnya telah dibahas terkait single index, tentunya pada sub bab ini akan bahas multi index atau disebut juga dengan hierarchical indexing.
Untuk membuat multi index (hierarchical indexing) dengan pandas diperlukan kolom-kolom mana saja yang perlu disusun agar index dari dataframe menjadi sebuah hirarki yang kemudian dapat dikenali.
```
import pandas as pd
# Baca file TSV sample_tsv.tsv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_tsv.tsv", sep="\t")
# Set multi index df
df_x = df.set_index(['order_date', 'city', 'customer_id'])
# Print nama dan level dari multi index
for name, level in zip(df_x.index.names, df_x.index.levels):
print(name,':',level)
```
# Indexing - Part 4
Terdapat beberapa cara untuk membuat index, salah satunya adalah seperti yang telah dilakukan pada sub bab sebelumnya dengan menggunakan method .set_index().
Di sub bab ini akan menggunakan assignment untuk menset index dari suatu dataframe. Untuk itu file "sample_excel.xlsx" yang digunakan
```
import pandas as pd
# Baca file sample_tsv.tsv untuk 10 baris pertama saja
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_tsv.tsv", sep="\t", nrows=10)
# Cetak data frame awal
print("Dataframe awal:\n", df)
# Set index baru
df.index = ["Pesanan ke-" + str(i) for i in range(1, 11)]
# Cetak data frame dengan index baru
print("Dataframe dengan index baru:\n", df)
```
# Indexing - Part 5
Jika file yang akan dibaca melalui penggunaan library pandas dapat di-preview terlebih dahulu struktur datanya maka melalui fungsi yang ditujukan untuk membaca file dapat diset mana kolom yang akan dijadikan index.
Fitur ini telah dimiliki oleh setiap fungsi yang digunakan dalam membaca data dengan pandas, yaitu penggunaan argumen index_col pada fungsi yang dimaksud
```
import pandas as pd
# Baca file sample_tsv.tsv dan set lah index_col sesuai instruksi
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_tsv.tsv", sep="\t", index_col=["order_date", "order_id"])
# Cetak data frame untuk 8 data teratas
print("Dataframe:\n", df.head(8))
df_week = pd.DataFrame({'day_number':[1,2,3,4,5,6,7],
'week_type':['weekday' for i in range(5)] + ['weekend' for i in range(2)]
})
df_week_ix = ['Mon','Tue','Wed','Thu','Fri','Sat','Sun']
df_week.index = [df_week_ix, df_week['day_number'].to_list()]
df_week.index.names = ['name','num']
```
# Slicing - Part 1
Seperti artinya slicing adalah cara untuk melakukan filter ke dataframe/series berdasarkan kriteria tertentu dari nilai kolomnya ataupun kriteria index-nya.
Terdapat 2 cara paling terkenal untuk slicing dataframe, yaitu dengan menggunakan method .loc dan .iloc pada variabel bertipe pandas DataFrame/Series. Method .iloc ditujukan untuk proses slicing berdasarkan index berupa nilai integer tertentu. Akan tetapi akan lebih sering menggunakan dengan method .loc karena lebih fleksibel.
```
import pandas as pd
# Baca file sample_csv.csv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
# Slice langsung berdasarkan kolom
df_slice = df.loc[(df["customer_id"] == "18055") &
(df["product_id"].isin(["P0029", "P0040", "P0041", "P0116", "P0117"]))
]
print("Slice langsung berdasarkan kolom:\n", df_slice)
```
# Slicing - Part 2
Dalam sub bab sebelumnya telah mempelajari bagaimana melakukan slicing/filtering dataset dengan menggunakan method .loc pada kolom dataset.
Sekarang, menerapkan berdasarkan index. Tentu syaratnya adalah dataset sudah dilakukan indexing terlebih dahulu melalui penerapan method .set_index
```
import pandas as pd
# Baca file sample_csv.csv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
# Set index dari df sesuai instruksi
df = df.set_index(["order_date", "order_id", "product_id"])
# Slice sesuai intruksi
df_slice = df.loc[("2019-01-01", 1612339, ["P2154", "P2159"]),:]
print("Slice df:\n", df_slice)
```
# Transforming - Part 1
Transform adalah ketika mengubah dataset yang ada menjadi entitas baru, dapat dilakukan dengan:
konversi dari satu data type ke data type yang lain,
transpose dataframe,
atau yang lainnya.
Hal yang biasa dilakukan pertama kali setelah data dibaca adalah mengecek tipe data di setiap kolomnya apakah sesuai dengan representasinya. Untuk itu dapat menggunakan atribut .dtypes pada dataframe yang telah kita baca tadi,
[nama_dataframe].dtypes
Untuk konversi tipe data, secara default system akan mendeteksi data yang tidak bisa di render as date type or numeric type sebagai object yang basically string. Tidak bisa di render oleh system ini karena berbagai hal, mungkin karena formatnya asing dan tidak dikenali oleh python secara umum (misal: date type data → '2019Jan01').
Data contoh tersebut tidak bisa di render karena bulannya Jan tidak bisa di translate menjadi in form of number (00-12) dan tidak ada ‘-’ di antara tahun, bulan dan harinya. Jika seluruh data pada kolom di order_date sudah tertulis dalam bentuk 'YYYY-MM-DD' maka ketika dibaca, kolom order_date sudah langsung dinyatakan bertipe data datetime.
Untuk merubah kolom date_order yang sebelumnya bertipe object menjadi kolom bertipe datetime, cara pertama yang dapat dilakukan adalah menggunakan:
pd.to_datetime(argumen)
dengan argumen adalah isi kolom dari dataframe yang akan dirubah tipe datanya, misal dalam format umum.
nama_dataframe["nama_kolom"]
Sehingga lengkapnya dapat ditulis sebagai:
nama_dataframe["nama_kolom"] =
```
import pandas as pd
# Baca file sample_csv.csv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
# Tampilkan tipe data
print("Tipe data df:\n", df.dtypes)
# Ubah tipe data kolom order_date menjadi datetime
df["order_date"] = pd.to_datetime(df["order_date"])
# Tampilkan tipe data df setelah transformasi
print("\nTipe data df setelah transformasi:\n", df.dtypes)
```
# Transforming - Part 2
Pada sub bab ini akan mengubah tipe data pada kolom dataframe yang telah dibaca menjadi tipe data float (kolom quantity) dan tipe kategori (kolom city).
Secara umum, untuk mengubah ke numerik dapat menggunakan pd.to_numeric(), yaitu:
nama_dataframe["nama_kolom"] = pd.to_numeric(nama_dataframe["nama_kolom"], downcast="tipe_data_baru")
Sedangkan untuk menjadi suatu kolom yang dapat dinyatakan sebagai kategori dapat menggunakan method .astype() pada dataframe, yaitu
nama_dataframe["nama_kolom"] = nama_dataframe["nama_kolom"].astype("category")
```
import pandas as pd
# Baca file sample_csv.csv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
# Tampilkan tipe data
print("Tipe data df:\n", df.dtypes)
# Ubah tipe data kolom quantity menjadi tipe data numerik float
df["quantity"] = pd.to_numeric(df["quantity"], downcast="float")
# Ubah tipe data kolom city menjadi tipe data category
df["city"] = df["city"].astype("category")
# Tampilkan tipe data df setelah transformasi
print("\nTipe data df setelah transformasi:\n", df.dtypes)
```
# Transforming - Part 3
Sekarang akan mempelajari teknik/cara berikutnya dalam proses transformasi suatu dataframe. Di sub bab ini akan memakai method .apply() dan .map() pada suatu dataframe.
Method .apply() digunakan untuk menerapkan suatu fungsi python (yang dibuat dengan def atau anonymous dengan lambda) pada dataframe/series atau hanya kolom tertentu dari dataframe.
Berikut ini adalah contohnya yaitu akan merubah setiap baris pada kolom brand menjadi lowercase.
```
import pandas as pd
# Baca file sample_csv.csv
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/sample_csv.csv")
# Cetak 5 baris teratas kolom brand
print("Kolom brand awal:\n", df["brand"].head())
# Gunakan method apply untuk merubah isi kolom menjadi lower case
df["brand"] = df["brand"].apply(lambda x: x.lower())
# Cetak 5 baris teratas kolom brand
print("Kolom brand setelah apply:\n", df["brand"].head())
# Gunakan method map untuk mengambil kode brand yaitu karakter terakhirnya
df["brand"] = df["brand"].map(lambda x: x[-1])
# Cetak 5 baris teratas kolom brand
print("Kolom brand setelah map:\n", df["brand"].head())
```
# Transforming - Part 4
Di sub bab sebelumnya sudah mengetahui bahwa map hanya dapat digunakan untuk pandas series. Pada sub bab ini akan menggunakan method .applymap pada dataframe.
```
import numpy as np
import pandas as pd
# number generator, set angka seed menjadi suatu angka, bisa semua angka, supaya hasil random nya selalu sama ketika kita run
np.random.seed(1234)
# create dataframe 3 baris dan 4 kolom dengan angka random
df_tr = pd.DataFrame(np.random.rand(3,4))
# Cetak dataframe
print("Dataframe:\n", df_tr)
# Cara 1 dengan tanpa define function awalnya, langsung pake fungsi anonymous lambda x
df_tr1 = df_tr.applymap(lambda x: x**2 + 3*x + 2)
print("\nDataframe - cara 1:\n", df_tr1)
# Cara 2 dengan define function
def qudratic_fun(x):
return x**2 + 3*x + 2
df_tr2 = df_tr.applymap(qudratic_fun)
print("\nDataframe - cara 2:\n", df_tr2)
```
# Inspeksi Missing Value
Value yang hilang/tidak lengkap dari dataframe akan membuat analisis atau model prediksi yang dibuat menjadi tidak akurat dan mengakibatkan keputusan salah yang diambil. Terdapat beberapa cara untuk mengatasi data yang hilang/tidak lengkap tersebut.
Data COVID-19 yang akan digunakan ini diambil dari google big query, tetapi sudah disediakan datasetnya dalam format csv dengan nama "public data covid19 jhu csse eu.csv". Ini adalah studi kasus untuk meng-handle missing value. Bagaimanakah langkah-langkahnya?
Di pandas data yang hilang umumnya direpresentasikan dengan NaN.
Langkah pertama, harus tahu kolom mana yang terdapat data hilang dan berapa banyak dengan cara:
Cara 1: menerapkan method .info() pada dataframe
```
import pandas as pd
# Baca file "public data covid19 jhu csse eu.csv"
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/CHAPTER%204%20-%20missing%20value%20-%20public%20data%20covid19%20.csv")
# Cetak info dari df
print(df.info())
# Cetak jumlah missing value di setiap kolom
mv = df.isna().sum()
print("\nJumlah missing value per kolom:\n", mv)
```
# Treatment untuk Missing Value - Part 1
Terdapat beberapa cara untuk mengatasi missing value, antara lain:
dibiarkan saja,
hapus value itu, atau
isi value tersebut dengan value yang lain (biasanya interpolasi, mean, median, etc)
# Treatment untuk Missing Value - Part 2
Sekarang dapat menerapkan dua aksi yaitu
Membiarkannya saja
Menghapus kolom
Treatment pertama (membiarkannya saja) seperti pada kolom confirmed, death, dan recovered. Akan tetapi jika tidak ada yang terkonfirmasi, meninggal dan sembuh sebenarnya dapat menukar value ini dengan angka nol. Meskipun ini lebih make sense dalam representasi datanya, tetapi untuk sub bab ini ketiga kolom tersebut diasumsikan dibiarkan memiliki nilai missing value.
Treatment kedua yaitu dengan menghapus kolom, yang mana ini digunakan jika seluruh kolom dari dataset yang dipunyai semua barisnya adalah missing value. Untuk itu dapat menerapkan method .dropna() pada dataframe, bagaimana caranya?
nama_dataframe.dropna(axis=1, how="all")
Pada method .dropna() ada dua keyword argumen yang harus diisikan yaitu axis dan how. Keyword axis digunakan untuk menentukan arah dataframe yang akan dibuang angka 1 untuk menyatakan kolom (column-based) atau dapat ditulis dalam string "column". Jika digunakan angka 0 berarti itu dalam searah index (row-based) atau dapat ditulis dalam string "index".
Sementara, keyword how digunakan untuk bagaimana cara membuangnya. Opsi yang dapat diterimanya (dalam string) adalah
"all" artinya jika seluruh data di satu/beberapa kolom atau di satu/beberapa baris adalah missing value.
"any" artinya jika memiliki 1 saja data yang hilang maka buanglah baris/kolom tersebut.
```
import pandas as pd
# Baca file "public data covid19 jhu csse eu.csv"
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/CHAPTER%204%20-%20missing%20value%20-%20public%20data%20covid19%20.csv")
# Cetak ukuran awal dataframe
print("Ukuran awal df: %d baris, %d kolom." % df.shape)
# Drop kolom yang seluruhnya missing value dan cetak ukurannya
df = df.dropna(axis=1, how="all")
print("Ukuran df setelah buang kolom dengan seluruh data missing: %d baris, %d kolom." % df.shape)
# Drop baris jika ada satu saja data yang missing dan cetak ukurannya
df = df.dropna(axis=0, how="any")
print("Ukuran df setelah dibuang baris yang memiliki sekurangnya 1 missing value: %d baris, %d kolom." % df.shape)
```
# Treatment untuk Missing Value - Part 3
Sekarang, akan melakukan treatment ketiga untuk melakukan handle missing value pada dataframe. Treatment ini dilakukan dengan cara mengisi missing value dengan nilai lain, yang dapat berupa :
nilai statistik seperti mean atau median
interpolasi data
text tertentu
Akan mulai pada kolom yang missing yang tipe datanya adalah berupa object. Kolom tersebut adalah province_state, karena tidak tahu secara persis province_state mana yang dimaksud, bisa menempatkan string "unknown" sebagai substitusi missing value. Meskipun keduanya berarti sama-sama tidak tahu tetapi berbeda dalam representasi datanya.
Untuk melakukan hal demikian dapat menggunakan method .fillna() pada kolom dataframe yang dimaksud.
```
import pandas as pd
# Baca file "public data covid19 jhu csse eu.csv"
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/CHAPTER%204%20-%20missing%20value%20-%20public%20data%20covid19%20.csv")
# Cetak unique value pada kolom province_state
print("Unique value awal:\n", df["province_state"].unique())
# Ganti missing value dengan string "unknown_province_state"
df["province_state"] = df["province_state"].fillna("unknown_province_state")
# Cetak kembali unique value pada kolom province_state
print("Unique value setelah fillna:\n", df["province_state"].unique())
```
# Treatment untuk Missing Value - Part 4
Masih melanjutkan bagaimana melakukan handle missing value tentunya dengan jalan mengganti missing value dengan nilai lainnya. Pada bab sebelumnya telah mengganti kolom bertipe objek dengan sesuatu string/teks.
Dalam sub bab ini akan mengganti missing value dengan nilai statistik kolom bersangkutan, baik median atau mean (nilai rata-rata). Misalnya akan menggunakan kolom active. Dengan mengabaikan terlebih dahulu sebaran berdasarkan negara (univariate), jika mengisi dengan nilai rata-rata maka harus melihat terlebih dahulu data apakah memiliki outliers atau tidak. Jika ada outliers dari data maka menggunakan nilai tengah (median) data adalah cara yang lebih safe.
Untuk itu diputuskan dengan mengecek nilai median dan nilai mean kolom active juga nilai min dan max-nya. Jika data pada kolom active terdistribusi normal maka nilai mean dan median akan hampir sama.
Terlihat data memiliki distribusi yang skewness, karena nilai mean dan median yang cukup jauh serta range data yang cukup lebar. Di sini pada kolom active data memiliki outliers. Jadi akan mengisi missing value dengan median.
```
import pandas as pd
# Baca file "https://dqlab-dataset.s3-ap-southeast-1.amazonaws.com/CHAPTER+4+-+missing+value+-+public+data+covid19+.csv"
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/CHAPTER%204%20-%20missing%20value%20-%20public%20data%20covid19%20.csv")
# Cetak nilai mean dan median awal
print("Awal: mean = %f, median = %f." % (df["active"].mean(), df["active"].median()))
# Isi missing value kolom active dengan median
df_median = df["active"].fillna(df["active"].median())
# Cetak nilai mean dan median awal setelah diisi dengan median
print("Fillna median: mean = %f, median = %f." % (df_median.mean(), df_median.median()))
# Isi missing value kolom active dengan mean
df_mean = df["active"].fillna(df["active"].mean())
# Cetak nilai mean dan median awal setelah diisi dengan mean
print("Fillna mean: mean = %f, median = %f." % (df_mean.mean(), df_mean.median()))
```
# Treatment untuk Missing Value - Part 5
Di bagian ini akan menggunakan teknik interpolasi dalam mengisi nilai missing value pada suatu dataset.
Data yang menggunakan interpolasi untuk mengisi data yang hilang adalah time series data, yang secara default akan diisi dengan interpolasi linear.
```
import numpy as np
import pandas as pd
# Data
ts = pd.Series({
"2020-01-01":9,
"2020-01-02":np.nan,
"2020-01-05":np.nan,
"2020-01-07":24,
"2020-01-10":np.nan,
"2020-01-12":np.nan,
"2020-01-15":33,
"2020-01-17":np.nan,
"2020-01-16":40,
"2020-01-20":45,
"2020-01-22":52,
"2020-01-25":75,
"2020-01-28":np.nan,
"2020-01-30":np.nan
})
# Isi missing value menggunakan interpolasi linier
ts = ts.interpolate()
# Cetak time series setelah interpolasi linier
print("Setelah diisi missing valuenya:\n", ts)
```
# Project
Diberikan dataset ‘retail_raw_test.csv’
1. Baca dataset
2. Tipe data diubah menjadi tipe yang seharusnya
- customer_id dari string ke int64,
- quantity dari string ke int64,
- item_price dari string ke int64
3. transform product_value supaya bentuknya seragam dengan format PXXXX, assign ke kolom baru "product_id", dan drop kolom "product_value", jika terdapat nan gantilah dengan "unknown".
4. trasnform order_date menjadi value dengan format YYYY-mm-dd
5. cek data hilang dari tiap kolom dan kemudian isi missing value
- di brand dengan "no_brand", dan
- cek dulu bagaimana missing value di city & province - isi missing value di city dan province dengan "unknown"
6. create column city/province dari gabungan city & province
7. membuat index berdasarkan city_provice, order_date, customer_id, order_id, product_id (cek index)
8. membuat kolom "total_price" sebagai hasil perkalian quantity dengan item_price
9. slice data hanya untuk Jan 2019
```
import pandas as pd
# 1. Baca dataset
print("[1] BACA DATASET")
df = pd.read_csv("https://storage.googleapis.com/dqlab-dataset/retail_raw_test.csv", low_memory=False)
print(" Dataset:\n", df.head())
print(" Info:\n", df.info())
# 2. Ubah tipe data
print("\n[2] UBAH TIPE DATA")
df["customer_id"] = df["customer_id"].apply(lambda x: x.split("'")[1]).astype("int64")
df["quantity"] = df["quantity"].apply(lambda x: x.split("'")[1]).astype("int64")
df["item_price"] = df["item_price"].apply(lambda x: x.split("'")[1]).astype("int64")
print(" Tipe data:\n", df.dtypes)
# 3. Transform "product_value" supaya bentuknya seragam dengan format "PXXXX", assign ke kolom baru "product_id", dan drop kolom "product_value", jika terdapat nan gantilah dengan "unknown"
print("\n[3] TRANSFORM product_value MENJADI product_id")
# Buat fungsi
import math
def impute_product_value(val):
if math.isnan(val):
return "unknown"
else:
return 'P' + '{:0>4}'.format(str(val).split('.')[0])
# Buat kolom "product_id"
df["product_id"] = df["product_value"].apply(lambda x: impute_product_value(x))
# Hapus kolom "product_value"
df.drop(["product_value"], axis=1, inplace=True)
# Cetak 5 data teratas
print(df.head())
# 4. Tranform order_date menjadi value dengan format "YYYY-mm-dd"
print("\n[4] TRANSFORM order_date MENJADI FORMAT YYYY-mm-dd")
months_dict = {
"Jan":"01",
"Feb":"02",
"Mar":"03",
"Apr":"04",
"May":"05",
"Jun":"06",
"Jul":"07",
"Aug":"08",
"Sep":"09",
"Oct":"10",
"Nov":"11",
"Dec":"12"
}
df["order_date"] = pd.to_datetime(df["order_date"].apply(lambda x: str(x)[-4:] + "-" + months_dict[str(x)[:3]] + "-" + str(x)[4:7]))
print(" Tipe data:\n", df.dtypes)
# 5. Mengatasi data yang hilang di beberapa kolom
print("\n[5] HANDLING MISSING VALUE")
# Kolom "city" dan "province" masih memiliki missing value, nilai yang hilang di kedua kolom ini diisi saja dengan "unknown"
df[["city","province"]] = df[["city","province"]].fillna("unknown")
# Kolom brand juga masih memiliki missing value, Ganti value NaN menjadi "no_brand"
df["brand"] = df["brand"].fillna("no_brand")
# Cek apakah masih terdapat missing value di seluruh kolom
print(" Info:\n", df.info())
# 6. Membuat kolom baru "city/province" dengan menggabungkan kolom "city" dan kolom "province" dan delete kolom asalnya
print("\n[6] MEMBUAT KOLOM BARU city/province")
df["city/province"] = df["city"] + "/" + df["province"]
# drop kolom "city" dan "province" karena telah digabungkan
df.drop(["city","province"], axis=1, inplace=True)
# Cetak 5 data teratas
print(df.head())
# 7. Membuat hierarchical index yang terdiri dari kolom "city/province", "order_date", "customer_id", "order_id", "product_id"
print("\n[7] MEMBUAT HIERACHICAL INDEX")
df = df.set_index(["city/province","order_date","customer_id","order_id","product_id"])
# urutkanlah berdasarkan index yang baru
df = df.sort_index()
# Cetak 5 data teratas
print(df.head())
# 8. Membuat kolom "total_price" yang formula nya perkalian antara kolom "quantity" dan kolom "item_price"
print("\n[8] MEMBUAT KOLOM total_price")
df["total_price"] = df["quantity"] * df["item_price"]
# Cetak 5 data teratas
print(df.head())
# 9. Slice dataset agar hanya terdapat data bulan Januari 2019
print("\n[9] SLICE DATASET UNTUK BULAN JANUARI 2019 SAJA")
idx = pd.IndexSlice
df_jan2019 = df.loc[idx[:, "2019-01-01":"2019-01-31"], :]
print("Dataset akhir:\n", df_jan2019)
# END OF PROJECT
```
# Evaluasi Project
Mengapa di langkah ketiga, dicari tahu terlebih dulu nilai null. Mengapa tidak diconvert to string secara langsung?”
karena di df.info()nya masih ada yang kosong di kolom ‘product_value’. Kalau langsung convert to string, value NaN akan berubah menjadi string ‘nan’, kemudian ketika pad 0 di depan dan concat dengan char ‘P’, hasilnya akan menjadi ‘P0nan’ yang aneh sekali.
Kenapa kamu memakai langkah ke-4? Mengapa tidak langsung menggunakan kolom date yang sudah ada. Bukankah format waktunya sudah ideal?
Tidak semua format datetime yang ideal pada umumnya akan ideal di dalam pandas environment. Seenggaknya harus translate dulu menjadi format yang ideal di dalam pandas sehingga pandas bisa mengenali.
|
github_jupyter
|
```
from aide_design.play import*
from aide_design import floc_model as floc
from aide_design import cdc_functions as cdc
from aide_design.unit_process_design.prefab import lfom_prefab_functional as lfom
from pytexit import py2tex
import math
```
# 1 L/s Plants in Parallel
# CHANCEUX
## Priya Aggarwal, Sung Min Kim, Felix Yang
AguaClara has been designing and building water treatment plants since 2005 in Honduras, 2013 in India, and 2017 in Nicaragua. It has been providing gravity powered water treatment systems to thousands of people in rural communities. However, there were populations that could not be targeted due to the technology only being scaled up from 6 L/s. For towns and rural areas with populations with smaller needs, AguaClara technologies were out of their reach.
Recently a one liter per second (1 LPS) plant was developed based on traditional AguaClara technology, to bring sustainable water treatment to towns with populations of 300 people per plant.
The first 1 LPS plant fabricated was sent to Cuatro Comunidades in Honduras, where a built in place plant already exists, and is currently operating without the filter attachment, also known as Enclosed Stacked Rapid Sand Filter (EStaRS). EStaRS is the last step in the 1 LPS plant processes before chlorination and completes the 4 step water treatment process: flocculation, sedimentation, filtration, and chlorination.
Having water treatment plants for smaller flow rates would increase AguaClara’s reach and allow it to help more people. Despite being in its initial stages, the demand for this technology is increasing. Three 1 LPS plants were recently ordered for a town that did not have water treatment. However, the implementation of 1 LPS plants is a problem that has not yet been solved.
This project has stemmed from the possibility of implementing AguaClara technologies to be helpful in Puerto Rico’s post hurricane rebuild effort. The goal of this project is to assess whether the portable 1 L/s plant could be a viable option to help rural communities have safe drinking water. The project models multiple 1 L/s plants working in parallel to provide for the community and plans for the future when communities would need to add capacity. For this project, the team has set 6 L/s as the design constraint. We need experience building and deploying 1 LPS plants to determine the economics and ease of operation to compare to those of built in place plants. For example, if we need 12 L/s, it could still be reasonable to use the 1 LPS plants in parallel or select a 16 L/s built in place plant if more than 12 L/s is needed. Because the dividing line between the modular prefabricated 1 LPS plants and the build in place plants is unknown, the team chose 6 L/s because it is the smallest built in place plant capacity.
Our model is based on the following:
* Standardization modular designs for each plant (1 plant has one EStaRs and Flocculator)
* One entrance tank and chemical dosing controller
* Entrance Tank accomodates to 6 L/s flow
* Coagulant/ Chlorine dosing according to flow by operator
* Parallel Layout for convenience
* Extendable shelter walls to add capacity using chain-link fencing
* Manifolds connecting up to 3 plants (accounting for 3 L/s) from the sedimentation tank to the ESTaRS and after filtration for chlorination (using Ts and fernco caps)
* Manifolds to prevent flow to other filters being cut off if filters need to be backwashed and lacks enough flow
* Equal flow to the filters and chlorination from the manifolds
Calculations follow below.
### Chemical Dosing Flow Rates
Below the functions for calculating the flow rate of the coagulant and chlorine based on the target plant flow rate are shown. The Q_Plant and concentrations of PACL and Cl can be set by the engineer and is set to 3 L/s in this sample calculation.
Chlorine would be ideally done at the end of the filtration where flow recombines so that the operator would only have to administer chlorine at one point. However our drafts did not account for that and instead lack piping that unites the top and bottom 1 L/s plants. Only the 6 L/s draft reflects this optimal design for chlorination.
```
#using Q_plant as the target variable, sample values of what a plant conditions might be are included below
Temperature = u.Quantity(20,u.degC)
Desired_PACl_Concentration=3*u.mg/u.L
Desired_Cl_Concentration=3*u.mg/u.L
C_stock_PACl=70*u.gram/u.L
C_stock_Cl=51.4*u.gram/u.L
NuPaCl = cdc.viscosity_kinematic_pacl(C_stock_PACl,Temperature)
RatioError = 0.1
KMinor = 2
Q_Plant= 3*u.L/u.s
def CDC(Q_Plant, DesiredCl_Concentration,C_stock_PACl):
Q_CDC=(Q_Plant*Desired_PACl_Concentration/C_stock_PACl).to(u.mL/u.s)
return (Q_CDC)
def Chlorine_Dosing(Q_Plant,Desired_Cl_Concentration,C_stock_Cl):
Q_Chlorine=(Q_Plant*Desired_Cl_Concentration/C_stock_Cl).to(u.mL/u.s)
return (Q_Chlorine)
print('The flow rate of coagulant is ',CDC(Q_Plant, Desired_PACl_Concentration, C_stock_PACl).to(u.L/u.hour))
print('The flow rate of chlorine is ',Chlorine_Dosing(Q_Plant, Desired_Cl_Concentration, C_stock_Cl).to(u.L/u.hour))
```
### SPACE CONSTRAINTS
In the code below the team is calculating the floor plan area. The X distance and Y distance are the length and width of the floor plan respectively. The dimensions of the sedimentation tank, flocculator, and entrance tank are accounted for in this calculation.
```
#Claculting the Y distance For the Sed Tank
#properties of sedimentation tank
Sed_Tank_Diameter=0.965*u.m
Length_Top_Half=1.546*u.m #See image for clearer understanding
Y_Sed_Top_Half=Length_Top_Half*math.cos(60*u.degrees)
print(Y_Sed_Top_Half)
Y_Sed_Total=Sed_Tank_Diameter+Y_Sed_Top_Half
print(Y_Sed_Total)
```
SED TANK: Based on the calculation above, the space the Sedimentation tank would take on the floor plant is found to be 1.738 m.

This is a picture of the sedimentation tank with dimensions showing the distance jutting out from the sedimentation tank. This distance of 0.773 m is added to the sedimentation tank diameter totalling 1.738 meters.
ESTaRS: The dimensions of the ESTaRS are set and did not need to be calculated. A single manifold can collect water from the sed tanks and send it to the EStaRS. There will be valves on the manifold system installed before the entrance to the ESTaRS to allow for backwashing. These valves can be shut to allow for enough flow to provide backwashing capacity. There will be a manifold connecting flow after filtration to equate the flow for chlorination.
FLOCCULATOR: We want symmetrical piping systems coming out of the flocculator. There is a flocculator for each plant so that available head going into the parallel sedimentation tanks will be the same. We will have an asymmetrical exit lauder system coming out of the sedimentation tanks going into the ESTaRS (diagram).
ENTRANCE TANK: The entrance tank is set to be at the front of the plant. The focus of this project is to calculate the dimensions and design the plant. The entrance tank dimensions should be left to be designed in the future. An estimated dimension was set in the drawing included in this project. There will be a grit chamber included after the entrance tank. The traditional design for rapid mix that is used in AguaClara plants will be included in the entrance tank.
CONTACT CHAMBER: A contact chamber is included after the entrance tank to ensure that the coagulant is mixed with all of the water before it separates into the multiple treatment trains. Like the entrance tank, contact chamber dimensions should be left to be designed in the future. An estimated dimension was set in the drawing included in this project.
WOODEN PLATFORM: The wooden platform is 4m long, 0.8m wide, and is 1.4 meters high allowing for the operator to be able to access the top of the sedimentation tank, flocculator, and ESTaRS. It would be placed in between every sedimentation tank. In the case of only a single sedimentation tank it would go on the right of the tank because the plant expands to the right.
```
#Spacing due to Entrance Tank and contact chamber #estimated values
Space_ET=0.5*u.m
CC_Diameter=0.4*u.m
Space_Between_ET_CC=0.1*u.m
Space_CC_ET=1*u.m
#Spacing due to Manifold between contact chamber and flocculators
Space_CC_Floc=1.116*u.m
#Spacing due to Flocculator
Space_Flocc_Sed=.1*u.m
Space_Flocculator=0.972*u.m
#Spacing due to the Manifold
Space_Manifold=0.40*u.m
#Spacing due to ESTaRS
Space_ESTaRS=0.607*u.m
#Spacing for ESTaRS Manifold to the wall
Space_ESTaRS_Wall=0.962*u.m
```
The Y distance below 3 L/s is set to be as a sum of the total Y distance of the flocculator, sedimentation tank, and ESTaRS. An additional 2 meters of Y distance is added for operator access around the plant. The lengths between the sedimentation tank, flocculator and ESTarS were kept minimal but additional Y distance can be taken off between the sedimentation tank and ESTaRS. This is because the ESTaRS can hide under the sloping half of the sedimentation tank but this orientation would not account for the manifold drawn in the picture.
The total Y distance is calculated below.
```
Y_Length_Top=(Space_CC_ET+Space_CC_Floc+Space_Flocc_Sed
+Space_Flocculator+Y_Sed_Total+Space_Manifold+Space_ESTaRS+
Space_ESTaRS_Wall)
Y_Length_Bottom=Y_Length_Top-0.488*u.m
```
Below are functions that can be used to design a plant based on the desired flow rate
```
def X(Q):
if Q>3*u.L/u.s:
X_Distance_Bottom=X(Q-3*u.L/u.s)
X_Distance_Top=6.9*u.m
return(X_Distance_Top,X_Distance_Bottom)
else:
Q_Plant=Q.to(u.L/u.s)
Extra_Space=2*u.m
X_Distance=(Q_Plant.magnitude-1)*1*u.m+(Q_Plant.magnitude)*.965*u.m+Extra_Space
return(X_Distance.to(u.m))
def Y(Q):
if Q>3*u.L/u.s:
return(Y_Length_Top+Y_Length_Bottom)
else:
return(Y_Length_Top)
print(X(Q_Plant_2).to(u.m))
def Area_Plant(Q):
if Q>3*u.L/u.s:
X_Distance_Bottom=X(Q-3*u.L/u.s)
Area_Bottom=X_Distance_Bottom*Y_Length_Bottom*((Q/u.L*u.s-3))
Area_Top=X(3*u.L/u.s)*Y_Length_Top
Area_Total=Area_Top+Area_Bottom
return(Area_Total)
else:
H_Distance=X(Q_Plant)
Y_Distance=Y_Length_Top
Area_Total=H_Distance*Y_Distance
return(Area.to(u.m**2))
```

This is a layout of a sample plant for three 1 L/s tanks running in parallel. Check bottom of document for additional drafts.
A platform will be in between sedimentation tanks as a way for the operators to have access to the sedimentation tanks. The platform height will be 1.4m to allow the plant operators 0.5m to view the sedimentation tanks just as in the built in place plants. The operator access requirements influence the optimal plant layout because the operators movements and safety have to be considered. The manifold will be built underneath the platform for space efficiency. The image below shows the wooden platform with 4m of length but could be truncated or extended to depending on the situation. The last image shows the platform in between the sedimentation tanks in the 3 L/s sample plant.

Wooden platforms would fill up the space in between sedimentation tanks to allow for operator access to the top of sedimentation tanks, ESTaRS and flocculators.

### Adding Capacity
When adding capacity up to plant flow rates of 3 L/s, vertical distance will be constant so adding capacity will only change the horizontal distance of the plant. We define a set of flocculator, sedimentation tank, and EStARS as a 1 L/s plant.
After the capacity of the plant reaches 3 L/s, additional 1 L/s plants will be added to the bottom half of the building, using a mirrored layout as the top half of the building. The only difference between the spacing is that the additions no longer need another entrance tank so the width of the bottom half of the plant is shorter than the width of the top half. This was done instead of simply increasing the length of the plant each time capacity was added because the length of the pipe between the contact chamber and the farthest flocculator would become increasingly large. This addition of major losses would cause different flow rates between the farther 1LPS plant and the closest one.
The following function will only account for adding 1 L/s plants one at at a time
```
def Additional_Area(Q_Plant,Q_Extra):
if (Q_Plant+Q_Extra>3*u.L/u.s):
X_Distance_Extra=X(Q_Extra)
Y_Distance_Extra=Y_Length_Bottom
Area=(X_Distance_Extra*Y_Distance_Extra).to(u.m**2)
return(Area)
else:
Q=Q_Extra.to(u.L/u.s)
Horizontal=(Q_Extra.magnitude)*.965*u.m+(Q_Extra.magnitude)*1*u.m
Vertical=5.512*u.m
Extra_Area=Vertical*Horizontal
print('Extra length that has to be added is '+ut.sig(Horizontal,4))
return(ut.sig(Extra_Area,2))
```
### ESTaRS
The total surface area required for the ESTaRS filter is simply a product of the area one ESTaRS requires and the flow rate coming into the plant. The surface area required for an ESTaRS was measured in the DeFrees lab. It is approximately a square meter.
```
ESTaRS_SA=1*u.m**2/u.L
def Area_ESTaRS(Q):
Q_Plant=Q.to(u.L/u.s)
Surface_Area_ESTaRS=(ESTaRS_SA.magnitude)*Q_Plant.magnitude
return(Surface_Area_ESTaRS*u.m**2)
print('Surface area required for the ESTaR(s) is',Area_ESTaRS(Q_Plant))
```
### Flocculators
The total surface area required for the ESTaRS filter is simply a product of the area one ESTaRS requires and the flow rate coming into the plant. The surface area required for an ESTaRS was measured in the DeFrees lab. It is approximately a square meter.
```
Flocc_SA=0.972*u.m*0.536*u.m*u.L/u.s
def Area_Flocc(Q):
Q_Plant=Q.to(u.L/u.s)
Surface_Area_Flocc=(Flocc_SA.magnitude)*Q_Plant.magnitude
return(Surface_Area_Flocc*u.m**2)
print('Surface area required for the flocculator(s) is',Area_Flocc(Q_Plant))
```
### Manifold Headloss Calculations
The amount of headloss has to be minimal so that the amount of head availible coming out of the exit launder is enough to drive water fast enough to fluidize the sand bed in ESTaRS. This fluidization is required for backwashing the filter. Since the calculation for 4 inch pipe has a headloss for less than 1mm we conclude that the manifold is economically feasible. Any futher increase in the diameter of the manifold would become increasingly expensive.
```
SDR = 26
SF=1.33
Q_Manifold = 1 * u.L/u.s #max flowrate for a manifold
Q_UpperBound=SF*Q_Manifold
L_pipe = 5*u.m #Length sed tank to it’s ESTaRS
K_minor_bend=0.3
K_minor_branch=1
K_minor_contractions=1
K_minor_total= 2*(K_minor_bend+K_minor_branch+K_minor_contractions) # (two bends, two dividing branch, and two contractions)
# The maximum viscosity will occur at the lowest temperature.
T_crit = u.Quantity(10,u.degC)
nu = pc.viscosity_kinematic(T_crit)
e = 0.1 * u.mm
Manifold_1LPS_ID=4*u.inch
Headloss_Max=10*u.mm
Manifold_Diam=pc.diam_pipe(Q_Manifold,Headloss_Max,L_pipe,nu,e,K_minor_total).to(u.inch)
print(Manifold_Diam.to(u.inch))
print('The minimum pipe inner diameter is '+ ut.sig(Manifold_Diam,2)+'.')
Manifold_ND = pipe.ND_SDR_available(Manifold_Diam,SDR)
print('The nominal diameter of the manifold is '+ut.sig(Manifold_ND,2)+' ('+ut.sig(Manifold_ND.to(u.inch),2)+').')
HLCheck = pc.headloss(Q_UpperBound,Manifold_1LPS_ID,L_pipe,nu,e,K_minor_total)
print('The head loss is',HLCheck.to(u.mm))
```
# Drafts of 1 L/s Plant to 6 L/s Plant

A sample 1 L/s plant. The red t's indicate where the piping system can be expanded to include more 1 L/s systems. Additionally the t would be covered by a fernco cap so that the pipe can be removed when the plant is adding capacity. See cell below for pictures of manifolds with caps.

The sample 2 L/s plant. The red t's indicate where the piping system can be expanded to include more 1 L/s plants. Additionally the t exit that isn't connected to any piping would be covered by a fernco cap so that the pipe can be removed when the plant is adding capacity.

The sample 3 L/s plant. There are now no more t's that can be extended because the manifold was designed for up to 3 1 L/s plants. Further capacities are added on the bottom half of the plant like in the next 3 pictures.

The sample 4 L/s plant. Like in the 1 L/s plant the red t's indicate the start of the 2nd manifold system.

The sample 5 L/s plant. The length (x-direction) is extended by the diameter of a sedimentation tank and one meter like in the top half of the plant. However the width of the bottom half is slightly lower because it can use the already built entrance tank used for the first 3 L/s systems.

The sample 6 L/s plant. The building is now at full capacity with an area of 91.74 m^2. The flow reunites to allow for chlorination to be administered at one point.
# Manifold Drafts

The manifold with 1 L/s. The elbow at the top is connected to the exit launder of the sedimentation tank. The flow goes from the exit launder into the reducer which is not yet connected in the draft to the ESTaRS. The removeable fernco cap that allows for further expansions of the manifold pipe system can be seen in the picture.

The manifold with 2 L/s. Again a fernco cap is used to allow for future expansions up to 3 L/s.

The manifold with 3 L/s. Here there are no fernco caps because the manifold is designed for up to connections with three 1 L/s plants.
|
github_jupyter
|
```
import sqlite3
conn = sqlite3.connect('nominations.db')
#Checking Schema
schema = conn.execute("pragma table_info(nominations)")
schema.fetchall()
first_ten = conn.execute("select * from nominations limit 10").fetchall()
for i in first_ten:
print(i)
#Creating a ceremonies table that contains the list of tuples connecting ceremonial hosts corresponding to year
#List of tuples
years_hosts = [(2010, "Steve Martin"),
(2009, "Hugh Jackman"),
(2008, "Jon Stewart"),
(2007, "Ellen DeGeneres"),
(2006, "Jon Stewart"),
(2005, "Chris Rock"),
(2004, "Billy Crystal"),
(2003, "Steve Martin"),
(2002, "Whoopi Goldberg"),
(2001, "Steve Martin"),
(2000, "Billy Crystal"),
]
#Creating table
query = '''create table ceremonies(
id integer primary key,
Year integer,
Host text
);'''
f = conn.execute(query)
#Inserting years_host list into ceremonies table
insert_query = ''' insert into ceremonies (Year,Host) values (?,?)'''
conn.executemany(insert_query,years_hosts)
f = conn.execute("pragma table_info(ceremonies)").fetchall()
f
f = conn.execute('select * from ceremonies limit 10').fetchall()
f
f
```
# Fixes
Fixing the schema when the column names are incorrect.
Rename the table(with errors) to tempName and then recreate the original tableName and then insert the values into newly created table.
https://stackoverflow.com/questions/805363/how-do-i-rename-a-column-in-a-sqlite-database-table
fix1 = '''alter table ceremonies rename to tmp_table'''
conn.execute(fix1)
Removing the old tmp table:
fix2 = "drop table tmp_table"
conn.execute(fix2)
# Foreign Keys
PRAGMA foreign_keys = ON;
The above query needs to be run every time you connect to a database where you'll be inserting foreign keys.
```
conn.execute('pragma foreign_keys = on')
#Creating an append listfrom old table to insert into new table.
query = '''SELECT ceremonies.id, nominations.category, nominations.nominee, nominations.movie,
nominations.charachter, nominations.won
FROM nominations
INNER JOIN ceremonies ON
nominations.year == ceremonies.year
;'''
conn.execute("pragma table_info(nominations)").fetchall()
join_list = conn.execute(query).fetchall()
for i in join_list[:10]:
print(i)
fix1 = '''alter table nominations rename to tmp_table2'''
conn.execute(fix1)
#Creating the new table with desired schema
create_table = '''create table nominations(
id integer primary key,
category text,
nominee text,
movie text,
charachter text,
Won integer,
ceremony_id integer,
foreign key(ceremony_id) references ceremonies(id)
);
'''
conn.execute(create_table)
insert_query = 'insert into nominations (ceremony_id,category,nominee,movie,charachter,Won) values (?,?,?,?,?,?)'
conn.executemany(insert_query,join_list)
f = conn.execute('pragma table_info(nominations)').fetchall()
f
f = conn.execute('select * from nominations limit 10').fetchall()
#Drop tmp_table
fix1 = '''alter table actors rename to tmp_table'''
conn.execute(fix1)
fix2 = "drop table movies_actors"
conn.execute(fix2)
```
# Many to Many relations through a join table
```
#Creating the tables
actors = '''create table actors(
id integer primary key,
actor text
)'''
conn.execute(actors)
movies = '''create table movies(
id integer primary key,
movie text
)
'''
conn.execute(movies)
movies_actors = '''create table movies_actors(
id integer primary key,
movie_id integer references movies(id),
actor_id integer references actors(id)
);'''
conn.execute(movies_actors)
actor_sql= "select distinct nominations.nominee from nominations;"
actor_list = conn.execute(actor_sql).fetchall()
actor_list[:5]
conn.executemany("insert into actors (actor) values (?);",actor_list)
movie_sql = "select distinct nominations.movie from nominations;"
movie_list = conn.execute(movie_sql).fetchall()
movie_list[:5]
conn.executemany("insert into movies (movie) values(?)",movie_list)
query = "select * from movies"
f = conn.execute(query).fetchall()
f[:5]
query = "select * from actors"
f = conn.execute(query).fetchall()
f[:5]
joint_query = '''select * from actors
inner join nominations on actors.actor == nominations.nominee'''
f = conn.execute(joint_query)
for i in f.fetchall()[:10]:
print(i)
f.fetchall()
f = conn.execute("pragma table_info(movies_actors)").fetchall()
f
query = "select * from movies_actors"
f = conn.execute(query).fetchall()
f[:5]
query = '''select ceremonies.year, nominations.movie from nominations
inner join ceremonies on
nominations.ceremony_id == ceremonies.id
where nominations.nominee == 'Natalie Portman';
'''
f = conn.execute(query)
portman_movies = f.fetchall()
print(portman_movies)
query = '''SELECT * FROM movies
INNER JOIN movies_actors ON movies.id == movies_actors.movie_id'''
f = conn.execute(query)
f.fetchall()
```
|
github_jupyter
|
```
'''
# IoU_old
usage of loss func
criterion = nn.NLLLoss()
def step(x, y, is_train=True):
x = x.reshape(-1, 28 * 28)
y_pred = model(x)
loss = criterion(y_pred, y)
if is_train:
opt.zero_grad()
loss.backward()
opt.step()
return loss, y_pred
'''
torch.nn.Module
class IoU_old(nn.Module):
def __init__(self, thresh: float = 0.5):
super().__init__()
self.thresh = thresh
def forward(self, inputs: torch.Tensor, targets:torch.Tensor, weights: Optional[torch.Tensor] = None, smooth: float = 0.0) -> Tensor:
inputs = torch.where(inputs < self.thresh, 0, 1)
batch_size = targets.shape[0]
intersect = torch.logical_and(inputs, targets)
intersect = intersect.view(batch_size, -1).sum(-1)
union = torch.logical_or(inputs, targets)
union = union.view(batch_size, -1).sum(-1)
print(intersect)
print(union)
print(union.shape)
IoU = (intersect + smooth) / (union + smooth)
IoU = torch.nan_to_num(IoU)
return IoU
def iou2(outputs: torch.Tensor, labels: torch.Tensor, smooth: float=0, threshold: float = 0.5):
# intersection = (outputs & labels).sum((1, 2)) # Will be zero if Truth=0 or Prediction=0
# union = (outputs | labels).sum((1, 2)) # Will be zzero if both are 0
# iou = (intersection + SMOOTH) / (union + SMOOTH) # We smooth our devision to avoid 0/0
# # thresholded = torch.clamp(20 * (iou - 0.5), 0, 10).ceil() / 10 # This is equal to comparing with thresolds
# return iou
outputs = torch.where(outputs < threshold, 0, 1)
print(f"num of labels: {len(torch.nonzero(labels))}")
intersect = torch.logical_and(outputs, labels)
intersect = intersect.long()
print(intersect)
# intersect = torch.where(outputs == labels, 1, 0)
# intersect = torch.where(outputs == intersect, 1, 0)
print(f"num of interesect: {len(torch.nonzero(intersect))}")
union = torch.logical_or(outputs, labels)
print(f"num of union: {len(torch.nonzero(union))}")
# print(f"intersect sum: {intersect.sum()}")
# print(f"union sum: {union.sum()}")
iou_score = torch.sum(intersect)/torch.sum(union)
print(iou_score)
# # You can comment out this line if you are passing tensors of equal shape
# # But if you are passing output from UNet or something it will most probably
# # be with the BATCH x 1 x H x W shape
# # outputs = outputs.squeeze(1) # BATCH x 1 x H x W => BATCH x H x W
# # intersection = (outputs & labels).sum((1, 2)) # Will be zero if Truth=0 or Prediction=0
# # union = (outputs | labels).float().sum((1, 2)) # Will be zzero if both are 0
iou = (intersect + smooth) / (union + smooth) # We smooth our devision to avoid 0/0
iou_score = torch.sum(iou)
print(iou_score)
return iou_score # Or thresholded.mean() if you are interested in average across the batch
'''
# IoU soft
note: "hard" probabilistic IoU calculation is not differentiable,
so be sure to use soft probabilistic loss func
'''
def iou_soft(inputs: torch.Tensor, labels: torch.Tensor,
smooth: float=0.1, threshold: float = 0.5, alpha: float = 1.0):
'''
- alpha: a parameter that sharpen the thresholding.
if alpha = 1 -> thresholded input is the same as raw input.
'''
thresholded_inputs = inputs**alpha / (inputs**alpha + (1 - inputs)**alpha)
# inputs = torch.where(thresholded_inputs < threshold, 0, 1)
thresholded_inputs = torch.where(thresholded_inputs < threshold, 0, 1)
inputs = (inputs + thresholded_inputs) - inputs.detach()
batch_size = inputs.shape[0]
# instead of hard prob calc: intersect = torch.logical_and(outputs, labels)
intersect_tensor = (inputs * labels).view(batch_size, -1)
intersect = intersect_tensor.sum(-1)
# insetad of using the hard prob: union = torch.logical_or(outputs, labels)
union_tensor = torch.max(inputs, labels).view(batch_size, -1)
union = union_tensor.sum(-1)
iou = (intersect + smooth) / (union + smooth) # We smooth our devision to avoid 0/0
iou_score = iou.mean()
# print(f"num of labels: {len(torch.nonzero(labels))}")
# print(f"intersection tensor: {intersect_tensor}")
# print(f"union tensor: {union_tensor}\n")
# print(f"intersect sum: {intersect}")
# print(f"union sum: {union}\n")
# print(f"iou error: {1- iou_score}")
return 1- iou_score
```
|
github_jupyter
|
```
import h5py
import keras
import numpy as np
import json
import os
import uuid
import yaml
from attlayer import AttentionWeightedAverage
#from avglayer import MaskAverage
from copy import deepcopy
#from finetuning import (sampling_generator, finetuning_callbacks)
from operator import itemgetter
#from global_variables import NB_TOKENS, NB_EMOJI_CLASSES
from keras.layers import *
from keras.layers.merge import concatenate
from keras.layers import Input, Bidirectional, Embedding, Dense, Dropout, SpatialDropout1D, LSTM, Activation
from keras.models import Model, Sequential
from keras.optimizers import Adam
from keras.regularizers import L1L2
from pathlib import Path
from sklearn.metrics import classification_report, recall_score, precision_score, f1_score
from os.path import exists
def elsa_architecture(nb_classes, nb_tokens, maxlen, feature_output=False, embed_dropout_rate=0, final_dropout_rate=0, embed_dim=300,
embed_l2=1E-6, return_attention=False, load_embedding=False, pre_embedding=None, high=False, LSTM_hidden=512, LSTM_drop=0.5):
"""
Returns the DeepMoji architecture uninitialized and
without using the pretrained model weights.
# Arguments:
nb_classes: Number of classes in the dataset.
nb_tokens: Number of tokens in the dataset (i.e. vocabulary size).
maxlen: Maximum length of a token.
feature_output: If True the model returns the penultimate
feature vector rather than Softmax probabilities
(defaults to False).
embed_dropout_rate: Dropout rate for the embedding layer.
final_dropout_rate: Dropout rate for the final Softmax layer.
embed_l2: L2 regularization for the embedding layerl.
high: use or not the highway network
# Returns:
Model with the given parameters.
"""
class NonMasking(Layer):
def __init__(self, **kwargs):
self.supports_masking = True
super(NonMasking, self).__init__(**kwargs)
def build(self, input_shape):
input_shape = input_shape
def compute_mask(self, input, input_mask=None):
# do not pass the mask to the next layers
return None
def call(self, x, mask=None):
return x
def get_output_shape_for(self, input_shape):
return input_shape
# define embedding layer that turns word tokens into vectors
# an activation function is used to bound the values of the embedding
model_input = Input(shape=(maxlen,), dtype='int32')
embed_reg = L1L2(l2=embed_l2) if embed_l2 != 0 else None
if not load_embedding and pre_embedding is None:
embed = Embedding(input_dim=nb_tokens, output_dim=embed_dim, mask_zero=True,input_length=maxlen,embeddings_regularizer=embed_reg,
name='embedding')
else:
embed = Embedding(input_dim=nb_tokens, output_dim=embed_dim, mask_zero=True,input_length=maxlen, weights=[pre_embedding],
embeddings_regularizer=embed_reg,trainable=True, name='embedding')
if high:
x = NonMasking()(embed(model_input))
else:
x = embed(model_input)
x = Activation('tanh')(x)
# entire embedding channels are dropped out instead of the
# normal Keras embedding dropout, which drops all channels for entire words
# many of the datasets contain so few words that losing one or more words can alter the emotions completely
if embed_dropout_rate != 0:
embed_drop = SpatialDropout1D(embed_dropout_rate, name='embed_drop')
x = embed_drop(x)
# skip-connection from embedding to output eases gradient-flow and allows access to lower-level features
# ordering of the way the merge is done is important for consistency with the pretrained model
lstm_0_output = Bidirectional(LSTM(LSTM_hidden, return_sequences=True, dropout=LSTM_drop), name="bi_lstm_0" )(x)
lstm_1_output = Bidirectional(LSTM(LSTM_hidden, return_sequences=True, dropout=LSTM_drop), name="bi_lstm_1" )(lstm_0_output)
x = concatenate([lstm_1_output, lstm_0_output, x])
if high:
x = TimeDistributed(Highway(activation='tanh', name="high"))(x)
# if return_attention is True in AttentionWeightedAverage, an additional tensor
# representing the weight at each timestep is returned
weights = None
x = AttentionWeightedAverage(name='attlayer', return_attention=return_attention)(x)
#x = MaskAverage(name='attlayer', return_attention=return_attention)(x)
if return_attention:
x, weights = x
if not feature_output:
# output class probabilities
if final_dropout_rate != 0:
x = Dropout(final_dropout_rate)(x)
if nb_classes > 2:
outputs = [Dense(nb_classes, activation='softmax', name='softmax')(x)]
else:
outputs = [Dense(1, activation='sigmoid', name='softmax')(x)]
else:
# output penultimate feature vector
outputs = [x]
if return_attention:
# add the attention weights to the outputs if required
outputs.append(weights)
return Model(inputs=[model_input], outputs=outputs)
os.environ['CUDA_VISIBLE_DEVICES'] = "2"
cur_lan = "elsa_pt"
maxlen = 20
batch_size = 250
lr = 3e-4
epoch_size = 25000
nb_epochs = 1000
patience = 5
checkpoint_weight_path = "./ckpt"
loss = "categorical_crossentropy"
optim = "adam"
vocab_path = "/data/elsa"
nb_classes=64
LSTM_hidden = 512
LSTM_drop = 0.5
final_dropout_rate = 0.5
embed_dropout_rate = 0.0
high = False
load_embedding = True
embed_dim = 200
steps = int(epoch_size/batch_size)
wv_path = Path(vocab_path).joinpath("{:s}_wv.npy".format(cur_lan)).as_posix()
X_path = Path(vocab_path).joinpath("{:s}_X.npy".format(cur_lan)).as_posix()
y_path = Path(vocab_path).joinpath("{:s}_y.npy".format(cur_lan)).as_posix()
word_vec = np.load(wv_path, allow_pickle=True)
input_vec, input_label = np.load(X_path, allow_pickle=True), np.load(y_path, allow_pickle=True)
nb_tokens, input_len = len(word_vec), len(input_label)
train_end = int(input_len*0.7)
val_end = int(input_len*0.9)
(X_train, y_train) = (input_vec[:train_end], input_label[:train_end])
(X_val, y_val) = (input_vec[train_end:val_end], input_label[train_end:val_end])
(X_test, y_test) = (input_vec[val_end:], input_label[val_end:])
input_vec.shape
model = elsa_architecture(nb_classes=nb_classes, nb_tokens=nb_tokens, maxlen=maxlen, final_dropout_rate=final_dropout_rate, embed_dropout_rate=embed_dropout_rate,
load_embedding=True, pre_embedding=word_vec, high=high, embed_dim=embed_dim)
model.summary()
if optim == 'adam':
adam = Adam(clipnorm=1, lr=lr)
model.compile(loss=loss, optimizer=adam, metrics=['accuracy'])
elif optim == 'rmsprop':
model.compile(loss=loss, optimizer='rmsprop', metrics=['accuracy'])
model.fit(X_train,
y_train,
batch_size=batch_size,
epochs=nb_epochs,
validation_data=(X_val, y_val),
callbacks=[keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=0, patience=patience, verbose=0, mode='auto')],
verbose=True)
_, acc = model.evaluate(X_test, y_test, batch_size=batch_size, verbose=0)
print(acc)
token2index = json.loads(open("/data/elsa/elsa_pt_vocab.txt", "r").read())
freq = {line.split()[0]: int(line.split()[1]) for line in open("/data/elsa/elsa_pt_emoji.txt").readlines()}
freq_topn = sorted(freq.items(), key=itemgetter(1), reverse=True)[:nb_classes]
y_pred = model.predict(X_test)
print(classification_report(y_test.argmax(axis=1), y_pred.argmax(axis=1), target_names=[e[0] for e in freq_topn]))
```
|
github_jupyter
|
**Import libraries**
```
import os
import logging
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Subset, DataLoader
from torch.backends import cudnn
import torch.utils.data
import torchvision
from torchvision import transforms
from torchvision.models import alexnet
from torchvision.datasets import ImageFolder
from torchvision import datasets
from PIL import Image
from tqdm import tqdm
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
import pretrainedmodels
import pickle
```
**Definitions**
```
from torch.autograd import Function
class ReverseLayerF(Function):
@staticmethod
def forward(ctx, x, alpha):
ctx.alpha = alpha
return x.view_as(x)
@staticmethod
def backward(ctx, grad_output):
output = grad_output.neg() * ctx.alpha
return output, None
```
**Set Arguments**
```
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 'cuda' or 'cpu'
DATA_DIR = 'PACS\\' # directory of dataset
NUM_CLASSES = 7
NUM_DOMAINS = 2
image_size = 224 # the size required by AlexNet
BATCH_SIZE = 256 # Higher batch sizes allows for larger learning rates. An empirical heuristic suggests that, when changing
# the batch size, learning rate should change by the same factor to have comparable results
LR = 1e-3 # The initial Learning Rate
NUM_EPOCHS = 35 # Total number of training epochs (iterations over dataset)
```
**Define Data Preprocessing**
```
# Define transforms for training phase
source_transform = transforms.Compose([
transforms.ColorJitter(),
transforms.RandomHorizontalFlip(),
transforms.Resize((224, 224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])]) # Normalizes tensor with mean and standard deviation of ImageNet
# Define transforms for the evaluation phase
target_transform = transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])])
```
**Prepare Dataset**
```
source_dataset = ImageFolder(DATA_DIR+'photo//', transform=source_transform)
target_dataset = ImageFolder(DATA_DIR+'art_painting//', transform=target_transform)
print('source Dataset: {}'.format(len(source_dataset)))
print('target Dataset: {}'.format(len(target_dataset)))
```
<!-- # xx=Caltech(DATA_DIR, split='train')
# xx.__getitem__(36) -->
**Prepare Dataloaders**
```
# Dataloaders iterate over pytorch datasets and transparently provide useful functions (e.g. parallelization and shuffling)
source_dataloader = DataLoader(source_dataset, batch_size=BATCH_SIZE, shuffle=True)
target_dataloader = DataLoader(target_dataset, batch_size=BATCH_SIZE, shuffle=True)
```
**Define Network**
```
import torch
import torch.nn as nn
from torch.hub import load_state_dict_from_url
__all__ = ['AlexNet', 'alexnet']
model_urls = {
'alexnet': 'https://download.pytorch.org/models/alexnet-owt-4df8aa71.pth',
}
class AlexNetDANN(nn.Module):
def __init__(self, num_classes=1000, num_domains=2):
super(AlexNetDANN, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(64, 192, kernel_size=5, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(192, 384, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(256, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.class_classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(256 * 6 * 6, 4096),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Linear(4096, num_classes),
)
self.domain_classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(256 * 6 * 6, 4096),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Linear(4096, num_domains),
)
def forward(self, input_data, alpha):
input_data = input_data.expand(input_data.data.shape[0], 3, 224, 224)
feature = self.features(input_data)
feature = feature.view(feature.size(0), -1)
reverse_feature = ReverseLayerF.apply(feature, alpha)
class_output = self.class_classifier(feature)
domain_output = self.domain_classifier(reverse_feature)
return class_output, domain_output
def alexnetdann(pretrained=False, progress=True, **kwargs):
r"""AlexNet model architecture from the
`"One weird trick..." <https://arxiv.org/abs/1404.5997>`_ paper.
Args:
pretrained (bool): If True, returns a model pre-trained on ImageNet
progress (bool): If True, displays a progress bar of the download to stderr
"""
model = AlexNetDANN(**kwargs)
if pretrained:
state_dict = load_state_dict_from_url(model_urls['alexnet'],
progress=progress)
model.load_state_dict(state_dict, strict=False)
r"""
something of great importace:
Whether you are loading from a partial state_dict, which is missing some keys, or loading a state_dict with more keys than the model that you are loading into, you can set the strict argument to False in the load_state_dict() function to ignore non-matching keys.
"""
return model
```
**Prepare Network Training Functions**
```
# Define model
my_net = alexnetdann(pretrained=True,progress=True, num_classes=NUM_CLASSES, num_domains=NUM_DOMAINS)
# Define loss function
loss_class = nn.CrossEntropyLoss()
loss_domain = nn.CrossEntropyLoss()
# Choose parameters to optimize
parameters_to_optimize = my_net.parameters() # In this case we optimize over all the parameters of AlexNet
# Define optimizer
# An optimizer updates the weights based on loss
optimizer = optim.SGD(parameters_to_optimize, lr=LR)
#move network to GPU
my_net = my_net.to(device)
loss_class = loss_class.to(device)
loss_domain = loss_domain.to(device)
#to train
for p in my_net.parameters():
p.requires_grad = True
```
**Test Function**
```
def test(dataset_name,epoch):
batch_size = BATCH_SIZE
if dataset_name == source_dataloader:
dataloader = source_dataloader
else:
dataloader = target_dataloader
global my_net
my_net = my_net.to(device)
my_net = my_net.eval()
len_dataloader = len(dataloader)
data_target_iter = iter(dataloader)
i = 0
n_total = 0
n_correct = 0
while i < len_dataloader:
data_target = data_target_iter.next()
t_img, t_label = data_target
batch_size = len(t_label)
input_img = torch.FloatTensor(batch_size, 3, image_size, image_size)
class_label = torch.LongTensor(batch_size)
t_img = t_img.to(device)
t_label = t_label.to(device)
input_img = input_img.to(device)
class_label = class_label.to(device)
input_img.resize_as_(t_img).copy_(t_img)
class_label.resize_as_(t_label).copy_(t_label)
class_output, _ = my_net(input_data=input_img, alpha=alpha)
pred = class_output.data.max(1, keepdim=True)[1]
n_correct += pred.eq(class_label.data.view_as(pred)).cpu().sum()
n_total += batch_size
i += 1
accu = n_correct.data.numpy() * 1.0 / n_total
if dataset_name == source_dataloader:
print ('epoch: %d, accuracy of the source_dataset: %f' % (epoch+1, accu))
else:
print ('epoch: %d, accuracy of the target_dataset: %f' % (epoch+1, accu))
return accu
```
**Train & Test**
```
cudnn.benchmark # Calling this optimizes runtime
all_err_s_label=[]
all_err_s_domain=[]
all_err_t_domain=[]
all_acc_source_dataset=[]
all_acc_target_dataset=[]
# Start iterating over the epochs
for epoch in range(NUM_EPOCHS):
it_err_s_label=[]
it_err_s_domain=[]
it_err_t_domain=[]
len_dataloader = min(len(source_dataloader), len(target_dataloader))
data_source_iter = iter(source_dataloader)
data_target_iter = iter(target_dataloader)
i = 0
while i < len_dataloader:
p = float(i + epoch * len_dataloader) / NUM_EPOCHS / len_dataloader
alpha = 2. / (1. + np.exp(-10 * p)) - 1
# training model using source data
data_source = data_source_iter.next()
s_img, s_label = data_source
my_net.zero_grad()
my_net.train()
batch_size = len(s_label)
input_img = torch.FloatTensor(batch_size, 3, image_size, image_size)
class_label = torch.LongTensor(batch_size)
domain_label = torch.zeros(batch_size)
domain_label = domain_label.long()
s_img = s_img.to(device)
s_label = s_label.to(device)
input_img = input_img.to(device)
class_label = class_label.to(device)
domain_label = domain_label.to(device)
input_img.resize_as_(s_img).copy_(s_img)
class_label.resize_as_(s_label).copy_(s_label)
class_output, domain_output = my_net(input_data=input_img, alpha=alpha)
err_s_label = loss_class(class_output, class_label)
err_s_domain = loss_domain(domain_output, domain_label)
# training model using target data
data_target = data_target_iter.next()
t_img, _ = data_target
batch_size = len(t_img)
input_img = torch.FloatTensor(batch_size, 3, image_size, image_size)
domain_label = torch.ones(batch_size)
domain_label = domain_label.long()
t_img = t_img.to(device)
input_img = input_img.to(device)
domain_label = domain_label.to(device)
input_img.resize_as_(t_img).copy_(t_img)
_, domain_output = my_net(input_data=input_img, alpha=alpha)
err_t_domain = loss_domain(domain_output, domain_label)
err = err_t_domain + err_s_domain + err_s_label
err.backward()
optimizer.step()
i += 1
print ('epoch: %d, [iter: %d / %d], err_s_label: %f, err_s_domain: %f, err_t_domain: %f' \
% (epoch+1, i, len_dataloader, err_s_label.data.cpu().numpy(),
err_s_domain.data.cpu().numpy(), err_t_domain.data.cpu().item()))
it_err_s_label.append(err_s_label.data.cpu().numpy())
it_err_s_domain.append(err_s_domain.data.cpu().numpy())
it_err_t_domain.append(err_t_domain.data.cpu().item())
all_err_s_label.append(min(it_err_s_label))
all_err_s_domain.append(min(it_err_s_domain))
all_err_t_domain.append(min(it_err_t_domain))
all_acc_source_dataset.append(test(source_dataloader,epoch))
all_acc_target_dataset.append(test(target_dataloader,epoch))
```
**Saving & Plotting Results**
```
# Error plots
plt.figure(figsize=(10, 7))
plt.plot(all_err_s_label, color='green', label='err_s_label')
plt.plot(all_err_s_domain, color='blue', label='err_s_domain')
plt.plot(all_err_t_domain, color='orange', label='err_t_domain')
plt.xlabel('Epochs')
plt.ylabel('Error')
plt.legend()
plt.savefig('Errors.png')
# accuracy plots
plt.figure(figsize=(10, 7))
plt.plot(all_acc_source_dataset, color='green', label='accuracy of the source_dataset')
plt.plot(all_acc_target_dataset, color='blue', label='accuracy of the target_dataset')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.savefig('accuracy.png')
```
|
github_jupyter
|
# Reset Put Option
A reset put option is similar to a standard put option except that the exercise price is reset equal to the stock price on the pre-specified reset date if this stock price exceeds the original exercise price. Unlike the standard put option, a Reset put option has a stochastic strike price. On issue date, the reset put option has a strike price equal to the stock price. However, if the stock price exceeds the original strike price on a pre-specified future reset date, then the strike price is reset to the current strike price.
This notebook proposes three approaches to pricing the exotic option: the binomial tree approach, Monte Carlo simulation approach, and the closed form solution. The presentation accompanying this notebook can be found in my [website](https://www.brianlim.xyz/files/Reset%20Put%20Option.pdf).
To read more about Reset Put Option, you can refer to the paper by [Gray and Whaley (1999)](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.8221&rep=rep1&type=pdf).
## Load Libraries
First, we import the necessary libraries
```
import numpy as np
import pandas as pd
from scipy.stats import multivariate_normal as mvn
from scipy.stats import norm
import plotly.express as px
import plotly.io as pio
pio.templates.default = "plotly_white"
```
## Binomial Tree
For the binomial tree implementation, instead of doing the naive approach of doing path dependent options, we can optimize our calculations since we are only concerned with the value at $T_1$. The formula used is from [Shparber and Resheff (2004)](https://www.researchgate.net/publication/240390357_Valuation_of_Cliquet_Options).
$$p_0 = e^{-rT_2} \sum_{j=0}^{n_1}\sum_{i=j}^{n_2-n_1+j} \frac{n_1! (n_2 - n_1)!}{j! (n_1 - j)! (i - j)! (n_2 - n_1 - i + j)!} p^i (1-p)^{n_2-i} \max(S_0 - S_0 u^{i}d^{n_2-i}, S_0 u^{j}d^{n_1-j} - S_0 u^i d^{n_2-i}, 0)$$
To further optimize the performance of this implementation, we can use the recursive form of the combination function and apply dynamic programming.
$${n \choose r} = {{n-1} \choose {r}} + {{n-1} \choose {r-1}}$$
```
memo = [[-1 for _ in range(1000)] for _ in range(1000)]
def choose(n,r):
if r > n or r < 0:
return 0
elif n == 1:
return 1
elif memo[n][r] == -1:
memo[n][r] = choose(n-1, r-1) + choose(n-1, r)
return memo[n][r]
def BT_option_price(S0, T2, n1, n2, r, q, sigma):
dt = T2 / n2
u = np.exp( sigma * np.sqrt(dt))
d = np.exp(- sigma * np.sqrt(dt))
pu = (np.exp( (r - q) * dt) - d) / (u - d)
pd = (u - np.exp( (r - q) * dt)) / (u - d)
ans = 0
for j in range(n1+1):
for i in range(j, n2 - n1 + j + 1):
ans += (
choose(n1, j) * choose (n2 - n1, i - j) * pow(pu, i) * pow(pd, n2 - i) *
max(
S0 - S0 * pow(u, i) * pow(d, n2 - i),
S0 * pow(u, j) * pow(d, n1 - j) - S0 * pow(u, i) * pow(d, n2 - i),
0
)
)
return np.exp(-r * T2) * ans
print("Binomial Tree: ", BT_option_price(
S0 = 100,
T2 = 1,
n1 = 500,
n2 = 1000,
r = 0.1,
q = 0.05,
sigma = 0.3)
)
```
## Monte Carlo Simulation
For the Monte Carlo Simulation, we will use the discretized GBM to determine trajectories of the stock price. The discretized GBM is given as
$$S_{t + \Delta t} = S_t \left[1 + (r - q) \Delta t + \sigma \sqrt{\Delta t} Z\right],$$
where $Z \sim N(0,1)$. After simulating each trajectory, we get the present value of the mean of the payoffs.
```
def generate_trajectory(S0, T2, n2, r, q, sigma):
dt = T2 / n2
trajectory = [S0]
for _ in range (n2):
trajectory.append(
trajectory[-1] * (1 + ( r - q ) * dt + sigma * np.sqrt(dt) * np.random.randn())
)
return trajectory
def MC_option_price(S0, T2, n1, n2, r, q, sigma):
res = []
for _ in range(100000):
tmp = generate_trajectory(S0, T2, n2, r, q, sigma)
res.append( max(max(S0, tmp[n1]) - tmp[-1] ,0) )
return np.exp(- r * T2) * np.mean(res)
print("Monte Carlo: ", MC_option_price(
S0 = 100,
T2 = 1,
n1 = 50,
n2 = 100,
r = 0.1,
q = 0.05,
sigma = 0.3)
)
```
## Closed Form
According to [Gray and Whaley (1999)](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.8221&rep=rep1&type=pdf), the closed form of the reset put option price is
\begin{align*}
p_0 &= S_0 e^{-qT_1 -r(T_2-T_1)} N(a_1) N(-c_2) - S_0 e^{-qT_2} N(a_1) N(-c_1) \\
& \qquad + S_0 e^{-rT_2} N_2\left(-b_2, -a_2, \sqrt{\frac{T_1}{T_2}}\right) - S_0 e^{-qT_2} N_2\left(-b_1, -a_1, \sqrt{\frac{T_1}{T_2}}\right),
\end{align*}
where
\begin{align*}
& a_1 = \dfrac{(r-q+\frac{1}{2}\sigma^2)T_1}{\sigma\sqrt{T_1}}, a_2 = a_1 - \sigma\sqrt{T_1},\\
& b_1 = \dfrac{(r-q+\frac{1}{2}\sigma^2)T_2}{\sigma\sqrt{T_2}}, b_2 = b_1 - \sigma\sqrt{T_2}, \\
& c_1 = \dfrac{(r-q+\frac{1}{2}\sigma^2)(T_2-T_1)}{\sigma\sqrt{T_2-T_1}}, c_2 = c_1 - \sigma\sqrt{T_2-T_1}.
\end{align*}
```
def closed_form_option_price(S0, T1, T2, r, q, sigma):
a1 = ( (r - q + 0.5 * sigma**2) * T1 ) / (sigma * np.sqrt(T1))
a2 = ( (r - q - 0.5 * sigma**2) * T1 ) / (sigma * np.sqrt(T1))
b1 = ( (r - q + 0.5 * sigma**2) * T2 ) / (sigma * np.sqrt(T2))
b2 = ( (r - q - 0.5 * sigma**2) * T2 ) / (sigma * np.sqrt(T2))
c1 = ( (r - q + 0.5 * sigma**2) * (T2 - T1) ) / (sigma * np.sqrt(T2 - T1))
c2 = ( (r - q - 0.5 * sigma**2) * (T2 - T1) ) / (sigma * np.sqrt(T2 - T1))
rho = np.sqrt(T1 / T2)
Sigma = np.array(
[[1, rho],
[rho, 1]]
)
return (
S0 * np.exp(-q * T1 - r * (T2 - T1)) * norm.cdf(a1) * norm.cdf(-c2)
- S0 * np.exp(-q * T2) * norm.cdf(a1) * norm.cdf(-c1)
+ S0 * np.exp(-r * T2) * mvn.cdf(np.array([-b2, -a2]), mean = np.zeros(2), cov = Sigma)
- S0 * np.exp(-q * T2) * mvn.cdf(np.array([-b1, -a1]), mean = np.zeros(2), cov = Sigma)
)
print("Closed Form: ", closed_form_option_price(
S0 = 100,
T1 = 0.5,
T2 = 1,
r = 0.1,
q = 0.05,
sigma = 0.3)
)
```
## Sensitivity Analysis
Next, we can perform a sensitivity analysis on the exotic option and compare its valuation against a vanilla European put option.
```
def vanilla_price(S0, T, r, q, sigma):
d1 = ( (r - q + 0.5 * sigma**2) * T ) / (sigma * np.sqrt(T))
d2 = ( (r - q - 0.5 * sigma**2) * T ) / (sigma * np.sqrt(T))
return (
S0 * np.exp(-r * T) * norm.cdf(-d2)
- S0 * np.exp(- q * T) * norm.cdf(-d1)
)
```
### Reset Date
First, we perform sensitivity analysis on the reset date.
```
df = []
for T1 in np.linspace(0.0001,0.9999,50):
df.append([
T1,
closed_form_option_price(S0 = 100, T1 = T1,
T2 = 1, r = 0.1, q = 0.05, sigma = 0.3),
vanilla_price(S0 = 100, T = 1, r = 0.1, q = 0.05, sigma = 0.3)
])
df = pd.DataFrame(df, columns = ["Reset Date", "Reset Put Option", "Put Option"])
df = df.melt(id_vars = ["Reset Date"])
px.line(df, x = "Reset Date", y = "value", color = "variable",
labels = {"value" : "Price", "variable" : "Type"})
```
### Risk-Free Rate
Next, we perform sensitivity analysis on the risk-free rate.
```
df = []
for r in np.linspace(0,0.2,50):
df.append([
r,
closed_form_option_price(S0 = 100, T1 = 0.5,
T2 = 1, r = r, q = 0.05, sigma = 0.3),
vanilla_price(S0 = 100, T = 1, r = r, q = 0.05, sigma = 0.3)
])
df = pd.DataFrame(df, columns = ["Risk-Free Rate", "Reset Put Option", "Put Option"])
df = df.melt(id_vars = ["Risk-Free Rate"])
px.line(df, x = "Risk-Free Rate", y = "value", color = "variable",
labels = {"value" : "Price", "variable" : "Type"})
```
### Dividend Yield
Afterwards, we perform sensitivity analysis on the dividend yield.
```
df = []
for q in np.linspace(0,0.1,50):
df.append([
q,
closed_form_option_price(S0 = 100, T1 = 0.5,
T2 = 1, r = 0.1, q = q, sigma = 0.3),
vanilla_price(S0 = 100, T = 1, r = 0.1, q = q, sigma = 0.3)
])
df = pd.DataFrame(df, columns = ["Dividend Yield", "Reset Put Option", "Put Option"])
df = df.melt(id_vars = ["Dividend Yield"])
px.line(df, x = "Dividend Yield", y = "value", color = "variable",
labels = {"value" : "Price", "variable" : "Type"})
```
### Volatility
Finally, we perform sensitivity analysis on the volatility.
```
df = []
for sigma in np.linspace(0.0001,0.5,50):
df.append([
sigma,
closed_form_option_price(S0 = 100, T1 = 0.5,
T2 = 1, r = 0.1, q = 0.05, sigma = sigma),
vanilla_price(S0 = 100, T = 1, r = 0.1, q = 0.05, sigma = sigma)
])
df = pd.DataFrame(df, columns = ["Volatility", "Reset Put Option", "Put Option"])
df = df.melt(id_vars = ["Volatility"])
px.line(df, x = "Volatility", y = "value", color = "variable",
labels = {"value" : "Price", "variable" : "Type"})
```
|
github_jupyter
|
```
from pysead import Truss_2D
import numpy as np
from random import random
import matplotlib.pyplot as plt
# initialize node dictionary
nodes = {}
# compute distances
distances_1 = np.arange(0,5*240,240)
distances_2 = np.arange(0,9*120,120)
# from node 1 to node 5
for i, distance in enumerate(distances_1):
nodes.update({i+1: [distance, 360+144*10]})
# from node 6 to node 14
for i, distance in enumerate(distances_2):
nodes.update({i+6: [distance, 360+144*9]})
# from node 15 to node 19
for i, distance in enumerate(distances_1):
nodes.update({i+15: [distance, 360+144*8]})
# from node 20 to node 28
for i, distance in enumerate(distances_2):
nodes.update({i+20: [distance, 360+144*7]})
# from node 29 to node 33
for i, distance in enumerate(distances_1):
nodes.update({i+29: [distance, 360+144*6]})
# from node 34 to node 42
for i, distance in enumerate(distances_2):
nodes.update({i+34: [distance, 360+144*5]})
# from node 43 to node 47
for i, distance in enumerate(distances_1):
nodes.update({i+43: [distance, 360+144*4]})
# from node 48 to node 56
for i, distance in enumerate(distances_2):
nodes.update({i+48: [distance, 360+144*3]})
# from node 57 to node 61
for i, distance in enumerate(distances_1):
nodes.update({i+57: [distance, 360+144*2]})
# from node 62 to node 70
for i, distance in enumerate(distances_2):
nodes.update({i+62: [distance, 360+144*1]})
# from node 71 to node 75
for i, distance in enumerate(distances_1):
nodes.update({i+71: [distance, 360]})
nodes.update({76:[240,0], 77:[120*6,0]})
elements = {1:[1,2], 2:[2,3], 3:[3,4], 4:[4,5],
5:[6,1], 6:[7,1], 7:[7,2], 8:[8,2], 9:[9,2], 10:[9,3], 11:[10,3], 12:[11,3], 13:[11,4], 14:[12,4], 15:[13,4], 16:[13,5], 17:[14,5],
18:[6,7], 19:[7,8], 20:[8,9], 21:[9,10], 22:[10,11], 23:[11,12], 24:[12,13], 25:[13,14],
26:[15,6], 27:[15,7], 28:[16,7], 29:[16,8], 30:[16,9], 31:[17,9], 32:[17,10], 33:[17,11], 34:[18,11], 35:[18,12], 36:[18,13], 37:[19,13], 38:[19,14],
39:[15,16], 40:[16,17], 41:[17,18], 42:[18,19],
43:[20,15], 44:[21,15], 45:[21,16], 46:[22,16], 47:[23,16], 48:[23,17], 49:[24,17], 50:[25,17], 51:[25,18], 52:[26,18], 53:[27,18], 54:[27,19], 55:[28,19],
56:[20,21], 57:[21,22], 58:[22,23], 59:[23,24], 60:[24,25], 61:[25,26], 62:[26,27], 63:[27,28],
64:[29,20], 65:[29,21], 66:[30,21], 67:[30,22], 68:[30,23], 69:[31,23], 70:[31,24], 71:[31,25], 72:[32,25], 73:[32,26], 74:[32,27], 75:[33,27], 76:[33,28],
77:[29,30], 78:[30,31], 79:[31,32], 80:[32,33],
81:[34,29], 82:[35,29], 83:[35,30], 84:[36,30], 85:[37,30], 86:[37,31], 87:[38,31], 88:[39,31], 89:[39,32], 90:[40,32], 91:[41,32], 92:[41,33], 93:[42,33],
94:[34,35], 95:[35,36], 96:[36,37], 97:[37,38], 98:[38,39], 99:[39,40], 100:[40,41], 101:[41,42],
102:[43,34], 103:[43,35], 104:[44,35], 105:[44,36], 106:[44,37], 107:[45,37], 108:[45,38], 109:[45,39], 110:[46,39], 111:[46,40], 112:[46,41], 113:[47,41], 114:[47,42],
115:[43,44], 116:[44,45], 117:[45,46], 118:[46,47], 119:[48,43], 120:[49,43], 121:[49,44], 122:[50,44], 123:[51,44], 124:[51,45], 125:[52,45], 126:[53,45], 127:[53,46], 128:[54,46], 129:[55,46], 130:[55,47], 131:[56,47],
132:[48,49], 133:[49,50], 134:[50,51], 135:[51,52], 136:[52,53], 137:[53,54], 138:[54,55], 139:[55,56], 140:[57,48], 141:[57,49], 142:[58,49], 143:[58,50], 144:[58,51], 145:[59,51], 146:[59,52], 147:[59,53], 148:[60,53], 149:[60,54], 150:[60,55], 151:[61,55], 152:[61,56],
153:[57,58], 154:[58,59], 155:[59,60], 156:[60,61],
157:[62,57], 158:[63,57], 159:[63,58], 160:[64,58], 161:[65,58], 162:[65,59], 163:[66,59], 164:[67,59], 165:[67,60], 166:[68,60], 167:[69,60], 168:[69,61], 169:[70,61],
170:[62,63], 171:[63,64], 172:[64,65], 173:[65,66], 174:[66,67], 175:[67,68], 176:[68,69], 177:[69,70],
178:[71,62], 179:[71,63], 180:[72,63], 181:[72,64], 182:[72,65], 183:[73,65], 184:[73,66], 185:[73,67], 186:[74,67], 187:[74,68], 188:[74,69], 189:[75,69], 190:[75,70],
191:[71,72], 192:[72,73], 193:[73,74], 194:[74,75],
195:[76,71], 196:[76,72], 197:[76,73], 198:[77,73], 199:[77,74], 200:[77,75]}
supports = {76:[1,1], 77:[1,1]}
elasticity = {key: 30_000 for key in elements}
forces = {key: [0,-10] for key in [1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 15, 16, 17, 18, 19, 20, 22, 24, 26, 28, 29, 30, 31, 32, 33, 34, 36, 38, 40, 42, 43, 44, 45, 46, 47, 48, 50, 52, 54, 56, 57, 58, 59, 60, 61, 62, 64, 66, 68, 70, 71,72, 73, 74,75]}
forces.update({key: [1,-10] for key in [1,6,15,20,29,34,43,48,57,62,71]})
def Truss_solver(cross_sectional_areas):
cross_area = {key: cross_sectional_areas[key - 1] for key in elements}
Two_Hundred_Truss_Case_1 = Truss_2D(nodes = nodes,
elements= elements,
supports= supports,
forces = forces,
elasticity= elasticity,
cross_area= cross_area)
Two_Hundred_Truss_Case_1.Solve()
return (Two_Hundred_Truss_Case_1.member_lengths_, Two_Hundred_Truss_Case_1.member_stresses_, Two_Hundred_Truss_Case_1.displacements_)
```
## Step 2: Define Objective Function
```
def Objective_Function(areas):
member_lengths, member_stresses, node_displacements = Truss_solver(areas)
total_area = np.array(areas)
total_member_lengths = []
for length in member_lengths:
total_member_lengths.append(member_lengths[length])
total_member_lengths = np.array(total_member_lengths)
weight = total_area.dot(np.array(total_member_lengths))
weight = weight.sum() * 0.283 # lb/in^3
return (weight, member_stresses, node_displacements)
```
## Step 3: Define Constraints
```
def stress_constraint(stress_new):
if stress_new > 30 or stress_new < -30:
stress_counter = 1
else:
stress_counter = 0
return stress_counter
def displacement_constraint(node_displacement_new):
x = node_displacement_new[0]
y = node_displacement_new[1]
if x > 0.5 or x < -0.5:
displacement_counter = 1
elif y > 0.5 or y < -0.5:
displacement_counter = 1
else:
displacement_counter = 0
return displacement_counter
```
Step 4: Define Algorithm
Step 4.1: Initialize Parameters
```
D = [0.100, 0.347, 0.440, 0.539, 0.954, 1.081, 1.174, 1.333, 1.488,
1.764, 2.142, 2.697, 2.800, 3.131, 3.565, 3.813, 4.805, 5.952, 6.572,
7.192, 8.525, 9.300, 10.850, 13.330, 14.290, 17.170, 19.180, 23.680,
28.080, 33.700]
def closest(list_of_areas, area_values_list):
for i, area_value in enumerate(area_values_list):
idx = (np.abs(list_of_areas - area_value)).argmin()
area_values_list[i] = list_of_areas[idx]
return area_values_list
cross_area_groupings = {1:[1,4], 2:[2,3], 3:[5,17], 4:[6,16], 5:[7,15], 6:[8,14], 7:[9,13], 8:[10,12], 9:[11], 10:[132,139,170,177,18,25,56,63],
11:[19,20,23,24], 12:[21,22], 13:[26,38], 14:[27,37], 15:[28,36], 16:[29,35], 17:[30,34], 18:[31,33], 19:[32], 20:[39,42],
21:[40,41], 22:[43,55], 23:[44,54], 24:[45,53], 25:[46,52], 26:[47,51], 27:[48,50], 28:[49], 29:[57,58,61,62], 30:[59,60],
31:[64,76], 32:[65,75], 33:[66,74], 34:[67,73], 35:[68,72], 36:[69,71], 37:[70], 38:[77,80], 39:[78,79], 40:[81,93],
41:[82,92], 42:[83,91], 43:[84,90], 44:[85,89], 45:[86,88], 46:[87], 47:[95,96,99,100], 48:[97,98], 49:[102,114], 50:[103,113],
51:[104,112], 52:[105,111], 53:[106,110], 54:[107, 109], 55:[108], 56:[115,118], 57:[116,117], 58:[119,131], 59:[120,130], 60:[121,129],
61:[122,128], 62:[123,127], 63:[124,126], 64:[125], 65:[133,134,137,138], 66:[135,136], 67:[140,152], 68:[141,151], 69:[142,150], 70:[143,149],
71:[144,148], 72:[145,147], 73:[146], 74:[153,156], 75:[154,155], 76:[157,169], 77:[158,168], 78:[159,167], 79:[160,166], 80:[161,165],
81:[162,164], 82:[163], 83:[171,172,175,176], 84:[173,174], 85:[178,190], 86:[179,189], 87:[180,188], 88:[181,187], 89:[182,186], 90:[183,185],
91:[184], 92:[191,194], 93:[192,193], 94:[195,200], 95:[196,199], 96:[197,198], 97:[94,101]}
area_old = [35 for i in range(len(elements))]
# intermediate variables
k = 0.05 # move variable's constant
M = 1000 # number of loops to be performed
T0 = 10000 # initial temperature
N = 20 # initial number of neighbors per search space loop
alpha = 0.85 # cooling parameter
temp = [] # storing of values for the temperature per loop M
min_weight = [] # storing best value of the objective function per loop M
area_list = [] # storing x values per loop for plotting purposes
def Random_Number_Check(objective_old, objective_new, Init_temp):
return 1/((np.exp(objective_old - objective_new)) / Init_temp)
%%time
for m in range(M):
for n in range(N):
# generate random area from choices
# create random area array from area choices
area_random_array = np.random.choice(D,len(cross_area_groupings))
# create dictionary from random array
cross_area_dict = {key+1: area_random_array[key] for key in range(len(area_random_array))}
# create dictionary from cross area dictionary that follows the groupings dictionary
cross_area = {}
for group in cross_area_groupings:
value = cross_area_dict[group]
for element in cross_area_groupings[group]:
dict_append = {element: value}
cross_area.update(dict_append)
# Sort the cross area groupings dictionary in asending order
cross_area = {k: v for k, v in sorted(cross_area.items(), key=lambda item: item[0])}
# flatten the cross area groupings dictionary to a list
area_new = []
for area in cross_area:
area_new.append(cross_area[area])
area_new = np.array(area_new)
for i,area in enumerate(area_old):
random_area = random()
if random_area >= 0.5:
area_new[i] = k*random_area
else:
area_new[i] = -k*random_area
for i, area in enumerate(area_old):
area_new[i] = area_old[i] + area_new[i]
closest(D,area_new)
weight_computed, stresses_new, node_displacement_new = Objective_Function(area_new)
weight_old, _, _ = Objective_Function(area_old)
check = Random_Number_Check(weight_computed, weight_old, T0)
random_number = random()
# Contraint 1: stresses should be within 25ksi and -25ksi
stress_counter = []
for j in stresses_new:
stress_counter.append(stress_constraint(stresses_new[j]))
stress_counter = sum(stress_counter)
# Constraint 2: Node Displacement should be limited to -2in and 2in
displacement_counter = 0
for k in node_displacement_new:
displacement_counter = displacement_counter + displacement_constraint(node_displacement_new[k])
if stress_counter >= 1 or displacement_counter >= 1:
area_old = area_old
else:
if weight_computed <= weight_old:
area_old = area_new
elif random_number <= check:
area_old = area_new
else:
area_old = area_old
temp.append(T0)
min_weight.append(weight_old)
area_list.append(area_old)
T0 = alpha * T0
plt.figure(figsize=[12,6])
plt.grid(True)
plt.xlabel('Iterations')
plt.ylabel('Weight')
plt.title('Iterations VS Weight')
plt.plot(min_weight)
area_list[-1]
cross_area = {key: area_list[-1][key-1] for key in elements}
Two_Hundred_Truss_Case_1 = Truss_2D(nodes = nodes,
elements= elements,
supports= supports,
forces = forces,
elasticity= elasticity,
cross_area= cross_area)
Two_Hundred_Truss_Case_1.Solve()
Two_Hundred_Truss_Case_1.Draw_Truss_Displacements(figure_size=[15,25])
Two_Hundred_Truss_Case_1.displacements_
weight, _, _ = Objective_Function(area_list[-1])
weight
```
|
github_jupyter
|
```
import os
import sys
import keras
import numpy as np
import tensorflow as tf
from keras import datasets
import matplotlib
import matplotlib.pyplot as plt
sys.path.append(os.getcwd() + "/../")
from bfcnn import BFCNN, collage, get_conv2d_weights
# setup environment
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
tf.compat.v1.disable_eager_execution()
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)
# get dataset
(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
x_train = x_train.astype(np.float32)
x_train = np.expand_dims(x_train, axis=3)
x_test = x_test.astype(np.float32)
x_test = np.expand_dims(x_test, axis=3)
EPOCHS = 10
FILTERS = 32
NO_LAYERS = 5
MIN_STD = 1.0
MAX_STD = 100.0
LR_DECAY = 0.9
LR_INITIAL = 0.1
BATCH_SIZE = 64
CLIP_NORMAL = 1.0
INPUT_SHAPE = (28, 28, 1)
PRINT_EVERY_N_BATCHES = 2000
# build model
model = \
BFCNN(
input_dims=INPUT_SHAPE,
no_layers=NO_LAYERS,
filters=FILTERS,
kernel_regularizer=keras.regularizers.l2(0.001))
# train dataset
trained_model, history = \
BFCNN.train(
model=model,
input_dims=INPUT_SHAPE,
dataset=x_train,
epochs=EPOCHS,
batch_size=BATCH_SIZE,
min_noise_std=MIN_STD,
max_noise_std=MAX_STD,
lr_initial=LR_INITIAL,
lr_decay=LR_DECAY,
print_every_n_batches=PRINT_EVERY_N_BATCHES)
matplotlib.use("nbAgg")
# summarize history for loss
plt.figure(figsize=(15,5))
plt.plot(history.history["loss"],
marker="o",
color="red",
linewidth=3,
markersize=6)
plt.grid(True)
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train"], loc="upper right")
plt.show()
from math import log10
# calculate mse for different std
sample_test = x_test[0:1024,:,:,:]
sample_test_mse = []
sample_train = x_train[0:1024,:,:,:]
sample_train_mse = []
sample_std = []
for std_int in range(0, int(MAX_STD), 5):
std = float(std_int)
#
noisy_sample_test = sample_test + np.random.normal(0.0, std, sample_test.shape)
noisy_sample_test = np.clip(noisy_sample_test, 0.0, 255.0)
results_test = trained_model.model.predict(noisy_sample_test)
mse_test = np.mean(np.power(sample_test - results_test, 2.0))
sample_test_mse.append(mse_test)
#
noisy_sample_train = sample_train + np.random.normal(0.0, std, sample_train.shape)
noisy_sample_train = np.clip(noisy_sample_train, 0.0, 255.0)
results_train = trained_model.model.predict(noisy_sample_train)
mse_train = np.mean(np.power(sample_train - results_train, 2.0))
sample_train_mse.append(mse_train)
#
sample_std.append(std)
matplotlib.use("nbAgg")
# summarize history for loss
plt.figure(figsize=(16,8))
plt.plot(sample_std,
[20 * log10(255) -10 * log10(m) for m in sample_test_mse],
color="red",
linewidth=2)
plt.plot(sample_std,
[20 * log10(255) -10 * log10(m) for m in sample_train_mse],
color="green",
linewidth=2)
plt.grid(True)
plt.title("Peak Signal-to-Noise Ratio")
plt.ylabel("PSNR")
plt.xlabel("Additive normal noise standard deviation")
plt.legend(["test", "train"], loc="lower right")
plt.show()
# draw test samples, predictions and diff
matplotlib.use("nbAgg")
sample = x_test[0:64,:,:,:]
noisy_sample = sample + np.random.normal(0.0, MAX_STD, sample.shape)
noisy_sample = np.clip(noisy_sample, 0.0, 255.0)
results = trained_model.model.predict(noisy_sample)
plt.figure(figsize=(14,14))
plt.subplot(2, 2, 1)
plt.imshow(collage(sample), cmap="gray_r")
plt.subplot(2, 2, 2)
plt.imshow(collage(noisy_sample), cmap="gray_r")
plt.subplot(2, 2, 3)
plt.imshow(collage(results), cmap="gray_r")
plt.subplot(2, 2, 4)
plt.imshow(collage(np.abs(sample - results)), cmap="gray_r")
plt.show()
trained_model.save("./model.h5")
m = trained_model.model
weights = get_conv2d_weights(m)
matplotlib.use("nbAgg")
plt.figure(figsize=(14,5))
plt.grid(True)
plt.hist(x=weights, bins=500, range=(-0.4,+0.4), histtype="bar", log=True)
plt.show()
```
|
github_jupyter
|
### OkCupid DataSet: Classify using combination of text data and metadata
### Meeting 5, 03- 03- 2020
### Recap last meeting's decisions:
<ol>
<p>Meeting 4, 28- 01- 2020</p>
<li> Approach 1: </li>
<ul>
<li>Merge classs 1, 3 and 5</li>
<li>Under sample class 6 </li>
<li> Merge classes 6, 7, 8</li>
</ul>
<li> Approach 2:</li>
<ul>
<li>Merge classs 1, 3 and 5 as class 1</li>
<li> Merge classes 6, 7, 8 as class 8</li>
<li>Under sample class 8 </li>
</ul>
<li> collect metadata: </li>
<ul>
<li> Number of misspelled </li>
<li> Number of unique words </li>
<li> Avg no wordlength </li>
</ul>
</ol>
## Education level summary
<ol>
<p></p>
<img src="rep2_image/count_diag.JPG">
</ol>
<ol>
<p></p>
<img src="rep2_image/count_table.JPG">
</ol>
## Logistic regression after removing minority classes and undersampling
<ol>
<p></p>
<img src="rep2_image/log1.JPG">
</ol>
## Merge levels:
- Merge classs 1, 3 and 5 as class 1
- Merge classes 6, 7, 8 as class 8
- weight classes while classifying using Logistic regression
<ol>
<p></p>
<img src="rep2_image/count_table2.JPG">
</ol>
<ol>
<p></p>
### Logistic regression with undersampling
<img src="rep2_image/log_undersampling.JPG">
</ol>
<ol>
<p></p>
### Logistic regression with weighting
<img src="rep2_image/log_weight.JPG">
</ol>
### Add metadata to the dataset
```
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score
from sklearn.multiclass import OneVsRestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.feature_extraction.text import TfidfVectorizer
import seaborn as sns
from sklearn.metrics import classification_report
from sklearn.preprocessing import StandardScaler
from sklearn import preprocessing
from sklearn.preprocessing import FunctionTransformer
from sklearn.pipeline import Pipeline
from sklearn.multiclass import OneVsRestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import FeatureUnion
from collections import Counter
from sklearn.naive_bayes import MultinomialNB
import numpy as np
import itertools
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.utils import resample
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0])
, range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
df = pd.read_csv (r'../../../data/processed/stylo_cupid2.csv')
df.columns
# import readability
# from tqdm._tqdm_notebook import tqdm_notebook
# tqdm_notebook.pandas()
# def text_readability(text):
# results = readability.getmeasures(text, lang='en')
# return results['readability grades']['FleschReadingEase']
# df['readability'] = df.progress_apply(lambda x:text_readability(x['text']), axis=1)
df.head()
# Read metadata dataset to dataframe
# df = pd.read_csv (r'../../../data/processed/stylo_cupid2.csv')
df['sex'].mask(df['sex'].isin(['m']) , 0.0, inplace=True)
df['sex'].mask(df['sex'].isin(['f']) , 1.0, inplace=True)
# print(df['sex'].value_counts())
df['isced'].mask(df['isced'].isin([3.0, 5.0]) , 1.0, inplace=True)
df['isced'].mask(df['isced'].isin([6.0, 7.0]) , 8.0, inplace=True)
# # Separate majority and minority classes
# df_majority = df[df.isced==8.0]
# df_minority = df[df.isced==1.0]
# # Downsample majority class
# df_majority_downsampled = resample(df_majority,
# replace=False, # sample without replacement
# n_samples=10985, # to match minority class
# random_state=123) # reproducible results
# # Combine minority class with downsampled majority class
# df = pd.concat([df_majority_downsampled, df_minority])
print(sorted(Counter(df['isced']).items()))
df = df.dropna(subset=['clean_text', 'isced'])
corpus = df[['clean_text', 'count_char','count_word', '#anwps', 'count_punct', 'avg_wordlength', 'count_misspelled', 'word_uniqueness', 'age', 'sex']]
target = df["isced"]
# vectorization
X_train, X_val, y_train, y_val = train_test_split(corpus, target, train_size=0.75, stratify=target,
test_size=0.25, random_state = 0)
get_text_data = FunctionTransformer(lambda x: x['clean_text'], validate=False)
get_numeric_data = FunctionTransformer(lambda x: x[['count_char','count_word', '#anwps', 'count_punct', 'avg_wordlength', 'count_misspelled', 'word_uniqueness', 'age', 'sex']], validate=False)
# Solver = lbfgs
# merge vectorized text data and scaled numeric data
process_and_join_features = Pipeline([
('features', FeatureUnion([
('numeric_features', Pipeline([
('selector', get_numeric_data),
('scaler', preprocessing.StandardScaler())
])),
('text_features', Pipeline([
('selector', get_text_data),
('vec', CountVectorizer(binary=False, ngram_range=(1, 2), lowercase=True))
]))
])),
('clf', LogisticRegression(random_state=0,max_iter=1000, solver='lbfgs', penalty='l2', class_weight='balanced'))
])
# merge vectorized text data and scaled numeric data
process_and_join_features.fit(X_train, y_train)
predictions = process_and_join_features.predict(X_val)
print("Final Accuracy for Logistic: %s"% accuracy_score(y_val, predictions))
cm = confusion_matrix(y_val,predictions)
plt.figure()
plot_confusion_matrix(cm, classes=[0,1], normalize=False,
title='Confusion Matrix')
print(classification_report(y_val, predictions))
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
# scores = cross_val_score(process_and_join_features, X_train, y_train, cv=5)
# print(scores)
# print(scores.mean())
process_and_join_features.fit(X_train, y_train)
y_pred = cross_val_predict(process_and_join_features, corpus, target, cv=5)
conf_mat = confusion_matrix(target, y_pred)
print(conf_mat)
from sklearn.model_selection import cross_val_score, cross_val_predict
scores = cross_val_score(process_and_join_features, corpus, target, cv=5)
print(scores)
print(scores.mean())
from sklearn.model_selection import cross_val_score, cross_val_predict
scores = cross_val_score(process_and_join_features, corpus, target, cv=5)
print(scores)
print(scores.mean())
# Solver = sag
# merge vectorized text data and scaled numeric data
process_and_join_features = Pipeline([
('features', FeatureUnion([
('numeric_features', Pipeline([
('selector', get_numeric_data),
('scaler', preprocessing.StandardScaler())
])),
('text_features', Pipeline([
('selector', get_text_data),
('vec', CountVectorizer(binary=False, ngram_range=(1, 2), lowercase=True))
]))
])),
('clf', LogisticRegression(random_state=0,max_iter=5000, solver='sag', penalty='l2', class_weight='balanced'))
])
#
process_and_join_features.fit(X_train, y_train)
predictions = process_and_join_features.predict(X_val)
print("Final Accuracy for Logistic: %s"% accuracy_score(y_val, predictions))
cm = confusion_matrix(y_val,predictions)
plt.figure()
plot_confusion_matrix(cm, classes=[0,1], normalize=False,
title='Confusion Matrix')
print(classification_report(y_val, predictions))
# Solver='saga'
# merge vectorized text data and scaled numeric data
process_and_join_features = Pipeline([
('features', FeatureUnion([
('numeric_features', Pipeline([
('selector', get_numeric_data),
('scaler', preprocessing.StandardScaler())
])),
('text_features', Pipeline([
('selector', get_text_data),
('vec', CountVectorizer(binary=False, ngram_range=(1, 2), lowercase=True))
]))
])),
('clf', LogisticRegression(n_jobs=-1, random_state=0,max_iter=3000, solver='saga', penalty='l2', class_weight='balanced'))
])
#
process_and_join_features.fit(X_train, y_train)
predictions = process_and_join_features.predict(X_val)
print("Final Accuracy for Logistic: %s"% accuracy_score(y_val, predictions))
cm = confusion_matrix(y_val,predictions)
plt.figure()
plot_confusion_matrix(cm, classes=[0,1], normalize=False,
title='Confusion Matrix')
print(classification_report(y_val, predictions))
```
|
github_jupyter
|
# Task 4: Classification
_All credit for the code examples of this notebook goes to the book "Hands-On Machine Learning with Scikit-Learn & TensorFlow" by A. Geron. Modifications were made and text was added by K. Zoch in preparation for the hands-on sessions._
# Setup
First, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Function to save a figure. This also decides that all output files
# should stored in the subdirectorz 'classification'.
PROJECT_ROOT_DIR = "."
EXERCISE = "classification"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "output", EXERCISE, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# Preparing the dataset
Define a function to sort the dataset into the 'targets' train and test data. This is needed because we want to use the same 60,000 data points for training, and the sam e10,000 data points for testing on every machine (and the dataset provided through Scikit-Learn is already prepared in this way).
```
def sort_by_target(mnist):
reorder_train = np.array(sorted([(target, i) for i, target in enumerate(mnist.target[:60000])]))[:, 1]
reorder_test = np.array(sorted([(target, i) for i, target in enumerate(mnist.target[60000:])]))[:, 1]
mnist.data[:60000] = mnist.data[reorder_train]
mnist.target[:60000] = mnist.target[reorder_train]
mnist.data[60000:] = mnist.data[reorder_test + 60000]
mnist.target[60000:] = mnist.target[reorder_test + 60000]
```
Now fetch the dataset using the SciKit-Learn function (this might take a moment ...).
```
# We need this try/except for different Scikit-Learn versions.
try:
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, cache=True)
mnist.target = mnist.target.astype(np.int8) # fetch_openml() returns targets as strings
sort_by_target(mnist) # fetch_openml() returns an unsorted dataset
except ImportError:
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')
mnist["data"], mnist["target"]
```
Let's have a look at what the 'data' key contains: it is a numpy array with one row per instance and one column per feature.
```
mnist["data"]
```
And the same for the 'target' key which is an array of labels.
```
mnist["target"]
```
Now, let's first define the more useful `x` and `y` aliases for the data and target keys, and let's have a look at the type of data using the `shape` function: we see 70,000 entries in the data array, with 784 features each. The 784 correspond to 28x28 pixels of an image with brightness values between 0 and 255.
```
X, y = mnist["data"], mnist["target"]
X.shape # get some information about its shape
28*28 # just a little cross-check we're doing the correct arithmetics here ...
X[36000][160:200] # Plot brightness values [160:200] of the random image X[36000].
```
Now let's have a look at one of the images. We just pick a random image and use the `numpy.reshape()` function to reshape it into an array of 28x28 pixels. Then we can plot it with `matplotlib.pyplot.imshow()`:
```
some_digit = X[36000]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap = mpl.cm.binary,
interpolation="nearest")
plt.axis("off")
save_fig("some_digit_plot")
plt.show()
```
Let's quickly define a function to plot one of the digits, we will need it later down the line. It might also be useful to have a function to plot multiple digits in a batch (we will also use this function later). The following two cells will not produce any output.
```
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.binary,
interpolation="nearest")
plt.axis("off")
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = mpl.cm.binary, **options)
plt.axis("off")
```
Great, now we can plot multiple digits at once. Let's ignore the details of the `np.r_[]` function and the indexing used within it for now and focus on what it does: it takes ten examples of each digit from the data array, which we can then plot with our `plot_digits()` function.
```
plt.figure(figsize=(9,9))
example_images = np.r_[X[:12000:600], X[13000:30600:600], X[30600:60000:590]]
plot_digits(example_images, images_per_row=10)
save_fig("more_digits_plot")
plt.show()
```
Ok, at this point we have a fairly good idea how our data array looks like: we have an array of 70,000 images with 28x28 pixels each. The entries in the array are sorted according to ascending digits, i.e. it starts with images of zeros and ends with images of nines at entry 59,999. Entries `x[60000:]` onwards are meant to be used for testing and again contain images of all digits in ascending order.
Before starting with binary classification, let's quickly confirm that the labels stored in `y` actually make sense. We previously looked at entry `X[36000]` and it looked like a five. Does `y[36000]` say the same?
```
y[36000]
```
Good! As a very last step, let's split train and test and store them separately. Because we also don't want our training to be biased, we should shuffle the entries randomly (i.e. not sort them in ascending order anymore). We can do this with the `np.random.permutation(60000)` function which returns a random permutation of the numbers between zero and 60,000.
```
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
import numpy as np
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
```
# Binary classifier
Before going towards a classifier, which can distinguish _all_ digits, let's start with something simple. Since our random digit `X[36000]` was a five, why not design a classifier that can distinguish fives from other digits? Let's first rewrite our labels from integers to booleans:
```
y_train_5 = (y_train == 5) # an array of booleans which is 'True' whenever y_train is == 5
y_test_5 = (y_test == 5)
y_train_5 # let's look at the array
```
A good model for the classification is the Stochastic Gradient Descent that was introduced in the lecture. Conveniently, Skiki-Learn already has such a classifier implemented, so let's import it and give it our training data `X_train` with the true labels `y_train_5`.
```
from sklearn.linear_model import SGDClassifier
# SDG relies on randomness, but by fixing the `random_state` we can get reproducible results.
# The other values are just to avoid a warning issued by Skikit-Learn ...
sgd_clf = SGDClassifier(random_state=42, max_iter=5, tol=-np.infty)
sgd_clf.fit(X_train, y_train_5)
```
If the training of the classifier was successful, it should be able to predict the label of our example instance `X[36000]` correctly.
```
sgd_clf.predict([some_digit])
```
That's good, but it doesn't really give us an idea about the overall performance of the classifier. One good measure for this introduced in the lecture is the cross-validation score. In k-fold cross-validation, the training data is split into k equal subsets. Then the classifier is trained on k-1 sets and evaluated on set k. It's called cross-validation, because this is done for all k possible (and non-redundant) permutations. In case of a 3-fold, this means we train on subsets 1 and 2 and validated on 3, train on 1 and 3 and validate on 2, and train on 2 and 3 and validate on 1. The _score_ represents the prediction accuracy on the validation fold.
```
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
```
While these numbers seem amazingly good, keep in mind, that only 10% of our training data are images of fives, so even a classifier which always predicts 'not five' would reach an accuracy of about 90% ...
In the following box, maybe you can try to implement the cross validation yourself! The `StratifiedKFold` creates k non-biased subsets of the training data. The input to the `StratifiedKFold.split(X, y)` are the training data `X` (in our case called `X_train`) and the labels (in our case for the five-classifier `y_train_5`). The `sklearn.base.clone` function will help to make a copy of the classifier object.
```
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_indices, test_indices in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf) # make a clone of the classifier
# [...] some code is missing here
X_train_folds = X_train[train_indices]
y_train_folds = y_train_5[train_indices]
clone_clf.fit(X_train_folds, y_train_folds)
X_test_fold = X_train[test_indices]
y_test_fold = y_train_5[test_indices]
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print("Fraction of correct predictions: %s" % (n_correct / len(y_pred)))
```
Let's move on to another performance measure: the confusion matrix. The confusion matrix is a 2x2 matrix and includes the number of true positives, false positives (type-I error), true negatives and false negatives (type-II error). First, let's use another of Scitkit-Learn's functions: `cross_val_predict` takes our classifier, our training data and our true labels, and automatically performs a k-fold cross-validation. It returns an array of the predicted labels.
```
from sklearn.model_selection import cross_val_predict
# Take our SGD classifer and perform a 3-fold cross-validation.
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
# Print some of the predicted labels.
print(y_train_pred)
```
Using cross-validation always gives us a 'clean', i.e. unbiased estimate of our prediction power, because the performance of the classifier is evaluated on data it hadn't seen during training. Now we have our predicted labels in `y_train_pred` and can compare them to the true labels `y_train_5`. So let's create a confusion matrix.
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
```
How do we read this? The rows correspond to the _true_ classes, the columns to the _predicted_ classes. So the 53,272 means that about fifty-three thousand numbers that are 'not five' were predicted as such, while 1307 were predicted to be fives. 4344 true fives were predicted to be fives, but 1077 were not. Sometimes it makes sense to normalise the confusion matrix by rows, so that the values in the cells give an idea how large the _fraction_ of correctly and incorrectly predicted instances is. So let's try this:
```
matrix = confusion_matrix(y_train_5, y_train_pred)
row_sums = matrix.sum(axis=1)
matrix / row_sums[:, np.newaxis]
```
There are other metrics to evaluate the performance of classifiers as we saw in the lecture. One example is the _precision_ which is the rate of true positives among all positives. The precision is a measure how many of our predicted positives are _actually_ positives, i.e. it can be calculated as TP / (TP + FP) (TP = true positives, FP = false positives).
```
from sklearn.metrics import precision_score, recall_score
print(precision_score(y_train_5, y_train_pred))
# Can you reproduce this value by hand? All info should be in the confusion matrix.
tp = matrix[1][1]
fp = matrix[0][1]
precision_by_hand = tp / (tp + fp)
print("By hand: %s" % precision_by_hand)
```
Or in words: 77% of our predicted fives are _actually_ fives, while 23% of the predicted fives are other numbers.
Another metric, which is often used in conjunction with the _precision_, is the _recall_. The recall is a measure of how many of the true positives as predicted as such, i.e. "how many true positives do we identify". It is easy to reach perfect precision if you just make your classifier reject all negatives, but it's impossible to keep a high recall score in that case. Let's look at our classifier's recall:
```
print(recall_score(y_train_5, y_train_pred))
# Again, it should be straight-forward to make this calculation by hand. Can you try?
tp = matrix[1][1]
fn = matrix[1][0]
recall_by_hand = tp / (tp + fn)
print("By hand: %s" % recall_by_hand)
```
In words: only 80% of the fives are correctly predicted to be fives. Doesn't look as great as the 95% prediction rate, does it? A nice combination for precision and recall is their harmonic mean, usually known (and in the lecture introduced as) the _F_1 score_. The harmonic mean (as opposed to the arithmetic mean) is very sensitive low values, so only a good balance between precision and recall will lead to a high F_1 score. Very conveniently, Scikit-Learn comes with an implementation of the score already, but can you also calculate it by hand?
```
from sklearn.metrics import f1_score
print(f1_score(y_train_5, y_train_pred))
# Once more, it is fairly easy to calculate this by hand. Give it a try!
f1_score_by_hand = 2 / (1/precision_by_hand + 1/recall_by_hand)
print("By hand: %s" % f1_score_by_hand)
```
Of course, a balanced precision and recall is not _always_ desirable. Whether you want both to be equally high, depends on the use case. Sometimes, you'd definitely want to classify as many true positives as such, with the tradeoff to have low precision (example: in a test for a virus you want every true positive to know that they might be infected, but you might get a few false positives). In other cases, you might want a high precision with the tradeoff that you don't detect all positives as such (example: it's ok to remove some harmless videos in a video filter, but you don't want harmful content to pass your filter).
## Decision function
When we use the `predict()` function, our classifier gives a boolean prediction. But how is that prediction done? The classifier calculates a score, called 'decision_function' in Scikit-Learn, and any instance above a certain threshold is classified as 'true', any instance below as 'false'. By retrieving the decision function directly, we can look at different tradeoffs between precision and recall.
```
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
method="decision_function")
print(y_scores) # Print scores to get an idea ...
```
This again gives us a numpy array with 60,000 entries, all of which contain a floating point value with the predicted score. Now, as we've seen before, Scikit-Learn provides many functions out-of-the-box to evaluate classifiers. The following `precision_recall_curve` metric gives us tuples of precision, recall and threshold values based on our training data. It takes the true labels, in our case `y_train_5` and the `y_scores` to calculate these. We can then use thes values to plot curves for precision and recall for different threshold values.
```
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
print(precisions)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.xlabel("Threshold", fontsize=16)
plt.legend(loc="upper left", fontsize=16)
plt.ylim([0, 1])
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
save_fig("precision_recall_vs_threshold_plot")
plt.show()
```
Looks good! Bonus question: why is the precision curve bumpier than the recall?
Let's assume we want to optimise our classfier for a precision value of 93%. Can you find a good threshold? The below threshold is just a test value and definitely too low.
```
threshold = -20000
y_train_pred_93 = (y_scores > threshold)
print("precision: %s" % precision_score(y_train_5, y_train_pred_93))
print("recall: %s" % recall_score(y_train_5, y_train_pred_93))
```
Sometimes, plotting precision vs. recall can also be helpful.
```
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
save_fig("precision_vs_recall_plot")
plt.show()
```
# ROC curves
Because it's an extremely common performance measure, we should also have a look at the ROC curve (_receiver operating characteristic_). ROC curves plot true positives vs. false positives, or usually the true positive _rate_ vs. the false positive _rate_. While the first is exactly what we called _recall_ so far, the latter is one minus the _true negative rate_, also called specificity. Let's import the ROC curve from Scikit-Learn, this will give us tuples of FPR, TPR and threshold values again.
```
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
```
Now we can plot them:
```
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
save_fig("roc_curve_plot")
plt.show()
```
It is always desirable to have the curve as close to the top left corner as above. As a measure for this, one usually calculates the _area under curve_. What is the AUC value for a random classifier?
```
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
```
# Multiclass classification
So far we have completely ignored the fact that our training data not only includes fives and 'other digits', but in fact ten different input labels (one for each digit). Multiclass classification will allow us to distinguish each of them individually and predict the _most likely class_ for each instance. Scikit-Learn is clever enough to realise, that our label array `y_train` contains ten different classes, so – without explicitly telling us – it runs ten binary classifiers when we call the `fit()` function on the SGD classifier. Each of these binary classifiers trains one class vs. all others ("one-versus-all"). Let's try it out:
```
sgd_clf.fit(X_train, y_train)
```
How does it classify our previous example of something that looked like a five?
```
sgd_clf.predict([some_digit])
```
Great! But what exactly happens under the hood? It actually calculates ten different scores for the ten different binary classifiers and picks the class with the highest score. We can see this by calling the `decision_function()` as we did earlier:
```
some_digit_scores = sgd_clf.decision_function([some_digit])
print(some_digit_scores) # Print us the array content
print("Largest entry: %s" % np.argmax(some_digit_scores)) # Get the index of the largest entry
```
Scikit-Learn even comes with a class to run the one-versus-one approach as well. We can just give it our SGD classifier instance and then call the `fit()` function on it:
```
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(sgd_clf)
ovo_clf.fit(X_train, y_train)
# What does it predict for our random five?
ovo_clf.predict([some_digit])
```
And how many classifiers does this one-versus-one approach need? Can you come up with the formula?
```
print("Number of estimators: %s" % len(ovo_clf.estimators_))
```
Back to the one-versus-all approach – how good are we? For that, we can calculate the cross-validation score once more to get values for the accuracy. Bear in mind that now we are running a _ten-class_ classification!
```
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
```
This is not bad at all, although you could probably spend hours optimising the hyperparameters of this model. How good does the onve-versus-one approach perform? Try it out!
Let's look at some other performance measures for the one-versus-all classifier. A good point to start is the confusing matrix.
```
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train, cv=3)
conf_mx = confusion_matrix(y_train_pred, y_train)
conf_mx
```
Ok, maybe it's better to display this in a plot:
```
def plot_confusion_matrix(matrix):
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)
plt.xlabel('Predicted class', fontsize=16)
plt.ylabel('True class', fontsize=16)
cax = ax.matshow(matrix)
fig.colorbar(cax)
plot_confusion_matrix(conf_mx)
save_fig("confusion_matrix_plot", tight_layout=False)
plt.show()
```
It's still very hard to see what's going on. So maybe we should (1) normalise the matrix by rows again, (2) "remove" all diagonal entries, because those are not interesting for us for the error analysis.
```
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
plot_confusion_matrix(norm_conf_mx)
save_fig("confusion_matrix_errors_plot", tight_layout=False)
plt.show()
```
It seems we're predicting many of the eights wrong. In particular, many of them are predicted to be a five! On the other hand, not many fives are misclassified as eights. Interesting, right? Let's pick out some eights and fives, each of which are either correctly predicted, or predicted as the other class. Maybe looking at the pictures with our "human learning" algorithm will see the problem.
```
cl_a, cl_b = 8, 5 # Define class a and class b for the plot
# Training data from class a, which is predicted as a.
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
# Training data from class a, which is predicted as b.
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
# Training data from class b, which is predicted as a.
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
# Training data from class b, which is predicted as b.
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
save_fig("error_analysis_digits_plot")
plt.show()
```
|
github_jupyter
|
# "Build Your First Neural Network with PyTorch"
* article <https://curiousily.com/posts/build-your-first-neural-network-with-pytorch/>
* dataset <https://www.kaggle.com/jsphyg/weather-dataset-rattle-package>
requires `torch 1.4.0`
```
import os
from os.path import dirname
import numpy as np
import pandas as pd
from tqdm import tqdm
import seaborn as sns
from pylab import rcParams
import matplotlib.pyplot as plt
from matplotlib import rc
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
import torch
from torch import nn, optim
import torch.nn.functional as F
%matplotlib inline
sns.set(style='whitegrid', palette='muted', font_scale=1.2)
HAPPY_COLORS_PALETTE = ["#01BEFE", "#FFDD00", "#FF7D00", "#FF006D", "#93D30C", "#8F00FF"]
sns.set_palette(sns.color_palette(HAPPY_COLORS_PALETTE))
rcParams["figure.figsize"] = 12, 8
RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
df = pd.read_csv(dirname(os.getcwd()) + "/dat/weatherAUS.csv")
df.describe()
df.shape
# data pre-processing
cols = [ "Rainfall", "Humidity3pm", "Pressure9am", "RainToday", "RainTomorrow" ]
df = df[cols]
df.head()
df["RainToday"].replace({"No": 0, "Yes": 1}, inplace = True)
df["RainTomorrow"].replace({"No": 0, "Yes": 1}, inplace = True)
df.head()
# drop missing values
df = df.dropna(how="any")
df.head()
sns.countplot(df.RainTomorrow);
df.RainTomorrow.value_counts() / df.shape[0]
X = df[["Rainfall", "Humidity3pm", "RainToday", "Pressure9am"]]
y = df[["RainTomorrow"]]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=RANDOM_SEED)
X_train = torch.from_numpy(X_train.to_numpy()).float()
X_test = torch.from_numpy(X_test.to_numpy()).float()
y_train = torch.squeeze(torch.from_numpy(y_train.to_numpy()).float())
y_test = torch.squeeze(torch.from_numpy(y_test.to_numpy()).float())
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
class Net (nn.Module):
def __init__ (self, n_features):
super(Net, self).__init__()
self.fc1 = nn.Linear(n_features, 5)
self.fc2 = nn.Linear(5, 3)
self.fc3 = nn.Linear(3, 1)
def forward (self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return torch.sigmoid(self.fc3(x))
net = Net(X_train.shape[1])
# training
criterion = nn.BCELoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
# weather forecast
def calculate_accuracy (y_true, y_pred):
predicted = y_pred.ge(.5).view(-1)
return (y_true == predicted).sum().float() / len(y_true)
def round_tensor (t, decimal_places=3):
return round(t.item(), decimal_places)
MAX_EPOCH = 5000
for epoch in range(MAX_EPOCH):
y_pred = net(X_train)
y_pred = torch.squeeze(y_pred)
train_loss = criterion(y_pred, y_train)
if epoch % 100 == 0:
train_acc = calculate_accuracy(y_train, y_pred)
y_test_pred = net(X_test)
y_test_pred = torch.squeeze(y_test_pred)
test_loss = criterion(y_test_pred, y_test)
test_acc = calculate_accuracy(y_test, y_test_pred)
print(
f'''epoch {epoch}
Train set - loss: {round_tensor(train_loss)}, accuracy: {round_tensor(train_acc)}
Test set - loss: {round_tensor(test_loss)}, accuracy: {round_tensor(test_acc)}
''')
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
# save the model
MODEL_PATH = "model.pth"
torch.save(net, MODEL_PATH)
# restore model
net = torch.load(MODEL_PATH)
# evaluation
classes = ["No rain", "Raining"]
y_pred = net(X_test)
y_pred = y_pred.ge(.5).view(-1).cpu()
y_test = y_test.cpu()
print(classification_report(y_test, y_pred, target_names=classes))
cm = confusion_matrix(y_test, y_pred)
df_cm = pd.DataFrame(cm, index=classes, columns=classes)
hmap = sns.heatmap(df_cm, annot=True, fmt="d")
hmap.yaxis.set_ticklabels(hmap.yaxis.get_ticklabels(), rotation=0, ha='right')
hmap.xaxis.set_ticklabels(hmap.xaxis.get_ticklabels(), rotation=30, ha='right')
plt.ylabel('True label')
plt.xlabel('Predicted label');
def will_it_rain (rainfall, humidity, rain_today, pressure):
t = torch.as_tensor([rainfall, humidity, rain_today, pressure]).float().cpu()
output = net(t)
print("net(t)", output.item())
return output.ge(0.5).item()
will_it_rain(rainfall=10, humidity=10, rain_today=True, pressure=2)
will_it_rain(rainfall=0, humidity=1, rain_today=False, pressure=100)
```
|
github_jupyter
|
# Scraping transfermarkt by html
```
from selenium.webdriver import (Chrome, Firefox)
import time
import requests
from bs4 import BeautifulSoup
from html_scraper import db
players = db['players']
player_urls = db['player_urls']
browser = Firefox()
url = 'https://www.transfermarkt.co.uk/primera-division/startseite/wettbewerb/AR1N'
browser.get(url)
elems = browser.find_elements_by_class_name("vereinprofil_tooltip")
url_links = []
for link in elems:
url = link.get_attribute('href')
if url not in url_links and 'startseite' in url:
url_links.append(url)
len(url_links)
club1 = url_links[0]
browser.get(club1)
```
### Go from club_url to detailed page club_url
```
detailed_url = []
for url in url_links:
change_url = url.replace('startseite', 'kader')
url_final = change_url + '/plus/1'
detailed_url.append(url_final)
detailed_url
```
### old code... skip down to scraping to DBMongo step
```
from html_scraper import scrape_player_info
scrape_player_info(detailed_url, delay=15)
db
club1 = detailed_url[0]
browser.get(club1)
sel = 'td.hauptlink a'
link_elements = browser.find_elements_by_css_selector(sel)
print(link_elements[0].text)
sel = 'td.zentriert'
link_elements = browser.find_elements_by_css_selector(sel)
print(link_elements[0].text)
for link in link_elements:
print(link.text)
sel = 'td.rechts.hauptlink'
link_elements = browser.find_elements_by_css_selector(sel)
test = '£4.05m '
chars = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'k', 'm', '.']
''.join(char for char in test if char in chars)
player_dict_odd = {}
for row in browser.find_elements_by_css_selector("tr.odd"):
player = row.find_element_by_css_selector('td.hauptlink a').text
squad_num = row.find_elements_by_css_selector('td.zentriert')[0].text
birthday = row.find_elements_by_css_selector('td.zentriert')[1].text
transfer_value = row.find_element_by_css_selector('td.rechts.hauptlink').text
player_dict_odd[player] = {'squad_num': squad_num, 'birthday': birthday, 'transfer_value': transfer_value}
player_dict_odd
# player_dict_even = {}
# for row in browser.find_elements_by_css_selector("tr.even"):
# player = row.find_element_by_css_selector('td.hauptlink a').text
# squad_num = row.find_elements_by_css_selector('td.zentriert')[0].text
# birthday = row.find_elements_by_css_selector('td.zentriert')[1].text
# # nationality = row.find_element_by_css_selector('td.zentriert.img')
# transfer_value = row.find_element_by_css_selector('td.rechts.hauptlink').text
# player_dict_even[player] = {'squad_num': squad_num, 'birthday': birthday, 'transfer_value': transfer_value}
# player_dict_even
player_dict = {**player_dict_even, **player_dict_odd}
len(player_dict)
# test = db['test']
# test.insert_one(player_dict)
```
# Scraping to DB Mongo
```
db_urls = detailed_url.copy()
db_urls
from html_scraper import get_all_player_data_from_url, team_scrape
teams = [get_all_player_data_from_url(url) for url in db_urls]
from html_scraper import add_player_to_db
import pandas as pd
for url in db_urls:
player_data = get_all_player_data_from_url(url)
print(url)
for player in player_data:
add_player_to_db(player)
```
# check db
```
db.players
players = db.players.find()
players.count()
master_list = []
for player in players:
master_list.append(player)
master_list
pd.DataFrame(master_list)
```
|
github_jupyter
|
```
import itertools
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
import pandas as pd
import numpy as np
import matplotlib.ticker as ticker
from sklearn import preprocessing
%matplotlib inline
# Load Data From CSV File
df = pd.read_csv('AnimeList.csv')
cols_id = list(df.columns)
# Clean some anime episodes that havent been updated. From personal experience, animes that are Hentai genre,
# Ova, Movie, Special anime type mainly have only 1 episode
df.loc[(df["genre"]=="Hentai") & (df["episodes"]==0),"episodes"] = 1
df.loc[(df["type"]=="OVA") & (df["episodes"]==0),"episodes"] = 1
df.loc[(df["type"] == "Movie") & (df["episodes"]==0), "episodes"] = 1
df.loc[(df["type"] == "Special") & (df["episodes"]==0), "episodes"] = 1
# Adjust NaN values
for col in cols_id:
try:
float(df_filtered[col][0])
df[col].fillna(df[col].median(),inplace = True)
except:
df[col].fillna(0, inplace = True)
df.head()
# Check number of individual values in each column
cols_id = list(df.columns)
for col in cols_id:
a = len(df[col].value_counts())
print(a, col)
print("==============================================================================")
df_filtered = df
new = pd.DataFrame(df_filtered.groupby("type").size())
new.columns = ['count']
new = new.sort_values(by = "count")
print(new)
a = new.index.tolist()
a
# Columns with less than 50 distinct values will beconverted to numbers,
# the values with more population will get higher index value
first_filtered = {}
for col in cols_id:
if len(df_filtered[col].value_counts()) < 50:
new = pd.DataFrame(df_filtered.groupby(col).size())
new.columns = ['count']
new = new.sort_values(by = "count")
a = new.index.tolist()
converted = {}
new_id = []
old_i = {}
start = 0
for i in new.values:
i = int(i)
if i not in list(old_i.keys()):
new_id.append(start)
old_i[i] = start
converted[a[start]] = start
start += 1
else:
new_id.append(old_i[i])
print(col)
print(converted)
first_filtered[col] = converted
print("=======================")
new["new_id"] = new_id
df_filtered[col] = df_filtered[col].replace(new.index,new.new_id)
print("All converted attributes: ")
print(first_filtered)
df_filtered
# Clean licensor column
new_license = []
a = pd.DataFrame(df_filtered.licensor.value_counts())
a.index.name = "lisence_id"
for count in a.licensor:
if count < 11:
new_license.append(1)
elif 10 < count < 50:
new_license.append(2)
elif count == 11105:
new_license.append(0)
else:
new_license.append(3)
a['new_license'] = new_license
df_filtered['licensor'] = df_filtered['licensor'].replace(a.index, a.new_license)
df_filtered
df_filtered.licensor.unique()
# Separate genres to columns
features = pd.concat([df_filtered["genre"].str.get_dummies(sep=", ")],axis=1)
features_cols = list(features.columns)
for feature_col in features_cols:
df_filtered[feature_col] = features[feature_col]
df_filtered
# Convert duration column to number
import re
new_duration = []
for time in df_filtered.duration:
test_string = time
temp = re.findall(r'\d+', test_string)
res = list(map(int, temp))
if len(res) == 2:
n = res[1] + 60 * res[0]
new_duration.append(n)
elif len(res) == 0:
new_duration.append(0)
else:
new_duration.append(res[0])
df_filtered['duration'] = new_duration
df_filtered['duration'] = df_filtered.duration.mask(df_filtered.duration == 0, df_filtered['duration'].mean(skipna=True))
df_filtered
# Convert Premiered Column to Year column and Season Column
new_year = []
seasons = []
for time in df_filtered.premiered:
test_string = str(time)
temp = re.findall(r'\d+', test_string)
res = list(map(int, temp))
if len(res) == 0:
new_year.append(0)
seasons.append(time)
else:
new_year.append(res[0])
seasons.append(str(time).replace(str(res[0]), ''))
df_filtered['year'] = new_year
df_filtered['season'] = seasons
df_filtered
cols_id = list(df_filtered.columns)
df_model = df_filtered[['title']]
df_not_use = df_filtered[['title']]
for col in cols_id:
try:
float(df_filtered[col][0])
df_model[col] = df_filtered[col]
except:
df_not_use[col] = df_filtered[col]
df_model.set_index('title')
df_not_use.set_index('title')
df_model
# I can see that there are some 0 values in episodes column
df_noeps = df_model[df_model.episodes == 0]
df_noeps.head()
# I can see that there are some 0 values in Score column as well
df_noscores = df_model[df_model.score == 0]
df_noscores.head()
# Now i see that in the episodes column and the rating column has some 0 values. Therefore, I tried to find an API
# called Encyclopedia API to update some missing episodes and ratings values
# Check eps and rating for anime Jinki:Extend
import xml.etree.ElementTree as ET
import urllib.request
from xml.etree.ElementTree import fromstring, ElementTree
url = "https://cdn.animenewsnetwork.com/encyclopedia/api.xml?anime=4658"
response = urllib.request.urlopen(url).read()
response = response.decode('utf-8')
tree = ET.fromstring(response)
for child in tree:
element = child.findall('episode')
print("Number of eps: "+ str(len(element)))
element = child.find('ratings').attrib
print("Rating: " + str(element["weighted_score"]))
df_report = pd.read_csv('report.csv')
anime_id = pd.DataFrame(df_report[['id', 'name']])
name_ls = list(anime_id.name)
anime_id.head()
# Check for similar missing episodes anime in my data compare to those of their data
# and update to a new dataframe called update_eps
df_report = pd.read_csv('report.csv')
anime_id = pd.DataFrame(df_report[['id', 'name']])
name_ls = list(anime_id.name)
anime_id = anime_id.set_index(['name'])
similar_eps = []
eps = []
count = 0
for n in df_noeps.title:
url = "https://cdn.animenewsnetwork.com/encyclopedia/api.xml?anime="
if n in name_ls and n != 0:
similar_eps.append(n)
try:
int(anime_id.loc[[n]].id[0])
new_id = int(anime_id.loc[[n]].id[0])
url += str(new_id)
response = urllib.request.urlopen(url).read()
response = response.decode('utf-8')
tree = ET.fromstring(response)
for child in tree:
element = child.findall('episode')
eps.append(len(element))
if len(element) != 0:
count += 1
except:
similar_eps.remove(n)
continue
update_eps = pd.DataFrame(eps, similar_eps, columns = ["episodes"])
print(str(count) + " of the missing episodes have been updated")
update_eps.sort_values(by=["episodes"], ascending = False).head()
# Check for similar missing scores anime in my data compare to those of their data
# and update to a new dataframe called update_scores
df_report = pd.read_csv('report.csv')
anime_id = pd.DataFrame(df_report[['id', 'name']])
name_ls = list(anime_id.name)
anime_id = anime_id.set_index(['name'])
similar_scores = []
scores = []
count = 0
for n in df_noscores.title:
url = "https://cdn.animenewsnetwork.com/encyclopedia/api.xml?anime="
if n in name_ls and n != 0:
similar_scores.append(n)
try:
int(anime_id.loc[[n]].id[0])
new_id = int(anime_id.loc[[n]].id[0])
url += str(new_id)
response = urllib.request.urlopen(url).read()
response = response.decode('utf-8')
tree = ET.fromstring(response)
for child in tree:
element = child.find('ratings').attrib
scores.append(float(element["weighted_score"]))
if float(element["weighted_score"]):
count += 1
except:
similar_scores.remove(n)
continue
update_scores = pd.DataFrame(scores, similar_scores, columns = ['score'])
print(str(count) + " of the missing scores have been updated")
update_scores.sort_values(by=['score'], ascending = False).head()
# Now Use the new found values to update the model dataFrame.
for name in df_model.title:
if name in similar_eps:
df_model.loc[(df_model["title"]==name) & (df_model["episodes"]==0),"episodes"] = update_eps.loc[name, "episodes"]
if name in similar_scores:
df_model.loc[(df_model["title"]==name) & (df_model["score"]==0),"score"] = update_scores.loc[name, "score"]
# For the remaining 0 episodes anime, I change them to 12 which is an average number of episodes per anime season
df_model['episodes']=df_model.episodes.mask(df_model.episodes == 0, 12)
df_not_use.drop(['genre', 'premiered'], axis=1).head()
# At this point we have a dataset for model called df_model and the remaining unused dataset called df_not_use
# KNN model application
# KNN with KNeighborsClassifier to predict anime Score
# To use scikit-learn library, we have to convert the Pandas data frame to a Numpy array:
# For this model, I round the score column to integers instead of floats
scores = []
for score in df_model.score:
scores.append(round(score))
Y = pd.DataFrame(scores)
df_model1 = df_model
df_model2 = df_model
use_cols = list(df_model1.columns)
if 'score' in use_cols:
use_cols.remove('score')
if 'title' in use_cols:
use_cols.remove('title')
X = df_model1[use_cols].values #.astype(float)
X[0:5]
y = Y[0].values
y[0:5]
#Normalize Data
x = preprocessing.StandardScaler().fit(X).transform(X.astype(float))
x[0:2]
#Train Test Split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( x, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape, y_train.shape)
print ('Test set:', X_test.shape, y_test.shape)
#K nearest neighbor (K-NN)
from sklearn.neighbors import KNeighborsClassifier
k = 7
#Train Model and Predict
neigh = KNeighborsClassifier(n_neighbors = k, algorithm='auto').fit(X_train,y_train)
neigh
#Predicting
yhat = neigh.predict(X_test)
yhat[0:5]
#Accuracy evaluation
from sklearn import metrics
print("Train set Accuracy: ", metrics.accuracy_score(y_train, neigh.predict(X_train)))
print("Test set Accuracy: ", metrics.accuracy_score(y_test, yhat))
#K value
Ks = 10
mean_acc = np.zeros((Ks-1))
std_acc = np.zeros((Ks-1))
ConfustionMx = [];
for n in range(1,Ks):
#Train Model and Predict
neigh = KNeighborsClassifier(n_neighbors = n).fit(X_train,y_train)
yhat=neigh.predict(X_test)
mean_acc[n-1] = metrics.accuracy_score(y_test, yhat)
std_acc[n-1]=np.std(yhat==y_test)/np.sqrt(yhat.shape[0])
mean_acc
#Plot model accuracy for Different number of Neighbors
plt.plot(range(1,Ks),mean_acc,'g')
plt.fill_between(range(1,Ks),mean_acc - 1 * std_acc,mean_acc + 1 * std_acc, alpha=0.10)
plt.legend(('Accuracy ', '+/- 3xstd'))
plt.ylabel('Accuracy ')
plt.xlabel('Number of Neighbors (K)')
plt.tight_layout()
plt.show()
print( "The best accuracy was with", mean_acc.max(), "with k=", mean_acc.argmax()+1)
# Apply Nearest Neighbor model for recommendation
from sklearn.neighbors import NearestNeighbors
X
# Here I use the Nearest Neighbor model to find the nearest 5 similar animes
# (closest distances between the animes' attributes)
rec_neigh = NearestNeighbors(n_neighbors=6, algorithm='auto').fit(X)
distances, indexs = rec_neigh.kneighbors(X)
# Return the Index of the anime if its name is given in full
# Warning, the name has to be exact, even the upper case letters.
def full_id(name):
try:
df_model1[df_model1["title"] == name].index.tolist()[0]
return df_model1[df_model1["title"] == name].index.tolist()[0]
except:
return "This is not a valid full name"
all_names = list(df_model1.title.values)
# If you only know a part of the anime name, you can get the list of possible full anime names,
# The input can be lower case
def part_id(part):
for name in all_names:
if part.lower() in name.lower():
print(name, all_names.index(name))
# Can get similar animes with input of anime name or anime index
def similar_animes(query=None,id=None):
if id:
for id in indexs[id][1:]:
print(df_model1.iloc[id]["title"])
if query:
found_id = full_id(query)
if found_id == "This is not a valid full name":
print(found_id)
else:
for id in indexs[found_id][1:]:
print(df_model1.iloc[id]["title"])
similar_animes(query="Naruto")
# It's well known that Naruto is a very popular anime, therefore, the 5 recommended options are very popular as well and
# some of them has many episodes and series such as Tokyo Ghoul and Code Geass with lots of fighting scenes.
# Personally, I would really recommend Angle Beats - a very touching anime
# When I put in a strange anime name it will cause error
similar_animes(query="Slime")
# Therefore I check the available names for "slime"
part_id("slime")
# After copy paste the name, it works!!
similar_animes(query="Slime Boukenki: Umi da, Yeah!")
# Now I will set up random user response to predict an anime score
# Some of the string attributes are categorized to numbers
print(first_filtered)
print(first_filtered.keys())
user_qs = []
for key in use_cols:
if key == "0":
break
user_qs.append(key)
print(user_qs)
genres = []
for key in use_cols:
if key not in user_qs:
genres.append(key)
genres.remove('year')
print(genres)
# Here are the attributes for the user to input
print(use_cols)
# Use random to random the user response invarious categories: 'type', 'source', 'status', 'airing', 'rating' and the genres
# The remaining attributes' default value would be the column's mean value, the anime year is set to 2017
import random
import numpy
user_response = {}
gen_choice = random.randint(1, 5)
gen_str = ""
for choice in range(gen_choice):
gen_str += ", "
gen_str += str(random.choice(genres))
gen_default = []
for gen in genres:
if gen in gen_str:
gen_default.append(1)
else:
gen_default.append(0)
response_default = []
for qs in use_cols:
if qs not in user_qs:
break
if qs in first_filtered.keys():
key_list = list(first_filtered[qs].keys())
val_list = list(first_filtered[qs].values())
first = random.choice(val_list)
response_default.append(first)
user_response[qs] = key_list[val_list.index(first)]
else:
response_default.append(df_model1[qs].mean())
user_response[qs] = df_model1[qs].mean()
response_default.extend(gen_default)
response_default.append(2017)
user_response['genre'] = gen_str
user_response['year'] = 2017
print("User input is:")
print("")
print(user_response)
# Return the anime score from the input
df2 = pd.DataFrame([response_default], columns=use_cols)
df_test = df_model1.append(df2, sort = True)
X_test = df_test[use_cols].values
x_test = preprocessing.StandardScaler().fit(X_test).transform(X_test.astype(float))
score = neigh.predict([x_test[len(x_test) - 1]])
print("The predicted anime score is: " + str(score))
# Here, an anime about Historical and Space for children which originate from Picture book has a decent score (7)
# This makes sense because this anime seems to be very interesting for children
# and would attract lots of viewers for education material
# Use random to random the user response invarious categories: 'type', 'source', 'status', 'airing', 'rating' and the genres
# The remaining attributes' default value would be the column's mean value, the anime year is set to 2017
import random
import numpy
user_response = {}
gen_choice = random.randint(1, 5)
gen_str = ""
for choice in range(gen_choice):
gen_str += ", "
gen_str += str(random.choice(genres))
gen_default = []
for gen in genres:
if gen in gen_str:
gen_default.append(1)
else:
gen_default.append(0)
response_default = []
for qs in use_cols:
if qs not in user_qs:
break
if qs in first_filtered.keys():
key_list = list(first_filtered[qs].keys())
val_list = list(first_filtered[qs].values())
first = random.choice(val_list)
response_default.append(first)
user_response[qs] = key_list[val_list.index(first)]
else:
response_default.append(df_model1[qs].mean())
user_response[qs] = df_model1[qs].mean()
response_default.extend(gen_default)
response_default.append(2017)
user_response['genre'] = gen_str
user_response['year'] = 2017
print("User input is:")
print("")
print(user_response)
# Return the anime score from the input
df2 = pd.DataFrame([response_default], columns=use_cols)
df_test = df_model1.append(df2, sort = True)
X_test = df_test[use_cols].values
x_test = preprocessing.StandardScaler().fit(X_test).transform(X_test.astype(float))
score = neigh.predict([x_test[len(x_test) - 1]])
print("The predicted anime score is: " + str(score))
# Here the anime that has an Unknown source with Music genre and has Rx-Hentai rate (censored info related) has a low score (4)
# This makes sense because it doesn't sound appealing to watch a porn anime that has music in it
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout,Activation,BatchNormalization
from tensorflow.keras.callbacks import ModelCheckpoint
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import keras
from keras.utils import np_utils
from tensorflow.keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
print(len(X_train))
print(len(X_test))
X_train = X_train.astype('float32')/255 #Scaling the data
X_test = X_test.astype('float32')/255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], '=train samples')
print(X_test.shape[0], '=test samples')
num_classes = 10
# print first ten (integer-valued) training labels
print('Integer-valued labels:')
print(y_train[:10])
# one-hot encode the labels
# convert class vectors to binary class matrices
y_train = np_utils.to_categorical(y_train, num_classes)
y_test = np_utils.to_categorical(y_test, num_classes)
# print first ten (one-hot) training labels
print('One-hot labels:')
print(y_train[:10])
img_rows, img_cols = 28, 28
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print('input_shape: ', input_shape)
print('x_train shape:', X_train.shape)
model = Sequential()
model.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu', input_shape=(28,28,1))) #26
model.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) #24
model.add(BatchNormalization())
model.add(Dropout(0.1))
model.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) # 22
model.add(BatchNormalization())
model.add(Dropout(0.1))
model.add(MaxPooling2D(pool_size=(2, 2))) #11
model.add(Conv2D(filters=16,kernel_size=(3,3), activation='relu')) # 9
model.add(BatchNormalization())
model.add(Dropout(0.1))
model.add(Conv2D(filters=10,kernel_size=(1,1), activation='relu')) # 9
model.add(BatchNormalization())
model.add(Dropout(0.1))
model.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) #7
model.add(BatchNormalization())
model.add(Dropout(0.1))
model.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) #5
model.add(BatchNormalization())
model.add(Dropout(0.1))
model.add(Conv2D(filters=10,kernel_size=(5,5))) #1
model.add(Flatten())
model.add(Activation('softmax'))
model.summary()
def scheduler(epoch, lr):
return round(0.003 * 1/(1 + 0.319 * epoch), 10)
model.compile(loss='categorical_crossentropy', optimizer=tf.keras.optimizers.Adam(lr=0.003), metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=128, epochs=30, verbose=1, validation_data=(X_test, y_test),
callbacks=[tf.keras.callbacks.LearningRateScheduler(scheduler, verbose=1)])
```
Here i run for 30 epochs but in 25 epcohs i got validation accuracy as 99.40%.
```
```
|
github_jupyter
|
```
import collections
import json
import pprint
from datetime import datetime
import pandas as pd
# Notebook to generate attack tree Graphviz file and Emacs Org mode
# table for attack tree analysis configuration. The input is itemized
# list of attack tree nodes with mark modifiers.
# Should use Python3.4+
# Name of the attack tree itemized input
tf = 'at/at-gather-intelligence-about.org'
# Prefix for the scenario
prefix = 'N'
# Not important, internal to grahviz
cluster_prefix = 'T'
step = 2
tab = 8
test = ''
# Output Graphviz or/and Org table
org = False
graphviz = True
##### Graphviz params
## Shape
#gshape = 'octagon'
#style=''
gshape = 'box'
style='rounded'
# Tree implementation, Python magic
def tree(): return collections.defaultdict(tree)
def add_tree(t, keys):
"""
Add elements to the tree
t: tree
keys: list of elements
"""
for key in keys:
t = t[key]
def print_tree(t):
print(json.dumps(t, indent=2, sort_keys=True))
def leaf_nodes(tree, k='', current=''):
"""
Finds tree leaf nodes, yields node identifiers build/concatenated
on the fly
k and current are important only for recursive calls
yields concatenated node identifiers
"""
current += '.' + k
path = current.lstrip('.')
if not tree.keys() and path != '':
yield path
for k in tree.keys():
yield from leaf_nodes(tree[k], k, current)
# Open org input file
with open(tf) as f:
test = f.readlines()
#### Itemize list input
branches = []
levels = []
st = []
# Parse simple/limited org input
# - st: list of lists, each list has two elements, one the concatenated
# levels and the other the description of the node
# - branches: list of branches of the tree, used to build the tree
for l in test:
# Modifiers
or_join = True
horizontal = True
double = False
triple = False
red = False
l = l.strip('\n')
l = l.replace('\t', ' '*tab)
n = l.split('-')
if len(n) == 1:
if st:
st[-1][1] = st[-1][1] + ' ' + n[0].lstrip()
continue
level = int(len(n[0])/step)
if level == 0:
pass
elif level > len(levels):
levels.append(1)
elif level == len(levels):
levels[-1] += 1
elif level < len(levels):
levels = levels[:level]
levels[-1] += 1
# Parse the label string for the modifiers
label = n[1].lstrip().rstrip()
ls = label.split(' ')
if ls[-1].find('[') >= 0:
mod = ls[-1]
# print('found modifier %s' % mod)
mod = mod.lstrip('[').rstrip(']')
if len(mod) >= 1 and mod[0] == 'a':
or_join = False
if len(mod) >= 2 and mod[1] == 'v':
horizontal = False
if mod.find('!') >= 0:
double = True
if mod.find('*') >= 0:
red = True
# print('modifier join:%s, direction:%s' % (or_join, horizontal))
label = ' '.join(ls[:-1])
e = []
e.append('.'.join(map(str, levels)))
e.append(label)
e.append([or_join, horizontal, double, red, triple])
branches.append('.'.join(map(str, levels)).split('.'))
st.append(e)
# Fill the tree, uses Python magic
tr = tree()
for b in branches:
add_tree(tr, b)
# Remove ORs on leaf nodes, subsuboptimal
for l in leaf_nodes(tr):
for e in st:
if e[0] == l:
e[2][0] = None
# Build a mapper between the levels and the names
# Build the list of tree nodes
at_nodes_mapper = {}
at_mod_mapper = {}
at_nodes = []
for e in st:
den = e[0]
if not e[0]:
den = 0
name = '%s_%s' % (prefix, den)
label = '<<FONT POINT-SIZE="9">%s<br/>%s</FONT>>' % (prefix, den)
st = style
# label = '\"%s\\n%s\"' % (prefix, den)
(or_join, horizontal, double, red, triple) = e[2]
template = '"%s" [shape=%s, label=%s, label="%s", xlabel=%s];'
if double:
template = '"%s" [shape=%s, style=%s, peripheries=2, label="%s", xlabel=%s];'
# template = '"%s" [shape=doubleoctagon, label="%s", xlabel="%s"];'
if red:
if st:
st = "\"%s,filled\"" % st
else:
st = 'filled'
template = '"%s" [shape=%s, style=%s, fillcolor=red, label="%s", xlabel=%s];'
at_nodes.append(template % (name, gshape, st, e[1], label))
at_nodes_mapper[den] = name
at_mod_mapper[den] = e[2]
#### Graphviz output
# Graphviz defaults
or_node = 'node [shape=%s, height=.0001, width=.0001, penwidth=0, label=""]' % gshape
or_style = '[style=dashed, weight=%s];'
and_style = '[weight=%s];'
full_style = '[dir=full, arrowhead=normal, weight=1000];'
or_node_def_templ = or_node + ' %s;'
or_line_templ = '%s ' + or_style
and_line_templ = '%s ' + and_style
rank = '{rank=same; %s;}'
# Prints graphviz subgraph
def print_graph(path, nodes, or_join=True, horizontal=True):
if nodes:
root = False
if nodes[0] == '':
root = True
path = 0
nodes = nodes[1:]
weight = 1
line_templ = or_line_templ
join_style = or_style
if not or_join:
line_templ = and_line_templ
join_style = and_style
num_or_nodes = len(nodes)
nodes_in = ['"%s_%s"' % (prefix, n) for n in nodes]
if path:
nodes_in = ['"%s_%s.%s"' % (prefix, path, n) for n in nodes]
or_nodes_in = ['"or%s_%s_%s"' % (cluster_prefix, path, e) for e in range(0, num_or_nodes)]
print('subgraph "cluster_%s%s" {' % (cluster_prefix, path))
extra_join_style = join_style % (weight*200)
join_style = join_style % weight
if horizontal:
print('# Horizontal')
if len(nodes)%2 == 0: # Add to even
num_or_nodes += 1
or_nodes_in = ['"or%s_%s_%s"' % (cluster_prefix, path, e) for e in range(0, num_or_nodes)]
print(or_node_def_templ % ', '.join(or_nodes_in))
print(line_templ % (' -> '.join(or_nodes_in), weight*100))
print(rank % ', '.join(or_nodes_in))
print(rank % ', '.join(nodes_in))
spare = or_nodes_in[int(len(nodes)/2)]
if len(nodes)%2 == 0:
or_nodes_in = or_nodes_in[:int(len(or_nodes_in)/2)] + or_nodes_in[int(len(or_nodes_in)/2)+1:]
assert(len(nodes_in) == len(or_nodes_in))
for i, n in enumerate(nodes_in):
print('%s -> %s %s' % (n, or_nodes_in[i], extra_join_style))
print('%s -> "%s" %s' % (spare, at_nodes_mapper[path], full_style))
else:
print('# Vertical')
print(or_node_def_templ % ', '.join(or_nodes_in))
print(line_templ % (' -> '.join(or_nodes_in), weight*700))
assert(len(nodes_in) == len(or_nodes_in))
for i, n in enumerate(nodes_in):
print(rank % ', '.join([n, or_nodes_in[i]]))
for i, n in enumerate(nodes_in):
print('%s -> %s %s' % (n, or_nodes_in[i], extra_join_style))
print('%s -> "%s" %s' % (or_nodes_in[-1], at_nodes_mapper[path], full_style))
print('}')
print()
# Ascii style tree visualisation
def pass_tree(tr, k='', me=''):
"""
Go through the tree and print the concatenated branches
"""
tree = tr
me += '.' + k
path = me.lstrip('.')
print(' '*path.count('.') + '-'*path.count('.') + path)
for k in tree.keys():
pass_tree(tree[k], k, me)
# Recursive through graphviz subgraphs
cluster = 0
def pass_graph(tr, k='', me=''):
"""
Pass through the graph and print it
"""
tree = tr
me += '.' + k
path = me.lstrip('.')
try:
(or_join, horizontal, double, red, triple) = at_mod_mapper[path]
print_graph(path, list(tree.keys()), or_join=or_join, horizontal=horizontal)
except:
(or_join, horizontal, double, red, triple) = at_mod_mapper[0]
print_graph(path, list(tree.keys()), or_join=or_join, horizontal=horizontal)
for k in tree.keys():
pass_graph(tree[k], k, me)
if graphviz:
# Print Graphviz nodes
for n in at_nodes:
print(n)
# Print Graphviz subraphs plot data
print()
pass_graph(tr)
#### Org mode table
# Print Org mode style table for nodes analysis
if org:
print()
for e in st:
den = e[0]
if not e[0]:
den = 0
name = '%s_%s' % (prefix, den)
print('|%s|%s||||' % (name.replace('_', '+'), e[1]))
```
|
github_jupyter
|
```
"Uni Face mask model"
#some important packages
from tensorflow.keras.applications.mobilenet_v2 import preprocess_input
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.models import model_from_json
from tensorflow.keras.models import load_model
from imutils.video import VideoStream
import numpy as np
import argparse
import cv2
import os
# Load your trained model
json_file = open('model_3class.json', 'r')
loaded_model_json = json_file.read()
json_file.close()# load json and create model
model = model_from_json(loaded_model_json)
# load weights into new model
model.load_weights("model_3class.h5")
print("Loaded model from disk")
# load our serialized face detector model from disk
print("[INFO] loading face detector model...")
prototxtPath = 'weights/deploy.prototxt.txt'
weightsPath = 'weights/res10_300x300_ssd_iter_140000.caffemodel'
net = cv2.dnn.readNet(prototxtPath, weightsPath)
"" "Application on image // Play with the parameters to choose the right probabilities"""
# load the image to test
#image = cv2.imread('images/pic1.jpeg')
image = cv2.imread('inputs/images/img4.jpeg')
orig = image.copy()
(h, w) = image.shape[:2]
# construct a blob from the image
blob = cv2.dnn.blobFromImage(image, 1.0, (300, 300),
(104.0, 177.0, 123.0))
# pass the blob through the network and obtain the face detections
print("[INFO] computing face detections...")
net.setInput(blob)
detections = net.forward()
# loop over the detections
for i in range(0, detections.shape[2]):
# extract the confidence (i.e., probability) associated with
# the detection
confidence = detections[0, 0, i, 2]
# filter out weak detections by ensuring the confidence is
# greater than the minimum confidence
if confidence > 0.5:
# compute the (x, y)-coordinates of the bounding box for
# the object
box = detections[0, 0, i, 3:7] * np.array([w, h, w, h])
(startX, startY, endX, endY) = box.astype("int")
# ensure the bounding boxes fall within the dimensions of
# the frame
(startX, startY) = (max(0, startX), max(0, startY))
(endX, endY) = (min(w - 1, endX), min(h - 1, endY))
# extract the face ROI, convert it from BGR to RGB channel
# ordering, resize it to 224x224, and preprocess it
face = image[startY:endY, startX:endX]
face = cv2.cvtColor(face, cv2.COLOR_BGR2RGB)
face = cv2.resize(face, (224, 224))
face = img_to_array(face)
face = preprocess_input(face)
face = np.expand_dims(face, axis=0)
# pass the face through the model to determine if the face
# has a mask or not
(notCorrect, mask, withoutMask) = model.predict(face)[0]
# determine the class label and color we'll use to draw
# the bounding box and text
if (mask < 0.70 and withoutMask < 0.70) or notCorrect > max(mask, withoutMask):
label, color = "Not correct", (0, 255, 255)
elif mask > max (withoutMask, notCorrect):
label, color = "Mask", (0, 255,0)
elif withoutMask > max (mask, notCorrect):
label, color = "No Mask", (0, 0, 255)
# label = "Mask" if mask > max (withoutMask, notCorrect) else "No Mask"
# color = (0, 255, 0) if label == "Mask" else (0, 0, 255)
# include the probability in the label
label = "{}: {:.2f}%".format(label, max(mask, withoutMask) * 100)
# display the label and bounding box rectangle on the output
# frame
cv2.putText(image, label, (startX, startY - 10),
cv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)
cv2.rectangle(image, (startX, startY), (endX, endY), color, 2)
#save the output image
cv2.imwrite('outputs/output_uni.jpg', image)
# show the output image
cv2.imshow("Output", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
"""" Application on webcam """"
def detect_and_predict_mask(frame, faceNet, maskNet):
# grab the dimensions of the frame and then construct a blob
# from it
(h, w) = frame.shape[:2]
blob = cv2.dnn.blobFromImage(frame, 1.0, (300, 300),
(104.0, 177.0, 123.0))
# pass the blob through the network and obtain the face detections
faceNet.setInput(blob)
detections = faceNet.forward()
# initialize our list of faces, their corresponding locations,
# and the list of predictions from our face mask network
faces = []
locs = []
preds = []
# loop over the detections
for i in range(0, detections.shape[2]):
# extract the confidence (i.e., probability) associated with
# the detection
confidence = detections[0, 0, i, 2]
# filter out weak detections by ensuring the confidence is
# greater than the minimum confidence
if confidence > 0.5:
# compute the (x, y)-coordinates of the bounding box for
# the object
box = detections[0, 0, i, 3:7] * np.array([w, h, w, h])
(startX, startY, endX, endY) = box.astype("int")
# ensure the bounding boxes fall within the dimensions of
# the frame
(startX, startY) = (max(0, startX), max(0, startY))
(endX, endY) = (min(w - 1, endX), min(h - 1, endY))
# extract the face ROI, convert it from BGR to RGB channel
# ordering, resize it to 224x224, and preprocess it
face = frame[startY:endY, startX:endX]
face = cv2.cvtColor(face, cv2.COLOR_BGR2RGB)
face = cv2.resize(face, (224, 224))
face = img_to_array(face)
face = preprocess_input(face)
face = np.expand_dims(face, axis=0)
# add the face and bounding boxes to their respective
# lists
faces.append(face)
locs.append((startX, startY, endX, endY))
# only make a predictions if at least one face was detected
if len(faces) > 0:
# for faster inference we'll make batch predictions on *all*
# faces at the same time rather than one-by-one predictions
# in the above `for` loop
preds = maskNet.predict(faces)
# return a 2-tuple of the face locations and their corresponding
# locations
return (locs, preds)
maskNet = model
size = 4
webcam = cv2.VideoCapture(0) #Use camera 0
# loop over the frames from the video stream
while True:
# grab the frame from the threaded video stream and resize it
# to have a maximum width of 400 pixels
#frame = vs.read()
#frame = imutils.resize(frame, width=400)
(rval, frame) = webcam.read()
#frame = imutils.resize(frame, width=400)
frame = cv2.flip(frame,1,1) #Flip to act as a mirror
frame = cv2.resize(frame, (frame.shape[1] // size, frame.shape[0] // size))# Resize the image to speed up detection
# detect faces in the frame and determine if they are wearing a
# face mask or not
(locs, preds) = detect_and_predict_mask(frame, net, maskNet)
# loop over the detected face locations and their corresponding
# locations
for (box, pred) in zip(locs, preds):
# unpack the bounding box and predictions
(startX, startY, endX, endY) = box
(notCorrect, mask, withoutMask) = pred
# determine the class label and color we'll use to draw
# the bounding box and text
if (mask < 0.70 and withoutMask < 0.70) or notCorrect > max(mask, withoutMask):
label, color = "Not correct", (0, 255, 255)
elif mask > max (withoutMask, notCorrect):
label, color = "Mask", (0, 255,0)
elif withoutMask > max (mask, notCorrect):
label, color = "No Mask", (0, 0, 255)
# include the probability in the label
label = "{}: {:.2f}%".format(label, max(notCorrect, mask, withoutMask) * 100)
# display the label and bounding box rectangle on the output
# frame
cv2.putText(frame, label, (startX-30, startY - 10),
cv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)
cv2.rectangle(frame, (startX, startY), (endX, endY), color, 2)
# show the output frame
cv2.namedWindow("LIVE", cv2.WND_PROP_FULLSCREEN)
cv2.setWindowProperty("LIVE",cv2.WND_PROP_FULLSCREEN, cv2.WINDOW_FULLSCREEN)
cv2.imshow("LIVE", frame)
key = cv2.waitKey(10)
if key==27:
break
# Stop video
webcam.release()
# Close all started windows
cv2.destroyAllWindows()
# Video
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Phân loại cơ bản: Dự đoán ảnh quần áo giày dép
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />Xem trên TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/vi/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Chạy trên Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/vi/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />Xem mã nguồn trên GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/vi/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Tải notebook</a>
</td>
</table>
**Lưu ý:** Cộng đồng TensorFlow tại Việt Nam đã và đang dịch những tài liệu này từ nguyên bản tiếng Anh.
Những bản dịch này được hoàn thiện dựa trên sự nỗ lực đóng góp từ cộng đồng lập trình viên sử dụng TensorFlow,
và điều này có thể không đảm bảo được tính cập nhật của bản dịch đối với [Tài liệu chính thức bằng tiếng Anh](https://www.tensorflow.org/?hl=en) này.
Nếu bạn có bất kỳ đề xuất nào nhằm cải thiện bản dịch này, vui lòng tạo Pull request đến
kho chứa trên GitHub của [tensorflow/docs-l10n](https://github.com/tensorflow/docs-l10n).
Để đăng ký dịch hoặc cải thiện nội dung bản dịch, các bạn hãy liên hệ và đặt vấn đề tại
[docs-vi@tensorflow.org](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-vi).
Trong hướng dẫn này, chúng ta sẽ huấn luyện một mô hình mạng neuron để phân loại các hình ảnh về quần áo và giày dép.
Đừng ngại nếu bạn không hiểu hết mọi chi tiết, vì chương trình trong hướng dẫn này là một chương trình TensorFlow hoàn chỉnh, và các chi tiết sẽ dần được giải thích ở những phần sau.
Hướng dẫn này dùng [tf.keras](https://www.tensorflow.org/guide/keras), một API cấp cao để xây dựng và huấn luyện các mô hình trong TensorFlow.
```
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## Import tập dữ liệu về quần áo và giày dép từ Fashion MNIST
Chúng ta sẽ dùng tập dữ liệu về quần áo và giày dép từ [Fashion MNIST](https://github.com/zalandoresearch/fashion-mnist), chứa khoảng 70,000 ảnh đen trắng phân thành 10 loại. Mỗi một ảnh là một loại quần áo hoặc giày dép với độ phân giải thấp (28 by 28 pixel), như hình minh hoạ bên dưới:
<table>
<tr><td>
<img src="https://tensorflow.org/images/fashion-mnist-sprite.png"
alt="Fashion MNIST sprite" width="600">
</td></tr>
<tr><td align="center">
<b>Figure 1.</b> <a href="https://github.com/zalandoresearch/fashion-mnist">Fashion-MNIST samples</a> (by Zalando, MIT License).<br/>
</td></tr>
</table>
Fashion MNIST là tập dữ liệu được dùng để thay thế cho tập dữ liệu [MNIST](http://yann.lecun.com/exdb/mnist/) kinh điển thường dùng cho các chương trình "Hello, World" của machine learning trong lĩnh vực thị giác máy tính. Tập dữ liệu kinh điển vừa đề cập gồm ảnh của các con số (ví dụ 0, 1, 2) được viết tay. Các ảnh này có cùng định dạng tệp và độ phân giải với các ảnh về quần áo và giầy dép chúng ta sắp dùng.
Hướng dẫn này sử dụng tập dữ liệu Fashion MNIST, vì đây là một bài toán tương đối phức tạp hơn so với bài toán nhận diện chữ số viết tay. Cả 2 tập dữ liệu (Fashion MNIST và MNIST kinh điển) đều tương đối nhỏ và thường dùng để đảm bảo một giải thuật chạy đúng, phù hợp cho việc kiểm thử và debug.
Với tập dữ liệu này, 60.000 ảnh sẽ được dùng để huấn luyện và 10.000 ảnh sẽ đường dùng để đánh giá khả năng phân loại nhận diện ảnh của mạng neuron. Chúng ta có dùng tập dữ liệu Fashion MNIST trực tiếp từ TensorFlow như sau:
```
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
```
Tập dữ liệu sau khi được tải sẽ trả về 4 mảng NumPy:
* 2 mảng `train_images` và `train_labels` là *tập huấn luyện*. Mô hình sẽ học từ dữ liệu của 2 mảng này.
* 2 mảng `test_images` vả `test_labels` là *tập kiểm thử*. Sau khi mô hình được huấn luyện xong, chúng ta sẽ chạy thử mô hình với dữ liệu đầu vào từ `test_images` để lấy kết quả, và so sánh kết quả đó với dữ liệu đối ứng từ `test_labels` để đánh giá chất lượng của mạng neuron.
Mỗi ảnh là một mảng NumPy 2 chiều, 28x28, với mỗi pixel có giá trị từ 0 đến 255. *Nhãn* là một mảng của các số nguyên từ 0 đến 9, tương ứng với mỗi *lớp* quần áo giày dép:
<table>
<tr>
<th>Nhãn</th>
<th>Lớp</th>
</tr>
<tr>
<td>0</td>
<td>Áo thun</td>
</tr>
<tr>
<td>1</td>
<td>Quần dài</td>
</tr>
<tr>
<td>2</td>
<td>Áo liền quần</td>
</tr>
<tr>
<td>3</td>
<td>Đầm</td>
</tr>
<tr>
<td>4</td>
<td>Áo khoác</td>
</tr>
<tr>
<td>5</td>
<td>Sandal</td>
</tr>
<tr>
<td>6</td>
<td>Áo sơ mi</td>
</tr>
<tr>
<td>7</td>
<td>Giày</td>
</tr>
<tr>
<td>8</td>
<td>Túi xách</td>
</tr>
<tr>
<td>9</td>
<td>Ủng</td>
</tr>
</table>
Mỗi ảnh sẽ được gán với một nhãn duy nhất. Vì tên của mỗi lớp không có trong tập dữ liệu, nên chúng ta có thể định nghĩa ở đây để dùng về sau:
```
class_names = ['Áo thun', 'Quần dài', 'Áo liền quần', 'Đầm', 'Áo khoác',
'Sandal', 'Áo sơ mi', 'Giày', 'Túi xách', 'Ủng']
```
## Khám phá dữ liệu
Chúng ta có thể khám phá dữ liệu một chút trước khi huấn luyện mô hình. Câu lệnh sau sẽ cho ta thấy có 60.000 ảnh trong tập huấn luyện, với mỗi ảnh được biểu diễn theo dạng 28x28 pixel:
```
train_images.shape
```
Tương tự, tập huấn luyện cũng có 60.000 nhãn đối ứng:
```
len(train_labels)
```
Mỗi nhãn là một số nguyên từ 0 đến 9:
```
train_labels
```
Có 10.000 ảnh trong tập kiểm thử, mỗi ảnh cũng được biểu diễn ở dãng 28 x 28 pixel:
```
test_images.shape
```
Và tập kiểm thử cũng chứa 10,000 nhãn:
```
len(test_labels)
```
## Tiền xử lý dữ liệu
Dữ liệu cần được tiền xử lý trước khi được dùng để huấn luyện mạng neuron. Phân tích ảnh đầu tiên trong tập dữ liệu, chúng ta sẽ thấy các pixel có giá trị từ 0 đến 255:
```
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
```
Chúng ta cần tiền xử lý để mỗi một điểm ảnh có giá trị từ 0 đến 1 (có thể hiểu là 0% đến 100%). Để làm điều này, chúng ta chỉ cần lấy giá trị của pixel chia cho 255. Cần lưu ý rằng việc tiền xử lý này phải được áp dụng đồng thời cho cả *tập huấn luyện* và *tập kiểm thử*:
```
train_images = train_images / 255.0
test_images = test_images / 255.0
```
Để chắc chắn việc tiền xử lý diễn ra chính xác, chúng ta có thể in ra 25 ảnh đầu trong *tập huấn luyện* cùng với tên lớp dưới mỗi ảnh.
```
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
```
## Xây dựng mô hình
Để xây dựng mạng neuron, chúng tay cần cấu hình các layer của mô hình, và sau đó biên dịch mô hình.
### Thiết lập các layers
Thành phần cơ bản của một mạng neuron là các *layer*. Các layer trích xuất các điểm đặc biệt từ dữ liệu mà chúng đón nhận. Khi thực hiện tốt, những điểm đặc biệt này mang nhiều ý nghĩa và phục vụ cho toán của chúng ta.
Đa số các mô hình deep learning đều chứa các layer đơn gian được xâu chuỗi lại với nhau. Đa số các layer, ví dụ `tf.keras.layers.Dense`, đều có các trọng số sẽ được học trong quá trình huấn luyện.
```
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
```
Trong mạng neuron trên, lớp đầu tiên, `tf.keras.layers.Flatten`, chuyển đổi định dạng của hình ảnh từ mảng hai chiều (28x28) thành mảng một chiều (28x28 = 784). Tưởng tương công việc của layer này là cắt từng dòng của anh, và ghép nối lại thành một dòng duy nhất nhưng dài gấp 28 lần. Lớp này không có trọng số để học, nó chỉ định dạng lại dữ liệu.
Sau layer làm phẳng ảnh (từ 2 chiều thành 1 chiều), phần mạng neuron còn lại gồm một chuỗi hai layer `tf.keras.layers.Dense`. Đây là các layer neuron được kết nối hoàn toàn (mỗi một neuron của layer này kết nối đến tất cả các neuron của lớp trước và sau nó). Layer `Dense` đầu tiên có 128 nút (hoặc neuron). Layer thứ hai (và cuối cùng) là lớp *softmax* có 10 nút, với mỗi nút tương đương với điểm xác suất, và tổng các giá trị của 10 nút này là 1 (tương đương 100%). Mỗi nút chứa một giá trị cho biết xác suất hình ảnh hiện tại thuộc về một trong 10 lớp.
### Biên dịch mô hình
Trước khi mô hình có thể được huấn luyện, chúng ta cần thêm vài chỉnh sửa. Các chỉnh sửa này được thêm vào trong bước *biên dịch* của mô hình:
* *Hàm thiệt hại* — dùng để đo lường mức độ chính xác của mô hình trong quá trình huấn luyện. Chúng ta cần giảm thiểu giá trị của hạm này "điều khiển" mô hình đi đúng hướng (thiệt hại càng ít, chính xác càng cao).
* *Trình tối ưu hoá* — Đây là cách mô hình được cập nhật dựa trên dữ liệu huấn luyện được cung cấp và hàm thiệt hại.
* *Số liệu* — dùng để theo dõi các bước huấn luyện và kiểm thử. Ví dụ sau dùng *accuracy*, tỉ lệ ảnh được phân loại chính xác.
```
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
```
## Huấn luyện mô hình
Huấn luyện mô hình mạng neuron cần các bước sau:
1. Cung cấp dữ liệu huấn luyện cho mô hình. Trong ví dụ này, dữ liệu huấn luyện năm trong 2 mảng `train_images` và `train_labels`
2. Mô hình sẽ học cách liên kết ảnh với nhãn.
3. Chúng ta sẽ yêu cầu mô hình đưa ra dự đoán từ dữ liệu của tập kiểm thử, trong ví dụ này là mảng `test_images`, sau đó lấy kết quả dự đoán đối chiếu với nhãn trong mảng `test_labels`.
Để bắt đầu huấn luyện, gọi hàm `model.fit`. Hàm này được đặt tên `fit` vì nó sẽ "fit" ("khớp") mô hình với dữ liệu huấn luyện:
```
model.fit(train_images, train_labels, epochs=10)
```
Trong quá trình huấn luyện, các số liệu như thiệt hại và hay độ chính xác được hiển thị. Với dữ liệu huấn luyện này, mô hình đạt đến độ accuracy vào khoảng 0.88 (88%).
## Đánh giá mô hình
Tiếp theo, chúng đánh giá các chất lượng của mô hình bằng tập kiểm thử:
```
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('\nTest accuracy:', test_acc)
```
Đến thời điểm này, chúng ta thấy rằng độ accuracy của mô hình, khi đánh giá bằng tập kiểm thử, hơi thấp hơn so với số liệu trong quá trình huấn luyện. Khoảng cách giữa hai độ accuracy khi huấn luyện và khi kiểm thử thể hiện sự *overfitting*. Overfitting xảy ra khi một mô hình ML hoạt động kém hơn khi được cung cấp các đầu vào mới, mà mô hình chưa từng thấy trước đây trong quá trình đào tạo.
## Đưa ra dự đoán
Với một mô hình đã được đào tạo, chúng ta có thể dùng nó để đưa ra dự đoán với một số ảnh.
```
predictions = model.predict(test_images)
```
Ở đây, mô hình sẽ dự đoán nhãn cho từng hình ảnh trong bộ thử nghiệm. Hãy xem dự đoán đầu tiên:
```
predictions[0]
```
Trong ví dụ này, dự đoán là một mảng 10 số thực, mỗi số tương ứng với "độ tự tin" của mô hình rằng ảnh đó thuộc về nhãn đó. Chúng ta có thể thấy nhãn nào có độ tư tin cao nhất:
```
np.argmax(predictions[0])
```
Vậy là mô hình tự tin nhất rằng ảnh này là một loại ủng, hoặc `class_names[9]`. Đối chiếu với nhãn trong tập kiểm thử, ta thấy dự đoán này là đúng:
```
test_labels[0]
```
Ta thử vẽ biểu đồ để xem các dự đoán trên cả 10 lớp của mô hình.
```
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array, true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
```
Chúng ta có thể nhìn vào ảnh 0th, các dự đoán, và mảng dự đoán.
Nhãn dự đoán đúng màu xanh và nhãn sai màu đỏ. Con số là số phần trăm của các nhãn được dự đoán.
```
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], test_labels)
plt.show()
i = 12
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], test_labels)
plt.show()
```
Thử vẽ biểu đồ với vài ảnh và dự đoán đi kèm. Chú ý thấy rằng mô hình đôi khi dự đoán sai dù điểm tự tin rất cao.
```
# Plot the first X test images, their predicted labels, and the true labels.
# Color correct predictions in blue and incorrect predictions in red.
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions[i], test_labels)
plt.tight_layout()
plt.show()
```
Cuối cùng, dùng mô hình để đưa ra dự đoán về một ảnh duy nhất.
```
# Grab an image from the test dataset.
img = test_images[1]
print(img.shape)
```
Các mô hình `tf.keras` được tối ưu hóa để đưa ra dự đoán về một *lô* hoặc bộ sưu tập các ví dụ cùng một lúc. Theo đó, mặc dù bạn đang sử dụng một ảnh duy nhất, bạn cần thêm nó vào list:
```
# Add the image to a batch where it's the only member.
img = (np.expand_dims(img,0))
print(img.shape)
```
Dự đoán nhãn cho ảnh này:
```
predictions_single = model.predict(img)
print(predictions_single)
plot_value_array(1, predictions_single[0], test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)
```
`model.predict` trả về một list của lists — mỗi list cho mỗi ảnh trong lô dữ liệu. Lấy dự đoán cho hình ảnh trong lô:
```
np.argmax(predictions_single[0])
```
Mô hình dự đoán ảnh này có nhãn là đúng như mong muốn.
|
github_jupyter
|
# Convolutional Neural Networks: Application
Welcome to Course 4's second assignment! In this notebook, you will:
- Implement helper functions that you will use when implementing a TensorFlow model
- Implement a fully functioning ConvNet using TensorFlow
**After this assignment you will be able to:**
- Build and train a ConvNet in TensorFlow for a classification problem
We assume here that you are already familiar with TensorFlow. If you are not, please refer the *TensorFlow Tutorial* of the third week of Course 2 ("*Improving deep neural networks*").
## 1.0 - TensorFlow model
In the previous assignment, you built helper functions using numpy to understand the mechanics behind convolutional neural networks. Most practical applications of deep learning today are built using programming frameworks, which have many built-in functions you can simply call.
As usual, we will start by loading in the packages.
```
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *
%matplotlib inline
np.random.seed(1)
```
Run the next cell to load the "SIGNS" dataset you are going to use.
```
# Loading the data (signs)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
```
As a reminder, the SIGNS dataset is a collection of 6 signs representing numbers from 0 to 5.
<img src="images/SIGNS.png" style="width:800px;height:300px;">
The next cell will show you an example of a labelled image in the dataset. Feel free to change the value of `index` below and re-run to see different examples.
```
# Example of a picture
index = 5
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[:,index])))
```
In Course 2, you had built a fully-connected network for this dataset. But since this is an image dataset, it is more natural to apply a ConvNet to it.
To get started, let's examine the shapes of your data.
```
X_train = X_train_orig/255
X_test = X_test_orig/255
Y_train = convert_to_one_hot(Y_train_orig, 6).T #.T used for transpose
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}
```
### 1.1 - Create placeholders
TensorFlow requires that you create placeholders for the input data that will be fed into the model when running the session.
**Exercise**: Implement the function below to create placeholders for the input image X and the output Y. You should not define the number of training examples for the moment. To do so, you could use "None" as the batch size, it will give you the flexibility to choose it later. Hence X should be of dimension **[None, n_H0, n_W0, n_C0]** and Y should be of dimension **[None, n_y]**. [Hint](https://www.tensorflow.org/api_docs/python/tf/placeholder).
```
# GRADED FUNCTION: create_placeholders
def create_placeholders(n_H0, n_W0, n_C0, n_y):
"""
Creates the placeholders for the tensorflow session.
Arguments:
n_H0 -- scalar, height of an input image
n_W0 -- scalar, width of an input image
n_C0 -- scalar, number of channels of the input
n_y -- scalar, number of classes
Returns:
X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
"""
### START CODE HERE ### (≈2 lines)
X = tf.placeholder(tf.float32, shape=(None,n_H0, n_W0, n_C0))
Y = tf.placeholder(tf.float32, shape=(None, n_y))
### END CODE HERE ###
return X, Y
X, Y = create_placeholders(64, 64, 3, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))
```
**Expected Output**
<table>
<tr>
<td>
X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
</td>
</tr>
<tr>
<td>
Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)
</td>
</tr>
</table>
### 1.2 - Initialize parameters
You will initialize weights/filters $W1$ and $W2$ using `tf.contrib.layers.xavier_initializer(seed = 0)`. You don't need to worry about bias variables as you will soon see that TensorFlow functions take care of the bias. Note also that you will only initialize the weights/filters for the conv2d functions. TensorFlow initializes the layers for the fully connected part automatically. We will talk more about that later in this assignment.
**Exercise:** Implement initialize_parameters(). The dimensions for each group of filters are provided below. Reminder - to initialize a parameter $W$ of shape [1,2,3,4] in Tensorflow, use:
```python
W = tf.get_variable("W", [1,2,3,4], initializer = ...)
```
[More Info](https://www.tensorflow.org/api_docs/python/tf/get_variable).
```
# GRADED FUNCTION: initialize_parameters
def initialize_parameters():
"""
Initializes weight parameters to build a neural network with tensorflow. The shapes are:
W1 : [4, 4, 3, 8]
W2 : [2, 2, 8, 16]
Returns:
parameters -- a dictionary of tensors containing W1, W2
"""
tf.set_random_seed(1) # so that your "random" numbers match ours
### START CODE HERE ### (approx. 2 lines of code)
W1 = tf.get_variable("W1", shape= [4, 4, 3, 8], initializer = tf.contrib.layers.xavier_initializer(seed = 0))
W2 = tf.get_variable("W2", shape= [2, 2, 8, 16], initializer = tf.contrib.layers.xavier_initializer(seed = 0))
### END CODE HERE ###
parameters = {"W1": W1,
"W2": W2}
return parameters
tf.reset_default_graph()
with tf.Session() as sess_test:
parameters = initialize_parameters()
init = tf.global_variables_initializer()
sess_test.run(init)
print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
print("W2 = " + str(parameters["W2"].eval()[1,1,1]))
```
** Expected Output:**
<table>
<tr>
<td>
W1 =
</td>
<td>
[ 0.00131723 0.14176141 -0.04434952 0.09197326 0.14984085 -0.03514394 <br>
-0.06847463 0.05245192]
</td>
</tr>
<tr>
<td>
W2 =
</td>
<td>
[-0.08566415 0.17750949 0.11974221 0.16773748 -0.0830943 -0.08058 <br>
-0.00577033 -0.14643836 0.24162132 -0.05857408 -0.19055021 0.1345228 <br>
-0.22779644 -0.1601823 -0.16117483 -0.10286498]
</td>
</tr>
</table>
### 1.2 - Forward propagation
In TensorFlow, there are built-in functions that carry out the convolution steps for you.
- **tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = 'SAME'):** given an input $X$ and a group of filters $W1$, this function convolves $W1$'s filters on X. The third input ([1,f,f,1]) represents the strides for each dimension of the input (m, n_H_prev, n_W_prev, n_C_prev). You can read the full documentation [here](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d)
- **tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = 'SAME'):** given an input A, this function uses a window of size (f, f) and strides of size (s, s) to carry out max pooling over each window. You can read the full documentation [here](https://www.tensorflow.org/api_docs/python/tf/nn/max_pool)
- **tf.nn.relu(Z1):** computes the elementwise ReLU of Z1 (which can be any shape). You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/nn/relu)
- **tf.contrib.layers.flatten(P)**: given an input P, this function flattens each example into a 1D vector it while maintaining the batch-size. It returns a flattened tensor with shape [batch_size, k]. You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/contrib/layers/flatten)
- **tf.contrib.layers.fully_connected(F, num_outputs):** given a the flattened input F, it returns the output computed using a fully connected layer. You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/contrib/layers/fully_connected)
In the last function above (`tf.contrib.layers.fully_connected`), the fully connected layer automatically initializes weights in the graph and keeps on training them as you train the model. Hence, you did not need to initialize those weights when initializing the parameters.
**Exercise**:
Implement the `forward_propagation` function below to build the following model: `CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED`. You should use the functions above.
In detail, we will use the following parameters for all the steps:
- Conv2D: stride 1, padding is "SAME"
- ReLU
- Max pool: Use an 8 by 8 filter size and an 8 by 8 stride, padding is "SAME"
- Conv2D: stride 1, padding is "SAME"
- ReLU
- Max pool: Use a 4 by 4 filter size and a 4 by 4 stride, padding is "SAME"
- Flatten the previous output.
- FULLYCONNECTED (FC) layer: Apply a fully connected layer without an non-linear activation function. Do not call the softmax here. This will result in 6 neurons in the output layer, which then get passed later to a softmax. In TensorFlow, the softmax and cost function are lumped together into a single function, which you'll call in a different function when computing the cost.
```
# GRADED FUNCTION: forward_propagation
def forward_propagation(X, parameters):
"""
Implements the forward propagation for the model:
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
Arguments:
X -- input dataset placeholder, of shape (input size, number of examples)
parameters -- python dictionary containing your parameters "W1", "W2"
the shapes are given in initialize_parameters
Returns:
Z3 -- the output of the last LINEAR unit
"""
# Retrieve the parameters from the dictionary "parameters"
W1 = parameters['W1']
W2 = parameters['W2']
### START CODE HERE ###
# CONV2D: stride of 1, padding 'SAME'
Z1 = tf.nn.conv2d(X,W1,strides=[1,1,1,1],padding="SAME")
# RELU
A1 = tf.nn.relu(Z1)
# MAXPOOL: window 8x8, sride 8, padding 'SAME'
P1 = tf.nn.max_pool(A1,ksize=[1,8,8,1],strides=[1,8,8,1],padding="SAME")
# CONV2D: filters W2, stride 1, padding 'SAME'
Z2 = tf.nn.conv2d(P1,W2,strides=[1,1,1,1],padding="SAME")
# RELU
A2 = tf.nn.relu(Z2)
# MAXPOOL: window 4x4, stride 4, padding 'SAME'
P2 = tf.nn.max_pool(A2,ksize=[1,4,4,1],strides=[1,4,4,1],padding="SAME")
# FLATTEN
P2 = tf.contrib.layers.flatten(P2)
# FULLY-CONNECTED without non-linear activation function (not not call softmax).
# 6 neurons in output layer. Hint: one of the arguments should be "activation_fn=None"
Z3 = tf.contrib.layers.fully_connected(P2, 6,activation_fn= None)
### END CODE HERE ###=None
return Z3
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(Z3, {X: np.random.randn(2,64,64,3), Y: np.random.randn(2,6)})
print("Z3 = " + str(a))
```
**Expected Output**:
<table>
<td>
Z3 =
</td>
<td>
[[-0.44670227 -1.57208765 -1.53049231 -2.31013036 -1.29104376 0.46852064] <br>
[-0.17601591 -1.57972014 -1.4737016 -2.61672091 -1.00810647 0.5747785 ]]
</td>
</table>
### 1.3 - Compute cost
Implement the compute cost function below. You might find these two functions helpful:
- **tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y):** computes the softmax entropy loss. This function both computes the softmax activation function as well as the resulting loss. You can check the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits)
- **tf.reduce_mean:** computes the mean of elements across dimensions of a tensor. Use this to sum the losses over all the examples to get the overall cost. You can check the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/reduce_mean)
** Exercise**: Compute the cost below using the function above.
```
# GRADED FUNCTION: compute_cost
def compute_cost(Z3, Y):
"""
Computes the cost
Arguments:
Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
Y -- "true" labels vector placeholder, same shape as Z3
Returns:
cost - Tensor of the cost function
"""
### START CODE HERE ### (1 line of code)
cost = tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y)
### END CODE HERE ###
return cost
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})
a = sess.run(tf.reduce_mean(a))
print("cost = "+ str(a))
```
**Expected Output**:
<table>
<td>
cost =
</td>
<td>
2.91034
</td>
</table>
## 1.4 Model
Finally you will merge the helper functions you implemented above to build a model. You will train it on the SIGNS dataset.
You have implemented `random_mini_batches()` in the Optimization programming assignment of course 2. Remember that this function returns a list of mini-batches.
**Exercise**: Complete the function below.
The model below should:
- create placeholders
- initialize parameters
- forward propagate
- compute the cost
- create an optimizer
Finally you will create a session and run a for loop for num_epochs, get the mini-batches, and then for each mini-batch you will optimize the function. [Hint for initializing the variables](https://www.tensorflow.org/api_docs/python/tf/global_variables_initializer)
```
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
num_epochs = 100, minibatch_size = 64, print_cost = True):
"""
Implements a three-layer ConvNet in Tensorflow:
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
Arguments:
X_train -- training set, of shape (None, 64, 64, 3)
Y_train -- test set, of shape (None, n_y = 6)
X_test -- training set, of shape (None, 64, 64, 3)
Y_test -- test set, of shape (None, n_y = 6)
learning_rate -- learning rate of the optimization
num_epochs -- number of epochs of the optimization loop
minibatch_size -- size of a minibatch
print_cost -- True to print the cost every 100 epochs
Returns:
train_accuracy -- real number, accuracy on the train set (X_train)
test_accuracy -- real number, testing accuracy on the test set (X_test)
parameters -- parameters learnt by the model. They can then be used to predict.
"""
ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables
tf.set_random_seed(1) # to keep results consistent (tensorflow seed)
seed = 3 # to keep results consistent (numpy seed)
(m, n_H0, n_W0, n_C0) = X_train.shape
n_y = Y_train.shape[1]
costs = [] # To keep track of the cost
# Create Placeholders of the correct shape
### START CODE HERE ### (1 line)
X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
### END CODE HERE ###
# Initialize parameters
### START CODE HERE ### (1 line)
parameters = initialize_parameters()
### END CODE HERE ###
# Forward propagation: Build the forward propagation in the tensorflow graph
### START CODE HERE ### (1 line)
Z3 = forward_propagation(X, parameters)
### END CODE HERE ###
# Cost function: Add cost function to tensorflow graph
### START CODE HERE ### (1 line)
cost = compute_cost(Z3, Y)
### END CODE HERE ###
# Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
### START CODE HERE ### (1 line)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
### END CODE HERE ###
# Initialize all the variables globally
init = tf.global_variables_initializer()
# Start the session to compute the tensorflow graph
with tf.Session() as sess:
# Run the initialization
sess.run(init)
# Do the training loop
for epoch in range(num_epochs):
minibatch_cost = 0.
num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# IMPORTANT: The line that runs the graph on a minibatch.
# Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
### START CODE HERE ### (1 line)
_ , temp_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
### END CODE HERE ###
minibatch_cost += (sess.run(tf.reduce_mean(temp_cost)) / num_minibatches)
# Print the cost every epoch
if print_cost == True and epoch % 5 == 0:
print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
if print_cost == True and epoch % 1 == 0:
costs.append(minibatch_cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# Calculate the correct predictions
predict_op = tf.argmax(Z3, 1)
correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
# Calculate accuracy on the test set
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(accuracy)
train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
print("Train Accuracy:", train_accuracy)
print("Test Accuracy:", test_accuracy)
# Predict random examples
index = 10
Xin = np.array(X_test[[index],:,:,:],dtype="float")
pred = tf.argmax(Z3,1)
a = sess.run(pred, {X: Xin})
print("Number = " + str(a))
plt.imshow(X_test[index])
return train_accuracy, test_accuracy, parameters
```
Run the following cell to train your model for 100 epochs. Check if your cost after epoch 0 and 5 matches our output. If not, stop the cell and go back to your code!
```
_, _, parameters = model(X_train, Y_train, X_test, Y_test)
```
**Expected output**: although it may not match perfectly, your expected output should be close to ours and your cost value should decrease.
<table>
<tr>
<td>
**Cost after epoch 0 =**
</td>
<td>
1.917929
</td>
</tr>
<tr>
<td>
**Cost after epoch 5 =**
</td>
<td>
1.506757
</td>
</tr>
<tr>
<td>
**Train Accuracy =**
</td>
<td>
0.940741
</td>
</tr>
<tr>
<td>
**Test Accuracy =**
</td>
<td>
0.783333
</td>
</tr>
</table>
|
github_jupyter
|
```
%matplotlib inline
import pandas as pd
import xgboost as xgb
import numpy as np
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import graphviz
from sklearn.preprocessing import LabelEncoder
data = pd.read_csv("data/telco-churn.csv")
data.head()
data.shape
data.drop('customerID', axis = 1, inplace = True)
data.iloc[0]
data['gender'] = LabelEncoder().fit_transform(data['gender'])
data['Partner'] = LabelEncoder().fit_transform(data['Partner'])
data['Dependents'] = LabelEncoder().fit_transform(data['Dependents'])
data['PhoneService'] = LabelEncoder().fit_transform(data['PhoneService'])
data['MultipleLines'] = LabelEncoder().fit_transform(data['MultipleLines'])
data['InternetService'] = LabelEncoder().fit_transform(data['InternetService'])
data['OnlineSecurity'] = LabelEncoder().fit_transform(data['OnlineSecurity'])
data['OnlineBackup'] = LabelEncoder().fit_transform(data['OnlineBackup'])
data['DeviceProtection'] = LabelEncoder().fit_transform(data['DeviceProtection'])
data['TechSupport'] = LabelEncoder().fit_transform(data['TechSupport'])
data['StreamingTV'] = LabelEncoder().fit_transform(data['StreamingTV'])
data['StreamingMovies'] = LabelEncoder().fit_transform(data['StreamingMovies'])
data['Contract'] = LabelEncoder().fit_transform(data['Contract'])
data['PaperlessBilling'] = LabelEncoder().fit_transform(data['PaperlessBilling'])
data['PaymentMethod'] = LabelEncoder().fit_transform(data['PaymentMethod'])
data['Churn'] = LabelEncoder().fit_transform(data['Churn'])
data.dtypes
data.TotalCharges = pd.to_numeric(data.TotalCharges, errors='coerce')
X = data.copy()
X.drop("Churn", inplace = True, axis = 1)
Y = data.Churn
X_train, X_test = X[:int(X.shape[0]*0.8)].values, X[int(X.shape[0]*0.8):].values
Y_train, Y_test = Y[:int(Y.shape[0]*0.8)].values, Y[int(Y.shape[0]*0.8):].values
train = xgb.DMatrix(X_train, label=Y_train)
test = xgb.DMatrix(X_test, label=Y_test)
test_error = {}
for i in range(20):
param = {'max_depth':i, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}
num_round = 50
model_metrics = xgb.cv(param, train, num_round, nfold = 10)
test_error[i] = model_metrics.iloc[-1]['test-error-mean']
plt.scatter(test_error.keys(),test_error.values())
plt.xlabel('Max Depth')
plt.ylabel('Test Error')
plt.show()
param = {'max_depth':4, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}
num_round = 300
model_metrics = xgb.cv(param, train, num_round, nfold = 10)
plt.scatter(range(300),model_metrics['test-error-mean'], s = 0.7, label = 'Test Error')
plt.scatter(range(300),model_metrics['train-error-mean'], s = 0.7, label = 'Train Error')
plt.legend()
plt.show()
param = {'max_depth':4, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}
num_round = 100
model = xgb.train(param, train, num_round)
preds = model.predict(test)
accuracy = accuracy_score(Y[int(Y.shape[0]*0.8):].values, preds)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
model.save_model('churn-model.model')
```
|
github_jupyter
|
# Slow Stochastic
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
# yfinance is used to fetch data
import yfinance as yf
yf.pdr_override()
# input
symbol = 'AAPL'
start = '2018-08-01'
end = '2019-01-01'
# Read data
df = yf.download(symbol,start,end)
# View Columns
df.head()
n = 14 # number of days
s = 3 # smoothing
df['High_Highest'] = df['Adj Close'].rolling(n).max()
df['Low_Lowest'] = df['Adj Close'].rolling(n).min()
df['Fast_%K'] = ((df['Adj Close'] - df['Low_Lowest']) / (df['High_Highest'] - df['Low_Lowest'])) * 100
df['Slow_%K'] = df['Fast_%K'].rolling(s).mean()
df['Slow_%D'] = df['Slow_%K'].rolling(s).mean()
df.head(30)
fig = plt.figure(figsize=(14,10))
ax1 = plt.subplot(2, 1, 1)
ax1.plot(df['Adj Close'])
ax1.set_title('Stock '+ symbol +' Closing Price')
ax1.set_ylabel('Price')
ax2 = plt.subplot(2, 1, 2)
ax2.plot(df['Slow_%K'], label='Slow %K')
ax2.plot(df['Slow_%D'], label='Slow %D')
ax2.text(s='Overbought', x=df.index[30], y=80, fontsize=14)
ax2.text(s='Oversold', x=df.index[30], y=20, fontsize=14)
ax2.axhline(y=80, color='red')
ax2.axhline(y=20, color='red')
ax2.grid()
ax2.set_ylabel('Slow Stochastic')
ax2.legend(loc='best')
ax2.set_xlabel('Date')
```
## Candlestick with Slow Stochastic
```
from matplotlib import dates as mdates
import datetime as dt
dfc = df.copy()
dfc['VolumePositive'] = dfc['Open'] < dfc['Adj Close']
#dfc = dfc.dropna()
dfc = dfc.reset_index()
dfc['Date'] = mdates.date2num(dfc['Date'].astype(dt.date))
dfc.head()
from mpl_finance import candlestick_ohlc
fig = plt.figure(figsize=(14,10))
ax1 = plt.subplot(2, 1, 1)
candlestick_ohlc(ax1,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax1.xaxis_date()
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax1.grid(True, which='both')
ax1.minorticks_on()
ax1v = ax1.twinx()
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
ax1v.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
ax1v.axes.yaxis.set_ticklabels([])
ax1v.set_ylim(0, 3*df.Volume.max())
ax1.set_title('Stock '+ symbol +' Closing Price')
ax1.set_ylabel('Price')
ax2 = plt.subplot(2, 1, 2)
ax2.plot(df['Slow_%K'], label='Slow %K')
ax2.plot(df['Slow_%D'], label='Slow %D')
ax2.text(s='Overbought', x=df.index[30], y=80, fontsize=14)
ax2.text(s='Oversold', x=df.index[30], y=20, fontsize=14)
ax2.axhline(y=80, color='red')
ax2.axhline(y=20, color='red')
ax2.grid()
ax2.set_ylabel('Slow Stochastic')
ax2.legend(loc='best')
ax2.set_xlabel('Date')
```
|
github_jupyter
|
# ロジスティック写像
$$
f(x, a) = a x (1 - x)
$$
```
import numpy as np
import pathfollowing as pf
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set('poster', 'whitegrid', 'dark', rc={"lines.linewidth": 2, 'grid.linestyle': '-'})
def func(x, a):
return np.array([a[0] * x[0] * (1.0 - x[0])])
def dfdx(x,a):
return np.array([[a[0]*(1.0 - 2*x[0])]])
def dfda(x,a):
return np.array([x[0]*(1.0 - x[0])])
```
## 不動点の追跡
- $(x, a) = (2/3, 3)$で周期倍分岐が起こる
```
x=np.array([0.5])
a=np.array([2.0])
bd,bp,lp,pd=pf.pathfollow(x, a, func, dfdx, dfda,nmax=45, h=0.05, epsr=1.0e-10, epsb=1.0e-10, amin=0.0,amax=4.0,problem='map', quiet=True)
```
周期倍分岐点
```
bd[pd[0]]
```
## 周期点の追跡
周期2の周期点の枝に切り替える
```
v2 = pf.calcSwitchingVectorPD(bd[pd[0]], func, dfdx, dfda, period=2)
x2=bd[pd[0]]['x']
a2=bd[pd[0]]['a']
bd2,bp2,lp2, pd2=pf.pathfollow(x2, a2, func, dfdx, dfda, w=v2, nmax=65, h=0.025, epsr=1.0e-10, epsb=1.0e-10, amin=0.0,amax=4.0,problem='map', quiet=True,period=2)
```
周期点の周期倍分岐
```
bd2[pd2[0]]
```
周期4の周期点の枝に切り替える
```
v4 = pf.calcSwitchingVectorPD(bd2[pd2[0]], func, dfdx, dfda, period=4)
x4=bd2[pd2[0]]['x']
a4=bd2[pd2[0]]['a']
bd4,bp4,lp4, pd4=pf.pathfollow(x4, a4, func, dfdx, dfda, w=v4, nmax=65, h=0.0125, epsr=1.0e-10, amin=0.0,amax=4.0,epsb=1.0e-12, problem='map', quiet=True,period=4)
```
周期8の周期点の枝に切り替える
```
v8 = pf.calcSwitchingVectorPD(bd4[pd4[0]], func, dfdx, dfda, period=8)
x8=bd4[pd4[0]]['x']
a8=bd4[pd4[0]]['a']
bd8,bp8,lp8, pd8=pf.pathfollow(x8, a8, func, dfdx, dfda, w=v8, nmax=130, h=0.00625, epsr=1.0e-10, amin=0.0,amax=4.0,epsb=1.0e-12, problem='map', quiet=True,period=8)
```
これまでにもとめた周期倍分岐点のパラメータ値$a$
```
print(bd[pd[0]]['a'], bd2[pd2[0]]['a'], bd4[pd4[0]]['a'], bd8[pd8[0]]['a'])
print(pd8)
bd_r = np.array([bd[m]['a'][0] for m in range(len(bd))])
bd_x = np.array([bd[m]['x'][0] for m in range(len(bd))])
bd_r2 = np.array([bd2[m]['a'][0] for m in range(len(bd2))])
bd_x2 = np.array([bd2[m]['x'][0] for m in range(len(bd2))])
bd_r4 = np.array([bd4[m]['a'][0] for m in range(len(bd4))])
bd_x4 = np.array([bd4[m]['x'][0] for m in range(len(bd4))])
bd_r8 = np.array([bd8[m]['a'][0] for m in range(len(bd8))])
bd_x8 = np.array([bd8[m]['x'][0] for m in range(len(bd8))])
def f(x,a):
return a*x*(1-x)
bd_x22 = np.array([f(bd_x2[m], bd_r2[m]) for m in range(len(bd2))])
bd_x42 = np.array([f(bd_x4[m], bd_r4[m]) for m in range(len(bd4))])
bd_x43 = np.array([f(bd_x42[m], bd_r4[m]) for m in range(len(bd4))])
bd_x44 = np.array([f(bd_x43[m], bd_r4[m]) for m in range(len(bd4))])
bd_x82 = np.array([f(bd_x8[m], bd_r8[m]) for m in range(len(bd8))])
bd_x83 = np.array([f(bd_x82[m], bd_r8[m]) for m in range(len(bd8))])
bd_x84 = np.array([f(bd_x83[m], bd_r8[m]) for m in range(len(bd8))])
bd_x85 = np.array([f(bd_x84[m], bd_r8[m]) for m in range(len(bd8))])
bd_x86 = np.array([f(bd_x85[m], bd_r8[m]) for m in range(len(bd8))])
bd_x87 = np.array([f(bd_x86[m], bd_r8[m]) for m in range(len(bd8))])
bd_x88 = np.array([f(bd_x87[m], bd_r8[m]) for m in range(len(bd8))])
fig = plt.figure(figsize=(8, 5))
ax = fig.add_subplot(111)
ax.set_xlim(2,4)
ax.set_ylim(0.2, 1)
ax.set_xlabel("$a$")
ax.set_ylabel("$x$")
ax.plot(bd_r ,bd_x, '-k')
ax.plot(bd_r2, bd_x2, '-k')
ax.plot(bd_r2, bd_x22, '-k')
ax.plot(bd_r4, bd_x4, '-k')
ax.plot(bd_r4, bd_x42, '-k')
ax.plot(bd_r4, bd_x43, '-k')
ax.plot(bd_r4, bd_x44, '-k')
ax.plot(bd_r8, bd_x8, '-k')
ax.plot(bd_r8, bd_x82, '-k')
ax.plot(bd_r8, bd_x83, '-k')
ax.plot(bd_r8, bd_x84, '-k')
ax.plot(bd_r8, bd_x85, '-k')
ax.plot(bd_r8, bd_x86, '-k')
ax.plot(bd_r8, bd_x87, '-k')
ax.plot(bd_r8, bd_x88, '-k')
# plt.savefig("bd_logistic.pdf", bbox_inches='tight')
```
|
github_jupyter
|
## Part 2: Introduction to Feed Forward Networks
### 1. What is a neural network?
#### 1.1 Neurons
A neuron is software that is roughly modeled after the neuons in your brain. In software, we model it with an _affine function_ and an _activation function_.
One type of neuron is the perceptron, which outputs a binary output 0 or 1 given an input [7]:
<img src="perceptron.jpg" width="600" height="480" />
You can add an activation function to the end isntead of simply thresholding values to clip values from 0 to 1. One common activiation function is the logistic function.
<img src="sigmoid_neuron.jpg" width="600" height="480" />
The most common activation function used nowadays is the rectified linear unit, which is simply max(0, z) where z = w * x + b, or the neurons output.
#### 1.2 Hidden layers and multi-layer perceptrons
A multi-layer perceptron (MLP) is quite simply layers on these perceptrons that are wired together. The layers between the input layer and the output layer are known as the hidden layers. The below is a four layer network with two hidden layers [7]:
<img src="hidden_layers.jpg" width="600" height="480" />
### 2. Tensorflow
Tensorflow (https://www.tensorflow.org/install/) is an extremely popular deep learning library built by Google and will be the main library used for of the rest of these notebooks (in the last lesson, we briefly used numpy, a numerical computation library that's useful but does not have deep learning functionality). NOTE: Other popular deep learning libraries include Pytorch and Caffe2. Keras is another popular one, but its API has since been absorbed into Tensorflow. Tensorflow is chosen here because:
* it has the most active community on Github
* it's well supported by Google in terms of core features
* it has Tensorflow serving, which allows you to serve your models online (something we'll see in a future notebook)
* it has Tensorboard for visualization (which we will use in this lesson)
Let's train our first model to get a sense of how powerful Tensorflow can be!
```
# Some initial setup. Borrowed from:
# https://github.com/ageron/handson-ml/blob/master/09_up_and_running_with_tensorflow.ipynb
# Common imports
import numpy as np
import os
import tensorflow as tf
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "tensorflow"
def save_fig(fig_id):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
def stabilize_output():
tf.reset_default_graph()
# needed to avoid the following error: https://github.com/RasaHQ/rasa_core/issues/80
tf.keras.backend.clear_session()
tf.set_random_seed(seed=42)
np.random.seed(seed=42)
print "Done"
```
Below we will train our first model using the example from the Tensorflow tutorial: https://www.tensorflow.org/tutorials/
This will show you the basics of training a model!
```
# The example below is also in https://colab.research.google.com/github/tensorflow/models/blob/master/samples/core/get_started/_index.ipynb
# to ensure relatively stable output across sessions
stabilize_output()
mnist = tf.keras.datasets.mnist
# load data (requires Internet connection)
(x_train, y_train),(x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# build a model
model = tf.keras.models.Sequential([
# flattens the input
tf.keras.layers.Flatten(),
# 1 "hidden" layer with 512 units - more on this in the next notebook
tf.keras.layers.Dense(512, activation=tf.nn.relu),
# example of regularization - dropout is a way of dropping hidden units at a certain factor
# this essentially results in a model averaging across a large set of possible configurations of the hidden layer above
# and results in model that should generalize better
tf.keras.layers.Dropout(0.2),
# 10 because there's possible didigts - 0 to 9
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# train a model (using 5 epochs -> notice the accuracy improving with each epoch)
model.fit(x_train, y_train, epochs=5)
print model.metrics_names # see https://keras.io/models/model/ for the full API
# evaluate model accuracy
model.evaluate(x_test, y_test)
```
You should see something similar to [0.06788356024027743, 0.9806]. The first number is the final loss and the second number is the accuracy.
Congratulations, it means you've trained a classifier that classifies digit images in the MNIST Dataset with __98% accuracy__! We'll break down how the model is optimizing to achieve this accuracy below.
### 3. More Training of Neural Networks in Tensorflow
#### 3.1: Data Preparation
We load the CIFAR-10 dataset using the tf.keras API.
```
# Borrowed from http://cs231n.github.io/assignments2018/assignment2/
def load_cifar10(num_training=49000, num_validation=1000, num_test=10000):
"""
Fetch the CIFAR-10 dataset from the web and perform preprocessing to prepare
it for the two-layer neural net classifier. These are the same steps as
we used for the SVM, but condensed to a single function.
"""
# Load the raw CIFAR-10 dataset and use appropriate data types and shapes
# NOTE: Download will take a few minutes but once downloaded, it should be cached.
cifar10 = tf.keras.datasets.cifar10.load_data()
(X_train, y_train), (X_test, y_test) = cifar10
X_train = np.asarray(X_train, dtype=np.float32)
y_train = np.asarray(y_train, dtype=np.int32).flatten()
X_test = np.asarray(X_test, dtype=np.float32)
y_test = np.asarray(y_test, dtype=np.int32).flatten()
# Subsample the data
mask = range(num_training, num_training + num_validation)
X_val = X_train[mask]
y_val = y_train[mask]
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
# Normalize the data: subtract the mean pixel and divide by std
mean_pixel = X_train.mean(axis=(0, 1, 2), keepdims=True)
std_pixel = X_train.std(axis=(0, 1, 2), keepdims=True)
X_train = (X_train - mean_pixel) / std_pixel
X_val = (X_val - mean_pixel) / std_pixel
X_test = (X_test - mean_pixel) / std_pixel
return X_train, y_train, X_val, y_val, X_test, y_test
# Invoke the above function to get our data.
# N - index of the number of datapoints (minibatch size)
# H - index of the the height of the feature map
# W - index of the width of the feature map
NHW = (0, 1, 2)
X_train, y_train, X_val, y_val, X_test, y_test = load_cifar10()
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape, y_train.dtype)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
```
#### 3.2 Preparation: Dataset object
Borrowed from CS231N [2], we will define a `Dataset` class for iteration to store data and labels.
```
class Dataset(object):
def __init__(self, X, y, batch_size, shuffle=False):
"""
Construct a Dataset object to iterate over data X and labels y
Inputs:
- X: Numpy array of data, of any shape
- y: Numpy array of labels, of any shape but with y.shape[0] == X.shape[0]
- batch_size: Integer giving number of elements per minibatch
- shuffle: (optional) Boolean, whether to shuffle the data on each epoch
"""
assert X.shape[0] == y.shape[0], 'Got different numbers of data and labels'
self.X, self.y = X, y
self.batch_size, self.shuffle = batch_size, shuffle
def __iter__(self):
N, B = self.X.shape[0], self.batch_size
idxs = np.arange(N)
if self.shuffle:
np.random.shuffle(idxs)
return iter((self.X[i:i+B], self.y[i:i+B]) for i in range(0, N, B))
train_dset = Dataset(X_train, y_train, batch_size=64, shuffle=True)
val_dset = Dataset(X_val, y_val, batch_size=64, shuffle=False)
test_dset = Dataset(X_test, y_test, batch_size=64)
print "Done"
# We can iterate through a dataset like this:
for t, (x, y) in enumerate(train_dset):
print(t, x.shape, y.shape)
if t > 5: break
# You can also optionally set GPU to true if you are working on AWS/Google Cloud (more on that later). For now,
# we to false
# Set up some global variables
USE_GPU = False
if USE_GPU:
device = '/device:GPU:0'
else:
device = '/cpu:0'
# Constant to control how often we print when training models
print_every = 100
print('Using device: ', device)
# Borrowed fromcs231n.github.io/assignments2018/assignment2/
# We define a flatten utility function to help us flatten our image data - the 32x32x3
# (or 32 x 32 image size with three channels for RGB) flattens into 3072
def flatten(x):
"""
Input:
- TensorFlow Tensor of shape (N, D1, ..., DM)
Output:
- TensorFlow Tensor of shape (N, D1 * ... * DM)
"""
N = tf.shape(x)[0]
return tf.reshape(x, (N, -1))
def two_layer_fc(x, params):
"""
A fully-connected neural network; the architecture is:
fully-connected layer -> ReLU -> fully connected layer.
Note that we only need to define the forward pass here; TensorFlow will take
care of computing the gradients for us.
The input to the network will be a minibatch of data, of shape
(N, d1, ..., dM) where d1 * ... * dM = D. The hidden layer will have H units,
and the output layer will produce scores for C classes.
Inputs:
- x: A TensorFlow Tensor of shape (N, d1, ..., dM) giving a minibatch of
input data.
- params: A list [w1, w2] of TensorFlow Tensors giving weights for the
network, where w1 has shape (D, H) and w2 has shape (H, C).
Returns:
- scores: A TensorFlow Tensor of shape (N, C) giving classification scores
for the input data x.
"""
w1, w2 = params # Unpack the parameters
x = flatten(x) # Flatten the input; now x has shape (N, D)
h = tf.nn.relu(tf.matmul(x, w1)) # Hidden layer: h has shape (N, H)
scores = tf.matmul(h, w2) # Compute scores of shape (N, C)
return scores
def two_layer_fc_test():
# TensorFlow's default computational graph is essentially a hidden global
# variable. To avoid adding to this default graph when you rerun this cell,
# we clear the default graph before constructing the graph we care about.
tf.reset_default_graph()
hidden_layer_size = 42
# Scoping our computational graph setup code under a tf.device context
# manager lets us tell TensorFlow where we want these Tensors to be
# placed.
with tf.device(device):
# Set up a placehoder for the input of the network, and constant
# zero Tensors for the network weights. Here we declare w1 and w2
# using tf.zeros instead of tf.placeholder as we've seen before - this
# means that the values of w1 and w2 will be stored in the computational
# graph itself and will persist across multiple runs of the graph; in
# particular this means that we don't have to pass values for w1 and w2
# using a feed_dict when we eventually run the graph.
x = tf.placeholder(tf.float32)
w1 = tf.zeros((32 * 32 * 3, hidden_layer_size))
w2 = tf.zeros((hidden_layer_size, 10))
# Call our two_layer_fc function to set up the computational
# graph for the forward pass of the network.
scores = two_layer_fc(x, [w1, w2])
# Use numpy to create some concrete data that we will pass to the
# computational graph for the x placeholder.
x_np = np.zeros((64, 32, 32, 3))
with tf.Session() as sess:
# The calls to tf.zeros above do not actually instantiate the values
# for w1 and w2; the following line tells TensorFlow to instantiate
# the values of all Tensors (like w1 and w2) that live in the graph.
sess.run(tf.global_variables_initializer())
# Here we actually run the graph, using the feed_dict to pass the
# value to bind to the placeholder for x; we ask TensorFlow to compute
# the value of the scores Tensor, which it returns as a numpy array.
scores_np = sess.run(scores, feed_dict={x: x_np})
print scores_np
print(scores_np.shape)
two_layer_fc_test()
# should print a bunch of zeros
# should print {64, 10}
print "Done"
```
#### 3.3 Training
We will now train using the gradient descent algorithm explained in the previous notebook. The check_accuracy function below lets us check the accuracy of our neural network.
As explained in CS231N:
"The `training_step` function has three basic steps:
1. Compute the loss
2. Compute the gradient of the loss with respect to all network weights
3. Make a weight update step using (stochastic) gradient descent.
Note that the step of updating the weights is itself an operation in the computational graph - the calls to `tf.assign_sub` in `training_step` return TensorFlow operations that mutate the weights when they are executed. There is an important bit of subtlety here - when we call `sess.run`, TensorFlow does not execute all operations in the computational graph; it only executes the minimal subset of the graph necessary to compute the outputs that we ask TensorFlow to produce. As a result, naively computing the loss would not cause the weight update operations to execute, since the operations needed to compute the loss do not depend on the output of the weight update. To fix this problem, we insert a **control dependency** into the graph, adding a duplicate `loss` node to the graph that does depend on the outputs of the weight update operations; this is the object that we actually return from the `training_step` function. As a result, asking TensorFlow to evaluate the value of the `loss` returned from `training_step` will also implicitly update the weights of the network using that minibatch of data.
We need to use a few new TensorFlow functions to do all of this:
- For computing the cross-entropy loss we'll use `tf.nn.sparse_softmax_cross_entropy_with_logits`: https://www.tensorflow.org/api_docs/python/tf/nn/sparse_softmax_cross_entropy_with_logits
- For averaging the loss across a minibatch of data we'll use `tf.reduce_mean`:
https://www.tensorflow.org/api_docs/python/tf/reduce_mean
- For computing gradients of the loss with respect to the weights we'll use `tf.gradients`: https://www.tensorflow.org/api_docs/python/tf/gradients
- We'll mutate the weight values stored in a TensorFlow Tensor using `tf.assign_sub`: https://www.tensorflow.org/api_docs/python/tf/assign_sub
- We'll add a control dependency to the graph using `tf.control_dependencies`: https://www.tensorflow.org/api_docs/python/tf/control_dependencies"
```
# Borrowed from cs231n.github.io/assignments2018/assignment2/
def training_step(scores, y, params, learning_rate):
"""
Set up the part of the computational graph which makes a training step.
Inputs:
- scores: TensorFlow Tensor of shape (N, C) giving classification scores for
the model.
- y: TensorFlow Tensor of shape (N,) giving ground-truth labels for scores;
y[i] == c means that c is the correct class for scores[i].
- params: List of TensorFlow Tensors giving the weights of the model
- learning_rate: Python scalar giving the learning rate to use for gradient
descent step.
Returns:
- loss: A TensorFlow Tensor of shape () (scalar) giving the loss for this
batch of data; evaluating the loss also performs a gradient descent step
on params (see above).
"""
# First compute the loss; the first line gives losses for each example in
# the minibatch, and the second averages the losses acros the batch
losses = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=scores)
loss = tf.reduce_mean(losses)
# Compute the gradient of the loss with respect to each parameter of the the
# network. This is a very magical function call: TensorFlow internally
# traverses the computational graph starting at loss backward to each element
# of params, and uses backpropagation to figure out how to compute gradients;
# it then adds new operations to the computational graph which compute the
# requested gradients, and returns a list of TensorFlow Tensors that will
# contain the requested gradients when evaluated.
grad_params = tf.gradients(loss, params)
# Make a gradient descent step on all of the model parameters.
new_weights = []
for w, grad_w in zip(params, grad_params):
new_w = tf.assign_sub(w, learning_rate * grad_w)
new_weights.append(new_w)
# Insert a control dependency so that evaluting the loss causes a weight
# update to happen; see the discussion above.
with tf.control_dependencies(new_weights):
return tf.identity(loss)
# Train using stochastic gradient descent without momentum
def train(model_fn, init_fn, learning_rate):
"""
Train a model on CIFAR-10.
Inputs:
- model_fn: A Python function that performs the forward pass of the model
using TensorFlow; it should have the following signature:
scores = model_fn(x, params) where x is a TensorFlow Tensor giving a
minibatch of image data, params is a list of TensorFlow Tensors holding
the model weights, and scores is a TensorFlow Tensor of shape (N, C)
giving scores for all elements of x.
- init_fn: A Python function that initializes the parameters of the model.
It should have the signature params = init_fn() where params is a list
of TensorFlow Tensors holding the (randomly initialized) weights of the
model.
- learning_rate: Python float giving the learning rate to use for SGD.
"""
# First clear the default graph
tf.reset_default_graph()
is_training = tf.placeholder(tf.bool, name='is_training')
# Set up the computational graph for performing forward and backward passes,
# and weight updates.
with tf.device(device):
# Set up placeholders for the data and labels
x = tf.placeholder(tf.float32, [None, 32, 32, 3])
y = tf.placeholder(tf.int32, [None])
params = init_fn() # Initialize the model parameters
scores = model_fn(x, params) # Forward pass of the model
loss = training_step(scores, y, params, learning_rate)
# Now we actually run the graph many times using the training data
with tf.Session() as sess:
# Initialize variables that will live in the graph
sess.run(tf.global_variables_initializer())
for t, (x_np, y_np) in enumerate(train_dset):
# Run the graph on a batch of training data; recall that asking
# TensorFlow to evaluate loss will cause an SGD step to happen.
feed_dict = {x: x_np, y: y_np}
loss_np = sess.run(loss, feed_dict=feed_dict)
# Periodically print the loss and check accuracy on the val set
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss_np))
check_accuracy(sess, val_dset, x, scores, is_training)
# Helper method for evaluating our model accuracy (note it also runs the computational graph but doesn't update loss)
def check_accuracy(sess, dset, x, scores, is_training=None):
"""
Check accuracy on a classification model.
Inputs:
- sess: A TensorFlow Session that will be used to run the graph
- dset: A Dataset object on which to check accuracy
- x: A TensorFlow placeholder Tensor where input images should be fed
- scores: A TensorFlow Tensor representing the scores output from the
model; this is the Tensor we will ask TensorFlow to evaluate.
Returns: Nothing, but prints the accuracy of the model
"""
num_correct, num_samples = 0, 0
for x_batch, y_batch in dset:
feed_dict = {x: x_batch, is_training: 0}
scores_np = sess.run(scores, feed_dict=feed_dict)
y_pred = scores_np.argmax(axis=1)
num_samples += x_batch.shape[0]
num_correct += (y_pred == y_batch).sum()
acc = float(num_correct) / num_samples
print('Got %d / %d correct (%.2f%%)' % (num_correct, num_samples, 100 * acc))
print "Done"
# Borrowed from cs231n.github.io/assignments2018/assignment2/
# We initialize the weight matrices for our models using a method known as Kaiming's normalization method [8]
def kaiming_normal(shape):
if len(shape) == 2:
fan_in, fan_out = shape[0], shape[1]
elif len(shape) == 4:
fan_in, fan_out = np.prod(shape[:3]), shape[3]
return tf.random_normal(shape) * np.sqrt(2.0 / fan_in)
def two_layer_fc_init():
"""
Initialize the weights of a two-layer network (one hidden layer), for use with the
two_layer_network function defined above.
Inputs: None
Returns: A list of:
- w1: TensorFlow Variable giving the weights for the first layer
- w2: TensorFlow Variable giving the weights for the second layer
"""
# Numer of neurons in hidden layer
hidden_layer_size = 4000
# Now we initialize the weights of our two layer network using tf.Variable
# "A TensorFlow Variable is a Tensor whose value is stored in the graph and persists across runs of the
# computational graph; however unlike constants defined with `tf.zeros` or `tf.random_normal`,
# the values of a Variable can be mutated as the graph runs; these mutations will persist across graph runs.
# Learnable parameters of the network are usually stored in Variables."
w1 = tf.Variable(kaiming_normal((3 * 32 * 32, hidden_layer_size)))
w2 = tf.Variable(kaiming_normal((hidden_layer_size, 10)))
return [w1, w2]
print "Done"
# Now we actually train our model with one *epoch* ! We use a learning rate of 0.01
learning_rate = 1e-2
train(two_layer_fc, two_layer_fc_init, learning_rate)
# You should see an accuracy of >40% with just one epoch (an epoch in this case consists of 700 iterations
# of gradient descent but can be tuned)
```
#### 3.3 Keras
Note in the first cell, we used the tf.keras Sequential API to make a neural network but here we use "barebones" Tensorflow. One of the good (and possibly bad) things about Tensorflow is that there are several ways to create a neural network and train it. Here are some possible ways:
* Barebones tensorflow
* tf.keras Model API
* tf.keras Sequential API
Here is a table of comparison borrowed from [2]:
| API | Flexibility | Convenience |
|---------------|-------------|-------------|
| Barebone | High | Low |
| `tf.keras.Model` | High | Medium |
| `tf.keras.Sequential` | Low | High |
Note that with the tf.keras Model API, you have the options of using the **object-oriented API**, where each layer of the neural network is represented as a Python object (like `tf.layers.Dense`) or the **functional API**, where each layer is a Python function (like `tf.layers.dense`). We will only use the Sequential API and skip the Model API in the cells below because we will simply trade off lots of flexiblity for convenience.
```
# Now we will train the same model using the Sequential API.
# First we set up our training and model initializiation functions
def train_keras(model_init_fn, optimizer_init_fn, num_epochs=1):
"""
Simple training loop for use with models defined using tf.keras. It trains
a model for one epoch on the CIFAR-10 training set and periodically checks
accuracy on the CIFAR-10 validation set.
Inputs:
- model_init_fn: A function that takes no parameters; when called it
constructs the model we want to train: model = model_init_fn()
- optimizer_init_fn: A function which takes no parameters; when called it
constructs the Optimizer object we will use to optimize the model:
optimizer = optimizer_init_fn()
- num_epochs: The number of epochs to train for
Returns: Nothing, but prints progress during trainingn
"""
tf.reset_default_graph()
with tf.device(device):
# Construct the computational graph we will use to train the model. We
# use the model_init_fn to construct the model, declare placeholders for
# the data and labels
x = tf.placeholder(tf.float32, [None, 32, 32, 3])
y = tf.placeholder(tf.int32, [None])
# We need a place holder to explicitly specify if the model is in the training
# phase or not. This is because a number of layers behaves differently in
# training and in testing, e.g., dropout and batch normalization.
# We pass this variable to the computation graph through feed_dict as shown below.
is_training = tf.placeholder(tf.bool, name='is_training')
# Use the model function to build the forward pass.
scores = model_init_fn(x, is_training)
# Compute the loss like we did in Part II
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=scores)
loss = tf.reduce_mean(loss)
# Use the optimizer_fn to construct an Optimizer, then use the optimizer
# to set up the training step. Asking TensorFlow to evaluate the
# train_op returned by optimizer.minimize(loss) will cause us to make a
# single update step using the current minibatch of data.
# Note that we use tf.control_dependencies to force the model to run
# the tf.GraphKeys.UPDATE_OPS at each training step. tf.GraphKeys.UPDATE_OPS
# holds the operators that update the states of the network.
# For example, the tf.layers.batch_normalization function adds the running mean
# and variance update operators to tf.GraphKeys.UPDATE_OPS.
optimizer = optimizer_init_fn()
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops):
train_op = optimizer.minimize(loss)
# Now we can run the computational graph many times to train the model.
# When we call sess.run we ask it to evaluate train_op, which causes the
# model to update.
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
t = 0
for epoch in range(num_epochs):
print('Starting epoch %d' % epoch)
for x_np, y_np in train_dset:
feed_dict = {x: x_np, y: y_np, is_training:1}
loss_np, _ = sess.run([loss, train_op], feed_dict=feed_dict)
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss_np))
check_accuracy(sess, val_dset, x, scores, is_training=is_training)
print()
t += 1
def model_init_fn(inputs, is_training):
input_shape = (32, 32, 3)
hidden_layer_size, num_classes = 4000, 10
initializer = tf.variance_scaling_initializer(scale=2.0)
layers = [
tf.layers.Flatten(input_shape=input_shape),
tf.layers.Dense(hidden_layer_size, activation=tf.nn.relu,
kernel_initializer=initializer),
tf.layers.Dense(num_classes, kernel_initializer=initializer),
]
model = tf.keras.Sequential(layers)
return model(inputs)
def optimizer_init_fn():
return tf.train.GradientDescentOptimizer(learning_rate)
print "Done"
# Now the actual training
learning_rate = 1e-2
train_keras(model_init_fn, optimizer_init_fn)
# Again, you should see accuracy > 40% after one epoch (700 iterations) of gradient descent
```
### 4. Backpropagation
You'll often hear the term "backpropagation" or "backprop," which is a way of updating a neural network. Google has a great demo that walks you through the backpropagation algorithm in detail. I encourage you to check it out!
https://google-developers.appspot.com/machine-learning/crash-course/backprop-scroll/
See also this seminar by Geoffrey Hinton, a premier deep learning researcher, on whether the brain can do back-propagation. It's an interesting lecture with relatively : https://www.youtube.com/watch?v=VIRCybGgHts
### 5. References
<pre>
[1] Fast.ai (http://course.fast.ai/)
[2] CS231N (http://cs231n.github.io/)
[3] CS224D (http://cs224d.stanford.edu/syllabus.html)
[4] Hands on Machine Learning (https://github.com/ageron/handson-ml)
[5] Deep learning with Python Notebooks (https://github.com/fchollet/deep-learning-with-python-notebooks)
[6] Deep learning by Goodfellow et. al (http://www.deeplearningbook.org/)
[7] Neural networks online book (http://neuralnetworksanddeeplearning.com/)
[8] He et al, *Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
*, ICCV 2015, https://arxiv.org/abs/1502.01852
</pre>
|
github_jupyter
|
```
import gc
import locale
import pickle
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import ListedColormap
from all_stand_var import conv_dict, lab_cols, used_cols
from all_own_funct import cnfl, value_filtering,y_modelling,x_modelling,evaluate,lin_reg_coef,split_stratified_into_train_val_test
from seaborn import heatmap
from sklearn.metrics import roc_curve, accuracy_score, roc_auc_score
from sklearn.metrics import classification_report, confusion_matrix,average_precision_score,f1_score,roc_curve,roc_auc_score,plot_confusion_matrix
from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier
from matplotlib.backends.backend_pdf import PdfPages
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import kurtosis
locale.setlocale(locale.LC_ALL, 'fr_FR')
# output folder in which al results are saved
output_folder = os.path.join(os.getcwd(), 'Results_LR_RF_v2','1u_Results_no_mis')
if not os.path.exists(output_folder):
os.makedirs(output_folder)
#Create processed dataframe, if not already run LR_build.py
"""
used_cols = ['pat_hosp_id', 'pat_bd', 'pat_datetime', 'AdmissionDate', 'DischargeDate', 'mon_rr', 'mon_hr', 'mon_sat',
'mon_etco2', 'vent_m_ppeak','vent_m_peep','vent_m_fio2',
'mon_ibp_mean', 'pat_weight_act', 'vent_m_rr', 'vent_m_tv_exp']
dtype_dict={'vent_cat': 'category','vent_machine':'category','vent_mode':'category'}
df_raw=pd.read_csv(r'data\sorted_bron_date.csv',delimiter=';',converters=conv_dict,usecols=used_cols,dtype=dtype_dict,parse_dates=['pat_bd','pat_datetime','AdmissionDate', 'DischargeDate'],na_values=['NULL','null', 'Null','nUll','nuLl','nulL'],dayfirst=True)
#df = pp.data_pp_function(df_raw,path=output_folder,timestep='12H')
#df=df.groupby('Admissionnumber',sort=False).fillna(method='ffill').fillna(method='bfill')
"""
import importlib
import LR_build as pp
importlib.reload(pp)
# Load processed dataframe
f = open(os.path.join('./Results_LR_RF_v2/', 'processed_df.txt'), 'rb')
df = pickle.load(f)
f.close()
#informative plots and descriptive information
"""
used_cols = [ 'pat_datetime', 'mon_rr', 'mon_hr', 'mon_sat',
'mon_etco2', 'vent_m_fio2', 'vent_m_ppeak','vent_m_peep',
'mon_ibp_mean','pat_weight_act','vent_m_rr', 'vent_m_tv_exp','Age']
for col in used_cols:
print(df[col].describe())
print(df[df.index.get_level_values('pat_hosp_id') == 5407]['Reintub'].value_counts())
print(df[df.index.get_level_values('pat_hosp_id') == 5150574]['pat_datetime'].tail(100))
plt.plot(np.linspace(start=0,stop=720,num=720),df[df.index.get_level_values('pat_hosp_id') == 5407]['vent_m_peep'],'b-')
plt.plot(np.linspace(start=0,stop=720,num=720),df[df.index.get_level_values('pat_hosp_id')==5150574]['vent_m_tv_exp'],'r-')
fig=plt.gcf()
fig.set_size_inches(18.5, 10.5)
plt.show()
"""
# calculate the hour intervals, and also the missingness parameter
df=df.reset_index(drop=False)
df.info()
def index_1hr(group):
group['tim']=pd.date_range(start='1/1/2018', periods=len(group), freq='1min')
grouped = pd.Grouper(key='tim', freq='1H')
group['idx_1hr']=group.groupby(grouped,sort=False).ngroup().add(1)
group['mis']=(group['pat_datetime'].max()-group['pat_datetime'].min()).total_seconds()/60
del group['tim']
return group
df=df.groupby('Adnum',sort=False,as_index=False).apply(index_1hr)
print((df['Adnum'].value_counts()))
print(df.info())
df['idx_1hr']=df['idx_1hr'].astype(str)
print(df['idx_1hr'].unique())
df[['mis']]=StandardScaler().fit_transform(df[['mis']])
df=df.set_index(['pat_hosp_id','AdmissionDate','DischargeDate'])
# Stratified spit of dataframe into train, test and validation
pat=pd.read_excel(r'Results\admissiondate_v2.xlsx', parse_dates=[
'AdmissionDate', 'DischargeDate'])
group=pat.groupby('pat_hosp_id',sort=False).max().reset_index()
group.drop_duplicates('pat_hosp_id',inplace=True)
df_train,df_val,df_test=split_stratified_into_train_val_test(group, stratify_colname='Reintub',
frac_train=0.7, frac_val=0.1, frac_test=0.2,
random_state=1)
train_pat=df_train['pat_hosp_id'].unique()
test_pat=df_test['pat_hosp_id'].unique()
val_pat=df_val['pat_hosp_id'].unique()
df_train = df[df.index.get_level_values('pat_hosp_id').isin(train_pat)]
df_val = df[df.index.get_level_values('pat_hosp_id').isin(val_pat)]
df_test = df[df.index.get_level_values('pat_hosp_id').isin(test_pat)]
print(df_train.info())
def y_modelling(df):
y = df[['Reintub', 'Adnum', 'idx_1hr']]
y = y.groupby(['Adnum', 'idx_1hr'], sort=False).agg(['max'])
y.columns = ["_".join(a) for a in y.columns.to_flat_index()]
y.reset_index(drop=True, inplace=True, level='idx_1hr')
y = y.reset_index().drop_duplicates().set_index(
['Adnum'])
y = y[~y.index.duplicated(keep='last')]
y = y.fillna(value=0)
return y
# from dataframwe with label per minute, to array with label per admission
Y_TRAIN=y_modelling(df_train)
Y_TEST=y_modelling(df_test)
Y_VAL=y_modelling(df_val)
Y_TRAIN=Y_TRAIN['Reintub_max'].to_numpy()
Y_TEST=Y_TEST['Reintub_max'].to_numpy()
Y_VAL=Y_VAL['Reintub_max'].to_numpy()
Y_TRAIN=np.append(Y_TRAIN,Y_VAL)
def x_modelling(df):
temp = df[['Age', 'Adnum', 'idx_1hr','pat_weight_act']]
df = df.drop(['Age','pat_weight_act','Extubation_date','level_0','pat_datetime', 'Reintub'], axis=1)
df = df.groupby(['Adnum', 'idx_1hr'], sort=False).agg(['mean', 'std',lin_reg_coef])
df.columns = ["_".join(a) for a in df.columns.to_flat_index()]
df = df.stack().unstack([2, 1])
df.columns = ["_".join(a) for a in df.columns.to_flat_index()]
df = df.reset_index().drop_duplicates().set_index('Adnum')
df = df.fillna(method='ffill').fillna(method='bfill')
temp = temp.groupby('Adnum', sort=False).agg(['mean'])
temp.columns = ["_".join(a) for a in temp.columns.to_flat_index()]
temp = temp.reset_index().drop_duplicates().set_index('Adnum')
temp = temp[~temp.index.duplicated(keep='last')]
"""
df_temp = df_temp.drop('idx_1hr',axis=1)
df_temp = df_temp.groupby('Adnum',sort=False).agg([lin_reg_coef])
df_temp.columns = ["_".join(a) for a in df_temp.columns.to_flat_index()]
df_temp = df_temp.reset_index().drop_duplicates().set_index('Adnum')
df_temp = df_temp[~df_temp.index.duplicated(keep='last')]
"""
df = df.merge(temp, right_index=True, left_index=True, how='left')
#df = df.merge(df_temp, right_index=True, left_index=True, how='left')
del temp
return df
# Calculate features per admission
X_TRAIN=x_modelling(df_train)
X_TEST=x_modelling(df_test)
X_VAL=x_modelling(df_val)
print(X_TRAIN.info())
print(X_TEST.info())
X_TRAIN=X_TRAIN.fillna(value=0)
X_VAL=X_VAL.fillna(value=0)
X_TEST=X_TEST.fillna(value=0)
X_TRAIN=X_TRAIN.append(X_VAL)
# Save Train and test data to file
f = open(os.path.join(output_folder, 'x_train.txt'), 'wb')
pickle.dump(X_TRAIN, f)
f.close()
f = open(os.path.join(output_folder, 'x_test.txt'), 'wb')
pickle.dump(X_TEST, f)
f.close()
f = open(os.path.join(output_folder, 'y_train.txt'), 'wb')
pickle.dump(Y_TRAIN, f)
f.close()
f = open(os.path.join(output_folder, 'y_test.txt'), 'wb')
pickle.dump(Y_TEST, f)
f.close()
# Randomised search for random forest mode
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(10, 50, num = 11)]
max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 4]
# Method of selecting samples for training each tree
bootstrap = [True, False]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
'bootstrap': bootstrap}
# Use the random grid to search for best hyperparameters
# First create the base model to tune
rf = RandomForestClassifier()
# Random search of parameters, using 3 fold cross validation,
# search across 100 different combinations, and use all available cores
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 20, cv = 3, verbose=2, random_state=42, n_jobs = -1)
# Fit the random search model
rf_random.fit(X_TRAIN, Y_TRAIN)
# Evaluate the base model vs the optimized model
base_model = RandomForestClassifier(n_estimators = 10, random_state = 42,max_depth=10)
base_model.fit(X_TRAIN, Y_TRAIN)
base_accuracy = evaluate(base_model, X_TEST, Y_TEST,'base_accuracy RF',output_folder)
best_random = rf_random.best_estimator_
random_accuracy = evaluate(best_random, X_TEST,Y_TEST,'Best_random RF',output_folder)
if base_accuracy > random_accuracy:
best_random = base_model
# Create AUROC plot, confusion matrix and other results
from all_own_funct import roc_auc_ci
try:
pdf = PdfPages(os.path.join(output_folder,f"Figures_all_.pdf"))
except PermissionError:
os.remove(os.path.join(output_folder,f"Figures_all.pdf"))
os.remove(os.path.join(output_folder,f"Result_scores_all.txt"))
clf = best_random
y_pred_clas=clf.predict(X_TEST)
# Predict the probabilities, function depends on used classifier
try:
y_pred_prob=clf.predict_proba(X_TEST)
y_pred_prob=y_pred_prob[:,1]
except:
try:
y_pred_prob=clf.decision_function(X_TEST)
except:
y_pred_prob=y_pred_clas
report=classification_report(Y_TEST,y_pred_clas,target_names=['No Reintubation','Reintubation'])
score=clf.score(X_TEST,Y_TEST)
average_precision = average_precision_score(Y_TEST, y_pred_prob)
f1_s=f1_score(Y_TEST, y_pred_clas)
# write scoring metrics to file
with open(os.path.join(output_folder,f"Result_scores_all.txt"),'a') as file:
file.write(f"Results for RF on training set\n\n")
file.write(f"Classification report \n {report} \n")
file.write(f"Hold_out_scores {score} \n")
file.write(f"Average precision score {average_precision} \n")
file.write(f"F1 score {f1_s} \n\n\n")
plot_confusion_matrix(clf,X_TEST,Y_TEST)
plt.title(f"Confusion matrix of random forrest")
fig=plt.gcf()
pdf.savefig(fig)
plt.close(fig)
fpr, tpr, _ = roc_curve(Y_TEST, y_pred_prob)
auc = roc_auc_score(Y_TEST, y_pred_prob)
# 95%CI calculation using bootstrapping
n_bootstraps = 2000
rng_seed = 42 # control reproducibility
bootstrapped_scores = []
rng = np.random.RandomState(rng_seed)
for i in range(n_bootstraps):
# bootstrap by sampling with replacement on the prediction indices
indices = rng.randint(0, len(y_pred_prob), len(y_pred_prob))
if len(np.unique(Y_TEST[indices])) < 2:
# We need at least one positive and one negative sample for ROC AUC
# to be defined: reject the sample
continue
score = roc_auc_score(Y_TEST[indices], y_pred_prob[indices])
bootstrapped_scores.append(score)
#print("Bootstrap #{} ROC area: {:0.3f}".format(i + 1, score))
sorted_scores = np.array(bootstrapped_scores)
sorted_scores.sort()
# Computing the lower and upper bound of the 90% confidence interval
# You can change the bounds percentiles to 0.025 and 0.975 to get
# a 95% confidence interval instead.
confidence_lower = sorted_scores[int(0.05 * len(sorted_scores))]
confidence_upper = sorted_scores[int(0.95 * len(sorted_scores))]
with open(os.path.join(output_folder,f"Result_scores_all.txt"),'a') as file:
file.write("\nConfidence interval for the score: [{:0.3f} - {:0.3}]\n".format(
confidence_lower, confidence_upper))
a=roc_auc_ci(Y_TEST,y_pred_prob)
print(a)
plt.plot(fpr,tpr,label=f"auc={auc}",linewidth=1.5,markersize=1)
plt.legend(loc=4,fontsize='xx-small')
plt.title(f'ROC of Random Forrest hour data')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
axes = plt.gca()
axes.set_xlim([0,1])
axes.set_ylim([0,1])
fig=plt.gcf()
pdf.savefig(fig)
plt.close(fig)
# Hyperparameters for Logistic Regression
# The solvers
solver =['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']
# Class weight optimizer
class_weight=[{0:0.1,1:0.9},'balanced',None]
# Penalty
penalty=['l1', 'l2', 'elasticnet', None]
# Inverse of regularization strength
C=np.logspace(-3,3,7)
# Bootsrapping
bootstrap = [True, False]
# Create the random grid
random_grid = {'solver':solver,
'class_weight':class_weight,
'penalty':penalty,
'C':C,
'penalty':penalty}
# First create the base model to tune
lr = LogisticRegression(max_iter=500)
# Random search of parameters, using 3 fold cross validation,
# search across 60 different combinations, and use all available cores
lr_random = RandomizedSearchCV(estimator = lr , param_distributions = random_grid, n_iter = 20, cv = 3, verbose=2, random_state=42, n_jobs = -1)
# Fit the random search model
lr_random.fit(X_TRAIN, Y_TRAIN)
# Evaluate the models based on AUROC
base_model_lr = LogisticRegression(max_iter=500)
base_model_lr.fit(X_TRAIN, Y_TRAIN)
base_accuracy_lr = evaluate(base_model, X_TEST, Y_TEST,'base_model LR',output_folder)
best_random_lr = lr_random.best_estimator_
random_accuracy_lr = evaluate(best_random, X_TEST,Y_TEST,'Best random LR',output_folder)
if base_accuracy_lr > random_accuracy_lr:
best_random_lr = base_model_lr
# Create AUROC plot, confusion matrix and other results for Logistic regression
clf = best_random_lr
y_pred_clas=clf.predict(X_TEST)
# Predict the probabilities, function depends on used classifier
try:
y_pred_prob=clf.predict_proba(X_TEST)
y_pred_prob=y_pred_prob[:,1]
except:
try:
y_pred_prob=clf.decision_function(X_TEST)
except:
y_pred_prob=y_pred_clas
report=classification_report(Y_TEST,y_pred_clas,target_names=['No Reintubation','Reintubation'])
score=clf.score(X_TEST,Y_TEST)
average_precision = average_precision_score(Y_TEST, y_pred_prob)
f1_s=f1_score(Y_TEST, y_pred_clas)
with open(os.path.join(output_folder,f"Result_scores_all.txt"),'a') as file:
file.write(f"Results for LR on training\n\n")
file.write(f"Classification report \n {report} \n")
file.write(f"Hold_out_scores {score} \n")
file.write(f"Average precision score {average_precision} \n")
file.write(f"F1 score {f1_s} \n\n\n")
plot_confusion_matrix(clf,X_TEST,Y_TEST)
plt.title(f"Confusion matrix of logistic regression")
fig=plt.gcf()
pdf.savefig(fig)
plt.close(fig)
fpr, tpr, _ = roc_curve(Y_TEST, y_pred_prob)
auc = roc_auc_score(Y_TEST, y_pred_prob)
n_bootstraps = 2000
rng_seed = 42 # control reproducibility
bootstrapped_scores = []
rng = np.random.RandomState(rng_seed)
for i in range(n_bootstraps):
# bootstrap by sampling with replacement on the prediction indices
indices = rng.randint(0, len(y_pred_prob), len(y_pred_prob))
if len(np.unique(Y_TEST[indices])) < 2:
# We need at least one positive and one negative sample for ROC AUC
# to be defined: reject the sample
continue
score = roc_auc_score(Y_TEST[indices], y_pred_prob[indices])
bootstrapped_scores.append(score)
#print("Bootstrap #{} ROC area: {:0.3f}".format(i + 1, score))
sorted_scores = np.array(bootstrapped_scores)
sorted_scores.sort()
# Computing the lower and upper bound of the 90% confidence interval
# You can change the bounds percentiles to 0.025 and 0.975 to get
# a 95% confidence interval instead.
confidence_lower = sorted_scores[int(0.05 * len(sorted_scores))]
confidence_upper = sorted_scores[int(0.95 * len(sorted_scores))]
with open(os.path.join(output_folder,f"Result_scores_all.txt"),'a') as file:
file.write("\nConfidence interval for the score: [{:0.3f} - {:0.3}]\n".format(
confidence_lower, confidence_upper))
a=roc_auc_ci(Y_TEST,y_pred_prob)
print(a)
plt.plot(fpr,tpr,label=f"auc={auc}",linewidth=1.5,markersize=1)
plt.legend(loc=4,fontsize='xx-small')
plt.title(f'ROC of Logistic Regression data')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
axes = plt.gca()
axes.set_xlim([0,1])
axes.set_ylim([0,1])
fig=plt.gcf()
pdf.savefig(fig)
plt.close(fig)
pdf.close()
# Save the best models
import pickle
f = open(os.path.join(output_folder,'ran_for.sav'), 'wb')
pickle.dump(best_random, f)
f.close()
f = open(os.path.join(output_folder,'log_reg.sav'), 'wb')
pickle.dump(best_random_lr, f)
f.close()
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Scale-heights-for-typical-atmospheric-soundings" data-toc-modified-id="Scale-heights-for-typical-atmospheric-soundings-1"><span class="toc-item-num">1 </span>Scale heights for typical atmospheric soundings</a></span><ul class="toc-item"><li><span><a href="#Plot-McClatchey's-US-Standard-Atmospheres" data-toc-modified-id="Plot-McClatchey's-US-Standard-Atmospheres-1.1"><span class="toc-item-num">1.1 </span>Plot McClatchey's US Standard Atmospheres</a></span><ul class="toc-item"><li><span><a href="#Reading-the-soundings-files-into-pandas" data-toc-modified-id="Reading-the-soundings-files-into-pandas-1.1.1"><span class="toc-item-num">1.1.1 </span>Reading the soundings files into pandas</a></span></li></ul></li></ul></li><li><span><a href="#Use-pd.DataFrame.head-to-see-first-5-lines" data-toc-modified-id="Use-pd.DataFrame.head-to-see-first-5-lines-2"><span class="toc-item-num">2 </span>Use pd.DataFrame.head to see first 5 lines</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Plot--temp-and-vapor-mixing-ratio-rmix-($\rho_{H2O}/\rho_{air}$)" data-toc-modified-id="Plot--temp-and-vapor-mixing-ratio-rmix-($\rho_{H2O}/\rho_{air}$)-2.0.1"><span class="toc-item-num">2.0.1 </span>Plot temp and vapor mixing ratio rmix ($\rho_{H2O}/\rho_{air}$)</a></span></li></ul></li><li><span><a href="#Calculating-scale-heights-for-temperature-and-air-density" data-toc-modified-id="Calculating-scale-heights-for-temperature-and-air-density-2.1"><span class="toc-item-num">2.1 </span>Calculating scale heights for temperature and air density</a></span><ul class="toc-item"><li><span><a href="#How-do-$\overline{H_p}$-and-$\overline{H_\rho}$-compare-for-the-tropical-sounding?" data-toc-modified-id="How-do-$\overline{H_p}$-and-$\overline{H_\rho}$-compare-for-the-tropical-sounding?-2.1.1"><span class="toc-item-num">2.1.1 </span>How do $\overline{H_p}$ and $\overline{H_\rho}$ compare for the tropical sounding?</a></span></li><li><span><a href="#How-well-do-these-average-values-represent-the-pressure-and-density-profiles?" data-toc-modified-id="How-well-do-these-average-values-represent-the-pressure-and-density-profiles?-2.1.2"><span class="toc-item-num">2.1.2 </span>How well do these average values represent the pressure and density profiles?</a></span></li><li><span><a href="#Assignment-for-Tuesday" data-toc-modified-id="Assignment-for-Tuesday-2.1.3"><span class="toc-item-num">2.1.3 </span>Assignment for Tuesday</a></span></li></ul></li></ul></li></ul></div>
# Scale heights for typical atmospheric soundings
## Plot McClatchey's US Standard Atmospheres
There are five different average profiles for the tropics, subarctic summer, subarctic winter, midlatitude summer, midlatitude winter. These are called the US Standard Atmospheres. This notebook shows how to read and plot the soundings, and calculate the pressure and density scale heights.
```
from matplotlib import pyplot as plt
import matplotlib.ticker as ticks
import numpy as np
import a301
from pathlib import Path
import pandas as pd
import pprint
soundings_folder= a301.test_dir / Path('soundings')
sounding_files = list(soundings_folder.glob("*csv"))
```
### Reading the soundings files into pandas
There are five soundings.
The soundings have six columns and 33 rows (i.e. 33 height levels). The variables are
z, press, temp, rmix, den, o3den -- where rmix is the mixing ratio of water vapor, den is the dry air density and o3den is the ozone density. The units are
m, pa, K, kg/kg, kg/m^3, kg/m^3
I will read the 6 column soundings into a [pandas (panel data) DataFrame](http://pandas.pydata.org/pandas-docs/stable/dsintro.html), which is like a matrix except the columns can be accessed by column name in addition to column number. The main advantage for us is that it's easier to keep track of which variables we're plotting
```
name_dict=dict()
sound_dict=dict()
for item in sounding_files:
name_dict[item.stem]=item
pprint.pprint(name_dict)
for item in sounding_files:
sound_dict[item.stem]=pd.read_csv(item)
```
# Use pd.DataFrame.head to see first 5 lines
```
for key,value in sound_dict.items():
print(f"sounding: {key}\n{sound_dict[key].head()}")
```
We use these keys to get a dataframe with 6 columns, and 33 levels. Here's an example for the midsummer sounding
```
midsummer=sound_dict['midsummer']
print(midsummer.head())
list(midsummer.columns)
```
### Plot temp and vapor mixing ratio rmix ($\rho_{H2O}/\rho_{air}$)
```
%matplotlib inline
plt.style.use('ggplot')
meters2km=1.e-3
plt.close('all')
fig,(ax1,ax2)=plt.subplots(1,2,figsize=(11,8))
for a_name,df in sound_dict.items():
ax1.plot(df['temp'],df['z']*meters2km,label=a_name)
ax1.set(ylim=(0,40),title='Temp soundings',ylabel='Height (km)',
xlabel='Temperature (K)')
ax2.plot(df['rmix']*1.e3,df['z']*meters2km,label=a_name)
ax2.set(ylim=(0,8),title='Vapor soundings',ylabel='Height (km)',
xlabel='vapor mixing ratio (g/kg)')
ax1.legend();
```
## Calculating scale heights for temperature and air density
Here is equation 1 of the [hydrostatic balance notes](http://clouds.eos.ubc.ca/~phil/courses/atsc301/hydrostat.html#equation-hydro)
$$\frac{ 1}{\overline{H_p}} = \overline{ \left ( \frac{1 }{H} \right )} = \frac{\int_{0 }^{z}\!\frac{1}{H} dz^\prime }{z-0} $$
where
$$H=R_d T/g$$
and here is the Python code to do that integral:
```
g=9.8 #don't worry about g(z) for this exercise
Rd=287. #kg/m^3
def calcScaleHeight(T,p,z):
"""
Calculate the pressure scale height H_p
Parameters
----------
T: vector (float)
temperature (K)
p: vector (float) of len(T)
pressure (pa)
z: vector (float) of len(T
height (m)
Returns
-------
Hbar: vector (float) of len(T)
pressure scale height (m)
"""
dz=np.diff(z)
TLayer=(T[1:] + T[0:-1])/2.
oneOverH=g/(Rd*TLayer)
Zthick=z[-1] - z[0]
oneOverHbar=np.sum(oneOverH*dz)/Zthick
Hbar = 1/oneOverHbar
return Hbar
```
Similarly, equation (5) of the [hydrostatic balance notes](http://clouds.eos.ubc.ca/~phil/courses/atsc301/hydrostat.html#equation-hydro)
is:
$$\frac{d\rho }{\rho} = - \left ( \frac{1 }{H} +
\frac{1 }{T} \frac{dT }{dz} \right ) dz \equiv - \frac{dz }{H_\rho} $$
Which leads to
$$\frac{ 1}{\overline{H_\rho}} = \frac{\int_{0 }^{z}\!\left [ \frac{1}{H} + \frac{1 }{T} \frac{dT }{dz} \right ] dz^\prime }{z-0} $$
and the following python function:
```
def calcDensHeight(T,p,z):
"""
Calculate the density scale height H_rho
Parameters
----------
T: vector (float)
temperature (K)
p: vector (float) of len(T)
pressure (pa)
z: vector (float) of len(T
height (m)
Returns
-------
Hbar: vector (float) of len(T)
density scale height (m)
"""
dz=np.diff(z)
TLayer=(T[1:] + T[0:-1])/2.
dTdz=np.diff(T)/np.diff(z)
oneOverH=g/(Rd*TLayer) + (1/TLayer*dTdz)
Zthick=z[-1] - z[0]
oneOverHbar=np.sum(oneOverH*dz)/Zthick
Hbar = 1/oneOverHbar
return Hbar
```
### How do $\overline{H_p}$ and $\overline{H_\rho}$ compare for the tropical sounding?
```
sounding='tropics'
#
# grab the dataframe and get the sounding columns
#
df=sound_dict[sounding]
z=df['z'].values
Temp=df['temp'].values
press=df['press'].values
#
# limit calculation to bottom 10 km
#
hit=z<10000.
zL,pressL,TempL=(z[hit],press[hit],Temp[hit])
rhoL=pressL/(Rd*TempL)
Hbar= calcScaleHeight(TempL,pressL,zL)
Hrho= calcDensHeight(TempL,pressL,zL)
print("pressure scale height for the {} sounding is {:5.2f} km".format(sounding,Hbar*1.e-3))
print("density scale height for the {} is {:5.2f} km".format(sounding,Hrho*1.e-3))
```
### How well do these average values represent the pressure and density profiles?
```
theFig,theAx=plt.subplots(1,1)
theAx.semilogy(Temp,press/100.)
#
# need to flip the y axis since pressure decreases with height
#
theAx.invert_yaxis()
tickvals=[1000,800, 600, 400, 200, 100, 50,1]
theAx.set_yticks(tickvals)
majorFormatter = ticks.FormatStrFormatter('%d')
theAx.yaxis.set_major_formatter(majorFormatter)
theAx.set_yticklabels(tickvals)
theAx.set_ylim([1000.,50.])
theAx.set_title('{} temperature profile'.format(sounding))
theAx.set_xlabel('Temperature (K)')
theAx.set_ylabel('pressure (hPa)');
```
Now check the hydrostatic approximation by plotting the pressure column against
$$p(z) = p_0 \exp \left (-z/\overline{H_p} \right )$$
vs. the actual sounding p(T):
```
fig,theAx=plt.subplots(1,1)
hydroPress=pressL[0]*np.exp(-zL/Hbar)
theAx.plot(pressL/100.,zL/1000.,label='sounding')
theAx.plot(hydroPress/100.,zL/1000.,label='hydrostat approx')
theAx.set_title('height vs. pressure for tropics')
theAx.set_xlabel('pressure (hPa)')
theAx.set_ylabel('height (km)')
theAx.set_xlim([500,1000])
theAx.set_ylim([0,5])
tickVals=[500, 600, 700, 800, 900, 1000]
theAx.set_xticks(tickVals)
theAx.set_xticklabels(tickVals)
theAx.legend(loc='best');
```
Again plot the hydrostatic approximation
$$\rho(z) = \rho_0 \exp \left (-z/\overline{H_\rho} \right )$$
vs. the actual sounding $\rho(z)$:
```
fig,theAx=plt.subplots(1,1)
hydroDens=rhoL[0]*np.exp(-zL/Hrho)
theAx.plot(rhoL,zL/1000.,label='sounding')
theAx.plot(hydroDens,zL/1000.,label='hydrostat approx')
theAx.set_title('height vs. density for the tropics')
theAx.set_xlabel('density ($kg\,m^{-3}$)')
theAx.set_ylabel('height (km)')
theAx.set_ylim([0,5])
theAx.legend(loc='best');
```
<a name="oct7assign"></a>
### Assignment for Tuesday
Add cells to this notebook to:
1\. Print out the density and pressure scale heights for each of the five soundings
2\. Define a function that takes a sounding dataframe and returns the "total precipitable water", which is defined as:
$$W = \int_0^{z_{top}} \rho_v dz $$
Do a change of units to convert $kg\,m^{-2}$ to $cm\,m^{-2}$ using the density of liquid water (1000 $kg\,m^{-3}$) -- that is, turn the kg of water in the 1 square meter column into cubic meters and turn that into $cm/m^{-2}$
3\. Use your function to print out W for all five soundings
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
sns.set_style('whitegrid')
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import cross_val_predict,cross_val_score
from sklearn.metrics import roc_auc_score,roc_curve
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import mean_squared_error
from sklearn.svm import SVC
training_data = pd.read_csv("../Data/aps_failure_training_set.csv",na_values="na")
training_data.head()
```
# Preprocessing
```
plt.figure(figsize=(20,12))
sns.heatmap(training_data.isnull(),yticklabels=False,cbar=False,cmap = 'viridis')
```
# Missing value handling
We are going to use different approches with missing values:
1. Removing the column having 80% missing values (**Self intuition)
2. Keeping all the features
3. Later, we will try to implement some feature engineering
**For the rest of the missing values, we are replacing them with their mean() for now (**Ref)
<big><b>Second Approach</b>
```
sample_training_data = training_data
sample_training_data.fillna(sample_training_data.mean(),inplace=True)
#after replacing with mean()
plt.figure(figsize=(20,12))
sns.heatmap(sample_training_data.isnull(),yticklabels=False,cbar=False,cmap='viridis')
#as all the other values are numerical except Class column so we can replace them with 1 and 0
sample_training_data = sample_training_data.replace('neg',0)
sample_training_data = sample_training_data.replace('pos',1)
sample_training_data.head()
```
# Testing Data preprocessing
```
testing_data = pd.read_csv("../Data/aps_failure_test_set.csv",na_values="na")
testing_data.head()
sample_testing_data = testing_data
sample_testing_data.fillna(sample_testing_data.mean(),inplace=True)
#after replacing with mean()
plt.figure(figsize=(20,12))
sns.heatmap(sample_testing_data.isnull(),yticklabels=False,cbar=False,cmap='viridis')
#as all the other values are numerical except Class column so we can replace them with 1 and 0
sample_testing_data = sample_testing_data.replace('neg',0)
sample_testing_data = sample_testing_data.replace('pos',1)
sample_testing_data.head()
```
# Implemented Methods
```
def getCost(y_test,prediction):
'''
evaluate the total cost without modified threshold
'''
tn, fp, fn, tp = confusion_matrix(y_test,prediction).ravel()
confusionData = [[tn,fp],[fn,tp]]
print("Confusion Matrix\n")
print(pd.DataFrame(confusionData,columns=['FN','FP'],index=['TN','TP']))
cost = 10*fp+500*fn
values = {'Score':[cost],'Number of Type 1 faults':[fp],'Number of Type 2 faults':[fn]}
print("\n\nCost\n")
print(pd.DataFrame(values))
def getCostWithThreshold(X_test,y_test,prediction,threshold,model):
"""
evaluate the total cost with modified threshold
model = model instance
"""
THRESHOLD = threshold #optimal one chosen from the roc curve
thresholdPrediction = np.where(model.predict_proba(X_test)[:,1] > THRESHOLD, 1,0)
tn, fp, fn, tp = confusion_matrix(y_test,thresholdPrediction).ravel()
cost = 10*fp+500*fn
values = {'Score':[cost],'Number of Type 1 faults':[fp],'Number of Type 2 faults':[fn]}
pd.DataFrame(values)
def aucForThreshold(X_test,y_test,model):
"""
return roc auc curve for determining the optimal threshold
model = desired model's instance
"""
from sklearn.metrics import roc_auc_score,roc_curve
logit_roc_auc = roc_auc_score(y_test, model.predict_proba(X_test)[:,1])
fpr, tpr, thresholds = roc_curve(y_test,model.predict_proba(X_test)[:,1])
plt.figure()
plt.plot(fpr, tpr, label='Logistic Regression (area = %0.2f)' % logit_roc_auc)
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="upper center")
plt.savefig('Log_ROC')
# create the axis of thresholds (scores)
ax2 = plt.gca().twinx()
ax2.plot(fpr, thresholds, markeredgecolor='g',linestyle='dashed', color='g',label = 'Threshold')
ax2.set_ylabel('Threshold',color='g')
ax2.set_ylim([thresholds[-1],thresholds[0]])
ax2.set_xlim([fpr[0],fpr[-1]])
plt.legend(loc="lower right")
plt.savefig('roc_and_threshold.png')
plt.show()
def evaluationScored(y_test,prediction):
acc = metrics.accuracy_score(y_test, prediction)
r2 = metrics.r2_score(y_test, prediction)
f1 = metrics.f1_score(y_test, prediction)
mse = metrics.mean_squared_error(y_test, prediction)
values = {'Accuracy Score':[acc],'R2':[r2],'F1':[f1],'MSE':[mse]}
print("\n\nScores")
print (pd.DataFrame(values))
```
# Model implementation with Cross validation
```
X = sample_training_data.drop('class',axis=1)
y = sample_training_data['class']
CV_prediction = cross_val_predict(SVC(),X,y,cv = 5)
CV_score = cross_val_score(SVC(),X,y,cv = 5)
#mean cross validation score
np.mean(CV_score)
print(classification_report(y,CV_prediction))
evaluationScores(y,CV_prediction)
CV_prediction = cross_val_predict(SVC(),X,y,cv = 10)
print(classification_report(y,CV_prediction))
evaluationScores(y,CV_prediction)
```
# Try with test train split
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
svc_model = SVC()
svc_model.fit(X_train,y_train)
trainingPrediction = svc_model.predict(X_test)
evaluationScored(y_test,trainingPrediction)
getCost(y_test,trainingPrediction)
```
<b>With threshold</b>
```
aucForThreshold(X_test,y_test,svc_model)
#need to implement
getCostWithThreshold(X_test,y_test,trainingPrediction,threshold,svc_model)
```
<b>With Gridsearch</b>
```
param_grid = {'C': [0.1,1], 'gamma': [1,0.1], 'kernel': ['rbf']}
from sklearn.model_selection import GridSearchCV
grid = GridSearchCV(SVC(),param_grid,refit=True,verbose=3)
#fitting again
grid.fit(X_train,y_train)
grid.best_params_
grid.best_estimator_
grid_predictions = grid.predict(X_test)
evaluationScored(y_test,grid_predictions)
getCost(y_test,grid_predictions)
aucForThreshold(X_test,y_test,grid)
#need to implement
getCostWithThreshold(X_test,y_test,trainingPrediction,threshold,grid)
```
# Testing Data implementation
|
github_jupyter
|
```
import tensorflow as tf
print(tf.__version__)
import tensorflow_datasets as tfds
print(tfds.__version__)
```
# Get dataset
```
SPLIT_WEIGHTS = (8, 1, 1)
splits = tfds.Split.TRAIN.subsplit(weighted=SPLIT_WEIGHTS)
(raw_train, raw_validation, raw_test), metadata = tfds.load('cats_vs_dogs',
split=list(splits),
with_info=True,
as_supervised=True)
print(metadata.features)
import matplotlib.pyplot as plt
%matplotlib inline
get_label_name = metadata.features['label'].int2str
for image, label in raw_train.take(2):
plt.figure()
plt.imshow(image)
plt.title(get_label_name(label))
```
# Prepare input pipelines
```
IMG_SIZE = 160
BATCH_SIZE = 32
SHUFFLE_BUFFER_SIZE = 1000
def normalize_img(image, label):
image = tf.cast(image, tf.float32)
image = (image / 127.5) - 1.0
image = tf.image.resize(image, (IMG_SIZE, IMG_SIZE))
return image, label
ds_train = raw_train.map(normalize_img)
ds_validation = raw_validation.map(normalize_img)
ds_test = raw_test.map(normalize_img)
ds_train = ds_train.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)
ds_validation = ds_validation.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)
ds_test = ds_test.batch(BATCH_SIZE)
```
# Get pretrained model
```
base_model = tf.keras.applications.MobileNetV2(input_shape=(IMG_SIZE, IMG_SIZE, 3),
include_top=False,
weights='imagenet')
base_model.trainable = False
model = tf.keras.Sequential([
base_model,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(1)
])
model.summary()
```
# (Optional): Use Tensorflow Hub
```
import tensorflow_hub as hub
print(hub.__version__)
feature_extractor_url = "https://tfhub.dev/google/imagenet/mobilenet_v2_035_160/classification/4"
base_model = hub.KerasLayer(feature_extractor_url, input_shape=(IMG_SIZE, IMG_SIZE, 3), trainable=False)
model = tf.keras.Sequential([
base_model,
tf.keras.layers.Dense(1)
])
model.summary()
```
# Compile model
```
base_learning_rate = 1e-4
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=base_learning_rate),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
```
# Evaluate random model
```
loss0, accuracy0 = model.evaluate(ds_validation)
```
# Train model
```
initial_epochs = 3
history = model.fit(ds_train,
epochs=initial_epochs,
validation_data=ds_validation)
```
# Fine-tune
```
base_model.trainable = True
base_learning_rate = 1e-5
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=base_learning_rate),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
model.summary()
fine_tune_epochs = 3
total_epochs = initial_epochs + fine_tune_epochs
history_fine = model.fit(ds_train,
epochs=total_epochs,
initial_epoch=history.epoch[-1],
validation_data=ds_validation)
```
|
github_jupyter
|
```
#default_exp tabular.core
#export
from fastai2.torch_basics import *
from fastai2.data.all import *
from nbdev.showdoc import *
#export
pd.set_option('mode.chained_assignment','raise')
```
# Tabular core
> Basic function to preprocess tabular data before assembling it in a `DataLoaders`.
## Initial preprocessing
```
#export
def make_date(df, date_field):
"Make sure `df[date_field]` is of the right date type."
field_dtype = df[date_field].dtype
if isinstance(field_dtype, pd.core.dtypes.dtypes.DatetimeTZDtype):
field_dtype = np.datetime64
if not np.issubdtype(field_dtype, np.datetime64):
df[date_field] = pd.to_datetime(df[date_field], infer_datetime_format=True)
df = pd.DataFrame({'date': ['2019-12-04', '2019-11-29', '2019-11-15', '2019-10-24']})
make_date(df, 'date')
test_eq(df['date'].dtype, np.dtype('datetime64[ns]'))
#export
def add_datepart(df, field_name, prefix=None, drop=True, time=False):
"Helper function that adds columns relevant to a date in the column `field_name` of `df`."
make_date(df, field_name)
field = df[field_name]
prefix = ifnone(prefix, re.sub('[Dd]ate$', '', field_name))
attr = ['Year', 'Month', 'Week', 'Day', 'Dayofweek', 'Dayofyear', 'Is_month_end', 'Is_month_start',
'Is_quarter_end', 'Is_quarter_start', 'Is_year_end', 'Is_year_start']
if time: attr = attr + ['Hour', 'Minute', 'Second']
for n in attr: df[prefix + n] = getattr(field.dt, n.lower())
df[prefix + 'Elapsed'] = field.astype(np.int64) // 10 ** 9
if drop: df.drop(field_name, axis=1, inplace=True)
return df
df = pd.DataFrame({'date': ['2019-12-04', '2019-11-29', '2019-11-15', '2019-10-24']})
df = add_datepart(df, 'date')
test_eq(df.columns, ['Year', 'Month', 'Week', 'Day', 'Dayofweek', 'Dayofyear', 'Is_month_end', 'Is_month_start',
'Is_quarter_end', 'Is_quarter_start', 'Is_year_end', 'Is_year_start', 'Elapsed'])
df.head()
#export
def _get_elapsed(df,field_names, date_field, base_field, prefix):
for f in field_names:
day1 = np.timedelta64(1, 'D')
last_date,last_base,res = np.datetime64(),None,[]
for b,v,d in zip(df[base_field].values, df[f].values, df[date_field].values):
if last_base is None or b != last_base:
last_date,last_base = np.datetime64(),b
if v: last_date = d
res.append(((d-last_date).astype('timedelta64[D]') / day1))
df[prefix + f] = res
return df
#export
def add_elapsed_times(df, field_names, date_field, base_field):
"Add in `df` for each event in `field_names` the elapsed time according to `date_field` grouped by `base_field`"
field_names = list(L(field_names))
#Make sure date_field is a date and base_field a bool
df[field_names] = df[field_names].astype('bool')
make_date(df, date_field)
work_df = df[field_names + [date_field, base_field]]
work_df = work_df.sort_values([base_field, date_field])
work_df = _get_elapsed(work_df, field_names, date_field, base_field, 'After')
work_df = work_df.sort_values([base_field, date_field], ascending=[True, False])
work_df = _get_elapsed(work_df, field_names, date_field, base_field, 'Before')
for a in ['After' + f for f in field_names] + ['Before' + f for f in field_names]:
work_df[a] = work_df[a].fillna(0).astype(int)
for a,s in zip([True, False], ['_bw', '_fw']):
work_df = work_df.set_index(date_field)
tmp = (work_df[[base_field] + field_names].sort_index(ascending=a)
.groupby(base_field).rolling(7, min_periods=1).sum())
tmp.drop(base_field,1,inplace=True)
tmp.reset_index(inplace=True)
work_df.reset_index(inplace=True)
work_df = work_df.merge(tmp, 'left', [date_field, base_field], suffixes=['', s])
work_df.drop(field_names,1,inplace=True)
return df.merge(work_df, 'left', [date_field, base_field])
df = pd.DataFrame({'date': ['2019-12-04', '2019-11-29', '2019-11-15', '2019-10-24'],
'event': [False, True, False, True], 'base': [1,1,2,2]})
df = add_elapsed_times(df, ['event'], 'date', 'base')
df
#export
def cont_cat_split(df, max_card=20, dep_var=None):
"Helper function that returns column names of cont and cat variables from given `df`."
cont_names, cat_names = [], []
for label in df:
if label == dep_var: continue
if df[label].dtype == int and df[label].unique().shape[0] > max_card or df[label].dtype == float:
cont_names.append(label)
else: cat_names.append(label)
return cont_names, cat_names
```
## Tabular -
```
#export
class _TabIloc:
"Get/set rows by iloc and cols by name"
def __init__(self,to): self.to = to
def __getitem__(self, idxs):
df = self.to.items
if isinstance(idxs,tuple):
rows,cols = idxs
cols = df.columns.isin(cols) if is_listy(cols) else df.columns.get_loc(cols)
else: rows,cols = idxs,slice(None)
return self.to.new(df.iloc[rows, cols])
#export
class Tabular(CollBase, GetAttr, FilteredBase):
"A `DataFrame` wrapper that knows which cols are cont/cat/y, and returns rows in `__getitem__`"
_default,with_cont='procs',True
def __init__(self, df, procs=None, cat_names=None, cont_names=None, y_names=None, y_block=None, splits=None,
do_setup=True, device=None, inplace=False, reduce_memory=True):
if inplace and splits is not None and pd.options.mode.chained_assignment is not None:
warn("Using inplace with splits will trigger a pandas error. Set `pd.options.mode.chained_assignment=None` to avoid it.")
if not inplace: df = df.copy()
if splits is not None: df = df.iloc[sum(splits, [])]
self.dataloaders = delegates(self._dl_type.__init__)(self.dataloaders)
super().__init__(df)
self.y_names,self.device = L(y_names),device
if y_block is None and self.y_names:
# Make ys categorical if they're not numeric
ys = df[self.y_names]
if len(ys.select_dtypes(include='number').columns)!=len(ys.columns): y_block = CategoryBlock()
else: y_block = RegressionBlock()
if y_block is not None and do_setup:
if callable(y_block): y_block = y_block()
procs = L(procs) + y_block.type_tfms
self.cat_names,self.cont_names,self.procs = L(cat_names),L(cont_names),Pipeline(procs)
self.split = len(df) if splits is None else len(splits[0])
if reduce_memory:
if len(self.cat_names) > 0: self.reduce_cats()
if len(self.cont_names) > 0: self.reduce_conts()
if do_setup: self.setup()
def new(self, df):
return type(self)(df, do_setup=False, reduce_memory=False, y_block=TransformBlock(),
**attrdict(self, 'procs','cat_names','cont_names','y_names', 'device'))
def subset(self, i): return self.new(self.items[slice(0,self.split) if i==0 else slice(self.split,len(self))])
def copy(self): self.items = self.items.copy(); return self
def decode(self): return self.procs.decode(self)
def decode_row(self, row): return self.new(pd.DataFrame(row).T).decode().items.iloc[0]
def reduce_cats(self): self.train[self.cat_names] = self.train[self.cat_names].astype('category')
def reduce_conts(self): self[self.cont_names] = self[self.cont_names].astype(np.float32)
def show(self, max_n=10, **kwargs): display_df(self.new(self.all_cols[:max_n]).decode().items)
def setup(self): self.procs.setup(self)
def process(self): self.procs(self)
def loc(self): return self.items.loc
def iloc(self): return _TabIloc(self)
def targ(self): return self.items[self.y_names]
def x_names (self): return self.cat_names + self.cont_names
def n_subsets(self): return 2
def y(self): return self[self.y_names[0]]
def new_empty(self): return self.new(pd.DataFrame({}, columns=self.items.columns))
def to_device(self, d=None):
self.device = d
return self
def all_col_names (self):
ys = [n for n in self.y_names if n in self.items.columns]
return self.x_names + self.y_names if len(ys) == len(self.y_names) else self.x_names
properties(Tabular,'loc','iloc','targ','all_col_names','n_subsets','x_names','y')
#export
class TabularPandas(Tabular):
def transform(self, cols, f, all_col=True):
if not all_col: cols = [c for c in cols if c in self.items.columns]
if len(cols) > 0: self[cols] = self[cols].transform(f)
#export
def _add_prop(cls, nm):
@property
def f(o): return o[list(getattr(o,nm+'_names'))]
@f.setter
def fset(o, v): o[getattr(o,nm+'_names')] = v
setattr(cls, nm+'s', f)
setattr(cls, nm+'s', fset)
_add_prop(Tabular, 'cat')
_add_prop(Tabular, 'cont')
_add_prop(Tabular, 'y')
_add_prop(Tabular, 'x')
_add_prop(Tabular, 'all_col')
df = pd.DataFrame({'a':[0,1,2,0,2], 'b':[0,0,0,0,1]})
to = TabularPandas(df, cat_names='a')
t = pickle.loads(pickle.dumps(to))
test_eq(t.items,to.items)
test_eq(to.all_cols,to[['a']])
#export
class TabularProc(InplaceTransform):
"Base class to write a non-lazy tabular processor for dataframes"
def setup(self, items=None, train_setup=False): #TODO: properly deal with train_setup
super().setup(getattr(items,'train',items), train_setup=False)
# Procs are called as soon as data is available
return self(items.items if isinstance(items,Datasets) else items)
#export
def _apply_cats (voc, add, c):
if not is_categorical_dtype(c):
return pd.Categorical(c, categories=voc[c.name][add:]).codes+add
return c.cat.codes+add #if is_categorical_dtype(c) else c.map(voc[c.name].o2i)
def _decode_cats(voc, c): return c.map(dict(enumerate(voc[c.name].items)))
#export
class Categorify(TabularProc):
"Transform the categorical variables to that type."
order = 1
def setups(self, to):
self.classes = {n:CategoryMap(to.iloc[:,n].items, add_na=(n in to.cat_names)) for n in to.cat_names}
def encodes(self, to): to.transform(to.cat_names, partial(_apply_cats, self.classes, 1))
def decodes(self, to): to.transform(to.cat_names, partial(_decode_cats, self.classes))
def __getitem__(self,k): return self.classes[k]
#export
@Categorize
def setups(self, to:Tabular):
if len(to.y_names) > 0:
self.vocab = CategoryMap(getattr(to, 'train', to).iloc[:,to.y_names[0]].items)
self.c = len(self.vocab)
return self(to)
@Categorize
def encodes(self, to:Tabular):
to.transform(to.y_names, partial(_apply_cats, {n: self.vocab for n in to.y_names}, 0), all_col=False)
return to
@Categorize
def decodes(self, to:Tabular):
to.transform(to.y_names, partial(_decode_cats, {n: self.vocab for n in to.y_names}), all_col=False)
return to
show_doc(Categorify, title_level=3)
df = pd.DataFrame({'a':[0,1,2,0,2]})
to = TabularPandas(df, Categorify, 'a')
cat = to.procs.categorify
test_eq(cat['a'], ['#na#',0,1,2])
test_eq(to['a'], [1,2,3,1,3])
to.show()
df1 = pd.DataFrame({'a':[1,0,3,-1,2]})
to1 = to.new(df1)
to1.process()
#Values that weren't in the training df are sent to 0 (na)
test_eq(to1['a'], [2,1,0,0,3])
to2 = cat.decode(to1)
test_eq(to2['a'], [1,0,'#na#','#na#',2])
#test with splits
cat = Categorify()
df = pd.DataFrame({'a':[0,1,2,3,2]})
to = TabularPandas(df, cat, 'a', splits=[[0,1,2],[3,4]])
test_eq(cat['a'], ['#na#',0,1,2])
test_eq(to['a'], [1,2,3,0,3])
df = pd.DataFrame({'a':pd.Categorical(['M','H','L','M'], categories=['H','M','L'], ordered=True)})
to = TabularPandas(df, Categorify, 'a')
cat = to.procs.categorify
test_eq(cat['a'], ['#na#','H','M','L'])
test_eq(to.items.a, [2,1,3,2])
to2 = cat.decode(to)
test_eq(to2['a'], ['M','H','L','M'])
#test with targets
cat = Categorify()
df = pd.DataFrame({'a':[0,1,2,3,2], 'b': ['a', 'b', 'a', 'b', 'b']})
to = TabularPandas(df, cat, 'a', splits=[[0,1,2],[3,4]], y_names='b')
test_eq(to.vocab, ['a', 'b'])
test_eq(to['b'], [0,1,0,1,1])
to2 = to.procs.decode(to)
test_eq(to2['b'], ['a', 'b', 'a', 'b', 'b'])
#test with targets and train
cat = Categorify()
df = pd.DataFrame({'a':[0,1,2,3,2], 'b': ['a', 'b', 'a', 'c', 'b']})
to = TabularPandas(df, cat, 'a', splits=[[0,1,2],[3,4]], y_names='b')
test_eq(to.vocab, ['a', 'b'])
#export
class NormalizeTab(TabularProc):
"Normalize the continuous variables."
order = 2
def setups(self, dsets): self.means,self.stds = dsets.conts.mean(),dsets.conts.std(ddof=0)+1e-7
def encodes(self, to): to.conts = (to.conts-self.means) / self.stds
def decodes(self, to): to.conts = (to.conts*self.stds ) + self.means
#export
@Normalize
def setups(self, to:Tabular):
self.means,self.stds = getattr(to, 'train', to).conts.mean(),getattr(to, 'train', to).conts.std(ddof=0)+1e-7
return self(to)
@Normalize
def encodes(self, to:Tabular):
to.conts = (to.conts-self.means) / self.stds
return to
@Normalize
def decodes(self, to:Tabular):
to.conts = (to.conts*self.stds ) + self.means
return to
norm = Normalize()
df = pd.DataFrame({'a':[0,1,2,3,4]})
to = TabularPandas(df, norm, cont_names='a')
x = np.array([0,1,2,3,4])
m,s = x.mean(),x.std()
test_eq(norm.means['a'], m)
test_close(norm.stds['a'], s)
test_close(to['a'].values, (x-m)/s)
df1 = pd.DataFrame({'a':[5,6,7]})
to1 = to.new(df1)
to1.process()
test_close(to1['a'].values, (np.array([5,6,7])-m)/s)
to2 = norm.decode(to1)
test_close(to2['a'].values, [5,6,7])
norm = Normalize()
df = pd.DataFrame({'a':[0,1,2,3,4]})
to = TabularPandas(df, norm, cont_names='a', splits=[[0,1,2],[3,4]])
x = np.array([0,1,2])
m,s = x.mean(),x.std()
test_eq(norm.means['a'], m)
test_close(norm.stds['a'], s)
test_close(to['a'].values, (np.array([0,1,2,3,4])-m)/s)
#export
class FillStrategy:
"Namespace containing the various filling strategies."
def median (c,fill): return c.median()
def constant(c,fill): return fill
def mode (c,fill): return c.dropna().value_counts().idxmax()
#export
class FillMissing(TabularProc):
"Fill the missing values in continuous columns."
def __init__(self, fill_strategy=FillStrategy.median, add_col=True, fill_vals=None):
if fill_vals is None: fill_vals = defaultdict(int)
store_attr(self, 'fill_strategy,add_col,fill_vals')
def setups(self, dsets):
missing = pd.isnull(dsets.conts).any()
self.na_dict = {n:self.fill_strategy(dsets[n], self.fill_vals[n])
for n in missing[missing].keys()}
def encodes(self, to):
missing = pd.isnull(to.conts)
for n in missing.any()[missing.any()].keys():
assert n in self.na_dict, f"nan values in `{n}` but not in setup training set"
for n in self.na_dict.keys():
to[n].fillna(self.na_dict[n], inplace=True)
if self.add_col:
to.loc[:,n+'_na'] = missing[n]
if n+'_na' not in to.cat_names: to.cat_names.append(n+'_na')
show_doc(FillMissing, title_level=3)
fill1,fill2,fill3 = (FillMissing(fill_strategy=s)
for s in [FillStrategy.median, FillStrategy.constant, FillStrategy.mode])
df = pd.DataFrame({'a':[0,1,np.nan,1,2,3,4]})
df1 = df.copy(); df2 = df.copy()
tos = (TabularPandas(df, fill1, cont_names='a'),
TabularPandas(df1, fill2, cont_names='a'),
TabularPandas(df2, fill3, cont_names='a'))
test_eq(fill1.na_dict, {'a': 1.5})
test_eq(fill2.na_dict, {'a': 0})
test_eq(fill3.na_dict, {'a': 1.0})
for t in tos: test_eq(t.cat_names, ['a_na'])
for to_,v in zip(tos, [1.5, 0., 1.]):
test_eq(to_['a'].values, np.array([0, 1, v, 1, 2, 3, 4]))
test_eq(to_['a_na'].values, np.array([0, 0, 1, 0, 0, 0, 0]))
fill = FillMissing()
df = pd.DataFrame({'a':[0,1,np.nan,1,2,3,4], 'b': [0,1,2,3,4,5,6]})
to = TabularPandas(df, fill, cont_names=['a', 'b'])
test_eq(fill.na_dict, {'a': 1.5})
test_eq(to.cat_names, ['a_na'])
test_eq(to['a'].values, np.array([0, 1, 1.5, 1, 2, 3, 4]))
test_eq(to['a_na'].values, np.array([0, 0, 1, 0, 0, 0, 0]))
test_eq(to['b'].values, np.array([0,1,2,3,4,5,6]))
```
## TabularPandas Pipelines -
```
procs = [Normalize, Categorify, FillMissing, noop]
df = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,1,np.nan,1,2,3,4]})
to = TabularPandas(df, procs, cat_names='a', cont_names='b')
#Test setup and apply on df_main
test_eq(to.cat_names, ['a', 'b_na'])
test_eq(to['a'], [1,2,3,2,2,3,1])
test_eq(to['b_na'], [1,1,2,1,1,1,1])
x = np.array([0,1,1.5,1,2,3,4])
m,s = x.mean(),x.std()
test_close(to['b'].values, (x-m)/s)
test_eq(to.classes, {'a': ['#na#',0,1,2], 'b_na': ['#na#',False,True]})
#Test apply on y_names
df = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,1,np.nan,1,2,3,4], 'c': ['b','a','b','a','a','b','a']})
to = TabularPandas(df, procs, 'a', 'b', y_names='c')
test_eq(to.cat_names, ['a', 'b_na'])
test_eq(to['a'], [1,2,3,2,2,3,1])
test_eq(to['b_na'], [1,1,2,1,1,1,1])
test_eq(to['c'], [1,0,1,0,0,1,0])
x = np.array([0,1,1.5,1,2,3,4])
m,s = x.mean(),x.std()
test_close(to['b'].values, (x-m)/s)
test_eq(to.classes, {'a': ['#na#',0,1,2], 'b_na': ['#na#',False,True]})
test_eq(to.vocab, ['a','b'])
df = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,1,np.nan,1,2,3,4], 'c': ['b','a','b','a','a','b','a']})
to = TabularPandas(df, procs, 'a', 'b', y_names='c')
test_eq(to.cat_names, ['a', 'b_na'])
test_eq(to['a'], [1,2,3,2,2,3,1])
test_eq(df.a.dtype,int)
test_eq(to['b_na'], [1,1,2,1,1,1,1])
test_eq(to['c'], [1,0,1,0,0,1,0])
df = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,np.nan,1,1,2,3,4], 'c': ['b','a','b','a','a','b','a']})
to = TabularPandas(df, procs, cat_names='a', cont_names='b', y_names='c', splits=[[0,1,4,6], [2,3,5]])
test_eq(to.cat_names, ['a', 'b_na'])
test_eq(to['a'], [1,2,2,1,0,2,0])
test_eq(df.a.dtype,int)
test_eq(to['b_na'], [1,2,1,1,1,1,1])
test_eq(to['c'], [1,0,0,0,1,0,1])
#export
def _maybe_expand(o): return o[:,None] if o.ndim==1 else o
#export
class ReadTabBatch(ItemTransform):
def __init__(self, to): self.to = to
def encodes(self, to):
if not to.with_cont: res = (tensor(to.cats).long(),)
else: res = (tensor(to.cats).long(),tensor(to.conts).float())
ys = [n for n in to.y_names if n in to.items.columns]
if len(ys) == len(to.y_names): res = res + (tensor(to.targ),)
if to.device is not None: res = to_device(res, to.device)
return res
def decodes(self, o):
o = [_maybe_expand(o_) for o_ in to_np(o) if o_.size != 0]
vals = np.concatenate(o, axis=1)
try: df = pd.DataFrame(vals, columns=self.to.all_col_names)
except: df = pd.DataFrame(vals, columns=self.to.x_names)
to = self.to.new(df)
return to
#export
@typedispatch
def show_batch(x: Tabular, y, its, max_n=10, ctxs=None):
x.show()
from torch.utils.data.dataloader import _MultiProcessingDataLoaderIter,_SingleProcessDataLoaderIter,_DatasetKind
_loaders = (_MultiProcessingDataLoaderIter,_SingleProcessDataLoaderIter)
#export
@delegates()
class TabDataLoader(TfmdDL):
do_item = noops
def __init__(self, dataset, bs=16, shuffle=False, after_batch=None, num_workers=0, **kwargs):
if after_batch is None: after_batch = L(TransformBlock().batch_tfms)+ReadTabBatch(dataset)
super().__init__(dataset, bs=bs, shuffle=shuffle, after_batch=after_batch, num_workers=num_workers, **kwargs)
def create_batch(self, b): return self.dataset.iloc[b]
TabularPandas._dl_type = TabDataLoader
```
## Integration example
```
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
df_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()
df_test.drop('salary', axis=1, inplace=True)
df_main.head()
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
splits = RandomSplitter()(range_of(df_main))
to = TabularPandas(df_main, procs, cat_names, cont_names, y_names="salary", splits=splits)
dls = to.dataloaders()
dls.valid.show_batch()
to.show()
row = to.items.iloc[0]
to.decode_row(row)
to_tst = to.new(df_test)
to_tst.process()
to_tst.items.head()
tst_dl = dls.valid.new(to_tst)
tst_dl.show_batch()
```
## Other target types
### Multi-label categories
#### one-hot encoded label
```
def _mock_multi_label(df):
sal,sex,white = [],[],[]
for row in df.itertuples():
sal.append(row.salary == '>=50k')
sex.append(row.sex == ' Male')
white.append(row.race == ' White')
df['salary'] = np.array(sal)
df['male'] = np.array(sex)
df['white'] = np.array(white)
return df
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
df_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()
df_main = _mock_multi_label(df_main)
df_main.head()
#export
@EncodedMultiCategorize
def encodes(self, to:Tabular): return to
@EncodedMultiCategorize
def decodes(self, to:Tabular):
to.transform(to.y_names, lambda c: c==1)
return to
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
splits = RandomSplitter()(range_of(df_main))
y_names=["salary", "male", "white"]
%time to = TabularPandas(df_main, procs, cat_names, cont_names, y_names=y_names, y_block=MultiCategoryBlock(encoded=True, vocab=y_names), splits=splits)
dls = to.dataloaders()
dls.valid.show_batch()
```
#### Not one-hot encoded
```
def _mock_multi_label(df):
targ = []
for row in df.itertuples():
labels = []
if row.salary == '>=50k': labels.append('>50k')
if row.sex == ' Male': labels.append('male')
if row.race == ' White': labels.append('white')
targ.append(' '.join(labels))
df['target'] = np.array(targ)
return df
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
df_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()
df_main = _mock_multi_label(df_main)
df_main.head()
@MultiCategorize
def encodes(self, to:Tabular):
#to.transform(to.y_names, partial(_apply_cats, {n: self.vocab for n in to.y_names}, 0))
return to
@MultiCategorize
def decodes(self, to:Tabular):
#to.transform(to.y_names, partial(_decode_cats, {n: self.vocab for n in to.y_names}))
return to
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
splits = RandomSplitter()(range_of(df_main))
%time to = TabularPandas(df_main, procs, cat_names, cont_names, y_names="target", y_block=MultiCategoryBlock(), splits=splits)
to.procs[2].vocab
```
### Regression
```
#export
@RegressionSetup
def setups(self, to:Tabular):
if self.c is not None: return
self.c = len(to.y_names)
return to
@RegressionSetup
def encodes(self, to:Tabular): return to
@RegressionSetup
def decodes(self, to:Tabular): return to
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
df_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()
df_main = _mock_multi_label(df_main)
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
splits = RandomSplitter()(range_of(df_main))
%time to = TabularPandas(df_main, procs, cat_names, cont_names, y_names='age', splits=splits)
to.procs[-1].means
dls = to.dataloaders()
dls.valid.show_batch()
```
## Not being used now - for multi-modal
```
class TensorTabular(Tuple):
def get_ctxs(self, max_n=10, **kwargs):
n_samples = min(self[0].shape[0], max_n)
df = pd.DataFrame(index = range(n_samples))
return [df.iloc[i] for i in range(n_samples)]
def display(self, ctxs): display_df(pd.DataFrame(ctxs))
class TabularLine(pd.Series):
"A line of a dataframe that knows how to show itself"
def show(self, ctx=None, **kwargs): return self if ctx is None else ctx.append(self)
class ReadTabLine(ItemTransform):
def __init__(self, proc): self.proc = proc
def encodes(self, row):
cats,conts = (o.map(row.__getitem__) for o in (self.proc.cat_names,self.proc.cont_names))
return TensorTabular(tensor(cats).long(),tensor(conts).float())
def decodes(self, o):
to = TabularPandas(o, self.proc.cat_names, self.proc.cont_names, self.proc.y_names)
to = self.proc.decode(to)
return TabularLine(pd.Series({c: v for v,c in zip(to.items[0]+to.items[1], self.proc.cat_names+self.proc.cont_names)}))
class ReadTabTarget(ItemTransform):
def __init__(self, proc): self.proc = proc
def encodes(self, row): return row[self.proc.y_names].astype(np.int64)
def decodes(self, o): return Category(self.proc.classes[self.proc.y_names][o])
# tds = TfmdDS(to.items, tfms=[[ReadTabLine(proc)], ReadTabTarget(proc)])
# enc = tds[1]
# test_eq(enc[0][0], tensor([2,1]))
# test_close(enc[0][1], tensor([-0.628828]))
# test_eq(enc[1], 1)
# dec = tds.decode(enc)
# assert isinstance(dec[0], TabularLine)
# test_close(dec[0], pd.Series({'a': 1, 'b_na': False, 'b': 1}))
# test_eq(dec[1], 'a')
# test_stdout(lambda: print(show_at(tds, 1)), """a 1
# b_na False
# b 1
# category a
# dtype: object""")
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
|
github_jupyter
|
# Optimización
Author: Jesús Cid-Sueiro
Jerónimo Arenas-García
Versión: 0.1 (2019/09/13)
0.2 (2019/10/02): Solutions added
## Exercise: compute the minimum of a real-valued function
The goal of this exercise is to implement and test optimization algorithms for the minimization of a given function. Gradient descent and Newton's method will be explored.
Our goal it so find the minimizer of the real-valued function
$$
f(w) = - w exp(-w)
$$
but the whole code will be easily modified to try with other alternative functions.
You will need to import some libraries (at least, `numpy` and `matplotlib`). Insert below all the imports needed along the whole notebook. Remind that numpy is usually abbreviated as np and `matplotlib.pyplot` is usually abbreviated as `plt`.
```
# <SOL>
# </SOL>
```
### Part 1: The function and its derivatives.
**Question 1.1**: Implement the following three methods:
* Method **`f`**: given $w$, it returns the value of function $f(w)$.
* Method **`df`**: given $w$, it returns the derivative of $f$ at $w$
* Medhod **`d2f`**: given $w$, it returns the second derivative of $f$ at $w$
```
# Funcion f
# <SOL>
# </SOL>
# First derivative
# <SOL>
# </SOL>
# Second derivative
# <SOL>
# </SOL>
```
### Part 2: Gradient descent.
**Question 2.1**: Implement a method **`gd`** that, given `w` and a learning rate parameter `rho` applies a single iteration of the gradien descent algorithm
```
# <SOL>
# </SOL>
```
**Question 2.2**: Apply the gradient descent to optimize the given function. To do so, start with an initial value $w=0$ and iterate $20$ times. Save two lists:
* A list of succesive values of $w_n$
* A list of succesive values of the function $f(w_n)$.
```
# <SOL>
# </SOL>
```
**Question 2.3**: Plot, in a single figure:
* The given function, for values ranging from 0 to 20.
* The sequence of points $(w_n, f(w_n))$.
```
# <SOL>
# </SOL>
```
You can check the effect of modifying the value of the learning rate.
### Part 2: Newton's method.
**Question 3.1**: Implement a method **`newton`** that, given `w` and a learning rate parameter `rho` applies a single iteration of the Newton's method
```
# <SOL>
# </SOL>
```
**Question 3**: Apply the Newton's method to optimize the given function. To do so, start with an initial value $w=0$ and iterate $20$ times. Save two lists:
* A list of succesive values of $w_n$
* A list of succesive values of the function $f(w_n)$.
```
# <SOL>
# </SOL>
```
**Question 4**: Plot, in a single figure:
* The given function, for values ranging from 0 to 20.
* The sequence of points $(w_n, f(w_n))$.
```
# <SOL>
# </SOL>
```
You can check the effect of modifying the value of the learning rate.
### Part 3: Optimize other cost functions
Now you are ready to explore these optimization algorithms with other more sophisticated functions. Try with them.
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.