code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
# <img style="float: left; padding-right: 10px; width: 45px" src="https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/iacs.png"> CS109A Introduction to Data Science
## Standard Section 3: Multiple Linear Regression and Polynomial Regression
**Harvard University**<br/>
**Fall 2019**<br/>
**Instructors**: Pavlos Protopapas, Kevin Rader, and Chris Tanner<br/>
**Section Leaders**: Marios Mattheakis, Abhimanyu (Abhi) Vasishth, Robbert (Rob) Struyven<br/>
<hr style='height:2px'>
```
#RUN THIS CELL
import requests
from IPython.core.display import HTML
styles = requests.get("http://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/cs109.css").text
HTML(styles)
```
For this section, our goal is to get you familiarized with Multiple Linear Regression. We have learned how to model data with kNN Regression and Simple Linear Regression and our goal now is to dive deep into Linear Regression.
Specifically, we will:
- Load in the titanic dataset from seaborn
- Learn a few ways to plot **distributions** of variables using seaborn
- Learn about different **kinds of variables** including continuous, categorical and ordinal
- Perform single and multiple linear regression
- Learn about **interaction** terms
- Understand how to **interpret coefficients** in linear regression
- Look at **polynomial** regression
- Understand the **assumptions** being made in a linear regression model
- (Extra): look at some cool plots to raise your EDA game

```
# Data and Stats packages
import numpy as np
import pandas as pd
# Visualization packages
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
```
# Extending Linear Regression
## Working with the Titanic Dataset from Seaborn
For our dataset, we'll be using the passenger list from the Titanic, which famously sank in 1912. Let's have a look at the data. Some descriptions of the data are at https://www.kaggle.com/c/titanic/data, and here's [how seaborn preprocessed it](https://github.com/mwaskom/seaborn-data/blob/master/process/titanic.py).
The task is to build a regression model to **predict the fare**, based on different attributes.
Let's keep a subset of the data, which includes the following variables:
- age
- sex
- class
- embark_town
- alone
- **fare** (the response variable)
```
# Load the dataset from seaborn
titanic = sns.load_dataset("titanic")
titanic.head()
# checking for null values
chosen_vars = ['age', 'sex', 'class', 'embark_town', 'alone', 'fare']
titanic = titanic[chosen_vars]
titanic.info()
```
**Exercise**: check the datatypes of each column and display the statistics (min, max, mean and any others) for all the numerical columns of the dataset.
```
## your code here
titanic.dtypes
titanic.describe()
# %load 'solutions/sol1.py'
```
**Exercise**: drop all the non-null *rows* in the dataset. Is this always a good idea?
```
## your code here
titanic = titanic.dropna(axis=0)
titanic.info()
#inputation is an alternative to addressing null values
# %load 'solutions/sol2.py'
```
Now let us visualize the response variable. A good visualization of the distribution of a variable will enable us to answer three kinds of questions:
- What values are central or typical? (e.g., mean, median, modes)
- What is the typical spread of values around those central values? (e.g., variance/stdev, skewness)
- What are unusual or exceptional values (e.g., outliers)
```
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(24, 6))
ax = ax.ravel()
sns.distplot(titanic['fare'], ax=ax[0])
ax[0].set_title('Seaborn distplot')
ax[0].set_ylabel('Normalized frequencies')
sns.violinplot(x='fare', data=titanic, ax=ax[1])
ax[1].set_title('Seaborn violin plot')
ax[1].set_ylabel('Frequencies')
sns.boxplot(x='fare', data=titanic, ax=ax[2])
ax[2].set_title('Seaborn box plot')
ax[2].set_ylabel('Frequencies')
fig.suptitle('Distribution of count');
```
How do we interpret these plots?
## Train-Test Split
```
from sklearn.model_selection import train_test_split
titanic_train, titanic_test = train_test_split(titanic, train_size=0.7, random_state=99)
titanic_train = titanic_train.copy()
titanic_test = titanic_test.copy()
print(titanic_train.shape, titanic_test.shape)
```
## Simple one-variable OLS
**Exercise**: You've done this before: make a simple model using the OLS package from the statsmodels library predicting **fare** using **age** using the training data. Name your model `model_1` and display the summary
```
from statsmodels.api import OLS
import statsmodels.api as sm
# Your code here
# %load 'solutions/sol3.py'
age_ca = sm.add_constant(titanic_train['age'])
model_1 = OLS(titanic_train['fare'], age_ca).fit()
model_1.summary()
```
## Dealing with different kinds of variables
In general, you should be able to distinguish between three kinds of variables:
1. Continuous variables: such as `fare` or `age`
2. Categorical variables: such as `sex` or `alone`. There is no inherent ordering between the different values that these variables can take on. These are sometimes called nominal variables. Read more [here](https://stats.idre.ucla.edu/other/mult-pkg/whatstat/what-is-the-difference-between-categorical-ordinal-and-interval-variables/).
3. Ordinal variables: such as `class` (first > second > third). There is some inherent ordering of the values in the variables, but the values are not continuous either.
*Note*: While there is some inherent ordering in `class`, we will be treating it like a categorical variable.
```
titanic_orig = titanic_train.copy()
```
Let us now examine the `sex` column and see the value counts.
```
titanic_train['sex'].value_counts()
```
**Exercise**: Create a column `sex_male` that is 1 if the passenger is male, 0 if female. The value counts indicate that these are the two options in this particular dataset. Ensure that the datatype is `int`.
```
# your code here
titanic_train['sex_male'] = (titanic_train.sex == 'male').astype(int)
titanic_train['sex_male'].value_counts()
# %load 'solutions/sol4.py'
```
Do we need a `sex_female` column, or a `sex_others` column? Why or why not?
Now, let us look at `class` in greater detail.
```
titanic_train['class_Second'] = (titanic_train['class'] == 'Second').astype(int)
titanic_train['class_Third'] = 1 * (titanic_train['class'] == 'Third') # just another way to do it
titanic_train['class_Second'].value_counts()
titanic_train['class_Third'].value_counts()
titanic_train.info()
# This function automates the above:
titanic_train_copy = pd.get_dummies(titanic_train, columns=['sex', 'class'], drop_first=True)
titanic_train_copy.head()
```
## Linear Regression with More Variables
**Exercise**: Fit a linear regression including the new sex and class variables. Name this model `model_2`. Don't forget the constant!
```
# your code here
# %load 'solutions/sol5.py'
model_2 = sm.OLS(titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third']])).fit()
# add constant just once for B0 value)
model_2.summary()
```
### Interpreting These Results
1. Which of the predictors do you think are important? Why?
2. All else equal, what does being male do to the fare?
### Going back to the example from class

3. What is the interpretation of $\beta_0$ and $\beta_1$?
Beta 0 = male; beta 1 = male - female (difference b/w male and female)
## Exploring Interactions
```
sns.lmplot(x="age", y="fare", hue="sex", data=titanic_train, size=6)
```
The slopes seem to be different for male and female. What does that indicate?
Let us now try to add an interaction effect into our model.
```
# It seemed like gender interacted with age and class. Can we put that in our model?
titanic_train['sex_male_X_age'] = titanic_train['age'] * titanic_train['sex_male']
model_3 = sm.OLS(
titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age']])
).fit()
model_3.summary()
```
**What happened to the `age` and `male` terms?**
```
# It seemed like gender interacted with age and class. Can we put that in our model?
titanic_train['sex_male_X_class_Second'] = titanic_train['age'] * titanic_train['class_Second']
titanic_train['sex_male_X_class_Third'] = titanic_train['age'] * titanic_train['class_Third']
model_4 = sm.OLS(
titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second', 'sex_male_X_class_Third']])
).fit()
model_4.summary()
```
## Polynomial Regression

Perhaps we now believe that the fare also depends on the square of age. How would we include this term in our model?
```
fig, ax = plt.subplots(figsize=(12,6))
ax.plot(titanic_train['age'], titanic_train['fare'], 'o')
x = np.linspace(0,80,100)
ax.plot(x, x, '-', label=r'$y=x$')
ax.plot(x, 0.04*x**2, '-', label=r'$y=c x^2$')
ax.set_title('Plotting Age (x) vs Fare (y)')
ax.set_xlabel('Age (x)')
ax.set_ylabel('Fare (y)')
ax.legend();
```
**Exercise**: Create a model that predicts fare from all the predictors in `model_4` + the square of age. Show the summary of this model. Call it `model_5`. Remember to use the training data, `titanic_train`.
```
# your code here
# %load 'solutions/sol6.py'
titanic_train['age^2'] = titanic_train['age'] **2
model_5 = sm.OLS(
titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second', 'sex_male_X_class_Third', 'age^2']])
).fit()
model_5.summary()
```
## Looking at All Our Models: Model Selection
What has happened to the $R^2$ as we added more features? Does this mean that the model is better? (What if we kept adding more predictors and interaction terms? **In general, how should we choose a model?** We will spend a lot more time on model selection and learn about ways to do so as the course progresses.
```
models = [model_1, model_2, model_3, model_4, model_5]
fig, ax = plt.subplots(figsize=(12,6))
ax.plot([model.df_model for model in models], [model.rsquared for model in models], 'x-')
ax.set_xlabel("Model degrees of freedom")
ax.set_title('Model degrees of freedom vs training $R^2$')
ax.set_ylabel("$R^2$");
```
**What about the test data?**
We added a lot of columns to our training data and must add the same to our test data in order to calculate $R^2$ scores.
```
# Added features for model 1
# Nothing new to be added
# Added features for model 2
titanic_test = pd.get_dummies(titanic_test, columns=['sex', 'class'], drop_first=True)
# Added features for model 3
titanic_test['sex_male_X_age'] = titanic_test['age'] * titanic_test['sex_male']
# Added features for model 4
titanic_test['sex_male_X_class_Second'] = titanic_test['age'] * titanic_test['class_Second']
titanic_test['sex_male_X_class_Third'] = titanic_test['age'] * titanic_test['class_Third']
# Added features for model 5
titanic_test['age^2'] = titanic_test['age'] **2
```
**Calculating R^2 scores**
```
from sklearn.metrics import r2_score
r2_scores = []
y_preds = []
y_true = titanic_test['fare']
# model 1
y_preds.append(model_1.predict(sm.add_constant(titanic_test['age'])))
# model 2
y_preds.append(model_2.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third']])))
# model 3
y_preds.append(model_3.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third',
'sex_male_X_age']])))
# model 4
y_preds.append(model_4.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third',
'sex_male_X_age', 'sex_male_X_class_Second',
'sex_male_X_class_Third']])))
# model 5
y_preds.append(model_5.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second',
'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second',
'sex_male_X_class_Third', 'age^2']])))
for y_pred in y_preds:
r2_scores.append(r2_score(y_true, y_pred))
models = [model_1, model_2, model_3, model_4, model_5]
fig, ax = plt.subplots(figsize=(12,6))
ax.plot([model.df_model for model in models], r2_scores, 'x-')
ax.set_xlabel("Model degrees of freedom")
ax.set_title('Model degrees of freedom vs test $R^2$')
ax.set_ylabel("$R^2$");
```
## Regression Assumptions. Should We Even Regress Linearly?

**Question**: What are the assumptions of a linear regression model?
We find that the answer to this question can be found on closer examimation of $\epsilon$. What is $\epsilon$? It is assumed that $\epsilon$ is normally distributed with a mean of 0 and variance $\sigma^2$. But what does this tell us?
1. Assumption 1: Constant variance of $\epsilon$ errors. This means that if we plot our **residuals**, which are the differences between the true $Y$ and our predicted $\hat{Y}$, they should look like they have constant variance and a mean of 0. We will show this in our plots.
2. Assumption 2: Independence of $\epsilon$ errors. This again comes from the distribution of $\epsilon$ that we decide beforehand.
3. Assumption 3: Linearity. This is an implicit assumption as we claim that Y can be modeled through a linear combination of the predictors. **Important Note:** Even though our predictors, for instance $X_2$, can be created by squaring or cubing another variable, we still use them in a linear equation as shown above, which is why polynomial regression is still a linear model.
4. Assumption 4: Normality. We assume that the $\epsilon$ is normally distributed, and we can show this in a histogram of the residuals.
**Exercise**: Calculate the residuals for model 5, our most recent model. Optionally, plot and histogram these residuals and check the assumptions of the model.
```
# your code here
# %load 'solutions/sol7.py'
predictors = sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second', 'sex_male_X_class_Third', 'age^2']])
y_hat = model_5.predict(predictors)
residuals = titanic_train['fare'] - y_hat
# plotting
fig, ax = plt.subplots(ncols=2, figsize=(16,5))
ax = ax.ravel()
ax[0].set_title('Plot of Residuals')
ax[0].scatter(y_hat, residuals, alpha=0.2)
ax[0].set_xlabel(r'$\hat{y}$')
ax[0].set_ylabel('residuals')
ax[1].set_title('Histogram of Residuals')
ax[1].hist(residuals, alpha=0.7)
ax[1].set_xlabel('residuals')
ax[1].set_ylabel('frequency');
# Mean of residuals
print('Mean of residuals: {}'.format(np.mean(residuals)))
```
**What can you say about the assumptions of the model?**
----------------
### End of Standard Section
---------------
## Extra: Visual exploration of predictors' correlations
The dataset for this problem contains 10 simulated predictors and a response variable.
```
# read in the data
data = pd.read_csv('../data/dataset3.txt')
data.head()
# this effect can be replicated using the scatter_matrix function in pandas plotting
sns.pairplot(data);
```
Predictors x1, x2, x3 seem to be perfectly correlated while predictors x4, x5, x6, x7 seem correlated.
```
data.corr()
sns.heatmap(data.corr())
```
## Extra: A Handy Matplotlib Guide

source: http://matplotlib.org/faq/usage_faq.html
See also [this](http://matplotlib.org/faq/usage_faq.html) matplotlib tutorial.

See also [this](https://mode.com/blog/violin-plot-examples) violin plot tutorial.
---
|
github_jupyter
|
# Example 3. CNN + DDA
Here, we train the same CNN as in previous notebook but applying the Direct Domain Adaptation method (DDA) to reduce the gap between MNIST and MNIST-M datasets.
-------
This code is modified from [https://github.com/fungtion/DANN_py3](https://github.com/fungtion/DANN_py3).
```
import os
import sys
import tqdm
import random
import numpy as np
from numpy.fft import rfft2, irfft2, fftshift, ifftshift
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.nn as nn
import torch.utils.data
from torchvision import datasets
from torchvision import transforms
from components.data_loader import GetLoader
from components.model import CNNModel
from components.test import test
import components.shared as sd
# os.environ["CUDA_VISIBLE_DEVICES"] = "2"
```
### Init paths
```
# Paths to datasets
source_dataset_name = 'MNIST'
target_dataset_name = 'mnist_m'
source_image_root = os.path.join('dataset', source_dataset_name)
target_image_root = os.path.join('dataset', target_dataset_name)
os.makedirs('./dataset', exist_ok=True)
# Where to save outputs
model_root = './out_ex3_cnn_da'
os.makedirs(model_root, exist_ok=True)
```
### Init training
```
cuda = True
cudnn.benchmark = True
# Hyperparameters
lr = 1e-3
batch_size = 128
image_size = 28
n_epoch = 100
# manual_seed = random.randint(1, 10000)
manual_seed = 222
random.seed(manual_seed)
torch.manual_seed(manual_seed)
print(f'Random seed: {manual_seed}')
```
### Data
```
# Transformations / augmentations
img_transform_source = transforms.Compose([
transforms.Resize(image_size),
transforms.ToTensor(),
transforms.Normalize(mean=(0.1307,), std=(0.3081,)),
transforms.Lambda(lambda x: x.repeat(3, 1, 1)),
])
img_transform_target = transforms.Compose([
transforms.Resize(image_size),
transforms.ToTensor(),
transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5))
])
# Load MNIST dataset
dataset_source = datasets.MNIST(
root='dataset',
train=True,
transform=img_transform_source,
download=True
)
# Load MNIST-M dataset
train_list = os.path.join(target_image_root, 'mnist_m_train_labels.txt')
dataset_target = GetLoader(
data_root=os.path.join(target_image_root, 'mnist_m_train'),
data_list=train_list,
transform=img_transform_target
)
```
# Direct Domain Adaptation (DDA)
## Average auto-correlation
For entire dataset
```
def get_global_acorr_for_loader(loader):
""" The average auto-correlation of all images in the dataset """
global_acorr = np.zeros((3, 28, 15), dtype=np.complex128)
prog_bar = tqdm.tqdm(loader)
for data, _ in prog_bar:
data_f = np.fft.rfft2(data, s=data.shape[-2:], axes=(-2, -1))
# Auto-correlation is multiplication with the conjucate of self
# in frequency domain
global_acorr += data_f * np.conjugate(data_f)
global_acorr /= len(loader)
print(global_acorr.shape)
return np.fft.fftshift(global_acorr)
def route_to(fname):
""" Shortcut for routing to the save folder """
return os.path.join(model_root, fname)
# Compute global acorr if not in the folder, load otherwise
if not 'gacorr_dst_tr.npy' in os.listdir(model_root):
print('Save global acorr')
gacorr_dst_tr = get_global_acorr_for_loader(dataset_target)
gacorr_src_tr = get_global_acorr_for_loader(dataset_source)
np.save(route_to('gacorr_dst_tr.npy'), gacorr_dst_tr)
np.save(route_to('gacorr_src_tr.npy'), gacorr_src_tr)
else:
print('Load global acorr')
gacorr_dst_tr = np.load(route_to('gacorr_dst_tr.npy'))
gacorr_src_tr = np.load(route_to('gacorr_src_tr.npy'))
```
## Average cross-correlation
Pick a random pixel(-s) from each image in the dataset and average
```
# Window size
crop_size = 1
print(f'Use the crop size for xcorr = {crop_size}')
def crop_ref(x, n=1, edge=5):
"""Crop a window from the image
Args:
x(np.ndarray): image [c, h, w]
n(int): window size
edge(int): margin to avoid from edges of the image
"""
if n % 2 == 0: n+=1;
k = int((n - 1) / 2)
nz, nx = x.shape[-2:]
dim1 = np.random.randint(0+k+edge, nz-k-edge)
dim2 = np.random.randint(0+k, nx-k)
out = x[..., dim1-k:dim1+k+1, dim2-k:dim2+k+1]
return out
# crop_ref(np.ones((2, 100, 100)), n=5).shape
def get_global_xcorr_for_loader(loader, crop_size=1):
# Init the placeholder for average
rand_pixel = np.zeros((3, crop_size, crop_size))
# Loop over all images in the dataset
prog_bar = tqdm.tqdm(loader)
for data, _ in prog_bar:
rand_pixel += np.mean(crop_ref(data, crop_size).numpy(), axis=0)
rand_pixel /= len(loader)
# Place the mean pixel into center of an empty image
c, h ,w = data.shape
mid_h, mid_w = int(h // 2), int(w // 2)
embed = np.zeros_like(data)
embed[..., mid_h:mid_h+1, mid_w:mid_w+1] = rand_pixel
global_xcorr = np.fft.rfft2(embed, s=data.shape[-2:], axes=(-2, -1))
return np.fft.fftshift(global_xcorr)
# Compute global xcorr if not in the folder, load otherwise
if not 'gxcorr_dst_tr.npy' in os.listdir(model_root):
# if True:
print('Save global xcorr')
gxcorr_dst_tr = get_global_xcorr_for_loader(dataset_target, crop_size)
gxcorr_src_tr = get_global_xcorr_for_loader(dataset_source, crop_size)
np.save(route_to('gxcorr_dst_tr.npy'), gxcorr_dst_tr)
np.save(route_to('gxcorr_src_tr.npy'), gxcorr_src_tr)
else:
print('Load global xcorr')
gxcorr_dst_tr = np.load(route_to('gxcorr_dst_tr.npy'))
gxcorr_src_tr = np.load(route_to('gxcorr_src_tr.npy'))
```
## Train Loader
```
def flip_channels(x):
"""Reverse polarity of random channels"""
flip_matrix = np.random.choice([-1, 1], 3)[..., np.newaxis, np.newaxis]
return (x * flip_matrix).astype(np.float32)
def shuffle_channels(x):
"""Change order of channels"""
return np.random.permutation(x)
def normalize_channels(x):
"""Map data to [-1,1] range. The scaling after conv(xcorr, acorr) is not
suitable for image processing so this function fixes it"""
cmin = np.min(x, axis=(-2,-1))[..., np.newaxis, np.newaxis]
x -= cmin
cmax = np.max(np.abs(x), axis=(-2,-1))[..., np.newaxis, np.newaxis]
x /= cmax
x *= 2
x -= 1
return x.astype(np.float32)
class DDALoaderTrain(torch.utils.data.Dataset):
def __init__(self, loader1, avg_acorr2, p=0.5, crop_size=1):
super().__init__()
self.loader1 = loader1
self.avg_acorr2 = avg_acorr2
self.p = p
self.crop_size = crop_size
def __len__(self):
return len(self.loader1)
def __getitem__(self, item):
# Get main data (data, label)
data, label = self.loader1.__getitem__(item)
data_fft = fftshift(rfft2(data, s=data.shape[-2:], axes=(-2, -1)))
# Get random pixel from another data from the same dataset
random_index = np.random.randint(0, len(self.loader1))
another_data, _ = self.loader1.__getitem__(random_index)
rand_pixel = crop_ref(another_data, self.crop_size)
# Convert to Fourier domain
c, h ,w = another_data.shape
mid_h, mid_w = int(h // 2), int(w // 2)
embed = np.zeros_like(another_data)
embed[:, mid_h:mid_h+1, mid_w:mid_w+1] = rand_pixel
pixel_fft = np.fft.rfft2(embed, s=another_data.shape[-2:], axes=(-2, -1))
pixel_fft = np.fft.fftshift(pixel_fft)
# Cross-correlate the data sample with the random pixel from the same dataset
xcorr = data_fft * np.conjugate(pixel_fft)
# Convolve the ruslt with the auto-correlation of another dataset
conv = xcorr * self.avg_acorr2
# Reverse Fourier domain and map channels to [-1, 1] range
data_da = fftshift(irfft2(ifftshift(conv), axes=(-2, -1)))
data_da = normalize_channels(data_da)
# Apply data augmentations
if np.random.rand() < self.p:
data_da = flip_channels(data_da)
if np.random.rand() < self.p:
data_da = shuffle_channels(data_da)
# Return a pair of data / label
return data_da.astype(np.float32), label
dataset_source = DDALoaderTrain(dataset_source, gacorr_dst_tr)
dataset_target = DDALoaderTrain(dataset_target, gacorr_src_tr)
dummy_data, dummy_label = dataset_source.__getitem__(0)
print('Image shape: {}\t Label: {}'.format(dummy_data.shape, dummy_label))
```
# Test Loader
```
class DDALoaderTest(torch.utils.data.Dataset):
def __init__(self, loader1, avg_acorr2, avg_xcorr1):
super().__init__()
self.loader1 = loader1
self.avg_acorr2 = avg_acorr2
self.avg_xcorr1 = avg_xcorr1
def __len__(self):
return len(self.loader1)
def __getitem__(self, item):
data, label = self.loader1.__getitem__(item)
data_fft = fftshift(rfft2(data, s=data.shape[-2:], axes=(-2, -1)))
xcorr = data_fft * np.conjugate(self.avg_xcorr1)
conv = xcorr * self.avg_acorr2
data_da = fftshift(irfft2(ifftshift(conv), axes=(-2, -1)))
data_da = normalize_channels(data_da)
return data_da.astype(np.float32), label
```
Re-define the test function so it accounts for the average cross-correlation and auto-correlation from source and target datasets
```
def test(dataset_name, model_root, crop_size=1):
image_root = os.path.join('dataset', dataset_name)
if dataset_name == 'mnist_m':
test_list = os.path.join(image_root, 'mnist_m_test_labels.txt')
dataset = GetLoader(
data_root=os.path.join(image_root, 'mnist_m_test'),
data_list=test_list,
transform=img_transform_target
)
if not 'gxcorr_dst_te.npy' in os.listdir(model_root):
print('Save global acorr and xcorr')
# acorr
gacorr_src_te = get_global_acorr_for_loader(dataset)
np.save(route_to('gacorr_src_te.npy'), gacorr_src_te)
# xcorr
gxcorr_dst_te = get_global_xcorr_for_loader(dataset, crop_size)
np.save(route_to('gxcorr_dst_te.npy'), gxcorr_dst_te)
else:
gacorr_src_te = np.load(route_to('gacorr_src_te.npy'))
gxcorr_dst_te = np.load(route_to('gxcorr_dst_te.npy'))
# Init loader for MNIST-M
dataset = DDALoaderTest(dataset, gacorr_src_te, gxcorr_dst_te)
else:
dataset = datasets.MNIST(
root='dataset',
train=False,
transform=img_transform_source,
)
if not 'gxcorr_src_te.npy' in os.listdir(model_root):
print('Save global acorr and xcorr')
# acorr
gacorr_dst_te = get_global_acorr_for_loader(dataset)
np.save(route_to('gacorr_dst_te.npy'), gacorr_dst_te)
# xcorr
gxcorr_src_te = get_global_xcorr_for_loader(dataset, crop_size)
np.save(route_to('gxcorr_src_te.npy'), gxcorr_src_te)
else:
gacorr_dst_te = np.load(route_to('gacorr_dst_te.npy'))
gxcorr_src_te = np.load(route_to('gxcorr_src_te.npy'))
# Init loader for MNIST
dataset = DDALoaderTest(dataset, gacorr_dst_te, gxcorr_src_te)
dataloader = torch.utils.data.DataLoader(
dataset=dataset,
batch_size=batch_size,
shuffle=False,
num_workers=8
)
""" test """
my_net = torch.load(os.path.join(model_root, 'mnist_mnistm_model_epoch_current.pth'))
my_net = my_net.eval()
if cuda:
my_net = my_net.cuda()
len_dataloader = len(dataloader)
data_target_iter = iter(dataloader)
i = 0
n_total = 0
n_correct = 0
while i < len_dataloader:
# test model using target data
data_target = data_target_iter.next()
t_img, t_label = data_target
_batch_size = len(t_label)
if cuda:
t_img = t_img.cuda()
t_label = t_label.cuda()
class_output, _ = my_net(input_data=t_img, alpha=0)
pred = class_output.data.max(1, keepdim=True)[1]
n_correct += pred.eq(t_label.data.view_as(pred)).cpu().sum()
n_total += _batch_size
i += 1
accu = n_correct.data.numpy() * 1.0 / n_total
return accu
```
# Training
```
dataloader_source = torch.utils.data.DataLoader(
dataset=dataset_source,
batch_size=batch_size,
shuffle=True,
num_workers=8)
dataloader_target = torch.utils.data.DataLoader(
dataset=dataset_target,
batch_size=batch_size,
shuffle=True,
num_workers=8)
class CNNModel(nn.Module):
def __init__(self):
super(CNNModel, self).__init__()
self.feature = nn.Sequential()
self.feature.add_module('f_conv1', nn.Conv2d(3, 64, kernel_size=5))
self.feature.add_module('f_bn1', nn.BatchNorm2d(64))
self.feature.add_module('f_pool1', nn.MaxPool2d(2))
self.feature.add_module('f_relu1', nn.ReLU(True))
self.feature.add_module('f_conv2', nn.Conv2d(64, 50, kernel_size=5))
self.feature.add_module('f_bn2', nn.BatchNorm2d(50))
self.feature.add_module('f_drop1', nn.Dropout2d())
self.feature.add_module('f_pool2', nn.MaxPool2d(2))
self.feature.add_module('f_relu2', nn.ReLU(True))
self.class_classifier = nn.Sequential()
self.class_classifier.add_module('c_fc1', nn.Linear(50 * 4 * 4, 100))
self.class_classifier.add_module('c_bn1', nn.BatchNorm1d(100))
self.class_classifier.add_module('c_relu1', nn.ReLU(True))
self.class_classifier.add_module('c_drop1', nn.Dropout())
self.class_classifier.add_module('c_fc2', nn.Linear(100, 100))
self.class_classifier.add_module('c_bn2', nn.BatchNorm1d(100))
self.class_classifier.add_module('c_relu2', nn.ReLU(True))
self.class_classifier.add_module('c_fc3', nn.Linear(100, 10))
self.class_classifier.add_module('c_softmax', nn.LogSoftmax(dim=1))
def forward(self, input_data, alpha):
input_data = input_data.expand(input_data.data.shape[0], 3, 28, 28)
feature = self.feature(input_data)
feature = feature.view(-1, 50 * 4 * 4)
class_output = self.class_classifier(feature)
return class_output, 0
# load model
my_net = CNNModel()
# setup optimizer
optimizer = optim.Adam(my_net.parameters(), lr=lr)
loss_class = torch.nn.NLLLoss()
if cuda:
my_net = my_net.cuda()
loss_class = loss_class.cuda()
for p in my_net.parameters():
p.requires_grad = True
# Record losses for each epoch (used in compare.ipynb)
losses = {'test': {'acc_bw': [], 'acc_color': []}}
name_losses = 'losses.pkl'
if not name_losses in os.listdir(model_root):
# if True:
# training
best_accu_t = 0.0
for epoch in range(n_epoch):
len_dataloader = min(len(dataloader_source), len(dataloader_target))
data_source_iter = iter(dataloader_source)
data_target_iter = iter(dataloader_target)
for i in range(len_dataloader):
p = float(i + epoch * len_dataloader) / n_epoch / len_dataloader
alpha = 2. / (1. + np.exp(-10 * p)) - 1
# training model using source data
data_source = data_source_iter.next()
s_img, s_label = data_source
my_net.zero_grad()
batch_size = len(s_label)
if cuda:
s_img = s_img.cuda()
s_label = s_label.cuda()
class_output, _ = my_net(input_data=s_img, alpha=alpha)
err_s_label = loss_class(class_output, s_label)
err = err_s_label
err.backward()
optimizer.step()
sys.stdout.write('\r epoch: %d, [iter: %d / all %d], err_s_label: %f' \
% (epoch, i + 1, len_dataloader, err_s_label.data.cpu().numpy()))
sys.stdout.flush()
torch.save(my_net, '{0}/mnist_mnistm_model_epoch_current.pth'.format(model_root))
print('\n')
accu_s = test(source_dataset_name, model_root)
print('Accuracy of the %s dataset: %f' % ('mnist', accu_s))
accu_t = test(target_dataset_name, model_root)
print('Accuracy of the %s dataset: %f\n' % ('mnist_m', accu_t))
losses['test']['acc_bw'].append(accu_s)
losses['test']['acc_color'].append(accu_t)
if accu_t > best_accu_t:
best_accu_s = accu_s
best_accu_t = accu_t
torch.save(my_net, '{0}/mnist_mnistm_model_epoch_best.pth'.format(model_root))
print('============ Summary ============= \n')
print('Accuracy of the %s dataset: %f' % ('mnist', best_accu_s))
print('Accuracy of the %s dataset: %f' % ('mnist_m', best_accu_t))
print('Corresponding model was save in ' + model_root + '/mnist_mnistm_model_epoch_best.pth')
sd.save_dict(os.path.join(model_root, 'losses.pkl'), losses)
else:
path_losses = os.path.join(model_root, name_losses)
print(f'Losses from previous run found!')
losses = sd.load_dict(path_losses)
sd.plot_curves(losses)
print('============ Summary ============= \n')
print('Accuracy of the %s dataset: %f' % ('mnist', max(losses['test']['acc_bw'])))
print('Accuracy of the %s dataset: %f' % ('mnist_m', max(losses['test']['acc_color'])))
print('Corresponding model was saved into ' + model_root + '/mnist_mnistm_model_epoch_best.pth')
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv("E:\Downlload\AAPL.csv")
df
df1 = df[['Date','Close']]
df1
df1 = df1.rename(columns={"Close":'Close'})
df1
df1 = df1.set_index(['Date'])
df1
import math
data = df1.diff()
data = data[1:]
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(df1)
plt.title('ACF Before Diff')
plot_acf(data)
plt.title('ACF After Diff')
#df.plot(figsize=(15,5),color='red')
plt.rcParams["figure.figsize"] = 15,8
plt.title('price history')
plt.plot(data['Close'],color = 'black',linewidth=4)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Open Price $',fontsize=18)
ax = plt.axes()
ax.set_facecolor("orange")
plt.show()
dataset = data.values
training_data_len = math.ceil(len(dataset)*.8)
training_data_len
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0,1))
scaled_data = scaler.fit_transform(dataset)
scaled_data
train_data = scaled_data[0:training_data_len,:]
x_train=[]
y_train=[]
for i in range(60,len(train_data)):
x_train.append(train_data[i-60:i,0])
y_train.append(train_data[i,0])
if i<= 61:
print(x_train)
print(y_train)
print()
x_train,y_train = np.array(x_train),np.array(y_train)
x_train=np.reshape(x_train,(x_train.shape[0],x_train.shape[1],1))
x_train.shape
from keras.models import Sequential
from keras.layers import Dense, LSTM
model = Sequential()
model.add(LSTM(50,return_sequences=True, input_shape=(x_train.shape[1],1)))
model.add(LSTM(50,return_sequences=False))
model.add(Dense(25))
model.add(Dense(1))
model.compile(optimizer="adam",loss="mean_squared_error")
model.fit(x_train,y_train,batch_size=1,epochs=1)
test_data = scaled_data[training_data_len - 60:,:]
x_test =[]
y_test = dataset[training_data_len:,:]
for i in range(60,len(test_data)):
x_test.append(test_data[i-60:i,0])
x_test = np.array(x_test)
print(x_test.shape)
x_test = np.reshape(x_test,(x_test.shape[0],x_test.shape[1],1))
print(x_test.shape)
predictions = model.predict(x_test)
predictions = scaler.inverse_transform(predictions)
rmse = np.sqrt(np.mean(predictions - y_test)**2)
rmse
train = data[:training_data_len]
valid = data[training_data_len:]
valid['predictions'] = predictions
plt.figure(figsize=(16,6))
plt.title('model')
plt.xlabel('Date' , fontsize=18)
plt.ylabel('Close price' , fontsize=18)
plt.plot(train['Close'],color = 'black',linewidth=4)
plt.plot(valid['Close'],color = 'red',linewidth=4)
plt.grid()
ax = plt.axes()
ax.set_facecolor("orange")
x = df.values
x.size
train = x[0:150]
test = x[150:]
train,test
predictions=[]
from statsmodels.tsa.ar_model import AR
from sklearn.metrics import mean_squared_error
model_ar = AR(train)
model_ar_fit = model_ar.fit()
AR_prediction=model_ar_fit.predict(start =120, end =154)
AR_prediction
model_ar_fit.summary()
train = data[:training_data_len]
valid = data[training_data_len:]
valid['AR_predictions'] = AR_prediction
plt.plot(train,color = 'black',linewidth=4)
plt.plot(valid,color = 'Red',linewidth=4)
plt.title("Train vs AR_Predictions")
plt.grid()
ax = plt.axes()
ax.set_facecolor("orange")
from statsmodels.tsa.arima_model import ARIMA
model_arima = ARIMA(train,order=(3,1,1))
model_arima_fit = model_arima.fit()
model_arima_fit
pred = model_arima_fit.forecast(steps=36)[0]
pred
model_arima_fit.summary()
len(train),len(valid)
len(pred)
train = data[:training_data_len]
valid = data[training_data_len:]
valid['ARIMA_predictions'] = pred
plt.plot(train,color = 'black',linewidth=4)
plt.plot(valid,color = 'Red',linewidth=4)
plt.title("Train vs ARIMA_Predictions")
plt.grid()
ax = plt.axes()
ax.set_facecolor("orange")
from statsmodels.tsa.statespace.sarimax import SARIMAX
model_sarimax = SARIMAX(train, order = (1, 1, 1), seasonal_order =(2, 1, 1, 12))
model_sarimax_fit = model_sarimax.fit()
sr_pred = model_sarimax_fit.predict(start =151, end =186,typ = 'levels',dynamic =True)
len(sr_pred)
model_sarimax_fit.summary()
train = data[:training_data_len]
valid = data[training_data_len:]
valid['SARIMAX_predictions'] = sr_pred
plt.plot(train,color = 'black',linewidth=4)
plt.plot(valid,color = 'Red',linewidth=4)
plt.title("Train vs SARIMAX_predictions")
plt.grid()
ax = plt.axes()
ax.set_facecolor("orange")
```
|
github_jupyter
|
## Swow On and Free Scenes
```
from plot_helpers import *
plt.style.use('fivethirtyeight')
casi_data = PixelClassifier(CASI_DATA, CLOUD_MASK, VEGETATION_MASK)
hillshade = RasterFile(HILLSHADE, band_number=1).band_values()
snow_on_diff_data = RasterFile(SNOW_ON_DIFF, band_number=1)
band_values_snow_on_diff = snow_on_diff_data.band_values()
band_values_snow_on_diff_mask = band_values_snow_on_diff.mask.copy()
snow_free_diff_data = RasterFile(SNOW_FREE_DIFF, band_number=1)
band_values_snow_free_diff = snow_free_diff_data.band_values()
band_values_snow_free_diff_mask = band_values_snow_free_diff.mask.copy()
```
## Snow Pixels comparison
```
band_values_snow_free_diff.mask = casi_data.snow_surfaces(band_values_snow_free_diff_mask)
band_values_snow_on_diff.mask = casi_data.snow_surfaces(band_values_snow_on_diff_mask)
ax = box_plot_compare(
[
band_values_snow_free_diff,
band_values_snow_on_diff,
],
[
'SfM Bare Ground\n- Lidar Bare Ground',
'SfM Snow\n- Lidar Snow',
],
)
ax.set_ylabel('$\Delta$ Elevation (m)')
ax.set_ylim([-1, 1]);
color_map = LinearSegmentedColormap.from_list(
'snow_pixels',
['royalblue', 'none'],
N=2
)
plt.figure(figsize=(6,6), dpi=150)
plt.imshow(hillshade, cmap='gray', clim=(1, 255), alpha=0.5)
plt.imshow(
band_values_snow_on_diff.mask,
cmap=color_map,
)
set_axes_style(plt.gca())
plt.xticks([])
plt.yticks([]);
```
## Stable Ground
```
lidar_data = RasterFile(LIDAR_SNOW_DEPTH, band_number=1)
band_values_lidar = lidar_data.band_values()
sfm_data = RasterFile(SFM_SNOW_DEPTH, band_number=1)
band_values_sfm = sfm_data.band_values()
band_values_lidar.mask = casi_data.stable_surfaces(band_values_lidar.mask)
band_values_sfm.mask = casi_data.stable_surfaces(band_values_sfm.mask)
band_values_snow_on_diff.mask = casi_data.stable_surfaces(band_values_snow_on_diff_mask)
band_values_snow_free_diff.mask = casi_data.stable_surfaces(band_values_snow_free_diff_mask)
data_sources = [
band_values_lidar,
band_values_sfm,
band_values_snow_on_diff,
band_values_snow_free_diff,
]
labels=[
'Lidar Snow\n Depth',
'SfM Snow\n Depth',
'Snow On\n Scenes',
'Bare Ground\n Scenes',
]
ax = box_plot_compare(data_sources, labels)
ax.set_ylim([-1.2, 1.2]);
color_map = LinearSegmentedColormap.from_list(
'snow_pixels',
['sienna', 'none'],
N=2
)
plt.figure(figsize=(6,6), dpi=150)
plt.imshow(hillshade, cmap='gray', clim=(1, 255), alpha=0.5)
plt.imshow(
band_values_snow_on_diff.mask,
cmap=color_map,
)
set_axes_style(plt.gca())
plt.xticks([])
plt.yticks([]);
```
|
github_jupyter
|
This tutorial provides simple examples to learn how to use the functions provided by Preprocesspack package. First we are going to load the modules needed.
```
from preprocesspack import utils, Attribute, DataSet, graphics
```
First we are going to create an Attribute object. There are several ways of creating an object. In this example we have created three Attributes.
```
attr=Attribute.Attribute(name="age",vector=[34,16,78,90,12])
attrContinuous=Attribute.Attribute(name="mark",vector=[1.2,3.4,6.7,8.9,4.7])
attrPass=Attribute.Attribute(name="pass",vector=[0,0,1,1,0])
attr.printAttribute()
```
To create a DataSet we can add a previously defined attribute or pass a vector. The name of each column will be the attribute name.
```
ds=DataSet.DataSet([],name="Students")
ds.addAttribute(attr)
ds.addAttribute(attrContinuous)
ds.addAttribute(attrPass)
ds.printDataSet()
```
From now on the tutorial will focus in how to use the preprocesspack in an external DataSet. We will use a DataSet called wine data that includes the information (alcohol quantity, color intensity, magnesium...) of two wine types. In this step we have loaded the data from a csv file using loadDataSet function. This function loads the csv file content into a DataSet. In this example the loaded file is separated by , and the first row works as the column name for the file.
```
wineData=DataSet.loadDataSet("wine_data_reduced.csv")
wineData.printDataSet()
```
The first step with this DataSet will be to discretize the Alcohol and Magnesium columns of the data, as it can be easily noticed that both can be divided into three intervals. DataSet and Attribute objects can be discretized using the function discretize. This function computes two types of discretization: on the one hand, by assigning the "EW" value to the type parameter equal width discretization is computed. On the other hand, assigning "EF" value to the parameter computes equal width discretization. Num.bins parameter indicates how many intervals are going to be made. In the following example we will compute an equal width discretization of the both columns (2 and 6). Moreover, we will compute an Equal Frecuency discretization in the last attribute, using num.bins=5
```
wineData=wineData.discretize(3,"EW",[1,5])
wineData=wineData.discretize(5,"EF",[6])
wineData.printDataSet()
```
Single attributes can also be discretized:
```
attr=Attribute.Attribute(name="age",vector=[34,16,78,90,12])
age_category=attr.discretize(2,"EW")
age_category.printAttribute()
```
The function normalize is used to normalize the data or an attribute. When applied to a DataSet, columns parameter indicate to which columns the normalization have to be applied. In this case I will apply it to the following columns: 2,3,4,6.
```
wineDataNormalized=wineData.normalize([2,3,4,6])
wineDataNormalized.printDataSet()
```
If the columns parameter is empty and the normalize function is applied to the hole DataSet it will return the original attribute if applied to categorical attributes and will normalize the rest.
```
wineDataNormalized=wineData.normalize()
wineDataNormalized.printDataSet()
```
Single attributes can also be normalized. If the attribute is categorical the result will be the original attribute
```
attrNorm=attrContinuous.normalize()
attrNorm.printAttribute()
attrNorm=age_category.normalize()
attrNorm.printAttribute()
```
To standardize the data or an attribute the function standardize can be used. When applied to a DataSet, columns parameter indicate to which columns the normalization have to be applied. In this case I will apply it to the following columns: 2,3,4,6.
```
wineDataStandardized=wineData.standardize([2,3,4,6])
wineDataStandardized.printDataSet()
```
If the columns parameter is empty and the standardize function is applied to the hole DataSet it will return the original attribute if applied to categorical attributes and will standardize the rest.
```
wineDataStandardized=wineData.standardize()
wineDataStandardized.printDataSet()
```
Single attributes can also be standardized. If the attribute is categorical the result will be the original attribute
```
attrStd=attrContinuous.standardize()
attrStd.printAttribute()
attrStd=age_category.standardize()
attrStd.printAttribute()
```
Entropy function computes the entropy of an Attribute or a complete DataSet. In the case of continuous variables it returns None. The entropy of a given DataSet can be plotted using the entropyPlot function. In the following example we have computed the entropy of the Wine Data dataset, as there are only 4 categorical or discrete variables we have only 4 results.
```
print(str(wineData.entropy()))
graphics.entropyPlot(wineData)
```
The entropy of single attributes can also be computed. If the attribute is not categorical the result will be None.
```
print(attrContinuous.entropy())
print (age_category.entropy())
```
The package also includes a function to compute the variance of a DataDet or an Attribute. The variance function returns a vector with the variance of each column of the DataSet or a value in the case of the Attribute. If the attribute is a factor it will return None.
```
print(wineData.variance())
```
The variance function can also be applied to Attributes.
```
print(attrContinuous.variance())
print (age_category.variance())
```
In order to analyze the relation between the data, the correlation function computes the correlation between the Attribute pairs of a DataSet. It calculates the correlation matrix between continuous variables and the mutual information between categorical ones. In the case where one of the variables is categorical and the other one discrete a discretization is computed in the continuous one. The parameters of the correlation function are the DataSet, num.bins and discretizationType. The default value of the last two is 3 and "EW". In the following example the correlation between the standardized wineData DataSet is computed.
```
print(wineDataStandardized.correlation())
```
With the correlationPlot function the correlation can be displayed graphically. The plot type used for that is a HeatMap that is darker where the correlation between the Attributes is higher.
```
graphics.correlationPlot(wineDataStandardized)
```
Another useful function of this package is the filter function. This function removes from the data the attributes with a correlation above the given threshold. If a function is passed through FUN parameter is given the filter function will apply the function to the data and remove the attributes that have a higher score than the threshold for the given function. Inverse parameter indicates whether the attributes have to be behind the thresshold in order to be removed, its default value is False. In the following example, first the attributes with a correlation higher than 0.4 are removed: Class.
```
filteredWineData=wineDataStandardized.filter(0.4)
filteredWineData.printDataSet()
```
In the following example the attributes with a variance higher than 2 will be removed. If we compute the variance we see that the attributes that have to be removed are the fifth (Alcalinity of ash) and the 11th one (Color intensity).
```
import numpy as np
print(wineData.variance())
filteredWineData=wineData.filter(13,np.mean)
filteredWineData.printDataSet()
```
Using the RocAuc function the area behind the ROC curve can be calculated. The RocAuc function takes as parameters: a DataSet, a variable and a class index and returns the area behind the ROC curve. In order to visualize the curve, the function RocPlot plots the Roc curve of the given variable index. In the example the Iris dataset is loaded and the roc
```
print(ds.rocAuc(1,2))
graphics.rocPlot(ds,1,2)
```
|
github_jupyter
|
# Modelling CpG islands with Hidden Markov Models
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Introduction" data-toc-modified-id="Introduction-1"><span class="toc-item-num">1 </span>Introduction</a></span><ul class="toc-item"><li><span><a href="#General" data-toc-modified-id="General-1.1"><span class="toc-item-num">1.1 </span>General</a></span></li><li><span><a href="#Viterbi,-Forward/Backward-Algorithm" data-toc-modified-id="Viterbi,-Forward/Backward-Algorithm-1.2"><span class="toc-item-num">1.2 </span>Viterbi, Forward/Backward Algorithm</a></span></li></ul></li><li><span><a href="#Imports" data-toc-modified-id="Imports-2"><span class="toc-item-num">2 </span>Imports</a></span></li><li><span><a href="#Matrices" data-toc-modified-id="Matrices-3"><span class="toc-item-num">3 </span>Matrices</a></span></li><li><span><a href="#Forward-Algorithm" data-toc-modified-id="Forward-Algorithm-4"><span class="toc-item-num">4 </span>Forward Algorithm</a></span></li><li><span><a href="#Backward-Algorithm" data-toc-modified-id="Backward-Algorithm-5"><span class="toc-item-num">5 </span>Backward Algorithm</a></span></li><li><span><a href="#Test-Sequence" data-toc-modified-id="Test-Sequence-6"><span class="toc-item-num">6 </span>Test Sequence</a></span></li><li><span><a href="#Test-Sequence-Modification" data-toc-modified-id="Test-Sequence-Modification-7"><span class="toc-item-num">7 </span>Test Sequence Modification</a></span></li></ul></div>
## Introduction
### General
We model CpG islands by creating a Hidden Markov Model of the 1st order.
The model assumes the presence of two “hidden” states: **CpG island** and **nonCpG island**.
We estimate parameters of the model by calculating **transition, emission and initiation** probabilities. For this use sequences from the file “Sequences.txt” with the known location of CpG islands described in the file “Keys.txt”.
Each line of the file “Sequences.txt” corresponds to a single sequence of bases “A”, “T”, “G” and “C”. The file contains 500 sequences in total.
The file “Keys.txt” specifies states of sequence bases: “+” – the base belongs to a CpG island, “-” – the base does not belong to a CpG island.
Note that in this exercise we do not require that the emission of the base at the
position i depends on the base at the position i+1.
look in most probable state for an observation
### Viterbi, Forward/Backward Algorithm
1. **Transition probability:** go from state k to state l: 𝑎𝑎𝑘𝑘,𝑙𝑙 = 𝑃𝑃(𝜋𝜋𝑖𝑖 = 𝑙𝑙 | 𝜋𝜋𝑖𝑖−1 = 𝑘𝑘)
2. **Emission probabilities:** emit a base 𝛽𝛽 at state l: 𝑒𝑒𝑙𝑙(𝛽𝛽) = 𝑃𝑃(𝑥𝑥𝑖𝑖 = 𝛽𝛽 | 𝜋𝜋𝑖𝑖 = 𝑙𝑙)
3. **Initiation probability:** genomic sequence starts at certain state (CpG or non-CpG)
## Imports
```
from matplotlib.patches import Rectangle
import re
import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
transitions = np.zeros((2, 2)) # +- / +-
emissions = np.zeros((4, 2)) # +- / ACTG
initiations = np.zeros((1, 2)) # +- / Probability
```
## Matrices
```
sequences = pd.read_csv('Sequences.txt', header=None)[0]
keys = pd.read_csv('keys.txt', header=None)[0]
keys_ohe = [x.replace('+', "1").replace('-', "0") for x in keys] # binary
totals = [60278, 29119]
# Transition Array
for i in range(2):
for x in range(2):
query = str(i)+str(x)
transitions[i][x] = np.sum(
[len(re.findall('(?=%s)' % query, keys_ohe[n])) for n in range(len(keys))])/totals[i]
print('Transitions: -+ / -+')
print(transitions)
print('\n')
non_cpgs = [[m.start() for m in re.finditer('0', n)] for n in keys_ohe]
cpgs = [[m.start() for m in re.finditer('1', n)] for n in keys_ohe]
cp_nuc = [[sequences[r][i] for i in cpgs[r]] for r in range(len(sequences))]
non_cp_nuc = [[sequences[r][i] for i in non_cpgs[r]]
for r in range(len(sequences))]
states = [non_cp_nuc, cp_nuc]
nucs = ['A', 'T', 'G', 'C']
totals2 = [np.sum([len(x) for x in non_cp_nuc]),
np.sum([len(x) for x in cp_nuc])]
# Emisssion Array
for nuc in range(len(nucs)):
for state in range(len(states)):
emissions[nuc][state] = np.sum(
[n.count(nucs[nuc]) for n in states[state]])/totals2[state]
print('Emissions: ATGC/-+')
print(emissions)
print('\n')
# Initiation Array (occurence in sequence)
pos = np.sum([int(n[0]) for n in keys_ohe])
initiations = [pos/500, 1-pos/500]
print('Initiations: -+/Probabilites')
print(initiations)
```
Using Viterbi algorithm we find the most likely assignment of CpG islands in the
“Test_sequence”.
## Forward Algorithm
```
def forward(sequence, initmat, a, e):
states = [0, 1]
seqlen = len(sequence)
f = [[0]*seqlen, [0]*seqlen]
ptr = [[0]*seqlen]
nucleotide = {"A": 0, "T": 1, "G": 2, "C": 3}
for k in states:
f[k][0] = initmat[k]*e[k][nucleotide[sequence[0]]]
for i in range(1, seqlen):
for k in states:
# Sum of both last previous probs*transitions for each state
f[k][i] = f[states[0]][i-1]*a[states[0]][k]
# Remaining state
for l in states[1:]:
f[k][i] += f[l][i-1]*a[l][k]
f[k][i] = f[k][i]*e[k][nucleotide[sequence[i]]]
return f
```
## Backward Algorithm
```
def backward(sequence, initmat, a, e):
states = [0, 1]
seqlen = len(sequence)
b = [[0]*seqlen, [0]*seqlen]
nucleotide = {"A": 0, "T": 1, "C": 2, "G": 3}
for k in states:
b[k][-1] = 1
for i in np.arange(seqlen-2, -1, -1):
# -1 for index shift, -1 for second last column
for k in states:
b[k][i] = b[states[0]][i+1] * a[k][states[0]] * \
e[states[0]][nucleotide[sequence[i+1]]]
# Remaining state
for l in states[1:]:
b[k][i] += b[l][i+1]*a[k][l]*e[l][nucleotide[sequence[i+1]]]
b[k][i] = b[k][i]
start = 0
for k in states:
start += b[k][0]*e[k][nucleotide[sequence[0]]]*initmat[k]
return b
```
## Test Sequence
```
test_sequence="AACAATAATTTTGTTCTCCAATATAATCATCGACGCGTCGCGACGCGCGGGGGCGCCGGGTGACCCTATACTTCACTTGAATGCCATCCG"
states = [0,1]
start_p = [0.558, 0.442]
trans_p = [[0.9871429, 0.0128571], [0.02558467, 0.97441533]]
emit_p = [[0.25910751, 0.26115618, 0.24023989, 0.23949642],
[0.14164113, 0.14501192, 0.35263875, 0.36070821]]
```
For every base of the “Test_sequence” calculate the probability to be in a CpG island. Use Forward and Backward algorithms. Calculate the probability of the “Test_sequence” using Forward and Backward algorithms. Obtained values should be the same. Plot the result: x-axis defines the position of the base, the y-axis defines the probability of the base to be in a CpG island.
```
f1 = forward(test_sequence, start_p, trans_p, emit_p)
b1 = backward(test_sequence, start_p, trans_p, emit_p)
probs = np.multiply(f1, b1) / np.sum(f1, axis=0)[-1]
island = ["-"]*len(test_sequence)
state=np.argmax(probs1,axis=0)
for i in range(len(test_sequence)):
if state[i]==1:
island[i]="+"
print('Most likely states: ' + "".join(island))
plt.figure(figsize=(16, 3))
plt.plot(probs[1], label='Probability')
plt.title('Probability Estimates for CpG Island')
plt.xlabel('Base Position')
plt.ylabel('Probability')
plt.legend(loc='best')
plt.show()
```
## Test Sequence Modification
Change a single letter of the “Test_sequence” from G to T (red):
```
test_sequence2="AACAATAATTTTGTTCTCCAATATAATCATCGACGCGTCGCGACTCGCGGGGGCGCCGGGTGACCCTATACTTCACTTGAATGCCATCCG"
f2 = forward(test_sequence2, start_p, trans_p, emit_p)
b2 = backward(test_sequence2, start_p, trans_p, emit_p)
probs2 = np.multiply(f2, b2) / np.sum(f2, axis=0)[-1]
island2 = ["-"]*len(test_sequence2)
state2=np.argmax(probs2,axis=0)
for i in range(len(test_sequence2)):
if state2[i]==1:
island2[i]="+"
print('Most likely states: ' + "".join(island2))
plt.figure(figsize=(16, 3))
plt.plot(probs[1], label='Original')
plt.plot(probs2[1], label='Modified')
plt.title('Modified Probability Estimates of CpG Island')
plt.xlabel('Base Position')
plt.ylabel('Probability')
plt.legend(loc='best')
plt.show()
```
Run Viterbi, Forward and Backward algorithms for the modified “Test_sequence”. For every base of the “Test_sequence” calculate the probability to be in a CpG island. Discuss the impact of the modification of one letter of the “Test_sequence” on the performance of Viterbi algorithm and on the probability of bases to belong to a CpG island.
**Answer:**
Changing a single nucleotide affects neighbors because we use the forward/backward algorithm.
|
github_jupyter
|
```
import sys
sys.path.append('../modules')
import likelihood_predictor
from likelihood_predictor import PlastPredictor
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.stats import zscore
import pickle
pl_full = pd.read_pickle('../database/plasticizer_data_v10_polarity.pkl')
pl_pol = pd.concat([pl_full[pl_full.columns[1:195]], pl_full['Polarity']], axis=1)
all_cols = pl_pol.columns.to_numpy()
pl_data = pl_pol[all_cols].to_numpy()
lin_data = pd.read_pickle('../database/linolein_test.pkl')
lin_data['Polarity'] = 0.048856
lin_data = lin_data[all_cols].to_numpy()
org_full = pd.read_pickle('../database/org_polarity_v2.pkl')
psim1 = open("pubs_similarity.txt", 'r')
psim11 = [line.rstrip('\n') for line in psim1]
psim2 = open("pubs_othersim.txt", 'r')
psim22 = [line.rstrip('\n') for line in psim2]
org_full
org_full['Dsim'] = psim11
org_full['Nasim'] = psim22
org_full = org_full.sort_values(by ='Dsim')
org_full = org_full[:5000]
org_data = org_full[all_cols].to_numpy()
pp = PlastPredictor()
pp_model = pp.fit_model(pl_data, org_data)
clf_file = 'savemodel.pkl'
scaler_file = 'savescaler.pkl'
pp.save_model(clf_file, scaler_file)
org_acc = pp.predict(org_data, type='binary', class_id='neg')
pl_acc = pp.predict(pl_data, type='binary', class_id='pos')
lin_prob = pp.predict(lin_data)
org_acc, pl_acc, lin_prob
pl_probs = pp.predict(pl_data)
pl_smiles = pl_full['SMILES'].to_numpy()
org_probs = pp.predict(org_data)
org_smiles = org_full['SMILES'].to_numpy()
sns.distplot(pl_probs, hist=False)
sns.distplot(org_probs, hist=False)
plt.show()
p1=PlastPredictor(reg_param=0.9)
p1.fit_model(pl_data, org_data)
org_acc = p1.predict(org_data, type='binary', class_id='neg')
pl_acc = p1.predict(pl_data, type='binary', class_id='pos')
lin_prob = p1.predict(lin_data)
pl_probs2 = p1.predict(pl_data)
pl_smiles = pl_full['SMILES'].to_numpy()
org_probs2 = p1.predict(org_data)
org_smiles = org_full['SMILES'].to_numpy()
sns.distplot(pl_probs2, hist=False)
sns.distplot(org_probs2, hist=False)
plt.show()
p1=PlastPredictor(reg_param=0.6)
p1.fit_model(pl_data, org_data)
org_acc = p1.predict(org_data, type='binary', class_id='neg')
pl_acc = p1.predict(pl_data, type='binary', class_id='pos')
lin_prob = p1.predict(lin_data)
pl_probs2 = p1.predict(pl_data)
pl_smiles = pl_full['SMILES'].to_numpy()
org_probs2 = p1.predict(org_data)
org_smiles = org_full['SMILES'].to_numpy()
sns.distplot(pl_probs2, hist=False)
sns.distplot(org_probs2, hist=False)
plt.show()
p1=PlastPredictor(reg_param=0.4)
p1.fit_model(pl_data, org_data)
org_acc = p1.predict(org_data, type='binary', class_id='neg')
pl_acc = p1.predict(pl_data, type='binary', class_id='pos')
lin_prob = p1.predict(lin_data)
pl_probs2 = p1.predict(pl_data)
pl_smiles = pl_full['SMILES'].to_numpy()
org_probs2 = p1.predict(org_data)
org_smiles = org_full['SMILES'].to_numpy()
sns.distplot(pl_probs2, hist=False)
sns.distplot(org_probs2, hist=False)
plt.show()
p1=PlastPredictor(reg_param=0.2)
p1.fit_model(pl_data, org_data)
org_acc = p1.predict(org_data, type='binary', class_id='neg')
pl_acc = p1.predict(pl_data, type='binary', class_id='pos')
lin_prob = p1.predict(lin_data)
pl_probs2 = p1.predict(pl_data)
pl_smiles = pl_full['SMILES'].to_numpy()
org_probs2 = p1.predict(org_data)
org_smiles = org_full['SMILES'].to_numpy()
sns.distplot(pl_probs2, hist=False)
sns.distplot(org_probs2, hist=False)
plt.show()
p1=PlastPredictor(reg_param=0.1)
p1.fit_model(pl_data, org_data)
org_acc = p1.predict(org_data, type='binary', class_id='neg')
pl_acc = p1.predict(pl_data, type='binary', class_id='pos')
lin_prob = p1.predict(lin_data)
pl_probs2 = p1.predict(pl_data)
pl_smiles = pl_full['SMILES'].to_numpy()
org_probs2 = p1.predict(org_data)
org_smiles = org_full['SMILES'].to_numpy()
sns.distplot(pl_probs2, hist=False)
sns.distplot(org_probs2, hist=False)
plt.show()
```
|
github_jupyter
|
## Dependencies
```
!pip install --quiet efficientnet
import warnings, time
from kaggle_datasets import KaggleDatasets
from sklearn.model_selection import KFold
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
from tensorflow.keras import optimizers, Sequential, losses, metrics, Model
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
import efficientnet.tfkeras as efn
from cassava_scripts import *
from scripts_step_lr_schedulers import *
import tensorflow_addons as tfa
seed = 0
seed_everything(seed)
warnings.filterwarnings('ignore')
```
### Hardware configuration
```
# TPU or GPU detection
# Detect hardware, return appropriate distribution strategy
strategy, tpu = set_up_strategy()
AUTO = tf.data.experimental.AUTOTUNE
REPLICAS = strategy.num_replicas_in_sync
print(f'REPLICAS: {REPLICAS}')
# Mixed precision
from tensorflow.keras.mixed_precision import experimental as mixed_precision
policy = mixed_precision.Policy('mixed_bfloat16')
mixed_precision.set_policy(policy)
# XLA
tf.config.optimizer.set_jit(True)
```
# Model parameters
```
BATCH_SIZE = 64 * REPLICAS #32 * REPLICAS
LEARNING_RATE = 3e-5 * REPLICAS # 1e-5 * REPLICAS
EPOCHS_CL = 5
EPOCHS = 15
HEIGHT = 512
WIDTH = 512
HEIGHT_DT = 512
WIDTH_DT = 512
CHANNELS = 3
N_CLASSES = 5
N_FOLDS = 5
FOLDS_USED = 1
ES_PATIENCE = 5
```
# Load data
```
database_base_path = '/kaggle/input/cassava-leaf-disease-classification/'
train = pd.read_csv(f'{database_base_path}train.csv')
print(f'Train samples: {len(train)}')
GCS_PATH = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-center-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord)
GCS_PATH_EXT = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-external-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord) (External)
GCS_PATH_CLASSES = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-classes-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord) by classes
GCS_PATH_EXT_CLASSES = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-classes-ext-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord) (External) by classes
FILENAMES_COMP = tf.io.gfile.glob(GCS_PATH + '/*.tfrec')
# FILENAMES_2019 = tf.io.gfile.glob(GCS_PATH_EXT + '/*.tfrec')
# FILENAMES_COMP_CBB = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CBB*.tfrec')
# FILENAMES_COMP_CBSD = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CBSD*.tfrec')
# FILENAMES_COMP_CGM = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CGM*.tfrec')
# FILENAMES_COMP_CMD = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CMD*.tfrec')
# FILENAMES_COMP_Healthy = tf.io.gfile.glob(GCS_PATH_CLASSES + '/Healthy*.tfrec')
# FILENAMES_2019_CBB = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CBB*.tfrec')
# FILENAMES_2019_CBSD = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CBSD*.tfrec')
# FILENAMES_2019_CGM = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CGM*.tfrec')
# FILENAMES_2019_CMD = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CMD*.tfrec')
# FILENAMES_2019_Healthy = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/Healthy*.tfrec')
TRAINING_FILENAMES = FILENAMES_COMP
NUM_TRAINING_IMAGES = count_data_items(TRAINING_FILENAMES)
print(f'GCS: train images: {NUM_TRAINING_IMAGES}')
display(train.head())
```
# Augmentation
```
def data_augment(image, label):
# p_rotation = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_spatial = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_rotate = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_pixel_1 = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_pixel_2 = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_pixel_3 = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
# p_shear = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_crop = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
p_cutout = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
# # Shear
# if p_shear > .2:
# if p_shear > .6:
# image = transform_shear(image, HEIGHT, shear=20.)
# else:
# image = transform_shear(image, HEIGHT, shear=-20.)
# # Rotation
# if p_rotation > .2:
# if p_rotation > .6:
# image = transform_rotation(image, HEIGHT, rotation=45.)
# else:
# image = transform_rotation(image, HEIGHT, rotation=-45.)
# Flips
image = tf.image.random_flip_left_right(image)
image = tf.image.random_flip_up_down(image)
if p_spatial > .75:
image = tf.image.transpose(image)
# Rotates
if p_rotate > .75:
image = tf.image.rot90(image, k=3) # rotate 270º
elif p_rotate > .5:
image = tf.image.rot90(image, k=2) # rotate 180º
elif p_rotate > .25:
image = tf.image.rot90(image, k=1) # rotate 90º
# Pixel-level transforms
if p_pixel_1 >= .4:
image = tf.image.random_saturation(image, lower=.7, upper=1.3)
if p_pixel_2 >= .4:
image = tf.image.random_contrast(image, lower=.8, upper=1.2)
if p_pixel_3 >= .4:
image = tf.image.random_brightness(image, max_delta=.1)
# Crops
if p_crop > .6:
if p_crop > .9:
image = tf.image.central_crop(image, central_fraction=.5)
elif p_crop > .8:
image = tf.image.central_crop(image, central_fraction=.6)
elif p_crop > .7:
image = tf.image.central_crop(image, central_fraction=.7)
else:
image = tf.image.central_crop(image, central_fraction=.8)
elif p_crop > .3:
crop_size = tf.random.uniform([], int(HEIGHT*.6), HEIGHT, dtype=tf.int32)
image = tf.image.random_crop(image, size=[crop_size, crop_size, CHANNELS])
image = tf.image.resize(image, size=[HEIGHT, WIDTH])
if p_cutout > .5:
image = data_augment_cutout(image)
return image, label
```
## Auxiliary functions
```
# CutOut
def data_augment_cutout(image, min_mask_size=(int(HEIGHT * .1), int(HEIGHT * .1)),
max_mask_size=(int(HEIGHT * .125), int(HEIGHT * .125))):
p_cutout = tf.random.uniform([], 0, 1.0, dtype=tf.float32)
if p_cutout > .85: # 10~15 cut outs
n_cutout = tf.random.uniform([], 10, 15, dtype=tf.int32)
image = random_cutout(image, HEIGHT, WIDTH,
min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=n_cutout)
elif p_cutout > .6: # 5~10 cut outs
n_cutout = tf.random.uniform([], 5, 10, dtype=tf.int32)
image = random_cutout(image, HEIGHT, WIDTH,
min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=n_cutout)
elif p_cutout > .25: # 2~5 cut outs
n_cutout = tf.random.uniform([], 2, 5, dtype=tf.int32)
image = random_cutout(image, HEIGHT, WIDTH,
min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=n_cutout)
else: # 1 cut out
image = random_cutout(image, HEIGHT, WIDTH,
min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=1)
return image
# Datasets utility functions
def random_crop(image, label):
"""
Resize and reshape images to the expected size.
"""
image = tf.image.random_crop(image, size=[HEIGHT, WIDTH, CHANNELS])
return image, label
def prepare_image(image, label):
"""
Resize and reshape images to the expected size.
"""
image = tf.image.resize(image, [HEIGHT, WIDTH])
image = tf.reshape(image, [HEIGHT, WIDTH, CHANNELS])
return image, label
def center_crop_(image, label, height_rs, width_rs, height=HEIGHT_DT, width=WIDTH_DT, channels=3):
image = tf.reshape(image, [height, width, channels]) # Original shape
h, w = image.shape[0], image.shape[1]
if h > w:
image = tf.image.crop_to_bounding_box(image, (h - w) // 2, 0, w, w)
else:
image = tf.image.crop_to_bounding_box(image, 0, (w - h) // 2, h, h)
image = tf.image.resize(image, [height_rs, width_rs]) # Expected shape
return image, label
def read_tfrecord_(example, labeled=True, n_classes=5):
"""
1. Parse data based on the 'TFREC_FORMAT' map.
2. Decode image.
3. If 'labeled' returns (image, label) if not (image, name).
"""
if labeled:
TFREC_FORMAT = {
'image': tf.io.FixedLenFeature([], tf.string),
'target': tf.io.FixedLenFeature([], tf.int64),
}
else:
TFREC_FORMAT = {
'image': tf.io.FixedLenFeature([], tf.string),
'image_name': tf.io.FixedLenFeature([], tf.string),
}
example = tf.io.parse_single_example(example, TFREC_FORMAT)
image = decode_image(example['image'])
if labeled:
label_or_name = tf.cast(example['target'], tf.int32)
# One-Hot Encoding needed to use "categorical_crossentropy" loss
# label_or_name = tf.one_hot(tf.cast(label_or_name, tf.int32), n_classes)
else:
label_or_name = example['image_name']
return image, label_or_name
def get_dataset(filenames, labeled=True, ordered=False, repeated=False,
cached=False, augment=False):
"""
Return a Tensorflow dataset ready for training or inference.
"""
ignore_order = tf.data.Options()
if not ordered:
ignore_order.experimental_deterministic = False
dataset = tf.data.Dataset.list_files(filenames)
dataset = dataset.interleave(tf.data.TFRecordDataset, num_parallel_calls=AUTO)
else:
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=AUTO)
dataset = dataset.with_options(ignore_order)
dataset = dataset.map(lambda x: read_tfrecord_(x, labeled=labeled), num_parallel_calls=AUTO)
if augment:
dataset = dataset.map(data_augment, num_parallel_calls=AUTO)
dataset = dataset.map(scale_image, num_parallel_calls=AUTO)
dataset = dataset.map(prepare_image, num_parallel_calls=AUTO)
if labeled:
dataset = dataset.map(conf_output, num_parallel_calls=AUTO)
if not ordered:
dataset = dataset.shuffle(2048)
if repeated:
dataset = dataset.repeat()
dataset = dataset.batch(BATCH_SIZE)
if cached:
dataset = dataset.cache()
dataset = dataset.prefetch(AUTO)
return dataset
def conf_output(image, label):
"""
Configure the output of the dataset.
"""
aux_label = [0.]
aux_2_label = [0.]
# if tf.math.argmax(label, axis=-1) == 4: # Healthy
if label == 4: # Healthy
aux_label = [1.]
# if tf.math.argmax(label, axis=-1) == 3: # CMD
if label == 3: # CMD
aux_2_label = [1.]
return (image, (label, aux_label, aux_2_label))
```
# Training data samples (with augmentation)
```
# train_dataset = get_dataset(FILENAMES_COMP, ordered=True, augment=True)
# train_iter = iter(train_dataset.unbatch().batch(20))
# display_batch_of_images(next(train_iter))
# display_batch_of_images(next(train_iter))
```
# Model
```
def encoder_fn(input_shape):
inputs = L.Input(shape=input_shape, name='input_image')
base_model = efn.EfficientNetB5(input_tensor=inputs,
include_top=False,
weights='noisy-student',
pooling=None)
outputs = L.GlobalAveragePooling2D()(base_model.output)
model = Model(inputs=inputs, outputs=outputs)
return model
def add_projection_head(input_shape, encoder):
inputs = L.Input(shape=input_shape, name='input_image')
features = encoder(inputs)
outputs = L.Dense(128, activation='relu', name='projection_head', dtype='float32')(features)
model = Model(inputs=inputs, outputs=outputs)
return model
def classifier_fn(input_shape, N_CLASSES, encoder, trainable=True):
for layer in encoder.layers:
layer.trainable = trainable
inputs = L.Input(shape=input_shape, name='input_image')
features = encoder(inputs)
features = L.Dropout(.5)(features)
features = L.Dense(1000, activation='relu')(features)
features = L.Dropout(.5)(features)
output = L.Dense(N_CLASSES, activation='softmax', name='output', dtype='float32')(features)
output_healthy = L.Dense(1, activation='sigmoid', name='output_healthy', dtype='float32')(features)
output_cmd = L.Dense(1, activation='sigmoid', name='output_cmd', dtype='float32')(features)
model = Model(inputs=inputs, outputs=[output, output_healthy, output_cmd])
return model
temperature = 0.1
class SupervisedContrastiveLoss(losses.Loss):
def __init__(self, temperature=0.1, name=None):
super(SupervisedContrastiveLoss, self).__init__(name=name)
self.temperature = temperature
def __call__(self, labels, feature_vectors, sample_weight=None):
# Normalize feature vectors
feature_vectors_normalized = tf.math.l2_normalize(feature_vectors, axis=1)
# Compute logits
logits = tf.divide(
tf.matmul(
feature_vectors_normalized, tf.transpose(feature_vectors_normalized)
),
temperature,
)
return tfa.losses.npairs_loss(tf.squeeze(labels), logits)
```
### Learning rate schedule
```
lr_start = 1e-8
lr_min = 1e-6
lr_max = LEARNING_RATE
num_cycles = 1
warmup_epochs = 3
hold_max_epochs = 0
total_epochs = EPOCHS
step_size = (NUM_TRAINING_IMAGES//BATCH_SIZE)
hold_max_steps = hold_max_epochs * step_size
total_steps = total_epochs * step_size
warmup_steps = warmup_epochs * step_size
def lrfn(total_steps, warmup_steps=0, lr_start=1e-4, lr_max=1e-3, lr_min=1e-4, num_cycles=1.):
@tf.function
def cosine_with_hard_restarts_schedule_with_warmup_(step):
""" Create a schedule with a learning rate that decreases following the
values of the cosine function with several hard restarts, after a warmup
period during which it increases linearly between 0 and 1.
"""
if step < warmup_steps:
lr = (lr_max - lr_start) / warmup_steps * step + lr_start
else:
progress = (step - warmup_steps) / (total_steps - warmup_steps)
lr = lr_max * (0.5 * (1.0 + tf.math.cos(np.pi * ((num_cycles * progress) % 1.0))))
if lr_min is not None:
lr = tf.math.maximum(lr_min, float(lr))
return lr
return cosine_with_hard_restarts_schedule_with_warmup_
lrfn_fn = lrfn(total_steps, warmup_steps, lr_start, lr_max, lr_min, num_cycles)
rng = [i for i in range(total_steps)]
y = [lrfn_fn(tf.cast(x, tf.float32)) for x in rng]
sns.set(style='whitegrid')
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print(f'{total_steps} total steps and {step_size} steps per epoch')
print(f'Learning rate schedule: {y[0]:.3g} to {max(y):.3g} to {y[-1]:.3g}')
```
# Training
```
skf = KFold(n_splits=N_FOLDS, shuffle=True, random_state=seed)
oof_pred = []; oof_labels = []; oof_names = []; oof_folds = []; history_list = []; oof_embed = []
for fold,(idxT, idxV) in enumerate(skf.split(np.arange(15))):
if fold >= FOLDS_USED:
break
if tpu: tf.tpu.experimental.initialize_tpu_system(tpu)
K.clear_session()
print(f'\nFOLD: {fold+1}')
print(f'TRAIN: {idxT} VALID: {idxV}')
# Create train and validation sets
TRAIN_FILENAMES = tf.io.gfile.glob([GCS_PATH + '/Id_train%.2i*.tfrec' % x for x in idxT])
# FILENAMES_COMP_CBB = tf.io.gfile.glob([GCS_PATH_CLASSES + '/CBB%.2i*.tfrec' % x for x in idxT])
# FILENAMES_COMP_CBSD = tf.io.gfile.glob([GCS_PATH_CLASSES + '/CBSD%.2i*.tfrec' % x for x in idxT])
# FILENAMES_COMP_CGM = tf.io.gfile.glob([GCS_PATH_CLASSES + '/CGM%.2i*.tfrec' % x for x in idxT])
# FILENAMES_COMP_Healthy = tf.io.gfile.glob([GCS_PATH_CLASSES + '/Healthy%.2i*.tfrec' % x for x in idxT])
np.random.shuffle(TRAIN_FILENAMES)
VALID_FILENAMES = tf.io.gfile.glob([GCS_PATH + '/Id_train%.2i*.tfrec' % x for x in idxV])
ct_train = count_data_items(TRAIN_FILENAMES)
ct_valid = count_data_items(VALID_FILENAMES)
step_size = (ct_train // BATCH_SIZE)
warmup_steps = (warmup_epochs * step_size)
total_steps = (total_epochs * step_size)
total_steps_cl = (EPOCHS_CL * step_size)
warmup_steps_cl = 1
### Pre-train the encoder
print('Pre-training the encoder using "Supervised Contrastive" Loss')
with strategy.scope():
encoder = encoder_fn((None, None, CHANNELS))
encoder_proj = add_projection_head((None, None, CHANNELS), encoder)
encoder_proj.summary()
lrfn_fn = lrfn(total_steps, warmup_steps, lr_start, lr_max, lr_min, num_cycles)
# optimizer = optimizers.SGD(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)),
# momentum=0.95, nesterov=True)
optimizer = optimizers.Adam(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)))
encoder_proj.compile(optimizer=optimizer,
loss=SupervisedContrastiveLoss(temperature))
es = EarlyStopping(patience=ES_PATIENCE, restore_best_weights=True,
monitor='val_loss', mode='max', verbose=1)
history_enc = encoder_proj.fit(x=get_dataset(TRAIN_FILENAMES, repeated=True, augment=True),
validation_data=get_dataset(VALID_FILENAMES, ordered=True),
steps_per_epoch=step_size,
# callbacks=[es],
batch_size=BATCH_SIZE,
epochs=EPOCHS,
verbose=2).history
### Train the classifier with the frozen encoder
print('Training the classifier with the frozen encoder')
with strategy.scope():
model = classifier_fn((None, None, CHANNELS), N_CLASSES, encoder, trainable=False)
model.summary()
lrfn_fn = lrfn(total_steps_cl, warmup_steps_cl, lr_start, lr_max, lr_min, num_cycles)
# optimizer = optimizers.SGD(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)),
# momentum=0.95, nesterov=True)
optimizer = optimizers.Adam(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)))
model.compile(optimizer=optimizer,
loss={'output': losses.SparseCategoricalCrossentropy(),
'output_healthy': losses.BinaryCrossentropy(),
'output_cmd': losses.BinaryCrossentropy()},
loss_weights={'output': 1.,
'output_healthy': .1,
'output_cmd': .1},
metrics={'output': metrics.SparseCategoricalAccuracy(),
'output_healthy': metrics.BinaryAccuracy(),
'output_cmd': metrics.BinaryAccuracy()})
model_path = f'model_{fold}.h5'
chkpt = ModelCheckpoint(model_path, mode='max',
monitor='val_output_sparse_categorical_accuracy',
save_best_only=True, save_weights_only=True)
history = model.fit(x=get_dataset(TRAIN_FILENAMES, repeated=True, augment=True),
validation_data=get_dataset(VALID_FILENAMES, ordered=True),
steps_per_epoch=step_size,
callbacks=[chkpt],
epochs=EPOCHS_CL,
verbose=2).history
### RESULTS
print(f"#### FOLD {fold+1} OOF Accuracy = {np.max(history['val_output_sparse_categorical_accuracy']):.3f}")
history_list.append(history)
# Load best model weights
model.load_weights(model_path)
# OOF predictions
ds_valid = get_dataset(VALID_FILENAMES, ordered=True)
oof_folds.append(np.full((ct_valid), fold, dtype='int8'))
oof_labels.append([target[0].numpy() for img, target in iter(ds_valid.unbatch())])
x_oof = ds_valid.map(lambda image, target: image)
oof_pred.append(np.argmax(model.predict(x_oof)[0], axis=-1))
# OOF names
ds_valid_names = get_dataset(VALID_FILENAMES, labeled=False, ordered=True)
oof_names.append(np.array([img_name.numpy().decode('utf-8') for img, img_name in iter(ds_valid_names.unbatch())]))
oof_embed.append(encoder.predict(x_oof)) # OOF embeddings
```
## Model loss graph
```
for fold, history in enumerate(history_list):
print(f'\nFOLD: {fold+1}')
plot_metrics(history, acc_name='output_sparse_categorical_accuracy')
```
# Model evaluation
```
y_true = np.concatenate(oof_labels)
y_pred = np.concatenate(oof_pred)
folds = np.concatenate(oof_folds)
names = np.concatenate(oof_names)
acc = accuracy_score(y_true, y_pred)
print(f'Overall OOF Accuracy = {acc:.3f}')
df_oof = pd.DataFrame({'image_id':names, 'fold':fold,
'target':y_true, 'pred':y_pred})
df_oof.to_csv('oof.csv', index=False)
display(df_oof.head())
print(classification_report(y_true, y_pred, target_names=CLASSES))
```
# Confusion matrix
```
fig, ax = plt.subplots(1, 1, figsize=(20, 12))
cfn_matrix = confusion_matrix(y_true, y_pred, labels=range(len(CLASSES)))
cfn_matrix = (cfn_matrix.T / cfn_matrix.sum(axis=1)).T
df_cm = pd.DataFrame(cfn_matrix, index=CLASSES, columns=CLASSES)
ax = sns.heatmap(df_cm, cmap='Blues', annot=True, fmt='.2f', linewidths=.5).set_title('Train', fontsize=30)
plt.show()
```
# Visualize embeddings outputs
```
y_true = np.concatenate(oof_labels)
y_pred = np.concatenate(oof_pred)
y_embeddings = np.concatenate(oof_embed)
visualize_embeddings(y_embeddings, y_true)
```
# Visualize predictions
```
# train_dataset = get_dataset(TRAINING_FILENAMES, ordered=True)
# x_samp, y_samp = dataset_to_numpy_util(train_dataset, 18)
# y_samp = np.argmax(y_samp, axis=-1)
# x_samp_1, y_samp_1 = x_samp[:9,:,:,:], y_samp[:9]
# samp_preds_1 = model.predict(x_samp_1, batch_size=9)
# display_9_images_with_predictions(x_samp_1, samp_preds_1, y_samp_1)
# x_samp_2, y_samp_2 = x_samp[9:,:,:,:], y_samp[9:]
# samp_preds_2 = model.predict(x_samp_2, batch_size=9)
# display_9_images_with_predictions(x_samp_2, samp_preds_2, y_samp_2)
```
|
github_jupyter
|
```
# Ricordati di eseguire questa cella con Shift+Invio
import sys
sys.path.append('../')
import jupman
```
# Stringhe 4 - iterazione e funzioni
## [Scarica zip esercizi](../_static/generated/strings.zip)
[Naviga file online](https://github.com/DavidLeoni/softpython-it/tree/master/strings)
### Che fare
- scompatta lo zip in una cartella, dovresti ottenere qualcosa del genere:
```
strings
strings1.ipynb
strings1-sol.ipynb
strings2.ipynb
strings2-sol.ipynb
strings3.ipynb
strings3-sol.ipynb
jupman.py
```
<div class="alert alert-warning">
**ATTENZIONE**: Per essere visualizzato correttamente, il file del notebook DEVE essere nella cartella szippata.
</div>
- apri il Jupyter Notebook da quella cartella. Due cose dovrebbero aprirsi, prima una console e poi un browser. Il browser dovrebbe mostrare una lista di file: naviga la lista e apri il notebook `strings1.ipynb`
- Prosegui leggendo il file degli esercizi, ogni tanto al suo interno troverai delle scritte **ESERCIZIO**, che ti chiederanno di scrivere dei comandi Python nelle celle successive. Gli esercizi sono graduati per difficoltà, da una stellina ✪ a quattro ✪✪✪✪
Scorciatoie da tastiera:
* Per eseguire il codice Python dentro una cella di Jupyter, premi `Control+Invio`
* Per eseguire il codice Python dentro una cella di Jupyter E selezionare la cella seguente, premi `Shift+Invio`
* Per eseguire il codice Python dentro una cella di Jupyter E creare una nuova cella subito dopo, premi `Alt+Invio`
* Se per caso il Notebook sembra inchiodato, prova a selezionare `Kernel -> Restart`
## Esercizi con le funzioni
<div class="alert alert-warning">
**ATTENZIONE: Gli esercizi seguenti richiedono di conoscere:**
<ul>
<li>Tutti gli esercizi sulle stringhe precedenti</li>
<li>[Controllo di flusso](https://it.softpython.org/#control-flow)</li>
<li>[Funzioni](https://it.softpython.org/functions/functions-sol.html)</li>
</ul>
<br/>
**Se sei alle prime armi con la programmazione, ti conviene saltarli e ripassare in seguito**
</div>
### lung
✪ a. Scrivi una funzione `lung1(stringa)` in cui data una stringa, RITORNI quanto è lunga la stringa. Usa `len` Per esempio, con la stringa `"ciao"`, la vostra funzione dovrebbe ritornare `4` mentre con `"hi"` dovrebbe ritornare `2`
```python
>>> x = lung1("ciao")
>>> x
4
```
✪ b. Scrivi una funzione `lung2` che come prima calcola la lunghezza della stringa, ma SENZA usare `len` (usa un ciclo `for`)
```python
>>> y = lung2("mondo")
>>> y
5
```
```
# scrivi qui
# versione con len, più veloce perchè python assieme ad una stringa mantiene sempre in memoria
# il numero della lunghezza immediatamente disponibile
def lung1(stringa):
return len(stringa)
# versione con contatore, più lenta
def lung2(parola):
contatore = 0
for lettera in parola:
contatore = contatore + 1
return contatore
```
### contin
✪ Scrivi la funzione `contin(parola, stringa)`, che RITORNA `True` se `parola` contiene la `stringa` indicata, altrimenti RITORNA `False`
- Usa l'operatore `in`
```python
>>> x = contin('carpenteria', 'ent')
>>> x
True
>>> y = contin('carpenteria', 'zent')
>>> y
False
```
```
# scrivi qui
def contin(parola, stringa):
return stringa in parola
```
### invertilet
✪ Scrivi la funzione `invertilet(primo, secondo)` che prende in input due stringhe di lunghezza maggiore di 3, e RESTITUISCE una nuova stringa in cui le parole sono concatenate e separate da uno spazio, le ultime lettere delle due parole sono invertite. Questo significa che passando in input 'ciao' e 'world', la funzione dovrebbe restituire 'ciad worlo'
Se le stringhe non sono di lunghezza adeguata, il programma STAMPA _errore!_
SUGGERIMENTO: usa _le slice_
```python
>>> x = invertilet('hi','mondo')
'errore!'
>>> x
None
>>> x = invertilet('cirippo', 'bla')
'errore!'
>>> x
None
```
```
# scrivi qui
def invertilet(primo,secondo):
if len(primo) <= 3 or len(secondo) <=3:
print("errore!")
else:
return primo[:-1] + secondo[-1] + " " + secondo[:-1] + primo[-1]
```
### nspazio
✪ Scrivi la funzione `nspazio` che data una stringa in input, RITORNA una nuova stringa in
cui l’n-esimo carattere è uno spazio. Per esempio, data la stringa 'largamente' e il carattere all'indice 5, il programma deve RITORNARE `'larga ente'`. Nota: se il numero
dovesse essere troppo grande (i.e., la parola ha 6 caratteri e chiedo di rimuovere
il numero 9), il programma STAMPA _errore!_
```python
>>> x = nspazio('largamente', 5)
>>> x
'larga ente'
>>> x = nspazio('ciao', 9)
errore!
>>> x
None
>>> x = nspazio('ciao', 4)
errore!
>>> x
None
```
```
# scrivi qui
def nspazio(parola, indice):
if indice >= len(parola):
print("errore!")
return parola[:indice]+' '+parola[indice+1:]
#nspazio("largamente", 5)
```
### inifin
✪ Scrivi un programma in Python prende una stringa, e se la stringa ha una lunghezza maggiore di 4, il programma STAMPA le prime e le ultime due lettere. Altrimenti, nel caso in cui la lunghezza della stringa sia minore di 4, STAMPA `voglio almeno 4 caratteri`. Per esempio, passando alla funzione `"ciaomondo"`, la funzione dovrebbe stampare `"cido"`. Passando `"ciao"` dovrebbe stampare `ciao` e passando `"hi"` dovrebbe stampare `voglio almeno 4 caratteri`
```python
>>> inifin('ciaomondo')
cido
>>> inifin('hi')
Voglio almeno 4 caratteri
```
```
# scrivi qui
def inifin(stringa):
if len(stringa) >= 4:
print(stringa[:2] + stringa[-2:])
else:
print("Voglio almeno 4 caratteri")
```
### scambia
Scrivere una funzione che data una stringa, inverte il primo e l’ultimo carattere, e STAMPA il risultato.
Quindi, data la stringa “mondo”, il programma stamperà “oondm”
```python
>>> scambia('mondo')
oondm
```
```
# scrivi qui
def scambia(stringa):
print(stringa[-1] + stringa[1:-1] + stringa[0])
```
## Esercizi con eccezioni e test
<div class="alert alert-warning">
**ATTENZIONE: Gli esercizi seguenti richiedono di conoscere:**
<ul>
<li>[Controllo di flusso](https://it.softpython.org/#control-flow)</li>
<li>[Funzioni](https://it.softpython.org/functions/functions-sol.html)</li>
<li>**e anche**: [Eccezioni e test con assert](https://it.softpython.org/errors-and-testing/errors-and-testing-sol.html)
</ul>
<br/>
<strong>Se sei alle prime armi con la programmazione, ti conviene saltarli e ripassare in seguito</strong>
</div>
### halet
✪ RITORNA `True` se parola contiene lettera, `False` altrimenti
- usare ciclo `while`
```
def halet(parola, lettera):
#jupman-raise
indice = 0 # inizializziamo indice
while indice < len(parola):
if parola[indice] == lettera:
return True # abbiamo trovato il carattere, possiamo interrompere la ricerca
indice += 1 # è come scrivere indice = indice + 1
# se arriviamo DOPO il while, c'è una sola ragione:
# non abbiamo trovato nulla, quindi dobbiamo ritornare False
return False
#/jupman-raise
# INIZIO TEST - NON TOCCARE !
# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError
assert halet("ciao", 'a')
assert not halet("ciao", 'A')
assert halet("ciao", 'c')
assert not halet("", 'a')
assert not halet("ciao", 'z')
# FINE TEST
```
### conta
✪ RITORNA il numero di occorrenze di lettera in parola
NOTA: NON VOGLIO UNA STAMPA, VOGLIO CHE *RITORNI* IL VALORE!
- Usare ciclo for in
```
def conta(parola, lettera):
#jupman-raise
occorrenze = 0
for carattere in parola:
# print("carattere corrente = ", carattere) # le print di debug sono ammesse
if carattere == lettera:
# print("trovata occorrenza !") # le print di debug sono ammesse
occorrenze += 1
return occorrenze # L'IMPORTANTE E' _RITORANRE_ IL VALORE COME DA TESTO DELL'ESERCIZIO !!!!!
#/jupman-raise
# INIZIO TEST - NON TOCCARE !
# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError
assert conta("ciao", "z") == 0
assert conta("ciao", "c") == 1
assert conta("babbo", "b") == 3
assert conta("", "b") == 0
assert conta("ciao", "C") == 0
# FINE TEST
```
### contiene_minuscola
✪ Esercizio ripreso dall' Esercizio 4 del libro Pensare in Python Capitolo Stringhe
leggere in fondo qua: https://davidleoni.github.io/ThinkPythonItalian/html/thinkpython2009.html
- RITORNA True se la parola contiene almeno una lettera minuscola
- RITORNA False altrimenti
- Usare ciclo `while`
```
def contiene_minuscola(s):
#jupman-raise
i = 0
while i < len(s):
if s[i] == s[i].lower():
return True
i += 1
return False
#/jupman-raise
# INIZIO TEST - NON TOCCARE !
# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError
assert contiene_minuscola("David")
assert contiene_minuscola("daviD")
assert not contiene_minuscola("DAVID")
assert not contiene_minuscola("")
assert contiene_minuscola("a")
assert not contiene_minuscola("A")
```
### dialetto
✪✪ Esiste un dialetto in cui tutte le “a” devono per forza essere precedute da una “g”. Nel caso una parola dovesse contenere “a” _non_ preceduta da una “g”, possiamo dire con certezza che questa parola non fa parte di quel dialetto. Scrivere una funzione che data una parola, RITORNI `True` se la parola rispetta le regole del dialetto, `False` altrimenti.
```python
>>> dialetto("ammot")
False
>>> print(dialetto("paganog")
False
>>> print(dialetto("pgaganog")
True
>>> print(dialetto("ciao")
False
>>> dialetto("cigao")
True
>>> dialetto("zogava")
False
>>> dialetto("zogavga")
True
```
```
def dialetto(parola):
#jupman-raise
n = 0
for i in range(0,len(parola)):
if parola[i] == "a":
if i == 0 or parola[i - 1] != "g":
return False
return True
#/jupman-raise
# INIZIO TEST - NON TOCCARE !
# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError
assert dialetto("a") == False
assert dialetto("ab") == False
assert dialetto("ag") == False
assert dialetto("ag") == False
assert dialetto("ga") == True
assert dialetto("gga") == True
assert dialetto("gag") == True
assert dialetto("gaa") == False
assert dialetto("gaga") == True
assert dialetto("gabga") == True
assert dialetto("gabgac") == True
assert dialetto("gabbgac") == True
assert dialetto("gabbgagag") == True
# FINE TEST
```
### contavoc
✪✪ Data una stringa, scrivere una funzione che conti il numero di vocali.
Se il numero di vocali è pari RITORNA il numero di vocali, altrimenti solleva l'eccezione `ValueError`
```python
>>> conta_vocali("asso")
2
>>> conta_vocali("ciao")
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-15-058310342431> in <module>()
16 contavoc("arco")
---> 19 contavoc("ciao")
ValueError: Vocali dispari !
```
```
def contavoc(parola):
#jupman-raise
n_vocali = 0
vocali = ["a","e","i","o","u"]
for lettera in parola:
if lettera.lower() in vocali:
n_vocali = n_vocali + 1
if n_vocali % 2 == 0:
return n_vocali
else:
raise ValueError("Vocali dispari !")
#/jupman-raise
# INIZIO TEST - NON TOCCARE !
# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError
assert contavoc("arco") == 2
assert contavoc("scaturire") == 4
try:
contavoc("ciao") # con questa stringa ci attendiamo che sollevi l'eccezione ValueError
raise Exception("Non dovrei arrivare fin qui !")
except ValueError: # se solleva l'eccezione ValueError,si sta comportando come previsto e non facciamo niente
pass
try:
contavoc("aiuola") # con questa stringa ci attendiamo che sollevi l'eccezione ValueError
raise Exception("Non dovrei arrivare fin qui !")
except ValueError: # se solleva l'eccezione ValueError,si sta comportando come previsto e non facciamo niente
pass
```
### palindroma
✪✪✪ Una parola è palindroma quando è esattamente la stessa se letta al contrario
Scrivi una funzione che RITORNA `True` se una parola è palindroma, `False` altrimenti
* assumi che la stringa vuota sia palindroma
Esempio:
```python
>>> x = palindroma('radar')
>>> x
True
>>> x = palindroma('scatola')
>>> x
False
```
```
def palindroma(parola):
#jupman-raise
for i in range(len(parola) // 2):
if parola[i] != parola[len(parola)- i - 1]:
return False
return True # nota che è FUORI dal for: superati tutti i controlli,
# possiamo concludere che la parola è palindroma
#/jupman-raise
# INIZIO TEST - NON TOCCARE !
# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError
assert palindroma('') == True # assumiamo che la stringa vuota sia palindroma
assert palindroma('a') == True
assert palindroma('aa') == True
assert palindroma('ab') == False
assert palindroma('aba') == True
assert palindroma('bab') == True
assert palindroma('bba') == False
assert palindroma('abb') == False
assert palindroma('abba') == True
assert palindroma('baab') == True
assert palindroma('abbb') == False
assert palindroma('bbba') == False
assert palindroma('radar') == True
assert palindroma('scatola') == False
# FINE TEST
```
## Prosegui
Continua con le [challenges](https://it.softpython.org/strings/strings5-chal.html)
|
github_jupyter
|
## Unit 5 - Financial Planning
```
%%capture
# Initial imports
import os
import requests
import pandas as pd
from dotenv import load_dotenv
import alpaca_trade_api as tradeapi
from MCForecastTools import MCSimulation
# Load .env enviroment variables
load_dotenv()
```
## Part 1 - Personal Finance Planner
```
# Set monthly household income
monthly_income = 12000
```
### Collect Crypto Prices Using the requests Library
```
# Current amount of crypto assets
my_btc = 1.2
my_eth = 5.3
# Crypto API URLs
btc_url = "https://api.alternative.me/v2/ticker/Bitcoin/?convert=USD"
eth_url = "https://api.alternative.me/v2/ticker/Ethereum/?convert=USD"
requests.get(btc_url)
btc_url_data = requests.get(btc_url)
btc_data = btc_url_data.json()
requests.get(eth_url)
eth_url_data = requests.get(eth_url)
eth_data = eth_url_data.json()
# Fetch current BTC price
current = float(btc_data['data']['1']['quotes']['USD']['price'])
# Fetch current ETH price
current2 = float(eth_data['data']['1027']['quotes']['USD']['price'])
# Compute current value of my crpto
my_btc_value = my_btc * current
my_eth_value = my_eth * current2
print(f"The current value of your {my_btc} BTC is ${my_btc_value:0.2f}")
print(f"The current value of your {my_eth} ETH is ${my_eth_value:0.2f}")
```
### Collect Investments Data Using Alpaca: SPY (stocks) and AGG (bonds)
```
# Current amount of shares
my_agg = 200
my_spy = 50
# Set Alpaca API key and secret
alpaca_api_key = os.getenv("ALPACA_API_KEY")
alpaca_secret_key = os.getenv("ALPACA_SECRET_KEY")
# Create the Alpaca API object
alpaca = tradeapi.REST(
alpaca_api_key,
alpaca_secret_key,
api_version="v2"
)
# Set timeframe to '1D' for Alpaca API
timeframe = "1D"
start_date = pd.Timestamp("2020-10-21", tz="America/New_York").isoformat()
end_date = pd.Timestamp("2020-10-21", tz="America/New_York").isoformat()
# today_now = pd.Timestamp.today().isoformat()
# Set the tickers
tickers = ["AGG", "SPY"]
# Get current closing prices for SPY and AGG
df_ticker = alpaca.get_barset(
tickers,
timeframe,
start=start_date,
end=end_date
).df
df_ticker.head()
# Create and empty DataFrame for closing prices
closing_prices = pd.DataFrame()
# Pick AGG and SPY close prices
closing_prices["AGG"] = df_ticker["AGG"]["close"]
closing_prices["SPY"] = df_ticker["SPY"]["close"]
closing_prices
# Drop the time component of the date
closing_prices.index = closing_prices.index.date
closing_prices.head()
agg_close_price = closing_prices['AGG'][0]
spy_close_price = closing_prices['SPY'][0]
print(f"Current AGG closing price: ${agg_close_price:0.2f}")
print(f"Current SPY closing price: ${spy_close_price:0.2f}")
# Compute the current value of shares
my_spy_value = spy_close_price * my_spy
my_agg_value = agg_close_price * my_agg
# Print current value of share
print(f"The current value of your {my_spy} SPY shares is ${my_spy_value:0.2f}")
print(f"The current value of your {my_agg} AGG shares is ${my_agg_value:0.2f}")
```
#### Savings Health Analysis
```
# Create savings DataFrame
shares = my_spy_value + my_agg_value
crypto = my_btc_value + my_eth_value
savings = [['shares',shares],['crypto', crypto]]
df_savings = pd.DataFrame(savings, columns =['','amount'])
df_savings.set_index(df_savings[''], inplace=True)
# Use the `drop` function to drop specific columns
df_savings.drop(columns=[''], inplace=True)
df_savings
%%capture
df_savings = pd.DataFrame({"Amount": [shares, crypto]},
index=['Shares', 'Crypto'])
plot = df_savings.plot.pie(subplots=True)
# Set ideal emergency fund
emergency_fund = monthly_income * 3
# Calculate total amount of savings
my_savings = shares + crypto
# Validate saving health
if my_savings > emergency_fund:
print("Congratulations! You have enough money in your emergency fund.")
else:
print("Your need more funds")
```
#### Part 2 - Retirement Planning
Monte Carlo Simulation
```
# Set start and end dates of five years back from today.
# Sample results may vary from the solution based on the time frame chosen
start_date1 = pd.Timestamp('2015-10-21', tz='America/New_York').isoformat()
end_date1 = pd.Timestamp('2020-10-21', tz='America/New_York').isoformat()
# Get 5 years' worth of historical data for SPY and AGG!
# Set the tickers
ticker = ["AGG", "SPY"]
df_stock_data = alpaca.get_barset(
ticker,
timeframe,
start=start_date1,
end=end_date1
).df
# Display sample data
df_stock_data.head().append(df_stock_data.tail())
# ?MCSimulation
# Configuring a Monte Carlo simulation to forecast 30 years cumulative returnss
MC_30year = MCSimulation(
portfolio_data = df_stock_data,
weights = [.40,.60],
num_simulation = 500,
num_trading_days = 252*30
)
MC_30year.portfolio_data.head()
MC_30year.calc_cumulative_return()
# Plot simulation outcomes
line_plot = MC_30year.plot_simulation()
# Save the plot for future usage
line_plot.get_figure().savefig("MC_30year_sim_plot.png", bbox_inches="tight")
# Plot probability distribution and confidence intervals
dist_plot = MC_30year.plot_distribution()
# Save the plot for future usage
dist_plot.get_figure().savefig('MC_30year_dist_plot.png',bbox_inches='tight')
# Fetch summary statistics from the Monte Carlo simulation results
tbl = MC_30year.summarize_cumulative_return()
# Print summary statistics
print(tbl)
```
#### Given an initial investment of $20,000, what is the expected portfolio return in dollars at the 95% lower and upper confidence intervals?
```
# Set initial investment
initial_investment = 20000
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $20,000
ci_lower = round(tbl[8]*20000,2)
ci_upper = round(tbl[9]*20000,2)
# Print results
print(f"There is a 95% chance that an initial investment of ${initial_investment} in the portfolio"
f" over the next 30 years will end within in the range of"
f" ${ci_lower} and ${ci_upper}")
```
#### How would a 50% increase in the initial investment amount affect the expected portfolio return in dollars at the 95% lower and upper confidence intervals
```
# Set initial investment
initial_investment1 = 20000 * 1.5
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $30,000
ci_lower1 = round(tbl[8]*(20000*1.5),2)
ci_upper1 = round(tbl[9]*(20000*1.5),2)
# Print results
print(f"There is a 95% chance that an initial investment of ${initial_investment1} in the portfolio"
f" over the next 30 years will end within in the range of"
f" ${ci_lower1} and ${ci_upper1}")
```
#### Optional Challenge - Early Retirement
Five Years Retirement Option
```
# Configuring a Monte Carlo simulation to forecast 5 years cumulative returns
start_date5 = pd.Timestamp('2015-10-21', tz='America/New_York').isoformat()
end_date5 = pd.Timestamp('2020-10-21', tz='America/New_York').isoformat()
ticker5 = ["AGG", "SPY"]
five_stock_data = alpaca.get_barset(
ticker5,
timeframe,
start=start_date5,
end=end_date5
).df
# Display sample data
MC_fiveyear = MCSimulation(
portfolio_data = five_stock_data,
weights = [.40,.60],
num_simulation = 500,
num_trading_days = 252*5
)
# Running a Monte Carlo simulation to forecast 5 years cumulative returns
MC_fiveyear.calc_cumulative_return()
# Plot simulation outcomes
line_plot_5 = MC_fiveyear.plot_simulation()
# Save the plot for future usage
line_plot_5.get_figure().savefig("MC_fiveyear_sim_plot.png", bbox_inches="tight")
# Plot probability distribution and confidence intervals
dist_plot_5 = MC_fiveyear.plot_distribution()
# Save the plot for future usage
dist_plot_5.get_figure().savefig('MC_fiveyear_dist_plot.png',bbox_inches='tight')
# Fetch summary statistics from the Monte Carlo simulation results
tbl_five = MC_fiveyear.summarize_cumulative_return()
# Print summary statistics
print(tbl_five)
# Set initial investment
initial_investment_five = 60000
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $60,000
ci_lower_five = round(tbl_five[8]*60000,2)
ci_upper_five = round(tbl_five[9]*60000,2)
# Print results
print(f"There is a 95% chance that an initial investment of ${initial_investment_five} in the portfolio"
f" over the next 5 years will end within in the range of"
f" ${ci_lower_five} and ${ci_upper_five}")
```
##### Ten Years Retirement Option
```
# Configuring a Monte Carlo simulation to forecast 10 years cumulative returns
start_date_10 = pd.Timestamp('2015-10-21', tz='America/New_York').isoformat()
end_date_10 = pd.Timestamp('2020-10-21', tz='America/New_York').isoformat()
ticker_10 = ["AGG", "SPY"]
ten_stock_data = alpaca.get_barset(
ticker_10,
timeframe,
start=start_date_10,
end=end_date_10
).df
# Display sample data
MC_tenyear = MCSimulation(
portfolio_data = ten_stock_data,
weights = [.40,.60],
num_simulation = 500,
num_trading_days = 252*10
)
# Running a Monte Carlo simulation to forecast 10 years cumulative returns
MC_tenyear.calc_cumulative_return()
# Plot simulation outcomes
line_plot_10= MC_tenyear.plot_simulation()
# Save the plot for future usage
line_plot_10.get_figure().savefig("MC_tenyear_sim_plot.png", bbox_inches="tight")
# Plot probability distribution and confidence intervals
dist_plot_10 = MC_tenyear.plot_distribution()
# Save the plot for future usage
dist_plot_10.get_figure().savefig('MC_tenyear_dist_plot.png',bbox_inches='tight')
# Fetch summary statistics from the Monte Carlo simulation results
tbl_ten = MC_tenyear.summarize_cumulative_return()
# Print summary statistics
print(tbl_ten)
# Set initial investment
initial_investment_ten = 60000
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $60,000
ci_lower_ten = round(tbl_ten[8]*60000,2)
ci_upper_ten = round(tbl_ten[9]*60000,2)
# Print results
print(f"There is a 95% chance that an initial investment of ${initial_investment_ten} in the portfolio"
f" over the next 10 years will end within in the range of"
f" ${ci_lower_ten} and ${ci_upper_ten}")
```
|
github_jupyter
|
```
# IMPORT PACKAGES
import spacy, string
nlp = spacy.load('de_core_news_sm')
from spacy.lang.de import German
# LOAD DATA S.T. 1 LINE IN XLSX = 1 DOCUMENT
def load (path):
data_raw = open(path + '.csv', encoding = 'utf-8').read().replace('\"', '').replace('\ufeff', '')
data_1row_1string = data_raw.split('\n')
data_list_remove_empty_last_line = []
for row in range(0, len(data_1row_1string)-1):
data_list_remove_empty_last_line.append(data_1row_1string[row])
data_1row_stringlist = [row.split(';') for row in data_list_remove_empty_last_line]
print('data from ' + path + ' is loaded')
return data_1row_stringlist
# EXTRACT TRANSCRIPTIONS
def extract (data_1row_stringlist):
column1 = [row[0] for row in data_1row_stringlist]
column1_1row_tokenlist = [nlp(row) for row in column1]
print('column extraction is done')
return column1_1row_tokenlist
# normalization, spacy lemmatization
def normalize (column1_1row_tokenlist):
column1_normalized = []
for row in column1_1row_tokenlist:
row_lemmatized = [token.lemma_.lower().replace('ß', 'ss').replace('\'s', '').replace('’s', '') for token in row if (not token.text.isdigit() and token.is_punct == False and len(token) > 1)]
column1_normalized.append(row_lemmatized)
print('spacy normalization is done')
return column1_normalized
# optimization with gerTwol
def gertwol_optimize (column1_normalized):
gertwol_raw = nlp(open('GERTWOL_LIST.csv', encoding = 'utf-8').read().replace('\ufeff', ''))
gertwol_list = [row.text.split(';') for row in gertwol_raw if row.text != '\n']
lemma_dict = {}
for i in range(0, len(gertwol_list)-1):
row = gertwol_list[i]
lemma_dict[row[0]] = [row[1]]
column1_gertwoled = []
j = 0
with open('GerTwol_check.csv', 'w') as test:
for row in column1_normalized:
for i in range (0, len(row)):
if (row[i] in lemma_dict.keys() and row[i] != lemma_dict[row[i]][0]):
test.write(row[i] + ': ' + lemma_dict[row[i]][0] + '\n')
row[i] = lemma_dict[row[i]][0] #returns value
j = j + 1
column1_gertwoled.append(row)
print('gertwol optimization is done, nr of changed items: ' + str(j))
return column1_gertwoled
# REMOVE STOPWORDS
def remove_stopwords (column1):
column1_nostops = []
stopwords = open('STOPWORDS.csv', encoding = 'utf-8').read().replace('\ufeff', '').split('\n')
for row in column1:
row_nostops = [word for word in row if word not in stopwords]
column1_nostops.append(row_nostops)
print('stopword removal is done')
return column1_nostops
#insert transcription back to table and print
def reinsert_and_save(data_1row_stringlist, column1_normalized, path):
i = 0
for row in column1_normalized:
data_to_string = ''
for word in row:
if word.strip() != '':
data_to_string = data_to_string + word.strip() + ' '
data_1row_stringlist[i][0] = data_to_string
i = i + 1
data_no_empty_record = [row for row in data_1row_stringlist if row[0].strip() != '']
with open(path + 'norm.csv', 'w', encoding = 'utf-8') as doc_out:
for row in data_no_empty_record:
for cell in row:
doc_out.write(cell + ';')
doc_out.write('\n')
print(path + ' output is saved')
return doc_out
# EXECUTE
paths = ['./IO_YO/all', './IO_YO/Test']
doc_in = load(paths[0] + '_in_v2')
doc_norm = normalize(extract(doc_in))
doc_gert = gertwol_optimize (doc_norm)
#doc_out = reinsert_and_save(doc_in, doc_norm, paths[0] + '_1')
#doc_out = reinsert_and_save(doc_in, doc_gert, paths[0] + '_2')
#doc_out = reinsert_and_save(doc_in, remove_stopwords (doc_norm), paths[0] + '_1S')
doc_out = reinsert_and_save(doc_in, remove_stopwords (doc_gert), paths[0] + '_2S')
```
|
github_jupyter
|
## Indexing in NumPy
### np.where vs masking
* np.where returns just the indices where the equivalent mask is true
* this is useful if you need the actual indices (maybe for counts)
* otherwise the shorthand notation (masking) is perhaps easier
* np.where returns a tuple
### Why do I care?
You may need to work directly in NumPy due to the size of your data. NumPy has a number of tricks that can speed up your code. Even if you already knew the **trick** shown here you may like to see some code that can help you compare the speeds of different methods... This is important aspect of performance tuning or more specifically code optimization.
```
import numpy as np
%matplotlib inline
x = np.arange(5)
print(np.where(x < 3))
print(x < 3)
```
### Chaining logic statements
```
x = np.arange(10)
y1 = np.intersect1d(np.where(x > 3),np.where(x<7))
y2 = np.where((x > 3) & (x < 7))
y3 = np.where(np.logical_and(x > 3, x < 7))
y4 = x[(x > 3) & (x < 7)]
print(y1,y2,y3,y4)
```
### Random helpful things in NumPy
```
a = np.array(['a','b','c','c'])
#a = np.sort(np.unique(a))
b = np.array(['c','d','e','c','f'])
mask1a = np.in1d(a,b)
mask1b = [np.where(b==i)[0].tolist() for i in a]
mask2a = np.in1d(b,a)
mask2b = [np.where(a==i)[0].tolist() for i in b]
print("1")
print(mask1a)
print(mask1b)
print("2")
print(mask2a)
print(mask2b)
```
### How does one array compare to another?
This example is also the real reason to read this notebook.
```python
a = np.array(['a','b','c'])
b = np.array(['c','d','e','c','f'])
```
* Where do we find elements of a in b?
* Where do we find elements of b in a?
* If you can use np.in1d
[np.in1d](http://docs.scipy.org/doc/numpy/reference/generated/numpy.in1d.html) is fast. But alway make sure you understand **when** it can be used before using it.
* if we have a query(a) and a search(b) list it can be helpful if you sort and make unique the query list
* it also helps to only look for things you can find
You might be suprised how often this comes up.
* matrix of hospital visits give me only data on subjects from $a$
* matrix of test scores use only subjects where name is in list $a$
```
## Get rid of nans
x = np.array([[1., 2., np.nan, 3., np.nan, np.nan]])
x[~np.isnan(x)]
## carry around indices
labels = np.array(['x' + str(i)for i in range(10)])
x = np.random.randint(1,14,10)
sortedInds = np.argsort(x)
print("sorted labels: %s"%labels[sortedInds])
## make x have exactly 5 evenly spaced points in the range 11 to 23
np.linspace(11,23,5)
## numpy has very efficient set operations
print(np.intersect1d(np.array([1,2,3]),np.arange(10)))
import matplotlib.pyplot as plt
import time
sizes = [100,1000,5000,10000]
times1,times2,times3 = [],[],[]
for n1 in sizes:
n2 = n1 * 100
a = np.random.randint(0,200,n1)
b = np.random.randint(0,100,n2)
b_list = b.tolist()
## attempt 1
time_start = time.time()
a = np.sort(np.unique(a))
a = a[np.in1d(a,b)]
times1.append(time.time()-time_start)
## attempt 2
time_start = time.time()
inds2 = [np.where(b==i)[0] for i in a]
inds2 = [item for sublist in inds2 for item in sublist]
inds2 = np.sort(np.array(inds2))
times2.append(time.time()-time_start)
## attempt 3
time_start = time.time()
inds3 = np.array([i for i,x in enumerate(b_list) if x in a])
inds3.sort()
times3.append(time.time()-time_start)
times1,times2,times3 = [np.array(t) for t in [times1,times2,times3]]
fig = plt.figure(figsize=(6,4),dpi=400)
ax = fig.add_subplot(111)
index = np.arange(len(sizes))
bar_width = 0.25
opacity = 0.4
rects1 = plt.bar(index, times1, bar_width,
alpha=opacity,
color='b',
label='np.in1d')
rects1 = plt.bar(index + bar_width, times2, bar_width,
alpha=opacity,
color='k',
label='np.where')
rects2 = plt.bar(index + (bar_width * 2.0), times3, bar_width,
alpha=opacity,
color='c',
label='list-only')
plt.xlabel('len(query_vector) by method')
plt.ylabel('Compute time (s)')
plt.title('Comparing two vectors')
plt.xticks(index + bar_width + (bar_width/2.0), [str(s) for s in sizes] )
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
## Bayesian Optimisation Verification
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from matplotlib.colors import LogNorm
from scipy.interpolate import interp1d
from scipy import interpolate
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
from scipy import stats
from scipy.stats import norm
from sklearn.metrics.pairwise import euclidean_distances
from scipy.spatial.distance import cdist
from scipy.optimize import fsolve
import math
def warn(*args, **kwargs):
pass
import warnings
warnings.warn = warn
```
## Trial on TiOx/SiOx
Tempeature vs. S10_HF
```
#import normal data sheet at 85 C (time:0~5000s)
address = 'data/degradation.xlsx'
x_normal = []
y_normal = []
df = pd.read_excel(address,sheet_name = 'normal data',usecols = [0],names = None,nrows = 5000)
df_85 = df.values.tolist()
df = pd.read_excel(address,sheet_name = 'normal data',usecols = [3],names = None,nrows = 5000)
df_85L = df.values.tolist()
#import smooth data sheet at 85 C (time:0~5000s)
address = 'data/degradation.xlsx'
df = pd.read_excel(address,sheet_name = 'smooth data',usecols = [0],names = None,nrows = 5000)
df_85s = df.values.tolist()
df = pd.read_excel(address,sheet_name = 'smooth data',usecols = [3],names = None,nrows = 5000)
df_85Ls = df.values.tolist()
#import normal data sheet at 120 C (time:0~5000s)
address = 'data/degradation.xlsx'
x_normal = []
y_normal = []
df = pd.read_excel(address,sheet_name = 'normal data',usecols = [0],names = None,nrows = 5000)
df_120 = df.values.tolist()
df = pd.read_excel(address,sheet_name = 'normal data',usecols = [3],names = None,nrows = 5000)
df_120L = df.values.tolist()
#import smooth data sheet at 120 C (time:0~5000s)
address = 'data/degradation.xlsx'
df = pd.read_excel(address,sheet_name = 'smooth data',usecols = [0],names = None,nrows = 5000)
df_120s = df.values.tolist()
df = pd.read_excel(address,sheet_name = 'smooth data',usecols = [3],names = None,nrows = 5000)
df_120Ls = df.values.tolist()
# randomly select 7 points from normal data
x_normal = np.array(df_120).T
y_normal = np.array(df_li_L).T
x_normal = x_normal.reshape((5000))
y_normal = y_normal.reshape((5000))
def plot (X,X_,y_mean,y,y_cov,gp,kernel):
#plot function
plt.figure()
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - np.sqrt(np.diag(y_cov)),y_mean + np.sqrt(np.diag(y_cov)),alpha=0.5, color='k')
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.tick_params(axis='y', colors = 'white')
plt.tick_params(axis='x', colors = 'white')
plt.ylabel('Lifetime',color = 'white')
plt.xlabel('Time',color = 'white')
plt.tight_layout()
# Preparing training set
# For log scaled plot
x_loop = np.array([1,10,32,100,316,1000,3162])
X = x_normal[x_loop].reshape(x_loop.size)
y = y_normal[x_loop]
X = X.reshape(x_loop.size,1)
X = np.log10(X)
MAX_x_value = np.log10(5000)
X_ = np.linspace(0,MAX_x_value, 5000)
# Kernel setting
length_scale_bounds_MAX = 0.5
length_scale_bounds_MIN = 1e-4
for length_scale_bounds_MAX in (0.3,0.5,0.7):
kernel = 1.0 * RBF(length_scale=20,length_scale_bounds=(length_scale_bounds_MIN, length_scale_bounds_MAX)) + WhiteKernel(noise_level=0.00000001)
gp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, y)
y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)
plot (X,X_,y_mean,y,y_cov,gp,kernel)
# Find the minimum value in the bound
# 5000 * 5000
# Find minimum value in the last row as the minimum value for the bound
def ucb(X , gp, dim, delta):
"""
Calculates the GP-UCB acquisition function values
Inputs: gp: The Gaussian process, also contains all data
x:The point at which to evaluate the acquisition function
Output: acq_value: The value of the aquisition function at point x
"""
mean, var = gp.predict(X[:, np.newaxis], return_cov=True)
#var.flags['WRITEABLE']=True
#var[var<1e-10]=0
mean = np.atleast_2d(mean).T
var = np.atleast_2d(var).T
beta = 2*np.log(np.power(5000,2.1)*np.square(math.pi)/(3*delta))
return mean - np.sqrt(beta)* np.sqrt(np.diag(var))
acp_value = ucb(X_, gp, 0.1, 5)
X_min = np.argmin(acp_value[-1])
print(acp_value[-1,X_min])
print(np.argmin(acp_value[-1]))
print(min(acp_value[-1]))
# Preparing training set
x_loop = np.array([1,10,32,100,316,1000,3162])
X = x_normal[x_loop].reshape(x_loop.size)
y = y_normal[x_loop]
X = X.reshape(x_loop.size,1)
X = np.log10(X)
MAX_x_value = np.log10(5000)
X_ = np.linspace(0,MAX_x_value, 5000)
# Kernel setting
length_scale_bounds_MAX = 0.4
length_scale_bounds_MIN = 1e-4
kernel = 1.0 * RBF(length_scale=20,length_scale_bounds=(length_scale_bounds_MIN, length_scale_bounds_MAX)) + WhiteKernel(noise_level=0.0001)
gp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, y)
y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)
acp_value = ucb(X_, gp, 0.1, 5)
ucb_y_min = acp_value[-1]
print (min(ucb_y_min))
X_min = np.argmin(acp_value[-1])
print(acp_value[-1,X_min])
print(np.argmin(acp_value[-1]))
print(min(acp_value[-1]))
plt.figure()
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.plot(X_, ucb_y_min, 'x', lw=3, zorder=9)
# plt.fill_between(X_, y_mean, ucb_y_min,alpha=0.5, color='k')
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.tick_params(axis='y', colors = 'white')
plt.tick_params(axis='x', colors = 'white')
plt.ylabel('Lifetime',color = 'white')
plt.xlabel('Time',color = 'white')
plt.tight_layout()
acp_value = ucb(X_, gp, 0.1, 5)
X_min = np.argmin(acp_value[-1])
print(acp_value[-1,X_min])
print(np.argmin(acp_value[-1]))
print(min(acp_value[-1]))
# Iterate i times with mins value point of each ucb bound
# Initiate with 7 data points, apply log transformation to them
x_loop = np.array([1,10,32,100,316,1000,3162])
X = x_normal[x_loop].reshape(x_loop.size)
Y = y_normal[x_loop]
X = X.reshape(x_loop.size,1)
X = np.log10(X)
MAX_x_value = np.log10(5000)
X_ = np.linspace(0,MAX_x_value, 5000)
# Kernel setting
length_scale_bounds_MAX = 0.5
length_scale_bounds_MIN = 1e-4
kernel = 1.0 * RBF(length_scale=20,length_scale_bounds=(length_scale_bounds_MIN, length_scale_bounds_MAX)) + WhiteKernel(noise_level=0.0001)
gp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, Y)
y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)
acp_value = ucb(X_, gp, 0.1, 5)
ucb_y_min = acp_value[-1]
plt.figure()
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean, ucb_y_min,alpha=0.5, color='k')
plt.scatter(X[:, 0], Y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.tick_params(axis='y', colors = 'white')
plt.tick_params(axis='x', colors = 'white')
plt.ylabel('Lifetime',color = 'white')
plt.xlabel('Time',color = 'white')
plt.tight_layout()
# Change i to set extra data points
i=0
while i < 5 :
acp_value = ucb(X_, gp, 0.1, 5)
ucb_y_min = acp_value[-1]
index = np.argmin(acp_value[-1])
print(acp_value[-1,X_min])
print(min(acp_value[-1]))
# Protection to stop equal x value
while index in x_loop:
index = index - 50
x_loop = np.append(x_loop, index)
x_loop = np.sort(x_loop)
print (x_loop)
X = x_normal[x_loop].reshape(x_loop.size)
Y = y_normal[x_loop]
X = X.reshape(x_loop.size,1)
X = np.log10(X)
gp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, Y)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean, ucb_y_min,alpha=0.5, color='k')
plt.scatter(X[:, 0], Y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.tick_params(axis='y', colors = 'white')
plt.tick_params(axis='x', colors = 'white')
plt.ylabel('Lifetime',color = 'white')
plt.xlabel('Time',color = 'white')
plt.title('cycle %d'%(i), color = 'white')
plt.tight_layout()
plt.show()
i+=1
print('X:', X, '\nY:', Y)
s = interpolate.InterpolatedUnivariateSpline(x_loop,Y)
x_uni = np.arange(0,5000,1)
y_uni = s(x_uni)
# Plot figure
plt.plot(df_120s,df_120Ls,'-',color = 'gray')
plt.plot(x_uni,y_uni,'-',color = 'red')
plt.plot(x_loop, Y,'x',color = 'black')
plt.tick_params(axis='y', colors = 'white')
plt.tick_params(axis='x', colors = 'white')
plt.ylabel('Lifetime',color = 'white')
plt.xlabel('Time',color = 'white')
plt.title('cycle %d'%(i+1), color = 'white')
plt.show()
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from IPython.display import Image
from sklearn import tree
from os import system
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
credit_df = pd.read_csv("credit.csv")
credit_df.head()
credit_df.shape
credit_df.describe()
credit_df.info()
for feature in credit_df.columns:
if credit_df[feature].dtype == 'object':
credit_df[feature] = pd.Categorical(credit_df[feature])
credit_df.head(5)
print(credit_df.checking_balance.value_counts())
print(credit_df.credit_history.value_counts())
print(credit_df.purpose.value_counts())
print(credit_df.savings_balance.value_counts())
print(credit_df.employment_duration.value_counts())
print(credit_df.other_credit.value_counts())
print(credit_df.housing.value_counts())
print(credit_df.job.value_counts())
print(credit_df.phone.value_counts())
replace_struc = {
"checking_balance": { "unknown": 0, "< 0 DM" : -1, "1 - 200 DM":1, "> 200 DM":2},
"credit_history": { "good": 3, "critical" : 1, "poor":2, "very good":4, "perfect":5},
"savings_balance": { "< 100 DM": 1, "100 - 500 DM" : 3, "500 - 1000 DM":7.5, "> 1000 DM":13, "unknown":0},
"employment_duration": { "< 1 year": 1, "1 - 4 years" : 3, "4 - 7 years":5.5, "> 7 years":10, "unemployed":0},
"phone": { "no": 1, "yes" : 2},
"default": { "no": 0, "yes" : 1},
}
oneHotCols = ["purpose", "housing", "other_credit", "job"]
credit_df = credit_df.replace(replace_struc)
credit_df = pd.get_dummies(credit_df, columns = oneHotCols)
credit_df.head(10)
credit_df.info()
x = credit_df.drop("default", axis = 1)
y = credit_df.pop("default")
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 101)
d_tree = DecisionTreeClassifier(criterion = 'gini', random_state = 1)
d_tree.fit(x_train, y_train)
print(d_tree.score(x_train, y_train))
print(d_tree.score(x_test, y_test))
train_char_label = ["no", "yes"]
Credit_Tree_File = open("credit_tree.dot", "w")
dot_data = tree.export_graphviz(d_tree, out_file = Credit_Tree_File, feature_names = list(x_train), class_names = list(train_char_label))
Credit_Tree_File.close()
retCode = system("dot - Tpng credit_tree.dot -o credit_tree.png")
if (retCode > 0):
print("Failed" + str(retCode))
else:
display(Image("credit_tree.png"))
d_tree_R = DecisionTreeClassifier(criterion = "gini", max_depth = 3, random_state = 1)
d_tree_R.fit (x_train, y_train)
print (d_tree_R.score(x_train,y_train))
print (d_tree_R.score(x_test,y_test))
train_char_label = ["no", "yes"]
Credit_Tree_File = open("credit_tree.dot", "w")
dot_data = tree.export_graphviz(d_tree_R, out_file = Credit_Tree_File, feature_names = list(x_train), class_names = list(train_char_label))
Credit_Tree_File.close()
retCode = system("dot - Tpng credit_tree.dot -o credit_tree.png")
if (retCode > 0):
print("Failed" + str(retCode))
else:
display(Image("credit_tree.png"))
print (pd.DataFrame(d_tree_R.feature_importances_,columns = ["Imp"], index = x_train.columns))
print(d_tree_R.score (x_test, y_test))
y_pred = d_tree_R.predict(x_test)
cm = confusion_matrix(y_test, y_pred, labels = [0,1])
df_cm = pd.DataFrame(cm, index = ["No", "Yes"], columns = ["No", "Yes"])
plt.figure (figsize = (7,5))
sns.heatmap(df_cm, annot = True, fmt = "g")
from sklearn.ensemble import bagging, AdaBoostClassifier
ada_boost = AdaBoostClassifier(base_estimator=d_tree, n_estimators=50, random_state = 1)
ada_boost.fit(x_train, y_train)
from sklearn.ensemble import BaggingClassifier
bag_ = BaggingClassifier(base_estimator=d_tree, n_estimators=100, random_state = 1)
bag_.fit(x_train, y_train)
y_pred = bag_.predict(x_test)
print(bag_.score(x_test, y_test))
cm = confusion_matrix(y_test, y_pred, labels = [0,1])
df_cm = pd.DataFrame(cm, columns = ["no","yes"], index = ["no","yes"])
sns.heatmap(df_cm,annot = True)
y_pred = ada_boost.predict(x_test)
print(ada_boost.score(x_test, y_test))
cm = confusion_matrix(y_test, y_pred, labels = [0,1])
df_cm = pd.DataFrame(cm, columns = ["no","yes"], index = ["no","yes"])
sns.heatmap(df_cm,annot = True)
ada_boost = AdaBoostClassifier(n_estimators=100, random_state = 1)
ada_boost.fit(x_train, y_train)
y_pred = ada_boost.predict(x_test)
print(ada_boost.score(x_test, y_test))
cm = confusion_matrix(y_test, y_pred, labels = [0,1])
df_cm = pd.DataFrame(cm, columns = ["no","yes"], index = ["no","yes"])
sns.heatmap(df_cm,annot = True)
from sklearn.ensemble import GradientBoostingClassifier
grb_ = GradientBoostingClassifier(n_estimators=100, random_state = 1)
grb_.fit(x_train, y_train)
y_pred = grb_.predict(x_test)
print(grb_.score(x_test, y_test))
cm = confusion_matrix(y_test, y_pred, labels = [0,1])
df_cm = pd.DataFrame(cm, columns = ["no","yes"], index = ["no","yes"])
sns.heatmap(df_cm,annot = True)
from sklearn.ensemble import RandomForestClassifier
random_forest = RandomForestClassifier(n_estimators=100, random_state = 1, max_features = 6)
random_forest.fit(x_train, y_train)
y_pred = random_forest.predict(x_test)
print(random_forest.score(x_test, y_test))
cm = confusion_matrix(y_test, y_pred, labels = [0,1])
df_cm = pd.DataFrame(cm, columns = ["no","yes"], index = ["no","yes"])
sns.heatmap(df_cm,annot = True)
ada_boost.predict_proba(x_test)
bag_.predict_proba(x_test)
grb_.predict_proba(x_test)
random_forest.predict_proba(x_test)
```
|
github_jupyter
|
# How to create Data objects
The SciDataTool python module has been created to **ease the handling of scientific data**, and considerately simplify plot commands. It unifies the extraction of relevant data (e.g. slices), whether they are stored in the time/space or in the frequency domain. The call to Fourier Transform functions is **transparent**, although it still can be parameterized through the use of a dictionary.
This tutorial explains the **structure** of the `Data` classes, then shows **how to create axes and fields objects**.
The following example demonstrates the syntax to **quickly create a 2D data field** (airgap radial flux density) depending on time and angle:
```
# Add SciDataTool to the Python path
import sys
sys.path.append('..')
# Import useful packages
from os.path import join
from numpy import pi, squeeze
from pandas import ExcelFile, read_excel
# Import SciDataTool modules
from SciDataTool import Data1D, DataTime
# Import scientific data
from Tests import DATA_DIR
xls_file = ExcelFile(join(DATA_DIR, "tutorials_data.xlsx"))
time = read_excel(xls_file, sheet_name="time", header=None, nrows=1, squeeze=True).to_numpy()
angle = read_excel(xls_file, sheet_name="angle", header=None, nrows=1, squeeze=True).to_numpy()
field = read_excel(xls_file, sheet_name="Br", header=None, nrows=2016, squeeze=True).to_numpy()
#---------------------------------------------------------------
# Create Data objects
Time = Data1D(name="time", unit="s", values=time)
Angle = Data1D(name="angle", unit="rad", values=angle)
Br = DataTime(
name="Airgap radial flux density",
unit="T",
symbol="B_r",
axes=[Time, Angle],
values=field,
)
#---------------------------------------------------------------
```
Your `Data`objects have been successfully created. Other features of the `SciDataTool` package are also available:
- reduce storage if an axis is regularly spaced
- reduce storage if the field presents a symmetry along one of its axes
- store a field in the frequency domain
- specifiy normalizations
These functionalities are described in the following sections.
## 1. Data class structure
The `Data` class is composed of:
- classes describing **axes**: `Data1D`, or `DataLinspace` if the axis is regularly spaced (see [section 2](#How-to-reduce-storage-if-an-axis-is-regularly-spaced))
- classes describing **fields** stored in the time/space domain (`DataTime`) or in the frequential domain (`DataFreq`)
The following UML summarizes this structure:
<div>
<img src="_static/UML_Data_Object.png" width="450"/>
</div>
The attributes in red are **mandatory**, those in gray are **optional**. To correctly fill the mandatory attributes, it is advised to follow these principles:
- `values` is a **numpy array**
- `axes` is a **list** of `Data1D` or `DataLinspace`
- `name` is **string** corresponding to a short description of the field, or the
- `symbol` is a **string** giving the symbol of the field in LaTeX format
- `unit` is a **string** among the list: `[dimless, m, rad, °, g, s, min, h, Hz, rpm, degC, A, J, W, N, C, T, G, V, F, H, Ohm, At, Wb, Mx]`, with a prefix `[k, h, da, d, c, m, etc.]`. Composed units are also available (e.g. `mm/s^2`). It is best to use such a LaTeX formatting for axis labelling. Other units can be added in [conversions.py](https://github.com/Eomys/SciDataTool/blob/master/Functions/conversions.py).
- for `Data1D` and `DataLinspace`, `name` + `[unit]` can be used to label axes
- for `DataTime` and `DataFreq`, `name` can be used as plot title, and `symbol` + `[unit]` as label
When a `Data1D` is created, the array `values` is **squeezed** to avoid dimension problems. When a `DataTime` or `DataFreq` is created, `values` is also squeezed, and a `CheckDimError` is raised if **dimensions** of `axes` and `values` do not match.
The following sections explain how to use the optional attributes to optimize storage.
## 2. How to reduce storage if an axis is regularly spaced
Axes often have a **regular distribution**, so that the use of `DataLinspace` allows to reduce the storage.
A `DataLinspace` object has five properties instead of the `values` array: `initial`, `final`, `step` and `number` allow to define the linspace vector (3 out of these 4 suffice), and `include_endpoint` is a boolean used to indicate whether the final point should be included or not (default `False`).
In the following example, the angle vector is defined as a linspace:
```
from SciDataTool import DataLinspace
#---------------------------------------------------------------
# Create Data objects
Angle = DataLinspace(
name="angle",
unit="rad",
symmetries={},
initial=0,
final=2*pi,
number=2016,
)
#---------------------------------------------------------------
```
## 3. How to reduce storage if a field presents a symmetry/periodicity
If a signal shows a **symmetry** or a **periodicity** along one or several of its axes, it is possible to store only the relevant part of the signal, and save the information necessary to rebuild it within the optional attribute `symmetries`. A repeting signal can either be periodic: $f(t+T)=f(t)$, or antiperiodic: $f(t+T)=-f(t)$. Indeed, we can consider that a symmetric signal is a periodic signal of period $T=N/2$.
`symmetries` is a dictionary containing the **name of the axis** and a **dictionary** of its symmetry (`{"period": n}` or `{"antiperiod": n}`, with *n* the number of periods in the complete signal. Note that the symmetries dictionary must be shared with the field itself (`DataTime` or `DataFreq`).
In the following example, the time vector and the field are reduced to one third before being stored.
```
time_reduced = time[0:time.size//3]
field_reduced = field[0:time.size//3,:]
#---------------------------------------------------------------
# Create Data objects
Time_reduced = Data1D(name="time", unit="s", symmetries={"time": {"period": 3}}, values=time_reduced)
Br_reduced = DataTime(
name="Airgap radial flux density",
unit="T",
symbol="B_r",
axes=[Time, Angle],
values=field,
symmetries={"time": {"period": 3}},
)
#---------------------------------------------------------------
```
## 4. How to store a field in the frequency domain
If one prefers to store data in the frequency domain, for example because most postprocessings will handle spectra, or because a small number of harmonics allow to reduce storage, the `DataFreq` class can be used.
The definition is similar to the `DataTime` one, with the difference that the axes now have to be **frequencies** or **wavenumbers** and a `DataFreq` object is created.
Since we want to be able to go back to the time/space domain, there must exist a corresponding axis name. For the time being, the existing **correspondances** are:
+ `"time"` ↔ `"freqs"`
+ `"angle"` ↔ `"wavenumber"`
This list is to be expanded, and a possibility to manually add a correspondance will be implemented soon.
In the following example, a field is stored in a `DataFreq` object.
```
from SciDataTool import DataFreq
# Import scientific data
freqs = read_excel(xls_file, sheet_name="freqs", header=None, nrows=1, squeeze=True).to_numpy()
wavenumber = read_excel(xls_file, sheet_name="wavenumber", header=None, nrows=1, squeeze=True).to_numpy()
field_fft2 = read_excel(xls_file, sheet_name="Br_fft2", header=None, nrows=2016, squeeze=True).to_numpy()
#---------------------------------------------------------------
# Create Data objects
Freqs = Data1D(name="freqs", unit="Hz", values=freqs)
Wavenumber = Data1D(name="wavenumber", unit="dimless", values=wavenumber)
Br_fft = DataFreq(
name="Airgap radial flux density",
unit="T",
symbol="B_r",
axes=[Freqs, Wavenumber],
values=field_fft2,
)
#---------------------------------------------------------------
```
## 5. How to specify normalizations (axes or field)
If you plan to **normalize** your field or its axes during certain postprocessings (but not all), you might want to store the normalizations values. To do so, you can use the `normalizations` attribute, which is a dictionaray:
- for a normalization of the **field**, use `"ref"` (e.g. `{"ref": 0.8}`)
- for a normalization of an **axis**, use the name of the normalized axis unit (e.g. `{"elec_order": 60}`). There is no list of predefined normalized axis units, you simply must make sure to request it when you extract data (see [How to extract slices](https://github.com/Eomys/SciDataTool/tree/master/Tutorials/tuto_Slices.ipynb))
- to **convert** to a unit which does not exist in the predefined units, and if there exists a proportionality relation, it is also possible to add it in the `normalizations` dictionary (e.g. `{"nameofmyunit": 154}`)
This dictionary can also be updated later.
See below examples of use of `normalizations`:
```
#---------------------------------------------------------------
Br = DataTime(
name="Airgap radial flux density",
unit="T",
symbol="B_r",
axes=[Time, Angle],
normalizations={"ref": 0.8, "elec_order": 60},
values=field,
)
Br.normalizations["space_order"] = 3
#---------------------------------------------------------------
```
## 6. How to store a field with multiple components
It is more efficient to store all the **components** of a same field (e.g. $x$, $y$, $z$ components of a vector field, phases of a signal, etc.) in the same `Data` object. To do so, the `is_components` key can be used to easily recognize it, and strings can be used as values.
```
from numpy import roll, array
fieldB = roll(field, 100, axis=0)
fieldC = roll(field, 200, axis=0)
new_field = array([field, fieldB, fieldC])
#---------------------------------------------------------------
Phases = Data1D(name="phases", unit="", values=["Phase A","Phase B","Phase C"], is_components=True)
Br = DataTime(
name="Airgap radial flux density",
unit="T",
symbol="B_r",
axes=[Phases, Time, Angle],
values=new_field,
)
#---------------------------------------------------------------
```
Now that the `Data` objects have been created, we can:
- [extract slices](https://nbviewer.jupyter.org/github/Eomys/SciDataTool/blob/master/Tutorials/tuto2_Slices.ipynb)
- [compare several fields](https://nbviewer.jupyter.org/github/Eomys/SciDataTool/blob/master/Tutorials/tuto3_Compare.ipynb)
- [perform advanced Fourier Transforms](https://nbviewer.jupyter.org/github/Eomys/SciDataTool/blob/master/Tutorials/tuto4_Fourier.ipynb)
|
github_jupyter
|
**On my honor I have neither given nor received any unauthorized aid.**
**Your name here**
# Test 2
On this test we are going use a dataset that researchers collected about 649 high school students in Portugal, and attempt to determine how their grades are affected by several of the variables that they collected information about.
P. Cortez and A. Silva. Using Data Mining to Predict Secondary School Student Performance. In A. Brito and J. Teixeira Eds., Proceedings of 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008) pp. 5-12, Porto, Portugal, April, 2008, EUROSIS, ISBN 978-9077381-39-7.
**As always load up the libraries**
```
library(dplyr)
library(ggplot2)
```
We will load the data using the command:
```
student<-read.csv("student-por.csv")
```
## Dataset student
The student dataset looks at the relationship between variables describing students lives and their performance in Portuguese class.
| Attribute | Explanation|
|-----------|------------|
|age|student's age (numeric: from 15 to 22) |
|studytime|hours studied weekly |
|Walc| Alcoholic drinks consumed weekly |
|absences| number of school absences (numeric: from 0 to 32) |
|G3| final grade (numeric: from 0 to 20, output target)|
```
str(student)
```
### Task 1
Create a scatterplot that shows the relationship between G3 and Walc.
### Task 2
Create a linear model that predicts the G3 based on the Walc. **Write a markdown cell that gives the equation that predicts G3 from Walc. Does your calculation indicate that Walc is a useful predictor for G3?**
### Task 3
**Create a scatterplot that shows the relationship between the G3 and Walc and add in the line of best fit that you found in Task 2.**
### Task 4
Create a table that shows the correlations between the all the quantitative variables in this dataset. **Write a markdown cell indicating the strength of the correlation between G3 and the other attributes.**
### Task 5
Create a residual plot for the model that you have found in Task 2. **What does the residual plot say about the model that we have found in Task 2?**
### Task 6
Create a multilinear model for G3 from the attributes in this dataset. Only use those attributes that seem demonstrated to be relevant to G3. **In a markdown cell, write the equation for G3 that is given by your model. And then describe what the is the meaning of the $R^2$ value given by the model.**
```
```
### Task 7
**Explain what each of the coefficients of your multilinear model from Task 6 mean in context of the dataset.**
### Task 8
**Make a prediction for the final grade of a student with the attributes described below.**
|Attribute|Value|
|---------|-----|
|age|19 |
|studytime|1 |
|Walc| 4 |
|absences| 22 |
### Task 9
Based on information what you know of the model used in the prediction above describe in words (with numerical support) how accurate you believe the prediction to be.
# Extra-Credit
Calculate the z-score of the prediction you made in Task 8.
|
github_jupyter
|
# MODIS
MODIS Terra: https://lpdaac.usgs.gov/products/mod11c1v006/
MODIS Acqua: https://lpdaac.usgs.gov/products/myd11c1v061/
Docs: https://lpdaac.usgs.gov/documents/118/MOD11_User_Guide_V6.pdf
```
! wget https://e4ftl01.cr.usgs.gov/MOLA/MYD11C1.061/2018.04.19/MYD11C1.A2018109.061.2021330052306.hdf -O /network/group/aopp/predict/TIP016_PAXTON_RPSPEEDY/ML4L/MODIS.hdf
import xarray as xr
import rioxarray as rxr
modis_xarray= rxr.open_rasterio('/network/group/aopp/predict/TIP016_PAXTON_RPSPEEDY/ML4L/MODIS.hdf',masked=True)
modis_xarray['Day_view_time']
modis_df = modis_xarray.to_dataframe().reset_index()
lite = modis_df[['y','x', 'LST_Day_CMG','Day_view_time', 'LST_Night_CMG', 'Night_view_time']]
L = lite.dropna().copy()
L['T_Day'] = L['LST_Day_CMG']*0.02
L['T_Night'] = L['LST_Night_CMG']*0.02
L['Time_Day'] = L['Day_view_time']*0.2
L['Time_Night'] = L['Night_view_time']*0.2
L['Time_Day_UTC'] = L['Time_Day'] - L['x']/15
window = L.query('-70 < y < 70')
w = window.copy()
import pandas as pd
#Create time delta to change local to UTC
#time_delta = pd.to_timedelta(window.x/15,unit='H')
#Convert local satellite time to UTC and round to nearest hour
# time = (pd.to_datetime([file_date + " " + local_times[satellite]]*time_delta.shape[0]) - time_delta).round('H')
w['ideal_UTC'] = (pd.to_datetime("2022-01-01 13:30") - pd.to_timedelta(w.x/15))#.dt.time
w['actual_utc'] = (pd.to_datetime("2022-01-01 00:00") + pd.to_timedelta(w.Time_Day_UTC,unit='hours'))#.dt.time
#w['dfdf'] = w.ideal_UTC.dt.time
#w['actual_utc'] = (pd.to_datetime("00:00") + pd.to_timedelta(w.Time_Day_UTC,unit='hours')).dt.time #.dt.components['hours']
w['difference'] = pd.to_timedelta(w.ideal_UTC - w.actual_utc,unit='s').dt.total_seconds() / 60
w
import matplotlib.pyplot as plt
import matplotlib.colors as mc
import matplotlib.colorbar as cb
#Get all data as vectors
x = w.x.values
y = w.y.values
z1 = w.difference.values
cmap = plt.cm.coolwarm
#Scatter plot it
# init the figure
fig,[ax,cax] = plt.subplots(1,2, gridspec_kw={"width_ratios":[50,1]},figsize=(30, 20))
vmin = -1500
vmax= +1500
norm = mc.Normalize(vmin=vmin, vmax=vmax)
cb1 = cb.ColorbarBase(cax, cmap=cmap,norm=norm,orientation='vertical')
sc = ax.scatter(x, y,s=1,c=cmap(norm(z1)),linewidths=1, alpha=1)
#ax.set_title(z)
plt.show()
modis_xarray.LST_Day_CMG.data.dropna()
t = modis_xarray.Day_view_time.data
tt = t.flatten()
sum(tt)
import numpy as np
tnn = t[~np.isnan(t)]*0.2
len(tnn)
min(tnn)
max(tnn)
np.unique(tnn)
[[[-19.0715515614,-1.4393790966],
[53.2624328136,-1.4393790966],
[53.2624328136,36.0044133726],
[-19.0715515614,36.0044133726],
[-19.0715515614,-1.4393790966]]]
-19 56
-1.4 36
```
|
github_jupyter
|
# ODE solver
In this notebook, we show some examples of solving an ODE model. For the purposes of this example, we use the Scipy solver, but the syntax remains the same for other solvers
```
%pip install pybamm -q # install PyBaMM if it is not installed
import pybamm
import tests
import numpy as np
import os
import matplotlib.pyplot as plt
from pprint import pprint
os.chdir(pybamm.__path__[0]+'/..')
# Create solver
ode_solver = pybamm.ScipySolver()
```
## Integrating ODEs
In PyBaMM, a model is solved by calling a solver with `solve`. This sets up the model to be solved, and then calls the method `_integrate`, which is specific to each solver. We begin by setting up and discretising a model
```
# Create model
model = pybamm.BaseModel()
u = pybamm.Variable("u")
v = pybamm.Variable("v")
model.rhs = {u: -v, v: u}
model.initial_conditions = {u: 2, v: 1}
model.variables = {"u": u, "v": v}
# Discretise using default discretisation
disc = pybamm.Discretisation()
disc.process_model(model);
```
Now the model can be solved by calling `solver.solve` with a specific time vector at which to evaluate the solution
```
# Solve ########################
t_eval = np.linspace(0, 5, 30)
solution = ode_solver.solve(model, t_eval)
################################
# Extract u and v
t_sol = solution.t
u = solution["u"]
v = solution["v"]
# Plot
t_fine = np.linspace(0,t_eval[-1],1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13,4))
ax1.plot(t_fine, 2 * np.cos(t_fine) - np.sin(t_fine), t_sol, u(t_sol), "o")
ax1.set_xlabel("t")
ax1.legend(["2*cos(t) - sin(t)", "u"], loc="best")
ax2.plot(t_fine, 2 * np.sin(t_fine) + np.cos(t_fine), t_sol, v(t_sol), "o")
ax2.set_xlabel("t")
ax2.legend(["2*sin(t) + cos(t)", "v"], loc="best")
plt.tight_layout()
plt.show()
```
Note that, where possible, the solver makes use of the mass matrix and jacobian for the model. However, the discretisation or solver will have created the mass matrix and jacobian algorithmically, using the expression tree, so we do not need to calculate and input these manually.
The solution terminates at the final simulation time:
```
solution.termination
```
### Events
It is possible to specify events at which a solution should terminate. This is done by adding events to the `model.events` dictionary. In the following example, we solve the same model as before but add a termination event when `v=-2`.
```
# Create model
model = pybamm.BaseModel()
u = pybamm.Variable("u")
v = pybamm.Variable("v")
model.rhs = {u: -v, v: u}
model.initial_conditions = {u: 2, v: 1}
model.events.append(pybamm.Event('v=-2', v + 2)) # New termination event
model.variables = {"u": u, "v": v}
# Discretise using default discretisation
disc = pybamm.Discretisation()
disc.process_model(model)
# Solve ########################
t_eval = np.linspace(0, 5, 30)
solution = ode_solver.solve(model, t_eval)
################################
# Extract u and v
t_sol = solution.t
u = solution["u"]
v = solution["v"]
# Plot
t_fine = np.linspace(0,t_eval[-1],1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13,4))
ax1.plot(t_fine, 2 * np.cos(t_fine) - np.sin(t_fine), t_sol, u(t_sol), "o")
ax1.set_xlabel("t")
ax1.legend(["2*cos(t) - sin(t)", "u"], loc="best")
ax2.plot(t_fine, 2 * np.sin(t_fine) + np.cos(t_fine), t_sol, v(t_sol), "o", t_fine, -2 * np.ones_like(t_fine), "k")
ax2.set_xlabel("t")
ax2.legend(["2*sin(t) + cos(t)", "v", "v = -2"], loc="best")
plt.tight_layout()
plt.show()
```
Now the solution terminates because the event has been reached
```
solution.termination
print("event time: ", solution.t_event, "\nevent state", solution.y_event.flatten())
```
## References
The relevant papers for this notebook are:
```
pybamm.print_citations()
```
|
github_jupyter
|
## 初始化
```
import sys,os
root_path = os.path.abspath('../../../../')
sys.path.append(root_path)
root_path
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import src.features.factors.consolidate_factor as cf
import src.visualization.plotting as pt
```
## 整理数据
```
fp = root_path + "/xxx.parquet" # 需要用到的其它类型的数据
mf = pd.read_parquet(fp)
md_fp = root_path + "/data/example/IF/md.parquet" # 需要用到的行情数据
md = pd.read_parquet(md_fp)
df = pd.concat([mf, md], axis=1).dropna(axis=0) # 将数据源进行整合
df['return'] = df['close'].diff() # 基准收益
```
## 生成因子
## 设置因子的类型、名称、参数值
```
factor_type = 'tmom'
factor_signature = 'xxx'
param_signatures = [560, 720, 960, 1200, 1800]
raw_factor_name = f"factor_{factor_type}_{factor_signature}"
raw_factor_name
def factor_tmom_xxx(df: pd.DataFrame, w) -> pd.Series:
"""
最好在这里规范描述因子逻辑,以便后期整理
"""
df['factor'] = df['return'].rolling(w).mean() / df['return'].rolling(w).max() # 生成因子
return df['factor']
```
## 开启一个循环,用以检验因子在不同参数下的表现
```
# set signal shift
sig_shift = 1
compare_df, compare_df_2 = pd.DataFrame(), pd.DataFrame()
for i in param_signatures:
factor = factor_tmom_xxx(df, i)
signal = np.sign(factor)
ret_cumsum_df = pd.DataFrame((df['return'] * signal.shift(sig_shift)).cumsum(), columns=[i])
ret_df = pd.DataFrame((df['return'] * signal.shift(sig_shift)), columns=[i])
compare_df = pd.concat([compare_df, ret_cumsum_df], axis=1)
compare_df_2 = pd.concat([compare_df_2, ret_df], axis=1)
compare_df['benchmark'] = base_return.cumsum()
compare_df['close'] = df['close']
compare_df_2['benchmark'] = base_return
compare_df.plot(figsize=(16,9), secondary_y='close')
compare_df.drop(columns=['close'], inplace=True)
vol_on_return = pd.DataFrame((compare_df - compare_df.mean()).std(), columns=['volitility'])
final_return = pd.DataFrame(compare_df.iloc[-1])
final_return.columns = ['return']
sample_df = pd.concat([vol_on_return, final_return], axis=1)
sample_df.plot(kind='bar', secondary_y='volitility', figsize=(16,9))
compare_df.describe()
compare_df_2.describe()
```
## 选取你认为表现比较好的因子,将因子函数固化
```
param_signature = 1200
factor_name = f"factor_{factor_type}_{factor_signature}_{param_signature}"
factor_name
```
#### 现在,你的因子函数应该有固定的参数,而非传入参数。
```
def factor_tmom_xxx_1200(df: pd.DataFrame):
"""
衡量北向资金净买入量在1200期内的投票结果
"""
df['factor'] = df['return'].rolling(w).mean() / df['return'].rolling(w).max() # 生成因子
return df['factor']
factor = factor_tmom_xxx_1200(df)
```
## 再次对固化的因子进行回测检验
```
# set signal shift
sig_shift = 1
```
## 确认因子转换为信号的逻辑
```
signal = np.sign(factor)
```
## 确认回测结果
```
(df['return'] * signal.shift(sig_shift)).cumsum().describe()
(df['return'] * signal.shift(sig_shift)).cumsum().plot(figsize=(16,9))
data = pd.DataFrame([factor.shift(sig_shift), base_return]).T
data.columns = ['factor', 'return']
fig = plt.figure(figsize=(16,9))
sns.scatterplot(data=data, x='factor', y='return')
data = pd.DataFrame([signal.shift(sig_shift), base_return]).T
data.columns = ['signal', 'return']
fig = plt.figure(figsize=(16,9))
sns.scatterplot(data=data, x='signal', y='return')
```
-----------------
# <font color=red>CAUTION! </font>
#### <font color=red>YOU ARE ABOUT TO CONSOLIDATE A FACTOR FUNCTION AND ITS DATA. </font>
#### <font color=red>ENTER FOLLOWING STEPS WITH CAUTION!</font>
-------------------------
## consolidate factor
```
cf.record_source(factor_tmom_xxx_1200)
```
## set instrument name:
```
instrument = 'IF'
```
## save factor to parquet
```
factor_df = pd.DataFrame(factor)
factor_df.columns=['factor']
factor_df
factor_fp = root_path + f"/factor/{instrument}/"
# os.mkdir(factor_fp)
cf.save_factor(factor_df, factor_fp, factor_name)
```
## save signal to parquet
```
signal_df = pd.DataFrame(signal)
signal_df.columns=['signal']
signal_df
signal_fp = root_path + f"/signal/{instrument}"
# os.mkdir(signal_fp)
cf.save_signal(signal_df, signal_fp, factor_name)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/muhdlaziem/DR/blob/master/Testing_3_all.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/gdrive')
%cd /gdrive/'My Drive'/
%tensorflow_version 1.x
# import libraries
import json
import math
from tqdm import tqdm, tqdm_notebook
import gc
import warnings
import os
import cv2
from PIL import Image
import pandas as pd
import scipy
import matplotlib.pyplot as plt
from keras import backend as K
from keras import layers
from keras.applications.densenet import DenseNet121
from keras.callbacks import Callback, ModelCheckpoint
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.optimizers import Adam
from sklearn.model_selection import train_test_split
from sklearn.metrics import cohen_kappa_score, accuracy_score
import numpy as np
warnings.filterwarnings("ignore")
%matplotlib inline
# Image size
im_size = 320
import pandas as pd
# %cd diabetic-retinopathy-resized/
DR = pd.read_csv('/gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/label_for_out_MYRRC_data2_256x256.csv')
DR.head()
def preprocess_image(image_path, desired_size=224):
img = cv2.imread(image_path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
#img = crop_image_from_gray(img)
img = cv2.resize(img, (desired_size,desired_size))
img = cv2.addWeighted(img,4,cv2.GaussianBlur(img, (0,0), desired_size/40) ,-4 ,128)
return img
# testing set
%cd /gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/image
N = DR.shape[0]
x_test = np.empty((N, im_size, im_size, 3), dtype=np.uint8)
for i, image_id in enumerate(tqdm_notebook(DR['file'])):
x_test[i, :, :, :] = preprocess_image(
f'{image_id}',
desired_size = im_size
)
y_test = pd.get_dummies(DR['class']).values
print(y_test.shape)
print(x_test.shape)
y_test_multi = np.empty(y_test.shape, dtype=y_test.dtype)
y_test_multi[:, 2] = y_test[:, 2]
for i in range(1, -1, -1):
y_test_multi[:, i] = np.logical_or(y_test[:, i], y_test_multi[:, i+1])
print("Y_test multi: {}".format(y_test_multi.shape))
# from keras.models import load_model
import tensorflow as tf
model = tf.keras.models.load_model('/gdrive/My Drive/diabetic-retinopathy-resized/resized_train_cropped/denseNet_3_all.h5')
model.summary()
y_val_pred = model.predict(x_test)
def compute_score_inv(threshold):
y1 = y_val_pred > threshold
y1 = y1.astype(int).sum(axis=1) - 1
y2 = y_test_multi.sum(axis=1) - 1
score = cohen_kappa_score(y1, y2, weights='quadratic')
return 1 - score
simplex = scipy.optimize.minimize(
compute_score_inv, 0.5, method='nelder-mead'
)
best_threshold = simplex['x'][0]
y1 = y_val_pred > best_threshold
y1 = y1.astype(int).sum(axis=1) - 1
# y1 = np.where(y1==2,1,y1)
# y1 = np.where(y1==3,2,y1)
# y1 = np.where(y1==4,2,y1)
y2 = y_test_multi.sum(axis=1) - 1
score = cohen_kappa_score(y1, y2, weights='quadratic')
print('Threshold: {}'.format(best_threshold))
print('Validation QWK score with best_threshold: {}'.format(score))
y1 = y_val_pred > .5
y1 = y1.astype(int).sum(axis=1) - 1
# y1 = np.where(y1==2,1,y1)
# y1 = np.where(y1==3,2,y1)
# y1 = np.where(y1==4,2,y1)
score = cohen_kappa_score(y1, y2, weights='quadratic')
print('Validation QWK score with .5 threshold: {}'.format(score))
from sklearn.metrics import classification_report, confusion_matrix
y_best = y_val_pred > best_threshold
y_best = y_best.astype(int).sum(axis=1) - 1
# y_best = np.where(y_best==2,1,y_best)
# y_best = np.where(y_best==3,2,y_best)
# y_best = np.where(y_best==4,2,y_best)
print('Confusion Matrix')
print(confusion_matrix(y_best, y2))
print('Classification Report')
target_names = ['No DR', 'Moderate', 'Severe']
print(classification_report(y_best, y2, target_names=target_names))
print(y_best)
print(y2)
DR['predicted'] = y_best
DR.to_excel("/gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/result_3_all.xlsx")
```
|
github_jupyter
|
[View in Colaboratory](https://colab.research.google.com/github/DillipKS/MLCC_assignments/blob/master/feature_sets.ipynb)
#### Copyright 2017 Google LLC.
```
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Feature Sets
**Learning Objective:** Create a minimal set of features that performs just as well as a more complex feature set
So far, we've thrown all of our features into the model. Models with fewer features use fewer resources and are easier to maintain. Let's see if we can build a model on a minimal set of housing features that will perform equally as well as one that uses all the features in the data set.
## Setup
As before, let's load and prepare the California housing data.
```
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from sklearn import metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
california_housing_dataframe = pd.read_csv("https://storage.googleapis.com/mledu-datasets/california_housing_train.csv", sep=",")
california_housing_dataframe = california_housing_dataframe.reindex(
np.random.permutation(california_housing_dataframe.index))
def preprocess_features(california_housing_dataframe):
"""Prepares input features from California housing data set.
Args:
california_housing_dataframe: A Pandas DataFrame expected to contain data
from the California housing data set.
Returns:
A DataFrame that contains the features to be used for the model, including
synthetic features.
"""
selected_features = california_housing_dataframe[
["latitude",
"longitude",
"housing_median_age",
"total_rooms",
"total_bedrooms",
"population",
"households",
"median_income"]]
processed_features = selected_features.copy()
# Create a synthetic feature.
processed_features["rooms_per_person"] = (
california_housing_dataframe["total_rooms"] /
california_housing_dataframe["population"])
return processed_features
def preprocess_targets(california_housing_dataframe):
"""Prepares target features (i.e., labels) from California housing data set.
Args:
california_housing_dataframe: A Pandas DataFrame expected to contain data
from the California housing data set.
Returns:
A DataFrame that contains the target feature.
"""
output_targets = pd.DataFrame()
# Scale the target to be in units of thousands of dollars.
output_targets["median_house_value"] = (
california_housing_dataframe["median_house_value"] / 1000.0)
return output_targets
# Choose the first 12000 (out of 17000) examples for training.
training_examples = preprocess_features(california_housing_dataframe.head(12000))
training_targets = preprocess_targets(california_housing_dataframe.head(12000))
# Choose the last 5000 (out of 17000) examples for validation.
validation_examples = preprocess_features(california_housing_dataframe.tail(5000))
validation_targets = preprocess_targets(california_housing_dataframe.tail(5000))
# Double-check that we've done the right thing.
print("Training examples summary:")
display.display(training_examples.describe())
print("Validation examples summary:")
display.display(validation_examples.describe())
print("Training targets summary:")
display.display(training_targets.describe())
print("Validation targets summary:")
display.display(validation_targets.describe())
```
## Task 1: Develop a Good Feature Set
**What's the best performance you can get with just 2 or 3 features?**
A **correlation matrix** shows pairwise correlations, both for each feature compared to the target and for each feature compared to other features.
Here, correlation is defined as the [Pearson correlation coefficient](https://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient). You don't have to understand the mathematical details for this exercise.
Correlation values have the following meanings:
* `-1.0`: perfect negative correlation
* `0.0`: no correlation
* `1.0`: perfect positive correlation
```
correlation_dataframe = training_examples.copy()
correlation_dataframe["target"] = training_targets["median_house_value"]
correlation_dataframe.corr()
```
Features that have strong positive or negative correlations with the target will add information to our model. We can use the correlation matrix to find such strongly correlated features.
We'd also like to have features that aren't so strongly correlated with each other, so that they add independent information.
Use this information to try removing features. You can also try developing additional synthetic features, such as ratios of two raw features.
For convenience, we've included the training code from the previous exercise.
```
def construct_feature_columns(input_features):
"""Construct the TensorFlow Feature Columns.
Args:
input_features: The names of the numerical input features to use.
Returns:
A set of feature columns
"""
return set([tf.feature_column.numeric_column(my_feature)
for my_feature in input_features])
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""Trains a linear regression model.
Args:
features: pandas DataFrame of features
targets: pandas DataFrame of targets
batch_size: Size of batches to be passed to the model
shuffle: True or False. Whether to shuffle the data.
num_epochs: Number of epochs for which data should be repeated. None = repeat indefinitely
Returns:
Tuple of (features, labels) for next data batch
"""
# Convert pandas data into a dict of np arrays.
features = {key:np.array(value) for key,value in dict(features).items()}
# Construct a dataset, and configure batching/repeating.
ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit
ds = ds.batch(batch_size).repeat(num_epochs)
# Shuffle the data, if specified.
if shuffle:
ds = ds.shuffle(10000)
# Return the next batch of data.
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
def train_model(
learning_rate,
steps,
batch_size,
training_examples,
training_targets,
validation_examples,
validation_targets):
"""Trains a linear regression model.
In addition to training, this function also prints training progress information,
as well as a plot of the training and validation loss over time.
Args:
learning_rate: A `float`, the learning rate.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
training_examples: A `DataFrame` containing one or more columns from
`california_housing_dataframe` to use as input features for training.
training_targets: A `DataFrame` containing exactly one column from
`california_housing_dataframe` to use as target for training.
validation_examples: A `DataFrame` containing one or more columns from
`california_housing_dataframe` to use as input features for validation.
validation_targets: A `DataFrame` containing exactly one column from
`california_housing_dataframe` to use as target for validation.
Returns:
A `LinearRegressor` object trained on the training data.
"""
periods = 10
steps_per_period = steps / periods
# Create a linear regressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=construct_feature_columns(training_examples),
optimizer=my_optimizer
)
# Create input functions.
training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
batch_size=batch_size)
predict_training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
num_epochs=1,
shuffle=False)
predict_validation_input_fn = lambda: my_input_fn(validation_examples,
validation_targets["median_house_value"],
num_epochs=1,
shuffle=False)
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
training_rmse = []
validation_rmse = []
for period in range (0, periods):
# Train the model, starting from the prior state.
linear_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period,
)
# Take a break and compute predictions.
training_predictions = linear_regressor.predict(input_fn=predict_training_input_fn)
training_predictions = np.array([item['predictions'][0] for item in training_predictions])
validation_predictions = linear_regressor.predict(input_fn=predict_validation_input_fn)
validation_predictions = np.array([item['predictions'][0] for item in validation_predictions])
# Compute training and validation loss.
training_root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(training_predictions, training_targets))
validation_root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(validation_predictions, validation_targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, training_root_mean_squared_error))
# Add the loss metrics from this period to our list.
training_rmse.append(training_root_mean_squared_error)
validation_rmse.append(validation_root_mean_squared_error)
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.ylabel("RMSE")
plt.xlabel("Periods")
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(training_rmse, label="training")
plt.plot(validation_rmse, label="validation")
plt.legend()
return linear_regressor
```
Spend 5 minutes searching for a good set of features and training parameters. Then check the solution to see what we chose. Don't forget that different features may require different learning parameters.
```
#
# Your code here: add your features of choice as a list of quoted strings.
#
minimal_features = ["median_income", "rooms_per_person"]
assert minimal_features, "You must select at least one feature!"
minimal_training_examples = training_examples[minimal_features]
minimal_validation_examples = validation_examples[minimal_features]
#
# Don't forget to adjust these parameters.
#
train_model(
learning_rate=0.03,
steps=500,
batch_size=10,
training_examples=minimal_training_examples,
training_targets=training_targets,
validation_examples=minimal_validation_examples,
validation_targets=validation_targets)
```
### Solution
Click below for a solution.
```
minimal_features = [
"median_income",
"latitude",
]
minimal_training_examples = training_examples[minimal_features]
minimal_validation_examples = validation_examples[minimal_features]
_ = train_model(
learning_rate=0.01,
steps=500,
batch_size=5,
training_examples=minimal_training_examples,
training_targets=training_targets,
validation_examples=minimal_validation_examples,
validation_targets=validation_targets)
```
## Task 2: Make Better Use of Latitude
Plotting `latitude` vs. `median_house_value` shows that there really isn't a linear relationship there.
Instead, there are a couple of peaks, which roughly correspond to Los Angeles and San Francisco.
```
plt.scatter(training_examples["latitude"], training_targets["median_house_value"])
```
**Try creating some synthetic features that do a better job with latitude.**
For example, you could have a feature that maps `latitude` to a value of `|latitude - 38|`, and call this `distance_from_san_francisco`.
Or you could break the space into 10 different buckets. `latitude_32_to_33`, `latitude_33_to_34`, etc., each showing a value of `1.0` if `latitude` is within that bucket range and a value of `0.0` otherwise.
Use the correlation matrix to help guide development, and then add them to your model if you find something that looks good.
What's the best validation performance you can get?
```
# YOUR CODE HERE: Train on a new data set that includes synthetic features based on latitude.
train_lat_bins = [0,0,0,0,0,0,0,0,0,0] #bins for a unit latitude range
for lat in training_examples["latitude"]:
if int(lat)==32: train_lat_bins[0]+=1
elif int(lat)==33: train_lat_bins[1]+=1
elif int(lat)==34: train_lat_bins[2]+=1
elif int(lat)==35: train_lat_bins[3]+=1
elif int(lat)==36: train_lat_bins[4]+=1
elif int(lat)==37: train_lat_bins[5]+=1
elif int(lat)==38: train_lat_bins[6]+=1
elif int(lat)==39: train_lat_bins[7]+=1
elif int(lat)==40: train_lat_bins[8]+=1
elif int(lat)==41: train_lat_bins[9]+=1
train_lat_bins
val_lat_bins = [0,0,0,0,0,0,0,0,0,0] #bins for a unit latitude range
for lat in validation_examples["latitude"]:
if int(lat)==32: val_lat_bins[0]+=1
elif int(lat)==33: val_lat_bins[1]+=1
elif int(lat)==34: val_lat_bins[2]+=1
elif int(lat)==35: val_lat_bins[3]+=1
elif int(lat)==36: val_lat_bins[4]+=1
elif int(lat)==37: val_lat_bins[5]+=1
elif int(lat)==38: val_lat_bins[6]+=1
elif int(lat)==39: val_lat_bins[7]+=1
elif int(lat)==40: val_lat_bins[8]+=1
elif int(lat)==41: val_lat_bins[9]+=1
val_lat_bins
```
### Solution
Click below for a solution.
Aside from `latitude`, we'll also keep `median_income`, to compare with the previous results.
We decided to bucketize the latitude. This is fairly straightforward in Pandas using `Series.apply`.
```
LATITUDE_RANGES = zip(range(32, 44), range(33, 45))
def select_and_transform_features(source_df):
selected_examples = pd.DataFrame()
selected_examples["median_income"] = source_df["median_income"]
for r in LATITUDE_RANGES:
selected_examples["latitude_%d_to_%d" % r] = source_df["latitude"].apply(
lambda l: 1.0 if l >= r[0] and l < r[1] else 0.0)
return selected_examples
selected_training_examples = select_and_transform_features(training_examples)
selected_validation_examples = select_and_transform_features(validation_examples)
selected_training_examples.head()
_ = train_model(
learning_rate=0.03,
steps=500,
batch_size=10,
training_examples=selected_training_examples,
training_targets=training_targets,
validation_examples=selected_validation_examples,
validation_targets=validation_targets)
```
|
github_jupyter
|
### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to Change These)
HeroesOfPymoli = "Resources/purchase_data.csv"
# Read Purchasing File and store into Pandas data frame
HoP_df = pd.read_csv(HeroesOfPymoli)
HoP_df.head()
```
## Player Count
* Display the total number of players
```
Player_Count = HoP_df["SN"].nunique()
Player_Count
data = {'Total Players':[Player_Count]}
PC_df = pd.DataFrame(data)
PC_df
```
## Purchasing Analysis (Total)
* Run basic calculations to obtain number of unique items, average price, etc.
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
# Number of Unique Items
U_Items_Count = HoP_df["Item ID"].nunique()
U_Items_Count
#Average Price
Average_Price = HoP_df["Price"].mean()
Average_Price
#Total Number of Purchases
Number_P = HoP_df["Purchase ID"].count()
Number_P
#Total Revenue
T_Revenue= Number_P * Average_Price
T_Revenue
PAdata = {'Number of Unique Items':[U_Items_Count], 'Average Price':[Average_Price], 'Number of Purchases' :[Number_P], 'Total Revenue' :[T_Revenue]}
PA_df = pd.DataFrame(PAdata)
PA_df
```
## Gender Demographics
* Percentage and Count of Male Players
* Percentage and Count of Female Players
* Percentage and Count of Other / Non-Disclosed
```
#Count of Players
G_Players_df = HoP_df.loc[1:, ["SN","Gender","Price","Purchase ID"]]
GP=G_Players_df.drop_duplicates()
GP
Gender_Count=GP['Gender'].value_counts()
Gender_Count
Percent_of_Players= (Gender_Count / Player_Count)*100
Percent_of_Players
GAdata = {'Total Count':[Gender_Count], 'Percentage of Players':[Percent_of_Players]}
GA_df = pd.DataFrame(GAdata)
GA_df
```
## Purchasing Analysis (Gender)
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. by gender
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
# Purchase analysis
Purchase_Analysis_df = HoP_df.loc[ 1:,["Gender","Price",]]
Purchase_Analysis_df
PA_Count = Purchase_Analysis_df['Gender'].value_counts()
PA_Count
#AVG purchase price per member
Avg_Purchase_Price = HoP_df.loc[ 1:,["Price"]]
Avg_Purchase_Price.mean()
```
## Age Demographics
* Establish bins for ages
* Categorize the existing players using the age bins. Hint: use pd.cut()
* Calculate the numbers and percentages by age group
* Create a summary data frame to hold the results
* Optional: round the percentage column to two decimal points
* Display Age Demographics Table
```
Age_df = HoP_df.loc[1:, ["SN","Age"]]
AG=Age_df.drop_duplicates()
AgeD=pd.DataFrame(AG)
AgeD
#Establish Bins
bins= [0,10,15,20,25,30,35,40,100]
group_names = ["<10","10-14","15-19","20-24","25-29","30-34","35-39","40+"]
AgeD["age ranges"] = pd.cut(AgeD["Age"], bins, labels=group_names)
AgeD.head()
#Total Counts
Total_Count = AgeD['age ranges'].value_counts()
Total_Count
#Percentage of Players
Percent_of_GPlayers= (Total_Count / Player_Count)*100
Percent_of_GPlayers
```
## Purchasing Analysis (Age)
* Bin the purchase_data data frame by age
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. in the table below
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
PurchaseAnalysis_df = HoP_df.loc[1:, ["SN","Age","Price","Purchase ID"]]
PurchaseAnalysis_df
P_Analysis=PurchaseAnalysis_df.drop_duplicates()
PurchaseAS=pd.DataFrame(PurchaseAnalysis_df)
PurchaseAS
#Establish Bins
bins= [0,10,15,20,25,30,35,40,100]
group_names = ["<10","10-14","15-19","20-24","25-29","30-34","35-39","40+"]
PurchaseAS["age ranges"] = pd.cut(PurchaseAS["Age"], bins, labels=group_names)
PurchaseAS
PA_age_Count = PurchaseAS['age ranges'].value_counts()
PA_age_Count
```
## Top Spenders
* Run basic calculations to obtain the results in the table below
* Create a summary data frame to hold the results
* Sort the total purchase value column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
```
T_Spenders_df = HoP_df.loc[1:, ["SN","Price"]]
T_Spenders_df
#Cant figure this out
T_Spenders1_df = T_Spenders_df.()
T_Spenders1_df
```
## Most Popular Items
* Retrieve the Item ID, Item Name, and Item Price columns
* Group by Item ID and Item Name. Perform calculations to obtain purchase count, item price, and total purchase value
* Create a summary data frame to hold the results
* Sort the purchase count column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
```
PopItems_df = HoP_df.loc[1:, ["Item Name","Price","Item ID"]]
PopItems_df
#???
PopItems1_df = PopItems_df.groupby(by="Item Name")
PopItems1_df
```
## Most Profitable Items
* Sort the above table by total purchase value in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the data frame
|
github_jupyter
|
# Population Segmentation with SageMaker
In this notebook, we'll employ two, unsupervised learning algorithms to do **population segmentation**. Population segmentation aims to find natural groupings in population data that reveal some feature-level similarities between different regions in the US.
Using **principal component analysis** (PCA) you will reduce the dimensionality of the original census data. Then, we'll use **k-means clustering** to assign each US county to a particular cluster based on where a county lies in component space. How each cluster is arranged in component space can tell us which US counties are most similar and what demographic traits define that similarity; this information is most often used to inform targeted, marketing campaigns that want to appeal to a specific group of people. This cluster information is also useful for learning more about a population by revealing patterns between regions that you otherwise may not have noticed.
### US Census Data
We'll be using data collected by the [US Census](https://en.wikipedia.org/wiki/United_States_Census), which aims to count the US population, recording demographic traits about labor, age, population, and so on, for each county in the US.
### Machine Learning Workflow
To implement population segmentation, we'll go through a number of steps:
* Data loading and exploration
* Data cleaning and pre-processing
* Dimensionality reduction with PCA
* Feature engineering and data transformation
* Clustering transformed data with k-means
* Extracting trained model attributes and visualizing k clusters
These tasks make up a complete, machine learning workflow from data loading and cleaning to model deployment.
---
First, import the relevant libraries into this SageMaker notebook.
```
# data managing and display libs
import pandas as pd
import numpy as np
import os
import io
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
# sagemaker libraries
import boto3
import sagemaker
```
## Loading the Data from Amazon S3
This particular dataset is already in an Amazon S3 bucket; you can load the data by pointing to this bucket and getting a data file by name.
> You can interact with S3 using a `boto3` client.
```
# boto3 client to get S3 data
s3_client = boto3.client('s3')
bucket_name='aws-sagemaker-census-segmentation'
```
Take a look at the contents of this bucket; get a list of objects that are contained within the bucket and print out the names of the objects. You should see that there is one file, 'Census_Data_for_SageMaker.csv'.
```
# get a list of objects in the bucket
obj_list=s3_client.list_objects(Bucket=bucket_name)
# print object(s)in S3 bucket
files=[]
for contents in obj_list['Contents']:
files.append(contents['Key'])
print(files)
# there is one file --> one key
file_name=files[0]
print(file_name)
```
Retrieve the data file from the bucket with a call to `client.get_object()`.
```
# get an S3 object by passing in the bucket and file name
data_object = s3_client.get_object(Bucket=bucket_name, Key=file_name)
# what info does the object contain?
display(data_object)
# information is in the "Body" of the object
data_body = data_object["Body"].read()
print('Data type: ', type(data_body))
```
This is a `bytes` datatype, which you can read it in using [io.BytesIO(file)](https://docs.python.org/3/library/io.html#binary-i-o).
```
# read in bytes data
data_stream = io.BytesIO(data_body)
# create a dataframe
counties_df = pd.read_csv(data_stream, header=0, delimiter=",")
counties_df.head()
```
## Exploratory Data Analysis (EDA)
Now that we've loaded in the data, it is time to clean it up, explore it, and pre-process it. Data exploration is one of the most important parts of the machine learning workflow because it allows you to notice any initial patterns in data distribution and features that may inform how you proceed with modeling and clustering the data.
### Explore data & drop any incomplete rows of data
When you first explore the data, it is good to know what you are working with. How many data points and features are you starting with, and what kind of information can you get at a first glance? In this notebook, we will use complete data points to train a model. So, our first exercise will be to investigate the shape of this data and implement a simple, data cleaning step: dropping any incomplete rows of data.
You should be able to answer the **question**: How many data points and features are in the original, provided dataset? (And how many points are left after dropping any incomplete rows?)
```
# print out stats about data
print('Original data stats:\n', counties_df.shape)
# drop any incomplete rows of data, and create a new df
clean_counties_df = counties_df.dropna()
print('Cleaned data stats:\n', clean_counties_df.shape)
```
### Create a new DataFrame, indexed by 'State-County'
Eventually, you'll want to feed these features into a machine learning model. Machine learning models need numerical data to learn from and not categorical data like strings (State, County). So, you'll reformat this data such that it is indexed by region and you'll also drop any features that are not useful for clustering.
To complete this task, perform the following steps, using your *clean* DataFrame, generated above:
1. Combine the descriptive columns, 'State' and 'County', into one, new categorical column, 'State-County'.
2. Index the data by this unique State-County name.
3. After doing this, drop the old State and County columns and the CensusId column, which does not give us any meaningful demographic information.
After completing this task, you should have a DataFrame with 'State-County' as the index, and 34 columns of numerical data for each county. You should get a resultant DataFrame that looks like the following (truncated for display purposes):
```
TotalPop Men Women Hispanic ...
Alabama-Autauga 55221 26745 28476 2.6 ...
Alabama-Baldwin 195121 95314 99807 4.5 ...
Alabama-Barbour 26932 14497 12435 4.6 ...
...
```
```
# index data by 'State-County'
clean_counties_df.index = clean_counties_df['State'] + '-' + clean_counties_df['County']
# drop the old State and County columns, and the CensusId column
# clean df should be modified or created anew
clean_counties_df = clean_counties_df.drop(['State', 'County', 'CensusId'], axis=1)
clean_counties_df.head()
```
Now, what features do you have to work with?
```
# features
features_list = clean_counties_df.columns.values
print('Features: \n', features_list)
```
## Visualizing the Data
In general, you can see that features come in a variety of ranges, mostly percentages from 0-100, and counts that are integer values in a large range. Let's visualize the data in some of our feature columns and see what the distribution, over all counties, looks like.
The below cell displays **histograms**, which show the distribution of data points over discrete feature ranges. The x-axis represents the different bins; each bin is defined by a specific range of values that a feature can take, say between the values 0-5 and 5-10, and so on. The y-axis is the frequency of occurrence or the number of county data points that fall into each bin. I find it helpful to use the y-axis values for relative comparisons between different features.
Below, I'm plotting a histogram comparing methods of commuting to work over all of the counties. I just copied these feature names from the list of column names, printed above. I also know that all of these features are represented as percentages (%) in the original data, so the x-axes of these plots will be comparable.
```
# transportation (to work)
transport_list = ['Drive', 'Carpool', 'Transit', 'Walk', 'OtherTransp']
n_bins = 30 # can decrease to get a wider bin (or vice versa)
for column_name in transport_list:
ax=plt.subplots(figsize=(6,3))
# get data by column_name and display a histogram
ax = plt.hist(clean_counties_df[column_name], bins=n_bins)
title="Histogram of " + column_name
plt.title(title, fontsize=12)
plt.show()
```
### EXERCISE: Create histograms of your own
Commute transportation method is just one category of features. If you take a look at the 34 features, you can see data on profession, race, income, and more. Display a set of histograms that interest you!
```
# create a list of features that you want to compare or examine
my_list = ['Hispanic', 'White', 'Black', 'Native', 'Asian']
n_bins = 50
# histogram creation code is similar to above
for column_name in my_list:
ax=plt.subplots(figsize=(6,3))
# get data by column_name and display a histogram
ax = plt.hist(clean_counties_df[column_name], bins=n_bins)
title="Histogram of " + column_name
plt.title(title, fontsize=12)
plt.show()
# create a list of features that you want to compare or examine
my_list = ['WorkAtHome', 'Employed', 'SelfEmployed', 'Unemployment']
n_bins = 50
# histogram creation code is similar to above
for column_name in my_list:
ax=plt.subplots(figsize=(6,3))
# get data by column_name and display a histogram
ax = plt.hist(clean_counties_df[column_name], bins=n_bins)
title="Histogram of " + column_name
plt.title(title, fontsize=12)
plt.show()
```
### Normalize the data
You need to standardize the scale of the numerical columns in order to consistently compare the values of different features. You can use a [MinMaxScaler](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) to transform the numerical values so that they all fall between 0 and 1.
```
# scale numerical features into a normalized range, 0-1
# store them in this dataframe
from sklearn.preprocessing import MinMaxScaler
min_max = MinMaxScaler()
counties_scaled = pd.DataFrame(min_max.fit_transform(clean_counties_df))
counties_scaled.columns = clean_counties_df.columns
counties_scaled.index = clean_counties_df.index
counties_scaled.head()
counties_scaled.describe()
```
---
# Data Modeling
Now, the data is ready to be fed into a machine learning model!
Each data point has 34 features, which means the data is 34-dimensional. Clustering algorithms rely on finding clusters in n-dimensional feature space. For higher dimensions, an algorithm like k-means has a difficult time figuring out which features are most important, and the result is, often, noisier clusters.
Some dimensions are not as important as others. For example, if every county in our dataset has the same rate of unemployment, then that particular feature doesn’t give us any distinguishing information; it will not help t separate counties into different groups because its value doesn’t *vary* between counties.
> Instead, we really want to find the features that help to separate and group data. We want to find features that cause the **most variance** in the dataset!
So, before I cluster this data, I’ll want to take a dimensionality reduction step. My aim will be to form a smaller set of features that will better help to separate our data. The technique I’ll use is called PCA or **principal component analysis**
## Dimensionality Reduction
PCA attempts to reduce the number of features within a dataset while retaining the “principal components”, which are defined as *weighted*, linear combinations of existing features that are designed to be linearly independent and account for the largest possible variability in the data! You can think of this method as taking many features and combining similar or redundant features together to form a new, smaller feature set.
We can reduce dimensionality with the built-in SageMaker model for PCA.
### Roles and Buckets
> To create a model, you'll first need to specify an IAM role, and to save the model attributes, you'll need to store them in an S3 bucket.
The `get_execution_role` function retrieves the IAM role you created at the time you created your notebook instance. Roles are essentially used to manage permissions and you can read more about that [in this documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html). For now, know that we have a FullAccess notebook, which allowed us to access and download the census data stored in S3.
You must specify a bucket name for an S3 bucket in your account where you want SageMaker model parameters to be stored. Note that the bucket must be in the same region as this notebook. You can get a default S3 bucket, which automatically creates a bucket for you and in your region, by storing the current SageMaker session and calling `session.default_bucket()`.
```
from sagemaker import get_execution_role
session = sagemaker.Session() # store the current SageMaker session
# get IAM role
role = get_execution_role()
print(role)
# get default bucket
bucket_name = session.default_bucket()
print(bucket_name)
print()
```
## Define a PCA Model
To create a PCA model, I'll use the built-in SageMaker resource. A SageMaker estimator requires a number of parameters to be specified; these define the type of training instance to use and the model hyperparameters. A PCA model requires the following constructor arguments:
* role: The IAM role, which was specified, above.
* train_instance_count: The number of training instances (typically, 1).
* train_instance_type: The type of SageMaker instance for training.
* num_components: An integer that defines the number of PCA components to produce.
* sagemaker_session: The session used to train on SageMaker.
Documentation on the PCA model can be found [here](http://sagemaker.readthedocs.io/en/latest/pca.html).
Below, I first specify where to save the model training data, the `output_path`.
```
# define location to store model artifacts
prefix = 'counties'
output_path='s3://{}/{}/'.format(bucket_name, prefix)
print('Training artifacts will be uploaded to: {}'.format(output_path))
# define a PCA model
from sagemaker import PCA
# this is current features - 1
# you'll select only a portion of these to use, later
N_COMPONENTS=33
pca_SM = PCA(role=role,
train_instance_count=1,
train_instance_type='ml.c4.xlarge',
output_path=output_path, # specified, above
num_components=N_COMPONENTS,
sagemaker_session=session)
```
### Convert data into a RecordSet format
Next, prepare the data for a built-in model by converting the DataFrame to a numpy array of float values.
The *record_set* function in the SageMaker PCA model converts a numpy array into a **RecordSet** format that is the required format for the training input data. This is a requirement for _all_ of SageMaker's built-in models. The use of this data type is one of the reasons that allows training of models within Amazon SageMaker to perform faster, especially for large datasets.
```
# convert df to np array
train_data_np = counties_scaled.values.astype('float32')
# convert to RecordSet format
formatted_train_data = pca_SM.record_set(train_data_np)
```
## Train the model
Call the fit function on the PCA model, passing in our formatted, training data. This spins up a training instance to perform the training job.
Note that it takes the longest to launch the specified training instance; the fitting itself doesn't take much time.
```
%%time
# train the PCA mode on the formatted data
pca_SM.fit(formatted_train_data)
```
## Accessing the PCA Model Attributes
After the model is trained, we can access the underlying model parameters.
### Unzip the Model Details
Now that the training job is complete, you can find the job under **Jobs** in the **Training** subsection in the Amazon SageMaker console. You can find the job name listed in the training jobs. Use that job name in the following code to specify which model to examine.
Model artifacts are stored in S3 as a TAR file; a compressed file in the output path we specified + 'output/model.tar.gz'. The artifacts stored here can be used to deploy a trained model.
```
# Get the name of the training job, it's suggested that you copy-paste
# from the notebook or from a specific job in the AWS console
training_job_name='pca-2021-04-21-10-18-40-888'
# where the model is saved, by default
model_key = os.path.join(prefix, training_job_name, 'output/model.tar.gz')
print(model_key)
# download and unzip model
boto3.resource('s3').Bucket(bucket_name).download_file(model_key, 'model.tar.gz')
# unzipping as model_algo-1
os.system('tar -zxvf model.tar.gz')
os.system('unzip model_algo-1')
```
### MXNet Array
Many of the Amazon SageMaker algorithms use MXNet for computational speed, including PCA, and so the model artifacts are stored as an array. After the model is unzipped and decompressed, we can load the array using MXNet.
You can take a look at the MXNet [documentation, here](https://aws.amazon.com/mxnet/).
```
import mxnet as mx
# loading the unzipped artifacts
pca_model_params = mx.ndarray.load('model_algo-1')
# what are the params
print(pca_model_params)
```
## PCA Model Attributes
Three types of model attributes are contained within the PCA model.
* **mean**: The mean that was subtracted from a component in order to center it.
* **v**: The makeup of the principal components; (same as ‘components_’ in an sklearn PCA model).
* **s**: The singular values of the components for the PCA transformation. This does not exactly give the % variance from the original feature space, but can give the % variance from the projected feature space.
We are only interested in v and s.
From s, we can get an approximation of the data variance that is covered in the first `n` principal components. The approximate explained variance is given by the formula: the sum of squared s values for all top n components over the sum over squared s values for _all_ components:
\begin{equation*}
\frac{\sum_{n}^{ } s_n^2}{\sum s^2}
\end{equation*}
From v, we can learn more about the combinations of original features that make up each principal component.
```
# get selected params
s=pd.DataFrame(pca_model_params['s'].asnumpy())
v=pd.DataFrame(pca_model_params['v'].asnumpy())
```
## Data Variance
Our current PCA model creates 33 principal components, but when we create new dimensionality-reduced training data, we'll only select a few, top n components to use. To decide how many top components to include, it's helpful to look at how much **data variance** the components capture. For our original, high-dimensional data, 34 features captured 100% of our data variance. If we discard some of these higher dimensions, we will lower the amount of variance we can capture.
### Tradeoff: dimensionality vs. data variance
As an illustrative example, say we have original data in three dimensions. So, three dimensions capture 100% of our data variance; these dimensions cover the entire spread of our data. The below images are taken from the PhD thesis, [“Approaches to analyse and interpret biological profile data”](https://publishup.uni-potsdam.de/opus4-ubp/frontdoor/index/index/docId/696) by Matthias Scholz, (2006, University of Potsdam, Germany).
<img src='notebook_ims/3d_original_data.png' width=35% />
Now, you may also note that most of this data seems related; it falls close to a 2D plane, and just by looking at the spread of the data, we can visualize that the original, three dimensions have some correlation. So, we can instead choose to create two new dimensions, made up of linear combinations of the original, three dimensions. These dimensions are represented by the two axes/lines, centered in the data.
<img src='notebook_ims/pca_2d_dim_reduction.png' width=70% />
If we project this in a new, 2D space, we can see that we still capture most of the original data variance using *just* two dimensions. There is a tradeoff between the amount of variance we can capture and the number of component-dimensions we use to represent our data.
When we select the top n components to use in a new data model, we'll typically want to include enough components to capture about 80-90% of the original data variance. In this project, we are looking at generalizing over a lot of data and we'll aim for about 80% coverage.
**Note**: The _top_ principal components, with the largest s values, are actually at the end of the s DataFrame. Let's print out the s values for the top n, principal components.
```
# looking at top 5 components
n_principal_components = 5
start_idx = N_COMPONENTS - n_principal_components # 33-n
# print a selection of s
print(s.iloc[start_idx:, :])
```
### Calculate the explained variance
In creating new training data, you'll want to choose the top n principal components that account for at least 80% data variance.
Complete a function, `explained_variance` that takes in the entire array `s` and a number of top principal components to consider. Then return the approximate, explained variance for those top n components.
For example, to calculate the explained variance for the top 5 components, calculate s squared for *each* of the top 5 components, add those up and normalize by the sum of *all* squared s values, according to this formula:
\begin{equation*}
\frac{\sum_{5}^{ } s_n^2}{\sum s^2}
\end{equation*}
> Using this function, you should be able to answer the **question**: What is the smallest number of principal components that captures at least 80% of the total variance in the dataset?
```
# Calculate the explained variance for the top n principal components
# you may assume you have access to the global var N_COMPONENTS
def explained_variance(s, n_top_components):
'''Calculates the approx. data variance that n_top_components captures.
:param s: A dataframe of singular values for top components;
the top value is in the last row.
:param n_top_components: An integer, the number of top components to use.
:return: The expected data variance covered by the n_top_components.'''
# your code here
start_idx = N_COMPONENTS - n_top_components
exp_var = np.square(s.iloc[start_idx:, :]).sum() / np.square(s).sum()
return exp_var[0]
pass
```
### Test Cell
Test out your own code by seeing how it responds to different inputs; does it return a reasonable value for the single, top component? What about for the top 5 components?
```
# test cell
n_top_components = 8 # select a value for the number of top components
# calculate the explained variance
exp_variance = explained_variance(s, n_top_components)
print('Explained variance: ', exp_variance)
```
As an example, you should see that the top principal component accounts for about 32% of our data variance! Next, you may be wondering what makes up this (and other components); what linear combination of features make these components so influential in describing the spread of our data?
Below, let's take a look at our original features and use that as a reference.
```
# features
features_list = counties_scaled.columns.values
print('Features: \n', features_list)
```
## Component Makeup
We can now examine the makeup of each PCA component based on **the weightings of the original features that are included in the component**. The following code shows the feature-level makeup of the first component.
Note that the components are again ordered from smallest to largest and so I am getting the correct rows by calling N_COMPONENTS-1 to get the top, 1, component.
```
import seaborn as sns
def display_component(v, features_list, component_num, n_weights=10):
# get index of component (last row - component_num)
row_idx = N_COMPONENTS-component_num
# get the list of weights from a row in v, dataframe
v_1_row = v.iloc[:, row_idx]
v_1 = np.squeeze(v_1_row.values)
# match weights to features in counties_scaled dataframe, using list comporehension
comps = pd.DataFrame(list(zip(v_1, features_list)),
columns=['weights', 'features'])
# we'll want to sort by the largest n_weights
# weights can be neg/pos and we'll sort by magnitude
comps['abs_weights']=comps['weights'].apply(lambda x: np.abs(x))
sorted_weight_data = comps.sort_values('abs_weights', ascending=False).head(n_weights)
# display using seaborn
ax=plt.subplots(figsize=(10,6))
ax=sns.barplot(data=sorted_weight_data,
x="weights",
y="features",
palette="Blues_d")
ax.set_title("PCA Component Makeup, Component #" + str(component_num))
plt.show()
# display makeup of first component
num=8
display_component(v, counties_scaled.columns.values, component_num=num, n_weights=20)
```
# Deploying the PCA Model
We can now deploy this model and use it to make "predictions". Instead of seeing what happens with some test data, we'll actually want to pass our training data into the deployed endpoint to create principal components for each data point.
Run the cell below to deploy/host this model on an instance_type that we specify.
```
%%time
# this takes a little while, around 7mins
pca_predictor = pca_SM.deploy(initial_instance_count=1,
instance_type='ml.t2.medium')
```
We can pass the original, numpy dataset to the model and transform the data using the model we created. Then we can take the largest n components to reduce the dimensionality of our data.
```
# pass np train data to the PCA model
train_pca = pca_predictor.predict(train_data_np)
# check out the first item in the produced training features
data_idx = 0
print(train_pca[data_idx])
```
### Create a transformed DataFrame
For each of our data points, get the top n component values from the list of component data points, returned by our predictor above, and put those into a new DataFrame.
You should end up with a DataFrame that looks something like the following:
```
c_1 c_2 c_3 c_4 c_5 ...
Alabama-Autauga -0.060274 0.160527 -0.088356 0.120480 -0.010824 ...
Alabama-Baldwin -0.149684 0.185969 -0.145743 -0.023092 -0.068677 ...
Alabama-Barbour 0.506202 0.296662 0.146258 0.297829 0.093111 ...
...
```
```
# create dimensionality-reduced data
def create_transformed_df(train_pca, counties_scaled, n_top_components):
''' Return a dataframe of data points with component features.
The dataframe should be indexed by State-County and contain component values.
:param train_pca: A list of pca training data, returned by a PCA model.
:param counties_scaled: A dataframe of normalized, original features.
:param n_top_components: An integer, the number of top components to use.
:return: A dataframe, indexed by State-County, with n_top_component values as columns.
'''
# create a dataframe of component features, indexed by State-County
# your code here
df = pd.DataFrame()
for data in train_pca:
comp = data.label['projection'].float32_tensor.values
df = df.append([list(comp)])
df.index = counties_scaled.index
start_idx = N_COMPONENTS - n_top_components
df = df.iloc[:, start_idx:]
return df.iloc[:, ::-1]
pass
```
Now we can create a dataset where each county is described by the top n principle components that we analyzed earlier. Each of these components is a linear combination of the original feature space. We can interpret each of these components by analyzing the makeup of the component, shown previously.
### Define the `top_n` components to use in this transformed data
Your code should return data, indexed by 'State-County' and with as many columns as `top_n` components.
You can also choose to add descriptive column names for this data; names that correspond to the component number or feature-level makeup.
```
## Specify top n
top_n = 8
# call your function and create a new dataframe
counties_transformed = create_transformed_df(train_pca, counties_scaled, n_top_components=top_n)
## TODO: Add descriptive column names
cols = ['col_1', 'col_2', 'col_3', 'col_4', 'col_5', 'col_6', 'col_7', 'col_8']
counties_transformed.columns = cols
# print result
counties_transformed.head()
```
### Delete the Endpoint!
Now that we've deployed the mode and created our new, transformed training data, we no longer need the PCA endpoint.
As a clean up step, you should always delete your endpoints after you are done using them (and if you do not plan to deploy them to a website, for example).
```
# delete predictor endpoint
session.delete_endpoint(pca_predictor.endpoint)
```
---
# Population Segmentation
Now, you’ll use the unsupervised clustering algorithm, k-means, to segment counties using their PCA attributes, which are in the transformed DataFrame we just created. K-means is a clustering algorithm that identifies clusters of similar data points based on their component makeup. Since we have ~3000 counties and 34 attributes in the original dataset, the large feature space may have made it difficult to cluster the counties effectively. Instead, we have reduced the feature space to 7 PCA components, and we’ll cluster on this transformed dataset.
### Define a k-means model
Your task will be to instantiate a k-means model. A `KMeans` estimator requires a number of parameters to be instantiated, which allow us to specify the type of training instance to use, and the model hyperparameters.
You can read about the required parameters, in the [`KMeans` documentation](https://sagemaker.readthedocs.io/en/stable/kmeans.html); note that not all of the possible parameters are required.
### Choosing a "Good" K
One method for choosing a "good" k, is to choose based on empirical data. A bad k would be one so *high* that only one or two very close data points are near it, and another bad k would be one so *low* that data points are really far away from the centers.
You want to select a k such that data points in a single cluster are close together but that there are enough clusters to effectively separate the data. You can approximate this separation by measuring how close your data points are to each cluster center; the average centroid distance between cluster points and a centroid. After trying several values for k, the centroid distance typically reaches some "elbow"; it stops decreasing at a sharp rate and this indicates a good value of k. The graph below indicates the average centroid distance for value of k between 5 and 12.
<img src='notebook_ims/elbow_graph.png' width=50% />
A distance elbow can be seen around 8 when the distance starts to increase and then decrease at a slower rate. This indicates that there is enough separation to distinguish the data points in each cluster, but also that you included enough clusters so that the data points aren’t *extremely* far away from each cluster.
```
# define a KMeans estimator
from sagemaker import KMeans
n_clusters = 7
kmeans_est = KMeans(role=role,
sagemaker_session=session,
instance_count=1,
instance_type='ml.c4.xlarge',
output_path=output_path,
k=n_clusters)
```
### Create formatted, k-means training data
Just as before, you should convert the `counties_transformed` df into a numpy array and then into a RecordSet. This is the required format for passing training data into a `KMeans` model.
```
# convert the transformed dataframe into record_set data
training_data_np = counties_transformed.values.astype('float32')
training_data = kmeans_est.record_set(training_data_np)
```
### Train the k-means model
Pass in the formatted training data and train the k-means model.
```
%%time
# train kmeans
kmeans_est.fit(training_data)
```
### Deploy the k-means model
Deploy the trained model to create a `kmeans_predictor`.
```
%%time
# deploy the model to create a predictor
kmeans_predictor = kmeans_est.deploy(initial_instance_count=1, instance_type='ml.t2.medium')
```
### Pass in the training data and assign predicted cluster labels
After deploying the model, you can pass in the k-means training data, as a numpy array, and get resultant, predicted cluster labels for each data point.
```
# get the predicted clusters for all the kmeans training data
cluster_info = kmeans_predictor.predict(training_data_np)
```
## Exploring the resultant clusters
The resulting predictions should give you information about the cluster that each data point belongs to.
You should be able to answer the **question**: which cluster does a given data point belong to?
```
# print cluster info for first data point
data_idx = 0
print('County is: ', counties_transformed.index[data_idx])
print()
print(cluster_info[data_idx])
```
### Visualize the distribution of data over clusters
Get the cluster labels for each of our data points (counties) and visualize the distribution of points over each cluster.
```
# get all cluster labels
cluster_labels = [c.label['closest_cluster'].float32_tensor.values[0] for c in cluster_info]
# count up the points in each cluster
cluster_df = pd.DataFrame(cluster_labels)[0].value_counts()
print(cluster_df)
```
Now, you may be wondering, what do each of these clusters tell us about these data points? To improve explainability, we need to access the underlying model to get the cluster centers. These centers will help describe which features characterize each cluster.
### Delete the Endpoint!
Now that you've deployed the k-means model and extracted the cluster labels for each data point, you no longer need the k-means endpoint.
```
# delete kmeans endpoint
session.delete_endpoint(kmeans_predictor.endpoint)
```
---
# Model Attributes & Explainability
Explaining the result of the modeling is an important step in making use of our analysis. By combining PCA and k-means, and the information contained in the model attributes within a SageMaker trained model, you can learn about a population and remark on some patterns you've found, based on the data.
### Access the k-means model attributes
Extract the k-means model attributes from where they are saved as a TAR file in an S3 bucket.
You'll need to access the model by the k-means training job name, and then unzip the file into `model_algo-1`. Then you can load that file using MXNet, as before.
```
# download and unzip the kmeans model file
# use the name model_algo-1
training_job_name='kmeans-2021-04-21-14-23-50-011'
model_key = os.path.join(prefix, training_job_name, 'output/model.tar.gz')
print(model_key)
boto3.resource('s3').Bucket(bucket_name).download_file(model_key, 'model.tar.gz')
os.system('tar -zxvf model.tar.gz')
os.system('unzip model_algo-1')
# get the trained kmeans params using mxnet
kmeans_model_params = mx.ndarray.load('model_algo-1')
print(kmeans_model_params)
```
There is only 1 set of model parameters contained within the k-means model: the cluster centroid locations in PCA-transformed, component space.
* **centroids**: The location of the centers of each cluster in component space, identified by the k-means algorithm.
```
# get all the centroids
cluster_centroids=pd.DataFrame(kmeans_model_params[0].asnumpy())
cluster_centroids.columns=counties_transformed.columns
display(cluster_centroids)
```
### Visualizing Centroids in Component Space
You can't visualize 7-dimensional centroids in space, but you can plot a heatmap of the centroids and their location in the transformed feature space.
This gives you insight into what characteristics define each cluster. Often with unsupervised learning, results are hard to interpret. This is one way to make use of the results of PCA + clustering techniques, together. Since you were able to examine the makeup of each PCA component, you can understand what each centroid represents in terms of the PCA components.
```
# generate a heatmap in component space, using the seaborn library
plt.figure(figsize = (12,9))
ax = sns.heatmap(cluster_centroids.T, cmap = 'YlGnBu')
ax.set_xlabel("Cluster")
plt.yticks(fontsize = 16)
plt.xticks(fontsize = 16)
ax.set_title("Attribute Value by Centroid")
plt.show()
```
If you've forgotten what each component corresponds to at an original-feature-level, that's okay! You can use the previously defined `display_component` function to see the feature-level makeup.
```
# what do each of these components mean again?
# let's use the display function, from above
component_num=7
display_component(v, counties_scaled.columns.values, component_num=component_num)
```
### Natural Groupings
You can also map the cluster labels back to each individual county and examine which counties are naturally grouped together.
```
# add a 'labels' column to the dataframe
counties_transformed['labels']=list(map(int, cluster_labels))
# sort by cluster label 0-6
sorted_counties = counties_transformed.sort_values('labels', ascending=True)
# view some pts in cluster 0
sorted_counties.head(20)
```
You can also examine one of the clusters in more detail, like cluster 1, for example. A quick glance at the location of the centroid in component space (the heatmap) tells us that it has the highest value for the `comp_6` attribute. You can now see which counties fit that description.
```
# get all counties with label == 1
cluster=counties_transformed[counties_transformed['labels']==1]
cluster.head()
```
## Final Cleanup!
* Double check that you have deleted all your endpoints.
* I'd also suggest manually deleting your S3 bucket, models, and endpoint configurations directly from your AWS console.
You can find thorough cleanup instructions, [in the documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/ex1-cleanup.html).
---
# Conclusion
You have just walked through a machine learning workflow for unsupervised learning, specifically, for clustering a dataset using k-means after reducing the dimensionality using PCA. By accessing the underlying models created within SageMaker, you were able to improve the explainability of your model and draw insights from the resultant clusters.
Using these techniques, you have been able to better understand the essential characteristics of different counties in the US and segment them into similar groups, accordingly.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/desaibhargav/VR/blob/main/notebooks/Semantic_Search.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## **Dependencies**
```
!pip install -U -q sentence-transformers
!git clone https://github.com/desaibhargav/VR.git
```
## **Imports**
```
import pandas as pd
import numpy as np
import torch
import time
from typing import Generator
from sentence_transformers import SentenceTransformer, CrossEncoder, util
from VR.backend.chunker import Chunker
```
## **Dataset**
```
# load scrapped data (using youtube_client.py)
dataset = pd.read_pickle('VR/datasets/youtube_scrapped.pickle')
# split transcripts of videos to smaller blocks or chunks (using chunker.py)
chunked = Chunker(chunk_by='length', expected_threshold=100, min_tolerable_threshold=75).get_chunks(dataset)
# finally, create dataset
dataset_untagged = dataset.join(chunked).drop(columns=['subtitles', 'timestamps'])
df = dataset_untagged.copy().dropna()
print(f"Average length of block: {df.length_of_block.mean()}, Standard Deviation: {df.length_of_block.std()}")
```
## **Semantic Search**
---
The idea is to compute embeddings of the query (entered by user) and use cosine similarity to find the `top_k` most similar blocks.
Blocks are nothing but the entire video transcript (big string) split into fixed length strings (small strings, ~100 words).
---
The reason for such a design choice was threefold, handled by `chunker.py` (refer the repo):
1. First and foremost, some videoes can be very long (over ~40 minutes) which means the transcript for the same is a **massive** string, and we need to avoid hitting the processing length limits of pre-trained models.
2. Secondly, and more importantly, it is always good to maintain the inputs at a length on which the models being used were trained (to stay as close as poossible to the training set for optimum results).
3. But perhaps, most importantly, the purpose for splitting transcripts to blocks is so that the recommendations can be targeted to a snippet within a video. The vision is to recommend many snippets from various videoes highly relevant to the query, rather than entire videoes themselves in which matching snippets have been found (which may sometimes be long and the content may not always be related to the query).
---
```
# request to enable GPU
if not torch.cuda.is_available():
print("Warning: No GPU found. Please add GPU to your notebook")
# load model (to encode the dataset)
bi_encoder = SentenceTransformer('paraphrase-distilroberta-base-v1')
# number of blocks we want to retrieve with the bi-encoder
top_k = 200
# the bi-encoder will retrieve 50 blocks (top_k).
# we use a cross-encoder, to re-rank the results list to improve the quality.
cross_encoder = CrossEncoder('cross-encoder/ms-marco-electra-base')
# encode dataset
corpus_embeddings = bi_encoder.encode(df.block.to_list(), convert_to_tensor=True, show_progress_bar=True)
# send corpus embeddings to GPU
corpus_embeddings = torch.tensor(corpus_embeddings).cuda()
# this function will search the dataset for passages that answer the query
def search(query):
start_time = time.time()
# encode the query using the bi-encoder and find potentially relevant passages
question_embedding = bi_encoder.encode(query, convert_to_tensor=True)
# send query embeddings to GPU
question_embedding = question_embedding.cuda()
# perform sematic search by computing cosine similarity between corpus and query embeddings
# return top_k highest similarity matches
hits = util.semantic_search(question_embedding, corpus_embeddings, top_k=top_k)[0]
# now, score all retrieved passages with the cross_encoder
cross_inp = [[query, df.block.to_list()[hit['corpus_id']]] for hit in hits]
cross_scores = cross_encoder.predict(cross_inp)
# sort results by the cross-encoder scores
for idx in range(len(cross_scores)):
hits[idx]['cross-score'] = cross_scores[idx]
hits = sorted(hits, key=lambda x: x['cross-score'], reverse=True)
end_time = time.time()
# print output of top-5 hits (for iteractive environments only)
print(f"Input query: {query}")
print(f"Results (after {round(end_time - start_time, 2)} seconds):")
for hit in hits[0:10]:
print("\t{:.3f}\t{}".format(hit['cross-score'], df.block.to_list()[hit['corpus_id']].replace("\n", " ")))
```
## **Try some queries!**
```
query = "I feel lost in life. I feel like there is no purpose of living. How should I deal with this?"
search(query)
query = "I just recently became a parent and I am feeling very nervous. What is the best way to bring up a child?"
search(query)
query = "I had a divorce. I feel like a failure. How should I handle this heartbreak?"
search(query)
query = "How to be confident while making big decisions in life?"
search(query)
```
## **Semantic Search x Auxiliary Features**
This section is under active development.
---
This purpose of this section is to explore two primary frontiers:
1. Just semantic search yields satisfactory results, but comes at the cost of compute power. The bottleneck for compute power is the cross-encoder step. This section explores how to reduce the search area, so that semantic search (by the cross-encoder) is performed over a small number blocks, significantly cutting down on the recommendation time.
2. Other than the content itself, several other features such as video statistics (views, likes, dislikes), video titles, video descriptions, video tags present in the dataset can be leveraged to improve the recommendations.
---
```
```
|
github_jupyter
|
# Think Bayes: Chapter 7
This notebook presents code and exercises from Think Bayes, second edition.
Copyright 2016 Allen B. Downey
MIT License: https://opensource.org/licenses/MIT
```
from __future__ import print_function, division
% matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import math
import numpy as np
from thinkbayes2 import Pmf, Cdf, Suite, Joint
import thinkplot
```
## Warm-up exercises
**Exercise:** Suppose that goal scoring in hockey is well modeled by a
Poisson process, and that the long-run goal-scoring rate of the
Boston Bruins against the Vancouver Canucks is 2.9 goals per game.
In their next game, what is the probability
that the Bruins score exactly 3 goals? Plot the PMF of `k`, the number
of goals they score in a game.
```
# Solution goes here
# Solution goes here
# Solution goes here
```
**Exercise:** Assuming again that the goal scoring rate is 2.9, what is the probability of scoring a total of 9 goals in three games? Answer this question two ways:
1. Compute the distribution of goals scored in one game and then add it to itself twice to find the distribution of goals scored in 3 games.
2. Use the Poisson PMF with parameter $\lambda t$, where $\lambda$ is the rate in goals per game and $t$ is the duration in games.
```
# Solution goes here
# Solution goes here
```
**Exercise:** Suppose that the long-run goal-scoring rate of the
Canucks against the Bruins is 2.6 goals per game. Plot the distribution
of `t`, the time until the Canucks score their first goal.
In their next game, what is the probability that the Canucks score
during the first period (that is, the first third of the game)?
Hint: `thinkbayes2` provides `MakeExponentialPmf` and `EvalExponentialCdf`.
```
# Solution goes here
# Solution goes here
# Solution goes here
```
**Exercise:** Assuming again that the goal scoring rate is 2.8, what is the probability that the Canucks get shut out (that is, don't score for an entire game)? Answer this question two ways, using the CDF of the exponential distribution and the PMF of the Poisson distribution.
```
# Solution goes here
# Solution goes here
```
## The Boston Bruins problem
The `Hockey` suite contains hypotheses about the goal scoring rate for one team against the other. The prior is Gaussian, with mean and variance based on previous games in the league.
The Likelihood function takes as data the number of goals scored in a game.
```
from thinkbayes2 import MakeNormalPmf
from thinkbayes2 import EvalPoissonPmf
class Hockey(Suite):
"""Represents hypotheses about the scoring rate for a team."""
def __init__(self, label=None):
"""Initializes the Hockey object.
label: string
"""
mu = 2.8
sigma = 0.3
pmf = MakeNormalPmf(mu, sigma, num_sigmas=4, n=101)
Suite.__init__(self, pmf, label=label)
def Likelihood(self, data, hypo):
"""Computes the likelihood of the data under the hypothesis.
Evaluates the Poisson PMF for lambda and k.
hypo: goal scoring rate in goals per game
data: goals scored in one game
"""
lam = hypo
k = data
like = EvalPoissonPmf(k, lam)
return like
```
Now we can initialize a suite for each team:
```
suite1 = Hockey('bruins')
suite2 = Hockey('canucks')
```
Here's what the priors look like:
```
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
```
And we can update each suite with the scores from the first 4 games.
```
suite1.UpdateSet([0, 2, 8, 4])
suite2.UpdateSet([1, 3, 1, 0])
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.Mean(), suite2.Mean()
```
To predict the number of goals scored in the next game we can compute, for each hypothetical value of $\lambda$, a Poisson distribution of goals scored, then make a weighted mixture of Poissons:
```
from thinkbayes2 import MakeMixture
from thinkbayes2 import MakePoissonPmf
def MakeGoalPmf(suite, high=10):
"""Makes the distribution of goals scored, given distribution of lam.
suite: distribution of goal-scoring rate
high: upper bound
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakePoissonPmf(lam, high)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
```
Here's what the results look like.
```
goal_dist1 = MakeGoalPmf(suite1)
goal_dist2 = MakeGoalPmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(goal_dist1)
thinkplot.Pmf(goal_dist2)
thinkplot.Config(xlabel='Goals',
ylabel='Probability',
xlim=[-0.7, 11.5])
goal_dist1.Mean(), goal_dist2.Mean()
```
Now we can compute the probability that the Bruins win, lose, or tie in regulation time.
```
diff = goal_dist1 - goal_dist2
p_win = diff.ProbGreater(0)
p_loss = diff.ProbLess(0)
p_tie = diff.Prob(0)
print('Prob win, loss, tie:', p_win, p_loss, p_tie)
```
If the game goes into overtime, we have to compute the distribution of `t`, the time until the first goal, for each team. For each hypothetical value of $\lambda$, the distribution of `t` is exponential, so the predictive distribution is a mixture of exponentials.
```
from thinkbayes2 import MakeExponentialPmf
def MakeGoalTimePmf(suite):
"""Makes the distribution of time til first goal.
suite: distribution of goal-scoring rate
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakeExponentialPmf(lam, high=2.5, n=1001)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
```
Here's what the predictive distributions for `t` look like.
```
time_dist1 = MakeGoalTimePmf(suite1)
time_dist2 = MakeGoalTimePmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(time_dist1)
thinkplot.Pmf(time_dist2)
thinkplot.Config(xlabel='Games until goal',
ylabel='Probability')
time_dist1.Mean(), time_dist2.Mean()
```
In overtime the first team to score wins, so the probability of winning is the probability of generating a smaller value of `t`:
```
p_win_in_overtime = time_dist1.ProbLess(time_dist2)
p_adjust = time_dist1.ProbEqual(time_dist2)
p_win_in_overtime += p_adjust / 2
print('p_win_in_overtime', p_win_in_overtime)
```
Finally, we can compute the overall chance that the Bruins win, either in regulation or overtime.
```
p_win_overall = p_win + p_tie * p_win_in_overtime
print('p_win_overall', p_win_overall)
```
## Exercises
**Exercise:** To make the model of overtime more correct, we could update both suites with 0 goals in one game, before computing the predictive distribution of `t`. Make this change and see what effect it has on the results.
```
# Solution goes here
```
**Exercise:** In the final match of the 2014 FIFA World Cup, Germany defeated Argentina 1-0. What is the probability that Germany had the better team? What is the probability that Germany would win a rematch?
For a prior distribution on the goal-scoring rate for each team, use a gamma distribution with parameter 1.3.
**Exercise:** In the 2014 FIFA World Cup, Germany played Brazil in a semifinal match. Germany scored after 11 minutes and again at the 23 minute mark. At that point in the match, how many goals would you expect Germany to score after 90 minutes? What was the probability that they would score 5 more goals (as, in fact, they did)?
Note: for this one you will need a new suite that provides a Likelihood function that takes as data the time between goals, rather than the number of goals in a game.
**Exercise:** Which is a better way to break a tie: overtime or penalty shots?
**Exercise:** Suppose that you are an ecologist sampling the insect population in a new environment. You deploy 100 traps in a test area and come back the next day to check on them. You find that 37 traps have been triggered, trapping an insect inside. Once a trap triggers, it cannot trap another insect until it has been reset.
If you reset the traps and come back in two days, how many traps do you expect to find triggered? Compute a posterior predictive distribution for the number of traps.
#### Exercise 7-1.
If buses arrive at a bus stop every 20 minutes, and you arrive at the bus stop at a random
time, your wait time until the bus arrives is uniformly distributed from 0 to 20
minutes.
But in reality, there is variability in the time between buses. Suppose you are waiting
for a bus, and you know the historical distribution of time between buses. Compute
your distribution of wait times.
Hint: Suppose that the time between buses is either 5 or 10 minutes with equal probability.
What is the probability that you arrive during one of the 10 minute intervals?
I solve a version of this problem in the next chapter.
#### Exercise 7-2.
Suppose that passengers arriving at the bus stop are well-modeled by a Poisson process
with parameter λ. If you arrive at the stop and find 3 people waiting, what is your
posterior distribution for the time since the last bus arrived.
I solve a version of this problem in the next chapter.
#### Exercise 7-4.
Suppose you are the manager of an apartment building with 100 light bulbs in common
areas. It is your responsibility to replace light bulbs when they break.
On January 1, all 100 bulbs are working. When you inspect them on February 1, you
find 3 light bulbs out. If you come back on April 1, how many light bulbs do you
expect to find broken?
In the previous exercise, you could reasonably assume that an event is equally likely at
any time. For light bulbs, the likelihood of failure depends on the age of the bulb.
Specifically, old bulbs have an increasing failure rate due to evaporation of the filament.
This problem is more open-ended than some; you will have to make modeling decisions.
You might want to read about the Weibull distribution (http://en.wikipedia.org/
wiki/Weibull_distribution). Or you might want to look around for information about
light bulb survival curves.
|
github_jupyter
|
# Adsorbed Phases on Graphene
```
import numpy as np
import matplotlib.pyplot as plt
from graphenetools import gt
import re,glob,os,sys
from scipy.signal import argrelextrema
import dgutils.colors as colortools
import dgutils.pypov as pypov
from collections import defaultdict
import importlib
from PIL import Image,ImageOps
from vapory import *
π = np.pi
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
# plot style
plot_style = {'notebook':'../include/notebook.mplstyle','aps':'../include/aps.mplstyle'}
plt.style.reload_library()
plt.style.use(plot_style['notebook'])
figsize = plt.rcParams['figure.figsize']
included = ["colors.inc","textures.inc","functions.inc"]
filename = "../plots/graphene_cell.pov"
```
## Setting the colors
```
blue = colortools.hex_to_rgb('#0073CD')
grey = colortools.hex_to_rgb('#a7a7a7')
brown = colortools.hex_to_rgb('#e9b68c')
brown = colortools.hex_to_rgb('#926f34')
green = colortools.hex_to_rgb('#15A05E')
red = colortools.hex_to_rgb('#8c0a07')
```
## Construct the graphene lattice, $\sqrt{3}\times\sqrt{3}$ adsorbant and bonds
```
# lattice vectors
aₒ = 1.42
a = (aₒ/2)*np.array([[np.sqrt(3),-np.sqrt(3)],[3,3]])
#√3 x √3
θ = π/6
R = np.array([[np.cos(θ),-np.sin(θ)],[np.sin(θ),np.cos(θ)]])
α = np.matmul(R,np.sqrt(3)*a)
# basis vectors
b = aₒ*np.array([[np.sqrt(3)/2,0],[1/2,1]])
# Box size
L = [8,8]
import sympy
sympy.init_printing(use_unicode=True)
sympy.Matrix(α)
```
### The Lattice
```
C_positions = []
G_centers = []
hex_centers = []
for n1 in range(-12,12):
for n2 in range(-12,12):
G_centers.append(n1*α[:,0] + n2*α[:,1])
C_positions.append(n1*a[:,0] + n2*a[:,1] + b[:,0])
C_positions.append(n1*a[:,0] + n2*a[:,1] + b[:,1])
hex_centers.append(n1*a[:,0] + n2*a[:,1])
C_positions = np.array(C_positions)
G_centers = np.array(G_centers)
hex_centers = np.array(hex_centers)
C_positions_big = np.array(C_positions[np.intersect1d(np.where(np.abs(C_positions[:,0])<2*L[0])[0],np.where(np.abs(C_positions[:,1])<1.9*L[1])[0])])
He_positions_big = np.array(G_centers[np.intersect1d(np.where(np.abs(G_centers[:,0])<2*L[0])[0],np.where(np.abs(G_centers[:,1])<1.8*L[1])[0])])
hex_centers_big = np.array(hex_centers[np.intersect1d(np.where(np.abs(hex_centers[:,0])<2*L[0])[0],np.where(np.abs(hex_centers[:,1])<1.8*L[1])[0])])
C_positions = np.array(C_positions[np.intersect1d(np.where(np.abs(C_positions[:,0])<L[0])[0],np.where(np.abs(C_positions[:,1])<L[1])[0])])
He_positions = np.array(G_centers[np.intersect1d(np.where(np.abs(G_centers[:,0])<L[0])[0],np.where(np.abs(G_centers[:,1])<L[1])[0])])
hex_centers = np.array(hex_centers[np.intersect1d(np.where(np.abs(hex_centers[:,0])<L[0])[0],np.where(np.abs(hex_centers[:,1])<L[1])[0])])
fig,ax = plt.subplots()
ax.scatter(C_positions[:,0],C_positions[:,1], s=4, color='k')
ax.scatter(He_positions[:,0],He_positions[:,1], s=8, color='b')
ax.set_aspect('equal')
ax.set_xlabel('x / Å')
ax.set_ylabel('y / Å')
```
### Visualizing the Lattice Vectors
```
fig,ax = plt.subplots()
#ax.scatter(He_positions[:,0],He_positions[:,1], s=8, color='b')
ax.annotate("",
xy=(a[0,0], a[1,0]), xycoords='data',
xytext=(0, 0), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3",ec='k'),
)
ax.annotate(r"$\vec{a}_1$",
xy=(a[0,0], a[1,0]), xycoords='data',
xytext=(1, 1), textcoords='offset points',
)
ax.annotate("",
xy=(a[0,1], a[1,1]), xycoords='data',
xytext=(0, 0), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3",ec='r'),
)
ax.annotate(r"$\vec{a}_2$",
xy=(a[0,1], a[1,1]), xycoords='data',
xytext=(1, 1), textcoords='offset points', color='r'
)
ax.annotate("",
xy=(b[0,0], b[1,0]), xycoords='data',
xytext=(0, 0), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3",ec='b'),
)
ax.annotate(r"$\vec{b}_1$",
xy=(b[0,0], b[1,0]), xycoords='data',
xytext=(2, 2), textcoords='offset points', color='b'
)
ax.annotate("",
xy=(b[0,1], b[1,1]), xycoords='data',
xytext=(0, 0), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3",ec='g'),
)
ax.annotate(r"$\vec{b}_2$",
xy=(b[0,1], b[1,1]), xycoords='data',
xytext=(2, 2), textcoords='offset points', color='g'
)
ax.annotate("",
xy=(α[0,0], α[1,0]), xycoords='data',
xytext=(0, 0), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3",ec='y'),
)
ax.annotate(r"$\vec{\alpha}_1$",
xy=(α[0,0], α[1,0]), xycoords='data',
xytext=(2, 2), textcoords='offset points', color='y'
)
ax.annotate("",
xy=(α[0,1], α[1,1]), xycoords='data',
xytext=(0, 0), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3",ec='y',zorder=-10),
)
ax.annotate(r"$\vec{\alpha}_2$",
xy=(α[0,1], α[1,1]), xycoords='data',
xytext=(2, 2), textcoords='offset points', color='y',zorder=-10
)
ax.scatter(C_positions[:,0],C_positions[:,1], s=4, color='k')
ax.set_aspect('equal')
ax.set_xlim(-6,6)
ax.set_ylim(-1,6)
ax.set_xlabel('x / Å')
ax.set_ylabel('y / Å')
```
### The Bonds
```
bonds = np.empty([0,4])
fig,ax = plt.subplots()
NG = len(C_positions)
for i in range(NG):
ri = C_positions[i]
for j in range(i,NG):
rj = C_positions[j]
d = np.linalg.norm(ri-rj)
if d > 0.1 and d < (aₒ+0.1):
ax.plot([ri[0],rj[0]],[ri[1],rj[1]],'-', zorder=-1, lw=0.5,color=grey)
bonds = np.vstack((bonds,[ri[0],rj[0],ri[1],rj[1]]))
ax.scatter(C_positions[:,0],C_positions[:,1], s=4, color='k')
ax.scatter(He_positions[:,0],He_positions[:,1], s=8, color=blue)
ax.set_aspect('equal')
ax.set_xlabel('x / Å')
ax.set_ylabel('y / Å')
x,y = C_positions[:,0],C_positions[:,1]
x1,x2,y1,y2 = bonds[:,0],bonds[:,1],bonds[:,2],bonds[:,3]
```
## Create a graphic of the dual triangular lattice
```
dual_bonds = np.empty([0,4])
NA = len(hex_centers)
for i in range(NA):
ri = hex_centers[i]
for j in range(i,NA):
rj = hex_centers[j]
d = np.linalg.norm(ri-rj)
if d > 0.1 and d < (np.sqrt(3)*aₒ+0.1):
dual_bonds = np.vstack((dual_bonds,[ri[0],rj[0],ri[1],rj[1]]))
```
## Images of Adsorbed Phases
### Setting the colors and sizes for some objects
```
col_C = Texture(Finish('ambient','0.2','diffuse','0.8'),Pigment('color',brown,'transmit',0.0))
col_bond = Texture(Finish('phong','0.2'),Pigment('color',brown,'transmit',0.0))
col_He = Texture(Finish('phong','0.9','phong_size',400),Pigment('color',green,'transmit',0.0))
col_He_link = Texture(Finish('phong','0.9','phong_size',400),Pigment('color',green,'transmit',0.6))
col_box = Texture(Finish('specular',0.5,'roughness',0.001,
'ambient',0,'diffuse',0.6,'conserve_energy'),
Pigment('color','Gray','transmit',0.0))
col_int = Texture(Finish('specular',0.5,'roughness',0.001,
'ambient',0,'diffuse',0.6,'conserve_energy'),
Pigment('color','Gray','transmit',0.5))
col_floor = Texture(Pigment('color','White','transmit',0.0))
r_C = 0.30 # radius of C-atoms in graphene
r_He = 3*r_C #/2.258# radius of He-atoms
```
## C1/3 Solid
### Generate the graphene lattice
```
sphere = [Sphere([x[i],0, y[i]], r_C, col_C) for i in range(len(x))]
cylinder = [Cylinder([x1[i],0.0,y1[i]],[x2[i],0.0,y2[i]], 0.075,col_bond) for i in range(len(x1))]
sphere.extend([Sphere([cr[0],1.1, cr[1]], r_He, col_He) for cr in He_positions])
```
### Output image to disk
```
cam = Camera('location',[0,75,0],'look_at',[0,0,0])
bg = Background("color", "White",'transmit',1.0)
lights = [LightSource( [0,80,0], 'color','White','parallel')]
#lights.extend([LightSource( [0,75,0], 'color','White shadowless')])
obj = [bg] + lights + sphere + cylinder
scene = Scene(camera=cam,objects=obj,included=included)
#scene.render('ipython', width=400, height=200,remove_temp=False)
filename = '../plots/graphene_solid.png'
povstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,
output_alpha=True,remove_temp=False)
# autocrop the image
image = Image.open(filename)
cropped = image.crop(image.getbbox())
cropped.save(filename)
```
## Superfluid
```
import importlib
importlib.reload(vapory)
# graphene
sphere = [Sphere([x[i],0, y[i]], r_C, col_C) for i in range(len(x))]
cylinder = [Cylinder([x1[i],0.0,y1[i]],[x2[i],0.0,y2[i]], 0.075,col_bond) for i in range(len(x1))]
# Helium
atoms = [Sphere([cr[0],1.1, cr[1]], r_He/3.0, col_He_link) for cr in hex_centers]
bonds = []
sphere_path = []
num_atoms = hex_centers.shape[0]
num_points = 21
num_shift = 2
s = ''
rmin = 0.4*r_He/3.0
rmax = 0.8*r_He/3.0
m = (rmax-rmin)/int(num_points/2)
for i in range(num_atoms):
r1 = hex_centers[i,:]
for j in range(i,num_atoms):
r2 = hex_centers[j,:]
Δr = r2-r1
if Δr[0]**2 + Δr[1]**2 <= 1.05*3*aₒ**2:
if Δr[1] > 0 or (Δr[1]< 0.001 and Δr[0] > 0):
path = pypov.generate_linear_path(r1,r2,num_points)
s = '\n'
for n in range(num_shift,num_points-num_shift):
rad = m*np.abs((n-int(num_points/2)))+rmin
loc = [path[n][0]+np.random.uniform(low=-0.001,high=0.001),1.1,path[n][1]+np.random.uniform(low=-0.001,high=0.001)]
s += vectorize(loc) + f', {rad}'
if n < num_points-1-num_shift:
s += ',\n'
else:
s+= '\n'
s += str(format_if_necessary(col_He_link))
bonds.append(Macro("sphere_sweep",f"linear_spline\n{num_points-2*num_shift}",s))
cam = Camera('location',[0,75,0],'look_at',[0,0,0])
bg = Background("color", "White",'transmit',1.0)
lights = [LightSource( [0,20,0], 'color','White','parallel')]
#lights.extend([LightSource( [0,75,0], 'color','White shadowless')])
obj = [bg] + lights + sphere + cylinder + [Merge(*bonds,*atoms)]
scene = Scene(camera=cam,objects=obj,included=included)
#scene.render('ipython', width=400, height=200,remove_temp=False)
filename = '../plots/graphene_superfluid.png'
povstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,
output_alpha=True,remove_temp=False)
# autocrop the image
image = Image.open(filename)
cropped = image.crop(image.getbbox())
cropped.save(filename)
```
## Supersolid
```
# graphene
sphere = [Sphere([x[i],0, y[i]], r_C, col_C) for i in range(len(x))]
cylinder = [Cylinder([x1[i],0.0,y1[i]],[x2[i],0.0,y2[i]], 0.075,col_bond) for i in range(len(x1))]
# Helium
atoms = [Sphere([cr[0],1.1, cr[1]], r_He/4.0, col_He_link) for cr in hex_centers]
atoms.extend([Sphere([cr[0],1.1, cr[1]], r_He/2.0, col_He) for cr in He_positions])
bonds = []
sphere_path = []
num_atoms = hex_centers.shape[0]
num_points = 21
num_shift = 2
s = ''
rmin = 0.4*r_He/4.0
rmax = 0.8*r_He/4.0
m = (rmax-rmin)/int(num_points/2)
for i in range(num_atoms):
r1 = hex_centers[i,:]
for j in range(i,num_atoms):
r2 = hex_centers[j,:]
Δr = r2-r1
if Δr[0]**2 + Δr[1]**2 <= 1.05*3*aₒ**2:
if Δr[1] > 0 or (Δr[1]< 0.001 and Δr[0] > 0):
path = pypov.generate_linear_path(r1,r2,num_points)
s = '\n'
for n in range(num_shift,num_points-num_shift):
rad = m*np.abs((n-int(num_points/2)))+rmin
loc = [path[n][0]+np.random.uniform(low=-0.001,high=0.001),1.1,path[n][1]+np.random.uniform(low=-0.001,high=0.001)]
s += vectorize(loc) + f', {rad}'
if n < num_points-1-num_shift:
s += ',\n'
else:
s+= '\n'
s += str(format_if_necessary(col_He_link))
bonds.append(Macro("sphere_sweep",f"linear_spline\n{num_points-2*num_shift}",s))
cam = Camera('location',[0,75,0],'look_at',[0,0,0])
bg = Background("color", "White",'transmit',1.0)
lights = [LightSource( [0,20,0], 'color','White','parallel')]
#lights.extend([LightSource( [0,75,0], 'color','White shadowless')])
obj = [bg] + lights + sphere + cylinder + [Merge(*bonds,*atoms)]
scene = Scene(camera=cam,objects=obj,included=included)
#scene.render('ipython', width=400, height=200,remove_temp=False)
filename = '../plots/graphene_supersolid.png'
povstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,
output_alpha=True,remove_temp=False)
# autocrop the image
image = Image.open(filename)
cropped = image.crop(image.getbbox())
cropped.save(filename)
```
## Suspended Wetting
We first construct the bonds for the larger graphene lattice used in wetting.
```
bonds_big = np.empty([0,4])
NG_big = len(C_positions_big)
for i in range(NG_big):
ri = C_positions_big[i]
for j in range(i,NG_big):
rj = C_positions_big[j]
d = np.linalg.norm(ri-rj)
if d > 0.1 and d < (aₒ+0.1):
bonds_big = np.vstack((bonds_big,[ri[0],rj[0],ri[1],rj[1]]))
x_big,y_big = C_positions_big[:,0],C_positions_big[:,1]
x1_big,x2_big,y1_big,y2_big = bonds_big[:,0],bonds_big[:,1],bonds_big[:,2],bonds_big[:,3]
# graphene
sphere = [Sphere([x_big[i],0, y_big[i]], r_C, col_C) for i in range(len(x_big))]
cylinder = [Cylinder([x1_big[i],0.0,y1_big[i]],[x2_big[i],0.0,y2_big[i]], 0.075,col_bond) for i in range(len(x1_big))]
atoms = []
zspace = 1.1
r_He = 1.2*r_C
for n in range(1,12):
if n == 1:
shift = 0.05
else:
shift = 0.1
for i,cr in enumerate(He_positions_big):
ccx = cr[0] + np.random.uniform(low=-shift*n, high=shift*n) - np.sqrt(3)*aₒ*(n%2)
if ccx < -2*L[0]:
ccx += 4*L[0]
ccy = cr[1] + np.random.uniform(low=-shift*n, high=shift*n)
ccz = n*zspace + np.random.uniform(low=-shift*n, high=shift*n)
if np.abs(ccx) < 2*L[0] and np.abs(ccy) < 2*L[1]:
atoms.append(Sphere([ccx,ccz,ccy], r_He, col_He))
# shift to get 2/3 filling
ccx = cr[0] + np.random.uniform(low=-shift*n, high=shift*n) - np.sqrt(3)*aₒ*(n%2) + a[0,0]
if ccx < -2*L[0]:
ccx += 4*L[0]
ccy = cr[1] + np.random.uniform(low=-shift*n, high=shift*n) + a[1,0]
ccz = n*zspace + np.random.uniform(low=-shift*n, high=shift*n)
if np.abs(ccx) < 2*L[0] and np.abs(ccy) < 2*L[1]:
atoms.append(Sphere([ccx,ccz,ccy], r_He, col_He))
# now do the vapor
vapor = False
if vapor:
n_min = n
n_max = n+8
trans = pypov.linear([n_min,0.1],[n_max,0.9])
lin_shift = pypov.linear([n_min,0.1],[n_max,0.5])
freq = pypov.linear([n_min,2/3],[n_max,0.1])
rad = pypov.linear([n_min,r_He],[n_max,0.4*r_He])
for n in range(n_min,n_max):
shift = lin_shift(n)
col_He_gas = Texture(Finish('phong','0.9','phong_size',400),Pigment('color',green,'transmit',trans(n)))
for i,cr in enumerate(hex_centers_big):
ccx = cr[0] + np.random.uniform(low=-shift*n, high=shift*n) - np.sqrt(3)*aₒ*(n%2)
ccy = cr[1] + np.random.uniform(low=-shift*n, high=shift*n)
ccz = n*zspace + np.random.uniform(low=-shift*n, high=shift*n)
if np.abs(ccx) < 2*L[0] and np.abs(ccy) < 2*L[1] and np.random.random() < freq(n):
atoms.append(Sphere([ccx,ccz,ccy], rad(n), col_He_gas))
cam = Camera('location',[0,25,-80],'look_at',[0,0,0])
bg = Background("color", "White",'transmit',1.0)
lights = [LightSource( [0,25,-80], 'color','White shadowless')]
# cam = Camera('location',[0,80,0],'look_at',[0,0,0])
# bg = Background("color", "White",'transmit',1.0)
# lights = [LightSource( [0,80,0], 'color','White','parallel')]
obj = [bg] + lights + sphere + cylinder + atoms
scene = Scene(camera=cam,objects=obj,included=included)
filename = '../plots/graphene_suspended.png'
povstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,
output_alpha=True,remove_temp=False)
# autocrop the image
image = Image.open(filename)
cropped = image.crop(image.getbbox())
cropped.save(filename)
```
|
github_jupyter
|
# USGS Earthquakes with the Mapboxgl-Jupyter Python Library
https://github.com/mapbox/mapboxgl-jupyter
```
# Python 3.5+ only!
import asyncio
from aiohttp import ClientSession
import json, geojson, os, time
import pandas as pd
from datetime import datetime, timedelta
from mapboxgl.viz import *
from mapboxgl.utils import *
import pysal.esda.mapclassify as mapclassify
# Get Data from the USGS API
data = []
async def fetch(url, headers, params, session):
async with session.get(url, headers=headers, params=params) as resp:
tempdata = await resp.json()
data.append(tempdata)
return tempdata
async def bound_fetch(sem, url, headers, params, session):
# Getter function with semaphore.
async with sem:
await fetch(url, headers, params, session)
async def get_quakes(param_list, headers):
# Store tasks to run
tasks = []
# create instance of Semaphore
sem = asyncio.Semaphore(1000)
# Generate URL from parameters
endpoint = '/query'
url = '{base_url}{endpoint}'.format(base_url=base_url, endpoint=endpoint)
async with ClientSession() as session:
for i in range(len(param_list)):
task = asyncio.ensure_future(bound_fetch(sem, url, headers, param_list[i], session))
tasks.append(task)
responses = await asyncio.gather(*tasks)
return responses
def create_params(starttime, endtime, minmagnitude):
return {
'format': 'geojson',
'starttime': starttime,
'endtime': endtime,
'minmagnitude': minmagnitude
}
# Default parameters
base_url = 'https://earthquake.usgs.gov/fdsnws/event/1'
HEADERS = {
'user-agent': ('Mozilla/5.0 (Macintosh; Intel Mac OS X 10_10_5) '
'AppleWebKit/537.36 (KHTML, like Gecko) '
'Chrome/45.0.2454.101 Safari/537.36'),
}
# Make a list of data to get in a date range
api_args = []
startdate = '2012-01-01'
date = datetime.strptime(startdate, "%Y-%m-%d")
for i in range(1000):
low = datetime.strftime(date + timedelta(days=i*10), "%Y-%m-%d")
high = datetime.strftime(date + timedelta(days=(i+1)*10), "%Y-%m-%d")
api_args.append(create_params(low, high, 2))
#Run api queries for all queries generated
loop = asyncio.get_event_loop()
future = asyncio.ensure_future(get_quakes(api_args, HEADERS))
temp = loop.run_until_complete(future)
#Collect results into a Pandas dataframe
keep_props = ['felt', 'mag', 'magType', 'place', 'time', 'tsunami', 'longitude', 'latitude']
df = pd.DataFrame(columns=keep_props, index=[0])
features = []
for fc in data:
for f in fc['features']:
feature = {}
for k in f['properties']:
if k in keep_props:
feature[k] = f['properties'][k]
feature['longitude'] = f['geometry']['coordinates'][0]
feature['latitude'] = f['geometry']['coordinates'][1]
feature['timestamp'] = time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(feature['time']/1000))
features.append(feature)
df = pd.DataFrame.from_dict(features)
print(df.shape)
df.head(1)
```
# Set your Mapbox access token.
Set a MAPBOX_ACCESS_TOKEN environment variable, or copy your token to use this notebook.
If you do not have a Mapbox access token, sign up for an account at https://www.mapbox.com/
If you already have an account, you can grab your token at https://www.mapbox.com/account/
```
token = os.getenv('MAPBOX_ACCESS_TOKEN')
# Generate a geojson file from the dataframe
df_to_geojson(df, filename='points.geojson', precision=4, lon='longitude', lat='latitude',
properties=['mag','timestamp'])
# Create the visualization
#Calculate the visualization to create
color_breaks = mapclassify.Natural_Breaks(df['mag'], k=6, initial=0).bins
color_stops = create_color_stops(color_breaks, colors='YlOrRd')
radius_breaks = mapclassify.Natural_Breaks(df['mag'], k=6, initial=0).bins
radius_stops = create_radius_stops(radius_breaks, 1, 10)
viz = GraduatedCircleViz('https://dl.dropbox.com/s/h4xjjlc9ggnr88b/earthquake-points-180223.geojson', #'points.geojson',
color_property = 'mag',
color_stops = color_stops,
radius_property = 'mag',
radius_stops = radius_stops,
opacity=0.8,
below_layer='waterway-label',
zoom=2,
center= [-95, 37],
access_token=token)
viz.show()
```
|
github_jupyter
|
Using min and max in another way
Just passing minrange and maxrange
r
/ \
/ \
min, r-1 r, max
```
import queue
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def minTree(root):
if root == None:
return 1000000
leftMin = minTree(root.left)
rightMin = minTree(root.right)
return min(leftMin, rightMin, root.data)
def maxTree(root):
if root == None:
return -10000000
leftMax = maxTree(root.left)
rightMax = maxTree(root.right)
return max(leftMax, rightMax, root.data)
def isBST(root):
if root == None:
return True
leftMax = maxTree(root.left)
rightMin = minTree(root.right)
if root.data > rightMin or root.data <= leftMax:
return False
isLeftBST = isBST(root.left)
isRightBST = isBST(root.right)
return isLeftBST and isRightBST
def isBST2(root):
if root == None:
return 1000000, -1000000, True
leftMin, leftMax, isLeftBST = isBST2(root.left)
rightMin, rightMax, isRightBST = isBST2(root.right)
minimum = min(leftMin, rightMin, root.data)
maximum = max(leftMax, rightMax, root.data)
isTreeBST = True
if root.data <= leftMax or root.data > rightMin:
isTreeBST = False
if not(isLeftBST) or not(isRightBST):
isTreeBST = False
return minimum, maximum, isTreeBST
def isBST3(root, min_range, max_range):
if root == None:
return True
if root.data < min_range or root.data > max_range:
return False
isLeftWithinConstraints = isBST3(root.left, min_range, root.data -1)
isRightWithinConstraints = isBST3(root.right, root.data, max_range)
return isLeftWithinConstraints and isRightWithinConstraints
def printTreeDetailed(root):
if root == None:
return
print(root.data, end = ":")
if root.left is not None:
print(root.left.data, end = ",")
if root.right is not None:
print(root.right.data, end = " ")
print()
printTreeDetailed(root.left)
printTreeDetailed(root.right)
def takeLevelWiseTreeInput():
q = queue.Queue()
print("Enter root")
rootData = int(input())
if rootData == -1:
return None
root = BinaryTreeNode(rootData)
q.put(root)
while (not(q.empty())):
current_node = q.get()
print("Enter left child of ", current_node.data)
leftChildData = int(input())
if leftChildData != -1:
leftChild = BinaryTreeNode(leftChildData)
current_node.left = leftChild
q.put(leftChild)
print("Enter right child of ", current_node.data)
rightChildData = int(input())
if rightChildData != -1:
rightChild = BinaryTreeNode(rightChildData)
current_node.right = rightChild
q.put(rightChild)
return root
root = takeLevelWiseTreeInput()
printTreeDetailed(root)
isBST3(root, -10000, 10000)
```
|
github_jupyter
|
```
# Tensorflowが使うCPUの数を制限します。(VMを使う場合)
%env OMP_NUM_THREADS=1
%env TF_NUM_INTEROP_THREADS=1
%env TF_NUM_INTRAOP_THREADS=1
from tensorflow.config import threading
num_threads = 1
threading.set_inter_op_parallelism_threads(num_threads)
threading.set_intra_op_parallelism_threads(num_threads)
#ライブラリのインポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
```
## MLP モデルのKerasによる実装
基礎編で使った2次元データを基に、MLPモデルをTensorflow/Kerasで書いてみます。
```
# 二次元ガウス分布と一様分布
def getDataset2():
state = np.random.get_state()
np.random.seed(0) # 今回はデータセットの乱数を固定させます。
nSignal = 100 # 生成するシグナルイベントの数
nBackground = 1000 # 生成するバックグラウンドイベントの数
# データ点の生成
xS = np.random.multivariate_normal([1.0, 0], [[1, 0], [0, 1]], size=nSignal) # 平均(x1,x2) = (1.0, 0.0)、分散=1の2次元ガウス分布
tS = np.ones(nSignal) # Signalは1にラベリング
xB = np.random.uniform(low=-5, high=5, size=(nBackground, 2)) # (-5, +5)の一様分布
tB = np.zeros(nBackground) # Backgroundは0にラベリング
# 2つのラベルを持つ学習データを1つにまとめる
x = np.concatenate([xS, xB])
t = np.concatenate([tS, tB]).reshape(-1, 1)
# データをランダムに並び替える
p = np.random.permutation(len(x))
x = x[p]
t = t[p]
np.random.set_state(state)
return x, t
# ラベル t={0,1}を持つデータ点のプロット
def plotDataPoint(x, t):
# シグナル/バックグラウンドの抽出
xS = x[t[:, 0] == 1] # シグナルのラベルだけを抽出
xB = x[t[:, 0] == 0] # バックグラウンドのラベルだけを抽出
# プロット
plt.scatter(xS[:, 0], xS[:, 1], label='Signal', c='red', s=10) # シグナルをプロット
plt.scatter(xB[:, 0], xB[:, 1], label='Background', c='blue', s=10) # バックグラウンドをプロット
plt.xlabel('x1') # x軸ラベルの設定
plt.ylabel('x2') # y軸ラベルの設定
plt.legend() # legendの表示
plt.show()
# prediction関数 の等高線プロット (fill)
def PlotPredictionContour(prediction, *args):
# 等高線を描くためのメッシュの生成
x1, x2 = np.mgrid[-5:5:100j, -5:5:100j] # x1 = (-5, 5), x2 = (-5, 5) の範囲で100点x100点のメッシュを作成
x1 = x1.flatten() # 二次元配列を一次元配列に変換 ( shape=(100, 100) => shape(10000, ))
x2 = x2.flatten() # 二次元配列を一次元配列に変換 ( shape=(100, 100) => shape(10000, ))
x = np.array([x1, x2]).T
# 関数predictionを使って入力xから出力yを計算し、等高線プロットを作成
y = prediction(x, *args)
cs = plt.tricontourf(x[:, 0], x[:, 1], y.flatten(), levels=10)
plt.colorbar(cs)
```
中間層が2層、それぞれの層のノード数がそれぞれ3つ、1つのMLPを構成します。
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
# データ点の取得
x, t = getDataset2()
# モデルの定義
model = Sequential([
Dense(units=3, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。
])
# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法
model.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=1.0))
# トレーニング
model.fit(
x=x,
y=t,
batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。
epochs=3000, # 学習のステップ数
verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される
)
# プロット
## パーセプトロンの出力を等高線プロット
PlotPredictionContour(model.predict)
## データ点をプロット
plotDataPoint(x, t)
```
`Dense` は1層の隠れ層を作成する関数です。
`Dense`の詳細は[公式のドキュメント](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense)を参照することでわかります。
ドキュメントを見ると、
```python
tf.keras.layers.Dense(
units, activation=None, use_bias=True,
kernel_initializer='glorot_uniform',
bias_initializer='zeros', kernel_regularizer=None,
bias_regularizer=None, activity_regularizer=None, kernel_constraint=None,
bias_constraint=None, **kwargs
)
```
のような引数を持つことがわかります。また、各引数の意味は、
* `units`: Positive integer, dimensionality of the output space.
* `activation`: Activation function to use. If you don't specify anything, no activation is applied (ie. "linear" activation: a(x) = x).
* `use_bias`: Boolean, whether the layer uses a bias vector.
* `kernel_initializer`: Initializer for the kernel weights matrix.
* `bias_initializer`: Initializer for the bias vector.
* `kernel_regularizer`: Regularizer function applied to the kernel weights matrix.
* `bias_regularizer`: Regularizer function applied to the bias vector.
* `activity_regularizer`: Regularizer function applied to the output of the layer (its "activation").
* `kernel_constraint`: Constraint function applied to the kernel weights matrix.
* `bias_constraint`: Constraint function applied to the bias vector.
のようになっています。隠れ層のノード数、重みの初期化方法、正規化方法、制約方法などを指定できることがわかります。
知らない関数を使うときは、必ずドキュメントを読んで、関数の入出力、引数、デフォルトの値などを確認するようにしましょう。
例えばこのDense関数は
```python
Dense(units=10)
```
のように、`units`(ノード数)だけを指定すれば動作しますが、その場合、暗に活性化関数は適用されず、重みの初期化は`glorot_uniform`で行われます。
`input_dim`は最初の層だけに対して必要となります。
Keras Model (上の例では`model`)は`summary`関数を使用することで、その構成が確認できます。
```
model.summary()
```
このモデルは、1層目の隠れ層の出力が3, 学習可能なパラメータ数が9, 2層目の隠れ層の出力が1, 学習可能なパラメータ数が4 であることがわかります。"Output Shape"の"None"はサイズが未確定であることを表しています。ここでは、バッチサイズ用の次元になります。
モデルの構成図を作ってくれる便利なAPIも存在します。
```
from tensorflow.keras.utils import plot_model
plot_model(model, to_file='model.png', show_shapes=True)
```
層の数を増やしてみましょう。新たな層を重ねることで層の数を増やすことができます。
```python
model = Sequential([
Dense(units=3, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=3, activation='sigmoid') # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=3, activation='sigmoid') # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。
])
```
```
model = Sequential([
Dense(units=3, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。
])
model.summary()
```
モデルのパラメータの数が増えていることがわかります。
次に、ノードの数を増やしてみましょう。
```
model = Sequential([
Dense(units=128, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。
Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。
Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。
Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。
Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。
Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。
])
model.summary()
```
パラメータの数が大きく増えたことがわかります。
MLPにおいては、パラメータの数は、ノード数の2乗で増加します。
このモデルを使って学習させてみましょう。
```
# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法
model.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.01))
# トレーニング
model.fit(
x=x,
y=t,
batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。
epochs=3000, # 学習のステップ数
verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される
)
# プロット
## パーセプトロンの出力を等高線プロット
PlotPredictionContour(model.predict)
## データ点をプロット
plotDataPoint(x, t)
```
これまでは活性化関数としてシグモイド関数(`sigmoid`)を使っていました。昔はsigmoid関数やtanh関数がよく使われていましたが、最近はReLU関数がよく使われます。
$$
ReLU = \begin{cases}
x & (x \geq 0) \\
0 & (x < 0)
\end{cases}
$$
ReLUが好まれる理由については、別の資料を参照してください。
ReLUを使って学習がどのようになるか確認してみましょう。
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
# データ点の取得
x, t = getDataset2()
# モデルの定義
model = Sequential([
Dense(units=128, activation='relu', input_dim=2), # ノード数が3の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。
])
# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法
model.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.01))
# トレーニング
model.fit(
x=x,
y=t,
batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。
epochs=3000, # 学習のステップ数
verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される
)
# プロット
## パーセプトロンの出力を等高線プロット
PlotPredictionContour(model.predict)
## データ点をプロット
plotDataPoint(x, t)
```
深層学習をトレーニングするにあたって、最適化関数(optimizer)も非常に重要な要素です。
確率的勾配降下法(SGD)の他によく使われるアルゴリズムとして adam があります。
adamを使ってみると、どのようになるでしょうか。
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
# データ点の取得
x, t = getDataset2()
# モデルの定義
model = Sequential([
Dense(units=128, activation='relu', input_dim=2), # ノード数が3の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。
Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。
])
# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法
model.compile(loss='binary_crossentropy', optimizer='adam')
# トレーニング
model.fit(
x=x,
y=t,
batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。
epochs=3000, # 学習のステップ数
verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される
)
# プロット
## パーセプトロンの出力を等高線プロット
PlotPredictionContour(model.predict)
## データ点をプロット
plotDataPoint(x, t)
```
## Keras モデルの定義方法
Kerasモデルを定義する方法はいくつかあります。
最も簡単なのが`Sequential`を使った方法で、これまでの例では全てこの方法でモデルを定義してきました。
一方で、少し複雑なモデルを考えると、`Sequential`モデルで対応できなくなってきます。
一例としてResidual Network(ResNet)で使われるskip connectionを考えてみます。
skip connectionは
$$
y = f_2(f_1(x) + x)
$$
のように、入力を2つの経路に分け、片方はMLP、もう片方はそのまま後ろのレイヤーに接続するつなげ方です。
このようなモデルは、途中入出力の分岐があるため、`Sequential`モデルでは実装できません。
かわりに`Function API`を使うとこれを実装することができます。
`Functional API`では以下のようにしてモデルを定義します。
```
from tensorflow.keras import Input, Model
input = Input(shape=(2,))
x = Dense(units=128, activation='relu')(input)
x = Dense(units=128, activation='relu')(x)
x = Dense(units=128, activation='relu')(x)
x = Dense(units=128, activation='relu')(x)
x = Dense(units=128, activation='relu')(x)
output = Dense(units=1, activation='sigmoid')(x)
model = Model(input, output)
```
入力(`Input`)をモジュールに順々に適用していき、
```python
x = Dense()(x)
```
最終的な出力(`output`)とはじめの入力を使って`Model`クラスを定義する、という流れになっています。
`Functional API`でskip connectionを実装すると、以下のようになります。
```
from tensorflow.keras import Input, Model
from tensorflow.keras.layers import Add
input = Input(shape=(2,))
x = Dense(units=128, activation='relu')(input)
z = Dense(units=128, activation='relu')(x)
x = Add()([x, z])
z = Dense(units=128, activation='relu')(x)
x = Add()([x, z])
output = Dense(units=1, activation='sigmoid')(x)
model = Model(input, output)
from tensorflow.keras.utils import plot_model
plot_model(model, to_file='model.png', show_shapes=True)
```
Kerasモデルを定義する方法として、`Model`クラスのサブクラスを作る方法もあります。
`Model`クラスをカスタマイズすることができるので、特殊な学習をさせたいときなど、高度な深層学習モデルを扱うときに使われることもあります。
```
# Modelクラスを継承して新しいクラスを作成します
from tensorflow.keras import Model
class myModel(Model):
def __init__(self):
super().__init__()
self.dense_1 = Dense(units=128, activation='relu')
self.dense_2 = Dense(units=128, activation='relu')
self.dense_3 = Dense(units=128, activation='relu')
self.dense_4 = Dense(units=128, activation='relu')
self.dense_5 = Dense(units=128, activation='relu')
self.dense_6 = Dense(units=1, activation='sigmoid')
def call(self, inputs):
x = self.dense_1(inputs)
x = self.dense_2(x)
x = self.dense_3(x)
x = self.dense_4(x)
x = self.dense_5(x)
x = self.dense_6(x)
return x
model = myModel()
```
|
github_jupyter
|
<a href="http://colab.research.google.com/github/dipanjanS/nlp_workshop_odsc19/blob/master/Module05%20-%20NLP%20Applications/Project07C%20-%20Text%20Classification%20Deep%20Learning%20Sequential%20Models%20LSTMs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!nvidia-smi
!pip install contractions
!pip install textsearch
!pip install tqdm
import nltk
nltk.download('punkt')
import pandas as pd
import numpy as np
# fix random seed for reproducibility
seed = 42
np.random.seed(seed)
import zipfile
from google.colab import drive
drive.mount("/content/drive")
z= zipfile.ZipFile("/content/drive/MyDrive/Colab Notebooks/YouTube-Spam-Collection-v1.zip")
Psy=pd.read_csv(z.open("Youtube01-Psy.csv"))
KatyPerry =pd.read_csv(z.open("Youtube02-KatyPerry.csv"))
LMFAQ =pd.read_csv(z.open("Youtube03-LMFAO.csv"))
Eminem =pd.read_csv(z.open("Youtube04-Eminem.csv"))
Shakira =pd.read_csv(z.open("Youtube05-Shakira.csv"))
frames = [Psy,LMFAQ,Eminem,Shakira,KatyPerry]
dataset = pd.concat(frames)
dataset.head(10)
dataset.info()
dataset.head()
# build train and test datasets
reviews = dataset['CONTENT'].values
sentiments = dataset['CLASS'].values
train_reviews = reviews[:3500]
train_sentiments = sentiments[:3500]
test_reviews = reviews[3500:]
test_sentiments = sentiments[3500:]
import contractions
from bs4 import BeautifulSoup
import numpy as np
import re
import tqdm
import unicodedata
def strip_html_tags(text):
soup = BeautifulSoup(text, "html.parser")
[s.extract() for s in soup(['iframe', 'script'])]
stripped_text = soup.get_text()
stripped_text = re.sub(r'[\r|\n|\r\n]+', '\n', stripped_text)
return stripped_text
def remove_accented_chars(text):
text = unicodedata.normalize('NFKD', text).encode('ascii', 'ignore').decode('utf-8', 'ignore')
return text
def pre_process_corpus(docs):
norm_docs = []
for doc in tqdm.tqdm(docs):
doc = strip_html_tags(doc)
doc = doc.translate(doc.maketrans("\n\t\r", " "))
doc = doc.lower()
doc = remove_accented_chars(doc)
doc = contractions.fix(doc)
# lower case and remove special characters\whitespaces
doc = re.sub(r'[^a-zA-Z0-9\s]', '', doc, re.I|re.A)
doc = re.sub(' +', ' ', doc)
doc = doc.strip()
norm_docs.append(doc)
return norm_docs
%%time
norm_train_reviews = pre_process_corpus(train_reviews)
norm_test_reviews = pre_process_corpus(test_reviews)
```
## Preprocessing
To prepare text data for our deep learning model, we transform each review into a sequence.
Every word in the review is mapped to an integer index and thus the sentence turns into a sequence of numbers.
To perform this transformation, keras provides the ```Tokenizer```
```
import tensorflow as tf
t = tf.keras.preprocessing.text.Tokenizer(oov_token='<UNK>')
# fit the tokenizer on the documents
t.fit_on_texts(norm_train_reviews)
t.word_index['<PAD>'] = 0
max([(k, v) for k, v in t.word_index.items()], key = lambda x:x[1]), min([(k, v) for k, v in t.word_index.items()], key = lambda x:x[1]), t.word_index['<UNK>']
train_sequences = t.texts_to_sequences(norm_train_reviews)
test_sequences = t.texts_to_sequences(norm_test_reviews)
print("Vocabulary size={}".format(len(t.word_index)))
print("Number of Documents={}".format(t.document_count))
import matplotlib.pyplot as plt
%matplotlib inline
train_lens = [len(s) for s in train_sequences]
test_lens = [len(s) for s in test_sequences]
fig, ax = plt.subplots(1,2, figsize=(12, 6))
h1 = ax[0].hist(train_lens)
h2 = ax[1].hist(test_lens)
MAX_SEQUENCE_LENGTH = 1000
```
```
# pad dataset to a maximum review length in words
X_train = tf.keras.preprocessing.sequence.pad_sequences(train_sequences, maxlen=MAX_SEQUENCE_LENGTH)
X_test = tf.keras.preprocessing.sequence.pad_sequences(test_sequences, maxlen=MAX_SEQUENCE_LENGTH)
X_train.shape, X_test.shape
```
### Encoding Labels
```
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
num_classes=2 # positive -> 1, negative -> 0
y_train = le.fit_transform(train_sentiments)
y_test = le.transform(test_sentiments)
VOCAB_SIZE = len(t.word_index)
```
# LSTM Model
```
EMBEDDING_DIM = 300 # dimension for dense embeddings for each token
LSTM_DIM = 128 # total LSTM units
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Embedding(input_dim=VOCAB_SIZE, output_dim=EMBEDDING_DIM, input_length=MAX_SEQUENCE_LENGTH))
model.add(tf.keras.layers.SpatialDropout1D(0.1))
model.add(tf.compat.v1.keras.layers.CuDNNLSTM(LSTM_DIM, return_sequences=False))
model.add(tf.keras.layers.Dense(256, activation='relu'))
model.add(tf.keras.layers.Dense(1, activation="sigmoid"))
model.compile(loss="binary_crossentropy", optimizer="adam",
metrics=["accuracy"])
model.summary()
```
## Train Model
```
Metrics = [tf.keras.metrics.BinaryAccuracy(name = 'accuracy'),
tf.keras.metrics.Precision(name = 'precision'),
tf.keras.metrics.Recall(name = 'recall')
]
# compiling our model
model.compile(optimizer ='adam',
loss = 'binary_crossentropy',
metrics = Metrics)
batch_size = 100
history=model.fit(X_train, y_train, epochs=5, batch_size=batch_size,
shuffle=True, validation_split=0.1, verbose=1)
from matplotlib import pyplot
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
```
|
github_jupyter
|
```
%matplotlib inline
```
Saving and loading models for inference in PyTorch
==================================================
There are two approaches for saving and loading models for inference in
PyTorch. The first is saving and loading the ``state_dict``, and the
second is saving and loading the entire model.
Introduction
------------
Saving the model’s ``state_dict`` with the ``torch.save()`` function
will give you the most flexibility for restoring the model later. This
is the recommended method for saving models, because it is only really
necessary to save the trained model’s learned parameters.
When saving and loading an entire model, you save the entire module
using Python’s
`pickle <https://docs.python.org/3/library/pickle.html>`__ module. Using
this approach yields the most intuitive syntax and involves the least
amount of code. The disadvantage of this approach is that the serialized
data is bound to the specific classes and the exact directory structure
used when the model is saved. The reason for this is because pickle does
not save the model class itself. Rather, it saves a path to the file
containing the class, which is used during load time. Because of this,
your code can break in various ways when used in other projects or after
refactors.
In this recipe, we will explore both ways on how to save and load models
for inference.
Setup
-----
Before we begin, we need to install ``torch`` if it isn’t already
available.
::
pip install torch
Steps
-----
1. Import all necessary libraries for loading our data
2. Define and intialize the neural network
3. Initialize the optimizer
4. Save and load the model via ``state_dict``
5. Save and load the entire model
1. Import necessary libraries for loading our data
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For this recipe, we will use ``torch`` and its subsidiaries ``torch.nn``
and ``torch.optim``.
```
import torch
import torch.nn as nn
import torch.optim as optim
```
2. Define and intialize the neural network
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For sake of example, we will create a neural network for training
images. To learn more see the Defining a Neural Network recipe.
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
print(net)
```
3. Initialize the optimizer
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We will use SGD with momentum.
```
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
```
4. Save and load the model via ``state_dict``
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let’s save and load our model using just ``state_dict``.
```
# Specify a path
PATH = "state_dict_model.pt"
# Save
torch.save(net.state_dict(), PATH)
# Load
model = Net()
model.load_state_dict(torch.load(PATH))
model.eval()
```
A common PyTorch convention is to save models using either a ``.pt`` or
``.pth`` file extension.
Notice that the ``load_state_dict()`` function takes a dictionary
object, NOT a path to a saved object. This means that you must
deserialize the saved state_dict before you pass it to the
``load_state_dict()`` function. For example, you CANNOT load using
``model.load_state_dict(PATH)``.
Remember too, that you must call ``model.eval()`` to set dropout and
batch normalization layers to evaluation mode before running inference.
Failing to do this will yield inconsistent inference results.
5. Save and load entire model
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now let’s try the same thing with the entire model.
```
# Specify a path
PATH = "entire_model.pt"
# Save
torch.save(net, PATH)
# Load
model = torch.load(PATH)
model.eval()
```
Again here, remember that you must call model.eval() to set dropout and
batch normalization layers to evaluation mode before running inference.
Congratulations! You have successfully saved and load models for
inference in PyTorch.
Learn More
----------
Take a look at these other recipes to continue your learning:
- `Saving and loading a general checkpoint in PyTorch <https://pytorch.org/tutorials/recipes/recipes/saving_and_loading_a_general_checkpoint.html>`__
- `Saving and loading multiple models in one file using PyTorch <https://pytorch.org/tutorials/recipes/recipes/saving_multiple_models_in_one_file.html>`__
|
github_jupyter
|
## Autograd: automatic differentiation
Central to all neural networks in PyTorch is the `autograd` package. Let's first briefly visit this, and we will then go to train our first neural network.
The `autograd` package provides automatic differentiation for all operation on Tensors. It is a define-by-run framework, which means that your backprop is defined by how your code is run, and that every single iteration can be different.
Let us see this in more simple terms with some examples.
#### Tensor
`torch.Tensor` is the central class of the package. If you set its attribute `.requires_grad` as True, it starts to track all operations on it. When you finish your computation you can call `.backward()` and have all the gradients computed automatically. The gradient for this tensor will be accumulated into `.grad` attribute.
To stop a tensor from tracking history, you can call `.detach()` to detach it from the computation history, and to prevent future computation from being tracked.
To prevent tracking history (and using memory), you can also wrap the code block in `with torch.no_grad():`. This can be particularly helpful when evaluating a model because the model may have trainable parameters with `requires_grad=True`, but for which we don’t need the gradients.
There’s one more class which is very important for autograd implementation - a `Function`.
`Tensor` and `Function` are interconnected and build up an acyclic graph, that encodes a complete history of computation. Each tensor has a `.grad_fn` attribute that references a `Function` that has created the `Tensor` (except for Tensors created by the user - their `grad_fn` is None).
If you want to compute the derivatives, you can call `.backward()` on a `Tensor`. If `Tensor` is a scalar (i.e. it holds a one element data), you don’t need to specify any arguments to `backward()`, however if it has more elements, you need to specify a `gradient` argument that is a tensor of matching shape.
```
import torch
# Create a tensor and set `requires_grad=True` to track computation with it.
x = torch.ones(2, 2, requires_grad=True)
print(x)
# Do a tensor operation:
y = x + 2
print(y)
# y was created as a result of an operation, so it has a grad_fn
print(y.grad_fn)
z = y * y * 3
out = z.mean()
print(z, out)
a = torch.randn(2, 2)
a = ((a * 3) / (a -1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)
out.backward()
print(x.grad)
x = torch.randn(3 ,requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y *= 2
print(y)
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)
# You can also stop autograd from tracking history on Tensors
# with .requires_grad=True either by wrapping the code block in with torch.no_grad():
print(x.requires_grad)
print((x ** 2).requires_grad)
with torch.no_grad():
print((x ** 2).requires_grad)
# Or by using .detach() to get a new Tensor with the same content but that does not require gradients:
print(x.requires_grad)
y = x.detach()
print(y.requires_grad)
print(x.eq(y).all())
```
|
github_jupyter
|
# Sampling the potential energy surface
## Introduction
This interactive notebook demonstrates how to utilize the Potential Energy Surface (PES) samplers algorithm of qiskit chemistry to generate the dissociation profile of a molecule. We use the Born-Oppenhemier Potential Energy Surface (BOPES)and demonstrate how to exploit bootstrapping and extrapolation to reduce the total number of function evaluations in computing the PES using the Variational Quantum Eigensolver (VQE).
```
# import common packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from functools import partial
# qiskit
from qiskit.aqua import QuantumInstance
from qiskit import BasicAer
from qiskit.aqua.algorithms import NumPyMinimumEigensolver, VQE, IQPE
from qiskit.aqua.components.optimizers import SLSQP
from qiskit.circuit.library import ExcitationPreserving
from qiskit import BasicAer
from qiskit.aqua.algorithms import NumPyMinimumEigensolver, VQE
from qiskit.aqua.components.optimizers import SLSQP
# chemistry components
from qiskit.chemistry.components.initial_states import HartreeFock
from qiskit.chemistry.components.variational_forms import UCCSD
from qiskit.chemistry.drivers import PySCFDriver, UnitsType
from qiskit.chemistry.core import Hamiltonian, TransformationType, QubitMappingType
from qiskit.aqua.algorithms import VQAlgorithm, VQE, MinimumEigensolver
from qiskit.chemistry.transformations import FermionicTransformation
from qiskit.chemistry.drivers import PySCFDriver
from qiskit.chemistry.algorithms.ground_state_solvers import GroundStateEigensolver
from qiskit.chemistry.algorithms.pes_samplers.bopes_sampler import BOPESSampler
from qiskit.chemistry.drivers.molecule import Molecule
from qiskit.chemistry.algorithms.pes_samplers.extrapolator import *
import warnings
warnings.simplefilter('ignore', np.RankWarning)
```
Here, we use the H2 molecule as a model sysem for testing.
```
ft = FermionicTransformation()
driver = PySCFDriver()
solver = VQE(quantum_instance=
QuantumInstance(backend=BasicAer.get_backend('statevector_simulator')))
me_gsc = GroundStateEigensolver(ft, solver)
stretch1 = partial(Molecule.absolute_stretching, atom_pair=(1, 0))
mol = Molecule(geometry=[('H', [0., 0., 0.]),
('H', [0., 0., 0.3])],
degrees_of_freedom=[stretch1],
)
# pass molecule to PSYCF driver
driver = PySCFDriver(molecule=mol)
print(mol.geometry)
```
### Make a perturbation to the molecule along the absolute_stretching dof
```
mol.perturbations = [0.2]
print(mol.geometry)
mol.perturbations = [0.6]
print(mol.geometry)
```
# Calculate bond dissociation profile using BOPES Sampler
Here, we pass the molecular information and the VQE to a built-in type called the BOPES Sampler. The BOPES Sampler allows the computation of the potential energy surface for a specified set of degrees of freedom/points of interest.
## First we compare no bootstrapping vs bootstrapping
Bootstrapping the BOPES sampler involves utilizing the optimal variational parameters for a given degree of freedom, say r (ex. interatomic distance) as the initial point for VQE at a later degree of freedom, say r + $\epsilon$. By default, if boostrapping is set to True, all previous optimal parameters are used as initial points for the next runs.
```
stretch1 = partial(Molecule.absolute_stretching, atom_pair=(1, 0))
mol = Molecule(geometry=[('H', [0., 0., 0.]),
('H', [0., 0., 0.3])],
degrees_of_freedom=[stretch1],
)
# pass molecule to PSYCF driver
driver = PySCFDriver(molecule=mol)
# Specify degree of freedom (points of interest)
points = np.linspace(0.1, 2, 20)
results_full = {} # full dictionary of results for each condition
results = {} # dictionary of (point,energy) results for each condition
conditions = {False: 'no bootstrapping', True: 'bootstrapping'}
for value, bootstrap in conditions.items():
# define instance to sampler
bs = BOPESSampler(
gss=me_gsc
,bootstrap=value
,num_bootstrap=None
,extrapolator=None)
# execute
res = bs.sample(driver,points)
results_full[f'{bootstrap}'] = res.raw_results
results[f'points_{bootstrap}'] = res.points
results[f'energies_{bootstrap}'] = res.energies
```
# Compare to classical eigensolver
```
# define numpy solver
solver_numpy = NumPyMinimumEigensolver()
me_gsc_numpy = GroundStateEigensolver(ft, solver_numpy)
bs_classical = BOPESSampler(
gss=me_gsc_numpy
,bootstrap=False
,num_bootstrap=None
,extrapolator=None)
# execute
res_np = bs_classical.sample(driver, points)
results_full['np'] = res_np.raw_results
results['points_np'] = res_np.points
results['energies_np'] = res_np.energies
```
## Plot results
```
fig = plt.figure()
for value, bootstrap in conditions.items():
plt.plot(results[f'points_{bootstrap}'], results[f'energies_{bootstrap}'], label = f'{bootstrap}')
plt.plot(results['points_np'], results['energies_np'], label = 'numpy')
plt.legend()
plt.title('Dissociation profile')
plt.xlabel('Interatomic distance')
plt.ylabel('Energy')
```
# Compare number of evaluations
```
for condition, result_full in results_full.items():
print(condition)
print('Total evaluations for ' + condition + ':')
sum = 0
for key in result_full:
if condition is not 'np':
sum += result_full[key]['raw_result']['cost_function_evals']
else:
sum = 0
print(sum)
```
# Extrapolation
Here, an extrapolator added that will try to fit each (param,point) set to some specified function and suggest an initial parameter set for the next point (degree of freedom).
- Extrapolator is based on an external extrapolator that sets the 'window', that is, the number of previous points to use for extrapolation, while the internal extrapolator proceeds with the actual extrapolation.
- In practice, the user sets the window by specifies an integer value to num_bootstrap - which also the number of previous points to use for bootstrapping. Additionally, the external extrapolator defines the space within how to extrapolate - here PCA, clustering and the standard window approach.
In practice, if no extrapolator is defined and bootstrapping is True, then all previous points will be bootstrapped. If an extrapolator list is defined and no points are specified for bootstrapping, then the extrapolation will be done based on all previous points.
1. Window Extrapolator: An extrapolator which wraps another extrapolator, limiting the internal extrapolator's ground truth parameter set to a fixed window size
2. PCA Extrapolator: A wrapper extrapolator which reduces the points' dimensionality with PCA, performs extrapolation in the transformed pca space, and untransforms the results before returning.
3. Sieve Extrapolator: A wrapper extrapolator which performs an extrapolation, then clusters the extrapolated parameter values into two large and small clusters, and sets the small clusters' parameters to zero.
4. Polynomial Extrapolator: An extrapolator based on fitting each parameter to a polynomial function of a user-specified degree.
5. Differential Extrapolator: An extrapolator based on treating each param set as a point in space, and performing regression to predict the param set for the next point. A user-specified degree also adds derivatives to the values in the point vectors which serve as features in the training data for the linear regression.
## Here we test two different extrapolation techniques
```
# define different extrapolators
degree = 1
extrap_poly = Extrapolator.factory("poly", degree = degree)
extrap_diff = Extrapolator.factory("diff_model", degree = degree)
extrapolators = {'poly': extrap_poly, 'diff_model': extrap_diff}
for key in extrapolators:
extrap_internal = extrapolators[key]
extrap = Extrapolator.factory("window", extrapolator = extrap_internal)
# define extrapolator
# BOPES sampler
bs_extr = BOPESSampler(
gss=me_gsc
,bootstrap=True
,num_bootstrap=None
,extrapolator=extrap)
# execute
res = bs_extr.sample(driver, points)
results_full[f'{key}']= res.raw_results
results[f'points_{key}'] = res.points
results[f'energies_{key}'] = res.energies
```
## Plot results
```
fig = plt.figure()
for value, bootstrap in conditions.items():
plt.plot(results[f'points_{bootstrap}'], results[f'energies_{bootstrap}'], label = f'{bootstrap}')
plt.plot(results['points_np'], results['energies_np'], label = 'numpy')
for condition in extrapolators.keys():
print(condition)
plt.plot(results[f'points_{condition}'], results[f'energies_{condition}'], label = condition)
plt.legend()
plt.title('Dissociation profile')
plt.xlabel('Interatomic distance')
plt.ylabel('Energy')
```
# Compare number of evaluations
```
for condition, result_full in results_full.items():
print(condition)
print('Total evaluations for ' + condition + ':')
sum = 0
for key in results_full[condition].keys():
if condition is not 'np':
sum += results_full[condition][key]['raw_result']['cost_function_evals']
else:
sum = 0
print(sum)
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
|
github_jupyter
|
# Weight Initialization
In this lesson, you'll learn how to find good initial weights for a neural network. Weight initialization happens once, when a model is created and before it trains. Having good initial weights can place the neural network close to the optimal solution. This allows the neural network to come to the best solution quicker.
<img src="notebook_ims/neuron_weights.png" width=40%/>
## Initial Weights and Observing Training Loss
To see how different weights perform, we'll test on the same dataset and neural network. That way, we know that any changes in model behavior are due to the weights and not any changing data or model structure.
> We'll instantiate at least two of the same models, with _different_ initial weights and see how the training loss decreases over time, such as in the example below.
<img src="notebook_ims/loss_comparison_ex.png" width=60%/>
Sometimes the differences in training loss, over time, will be large and other times, certain weights offer only small improvements.
### Dataset and Model
We'll train an MLP to classify images from the [Fashion-MNIST database](https://github.com/zalandoresearch/fashion-mnist) to demonstrate the effect of different initial weights. As a reminder, the FashionMNIST dataset contains images of clothing types; `classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']`. The images are normalized so that their pixel values are in a range [0.0 - 1.0). Run the cell below to download and load the dataset.
---
#### EXERCISE
[Link to normalized distribution, exercise code](#normalex)
---
### Import Libraries and Load [Data](http://pytorch.org/docs/stable/torchvision/datasets.html)
```
import torch
import numpy as np
from torchvision import datasets
import torchvision.transforms as transforms
from torch.utils.data.sampler import SubsetRandomSampler
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 100
# percentage of training set to use as validation
valid_size = 0.2
# convert data to torch.FloatTensor
transform = transforms.ToTensor()
# choose the training and test datasets
train_data = datasets.FashionMNIST(root='data', train=True,
download=True, transform=transform)
test_data = datasets.FashionMNIST(root='data', train=False,
download=True, transform=transform)
# obtain training indices that will be used for validation
num_train = len(train_data)
indices = list(range(num_train))
np.random.shuffle(indices)
split = int(np.floor(valid_size * num_train))
train_idx, valid_idx = indices[split:], indices[:split]
# define samplers for obtaining training and validation batches
train_sampler = SubsetRandomSampler(train_idx)
valid_sampler = SubsetRandomSampler(valid_idx)
# prepare data loaders (combine dataset and sampler)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=train_sampler, num_workers=num_workers)
valid_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=valid_sampler, num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
# specify the image classes
classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
```
### Visualize Some Training Data
```
import matplotlib.pyplot as plt
%matplotlib inline
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
ax.set_title(classes[labels[idx]])
```
## Define the Model Architecture
We've defined the MLP that we'll use for classifying the dataset.
### Neural Network
<img style="float: left" src="notebook_ims/neural_net.png" width=50%/>
* A 3 layer MLP with hidden dimensions of 256 and 128.
* This MLP accepts a flattened image (784-value long vector) as input and produces 10 class scores as output.
---
We'll test the effect of different initial weights on this 3 layer neural network with ReLU activations and an Adam optimizer.
The lessons you learn apply to other neural networks, including different activations and optimizers.
---
## Initialize Weights
Let's start looking at some initial weights.
### All Zeros or Ones
If you follow the principle of [Occam's razor](https://en.wikipedia.org/wiki/Occam's_razor), you might think setting all the weights to 0 or 1 would be the best solution. This is not the case.
With every weight the same, all the neurons at each layer are producing the same output. This makes it hard to decide which weights to adjust.
Let's compare the loss with all ones and all zero weights by defining two models with those constant weights.
Below, we are using PyTorch's [nn.init](https://pytorch.org/docs/stable/nn.html#torch-nn-init) to initialize each Linear layer with a constant weight. The init library provides a number of weight initialization functions that give you the ability to initialize the weights of each layer according to layer type.
In the case below, we look at every layer/module in our model. If it is a Linear layer (as all three layers are for this MLP), then we initialize those layer weights to be a `constant_weight` with bias=0 using the following code:
>```
if isinstance(m, nn.Linear):
nn.init.constant_(m.weight, constant_weight)
nn.init.constant_(m.bias, 0)
```
The `constant_weight` is a value that you can pass in when you instantiate the model.
```
import torch.nn as nn
import torch.nn.functional as F
# define the NN architecture
class Net(nn.Module):
def __init__(self, hidden_1=256, hidden_2=128, constant_weight=None):
super(Net, self).__init__()
# linear layer (784 -> hidden_1)
self.fc1 = nn.Linear(28 * 28, hidden_1)
# linear layer (hidden_1 -> hidden_2)
self.fc2 = nn.Linear(hidden_1, hidden_2)
# linear layer (hidden_2 -> 10)
self.fc3 = nn.Linear(hidden_2, 10)
# dropout layer (p=0.2)
self.dropout = nn.Dropout(0.2)
# initialize the weights to a specified, constant value
if(constant_weight is not None):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.constant_(m.weight, constant_weight)
nn.init.constant_(m.bias, 0)
def forward(self, x):
# flatten image input
x = x.view(-1, 28 * 28)
# add hidden layer, with relu activation function
x = F.relu(self.fc1(x))
# add dropout layer
x = self.dropout(x)
# add hidden layer, with relu activation function
x = F.relu(self.fc2(x))
# add dropout layer
x = self.dropout(x)
# add output layer
x = self.fc3(x)
return x
```
### Compare Model Behavior
Below, we are using `helpers.compare_init_weights` to compare the training and validation loss for the two models we defined above, `model_0` and `model_1`. This function takes in a list of models (each with different initial weights), the name of the plot to produce, and the training and validation dataset loaders. For each given model, it will plot the training loss for the first 100 batches and print out the validation accuracy after 2 training epochs. *Note: if you've used a small batch_size, you may want to increase the number of epochs here to better compare how models behave after seeing a few hundred images.*
We plot the loss over the first 100 batches to better judge which model weights performed better at the start of training. **I recommend that you take a look at the code in `helpers.py` to look at the details behind how the models are trained, validated, and compared.**
Run the cell below to see the difference between weights of all zeros against all ones.
```
# initialize two NN's with 0 and 1 constant weights
model_0 = Net(constant_weight=0)
model_1 = Net(constant_weight=1)
import helpers
import importlib
importlib.reload(helpers)
# put them in list form to compare
model_list = [(model_0, 'All Zeros'),
(model_1, 'All Ones')]
# plot the loss over the first 100 batches
helpers.compare_init_weights(model_list,
'All Zeros vs All Ones',
train_loader,
valid_loader)
```
As you can see the accuracy is close to guessing for both zeros and ones, around 10%.
The neural network is having a hard time determining which weights need to be changed, since the neurons have the same output for each layer. To avoid neurons with the same output, let's use unique weights. We can also randomly select these weights to avoid being stuck in a local minimum for each run.
A good solution for getting these random weights is to sample from a uniform distribution.
### Uniform Distribution
A [uniform distribution](https://en.wikipedia.org/wiki/Uniform_distribution) has the equal probability of picking any number from a set of numbers. We'll be picking from a continuous distribution, so the chance of picking the same number is low. We'll use NumPy's `np.random.uniform` function to pick random numbers from a uniform distribution.
>#### [`np.random_uniform(low=0.0, high=1.0, size=None)`](https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.uniform.html)
>Outputs random values from a uniform distribution.
>The generated values follow a uniform distribution in the range [low, high). The lower bound minval is included in the range, while the upper bound maxval is excluded.
>- **low:** The lower bound on the range of random values to generate. Defaults to 0.
- **high:** The upper bound on the range of random values to generate. Defaults to 1.
- **size:** An int or tuple of ints that specify the shape of the output array.
We can visualize the uniform distribution by using a histogram. Let's map the values from `np.random_uniform(-3, 3, [1000])` to a histogram using the `helper.hist_dist` function. This will be `1000` random float values from `-3` to `3`, excluding the value `3`.
```
import importlib
importlib.reload(helpers)
helpers.hist_dist('Random Uniform (low=-3, high=3)', np.random.uniform(-3, 3, [1000]))
```
The histogram used 500 buckets for the 1000 values. Since the chance for any single bucket is the same, there should be around 2 values for each bucket. That's exactly what we see with the histogram. Some buckets have more and some have less, but they trend around 2.
Now that you understand the uniform function, let's use PyTorch's `nn.init` to apply it to a model's initial weights.
### Uniform Initialization, Baseline
Let's see how well the neural network trains using a uniform weight initialization, where `low=0.0` and `high=1.0`. Below, I'll show you another way (besides in the Net class code) to initialize the weights of a network. To define weights outside of the model definition, you can:
>1. Define a function that assigns weights by the type of network layer, *then*
2. Apply those weights to an initialized model using `model.apply(fn)`, which applies a function to each model layer.
This time, we'll use `weight.data.uniform_` to initialize the weights of our model, directly.
```
# takes in a module and applies the specified weight initialization
def weights_init_uniform(m):
classname = m.__class__.__name__
# for every Linear layer in a model..
if classname.find('Linear') != -1:
# apply a uniform distribution to the weights and a bias=0
m.weight.data.uniform_(0.0, 1.0)
m.bias.data.fill_(0)
# create a new model with these weights
model_uniform = Net()
model_uniform.apply(weights_init_uniform)
# evaluate behavior
helpers.compare_init_weights([(model_uniform, 'Uniform Weights')],
'Uniform Baseline',
train_loader,
valid_loader)
```
---
The loss graph is showing the neural network is learning, which it didn't with all zeros or all ones. We're headed in the right direction!
## General rule for setting weights
The general rule for setting the weights in a neural network is to set them to be close to zero without being too small.
>Good practice is to start your weights in the range of $[-y, y]$ where $y=1/\sqrt{n}$
($n$ is the number of inputs to a given neuron).
Let's see if this holds true; let's create a baseline to compare with and center our uniform range over zero by shifting it over by 0.5. This will give us the range [-0.5, 0.5).
```
# takes in a module and applies the specified weight initialization
def weights_init_uniform_center(m):
classname = m.__class__.__name__
# for every Linear layer in a model..
if classname.find('Linear') != -1:
# apply a centered, uniform distribution to the weights
m.weight.data.uniform_(-0.5, 0.5)
m.bias.data.fill_(0)
# create a new model with these weights
model_centered = Net()
model_centered.apply(weights_init_uniform_center)
```
Then let's create a distribution and model that uses the **general rule** for weight initialization; using the range $[-y, y]$, where $y=1/\sqrt{n}$ .
And finally, we'll compare the two models.
```
# takes in a module and applies the specified weight initialization
def weights_init_uniform_rule(m):
classname = m.__class__.__name__
# for every Linear layer in a model..
if classname.find('Linear') != -1:
# get the number of the inputs
n = m.in_features
y = 1.0/np.sqrt(n)
m.weight.data.uniform_(-y, y)
m.bias.data.fill_(0)
# create a new model with these weights
model_rule = Net()
model_rule.apply(weights_init_uniform_rule)
# compare these two models
model_list = [(model_centered, 'Centered Weights [-0.5, 0.5)'),
(model_rule, 'General Rule [-y, y)')]
# evaluate behavior
helpers.compare_init_weights(model_list,
'[-0.5, 0.5) vs [-y, y)',
train_loader,
valid_loader)
```
This behavior is really promising! Not only is the loss decreasing, but it seems to do so very quickly for our uniform weights that follow the general rule; after only two epochs we get a fairly high validation accuracy and this should give you some intuition for why starting out with the right initial weights can really help your training process!
---
Since the uniform distribution has the same chance to pick *any value* in a range, what if we used a distribution that had a higher chance of picking numbers closer to 0? Let's look at the normal distribution.
### Normal Distribution
Unlike the uniform distribution, the [normal distribution](https://en.wikipedia.org/wiki/Normal_distribution) has a higher likelihood of picking number close to it's mean. To visualize it, let's plot values from NumPy's `np.random.normal` function to a histogram.
>[np.random.normal(loc=0.0, scale=1.0, size=None)](https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.normal.html)
>Outputs random values from a normal distribution.
>- **loc:** The mean of the normal distribution.
- **scale:** The standard deviation of the normal distribution.
- **shape:** The shape of the output array.
```
helpers.hist_dist('Random Normal (mean=0.0, stddev=1.0)', np.random.normal(0, 2, size=[1000]))
```
Let's compare the normal distribution against the previous, rule-based, uniform distribution.
<a id='normalex'></a>
#### TODO: Define a weight initialization function that gets weights from a normal distribution
> The normal distribution should have a mean of 0 and a standard deviation of $y=1/\sqrt{n}$
```
## complete this function
def weights_init_normal(m):
'''Takes in a module and initializes all linear layers with weight
values taken from a normal distribution.'''
classname = m.__class__.__name__
# for every Linear layer in a model
# m.weight.data shoud be taken from a normal distribution
# m.bias.data should be 0
if classname.find('Linear') != -1:
# get the number of the inputs
n = m.in_features
y = 1.0/np.sqrt(n)
m.weight.data.normal_(0, y)
m.bias.data.fill_(0)
## -- no need to change code below this line -- ##
# create a new model with the rule-based, uniform weights
model_uniform_rule = Net()
model_uniform_rule.apply(weights_init_uniform_rule)
# create a new model with the rule-based, NORMAL weights
model_normal_rule = Net()
model_normal_rule.apply(weights_init_normal)
# compare the two models
model_list = [(model_uniform_rule, 'Uniform Rule [-y, y)'),
(model_normal_rule, 'Normal Distribution')]
# evaluate behavior
helpers.compare_init_weights(model_list,
'Uniform vs Normal',
train_loader,
valid_loader)
```
The normal distribution gives us pretty similar behavior compared to the uniform distribution, in this case. This is likely because our network is so small; a larger neural network will pick more weight values from each of these distributions, magnifying the effect of both initialization styles. In general, a normal distribution will result in better performance for a model.
---
### Automatic Initialization
Let's quickly take a look at what happens *without any explicit weight initialization*.
```
## Instantiate a model with _no_ explicit weight initialization
model_no_rule = Net()
# create a new model with the rule-based, uniform weights
model_uniform_rule = Net()
model_uniform_rule.apply(weights_init_uniform_rule)
# create a new model with the rule-based, NORMAL weights
model_normal_rule = Net()
model_normal_rule.apply(weights_init_normal)
# compare the two models
model_list = [(model_uniform_rule, 'Uniform Rule [-y, y)'),
(model_normal_rule, 'Normal Distribution'),
(model_no_rule, 'no')]
# evaluate behavior
helpers.compare_init_weights(model_list,
'Uniform vs Normal',
train_loader,
valid_loader)
## evaluate the behavior using helpers.compare_init_weights
```
As you complete this exercise, keep in mind these questions:
* What initializaion strategy has the lowest training loss after two epochs? What about highest validation accuracy?
* After testing all these initial weight options, which would you decide to use in a final classification model?
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
from os import path
import sys, inspect
current_dir = path.dirname(path.abspath(inspect.getfile(inspect.currentframe())))
parent_dir = path.dirname(current_dir)
sys.path.insert(0, parent_dir)
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from nu_aesthetics.single_colors import brand, design
from matplotlib.cm import register_cmap
from support.shared_consts import *
from support.utils import *
```
# Model
$Y = \beta_0 + \beta_1 x_1 + \dots + \beta_k x_k + \epsilon$
$\epsilon_i$ i.i.d. $N(0, 1)$
$E = Y - \hat{Y}$
## Canonical X
$Y = 6 + 1.3 x + \epsilon$
$\epsilon_i$ i.i.d. $N(0, 1)$
```
x = x_fix.copy()
e = e_fix.copy()
y = y_fix.copy()
data = pd.DataFrame({"x": x, "e": e, "y": y})
regressor = smf.ols(formula="y ~ x", data=data).fit()
print(regressor.summary())
ax = plot_lmreg(data=data)
plt.savefig(f"../imgs/simul_model_canonical.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
plot_resid(regressor, data)
plt.savefig(f"../imgs/simul_resid_canonical.png", bbox_inches="tight")
plt.show()
```
## Model validity
Normality: the OLS is `robust`, having its `validity` even when their assumptions are false - hypothesis tests and confidence intervals are approximately correct for **non-normal large samples**.<br/>
The OLS might not be `efficient`, specially for **heavy-tailed** distributed errors.
When the errors have a **skewed distribution**, the mean is no more a good measure of centrality and this compromises the `interpretation` of the OLS coefficients even though they might be valid. The remedy to this is usually a transformation on $Y$ to make it more symmetrical.
**Non linearity on covariate**
$Y = 6 + 1.3 x ^2 + \epsilon$
```
x = x_fix.copy() / 10
e = e_fix.copy()
y = true_params["b0"] + true_params["b1"] * x**2 + e
data = pd.DataFrame({"x": x, "e": e, "y": y})
print("Model: y ~ x")
regressor = smf.ols(formula="y ~ x", data=data).fit()
ax = plot_lmreg(data=data, x="x", y="y", lowess=True)
plt.savefig(f"../imgs/simul_model_nonlin_cov_false.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
plot_resid(regressor, data)
plt.savefig(f"../imgs/simul_resid_nonlin_cov_false.png", bbox_inches="tight")
plt.show()
print("Model: y ~ x**2")
data["x2"] = data["x"]**2
regressor = smf.ols(formula="y ~ x2", data=data).fit()
ax = plot_lmreg(data=data, x="x2", y="y", lowess=True)
plt.savefig(f"../imgs/simul_model_nonlin_cov_true.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data, x="x2")
plot_resid(regressor, data, x="x2")
plt.savefig(f"../imgs/simul_resid_nonlin_cov_true.png", bbox_inches="tight")
plt.show()
```
**Non linearity on response**
$Y^2 = 6 + 1.3 x + \epsilon$
```
setting = "canonical"
x = x_fix.copy()
e = e_fix.copy()
y = 100+true_params["b0"] + true_params["b1"] * x + e
y = y**2
data = pd.DataFrame({"x": x, "e": e, "y": y})
print("Model: y ~ x")
regressor = smf.ols(formula="y ~ x", data=data).fit()
ax = plot_lmreg(data=data, x="x", y="y", lowess=True)
plt.savefig(f"../imgs/simul_model_nonlin_y_false.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
data["qresid"] = calculate_qresid(regressor, data)
plot_resid(regressor, data)
plt.savefig(f"../imgs/simul_resid_nonlin_y_false.png", bbox_inches="tight")
plt.show()
print("Model: sqrt(y) ~ x")
data["sqrt_y"] = np.sqrt(data["y"])
regressor = smf.ols(formula="sqrt_y ~ x", data=data).fit()
ax = plot_lmreg(data=data, x="x", y="sqrt_y", lowess=True)
plt.savefig(f"../imgs/simul_model_nonlin_y_true.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
data["qresid"] = calculate_qresid(regressor, data, y="sqrt_y")
plot_resid(regressor, data, y="sqrt_y")
plt.savefig(f"../imgs/simul_resid_nonlin_y_true.png", bbox_inches="tight")
plt.show()
```
**Non independent**
Positive-correlated data in a same with independent data between days.
```
x = x_fix.copy()
data = pd.DataFrame({"x": x, "e": None, "y": None})
data["date"] = pd.Series(range(n//5)).sample(n, replace=True, random_state=0).values
for idx, [group, df_group] in enumerate(data.groupby("date")):
m = len(df_group)
cov = np.full((m, m), 0.9 * true_params["scale"]**2)
np.fill_diagonal(cov, true_params["scale"]**2)
np.random.seed(idx)
data.loc[data["date"] == group, "e"] = np.random.multivariate_normal(np.zeros(m), cov, 1)[0]
# e = np.random.normal(0, true_params["scale"], 1)
# np.random.seed(seed)
# data.loc[data["date"] == group, "e"] = e + np.random.normal(0, true_params["scale"]/2, m)
data["y"] = true_params["b0"] + true_params["b1"] * data["x"] + data["e"]
data = data.astype("float")
print("Model: y ~ x")
regressor = smf.ols(formula="y ~ x", data=data).fit()
print(regressor.summary())
ax = plot_lmreg(data=data, x="x", y="y")
plt.savefig(f"../imgs/simul_model_dep.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
plot_resid(regressor, data.set_index("date"))
plt.savefig(f"../imgs/simul_resid_dep.png", bbox_inches="tight")
plt.show()
print("Model: y ~ x; aggregated residuals")
regressor = smf.ols(formula="y ~ x", data=data).fit()
print(regressor.summary())
ax = plot_lmreg(data=data, x="x", y="y")
plt.savefig(f"../imgs/simul_model_dep_agg.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
data = data.groupby("date").mean()
plot_resid(regressor, data.set_index("x"))
plt.savefig(f"../imgs/simul_resid_dep_agg.png", bbox_inches="tight")
plt.show()
print("Model: y ~ date")
data = data.groupby("date").mean().reset_index()
regressor = smf.ols(formula="y ~ date", data=data).fit()
print(regressor.summary())
ax = plot_lmreg(data=data, x="date", y="y", lowess=True)
plt.savefig(f"../imgs/simul_model_dep_date.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data, x="date")
plot_resid(regressor, data.set_index("date"), x="date")
plt.savefig(f"../imgs/simul_resid_dep_date.png", bbox_inches="tight")
plt.show()
```
**Non-constant variance**
```
setting = "canonical"
x = x_fix.copy()
e = e_fix.copy()
mu = 100 + true_params["b1"] * x
e = (mu)**0.5 * e
y = true_params["b0"] + true_params["b1"] * x + e
data = pd.DataFrame({"x": x, "e": e, "y": y})
print("Model: y ~ x")
regressor = smf.ols(formula="y ~ x", data=data).fit()
ax = plot_lmreg(data=data, x="x", y="y")
sns.regplot(x="x",y="y", data=data, ax=ax,
lowess=True, scatter=False,
color=brand.NU_DARK_PURPLE_MATPLOT, line_kws={"linestyle": "--"})
plt.savefig(f"../imgs/simul_model_nonconst_var.png", bbox_inches="tight")
plt.show()
data["pred"] = predict(regressor, data)
data["qresid"] = calculate_qresid(regressor, data)
plot_resid(regressor, data)
plt.savefig(f"../imgs/simul_model_nonconst_var.png", bbox_inches="tight")
plt.show()
```
|
github_jupyter
|
# 實驗:實作InceptionV3網路架構
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/taipeitechmmslab/MMSLAB-TF2/blob/master/Lab8.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/taipeitechmmslab/MMSLAB-TF2/blob/master/Lab8.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
### Import必要套件
```
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
```
---
## Keras Applications
### 創建InceptionV3網路架構
- 輸入大小(預設):(299, 299, 3)
- 權重(預設):`imagenet`
- 輸出類別(預設):1000個類別
```
model = tf.keras.applications.InceptionV3(include_top=True, weights='imagenet')
```
透過`model.summary`可以察看網路模型的每一層資訊:
```
model.summary()
```
將網路模型儲存到TensorBoard上:
```
model_tb = tf.keras.callbacks.TensorBoard(log_dir='lab8-logs-inceptionv3-keras')
model_tb.set_model(model)
```
### 資料前處理和輸出解碼
使用別人提供的模型預測,需要注意兩件事情,1)訓練時的資料前處理,2)輸出結果對應到的類別。
Keras很貼心的提供每個模型相對應的資料預處理和輸出解碼的函式。
- preprocess_input:網路架構的影像前處理(注意:每一個模型在訓練時做的資料正規化並不會相同,例如:VGG、ResNet-50輸入影像為0~255的數值,而inception_v3、xception輸入影像為-1~1的數值)。
- decode_predictions:對應網路架構的輸出解碼。
Import資料預處理和輸出解碼的函式:
```
from tensorflow.keras.applications.inception_v3 import preprocess_input
from tensorflow.keras.applications.inception_v3 import decode_predictions
```
### 預測輸出結果
創建影像讀取的函式:讀取影像,並將影像大小縮放大299x299x3的尺寸。
```
def read_img(img_path, resize=(299,299)):
img_string = tf.io.read_file(img_path) # 讀取檔案
img_decode = tf.image.decode_image(img_string) # 將檔案以影像格式來解碼
img_decode = tf.image.resize(img_decode, resize) # 將影像resize到網路輸入大小
# 將影像格式增加到4維(batch, height, width, channels),模型預測要求格式
img_decode = tf.expand_dims(img_decode, axis=0)
return img_decode
```
從資料夾中讀取一張影像(elephant.jpg)作為測試:
```
img_path = 'image/elephant.jpg'
img = read_img(img_path) # 透過剛創建的函式讀取影像
plt.imshow(tf.cast(img, tf.uint8)[0]) # 透過matplotlib顯示圖片需將影像轉為Integers
```
預測結果:
```
img = preprocess_input(img) # 影像前處理
preds = model.predict(img) # 預測圖片
print("Predicted:", decode_predictions(preds, top=3)[0]) # 輸出預測最高的三個類別
```
---
## TensorFlow Hub
Install:
```
pip install tensorflow-hub
```
Search:
https://tfhub.dev/
```
import tensorflow as tf
import tensorflow_hub as hub
```
### 創建Inception V3模型
Model:
https://tfhub.dev/google/tf2-preview/inception_v3/classification/2
num_classes = 1001 classes of the classification from the original training
Image:height x width = 299 x 299 pixels, 3 RGB color values in the range 0~1
labels file: https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt
```
# Inception V3預訓練模型的URL
module_url = "https://tfhub.dev/google/tf2-preview/inception_v3/classification/4"
# 創建一個Sequential Model,網路模型裡面包含了Inception V3網路層
model = tf.keras.Sequential([
# hub.KerasLayer將載入的Inception V3模型封裝成網路層(Keras Layer)
hub.KerasLayer(module_url,
input_shape=(299, 299, 3), # 模型輸入大小
output_shape=(1001, ), # 模型輸出大小
name='Inception_v3') # 網路層名稱
])
model.summary()
```
### 資料前處理和輸出解碼
創建資料前處理函式:
```
def read_img(img_path, resize=(299,299)):
img_string = tf.io.read_file(img_path) # 讀取檔案
img_decode = tf.image.decode_image(img_string) # 將檔案以影像格式來解碼
img_decode = tf.image.resize(img_decode, resize) # 將影像resize到網路輸入大小
img_decode = img_decode / 255.0 # 對影像做正規畫,將數值縮放到0~1之間
# 將影像格式增加到4維(batch, height, width, channels),模型預測要求格式
img_decode = tf.expand_dims(img_decode, axis=0) #
return img_decode
```
創建輸出解碼器:
```
# 下載ImageNet 的標籤檔
labels_path = tf.keras.utils.get_file('ImageNetLabels.txt', 'https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt')
# 讀取標籤檔中的數據
with open(labels_path) as file:
lines = file.read().splitlines()
print(lines) # 顯示讀取的標籤
imagenet_labels = np.array(lines) # 將標籤轉成numpy array做為網路輸出的解碼器
```
### 預測輸出結果
從資料夾中讀取一張影像(elephant.jpg)作為測試:
```
img_path = 'image/elephant.jpg'
img = read_img(img_path) # 透過剛創建的函式讀取影像
plt.imshow(img[0])
```
預測結果:
```
preds = model.predict(img) # 預測圖片
index = np.argmax(preds) # 取得預測結果最大的Index
print("Predicted:", imagenet_labels[index]) # 透過解碼器將輸出轉成標籤
```
顯示最好的三個預測:
```
# 取得預測結果最大的三個indexs
top3_indexs = np.argsort(preds)[0, ::-1][:3]
print("Predicted:", imagenet_labels[top3_indexs]) # 透過解碼器將輸出轉成標籤
```
|
github_jupyter
|
# Distribuciones de probabilidad
```
# Importamos librerías a trabajar en todas las simulaciones
import matplotlib.pyplot as plt
import numpy as np
from itertools import cycle # Librería para hacer ciclos
import scipy.stats as st # Librería estadística
from math import factorial as fac # Importo la operación factorial
%matplotlib inline
```
## 1. Distrución de probabilidad uniforme
$X\sim U(a,b)$ Parámetros $a,b \rightarrow $ intervalo
$$\textbf{Función de densidad de probabilidad}\\f(x)=\begin{cases}\frac{1}{b-a} & a\leq x \leq b\\0& \text{otro caso}\end{cases}$$
$$ \textbf{Función de distribución de probabilidad}\\F(x)=\begin{cases}0& x<a\\\frac{x-a}{b-a} & a\leq x \leq b\\1& x\geq b\end{cases}$$

### Uso en python
```
a,b=1,2 # Interval
U = np.random.uniform(a,b)
U
st.uniform.rvs(loc=a, scale=b, size=2)
```
## 2. Distribución normal
$X\sim N(\mu,\sigma^2)$ Parámetros: Media=$\mu$ y varianza=$\sigma^2$
$$ \textbf{Función de densidad de probabilidad}\\ f(x)= \frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}$$
$$ \textbf{Función de distribución de probabilidad}\\ F(x)= \frac{1}{\sigma\sqrt(2\pi)}\int_{-\infty}^{x}e^{\frac{-(v-\mu)^2}{2\sigma^2}}dv$$

### Propiedades

### Estandarización de variables aleatorias normales
Como consecuencia de que la función normal es simétrica en $\mu$ es posible relacionar todas las variables aleatorias normales con la distribución normal estándar.
Si $X\sim N(\mu ,\sigma ^{2})$, entonces
$$Z = \frac{X - \mu}{\sigma}$$
es una variable aleatoria normal estándar: $Z\sim N(0,1)$.
### El Teorema del Límite Central
El Teorema del límite central establece que bajo ciertas condiciones (como pueden ser independientes e idénticamente distribuidas con varianza finita), la suma de un gran número de variables aleatorias se distribuye aproximadamente como una normal. **(Hablar de la importancia del uso)**
### Incidencia
Cuando en un fenómeno se sospecha la presencia de un gran número de pequeñas causas actuando de forma aditiva e independiente es razonable pensar que las observaciones serán "normales". **(Debido al TLC)**
Hay causas que pueden actuar de forma multiplicativa (más que aditiva). En este caso, la suposición de normalidad no está justificada y es el logaritmo de la variable en cuestión el que estaría normalmente distribuido. **(log-normal)**.
### Ejemplo de aplicación
En variables financieras, el modelo de Black-Scholes, el cúal es empleado para estimar el valor actual de una opción europea para la compra (Call), o venta (Put), de acciones en una fecha futura, supone normalidad en algunas variables económicas. ver:https://es.wikipedia.org/wiki/Modelo_de_Black-Scholes para información adicional.
> Referencia: https://es.wikipedia.org/wiki/Distribuci%C3%B3n_normal
### Uso en python
```
mu, sigma = 0, 0.1 # mean and standard deviation
N = np.random.normal(mu, sigma,5)
N
st.norm.rvs(loc=a, scale=sigma, size=5)
```
## 3. Distribución exponencial
$X\sim Exp(\beta)$ Parámetros: Media $\beta>0$ o tasa = $\lambda = 1/\beta$
$$\textbf{Función de densidad de probabilidad}\\f(x) = \frac{1}{\beta} e^{-\frac{x}{\beta}}$$
$$\textbf{Función de distribución de probabilidad}\\F(x) = 1-e^{-\frac{x}{\beta}}$$

### Ejemplos
Ejemplos para la distribución exponencial **es la distribución de la longitud de los intervalos de una variable continua que transcurren entre dos sucesos**, que se distribuyen según la distribución de Poisson.
- El tiempo transcurrido en un centro de llamadas hasta recibir la primera llamada del día se podría modelar como una exponencial.
- El intervalo de tiempo entre terremotos (de una determinada magnitud) sigue una distribución exponencial.
- Supongamos una máquina que produce hilo de alambre, la cantidad de metros de alambre hasta encontrar una falla en el alambre se podría modelar como una exponencial.
- En fiabilidad de sistemas, un dispositivo con tasa de fallo constante sigue una distribución exponencial.
### Relaciones
La suma de k variables aleatorias independientes de distribución exponencial con parámetro $\lambda$ es una variable aleatoria de distribución de Erlang.
> Referencia: https://en.wikipedia.org/wiki/Exponential_distribution
### Uso en python
```
beta = 4
E = np.random.exponential(beta,1)
E
st.expon
```
## 4. Distribución erlang
Parámetros: Tamaño $k \in \mathbb{N}$, escala=$\frac{1}{\beta}$
$$\textbf{Función de densidad de probabilidad}\\f(x)=x^{k-1}\frac{e^{-x/\beta}}{\beta^k\Gamma(k)}\equiv x^{k-1}\frac{e^{-x/\beta}}{\beta^k(k-1)!}$$
$$\textbf{Función de distribución de probabilidad}\\F(x)=1-\sum_{n=0}^{k-1}\frac{1}{n!}e^{-\frac{1}{\beta}x}\big(\frac{x}{\beta}\big)^n$$

### Simplificaciones
La distribución Erlang con tamaño $k=1$ se simplifica a una distribución exponencial. Esta es una distribución de la suma de $k$ variables exponenciales donde cada una tiene media $\beta$
### Ocurrencia
**Tiempos de espera**
Los eventos que ocurren de forma independiente con una tasa promedio se modelan con un proceso de Poisson. Los tiempos de espera entre k ocurrencias del evento son distribuidos Erlang. (La cuestión relacionada con el número de eventos en una cantidad de tiempo dada descrita por una distribución de Poisson).
Las fórmulas de Erlang se han utilizado en economía de negocios para describir los tiempos entre compras de un activo.
> Referencia: https://en.wikipedia.org/wiki/Erlang_distribution
### Uso en python
```
N = 10000 # Número de muestras
k,scale = 3,1/4 # Parámetros de la distribución
E1 = st.erlang.rvs(k,scale=scale,size=N)
E2 = np.random.gamma(k,scale,N) # Erlang como caso particular de la distribución gamma
plt.figure(1,figsize=[12,4])
plt.subplot(121)
plt.hist(E1,50,density=True,label='Usando Lib. scipy')
plt.legend()
plt.subplot(122)
plt.hist(E2,50,density=True,label='Usando Lib. numpy')
plt.legend()
plt.show()
```
## 5. Distribución binomial
$X\sim B(n,p)$ Parámetros: $n$ y $p$
$$\textbf{Función de densidad de probabilidad}\\p_i=P(X=i)={n \choose i}p^i(1-p)^{n-i}= \frac{n!}{i!(n-i)!}p^i(1-p)^{n-i},\quad i=0,1,\cdots,n$$
>Recordar:$$p_{i+1}=\frac{n-i}{i+1}\frac{p}{1-p} p_i $$
$$\textbf{Función de distribución de probabilidad}\\F(x)=\sum_{i=0}^{k-1}\frac{n!}{i!(n-i)!}p^i(1-p)^{n-i}$$
## Método vectorizado
```
# Función que calcula la probabilidad acumulada optimizada
def proba_binomial(n:'Cantidad de ensayos',p:'Probabilidad de los eventos',
N:'Cantidad de puntos a graficar'):
Pr = np.zeros(N)
Pr[0] = (1-p)**n
def pr(i):
nonlocal Pr
c = p/(1-p)
Pr[i+1]=(c*(n-i)/(i+1))*Pr[i]
# Lleno el vector Pr usando compresión de listas
[pr(i) for i in range(N-1)]
return Pr
# Comprobación de función creada
# Distintos parámetros para graficar la función binomial
n = [50,100,150]
# Parámetro p de la dristribución
p = 0.5
# Resultado usando método convencional
P = list(map(lambda x,n: proba_binomial(n,p,100),range(len(n)),n))
P = np.asmatrix(P)
print(P.shape)
def grafica_distribucion_prob(P:'Matriz de probabilidades binomiales'):
# Gráfica de densidad de probabilidad
fig,(ax1,ax2) = plt.subplots(1,2)
fig.set_figwidth(10)
ax1.plot(P.T,'o',markersize=3)
ax1.legend(['n=50','n=100','n=150'])
ax1.set_title('Densidad de probabilidad')
# ax1.show()
# Probabilidad acumulada
F = np.cumsum(P,axis=1)
# plt.figure(2)
ax2.plot(F.T,'o',markersize=3)
ax2.legend(['n=%d'%n[0],'n=%d'%n[1],'n=%d'%n[2]])
ax2.set_title('Distribución acumulada')
plt.show()
st.binom
# Gráfica del método convencional y vectorizado
grafica_distribucion_prob(P)
```
### Características
La distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de **n ensayos de Bernoulli independientes entre sí**, con una probabilidad `fija` p de ocurrencia del éxito entre los ensayos. A lo que se denomina «éxito», tiene una probabilidad de ocurrencia p y al otro, «fracaso», tiene una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se designa por $X$ a la variable que mide el número de éxitos que se han producido en los n experimentos.
Cuando se dan estas circunstancias, se dice que la variable $X$ sigue una distribución de probabilidad binomial, y se denota $X\sim B(n,p)$.
### Ejemplo
Supongamos que se lanza un dado (con 6 caras) 51 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una $X \sim B(51, 1/6)$ y la probabilidad sería $P(X=20)$:
$$P(X=20)={51 \choose 20}(1/6)^{20}(1-1/6)^{51-20} $$
```
n = 51; p=1/6; X=20
print('P(X=20)=',st.binom(n,p).pmf(X))
```
### Relaciones con otras variables aleatorias
Si n tiende a infinito y p es tal que el producto entre ambos parámetros tiende a $\lambda$, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro $\lambda$.
Por último, se cumple que cuando $p =0.5$ y n es muy grande (usualmente se exige que $n\geq 30$) la distribución binomial puede aproximarse mediante la distribución normal, con parámetros $\mu=np,\sigma^2=np(1-p)$.
> Referencia: https://en.wikipedia.org/wiki/Binomial_distribution
```
p = .5; n = 50
mu = n*p; sigma = np.sqrt(n*p*(1-p))
# Usando nuetra función creada
Bi = proba_binomial(n,p,n)
plt.figure(1,figsize=[10,5])
plt.subplot(121)
plt.plot(Bi,'o')
plt.title('Distribución binomial n=%i,p=%0.2f'%(n,p))
# Usando la función de la librería scipy para graficar la normal
x = np.arange(0,n)
Bi_norm = st.norm.pdf(x,loc=mu,scale=sigma)
plt.subplot(122)
plt.plot(Bi_norm,'o')
plt.title('Distribución~normal(np,np(1-p))')
plt.show()
```
## 6. Distribución Poisson
Parámetros: media=$\lambda>0 \in \mathbb{R}$, N°Ocurrencias = k
- k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
- λ es un parámetro positivo que representa el <font color ='red'>**número de veces que se espera que ocurra el fenómeno durante un intervalo dado**</font>. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40
$$\textbf{Función de densidad de probabilidad}\\p(k)=\frac{\lambda^k e^{-\lambda}}{k!},\quad k\in \mathbb{N}$$
### Aplicación
El número de sucesos en un intervalo de tiempo dado es una variable aleatoria de distribución de Poisson donde $\lambda$ es la media de números de sucesos en este intervalo.
### Relación con distribución Erlang o Gamma
El tiempo hasta que ocurre el suceso número k en un proceso de Poisson de intensidad $\lambda$ es una variable aleatoria con distribución gamma o (lo mismo) con distribución de Erlang con $ \beta =1/\lambda $
### Aproximación normal
Como consecuencia del teorema central del límite, para valores grandes de $\lambda$ , una variable aleatoria de Poisson X puede aproximarse por otra normal, con parámetros $\mu=\sigma^2=\lambda$. Por otro lado, si el cociente
$$Y=\frac{X-\lambda}{\sqrt{\lambda}}$$
converge a una distribución normal de media 0 y varianza 1.
### Ejemplo
Si el 2% de los libros encuadernados en cierto taller tiene encuadernación defectuosa, para obtener la probabilidad de que 5 de 400 libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson. En este caso concreto, k es 5 y, λ, el valor esperado de libros defectuosos es el 2% de 400, es decir, 8. Por lo tanto, la probabilidad buscada es
$$P(5;8)={\frac {8^{5}e^{-8}}{5!}}=0,092$$
> Referencia: https://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Poisson
```
k=5; Lamda = 8
print('P(5;8)=',st.poisson(Lamda).pmf(k))
```
## Usando el paquete estadístico `stats`
```
# Parámetros
Lamda = [8,20]
k=np.arange(0,40);
# Distribución de probabilidad
P = np.array([st.poisson(Lamda[i]).pmf(k) for i in range(len(Lamda))])
# Distribución de probabilidad acumulada
P_acum = np.array([st.poisson(Lamda[i]).cdf(k) for i in range(len(Lamda))])
fig,[ax1,ax2] = plt.subplots(1,2,sharey=False,figsize=[12,4])
ax1.plot(P.T,'o',markersize=3)
ax1.legend(['$\lambda$=%d'%i for i in Lamda])
ax1.title.set_text('Distribución de probabilidad')
ax2.plot(P_acum.T,'o',markersize=3)
[ax2.hlines(P_acum[i,:],range(len(k)),range(1,len(k)+1)) for i in range(len(Lamda))]
plt.legend(['$\lambda$=%d'%i for i in Lamda])
ax2.title.set_text('Distribución de probabilidad')
plt.show()
# P_acum.shape
```
## Usando las expresiones matemáticas
```
import scipy.special as sps
p = lambda k,l:(l**k*np.exp(-l))/sps.gamma(k+1)
k = np.arange(0,50)
l = [1,10,20,30]
P = np.asmatrix(list(map(lambda x:p(k,x*np.ones(len(k))),l))).T
print(P.shape)
plt.figure(1,figsize=[12,4])
plt.subplot(121)
plt.plot(P,'o',markersize=3)
plt.legend(['$\lambda$=%d'%i for i in l])
plt.title('Distribución de probabilidad')
# Probabilidad acumulada
P_ac = np.cumsum(P,axis=0)
plt.subplot(122)
plt.plot(P_ac,'o',markersize=3)
[plt.hlines(P_ac[:,i],range(len(P_ac)),range(1,len(P_ac)+1)) for i in range(len(l))]
plt.legend(['$\lambda$=%d'%i for i in l])
plt.title('Distribución de probabilidad acumulada')
plt.show()
```

## 7. Distribuciónn triangular
Parámetros:
- a : $a\in (-\infty ,\infty)$
- b : $b > a$
- c : $a\leq c\leq b$
- Soporte: $a\leq x\leq b$
$$\textbf{Función de densidad de probabilidad}\\f(x|a,b,c)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{para }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{para }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{para }}c<x\leq b,\\[4pt]0&{\text{para otros casos}}\end{cases}}$$
$$\textbf{Función de distribución de probabilidad}\\F(x|a,b,c)={\begin{cases}{0}&{\text{para }}x\leq a,\\[4pt]{\frac {(x-a)^2}{(b-a)(c-a)}}&{\text{para }}a< x\leq c,\\[4pt]{1-\frac{(b-x)^2}{(b-a)(b-c)}}&{\text{para }}c<x< b,\\[4pt]1&{\text{para }}b\leq x\end{cases}}$$

### Uso de la distribución triangular
La distribución triangular es habitualmente empleada como una descripción subjetiva de una población para la que sólo se cuenta con una cantidad limitada de datos muestrales y, especialmente en casos en que la relación entre variables es conocida pero los **datos son escasos** (posiblemente porque es alto el costo de recolectarlos). Está basada en un conocimiento del mínimo y el máximo como el del valor modal. Por estos motivos, la Distribución Triangular ha sido denominada como la de "falta de precisión" o de información.
> Referencia: https://en.wikipedia.org/wiki/Triangular_distribution
# <font color ='red'> Tarea (Opcional)
Generar valores aleatorios para la siguiente distribución de probabilidad
$$f(x)=\begin{cases}\frac{2}{(c-a)(b-a)}(x-a), & a\leq x \leq b\\ \frac{-2}{(c-a)(c-b)}(x-c),& b\leq x \leq c \end{cases}$$ con a=1; b=2; c=5
1. Usando el método de la transformada inversa.
2. Usando el método de aceptación y rechazo.
3. En la librería `import scipy.stats as st` hay una función que genera variables aleatorias triangulares `st.triang.pdf(x, c, loc, scale)` donde "c,loc,scale" son los parámetros de esta distribución (similares a los que nuestra función se llaman a,b,c, PERO NO IGUALES). Explorar el help de python para encontrar la equivalencia entre los parámetros "c,loc,scale" y los parámetros de nuestra función con parámetros "a,b,c". La solución esperada es como se muestra a continuación:

4. Generar 1000 variables aleatorias usando la función creada en el punto 2 y usando la función `st.triang.rvs` y graficar el histograma en dos gráficas diferentes de cada uno de los conjuntos de variables aleatorios creado. Se espera algo como esto:

### La pongo como opcional por que puede aparecer en un quiz o un examen.
# <font color ='red'>Tarea distribuciones de probabilidad:</font>
La tarea debe de realizarse en grupos, los cuales están nombrados en la siguiente tabla. La tarea consiste en modificar una de las páginas que corresponde a el grupo conformado, por ejemplo si eres el grupo 1, debes de modificar la página que corresponde a tu grupo, no ninguna de las otras páginas. En dicha página les voy a pedir que respondan a cada una de las siguientes pregutas, para el próximo viernes 9 de octubre, donde consultan acerca de cada una de las distribuciones de probabilidad asignadas. Lo que necesito que consulten es:
1. Explicación del uso de cada distribución de probabilidad.
2. Utilizar recursos audiovisuales, como videos, tablas, gifts, imágenes, enlace externos, etc, los cuales desde esta plataforma de canvas es posible introducir, en donde expliquen de la forma mas amigable y simple posible, las aplicaciones y usos de las distribuciones de probabilidad asignadas.
3. Consultar en libros, internet, aplicaciones de como usar dichas distribuciones, por qué usarlas y posibles aplicaciones en finanzas.
4. También pueden poner la descripción matemática de dichas distribuciones. Noten que pueden ingresar código latex para poder ingresar ecuaciones y demás.
5. Poner pantallazos del código y resultados de como usar dicha función de distribución de probabilidad en python. Algo como esto
> Distribución poisson
> - Distribución de probabilidad y distribución acumulada (usando el paquete estadístico stats)
> 
> - Gráficas para distintos parámetros en este caso $\lambda = [8,30]$
> 
6. ¿Cómo pudieran responder la pregunta P(X<b)=** ? Para el caso de la distribución poisson exploren el comando `st.poisson(Lamda).ppf(b)`
La calificación estará basada, en la creatividad y el manejo que tengan de cada una de sus distribuciones de probabilidad a la hora de la exposición.
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Oscar David Jaramillo Zuluaga
</footer>
|
github_jupyter
|
```
%matplotlib notebook
import pickle
import numpy as np
import matplotlib.pyplot as plt
from refnx.reflect import SLD, Slab, ReflectModel, MixedReflectModel
from refnx.dataset import ReflectDataset as RD
from refnx.analysis import Objective, CurveFitter, PDF, Parameter, process_chain, load_chain
from FreeformVFP import FreeformVFP
# Version numbers allow you to repeat the analysis on your computer and obtain identical results.
import refnx, scipy
refnx.version.version, np.version.version, scipy.version.version
```
# Load data
Three datasets are included, pNIPAM at 25 °C, 32.5 °C and 40 °C.
pNIPAM is thermoresponsive; the 25 °C is a swollen, diffuse layer, whilst the 40 °C data is a collapsed slab.
```
data = RD("pNIPAM brush in d2o at 25C.dat")
# data = RD("pNIPAM brush in d2o at 32C.dat")
# data = RD("pNIPAM brush in d2o at 40C.dat")
```
# Define materials and slab components
For simplicity some parameters that may normally have been allowed to vary have been set to predetermined optimum values.
```
si = SLD(2.07, 'si')
sio2 = SLD(2.9, 'sio2')
d2o = SLD(6.23 , 'd2o')
polymer = SLD(0.81, 'polymer')
si_l = si(0, 0)
sio2_l = sio2(20, 4.8)
d2o_l = d2o(0, 0)
```
# Create the freeform component
```
NUM_KNOTS = 4
#Polymer layer 1
polymer_0 = polymer(2, 0.5)
# Polymer-Solvent interface (spline)
polymer_vfp = FreeformVFP(adsorbed_amount=120,
vff=[0.6] * NUM_KNOTS,
dzf=[1/(NUM_KNOTS + 1)] * (NUM_KNOTS + 1),
polymer_sld=polymer,
name='freeform vfp',
left_slabs=[polymer_0])
```
# Set parameter bounds
```
sio2.real.setp(vary=True, bounds=(2.8, 3.47))
polymer_0.thick.setp(vary=True, bounds=(2, 20))
polymer_0.vfsolv.setp(vary=True, bounds=(0.1, 0.7))
polymer_vfp.adsorbed_amount.setp(vary=True, bounds=(100, 130))
# We can enforce monotonicity through the bounds we place on the fractional volume fraction changes.
enforce_mono = True
if enforce_mono:
bounds = (0.1, 1)
else:
bounds = (0.1, 1.5)
# Here we set the bounds on the knot locations
for idx in range(NUM_KNOTS):
polymer_vfp.vff[idx].setp(vary=True, bounds=bounds)
polymer_vfp.dzf[idx].setp(vary=True, bounds=(0.05, 1))
polymer_vfp.dzf[-1].setp(vary=True, bounds=(0.05, 1))
polymer_vfp.dzf[0].setp(vary=True, bounds=(0.005, 1))
```
# Create the structure, model, objective
```
structure = si_l | sio2_l | polymer_0 | polymer_vfp | d2o_l
# contracting the slab representation reduces computation time.
structure.contract = 1.5
model = ReflectModel(structure)
model.bkg.setp(vary=True, bounds=(1e-6, 1e-5))
objective = Objective(model, data)
fitter= CurveFitter(objective)
fitter.fit('differential_evolution');
fig, [ax_vfp, ax_sld, ax_refl] = plt.subplots(1, 3, figsize=(10,3), dpi=90)
z = np.linspace(-50, 1750, 2000)
ax_vfp.plot(*polymer_vfp.profile())
ax_sld.plot(*structure.sld_profile(z))
ax_refl.plot(data.x, objective.generative())
ax_refl.errorbar(data.x, data.y, yerr=data.y_err)
ax_refl.set_yscale('log')
fig.tight_layout()
```
|
github_jupyter
|
# Iterative reconstruction of undersampled MR data
This demonstration shows how to hande undersampled data
and how to write a simple iterative reconstruction algorithm with
the acquisition model.
This demo is a 'script', i.e. intended to be run step by step in a
Python notebook such as Jupyter. It is organised in 'cells'. Jupyter displays these
cells nicely and allows you to run each cell on its own.
First version: 27th of March 2019
Updated: 26nd of June 2021
Author: Johannes Mayer, Christoph Kolbitsch
CCP SyneRBI Synergistic Image Reconstruction Framework (SIRF).
Copyright 2015 - 2017 Rutherford Appleton Laboratory STFC.
Copyright 2015 - 2017 University College London.
Copyright 2015 - 2017, 2019, 2021 Physikalisch-Technische Bundesanstalt.
This is software developed for the Collaborative Computational
Project in Positron Emission Tomography and Magnetic Resonance imaging
(http://www.ccppetmr.ac.uk/).
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
```
#%% make sure figures appears inline and animations works
%matplotlib notebook
# Setup the working directory for the notebook
import notebook_setup
from sirf_exercises import cd_to_working_dir
cd_to_working_dir('MR', 'd_undersampled_reconstructions')
__version__ = '0.1.0'
# import engine module
import sirf.Gadgetron as pMR
from sirf.Utilities import examples_data_path
from sirf_exercises import exercises_data_path
# import further modules
import os, numpy
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from tqdm.auto import trange
```
### Undersampled Reconstruction
#### Goals of this notebook:
- Write a fully sampled reconstruction on your own.
- Obtain knowledge of how to deal with undersampled data.
- User SIRF and Gadgetron to perform a GRAPPA reconstruction.
- Implement an iterative parallel imaging SENSE reconstruction algorithm from scratch.
```
# This is just an auxiliary function
def norm_array( arr ):
min_a = abs(arr).min()
max_a = abs(arr).max()
return (arr - min_a)/(max_a - min_a)
```
### Time to get warmed up again:
Since we deal with undersampled data in this last section, we need to compare it to a reference.
So we need to reconstruct the fully sampled dataset we encountered before.
This is an ideal opportunity to test what we learned and employ the `pMR.FullSampledReconstructor` class from before.
### Programming Task: Fully sampled reconstruction
__Please write code that does the following:__
- create a variable called `full_acq_data` of type `pMR.AcquisitionData` from the file `ptb_resolutionphantom_fully_ismrmrd.h5`
- create a variable called `prep_full_data` and assign it the preprocessed data by calling the function `pMR.preprocess_acquisition_data` on our variable `full_acq_data`
- create a variable called `recon` of type `pMR.FullySampledReconstructor()`
- call the `set_input` method of `recon` on `prep_full_data` to assign our fully sampled dataset to our reconstructor
- call the `process()` method of `recon` without arguments.
- create a variable called `fs_image` and assign it the output of the `get_output` method of `recon`
__Hint:__ if you call a function without arguments, don't forget the empty parenthesis.
#### Don't look at the solution before you tried!
```
# YOUR CODE GOES HERE
# VALIDATION CELL
fs_image_array = fs_image.as_array()
fs_image_array = norm_array(fs_image_array)
fig = plt.figure()
plt.set_cmap('gray')
ax = fig.add_subplot(1,1,1)
ax.imshow( abs(fs_image_array[0,:,:]), vmin=0, vmax=1)
ax.set_title('Fully sampled reconstruction')
ax.axis('off')
# Solution Cell. Don't look if you didn't try!
data_path = exercises_data_path('MR', 'PTB_ACRPhantom_GRAPPA')
filename_full_file = os.path.join(data_path, 'ptb_resolutionphantom_fully_ismrmrd.h5')
full_acq_data = pMR.AcquisitionData(filename_full_file)
prep_full_data = pMR.preprocess_acquisition_data(full_acq_data)
recon = pMR.FullySampledReconstructor()
recon.set_input(prep_full_data)
recon.process()
fs_image = recon.get_output()
# VALIDATION CELL
fs_image_array = fs_image.as_array()
fs_image_array = norm_array(fs_image_array)
fig = plt.figure()
plt.set_cmap('gray')
ax = fig.add_subplot(1,1,1)
ax.imshow( abs(fs_image_array[0,:,:]), vmin=0, vmax=1)
ax.set_title('Fully sampled reconstruction')
ax.axis('off')
# LOADING AND PREPROCESSING DATA FOR THIS SET
filename_grappa_file = os.path.join(data_path, 'ptb_resolutionphantom_GRAPPA4_ismrmrd.h5')
acq_data = pMR.AcquisitionData(filename_grappa_file)
preprocessed_data = pMR.preprocess_acquisition_data(acq_data)
preprocessed_data.sort()
print('Is the data we loaded undersampled? %s' % preprocessed_data.is_undersampled())
#%% RETRIEVE K-SPACE DATA
k_array = preprocessed_data.as_array()
print('Size of k-space %dx%dx%d' % k_array.shape)
#%% SELECT VIEW DATA FROM DIFFERENT COILS
print('Size of k-space %dx%dx%d' % k_array.shape)
num_channels = k_array.shape[1]
print(num_channels)
k_array = norm_array(k_array)
fig = plt.figure()
plt.set_cmap('gray')
for c in range(num_channels):
ax = fig.add_subplot(2,num_channels//2,c+1)
ax.imshow(abs(k_array[:,c,:]), vmin=0, vmax=0.05)
ax.set_title('Coil '+str(c+1))
ax.axis('off')
```
This looks pretty similar to what we had before, so we should be good.
```
# we define a quick fft with sos coil combination to do a standard reconstruction.
def our_fft( k_array ):
image_array = numpy.zeros(k_array.shape, numpy.complex128)
for c in range(num_channels):
image_array[:,c,:] = numpy.fft.fftshift( numpy.fft.ifft2( numpy.fft.ifftshift(k_array[:,c,:])))
# image_array = image_array/image_array.max()
image_array = numpy.sqrt(numpy.sum(numpy.square(numpy.abs(image_array)),1))
return image_array
# now we make a FFT of the data we looked at and compare it to our fully sampled image
image_array_sos = our_fft(k_array)
image_array_sos = norm_array(image_array_sos)
fig = plt.figure()
ax = fig.add_subplot(1,2,1)
ax.imshow(abs(image_array_sos), vmin=0, vmax=1)
ax.set_title('Undersampled')
ax.axis('off')
ax = fig.add_subplot(1,2,2)
ax.imshow(abs(fs_image_array[0,:,:]), vmin=0, vmax=1)
ax.set_title('Fully sampled')
ax.axis('off')
```
### Question:
Please answer the following question for yourself:
- Why is the undersampled reconstruction squeezed, but covers the whole FOV?
```
# NOW LET'S LOOK WHICH PARTS ARE SAMPLED AND WHICH ARE LEFT OUT
# kspace_encode_step_1 gives the phase encoding steps which were performed
which_pe = preprocessed_data.get_ISMRMRD_info('kspace_encode_step_1')
print('The following Phase Encoding (PE) points were sampled: \n')
print(which_pe)
```
#### Observation: approximately 3 out of 4 phase encoding steps are missing.
```
# Fill an array with 1 only if a datapoint was acquired
sampling_mask = numpy.zeros([256,256])
for pe in which_pe:
sampling_mask[pe,:] = 1
# PLOT THE SAMPLING MASK
fig = plt.figure()
plt.set_cmap('gray')
ax = fig.add_subplot(1,1,1)
ax.imshow( sampling_mask, vmin=0, vmax=1)
ax.set_title('Sampling pattern of a GRAPPA acquisition')
plt.xlabel('Frequency encoding')
plt.ylabel('Phase encoding')
#ax.axis('off')
```
We notice that $112 = \frac{256}{4} + 48$.
This means the around the center of k-space is densely sampled containing 48 readout lines.
The outside of k-space is undersampled by a factor of 4.
### Workaround: 'zero-fill' the k-space data
Since the artifacts seem to be related to the shape of the data, let's just unsqueeze the shape into the correct one.
Somehow we need to supply more datapoints to our FFT. But can we just add datapoints? This will corrupt the data!
Actually, a Fourier transform is just a sum weighted by a phase:
$$
f(x) = \sum_k e^{j k x} \cdot F(k)
$$
So it does not mind if we add a data point $F(k) = 0$ at a position we didn't sample!
This means we make a larger array, __add our data in the correct spots__, and the gaps we fill with zeros. The correct spots are given by our sampling mask!
```
k_shape = [sampling_mask.shape[0], num_channels, sampling_mask.shape[1]]
zf_k_array = numpy.zeros(k_shape, numpy.complex128)
for i in range(k_array.shape[0]):
zf_k_array[which_pe[i],:,:] = k_array[i,:,:]
fig = plt.figure()
plt.set_cmap('gray')
for c in range(num_channels):
ax = fig.add_subplot(2,num_channels//2,c+1)
ax.imshow(abs(zf_k_array[:,c,:]), vmin=0, vmax=0.05)
ax.set_title('Coil '+str(c+1))
ax.axis('off')
# Reconstruct the zero-filled data and take a look
zf_recon = our_fft( zf_k_array)
zf_recon = norm_array(zf_recon)
fig = plt.figure()
ax = fig.add_subplot(1,2,1)
ax.imshow(abs(zf_recon), vmin=0, vmax=1)
ax.set_title('Zero-filled Undersampled ')
ax.axis('off')
ax = fig.add_subplot(1,2,2)
ax.imshow(abs(fs_image_array[0,:,:]), vmin=0, vmax=1)
ax.set_title('Fully Sampled ')
ax.axis('off')
```
### Observation:
Bummer. Now the shape is correct, however the artifacts are still present.
- What artifacts appear in the zero-filled reconstruction?
- Why are they artifacts all fine-lined?
- How come they only appear in one direction?
To get rid of these we will need some parallel imaging techniques.
### Coil Sensitivity Map computation
Parallel imaging, this has something to do with exploiting the spatially varying coil sensitivities.
```
# WHICH COILMAPS DO WE GET FROM THIS DATASET?
csm = pMR.CoilSensitivityData()
csm.smoothness = 50
csm.calculate(preprocessed_data)
csm_array = numpy.squeeze(csm.as_array())
csm_array = csm_array.transpose([1,0,2])
fig = plt.figure()
plt.set_cmap('jet')
for c in range(csm_array.shape[1]):
ax = fig.add_subplot(2,num_channels//2,c+1)
ax.imshow(abs(csm_array[:,c,:]))
ax.set_title('Coil '+str(c+1))
ax.axis('off')
plt.set_cmap('gray')
```
### Question:
In practice we would want to use a weighted sum (WS) coil combination technique so any artifacts in the coilmap would directly translate into the combined image. But we didn't see any of the high frequency artifacts!
Please answer the following question:
- Why are there are artifacts in the reconstruction but not in the coilmaps?
We learned before, that parallel imaging is easily able to get rid of undersampling factor R=4.
But to have enough information to estimate coilmaps the center must be fully sampled.
Ergo a perfect acceleration by R=4 is not possible, one needs to spends some time to sample the center densely, to obtain coil sensitivities. Still, $\frac{112}{256} = 0.44$, we acquired 56% faster.
### GRAPPA Reconstruction
GRAPPA is a parallel imaging technique which promises to get rid of undersampling artifacts.
So let's use one of our SIRF classes and see what it can do!
```
# WE DO A GRAPPA RECONSTRUCTION USING SIRF
recon = pMR.CartesianGRAPPAReconstructor()
recon.set_input(preprocessed_data)
recon.compute_gfactors(False)
print('---\n reconstructing...')
recon.process()
# for undersampled acquisition data GRAPPA computes Gfactor images
# in addition to reconstructed ones
grappa_images = recon.get_output()
grappa_images_array = grappa_images.as_array()
grappa_images_array = norm_array(grappa_images_array)
# PLOT THE RESULTS
fig = plt.figure(figsize=(9, 4))
ax = fig.add_subplot(1,3,1)
ax.imshow(abs(zf_recon), vmin=0, vmax=1)
ax.set_title('Zero-filled Undersampled ')
ax.axis('off')
ax = fig.add_subplot(1,3,2)
ax.imshow(abs(grappa_images_array[0,:,:]), vmin=0, vmax=1)
ax.set_title('GRAPPA')
ax.axis('off')
ax = fig.add_subplot(1,3,3)
ax.imshow(abs(fs_image_array[0,:,:]), vmin=0, vmax=1)
ax.set_title('Fully Sampled')
ax.axis('off')
plt.tight_layout()
```
__Well, that was very little code to perform a difficult task!__ That is because we sent our data off to The Gadgetron and they did all the work.
### Question:
In what respect did a GRAPPA reconstruction:
* improve the resulting image?
* deterioate the resulting image?
# GREAT! Now we want to develop our own algorithm and be better than the GRAPPA reconstruction!
## Urgh, let's rather not because we are annoyed by how much code we have to write all the time! Zero filling, coil combining, inverse FFTs. Frankly: terrible!
We want to capture our entire imaging and reconstruction process in one single object and don't care about data structure. Also we don't want to have to sum over coil channels all the time and take care of zero filling, this is just too much work!
When we want to develop some reconstruction algorithm, we want to be able to go from an image $x$ __forward__ to k-space data $y$:
$$ E: x \rightarrow y,$$
implicitly performing multiplication of the image with the coil sensitivities $C_c$ for each channel $c$ and performing an FFT:
$$
E x = y_c = \mathcal{F}( C_c \cdot x).
$$
In iterative image reconstruction we often to apply the so-called __backward__ or __adjoint__ to transform the k-space data into image space. This bundles doing the zero-filling, inverse FFT, and coil combination into one operation:
$$ E^H: y \rightarrow x,$$
implicitly performing everything:
$$
E^H y = x = \sum_c C_c^*\mathcal{F}^{-1}(y)
$$
$E^H$ in this case is the hermitian conjugate of the complex valued operator $E$. It is the combination of transposing and complex conjugation of a matrix: $ E^H = (E^T)^* $. Note, that this is not generally the inverse: $ E^H \neq E^{-1}$
### Enter: AcquisitionModel
In SIRF there exists something called `AcquisitionModel`, in the literature also referenced as and Encoding operator $E$, *E* for encoding.
```
# NOW WE GENERATE THE ACQUISITION MODEL
E = pMR.AcquisitionModel(preprocessed_data, grappa_images)
# We need help again to see what this thing here can do
help(E)
# to supply coil info to the acquisition model we use the dedicated method
E.set_coil_sensitivity_maps(csm)
# Now we can hop back from k-space into image space in just one line:
aq_model_image = E.backward( preprocessed_data )
```
Well this is not much code any more. Suddenly implementing our own iterative algorithm seems feasible!
### QUESTION
BEFORE YOU RUN THE NEXT CELL AND LOOK AT THE PLOT:
In the next plot the image stored in `aq_model_image_array` will be shown, i.e. $x = E^H y$.
Based on the discussion what the AcquisitionModel E does, what do you expect the reconstruction to look like?
- Is it squeezed or is it the correct size?
- Does it contain artifacts? If so, which ones?
```
aq_model_image_array = norm_array(aq_model_image.as_array())
fig = plt.figure()
plt.set_cmap('gray')
ax = fig.add_subplot(1,1,1)
ax.imshow(abs(aq_model_image_array[0,:,:]))
ax.set_title('Result Backward Method of E ')
ax.axis('off')
```
__Well, bummer again, the artifacts are still there!__ Of course, the acquisition model is just a compact version of our above code. We need something smarter to kill them off. But it got a bit more homogeneous, due to the weighted coil combination.
# Image Reconstruction as an Inverse Problem
## Iterative Parallel Imaging Reconstruction
In order to employ parallel imagaing, we should look at image reconstruction as an inverse problem.
By "image reconstruction" we actually mean to achieve the following equality:
$$ E x = y,$$ or equivalently
$$ E^H E \, x = E^H y,$$
where $E$ is the encoding operator $x$ is the true image object and $y$ is the MR raw data we acquired.
The task of image reconstruction boils down to optimizing the following function:
$$ \mathcal{C}(x) = \frac{1}{2} \bigl{|} \bigl{|} E \, x - y \bigr{|} \bigr{|}_2^2 \\
\tilde{x} = \min_x \mathcal{C}(x)
$$
To iteratively find the minimum of this cost function, $\tilde{x}$, we need to go through steps of the kind:
1. have a first guess for our image (usually an empty image)
2. generate k-space data from this guess and compute the discrepancy to our acquired data (i.e. evaluate the cost fuction).
3. update our image guess based on the computed discrepancy s.t. the cost will be lowered.
__By iterating steps 2 and 3 many times we will end up at $\tilde{x}$.__
Is that going to be better than a GRAPPA reconstruction?
## Implementing Conjugate Gradient Descent SENSE
Conjugate Gradient (CG) optimization is such an iterative procedure which will quickly result in finding $\tilde{x}$.
We can study the corresponding [Wikipedia Article](https://en.wikipedia.org/wiki/Conjugate_gradient_method#Description_of_the_problem_addressed_by_conjugate_gradients).
This looks like our thang!
For that we need to write a bit of code:
- We already have this encoding operator `E` defined where we can go from image to k-space and back.
- Now we need to implement our first guess
- and somehow we loop through steps 2 and 3 updating our image s.t. the costs are lowered.
They want to compute x in $Ax = b$, we want to compute x in $E^H E x = E^H y$.
This means we need to translate what it says on Wikipedia:
- $x$ = reconstructed image
- $A$ = $E^HE$
- $b$ = $E^H y$
### Programming task
Please write code executing the following task:
- define a fuction named `A_operator`
- it should have one single argument `image`
- it should return $E^H( E (image))$
__Hint 1:__ We defined `E` already. Use it methods `forward` and `backward`. `forward` goes from image space to k-space and `backward` the other way round.
__Hint 2:__ Short reminder on the syntax. The function should look like:
```
def function_name( arugment_name):
variable = code_that_does_something_with ( argument_name )
return variable
```
```
# Write your code here (this is as much space as you need!)
# make sure the name of your function is A_operator
# Don't look at the solution before you tried!
# With this guy we will write our optimization
def A_operator( image ):
return E.backward( E.forward(image) )
```
#### Back to Wikipedia!
Now we have all the tools we need. Now let's write the code to optimize our cost function iteratively.
We don't care too much about maths, but we want the [algorithm](https://en.wikipedia.org/wiki/Conjugate_gradient_method#The_resulting_algorithm).
```
# our images should be the same shape as the GRAPPA output
recon_img = grappa_images
# since we have no knowledge at all of what the image is we start from zero
zero_array = recon_img.as_array()
zero_array.fill(0)
recon_img.fill(zero_array)
# now name the variables the same as in the Wikipedia article:
x = recon_img
y = preprocessed_data
```
### Programming task: Initialize Iterative Reconstruction
Please write code executing the following task:
- Initialize a variable `r` with `r` = $b - Ax$ (`r` stands for residual).
__Hint 0:__ Remember: $b=E^H y$. Don't forget we just defined the A operator!
- Print the type of `r` using Pythons built-in `type` and `print` function. What type of r do you expect? Is it an image, or is it acquisition data?
- After you wrote these two lines run your cell pressing `Ctrl+Enter`, to get the output of the print statement. This will tell you the class of `r`.
- Afterwards, initialize a variable named `rr` with `rr` = $r^\dagger r$. (`rr` stands for r times r). `rr` is the value of the cost function by the way.
__Hint 1:__ No need to access any numpy arrays! Objects of type `sirf.Gadgetron.ImageData` have the method called ` norm()` giving you the square root of the quantity we are looking for.
__Hint 2:__ Python-Power: $c=a^b$ $\equiv$ `c = a**b`.
- Initialize a variable `rr0` with the value of `rr` to store the starting norm of the residuals.
- Initialize a variable `p` with the value of `r`.
```
## WRITE YOUR CODE IN THIS CELL
## Please make sure to name the variables correctly
##### Don't look at the solution before you tried! #############################
############################################################################
# this is our first residual
r = E.backward( y ) - A_operator(x)
# print the type
print('The type of r is: ' + str( type(r) ) )
# this is our cost function at the start
rr = r.norm() ** 2
rr0 = rr
# initialize p
p = r
# now we write down the algorithm
# how many iterative steps do we want
# how low should the cost be
num_iter = 15
sufficiently_small = 1e-7
#prep a container to store the updated image after each iteration, this is just for plotting reasons!
data_shape = numpy.array( x.as_array().shape )
data_shape[0] = num_iter
array_with_iterations = numpy.zeros(data_shape, numpy.complex128)
# HERE WE RUN THE LOOP.
print('Cost for k = 0: ' + str( rr/ rr0) )
with trange(num_iter) as iters:
for k in iters:
Ap = A_operator( p )
alpha = rr / Ap.dot(p)
x = x + alpha * p
r = r - alpha * Ap
beta = r.norm()**2 / rr
rr = r.norm()**2
p = r + beta * p
relative_residual = numpy.sqrt(rr/rr0)
array_with_iterations[k,:,:] = x.as_array()
iters.write('Cost for k = ' +str(k+1) + ': ' + str(relative_residual) )
iters.set_postfix(cost=relative_residual)
if( relative_residual < sufficiently_small ):
iters.write('We achieved our desired accuracy. Stopping iterative reconstruction')
break
if k is num_iter-1:
print('Reached maximum number of iterations. Stopping reconstruction.')
# See how the reconstructed image evolves
fig = plt.figure()
ims = []
for i in range(k):
im = plt.imshow(abs( array_with_iterations[i,:,:]), animated=True)
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=500, blit=True, repeat_delay=0)
plt.show()
## now check out the final result as a still image
recon_arr = norm_array( x.as_array())
plt.set_cmap('gray')
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.imshow(abs(recon_arr[0,:,:]))
ax.set_title('SENSE RECONSTRUCTION')
ax.axis('off')
# Let's Plot
recon_arr = x.as_array()
fig = plt.figure(figsize=(9, 9))
ax = fig.add_subplot(2,2,1)
ax.imshow(abs(aq_model_image_array[0,:,:]))
ax.set_title('UNDERSAMPLED RECONSTRUCTION')
ax.axis('off')
ax = fig.add_subplot(2,2,2)
ax.imshow(abs(grappa_images_array[0,:,:]))
ax.set_title('GRAPPA RECONSTRUCTION')
ax.axis('off')
ax = fig.add_subplot(2,2,3)
ax.imshow(abs(recon_arr[0,:,:]))
ax.set_title('SENSE RECONSTRUCTION')
ax.axis('off')
ax = fig.add_subplot(2,2,4)
ax.imshow(abs(fs_image_array[0,:,:]))
ax.set_title('FULLY SAMPLED RECONSTRUCTION')
ax.axis('off')
plt.tight_layout()
```
### Question: Evaluation SENSE Reconstruction
[So what is better, GRAPPA or SENSE?](https://www.youtube.com/watch?v=XVCtkzIXYzQ)
Please answer the following questions:
- Where is the noise coming from?
- Why has not every high-frequency artifact vanished?
And if you had typed the above code into your computer in 2001 and written a [paper](https://scholar.google.de/scholar?hl=de&as_sdt=0%2C5&q=Advances+in+sensitivity+encoding+with+arbitrary+k%E2%80%90space+trajectories&btnG=) on it, then 18 years later you had a good 1000 citations (plus 6k from the [previous one](https://scholar.google.de/scholar?hl=de&as_sdt=0%2C5&q=SENSE%3A+sensitivity+encoding+for+fast+MRI&btnG=)).
### Undersampled Reconstruction
#### Recap:
In this notebook you
- wrote your own fully sampled recon using SIRF.
- saw the undersampling structure of GRAPPA files
- discovered high-frequency undersampling artifacts.
- implemented our own version of SENSE and beat (?) GRAPPA.
### Fin
This was the last exercise. We hoped you learned some new things about MRI and had a pleasant experience with SIRF and Python.
See you later!
|
github_jupyter
|
# k-Nearest Neighbor (kNN) exercise
*Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the [assignments page](http://vision.stanford.edu/teaching/cs231n/assignments.html) on the course website.*
The kNN classifier consists of two stages:
- During training, the classifier takes the training data and simply remembers it
- During testing, kNN classifies every test image by comparing to all training images and transfering the labels of the k most similar training examples
- The value of k is cross-validated
In this exercise you will implement these steps and understand the basic Image Classification pipeline, cross-validation, and gain proficiency in writing efficient, vectorized code.
```
# Run some setup code for this notebook.
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0)
# set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print 'Training data shape: ', X_train.shape
print 'Training labels shape: ', y_train.shape
print 'Test data shape: ', X_test.shape
print 'Test labels shape: ', y_test.shape
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
# select $samples_per_class different samples from a class
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
# Subsample the data for more efficient code execution in this exercise
num_training = 5000
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print X_train.shape, X_test.shape
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
```
We would now like to classify the test data with the kNN classifier. Recall that we can break down this process into two steps:
1. First we must compute the distances between all test examples and all train examples.
2. Given these distances, for each test example we find the k nearest examples and have them vote for the label
Lets begin with computing the distance matrix between all training and test examples. For example, if there are **Ntr** training examples and **Nte** test examples, this stage should result in a **Nte x Ntr** matrix where each element (i,j) is the distance between the i-th test and j-th train example.
First, open `cs231n/classifiers/k_nearest_neighbor.py` and implement the function `compute_distances_two_loops` that uses a (very inefficient) double loop over all pairs of (test, train) examples and computes the distance matrix one element at a time.
```
# Open cs231n/classifiers/k_nearest_neighbor.py and implement
# compute_distances_two_loops.
# Test your implementation:
dists = classifier.compute_distances_two_loops(X_test)
print dists.shape
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
```
**Inline Question #1:** Notice the structured patterns in the distance matrix.
- What is the cause behind the distinctly visible rows?
- What causes the columns?
**Your Answer**:
* Each test image will have variant L2 distance to the training images
* Each training image have distinct L2 distance to the test images
```
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)
# Now lets speed up distance matrix computation by using partial vectorization
# with one loop. Implement the function compute_distances_one_loop and run the
# code below:
dists_one = classifier.compute_distances_one_loop(X_test)
# To ensure that our vectorized implementation is correct, we make sure that it
# agrees with the naive implementation. There are many ways to decide whether
# two matrices are similar; one of the simplest is the Frobenius norm. In case
# you haven't seen it before, the Frobenius norm of two matrices is the square
# root of the squared sum of differences of all elements; in other words, reshape
# the matrices into vectors and compute the Euclidean distance between them.
difference = np.linalg.norm(dists - dists_one, ord='fro')
print 'Difference was: %f' % (difference, )
if difference < 0.001:
print 'Good! The distance matrices are the same'
else:
print 'Uh-oh! The distance matrices are different'
# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print 'Difference was: %f' % (difference, )
if difference < 0.001:
print 'Good! The distance matrices are the same'
else:
print 'Uh-oh! The distance matrices are different'
# Let's compare how fast the implementations are
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print 'Two loop version took %f seconds' % two_loop_time
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print 'One loop version took %f seconds' % one_loop_time
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print 'No loop version took %f seconds' % no_loop_time
# you should see significantly faster performance with the fully vectorized implementation
```
### Cross-validation
We have implemented the k-Nearest Neighbor classifier but we set the value k = 5 arbitrarily. We will now determine the best value of this hyperparameter with cross-validation.
```
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
idxes = range(num_training)
idx_folds = np.array_split(idxes, num_folds)
for idx in idx_folds:
# mask = np.ones(num_training, dtype=bool)
# mask[idx] = False
# X_train_folds.append( (X_train[mask], X_train[~mask]) )
# y_train_folds.append( (y_train[mask], y_train[~mask]) )
X_train_folds.append( X_train[idx] )
y_train_folds.append( y_train[idx] )
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
import sys
classifier = KNearestNeighbor()
Verbose = False
for k in k_choices:
if Verbose: print "processing k=%f" % k
else: sys.stdout.write('.')
k_to_accuracies[k] = list()
for num in xrange(num_folds):
if Verbose: print "processing fold#%i/%i" % (num, num_folds)
X_cv_train = np.vstack( [ X_train_folds[x] for x in xrange(num_folds) if x != num ])
y_cv_train = np.hstack( [ y_train_folds[x].T for x in xrange(num_folds) if x != num ])
X_cv_test = X_train_folds[num]
y_cv_test = y_train_folds[num]
# train k-nearest neighbor classifier
classifier.train(X_cv_train, y_cv_train)
# calculate trained matrix
dists = classifier.compute_distances_no_loops(X_cv_test)
y_cv_test_pred = classifier.predict_labels(dists, k=k)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_cv_test_pred == y_cv_test)
k_to_accuracies[k].append( float(num_correct) / y_cv_test.shape[0] )
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print 'k = %d, accuracy = %f' % (k, accuracy)
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data.
best_k = 6
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)
```
|
github_jupyter
|
### Forced Alignment with Wav2Vec2
In this notebook we are going to follow [this pytorch tutorial](https://pytorch.org/tutorials/intermediate/forced_alignment_with_torchaudio_tutorial.html) to align script to speech with torchaudio using the CTC segmentation algorithm described in [ CTC-Segmentation of Large Corpora for German End-to-end Speech Recognition](https://arxiv.org/abs/2007.09127)
The process of alignment looks like the following.
1. Estimate the frame-wise label probability from audio waveform
Generate the trellis matrix which represents the probability of labels aligned at time step.
2. Find the most likely path from the trellis matrix.
3. In this example, we use torchaudio’s Wav2Vec2 model for acoustic feature extraction.
### Installation of `tourchaudio`
```
!pip install torchaudio
```
### Imports
```
import os, requests, torch, torchaudio, IPython
from dataclasses import dataclass
import matplotlib.pyplot as plt
SPEECH_URL = 'https://download.pytorch.org/torchaudio/test-assets/Lab41-SRI-VOiCES-src-sp0307-ch127535-sg0042.flac'
SPEECH_FILE = 'speech.flac'
if not os.path.exists(SPEECH_FILE):
with open(SPEECH_FILE, 'wb') as file:
with requests.get(SPEECH_URL) as resp:
resp.raise_for_status()
file.write(resp.content)
```
### Generate frame-wise label probability
The first step is to generate the label class porbability of each aduio frame. We can use a ``Wav2Vec2`` model that is trained for ASR.
``torchaudio`` provides easy access to pretrained models with associated labels.
**Note:** In the subsequent sections, we will compute the probability in log-domain to avoid numerical instability. For this purpose, we normalize the emission with ``log_softmax``.
```
bundle = torchaudio.pipelines.WAV2VEC2_ASR_BASE_960H
model = bundle.get_model()
labels = bundle.get_labels()
with torch.inference_mode():
waveform, _ = torchaudio.load(SPEECH_FILE)
emissions, _ = model(waveform)
emissions = torch.log_softmax(emissions, dim=-1)
emission = emissions[0].cpu().detach()
```
### Visualization
```
print(labels)
plt.imshow(emission.T)
plt.colorbar()
plt.title("Frame-wise class probability")
plt.xlabel("Time")
plt.ylabel("Labels")
plt.show()
```
### Generate alignment probability (trellis)
From the emission matrix, next we generate the trellis which represents
the probability of transcript labels occur at each time frame.
Trellis is 2D matrix with time axis and label axis. The label axis
represents the transcript that we are aligning. In the following, we use
$t$ to denote the index in time axis and $j$ to denote the
index in label axis. $c_j$ represents the label at label index
$j$.
To generate, the probability of time step $t+1$, we look at the
trellis from time step $t$ and emission at time step $t+1$.
There are two path to reach to time step $t+1$ with label
$c_{j+1}$. The first one is the case where the label was
$c_{j+1}$ at $t$ and there was no label change from
$t$ to $t+1$. The other case is where the label was
$c_j$ at $t$ and it transitioned to the next label
$c_{j+1}$ at $t+1$.
The follwoing diagram illustrates this transition.
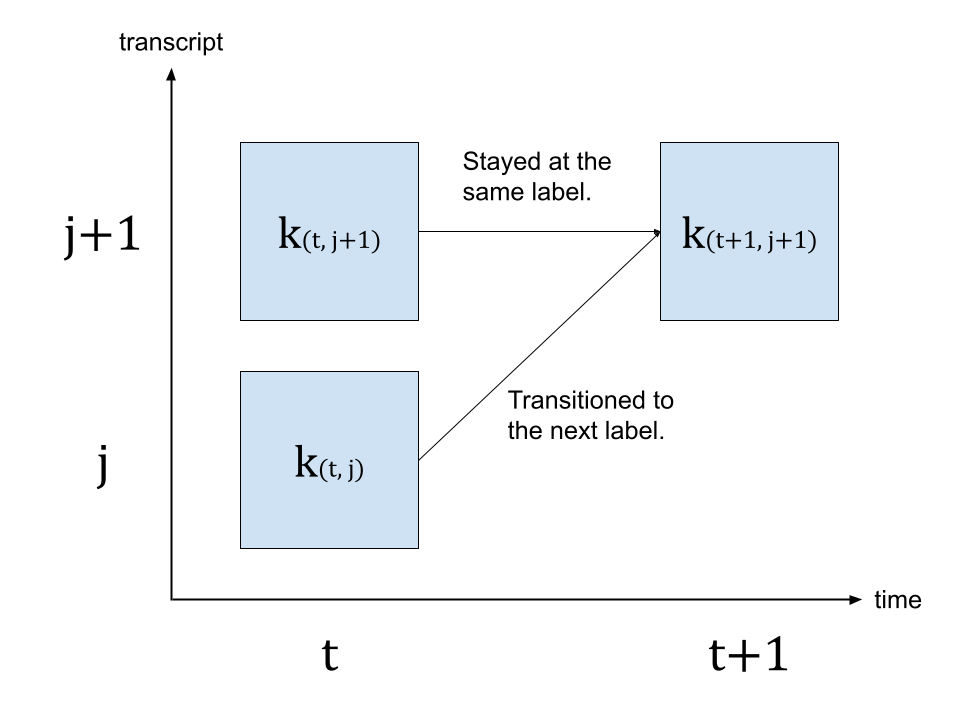
Since we are looking for the most likely transitions, we take the more
likely path for the value of $k_{(t+1, j+1)}$, that is
$ k_{(t+1, j+1)} = max( k_{(t, j)} p(t+1, c_{j+1}), k_{(t, j+1)} p(t+1,
repeat) ) $
where $k$ represents is trellis matrix, and $p(t, c_j)$
represents the probability of label $c_j$ at time step $t$.
$repeat$ represents the blank token from CTC formulation. (For the
detail of CTC algorithm, please refer to the `Sequence Modeling with CTC
[distill.pub] <https://distill.pub/2017/ctc/>`__)
```
transcript = 'I|HAD|THAT|CURIOSITY|BESIDE|ME|AT|THIS|MOMENT'
dictionary = {c: i for i, c in enumerate(labels)}
tokens = [dictionary[c] for c in transcript]
print(list(zip(transcript, tokens)))
def get_trellis(emission, tokens, blank_id=0):
num_frame = emission.size(0)
num_tokens = len(tokens)
# Trellis has extra diemsions for both time axis and tokens.
# The extra dim for tokens represents <SoS> (start-of-sentence)
# The extra dim for time axis is for simplification of the code.
trellis = torch.full((num_frame+1, num_tokens+1), -float('inf'))
trellis[:, 0] = 0
for t in range(num_frame):
trellis[t+1, 1:] = torch.maximum(
# Score for staying at the same token
trellis[t, 1:] + emission[t, blank_id],
# Score for changing to the next token
trellis[t, :-1] + emission[t, tokens],
)
return trellis
trellis = get_trellis(emission, tokens)
trellis
```
### Visualization.
```
plt.imshow(trellis[1:, 1:].T, origin='lower')
plt.annotate("- Inf", (trellis.size(1) / 5, trellis.size(1) / 1.5))
plt.colorbar()
plt.show()
```
>In the above visualization, we can see that there is a trace of high probability crossing the matrix diagonally.
### Find the most likely path (backtracking)
Once the trellis is generated, we will traverse it following the
elements with high probability.
We will start from the last label index with the time step of highest
probability, then, we traverse back in time, picking stay
($c_j \rightarrow c_j$) or transition
($c_j \rightarrow c_{j+1}$), based on the post-transition
probability $k_{t, j} p(t+1, c_{j+1})$ or
$k_{t, j+1} p(t+1, repeat)$.
Transition is done once the label reaches the beginning.
The trellis matrix is used for path-finding, but for the final
probability of each segment, we take the frame-wise probability from
emission matrix.
```
@dataclass
class Point:
token_index: int
time_index: int
score: float
def backtrack(trellis, emission, tokens, blank_id=0):
# Note:
# j and t are indices for trellis, which has extra dimensions
# for time and tokens at the beginning.
# When refering to time frame index `T` in trellis,
# the corresponding index in emission is `T-1`.
# Similarly, when refering to token index `J` in trellis,
# the corresponding index in transcript is `J-1`.
j = trellis.size(1) - 1
t_start = torch.argmax(trellis[:, j]).item()
path = []
for t in range(t_start, 0, -1):
# 1. Figure out if the current position was stay or change
# Note (again):
# `emission[J-1]` is the emission at time frame `J` of trellis dimension.
# Score for token staying the same from time frame J-1 to T.
stayed = trellis[t-1, j] + emission[t-1, blank_id]
# Score for token changing from C-1 at T-1 to J at T.
changed = trellis[t-1, j-1] + emission[t-1, tokens[j-1]]
# 2. Store the path with frame-wise probability.
prob = emission[t-1, tokens[j-1] if changed > stayed else 0].exp().item()
# Return token index and time index in non-trellis coordinate.
path.append(Point(j-1, t-1, prob))
# 3. Update the token
if changed > stayed:
j -= 1
if j == 0:
break
else:
raise ValueError('Failed to align')
return path[::-1]
path = backtrack(trellis, emission, tokens)
print(path)
```
### Visualization
```
def plot_trellis_with_path(trellis, path):
# To plot trellis with path, we take advantage of 'nan' value
trellis_with_path = trellis.clone()
for i, p in enumerate(path):
trellis_with_path[p.time_index, p.token_index] = float('nan')
plt.imshow(trellis_with_path[1:, 1:].T, origin='lower')
plot_trellis_with_path(trellis, path)
plt.title("The path found by backtracking")
plt.show()
```
Looking good. Now this path contains repetations for the same labels, so let’s merge them to make it close to the original transcript.
When merging the multiple path points, we simply take the average probability for the merged segments.
```
# Merge the labels
@dataclass
class Segment:
label: str
start: int
end: int
score: float
def __repr__(self):
return f"{self.label}\t({self.score:4.2f}): [{self.start:5d}, {self.end:5d})"
@property
def length(self):
return self.end - self.start
def merge_repeats(path):
i1, i2 = 0, 0
segments = []
while i1 < len(path):
while i2 < len(path) and path[i1].token_index == path[i2].token_index:
i2 += 1
score = sum(path[k].score for k in range(i1, i2)) / (i2 - i1)
segments.append(Segment(transcript[path[i1].token_index], path[i1].time_index, path[i2-1].time_index + 1, score))
i1 = i2
return segments
segments = merge_repeats(path)
for seg in segments:
print(seg)
```
### Visualization
```
def plot_trellis_with_segments(trellis, segments, transcript):
# To plot trellis with path, we take advantage of 'nan' value
trellis_with_path = trellis.clone()
for i, seg in enumerate(segments):
if seg.label != '|':
trellis_with_path[seg.start+1:seg.end+1, i+1] = float('nan')
plt.figure()
plt.title("Path, label and probability for each label")
ax1 = plt.axes()
ax1.imshow(trellis_with_path.T, origin='lower')
ax1.set_xticks([])
for i, seg in enumerate(segments):
if seg.label != '|':
ax1.annotate(seg.label, (seg.start + .7, i + 0.3))
ax1.annotate(f'{seg.score:.2f}', (seg.start - .3, i + 4.3))
plt.figure()
plt.title("Probability for each label at each time index")
ax2 = plt.axes()
xs, hs = [], []
for p in path:
label = transcript[p.token_index]
if label != '|':
xs.append(p.time_index + 1)
hs.append(p.score)
for seg in segments:
if seg.label != '|':
ax2.axvspan(seg.start+.4, seg.end+.4, color='gray', alpha=0.2)
ax2.annotate(seg.label, (seg.start + .8, -0.07))
ax2.bar(xs, hs, width=0.5)
ax2.axhline(0, color='black')
ax2.set_position(ax1.get_position())
ax2.set_xlim(ax1.get_xlim())
ax2.set_ylim(-0.1, 1.1)
plot_trellis_with_segments(trellis, segments, transcript)
plt.show()
```
Looks good. Now let’s merge the words. The Wav2Vec2 model uses ``'|'`` as the word boundary, so we merge the segments before each occurance of ``'|'``.
```
# Merge words
def merge_words(segments, separator='|'):
words = []
i1, i2 = 0, 0
while i1 < len(segments):
if i2 >= len(segments) or segments[i2].label == separator:
if i1 != i2:
segs = segments[i1:i2]
word = ''.join([seg.label for seg in segs])
score = sum(seg.score * seg.length for seg in segs) / sum(seg.length for seg in segs)
words.append(Segment(word, segments[i1].start, segments[i2-1].end, score))
i1 = i2 + 1
i2 = i1
else:
i2 += 1
return words
word_segments = merge_words(segments)
for word in word_segments:
print(word)
```
### Visualization
```
trellis_with_path = trellis.clone()
for i, seg in enumerate(segments):
if seg.label != '|':
trellis_with_path[seg.start+1:seg.end+1, i+1] = float('nan')
plt.imshow(trellis_with_path[1:, 1:].T, origin='lower')
ax1 = plt.gca()
ax1.set_yticks([])
ax1.set_xticks([])
for word in word_segments:
plt.axvline(word.start - 0.5)
plt.axvline(word.end - 0.5)
for i, seg in enumerate(segments):
if seg.label != '|':
plt.annotate(seg.label, (seg.start, i + 0.3))
plt.annotate(f'{seg.score:.2f}', (seg.start , i + 4), fontsize=8)
plt.show()
# The original waveform
ratio = waveform.size(1) / (trellis.size(0) - 1)
plt.plot(waveform[0])
for word in word_segments:
x0 = ratio * word.start
x1 = ratio * word.end
plt.axvspan(x0, x1, alpha=0.1, color='red')
plt.annotate(f'{word.score:.2f}', (x0, 0.8))
for seg in segments:
if seg.label != '|':
plt.annotate(seg.label, (seg.start * ratio, 0.9))
ax2 = plt.gca()
xticks = ax2.get_xticks()
plt.xticks(xticks, xticks / bundle.sample_rate)
plt.xlabel('time [second]')
ax2.set_position(ax1.get_position())
ax2.set_yticks([])
ax2.set_ylim(-1.0, 1.0)
ax2.set_xlim(0, waveform.size(-1))
plt.show()
# Generate the audio for each segment
print(transcript)
IPython.display.display(IPython.display.Audio(SPEECH_FILE))
for i, word in enumerate(word_segments):
x0 = int(ratio * word.start)
x1 = int(ratio * word.end)
filename = f"{i}_{word.label}.wav"
torchaudio.save(filename, waveform[:, x0:x1], bundle.sample_rate)
print(f"{word.label}: {x0 / bundle.sample_rate:.3f} - {x1 / bundle.sample_rate:.3f}")
IPython.display.display(IPython.display.Audio(filename))
```
|
github_jupyter
|
```
"""Keras-ImageDataGenerator
『本次練習內容』
學習使用Keras-ImageDataGenerator 與 Imgaug 做圖像增強
『本次練習目的』
熟悉Image Augmentation的實作方法
瞭解如何導入Imgae Augmentation到原本NN架構中"""
from keras.models import Sequential
from keras.layers import Convolution2D
from keras.layers import MaxPooling2D
from keras.layers import Flatten
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import BatchNormalization
from keras.datasets import cifar10
import numpy as np
import tensorflow as tf
from sklearn.preprocessing import OneHotEncoder
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print(x_train.shape) #(50000, 32, 32, 3)
## Normalize Data
def normalize(X_train,X_test):
mean = np.mean(X_train,axis=(0,1,2,3))
std = np.std(X_train, axis=(0, 1, 2, 3))
X_train = (X_train-mean)/(std+1e-7)
X_test = (X_test-mean)/(std+1e-7)
return X_train, X_test,mean,std
## Normalize Training and Testset
x_train, x_test,mean_train,std_train = normalize(x_train, x_test)
## OneHot Label 由(None, 1)-(None, 10)
## ex. label=2,變成[0,0,1,0,0,0,0,0,0,0]
one_hot=OneHotEncoder()
y_train=one_hot.fit_transform(y_train).toarray()
y_test=one_hot.transform(y_test).toarray()
classifier=Sequential()
input_shape=(32,32,3)
#卷積組合
classifier.add(Convolution2D(filters =32 ,kernel_size=(3,3),input_shape=input_shape,padding ="same"))#32,3,3,input_shape=(32,32,3),activation='relu''
classifier.add(BatchNormalization(momentum=0.8))
'''自己決定MaxPooling2D放在哪裡'''
#classifier.add(MaxPooling2D(pool_size=(2,2)))
#卷積組合
classifier.add(Convolution2D(filters =32 ,kernel_size=(3,3),input_shape=input_shape,padding ="same"))#32,3,3,input_shape=(32,32,3),activation='relu''
classifier.add(BatchNormalization(momentum=0.8))
#flatten
classifier.add(Flatten())
#FC
classifier.add(Dense(80)) #output_dim=100,activation=relu
#輸出
classifier.add(Dense(output_dim=10,activation='relu'))
#超過兩個就要選categorical_crossentrophy
classifier.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ['accuracy'])
classifier.fit(x_train,y_train,batch_size=100,epochs=100)
from keras.preprocessing.image import ImageDataGenerator
import matplotlib.pyplot as plt
import numpy as np
import cv2
%matplotlib inline
##定義使用的Augmentation
img_gen = ImageDataGenerator(
horizontal_flip=True)
width=224
height=224
batch_size=4
img = cv2.imread('Tano.JPG')
img = cv2.resize(img, (224,224))##改變圖片尺寸
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR,轉成RGB
img_origin=img.copy()
img= np.array(img, dtype=np.float32)
img_combine=np.array([img,img,img,img],dtype=np.uint8) ##輸入generator要是四維,(224,224,3)變成(4,224,224,3)
batch_gen = img_gen.flow(img_combine, batch_size=4)
assert next(batch_gen).shape==(batch_size, width, height, 3)
plt.figure(figsize=(20,10))
i = 1
for batch in batch_gen:
plt.subplot(1, 5, 1)
plt.imshow(img_origin) ##原圖
plt.subplot(1, 5, i+1)
plt.imshow(batch[0, :, :, :].astype(np.uint8))
plt.imshow(batch[1, :, :, :].astype(np.uint8))
plt.imshow(batch[2, :, :, :].astype(np.uint8))
plt.imshow(batch[3, :, :, :].astype(np.uint8))
plt.axis('off')
i += 1
if i > 4:
break # or the generator would loop infinitely
train_datagen = ImageDataGenerator(rescale = 2,shear_range = 0.2,zoom_range = 0.2,horizontal_flip = True)
#Test Generator,只需要Rescale,不需要其他增強
test_datagen = ImageDataGenerator(rescale = 1./255)
#將路徑給Generator,自動產生Label
training_set = train_datagen.flow_from_directory('training_set',
target_size = (64, 64),
batch_size = 32,
class_mode = 'categorical')
test_set = test_datagen.flow_from_directory('test_set',
target_size = (64, 64),
batch_size = 32,
class_mode = 'categorical')
#訓練
classifier.fit_generator(training_set,steps_per_epoch = 250,nb_epoch = 25,
validation_data = valid_set,validation_steps = 63)
#預測新照片
from keras.preprocessing import image as image_utils
test_image = image_utils.load_img('dataset/new_images/new_picture.jpg', target_size=(224, 224))
test_image = image_utils.img_to_array(test_image)
test_image = np.expand_dims(test_image, axis=0)
result = classifier.predict_on_batch(test_image)
from imgaug import augmenters as iaa
import matplotlib.pyplot as plt
import numpy as np
import cv2
img = cv2.imread('Tano.JPG')
img = cv2.resize(img, (224,224))##改變圖片尺寸
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR,轉成RGB
img_origin=img.copy()
img= np.array(img, dtype=np.float32)
images = np.random.randint(0, 255, (5, 224, 224, 3), dtype=np.uint8)##創造一個array size==(5, 224, 224, 3)
flipper = iaa.Fliplr(1.0) #水平翻轉機率==1.0
images[0] = flipper.augment_image(img)
vflipper = iaa.Flipud('''填入''') #垂直翻轉機率40%
images[1] = vflipper.augment_image(img)
blurer = iaa.GaussianBlur(3.0)
images[2] = blurer.augment_image(img) # 高斯模糊圖像( sigma of 3.0)
translater = iaa.Affine(translate_px={"x": -16}) #向左橫移16個像素
images[3] = translater.augment_image(img)
scaler = iaa.Affine(scale={"y":'''填入'''}) # 縮放照片,區間(0.8-1.2倍)
images[4] = scaler.augment_image(img)
i=1
plt.figure(figsize=(20,20))
for image in images:
plt.subplot(1, 6, 1)
plt.imshow(img_origin.astype(np.uint8))
plt.subplot(1, 6, i+1)
plt.imshow(image.astype(np.uint8))
plt.axis('off')
i+=1
"""第二Part
打包多種Augmentation
請學員自行練習新增以及改變Augmentation內容
可參考Github: https://github.com/aleju/imgaug"""
import numpy as np
import imgaug as ia
import imgaug.augmenters as iaa
import matplotlib.pyplot as plt
%matplotlib inline
##輸入照片
img = cv2.imread('Tano.JPG')
img = cv2.resize(img, (224,224))##改變圖片尺寸
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR,轉成RGB
img_origin=img.copy()
img= np.array(img, dtype=np.float32)
img_combine=np.array([img,img,img,img],dtype=np.float32)
sometimes = lambda aug: iaa.Sometimes(0.5, aug) # Sometimes(0.5, ...) 代表每次都有50%的機率運用不同的Augmentation
##包裝想運用之圖像強化方式
seq = iaa.Sequential([
iaa.Crop(px=(0, 16)),
iaa.Fliplr(0.4),
sometimes(iaa.CropAndPad(
percent=(-0.05, 0.1),
pad_mode=ia.ALL,
pad_cval=(0, 255)
)),
sometimes(iaa.Affine(
scale={"x": (0.8, 1.2), "y": (0.8, 1.2)},
translate_percent={"x": (-0.2, 0.2), "y": (-0.2, 0.2)},
rotate=(-10, 10),
shear=(-8, 8),
order=[0, 1],
cval=(0, 255),
mode=ia.ALL
)),
sometimes(iaa.Superpixels(p_replace=(0, 1.0), n_segments=(20, 200))), # convert images into their superpixel representation
sometimes(iaa.OneOf([
iaa.GaussianBlur((0, 3.0)), # blur images
iaa.AverageBlur(k=(1,3)), # blur image using local means with kernel sizes between 1 and 3
iaa.MedianBlur(k=(3, 5)), # blur image using local medians with kernel sizes between 3 and 5
])),
sometimes(iaa.Sharpen(alpha=(0, 0.2), lightness=(0.1, 0.4))), # sharpen images
sometimes(iaa.Emboss(alpha=(0, 0.3), strength=(0, 0.5))), # emboss images
],random_order=True)
images_aug = seq.augment_images(img_combine) ## Image Augmentation
##畫出來
i=1
plt.figure(figsize=(20,20))
for image in images_aug:
plt.subplot(1, 5, 1)
plt.imshow(img_origin.astype(np.uint8))
plt.subplot(1, 5, i+1)
plt.imshow(image.astype(np.uint8))
plt.axis('off')
i+=1
#包裝自定義Augmentation 與 Imgaug Augmentation
from PIL import Image
import os
import pickle
import numpy as np
import cv2
import glob
import pandas as pd
import time
import random
import imgaug as ia
import imgaug.augmenters as iaa
'''隨機改變亮度'''
class RandomBrightness(object):
'''Function to randomly make image brighter or darker
Parameters
----------
delta: float
the bound of random.uniform distribution
'''
def __init__(self, delta=16):
assert 0 <= delta <= 255
self.delta = delta
def __call__(self, image):
delta = random.uniform(-self.delta, self.delta)
if random.randint(0, 1):
image = image + delta
image = np.clip(image, 0.0, 255.0)
return image
'''隨機改變對比'''
class RandomContrast(object):
'''Function to strengthen or weaken the contrast in each image
Parameters
----------
lower: float
lower bound of random.uniform distribution
upper: float
upper bound of random.uniform distribution
'''
def __init__(self, lower=0.5, upper=1.5):
assert upper >= lower, "contrast upper must be >= lower."
assert lower >= 0, "contrast lower must be non-negative."
self.lower = lower
self.upper = upper
def __call__(self, image):
alpha = random.uniform(self.lower, self.upper)
if random.randint(0, 1):
image = image * alpha
image = np.clip(image, 0.0, 255.0)
return image
'''包裝所有Augmentation'''
class Compose(object):
def __init__(self, transforms):
self.transforms = transforms
def __call__(self, image):
for t in self.transforms:
image= t(image)
return image
'''包裝Imgaug'''
class ImgAugSequence(object):
def __init__(self, sequence):
self.sequence = sequence
def __call__(self, image):
image = self.sequence.augment_image(image)
return image
class TrainAugmentations(object):
def __init__(self):
#Define imgaug.augmenters Sequential transforms
sometimes = lambda aug: iaa.Sometimes(0.4, aug) # applies the given augmenter in 50% of all cases
img_seq = iaa.Sequential([
sometimes(iaa.AdditiveGaussianNoise(loc=0, scale=(0.0, 0.03*255), per_channel=0.5)),
sometimes(iaa.ContrastNormalization((0.5, 2.0), per_channel=1),),
sometimes(iaa.Sharpen(alpha=(0, 0.2), lightness=(0.1, 0.4))), # sharpen images
sometimes(iaa.Emboss(alpha=(0, 0.3), strength=(0, 0.5))), # emboss images
],random_order=True)
self.aug_pipeline = Compose([
RandomBrightness(16), #make image brighter or darker
RandomContrast(0.9, 1.1), #strengthen or weaken the contrast in each image
ImgAugSequence(img_seq),
])
def __call__(self, image):
image= self.aug_pipeline(image)
return image
Augmenation=TrainAugmentations()
import numpy as np
import imgaug as ia
import imgaug.augmenters as iaa
import matplotlib.pyplot as plt
%matplotlib inline
##輸入照片
img = cv2.imread('Tano.JPG')
img = cv2.resize(img, (224,224))##改變圖片尺寸
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR,轉成RGB
output=Augmenation(img)
##畫出來
plt.figure(figsize=(10,10))
for image in images_aug:
plt.imshow(output.astype(np.uint8))
plt.axis('off')
#鎖住隨機性-主要用在Semantic segmentation中
class MaskAugSequence(object):
def __init__(self, sequence):
self.sequence = sequence
def __call__(self, image, mask):
sequence = self.sequence.to_deterministic() ##用來關閉隨機性
image = sequence.augment_image(image)
mask = sequence.augment_image(mask)
image, mask= image.astype(np.float32), mask.astype(np.float32)
return image, mask
```
|
github_jupyter
|
```
import pandas as pd
import random
```
### Read the data
```
movies_df = pd.read_csv('mymovies.csv')
ratings_df = pd.read_csv('myratings.csv')
```
### Select the data
The recommender system should avoid bias, for example, the recommender system should not recommend movie with just 1 rating which is also a 5-star rating. But should recommend movies with more ratings.
Therefore, we only take into account movies with at least 200 ratings and users who have at least rated 50 movies.
```
user_threshold = 50
movie_threshold = 200
filtered_users = ratings_df['user'].value_counts()>=user_threshold
filtered_users = filtered_users[filtered_users].index.tolist()
filtered_movies = ratings_df['item'].value_counts()>=movie_threshold
filtered_movies = filtered_movies[filtered_movies].index.tolist()
filtered_df = ratings_df[(ratings_df['user'].isin(filtered_users)) & (ratings_df['item'].isin(filtered_movies))]
display(filtered_df)
```
### Select a group of n random users
Here we let n = 5, we select 5 random users from the filtered dataset
```
#Select a random group of user
user_ids = filtered_df['user'].unique()
group_users_ids = random.sample(list(user_ids), 5)
group_users_ids
```
### Select rated and unrated movies for the given group
We now can get the rated movies all users in the groups, and from that, we can also get the unrated movies for the whole group of 5
```
selected_group_rating = ratings_df.loc[ratings_df['user'].isin(group_users_ids)]
group_rated_movies_ids = selected_group_rating['item'].unique()
group_unrated_movies_ids = set(movies_df['item']) - set(group_rated_movies_ids)
group_rated_movies_df = movies_df.loc[movies_df['item'].isin(group_rated_movies_ids)]
group_unrated_movies_df = movies_df.loc[movies_df['item'].isin(group_unrated_movies_ids)]
group_rated_movies_df
group_unrated_movies_df
```
### Calculate expected ratings for unrated movies
For each users, we need to calculate the expected ratings for the user's unrated movies. To calculate unrated ratings, we first need to train
an algorithm, here, the SVD algorithm from Surprise is used
```
from surprise import Reader, Dataset, SVD
from surprise.model_selection.validation import cross_validate
```
We perform 5-fold cross validation on the whole ratings dataset to see how well SVD will perform
```
reader = Reader()
data = Dataset.load_from_df(ratings_df[['user', 'item', 'rating']], reader)
svd = SVD()
cross_validate(svd, data, measures=['RMSE', 'MAE'], cv=5, verbose=True)
```
Next, We train the SVD model on the dataset
```
trainset = data.build_full_trainset()
svd = svd.fit(trainset)
def predict(user):
unrated_movies = list(group_unrated_movies_df['item'].unique())
pred = pd.DataFrame()
i = 0
for item in unrated_movies:
pred = pred.append({'user':user,'item': item, 'predicted_rating':svd.predict(user, item)[3]}, ignore_index=True)
return pred
users_rating = []
for user in group_users_ids:
prediction = predict(user)
prediction = prediction.sort_values('predicted_rating')
prediction = prediction.merge(movies_df, on= 'item')
users_rating.append(prediction[['user','item','title','predicted_rating']])
```
The algorithm will iterate through 5 users, for each user, it will calculate the predicted rating for each unrated movie. Then the algorithm combines the predicted ratings of 5 users into one big dataset, to perform aggregation calculation
```
final = pd.concat([df for df in users_rating], ignore_index = True)
final
```
### Additive Strategy
```
additive = final.copy()
additive= additive.groupby(['item','title']).sum()
additive = additive.sort_values(by="predicted_rating", ascending=False).reset_index()
additive
```
### Most Pleasure Strategy
```
most_pleasure = final.copy()
most_pleasure = final.copy()
most_pleasure= most_pleasure.groupby(['item','title']).max()
most_pleasure = most_pleasure.sort_values(by="predicted_rating", ascending=False).reset_index()
most_pleasure
```
### Least Misery Strategy
```
least_misery = final.copy()
least_misery = final.copy()
least_misery= least_misery.groupby(['item','title']).min()
least_misery = least_misery.sort_values(by="predicted_rating", ascending=False).reset_index()
least_misery
def fairness():
titles = []
for uid in group_users_ids:
data = final.loc[final['user'] == uid]
data = data.sort_values(by = 'predicted_rating', ascending = False).reset_index().iloc[0]['title']
titles.append([uid,data])
return titles
tt = fairness()
print(tt)
def gen_rec_and_explain():
most_pleasure = final.copy()
most_pleasure= most_pleasure.groupby(['item','title']).max()
most_pleasure = most_pleasure.sort_values(by="predicted_rating", ascending=False).reset_index()
most_pleasure_movie = most_pleasure.iloc[0:5]['title']
least_misery = final.copy()
least_misery= least_misery.groupby(['item','title']).min()
least_misery = least_misery.sort_values(by="predicted_rating", ascending=False).reset_index()
least_misery_movie = least_misery.iloc[0:5]['title']
additive = final.copy()
additive= additive.groupby(['item','title']).sum()
additive = additive.sort_values(by="predicted_rating", ascending=False).reset_index()
additive_movie = additive.iloc[0:5]['title']
fairnesss = fairness()
print("#FAIR")
for uid, title in fairnesss:
print("The movie {} is the most favorite movie of user {}".format(title, uid))
print("#ADD: ")
print("The movies: {} was recommended to you because they have highest additive rating within your group".format(list(additive_movie)))
print("#LEAST: ")
print("The movies: {} was recommended to you because they are everyones' preferences ".format(list(least_misery_movie)))
print("#MOST: ")
print("The movies: {} was recommended to you because they are the most loved".format(list(most_pleasure_movie)))
gen_rec_and_explain()
import itertools
from lenskit.algorithms import Recommender
from lenskit.algorithms.user_knn import UserUser
user_user = UserUser(15, min_nbrs=3) # Minimum (3) and maximum (15) number of neighbors to consider
recsys = Recommender.adapt(user_user)
recsys.fit(ratings_df)
group_unseen_df = pd.DataFrame(list(itertools.product(group_users_ids, group_unrated_movies_ids)), columns=['user', 'item'])
group_unseen_df['predicted_rating'] = recsys.predict(group_unseen_df)
group_unseen_df = group_unseen_df.loc[group_unseen_df['predicted_rating'].notnull()]
display(group_unseen_df)
group_unseen_df
group_unseen_df.groupby('item').sum()
additive_df = group_unseen_df.groupby('item').sum()
additive_df = additive_df.join(movies_df['title'], on='item')
additive_df = additive_df.sort_values(by="predicted_rating", ascending=False).reset_index()[['item', 'title', 'predicted_rating']]
display(additive_df.head(10))
additive_df = group_unseen_df.groupby('item').sum()
additive_df
movies_df.loc[movies_df['item'] == 177593]
```
|
github_jupyter
|
# Call stacks and recursion
In this notebook, we'll take a look at *call stacks*, which will provide an opportunity to apply some of the concepts we've learned about both stacks and recursion.
### What is a *call stack*?
When we use functions in our code, the computer makes use of a data structure called a **call stack**. As the name suggests, a *call stack* is a type of stack—meaning that it is a *Last-In, First-Out* (LIFO) data structure.
So it's a type of stack—but a stack of *what*, exactly?
Essentially, a *call stack* is a stack of *frames* that are used for the *functions* that we are calling. When we call a function, say `print_integers(5)`, a *frame* is created in memory. All the variables local to the function are created in this memory frame. And as soon as this frame is created, it's pushed onto the call stack.
The frame that lies at the top of the call stack is executed first. And as soon as the function finishes executing, this frame is discarded from the *call stack*.
### An example
Let's consider the following function, which simply takes two integers and returns their sum
```
def add(num_one, num_two):
output = num_one + num_two
return output
result = add(5, 7)
print(result)
```
Before understanding what happens when a function is executed, it is important to remind ourselves that whenever an expression such as `product = 5 * 7` is evaluated, the right hand side of the `=` sign is evaluted first. When the right-hand side is completely evaluated, the result is stored in the variable name mentioned in the left-hand side.
When Python executes line 1 in the previous cell (`result = add(5, 7)`), the following things happen in memory:
* A frame is created for the `add` function. This frame is then pushed onto the *call stack*. We do not have to worry about this because Python takes care of this for us.
* Next, the parameters `num_one` and `num_two` get the values `5` and `7`, respectively
If we run this code in Python tutor website [http://pythontutor.com/](http://pythontutor.com/) , we can get a nice visualization of what's happening "behind the scenes" in memory:
<img src='./stack-frame-resources/01.png'>
* Python then moves on to the first line of the function. The first line of the function is
output = num_one + num_two
Here an expression is being evaluated and the result is stored in a new variable. The expression here is sum of two numbers the result of which is stored in the variable `output`. We know that whenever an expression is evaluated, the right-hand side of the `= sign` is evaluated first. So, the numbers `5 and 7` will be added first.
* Once the right-hand side is completely evaluated, then the assignment operation happens i.e. now the result of `5 + 7` will be stored in the variable `output`.
<img src='./stack-frame-resources/02.png'>
* In the next line, we are returning this value.
return output
Python acknowledged this return statement.
<img src='./stack-frame-resources/03.png'>
* Now the last line of the function has been executed. Therefore, this function can now be discarded from the stack frame. Also, the right-hand side of the expression `result = add(5, 7)` has finished evaluation. Now, the result of this evaluation will be stored in the variable `result`.
<img src='./stack-frame-resources/04.png'>
Now the next question is how does this behave like a stack?
The answer is pretty simple. We know that a stack is a Last-In First-Out (LIFO) structure, meaning the latest element inserted in the stack is the first to be removed.
You can play more with such "behind-the-scenes" of code execution on the Python tutor website: http://pythontutor.com/
### Another example
Here's another example. Let's say we have a function `add()` which adds two integers and then prints a custom message for us using the `custom_print()` function.
```
def add(num_one, num_two):
output = num_one + num_two
custom_print(output, num_one, num_two)
return output
def custom_print(output, num_one, num_two):
print("The sum of {} and {} is: {}".format(num_one, num_two, output))
result = add(5, 7)
```
What happens "behind-the-scenes" when `add()` is called, as in `result = add(5, 7)`?
Feel free to play with this on the Python tutor website. Here are a few points which might help aid the understanding.
* We know that when add function is called using `result = add(5, 7)`, a frame is created in the memory for the `add()` function. This frame is then pushed onto the call stack.
* Next, the two numbers are added and their result is stored in the variable `output`.
* On the next line we have a new function call - `custom_print(output, num_one, num_two)`. It's obvious that a new frame should be created for this function call as well. You must have realized that this new frame is now pushed into the call stack.
* We also know that the function which is at the top of the call stack is the one which Python executes. So, our `custom_print(output, num_one, num_two)` will now be executed.
* Python executes this function and as soon as it is finished with execution, the frame for `custom_print(output, num_one, num_two)` is discarded. If you recall, this is the LIFO behavior that we have discussed while studying stacks.
* Now, again the frame for `add()` function is at the top. Python resumes operation just after the line where it had left and returns the `output`.
### Call Stack and Recursion
#### Problem Statement
Consider the following problem:
Given a positive integer `n`, write a function, `print_integers`, that uses recursion to print all numbers from `n` to `1`.
For example, if `n` is `4`, the function shuld print `4 3 2 1`.
If we use iteration, the solution to the problem is simple. We can simply start at `4` and use a loop to print all numbers till `1`. However, instead of using an interative approach, our goal is to solve this problem using recursion.
```
def print_integers(n):
# TODO: Complete the function so that it uses recursion to print all integers from n to 1
if n <= 0:
return
print(n)
print_integers(n - 1)
```
<span class="graffiti-highlight graffiti-id_0usbivt-id_8peifb7"><i></i><button>Show Solution</button></span>
```
print_integers(5)
```
Now let's consider what happens in the call stack when `print_integers(5)` is called.
* As expected, a frame will be created for the `print_integers()` function and pushed onto the call stack.
* Next, the parameter `n` gets the value `5`.
* Following this, the function starts executing. The base condition is checked. For `n = 5`, the base case is `False`, so we move forward and print the value of `n`.
* In the next line, `print_integers()` is called again. This time it is called with the argument `n - 1`. The value of `n` in the current frame is `5`. So this new function call takes place with value `4`. Again, a new frame is created. **Note that for every new call a new frame will be created.** This frame is pushed onto the top of the stack.
* Python now starts executing this frame. Again the base case is checked. It's `False` for `n = 4`. Following this, the `n` is printed and then `print_integers()` is called with argument `n - 1 = 3`.
* The process keeps on like this until we hit the base case. When `n <= 0`, we return from the frame without calling the function `print_integers()` again. Because we have returned from the function call, the frame is discarded from the call stack and the next frame resumes execution right after the line where we left off.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/RajArPatra/MIDAS-task-2/blob/main/Results_Summary.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Libraries
```
from sklearn.preprocessing import StandardScaler,MinMaxScaler
import pandas as pd
import torchvision
import os
import numpy as np
from skimage import io,transform as ts
import torch
from torchvision import transforms
from torch.utils.data import Dataset
import torch
import torch.nn as nn
import torch.nn.functional as F
from PIL import Image
import imgaug as ia
import imgaug.augmenters as iaa
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
from torch.autograd import Variable
import distutils
from distutils import dir_util
from torch.utils.data.sampler import SubsetRandomSampler
from torch.utils.tensorboard import SummaryWriter
```
Mount Drive
```
from google.colab import drive
drive.mount('/content/drive')
```
# PART 1
Training and evaluation for part1 for whole of 62 classes
```
run_train(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part1',0,70,10,False)
print('====> After epoch {} '.format(con.epoch))
print('====>conv Time: {}'.format(con.time))
#print('====>conv Time: {}'.format(con.time))
print('====>Average train loss: {:.4f} +-{:.4f}'.format(
con.meter.value()[0],con.meter.value()[1]))
print('Train_accuracy:'.format(acc_meter.value())
train_labels,train_preds = get_all_preds(model, train_loader)
cm = confusion_matrix(train_labels, train_preds.argmax(dim=1))
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, lst1)
```
Training and evaluation for part1 for (0-9) classes
```
run(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_(0-9)_part1',0,100,10,False)
print('====> After epoch {} '.format(con.epoch))
print('====>conv Time: {}'.format(con.time))
#print('====>conv Time: {}'.format(con.time))
print('====>Average train loss: {:.4f} +-{:.4f}'.format(
con.meter.value()[0],con.meter.value()[1]))
acc_meter=AverageValueMeter()
model.eval()
for batch_idx, (data,label) in enumerate(train_loader):
data = data.to(device)
label=label.to(device)
data = data.expand(-1, 3, -1, -1)
output= model(data)
r=accuracy_fn(output.data,label.data,(1,3,5))
acc_meter.add(r[0].item())
print('Train_accuracy:{}'.format(acc_meter.value()))
cm=conf(model,train_loader,10)
cm=cm.cpu().numpy().astype('uint64')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, lst1)
```
# Part 2
Training and Evaluation Metrics for part2 without pretrained weights
```
run(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part2_nopre3',0,100,10,False,1)
print('====> After epoch {} '.format(con.epoch))
print('====>conv Time: {}'.format(con.time))
#print('====>conv Time: {}'.format(con.time))
print('====>Average train loss: {:.4f} +-{:.4f}'.format(
con.meter.value()[0],con.meter.value()[1]))
acc_meter=AverageValueMeter()
model.eval()
for batch_idx, (data,label) in enumerate(test_loader):
data = data.to(device)
label=label.to(device)
data = data.expand(-1, 3, -1, -1)
output= model(data)
r=accuracy_fn(output.data,label.data,(1,3,5))
acc_meter.add(r[0].item())
print('Test_accuracy:{}'.format(acc_meter.value()))
cm=conf(model,train_loader,10)
cm=cm.cpu().numpy().astype('uint64')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, lst1)
```
Training and Evaluation Metrics for part2 with pretrained weights from part 1
```
run_pre(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part2_pre3',0,100,10,False,1)
print('====> After epoch {} '.format(con.epoch))
print('====>conv Time: {}'.format(con.time))
#print('====>conv Time: {}'.format(con.time))
print('====>Average train loss: {:.4f} +-{:.4f}'.format(
con.meter.value()[0],con.meter.value()[1]))
acc_meter=AverageValueMeter()
model.eval()
for batch_idx, (data,label) in enumerate(test_loader):
data = data.to(device)
label=label.to(device)
data = data.expand(-1, 3, -1, -1)
output= model(data)
r=accuracy_fn(output.data,label.data,(1,3,5))
acc_meter.add(r[0].item())
print('Test_accuracy:{}'.format(acc_meter.value()))
def conf(model,test_loader,n_class):
nb_classes = n_class
model.to(device)
model.eval()
confusion_matrix = torch.zeros(nb_classes, nb_classes)
with torch.no_grad():
for i, (inputs, classes) in enumerate(test_loader):
inputs = inputs.to(device)
inputs=inputs.expand(-1, 3, -1, -1)
classes = classes.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
for t, p in zip(classes.view(-1), preds.view(-1)):
confusion_matrix[t.long(), p.long()] += 1
return confusion_matrix
cm=conf(model,train_loader,10)
cm=cm.cpu().numpy().astype('uint64')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, lst1)
```
# Part 3
Training and Evaluation Metrics for part3 without pretrained weights
```
run(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part3_nopre',0,100,10,False,1)
print('====> After epoch {} '.format(con.epoch))
print('====>conv Time: {}'.format(con.time))
#print('====>conv Time: {}'.format(con.time))
print('====>Average train loss: {:.4f} +-{:.4f}'.format(
con.meter.value()[0],con.meter.value()[1]))
acc_meter=AverageValueMeter()
model.eval()
for batch_idx, (data,label) in enumerate(test_loader):
data = data.to(device)
label=label.to(device)
data = data.expand(-1, 3, -1, -1)
output= model(data)
r=accuracy_fn(output.data,label.data,(1,3,5))
acc_meter.add(r[0].item())
print('Test_accuracy:{}'.format(acc_meter.value()))
cm=conf(model,train_loader,10)
cm=cm.cpu().numpy().astype('uint64')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, lst1)
```
Training and Evaluation Metrics for part3 with pretrained weights from part1
```
run_pre(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part3_pre2',0,100,10,False,1)
print('====> After epoch {} '.format(con.epoch))
print('====>conv Time: {}'.format(con.time))
#print('====>conv Time: {}'.format(con.time))
print('====>Average train loss: {:.4f} +-{:.4f}'.format(
con.meter.value()[0],con.meter.value()[1]))
acc_meter=AverageValueMeter()
model.eval()
for batch_idx, (data,label) in enumerate(test_loader):
data = data.to(device)
label=label.to(device)
data = data.expand(-1, 3, -1, -1)
output= model(data)
r=accuracy_fn(output.data,label.data,(1,3,5))
acc_meter.add(r[0].item())
print('Test_accuracy:{}'.format(acc_meter.value()))
cm=conf(model,train_loader,10)
cm=cm.cpu().numpy().astype('uint64')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, lst1)
```
|
github_jupyter
|
# How many cases of COVID-19 does each U.S. state really have?
> Reported U.S. case counts are based on the number of administered tests. Since not everyone is tested, this number is biased. We use Bayesian techniques to estimate the true number of cases.
- author: Joseph Richards
- image: images/covid-state-case-estimation.png
- hide: false
- comments: true
- categories: [MCMC, US, states, cases]
- permalink: /covid-19-us-case-estimation/
- toc: false
```
#hide
# Setup and imports
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import requests
from IPython.display import display, Markdown
#hide
# Data utilities:
def get_statewise_testing_data():
'''
Pull all statewise data required for model fitting and
prediction
Returns:
* df_out: DataFrame for model fitting where inclusion
requires testing data from 7 days ago
* df_pred: DataFrame for count prediction where inclusion
only requires testing data from today
'''
# Pull testing counts by state:
out = requests.get('https://covidtracking.com/api/states')
df_out = pd.DataFrame(out.json())
df_out.set_index('state', drop=True, inplace=True)
# Pull time-series of testing counts:
ts = requests.get('https://covidtracking.com/api/states/daily')
df_ts = pd.DataFrame(ts.json())
# Get data from last week
date_last_week = df_ts['date'].unique()[7]
df_ts_last_week = _get_test_counts(df_ts, df_out.index, date_last_week)
df_out['num_tests_7_days_ago'] = \
(df_ts_last_week['positive'] + df_ts_last_week['negative'])
df_out['num_pos_7_days_ago'] = df_ts_last_week['positive']
# Get data from today:
df_out['num_tests_today'] = (df_out['positive'] + df_out['negative'])
# State population:
df_pop = pd.read_excel(('https://github.com/jwrichar/COVID19-mortality/blob/'
'master/data/us_population_by_state_2019.xlsx?raw=true'),
skiprows=2, skipfooter=5)
r = requests.get(('https://raw.githubusercontent.com/jwrichar/COVID19-mortality/'
'master/data/us-state-name-abbr.json'))
state_name_abbr_lookup = r.json()
df_pop.index = df_pop['Geographic Area'].apply(
lambda x: str(x).replace('.', '')).map(state_name_abbr_lookup)
df_pop = df_pop.loc[df_pop.index.dropna()]
df_out['total_population'] = df_pop['Total Resident\nPopulation']
# Tests per million people, based on today's test coverage
df_out['tests_per_million'] = 1e6 * \
(df_out['num_tests_today']) / df_out['total_population']
df_out['tests_per_million_7_days_ago'] = 1e6 * \
(df_out['num_tests_7_days_ago']) / df_out['total_population']
# People per test:
df_out['people_per_test'] = 1e6 / df_out['tests_per_million']
df_out['people_per_test_7_days_ago'] = \
1e6 / df_out['tests_per_million_7_days_ago']
# Drop states with messed up / missing data:
# Drop states with missing total pop:
to_drop_idx = df_out.index[df_out['total_population'].isnull()]
print('Dropping %i/%i states due to lack of population data: %s' %
(len(to_drop_idx), len(df_out), ', '.join(to_drop_idx)))
df_out.drop(to_drop_idx, axis=0, inplace=True)
df_pred = df_out.copy(deep=True) # Prediction DataFrame
# Criteria for model fitting:
# Drop states with missing test count 7 days ago:
to_drop_idx = df_out.index[df_out['num_tests_7_days_ago'].isnull()]
print('Dropping %i/%i states due to lack of tests: %s' %
(len(to_drop_idx), len(df_out), ', '.join(to_drop_idx)))
df_out.drop(to_drop_idx, axis=0, inplace=True)
# Drop states with no cases 7 days ago:
to_drop_idx = df_out.index[df_out['num_pos_7_days_ago'] == 0]
print('Dropping %i/%i states due to lack of positive tests: %s' %
(len(to_drop_idx), len(df_out), ', '.join(to_drop_idx)))
df_out.drop(to_drop_idx, axis=0, inplace=True)
# Criteria for model prediction:
# Drop states with missing test count today:
to_drop_idx = df_pred.index[df_pred['num_tests_today'].isnull()]
print('Dropping %i/%i states in prediction data due to lack of tests: %s' %
(len(to_drop_idx), len(df_pred), ', '.join(to_drop_idx)))
df_pred.drop(to_drop_idx, axis=0, inplace=True)
# Cast counts to int
df_pred['negative'] = df_pred['negative'].astype(int)
df_pred['positive'] = df_pred['positive'].astype(int)
return df_out, df_pred
def _get_test_counts(df_ts, state_list, date):
ts_list = []
for state in state_list:
state_ts = df_ts.loc[df_ts['state'] == state]
# Back-fill any gaps to avoid crap data gaps
state_ts.fillna(method='bfill', inplace=True)
record = state_ts.loc[df_ts['date'] == date]
ts_list.append(record)
df_ts = pd.concat(ts_list, ignore_index=True)
return df_ts.set_index('state', drop=True)
#hide
# Model utilities
def case_count_model_us_states(df):
# Normalize inputs in a way that is sensible:
# People per test: normalize to South Korea
# assuming S.K. testing is "saturated"
ppt_sk = np.log10(51500000. / 250000)
df['people_per_test_normalized'] = (
np.log10(df['people_per_test_7_days_ago']) - ppt_sk)
n = len(df)
# For each country, let:
# c_obs = number of observed cases
c_obs = df['num_pos_7_days_ago'].values
# c_star = number of true cases
# d_obs = number of observed deaths
d_obs = df[['death', 'num_pos_7_days_ago']].min(axis=1).values
# people per test
people_per_test = df['people_per_test_normalized'].values
covid_case_count_model = pm.Model()
with covid_case_count_model:
# Priors:
mu_0 = pm.Beta('mu_0', alpha=1, beta=100, testval=0.01)
# sig_0 = pm.Uniform('sig_0', lower=0.0, upper=mu_0 * (1 - mu_0))
alpha = pm.Bound(pm.Normal, lower=0.0)(
'alpha', mu=8, sigma=3, shape=1)
beta = pm.Bound(pm.Normal, upper=0.0)(
'beta', mu=-1, sigma=1, shape=1)
# beta = pm.Normal('beta', mu=0, sigma=1, shape=3)
sigma = pm.HalfNormal('sigma', sigma=0.5, testval=0.1)
# sigma_1 = pm.HalfNormal('sigma_1', sigma=2, testval=0.1)
# Model probability of case under-reporting as logistic regression:
mu_model_logit = alpha + beta * people_per_test
tau_logit = pm.Normal('tau_logit',
mu=mu_model_logit,
sigma=sigma,
shape=n)
tau = np.exp(tau_logit) / (np.exp(tau_logit) + 1)
c_star = c_obs / tau
# Binomial likelihood:
d = pm.Binomial('d',
n=c_star,
p=mu_0,
observed=d_obs)
return covid_case_count_model
#hide
df, df_pred = get_statewise_testing_data()
# Initialize the model:
mod = case_count_model_us_states(df)
# Run MCMC sampler
with mod:
trace = pm.sample(500, tune=500, chains=1)
#hide_input
n = len(trace['beta'])
# South Korea:
ppt_sk = np.log10(51500000. / 250000)
# Compute predicted case counts per state right now
logit_now = pd.DataFrame([
pd.Series(np.random.normal((trace['alpha'][i] + trace['beta'][i] * (np.log10(df_pred['people_per_test']) - ppt_sk)),
trace['sigma'][i]), index=df_pred.index)
for i in range(len(trace['beta']))])
prob_missing_now = np.exp(logit_now) / (np.exp(logit_now) + 1)
predicted_counts_now = np.round(df_pred['positive'] / prob_missing_now.mean(axis=0)).astype(int)
predicted_counts_now_lower = np.round(df_pred['positive'] / prob_missing_now.quantile(0.975, axis=0)).astype(int)
predicted_counts_now_upper = np.round(df_pred['positive'] / prob_missing_now.quantile(0.025, axis=0)).astype(int)
case_increase_percent = list(map(lambda x, y: (((x - y) / float(y))),
predicted_counts_now, df_pred['positive']))
df_summary = pd.DataFrame(
data = {
'Cases Reported': df_pred['positive'],
'Cases Estimated': predicted_counts_now,
'Percent Increase': case_increase_percent,
'Tests per Million People': df_pred['tests_per_million'].round(1),
'Cases Estimated (range)': list(map(lambda x, y: '(%i, %i)' % (round(x), round(y)),
predicted_counts_now_lower, predicted_counts_now_upper)),
'Cases per Million': ((df_pred['positive'] / df_pred['total_population']) * 1e6),
'Positive Test Rate': (df_pred['positive'] / (df_pred['positive'] + df_pred['negative']))
},
index=df_pred.index)
from datetime import datetime
display(Markdown("## Summary for the United States on %s:" % str(datetime.today())[:10]))
display(Markdown(f"**Reported Case Count:** {df_summary['Cases Reported'].sum():,}"))
display(Markdown(f"**Predicted Case Count:** {df_summary['Cases Estimated'].sum():,}"))
case_increase_percent = 100. * (df_summary['Cases Estimated'].sum() - df_summary['Cases Reported'].sum()) / df_summary['Cases Estimated'].sum()
display(Markdown("**Percentage Underreporting in Case Count:** %.1f%%" % case_increase_percent))
#hide
df_summary.loc[:, 'Ratio'] = df_summary['Cases Estimated'] / df_summary['Cases Reported']
df_summary.columns = ['Reported Cases', 'Est Cases', '% Increase',
'Tests per Million', 'Est Range',
'Cases per Million', 'Positive Test Rate',
'Ratio']
df_display = df_summary[['Reported Cases', 'Est Cases', 'Est Range', 'Ratio',
'Tests per Million', 'Cases per Million',
'Positive Test Rate']].copy()
```
## COVID-19 Case Estimates, by State
### Definition Of Fields:
- **Reported Cases**: The number of cases reported by each state, which is a function of how many tests are positive.
- **Est Cases**: The predicted number of cases, accounting for the fact that not everyone is tested.
- **Est Range**: The 95% confidence interval of the predicted number of cases.
- **Ratio**: `Estimated Cases` divided by `Reported Cases`.
- **Tests per Million**: The number of tests administered per one million people. The less tests administered per capita, the larger the difference between reported and estimated number of cases, generally.
- **Cases per Million**: The number of **reported** cases per on million people.
- **Positive Test Rate**: The **reported** percentage of positive tests.
```
#hide_input
df_display.sort_values(
by='Est Cases', ascending=False).style.background_gradient(
cmap='Oranges').format(
{'Ratio': "{:.1f}"}).format(
{'Tests per Million': "{:.1f}"}).format(
{'Cases per Million': "{:.1f}"}).format(
{'Positive Test Rate': "{:.0%}"})
#hide_input
df_plot = df_summary.copy(deep=True)
# Compute predicted cases per million
df_plot['predicted_counts_now_pm'] = 1e6 * (
df_pred['positive'] / prob_missing_now.mean(axis=0)) / df_pred['total_population']
df_plot['predicted_counts_now_lower_pm'] = 1e6 * (
df_pred['positive'] / prob_missing_now.quantile(0.975, axis=0))/ df_pred['total_population']
df_plot['predicted_counts_now_upper_pm'] = 1e6 * (
df_pred['positive'] / prob_missing_now.quantile(0.025, axis=0))/ df_pred['total_population']
df_plot.sort_values('predicted_counts_now_pm', ascending=False, inplace=True)
xerr = [
df_plot['predicted_counts_now_pm'] - df_plot['predicted_counts_now_lower_pm'],
df_plot['predicted_counts_now_upper_pm'] - df_plot['predicted_counts_now_pm']]
fig, axs = plt.subplots(1, 1, figsize=(15, 15))
ax = plt.errorbar(df_plot['predicted_counts_now_pm'], range(len(df_plot)-1, -1, -1),
xerr=xerr, fmt='o', elinewidth=1, label='Estimate')
ax = plt.yticks(range(len(df_plot)), df_plot.index[::-1])
ax = plt.errorbar(df_plot['Cases per Million'], range(len(df_plot)-1, -1, -1),
xerr=None, fmt='.', color='k', label='Reported')
ax = plt.xlabel('COVID-19 Case Counts Per Million People', size=20)
ax = plt.legend(fontsize='xx-large', loc=4)
ax = plt.grid(linestyle='--', color='grey', axis='x')
```
## Appendix: Model Diagnostics
### Derived relationship between Test Capacity and Case Under-reporting
Plotted is the estimated relationship between test capacity (in terms of people per test -- larger = less testing) and the likelihood a COVID-19 case is reported (lower = more under-reporting of cases).
The lines represent the posterior samples from our MCMC run (note the x-axis is plotted on a log scale). The rug plot shows the current test capacity for each state (black '|') and the capacity one week ago (cyan '+'). For comparison, South Korea's testing capacity is currently at the very left of the graph (200 people per test).
```
#hide_input
# Plot pop/test vs. Prob of case detection for all posterior samples:
x = np.linspace(0.0, 4.0, 101)
logit_pcase = pd.DataFrame([
trace['alpha'][i] + trace['beta'][i] * x
for i in range(n)])
pcase = np.exp(logit_pcase) / (np.exp(logit_pcase) + 1)
fig, ax = plt.subplots(1, 1, figsize=(14, 9))
for i in range(n):
ax = plt.plot(10**(ppt_sk + x), pcase.iloc[i], color='grey', lw=.1, alpha=.5)
plt.xscale('log')
plt.xlabel('State-wise population per test', size=14)
plt.ylabel('Probability a true case is detected', size=14)
# rug plots:
ax=plt.plot(df_pred['people_per_test'], np.zeros(len(df_pred)),
marker='|', color='k', ls='', ms=20,
label='U.S. State-wise Test Capacity Now')
ax=plt.plot(df['people_per_test_7_days_ago'], np.zeros(len(df)),
marker='+', color='c', ls='', ms=10,
label='U.S. State-wise Test Capacity 7 Days Ago')
ax = plt.legend(fontsize='x-large')
```
## About this Analysis
This analysis was done by [Joseph Richards](https://twitter.com/joeyrichar).
This project[^1] uses the testing rates per state from [https://covidtracking.com/](https://covidtracking.com/), which reports case counts and mortality by state. This is used to **estimate the number of unreported (untested) COVID-19 cases in each U.S. state.**
The analysis makes a few assumptions:
1. The probability that a case is reported by a state is a function of the number of tests run per person in that state. Hence the degree of under-reported cases is a function of tests run per capita.
2. The underlying mortality rate is the same across every state.
3. Patients take time to succumb to COVID-19, so the mortality counts *today* reflect the case counts *7 days ago*. E.g., mortality rate = (cumulative deaths today) / (cumulative cases 7 days ago).
The model attempts to find the most likely relationship between state-wise test volume (per capita) and under-reporting, such that the true underlying mortality rates between the individual states are as similar as possible. The model simultaneously finds the most likely posterior distribution of mortality rates, the most likely *true* case count per state, and the test volume vs. case underreporting relationship.
[^1]: Full details about the model are available at: https://github.com/jwrichar/COVID19-mortality
|
github_jupyter
|
```
%matplotlib inline
%pylab inline
from parsing import parser, digit
from plotting import plotter, voronoi
from analysis import training, sampling, testing, classify
from config import settings
import warnings
warnings.filterwarnings('ignore')
n_observation_classes = 256
n_hidden_states = 30
n_iter = 10000
tol = 0.1
parse = parser.Parser();
train_digits = parse.parse_file('data/pendigits-train');
test_digits = parse.parse_file('data/pendigits-test')
pylab.rcParams['figure.figsize'] = (5, 5);
plotter.plot_digit(train_digits[6], True)
pylab.rcParams['figure.figsize'] = (15, 6);
plotter.plot_digits_heatmap(train_digits, True);
centroids = training.get_digit_kmeans_centroids(train_digits, n_observation_classes - 3)
pylab.rcParams['figure.figsize'] = (10, 10);
voronoi.plot_centroids(centroids);
training.set_digit_observations(train_digits, centroids, n_observation_classes)
pylab.rcParams['figure.figsize'] = (5, 5);
plotter.plot_digit_observations(train_digits[11], centroids, n_observation_classes, True)
hidden_markov_models = training.train_hmm(train_digits, n_observation_classes, n_hidden_states, n_iter, tol)
samplings = sampling.get_samplings(hidden_markov_models, n_observation_classes, centroids, 100)
pylab.rcParams['figure.figsize'] = (5, 5);
plotter.plot_digit(samplings[2][8], True)
pylab.rcParams['figure.figsize'] = (15, 6);
plotter.plot_digit_samples_heatmap(samplings)
test_labels_probabilities = classify.get_labels_probabilities(test_digits, hidden_markov_models, centroids, n_observation_classes, n_hidden_states,
n_iter, tol, True, True, "test_labels_probabilities.dat")
test_classifier = classify.WeightedClassifier(test_digits, test_labels_probabilities)
prediction_matrix = test_classifier.get_prediction_matrix()
for row in prediction_matrix:
print(row)
test_classifier.print_classification_performance()
gaussian_hidden_markov_models = training.train_gaussian_hmm(train_digits, n_hidden_states, n_iter, tol)
for i in range(0, 10):
print(classify.get_gaussian_hmm_probability(test_digits[0], gaussian_hidden_markov_models[i]))
gaussian_test_labels_probabilities = classify.get_gaussian_labels_probabilities(test_digits, gaussian_hidden_markov_models, n_observation_classes, n_hidden_states,
n_iter, tol, True, True, "gaussian_test_labels_probabilities.dat")
gaussian_test_classifier = classify.GaussianClassifier(test_digits, gaussian_test_labels_probabilities)
prediction_matrix = gaussian_test_classifier.get_prediction_matrix()
for row in prediction_matrix:
print(row)
gaussian_test_classifier.print_classification_performance()
```
# Dynamic Time Warping
\begin{equation}
y = \mathop{\arg\,\max}\limits{l \in L} \frac{1}{n_l} \sum_{i = 0}^{n_l} \text{fastdtw\_distance}(x_i^l, x_{\text{test}})
\end{equation}
```
import dtw
print(dtw.score())
```
|
github_jupyter
|
# GLM: Logistic Regression
* This is a reproduction with a few slight alterations of [Bayesian Log Reg](http://jbencook.github.io/portfolio/bayesian_logistic_regression.html) by J. Benjamin Cook
* Author: Peadar Coyle and J. Benjamin Cook
* How likely am I to make more than $50,000 US Dollars?
* Exploration of model selection techniques too - I use WAIC to select the best model.
* The convenience functions are all taken from Jon Sedars work.
* This example also has some explorations of the features so serves as a good example of Exploratory Data Analysis and how that can guide the model creation/ model selection process.
```
%matplotlib inline
import pandas as pd
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt
import seaborn
import warnings
warnings.filterwarnings('ignore')
from collections import OrderedDict
from time import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import fmin_powell
from scipy import integrate
import theano as thno
import theano.tensor as T
def run_models(df, upper_order=5):
'''
Convenience function:
Fit a range of pymc3 models of increasing polynomial complexity.
Suggest limit to max order 5 since calculation time is exponential.
'''
models, traces = OrderedDict(), OrderedDict()
for k in range(1,upper_order+1):
nm = 'k{}'.format(k)
fml = create_poly_modelspec(k)
with pm.Model() as models[nm]:
print('\nRunning: {}'.format(nm))
pm.glm.GLM.from_formula(fml, df, family=pm.glm.families.Normal())
traces[nm] = pm.sample(2000, chains=1, init=None, tune=1000)
return models, traces
def plot_traces(traces, retain=1000):
'''
Convenience function:
Plot traces with overlaid means and values
'''
ax = pm.traceplot(traces[-retain:], figsize=(12,len(traces.varnames)*1.5),
lines={k: v['mean'] for k, v in pm.summary(traces[-retain:]).iterrows()})
for i, mn in enumerate(pm.summary(traces[-retain:])['mean']):
ax[i,0].annotate('{:.2f}'.format(mn), xy=(mn,0), xycoords='data'
,xytext=(5,10), textcoords='offset points', rotation=90
,va='bottom', fontsize='large', color='#AA0022')
def create_poly_modelspec(k=1):
'''
Convenience function:
Create a polynomial modelspec string for patsy
'''
return ('income ~ educ + hours + age ' + ' '.join(['+ np.power(age,{})'.format(j)
for j in range(2,k+1)])).strip()
```
The [Adult Data Set](http://archive.ics.uci.edu/ml/datasets/Adult) is commonly used to benchmark machine learning algorithms. The goal is to use demographic features, or variables, to predict whether an individual makes more than \\$50,000 per year. The data set is almost 20 years old, and therefore, not perfect for determining the probability that I will make more than \$50K, but it is a nice, simple dataset that can be used to showcase a few benefits of using Bayesian logistic regression over its frequentist counterpart.
The motivation for myself to reproduce this piece of work was to learn how to use Odd Ratio in Bayesian Regression.
```
data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data", header=None, names=['age', 'workclass', 'fnlwgt',
'education-categorical', 'educ',
'marital-status', 'occupation',
'relationship', 'race', 'sex',
'captial-gain', 'capital-loss',
'hours', 'native-country',
'income'])
data.head(10)
```
## Scrubbing and cleaning
We need to remove any null entries in Income.
And we also want to restrict this study to the United States.
```
data = data[~pd.isnull(data['income'])]
data[data['native-country']==" United-States"]
income = 1 * (data['income'] == " >50K")
age2 = np.square(data['age'])
data = data[['age', 'educ', 'hours']]
data['age2'] = age2
data['income'] = income
income.value_counts()
```
## Exploring the data
Let us get a feel for the parameters.
* We see that age is a tailed distribution. Certainly not Gaussian!
* We don't see much of a correlation between many of the features, with the exception of Age and Age2.
* Hours worked has some interesting behaviour. How would one describe this distribution?
```
g = seaborn.pairplot(data)
# Compute the correlation matrix
corr = data.corr()
# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(11, 9))
# Generate a custom diverging colormap
cmap = seaborn.diverging_palette(220, 10, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
seaborn.heatmap(corr, mask=mask, cmap=cmap, vmax=.3,
linewidths=.5, cbar_kws={"shrink": .5}, ax=ax)
```
We see here not many strong correlations. The highest is 0.30 according to this plot. We see a weak-correlation between hours and income
(which is logical), we see a slighty stronger correlation between education and income (which is the kind of question we are answering).
## The model
We will use a simple model, which assumes that the probability of making more than $50K
is a function of age, years of education and hours worked per week. We will use PyMC3
do inference.
In Bayesian statistics, we treat everything as a random variable and we want to know the posterior probability distribution of the parameters
(in this case the regression coefficients)
The posterior is equal to the likelihood $$p(\theta | D) = \frac{p(D|\theta)p(\theta)}{p(D)}$$
Because the denominator is a notoriously difficult integral, $p(D) = \int p(D | \theta) p(\theta) d \theta $ we would prefer to skip computing it. Fortunately, if we draw examples from the parameter space, with probability proportional to the height of the posterior at any given point, we end up with an empirical distribution that converges to the posterior as the number of samples approaches infinity.
What this means in practice is that we only need to worry about the numerator.
Getting back to logistic regression, we need to specify a prior and a likelihood in order to draw samples from the posterior. We could use sociological knowledge about the effects of age and education on income, but instead, let's use the default prior specification for GLM coefficients that PyMC3 gives us, which is $p(θ)=N(0,10^{12}I)$. This is a very vague prior that will let the data speak for themselves.
The likelihood is the product of n Bernoulli trials, $\prod^{n}_{i=1} p_{i}^{y} (1 - p_{i})^{1-y_{i}}$,
where $p_i = \frac{1}{1 + e^{-z_i}}$,
$z_{i} = \beta_{0} + \beta_{1}(age)_{i} + \beta_2(age)^{2}_{i} + \beta_{3}(educ)_{i} + \beta_{4}(hours)_{i}$ and $y_{i} = 1$ if income is greater than 50K and $y_{i} = 0$ otherwise.
With the math out of the way we can get back to the data. Here I use PyMC3 to draw samples from the posterior. The sampling algorithm used is NUTS, which is a form of Hamiltonian Monte Carlo, in which parameteres are tuned automatically. Notice, that we get to borrow the syntax of specifying GLM's from R, very convenient! I use a convenience function from above to plot the trace infromation from the first 1000 parameters.
```
with pm.Model() as logistic_model:
pm.glm.GLM.from_formula('income ~ age + age2 + educ + hours', data, family=pm.glm.families.Binomial())
trace_logistic_model = pm.sample(2000, chains=1, init=None, tune=1000)
plot_traces(trace_logistic_model, retain=1000)
```
## Some results
One of the major benefits that makes Bayesian data analysis worth the extra computational effort in many circumstances is that we can be explicit about our uncertainty. Maximum likelihood returns a number, but how certain can we be that we found the right number? Instead, Bayesian inference returns a distribution over parameter values.
I'll use seaborn to look at the distribution of some of these factors.
```
plt.figure(figsize=(9,7))
trace = trace_logistic_model[1000:]
seaborn.jointplot(trace['age'], trace['educ'], kind="hex", color="#4CB391")
plt.xlabel("beta_age")
plt.ylabel("beta_educ")
plt.show()
```
So how do age and education affect the probability of making more than $$50K?$ To answer this question, we can show how the probability of making more than $50K changes with age for a few different education levels. Here, we assume that the number of hours worked per week is fixed at 50. PyMC3 gives us a convenient way to plot the posterior predictive distribution. We need to give the function a linear model and a set of points to evaluate. We will pass in three different linear models: one with educ == 12 (finished high school), one with educ == 16 (finished undergrad) and one with educ == 19 (three years of grad school).
```
# Linear model with hours == 50 and educ == 12
lm = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] +
samples['age']*x +
samples['age2']*np.square(x) +
samples['educ']*12 +
samples['hours']*50)))
# Linear model with hours == 50 and educ == 16
lm2 = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] +
samples['age']*x +
samples['age2']*np.square(x) +
samples['educ']*16 +
samples['hours']*50)))
# Linear model with hours == 50 and educ == 19
lm3 = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] +
samples['age']*x +
samples['age2']*np.square(x) +
samples['educ']*19 +
samples['hours']*50)))
```
Each curve shows how the probability of earning more than $ 50K$ changes with age. The red curve represents 19 years of education, the green curve represents 16 years of education and the blue curve represents 12 years of education. For all three education levels, the probability of making more than $50K increases with age until approximately age 60, when the probability begins to drop off. Notice that each curve is a little blurry. This is because we are actually plotting 100 different curves for each level of education. Each curve is a draw from our posterior distribution. Because the curves are somewhat translucent, we can interpret dark, narrow portions of a curve as places where we have low uncertainty and light, spread out portions of the curve as places where we have somewhat higher uncertainty about our coefficient values.
```
# Plot the posterior predictive distributions of P(income > $50K) vs. age
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm, samples=100, color="blue", alpha=.15)
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm2, samples=100, color="green", alpha=.15)
pm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm3, samples=100, color="red", alpha=.15)
import matplotlib.lines as mlines
blue_line = mlines.Line2D(['lm'], [], color='b', label='High School Education')
green_line = mlines.Line2D(['lm2'], [], color='g', label='Bachelors')
red_line = mlines.Line2D(['lm3'], [], color='r', label='Grad School')
plt.legend(handles=[blue_line, green_line, red_line], loc='lower right')
plt.ylabel("P(Income > $50K)")
plt.xlabel("Age")
plt.show()
b = trace['educ']
plt.hist(np.exp(b), bins=20, normed=True)
plt.xlabel("Odds Ratio")
plt.show()
```
Finally, we can find a credible interval (remember kids - credible intervals are Bayesian and confidence intervals are frequentist) for this quantity. This may be the best part about Bayesian statistics: we get to interpret credibility intervals the way we've always wanted to interpret them. We are 95% confident that the odds ratio lies within our interval!
```
lb, ub = np.percentile(b, 2.5), np.percentile(b, 97.5)
print("P(%.3f < O.R. < %.3f) = 0.95" % (np.exp(lb),np.exp(ub)))
```
## Model selection
One question that was immediately asked was what effect does age have on the model, and why should it be $age^2$ versus age? We'll run the model with a few changes to see what effect higher order terms have on this model in terms of WAIC.
```
models_lin, traces_lin = run_models(data, 4)
dfwaic = pd.DataFrame(index=['k1','k2','k3','k4'], columns=['lin'])
dfwaic.index.name = 'model'
for nm in dfwaic.index:
dfwaic.loc[nm, 'lin'] = pm.waic(traces_lin[nm],models_lin[nm])[0]
dfwaic = pd.melt(dfwaic.reset_index(), id_vars=['model'], var_name='poly', value_name='waic')
g = seaborn.factorplot(x='model', y='waic', col='poly', hue='poly', data=dfwaic, kind='bar', size=6)
```
WAIC confirms our decision to use age^2.
|
github_jupyter
|
# Indian food analysis
Firstly please read docs.md
## Table of contents
* Data preparation
* Load original dataset into dataframes
* Data cleansing
* Save dataset
* Load cleansed dataset
* Analysis
* Top 30 popular songs of all time
* Analyze by a single song
* Analyze track duration with frequency distribution chart
* Analyze average track details by year
## Data preparation
### Load original dataset into dataframes
fonte: https://www.kaggle.com/yamaerenay/spotify-dataset-19212020-160k-tracks
```
import numpy as np
import pandas as pd
# read dataset from csv
df_data_by_song : pd.DataFrame = pd.read_csv('dataset/original/data.csv', index_col='name')
df_data_by_artist : pd.DataFrame = pd.read_csv('dataset/original/data_by_artist.csv', index_col='artists')
df_data_by_genres : pd.DataFrame = pd.read_csv('dataset/original/data_by_genres.csv', index_col='genres')
df_data_by_year : pd.DataFrame = pd.read_csv('dataset/original/data_by_year.csv', index_col='year')
df_data_w_genres : pd.DataFrame = pd.read_csv('dataset/original/data_w_genres.csv', index_col='artists')
# show dataset
print(f'data_by_song:\tPK: {df_data_by_song.index.name}\t{str(list(df_data_by_song.columns))}')
print(f'data_by_artist:\tPK: {df_data_by_artist.index.name}\t{str(list(df_data_by_artist.columns))}')
print(f'data_by_genres:\tPK: {df_data_by_genres.index.name}\t{str(list(df_data_by_genres.columns))}')
print(f'data_by_year:\tPK: {df_data_by_year.index.name}\t{str(list(df_data_by_year.columns))}')
print(f'data_w_genres:\tPK: {df_data_w_genres.index.name}\t{str(list(df_data_w_genres.columns))}')
```
### Data cleansing
```
# some fixes
df_data_by_song = df_data_by_song.drop(columns=['id'])
df_data_by_artist.index.name = 'artist'
df_data_by_genres.index.name = 'genre'
df_data_w_genres.index.name = 'artist'
# reorder columns
df_data_by_song = df_data_by_song[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness', 'artists', 'year', 'explicit', 'release_date']]
df_data_by_artist = df_data_by_artist[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'count']]
df_data_by_genres = df_data_by_genres[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness']]
df_data_by_year = df_data_by_year[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness']]
df_data_w_genres = df_data_w_genres[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness', 'count', 'genres']]
```
### Savedataset
```
df_data_by_song.to_csv('dataset/cleansed/data_by_song.csv')
df_data_by_artist.to_csv('dataset/cleansed/data_by_artist.csv')
df_data_by_genres.to_csv('dataset/cleansed/data_by_genres.csv')
df_data_by_year.to_csv('dataset/cleansed/data_by_year.csv')
df_data_w_genres.to_csv('dataset/cleansed/data_w_genres.csv')
```
### Load cleansed dataset
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
df_data_by_song : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_song.csv', index_col='name')
df_data_by_artist : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_artist.csv', index_col='artist')
df_data_by_genres : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_genres.csv', index_col='genre')
df_data_by_year : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_year.csv', index_col='year')
df_data_w_genres : pd.DataFrame = pd.read_csv('dataset/cleansed/data_w_genres.csv', index_col='artist')
```
## Analysis
### Top 30 popular songs of all time
you can choose by and ascending or dicending
```
by = 'loudness' # choices: popularity duration_ms key loudness tempo year
ascending = False
import matplotlib.pyplot as plt
df_data_by_song_tops = df_data_by_song.sort_values(by=by, ascending=ascending).head(30)
fig, ax = plt.subplots(figsize=(10, 10))
ax.barh(list(df_data_by_song_tops.index.values), df_data_by_song_tops[by])
ax.invert_yaxis()
plt.title('Most ingredient used')
plt.show()
```
### Analyze by a single song
you can choose song_name
```
song_name = 'Stasera... Che Sera! - 1991 - Remaster;'
import matplotlib.pyplot as plt
from lib.complexRadar import ComplexRadar
if song_name not in df_data_by_song.index:
raise IndexError('Song doesn\'t exist')
song = df_data_by_song.loc[song_name]
if isinstance(song, pd.DataFrame): #if multiple song with same name, song is a Dataframe, so I have to save only the first row as pd.Series
song = song.iloc[0]
# duration milliseconds to seconds
song = song.rename({'duration_ms' : 'duration_s'})
song['duration_s'] = song['duration_s'] / 1000
# print release date
print('Release date: ' + song['release_date'])
print()
# print artists details
import ast
print('Artists: ')
print()
for artist in ast.literal_eval(song['artists']):
print('name: ' + artist)
if artist in df_data_by_artist.index:
print(df_data_by_artist.loc[artist].to_string())
print()
# print track details
print('track details:')
song: pd.Series = song.drop(index=['artists', 'release_date'])
variables = list(song.index)
data = list(song.values)
ranges = [(0, 100), (0, 1), (0, 1), (0, 6000), # popularity danceability valence duration_s
(0, 1), (0, 1), (0, 1), (0, 1), # energy acousticness instrumentalness liveness
(0, 11), (-60, 4), (-1, 250), (0, 1), # key loudness tempo mode
(0, 1), (1921, 2020), (0, 1)] # speechiness year explicit
# plotting
fig = plt.figure(figsize=(6, 6))
radar = ComplexRadar(fig, variables, ranges)
radar.plot(data)
radar.fill(data, alpha=0.2)
plt.show()
```
### Analyze track duration with frequency distribution chart
```
X = df_data_by_song.rename(columns={'duration_ms' : 'duration_s'})
X=X['duration_s'].loc[X['duration_s'] < 800000] / 10**3
# plotting
plt.figure(figsize=(20, 5))
sns.distplot(X)
plt.show()
```
### Analyze average track details by year
you can choose by which detail
```
by = 'duration_ms' #choices: popularity, duration_ms, key, loudness, tempo
df_data_by_song : pd.DataFrame = df_data_by_song
data = df_data_by_song[[by, 'year']].groupby(by='year').mean()
X = data.index
Y = data[by].values
# plotting
fig, ax = plt.subplots()
ax.plot(X, Y)
ax.grid()
ax.set_xlabel('year')
ax.set_ylabel(by)
fig.set_size_inches(20, 5)
fig.show()
```
|
github_jupyter
|
```
import numpy
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Activation
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization
from keras.utils import to_categorical
from keras import backend as K
from keras.wrappers.scikit_learn import KerasClassifier
from keras.utils import np_utils
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_val_score
import numpy as np
import pandas as pd
from sklearn import preprocessing
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import linear_model
from statistics import mean, stdev
from sklearn.preprocessing import scale
from keras.utils import to_categorical
from sklearn import metrics
SOXL = pd.read_csv('soxl_new.csv') #ETF growth cycle
TQQQ = pd.read_csv('tqqq_new.csv') #3X Index
MU = pd.read_csv('mu_new.csv') #high Beta
AMD = pd.read_csv('amd_new.csv') # high beta
NFLX = pd.read_csv('nflx_new.csv') #High growth
AMZN = pd.read_csv('amzn_new.csv') #High growth
V = pd.read_csv('visa_new.csv') #low volalitity
NVDA = pd.read_csv('nvda_new.csv') #high growth
NFLX['tar_3best_class'].unique()
features = ['Day_previous_roi','ma10','rsi10','ma20','rsi20','ma_chg20',
'ma60','rsi60','ma200','rsi200','obv','macd_diff','ma_chg10',
'macd_diff_hist','aroon_diff','slope60','r_sqr_60','ma_chg60',
'slope10','r_sqr_10','slope5','r_sqr_5','stDev20','ma_chg200',
'rsi_chg10','rsi_chg20','rsi_chg60','rsi_chg200',
'percent_down','sine','leadsine','tsf10','tsf20','tsf60','tsf200',
'up_dwn_prev','shawman','hammer','semi_pk_pr']
top_feats = ['ma200',
'macd_diff_hist',
'tsf200',
'r_sqr_60',
'slope60']#,
# 'macd_diff',
# 'tsf60',
# 'slope10',
# 'r_sqr_10',
# 'percent_down',
# 'rsi60',
# 'obv']
#Set stock or dataframe
df_cln = NFLX
target_name = 'tar_3best_class'
#.75 make a 25/75 split
stop = round(.80*len(df_cln))
#set features
features = df_cln[features].values
top_features = df_cln[top_feats].values
targets = df_cln[target_name].values
arr = []
end = targets.shape[0]
for i in range(end):
#print(targets[i])
if targets[i] == 'bel_1.02':
arr.append([1,0,0,0])
elif targets[i] == 'abv_1.02':
arr.append([0,1,0,0])
elif targets[i] == 'abv_1.04':
arr.append([0,0,1,0])
elif targets[i] == 'abv_1.07':
arr.append([0,0,0,1])
target_int = arr
feature_train = features[:stop]
feature_test = features[stop:]
top_feat_train = top_features[:stop]
top_feat_test = top_features[stop:]
target_test_int = target_int[stop:]
target_train_int = target_int[:stop]
#set my targets
# feature_train = np.array(feature_train)
# target_train = np.array(target_train)
# feature_test = np.array(feature_test)
# target_test = np.array(target_test)
feature_train.reshape(feature_train.shape[0],
feature_train.shape[1],
1).astype( 'float32' )
feature_test.reshape(feature_test.shape[0],
feature_test.shape[1],
1).astype( 'float32' )
#print(feature_train.shape,target_train.shape)
# from keras.utils.np_utils import to_categorical
# categorical_labels = to_categorical(target_int, num_classes=4)
# categorical_labels
#target_train_int
# # Standardize the train and test features
# scaled_train_features = scale(feature_train)
# scaled_test_features = scale(feature_test)
# # Create the model
# def baseline_model():
# model_1 = Sequential()
# model_1.add(Dense(200, input_dim=scaled_train_features.shape[1], activation='relu'))
# #model_1.add(Dropout(0.25))
# model_1.add(Dense(200, activation='relu'))
# #model_1.add(Dropout(0.25))
# model_1.add(Dense(100, activation='relu'))
# model_1.add(Dense(10, activation='relu'))
# model_1.add(Dense(4, activation='softmax'))
# model_1.compile(loss= 'categorical_crossentropy' ,
# optimizer= 'adam' ,
# metrics=[ 'accuracy' ])
# return model_1
# # Fit the model
# history = KerasClassifier(build_fn=baseline_model, epochs=40, batch_size=200, verbose=True)
# kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=42)
# results = cross_val_score(history,scaled_train_features , target_train, cv=kfold)
# print(results.mean())
# %matplotlib inline
# plt.plot(history.history['acc'],'b')
# plt.plot(history.history['val_acc'],'r')
# plt.show()
# model = baseline_model()
# model.fit(feature_train,target_train, epochs=40, verbose=2)
# target_test.unique()
# Standardize the train and test features
min_max_scaler = preprocessing.MinMaxScaler()
X_train = min_max_scaler.fit_transform(feature_train)
X_test = min_max_scaler.fit_transform(feature_test)
min_max_scaler = preprocessing.MinMaxScaler()
top_X_train = min_max_scaler.fit_transform(top_feat_train)
top_X_test = min_max_scaler.fit_transform(top_feat_test)
from keras.layers import Input, Dense, Dropout, BatchNormalization
from keras.models import Model, load_model
import keras.backend as K
from keras.callbacks import ModelCheckpoint
# Standardize the train and test features
K.clear_session()
target_test = np.array(target_test_int)
target_train = np.array(target_train_int)
# scaled_train_features = scale(feature_train)
# scaled_test_features = scale(feature_test)
# Create the model
K.clear_session()
inputs = Input(shape=(top_X_train.shape[1], ))
x1 = Dense(128)(inputs)
x1 = BatchNormalization()(x1)
x1 = Activation('relu')(x1)
x1 = Dropout(0.5)(x1)
# x2 = Dense(16, activation='relu')(x1)
# x2 = BatchNormalization()(x2)
# x2 = Activation('relu')(x2)
# x3 = Dense(16, activation='relu')(x2)
# x3 = BatchNormalization()(x3)
# x3 = Activation('relu')(x3)
# x4 = Dense(8, activation='relu')(x3)
# x4 = BatchNormalization()(x4)
# x4 = Activation('relu')(x4)
# x5 = Dense(16, activation='relu')(x4)
# x5 = BatchNormalization()(x5)
# x5 = Activation('relu')(x5)
# x6 = Dense(32, activation='relu')(x5)
# x6 = BatchNormalization()(x6)
# x6 = Activation('relu')(x6)
# x7 = Dense(64, activation='relu')(x6)
# x7 = BatchNormalization()(x7)
# x7 = Activation('relu')(x7)
x = Dense(4, activation='softmax')(x1)
checkpoint = ModelCheckpoint('3_layer_dense.h5',
monitor='val_loss',
save_best_only=True)
cb = [checkpoint]
# this compiles our model so it is ready to fit
model = Model(inputs, x)
model.compile(loss= 'categorical_crossentropy' ,
optimizer= 'adam' ,
metrics=[ 'accuracy' ])
model.summary()
2**7
#target_test = categorical_labels[stop:]
#target_train = categorical_labels[:stop]
# we actually fit the model here
history = model.fit(top_X_train,
target_train,
epochs=100,
validation_split=0.15,
callbacks=cb,
batch_size=200)
plt.plot(history.history['loss'], label = 'training loss')
plt.plot(history.history['val_loss'], label = 'validation loss')
plt.legend()
plt.show()
history = model.fit(top_X_train,
target_train,
epochs=100,
validation_split=0.15,
callbacks=cb,
batch_size=200)
target_pred = model.predict(top_X_test)
print("Accuracy:",metrics.accuracy_score(target_test_int, target_pred),'\n'
'Cohans Kappa:', metrics.cohen_kappa_score(target_test_int, target_pred),'\n'
'Train ACC:', metrics.accuracy_score(target_train_int, target_pred), '\n'
"Confusion Matrix:",'\n',
metrics.confusion_matrix(target_test, target_pred))
target_pred
target_train_int
targets = df_cln[target_name].values
targ_test = targets[stop:]
targ_train = targets[:stop]
targ_train[0:10]
history.predict_classes(feature_test)
top_X_train,
target_train,
epochs=100,
validation_split=0.15,
callbacks=cb,
batch_size=200
```
|
github_jupyter
|
```
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import zscore
import sklearn.preprocessing as preproc
from sklearn.cluster import KMeans, DBSCAN
from collections import Counter
from pract2_utils import *
RESULTS='results/accidentes/'
DATA='data/accidentes_2013.csv'
def readData(results_file):
return pd.read_csv(results_file,header=0,engine='python')
dataTot=readData(DATA)
dataTot
dataTot.columns
# Atributos numéricos que reflejan la gravedad del accidente, sobre los que haré clustering
atributos=['TOT_VICTIMAS','TOT_MUERTOS','TOT_HERIDOS_GRAVES','TOT_HERIDOS_LEVES','TOT_VEHICULOS_IMPLICADOS']
```
## Caso de uso 2: Estudio de los accidentes a altas horas de la madrugada
Filtramos los datos para quedarnos con accidentes que ocurren a altas horas de la madrugada.
```
data2=dataTot[dataTot.HORA<=6]
data=data2[atributos] # En data2 quedan el resto de variables
data
for a in atributos:
print(a)
print(Counter(data[a]))
# Box Plot
n_var = len(atributos)
fig, axes = plt.subplots(1, n_var, sharey=True, figsize=(15,5))
fig.subplots_adjust(wspace=0, hspace=0)
colors = sns.color_palette(palette=None, n_colors=1, desat=None)
rango = []
for j in range(n_var):
d=data[atributos[j]]
rango.append([d.min(), d.max()])
for i in range(1):
dat_filt = data
for j in range(n_var):
ax = sns.boxplot(x=dat_filt[atributos[j]],
color=colors[i],
flierprops={
'marker': 'o',
'markersize': 4
},
ax=axes[j], whis=3,showfliers=True)
if (i == 0):
axes[j].set_xlabel(atributos[j])
else:
axes[j].set_xlabel("")
if (j == 0):
axes[j].set_ylabel("")
else:
axes[j].set_ylabel("")
axes[j].set_yticks([])
axes[j].grid(axis='x',
linestyle='-',
linewidth='0.2',
color='gray')
axes[j].grid(axis='y', b=False)
ax.set_xlim(rango[j][0] - 0.05 * (rango[j][1] - rango[j][0]),
rango[j][1] + 0.05 * (rango[j][1] - rango[j][0]))
# Normalizar los datos
normalizer=preproc.MinMaxScaler()
data_norm=normalizer.fit_transform(data)
data_norm
```
### K-Means
```
# Elección de un número adecuado de Clústers atendiendo a las métricas
K=list(range(2,10))
silhouette=[]
calinski=[]
for k in K:
results = KMeans(n_clusters=k, random_state=0).fit(data_norm)
sil, cal = measures_silhoutte_calinski(data_norm, results.labels_)
silhouette.append(sil)
calinski.append(cal)
print(silhouette)
print(calinski)
plt.plot(K,calinski, 'bo-')
plt.xlabel('Nº de clústers. K')
plt.ylabel('Calinski')
plt.show()
plt.plot(K,silhouette,'bo-')
plt.ylabel('Silhouette')
plt.xlabel('Nº de clústers. K')
plt.show()
```
Nos quedaremos con K=3. Introducir más clústers no gana tanto score y hace la segmentación muy difícil de interpretar.
```
K=3
results = KMeans(n_clusters=K, random_state=0).fit(data_norm)
labels=results.labels_
centroids=results.cluster_centers_
```
Análisis.
```
Counter(labels)
visualize_centroids(centroids, np.array(data), atributos, denormCentroids=True)
pairplot(data,atributos,labels)
dataC=data.copy()
dataC['cluster']=labels
dataC
# Box Plot
n_var = len(atributos)
fig, axes = plt.subplots(K, n_var, sharey=True, figsize=(15, 15))
fig.subplots_adjust(wspace=0, hspace=0)
colors = sns.color_palette(palette=None, n_colors=K, desat=None)
rango = []
for j in range(n_var):
d=dataC[atributos[j]]
rango.append([d.min(), d.max()])
for i in range(K):
dat_filt = dataC.loc[dataC['cluster'] == i]
for j in range(n_var):
ax = sns.boxplot(x=dat_filt[atributos[j]],
color=colors[i],
flierprops={
'marker': 'o',
'markersize': 4
},
ax=axes[i, j], whis=3,showfliers=True)
if (i == K - 1):
axes[i, j].set_xlabel(atributos[j])
else:
axes[i, j].set_xlabel("")
if (j == 0):
axes[i, j].set_ylabel("Cluster " + str(i))
else:
axes[i, j].set_ylabel("")
axes[i, j].set_yticks([])
axes[i, j].grid(axis='x',
linestyle='-',
linewidth='0.2',
color='gray')
axes[i, j].grid(axis='y', b=False)
ax.set_xlim(rango[j][0] - 0.05 * (rango[j][1] - rango[j][0]),
rango[j][1] + 0.05 * (rango[j][1] - rango[j][0]))
```
Con K=6 también obtenemos una ganancia considerable en las métricas, pero el análisis es más complejo debido al mayor número de clústers.
```
K=6
results = KMeans(n_clusters=K, random_state=0).fit(data_norm)
labels=results.labels_
centroids=results.cluster_centers_
data2['cluster']=labels # Para después observar el resto de variables
print(Counter(labels))
# Introduce un clúster con muertos, antes los despreciaba
visualize_centroids(centroids, np.array(data), atributos, denormCentroids=True)
pairplot(data,atributos,labels)
dataC=data.copy()
dataC['cluster']=labels
dataC
# Box Plot
n_var = len(atributos)
fig, axes = plt.subplots(K, n_var, sharey=True, figsize=(15, 15))
fig.subplots_adjust(wspace=0, hspace=0)
colors = sns.color_palette(palette=None, n_colors=K, desat=None)
rango = []
for j in range(n_var):
d=dataC[atributos[j]]
rango.append([d.min(), d.max()])
for i in range(K):
dat_filt = dataC.loc[dataC['cluster'] == i]
for j in range(n_var):
ax = sns.boxplot(x=dat_filt[atributos[j]],
color=colors[i],
flierprops={
'marker': 'o',
'markersize': 4
},
ax=axes[i, j], whis=3,showfliers=True)
if (i == K - 1):
axes[i, j].set_xlabel(atributos[j])
else:
axes[i, j].set_xlabel("")
if (j == 0):
axes[i, j].set_ylabel("Cluster " + str(i))
else:
axes[i, j].set_ylabel("")
axes[i, j].set_yticks([])
axes[i, j].grid(axis='x',
linestyle='-',
linewidth='0.2',
color='gray')
axes[i, j].grid(axis='y', b=False)
ax.set_xlim(rango[j][0] - 0.05 * (rango[j][1] - rango[j][0]),
rango[j][1] + 0.05 * (rango[j][1] - rango[j][0]))
```
### DBSCAN
Ahora utilizaremos el algoritmo DBSCAN para formar los clústers
```
# Elección de un umbral de distancia por encima del cual no se mezclarán más clústers
#E=[0.1,0.15,0.2,0.25,0.3,0.35]
E=[0.1,0.11,0.12,0.13,0.14,0.15]
# Con 0.35 en adelante ya hace un sólo clúster
K=[]
silhouette=[]
calinski=[]
for e in E:
results = DBSCAN(eps=e, min_samples=50, n_jobs=4).fit(data_norm)
sil, cal = measures_silhoutte_calinski(data_norm, results.labels_)
silhouette.append(sil)
calinski.append(cal)
K.append(max(results.labels_)+1) # La etiqueta -1 corresponde a un clúster de muestras que el algoritmo considera ruidosas, luego lo desecharemos
print(silhouette)
print(calinski)
print(K)
plt.plot(E,calinski, 'bo-')
plt.ylabel('Calinski')
plt.xlabel('Radio')
plt.show()
plt.plot(E,silhouette,'bo-')
plt.ylabel('Silhouette')
plt.xlabel('Radio')
plt.show()
plt.plot(E,K,'bo-')
plt.ylabel('Nº de clústers. K')
plt.xlabel('Radio')
plt.show()
```
Elegimos epsilon=0.15
```
E=0.15 #0.12 produce 8 clústers y considera demasiados elementos (266) como ruidosos
results = DBSCAN(eps=E, min_samples=50, n_jobs=4).fit(data_norm)
labels=results.labels_
Counter(labels)
```
Calculamos los centroides a mano
```
dataC=data.copy()
dataC['cluster']=labels
dataC
# Eliminamos los 183 ejemplos que el algoritmo considera ruidosos
dataC.drop(dataC[dataC['cluster']==-1].index,inplace=True)
dataC
centroids = dataC.groupby('cluster').mean()
centroids
centroids=centroids.values
centroids
visualize_centroids(centroids, np.array(data), atributos, denormCentroids=False)
labels=[l for l in labels if l != -1]
pairplot(dataC,atributos,labels)
K=max(labels)+1
# Box Plot
n_var = len(atributos)
fig, axes = plt.subplots(K, n_var, sharey=True, figsize=(15, 15))
fig.subplots_adjust(wspace=0, hspace=0)
colors = sns.color_palette(palette=None, n_colors=K, desat=None)
rango = []
for j in range(n_var):
d=dataC[atributos[j]]
rango.append([d.min(), d.max()])
for i in range(K):
dat_filt = dataC.loc[dataC['cluster'] == i]
for j in range(n_var):
ax = sns.boxplot(x=dat_filt[atributos[j]],
color=colors[i],
flierprops={
'marker': 'o',
'markersize': 4
},
ax=axes[i, j], whis=3,showfliers=True)
if (i == K - 1):
axes[i, j].set_xlabel(atributos[j])
else:
axes[i, j].set_xlabel("")
if (j == 0):
axes[i, j].set_ylabel("Cluster " + str(i))
else:
axes[i, j].set_ylabel("")
axes[i, j].set_yticks([])
axes[i, j].grid(axis='x',
linestyle='-',
linewidth='0.2',
color='gray')
axes[i, j].grid(axis='y', b=False)
ax.set_xlim(rango[j][0] - 0.05 * (rango[j][1] - rango[j][0]),
rango[j][1] + 0.05 * (rango[j][1] - rango[j][0]))
print(sum(data.TOT_MUERTOS))
print(sum(data.TOT_HERIDOS_GRAVES))
```
### Estudio de variables circunstanciales y de tipo dentro en los clusters
```
Counter(data2.TIPO_ACCIDENTE)
cluster_3=data2[data2.cluster==3]
cluster_4=data2[data2.cluster==4]
data2.shape[0], cluster_3.shape[0], cluster_4.shape[0]
conjuntos=[data2,cluster_3,cluster_4]
def prop(condicion,data):
n=0
for i, row in data.iterrows():
if condicion(row):
n+=1
return n/data.shape[0]
def propChoques_front_lat(data):
condicion=(lambda x: '(Front' in x.TIPO_ACCIDENTE or '(Lateral)' in x.TIPO_ACCIDENTE)
return prop(condicion,data)
def propAlcances(data):
condicion=(lambda x: '(Alcance)' in x.TIPO_ACCIDENTE)
return prop(condicion,data)
def propInterurbanas(data):
condicion=(lambda x: x.ZONA_AGRUPADA=='VÍAS INTERURBANAS')
return prop(condicion,data)
def propUrbanas(data):
condicion=(lambda x: x.ZONA_AGRUPADA=='VÍAS URBANAS')
return prop(condicion,data)
def propAtropellos(data):
condicion=(lambda x: 'peatón' in x.TIPO_ACCIDENTE)
return prop(condicion,data)
for c in conjuntos: # Proporción de choques frontales y laterales
print(propChoques_front_lat(c))
for c in conjuntos: # Proporción de choques por alcance
print(propAlcances(c))
for c in conjuntos:
print(propUrbanas(c))
for c in conjuntos:
print(propInterurbanas(c))
for c in conjuntos:
print(propAtropellos(c))
```
|
github_jupyter
|
```
import os
import sys
import numpy as np
import pandas as pd
from scipy.io import mmread
from scipy.linalg import hessenberg
import scipy.linalg as sl
sys.path.append("../qr")
from qr import *
import sympy as sp
a = np.random.default_rng().random(size = (10, 10))
%%timeit
max(a[0])
%%timeit
np.max(a[0])
path = "../test_matrices"
mat_1_file = "west0381"
ext = ".mtx.gz"
mat = mmread(os.path.join(path, "".join((mat_1_file, ext))))
m = mat.toarray()
m
import mpmath as mpm
mpm.dps = 15
def complex_matrix(n: int, a: float, b: float) -> np.ndarray:
if a >= b:
raise ValueError("Required: b > a")
r = (b - a) * np.random.default_rng().random(size = (n, n)) + a
c = (b - a) * np.random.default_rng().random(size = (n, n)) + a
m = r + 1j * c
return m.astype(np.complex128)
def householder_reflector(x: np.array):
"""
Produces the Householder
vector based on the input
vector x. The householder
vector acts as:
|a_1| |alpha|
|a_2| -> |0|
|a_3| |0|
Parameters
----------
x:
A numpy array who's entries
after the 1st element needs to
be 0ed.
Returns
-------
A numpy array that acts as the
Householder vector.
"""
u = x.copy()
rho = -np.exp(1j * np.angle(u[0]), dtype = np.complex128)
# Set the Householder vector
# to u = u \pm alpha e_1 to
# avoid cancellation.
u[0] -= rho * mpm.norm(u)
# Vector needs to have 1
# in the 2nd dimension.
# print(u)
return u.reshape(-1, 1)
def hessenberg_transform_1(M: np.ndarray) -> np.ndarray:
"""
Converts a given matrix to
Hessenberg form using
Houeholder transformations.
Parameters
----------
M:
A complex square
numpy 2darray.
Returns
-------
A tuple consisting of numpy
2-D arrays which are the
hessenberg form and the
permutation matrix.
"""
h = M.copy()
n = np.array(h.tolist()).shape[0]
u = np.eye(n, dtype = np.complex128)
householder_vectors = list()
# MAIN LOOP.
for l in range(n - 2):
# Get the Householder vector for h.
t = householder_reflector(h[l + 1 :, l])
# Norm**2 of the Householder vector.
t_norm_squared = t.conj().T @ t
# p = np.eye(h[l + 1:, l].shape[0]) - 2 * (np.outer(t, t)) / t_norm_squared
# # Resize and refactor the Householder matrix.
# p = np.pad(p, ((l + 1, 0), (l + 1, 0)), mode = "constant", constant_values = ((0, 0), (0, 0)))
# for k in range(l + 1):
# p[k, k] = 1
# Perform a similarity transformation on h
# using the Householder matrix.
# h = p @ h @ p.
# --- REAL --- #
# Left multiplication by I - 2uu^{*}.
# h_real[l + 1 :, l :] -= 2 * (t @ (t.conj().T @ h_real[l + 1 :, l :])) / t_norm_squared
# Right multiplication by I - 2uu^{*}.
# h_real[ :, l + 1 :] -= 2 * ((h[ :, l + 1 :] @ t) @ t.conj().T) / t_norm_squared
# print(f"{np.array(h[l + 1 :, l :].tolist()).shape = }")
# print(f"{np.array(t.transpose_conj().tolist()).shape = }")
# print(f"{np.array((t.transpose_conj() * h[l + 1 :, l :]).tolist()).shape = }")
factor = 2 / t_norm_squared
h[l + 1 :, l :] -= factor * (t @ (t.conj().T @ h[l + 1 :, l :]))
# --- IMAGINARY --- #
# Left multiplication by I - 2uu^{*}.
# h_imag[l + 1 :, l :] -= 2 * (t @ (t.conj().T @ h_imag[l + 1 :, l :])) / t_norm_squared
# Right multiplication by I - 2uu^{*}.
# h_imag[ :, l + 1 :] -= 2 * ((h[ :, l + 1 :] @ t) @ t.conj().T) / t_norm_squared
h[ :, l + 1 :] -= factor * ((h[ :, l + 1 :] @ t) @ t.conj().T)
# Force elements below main
# subdiagonal to be 0.
h[l + 2 :, l] = 0.0
# Store the transformations
# to compute u.
householder_vectors.append(t)
# Store the transformations.
for k in reversed(range(n - 2)):
t = householder_vectors[k]
t_norm_squared = np.dot(t.conj().T, t)
u[k + 1 :, k + 1 :] = 2 * t * (t.conj().T @ u[k + 1 :, k + 1 :]) / t_norm_squared
# h = h_real + 1j * h_imag
return h, u
n = 1000
a = 10.0
b = 20.0
# m = complex_matrix(n, a, b)
# M = mpm.matrix(m.tolist())
hess_from_alg, _ = hessenberg_transform_1(m)
hess_from_scipy = hessenberg(m)
%%capture cap --no-stderr
pd.options.display.max_columns = 200
pd.set_option("display.width", 1000)
pd.set_option("display.max_columns", 200)
pd.set_option("display.max_rows", 1000)
# print(f" Hessenberged:\n {pd.DataFrame(hess_alg)}")
# print(f"Hessenberged (scipy):\n {pd.DataFrame(hess_from_scipy)}")
eigs = np.sort(np.linalg.eig(hess_from_alg)[0])
eigs_scipy = np.sort(np.linalg.eig(hess_from_scipy)[0])
print(f"Eigs:\n {pd.DataFrame(np.vstack([eigs, eigs_scipy]).T)}")
print(f"Equality of eigs: {np.testing.assert_allclose(eigs_scipy, eigs, rtol = 1e-6)}")
with open("test_ipynb_output.txt", "w") as f:
f.write(cap.stdout)
sl.blas.daxpy([1, 2, 3], [1, 2, 3], a = 0.5)
def sign(z: complex) -> complex:
if z == 0:
return 1
return z / abs(z)
sign(-2.0 + 2.j)
a = np.array([1.00345345, 2, 1, -1, 2])
b = np.array([1.00354, 2, 1, -1, 2])
[i for i, _ in enumerate(a) if np.isclose(_, 1.00354, 1e-3)]
np.round(1.011234, 1) == 1.0
dec = 6
a = f"{0:.{dec}f}"
print(float(a))
np.prod([1, 2, 3, 4])
```
|
github_jupyter
|
```
import os
import sys
module_path = os.path.abspath('..')
sys.path.append(module_path)
from lc.measurements import CurveMeasurements
from lc.curve import LearningCurveEstimator
from omegaconf import OmegaConf
```
Load error measurements using `CurveMeasurements`. See `notebooks/measurements.ipynb` for more about reading error measurements.
```
curvems = CurveMeasurements()
curvems.load_from_json('../data/no_pretr_ft.json')
print(curvems)
```
Load default config. Modify `config.yaml` directly or update parameters once loaded.
```
cfg = OmegaConf.load('../lc/config.yaml')
print('-'*20)
print('Default config')
print('-'*20)
print(OmegaConf.to_yaml(cfg))
cfg.gamma_search = False
print('-'*20)
print('Modified config')
print('-'*20)
print(OmegaConf.to_yaml(cfg))
curve_estimator = LearningCurveEstimator(cfg)
curve, objective = curve_estimator.estimate(curvems)
print('Quality of the fit:',objective)
curve.print_summary(cfg.N)
```
Searching for gamma leads to better fit. To enable gamma search set `gamma_search` to `True` (default). When gamma search is disabled, `curve_estimator.estimate()` uses `cfg.gamma` to estimate the curve.
```
cfg.gamma_search = True
curve, objective = curve_estimator.estimate(curvems)
print('Quality of the fit:',objective)
curve.print_summary(cfg.N)
```
Use `curve_estimator.plot()` to visualizes the learning curve and the error measurements.
```
curve_estimator.plot(curve,curvems,label='No Pretr; Ft')
```
You may also want to visualize the variance estimates. We recommend using the smoothed variance estimate but you can switch to using sample variance for curve estimation by setting `cfg.variance_type='sample'`. See `notebooks/variance.ipynb` for details on smooth variance estimation.
```
curve_estimator.err_mean_var_estimator.visualize(curvems)
```
Plot multiple curves for easy comparison.
```
plot_metadata = [
['../data/no_pretr_linear.json','No Pretr; Lin','r','--'],
['../data/no_pretr_ft.json','No Pretr; Ft','g','-'],
['../data/pretr_linear.json','Pretr; Lin','b','--'],
['../data/pretr_ft.json','Pretr; Ft','m','-']
]
for (json_path,label,color,linestyle) in plot_metadata:
curvems.load_from_json(json_path)
curve, _ = curve_estimator.estimate(curvems)
curve_estimator.plot(curve,curvems,label,color,linestyle)
```
## What if you don't have all recommended error measurements?
Technically, it is possible to use just 2 training set sizes to estimate the learning curve but the results may be susceptible to high variance. For instance, here we estimate the learning curve using only measurements on training set sizes of 400 and 200. Note that below, we plot all error measurements and not just the ones used to estimate the curve.
```
import copy
for (json_path,label,color,linestyle) in plot_metadata:
curvems.load_from_json(json_path)
curvems_filtered = copy.deepcopy(curvems)
curvems_filtered.curvems = [errms for errms in curvems if errms.num_train_samples in [400,200]]
curve, _ = curve_estimator.estimate(curvems_filtered)
curve_estimator.plot(curve,curvems,label,color,linestyle)
```
However, results improve considerably when using 3 training set sizes. Below, we estimate learning curve using measurements on training sets of sizes 400, 200, and 100.
```
for (json_path,label,color,linestyle) in plot_metadata:
curvems.load_from_json(json_path)
curvems_filtered = copy.deepcopy(curvems)
curvems_filtered.curvems = [errms for errms in curvems if errms.num_train_samples in [400,200,100]]
curve, _ = curve_estimator.estimate(curvems_filtered)
curve_estimator.plot(curve,curvems,label,color,linestyle)
```
It may be possible to use much smaller training set sizes to compute learning curves as shown below. Note that the errors predicted by the curve at 200 and 400 training set sizes, which were not used to estimate the curve, are reasonably accurate.
```
for (json_path,label,color,linestyle) in plot_metadata:
curvems.load_from_json(json_path)
curvems_filtered = copy.deepcopy(curvems)
curvems_filtered.curvems = [errms for errms in curvems if errms.num_train_samples in [100,50,25]]
curve, _ = curve_estimator.estimate(curvems_filtered)
curve_estimator.plot(curve,curvems,label,color,linestyle)
```
## Quick and Lazy Approach
It is possible to compute a decent learning curve with only 3 error measurments - 1 for each of full, half, and quarter dataset sizes. In this case, simply set `cfg.v_1` to a reasonable value and proceed as before. This is our recommended approach if you are in a rush. See `notebooks/basic_lazy_usage.ipynb` for more details on this quick and lazy approach.
```
cfg.v_1 = 10
for (json_path,label,color,linestyle) in plot_metadata:
curvems.load_from_json(json_path)
curvems_filtered = copy.deepcopy(curvems)
curvems_filtered.curvems = [errms for errms in curvems if errms.num_train_samples in [400,200,100]]
for errms in curvems_filtered:
# Through away all but 1 error measurment per train set size
errms.test_errors = [errms.test_errors[0]]
errms.num_ms = 1
curve, _ = curve_estimator.estimate(curvems_filtered)
curve_estimator.plot(curve,curvems,label,color,linestyle)
```
|
github_jupyter
|
<h3 style='color:blue'>Exercise: GPU performance for fashion mnist dataset</h3>
This notebook is derived from a tensorflow tutorial here: https://www.tensorflow.org/tutorials/keras/classification
So please refer to it before starting work on this exercise
You need to write code wherever you see `your code goes here` comment. You are going to do image classification for fashion mnist dataset and then you will benchmark the performance of GPU vs CPU for 1 hidden layer and then for 5 hidden layers. You will eventually fill out this table with your performance benchmark numbers
| Hidden Layer | CPU | GPU |
|:------|:------|:------|
| 1 | ? | ? |
| 5 | ? | ? |
```
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
train_images.shape
plt.imshow(train_images[0])
train_labels[0]
class_names[train_labels[0]]
plt.figure(figsize=(3,3))
for i in range(5):
plt.imshow(train_images[i])
plt.xlabel(class_names[train_labels[i]])
plt.show()
train_images_scaled = train_images / 255.0
test_images_scaled = test_images / 255.0
def get_model(hidden_layers=1):
layers = []
# Your code goes here-----------START
# Create Flatten input layers
# Create hidden layers that are equal to hidden_layers argument in this function
# Create output
# Your code goes here-----------END
model = keras.Sequential(layers)
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
return model
model = get_model(1)
model.fit(train_images_scaled, train_labels, epochs=5)
model.predict(test_images_scaled)[2]
test_labels[2]
tf.config.experimental.list_physical_devices()
```
<h4 style="color:purple">5 Epochs performance comparison for 1 hidden layer</h4>
```
%%timeit -n1 -r1
with tf.device('/CPU:0'):
# your code goes here
%%timeit -n1 -r1
with tf.device('/GPU:0'):
# your code goes here
```
<h4 style="color:purple">5 Epocs performance comparison with 5 hidden layers</h4>
```
%%timeit -n1 -r1
with tf.device('/CPU:0'):
# your code here
%%timeit -n1 -r1
with tf.device('/GPU:0'):
# your code here
```
[Click me to check solution for this exercise](https://github.com/codebasics/py/blob/master/DeepLearningML/10_gpu_benchmarking/Exercise/exercise_solution.ipynb)
|
github_jupyter
|
# Chapter 7
This is the seventh in a series of notebooks related to astronomy data.
As a continuing example, we will replicate part of the analysis in a recent paper, "[Off the beaten path: Gaia reveals GD-1 stars outside of the main stream](https://arxiv.org/abs/1805.00425)" by Adrian M. Price-Whelan and Ana Bonaca.
In the previous notebook we selected photometry data from Pan-STARRS and used it to identify stars we think are likely to be in GD-1
In this notebook, we'll take the results from previous lessons and use them to make a figure that tells a compelling scientific story.
## Outline
Here are the steps in this notebook:
1. Starting with the figure from the previous notebook, we'll add annotations to present the results more clearly.
2. The we'll see several ways to customize figures to make them more appealing and effective.
3. Finally, we'll see how to make a figure with multiple panels or subplots.
After completing this lesson, you should be able to
* Design a figure that tells a compelling story.
* Use Matplotlib features to customize the appearance of figures.
* Generate a figure with multiple subplots.
## Installing libraries
If you are running this notebook on Colab, you can run the following cell to install Astroquery and the other libraries we'll use.
If you are running this notebook on your own computer, you might have to install these libraries yourself. See the instructions in the preface.
```
# If we're running on Colab, install libraries
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install astroquery astro-gala pyia python-wget
```
## Making Figures That Tell a Story
So far the figure we've made have been "quick and dirty". Mostly we have used Matplotlib's default style, although we have adjusted a few parameters, like `markersize` and `alpha`, to improve legibility.
Now that the analysis is done, it's time to think more about:
1. Making professional-looking figures that are ready for publication, and
2. Making figures that communicate a scientific result clearly and compellingly.
Not necessarily in that order.
Let's start by reviewing Figure 1 from the original paper. We've seen the individual panels, but now let's look at the whole thing, along with the caption:
<img width="500" src="https://github.com/datacarpentry/astronomy-python/raw/gh-pages/fig/gd1-5.png">
**Exercise:** Think about the following questions:
1. What is the primary scientific result of this work?
2. What story is this figure telling?
3. In the design of this figure, can you identify 1-2 choices the authors made that you think are effective? Think about big-picture elements, like the number of panels and how they are arranged, as well as details like the choice of typeface.
4. Can you identify 1-2 elements that could be improved, or that you might have done differently?
Some topics that might come up in this discussion:
1. The primary result is that the multiple stages of selection make it possible to separate likely candidates from the background more effectively than in previous work, which makes it possible to see the structure of GD-1 in "unprecedented detail".
2. The figure documents the selection process as a sequence of steps. Reading right-to-left, top-to-bottom, we see selection based on proper motion, the results of the first selection, selection based on color and magnitude, and the results of the second selection. So this figure documents the methodology and presents the primary result.
3. It's mostly black and white, with minimal use of color, so it will work well in print. The annotations in the bottom left panel guide the reader to the most important results. It contains enough technical detail for a professional audience, but most of it is also comprehensible to a more general audience. The two left panels have the same dimensions and their axes are aligned.
4. Since the panels represent a sequence, it might be better to arrange them left-to-right. The placement and size of the axis labels could be tweaked. The entire figure could be a little bigger to match the width and proportion of the caption. The top left panel has unnused white space (but that leaves space for the annotations in the bottom left).
## Plotting GD-1
Let's start with the panel in the lower left. The following cell reloads the data.
```
import os
from wget import download
filename = 'gd1_merged.hdf5'
path = 'https://github.com/AllenDowney/AstronomicalData/raw/main/data/'
if not os.path.exists(filename):
print(download(path+filename))
import pandas as pd
selected = pd.read_hdf(filename, 'selected')
import matplotlib.pyplot as plt
def plot_second_selection(df):
x = df['phi1']
y = df['phi2']
plt.plot(x, y, 'ko', markersize=0.7, alpha=0.9)
plt.xlabel('$\phi_1$ [deg]')
plt.ylabel('$\phi_2$ [deg]')
plt.title('Proper motion + photometry selection', fontsize='medium')
plt.axis('equal')
```
And here's what it looks like.
```
plt.figure(figsize=(10,2.5))
plot_second_selection(selected)
```
## Annotations
The figure in the paper uses three other features to present the results more clearly and compellingly:
* A vertical dashed line to distinguish the previously undetected region of GD-1,
* A label that identifies the new region, and
* Several annotations that combine text and arrows to identify features of GD-1.
As an exercise, choose any or all of these features and add them to the figure:
* To draw vertical lines, see [`plt.vlines`](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.vlines.html) and [`plt.axvline`](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.axvline.html#matplotlib.pyplot.axvline).
* To add text, see [`plt.text`](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.text.html).
* To add an annotation with text and an arrow, see [plt.annotate]().
And here is some [additional information about text and arrows](https://matplotlib.org/3.3.1/tutorials/text/annotations.html#plotting-guide-annotation).
```
# Solution
# plt.axvline(-55, ls='--', color='gray',
# alpha=0.4, dashes=(6,4), lw=2)
# plt.text(-60, 5.5, 'Previously\nundetected',
# fontsize='small', ha='right', va='top');
# arrowprops=dict(color='gray', shrink=0.05, width=1.5,
# headwidth=6, headlength=8, alpha=0.4)
# plt.annotate('Spur', xy=(-33, 2), xytext=(-35, 5.5),
# arrowprops=arrowprops,
# fontsize='small')
# plt.annotate('Gap', xy=(-22, -1), xytext=(-25, -5.5),
# arrowprops=arrowprops,
# fontsize='small')
```
## Customization
Matplotlib provides a default style that determines things like the colors of lines, the placement of labels and ticks on the axes, and many other properties.
There are several ways to override these defaults and customize your figures:
* To customize only the current figure, you can call functions like `tick_params`, which we'll demonstrate below.
* To customize all figures in a notebook, you use `rcParams`.
* To override more than a few defaults at the same time, you can use a style sheet.
As a simple example, notice that Matplotlib puts ticks on the outside of the figures by default, and only on the left and bottom sides of the axes.
To change this behavior, you can use `gca()` to get the current axes and `tick_params` to change the settings.
Here's how you can put the ticks on the inside of the figure:
```
plt.gca().tick_params(direction='in')
```
**Exercise:** Read the documentation of [`tick_params`](https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.axes.Axes.tick_params.html) and use it to put ticks on the top and right sides of the axes.
```
# Solution
# plt.gca().tick_params(top=True, right=True)
```
## rcParams
If you want to make a customization that applies to all figures in a notebook, you can use `rcParams`.
Here's an example that reads the current font size from `rcParams`:
```
plt.rcParams['font.size']
```
And sets it to a new value:
```
plt.rcParams['font.size'] = 14
```
**Exercise:** Plot the previous figure again, and see what font sizes have changed. Look up any other element of `rcParams`, change its value, and check the effect on the figure.
If you find yourself making the same customizations in several notebooks, you can put changes to `rcParams` in a `matplotlibrc` file, [which you can read about here](https://matplotlib.org/3.3.1/tutorials/introductory/customizing.html#customizing-with-matplotlibrc-files).
## Style sheets
The `matplotlibrc` file is read when you import Matplotlib, so it is not easy to switch from one set of options to another.
The solution to this problem is style sheets, [which you can read about here](https://matplotlib.org/3.1.1/tutorials/introductory/customizing.html).
Matplotlib provides a set of predefined style sheets, or you can make your own.
The following cell displays a list of style sheets installed on your system.
```
plt.style.available
```
Note that `seaborn-paper`, `seaborn-talk` and `seaborn-poster` are particularly intended to prepare versions of a figure with text sizes and other features that work well in papers, talks, and posters.
To use any of these style sheets, run `plt.style.use` like this:
```
plt.style.use('fivethirtyeight')
```
The style sheet you choose will affect the appearance of all figures you plot after calling `use`, unless you override any of the options or call `use` again.
**Exercise:** Choose one of the styles on the list and select it by calling `use`. Then go back and plot one of the figures above and see what effect it has.
If you can't find a style sheet that's exactly what you want, you can make your own. This repository includes a style sheet called `az-paper-twocol.mplstyle`, with customizations chosen by Azalee Bostroem for publication in astronomy journals.
The following cell downloads the style sheet.
```
import os
filename = 'az-paper-twocol.mplstyle'
path = 'https://github.com/AllenDowney/AstronomicalData/raw/main/data/'
if not os.path.exists(filename):
print(download(path+filename))
```
You can use it like this:
```
plt.style.use('./az-paper-twocol.mplstyle')
```
The prefix `./` tells Matplotlib to look for the file in the current directory.
As an alternative, you can install a style sheet for your own use by putting it in your configuration directory. To find out where that is, you can run the following command:
```
import matplotlib as mpl
mpl.get_configdir()
```
## LaTeX fonts
When you include mathematical expressions in titles, labels, and annotations, Matplotlib uses [`mathtext`](https://matplotlib.org/3.1.0/tutorials/text/mathtext.html) to typeset them. `mathtext` uses the same syntax as LaTeX, but it provides only a subset of its features.
If you need features that are not provided by `mathtext`, or you prefer the way LaTeX typesets mathematical expressions, you can customize Matplotlib to use LaTeX.
In `matplotlibrc` or in a style sheet, you can add the following line:
```
text.usetex : true
```
Or in a notebook you can run the following code.
```
plt.rcParams['text.usetex'] = True
```
```
plt.rcParams['text.usetex'] = True
```
If you go back and draw the figure again, you should see the difference.
If you get an error message like
```
LaTeX Error: File `type1cm.sty' not found.
```
You might have to install a package that contains the fonts LaTeX needs. On some systems, the packages `texlive-latex-extra` or `cm-super` might be what you need. [See here for more help with this](https://stackoverflow.com/questions/11354149/python-unable-to-render-tex-in-matplotlib).
In case you are curious, `cm` stands for [Computer Modern](https://en.wikipedia.org/wiki/Computer_Modern), the font LaTeX uses to typeset math.
## Multiple panels
So far we've been working with one figure at a time, but the figure we are replicating contains multiple panels, also known as "subplots".
Confusingly, Matplotlib provides *three* functions for making figures like this: `subplot`, `subplots`, and `subplot2grid`.
* [`subplot`](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.subplot.html) is simple and similar to MATLAB, so if you are familiar with that interface, you might like `subplot`
* [`subplots`](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.subplots.html) is more object-oriented, which some people prefer.
* [`subplot2grid`](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.subplot2grid.html) is most convenient if you want to control the relative sizes of the subplots.
So we'll use `subplot2grid`.
All of these functions are easier to use if we put the code that generates each panel in a function.
## Upper right
To make the panel in the upper right, we have to reload `centerline`.
```
import os
filename = 'gd1_dataframe.hdf5'
path = 'https://github.com/AllenDowney/AstronomicalData/raw/main/data/'
if not os.path.exists(filename):
print(download(path+filename))
import pandas as pd
centerline = pd.read_hdf(filename, 'centerline')
```
And define the coordinates of the rectangle we selected.
```
pm1_min = -8.9
pm1_max = -6.9
pm2_min = -2.2
pm2_max = 1.0
pm1_rect = [pm1_min, pm1_min, pm1_max, pm1_max]
pm2_rect = [pm2_min, pm2_max, pm2_max, pm2_min]
```
To plot this rectangle, we'll use a feature we have not seen before: `Polygon`, which is provided by Matplotlib.
To create a `Polygon`, we have to put the coordinates in an array with `x` values in the first column and `y` values in the second column.
```
import numpy as np
vertices = np.transpose([pm1_rect, pm2_rect])
vertices
```
The following function takes a `DataFrame` as a parameter, plots the proper motion for each star, and adds a shaded `Polygon` to show the region we selected.
```
from matplotlib.patches import Polygon
def plot_proper_motion(df):
pm1 = df['pm_phi1']
pm2 = df['pm_phi2']
plt.plot(pm1, pm2, 'ko', markersize=0.3, alpha=0.3)
poly = Polygon(vertices, closed=True,
facecolor='C1', alpha=0.4)
plt.gca().add_patch(poly)
plt.xlabel('$\mu_{\phi_1} [\mathrm{mas~yr}^{-1}]$')
plt.ylabel('$\mu_{\phi_2} [\mathrm{mas~yr}^{-1}]$')
plt.xlim(-12, 8)
plt.ylim(-10, 10)
```
Notice that `add_patch` is like `invert_yaxis`; in order to call it, we have to use `gca` to get the current axes.
Here's what the new version of the figure looks like. We've changed the labels on the axes to be consistent with the paper.
```
plt.rcParams['text.usetex'] = False
plt.style.use('default')
plot_proper_motion(centerline)
```
## Upper left
Now let's work on the panel in the upper left. We have to reload `candidates`.
```
import os
filename = 'gd1_candidates.hdf5'
path = 'https://github.com/AllenDowney/AstronomicalData/raw/main/data/'
if not os.path.exists(filename):
print(download(path+filename))
import pandas as pd
filename = 'gd1_candidates.hdf5'
candidate_df = pd.read_hdf(filename, 'candidate_df')
```
Here's a function that takes a `DataFrame` of candidate stars and plots their positions in GD-1 coordindates.
```
def plot_first_selection(df):
x = df['phi1']
y = df['phi2']
plt.plot(x, y, 'ko', markersize=0.3, alpha=0.3)
plt.xlabel('$\phi_1$ [deg]')
plt.ylabel('$\phi_2$ [deg]')
plt.title('Proper motion selection', fontsize='medium')
plt.axis('equal')
```
And here's what it looks like.
```
plot_first_selection(candidate_df)
```
## Lower right
For the figure in the lower right, we need to reload the merged `DataFrame`, which contains data from Gaia and photometry data from Pan-STARRS.
```
import pandas as pd
filename = 'gd1_merged.hdf5'
merged = pd.read_hdf(filename, 'merged')
```
From the previous notebook, here's the function that plots the color-magnitude diagram.
```
import matplotlib.pyplot as plt
def plot_cmd(table):
"""Plot a color magnitude diagram.
table: Table or DataFrame with photometry data
"""
y = table['g_mean_psf_mag']
x = table['g_mean_psf_mag'] - table['i_mean_psf_mag']
plt.plot(x, y, 'ko', markersize=0.3, alpha=0.3)
plt.xlim([0, 1.5])
plt.ylim([14, 22])
plt.gca().invert_yaxis()
plt.ylabel('$g_0$')
plt.xlabel('$(g-i)_0$')
```
And here's what it looks like.
```
plot_cmd(merged)
```
**Exercise:** Add a few lines to `plot_cmd` to show the Polygon we selected as a shaded area.
Run these cells to get the polygon coordinates we saved in the previous notebook.
```
import os
filename = 'gd1_polygon.hdf5'
path = 'https://github.com/AllenDowney/AstronomicalData/raw/main/data/'
if not os.path.exists(filename):
print(download(path+filename))
coords_df = pd.read_hdf(filename, 'coords_df')
coords = coords_df.to_numpy()
coords
# Solution
#poly = Polygon(coords, closed=True,
# facecolor='C1', alpha=0.4)
#plt.gca().add_patch(poly)
```
## Subplots
Now we're ready to put it all together. To make a figure with four subplots, we'll use `subplot2grid`, [which requires two arguments](https://matplotlib.org/3.3.1/api/_as_gen/matplotlib.pyplot.subplot2grid.html):
* `shape`, which is a tuple with the number of rows and columns in the grid, and
* `loc`, which is a tuple identifying the location in the grid we're about to fill.
In this example, `shape` is `(2, 2)` to create two rows and two columns.
For the first panel, `loc` is `(0, 0)`, which indicates row 0 and column 0, which is the upper-left panel.
Here's how we use it to draw the four panels.
```
shape = (2, 2)
plt.subplot2grid(shape, (0, 0))
plot_first_selection(candidate_df)
plt.subplot2grid(shape, (0, 1))
plot_proper_motion(centerline)
plt.subplot2grid(shape, (1, 0))
plot_second_selection(selected)
plt.subplot2grid(shape, (1, 1))
plot_cmd(merged)
poly = Polygon(coords, closed=True,
facecolor='C1', alpha=0.4)
plt.gca().add_patch(poly)
plt.tight_layout()
```
We use [`plt.tight_layout`](https://matplotlib.org/3.3.1/tutorials/intermediate/tight_layout_guide.html) at the end, which adjusts the sizes of the panels to make sure the titles and axis labels don't overlap.
**Exercise:** See what happens if you leave out `tight_layout`.
## Adjusting proportions
In the previous figure, the panels are all the same size. To get a better view of GD-1, we'd like to stretch the panels on the left and compress the ones on the right.
To do that, we'll use the `colspan` argument to make a panel that spans multiple columns in the grid.
In the following example, `shape` is `(2, 4)`, which means 2 rows and 4 columns.
The panels on the left span three columns, so they are three times wider than the panels on the right.
At the same time, we use `figsize` to adjust the aspect ratio of the whole figure.
```
plt.figure(figsize=(9, 4.5))
shape = (2, 4)
plt.subplot2grid(shape, (0, 0), colspan=3)
plot_first_selection(candidate_df)
plt.subplot2grid(shape, (0, 3))
plot_proper_motion(centerline)
plt.subplot2grid(shape, (1, 0), colspan=3)
plot_second_selection(selected)
plt.subplot2grid(shape, (1, 3))
plot_cmd(merged)
poly = Polygon(coords, closed=True,
facecolor='C1', alpha=0.4)
plt.gca().add_patch(poly)
plt.tight_layout()
```
This is looking more and more like the figure in the paper.
**Exercise:** In this example, the ratio of the widths of the panels is 3:1. How would you adjust it if you wanted the ratio to be 3:2?
## Summary
In this notebook, we reverse-engineered the figure we've been replicating, identifying elements that seem effective and others that could be improved.
We explored features Matplotlib provides for adding annotations to figures -- including text, lines, arrows, and polygons -- and several ways to customize the appearance of figures. And we learned how to create figures that contain multiple panels.
## Best practices
* The most effective figures focus on telling a single story clearly and compellingly.
* Consider using annotations to guide the readers attention to the most important elements of a figure.
* The default Matplotlib style generates good quality figures, but there are several ways you can override the defaults.
* If you find yourself making the same customizations on several projects, you might want to create your own style sheet.
|
github_jupyter
|
# Exercises
## Playing with the interpreter
Try to execute some simple statements and expressions (one at a time) e.g
```
print("Hello!")
1j**2
1 / 2
1 // 2
5 + 5
10 / 2 + 5
my_tuple = (1, 2, 3)
my_tuple[0] = 1
2.3**4.5
```
Do you understand what is going on in all cases?
Most Python functions and objects can provide documentation via **help** function. Look the documentation of e.g open function with ```help(open)```
Play with tabulator completion, by typing just ```pr``` and pressing then tabulator key. Pressing Shift-tab (after finalising completion) one sees also short documentation about the function or object. This works also on variable names, try e.g.
```
my_extremely_long_variable_name = 5
my <TAB>
```
## Basic syntax
Try to assign the value 6 to the following variable names
````
first-name
family_name
3PO
____variable
inb4tool8
print
in
```
Which of them are valid to assign to?
Extra: why do you think the ones that cause an error are not valid? What's the reason?
You probably noticed that even though ``print`` is a method in the namespace it was still valid to create a variable called ``print``. If you now try to actually print something, you will get an error. For built-in functions (such as print) one can recover with the following code
```
print = __builtin__.print
print("hello")
```
Are the following pieces valid Python code?
** Case 1 **
```
numbers = [4, 5, 6, 9, 11]
sum = 0
for n in numbers:
sum += n
print("Sum is now"), sum
```
** Case 2 **
```
x = 11
test(x)
def test(a):
if a < 0:
print("negative number")
```
## Tuples and lists
1. Create a tuple called ``mytuple``, with the following strings: "sausage", "eggs" and "bacon"
2. check it's type using ``type()``
3. Create than a list called ``mylist`` with the same contents. You use can the normal list definition syntax (``[]``) or coerce it from the tuple with the ``list()`` function.
Attempt to append the string "spam"
to ``mylist`` and ``mytuple`` using ``append``.
List objects have a sort()
function, use that for sorting the list alphabetically (e.g.
mylist.sort() ). What is now the first item of the list?
Next, remove the first item from the list, investigate the contents and remove then last item from the list.
### Slicing
Using ``range()`` create a list that has the numbers from 50 to 0 with a step of -2. Note that in Python 3 ``range()`` returns an *iterator* (we'll discuss iterators more later on), ``list(range(args))`` returns an actual list.
Using slicing syntax, select
* the last 4 items from the list
* the items from index 10 to index 13
* the first 5 items from the list
Read up on the [stride syntax](https://en.wikipedia.org/wiki/Array_slicing#1991:_Python) . Then using it select
* every third value in the list
* the values with an odd-numbered index in the list
### Multidimensional lists
Create a two dimensional list of (x,y) value pairs, i.e.
arbitrary long list whose elements are two element lists.
Are you able to use slicing for extracting only the y values? (Answer is no, but try it in any case)
## Dictionaries
Create a dictionary whose keys are the fruits “pineapple”, “strawberry”, and “banana”. As values use numbers
representing e.g. prices.
Add “orange” to the dictionary and then remove “banana” from the dictionary. Investigate the contents of dictionary and pay attention to the order of key-value pairs.
# Bonus exercises
Create a new “fruits” dictionary where the values are also
dictionaries containing key-value pairs for color and weight,
e.g.
```
fruits['apple'] = {'color':'green', 'weight': 120}
```
Change the color of *apple* from green to red
It is often useful idiom to create empty lists or dictionaries
and add contents little by little.
Create first an empty dictionary for a mid-term grades of
students. Then, add a key-value pairs where the keys are
student names and the values are empty lists.
Finally, add values to the lists and investigate the contents of the
dictionary.
|
github_jupyter
|
<h1> Data Transformation </h1>
## Logistic Regression - on [Titanic Dataset](https://www.kaggle.com/c/titanic)
- Models the probability an object belongs to a class
- Values ranges from 0 to 1
- Can use threshold to classify into which classes a class belongs
- An S-shaped curve
$
\begin{align}
\sigma(t) = \frac{1}{1 + e^{-t}}
\end{align}
$
#### Read the data
```
import pandas as pd
df_train = pd.read_csv('../data/titanic_train.csv')
df_train.head(8)
```
## Data Statistics
#### Describing the statistics for numerical features
```
df_train.describe()
```
#### Find the count of the non-NaN values per feature
```
df_train.count()
```
## What features can be removed?
### Remove features that are not related to your outcome
```
df_train.drop(['Name', 'Ticket'], axis=1, inplace=True)
```
### Remove column with missing data
```
df_train.drop(['Cabin'], axis=1, inplace=True)
```
## Data Imputation - Filling in missing values
- Select a percentage threshold that you would want to accomodate
- Around 1/5th to 1/3rd of the data (20% to 33.3%)
- if more than 50% of the data is missing, you will be generating data for the majority of your dataset - Not a good thing to do
```
from matplotlib import pyplot as plt
import seaborn as sns
plt.figure(figsize=(7,5))
sns.boxplot(x='Pclass',y='Age',data=df_train)
from matplotlib import pyplot as plt
import seaborn as sns
plt.figure(figsize=(7,5))
sns.boxplot(x='Sex',y='Age',data=df_train)
from matplotlib import pyplot as plt
import seaborn as sns
plt.figure(figsize=(7,5))
sns.boxplot(x='Embarked',y='Age',data=df_train)
def add_age(cols):
Age = cols[0]
Pclass = cols[1]
if pd.isnull(Age):
return int(df_train[df_train["Pclass"] == Pclass]["Age"].mean())
else:
return Age
df_train['Age'] = df_train[['Age', 'Pclass']].apply(add_age,axis=1)
df_train.count()
```
### Drop Rows
```
df_train.dropna(inplace=True)
df_train.count()
```
## Data Transformation
#### Convert the categorical values to numeric
- Find the columns that are explicitly categorical - like male, female
- Find the columns that are although numerical, represent categorical features
### One-Hot Encoding
- A technique to create multiple feature for each corrsponding value
<img src='img/one_hot_encoding.png'>
```
import numpy as np
col = 'Sex'
print(np.unique(df_train[col]))
import numpy as np
col = 'Embarked'
print(np.unique(df_train[col]))
import numpy as np
col = 'Pclass'
print(np.unique(df_train[col]))
sex = pd.get_dummies(df_train["Sex"],drop_first=True)
embarked = pd.get_dummies(df_train["Embarked"],drop_first=True)
pclass = pd.get_dummies(df_train["Pclass"],drop_first=True)
```
### Drop the columns that were used for transformation
```
df_train.drop(['Sex', 'Embarked', 'Pclass', 'PassengerId'], axis=1, inplace=True)
df_train.head()
```
### Add encoded columns to the training dataset
```
df_train = pd.concat([df_train,pclass,sex,embarked],axis=1)
df_train.head()
```
# Save the transformed file as a pickle file
```
df_train.shape
import pickle as pkl
df_train.to_pickle('../data/titanic_tansformed.pkl')
```
## Logistic Regression
```
data = df_train.drop("Survived",axis=1)
label = df_train["Survived"]
data.head()
from sklearn.cross_validation import train_test_split
data_train, data_test, label_train, label_test = train_test_split(data, label, test_size = 0.3, random_state = 101)
from sklearn.linear_model import LogisticRegression
# Run Logistic Regression
log_regr = LogisticRegression()
log_regr.fit(data_train, label_train)
predictions = log_regr.predict(data_test)
```
### Accuracy
```
print('Accuracy', log_regr.score(data_test, label_test))
print('Coefficients', log_regr.coef_)
print('Intercept', log_regr.intercept_)
```
### Precision Recall
```
from sklearn.metrics import classification_report
print(classification_report(label_test, predictions))
```
## Cross Validation
```
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
# skf = StratifiedKFold(n_splits=5)
log_regr = LogisticRegression()
log_regr.fit(data_train, label_train)
score = log_regr.score(data_train, label_train)
print('Train accuracy score', score)
score_cv = cross_val_score(log_regr, data_train, label_train, cv=10, scoring='accuracy')
print('Cross Val Accuracy for each run', score_cv)
print('CrossVal Accuracy', score_cv.mean())
```
## AUC - Receiver Operating Characteristics
- How much a model is capable of distinguishing between classes
- Higher the AUC, better the model is
$
\begin{align}
True Positive Rate = \frac{TP}{TP + FN}
\end{align}
$
<br>
$
\begin{align}
\ False Positive Rate = 1 - \frac{TN}{TN + FP} = \frac{FP}{TN + FP}
\end{align}
$
```
from sklearn import metrics
fpr, tpr, threshold = metrics.roc_curve(label_test, log_regr.predict(data_test))
roc_auc = metrics.auc(fpr, tpr)
print('AUCROC Stage1 vs Healthy: ' , roc_auc)
import matplotlib.pyplot as plt
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b', label = 'AUC = %0.2f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
```
|
github_jupyter
|
**_Privacy and Confidentiality Exercises_**
This notebook shows you how to prepare your results for export and what you have to keep in mind in general when you want to export output. You will learn how to prepare files for export so they meet our export requirements.
```
# Load packages
%pylab inline
from __future__ import print_function
import os
import pandas as pd
import numpy as np
import psycopg2
import matplotlib.pyplot as plt
%matplotlib inline
matplotlib.style.use('ggplot')
```
# General Remarks on Disclosure Review
This notebook provides you with information on how to prepare research output for disclosure control. It outlines how to prepare different kind of outputs before submitting an export request and gives you an overview of the information needed for disclosure review.
## Files you can export
In general you can export any kind of file format. However, most research results that researchers typically export are tables, graphs, regression output and aggregated data. Thus, we ask you to export one of these types which implies that every result you would like to export needs to be saved in either .csv, .txt or graph format.
## Jupyter notebooks are only exported to retrieve code
Unfortunately, you can't export results in a jupyter notebook. Doing disclosure reviews on output in jupyter notebooks is too burdensome for us. Jupyter notebooks will only be exported when the output is deleted for the purpose of exporting code. This does not mean that you won't need your jupyter notebooks during the export process.
## Documentation of code is important
During the export process we ask you to provide the code for every output you are asking to export. It is important for ADRF staff to have the code to better understand what you exactly did. Understanding how research results are created is important to understand your research output. Thus, it is important to document every single step of your analysis in your jupyter notebook.
## General rules to keep in mind
A more detailed description of the rules for exporting results can be found on the class website. This is just a quick overview. We recommend that you to go to the class website and read the entire guidelines before you prepare your files for export.
- The disclosure review is based on the underlying observations of your study. Every statistic you want to export should be based on at least 10 individual data points
- Document your code so the reviewer can follow your data work. Assessing re-identification risks highly depends on the context. Thus it is important that you provide context info with your anlysis for the reviewer
- Save the requested output with the corresponding code in you input and output folder. Make sure the code is executable. The code should exactly produce the output you requested
- In case you are exporting powerpoint slides that show project results you have to provide the code which produces the output in the slide
- Please export results only when there are final and you need them for your presentation or final projcet report
# Disclosure Review Walkthrough
We will IL DES data and MO DES to construct our statistics we are interested in, and prepare it in a way so we can submit the output for disclosure review.
```
# get working directory
mypath = (os.getcwd())
print(mypath)
# connect to database
db_name = "appliedda"
hostname = "10.10.2.10"
conn = psycopg2.connect(database=db_name, host = hostname)
```
## pull data
In this example we will use the workers who had a job in both MO and IL at some point over the course of our datasets (2005-2016)
```
# Get data
query = """
SELECT *, il_wage + mo_wage AS earnings
FROM ada_18_uchi.il_mo_overlap_by_qtr
WHERE year = 2011
AND quarter IN (2,3)"""
# Save query in dataframe
df = pd.read_sql( query, con = conn )
# Check dataframe
df.head()
# another way to check dataframe
df.info()
# basic stats of
df.describe()
# let's add an earnings categorization for "low", "mid" and "high" using a simple function
def earn_calc(earn):
if earn < 16500:
return('low')
elif earn < 45000:
return('mid')
else:
return('high')
earn_calc(24000)
df['earn_cat'] = df['earnings'].apply(lambda x: earn_calc(x))
```
We now have loaded the data that we need to generate some basic statistics about our populations we want to compare
```
# Let's look at some first desccriptives by group
grouped = df.groupby('earn_cat')
grouped.describe()
grouped.describe().T
```
Statistics in this table will be released if the statistic is based on at least 10 entities (in this example individuals). We can see that the total number of individuals we observe in each group completely satisfies this (see cell count). However, we also report percentiles, and we report the minimum and maximum value. Especially the minimum and maximum value are most likely representing one individual person.
Thus, during disclosure review these values will be supressed.
```
# Now let's export the statistics. Ideally we want to have a csv file
# We can safe the statistics in a dataframe
export1 = grouped.describe()
# and then print to csv
export1.to_csv('descriptives_by_group.csv')
```
### Reminder: Export of Statistics
You can save any dataframe as a csv file and export this csv file. The only thing you have to keep in mind is that besides the statistic X you are interested in you have to include a variable count of X so we can see on how many observations the statistic is based on. This also applies if you aggregate data. For example if you agregate by benefit type, we need to know how many observations are in each benefit program (because after the aggregation each benefit type will be only one data point).
### Problematic Output
Some subgroups (eg for some of the Illinois datasets dealing with race and gender) will result in cell sizes representing less than 10 people.
Tables with cells representing less than 10 individuals won't be released. In this case, disclosure review would mean to delete all cells with counts of less than 10. In addition, secondary suppression has to take place. The disclosure reviewer has to delete as many cells as needed to make it impossible to recalculate the suppressed values.
### How to do it better
Instead of asking for export of a tables like this, you should prepare your tables in advance that all cell sizes are at least represented by a minimum of 10 observations.
### Reminder: Export of Tables
For tables of any kind you need to provide the underlying counts of the statistics presented in the table. Make sure you provide all counts. If you calculate ratios, for example employment rates you need to provide the count of individuals who are employed and the count of the ones who are not. If you are interested in percentages we still need the underlying counts for disclosure review. Please label the table in a way that we can easily understand what you are plotting.
```
df[['il_flag', 'mo_flag']].describe(percentiles = [.5, .9, .99, .999])
# for this example let's cap the job counts to 5
df['il_flag'] = df['il_flag'].apply(lambda x: x if x < 5 else 5)
df['mo_flag'] = df['mo_flag'].apply(lambda x: x if x < 5 else 5)
# Let's say we are interested in plotting parts of the crosstabulation as a graph, for example benefit type and race
# First we need to calulate the counts
graph = df.groupby(['earn_cat', 'il_flag'])['ssn'].count()
# Note: we need to add the unstack command here because our dataframe has nested indices.
# We need to flatten out the data before plotting the graph
print(graph)
print(graph.unstack())
# Now we can generate the graph
mygraph = graph.unstack().plot(kind='bar')
```
In this graph it is not clearly visible how many observations are in each bar. Thus we either have to provide a corresponding table (as we generated earlier), or we can use the table=True option to add a table of counts to the graph. In addition, we wnat to make sure that all our axes and legend are labeled properly.
```
# Graphical representation including underlying values: the option table=True displays the underlying counts
mygraph = graph.unstack().plot(kind='bar', table=True, figsize=(7,5), fontsize=7)
# Adjust legend and axes
mygraph.legend(["Unknown","1", "2", "3", "4", '5'], loc = 1, ncol= 3, fontsize=9)
mygraph.set_ylabel("Number of Observations", fontsize=9)
# Add table with counts
# We don't need an x axis if we display table
mygraph.axes.get_xaxis().set_visible(False)
# Grab table info
table = mygraph.tables[0]
# Format table and figure
table.set_fontsize(9)
```
> in this example there is a problematic value, we will instead cap to 4 maximum jobs to ensure all cells are more than 10
```
# for this example let's cap the job counts to 5
df['il_flag'] = df['il_flag'].apply(lambda x: x if x < 4 else 4)
df['mo_flag'] = df['mo_flag'].apply(lambda x: x if x < 4 else 4)
# create our new "graph" dataframe to plot with
graph = df.groupby(['earn_cat', 'il_flag'])['ssn'].count()
# confirm we solved the issue
mygraph = graph.unstack().plot(kind='bar', table=True, figsize=(7,5), fontsize=7)
# Adjust legend and axes
mygraph.legend(["Unknown","1", "2", "3", "4", '5'], loc = 1, ncol= 3, fontsize=9)
mygraph.set_ylabel("Number of Observations", fontsize=9)
# Add table with counts
# We don't need an x axis if we display table
mygraph.axes.get_xaxis().set_visible(False)
# Grab table info
table = mygraph.tables[0]
# Format table and figure
table.set_fontsize(9)
# We want to export the graph without the table though
# Because we already generated the crosstab earlier which shows the counts
mygraph = graph.unstack().plot(kind='bar', figsize=(7,5), fontsize=7, rot=0)
# Adjust legend and axes
mygraph.legend(["Unknown","1", "2", "3", "4", '5'], loc = 1, ncol= 3, fontsize=9)
mygraph.set_ylabel("Number of Observations", fontsize=9)
mygraph.set_xlabel("Income category", fontsize=9)
mygraph.annotate('Source: IL & MO DES', xy=(0.7,-0.2), xycoords="axes fraction");
# Now we can export the graph as pdf
# Save plot to file
export2 = mygraph.get_figure()
export2.set_size_inches(15,10, forward=True)
export2.savefig('barchart_jobs_income_category.pdf', bbox_inches='tight', dpi=300)
```
### Reminder: Export of Graphs
It is important that every point which is plotted in a graph is based on at least 10 observations. Thus scatterplots for example cannot be released. In case you are interested in a histogram you have to change the bin size to make sure that every bin contains at least 10 people. In addition to the graph you have to provide the ADRF with the underlying table in a .csv or .txt file. This file should have the same name as the graph so ADRF can directly see which files go together. Alternatively you can include the counts in the graph as shown in the example above.
|
github_jupyter
|
```
import pandas as pd
import os
import glob
import shutil
import random
import time
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
import pickle
import numpy as np
es_url = 'http://ckg07:9200'
es_index = 'wikidatadwd-augmented'
# GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/t2dv2-train-canonical/
train_path = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-train-canonical/'
# GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/t2dv2-dev-canonical/
dev_path = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-dev-canonical/'
# GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/t2dv2-train-candidates-dwd-v2/
train_candidate_path = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-train-candidates-dwd-v2/'
# GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/t2dv2-dev-candidates-dwd-v2/
dev_candidate_path = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-dev-candidates-dwd-v2/'
# GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/ground_truth/Xinting_GT_csv
ground_truth_files = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/Xinting_GT_csv/round_1/'
aux_field = 'graph_embedding_complex,class_count,property_count'
temp_dir = './temp' #temp directory to store intermediate files
#directory to store the property count file for each table. Can be directly used for computing the tf-idf features
#without running the candidate generation process again which is expensive
#GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/train_prop_count/
train_prop_count = './train_prop_count/'
#GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/dev_prop_count/
dev_prop_count = './dev_prop_count/'
#GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/train_class_count/
train_class_count = './train_class_count/'
#GDrive Path: /table-linker-dataset/2019-iswc_challenge_data/t2dv2/canonical-with-context/dev_class_count/
dev_class_count = './dev_class_count/'
!mkdir -p $temp_dir
!mkdir -p $train_prop_count
!mkdir -p $dev_prop_count
!mkdir -p $train_class_count
!mkdir -p $dev_class_count
candidates = os.path.join(temp_dir,'candidates.csv')
embedding_file = os.path.join(temp_dir, 'graph_embedding_complex.tsv')
print(candidates)
def cand_feat_generation(path, gt_path, output_path, class_count, prop_count):
for file in glob.glob(path + '*.csv')[-1:]:
st = time.time()
filename = file.split('/')[-1]
print(filename)
gt_file = os.path.join(ground_truth_files, filename)
output_file = os.path.join(output_path, filename)
!tl clean -c label -o label_clean $file / \
--url $es_url --index $es_index \
get-fuzzy-augmented-matches -c label_clean \
--auxiliary-fields {aux_field} \
--auxiliary-folder $temp_dir / \
--url $es_url --index $es_index \
get-exact-matches -c label_clean \
--auxiliary-fields {aux_field} \
--auxiliary-folder {temp_dir} / \
ground-truth-labeler --gt-file $gt_file > $candidates
for field in aux_field.split(','):
aux_list = []
for f in glob.glob(f'{temp_dir}/*{field}.tsv'):
aux_list.append(pd.read_csv(f, sep='\t', dtype=object))
aux_df = pd.concat(aux_list).drop_duplicates(subset=['qnode'])
if field == 'class_count':
class_count_file = os.path.join(class_count, filename.strip('.csv') + '_class_count.tsv')
aux_df.to_csv(class_count_file, sep='\t', index=False)
elif field == 'property_count':
prop_count_file = os.path.join(prop_count, filename.strip('.csv') + '_prop_count.tsv')
aux_df.to_csv(prop_count_file, sep='\t', index=False)
else:
aux_df.to_csv(f'{temp_dir}/{field}.tsv', sep='\t', index=False)
!tl string-similarity -i --method symmetric_monge_elkan:tokenizer=word -o monge_elkan $candidates \
/ string-similarity -i --method jaccard:tokenizer=word -c kg_descriptions context -o des_cont_jaccard \
/ string-similarity -i --method jaro_winkler -o jaro_winkler \
/ score-using-embedding --column-vector-strategy centroid-of-singletons -o graph-embedding-score \
--embedding-file $embedding_file \
/ create-singleton-feature -o singleton\
/ generate-reciprocal-rank -c graph-embedding-score -o reciprocal_rank\
/ mosaic-features -c kg_labels --num-char --num-tokens > $output_file
print(time.time() - st)
cand_feat_generation(train_path, ground_truth_files, train_candidate_path, train_class_count, train_prop_count)
candidate_generation(dev_path, ground_truth_files, dev_candidate_path, dev_class_count, dev_prop_count)
```
### Generate Balanced Training Data
```
training_datapath = '../random_forest_ranking/training_data_dwd.csv'
final_list = []
for i,file in enumerate(glob.glob(train_candidate_path + '*.csv')):
file_name = file.split('/')[-1]
print(file_name)
try:
d_sample = pd.read_csv(file)
grouped_obj = d_sample.groupby(['row', 'column'])
for cell in grouped_obj:
num_rows = random.randint(2,5)
sorted_df = cell[1].sort_values('graph-embedding-score',ascending=False)
if 0 in sorted_df['evaluation_label'].tolist():
continue
if sorted_df.empty:
continue
if num_rows < len(sorted_df):
top_sample_df = sorted_df[sorted_df['evaluation_label'] == -1][:10].sample(n=num_rows)
bottom_sample_df = sorted_df[sorted_df['evaluation_label'] == -1][-10:].sample(n=num_rows)
final_list.extend(top_sample_df.to_dict(orient='records'))
final_list.extend(bottom_sample_df.to_dict(orient='records'))
else:
sample_df = sorted_df[sorted_df['evaluation_label'] == -1]
final_list.extend(sample_df.to_dict(orient='records'))
a = cell[1][cell[1]['evaluation_label'] == 1]
if a.empty:
continue
final_list.extend(a.to_dict(orient='records'))
except:
pass
train_df = pd.DataFrame(final_list)
train_df.to_csv(training_datapath, index=False)
```
### Data Exploration
```
train_datapath = '../random_forest_ranking/training_data_dwd.csv'
df = pd.read_csv(train_datapath)
df.info()
# Features we need to include in training
features = ['pagerank','retrieval_score','monge_elkan',
'des_cont_jaccard','jaro_winkler','graph-embedding-score',
'singleton','num_char','num_tokens','reciprocal_rank']
evaluation_label = ['evaluation_label']
df[features].info()
df['graph-embedding-score'] = df['graph-embedding-score'].fillna(0.0)
df['reciprocal_rank'] = df['reciprocal_rank'].fillna(0.0)
df[features].info()
```
### Train a Random Forest Regressor
```
train_data = df[features]
y_label = df[evaluation_label]
model = RandomForestRegressor(n_estimators=100, max_features="log2",min_samples_leaf=3)
model.fit(train_data,y_label)
y_pred = model.predict(train_data)
mean_squared_error(y_label, y_pred)
model_save_path = '../random_forest_ranking/rf_tuned_dwd_ranking.pkl'
pickle.dump(model,open(model_save_path,'wb'))
saved_model = pickle.load(open(model_save_path, 'rb'))
```
### Predicting Scores for Train set
```
train_candidate_path = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-train-candidates-dwd-v2/'
train_pred_output = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-train-rf-pred-dwd-2/'
train_mse = []
for file in glob.glob(train_candidate_path + '*.csv'):
try:
file_name = file.split('/')[-1]
print(file_name)
df_file = pd.read_csv(file)
data = df_file[features]
y_file_label = df_file[evaluation_label]
y_file_pred = saved_model.predict(data)
df_file['rf_model_pred'] = y_file_pred
file_mse = mean_squared_error(y_file_label,y_file_pred)
train_mse.append(file_mse)
df_file.to_csv(os.path.join(train_pred_output,file_name),index=False)
except:
pass
print("Train MSE is: ", sum(train_mse)/len(train_mse))
```
### Predicting Scores for dev set
```
dev_candidate_path = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-dev-candidates-dwd-v2/'
dev_pred_output = '/Users/rijulvohra/Documents/work/Novartis-ISI/novartis-isi-git/entity_linking/t2dv2-raw/t2dv2/canonical-with-context/t2dv2-dev-rf-pred-dwd-2/'
dev_mse = []
for file in glob.glob(dev_candidate_path + '*.csv'):
file_name = file.split('/')[-1]
print(file_name)
df_file = pd.read_csv(file)
data = df_file[features]
y_file_label = df_file[evaluation_label]
y_file_pred = saved_model.predict(data)
df_file['rf_model_pred'] = y_file_pred
file_mse = mean_squared_error(y_file_label,y_file_pred)
dev_mse.append(file_mse)
df_file.to_csv(os.path.join(dev_pred_output,file_name),index=False)
print("Dev MSE is: ", sum(dev_mse)/len(dev_mse))
```
### Evaluation
```
final_score_path = dev_pred_output
import os
eval_file_names = []
for (dirpath, dirnames, filenames) in os.walk(final_score_path):
for fn in filenames:
if "csv" not in fn:
continue
abs_fn = dirpath + fn
assert os.path.isfile(abs_fn)
if os.path.getsize(abs_fn) == 0:
continue
eval_file_names.append(abs_fn)
len(eval_file_names)
# merge all eval files in one df
def merge_df(file_names: list):
df_list = []
for fn in file_names:
fid = fn.split('/')[-1].split('.csv')[0]
df = pd.read_csv(fn)
df['table_id'] = fid
# df = df.fillna('')
df_list.append(df)
return pd.concat(df_list)
all_data = merge_df(eval_file_names)
all_data
# parse eval file
from pandas.core.common import SettingWithCopyError
pd.options.mode.chained_assignment = 'raise'
def parse_eval_files_stats(eval_data,method):
res = {}
candidate_eval_data = eval_data.groupby(['table_id', 'row', 'column'])['table_id'].count().reset_index(name="count")
res['num_tasks'] = len(eval_data.groupby(['table_id', 'row', 'column']))
res['num_tasks_with_gt'] = len(eval_data[pd.notna(eval_data['GT_kg_id'])].groupby(['table_id', 'row', 'column']))
res['num_tasks_with_gt_in_candidate'] = len(eval_data[eval_data['evaluation_label'] == 1].groupby(['table_id', 'row', 'column']))
res['num_tasks_with_singleton_candidate'] = len(candidate_eval_data[candidate_eval_data['count'] == 1].groupby(['table_id', 'row', 'column']))
singleton_eval_data = candidate_eval_data[candidate_eval_data['count'] == 1]
num_tasks_with_singleton_candidate_with_gt = 0
for i, row in singleton_eval_data.iterrows():
table_id, row_idx, col_idx = row['table_id'], row['row'], row['column']
c_e_data = eval_data[(eval_data['table_id'] == table_id) & (eval_data['row'] == row_idx) & (eval_data['column'] == col_idx)]
assert len(c_e_data) == 1
if c_e_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_singleton_candidate_with_gt += 1
res['num_tasks_with_singleton_candidate_with_gt'] = num_tasks_with_singleton_candidate_with_gt
num_tasks_with_graph_top_one_accurate = []
num_tasks_with_graph_top_five_accurate = []
num_tasks_with_graph_top_ten_accurate = []
num_tasks_with_final_score_top_one_accurate = []
num_tasks_with_final_score_top_five_accurate = []
num_tasks_with_final_score_top_ten_accurate = []
num_tasks_with_model_score_top_one_accurate = []
num_tasks_with_model_score_top_five_accurate = []
num_tasks_with_model_score_top_ten_accurate = []
ndcg_score_g_list = []
ndcg_model_score_list = []
has_gt_list = []
has_gt_in_candidate = []
# candidate_eval_data = candidate_eval_data[:1]
for i, row in candidate_eval_data.iterrows():
#print(i)
table_id, row_idx, col_idx = row['table_id'], row['row'], row['column']
c_e_data = eval_data[(eval_data['table_id'] == table_id) & (eval_data['row'] == row_idx) & (eval_data['column'] == col_idx)]
assert len(c_e_data) > 0
if np.nan not in set(c_e_data['GT_kg_id']):
has_gt_list.append(1)
else:
has_gt_list.append(0)
if 1 in set(c_e_data['evaluation_label']):
has_gt_in_candidate.append(1)
else:
has_gt_in_candidate.append(0)
# handle graph-embedding-score
s_data = c_e_data.sort_values(by=['graph-embedding-score'], ascending=False)
if s_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_graph_top_one_accurate.append(1)
else:
num_tasks_with_graph_top_one_accurate.append(0)
if 1 in set(s_data.iloc[0:5]['evaluation_label']):
num_tasks_with_graph_top_five_accurate.append(1)
else:
num_tasks_with_graph_top_five_accurate.append(0)
if 1 in set(s_data.iloc[0:10]['evaluation_label']):
num_tasks_with_graph_top_ten_accurate.append(1)
else:
num_tasks_with_graph_top_ten_accurate.append(0)
#rank on model score
s_data = c_e_data.sort_values(by=[method], ascending=False)
if s_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_model_score_top_one_accurate.append(1)
else:
num_tasks_with_model_score_top_one_accurate.append(0)
if 1 in set(s_data.iloc[0:5]['evaluation_label']):
num_tasks_with_model_score_top_five_accurate.append(1)
else:
num_tasks_with_model_score_top_five_accurate.append(0)
if 1 in set(s_data.iloc[0:10]['evaluation_label']):
num_tasks_with_model_score_top_ten_accurate.append(1)
else:
num_tasks_with_model_score_top_ten_accurate.append(0)
cf_e_data = c_e_data.copy()
#cf_e_data['evaluation_label'] = cf_e_data['evaluation_label'].replace(-1, 0)
# cf_e_data['text-embedding-score'] = cf_e_data['text-embedding-score'].replace(np.nan, 0)
cf_e_data['graph-embedding-score'] = cf_e_data['graph-embedding-score'].replace(np.nan, 0)
cf_e_data[method] = cf_e_data[method].replace(np.nan, 0)
candidate_eval_data['graph_top_one_accurate'] = num_tasks_with_graph_top_one_accurate
candidate_eval_data['graph_top_five_accurate'] = num_tasks_with_graph_top_five_accurate
candidate_eval_data['graph_top_ten_accurate'] = num_tasks_with_graph_top_five_accurate
candidate_eval_data['model_top_one_accurate'] = num_tasks_with_model_score_top_one_accurate
candidate_eval_data['model_top_five_accurate'] = num_tasks_with_model_score_top_five_accurate
candidate_eval_data['model_top_ten_accurate'] = num_tasks_with_model_score_top_ten_accurate
candidate_eval_data['has_gt'] = has_gt_list
candidate_eval_data['has_gt_in_candidate'] = has_gt_in_candidate
res['num_tasks_with_graph_top_one_accurate'] = sum(num_tasks_with_graph_top_one_accurate)
res['num_tasks_with_graph_top_five_accurate'] = sum(num_tasks_with_graph_top_five_accurate)
res['num_tasks_with_graph_top_ten_accurate'] = sum(num_tasks_with_graph_top_ten_accurate)
res['num_tasks_with_model_score_top_one_accurate'] = sum(num_tasks_with_model_score_top_one_accurate)
res['num_tasks_with_model_score_top_five_accurate'] = sum(num_tasks_with_model_score_top_five_accurate)
res['num_tasks_with_model_score_top_ten_accurate'] = sum(num_tasks_with_model_score_top_ten_accurate)
return res, candidate_eval_data
res, candidate_eval_data = parse_eval_files_stats(all_data,'rf_model_pred')
print(res)
display(candidate_eval_data)
# Conclusion of exact-match on all tasks with ground truth (no filtering)
print(f"number of tasks: {res['num_tasks']}")
print(f"number of tasks with ground truth: {res['num_tasks_with_gt']}")
print(f"number of tasks with ground truth in candidate set: {res['num_tasks_with_gt_in_candidate']}, which is {res['num_tasks_with_gt_in_candidate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks has singleton candidate set: {res['num_tasks_with_singleton_candidate']}, which is {res['num_tasks_with_singleton_candidate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks has singleton candidate set which is ground truth: {res['num_tasks_with_singleton_candidate_with_gt']}, which is {res['num_tasks_with_singleton_candidate_with_gt']/res['num_tasks_with_gt'] * 100}%")
print()
print(f"number of tasks with top-1 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_one_accurate']}, which is {res['num_tasks_with_graph_top_one_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-5 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_five_accurate']}, which is {res['num_tasks_with_graph_top_five_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-10 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_ten_accurate']}, which is {res['num_tasks_with_graph_top_ten_accurate']/res['num_tasks_with_gt'] * 100}%")
print()
print(f"number of tasks with top-1 accuracy in terms of model score: {res['num_tasks_with_model_score_top_one_accurate']}, which is {res['num_tasks_with_model_score_top_one_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-5 accuracy in terms of model score: {res['num_tasks_with_model_score_top_five_accurate']}, which is {res['num_tasks_with_model_score_top_five_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-10 accuracy in terms of model score: {res['num_tasks_with_model_score_top_ten_accurate']}, which is {res['num_tasks_with_model_score_top_ten_accurate']/res['num_tasks_with_gt'] * 100}%")
print()
candidate_eval_data_with_gt = candidate_eval_data[candidate_eval_data['has_gt'] == 1]
c = candidate_eval_data.groupby(['table_id']).agg({
'graph_top_one_accurate':lambda x: sum(x)/len(x),
'model_top_one_accurate':lambda x: sum(x)/len(x),
'graph_top_five_accurate':lambda x: sum(x)/len(x),
'model_top_five_accurate':lambda x: sum(x)/len(x)
})
c['table type'] = [
'country II',
'companies',
'pope',
'video games',
'movies',
'players I',
'players II',
'magazines'
]
c
```
|
github_jupyter
|
# Logistic Regression with Hyperparameter Optimization (scikit-learn)
<a href="https://colab.research.google.com/github/VertaAI/modeldb/blob/master/client/workflows/examples-without-verta/notebooks/sklearn-census.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Imports
```
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings("ignore", category=ConvergenceWarning)
import itertools
import time
import numpy as np
import pandas as pd
from sklearn import model_selection
from sklearn import linear_model
from sklearn import metrics
```
---
## Prepare Data
```
try:
import wget
except ImportError:
!pip install wget # you may need pip3
import wget
train_data_url = "http://s3.amazonaws.com/verta-starter/census-train.csv"
train_data_filename = wget.download(train_data_url)
test_data_url = "http://s3.amazonaws.com/verta-starter/census-test.csv"
test_data_filename = wget.download(test_data_url)
df_train = pd.read_csv("census-train.csv")
X_train = df_train.iloc[:,:-1].values
y_train = df_train.iloc[:, -1]
df_train.head()
```
## Prepare Hyperparameters
```
hyperparam_candidates = {
'C': [1e-4, 1e-1, 1, 10, 1e3],
'solver': ['liblinear', 'lbfgs'],
'max_iter': [15, 28],
}
# total models 20
# create hyperparam combinations
hyperparam_sets = [dict(zip(hyperparam_candidates.keys(), values))
for values
in itertools.product(*hyperparam_candidates.values())]
```
## Run Validation
```
# create validation split
(X_val_train, X_val_test,
y_val_train, y_val_test) = model_selection.train_test_split(X_train, y_train,
test_size=0.2,
shuffle=True)
def run_experiment(hyperparams):
# create and train model
model = linear_model.LogisticRegression(**hyperparams)
model.fit(X_train, y_train)
# calculate and log validation accuracy
val_acc = model.score(X_val_test, y_val_test)
print(hyperparams, end=' ')
print("Validation accuracy: {:.4f}".format(val_acc))
# NOTE: run_experiment() could also be defined in a module, and executed in parallel
for hyperparams in hyperparam_sets:
run_experiment(hyperparams)
```
## Pick the best hyperparameters and train the full data
```
best_hyperparams = {}
model = linear_model.LogisticRegression(multi_class='auto', **best_hyperparams)
model.fit(X_train, y_train)
```
## Calculate Accuracy on Full Training Set
```
train_acc = model.score(X_train, y_train)
print("Training accuracy: {:.4f}".format(train_acc))
```
---
|
github_jupyter
|
# Sesiones prácticas
## 0
Instalación de Python + ecosistema científico + opencv + opengl
- aula virtual -> página web -> install
- git o unzip master
- anaconda completo o miniconda
- linux, windows, mac
- probar scripts con webcam y verificar opengl, dlib etc.
- manejo básico de jupyter
- repaso Python
- Ejercicio: recortar y unir imágenes para conseguir [algo como esto](../images/demos/ej-c0.png).
Opcional:
- compilación opencv
- docker
## 1
Ejercicio de comprobación de FOV/tamaños/distancias.
Dispositivos de captura
- umucv (install con --upgrade) (update_umucv.sh)
- webcam.py con opencv crudo
- stream.py, opciones de autostream, efecto de teclas, --help, --dev=help
- webcams
- videos
- carpeta de imágenes
- teléfono
- youtube
- urls de tv
- ejemplo de recorte invertido
## 2
Más utilidades
- spyder
- PYTHONPATH
- control de webcam v4l2-ctl, vlc, gucview
- wzoom.py (para las ventanas de Windows que no tienen zoom)
- help_window.py
- save_video.py
- ampliar mouse.py:
- círculos en las posiciones marcadas (cv.circle)
- coordenadas textuales (cv.putText (ej. en hello.py) o umucv.util.putText)
- marcar solo los dos últimos (pista: collections.deque)
- reproducir code/medidor.py indicando la distancia en pixels
- Dado el FOV: indicar el ángulo de las direcciones marcadas.
## 3
deque.py
roi.py:
- añadir la media del nivel de gris del recorte
- guardar el recorte y mostrar cv.absdiff respecto al frame actual, mostrando su media o su máximo.
(Sirve de punto de partida para el ejercicio ACTIVIDAD)
## 4
- aclaraciones ejercicio COLOR
- demo spectral
- trackbar.py
- demo filtros
Ejercicio:
- implementación de filtro gaussiano con tracker sigma en toda la imagen, monocromo ([ejemplo](../images/demos/ej-c4-0.png)).
- add box y median
- medir y mostrar tiempos de cómputo en diferentes casos
(Sirve de punto de partida para el ejercicio opcional FILTROS)
## 5
HOG
- (captura asíncrona)
- (teoría de HOG, implementación sencilla)
- hog0.py en detalle
- pedestrian.py, detección multiescala
- DLIB facelandmarks.py: HOG face detector con landmarks
Ejercicio: blink detection, inpainting eyes, etc.
## 6
Detección de corners y Flujo óptico de Lucas-Kanade
- LK/*.py
Vamos a construir un "tracker" de puntos de interés basado en el método de Lucas-Kanade.
El primer paso es construir un detector de corners partiendo de cero, calculando la imagen de respuesta correspondiente al menor valor propio de la matriz de covarianza de la distribución local del gradiente en cada pixel (`corners0.py`). En realidad esta operación está directamente disponible en opencv mediante cv.goodFeaturesToTrack (`corners1.py`, `corners2.py ).
El siguiente ejemplo muestra cómo encontrar directamente con `cv.calcOpticalFlowPyrLK` la posición de los puntos detectados en el fotograma siguiente, sin necesidad de recalcular puntos nuevos y asociarlos con los anteriores (`lk_track0.py`).
A continuación ampliamos el código para generar puntos nuevos periódicamente y crear una lista de trayectorias "tracks" que se mantiene actualizada en cada fotograma (`lk_track1.py`).
Finalmente, ampliamos el código anterior para que solo se generen puntos nuevos en zonas de la imagen donde no los haya, y mejoramos la detección de las posiciones siguientes con un criterio de calidad muy robusto que exige que la predicción hacia el pasado de los puntos nuevos coincida con el punto inicial. Si no hay una asociación mutua el punto y su trayectoria se descartan (`lk_tracks.py`).
Ejercicios:
- Analizar los tracks para determinar en qué dirección se mueve la cámara (UP,DOWN,LEFT,RIGHT, [FORWARD, BACKWARD])
- Estudiar la posibilidad de hacer tracking de un ROI.
## 7
Experimentamos con el detector de puntos de interés SIFT.
Nuestro objetivo es obtener un conjunto de "keypoints", cada uno con su descriptor (vector de características que describe el entorno del punto), que permita encontrarlo en imágenes futuras. Esto tiene una aplicación inmediata para reconocer objetos y más adelante en geometría visual.
Empezamos con el ejemplo de código code/SIFT/sift0.py, que simplemente calcula y muestra los puntos de interés. Es interesante observar el efecto de los parámetros del método y el tiempo de cómputo en función del tamaño de la imagen (que puedes cambiar con --size o --resize).
El siguiente ejemplo code/SIFT/sift1.py muestra un primer ataque para establecer correspondencias. Los resultados son bastante pobres porque se aceptan todas las posibles coincidencias.
Finalmente, en code/SIFT/sift.py aplicamos un criterio de selección para eliminar muchas correspondencias erróneas (aunque no todas). Esto es en principio suficiente para el reconocimiento de objetos. (Más adelante veremos una forma mucho mejor de eliminar correspondencias erróneas, necesaria para aplicaciones de geometría.)
El ejercicio obligatorio **SIFT** es una ampliación sencilla de este código. Se trata de almacenar un conjunto de modelos (¡con textura! para que tengan suficientes keypoints) como portadas de libros, discos, videojuegos, etc. y reconocerlos en base a la proporción de coincidencias detectadas.
En la segunda parte de la clase experimentamos con un servidor mjpg y creamos bots de telegram (explicados al final de este documento) para comunicarnos fácilmente con las aplicaciones de visión artificial desde el móvil.
## 8
Reconocimiento de formas mediante descriptores frecuenciales.
Nuestro objetivo es hacer un programa que reconozca la forma de trébol, como se muestra [en este pantallazo](../images/demos/shapedetect.png). Si no tenéis a mano un juego de cartas podéis usar --dev=dir:../images/card*.png para hacer las pruebas, aunque lo ideal es hacerlo funcionar con una cámara en vivo.
Trabajaremos con los ejemplos de código de la carpeta `code/shapes` y, como es habitual, iremos añadiendo poco a poco funcionalidad. En cada nuevo paso los comentarios explican los cambios respecto al paso anterior.
Empezamos con el ejemplo shapes/trebol1.py, que simplemente prepara un bucle de captura básico, binariza la imagen y muestra los contornos encontrados. Se muestran varias formas de realizar la binarización y se puede experimentar con ellas, pero en principio el método automático propuesto suele funcionar bien en muchos casos.
El segundo paso en shapes/trebol2.py junta la visualización en una ventana y selecciona los contornos oscuros de tamaño razonable. Esto no es imprescincible para nuestra aplicación, pero es conveniente familiarizarse con el concepto de orientación de un contorno.
En shapes/trebol3.py leemos un modelo de la silueta trébol de una imagen que tenemos en el repositorio y la mostramos en una ventana.
En shapes/trebol3b.py hacemos una utilidad para ver gráficamente las componentes frecuenciales como elipses que componen la figura. Podemos ver las componentes en su tamaño natural, incluyendo la frecuencia principal, [como aquí](../images/demos/full-components.png), o quitando la frecuencia principal y ampliando el tamaño de las siguientes, que son la base del descriptor de forma, [como se ve aquí](../images/demos/shape-components.png). Observa que las configuraciones de elipses son parecidas cuando corresponden a la misma silueta.
En shapes/trebol4.py definimos la función que calcula el descriptor invariante. Se basa esencialmente en calcular los tamaños relativos de estas elipses. En el código se explica cómo se consigue la invarianza a las transformaciones deseadas: posición, tamaño, giros, punto de partida del contorno y ruido de medida.
Finalmente, en shapes/trebol5.py calculamos el descriptor del modelo y en el bucle de captura calculamos los descriptores de los contornos oscuros detectados para marcar las siluetas que tienen un descriptor muy parecido al del trébol.
## 8b
En esta subsesión vamos a hacer varias actividades. Necesitamos algunos paquetes. En Linux son:
sudo apt install tesseract-ocr tesseract-ocr-spa libtesseract-dev
pip install tesserocr
sudo apt install libzbar-dev
pip install pyzbar
[zbar Windows instaler](http://zbar.sourceforge.net) -> download
Usuarios de Mac y Windows: investigad la forma de instalar tesseract.
1) En primer lugar nos fijamos en el script [code/ocr.py](../code/ocr.py), cuya misión es poner en marcha el OCR con la cámara en vivo. Usamos el paquete de python `tesserocr`. Vamos a verificar el funcionamiento con una imagen estática, pero lo ideal es probarlo con la cámara en vivo.
./ocr.py --dev=dir:../images/texto/bo0.png
Está pensado para marcar una sola línea de texto, [como se muestra aquí](../images/demos/ocr.png). Este pantallazo se ha hecho con la imagen bo1.png disponible en la misma carpeta, que está desenfocada, pero aún así el OCR funciona bien.
(En windows parece que hay que usar pytesseract en lugar de tesserocr, lo que requiere adaptar del script.)
Para mostrar la complejidad de un ocr mostramos el resultado del script `crosscorr.py` sobre images/texto.png, para observar que la comparación pixel a pixel no es suficiente para obtener resultados satisfactorios. En esa misma imagen la binarización y extracción de componentes conexas no consigue separar letras individuales.
Finalmente demostramos mediante `spectral.py` que la transormada de Fourier 2D permite detectar el ángulo y la separación entre renglones.
2) El segundo ejemplo es `code/zbardemo.png` que muestra el uso del paquete pyzbar para leer códigos de barras ([ejemplo](../images/demos/barcode.png)) y códigos QR ([ejemplo](../images/demos/qr.png)) con la cámara. En los códigos de barras se detectan puntos de referencia, y en los QR se detectan las 4 esquinas del cuadrado, que pueden ser útiles como referencia en algunas aplicaciones de geometría.
4) demo de `grabcut.py` para segmentar interactivamente una imagen. Lo probamos con images/puzzle3.png.
5) Ponemos en marcha el detector de caras de opencv con la webcam en vivo y comparamos con el detector de DLIB.
## 9
Hoy vamos a rectificar el plano de la mesa apoyándonos en marcadores artificiales.
En primer lugar trabajaremos con marcadores poligonales. Nuestro objetivo es detectar un marcador como el que aparece en el vídeo `images/rot4.mjpg`. Nos vamos a la carpeta `code/polygon`.
El primer paso (`polygon0.py`) es detectar figuras poligonales con el número de lados correcto a partir de los contornos detectados.
A continuación (`polygon1.py`) nos quedamos con los polígonos que realmente pueden corresponder al marcador. Esto se hace viendo si existe una homografía que relaciona con precisión suficiente el marcador real y su posible imagen.
Finalmente (`polygon2.py`) obtiene el plano rectificado
También se puede añadir información "virtual" a la imagen original, como por ejemplo los ejes de coordenadas definidos por el marcador (`polygon3.py`).
Como segunda actividad, en la carpeta `code/elipses` se muestra la forma de detectar un marcador basado en 4 círculos.
## 10
En esta sesión vamos a extraer la matriz de cámara a partir del marcador utilizado en la sesión anterior, lo que nos permitirá añadir objetos virtuales tridimensionales a la escena y determinar la posición de la cámara en el espacio.
Nos vamos a la carpeta `code/pose`, donde encontraremos los siguientes ejemplos de código:
`pose0.py` incluye el código completo para extraer contornos, detectar el marcador poligonal, extraer la matriz de cámara y dibujar un cubo encima del marcador.
`pose1.py` hace lo mismo con funciones de umucv.
`pose2.py` trata de ocultar el marcador y dibuja un objeto que cambia de tamaño.
`pose3.py` explica la forma de proyectar una imagen en la escena escapando del plano del marcador.
`pose3D.py` es un ejemplo un poco más avanzado que utiliza el paquete pyqtgraph para mostrar en 3D la posición de la cámara en el espacio.
En el ejercicio **RA** puedes intentar que el comportamiento del objeto virtual dependa de acciones del usuario (p. ej. señalando con el ratón un punto del plano) o de objetos que se encuentran en la escena.
## 11
Breve introducción a scikit-learn y keras.
En primer lugar repasaremos algunos conceptos básicos en el notebook [machine learning](machine-learning.ipynb).
Esta sesión está dedicada a poner en marcha una red convolucional sencilla. La tarea que vamos a resolver es el reconocimiento de dígitos manuscritos. Por eso, en primer lugar es conveniente escribir unos cuantos números en una hoja de papel, con un bolígrafo que tenga un trazo no demasiado fino, y sin preocuparnos mucho de que estén bien escritos. Pueden tener distintos tamaños, pero no deben estar muy girados. Para desarrollar el programa y hacer pruebas cómodamente se puede trabajar con una imagen fija, pero la idea es que nuestro programa funcione con la cámara en vivo.
Trabajaremos en la carpeta [code/DL/CNN](../code/DL/CNN), donde tenemos las diferentes etapas de ejercicio y una imagen de prueba.
El primer paso es `digitslive-1.py` que simplemente encuentra las manchas de tinta que pueden ser posibles números.
En `digitslive-2.py` normalizamos el tamaño de las detecciones para poder utilizar la base de datos MNIST.
En `digitslive-3.py` implementamos un clasificador gaussiano con reducción de dimensión mediante PCA y lo ponemos en marcha con la imagen en vivo. (Funciona bastante bien pero, p.ej., en la imagen de prueba comete un error).
Finalmente, en `digitslive-4.py` implementamos la clasificación mediante una red convolucional mediante el paquete **keras**. Usamos unos pesos precalculados. (Esta máquina ya no comete el error anterior.)
Como siempre, en cada fase del ejercicio los comentarios explican el código que se va añadiendo.
Una vez conseguido esto, la sesión práctica tiene una segunda actividad que consiste en **entrenar los pesos** de (por ejemplo) esta misma red convolucional. Para hacerlo en nuestro ordenador sin perder la paciencia necesitamos una GPU con CUDA y libCUDNN. La instalación de todo lo necesario puede no ser trivial.
Una alternativa muy práctica es usar [google colab](https://colab.research.google.com/), que proporciona gratuitamente máquinas virtuales con GPU y un entorno de notebooks jupyter (un poco modificados pero compatibles). Para probarlo, entrad con vuestra cuenta de google y abrid un nuevo notebook. En la opción de menú **Runtime** hay que seleccionar **Change runtime type** y en hardware accelerator ponéis GPU. En una celda del notebook copiáis directamente el contenido del archivo `cnntest.py` que hay en este mismo directorio donde estamos trabajando hoy. Al evaluar la celda se descargará la base de datos y se lanzará un proceso de entrenamiento. Cada epoch tarda unos 4s. Podéis comparar con lo que se consigue con la CPU en vuestro propio ordenador. Se puede lanzar un entrenamiento más completo, guardar los pesos y descargarlos a vuestra máquina.
Como curiosidad, podéis comparar con lo que conseguiría el OCR tesseract, y guardar algunos casos de dígitos que estén bien dibujados pero que la red clasifique mal.
Finalmente, entrenamos un autoencoder (notebook [bottleneck](bottleneck.ipynb)) y comparamos el resultado con la reducción de dimensión PCA explicada al principio.
## 12
En esta sesión vamos a poner en marcha algunos modelos más avanzados de deep learning.
Los ejemplos de código se han probado sobre LINUX. En Windows o Mac puede ser necesario hacer modificaciones; para no perder mucho tiempo mi recomendación es probarlo primero en una máquina virtual.
Si tenéis una GPU nvidia reciente lo ideal es instalar CUDA y libCUDNN para conseguir una mayor velocidad de proceso. Si no tenéis GPU no hay ningún problema, todos los modelos funcionan con CPU. (Los ejercicios de deep learning que requieren entrenamiento son opcionales y se pueden entrenar en COLAB.)
1) Para probar el **reconocimiento de caras** nos vamos a la carpeta code/DL/facerec. Debe estar correctamente instalado DLIB.
En el directorio `gente` se guardan los modelos. Como ejemplo tenemos a los miembros de Monty Python:
./facerec.py --dev=dir:../../../images/monty-python*
(Recuerda que las imágenes seleccionadas con --dev=dir: se avanzan pinchando con el ratón en la ventana pequeña de muestra).
Puedes meter fotos tuyas y de tu familia en la carpeta `gente` para probar con la webcam o con otras fotos.
Esta versión del reconocimiento de caras no tiene aceleración con GPU (tal vez se puede configurar). Si reducimos un poco el tamaño de la imagen funciona con bastante fluidez.
Ejercicio: selecciona una cara en la imagen en vivo pinchando con el ratón para ocultarla (emborronándola o pixelizándola) cuando se reconozca en las imágenes siguientes.
2) Para probar la máquina **inception** nos movemos a la carpeta code/DL/inception.
./inception0.py
(Se descargará el modelo del la red). Se puede probar con las fotos incluidas en la carpeta con `--dev=dir:*.png`. La versión `inception1.py` captura en hilo aparte y muestra en consola las 5 categorías más probables.
Aunque se supone que consigue buenos resultados en las competiciones, sobre imágenes naturales comete bastante errores.
3) El funcionamiento de **YOLO** es mucho mejor. Puede ponerse en marcha fácilmente siguiendo las instrucciones en
https://github.com/zzh8829/yolov3-tf2
El artículo de [YOLO V3](https://pjreddie.com/media/files/papers/YOLOv3.pdf) es interesante. En la sección 5 el autor explica que abandonó esta línea de investigación por razones éticas. Os recomiendo que la leáis. Posteriormente apareció [YOLO V4](https://arxiv.org/abs/2004.10934).
4) mediapipe proporciona unos detectorses de "human pose" and "hand pose" muy fáciles de usar.
En la carpeta `docker` hay un script para ejecutar una imagen docker que tiene instalados todos los paquetes que hemos estamos usando en la asignatura. Es experimental. No perdaís ahora tiempo con esto si no estáis familiarizados con docker.
El tema de deep learning en visión artificial es amplísimo. Para estudiarlo en detalle hace falta (como mínimo) una asignatura avanzada (master). Nuestro objetivo es familizarizarnos un poco con algunas de las máquinas preentrenadas disponibles para hacernos una idea de sus ventajas y limitaciones.
Si estáis interesados en estos temas el paso siguiente es adaptar alguno de estos modelos a un problema propio mediante "transfer learning", que consiste en utilizar las primeras etapas de una red preentrenada para transformar nuestros datos y ajustar un clasificador sencillo. Alternativamente, se puede reajustar los pesos de un modelo preentrenado, fijando las capas iniciales al principio. Para remediar la posible falta de ejemplos se utilizan técnicas de "data augmentation", que generan variantes de los ejemplos de entrenamiento con múltiples transformaciones.
## 13
Repaso y dudas.
## otros modelos
UNET
Variational autoencoder
Transformers
## entrenar dlib
- (opcional) DLIB herramienta de etiquetado imglab. Entrenamiento de detector HOG SVM con herramientas de DLIB:
- descargar y descomprimir dlib source
- ir a los ejemplos/faces
- meter dentro imglab (que hay que compilar pero tenemos versión precompilada en robot/material/va)
- mostrar los training.xml y testing.xml (se pueden crear otros)
- meter dentro train_detector.py y run_detector.py de code/hog
- ./train_detector training.xml testing.xml (crea detector.svm)
- ./run_detector detector.svm --dev=dir:\*.jpg (o también --dev=dir:/path/to/umucv/images/monty\*)
## correlation filter
Comentamos el método de detección de objetos por correlación cruzada, que es el mismo criterio que se usa para buscar la posición de *corners* en imágenes sucesivas, y luego vemos la demostración del discriminative correlation filter.
- crosscorr.py
- dcf.py
## flask server
El ejemplo `server.py` explica cómo hacer un servidor web sencillo con *flask* para enviar un pantallazo de la imagen actual de la webcam, y `mjpegserver.py` explica cómo hacer un servidor de streaming en formato mjpeg.
## telegram bot
Vamos a jugar con un bot de telegram que nos permite comunicarnos cómodamente con nuestro ordenador desde el teléfono móvil, sin necesidad de tener una dirección pública de internet.
Simplemente necesitamos:
pip install python-telegram-bot
El ejemplo `bot/bot0.py` nos envía al teléfono la IP del ordenador (es útil si necesitamos conectarnos por ssh con una máquina que tiene IP dinámica).
El ejemplo `bot/bot1.py` explica la forma de enviar una imagen nuestro teléfono cuando ocurre algo. En este caso se envía cuando se pulsa una tecla, pero lo normal es detectar automáticamente algún evento con las técnicas de visión artificial que estamos estudiando.
El ejemplo `bot/bot2.py` explica la forma de hacer que el bot responda a comandos. El comando /hello nos devuelve el saludo, el comando /stop detiene el programa y el comando /image nos devuelve una captura de nuestra webcam. (Se ha usado la captura en un hilo).
El ejemplo `bot/bot3.py` explica la forma de capturar comandos con argumentos y el procesamiento de una imagen enviada por el usuario.
Esta práctica es muy útil para enviar cómodamente a nuestros programas de visión artificial una imagen tomada con la cámara sin necesidad de escribir una aplicación específica para el móvil. Algunos ejercicios que estamos haciendo se pueden adaptar fácilmente para probarlos a través de un bot de este tipo.
Para crearos vuestro propio bot tenéis que contactar con el bot de telegram "BotFather", que os guiará paso a paso y os dará el token de acceso. Y luego el "IDBot" os dirá el id numérico de vuestro usuario.
|
github_jupyter
|
# Other widget libraries
We would have loved to show you everything the Jupyter Widgets ecosystem has to offer today, but we are blessed to have such an active community of widget creators and unfortunately can't fit all widgets in a single session, no matter how long.
This notebook lists some of the widget libraries we wanted to demo but did not have enough time to include in the session. Enjoy!
# ipyleaflet: Interactive maps
## A Jupyter - LeafletJS bridge
## https://github.com/jupyter-widgets/ipyleaflet
ipyleaflet is a jupyter interactive widget library which provides interactive maps to the Jupyter notebook.
- MIT Licensed
**Installation:**
```bash
conda install -c conda-forge ipyleaflet
```
```
from ipywidgets import Text, HTML, HBox
from ipyleaflet import GeoJSON, WidgetControl, Map
import json
m = Map(center = (43,-100), zoom = 4)
geo_json_data = json.load(open('us-states-density-colored.json'))
geojson = GeoJSON(data=geo_json_data, hover_style={'color': 'black', 'dashArray': '5, 5', 'weight': 2})
m.add_layer(geojson)
html = HTML('''
<h4>US population density</h4>
Hover over a state
''')
html.layout.margin = '0px 20px 20px 20px'
control = WidgetControl(widget=html, position='topright')
m.add_control(control)
def update_html(properties, **kwargs):
html.value = '''
<h4>US population density</h4>
<h2><b>{}</b></h2>
{} people / mi^2
'''.format(properties['name'], properties['density'])
geojson.on_hover(update_html)
m
```
# pythreejs: 3D rendering in the browser
## A Jupyter - threejs bridge
## https://github.com/jupyter-widgets/pythreejs
Pythreejs is a jupyter interactive widget bringing fast WebGL 3d visualization to the Jupyter notebook.
- Originally authored by Jason Grout, currently maintained by Vidar Tonaas Fauske
- BSD Licensed
Pythreejs is *not* a 3d plotting library, it only exposes the threejs scene objects to the Jupyter kernel.
**Installation:**
```bash
conda install -c conda-forge pythreejs
```
```
from pythreejs import *
import numpy as np
from IPython.display import display
from ipywidgets import HTML, Text, Output, VBox
from traitlets import link, dlink
# Generate surface data:
view_width = 600
view_height = 400
nx, ny = (20, 20)
xmax=1
x = np.linspace(-xmax, xmax, nx)
y = np.linspace(-xmax, xmax, ny)
xx, yy = np.meshgrid(x, y)
z = xx ** 2 - yy ** 2
#z[6,1] = float('nan')
# Generate scene objects from data:
surf_g = SurfaceGeometry(z=list(z[::-1].flat),
width=2 * xmax,
height=2 * xmax,
width_segments=nx - 1,
height_segments=ny - 1)
surf = Mesh(geometry=surf_g,
material=MeshLambertMaterial(map=height_texture(z[::-1], 'YlGnBu_r')))
surfgrid = SurfaceGrid(geometry=surf_g, material=LineBasicMaterial(color='black'),
position=[0, 0, 1e-2]) # Avoid overlap by lifting grid slightly
# Set up picking bojects:
hover_point = Mesh(geometry=SphereGeometry(radius=0.05),
material=MeshLambertMaterial(color='green'))
click_picker = Picker(controlling=surf, event='dblclick')
hover_picker = Picker(controlling=surf, event='mousemove')
# Set up scene:
key_light = DirectionalLight(color='white', position=[3, 5, 1], intensity=0.4)
c = PerspectiveCamera(position=[0, 3, 3], up=[0, 0, 1], aspect=view_width / view_height,
children=[key_light])
scene = Scene(children=[surf, c, surfgrid, hover_point, AmbientLight(intensity=0.8)])
renderer = Renderer(camera=c, scene=scene,
width=view_width, height=view_height,
controls=[OrbitControls(controlling=c), click_picker, hover_picker])
# Set up picking responses:
# Add a new marker when double-clicking:
out = Output()
def f(change):
value = change['new']
with out:
print('Clicked on %s' % (value,))
point = Mesh(geometry=SphereGeometry(radius=0.05),
material=MeshLambertMaterial(color='hotpink'),
position=value)
scene.add(point)
click_picker.observe(f, names=['point'])
# Have marker follow picker point:
link((hover_point, 'position'), (hover_picker, 'point'))
# Show picker point coordinates as a label:
h = HTML()
def g(change):
h.value = 'Green point at (%.3f, %.3f, %.3f)' % tuple(change['new'])
h.value += ' Double-click to add marker'
g({'new': hover_point.position})
hover_picker.observe(g, names=['point'])
display(VBox([h, renderer, out]))
```
# bqplot: complex interactive visualizations
## https://github.com/bloomberg/bqplot
## A Jupyter - d3.js bridge
bqplot is a jupyter interactive widget library bringing d3.js visualization to the Jupyter notebook.
- Apache Licensed
bqplot implements the abstractions of Wilkinson’s “The Grammar of Graphics” as interactive Jupyter widgets.
bqplot provides both
- high-level plotting procedures with relevant defaults for common chart types,
- lower-level descriptions of data visualizations meant for complex interactive visualization dashboards and applications involving mouse interactions and user-provided Python callbacks.
**Installation:**
```bash
conda install -c conda-forge bqplot
```
```
import numpy as np
import bqplot as bq
xs = bq.LinearScale()
ys = bq.LinearScale()
x = np.arange(100)
y = np.cumsum(np.random.randn(2, 100), axis=1) #two random walks
line = bq.Lines(x=x, y=y, scales={'x': xs, 'y': ys}, colors=['red', 'green'])
xax = bq.Axis(scale=xs, label='x', grid_lines='solid')
yax = bq.Axis(scale=ys, orientation='vertical', tick_format='0.2f', label='y', grid_lines='solid')
fig = bq.Figure(marks=[line], axes=[xax, yax], animation_duration=1000)
display(fig)
# update data of the line mark
line.y = np.cumsum(np.random.randn(2, 100), axis=1)
```
# ipympl: The Matplotlib Jupyter Widget Backend
## https://github.com/matplotlib/ipympl
Enabling interaction with matplotlib charts in the Jupyter notebook and JupyterLab
- BSD-3-Clause
**Installation:**
```bash
conda install -c conda-forge ipympl
```
Enabling the `widget` backend. This requires ipympl. ipympl can be install via pip or conda.
```
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import VBox, FloatSlider
```
When using the `widget` backend from ipympl, fig.canvas is a proper Jupyter interactive widget, which can be embedded in Layout classes like HBox and Vbox.
One can bound figure attributes to other widget values.
```
plt.ioff()
plt.clf()
slider = FloatSlider(
value=1.0,
min=0.02,
max=2.0
)
fig1 = plt.figure(1)
x1 = np.linspace(0, 20, 500)
lines = plt.plot(x1, np.sin(slider.value * x1))
def update_lines(change):
lines[0].set_data(x1, np.sin(change.new * x1))
fig1.canvas.draw()
fig1.canvas.flush_events()
slider.observe(update_lines, names='value')
VBox([slider, fig1.canvas])
```
# ipytree: Interactive tree view based on ipywidgets
## https://github.com/QuantStack/ipytree/
ipytree is a jupyter interactive widget library which provides a tree widget to the Jupyter notebook.
- MIT Licensed
**Installation:**
```bash
conda install -c conda-forge ipytree
```
## Create a tree
```
from ipywidgets import Text, link
from ipytree import Tree, Node
tree = Tree()
tree.add_node(Node('node1'))
node2 = Node('node2')
tree.add_node(node2)
tree
node3 = Node('node3', disabled=True)
node4 = Node('node4')
node5 = Node('node5', [Node('1'), Node('2')])
node2.add_node(node3)
node2.add_node(node4)
node2.add_node(node5)
```
|
github_jupyter
|
[Schema](Schema.ipynb) <- vorige - [Inhoudsopgave](Inhoud.ipynb) - volgende -> [JSON-LD en linked data](json-ld-linked-data.ipynb)
# JSON-schema
Met JSON-schema kun je schema's voor JSON-objecten maken.
Deze kun je gebruiken als documentatie van JSON-objecten die bijvoorbeeld in een web-API gebruikt worden.
Vervolgens kun je JSON-objecten valideren tegen een schema.
Dit kan handig zijn voor JSON-objecten in web-API's,
zowel bij het genereren als bij het accepteren van JSON objecten.
## JSON-schema in MongoDB
In MongoDB kun je schema's in de JSON-schema notatie gebruiken voor het valideren van documenten in een collection.
## Definiëren van een schema
### Annotaties
Deze annotaties zijn niet verplicht, maar wel "good practice".
* `$schema` - welke (standaard)notatie gebruiken we hier? ("schema van het schema")
* `title` - de naam van het schema
* `description` - een beschrijving van het schema
### Type, object, properties
Een document heeft als type: `object`.
Per veld (*property*) van dit object geef je de naam en het type.
Je kunt ook aangeven of welke velden verplicht (*required*) zijn.
```
contact_schema = {
"$schema": "http://json-schema.org/draft-07/schema#",
"title": "Contact",
"description": "schema for documents in the contacts collection",
"type": "object",
"properties": {
"name": {"type": "string"},
"email": {"type": "string"},
"telephone": {"type": "string"},
},
"required": ["name", "email", "telephone"]
}
```
## JSON-schema in Python
Je kunt in Python een schema definiëren als een Python dictionary.
(Dit is vrijwel dezelfde notatie als JSON.)
De libraries `jsonschema` (https://python-jsonschema.readthedocs.io) en `fastjsonschema` geven je functies om JSON-objecten te valideren tegen een schema.
```
from jsonschema import validate
mycontact = {
"name": "Harry van Doorn",
"email": "harryvdoorm@friendmail.org",
"tel": "06-1357 8642"
}
validate(instance=mycontact, schema=contact_schema)
```
* Verbeter `mycontact` en valideer opnieuw.
### Arrays
Als we meerdere e-mailadressen toestaan dan kunnen we daarvan een `array` maken:
```
contact_schema_1 = {
"$schema": "http://json-schema.org/draft-07/schema#",
"title": "Contact",
"description": "schema for documents in the contacts collection",
"type": "object",
"properties": {
"name": {"type": "string"},
"email": {"type": "array",
"items": {"type": "string"}},
"telephone": {"type": "string"},
},
"required": ["name", "email", "telephone"]
}
mycontact_1 = {
"name": "Harry van Doorn",
"email": "harryvdoorm@friendmail.org",
"telephone": "06-1357 8642"
}
validate(instance=mycontact_1, schema=contact_schema_1)
```
* Verbeter het veld `email` door daar een array van te maken, en valideer opnieuw.
## Alternatieven
In een contact moeten we tenminste een e-mailadres opnemen of een telefoonnummer, beide is niet verplicht.
We gebruiken hiervoor het keyword `anyOf`, met een lijst van alternatieven.
```
contact_schema_2 = {
"$schema": "http://json-schema.org/draft-07/schema#",
"title": "Contact",
"description": "schema for documents in the contacts collection",
"type": "object",
"required": ["name"],
"properties": {
"name": {"type": "string"}
},
"anyOf": [
{"properties": {"email": {"type": "array",
"items": {"type": "string"}
}
},
"required": ["email"]},
{"properties": {"telephone": {"type": "string"}},
"required": ["telephone"]}
]
}
mycontact_2 = {
"name": "Harry van Doorn"
}
validate(instance=mycontact_2, schema=contact_schema_2)
```
* verbeter `mycontact2` door een e-mailadres of een telefoonnummer toe te voegen, en valideer opnieuw.
(Merk op dat het eerste missende alternatief als ontbrekend gemeld wordt,
terwijl je natuurlijk ook de andere alternatieven kunt opgeven.
## Patronen (reguliere expressies)
Zoals je ziet is een waarde van een veld vaak een string.
In veel gevallen moet die string aan een bepaald patroon (reguliere expressie) voldoen.
Dit patronen kun je ook beschrijven in JSON-schema.
Zie: https://json-schema.org/understanding-json-schema/reference/regular_expressions.html
## Gestandaardiseerde schema's
Voor veel voorkomende domeinen zijn standaard-schema's gemaakt.
Je vindt deze bijvoorbeeld via (in json-schema formaat).
Schema.org bevat een *ontologie* van veel-voorkomende begrippen.
Deze begrippen zijn in samenhang met elkaar gedefinieerd.
Zie bijvoorbeeld:
* https://schema.org/ContactPoint
* https://json.schemastore.org/schema-org-contact-point (hetzelfde, in json-ld)
* en de lijst:
* https://schema.org/Person
** met bijvoorbeeld: `givenName` en `familyName`.
(Dit vormt een opstapje naar Linked Open Data.)
|
github_jupyter
|
```
from IPython import display
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
from utils import Logger
import tensorflow as tf
import numpy as np
DATA_FOLDER = './tf_data/VGAN/MNIST'
IMAGE_PIXELS = 28*28
NOISE_SIZE = 100
BATCH_SIZE = 100
def noise(n_rows, n_cols):
return np.random.normal(size=(n_rows, n_cols))
def xavier_init(size):
in_dim = size[0] if len(size) == 1 else size[1]
stddev = 1. / np.sqrt(float(in_dim))
return tf.random_uniform(shape=size, minval=-stddev, maxval=stddev)
def images_to_vectors(images):
return images.reshape(images.shape[0], 784)
def vectors_to_images(vectors):
return vectors.reshape(vectors.shape[0], 28, 28, 1)
```
## Load Data
```
def mnist_data():
compose = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((.5, .5, .5), (.5, .5, .5))
])
out_dir = '{}/dataset'.format(DATA_FOLDER)
return datasets.MNIST(root=out_dir, train=True, transform=compose, download=True)
# Load data
data = mnist_data()
# Create loader with data, so that we can iterate over it
data_loader = DataLoader(data, batch_size=BATCH_SIZE, shuffle=True)
# Num batches
num_batches = len(data_loader)
```
## Initialize Graph
```
## Discriminator
# Input
X = tf.placeholder(tf.float32, shape=(None, IMAGE_PIXELS))
# Layer 1 Variables
D_W1 = tf.Variable(xavier_init([784, 1024]))
D_B1 = tf.Variable(xavier_init([1024]))
# Layer 2 Variables
D_W2 = tf.Variable(xavier_init([1024, 512]))
D_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
D_W3 = tf.Variable(xavier_init([512, 256]))
D_B3 = tf.Variable(xavier_init([256]))
# Out Layer Variables
D_W4 = tf.Variable(xavier_init([256, 1]))
D_B4 = tf.Variable(xavier_init([1]))
# Store Variables in list
D_var_list = [D_W1, D_B1, D_W2, D_B2, D_W3, D_B3, D_W4, D_B4]
## Generator
# Input
Z = tf.placeholder(tf.float32, shape=(None, NOISE_SIZE))
# Layer 1 Variables
G_W1 = tf.Variable(xavier_init([100, 256]))
G_B1 = tf.Variable(xavier_init([256]))
# Layer 2 Variables
G_W2 = tf.Variable(xavier_init([256, 512]))
G_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
G_W3 = tf.Variable(xavier_init([512, 1024]))
G_B3 = tf.Variable(xavier_init([1024]))
# Out Layer Variables
G_W4 = tf.Variable(xavier_init([1024, 784]))
G_B4 = tf.Variable(xavier_init([784]))
# Store Variables in list
G_var_list = [G_W1, G_B1, G_W2, G_B2, G_W3, G_B3, G_W4, G_B4]
def discriminator(x):
l1 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(x, D_W1) + D_B1, .2), .3)
l2 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l1, D_W2) + D_B2, .2), .3)
l3 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l2, D_W3) + D_B3, .2), .3)
out = tf.matmul(l3, D_W4) + D_B4
return out
def generator(z):
l1 = tf.nn.leaky_relu(tf.matmul(z, G_W1) + G_B1, .2)
l2 = tf.nn.leaky_relu(tf.matmul(l1, G_W2) + G_B2, .2)
l3 = tf.nn.leaky_relu(tf.matmul(l2, G_W3) + G_B3, .2)
out = tf.nn.tanh(tf.matmul(l3, G_W4) + G_B4)
return out
G_sample = generator(Z)
D_real = discriminator(X)
D_fake = discriminator(G_sample)
# Losses
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_real, labels=tf.ones_like(D_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.zeros_like(D_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.ones_like(D_fake)))
# Optimizers
D_opt = tf.train.AdamOptimizer(2e-4).minimize(D_loss, var_list=D_var_list)
G_opt = tf.train.AdamOptimizer(2e-4).minimize(G_loss, var_list=G_var_list)
```
## Train
#### Testing
```
num_test_samples = 16
test_noise = noise(num_test_samples, NOISE_SIZE)
```
#### Inits
```
num_epochs = 200
# Start interactive session
session = tf.InteractiveSession()
# Init Variables
tf.global_variables_initializer().run()
# Init Logger
logger = Logger(model_name='DCGAN1', data_name='CIFAR10')
```
#### Train
```
# Iterate through epochs
for epoch in range(num_epochs):
for n_batch, (batch,_) in enumerate(data_loader):
# 1. Train Discriminator
X_batch = images_to_vectors(batch.permute(0, 2, 3, 1).numpy())
feed_dict = {X: X_batch, Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, d_error, d_pred_real, d_pred_fake = session.run(
[D_opt, D_loss, D_real, D_fake], feed_dict=feed_dict
)
# 2. Train Generator
feed_dict = {Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, g_error = session.run(
[G_opt, G_loss], feed_dict=feed_dict
)
if n_batch % 100 == 0:
display.clear_output(True)
# Generate images from test noise
test_images = session.run(
G_sample, feed_dict={Z: test_noise}
)
test_images = vectors_to_images(test_images)
# Log Images
logger.log_images(test_images, num_test_samples, epoch, n_batch, num_batches, format='NHWC');
# Log Status
logger.display_status(
epoch, num_epochs, n_batch, num_batches,
d_error, g_error, d_pred_real, d_pred_fake
)
```
|
github_jupyter
|
# 基本程序设计
- 一切代码输入,请使用英文输入法
```
print('hello world')
```
## 编写一个简单的程序
- 圆公式面积: area = radius \* radius \* 3.1415
```
radius = int(input('请输入一个半径:'))
area = radius * radius * 3.1433223
print(area)
```
### 在Python里面不需要定义数据的类型
## 控制台的读取与输入
- input 输入进去的是字符串
- eval
- 在jupyter用shift + tab 键可以跳出解释文档
## 变量命名的规范
- 由字母、数字、下划线构成
- 不能以数字开头 \*
- 标识符不能是关键词(实际上是可以强制改变的,但是对于代码规范而言是极其不适合)
- 可以是任意长度
- 驼峰式命名
## 变量、赋值语句和赋值表达式
- 变量: 通俗理解为可以变化的量
- x = 2 \* x + 1 在数学中是一个方程,而在语言中它是一个表达式
- test = test + 1 \* 变量在赋值之前必须有值
## 同时赋值
var1, var2,var3... = exp1,exp2,exp3...
## 定义常量
- 常量:表示一种定值标识符,适合于多次使用的场景。比如PI
- 注意:在其他低级语言中如果定义了常量,那么,该常量是不可以被改变的,但是在Python中一切皆对象,常量也是可以被改变的
## 数值数据类型和运算符
- 在Python中有两种数值类型(int 和 float)适用于加减乘除、模、幂次
<img src = "../Photo/01.jpg"></img>
## 运算符 /、//、**
## 运算符 %
## EP:
- 25/4 多少,如果要将其转变为整数该怎么改写
- 输入一个数字判断是奇数还是偶数
- 进阶: 输入一个秒数,写一个程序将其转换成分和秒:例如500秒等于8分20秒
- 进阶: 如果今天是星期六,那么10天以后是星期几? 提示:每个星期的第0天是星期天
```
25/4
25//4
num = int(input('请输入一个整数:'))
if num%2==0:
print('该数为偶数')
else:
print('该数为奇数')
s = eval(input('请输入一个秒数:'))
min = s//60
s1 = s%60
print (str(min)+'分'+str(s1)+'秒')
```
## 科学计数法
- 1.234e+2
- 1.234e-2
## 计算表达式和运算优先级
<img src = "../Photo/02.png"></img>
<img src = "../Photo/03.png"></img>
## 增强型赋值运算
<img src = "../Photo/04.png"></img>
## 类型转换
- float -> int
- 四舍五入 round
## EP:
- 如果一个年营业税为0.06%,那么对于197.55e+2的年收入,需要交税为多少?(结果保留2为小数)
- 必须使用科学计数法
# Project
- 用Python写一个贷款计算器程序:输入的是月供(monthlyPayment) 输出的是总还款数(totalpayment)

# Homework
- 1
<img src="../Photo/06.png"></img>
```
celsius = eval(input('请输入一个温度:'))
fahrenheit = (9/5)*celsius+32
print (fahrenheit)
```
- 2
<img src="../Photo/07.png"></img>
```
import math
radius = eval(input('请输入一个半径:'))
length = eval(input('请输入一个高:'))
area = radius*radius*math.pi
volume = area*length
print (round(area,1))
print (round(volume,1))
```
- 3
<img src="../Photo/08.png"></img>
```
feet = eval(input('请输入一个英尺数:'))
meters = feet*0.305
print (meters)
```
- 4
<img src="../Photo/10.png"></img>
```
M = eval(input('请输入以kg为单位的水的质量:'))
initialTemperature = eval(input('请输入水的初始温度:'))
finalTemperature = eval(input('请输入水的最终温度:'))
Q = M*(finalTemperature-initialTemperature)*4184
print (Q)
```
- 5
<img src="../Photo/11.png"></img>
```
balance = eval(input('请输入差额:'))
rate = eval(input('请输入年利率:'))
interest = (balance*(rate/1200))
print (interest)
```
- 6
<img src="../Photo/12.png"></img>
```
v0 = eval(input('请输入初速度:'))
v1 = eval(input('请输入末速度:'))
t = eval(input('以秒为单位速度变化所占用的时间:'))
a = (v1-v0)/t
print (a)
```
- 7 进阶
<img src="../Photo/13.png"></img>
```
money = eval(input('请输入每月的存钱数:'))
one = money*(1+0.00417)
two = (money+one)*(1+0.00417)
three = (money+two)*(1+0.00417)
four = (money+three)*(1+0.00417)
five = (money+four)*(1+0.00417)
six = (money+five)*(1+0.00417)
print (round(six,2))
```
- 8 进阶
<img src="../Photo/14.png"></img>
```
num = eval(input('请输入一个0到1000的整数:'))
a = num%10
b = num//10
c = b%10
d = b//10
print (a+c+d)
```
|
github_jupyter
|
# Import Required Packages
```
# Imports
import os
import datetime
import glob
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import time
```
# Input data from User
```
#Market analysed: 'Investment','FullYear','DayAhead','Balancing' (choose one or several)
market_analysed=['DayAhead','Balancing']
output='CurtailmentHourly'
first_timestep="2012-01-02"
#Number of timesteps (total number of combination of SSS and TTT)
number_periods=8736*12
#Time size of each time step for creating timestamp
size_timestep="300s"
#Time size of each TTT calculating energy values
size_t=1/12;
#Countries in focus
ccc_in_focus = ['DENMARK', 'GERMANY', 'NORWAY', 'GREAT_BRITAIN','BELGIUM','HOLLAND']
```
# Plot Settings
```
# Set plotting specifications
% matplotlib inline
plt.rcParams.update({'font.size': 21})
plt.rcParams['xtick.major.pad']='12'
plt.rc('legend', fontsize=16)
y_limit = 1.1
lw = 3
```
# Read Input Files
```
data=pd.DataFrame()
for market in market_analysed:
csvfiles = []
for file in glob.glob("./input/results/" + market + "/*.csv"):
csvfiles.append(file)
csvfiles=[file.replace('./input\\','') for file in csvfiles]
csvfiles=[file.replace('.csv','') for file in csvfiles]
csvfiles=[file.split('_') for file in csvfiles]
csvfiles = np.asarray(csvfiles)
csvfiles=pd.DataFrame.from_records(csvfiles)
csvfiles.rename(columns={0: 'Output', 1: 'Scenario',2: 'Year',3:'Subset'}, inplace=True)
scenarios=csvfiles.Scenario.unique().tolist()
years=csvfiles.Year.unique().tolist()
subsets=csvfiles.Subset.unique().tolist()
for scenario in scenarios:
for year in years:
for subset in subsets:
file = "./input/results/"+ market + "/"+ output + "_" + scenario + "_" + year + "_" + subset + ".csv"
if os.path.isfile(file):
df=pd.read_csv(file,encoding='utf8')
df['Scenario'] = scenario
df['Market'] = market
#Renaming columns just in case timeconversion was required
df.rename(columns = {'G':'GGG', 'C':'CCC', 'Y':'YYY','TTT_NEW':'TTT','SSS_NEW':'SSS'}, inplace = True)
data=data.append(df)
#Timestamp addition
full_timesteps = pd.read_csv('./input/full_timesteps.csv')
full_timesteps.Key=full_timesteps['SSS']+full_timesteps['TTT']
full_timesteps['timestamp']= pd.date_range(first_timestep, periods = number_periods, freq =size_timestep)
dict_timestamp=dict(zip(full_timesteps.Key, full_timesteps.timestamp))
data['timestamp']=data['SSS']+data['TTT']
data['timestamp']=data['timestamp'].map(dict_timestamp)
data.to_csv(r'./output/test.csv')
```
# Additional set declaration
```
ccc = list(data.CCC.unique())
rrr = list(data.RRR.unique())
tech_type = list(data.TECH_TYPE.unique())
commodity = list(data.COMMODITY.unique())
fff = list(data.FFF.unique())
sss = list(full_timesteps.SSS.unique())
ttt = list(full_timesteps.TTT.unique())
```
# Time step selection
```
# Seasons to investigate
# season_names = ['S01', 'S07', 'S20', 'S24', 'S28', 'S38', 'S42', 'S43']
# Make a list of every nth element of sss (1 <= nth <= number of elements in sss)
nth = 1
s = sss[0::nth]
# Or select seasons by names
# s = season_names
# Terms to investigate
# term_names = ['T005', 'T019', 'T033', 'T047', 'T061', 'T075', 'T089', 'T103', 'T117', 'T131', 'T145', 'T159']
# Make a list of every nth element of ttt (1 <= nth <= number of elements in ttt)
nth = 1
t = ttt[0::nth]
# Or select terms by name
# t = term_names
```
# Make Directories
```
# Make output folder
if not os.path.isdir('output'):
os.makedirs('output')
# Make CurtailmentHourly folder
if not os.path.isdir('output/' + output):
os.makedirs('output/' + output)
# Make market folder
for market in market_analysed:
if not os.path.isdir('output/' + output + '/'+ market +'/Country_wise'):
os.makedirs('output/' + output + '/'+ market +'/Country_wise')
# Make country folder
if not os.path.isdir('output/' + output + '/'+ market +'/Country_wise'):
os.makedirs('output/' + output + '/'+ market +'/Country_wise')
# Make country wise folders
for c in ccc:
if not os.path.isdir('output/' + output + '/'+ market +'/Country_wise/' + c):
os.makedirs('output/' + output + '/'+ market +'/Country_wise/' + c)
```
# Plotting
```
# Make data frames to plot
data_plot = data[(data.SSS.isin(s)) & (data.TTT.isin(t))]
data_plot = data[data.CCC.isin(ccc_in_focus)]
```
## Plot per year, scenario, market
```
df_plot=(pd.DataFrame(data_plot.groupby(['YYY', 'Scenario', 'Market'])['Val'].agg('sum')/1000000*size_t))
df_plot
df_plot.reset_index(inplace=True)
df_plot
for scenario in Scenarios:
df_plot
plt.bar(df_plot.YYY, df_plot.Val)
for i in years:
spp_plot[data.SSS.isin([i])][ccc[:2]].plot(figsize=(16,9), lw=lw)
plt.ylim([0, y_limit])
plt.legend(loc=1)
plt.title('Curtailment in ' + i)
plt.xlabel('Terms')
plt.xticks(t_marker, t_selected, rotation=45)
for x_pos in t_marker:
plt.axvline(x=x_pos, c='black', lw=6, alpha=0.3)
plt.tight_layout()
plt.savefig('output/pv_production/spp_' + i + '.png', compression=None)
# plt.show()
plt.close()
plt.close()
#Plot example with several x axis
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax2 = ax1.twiny()
# Add some extra space for the second axis at the bottom
fig.subplots_adjust(bottom=0.2)
ax1.set_xticks([1,2,4,5,7,8])
ax1.set_xlim(0,9)
ax1.set_xticklabels(('2015','2016','2015','2016','2015','2016'))
ax2.spines["bottom"].set_position(("axes", -0.15))
ax2.xaxis.set_ticks_position("bottom")
ax2.spines["bottom"].set_visible(True)
ax2.set_xticks([1.5,4.5,7.5])
ax2.set_xticklabels(('1','2','3'))
ax2.set_xlim(0,9)
b1 = np.random.randint(0,100,6)
b2 = np.random.randint(0,100,6)
b3 = np.random.randint(0,100,6)
plt.bar(np.array([1,2,4,5,7,8])-0.4,b1,color='blue')
plt.bar(np.array([1,2,4,5,7,8])-0.4,b2,color='orange',bottom=b1)
plt.bar(np.array([1,2,4,5,7,8])-0.4,b3,color='yellow',bottom=b1+b2)
plt.show()
```
|
github_jupyter
|
# Mining the Social Web, 2nd Edition
## Appendix B: OAuth Primer
This IPython Notebook provides an interactive way to follow along with and explore the numbered examples from [_Mining the Social Web (3rd Edition)_](http://bit.ly/Mining-the-Social-Web-3E). The intent behind this notebook is to reinforce the concepts from the sample code in a fun, convenient, and effective way. This notebook assumes that you are reading along with the book and have the context of the discussion as you work through these exercises.
In the somewhat unlikely event that you've somehow stumbled across this notebook outside of its context on GitHub, [you can find the full source code repository here](http://bit.ly/Mining-the-Social-Web-3E).
## Copyright and Licensing
You are free to use or adapt this notebook for any purpose you'd like. However, please respect the [Simplified BSD License](https://github.com/mikhailklassen/Mining-the-Social-Web-3rd-Edition/blob/master/LICENSE) that governs its use.
## Notes
While the chapters in the book opt to simplify the discussion by avoiding a discussion of OAuth and instead opting to use application credentials provided by social web properties for API access, this notebook demonstrates how to implement some OAuth flows for several of the more prominent social web properties. While IPython Notebook is used for consistency and ease of learning, and in some cases, this actually adds a little bit of extra complexity in some cases given the nature of embedding a web server and handling asynchronous callbacks. (Still, the overall code should be straightforward to adapt as needed.)
# Twitter OAuth 1.0a Flow with IPython Notebook
Twitter implements OAuth 1.0A as its standard authentication mechanism, and in order to use it to make requests to Twitter's API, you'll need to go to https://dev.twitter.com/apps and create a sample application. There are three items you'll need to note for an OAuth 1.0A workflow, a consumer key and consumer secret that identify the application as well as the oauth_callback URL that tells Twitter where redirect back to after the user has authorized the application. Note that you will need an ordinary Twitter account in order to login, create an app, and get these credentials. Keep in mind that for development purposes or for accessing your own account's data, you can simply use the oauth token and oauth token secret that are provided in your appliation settings to authenticate as opposed to going through the steps here. The process of obtaining an the oauth token and oauth token secret is fairly straight forward (especially with the help of a good library), but an implementation in IPython Notebook is a bit tricker due to the nature of embedding a web server, capturing information within web server contexts, and handling the various redirects along the way.
You must ensure that your browser is not blocking popups in order for this script to work.
<img src="files/resources/ch01-twitter/images/Twitter-AppCredentials-oauth_callback.png" width="600px">
## Example 1. Twitter OAuth 1.0a Flow
```
import json
from flask import Flask, request
from threading import Timer
from IPython.display import IFrame
from IPython.display import display
from IPython.display import Javascript as JS
import twitter
from twitter.oauth_dance import parse_oauth_tokens
from twitter.oauth import read_token_file, write_token_file
OAUTH_FILE = "/tmp/twitter_oauth"
# XXX: Go to http://twitter.com/apps/new to create an app and get values
# for these credentials that you'll need to provide in place of these
# empty string values that are defined as placeholders.
# See https://dev.twitter.com/docs/auth/oauth for more information
# on Twitter's OAuth implementation and ensure that *oauth_callback*
# is defined in your application settings as shown below if you are
# using Flask in this IPython Notebook
# Define a few variables that will bleed into the lexical scope of a couple of
# functions below
CONSUMER_KEY = ''
CONSUMER_SECRET = ''
oauth_callback = 'http://127.0.0.1:5000/oauth_helper'
# Setup a callback handler for when Twitter redirects back to us after the user authorizes the app
webserver = Flask("TwitterOAuth")
@webserver.route("/oauth_helper")
def oauth_helper():
oauth_verifier = request.args.get('oauth_verifier')
# Pick back up credentials from ipynb_oauth_dance
oauth_token, oauth_token_secret = read_token_file(OAUTH_FILE)
_twitter = twitter.Twitter(
auth=twitter.OAuth(
oauth_token, oauth_token_secret, CONSUMER_KEY, CONSUMER_SECRET),
format='', api_version=None)
oauth_token, oauth_token_secret = parse_oauth_tokens(
_twitter.oauth.access_token(oauth_verifier=oauth_verifier))
# This web server only needs to service one request, so shut it down
shutdown_after_request = request.environ.get('werkzeug.server.shutdown')
shutdown_after_request()
# Write out the final credentials that can be picked up after the blocking
# call to webserver.run() below.
write_token_file(OAUTH_FILE, oauth_token, oauth_token_secret)
return "%s %s written to %s" % (oauth_token, oauth_token_secret, OAUTH_FILE)
# To handle Twitter's OAuth 1.0a implementation, we'll just need to implement a custom
# "oauth dance" and will closely follower the pattern defined in twitter.oauth_dance.
def ipynb_oauth_dance():
_twitter = twitter.Twitter(
auth=twitter.OAuth('', '', CONSUMER_KEY, CONSUMER_SECRET),
format='', api_version=None)
oauth_token, oauth_token_secret = parse_oauth_tokens(
_twitter.oauth.request_token(oauth_callback=oauth_callback))
# Need to write these interim values out to a file to pick up on the callback from Twitter
# that is handled by the web server in /oauth_helper
write_token_file(OAUTH_FILE, oauth_token, oauth_token_secret)
oauth_url = ('http://api.twitter.com/oauth/authorize?oauth_token=' + oauth_token)
# Tap the browser's native capabilities to access the web server through a new window to get
# user authorization
display(JS("window.open('%s')" % oauth_url))
# After the webserver.run() blocking call, start the oauth dance that will ultimately
# cause Twitter to redirect a request back to it. Once that request is serviced, the web
# server will shutdown, and program flow will resume with the OAUTH_FILE containing the
# necessary credentials
Timer(1, lambda: ipynb_oauth_dance()).start()
webserver.run(host='0.0.0.0')
# The values that are read from this file are written out at
# the end of /oauth_helper
oauth_token, oauth_token_secret = read_token_file(OAUTH_FILE)
# These 4 credentials are what is needed to authorize the application
auth = twitter.oauth.OAuth(oauth_token, oauth_token_secret,
CONSUMER_KEY, CONSUMER_SECRET)
twitter_api = twitter.Twitter(auth=auth)
print(twitter_api)
```
# Facebook OAuth 2.0 Flow with IPython Notebook
Facebook implements OAuth 2.0 as its standard authentication mechanism, and this example demonstrates how get an access token for making API requests once you've created an app and gotten a "client id" value that can be used to initiate an OAuth flow. Note that you will need an ordinary Facebook account in order to login, create an app, and get these credentials. You can create an app through the "Developer" section of your account settings as shown below or by navigating directly to https://developers.facebook.com/apps/. During development or debugging cycles, or to just access data in your own account, you may sometimes find it convenient to also reference the access token that's available to you through the Graph API Explorer tool at https://developers.facebook.com/tools/explorer as opposed to using the flow described here. The process of obtaining an access token is fairly straight forward, but an implementation in IPython Notebook is a bit tricker due to the nature of embedding a web server, capturing information within web server contexts, and handling the various redirects along the way.
You must ensure that your browser is not blocking popups in order for this script to work.
<br />
<br />
<img src="files/resources/ch02-facebook/images/fb_create_app.png" width="400px"><br />
Create apps at https://developers.facebook.com/apps/<br />
<br />
<img src="files/resources/ch02-facebook/images/fb_edit_app.png" width="400px"><br />
Clicking on the app in your list to see the app dashboard and access app settings.
## Example 2. Facebook OAuth 2.0 Flow
```
import urllib
from flask import Flask, request
from threading import Timer
from IPython.display import display
from IPython.display import Javascript as JS
# XXX: Get this value from your Facebook application's settings for the OAuth flow
# at https://developers.facebook.com/apps
APP_ID = ''
# This value is where Facebook will redirect. We'll configure an embedded
# web server to be serving requests here
REDIRECT_URI = 'http://localhost:5000/oauth_helper'
# You could customize which extended permissions are being requested for your app
# by adding additional items to the list below. See
# https://developers.facebook.com/docs/reference/login/extended-permissions/
EXTENDED_PERMS = ['user_likes']
# A temporary file to store a code from the web server
OAUTH_FILE = 'resources/ch02-facebook/access_token.txt'
# Configure an emedded web server that accepts one request, parses
# the fragment identifier out of the browser window redirects to another
# handler with the parsed out value in the query string where it can be captured
# and stored to disk. (A webserver cannot capture information in the fragment
# identifier or that work would simply be done in here.)
webserver = Flask("FacebookOAuth")
@webserver.route("/oauth_helper")
def oauth_helper():
return '''<script type="text/javascript">
var at = window.location.hash.substring("access_token=".length+1).split("&")[0];
setTimeout(function() { window.location = "/access_token_capture?access_token=" + at }, 1000 /*ms*/);
</script>'''
# Parses out a query string parameter and stores it to disk. This is required because
# the address space that Flask uses is not shared with IPython Notebook, so there is really
# no other way to share the information than to store it to a file and access it afterward
@webserver.route("/access_token_capture")
def access_token_capture():
access_token = request.args.get('access_token')
f = open(OAUTH_FILE, 'w') # Store the code as a file
f.write(access_token)
f.close()
# It is safe (and convenient) to shut down the web server after this request
shutdown_after_request = request.environ.get('werkzeug.server.shutdown')
shutdown_after_request()
return access_token
# Send an OAuth request to Facebook, handle the redirect, and display the access
# token that's included in the redirect for the user to copy and paste
args = dict(client_id=APP_ID, redirect_uri=REDIRECT_URI,
scope=','.join(EXTENDED_PERMS), type='user_agent', display='popup'
)
oauth_url = 'https://facebook.com/dialog/oauth?' + urllib.parse.urlencode(args)
Timer(1, lambda: display(JS("window.open('%s')" % oauth_url))).start()
webserver.run(host='0.0.0.0')
access_token = open(OAUTH_FILE).read()
print(access_token)
```
# LinkedIn OAuth 2.0 Flow with IPython Notebook
LinkedIn implements OAuth 2.0 as one of its standard authentication mechanism, and "Example 3" demonstrates how to use it to get an access token for making API requests once you've created an app and gotten the "API Key" and "Secret Key" values that are part of the OAuth flow. Note that you will need an ordinary LinkedIn account in order to login, create an app, and get these credentials. You can create an app through the "Developer" section of your account settings as shown below or by navigating directly to https://www.linkedin.com/secure/developer.
You must ensure that your browser is not blocking popups in order for this script to work.
<img src="files/resources/ch04-linkedin/images/LinkedIn-app.png" width="600px">
## Example 3. Using LinkedIn OAuth credentials to receive an access token an authorize an application
Note: You must ensure that your browser is not blocking popups in order for this script to work. LinkedIn's OAuth flow appears to expressly involve opening a new window, and it does not appear that an inline frame can be used as is the case with some other social web properties. You may also find it very convenient to ensure that you are logged into LinkedIn at http://www.linkedin.com/ with this browser before executing this script, because the OAuth flow will prompt you every time you run it if you are not already logged in. If for some reason you cause IPython Notebook to hang, just select "Kernel => Interrupt" from its menu.
```
import os
from threading import Timer
from flask import Flask, request
from linkedin import linkedin # pip install python3-linkedin
from IPython.display import display
from IPython.display import Javascript as JS
# XXX: Get these values from your application's settings for the OAuth flow
CONSUMER_KEY = ''
CONSUMER_SECRET = ''
# This value is where LinkedIn will redirect. We'll configure an embedded
# web server to be serving requests here. Make sure to add this to your
# app settings
REDIRECT_URL = 'http://localhost:5000/oauth_helper'
# A temporary file to store a code from the web server
OAUTH_FILE = 'resources/ch04-linkedin/linkedin.authorization_code'
# These should match those in your app settings
permissions = {'BASIC_PROFILE': 'r_basicprofile',
'EMAIL_ADDRESS': 'r_emailaddress',
'SHARE': 'w_share',
'COMPANY_ADMIN': 'rw_company_admin'}
# Configure an emedded web server that accepts one request, stores a file
# that will need to be accessed outside of the request context, and
# immediately shuts itself down
webserver = Flask("OAuthHelper")
@webserver.route("/oauth_helper")
def oauth_helper():
code = request.args.get('code')
f = open(OAUTH_FILE, 'w') # Store the code as a file
f.write(code)
f.close()
shutdown_after_request = request.environ.get('werkzeug.server.shutdown')
shutdown_after_request()
return """<p>Handled redirect and extracted code <strong>%s</strong>
for authorization</p>""" % (code,)
# Send an OAuth request to LinkedIn, handle the redirect, and display the access
# token that's included in the redirect for the user to copy and paste
auth = linkedin.LinkedInAuthentication(CONSUMER_KEY, CONSUMER_SECRET, REDIRECT_URL,
permissions.values())
# Display popup after a brief delay to ensure that the web server is running and
# can handle the redirect back from LinkedIn
Timer(1, lambda: display(JS("window.open('%s')" % auth.authorization_url))).start()
# Run the server to accept the redirect back from LinkedIn and capture the access
# token. This command blocks, but the web server is configured to shut itself down
# after it serves a request, so after the redirect occurs, program flow will continue
webserver.run(host='0.0.0.0')
# As soon as the request finishes, the web server shuts down and these remaining commands
# are executed, which exchange an authorization code for an access token. This process
# seems to need full automation because the authorization code expires very quickly.
auth.authorization_code = open(OAUTH_FILE).read()
auth.get_access_token()
# Prevent stale tokens from sticking around, which could complicate debugging
os.remove(OAUTH_FILE)
# How you can use the application to access the LinkedIn API...
app = linkedin.LinkedInApplication(auth)
print(app.get_profile())
```
|
github_jupyter
|
# Homework 9 - Berkeley STAT 157
**Your name: XX, SID YY, teammates A,B,C** (Please add your name, SID and teammates to ease Ryan and Rachel to grade.)
**Please submit your homework through [gradescope](http://gradescope.com/)**
Handout 4/18/2019, due 4/25/2019 by 4pm.
This homework deals with sequence models for numbers. It builds on Homework 8 in terms of modeling. The main difference to last week is that we're modeling *real valued numbers* of stocks rather than characters.
**This is teamwork.**
## 1. Time Series Model
The goal is to develop multivariate regression models where the numbers are *nonnegative* and where changes are *relative*. That is, a stock price can never assume negative values and for convenience we assume that the companies listed do not go bankrupt, i.e. their stock price will never be zero. Moreover, we assume that we can ignore quantization of prices, i.e. the fact that stocks aren't traded at arbitrary prices in $\mathbb{R}$ but only at fractions of a cent (see [this link for a backstory](https://www.investopedia.com/ask/answers/why-nyse-switch-fractions-to-decimals/)).
The prices $x_{st}$ for a security $s$ at time $t$ typically reported at a given date are `(open, high, low, close, volume)`. Here `open` denotes the price when the market opens, `high` the highest price that it was traded for during that day, `low` the lowest, and `close` is the price of the security at closing. Lastly `volume` is an indicator for how many units were sold at that day. We index the respective values with $x_{st} = (o, h, l, c, v) \in \mathbb{R}^{5}$. To process them we transform $x_{st}$ as follows:
$$z_{st} := \left(\log o, 10 \cdot (\log h - \log o), 100 \cdot (\log l - \log o), \log c, \log v\right)$$
Moreover, we assume that $z_{st}$ is obtained as part of a regression problem with squared loss, i.e.\ for an estimate $\hat{z}_{st}$ we compute the loss as
$$l(z_{st}, \hat{z}_{st}) = \frac{1}{2} \|z_{st} - \hat{z}_{st}\|^2$$
1. Why is converting values into logarithms (and logarithms of ratios) a good idea? Explain this for each variable.
1. Why would we want to rescale the ratios by 10?
1. Explain why this model assumes a *lognormal* distribution of prediction errors between the values of the securities ${z}_{st}$ and their estimates $\hat{z}_{st}$. That is, rather than being drawn from a Gaussian, they're drawn from another distribution. Characterize it (hint - exploit the connection between squared loss and the normal distribution).
1. Now assume that we have not just one security but the top 500 stocks over some period of time. Why might it make
sense to estimate the share prices jointly?
## 2. Load Data
1. Obtain data from the S&P500 for the past 5 years and convert it into a time series. You can get the data either from Kaggle [www.kaggle.com/camnugent/sandp500](https://www.kaggle.com/camnugent/sandp500) or crawl it directly using the Python script given here: [github.com/CNuge/kaggle-code/blob/master/stock_data/getSandP.py](https://github.com/CNuge/kaggle-code/blob/master/stock_data/getSandP.py). Your dataset will contain tuples of the form
`(date, open, high, low, close, volume, Name)`.
1. Import this data into an NDArray dataset where you have a vector containing `(open, high, low, close, volume)` for each security. That is, this is a 2,500 dimensional vector and you have 5 years' worth of data.
1. Preprocess the data into logarithmic representation as outlined in problem 1.
1. Split the data into observations for the first 4 years and a dataset for the last year.
1. Load data into an MXNet dataset iterator.
1. Why do you need to do this as opposed to splitting into random segments?
## 3. Time Series Implementation
1. Implement a model similar to `RNNModel` of section [d2l.ai/chapter_recurrent-neural-networks/rnn-concise.html](http://en.d2l.ai/chapter_recurrent-neural-networks/rnn-concise.html) suitable for regression. It should take as input vector-valued data, such as the time series mentioned above and it should output vector-valued data (of some other dimensionality).
1. Train the model on the first 4 years of data using plain RNN, GRU and LSTM cells (for a single layer). How well can the model
* Predict the stock value the next day on the last 1 year of data (price at opening).
* Plot how the quality of the model degrades as we apply it throughout the year (i.e. we ingest all the data up to day $t$ and predict forward at day $t+1$).
* Predict the stock value the next week on the last 1 year of data (price at opening).
1. Train the model on each stock separately (with much lower dimensionality) and compare the performance of the above model with the one you get by using each stock separately.
1. Improve the model using better features, e.g. the fact that time is not uniformly spaced (Saturday, Sunday and holidays do not see any trades). For that use the day of the week as an additional input feature.
1. Improve the model further by using a deeper RNN, e.g. with 2 layers.
Note, there are many cases where we might want to know the *sequence* of stock prices over a period of time rather than just knowing the value, say one month from now. This is relevant e.g. for options pricing where investors can bet on or bet against volatility of a stock price. For a detailed description of this see e.g. [en.wikipedia.org/wiki/Options_strategy](https://en.wikipedia.org/wiki/Options_strategy).
|
github_jupyter
|
# 2 Data Acquisition
In this chapter we will discuss data acquisition and data formatting for four online Assyriological projects: [ORACC](http://oracc.org) (2.1), [ETCSL](https://etcsl.orinst.ox.ac.uk/), (2.2) [CDLI](http://cdli.ucla.edu) (2.3) and [BDTNS](http://bdtns.filol.csic.es/) (2.4).
The data in [CDLI](http://cdli.ucla.edu) and [BDTNS](http://bdtns.filol.csic.es/) are made available in raw-text format, with transliteration only. For instance (atf text format as used by [CDLI](http://cdli.ucla.edu)):
```{admonition} ATF
:class: tip, dropdown
ATF is short for ASCII Text Format. [ORACC](http://oracc.org) and [CDLI](http://cdli.ucla.edu) use different versions of the ATF format. The various symbols and conventions are explained [here](http://oracc.org/doc/help/editinginatf/cdliatf/).
```
&P100001 = AAS 013
#atf: lang sux
@tablet
@obverse
@column 1
$ beginning broken
1'. a2-bi u4 [...] 5(u) 4(disz) 2/3(disz)-kam
2'. 8(gesz2) 3(u) 5(disz) gurusz u4 1(disz)-sze3
3'. si-i3-tum nig2-ka9-ak mu en-mah-gal-an-na ba-hun
4'. 2(asz) 2(barig) sze gur
This data format is easy to read for humans (those humans who know Sumerian), but less so for computers. It is necessary to tell the software which data elements belong to the text and which do not (for instance, line numbers and surface labels) and what the various non-textual elements mean. We will see examples of how such data sets may be used in the sections 2.3 ([CDLI](http://cdli.ucla.edu)) and 2.4 ([BDTNS](http://bdtns.filol.csic.es/)). Section 2.4 will also demonstrate code for constructing a search engine for [BDTNS](http://bdtns.filol.csic.es/) that ignores sign values - that is, searching for `luh` will also find `sukkal`, etc. The code uses both [BDTNS](http://bdtns.filol.csic.es/) data and the [ORACC Global Sign List](http://orac.org/ogsl), showing how data from different projects can be mashed into a single tool.
The data in [ORACC](http://oracc.org) and [ETCSL](https://etcsl.orinst.ox.ac.uk/) are made available in [JSON](http://json.org) and [XML](http://xml.org), respectively. Those formats are very explicit and atomistic. They less easy to read for humans, but are very flexible for computational usage and allow for multiple levels of annotation (with e.g. lexical, morphological, and graphemic information) at the same time. The data in [ORACC](http://oracc.org) and [ETCSL](https://etcsl.orinst.ox.ac.uk/) includes lemmatization, linking each word to an entry in a glossary. The following is an example of a JSON file, one may click on any of the lines with an arrow to expose more or less of the hierarchical structure. The usage of JSON and XML files will be discussed in sections 2.1 and 2.2.
```
import json
import panel as pn
pn.extension()
with open('P100001.json', 'r', encoding='utf8') as p:
P100001 = json.load(p)
json_object = pn.pane.JSON(P100001, name='P100001', depth=1, height=300, width=500, theme = 'light')
json_object
```
This represents the same text as the one shown in raw text format above ([P100001 = AAS 13](http://oracc.org/epsd2/P100001)), but in this case provided with lemmatization and explicit information on the various data types.
```{admonition} Full JSON file
:class: tip, dropdown
To see the full JSON file of P100001 click [here](https://github.com/niekveldhuis/compass/blob/master/2_Data_Acquisition/P100001.json)
```
The Compass project mostly deals with [ORACC](http://oracc.org) data, and much of this chapter will provide code and explanations for how to extract the various types of information that are included in the JSON files. The parsing of the [ETCSL](https://etcsl.orinst.ox.ac.uk/) XML files (section [2.2](2.2) is, to some extent, redundant, because all of the [ETCSL](https://etcsl.orinst.ox.ac.uk/) data have been incorporated into [epsd2/literary](http://oracc.org/epsd2/literary) and can be parsed with the tools for regular [ORACC](http://oracc.org) projects.
The Chapters 3-6 of Compass will work with [ORACC](http://oracc.org) data and will parse that data with the tools demonstrated and explained in section [2.1](2.1). Chapter 2 is not needed to follow along in those chapters. The present chapter is primarily meant for researchers who wish to pursue their own computational projects and need a deeper understanding of how the data is acquired and formatted.
|
github_jupyter
|
# Hello World API with Flask
```
# We'll create the script - we created our folder structure with cookiecutter
import os
hello_world_script_file = os.path.join(os.path.pardir,'src','models','hello_world_api2.py')
%%writefile $hello_world_script_file
from flask import Flask, request
app = Flask(__name__)
@app.route('/api', methods=['POST']) #api will take an input, process it, and return it
def say_hello():
data = request.get_json(force=True) #we will pass json, so use get_json to get extract the data
name = data['name']
return "hello {0}".format(name)
if __name__ == '__main__': # script entry point, the flask app will run on port 10001 - can be any available port
app.run(port=10001, debug=True,use_reloader=False) # debug = true for troubleshooting in dev
# We have started the process via the command line with python3 hellow_world_api2.py
import json
import requests
# create a call to the API endpoint
url = 'http://127.0.0.1:10001/api'
#create the data we are sending
data = json.dumps({'name':'graeme'}) #dumps creates the data in a json object
r = requests.post(url, data) #call the API and store response in r.
print(r.text)
# This is calling the API and returning correctly :D
```
# API for Machine Learning with Flask
```
# We'll create the script - we created our folder structure with cookiecutter
import os
machine_learning_api_script_file = os.path.join(os.path.pardir,'src','models','machine_learning_api.py')
%%writefile $machine_learning_api_script_file
# Now this is the code we used from all the previous steps we performed.
from flask import Flask, request
import pandas as pd
import numpy as np
import json
import pickle
import os
app = Flask(__name__)
#load the model and scaler files
model_path = os.path.join(os.path.pardir, os.path.pardir,'models')
model_filepath = os.path.join(model_path, 'lr_model.pkl')
scaler_filepath = os.path.join(model_path, 'lr_scaler.pkl')
#load them in
scaler = pickle.load(open(scaler_filepath,'rb')) #remember to set read more binary
model = pickle.load(open(model_filepath,'rb'))
# columns put in order that the ML model will expect
columns = [ u'Age', u'Fare', u'FamilySize', \
u'IsMother', u'IsMale', u'Deck_A', u'Deck_B', u'Deck_C', u'Deck_D', \
u'Deck_E', u'Deck_F', u'Deck_G', u'Deck_Z', u'Pclass_1', u'Pclass_2', \
u'Pclass_3', u'Title_Lady', u'Title_Master', u'Title_Miss', u'Title_Mr', \
u'Title_Mrs', u'Title_Officer', u'Title_Sir', u'Fare_Bin_very_low', \
u'Fare_Bin_low', u'Fare_Bin_high', u'Fare_Bin_very_high', u'Embarked_C', \
u'Embarked_Q', u'Embarked_S', u'AgeState_Adult', u'AgeState_Child']
@app.route('/api', methods=['POST'])
def make_predicitions():
#This will be executed with the API is called
#Read the json object and convert it to a json string
data = json.dumps(request.get_json(force='TRUE'))
#create a data frame from the json string
df = pd.read_json(data)
#extract the index passenger id
passenger_ids = df['PassengerId'].ravel()
# capture the actual survived values -- we do not have all the actuals, those are on Kaggle, but this is how
# this API process would work, if we did have a store of all the actual survival data
actuals = df['Survived'].ravel()
# extract all the columns from the data and convert into a matrix
X = df[columns].as_matrix().astype('float')
# transform the data into the scaled object
X_scaled = scaler.transform(X)
# make the predicitions
predictions = model.predict(X_scaled)
# create response object dataframe
df_response = pd.DataFrame({'PassengerId': passenger_ids, 'Predicted': predictions, 'Actual': actuals})
# return our JSON object
return df_response.to_json()
if __name__ == '__main__':
#host the flask app
app.run(port=10001, debug=True,use_reloader=False) # debug = true for troubleshooting in dev
# now we run the flask server from the command line
# $ python3 machine_learning_api.py
```
## Invoke API using the Requests feature
```
import os
import numpy as np
import pandas as pd
processed_data_path = os.path.join(os.path.pardir,'data','processed')
train_file_path = os.path.join(processed_data_path, 'train.csv')
train_df = pd.read_csv(train_file_path)
# the processed training data will be used to check the API is working
# let's use 5 passengers to check to see if they Survived
survived_passengers = train_df[train_df['Survived'] == 1][:5]
survived_passengers
# We should get same response from API. Let's create a helper
import requests
def make_api_request(data):
# url where the API is exposed
url = "http://127.0.0.1:10001/api"
#request
r = requests.post(url, data)
#return
# return r.text - check we get something
return r.json()
# This should retrn the same output of Survived, as a check that hte API is working
make_api_request(survived_passengers.to_json())
# As we can see, all Survived
# Now pass the entire Training df to the api function
# then convert the result to JSON and put it into a result df
# Have a look at the top 5, then check accuracy by compare Actual to Predicted
# Then we will convert that into a Mean value, to get the accuracy.
result = make_api_request(train_df.to_json())
df_result = pd.read_json(json.dumps(result))
df_result.head()
# what is the oveall accuracy?
np.mean(df_result.Actual == df_result.Predicted)
# This is as expected from our previous modeling persistence demo
# So now we have a machine learning API
#
# How could we improve the API?
# We should be able to tinker to allow the raw data to be feed, to be processed then passing that dat to the model
```
|
github_jupyter
|
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import dill as pickle
import os, sys
import scipy.interpolate as intp
import bead_util as bu
plt.rcParams['figure.figsize'] = (12,8)
plt.rcParams['xtick.labelsize'] = 15
plt.rcParams['ytick.labelsize'] = 15
%matplotlib inline
from symmetric_attractor_profile import attractor_profile
from holes_analysis import holes_data, holes_analysis
parent = '/home/emmetth/gravity_sim'
os.chdir(parent)
full_path = parent+'/sim_data/modulated/'
PS = holes_data(data_dir=full_path)
data = PS.data
hrs = sorted(PS.hrs)
separations = sorted(PS.from_edges)
hrs
separations
p0 = 7,separations[-1],hrs[0],10.0,5.0
FM0 = holes_analysis(data, p0)
FM0.sum_harmonics(w=1, fsamp=5e3, num_harmonics=10, verbose=True)
times, newt, (yuka, lambdas) = FM0.sample_Gdata(w=1, tint=1)
yuka.shape
plt.plot(times, yuka[1,0,:]-np.mean(yuka[1,0,:]))
plt.plot(times, newt[0,:]-np.mean(newt[0,:]))
plt.rcParams['figure.figsize'] = 12,8
plt.xlim(0,0.5)
plt.close('all')
fig, ax = FM0.plot_signals(log=False, fsamp=5e3, f0=7, num_harmonics=15)
fig
%matplotlib inline
fig,ax = FM0.plot_asd()
harms_rad = np.zeros((len(separations), len(hrs), 3))
sep, height = 5.0,5.0
axes_ind = {'radial': 0, 'angular': 1, 'axial': 2}
axis = axes_ind['radial']
for i,edge in enumerate(separations):
for j,hr in enumerate(hrs):
p = 7,edge,hr,sep,height
FM = holes_analysis(data, p)
harms = FM.sum_harmonics(w=1, fsamp=5e3, num_harmonics=10)
harms_rad[i,j,:] = harms[:,axis]
np.save('holes_harm_rad_new.npy', harms_rad)
%matplotlib inline
plt.rcParams['figure.figsize'] = (12,8)
plt.contourf(separations, hrs, harms_rad[:,:,0].T, levels=25)
plt.colorbar()
plt.xlabel('Modulation Distance [frac. of hr]', fontsize=18)
plt.ylabel('Hole Radius [$\mu m$]', fontsize=18)
plt.title('Hole Harmonic Content\nRadial Newtonian', fontsize=20, y=1.02)
plt.tick_params('both', length=10, width=2.5, which='major', labelsize=15)
plt.tick_params('both', length=10, width=2.5, which='minor')
# plt.savefig('dist_radius.png', dpi=150)
plt.show()
```
This is not at all what I expected, but it makes sense as the absolute magnitude increases with both hole size and distance from edge, so to see the feature matching in a colorbar one would need to normalize the peaks to each other or something similar.
```
for i,hr in enumerate(hrs):
plt.plot(separations, harms_rad[:,i,:], 'o-')
plt.legend(['newtonian', '$\lambda=1\mu m$', '$\lambda=10\mu m$'])
plt.xlabel('modulation separation [$\mu m$]', fontsize=18)
plt.ylabel('harmonic strength [N/$\sqrt{Hz}$]', fontsize=18)
# plt.axvline(hr, ls='--', alpha=0.7)
plt.title(f'{hr} $\mu m$ hole radius harmonics vs distance', fontsize=18, y=1)
# plt.savefig(f'new_feature_matching_plots/edge/{hr}.png', dpi=150)
plt.show()
for i,edge in enumerate(separations):
plt.plot(hrs, harms_rad[i,:,:], 'o-')
plt.legend(['newtonian', '$\lambda=1\mu m$', '$\lambda=10\mu m$'])
plt.xlabel('hole radius [$\mu m$]', fontsize=18)
plt.ylabel('harmonic strength [N/$\sqrt{Hz}$]', fontsize=18)
# plt.axvline(edge, ls='--', alpha=0.7)
plt.title(f'{edge}x modulation distance harmonics vs radius', fontsize=18)
# plt.savefig(f'new_feature_matching_plots/radius/{edge}.png', dpi=150)
plt.show()
```
|
github_jupyter
|
```
#default_exp data.transform
#export
from local.torch_basics import *
from local.test import *
from local.notebook.showdoc import show_doc
from PIL import Image
```
# Transforms
## Helpers
```
#exports
def type_hints(f):
"Same as `typing.get_type_hints` but returns `{}` if not allowed type"
return typing.get_type_hints(f) if isinstance(f, typing._allowed_types) else {}
#export
def anno_ret(func):
"Get the return annotation of `func`"
if not func: return None
ann = type_hints(func)
if not ann: return None
return ann.get('return')
#hide
def f(x) -> float: return x
test_eq(anno_ret(f), float)
def f(x) -> Tuple[float,float]: return x
test_eq(anno_ret(f), Tuple[float,float])
def f(x) -> None: return x
test_eq(anno_ret(f), NoneType)
def f(x): return x
test_eq(anno_ret(f), None)
test_eq(anno_ret(None), None)
#export
cmp_instance = functools.cmp_to_key(lambda a,b: 0 if a==b else 1 if issubclass(a,b) else -1)
td = {int:1, numbers.Number:2, numbers.Integral:3}
test_eq(sorted(td, key=cmp_instance), [numbers.Number, numbers.Integral, int])
#export
def _p1_anno(f):
"Get the annotation of first param of `f`"
hints = type_hints(f)
ann = [o for n,o in hints.items() if n!='return']
return ann[0] if ann else object
def _f(a, b): pass
test_eq(_p1_anno(_f), object)
def _f(a, b)->str: pass
test_eq(_p1_anno(_f), object)
def _f(a, b:str)->float: pass
test_eq(_p1_anno(_f), str)
def _f(a:int, b:int)->float: pass
test_eq(_p1_anno(_f), int)
test_eq(_p1_anno(attrgetter('foo')), object)
```
## Types
```
#export
@delegates(plt.subplots, keep=True)
def subplots(nrows=1, ncols=1, **kwargs):
fig,ax = plt.subplots(nrows,ncols,**kwargs)
if nrows*ncols==1: ax = array([ax])
return fig,ax
#export
class TensorImageBase(TensorBase):
_show_args = {'cmap':'viridis'}
def show(self, ctx=None, **kwargs):
return show_image(self, ctx=ctx, **{**self._show_args, **kwargs})
def get_ctxs(self, max_n=10, rows=None, cols=None, figsize=None, **kwargs):
n_samples = min(self.shape[0], max_n)
rows = rows or int(np.ceil(math.sqrt(n_samples)))
cols = cols or int(np.ceil(math.sqrt(n_samples)))
figsize = (cols*3, rows*3) if figsize is None else figsize
_,axs = subplots(rows, cols, figsize=figsize)
return axs.flatten()
#export
class TensorImage(TensorImageBase): pass
#export
class TensorImageBW(TensorImage): _show_args = {'cmap':'Greys'}
#export
class TensorMask(TensorImageBase): _show_args = {'alpha':0.5, 'cmap':'tab20'}
im = Image.open(TEST_IMAGE)
im_t = TensorImage(array(im))
test_eq(type(im_t), TensorImage)
im_t2 = TensorMask(tensor(1))
test_eq(type(im_t2), TensorMask)
test_eq(im_t2, tensor(1))
ax = im_t.show(figsize=(2,2))
test_fig_exists(ax)
#hide
axes = im_t.get_ctxs(1)
test_eq(axes.shape,[1])
plt.close()
axes = im_t.get_ctxs(4)
test_eq(axes.shape,[4])
plt.close()
```
## TypeDispatch -
```
#export
class TypeDispatch:
"Dictionary-like object; `__getitem__` matches keys of types using `issubclass`"
def __init__(self, *funcs):
self.funcs,self.cache = {},{}
for f in funcs: self.add(f)
self.inst = None
def _reset(self):
self.funcs = {k:self.funcs[k] for k in sorted(self.funcs, key=cmp_instance, reverse=True)}
self.cache = {**self.funcs}
def add(self, f):
"Add type `t` and function `f`"
self.funcs[_p1_anno(f) or object] = f
self._reset()
def returns(self, x): return anno_ret(self[type(x)])
def returns_none(self, x):
r = anno_ret(self[type(x)])
return r if r == NoneType else None
def __repr__(self): return str({getattr(k,'__name__',str(k)):v.__name__ for k,v in self.funcs.items()})
def __call__(self, x, *args, **kwargs):
f = self[type(x)]
if not f: return x
if self.inst: f = types.MethodType(f, self.inst)
return f(x, *args, **kwargs)
def __get__(self, inst, owner):
self.inst = inst
return self
def __getitem__(self, k):
"Find first matching type that is a super-class of `k`"
if k in self.cache: return self.cache[k]
types = [f for f in self.funcs if issubclass(k,f)]
res = self.funcs[types[0]] if types else None
self.cache[k] = res
return res
def f_col(x:typing.Collection): return x
def f_nin(x:numbers.Integral)->int: return x+1
def f_bti(x:TensorMask): return x
def f_fti(x:TensorImage): return x
def f_bll(x:bool): return x
def f_num(x:numbers.Number): return x
t = TypeDispatch(f_nin,f_fti,f_num,f_bti,f_bll)
test_eq(t[int], f_nin)
test_eq(t[str], None)
test_eq(t[TensorImage], f_fti)
test_eq(t[float], f_num)
t.add(f_col)
test_eq(t[str], f_col)
test_eq(t[int], f_nin)
test_eq(t(1), 2)
test_eq(t.returns(1), int)
t
def m_nin(self, x:numbers.Integral): return x+1
def m_bll(self, x:bool): return x
def m_num(self, x:numbers.Number): return x
t = TypeDispatch(m_nin,m_num,m_bll)
class A: f = t
a = A()
test_eq(a.f(1), 2)
test_eq(a.f(1.), 1.)
```
## Transform -
```
#export
class _TfmDict(dict):
def __setitem__(self,k,v):
if k=='_': k='encodes'
if k not in ('encodes','decodes') or not isinstance(v,Callable): return super().__setitem__(k,v)
if k not in self: super().__setitem__(k,TypeDispatch())
res = self[k]
res.add(v)
#export
class _TfmMeta(type):
def __new__(cls, name, bases, dict):
res = super().__new__(cls, name, bases, dict)
res.__signature__ = inspect.signature(res.__init__)
return res
def __call__(cls, *args, **kwargs):
f = args[0] if args else None
n = getattr(f,'__name__',None)
if not hasattr(cls,'encodes'): cls.encodes=TypeDispatch()
if not hasattr(cls,'decodes'): cls.decodes=TypeDispatch()
if isinstance(f,Callable) and n in ('decodes','encodes','_'):
getattr(cls,'encodes' if n=='_' else n).add(f)
return f
return super().__call__(*args, **kwargs)
@classmethod
def __prepare__(cls, name, bases): return _TfmDict()
#export
class Transform(metaclass=_TfmMeta):
"Delegates (`__call__`,`decode`) to (`encodes`,`decodes`) if `filt` matches"
filt,init_enc,as_item_force,as_item,order = None,False,None,True,0
def __init__(self, enc=None, dec=None, filt=None, as_item=False):
self.filt,self.as_item = ifnone(filt, self.filt),as_item
self.init_enc = enc or dec
if not self.init_enc: return
# Passing enc/dec, so need to remove (base) class level enc/dec
del(self.__class__.encodes,self.__class__.decodes)
self.encodes,self.decodes = (TypeDispatch(),TypeDispatch())
if enc:
self.encodes.add(enc)
self.order = getattr(self.encodes,'order',self.order)
if dec: self.decodes.add(dec)
@property
def use_as_item(self): return ifnone(self.as_item_force, self.as_item)
def __call__(self, x, **kwargs): return self._call('encodes', x, **kwargs)
def decode (self, x, **kwargs): return self._call('decodes', x, **kwargs)
def __repr__(self): return f'{self.__class__.__name__}: {self.use_as_item} {self.encodes} {self.decodes}'
def _call(self, fn, x, filt=None, **kwargs):
if filt!=self.filt and self.filt is not None: return x
f = getattr(self, fn)
if self.use_as_item or not is_listy(x): return self._do_call(f, x, **kwargs)
res = tuple(self._do_call(f, x_, **kwargs) for x_ in x)
return retain_type(res, x)
def _do_call(self, f, x, **kwargs):
return x if f is None else retain_type(f(x, **kwargs), x, f.returns_none(x))
add_docs(Transform, decode="Delegate to `decodes` to undo transform")
show_doc(Transform)
```
Base class that delegates `__call__` and `decode` to `encodes` and `decodes`, doing nothing if param annotation doesn't match type. If called with listy `x` then it calls function with each item (unless `whole_typle`, in which case it's passed directly as a whole). The function (if matching 1st param type) will cast the result to the same as the input type, unless there's a return annotation (in which case it's cast to that), or the return annotation is `None` (in which case no casting is done).
Details: `Transform` is a base class where you override encodes and/or decodes. e.g. `__call__` uses `call` which looks up what to call using `func`. If `whole_tuple` is set, that just returns `encodes` (or `decodes` if not `is_enc`). Otherwise we find the first annotated param with `_p1_anno` and check if `x` is an instance of that (if not `is_listy(x)`). If it is, we return the function (encodes/decodes), otherwise None. `call` then passes on to `_do_call` which does nothing if function is `None`. If `x` is listy, then we return a *list* of {functions or `None`}, and a list of results from `_do_call` for each function is returned.
```
class A(Transform): pass
@A
def encodes(self, x): return x+1
f1 = A()
test_eq(f1(1), 2)
class B(A): pass
f2 = B()
test_eq(f2(1), 2)
class A(Transform): pass
f3 = A()
test_eq_type(f3(2), 2)
test_eq_type(f3.decode(2.0), 2.0)
```
`Transform` can be used as a decorator, to turn a function into a `Transform`.
```
@Transform
def f(x): return x//2
test_eq_type(f(2), 1)
test_eq_type(f.decode(2.0), 2.0)
```
You can derive from `Transform` and use either `_` or `encodes` for your encoding function.
```
class A(Transform):
def _(self, x:TensorImage): return -x
f = A()
t = f(im_t)
test_eq(t, -im_t)
test_eq(f(1), 1)
test_eq(type(t), TensorImage)
f
```
Without return annotation we get an `Int` back since that's what was passed.
```
class A(Transform): pass
@A
def _(self, x:Int): return x//2 # `_` is an abbreviation for `encodes`
@A
def encodes(self, x:float): return x+1
f = A()
test_eq_type(f(Int(2)), Int(1))
test_eq_type(f(2), 2)
test_eq_type(f(2.), 3.)
```
Without return annotation we don't cast if we're not a subclass of the input type.
```
class A(Transform):
def encodes(self, x:Int): return x/2
def _(self, x:float): return x+1
f = A()
test_eq_type(f(Int(2)), 1.)
test_eq_type(f(2), 2)
test_eq_type(f(Float(2.)), Float(3.))
```
With return annotation `None` we get back whatever Python creates usually.
```
def func(x)->None: return x/2
f = Transform(func)
test_eq_type(f(2), 1.)
test_eq_type(f(2.), 1.)
```
Since `decodes` has no return annotation, but `encodes` created an `Int` and we pass that result here to `decode`, we end up with an `Int`.
```
def func(x): return Int(x+1)
def dec (x): return x-1
f = Transform(func,dec)
t = f(1)
test_eq_type(t, Int(2))
test_eq_type(f.decode(t), Int(1))
```
If the transform has `filt` then it's only applied if `filt` param matches.
```
f.filt = 1
test_eq(f(1, filt=1),2)
test_eq_type(f(1, filt=0), 1)
class A(Transform):
def encodes(self, xy): x,y=xy; return (x+y,y)
def decodes(self, xy): x,y=xy; return (x-y,y)
f = A(as_item=True)
t = f((1,2))
test_eq(t, (3,2))
test_eq(f.decode(t), (1,2))
f.filt = 1
test_eq(f((1,2), filt=1), (3,2))
test_eq(f((1,2), filt=0), (1,2))
class AL(Transform): pass
@AL
def encodes(self, x): return L(x_+1 for x_ in x)
@AL
def decodes(self, x): return L(x_-1 for x_ in x)
f = AL(as_item=True)
t = f([1,2])
test_eq(t, [2,3])
test_eq(f.decode(t), [1,2])
def neg_int(x:numbers.Integral): return -x
f = Transform(neg_int, as_item=False)
test_eq(f([1]), (-1,))
test_eq(f([1.]), (1.,))
test_eq(f([1.,2,3.]), (1.,-2,3.))
test_eq(f.decode([1,2]), (1,2))
#export
class InplaceTransform(Transform):
"A `Transform` that modifies in-place and just returns whatever it's passed"
def _call(self, fn, x, filt=None, **kwargs):
super()._call(fn,x,filt,**kwargs)
return x
```
## TupleTransform
```
#export
class TupleTransform(Transform):
"`Transform` that always treats `as_item` as `False`"
as_item_force=False
#export
class ItemTransform (Transform):
"`Transform` that always treats `as_item` as `True`"
as_item_force=True
def float_to_int(x:(float,int)): return Int(x)
f = TupleTransform(float_to_int)
test_eq_type(f([1.]), (Int(1),))
test_eq_type(f([1]), (Int(1),))
test_eq_type(f(['1']), ('1',))
test_eq_type(f([1,'1']), (Int(1),'1'))
test_eq(f.decode([1]), [1])
test_eq_type(f(TupleBase((1.,))), TupleBase((Int(1),)))
class B(TupleTransform): pass
class C(TupleTransform): pass
f = B()
test_eq(f([1]), [1])
@B
def _(self, x:int): return x+1
@B
def _(self, x:str): return x+'1'
@B
def _(self, x)->None: return str(x)+'!'
b,c = B(),C()
test_eq(b([1]), [2])
test_eq(b(['1']), ('11',))
test_eq(b([1.0]), ('1.0!',))
test_eq(c([1]), [1])
test_eq(b([1,2]), (2,3))
test_eq(b.decode([2]), [2])
assert pickle.loads(pickle.dumps(b))
@B
def decodes(self, x:int): return x-1
test_eq(b.decode([2]), [1])
test_eq(b.decode(('2',)), ('2',))
```
Non-type-constrained functions are applied to all elements of a tuple.
```
class A(TupleTransform): pass
@A
def _(self, x): return x+1
@A
def decodes(self, x): return x-1
f = A()
t = f((1,2.0))
test_eq_type(t, (2,3.0))
test_eq_type(f.decode(t), (1,2.0))
```
Type-constrained functions are applied to only matching elements of a tuple, and return annotations are only applied where matching.
```
class B(TupleTransform):
def encodes(self, x:int): return Int(x+1)
def encodes(self, x:str): return x+'1'
def decodes(self, x:Int): return x//2
f = B()
start = (1.,2,'3')
t = f(start)
test_eq_type(t, (1.,Int(3),'31'))
test_eq(f.decode(t), (1.,Int(1),'31'))
```
The same behavior also works with `typing` module type classes.
```
class A(Transform): pass
@A
def _(self, x:numbers.Integral): return x+1
@A
def _(self, x:float): return x*3
@A
def decodes(self, x:int): return x-1
f = A()
start = 1.0
t = f(start)
test_eq(t, 3.)
test_eq(f.decode(t), 3)
f = A(as_item=False)
start = (1.,2,3.)
t = f(start)
test_eq(t, (3.,3,9.))
test_eq(f.decode(t), (3.,2,9.))
```
Transform accepts lists
```
def a(x): return L(x_+1 for x_ in x)
def b(x): return L(x_-1 for x_ in x)
f = TupleTransform(a,b)
t = f((L(1,2),))
test_eq(t, (L(2,3),))
test_eq(f.decode(t), (L(1,2),))
```
## Export -
```
#hide
from local.notebook.export import notebook2script
notebook2script(all_fs=True)
```
|
github_jupyter
|
# Text Generation with Neural Networks
Import necessary packages for preprocessing, model building, etc. We follow the steps described in the theoretical part of this summer school as follows:
0. Define Reseach Goal (already done)
2. Retrieve Data
3. Prepare Data
4. Explore Data
5. Model Data
6. Present and automate Model
```
from keras.callbacks import LambdaCallback
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
from keras.models import load_model
from keras import backend as K
import numpy as np
import random
import sys
import io
```
# 1. Retrieve Data
Load your data! You can pick up data from everywhere, such as plain text, HTML, source code, etc.
You can either automatically download with Keras get_file function or download it manually and import it in this notebook.
## Example Data Set
[trump.txt](https://raw.githubusercontent.com/harshilkamdar/trump-tweets/master/trump.txt)
```
#path = get_file('trump.txt', origin='https://raw.githubusercontent.com/harshilkamdar/trump-tweets/master/trump.txt')
text = io.open('resources/shakespeare.txt', encoding='utf-8').read().lower()
print('corpus length:', len(text))
```
# 2. Prepare Data
As described in the theoretical part of this workshop we need to convert our text into a word embedding that can be processed by a (later) defined Neural Network.
## 2.1. Create Classes
The goal after this step is to have a variable which contains the distinct characters of the text. Characters can be letters, digits, punctions, new lines, spaces, etc.
### Example:
Let's assume we have the following text as input: "hallo. "
After the following step, we want to have all distinct characters, i.e.:
``[ "h", "a", "l", "o", ".", " " ] ``
```
chars = sorted(list(set(text)))
print('total chars:', len(chars))
```
## 2.2. Create Training Set
In the following section we need to create our test set based on our text. The idea is to map a sequence of characters to a class. In this case, a class is one of our distinct characters defined in the previous task. This means that a sequence of characters predicts the next character. This is important for the later model to know which characters come after specific sequences. The sequence length can be chosen. So try out different squence length.
### Example:
Our text is still: "hallo. "
Sequence length: 2 (i.e. 2 characters predict the next character)
The result (training set) should be defined as follows:
``
Seuences --> Class
"ha" --> "l"
"al" --> "l"
"ll" --> "o"
"lo" --> "."
"o." --> " "
``
You can read the previous example like this: Squence "ha" predicts the next character " l ", sequence "al" predicts next character " l " and so on.
```
seqlen = 40 # Sequence length parameter
step = 5 # Determines the how many characters the window should be shifted in the text
sequences = [] # List of sequences
char_class = [] # Corresponding class of each sequence
for i in range(0, len(text) - seqlen, step):
sequences.append(text[i: i + seqlen])
char_class.append(text[i + seqlen])
print('#no sequences:', len(sequences))
```
## 2.3. Check your Data
Now that we processed our data, it's time to understand what we have built so far.
```
for idx in range(len(sequences[:10])):
print(sequences[idx], ":" , char_class[idx])
# Print from 1st to 10th character
chars[:10]
# Print from 150th to 160th character :-)
chars[150:160]
```
## 2.4. Vectorization of Training Sequences
The following section describes the desired form of our final training set.
text: "hallo. ".
As defined above we have a couple of sequences mapping to the next appearing character in the text (e.g. "ha" mapping to "l"). But first of all, we transform each sequence to the following one-hot-encoded matrix.
**Example:**
sequence "ha" maps to the following matrix
| | h | a | l | o | . | ' ' |
|-----|-----|-----|-----|-----|-----|-----|
| h | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 0 | 1 | 0 | 0 | 0 | 0 |
next sequence "al" maps to the following matrix
| | h | a | l | o | . | ' ' |
|-----|-----|-----|-----|-----|-----|-----|
| a | 0 | 1 | 0 | 0 | 0 | 0 |
| l | 0 | 0 | 1 | 0 | 0 | 0 |
... And so on
## 2.5. Vectorization of Target Classes
We build our target classes similar to the training set. We need a one hot-encoded vector for each target (which is a character).
**Example:** for target char "l" the vector looks like this
| | h | a | l | o | . | ' ' |
|-----|-----|-----|-----|-----|-----|-----|
| l | 0 | 0 | 1 | 0 | 0 | 0 |
```
# Indexed characters as dictionary
char_indices = dict((c, i) for i, c in enumerate(chars))
# Both matrices will initialized with zeros
training_set = np.zeros((len(sequences), seqlen, len(chars)), dtype=np.bool)
target_char = np.zeros((len(sequences), len(chars)), dtype=np.bool)
for i, sequence in enumerate(sequences):
for t, char in enumerate(sequence):
training_set[i, t, char_indices[char]] = 1
target_char[i, char_indices[char_class[i]]] = 1
```
# 3. Explore Data
```
# Let's check the shape of the training_set
training_set.shape
```
Output: (x, y, z)
x = number of all sequences to test
y = window size to predict the next character
z = number of all appearing characters in text (for one-hot-enconding)
```
# Let's check the shape of the target_char (act as our target classes)
target_char.shape
```
Output: (x, y)
x = number of all sequences to test
y = the mapping of each sequence to the next character
# 4. Model data
Let's get down to business! Create your model.
Try different model configuration (see [keras doc](https://keras.io/models/about-keras-models/#about-keras-models))
```
model = Sequential()
# build the model: a LSTM
model = Sequential()
model.add(LSTM(128, input_shape=(seqlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
model.summary()
def getNextCharIdx(preds, temperature=1.0):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / temperature
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
# Creation of reverse char index, to get the char for the predicted class
indices_char = dict((i, c) for i, c in enumerate(chars))
def on_epoch_end(epoch, logs):
# Function invoked at end of each epoch. Prints generated text.
print()
print('----- Generating text after Epoch: %d' % epoch)
start_index = random.randint(0, len(text) - seqlen - 1)
for diversity in [1, 0.1, 0.5]:
print('----- diversity:', diversity)
generated = ''
sentence = text[start_index: start_index + seqlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(1000):
x_pred = np.zeros((1, seqlen, len(chars)))
for t, char in enumerate(sentence):
x_pred[0, t, char_indices[char]] = 1.
preds = model.predict(x_pred, verbose=0)[0]
next_index = getNextCharIdx(preds, diversity)
next_char = indices_char[next_index]
generated += next_char
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
```
# 5. Evaluate Model
We are not at the sweet part of the model. Let's fit our model and see what it prints!
```
model.fit(training_set, target_char,
batch_size=128,
epochs=150,
callbacks=[print_callback])
```
# Present and Automate
Having a model trained for hours is a valuable asset! We need now to store the model and use it to solve the problem we wanted to solve with Machine Learning. Keras has a simple function to save a model to the local file system and also a function to load the model again and have it ready for our task!
```
model.save('shakespeareModel.h5')
model = load_model('shakespeareModel.h5')
```
|
github_jupyter
|
```
##take Max cosine/jaccard similarity from 5 annotators
from sklearn.metrics import cohen_kappa_score
import pandas as pd
import sklearn
from rouge_score import rouge_scorer
from similarity.cosine import Cosine
from similarity.jaccard import Jaccard
import numpy as np
def compute_similarity_cosine(text1,text2):
cosine = Cosine(2)
p0 = cosine.get_profile(text1)
p1 = cosine.get_profile(text2)
score = cosine.similarity_profiles(p0, p1)
return score
def compute_similarity_jaccard(text1,text2):
jaccard = Jaccard(2)
score = jaccard.similarity(text1, text2)
return score
new_labels = pd.read_excel('proposed_gs_otherapproaches_1750news.xlsx',sheet_name=1)
new_labels.columns
#annotators = ['Zainab GS','Solat GS','Noor GS','Dr. Sajjad GS','Sumaira GS']
annotators = ['Majority Voting']
comparison_methods = new_labels.columns[7:len(new_labels.columns)]
comparison_methods
#cosine similarity
cosine_scores_method=[] #average cosine score for each method
for x in comparison_methods:
cosine_score = []
print("Method: %s"%x)
for index,row in new_labels.iterrows():
cs_for_each_annotator=[]
for a in annotators:
print(a)
cs_for_each_annotator.append(compute_similarity_cosine(row[x],row[a]))
print(cs_for_each_annotator)
cosine_score.append(np.max(cs_for_each_annotator))
cosine_scores_method.append(np.average(cosine_score))
arr = np.array(cosine_scores_method)
top_3_methods_index = arr.argsort()[-4:][::-1]
for x in top_3_methods_index:
print(cosine_scores_method[x])
print(comparison_methods[x])
comparison_results = pd.DataFrame({'Method':comparison_methods,'Cosine_Similarity': cosine_scores_method})
comparison_results
#jaccard similarity
jaccard_scores_method=[] #average cosine score for each method
for x in comparison_methods:
jaccard_score = []
print("Method: %s"%x)
for index,row in new_labels.iterrows():
js_for_each_annotator=[]
for a in annotators:
print(a)
js_for_each_annotator.append(compute_similarity_jaccard(row[x],row[a]))
print(cs_for_each_annotator)
jaccard_score.append(np.max(js_for_each_annotator))
jaccard_scores_method.append(np.average(jaccard_score))
arr = np.array(jaccard_scores_method)
top_3_methods_index = arr.argsort()[-4:][::-1]
for x in top_3_methods_index:
print(jaccard_scores_method[x])
print(comparison_methods[x])
comparison_results['Jaccard Similarity'] = jaccard_scores_method
comparison_results
fname="automatic evaluation 1750newsheadlines_UsingMaxofAnnotators"+".csv"
comparison_results.to_csv(fname,sep='\t',index=False)
```
## Gold Standard Cosine Similarity
```
gold_standard = new_labels.columns[1:7]
gold_standard
cs_annotators = pd.DataFrame(columns=gold_standard)
for x in gold_standard:
cosine_scores_method_x=[] #average cosine score for each method
for y in gold_standard:
cosine_score = []
for index,row in new_labels.iterrows():
cosine_score.append(compute_similarity_cosine(row[x],row[y]))
cosine_scores_method_x.append(np.average(cosine_score))
cs_annotators[x] = cosine_scores_method_x
cs_annotators
cs_annotators.to_csv('cosine_similarity_annotators.csv',sep='\t',index=False)
js_annotators = pd.DataFrame(columns=gold_standard)
for x in gold_standard:
jaccard_scores_method_x=[] #average jaccard score for each method
for y in gold_standard:
jaccard_score = []
for index,row in new_labels.iterrows():
jaccard_score.append(compute_similarity_jaccard(row[x],row[y]))
jaccard_scores_method_x.append(np.average(jaccard_score))
js_annotators[x] = jaccard_scores_method_x
js_annotators
js_annotators.to_csv('jaccard_similarity_annotators.csv',sep='\t',index=False)
```
|
github_jupyter
|
## Variant of the Blocked Input Model in which the stop process decelerates the go process by a rate that varies across trials
```
import numpy
import random
import matplotlib.pyplot as plt
import matplotlib
import seaborn
import pandas
import matplotlib.patches as patches
from matplotlib.ticker import FormatStrFormatter
%matplotlib inline
params={'mugo':.2,
'mustop':.8,
'threshold':60,
'nondecisiongo':50,
'nondecisionstop':50,
'inhibitionParam':1,
'ssds':[1,50,100,150, 200,250, 300, 350, 400, 450, 500,3000],
'nreps':1000,
'maxtime':1000}
def interactiverace(params):
stopaccumsave = []
mustopsave = []
stopsave = []
meanrtgo = numpy.zeros(len(params['ssds']))
presp = numpy.zeros(len(params['ssds']));
for irep in range(params['nreps']):
for j,ssd in enumerate(params['ssds']):
stopsignaldelay = ssd
goaccumulator = 0
stopaccumulator = 0
rtgo = 0
itime = 0
mustop = params['mustop']+numpy.random.normal(loc=0, scale=.7)
if mustop < 0:
mustop = 0
mustopsave.append(mustop)
while itime < params['maxtime'] and rtgo == 0: # single trial
itime = itime + 1
if itime < stopsignaldelay + params['nondecisionstop']:
inhibition = 0
else:
inhibition = params['inhibitionParam']
stopaccumulator = mustop + numpy.random.normal(loc=0, scale=.008)
if stopaccumulator <= 0:
stopaccumulator = 0;
stopaccumsave.append(stopaccumulator)
if itime >= params['nondecisiongo']:
goaccumulator = goaccumulator + params['mugo'] - inhibition*stopaccumulator + numpy.random.normal(loc=0, scale=1)
if goaccumulator <= 0:
goaccumulator = 0;
if goaccumulator > params['threshold']:
if rtgo == 0:
rtgo = itime;
meanrtgo[j] += rtgo;
if rtgo > 0:
presp[j] += 1;
for ssd in range(len(params['ssds'])):
if presp[ssd] > 0:
meanrtgo[ssd] = meanrtgo[ssd]/presp[ssd];
presp[ssd] = presp[ssd]/params['nreps'];
return(meanrtgo,presp,mustopsave,stopaccumsave)
meanrtgo,presp,mustopsave,stopaccumsave=interactiverace(params)
print(meanrtgo)
print(presp)
#print(stopaccumsave)
#print(mustopsave)
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.plot(params['ssds'][:11],meanrtgo[:11] - meanrtgo[11])
plt.plot([params['ssds'][0],params['ssds'][10]],[0,0],'k:')
plt.xlabel('Stop signal delay')
plt.ylabel('Violation (Stop Failure RT - No-Stop RT)')
plt.subplot(1,2,2)
plt.plot(params['ssds'][:11],presp[:11])
plt.xlabel('Stop signal delay')
plt.ylabel('Probability of responding')
plt.axis([params['ssds'][0],params['ssds'][10],0,1])
```
|
github_jupyter
|
# ELEC 400M / EECE 571M Assignment 2: Neural networks
(This assignment is a modified version of an assignment used in ECE 421 at the University of Toronto and kindly made available to us by the instructor.)
In this assignment, you will implement a neural network model for multi-class classification. The purpose is to demonstrate an understanding of the basic elements including training of neural network models. Hence, your implementation will be from scratch only using functions from the NumPy library.
The neural network you will be implementing has the following structure:
* 3 layers: 1 input layer, 1 hidden layer with ReLU activation and 1 output layer with Softmax function
* The loss function is the Cross Entropy Loss.
* Training will be done using Gradient Descent with Momentum.
## Data Set
We again consider the dataset of images of letters in different fonts contained in file notMNIST.npz (which btw is from http://yaroslavvb.blogspot.com/2011/09/notmnist-dataset.html). This time we consider 10 letters ("A" to "J"), which are all the letters contained in this data set, and we want to classfiy the images according to the letter they display. The figure below shows 30 randomly selected image samples for the letters.

You will apply the function `loadData` given below to load the data set, which includes 18720 images and their labels, which we also refer to as targets. This script organizes the data set into training, validation and test sets.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def loadData():
with np.load('notMNIST.npz') as data:
Data, Target = data['images'], data['labels']
np.random.seed(521)
randIndx = np.arange(len(Data))
np.random.shuffle(randIndx)
Data = Data[randIndx]/255.0
Target = Target[randIndx]
trainData, trainTarget = Data[:15000], Target[:15000]
validData, validTarget = Data[15000:16000], Target[15000:16000]
testData, testTarget = Data[16000:], Target[16000:]
return trainData, validData, testData, trainTarget, validTarget, testTarget
```
## Data preprocessing [5 points]
Input data: The classification should be based on the $d=28\times 28=784$ intensity values in an image (as for Assignment 1).
Output data: Since you will be performing multi-class classification, the labels will be converted into a one-hot encoding format.
Please first briefly explain the meaning of one-hot encoding and why it is used (instead of keeping the numerical label values provided by the data set). State an example for a one-hot encoded label for the data set considered in this assignment.
**Solution:**
One-hot encoding is a way of encoding or representing labels or other categorical data. For instance, if there are 'n' classes that have unique labels, they may be numerically labeled using numbers from 0 to (n-1). Alternatively, they may also be one-hot encoded using a label that is n-bits wide and has the nth bit (coresponding to the nth numerical label) set to 1.
For most classification problems, machine learning algorithms may misinterpret numerical data and infer some sort of hierarchy or relationship amongst the data that is not necessarily relevant to the problem at hand. This can ultimately lead the algorithm to learn a false hypothesis. One-hot encoding is a way of pre-processing the labels to remove any such hierarchical relationship so that the machine learning algorithm does not infer anything that is otherwise not useful to the task it is trying to accomplish.
__Example of One-Hot-Encoding__
Consider a few numerical labels from the training data-set (numbered from 0-9), their corresponding one-hot encoded values are represented alongside.
| Categorical Data (From Dataset) | Numerical Label | One-Hot Encoded Label |
|:-------------------------------:|:---------------:|:---------------------:|
| A | 0 | [1;0;0;0;0;0;0;0;0;0] |
| B | 1 | [0;1;0;0;0;0;0;0;0;0] |
| H | 8 | [0;0;0;0;0;0;0;0;1;0] |
| E | 5 | [0;0;0;0;0;1;0;0;0;0] |
Now implement a function that one-hot encodes the labels (or targets) for the training, validation and test sets.
```
def convertOneHot(trainTarget, validTarget, testTarget):
trainTargetOneHot = np.zeros([trainTarget.shape[0],10])
trainTargetOneHot[np.arange(trainTarget.size),trainTarget]=1
validTargetOneHot = np.zeros([validTarget.shape[0],10])
validTargetOneHot[np.arange(validTarget.size),validTarget] = 1
testTargetOneHot = np.zeros([testTarget.shape[0],10])
testTargetOneHot[np.arange(testTarget.size),testTarget]=1
return trainTargetOneHot, validTargetOneHot, testTargetOneHot
```
## Structure of the network [2 points]
Sketch the structure of the network to classify the letters from the data set. Identify the dimensions of the network layers, include the activation functions, and do not forget the bias nodes. (You may sketch this by hand and upload a photo of your sketch.)
**Solution:**
*Note: A scaled down version of the actual network has been sketched for the sake of space and clarity.*

The activation function in the hidden layer is the ReLU : $\mathrm{ReLU}(x)=\max(0,x).$
The activation function in the output layer is the Softmax : $ P_j = [\sigma(\mathbf{z})]_j = \frac{\mathrm{e}^{z_j}}{\sum\limits_{k=1}^{10}\mathrm{e}^{z_{10}}}$ where $j=1,2,\ldots, 10$, for $10$ classes.
## Helper functions [6 points]
To give the implementation of the network some structure, you will first implement five helper functions.
Use Numpy arrays for your implementations, and organize data in vectors and matrices as appropriate for compact programming.
1. `relu`: This function will accept one argument and return the ReLU activation:
$$\mathrm{ReLU}(x)=\max(0,x).$$
2. `softmax`: This function will accept one argument and return the softmax activations:
$$ [\sigma(\mathbf{z})]_j = \frac{\mathrm{e}^{z_j}}{\sum\limits_{k=1}^K\mathrm{e}^{z_k}},$$ $j=1,2,\ldots, K$, for $K$ classes.
3. `computeLayer`: This function will accept two arguments, the input vector $\mathbf{x}$ for a layer and the weight matrix $\mathbf{W}$, and return a vector $\mathbf{s}=\mathbf{W}^T\mathbf{x}$, i.e., the input to the activation function of the layer (the notation for variables from the textbook is used). Don't forget to account for the bias term (which can be included in an augmented vector $\mathbf{x}$ as in the textbook).
4. `CE`: This function will accept two arguments, the one-hot encoded labels $\mathbf{y}_n$ and the inputs $\mathbf{s}_n$ to the softmax function, $n=1,2,\ldots N$. It will return the cross entropy loss
$$\mathrm{E}_{\mathrm{in}}=-\frac{1}{N}\sum\limits_{n=1}^N\sum\limits_{k=1}^Ky_{n,k}\log([\sigma(\mathbf{s}_n)]_k)$$
5. `gradCE`: This function will accept two arguments, the labels and the inputs to the softmax function. It will return the gradient of the cross entropy loss with respect to the inputs (i.e., it returns the sensivity vector for the output layer as introduced in the textbook).
First state the analytical expression for the gradient used in `gradCE` and then implement the five helper functions.
**Solution:**
The analytical expression for the gradient used in gradCE is given by,
$$\delta^{\left(L\right)}_{n}=\frac{\partial e_{n}}{\partial S^{L}_{n}}=\sigma\left(S^{L}_{n}\right)-y_{n}$$
Where $\sigma$ refers to the softmax function and $n$ is associated with the $n^{th}$ input. That is, $n \in [0,N]$
```
def relu(x):
return np.maximum(0,x)
def softmax(x):
maxes = np.amax(x,axis=0)
maxes = maxes.reshape(1,maxes.shape[0])
x = x - maxes
op = np.exp(x)/sum(np.exp(x))
return op
def computeLayer(x,W):
return np.matmul(W.T,x)
def CE(target, prediction):
return (-1/target.shape[1])*(np.sum(np.multiply(target,np.log(1E-15+softmax(prediction)))))
def gradCE(target, prediction):
return softmax(prediction)-target
```
## Backpropagation [2 points]
The training of the network will be done via backpropagation. First derive the following gradients:
1. $\frac{\partial E_{\mathrm{in}}}{\partial \mathbf{W}^{\mathrm{o}}}$, where $\mathbf{W}^{\mathrm{o}}$ is the weight matrix of the output layer.
2. $\frac{\partial E_{\mathrm{in}}}{\partial \mathbf{W}^{\mathrm{h}}}$, where $\mathbf{W}^{\mathrm{h}}$ is the weight matrix of the hidden layer.
Write the results using the steps and notation used in the textbook.
**Solution:**
We know that,
$$E_{in}=\frac{1}{N}\sum_{n=1}^{N}e_{n}$$
$$\frac{\partial E_{in}}{\partial W^{\left(l\right)}}=\frac{1}{N}\sum_{n=1}^{N}\frac{\partial e_{n}}{\partial W^{\left(l\right)}}$$
where,
$$\frac{\partial e_{n}}{\partial W^{\left(l\right)}}=\frac{\partial S_n^{\left(l\right)}}{\partial W^{\left(l\right)}} . \frac{\partial e_n}{\partial S_n^{\left(l\right)}}=\frac{\partial \left( \left(W^{\left(l\right)}\right)^T.x_n^{l-1}\right)}{\partial W^{\left(l\right)}}.\frac{\partial e_n}{\partial S_n^{\left(l\right)}}$$
thus,
$$\frac{\partial e_{n}}{\partial W^{\left(l\right)}}=x_n^{l-1}.\frac{\partial e_n}{\partial S_n^{\left(l\right)}}=x_n^{l-1}\left(\delta_n^{l}\right)^T\ \ -----\ Equation\ 1$$
Where $\frac{\partial e_n}{\partial S_n^{\left(l\right)}}=\delta_n^{l}$ is the sensitivity vector at layer $l$. The gradients for each layer is given by,
**1. $\frac{\partial E_{in}}{\partial W^{O}}$ where $W^{O}$ is the weight matrix of the output layer.**
$$\frac{\partial E_{in}}{\partial W^{O}}=\frac{1}{N}\sum_{n=1}^{N}\frac{\partial e_{n}}{\partial W^{O}}=\frac{1}{N}\sum_{n=1}^{N}\left(x_n^{O-1}\left(\delta_n^{O}\right)^T\right)$$
The sensitivity at the output layer, $\delta_n^{O}$ is given by,
$$\delta_n^{O}=\frac{\partial e_n}{\partial S_n^{\left(O\right)}}$$
where, $e_n=-\sum_jy_{n,j}\log{[\sigma(\mathbf{S}_n)]_j}$ and $\sigma(\mathbf{S}_n)=\frac{e^{S_n}}{\sum_{k=1}^Ne^{\left(S_n\right)_k}}$ where $\sigma$ is the activation (softmax) at the output layer.
Applying the analytical expression for gradCE from the previous section,
$$\delta_n^{O}=\frac{\partial e_n}{\partial S_n^{\left(O\right)}}=\frac{\partial e_{n}}{\partial S^{O}_{n}}=\sigma\left(S^{O}_{n}\right)-y_{n}\ \ -----\ Equation\ 1.A$$
Applying $Equation\ 1.A$ in $Equation\ 1$
$$\frac{\partial E_{in}}{\partial W^{O}}=\frac{1}{N}\sum_{n=1}^{N}\left(x_n^{O-1}\left(\sigma\left(S^{O}_{n}\right)-y_{n}\right)^T\right)$$
**2. $\frac{\partial E_{in}}{\partial W^{h}}$ where $W^{h}$ is the weight matrix of the hidden layer.**
$$\frac{\partial E_{in}}{\partial W^{h}}=\frac{1}{N}\sum_{n=1}^{N}\frac{\partial e_{n}}{\partial W^{h}}=\frac{1}{N}\sum_{n=1}^{N}\left(x_n^{h-1}\left(\delta_n^{h}\right)^T\right)\ \ -----\ Equation\ 2.A$$
The sensitivity at the hidden layer, $\delta_n^{h}$ is given by,
$$\delta_n^{h}=\frac{\partial e_n}{\partial S_n^{\left(h\right)}}=\frac{\partial e_n}{\partial x_n^{h}}.\frac{\partial x_n^{h}}{\partial S_n^{h}}=\frac{\partial e_n}{\partial x_n^{h}}.\theta'\left(S_n^{h}\right)\ \ -----\ Equation\ 2.B$$
Where $x_n^{h}=\theta\left(S_n^{h}\right)$ and $\theta$ is the activation function (ReLU) at the hidden layer.
Finally,
$$\frac{\partial e_n}{\partial x_n^{h}}=\left[W^O\delta^O\right]_1^{d^{\left(h\right)}}$$
Applying this to $Equation\ 2.B$,
$$\delta_n^{h}=\theta'\left(S_n^{h}\right)\otimes\left[W^O\delta_n^O\right]_1^{d^{\left(h\right)}}\ \ -----\ Equation\ 2.C$$
Where $\otimes$ denotes element-wise multiplication.
Applying $Equation\ 2.C$ in $Equation\ 2.A$, we finally get
$$\frac{\partial E_{in}}{\partial W^{h}}=\frac{1}{N}\sum_{n=1}^{N}x_n^{h-1}\left[\theta'\left(S_n^{h}\right)\otimes\left[W^O\delta_n^O\right]_1^{d^{\left(h\right)}}\right]^T$$
## Network training [8 points]
Implement a function to train the network. The function uses the helper functions from above. The optimization technique for backpropagation will be Gradient Descent with Momentum:
$$\mathbf{V}(t)=\alpha \mathbf{V}(t-1)-\eta\frac{\partial E_{\mathrm{in}}}{\partial \mathbf{W}(t)}$$
and
$$\mathbf{W}(t+1)=\mathbf{W}(t)+\mathbf{V}(t),$$
where $\eta$ is the learning rate and $\alpha$ is the momentum hyperparameter.
The training function accepts the following inputs: training data (features), training labels, weight matrix of the hidden layer, weight matrix of the output layer, number of iterations, parameters $\eta$ and $\alpha$, validation data, validation labels, test data, test labels. The validation and test inputs are initialized to "None" and need not be passed on. You will also need to initialize the velocity matrices $\mathbf{V}$ for both hidden layer and output layer weights to small values, e.g. $10^{-5}%$.
The function outputs the updated weight matrices, the losses and classification accuracies for the training data, and if validation and test inputs were provided, then it also outputs the classification accuracies for the validation and test data.
```
# Utility Functions
# A. Easy ForwardProp
def forwardProp(inputData,targetLabel,weightHidd,weightOp):
# 1. Hidden Layer
# Add Bias and Multiply with Weights to get S(1)
sToHidd = computeLayer((np.append(np.ones((inputData.shape[0],1)),inputData,axis=1)).T,weightHidd)
# Calculate Activation to get X(1)
xToOp = relu(sToHidd)
# 2. Output Layer
# Add Bias and Multiply with Weights to get S(L)
sToOp = computeLayer((np.append(np.ones((1,xToOp.shape[1])),xToOp,axis=0)),weightOp)
# Calculate Activation to get h(x)
fpassResult = softmax(sToOp)
# Calculate Loss
fpassLoss = CE(targetLabel.T,sToOp)
return fpassResult, fpassLoss
# B. Easy Classification Accuracies
def classAccuracy(fpassResult,targetLabel):
# Fpass Classification
fpassClass = np.argmax(fpassResult,axis=0)
# True Classification
trueClass = np.argmax(targetLabel,axis=0)
return np.sum(fpassClass==trueClass)/targetLabel.shape[1]
def trainNN(trainingData, trainingTarget, weightHidd, weightOp, numIter, eta, alpha, validationData, validationTarget, testData, testTarget):
# eta --> Learning Rate
# alpha --> Momentum
# Grab NN Dimensions
numHiddenUnits = weightHidd.shape[1]
numOpUnits = weightOp.shape[1]
numIpVectors = trainingData.shape[0]
numInputs = trainingData.shape[1]
# Initialize Matrices
velocityHidd = 1E-5 * (np.ones([weightHidd.shape[0],weightHidd.shape[1]]))
velocityOp = 1E-5 * (np.ones([weightOp.shape[0],weightOp.shape[1]]))
sToHidd = np.zeros([trainingData.shape[0],numHiddenUnits])
sToOp = np.zeros([trainingData.shape[0],numOpUnits])
lossesTrain = np.zeros([numIter,1])
lossesValid = np.zeros([numIter,1])
lossesTest = np.zeros([numIter,1])
accuracyTrain = np.zeros([numIter,1])
accuracyValid = np.zeros([numIter,1])
accuracyTest = np.zeros([numIter,1])
i = 1
while (i != numIter+1):
# 1. Hidden Layer
# Add Bias and Multiply with Weights to get S(1)
sToHidd = computeLayer((np.append(np.ones((trainingData.shape[0],1)),trainingData,axis=1)).T,weightHidd)
# Calculate Activation to get X(1)
xToOp = relu(sToHidd)
# 2. Output Layer
# Add Bias and Multiply with Weights to get S(L)
sToOp = computeLayer((np.append(np.ones((1,xToOp.shape[1])),xToOp,axis=0)),weightOp)
# Calculate Activation to get h(x)
hx = softmax(sToOp)
# Calculate Loss
lossesTrain[i-1,0] = CE(trainingTarget.T,sToOp)
# Back Propagation
# Part 1 : At OP
# 1. Grad w.r.t weightOp
dEdWL = (1/1)*(np.matmul((np.append(np.ones((1,xToOp.shape[1])),xToOp,axis=0)),gradCE(trainingTarget.T,sToOp).T))
# 2. Velocity OP
velocityOp = (alpha*velocityOp)-(eta*dEdWL)
# 3. weightOp Update
weightOp = weightOp + velocityOp
# Part 2 : At Hidden
# 1. Grad w.r.t weightHidd
dedxl = (np.matmul(weightOp[1:,:],gradCE(trainingTarget.T,sToOp)))
derRelu = (sToHidd>0).astype(int) # Derivative of ReLU
temp = np.multiply((derRelu),(dedxl)) # [n x numberHiddenNeuron]
dEdWl = (1/1)*(np.matmul((np.append(np.ones((trainingData.shape[0],1)),trainingData,axis=1)).T,temp.T))
# 2. Velocity Hidden
velocityHidd = (alpha*velocityHidd)-(eta*dEdWl)
# 3. weightHidd Update
weightHidd = weightHidd + velocityHidd
# Report Accuracies and Losses
# 1. Training Accuracy
accuracyTrain[i-1,0] = classAccuracy(hx,trainingTarget.T)
# 2. Validation Accuracy
fpassResValid, lossesValid[i-1,0] = forwardProp(validationData,validationTarget,weightHidd,weightOp)
accuracyValid[i-1,0] = classAccuracy(fpassResValid,validationTarget.T)
# 3. Testing Accuracy
fpassResTest, lossesTest[i-1,0] = forwardProp(testData,testTarget,weightHidd,weightOp)
accuracyTest[i-1,0] = classAccuracy(fpassResTest,testTarget.T)
# Increment Index
i = i + 1
return weightHidd, weightOp, lossesTrain, lossesValid, lossesTest, accuracyTrain, accuracyValid, accuracyTest
```
## Network test [4 points]
Write a script that constructs the neural network.
Initialize your weight matrices by drawing the elements i.i.d. at random from a zero-mean Gaussian distribution with variance equal to $$\sigma_w^2=\frac{2}{\mbox{# of input nodes + # of output nodes}}$$ (Xavier normalization http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)
Build a network with 1000 hidden units and train it for 200 epochs using $\alpha=0.9$ and $\eta=10^{-5}$. Plot the training, validation and testing accuracy curves. State the training, validation and testing accuracies after training. Show the plot and the accuracies in the next markdown cell.
```
# Load Data
trainData, validData, testData, trainTarget, validTarget, testTarget = loadData()
trainData = trainData.reshape(trainData.shape[0],-1)
validData = validData.reshape(validData.shape[0],-1)
testData = testData.reshape(testData.shape[0],-1)
trainTargetOneHot, validTargetOneHot, testTargetOneHot = convertOneHot(trainTarget, validTarget, testTarget)
alpha = 0.9 # Momentum
eta = 0.6*(1e-05) # Learning Rate
numIter = 200 # Epochs
numHiddenNeurons = 1000 # Number of Hidden Layer Neurons
numInputNodes = 784 # Excluding Bias
numOpNodes = 10 # 10 Classes
centre = 0 # Mean of Distribution to Draw Weights
# Weight Matrix Initialization
# Function To Generate Standard Deviation for Xavier Init
def standDevDistr(ipNodes,opNodes):
variance = 2/(ipNodes+opNodes)
return np.sqrt(variance)
def constructAndTrainNN(alpha,eta,numIter,numHiddenNeurons,numInputNodes,numOpNodes,centre,trainData,trainTargetOneHot,validData,validTargetOneHot,testData,testTargetOneHot):
standDevHidd = standDevDistr(numInputNodes,numHiddenNeurons)
standDevOp = standDevDistr(numHiddenNeurons,numOpNodes)
weightHiddenLayer = np.random.normal(loc=centre,scale=standDevHidd,size=(numInputNodes+1,numHiddenNeurons))
#weightHiddenLayer = np.zeros([numInputNodes+1,numHiddenNeurons])
weightOpLayer = np.random.normal(loc=centre,scale=standDevOp,size=(numHiddenNeurons+1,numOpNodes))
#weightOpLayer = np.zeros([numHiddenNeurons+1,numOpNodes])
wHid, wOp, ltrain, lvalid, ltest, atrain, avalid, atest = trainNN(trainData, trainTargetOneHot, weightHiddenLayer, weightOpLayer,numIter,eta,alpha,validData,validTargetOneHot,testData,testTargetOneHot)
plt.plot(atrain,"-r",label="Training Set")
plt.plot(avalid,"-b",label="Validation Set")
plt.plot(atest,"-g",label="Test Set")
plt.xlabel('Epochs')
plt.ylabel('Classification Accuracy')
plt.legend(loc="lower right")
plt.title("Classification Accuracy vs Number of Epochs")
plt.show()
plt.plot(ltrain,"-r",label="Training Set")
plt.plot(lvalid,"-b",label="Validation Set")
plt.plot(ltest,"-g",label="Testing Set")
plt.xlabel('Epochs')
plt.ylabel('Cross Entropy Loss')
plt.legend(loc="upper right")
plt.title("Cross Entropy Loss vs Epochs")
plt.show()
return wHid, wOp, ltrain, lvalid, ltest, atrain, avalid, atest
np.random.seed(7)
# Construct Network With 1000 Hidden Nodes and Run Test
wHid, wOp, ltrain, lvalid, ltest, atrain, avalid, atest = constructAndTrainNN(alpha,eta,numIter,numHiddenNeurons,numInputNodes,numOpNodes,centre,trainData,trainTargetOneHot,validData,validTargetOneHot,testData,testTargetOneHot)
```
**Solution:**
**Accuracy Curves**

For this network with 1000 hidden nodes, the accuracies at the end of 200 Epochs are,
| Dataset | Accuracy |
|:----------:|:--------:|
| Training | 95.45% |
| Validation | 92.90% |
| Testing | 90.89% |
**Cross Entropy Loss**

*Note: I noticed that at the learning rate of 1E-5, the solution often failed to converge. That is, after a few initial iterations, the loss would shoot up and never come down. As a result, the learning rate was lowered to 60% of 1E-5 to capture the outputs. No other aspect of the network was modified.*
## Hyperparameter investigation [3 points]
Continue to use $\alpha=0.9$ and $\eta=10^{-5}$.
Test your network with 500, 1500, 2500 hidden nodes and train for 200 epochs. Comment based on the validation accuracy after how many epochs training could be terminated early.
Plot the training and validation accuracy curves for all three network sizes and 200 training epochs, and report the test accuracy for your selected network size and training length. Show the plot and the accuracies in the next markdown cell.
(Training of the large network for 200 epochs should take about 30-60 mins.)
```
print('Number of Hidden Units = 500')
wHid500, wOp500, ltrain500, lvalid500, ltest500, atrain500, avalid500, atest500 = constructAndTrainNN(alpha,eta,numIter,500,numInputNodes,numOpNodes,centre,trainData,trainTargetOneHot,validData,validTargetOneHot,testData,testTargetOneHot)
print('Number of Hidden Units = 1500')
wHid1500, wOp1500, ltrain1500, lvalid1500, ltest1500, atrain1500, avalid1500, atest1500 = constructAndTrainNN(alpha,eta,numIter,1500,numInputNodes,numOpNodes,centre,trainData,trainTargetOneHot,validData,validTargetOneHot,testData,testTargetOneHot)
print('Number of Hidden Units = 2500')
wHid2500, wOp2500, ltrain2500, lvalid2500, ltest2500, atrain2500, avalid2500, atest2500 = constructAndTrainNN(alpha,eta,numIter,2500,numInputNodes,numOpNodes,centre,trainData,trainTargetOneHot,validData,validTargetOneHot,testData,testTargetOneHot)
```
**Solution:**
**Number of Hidden Units = 500**
Accuracy Curves

**Number of Hidden Units = 1500**
Accuracy Curves

**Number of Hidden Units = 2500**
Accuracy Curves

**Summary of Accuracies**
| | | | Accuracy | |
|:------------:|:-----:|:------------:|:--------------:|:-----------:|
| Hidden Units | Epoch | Training Set | Validation Set | Testing Set |
| 500 | 200 | 95.11% | 92.40% | 90.93% |
| 1500 | 200 | 95.65% | 92.10% | 91.26% |
| 2500 | 200 | 95.93% | 92.60% | 91.18% |
With respect to the validation accuracies, the highest validation accuracies were achieved at the following epochs for the each network.
| Hidden Units | Epoch Count at Highest Validation Accuracy |
|:------------:|:------------------------------------------:|
| 500 | 193 |
| 1500 | 183 |
| 2500 | 189 |
Accuracies at the corresponding epochs have been tabulated below.
| | | | Accuracy | |
|:------------:|:-----:|:------------:|:--------------:|:-----------:|
| Hidden Units | Epoch | Training Set | Validation Set | Testing Set |
| 500 | 193 | 94.95% | 92.40% | 90.97% |
| 1500 | 183 | 95.27% | 92.10% | 91.19% |
| 2500 | 189 | 95.66% | 92.70% | 91.12% |
|
github_jupyter
|
```
!pip install --upgrade progressbar2
from torch import nn
from collections import OrderedDict
import torch.nn.functional as F
import torch
from torch.utils.data import DataLoader
import torchvision
import random
from torch.utils.data import Subset
from matplotlib import pyplot as plt
from torchsummary import summary
from torchvision import transforms
import progressbar as pb
import numpy as np
SUM = lambda x,y : x+y
def check_equity(property,a,b):
pa = getattr(a,property)
pb = getattr(b,property)
assert pa==pb, "Different {}: {}!={}".format(property,pa,pb)
return pa
def module_unwrap(mod:nn.Module,recursive=False):
children = OrderedDict()
try:
for name, module in mod.named_children():
if (recursive):
recursive_call = module_unwrap(module,recursive=True)
if (len(recursive_call)>0):
for k,v in recursive_call.items():
children[name+"_"+k] = v
else:
children[name] = module
else:
children[name] = module
except AttributeError:
pass
return children
class VGGBlock(nn.Module):
def __init__(self, in_channels, out_channels,batch_norm=False):
super().__init__()
conv2_params = {'kernel_size': (3, 3),
'stride' : (1, 1),
'padding' : 1
}
noop = lambda x : x
self._batch_norm = batch_norm
self.conv1 = nn.Conv2d(in_channels=in_channels,out_channels=out_channels , **conv2_params)
#self.bn1 = nn.BatchNorm2d(out_channels) if batch_norm else noop
self.bn1 = nn.GroupNorm(32, out_channels) if batch_norm else noop
self.conv2 = nn.Conv2d(in_channels=out_channels,out_channels=out_channels, **conv2_params)
#self.bn2 = nn.BatchNorm2d(out_channels) if batch_norm else noop
self.bn2 = nn.GroupNorm(32, out_channels) if batch_norm else noop
self.max_pooling = nn.MaxPool2d(kernel_size=(2, 2), stride=(2, 2))
@property
def batch_norm(self):
return self._batch_norm
def forward(self,x):
x = self.conv1(x)
x = self.bn1(x)
x = F.relu(x)
x = self.conv2(x)
x = self.bn2(x)
x = F.relu(x)
x = self.max_pooling(x)
return x
class Classifier(nn.Module):
def __init__(self,num_classes=10):
super().__init__()
self.classifier = nn.Sequential(
nn.Linear(2048, 2048),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(2048, 512),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(512, num_classes)
)
def forward(self,x):
return self.classifier(x)
class VGG16(nn.Module):
def __init__(self, input_size, batch_norm=False):
super(VGG16, self).__init__()
self.in_channels,self.in_width,self.in_height = input_size
self.block_1 = VGGBlock(self.in_channels,64,batch_norm=batch_norm)
self.block_2 = VGGBlock(64, 128,batch_norm=batch_norm)
self.block_3 = VGGBlock(128, 256,batch_norm=batch_norm)
self.block_4 = VGGBlock(256,512,batch_norm=batch_norm)
@property
def input_size(self):
return self.in_channels,self.in_width,self.in_height
def forward(self, x):
x = self.block_1(x)
x = self.block_2(x)
x = self.block_3(x)
x = self.block_4(x)
# x = self.avgpool(x)
x = torch.flatten(x,1)
return x
class CombinedLoss(nn.Module):
def __init__(self, loss_a, loss_b, loss_combo, _lambda=1.0):
super().__init__()
self.loss_a = loss_a
self.loss_b = loss_b
self.loss_combo = loss_combo
self.register_buffer('_lambda',torch.tensor(float(_lambda),dtype=torch.float32))
def forward(self,y_hat,y):
return self.loss_a(y_hat[0],y[0]) + self.loss_b(y_hat[1],y[1]) + self._lambda * self.loss_combo(y_hat[2],torch.cat(y,0))
DO='TRAIN'
random.seed(47)
combo_fn = SUM
lambda_reg = 1
def test(net,classifier, loader):
net.to(dev)
classifier.to(dev)
net.eval()
sum_accuracy = 0
# Process each batch
for j, (input, labels) in enumerate(loader):
input = input.to(dev)
labels = labels.float().to(dev)
features = net(input)
pred = torch.squeeze(classifier(features))
# https://discuss.pytorch.org/t/bcewithlogitsloss-and-model-accuracy-calculation/59293/ 2
#pred_labels = (pred >= 0.0).long() # Binarize predictions to 0 and 1
_,pred_label = torch.max(pred, dim = 1)
pred_labels = (pred_label == labels).float()
batch_accuracy = pred_labels.sum().item() / len(labels)
# Update accuracy
sum_accuracy += batch_accuracy
epoch_accuracy = sum_accuracy / len(loader)
return epoch_accuracy
#print(f"Accuracy test: {epoch_accuracy:0.5}")
def train(nets, loaders, optimizer, criterion, epochs=20, dev=None, save_param=False, model_name="federated_mnist"):
# try:
nets = [n.to(dev) for n in nets]
model_a = module_unwrap(nets[0], True)
model_b = module_unwrap(nets[1], True)
model_c = module_unwrap(nets[2], True)
reg_loss = nn.MSELoss()
criterion.to(dev)
reg_loss.to(dev)
# Initialize history
history_loss = {"train": [], "val": [], "test": []}
history_accuracy = {"train": [], "val": [], "test": []}
history_test = []
# Store the best val accuracy
best_val_accuracy = 0
# Store best accuracy to save the model
best_accuracy = 0
# Process each epoch
for epoch in range(epochs):
# Initialize epoch variables
sum_loss = {"train": 0, "val": 0, "test": 0}
sum_accuracy = {"train": [0,0,0], "val": [0,0,0], "test": [0,0,0]}
progbar = None
# Process each split
for split in ["train", "val", "test"]:
if split == "train":
for n in nets:
n.train()
widgets = [
' [', pb.Timer(), '] ',
pb.Bar(),
' [', pb.ETA(), '] ', pb.Variable('ta','[Train Acc: {formatted_value}]')
]
progbar = pb.ProgressBar(max_value=len(loaders[split][0]),widgets=widgets,redirect_stdout=True)
else:
for n in nets:
n.eval()
# Process each batch
for j,((input_a, labels_a),(input_b, labels_b)) in enumerate(zip(loaders[split][0],loaders[split][1])):
input_a = input_a.to(dev)
input_b = input_b.to(dev)
labels_a = labels_a.long().to(dev)
labels_b = labels_b.long().to(dev)
inputs = torch.cat([input_a,input_b],axis=0)
labels = torch.cat([labels_a, labels_b])
# Reset gradients
optimizer.zero_grad()
# Compute output
features_a = nets[0](input_a)
features_b = nets[1](input_b)
features_c = nets[2](inputs)
pred_a = torch.squeeze(nets[3](features_a))
pred_b = torch.squeeze(nets[3](features_b))
pred_c = torch.squeeze(nets[3](features_c))
loss = criterion(pred_a, labels_a) + criterion(pred_b, labels_b) + criterion(pred_c, labels)
for n in model_a:
layer_a = model_a[n]
layer_b = model_b[n]
layer_c = model_c[n]
if (isinstance(layer_a,nn.Conv2d)):
loss += lambda_reg * reg_loss(combo_fn(layer_a.weight,layer_b.weight),layer_c.weight)
if (layer_a.bias is not None):
loss += lambda_reg * reg_loss(combo_fn(layer_a.bias, layer_b.bias), layer_c.bias)
# Update loss
sum_loss[split] += loss.item()
# Check parameter update
if split == "train":
# Compute gradients
loss.backward()
# Optimize
optimizer.step()
# Compute accuracy
#https://discuss.pytorch.org/t/bcewithlogitsloss-and-model-accuracy-calculation/59293/ 2
#pred_labels_a = (pred_a >= 0.0).long() # Binarize predictions to 0 and 1
#pred_labels_b = (pred_b >= 0.0).long() # Binarize predictions to 0 and 1
#pred_labels_c = (pred_c >= 0.0).long() # Binarize predictions to 0 and 1
#print(pred_a.shape)
_,pred_label_a = torch.max(pred_a, dim = 1)
pred_labels_a = (pred_label_a == labels_a).float()
_,pred_label_b = torch.max(pred_b, dim = 1)
pred_labels_b = (pred_label_b == labels_b).float()
_,pred_label_c = torch.max(pred_c, dim = 1)
pred_labels_c = (pred_label_c == labels).float()
batch_accuracy_a = pred_labels_a.sum().item() / len(labels_a)
batch_accuracy_b = pred_labels_b.sum().item() / len(labels_b)
batch_accuracy_c = pred_labels_c.sum().item() / len(labels)
# Update accuracy
sum_accuracy[split][0] += batch_accuracy_a
sum_accuracy[split][1] += batch_accuracy_b
sum_accuracy[split][2] += batch_accuracy_c
if (split=='train'):
progbar.update(j, ta=batch_accuracy_c)
if (progbar is not None):
progbar.finish()
# Compute epoch loss/accuracy
epoch_loss = {split: sum_loss[split] / len(loaders[split][0]) for split in ["train", "val", "test"]}
epoch_accuracy = {split: [sum_accuracy[split][i] / len(loaders[split][0]) for i in range(len(sum_accuracy[split])) ] for split in ["train", "val", "test"]}
print(f"Epoch {epoch + 1}:")
# Update history
for split in ["train", "val", "test"]:
history_loss[split].append(epoch_loss[split])
history_accuracy[split].append(epoch_accuracy[split])
# Print info
print(f"\t{split}\tLoss: {epoch_loss[split]:0.5}\tVGG 1:{epoch_accuracy[split][0]:0.5}"
f"\tVGG 2:{epoch_accuracy[split][1]:0.5}\tVGG *:{epoch_accuracy[split][2]:0.5}")
if save_param:
torch.save({'vgg_a':nets[0].state_dict(),'vgg_b':nets[1].state_dict(),'vgg_star':nets[2].state_dict(),'classifier':nets[3].state_dict()},f'{model_name}.pth')
print(f"Accuracy test VGGA: {test(nets[0], nets[3], test_loader_all):0.5}")
print(f"Accuracy test VGGB: {test(nets[1], nets[3], test_loader_all):0.5}")
print(f"Accuracy test VGG*: {test(nets[2], nets[3], test_loader_all):0.5}")
summed_state_dict = OrderedDict()
for key in nets[2].state_dict():
if key.find('conv') >=0:
#print(key)
summed_state_dict[key] = combo_fn(nets[0].state_dict()[key],nets[1].state_dict()[key])
else:
summed_state_dict[key] = nets[2].state_dict()[key]
nets[2].load_state_dict(summed_state_dict)
accuracy_star = test(nets[2], nets[3], test_loader_all)
print(f"Accuracy test VGGSTAR: {accuracy_star:0.5}")
history_test.append(accuracy_star)
# Store params at the best validation accuracy
if save_param and accuracy_star > best_accuracy:
# torch.save(net.state_dict(), f"{net.__class__.__name__}_best_val.pth")
torch.save({'vgg_a':nets[0].state_dict(),'classifier':nets[3].state_dict()}, f"{model_name}_best_test.pth")
best_accuracy = accuracy_star
print(f"Best accuracy test is: {best_accuracy:0.5}")
# Plot accuracy
plt.title("Accuracy VGGSTAR over epochs")
plt.plot(history_test)
#plt.legend()
plt.show()
```
MNIST
```
root_dir = './'
rescale_data = transforms.Lambda(lambda x : x/255)
# Compose transformations
data_transform = transforms.Compose([
transforms.Resize(32),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
rescale_data,
#transforms.Normalize((-0.7376), (0.5795))
])
test_transform = transforms.Compose([
transforms.Resize(32),
transforms.ToTensor(),
rescale_data,
#transforms.Normalize((0.1327), (0.2919))
])
# Load MNIST dataset with transforms
train_set = torchvision.datasets.MNIST(root=root_dir, train=True, download=True, transform=data_transform)
test_set = torchvision.datasets.MNIST(root=root_dir, train=False, download=True, transform=test_transform)
# Dataset len
num_train = len(train_set)
num_test = len(test_set)
print(f"Num. training samples: {num_train}")
print(f"Num. test samples: {num_test}")
train_idx = np.random.permutation(np.arange(len(train_set)))
test_idx = np.arange(len(test_set))
# Fraction of the original train set that we want to use as validation set
val_frac = 0.1
# Number of samples of the validation set
num_val = int(num_train * val_frac)
num_train = num_train - num_val
# Split training set
val_idx = train_idx[num_train:]
train_idx = train_idx[:num_train]
print(f"{num_train} samples used as train set")
print(f"{num_val} samples used as val set")
print(f"{len(test_set)} samples used as test set")
val_set_a = Subset(train_set, val_idx)
train_set_a = Subset(train_set, train_idx)
test_set_a = test_set
```
MNIST PERTURBATO
```
root_dir = './'
rescale_data = transforms.Lambda(lambda x : x/255)
class AddGaussianNoise(object):
def __init__(self, mean=0., std=1.):
self.std = std
self.mean = mean
def __call__(self, tensor):
return tensor + torch.randn(tensor.size()) * self.std + self.mean
def __repr__(self):
return self.__class__.__name__ + '(mean={0}, std={1})'.format(self.mean, self.std)
# Compose transformations
data_transform = transforms.Compose([
transforms.Resize(32),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
AddGaussianNoise(0., 0.2),
rescale_data,
])
test_transform = transforms.Compose([
transforms.Resize(32),
transforms.ToTensor(),
AddGaussianNoise(0., 0.2),
rescale_data,
])
# Load MNIST dataset with transforms
train_set = torchvision.datasets.MNIST(root=root_dir, train=True, download=True, transform=data_transform)
test_set = torchvision.datasets.MNIST(root=root_dir, train=False, download=True, transform=test_transform)
# Dataset len
num_train = len(train_set)
num_test = len(test_set)
print(f"Num. training samples: {num_train}")
print(f"Num. test samples: {num_test}")
train_idx = np.random.permutation(np.arange(len(train_set)))
test_idx = np.arange(len(test_set))
# Fraction of the original train set that we want to use as validation set
val_frac = 0.1
# Number of samples of the validation set
num_val = int(num_train * val_frac)
num_train = num_train - num_val
# Split training set
val_idx = train_idx[num_train:]
train_idx = train_idx[:num_train]
print(f"{num_train} samples used as train set")
print(f"{num_val} samples used as val set")
print(f"{len(test_set)} samples used as test set")
val_set_b = Subset(train_set, val_idx)
train_set_b = Subset(train_set, train_idx)
test_set_b = test_set
test_set = torch.utils.data.ConcatDataset([test_set_a, test_set_b])
# Define loaders
train_loader_a = DataLoader(train_set_a, batch_size=128, num_workers=0, shuffle=True, drop_last=True)
val_loader_a = DataLoader(val_set_a, batch_size=128, num_workers=0, shuffle=False, drop_last=False)
test_loader_a = DataLoader(test_set_a, batch_size=128, num_workers=0, shuffle=False, drop_last=False)
train_loader_b = DataLoader(train_set_b, batch_size=128, num_workers=0, shuffle=True, drop_last=True)
val_loader_b = DataLoader(val_set_b, batch_size=128, num_workers=0, shuffle=False, drop_last=False)
test_loader_b = DataLoader(test_set_b, batch_size=128, num_workers=0, shuffle=False, drop_last=False)
test_loader_all = DataLoader(test_set,batch_size=128, num_workers=0,shuffle=False,drop_last=False)
# Define dictionary of loaders
loaders = {"train": [train_loader_a,train_loader_b],
"val": [val_loader_a,val_loader_b],
"test": [test_loader_a,test_loader_b]}
image, label = train_set_a[1]
plt.imshow(image.squeeze(), cmap='gray')
print('Label:', label)
image, label = train_set_b[7]
plt.imshow(image.squeeze(), cmap='gray')
print('Label:', label)
model1 = VGG16((1,32,32),batch_norm=True)
model2 = VGG16((1,32,32),batch_norm=True)
model3 = VGG16((1,32,32),batch_norm=True)
classifier = Classifier(num_classes=10)
nets = [model1,model2,model3,classifier]
dev = torch.device('cuda')
parameters = set()
for n in nets:
parameters |= set(n.parameters())
optimizer = torch.optim.SGD(parameters, lr = 0.01)
# Define a loss
#criterion = nn.BCEWithLogitsLoss()#,nn.BCEWithLogitsLoss(),nn.BCEWithLogitsLoss(),_lambda = 1)
criterion = nn.CrossEntropyLoss()
n_params = 0
DO = 'TRAIN'
if (DO=='TRAIN'):
train(nets, loaders, optimizer, criterion, epochs=50, dev=dev,save_param=True)
else:
state_dicts = torch.load('model.pth')
model1.load_state_dict(state_dicts['vgg_a']) #questi state_dict vengono dalla funzione di training
model2.load_state_dict(state_dicts['vgg_b'])
model3.load_state_dict(state_dicts['vgg_star'])
classifier.load_state_dict(state_dicts['classifier'])
test(model1,classifier,test_loader_all)
test(model2, classifier, test_loader_all)
test(model3, classifier, test_loader_all)
summed_state_dict = OrderedDict()
for key in state_dicts['vgg_star']:
if key.find('conv') >=0:
print(key)
summed_state_dict[key] = combo_fn(state_dicts['vgg_a'][key],state_dicts['vgg_b'][key])
else:
summed_state_dict[key] = state_dicts['vgg_star'][key]
model3.load_state_dict(summed_state_dict)
test(model3, classifier, test_loader_all)
```
Now you can download federated_mnist_best_test.pth
|
github_jupyter
|
## Quaxis Corporation for Research & Innovation 2020
### Written by: JP Aldama
#### MIT License, feel free to do whatever you want with this code.
### Goal: Object detection using opencv-python and numpy.
***Requirements: opencv-python, numpy. It is highly recommended to install Anaconda for python 3.x. Using cv2 we will detect objects. For best results use still video (no camera movement).***
#### Step 1: Import required libraries. Install opencv-python and numpy.
***pip install opencv-python numpy***
```
import cv2
import numpy as np
```
#### Step 2: Path to video source and invoke VideoCapture using source video.
```
SOURCE = 'data/qxdatasets/test_videos/walk_australia_372020.mp4'
capture = cv2.VideoCapture(SOURCE)
```
#### Step 3: Read first and second frame.
```
ret, frame1 = capture.read()
ret, frame2 = capture.read()
```
#### Step 4: The main loop
***4a: Calculate the absolute difference between frame1 and frame2.
4b: Convert frames to grayscale.
4c: Apply Gaussian blur to the grayscale frames.
4d: Set a threshold.
4e: Apply dilation, find contours.
4f: For each contour found in frames apply bounding rectangles to each contour found in total contours.
4g: If movement is detected, display text on screen. If no movement is detected remove the text
4h: Show the video
4i: If 'q' is pressed, terminate the main loop and exit program.***
```
# KNOWN BUG: Program freezes if you try to exit the program.
# Do not worry, this only applies if you are using Jupyter Notebook.
# Just code in your IDE and everything will be fine.
while capture.isOpened():
difference = cv2.absdiff(frame1, frame2)
grayscale = cv2.cvtColor(difference, cv2.COLOR_BGR2GRAY)
blur = cv2.GaussianBlur(grayscale, (5,5), 0)
_, threshold = cv2.threshold(blur, 30, 255, cv2.THRESH_BINARY)
dilated = cv2.dilate(threshold, None, iterations=1)
contours, _ = cv2.findContours(dilated, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
for contour in contours:
(x,y,w,h) = cv2.boundingRect(contour)
if cv2.contourArea(contour) < 1300:
continue
cv2.rectangle(frame1, (x,y), (x+w,y+h),(255,0,255), 2)
cv2.putText(frame1, 'STATUS: {}'.format('MOVEMENT!'),(10,50),cv2.FONT_HERSHEY_SIMPLEX,
1,(0,255,0), 2)
cv2.imshow('video', frame1)
frame1 = frame2
ret, frame2 = capture.read()
key = cv2.waitKey(1) & 0xFF
if key == ord('q'):
break
```
#### Step 5: Close the video and exit the program.
```
capture.release()
cv2.destroyAllWindows()
```
### Conclusion:
***We have implemented very basic object detection using opencv-python. You can further adjust thresholds so you may 'tune' your threshold. Try extreme values so you can see the difference and learn how to enhance its functionality.***
|
github_jupyter
|
<table>
<tr><td><img style="height: 150px;" src="images/geo_hydro1.jpg"></td>
<td bgcolor="#FFFFFF">
<p style="font-size: xx-large; font-weight: 900; line-height: 100%">AG Dynamics of the Earth</p>
<p style="font-size: large; color: rgba(0,0,0,0.5);">Jupyter notebooks</p>
<p style="font-size: large; color: rgba(0,0,0,0.5);">Georg Kaufmann</p>
</td>
</tr>
</table>
# Dynamic systems: 5. Gravity
## Spherical harmonics
---
*Georg Kaufmann,
Geophysics Section,
Institute of Geological Sciences,
Freie Universität Berlin,
Germany*
In this notebook, we introduce **spherical harmonics** as function space.
We discuss:
- **Legendre** polynomials $P_n$
- **Associated Legendre** polynomials $P_{nm}$
- **Spherical harmonics** $Y_{nm}$
We start importing libraries first:
```
import matplotlib.pyplot as plt
import numpy as np
import math
from scipy.special import lpn,lpmn
from scipy.special import sph_harm
```
----
## Legendre polynomials
We refer to the recursive equation for Legendre polynomials, defined on $x \in [-1,1]$:
$$
P_n(x) = -\frac{n-1}{n} P_{n-2}(x)
+\frac{2n-1}{n} x P_{n-1}(x),
$$
where we have to know the first two polynomials:
$$
\begin{array}{rcl}
P_0(x) &=& 1 \\
P_1(x) &=& x
\end{array}
$$
We start defining the array for the argument $x$, then we call the function `lpn` from
the `scipy.special` package for degree $n \in [0,n_{max}]$.
```
nmax = 5
x = np.linspace(-1,1,51)
Pn = np.zeros(len(x)*(nmax+1)).reshape(nmax+1,len(x))
print(Pn.shape)
for i in range(len(x)):
tmp = lpn(nmax,x[i])
for n in range(nmax+1):
Pn[n,i] = tmp[0][n]
plt.figure(figsize=(10,6))
plt.xlim([-1.1,1.1])
plt.ylim([-1.1,1.1])
plt.xlabel('x')
plt.ylabel('P$_{n}$(x)')
plt.grid(linestyle='--')
for n in range(nmax+1):
plt.plot(x,Pn[n,:],linewidth=3,label='P$_{'+str(n)+'}$')
plt.legend()
```
----
## Associated Legendre polynomials
Next, we refer to the **associated Legendre Polynomials**, $P_n^m(x)$ with the
recursive equation:
$$
(n-m+1) P_{n+1}^{m}(x) = (2n+1) x P_{n}^{m}(x) - (l+m) P_{n-1}^{m}(x)
$$
We normalize the calculated associated Legendre polynomials:
$$
P_{nm} = \sqrt{2n+1} \frac{(n-m)!}{(n+m)!} P_n^m
$$
```
nmax = 5
mmax = nmax
x = np.linspace(-1,1,101)
Pnm = np.zeros(len(x)*(nmax+1)*(mmax+1)).reshape(nmax+1,mmax+1,len(x))
print(Pnm.shape)
for i in range(len(x)):
tmp = lpmn(mmax,nmax,x[i])
for n in range(nmax+1):
for m in range(nmax+1):
#print(n,m)
if (m == 0):
norm = np.sqrt(2*(2*n+1))
elif (m > n):
norm = 0.
else:
norm = np.sqrt((2*n+1)*math.factorial(n-m)/math.factorial(n+m))
Pnm[n,m,i] = norm*tmp[0][m,n]
plt.figure(figsize=(10,6))
plt.xlim([-1.1,1.1])
plt.ylim([-3,3])
plt.xlabel('x')
plt.ylabel('P$_{nm}$(x)')
plt.grid(linestyle='--')
n = nmax
for m in range(n+1):
plt.plot(x,Pnm[n,m,:],linewidth=3,label='P$_{'+str(n)+str(m)+'}$')
plt.legend()
```
----
## Spherical harmonics
$$
Y_{nm}(\vartheta,\Phi) = \sqrt{\frac{2n+1}{4\pi} \frac{(n-m)!}{(n+m)!}} P_n^m(\cos\vartheta) e^{im \Phi}
$$
with
- $\Theta \in [90,-90]$ latitude
- $\vartheta \in [0,180]$ co-latitude
- $\Phi \in [0,360]$ longitude
Note: $x=\cos(\vartheta)$.
Note: **Latitude** $\Theta$ and **Co-latitude** $\vartheta$ are (roughly) related through:
$$
\Theta = 90 - \vartheta
$$
```
# define coordinates
d2r = np.pi/180.
dlong = 101 #21
dcolat = 51 #11
colat = np.linspace(0, np.pi, dcolat)
long = np.linspace(0, 2*np.pi, dlong)
colat, long = np.meshgrid(colat, long)
print(colat.shape)
n=2;m=0
Ynm = sph_harm(m, n, long, colat)
fig,axs = plt.subplots(2,1,figsize=(10,10))
axs[0].set_title('P$_{'+str(n)+str(m)+'}(\\theta) cos(\\phi)$')
axs[0].set_ylabel('Latitude [$^{\circ}$]')
axs[0].contourf(long/d2r,90-colat/d2r,Ynm.real)
axs[1].set_title('P$_{'+str(n)+str(m)+'}(\\theta) sin(\\phi)$')
axs[1].contourf(long/d2r,90-colat/d2r,Ynm.imag)
axs[1].set_xlabel('Longitude [$^{\circ}$]')
axs[1].set_ylabel('Latitude [$^{\circ}$]')
n=2;m=1
Ynm = sph_harm(m, n, long, colat)
fig,axs = plt.subplots(2,1,figsize=(10,10))
axs[0].set_title('P$_{'+str(n)+str(m)+'}(\\theta) cos(\\phi)$')
axs[0].set_ylabel('Latitude [$^{\circ}$]')
axs[0].contourf(long/d2r,90-colat/d2r,Ynm.real)
axs[1].set_title('P$_{'+str(n)+str(m)+'}(\\theta) sin(\\phi)$')
axs[1].contourf(long/d2r,90-colat/d2r,Ynm.imag)
axs[1].set_xlabel('Longitude [$^{\circ}$]')
axs[1].set_ylabel('Latitude [$^{\circ}$]')
n=2;m=2
Ynm = sph_harm(m, n, long, colat)
fig,axs = plt.subplots(2,1,figsize=(10,10))
axs[0].set_title('P$_{'+str(n)+str(m)+'}(\\theta) cos(\\phi)$')
axs[0].set_ylabel('Latitude [$^{\circ}$]')
axs[0].contourf(long/d2r,90-colat/d2r,Ynm.real)
axs[1].set_title('P$_{'+str(n)+str(m)+'}(\\theta) sin(\\phi)$')
axs[1].contourf(long/d2r,90-colat/d2r,Ynm.imag)
axs[1].set_xlabel('Longitude [$^{\circ}$]')
axs[1].set_ylabel('Latitude [$^{\circ}$]')
```
... done
|
github_jupyter
|

## Amazon Access Samples Data Set
Let's apply our boosting algorithm to a real dataset! We are going to use the __Amazon Access Samples dataset__.
We download this dataset from UCI ML repository from this [link](https://archive.ics.uci.edu/ml/datasets/Amazon+Access+Samples). Dua, D. and Graff, C. (2019). [UCI Machine Learning Repository](http://archive.ics.uci.edu/ml). Irvine, CA: University of California, School of Information and Computer Science.
__Dataset description:__
Employees need to request certain resources to fulfill their daily duties. This data consists of anonymized historical data of employee IT access requests. Data fields look like this:
#### Column Descriptions
* __ACTION__: 1 if the resource was approved, 0 if not.
* __RESOURCE__: An ID for each resource
* __PERSON_MGR_ID__: ID of the user's manager
* __PERSON_ROLLUP_1__: User grouping ID
* __PERSON_ROLLUP_2__: User grouping ID
* __PERSON_BUSINESS_TITLE__: Title ID
* __PERSON_JOB_FAMILY__: Job family ID
* __PERSON_JOB_CODE__: Job code ID
Our task is to build a machine learning model that can automatically provision an employee's access to company resources given employee profile information and the resource requested.
### 1. Download and process the dataset
In this section, we will download our dataset and process it. It consists of two files, we will run the following code cells to get our dataset as a single file at the end. One of the files is large (4.8GB), so make sure you have enough storage.
```
! wget https://archive.ics.uci.edu/ml/machine-learning-databases/00216/amzn-anon-access-samples.tgz
! tar -zxvf amzn-anon-access-samples.tgz
```
We have the following files:
* __amzn-anon-access-samples-2.0.csv__: Employee profile data.
* __amzn-anon-access-samples-history-2.0.csv__: Resource provision history
Below, we first read the amzn-anon-access-samples-2.0.csv file (it is a large file) and use some employee fields.
```
import pandas as pd
import random
person_fields = ["PERSON_ID", "PERSON_MGR_ID",
"PERSON_ROLLUP_1", "PERSON_ROLLUP_2",
"PERSON_DEPTNAME", "PERSON_BUSINESS_TITLE",
"PERSON_JOB_FAMILY", "PERSON_JOB_CODE"]
people = {}
for chunk in pd.read_csv('amzn-anon-access-samples-2.0.csv', usecols = person_fields, chunksize=5000):
for index, row in chunk.iterrows():
people[row["PERSON_ID"]] = [row["PERSON_MGR_ID"], row["PERSON_ROLLUP_1"],
row["PERSON_ROLLUP_2"], row["PERSON_DEPTNAME"],
row["PERSON_BUSINESS_TITLE"], row["PERSON_JOB_FAMILY"],
row["PERSON_JOB_CODE"]]
```
Now, let's read the resource provision history file. Here, we will create our dataset. We will read the add access and remove access actions and save them.
```
add_access_data = []
remove_access_data = []
df = pd.read_csv('amzn-anon-access-samples-history-2.0.csv')
# Loop through unique logins (employee ids)
for login in df["LOGIN"].unique():
login_df = df[df["LOGIN"]==login].copy()
# Save actions
for target in login_df["TARGET_NAME"].unique():
login_target_df = login_df[login_df["TARGET_NAME"]==target]
unique_actions = login_target_df["ACTION"].unique()
if((len(unique_actions)==1) and (unique_actions[0]=="remove_access")):
remove_access_data.append([0, target] + people[login])
elif((len(unique_actions)==1) and (unique_actions[0]=="add_access")):
add_access_data.append([1, target] + people[login])
# Create random seed
random.seed(30)
# We will use only 8000 random add_access data
add_access_data = random.sample(add_access_data, 8000)
# Add them together
data = add_access_data + remove_access_data
# Let's shuffle it
random.shuffle(data)
```
Let's save this data so that we can use it later
```
df = pd.DataFrame(data, columns=["ACTION", "RESOURCE",
"MGR_ID", "ROLLUP_1",
"ROLLUP_2", "DEPTNAME",
"BUSINESS_TITLE", "JOB_FAMILY",
"JOB_CODE"])
df.to_csv("data.csv", index=False)
```
Here is how our data look like:
```
df.head()
# Delete the downloaded files
! rm amzn-anon-access-samples-2.0.csv amzn-anon-access-samples-history-2.0.csv amzn-anon-access-samples.tgz
```
### 2. LightGBM
Let's use LightGBM on this dataset.
```
! pip install -q lightgbm
```
Let's read the dataset
```
import pandas as pd
import numpy as np
data = pd.read_csv("data.csv")
data.head()
data.info()
data["ACTION"].value_counts()
```
We will fix the column types below to make sure they are handled as categorical variables.
```
from sklearn.model_selection import train_test_split
y = data["ACTION"].values
X = data.drop(columns='ACTION')
for c in X.columns:
X[c] = X[c].astype('category')
X_train, X_valid, y_train, y_valid = train_test_split(X,
y,
test_size=0.15,
random_state=136,
stratify=y
)
```
Let's fit the lightGBM model below.
```
import lightgbm as lgb
# Create dataset for lightgbm
lgb_train = lgb.Dataset(X_train, y_train)
lgb_eval = lgb.Dataset(X_valid, y_valid, reference=lgb_train)
# Let's see our parameters
# boosting_type (string, optional (default='gbdt'))
# ‘gbdt’, traditional Gradient Boosting Decision Tree.
# ‘dart’, Dropouts meet Multiple Additive Regression Trees.
# ‘goss’, Gradient-based One-Side Sampling.
# ‘rf’, Random Forest.
params = {
'boosting_type': 'gbdt',
'objective': 'binary', # ‘regression’ for LGBMRegressor, ‘binary’ or ‘multiclass’ for LGBMClassifier
'metric': ['auc'],
'n_estimators': 50, # We can change it, by default 100
'learning_rate': 0.1, # Default 0.1
'num_iterations': 1000, # Default 100
'is_unbalance': True, # Used to fix the class imbalance in the dataset
'verbose': 1
}
#Train
gbm = lgb.train(params,
lgb_train,
valid_sets=lgb_eval,
early_stopping_rounds=20
)
```
Let's see the overall performance on validation set.
```
from sklearn.metrics import classification_report
y_pred = gbm.predict(X_valid, num_iteration=gbm.best_iteration)
print(classification_report(y_valid, np.round(y_pred)))
```
|
github_jupyter
|
## Preprocessing
```
# Import our dependencies
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import pandas as pd
import tensorflow as tf
# Import and read the charity_data.csv.
import pandas as pd
application_df = pd.read_csv("/Users/melissa/Downloads/Deep Learning Hw/Resources /charity_data.csv")
application_df.head()
# Drop the non-beneficial ID columns, 'EIN' and 'NAME'.
application_df = application_df.drop(['EIN', 'NAME', 'STATUS'], axis=1)
# Determine the number of unique values in each column.
print(application_df.nunique())
# Look at APPLICATION_TYPE value counts for binning
app_vc = application_df['APPLICATION_TYPE'].value_counts()
app_vc
# Choose a cutoff value and create a list of application types to be replaced
# use the variable name `application_types_to_replace`
application_types_to_replace = app_vc[app_vc < 50].index
# Replace in dataframe
for app in application_types_to_replace:
application_df['APPLICATION_TYPE'] = application_df['APPLICATION_TYPE'].replace(app,"Other")
# Check to make sure binning was successful
application_df['APPLICATION_TYPE'].value_counts()
# Look at CLASSIFICATION value counts for binning
class_vc = application_df['CLASSIFICATION'].value_counts()
class_vc
# You may find it helpful to look at CLASSIFICATION value counts >1
class_vc_1 = class_vc[class_vc > 1]
class_vc_1
# Choose a cutoff value and create a list of classifications to be replaced
# use the variable name `classifications_to_replace`
classifications_to_replace = class_vc[class_vc < 500].index
# Replace in dataframe
for cls in classifications_to_replace:
application_df['CLASSIFICATION'] = application_df['CLASSIFICATION'].replace(cls,"Other")
# Check to make sure binning was successful
application_df['CLASSIFICATION'].value_counts()
# Convert categorical data to numeric with `pd.get_dummies`
df = pd.get_dummies(application_df)
print(df.columns)
# Split our preprocessed data into our features and target arrays
y = df["IS_SUCCESSFUL"].values
X = df.drop(columns=['IS_SUCCESSFUL']).values
# Split the preprocessed data into a training and testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42, stratify=y)
# Create a StandardScaler instances
scaler = StandardScaler()
# Fit the StandardScaler
X_scaler = scaler.fit(X_train)
# Scale the data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
```
## Compile, Train and Evaluate the Model
```
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
number_input_features = len(X_train[0])
hidden_nodes_layer1 = 100
hidden_nodes_layer2 = 70
hidden_nodes_layer2 = 40
nn = tf.keras.models.Sequential()
# First hidden layer
nn.add(
tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=number_input_features, activation="relu")
)
# Second hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation="relu"))
# third layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation="softplus"))
# output layer
nn.add(tf.keras.layers.Dense(units=1, activation="tanh"))
# Check the structure of the model
nn.summary()
# Compile the model
nn.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
# Train the model
fit_model = nn.fit(X_train_scaled,y_train,epochs=40)
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export our model to HDF5 file
nn.save('AlphabetSoupCharity_Optimization.h5')
```
|
github_jupyter
|
# ML Scripts
So far, we've done everything inside the Jupyter notebooks but we're going to now move our code into individual python scripts. We will lay out the code that needs to be inside each script but checkout the `API` lesson to see how it all comes together.
<div align="left">
<a href="https://github.com/madewithml/lessons/blob/master/notebooks/03_APIs/02_ML_Scripts/02_PT_ML_Scripts.ipynb" role="button"><img class="notebook-badge-image" src="https://img.shields.io/static/v1?label=&message=View%20On%20GitHub&color=586069&logo=github&labelColor=2f363d"></a>
<a href="https://colab.research.google.com/github/madewithml/lessons/blob/master/notebooks/03_APIs/02_ML_Scripts/02_PT_ML_Scripts.ipynb"><img class="notebook-badge-image" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"></a>
</div>
# data.py
## Load data
```
import numpy as np
import pandas as pd
import random
import urllib
SEED = 1234
DATA_FILE = 'news.csv'
INPUT_FEATURE = 'title'
OUTPUT_FEATURE = 'category'
# Set seed for reproducibility
np.random.seed(SEED)
random.seed(SEED)
# Load data from GitHub to notebook's local drive
url = "https://raw.githubusercontent.com/madewithml/lessons/master/data/news.csv"
response = urllib.request.urlopen(url)
html = response.read()
with open(DATA_FILE, 'wb') as fp:
fp.write(html)
# Load data
df = pd.read_csv(DATA_FILE, header=0)
X = df[INPUT_FEATURE].values
y = df[OUTPUT_FEATURE].values
df.head(5)
```
## Preprocessing
```
import re
LOWER = True
FILTERS = r"[!\"'#$%&()*\+,-./:;<=>?@\\\[\]^_`{|}~]"
def preprocess_texts(texts, lower, filters):
preprocessed_texts = []
for text in texts:
if lower:
text = ' '.join(word.lower() for word in text.split(" "))
text = re.sub(r"([.,!?])", r" \1 ", text)
text = re.sub(filters, r"", text)
text = re.sub(' +', ' ', text) # remove multiple spaces
text = text.strip()
preprocessed_texts.append(text)
return preprocessed_texts
original_text = X[0]
X = np.array(preprocess_texts(X, lower=LOWER, filters=FILTERS))
print (f"{original_text} → {X[0]}")
```
## Split data
```
import collections
from sklearn.model_selection import train_test_split
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
SHUFFLE = True
def train_val_test_split(X, y, val_size, test_size, shuffle):
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, stratify=y, shuffle=shuffle)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=val_size, stratify=y_train, shuffle=shuffle)
return X_train, X_val, X_test, y_train, y_val, y_test
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
class_counts = dict(collections.Counter(y))
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"{X_train[0]} → {y_train[0]}")
print (f"Classes: {class_counts}")
```
# tokenizers.py
## Tokenizer
```
import json
import re
SEPARATOR = ' ' # word level
class Tokenizer(object):
def __init__(self, separator, pad_token='<PAD>', oov_token='<UNK>',
token_to_index={'<PAD>': 0, '<UNK>': 1}):
self.separator = separator
self.oov_token = oov_token
self.token_to_index = token_to_index
self.index_to_token = {v: k for k, v in self.token_to_index.items()}
def __len__(self):
return len(self.token_to_index)
def __str__(self):
return f"<Tokenizer(num_tokens={len(self)})>"
def fit_on_texts(self, texts):
for text in texts:
for token in text.split(self.separator):
if token not in self.token_to_index:
index = len(self)
self.token_to_index[token] = index
self.index_to_token[index] = token
return self
def texts_to_sequences(self, texts):
sequences = []
for text in texts:
sequence = []
for token in text.split(self.separator):
sequence.append(self.token_to_index.get(
token, self.token_to_index[self.oov_token]))
sequences.append(sequence)
return sequences
def sequences_to_texts(self, sequences):
texts = []
for sequence in sequences:
text = []
for index in sequence:
text.append(self.index_to_token.get(index, self.oov_token))
texts.append(self.separator.join([token for token in text]))
return texts
def save(self, fp):
with open(fp, 'w') as fp:
contents = {
'separator': self.separator,
'oov_token': self.oov_token,
'token_to_index': self.token_to_index
}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Input vectorizer
X_tokenizer = Tokenizer(separator=SEPARATOR)
X_tokenizer.fit_on_texts(texts=X_train)
vocab_size = len(X_tokenizer)
print (X_tokenizer)
# Convert text to sequence of tokens
original_text = X_train[0]
X_train = np.array(X_tokenizer.texts_to_sequences(X_train))
X_val = np.array(X_tokenizer.texts_to_sequences(X_val))
X_test = np.array(X_tokenizer.texts_to_sequences(X_test))
preprocessed_text = X_tokenizer.sequences_to_texts([X_train[0]])
print (f"{original_text} \n\t→ {preprocessed_text} \n\t→ {X_train[0]}")
# Save tokenizer
X_tokenizer.save(fp='X_tokenizer.json')
# Load tokenizer
X_tokenizer = Tokenizer.load(fp='X_tokenizer.json')
print (X_tokenizer)
```
## Label Encoder
```
class LabelEncoder(object):
def __init__(self, class_to_index={}):
self.class_to_index = class_to_index
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
def __len__(self):
return len(self.class_to_index)
def __str__(self):
return f"<LabelEncoder(num_classes={len(self)})>"
def fit(self, y_train):
for i, class_ in enumerate(np.unique(y_train)):
self.class_to_index[class_] = i
self.index_to_class = {v: k for k, v in self.class_to_index.items()}
self.classes = list(self.class_to_index.keys())
return self
def transform(self, y):
return np.array([self.class_to_index[class_] for class_ in y])
def decode(self, index):
return self.index_to_class.get(index, None)
def save(self, fp):
with open(fp, 'w') as fp:
contents = {
'class_to_index': self.class_to_index
}
json.dump(contents, fp, indent=4, sort_keys=False)
@classmethod
def load(cls, fp):
with open(fp, 'r') as fp:
kwargs = json.load(fp=fp)
return cls(**kwargs)
# Output vectorizer
y_tokenizer = LabelEncoder()
# Fit on train data
y_tokenizer = y_tokenizer.fit(y_train)
print (y_tokenizer)
classes = y_tokenizer.classes
print (f"classes: {classes}")
# Convert labels to tokens
class_ = y_train[0]
y_train = y_tokenizer.transform(y_train)
y_val = y_tokenizer.transform(y_val)
y_test = y_tokenizer.transform(y_test)
print (f"{class_} → {y_train[0]}")
# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"class counts: {counts},\nclass weights: {class_weights}")
# Save label encoder
y_tokenizer.save(fp='y_tokenizer.json')
# Load label encoder
y_tokenizer = LabelEncoder.load(fp='y_tokenizer.json')
print (y_tokenizer)
```
# datasets.py
```
import math
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
BATCH_SIZE = 128
FILTER_SIZES = [2, 3, 4]
# Set seed for reproducibility
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.cuda.manual_seed_all(SEED) # multi-GPU.
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
USE_CUDA = True
DEVICE = torch.device('cuda' if (torch.cuda.is_available() and USE_CUDA) else 'cpu')
print (DEVICE)
```
## Pad
```
def pad_sequences(X, max_seq_len):
sequences = np.zeros((len(X), max_seq_len))
for i, sequence in enumerate(X):
sequences[i][:len(sequence)] = sequence
return sequences
# Pad sequences
inputs = [[1,2,3], [1,2,3,4], [1,2]]
max_seq_len = max(len(x) for x in inputs)
padded_inputs = pad_sequences(X=inputs, max_seq_len=max_seq_len)
print (padded_inputs.shape)
print (padded_inputs)
```
## Dataset
```
class TextDataset(Dataset):
def __init__(self, X, y, batch_size, max_filter_size):
self.X = X
self.y = y
self.batch_size = batch_size
self.max_filter_size = max_filter_size
def __len__(self):
return len(self.y)
def __str__(self):
return f"<Dataset(N={len(self)}, batch_size={self.batch_size}, num_batches={self.get_num_batches()})>"
def __getitem__(self, index):
X = self.X[index]
y = self.y[index]
return X, y
def get_num_batches(self):
return math.ceil(len(self)/self.batch_size)
def collate_fn(self, batch):
"""Processing on a batch."""
# Get inputs
X = np.array(batch)[:, 0]
y = np.array(batch)[:, 1]
# Pad inputs
max_seq_len = max(self.max_filter_size, max([len(x) for x in X]))
X = pad_sequences(X=X, max_seq_len=max_seq_len)
return X, y
def generate_batches(self, shuffle=False, drop_last=False):
dataloader = DataLoader(dataset=self, batch_size=self.batch_size,
collate_fn=self.collate_fn, shuffle=shuffle,
drop_last=drop_last, pin_memory=True)
for (X, y) in dataloader:
X = torch.LongTensor(X.astype(np.int32))
y = torch.LongTensor(y.astype(np.int32))
yield X, y
# Create datasets
train_set = TextDataset(X=X_train, y=y_train, batch_size=BATCH_SIZE, max_filter_size=max(FILTER_SIZES))
val_set = TextDataset(X=X_val, y=y_val, batch_size=BATCH_SIZE, max_filter_size=max(FILTER_SIZES))
test_set = TextDataset(X=X_test, y=y_test, batch_size=BATCH_SIZE, max_filter_size=max(FILTER_SIZES))
print (train_set)
print (train_set[0])
# Generate batch
batch_X, batch_y = next(iter(test_set.generate_batches()))
print (batch_X.shape)
print (batch_y.shape)
```
# utils.py
## Embeddings
```
from io import BytesIO
from urllib.request import urlopen
from zipfile import ZipFile
EMBEDDING_DIM = 100
def load_glove_embeddings(embeddings_file):
"""Load embeddings from a file."""
embeddings = {}
with open(embeddings_file, "r") as fp:
for index, line in enumerate(fp):
values = line.split()
word = values[0]
embedding = np.asarray(values[1:], dtype='float32')
embeddings[word] = embedding
return embeddings
def make_embeddings_matrix(embeddings, token_to_index, embedding_dim):
"""Create embeddings matrix to use in Embedding layer."""
embedding_matrix = np.zeros((len(token_to_index), embedding_dim))
for word, i in token_to_index.items():
embedding_vector = embeddings.get(word)
if embedding_vector is not None:
embedding_matrix[i] = embedding_vector
return embedding_matrix
# Unzip the file (may take ~3-5 minutes)
resp = urlopen('http://nlp.stanford.edu/data/glove.6B.zip')
zipfile = ZipFile(BytesIO(resp.read()))
zipfile.namelist()
# Write embeddings to file
embeddings_file = 'glove.6B.{0}d.txt'.format(EMBEDDING_DIM)
zipfile.extract(embeddings_file)
!ls
# Create embeddings
embeddings_file = 'glove.6B.{0}d.txt'.format(EMBEDDING_DIM)
glove_embeddings = load_glove_embeddings(embeddings_file=embeddings_file)
embedding_matrix = make_embeddings_matrix(
embeddings=glove_embeddings, token_to_index=X_tokenizer.token_to_index,
embedding_dim=EMBEDDING_DIM)
print (embedding_matrix.shape)
```
# model.py
## Model
```
import torch.nn.functional as F
NUM_FILTERS = 50
HIDDEN_DIM = 128
DROPOUT_P = 0.1
class TextCNN(nn.Module):
def __init__(self, embedding_dim, vocab_size, num_filters, filter_sizes,
hidden_dim, dropout_p, num_classes, pretrained_embeddings=None,
freeze_embeddings=False, padding_idx=0):
super(TextCNN, self).__init__()
# Initialize embeddings
if pretrained_embeddings is None:
self.embeddings = nn.Embedding(
embedding_dim=embedding_dim, num_embeddings=vocab_size,
padding_idx=padding_idx)
else:
pretrained_embeddings = torch.from_numpy(pretrained_embeddings).float()
self.embeddings = nn.Embedding(
embedding_dim=embedding_dim, num_embeddings=vocab_size,
padding_idx=padding_idx, _weight=pretrained_embeddings)
# Freeze embeddings or not
if freeze_embeddings:
self.embeddings.weight.requires_grad = False
# Conv weights
self.filter_sizes = filter_sizes
self.conv = nn.ModuleList(
[nn.Conv1d(in_channels=embedding_dim,
out_channels=num_filters,
kernel_size=f) for f in filter_sizes])
# FC weights
self.dropout = nn.Dropout(dropout_p)
self.fc1 = nn.Linear(num_filters*len(filter_sizes), hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, x_in, channel_first=False):
# Embed
x_in = self.embeddings(x_in)
if not channel_first:
x_in = x_in.transpose(1, 2) # (N, channels, sequence length)
# Conv + pool
z = []
conv_outputs = [] # for interpretability
max_seq_len = x_in.shape[2]
for i, f in enumerate(self.filter_sizes):
# `SAME` padding
padding_left = int((self.conv[i].stride[0]*(max_seq_len-1) - max_seq_len + self.filter_sizes[i])/2)
padding_right = int(math.ceil((self.conv[i].stride[0]*(max_seq_len-1) - max_seq_len + self.filter_sizes[i])/2))
# Conv + pool
_z = self.conv[i](F.pad(x_in, (padding_left, padding_right)))
conv_outputs.append(_z)
_z = F.max_pool1d(_z, _z.size(2)).squeeze(2)
z.append(_z)
# Concat conv outputs
z = torch.cat(z, 1)
# FC layers
z = self.fc1(z)
z = self.dropout(z)
logits = self.fc2(z)
return conv_outputs, logits
# Initialize model
model = TextCNN(embedding_dim=EMBEDDING_DIM,
vocab_size=vocab_size,
num_filters=NUM_FILTERS,
filter_sizes=FILTER_SIZES,
hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P,
num_classes=len(classes),
pretrained_embeddings=embedding_matrix,
freeze_embeddings=False).to(DEVICE)
print (model.named_parameters)
```
# train.py
## Training
```
from pathlib import Path
from torch.optim import Adam
from torch.optim.lr_scheduler import ReduceLROnPlateau
from torch.utils.tensorboard import SummaryWriter
%load_ext tensorboard
LEARNING_RATE = 1e-4
PATIENCE = 3
NUM_EPOCHS = 100
def train_step(model, device, dataset, optimizer):
"""Train step."""
# Set model to train mode
model.train()
train_loss = 0.
correct = 0
# Iterate over train batches
for i, (X, y) in enumerate(dataset.generate_batches()):
# Set device
X, y = X.to(device), y.to(device)
# Reset gradients
optimizer.zero_grad()
# Forward pass
_, logits = model(X)
# Define loss
loss = F.cross_entropy(logits, y)
# Backward pass
loss.backward()
# Update weights
optimizer.step()
# Metrics
y_pred = logits.max(dim=1)[1]
correct += torch.eq(y_pred, y).sum().item()
train_loss += (loss.item() - train_loss) / (i + 1)
train_acc = 100. * correct / len(dataset)
return train_loss, train_acc
def test_step(model, device, dataset):
"""Validation or test step."""
# Set model to eval mode
model.eval()
loss = 0.
correct = 0
y_preds = []
y_targets = []
# Iterate over val batches
with torch.no_grad():
for i, (X, y) in enumerate(dataset.generate_batches()):
# Set device
X, y = X.to(device), y.to(device)
# Forward pass
_, logits = model(X)
# Metrics
loss += F.cross_entropy(logits, y, reduction='sum').item()
y_pred = logits.max(dim=1)[1]
correct += torch.eq(y_pred, y).sum().item()
# Outputs
y_preds.extend(y_pred.cpu().numpy())
y_targets.extend(y.cpu().numpy())
loss /= len(dataset)
accuracy = 100. * correct / len(dataset)
return y_preds, y_targets, loss, accuracy
def train(model, optimizer, scheduler,
train_set, val_set, test_set, writer):
# Epochs
best_val_loss = np.inf
for epoch in range(NUM_EPOCHS):
# Steps
train_loss, train_acc = train_step(model, DEVICE, train_set, optimizer)
_, _, val_loss, val_acc = test_step(model, DEVICE, val_set)
# Metrics
print (f"Epoch: {epoch} | train_loss: {train_loss:.2f}, train_acc: {train_acc:.1f}, val_loss: {val_loss:.2f}, val_acc: {val_acc:.1f}")
writer.add_scalar(tag='training loss', scalar_value=train_loss, global_step=epoch)
writer.add_scalar(tag='training accuracy', scalar_value=train_acc, global_step=epoch)
writer.add_scalar(tag='validation loss', scalar_value=val_loss, global_step=epoch)
writer.add_scalar(tag='validation accuracy', scalar_value=val_acc, global_step=epoch)
# Adjust learning rate
scheduler.step(val_loss)
# Early stopping
if val_loss < best_val_loss:
best_val_loss = val_loss
patience = PATIENCE # reset patience
torch.save(model.state_dict(), MODEL_PATH)
else:
patience -= 1
if not patience: # 0
print ("Stopping early!")
break
# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
scheduler = ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=3)
# Path to save model
MODEL_NAME = 'TextCNN'
MODEL_PATH = Path(f'models/{MODEL_NAME}.h5')
Path(MODEL_PATH.parent).mkdir(parents=True, exist_ok=True)
# TensorBoard writer
log_dir = f'tensorboard/{MODEL_NAME}'
!rm -rf {log_dir} # remove if it already exists
writer = SummaryWriter(log_dir=log_dir)
# Training
train(model, optimizer, scheduler,
train_set, val_set, test_set, writer)
%tensorboard --logdir {log_dir}
```
## Evaluation
```
import io
import itertools
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_recall_fscore_support
def plot_confusion_matrix(y_pred, y_target, classes, cmap=plt.cm.Blues):
"""Plot a confusion matrix using ground truth and predictions."""
# Confusion matrix
cm = confusion_matrix(y_target, y_pred)
cm_norm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
# Figure
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(cm, cmap=plt.cm.Blues)
fig.colorbar(cax)
# Axis
plt.title("Confusion matrix")
plt.ylabel("True label")
plt.xlabel("Predicted label")
ax.set_xticklabels([''] + classes)
ax.set_yticklabels([''] + classes)
ax.xaxis.set_label_position('bottom')
ax.xaxis.tick_bottom()
# Values
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, f"{cm[i, j]:d} ({cm_norm[i, j]*100:.1f}%)",
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
# Display
plt.show()
def get_performance(y_pred, y_target, classes):
"""Per-class performance metrics. """
performance = {'overall': {}, 'class': {}}
metrics = precision_recall_fscore_support(y_target, y_pred)
# Overall performance
performance['overall']['precision'] = np.mean(metrics[0])
performance['overall']['recall'] = np.mean(metrics[1])
performance['overall']['f1'] = np.mean(metrics[2])
performance['overall']['num_samples'] = np.float64(np.sum(metrics[3]))
# Per-class performance
for i in range(len(classes)):
performance['class'][classes[i]] = {
"precision": metrics[0][i],
"recall": metrics[1][i],
"f1": metrics[2][i],
"num_samples": np.float64(metrics[3][i])
}
return performance
# Test
y_preds, y_targets, test_loss, test_acc = test_step(model, DEVICE, test_set)
print (f"test_loss: {test_loss:.2f}, test_acc: {test_acc:.1f}")
# Class performance
performance = get_performance(y_preds, y_targets, classes)
print (json.dumps(performance, indent=4))
# Confusion matrix
plt.rcParams["figure.figsize"] = (7,7)
plot_confusion_matrix(y_preds, y_targets, classes)
print (classification_report(y_targets, y_preds))
```
# inference.py
## Load model
```
# Load model
model = TextCNN(embedding_dim=EMBEDDING_DIM,
vocab_size=vocab_size,
num_filters=NUM_FILTERS,
filter_sizes=FILTER_SIZES,
hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P,
num_classes=len(classes),
pretrained_embeddings=embedding_matrix,
freeze_embeddings=False).to(DEVICE)
model.load_state_dict(torch.load(MODEL_PATH))
model.eval()
```
## Inference
```
import collections
def get_probability_distribution(y_prob, classes):
results = {}
for i, class_ in enumerate(classes):
results[class_] = np.float64(y_prob[i])
sorted_results = {k: v for k, v in sorted(
results.items(), key=lambda item: item[1], reverse=True)}
return sorted_results
def get_top_n_grams(tokens, conv_outputs, filter_sizes):
# Process conv outputs for each unique filter size
n_grams = {}
for i, filter_size in enumerate(filter_sizes):
# Identify most important n-gram (excluding last token)
popular_indices = collections.Counter([np.argmax(conv_output) \
for conv_output in conv_outputs[filter_size]])
# Get corresponding text
start = popular_indices.most_common(1)[-1][0]
n_gram = " ".join([token for token in tokens[start:start+filter_size]])
n_grams[filter_size] = n_gram
return n_grams
# Inputs
texts = ["The Wimbledon tennis tournament starts next week!",
"The President signed in the new law."]
texts = preprocess_texts(texts, lower=LOWER, filters=FILTERS)
X_infer = np.array(X_tokenizer.texts_to_sequences(texts))
print (f"{texts[0]} \n\t→ {X_tokenizer.sequences_to_texts(X_infer)[0]} \n\t→ {X_infer[0]}")
y_filler = np.array([0]*len(texts))
# Dataset
infer_set = TextDataset(X=X_infer, y=y_filler, batch_size=BATCH_SIZE,
max_filter_size=max(FILTER_SIZES))
# Iterate over infer batches
conv_outputs = collections.defaultdict(list)
y_probs = []
with torch.no_grad():
for i, (X, y) in enumerate(infer_set.generate_batches()):
# Set device
X, y = X.to(DEVICE), y.to(DEVICE)
# Forward pass
conv_outputs_, logits = model(X)
y_prob = F.softmax(logits, dim=1)
# Save probabilities
y_probs.extend(y_prob.cpu().numpy())
for i, filter_size in enumerate(FILTER_SIZES):
conv_outputs[filter_size].extend(conv_outputs_[i].cpu().numpy())
# Results
results = []
for index in range(len(X_infer)):
results.append({
'raw_input': texts[index],
'preprocessed_input': X_tokenizer.sequences_to_texts([X_infer[index]])[0],
'probabilities': get_probability_distribution(y_prob[index], y_tokenizer.classes),
'top_n_grams': get_top_n_grams(
tokens=preprocessed_input.split(' '),
conv_outputs={k:v[index] for k,v in conv_outputs.items()},
filter_sizes=FILTER_SIZES)})
print (json.dumps(results, indent=4))
```
Use inferences to collect information how the model performs on your real world data and use it to improve it over time.
- Use a probability threshold for the top class (ex. If the predicted class is less than 75%, send the inference for review).
- Combine the above with Use probability thresholds for each class (ex. if the predicted class is `Sports` at 85% but that class's precision/recall is low, then send it for review but maybe you don't do this when the predicted class is `Sports` but above 90%.
- If the preprocessed sentence has <UNK> tokens, send the inference for further review.
- When latency is not an issue, use the n-grams to validate the prediction.
Check out the `API` lesson to see how all of this comes together to create an ML service.
---
Share and discover ML projects at <a href="https://madewithml.com/">Made With ML</a>.
<div align="left">
<a class="ai-header-badge" target="_blank" href="https://github.com/madewithml/lessons"><img src="https://img.shields.io/github/stars/madewithml/lessons.svg?style=social&label=Star"></a>
<a class="ai-header-badge" target="_blank" href="https://www.linkedin.com/company/madewithml"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a class="ai-header-badge" target="_blank" href="https://twitter.com/madewithml"><img src="https://img.shields.io/twitter/follow/madewithml.svg?label=Follow&style=social"></a>
</div>
|
github_jupyter
|
# Model Selection, Underfitting, and Overfitting
:label:`sec_model_selection`
As machine learning scientists,
our goal is to discover *patterns*.
But how can we be sure that we have
truly discovered a *general* pattern
and not simply memorized our data?
For example, imagine that we wanted to hunt
for patterns among genetic markers
linking patients to their dementia status,
where the labels are drawn from the set
$\{\text{dementia}, \text{mild cognitive impairment}, \text{healthy}\}$.
Because each person's genes identify them uniquely
(ignoring identical siblings),
it is possible to memorize the entire dataset.
We do not want our model to say
*"That's Bob! I remember him! He has dementia!"*
The reason why is simple.
When we deploy the model in the future,
we will encounter patients
that the model has never seen before.
Our predictions will only be useful
if our model has truly discovered a *general* pattern.
To recapitulate more formally,
our goal is to discover patterns
that capture regularities in the underlying population
from which our training set was drawn.
If we are successful in this endeavor,
then we could successfully assess risk
even for individuals that we have never encountered before.
This problem---how to discover patterns that *generalize*---is
the fundamental problem of machine learning.
The danger is that when we train models,
we access just a small sample of data.
The largest public image datasets contain
roughly one million images.
More often, we must learn from only thousands
or tens of thousands of data examples.
In a large hospital system, we might access
hundreds of thousands of medical records.
When working with finite samples, we run the risk
that we might discover apparent associations
that turn out not to hold up when we collect more data.
The phenomenon of fitting our training data
more closely than we fit the underlying distribution is called *overfitting*, and the techniques used to combat overfitting are called *regularization*.
In the previous sections, you might have observed
this effect while experimenting with the Fashion-MNIST dataset.
If you altered the model structure or the hyperparameters during the experiment, you might have noticed that with enough neurons, layers, and training epochs, the model can eventually reach perfect accuracy on the training set, even as the accuracy on test data deteriorates.
## Training Error and Generalization Error
In order to discuss this phenomenon more formally,
we need to differentiate between training error and generalization error.
The *training error* is the error of our model
as calculated on the training dataset,
while *generalization error* is the expectation of our model's error
were we to apply it to an infinite stream of additional data examples
drawn from the same underlying data distribution as our original sample.
Problematically, we can never calculate the generalization error exactly.
That is because the stream of infinite data is an imaginary object.
In practice, we must *estimate* the generalization error
by applying our model to an independent test set
constituted of a random selection of data examples
that were withheld from our training set.
The following three thought experiments
will help illustrate this situation better.
Consider a college student trying to prepare for his final exam.
A diligent student will strive to practice well
and test his abilities using exams from previous years.
Nonetheless, doing well on past exams is no guarantee
that he will excel when it matters.
For instance, the student might try to prepare
by rote learning the answers to the exam questions.
This requires the student to memorize many things.
She might even remember the answers for past exams perfectly.
Another student might prepare by trying to understand
the reasons for giving certain answers.
In most cases, the latter student will do much better.
Likewise, consider a model that simply uses a lookup table to answer questions. If the set of allowable inputs is discrete and reasonably small, then perhaps after viewing *many* training examples, this approach would perform well. Still this model has no ability to do better than random guessing when faced with examples that it has never seen before.
In reality the input spaces are far too large to memorize the answers corresponding to every conceivable input. For example, consider the black and white $28\times28$ images. If each pixel can take one among $256$ grayscale values, then there are $256^{784}$ possible images. That means that there are far more low-resolution grayscale thumbnail-sized images than there are atoms in the universe. Even if we could encounter such data, we could never afford to store the lookup table.
Last, consider the problem of trying
to classify the outcomes of coin tosses (class 0: heads, class 1: tails)
based on some contextual features that might be available.
Suppose that the coin is fair.
No matter what algorithm we come up with,
the generalization error will always be $\frac{1}{2}$.
However, for most algorithms,
we should expect our training error to be considerably lower,
depending on the luck of the draw,
even if we did not have any features!
Consider the dataset {0, 1, 1, 1, 0, 1}.
Our feature-less algorithm would have to fall back on always predicting
the *majority class*, which appears from our limited sample to be *1*.
In this case, the model that always predicts class 1
will incur an error of $\frac{1}{3}$,
considerably better than our generalization error.
As we increase the amount of data,
the probability that the fraction of heads
will deviate significantly from $\frac{1}{2}$ diminishes,
and our training error would come to match the generalization error.
### Statistical Learning Theory
Since generalization is the fundamental problem in machine learning,
you might not be surprised to learn
that many mathematicians and theorists have dedicated their lives
to developing formal theories to describe this phenomenon.
In their [eponymous theorem](https://en.wikipedia.org/wiki/Glivenko%E2%80%93Cantelli_theorem), Glivenko and Cantelli
derived the rate at which the training error
converges to the generalization error.
In a series of seminal papers, [Vapnik and Chervonenkis](https://en.wikipedia.org/wiki/Vapnik%E2%80%93Chervonenkis_theory)
extended this theory to more general classes of functions.
This work laid the foundations of statistical learning theory.
In the standard supervised learning setting, which we have addressed up until now and will stick with throughout most of this book,
we assume that both the training data and the test data
are drawn *independently* from *identical* distributions.
This is commonly called the *i.i.d. assumption*,
which means that the process that samples our data has no memory.
In other words,
the second example drawn and the third drawn
are no more correlated than the second and the two-millionth sample drawn.
Being a good machine learning scientist requires thinking critically,
and already you should be poking holes in this assumption,
coming up with common cases where the assumption fails.
What if we train a mortality risk predictor
on data collected from patients at UCSF Medical Center,
and apply it on patients at Massachusetts General Hospital?
These distributions are simply not identical.
Moreover, draws might be correlated in time.
What if we are classifying the topics of Tweets?
The news cycle would create temporal dependencies
in the topics being discussed, violating any assumptions of independence.
Sometimes we can get away with minor violations of the i.i.d. assumption
and our models will continue to work remarkably well.
After all, nearly every real-world application
involves at least some minor violation of the i.i.d. assumption,
and yet we have many useful tools for
various applications such as
face recognition,
speech recognition, and language translation.
Other violations are sure to cause trouble.
Imagine, for example, if we try to train
a face recognition system by training it
exclusively on university students
and then want to deploy it as a tool
for monitoring geriatrics in a nursing home population.
This is unlikely to work well since college students
tend to look considerably different from the elderly.
In subsequent chapters, we will discuss problems
arising from violations of the i.i.d. assumption.
For now, even taking the i.i.d. assumption for granted,
understanding generalization is a formidable problem.
Moreover, elucidating the precise theoretical foundations
that might explain why deep neural networks generalize as well as they do
continues to vex the greatest minds in learning theory.
When we train our models, we attempt to search for a function
that fits the training data as well as possible.
If the function is so flexible that it can catch on to spurious patterns
just as easily as to true associations,
then it might perform *too well* without producing a model
that generalizes well to unseen data.
This is precisely what we want to avoid or at least control.
Many of the techniques in deep learning are heuristics and tricks
aimed at guarding against overfitting.
### Model Complexity
When we have simple models and abundant data,
we expect the generalization error to resemble the training error.
When we work with more complex models and fewer examples,
we expect the training error to go down but the generalization gap to grow.
What precisely constitutes model complexity is a complex matter.
Many factors govern whether a model will generalize well.
For example a model with more parameters might be considered more complex.
A model whose parameters can take a wider range of values
might be more complex.
Often with neural networks, we think of a model
that takes more training iterations as more complex,
and one subject to *early stopping* (fewer training iterations) as less complex.
It can be difficult to compare the complexity among members
of substantially different model classes
(say, decision trees vs. neural networks).
For now, a simple rule of thumb is quite useful:
a model that can readily explain arbitrary facts
is what statisticians view as complex,
whereas one that has only a limited expressive power
but still manages to explain the data well
is probably closer to the truth.
In philosophy, this is closely related to Popper's
criterion of falsifiability
of a scientific theory: a theory is good if it fits data
and if there are specific tests that can be used to disprove it.
This is important since all statistical estimation is
*post hoc*,
i.e., we estimate after we observe the facts,
hence vulnerable to the associated fallacy.
For now, we will put the philosophy aside and stick to more tangible issues.
In this section, to give you some intuition,
we will focus on a few factors that tend
to influence the generalizability of a model class:
1. The number of tunable parameters. When the number of tunable parameters, sometimes called the *degrees of freedom*, is large, models tend to be more susceptible to overfitting.
1. The values taken by the parameters. When weights can take a wider range of values, models can be more susceptible to overfitting.
1. The number of training examples. It is trivially easy to overfit a dataset containing only one or two examples even if your model is simple. But overfitting a dataset with millions of examples requires an extremely flexible model.
## Model Selection
In machine learning, we usually select our final model
after evaluating several candidate models.
This process is called *model selection*.
Sometimes the models subject to comparison
are fundamentally different in nature
(say, decision trees vs. linear models).
At other times, we are comparing
members of the same class of models
that have been trained with different hyperparameter settings.
With MLPs, for example,
we may wish to compare models with
different numbers of hidden layers,
different numbers of hidden units,
and various choices of the activation functions
applied to each hidden layer.
In order to determine the best among our candidate models,
we will typically employ a validation dataset.
### Validation Dataset
In principle we should not touch our test set
until after we have chosen all our hyperparameters.
Were we to use the test data in the model selection process,
there is a risk that we might overfit the test data.
Then we would be in serious trouble.
If we overfit our training data,
there is always the evaluation on test data to keep us honest.
But if we overfit the test data, how would we ever know?
Thus, we should never rely on the test data for model selection.
And yet we cannot rely solely on the training data
for model selection either because
we cannot estimate the generalization error
on the very data that we use to train the model.
In practical applications, the picture gets muddier.
While ideally we would only touch the test data once,
to assess the very best model or to compare
a small number of models to each other,
real-world test data is seldom discarded after just one use.
We can seldom afford a new test set for each round of experiments.
The common practice to address this problem
is to split our data three ways,
incorporating a *validation dataset* (or *validation set*)
in addition to the training and test datasets.
The result is a murky practice where the boundaries
between validation and test data are worryingly ambiguous.
Unless explicitly stated otherwise, in the experiments in this book
we are really working with what should rightly be called
training data and validation data, with no true test sets.
Therefore, the accuracy reported in each experiment of the book is really the validation accuracy and not a true test set accuracy.
### $K$-Fold Cross-Validation
When training data is scarce,
we might not even be able to afford to hold out
enough data to constitute a proper validation set.
One popular solution to this problem is to employ
$K$*-fold cross-validation*.
Here, the original training data is split into $K$ non-overlapping subsets.
Then model training and validation are executed $K$ times,
each time training on $K-1$ subsets and validating
on a different subset (the one not used for training in that round).
Finally, the training and validation errors are estimated
by averaging over the results from the $K$ experiments.
## Underfitting or Overfitting?
When we compare the training and validation errors,
we want to be mindful of two common situations.
First, we want to watch out for cases
when our training error and validation error are both substantial
but there is a little gap between them.
If the model is unable to reduce the training error,
that could mean that our model is too simple
(i.e., insufficiently expressive)
to capture the pattern that we are trying to model.
Moreover, since the *generalization gap*
between our training and validation errors is small,
we have reason to believe that we could get away with a more complex model.
This phenomenon is known as *underfitting*.
On the other hand, as we discussed above,
we want to watch out for the cases
when our training error is significantly lower
than our validation error, indicating severe *overfitting*.
Note that overfitting is not always a bad thing.
With deep learning especially, it is well known
that the best predictive models often perform
far better on training data than on holdout data.
Ultimately, we usually care more about the validation error
than about the gap between the training and validation errors.
Whether we overfit or underfit can depend
both on the complexity of our model
and the size of the available training datasets,
two topics that we discuss below.
### Model Complexity
To illustrate some classical intuition
about overfitting and model complexity,
we give an example using polynomials.
Given training data consisting of a single feature $x$
and a corresponding real-valued label $y$,
we try to find the polynomial of degree $d$
$$\hat{y}= \sum_{i=0}^d x^i w_i$$
to estimate the labels $y$.
This is just a linear regression problem
where our features are given by the powers of $x$,
the model's weights are given by $w_i$,
and the bias is given by $w_0$ since $x^0 = 1$ for all $x$.
Since this is just a linear regression problem,
we can use the squared error as our loss function.
A higher-order polynomial function is more complex
than a lower-order polynomial function,
since the higher-order polynomial has more parameters
and the model function's selection range is wider.
Fixing the training dataset,
higher-order polynomial functions should always
achieve lower (at worst, equal) training error
relative to lower degree polynomials.
In fact, whenever the data examples each have a distinct value of $x$,
a polynomial function with degree equal to the number of data examples
can fit the training set perfectly.
We visualize the relationship between polynomial degree
and underfitting vs. overfitting in :numref:`fig_capacity_vs_error`.

:label:`fig_capacity_vs_error`
### Dataset Size
The other big consideration to bear in mind is the dataset size.
Fixing our model, the fewer samples we have in the training dataset,
the more likely (and more severely) we are to encounter overfitting.
As we increase the amount of training data,
the generalization error typically decreases.
Moreover, in general, more data never hurt.
For a fixed task and data distribution,
there is typically a relationship between model complexity and dataset size.
Given more data, we might profitably attempt to fit a more complex model.
Absent sufficient data, simpler models may be more difficult to beat.
For many tasks, deep learning only outperforms linear models
when many thousands of training examples are available.
In part, the current success of deep learning
owes to the current abundance of massive datasets
due to Internet companies, cheap storage, connected devices,
and the broad digitization of the economy.
## Polynomial Regression
We can now explore these concepts interactively
by fitting polynomials to data.
```
from d2l import tensorflow as d2l
import tensorflow as tf
import numpy as np
import math
```
### Generating the Dataset
First we need data. Given $x$, we will use the following cubic polynomial to generate the labels on training and test data:
$$y = 5 + 1.2x - 3.4\frac{x^2}{2!} + 5.6 \frac{x^3}{3!} + \epsilon \text{ where }
\epsilon \sim \mathcal{N}(0, 0.1^2).$$
The noise term $\epsilon$ obeys a normal distribution
with a mean of 0 and a standard deviation of 0.1.
For optimization, we typically want to avoid
very large values of gradients or losses.
This is why the *features*
are rescaled from $x^i$ to $\frac{x^i}{i!}$.
It allows us to avoid very large values for large exponents $i$.
We will synthesize 100 samples each for the training set and test set.
```
max_degree = 20 # Maximum degree of the polynomial
n_train, n_test = 100, 100 # Training and test dataset sizes
true_w = np.zeros(max_degree) # Allocate lots of empty space
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1) # `gamma(n)` = (n-1)!
# Shape of `labels`: (`n_train` + `n_test`,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)
```
Again, monomials stored in `poly_features`
are rescaled by the gamma function,
where $\Gamma(n)=(n-1)!$.
Take a look at the first 2 samples from the generated dataset.
The value 1 is technically a feature,
namely the constant feature corresponding to the bias.
```
# Convert from NumPy ndarrays to tensors
true_w, features, poly_features, labels = [tf.constant(x, dtype=
tf.float32) for x in [true_w, features, poly_features, labels]]
features[:2], poly_features[:2, :], labels[:2]
```
### Training and Testing the Model
Let us first implement a function to evaluate the loss on a given dataset.
```
def evaluate_loss(net, data_iter, loss): #@save
"""Evaluate the loss of a model on the given dataset."""
metric = d2l.Accumulator(2) # Sum of losses, no. of examples
for X, y in data_iter:
l = loss(net(X), y)
metric.add(tf.reduce_sum(l), tf.size(l).numpy())
return metric[0] / metric[1]
```
Now define the training function.
```
def train(train_features, test_features, train_labels, test_labels,
num_epochs=400):
loss = tf.losses.MeanSquaredError()
input_shape = train_features.shape[-1]
# Switch off the bias since we already catered for it in the polynomial
# features
net = tf.keras.Sequential()
net.add(tf.keras.layers.Dense(1, use_bias=False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels), batch_size)
test_iter = d2l.load_array((test_features, test_labels), batch_size,
is_train=False)
trainer = tf.keras.optimizers.SGD(learning_rate=.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
xlim=[1, num_epochs], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
evaluate_loss(net, test_iter, loss)))
print('weight:', net.get_weights()[0].T)
```
### Third-Order Polynomial Function Fitting (Normal)
We will begin by first using a third-order polynomial function, which is the same order as that of the data generation function.
The results show that this model's training and test losses can be both effectively reduced.
The learned model parameters are also close
to the true values $w = [5, 1.2, -3.4, 5.6]$.
```
# Pick the first four dimensions, i.e., 1, x, x^2/2!, x^3/3! from the
# polynomial features
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
labels[:n_train], labels[n_train:])
```
### Linear Function Fitting (Underfitting)
Let us take another look at linear function fitting.
After the decline in early epochs,
it becomes difficult to further decrease
this model's training loss.
After the last epoch iteration has been completed,
the training loss is still high.
When used to fit nonlinear patterns
(like the third-order polynomial function here)
linear models are liable to underfit.
```
# Pick the first two dimensions, i.e., 1, x, from the polynomial features
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
labels[:n_train], labels[n_train:])
```
### Higher-Order Polynomial Function Fitting (Overfitting)
Now let us try to train the model
using a polynomial of too high degree.
Here, there are insufficient data to learn that
the higher-degree coefficients should have values close to zero.
As a result, our overly-complex model
is so susceptible that it is being influenced
by noise in the training data.
Though the training loss can be effectively reduced,
the test loss is still much higher.
It shows that
the complex model overfits the data.
```
# Pick all the dimensions from the polynomial features
train(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:], num_epochs=1500)
```
In the subsequent sections, we will continue
to discuss overfitting problems
and methods for dealing with them,
such as weight decay and dropout.
## Summary
* Since the generalization error cannot be estimated based on the training error, simply minimizing the training error will not necessarily mean a reduction in the generalization error. Machine learning models need to be careful to safeguard against overfitting so as to minimize the generalization error.
* A validation set can be used for model selection, provided that it is not used too liberally.
* Underfitting means that a model is not able to reduce the training error. When training error is much lower than validation error, there is overfitting.
* We should choose an appropriately complex model and avoid using insufficient training samples.
## Exercises
1. Can you solve the polynomial regression problem exactly? Hint: use linear algebra.
1. Consider model selection for polynomials:
1. Plot the training loss vs. model complexity (degree of the polynomial). What do you observe? What degree of polynomial do you need to reduce the training loss to 0?
1. Plot the test loss in this case.
1. Generate the same plot as a function of the amount of data.
1. What happens if you drop the normalization ($1/i!$) of the polynomial features $x^i$? Can you fix this in some other way?
1. Can you ever expect to see zero generalization error?
[Discussions](https://discuss.d2l.ai/t/234)
|
github_jupyter
|
```
import numpy as np
import math
import random
import pandas as pd
import os
import matplotlib.pyplot as plt
import cv2
import glob
import gc
from google.colab import files
src = list(files.upload().values())[0]
open('utils.py','wb').write(src)
from utils import *
from tqdm import tqdm
import pickle
from keras.optimizers import *
from keras.models import Model
from keras.layers import *
from keras.layers.core import *
from keras.layers.convolutional import *
from keras import backend as K
import tensorflow as tf
```
# Initialize the setting
```
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"]="1"
random.seed(123)
class Config():
def __init__(self):
self.frame_l = 32 # the length of frames
self.joint_n = 15 # the number of joints
self.joint_d = 2 # the dimension of joints
self.clc_num = 21 # the number of class
self.feat_d = 105
self.filters = 16
self.data_dir = '/mnt/nasbi/homes/fan/projects/action/skeleton/data/JHMDB/'
C = Config()
def data_generator(T,C,le):
X_0 = []
X_1 = []
Y = []
for i in tqdm(range(len(T['pose']))):
p = np.copy(T['pose'][i])
p = zoom(p,target_l=C.frame_l,joints_num=C.joint_n,joints_dim=C.joint_d)
label = np.zeros(C.clc_num)
label[le.transform(T['label'])[i]-1] = 1
M = get_CG(p,C)
X_0.append(M)
X_1.append(p)
Y.append(label)
X_0 = np.stack(X_0)
X_1 = np.stack(X_1)
Y = np.stack(Y)
return X_0,X_1,Y
```
# Building the model
```
def poses_diff(x):
H, W = x.get_shape()[1],x.get_shape()[2]
x = tf.subtract(x[:,1:,...],x[:,:-1,...])
x = tf.image.resize_nearest_neighbor(x,size=[H.value,W.value],align_corners=False) # should not alignment here
return x
def pose_motion(P,frame_l):
P_diff_slow = Lambda(lambda x: poses_diff(x))(P)
P_diff_slow = Reshape((frame_l,-1))(P_diff_slow)
P_fast = Lambda(lambda x: x[:,::2,...])(P)
P_diff_fast = Lambda(lambda x: poses_diff(x))(P_fast)
P_diff_fast = Reshape((int(frame_l/2),-1))(P_diff_fast)
return P_diff_slow,P_diff_fast
def c1D(x,filters,kernel):
x = Conv1D(filters, kernel_size=kernel,padding='same',use_bias=False)(x)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x)
return x
def block(x,filters):
x = c1D(x,filters,3)
x = c1D(x,filters,3)
return x
def d1D(x,filters):
x = Dense(filters,use_bias=False)(x)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x)
return x
def build_FM(frame_l=32,joint_n=22,joint_d=2,feat_d=231,filters=16):
M = Input(shape=(frame_l,feat_d))
P = Input(shape=(frame_l,joint_n,joint_d))
diff_slow,diff_fast = pose_motion(P,frame_l)
x = c1D(M,filters*2,1)
x = SpatialDropout1D(0.1)(x)
x = c1D(x,filters,3)
x = SpatialDropout1D(0.1)(x)
x = c1D(x,filters,1)
x = MaxPooling1D(2)(x)
x = SpatialDropout1D(0.1)(x)
x_d_slow = c1D(diff_slow,filters*2,1)
x_d_slow = SpatialDropout1D(0.1)(x_d_slow)
x_d_slow = c1D(x_d_slow,filters,3)
x_d_slow = SpatialDropout1D(0.1)(x_d_slow)
x_d_slow = c1D(x_d_slow,filters,1)
x_d_slow = MaxPool1D(2)(x_d_slow)
x_d_slow = SpatialDropout1D(0.1)(x_d_slow)
x_d_fast = c1D(diff_fast,filters*2,1)
x_d_fast = SpatialDropout1D(0.1)(x_d_fast)
x_d_fast = c1D(x_d_fast,filters,3)
x_d_fast = SpatialDropout1D(0.1)(x_d_fast)
x_d_fast = c1D(x_d_fast,filters,1)
x_d_fast = SpatialDropout1D(0.1)(x_d_fast)
x = concatenate([x,x_d_slow,x_d_fast])
x = block(x,filters*2)
x = MaxPool1D(2)(x)
x = SpatialDropout1D(0.1)(x)
x = block(x,filters*4)
x = MaxPool1D(2)(x)
x = SpatialDropout1D(0.1)(x)
x = block(x,filters*8)
x = SpatialDropout1D(0.1)(x)
return Model(inputs=[M,P],outputs=x)
def build_DD_Net(C):
M = Input(name='M', shape=(C.frame_l,C.feat_d))
P = Input(name='P', shape=(C.frame_l,C.joint_n,C.joint_d))
FM = build_FM(C.frame_l,C.joint_n,C.joint_d,C.feat_d,C.filters)
x = FM([M,P])
x = GlobalMaxPool1D()(x)
x = d1D(x,128)
x = Dropout(0.5)(x)
x = d1D(x,128)
x = Dropout(0.5)(x)
x = Dense(C.clc_num, activation='softmax')(x)
######################Self-supervised part
model = Model(inputs=[M,P],outputs=x)
return model
DD_Net = build_DD_Net(C)
DD_Net.summary()
```
## Train and test on GT_split 1
```
from google.colab import drive
import pickle
drive.mount('/content/drive')
DATA_PATH1 = "/content/drive/My Drive/Colab Notebooks/Data"
infile = open(DATA_PATH1+'/GT_train_1.pkl','rb')
Train = pickle.load(infile)
DATA_PATH2 = "/content/drive/My Drive/Colab Notebooks/Data"
testfile= open(DATA_PATH2+'/GT_test_1.pkl','rb')
Test = pickle.load(testfile)
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit(Train['label'])
X_0,X_1,Y = data_generator(Train,C,le)
X_test_0,X_test_1,Y_test = data_generator(Test,C,le)
import keras
lr = 1e-3
DD_Net.compile(loss="categorical_crossentropy",optimizer=adam(lr),metrics=['accuracy'])
lrScheduler = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=5, cooldown=5, min_lr=1e-5)
history = DD_Net.fit([X_0,X_1],Y,
batch_size=len(Y),
epochs=600,
verbose=True,
shuffle=True,
callbacks=[lrScheduler],
validation_data=([X_test_0,X_test_1],Y_test)
)
lr = 1e-3
DD_Net.compile(loss="categorical_crossentropy",optimizer=adam(lr),metrics=['accuracy'])
lrScheduler = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=5, cooldown=5, min_lr=5e-6)
history = DD_Net.fit([X_0,X_1],Y,
batch_size=len(Y),
epochs=500,
verbose=True,
shuffle=True,
callbacks=[lrScheduler],
validation_data=([X_test_0,X_test_1],Y_test)
)
# Plot training & validation accuracy values
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
```
## Train and test on GT_split 2
```
from google.colab import drive
import pickle
drive.mount('/content/drive')
DATA_PATH1 = "/content/drive/My Drive/Colab Notebooks/Data"
infile = open(DATA_PATH1+'/GT_train_2.pkl','rb')
Train = pickle.load(infile)
DATA_PATH2 = "/content/drive/My Drive/Colab Notebooks/Data"
testfile= open(DATA_PATH2+'/GT_test_2.pkl','rb')
Test = pickle.load(testfile)
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit(Train['label'])
X_0,X_1,Y = data_generator(Train,C,le)
X_test_0,X_test_1,Y_test = data_generator(Test,C,le)
# Re-initialize weights, since training and testing data switch
DD_Net = build_DD_Net(C)
import keras
lr = 1e-3
DD_Net.compile(loss="categorical_crossentropy",optimizer=adam(lr),metrics=['accuracy'])
lrScheduler = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=5, cooldown=5, min_lr=1e-5)
history = DD_Net.fit([X_0,X_1],Y,
batch_size=len(Y),
epochs=600,
verbose=True,
shuffle=True,
callbacks=[lrScheduler],
validation_data=([X_test_0,X_test_1],Y_test)
)
lr = 1e-4
DD_Net.compile(loss="categorical_crossentropy",optimizer=adam(lr),metrics=['accuracy'])
lrScheduler = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=5, cooldown=5, min_lr=5e-6)
history = DD_Net.fit([X_0,X_1],Y,
batch_size=len(Y),
epochs=500,
verbose=True,
shuffle=True,
callbacks=[lrScheduler],
validation_data=([X_test_0,X_test_1],Y_test)
)
# Plot training & validation accuracy values
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
```
## Train and test on GT_split 3
```
from google.colab import drive
import pickle
drive.mount('/content/drive')
DATA_PATH1 = "/content/drive/My Drive/Colab Notebooks/Data"
infile = open(DATA_PATH1+'/GT_train_3.pkl','rb')
Train = pickle.load(infile)
DATA_PATH2 = "/content/drive/My Drive/Colab Notebooks/Data"
testfile= open(DATA_PATH2+'/GT_test_3.pkl','rb')
Test = pickle.load(testfile)
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit(Train['label'])
X_0,X_1,Y = data_generator(Train,C,le)
X_test_0,X_test_1,Y_test = data_generator(Test,C,le)
# Re-initialize weights, since training and testing data switch
DD_Net = build_DD_Net(C)
import keras
lr = 1e-3
DD_Net.compile(loss="categorical_crossentropy",optimizer=adam(lr),metrics=['accuracy'])
lrScheduler = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=5, cooldown=5, min_lr=1e-5)
history = DD_Net.fit([X_0,X_1],Y,
batch_size=len(Y),
epochs=600,
verbose=True,
shuffle=True,
callbacks=[lrScheduler],
validation_data=([X_test_0,X_test_1],Y_test)
)
lr = 1e-3
DD_Net.compile(loss="categorical_crossentropy",optimizer=adam(lr),metrics=['accuracy'])
lrScheduler = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=5, cooldown=5, min_lr=5e-6)
history = DD_Net.fit([X_0,X_1],Y,
batch_size=len(Y),
epochs=500,
verbose=True,
shuffle=True,
callbacks=[lrScheduler],
validation_data=([X_test_0,X_test_1],Y_test)
)
# Plot training & validation accuracy values
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
```
## Calculate average
```
(0.63+0.66+0.68)/3
```
|
github_jupyter
|
# Face Recognition & Verification for Person Identification
Inspired by Coursera deeplearning.ai's assignment of programming a face recognition for happy house, I wanted to give it a try implementing a face recognition system by using face detection library(https://github.com/ageitgey/face_recognition) and face_recognition model from deeplearning.ai course specialization.
In this notebook, I implemented a person identification system by using pre-trained model to map face images into 128 dimensional encodings.
In the notebook,
- I tried to implement pre-processing process for the images by using face detection library
- Kept track of encodings of a person and try to improve performance by adding more pictures of a person (more embeddings of the same person)
- Detect and identify people given an specific image
- Implement triple loss function
- Implement face verification and face recognition step
- I save unknown encodings in the database dictionary for later identification
```
#import the necessary packages
from keras.models import Sequential
from keras.layers import Conv2D, ZeroPadding2D, Activation, Input, concatenate
from keras.models import Model
from keras.layers.normalization import BatchNormalization
from keras.layers.pooling import MaxPooling2D, AveragePooling2D
from keras.layers.merge import Concatenate
from keras.layers.core import Lambda, Flatten, Dense
from keras.initializers import glorot_uniform
from keras.engine.topology import Layer
from keras import backend as K
K.set_image_data_format('channels_first')
import cv2
import os
import numpy as np
from numpy import genfromtxt
import pandas as pd
import tensorflow as tf
from fr_utils import *
from inception_blocks import *
import matplotlib.pyplot as plt
import face_recognition
from PIL import Image
%matplotlib inline
%load_ext autoreload
%autoreload 2
np.set_printoptions(threshold=np.nan)
# Initialize the model
# The model takes images with shape (3, 96, 96) 'channels first'
FRmodel = faceRecoModel(input_shape=(3, 96, 96))
#Showing the architecture of the model
FRmodel.summary()
# using triplets of images, for triplet loss function
# anchor (A): picture of the person
# positive (P): picture of the same person of the anchor image
# negative (N): picture of a different person than the anchor image(person)
# Goal: Individual's encoding should be closer to the positive image and further away from negative image by margin alpha
def triplet_loss(y_true, y_pred, alpha = 0.2):
"""
Implementation of the triplet loss
Arguments:
y_true -- true labels, required when you define a loss in Keras, you don't need it in this function.
y_pred -- python list containing three objects:
anchor -- the encodings for the anchor images, of shape (None, 128)
positive -- the encodings for the positive images, of shape (None, 128)
negative -- the encodings for the negative images, of shape (None, 128)
Returns:
loss -- real number, value of the loss
"""
anchor, positive, negative = y_pred[0], y_pred[1], y_pred[2]
# (encoding) distance between the anchor and the positive
pos_dist = tf.square(tf.subtract(anchor, positive))
# (encoding) distance between the anchor and the negative
neg_dist = tf.square(tf.subtract(anchor, negative))
# Subtracting the two previous distances and adding an alpha.
basic_loss = tf.add(tf.reduce_sum(tf.subtract(pos_dist, neg_dist)), alpha)
# Taking the maximum of basic_loss and 0.0. Summing over the training examples.
loss = tf.reduce_sum(tf.maximum(basic_loss, 0))
return loss
# Compile the model
FRmodel.compile(optimizer = 'adam', loss = triplet_loss, metrics = ['accuracy'])
load_weights_from_FaceNet(FRmodel)
#Function for resizing an image
def pre_process_image(img, image_size):
"""
Resizes an image into given image_size (height, width, channel)
Arguments:
img -- original image, array
image_size -- tuple containing width, height, channel of the image (h, w, c)
Returns:
img -- resized image
"""
height, width, channels = image_size
img = cv2.resize(img, dsize=(height, width))
return img
# Function for identifying face locations on an image
def find_face_locations(image_path):
"""
returns the bounding box locations of the faces, image from the path
Arguments:
image_path -- destination of the original image
image_size -- tuple containing width and height of the image (h, w)
Returns:
(top, right, bottom, left), image -- bounding box
if multiple faces present in the picture returns a list of tuples,
image obtained from image_path
"""
# Use face recognition module to detect faces
image = face_recognition.load_image_file(image_path)
#Test: print("Shape of the image: " + str(image.shape))
face_locations = face_recognition.face_locations(image)
for face_location in face_locations:
# Print the location of each face in this image
top, right, bottom, left = face_location
print("A face is located at pixel location Top: {}, Left: {}, Bottom: {}, Right: {}".format(top, left, bottom, right))
return face_locations, image
# access the actual face itself and print
#face_image = image[top:bottom, left:right]
#pil_image = Image.fromarray(face_image)
#pil_image.show()
```
## Image to Embedding
`face_img_to_encoding(image_path, model)` : basically runs the forward propagation of the model on the specified image.
```
def face_img_to_encoding(image_path, model):
"""
returns the embedding vector of the specific image from the path
Arguments:
image_path -- Destination of the original image
model -- Inception model instance in Keras
Returns:
embeddings -- List containing embeddings of the people in the image
"""
# obtain the face locations and the image
face_locations, image = find_face_locations(image_path)
#initialize the embeddings list
embeddings = []
#initialize embeddings list
for face_location in face_locations:
# Print the location of each face in this image
top, right, bottom, left = face_location
# access the actual face itself
face_image = image[top:bottom, left:right]
# resize the cropped face image
image_size = (96, 96, 3)
img = pre_process_image(face_image, image_size)
# pre-process the face image
img = img[...,::-1]
img = np.around(np.transpose(img, (2,0,1))/255.0, decimals=12)
x_train = np.array([img])
embedding = model.predict_on_batch(x_train)
embeddings.append(embedding)
return embeddings
```
## Create the Database
```
# Create a initial database for identifying people
database = {}
database["leonardo dicaprio"] = face_img_to_encoding("my_images/dicaprio.jpg", FRmodel)
database["brad pitt"] = face_img_to_encoding("my_images/bradPitt1.jpg", FRmodel)
database["matt damon"] = face_img_to_encoding("my_images/mattDamon.jpg", FRmodel)
database["unknown"] = face_img_to_encoding("my_images/unknown.jpg", FRmodel)
# Test for face_img_to_encoding
embedding = face_img_to_encoding("my_images/dicaprio.jpg", FRmodel)
img = cv2.imread("my_images/dicaprio.jpg")
#Visualize the image
plt.imshow(img)
#Visualize the embedding
print(embedding)
```
## Face Verification
Face Verification is a 1:1 matching problem given identity of a person program identifies if the picture of a person matches with identity
- verify() function below implements simple face-verification functionality
```
def verify(image_path, identity, database, model):
"""
Function that verifies if the person on the "image_path" image is "identity".
Arguments:
image_path -- path to an image
identity -- string, name of the person.
database -- python dictionary mapping names of allowed people's names (strings) to their encodings (vectors).
model -- Inception model instance in Keras
Returns:
dist -- distance between the image_path and the image of "identity" in the database.
match -- True, if person(embedding) matches with the identity(embedding) .
"""
# Encodings in the image.
encodings = face_img_to_encoding(image_path, FRmodel)
#Loop inside encodings to obtain encoding of each person
for encoding in encodings:
# Step 2: Compute distance with identity's image
dist = np.linalg.norm(encoding - database[identity])
# Step 3: Match if dist < 0.8
if dist < 0.8:
print(str(identity) + ", you are verified")
match = True
else:
print("You're not " + str(identity) + "!!!")
match = False
return dist, match
```
## Let's see if we can verify Matt Damon
```
verify("my_images/dicaprio.jpg", "matt damon", database, FRmodel)
verify("my_images/mattDamon1.jpg", "matt damon", database, FRmodel)
```
## Face Recognition
Identifies the person withou needing to provide an identity. This is a 1:K matching problem.
Steps:
1. Compute the target encoding of the image from image_path
2. Find the encoding from the database that has smallest distance with the target encoding.
```
def recognize(image_path, database, model):
"""
Implements face recognition by finding who is the person on the image_path image.
Arguments:
image_path -- path to an image
database -- database containing image encodings along with the name of the person on the image
model -- Inception model instance in Keras
Returns:
identities -- list, containing names of the predicted people on the image_path image
"""
## Step 1: Compute the encodings
encodings = face_img_to_encoding(image_path, model)
# Initialize the lists for keeping track of people in the picture
identities = []
unknown_encodings = []
# Loop over person encodings in the specific image
for encoding in encodings:
## Step 2: Find the closest encoding ##
# Initializing "min_dist" to a large value, say 100
min_dist = 100
# Loop over the database dictionary's names and encodings.
for (name, db_encodings) in database.items():
for db_enc in db_encodings:
# Compute L2 distance between the target "encoding" and the current "emb" from the database.
dist = np.linalg.norm(encoding - db_enc)
# If this distance is less than the min_dist, then set min_dist to dist, and identity to name.
if dist < min_dist:
min_dist = dist
identity = name
if min_dist > 0.8:
print("Not in the database.")
#Add the encoding in the database for unknown encodings
unknown_encodings.append(encoding)
else:
if identity not in identities and identity != "unknown":
print ("You're " + str(identity) + ", the distance is " + str(min_dist))
#Add the encoding to the known person's encoding list so that model can become more robust.
identities.append(identity)
face_encodings = database[str(identity)]
face_encodings.append(encoding)
database[str(identity)] = face_encodings
for encoding in unknown_encodings:
unknown = database["unknown"]
unknown.append(encoding)
database["unknown"] = unknown
return identities
```
## Let's see if the database can recognize unseen picture of Matt Damon
```
recognize("my_images/mattDamon1.jpg", database, FRmodel)
```
### End of The Recognition & Verification, Congratulations
Keep Learning...
|
github_jupyter
|
<a href="https://colab.research.google.com/github/meisben/docs/blob/master/bmcCompletedTutorials/tutorials/keras/basic_text_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Text classification with movie reviews
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/basic_text_classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/keras/basic_text_classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/keras/basic_text_classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
This notebook classifies movie reviews as *positive* or *negative* using the text of the review. This is an example of *binary*—or two-class—classification, an important and widely applicable kind of machine learning problem.
We'll use the [IMDB dataset](https://www.tensorflow.org/api_docs/python/tf/keras/datasets/imdb) that contains the text of 50,000 movie reviews from the [Internet Movie Database](https://www.imdb.com/). These are split into 25,000 reviews for training and 25,000 reviews for testing. The training and testing sets are *balanced*, meaning they contain an equal number of positive and negative reviews.
This notebook uses [tf.keras](https://www.tensorflow.org/guide/keras), a high-level API to build and train models in TensorFlow. For a more advanced text classification tutorial using `tf.keras`, see the [MLCC Text Classification Guide](https://developers.google.com/machine-learning/guides/text-classification/).
```
# keras.datasets.imdb is broken in 1.13 and 1.14, by np 1.16.3
!pip install tf_nightly
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow as tf
from tensorflow import keras
import numpy as np
print(tf.__version__)
```
## Download the IMDB dataset
The IMDB dataset comes packaged with TensorFlow. It has already been preprocessed such that the reviews (sequences of words) have been converted to sequences of integers, where each integer represents a specific word in a dictionary.
The following code downloads the IMDB dataset to your machine (or uses a cached copy if you've already downloaded it):
```
imdb = keras.datasets.imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
```
The argument `num_words=10000` keeps the top 10,000 most frequently occurring words in the training data. The rare words are discarded to keep the size of the data manageable.
## Explore the data
Let's take a moment to understand the format of the data. The dataset comes preprocessed: each example is an array of integers representing the words of the movie review. Each label is an integer value of either 0 or 1, where 0 is a negative review, and 1 is a positive review.
```
print("Training entries: {}, labels: {}".format(len(train_data), len(train_labels)))
```
The text of reviews have been converted to integers, where each integer represents a specific word in a dictionary. Here's what the first review looks like:
```
print(train_data[0])
```
Movie reviews may be different lengths. The below code shows the number of words in the first and second reviews. Since inputs to a neural network must be the same length, we'll need to resolve this later.
```
len(train_data[0]), len(train_data[1])
dir(imdb)
imdb.get_word_index?
```
### Convert the integers back to words
It may be useful to know how to convert integers back to text. Here, we'll create a helper function to query a dictionary object that contains the integer to string mapping:
```
# A dictionary mapping words to an integer index
word_index = imdb.get_word_index()
# The first indices are reserved
word_index = {k:(v+3) for k,v in word_index.items()}
word_index["<PAD>"] = 0
word_index["<START>"] = 1
word_index["<UNK>"] = 2 # unknown
word_index["<UNUSED>"] = 3
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
def decode_review(text):
return ' '.join([reverse_word_index.get(i, '?') for i in text])
```
Let's have a look at the propterties of the word_index dictionary
```
#imdb.load_data?
print(type(word_index))
print(len(word_index))
#print(word_index)
print(decode_review([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]))
print(decode_review([10003,1002,10001,10000]))
```
Now we can use the `decode_review` function to display the text for the first review:
```
decode_review(train_data[0])
```
## Prepare the data
The reviews—the arrays of integers—must be converted to tensors before fed into the neural network. This conversion can be done a couple of ways:
* Convert the arrays into vectors of 0s and 1s indicating word occurrence, similar to a one-hot encoding. For example, the sequence [3, 5] would become a 10,000-dimensional vector that is all zeros except for indices 3 and 5, which are ones. Then, make this the first layer in our network—a Dense layer—that can handle floating point vector data. This approach is memory intensive, though, requiring a `num_words * num_reviews` size matrix.
* Alternatively, we can pad the arrays so they all have the same length, then create an integer tensor of shape `max_length * num_reviews`. We can use an embedding layer capable of handling this shape as the first layer in our network.
In this tutorial, we will use the second approach.
Since the movie reviews must be the same length, we will use the [pad_sequences](https://keras.io/preprocessing/sequence/#pad_sequences) function to standardize the lengths:
```
train_data = keras.preprocessing.sequence.pad_sequences(train_data,
value=word_index["<PAD>"],
padding='post',
maxlen=256)
test_data = keras.preprocessing.sequence.pad_sequences(test_data,
value=word_index["<PAD>"],
padding='post',
maxlen=256)
```
Let's look at the length of the examples now:
```
len(train_data[0]), len(train_data[1])
```
And inspect the (now padded) first review:
```
print(train_data[0])
```
## Build the model
The neural network is created by stacking layers—this requires two main architectural decisions:
* How many layers to use in the model?
* How many *hidden units* to use for each layer?
In this example, the input data consists of an array of word-indices. The labels to predict are either 0 or 1. Let's build a model for this problem:
```
# input shape is the vocabulary count used for the movie reviews (10,000 words)
vocab_size = 10000
model = keras.Sequential()
model.add(keras.layers.Embedding(vocab_size, 16))
model.add(keras.layers.GlobalAveragePooling1D())
model.add(keras.layers.Dense(16, activation=tf.nn.relu))
model.add(keras.layers.Dense(1, activation=tf.nn.sigmoid))
model.summary()
```
The layers are stacked sequentially to build the classifier:
1. The first layer is an `Embedding` layer. This layer takes the integer-encoded vocabulary and looks up the embedding vector for each word-index. These vectors are learned as the model trains. The vectors add a dimension to the output array. The resulting dimensions are: `(batch, sequence, embedding)`.
2. Next, a `GlobalAveragePooling1D` layer returns a fixed-length output vector for each example by averaging over the sequence dimension. This allows the model to handle input of variable length, in the simplest way possible.
3. This fixed-length output vector is piped through a fully-connected (`Dense`) layer with 16 hidden units.
4. The last layer is densely connected with a single output node. Using the `sigmoid` activation function, this value is a float between 0 and 1, representing a probability, or confidence level.
### Hidden units
The above model has two intermediate or "hidden" layers, between the input and output. The number of outputs (units, nodes, or neurons) is the dimension of the representational space for the layer. In other words, the amount of freedom the network is allowed when learning an internal representation.
If a model has more hidden units (a higher-dimensional representation space), and/or more layers, then the network can learn more complex representations. However, it makes the network more computationally expensive and may lead to learning unwanted patterns—patterns that improve performance on training data but not on the test data. This is called *overfitting*, and we'll explore it later.
### Loss function and optimizer
A model needs a loss function and an optimizer for training. Since this is a binary classification problem and the model outputs a probability (a single-unit layer with a sigmoid activation), we'll use the `binary_crossentropy` loss function.
This isn't the only choice for a loss function, you could, for instance, choose `mean_squared_error`. But, generally, `binary_crossentropy` is better for dealing with probabilities—it measures the "distance" between probability distributions, or in our case, between the ground-truth distribution and the predictions.
Later, when we are exploring regression problems (say, to predict the price of a house), we will see how to use another loss function called mean squared error.
Now, configure the model to use an optimizer and a loss function:
```
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['acc'])
```
## Create a validation set
When training, we want to check the accuracy of the model on data it hasn't seen before. Create a *validation set* by setting apart 10,000 examples from the original training data. (Why not use the testing set now? Our goal is to develop and tune our model using only the training data, then use the test data just once to evaluate our accuracy).
```
x_val = train_data[:10000]
partial_x_train = train_data[10000:]
y_val = train_labels[:10000]
partial_y_train = train_labels[10000:]
```
## Train the model
Train the model for 40 epochs in mini-batches of 512 samples. This is 40 iterations over all samples in the `x_train` and `y_train` tensors. While training, monitor the model's loss and accuracy on the 10,000 samples from the validation set:
```
history = model.fit(partial_x_train,
partial_y_train,
epochs=40,
batch_size=512,
validation_data=(x_val, y_val),
verbose=1)
```
## Evaluate the model
And let's see how the model performs. Two values will be returned. Loss (a number which represents our error, lower values are better), and accuracy.
```
results = model.evaluate(test_data, test_labels)
print(results)
```
This fairly naive approach achieves an accuracy of about 87%. With more advanced approaches, the model should get closer to 95%.
## Create a graph of accuracy and loss over time
`model.fit()` returns a `History` object that contains a dictionary with everything that happened during training:
```
history_dict = history.history
history_dict.keys()
```
There are four entries: one for each monitored metric during training and validation. We can use these to plot the training and validation loss for comparison, as well as the training and validation accuracy:
```
import matplotlib.pyplot as plt
acc = history_dict['acc']
val_acc = history_dict['val_acc']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = range(1, len(acc) + 1)
# "bo" is for "blue dot"
plt.plot(epochs, loss, 'bo', label='Training loss')
# b is for "solid blue line"
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() # clear figure
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
In this plot, the dots represent the training loss and accuracy, and the solid lines are the validation loss and accuracy.
Notice the training loss *decreases* with each epoch and the training accuracy *increases* with each epoch. This is expected when using a gradient descent optimization—it should minimize the desired quantity on every iteration.
This isn't the case for the validation loss and accuracy—they seem to peak after about twenty epochs. This is an example of overfitting: the model performs better on the training data than it does on data it has never seen before. After this point, the model over-optimizes and learns representations *specific* to the training data that do not *generalize* to test data.
For this particular case, we could prevent overfitting by simply stopping the training after twenty or so epochs. Later, you'll see how to do this automatically with a callback.
|
github_jupyter
|
# Fetching Hydrology Data
We have prepared shapefiles containing the USGS quarter quadrangles that have good coverage of forest stand delineations that we want to grab other data for.
# Mount Google Drive
So we can access our files showing tile locations, and save the rasters we will generate from the elevation data.
```
from google.colab import drive
drive.mount('/content/drive', force_remount=True)
! sudo apt-get install -y libspatialindex-dev
! pip install geopandas rtree -q
import numpy as np
import geopandas as gpd
import os
import requests
from shapely.geometry import box, Polygon
```
The following function will retrieve the hydro data from The National Map's web service.
```
def nhd_from_tnm(nhd_layer,
bbox,
inSR=4326,
**kwargs):
"""Returns features from the National Hydrography Dataset Plus High
Resolution web service from The National Map.
Available layers are:
========= ======================
NHD Layer Description
========= ======================
0 NHDPlusSink
1 NHDPoint
2 NetworkNHDFlowline
3 NonNetworkNHDFlowline
4 FlowDirection
5 NHDPlusWall
6 NHDPlusBurnLineEvent
7 NHDLine
8 NHDArea
9 NHDWaterbody
10 NHDPlusCatchment
11 WBDHU12
========= ======================
Parameters
----------
nhd_layer : int
a value from 0-11 indicating the feature layer to retrieve.
bbox : list-like
list of bounding box coordinates (minx, miny, maxx, maxy).
inSR : int
spatial reference for bounding box, such as an EPSG code (e.g., 4326)
Returns
-------
clip_gdf : GeoDataFrame
features in vector format, clipped to bbox
"""
BASE_URL = ''.join([
'https://hydro.nationalmap.gov/arcgis/rest/services/NHDPlus_HR/',
'MapServer/',
str(nhd_layer), '/query?'
])
params = dict(where=None,
text=None,
objectIds=None,
time=None,
geometry=','.join([str(x) for x in bbox]),
geometryType='esriGeometryEnvelope',
inSR=inSR,
spatialRel='esriSpatialRelIntersects',
relationParam=None,
outFields='*',
returnGeometry='true',
returnTrueCurves='false',
maxAllowableOffset=None,
geometryPrecision=None,
outSR=inSR,
having=None,
returnIdsOnly='false',
returnCountOnly='false',
orderByFields=None,
groupByFieldsForStatistics=None,
outStatistics=None,
returnZ='false',
returnM='false',
gdbVersion=None,
historicMoment=None,
returnDistinctValues='false',
resultOffset=None,
resultRecordCount=None,
queryByDistance=None,
returnExtentOnly='false',
datumTransformation=None,
parameterValues=None,
rangeValues=None,
quantizationParameters=None,
featureEncoding='esriDefault',
f='geojson')
for key, value in kwargs.items():
params.update({key: value})
r = requests.get(BASE_URL, params=params)
jsn = r.json()
if len(jsn['features']) == 0:
clip_gdf = gpd.GeoDataFrame(geometry=[Polygon()], crs=inSR)
else:
try:
gdf = gpd.GeoDataFrame.from_features(jsn, crs=inSR)
# this API seems to return M and Z values even if not requested
# this catches the error and keeps only the first two coordinates (x and y)
except AssertionError:
for f in jsn['features']:
f['geometry'].update({
'coordinates': [c[0:2] for c in f['geometry']['coordinates']]
})
gdf = gpd.GeoDataFrame.from_features(jsn)
clip_gdf = gpd.clip(gdf, box(*bbox))
if len(clip_gdf) == 0:
clip_gdf = gpd.GeoDataFrame(geometry=[Polygon()], crs=inSR)
return clip_gdf
```
# Download Data for Training Tiles
This function will loop through a GeoDataFrame, fetch the relevant data, and write data to disk in the appropriate format.
```
def fetch_hydro(gdf, state, overwrite=False):
epsg = gdf.crs.to_epsg()
print('Fetching hydro data for {:,d} tiles'.format(len(gdf)))
## loop through all the geometries in the geodataframe
for idx, row in gdf.iterrows():
xmin, ymin, xmax, ymax = row['geometry'].bounds
xmin, ymin = np.floor((xmin, ymin))
xmax, ymax = np.ceil((xmax, ymax))
bbox = [xmin, ymin, xmax, ymax]
## don't bother fetching data if we already have processed this tile
OUTROOT = '/content/drive/Shared drives/stand_mapping/data/interim/training_tiles'
outfolder = f'{state.lower()}/hydro'
outdir = os.path.join(OUTROOT, outfolder)
flow_outname = f'{row.CELL_ID}_flowlines.geojson'
waterbody_outname = f'{row.CELL_ID}_waterbodies.geojson'
flow_outfile = os.path.join(outdir, flow_outname)
waterbody_outfile = os.path.join(outdir, waterbody_outname)
if (os.path.exists(flow_outfile) and os.path.exists(waterbody_outfile)) and not overwrite:
if idx % 100 == 0:
print()
if idx % 10 == 0:
print(idx, end='')
else:
print('.', end='')
continue
flow = nhd_from_tnm(4, bbox, epsg)
waterbody = nhd_from_tnm(9, bbox, epsg)
flow.to_file(flow_outfile, driver='GeoJSON')
waterbody.to_file(waterbody_outfile, driver='GeoJSON')
## report progress
if idx % 100 == 0:
print()
if idx % 10 == 0:
print(idx, end='')
else:
print('.', end='')
```
## Fetch Hydro Layers for each tile
```
SHP_DIR = '/content/drive/Shared drives/stand_mapping/data/interim'
WA11_SHP = 'washington_utm11n_training_quads_epsg6340.shp'
WA10_SHP = 'washington_utm10n_training_quads_epsg6339.shp'
OR10_SHP = 'oregon_utm10n_training_quads_epsg6339.shp'
OR11_SHP = 'oregon_utm11n_training_quads_epsg6340.shp'
or10_gdf = gpd.read_file(os.path.join(SHP_DIR, OR10_SHP))
or11_gdf = gpd.read_file(os.path.join(SHP_DIR, OR11_SHP))
wa10_gdf = gpd.read_file(os.path.join(SHP_DIR, WA10_SHP))
wa11_gdf = gpd.read_file(os.path.join(SHP_DIR, WA11_SHP))
GDF = wa11_gdf
STATE = 'washington'
fetch_hydro(GDF, STATE)
GDF = wa10_gdf
STATE = 'washington'
fetch_hydro(GDF, STATE)
GDF = or10_gdf
STATE = 'oregon'
fetch_hydro(GDF, STATE)
GDF = or11_gdf
STATE = 'oregon'
fetch_hydro(GDF, STATE)
```
|
github_jupyter
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Installation
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
This book is written in Jupyter Notebook, a browser based interactive Python environment that mixes Python, text, and math. I choose it because of the interactive features - I found Kalman filtering nearly impossible to learn until I started working in an interactive environment. It is difficult to form an intuition about many of the parameters until you can change them and immediately see the output. An interactive environment also allows you to play 'what if' scenarios. "What if I set $\mathbf{Q}$ to zero?" It is trivial to find out with Jupyter Notebook.
Another reason I choose it is because most textbooks leaves many things opaque. For example, there might be a beautiful plot next to some pseudocode. That plot was produced by software, but software that is not available to the reader. I want everything that went into producing this book to be available to you. How do you plot a covariance ellipse? You won't know if you read most books. With Jupyter Notebook all you have to do is look at the source code.
Even if you choose to read the book online you will want Python and the SciPy stack installed so that you can write your own Kalman filters. There are many different ways to install these libraries, and I cannot cover them all, but I will cover a few typical scenarios.
## Installing the SciPy Stack
This book requires IPython, Jupyter, NumPy, SciPy, SymPy, and Matplotlib. The SciPy stack of NumPy, SciPy, and Matplotlib depends on third party Fortran and C code, and is not trivial to install from source code. The SciPy website strongly urges using a pre-built installation, and I concur with this advice.
Jupyter notebook is the software that allows you to run Python inside of the browser - the book is a collection of Jupyter notebooks. IPython provides the infrastructure for Jupyter and data visualization. NumPy and Scipy are packages which provide the linear algebra implementation that the filters use. Sympy performs symbolic math - I use it to find derivatives of algebraic equations. Finally, Matplotlib provides plotting capability.
I use the Anaconda distribution from Continuum Analytics. This is an excellent distribution that combines all of the packages listed above, plus many others. IPython recommends this package to install Ipython. Installation is very straightforward, and it can be done alongside other Python installations you might already have on your machine. It is free to use. You may download it from here: http://continuum.io/downloads I strongly recommend using the latest Python 3 version that they provide. For now I support Python 2.7, but perhaps not much longer.
There are other choices for installing the SciPy stack. You can find instructions here: http://scipy.org/install.html It can be very cumbersome, and I do not support it or provide any instructions on how to do it.
Many Linux distributions come with these packages pre-installed. However, they are often somewhat dated and they will need to be updated as the book depends on recent versions of all. Updating a specific Linux installation is beyond the scope of this book. An advantage of the Anaconda distribution is that it does not modify your local Python installation, so you can install it and not break your linux distribution. Some people have been tripped up by this. They install Anaconda, but the installed Python remains the default version and then the book's software doesn't run correctly.
I do not run regression tests on old versions of these libraries. In fact, I know the code will not run on older versions (say, from 2014-2015). I do not want to spend my life doing tech support for a book, thus I put the burden on you to install a recent version of Python and the SciPy stack.
You will need Python 2.7 or later installed. Almost all of my work is done in Python 3.6, but I periodically test on 2.7. I do not promise any specific check in will work in 2.7 however. I use Python's `from __future__ import ...` statement to help with compatibility. For example, all prints need to use parenthesis. If you try to add, say, `print x` into the book your script will fail; you must write `print(x)` as in Python 3.X.
Please submit a bug report at the book's [github repository](https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python) if you have installed the latest Anaconda and something does not work - I will continue to ensure the book will run with the latest Anaconda release. I'm rather indifferent if the book will not run on an older installation. I'm sorry, but I just don't have time to provide support for everyone's different setups. Packages like `jupyter notebook` are evolving rapidly, and I cannot keep up with all the changes *and* remain backwards compatible as well.
If you need older versions of the software for other projects, note that Anaconda allows you to install multiple versions side-by-side. Documentation for this is here:
https://conda.io/docs/user-guide/tasks/manage-python.html
## Installing FilterPy
FilterPy is a Python library that implements all of the filters used in this book, and quite a few others. Installation is easy using `pip`. Issue the following from the command prompt:
pip install filterpy
FilterPy is written by me, and the latest development version is always available at https://github.com/rlabbe/filterpy.
## Downloading and Running the Book
The book is stored in a github repository. From the command line type the following:
git clone --depth=1 https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python.git
This will create a directory named Kalman-and-Bayesian-Filters-in-Python. The `depth` parameter just gets you the latest version. Unless you need to see my entire commit history this is a lot faster and saves space.
If you do not have git installed, browse to https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python where you can download the book via your browser.
Now, from the command prompt change to the directory that was just created, and then run Jupyter notebook:
cd Kalman-and-Bayesian-Filters-in-Python
juptyer notebook
A browser window should launch showing you all of the chapters in the book. Browse to the first chapter by clicking on it, then open the notebook in that subdirectory by clicking on the link.
More information about running the notebook can be found here:
http://jupyter-notebook-beginner-guide.readthedocs.org/en/latest/execute.html
## Companion Software
Code that is specific to the book is stored with the book in the subdirectory *./kf_book*. This code is in a state of flux; I do not wish to document it here yet. I do mention in the book when I use code from this directory, so it should not be a mystery.
In the *kf_book* subdirectory there are Python files with a name like *xxx*_internal.py. I use these to store functions that are useful for a specific chapter. This allows me to hide away Python code that is not particularly interesting to read - I may be generating a plot or chart, and I want you to focus on the contents of the chart, not the mechanics of how I generate that chart with Python. If you are curious as to the mechanics of that, just go and browse the source.
Some chapters introduce functions that are useful for the rest of the book. Those functions are initially defined within the Notebook itself, but the code is also stored in a Python file that is imported if needed in later chapters. I do document when I do this where the function is first defined, but this is still a work in progress. I try to avoid this because then I always face the issue of code in the directory becoming out of sync with the code in the book. However, IPython Notebook does not give us a way to refer to code cells in other notebooks, so this is the only mechanism I know of to share functionality across notebooks.
There is an undocumented directory called **experiments**. This is where I write and test code prior to putting it in the book. There is some interesting stuff in there, and feel free to look at it. As the book evolves I plan to create examples and projects, and a lot of this material will end up there. Small experiments will eventually just be deleted. If you are just interested in reading the book you can safely ignore this directory.
The subdirectory *./kf_book* contains a css file containing the style guide for the book. The default look and feel of IPython Notebook is rather plain. Work is being done on this. I have followed the examples set by books such as [Probabilistic Programming and Bayesian Methods for Hackers](http://nbviewer.ipython.org/github/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/blob/master/Chapter1_Introduction/Chapter1.ipynb). I have also been very influenced by Professor Lorena Barba's fantastic work, [available here](https://github.com/barbagroup/CFDPython). I owe all of my look and feel to the work of these projects.
## Using Juptyer Notebook
A complete tutorial on Jupyter Notebook is beyond the scope of this book. Many are available online. In short, Python code is placed in cells. These are prefaced with text like `In [1]:`, and the code itself is in a boxed area. If you press CTRL-ENTER while focus is inside the box the code will run and the results will be displayed below the box. Like this:
```
print(3+7.2)
```
If you have this open in Jupyter Notebook now, go ahead and modify that code by changing the expression inside the print statement and pressing CTRL+ENTER. The output should be changed to reflect what you typed in the code cell.
## SymPy
SymPy is a Python package for performing symbolic mathematics. The full scope of its abilities are beyond this book, but it can perform algebra, integrate and differentiate equations, find solutions to differential equations, and much more. For example, we use use it to compute the Jacobian of matrices and expected value integral computations.
First, a simple example. We will import SymPy, initialize its pretty print functionality (which will print equations using LaTeX). We will then declare a symbol for SymPy to use.
```
import sympy
sympy.init_printing(use_latex='mathjax')
phi, x = sympy.symbols('\phi, x')
phi
```
Notice how it prints the symbol `phi` using LaTeX. Now let's do some math. What is the derivative of $\sqrt{\phi}$?
```
sympy.diff('sqrt(phi)')
```
We can factor equations
```
sympy.factor(phi**3 -phi**2 + phi - 1)
```
and we can expand them.
```
((phi+1)*(phi-4)).expand()
```
You can evauate an equation for specific values of its variables:
```
w =x**2 -3*x +4
print(w.subs(x, 4))
print(w.subs(x, 12))
```
You can also use strings for equations that use symbols that you have not defined:
```
x = sympy.expand('(t+1)*2')
x
```
Now let's use SymPy to compute the Jacobian of a matrix. Given the function
$$h=\sqrt{(x^2 + z^2)}$$
find the Jacobian with respect to x, y, and z.
```
x, y, z = sympy.symbols('x y z')
H = sympy.Matrix([sympy.sqrt(x**2 + z**2)])
state = sympy.Matrix([x, y, z])
H.jacobian(state)
```
Now let's compute the discrete process noise matrix $\mathbf Q$ given the continuous process noise matrix
$$\mathbf Q = \Phi_s \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix}$$
The integral is
$$\mathbf Q = \int_0^{\Delta t} \mathbf F(t)\mathbf Q\mathbf F^T(t)\, dt$$
where
$$\mathbf F(\Delta t) = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
```
dt = sympy.symbols('\Delta{t}')
F_k = sympy.Matrix([[1, dt, dt**2/2],
[0, 1, dt],
[0, 0, 1]])
Q = sympy.Matrix([[0,0,0],
[0,0,0],
[0,0,1]])
sympy.integrate(F_k*Q*F_k.T,(dt, 0, dt))
```
## Various Links
https://ipython.org/
https://jupyter.org/
https://www.scipy.org/
|
github_jupyter
|
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import os
kdata = np.load('KeplerSampleFullQ.npy',encoding='bytes')
print(kdata.shape)
print(len(kdata[250][0]))
import os
dmints = [-1.2,-0.3,-0.1,-0.05, -0.02,-0.01, -0.006, -0.005, -0.004, -0.0012,
-0.001, -0.0006, -0.0003, 0, 0.0003, 0.0006, 0.001, 0.0012, 0.003,
0.004, 0.005, 0.006, 0.01, 0.02, 0.05, 0.1, 0.3, 0.6, 1.2]
dtints = [-1.0/145, 1.0/47, 2.0/47, 3.0/47, 4.0/47, 6.0/47, 10.0/47, 15.0/47,
20.0/47, 30.0/47, 40.0/47, 1.0, 1.2,
1.4, 1.5, 1.7, 2, 2.25, 2.5, 3.0, 4, 6 , 9, 15, 20, 30, 45, 60, 90]
def pairwisediffs(arrayoned):
x = arrayoned.reshape((1,len(arrayoned)))
xdm = x[:] - np.transpose(x[:])
xd = xdm[np.triu_indices(len(x[0]), k = 1)]
return(xd)
def get2dhist(lightcurve):
xd = pairwisediffs(lightcurve[0])
yd = pairwisediffs(lightcurve[1])
H,xe,ye = np.histogram2d(xd,yd,bins=[dtints,dmints],range=None,normed=False)
G = 255*H/np.sum(H)
return G
def load_data():
data = []
for file in os.listdir("full_dmdt"):
data.append(np.load("full_dmdt/"+file))
data = np.array(data)
return data
data = load_data()
import umap
import sklearn
from sklearn.manifold import TSNE
tt = data.reshape(2500, 784)
x_embedded_tsne_first = TSNE(n_components=2).fit_transform(tt)
x_embedded_umap_first = umap.UMAP().fit_transform(tt)
plt.scatter(x_embedded_tsne_first[:, 0], x_embedded_tsne_first[:, 1])
plt.scatter(x_embedded_umap_first[:, 0], x_embedded_umap_first[:, 1])
```
# first 30 points
```
kdata = np.load('KeplerSampleFullQ.npy',encoding='bytes')
print(kdata.shape)
print(len(kdata[250][0]))
kdata[0][0].shape
normalized_x_flux = []
normalized_y_flux = []
for i, _ in enumerate(kdata):
if len(kdata[i][1]) == 3534:
normalized_x_flux.append(kdata[i][0])
normalized_y_flux.append(kdata[i][1])
nx = np.array(normalized_x_flux)
ny = np.array(normalized_y_flux)
nx = nx[:, :1350]
ny = ny[:, :1350]
fastdmdt = get2dhist([nx[0],ny[0]])
plt.imshow(fastdmdt.T, norm = LogNorm(), origin="lower")
plt.colorbar()
first_30_points.shape
def first_n_points(n, dir_name):
normalized_x_flux = []
normalized_y_flux = []
for i, _ in enumerate(kdata):
if len(kdata[i][1]) == 3534:
normalized_x_flux.append(kdata[i][0])
normalized_y_flux.append(kdata[i][1])
nx = np.array(normalized_x_flux)
ny = np.array(normalized_y_flux)
nx = nx[:, :n]
ny = ny[:, :n]
data = []
for i, _ in enumerate(nx):
fastdmdt = get2dhist([nx[i],ny[i]])
np.save(dir_name + "/" + str(i), fastdmdt.T)
data.append(fastdmdt)
return np.array(data)
points_30 = first_n_points(30, "full_30_points")
print points_30.shape
tt = points_30.reshape(2196, 784)
x_embedded_tsne_first = TSNE(n_components=2).fit_transform(tt)
x_embedded_umap_first = umap.UMAP().fit_transform(tt)
plt.scatter(x_embedded_tsne_first[:, 0], x_embedded_tsne_first[:, 1])
plt.scatter(x_embedded_umap_first[:, 0], x_embedded_umap_first[:, 1])
```
# random 1/2 of the points
```
import random
def random_n_points(n, dir_name):
if not os.path.exists(dir_name):
os.makedirs(dir_name)
normalized_x_flux = []
normalized_y_flux = []
for i, _ in enumerate(kdata):
if len(kdata[i][1]) == 3534:
normalized_x_flux.append(kdata[i][0])
normalized_y_flux.append(kdata[i][1])
nx = np.array(normalized_x_flux)
ny = np.array(normalized_y_flux)
start = random.randint(1, len(normalized_x_flux[0])-n)
random_x_points = nx[:, start: start+n]
random_y_points = ny[:, start: start+n]
data = []
for i, _ in enumerate(nx):
fastdmdt = get2dhist([random_x_points[i],random_y_points[i]])
np.save(dir_name + "/" + str(i), fastdmdt.T)
data.append(fastdmdt)
if i%500 == 0:
print "ON ITERATION " + str(i)
return np.array(data)
r_half_points = random_n_points(1090, "random_half_points")
print r_half_points.shape
tt = r_half_points.reshape(2196, 784)
x_embedded_tsne_first = TSNE(n_components=2).fit_transform(tt)
x_embedded_umap_first = umap.UMAP().fit_transform(tt)
plt.scatter(x_embedded_tsne_first[:, 0], x_embedded_tsne_first[:, 1])
plt.scatter(x_embedded_umap_first[:, 0], x_embedded_umap_first[:, 1])
plt.scatter(x_embedded_umap_first[:, 0], x_embedded_umap_first[:, 1])
```
|
github_jupyter
|
# [ATM 623: Climate Modeling](index.ipynb)
A graduate-level course on the hands-on use of climate models for understanding climate processes.
### [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html)
University at Albany, Department of Atmospheric and Environmental Sciences
[Course home page](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2017/)
### About these notes:
This document uses the interactive [`Jupyter notebook`](https://jupyter.org) format. The notes can be accessed in several different ways:
- The interactive notebooks are hosted on `github` at https://github.com/brian-rose/ClimateModeling_courseware
- The latest versions can be viewed as static web pages [rendered on nbviewer](http://nbviewer.ipython.org/github/brian-rose/ClimateModeling_courseware/blob/master/index.ipynb)
- A complete snapshot of the notes as of May 2017 (end of spring semester) are [available on Brian's website](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2017/Notes/index.html).
[Also here is a legacy version from 2015](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/Notes/index.html).
Many of these notes make use of the `climlab` package, available at https://github.com/brian-rose/climlab
This page is the top-level notebook with links to all notes and assignments.
## Lecture notes
1. [Planetary energy budget](Lectures/Lecture01 -- Planetary energy budget.ipynb)
2. [Solving the zero-dimensional EBM](Lectures/Lecture02 -- Solving the zero-dimensional EBM.ipynb)
3. [Climate Sensitivity and Feedback](Lectures/Lecture03 -- Climate sensitivity and feedback.ipynb)
4. [The climate system and climate models](Lectures/Lecture04 -- Climate system and climate models.ipynb)
5. [A Brief Review of Radiation](Lectures/Lecture05 -- Radiation.ipynb)
6. [Elementary greenhouse models](Lectures/Lecture06 -- Elementary greenhouse models.ipynb)
7. [Grey radiation modeling with climlab](Lectures/Lecture07 -- Grey radiation modeling with climlab.ipynb)
8. [Modeling non-scattering radiative transfer](Lectures/Lecture08 -- Modeling non-scattering radiative transfer.ipynb)
9. [Who needs spectral bands? We do. Some baby steps...](Lectures/Lecture09 -- Who needs spectral bands.ipynb)
10. [Radiative-Convective Equilibrium](Lectures/Lecture10 -- Radiative-Convective Equilibrium.ipynb)
11. [Clouds and cloud feedback](Lectures/Lecture11 -- Clouds and cloud feedback.ipynb)
12. [Insolation](Lectures/Lecture12 -- Insolation.ipynb)
13. [Orbital variations, insolation, and the ice ages](Lectures/Lecture13 -- Orbital variations.ipynb)
14. [Heat transport](Lectures/Lecture14 -- Heat transport.ipynb)
15. [The one-dimensional energy balance model](Lectures/Lecture15 -- Diffusive energy balance model.ipynb)
16. [Seasonal cycle and heat capacity](Lectures/Lecture16 -- Seasonal cycle and heat capacity.ipynb)
17. [A peak at numerical methods for diffusion models](Lectures/Lecture17 -- Numerical methods for diffusion models.ipynb)
18. [Ice albedo feedback in the EBM](Lectures/Lecture18 -- Ice albedo feedback in the EBM.ipynb)
19. [Snowball Earth and Large Ice Cap Instability in the EBM](Lectures/Lecture19 -- Snowball Earth in the EBM.ipynb)
20. [The surface energy balance](Lectures/Lecture20 -- The surface energy balance.ipynb)
21. [Water, water everywhere](Lectures/Lecture21 -- Water, water everywhere!.ipynb)
## Assignments
1. [Feedback in the zero-dimensional EBM](Assignments/Assignment01 -- Feedback in the zero-dimensional EBM.ipynb)
2. [Introducing CESM](Assignments/Assignment02 -- Introducing CESM.ipynb)
3. [Energy budget in CESM](Assignments/Assignment03 -- Energy budget in CESM.ipynb)
4. [Radiative forcing in a grey radiation atmosphere](Assignments/Assignment04 -- Radiative forcing in a grey radiation atmosphere.ipynb)
5. [Height-Dependent Water Vapor Changes](Assignments/Assignment05 -- Height-Dependent Water Vapor Changes.ipynb)
6. [Orbital variations and insolation](Assignments/Assignment06 -- Orbital variations and insolation.ipynb)
7. Numerical solution of the diffusion equation using the implicit method (see end of [Lecture 17](Lectures/Lecture16 -- Numerical methods for diffusion models.ipynb))
____________
## Dependencies and installation
These notebooks use the following packages:
- Python (compatible with Python 2 and 3)
- numpy (array-based numerical computing)
- scipy (specialized numerical recipes)
- matplotlib (graphics and animation)
- xarray (labeled datasets)
- sympy (symbolic math)
- climlab (climate modeling engine)
- ffmpeg (video conversion tool used under-the-hood for interactive animations)
- version_information (display information about package version)
We highly recommend using [Anaconda Python](https://www.continuum.io/downloads). For example, the following commands will create a self-contained [conda environment](https://conda.io/docs/using/envs.html) with everything you need to run these notebooks (Mac, Linux and Windows):
```
conda config --add channels conda-forge
conda create --name atm623 python jupyter xarray sympy climlab version_information ffmpeg
```
____________
## Credits
The author of this notebook is [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany.
It was developed in support of [ATM 623: Climate Modeling](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/), a graduate-level course in the [Department of Atmospheric and Envionmental Sciences](http://www.albany.edu/atmos/index.php)
Development of these notes and the [climlab software](https://github.com/brian-rose/climlab) is partially supported by the National Science Foundation under award AGS-1455071 to Brian Rose. Any opinions, findings, conclusions or recommendations expressed here are mine and do not necessarily reflect the views of the National Science Foundation.
____________
|
github_jupyter
|
```
import ipywidgets as W
from wxyz.jsonld.widget_jsonld import Expand, Compact, Flatten, Frame, Normalize
from wxyz.lab.widget_dock import DockBox
from wxyz.lab.widget_editor import Editor
from wxyz.core.widget_json import JSON
flex = lambda x=1: dict(layout=dict(flex=f"{x}"))
context = JSON("""{
"@context": {
"@vocab": "http://schema.org/"
}
}""")
document = JSON("""{
"@graph": [{
"@type": "Person",
"@id": "this-guy",
"name": "Jekyll",
"jobTitle": "Doctor"
},{
"@type": "Person",
"@id": "this-guy",
"name": "Hyde",
"jobTitle": "Mister"
}]
}""")
context_source = Editor(description="JSON-LD Context", **flex())
document_source = Editor(description="JSON Document", **flex())
W.jslink((context, "source"), (context_source, "value"))
W.jslink((document, "source"), (document_source, "value"))
expand = Expand()
expand_output = Editor(description="Expanded")
W.jslink((expand, "value"), (expand_output, "value"))
W.jslink((document, "value"), (expand, "source"))
W.jslink((context, "value"), (expand, "expand_context"))
compact = Compact()
compact_output = Editor(description="Compacted")
W.jslink((compact, "value"), (compact_output, "value"))
W.jslink((document, "value"), (compact, "source"))
W.jslink((context, "value"), (compact, "context"))
W.jslink((context, "value"), (compact, "expand_context"))
flatten = Flatten()
flatten_output = Editor(description="Flattened")
W.jslink((flatten, "value"), (flatten_output, "value"))
W.jslink((document, "value"), (flatten, "source"))
W.jslink((context, "value"), (flatten, "context"))
W.jslink((context, "value"), (flatten, "expand_context"))
error = Editor("errors will appear here", description="errors be here", **flex(1))
W.jslink((expand, "error"), (error, "value"))
W.jslink((compact, "error"), (error, "value"))
W.jslink((flatten, "error"), (error, "value"))
jsonld_playground = DockBox([
document_source,
context_source,
expand_output,
compact_output,
flatten_output,
error
], layout=dict(height="60vh"))
@jsonld_playground.on_displayed
def on_display(*args, **kwargs):
jsonld_playground.dock_layout = {
'type': 'split-area',
'orientation': 'horizontal',
'children': [
{'type': 'split-area', 'orientation': 'vertical', 'children': [
{'type': 'tab-area', 'widgets': [0], 'currentIndex': 0},
{'type': 'tab-area', 'widgets': [1], 'currentIndex': 0},
], 'sizes': [2, 1]},
{'type': 'split-area', 'orientation': 'vertical', 'children': [
{'type': 'tab-area', 'widgets': [2], 'currentIndex': 0},
{'type': 'tab-area', 'widgets': [3], 'currentIndex': 0},
], 'sizes': [1, 1]},
{'type': 'split-area', 'orientation': 'vertical', 'children': [
{'type': 'tab-area', 'widgets': [4], 'currentIndex': 0},
{'type': 'tab-area', 'widgets': [5], 'currentIndex': 0}
], 'sizes': [1, 1]},
],
'sizes': [1, 1, 1]
}
jsonld_playground
```
|
github_jupyter
|
# A Whirlwind Tour of Python
*Jake VanderPlas*
<img src="fig/cover-large.gif">
These are the Jupyter Notebooks behind my O'Reilly report,
[*A Whirlwind Tour of Python*](http://www.oreilly.com/programming/free/a-whirlwind-tour-of-python.csp).
The full notebook listing is available [on Github](https://github.com/jakevdp/WhirlwindTourOfPython).
*A Whirlwind Tour of Python* is a fast-paced introduction to essential
components of the Python language for researchers and developers who are
already familiar with programming in another language.
The material is particularly aimed at those who wish to use Python for data
science and/or scientific programming, and in this capacity serves as an
introduction to my upcoming book, *The Python Data Science Handbook*.
These notebooks are adapted from lectures and workshops I've given on these
topics at University of Washington and at various conferences, meetings, and
workshops around the world.
## Index
1. [Introduction](00-Introduction.ipynb)
2. [How to Run Python Code](01-How-to-Run-Python-Code.ipynb)
3. [Basic Python Syntax](02-Basic-Python-Syntax.ipynb)
4. [Python Semantics: Variables](03-Semantics-Variables.ipynb)
5. [Python Semantics: Operators](04-Semantics-Operators.ipynb)
6. [Built-In Scalar Types](05-Built-in-Scalar-Types.ipynb)
7. [Built-In Data Structures](06-Built-in-Data-Structures.ipynb)
8. [Control Flow Statements](07-Control-Flow-Statements.ipynb)
9. [Defining Functions](08-Defining-Functions.ipynb)
10. [Errors and Exceptions](09-Errors-and-Exceptions.ipynb)
11. [Iterators](10-Iterators.ipynb)
12. [List Comprehensions](11-List-Comprehensions.ipynb)
13. [Generators and Generator Expressions](12-Generators.ipynb)
14. [Modules and Packages](13-Modules-and-Packages.ipynb)
15. [Strings and Regular Expressions](14-Strings-and-Regular-Expressions.ipynb)
16. [Preview of Data Science Tools](15-Preview-of-Data-Science-Tools.ipynb)
17. [Resources for Further Learning](16-Further-Resources.ipynb)
18. [Appendix: Code To Reproduce Figures](17-Figures.ipynb)
## License
This material is released under the "No Rights Reserved" [CC0](LICENSE)
license, and thus you are free to re-use, modify, build-on, and enhance
this material for any purpose.
That said, I request (but do not require) that if you use or adapt this material,
you include a proper attribution and/or citation; for example
> *A Whirlwind Tour of Python* by Jake VanderPlas (O’Reilly). Copyright 2016 O’Reilly Media, Inc., 978-1-491-96465-1
Read more about CC0 [here](https://creativecommons.org/share-your-work/public-domain/cc0/).
|
github_jupyter
|
## Content-Based Filtering Using Neural Networks
This notebook relies on files created in the [content_based_preproc.ipynb](./content_based_preproc.ipynb) notebook. Be sure to run the code in there before completing this notebook.
Also, we'll be using the **python3** kernel from here on out so don't forget to change the kernel if it's still Python2.
This lab illustrates:
1. how to build feature columns for a model using tf.feature_column
2. how to create custom evaluation metrics and add them to Tensorboard
3. how to train a model and make predictions with the saved model
Tensorflow Hub should already be installed. You can check that it is by using "pip freeze".
```
%bash
pip freeze | grep tensor
```
If 'tensorflow-hub' isn't one of the outputs above, then you'll need to install it. Uncomment the cell below and execute the commands. After doing the pip install, click **"Reset Session"** on the notebook so that the Python environment picks up the new packages.
```
#%bash
#pip install tensorflow-hub
import os
import tensorflow as tf
import numpy as np
import tensorflow_hub as hub
import shutil
PROJECT = 'cloud-training-demos' # REPLACE WITH YOUR PROJECT ID
BUCKET = 'cloud-training-demos-ml' # REPLACE WITH YOUR BUCKET NAME
REGION = 'us-central1' # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# do not change these
os.environ['PROJECT'] = PROJECT
os.environ['BUCKET'] = BUCKET
os.environ['REGION'] = REGION
os.environ['TFVERSION'] = '1.8'
%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
```
### Build the feature columns for the model.
To start, we'll load the list of categories, authors and article ids we created in the previous **Create Datasets** notebook.
```
categories_list = open("categories.txt").read().splitlines()
authors_list = open("authors.txt").read().splitlines()
content_ids_list = open("content_ids.txt").read().splitlines()
mean_months_since_epoch = 523
```
In the cell below we'll define the feature columns to use in our model. If necessary, remind yourself the [various feature columns](https://www.tensorflow.org/api_docs/python/tf/feature_column) to use.
For the embedded_title_column feature column, use a Tensorflow Hub Module to create an embedding of the article title. Since the articles and titles are in German, you'll want to use a German language embedding module.
Explore the text embedding Tensorflow Hub modules [available here](https://alpha.tfhub.dev/). Filter by setting the language to 'German'. The 50 dimensional embedding should be sufficient for our purposes.
```
embedded_title_column = hub.text_embedding_column(
key="title",
module_spec="https://tfhub.dev/google/nnlm-de-dim50/1",
trainable=False)
content_id_column = tf.feature_column.categorical_column_with_hash_bucket(
key="content_id",
hash_bucket_size= len(content_ids_list) + 1)
embedded_content_column = tf.feature_column.embedding_column(
categorical_column=content_id_column,
dimension=10)
author_column = tf.feature_column.categorical_column_with_hash_bucket(key="author",
hash_bucket_size=len(authors_list) + 1)
embedded_author_column = tf.feature_column.embedding_column(
categorical_column=author_column,
dimension=3)
category_column_categorical = tf.feature_column.categorical_column_with_vocabulary_list(
key="category",
vocabulary_list=categories_list,
num_oov_buckets=1)
category_column = tf.feature_column.indicator_column(category_column_categorical)
months_since_epoch_boundaries = list(range(400,700,20))
months_since_epoch_column = tf.feature_column.numeric_column(
key="months_since_epoch")
months_since_epoch_bucketized = tf.feature_column.bucketized_column(
source_column = months_since_epoch_column,
boundaries = months_since_epoch_boundaries)
crossed_months_since_category_column = tf.feature_column.indicator_column(tf.feature_column.crossed_column(
keys = [category_column_categorical, months_since_epoch_bucketized],
hash_bucket_size = len(months_since_epoch_boundaries) * (len(categories_list) + 1)))
feature_columns = [embedded_content_column,
embedded_author_column,
category_column,
embedded_title_column,
crossed_months_since_category_column]
```
### Create the input function.
Next we'll create the input function for our model. This input function reads the data from the csv files we created in the previous labs.
```
record_defaults = [["Unknown"], ["Unknown"],["Unknown"],["Unknown"],["Unknown"],[mean_months_since_epoch],["Unknown"]]
column_keys = ["visitor_id", "content_id", "category", "title", "author", "months_since_epoch", "next_content_id"]
label_key = "next_content_id"
def read_dataset(filename, mode, batch_size = 512):
def _input_fn():
def decode_csv(value_column):
columns = tf.decode_csv(value_column,record_defaults=record_defaults)
features = dict(zip(column_keys, columns))
label = features.pop(label_key)
return features, label
# Create list of files that match pattern
file_list = tf.gfile.Glob(filename)
# Create dataset from file list
dataset = tf.data.TextLineDataset(file_list).map(decode_csv)
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
num_epochs = 1 # end-of-input after this
dataset = dataset.repeat(num_epochs).batch(batch_size)
return dataset.make_one_shot_iterator().get_next()
return _input_fn
```
### Create the model and train/evaluate
Next, we'll build our model which recommends an article for a visitor to the Kurier.at website. Look through the code below. We use the input_layer feature column to create the dense input layer to our network. This is just a sigle layer network where we can adjust the number of hidden units as a parameter.
Currently, we compute the accuracy between our predicted 'next article' and the actual 'next article' read next by the visitor. We'll also add an additional performance metric of top 10 accuracy to assess our model. To accomplish this, we compute the top 10 accuracy metric, add it to the metrics dictionary below and add it to the tf.summary so that this value is reported to Tensorboard as well.
```
def model_fn(features, labels, mode, params):
net = tf.feature_column.input_layer(features, params['feature_columns'])
for units in params['hidden_units']:
net = tf.layers.dense(net, units=units, activation=tf.nn.relu)
# Compute logits (1 per class).
logits = tf.layers.dense(net, params['n_classes'], activation=None)
predicted_classes = tf.argmax(logits, 1)
from tensorflow.python.lib.io import file_io
with file_io.FileIO('content_ids.txt', mode='r') as ifp:
content = tf.constant([x.rstrip() for x in ifp])
predicted_class_names = tf.gather(content, predicted_classes)
if mode == tf.estimator.ModeKeys.PREDICT:
predictions = {
'class_ids': predicted_classes[:, tf.newaxis],
'class_names' : predicted_class_names[:, tf.newaxis],
'probabilities': tf.nn.softmax(logits),
'logits': logits,
}
return tf.estimator.EstimatorSpec(mode, predictions=predictions)
table = tf.contrib.lookup.index_table_from_file(vocabulary_file="content_ids.txt")
labels = table.lookup(labels)
# Compute loss.
loss = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits)
# Compute evaluation metrics.
accuracy = tf.metrics.accuracy(labels=labels,
predictions=predicted_classes,
name='acc_op')
top_10_accuracy = tf.metrics.mean(tf.nn.in_top_k(predictions=logits,
targets=labels,
k=10))
metrics = {
'accuracy': accuracy,
'top_10_accuracy' : top_10_accuracy}
tf.summary.scalar('accuracy', accuracy[1])
tf.summary.scalar('top_10_accuracy', top_10_accuracy[1])
if mode == tf.estimator.ModeKeys.EVAL:
return tf.estimator.EstimatorSpec(
mode, loss=loss, eval_metric_ops=metrics)
# Create training op.
assert mode == tf.estimator.ModeKeys.TRAIN
optimizer = tf.train.AdagradOptimizer(learning_rate=0.1)
train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step())
return tf.estimator.EstimatorSpec(mode, loss=loss, train_op=train_op)
```
### Train and Evaluate
```
outdir = 'content_based_model_trained'
shutil.rmtree(outdir, ignore_errors = True) # start fresh each time
tf.summary.FileWriterCache.clear() # ensure filewriter cache is clear for TensorBoard events file
estimator = tf.estimator.Estimator(
model_fn=model_fn,
model_dir = outdir,
params={
'feature_columns': feature_columns,
'hidden_units': [200, 100, 50],
'n_classes': len(content_ids_list)
})
train_spec = tf.estimator.TrainSpec(
input_fn = read_dataset("training_set.csv", tf.estimator.ModeKeys.TRAIN),
max_steps = 2000)
eval_spec = tf.estimator.EvalSpec(
input_fn = read_dataset("test_set.csv", tf.estimator.ModeKeys.EVAL),
steps = None,
start_delay_secs = 30,
throttle_secs = 60)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
```
This takes a while to complete but in the end, I get about **30% top 10 accuracy**.
### Make predictions with the trained model.
With the model now trained, we can make predictions by calling the predict method on the estimator. Let's look at how our model predicts on the first five examples of the training set.
To start, we'll create a new file 'first_5.csv' which contains the first five elements of our training set. We'll also save the target values to a file 'first_5_content_ids' so we can compare our results.
```
%%bash
head -5 training_set.csv > first_5.csv
head first_5.csv
awk -F "\"*,\"*" '{print $2}' first_5.csv > first_5_content_ids
```
Recall, to make predictions on the trained model we pass a list of examples through the input function. Complete the code below to make predicitons on the examples contained in the "first_5.csv" file we created above.
```
output = list(estimator.predict(input_fn=read_dataset("first_5.csv", tf.estimator.ModeKeys.PREDICT)))
import numpy as np
recommended_content_ids = [np.asscalar(d["class_names"]).decode('UTF-8') for d in output]
content_ids = open("first_5_content_ids").read().splitlines()
```
Finally, we map the content id back to the article title. Let's compare our model's recommendation for the first example. This can be done in BigQuery. Look through the query below and make sure it is clear what is being returned.
```
import google.datalab.bigquery as bq
recommended_title_sql="""
#standardSQL
SELECT
(SELECT MAX(IF(index=6, value, NULL)) FROM UNNEST(hits.customDimensions)) AS title
FROM `cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
AND (SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) = \"{}\"
LIMIT 1""".format(recommended_content_ids[0])
current_title_sql="""
#standardSQL
SELECT
(SELECT MAX(IF(index=6, value, NULL)) FROM UNNEST(hits.customDimensions)) AS title
FROM `cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
AND (SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) = \"{}\"
LIMIT 1""".format(content_ids[0])
recommended_title = bq.Query(recommended_title_sql).execute().result().to_dataframe()['title'].tolist()[0]
current_title = bq.Query(current_title_sql).execute().result().to_dataframe()['title'].tolist()[0]
print("Current title: {} ".format(current_title))
print("Recommended title: {}".format(recommended_title))
```
### Tensorboard
As usual, we can monitor the performance of our training job using Tensorboard.
```
from google.datalab.ml import TensorBoard
TensorBoard().start('content_based_model_trained')
for pid in TensorBoard.list()['pid']:
TensorBoard().stop(pid)
print("Stopped TensorBoard with pid {}".format(pid))
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import scale
wines=pd.read_csv("wine.csv")
wines
wines.describe()
wines.info()
wines_ary=wines.values
wines_ary
wines_normal = scale(wines_ary)
wines_normal
```
# PCA Implementation
```
pca = PCA()
pca_values = pca.fit_transform(wines_normal)
pca_values
var = pca.explained_variance_ratio_
var
var1 = np.cumsum(np.round(var,decimals = 4)*100)
var1
pca.components_
plt.plot(var1, color='red', marker = 'o',linestyle = '--')
# Final Dataframe
finalDf =pd.concat([wines['Type'],pd.DataFrame(pca_values[:,0:3], columns=['pc1','pc2','pc3'])] ,axis = 1)
finalDf
finalDf = pd.concat([pd.DataFrame(pca_values[:,0:3],columns=['pc1','pc2','pc3']), wines['Type']], axis = 1)
finalDf
# Visualization of PCAs
fig=plt.figure(figsize=(16,12))
sns.scatterplot(data=finalDf)
sns.scatterplot(data=finalDf,x='pc1',y='pc2', hue='Type')
sns.scatterplot(data=finalDf,x='pc1',y='pc3', hue='Type')
sns.scatterplot(data=finalDf,x='pc2',y='pc3', hue='Type')
```
# Checking with other Clustering Algorithms
# 1. Hierarchical Clustering
```
# Import Libraries
import scipy.cluster.hierarchy as sch
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import normalize
# As we already have normalized data, create Dendrograms
plt.figure(figsize=(10,8))
dendrogram=sch.dendrogram(sch.linkage(finalDf,method='average'))
hc=AgglomerativeClustering(n_clusters=6, affinity='euclidean', linkage = 'average')
hc
y_hc=pd.DataFrame(hc.fit_predict(finalDf),columns=['clustersid'])
y_hc['clustersid'].value_counts()
# Adding clusters to dataset
wine3=wines.copy()
wine3['clustersid']=hc.labels_
wine3
```
# 2. K-Means Clustering
```
# Import Libraries
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_wines= scaler.fit_transform(wines.iloc[:,1:])
scaled_wines
# within-cluster sum-of-squares criterion
wcss=[]
for i in range (1,11):
kmeans=KMeans(n_clusters=i,random_state=0)
kmeans.fit(finalDf)
wcss.append(kmeans.inertia_)
# Plot K values range vs WCSS to get Elbow graph for choosing K (no. of clusters)
plt.plot(range(1,11),wcss, marker = 'o', linestyle = '--')
plt.title('Elbow Graph')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
```
# Build Cluster algorithm using K=4
```
# Cluster algorithm using K=4
clusters3=KMeans(4,random_state=30).fit(finalDf)
clusters3
clusters3.labels_
# Assign clusters to the data set
wine4=wines.copy()
wine4['clustersid']=clusters3.labels_
wine4
wine4['clustersid'].value_counts()
scaled_wines
```
|
github_jupyter
|
## Final rescale for paper 1
Final figures for the scaling section of paper 1 and cleaner fits for:
* Maximum and minimum squeezing of isopyncals (max $N^2/N^2_0$, min $N^2/N^2_0$ )
* Effective stratification ($N_{eff}$)
* Upwelling flux induced by the canyon ($\Phi$)
* Maximum and minimum squeezing of isopyncals iso-concentration lines (max $\partial_zC/\partial_zC_0$, min $\partial_zC/\partial_zC_0$ ) *These won't be necessary for the paper(?)*
* Mean concentration just above the rim during the advective phase ($\bar{C}$)
* Tracer upwelling flux induced by the canyon ($\Phi_{Tr}$)
```
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import matplotlib.gridspec as gspec
from matplotlib.ticker import FormatStrFormatter
from netCDF4 import Dataset
import numpy as np
import os
import pandas as pd
import seaborn as sns
import sys
import scipy.stats
import warnings
warnings.filterwarnings("ignore")
import canyon_tools.readout_tools as rout
import canyon_tools.metrics_tools as mpt
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')
sns.set_context('paper')
sns.set_style('white')
CanyonGrid='/data/kramosmu/results/TracerExperiments/CNTDIFF/run38/gridGlob.nc'
CanyonGridOut = Dataset(CanyonGrid)
CanyonGridNoC='/data/kramosmu/results/TracerExperiments/CNTDIFF/run68/gridGlob.nc'
CanyonGridOutNoC = Dataset(CanyonGridNoC)
CanyonState='/data/kramosmu/results/TracerExperiments/CNTDIFF/run38/stateGlob.nc'
CanyonStateOut = Dataset(CanyonState)
# Grid variables
nx = 616
ny = 360
nz = 90
nt = 19 # t dimension size
time = CanyonStateOut.variables['T']
RC = CanyonGridOut.variables['RC']
# Constants and scales
g = 9.81 # accel. gravity
Hs = 149.8 # Shelf break depth
s = 0.0061 # shelf slope
def Dh(f,L,N):
'''Vertical scale Dh'''
return((f*L)/(N))
def Ro(U,f,R):
'''Rossby number'''
return(U/(f*R))
def F(Ro):
'''Function that estimates the ability of the flow to follow isobaths'''
return(Ro/(0.9+Ro))
def Bu(N,f,W,Hs):
'''Burger number'''
return((N*Hs)/(f*W))
def RossbyRad(N,Hs,f):
'''1st Rossby radius of deformation'''
return((N*Hs)/f)
def SE(s,N,f,Fw,Rl):
'''Slope effect '''
return((s*N)/(f*(Fw/Rl)**0.5))
# Information for all runs is stored in canyon_records.py
lib_path = os.path.abspath('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/PythonScripts/Paper1Figures/') # Add absolute path to my python scripts
sys.path.append(lib_path)
import canyon_records
records = canyon_records.main()
import nocanyon_records
recordsNoC = nocanyon_records.main()
```
### Not all runs are used to fit all variables
**records_dyn** has all runs where f, N or U vary. USe this list to fit upwelling flux $\Phi$ and modify *Howatt and Allen 2013*.
**records_epsilon** has all runs in records_dyn plus the runs with a heaviside Kv profile. Use this list to fit $\Phi$ with scaled N.
**records_real** has all runs in records_epsilon plus the runs with a Kv profile inspired in observations.
```
# Indices of all runs that will be considered for paper 1
select_rec = [0,1,2,3,4,5,51,6,7,8,9,10,17,18,19,20,21,
22,23,24,25,26,27,29,30,31,32,33,
34,35,38,39,41,42,43,44,45,46,47,48,49]#,52, 53, 54, 55, 56, 57, 58, 59, 60]
for ii in select_rec:
print(ii,records[ii].label2, records[ii].name)
# records_dyn has all the runs without the ones where K_bg changes. Use these ones for fitting the data HA2013
ind = [0,3,4,5,51,6,7,8,9,10,17,18,19,20,21,22]
records_dyn = []
for ii in ind:
records_dyn.append(records[ii])
# records_epsilon has all the runs in records_step plus the epsilon runs (use these to fit Nmax+Nmin)
ind = [0,3,4,5,51,6,7,8,9,10,17,18,19,20,21,22,29,30,31,32,33,
34,38,39,41,42,43,44,45,46,47,48,49]#,52, 53, 54, 55, 56, 57, 58, 59, 60]
records_epsilon = []
for ii in ind:
records_epsilon.append(records[ii])
# records_real has all the runs in records_epsilon plus the realistic runs
ind = [0,3,4,5,51,6,7,8,9,10,17,18,19,20,21,22,29,30,31,32,33,
34,38,41,42,39,43,44,45,46,47,48,49,24,25,26,27]#,52,53, 54, 55, 56, 57, 58, 59, 60]
records_real = []
for ii in ind:
records_real.append(records[ii])
records_sel = []
for ind in select_rec:
records_sel.append(records[ind])
file = ('/data/kramosmu/results/TracerExperiments/%s/HCW_TrMass_%s%s.csv'
%(records[ind].exp_code,records[ind].exp_code,records[ind].run_num))
dfcan = pd.read_csv(file)
records[ind].HCW = dfcan['HCW']
records[ind].HCWTr1 = dfcan['HCWTr1']
records[ind].TrMass = dfcan['TrMassHCW']
records[ind].TrMassTr1 = dfcan['TrMassHCWTr1']
records[ind].TrMassTr2 = dfcan['TrMassHCWTr2']
records[ind].TrMassTot = dfcan['TotTrMass']
records[ind].TrMassTotTr2 = dfcan['TotTrMassTr2']
records[ind].TrMassTotTr1 = dfcan['TotTrMassTr1']
t=6.5
stname = 'UwH' #Station downstream head of canyon
keys2 = ['N_tt12','N_tt14']
for ind in select_rec:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/N_%s_%s.csv' %
(records[ind].name,stname))
df = pd.read_csv(filename1)
Nab = np.empty(len(keys2))
Nbe = np.empty(len(keys2))
if records[ind].L > 13000:
print(records[ind].L)
for key,ii in zip(keys2, range(len(keys2))):
Nab[ii] = np.max(df[keys2[ii]][:])
Nbe[ii] = np.min(df[keys2[ii]][12:16])
elif (records[ind].L < 13000) & (records[ind].L > 8500):
print(records[ind].L)
for key,ii in zip(keys2, range(len(keys2))):
Nab[ii] = np.max(df[keys2[ii]][:])
Nbe[ii] = np.min(df[keys2[ii]][16:19])
else:
for key,ii in zip(keys2, range(len(keys2))):
Nab[ii] = np.max(df[keys2[ii]][:])
Nbe[ii] = np.min(df[keys2[ii]][20:23])
records[ind].Nab = np.mean(Nab)
records[ind].Nbe = np.mean(Nbe)
records[ind].Nab_std = np.std(Nab)
records[ind].Nbe_std = np.std(Nbe)
keys2 = ['dTrdz_tt08','dTrdz_tt10','dTrdz_tt12','dTrdz_tt14','dTrdz_tt16','dTrdz_tt18']
for ind in select_rec:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/dTr1dz_%s_%s.csv' %
(records[ind].name,stname))
df = pd.read_csv(filename1)
dTrab = 0
dTrbe = 0
if records[ind].L > 13000:
for key,ii in zip(keys2, range(len(keys2))):
dTrab = dTrab + np.min(df[keys2[ii]][:])
dTrbe = dTrbe + np.max(df[keys2[ii]][12:16])
records[ind].dTr0 = df['dTrdz_tt00'][10]
elif (records[ind].L < 13000) & (records[ind].L > 8500):
for key,ii in zip(keys2, range(len(keys2))):
dTrab = dTrab + np.min(df[keys2[ii]][:])
dTrbe = dTrbe + np.max(df[keys2[ii]][16:19])
records[ind].dTr0 = df['dTrdz_tt00'][10]
else:
for key,ii in zip(keys2, range(len(keys2))):
dTrab = dTrab + np.min(df[keys2[ii]][:]) #0:20
dTrbe = dTrbe + np.max(df[keys2[ii]][20:23]) #20:24
records[ind].dTr0 = df['dTrdz_tt00'][10]
records[ind].dTr_ab = dTrab/ len(keys2)
records[ind].dTr_be = dTrbe/ len(keys2)
keys2 = ['Tr_profile_tt08','Tr_profile_tt10','Tr_profile_tt12','Tr_profile_tt14','Tr_profile_tt16','Tr_profile_tt18']
for ind in select_rec:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/Tr1_profile_%s_%s.csv' %
(records[ind].name,stname))
df = pd.read_csv(filename1)
Nab = np.zeros(len(keys2))
if records[ind].L > 13000:
for key,ii in zip(keys2, range(len(keys2))):
Nab[ii] = np.nanmean(df[keys2[ii]][11:13]) # just above rim depth
records[ind].Tr0 = (df['Tr_profile_tt00'][13])
elif (records[ind].L < 13000) & (records[ind].L > 8500):
for key,ii in zip(keys2, range(len(keys2))):
Nab[ii] = np.nanmean(df[keys2[ii]][15:17]) # just above rim depth
records[ind].Tr0 = (df['Tr_profile_tt00'][17])
else:
for key,ii in zip(keys2, range(len(keys2))):
Nab[ii] = np.nanmean(df[keys2[ii]][19:21]) # just above rim depth
records[ind].Tr0 = (df['Tr_profile_tt00'][21])
records[ind].Tr = np.nanmean(Nab)
records[ind].Tr_std = np.std(Nab)
```
## Stratification and upwelling flux
In previous notebooks I found that the upwelling flux is porportional to an effective stratification $N_{eff}$ given by the weighted sum of the maximum stratification above the rim, near the head and the minimum stratification below the rim:
$$N_{eff} = {0.75N_{max}+0.25N_{min}}$$
So first, we scale $N_{max}$ and $N_{min}$ using the information we got from the 1D model and modifications to the 1D model due to the enhanced diffusion above the rim when $\epsilon$ is larger than the step case.
Once we get both N's, we can scale $N_{eff}$ and use it in the depth scale $D_h$ in the scaling for $\Phi$ by Howatt and Allen as $D_{eff}=fL/N_{eff}$, with proper fitting parameters.
```
# Get kv form initial files
records_kv_files = [24,25,26,27,29,30,31,32,33,34,38,39,41,42,43,44,45,46,47,48,49]
kv_dir = '/ocean/kramosmu/Building_canyon/BuildCanyon/Stratification/616x360x90/'
ini_kv_files = [kv_dir + 'KrDiff_Mty_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_Eel_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_Mty_rim_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_Asc_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e10_kv1E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e25_kv1E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e50_kv1E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e100_kv1E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e15_kv1E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e75_kv1E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_kv1E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_kv5E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e25_kv1E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e100_kv1E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e25_kv5E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e100_kv5E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_kv8E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_exact1p2E2_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_kv2p5E3_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_kv5E4_90zlev_616x360_Quad.bin',
kv_dir + 'KrDiff_e05_exact_nosmooth_90zlev_616x360_Quad.bin',
]
dt = np.dtype('>f8') # float 64 big endian
st = [240, 200] # y, x indices of UwH station
Hrim = 135
dd = 1
ini_kv_profiles = np.zeros((len(ini_kv_files,nz))
for file, ii in zip(ini_kv_files, records_kv_files):
data = np.fromfile(file, dt)
ini_kv = np.reshape(data,(90,360,616),order='C')
KK = ini_kv[:, st[0], st[1]]
records[ii].Zdif = (((KK[int(Hrim/5)+1]-KK[int(Hrim/5)-1]))*t*3600*24)**0.5
records[ii].dk = KK[int(Hrim/5)+1]-KK[int(Hrim/5)-1]
records[ii].Kz = KK[int(Hrim/5)-4]
records[ii].Kz_be = KK[int(Hrim/5)+4]
for rec in records_real:
Dz = abs(RC[int(Hrim/5)+1]-RC[int(Hrim/5)-1])
rec.Z = ((rec.f*rec.u_mod*F(Ro(rec.u_mod,rec.f,rec.R))*rec.L)**(0.5))/rec.N
if rec.kv == rec.kbg:
rec.Zdif = 0
rec.Sdif_min = np.exp(-0.15*rec.Zdif/Dz) # -0.1 comes from the 1D model
rec.dk = 0
rec.Kz = 1E-5
rec.Kz_be = 1E-5
rec.Sdif_max = (rec.Zdif/Dz)*np.exp(-(rec.Kz*t*3600*24)/((rec.epsilon)**2))
else:
rec.Sdif_min = np.exp(-0.15*rec.Zdif/Dz)
rec.Sdif_max = (rec.Zdif/Dz)*np.exp(-(rec.Kz*t*3600*24)/((rec.epsilon)**2))
rec.S_max = (rec.Z/rec.Hh)*np.exp(-rec.Kz*t*3600*24/rec.Z**2)
rec.S_min = (rec.Z/rec.Hh)*np.exp(-rec.Kz_be*t*3600*24/rec.Z**2)
print(rec.name)
X1_be = np.array([rec.S_min for rec in records_epsilon])
X2_be = np.array([rec.Sdif_min for rec in records_epsilon])
Y_be = np.array([(rec.Nbe)**2/(rec.N**2) for rec in records_epsilon])
X1_ab = np.array([rec.S_max for rec in records_epsilon])
X2_ab = np.array([rec.Sdif_max for rec in records_epsilon])
Y_ab = np.array([(rec.Nab)**2/(rec.N**2) for rec in records_epsilon])
from sklearn import linear_model
reg_be = linear_model.LinearRegression()
reg_be.fit (np.transpose([X1_be,X2_be]),np.transpose(Y_be) )
print(r'min $N^2/N^2_0$ = %1.2f $S^-$ + %1.2f $(1-S^-_{diff})$ %1.2f ' %
(reg_be.coef_[0],reg_be.coef_[1],reg_be.intercept_))
reg_ab = linear_model.LinearRegression()
reg_ab.fit (np.transpose([X1_ab, X2_ab]),np.transpose(Y_ab) )
print(r'max $N^2/N^2_0$ = %1.2f $S^+$ + %1.2f $S^+_{diff}$ + %1.2f ' %
(reg_ab.coef_[0],reg_ab.coef_[1],reg_ab.intercept_))
# Save values of N_eff and Phi
for rec in records_sel:
can_eff = rec.HCW
Phi = np.mean(np.array([(can_eff[ii]-can_eff[ii-1])/(time[ii]-time[ii-1])
for ii in range (8,18)]))
Phi_std = np.std(np.array([(can_eff[ii]-can_eff[ii-1])/(time[ii]-time[ii-1])
for ii in range (8,18)]))
rec.Phi = Phi
rec.Phi_std = Phi_std
for rec in records_real:
rec.Nbe_scaled = np.sqrt(reg_be.coef_[0]*rec.S_min +
reg_be.coef_[1]*rec.Sdif_min +
reg_be.intercept_)*rec.N
rec.Nab_scaled = np.sqrt(reg_ab.coef_[0]*rec.S_max +
reg_ab.coef_[1]*rec.Sdif_max +
reg_ab.intercept_)*rec.N
if (reg_be.coef_[0]*rec.S_min+ reg_be.coef_[1]*rec.Sdif_min +
reg_be.intercept_)< 0 :
rec.N_eff_scaled = (0.75*rec.Nab_scaled)
else:
rec.N_eff_scaled = (0.75*rec.Nab_scaled + 0.25*rec.Nbe_scaled)
rec.Neff = (0.75*rec.Nab+0.25*rec.Nbe)
# find best slope parameter to use
for param in np.linspace(0.4, 1.3, 80):
for rec in records_real:
Se = SE(s, rec.N, rec.f, F(Ro(rec.u_mod,rec.f,rec.Wiso)), Ro(rec.u_mod,rec.f,rec.L))
rec.X = ((F(Ro(rec.u_mod,rec.f,rec.Wiso)))**(1.5))*((Ro(rec.u_mod,rec.f,rec.L))**(0.5))*((1-param*Se)**3)
rec.Phi_nonDim = rec.Phi/(rec.u_mod*rec.W*Dh(rec.f,rec.L,rec.N_eff_scaled))
Y_array = np.array([rec.Phi_nonDim for rec in records_epsilon])
X_array = np.array([rec.X for rec in records_epsilon])
slope2, intercept2, r_value2, p_value2, std_err2 = scipy.stats.linregress(X_array,Y_array)
print('Using parameter %1.2f: slope = %1.2f, intercept = %1.3f, r-value = %1.3f' %(param, slope2, intercept2, r_value2))
# My re-fit of Howatt and Allen's function for Phi gave:
slope = 2.10
param = 0.40
intercept = -0.004
#Using parameter 0.86: slope = 5.00, intercept = -0.012, r-value = 0.974, choose largest r-value from above
slope2 = 5.00
param2 = 0.86
intercept2 = -0.012
for rec in records_real:
Se = SE(s, rec.N, rec.f, F(Ro(rec.u_mod,rec.f,rec.Wiso)), Ro(rec.u_mod,rec.f,rec.L))
HA2013=((slope*(F(Ro(rec.u_mod,rec.f,rec.Wiso))**(3/2))*(Ro(rec.u_mod,rec.f,rec.L)**(1/2))*((1-param*Se)**3))+intercept)
RA2018 = (slope2*(F(Ro(rec.u_mod,rec.f,rec.Wiso))**(3/2))*(Ro(rec.u_mod,rec.f,rec.L)**(1/2))*((1-param2*Se)**3))+intercept2
rec.HA2013 = HA2013
rec.HA2013_sqe = (rec.Phi-rec.HA2013)**2
rec.RA2018 = RA2018
rec.RA2018_sqe = (rec.Phi-rec.RA2018)**2
```
### Tracer gradient
```
X1_be = np.array([rec.S_min for rec in records_epsilon])
X2_be = np.array([rec.Sdif_min for rec in records_epsilon])
Y_be = np.array([(rec.dTr_be)/(rec.dTr0) for rec in records_epsilon])
X1_ab = np.array([rec.S_max for rec in records_epsilon])
X2_ab = np.array([rec.Sdif_max for rec in records_epsilon])
Y_ab = np.array([(rec.dTr_ab)/(rec.dTr0) for rec in records_epsilon])
from sklearn import linear_model
reg_be_dTr = linear_model.LinearRegression()
reg_be_dTr.fit (np.transpose([X1_be,X2_be]),np.transpose(Y_be) )
print(r'min $dzC/dzCo$ = %1.2f $S^-$ + %1.2f $S^-_{diff}$ %1.2f ' %
(reg_be_dTr.coef_[0],reg_be_dTr.coef_[1],reg_be_dTr.intercept_))
reg_ab_dTr = linear_model.LinearRegression()
reg_ab_dTr.fit (np.transpose([X1_ab, X2_ab]),np.transpose(Y_ab) )
print(r'max $dzC/dzCo$ = %1.2f $S^+$ + %1.2f $S^+_{diff}$ %1.2f ' %
(reg_ab_dTr.coef_[0],reg_ab_dTr.coef_[1],reg_ab_dTr.intercept_))
# save values of dTr scaled and PhiTr
for rec in records_sel:
can_eff = rec.TrMass
Phi_Tr = np.mean(np.array([(can_eff[ii]-can_eff[ii-1])/(time[ii]-time[ii-1]) for ii in range (12,18)]))
Phi_Tr_std = np.std(np.array([(can_eff[ii]-can_eff[ii-1])/(time[ii]-time[ii-1]) for ii in range (12,18)]))
rec.PhiTr = Phi_Tr
rec.PhiTr_std = Phi_Tr_std
for rec in records_real:
rec.dTr_ab_scaled = (reg_ab_dTr.coef_[0]*rec.S_max+
reg_ab_dTr.coef_[1]*rec.Sdif_max+
reg_ab_dTr.intercept_)*rec.dTr0
rec.dTr_be_scaled = (reg_be_dTr.coef_[0]*rec.S_min+
reg_be_dTr.coef_[1]*(1-rec.Sdif_min)+
reg_be_dTr.intercept_)*rec.dTr0
```
### Concentration
```
# Fit mean concentration just above the rim - I know using the max
# worked slightly better (smaller mse). Co is the initial concentration just above rim depth
X1_tr = np.array([rec.S_max for rec in records_epsilon])
X2_tr = np.array([rec.Sdif_max for rec in records_epsilon])
Y_tr = np.array([(rec.Tr/rec.Tr0) for rec in records_epsilon])
reg_Tr = linear_model.LinearRegression()
reg_Tr.fit (np.transpose([X1_tr,X2_tr]),np.transpose(Y_tr) )
print(r'$\bar{C}/Co$ = %1.2f $S^+$ + %1.2f $S^+_{diff}$ %1.2f ' %
(reg_Tr.coef_[0],reg_Tr.coef_[1],reg_Tr.intercept_))
for rec in records_real:
rec.Tr_scaled = (reg_Tr.coef_[0]*(rec.S_max)+ reg_Tr.coef_[1]*(rec.Sdif_max)+
reg_Tr.intercept_)*rec.Tr0
print(rec.Tr0)
print(rec.dTr0)
```
### Tracer flux
```
Y_array = np.array([rec.PhiTr for rec in records_epsilon])
X_array = np.array([rec.RA2018*(rec.u_mod*rec.W*Dh(rec.f,rec.L,rec.N_eff_scaled))*
(rec.Tr_scaled) for rec in records_epsilon])
slope6, intercept6, r_value6, p_value6, std_err6 = scipy.stats.linregress(np.squeeze(X_array),
np.squeeze(Y_array))
for rec in records_real:
depth_scale = Dh(rec.f,rec.L,rec.N_eff_scaled)
rec.Phi_scaled = rec.RA2018*(rec.u_mod*rec.W*depth_scale)
rec.PhiTr_scaled = np.squeeze((slope6*rec.Phi_scaled*(rec.Tr_scaled))+intercept6)
print('\Phi/UWD_{eff} = %1.2f Fw^{3/2} Ro^{1/2} (1-%1.2f *Se)^3 +%1.2f' %(slope2,param2,intercept2))
print('\Phi_{Tr} = %1.2f $\Phi \ bar{C}$ + %1.2f ' %(slope6, intercept6))
```
## Figures
```
sns.set_context('paper')
plt.rcParams['font.size'] = 11.0
f = plt.figure(figsize = (5,5)) # 190mm = 7.48 in, 230cm = 9.05in
gs = gspec.GridSpec(2, 2,wspace=0.2)
ax1 = plt.subplot(gs[0,0])
ax0 = plt.subplot(gs[0,1])
ax3 = plt.subplot(gs[1,0])
ax2 = plt.subplot(gs[1,1])
# ---- plot 1:1 line ----
ax0.plot(np.linspace(-0.1,3.5,20),np.linspace(-0.1,3.5,20), '-',color='0.5')
ax1.plot(np.linspace(2,8,20),np.linspace(2,8,20), '-', color='0.5')
ax2.plot(np.linspace(5, 17, 20),np.linspace(5,17, 20),'-', color='0.5')
ax3.plot(np.linspace(1, 1.8, 20),np.linspace(1, 1.8, 20),'-', color='0.5')
# ---- plot error -----
# MSE ax0
phi_array = np.array([(rec.Nbe_scaled/rec.N)**2 for rec in records_epsilon])
sca_array = np.array([(rec.Nbe)**2/(rec.N**2) for rec in records_epsilon])
x_fit = np.linspace(-0.1, 3.5, 50)
mean_sq_err = np.nanmean(((phi_array)-(sca_array))**2)
upper_bound = ax0.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax0.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# MSE ax1
phi_array = np.array([(rec.Nab_scaled/rec.N)**2 for rec in records_epsilon])
sca_array = np.array([(rec.Nab)**2/(rec.N**2) for rec in records_epsilon])
x_fit = np.linspace(2,8, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
upper_bound = ax1.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax1.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# MSE ax2
phi_array = np.array([rec.N_eff_scaled/1E-3 for rec in records_epsilon])
sca_array = np.array([rec.Neff/1E-3 for rec in records_epsilon])
x_fit = np.linspace(5,17, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
upper_bound = ax2.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax2.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# MSE ax3
phi_array = np.squeeze(np.array([rec.Tr_scaled/rec.Tr0 for rec in records_epsilon]))
sca_array = np.squeeze(np.array([rec.Tr/rec.Tr0 for rec in records_epsilon]))
x_fit = np.linspace(1,1.8, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
print('MSE for Cbar/Co is %f and RMSE is %f ' %(mean_sq_err, mean_sq_err**(1/2)))
upper_bound = ax3.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax3.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# ---- plot scaling ----
for rec in records_real:
plt0 = ax0.plot((rec.Nbe_scaled/rec.N)**2,(rec.Nbe)**2/(rec.N**2),
marker = rec.mstyle,
markersize = 7,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
plt1 = ax1.plot((rec.Nab_scaled/rec.N)**2,(rec.Nab)**2/(rec.N**2),
marker = rec.mstyle,
markersize = 7,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
plt2 = ax2.plot(rec.N_eff_scaled/1E-3,rec.Neff/1E-3,
marker = rec.mstyle,
markersize = 7,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
print(rec.name, rec.N_eff_scaled)
plt3 = ax3.plot(rec.Tr_scaled/rec.Tr0,
(rec.Tr/rec.Tr0),
marker = rec.mstyle,
markersize = 7,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
# ---- aesthetics -----
ax0.set_xlim(-0.1,3.5)
ax0.set_ylim(-0.1,3.5)
ax1.set_xlim(2,8)#
ax1.set_ylim(2,8)
ax2.set_xlim(7,15.5)
ax2.set_ylim(7,15.5)
ax3.set_xlim(1,1.62)
ax3.set_ylim(1,1.62)
ax0.set_ylabel('min $N^2/N^2_0$',labelpad=-1.5)
ax1.set_ylabel('max $N^2/N^2_0$',labelpad=-1.5)
ax0.set_xlabel(r'%1.2f$S^-$ + %1.2f$(1-S^-_{dif})$ %1.2f' %(reg_be.coef_[0],
reg_be.coef_[1],
reg_be.intercept_),labelpad=0.5)
ax1.set_xlabel(r'%1.2f$S^+$ + %1.2f$S^+_{dif}$ + %1.2f' %(reg_ab.coef_[0],
reg_ab.coef_[1],
reg_ab.intercept_),labelpad=0.5)
ax2.set_ylabel('$N_{eff}$ model / $10^{-3}$ s$^{-1}$', labelpad=0)
ax2.set_xlabel('$N_{eff}$ scaled / $10^{-3}$ s$^{-1}$',labelpad=0.0)
ax3.set_ylabel(r'$C_{rim}$ model /$C_0$', labelpad=0)
ax3.set_xlabel(r'$\bar{C}$ /$C_0$', labelpad=0.0)
ax0.tick_params(axis='x', pad=2)
ax1.tick_params(axis='x', pad=2)
ax3.tick_params(axis='x', pad=2)
ax2.tick_params(axis='x', pad=2)
ax0.tick_params(axis='y', pad=2)
ax1.tick_params(axis='y', pad=2)
ax3.tick_params(axis='y', pad=2)
ax2.tick_params(axis='y', pad=2)
ax0.legend(bbox_to_anchor=(1.05,1.3), ncol=1,columnspacing=0.1,labelspacing=0.1,frameon=True )
ax0.set_aspect(1)
ax1.set_aspect(1)
ax2.set_aspect(1)
ax3.set_aspect(1)
ax1.text(0.1,0.85,'Eqn. 22',transform=ax1.transAxes)
ax0.text(0.1,0.85,'Eqn. 24',transform=ax0.transAxes)
ax2.text(0.1,0.85,'Eqn. 27',transform=ax2.transAxes)
ax3.text(0.1,0.85,'Eqn. 25',transform=ax3.transAxes)
ax1.text(0.87,0.05,'(a)',transform=ax1.transAxes)
ax0.text(0.87,0.05,'(b)',transform=ax0.transAxes)
ax3.text(0.87,0.05,'(c)',transform=ax3.transAxes)
ax2.text(0.87,0.05,'(d)',transform=ax2.transAxes)
plt.savefig('figure10_v2.eps',format='eps',bbox_inches='tight')
sns.set_context('paper')
plt.rcParams['font.size'] = 11.0
f = plt.figure(figsize = (5,7)) # 190mm = 7.48 in, 230cm = 9.05in
gs = gspec.GridSpec(1, 2,wspace=0.4)
ax2 = plt.subplot(gs[0])
ax3 = plt.subplot(gs[1])
# ---- plot 1:1 line ----
ax3.plot(np.linspace(5, 17, 20),np.linspace(5,17, 20),'-', color='0.5')
ax2.plot(np.linspace(1, 1.8, 20),np.linspace(1, 1.8, 20),'-', color='0.5')
# ---- plot error -----
# MSE ax2
phi_array = np.array([rec.N_eff_scaled/1E-3 for rec in records_epsilon])
sca_array = np.array([rec.Neff/1E-3 for rec in records_epsilon])
x_fit = np.linspace(5,17, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
upper_bound = ax3.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax3.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# MSE ax3
phi_array = np.squeeze(np.array([rec.Tr_scaled/rec.Tr0 for rec in records_epsilon]))
sca_array = np.squeeze(np.array([rec.Tr/rec.Tr0 for rec in records_epsilon]))
x_fit = np.linspace(1,1.8, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
upper_bound = ax2.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax2.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
print('MSE for Cbar/Co is %f and RMSE is %f ' %(mean_sq_err, mean_sq_err**(1/2)))
# ---- plot scaling ----
for rec in records_real:
plt2 = ax3.plot(rec.N_eff_scaled/1E-3,rec.Neff/1E-3,
marker = rec.mstyle,
markersize = 7,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
plt3 = ax2.plot(rec.Tr_scaled/rec.Tr0,
(rec.Tr/rec.Tr0),
marker = rec.mstyle,
markersize = 7,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
# ---- aesthetics -----
#ax3.set_xlim(5,15.5)
#ax3.set_ylim(5,15.5)
#ax2.set_xlim(1,1.62)
#ax2.set_ylim(1,1.62)
ax3.set_ylabel('$N_{eff}$ model / $10^{-3}$ s$^{-1}$', labelpad=0)
ax3.set_xlabel('$N_{eff}$ scaled / $10^{-3}$ s$^{-1}$',labelpad=0.0)
ax2.set_ylabel(r'$C_{rim}$ model /$C_0$', labelpad=0)
ax2.set_xlabel(r'$\bar{C}$ /$C_0$', labelpad=0.0)
ax3.tick_params(axis='x', pad=2)
ax2.tick_params(axis='x', pad=2)
ax3.tick_params(axis='y', pad=2)
ax2.tick_params(axis='y', pad=2)
ax2.legend(bbox_to_anchor=(3.2,-0.2), ncol=5,columnspacing=0.1,labelspacing=0.1,frameon=True )
ax2.set_aspect(1)
ax3.set_aspect(1)
ax3.text(0.1,0.85,'Eqn. 27',transform=ax3.transAxes)
ax2.text(0.1,0.85,'Eqn. 25',transform=ax2.transAxes)
ax3.text(0.87,0.05,'(b)',transform=ax3.transAxes)
ax2.text(0.87,0.05,'(a)',transform=ax2.transAxes)
plt.savefig('scaling_w_Ls.eps',format='eps',bbox_inches='tight')
sns.set_context('paper')
plt.rcParams['font.size'] = 10.0
f = plt.figure(figsize = (6,3)) # 190mm = 7.48 in, 230cm = 9.05in
gs = gspec.GridSpec(1, 2)
ax0 = plt.subplot(gs[0,0])
ax1 = plt.subplot(gs[0,1])
# ---- plot 1:1 lines ----
ax0.plot(np.linspace(0,7,50),np.linspace(0,7,50),'-', color='0.5')
ax1.plot(np.linspace(0,5.5,50),np.linspace(0,5.5,50),'-', color='0.5')
# ---- plot errors ----
# MSE ax0
phi_array = np.array([rec.Phi/1E4 for rec in records_dyn])
sca_array = np.array([rec.Phi_scaled/1E4 for rec in records_dyn])
x_fit = np.linspace(0,8, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
upper_bound = ax0.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax0.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# MSE ax1
phi_array = np.array([rec.PhiTr_scaled/1E5 for rec in records_epsilon])
sca_array = np.array([rec.PhiTr/1E5 for rec in records_epsilon])
x_fit = np.linspace(0,6, 50)
mean_sq_err = np.mean(((phi_array)-(sca_array))**2)
upper_bound = ax1.plot(x_fit,x_fit+(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
lower_bound = ax1.plot(x_fit,x_fit-(mean_sq_err)**(0.5),linestyle = '--',color='0.5')
# ---- plot scaling ----
for rec in records_real:
plt1 = ax0.errorbar(rec.Phi_scaled/1E4,
rec.Phi/1E4,
yerr=rec.Phi_std/1E4,
marker = rec.mstyle,
markersize = 8,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
plt1 = ax1.errorbar(rec.PhiTr_scaled/1E5,
rec.PhiTr/1E5,
yerr=rec.PhiTr_std/1E5,
marker = rec.mstyle,
markersize = 8,
color = sns.xkcd_rgb[rec.color2],
markeredgewidth=0.5,
markeredgecolor = 'k',
label=rec.label2)
# ---- aesthetics ----
ax0.set_ylabel('Phi',labelpad=0.5)
ax0.set_ylabel('Upwelling flux / $10^4$ m$^3$s$^{-1}$', labelpad=-0.5)
ax1.set_ylabel('Tracer flux / $10^5$ $\mu$Mm$^3$s$^{-1}$', labelpad=-0.5)
ax0.set_xlabel(r'$\Phi$ / $10^4$ m$^3$s$^{-1}$', labelpad=-0.5 )
ax1.set_xlabel(r'$\Phi_{Tr}$ / $10^5$ $\mu$Mm$^3$s$^{-1}$', labelpad=-0.5)
ax0.set_xlim(-0.2,7.2)
ax0.set_ylim(-0.2,7.2)
ax1.set_xlim(-0.2,5.8)
ax1.set_ylim(-0.2,5.8)
ax0.text(0.1,0.85,'Eqn. 28',transform=ax0.transAxes)
ax1.text(0.1,0.85,'Eqn. 29',transform=ax1.transAxes)
ax0.text(0.9,0.05,'(a)',transform=ax0.transAxes)
ax1.text(0.9,0.05,'(b)',transform=ax1.transAxes)
ax0.tick_params(axis='x', pad=2)
ax1.tick_params(axis='x', pad=2)
ax0.tick_params(axis='y', pad=2)
ax1.tick_params(axis='y', pad=2)
ax0.set_aspect(1)
ax1.set_aspect(1)
#ax0.plot(57261.9871812/1E4,40630.372436/1E4, 'o', color='brown')
#ax1.plot(520483.538981/1E5,298566.920079/1E5, 'o', color='brown')
plt.savefig('figure11_v2.eps',format='eps',bbox_inches='tight')
sns.set_context('paper')
sns.set_style("white")
plt.rcParams['font.size'] = 10.0
f = plt.figure(figsize = (6,2.2)) # 190mm = 7.48 in, 230cm = 9.05in
gs = gspec.GridSpec(1, 2, width_ratios=(1.0,1), wspace=0.1)
ax0 = plt.subplot(gs[0])
ax1 = plt.subplot(gs[1])
# ---- plot scaling ----
for rec in records_real[:]:
print(rec.label)
plt1 = ax0.errorbar(rec.Phi/1E4,
rec.PhiTr/1E5,
yerr=rec.PhiTr_std/1E5,
xerr = rec.Phi_std/1E4,
marker = '.',
markersize = 12,
color = 'yellowgreen',
markeredgewidth=1,
markeredgecolor = 'k',
label=rec.label2,
capsize=2,
ecolor = '0.7')
if rec.kv <= 1E-5:
plt1 = ax1.scatter(Ro(U=rec.u_mod, f=rec.f, R=rec.Wiso),
Bu(rec.N, rec.f,rec.W,Hs),
c = rec.PhiTr/1E5,
vmin=0, vmax=5,
cmap='Blues',
marker = 'o',
s = (rec.PhiTr/1E5)*25,
linewidths=1,
edgecolors='k',
)
else:
plt1 = ax1.scatter(Ro(U=rec.u_mod, f=rec.f, R=rec.Wiso),
Bu(rec.N, rec.f,rec.W,Hs),
c = rec.PhiTr/1E5,
vmin=0, vmax=5,
cmap='Blues',
marker = 'o',
s = (rec.PhiTr/1E5)*25,
linewidths=1,
edgecolors='r',
)
# Longer canyon runs
cb=plt.colorbar(plt1 )
cb.set_label('$10^5$ $\mu$Mm$^3$s$^{-1}$')
# ---- aesthetics ----
ax0.set_xlabel('Upwelling flux / $10^4$ m$^3$s$^{-1}$', labelpad=-0.5)
ax0.set_ylabel('Tracer flux / $10^5$ $\mu$Mm$^3$s$^{-1}$', labelpad=-0.5)
ax1.set_xlabel('$R_W$', labelpad=-0.5)
ax1.set_ylabel('$Bu$', labelpad=-0.5)
ax1.set_xlim(0,0.65)
ax1.set_ylim(0.0,0.65)
ax0.tick_params(axis='x', pad=2)
ax0.tick_params(axis='y', pad=2)
ax1.tick_params(axis='x', pad=2)
ax1.tick_params(axis='y', pad=2)
ax0.set_aspect(1)
ax1.set_aspect(1)
ax1.text(0.11,0.05,'Tracer Flux')
ax0.text(0.9,0.05,'(a)',transform=ax0.transAxes)
ax1.text(0.9,0.05,'(b)',transform=ax1.transAxes)
plt.savefig('figure_fluxes_comparison.eps',format='eps',bbox_inches='tight')
```
### Tables
```
print ("\t".join(['Experiment &','$\kappa_{bg}$ &','$\kappa_{can}$&','$\epsilon$&'
]))
for rec in records_sel:
print ("\t".join(['%s\t&$%0.2e$\t&$%0.2e$\t&$%1.0f$\t '
% (rec.label2,
rec.kbg,
rec.kv,
rec.epsilon,
)
]))
print ("\t".join(['Experiment &', '$N$ (s$^{-1}$)$&',
'$f$ (s$^{-1}$)&', 'U (ms$^{-1}$)&', '$Bu$&','$R_L$' ,'$R_W$' ,
]))
for rec in records_sel:
print ("\t".join(['%s\t\t&$%.1e$\t&$%.2e$\t&$%.2f$\t&$%.2f$\t&$%.2f$\t&$%.2f$\t '
% (rec.label2,
rec.N,
rec.f,
rec.u_mod,
Bu(rec.N, rec.f, rec.W, Hs),
Ro(U=rec.u_mod, f=rec.f, R=rec.L),
Ro(U=rec.u_mod, f=rec.f, R=rec.Wiso),
)
]))
```
#### MISC.
Conversion form $\mu Mm^3$ of $NO^-_3$ to kg of $NO^-_3$:
molecular weight of $NO^-_3$ = 3x16 O + 1x14 N = 62 g/mol
$\mu$Mm$^3$ = 1 x $10^{-6}$ x mol/0.001 m$^3$ x 1 m$^3$ = $10^{-3}$ mol
$10^{-3}$ mol $NO_3$ = $10^{-3}$ mol x 62 g/mol = 0.062 g = $6.2 \times 10^{-5}$ kg
```
```
|
github_jupyter
|
```
# import packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.optimize import fmin_bfgs
%matplotlib inline
#loc = 'https://raw.githubusercontent.com/chenyuw1/coursera-ml-hw/master/hw2/ex2data2.txt'
loc = r'C:\Users\c0w00f8.WMSC\Documents\Coursera\1. Machine Learning\machine-learning-ex2\ex2\ex2data2.txt'
data = pd.read_csv(loc, sep = ',', header = None)
data.shape
data.columns = ['Test1', 'Test2', 'y']
data.head()
# visualizing the data
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
title = ax.set_title('Plot of Training Data')
plot1 = ax.scatter(data[data.y == 1].Test1, data[data.y == 1].Test2, marker = 'P', c = 'green',
label = 'y = 1')
plot2 = ax.scatter(data[data.y == 0].Test1, data[data.y == 0].Test2, marker = '8', c = 'brown',
label = 'y = 0')
ax.legend()
fig.canvas.draw()
# Feature mapping
def mapFeature(x1, x2, degree):
df0 = pd.DataFrame({'x1': x1, 'x2': x2})
#else:
# df0 = pd.concat([x1, x2], axis = 1)
df = pd.DataFrame()
for deg in range(degree + 1):
for i in range(deg + 1):
#print ("deg: ", deg)
#print ("i: ", i)
col1 = x1 ** i
col2 = x2 ** (deg - i)
col = [ col1[j] * col2[j] for j in range(len(df0)) ]
col = pd.DataFrame(col)
df = pd.concat([df, col], axis = 1)
#print (df.shape)
return df
data_mapped = mapFeature(data.iloc[:, 0], data.iloc[:, 1], 6)
data_mapped.shape
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# sigmoid for vector/matrix
sigmd = np.vectorize(sigmoid)
# cost func
def costRegOpt(theta, x, y, l):
m = len(y)
hx = sigmd(np.dot(x, theta))
if (hx.all() != 0) and ((1 - hx).all() != 0):
theta_2 = [ theta[i] ** 2 for i in range(len(theta)) ]
j = (-y.T * np.log(hx) - (1 - y.T) * np.log(1 - hx)).sum() / m + sum(theta_2) * l / 2 / m
else: j = 1000000
return j
def gradReg(theta, x, y, l):
m = len(y)
hx = sigmd(np.dot(x, theta))
grad = np.dot((hx - y), x) / m + l * theta / m
grad[0] = ((hx[0] - y[0]) * x.iloc[:, 0]).sum() / m
return grad
def init_theta(x):
n = x.shape[1]
return [0] * n
# prepare data
x = data_mapped
y = data.iloc[:, -1]
# cost function test
theta = init_theta(x)
costRegOpt(theta, x, y, 1)
# optimize using fmin_bfgs
theta = init_theta(x)
l = 1
myargs = (x, y, l)
theta_opt = fmin_bfgs(costRegOpt, theta, args = myargs)
theta_opt
# plot prep
u = np.linspace(-1, 1.5, 50)
v = np.linspace(-1, 1.5, 50)
z = np.zeros(shape=(len(u), len(v)))
for i in range(len(u)):
for j in range(len(v)):
ui = np.array([u[i]])
vj = np.array([v[j]])
z_i_j = mapFeature(ui, vj, 6)
z[i, j] = z_i_j.dot(theta_opt)
# plot
# visualizing the data
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
title = ax.set_title('lambda = %f' % l)
xlabel = ax.set_xlabel('Test 1')
ylabel = ax.set_ylabel('Test 2')
plot1 = ax.scatter(data[data.y == 1].Test1, data[data.y == 1].Test2, marker = 'P', c = 'green',
label = 'y = 1')
plot2 = ax.scatter(data[data.y == 0].Test1, data[data.y == 0].Test2, marker = '8', c = 'brown',
label = 'y = 0')
z = z.T
plot3 = ax.contour(u, v, z, levels = [0.5])
plot3.clabel(inline = True, fontsize = 9)
ax.legend()
fig.canvas.draw()
# test lambda = 0
theta = init_theta(x)
l = 0
myargs = (x, y, l)
theta_opt = fmin_bfgs(costRegOpt, theta, args = myargs)
theta_opt
# plot prep
u = np.linspace(-1, 1.5, 50)
v = np.linspace(-1, 1.5, 50)
z = np.zeros(shape=(len(u), len(v)))
for i in range(len(u)):
for j in range(len(v)):
ui = np.array([u[i]])
vj = np.array([v[j]])
z_i_j = mapFeature(ui, vj, 6)
z[i, j] = z_i_j.dot(theta_opt)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
title = ax.set_title('lambda = %f' % l)
xlabel = ax.set_xlabel('Test 1')
ylabel = ax.set_ylabel('Test 2')
plot1 = ax.scatter(data[data.y == 1].Test1, data[data.y == 1].Test2, marker = 'P', c = 'green',
label = 'y = 1')
plot2 = ax.scatter(data[data.y == 0].Test1, data[data.y == 0].Test2, marker = '8', c = 'brown',
label = 'y = 0')
z = z.T
plot3 = ax.contour(u, v, z, levels = [0.5])
plot3.clabel(inline = True, fontsize = 9)
ax.legend()
fig.canvas.draw()
# test lambda = 100
theta = init_theta(x)
l = 100
myargs = (x, y, l)
theta_opt = fmin_bfgs(costRegOpt, theta, args = myargs)
theta_opt
# plot prep
u = np.linspace(-1, 1.5, 50)
v = np.linspace(-1, 1.5, 50)
z = np.zeros(shape=(len(u), len(v)))
for i in range(len(u)):
for j in range(len(v)):
ui = np.array([u[i]])
vj = np.array([v[j]])
z_i_j = mapFeature(ui, vj, 6)
z[i, j] = z_i_j.dot(theta_opt)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
title = ax.set_title('lambda = %f' % l)
xlabel = ax.set_xlabel('Test 1')
ylabel = ax.set_ylabel('Test 2')
plot1 = ax.scatter(data[data.y == 1].Test1, data[data.y == 1].Test2, marker = 'P', c = 'green',
label = 'y = 1')
plot2 = ax.scatter(data[data.y == 0].Test1, data[data.y == 0].Test2, marker = '8', c = 'brown',
label = 'y = 0')
z = z.T
plot3 = ax.contour(u, v, z)
plot3.clabel(inline = True, fontsize = 9)
ax.legend()
fig.canvas.draw()
```
|
github_jupyter
|
# 循环结构
在程序中我们需要执行重复重复再重复的东东,使用循环结构。
一种是for-in循环
一种是while循环
```
"""
for循环实现1~100 求和
"""
sum = 0
for x in range(101):
sum += x
print(sum)
sum = 0
for x in range(1,101):
sum += x
print(sum)
####偶数求和
sum = 0
for x in range(2,101,2):
sum += x
print(sum)
```
while循环 :常用于死循环进行取值
```
"""
for循环实现1~100 求和
"""
sum = 0
num = 1
while num <= 100:
sum += num
num += 1
print(sum)
"""
for循环实现1~100 偶数求和
"""
sum = 0
num = 2
while num <= 100:
sum += num
num += 2
print(sum)
```
# 函数和模块的使用
def关键字来定义函数,和变量一样每个函数也有一个响亮的名字,而且命名规则跟变量的命名规则是一致的。在函数名后面的圆括号中可以放置传递给函数的参数,这一点和数学上的函数非常相似,程序中函数的参数就相当于是数学上说的函数的自变量,而函数执行完成后我们可以通过return关键字来返回一个值,这相当于数学上说的函数的因变量。
```
###在参数名前面的*表示args是一个可变参数(不定长参数)
###记载调用add函数时可以传入0个或多个参数
def add (*args):
total = 0
for val in args:
total += val
return total
print(add())
print(add(1))
print(add(1,2,3,4))
##1一元二次方程
def gongshi():
a = float(input('请输入a:'))
b = float(input('请输入b:'))
c = float(input('请输入c:'))
r1 = (-b + ((b ** 2) - 4*a*c)**0.5) / 2 * a
r2 = (-b - ((b ** 2) - 4*a*c)**0.5) / 2 * a
s = (b**2 - (4 * a * c))
if s > 0:
print(r1,r2)
elif s ==0:
print(r1)
else:
print('The equation has no real roots')
gongshi()
##2学习加法
import random
def chengxu():
## num1 = int(input())
## num2 = int(input())
num1 = random.randint(1,100)
num2 = random.randint(1,100)
num = int(input("输入两数之和:"))
if num == num1 + num2:
print('真')
else :
print("程序为假")
chengxu()
##3预测之后的天
def rizi():
a = int(input("星期"))
b = int(input("天数"))
tian = b % 7
xia = a + tian
tai = xia % 7
print(tai)
rizi()
##4三个整数比大小
def tishi():
one = input("请输入")
two = input("请输入")
three = input("请输入")
a = [one,two,three]
a.sort()
print(a)
tishi()
##5比较价钱
def tishi():
weight1 = float(input("package1"))
price1 = float(input())
weight2 = float(input("package2"))
price2 = float(input())
danjia1 = weight1 / price1
danjia2 = weight2 / price2
if danjia1 > danjia2:
print("package1 hao")
else :
print("package2 hao")
tishi()
##6。找出一个月中的天数
def tishi():
a = int(input("月"))
b = int(input("年"))
list1 = [1,3,5,7,8,10,12]
list2 = [4,6,9,11]
if a in list1 :
print("31天")
elif a in list2:
print("30天")
else:
if b % 4 != 0:
print("28天")
else:
print("29天")
tishi()
##7 猜硬币
import random
def tishi():
num1 = random.randint(1,3)
a = int(input(""))
if a == num1:
print("对了")
else:
print("错了")
tishi()
##8
import random
# import numpy as np
# res = np.random.choice(['石头','✂️','🙅🙅♀️'])
# print(res)
import os
# pywin32
C_res = random.randint(0,2)
U_res = int(input('0:石头,1:剪刀,2:布'))
if C_res == U_res:
print('平局')
else:
if C_res == 0 and U_res == 1:
print('电脑赢了 😢')
#os.system('say you loser.')
elif C_res == 1 and U_res == 2:
print('电脑赢了 😢')
# os.system('say you loser.')
elif C_res == 2 and U_res == 0:
print('电脑赢了 😢')
# os.system('say you loser.')
else:
print('你赢了 😄')
# os.system('say you winer.')
##9
def function():
year = int(input('年'))
mounth = int(input('月'))
data = int(input('天'))
k = year % 100
j = year / 100
h = (data + (26 * (mounth + 1) / 10) + k + (k / 4) +(j/4) + 5 * j ) % 7
print('这一天是星期%d'%h)
function()
##11。回文数
def tishi():
a = input()
gw = a[2]
bw = a[0]
if gw == bw:
print("回文")
else :
print("非回文")
tishi()
##12. 计算三角形的周长
def tishi():
a = int(input("请输入"))
b = int(input("请输入"))
c = int(input("请输入"))
zhaochang = (a + b + c)
if a + b > c and a + c > b and b + c > a:
print (zhaochang)
else :
print("错了")
tishi()
```
|
github_jupyter
|
This notebook contains a bunch of experiments to determine the optimal learning rate value for different optimizers. The reference model is a CNN with 3 convolutional blocks; the dataset is an augmented version of the CBIS dataset.
# Environment setup
```
# Connect to Google Drive
from google.colab import drive
drive.mount('/content/gdrive')
# Copy the dataset from Google Drive to local
!cp "/content/gdrive/My Drive/CBIS_DDSM.zip" .
!unzip -qq CBIS_DDSM.zip
!rm CBIS_DDSM.zip
cbis_path = 'CBIS_DDSM'
# Import libraries
%tensorflow_version 1.x
import os
import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import models
from tensorflow.keras import optimizers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint, LearningRateScheduler, Callback
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.optimizers import RMSprop, SGD, Adam, Nadam
```
# Data pre-processing
```
def load_training():
"""
Load the training set (excluding baseline patches)
"""
images = np.load(os.path.join(cbis_path, 'numpy data', 'train_tensor.npy'))[1::2]
labels = np.load(os.path.join(cbis_path, 'numpy data', 'train_labels.npy'))[1::2]
return images, labels
def load_testing():
"""
Load the test set (abnormalities patches and labels, no baseline)
"""
images = np.load(os.path.join(cbis_path, 'numpy data', 'public_test_tensor.npy'))[1::2]
labels = np.load(os.path.join(cbis_path, 'numpy data', 'public_test_labels.npy'))[1::2]
return images, labels
def remap_label(l):
"""
Remap the labels to 0->mass 1->calcification
"""
if l == 1 or l == 2:
return 0
elif l == 3 or l == 4:
return 1
else:
print("[WARN] Unrecognized label (%d)" % l)
return None
# Load training and test images (abnormalities only, no baseline)
train_images, train_labels= load_training()
test_images, test_labels= load_testing()
# Number of images
n_train_img = train_images.shape[0]
n_test_img = test_images.shape[0]
print("Train size: %d \t Test size: %d" % (n_train_img, n_test_img))
# Compute width and height of images
img_w = train_images.shape[1]
img_h = train_images.shape[2]
print("Image size: %dx%d" % (img_w, img_h))
# Remap labels
train_labels = np.array([remap_label(l) for l in train_labels])
test_labels = np.array([remap_label(l) for l in test_labels])
# Create a new dimension for color in the images arrays
train_images = train_images.reshape((n_train_img, img_w, img_h, 1))
test_images = test_images.reshape((n_test_img, img_w, img_h, 1))
# Convert from 16-bit (0-65535) to float (0-1)
train_images = train_images.astype('uint16') / 65535
test_images = test_images.astype('uint16') / 65535
# Shuffle the training set (originally sorted by label)
perm = np.random.permutation(n_train_img)
train_images = train_images[perm]
train_labels = train_labels[perm]
# Create a generator for training images
train_datagen = ImageDataGenerator(
validation_split=0.2,
rotation_range=180,
zoom_range=0.2,
horizontal_flip=True,
vertical_flip=True,
fill_mode='reflect'
)
# Fit the generator with some images
train_datagen.fit(train_images)
# Split train images into actual training and validation
train_generator = train_datagen.flow(train_images, train_labels, batch_size=128, subset='training')
validation_generator = train_datagen.flow(train_images, train_labels, batch_size=128, subset='validation')
# Visualize one image from the dataset and its label, just to make sure the data format is correct
idx = 0
plt.imshow(train_images[idx][:,:,0], cmap='gray')
plt.show()
print("Label: " + str(train_labels[idx]))
def create_cnn():
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(150, 150, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(48, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
return model
```
# Learning rate estimation
The following experiment involves four of the most popular optimizers for NNs: SGD, RMSprop, Adam and Nadam.
In order to roughly approximate the range of reasonable values of learning rate for each optimizer, a simple strategy is adopted. Starting with a very low LR, its value is slightly increased at the end of each epoch. Initially, the network will learn slowly, because a small LR does now allow large weight updates, hence the loss will remain more or less constant.
Then, the LR increases and the loss starts decreasing. At some point, however, the learning rate becomes so big that updates cause large and unpredictable fluctuations of the loss, and the network basically starts diverging.
In practice, the loss will start from a value around 0.69, corresponding to random prediction. After it gets lower a certain threshold, let's say 0.6, one can safely assume that the network started learning, and will eventually reach a loss minimum. Later, as soon as the weights diverge and the network goes back to random prediction, the training is stopped.
```
loss_lower_threshold = 0.60
loss_upper_threshold = 0.69
class StopOnDivergingLoss(Callback):
def on_epoch_end(self, epoch, logs={}):
global low_reached
if logs.get('loss') < loss_lower_threshold:
low_reached = True
if logs.get('loss') > loss_upper_threshold and low_reached:
print("\nStopping training!")
self.model.stop_training = True
# Callback for monitoring the loss at each learning rate
class LossLRCallback(Callback):
def on_epoch_end(self, epoch, logs=None):
lr2loss[opt][0].append(keras.backend.eval(self.model.optimizer.lr))
lr2loss[opt][1].append(logs['loss'])
# Callback to update the learning rate
lr_inc_rate = 1.1
def lr_scheduler(epoch):
new_lr = lr_begin*(lr_inc_rate**epoch)
print("Learning rate: %.7f" % new_lr)
return new_lr
opts = [SGD, RMSprop, Adam, Nadam]
initial_lr = {
SGD: 1e-3,
RMSprop: 1e-5,
Adam: 1e-6,
Nadam: 1e-6
}
lr2loss = {
SGD: [[], []],
RMSprop: [[], []],
Adam: [[], []],
Nadam: [[], []]
}
# For each optimizer, perform a run incrementing the learning rate after every
# epoch, and keep track of the results
for opt in opts:
print("Optimizer: " + opt.__name__)
cnn = create_cnn()
lr_begin = initial_lr[opt]
low_reached = False
stop_on_diverging_loss = StopOnDivergingLoss()
losslrcb = LossLRCallback()
lrschedulecb = keras.callbacks.LearningRateScheduler(lr_scheduler)
cnn.compile(
optimizer=opt(learning_rate=lr_begin),
loss='binary_crossentropy',
metrics=['accuracy'])
history = cnn.fit_generator(
train_generator,
steps_per_epoch=n_train_img // 128,
epochs=300,
validation_data=validation_generator,
callbacks=[stop_on_diverging_loss, losslrcb, lrschedulecb],
shuffle=True,
verbose=1,
initial_epoch=0)
# Plot the loss obtained at different learning rates
plt.figure(figsize=(9, 8), dpi=80, facecolor='w', edgecolor='k')
for opt in opts:
plt.xscale('log')
plt.ylim(0.35, 0.8)
plt.plot(lr2loss[opt][0], lr2loss[opt][1], label=opt.__name__)
plt.title(' Loss-LR curve')
plt.ylabel('Loss')
plt.xlabel('Learning rate')
plt.legend(loc='lower right')
plt.show()
```
The graph above clearly shows that learning rate plays a decisive role during the training. When it is too high, weight updates become too large and the network becomes unstable, failing to converge towards the loss minimum. On the other hand, if it set too low, the network learns slowly and we observe modest improvements between two consecutive epochs.
The global minimum of the Loss-LR curve indicates the point where the learning rate starts causing instabilities, hence choosing a greater value is discouraged.
Ideally, the best one is in the region with the fastest descent of loss function, that is where the plotted curve is steepest (negatively). It should be also noted that, in a stable network, loss variations naturally decrease over time, even if the LR remains constant, as a consequence of the gradual convergence of the weights towards the optimum. Thus, the steepest point represents may not directly represent the optimal LR, but a lower bound for it.
That said, a practical way to choose an adequate LR for an optimizer is to pick a value between the steepest point and the minimum, e.g. in the middle of this region.
In this case, reasonable choices are:
* **SGD** : 3e-2
* **RMSProp** : 1e-4
* **Adam** : 1e-4
* **Nadam** : 1e-4
Note how these values slightly differ from the Keras default ones.
# Optimizers comparison
In the following experiment each optimizer runs once for 100 epochs, with the previously determined learning rate.
```
# For each optimizer, execute a training run with the previously determined best learning rate
optimal_lr = {
SGD: 3e-2,
RMSprop: 1e-4,
Adam: 1e-4,
Nadam: 1e-4
}
histories = {}
for opt in opts:
print("Optimizer: " + opt.__name__)
cnn = create_cnn()
cnn.compile(
optimizer=opt(learning_rate=optimal_lr[opt]),
loss='binary_crossentropy',
metrics=['accuracy'])
histories[opt] = cnn.fit_generator(
train_generator,
steps_per_epoch=n_train_img // 128,
epochs=100,
validation_data=validation_generator,
shuffle=True,
verbose=1,
initial_epoch=0)
# Validation accuracy
plt.figure(figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.title('Validation accuracy comparison')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
for opt in opts:
val_acc = histories[opt].history['val_acc']
epochs = range(1, len(val_acc)+1)
plt.plot(epochs, val_acc, label=opt.__name__)
plt.legend(loc='lower right')
# Validation loss
plt.figure(figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.title('Validation loss comparison')
plt.ylabel('Loss')
plt.xlabel('Epoch')
for opt in opts:
val_loss = histories[opt].history['val_loss']
epochs = range(1, len(val_loss)+1)
plt.plot(epochs, val_loss, label=opt.__name__)
plt.legend(loc='lower right')
```
The graphs shows that SGD is relatively weak with respect to the other optimizers. Adam converges faster than RMSprop and Nadam, whose curves are quite similar.
# Learning rate verification
Now that approximate values for the learning rate have been discovered, one may try to directly experiment with different nearby values and find which one works best.
## RMSprop
```
# Try RMSprop with different learning rates
lr_to_test = (1e-5, 1e-4, 1e-3)
opt = RMSprop
histories = {}
for lr in lr_to_test:
print("RMS [lr = %.5f]: " % lr)
cnn = create_cnn()
cnn.compile(
optimizer=opt(learning_rate=lr),
loss='binary_crossentropy',
metrics=['accuracy'])
histories[lr] = cnn.fit_generator(
train_generator,
steps_per_epoch=n_train_img // 128,
epochs=100,
validation_data=validation_generator,
shuffle=True,
verbose=1,
initial_epoch=0)
# Validation accuracy
plt.figure(figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.title('Validation accuracy comparison')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
for lr in lr_to_test:
val_acc = histories[lr].history['val_acc']
epochs = range(1, len(val_acc)+1)
plt.plot(epochs, val_acc, label=("%s, lr=%f" % (opt.__name__, lr)))
plt.legend(loc='lower right')
# Validation loss
plt.figure(figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.title('Validation loss comparison')
plt.ylabel('Loss')
plt.xlabel('Epoch')
for lr in lr_to_test:
val_loss = histories[lr].history['val_loss']
epochs = range(1, len(val_loss)+1)
plt.plot(epochs, val_loss, label=("%s, lr=%f" % (opt.__name__, lr)))
plt.legend(loc='upper right');
```
**Result**: Values between 1e-4 and 1e-3 produce similar results. 1e-3 is more noisy, but converges a bit faster. On the other hand, 1e-5 represents an excessively low value.
## Adam
```
# Try Adam with different learning rates
lr_to_test = (1e-5, 1e-4, 1e-3)
opt = Adam
histories = {}
for lr in lr_to_test:
print("Adam [lr = %.5f]: " % lr)
cnn = create_cnn()
cnn.compile(
optimizer=opt(learning_rate=lr),
loss='binary_crossentropy',
metrics=['accuracy'])
histories[lr] = cnn.fit_generator(
train_generator,
steps_per_epoch=n_train_img // 128,
epochs=100,
validation_data=validation_generator,
shuffle=True,
verbose=1,
initial_epoch=0)
# Validation accuracy
plt.figure(figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.title('Validation accuracy comparison')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
for lr in lr_to_test:
val_acc = histories[lr].history['val_acc']
epochs = range(1, len(val_acc)+1)
plt.plot(epochs, val_acc, label=("%s, lr=%f" % (opt.__name__, lr)))
plt.legend(loc='lower right')
# Validation loss
plt.figure(figsize=(7, 7), dpi=80, facecolor='w', edgecolor='k')
plt.title('Validation loss comparison')
plt.ylabel('Loss')
plt.xlabel('Epoch')
for lr in lr_to_test:
val_loss = histories[lr].history['val_loss']
epochs = range(1, len(val_loss)+1)
plt.plot(epochs, val_loss, label=("%s, lr=%f" % (opt.__name__, lr)))
plt.legend(loc='upper right');
```
**Result**: 1e-5 is definitely a bad choice, as the network converges very slowly. Interestingly, 1e-4 produces better results than 1e-3.
```
```
|
github_jupyter
|
# Converting between the 4-metric $g_{\mu\nu}$ and ADM variables $\left\{\gamma_{ij}, \alpha, \beta^i\right\}$ or BSSN variables $\left\{h_{ij}, {\rm cf}, \alpha, {\rm vet}^i\right\}$
## Author: Zach Etienne
[comment]: <> (Abstract: TODO)
### We will often find it useful to convert between the 4-metric $g_{\mu\nu}$ and the ADM or BSSN variables. This notebook documents the NRPy+ Python module [`BSSN.ADMBSSN_tofrom_4metric`](../edit/BSSN/ADMBSSN_tofrom_4metric.py), which provides that functionality.
**Notebook Status:** <font color='orange'><b> Self-validated, some additional tests performed </b></font>
**Validation Notes:** This tutorial notebook has been confirmed to be self-consistent with its corresponding NRPy+ module, as documented [below](#code_validation). In addition, the construction of $g_{\mu\nu}$ and $g^{\mu\nu}$ from BSSN variables has passed the test $g^{\mu\nu}g_{\mu\nu}=4$ [below](#validationcontraction). **Additional validation tests may have been performed, but are as yet, undocumented. (TODO)**
### NRPy+ Source Code for this module: [BSSN/ADMBSSN_tofrom_4metric.py](../edit/BSSN/ADMBSSN_tofrom_4metric.py)
## Introduction:
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
This notebook is organized as follows
1. [Step 1](#setup_ADM_quantities): `setup_ADM_quantities(inputvars)`: If `inputvars="ADM"` declare ADM quantities $\left\{\gamma_{ij},\beta^i,\alpha\right\}$; if `inputvars="ADM"` define ADM quantities in terms of BSSN quantities
1. [Step 2](#admbssn_to_fourmetric): Write 4-metric $g_{\mu\nu}$ and its inverse $g^{\mu\nu}$ in terms of ADM or BSSN quantities
1. [Step 2.a](#admbssn_to_fourmetric_lower): 4-metric $g_{\mu\nu}$ in terms of ADM or BSSN quantities
1. [Step 2.b](#admbssn_to_fourmetric_inv): 4-metric inverse $g^{\mu\nu}$ in terms of ADM or BSSN quantities
1. [Step 2.c](#validationcontraction): Validation check: Confirm $g_{\mu\nu}g^{\mu\nu}=4$
1. [Step 3](#fourmetric_to_admbssn): Write ADM/BSSN metric quantities in terms of 4-metric $g_{\mu\nu}$ (Excludes extrinsic curvature $K_{ij}$ or the BSSN $\bar{A}_{ij}$, $K$)
1. [Step 3.a](#adm_ito_fourmetric_validate): ADM in terms of 4-metric validation: Confirm $\gamma_{ij}\gamma^{ij}=3$
1. [Step 3.b](#bssn_ito_fourmetric_validate): BSSN in terms of 4-metric validation: Confirm $\bar{\gamma}_{ij}\bar{\gamma}^{ij}=3$
1. [Step 4](#code_validation): Code Validation against `BSSN.ADMBSSN_tofrom_4metric` NRPy+ module
1. [Step 5](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='setup_ADM_quantities'></a>
# Step 1: `setup_ADM_quantities(inputvars)`: If `inputvars="ADM"` declare ADM quantities $\left\{\gamma_{ij},\beta^i,\alpha\right\}$; if `inputvars="ADM"` define ADM quantities in terms of BSSN quantities \[Back to [top](#toc)\]
$$\label{setup_ADM_quantities}$$
```
import sympy as sp
import NRPy_param_funcs as par
import indexedexp as ixp
import sys
def setup_ADM_quantities(inputvars):
if inputvars == "ADM":
gammaDD = ixp.declarerank2("gammaDD", "sym01")
betaU = ixp.declarerank1("betaU")
alpha = sp.symbols("alpha", real=True)
elif inputvars == "BSSN":
import BSSN.ADM_in_terms_of_BSSN as AitoB
# Construct gamma_{ij} in terms of cf & gammabar_{ij}
AitoB.ADM_in_terms_of_BSSN()
gammaDD = AitoB.gammaDD
# Next construct beta^i in terms of vet^i and reference metric quantities
import BSSN.BSSN_quantities as Bq
Bq.BSSN_basic_tensors()
betaU = Bq.betaU
alpha = sp.symbols("alpha", real=True)
else:
print("inputvars = " + str(inputvars) + " not supported. Please choose ADM or BSSN.")
sys.exit(1)
return gammaDD,betaU,alpha
```
<a id='admbssn_to_fourmetric'></a>
# Step 2: Write 4-metric $g_{\mu\nu}$ and its inverse $g^{\mu\nu}$ in terms of ADM or BSSN variables \[Back to [top](#toc)\]
$$\label{admbssn_to_fourmetric}$$
<a id='admbssn_to_fourmetric_lower'></a>
## Step 2.a: 4-metric $g_{\mu\nu}$ in terms of ADM or BSSN variables \[Back to [top](#toc)\]
$$\label{admbssn_to_fourmetric_lower}$$
Given ADM variables $\left\{\gamma_{ij},\beta^i,\alpha \right\}$, which themselves may be written in terms of the rescaled BSSN curvilinear variables $\left\{h_{ij},{\rm cf},\mathcal{V}^i,\alpha \right\}$ for our chosen reference metric via simple function calls to `ADM_in_terms_of_BSSN()` and `BSSN_quantities.BSSN_basic_tensors()`, we are to construct the 4-metric $g_{\mu\nu}$.
We accomplish this via Eq. 2.122 (which can be trivially derived from the ADM 3+1 line element) of Baumgarte & Shapiro's *Numerical Relativity* (henceforth B&S):
$$
g_{\mu\nu} = \begin{pmatrix}
-\alpha^2 + \beta^k \beta_k & \beta_i \\
\beta_j & \gamma_{ij}
\end{pmatrix},
$$
where the shift vector $\beta^i$ is lowered via (Eq. 2.121):
$$\beta_k = \gamma_{ik} \beta^i.$$
```
def g4DD_ito_BSSN_or_ADM(inputvars):
# Step 0: Declare g4DD as globals, to make interfacing with other modules/functions easier
global g4DD
# Step 1: Check that inputvars is set to a supported value
gammaDD,betaU,alpha = setup_ADM_quantities(inputvars)
# Step 2: Compute g4DD = g_{mu nu}:
# To get \gamma_{\mu \nu} = gamma4DD[mu][nu], we'll need to construct the 4-metric, using Eq. 2.122 in B&S:
g4DD = ixp.zerorank2(DIM=4)
# Step 2.a: Compute beta_i via Eq. 2.121 in B&S
betaD = ixp.zerorank1()
for i in range(3):
for j in range(3):
betaD[i] += gammaDD[i][j] * betaU[j]
# Step 2.b: Compute beta_i beta^i, the beta contraction.
beta2 = sp.sympify(0)
for i in range(3):
beta2 += betaU[i] * betaD[i]
# Step 2.c: Construct g4DD via Eq. 2.122 in B&S
g4DD[0][0] = -alpha ** 2 + beta2
for mu in range(1, 4):
g4DD[mu][0] = g4DD[0][mu] = betaD[mu - 1]
for mu in range(1, 4):
for nu in range(1, 4):
g4DD[mu][nu] = gammaDD[mu - 1][nu - 1]
```
<a id='admbssn_to_fourmetric_inv'></a>
## Step 2.b: Inverse 4-metric $g^{\mu\nu}$ in terms of ADM or BSSN variables \[Back to [top](#toc)\]
$$\label{admbssn_to_fourmetric_inv}$$
B&S also provide a convenient form for the inverse 4-metric (Eq. 2.119; also Eq. 4.49 in [Gourgoulhon](https://arxiv.org/pdf/gr-qc/0703035.pdf)):
$$
g^{\mu\nu} = \gamma^{\mu\nu} - n^\mu n^\nu =
\begin{pmatrix}
-\frac{1}{\alpha^2} & \frac{\beta^i}{\alpha^2} \\
\frac{\beta^i}{\alpha^2} & \gamma^{ij} - \frac{\beta^i\beta^j}{\alpha^2}
\end{pmatrix},
$$
where the unit normal vector to the hypersurface is given by $n^{\mu} = \left(\alpha^{-1},-\beta^i/\alpha\right)$.
```
def g4UU_ito_BSSN_or_ADM(inputvars):
# Step 0: Declare g4UU as globals, to make interfacing with other modules/functions easier
global g4UU
# Step 1: Check that inputvars is set to a supported value
gammaDD,betaU,alpha = setup_ADM_quantities(inputvars)
# Step 2: Compute g4UU = g_{mu nu}:
# To get \gamma^{\mu \nu} = gamma4UU[mu][nu], we'll need to use Eq. 2.119 in B&S.
g4UU = ixp.zerorank2(DIM=4)
# Step 3: Construct g4UU = g^{mu nu}
# Step 3.a: Compute gammaUU based on provided gammaDD:
gammaUU, gammaDET = ixp.symm_matrix_inverter3x3(gammaDD)
# Then evaluate g4UU:
g4UU = ixp.zerorank2(DIM=4)
g4UU[0][0] = -1 / alpha**2
for mu in range(1,4):
g4UU[0][mu] = g4UU[mu][0] = betaU[mu-1]/alpha**2
for mu in range(1,4):
for nu in range(1,4):
g4UU[mu][nu] = gammaUU[mu-1][nu-1] - betaU[mu-1]*betaU[nu-1]/alpha**2
```
<a id='validationcontraction'></a>
## Step 2.c: Validation check: Confirm $g_{\mu\nu}g^{\mu\nu}=4$ \[Back to [top](#toc)\]
$$\label{validationcontraction}$$
Next we compute $g^{\mu\nu} g_{\mu\nu}$ as a validation check. It should equal 4:
```
g4DD_ito_BSSN_or_ADM("BSSN")
g4UU_ito_BSSN_or_ADM("BSSN")
sum = 0
for mu in range(4):
for nu in range(4):
sum += g4DD[mu][nu]*g4UU[mu][nu]
if sp.simplify(sum) == sp.sympify(4):
print("TEST PASSED!")
else:
print("TEST FAILED: "+str(sum)+" does not apparently equal 4.")
sys.exit(1)
```
<a id='fourmetric_to_admbssn'></a>
# Step 3: Write ADM/BSSN metric quantities in terms of 4-metric $g_{\mu\nu}$ (Excludes extrinsic curvature $K_{ij}$, the BSSN $a_{ij}$, $K$, and $\lambda^i$) \[Back to [top](#toc)\]
$$\label{fourmetric_to_admbssn}$$
Given $g_{\mu\nu}$, we now compute ADM/BSSN metric quantities, excluding extrinsic curvature.
Let's start by computing the ADM quantities in terms of the 4-metric $g_{\mu\nu}$
Recall that
$$
g_{\mu\nu} = \begin{pmatrix}
-\alpha^2 + \beta^k \beta_k & \beta_i \\
\beta_j & \gamma_{ij}
\end{pmatrix}.
$$
From this equation we immediately obtain $\gamma_{ij}$. However we need $\beta^i$ and $\alpha$. After computing the inverse of $\gamma_{ij}$, $\gamma^{ij}$, we raise $\beta_j$ via $\beta^i=\gamma^{ij} \beta_j$ and then compute $\alpha$ via $\alpha = \sqrt{\beta^k \beta_k - g_{00}}$. To convert to BSSN variables $\left\{h_{ij},{\rm cf},\mathcal{V}^i,\alpha \right\}$, we need only convert from ADM via function calls to [`BSSN.BSSN_in_terms_of_ADM`](../edit/BSSN/BSSN_in_terms_of_ADM.py) ([**tutorial**](Tutorial-BSSN_in_terms_of_ADM.ipynb)).
```
def BSSN_or_ADM_ito_g4DD(inputvars):
# Step 0: Declare output variables as globals, to make interfacing with other modules/functions easier
if inputvars == "ADM":
global gammaDD,betaU,alpha
elif inputvars == "BSSN":
global hDD,cf,vetU,alpha
else:
print("inputvars = " + str(inputvars) + " not supported. Please choose ADM or BSSN.")
sys.exit(1)
# Step 1: declare g4DD as symmetric rank-4 tensor:
g4DD = ixp.declarerank2("g4DD","sym01",DIM=4)
# Step 2: Compute gammaDD & betaD
betaD = ixp.zerorank1()
gammaDD = ixp.zerorank2()
for i in range(3):
betaD[i] = g4DD[0][i]
for j in range(3):
gammaDD[i][j] = g4DD[i+1][j+1]
# Step 3: Compute betaU
# Step 3.a: Compute gammaUU based on provided gammaDD
gammaUU, gammaDET = ixp.symm_matrix_inverter3x3(gammaDD)
# Step 3.b: Use gammaUU to raise betaU
betaU = ixp.zerorank1()
for i in range(3):
for j in range(3):
betaU[i] += gammaUU[i][j]*betaD[j]
# Step 4: Compute alpha = sqrt(beta^2 - g_{00}):
# Step 4.a: Compute beta^2 = beta^k beta_k:
beta_squared = sp.sympify(0)
for k in range(3):
beta_squared += betaU[k]*betaD[k]
# Step 4.b: alpha = sqrt(beta^2 - g_{00}):
alpha = sp.sqrt(sp.simplify(beta_squared) - g4DD[0][0])
# Step 5: If inputvars == "ADM", we are finished. Return.
if inputvars == "ADM":
return
# Step 6: If inputvars == "BSSN", convert ADM to BSSN & return hDD, cf,
import BSSN.BSSN_in_terms_of_ADM as BitoA
dummyBU = ixp.zerorank1()
BitoA.gammabarDD_hDD( gammaDD)
BitoA.cf_from_gammaDD(gammaDD)
BitoA.betU_vetU( betaU,dummyBU)
hDD = BitoA.hDD
cf = BitoA.cf
vetU = BitoA.vetU
```
<a id='adm_ito_fourmetric_validate'></a>
## Step 3.a: ADM in terms of 4-metric validation: Confirm $\gamma_{ij}\gamma^{ij}=3$ \[Back to [top](#toc)\]
$$\label{adm_ito_fourmetric_validate}$$
Next we compute $\gamma^{ij} \gamma_{ij}$ as a validation check. It should equal 3:
```
BSSN_or_ADM_ito_g4DD("ADM")
gammaUU, gammaDET = ixp.symm_matrix_inverter3x3(gammaDD)
sum = sp.sympify(0)
for i in range(3):
for j in range(3):
sum += gammaDD[i][j]*gammaUU[i][j]
if sp.simplify(sum) == sp.sympify(3):
print("TEST PASSED!")
else:
print("TEST FAILED: "+str(sum)+" does not apparently equal 3.")
sys.exit(1)
```
<a id='bssn_ito_fourmetric_validate'></a>
## Step 3.b: BSSN in terms of 4-metric validation: Confirm $\bar{\gamma}_{ij}\bar{\gamma}^{ij}=3$ \[Back to [top](#toc)\]
$$\label{bssn_ito_fourmetric_validate}$$
Next we compute $\bar{\gamma}_{ij}\bar{\gamma}^{ij}$ as a validation check. It should equal 3:
```
import reference_metric as rfm
par.set_parval_from_str("reference_metric::CoordSystem","SinhCylindrical")
rfm.reference_metric()
BSSN_or_ADM_ito_g4DD("BSSN")
gammabarDD = ixp.zerorank2()
for i in range(3):
for j in range(3):
# gammabar_{ij} = h_{ij}*ReDD[i][j] + gammahat_{ij}
gammabarDD[i][j] = hDD[i][j] * rfm.ReDD[i][j] + rfm.ghatDD[i][j]
gammabarUU, gammabarDET = ixp.symm_matrix_inverter3x3(gammabarDD)
sum = sp.sympify(0)
for i in range(3):
for j in range(3):
sum += gammabarDD[i][j]*gammabarUU[i][j]
if sp.simplify(sum) == sp.sympify(3):
print("TEST PASSED!")
else:
print("TEST FAILED: "+str(sum)+" does not apparently equal 3.")
sys.exit(1)
```
<a id='code_validation'></a>
## Step 4: Code Validation against `BSSN.ADMBSSN_tofrom_4metric` NRPy+ module \[Back to [top](#toc)\]
$$\label{code_validation}$$
Here, as a code validation check, we verify agreement in the SymPy expressions for BrillLindquist initial data between
1. this tutorial and
2. the NRPy+ [BSSN.ADMBSSN_tofrom_4metric](../edit/BSSN/ADMBSSN_tofrom_4metric.py) module.
By default, we analyze these expressions in SinhCylindrical coordinates, though other coordinate systems may be chosen.
```
par.set_parval_from_str("reference_metric::CoordSystem","SinhCylindrical")
rfm.reference_metric()
import BSSN.ADMBSSN_tofrom_4metric as AB4m
for inputvars in ["BSSN","ADM"]:
g4DD_ito_BSSN_or_ADM(inputvars)
AB4m.g4DD_ito_BSSN_or_ADM(inputvars)
for i in range(4):
for j in range(4):
print(inputvars+" input: g4DD["+str(i)+"]["+str(j)+"] - g4DD_mod["+str(i)+"]["
+str(j)+"] = "+str(g4DD[i][j]-AB4m.g4DD[i][j]))
g4UU_ito_BSSN_or_ADM(inputvars)
AB4m.g4UU_ito_BSSN_or_ADM(inputvars)
for i in range(4):
for j in range(4):
print(inputvars+" input: g4UU["+str(i)+"]["+str(j)+"] - g4UU_mod["+str(i)+"]["
+str(j)+"] = "+str(g4UU[i][j]-AB4m.g4UU[i][j]))
BSSN_or_ADM_ito_g4DD("BSSN")
AB4m.BSSN_or_ADM_ito_g4DD("BSSN")
print("BSSN QUANTITIES (ito 4-metric g4DD)")
print("cf - mod_cf = " + str(cf - AB4m.cf))
print("alpha - mod_alpha = " + str(alpha - AB4m.alpha))
for i in range(3):
print("vetU["+str(i)+"] - mod_vetU["+str(i)+"] = " + str(vetU[i] - AB4m.vetU[i]))
for j in range(3):
print("hDD["+str(i)+"]["+str(j)+"] - mod_hDD["+str(i)+"]["+str(j)+"] = "
+ str(hDD[i][j] - AB4m.hDD[i][j]))
BSSN_or_ADM_ito_g4DD("ADM")
AB4m.BSSN_or_ADM_ito_g4DD("ADM")
print("ADM QUANTITIES (ito 4-metric g4DD)")
print("alpha - mod_alpha = " + str(alpha - AB4m.alpha))
for i in range(3):
print("betaU["+str(i)+"] - mod_betaU["+str(i)+"] = " + str(betaU[i] - AB4m.betaU[i]))
for j in range(3):
print("gammaDD["+str(i)+"]["+str(j)+"] - mod_gammaDD["+str(i)+"]["+str(j)+"] = "
+ str(gammaDD[i][j] - AB4m.gammaDD[i][j]))
```
<a id='latex_pdf_output'></a>
# Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename [Tutorial-ADMBSSN_tofrom_4metric.pdf](Tutorial-ADMBSSN_tofrom_4metric.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-ADMBSSN_tofrom_4metric")
```
|
github_jupyter
|
### Load Test deployed web application
This notebook pulls some images and tests them against the deployed web application. We submit requests asychronously which should reduce the contribution of latency.
```
import asyncio
import json
import random
import urllib.request
from timeit import default_timer
import aiohttp
import matplotlib.pyplot as plt
import testing_utilities
from tqdm import tqdm
%matplotlib inline
```
We will test our deployed service with 100 calls. We will only have 4 requests concurrently at any time. We have only deployed one pod on one node and increasing the number of concurrent calls does not really increase throughput. Feel free to try different values and see how the service responds.
```
NUMBER_OF_REQUESTS = 100 # Total number of requests
CONCURRENT_REQUESTS = 4 # Number of requests at a time
```
Get the IP address of our service
```
service_json = !kubectl get service azure-dl -o json
service_dict = json.loads(''.join(service_json))
app_url = service_dict['status']['loadBalancer']['ingress'][0]['ip']
scoring_url = 'http://{}/score'.format(app_url)
version_url = 'http://{}/version'.format(app_url)
!curl $version_url # Reports the Tensorflow Version
IMAGEURL = "https://upload.wikimedia.org/wikipedia/commons/thumb/6/68/Lynx_lynx_poing.jpg/220px-Lynx_lynx_poing.jpg"
plt.imshow(testing_utilities.to_img(IMAGEURL))
def gen_variations_of_one_image(num, label='image'):
out_images = []
img = testing_utilities.to_img(IMAGEURL).convert('RGB')
# Flip the colours for one-pixel
# "Different Image"
for i in range(num):
diff_img = img.copy()
rndm_pixel_x_y = (random.randint(0, diff_img.size[0]-1),
random.randint(0, diff_img.size[1]-1))
current_color = diff_img.getpixel(rndm_pixel_x_y)
diff_img.putpixel(rndm_pixel_x_y, current_color[::-1])
b64img = testing_utilities.to_base64(diff_img)
out_images.append(json.dumps({'input':{label:'\"{0}\"'.format(b64img)}}))
return out_images
url_list = [[scoring_url, jsonimg] for jsonimg in gen_variations_of_one_image(NUMBER_OF_REQUESTS)]
def decode(result):
return json.loads(result.decode("utf-8"))
async def fetch(url, session, data, headers):
start_time = default_timer()
async with session.request('post', url, data=data, headers=headers) as response:
resp = await response.read()
elapsed = default_timer() - start_time
return resp, elapsed
async def bound_fetch(sem, url, session, data, headers):
# Getter function with semaphore.
async with sem:
return await fetch(url, session, data, headers)
async def await_with_progress(coros):
results=[]
for f in tqdm(asyncio.as_completed(coros), total=len(coros)):
result = await f
results.append((decode(result[0]),result[1]))
return results
async def run(url_list, num_concurrent=CONCURRENT_REQUESTS):
headers = {'content-type': 'application/json'}
tasks = []
# create instance of Semaphore
sem = asyncio.Semaphore(num_concurrent)
# Create client session that will ensure we dont open new connection
# per each request.
async with aiohttp.ClientSession() as session:
for url, data in url_list:
# pass Semaphore and session to every POST request
task = asyncio.ensure_future(bound_fetch(sem, url, session, data, headers))
tasks.append(task)
return await await_with_progress(tasks)
```
Below we run the 100 requests against our deployed service
```
loop = asyncio.get_event_loop()
start_time = default_timer()
complete_responses = loop.run_until_complete(asyncio.ensure_future(run(url_list, num_concurrent=CONCURRENT_REQUESTS)))
elapsed = default_timer() - start_time
print('Total Elapsed {}'.format(elapsed))
print('Avg time taken {0:4.2f} ms'.format(1000*elapsed/len(url_list)))
```
Below we can see the output of some of our calls
```
complete_responses[:3]
num_succesful=[i[0]['result'][0]['image'][0][0] for i in complete_responses].count('n02127052 lynx, catamount')
print('Succesful {} out of {}'.format(num_succesful, len(url_list)))
# Example response
plt.imshow(testing_utilities.to_img(IMAGEURL))
complete_responses[0]
```
To tear down the cluster and all related resources go to the [deploy on AKS notebook](04_DeployOnAKS.ipynb)
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.