code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# [](https://githubtocolab.com/giswqs/leafmap/blob/master/examples/notebooks/52_netcdf.ipynb)
# [](https://gishub.org/leafmap-binder)
#
# **Visualizing NetCDF data**
#
# Uncomment the following line to install [leafmap](https://leafmap.org) if needed.
# +
# # !pip install leafmap xarray rioxarray netcdf4 localtileserver
# -
import leafmap
# Download a sample NetCDF dataset.
url = 'https://github.com/giswqs/leafmap/raw/master/examples/data/wind_global.nc'
filename = 'wind_global.nc'
leafmap.download_file(url, output=filename)
# Read the NetCDF dataset.
data = leafmap.read_netcdf(filename)
data
# Convert the NetCDF dataset to GeoTIFF. Note that the longitude range of the NetCDF dataset is `[0, 360]`. We need to convert it to `[-180, 180]` by setting `shift_lon=True` so that it can be displayed on the map.
tif = 'wind_global.tif'
leafmap.netcdf_to_tif(filename, tif, variables=['u_wind', 'v_wind'], shift_lon=True)
# Add the GeoTIFF to the map. We can also overlay the country boundary on the map.
geojson = 'https://github.com/giswqs/leafmap/raw/master/examples/data/countries.geojson'
m = leafmap.Map(layers_control=True)
m.add_geotiff(tif, band=[1], palette='coolwarm', layer_name='u_wind')
m.add_geojson(geojson, layer_name='Countries')
m
# You can also use the `add_netcdf()` function to add the NetCDF dataset to the map without having to convert it to GeoTIFF explicitly.
m = leafmap.Map(layers_control=True)
m.add_netcdf(
filename,
variables=['v_wind'],
palette='coolwarm',
shift_lon=True,
layer_name='v_wind',
)
m.add_geojson(geojson, layer_name='Countries')
m
# Visualizing wind velocity.
m = leafmap.Map(layers_control=True)
m.add_basemap('CartoDB.DarkMatter')
m.add_velocity(filename, zonal_speed='u_wind', meridional_speed='v_wind')
m
# 
|
examples/notebooks/52_netcdf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="9lAsyeOwFnoX"
# # CSCE 623 Homework Assignment 3
#
# + [markdown] id="46d-KBtJJxN1"
# ### Student Name: <font color="blue">Enter Name</font>
# + [markdown] id="Yna07rL4Jz43"
# ### Date: <font color="blue">Enter Date</font>
# + [markdown] id="P685WkBlKB2x"
# ## Disclosures
#
# * None
# + [markdown] id="zXzR22oMKEtf"
# ## Overview
#
# In this homework assignment, you will explore various methods of cross-validation.
#
# We will introduce you to a generated dataset that represents a polynomial function with gaussian noise. You will attempt to fit various models of increasing flexibility (polynomial order) to the data. You will analyze and evaluate each models using cross-validation to (1) determine the model that best fits the data, and (2) predict the performance of your model on new data.
#
# You will then compare the model you developed using machine learning techniques to the model indicated by statistical analysis.
#
# This assignment includes both written and programming components.
# + [markdown] id="qbbSOVyq7lYk"
# ### Written Components
# Full effort answers to written components should include not only the answer to the question, but they should also include supporting information. You should provide justification or supporting information even if the question only asks for a single number or short answer.
# + [markdown] id="a-5OaiNO7m6F"
# ### Programming Components
# Use Python to perform any manipulations you make to provided datasets, all calculations and mathematical transformations, and to generate graphs, figures, or other support to explain how you arrived at your written answers.
# + [markdown] id="a0Zjdxie-jWf"
# ### Helpful Tips
#
# You might find these Python packages/imports helpful
#
# ``` python
# import numpy as np
# import pandas as pd
# import matplotlib.pyplot as plt
# import math
# import seaborn as sns
#
# from sklearn.model_selection import KFold
# from sklearn.model_selection import ShuffleSplit
# from sklearn.model_selection import LeaveOneOut
# from sklearn.model_selection import cross_val_score
#
# from IPython.display import Markdown as md
#
# from sklearn.linear_model import LinearRegression
#
# from sklearn.metrics import mean_squared_error
#
# # # %matplotlib inline
# ```
# + [markdown] id="kS60EAw9MiU2"
# ## Cross-fold Validation
# + [markdown] id="A5yhrcvjN0AD"
# ### STEP 0: installs & configuration
# + [markdown] id="pFdGmA3GN3_q"
# Install any packages you need for your notebook. If using the Google Colab environment, you will not need to install any additional packages.
# + id="AqoMuH_YOJ3e"
"""
CSCE 623 HW3. Cross-fold Validation
"""
DEBUG = True
# install packages, set configuration, as needed
# + [markdown] id="1HI9buTTOPHH"
# Import any packages you need for your notebook
# + id="2yVNfQdnY7BW"
# import pacakages for your notebook
# %matplotlib inline
# + id="4pD5Jejhp70q" tags=["remove_cell"]
# instructor provided code
plot_x_min = -2.
plot_x_max = 2.
def generate_data(seed = 1, quantity = 200, test_data = False):
np.random.seed(seed)
x = np.random.uniform(low=plot_x_min,high=plot_x_max,size=quantity)
order = np.random.randint(3, 4)
betas = np.random.uniform(-2, 2, order)
y = sum((beta * x ** (idx+1) for idx, beta in enumerate(betas)))
beta0 = np.random.uniform(np.min(y), np.max(y))
noise = np.random.normal(size=quantity, scale = (np.max(y) - np.min(y)) / 8)
if test_data: # get new sample if we're generating test data
noise = np.random.normal(size=quantity, scale = (np.max(y) - np.min(y)) / 8)
y += noise + beta0
df = pd.DataFrame({'x': x, 'y': y})
globals()['global_betas'] = betas
globals()['global_beta0'] = beta0
return(df)
# + [markdown] id="xRPFmS9PJVGI"
# ### STEP A: provided functions
# + id="-feg5ea9I_sE"
# instructor provided functions
"""
returns a LaTeX style string representing a function defined by beta0 and betas
"""
def create_model_string(beta0, betas):
model_function = f'$f(x) = {beta0:.2f}'
for idx, beta in enumerate(betas):
model_function += f' + {beta:.2f}x^{idx+1}'
model_function += '$'
return model_function
"""
adds a plot of a function to the current plot
"""
def plot_function(x_min, x_max, beta0, betas, resolution = .1, style = None, label = ''):
plot_x = np.arange(x_min - .2 * abs(x_min), x_max + .2 * abs(x_max), resolution)
plot_y = sum((beta * plot_x ** (idx+1) for idx, beta in enumerate(betas))) + beta0
if style:
plt.plot(plot_x, plot_y, style, label=label)
else:
plt.plot(plot_x, plot_y, label=label)
# + [markdown] id="vnE14vxA2VvU"
# ### STEP 1: scikit-learn Functions
#
# Review the scikit-learn documentation for the following functions and answer the questions that follow:
#
# - [User Guide for cross validation iterators](https://scikit-learn.org/stable/modules/cross_validation.html#cross-validation-iterators)
# - Identically Distributed Data
# - [KFold](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.KFold.html#sklearn.model_selection.KFold)
# - [RepeatedKFold](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RepeatedKFold.html#sklearn.model_selection.RepeatedKFold)
# - [LeaveOneOut](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.LeaveOneOut.html)
# - [LeavePOut](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.LeavePOut.html#sklearn.model_selection.LeavePOut)
# - [ShuffleSplit](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.ShuffleSplit.html#sklearn.model_selection.ShuffleSplit)
# - Stratification with Class Data
# - [StratifiedKFold](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.StratifiedKFold.html#sklearn.model_selection.StratifiedKFold)
# - [RepeatedStratifiedKFold](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RepeatedStratifiedKFold.html#sklearn.model_selection.RepeatedStratifiedKFold)
# - [StratifiedShuffleSplit](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.StratifiedShuffleSplit.html#sklearn.model_selection.StratifiedShuffleSplit)
# - Grouped Data
# - [GroupKFold](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GroupKFold.html#sklearn.model_selection.GroupKFold)
# - [LeaveOneGroupOut](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GroupKFold.html#sklearn.model_selection.GroupKFold)
# - [LeavePGroupsOut](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.LeavePGroupsOut.html#sklearn.model_selection.LeavePGroupsOut)
# - [GroupShuffleSplit](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GroupShuffleSplit.html#sklearn.model_selection.GroupShuffleSplit)
#
#
#
# ### Discussion
#
# - Using one of the functions listed above, what is the most straight-forward way to implement "The Validation Set" approach discussed in _ISLR_, 5.1.1 on regression data? What function would you use? What argument values would you use?
#
# <font color=green class="student_answer">Student Answer</font>
#
# - What function and arguments would you use to implement LOOCV as discussed in _ISLR_ 5.1.2?
#
# <font color=green class="student_answer">Student Answer</font>
#
# - How would you implement k-fold Cross-Validation as discussedd in _ISLR_ 5.1.3? Assuming $k = 10$, what argument values would you use?
#
# <font color=green class="student_answer">Student Answer</font>
#
# - If the problem is a classification problem how would you ensure that each _k-fold_ had a balance of classes represented in the data? What function and argument values would you use assuming $k = 10$?
#
# <font color=green class="student_answer">Student Answer</font>
#
# - Suppose you wanted to train multiple models using k-fold cross-validation each with $k=10$ and compare their performance. What arguments would you use?
#
# <font color=green class="student_answer">Student Answer</font>
#
#
# + id="4Vi2UU9HDUVR"
STEP_1_COMPLETE = False
# + [markdown] id="Z4Lwf_jiXqXK"
# ### Data Analysis
#
# In steps 1-2, you'll load and conduct an analysis of a generated dataset.
# + [markdown] id="EwKDAUtjFnof"
# #### STEP 2: load dataset
# + [markdown] id="G7c6P84MOuJB"
# For this assignment, you will use a generated dataset. You have been provided a function that will generate a dataset. You need only provide a random seed value to generate a unique dataset.
#
# You'll initialize a dataset unique to yourself by choosing a random seed value. You can initialize the seed with the last 4 digits of your phone number, your street address, or some other number.
#
# You'll then generate the dataset and store it in a Dataframe named df:
# ```
# df = generate_data(seed)
# ```
#
# IMPORTANT: After choosing a seed value, you will not want to change this value, as changing the seed will result in your dataset changing. This will invalidate any analysis that you've completed.
#
# + id="_tQNDIVeFnog" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="4ca453b1-0722-4955-8426-63178a6dd95e"
#STEP 2
#STUDENT CODE - insert code to load a generated dataset using pandas
# store your data in a dataframe called 'df'
#---------------------------------------------
#---------------------------------------------
STEP_2_COMPLETE = False
# + [markdown] id="TawtbcrZBEuH"
# #### STEP 3: plot and analyze data
#
# Using a similar approach that you employed in homework assignments 1 and 2, plot and analyze the dataset.
#
# + id="pFCTBu8kCH38" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="3c4b56e0-6b00-4aa7-957a-e9688ba5a24b"
#STEP 3
#STUDENT CODE - insert code to plot and use pandas analysis tools on the dataset
#---------------------------------------------
#---------------------------------------------
# + [markdown] id="3rDHXs2IC2Bx"
# Discuss the dataset, being sure to answer such questions as:
# - How many observations are in the dataset?
# - How many features?
# - What is the nature of the target (regression or classification)?
# - What kind of relationship will best fit the data? Linear? Polynomial? If polynomial, what order?
#
# <font color=green class="student_answer">Student Discussion</font>
#
#
# + id="YxcxNljkDYRn"
STEP_3_COMPLETE = False
# + [markdown] id="GEjQYr2oB4pj"
# #### STEP 4: initial hypothesis
#
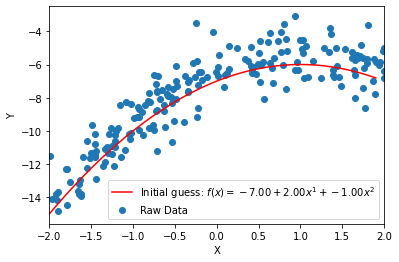
# Develop an initial hypothesis about the best model that will fit the data and overlay it on a scatterplot of the dataset. Be sure to use a model informed by your analysis above. I've provided an example below. While my example is quadratic, your model might not necessarily be quadratic. Feel free to use either of the functions provided in SETUP A above.
#
# 
# + id="9zBQSfynCYsN" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="644439f4-3de4-4137-eb84-39124f388d5d"
#STEP 4
#STUDENT CODE - insert code to overlay your initial hypothesis on a scatter plot of the dataset
#---------------------------------------------
#---------------------------------------------
STEP_4_COMPLETE = False
# + [markdown] id="80j7ZKyoDs_c"
# ### Feature Engineering
#
# In this section, you'll implement code to create a new dataframe with engineered features.
# + [markdown] id="RHKjj6oeEG4c"
# #### STEP 5: feature engineering
#
# `df` contains a feature and a target. You will create a function that will generate a new feature dataframe that will generate a new dataframe with $p$ columns, where column $p$ will contain the the values of $x^p$.
#
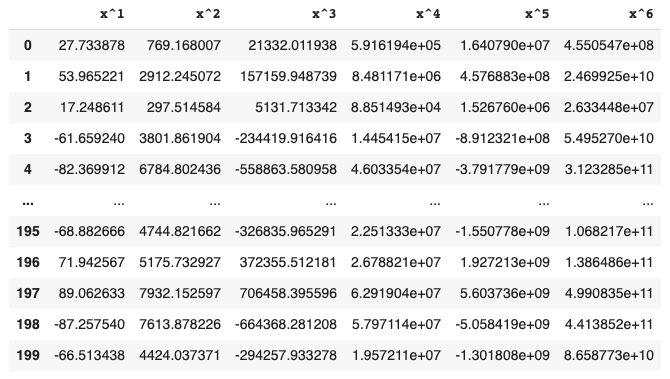
# Your function will have the signature `poly_df(x, p)` where `x` is a series of feature values and `p` is the highest order polynomial desired. The function will return a dataframe where the first column contains the original feature values ($x^1$), the second column contains the quadratic values ($x^2$), the third column has cubic values ($x^3$), and so forth. Provide header values of `x^1`, `x^2`, `x^3`, etc.
#
# This is an example of a displayed dataframe returned after calling `poly_df(df.x, 6)` (specific values will differ).
#
# 
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="XOGdRpJ3IEWM" outputId="6d51736c-c6ee-48cb-e4db-672873f51c70"
#STEP 5
#STUDENT CODE - insert code to implement poly_df
#---------------------------------------------
#---------------------------------------------
STEP_5_COMPLETE = False
# + [markdown] id="81Ntq_t1fi2C"
# ### 3 Ways to Cross Validate
#
# In the following section, we will explore the three methods of cross-validation discussed in the _ISLR_ text:
#
# - Validation Set
# - Leave One Out
# - K-Fold
#
# For each method, we'll execute three steps:
#
# 1. Write a function to calculate the root mean squared error using the intended cross-validation method.
# 2. Generate a DataFrame of root mean squared error values using the cross-validation technique for models of increasing flexibility. Specifically, you'll evaluate 8 models, polynomial models, ordered 1 through 8.
# 3. Plot the spaghetti chart of the root mean squared error values
#
#
# + [markdown] id="rak97xTA3pah"
# #### SETUP B: constants for cv
#
# Here are constants available for your use in STEPS 6-14
# + id="fvAFdvhD1xI-"
# instructor provided constants:
# feel free to use throughout the following STEPs
TRIALS = 10
MAX_ORDER = 8
COLUMNS = ['Trial 1', 'Trial 2', 'Trial 3', 'Trial 4', 'Trial 5', 'Trial 6', 'Trial 7', 'Trial 8', 'Trial 9', 'Trial 10']
INDICES = ['1st', '2nd', '3rd', '4th', '5th', '6th', '7th', '8th']
# + [markdown] id="PGvmAaG3DiE-"
# #### Validation Set Approach
#
# In this section, you will evaluate models of increasing flexibility (up to 8th order polynomial) fit to the generated data.
# + [markdown] id="mJ8SnNJIKycu"
# ##### STEP 6: validation set rmse
#
# In this step, you'll create `val_set_mse(X, y, random_state)` which returns the root mean squared error of a model fit to a training set and evaluated on a validation set.
#
# - `X` is a DataFrame of feature inputs
# - `y` is a Series of targets
# - return a scalar value representing the root mean squared error
#
# Hints:
# - The instructor's solution to this function uses only 4 lines of code--no Python tricks. If you're using more than 6-8 lines of code, you may not be doing something right
# - You'll use the scikit-learn [cross_val_score](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html) function to calculate the root mean squared error. The use of this function may be a bit non-standard for the typical programmer. While the `X` and `y` arguments are pretty straight-forward, three arguments in particular may be confounding:
# - `estimator` is the model type. Usually, you'll set this in advance and then pass in a reference to the model. For example, if you wanted to use a [LogisticRegression](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) model using the `liblinear` solver, you might do the following:
# ```
# model = LogisticRegression(solver='liblinear')
# ```
# and then you would pass in `model` as the `cross_val_score` estimator. There is an additional example on the bottom of page 73 in _HOML_ that uses a DecisionTreeRegressor defined near the top of the page.
# - `cv` is an integer or a cross-validation generator. Unless you're doing k-fold validation, you'll need to provide a generator. The generators are those iterators you reviewed in STEP 1. For example, if you wanted to train and validate on possible training/validaton sets when you remove 12 samples from the dataset, you might do the following:
# ```
# lpo = LeavePOut(p=12)
# ```
# and pass in `lpo` as the `cv` generator
# - `scoring` is a scoring methodology. You can create your own scoring function, but often, using a [predefined scoring method](https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter) is suitable. Note that all scoring methods follow the "greater is better" principal. Therefore, many of the regression scores are negated. To report the actual score of a negated value, you'll need to take the absolute value or negation of the score. See also pages 73-74 of _HOML_. Note that _HOML_ collects the root mean squared error from the `cross_val_score` method and then take the square root of the negation to calculate RMSE. Observe that the negated RMSE metric is available directly as a scoring methodology, so the square root step isn't be necessary.
# - An algorithm for completing this task:
# - Identify the correct cross validation iterator for this problem, and create the generator with all appropriate parameters, assigning it to a variable. NOTES (these are things to consider after you have basic functionality):
# - For the sake of repeatability, you'll want to set the `random_state` value. However, if you set `random_state` to a number, you'll get the exact same train/validation partition every time you call the function. Instead, use a seeded [RandomState](https://numpy.org/doc/1.16/reference/generated/numpy.random.RandomState.html).
# - Be sure that you're splitting the dataset in half for the train and validation sets
# - Identify the correct model type for this problem, and create the model with all appropriate parameters, assigning it to a variable
# - Call cross_val_score, selecting the appropriate scoring metric and assigning the result to a variable
# - Correct for negation and return the score
# + id="S7wrEbTiYq9K"
#STEP 6
#STUDENT CODE - insert code to implement val_set_mse(X, y, random_state)
#---------------------------------------------
#---------------------------------------------
STEP_6_COMPLETE = False
# + [markdown] id="KEgG-JYdf9tm"
# ##### STEP 7: dataframe of val set rmse
#
# In this step, you'll generate a DataFrame of RMSE values for 10 trials of 8 models using the Validation Set approach. Each model will represent an increasing order polynomial feature set. For example, the first value in the DataFrame for Trial 1 will be the the RMSE for a 1st order $(x^1)$ model, whereas the eighth value will be the MSE for an 8th order $(x^1, x^2, ... , x^8)$ model. The resulting DataFrame might look something like this:
#
# ```
# Trial 1 Trial 2 Trial 3 Trial 4 Trial 5 Trial 6 Trial 7 Trial 8 Trial 9 Trial 10
# 1 1.195520 1.307997 1.390264 1.299595 1.320461 1.170825 1.256463 1.321078 1.247050 1.212689
# 2 0.635550 0.621675 0.668410 0.627653 0.625856 0.639784 0.594125 0.638596 0.563780 0.633923
# 3 0.561838 0.582483 0.604784 0.639694 0.612064 0.593695 0.605464 0.569258 0.605322 0.665788
# 4 0.650670 0.655353 0.671473 0.638411 0.614336 0.609196 0.658455 0.709729 0.661375 0.595443
# 5 0.655897 0.670315 0.652939 0.663934 0.699677 0.587052 0.647100 0.669904 0.597044 0.573686
# 6 0.605551 0.559774 0.656311 0.617817 0.666769 0.577362 0.643648 0.622396 0.681107 0.689736
# 7 0.601836 0.633743 0.634507 0.635380 0.636882 0.633724 0.666757 0.676464 0.674024 0.639023
# 8 0.607631 0.639835 0.676559 0.668600 0.660138 0.654388 0.636267 0.659123 0.654003 0.642247
# ```
#
# Hints:
#
# - Adding each trial as a column is not necessarily intuitive. For many, it's more straight-forward to think of trials as rows with the each column representing the order of polynomial. The reason we use Trials as the columns is that the `matplotlib` package will plot lines using columns as the series values. It involves some Python gymnastics to plot rows instead of columns--better to handle it now.
# - You will use your `poly_df` function to generate polynomial feature data
# - The most straight-forward approach involves iterating over 10 trials and 8 orders of polynomials to assign the MSE values to an numpy array. Then, after you've filled your array, you'll create a DataFrame specifying indices (row labels 1-8) and column headers (Trial numbers)
# - Assuming you implemented RandomState in `val_set_mse`, here you'll initialize a RandomState object at the beginning of the cell and pass in to `val_set_mse`. In this way, every time you run this cell, you'll get the same sequence of random train/validation set partitions.
#
# + id="GONYy_mkkyI1" colab={"base_uri": "https://localhost:8080/", "height": 297} outputId="107ae609-c033-4574-dc89-81d244d1da8f"
#STEP 7
#STUDENT CODE - create DataFrame of Trial and Order data
#---------------------------------------------
#---------------------------------------------
STEP_7_COMPLETE = False
# + [markdown] id="2Hk42skZkz6O"
# ##### STEP 8: plot val set cv
#
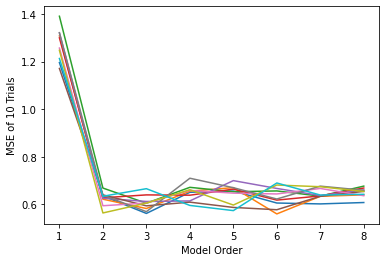
# In this step, create a spaghetti plot of each of the 10 trials. Be sure to label your axes.
#
# Example of resulting plot:
#
# 
# + id="4Ud1UJSokzCz" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="72294b08-9023-4ed6-b034-0a66314fa951"
#STEP 8
#STUDENT CODE - plot validation set spaghetti charts
#---------------------------------------------
#---------------------------------------------
STEP_8_COMPLETE = False
# + [markdown] id="CMSW4czeIXnX"
# #### Leave-One-Out Cross-Validation
#
# + [markdown] id="lFIpRurDxrvK"
# ##### STEP 9: loocv rmse
#
# In this step, you'll create loocv_mse(X, y, random_state) which returns the average root mean squared error of models fit to training sets and evaluated on the validation sets as defined by the Leave-One-Out Cross Validation approach.
#
# - X is a DataFrame of feature inputs
# - y is a Series of targets
# - return a scalar value representing the root mean squared error
#
# Hints:
# - See hints in STEP 6 for guidance here
# - One caveat to consider... what is the type/shape of the value returned by the `cross_val_score` method in STEP 6? What is it here? Another way to think about this question is how many models are being evaluated in the Validation Set approach (STEP 6)? How many models are being evaluted in LOOVC? If your function is expected to return a single RMSE, what will you do differently, here?
# - Your code will likely look nearly identical to that in STEP 6. Don't worry about avoiding repeatition... in practice, you will rarely implement more than one method of cross-validation in your research. Therefore, it's reasonable to generate the full workflow here as a possible source for your research later (apart from reuse of constants from the SETUP B step above).
# + id="xP_Ecu00OXQK"
#STEP 9
#STUDENT CODE - create loocv_mse(X, y, random_state)
#---------------------------------------------
#---------------------------------------------
STEP_9_COMPLETE = False
# + [markdown] id="KZonhX4oxuTH"
# ##### STEP 10: dataframe of loocv rmse
#
# In this step, you'll generate a DataFrame of RMSE values for 1 trial of 8 models using the Leave One Out Cross-Validation approach. As in STEP 7, each model will represent an increasing order polynomial feature set. For example, the first value in the DataFrame for Trial 1 will be the the RMSE for a 1st order $(x^1)$ model, whereas the eighth value will be the MSE for an 8th order $(x^1, x^2, ... , x^8)$ model.
#
# Hints:
# - Unlike STEP 7, you'll have only one column of data representing a single trial of 8 models of polynomials
# + id="PX4OBFELpgHb"
#STEP 10
#STUDENT CODE - create DataFrame of LOOCV Order data
#---------------------------------------------
#---------------------------------------------
STEP_10_COMPLETE = True
# + [markdown] id="N2ieXkh7xxSh"
# ##### STEP 11: plot loocv
#
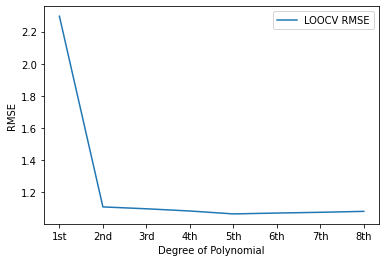
# In this step, create a spaghetti plot of LOOVC for each order polynomial model. Be sure to label your axes.
#
# - Your plot might look something like this (specific values will vary):
#
# 
# + id="2TthIazms3rL" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="953cbe1e-aa6a-4a95-e784-80128780ee26"
#STEP 11
#STUDENT CODE - plot loocv spaghetti chart
#---------------------------------------------
#---------------------------------------------
STEP_11_COMPLETE = False
# + [markdown] id="emh-0CO0Iqm5"
# #### k-Fold Cross Validation
# + [markdown] id="VPV2ZssE7ZAs"
# ##### STEP 12: kfold rmse
#
# In this step, you'll create kfold_mse(X, y, k, random_state) which returns the average root mean squared error of models fit to training sets and evaluated on the validation sets as defined by the k-fold cross-validation approach.
#
# - `X` is a DataFrame of feature inputs
# - `y` is a Series of targets
# - `k` is the number of folds
# - return a scalar value representing the root mean squared error
#
# Hints:
# - See hints in STEP 6 STEP 9 for guidance here
# - Though `cross_val_score` provides a mechanism to pass an integer via the `cv` argument to implement k-fold CV without a cross-validation iterator, this method does not randomize or shuffle the train and validation sets. As you the next step will require that you run multiple trials, do not use the short provided in `cross_val_score` to use k-fold CV. Instead, select the appropriate cross-validation generator with the appropriate `shuffle` and `random_state` values.
# + id="AlaH-SV4s2SU"
#STEP 12
#STUDENT CODE - create kfold_mse(X, y, k, random_state)
#---------------------------------------------
#---------------------------------------------
STEP_12_COMPLETE = False
# + [markdown] id="F0uDpcHF7i-_"
# ##### STEP 13: dataframe of kfold rmse
#
# In this step, you'll generate a DataFrame of RMSE values for 10 trials of 8 models using the 10-fold cross-validation approach.
# + id="TGwJgcKIxHXK" colab={"base_uri": "https://localhost:8080/", "height": 297} outputId="a809172d-e2de-4eea-fe1d-ba272b35f66c"
#STEP 13
#STUDENT CODE - create DataFrame of LOOCV Order data
#---------------------------------------------
#---------------------------------------------
STEP_13_COMPLETE = True
# + [markdown] id="cjMRS9oJ7o_Y"
# ##### STEP 14: plot kfold rmse
#
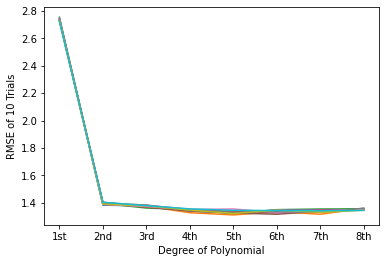
# In this step, create a spaghetti plot of the k-fold trials. Be sure to label your axes.
#
# - Your plot might look something like this (specific values will vary):
#
# 
# + id="ZF7lkpxrxBxf" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="eaa482fd-2780-409f-b942-79fe4985f10c"
#STEP 14
#STUDENT CODE - plot k-fold spaghetti charts
#---------------------------------------------
#---------------------------------------------
STEP_14_COMPLETE = False
# + [markdown] id="rcadU5rtBQty"
# #### Discussion
# + [markdown] id="5eeVWo-DBTzA"
# ##### STEP 15: analysis
#
# Review the spaghetti charts created in STEPS 8, 11, and 14, then answer the following questions.
#
# - For both the Validation Set and for k-fold approaches we conducted 10 trials, and there was variation between them. What would have occurred had we conducted 10 trials of LOOCV?
#
# <font color=green class="student_answer">Student Discussion</font>
#
#
# - Which cross-validation approach has the greatest variation from one trial to the next? Why?
#
# <font color=green class="student_answer">Student Discussion</font>
#
# - Which cross-validation approach has the least variation from one trial to the next? Why?
#
# <font color=green class="student_answer">Student Discussion</font>
#
# - Suppose you had observations whose targets (y-values) range from $[0-10]$. When you conduct cross-validation, you note that the model of polynomial order $p$ yields an RMSE of 0.0800, but the model of polynomial order $p+4$ yields an RMSE of 0.0792. In terms of $p$, which model will you use and why?
#
# <font color=green class="student_answer">Student Discussion</font>
#
# - Which CV approach do you think will be most appropriate for your machine learning research? Why?
#
# <font color=green class="student_answer">Student Discussion</font>
#
#
# + id="wlFt5LcDiR3s"
STEP_15_COMPLETE = False
# + [markdown] id="4vITNJhSEbQg"
# ##### STEP 16: model selection
#
# Based on your analysis of cross-validation, which order polynomial model will you choose? Why?
#
# <font color=green class="student_answer">Student Discussion</font>
#
# + id="G1MKk23PiUdk"
STEP_16_COMPLETE = False
# + [markdown] id="rcYHRbbiE7bm"
# #### Model Creation & Evaluation
# + [markdown] id="TppVvahYE-i5"
# ##### STEP 17: Model Creation
#
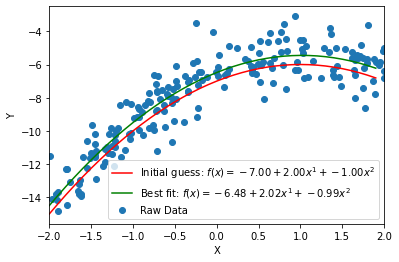
# In this step, you will generate a model of the polynomial order you identified in STEP 16 (using your `poly_df` function). Then, you will fit that model to your data.
#
# Finally, you'll plot your model, along with the original data and your initial guess. Be sure to label your plot. Here is an example of a possible result:
#
# 
# + id="ivtDGgQlFBop" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="389e0fc3-6bb8-4a5c-eb76-a997795320b4"
#STEP 17
#STUDENT CODE - fit model, plot initial guess and best fit line
#---------------------------------------------
#---------------------------------------------
STEP_17_COMPLETE = False
# + [markdown] id="9gyQOP6uPhqO"
# ##### STEP 18: Model Evaluation
#
# In this step, you will generate test data and evaluate the performance of your fitted model on that test data.
#
# Hints:
# - To generate test data, you will use the `generate_data()` function. It is critical you reuse the seed value that you used in STEP 2. Using a different seed value will result in you creating test data generated from a different data signal, and your model will inevitably perform disastrously. Also, you will need to set the optional argument `test_data` to `True`:
#
# `df_test = generate_data(seed, test_data=True)`
#
# You should use the actual value of `seed` unless you are ABSOLUTELY sure that you have not modified it somewhere in the notebook
#
# - After you have generated the data, be sure that you engineer a feature set of the appropriate polynomial order.
#
# - Page 80 of _HOML_ provides an example of how you can calculate the RMSE of your model on test data. Note that the text calculates the square root of the mean squared error. If you take a look at the [mean_squared_error](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_squared_error.html) function, you'll see that you can set an argument to return the RMSE, without a need to take a square root of the result.
#
# - Note that the instructor solution for this step involves approximately 5 steps. If you are using significantly more than that, you may not be effectively using the functions you've created or the scikit-learn tools.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} id="vMS5haVjWHMF" outputId="66919e24-4331-4069-e0e0-49285df51cb1"
#STEP 18
#STUDENT CODE - generate test data, calculate rmse on test data
#---------------------------------------------
#---------------------------------------------
STEP_18_COMPLETE = False
# + [markdown] id="lXQiXKD8jjsi"
# #### STEP 19: final model discussion
#
# Answer the following questions
#
# - What is your model's performance on test data?
#
# <font color=green class="student_answer">Student Discussion</font>
#
#
# - How does this compare to the cross-validation error that you used to determine the polynomial order for your model?
#
# <font color=green class="student_answer">Student Discussion</font>
#
# - What accounts for the difference between the cross-validation error and the error on the test data?
#
# <font color=green class="student_answer">Student Discussion</font>
#
# - What is the most appropriate metric to use when advertising the performance of your model?
#
# <font color=green class="student_answer">Student Discussion</font>
#
#
# + id="5o2lfeA6kVYn"
STEP_19_COMPLETE = False
# + id="gCsY--TI02Jw"
# Enter the number of hours you spend on this homework assignment as a floating point value
hours_spent = 0.0
STEP_20_COMPLETE = False
|
hw3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Detector Face with CV2
# +
import os,cv2,keras
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import time
cv2.setUseOptimized(True);
# -
# https://github.com/opencv/opencv/tree/master/data/haarcascades
path = "Image"
i = "1.jpg"
a = time.time()
img = cv2.imread(os.path.join(path,i))
detector = cv2.CascadeClassifier('model/haarcascade_frontalface_default.xml');
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY);
faces = detector.detectMultiScale(gray, 1.3, 5);
for (x,y,w,h) in faces:
cv2.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
b = time.time()
print(b-a)
|
Train/CV2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # MPIJob and Horovod Runtime
#
# ## Running distributed workloads
#
# Training a Deep Neural Network is a hard task. With growing datasets, wider and deeper networks, training our Neural Network can require a lot of resources (CPUs / GPUs / Mem and Time).
#
# There are two main reasons why we would like to distribute our Deep Learning workloads:
#
# 1. **Model Parallelism** — The **Model** is too big to fit a single GPU.
# In this case the model contains too many parameters to hold within a single GPU.
# To negate this we can use strategies like **Parameter Server** or slicing the model into slices of consecutive layers which we can fit in a single GPU.
# Both strategies require **Synchronization** between the layers held on different GPUs / Parameter Server shards.
#
# 2. **Data Parallelism** — The **Dataset** is too big to fit a single GPU.
# Using methods like **Stochastic Gradient Descent** we can send batches of data to our models for gradient estimation. This comes at the cost of longer time to converge since the estimated gradient may not fully represent the actual gradient.
# To increase the likelihood of estimating the actual gradient we could use bigger batches, by sending small batches to different GPUs running the same Neural Network, calculating the batch gradient and then running a **Synchronization Step** to calculate the average gradient over the batches and update the Neural Networks running on the different GPUs.
#
#
# > It is important to understand that the act of distribution adds extra **Synchronization Costs** which may vary according to your cluster's configuration.
# > <br>
# > As the gradients and NN needs to be propagated to each GPU in the cluster every epoch (or a number of steps), Networking can become a bottleneck and sometimes different configurations need to be used for optimal performance.
# > <br>
# > **Scaling Efficiency** is the metric used to show by how much each additional GPU should benefit the training process with Horovod showing up to 90% (When running with a well written code and good parameters).
#
# 
# ## How can we distribute our training
# There are two different cluster configurations (which can be combined) we need to take into account.
# - **Multi Node** — GPUs are distributed over multiple nodes in the cluster.
# - **Multi GPU** — GPUs are within a single Node.
#
# In this demo we show a **Multi Node Multi GPU** — **Data Parallel** enabled training using Horovod.
# However, you should always try and use the best distribution strategy for your use case (due to the added costs of the distribution itself, ability to run in an optimized way on specific hardware or other considerations that may arise).
# ## How Horovod works?
# Horovod's primary motivation is to make it easy to take a single-GPU training script and successfully scale it to train across many GPUs in parallel. This has two aspects:
#
# - How much modification does one have to make to a program to make it distributed, and how easy is it to run it?
# - How much faster would it run in distributed mode?
#
# Horovod Supports TensorFlow, Keras, PyTorch, and Apache MXNet.
#
# in MLRun we use Horovod with MPI in order to create cluster resources and allow for optimized networking.
# **Note:** Horovd and MPI may use [NCCL](https://developer.nvidia.com/nccl) when applicable which may require some specific configuration arguments to run optimally.
#
# Horovod uses this MPI and NCCL concepts for distributed computation and messaging to quickly and easily synchronize between the different nodes or GPUs.
#
# 
#
# Horovod will run your code on all the given nodes (Specific node can be addressed via `hvd.rank()`) while using an `hvd.DistributedOptimizer` wrapper to run the **synchronization cycles** between the copies of your Neural Network running at each node.
#
# **Note:** Since all the copies of your Neural Network must be the same, Your workers will adjust themselves to the rate of the slowest worker (simply by waiting for it to finish the epoch and receive its updates). Thus try not to make a specific worker do a lot of additional work on each epoch (Like a lot of saving, extra calculations, etc...) since this can affect the overall training time.
# ## How do we integrate TF2 with Horovod?
# As it's one of the main motivations, integration is fairly easy and requires only a few steps: ([You can read the full instructions for all the different frameworks on Horovod's documentation website](https://horovod.readthedocs.io/en/stable/tensorflow.html)).
#
# 1. Run `hvd.init()`.
# 2. Pin each GPU to a single process.
# With the typical setup of one GPU per process, set this to local rank. The first process on the server will be allocated the first GPU, the second process will be allocated the second GPU, and so forth.
# ```
# gpus = tf.config.experimental.list_physical_devices('GPU')
# for gpu in gpus:
# tf.config.experimental.set_memory_growth(gpu, True)
# if gpus:
# tf.config.experimental.set_visible_devices(gpus[hvd.local_rank()], 'GPU')
# ```
# 3. Scale the learning rate by the number of workers.
# Effective batch size in synchronous distributed training is scaled by the number of workers. An increase in learning rate compensates for the increased batch size.
# 4. Wrap the optimizer in `hvd.DistributedOptimizer`.
# The distributed optimizer delegates gradient computation to the original optimizer, averages gradients using allreduce or allgather, and then applies those averaged gradients.
# For TensorFlow v2, when using a `tf.GradientTape`, wrap the tape in `hvd.DistributedGradientTape` instead of wrapping the optimizer.
# 1. Broadcast the initial variable states from rank 0 to all other processes.
# This is necessary to ensure consistent initialization of all workers when training is started with random weights or restored from a checkpoint.
# For TensorFlow v2, use `hvd.broadcast_variables` after models and optimizers have been initialized.
# 1. Modify your code to save checkpoints only on worker 0 to prevent other workers from corrupting them.
# For TensorFlow v2, construct a `tf.train.Checkpoint` and only call `checkpoint.save()` when `hvd.rank() == 0`.
#
#
# You can go to [Horovod's Documentation](https://horovod.readthedocs.io/en/stable) to read more about horovod.
# ## Image classification use case
# See the end to end [**Image Classification with Distributed Training Demo**](https://github.com/mlrun/demos/tree/0.6.x/image-classification-with-distributed-training)
|
docs/runtimes/horovod.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import torch
torch.set_printoptions(edgeitems=2, precision=2)
import csv
wine_path = "../data/tabular-wine/winequality-white.csv"
wineq_numpy = np.loadtxt(wine_path, dtype=np.float32, delimiter=";", skiprows=1)
wineq_numpy
# +
col_list = next(csv.reader(open(wine_path), delimiter=';'))
wineq_numpy.shape, col_list
# +
wineq = torch.from_numpy(wineq_numpy)
wineq.shape, wineq.type()
# -
data = wineq[:, :-1] # <1>
data, data.shape
target = wineq[:, -1] # <2>
target, target.shape
target = wineq[:, -1].long()
target
data_mean = torch.mean(data, dim=0)
data_mean
data_var = torch.var(data, dim=0)
data_var
data_normalized = (data - data_mean) / torch.sqrt(data_var)
data_normalized
data_normalized.size()
np.unique(target.numpy())
np.unique(target.numpy() - 3)
target_shift = target - 3
np.unique(target_shift.numpy())
# +
n_samples = data_normalized.shape[0]
n_val = int(0.3 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_x = data_normalized[train_indices]
train_y = target_shift[train_indices]
val_x = data_normalized[val_indices]
val_y = target_shift[val_indices]
# -
train_x.size(), train_y.size()
def training_loop(model, n_epochs, optimizer, loss_fn, train_x, val_x, train_y, val_y):
for epoch in range(1, n_epochs + 1):
train_t_p = model(train_x) # ya no tenemos que pasar los params
train_loss = loss_fn(train_t_p, train_y)
with torch.no_grad(): # todos los args requires_grad=False
val_t_p = model(val_x)
val_loss = loss_fn(val_t_p, val_y)
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print(f"Epoch {epoch}, Training loss {train_loss}, Validation loss {val_loss}")
import torch.nn as nn
import torch.optim as optim
# +
class SimpleNet(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(11, 32)
self.fc2 = nn.Linear(32, 7)
def forward(self, x):
x = self.fc1(x)
x = self.fc2(x)
x = torch.softmax(x, dim=1)
return x
net = SimpleNet()
optimizer = optim.SGD(net.parameters(), lr=5e-3, momentum=0.9)
criterion = nn.CrossEntropyLoss()
# -
# %%time
training_loop(
n_epochs=1000,
optimizer=optimizer,
model=net,
loss_fn=criterion,
train_x = train_x,
val_x = val_x,
train_y = train_y,
val_y = val_y)
|
lectures/white_whine_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## The QLBS model for a European option
#
# Welcome to your 2nd assignment in Reinforcement Learning in Finance. In this exercise you will arrive to an option price and the hedging portfolio via standard toolkit of Dynamic Pogramming (DP).
# QLBS model learns both the optimal option price and optimal hedge directly from trading data.
#
# **Instructions:**
# - You will be using Python 3.
# - Avoid using for-loops and while-loops, unless you are explicitly told to do so.
# - Do not modify the (# GRADED FUNCTION [function name]) comment in some cells. Your work would not be graded if you change this. Each cell containing that comment should only contain one function.
# - After coding your function, run the cell right below it to check if your result is correct.
# - When encountering **```# dummy code - remove```** please replace this code with your own
#
#
# **After this assignment you will:**
# - Re-formulate option pricing and hedging method using the language of Markov Decision Processes (MDP)
# - Setup foward simulation using Monte Carlo
# - Expand optimal action (hedge) $a_t^\star(X_t)$ and optimal Q-function $Q_t^\star(X_t, a_t^\star)$ in basis functions with time-dependend coefficients
#
# Let's get started!
# ## About iPython Notebooks ##
#
# iPython Notebooks are interactive coding environments embedded in a webpage. You will be using iPython notebooks in this class. You only need to write code between the ### START CODE HERE ### and ### END CODE HERE ### comments. After writing your code, you can run the cell by either pressing "SHIFT"+"ENTER" or by clicking on "Run Cell" (denoted by a play symbol) in the upper bar of the notebook.
#
# We will often specify "(≈ X lines of code)" in the comments to tell you about how much code you need to write. It is just a rough estimate, so don't feel bad if your code is longer or shorter.
# +
#import warnings
#warnings.filterwarnings("ignore")
import numpy as np
import pandas as pd
from scipy.stats import norm
import random
import time
import matplotlib.pyplot as plt
import sys
sys.path.append("..")
import grading
# -
### ONLY FOR GRADING. DO NOT EDIT ###
submissions=dict()
assignment_key="<KEY>"
all_parts=["15mYc", "h1P6Y", "q9QW7","s7MpJ","Pa177"]
### ONLY FOR GRADING. DO NOT EDIT ###
COURSERA_TOKEN = # the key provided to the Student under his/her email on submission page
COURSERA_EMAIL = # the email
# ## Parameters for MC simulation of stock prices
# +
S0 = 100 # initial stock price
mu = 0.05 # drift
sigma = 0.15 # volatility
r = 0.03 # risk-free rate
M = 1 # maturity
T = 24 # number of time steps
N_MC = 10000 # number of paths
delta_t = M / T # time interval
gamma = np.exp(- r * delta_t) # discount factor
# -
# ### Black-Sholes Simulation
# Simulate $N_{MC}$ stock price sample paths with $T$ steps by the classical Black-Sholes formula.
#
# $$dS_t=\mu S_tdt+\sigma S_tdW_t\quad\quad S_{t+1}=S_te^{\left(\mu-\frac{1}{2}\sigma^2\right)\Delta t+\sigma\sqrt{\Delta t}Z}$$
#
# where $Z$ is a standard normal random variable.
#
# Based on simulated stock price $S_t$ paths, compute state variable $X_t$ by the following relation.
#
# $$X_t=-\left(\mu-\frac{1}{2}\sigma^2\right)t\Delta t+\log S_t$$
#
# Also compute
#
# $$\Delta S_t=S_{t+1}-e^{r\Delta t}S_t\quad\quad \Delta\hat{S}_t=\Delta S_t-\Delta\bar{S}_t\quad\quad t=0,...,T-1$$
#
# where $\Delta\bar{S}_t$ is the sample mean of all values of $\Delta S_t$.
#
# Plots of 5 stock price $S_t$ and state variable $X_t$ paths are shown below.
# +
# make a dataset
starttime = time.time()
np.random.seed(42)
# stock price
S = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
S.loc[:,0] = S0
# standard normal random numbers
RN = pd.DataFrame(np.random.randn(N_MC,T), index=range(1, N_MC+1), columns=range(1, T+1))
for t in range(1, T+1):
S.loc[:,t] = S.loc[:,t-1] * np.exp((mu - 1/2 * sigma**2) * delta_t + sigma * np.sqrt(delta_t) * RN.loc[:,t])
delta_S = S.loc[:,1:T].values - np.exp(r * delta_t) * S.loc[:,0:T-1]
delta_S_hat = delta_S.apply(lambda x: x - np.mean(x), axis=0)
# state variable
X = - (mu - 1/2 * sigma**2) * np.arange(T+1) * delta_t + np.log(S) # delta_t here is due to their conventions
endtime = time.time()
print('\nTime Cost:', endtime - starttime, 'seconds')
# +
# plot 10 paths
step_size = N_MC // 10
idx_plot = np.arange(step_size, N_MC, step_size)
plt.plot(S.T.iloc[:,idx_plot])
plt.xlabel('Time Steps')
plt.title('Stock Price Sample Paths')
plt.show()
plt.plot(X.T.iloc[:,idx_plot])
plt.xlabel('Time Steps')
plt.ylabel('State Variable')
plt.show()
# -
# Define function *terminal_payoff* to compute the terminal payoff of a European put option.
#
# $$H_T\left(S_T\right)=\max\left(K-S_T,0\right)$$
def terminal_payoff(ST, K):
# ST final stock price
# K strike
payoff = max(K - ST, 0)
return payoff
type(delta_S)
# ## Define spline basis functions
# +
import bspline
import bspline.splinelab as splinelab
X_min = np.min(np.min(X))
X_max = np.max(np.max(X))
print('X.shape = ', X.shape)
print('X_min, X_max = ', X_min, X_max)
p = 4 # order of spline (as-is; 3 = cubic, 4: B-spline?)
ncolloc = 12
tau = np.linspace(X_min,X_max,ncolloc) # These are the sites to which we would like to interpolate
# k is a knot vector that adds endpoints repeats as appropriate for a spline of order p
# To get meaninful results, one should have ncolloc >= p+1
k = splinelab.aptknt(tau, p)
# Spline basis of order p on knots k
basis = bspline.Bspline(k, p)
f = plt.figure()
# B = bspline.Bspline(k, p) # Spline basis functions
print('Number of points k = ', len(k))
basis.plot()
plt.savefig('Basis_functions.png', dpi=600)
# -
type(basis)
X.values.shape
# ### Make data matrices with feature values
#
# "Features" here are the values of basis functions at data points
# The outputs are 3D arrays of dimensions num_tSteps x num_MC x num_basis
# +
num_t_steps = T + 1
num_basis = ncolloc # len(k) #
data_mat_t = np.zeros((num_t_steps, N_MC,num_basis ))
print('num_basis = ', num_basis)
print('dim data_mat_t = ', data_mat_t.shape)
t_0 = time.time()
# fill it
for i in np.arange(num_t_steps):
x = X.values[:,i]
data_mat_t[i,:,:] = np.array([ basis(el) for el in x ])
t_end = time.time()
print('Computational time:', t_end - t_0, 'seconds')
# -
# save these data matrices for future re-use
np.save('data_mat_m=r_A_%d' % N_MC, data_mat_t)
print(data_mat_t.shape) # shape num_steps x N_MC x num_basis
print(len(k))
# ## Dynamic Programming solution for QLBS
#
# The MDP problem in this case is to solve the following Bellman optimality equation for the action-value function.
#
# $$Q_t^\star\left(x,a\right)=\mathbb{E}_t\left[R_t\left(X_t,a_t,X_{t+1}\right)+\gamma\max_{a_{t+1}\in\mathcal{A}}Q_{t+1}^\star\left(X_{t+1},a_{t+1}\right)\space|\space X_t=x,a_t=a\right],\space\space t=0,...,T-1,\quad\gamma=e^{-r\Delta t}$$
#
# where $R_t\left(X_t,a_t,X_{t+1}\right)$ is the one-step time-dependent random reward and $a_t\left(X_t\right)$ is the action (hedge).
#
# Detailed steps of solving this equation by Dynamic Programming are illustrated below.
# With this set of basis functions $\left\{\Phi_n\left(X_t^k\right)\right\}_{n=1}^N$, expand the optimal action (hedge) $a_t^\star\left(X_t\right)$ and optimal Q-function $Q_t^\star\left(X_t,a_t^\star\right)$ in basis functions with time-dependent coefficients.
# $$a_t^\star\left(X_t\right)=\sum_n^N{\phi_{nt}\Phi_n\left(X_t\right)}\quad\quad Q_t^\star\left(X_t,a_t^\star\right)=\sum_n^N{\omega_{nt}\Phi_n\left(X_t\right)}$$
#
# Coefficients $\phi_{nt}$ and $\omega_{nt}$ are computed recursively backward in time for $t=T−1,...,0$.
# Coefficients for expansions of the optimal action $a_t^\star\left(X_t\right)$ are solved by
#
# $$\phi_t=\mathbf A_t^{-1}\mathbf B_t$$
#
# where $\mathbf A_t$ and $\mathbf B_t$ are matrix and vector respectively with elements given by
#
# $$A_{nm}^{\left(t\right)}=\sum_{k=1}^{N_{MC}}{\Phi_n\left(X_t^k\right)\Phi_m\left(X_t^k\right)\left(\Delta\hat{S}_t^k\right)^2}\quad\quad B_n^{\left(t\right)}=\sum_{k=1}^{N_{MC}}{\Phi_n\left(X_t^k\right)\left[\hat\Pi_{t+1}^k\Delta\hat{S}_t^k+\frac{1}{2\gamma\lambda}\Delta S_t^k\right]}$$
#
# $$\Delta S_t=S_{t+1} - e^{-r\Delta t} S_t\space \quad t=T-1,...,0$$
# where $\Delta\hat{S}_t$ is the sample mean of all values of $\Delta S_t$.
#
# Define function *function_A* and *function_B* to compute the value of matrix $\mathbf A_t$ and vector $\mathbf B_t$.
# ## Define the option strike and risk aversion parameter
# +
risk_lambda = 0.001 # risk aversion
K = 100 # option stike
# Note that we set coef=0 below in function function_B_vec. This correspond to a pure risk-based hedging
# -
# ### Part 1 Calculate coefficients $\phi_{nt}$ of the optimal action $a_t^\star\left(X_t\right)$
#
# **Instructions:**
# - implement function_A_vec() which computes $A_{nm}^{\left(t\right)}$ matrix
# - implement function_B_vec() which computes $B_n^{\left(t\right)}$ column vector
# +
# functions to compute optimal hedges
def function_A_vec(t, delta_S_hat, data_mat, reg_param):
"""
function_A_vec - compute the matrix A_{nm} from Eq. (52) (with a regularization!)
Eq. (52) in QLBS Q-Learner in the Black-Scholes-Merton article
Arguments:
t - time index, a scalar, an index into time axis of data_mat
delta_S_hat - pandas.DataFrame of dimension N_MC x T
data_mat - pandas.DataFrame of dimension T x N_MC x num_basis
reg_param - a scalar, regularization parameter
Return:
- np.array, i.e. matrix A_{nm} of dimension num_basis x num_basis
"""
### START CODE HERE ### (≈ 5-6 lines of code)
# store result in A_mat for grading
### END CODE HERE ###
return A_mat
def function_B_vec(t,
Pi_hat,
delta_S_hat=delta_S_hat,
S=S,
data_mat=data_mat_t,
gamma=gamma,
risk_lambda=risk_lambda):
"""
function_B_vec - compute vector B_{n} from Eq. (52) QLBS Q-Learner in the Black-Scholes-Merton article
Arguments:
t - time index, a scalar, an index into time axis of delta_S_hat
Pi_hat - pandas.DataFrame of dimension N_MC x T of portfolio values
delta_S_hat - pandas.DataFrame of dimension N_MC x T
S - pandas.DataFrame of simulated stock prices of dimension N_MC x T
data_mat - pandas.DataFrame of dimension T x N_MC x num_basis
gamma - one time-step discount factor $exp(-r \delta t)$
risk_lambda - risk aversion coefficient, a small positive number
Return:
np.array() of dimension num_basis x 1
"""
# coef = 1.0/(2 * gamma * risk_lambda)
# override it by zero to have pure risk hedge
### START CODE HERE ### (≈ 5-6 lines of code)
# store result in B_vec for grading
### END CODE HERE ###
return B_vec
# +
### GRADED PART (DO NOT EDIT) ###
reg_param = 1e-3
np.random.seed(42)
A_mat = function_A_vec(T-1, delta_S_hat, data_mat_t, reg_param)
idx_row = np.random.randint(low=0, high=A_mat.shape[0], size=50)
np.random.seed(42)
idx_col = np.random.randint(low=0, high=A_mat.shape[1], size=50)
part_1 = list(A_mat[idx_row, idx_col])
try:
part1 = " ".join(map(repr, part_1))
except TypeError:
part1 = repr(part_1)
submissions[all_parts[0]]=part1
grading.submit(COURSERA_EMAIL, COURSERA_TOKEN, assignment_key,all_parts[:1],all_parts,submissions)
A_mat[idx_row, idx_col]
### GRADED PART (DO NOT EDIT) ###
# +
### GRADED PART (DO NOT EDIT) ###
np.random.seed(42)
risk_lambda = 0.001
Pi = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
Pi.iloc[:,-1] = S.iloc[:,-1].apply(lambda x: terminal_payoff(x, K))
Pi_hat = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
Pi_hat.iloc[:,-1] = Pi.iloc[:,-1] - np.mean(Pi.iloc[:,-1])
B_vec = function_B_vec(T-1, Pi_hat, delta_S_hat, S, data_mat_t, gamma, risk_lambda)
part_2 = list(B_vec)
try:
part2 = " ".join(map(repr, part_2))
except TypeError:
part2 = repr(part_2)
submissions[all_parts[1]]=part2
grading.submit(COURSERA_EMAIL, COURSERA_TOKEN, assignment_key,all_parts[:2],all_parts,submissions)
B_vec
### GRADED PART (DO NOT EDIT) ###
# -
# ## Compute optimal hedge and portfolio value
# Call *function_A* and *function_B* for $t=T-1,...,0$ together with basis function $\Phi_n\left(X_t\right)$ to compute optimal action $a_t^\star\left(X_t\right)=\sum_n^N{\phi_{nt}\Phi_n\left(X_t\right)}$ backward recursively with terminal condition $a_T^\star\left(X_T\right)=0$.
#
# Once the optimal hedge $a_t^\star\left(X_t\right)$ is computed, the portfolio value $\Pi_t$ could also be computed backward recursively by
#
# $$\Pi_t=\gamma\left[\Pi_{t+1}-a_t^\star\Delta S_t\right]\quad t=T-1,...,0$$
#
# together with the terminal condition $\Pi_T=H_T\left(S_T\right)=\max\left(K-S_T,0\right)$ for a European put option.
#
# Also compute $\hat{\Pi}_t=\Pi_t-\bar{\Pi}_t$, where $\bar{\Pi}_t$ is the sample mean of all values of $\Pi_t$.
#
# Plots of 5 optimal hedge $a_t^\star$ and portfolio value $\Pi_t$ paths are shown below.
# +
starttime = time.time()
# portfolio value
Pi = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
Pi.iloc[:,-1] = S.iloc[:,-1].apply(lambda x: terminal_payoff(x, K))
Pi_hat = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
Pi_hat.iloc[:,-1] = Pi.iloc[:,-1] - np.mean(Pi.iloc[:,-1])
# optimal hedge
a = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
a.iloc[:,-1] = 0
reg_param = 1e-3 # free parameter
for t in range(T-1, -1, -1):
A_mat = function_A_vec(t, delta_S_hat, data_mat_t, reg_param)
B_vec = function_B_vec(t, Pi_hat, delta_S_hat, S, data_mat_t, gamma, risk_lambda)
# print ('t = A_mat.shape = B_vec.shape = ', t, A_mat.shape, B_vec.shape)
# coefficients for expansions of the optimal action
phi = np.dot(np.linalg.inv(A_mat), B_vec)
a.loc[:,t] = np.dot(data_mat_t[t,:,:],phi)
Pi.loc[:,t] = gamma * (Pi.loc[:,t+1] - a.loc[:,t] * delta_S.loc[:,t])
Pi_hat.loc[:,t] = Pi.loc[:,t] - np.mean(Pi.loc[:,t])
a = a.astype('float')
Pi = Pi.astype('float')
Pi_hat = Pi_hat.astype('float')
endtime = time.time()
print('Computational time:', endtime - starttime, 'seconds')
# +
# plot 10 paths
plt.plot(a.T.iloc[:,idx_plot])
plt.xlabel('Time Steps')
plt.title('Optimal Hedge')
plt.show()
plt.plot(Pi.T.iloc[:,idx_plot])
plt.xlabel('Time Steps')
plt.title('Portfolio Value')
plt.show()
# -
# ## Compute rewards for all paths
# Once the optimal hedge $a_t^\star$ and portfolio value $\Pi_t$ are all computed, the reward function $R_t\left(X_t,a_t,X_{t+1}\right)$ could then be computed by
#
# $$R_t\left(X_t,a_t,X_{t+1}\right)=\gamma a_t\Delta S_t-\lambda Var\left[\Pi_t\space|\space\mathcal F_t\right]\quad t=0,...,T-1$$
#
# with terminal condition $R_T=-\lambda Var\left[\Pi_T\right]$.
#
# Plot of 5 reward function $R_t$ paths is shown below.
# +
# Compute rewards for all paths
starttime = time.time()
# reward function
R = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
R.iloc[:,-1] = - risk_lambda * np.var(Pi.iloc[:,-1])
for t in range(T):
R.loc[1:,t] = gamma * a.loc[1:,t] * delta_S.loc[1:,t] - risk_lambda * np.var(Pi.loc[1:,t])
endtime = time.time()
print('\nTime Cost:', endtime - starttime, 'seconds')
# plot 10 paths
plt.plot(R.T.iloc[:, idx_plot])
plt.xlabel('Time Steps')
plt.title('Reward Function')
plt.show()
# -
# ## Part 2: Compute the optimal Q-function with the DP approach
#
# Coefficients for expansions of the optimal Q-function $Q_t^\star\left(X_t,a_t^\star\right)$ are solved by
#
# $$\omega_t=\mathbf C_t^{-1}\mathbf D_t$$
#
# where $\mathbf C_t$ and $\mathbf D_t$ are matrix and vector respectively with elements given by
#
# $$C_{nm}^{\left(t\right)}=\sum_{k=1}^{N_{MC}}{\Phi_n\left(X_t^k\right)\Phi_m\left(X_t^k\right)}\quad\quad D_n^{\left(t\right)}=\sum_{k=1}^{N_{MC}}{\Phi_n\left(X_t^k\right)\left(R_t\left(X_t,a_t^\star,X_{t+1}\right)+\gamma\max_{a_{t+1}\in\mathcal{A}}Q_{t+1}^\star\left(X_{t+1},a_{t+1}\right)\right)}$$
# Define function *function_C* and *function_D* to compute the value of matrix $\mathbf C_t$ and vector $\mathbf D_t$.
#
# **Instructions:**
# - implement function_C_vec() which computes $C_{nm}^{\left(t\right)}$ matrix
# - implement function_D_vec() which computes $D_n^{\left(t\right)}$ column vector
# +
def function_C_vec(t, data_mat, reg_param):
"""
function_C_vec - calculate C_{nm} matrix from Eq. (56) (with a regularization!)
Eq. (56) in QLBS Q-Learner in the Black-Scholes-Merton article
Arguments:
t - time index, a scalar, an index into time axis of data_mat
data_mat - pandas.DataFrame of values of basis functions of dimension T x N_MC x num_basis
reg_param - regularization parameter, a scalar
Return:
C_mat - np.array of dimension num_basis x num_basis
"""
### START CODE HERE ### (≈ 5-6 lines of code)
# your code here ....
# C_mat = your code here ...
### END CODE HERE ###
return C_mat
def function_D_vec(t, Q, R, data_mat, gamma=gamma):
"""
function_D_vec - calculate D_{nm} vector from Eq. (56) (with a regularization!)
Eq. (56) in QLBS Q-Learner in the Black-Scholes-Merton article
Arguments:
t - time index, a scalar, an index into time axis of data_mat
Q - pandas.DataFrame of Q-function values of dimension N_MC x T
R - pandas.DataFrame of rewards of dimension N_MC x T
data_mat - pandas.DataFrame of values of basis functions of dimension T x N_MC x num_basis
gamma - one time-step discount factor $exp(-r \delta t)$
Return:
D_vec - np.array of dimension num_basis x 1
"""
### START CODE HERE ### (≈ 5-6 lines of code)
# your code here ....
# D_vec = your code here ...
### END CODE HERE ###
return D_vec
# +
### GRADED PART (DO NOT EDIT) ###
C_mat = function_C_vec(T-1, data_mat_t, reg_param)
np.random.seed(42)
idx_row = np.random.randint(low=0, high=C_mat.shape[0], size=50)
np.random.seed(42)
idx_col = np.random.randint(low=0, high=C_mat.shape[1], size=50)
part_3 = list(C_mat[idx_row, idx_col])
try:
part3 = " ".join(map(repr, part_3))
except TypeError:
part3 = repr(part_3)
submissions[all_parts[2]]=part3
grading.submit(COURSERA_EMAIL, COURSERA_TOKEN, assignment_key,all_parts[:3],all_parts,submissions)
C_mat[idx_row, idx_col]
### GRADED PART (DO NOT EDIT) ###
# +
### GRADED PART (DO NOT EDIT) ###
Q = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
Q.iloc[:,-1] = - Pi.iloc[:,-1] - risk_lambda * np.var(Pi.iloc[:,-1])
D_vec = function_D_vec(T-1, Q, R, data_mat_t,gamma)
part_4 = list(D_vec)
try:
part4 = " ".join(map(repr, part_4))
except TypeError:
part4 = repr(part_4)
submissions[all_parts[3]]=part4
grading.submit(COURSERA_EMAIL, COURSERA_TOKEN, assignment_key,all_parts[:4],all_parts,submissions)
D_vec
### GRADED PART (DO NOT EDIT) ###
# -
# Call *function_C* and *function_D* for $t=T-1,...,0$ together with basis function $\Phi_n\left(X_t\right)$ to compute optimal action Q-function $Q_t^\star\left(X_t,a_t^\star\right)=\sum_n^N{\omega_{nt}\Phi_n\left(X_t\right)}$ backward recursively with terminal condition $Q_T^\star\left(X_T,a_T=0\right)=-\Pi_T\left(X_T\right)-\lambda Var\left[\Pi_T\left(X_T\right)\right]$.
# +
starttime = time.time()
# Q function
Q = pd.DataFrame([], index=range(1, N_MC+1), columns=range(T+1))
Q.iloc[:,-1] = - Pi.iloc[:,-1] - risk_lambda * np.var(Pi.iloc[:,-1])
reg_param = 1e-3
for t in range(T-1, -1, -1):
######################
C_mat = function_C_vec(t,data_mat_t,reg_param)
D_vec = function_D_vec(t, Q,R,data_mat_t,gamma)
omega = np.dot(np.linalg.inv(C_mat), D_vec)
Q.loc[:,t] = np.dot(data_mat_t[t,:,:], omega)
Q = Q.astype('float')
endtime = time.time()
print('\nTime Cost:', endtime - starttime, 'seconds')
# plot 10 paths
plt.plot(Q.T.iloc[:, idx_plot])
plt.xlabel('Time Steps')
plt.title('Optimal Q-Function')
plt.show()
# -
# The QLBS option price is given by $C_t^{\left(QLBS\right)}\left(S_t,ask\right)=-Q_t\left(S_t,a_t^\star\right)$
#
# ## Summary of the QLBS pricing and comparison with the BSM pricing
# Compare the QLBS price to European put price given by Black-Sholes formula.
#
# $$C_t^{\left(BS\right)}=Ke^{-r\left(T-t\right)}\mathcal N\left(-d_2\right)-S_t\mathcal N\left(-d_1\right)$$
# +
# The Black-Scholes prices
def bs_put(t, S0=S0, K=K, r=r, sigma=sigma, T=M):
d1 = (np.log(S0/K) + (r + 1/2 * sigma**2) * (T-t)) / sigma / np.sqrt(T-t)
d2 = (np.log(S0/K) + (r - 1/2 * sigma**2) * (T-t)) / sigma / np.sqrt(T-t)
price = K * np.exp(-r * (T-t)) * norm.cdf(-d2) - S0 * norm.cdf(-d1)
return price
def bs_call(t, S0=S0, K=K, r=r, sigma=sigma, T=M):
d1 = (np.log(S0/K) + (r + 1/2 * sigma**2) * (T-t)) / sigma / np.sqrt(T-t)
d2 = (np.log(S0/K) + (r - 1/2 * sigma**2) * (T-t)) / sigma / np.sqrt(T-t)
price = S0 * norm.cdf(d1) - K * np.exp(-r * (T-t)) * norm.cdf(d2)
return price
# -
# ## The DP solution for QLBS
# +
# QLBS option price
C_QLBS = - Q.copy()
print('-------------------------------------------')
print(' QLBS Option Pricing (DP solution) ')
print('-------------------------------------------\n')
print('%-25s' % ('Initial Stock Price:'), S0)
print('%-25s' % ('Drift of Stock:'), mu)
print('%-25s' % ('Volatility of Stock:'), sigma)
print('%-25s' % ('Risk-free Rate:'), r)
print('%-25s' % ('Risk aversion parameter: '), risk_lambda)
print('%-25s' % ('Strike:'), K)
print('%-25s' % ('Maturity:'), M)
print('%-26s %.4f' % ('\nQLBS Put Price: ', C_QLBS.iloc[0,0]))
print('%-26s %.4f' % ('\nBlack-Sholes Put Price:', bs_put(0)))
print('\n')
# plot 10 paths
plt.plot(C_QLBS.T.iloc[:,idx_plot])
plt.xlabel('Time Steps')
plt.title('QLBS Option Price')
plt.show()
# +
### GRADED PART (DO NOT EDIT) ###
part5 = str(C_QLBS.iloc[0,0])
submissions[all_parts[4]]=part5
grading.submit(COURSERA_EMAIL, COURSERA_TOKEN, assignment_key,all_parts[:5],all_parts,submissions)
C_QLBS.iloc[0,0]
### GRADED PART (DO NOT EDIT) ###
# -
# ### make a summary picture
# +
# plot: Simulated S_t and X_t values
# optimal hedge and portfolio values
# rewards and optimal Q-function
f, axarr = plt.subplots(3, 2)
f.subplots_adjust(hspace=.5)
f.set_figheight(8.0)
f.set_figwidth(8.0)
axarr[0, 0].plot(S.T.iloc[:,idx_plot])
axarr[0, 0].set_xlabel('Time Steps')
axarr[0, 0].set_title(r'Simulated stock price $S_t$')
axarr[0, 1].plot(X.T.iloc[:,idx_plot])
axarr[0, 1].set_xlabel('Time Steps')
axarr[0, 1].set_title(r'State variable $X_t$')
axarr[1, 0].plot(a.T.iloc[:,idx_plot])
axarr[1, 0].set_xlabel('Time Steps')
axarr[1, 0].set_title(r'Optimal action $a_t^{\star}$')
axarr[1, 1].plot(Pi.T.iloc[:,idx_plot])
axarr[1, 1].set_xlabel('Time Steps')
axarr[1, 1].set_title(r'Optimal portfolio $\Pi_t$')
axarr[2, 0].plot(R.T.iloc[:,idx_plot])
axarr[2, 0].set_xlabel('Time Steps')
axarr[2, 0].set_title(r'Rewards $R_t$')
axarr[2, 1].plot(Q.T.iloc[:,idx_plot])
axarr[2, 1].set_xlabel('Time Steps')
axarr[2, 1].set_title(r'Optimal DP Q-function $Q_t^{\star}$')
# plt.savefig('QLBS_DP_summary_graphs_ATM_option_mu=r.png', dpi=600)
# plt.savefig('QLBS_DP_summary_graphs_ATM_option_mu>r.png', dpi=600)
plt.savefig('QLBS_DP_summary_graphs_ATM_option_mu>r.png', dpi=600)
plt.show()
# +
# plot convergence to the Black-Scholes values
# lam = 0.0001, Q = 4.1989 +/- 0.3612 # 4.378
# lam = 0.001: Q = 4.9004 +/- 0.1206 # Q=6.283
# lam = 0.005: Q = 8.0184 +/- 0.9484 # Q = 14.7489
# lam = 0.01: Q = 11.9158 +/- 2.2846 # Q = 25.33
lam_vals = np.array([0.0001, 0.001, 0.005, 0.01])
# Q_vals = np.array([3.77, 3.81, 4.57, 7.967,12.2051])
Q_vals = np.array([4.1989, 4.9004, 8.0184, 11.9158])
Q_std = np.array([0.3612,0.1206, 0.9484, 2.2846])
BS_price = bs_put(0)
# f, axarr = plt.subplots(1, 1)
fig, ax = plt.subplots(1, 1)
f.subplots_adjust(hspace=.5)
f.set_figheight(4.0)
f.set_figwidth(4.0)
# ax.plot(lam_vals,Q_vals)
ax.errorbar(lam_vals, Q_vals, yerr=Q_std, fmt='o')
ax.set_xlabel('Risk aversion')
ax.set_ylabel('Optimal option price')
ax.set_title(r'Optimal option price vs risk aversion')
ax.axhline(y=BS_price,linewidth=2, color='r')
textstr = 'BS price = %2.2f'% (BS_price)
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
# place a text box in upper left in axes coords
ax.text(0.05, 0.95, textstr, fontsize=11,transform=ax.transAxes, verticalalignment='top', bbox=props)
plt.savefig('Opt_price_vs_lambda_Markowitz.png')
plt.show()
# -
|
m3-ex2/dp_qlbs_oneset_m3_ex2_v3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + tags=["parameters"]
cfg_times = 3
cfg_lr = 0.02/4
cfg_classes = []
cfg_num_classes = 20
cfg_albu_p = 0.5
cfg_num_gpus = 2
cfg_mini_batch = 2
cfg_multi_scale = []
cfg_crop_size = 1280
cfg_load_from = None
cfg_frozen_stages = 1
cfg_experiment_path = './tmp/ipynbname'
cfg_train_data_root = '/workspace/notebooks/xxxx'
cfg_train_coco_file = 'keep_p_samples/01/train.json'
cfg_val_data_root = '/workspace/notebooks/xxxx'
cfg_val_coco_file = 'keep_p_samples/01/val.json'
cfg_test_data_root = '/workspace/notebooks/xxxx'
cfg_test_coco_file = 'keep_p_samples/01/test.json'
cfg_tmpl_path = '/usr/src/mmdetection/configs/faster_rcnn/faster_rcnn_r50_fpn_1x_coco.py'
# +
import os
#MMDET_PATH = '/usr/src/mmdetection'
#os.environ['MMDET_PATH'] = MMDET_PATH
#os.environ['MKL_THREADING_LAYER'] = 'GNU'
from cvtk.utils.notebook import clean_models
# +
# %%time
albu_train_transforms = [
dict(type='RandomRotate90', p=cfg_albu_p),
]
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
train_pipeline = [
dict(type='LoadImageFromFile'),
dict(type='LoadAnnotations', with_bbox=True),
dict(
type='Albu',
transforms=albu_train_transforms,
bbox_params=dict(
type='BboxParams',
format='pascal_voc',
label_fields=['gt_labels'],
min_visibility=0.0,
filter_lost_elements=True),
keymap={
'img': 'image',
'gt_masks': 'masks',
'gt_bboxes': 'bboxes'
},
update_pad_shape=False,
skip_img_without_anno=True),
dict(type='Resize', test_mode=(len(cfg_multi_scale) == 0), multi_scale=cfg_multi_scale),
dict(type='RandomCrop', height=cfg_crop_size, width=cfg_crop_size),
dict(type='RandomFlip', flip_ratio=0.5, direction=['horizontal', 'vertical', 'diagonal']),
dict(type='Normalize', **img_norm_cfg),
dict(type='Pad', size_divisor=32),
dict(type='DefaultFormatBundle'),
dict(type='Collect', keys=['img', 'gt_bboxes', 'gt_labels']),
]
test_pipeline = [
dict(type='LoadImageFromFile'),
dict(
type='MultiScaleFlipAug',
scale_factor=1.0,
transforms=[
dict(type='Resize', test_mode=True, multi_scale=cfg_multi_scale),
dict(type='Normalize', **img_norm_cfg),
dict(type='Pad', size_divisor=32),
dict(type='DefaultFormatBundle'),
dict(type='Collect', keys=['img']),
]),
]
cfg_data = dict(
samples_per_gpu=cfg_mini_batch,
workers_per_gpu=cfg_mini_batch,
train=dict(
type='CocoDataset',
data_root=cfg_train_data_root,
ann_file=cfg_train_coco_file,
classes=cfg_classes,
img_prefix='',
pipeline=train_pipeline),
val=dict(
type='CocoDataset',
data_root=cfg_val_data_root,
ann_file=cfg_val_coco_file,
classes=cfg_classes,
img_prefix='',
pipeline=test_pipeline),
test=dict(
type='CocoDataset',
data_root=cfg_test_data_root,
ann_file=cfg_test_coco_file,
classes=cfg_classes,
img_prefix='',
pipeline=test_pipeline))
cfg_model = dict(
type='FasterRCNN',
pretrained='torchvision://resnet50',
backbone=dict(
type='ResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=cfg_frozen_stages,
),
neck=dict(
num_outs=5,
start_level=1,
add_extra_convs='on_input',
relu_before_extra_convs=False,
),
rpn_head=dict(
anchor_generator=dict(
scales=[8],
ratios=[0.5, 1.0, 2.0],
strides=[8, 16, 32, 64, 128],
),
),
roi_head=dict(
bbox_roi_extractor=dict(
featmap_strides=[8, 16, 32, 64, 128],
finest_scale=56,
),
bbox_head=dict(
num_classes=cfg_num_classes,
),
),
)
cfg_lr_config = dict(
_delete_=True,
policy='Step',
step=[8 * cfg_times, 11 * cfg_times],
gamma=0.1,
warmup='linear',
warmup_iters=1500,
warmup_ratio=0.001,
)
cfg_log_config = dict(
interval=50,
hooks=[
dict(type='TextLoggerHook'),
],
)
cfg_options = dict(
optimizer=dict(type='SGD', lr=cfg_lr, momentum=0.9, weight_decay=0.0001),
runner=dict(type='EpochBasedRunner', max_epochs=12 * cfg_times),
evaluation=dict(interval=6, metric='bbox'),
checkpoint_config=dict(interval=1),
log_config=cfg_log_config,
lr_config=cfg_lr_config,
load_from=cfg_load_from,
model=cfg_model,
data=cfg_data)
os.environ['CFG_OPTIONS'] = str(cfg_options)
ARG_TRAIN = '{} --work-dir {} --launcher pytorch'.format(cfg_tmpl_path, cfg_experiment_path)
# !python -m torch.distributed.launch --nproc_per_node={cfg_num_gpus} dev/py_train.py {ARG_TRAIN}
DEL_FILES = ' '.join(clean_models(cfg_experiment_path, 3))
# logs = !rm -rfv {DEL_FILES}
cfg_experiment_path
# +
# %%time
import os
work_dir = cfg_experiment_path
config = os.path.basename(cfg_tmpl_path)
data_root = cfg_test_data_root#'/workspace/notebooks/xxxx'
coco_file = cfg_test_coco_file#'keep_p_samples/01/train.json'
gpus = cfg_num_gpus
config_file = os.path.join(work_dir, config)
checkpoint_file = os.path.join(work_dir, 'latest.pth')
batch_size = 1
workers_per_gpu = 2
ARG_TEST = f'{data_root} {coco_file} {gpus} {config_file} {checkpoint_file} {batch_size} {workers_per_gpu}'
# logs = !python dev/py_test.py {ARG_TEST}
print('\n'.join(logs))
from cvtk.utils.abc.discover import hardmini_test
[hardmini_test(logs, level='image', score=s, nok=True) for s in (0.3, 0.5, 0.85, 1.01)]
|
references/mmdetection/dev/tmpl_s1_step.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="ZlnGn4MT_1jC" outputId="1454afb8-4ca3-4951-c8c3-9fd52ee507f3" colab={"base_uri": "https://localhost:8080/"}
from google.colab import drive
#drive.flush_and_unmount()
drive.mount('/content/drive')
# + id="BXLv74lX_36R" outputId="f0240eef-73dc-4ea5-bbae-a95ca0d30120" colab={"base_uri": "https://localhost:8080/"}
# !pip install transformers
# + [markdown] id="02QnDOdqi6Co"
# # Deceptive Opinion Detection using BERT without Fine-Tune
# In this notebook, we are going to use pre-trained BERT to process text to learn features. Then, the encoded embeddings are used to train a logistic regression model for classifcation. The used corpus consists of truthful and deceptive hotel reviews of 20 Chicago hotels. The model will be used to classify the review as truthful or decpetive. The data is open in [Kaggle](https://www.kaggle.com/rtatman/deceptive-opinion-spam-corpus).
#
# ## Agenda
#
# 1. Data Loading
# 2. BaseLine Mode: BoW Features + Logistic Regression
# 3. BERT without Fine-Tune:
#
# 3.1 DistillBERT is used to process sentences to learn features
#
# 3.2 Features are fed into Logistic Regression for classifcation.
#
# DistilBERT is a smaller version of BERT developed and open sourced by the team at HuggingFace. It’s a lighter and faster version of BERT that roughly matches its performance.
#
# + [markdown] id="Jyx2kQxbnHbM"
#
# It should be noted that although the `[CLS]` acts as an "aggregate representation" for classification tasks, this is not the best choice for a high quality sentence embedding vector. [According to](https://github.com/google-research/bert/issues/164) BERT author <NAME>: "*I'm not sure what these vectors are, since BERT does not generate meaningful sentence vectors. It seems that this is is doing average pooling over the word tokens to get a sentence vector, but we never suggested that this will generate meaningful sentence representations*."
#
# (However, the [CLS] token does become meaningful if the model has been fine-tuned, where the last hidden layer of this token is used as the "sentence vector" for sequence classification.)
#
# + id="nRaix9bHHXox"
import pandas as pd
import re
from bs4 import BeautifulSoup
import seaborn as sns
import numpy as np
# + [markdown] id="t5kyz8fnFpmS"
# ## 1. Data Loading
# + id="VK1LGyI7A0AL"
basefn = "/content/drive/My Drive/fraud_analysis/datasets/"
df_corpus = pd.read_csv(basefn + "deceptive-opinion.csv")
df_corpus['LABEL'] = 1
df_corpus.loc[df_corpus['deceptive']=='truthful', 'LABEL'] = 0
# + id="Nx51SXztA_jG"
def review_to_words( raw_review ):
# Function to convert a raw review to a string of words
# The input is a single string (a raw movie review), and
# the output is a single string (a preprocessed movie review)
#
# 1. Remove HTML
review_text = BeautifulSoup(raw_review).get_text()
# 2. Only keep letters
letters_only = re.sub("[^a-zA-Z]", " ", review_text)
# 3. Convert to lower case, split into individual words
words = letters_only.lower().split()
return( " ".join(words))
# Get the number of reviews based on the dataframe column size
num_reviews = df_corpus["text"].size
# Initialize an empty list to hold the clean reviews
clean_train_reviews = []
# Loop over each review; create an index i that goes from 0 to the length
# of the movie review list
for i in range(0, num_reviews ):
# Call our function for each one, and add the result to the list of
# clean reviews
clean_train_reviews.append( review_to_words( df_corpus["text"][i] ) )
# + id="Qcgunp5oBENK" outputId="49ba4389-2d65-463a-9fb0-b6c3d3119fe4" colab={"base_uri": "https://localhost:8080/", "height": 191}
df_corpus['TEXT'] = clean_train_reviews
df_corpus = df_corpus[['TEXT', 'LABEL']]
df_corpus.head()
# + [markdown] id="w3yKK4sCI7QC"
# ## 2. Baseline Model
# + id="jK91GE59q6Xa"
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
# + id="sCQ9CXBer7L1"
df_train, df_test, train_labels, test_labels = train_test_split(df_corpus.TEXT, df_corpus.LABEL, test_size=0.25, random_state=123)
# + [markdown] id="khvI36JPJKe5"
# #### BoW Model
# + id="NSBUT1Hkr7Eg"
vectorizer = CountVectorizer()
X_train = vectorizer.fit_transform(df_train)
X_test =vectorizer.transform(df_test)
# + [markdown] id="FOXrqwlRJPZy"
# #### Logistic Regression
# + id="1mWO51wP0fa4" outputId="be148796-9b88-4183-e3cf-d183a7a72f63" colab={"base_uri": "https://localhost:8080/"}
lr_clf = LogisticRegression(max_iter=20000)
lr_clf.fit(X_train, train_labels)
# + [markdown] id="uPA7rOUkJVbK"
# #### Evaluating the baseline model
# + id="ZdrUakN607fu" outputId="a9475d28-42fb-4e9c-83f7-c4b02ed3fb75" colab={"base_uri": "https://localhost:8080/"}
lr_clf.score(X_test, test_labels)
# + [markdown] id="4TJ4_I7kKCpP"
# ## 3. BERT without Fine-Tune
# + [markdown] id="R8UGoznNmMLd"
# #### Load pre-trained model
# + id="8DifFkY-mLxz" outputId="fe273e81-eeec-47cb-f881-f37142b369c9" colab={"base_uri": "https://localhost:8080/", "height": 161, "referenced_widgets": ["7496c5ce218e40f88464e6db104176f2", "8277677b47724a04a9c6bf62ce38c604", "a5a73aab47b2448ead1a9a03d4c7ec23", "b3958af0a2ca4674836ce078b270f9df", "c4cd1c5b901c4dee8bec34795191fb21", "cc6869f3af7f4fc5a7b0aada6ff65887", "<KEY>", "<KEY>", "b97bfd58e9e442958dc9e5ca51d255bf", "<KEY>", "ea8e408e615641719e096f0e420af5be", "235d586dedf742a1bdc4781126c1fc40", "15e112e66d434c91bc5e862c3a40ee3f", "59d24d1f73c14cb9a2d4d3506caaffc0", "<KEY>", "<KEY>", "d21410b0cde246c6995ede92ffe7960c", "<KEY>", "<KEY>", "<KEY>", "57c16041d25947e288401051ff14f9f1", "<KEY>", "1f858a8f0ad34be999bbd44a2742be29", "0705517a0c194d11a89091a1dbae84a3"]}
import torch
from transformers import DistilBertTokenizer, DistilBertModel
# Load pre-trained model tokenizer (vocabulary)
tokenizer = DistilBertTokenizer.from_pretrained('distilbert-base-uncased')
# Load pre-trained model (weights)
model = DistilBertModel.from_pretrained('distilbert-base-uncased')
# + [markdown] id="QIWsQhd1UmRh"
# #### 3.1 Convert text into vectors using DistillBERT
# + [markdown] id="7Rv6rV00TMgp"
# ### Tokenization-Padding-Masking
# + id="iJetv3UkCY08"
tokenized = df_corpus['TEXT'].apply((lambda x: tokenizer.encode(x, add_special_tokens=True, max_length=512, truncation=True)))
max_len = 0
for i in tokenized.values:
if len(i) > max_len:
max_len = len(i)
padded = np.array([i + [0]*(max_len-len(i)) for i in tokenized.values])
attention_mask = np.where(padded != 0, 1, 0)
attention_mask.shape
# + id="mjCBxHOlCgWx"
max_len = 0
for i in tokenized.values:
if len(i) > max_len:
max_len = len(i)
padded = np.array([i + [0]*(max_len-len(i)) for i in tokenized.values])
# + id="88CAgeQID8oh" outputId="8e4279d0-8d27-467a-ebca-58e2daea0190" colab={"base_uri": "https://localhost:8080/"}
attention_mask = np.where(padded != 0, 1, 0)
attention_mask.shape
# + [markdown] id="l-ULfzAiTR4A"
# ### Batch Inference
#
# To save memory, 10 reviews are fed into the BERT model each time.
# + id="8S_tTF3JYLh1"
feature_list = []
with torch.no_grad():
for batch_idx in range(0,padded.shape[0],10):
# BERT check 10 sample each time.
input_ids = torch.tensor(padded[batch_idx:batch_idx+10])
used_attention_mask = torch.tensor(attention_mask[batch_idx:batch_idx+10])
last_hidden_states = model(input_ids, attention_mask=used_attention_mask)
# Get the embeddings for the [CLS] tag (position is 0)
features = last_hidden_states[0][:,0,:].numpy()
feature_list.append(features)
# + [markdown] id="dxw5dFL_TEKQ"
# It should be noted that although the `[CLS]` acts as an "aggregate representation" for classification tasks, this is not the best choice for a high quality sentence embedding vector. [According to](https://github.com/google-research/bert/issues/164) BERT author <NAME>: "*I'm not sure what these vectors are, since BERT does not generate meaningful sentence vectors. It seems that this is is doing average pooling over the word tokens to get a sentence vector, but we never suggested that this will generate meaningful sentence representations*."
#
# (However, the [CLS] token does become meaningful if the model has been fine-tuned, where the last hidden layer of this token is used as the "sentence vector" for sequence classification.)
# + [markdown] id="3SV3CLguSt4s"
# 
# + id="B1njbisCX6Yt" outputId="1d49f185-ae28-44b3-f9f6-7e316298d4f7" colab={"base_uri": "https://localhost:8080/"}
# preprare features
features = np.vstack(feature_list)
features.shape
# + [markdown] id="CWnF7yJYUfNB"
# #### 3.2 Build Logistic Regression
# + id="3yUNLup6O9iL"
# get labels
labels = df_corpus.LABEL.tolist()
# + id="EssDr8YvE547"
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.25, random_state=123)
# + id="g6DO0B0nOH4i" outputId="24328252-920b-4906-c858-eb4a8662bff3" colab={"base_uri": "https://localhost:8080/"}
lr_clf = LogisticRegression(max_iter=20000)
lr_clf.fit(train_features, train_labels)
# + id="xIBT4NkqZEFW" outputId="c0bfc243-01ce-4b72-94b0-8e2949573914" colab={"base_uri": "https://localhost:8080/"}
# validate the model
lr_clf.score(test_features, test_labels)
# + [markdown] id="WFOlC42SUB2x"
# So it is clear that the features encoded by pre-trained BERT is better than the BoW features.
# And that’s it! That’s a good first contact with BERT. The next step would be to head over to the documentation and try your hand at [fine-tuning](https://huggingface.co/transformers/examples.html#glue). You can also go back and switch from distilBERT to BERT and see how that works.
|
12_Deceptive_Opinion_Detection_using_BERT_without_Fine_Tune.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + run_control={"frozen": false, "read_only": false}
# This Youtube video walks through this notebook
from IPython.display import YouTubeVideo
YouTubeVideo('dGcLHtYLgDU')
# + run_control={"frozen": false, "read_only": false}
from jove.DotBashers import *
from jove.Def_md2mc import *
from jove.Def_DFA import *
# + [markdown] run_control={"frozen": false, "read_only": false}
# # Basic DFA Creation, Alphabet Expansion, Totalization
# + [markdown] run_control={"frozen": false, "read_only": false}
# <span style="color:blue"> **We can now write routines to print DFA using dot. The main routines are listed below.** </span>
#
# * dot_dfa_w_bh : lists all states of a DFA including black-hole states
# * dot_dfa : lists all isNotBH states (see below for a defn), i.e. suppress black-holes
# - Usually there are too many transitions to them and that clutters the view
#
# + run_control={"frozen": false, "read_only": false}
# Essential part of a DFA for even # of 0s
ev0 = md2mc('''
DFA
IF : 0 -> A
A : 0 -> IF
''')
dotObj_dfa(ev0)
# + run_control={"frozen": false, "read_only": false}
# Expand the Sigma of this DFA by adding '1' to it
ev0_bh = addtosigma_dfa(ev0, set({'1'}))
dotObj_dfa(ev0_bh)
# + run_control={"frozen": false, "read_only": false}
# Totalize this DFA so that the '1' moves land in a "black hole" state
ev0_bh_totalize = totalize_dfa(ev0_bh)
# But, viewing using dotObj_dfa still suppresses black-hole moves (reduces clutter)
dotObj_dfa(ev0_bh_totalize)
# + run_control={"frozen": false, "read_only": false}
# If you want to see all moves, display using dotObj_dfa_w_bh
dotObj_dfa_w_bh(ev0_bh_totalize)
# + run_control={"frozen": false, "read_only": false}
# For an even prettier depiction, set FuseEdges True so that multiple edges between the same states are fused
dotObj_dfa_w_bh(ev0_bh_totalize, FuseEdges=True)
# + [markdown] run_control={"frozen": false, "read_only": false}
# # Basic DFA Tests Illustrated
#
# We now illustrate some basic testing of consistency, language acceptance, etc
# + run_control={"frozen": false, "read_only": false}
# This is the DFA which accepts sequences of three 0's
# (hence the name DFA_Tz -- for "three zeros")
# Arrival of 1's cause the machine to "idle" in the same state
#
# This corresponds to Figure 4.6 in the book
DFA_Tz = md2mc('''DFA
IF : 0 -> A
A : 0 -> B
B : 0 -> IF
IF : 1 -> IF
A : 1 -> A
B : 1 -> B''')
dotObj_dfa(DFA_Tz)
# + code_folding=[] run_control={"frozen": false, "read_only": false}
# Some tests pertaining to totalize_dfa, is_consistent_dfa, etc
def tests_dfa_consist():
"""Some tests wrt DFA routines.
"""
DFA_Tz_Q = DFA_Tz["Q"]
DFA_Tz_Sigma = DFA_Tz["Sigma"]
randQ = random.choice(list(DFA_Tz_Q))
randSym = random.choice(list(DFA_Tz_Sigma))
DFA_Tz_deepcopy = copy.deepcopy(DFA_Tz)
print('is_consistent_dfa(DFA_Tz) =',
is_consistent_dfa(DFA_Tz) )
print('Removing mapping for ' +
"(" + randQ + "," + randSym + ")" +
"from DFA_Tz_deepcopy")
DFA_Tz_deepcopy["Delta"].pop((randQ,randSym))
print('is_consistent_dfa(DFA_Tz_deepcopy) =',
is_consistent_dfa(DFA_Tz_deepcopy) )
totalized = totalize_dfa(DFA_Tz_deepcopy)
print ( 'is_consistent_dfa(totalized) =',
is_consistent_dfa(totalized) )
assert(totalized == totalize_dfa(totalized)) # Must pass
tests_dfa_consist()
# + [markdown] run_control={"frozen": false, "read_only": false}
# Let us test functions step_dfa, run_dfa, and accepts_dfa
# + code_folding=[] run_control={"frozen": false, "read_only": false}
# Some tests of step, run, etc.
def step_run_accepts_tests():
print("step_dfa(DFA_Tz, 'IF', '1') = ",
step_dfa(DFA_Tz, 'IF', '1'))
print("step_dfa(DFA_Tz, 'A', '0') = ",
step_dfa(DFA_Tz, 'A', '0'))
print("run_dfa(DFA_Tz, '101001') = ",
run_dfa(DFA_Tz, '101001'))
print("run_dfa(DFA_Tz, '101000') = ",
run_dfa(DFA_Tz, '101000'))
print("accepts_dfa(DFA_Tz, '101001') = ",
accepts_dfa(DFA_Tz, '101001'))
print("accepts_dfa(DFA_Tz, '101000') = ",
accepts_dfa(DFA_Tz, '101000'))
step_run_accepts_tests()
# + [markdown] run_control={"frozen": false, "read_only": false}
# # Boolean Operations on DFA
#
# It is possible to take complements, union, and intersection of DFA.
#
# The union of two DFA produces a new DFA such that its language is the language-union of the input DFA
# (and similarly for the other set operations also)
# + run_control={"frozen": false, "read_only": false}
dotObj_dfa(DFA_Tz, "DFA_Tz")
# + run_control={"frozen": false, "read_only": false}
# Run a complementation test
DFA_Tz_comp = comp_dfa(DFA_Tz)
dotObj_dfa(DFA_Tz_comp)
# + run_control={"frozen": false, "read_only": false}
# One more test
# Clearly, the union of a DFA and its complement results in the universal language
du = union_dfa(DFA_Tz, DFA_Tz_comp)
dotObj_dfa(du, "orig union")
# + run_control={"frozen": false, "read_only": false}
# Clearly, the union of a DFA and its complement results in the universal language
# We can see this fact by minimizing the above diagram (DFA minimization will be shortly discussed)
dotObj_dfa(min_dfa(du), FuseEdges = True)
# + [markdown] run_control={"frozen": false, "read_only": false}
# # Language Equivalence and Isomorphism of DFA
#
# We will now illustrate ideas revolving around DFA language-equivalence and isomorphism
#
# + code_folding=[] run_control={"frozen": false, "read_only": false}
# It is convenient to have a DFA that is an artificially bloated variant of one you've seen earlier...
Tz_bloated = md2mc('''DFA
IF : 0 -> A
A : 0 -> B1
B : 0 -> IF
IF : 1 -> IF
A : 1 -> A1
B : 1 -> B1
A1 : 0 -> B
A1 : 1 -> A
B1 : 0 -> IF
B1 : 1 -> B
''')
dotObj_dfa(Tz_bloated)
# + run_control={"frozen": false, "read_only": false}
help(langeq_dfa)
help(iso_dfa)
# + run_control={"frozen": false, "read_only": false}
# Are these DFA language-equivalent?
is_langeq = langeq_dfa(DFA_Tz, Tz_bloated, False)
# These DFA are language equivalent, but not isomorphic -- because one is bloated
is_iso = iso_dfa(DFA_Tz, Tz_bloated)
print('is language-equivalent:', is_langeq)
print('is isomorphic:', is_iso)
# + run_control={"frozen": false, "read_only": false}
# By minimizing, we know what the bloated DFA corresponds to. Looks familiar?
dotObj_dfa(min_dfa(Tz_bloated), FuseEdges = True)
# + code_folding=[] run_control={"frozen": false, "read_only": false}
# We create a DFA that is a badly bloated variant of Tz_bloated
Tz_badBloat = md2mc('''DFA
IF : 0 -> A
A : 0 -> B1
B : 0 -> IF
IF : 1 -> IF
A : 1 -> A1
B : 1 -> IF
A1 : 0 -> B
A1 : 1 -> A
B1 : 0 -> IF
B1 : 1 -> B
''')
dotObj_dfa(Tz_badBloat, FuseEdges=True)
# + run_control={"frozen": false, "read_only": false}
# We minimize the badly bloated DFA and the minimized DFA does not look like Tz_bloated
# This itself suggests that we did not bloat it right
dotObj_dfa(min_dfa(Tz_badBloat), FuseEdges = True)
# + run_control={"frozen": false, "read_only": false}
# If we apply language equivalence, we find out how these DFAs differ (why they are not language-equivalent)
# Providing "True" as the last argument results in one example of a difference being printed
langeq_dfa(DFA_Tz, Tz_badBloat, True)
# + run_control={"frozen": false, "read_only": false}
# If you don't want to see the counterexample, supply "False" as the last argument
langeq_dfa(DFA_Tz, Tz_badBloat, False)
# + run_control={"frozen": false, "read_only": false}
# Clearly, DFAs that are not language equivalent are not isomorphic either
iso_dfa(DFA_Tz, Tz_badBloat)
# + [markdown] run_control={"frozen": false, "read_only": false}
# ## One more test, now illustrating intersection, union, isomorphism
# + run_control={"frozen": false, "read_only": false}
DFA_Tzv1 = md2mc('''DFA
IF : 0 -> A
A : 0 -> B
B : 0 -> IF
IF : 1 -> IF
A : 1 -> B
B : 1 -> B''')
dotObj_dfa(DFA_Tzv1)
# + run_control={"frozen": false, "read_only": false}
IntDFA = intersect_dfa(DFA_Tzv1, DFA_Tz)
dotObj_dfa(IntDFA)
# + run_control={"frozen": false, "read_only": false}
dotObj_dfa(min_dfa(IntDFA))
# + run_control={"frozen": false, "read_only": false}
UnionDFA = union_dfa(DFA_Tzv1, DFA_Tz)
dotObj_dfa(UnionDFA)
# + run_control={"frozen": false, "read_only": false}
# We did not expect the union and intersection to be isomorphic, and nor are they
iso_dfa(IntDFA, UnionDFA)
# + [markdown] run_control={"frozen": false, "read_only": false}
# ## Counterexample trace generation
# + run_control={"frozen": false, "read_only": false}
# Neither are the union and intersection language-equivalent
langeq_dfa(IntDFA, UnionDFA, True)
# + [markdown] run_control={"frozen": false, "read_only": false}
# # DFA minimization
# + [markdown] run_control={"frozen": false, "read_only": false}
# ## A first simple example
#
# <font size="4">
#
#
# ```
#
#
# Consider this DFA as an example
# --------------------------------
#
# DFA
# IF : 0 -> A IF : 1 -> IF
# A : 0 -> B1 A : 1 -> A1
# B : 0 -> IF B : 1 -> B1
# A1 : 0 -> B A1 : 1 -> A
# B1 : 0 -> IF B1 : 1 -> B
#
#
# This is the initial display of a matrix (only the lower half shown, as the upper half is symmetric). The matrix shows "." which are points at which state pairs "collide." The dots in this figure allow for these pairs to collide (we show pairs only one way, i.e. (P,Q) and not the other way i.e. (Q,P) also).
#
#
# A .
#
# A1 . .
#
# B . . .
#
# B1 . . . .
#
# IF A A1 B
#
#
# The above is a convenient arrangement to talk about these pairs:
#
#
# (A, IF),
#
# (A1, IF), (A1, A)
#
# (B, IF), (B, A), (B, A1)
#
# (B1, IF), (B1, A), (B1, A1), (B1, B)
#
# Now, here is how the computation proceeds for this example:
# ===========================================================
#
# Frame-0 Frame-1 Frame-2
#
# A -1 A 0 A 0
#
# A1 -1 -1 A1 0 -1 A1 0 -1
#
# B -1 -1 -1 B 0 -1 -1 B 0 1 1
#
# B1 -1 -1 -1 -1 B1 0 -1 -1 -1 B1 0 1 1 -1
#
# IF A A1 B IF A A1 B IF A A1 B
#
#
# Frame-3 = Frame-2
#
# A 0
#
# A1 0 -1
#
# B 0 1 1
#
# B1 0 1 1 -1
#
# IF A A1 B
# ```
#
#
#
# </font>
#
#
# __Now, given that there are no changes, we can form equivalence-classes of states__
#
# 1. A and A1 are in the same equivalence class
#
# 2. B and B1 are in the same equivalence class
#
# 3. No overlap between the equivalence classes. So we are done:
#
# a. Choose a representative (e.g., A) for {A,A1}
#
# b. Choose a representative (e.g., B) for {B,B1}
# + [markdown] run_control={"frozen": false, "read_only": false}
# ## A more elaborate example of DFA minimization
# + run_control={"frozen": false, "read_only": false}
bloated_dfa = md2mc('''
DFA
IS1 : a -> FS2
IS1 : b -> FS3
FS2 : a -> S4
FS2 : b -> S5
FS3 : a -> S5
FS3 : b -> S4
S4 : a | b -> FS6
S5 : a | b -> FS6
FS6 : a | b -> FS6
''')
dotObj_dfa(bloated_dfa)
# + [markdown] run_control={"frozen": false, "read_only": false}
#
# Now, here is how the computation proceeds for this example:
# --------------------------------------------------------
#
# <br>
#
# <font size="3">
#
#
# ```
#
# Frame-0 Frame-1 Frame-2
#
# FS2 -1 FS2 0 FS2 0
#
# FS3 -1 -1 FS3 0 -1 FS3 0 -1
#
# S4 -1 -1 -1 S4 -1 0 0 S4 2 0 0
#
# S5 -1 -1 -1 -1 S5 -1 0 0 -1 S5 2 0 0 -1
#
# FS6 -1 -1 -1 -1 -1 FS6 0 -1 -1 0 0 FS6 0 1 1 0 0
#
# IS1 FS2 FS3 S4 S5 IS1 FS2 FS3 S4 S5 IS1 IS2 FS3 S4 S5
#
# Initial 0-distinguishable 1-distinguishable
#
#
# Frame-3 Frame-4
# =
# Frame-3
#
# FS2 0
#
# FS3 0 -1
#
# S4 2 0 0
#
# S5 2 0 0 -1
#
# FS6 0 1 1 0 0
#
# IS1 IS2 FS3 S4 S5
#
# 2-distinguishable
#
# ```
# </font>
# + [markdown] run_control={"frozen": false, "read_only": false}
# Here is the algorithm, going frame by frame.
#
# - Initial Frame:
#
# The initial frame is drawn to clash all _combinations_ of states taken two at a time.
# Since we have 6 states, we have $6\choose 2$ = $15$ entries. We put a -1 against each
# such pair to denote that they have not been found distinguishable yet.
#
# - Frame *0-distinguishable*: We now put a 0 where a pair of states is 0-distinguishable. This means the states are distinguisable after consuming $\varepsilon$. This of course means that the states are themselves distinguishable. This is only possible if one is a final state and the other is not (in that case, one state, after consuming $\varepsilon$ accepts_dfa, and another state after consuming $\varepsilon$ does not accept.
#
# - So for instance, notice that (FS3,IS1) and (S4,FS2) are 0-distinguishable, meaning that one is a final and the other is a non-final state.
#
# - Frame *1-distinguishable*: We now put a 1 where a pair of states is 1-distinguishable. This means the states are distinguisable after consuming a string of length $1$ (a single symbol). This is only possible if one state transitions to a final state and the other transitions to a non-final state after consuming a member of $\Sigma$.
#
# State pairs (FS6,FS2) and (FS6,FS3) are of this kind. While both FS6 and FS2 are final states (hence _0-indistinguishable_), after consuming an 'a' (or a 'b') they respectively go to a final/non-final state.
# This means that
#
# - after processing **the same symbol** one state -- let's say pre_p -- finds itself landing in a state p and another state -- let's say pre_q -- finds itself landing in a state q such that (p,q) is 0-distinguishable.
#
# - When this happens, states pre-p and pre-q are **1-distinguishable**.
#
# - Frame *2-distinguishable*: We now put a 2 where a pair of states is 2-distinguishable. This means the states are distinguisable after consuming a string of length $2$ (a string of length $2$). This is only possible if one state transitions to a state (say p) and the other transitions to state (say q) after consuming a member of $\Sigma$ such that (p,q) is **1-distinguishable**. State pairs (S5,IS1) and (S4,IS1) are 2-distinguishable because
#
# - after processing **the same symbol** one state -- let's say pre_p -- finds itself landing in a state p and another state -- let's say pre_q -- finds itself landing in a state q such that (p,q) is 0-distinguishable.
#
# - When this happens, states pre-p and pre-q are **1-distinguishable**.
#
# - One example is this:
#
# - S5 and IS1 are 2-distinguishable.
#
# - This is because after seeing an 'aa', IS1 lands in a non-final state while S5 lands in a final state
#
# - Observe that "aa" = "a" + "a" . Thus, after eating the first "a", IS1 lands in S2 while S5 lands in FS6, and (S2,FS6) have already been deemed 1-distinguishable.
#
# - Thus, when we mark (S5,IS1) as 2-distinguishable, we are sending the matrix entry at (S5,IS1) from
# -1 to 2
#
#
#
# - Now, in search of 3-distinguishability, we catch hold of all pairs in the matrix and see if we can send another -1 entry to "3". This appears not to happen.
#
# - Thus, if (FS2,FS3) is pushed via any sequence of symbols (any string) of any length, it
# always stays in the same type of state. Thus, after seeing 'ababba', FS2 is in S6, while FS3
# is also in FS6.
#
#
# - Thus, given no changes in the matrix, we stop.
#
#
# __Now the equivalence classes are formed as follows:__
#
#
# * FS2 and FS3 in one equivalence class
#
# * S4 and S5 in another
#
# An example where equivalence-classes themselves are to be merged should be fun to try.
# + run_control={"frozen": false, "read_only": false}
# Results of minimizing the bloated DFA
dotObj_dfa(min_dfa(bloated_dfa), FuseEdges=True, dfaName="shrunkbloated_dfa")
# + [markdown] run_control={"frozen": false, "read_only": false}
# __Another fun DFA called "The blimp" :-) __
# + run_control={"frozen": false, "read_only": false}
blimp = md2mc('''
DFA
I1 : a -> F2
I1 : b -> F3
F2 : a -> S8
F2 : b -> S5
F3 : a -> S7
F3 : b -> S4
S4 : a | b -> F6
S5 : a | b -> F6
F6 : a | b -> F6
S7 : a | b -> F6
S8 : a -> F6
S8 : b -> F9
F9 : a -> F9
F9 : b -> F6
''')
dblimp = dotObj_dfa(blimp)
dblimp
# + run_control={"frozen": false, "read_only": false}
dblimp = dotObj_dfa(blimp, FuseEdges=True)
dblimp
# + run_control={"frozen": false, "read_only": false}
mblimp = min_dfa(blimp)
dmblimp = dotObj_dfa(mblimp, FuseEdges=True)
dmblimp
# + [markdown] run_control={"frozen": false, "read_only": false}
# # Illustration of DeMorgan's Law on DFA
#
# This is an extensive illustration of union, intersection and complementation, DFA minimization, isomorphism test, language equivalence test, and an application of DeMorgan's law
# + [markdown] run_control={"frozen": false, "read_only": false}
# Here is how our construction proceeds:
#
# * First we construct dfaOdd1s
#
# * Then we construct ends0101
#
# * Then obtain odd1sORends0101
#
# * Then minimize as per Minodd1sORends0101 = min_dfa(odd1sORends0101)
#
# * Check if isomorphism exists via iso_dfa(odd1sORends0101, Minodd1sORends0101) (should not)
#
# * Check and confirm via langeq_dfa(odd1sORends0101, Minodd1sORends0101) (should hold)
#
# * Then obtain intersection odd1sANDends0101 = intersect_dfa(dfaOdd1s,ends0101)
#
# * Then minimize via Minodd1sANDends0101 = min_dfa(odd1sANDends0101)
#
# * Then complement via CdfaOdd1s = comp_dfa(dfaOdd1s)
#
# * Then complement the other DFA via Cends0101 = comp_dfa(ends0101)
#
# * Now take complement of union via C_CdfaOdd1sORCends0101 = comp_dfa(union_dfa(CdfaOdd1s, Cends0101))
#
# * Now minimize via MinC_CdfaOdd1sORCends0101 = min_dfa(C_CdfaOdd1sORCends0101)
#
# * Now isomorphism holds via iso_dfa(MinC_CdfaOdd1sORCends0101, Minodd1sANDends0101)
# + run_control={"frozen": false, "read_only": false}
dfaOdd1s = md2mc('''
DFA
I : 0 -> I
I : 1 -> F
F : 0 -> F
F : 1 -> I
''')
dotObj_dfa(dfaOdd1s)
# + run_control={"frozen": false, "read_only": false}
ends0101 = md2mc('''
DFA
I : 0 -> S0
I : 1 -> I
S0 : 0 -> S0
S0 : 1 -> S01
S01 : 0 -> S010
S01 : 1 -> I
S010 : 0 -> S0
S010 : 1 -> F0101
F0101 : 0 -> S010
F0101 : 1 -> I
''')
dotObj_dfa(ends0101)
# + run_control={"frozen": false, "read_only": false}
odd1sORends0101 = union_dfa(dfaOdd1s,ends0101)
dotObj_dfa(odd1sORends0101)
# + run_control={"frozen": false, "read_only": false}
Minodd1sORends0101 = min_dfa(odd1sORends0101)
dotObj_dfa(Minodd1sORends0101)
# + run_control={"frozen": false, "read_only": false}
iso_dfa(odd1sORends0101, Minodd1sORends0101)
# + run_control={"frozen": false, "read_only": false}
langeq_dfa(odd1sORends0101, Minodd1sORends0101)
# + run_control={"frozen": false, "read_only": false}
odd1sANDends0101 = intersect_dfa(dfaOdd1s,ends0101)
dotObj_dfa(odd1sANDends0101)
# + run_control={"frozen": false, "read_only": false}
Minodd1sANDends0101 = min_dfa(odd1sANDends0101)
dotObj_dfa(Minodd1sANDends0101)
# + run_control={"frozen": false, "read_only": false}
CdfaOdd1s = comp_dfa(dfaOdd1s)
Cends0101 = comp_dfa(ends0101)
C_CdfaOdd1sORCends0101 = comp_dfa(union_dfa(CdfaOdd1s, Cends0101))
dotObj_dfa(C_CdfaOdd1sORCends0101)
# + run_control={"frozen": false, "read_only": false}
MinC_CdfaOdd1sORCends0101 = min_dfa(C_CdfaOdd1sORCends0101)
dotObj_dfa(MinC_CdfaOdd1sORCends0101)
# + run_control={"frozen": false, "read_only": false}
# This is where DeMorgan's Law is shown in its full glory!!
iso_dfa(MinC_CdfaOdd1sORCends0101, Minodd1sANDends0101)
|
notebooks/tutorial/DFAUnit2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
kos = '../out/rev_sequencing_kos.tsv'
# +
# %matplotlib inline
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('white')
plt.rc('font', size=12)
# -
import numpy as np
import pandas as pd
d = {'S288C': 'S288C',
'Y55': 'Y55',
'UWOPS87': 'UWOP',
'YPS606': 'YPS'}
inter = pd.read_csv(kos, sep='\t')
inter['size'] = inter['stop'] - inter['start']
inter = inter[inter['size'] > 100]
ci = inter.groupby(['target', 'strain'])['set'].nunique()
ci = ci[ci == 2]
inter = inter.set_index(['target', 'strain']).loc[ci.index].reset_index()
niter = inter.groupby(['set', 'strain', 'gene'])['sample'].count().loc['new']
oiter = inter.groupby(['set', 'strain', 'gene'])['sample'].count().loc['original']
m = niter.to_frame().join(oiter.to_frame(),
how='outer',
lsuffix='_new',
rsuffix='_original')
m[np.isnan(m)] = 0.0
# +
plt.figure(figsize=(4, 4))
plt.plot(m['sample_original'],
m['sample_new'],
'k.',
alpha=0.3)
plt.plot([-0.5, 13],
[-0.5, 13],
'--',
color='grey',
alpha=0.5)
plt.xlabel('Number of genes with no coverage\n(Original mutants)')
plt.ylabel('Number of genes with no coverage\n(New mutants)')
plt.title('All strains')
plt.xlim(-0.5, 13)
plt.ylim(-0.5, 13)
plt.savefig('ko_sequencing.png',
dpi=300, bbox_inches='tight',
transparent=True)
plt.savefig('ko_sequencing.svg',
dpi=300, bbox_inches='tight',
transparent=True);
# +
plt.figure(figsize=(8, 8))
for i, strain in enumerate(['S288C',
'Y55',
'YPS606',
'UWOPS87']):
plt.subplot(2, 2, i+1)
plt.plot(m.loc[strain]['sample_original'],
m.loc[strain]['sample_new'],
'k.',
alpha=0.3,
label='_')
plt.xlabel('Number of genes with no coverage\n(Original mutants)')
plt.ylabel('Number of genes with no coverage\n(New mutants)')
plt.title(d[strain])
plt.xlim(-0.5, 13)
plt.ylim(-0.5, 13)
plt.plot([-0.5, 13],
[-0.5, 13],
'--',
color='grey',
alpha=0.5)
plt.tight_layout()
plt.savefig('ko_sequencing_all.png',
dpi=300, bbox_inches='tight',
transparent=True)
plt.savefig('ko_sequencing_all.svg',
dpi=300, bbox_inches='tight',
transparent=True);
# -
g = None
for gene in ['URA3', 'CAN1', 'LYP1', 'LEU2', 'MET17']:
x = inter[inter['name'].isin([gene])
].groupby(['strain', 'set'])['sample'
].nunique() / inter.groupby(['strain', 'set'])[
'sample'].nunique()
x[np.isnan(x)] = 0.0
x.name = gene
if g is None:
g = x.to_frame()
else:
g = g.join(x.to_frame(), how='outer')
g
|
notebooks/sequencing_kos.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Naming of Gluon Parameter and Blocks
#
# In gluon, each Parameter or Block has a name (and prefix). Parameter names are specified by users and Block names can be either specified by users or automatically created.
#
# In this tutorial we talk about the best practices on naming. First, let's import MXNet and Gluon:
# ```python
# from __future__ import print_function
# import mxnet as mx
# from mxnet import gluon
# ```
#
# ## Naming Blocks
#
# When creating a block, you can assign a prefix to it:
# ```python
# mydense = gluon.nn.Dense(100, prefix='mydense_')
# print(mydense.prefix)
# ```
#
# When no prefix is given, Gluon will automatically generate one:
# ```python
# dense0 = gluon.nn.Dense(100)
# print(dense0.prefix)
# ```
#
# When you create more Blocks of the same kind, they will be named with incrementing suffixes to avoid collision:
# ```python
# dense1 = gluon.nn.Dense(100)
# print(dense1.prefix)
# ```
#
# ## Naming Parameters
#
# Parameters within a Block will be named by prepending the prefix of the Block to the name of the Parameter:
# ```python
# print(dense0.collect_params())
# ```
#
# ## Name scopes
#
# To manage the names of nested Blocks, each Block has a `name_scope` attached to it. All Blocks created within a name scope will have its parent Block's prefix prepended to its name.
#
# Let's demonstrate this by first defining a simple neural net:
# ```python
# class Model(gluon.Block):
# def __init__(self, **kwargs):
# super(Model, self).__init__(**kwargs)
# with self.name_scope():
# self.dense0 = gluon.nn.Dense(20)
# self.dense1 = gluon.nn.Dense(20)
# self.mydense = gluon.nn.Dense(20, prefix='mydense_')
#
# def forward(self, x):
# x = mx.nd.relu(self.dense0(x))
# x = mx.nd.relu(self.dense1(x))
# return mx.nd.relu(self.mydense(x))
# ```
#
# Now let's instantiate our neural net.
#
# - Note that `model0.dense0` is named as `model0_dense0_` instead of `dense0_`.
#
# - Also note that although we specified `mydense_` as prefix for `model.mydense`, its parent's prefix is automatically prepended to generate the prefix `model0_mydense_`.
# ```python
# model0 = Model()
# model0.initialize()
# model0(mx.nd.zeros((1, 20)))
# print(model0.prefix)
# print(model0.dense0.prefix)
# print(model0.dense1.prefix)
# print(model0.mydense.prefix)
# ```
#
# If we instantiate `Model` again, it will be given a different name like shown before for `Dense`.
#
# - Note that `model1.dense0` is still named as `dense0_` instead of `dense2_`, following dense layers in previously created `model0`. This is because each instance of model's name scope is independent of each other.
# ```python
# model1 = Model()
# print(model1.prefix)
# print(model1.dense0.prefix)
# print(model1.dense1.prefix)
# print(model1.mydense.prefix)
# ```
#
# **It is recommended that you manually specify a prefix for the top level Block, i.e. `model = Model(prefix='mymodel_')`, to avoid potential confusions in naming.**
#
# The same principle also applies to container blocks like Sequential. `name_scope` can be used inside `__init__` as well as out side of `__init__`:
# ```python
# net = gluon.nn.Sequential()
# with net.name_scope():
# net.add(gluon.nn.Dense(20))
# net.add(gluon.nn.Dense(20))
# print(net.prefix)
# print(net[0].prefix)
# print(net[1].prefix)
# ```
#
# `gluon.model_zoo` also behaves similarly:
# ```python
# net = gluon.nn.Sequential()
# with net.name_scope():
# net.add(gluon.model_zoo.vision.alexnet(pretrained=True))
# net.add(gluon.model_zoo.vision.alexnet(pretrained=True))
# print(net.prefix, net[0].prefix, net[1].prefix)
# ```
#
# ## Saving and loading
#
# Because model0 and model1 have different prefixes, their parameters also have different names:
# ```python
# print(model0.collect_params(), '\n')
# print(model1.collect_params())
# ```
#
# As a result, if you try to save parameters from model0 and load it with model1, you'll get an error due to unmatching names:
# ```python
# model0.collect_params().save('model.params')
# try:
# model1.collect_params().load('model.params', mx.cpu())
# except Exception as e:
# print(e)
# ```
#
# To solve this problem, we use `save_parameters`/`load_parameters` instead of `collect_params` and `save`/`load`. `save_parameters` uses model structure, instead of parameter name, to match parameters.
# ```python
# model0.save_parameters('model.params')
# model1.load_parameters('model.params')
# print(mx.nd.load('model.params').keys())
# ```
#
# ## Replacing Blocks from networks and fine-tuning
#
# Sometimes you may want to load a pretrained model, and replace certain Blocks in it for fine-tuning.
#
# For example, the alexnet in model zoo has 1000 output dimensions, but maybe you only have 100 classes in your application.
#
# To see how to do this, we first load a pretrained AlexNet.
#
# - In Gluon model zoo, all image classification models follow the format where the feature extraction layers are named `features` while the output layer is named `output`.
# - Note that the output layer is a dense block with 1000 dimension outputs.
# ```python
# alexnet = gluon.model_zoo.vision.alexnet(pretrained=True)
# print(alexnet.output)
# print(alexnet.output.prefix)
# ```
#
# To change the output to 100 dimension, we replace it with a new block.
# ```python
# with alexnet.name_scope():
# alexnet.output = gluon.nn.Dense(100)
# alexnet.output.initialize()
# print(alexnet.output)
# print(alexnet.output.prefix)
# ```
#
|
static_websites/python/docs/_sources/tutorials/packages/gluon/naming.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# # EDA - Explotary data analysis
# UCI
# dataset (Data taken from the Blood Transfusion Service Center in Hsin-Chu City in Taiwan.
# This is a classification problem. Number of instances is 748 and number of attributes is
# 5 which includes: R (Recency - months since last donation), F (Frequency - total number
# of donatios), M (Monetary - total blood donated in c.c.), T (Time - months since first donation), and a binary variable representing whether he/she donated blood in March 2007
# (1 stand for donating blood; 0 stands for not donating blood)2
# ).
df = pd.read_excel(r"C:\Users\siava\OneDrive - University of Manitoba\D\Computer science\Data Science Projects\UCI-data-set---Multivariate-data---classification\Data\transfusion.xlsx")
df.head()
df.info()
df.describe()
df["whether he/she donated blood in March 2007"].value_counts()
sns.distplot(df["Recency (months)"], kde=False)
sns.distplot(df["Frequency (times)"], kde=False)
df["Frequency (times)"].value_counts()
sns.distplot(df["Monetary (c.c. blood)"], kde=False)
sns.countplot(df["whether he/she donated blood in March 2007"])
# # Model Building: Hyper parameter Tuning
X = df.drop("whether he/she donated blood in March 2007", axis=1)
y = df["whether he/she donated blood in March 2007"]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
# +
best_score = np.zeros((1,2))
for i in range(4,50):
dt = DecisionTreeClassifier(criterion="entropy", max_depth=i)
scores = cross_val_score(dt, X_train, y_train, cv=4)
print(f"max_depth: {i}")
print(scores)
print(f"Scores mean: {scores.mean()}")
print("\n")
if scores.mean() > best_score[0,1]:
best_score[0,1] = scores.mean()
best_score[0,0] = i
print(f"entropy as heuristic:best_score and its max depth: {best_score}")
# +
best_score = np.zeros((1,2))
for i in range(4,50):
dt = DecisionTreeClassifier(criterion="gini", max_depth=i)
scores = cross_val_score(dt, X_train, y_train, cv=4)
print(f"max_depth: {i}")
print(scores)
print(f"Scores mean: {scores.mean()}")
print("\n")
if scores.mean() > best_score[0,1]:
best_score[0,1] = scores.mean()
best_score[0,0] = i
print(f"Gini as heuristic:best_score and its max depth: {best_score}")
# -
# # Model Building: entropy as the heuristic, Max_depth = 4
# +
dt = DecisionTreeClassifier(criterion="entropy", max_depth=4)
dt.fit(X_train, y_train)
predictions = dt.predict(X_test)
# -
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, predictions))
print("\n")
print(classification_report(y_test, predictions))
# # Model Building: gini as the heuristic, Max_depth = 4
# +
dt = DecisionTreeClassifier(criterion="gini", max_depth=4)
dt.fit(X_train, y_train)
predictions = dt.predict(X_test)
# -
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, predictions))
print("\n")
print(classification_report(y_test, predictions))
# # K fold validation on the whole dataset
# +
best_score = np.zeros((1,2))
for i in range(4,50):
dt = DecisionTreeClassifier(criterion="gini", max_depth=i)
scores = cross_val_score(dt, X, y, cv=4)
print(f"max_depth: {i}")
print(scores)
print(f"Scores mean: {scores.mean()}")
print("\n")
if scores.mean() > best_score[0,1]:
best_score[0,1] = scores.mean()
best_score[0,0] = i
print(f"Gini as heuristic:best_score and its max depth: {best_score}")
# +
best_score = np.zeros((1,2))
for i in range(4,50):
dt = DecisionTreeClassifier(criterion="entropy", max_depth=i)
scores = cross_val_score(dt, X_train, y_train, cv=4)
print(f"max_depth: {i}")
print(scores)
print(f"Scores mean: {scores.mean()}")
print("\n")
if scores.mean() > best_score[0,1]:
best_score[0,1] = scores.mean()
best_score[0,0] = i
print(f"Gini as heuristic:best_score and its max depth: {best_score}")
# -
# As can be seen from the results, we have reached the same proposed Max_depth form both models(entropy as criteria and gini as criteria) <br>
# Max_depth = 4
|
ipynb/UCI-data-set---Multivariate-data---classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import glob, os
import re
import PIL
from PIL import Image
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
import matplotlib.pyplot as plt
# +
def jpeg_to_8_bit_greyscale(path, maxsize):
# img = Image.open(path).convert('L') # convert image to 8-bit grayscale
img = Image.open(path) # convert image to 8-bit grayscale
# Make aspect ratio as 1:1, by applying image crop.
# Please note, croping works for this data set, but in general one
# needs to locate the subject and then crop or scale accordingly.
WIDTH, HEIGHT = img.size
if WIDTH != HEIGHT:
m_min_d = min(WIDTH, HEIGHT)
img = img.crop((0, 0, m_min_d, m_min_d))
# Scale the image to the requested maxsize by Anti-alias sampling.
img.thumbnail(maxsize, PIL.Image.ANTIALIAS)
return np.asarray(img)
# +
def load_image_dataset(path_dir, maxsize):
images = []
labels = []
os.chdir(path_dir)
for file in glob.glob("*.png"):
img = jpeg_to_8_bit_greyscale(file, maxsize)
if re.match('HourseMackerel*', file):
images.append(img)
labels.append(0)
elif re.match('RedMullet*', file):
images.append(img)
labels.append(1)
elif re.match('Shrimp*', file):
images.append(img)
labels.append(2)
return (np.asarray(images), np.asarray(labels))
# -
maxsize = 50, 50
(train_images, train_labels) = load_image_dataset('/media/jhonat/Home/documentos/UFRN/9-semestres-engcomp/INTELIGÊNCIA ARTIFICIAL/artificial-intelligence/machineLearning/deepLearning/dataset/peixes/Fish_Dataset/train', maxsize)
(test_images, test_labels) = load_image_dataset('/media/jhonat/Home/documentos/UFRN/9-semestres-engcomp/INTELIGÊNCIA ARTIFICIAL/artificial-intelligence/machineLearning/deepLearning/dataset/peixes/Fish_Dataset/test', maxsize)
class_names = ['HourseMackerel', 'RedeMullet', 'Shrimp']
train_images.shape
print(train_labels)
test_images.shape
print(test_labels)
def display_images(images, labels):
plt.figure(figsize=(10,10))
grid_size = min(50, len(images))
for i in range(grid_size):
plt.subplot(5, 5, i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[labels[i]])
# +
display_images(train_images, train_labels)
plt.show()
# +
train_images = train_images / 255.0
test_images = test_images / 255.0
# -
model = models.Sequential()
model.add(layers.Conv2D(64, (3, 3), activation='relu', input_shape=(50, 50, 3)))
model.add(layers.MaxPooling2D((4, 4)))
model.add(layers.Conv2D(32, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.summary()
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))
model.summary()
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
history = model.fit(train_images, train_labels, epochs=20,
validation_data=(test_images, test_labels))
# +
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
# -
print(history.history)
#PERFORM THE PREDICTION UPON THE DATA
predictions = model.predict(test_images)
#VISUAL EVALUATION OF THE MODEL
plt.figure(figsize=(10,10))
for i in range(50):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
if np.int(np.around(predictions[i][0])) >= 0 and np.int(np.around(predictions[i][0])) <= 9:
plt.imshow(test_images[i], cmap=plt.cm.binary)
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
t = np.argmax(predictions, axis=1)
plt.xlabel(class_names[t[i]])
plt.show()
model.save('model_fish')
|
machineLearning/deepLearning/.ipynb_checkpoints/CNN-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Math - Linear Algebra**
#
# *Linear Algebra is the branch of mathematics that studies [vector spaces](https://en.wikipedia.org/wiki/Vector_space) and linear transformations between vector spaces, such as rotating a shape, scaling it up or down, translating it (ie. moving it), etc.*
#
# *Machine Learning relies heavily on Linear Algebra, so it is essential to understand what vectors and matrices are, what operations you can perform with them, and how they can be useful.*
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/ageron/handson-ml2/blob/master/math_linear_algebra.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# </td>
# <td>
# <a target="_blank" href="https://kaggle.com/kernels/welcome?src=https://github.com/ageron/handson-ml2/blob/master/math_linear_algebra.ipynb"><img src="https://kaggle.com/static/images/open-in-kaggle.svg" /></a>
# </td>
# </table>
# # Vectors
# ## Definition
# A vector is a quantity defined by a magnitude and a direction. For example, a rocket's velocity is a 3-dimensional vector: its magnitude is the speed of the rocket, and its direction is (hopefully) up. A vector can be represented by an array of numbers called *scalars*. Each scalar corresponds to the magnitude of the vector with regards to each dimension.
#
# For example, say the rocket is going up at a slight angle: it has a vertical speed of 5,000 m/s, and also a slight speed towards the East at 10 m/s, and a slight speed towards the North at 50 m/s. The rocket's velocity may be represented by the following vector:
#
# **velocity** $= \begin{pmatrix}
# 10 \\
# 50 \\
# 5000 \\
# \end{pmatrix}$
#
# Note: by convention vectors are generally presented in the form of columns. Also, vector names are generally lowercase to distinguish them from matrices (which we will discuss below) and in bold (when possible) to distinguish them from simple scalar values such as ${meters\_per\_second} = 5026$.
#
# A list of N numbers may also represent the coordinates of a point in an N-dimensional space, so it is quite frequent to represent vectors as simple points instead of arrows. A vector with 1 element may be represented as an arrow or a point on an axis, a vector with 2 elements is an arrow or a point on a plane, a vector with 3 elements is an arrow or point in space, and a vector with N elements is an arrow or a point in an N-dimensional space… which most people find hard to imagine.
#
#
# ## Purpose
# Vectors have many purposes in Machine Learning, most notably to represent observations and predictions. For example, say we built a Machine Learning system to classify videos into 3 categories (good, spam, clickbait) based on what we know about them. For each video, we would have a vector representing what we know about it, such as:
#
# **video** $= \begin{pmatrix}
# 10.5 \\
# 5.2 \\
# 3.25 \\
# 7.0
# \end{pmatrix}$
#
# This vector could represent a video that lasts 10.5 minutes, but only 5.2% viewers watch for more than a minute, it gets 3.25 views per day on average, and it was flagged 7 times as spam. As you can see, each axis may have a different meaning.
#
# Based on this vector our Machine Learning system may predict that there is an 80% probability that it is a spam video, 18% that it is clickbait, and 2% that it is a good video. This could be represented as the following vector:
#
# **class_probabilities** $= \begin{pmatrix}
# 0.80 \\
# 0.18 \\
# 0.02
# \end{pmatrix}$
# ## Vectors in python
# In python, a vector can be represented in many ways, the simplest being a regular python list of numbers:
[10.5, 5.2, 3.25, 7.0]
# Since we plan to do quite a lot of scientific calculations, it is much better to use NumPy's `ndarray`, which provides a lot of convenient and optimized implementations of essential mathematical operations on vectors (for more details about NumPy, check out the [NumPy tutorial](tools_numpy.ipynb)). For example:
import numpy as np
video = np.array([10.5, 5.2, 3.25, 7.0])
video
# The size of a vector can be obtained using the `size` attribute:
video.size
# The $i^{th}$ element (also called *entry* or *item*) of a vector $\textbf{v}$ is noted $\textbf{v}_i$.
#
# Note that indices in mathematics generally start at 1, but in programming they usually start at 0. So to access $\textbf{video}_3$ programmatically, we would write:
video[2] # 3rd element
# ## Plotting vectors
# To plot vectors we will use matplotlib, so let's start by importing it (for details about matplotlib, check the [matplotlib tutorial](tools_matplotlib.ipynb)):
# %matplotlib inline
import matplotlib.pyplot as plt
# ### 2D vectors
# Let's create a couple very simple 2D vectors to plot:
# + jupyter={"outputs_hidden": true}
u = np.array([2, 5])
v = np.array([3, 1])
# -
# These vectors each have 2 elements, so they can easily be represented graphically on a 2D graph, for example as points:
x_coords, y_coords = zip(u, v)
plt.scatter(x_coords, y_coords, color=["r","b"])
plt.axis([0, 9, 0, 6])
plt.grid()
plt.show()
# Vectors can also be represented as arrows. Let's create a small convenience function to draw nice arrows:
def plot_vector2d(vector2d, origin=[0, 0], **options):
return plt.arrow(origin[0], origin[1], vector2d[0], vector2d[1],
head_width=0.2, head_length=0.3, length_includes_head=True,
**options)
# Now let's draw the vectors **u** and **v** as arrows:
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
plt.axis([0, 9, 0, 6])
plt.grid()
plt.show()
# ### 3D vectors
# Plotting 3D vectors is also relatively straightforward. First let's create two 3D vectors:
a = np.array([1, 2, 8])
b = np.array([5, 6, 3])
# Now let's plot them using matplotlib's `Axes3D`:
# +
from mpl_toolkits.mplot3d import Axes3D
subplot3d = plt.subplot(111, projection='3d')
x_coords, y_coords, z_coords = zip(a,b)
subplot3d.scatter(x_coords, y_coords, z_coords)
subplot3d.set_zlim3d([0, 9])
plt.show()
# -
# It is a bit hard to visualize exactly where in space these two points are, so let's add vertical lines. We'll create a small convenience function to plot a list of 3d vectors with vertical lines attached:
# +
def plot_vectors3d(ax, vectors3d, z0, **options):
for v in vectors3d:
x, y, z = v
ax.plot([x,x], [y,y], [z0, z], color="gray", linestyle='dotted', marker=".")
x_coords, y_coords, z_coords = zip(*vectors3d)
ax.scatter(x_coords, y_coords, z_coords, **options)
subplot3d = plt.subplot(111, projection='3d')
subplot3d.set_zlim([0, 9])
plot_vectors3d(subplot3d, [a,b], 0, color=("r","b"))
plt.show()
# -
# ## Norm
# The norm of a vector $\textbf{u}$, noted $\left \Vert \textbf{u} \right \|$, is a measure of the length (a.k.a. the magnitude) of $\textbf{u}$. There are multiple possible norms, but the most common one (and the only one we will discuss here) is the Euclidian norm, which is defined as:
#
# $\left \Vert \textbf{u} \right \| = \sqrt{\sum_{i}{\textbf{u}_i}^2}$
#
# We could implement this easily in pure python, recalling that $\sqrt x = x^{\frac{1}{2}}$
# +
def vector_norm(vector):
squares = [element**2 for element in vector]
return sum(squares)**0.5
print("||", u, "|| =")
vector_norm(u)
# -
# However, it is much more efficient to use NumPy's `norm` function, available in the `linalg` (**Lin**ear **Alg**ebra) module:
import numpy.linalg as LA
LA.norm(u)
# Let's plot a little diagram to confirm that the length of vector $\textbf{v}$ is indeed $\approx5.4$:
radius = LA.norm(u)
plt.gca().add_artist(plt.Circle((0,0), radius, color="#DDDDDD"))
plot_vector2d(u, color="red")
plt.axis([0, 8.7, 0, 6])
plt.grid()
plt.show()
# Looks about right!
# ## Addition
# Vectors of same size can be added together. Addition is performed *elementwise*:
print(" ", u)
print("+", v)
print("-"*10)
u + v
# Let's look at what vector addition looks like graphically:
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
plot_vector2d(v, origin=u, color="b", linestyle="dotted")
plot_vector2d(u, origin=v, color="r", linestyle="dotted")
plot_vector2d(u+v, color="g")
plt.axis([0, 9, 0, 7])
plt.text(0.7, 3, "u", color="r", fontsize=18)
plt.text(4, 3, "u", color="r", fontsize=18)
plt.text(1.8, 0.2, "v", color="b", fontsize=18)
plt.text(3.1, 5.6, "v", color="b", fontsize=18)
plt.text(2.4, 2.5, "u+v", color="g", fontsize=18)
plt.grid()
plt.show()
# Vector addition is **commutative**, meaning that $\textbf{u} + \textbf{v} = \textbf{v} + \textbf{u}$. You can see it on the previous image: following $\textbf{u}$ *then* $\textbf{v}$ leads to the same point as following $\textbf{v}$ *then* $\textbf{u}$.
#
# Vector addition is also **associative**, meaning that $\textbf{u} + (\textbf{v} + \textbf{w}) = (\textbf{u} + \textbf{v}) + \textbf{w}$.
# If you have a shape defined by a number of points (vectors), and you add a vector $\textbf{v}$ to all of these points, then the whole shape gets shifted by $\textbf{v}$. This is called a [geometric translation](https://en.wikipedia.org/wiki/Translation_%28geometry%29):
# +
t1 = np.array([2, 0.25])
t2 = np.array([2.5, 3.5])
t3 = np.array([1, 2])
x_coords, y_coords = zip(t1, t2, t3, t1)
plt.plot(x_coords, y_coords, "c--", x_coords, y_coords, "co")
plot_vector2d(v, t1, color="r", linestyle=":")
plot_vector2d(v, t2, color="r", linestyle=":")
plot_vector2d(v, t3, color="r", linestyle=":")
t1b = t1 + v
t2b = t2 + v
t3b = t3 + v
x_coords_b, y_coords_b = zip(t1b, t2b, t3b, t1b)
plt.plot(x_coords_b, y_coords_b, "b-", x_coords_b, y_coords_b, "bo")
plt.text(4, 4.2, "v", color="r", fontsize=18)
plt.text(3, 2.3, "v", color="r", fontsize=18)
plt.text(3.5, 0.4, "v", color="r", fontsize=18)
plt.axis([0, 6, 0, 5])
plt.grid()
plt.show()
# -
# Finally, subtracting a vector is like adding the opposite vector.
# ## Multiplication by a scalar
# Vectors can be multiplied by scalars. All elements in the vector are multiplied by that number, for example:
# +
print("1.5 *", u, "=")
1.5 * u
# -
# Graphically, scalar multiplication results in changing the scale of a figure, hence the name *scalar*. The distance from the origin (the point at coordinates equal to zero) is also multiplied by the scalar. For example, let's scale up by a factor of `k = 2.5`:
# +
k = 2.5
t1c = k * t1
t2c = k * t2
t3c = k * t3
plt.plot(x_coords, y_coords, "c--", x_coords, y_coords, "co")
plot_vector2d(t1, color="r")
plot_vector2d(t2, color="r")
plot_vector2d(t3, color="r")
x_coords_c, y_coords_c = zip(t1c, t2c, t3c, t1c)
plt.plot(x_coords_c, y_coords_c, "b-", x_coords_c, y_coords_c, "bo")
plot_vector2d(k * t1, color="b", linestyle=":")
plot_vector2d(k * t2, color="b", linestyle=":")
plot_vector2d(k * t3, color="b", linestyle=":")
plt.axis([0, 9, 0, 9])
plt.grid()
plt.show()
# -
# As you might guess, dividing a vector by a scalar is equivalent to multiplying by its multiplicative inverse (reciprocal):
#
# $\dfrac{\textbf{u}}{\lambda} = \dfrac{1}{\lambda} \times \textbf{u}$
# Scalar multiplication is **commutative**: $\lambda \times \textbf{u} = \textbf{u} \times \lambda$.
#
# It is also **associative**: $\lambda_1 \times (\lambda_2 \times \textbf{u}) = (\lambda_1 \times \lambda_2) \times \textbf{u}$.
#
# Finally, it is **distributive** over addition of vectors: $\lambda \times (\textbf{u} + \textbf{v}) = \lambda \times \textbf{u} + \lambda \times \textbf{v}$.
# ## Zero, unit and normalized vectors
# * A **zero-vector ** is a vector full of 0s.
# * A **unit vector** is a vector with a norm equal to 1.
# * The **normalized vector** of a non-null vector $\textbf{u}$, noted $\hat{\textbf{u}}$, is the unit vector that points in the same direction as $\textbf{u}$. It is equal to: $\hat{\textbf{u}} = \dfrac{\textbf{u}}{\left \Vert \textbf{u} \right \|}$
#
#
plt.gca().add_artist(plt.Circle((0,0),1,color='c'))
plt.plot(0, 0, "ko")
plot_vector2d(v / LA.norm(v), color="k")
plot_vector2d(v, color="b", linestyle=":")
plt.text(0.3, 0.3, "$\hat{u}$", color="k", fontsize=18)
plt.text(1.5, 0.7, "$u$", color="b", fontsize=18)
plt.axis([-1.5, 5.5, -1.5, 3.5])
plt.grid()
plt.show()
# ## Dot product
# ### Definition
# The dot product (also called *scalar product* or *inner product* in the context of the Euclidian space) of two vectors $\textbf{u}$ and $\textbf{v}$ is a useful operation that comes up fairly often in linear algebra. It is noted $\textbf{u} \cdot \textbf{v}$, or sometimes $⟨\textbf{u}|\textbf{v}⟩$ or $(\textbf{u}|\textbf{v})$, and it is defined as:
#
# $\textbf{u} \cdot \textbf{v} = \left \Vert \textbf{u} \right \| \times \left \Vert \textbf{v} \right \| \times cos(\theta)$
#
# where $\theta$ is the angle between $\textbf{u}$ and $\textbf{v}$.
#
# Another way to calculate the dot product is:
#
# $\textbf{u} \cdot \textbf{v} = \sum_i{\textbf{u}_i \times \textbf{v}_i}$
#
# ### In python
# The dot product is pretty simple to implement:
# +
def dot_product(v1, v2):
return sum(v1i * v2i for v1i, v2i in zip(v1, v2))
dot_product(u, v)
# -
# But a *much* more efficient implementation is provided by NumPy with the `dot` function:
np.dot(u,v)
# Equivalently, you can use the `dot` method of `ndarray`s:
u.dot(v)
# **Caution**: the `*` operator will perform an *elementwise* multiplication, *NOT* a dot product:
# +
print(" ",u)
print("* ",v, "(NOT a dot product)")
print("-"*10)
u * v
# -
# ### Main properties
# * The dot product is **commutative**: $\textbf{u} \cdot \textbf{v} = \textbf{v} \cdot \textbf{u}$.
# * The dot product is only defined between two vectors, not between a scalar and a vector. This means that we cannot chain dot products: for example, the expression $\textbf{u} \cdot \textbf{v} \cdot \textbf{w}$ is not defined since $\textbf{u} \cdot \textbf{v}$ is a scalar and $\textbf{w}$ is a vector.
# * This also means that the dot product is **NOT associative**: $(\textbf{u} \cdot \textbf{v}) \cdot \textbf{w} ≠ \textbf{u} \cdot (\textbf{v} \cdot \textbf{w})$ since neither are defined.
# * However, the dot product is **associative with regards to scalar multiplication**: $\lambda \times (\textbf{u} \cdot \textbf{v}) = (\lambda \times \textbf{u}) \cdot \textbf{v} = \textbf{u} \cdot (\lambda \times \textbf{v})$
# * Finally, the dot product is **distributive** over addition of vectors: $\textbf{u} \cdot (\textbf{v} + \textbf{w}) = \textbf{u} \cdot \textbf{v} + \textbf{u} \cdot \textbf{w}$.
# ### Calculating the angle between vectors
# One of the many uses of the dot product is to calculate the angle between two non-zero vectors. Looking at the dot product definition, we can deduce the following formula:
#
# $\theta = \arccos{\left ( \dfrac{\textbf{u} \cdot \textbf{v}}{\left \Vert \textbf{u} \right \| \times \left \Vert \textbf{v} \right \|} \right ) }$
#
# Note that if $\textbf{u} \cdot \textbf{v} = 0$, it follows that $\theta = \dfrac{π}{2}$. In other words, if the dot product of two non-null vectors is zero, it means that they are orthogonal.
#
# Let's use this formula to calculate the angle between $\textbf{u}$ and $\textbf{v}$ (in radians):
# +
def vector_angle(u, v):
cos_theta = u.dot(v) / LA.norm(u) / LA.norm(v)
return np.arccos(np.clip(cos_theta, -1, 1))
theta = vector_angle(u, v)
print("Angle =", theta, "radians")
print(" =", theta * 180 / np.pi, "degrees")
# -
# Note: due to small floating point errors, `cos_theta` may be very slightly outside of the $[-1, 1]$ interval, which would make `arccos` fail. This is why we clipped the value within the range, using NumPy's `clip` function.
# ### Projecting a point onto an axis
# The dot product is also very useful to project points onto an axis. The projection of vector $\textbf{v}$ onto $\textbf{u}$'s axis is given by this formula:
#
# $\textbf{proj}_{\textbf{u}}{\textbf{v}} = \dfrac{\textbf{u} \cdot \textbf{v}}{\left \Vert \textbf{u} \right \| ^2} \times \textbf{u}$
#
# Which is equivalent to:
#
# $\textbf{proj}_{\textbf{u}}{\textbf{v}} = (\textbf{v} \cdot \hat{\textbf{u}}) \times \hat{\textbf{u}}$
#
# +
u_normalized = u / LA.norm(u)
proj = v.dot(u_normalized) * u_normalized
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
plot_vector2d(proj, color="k", linestyle=":")
plt.plot(proj[0], proj[1], "ko")
plt.plot([proj[0], v[0]], [proj[1], v[1]], "b:")
plt.text(1, 2, "$proj_u v$", color="k", fontsize=18)
plt.text(1.8, 0.2, "$v$", color="b", fontsize=18)
plt.text(0.8, 3, "$u$", color="r", fontsize=18)
plt.axis([0, 8, 0, 5.5])
plt.grid()
plt.show()
# -
# # Matrices
# A matrix is a rectangular array of scalars (ie. any number: integer, real or complex) arranged in rows and columns, for example:
#
# \begin{bmatrix} 10 & 20 & 30 \\ 40 & 50 & 60 \end{bmatrix}
#
# You can also think of a matrix as a list of vectors: the previous matrix contains either 2 horizontal 3D vectors or 3 vertical 2D vectors.
#
# Matrices are convenient and very efficient to run operations on many vectors at a time. We will also see that they are great at representing and performing linear transformations such rotations, translations and scaling.
# ## Matrices in python
# In python, a matrix can be represented in various ways. The simplest is just a list of python lists:
[
[10, 20, 30],
[40, 50, 60]
]
# A much more efficient way is to use the NumPy library which provides optimized implementations of many matrix operations:
A = np.array([
[10,20,30],
[40,50,60]
])
A
# By convention matrices generally have uppercase names, such as $A$.
#
# In the rest of this tutorial, we will assume that we are using NumPy arrays (type `ndarray`) to represent matrices.
# ## Size
# The size of a matrix is defined by its number of rows and number of columns. It is noted $rows \times columns$. For example, the matrix $A$ above is an example of a $2 \times 3$ matrix: 2 rows, 3 columns. Caution: a $3 \times 2$ matrix would have 3 rows and 2 columns.
#
# To get a matrix's size in NumPy:
A.shape
# **Caution**: the `size` attribute represents the number of elements in the `ndarray`, not the matrix's size:
A.size
# ## Element indexing
# The number located in the $i^{th}$ row, and $j^{th}$ column of a matrix $X$ is sometimes noted $X_{i,j}$ or $X_{ij}$, but there is no standard notation, so people often prefer to explicitely name the elements, like this: "*let $X = (x_{i,j})_{1 ≤ i ≤ m, 1 ≤ j ≤ n}$*". This means that $X$ is equal to:
#
# $X = \begin{bmatrix}
# x_{1,1} & x_{1,2} & x_{1,3} & \cdots & x_{1,n}\\
# x_{2,1} & x_{2,2} & x_{2,3} & \cdots & x_{2,n}\\
# x_{3,1} & x_{3,2} & x_{3,3} & \cdots & x_{3,n}\\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# x_{m,1} & x_{m,2} & x_{m,3} & \cdots & x_{m,n}\\
# \end{bmatrix}$
#
# However in this notebook we will use the $X_{i,j}$ notation, as it matches fairly well NumPy's notation. Note that in math indices generally start at 1, but in programming they usually start at 0. So to access $A_{2,3}$ programmatically, we need to write this:
A[1,2] # 2nd row, 3rd column
# The $i^{th}$ row vector is sometimes noted $M_i$ or $M_{i,*}$, but again there is no standard notation so people often prefer to explicitely define their own names, for example: "*let **x**$_{i}$ be the $i^{th}$ row vector of matrix $X$*". We will use the $M_{i,*}$, for the same reason as above. For example, to access $A_{2,*}$ (ie. $A$'s 2nd row vector):
A[1, :] # 2nd row vector (as a 1D array)
# Similarly, the $j^{th}$ column vector is sometimes noted $M^j$ or $M_{*,j}$, but there is no standard notation. We will use $M_{*,j}$. For example, to access $A_{*,3}$ (ie. $A$'s 3rd column vector):
A[:, 2] # 3rd column vector (as a 1D array)
# Note that the result is actually a one-dimensional NumPy array: there is no such thing as a *vertical* or *horizontal* one-dimensional array. If you need to actually represent a row vector as a one-row matrix (ie. a 2D NumPy array), or a column vector as a one-column matrix, then you need to use a slice instead of an integer when accessing the row or column, for example:
A[1:2, :] # rows 2 to 3 (excluded): this returns row 2 as a one-row matrix
A[:, 2:3] # columns 3 to 4 (excluded): this returns column 3 as a one-column matrix
# ## Square, triangular, diagonal and identity matrices
# A **square matrix** is a matrix that has the same number of rows and columns, for example a $3 \times 3$ matrix:
#
# \begin{bmatrix}
# 4 & 9 & 2 \\
# 3 & 5 & 7 \\
# 8 & 1 & 6
# \end{bmatrix}
# An **upper triangular matrix** is a special kind of square matrix where all the elements *below* the main diagonal (top-left to bottom-right) are zero, for example:
#
# \begin{bmatrix}
# 4 & 9 & 2 \\
# 0 & 5 & 7 \\
# 0 & 0 & 6
# \end{bmatrix}
# Similarly, a **lower triangular matrix** is a square matrix where all elements *above* the main diagonal are zero, for example:
#
# \begin{bmatrix}
# 4 & 0 & 0 \\
# 3 & 5 & 0 \\
# 8 & 1 & 6
# \end{bmatrix}
# A **triangular matrix** is one that is either lower triangular or upper triangular.
# A matrix that is both upper and lower triangular is called a **diagonal matrix**, for example:
#
# \begin{bmatrix}
# 4 & 0 & 0 \\
# 0 & 5 & 0 \\
# 0 & 0 & 6
# \end{bmatrix}
#
# You can construct a diagonal matrix using NumPy's `diag` function:
np.diag([4, 5, 6])
# If you pass a matrix to the `diag` function, it will happily extract the diagonal values:
D = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
])
np.diag(D)
# Finally, the **identity matrix** of size $n$, noted $I_n$, is a diagonal matrix of size $n \times n$ with $1$'s in the main diagonal, for example $I_3$:
#
# \begin{bmatrix}
# 1 & 0 & 0 \\
# 0 & 1 & 0 \\
# 0 & 0 & 1
# \end{bmatrix}
#
# Numpy's `eye` function returns the identity matrix of the desired size:
np.eye(3)
# The identity matrix is often noted simply $I$ (instead of $I_n$) when its size is clear given the context. It is called the *identity* matrix because multiplying a matrix with it leaves the matrix unchanged as we will see below.
# ## Adding matrices
# If two matrices $Q$ and $R$ have the same size $m \times n$, they can be added together. Addition is performed *elementwise*: the result is also a $m \times n$ matrix $S$ where each element is the sum of the elements at the corresponding position: $S_{i,j} = Q_{i,j} + R_{i,j}$
#
# $S =
# \begin{bmatrix}
# Q_{11} + R_{11} & Q_{12} + R_{12} & Q_{13} + R_{13} & \cdots & Q_{1n} + R_{1n} \\
# Q_{21} + R_{21} & Q_{22} + R_{22} & Q_{23} + R_{23} & \cdots & Q_{2n} + R_{2n} \\
# Q_{31} + R_{31} & Q_{32} + R_{32} & Q_{33} + R_{33} & \cdots & Q_{3n} + R_{3n} \\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# Q_{m1} + R_{m1} & Q_{m2} + R_{m2} & Q_{m3} + R_{m3} & \cdots & Q_{mn} + R_{mn} \\
# \end{bmatrix}$
#
# For example, let's create a $2 \times 3$ matrix $B$ and compute $A + B$:
B = np.array([[1,2,3], [4, 5, 6]])
B
A
A + B
# **Addition is *commutative***, meaning that $A + B = B + A$:
B + A
# **It is also *associative***, meaning that $A + (B + C) = (A + B) + C$:
# +
C = np.array([[100,200,300], [400, 500, 600]])
A + (B + C)
# -
(A + B) + C
# ## Scalar multiplication
# A matrix $M$ can be multiplied by a scalar $\lambda$. The result is noted $\lambda M$, and it is a matrix of the same size as $M$ with all elements multiplied by $\lambda$:
#
# $\lambda M =
# \begin{bmatrix}
# \lambda \times M_{11} & \lambda \times M_{12} & \lambda \times M_{13} & \cdots & \lambda \times M_{1n} \\
# \lambda \times M_{21} & \lambda \times M_{22} & \lambda \times M_{23} & \cdots & \lambda \times M_{2n} \\
# \lambda \times M_{31} & \lambda \times M_{32} & \lambda \times M_{33} & \cdots & \lambda \times M_{3n} \\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# \lambda \times M_{m1} & \lambda \times M_{m2} & \lambda \times M_{m3} & \cdots & \lambda \times M_{mn} \\
# \end{bmatrix}$
#
# A more concise way of writing this is:
#
# $(\lambda M)_{i,j} = \lambda (M)_{i,j}$
#
# In NumPy, simply use the `*` operator to multiply a matrix by a scalar. For example:
2 * A
# Scalar multiplication is also defined on the right hand side, and gives the same result: $M \lambda = \lambda M$. For example:
A * 2
# This makes scalar multiplication **commutative**.
#
# It is also **associative**, meaning that $\alpha (\beta M) = (\alpha \times \beta) M$, where $\alpha$ and $\beta$ are scalars. For example:
2 * (3 * A)
(2 * 3) * A
# Finally, it is **distributive over addition** of matrices, meaning that $\lambda (Q + R) = \lambda Q + \lambda R$:
2 * (A + B)
2 * A + 2 * B
# ## Matrix multiplication
# So far, matrix operations have been rather intuitive. But multiplying matrices is a bit more involved.
#
# A matrix $Q$ of size $m \times n$ can be multiplied by a matrix $R$ of size $n \times q$. It is noted simply $QR$ without multiplication sign or dot. The result $P$ is an $m \times q$ matrix where each element is computed as a sum of products:
#
# $P_{i,j} = \sum_{k=1}^n{Q_{i,k} \times R_{k,j}}$
#
# The element at position $i,j$ in the resulting matrix is the sum of the products of elements in row $i$ of matrix $Q$ by the elements in column $j$ of matrix $R$.
#
# $P =
# \begin{bmatrix}
# Q_{11} R_{11} + Q_{12} R_{21} + \cdots + Q_{1n} R_{n1} &
# Q_{11} R_{12} + Q_{12} R_{22} + \cdots + Q_{1n} R_{n2} &
# \cdots &
# Q_{11} R_{1q} + Q_{12} R_{2q} + \cdots + Q_{1n} R_{nq} \\
# Q_{21} R_{11} + Q_{22} R_{21} + \cdots + Q_{2n} R_{n1} &
# Q_{21} R_{12} + Q_{22} R_{22} + \cdots + Q_{2n} R_{n2} &
# \cdots &
# Q_{21} R_{1q} + Q_{22} R_{2q} + \cdots + Q_{2n} R_{nq} \\
# \vdots & \vdots & \ddots & \vdots \\
# Q_{m1} R_{11} + Q_{m2} R_{21} + \cdots + Q_{mn} R_{n1} &
# Q_{m1} R_{12} + Q_{m2} R_{22} + \cdots + Q_{mn} R_{n2} &
# \cdots &
# Q_{m1} R_{1q} + Q_{m2} R_{2q} + \cdots + Q_{mn} R_{nq}
# \end{bmatrix}$
#
# You may notice that each element $P_{i,j}$ is the dot product of the row vector $Q_{i,*}$ and the column vector $R_{*,j}$:
#
# $P_{i,j} = Q_{i,*} \cdot R_{*,j}$
#
# So we can rewrite $P$ more concisely as:
#
# $P =
# \begin{bmatrix}
# Q_{1,*} \cdot R_{*,1} & Q_{1,*} \cdot R_{*,2} & \cdots & Q_{1,*} \cdot R_{*,q} \\
# Q_{2,*} \cdot R_{*,1} & Q_{2,*} \cdot R_{*,2} & \cdots & Q_{2,*} \cdot R_{*,q} \\
# \vdots & \vdots & \ddots & \vdots \\
# Q_{m,*} \cdot R_{*,1} & Q_{m,*} \cdot R_{*,2} & \cdots & Q_{m,*} \cdot R_{*,q}
# \end{bmatrix}$
#
# Let's multiply two matrices in NumPy, using `ndarray`'s `dot` method:
#
# $E = AD = \begin{bmatrix}
# 10 & 20 & 30 \\
# 40 & 50 & 60
# \end{bmatrix}
# \begin{bmatrix}
# 2 & 3 & 5 & 7 \\
# 11 & 13 & 17 & 19 \\
# 23 & 29 & 31 & 37
# \end{bmatrix} =
# \begin{bmatrix}
# 930 & 1160 & 1320 & 1560 \\
# 2010 & 2510 & 2910 & 3450
# \end{bmatrix}$
D = np.array([
[ 2, 3, 5, 7],
[11, 13, 17, 19],
[23, 29, 31, 37]
])
E = A.dot(D)
E
# Let's check this result by looking at one element, just to be sure: looking at $E_{2,3}$ for example, we need to multiply elements in $A$'s $2^{nd}$ row by elements in $D$'s $3^{rd}$ column, and sum up these products:
40*5 + 50*17 + 60*31
E[1,2] # row 2, column 3
# Looks good! You can check the other elements until you get used to the algorithm.
#
# We multiplied a $2 \times 3$ matrix by a $3 \times 4$ matrix, so the result is a $2 \times 4$ matrix. The first matrix's number of columns has to be equal to the second matrix's number of rows. If we try to multiply $D$ by $A$, we get an error because D has 4 columns while A has 2 rows:
try:
D.dot(A)
except ValueError as e:
print("ValueError:", e)
# This illustrates the fact that **matrix multiplication is *NOT* commutative**: in general $QR ≠ RQ$
#
# In fact, $QR$ and $RQ$ are only *both* defined if $Q$ has size $m \times n$ and $R$ has size $n \times m$. Let's look at an example where both *are* defined and show that they are (in general) *NOT* equal:
F = np.array([
[5,2],
[4,1],
[9,3]
])
A.dot(F)
F.dot(A)
# On the other hand, **matrix multiplication *is* associative**, meaning that $Q(RS) = (QR)S$. Let's create a $4 \times 5$ matrix $G$ to illustrate this:
G = np.array([
[8, 7, 4, 2, 5],
[2, 5, 1, 0, 5],
[9, 11, 17, 21, 0],
[0, 1, 0, 1, 2]])
A.dot(D).dot(G) # (AB)G
A.dot(D.dot(G)) # A(BG)
# It is also ***distributive* over addition** of matrices, meaning that $(Q + R)S = QS + RS$. For example:
(A + B).dot(D)
A.dot(D) + B.dot(D)
# The product of a matrix $M$ by the identity matrix (of matching size) results in the same matrix $M$. More formally, if $M$ is an $m \times n$ matrix, then:
#
# $M I_n = I_m M = M$
#
# This is generally written more concisely (since the size of the identity matrices is unambiguous given the context):
#
# $MI = IM = M$
#
# For example:
A.dot(np.eye(3))
np.eye(2).dot(A)
# **Caution**: NumPy's `*` operator performs elementwise multiplication, *NOT* a matrix multiplication:
A * B # NOT a matrix multiplication
# **The @ infix operator**
#
# Python 3.5 [introduced](https://docs.python.org/3/whatsnew/3.5.html#pep-465-a-dedicated-infix-operator-for-matrix-multiplication) the `@` infix operator for matrix multiplication, and NumPy 1.10 added support for it. If you are using Python 3.5+ and NumPy 1.10+, you can simply write `A @ D` instead of `A.dot(D)`, making your code much more readable (but less portable). This operator also works for vector dot products.
# +
import sys
print("Python version: {}.{}.{}".format(*sys.version_info))
print("Numpy version:", np.version.version)
# Uncomment the following line if your Python version is ≥3.5
# and your NumPy version is ≥1.10:
A @ D
# -
# Note: `Q @ R` is actually equivalent to `Q.__matmul__(R)` which is implemented by NumPy as `np.matmul(Q, R)`, not as `Q.dot(R)`. The main difference is that `matmul` does not support scalar multiplication, while `dot` does, so you can write `Q.dot(3)`, which is equivalent to `Q * 3`, but you cannot write `Q @ 3` ([more details](http://stackoverflow.com/a/34142617/38626)).
# ## Matrix transpose
# The transpose of a matrix $M$ is a matrix noted $M^T$ such that the $i^{th}$ row in $M^T$ is equal to the $i^{th}$ column in $M$:
#
# $ A^T =
# \begin{bmatrix}
# 10 & 20 & 30 \\
# 40 & 50 & 60
# \end{bmatrix}^T =
# \begin{bmatrix}
# 10 & 40 \\
# 20 & 50 \\
# 30 & 60
# \end{bmatrix}$
#
# In other words, ($A^T)_{i,j}$ = $A_{j,i}$
#
# Obviously, if $M$ is an $m \times n$ matrix, then $M^T$ is an $n \times m$ matrix.
#
# Note: there are a few other notations, such as $M^t$, $M′$, or ${^t}M$.
#
# In NumPy, a matrix's transpose can be obtained simply using the `T` attribute:
A
A.T
# As you might expect, transposing a matrix twice returns the original matrix:
A.T.T
# Transposition is distributive over addition of matrices, meaning that $(Q + R)^T = Q^T + R^T$. For example:
(A + B).T
A.T + B.T
# Moreover, $(Q \cdot R)^T = R^T \cdot Q^T$. Note that the order is reversed. For example:
(A.dot(D)).T
D.T.dot(A.T)
# A **symmetric matrix** $M$ is defined as a matrix that is equal to its transpose: $M^T = M$. This definition implies that it must be a square matrix whose elements are symmetric relative to the main diagonal, for example:
#
# \begin{bmatrix}
# 17 & 22 & 27 & 49 \\
# 22 & 29 & 36 & 0 \\
# 27 & 36 & 45 & 2 \\
# 49 & 0 & 2 & 99
# \end{bmatrix}
#
# The product of a matrix by its transpose is always a symmetric matrix, for example:
D.dot(D.T)
# ## Converting 1D arrays to 2D arrays in NumPy
# As we mentionned earlier, in NumPy (as opposed to Matlab, for example), 1D really means 1D: there is no such thing as a vertical 1D-array or a horizontal 1D-array. So you should not be surprised to see that transposing a 1D array does not do anything:
u
u.T
# We want to convert $\textbf{u}$ into a row vector before transposing it. There are a few ways to do this:
u_row = np.array([u])
u_row
# Notice the extra square brackets: this is a 2D array with just one row (ie. a 1x2 matrix). In other words it really is a **row vector**.
u[np.newaxis, :]
# This is quite explicit: we are asking for a new vertical axis, keeping the existing data as the horizontal axis.
u[np.newaxis]
# This is equivalent, but a little less explicit.
u[None]
# This is the shortest version, but you probably want to avoid it because it is unclear. The reason it works is that `np.newaxis` is actually equal to `None`, so this is equivalent to the previous version.
#
# Ok, now let's transpose our row vector:
u_row.T
# Great! We now have a nice **column vector**.
#
# Rather than creating a row vector then transposing it, it is also possible to convert a 1D array directly into a column vector:
u[:, np.newaxis]
# ## Plotting a matrix
# We have already seen that vectors can be represented as points or arrows in N-dimensional space. Is there a good graphical representation of matrices? Well you can simply see a matrix as a list of vectors, so plotting a matrix results in many points or arrows. For example, let's create a $2 \times 4$ matrix `P` and plot it as points:
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
x_coords_P, y_coords_P = P
plt.scatter(x_coords_P, y_coords_P)
plt.axis([0, 5, 0, 4])
plt.show()
# Of course we could also have stored the same 4 vectors as row vectors instead of column vectors, resulting in a $4 \times 2$ matrix (the transpose of $P$, in fact). It is really an arbitrary choice.
#
# Since the vectors are ordered, you can see the matrix as a path and represent it with connected dots:
plt.plot(x_coords_P, y_coords_P, "bo")
plt.plot(x_coords_P, y_coords_P, "b--")
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
# Or you can represent it as a polygon: matplotlib's `Polygon` class expects an $n \times 2$ NumPy array, not a $2 \times n$ array, so we just need to give it $P^T$:
from matplotlib.patches import Polygon
plt.gca().add_artist(Polygon(P.T))
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
# ## Geometric applications of matrix operations
# We saw earlier that vector addition results in a geometric translation, vector multiplication by a scalar results in rescaling (zooming in or out, centered on the origin), and vector dot product results in projecting a vector onto another vector, rescaling and measuring the resulting coordinate.
#
# Similarly, matrix operations have very useful geometric applications.
# ### Addition = multiple geometric translations
# First, adding two matrices together is equivalent to adding all their vectors together. For example, let's create a $2 \times 4$ matrix $H$ and add it to $P$, and look at the result:
# +
H = np.array([
[ 0.5, -0.2, 0.2, -0.1],
[ 0.4, 0.4, 1.5, 0.6]
])
P_moved = P + H
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_moved.T, alpha=0.3, color="r"))
for vector, origin in zip(H.T, P.T):
plot_vector2d(vector, origin=origin)
plt.text(2.2, 1.8, "$P$", color="b", fontsize=18)
plt.text(2.0, 3.2, "$P+H$", color="r", fontsize=18)
plt.text(2.5, 0.5, "$H_{*,1}$", color="k", fontsize=18)
plt.text(4.1, 3.5, "$H_{*,2}$", color="k", fontsize=18)
plt.text(0.4, 2.6, "$H_{*,3}$", color="k", fontsize=18)
plt.text(4.4, 0.2, "$H_{*,4}$", color="k", fontsize=18)
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
# -
# If we add a matrix full of identical vectors, we get a simple geometric translation:
# +
H2 = np.array([
[-0.5, -0.5, -0.5, -0.5],
[ 0.4, 0.4, 0.4, 0.4]
])
P_translated = P + H2
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_translated.T, alpha=0.3, color="r"))
for vector, origin in zip(H2.T, P.T):
plot_vector2d(vector, origin=origin)
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
# -
# Although matrices can only be added together if they have the same size, NumPy allows adding a row vector or a column vector to a matrix: this is called *broadcasting* and is explained in further details in the [NumPy tutorial](tools_numpy.ipynb). We could have obtained the same result as above with:
P + [[-0.5], [0.4]] # same as P + H2, thanks to NumPy broadcasting
# ### Scalar multiplication
# Multiplying a matrix by a scalar results in all its vectors being multiplied by that scalar, so unsurprisingly, the geometric result is a rescaling of the entire figure. For example, let's rescale our polygon by a factor of 60% (zooming out, centered on the origin):
# +
def plot_transformation(P_before, P_after, text_before, text_after, axis = [0, 5, 0, 4], arrows=False):
if arrows:
for vector_before, vector_after in zip(P_before.T, P_after.T):
plot_vector2d(vector_before, color="blue", linestyle="--")
plot_vector2d(vector_after, color="red", linestyle="-")
plt.gca().add_artist(Polygon(P_before.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_after.T, alpha=0.3, color="r"))
plt.text(P_before[0].mean(), P_before[1].mean(), text_before, fontsize=18, color="blue")
plt.text(P_after[0].mean(), P_after[1].mean(), text_after, fontsize=18, color="red")
plt.axis(axis)
plt.grid()
P_rescaled = 0.60 * P
plot_transformation(P, P_rescaled, "$P$", "$0.6 P$", arrows=True)
plt.show()
# -
# ### Matrix multiplication – Projection onto an axis
# Matrix multiplication is more complex to visualize, but it is also the most powerful tool in the box.
#
# Let's start simple, by defining a $1 \times 2$ matrix $U = \begin{bmatrix} 1 & 0 \end{bmatrix}$. This row vector is just the horizontal unit vector.
# + jupyter={"outputs_hidden": true}
U = np.array([[1, 0]])
# -
# Now let's look at the dot product $U \cdot P$:
U.dot(P)
# These are the horizontal coordinates of the vectors in $P$. In other words, we just projected $P$ onto the horizontal axis:
# +
def plot_projection(U, P):
U_P = U.dot(P)
axis_end = 100 * U
plot_vector2d(axis_end[0], color="black")
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
for vector, proj_coordinate in zip(P.T, U_P.T):
proj_point = proj_coordinate * U
plt.plot(proj_point[0][0], proj_point[0][1], "ro")
plt.plot([vector[0], proj_point[0][0]], [vector[1], proj_point[0][1]], "r--")
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
plot_projection(U, P)
# -
# We can actually project on any other axis by just replacing $U$ with any other unit vector. For example, let's project on the axis that is at a 30° angle above the horizontal axis:
# +
angle30 = 30 * np.pi / 180 # angle in radians
U_30 = np.array([[np.cos(angle30), np.sin(angle30)]])
plot_projection(U_30, P)
# -
# Good! Remember that the dot product of a unit vector and a matrix basically performs a projection on an axis and gives us the coordinates of the resulting points on that axis.
# ### Matrix multiplication – Rotation
# Now let's create a $2 \times 2$ matrix $V$ containing two unit vectors that make 30° and 120° angles with the horizontal axis:
#
# $V = \begin{bmatrix} \cos(30°) & \sin(30°) \\ \cos(120°) & \sin(120°) \end{bmatrix}$
angle120 = 120 * np.pi / 180
V = np.array([
[np.cos(angle30), np.sin(angle30)],
[np.cos(angle120), np.sin(angle120)]
])
V
# Let's look at the product $VP$:
print(V)
print(P)
V.dot(P)
# The first row is equal to $V_{1,*} P$, which is the coordinates of the projection of $P$ onto the 30° axis, as we have seen above. The second row is $V_{2,*} P$, which is the coordinates of the projection of $P$ onto the 120° axis. So basically we obtained the coordinates of $P$ after rotating the horizontal and vertical axes by 30° (or equivalently after rotating the polygon by -30° around the origin)! Let's plot $VP$ to see this:
P_rotated = V.dot(P)
plot_transformation(P, P_rotated, "$P$", "$VP$", [-2, 6, -2, 4], arrows=True)
plt.show()
# Matrix $V$ is called a **rotation matrix**.
# ### Matrix multiplication – Other linear transformations
# More generally, any linear transformation $f$ that maps n-dimensional vectors to m-dimensional vectors can be represented as an $m \times n$ matrix. For example, say $\textbf{u}$ is a 3-dimensional vector:
#
# $\textbf{u} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$
#
# and $f$ is defined as:
#
# $f(\textbf{u}) = \begin{pmatrix}
# ax + by + cz \\
# dx + ey + fz
# \end{pmatrix}$
#
# This transormation $f$ maps 3-dimensional vectors to 2-dimensional vectors in a linear way (ie. the resulting coordinates only involve sums of multiples of the original coordinates). We can represent this transformation as matrix $F$:
#
# $F = \begin{bmatrix}
# a & b & c \\
# d & e & f
# \end{bmatrix}$
#
# Now, to compute $f(\textbf{u})$ we can simply do a matrix multiplication:
#
# $f(\textbf{u}) = F \textbf{u}$
#
# If we have a matric $G = \begin{bmatrix}\textbf{u}_1 & \textbf{u}_2 & \cdots & \textbf{u}_q \end{bmatrix}$, where each $\textbf{u}_i$ is a 3-dimensional column vector, then $FG$ results in the linear transformation of all vectors $\textbf{u}_i$ as defined by the matrix $F$:
#
# $FG = \begin{bmatrix}f(\textbf{u}_1) & f(\textbf{u}_2) & \cdots & f(\textbf{u}_q) \end{bmatrix}$
#
# To summarize, the matrix on the left hand side of a dot product specifies what linear transormation to apply to the right hand side vectors. We have already shown that this can be used to perform projections and rotations, but any other linear transformation is possible. For example, here is a transformation known as a *shear mapping*:
F_shear = np.array([
[1, 1.5],
[0, 1]
])
plot_transformation(P, F_shear.dot(P), "$P$", "$F_{shear} P$",
axis=[0, 10, 0, 7])
plt.show()
# Let's look at how this transformation affects the **unit square**:
Square = np.array([
[0, 0, 1, 1],
[0, 1, 1, 0]
])
plot_transformation(Square, F_shear.dot(Square), "$Square$", "$F_{shear} Square$",
axis=[0, 2.6, 0, 1.8])
plt.show()
# Now let's look at a **squeeze mapping**:
F_squeeze = np.array([
[1.4, 0],
[0, 1/1.4]
])
plot_transformation(P, F_squeeze.dot(P), "$P$", "$F_{squeeze} P$",
axis=[0, 7, 0, 5])
plt.show()
# The effect on the unit square is:
plot_transformation(Square, F_squeeze.dot(Square), "$Square$", "$F_{squeeze} Square$",
axis=[0, 1.8, 0, 1.2])
plt.show()
# Let's show a last one: reflection through the horizontal axis:
F_reflect = np.array([
[1, 0],
[0, -1]
])
plot_transformation(P, F_reflect.dot(P), "$P$", "$F_{reflect} P$",
axis=[-2, 9, -4.5, 4.5])
plt.show()
# ## Matrix inverse
# Now that we understand that a matrix can represent any linear transformation, a natural question is: can we find a transformation matrix that reverses the effect of a given transformation matrix $F$? The answer is yes… sometimes! When it exists, such a matrix is called the **inverse** of $F$, and it is noted $F^{-1}$.
#
# For example, the rotation, the shear mapping and the squeeze mapping above all have inverse transformations. Let's demonstrate this on the shear mapping:
F_inv_shear = np.array([
[1, -1.5],
[0, 1]
])
P_sheared = F_shear.dot(P)
P_unsheared = F_inv_shear.dot(P_sheared)
plot_transformation(P_sheared, P_unsheared, "$P_{sheared}$", "$P_{unsheared}$",
axis=[0, 10, 0, 7])
plt.plot(P[0], P[1], "b--")
plt.show()
# We applied a shear mapping on $P$, just like we did before, but then we applied a second transformation to the result, and *lo and behold* this had the effect of coming back to the original $P$ (we plotted the original $P$'s outline to double check). The second transformation is the inverse of the first one.
#
# We defined the inverse matrix $F_{shear}^{-1}$ manually this time, but NumPy provides an `inv` function to compute a matrix's inverse, so we could have written instead:
F_inv_shear = LA.inv(F_shear)
F_inv_shear
# Only square matrices can be inversed. This makes sense when you think about it: if you have a transformation that reduces the number of dimensions, then some information is lost and there is no way that you can get it back. For example say you use a $2 \times 3$ matrix to project a 3D object onto a plane. The result may look like this:
plt.plot([0, 0, 1, 1, 0, 0.1, 0.1, 0, 0.1, 1.1, 1.0, 1.1, 1.1, 1.0, 1.1, 0.1],
[0, 1, 1, 0, 0, 0.1, 1.1, 1.0, 1.1, 1.1, 1.0, 1.1, 0.1, 0, 0.1, 0.1],
"r-")
plt.axis([-0.5, 2.1, -0.5, 1.5])
plt.show()
# Looking at this image, it is impossible to tell whether this is the projection of a cube or the projection of a narrow rectangular object. Some information has been lost in the projection.
#
# Even square transformation matrices can lose information. For example, consider this transformation matrix:
F_project = np.array([
[1, 0],
[0, 0]
])
plot_transformation(P, F_project.dot(P), "$P$", "$F_{project} \cdot P$",
axis=[0, 6, -1, 4])
plt.show()
# This transformation matrix performs a projection onto the horizontal axis. Our polygon gets entirely flattened out so some information is entirely lost and it is impossible to go back to the original polygon using a linear transformation. In other words, $F_{project}$ has no inverse. Such a square matrix that cannot be inversed is called a **singular matrix** (aka degenerate matrix). If we ask NumPy to calculate its inverse, it raises an exception:
try:
LA.inv(F_project)
except LA.LinAlgError as e:
print("LinAlgError:", e)
# Here is another example of a singular matrix. This one performs a projection onto the axis at a 30° angle above the horizontal axis:
angle30 = 30 * np.pi / 180
F_project_30 = np.array([
[np.cos(angle30)**2, np.sin(2*angle30)/2],
[np.sin(2*angle30)/2, np.sin(angle30)**2]
])
plot_transformation(P, F_project_30.dot(P), "$P$", "$F_{project\_30} \cdot P$",
axis=[0, 6, -1, 4])
plt.show()
# But this time, due to floating point rounding errors, NumPy manages to calculate an inverse (notice how large the elements are, though):
LA.inv(F_project_30)
# As you might expect, the dot product of a matrix by its inverse results in the identity matrix:
#
# $M \cdot M^{-1} = M^{-1} \cdot M = I$
#
# This makes sense since doing a linear transformation followed by the inverse transformation results in no change at all.
F_shear.dot(LA.inv(F_shear))
# Another way to express this is that the inverse of the inverse of a matrix $M$ is $M$ itself:
#
# $((M)^{-1})^{-1} = M$
LA.inv(LA.inv(F_shear))
# Also, the inverse of scaling by a factor of $\lambda$ is of course scaling by a factor or $\frac{1}{\lambda}$:
#
# $ (\lambda \times M)^{-1} = \frac{1}{\lambda} \times M^{-1}$
#
# Once you understand the geometric interpretation of matrices as linear transformations, most of these properties seem fairly intuitive.
#
# A matrix that is its own inverse is called an **involution**. The simplest examples are reflection matrices, or a rotation by 180°, but there are also more complex involutions, for example imagine a transformation that squeezes horizontally, then reflects over the vertical axis and finally rotates by 90° clockwise. Pick up a napkin and try doing that twice: you will end up in the original position. Here is the corresponding involutory matrix:
F_involution = np.array([
[0, -2],
[-1/2, 0]
])
plot_transformation(P, F_involution.dot(P), "$P$", "$F_{involution} \cdot P$",
axis=[-8, 5, -4, 4])
plt.show()
# Finally, a square matrix $H$ whose inverse is its own transpose is an **orthogonal matrix**:
#
# $H^{-1} = H^T$
#
# Therefore:
#
# $H \cdot H^T = H^T \cdot H = I$
#
# It corresponds to a transformation that preserves distances, such as rotations and reflections, and combinations of these, but not rescaling, shearing or squeezing. Let's check that $F_{reflect}$ is indeed orthogonal:
F_reflect.dot(F_reflect.T)
# ## Determinant
# The determinant of a square matrix $M$, noted $\det(M)$ or $\det M$ or $|M|$ is a value that can be calculated from its elements $(M_{i,j})$ using various equivalent methods. One of the simplest methods is this recursive approach:
#
# $|M| = M_{1,1}\times|M^{(1,1)}| - M_{2,1}\times|M^{(2,1)}| + M_{3,1}\times|M^{(3,1)}| - M_{4,1}\times|M^{(4,1)}| + \cdots ± M_{n,1}\times|M^{(n,1)}|$
#
# * Where $M^{(i,j)}$ is the matrix $M$ without row $i$ and column $j$.
#
# For example, let's calculate the determinant of the following $3 \times 3$ matrix:
#
# $M = \begin{bmatrix}
# 1 & 2 & 3 \\
# 4 & 5 & 6 \\
# 7 & 8 & 0
# \end{bmatrix}$
#
# Using the method above, we get:
#
# $|M| = 1 \times \left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right |
# - 2 \times \left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right |
# + 3 \times \left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right |$
#
# Now we need to compute the determinant of each of these $2 \times 2$ matrices (these determinants are called **minors**):
#
# $\left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | = 5 \times 0 - 6 \times 8 = -48$
#
# $\left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | = 4 \times 0 - 6 \times 7 = -42$
#
# $\left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right | = 4 \times 8 - 5 \times 7 = -3$
#
# Now we can calculate the final result:
#
# $|M| = 1 \times (-48) - 2 \times (-42) + 3 \times (-3) = 27$
# To get the determinant of a matrix, you can call NumPy's `det` function in the `numpy.linalg` module:
M = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 0]
])
LA.det(M)
# One of the main uses of the determinant is to *determine* whether a square matrix can be inversed or not: if the determinant is equal to 0, then the matrix *cannot* be inversed (it is a singular matrix), and if the determinant is not 0, then it *can* be inversed.
#
# For example, let's compute the determinant for the $F_{project}$, $F_{project\_30}$ and $F_{shear}$ matrices that we defined earlier:
LA.det(F_project)
# That's right, $F_{project}$ is singular, as we saw earlier.
LA.det(F_project_30)
# This determinant is suspiciously close to 0: it really should be 0, but it's not due to tiny floating point errors. The matrix is actually singular.
LA.det(F_shear)
# Perfect! This matrix *can* be inversed as we saw earlier. Wow, math really works!
# The determinant can also be used to measure how much a linear transformation affects surface areas: for example, the projection matrices $F_{project}$ and $F_{project\_30}$ completely flatten the polygon $P$, until its area is zero. This is why the determinant of these matrices is 0. The shear mapping modified the shape of the polygon, but it did not affect its surface area, which is why the determinant is 1. You can try computing the determinant of a rotation matrix, and you should also find 1. What about a scaling matrix? Let's see:
F_scale = np.array([
[0.5, 0],
[0, 0.5]
])
plot_transformation(P, F_scale.dot(P), "$P$", "$F_{scale} \cdot P$",
axis=[0, 6, -1, 4])
plt.show()
# We rescaled the polygon by a factor of 1/2 on both vertical and horizontal axes so the surface area of the resulting polygon is 1/4$^{th}$ of the original polygon. Let's compute the determinant and check that:
LA.det(F_scale)
# Correct!
#
# The determinant can actually be negative, when the transformation results in a "flipped over" version of the original polygon (eg. a left hand glove becomes a right hand glove). For example, the determinant of the `F_reflect` matrix is -1 because the surface area is preserved but the polygon gets flipped over:
LA.det(F_reflect)
# ## Composing linear transformations
# Several linear transformations can be chained simply by performing multiple dot products in a row. For example, to perform a squeeze mapping followed by a shear mapping, just write:
P_squeezed_then_sheared = F_shear.dot(F_squeeze.dot(P))
# Since the dot product is associative, the following code is equivalent:
P_squeezed_then_sheared = (F_shear.dot(F_squeeze)).dot(P)
# Note that the order of the transformations is the reverse of the dot product order.
#
# If we are going to perform this composition of linear transformations more than once, we might as well save the composition matrix like this:
# + jupyter={"outputs_hidden": true}
F_squeeze_then_shear = F_shear.dot(F_squeeze)
P_squeezed_then_sheared = F_squeeze_then_shear.dot(P)
# -
# From now on we can perform both transformations in just one dot product, which can lead to a very significant performance boost.
# What if you want to perform the inverse of this double transformation? Well, if you squeezed and then you sheared, and you want to undo what you have done, it should be obvious that you should unshear first and then unsqueeze. In more mathematical terms, given two invertible (aka nonsingular) matrices $Q$ and $R$:
#
# $(Q \cdot R)^{-1} = R^{-1} \cdot Q^{-1}$
#
# And in NumPy:
LA.inv(F_shear.dot(F_squeeze)) == LA.inv(F_squeeze).dot(LA.inv(F_shear))
# ## Singular Value Decomposition
# It turns out that any $m \times n$ matrix $M$ can be decomposed into the dot product of three simple matrices:
# * a rotation matrix $U$ (an $m \times m$ orthogonal matrix)
# * a scaling & projecting matrix $\Sigma$ (an $m \times n$ diagonal matrix)
# * and another rotation matrix $V^T$ (an $n \times n$ orthogonal matrix)
#
# $M = U \cdot \Sigma \cdot V^{T}$
#
# For example, let's decompose the shear transformation:
U, S_diag, V_T = LA.svd(F_shear) # note: in python 3 you can rename S_diag to Σ_diag
U
S_diag
# Note that this is just a 1D array containing the diagonal values of Σ. To get the actual matrix Σ, we can use NumPy's `diag` function:
S = np.diag(S_diag)
S
# Now let's check that $U \cdot \Sigma \cdot V^T$ is indeed equal to `F_shear`:
U.dot(np.diag(S_diag)).dot(V_T)
F_shear
# It worked like a charm. Let's apply these transformations one by one (in reverse order) on the unit square to understand what's going on. First, let's apply the first rotation $V^T$:
plot_transformation(Square, V_T.dot(Square), "$Square$", "$V^T \cdot Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
# Now let's rescale along the vertical and horizontal axes using $\Sigma$:
plot_transformation(V_T.dot(Square), S.dot(V_T).dot(Square), "$V^T \cdot Square$", "$\Sigma \cdot V^T \cdot Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
# Finally, we apply the second rotation $U$:
plot_transformation(S.dot(V_T).dot(Square), U.dot(S).dot(V_T).dot(Square),"$\Sigma \cdot V^T \cdot Square$", "$U \cdot \Sigma \cdot V^T \cdot Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
# And we can see that the result is indeed a shear mapping of the original unit square.
# ## Eigenvectors and eigenvalues
# An **eigenvector** of a square matrix $M$ (also called a **characteristic vector**) is a non-zero vector that remains on the same line after transformation by the linear transformation associated with $M$. A more formal definition is any vector $v$ such that:
#
# $M \cdot v = \lambda \times v$
#
# Where $\lambda$ is a scalar value called the **eigenvalue** associated to the vector $v$.
#
# For example, any horizontal vector remains horizontal after applying the shear mapping (as you can see on the image above), so it is an eigenvector of $M$. A vertical vector ends up tilted to the right, so vertical vectors are *NOT* eigenvectors of $M$.
#
# If we look at the squeeze mapping, we find that any horizontal or vertical vector keeps its direction (although its length changes), so all horizontal and vertical vectors are eigenvectors of $F_{squeeze}$.
#
# However, rotation matrices have no eigenvectors at all (except if the rotation angle is 0° or 180°, in which case all non-zero vectors are eigenvectors).
#
# NumPy's `eig` function returns the list of unit eigenvectors and their corresponding eigenvalues for any square matrix. Let's look at the eigenvectors and eigenvalues of the squeeze mapping matrix $F_{squeeze}$:
eigenvalues, eigenvectors = LA.eig(F_squeeze)
eigenvalues # [λ0, λ1, …]
eigenvectors # [v0, v1, …]
# Indeed the horizontal vectors are stretched by a factor of 1.4, and the vertical vectors are shrunk by a factor of 1/1.4=0.714…, so far so good. Let's look at the shear mapping matrix $F_{shear}$:
eigenvalues2, eigenvectors2 = LA.eig(F_shear)
eigenvalues2 # [λ0, λ1, …]
eigenvectors2 # [v0, v1, …]
# Wait, what!? We expected just one unit eigenvector, not two. The second vector is almost equal to $\begin{pmatrix}-1 \\ 0 \end{pmatrix}$, which is on the same line as the first vector $\begin{pmatrix}1 \\ 0 \end{pmatrix}$. This is due to floating point errors. We can safely ignore vectors that are (almost) colinear (ie. on the same line).
# ## Trace
# The trace of a square matrix $M$, noted $tr(M)$ is the sum of the values on its main diagonal. For example:
D = np.array([
[100, 200, 300],
[ 10, 20, 30],
[ 1, 2, 3],
])
np.trace(D)
# The trace does not have a simple geometric interpretation (in general), but it has a number of properties that make it useful in many areas:
# * $tr(A + B) = tr(A) + tr(B)$
# * $tr(A \cdot B) = tr(B \cdot A)$
# * $tr(A \cdot B \cdot \cdots \cdot Y \cdot Z) = tr(Z \cdot A \cdot B \cdot \cdots \cdot Y)$
# * $tr(A^T \cdot B) = tr(A \cdot B^T) = tr(B^T \cdot A) = tr(B \cdot A^T) = \sum_{i,j}X_{i,j} \times Y_{i,j}$
# * …
#
# It does, however, have a useful geometric interpretation in the case of projection matrices (such as $F_{project}$ that we discussed earlier): it corresponds to the number of dimensions after projection. For example:
np.trace(F_project)
# # What next?
# This concludes this introduction to Linear Algebra. Although these basics cover most of what you will need to know for Machine Learning, if you wish to go deeper into this topic there are many options available: Linear Algebra [books](http://linear.axler.net/), [Khan Academy](https://www.khanacademy.org/math/linear-algebra) lessons, or just [Wikipedia](https://en.wikipedia.org/wiki/Linear_algebra) pages.
|
math_linear_algebra.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import aiohttp
import asyncio
import time
from IPython.display import HTML
import pandas
from bs4 import BeautifulSoup
import datetime
# +
async def fetch(session, url):
async with session.get(url) as response:
return await response.text()
async def main(url):
async with aiohttp.ClientSession() as session:
html = await fetch(session, url)
return html
loop = asyncio.get_event_loop()
# -
html = loop.create_task(main('https://xappprod.aqmd.gov/aqdetail/AirQuality?AreaNumber=8'))
html.done()
tree = BeautifulSoup(html.result(), 'html.parser')
type(tree)
def parse_station_name(tree):
div = tree.find('div', attrs={'class': 'p20'})
station_label = div.find('label')
if station_label.text == 'Station Name:':
station_name = station_label.next_sibling
return station_name.strip()
parse_station_name(tree)
def parse_report_time(tree):
print(type(tree))
div = tree.find('div', attrs={'class': 'p20'})
time_label = div.find_all('label')[3].text.replace('\xa0', '')
time_label = time_label.split(': ')[1].lstrip()
time_label = time_label[:time_label.index('m')+1]
return datetime.datetime.strptime(time_label,'%m/%d/%Y %I:%M%p')
parse_report_time(tree)
# +
def parse_aqi(tree):
header = None
values = []
table = tree.find_all('table')[1]
for row in table.find_all('tr'):
parsed_row = []
if header is None:
for element in row.find_all('th'):
parsed_row.append(element.text.strip())
header = parsed_row
else:
for element in row.find_all('td'):
text = element.text.strip()
if len(text) > 0:
parsed_row.append(text)
values.append(parsed_row)
return pandas.DataFrame(values, columns=header)
parse_aqi(tree)
# +
def parse_standards(tree):
header = None
values = []
table = tree.find_all('table')[0]
for row in table.find_all('tr'):
parsed_row = []
for i, element in enumerate(row.find_all('td')):
parsed_row.append(element.text.strip())
if header is None:
header = parsed_row
else:
values.append(parsed_row)
return pandas.DataFrame(values, columns=header)
parse_standards(tree)
# -
https://xappprod.aqmd.gov/aqdetail/AirQuality/MonitoredData
forecast = loop.create_task(main('http://www.aqmd.gov/assets/forecast_today.txt'))
text = forecast.result()
def parse_forecast(text):
columns = ['id', 'name', 'O3-1hr', 'O3-8hr', 'CO', 'PM10', 'PM2.5', 'NO2', 'MAX AQI']
values = []
for line in [x.strip() for x in text.split('\r\n')]:
if len(line) > 0 and line[0].isdigit():
row = [
line[0:4].strip(),
line[4:28].strip(),
]
row.extend(line[28:].split())
values.append(row)
elif line.startswith('AIR QUALITY FORECAST'):
break
return pandas.DataFrame(values, columns=columns)
parse_forecast(text)
print(text)
max(3, 5, None)
html = loop.create_task(main('https://xappprod.aqmd.gov/aqdetail/AirQuality/MonitoredData?AreaNumber=8'))
html.done()
tree = BeautifulSoup(html.result())
HTML(str(tree.find_all('table')[0]))
|
explore-aqmd-urls.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Tutorial Goal
# This tutorial aims to show how RTApp performance metrics are computed
# and reported by the **perf analysis** module provided by LISA.
# +
import logging
reload(logging)
logging.basicConfig(
format='%(asctime)-9s %(levelname)-8s: %(message)s',
datefmt='%I:%M:%S')
# Enable logging at INFO level
logging.getLogger().setLevel(logging.INFO)
# -
# Execute this cell to report devlib debugging information
logging.getLogger('ssh').setLevel(logging.DEBUG)
# +
# Generate plots inline
# %pylab inline
import json
import os
# -
# # Collected results
# Let's use an example trace
res_dir = './example_rtapp'
trace_file = os.path.join(res_dir, 'trace.dat')
platform_file = os.path.join(res_dir, 'platform.json')
# !tree {res_dir}
# Inspect the JSON file used to run the application
with open('{}/simple_00.json'.format(res_dir), 'r') as fh:
rtapp_json = json.load(fh, )
logging.info('Generated RTApp JSON file:')
print json.dumps(rtapp_json, indent=4, sort_keys=True)
# # Trace inspection
# +
# Suport for FTrace events parsing and visualization
import trappy
# NOTE: The interactive trace visualization is available only if you run
# the workload to generate a new trace-file
trappy.plotter.plot_trace(res_dir)
# -
# # RTApp task performance plots
# +
# Support for performance analysis of RTApp workloads
from perf_analysis import PerfAnalysis
# Parse the RT-App generate log files to compute performance metrics
pa = PerfAnalysis(res_dir)
# For each task which has generated a logfile, plot its performance metrics
for task in pa.tasks():
pa.plotPerf(task, "Performance plots for task [{}] ".format(task))
|
ipynb/tutorial/07_PerfAnalysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="WWxwZ9wtnTZE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 222} outputId="b2a806cc-f097-492a-a73d-0ecd64530e1a" executionInfo={"status": "ok", "timestamp": 1548749286891, "user_tz": -180, "elapsed": 76854, "user": {"displayName": "<NAME>\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
# !apt-get install -y -qq software-properties-common python-software-properties module-init-tools
# !add-apt-repository -y ppa:alessandro-strada/ppa 2>&1 > /dev/null
# !apt-get update -qq 2>&1 > /dev/null
# !apt-get -y install -qq google-drive-ocamlfuse fuse
from google.colab import auth
auth.authenticate_user()
from oauth2client.client import GoogleCredentials
creds = GoogleCredentials.get_application_default()
import getpass
# !google-drive-ocamlfuse -headless -id={creds.client_id} -secret={creds.client_secret} < /dev/null 2>&1 | grep URL
vcode = getpass.getpass()
# !echo {vcode} | google-drive-ocamlfuse -headless -id={creds.client_id} -secret={creds.client_secret}
# + id="rLTv9uTWpVdd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="89ed48f6-0287-452d-c535-b64212a92e9a" executionInfo={"status": "ok", "timestamp": 1548749207868, "user_tz": -180, "elapsed": 3646, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
# !ls
# + id="tLsfwRLSnpq5" colab_type="code" colab={}
# !mkdir -p drive
# !google-drive-ocamlfuse drive
# + id="UcanFBNXnzxI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="c1638ebb-67a7-4c38-a1d5-e3d89f31fc04" executionInfo={"status": "ok", "timestamp": 1548749295840, "user_tz": -180, "elapsed": 3268, "user": {"displayName": "ef<NAME>\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
# cd drive/Houston
# + id="MJbSLHsfn1x4" colab_type="code" colab={}
import numpy as np
import cv2
# + id="c3Ilj3OSn4ZA" colab_type="code" colab={}
moment_hsi = []
for i in range(3):
for j in range(4):
img_path = "moment/pc_" + str(i) + "_" + str(j) + ".png"
img = cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)
moment_hsi.append(img)
moment_hsi = np.array(moment_hsi)
# + id="c2jsFjrZoOpm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="78d446ab-6bd3-4e52-e78d-69840e39759a" executionInfo={"status": "ok", "timestamp": 1548749313357, "user_tz": -180, "elapsed": 14741, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
print(moment_hsi.shape)
# + id="_MItUDSRoXxN" colab_type="code" colab={}
train_file_name = "labels/train.txt"
test_file_name = "labels/test.txt"
# + id="mDbvqF5BoZ0r" colab_type="code" colab={}
file = open(train_file_name)
triplets = file.read().split()
for i in range(0, len(triplets)):
triplets[i] = triplets[i].split(",")
train_array = np.array(triplets, dtype=int)
file.close()
file = open(test_file_name)
triplets = file.read().split()
for i in range(0, len(triplets)):
triplets[i] = triplets[i].split(",")
test_array = np.array(triplets, dtype=int)
file.close()
HEIGHT = train_array.shape[0]
WIDTH = train_array.shape[1]
# + id="gaWRCp74ock7" colab_type="code" colab={}
moment_hsi_train_data = []
moment_hsi_test_data = []
train_labels = []
test_labels = []
for i in range(HEIGHT):
for j in range(WIDTH):
if train_array[i, j] != 0:
moment_hsi_train_data.append(moment_hsi[:, i, j])
train_labels.append(train_array[i, j])
if test_array[i,j] != 0:
moment_hsi_test_data.append(moment_hsi[:, i, j])
test_labels.append(test_array[i, j])
# + id="ow_Tv9aJoj3c" colab_type="code" colab={}
moment_hsi_train_data = np.array(moment_hsi_train_data)
train_labels = np.array(train_labels)
test_labels = np.array(test_labels)
# + id="Yx9JfFuIooAt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 67} outputId="e3470249-1e1b-4c2c-db27-12f53a848101" executionInfo={"status": "ok", "timestamp": 1548749316913, "user_tz": -180, "elapsed": 9274, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
print(moment_hsi_train_data.shape)
print(train_labels.shape)
print(test_labels.shape)
# + id="sZKNt6rTos3O" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="de08d0ab-1d4b-4cdf-ba2f-82e42163ebb5" executionInfo={"status": "ok", "timestamp": 1548749318310, "user_tz": -180, "elapsed": 8470, "user": {"displayName": "ef<NAME>0131", "photoUrl": "", "userId": "05109145790333741779"}}
import keras
train_one_hot = keras.utils.to_categorical(train_labels-1)
test_one_hot = keras.utils.to_categorical(test_labels-1)
# + id="3rBaSfbCovDv" colab_type="code" colab={}
import keras
train_one_hot = keras.utils.to_categorical(train_labels-1)
test_one_hot = keras.utils.to_categorical(test_labels-1)
# + id="A_qVYbb1ox5q" colab_type="code" colab={}
HSI_PATCH_SIZE = 27
CONV1 = 500
CONV2 = 100
FC1 = 200
FC2 = 84
LEARNING_RATE = 0.005
# + id="4zRl2Zooozp_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="af764a5d-2d49-4e21-c0b5-069a8696b197" executionInfo={"status": "ok", "timestamp": 1548749318320, "user_tz": -180, "elapsed": 3410, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
padded_moment_hsi = np.lib.pad(moment_hsi, ((0,0), (HSI_PATCH_SIZE//2, HSI_PATCH_SIZE//2), (HSI_PATCH_SIZE//2,HSI_PATCH_SIZE//2)), 'reflect')
print(padded_moment_hsi.shape)
# + id="W-yvaHNdo4zi" colab_type="code" colab={}
def get_patches(data, patch_size, row, column):
offset = patch_size // 2
row_low = row - offset
row_high = row + offset
col_low = column - offset
col_high = column + offset
return data[0:, row_low:row_high + 1, col_low:col_high + 1].reshape(patch_size, patch_size, data.shape[0])
# + id="OfQnwbBfo68T" colab_type="code" colab={}
moment_hsi_train_patches = []
moment_hsi_test_patches = []
for i in range(HEIGHT):
for j in range(WIDTH):
if train_array[i, j] != 0:
moment_hsi_train_patches.append(get_patches(padded_moment_hsi, HSI_PATCH_SIZE, i+HSI_PATCH_SIZE//2, j+HSI_PATCH_SIZE//2))
if test_array[i, j] != 0:
moment_hsi_test_patches.append(get_patches(padded_moment_hsi, HSI_PATCH_SIZE, i+HSI_PATCH_SIZE//2, j+HSI_PATCH_SIZE//2))
# + id="9cptLoLoo_-q" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 50} outputId="1e5dc6c7-23ce-4617-ab8d-3aa87fe01e2b" executionInfo={"status": "ok", "timestamp": 1548749329358, "user_tz": -180, "elapsed": 987, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
moment_hsi_train_patches = np.array(moment_hsi_train_patches)
moment_hsi_test_patches = np.array(moment_hsi_test_patches)
print(moment_hsi_train_patches.shape)
print(moment_hsi_test_patches.shape)
# + id="ThQV0l52pFxK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 538} outputId="cca6e1f6-56a6-453f-de89-7d9a2da5e6be" executionInfo={"status": "ok", "timestamp": 1548749331839, "user_tz": -180, "elapsed": 1477, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
from tensorflow.python.keras.models import Sequential
from tensorflow.python.keras.layers import Conv2D, Dense, Flatten
from tensorflow.python.keras.layers import InputLayer
from tensorflow.python.keras.layers import MaxPooling2D
from tensorflow.python.keras.layers import BatchNormalization, Dropout
from tensorflow.python.keras.optimizers import Adam,SGD
BANDS = moment_hsi_train_patches.shape[3]
NUM_CLS = train_one_hot.shape[1]
BATCH_SIZE = 25
moment_hsi_model = Sequential()
moment_hsi_model.add(InputLayer(input_shape=(HSI_PATCH_SIZE, HSI_PATCH_SIZE, BANDS)))
moment_hsi_model.add(Conv2D(kernel_size=6, strides=2, filters=CONV1, padding='same', activation='relu', name='conv1'))
moment_hsi_model.add(BatchNormalization())
moment_hsi_model.add(MaxPooling2D(pool_size=2, strides=2))
moment_hsi_model.add(Conv2D(kernel_size=5, strides=2, filters=CONV2, padding='same', activation='relu', name='conv2'))
moment_hsi_model.add(BatchNormalization())
moment_hsi_model.add(MaxPooling2D(pool_size=2, strides=2))
moment_hsi_model.add(Flatten())
moment_hsi_model.add(Dense(FC1, activation='relu'))
moment_hsi_model.add(Dropout(0.6))
moment_hsi_model.add(Dense(FC2, activation='relu'))
moment_hsi_model.add(Dropout(0.4))
moment_hsi_model.add(Dense(NUM_CLS, activation='softmax'))
sgd = SGD(lr=LEARNING_RATE, decay=1e-6, momentum=0.9, nesterov=True)
moment_hsi_model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
moment_hsi_model.summary()
# + id="qb_swsXOpPIL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1697} outputId="9573bcd2-5d69-4f4f-94e4-7ffe3a043c7d" executionInfo={"status": "ok", "timestamp": 1548751339463, "user_tz": -180, "elapsed": 106035, "user": {"displayName": "ef<NAME>l\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
history = moment_hsi_model.fit(moment_hsi_train_patches, train_one_hot, batch_size=BATCH_SIZE, shuffle=True, epochs=50)
# + id="lAOB_vK0p6BB" colab_type="code" colab={}
from operator import truediv
def AA_andEachClassAccuracy(confusion_matrix):
counter = confusion_matrix.shape[0]
list_diag = np.diag(confusion_matrix)
list_raw_sum = np.sum(confusion_matrix, axis=1)
each_acc = np.nan_to_num(truediv(list_diag, list_raw_sum))
average_acc = np.mean(each_acc)
return each_acc, average_acc
# + id="Xbt_GRsip-s5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 370} outputId="770bbe4a-2979-43bf-d004-31c61363a3ea" executionInfo={"status": "ok", "timestamp": 1548751676650, "user_tz": -180, "elapsed": 3529, "user": {"displayName": "efkan durakl\u0131", "photoUrl": "", "userId": "05109145790333741779"}}
test_cls = test_labels - 1
prediction = moment_hsi_model.predict(moment_hsi_test_patches).argmax(axis=-1)
from sklearn import metrics, preprocessing
overall_acc = metrics.accuracy_score(prediction, test_cls)
kappa = metrics.cohen_kappa_score(prediction, test_cls)
confusion_matrix = metrics.confusion_matrix(prediction, test_cls)
each_acc, average_acc = AA_andEachClassAccuracy(confusion_matrix)
print("Overall Accuracy of training sapmles : ",overall_acc)
print("Average Accuracy of training samples : ",average_acc)
print("Kappa statistics of training samples : ",kappa)
print("Each class accuracy of training samples : ", each_acc)
print("Confusion matrix :", confusion_matrix)
# + id="3SBUuCg9rLkB" colab_type="code" colab={}
moment_hsi_model.save_weights('Models/moment_hsi_model_weights.h5')
|
Part2/moment_train/hsi.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/MaxwellHarper/HarmonySpace/blob/master/TEST_Zero_Shot_Pipeline.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="yTBP_QYuu6tc" colab_type="code" colab={}
# !pip install git+https://github.com/huggingface/transformers.git
# + id="TiU_ES5tzpMH" colab_type="code" colab={}
from transformers import pipeline
# + id="spkccRiv0CB3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 89} outputId="8378c6c4-4823-4709-f6ff-443abaa86124"
classifier = pipeline("zero-shot-classification")
# + [markdown] id="xWiovVJG9ei_" colab_type="text"
# We can use this pipeline by passing in a sequence and a list of candidate labels. The pipeline assumes by default that only one of the candidate labels is true, returning a list of scores for each label which add up to 1.
# + id="hkfE6NRA0Dzy" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 69} outputId="bc2583cd-aae1-46f5-ad39-a0f0078477c5"
sequence = "Who are you voting for in 2020?"
candidate_labels = ["politics", "public health", "economics"]
classifier(sequence, candidate_labels)
# + [markdown] id="PGXwxxyn9nOC" colab_type="text"
# To do multi-class classification, simply pass `multi_class=True`. In this case, the scores will be independent, but each will fall between 0 and 1.
# + id="ZvZeVb2h5RX0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 121} outputId="03b248fb-d08a-4699-f2bb-6ded805a7bb8"
sequence = "Who are you voting for in 2020?"
candidate_labels = ["politics", "public health", "economics", "elections"]
classifier(sequence, candidate_labels, multi_class=True)
# + [markdown] id="lLLeDT1r9-yQ" colab_type="text"
# Here's an example of sentiment classification:
# + id="f7AF53Wl5f8W" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 69} outputId="fd1c8c8c-b68b-440e-bc94-0d3c7dd8d283"
sequence = "I hated this movie. The acting sucked."
candidate_labels = ["positive", "negative"]
classifier(sequence, candidate_labels)
# + [markdown] id="uSoBpCpV6k4s" colab_type="text"
# So how does this method work?
#
# The underlying model is trained on the task of Natural Language Inference (NLI), which takes in two sequences and determines whether they contradict each other, entail each other, or neither.
#
# This can be adapted to the task of zero-shot classification by treating the sequence which we want to classify as one NLI sequence (called the premise) and turning a candidate label into the other (the hypothesis). If the model predicts that the constructed premise _entails_ the hypothesis, then we can take that as a prediction that the label applies to the text. Check out [this blog post](https://joeddav.github.io/blog/2020/05/29/ZSL.html) for a more detailed explanation.
#
# By default, the pipeline turns labels into hypotheses with the template `This example is {class_name}.`. This works well in many settings, but you can also customize this for your specific setting. Let's add another review to our above sentiment classification example that's a bit more challenging:
# + id="5yLx3pRr5xQA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 121} outputId="725212c9-4759-4457-ef4f-dc9b5ae20d84"
sequences = [
"I hated this movie. The acting sucked.",
"This movie didn't quite live up to my high expectations, but overall I still really enjoyed it."
]
candidate_labels = ["positive", "negative"]
classifier(sequences, candidate_labels)
# + [markdown] id="CfrpyGWM782R" colab_type="text"
# The second example is a bit harder. Let's see if we can improve the results by using a hypothesis template which is more specific to the setting of review sentiment analysis. Instead of the default, `This example is {}.`, we'll use, `The sentiment of this review is {}.` (where `{}` is replaced with the candidate class name)
# + id="kqx5hp7X8XNA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 121} outputId="73a84935-de37-4f2c-abdc-46dacd6614ea"
sequences = [
"I hated this movie. The acting sucked.",
"This movie didn't quite live up to my high expectations, but overall I still really enjoyed it."
]
candidate_labels = ["positive", "negative"]
hypothesis_template = "The sentiment of this review is {}."
classifier(sequences, candidate_labels, hypothesis_template=hypothesis_template)
# + [markdown] id="iArbRAe781-_" colab_type="text"
# By providing a more precise hypothesis template, we are able to see a more accurate classification of the second review.
#
# > Note that sentiment classification is used here just as an illustrative example. The [Hugging Face Model Hub](https://huggingface.co/models?filter=text-classification) has a number of models trained specifically on sentiment tasks which can be used instead.
|
TEST_Zero_Shot_Pipeline.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TensorFlow & Keras - Basics of Deep Learning
# ### Most importantly... resources
#
# https://www.tensorflow.org/api_docs
#
# https://keras.io/
#
# https://www.tensorflow.org/tutorials/
#
# https://www.google.com
# ## TF overview
#
# * #### "End-to-end machine learning platform"
#
# - Not the only one! Check out PyTorch, Theano, Cognitive Toolkit.
#
# * #### Integrates with high-level APIs like Keras
# * #### Plays nice with Pandas
# * #### Makes deep learning *fast* and *easy* *
# *<sup>"easy"</sup>
#
# ## Tasks for TensorFlow:
#
# * #### Regression
# - Predict house prices
# - Predict drug metabolic rates
# - Predict stock trends *
#
# *<sup>this is super hard</sup>
#
#
#
# * #### Classification
# - Cat or dog?
# - Malignant or benign cancer from images
# 
# <span style="font-size:0.75em;">Google AI Blog: Diabetic Retinopathy</span>
#
#
#
# * #### Dimensionality reduction
# - Visualize high-dimensional data in 2 or 3-D space
# - Compress representations for successive ML
#
#
#
# * #### Generative models
# - Create new molecules with desirable properties
# - Artificially enhance image resolution
# 
# <span style="font-size:0.75em;">Kadurin et al., 2017</span>
#
#
# * #### Reinforcement learning
# - Can't beat your friends at chess? Make your computer do it
#
#
#
# * #### Much more...
# - Generic math
# - Probabilistic programming with TFP
# - Automatic differentiation
# - ...
#
#
# ## Let's Regress
#
# ### Imports!
import numpy as np
import pandas as pd
# Name a more iconic duo, I'll wait
#
# #### New imports -- TF and Keras
import keras
import tensorflow as tf
# Check our versions for good measure -- these programs may have very different behavior version-to-version
print(keras.__version__)
print(tf.__version__)
# #### Loading in housing data as with SKLearn
data = pd.read_csv('kc_house_data.csv')
data
# +
column_selection = ["bedrooms","bathrooms","sqft_living","sqft_lot",
"floors","condition","grade","sqft_above",
"sqft_basement","sqft_living15","sqft_lot15",
"lat", "long","yr_built","yr_renovated","waterfront"]
selected_feature = np.array(data[column_selection])
price = np.array(data["price"])
selected_feature_train = selected_feature[:20000]
price_train = price[:20000]
selected_feature_test = selected_feature[20000:]
price_test = price[20000:]
# -
def score(y,y_pred):
return np.mean(np.abs(y-y_pred)/y)
model = keras.Sequential()
# +
input_len = len(column_selection)
model.add(keras.layers.Dense(50, input_dim=input_len, activation='relu'))
model.add(keras.layers.Dense(50, activation='relu'))
model.add(keras.layers.Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
# -
history = model.fit(selected_feature_train, price_train, epochs=50, batch_size=128)
preds = model.predict(selected_feature_test)
score(preds, price_test)
# ### Like SKLearn, it's easy to train and evaluate simple models.
# #### ... but we should try to do better
# ## Practical Deep Learning -- What you need to know
# ### Train, Validation, Test:
# * Optimize parameters with Train (weights, biases)
# * Optimize hyperparameters with Validation (layer width & depth, activation functions, etc.)
# * Optimize NOTHING with Test
# +
# Split out a validation set for hyperparameter optimization
selected_feature_train = selected_feature[:18000]
price_train = price[:18000]
selected_feature_val = selected_feature[18000:20000]
price_val = price[18000:20000]
selected_feature_test = selected_feature[20000:]
price_test = price[20000:]
# -
# #### In the future, try better validation schemes like [k-fold cross validation](https://chrisalbon.com/deep_learning/keras/k-fold_cross-validating_neural_networks/), though 80/20 or 90/10 train/val like this works in a pinch
# ### Try a hyperparameter optimization:
#
# ### Try three activation functions to use for dense layers in the neural network above. Save the model that achieves the best validation loss
# #### Hint: [activation functions](http://letmegooglethat.com/?q=keras+activation+functions)
#
# #### Hint: `model.fit` has argument "`validation_data`" which takes a tuple of features and targets
#
# #### Hint: Use `model.save("filename.h5")` to save a model locally. If you want to use it later, just call `keras.models.load_model("filename.h5")`
# +
# For easy looping, define neural network model as a function
def nn_model(optimizer='adam',
activation='relu',
layers=[20,20],
loss='mean_squared_error'):
model = keras.Sequential()
model.add(keras.layers.Dense(50, input_dim=input_len, activation=activ))
model.add(keras.layers.Dense(50, activation=activ))
model.add(keras.layers.Dense(1))
model.compile(loss='mean_absolute_error', optimizer='adam')
return model
# +
best_score = 1000.0 # bad
# loop over chosen activation functions, train, evaluate on validation
for activ in ['sigmoid', 'tanh', 'relu']:
model = nn_model(activation=activ)
history = model.fit(selected_feature_train, price_train,
epochs=50, batch_size=128,
validation_data=(selected_feature_val, price_val))
model_score = score(model.predict(selected_feature_val), price_val)
if model_score < best_score:
best_score = model_score
best_activ = activ
best_model = model
best_train = history
print(f"BEST ACTIVATION FUNCTION {best_activ} WITH SCORE {best_score}")
best_model.save("awesome_model.h5")
# -
# ### Visualize your training:
# +
import matplotlib.pyplot as plt
# plot loss during training
def plot_loss(hist):
# %matplotlib inline
plt.title('Training Curve')
plt.plot(hist.history['loss'], label='train')
plt.plot(hist.history['val_loss'], label='validation')
plt.xlabel("Epochs")
plt.ylabel("Mean squared error")
plt.legend()
plt.show()
plot_loss(best_train)
# -
#
#
# ### Standardize your features:
# * Typically assumes normally distributed feature, shifting mean to 0 and standard deviation to 1
# * In theory does not matter for neural networks
# * In practice tends to matter for neural networks
# * Scale if using:
# - Logistic regression
# - Support vector machines
# - Perceptrons
# - Neural networks
# - Principle component analysis
# * Don't bother if using:
# - "Forest" methods
# - Naive Bayes
# +
from sklearn.preprocessing import StandardScaler
# Instantiate StandardScaler
in_scaler = StandardScaler()
# Fit scaler to the training set and perform the transformation
selected_feature_train = in_scaler.fit_transform(selected_feature_train)
# Use the fitted scaler to transform validation and test features
selected_feature_val = in_scaler.transform(selected_feature_val)
selected_feature_test = in_scaler.transform(selected_feature_test)
# Check appropriate scaling
print(np.mean(selected_feature_train[:,0]))
print(np.std(selected_feature_train[:,0]))
print(np.mean(selected_feature_val[:,0]))
print(np.std(selected_feature_val[:,0]))
print(np.mean(selected_feature_test[:,0]))
print(np.std(selected_feature_test[:,0]))
# +
model = nn_model()
model.compile(loss='mean_squared_error', optimizer='adam')
history = model.fit(selected_feature_train, price_train,
epochs=100, batch_size=128,
validation_data=(selected_feature_val, price_val))
model_score = score(model.predict(selected_feature_val), price_val)
print(model_score)
plot_loss(history)
# -
# #### In the future, consider standardizing outputs as well
#
# ### Regularize:
# * Heavily parameterized models like neural networks are prone to overfitting
# * Popular off-the-shelf tools exist to regularize models and prevent overfitting:
# - L2 regularization (weight decay)
# - Dropout
# - Batch normalization
#
# #### These tools come as standard Keras/TF layers!
# `model.add(keras.layers.Dropout(rate)`
# `model.add(keras.layers.ActivityRegularization(l1=0.0, l2=0.0)`
# `model.add(keras.layers.BatchNormalization())`
# ### Early stopping and model checkpointing:
# #### It's unlikely the last iteration is the best, and who knows how long until the thing is converged. Just grab the best validation error.
# +
# Set callback functions to early stop training and save the
# best model so far
from keras.callbacks import EarlyStopping, ModelCheckpoint
callbacks = [EarlyStopping(monitor='val_loss', patience=5),
ModelCheckpoint(filepath='best_model.h5',
monitor='val_loss',
save_best_only=True,
verbose=1)]
model = nn_model(layers=[20,20,20])
model.compile(loss='mean_squared_error', optimizer='adam')
history = model.fit(selected_feature_train, price_train,
epochs=400, callbacks=callbacks, batch_size=128,
validation_data=(selected_feature_val, price_val))
model_score = score(model.predict(selected_feature_val), price_val)
print(f"Model score: {model_score}")
plot_loss(history)
# -
# ### You don't have to remember these resources because they're here when you need them
# https://www.tensorflow.org/api_docs
#
# https://keras.io/
#
# https://www.tensorflow.org/tutorials/
#
# https://www.google.com
#
# ### Don't trust me, trust your validation errors
# ### Don't look at your test set until you're actually going to test
|
Day03/deep_learning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ---
# layout: post
# title: "Basics of panda"
# categories: panda
# background: '/img/posts/panda/cheetSheet.png'
# ---
#
#
# [Taken reference from ](https://jakevdp.github.io/PythonDataScienceHandbook/)
# <br>
# <a href="\img\posts\numpy\cheetSheet.pdf" download>Download CheetSheet</a>
#
#
# - To display all the content of pandas documantation - pd.<tab>
# - pandas can be thought enhanced version of numpy
# - Three pandas data structure
# - series
# - data frame
# - index
# # Recap of numpy array
# These included indexing (e.g., arr[2, 1]), slicing (e.g., arr[:, 1:5]), masking (e.g., arr[arr > 0]), fancy indexing (e.g., arr[0, [1, 5]]),
# ## Series
# - Series is one dimensional index array
#
# - difference between np array and panda series
# - the difference is of index, np has implicit index always in integer . while series can have user defined index.
#
# - Series is like dictionary
# as dictionary has key value pair , panda series has index value pair
#
# - syntax
# - pd.Series(data, index=index)
#
# - in series , index can be user defined but they will implicity have integer index also , can be used by iloc func
#
# - First, the loc attribute allows indexing and slicing that always references the explicit index:
# - The iloc attribute allows indexing and slicing that always references the implicit Python-style index:
# +
import pandas as pd
import numpy as np
data = pd.Series([11,12,13,14,15], index=['a','b','c','d','e'])
print(data)
print(type(data))
# +
# how to check value of a series
print('value of a series \n', data.values)
print("\n"*4)
# check index of a series
print('index of a series \n',data.index)
print("\n"*4)
# accessing data using index
print('access data using index \n',data['b'])
print("\n"*4)
# data slicing
print('data slicing \n',data['b':'e'])
# slicing by explicit index
print(data['a':'c'])
# slicing by implicit integer index
print(data[0:2])
# masking
print(data[(data > 13) & (data < 18)])
# fancy indexing
print(data[['a', 'e']])
# +
# user defind index
data = pd.Series([0.25, 0.5, 0.75, 1.0],
index=['a', 'b', 'c', 'd'])
print(data)
# a panda series is more like dictionary
population_dict = {'California': 38332521,
'Texas': 26448193,
'New York': 19651127,
'Florida': 19552860,
'Illinois': 12882135}
population = pd.Series(population_dict)
print(population)
print("\n"*4)
print(population.index)
# using loc attribute
print('data at index california :',population.loc['California'])
print("\n"*4)
# using iloc attribute
print('data at using slixing \n',population.iloc[1:3])
# -
# # Dataframe
# - If a Series is an analog of a one-dimensional array with flexible indices,
# - DataFrame as a sequence of aligned Series objects. Here, by "aligned" we mean that they share the same index.
#
#
#
# - Index is immutable
#
#
# - lets say we want to compare two data frame based on some column , we can change them to index and get union and intersection of them using | and ^ operator
#COnstruction from single series object
population = pd.Series(np.random.randint(10, size = 5))
print(pd.DataFrame(population, columns=['population']))
# +
# Construction of series using two dimensional array
arr= np.random.randint(12, size =12).reshape(4,3)
x = pd.DataFrame(arr, index= ['a','b','c','d'])
print(x)
print('\n'*4)
x = pd.DataFrame(arr, index= ['a','b','c','d'], columns = ['col1', 'col2','col3'])
print(x)
# +
# access index
ind = x.index
print(x.index , end='\n'*3)
print(x.index[1], end='\n'*3)
print(ind.size, ind.shape, ind.ndim, ind.dtype)
# -
ind[1] = 0
|
_drafts/2021-02-01-Basic-of-pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matplotlib: Beyond the basics
#
# ## Status and plan for today
#
# By now you know the basics of:
#
# * Numpy array creation and manipulation.
# * Display of data in numpy arrays, sufficient for interactive exploratory work.
#
# Hopefully after this notebook you will:
#
# * Know how to polish those figures to the point where they can go to a journal.
# * Understand matplotlib's internal model enough to:
# - know where to look for knobs to fine-tune
# - better understand the help and examples online
# - use it as a development platform for complex visualization
#
# ## Resources
#
# * The [official matplotlib documentation](https://matplotlib.org/contents.html) is detailed and comprehensive. Particularly useful sections are:
# - The [gallery](https://matplotlib.org/gallery/index.html).
# - The [high level overview of its dual APIs, `pyplot` and object-oriented](https://matplotlib.org/api/pyplot_summary.html).
# - The [topical tutorials](https://matplotlib.org/tutorials/index.html).
#
#
#
# * A detailed [tutorial](https://www.labri.fr/perso/nrougier/teaching/matplotlib) by <NAME>, similar in style to the ones we saw for Numpy.
# * The fantastic [Python Graph Gallery](https://python-graph-gallery.com), which provides a large collection of plots with emphasis on statistical visualizations. It uses [Seaborn](https://seaborn.pydata.org) extensively.
# * In this tutorial we'll focus on "raw" matplotlib, but for a wide variety of statistical visualization tasks, using Seaborn makes life much easier. We'll dive into its [tutorial](https://seaborn.pydata.org/tutorial.html) later on.
#
# ## Matplotlib's main APIs: ``pyplot`` and object-oriented
#
# Matplotlib is a library that can be thought of as having two main ways of being
# used:
#
# - via ``pyplot`` calls, as a high-level, matlab-like library that automatically
# manages details like figure creation.
#
# - via its internal object-oriented structure, that offers full control over all
# aspects of the figure, at the cost of slightly more verbose calls for the
# common case.
#
# The pyplot api:
#
# - Easiest to use.
# - Sufficient for simple and moderately complex plots.
# - Does not offer complete control over all details.
#
# Before we look at our first simple example, we must activate matplotlib support in the notebook:
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# a few widely used tools from numpy
from numpy import sin, cos, exp, sqrt, pi, linspace, arange
# +
x = linspace(0, 2 * pi)
y = sin(x)
plt.plot(x, y, label='sin(x)')
plt.legend()
plt.title('Harmonic')
plt.xlabel('x')
plt.ylabel('y')
# Add one line to that plot
z = cos(x)
plt.plot(x, z, label='cos(x)')
# Make a second figure with a simple plot
plt.figure()
plt.plot(x, sin(2*x), label='sin(2x)')
plt.legend();
# -
# Here is how to create the same two plots, using explicit management of the figure and axis objects:
# +
f, ax = plt.subplots() # we manually make a figure and axis
ax.plot(x,y, label='sin(x)') # it's the axis who plots
ax.legend()
ax.set_title('Harmonic') # we set the title on the axis
ax.set_xlabel('x') # same with labels
ax.set_ylabel('y')
# Make a second figure with a simple plot. We can name the figure with a
# different variable name as well as its axes, and then control each
f1, ax1 = plt.subplots()
ax1.plot(x, sin(2*x), label='sin(2x)')
ax1.legend()
# Since we now have variables for each axis, we can add back to the first
# figure even after making the second
ax.plot(x, z, label='cos(x)');
# -
# It’s important to understand the existence of these objects, even if you use mostly the top-level pyplot calls most of the time. Many things can be accomplished in MPL with mostly pyplot and a little bit of tweaking of the underlying objects. We’ll revisit the object-oriented API later.
#
# Important commands to know about, and which matplotlib uses internally a lot:
#
# gcf() # get current figure
# gca() # get current axis
# ## Making subplots
#
#
# The simplest command is:
#
# f, ax = plt.subplots()
#
# which is equivalent to:
#
# f = plt.figure()
# ax = f.add_subplot(111)
#
# By passing arguments to `subplots`, you can easily create a regular plot grid:
# +
x = linspace(0, 2*pi, 400)
y = sin(x**2)
# Just a figure and one subplot
f, ax = plt.subplots()
ax.plot(x, y)
ax.set_title('Simple plot')
# Two subplots, unpack the output array immediately
f, (ax1, ax2) = plt.subplots(1, 2)
ax1.plot(x, y)
ax2.scatter(x, y)
# Put a figure-level title
f.suptitle('Two plots');
# -
# And finally, an arbitrarily complex grid can be made with ``subplot2grid``:
# +
f = plt.figure()
ax1 = plt.subplot2grid((3,3), (0,0), colspan=3)
ax2 = plt.subplot2grid((3,3), (1,0), colspan=2)
ax3 = plt.subplot2grid((3,3), (1, 2), rowspan=2)
ax4 = plt.subplot2grid((3,3), (2, 0))
ax5 = plt.subplot2grid((3,3), (2, 1))
# Let's turn off visibility of all tick labels here
for ax in f.axes:
for t in ax.get_xticklabels()+ax.get_yticklabels():
t.set_visible(False)
# And add a figure-level title at the top
f.suptitle('Subplot2grid');
# -
# ## Manipulating properties across matplotlib
#
# In matplotlib, most properties for lines, colors, etc, can be set directly in
# the call:
plt.plot([1,2,3], linestyle='--', color='r')
# But for finer control you can get a hold of the returned line object (more on
# these objects later):
#
# In [1]: line, = plot([1,2,3])
#
# These line objects have a lot of properties you can control, a full list is
# seen here by tab-completing in IPython:
#
# In [2]: line.set
# line.set line.set_drawstyle line.set_mec
# line.set_aa line.set_figure line.set_mew
# line.set_agg_filter line.set_fillstyle line.set_mfc
# line.set_alpha line.set_gid line.set_mfcalt
# line.set_animated line.set_label line.set_ms
# line.set_antialiased line.set_linestyle line.set_picker
# line.set_axes line.set_linewidth line.set_pickradius
# line.set_c line.set_lod line.set_rasterized
# line.set_clip_box line.set_ls line.set_snap
# line.set_clip_on line.set_lw line.set_solid_capstyle
# line.set_clip_path line.set_marker line.set_solid_joinstyle
# line.set_color line.set_markeredgecolor line.set_transform
# line.set_contains line.set_markeredgewidth line.set_url
# line.set_dash_capstyle line.set_markerfacecolor line.set_visible
# line.set_dashes line.set_markerfacecoloralt line.set_xdata
# line.set_dash_joinstyle line.set_markersize line.set_ydata
# line.set_data line.set_markevery line.set_zorder
#
#
# But the `setp` call (short for set property) can be very useful, especially
# while working interactively because it contains introspection support, so you
# can learn about the valid calls as you work:
#
# In [7]: line, = plot([1,2,3])
#
# In [8]: setp(line, 'linestyle')
# linestyle: [ ``'-'`` | ``'--'`` | ``'-.'`` | ``':'`` | ``'None'`` | ``' '`` | ``''`` ] and any drawstyle in combination with a linestyle, e.g. ``'steps--'``.
#
# In [9]: setp(line)
# agg_filter: unknown
# alpha: float (0.0 transparent through 1.0 opaque)
# animated: [True | False]
# antialiased or aa: [True | False]
# ...
# ... much more output elided
# ...
#
# In the first form, it shows you the valid values for the 'linestyle' property,
# and in the second it shows you all the acceptable properties you can set on the
# line object. This makes it very easy to discover how to customize your figures
# to get the visual results you need.
#
# Furthermore, setp can manipulate multiple objects at a time:
# +
x = linspace(0, 2*pi)
y1 = sin(x)
y2 = sin(2*x)
lines = plt.plot(x, y1, x, y2)
# We will set the width and color of all lines in the figure at once:
plt.setp(lines, linewidth=2, color='r')
# -
# Finally, if you know what properties you want to set on a specific object, a
# plain ``set`` call is typically the simplest form:
line, = plt.plot([1,2,3])
line.set(lw=2, c='red',ls='--')
# ## Understanding what matplotlib returns: lines, axes and figures
#
#
# ### Lines
#
#
# In a simple plot:
plt.plot([1,2,3])
# The return value of the plot call is a list of lines, which can be manipulated
# further. If you capture the line object (in this case it's a single line so we
# use a one-element tuple):
line, = plt.plot([1,2,3])
line.set_color('r')
# One line property that is particularly useful to be aware of is ``set_data``:
# +
# Create a plot and hold the line object
line, = plt.plot([1,2,3], label='my data')
plt.grid()
plt.title('My title')
# ... later, we may want to modify the x/y data but keeping the rest of the
# figure intact, with our new data:
x = linspace(0, 1)
y = x**2
# This can be done by operating on the data object itself
line.set_data(x, y)
# Now we must set the axis limits manually. Note that we can also use xlim
# and ylim to set the x/y limits separately.
plt.axis([0,1,0,1])
# Note, alternatively this can be done with:
ax = plt.gca() # get currently active axis object
ax.relim()
ax.autoscale_view()
# as well as requesting matplotlib to draw
plt.draw()
# -
# ### The next important component, axes
#
#
# The ``axis`` call above was used to set the x/y limits of the axis. And in
# previous examples we called ``.plot`` directly on axis objects. Axes are the
# main object that contains a lot of the user-facing functionality of matplotlib:
#
# In [15]: f = plt.figure()
#
# In [16]: ax = f.add_subplot(111)
#
# In [17]: ax.
# Display all 299 possibilities? (y or n)
# ax.acorr ax.hitlist
# ax.add_artist ax.hlines
# ax.add_callback ax.hold
# ax.add_collection ax.ignore_existing_data_limits
# ax.add_line ax.images
# ax.add_patch ax.imshow
#
# ... etc.
#
# Many of the commands in ``plt.<command>`` are nothing but wrappers around axis
# calls, with machinery to automatically create a figure and add an axis to it if
# there wasn't one to begin with. The output of most axis actions that draw
# something is a collection of lines (or other more complex geometric objects).
# ### Enclosing it all, the figure
#
#
# The enclosing object is the ``figure``, that holds all axes:
#
# In [17]: f = plt.figure()
#
# In [18]: f.add_subplot(211)
# Out[18]: <matplotlib.axes.AxesSubplot object at 0x9d0060c>
#
# In [19]: f.axes
# Out[19]: [<matplotlib.axes.AxesSubplot object at 0x9d0060c>]
#
# In [20]: f.add_subplot(212)
# Out[20]: <matplotlib.axes.AxesSubplot object at 0x9eacf0c>
#
# In [21]: f.axes
# Out[21]:
# [<matplotlib.axes.AxesSubplot object at 0x9d0060c>,
# <matplotlib.axes.AxesSubplot object at 0x9eacf0c>]
#
# The basic view of matplotlib is: a figure contains one or more axes, axes draw
# and return collections of one or more geometric objects (lines, patches, etc).
#
# For all the gory details on this topic, see the matplotlib [artist tutorial](http://matplotlib.sourceforge.net/users/artists.html).
# ## Anatomy of a common plot
#
#
# Let's make a simple plot that contains a few commonly used decorations
# +
f, ax = plt.subplots()
# Three simple polyniomials
x = linspace(-1, 1)
y1,y2,y3 = [x**i for i in [1,2,3]]
# Plot each with a label (for a legend)
ax.plot(x, y1, label='linear')
ax.plot(x, y2, label='cuadratic')
ax.plot(x, y3, label='cubic')
# Make all lines drawn so far thicker
plt.setp(ax.lines, linewidth=2)
# Add a grid and a legend that doesn't overlap the lines
ax.grid(True)
ax.legend(loc='lower right')
# Add black horizontal and vertical lines through the origin
ax.axhline(0, color='black')
ax.axvline(0, color='black')
# Set main text elements of the plot
ax.set_title('Some polynomials')
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
# -
# ## Common plot types
#
#
# ### Error plots
#
#
# First a very simple error plot
# +
# example data
x = arange(0.1, 4, 0.5)
y = exp(-x)
# example variable error bar values
yerr = 0.1 + 0.2*sqrt(x)
xerr = 0.1 + yerr
# First illustrate basic pyplot interface, using defaults where possible.
plt.figure()
plt.errorbar(x, y, xerr=0.2, yerr=0.4)
plt.title("Simplest errorbars, 0.2 in x, 0.4 in y")
# -
# Now a more elaborate one, using the OO interface to exercise more features.
# +
# same data/errors as before
x = arange(0.1, 4, 0.5)
y = exp(-x)
yerr = 0.1 + 0.2*sqrt(x)
xerr = 0.1 + yerr
fig, axs = plt.subplots(nrows=2, ncols=2)
ax = axs[0,0]
ax.errorbar(x, y, yerr=yerr, fmt='o')
ax.set_title('Vert. symmetric')
# With 4 subplots, reduce the number of axis ticks to avoid crowding.
ax.locator_params(nbins=4)
ax = axs[0,1]
ax.errorbar(x, y, xerr=xerr, fmt='o')
ax.set_title('Hor. symmetric')
ax = axs[1,0]
ax.errorbar(x, y, yerr=[yerr, 2*yerr], xerr=[xerr, 2*xerr], fmt='--o', label='foo')
ax.legend()
ax.set_title('H, V asymmetric')
ax = axs[1,1]
ax.set_yscale('log')
# Here we have to be careful to keep all y values positive:
ylower = np.maximum(1e-2, y - yerr)
yerr_lower = y - ylower
ax.errorbar(x, y, yerr=[yerr_lower, 2*yerr], xerr=xerr,
fmt='o', ecolor='g')
ax.set_title('Mixed sym., log y')
# Fix layout to minimize overlap between titles and marks
# https://matplotlib.org/users/tight_layout_guide.html
plt.tight_layout()
# -
# ### Logarithmic plots
#
# A simple log plot
# +
x = linspace(-5, 5)
y = exp(-x**2)
f, (ax1, ax2) = plt.subplots(2, 1)
ax1.plot(x, y)
ax2.semilogy(x, y)
# -
# A more elaborate log plot using 'symlog', that treats a specified range as
# linear (thus handling values near zero) and symmetrizes negative values:
# +
x = linspace(-50, 50, 100)
y = linspace(0, 100, 100)
# Create the figure and axes
f, (ax1, ax2, ax3) = plt.subplots(3, 1)
# Symlog on the x axis
ax1.plot(x, y)
ax1.set_xscale('symlog')
ax1.set_ylabel('symlogx')
# Grid for both axes
ax1.grid(True)
# Minor grid on too for x
ax1.xaxis.grid(True, which='minor')
# Symlog on the y axis
ax2.plot(y, x)
ax2.set_yscale('symlog')
ax2.set_ylabel('symlogy')
# Symlog on both
ax3.plot(x, sin(x / 3.0))
ax3.set_xscale('symlog')
ax3.set_yscale('symlog')
ax3.grid(True)
ax3.set_ylabel('symlog both')
# -
# ### Bar plots
# +
# a bar plot with errorbars
import numpy as np
import matplotlib.pyplot as plt
N = 5
menMeans = (20, 35, 30, 31, 27)
menStd = (2, 3, 4, 1, 2)
ind = arange(N) # the x locations for the groups
width = 0.35 # the width of the bars
fig = plt.figure()
ax = fig.add_subplot(111)
rects1 = ax.bar(ind, menMeans, width, color='r', yerr=menStd)
womenMeans = (25, 32, 34, 21, 29)
womenStd = (3, 5, 2, 3, 3)
rects2 = ax.bar(ind+width, womenMeans, width, color='y', yerr=womenStd)
# add some
ax.set_ylabel('Scores')
ax.set_title('Scores by group and gender')
ax.set_xticks(ind+width)
ax.set_xticklabels( ('G1', 'G2', 'G3', 'G4', 'G5') )
ax.legend( (rects1[0], rects2[0]), ('Men', 'Women') )
# -
# ### Scatter plots
#
# The ``scatter`` command produces scatter plots with arbitrary markers.
# +
from matplotlib import cm
t = linspace(0.0, 6*pi, 100)
y = exp(-0.1*t)*cos(t)
phase = t % 2*pi
f = plt.figure()
ax = f.add_subplot(111)
ax.scatter(t, y, s=100*abs(y), c=phase, cmap=cm.jet)
ax.set_ylim(-1,1)
ax.grid()
ax.axhline(0, color='k')
# -
# ### Exercise
#
# Consider you have the following data in a text file (The file `data/stations.txt` contains the full dataset):
#
# # Station Lat Long Elev
# BIRA 26.4840 87.2670 0.0120
# BUNG 27.8771 85.8909 1.1910
# GAIG 26.8380 86.6318 0.1660
# HILE 27.0482 87.3242 2.0880
# ... etc.
#
#
# These are the names of seismographic stations in the Himalaya, with their coordinates and elevations in Kilometers.
#
# 1. Make a scatter plot of all of these, using both the size and the color to (redundantly) encode elevation. Label each station by its 4-letter code, and add a colorbar on the right that shows the color-elevation map.
#
# 2. If you have the basemap toolkit installed, repeat the same exercise but draw a grid with parallels and meridians, add rivers in cyan and country boundaries in yellow. Also, draw the background using the NASA BlueMarble image of Earth. You can install it with `conda install basemap`.
#
#
# **Tips**
#
# * You can check whether you have Basemap installed with:
#
# from mpl_toolkits.basemap import Basemap
#
# * For the basemap part, choose a text label color that provides adequate reading contrast over the image background.
#
# * Create your Basemap with 'i' resolution, otherwise it will take forever to draw.
# ### Histograms
#
# Matplotlib has a built-in command for histograms.
# +
mu, sigma = 100, 15
x = mu + sigma * np.random.randn(10000)
# the histogram of the data
n, bins, patches = plt.hist(x, 50, normed=1, facecolor='g', alpha=0.75)
plt.xlabel('Smarts')
plt.ylabel('Probability')
plt.title('Histogram of IQ')
plt.text(60, .025, r'$\mu=100,\ \sigma=15$')
plt.axis([40, 160, 0, 0.03])
plt.grid(True)
# -
# ## Aribitrary text and LaTeX support
#
# In matplotlib, text can be added either relative to an individual axis object
# or to the whole figure.
#
# These commands add text to the Axes:
#
# - title() - add a title
# - xlabel() - add an axis label to the x-axis
# - ylabel() - add an axis label to the y-axis
# - text() - add text at an arbitrary location
# - annotate() - add an annotation, with optional arrow
#
# And these act on the whole figure:
#
# - figtext() - add text at an arbitrary location
# - suptitle() - add a title
#
# And any text field can contain LaTeX expressions for mathematics, as long as
# they are enclosed in ``$`` signs.
#
# This example illustrates all of them:
# +
fig = plt.figure()
fig.suptitle('bold figure suptitle', fontsize=14, fontweight='bold')
ax = fig.add_subplot(111)
fig.subplots_adjust(top=0.85)
ax.set_title('axes title')
ax.set_xlabel('xlabel')
ax.set_ylabel('ylabel')
ax.text(3, 8, 'boxed italics text in data coords', style='italic',
bbox={'facecolor':'red', 'alpha':0.5, 'pad':10})
ax.text(2, 6, r'an equation: $E=mc^2$', fontsize=15)
ax.text(3, 2, 'unicode: Institut für Festkörperphysik')
ax.text(0.95, 0.01, 'colored text in axes coords',
verticalalignment='bottom', horizontalalignment='right',
transform=ax.transAxes,
color='green', fontsize=15)
ax.plot([2], [1], 'o')
ax.annotate('annotate', xy=(2, 1), xytext=(3, 4),
arrowprops=dict(facecolor='black', shrink=0.05))
ax.axis([0, 10, 0, 10])
# -
# ## Image display
#
# The ``imshow`` command can display single or multi-channel images. A simple
# array of random numbers, plotted in grayscale:
from matplotlib import cm
plt.imshow(np.random.rand(128, 128), cmap=cm.gray, interpolation='nearest')
# A real photograph is a multichannel image, `imshow` interprets it correctly:
img = plt.imread('data/stained_glass_barcelona.png')
plt.imshow(img)
# ### Exercise
#
# Write a notebook where you can load an image and then perform the following operations on it:
#
# 1. Create a figure with four plots that show both the full-color image and color channel of the image with the right colormap for that color. Ensure that the axes are linked so zooming in one image zooms the same region in the others.
#
# 2. Compute a luminosity and per-channel histogram and display all four histograms in one figure, giving each a separate plot (hint: a 4x1 plot works best for this). Link the appropriate axes together.
#
# 3. Create a black-and-white (or more precisely, grayscale) version of the image. Compare the results from a naive average of all three channels with that of a model that uses 30% red, 59% green and 11% blue, by displaying all three (full color and both grayscales) side by side with linked axes for zooming.
#
# Hint: look for the matplotlib image tutorial.
|
lectures/10-matplotlib_beyond_basics/10-matplotlib_beyond_basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# # Retail Demo Store - Personalization Workshop
#
# Welcome to the Retail Demo Store Personalization Workshop. In this module we're going to be adding three core personalization features powered by [Amazon Personalize](https://aws.amazon.com/personalize/): related product recommendations on the product detail page, personalized recommendations on the Retail Demo Store homepage, and personalized ranking of items on the featured product page and product search results. This will allow us to give our users targeted recommendations based on their activity.
#
# Recommended Time: 2 Hours
# ## Setup
#
# To get started, we need to perform a bit of setup. Walk through each of the following steps to configure your environment to interact with the Amazon Personalize Service.
# ### Import Dependencies and Setup Boto3 Python Clients
#
# Throughout this workshop we will need access to some common libraries and clients for connecting to AWS services.
# +
# Import Dependencies
import boto3
import json
import pandas as pd
import numpy as np
import time
import requests
import csv
import sys
import botocore
import uuid
from packaging import version
from random import randint
from botocore.exceptions import ClientError
# Setup Clients
personalize = boto3.client('personalize')
personalize_runtime = boto3.client('personalize-runtime')
personalize_events = boto3.client('personalize-events')
servicediscovery = boto3.client('servicediscovery')
ssm = boto3.client('ssm')
# -
# Since we require a newer version of the botocore library, upgrade the local version if necessary. **Note that if the botocore is upgraded, you will need to restart the Jupyter notebook kernel and re-execute the cells from the top to resume.** An assertion error is thrown as a reminder if a kernel restart is required.
# +
# Minimum version of botocore we need for this workshop.
min_botocore_version = '1.16.24'
if version.parse(botocore.__version__) < version.parse(min_botocore_version):
print('Current version of botocore ({}) does not meet the minimum required version ({})'.format(botocore.__version__, min_botocore_version))
print('Upgrading to latest pip and botocore...')
# !{sys.executable} -m pip install --upgrade pip
# !{sys.executable} -m pip install --upgrade --no-deps --force-reinstall botocore
assert False, 'Restart the notebook kernel to pick up the latest botocore and begin at the top of this notebook'
else:
print('Version of botocore ({}) meets minimum requirement ({}) for this notebook'.format(botocore.__version__, min_botocore_version))
# -
# ### Configure Bucket and Data Output Location
# We will be configuring some variables that will store the location of our source data. When the Retail Demo Store stack was deployed in this account, an S3 bucket was created for you and the name of this bucket was stored in Systems Manager Parameter Store. Using the Boto3 client we can get the name of this bucket for use within our Notebook.
# +
response = ssm.get_parameter(
Name='retaildemostore-stack-bucket'
)
bucket = response['Parameter']['Value'] # Do Not Change
items_filename = "items.csv" # Do Not Change
users_filename = "users.csv" # Do Not Change
interactions_filename = "interactions.csv" # Do Not Change
print('Bucket: {}'.format(bucket))
# -
# ## Get, Prepare, and Upload User, Product, and Interaction Data
#
# Amazon Personalize provides predefined recipes, based on common use cases, for training models. A recipe is a machine learning algorithm that you use with settings, or hyperparameters, and the data you provide to train an Amazon Personalize model. The data you provide to train a model are organized into separate datasets by the type of data being provided. A collection of datasets are organized into a dataset group. The three dataset types supported by Personalize are items, users, and interactions. Depending on the recipe type you choose, a different combination of dataset types are required. For all recipe types, an interactions dataset is required. Interactions represent how users interact with items. For example, viewing a product, watching a video, listening to a recording, or reading an article. For this workshop, we will be using a recipe that supports all three dataset types.
#
# When we deployed the Retail Demo Store, it was deployed with an initial seed of fictitious User and Product data. We will use this data to train three models, or solutions, in the Amazon Personalize service which will be used to serve product recommendations, related items, and to rerank product lists for our users. The User and Product data can be accessed from the Retail Demo Store's [Users](https://github.com/aws-samples/retail-demo-store/tree/master/src/users) and [Products](https://github.com/aws-samples/retail-demo-store/tree/master/src/products) microservices, respectively. We will access our data through microservice data APIs, process the data, and upload them as CSVs to S3. Once our datasets are in S3, we can import them into the Amazon Personalize service.
#
# Let's get started.
# ### Get Products Service Instance
#
# We will be pulling our Product data from the [Products Service](https://github.com/aws-samples/retail-demo-store/tree/master/src/products) that was deployed in Amazon Elastic Container Service as part of the Retail Demo Store. To connect to this service we will use [AWS Cloud Map](https://aws.amazon.com/cloud-map/)'s Service Discovery to discover an instance of the Product Service running in ECS, and then connect directly to that service instances to access our data.
# +
response = servicediscovery.discover_instances(
NamespaceName='retaildemostore.local',
ServiceName='products',
MaxResults=1,
HealthStatus='HEALTHY'
)
products_service_instance = response['Instances'][0]['Attributes']['AWS_INSTANCE_IPV4']
print('Products Service Instance IP: {}'.format(products_service_instance))
# -
# #### Download and Explore the Products Dataset
# +
response = requests.get('http://{}/products/all'.format(products_service_instance))
products = response.json()
products_df = pd.DataFrame(products)
pd.set_option('display.max_rows', 5)
products_df
# -
# #### Prepare and Upload Data
#
# When training models in Amazon Personalize, we can provide meta data about our items. For this workshop we will add each product's category and style to the item dataset. The product's unique identifier is required. Then we will rename the columns in our dataset to match our schema (defined later) and those expected by Personalize. Finally, we will save our dataset as a CSV and copy it to our S3 bucket.
# +
products_dataset_df = products_df[['id','category','style']]
products_dataset_df = products_dataset_df.rename(columns = {'id':'ITEM_ID','category':'CATEGORY','style':'STYLE'})
products_dataset_df.to_csv(items_filename, index=False)
boto3.Session().resource('s3').Bucket(bucket).Object(items_filename).upload_file(items_filename)
# -
# ### Get Users Service Instance
#
# We will be pulling our User data from the [Users Service](https://github.com/aws-samples/retail-demo-store/tree/master/src/users) that is deployed as part of the Retail Demo Store. To connect to this service we will use Service Discovery to discover an instance of the User Service, and then connect directly to that service instance to access our data.
# +
response = servicediscovery.discover_instances(
NamespaceName='retaildemostore.local',
ServiceName='users',
MaxResults=1,
HealthStatus='HEALTHY'
)
users_service_instance = response['Instances'][0]['Attributes']['AWS_INSTANCE_IPV4']
print('Users Service Instance IP: {}'.format(users_service_instance))
# -
# #### Download and Explore the Users Dataset
# +
response = requests.get('http://{}/users/all?count=10000'.format(users_service_instance))
users = response.json()
users_df = pd.DataFrame(users)
pd.set_option('display.max_rows', 5)
users_df
# -
# #### Prepare and Upload Data
#
# Similar to the items dataset we created above, we can provide metadata on our users when training models in Personalize. For this workshop we will include each user's age and gender. As before, we will name the columns to match our schema, save the data as a CSV, and upload to our S3 bucket.
# +
users_dataset_df = users_df[['id','age','gender']]
users_dataset_df = users_dataset_df.rename(columns = {'id':'USER_ID','age':'AGE','gender':'GENDER'})
users_dataset_df.to_csv(users_filename, index=False)
boto3.Session().resource('s3').Bucket(bucket).Object(users_filename).upload_file(users_filename)
# -
# ### Create User-Items Interactions Dataset
#
# To mimic user behavior, we will be generating a new dataset that represents user interactions with items. To make the interactions more realistic, we will use the pre-defined shopper persona for each user to generate event types for products matching that persona. We will create events for viewing products, add products to a cart, checking out, and completing orders.
# +
# %%time
# Minimum number of interactions to generate
min_interactions = 500000
# Percentages of each event type to generate
product_added_percent = .08
cart_viewed_percent = .05
checkout_started_percent = .02
order_completed_percent = .01
# Count of interactions generated for each event type
product_viewed_count = 0
product_added_count = 0
cart_viewed_count = 0
checkout_started_count = 0
order_completed_count = 0
# How many days in the past (from now) to start generating interactions
days_back = 90
start_time = int(time.time())
next_timestamp = start_time - (days_back * 24 * 60 * 60)
seconds_increment = int((start_time - next_timestamp) / min_interactions)
next_update = start_time + 60
assert seconds_increment > 0, "Increase days_back or reduce min_interactions"
print('Minimum interactions to generate: {}'.format(min_interactions))
print('Days back: {}'.format(days_back))
print('Starting timestamp: {} ({})'.format(next_timestamp, time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(next_timestamp))))
print('Seconds increment: {}'.format(seconds_increment))
print("Generating interactions... (this may take a few minutes)")
interactions = 0
subsets_cache = {}
with open(interactions_filename, 'w') as outfile:
f = csv.writer(outfile)
f.writerow(["ITEM_ID", "USER_ID", "EVENT_TYPE", "TIMESTAMP"])
while interactions < min_interactions:
if (time.time() > next_update):
rate = interactions / (time.time() - start_time)
to_go = (min_interactions - interactions) / rate
print('Generated {} interactions so far ({:0.2f} seconds to go)'.format(interactions, to_go))
next_update += 60
# Pick a random user
user = users[randint(0, len(users)-1)]
# Determine category affinity from user's persona
persona = user['persona']
preferred_categories = persona.split('_')
# Select category based on weighted preference of category order.
category = np.random.choice(preferred_categories, 1, p=[0.6, 0.25, 0.15])[0]
gender = user['gender']
# Check if subset data frame is already cached for category & gender
prods_subset_df = subsets_cache.get(category + gender)
if prods_subset_df is None:
# Select products from selected category without gender affinity or that match user's gender
prods_subset_df = products_df.loc[(products_df['category'] == category) & ((products_df['gender_affinity'] == gender) | (products_df['gender_affinity'].isnull()))]
# Update cache
subsets_cache[category + gender] = prods_subset_df
# Pick a random product from gender filtered subset
product = prods_subset_df.sample().iloc[0]
this_timestamp = next_timestamp + randint(0, seconds_increment)
f.writerow([product['id'],
user['id'],
'ProductViewed',
this_timestamp])
next_timestamp += seconds_increment
product_viewed_count += 1
interactions += 1
if product_added_count < int(product_viewed_count * product_added_percent):
this_timestamp += randint(0, int(seconds_increment / 2))
f.writerow([product['id'],
user['id'],
'ProductAdded',
this_timestamp])
interactions += 1
product_added_count += 1
if cart_viewed_count < int(product_viewed_count * cart_viewed_percent):
this_timestamp += randint(0, int(seconds_increment / 2))
f.writerow([product['id'],
user['id'],
'CartViewed',
this_timestamp])
interactions += 1
cart_viewed_count += 1
if checkout_started_count < int(product_viewed_count * checkout_started_percent):
this_timestamp += randint(0, int(seconds_increment / 2))
f.writerow([product['id'],
user['id'],
'CheckoutStarted',
this_timestamp])
interactions += 1
checkout_started_count += 1
if order_completed_count < int(product_viewed_count * order_completed_percent):
this_timestamp += randint(0, int(seconds_increment / 2))
f.writerow([product['id'],
user['id'],
'OrderCompleted',
this_timestamp])
interactions += 1
order_completed_count += 1
print("Done")
print("Total interactions: " + str(interactions))
print("Total product viewed: " + str(product_viewed_count))
print("Total product added: " + str(product_added_count))
print("Total cart viewed: " + str(cart_viewed_count))
print("Total checkout started: " + str(checkout_started_count))
print("Total order completed: " + str(order_completed_count))
# -
# #### Open and Explore the Interactions Dataset
interactions_df = pd.read_csv(interactions_filename)
interactions_df
# #### Prepare and Upload Data
boto3.Session().resource('s3').Bucket(bucket).Object(interactions_filename).upload_file(interactions_filename)
# ## Configure Amazon Personalize
#
# Now that we've prepared our three datasets and uploaded them to S3 we'll need to configure the Amazon Personalize service to understand our data so that it can be used to train models for generating recommendations.
# ### Create Schemas for Datasets
#
# Amazon Personalize requires a schema for each dataset so it can map the columns in our CSVs to fields for model training. Each schema is declared in JSON using the [Apache Avro](https://avro.apache.org/) format.
#
# Let's define and create schemas in Personalize for our datasets.
# #### Items Datsaset Schema
# +
items_schema = {
"type": "record",
"name": "Items",
"namespace": "com.amazonaws.personalize.schema",
"fields": [
{
"name": "ITEM_ID",
"type": "string"
},
{
"name": "CATEGORY",
"type": "string",
"categorical": True,
},
{
"name": "STYLE",
"type": "string",
"categorical": True,
}
],
"version": "1.0"
}
create_schema_response = personalize.create_schema(
name = "retaildemostore-schema-items",
schema = json.dumps(items_schema)
)
items_schema_arn = create_schema_response['schemaArn']
print(json.dumps(create_schema_response, indent=2))
# -
# #### Users Dataset Schema
# +
users_schema = {
"type": "record",
"name": "Users",
"namespace": "com.amazonaws.personalize.schema",
"fields": [
{
"name": "USER_ID",
"type": "string"
},
{
"name": "AGE",
"type": "int"
},
{
"name": "GENDER",
"type": "string",
"categorical": True,
}
],
"version": "1.0"
}
create_schema_response = personalize.create_schema(
name = "retaildemostore-schema-users",
schema = json.dumps(users_schema)
)
users_schema_arn = create_schema_response['schemaArn']
print(json.dumps(create_schema_response, indent=2))
# -
# #### Interactions Dataset Schema
# +
interactions_schema = {
"type": "record",
"name": "Interactions",
"namespace": "com.amazonaws.personalize.schema",
"fields": [
{
"name": "ITEM_ID",
"type": "string"
},
{
"name": "USER_ID",
"type": "string"
},
{
"name": "EVENT_TYPE",
"type": "string"
},
{
"name": "TIMESTAMP",
"type": "long"
}
],
"version": "1.0"
}
create_schema_response = personalize.create_schema(
name = "retaildemostore-schema-interactions",
schema = json.dumps(interactions_schema)
)
interactions_schema_arn = create_schema_response['schemaArn']
print(json.dumps(create_schema_response, indent=2))
# -
# ### Create and Wait for Dataset Group
#
# Next we need to create the dataset group that will contain our three datasets.
# #### Create Dataset Group
# +
create_dataset_group_response = personalize.create_dataset_group(
name = 'retaildemostore'
)
dataset_group_arn = create_dataset_group_response['datasetGroupArn']
print(json.dumps(create_dataset_group_response, indent=2))
print(f'DatasetGroupArn = {dataset_group_arn}')
# -
# #### Wait for Dataset Group to Have ACTIVE Status
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_dataset_group_response = personalize.describe_dataset_group(
datasetGroupArn = dataset_group_arn
)
status = describe_dataset_group_response["datasetGroup"]["status"]
print("DatasetGroup: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(15)
# ### Create Items Dataset
#
# Next we will create the datasets in Personalize for our three dataset types. Let's start with the items dataset.
# +
dataset_type = "ITEMS"
create_dataset_response = personalize.create_dataset(
name = "retaildemostore-dataset-items",
datasetType = dataset_type,
datasetGroupArn = dataset_group_arn,
schemaArn = items_schema_arn
)
items_dataset_arn = create_dataset_response['datasetArn']
print(json.dumps(create_dataset_response, indent=2))
# -
# ### Create Users Dataset
# +
dataset_type = "USERS"
create_dataset_response = personalize.create_dataset(
name = "retaildemostore-dataset-users",
datasetType = dataset_type,
datasetGroupArn = dataset_group_arn,
schemaArn = users_schema_arn
)
users_dataset_arn = create_dataset_response['datasetArn']
print(json.dumps(create_dataset_response, indent=2))
# -
# ### Create Interactions Dataset
# +
dataset_type = "INTERACTIONS"
create_dataset_response = personalize.create_dataset(
name = "retaildemostore-dataset-interactions",
datasetType = dataset_type,
datasetGroupArn = dataset_group_arn,
schemaArn = interactions_schema_arn
)
interactions_dataset_arn = create_dataset_response['datasetArn']
print(json.dumps(create_dataset_response, indent=2))
# -
# ## Import Datasets to Personalize
#
# Up to this point we have generated CSVs containing data for our users, items, and interactions and staged them in an S3 bucket. We also created schemas in Personalize that define the columns in our CSVs. Then we created a datset group and three datasets in Personalize that will receive our data. In the following steps we will create import jobs with Personalize that will import the datasets from our S3 bucket into the service.
#
# ### Setup Permissions
#
# By default, the Personalize service does not have permission to acccess the data we uploaded into the S3 bucket in our account. In order to grant access to the Personalize service to read our CSVs, we need to set a Bucket Policy and create an IAM role that the Amazon Personalize service will assume.
# #### Attach policy to S3 bucket
# +
s3 = boto3.client("s3")
policy = {
"Version": "2012-10-17",
"Id": "PersonalizeS3BucketAccessPolicy",
"Statement": [
{
"Sid": "PersonalizeS3BucketAccessPolicy",
"Effect": "Allow",
"Principal": {
"Service": "personalize.amazonaws.com"
},
"Action": [
"s3:GetObject",
"s3:ListBucket"
],
"Resource": [
"arn:aws:s3:::{}".format(bucket),
"arn:aws:s3:::{}/*".format(bucket)
]
}
]
}
s3.put_bucket_policy(Bucket=bucket, Policy=json.dumps(policy));
# -
# #### Create S3 Read Only Access Role
# +
iam = boto3.client("iam")
role_name = "RetailDemoStorePersonalizeS3Role"
assume_role_policy_document = {
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Principal": {
"Service": "personalize.amazonaws.com"
},
"Action": "sts:AssumeRole"
}
]
}
create_role_response = iam.create_role(
RoleName = role_name,
AssumeRolePolicyDocument = json.dumps(assume_role_policy_document)
);
iam.attach_role_policy(
RoleName = role_name,
PolicyArn = "arn:aws:iam::aws:policy/AmazonS3ReadOnlyAccess"
);
role_arn = create_role_response["Role"]["Arn"]
print('IAM Role: {}'.format(role_arn))
# Pause to allow role to fully persist
time.sleep(10)
# -
# ### Create Import Jobs
#
# With the permissions in place to allow Personalize to access our CSV files, let's create three import jobs to import each file into its respective dataset. Each import job can take several minutes to complete so we'll create all three and then wait for them all to complete.
# #### Create Items Dataset Import Job
# +
items_create_dataset_import_job_response = personalize.create_dataset_import_job(
jobName = "retaildemostore-dataset-items-import-job",
datasetArn = items_dataset_arn,
dataSource = {
"dataLocation": "s3://{}/{}".format(bucket, items_filename)
},
roleArn = role_arn
)
items_dataset_import_job_arn = items_create_dataset_import_job_response['datasetImportJobArn']
print(json.dumps(items_create_dataset_import_job_response, indent=2))
# -
# #### Create Users Dataset Import Job
# +
users_create_dataset_import_job_response = personalize.create_dataset_import_job(
jobName = "retaildemostore-dataset-users-import-job",
datasetArn = users_dataset_arn,
dataSource = {
"dataLocation": "s3://{}/{}".format(bucket, users_filename)
},
roleArn = role_arn
)
users_dataset_import_job_arn = users_create_dataset_import_job_response['datasetImportJobArn']
print(json.dumps(users_create_dataset_import_job_response, indent=2))
# -
# #### Create Interactions Dataset Import Job
# +
interactions_create_dataset_import_job_response = personalize.create_dataset_import_job(
jobName = "retaildemostore-dataset-interactions-import-job",
datasetArn = interactions_dataset_arn,
dataSource = {
"dataLocation": "s3://{}/{}".format(bucket, interactions_filename)
},
roleArn = role_arn
)
interactions_dataset_import_job_arn = interactions_create_dataset_import_job_response['datasetImportJobArn']
print(json.dumps(interactions_create_dataset_import_job_response, indent=2))
# -
# ### Wait for Import Jobs to Complete
#
# It will take 10-15 minutes for the import jobs to complete, while you're waiting you can learn more about Datasets and Schemas here: https://docs.aws.amazon.com/personalize/latest/dg/how-it-works-dataset-schema.html
#
# We will wait for all three jobs to finish.
# #### Wait for Items Import Job to Complete
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_dataset_import_job_response = personalize.describe_dataset_import_job(
datasetImportJobArn = items_dataset_import_job_arn
)
status = describe_dataset_import_job_response["datasetImportJob"]['status']
print("DatasetImportJob: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# #### Wait for Users Import Job to Complete
#
# Since we submitted all three import jobs at the same time, it's likely that the users import job is already complete. Let's check to be sure.
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_dataset_import_job_response = personalize.describe_dataset_import_job(
datasetImportJobArn = users_dataset_import_job_arn
)
status = describe_dataset_import_job_response["datasetImportJob"]['status']
print("DatasetImportJob: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# #### Wait for Interactions Import Job to Complete
#
# Since we submitted all three import jobs at the same time, it's likely that the interactions import job is already complete. Let's check to be sure.
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_dataset_import_job_response = personalize.describe_dataset_import_job(
datasetImportJobArn = interactions_dataset_import_job_arn
)
status = describe_dataset_import_job_response["datasetImportJob"]['status']
print("DatasetImportJob: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# ## Create Solutions
#
# With our three datasets imported into our dataset group, we can now turn to training models. As a reminder, we will be training three models in this workshop to support three different personalization use-cases. One model will be used to make related product recommendations on the product detail view/page, another model will be used to make personalized product recommendations to users on the homepage, and the last model will be used to rerank product lists on the category and featured products page. In Amazon Personalize, training a model involves creating a Solution and Solution Version. So when we are finished we will have three solutions and a solution version for each solution.
#
# When creating a solution, you provide your dataset group and the recipe for training. Let's declare the recipes that we will need for our solutions.
# ### List Recipes
#
# First, let's list all available recipes.
list_recipes_response = personalize.list_recipes()
list_recipes_response
# As you can see above, there are several recipes to choose from. Let's declare the recipes for each Solution.
# #### Declare Personalize Recipe for Related Products
#
# On the product detail page we want to display related products so we'll create a campaign using the [SIMS](https://docs.aws.amazon.com/personalize/latest/dg/native-recipe-sims.html) recipe.
#
# > The Item-to-item similarities (SIMS) recipe is based on the concept of collaborative filtering. A SIMS model leverages user-item interaction data to recommend items similar to a given item. In the absence of sufficient user behavior data for an item, this recipe recommends popular items.
related_recipe_arn = "arn:aws:personalize:::recipe/aws-sims"
# #### Declare Personalize Recipe for Product Recommendations
#
# Since we are providing metadata for users and items, we will be using the [HRNN-Metadata](https://docs.aws.amazon.com/personalize/latest/dg/native-recipe-hrnn-metadata.html) recipe for our product recommendations solution.
#
# > The HRNN-Metadata recipe predicts the items that a user will interact with. It is similar to the HRNN recipe, with additional features derived from contextual, user, and item metadata (from Interactions, Users, and Items datasets, respectively). HRNN-Metadata provides accuracy benefits over non-metadata models when high quality metadata is available. Using this recipe might require longer training times.
recommend_recipe_arn = "arn:aws:personalize:::recipe/aws-hrnn-metadata"
# #### Declare Personalize Recipe for Personalized Ranking
#
# In use-cases where we have a curated list of products, we can use the [Personalized-Ranking](https://docs.aws.amazon.com/personalize/latest/dg/native-recipe-search.html) recipe to reorder the products for the current user.
#
# > The Personalized-Ranking recipe generates personalized rankings. A personalized ranking is a list of recommended items that are re-ranked for a specific user.
ranking_recipe_arn = "arn:aws:personalize:::recipe/aws-personalized-ranking"
# ### Create Solutions and Solution Versions
#
# With our recipes defined, we can now create our solutions and solution versions.
# #### Create Related Products Solution
# +
create_solution_response = personalize.create_solution(
name = "retaildemostore-related-products",
datasetGroupArn = dataset_group_arn,
recipeArn = related_recipe_arn,
eventType = "ProductViewed"
)
related_solution_arn = create_solution_response['solutionArn']
print(json.dumps(create_solution_response, indent=2))
# -
# #### Create Related Products Solution Version
# +
create_solution_version_response = personalize.create_solution_version(
solutionArn = related_solution_arn
)
related_solution_version_arn = create_solution_version_response['solutionVersionArn']
print(json.dumps(create_solution_version_response, indent=2))
# -
# #### Create Product Recommendation Solution
# +
create_solution_response = personalize.create_solution(
name = "retaildemostore-product-personalization",
datasetGroupArn = dataset_group_arn,
recipeArn = recommend_recipe_arn,
eventType = "ProductViewed"
)
recommend_solution_arn = create_solution_response['solutionArn']
print(json.dumps(create_solution_response, indent=2))
# -
# #### Create Product Recommendation Solution Version
# +
create_solution_version_response = personalize.create_solution_version(
solutionArn = recommend_solution_arn
)
recommend_solution_version_arn = create_solution_version_response['solutionVersionArn']
print(json.dumps(create_solution_version_response, indent=2))
# -
# #### Create Personalized Ranking Solution
# +
create_solution_response = personalize.create_solution(
name = "retaildemostore-personalized-ranking",
datasetGroupArn = dataset_group_arn,
recipeArn = ranking_recipe_arn,
eventType = "ProductViewed"
)
ranking_solution_arn = create_solution_response['solutionArn']
print(json.dumps(create_solution_response, indent=2))
# -
# #### Create Personalized Ranking Solution Version
# +
create_solution_version_response = personalize.create_solution_version(
solutionArn = ranking_solution_arn
)
ranking_solution_version_arn = create_solution_version_response['solutionVersionArn']
print(json.dumps(create_solution_version_response, indent=2))
# -
# ### Wait for Solution Versions to Complete
#
# It can take 40-60 minutes for all solution versions to be created. During this process a model is being trained and tested with the data contained within your datasets. The duration of training jobs can increase based on the size of the dataset, training parameters and using AutoML vs. manually selecting a recipe. We submitted requests for all three solutions and versions at once so they are trained in parallel and then below we will wait for all three to finish.
#
# While you are waiting for this process to complete you can learn more about solutions here: https://docs.aws.amazon.com/personalize/latest/dg/training-deploying-solutions.html
# #### Wait for Related Products Solution Version to Have ACTIVE Status
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_solution_version_response = personalize.describe_solution_version(
solutionVersionArn = related_solution_version_arn
)
status = describe_solution_version_response["solutionVersion"]["status"]
print("SolutionVersion: {}".format(status))
if status == 'CREATE FAILED':
print(describe_solution_version_response["solutionVersion"]["failureReason"])
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# #### Wait for Product Recommendation Solution Version to Have ACTIVE Status
#
# Since we created the solution versions at the same time, they were being created in parallel. Therefore, it's likely that our product recommendations and personalized ranking solution versions are already complete. Let's check to make sure.
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_solution_version_response = personalize.describe_solution_version(
solutionVersionArn = recommend_solution_version_arn
)
status = describe_solution_version_response["solutionVersion"]["status"]
print("SolutionVersion: {}".format(status))
if status == 'CREATE FAILED':
print(describe_solution_version_response["solutionVersion"]["failureReason"])
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# #### Wait for Personalized Ranking Solution Version to Have ACTIVE Status
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_solution_version_response = personalize.describe_solution_version(
solutionVersionArn = ranking_solution_version_arn
)
status = describe_solution_version_response["solutionVersion"]["status"]
print("SolutionVersion: {}".format(status))
if status == 'CREATE FAILED':
print(describe_solution_version_response["solutionVersion"]["failureReason"])
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# ### Evaluate Offline Metrics for Solution Versions
#
# Amazon Personalize provides [offline metrics](https://docs.aws.amazon.com/personalize/latest/dg/working-with-training-metrics.html#working-with-training-metrics-metrics) that allow you to evaluate the performance of the solution version before you deploy the model in your application. Metrics can also be used to view the effects of modifying a Solution's hyperparameters or to compare the metrics between solutions that use the same training data but created with different recipes.
#
# Let's retrieve the metrics for the solution versions we just created.
# #### Related Products Metrics
# +
get_solution_metrics_response = personalize.get_solution_metrics(
solutionVersionArn = related_solution_version_arn
)
print(json.dumps(get_solution_metrics_response, indent=2))
# -
# #### Product Recommendations Metrics
# +
get_solution_metrics_response = personalize.get_solution_metrics(
solutionVersionArn = recommend_solution_version_arn
)
print(json.dumps(get_solution_metrics_response, indent=2))
# -
# #### Personalized Ranking Metrics
# +
get_solution_metrics_response = personalize.get_solution_metrics(
solutionVersionArn = ranking_solution_version_arn
)
print(json.dumps(get_solution_metrics_response, indent=2))
# -
# ## Create Campaigns
#
# Once we're satisfied with our solution versions, we need to create Campaigns for each solution version. When creating a campaign you specify the minimum transactions per second (`minProvisionedTPS`) that you expect to make against the service for this campaign. Personalize will automatically scale the inference endpoint up and down for the campaign to match demand but will never scale below `minProvisionedTPS`.
#
# Let's create campaigns for our three solution versions with each set at `minProvisionedTPS` of 1.
# #### Create Related Products Campaign
# +
create_campaign_response = personalize.create_campaign(
name = "retaildemostore-related-products",
solutionVersionArn = related_solution_version_arn,
minProvisionedTPS = 1
)
related_campaign_arn = create_campaign_response['campaignArn']
print(json.dumps(create_campaign_response, indent=2))
# -
# #### Create Product Recommendation Campaign
# +
create_campaign_response = personalize.create_campaign(
name = "retaildemostore-product-personalization",
solutionVersionArn = recommend_solution_version_arn,
minProvisionedTPS = 1
)
recommend_campaign_arn = create_campaign_response['campaignArn']
print(json.dumps(create_campaign_response, indent=2))
# -
# #### Create Personalized Ranking Campaign
# +
create_campaign_response = personalize.create_campaign(
name = "retaildemostore-personalized-ranking",
solutionVersionArn = ranking_solution_version_arn,
minProvisionedTPS = 1
)
ranking_campaign_arn = create_campaign_response['campaignArn']
print(json.dumps(create_campaign_response, indent=2))
# -
# #### Wait for Related Products Campaign to Have ACTIVE Status
#
# It can take 20-30 minutes for the campaigns to be fully created.
#
# While you are waiting for this to complete you can learn more about campaigns here: https://docs.aws.amazon.com/personalize/latest/dg/campaigns.html
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_campaign_response = personalize.describe_campaign(
campaignArn = related_campaign_arn
)
status = describe_campaign_response["campaign"]["status"]
print("Campaign: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# #### Wait for Product Recommendation Campaign to Have ACTIVE Status
#
# Since we created our campaigns at the same time, they were being built in parallel. Therefore, it's likely that the product recommendation and personalized ranking campaigns are already active. Let's check to make sure.
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_campaign_response = personalize.describe_campaign(
campaignArn = recommend_campaign_arn
)
status = describe_campaign_response["campaign"]["status"]
print("Campaign: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# #### Wait for Personalized Ranking Campaign to Have ACTIVE Status
status = None
max_time = time.time() + 3*60*60 # 3 hours
while time.time() < max_time:
describe_campaign_response = personalize.describe_campaign(
campaignArn = ranking_campaign_arn
)
status = describe_campaign_response["campaign"]["status"]
print("Campaign: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(60)
# ## Test Campaigns
#
# Now that our campaigns have been fully created, let's test each campaign and evaluate the results.
# ### Test Related Product Recommendations Campaign
#
# Let's test the recommendations made by the related items/products campaign by selecting a product from the Retail Demo Store's [Products](https://github.com/aws-samples/retail-demo-store/tree/master/src/products) microservice and requesting related item recommendations for that product.
# #### Select a Product
#
# We'll just pick a random product for simplicity. Feel free to change the `productId` below and execute the following cells with a different product to get a sense for how the recommendations change.
# +
productId = 22
response = requests.get('http://{}/products/id/{}'.format(products_service_instance, productId))
product = response.json()
print(json.dumps(product, indent=4, sort_keys=True))
# -
# #### Get Related Product Recommendations for Product
#
# Now let's call Amazon Personalize to get related item/product recommendations for our product from the related item campaign.
# +
get_recommendations_response = personalize_runtime.get_recommendations(
campaignArn = related_campaign_arn,
itemId = str(productId),
numResults = 10
)
item_list = get_recommendations_response['itemList']
# -
print(json.dumps(item_list, indent=4))
# Since the `itemId`'s in the above response don't tell us much about the products being recommended, let's get detailed information for each item ID from the Products microservice.
for item in item_list:
response = requests.get('http://{}/products/id/{}'.format(products_service_instance, item['itemId']))
print(json.dumps(response.json(), indent = 4))
# ### Test Product Recommendations Campaign
#
# Let's test the recommendations made by the product recommendations campaign by selecting a user from the Retail Demo Store's Users microservice and requesting item recommendations for that user.
# #### Select a User
#
# We'll just pick a random user for simplicity. Feel free to change the `userId` below and execute the following cells with a different user to get a sense for how the recommendations change.
# +
userId = 10
response = requests.get('http://{}/users/id/{}'.format(users_service_instance, userId))
user = response.json()
persona = user['persona']
# -
print(json.dumps(user, indent=4, sort_keys=True))
# **Take note of the `persona` value for the user above. We should see recommendations for products consistent with this persona.**
print('Shopper persona for user {} is {}'.format(userId, persona))
# #### Get Product Recommendations for User
#
# Now let's call Amazon Personalize to get recommendations for our user from the product recommendations campaign.
# +
get_recommendations_response = personalize_runtime.get_recommendations(
campaignArn = recommend_campaign_arn,
userId = str(userId),
numResults = 10
)
item_list = get_recommendations_response['itemList']
# -
print(json.dumps(item_list, indent=4))
# Since the `itemId`'s in the above response don't tell us much about the products being recommended, let's retrieve product details from the Products microservice.
# +
print('User persona: ' + persona)
for item in item_list:
response = requests.get('http://{}/products/id/{}'.format(products_service_instance, item['itemId']))
print(json.dumps(response.json(), indent = 4))
# -
# Are the recommended products consistent with the persona? Note that this is a rather contrived example using a limited amount of generated interaction data without model parameter tuning. The purpose is to give you hands on experience building models and retrieving inferences from Amazon Personalize.
# ### Test Personalized Ranking Campaign
#
# Next let's evaluate the results of the personalized ranking campaign. As a reminder, given a list of items and a user, this campaign will rerank the items based on the preferences of the user. For the Retail Demo Store, we will use this campaign to rerank the products listed for each category and the featured products list as well as reranking catalog search results displayed in the search widget.
# #### Get Featured Products List
#
# First let's get the list of featured products from the Products microservice.
response = requests.get('http://{}/products/featured'.format(products_service_instance))
featured_products = response.json()
print(json.dumps(featured_products, indent = 4))
# #### ReRank Featured Products
#
# Using the featured products list just retrieved, first we'll create a list of item IDs that we want to rerank for a specific user. This reranking will allow us to provide ranked products based on the user's behavior. These behaviors should be consistent the same persona that was mentioned above.
# +
unranked_product_ids = []
for product in featured_products:
unranked_product_ids.append(product['id'])
print(unranked_product_ids)
# -
response = personalize_runtime.get_personalized_ranking(
campaignArn=ranking_campaign_arn,
inputList=unranked_product_ids,
userId=str(userId)
)
print(json.dumps(response['personalizedRanking'], indent = 4))
# Are the reranked results different than the original results from the Search service? Experiment with a different `userId` in the cells above to see how the item ranking changes.
# ## Enable Campaigns in Retail Demo Store Recommendations Service
#
# Now that we've tested our campaigns and can get related product, product recommendations, and reranked items for our users, we need to enable the campaigns in the Retail Demo Store's [Recommendations service](https://github.com/aws-samples/retail-demo-store/tree/master/src/recommendations). The Recommendations service is called by the Retail Demo Store Web UI when a signed in user visits a page with personalized content capabilities (home page, product detail page, and category page). The Recommendations service checks Systems Manager Parameters values to determine the Personalize campaign ARNs to use for each of our three personalization use-cases.
#
# Let's set the campaign ARNs for our campaigns in the expected parameter names.
# ### Update SSM Parameter To Enable Related Products
response = ssm.put_parameter(
Name='retaildemostore-related-products-campaign-arn',
Description='Retail Demo Store Related Products Campaign Arn Parameter',
Value='{}'.format(related_campaign_arn),
Type='String',
Overwrite=True
)
# ### Update SSM Parameter To Enable Product Recommendations
response = ssm.put_parameter(
Name='retaildemostore-product-recommendation-campaign-arn',
Description='Retail Demo Store Product Recommendation Campaign Arn Parameter',
Value='{}'.format(recommend_campaign_arn),
Type='String',
Overwrite=True
)
# ### Update SSM Parameter To Enable Search Personalization
response = ssm.put_parameter(
Name='retaildemostore-personalized-ranking-campaign-arn',
Description='Retail Demo Store Personalized Ranking Campaign Arn Parameter',
Value='{}'.format(ranking_campaign_arn),
Type='String',
Overwrite=True
)
# ## Evaluate Personalization in Retail Demo Store's Web UI
#
# Now that you've enabled each personalization feature by setting the respective campaign ARN, you can test these personalization features through the Web App UI. If you haven't already opened a browser window/tab to the Retail Demo Store Web UI, navigate to the CloudFormation console in this AWS account and check the Outputs section of the stack used to launch the Retail Demo Store. Make sure you're checking the base stack and not the nested stacks that were created. In the Outputs section look for the output named: WebURL and browse to the URL provided.
#
# 
#
# If you haven't already created a user account in your Retail Demo Store instance, let's create one now. Once you've accessed the Retail Demo Store Web UI, you can logon and create a new account. Click on the Sign In button and then the "**No account? Create account**" link to create an account. Follow the prompts and enter the required data. You will need to provide a valid mobile phone number in order to receive an SMS message with the confirmation code to validate your account.
#
# Once you've created and validated your account, click on the Sign In button again and sign in with the account you created.
# ### Emulate Shopper
#
# To confirm product recommendations are personalized, you can emulate a different user. Click on your username in the top right-corner and then select [**Profile**](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/authenticated/Profile.vue). Use the Switch User drop-down to select a different user. In the drop down you will see a user's First and Last Name and a Persona that matches that user's behavior. Product recommendations should match the persona of the user you've selected.
#
# 
# ### Viewing Related Product Recommendations
#
# Let's start with the Related Product Recommendations use-case. This campaign for this use-case is based on the [SIMS](https://docs.aws.amazon.com/personalize/latest/dg/native-recipe-sims.html) recipe which uses item-to-item collaborative filtering at its core to derive an understanding of how users interact with similar items.
#
# Browse to a [product detail page](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/public/ProductDetail.vue) and evaluate the products listed in the **What other items do customers view related to this product?** section. You should see the recipe name displayed below the section header. This tells you that results are actually coming from the related item campaign. If you don't see the recipe name, the page is using default behavior of displaying products from the same category (verify that the campaign was created successfully above **and** the campaign ARN is set as an SSM parameter).
#
# Given the shopper personas we used to generate historical data, do the related item recommendations make sense? For example, given that one of the shopper personas used across many of the customers is "footwear_outdoors", you should see related products from both of these categories when viewing a product from either category. Although this is a somewhat contrived example, it does illustrate how Personalize understands an affinity for products across these categories.
#
# 
# ### Viewing Product Recommendations
#
# With the user emulation saved, browse to the Retail Demo Store [home page](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/public/Main.vue) and evaluate the products listed in the **Inspired by your shopping trends** section (towards bottom of page). Do they appear consistent with the shopping persona you're emulating? For the screenshots listed here, the user was trained with historical data based on the "footwear_outdoors" persona so we should see product recommendations from the Footwear and Outdoors categories.
#
# 
#
# Note that if the section is titled **Featured** or you don't see the Personalize recipe name displayed, this indicates that either you are not signed in as a user or the campaign ARN is not set as the appropriate SSM parameter. Double check that the campaign was created successfully above and that the campaign ARN is set in SSM.
# ### Personalized Ranking
#
# Finally, let's evaluate the personalizated ranking use-case. There are two places where personalized ranking is implemented in the Retail Demo Store. With a user emulated, browse to the featured product category list by clicking on "Featured" from the Retail Demo Store home page. Note how for the emulated user with a persona of "footwear_outdoors" that the shoe is moved to the first product. (See [CategoryDetail.vue](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/public/CategoryDetail.vue)).
#
# 
#
# The other feature where personalized ranking is implemented is in [search results](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/public/Search.vue). Start typing a word in the search box and a search result widget will be displayed. If the results were reranked by Personalize, you will see a "Personalize Ranking" annotation in the search box. For the emulated user with a historical affinity for footwear and outdoors, notice that a search for product keywords starting with "s" will move shoes to the top of the results.
#
# 
#
# If the search functionality is not working at all for you, make sure that you completed the [Search workshop](../0-StartHere/Search.ipynb).
# ## Event Tracking - Keeping up with evolving user intent
#
# Up to this point we have trained and deployed three Amazon Personalize campaigns based on historical data that we generated in this workshop. This allows us to make related product, user recommendations, and rerank product lists based on already observed behavior of our users. However, user intent often changes in real-time such that what products the user is interested in now may be different than what they were interested in a week ago, a day ago, or even a few minutes ago. Making recommendations that keep up with evolving user intent is one of the more difficult challenges with personalization. Fortunately, Amazon Personalize has a mechanism for this exact issue.
#
# Amazon Personalize supports the ability to send real-time user events (i.e. clickstream) data into the service. Personalize uses this event data to improve recommendations. It will also save these events and automatically include them when solutions for the same dataset group are re-created (i.e. model retraining).
#
# The Retail Demo Store's Web UI already has [logic to send events](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/analytics/AnalyticsHandler.js) such as 'ProductViewed', 'ProductAdded', 'OrderCompleted', and others as they occur in real-time to a Personalize Event Tracker. These are the same event types we used to initially create the solutions and campaigns for our three use-cases. All we need to do is create an event tracker in Personalize, set the tracking Id for the tracker in an SSM parameter, and rebuild the Web UI service to pick up the change.
# ### Create Personalize Event Tracker
#
# Let's start by creating an event tracker for our dataset group.
# +
event_tracker_response = personalize.create_event_tracker(
datasetGroupArn=dataset_group_arn,
name='retaildemostore-event-tracker'
)
event_tracker_arn = event_tracker_response['eventTrackerArn']
event_tracking_id = event_tracker_response['trackingId']
print('Event Tracker ARN: ' + event_tracker_arn)
print('Event Tracking ID: ' + event_tracking_id)
# -
# ### Wait for Event Tracker Status to Become ACTIVE
#
# The event tracker should take a minute or so to become active.
status = None
max_time = time.time() + 60*60 # 1 hours
while time.time() < max_time:
describe_event_tracker_response = personalize.describe_event_tracker(
eventTrackerArn = event_tracker_arn
)
status = describe_event_tracker_response["eventTracker"]["status"]
print("EventTracker: {}".format(status))
if status == "ACTIVE" or status == "CREATE FAILED":
break
time.sleep(15)
# ### Update SSM Parameter To Enable Event Tracking
#
# The Retail Demo Store's Web UI service just needs a Personalize Event Tracking Id to be able to send events to Personalize. The CodeBuild configuration for the Web UI service will pull the event tracking ID from an SSM parameter.
#
# Let's set our tracking ID in an SSM parameter.
response = ssm.put_parameter(
Name='retaildemostore-personalize-event-tracker-id',
Description='Retail Demo Store Personalize Event Tracker ID Parameter',
Value='{}'.format(event_tracking_id),
Type='String',
Overwrite=True
)
# ### Trigger Web UI Service Release
#
# Next let's trigger a new release of the Retail Demo Store's Web UI service so that it will pick up our SSM parameter change.
#
# In the AWS console, browse to the AWS Code Pipeline service. Find the pipeline with **WebUIPipeline** in the name. Click on the pipeline name.
#
# 
# #### Trigger Release
#
# To manually trigger a new release, click the **Release change** button, click the **Release** button on the popup dialog window, and then wait for the pipeline to build and deploy. This will rebuild the web app, deploy it to the web UI S3 bucket, and invalidate the CloudFront distribution to force browsers to load from the origin rather than from their local cache.
#
# 
# ### Verify Event Tracking
#
# Return to your web browser tab/window where the Retail Demo Store Web UI is loaded and **reload the web app/page**. Reloading the page is important so that the web app is reloaded in your browser and the new event tracking configuration is loaded as well.
#
# There are a couple ways to verify that events are being sent to the Event Tracker. First, you can use your browser's developer tools to monitor the network calls made by the Retail Demo Store Web UI when you're browsing to product detail pages, adding items to carts, and completing orders. The other way you can verify that events are being received by the event tracker is in CloudWatch metrics for Personalize.
#
# 1. If you have done so, **reload the web app by refreshing/reloading your browser page.**
# 2. If not already signed in as a storefront user, sign in as (or create) a user.
# 3. In the Retail Demo Store Web app, view product detail pages, add items to your cart, complete an order.
# 4. Verify that the Web UI is making "events" calls to the Personalize Event Tracker.
# 5. In the AWS console, browse to CloudWatch and then Metrics.
#
# 
#
# If events are not being sent to the event tracker, make sure that the WebUIPipeline pipeline was built and deployed successfully and that you reloaded the web app in your browser.
#
# To assess the impact of real-time event tracking in recommendations made by the user recommendations on the home page, follow these steps.
#
# 1. Sign in as (or create) a storefront user.
# 2. View the product recommendations displayed on the home page under the "Inspired by your shopping trends" header. Take note of the products being recommended.
# 3. View products from categories that are not being recommended by clicking on their "Details" button. When you view the details for a product, an event is fired and sent to the Personalize event tracker.
# 4. Return to the home page and you should see products being recommended that are the same or similar to the ones you just viewed.
# ## Create Purchased Products Filter
#
# Amazon Personalize supports the ability to create [filters](https://docs.aws.amazon.com/personalize/latest/dg/filter.html) that can be used to exclude items from being recommended that meet a filter expression. Since it's a poor user experience to recommend products that a user has already purchased, we will create a filter that excludes recently purchased products. We'll do this by creating a filter expression that excludes items that have an interaction with an event type of `OrderCompleted` for the user.
#
# > As noted above, the Retail Demo Store web application streams clickstream events to Personalize when the user performs various actions such as viewing and purchasing products. The filter created below allows us to use those events as exclusion criteria. See the [AnalyticsHandler.js](https://github.com/aws-samples/retail-demo-store/blob/master/src/web-ui/src/analytics/AnalyticsHandler.js) file for the code that sends clickstream events.
# +
response = personalize.create_filter(
name = 'retaildemostore-filter-purchased-products',
datasetGroupArn = dataset_group_arn,
filterExpression = 'EXCLUDE itemId WHERE INTERACTIONS.event_type in ("OrderCompleted")'
)
filter_arn = response['filterArn']
print(f'Filter ARN: {filter_arn}')
# -
# ### Test Purchased Products Filter
#
# To test our purchased products filter, we will request recommendations for a random user. Then we will send an `OrderCompleted` event for one of the recommended products to Personalize using the event tracker created above. Finally, we will request recommendations again for the same user but this time specify our filter.
# +
# Pick a user ID in the range of test users and fetch 5 recommendations.
user_id = '456'
get_recommendations_response = personalize_runtime.get_recommendations(
campaignArn = recommend_campaign_arn,
userId = user_id,
numResults = 5
)
item_list = get_recommendations_response['itemList']
print(json.dumps(item_list, indent=2))
# -
# Next let's randomly select an item from the returned list of recommendations to be our product to purchase.
product_id_to_purchase = item_list[randint(0, len(item_list)-1)]['itemId']
print(f'Product ID to purchase: {product_id_to_purchase}')
# Next let's send an `OrderCompleted` event to Personalize to simulate that the product was just purchased. This will match the criteria for our filter. In the Retail Demo Store web application, this event is sent for each product in the order after the order is completed.
# +
response = personalize_events.put_events(
trackingId = event_tracking_id,
userId = user_id,
sessionId = str(uuid.uuid4()),
eventList = [
{
'eventId': str(uuid.uuid4()),
'eventType': 'OrderCompleted',
'properties': json.dumps({ 'itemId': product_id_to_purchase }),
'sentAt': int(time.time())
}
]
)
print(json.dumps(response, indent=2))
# -
# Finally, let's retrieve recommendations for the user again but this time specifying the filter to exclude recently purchased items. We do this by passing the filter's ARN via the `filterArn` parameter. In the Retail Demo Store, this is done in the [Recommendations](https://github.com/aws-samples/retail-demo-store/tree/master/src/recommendations) service.
# +
get_recommendations_response = personalize_runtime.get_recommendations(
campaignArn = recommend_campaign_arn,
userId = user_id,
numResults = 5,
filterArn = filter_arn
)
item_list = get_recommendations_response['itemList']
print(json.dumps(item_list, indent=2))
# -
# The following code will raise an assertion error if the product we just purchased is still recommended.
found_item = next((item for item in item_list if item['itemId'] == product_id_to_purchase), None)
if found_item:
assert found_item, 'Purchased item found unexpectedly in recommendations'
else:
print('Purchased item filtered from recommendations for user!')
# ### Update Filter SSM Parameter
#
# With our filter created and tested, the last step is to update the SSM parameter that is used throughout the Retail Demo Store project to detect the filter ARN.
#
# The [Recommendations](https://github.com/aws-samples/retail-demo-store/tree/master/src/recommendations) service already has logic to look for the purchased products filter ARN in SSM and use it when fetching recommendations. All we have to do is set the filter's ARN in SSM.
response = ssm.put_parameter(
Name='retaildemostore-personalize-filter-purchased-arn',
Description='Retail Demo Store Personalize Filter Purchased Products Arn Parameter',
Value='{}'.format(filter_arn),
Type='String',
Overwrite=True
)
# Now if you test completing an order for one or more items in the Retail Demo Store web application for a user, those products should no longer be included in recommendations for that user. Test it out by purchasing a recommended product from the "Inspired by your shopping trends" section of the home page and then verifying that the product is no longer recommended.
# ## Workshop Complete
#
# Congratulations! You have completed the Retail Demo Store Personalization Workshop.
#
# ### Cleanup
#
# If you launched the Retail Demo Store in your personal AWS account **AND** you're done with all workshops, you can follow the [Personalize workshop cleanup](./1.2-Personalize-Cleanup.ipynb) notebook to delete all of the Amazon Personalize resources created by this workshop. **IMPORTANT: since the Personalize resources were created by this notebook and not CloudFormation, deleting the CloudFormation stack for the Retail Demo Store will not remove the Personalize resources. You MUST run the [Personalize workshop cleanup](./1.2-Personalize-Cleanup.ipynb) notebook or manually clean up these resources.**
#
# If you are participating in an AWS managed event such as a workshop and using an AWS provided temporary account, you can skip the cleanup workshop unless otherwise instructed.
|
workshop/1-Personalization/1.1-Personalize.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## ノイズ耐性1
from ml.nn import *
from datasets.dataset import load_mnist
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import *
(x_train, t_train), (x_test, t_test) = load_mnist(one_hot=False)
# rateだけノイズを加える関数
def add_noise(data, rate):
n_noise = int(data.shape[1] * rate)
pixel = np.arange(0, data.shape[1], 1)
for d in data:
target_pixel = np.random.choice(pixel, n_noise, replace=False)
for i in target_pixel:
d[i] = np.random.rand()
return data
# ### 0%~25%のノイズを5%刻みで付与
rates = [0, 0.05, 0.10, 0.15, 0.20, 0.25]
noised_x_train = []
noised_x_test = []
# ノイズ付与
for rate in rates:
noised_x_train.append(add_noise(x_train, rate))
noised_x_test.append(add_noise(x_test, rate))
input_size = 784
output_size = 10
middle_layer_size = 50
lr = 0.001
optimizer = 'Adam'
model = Sequential()
model.addlayer(Linear(input_size, middle_layer_size, optimizer=optimizer, lr=lr))
model.addlayer(ReLU(optimizer=optimizer, lr=lr))
model.addlayer(Linear(middle_layer_size, middle_layer_size, optimizer=optimizer, lr=lr))
model.addlayer(ReLU(optimizer=optimizer, lr=lr))
model.addlayer(Linear(middle_layer_size, output_size, optimizer=optimizer, lr=lr))
network = Classifier(model)
# 各rateに対応するニューラルネットワーク生成
networks = []
for i in range(6):
networks.append(network)
batch_size = 100
epoch = 15
n_train = x_train.shape[0]
n_test = x_test.shape[0]
train_loss_list = []
train_acc_list = []
test_loss_list = []
test_acc_list = []
for i in range(6):
for e in range(epoch):
acctrain = 0
losstrain = 0
randinds = np.random.permutation(n_train)
for it in range(0, n_train, batch_size):
ind = randinds[it:it+batch_size]
x = noised_x_train[i][ind]
t = t_train[ind]
loss, acc = networks[i].update(x, t)
acctrain += int(acc * batch_size)
losstrain += loss
acctrain /= (1.0 * n_train)
losstrain /= (n_train // batch_size)
acctest = 0
losstest = 0
for it in range(0, n_test, batch_size):
# 10%のノイズを含むデータがtest
x = noised_x_test[2][it:it+batch_size]
t = t_test[it:it+batch_size]
loss, acc = networks[i].predict(x, t)
acctest += int(acc * batch_size)
losstest += loss
acctest /= (1.0 * n_test)
losstest /= (n_test // batch_size)
train_loss_list.append(losstrain)
train_acc_list.append(acctrain)
test_loss_list.append(losstest)
test_acc_list.append(acctest)
# +
fig = plt.figure(figsize=(10, 4))
loss_graph = fig.add_subplot(1, 2, 1)
acc_graph = fig.add_subplot(1, 2, 2)
loss_graph.set_xlabel('noise rate')
loss_graph.set_ylabel('loss')
acc_graph.set_xlabel('noise rate')
acc_graph.set_ylabel('accuracy')
loss_graph.plot(rates, train_loss_list, label='train')
loss_graph.plot(rates, test_loss_list, label='test')
loss_graph.legend()
acc_graph.plot(rates, train_acc_list, label='train')
acc_graph.plot(rates, test_acc_list, label='test')
acc_graph.legend()
plt.subplots_adjust(wspace=0.4, hspace=0.6)
plt.savefig('nn_noise.png')
# -
|
robot_intelligence_noise1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ! wget -N http://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data
# # Abalone
# <img src='https://cdn.shopify.com/s/files/1/2086/1263/products/1d89434927bffb6fd1786c19c2d921fb_2000x.jpg?v=1522240385' width='500px'/>
# Abalone vary in size from 20 mm (0.79 in) (Haliotis pulcherrima) to 200 mm (7.9 in) while Haliotis rufescens is the largest of the genus at 12 in (30 cm).
#
# The shell of abalones is convex, rounded to oval in shape, and may be highly arched or very flattened. The shell of the majority of species has a small, flat spire and two to three whorls. The last whorl, known as the body whorl, is auriform, meaning that the shell resembles an ear, giving rise to the common name "ear shell". Haliotis asinina has a somewhat different shape, as it is more elongated and distended. The shell of Haliotis cracherodii cracherodii is also unusual as it has an ovate form, is imperforate, shows an exserted spire, and has prickly ribs.
#
# A mantle cleft in the shell impresses a groove in the shell, in which are the row of holes characteristic of the genus. These holes are respiratory apertures for venting water from the gills and for releasing sperm and eggs into the water column. They make up what is known as the selenizone which forms as the shell grows. This series of eight to 38 holes is near the anterior margin. Only a small number is generally open. The older holes are gradually sealed up as the shell grows and new holes form. Each species has a typical number of open holes, between four and 10, in the selenizone. An abalone has no operculum. The aperture of the shell is very wide and nacreous.
# +
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
# %matplotlib inline
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.decomposition import PCA
# -
data = pd.read_csv('abalone.data', names=['Sex', 'Length', 'Diameter', 'Height', 'Whole weight', 'Shucked weight', 'Viscera weight', 'Shell weight', 'Rings'])
data.head()
# Now let's convert categorical feature 'Sex' to numerical via **one-hot encoding**
data = pd.get_dummies(data)
data.head()
# ## Analysis
data.describe()
corr = data.corr()
fig, ax = plt.subplots(figsize=(18,10))
sns.heatmap(corr)
corr
fig, ((ax1, ax2), (ax3, ax4),(ax5, ax6),(ax7,ax8)) = plt.subplots(4, 2, figsize = (15,10), sharex=False)
axs = [ax1,ax2,ax3,ax4,ax5,ax6,ax7,ax8]
plt.tight_layout()
for n in range(0, 8):
axs[n].hist(data[data.columns[n]], bins=30)
axs[n].set_title(data.columns[n], fontsize=10)
plt.figure(figsize=(18, 10))
plt.hist(data['Rings'], bins=30)
plt.title("Rings", fontsize=16)
plt.show()
X_train, X_test, y_train, y_test = train_test_split(data.drop(columns=['Rings']), data['Rings'], test_size=.2, random_state=17)
sc = StandardScaler().fit(X_train)
X_train, X_test = sc.transform(X_train), sc.transform(X_test)
# # Classification
# +
def approx(y_pred, y_true):
predictions = list(zip(y_pred, y_true))
return [len(list(filter(lambda a: abs(a[0] - a[1]) <= d, predictions))) / len(predictions) for d in [0.5, 1, 2]]
def score(model):
model.fit(X_train, y_train)
print('Train score: {}'.format(approx(model.predict(X_train), y_train)))
print('Test score: {}'.format(approx(model.predict(X_test), y_test)))
def grid_search(model, params):
gs = GridSearchCV(model, params)
return gs.fit(X_train, y_train)
# -
# ## K-Neighbors
score(KNeighborsClassifier(29))
# ## SVM + linear kernel
score(SVC(kernel='linear'))
# ## Decision tree
import graphviz
from sklearn.tree import export_graphviz
dt = DecisionTreeClassifier(max_depth=5)
score(dt)
dot_data = export_graphviz(dt, out_file=None,
feature_names=data.drop(columns=['Rings']).columns,
class_names=[str(i + 1) for i in range(29)],
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
# ## Random forest
score(RandomForestClassifier(max_depth=4, n_estimators=83, max_features=1))
# ## Multi-layer perceptron
score(MLPClassifier(alpha=2))
# ## AdaBoost
score(AdaBoostClassifier())
# # Regression
from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
from sklearn.tree import DecisionTreeRegressor
from sklearn.neural_network import MLPRegressor
# ## Linear regression
score(LinearRegression())
# ## SVM + RBF kernel
score(SVR(C=250, gamma=0.01))
# ## SVM + polynomial kernel
score(SVR(kernel='poly', C=100, degree=4))
# ## Decision tree
score(DecisionTreeRegressor(max_depth=6, criterion="mse", min_samples_leaf=20))
# ## Multi-layer perceptron
score(MLPRegressor(alpha=1e-2))
# # TensorFlow
# +
import urllib
import tempfile
import tensorflow as tf
# +
FLAGS = None
LEARNING_RATE = 0.001
tf.logging.set_verbosity(tf.logging.INFO)
# -
def maybe_download(train_data=None, test_data=None, predict_data=None):
"""Maybe downloads training data and returns train and test file names."""
if train_data:
train_file_name = train_data
else:
train_file = tempfile.NamedTemporaryFile(delete=False)
urllib.request.urlretrieve(
"http://download.tensorflow.org/data/abalone_train.csv",
train_file.name)
train_file_name = train_file.name
train_file.close()
print("Training data is downloaded to %s" % train_file_name)
if test_data:
test_file_name = test_data
else:
test_file = tempfile.NamedTemporaryFile(delete=False)
urllib.request.urlretrieve(
"http://download.tensorflow.org/data/abalone_test.csv", test_file.name)
test_file_name = test_file.name
test_file.close()
print("Test data is downloaded to %s" % test_file_name)
if predict_data:
predict_file_name = predict_data
else:
predict_file = tempfile.NamedTemporaryFile(delete=False)
urllib.request.urlretrieve(
"http://download.tensorflow.org/data/abalone_predict.csv",
predict_file.name)
predict_file_name = predict_file.name
predict_file.close()
print("Prediction data is downloaded to %s" % predict_file_name)
return train_file_name, test_file_name, predict_file_name
def model_fn(features, labels, mode, params):
first_hidden_layer = tf.layers.dense(features["x"], 10, activation=tf.nn.relu)
second_hidden_layer = tf.layers.dense(
first_hidden_layer, 10, activation=tf.nn.relu)
output_layer = tf.layers.dense(second_hidden_layer, 1)
predictions = tf.reshape(output_layer, [-1])
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions={"ages": predictions})
loss = tf.losses.mean_squared_error(labels, predictions)
optimizer = tf.train.GradientDescentOptimizer(
learning_rate=params["learning_rate"])
train_op = optimizer.minimize(
loss=loss, global_step=tf.train.get_global_step())
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(
tf.cast(labels, tf.float64), predictions)
}
return tf.estimator.EstimatorSpec(
mode=mode,
loss=loss,
train_op=train_op,
eval_metric_ops=eval_metric_ops)
# +
abalone_train, abalone_test, abalone_predict = maybe_download()
training_set = tf.contrib.learn.datasets.base.load_csv_without_header(
filename=abalone_train, target_dtype=np.int, features_dtype=np.float64)
test_set = tf.contrib.learn.datasets.base.load_csv_without_header(
filename=abalone_test, target_dtype=np.int, features_dtype=np.float64)
prediction_set = tf.contrib.learn.datasets.base.load_csv_without_header(
filename=abalone_predict, target_dtype=np.int, features_dtype=np.float64)
# +
model_params = {"learning_rate": LEARNING_RATE}
nn = tf.estimator.Estimator(model_fn=model_fn, params=model_params)
train_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"x": np.array(training_set.data)},
y=np.array(training_set.target),
num_epochs=None,
shuffle=True)
nn.train(input_fn=train_input_fn, steps=5000)
test_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"x": np.array(test_set.data)},
y=np.array(test_set.target),
num_epochs=1,
shuffle=False)
ev = nn.evaluate(input_fn=test_input_fn)
print("Loss: %s" % ev["loss"])
print("Root Mean Squared Error: %s" % ev["rmse"])
predict_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"x": prediction_set.data},
num_epochs=1,
shuffle=False)
predictions = nn.predict(input_fn=predict_input_fn)
for i, p in enumerate(predictions):
print("Prediction %s: %s" % (i + 1, p["ages"]))
# +
t_fn = tf.estimator.inputs.numpy_input_fn(
x={"x": test_set.data},
num_epochs=1,
shuffle=False)
t_pred = nn.predict(input_fn=t_fn)
t_pred = list(map(lambda x: x['ages'], t_pred))
approx(t_pred, test_set.target)
|
ml/lab1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
x = [i/10. for i in range(5, 11)]
y = [0.867, 0.807, 0.685, 0.366, 0.040, 0]
print y
# y = [0.855, 0.84, 0.835, 0.815, 0.81]
# y1=[0.86,0.85,0.853,0.849,0.83]
plt.plot(x, y, 'r')
#plt.plot(x, y1, 'bo-')
plt.xlim(0.5, 1) # 限定横轴的范围
plt.ylim(0, 1) # 限定纵轴的范围
# plt.plot(x, y, marker='o', mec='r', mfc='w',label=u'y=x^2曲线图')
# plt.plot(x, y1, marker='*', ms=10,label=u'y=x^3曲线图')
# plt.legend() # 让图例生效
# plt.xticks(x, names, rotation=45)
# plt.margins(0)
# plt.subplots_adjust(bottom=0.15)
# plt.xlabel(u"time(s)邻居") #X轴标签
# plt.ylabel("RMSE") #Y轴标签
# plt.title("A simple plot") #标题
plt.show()
# +
from scipy import optimize
#直线方程函数
def f_1(x, A, B):
return A*x + B
#二次曲线方程
def f_2(x, A, B, C):
return A*x*x + B*x + C
#三次曲线方程
def f_3(x, A, B, C, D):
return A*x*x*x + B*x*x + C*x + D
def plot_test():
plt.figure()
#拟合点
x0 = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
y0 = [0.867, 0.807, 0.685, 0.366, 0.040, 0]
#绘制散点
plt.scatter(x0[:], y0[:], 25, "red")
#直线拟合与绘制
A1, B1 = optimize.curve_fit(f_1, x0, y0)[0]
x1 = np.arange(0, 6, 0.01)
y1 = A1*x1 + B1
plt.plot(x1, y1, "blue")
#二次曲线拟合与绘制
A2, B2, C2 = optimize.curve_fit(f_2, x0, y0)[0]
x2 = np.arange(0, 6, 0.01)
y2 = A2*x2*x2 + B2*x2 + C2
plt.plot(x2, y2, "green")
#三次曲线拟合与绘制
A3, B3, C3, D3= optimize.curve_fit(f_3, x0, y0)[0]
x3 = np.arange(0, 6, 0.01)
y3 = A3*x3*x3*x3 + B3*x3*x3 + C3*x3 + D3
plt.plot(x3, y3, "purple")
plt.title("test")
plt.xlabel('x')
plt.ylabel('y')
plt.show()
return
# -
plot_test()
|
tools/.ipynb_checkpoints/draw_bbox_recall-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Lemmatizing
from nltk.stem import WordNetLemmatizer
lem = WordNetLemmatizer()
words = ['drive', 'driving', 'driver', 'drives', 'drove', 'cats', 'children']
for w in words:
print(lem.lemmatize(w))
lem.lemmatize('drive','v')
|
lemmatizing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Huggingface Sagemaker-sdk - Getting Started Demo
# ### Binary Classification with `Trainer` and `imdb` dataset
# 1. [Introduction](#Introduction)
# 2. [Development Environment and Permissions](#Development-Environment-and-Permissions)
# 1. [Installation](#Installation)
# 2. [Development environment](#Development-environment)
# 3. [Permissions](#Permissions)
# 3. [Processing](#Preprocessing)
# 1. [Tokenization](#Tokenization)
# 2. [Uploading data to sagemaker_session_bucket](#Uploading-data-to-sagemaker_session_bucket)
# 4. [Fine-tuning & starting Sagemaker Training Job](#Fine-tuning-\&-starting-Sagemaker-Training-Job)
# 1. [Creating an Estimator and start a training job](#Creating-an-Estimator-and-start-a-training-job)
# 2. [Estimator Parameters](#Estimator-Parameters)
# 3. [Download fine-tuned model from s3](#Download-fine-tuned-model-from-s3)
# 3. [Attach to old training job to an estimator ](#Attach-to-old-training-job-to-an-estimator)
# 5. [_Coming soon_:Push model to the Hugging Face hub](#Push-model-to-the-Hugging-Face-hub)
# # Introduction
#
# Welcome to our end-to-end binary Text-Classification example. In this demo, we will use the Hugging Faces `transformers` and `datasets` library together with a custom Amazon sagemaker-sdk extension to fine-tune a pre-trained transformer on binary text classification. In particular, the pre-trained model will be fine-tuned using the `imdb` dataset. To get started, we need to set up the environment with a few prerequisite steps, for permissions, configurations, and so on.
#
# 
#
# _**NOTE: You can run this demo in Sagemaker Studio, your local machine or Sagemaker Notebook Instances**_
# # Development Environment and Permissions
# ## Installation
#
# _*Note:* we only install the required libraries from Hugging Face and AWS. You also need PyTorch or Tensorflow, if you haven´t it installed_
# !pip install "sagemaker>=2.48.0" "transformers==4.6.1" "datasets[s3]==1.6.2" --upgrade
# ## Development environment
# **upgrade ipywidgets for `datasets` library and restart kernel, only needed when prerpocessing is done in the notebook**
# %%capture
import IPython
# !conda install -c conda-forge ipywidgets -y
IPython.Application.instance().kernel.do_shutdown(True) # has to restart kernel so changes are used
import sagemaker.huggingface
# ## Permissions
# _If you are going to use Sagemaker in a local environment. You need access to an IAM Role with the required permissions for Sagemaker. You can find [here](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html) more about it._
# +
import sagemaker
sess = sagemaker.Session()
# sagemaker session bucket -> used for uploading data, models and logs
# sagemaker will automatically create this bucket if it not exists
sagemaker_session_bucket=None
if sagemaker_session_bucket is None and sess is not None:
# set to default bucket if a bucket name is not given
sagemaker_session_bucket = sess.default_bucket()
role = sagemaker.get_execution_role()
sess = sagemaker.Session(default_bucket=sagemaker_session_bucket)
print(f"sagemaker role arn: {role}")
print(f"sagemaker bucket: {sess.default_bucket()}")
print(f"sagemaker session region: {sess.boto_region_name}")
# -
# # Preprocessing
#
# We are using the `datasets` library to download and preprocess the `imdb` dataset. After preprocessing, the dataset will be uploaded to our `sagemaker_session_bucket` to be used within our training job. The [imdb](http://ai.stanford.edu/~amaas/data/sentiment/) dataset consists of 25000 training and 25000 testing highly polar movie reviews.
# ## Tokenization
# +
from datasets import load_dataset
from transformers import AutoTokenizer
# tokenizer used in preprocessing
tokenizer_name = 'distilbert-base-uncased'
# dataset used
dataset_name = 'imdb'
# s3 key prefix for the data
s3_prefix = 'samples/datasets/imdb'
# +
# load dataset
dataset = load_dataset(dataset_name)
# download tokenizer
tokenizer = AutoTokenizer.from_pretrained(tokenizer_name)
# tokenizer helper function
def tokenize(batch):
return tokenizer(batch['text'], padding='max_length', truncation=True)
# load dataset
train_dataset, test_dataset = load_dataset('imdb', split=['train', 'test'])
test_dataset = test_dataset.shuffle().select(range(10000)) # smaller the size for test dataset to 10k
# tokenize dataset
train_dataset = train_dataset.map(tokenize, batched=True)
test_dataset = test_dataset.map(tokenize, batched=True)
# set format for pytorch
train_dataset = train_dataset.rename_column("label", "labels")
train_dataset.set_format('torch', columns=['input_ids', 'attention_mask', 'labels'])
test_dataset = test_dataset.rename_column("label", "labels")
test_dataset.set_format('torch', columns=['input_ids', 'attention_mask', 'labels'])
# -
# ## Uploading data to `sagemaker_session_bucket`
#
# After we processed the `datasets` we are going to use the new `FileSystem` [integration](https://huggingface.co/docs/datasets/filesystems.html) to upload our dataset to S3.
# +
import botocore
from datasets.filesystems import S3FileSystem
s3 = S3FileSystem()
# save train_dataset to s3
training_input_path = f's3://{sess.default_bucket()}/{s3_prefix}/train'
train_dataset.save_to_disk(training_input_path,fs=s3)
# save test_dataset to s3
test_input_path = f's3://{sess.default_bucket()}/{s3_prefix}/test'
test_dataset.save_to_disk(test_input_path,fs=s3)
# -
# # Fine-tuning & starting Sagemaker Training Job
#
# In order to create a sagemaker training job we need an `HuggingFace` Estimator. The Estimator handles end-to-end Amazon SageMaker training and deployment tasks. In a Estimator we define, which fine-tuning script should be used as `entry_point`, which `instance_type` should be used, which `hyperparameters` are passed in .....
#
#
#
# ```python
# huggingface_estimator = HuggingFace(entry_point='train.py',
# source_dir='./scripts',
# base_job_name='huggingface-sdk-extension',
# instance_type='ml.p3.2xlarge',
# instance_count=1,
# transformers_version='4.4',
# pytorch_version='1.6',
# py_version='py36',
# role=role,
# hyperparameters = {'epochs': 1,
# 'train_batch_size': 32,
# 'model_name':'distilbert-base-uncased'
# })
# ```
#
# When we create a SageMaker training job, SageMaker takes care of starting and managing all the required ec2 instances for us with the `huggingface` container, uploads the provided fine-tuning script `train.py` and downloads the data from our `sagemaker_session_bucket` into the container at `/opt/ml/input/data`. Then, it starts the training job by running.
#
# ```python
# /opt/conda/bin/python train.py --epochs 1 --model_name distilbert-base-uncased --train_batch_size 32
# ```
#
# The `hyperparameters` you define in the `HuggingFace` estimator are passed in as named arguments.
#
# Sagemaker is providing useful properties about the training environment through various environment variables, including the following:
#
# * `SM_MODEL_DIR`: A string that represents the path where the training job writes the model artifacts to. After training, artifacts in this directory are uploaded to S3 for model hosting.
#
# * `SM_NUM_GPUS`: An integer representing the number of GPUs available to the host.
#
# * `SM_CHANNEL_XXXX:` A string that represents the path to the directory that contains the input data for the specified channel. For example, if you specify two input channels in the HuggingFace estimator’s fit call, named `train` and `test`, the environment variables `SM_CHANNEL_TRAIN` and `SM_CHANNEL_TEST` are set.
#
#
# To run your training job locally you can define `instance_type='local'` or `instance_type='local_gpu'` for gpu usage. _Note: this does not working within SageMaker Studio_
#
# !pygmentize ./scripts/train.py
# ## Creating an Estimator and start a training job
# +
from sagemaker.huggingface import HuggingFace
# hyperparameters, which are passed into the training job
hyperparameters={'epochs': 1,
'train_batch_size': 32,
'model_name':'distilbert-base-uncased'
}
# -
huggingface_estimator = HuggingFace(entry_point='train.py',
source_dir='./scripts',
instance_type='ml.p3.2xlarge',
instance_count=1,
role=role,
transformers_version='4.6',
pytorch_version='1.7',
py_version='py36',
hyperparameters = hyperparameters)
# starting the train job with our uploaded datasets as input
huggingface_estimator.fit({'train': training_input_path, 'test': test_input_path})
# ## Deploying the endpoint
#
# To deploy our endpoint, we call `deploy()` on our HuggingFace estimator object, passing in our desired number of instances and instance type.
predictor = huggingface_estimator.deploy(1,"ml.g4dn.xlarge")
# Then, we use the returned predictor object to call the endpoint.
# +
sentiment_input= {"inputs":"I love using the new Inference DLC."}
predictor.predict(sentiment_input)
# -
# Finally, we delete the endpoint again.
predictor.delete_endpoint()
# # Extras
# ### Estimator Parameters
# +
# container image used for training job
print(f"container image used for training job: \n{huggingface_estimator.image_uri}\n")
# s3 uri where the trained model is located
print(f"s3 uri where the trained model is located: \n{huggingface_estimator.model_data}\n")
# latest training job name for this estimator
print(f"latest training job name for this estimator: \n{huggingface_estimator.latest_training_job.name}\n")
# -
# access the logs of the training job
huggingface_estimator.sagemaker_session.logs_for_job(huggingface_estimator.latest_training_job.name)
# ### Attach to old training job to an estimator
#
# In Sagemaker you can attach an old training job to an estimator to continue training, get results etc..
# +
from sagemaker.estimator import Estimator
# job which is going to be attached to the estimator
old_training_job_name=''
# +
# attach old training job
huggingface_estimator_loaded = Estimator.attach(old_training_job_name)
# get model output s3 from training job
huggingface_estimator_loaded.model_data
|
sagemaker/01_getting_started_pytorch/sagemaker-notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Al-x-R/Colab-examples/blob/master/titanic.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="GMjIbGjzd0VP" colab_type="code" outputId="0821d467-8773-40cb-818b-7e350c454397" colab={"base_uri": "https://localhost:8080/", "height": 937}
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/an-2-an/data/master/titanic_train.csv', index_col='PassengerId')
df.head(10)
# + id="tlKBjUcmd3u4" colab_type="code" outputId="e1895508-fa6a-40c7-aaad-b6b9ff18733e" colab={"base_uri": "https://localhost:8080/", "height": 297}
df.describe()
# + id="B6pYboCbd3xl" colab_type="code" outputId="adfb2d83-eafa-4044-a39d-7a8623ef1d34" colab={"base_uri": "https://localhost:8080/", "height": 34}
#подчищаем
df.drop('Cabin', axis=1, inplace=True)
df.dropna(inplace=True) #удаляем пустые значения
df.shape
# + id="Oj_7Lkx6d30l" colab_type="code" outputId="0ebc2736-677a-4266-da47-0978c366eac9" colab={"base_uri": "https://localhost:8080/", "height": 637}
#изобразим попарно матрицу графиков
from pandas.plotting import scatter_matrix
fields = ['Age', 'Pclass', 'Sex', 'Fare']
scatter_matrix(df[fields], figsize=(15, 10));
# + id="8JIYgzrjd3_8" colab_type="code" outputId="bfc499bf-57d5-4175-b4ac-eb132e3e33cb" colab={"base_uri": "https://localhost:8080/", "height": 301}
#как плата за билет зависит от класса каюты
df.boxplot(column='Fare', by='Pclass');
# + id="OaoW1pdhhVcQ" colab_type="code" outputId="36f9a740-694a-49a0-ddd2-eb25772851f3" colab={"base_uri": "https://localhost:8080/", "height": 283}
#соотношение погибших и выживших в зависимости от пола
import seaborn as sns
sns.countplot(x='Sex', hue='Survived', data=df);
# + id="aVLlKR9vhVe-" colab_type="code" outputId="dc98fff7-3c25-4fd1-f377-4ae5cb9198bc" colab={"base_uri": "https://localhost:8080/", "height": 173}
df.pivot_table(index='Sex', values='Survived', aggfunc=['count','sum', 'mean'])
# + id="tHqLr12mhVhn" colab_type="code" outputId="19319e94-f1e2-4f7d-a145-8135c5a44ce8" colab={"base_uri": "https://localhost:8080/", "height": 283}
#соотношение погибших и выживших в зависимости от класса кают
sns.countplot(x='Pclass', hue='Survived', data=df);
# + id="p99B1uyYjVFK" colab_type="code" outputId="16fed6d7-df3a-4af8-9803-07f7d364e941" colab={"base_uri": "https://localhost:8080/", "height": 527}
#молодые(до 30) выживали чаще?
df['Young'] = (df['Age'] < 30).astype(int)
df.head()
# + id="YCGa4pLEjVIx" colab_type="code" outputId="860f4470-7f1a-4af2-8c34-40dde66a9109" colab={"base_uri": "https://localhost:8080/", "height": 85}
df.groupby('Young')['Survived'].mean() * 100.0
# + id="7mkJAoGZhVlI" colab_type="code" outputId="9719bb97-e671-4968-8ac6-81f5f596b527" colab={"base_uri": "https://localhost:8080/", "height": 255}
df[df['Young']==1]['Survived'].value_counts().plot.pie(autopct='%1.1f%%');
# + id="h5GmlvQ-hVpO" colab_type="code" outputId="65af4d67-ab69-4e60-932a-dd6f628f31a7" colab={"base_uri": "https://localhost:8080/", "height": 255}
df[df['Young']==0]['Survived'].value_counts().plot.pie(autopct='%1.1f%%');
|
titanic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 02- Array & Linked List
# ## Table of Contents:
# * [1. Array](#array)
# * [2. Linked List](#linked-list)
# * [3. Array vs. Linked List](#array-vs-linked-list)
# <a class="anchor" id="array"></a>
# ## 1. Array
# An array is defined as a set of a definite number of homogeneous elements or data items. It means an array can contain one type of data only, either all integers, all floating-point numbers, or all characters.
#
# Declaration of an array is as follows:
#
# C:
# ```C
# int a [10];
# ```
#
# Python:
# ```python
# mylist = []
# ```
# The individual elements of an array can be accessed by describing the name of the array, followed by index or subscript (determining the location of the element in the array) inside the square brackets.
#
# For example, to retrieve 5th element of the array, we need to write a statement `a[4]`.
# 
# <a class="anchor" id="linked-list"></a>
# ## 2. Linked List
# Linked list is a particular list of some data elements linked to one other. In this every element point to the next element which represents the logical ordering. Each element is called a node, which has two parts
# **INFO** part which stores the information and **POINTER** which points to the next element. As you know for storing address, we have a unique data structures in C called pointers. Hence the second field of the list must be a pointer type.
# 
# 
# <a class="anchor" id="array-vs-linked-list"></a>
# ## 3. Array vs. Linked List
# |Basis for Comparison|Array|Linked List|
# |:--|:--|:--|
# |**Basic**|It is a consistent set of a fixed number of data items. |It is an ordered set comprising a variable number of data items.|
# |**Size**| Specified during declaration.| No need to specify; grow and shrink during execution.|
# |**Storage**| Allocation| Element location is allocated during compile time. Element position is assigned during run time.|
# |**Order of the elements**| Stored consecutively| Stored randomly|
# |**Accessing the element**| Direct or randomly accessed, i.e., Specify the array index or subscript.| Sequentially accessed, i.e., Traverse starting from the first node in the list by the pointer.|
# |**Insertion and deletion of element**| Slow relatively as shifting is required.|Easier, fast and efficient.
# |**Searching**| Binary search and linear search|Linear search|
# |**Memory required**| Less| More|
# |**Memory Utilization**| Ineffective| Efficient|
|
03. Data Structure and Algorithm/02- Array & Linked List.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import mindspore
import mindspore.nn as nn
from mindspore import Parameter, Tensor
import numpy as np
import mindspore.ops as ops
class TextCNN(nn.Cell):
def __init__(self, embedding_size, sequence_length, num_classes, filter_sizes, num_filters, vocab_size):
super(TextCNN, self).__init__()
self.num_filters_total = num_filters * len(filter_sizes)
self.filter_sizes = filter_sizes
self.sequence_length = sequence_length
self.W = nn.Embedding(vocab_size, embedding_size)
self.Weight = nn.Dense(self.num_filters_total, num_classes, has_bias=False)
self.Bias = Parameter(Tensor(np.ones(num_classes), mindspore.float32))
self.filter_list = nn.CellList()
for size in filter_sizes:
seq_cell = nn.SequentialCell([
nn.Conv2d(1, num_filters, (size, embedding_size), pad_mode='valid'),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(sequence_length - size + 1, 1))
])
self.filter_list.append(seq_cell)
self.expand_dims = ops.ExpandDims()
self.transpose = ops.Transpose()
self.concat = ops.Concat(axis=len(filter_sizes))
self.reshape = ops.Reshape()
def construct(self, X):
embedded_chars = self.W(X)
embedded_chars = self.expand_dims(embedded_chars, 1)
pooled_outputs= []
for conv in self.filter_list:
pooled = conv(embedded_chars)
pooled = self.transpose(pooled,(0,3,2,1))
pooled_outputs.append(pooled)
h_pool = self.concat((pooled_outputs[0], pooled_outputs[1], pooled_outputs[2]))
h_pool_flat = ops.reshape(h_pool,(-1, self.num_filters_total))
model = self.Weight(h_pool_flat) + self.Bias
return model
# +
embedding_size = 2
sequence_length = 3
num_classes = 2
filter_sizes = [2, 2, 2]
num_filters = 3
sentences = ["i love you", "he loves me", "she likes baseball", " i hate you", "sorry for that", "this is awful"]
labels = [1, 1, 1, 0, 0, 0] # 1 is good, 0 is not good.
word_list = " ".join(sentences).split()
word_list = list(set(word_list))
word_dict = {w: i for i, w in enumerate(word_list)}
vocab_size = len(word_dict)
model = TextCNN(embedding_size, sequence_length, num_classes, filter_sizes, num_filters, vocab_size)
# -
criterion = nn.SoftmaxCrossEntropyWithLogits(sparse=True,reduction='mean')
optimizer = nn.Adam(model.trainable_params(), learning_rate=0.001)
inputs = Tensor([np.asarray([word_dict[n] for n in sen.split()]) for sen in sentences], mindspore.int32)
targets = Tensor([out for out in labels], mindspore.int32)
# +
from mindspore import context
context.set_context(mode=context.GRAPH_MODE, device_target="CPU")
net_with_criterion = nn.WithLossCell(model, criterion)
train_network = nn.TrainOneStepCell(net_with_criterion, optimizer)
train_network.set_train()
# -
epoch = 5000
for step in range(epoch):
loss = train_network(inputs, targets)
if (step + 1) % 1000 == 0:
print('Epoch:', '%04d' % (step + 1), 'cost =', '{:.6f}'.format(loss.asnumpy()))
# +
test_text = 'sorry hate you'
tests = [np.asarray([word_dict[n] for n in test_text.split()])]
test_batch = Tensor(tests, mindspore.int32 )
# Predict
predict = model(test_batch).asnumpy().argmax(1)
if predict[0] == 0:
print(test_text,"is Bad Mean...")
else:
print(test_text,"is Good Mean!!")
# -
|
2-1.TextCNN/TextCNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
# <script>
# window.dataLayer = window.dataLayer || [];
# function gtag(){dataLayer.push(arguments);}
# gtag('js', new Date());
#
# gtag('config', 'UA-59152712-8');
# </script>
#
# # Tetrads for Evaluating the Outgoing Gravitational Wave Weyl scalar $\psi_4$
#
# ## Authors: <NAME> & <NAME>
#
# [comment]: <> (Abstract: TODO)
#
# **Notebook Status:** <font color='green'><b> Validated </b></font>
#
# **Validation Notes:** This module has been validated to agree at roundoff error with the WeylScal4 ETK thorn in Cartesian coordinates (as it agrees to roundoff error with Patrick Nelson's [Cartesian Weyl Scalars & Invariants NRPy+ tutorial notebook](Tutorial-WeylScalarsInvariants-Cartesian.ipynb), which itself was validated against WeylScal4). In addition, in SinhSpherical coordinates it yields results for a ringing Brill-Lindquist black hole remnant that agree with black hole perturbation theory to more than 7 decades in amplitude, surpassing the agreement seen in Fig. 6 of [Ruchlin, Etienne, & Baumgarte](https://arxiv.org/pdf/1712.07658.pdf).
#
# ### NRPy+ Source Code for this module: [BSSN/Psi4_tetrads.py](../edit/BSSN/Psi4_tetrads.py)
#
# ## Introduction:
# This module constructs tetrad vectors $l^\mu$, $m^\mu$, and $n^\mu$ for the $\psi_4$ Weyl scalar, a quantity that is immensely useful when extracting gravitational wave content from a numerical relativity simulation. $\psi_4$ is related to the gravitational wave strain via
#
# $$
# \psi_4 = \ddot{h}_+ - i \ddot{h}_\times.
# $$
#
# We construct $\psi_4$ from the standard ADM spatial metric $\gamma_{ij}$ and extrinsic curvature $K_{ij}$, and their derivatives. The full expression is given by Eq. 5.1 in [Baker, Campanelli, Lousto (2001)](https://arxiv.org/pdf/gr-qc/0104063.pdf):
#
# \begin{align}
# \psi_4 &= \left[ {R}_{ijkl}+2K_{i[k}K_{l]j}\right]
# {n}^i\bar{m}^j{n}^k\bar{m}^l \\
# & -8\left[ K_{j[k,l]}+{\Gamma }_{j[k}^pK_{l]p}\right]
# {n}^{[0}\bar{m}^{j]}{n}^k\bar{m}^l \\
# & +4\left[ {R}_{jl}-K_{jp}K_l^p+KK_{jl}\right]
# {n}^{[0}\bar{m}^{j]}{n}^{[0}\bar{m}^{l]},
# \end{align}
#
# Note that $\psi_4$ is complex, with the imaginary components originating from the tetrad vector $m^\mu$. This module does not specify a tetrad; instead it only constructs the above expression leaving $m^\mu$ and $n^\mu$ unspecified. This module defines these tetrad quantities, implementing the quasi-Kinnersley tetrad of [Baker, Campanelli, Lousto (2001)](https://arxiv.org/pdf/gr-qc/0104063.pdf), also referred to as "***the BCL paper***".
#
# ### A Note on Notation:
#
# As is standard in NRPy+,
#
# * Greek indices range from 0 to 3, inclusive, with the zeroth component denoting the temporal (time) component.
# * Latin indices range from 0 to 2, inclusive, with the zeroth component denoting the first spatial component.
#
# As a corollary, any expressions involving mixed Greek and Latin indices will need to offset one set of indices by one: A Latin index in a four-vector will be incremented and a Greek index in a three-vector will be decremented (however, the latter case does not occur in this tutorial notebook).
#
#
#
# <a id='toc'></a>
#
# # Table of Contents
# $$\label{toc}$$
#
# This tutorial notebook is organized as follows
#
# 1. [Step 1](#initializenrpy): Initialize needed NRPy+ modules
# 1. [Step 2](#quasikinnersley): The quasi-Kinnersley tetrad
# 1. [Step 3](#code_validation): Code Validation against `BSSN.Psi4_tetrads` NRPy+ module
# 1. [Step 4](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
# <a id='initializenrpy'></a>
#
# # Step 1: Initialize core NRPy+ modules \[Back to [top](#toc)\]
# $$\label{initializenrpy}$$
# +
# Step 1.a: import all needed modules from NRPy+:
import sympy as sp # SymPy: The Python computer algebra package upon which NRPy+ depends
import NRPy_param_funcs as par # NRPy+: Parameter interface
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
import sys # Standard Python modules for multiplatform OS-level functions
# Step 1.b: Set the coordinate system for the numerical grid
par.set_parval_from_str("reference_metric::CoordSystem","Spherical")
# Step 1.c: Given the chosen coordinate system, set up
# corresponding reference metric and needed
# reference metric quantities
# The following function call sets up the reference metric
# and related quantities, including rescaling matrices ReDD,
# ReU, and hatted quantities.
rfm.reference_metric()
# Step 1.d: Set spatial dimension (must be 3 for BSSN, as BSSN is
# a 3+1-dimensional decomposition of the general
# relativistic field equations)
DIM = 3
# Step 1.e: Import all ADM quantities as written in terms of BSSN quantities
import BSSN.ADM_in_terms_of_BSSN as AB
AB.ADM_in_terms_of_BSSN()
# Step 1.f: Initialize TetradChoice parameter
thismodule = __name__
# Current option: QuasiKinnersley = choice made in Baker, Campanelli, and Lousto. PRD 65, 044001 (2002)
par.initialize_param(par.glb_param("char", thismodule, "TetradChoice", "QuasiKinnersley"))
# -
# <a id='quasikinnersley'></a>
#
# # Step 2: The quasi-Kinnersley tetrad of [Baker, Campanelli, Lousto (2001)](https://arxiv.org/pdf/gr-qc/0104063.pdf) \[Back to [top](#toc)\]
# $$\label{quasikinnersley}$$
#
# To define the Weyl scalars, first a tetrad must be chosen. Below, for compatibility with the [WeylScal4 diagnostic module](https://bitbucket.org/einsteintoolkit/einsteinanalysis/src/master/WeylScal4/), we implement the quasi-Kinnersley tetrad of [Baker, Campanelli, Lousto (2001)](https://arxiv.org/pdf/gr-qc/0104063.pdf).
#
# We begin with the vectors given in eqs. 5.6 and 5.7 of the BCL paper, which are orthogonal to each other in flat spacetime; one is in the $\phi$ direction, one is in $r$, and the third is the cross product of the first two:
# \begin{align}
# v_1^a &= [-y,x,0] \\
# v_2^a &= [x,y,z] \\
# v_3^a &= {\rm det}(\gamma)^{1/2} \gamma^{ad} \epsilon_{dbc} v_1^b v_2^c,
# \end{align}
#
# Notice that $v_1^a$ and $v_2^a$ assume the Cartesian basis, but $\gamma^{ad}$ will be in the $xx^i$ basis given by the chosen `reference_metric::CoordSystem`. Thus to construct $v_3^a$, we must first perform a change of basis on $v_1^a$ and $v_2^a$:
#
# $$
# v_{1,{\rm xx}}^a = \frac{\partial xx^a}{\partial x_{\rm Cart}^b} v_{1,{\rm Cart}}^b.
# $$
# This equation is problematic because we generally do not have a closed-form expression for components of the $xx^a$ vector as functions of the Cartesian coordinate vector components $x_{\rm Cart}^a$. However we do have closed-form expressions for components of $x_{\rm Cart}^a$ as functions of $xx^a$. Thus we can construct the needed Jacobian matrix $\frac{\partial xx^a}{\partial x_{\rm Cart}^b}$ by evaluating the derivative $\frac{\partial x_{\rm Cart}^b}{\partial xx^a}$ and performing a simple matrix inversion:
# $$
# \frac{\partial xx^a}{\partial x_{\rm Cart}^b} = \left(\frac{\partial x_{\rm Cart}^b}{\partial xx^a} \right)^{-1}.
# $$
# +
# Step 2.a: Declare the Cartesian x,y,z in terms of
# xx0,xx1,xx2.
x = rfm.xxCart[0]
y = rfm.xxCart[1]
z = rfm.xxCart[2]
# Step 2.b: Declare v_1^a, v_2^a, and v_3^a tetrads,
# as well as detgamma and gammaUU from
# BSSN.ADM_in_terms_of_BSSN
v1UCart = ixp.zerorank1()
v2UCart = ixp.zerorank1()
detgamma = AB.detgamma
gammaUU = AB.gammaUU
# Step 2.c: Define v1U and v2U
v1UCart = [-y, x, sp.sympify(0)]
v2UCart = [x, y, z]
# Step 2.d: Construct the Jacobian d x_Cart^i / d xx^j
Jac_dUCart_dDrfmUD = ixp.zerorank2()
for i in range(DIM):
for j in range(DIM):
Jac_dUCart_dDrfmUD[i][j] = sp.simplify(sp.diff(rfm.xxCart[i], rfm.xx[j]))
# Step 2.e: Invert above Jacobian to get needed d xx^j / d x_Cart^i
Jac_dUrfm_dDCartUD, dummyDET = ixp.generic_matrix_inverter3x3(Jac_dUCart_dDrfmUD)
# Step 2.e.i: Simplify expressions for d xx^j / d x_Cart^i:
for i in range(DIM):
for j in range(DIM):
Jac_dUrfm_dDCartUD[i][j] = sp.simplify(Jac_dUrfm_dDCartUD[i][j])
# Step 2.f: Transform v1U and v2U from the Cartesian to the xx^i basis
v1U = ixp.zerorank1()
v2U = ixp.zerorank1()
for i in range(DIM):
for j in range(DIM):
v1U[i] += Jac_dUrfm_dDCartUD[i][j] * v1UCart[j]
v2U[i] += Jac_dUrfm_dDCartUD[i][j] * v2UCart[j]
# -
# ... next we construct the third tetrad vector $v_3^a={\rm det}(\gamma)^{1/2} \gamma^{ad} \epsilon_{dbc} v_1^b v_2^c$:
#
# Let's start by defining the Levi-Civita symbol $\epsilon_{dbc}$:
# +
# Step 2.g: Define the rank-3 version of the Levi-Civita symbol. Amongst
# other uses, this is needed for the construction of the approximate
# quasi-Kinnersley tetrad.
def define_LeviCivitaSymbol_rank3(DIM=-1):
if DIM == -1:
DIM = par.parval_from_str("DIM")
LeviCivitaSymbol = ixp.zerorank3()
for i in range(DIM):
for j in range(DIM):
for k in range(DIM):
# From https://codegolf.stackexchange.com/questions/160359/levi-civita-symbol :
LeviCivitaSymbol[i][j][k] = (i - j) * (j - k) * (k - i) / 2
return LeviCivitaSymbol
# Step 2.h: Define v3U
v3U = ixp.zerorank1()
LeviCivitaSymbolDDD = define_LeviCivitaSymbol_rank3(DIM=3)
for a in range(DIM):
for b in range(DIM):
for c in range(DIM):
for d in range(DIM):
v3U[a] += sp.sqrt(detgamma)*gammaUU[a][d]*LeviCivitaSymbolDDD[d][b][c]*v1U[b]*v2U[c]
# Step 2.h.i: Simplify expressions for v1U,v2U,v3U. This greatly expedites the C code generation (~10x faster)
for a in range(DIM):
v1U[a] = sp.simplify(v1U[a])
v2U[a] = sp.simplify(v2U[a])
v3U[a] = sp.simplify(v3U[a])
# -
# As our next step, we carry out the Gram-Schmidt orthonormalization process. The vectors $v_i^a$ are placeholders in the code; the final product of the orthonormalization is the vectors $e_i^a$. So,
# \begin{align}
# e_1^a &= \frac{v_1^a}{\sqrt{\omega_{11}}} \\
# e_2^a &= \frac{v_2^a - \omega_{12} e_1^a}{\sqrt{\omega_{22}}} \\
# e_3^a &= \frac{v_3^a - \omega_{13} e_1^a - \omega_{23} e_2^a}{\sqrt{\omega_{33}}}, \text{ where}\\
# \omega_{ij} &= v_i^a v_j^b \gamma_{ab}
# \end{align}
#
# Note that the above expressions must be evaluated with the numerators first, so that the denominators generate the proper normalization.
# +
# Step 2.i: Define omega_{ij}
omegaDD = ixp.zerorank2()
gammaDD = AB.gammaDD
def v_vectorDU(v1U,v2U,v3U, i,a):
if i==0:
return v1U[a]
elif i==1:
return v2U[a]
elif i==2:
return v3U[a]
else:
print("ERROR: unknown vector!")
sys.exit(1)
def update_omega(omegaDD, i,j, v1U,v2U,v3U,gammaDD):
omegaDD[i][j] = sp.sympify(0)
for a in range(DIM):
for b in range(DIM):
omegaDD[i][j] += v_vectorDU(v1U,v2U,v3U, i,a)*v_vectorDU(v1U,v2U,v3U, j,b)*gammaDD[a][b]
# Step 2.j: Define e^a_i. Note that:
# omegaDD[0][0] = \omega_{11} above;
# omegaDD[1][1] = \omega_{22} above, etc.
e1U = ixp.zerorank1()
e2U = ixp.zerorank1()
e3U = ixp.zerorank1()
# First e_1^a: Orthogonalize & normalize:
update_omega(omegaDD, 0,0, v1U,v2U,v3U,gammaDD)
for a in range(DIM):
e1U[a] = v1U[a]/sp.sqrt(omegaDD[0][0])
# Next e_2^a: First orthogonalize:
update_omega(omegaDD, 0,1, e1U,v2U,v3U,gammaDD)
for a in range(DIM):
e2U[a] = (v2U[a] - omegaDD[0][1]*e1U[a])
# Then normalize:
update_omega(omegaDD, 1,1, e1U,e2U,v3U,gammaDD)
for a in range(DIM):
e2U[a] /= sp.sqrt(omegaDD[1][1])
# Next e_3^a: First orthogonalize:
update_omega(omegaDD, 0,2, e1U,e2U,v3U,gammaDD)
update_omega(omegaDD, 1,2, e1U,e2U,v3U,gammaDD)
for a in range(DIM):
e3U[a] = (v3U[a] - omegaDD[0][2]*e1U[a] - omegaDD[1][2]*e2U[a])
# Then normalize:
update_omega(omegaDD, 2,2, e1U,e2U,e3U,gammaDD)
for a in range(DIM):
e3U[a] /= sp.sqrt(omegaDD[2][2])
# -
# Once we have orthogonal, normalized vectors, we can construct the tetrad itself, again drawing on eqs. 5.6. We can draw on SymPy's built-in tools for complex numbers to build the complex vector $m^a$:
# \begin{align}
# l^\mu &= \frac{1}{\sqrt{2}} \left(u^\mu + r^\mu\right) \\
# n^\mu &= \frac{1}{\sqrt{2}} \left(u^\mu - r^\mu\right) \\
# \Re(m^\mu) &= \frac{1}{\sqrt{2}} \theta^\mu \\
# \Im(m^\mu) &= \frac{1}{\sqrt{2}} \phi^\mu,
# \end{align}
# where $r^\mu=\{0,e_2^i\}$, $\theta^\mu=\{0,e_3^i\}$, $\phi^\mu=\{0,e_1^i\}$, and $u^\mu$ is the time-like unit normal to the hypersurface.
# +
# Step 2.k: Construct l^mu, n^mu, and m^mu, based on r^mu, theta^mu, phi^mu, and u^mu:
r4U = ixp.zerorank1(DIM=4)
u4U = ixp.zerorank1(DIM=4)
theta4U = ixp.zerorank1(DIM=4)
phi4U = ixp.zerorank1(DIM=4)
for a in range(DIM):
r4U[ a+1] = e2U[a]
theta4U[a+1] = e3U[a]
phi4U[ a+1] = e1U[a]
# FIXME? assumes alpha=1, beta^i = 0
u4U[0] = 1
l4U = ixp.zerorank1(DIM=4)
n4U = ixp.zerorank1(DIM=4)
mre4U = ixp.zerorank1(DIM=4)
mim4U = ixp.zerorank1(DIM=4)
# M_SQRT1_2 = 1 / sqrt(2) (defined in math.h on Linux)
M_SQRT1_2 = par.Cparameters("#define",thismodule,"M_SQRT1_2","")
isqrt2 = M_SQRT1_2 #1/sp.sqrt(2) <- SymPy drops precision to 15 sig. digits in unit tests
for mu in range(4):
l4U[mu] = isqrt2*(u4U[mu] + r4U[mu])
n4U[mu] = isqrt2*(u4U[mu] - r4U[mu])
mre4U[mu] = isqrt2*theta4U[mu]
mim4U[mu] = isqrt2* phi4U[mu]
# ltetU,ntetU,remtetU,immtetU,e1U,e2U,e3U
for mu in range(4):
l4U[mu] = isqrt2*(u4U[mu] + r4U[mu])
n4U[mu] = isqrt2*(u4U[mu] - r4U[mu])
mre4U[mu] = isqrt2*theta4U[mu]
mim4U[mu] = isqrt2* phi4U[mu]
# -
# <a id='code_validation'></a>
#
# # Step 3: Code validation against `BSSN.Psi4_tetrads` NRPy+ module \[Back to [top](#toc)\]
# $$\label{code_validation}$$
#
# As a code validation check, we verify agreement in the SymPy expressions for the RHSs of the BSSN equations between
# 1. this tutorial and
# 2. the NRPy+ [BSSN.Psi4_tetrads](../edit/BSSN/Psi4_tetrads.py) module.
#
# By default, we compare all quantities in Spherical coordinates, though other coordinate systems may be chosen.
# +
all_passed=True
def comp_func(expr1,expr2,basename,prefixname2="BP4T."):
if str(expr1-expr2)!="0":
print(basename+" - "+prefixname2+basename+" = "+ str(expr1-expr2))
all_passed=False
def gfnm(basename,idx1,idx2=None,idx3=None):
if idx2==None:
return basename+"["+str(idx1)+"]"
if idx3==None:
return basename+"["+str(idx1)+"]["+str(idx2)+"]"
return basename+"["+str(idx1)+"]["+str(idx2)+"]["+str(idx3)+"]"
expr_list = []
exprcheck_list = []
namecheck_list = []
import BSSN.Psi4_tetrads as BP4T
BP4T.Psi4_tetrads()
for mu in range(4):
namecheck_list.extend([gfnm("l4U",mu),gfnm("n4U",mu),gfnm("mre4U",mu),gfnm("mim4U",mu)])
exprcheck_list.extend([BP4T.l4U[mu],BP4T.n4U[mu],BP4T.mre4U[mu],BP4T.mim4U[mu]])
expr_list.extend([l4U[mu],n4U[mu],mre4U[mu],mim4U[mu]])
for i in range(len(expr_list)):
comp_func(expr_list[i],exprcheck_list[i],namecheck_list[i])
if all_passed:
print("ALL TESTS PASSED!")
# -
# <a id='latex_pdf_output'></a>
#
# # Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
# $$\label{latex_pdf_output}$$
#
# The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
# [Tutorial-Psi4_tetrads.pdf](Tutorial-Psi4_tetrads.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
# !jupyter nbconvert --to latex --template latex_nrpy_style.tplx --log-level='WARN' Tutorial-Psi4_tetrads.ipynb
# !pdflatex -interaction=batchmode Tutorial-Psi4_tetrads.tex
# !pdflatex -interaction=batchmode Tutorial-Psi4_tetrads.tex
# !pdflatex -interaction=batchmode Tutorial-Psi4_tetrads.tex
# !rm -f Tut*.out Tut*.aux Tut*.log
|
Tutorial-Psi4_tetrads.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# # Introduction
# ### Download the raw data
# This notebook is the first of three notebooks on combining natural language processing with time series forecasting using Amazon SageMaker and Amazon Forecast. As a first step, we download the raw dataset from UCI: the dataset consists of news articles and their headlines and titles and their source on 4 major topics. Associated sentiment scores and article ratings on Facebook, GooglePlus and LinkedIn are provided.
#
# The dataset can be viewed in 2 ways:
#
# 1) Regression: given an article, predict its popularity
#
# 2) Given a topic, forecast the popularity of the topic on various social media channels from historical data out into the future.
#
# Since we want to leverage Amazon Forecast, we treat it as the latter problem. A major thrust of this workshop is to demonstrate how unstructured text data can be included in Forecasting problems. That will be the topic of Notebook 2 (2_NTM.ipynb) and 3 (3_Forecast.ipynb).
#
# But first, we need to download the preprocess the dataset.
import os
import pandas as pd
import requests
if os.path.exists('data/'):
pass
else:
os.mkdir('data')
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00432/Data/News_Final.csv'
r = requests.get(url, allow_redirects=True, verify=False)
with open ('data/News_Final.csv', 'wb') as fd:
fd.write(r.content)
# ### Load the data
df = pd.read_csv('data/News_Final.csv')
df.head()
df.Source.value_counts()
# This exercise is primarily focused on extracting content from the headlines and title. So let's drop the source column and the IDLink relating the dataset to an internal ID.
df = df.drop(columns = ['Source', 'IDLink'])
# ### Basic Data Exploration
# Take a small sample of the dataset for visualization
df_small = df.sample(frac = 0.2)
import matplotlib.pyplot as plt
plt.xlabel('Articles')
plt.ylabel('Popularity')
plt.title('Facebook News Articles')
n, bins, patches = plt.hist(df_small['Facebook'], bins = 100, density=True, range = (0,600), alpha=0.75)
plt.xlabel('Articles')
plt.ylabel('Popularity')
plt.title('GooglePlus News Articles')
n, bins, patches = plt.hist(df_small['GooglePlus'], bins = 100, density=True, range = (0,600), alpha=0.75)
# Notice that the popularity of articles is extremely skewed. For this exercise, we may just choose to forecast the popularity on one of the platforms. In order to convert this into a usable time series for Machine Learning, we need to aggregate the news articles. We have 4 categories, let's aggregate the news datasets from all the 4 categories into 4 timeseries.
# First we replace the Original Topics with Numerical "item_id"
df =df.replace({'Topic': {'economy':0, 'obama': 1, 'microsoft': 2, 'palestine': 3}})
df.head()
df.Topic.value_counts()
# ### Preprocess the data
# First we convert the PublishDate column to a datetime column using pandas to_datetime function.
df['PublishDate'] = pd.to_datetime(df['PublishDate'], infer_datetime_format=True)
df = df.sort_values(by = ['Topic', 'PublishDate'])
df.head()
df.to_csv('data/NewsRatingsdataset.csv', index = None)
# ### End
#
# In this notebook, we downloaded the dataset and did some very basic preprocessing and cleaning as well as some simple visualizations.
#
# Next move on to the 2_NTM.ipynb notebook to preprocess the text data even further and build a neural topic model to generate topic vectors from all the Headlines. This will then become the input to a DeepAR+ forecasting algorithm in the last notebook for the Amazon Forecast service in 3_Forecast.ipynb.
#
# Enjoy!
|
notebooks/blog_materials/Time_Series_Forecasting_with_Unstructured_Data_and_Amazon_SageMaker_Neural_Topic_Model/1_preprocess.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py35]
# language: python
# name: conda-env-py35-py
# ---
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
#loading iris dataset setting petal and sepal length as feature matrix and class label as targets
iris = datasets.load_iris()
X = iris.data[:, [2,3]]
y = iris.target
#Splitting the dataset in test ans train dataset to test aor model's performance on unseen data
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3 , random_state = 1, stratify = y)
#stratify function ensures all the classes have equal proportion of representaion in both test and train sets
# performing feature scaling for better preformance of the optimizer
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train) # fit method will estimate the parameters mean and standars deviation of the sample given
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
from matplotlib.colors import ListedColormap
def plotDecisionRegion(X, y, classifier, test_idx = None, resolution = 0.02):
markers = ('s','x','o','^','v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:, 0].min() - 1,X[:,0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1,X[:,1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
np.arange(x2_min,x2_max, resolution))
#xx1, xx2 are the coordinates of x and y respectively, we pair each value of the two corresponding matrices and get a grid
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1,xx2, Z, alpha = 0.3, cmap = cmap)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
for idx, c1 in enumerate(np.unique(y)):
plt.scatter(x =X[y==c1,0],
y = X[y==c1,1],
alpha =0.8,
c = colors[idx],
marker = markers[idx],
label = c1, edgecolor='black')
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:,0], X_test[:,1], c= '', edgecolors='black',
alpha=1.0, linewidths=1, marker='o', s=100, label='test set')
from sklearn.svm import SVC
svm = SVC(C=1.0, kernel='linear', random_state=1)
svm.fit(X_test_std, y_test)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plotDecisionRegion(X_combined_std, y_combined, classifier=svm, test_idx=range(105,150))
plt.ylabel('Petal length (standardized)')
plt.xlabel('Petal width (standardized)')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
# When the data is too large to fit the computer memory,we would like to use SGDClassifier class which is similar to stochastic gradient algorithm, which also supports online learning via the method partial_fit
from sklearn.linear_model import SGDClassifier
# SGDClassifier with different loss functions which amounts to different classifiers
ppn = SGDClassifier(loss='perceptron')
lr = SGDClassifier(loss='log')
svm = SGDClassifier(loss='hinge')
|
SVM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 文本处理与增强
#
# [](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/programming_guide/source_zh_cn/tokenizer.ipynb) [](https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/master/programming_guide/zh_cn/mindspore_tokenizer.ipynb) [](https://authoring-modelarts-cnnorth4.huaweicloud.com/console/lab?share-url-b64=aHR0cHM6Ly9vYnMuZHVhbHN0YWNrLmNuLW5vcnRoLTQubXlodWF3ZWljbG91ZC5jb20vbWluZHNwb3JlLXdlYnNpdGUvbm90ZWJvb2svbW9kZWxhcnRzL3Byb2dyYW1taW5nX2d1aWRlL21pbmRzcG9yZV90b2tlbml6ZXIuaXB5bmI=&imageid=65f636a0-56cf-49df-b941-7d2a07ba8c8c)
# ## 概述
#
# 分词就是将连续的字序列按照一定的规范重新组合成词序列的过程,合理的进行分词有助于语义的理解。
#
# MindSpore提供了多种用途的分词器(Tokenizer),能够帮助用户高性能地处理文本,用户可以构建自己的字典,使用适当的标记器将句子拆分为不同的标记,并通过查找操作获取字典中标记的索引。
#
# MindSpore目前提供的分词器如下表所示。此外,用户也可以根据需要实现自定义的分词器。
#
# | 分词器 | 分词器说明 |
# | :-- | :-- |
# | BasicTokenizer | 根据指定规则对标量文本数据进行分词。 |
# | BertTokenizer | 用于处理Bert文本数据的分词器。 |
# | JiebaTokenizer | 基于字典的中文字符串分词器。 |
# | RegexTokenizer | 根据指定正则表达式对标量文本数据进行分词。 |
# | SentencePieceTokenizer | 基于SentencePiece开源工具包进行分词。 |
# | UnicodeCharTokenizer | 将标量文本数据分词为Unicode字符。 |
# | UnicodeScriptTokenizer | 根据Unicode边界对标量文本数据进行分词。 |
# | WhitespaceTokenizer | 根据空格符对标量文本数据进行分词。 |
# | WordpieceTokenizer | 根据单词集对标量文本数据进行分词。 |
#
# 更多分词器的详细说明,可以参见[API文档](https://www.mindspore.cn/docs/api/zh-CN/master/api_python/mindspore.dataset.text.html)。
# ## MindSpore分词器
#
# 下面介绍几种常用分词器的使用方法。
#
# ### BertTokenizer
#
# `BertTokenizer`是通过调用`BasicTokenizer`和`WordpieceTokenizer`来进行分词的。
#
# 下面的样例首先构建了一个文本数据集和字符串列表,然后通过`BertTokenizer`对数据集进行分词,并展示了分词前后的文本结果。
# +
import mindspore.dataset as ds
import mindspore.dataset.text as text
input_list = ["床前明月光", "疑是地上霜", "举头望明月", "低头思故乡", "I am making small mistakes during working hours",
"😀嘿嘿😃哈哈😄大笑😁嘻嘻", "繁體字"]
dataset = ds.NumpySlicesDataset(input_list, column_names=["text"], shuffle=False)
print("------------------------before tokenization----------------------------")
for data in dataset.create_dict_iterator(output_numpy=True):
print(text.to_str(data['text']))
vocab_list = [
"床", "前", "明", "月", "光", "疑", "是", "地", "上", "霜", "举", "头", "望", "低", "思", "故", "乡",
"繁", "體", "字", "嘿", "哈", "大", "笑", "嘻", "i", "am", "mak", "make", "small", "mistake",
"##s", "during", "work", "##ing", "hour", "😀", "😃", "😄", "😁", "+", "/", "-", "=", "12",
"28", "40", "16", " ", "I", "[CLS]", "[SEP]", "[UNK]", "[PAD]", "[MASK]", "[unused1]", "[unused10]"]
vocab = text.Vocab.from_list(vocab_list)
tokenizer_op = text.BertTokenizer(vocab=vocab)
dataset = dataset.map(operations=tokenizer_op)
print("------------------------after tokenization-----------------------------")
for i in dataset.create_dict_iterator(num_epochs=1, output_numpy=True):
print(text.to_str(i['text']))
# -
# ### JiebaTokenizer
#
# `JiebaTokenizer`是基于jieba的中文分词。
#
# 下载字典文件`hmm_model.utf8`和`jieba.dict.utf8`,并将其放到指定位置,在Jupyter Notebook中执行如下命令。
# !wget -N https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/datasets/hmm_model.utf8 --no-check-certificate
# !wget -N https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/datasets/jieba.dict.utf8 --no-check-certificate
# !mkdir -p ./datasets/tokenizer/
# !mv hmm_model.utf8 jieba.dict.utf8 -t ./datasets/tokenizer/
# !tree ./datasets/tokenizer/
# 下面的样例首先构建了一个文本数据集,然后使用HMM与MP字典文件创建`JiebaTokenizer`对象,并对数据集进行分词,最后展示了分词前后的文本结果。
# +
import mindspore.dataset as ds
import mindspore.dataset.text as text
input_list = ["今天天气太好了我们一起去外面玩吧"]
dataset = ds.NumpySlicesDataset(input_list, column_names=["text"], shuffle=False)
print("------------------------before tokenization----------------------------")
for data in dataset.create_dict_iterator(output_numpy=True):
print(text.to_str(data['text']))
# files from open source repository https://github.com/yanyiwu/cppjieba/tree/master/dict
HMM_FILE = "./datasets/tokenizer/hmm_model.utf8"
MP_FILE = "./datasets/tokenizer/jieba.dict.utf8"
jieba_op = text.JiebaTokenizer(HMM_FILE, MP_FILE)
dataset = dataset.map(operations=jieba_op, input_columns=["text"], num_parallel_workers=1)
print("------------------------after tokenization-----------------------------")
for i in dataset.create_dict_iterator(num_epochs=1, output_numpy=True):
print(text.to_str(i['text']))
# -
# ### SentencePieceTokenizer
#
# `SentencePieceTokenizer`是基于[SentencePiece](https://github.com/google/sentencepiece)这个开源的自然语言处理工具包。
#
# 下载文本数据集文件`botchan.txt`,并将其放置到指定位置,在Jupyter Notebook中执行如下命令。
# !wget -N https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/datasets/botchan.txt --no-check-certificate
# !mkdir -p ./datasets/tokenizer/
# !mv botchan.txt ./datasets/tokenizer/
# !tree ./datasets/tokenizer/
# 下面的样例首先构建了一个文本数据集,然后从`vocab_file`文件中构建一个`vocab`对象,再通过`SentencePieceTokenizer`对数据集进行分词,并展示了分词前后的文本结果。
# +
import mindspore.dataset as ds
import mindspore.dataset.text as text
from mindspore.dataset.text import SentencePieceModel, SPieceTokenizerOutType
input_list = ["I saw a girl with a telescope."]
dataset = ds.NumpySlicesDataset(input_list, column_names=["text"], shuffle=False)
print("------------------------before tokenization----------------------------")
for data in dataset.create_dict_iterator(output_numpy=True):
print(text.to_str(data['text']))
# file from MindSpore repository https://gitee.com/mindspore/mindspore/blob/master/tests/ut/data/dataset/test_sentencepiece/botchan.txt
vocab_file = "./datasets/tokenizer/botchan.txt"
vocab = text.SentencePieceVocab.from_file([vocab_file], 5000, 0.9995, SentencePieceModel.UNIGRAM, {})
tokenizer_op = text.SentencePieceTokenizer(vocab, out_type=SPieceTokenizerOutType.STRING)
dataset = dataset.map(operations=tokenizer_op)
print("------------------------after tokenization-----------------------------")
for i in dataset.create_dict_iterator(num_epochs=1, output_numpy=True):
print(text.to_str(i['text']))
# -
# ### UnicodeCharTokenizer
#
# `UnicodeCharTokenizer`是根据Unicode字符集来分词的。
#
# 下面的样例首先构建了一个文本数据集,然后通过`UnicodeCharTokenizer`对数据集进行分词,并展示了分词前后的文本结果。
# +
import mindspore.dataset as ds
import mindspore.dataset.text as text
input_list = ["Welcome to Beijing!", "北京欢迎您!", "我喜欢English!"]
dataset = ds.NumpySlicesDataset(input_list, column_names=["text"], shuffle=False)
print("------------------------before tokenization----------------------------")
for data in dataset.create_dict_iterator(output_numpy=True):
print(text.to_str(data['text']))
tokenizer_op = text.UnicodeCharTokenizer()
dataset = dataset.map(operations=tokenizer_op)
print("------------------------after tokenization-----------------------------")
for i in dataset.create_dict_iterator(num_epochs=1, output_numpy=True):
print(text.to_str(i['text']).tolist())
# -
# ### WhitespaceTokenizer
#
# `WhitespaceTokenizer`是根据空格来进行分词的。
#
# 下面的样例首先构建了一个文本数据集,然后通过`WhitespaceTokenizer`对数据集进行分词,并展示了分词前后的文本结果。
# +
import mindspore.dataset as ds
import mindspore.dataset.text as text
input_list = ["Welcome to Beijing!", "北京欢迎您!", "我喜欢English!"]
dataset = ds.NumpySlicesDataset(input_list, column_names=["text"], shuffle=False)
print("------------------------before tokenization----------------------------")
for data in dataset.create_dict_iterator(output_numpy=True):
print(text.to_str(data['text']))
tokenizer_op = text.WhitespaceTokenizer()
dataset = dataset.map(operations=tokenizer_op)
print("------------------------after tokenization-----------------------------")
for i in dataset.create_dict_iterator(num_epochs=1, output_numpy=True):
print(text.to_str(i['text']).tolist())
# -
# ### WordpieceTokenizer
#
# `WordpieceTokenizer`是基于单词集来进行划分的,划分依据可以是单词集中的单个单词,或者多个单词的组合形式。
#
# 下面的样例首先构建了一个文本数据集,然后从单词列表中构建`vocab`对象,通过`WordpieceTokenizer`对数据集进行分词,并展示了分词前后的文本结果。
# +
import mindspore.dataset as ds
import mindspore.dataset.text as text
input_list = ["my", "favorite", "book", "is", "love", "during", "the", "cholera", "era", "what",
"我", "最", "喜", "欢", "的", "书", "是", "霍", "乱", "时", "期", "的", "爱", "情", "您"]
vocab_english = ["book", "cholera", "era", "favor", "##ite", "my", "is", "love", "dur", "##ing", "the"]
vocab_chinese = ["我", '最', '喜', '欢', '的', '书', '是', '霍', '乱', '时', '期', '爱', '情']
dataset = ds.NumpySlicesDataset(input_list, column_names=["text"], shuffle=False)
print("------------------------before tokenization----------------------------")
for data in dataset.create_dict_iterator(output_numpy=True):
print(text.to_str(data['text']))
vocab = text.Vocab.from_list(vocab_english+vocab_chinese)
tokenizer_op = text.WordpieceTokenizer(vocab=vocab)
dataset = dataset.map(operations=tokenizer_op)
print("------------------------after tokenization-----------------------------")
for i in dataset.create_dict_iterator(num_epochs=1, output_numpy=True):
print(text.to_str(i['text']))
|
docs/mindspore/programming_guide/source_zh_cn/tokenizer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Aplicando Python para análisis de precios: descarga, manejo y análisis de datos
# <img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/0/0a/Python.svg" width="300px" height="100px" />
#
# > En esta y en las siguientes dos clases veremos un caso de aplicación de simulación montecarlo en la toma de decisiones. Para lograr este objetivo, primero veremos (en esta clase) como manipular datos con *pandas*, tanto desde un archivo local de excel como remotamente desde Yahoo Finance.
#
# > Python Data Analysis Library: pandas es una librería de código abierto, fácil de usar y que provee alto rendimiento en estructuras de datos y herramientas de análisis de datos para el lenguaje de programación Python.
#
# **Referencias:**
# - http://pandas.pydata.org/
# - http://www.learndatasci.com/python-finance-part-yahoo-finance-api-pandas-matplotlib/
# - https://www.datacamp.com/community/tutorials/python-excel-tutorial
# - https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.html
# ## 0. Motivación
#
# <img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/d/d7/Philippine-stock-market-board.jpg" width="400px" height="125px" />
#
# Hace menos de una década, los instrumentos financieros estaban en la cúspide de la popularidad. Las instituciones financieras de todo el mundo estaban negociando miles de millones de dólares de estos instrumentos a diario, y los analistas cuantitativos estaban modelándolos utilizando el cálculo estocástico y el poderoso `C++`.
#
# Sin embargo, el avance en los últimos años ha sido impresionante y las cosas han cambiado. Por una parte, la [crisis financiera del 2008](https://es.wikipedia.org/wiki/Crisis_financiera_de_2008) fue producida por los instrumentos financieros llamados *derivados*. Por otra parte, los volúmenes transaccionales han bajado y la demanda de modelado con `C++` se ha marchitado con ellos. Además, un nuevo jugador entró en la competencia... `¡Python!`
#
# `Python` ha estado ganando muchos seguidores en la industria financiera en los últimos años y con razón. No en vano, junto a `R` son los lenguajes de programación más utilizados en cuanto a análisis financiero.
# ## 1. Descarga de datos de Yahoo! Finance
# Para esto utilizaremos el paquete *pandas_datareader*.
#
# **Nota**: Usualmente, las distribuciones de Python no cuentan, por defecto, con el paquete *pandas_datareader*. Por lo que será necesario instalarlo aparte:
# - buscar en inicio "Anaconda prompt" y ejecutarlo como administrador;
# - el siguiente comando instala el paquete en Anaconda: *conda install pandas-datareader*;
# - una vez finalice la instalación correr el comando: *conda list*, y buscar que sí se haya instalado pandas-datareader
# Importar el modulo data del paquete pandas_datareader. La comunidad lo importa con el nombre de web
import pandas as pd
import pandas_datareader as web
# Librerías estándar para arreglos y gráficos
import numpy as np
import matplotlib.pyplot as plt
# Primero importaremos datos desde un archivo con extensión `.csv`
#Importar datos de un archivo csv
name = "WMT.csv"
datos = pd.read_csv(name)
datos
# Ahora lo haremos desde Yahoo Finance
# +
# web.DataReader?
# -
datos = web.DataReader('WMT','yahoo','1972-08-25','2020-11-03')
datos["Adj Close"]
# Escribir una función para generalizar la importación desde Yahoo
def get_closes(names,start,end):
precios = web.DataReader(names,'yahoo',start,end)
closes = precios["Adj Close"]
return closes
# +
# Instrumentos a descargar
names = ['BIMBOA.MX','AEROMEX.MX', 'GFAMSAA.MX']
# Fechas: inicios 2015 a finales de 2019
start = '2015-01-01'
end = '2020-11-03'
# -
# Obtenemos los precios ajustados en el cierre
datos_MX = get_closes(names,start,end)
datos_MX
# ¿Cómo lucen estos datos?
# Graficar
datos_MX.plot(figsize=(15,8))
# Una vez tenemos los datos, podemos operar con ellos. Por ejemplo un resumen de datos estadísticos se podría obtener con
# Método describe
datos_MX.describe()
# ## 2. Rendimientos diarios
#
# Para una sucesión de precios $\{S_t\}_{t=0}^{n}$, el rendimiento simple $R_t$ se define como el el cambio porcentual
# $$
# R_t=\frac{S_t-S_{t-1}}{S_{t-1}}
# $$
# para $t=1,\ldots,n$.
#
# Para el ejemplo en curso, ¿cómo calcular esto?
# Método shift
datos_MX.shift()
# Entonces los rendimientos se calculan como
ret_MX = (datos_MX - datos_MX.shift())/datos_MX.shift()
ret_MX = ret_MX.dropna()
ret_MX
# Método pct_change
datos_MX.pct_change().dropna()
# y la gráfica de los rendimientos se puede obtener como...
# Gráfica
ret_MX.plot(figsize=(15,8))
# Donde se observa que el rendimiento tiene una tendencia constante y, por tanto, se puede plantear la hipótesis de que se puede modelar usando un proceso estocástico estacionario en media.
# Otro rendimiento usado con frecuencia es el rendimiento continuamente compuesto o rendimiento logaritmico. Éste, está definido como
#
# $$
# r_t=\ln\left(\frac{S_t}{S_{t-1}}\right).
# $$
#
# **Esta ecuación sólo es válida cuando se tienen periodos cortos de tiempo**
# Es fácil darse cuenta que $r_t=\ln(1+R_t)$.
#
# **Nota:** ver gráficamente que si $0\leq|x|\ll 1$, entonces $\ln(1+x)\approx x$.
#
# Para este caso, la fórmula del rendimiento continuamente compuesto se translada facilmente a código Python (obtener, graficar y comparar).
# Rendimiento logarítmico
ret_log = np.log(datos_MX/datos_MX.shift())
ret_log
# Gráfica
ret_log.plot(figsize=(15,8))
# Valor absoluto de la diferencia
# Donde se observa que el rendimiento tiene una tendencia constante y, por tanto, se puede plantear la hipótesis de que se puede modelar usando un proceso estocástico estacionario en media.
#
# Podemos incluso plantear la hipótesis de que los log rendimientos son normales...
# Media y volatilidad de rendimientos
ret_MX.mean()['BIMBOA.MX']
ret_MX.std()
ret_MX.std()['GFAMSAA.MX']
# ___
# Recapitulando, hoy aprendimos a obtener datos con pandas-datareader directamente desde un archivo local ó fuentes remotas.
#
# Por otra parte, estudiamos los rendimientos diarios y dimos con la conclusión de que se podrían modelar como un proceso estocástico estacionario normal.
# La siguiente clase veremos como simular escenarios de comportamiento de los precios futuros (no determinístico, no sabemos como se comporta, muchas posibilidades: montecarlo) a partir de datos de ingresos diarios.
#
# Luego, con esas predicciones veremos la probabilidad de que el precio de las acciones quede por encima (debajo) de cierto umbral y con ello tomar decisiones de vender (comprar) estas acciones.
# <script>
# $(document).ready(function(){
# $('div.prompt').hide();
# $('div.back-to-top').hide();
# $('nav#menubar').hide();
# $('.breadcrumb').hide();
# $('.hidden-print').hide();
# });
# </script>
#
# <footer id="attribution" style="float:right; color:#808080; background:#fff;">
# Created with Jupyter by <NAME>.
# </footer>
|
Módulo 2/Clase12_ManejoAnalisisDatosPandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Download this page as a jupyter notebook at [Lesson 3](http://192.168.3.11/engr-1330-webroot/1-Lessons/Lesson03/ENGR-1330-Lesson03.ipynb)
# # ENGR 1330 Computational Thinking with Data Science
# Copyright © 2021 <NAME> and <NAME>
#
# Last GitHub Commit Date: 13 July 2021
#
# ## Lesson 3 Data Structures:
# - Data structures; lists, arrays, tuples, sets, dictionaries
# - Name, index, contents; keys
#
# ---
# Script block to identify host, user, and kernel
import sys
# ! hostname; ! whoami; ! pwd;
print(sys.executable)
# + language="html"
# <!-- Script Block to set tables to left alignment -->
# <style>
# table {margin-left: 0 !important;}
# </style>
# -
# ---
# ## Objectives
#
# 1. Awareness of data structures available in Python to store and manipulate data
# 2. Implement arrays (lists), dictionaries, and tuples
# 2. Address contents of lists , dictionaries, and tuples
# ---
# ## Data Structures and Conditional Statements
#
# **Computational thinking (CT)** concepts involved are:
#
# - `Decomposition` : Data interpretation, manipulation, and analysis of NumPy arrays
# - `Abstraction` : Data structures; Arrays, lists, tuples, sets, and dictionaries
# - `Algorithms` : Conditional statements
#
# ## What is a data structure?
#
# Data Structures are a specialized means of organizing and storing data in computers in such a way that we can perform operations on the stored data more efficiently.
#
# In our iPython world the structures are illustrated in the figure below
#
# 
# <!--  -->
# ### Lists
#
# A list is a collection of data that are somehow related. It is a convenient way to refer to a
# collection of similar things by a single name, and using an index (like a subscript in math)
# to identify a particular item.
#
# Consider the "math-like" variable $x$ below:
#
# \begin{gather}
# x_0= 7 \\
# x_1= 11 \\
# x_2= 5 \\
# x_3= 9 \\
# x_4= 13 \\
# \dots \\
# x_N= 223 \\
# \end{gather}
#
# The variable name is $x$ and the subscripts correspond to different values.
# Thus the `value` of the variable named $x$ associated with subscript $3$ is the number $9$.
#
# The figure below is a visual representation of a the concept that treats a variable as a collection of cells.
#
# 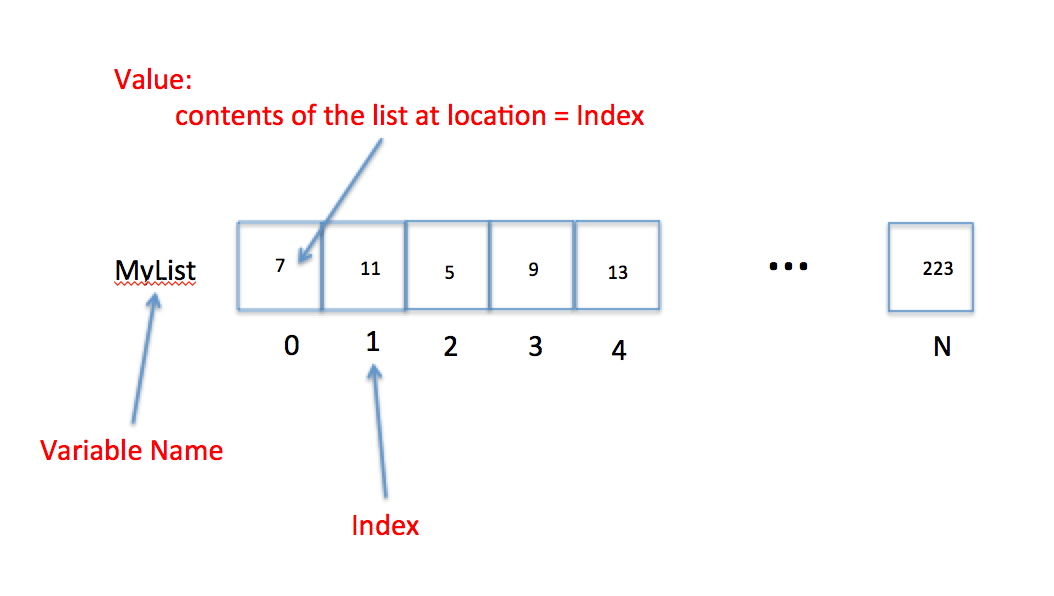
# <!--  -->
#
# In the figure, the variable name is `MyList`, the subscripts are replaced by an index
# which identifies which cell is being referenced.
# The value is the cell content at the particular index.
#
# So in the figure the value of `MyList` at Index = 3 is the number 9.'
#
# In engineering and data science we use lists a lot - we often call then vectors, arrays, matrices and such, but they are ultimately just lists.
#
# To declare a list you can write the list name and assign it values.
# The square brackets are used to identify that the variable is a list.
# Like:
#
# MyList = [7,11,5,9,13,66,99,223]
#
# One can also declare a null list and use the `append()` method to fill it as needed.
#
# MyOtherList = [ ]
#
# Python indices start at **ZERO**.
# A lot of other languages start at ONE.
# It's just the convention.
#
# The first element in a list has an index of 0, the second an index of 1, and so on.
# We access the contents of a list by referring to its name and index.
# For example
#
# MyList[3] has a value of the number 9.
# ### Arrays
#
# Arrays are special lists that are used to store only elements of a specific data type, and require use of an external dependency (package) named **array**. The package is installed with core python, so other than importing it into a script nothing else special is needed.
#
# Arrays are:
# - Ordered: Elements in an array can be indexed
# - Mutable: Elements in an array can be altered
#
# <!---->
#
# 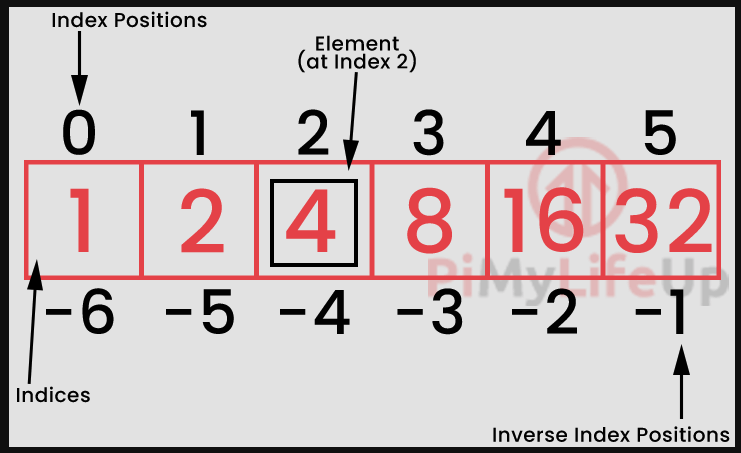
#
# <!--  -->
#
# Data type that an array must hold is specified using the type code when it is created
# - ‘f’ for float
# - ‘d’ for double
# - ‘i’ for signed int
# - ‘I’ for unsigned int
#
# More types are listed below
#
#
# |Type Code|C Data Type|Python Data Type|Minimum Size in Bytes|
# |:---|---|---|---:|
# |'b'| signed char|int |1|
# |'B'| unsigned char |int |1|
# |'h'| signed short |int |2|
# |'H'| unsigned short |int |2|
# |'i'| signed int |int |2|
# |'I'| unsigned int |int |2|
# |'l'| signed long |int |4|
# |'L'| unsigned long |int |4|
# |'q'| signed long long |int |8|
# |'Q'| unsigned long long |int |8|
# |'f'| float |float |4|
# |'d'| double |float |8|
#
# To use arrays, a library named ‘array’ must be imported
import array
# Creating an array that contains signed integer numbers
myarray = array.array('i', [1, 2, 4, 8, 16, 32])
myarray[0] #1-st element, 0-th position
import array as arr #import using an alias so the calls don't look so funny
myarray = arr.array('i', [1, 2, 4, 8, 16, 32])
myarray[0] #1-st element, 0-th position
# Lists: Can store elements of different data types; like arrays they are (arrays are lists, but lists are not quite arrays!)
# - Ordered: Elements in a list can be indexed
# - Mutable: Elements in a list can be altered
# - Mathematical operations must be applied to each element of the list
# ### Tuple - A special list
#
# A tuple is a special kind of list where the **values cannot be changed** after the list is created.
# Such a property is called `immutable`
# It is useful for list-like things that are static - like days in a week, or months of a year.
# You declare a tuple like a list, except use round brackets instead of square brackets.
#
# MyTupleName = ("Jan","Feb","Mar","Apr","May","Jun","Jul","Aug","Sep","Oct","Nov","Dec")
#
# Tuples are often created as output from packages and functions.
#
#
# ### Dictionary - A special list
#
# A dictionary is a special kind of list where the items are related data `PAIRS`.
# It is a lot like a relational database (it probably is one in fact) where the first item in the pair is called the key, and must be unique in a dictionary, and the second item in the pair is the data.
# The second item could itself be a list, so a dictionary would be a meaningful way to build a
# database in Python.
#
# To declare a dictionary using `curly` brackets
#
# MyPetsNamesAndMass = { "Dusty":7.8 , "Aspen":6.3, "Merrimee":0.03}
#
# To declare a dictionary using the `dict()` method
#
# MyPetsNamesAndMassToo = dict(Dusty = 7.8 , Aspen = 6.3, Merrimee = 0.03)
#
# Dictionary properties
# - Unordered: Elements in a dictionary cannot be
# - Mutable elements: Elements in a dictionary can be altered
# - Immutable keys: Keys in a dictionary cannot be altered
# ### Sets - A special list
#
# Sets: Are used to store elements of different data types
# - Unordered: Elements in a set cannot be indexed
# - Mutable: Elements in a set can be altered
# - Non-repetition: Elements in a set are unique
#
# Elements of a set are enclosed in curly brackets { }
# - Creating sets that contains different data types
# - Sets cannot be nested
#
# #### What's the difference between a set and dictionary?
#
# From [https://stackoverflow.com/questions/34370599/difference-between-dict-and-set-python](https://stackoverflow.com/questions/34370599/difference-between-dict-and-set-python)
#
# "Well, a set is like a dict with keys but no values, and they're both implemented using a hash table. But yes, it's a little annoying that the `{}` notation denotes an empty `dict` rather than an empty `set`, but that's a historical artifact."
# ## Readings
#
# 1. Computational and Inferential Thinking <NAME> and <NAME>, Computational and Inferential Thinking, The Foundations of Data Science, Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND) Chapter 4 Subpart 3 https://www.inferentialthinking.com/chapters/04/3/Comparison.html
#
# 2. Computational and Inferential Thinking <NAME> and <NAME>, Computational and Inferential Thinking, The Foundations of Data Science, Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND) Chapter 4
# https://www.inferentialthinking.com/chapters/04/Data_Types.html
#
# 3. Learn Python in One Day and Learn It Well. Python for Beginners with Hands-on Project. (Learn Coding Fast with Hands-On Project Book -- Kindle Edition by LCF Publishing (Author), <NAME> https://www.amazon.com/Python-2nd-Beginners-Hands-Project-ebook/dp/B071Z2Q6TQ/ref=sr_1_3?dchild=1&keywords=learn+python+in+a+day&qid=1611108340&sr=8-3
#
# 4. <NAME>, <NAME>, <NAME>, <NAME> (Batu), <NAME>, <NAME>, and <NAME>. (2021) Computational Thinking and Data Science: A WebBook to Accompany ENGR 1330 at TTU, Whitacre College of Engineering, DOI (pending)<!--[https://172.16.58.3/engr-1330-webroot/engr-1330-webbook/ctds-psuedocourse/site/](https://172.16.58.3/engr-1330-webroot/engr-1330-webbook/ctds-psuedocourse/site/)-->
|
1-Lessons/Lesson03/dev_src/.ipynb_checkpoints/ENGR-1330-Lesson03old-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from numpy import log10, asarray, polyfit, ceil, arange
import csv
import matplotlib.pyplot as plt
from numpy import log10, asarray, polyfit, ceil, arange
import csv
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import json
import os.path
from os import path
import matplotlib.dates as mdates
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
def read_covid_data(data_type):
if (data_type in ['confirmed', 'deaths', 'recovered']):
COVID_directory = "/Users/kootsoop/git/COVID-19/csse_covid_19_data/csse_covid_19_time_series/"
first_row = None
with open(COVID_directory + 'time_series_covid19_' + data_type + '_global.csv') as csvfile:
confirmed = csv.reader(csvfile)
for row in confirmed:
if (first_row == None):
first_row = row
if (row[1] == 'US'):
us_data = row
break
else:
raise Exception('Invalid data_type', data_type)
return(first_row, us_data)
FORECAST_FILE = 'forecasts500k.txt'
if (path.exists(FORECAST_FILE)):
forecast_file = open(FORECAST_FILE, 'r')
forecasts500k = json.load(forecast_file)
forecast_file.close()
else:
forecasts500k = {}
(first_row, confirmed) = read_covid_data('confirmed')
(first_row2, recovered) = read_covid_data('recovered')
(first_row3, deaths) = read_covid_data('deaths')
death_data = [(float(data)) for data in deaths[4:(len(first_row))]]
recovered_data = [(float(data)) for data in recovered[4:(len(first_row))]]
confirmed_data = [(float(data)) for data in confirmed[4:(len(first_row))]]
first_row_shifted = [ data for data in first_row[4:(len(first_row))]]
x_axis = arange(len(death_data))
NumberInEstimateWindow = 20
# Started at 70 @ 2020/5/10
# 133 2020/06/24
# 137 2020/06/28
start_fit = len(death_data) - (NumberInEstimateWindow + 1)
# Started 20 more than start_fit
end_fit = start_fit + NumberInEstimateWindow
y_fit_data = death_data[start_fit:end_fit+1]
x_fit_data = arange(start_fit,end_fit+1)
y_pre = death_data[1:start_fit]
x_pre = arange(1,start_fit)
y_new_data = death_data[end_fit+1:len(death_data)]
x_new_data = arange(end_fit+1, len(death_data))
x_forecast = arange(end_fit, len(death_data) + 20)
[m, b] = polyfit(x_fit_data, y_fit_data, 1)
day_for_500k = (500000-b)/m
day_for_300k = (300000-b)/m
days_until = day_for_500k - len(first_row_shifted)
days_until_300k = day_for_300k - len(first_row_shifted)
print('Days until 500k: ' + str(day_for_500k - len(first_row_shifted) ))
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.tick_params(axis='both', which='minor', labelsize=8)
date_for_500k = (datetime.now() + timedelta(days=days_until)).date()
date_for_300k = (datetime.now() + timedelta(days=days_until_300k)).date()
print('300k:' + str(date_for_300k))
if (not first_row_shifted[end_fit] in forecasts500k):
print("Updating file.")
forecasts500k.update({ first_row_shifted[end_fit] : str(date_for_500k) })
forecast_file = open(FORECAST_FILE, 'w+')
json.dump(forecasts500k, forecast_file)
forecast_file.close()
dates = []
forecasts = []
for date in forecasts500k:
forecasts.append(datetime.strptime(forecasts500k[date], '%Y-%m-%d'))
dates.append(datetime.strptime(date, '%m/%d/%y'))
election_date = datetime.strptime('2020-11-03', '%Y-%m-%d')
election_day_of_year = (election_date - datetime(election_date.year, 1, 1)).days + 1
start_data_date = datetime.strptime(first_row_shifted[start_fit], '%m/%d/%y')
deaths_at_election = int(m*(election_day_of_year)+b)
deaths_at_election_end = int(m*(election_day_of_year+1)+b)
end_of_year_date = datetime.strptime('2020-12-31', '%Y-%m-%d')
end_of_year_day = (end_of_year_date - datetime(end_of_year_date.year, 1, 1)).days + 1
deaths_at_end_of_year = int(m*(end_of_year_day)+b)
nine_eleven_date = datetime.strptime('2020-09-11', '%Y-%m-%d')
nine_eleven_day = (nine_eleven_date - datetime(nine_eleven_date.year, 1, 1)).days + 1
deaths_at_nine_eleven_day = int(m*(nine_eleven_day)+b)
print(election_date)
print(start_data_date)
print(first_row_shifted[start_fit])
print(election_day_of_year)
print(deaths_at_election)
print(deaths_at_election_end)
print(deaths_at_end_of_year)
print(deaths_at_nine_eleven_day)
print(deaths_at_nine_eleven_day/2977)
print('Estimated deaths per day: ' + str(m))
plt.figure(1)
plt.plot(x_pre, y_pre, 'g.', label='Prior data')
plt.plot(x_fit_data, y_fit_data,'o', markersize=20, label='Data used in forecast')
plt.plot([election_day_of_year, election_day_of_year], [deaths_at_election, deaths_at_election_end],'r+',markersize=20, label='Deaths at election: ' + str(deaths_at_election))
plt.plot(x_forecast, m*x_forecast + b,'k:',markersize=14, label='Line of best fit (forecast)')
plt.plot(day_for_500k, 500000, 'rx', markersize=50, label='500,000 deaths on ' + str(date_for_500k))
plt.ylim(0,300000)
plt.xlim(60,350)
plt.title('Data used in forecast is from ' + first_row_shifted[start_fit] + ' to ' + first_row_shifted[end_fit], fontsize=40)
ax.legend(loc='upper left', shadow=True, fontsize=30)
plt.savefig('/Users/kootsoop/Pictures/COVID-19-FORECAST-' + first_row_shifted[end_fit].replace('/','-') + '.png')
death_percent = [i / j * 100.0 for i, j in zip(death_data, confirmed_data)]
plt.figure(2)
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.yaxis.set_major_formatter(mdates.DateFormatter("%B %d"))
ax.xaxis.set_major_formatter(mdates.DateFormatter("%B %d"))
plt.xticks(rotation=90)
ax.xaxis.set_major_locator(MultipleLocator(2))
ax.yaxis.set_major_locator(MultipleLocator(1))
ax.tick_params(axis='both', which='minor', labelsize=8)
plt.plot(dates, forecasts,'g+', markersize=50)
plt.title('Forecast 500k date over time', fontsize=40)
plt.savefig('/Users/kootsoop/Pictures/COVID-19-FORECAST-HISTORY-' + first_row_shifted[end_fit].replace('/','-') + '.png')
# Doesn't seem to do the right thing: ax.set_xticklabels(dates)
plt.figure(3)
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.tick_params(axis='both', which='minor', labelsize=8)
death_by_delay = {}
for delay in arange(22):
death_percent_with_delay = [i / j * 100.0 for i, j in zip(death_data[0:len(death_data)-delay], confirmed_data[delay:len(confirmed_data)])]
plt.plot(x_axis[0:len(death_data)-delay], death_percent_with_delay)
death_by_delay[delay] = death_percent_with_delay[len(death_percent_with_delay)-1]
plt.title('Deaths as a percentage of confirmed cases, max delay:' + str(delay), fontsize=40)
plt.savefig('/Users/kootsoop/Pictures/COVID-19-DEATH-RATE-DELAY.png')
plt.figure(4)
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.tick_params(axis='both', which='minor', labelsize=8)
death_list = sorted(death_by_delay.items())
x,y = zip(*death_list)
plt.plot(x, y)
plt.title('Deaths as a percentage of confirmed cases (delay in days vs percentage)', fontsize=40)
plt.savefig('/Users/kootsoop/Pictures/COVID-19-DEATH-RATE-ESTIMATE.png')
plt.figure(5)
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.tick_params(axis='both', which='minor', labelsize=8)
plt.plot(x_axis , death_data)
# plt.plot(x_axis, confirmed_data, 'r')
plt.title('Deaths and confirmed numbers.', fontsize=40)
plt.savefig('/Users/kootsoop/Pictures/COVID-19-DEATH-RATE-DEATHS-AND-CONFIRMED.png')
plt.figure(6)
plt.plot(x_pre, y_pre, 'g.', label='Prior data')
plt.plot(x_fit_data, y_fit_data,'o', markersize=20, label='Data used in forecast')
plt.plot([election_day_of_year, election_day_of_year], [deaths_at_election, deaths_at_election_end],'r+',markersize=20, label='Deaths at election: ' + str(deaths_at_election))
plt.plot(x_forecast, m*x_forecast + b,'k:',markersize=14, label='Line of best fit (forecast)')
plt.plot(day_for_500k, 500000, 'rx', markersize=50, label='500,000 deaths on ' + str(date_for_500k))
plt.ylim(125000,210000)
plt.xlim(150,275)
plt.title('Data used in forecast is from ' + first_row_shifted[start_fit] + ' to ' + first_row_shifted[end_fit], fontsize=40)
ax.legend(loc='upper left', shadow=True, fontsize=30)
# +
import numpy as np
from scipy import stats
mean_forecast = np.mean([x - min(forecasts) for x in forecasts ]) + min(forecasts)
median_forecast = np.median([x - min(forecasts) for x in forecasts ]) + min(forecasts)
print("mean : " + str(mean_forecast))
print("median : " + str(median_forecast))
# print("mode. : " + str(stats.mode([x - min(forecasts) for x in forecasts ]) + min(forecasts)))
start_of_forecasts = datetime.strptime('2020-06-24', '%Y-%m-%d')
end_of_forecasts = datetime.strptime('2020-09-20', '%Y-%m-%d')
plt.figure(0)
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.yaxis.set_major_formatter(mdates.DateFormatter("%B %d"))
ax.xaxis.set_major_formatter(mdates.DateFormatter("%B %d"))
plt.xticks(rotation=90)
ax.xaxis.set_major_locator(MultipleLocator(2))
ax.yaxis.set_major_locator(MultipleLocator(1))
ax.tick_params(axis='both', which='minor', labelsize=8)
plt.plot(dates, forecasts,'g+', markersize=50)
plt.plot([start_of_forecasts, end_of_forecasts], [median_forecast,median_forecast],'r')
plt.plot([start_of_forecasts, end_of_forecasts], [mean_forecast,mean_forecast],'b')
plt.title('Forecast 500k date over time', fontsize=40)
plt.savefig('/Users/kootsoop/Pictures/COVID-19-FORECAST-HISTORY-FINAL.png')
# Doesn't seem to do the right thing: ax.set_xticklabels(dates)
# -
plt.figure(0)
plt.figure(figsize=(20,20))
plt.plot(first_row_shifted, death_data)
# +
from numpy import log10, asarray, polyfit, ceil, arange
import csv
import matplotlib.pyplot as plt
from numpy import log10, asarray, polyfit, ceil, arange
import csv
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import json
import os.path
from os import path
import matplotlib.dates as mdates
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
def read_covid_data(data_type):
if (data_type in ['confirmed', 'deaths', 'recovered']):
COVID_directory = "/Users/kootsoop/git/COVID-19/csse_covid_19_data/csse_covid_19_time_series/"
first_row = None
with open(COVID_directory + 'time_series_covid19_' + data_type + '_global.csv') as csvfile:
confirmed = csv.reader(csvfile)
for row in confirmed:
if (first_row == None):
first_row = row
if (row[1] == 'US'):
us_data = row
break
else:
raise Exception('Invalid data_type', data_type)
return(first_row, us_data)
FORECAST_FILE = 'forecasts500k.txt'
if (path.exists(FORECAST_FILE)):
forecast_file = open(FORECAST_FILE, 'r')
forecasts500k = json.load(forecast_file)
forecast_file.close()
else:
forecasts500k = {}
(first_row, confirmed) = read_covid_data('confirmed')
(first_row2, recovered) = read_covid_data('recovered')
(first_row3, deaths) = read_covid_data('deaths')
death_data = [(float(data)) for data in deaths[4:(len(first_row))]]
recovered_data = [(float(data)) for data in recovered[4:(len(first_row))]]
confirmed_data = [(float(data)) for data in confirmed[4:(len(first_row))]]
first_row_shifted = [ data for data in first_row[4:(len(first_row))]]
x_axis = arange(len(death_data))
NumberInEstimateWindow = 20
# Started at 70 @ 2020/5/10
# 133 2020/06/24
# 137 2020/06/28
start_fit = len(death_data) - (NumberInEstimateWindow + 1)
# Started 20 more than start_fit
end_fit = start_fit + NumberInEstimateWindow
y_fit_data = death_data[start_fit:end_fit+1]
x_fit_data = arange(start_fit,end_fit+1)
y_pre = death_data[1:start_fit]
x_pre = arange(1,start_fit)
y_new_data = death_data[end_fit+1:len(death_data)]
x_new_data = arange(end_fit+1, len(death_data))
x_forecast = arange(end_fit, len(death_data) + 20)
[m, b] = polyfit(x_fit_data, y_fit_data, 1)
day_for_500k = (500000-b)/m
day_for_300k = (300000-b)/m
days_until = day_for_500k - len(first_row_shifted)
days_until_300k = day_for_300k - len(first_row_shifted)
print('Days until 500k: ' + str(day_for_500k - len(first_row_shifted) ))
plt.figure(figsize=(20,20))
ax = plt.gca()
# We change the fontsize of minor ticks label
ax.tick_params(axis='both', which='major', labelsize=30)
ax.tick_params(axis='both', which='minor', labelsize=8)
date_for_500k = (datetime.now() + timedelta(days=days_until)).date()
date_for_300k = (datetime.now() + timedelta(days=days_until_300k)).date()
print('300k:' + str(date_for_300k))
print('500k:' + str(date_for_500k))
# -
read_covid_data('deaths')
|
Python/COVID-19 Plots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="1BtkMGSYQOTQ"
# # Train a gesture recognition model for microcontroller use
# + [markdown] colab_type="text" id="BaFfr7DHRmGF"
# This notebook demonstrates how to train a 20kb gesture recognition model for [TensorFlow Lite for Microcontrollers](https://tensorflow.org/lite/microcontrollers/overview). It will produce the same model used in the [magic_wand](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/magic_wand) example application.
#
# The model is designed to be used with [Google Colaboratory](https://colab.research.google.com).
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/magic_wand/train/train_magic_wand_model.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/magic_wand/train/train_magic_wand_model.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
#
# + [markdown] colab_type="text" id="xXgS6rxyT7Qk"
# Training is much faster using GPU acceleration. Before you proceed, ensure you are using a GPU runtime by going to **Runtime -> Change runtime type** and selecting **GPU**. Training will take around 5 minutes on a GPU runtime.
# + [markdown] colab_type="text" id="LG6ErX5FRIaV"
# ## Configure dependencies
#
# Run the following cell to ensure the correct version of TensorFlow is used.
# + [markdown] colab_type="text" id="STNft9TrfoVh"
# We'll also clone the TensorFlow repository, which contains the training scripts, and copy them into our workspace.
# + colab={} colab_type="code" id="ygkWw73dRNda"
# Clone the repository from GitHub
# !git clone --depth 1 -q https://github.com/tensorflow/tensorflow
# Copy the training scripts into our workspace
# !cp -r tensorflow/tensorflow/lite/micro/examples/magic_wand/train train
# + [markdown] colab_type="text" id="pXI7R4RehFdU"
# ## Prepare the data
#
# Next, we'll download the data and extract it into the expected location within the training scripts' directory.
# + colab={} colab_type="code" id="W2Sg2AKzVr2L"
# Download the data we will use to train the model
# !wget http://download.tensorflow.org/models/tflite/magic_wand/data.tar.gz
# Extract the data into the train directory
# !tar xvzf data.tar.gz -C train 1>/dev/null
# + [markdown] colab_type="text" id="DNjukI1Sgl2C"
# We'll then run the scripts that split the data into training, validation, and test sets.
# + colab={} colab_type="code" id="XBqSVpi6Vxss"
# The scripts must be run from within the train directory
# %cd train
# Prepare the data
# !python data_prepare.py
# Split the data by person
# !python data_split_person.py
# + [markdown] colab_type="text" id="5-cmVbFvhTvy"
# ## Load TensorBoard
#
# Now, we set up TensorBoard so that we can graph our accuracy and loss as training proceeds.
# + colab={} colab_type="code" id="CCx6SN9NWRPw"
# Load TensorBoard
# %load_ext tensorboard
# %tensorboard --logdir logs/scalars
# + [markdown] colab_type="text" id="ERC2Cr4PhaOl"
# ## Begin training
#
# The following cell will begin the training process. Training will take around 5 minutes on a GPU runtime. You'll see the metrics in TensorBoard after a few epochs.
# + colab={} colab_type="code" id="DXmQZgbuWQFO"
# !python train.py --model CNN --person true
# + [markdown] colab_type="text" id="4gXbVzcXhvGD"
# ## Create a C source file
#
# The `train.py` script writes a model, `model.tflite`, to the training scripts' directory.
#
# In the following cell, we convert this model into a C++ source file we can use with TensorFlow Lite for Microcontrollers.
# + colab={} colab_type="code" id="8wgei4OGe3Nz"
# Install xxd if it is not available
# !apt-get -qq install xxd
# Save the file as a C source file
# !xxd -i model.tflite > /content/model.cc
# Print the source file
# !cat /content/model.cc
|
tensorflow/lite/micro/examples/magic_wand/train/train_magic_wand_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: adelaideswarbler
# language: python
# name: adelaideswarbler
# ---
# # Segment
#
# Description
# +
# %load_ext autoreload
# %autoreload 2
import sys
from pathlib import Path
path = str(Path.cwd().parent)
sys.path.append(path)
# +
import librosa
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from avgn.dataset import DataSet
from avgn.signalprocessing.create_spectrogram_dataset import (
create_label_df,
get_row_audio,
log_resize_spec,
make_spec,
pad_spectrogram,
)
from avgn.utils.hparams import HParams
from avgn.visualization.spectrogram import draw_spec_set
from parameters import PARAMETERS
from joblib import Parallel, delayed
from path import INDIVIDUALS
from tqdm.autonotebook import tqdm
# +
# [Optional]
# Normalize the spectrograms into uint8
# This will make the dataset smaller
def norm(x):
return (x - np.min(x)) / (np.max(x) - np.min(x))
# Create a set of parameters for processing the dataset
hparams = HParams(
n_fft=PARAMETERS.get('n_fft'),
hop_length_ms=PARAMETERS.get('hop_length_ms'),
win_length_ms=PARAMETERS.get('win_length_ms'),
ref_level_db=PARAMETERS.get('ref_level_db'),
pre=PARAMETERS.get('pre'),
min_level_db=PARAMETERS.get('min_level_db'),
min_level_db_floor=PARAMETERS.get('min_level_db_floor'),
db_delta=PARAMETERS.get('db_delta'),
silence_threshold=PARAMETERS.get('silence_threshold'),
min_silence_for_spec=PARAMETERS.get('min_silence_for_spec'),
max_vocal_for_spec=PARAMETERS.get('max_vocal_for_spec'),
min_syllable_length_s=PARAMETERS.get('min_syllable_length_s'),
spectral_range=PARAMETERS.get('spectral_range'),
num_mel_bins=PARAMETERS.get('num_mel_bins'),
mel_lower_edge_hertz=PARAMETERS.get('mel_lower_edge_hertz'),
mel_upper_edge_hertz=PARAMETERS.get('mel_upper_edge_hertz'),
butter_lowcut=PARAMETERS.get('butter_lowcut'),
butter_highcut=PARAMETERS.get('butter_highcut'),
mask_spec=PARAMETERS.get('mask_spec'),
nex=PARAMETERS.get('nex'),
n_jobs=PARAMETERS.get('n_jobs'),
verbosity=PARAMETERS.get('verbosity')
)
dataset = DataSet(INDIVIDUALS, hparams=hparams)
n_jobs = PARAMETERS.get('n_jobs')
verbosity = PARAMETERS.get('verbosity')
# +
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllable_dfs = parallel(
delayed(create_label_df)(
dataset.data_files[key].data,
hparams=dataset.hparams,
labels_to_retain=["labels", "sequence_num"],
unit="notes",
dict_features_to_retain=[],
key=key,
)
for key in tqdm(dataset.data_files.keys())
)
syllable_df = pd.concat(syllable_dfs)
# +
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllable_dfs = parallel(
delayed(get_row_audio)(
syllable_df[syllable_df.key == key],
dataset.data_files[key].data['wav_loc'],
dataset.hparams
)
for key in tqdm(syllable_df.key.unique())
)
syllable_df = pd.concat(syllable_dfs)
# +
# Get rid of syllables that are zero seconds,
# which will produce errors in segmentation
df_mask = np.array(
[len(i) > 0 for i in tqdm(syllable_df.audio.values)]
)
syllable_df = syllable_df[np.array(df_mask)]
syllable_df['audio'] = [
librosa.util.normalize(i) for i in syllable_df.audio.values
]
# Plot some example audio
nrows = 5
ncols = 10
zoom = 2
fig, axs = plt.subplots(
ncols=ncols,
nrows=nrows,
figsize=(ncols * zoom, nrows + zoom / 1.5)
)
for i, syll in tqdm(enumerate(syllable_df['audio'].values), total=nrows*ncols):
ax = axs.flatten()[i]
ax.plot(syll)
if i == nrows * ncols - 1:
break
plt.show()
# +
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
# Create spectrograms
syllables_spec = parallel(
delayed(make_spec)(
syllable,
rate,
hparams=dataset.hparams,
mel_matrix=dataset.mel_matrix,
use_mel=True,
use_tensorflow=False,
)
for syllable, rate in tqdm(
zip(syllable_df.audio.values, syllable_df.rate.values),
total=len(syllable_df),
desc="Getting syllable spectrograms",
leave=False,
)
)
plt.matshow(syllables_spec[10])
# +
# A hyperparameter where larger = higher dimensional spectrogram
log_scaling_factor = 10
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllables_spec = parallel(
delayed(log_resize_spec)(spec, scaling_factor=log_scaling_factor)
for spec in tqdm(
syllables_spec,
desc="scaling spectrograms",
leave=False
)
)
# Lets take a look at these spectrograms
draw_spec_set(
syllables_spec,
zoom=1,
maxrows=10,
colsize=25
)
plt.show()
syllables_spec = [
(norm(i) * 255).astype('uint8') for i in tqdm(syllables_spec)
]
syll_lens = [np.shape(i)[1] for i in syllables_spec]
plt.hist(syll_lens)
plt.show()
pad_length = np.max(syll_lens)
# +
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllables_spec = parallel(
delayed(pad_spectrogram)(spec, pad_length)
for spec in tqdm(
syllables_spec, desc="padding spectrograms", leave=False
)
)
draw_spec_set(syllables_spec, zoom=1, maxrows=10, colsize=25)
plt.show()
# What is the dimensionality of the dataset
print(np.shape(syllables_spec))
# convert to uint8 to save space
syllables_spec = [
(norm(i) * 255).astype('uint8') for i in tqdm(syllables_spec)
]
syllable_df['spectrogram'] = syllables_spec
|
notebook/segment/2.0-segment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Profiling PyTorch Multi GPU Single Node Training Job with Amazon SageMaker Debugger
#
# This notebook will walk you through creating a PyTorch training job with the SageMaker Debugger profiling feature enabled. It will create a multi GPU single node training using Horovod.
#
# ## 1. Create a Training Job with Profiling Enabled<a class="anchor" id="option-1"></a>
#
# You will use the standard [SageMaker Estimator API for PyTorch ](https://sagemaker.readthedocs.io/en/stable/frameworks/tensorflow/sagemaker.pytorch.html) to create training jobs. To enable profiling, create a `ProfilerConfig` object and pass it to the `profiler_config` parameter of the `PyTorch` estimator.
#
# ### Define hyperparameters
#
# Define hyperparameters such as number of epochs, batch size, and data augmentation. You can increase batch size to increases system utilization, but it may result in CPU bottlneck problems. Data preprocessing of a large batch size with augmentation requires a heavy computation. You can disable data_augmentation to see the impact on the system utilization.
#
# For demonstration purpose, the following hyperparameters are prepared to increase CPU usage, leading to GPU starvation.
hyperparameters = {"script":"pt_res50_cifar10_horovod_dataloader.py",
"model":"resnext101_32x8d",
"batch_size":2048,
"epoch":5}
# ### Configure rules
# We specify the following rules:
# - loss_not_decreasing: checks if loss is decreasing and triggers if the loss has not decreased by a certain persentage in the last few iterations
# - LowGPUUtilization: checks if GPU is under-utilizated
# - ProfilerReport: runs the entire set of performance rules and create a final output report with further insights and recommendations.
# +
from sagemaker.debugger import Rule, ProfilerRule, rule_configs
rules=[
Rule.sagemaker(rule_configs.loss_not_decreasing()),
ProfilerRule.sagemaker(rule_configs.LowGPUUtilization()),
ProfilerRule.sagemaker(rule_configs.ProfilerReport()),
]
# -
# ### Specify a profiler configuration
# The following configuration will capture system metrics at 500 milliseconds. The system metrics include utilization per CPU, GPU, memory utilization per CPU, GPU as well I/O and network.
#
# Debugger will capture detailed profiling information from step 5 to step 15. This information includes Horovod metrics, dataloading, preprocessing, operators running on CPU and GPU.
# +
from sagemaker.debugger import ProfilerConfig, FrameworkProfile
profiler_config = ProfilerConfig(
system_monitor_interval_millis=500,
framework_profile_params=FrameworkProfile(num_steps=10)
)
# -
# ### Define estimator
#
# We just need to pass in the profiler configuration and the list of rules and Debugger will take care of the rest.
# +
import sagemaker
from sagemaker.pytorch import PyTorch
estimator = PyTorch(
role=sagemaker.get_execution_role(),
train_instance_count=1,
train_instance_type='ml.p3.8xlarge',
source_dir='entry_point',
entry_point='horovod_test_launcher.py',
framework_version='1.6.0',
hyperparameters=hyperparameters,
profiler_config=profiler_config,
rules=[rules])
# -
# ### Start training job
#
# The following `estimator.fit()` with `wait=False` argument initiates the training job in the background. You can proceed to run the dashboard or analysis notebooks.
estimator.fit(wait=False)
# ## 2. Analyze Profiling Data
#
# Copy outputs of the following cell (`training_job_name` and `region`) to run the analysis notebooks `profiling_generic_dashboard.ipynb`, `analyze_performance_bottlenecks.ipynb`, and `profiling_interactive_analysis.ipynb`.
# +
import boto3
session = boto3.session.Session()
region = session.region_name
training_job_name = estimator.latest_training_job.name
print(f"Training jobname: {training_job_name}")
print(f"Region: {region}")
# -
# While the training is still in progress you can visualize the performance data in SageMaker Studio or in the notebook.
# Debugger provides utilities to plot system metrics in form of timeline charts or heatmaps. Checkout out the notebook
# [profiling_interactive_analysis.ipynb](analysis_tools/profiling_interactive_analysis.ipynb) for more details. In the following code cell we plot the total CPU and GPU utilization as timeseries charts. To visualize other metrics such as I/O, memory, network you simply need to extend the list passed to `select_dimension` and `select_events`.
from smdebug.profiler.analysis.notebook_utils.training_job import TrainingJob
tj = TrainingJob(training_job_name, region)
tj.wait_for_sys_profiling_data_to_be_available()
# +
from smdebug.profiler.analysis.notebook_utils.timeline_charts import TimelineCharts
system_metrics_reader.refresh_event_file_list()
view_timeline_charts = TimelineCharts(system_metrics_reader,
framework_metrics_reader=None,
select_dimensions=["CPU", "GPU"],
select_events=["total"])
# -
# ## 3. Download Debugger Profiling Report
# The profiling report rule will create an html report `profiler-report.html` with a summary of builtin rules and recommenades of next steps. You can find this report in your S3 bucket.
rule_output_path = estimator.output_path + estimator.latest_training_job.job_name + "/rule-output"
print(f"You will find the profiler report in {rule_output_path}")
# For more information about how to download and open the Debugger profiling report, see [SageMaker Debugger Profiling Report](https://docs.aws.amazon.com/sagemaker/latest/dg/debugger-profiling-report.html) in the SageMaker developer guide.
|
sagemaker-debugger/pytorch_profiling/pt-resnet-profiling-multi-gpu-single-node.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Dummy data for classification
# +
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
from sklearn.datasets import make_blobs
data, labels = make_blobs(n_features=2, centers=2,cluster_std=2,random_state=3)
plt.scatter(data[:,0], data[:,1], c = labels, cmap='coolwarm');
# -
# ### Attempt to Classify Data
# +
#Import LinearSVC
from sklearn.svm import LinearSVC
#Create instance of Support Vector Classifier
svc = LinearSVC()
#Fit estimator to 70% of the data
svc.fit(data[:70], labels[:70])
#Predict final 30%
y_pred = svc.predict(data[70:])
#Establish true y values
y_true = labels[70:]
# -
# ### Metrics
# #### Precision Score
#
# TP - True Positives<br>
# FP - False Positives<br>
#
# Precision - Accuracy of positive predictions.<br>
# Precision = TP/(TP + FP)
# +
from sklearn.metrics import precision_score
print("Precision score: {}".format(precision_score(y_true,y_pred)))
# -
# #### Recall Score
#
# FN - False Negatives<br>
#
# Recall (aka sensitivity or true positive rate): Fraction of positives That were correctly identified.<br>
# Recall = TP/(TP+FN)
# +
from sklearn.metrics import recall_score
print("Recall score: {}".format(recall_score(y_true,y_pred)))
# -
# #### Accuracy Score
# +
from sklearn.metrics import accuracy_score
print("Accuracy score: {}".format(accuracy_score(y_true,y_pred)))
# -
# #### Confusion Matrix
# +
from sklearn.metrics import confusion_matrix
import pandas as pd
confusion_df = pd.DataFrame(confusion_matrix(y_true,y_pred),
columns=["Predicted Class " + str(class_name) for class_name in [0,1]],
index = ["Class " + str(class_name) for class_name in [0,1]])
print(confusion_df)
# -
# #### Classification Report
# +
from sklearn.metrics import classification_report
print(classification_report(y_true,y_pred))
# -
# #### F1 Score
# +
from sklearn.metrics import f1_score
print("F1 Score: {}".format(f1_score(y_true,y_pred)))
# -
# #### Accuracy Score
# +
from sklearn.metrics import accuracy_score
print("Accuracy score: {}".format(accuracy_score(y_true,y_pred)))
# -
# ### Metric Curves
# +
from sklearn.metrics import precision_recall_curve
precisions,recalls, thresholds
# -
# ### Other classification metrics available from sklearn.metrics
#
#
# - auc
# - average_precision_score
# - brier_score_loss
# - cohen_kappa_score
# - dcg_score
# - fbeta_score
# - hamming_loss
# - hinge_loss
# - jaccard_similarity_score
# - loss..matthews_corrcoef
# - precision_recall_curve
# - precision_recall_fscore_support
# - roc_auc_score
# - roc_curve
# - zero_one_loss
#
# sklearn.metrics also offers Regression Metrics, Model Selection Scorer, Multilabel ranking metrics, Clusterin Metrics, Biclustering metrics, and Pairwise metrics.
|
content/sklearn/.ipynb_checkpoints/Metrics - Classification Report Breakdown (Precision, Recall, F1)-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table>
# <tr><td align="right" style="background-color:#ffffff;">
# <img src="../images/logo.jpg" width="20%" align="right">
# </td></tr>
# <tr><td align="right" style="color:#777777;background-color:#ffffff;font-size:12px;">
# Prepared by <NAME>
# </td></tr>
# <tr><td align="right" style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;">
# This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros.
# </td></tr>
# </table>
# $ \newcommand{\bra}[1]{\langle #1|} $
# $ \newcommand{\ket}[1]{|#1\rangle} $
# $ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
# $ \newcommand{\dot}[2]{ #1 \cdot #2} $
# $ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
# $ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
# $ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
# $ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
# $ \newcommand{\mypar}[1]{\left( #1 \right)} $
# $ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
# $ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
# $ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
# $ \newcommand{\onehalf}{\frac{1}{2}} $
# $ \newcommand{\donehalf}{\dfrac{1}{2}} $
# $ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
# $ \newcommand{\vzero}{\myvector{1\\0}} $
# $ \newcommand{\vone}{\myvector{0\\1}} $
# $ \newcommand{\vhadamardzero}{\myvector{ \sqrttwo \\ \sqrttwo } } $
# $ \newcommand{\vhadamardone}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
# $ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
# $ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
# $ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
# $ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
# $ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
# $ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
# <h2>Quantum Coin Flipping</h2>
#
# We will do a series of experiments, and try to understand the behaviors of "particles".
# <h3> The first experiment</h3>
#
# We will trace the behavior of a photon.
#
# For quantum coin-flipping, we use a beam splitter.
#
# For measurements, we use two photon detectors.
#
# <ul>
# <li> Photon is our coin. </li>
# <li> Beam splitter flips the photon. </li>
# <li> Photon detectors are our eyes.</li>
# </li>
# <h4> The setup </h4>
#
# </b>We send photons to a beam splitter as shown below.
#
# We expect two behaviors: the beam splitter either transmits or reflects the photon.
#
# <img src="../images/photon1.jpg" width="50%">
# <hr>
# <center><font size="+1" style="color:blue;">
# We can use an open-source interactive tool <a href="http://play.quantumgame.io" target="_blank">quantumgame</a> (requiring internet connection).
# </font></center>
# <hr>
# <h4> Experimental results </h4>
#
# After many experiments, we observe the photons in each photon detector almost evenly ($ \approx \% 50 $ and $ \approx \% 50 $).
#
# <img src="../images/photon2.jpg" width="50%">
# <h4> The first interpretation </h4>
#
# So, a beam splitter behaves similarly to a fair coin.
#
# <ul>
# <li> Head (state 0): Trasmitted </li>
# <li> Tail (state 1): Reflected </li>
# </ul>
# <h4> Modeling </h4>
#
# We describe our first experiment by a single (probabilistic) bit.
#
# We start in state 0.
#
# With half probability, the photon transmits, and the state does not change.
#
# With half probability, the photon is reflected, and the state is flipped.
#
# <img src="../images/photon3.jpg" width="50%">
# <h3> The second experiment </h3>
#
# We extend our experiment with two mirrors and another beam splitter.
#
# Then, we try to validate our <u>interpretation</u> and <u>model</u>.
# <img src="../images/photon4.jpg" width="60%">
# In this setup, we have three photon detectors.
#
# By using our model described above, we expect to observe a photon
# <ul>
# <li> in $ A $ with probability $ 0.5 $, </li>
# <li> and in $ B1 $ and $ B2 $ with probabilities $ 0.25 $. </li>
# </ul>
#
# Thus, our prediction for the frequencies of observing the photons in $ A $, $ B1 $, and $ B2 $ are respectively
#
# $$
# \approx \% 50, \approx \% 25, \mbox{ and } \approx \% 25.
# $$
# <h4> Experimental results </h4>
#
# Experiments confirm our predictions.
#
# Our model explains the second experiment.
# <img src="../images/photon5.jpg" width="65%">
# <h3> The third experiment </h3>
#
# In the third experiment, we remove the photon detector $ A $.
#
# So we have only the detectors $ B1 $ and $ B2 $.
#
# <img src="../images/photon6.jpg" width="65%">
# <h4> Our prediction </h4>
#
# The third setup is similar to flipping a fair coin twice.
#
# Our prediciton is to observe the photons in $ B1 $ and $ B2 $ almost evenly ($ \approx \% 50 $ and $ \approx \% 50 $)
# <h4>Let's do the math of our prediction</h4>
#
# 0) At the initial step, we are in state $ 0 $. If we use our vector representation, it is
#
# $$ v_0 = \myvector{1 \\ 0}. $$
#
# 1) We flip a fair coin. The new probabilistic state is expected to be in both states ($0$ and $1$) with half probability ($ \frac{1}{2} = 0.5 $).
#
# $$
# v_1 = \myvector{\frac{1}{2} \\ \frac{1}{2}}
# = \mymatrix{cc}{ \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} }
# \myvector{1 \\ 0}.
# $$
#
# Here the transitions of a fair coin can be represented by the matrix (table): $ \mymatrix{cc}{ \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} } $ .
#
# 2) Then, we flip a fair coin again. The new probabilistic state will be the same:
#
# $$
# v_2 = \myvector{\frac{1}{2} \\ \frac{1}{2}} =
# \mymatrix{cc}{ \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} }
# \myvector{\frac{1}{2} \\ \frac{1}{2}}.
# $$
#
# <b><i> Our predicition is fine with mathematical calculation. </i></b>
# <img src="../images/prediction1.jpg" width="50%">
# <h4> Experimental results </h4>
#
# <b style="color:red;">However, the experiment results do not confirm our prediction.<b>
# <img src="../images/photon7.jpg" width="65%">
# We observe the photons <b>only</b> in the detector $ B1 $, and we <b>never</b> observe any photon in the detector $ B2 $.
#
# <b> How could this be possible?</b>
# We can conclude that the "classical" (Newtonian) mechanics fail to explain the behaviors of particles.
# We need a new (mathematical) model.
#
# We can explain our experiments by using <u>quantum mechanics</u>.
|
bronze/B20_Quantum_Coin_Flipping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Comparison of LDA and PCA 2D projection of Iris dataset
#
#
# The Iris dataset represents 3 kind of Iris flowers (Setosa, Versicolour
# and Virginica) with 4 attributes: sepal length, sepal width, petal length
# and petal width.
#
# Principal Component Analysis (PCA) applied to this data identifies the
# combination of attributes (principal components, or directions in the
# feature space) that account for the most variance in the data. Here we
# plot the different samples on the 2 first principal components.
#
# Linear Discriminant Analysis (LDA) tries to identify attributes that
# account for the most variance *between classes*. In particular,
# LDA, in contrast to PCA, is a supervised method, using known class labels.
#
#
# +
print(__doc__)
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)
lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
# Percentage of variance explained for each components
print('explained variance ratio (first two components): %s'
% str(pca.explained_variance_ratio_))
plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of IRIS dataset')
plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], alpha=.8, color=color,
label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of IRIS dataset')
plt.show()
|
scikit-learn-official-examples/decomposition/plot_pca_vs_lda.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/dustin-py/DS-Unit-1-Sprint-2-Statistics/blob/master/module1/LS_DS_121_Statistics_Probability_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Sa5KWMO1ngPN" colab_type="text"
# <img align="left" src="https://lever-client-logos.s3.amazonaws.com/864372b1-534c-480e-acd5-9711f850815c-1524247202159.png" width=200>
# <br></br>
# <br></br>
#
# ## *Data Science Unit 1 Sprint 2 Assignment 1*
#
# # Apply the t-test to real data
#
# Your assignment is to determine which issues have "statistically significant" differences between political parties in this [1980s congressional voting data](https://archive.ics.uci.edu/ml/datasets/Congressional+Voting+Records). The data consists of 435 instances (one for each congressperson), a class (democrat or republican), and 16 binary attributes (yes or no for voting for or against certain issues). Be aware - there are missing values!
#
# Your goals:
#
# 1. Load and clean the data (or determine the best method to drop observations when running tests)
# 2. Using hypothesis testing, find an issue that democrats support more than republicans with p < 0.01
# 3. Using hypothesis testing, find an issue that republicans support more than democrats with p < 0.01
# 4. Using hypothesis testing, find an issue where the difference between republicans and democrats has p > 0.1 (i.e. there may not be much of a difference)
#
# Note that this data will involve *2 sample* t-tests, because you're comparing averages across two groups (republicans and democrats) rather than a single group against a null hypothesis.
# + [markdown] id="RLAEIGaPJnpd" colab_type="text"
#
#
# ---
#
#
# + [markdown] id="FQjajFEvJo2-" colab_type="text"
# # 1. Load and clean the data (or determine the best method to drop observations when running tests)
# + id="ZKwspo2CngPP" colab_type="code" outputId="96c84c5e-44be-4358-d8ca-c480d07c90d6" colab={"base_uri": "https://localhost:8080/", "height": 823}
# Import external libraries:
import pandas as pd
import numpy as np
from scipy.stats import ttest_ind, ttest_1samp
# Load in csv file of house votes from '84:
house_votes = pd.read_csv('house-votes-84.data', header=None, na_values='?')
# Check to see if the data loades with the frist 5 rows:
# display(house_votes.head())
# View the shape of our data to see if it matches the original data repo:
# print(house_votes.shape)
# Open the names document to get the attribute names
with open('house-votes-84.names','r') as file:
names_file = file.read()
# print(names_file)
# Create a list of Attribute names to use as columns:
cols = ['party','handicap-infants','water-project-cost-sharing',
'adoption-of-the-budget-resolution','physician-fee-freeze',
'el-salvador-aid','religious-groups-in-schools',
'anti-satellite-test-ban','aid-to-nicaraguan-contras','mx-missile',
'immigration','synfuels-corporation','education-spending',
'superfund-right-to-sue','crime','duty-free-exports',
'export-administration-act-south-africa']
# Apply cols list to our data frame:
house_votes.columns = cols
# View the first five rows to confirm the change was saved:
# house_votes.head()
# Here we will map our yes and no values:
house_votes = house_votes.replace({'y':1,'n':0})
# Now I want to create a group for republicans and a group ro democrats:
republicans = house_votes[house_votes['party']=='republican']
democrats = house_votes[house_votes['party']=='democrat']
# Display the groupped DataFrames to make sure it worked:
display(republicans.head(10))
display(democrats.head(10))
# + id="Wrjnf5WcySh7" colab_type="code" colab={}
# Function to remove nans from columns
def removeNan(df,col_name=[]):
'''Function to remove nans from dataframe columns'''
col = df[col_name]
np.isnan(col)
return col[~np.isnan(col)]
# + id="5SrWxYU401wN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 731} outputId="b12f83bd-f5b9-427f-c613-4f254f620509"
# Further Cleaning and Exploring:
# Remove NaN values from adoption-of-the-budget-resolution column:
republicans_no_nans = removeNan(republicans,['adoption-of-the-budget-resolution','education-spending','immigration'])
democrats_no_nans = removeNan(democrats,['adoption-of-the-budget-resolution','education-spending','immigration'])
# Simple visual.
republicans_no_nans.plot(kind='density',color=['red','orange','black'],figsize=(9,6)); # Red
democrats_no_nans.plot(kind='density',color=['blue','orange','black'],figsize=(9,6)); # Blue
# + [markdown] id="B4flTQU6YEJ4" colab_type="text"
# # 2. Using hypothesis testing, find an issue that democrats support more than republicans with p < 0.01
# + id="amXWp2rnDHle" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 207} outputId="04a8d923-9281-4fcc-eb3f-a9269dcfe447"
# State NULL Hypothesis:
print("NULL HYPOTHESIS:",
"\nThere is no difference in voting averages between republicans and",
"democrats on adoption of the budget resolutionis.")
print("\nALT HYPOTHESIS:",
"\nDemocrats are more likely to vote 'yes' on the topic of adoption of the budget resolution than Republicans.")
# Run our ttest to compare the means of yes in our two groups.
print("\nIndependent T-test results:")
ttest1 = ttest_ind(democrats['adoption-of-the-budget-resolution'],
republicans['adoption-of-the-budget-resolution'],
nan_policy='omit')
print(ttest1)
# Check to confirm pvalue is < 0.01
if ttest1.pvalue < 0.01:
print("\nThe pvalue is less than 0.01")
# + [markdown] id="qHPT30mWYM_g" colab_type="text"
# # 3. Using hypothesis testing, find an issue that republicans support more than democrats with p < 0.01
# + id="mt8ppJKZ7Gf2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 187} cellView="code" outputId="c17dcb75-a3b6-42e7-d97a-005ddf92f52e"
#@title Default title text
# State NULL Hypothesis:
print("NULL HYPOTHESIS:",
"\nThere is no difference in voting averages between republicans and",
"democrats on education.")
# State ALT Hypothesis:
print("\nALT HYPOTHESIS:",
"\nRepublicans are more likely to vote 'yes' on the topic of education spending than Democrats.")
# Run our ttest to compare the means of yes in our two groups.
print("\nIndependent T-test results:")
ttest2 = ttest_ind(republicans['education-spending'],
democrats['education-spending'],
nan_policy='omit')
print(ttest2)
# Check to confirm pvalue is > 0.01
if ttest2.pvalue < 0.01:
print("\nThe pvalue is less than 0.01")
# + [markdown] id="qFvrsNPdYVVf" colab_type="text"
# # 4. Using hypothesis testing, find an issue where the difference between republicans and democrats has p > 0.1 (i.e. there may not be much of a difference)
# + id="zoRP5K4Qy4qL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 153} outputId="9ddca19a-bef4-4221-d8d6-c90bdf68e971"
# State NULL Hypothesis:
print("NULL HYPOTHESIS:",
"\nThere is no difference in voting averages between republicans and",
"democrats on immigration.")
# State ALT Hypothesis:
print("\nALT HYPOTHESIS:",
"\nRepublicans are more likely to vote 'yes' on the topic of immigration than Democrats.")
# Run our ttest to compare the means of yes in our two groups.
print("\nIndependent T-test results:")
ttest3 = ttest_ind(republicans['immigration'],
democrats['immigration'],
nan_policy='omit')
ttest3
if ttest3.pvalue > 0.01:
print("\nThe pvalue is greater than 0.01")
# + id="ugMyvv1nKxZo" colab_type="code" colab={}
# + [markdown] id="wcA_AvvRAqW_" colab_type="text"
# ## Stretch Goals:
#
# 1. Refactor your code into functions so it's easy to rerun with arbitrary variables
# 2. Work on Performing a T-test without using Scipy in order to get "under the hood" and learn more thoroughly about this topic.
# ### Start with a 1-sample t-test
# - Establish the conditions for your test
# - [Calculate the T Statistic](https://blog.minitab.com/hs-fs/hubfs/Imported_Blog_Media/701f9c0efa98a38fb397f3c3ec459b66.png?width=247&height=172&name=701f9c0efa98a38fb397f3c3ec459b66.png) (You'll need to omit NaN values from your sample).
# - Translate that t-statistic into a P-value. You can use a [table](https://www.google.com/search?q=t+statistic+table) or the [University of Iowa Applet](https://homepage.divms.uiowa.edu/~mbognar/applets/t.html)
#
# ### Then try a 2-sample t-test
# - Establish the conditions for your test
# - [Calculate the T Statistic](https://lh3.googleusercontent.com/proxy/rJJ5ZOL9ZDvKOOeBihXoZDgfk7uv1YsRzSQ1Tc10RX-r2HrRpRLVqlE9CWX23csYQXcTniFwlBg3H-qR8MKJPBGnjwndqlhDX3JxoDE5Yg) (You'll need to omit NaN values from your sample).
# - Translate that t-statistic into a P-value. You can use a [table](https://www.google.com/search?q=t+statistic+table) or the [University of Iowa Applet](https://homepage.divms.uiowa.edu/~mbognar/applets/t.html)
#
# ### Then check your Answers using Scipy!
# + id="dPmXOHh1Cfea" colab_type="code" colab={}
|
DataScience/DS-Unit-1-Sprint-2-Statistics/module1/LS_DS_121_Statistics_Probability_Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Step 5.3 Parameter Tuning with C
# In this notebook, we tune the SVC model with three different values for the C parameter.
import pandas as pd
import numpy as np
from pandas import plotting
import matplotlib.pyplot as plt
from datetime import datetime as dt
import io, s3fs, json, traceback
pd.set_option('display.max_columns', None)
print('Program run at', dt.now())
# Load modules, data, and write functions
# +
# Ignore warnings from scikit-learn to make this notebook a bit nicer
import warnings
warnings.simplefilter('ignore')
# Models may be implemented as pipelines
from sklearn.pipeline import Pipeline
# Used to divide our dataseets into train/test splits
# Data will be randomly shuffled so running this notebook multiple times may lead to different results
from sklearn.model_selection import train_test_split as tts
# Visual analysis of model performance
from yellowbrick.classifier import confusion_matrix
from yellowbrick.classifier import classification_report
from yellowbrick.regressor import prediction_error, ResidualsPlot
from yellowbrick.classifier import ROCAUC
# Set the default figure size for matplotlib
plt.rcParams['figure.figsize'] = (9, 6)
#Model toolset
from sklearn.metrics import f1_score
from sklearn.pipeline import Pipeline
from sklearn.svm import LinearSVC, NuSVC, SVC
#Pipeline toolset
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer, make_column_selector
from sklearn.preprocessing import RobustScaler, OneHotEncoder, OrdinalEncoder, StandardScaler, MinMaxScaler
from sklearn.impute import SimpleImputer
from sklearn.utils import resample
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from sklearn.model_selection import train_test_split as tts
#Evaluation toolset
from sklearn.model_selection import StratifiedKFold, cross_val_score
from yellowbrick.classifier import ConfusionMatrix
from yellowbrick.classifier import ClassificationReport
from yellowbrick.features import FeatureImportances
from yellowbrick.target import ClassBalance
from sklearn.metrics import accuracy_score
# -
est_rmv = pd.read_csv('s3://bleeding-hearts/workingdata/est_rmv.csv')
cat_labels = ['Very Low', 'Low', 'Moderate', 'High', 'Very High']
categorical = make_column_selector(dtype_include=np.object)
numeric = make_column_selector(dtype_include=np.int64)
numeric2 = make_column_selector(dtype_include=np.float64)
def train_test(X,y):
X_train, X_test, y_train, y_test = tts(X, y, test_size=.2)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
def score_model(X, y, estimator, **kwargs):
"""
Test various estimators.
"""
y = LabelEncoder().fit_transform(y)
model = Pipeline([
("columns", ColumnTransformer([
('onehot', OneHotEncoder(), categorical),
('scalar', RobustScaler(), numeric),
('scalar2', RobustScaler(), numeric2),
], remainder='drop')),
("imputer",SimpleImputer(missing_values=np.nan, strategy='mean')),
('estimator', estimator)
])
# Instantiate the classification model and visualizer
model.fit(X, y, **kwargs)
expected = y
predicted = model.predict(X)
# Compute and return F1 (harmonic mean of precision and recall)
print("F1 SCORE {}: {}".format(estimator.__class__.__name__, f1_score(expected, predicted,average='micro')))
def visualize_model(X, y, estimator,label_lst, **kwargs):
"""
Test various estimators.
"""
y = LabelEncoder().fit_transform(y)
model = Pipeline([
("columns", ColumnTransformer([
('onehot', OneHotEncoder(), categorical),
('scalar', RobustScaler(), numeric),
('scalar2', RobustScaler(), numeric2),
], remainder='drop')),
("imputer",SimpleImputer(missing_values=np.nan, strategy='mean')),
('estimator', estimator)
])
X_train, X_test, y_train, y_test = tts(X, y, test_size=0.2)
# Instantiate the classification model and visualizer
visualizer = ClassificationReport(
model, classes=label_lst,
cmap="YlGn", size=(600, 360), support=True, **kwargs
)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show()
def conf_matrix(X,y,estimator,label_lst, **kwargs):
y = LabelEncoder().fit_transform(y)
model = Pipeline([
("columns", ColumnTransformer([
('onehot', OneHotEncoder(), categorical),
('scalar', RobustScaler(), numeric),
('scalar2', RobustScaler(), numeric2),
], remainder='drop')),
("imputer",SimpleImputer(missing_values=np.nan, strategy='mean')),
('estimator', estimator)
])
#Create the train and test data
X_train, X_test, y_train, y_test = tts(X, y, test_size=0.2)
model.fit(X, y)
# Instantiate the visualizer with the classification model
confusion_matrix(
model,
X_train, y_train, X_test, y_test,
classes=label_lst
).show()
#plt.tight_layout()
#plt.show()
def roc_auc(X,y,estimator,**kwargs):
y = LabelEncoder().fit_transform(y)
model = Pipeline([
("columns", ColumnTransformer([
('onehot', OneHotEncoder(), categorical),
('scalar', RobustScaler(), numeric),
('scalar2', RobustScaler(), numeric2),
], remainder='drop')),
("imputer",SimpleImputer(missing_values=np.nan, strategy='mean')),
('estimator', estimator)
])
#Create the train and test data
X_train, X_test, y_train, y_test = tts(X, y, test_size=0.2)
# Instantiate the visualizer with the classification model
visualizer = ROCAUC(model, classes=cat_labels)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and show the figure
# Different values of C below - 1, 10, and 100
models = [
SVC(
kernel='linear', #How does using a linear kernel affect model performance?
C=1.0,
gamma='scale'),
SVC(
kernel='linear',
C=10,
gamma='scale'),
SVC(kernel='linear',
C=100,
gamma='scale'
)]
# Run the model with different C parameters below. First output is C of 1, second is C of 10, and third is C of 100.
X = est_rmv.loc[:, est_rmv.columns != 'Child Opportunity Levels, overall COI, nationally-normed']
y = est_rmv['Child Opportunity Levels, overall COI, nationally-normed']
train_test(X,y)
for model in models:
try:
score_model(X, y, model)
visualize_model(X, y, model, cat_labels)
conf_matrix(X, y, model,cat_labels)
roc_auc(X, y, model)
except Exception as exc:
print(model,
traceback.format_exc(),
exc)
|
Step_5.3_Parameter_Tuning_C.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Python Cleaning Up Text Files
import os
fname = "Veidenbaums.txt"
fpath = os.path.join(os.getcwd(), 'data', fname)
fpath
newpath = os.path.join(os.getcwd(), 'data', 'cleaned.txt')
newpath
with open(fpath) as f:
mylist = f.readlines()
len(mylist)
print("Hello Python")
# !python --version
# we can check filesize first if we are worried about reading whole file into our RAM
os.path.getsize(fpath)
with open(fpath, encoding="utf-8") as f:
mylist = f.readlines()
len(mylist)
with open(fpath, encoding="utf-8") as f:
rawtext = f.read()
len(rawtext)
mylist[:10]
mylist[:50]
mylist[-10:]
stars = "***"
stars
stars in mylist[0]
stars in mylist[2]
rawtext.count(stars)
total = 0
lcount = 0
for line in mylist:
if stars in line:
total += 1
lcount += 1
print("Total lines", lcount)
print("Starred lines", total)
# +
# for those times when we need an index, we can use enumerate
total = 0
for i, line in enumerate(mylist):
if stars in line:
total += 1
print("Found ",stars, "on Line:", i)
print("Total lines", i)
print("Starred lines", total)
# -
badwords = ['***','ReallyBadWord']
# This recipe will clean small,big and huge files
# from all lines containing bad words in the list badwords
with open(fpath, encoding='utf-8') as oldfile, open(newpath, mode='w', encoding='utf-8') as newfile:
for line in oldfile:
if not any(badword in line for badword in badwords):
newfile.write(line)
with open(newpath, encoding='utf-8') as f:
txt=f.read()
len(txt)
len(rawtext),len(txt)
# # Exercise
#
# 1. Saskaitīt tekstā sastopamo vārdu biežumu
# 2. Izdrukāt unikālo vārdu skaitu
# 3. Izdrukāt 20. biežāk sastopamo vārdu sarakstu
# 4. Kādi ir tekstā visretāk sastopamie vārdi?
mylist[100:130]
badchars = ',;:!?."\'-'
badchars
newname = 'Valdis'.replace('al', 'od')
newname
newname.replace()
# with this recipe we can clear the text of all bad chars
for char in badchars:
print("Cleaning text from ", char)
txt = txt.replace(char, '') # suggestion to use regular expressions for heavier tasks
len(txt)
txt[:50]
# +
# <NAME>'s extra whitespace cleaner
# ' '.join(mystring.split())
# -
words = txt.split()
len(words)
words[:10]
words[-10:]
nums = list(range(10))
nums
numtxt = str(nums)
numtxt
mynums = numtxt.split(", ")
mynums
type(mynums)
type(mynums[0])
"Valdis".lower()
# generate a list with all words in lowercase from words list
newlist = []
for word in words:
newlist.append(word.lower())
print(len(newlist))
nlist = [w.lower() for w in words]
len(nlist)
newlist[:10]
# List Comprehension
nlist = [word.lower() for word in words]
nlist
cwords = [word.title() for word in words]
len(cwords)
nlist.count('alus')
uniq = set(nlist)
len(uniq)
mytemp = { 'alus' : nlist.count('alus')}
mytemp
# Dictionary comprehension
mydict = { word : nlist.count(word) for word in set(nlist)}
len(mydict)
mydict['alus']
newdict = {}
for word in nlist:
if word in newdict.keys():
newdict[word] += 1
else:
newdict[word] = 1
len(newdict)
newdict['alus']
sorted(mydict.items())[:10]
# the el[1] refers to second element of the tuple in mydict.items() list
sortedfrequency = sorted(mydict.items(),key=lambda el: el[1], reverse=True)
sorted(list('kartupelis'))
sortedfrequency[:10]
somewords = [item[0] for item in longcnt.most_common(10)]
somewords
sorted(somewords)
def mycomparison(el):
return el[::-1]
sorted(somewords, key = mycomparison)
# in lambda functions return is implied and comes right after the first :
sorted(somewords, key = lambda el: el[::-1])
vdict = { word: cwords.count(word) for word in set(cwords)}
len(vdict)
list(vdict.keys())[:5]
max(vdict, key = lambda k: vdict[k])
vdict['Un']
sortedWords = sorted(vdict.items(), key = lambda x: x[1])
len(sortedWords)
type(vdict.items())
sortedWords.reverse()
sortedWords[:10]
sortedWords[:50]
from collections import Counter
wcount = Counter('abracadabra')
wcount.most_common()
ncount = Counter(nlist)
ncount.most_common(20)
# we filter out all words that are shorter than 3 or less characters
longlist = [word for word in nlist if len(word) > 3]
len(longlist)
longcnt = Counter(longlist)
longcnt.most_common(20)
type(longcnt)
type(longcnt.most_common())
commonlongwords = longcnt.most_common(20)
commonlongwords
longlist[:10]
# we can update counter values manually it will add new values
longcnt.update({'sirds':13})
longcnt.most_common(10)
longcnt['sirds'] += 3
longcnt.most_common(5)
longcnt.update({'sirds':20, 'gars':50})
longcnt.most_common(10)
cnt = Counter(nlist)
cnt.most_common(10)
cnt.most_common(50)
# +
# Reading files from URL
# https://docs.python.org/3.7/library/urllib.request.html#module-urllib.request
# -
from collections import Counter
wcnt = Counter("abbbbbbaabbbccdfdfad")
wcnt.most_common()
|
Python Cleaning Up Text Files.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from gs_quant.common import PayReceive, Currency
from gs_quant.instrument import IRSwap
from gs_quant.session import Environment, GsSession
from gs_quant.risk import DollarPrice, IRDelta, IRDeltaParallelLocalCcy
from gs_quant.markets import HistoricalPricingContext
from datetime import date
# external users should substitute their client id and secret; please skip this step if using internal jupyterhub
GsSession.use(Environment.PROD, client_id = None, client_secret=None, scopes=('run_analytics',))
swap_10bps = IRSwap(PayReceive.Receive, '5y', Currency.EUR, fixed_rate='atm+10')
with HistoricalPricingContext(date(2020, 3, 2), date(2020, 4, 1), show_progress=True):
res_f = swap_10bps.calc((DollarPrice, IRDelta, IRDeltaParallelLocalCcy))
print(res_f.result()) # retrieve all results
print(res_f[DollarPrice]) # retrieve historical prices
|
gs_quant/documentation/02_pricing_and_risk/00_instruments_and_measures/examples/01_rates/000107_calc_swap_risk_historically.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Perform Analysis on Athletes
#
# This file reads the detailed athlete information and performs Linear Regression analysis on this data.
#
# The following areas are examined in this code
#
# * <a href=#Visualize>Visualize Data</a>
#
# * <a href=#LinearRegression>Linear Regression</a>
#
# * <a href=#LASSO>LASSO</a>
#
# * <a href=#MixedEffect>Mixed Effect</a>
#
# * <a href=#Algebraic>Algebraic Model</a>
#
# +
# Necessary imports
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import patsy
from math import sqrt
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import kurtosis, skew
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import Lasso
from sklearn import linear_model
# %matplotlib inline
# -
# ## Read data
# +
boy1600 = pd.read_csv("1allDistrict_boy1600.csv")
girl1600 = pd.read_csv("1allDistrict_girl1600.csv")
girl400 = pd.read_csv("1allDistrict_girl400.csv")
boy400 = pd.read_csv("1allDistrict_boy400.csv")
boy1600['sex'] = 'boy'
girl1600['sex'] = 'girl'
boy400['sex'] = 'boy'
girl400['sex'] = 'girl'
print(f"Girl 1600: {girl1600.shape}")
print(f"Boy 1600: {boy1600.shape}")
print(f"Girl 400: {girl400.shape}")
print(f"Boy 400: {boy400.shape}")
# +
athlete_data = pd.concat([boy1600,girl1600])
#athlete_data = pd.concat([boy400,girl400])
print(athlete_data.shape)
print(athlete_data.columns)
# +
# rename columns because statsmodels doesn't like the 12_PR format
# add a numerical column for sex of the athlete
athlete_data['PR12'] = athlete_data['12_PR']
athlete_data['PR11'] = athlete_data['11_PR']
athlete_data['PR10'] = athlete_data['10_PR']
athlete_data['PR9'] = athlete_data['9_PR']
athlete_data['Nsex'] = [1 if s == 'boy' else 0 for s in athlete_data['sex']]
# -
print('number of unique schools: ',len(athlete_data['School'].unique()))
# ## Set up X and y
# How many unique athletes in each district
athlete_data.District.value_counts()
print(athlete_data.District[athlete_data.District == 'District 7'])
print(athlete_data.District[athlete_data.District == 'District 8'])
# +
# for 1600 data
# drop the 3 athletes from District 7 and 8
athlete_data.drop(index=104,inplace=True)
athlete_data.drop(index=201,inplace=True)
athlete_data.drop(index=252,inplace=True)
# -
print(athlete_data.District[athlete_data.District == 'District 7'])
print(athlete_data.District[athlete_data.District == 'District 8'])
# +
# for 400 data
# drop the athlete from District 8
athlete_data.drop(index=132,inplace=True)
# -
athlete_data.head()
# Variable |Description |Value
# ----------|------------------------------:|:----
# District 1|Athlete school in this district| 0 or 1
# District 2|Athlete school in this district| 0 or 1
# District 3|Athlete school in this district| 0 or 1
# District 4|Athlete school in this district| 0 or 1
# District 5|Athlete school in this district| 0 or 1
# District 6|Athlete school in this district| 0 or 1
# Sex |Athlete girl or boy | 1=boy, 0=girl
# Grad Year |Graduation Year | int
# 9th Grade PR|Best time in 9th Grade | float
# 10th Grade PR|Best time in 10th Grade | float
# 11th Grade PR|Best time in 11th Grade | float|
# +
#given the athlete_data read from files, generate the X & y dataframes
def get_Xy(athlete_data,Dist=100):
X = pd.DataFrame()
if Dist == 100:
# create one-hot columns for District
X = pd.get_dummies(athlete_data[['District']])
X = pd.concat([X, athlete_data[['PR9','PR10','PR11','Nsex','Grad_Yr']]], axis=1, sort=False)
y = athlete_data['PR12']
else:
filtered_data = athlete_data[athlete_data['District'] == 'District '+str(Dist)]
X = filtered_data[['PR9','PR10','PR11','Nsex','Grad_Yr']]
y = filtered_data['PR12']
#y = pd.DataFrame(y.values.reshape((len(y),1)))
return(X,y)
X,y = get_Xy(athlete_data,100)
# -
X.shape
y.shape
type(y)
# ## Visualize Data <a name='Visualize' />
X.corr()
X.info()
sns.distplot(athlete_data['PR12'])
plt.show()
sns.distplot(athlete_data['PR12'],label = '12th Grade',norm_hist=False)
sns.distplot(athlete_data['PR11'],label = '11th Grade',norm_hist=False)
sns.distplot(athlete_data['PR10'],label = '10th Grade',norm_hist=False)
sns.distplot(athlete_data['PR9'],label = '9th Grade',norm_hist=False)
plt.legend()
plt.show();
# plot 9th grade PR vs 12th grade PR for boys by district
grid=sns.lmplot(x = "PR9",y = "PR12",col="District",
col_wrap=3,
data=athlete_data[athlete_data['Nsex'] == 1])
plt.ylim(top=450) # adjust the top leaving bottom unchanged
plt.ylim(bottom=240) # adjust the top leaving bottom unchanged
# +
sns.catplot(x="District",y="PR12",
data=athlete_data[(athlete_data['Nsex'] == 1)]);
#plt.figure(figsize=(10,2))
plt.ylabel('12th grade PR (Seconds)')
plt.xlabel('District')
plt.xticks(range(0,6),('1','2','3','4','5','6'));
plt.title('Variation in 12th grade times by district');
#plt.figure(figsize=(6,3))
#plt.savefig('12_PR_by_District.png')
# +
#boxplot = athlete_data.boxplot(column=[athlete_data[athlete_data[District == 'District 1'['PR12'],
# athlete_data[athlete_data[District == 'District 2'['PR12']])
data = ([athlete_data[athlete_data.District == 'District 1']['PR12'],
athlete_data[athlete_data.District == 'District 2']['PR12'],
athlete_data[athlete_data.District == 'District 3']['PR12'],
athlete_data[athlete_data.District == 'District 4']['PR12'],
athlete_data[athlete_data.District == 'District 5']['PR12'],
athlete_data[athlete_data.District == 'District 6']['PR12']])
fig_box, fig = plt.subplots()
fig.set_title('12th grade PR for each district')
fig.boxplot(data)
plt.xlabel('District')
plt.ylabel('time (seconds)')
plt.show()
# -
# How many unique athletes in each district
athlete_data.School.value_counts()
# ## Linear Regression Model <a name='LinearRegression' />
#divide in to train and test sets
X_train,X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,random_state=42,stratify=X['Nsex'])
X_train.shape
X_test.shape
# +
# Create an empty model
lr = LinearRegression()
# Fit the model to the full dataset
lr.fit(X_train, y_train)
# Print out the R^2 for the model against the full dataset
lr.score(X_train,y_train)
# -
y_pred = lr.predict(X_test)
X.columns
RMSE = sqrt(((y_test-y_pred)**2).values.mean())
print(RMSE)
# +
plt.scatter(y_pred,y_test,alpha=0.5);
plt.ylabel('y_test (seconds)');
plt.xlabel('y_predicted (seconds)');
plt.plot([max(y_pred),min(y_pred)],[max(y_pred),min(y_pred)],color='r')
#plt.plot([240,470],[240,470],color='r')
#plt.savefig('test_vs_pred.png');
# +
print('Using all data (9th, 10th & 11th grades) to predict 12th grade PR')
print('Train R^2: ',lr.score(X_train, y_train))
print('Train RMSE:',
sqrt(mean_squared_error(y_train, lr.predict(X_train))))
print('Test R^2: ', lr.score(X_test, y_test))
print('Test RMSE:',
sqrt(mean_squared_error(y_test, lr.predict(X_test))))
data = y_test-lr.predict(X_test)
print('Skew:',skew(data))
print("mean : ", np.mean(data))
print("var : ", np.var(data))
print("skew : ",skew(data))
print("kurt : ",kurtosis(data))
# +
#remove 9th grade PR data - how good does it do now
X1_train = X_train.drop(['PR9'],axis=1)
X1_test = X_test.drop(['PR9'],axis=1)
lr.fit(X1_train,y_train)
# -
print('Using only 10th & 11th to predict 12th grade PR')
print('Train R^2: ',lr.score(X1_train, y_train))
print('Train RMSE:',
sqrt(mean_squared_error(y_train, lr.predict(X1_train))))
print('Test R^2: ', lr.score(X1_test, y_test))
print('Test RMSE:',
sqrt(mean_squared_error(y_test, lr.predict(X1_test))))
# +
#remove 9th grade PR data - how good does it do now
# only select boys
athlete_data_boy = athlete_data[athlete_data.sex == 'boy'].copy()
X1,y1 = get_Xy(athlete_data_boy,100)
X1_train, X1_test, y1_train, y1_test = train_test_split(X1, y1, test_size=0.4,random_state=42)
X1_train.drop(['PR9'],axis=1)
lr = LinearRegression()
lr.fit(X1_train,y1_train)
print('Using only 10th & 11th to predict 12th grade PR for boys')
print('Train R^2: ',lr.score(X1_train, y1_train))
print('Train RSSE:',
sqrt(mean_squared_error(y1_train, lr.predict(X1_train))))
print('Test R^2: ', lr.score(X1_test, y1_test))
print('Test RSSE:',
sqrt(mean_squared_error(y1_test, lr.predict(X1_test))))
# +
#remove 10th and 11th grade PR data - how good does it do now
X2_train = X_train.drop(['PR10','PR11'],axis=1)
X2_test = X_test.drop(['PR10','PR11'],axis=1)
lr.fit(X2_train,y_train)
# -
print('Using only 9th grade to predict 12th grade PR')
print('Train R^2: ',lr.score(X2_train, y_train))
print('Train SSE:',
mean_squared_error(y_train, lr.predict(X2_train)))
print('Test R^2: ', lr.score(X2_test, y_test))
print('Test SSE:',
mean_squared_error(y_test, lr.predict(X2_test)))
# +
# add a PR11**2 and PR10**2 term to linear regression
X3_train = X_train.copy()
X3_train['PR11squared'] = X_train['PR11']**2
X3_train['PR10squared'] = X_train['PR10']**2
X3_test = X_test.copy()
X3_test['PR11squared'] = X_test['PR11']**2
X3_test['PR10squared'] = X_test['PR10']**2
# Create an empty model
lr = LinearRegression()
lr.fit(X3_train,y_train)
print('Using squared terms as well to predict 12th grade PR')
print('Train R^2: ',lr.score(X3_train, y_train))
print('Train RMSE:',
sqrt(mean_squared_error(y_train, lr.predict(X3_train))))
print('Test R^2: ', lr.score(X3_test, y_test))
print('Test RMSE:',
sqrt(mean_squared_error(y_test, lr.predict(X3_test))))
# +
# add a PR11**2 and PR10**2 term to linear regression
X4_train = X_train.copy()
X4_train['PR11squared'] = X_train['PR11']**2
X4_train['PR10squared'] = X_train['PR10']**2
#X4_train['PR11_o_PR10'] = X_train['PR11']/X_train['PR10']
#X4_train['PR10_o_PR9'] = X_train['PR10']/X_train['PR9']
X4_test = X_test.copy()
X4_test['PR11squared'] = X_test['PR11']**2
X4_test['PR10squared'] = X_test['PR10']**2
#X4_test['PR11_o_PR10'] = X_test['PR11']/X_test['PR10']
#X4_test['PR10_o_PR9'] = X_test['PR11']/X_test['PR9']
# Create an empty model
lr = LinearRegression()
lr.fit(X4_train,y_train)
print('Using squared terms as well to predict 12th grade PR')
print('Train R^2: ',lr.score(X4_train, y_train))
print('Train RMSE:',
sqrt(mean_squared_error(y_train, lr.predict(X4_train))))
print('Test R^2: ', lr.score(X4_test, y_test))
print('Test RMSE:',
sqrt(mean_squared_error(y_test, lr.predict(X4_test))))
data = y_test-lr.predict(X4_test)
print('Skew:',skew(data))
print("mean : ", np.mean(data))
print("var : ", np.var(data))
print("skew : ",skew(data))
print("kurt : ",kurtosis(data))
# +
import yellowbrick
from sklearn.linear_model import Ridge
from yellowbrick.regressor import ResidualsPlot
# Instantiate the linear model and visualizer
visualizer = ResidualsPlot(model = lr)
visualizer.fit(X3_train, y_train) # Fit the training data to the model
visualizer.poof()
# -
# Now do it with statsmodels
# +
X = pd.DataFrame()
# create one-hot columns for District
X = pd.get_dummies(athlete_data[['District']])
X = pd.concat([X, athlete_data[['PR9','PR10','PR11','Nsex','Grad_Yr']]], axis=1, sort=False)
y = athlete_data['PR12']
#y = pd.DataFrame(y.values.reshape((len(y),1)))
# -
X.shape,y.shape
# +
sm_data = pd.DataFrame()
# create one-hot columns for District
sm_data = pd.get_dummies(athlete_data[['District']])
sm_data = pd.concat([X, athlete_data[['PR9','PR10','PR11','PR12','Nsex','Grad_Yr']]], axis=1, sort=False)
# +
y_train_sm, X_train_sm = patsy.dmatrices('PR12 ~ PR9 + PR10 + PR11 + Nsex + Grad_Yr',data = sm_data, return_type='dataframe')
model = sm.OLS(y_train_sm,X_train_sm)
fit = model.fit()
print(fit.summary())
# -
# Explore the effect of sample size on the results.
# Set District to filter for only one district, Dist=100 is all districts
Dist = 100
filtered_X, filtered_y = get_Xy(athlete_data,Dist)
# +
#divide into train and test sets
X_train, X_test, y_train, y_test = train_test_split(filtered_X, filtered_y, test_size=0.4,
random_state=42,stratify=filtered_X['Nsex'])
# Create an empty model
output_data = pd.DataFrame()
max_sample_size = min(401,len(X_train))
for sample_size in range(10,max_sample_size,1):
X2_train = X_train.sample(n=sample_size,random_state=1)
y2_train = y_train.sample(n=sample_size,random_state=1)
#X2_test = X_test.sample(n=sample_size,random_state=1)
#y2_test = y_test.sample(n=sample_size,random_state=1)
lr = LinearRegression()
lr.fit(X2_train, y2_train)
y2_predict = lr.predict(X_test)
test_score = lr.score(X_test,y_test)
train_score = lr.score(X2_train,y2_train)
train_error = mean_squared_error(y2_train, lr.predict(X2_train))
test_error = mean_squared_error(y_test, lr.predict(X_test))
#test_error = mean_squared_error(y2_test, lr.predict(X2_test))
#print(sample_size,train_error,test_error)
output_data = output_data.append([[sample_size,test_score,train_score,train_error,test_error]])
#print('Train R^2: ', train_score)
#print('Train SSE:', train_error)
#print('Test R^2: ', test_score)
#print('Test SSE:', test_error)
plt.plot(output_data[0],output_data[3],label='Train Error')
plt.plot(output_data[0],output_data[4],label='Test Error')
plt.legend()
plt.title('Model error vs. number of data points');
plt.xlabel('Number of data points');
plt.ylabel('RMS Error');
# -
print('boys in train set: ',X_train[X_train.Nsex == 1]['Nsex'].count())
print('girls in train set:',X_train[X_train.Nsex == 0]['Nsex'].count())
print('boys in test set: ',X_test[X_test.Nsex == 1]['Nsex'].count())
print('girls in test set: ',X_test[X_test.Nsex == 0]['Nsex'].count())
# ## LASSO shows feature importance <a name='LASSO' />
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
random_state=42,stratify=X['Nsex'])
lr_lasso = linear_model.Lasso(alpha=0.1)
lr_fit = lr_lasso.fit(X_train, y_train)
# Print out the R^2 for the model against the full dataset
lr_lasso.score(X_train,y_train)
# -
#lr_lasso.get_params()['lassocv'].alpha_
lr_lasso.get_params()
X_train.columns
print(X_train.shape)
print(y_train.shape,lr_lasso.predict(X_train).shape)
X_train.head()
print('Train R^2: ',lr_lasso.score(X_train, y_train))
print('Train RMSE:', sqrt(mean_squared_error(y_train,lr_lasso.predict(X_train))))
print('Test R^2: ', lr_lasso.score(X_test, y_test))
print('Test RMSE:', sqrt(mean_squared_error(y_test, lr_lasso.predict(X_test))))
# +
alpha_list = [1e-4, 1e-3, 1e-2, .05, 1e-1,.3,.5,.7]
lasso_results = []
for alpha in alpha_list:
lr_lasso = linear_model.Lasso(alpha=alpha)
lr_lasso_fit = lr_lasso.fit(X_train, y_train)
score = lr_lasso.score(X_train,y_train)
RMSE = sqrt(mean_squared_error(y_test, lr_lasso.predict(X_test)))
coef = lr_lasso_fit.coef_.tolist()
#print(coef)
lasso_results.append([alpha,score,coef,RMSE])
# +
num_features = X.shape[1]
for alpha,score,coef,RMSE in lasso_results:
#print(alpha,score,coef)
test = (alpha == 0.7)
test = True
if test:
plt.plot(range(1,num_features+1),coef,label=f"alpha = {alpha}")
plt.legend()
plt.xticks(np.linspace(0,num_features+1, num=num_features+2));
plt.xlabel('Feature')
plt.ylabel('Lasso coefficient');
# +
num_features = X.shape[1]
for alpha,score,coef,RMSE in lasso_results:
#print(alpha,score,coef)
#test = (alpha == 0.7)
test = (alpha >= 0.001) and (alpha <= .3)
if test:
plt.plot(range(1,num_features+1),coef,label=f"alpha = {alpha}")
plt.legend()
plt.xticks(np.linspace(0,num_features+1, num=num_features+2));
plt.xlabel('Feature')
plt.ylabel('Lasso coefficient');
# -
X_train.columns
pd.DataFrame(lasso_results)
lasso_results[5][2]
xx = [row[0] for row in lasso_results]
yy = [row[3] for row in lasso_results]
plt.semilogx(xx,yy);
plt.xlabel('alpha')
plt.ylabel('RMSE');
# ## Modeling District as a mixed effect <a name='MixedEffect' />
# Random effect - District
# Fixed effect - PRs from each year, grad year
#
# We expect to see some clustering due to the random effect variable.
# +
sm_data = athlete_data[['District','PR9','PR10','PR11','PR12','Nsex','Grad_Yr']]
y_train_sm, X_train_sm = patsy.dmatrices('PR12 ~ PR9 + PR10 + PR11 + Nsex + Grad_Yr',
data = sm_data, return_type='dataframe')
# -
print(sm_data.shape)
sm_data.head()
print(y_train_sm.shape,X_train_sm.shape)
# +
#X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,random_state=42)
#data_train = pd.concat([y_train,X_train],axis=1,sort=False)
#data_test = pd.concat([y_test,X_test],axis=1,sort=False)
# +
#md = smf.mixedlm("12_PR ~ 9_PR + 10_PR + 11_PR + sex + Grad_Yr",
# data = athlete_data,
# groups = athlete_data["District"])
md = smf.mixedlm('PR12 ~ PR9 + PR10 + PR11 + Nsex + Grad_Yr',
data = sm_data,
groups = sm_data['District'])
mdf = md.fit()
print(mdf.summary())
# -
y_sm = sm_data['PR12']
#X_sm = sm_data = athlete_data[['District','PR9','PR10','PR11','Nsex','Grad_Yr']]
#y_sm_predict = mdf.predict(X_sm)
y_sm_predict = mdf.fittedvalues
RMSE = sqrt(((y_sm-y_sm_predict)**2).values.mean())
print(RMSE)
# +
# and let's plot the predictions
performance = pd.DataFrame()
performance["predicted"] = mdf.fittedvalues
performance["residuals"] = mdf.resid.values
#performance["PR12"] = data.age_scaled
sns.lmplot(x = "predicted", y = "residuals", data = performance)
# -
# ## Algebraic Model <a name='Algebraic' />
# How well can you predict 12th grade scores if you use a brute force method. Assume the ratio in the decrease in times from 10th grade to 11th grade is the same as from 11th grade to 12th grade. In this way with the competition times in 10th and 11th grade you can predict the time for 12th grade.
athlete_data.head()
# +
RMSE = 0
average = 0
total = 0
growth = []
growth1 = []
residual = []
max_val = []
#for index,athlete in athlete_data[athlete_data.sex=='boy'].iterrows():
for index,athlete in athlete_data.iterrows():
g12 = athlete['PR12']
g11 = athlete['PR11']
g10 = athlete['PR10']
g9 = athlete['PR9']
g12_predict = g11 + (g11/g10)*(g11-g10)
#g12_predict = g11**2/g10
RMSE += (g12_predict - g12)**2
average += g12
total += 1
growth.append((g12/g11)/(g11/g10))
residual.append(g12_predict - g12)
if (g11-g10) != 0:
g = (g12-g11)/(g11-g10)
if g < 5: growth1.append(g)
max_val.append(g12)
RMSE = sqrt(RMSE/total)
average = average/total
print('RMSE:',RMSE)
print('12th grade average time:',average)
#plt.scatter(max,growth)
#plt.hist(growth1,1000);
plt.hist(growth,100);
plt.title('Histogram of ratio of 12/11 grade times to 11/10 grade times');
#plt.xlim(-10,10)
plt.plot([1,1],[0,130],color='r')
#plt.plot([0,0],[0,130],color='y')
# -
plt.hist(residual,50)
plt.plot([0,0],[0,370],color='r')
plt.title('histogram of residuals')
plt.xlabel('y_predicted - y')
|
2-Luther_Project/code/.ipynb_checkpoints/Luther_Regression-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Importazione dati
# Questo notebook verrà usato per l'importazione di tutti i database che ci servono \
# I dati saranno salvati quindi nella cartella data\processed
# +
import numpy as np
import pandas as pd
import geopandas as gpd
import matplotlib.pyplot as plt
import make_dataset as m_d
### Per usare multi cartelle
#import sys
#sys.path.append('./../src')
#print(sys.path)
# -
# ## Grid data
# +
#GRID
grid=m_d.safe_import("grid")
grid.plot('cellId')
grid
## Non da' problemi, poi dovrò mergiarlo
# -
# # Social Pulse
# +
#Questo fallisce ad importare, come mostrato a lezione 24
import json
tweets_json = json.load( open(m_d.data_path / m_d.files['twitter'][0]) )
tweets = gpd.GeoDataFrame(tweets_json['features'])
#Creiamo il punto smontando la casella point
from shapely.geometry import Point
tweets['geometry'] = tweets['geomPoint.geom'].apply(lambda x:Point(x['coordinates'][0], x['coordinates'][1]))
tweets.drop(columns=['geomPoint.geom'],inplace=True)
#Droppo roba inutile
tweets.drop(columns=['municipality.acheneID'],inplace=True)
tweets.drop(columns=['entities'],inplace=True)
tweets.head(3)
# -
# # Weather
# +
"""
#Fallisce ad importare
weather=m_d.safe_import("weather")
weather
"""
weather_json = json.load( open(m_d.data_path / m_d.files['weather'][0]) )
print(tweets_json.keys())
print(tweets_json['crs'])
print(tweets_json['type'])
#Come prima ho metadati
weather = gpd.GeoDataFrame(weather_json['features'])
weather.head(10)
# +
#Elimino le colonne del vento (dati molto incompleti)
weather.drop(weather.columns[list(range(202,298))], axis=1, inplace=True)
weather.drop(columns=['minWind', "maxWind"], inplace=True)
pd.set_option('display.max_columns', None)
weather.head(5)
#plt.plot(weather["precipitations.0000"]) #Sanity check per verificare che i dati sulle precipitazioni non siano nulli
# -
#Svolgiamo infine i punti
weather['geometry'] = weather['geomPoint.geom'].apply(lambda x:Point(x['coordinates'][0], x['coordinates'][1]))
weather.drop(columns=['geomPoint.geom'],inplace=True)
# # Precipitazioni
# +
#Questo si comporta bene
#Non è utile importare i data availability tendenzialmente
colnames = ['time', ]
precipitation = pd.DataFrame
precipitation(columns = )
precipitation=m_d.safe_import('precip')
precipitation
# -
# # DA INSERIRE: DATABASE PRECIPITAZIONI (C'è NE è UN ALTRO) E QUELLO ELETTRICITò, E DB ELETTRICITà E REGIONI AMMINISTRATIVE
# ## ADMINISTRATIVE REGIONS
# +
#ADMINISTRATIVE REGIONS
adm_reg=m_d.safe_import("adm_reg")
adm_reg
# +
#Vediamo cosa contiene e come è importato
"""
#Opzioni di prints per i dataframe panda per visualizzare intere righe
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
pd.set_option('display.max_colwidth', -1)
print(adm_reg.loc[[0]]) #E' chiaro che molte delle info sono contenute nella colonna 2 che è una mappa non svolta
print(adm_reg.count) #Questi valori sono tutti uguali
#Visto che anche la terza colonna ci è inutile, l'effettivo database consiste nello svolgere la colonna 2
"""
adm_reg=pd.DataFrame(list(adm_reg['items']))
adm_reg.head(5)
# -
# ## NOTE PER RIALLACCIARE I DATI:
# I dati vanno riallacciati mediante appropriata conversione, dovrò \
# 1) Discretizzare il tempo, scegliere un tempo base per fare un binning della
# 2) Collegare tramite la grid i dati ad un punto del plot (binning su posizioni)
# 3) Svolgo la divisione in minuti della tabella weather, dovrò abbastanza binnare comunque
# 4) Svolgo i tweets vanno binnati agli intervalli temporali
#
# Alt: creo una funzione temperatura che sia continua (connetto linearmente punti distanti 15 minuti, non dovrebbero cambiar molto), e poi tratto il tempo continuo
|
SocialPulse(noCC)/.ipynb_checkpoints/Import+Merge_Final-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="aFifDWoz20QY"
# # 0. Setup
#
# + id="IWemigXMuUqk"
import numpy as np
import pandas as pd
import torchvision
from torchvision import transforms, datasets, models
import torch
from PIL import Image
from pathlib import Path
from bs4 import BeautifulSoup
import os
import io
import cv2
import torch.nn.functional as F
# + [markdown] id="7y_g93YMKedb"
# # 1. Check is GPU available
# + id="ASflVQJpKdwm" colab={"base_uri": "https://localhost:8080/"} outputId="9528222f-d63b-4992-b79e-f0b7952cede4"
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
if torch.cuda.is_available():
print("GPU is available")
else:
print("GPU is not available")
# + [markdown] id="0LWKvs-oK7SM"
# # 2. Mount Google Drive
# + id="Mo8G_KsJK6cu" colab={"base_uri": "https://localhost:8080/"} outputId="fc300082-979b-478d-de8b-079aa7901a5d"
from google.colab import drive
drive.mount('/gdrive')
root = '/gdrive/My Drive/CS470/Project/dataset'
# + [markdown] id="0EFhO3f0NdGs"
# # 3. Define datasets
# + id="gl9BYYPtNjLB"
from PIL import Image, ImageFile
ImageFile.LOAD_TRUNCATED_IMAGES = True
class MaskDataset(object):
def __init__(self, transforms):
self.transforms = transforms
def __getitem__(self, idx):
folder=idx // 1000
num= idx % 1000
folder_name = 'data'+str(folder)
file_list=list(sorted(os.listdir(Path(root)/folder_name)))
file_name=file_list[num]
img_path = os.path.join(Path(root)/folder_name,file_name)
img=Image.open(img_path).convert("RGB")
#~~~~~~.jpg 0 ; without mask
#00001_Mask.jpg 1
#00001_Mask_Chin.jpg. 2
#00001_Mask_Mouth_Chin.jpg 3
#00001_Mask_Nose_Mouth.jpg 4
p_list=str(file_name).split('_')
if len(p_list)==1:
label=0
elif len(p_list)==2:
label=1
elif len(p_list)==3:
label=2
elif p_list[-1]=='Chin.jpg':
label=3
else:
label=4
#Generate Label
if self.transforms is not None:
img = self.transforms(img)
return img, label
def __len__(self):
return 39000
# + [markdown] id="_dNa-kYyLy4F"
# # 4. Build dataloader and transform
# + id="Dts-OlpGOP_S"
preprocess = transforms.Compose([
transforms.Resize((224,224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
])
# + id="0bK1F9MFRcsS"
dataset = MaskDataset(preprocess)
train_size = int(0.8 * len(dataset))
test_size = len(dataset) - train_size
train_dataset, test_dataset = torch.utils.data.random_split(dataset, [train_size, test_size])
train_loader = torch.utils.data.DataLoader(train_dataset,batch_size=256, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset,batch_size=256, shuffle=True)
# + id="KGs60j8MUNNt" colab={"base_uri": "https://localhost:8080/"} outputId="1499342c-72c7-4f90-b6ac-98fb6b4be76a"
import cv2
print('size of train datasets :',len(train_loader.dataset))
print('size of test datasets :',len(test_loader.dataset))
# + [markdown] id="yR2vpmVLXN2i"
# # 5. Define model
# + id="Ias2d-IevhPI" colab={"base_uri": "https://localhost:8080/", "height": 1000, "referenced_widgets": ["1d4d774f67484628a9b20e032eea3766", "e1d8ec000e2447059cc69a95542dac48", "410631d4e0c24d34b22c6e29d9457465", "190d086d98e7447dbccf3beb73584a17", "bf5b5f6143c14c109fe94d45c90ef003", "8921d6761c74494e8f7ed3711ef8fb30", "258ca161392b4a89b56a9146130f902c", "192171251f04459e85a94d41314255b7"]} outputId="cc4138cb-3199-42b9-e22e-55263363b335"
model = torchvision.models.mobilenet_v2(pretrained=True)
model.classifier[1] = torch.nn.Linear(in_features=model.classifier[1].in_features, out_features=5)
model.eval()
model.to(device)
# + id="8lfRyWnffCRL"
from torch.utils.mobile_optimizer import optimize_for_mobile
# name should be a string ex) model.pt
def model_save(model, name):
t_model = torch.jit.trace(model, torch.rand(1,3,224,224).to(device))
torch.jit.save(t_model, "/gdrive/My Drive/CS470/Project/"+"scripted_"+name)
q_model = torch.quantization.convert(model)
traced_script_module = torch.jit.trace(q_model, torch.rand(1,3,224,224).to(device))
opt_model = optimize_for_mobile(traced_script_module)
torch.jit.save(opt_model, "/gdrive/My Drive/CS470/Project/"+"quantized_" + name)
# + [markdown] id="Rwj4TMsyhIor"
# # 6. Training
# + id="DDjaLKOd3mAt"
# pre-setup
num_epochs = 20
params = [p for p in model.parameters() if p.requires_grad]
learning_rate = 0.0005
optimizer = torch.optim.SGD(params, lr=learning_rate, momentum=0.9, weight_decay=0.000001)
loss_func = torch.nn.CrossEntropyLoss().to(device)
# + id="rxO2GOrUg3RP"
# for plotting
from matplotlib import pyplot as plt
train_loss_list = []
test_loss_list = []
# + id="ZhDSfvXv3s13"
for epoch in range(num_epochs):
epoch_loss = 0
test_loss = 0
best_test_loss = 1
for i, samples in enumerate(train_loader):
model.train()
imgs, annotations = samples
imgs, annotations = imgs.to(device), annotations.to(device)
output = model(imgs)
loss = loss_func(output,annotations)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(f'Iteration: {i+1}/{len(train_loader)}, Loss: {loss.item()}')
epoch_loss += loss.item()
avg_train_loss = epoch_loss/len(train_loader)
# Save result for plotting
train_loss_list.append(avg_train_loss)
# Print epoch's test loss
print(f'Epoch {epoch} train loss: {avg_train_loss}')
# validation
for i,test_samples in enumerate(test_loader):
with torch.no_grad():
model.eval()
test_imgs, test_annotations = test_samples
test_imgs, test_annotations = test_imgs.to(device), test_annotations.to(device)
test_output = model(test_imgs)
loss = loss_func(test_output, test_annotations)
test_loss += loss.item()
# print(f'Iteration: {i+1}/{len(test_loader)}, Loss: {loss.item()}')
avg_test_loss = test_loss/len(test_loader)
# Save result for plotting
test_loss_list.append(avg_test_loss)
# Print epoch's test loss
print(f'Epoch {epoch} test loss: {avg_test_loss}')
# save best
if best_test_loss > avg_test_loss:
best_test_loss = avg_test_loss
model_save(model, 'best.pt')
print('-------------------------------------')
# + id="9iigMuWghd27" colab={"base_uri": "https://localhost:8080/", "height": 349} outputId="bb0d2d07-f3f1-4116-b7ab-de7f166897dd"
# Plot
print(train_loss_list)
print(test_loss_list)
plt.plot(train_loss_list)
plt.plot(test_loss_list)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Train/Test Loss')
plt.legend(['Train', 'Test'])
plt.show()
|
CS470_PJ.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# +
import pandas as pd
url1 = 'https://www.cbssports.com/mlb/standings/'
data = pd.read_html(url1)
standings = data[0]
columns = standings.iloc[0].tolist()
columns[0]='Team'
standings.columns = columns
x = standings[standings['Day'] != 'Day']
x.sort_values('L Losses', ascending=False)
# -
|
content/lessons/12/End-To-End-Example/CBS Sports.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib
import torch
import seaborn as sns
from privacy_utils import get_sigma_epsilon
sns.set_style("whitegrid")
plt.rcParams['text.usetex'] = True #Let TeX do the typsetting
plt.rcParams['text.latex.preamble'] = r"""
\usepackage{sansmath}
\sansmath
""" #Force sans-serif math mode (for axes labels)
plt.rcParams['font.family'] = 'sans-serif' # ... for regular text
plt.rcParams['font.sans-serif'] = 'Helvetica, Avant Garde, Computer Modern Sans serif' # Choose a nice font here
fontsize = 15
base_path = "./data"
# +
def plot_fig(results, iwerm_gap, erm_gap, output_path=None):
plt.plot(results['sigma'], results['trn wg acc'] - results['tst wg acc'], label="DP")
plt.plot(results['sigma'], iwerm_gap * np.ones(len(results['sigma'])), label="IWERM")
plt.plot(results['sigma'], erm_gap * np.ones(len(results['sigma'])), label="ERM")
plt.xscale("log")
plt.xticks(fontsize=fontsize)
plt.yticks(fontsize=fontsize)
plt.xlabel("sigma", fontsize=fontsize)
plt.ylabel("worst-group accuracy gap", fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.tight_layout()
if output_path is not None:
plt.savefig(output_path)
def get_losses(model, loader):
losses = []
for X, y in loader:
y_pred = model(X.cuda())
loss = torch.nn.functional.nll_loss(
y_pred, y.cuda(), reduction="none").detach().cpu().numpy()
losses.append(loss)
return np.concatenate(losses)
#def mia_opt_loss_threshold(train_losses, test_losses):
# # MIA metric is balanced accuracy.
# def _compute_mia_metric(threshold, train_losses, test_losses):
# return 0.5 * (np.mean(train_losses <= threshold) + np.mean(test_losses > threshold))
#
# best_mia_acc = 0.
# for thresh in np.concatenate([train_losses, test_losses]):
# mia_acc = _compute_mia_metric(thresh, train_losses, test_losses)
# if mia_acc > best_mia_acc:
# best_mia_acc = mia_acc
#
# return best_mia_acc, thresh
def mia_opt_loss_threshold(train_losses, test_losses):
# MIA metric is balanced accuracy.
losses = np.concatenate([train_losses, test_losses])
ans = np.concatenate([np.zeros(len(train_losses)), np.ones(len(test_losses))])
ind = np.argsort(losses)
losses, ans = losses[ind], ans[ind]
weights = [1 / 2 / (ans==0).sum(), 1 / 2 / (ans==1).sum()]
mia_acc = 0.5
best_mia_acc = (0., losses[0])
for i, thresh in enumerate(losses):
if (i+1) < len(losses) and losses[i+1] == thresh:
continue
if ans[i] == 0:
mia_acc = mia_acc + weights[0]
else:
mia_acc = mia_acc - weights[1]
if mia_acc > best_mia_acc[0]:
best_mia_acc = (mia_acc, thresh)
return best_mia_acc[0], best_mia_acc[1]
#train_losses = get_losses(model, train_loader)
#test_losses = get_losses(model, test_loader)
#mia_acc, _ = mia_opt_loss_threshold(train_losses, test_losses) # Attack accuracy from 50% to 100%
#mia_adv = 2 * mia_acc - 1 # Attack advantage from 0 to 1
# +
ds_name = "celebA"
sigmas = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0]
log_paths = []
for sigma in sigmas:
log_paths.append(f"erm-dp_resnet50-lr1e-3-dpsgd_1e-5_{sigma}_1.0_0.0001")
cols = ["acc_avg", "acc_wg", "acc_y:notblond_male:0", "acc_y:notblond_male:1", "acc_y:blond_male:0", "acc_y:blond_male:1"]
col_names = ["acc", "acc_wg", "notblond_male:0", "notblond_male:1", "blond_male:0", "blond_male:1"]
results = {}
for sigma, log_path in zip(sigmas, log_paths):
results.setdefault("sigma", []).append(sigma)
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
train_res = df[["epoch", "acc_avg", "acc_wg"]].values
results.setdefault("trn acc", []).append(train_res[-1][1])
results.setdefault("trn wg acc", []).append(train_res[-1][2])
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/val_eval.csv"))
res = df[["epoch", "acc_avg", "acc_wg"]].values
results.setdefault("val acc", []).append(res[-1][1])
results.setdefault("val wg acc", []).append(res[-1][2])
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
res = df[["epoch", "acc_avg", "acc_wg", "epsilon"]].values.tolist()
results.setdefault("tst acc", []).append(res[-1][1])
results.setdefault("tst wg acc", []).append(res[-1][2])
results.setdefault("epsilon", []).append(res[-1][3])
#preds = joblib.load(f"../logs/{ds_name}/{log_path}/preds.pkl")
#trn_losses = torch.nn.functional.nll_loss(preds["trn"], torch.cat(preds["trny"]), reduction="none").detach().cpu().numpy()
#tst_losses = torch.nn.functional.nll_loss(preds["tst"], torch.cat(preds["tsty"]), reduction="none").detach().cpu().numpy()
#mia_acc, _ = mia_opt_loss_threshold(trn_losses, tst_losses) # Attack accuracy from 50% to 100%
#mia_adv = 2 * mia_acc - 1 # Attack advantage from 0 to 1
#results.setdefault("attack adv", []).append(mia_adv)
for k, v in results.items():
results[k] = np.array(v)
log_path = "erm-resnet50"
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
erm_trn_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
erm_tst_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
#erm_gap = (erm_trn_acc_wg - erm_tst_acc_wg)
#preds = joblib.load(f"../logs/{ds_name}/{log_path}/preds.pkl")
#trn_losses = torch.nn.functional.nll_loss(preds["trn"], torch.cat(preds["trny"]), reduction="none").detach().cpu().numpy()
#tst_losses = torch.nn.functional.nll_loss(preds["tst"], torch.cat(preds["tsty"]), reduction="none").detach().cpu().numpy()
#mia_acc, _ = mia_opt_loss_threshold(trn_losses, tst_losses) # Attack accuracy from 50% to 100%
#erm_mia_adv = 2 * mia_acc - 1 # Attack advantage from 0 to 1
# +
epsilon = np.concatenate([[1e20], results['epsilon']])
trn_wg_acc = np.concatenate(([erm_trn_acc_wg], results['trn wg acc']))
tst_wg_acc = np.concatenate(([erm_tst_acc_wg], results['tst wg acc']))
joblib.dump({
'epsilon': epsilon,
'trn_wg_acc': trn_wg_acc,
'tst_wg_acc': tst_wg_acc,
}, f"data/dpdg_wgacc_{ds_name}.pkl")
ticks_ = [-1, 2, 5, 10, 15, 20]
line, = plt.plot(epsilon[1:], trn_wg_acc[1:], label="trn")
plt.plot(epsilon[0: 2], trn_wg_acc[0: 2], color=line.get_color(), ls='--')
line, = plt.plot(epsilon[1:], tst_wg_acc[1:], label="tst")
plt.plot(epsilon[0: 2], tst_wg_acc[0: 2], color=line.get_color(), ls='--')
plt.xscale("log")
plt.xticks(fontsize=fontsize, ticks=[float(10**i) for i in ticks_], labels=[f"$10^{{{eps}}}$" for eps in ticks_[:-1]] + ['$\infty$'])
plt.yticks(fontsize=fontsize)
plt.xlabel("Privacy budget $\epsilon$", fontsize=fontsize)
plt.ylabel("Worst-group accuracy", fontsize=fontsize)
plt.legend(fontsize=fontsize, frameon=False)
plt.tight_layout()
plt.savefig(f"figs/dpdg_wgacc_{ds_name}.png")
# +
ds_name = "utkface"
sigmas = [1.0, 0.1, 0.01, 0.001, 0.0001][::-1]
log_paths = []
for sigma in sigmas:
log_paths.append(f"erm-dp_resnet50-lr1e-3-dpsgd_1e-5_{sigma}_1.0_0.001")
#cols = ["acc_avg", "acc_wg", "acc_y:notblond_male:0", "acc_y:notblond_male:1", "acc_y:blond_male:0", "acc_y:blond_male:1"]
#col_names = ["acc", "acc_wg", "notblond_male:0", "notblond_male:1", "blond_male:0", "blond_male:1"]
subgroup_names = [
'acc_y:male_race:White',
'acc_y:male_race:Black',
'acc_y:male_race:Asian',
'acc_y:male_race:Indian',
'acc_y:male_race:Others',
'acc_y:female_race:White',
'acc_y:female_race:Black',
'acc_y:female_race:Asian',
'acc_y:female_race:Indian',
'acc_y:female_race:Others',
]
results = {}
for sigma, log_path in zip(sigmas, log_paths):
results.setdefault("sigma", []).append(sigma)
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
train_res = df[["epoch", "acc_avg", "acc_wg"] + subgroup_names].values
results.setdefault("trn acc", []).append(train_res[-1][1])
results.setdefault("trn wg acc", []).append(train_res[-1][2])
for i, name in enumerate(subgroup_names):
results.setdefault(f"trn {name}", []).append(train_res[-1][i+3])
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/val_eval.csv"))
val_res = df[["epoch", "acc_avg", "acc_wg"]].values
results.setdefault("val acc", []).append(res[-1][1])
results.setdefault("val wg acc", []).append(res[-1][2])
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
res = df[["epoch", "acc_avg", "acc_wg", "epsilon"] + subgroup_names].values.tolist()
results.setdefault("tst acc", []).append(res[-1][1])
results.setdefault("tst wg acc", []).append(res[-1][2])
results.setdefault("epsilon", []).append(res[-1][3])
for i, name in enumerate(subgroup_names):
results.setdefault(f"tst {name}", []).append(res[-1][i+4])
for k, v in results.items():
results[k] = np.array(v)
log_path = "iwerm-resnet50"
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
trn_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
tst_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
iwerm_gap = (trn_acc_wg - tst_acc_wg)
log_path = "erm-resnet50"
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
trn_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
tst_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
erm_gap = (trn_acc_wg - tst_acc_wg)
# +
epsilon = np.concatenate([[1e18], results['epsilon']])
trn_wg_acc = np.concatenate(([erm_trn_acc_wg], results['trn wg acc']))
tst_wg_acc = np.concatenate(([erm_tst_acc_wg], results['tst wg acc']))
joblib.dump({
'epsilon': epsilon,
'trn_wg_acc': trn_wg_acc,
'tst_wg_acc': tst_wg_acc,
}, f"data/dpdg_wgacc_{ds_name}.pkl")
ticks_ = [-1, 2, 5, 10, 15, 18]
line, = plt.plot(epsilon[1:], trn_wg_acc[1:], label="trn")
plt.plot(epsilon[0: 2], trn_wg_acc[0: 2], color=line.get_color(), ls='--')
line, = plt.plot(epsilon[1:], tst_wg_acc[1:], label="tst")
plt.plot(epsilon[0: 2], tst_wg_acc[0: 2], color=line.get_color(), ls='--')
plt.xscale("log")
plt.xticks(fontsize=fontsize, ticks=[float(10**i) for i in ticks_], labels=[f"$10^{{{eps}}}$" for eps in ticks_[:-1]] + ['$\infty$'])
plt.yticks(fontsize=fontsize)
plt.xlabel("Privacy budget $\epsilon$", fontsize=fontsize)
plt.ylabel("Worst-group accuracy", fontsize=fontsize)
plt.legend(fontsize=fontsize, frameon=False)
plt.tight_layout()
plt.savefig(f"figs/dpdg_wgacc_{ds_name}.png")
# -
# # iNaturalist
# +
ds_name = "inaturalist"
base_path = "../logs/"
clip = "100.0"
sigmas = [0.0001, "0.00001", "0.000001"][::-1]
#clip = "1.0"
#sigmas = [1.0, 0.1, 0.01, 0.001, 0.0001][::-1]
clip = "10.0"
sigmas = [0.001, 0.0001, "0.00001", "0.000001"][::-1]
log_paths = []
for sigma in sigmas:
log_paths.append(f"erm-dp_resnet18-lr1e-3-dpsgd_1e-5_{sigma}_{clip}_0.0001")
results = {}
for sigma, log_path in zip(sigmas, log_paths):
results.setdefault("sigma", []).append(sigma)
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
train_res = df[["epoch", "acc_avg", "acc_wg"]].values
results.setdefault("trn acc", []).append(train_res[-1][1])
results.setdefault("trn wg acc", []).append(train_res[-1][2])
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/val_eval.csv"))
res = df[["epoch", "acc_avg", "acc_wg"]].values
results.setdefault("val acc", []).append(res[-1][1])
results.setdefault("val wg acc", []).append(res[-1][2])
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
res = df[["epoch", "acc_avg", "acc_wg", "epsilon"]].values.tolist()
results.setdefault("tst acc", []).append(res[-1][1])
results.setdefault("tst wg acc", []).append(res[-1][2])
results.setdefault("epsilon", []).append(res[-1][3])
for k, v in results.items():
results[k] = np.array(v)
log_path = "erm-resnet18-lr1e-3"
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/train_eval.csv"))
trn_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
df = pd.read_csv(os.path.join(base_path, f"{ds_name}/{log_path}/test_eval.csv"))
tst_acc_wg = df[["epoch", "acc_avg", "acc_wg"]].values[-1][2]
erm_gap = (trn_acc_wg - tst_acc_wg)
# +
epsilon = np.concatenate([[1e18], results['epsilon']])
trn_wg_acc = np.concatenate(([trn_acc_wg], results['trn wg acc']))
tst_wg_acc = np.concatenate(([tst_acc_wg], results['tst wg acc']))
joblib.dump({
'epsilon': epsilon,
'trn_wg_acc': trn_wg_acc,
'tst_wg_acc': tst_wg_acc,
}, f"data/dpdg_wgacc_{ds_name}.pkl")
ticks_ = [-1, 2, 5, 10, 15, 18]
line, = plt.plot(epsilon[1:], trn_wg_acc[1:], label="trn")
plt.plot(epsilon[0: 2], trn_wg_acc[0: 2], color=line.get_color(), ls='--')
line, = plt.plot(epsilon[1:], tst_wg_acc[1:], label="tst")
plt.plot(epsilon[0: 2], tst_wg_acc[0: 2], color=line.get_color(), ls='--')
plt.xscale("log")
plt.xticks(fontsize=fontsize, ticks=[float(10**i) for i in ticks_], labels=[f"$10^{{{eps}}}$" for eps in ticks_[:-1]] + ['$\infty$'])
plt.yticks(fontsize=fontsize)
plt.xlabel("Privacy budget $\epsilon$", fontsize=fontsize)
plt.ylabel("Worst-group accuracy", fontsize=fontsize)
plt.legend(fontsize=fontsize, frameon=False)
plt.tight_layout()
plt.savefig(f"figs/dpdg_wgacc_{ds_name}_{clip}_old.png")
# -
# # Other methods
def get_data(ds_name, wds, paths, early_stopping=False):
results = {}
for wd, log_path in zip(wds, paths):
results.setdefault("wds", []).append(wd)
df = pd.read_csv(f"../logs/{ds_name}/{log_path}/val_eval.csv")
res = df[["epoch", "acc_avg", "acc_wg"]].values.tolist()
if early_stopping:
val_res = sorted(res, key=lambda x: x[2])
best_epoch_no = int(val_res[-1][0])
else:
best_epoch_no = -1
results.setdefault("val acc", []).append(res[best_epoch_no][1])
results.setdefault("val wg acc", []).append(res[best_epoch_no][2])
df = pd.read_csv(f"../logs/{ds_name}/{log_path}/train_eval.csv")
res = df[["epoch", "acc_avg", "acc_wg"]].values
results.setdefault("trn acc", []).append(res[best_epoch_no][1])
results.setdefault("trn wg acc", []).append(res[best_epoch_no][2])
df = pd.read_csv(f"../logs/{ds_name}/{log_path}/test_eval.csv")
res = df[["epoch", "acc_avg", "acc_wg"]].values.tolist()
results.setdefault("tst acc", []).append(res[best_epoch_no][1])
results.setdefault("tst wg acc", []).append(res[best_epoch_no][2])
for k, v in results.items():
results[k] = np.array(v)
return results
# +
ds_name = "celebA"
paths = ["iwerm-resnet50"]
wds = [0., 0.01, 0.1]
for wd in wds[1:]:
paths.append(f"iwerm-resnet50_wd{wd}")
results = get_data(ds_name, wds, paths, False)
stop_results = get_data(ds_name, wds, paths, True)
plt.plot(results['wds'], results['trn wg acc'], ls='--', label="trn", marker='o')
plt.plot(results['wds'], results['tst wg acc'], ls='--', label="tst", marker='o')
plt.plot(stop_results['wds'], stop_results['trn wg acc'], label="trn early stop")
plt.plot(stop_results['wds'], stop_results['tst wg acc'], label="tst early stop")
plt.xscale("symlog")
plt.xticks(fontsize=fontsize)
plt.yticks(fontsize=fontsize)
plt.xlabel("Weight decay", fontsize=fontsize)
plt.ylabel("Worst-group accuracy", fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.tight_layout()
plt.savefig(f"figs/dpdg_wgacc_iwerm_wd_{ds_name}.png")
# +
ds_name = "utkface"
paths = ["iwerm-resnet50"]
wds = [0., 0.001, 0.01, 0.1, 1.0]
for wd in wds[1:]:
paths.append(f"iwerm-resnet50_wd{wd}")
results = get_data(ds_name, wds, paths, False)
stop_results = get_data(ds_name, wds, paths, True)
plt.plot(results['wds'], results['trn wg acc'], ls='--', label="trn", )
plt.plot(results['wds'], results['tst wg acc'], ls='--', label="tst")
plt.plot(stop_results['wds'], stop_results['trn wg acc'], label="trn early stop")
plt.plot(stop_results['wds'], stop_results['tst wg acc'], label="tst early stop")
plt.xscale("symlog")
plt.xticks(fontsize=fontsize)
plt.yticks(fontsize=fontsize)
plt.xlabel("Weight decay", fontsize=fontsize)
plt.ylabel("Worst-group accuracy", fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.tight_layout()
plt.savefig(f"figs/dpdg_wgacc_iwerm_wd_{ds_name}.png")
# +
ds_name = "utkface"
paths = ["groupDRO-resnet50"]
wds = [0., 0.001, 0.01, 0.1, 1.0]
for wd in wds[1:]:
paths.append(f"groupDRO-resnet50_wd{wd}")
results = get_data(ds_name, wds, paths, False)
stop_results = get_data(ds_name, wds, paths, True)
plt.plot(results['wds'], results['trn wg acc'], ls='--', label="trn", )
plt.plot(results['wds'], results['tst wg acc'], ls='--', label="tst")
plt.plot(stop_results['wds'], stop_results['trn wg acc'], label="trn early stop")
plt.plot(stop_results['wds'], stop_results['tst wg acc'], label="tst early stop")
plt.xscale("symlog")
plt.xticks(fontsize=fontsize)
plt.yticks(fontsize=fontsize)
plt.xlabel("Weight decay", fontsize=fontsize)
plt.ylabel("Worst-group accuracy", fontsize=fontsize)
plt.legend(fontsize=fontsize)
plt.tight_layout()
plt.savefig(f"figs/dpdg_wgacc_gdro_wd_{ds_name}.png")
|
notebooks/dpdg.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
#
# # OpTaliX: Lens data items surface
# These are ...
# + tags=["remove_input"]
import pandas as pd
import itables
from itables import init_notebook_mode, show
import itables.options as opt
init_notebook_mode(all_interactive=True)
opt.lengthMenu = [50, 100, 200, 500]
#opt.classes = ["display", "cell-border"]
#opt.classes = ["display", "nowrap"]
opt.columnDefs = [{"className": "dt-left", "targets": "_all"}, {"width": "500px", "targets": 1}]
# + tags=["remove_input"]
import os
cwd = os.getcwd()
filename = os.path.join(cwd, os.path.join('Excel', 'OpTaliX_optimization_operands.xlsx'))
df_var = pd.read_excel(filename, sheet_name = "LDI_surface", header = 0, index_col = 0)
df_var = df_var.dropna() # drop nan values
# + tags=["remove_input"]
df_var
# -
|
_build/html/_sources/OpTaliX_LDI_surface.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# +
"""
Simple TensorFlow exercises
You should thoroughly test your code
"""
import tensorflow as tf
import pandas as pd
from sklearn.cross_validation import train_test_split
# -
# # Problem1: Ops exercises
# +
###############################################################################
# 1a: Create two random 0-d tensors x and y of any distribution.
# Create a TensorFlow object that returns x + y if x < y, and x - y otherwise.
# Hint: look up tf.cond()
# I do the first problem for you
###############################################################################
x = tf.random_uniform([]) # Empty array as shape creates a scalar.
y = tf.random_uniform([])
out = tf.cond(tf.less(x, y), lambda: tf.add(x, y), lambda: tf.subtract(x, y))
with tf.Session() as sess:
x, y, result = sess.run([x, y, out])
print("x: ",x)
print("y: ", y)
print("1a result: ", result)
print()
###############################################################################
# 1b: Create two 0-d tensors x and y randomly selected from -1 and 1.
# Return x + y if x < y, x - y if x > y, 0 otherwise.
# Hint: Look up tf.case().
###############################################################################
x = tf.random_uniform([], -1, 1, dtype=tf.float32)
y = tf.random_uniform([], -1, 1, dtype=tf.float32)
def f1(): return tf.add(x, y)
def f2(): return tf.subtract(x, y)
def f3(): return tf.constant(0.0)
out = tf.case({tf.less(x, y): f1, tf.greater(x, y): f2}, default=f3, exclusive=True)
with tf.Session() as sess:
x, y, result = sess.run([x, y, out])
print("x: ",x)
print("y: ", y)
print("1b result: ", result)
print()
###############################################################################
# 1c: Create the tensor x of the value [[0, -2, -1], [0, 1, 2]]
# and y as a tensor of zeros with the same shape as x.
# Return a boolean tensor that yields Trues if x equals y element-wise.
# Hint: Look up tf.equal().
###############################################################################
x = tf.constant([[0, -2, -1], [0, 1, 2]])
y = tf.zeros_like(x)
out = tf.equal(x, y)
with tf.Session() as sess:
x, y, result = sess.run([x, y, out])
print("x: ", x)
print("y: ", y)
print("1c result: ", result)
print()
###############################################################################
# 1d: Create the tensor x of value
# [29.05088806, 27.61298943, 31.19073486, 29.35532951,
# 30.97266006, 26.67541885, 38.08450317, 20.74983215,
# 34.94445419, 34.45999146, 29.06485367, 36.01657104,
# 27.88236427, 20.56035233, 30.20379066, 29.51215172,
# 33.71149445, 28.59134293, 36.05556488, 28.66994858].
# Get the indices of elements in x whose values are greater than 30.
# Hint: Use tf.where().
# Then extract elements whose values are greater than 30.
# Hint: Use tf.gather().
###############################################################################
x = tf.constant([29.05088806, 27.61298943, 31.19073486, 29.35532951,
30.97266006, 26.67541885, 38.08450317, 20.74983215,
34.94445419, 34.45999146, 29.06485367, 36.01657104,
27.88236427, 20.56035233, 30.20379066, 29.51215172,
33.71149445, 28.59134293, 36.05556488, 28.66994858])
indices = tf.where(condition=x>30)
result = tf.gather(params=x, indices=indices)
with tf.Session() as sess:
indices, result = sess.run([indices, result])
print("1d indices: ", indices)
print("1d elements: ", result)
print()
###############################################################################
# 1e: Create a diagnoal 2-d tensor of size 6 x 6 with the diagonal values of 1,
# 2, ..., 6
# Hint: Use tf.range() and tf.diag().
###############################################################################
out = tf.diag(tf.range(1,7))
with tf.Session() as sess:
result = sess.run(out)
print("1e result: ", result)
print()
###############################################################################
# 1f: Create a random 2-d tensor of size 10 x 10 from any distribution.
# Calculate its determinant.
# Hint: Look at tf.matrix_determinant().
###############################################################################
x = tf.random_normal(shape=(10, 10))
out = tf.matrix_determinant(x)
with tf.Session() as sess:
matrix, result = sess.run([x, out])
print("matrix: ", matrix)
print("1f result: ", result)
print()
###############################################################################
# 1g: Create tensor x with value [5, 2, 3, 5, 10, 6, 2, 3, 4, 2, 1, 1, 0, 9].
# Return the unique elements in x
# Hint: use tf.unique(). Keep in mind that tf.unique() returns a tuple.
###############################################################################
x = tf.constant([5, 2, 3, 5, 10, 6, 2, 3, 4, 2, 1, 1, 0, 9])
out = tf.unique(x)
with tf.Session() as sess:
result = sess.run(out)
print("1g result: ", result)
print()
###############################################################################
# 1h: Create two tensors x and y of shape 300 from any normal distribution,
# as long as they are from the same distribution.
# Use tf.less() and tf.select() to return:
# - The mean squared error of (x - y) if the average of all elements in (x - y)
# is negative, or
# - The sum of absolute value of all elements in the tensor (x - y) otherwise.
# Hint: see the Huber loss function in the lecture slides 3.
###############################################################################
x = tf.random_normal([300])
y = tf.random_normal([300])
residual = tf.reduce_mean(x - y)
mse = tf.reduce_mean(tf.square(x - y))
sav = tf.reduce_sum(tf.abs(x - y))
condition = tf.less(residual, 0)
out = tf.cond(condition, lambda: mse, lambda: sav)
with tf.Session() as sess:
residual, result = sess.run([residual, out])
print("average of all elements in (x-y)", residual)
print("1h result: ", result)
print()
# -
# # Problem2: Logistic regression
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time
# +
# step 1: read in data
print("Loading data......")
MNIST = input_data.read_data_sets("MNIST_data/", one_hot=True)
print("Done!")
# step 2: define parameters for the model
LEARNING_RATE = 1e-2
BATCH_SIZE = 128
N_EPOCHS = 45
H1_UNITS = 512
H2_UNITS = 380
KEEP_PROB = 0.5
# step 3: create placeholders for features and labels
# each image in the MNIST data is of shape 28*28 = 784
# therefore, each image is represented with a 1x784 tensor
# there are 10 classes for each image, corresponding to digits 0 - 9.
# each label is one hot vector.
X = tf.placeholder(tf.float32, [BATCH_SIZE, 784])
Y = tf.placeholder(tf.float32, [BATCH_SIZE, 10])
keep_prob = tf.placeholder(tf.float32)
# step 4: create weights and bias
# w is initialized to random variables with mean of 0, stddev of 0.01
# b is initialized to 0
# shape of w depends on the dimension of X and Y so that Y = tf.matmul(X, w)
# shape of b depends on Y
W1 = tf.Variable(tf.random_normal(shape=[784, H1_UNITS], stddev=0.01), name="W1")
b1 = tf.Variable(tf.zeros([1, H1_UNITS]), name="b1")
h1 = tf.nn.relu(tf.matmul(X, W1)+b1)
h1_drop = tf.nn.dropout(h1, KEEP_PROB)
W2 = tf.Variable(tf.random_normal(shape=[H1_UNITS, H2_UNITS], stddev=0.01), name="W2")
b2 = tf.Variable(tf.zeros([1, H2_UNITS]), name="b2")
h2 = tf.nn.relu(tf.matmul(h1_drop, W2)+b2)
W_out = tf.Variable(tf.random_normal(shape=[H2_UNITS, 10], stddev=0.01), name="W_out")
b_out = tf.Variable(tf.zeros([1, 10]), name="b_out")
# step 5: predict Y from X and w, b
# the model that returns probability distribution of possible label of the image
# through the softmax layer
# a batch_size x 10 tensor that represents the possibility of the digits
logits = tf.matmul(h2, W_out) + b_out
# step 6: define loss function
# use softmax cross entropy with logits as the loss function
# compute mean cross entropy, softmax is applied internally
Y_ = tf.nn.softmax(logits)
cross_entropy_loss = tf.reduce_mean(-tf.reduce_sum(Y*tf.log(Y_), reduction_indices=[1]))
# Step 7: define training op
# using gradient descent with learning rate of 0.01 to minimize cost
optimizer = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(cross_entropy_loss)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
n_batches = int(MNIST.train.num_examples/BATCH_SIZE)
for i in range(N_EPOCHS):
total_loss = 0.0
for _ in range(n_batches):
X_batch, Y_batch = MNIST.train.next_batch(BATCH_SIZE)
_, loss = sess.run([optimizer, cross_entropy_loss], feed_dict={X:X_batch, Y:Y_batch})
total_loss += loss
print("Total loss in iter%d: " % i, total_loss)
# test model
n_batches = int(MNIST.test.num_examples/BATCH_SIZE)
total_correct_preds = 0.0
for i in range(n_batches):
X_batch, Y_batch = MNIST.test.next_batch(BATCH_SIZE)
_, loss_batch, pred = sess.run([optimizer, cross_entropy_loss, Y_], feed_dict={X:X_batch, Y:Y_batch})
correct_preds = tf.equal(tf.argmax(pred,1), tf.argmax(Y_batch,1))
accuracy = tf.reduce_sum(tf.cast(correct_preds, tf.float32))
total_correct_preds += sess.run(accuracy)
print("Accuracy {0}".format(total_correct_preds / MNIST.test.num_examples))
# -
# # Logistic regression model to predict whether someone has coronary heart disease
data = pd.read_csv('heart.csv')
data.head()
data.famhist[data['famhist']=='Present'] = 1
data.famhist[data['famhist']=='Absent'] = 0
data['chd_0'] = 0
data.chd_0[data['chd']==0] = 1.0
data.chd[data['chd']==1] = 1.0
data.head()
Y = pd.concat([data.chd, data.chd_0], axis=1)
X = data.drop('chd', axis=1).drop('chd_0', axis=1)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.13, random_state=0)
print("train data count: ", X_train.shape)
print("test data count: ", X_test.shape)
LEARNING_RATE = 1e-4
N_EPOCH = 100
BATCH_SIZE = 10
X = tf.placeholder(tf.float32, [BATCH_SIZE, 9])
Y = tf.placeholder(tf.float32, [BATCH_SIZE, 2])
W = tf.Variable(tf.zeros([9, 2]))
b = tf.Variable(tf.zeros([1, 2]))
y = tf.matmul(X, W) + b
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y, labels=Y))
optimizer = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(loss)
init = tf.global_variables_initializer()
with tf.Session() as sess:
writer = tf.summary.FileWriter('./graphs', sess.graph)
sess.run(init)
n_batches = int(len(X_train)/BATCH_SIZE)
for i in range(N_EPOCH):
total_loss = 0.0
for n in range(n_batches):
X_batch = X_train[n*BATCH_SIZE:(n+1)*BATCH_SIZE]
Y_batch = Y_train[n*BATCH_SIZE:(n+1)*BATCH_SIZE]
_, loss_batch = sess.run([optimizer, loss], feed_dict={X:X_batch, Y:Y_batch})
total_loss += loss_batch
if i % 20 == 0:
print("Average loss epoch {0}:{1}".format(i, total_loss/n_batches))
n_batches = int(len(X_test) / BATCH_SIZE)
total_correct_preds = 0
for n in range(n_batches):
X_batch = X_test[n*BATCH_SIZE:(n+1)*BATCH_SIZE]
Y_batch = Y_test[n*BATCH_SIZE:(n+1)*BATCH_SIZE]
_, loss_batch, logits_batch = sess.run([optimizer, loss, y], feed_dict={X: X_batch, Y: Y_batch})
preds = tf.nn.softmax(logits_batch)
correct_preds = tf.equal(tf.argmax(preds, 1), tf.argmax(Y_batch.as_matrix(), 1))
accuracy = tf.reduce_sum(tf.cast(correct_preds, tf.float32)) # need numpy.count_nonzero(boolarr) :(
total_correct_preds += sess.run(accuracy)
print('Accuracy {0}%'.format(100 * total_correct_preds / (n_batches * BATCH_SIZE)))
writer.close()
# # Word2Vec
import time
import numpy as np
import tensorflow as tf
import collections
import random
import os
import math
import urllib
from urllib import request
import zipfile
# +
def read_data(filename):
def build_vocab(words, vocab_size):
""" Build vocabulary of VOCAB_SIZE most frequent words """
dictionary = dict()
count = [('UNK', -1)]
count.extend(Counter(words).most_common(vocab_size - 1))
# >> 原来的写法
index = 0
with open('processed/vocab_1000.tsv', "w") as f:
# f.write("Name\n")
for word, _ in count:
dictionary[word] = index
if index < 1000:
f.write(word + "\n")
index += 1
index_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
with zipfile.ZipFile(filename) as f:
data = tf.compat.as_str(f.read(f.namelist()[0])).split()
return data
words = read_data('text8.zip')
print('data size', len(words))
# -
def build_vocab(words, vocab_size):
""" Build vocabulary of VOCAB_SIZE most frequent words """
dictionary = dict()
count = [('UNK', -1)]
count.extend(collection.Counter(words).most_common(vocab_size - 1))
# >> 原来的写法
index = 0
with open('processed/vocab_1000.tsv', "w") as f:
# f.write("Name\n")
for word, _ in count:
dictionary[word] = index
if index < 1000:
f.write(word + "\n")
index += 1
index_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
def convert_words_to_index(words, dictionary):
|
Assignment1/assignment1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_mxnet_p36
# language: python
# name: conda_mxnet_p36
# ---
# ## Please input your directory for the top level folder
# folder name : SUBMISSION MODEL
dir_ = 'INPUT-PROJECT-DIRECTORY/submission_model/' # input only here
# #### setting other directory
raw_data_dir = dir_+'2. data/'
processed_data_dir = dir_+'2. data/processed/'
log_dir = dir_+'4. logs/'
model_dir = dir_+'5. models/'
submission_dir = dir_+'6. submissions/'
# +
####################################################################################
################## 2-3. nonrecursive model by store & dept #########################
####################################################################################
# -
cvs = ['private']
STORES = ['CA_1', 'CA_2', 'CA_3', 'CA_4', 'TX_1', 'TX_2', 'TX_3', 'WI_1', 'WI_2', 'WI_3']
DEPTS = ['HOBBIES_1', 'HOBBIES_2', 'HOUSEHOLD_1', 'HOUSEHOLD_2', 'FOODS_1', 'FOODS_2', 'FOODS_3']
# +
from datetime import datetime, timedelta
import gc
import numpy as np, pandas as pd
import lightgbm as lgb
import os, sys, gc, time, warnings, pickle, psutil, random
warnings.filterwarnings('ignore')
# -
def reduce_mem_usage(df, verbose=False):
numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
start_mem = df.memory_usage().sum() / 1024**2
for col in df.columns:
col_type = df[col].dtypes
if col_type in numerics:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
end_mem = df.memory_usage().sum() / 1024**2
if verbose: print('Mem. usage decreased to {:5.2f} Mb ({:.1f}% reduction)'.format(end_mem, 100 * (start_mem - end_mem) / start_mem))
return df
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
FIRST_DAY = 710
remove_feature = ['id',
'state_id',
'store_id',
# 'item_id',
'dept_id',
'cat_id',
'date','wm_yr_wk','d','sales']
cat_var = ['item_id', 'dept_id','store_id', 'cat_id', 'state_id'] + ["event_name_1", "event_name_2", "event_type_1", "event_type_2"]
cat_var = list(set(cat_var) - set(remove_feature))
# +
grid2_colnm = ['sell_price', 'price_max', 'price_min', 'price_std',
'price_mean', 'price_norm', 'price_nunique', 'item_nunique',
'price_momentum', 'price_momentum_m', 'price_momentum_y']
grid3_colnm = ['event_name_1', 'event_type_1', 'event_name_2',
'event_type_2', 'snap_CA', 'snap_TX', 'snap_WI', 'tm_d', 'tm_w', 'tm_m',
'tm_y', 'tm_wm', 'tm_dw', 'tm_w_end']
lag_colnm = [ 'sales_lag_28', 'sales_lag_29', 'sales_lag_30',
'sales_lag_31', 'sales_lag_32', 'sales_lag_33', 'sales_lag_34',
'sales_lag_35', 'sales_lag_36', 'sales_lag_37', 'sales_lag_38',
'sales_lag_39', 'sales_lag_40', 'sales_lag_41', 'sales_lag_42',
'rolling_mean_7', 'rolling_std_7', 'rolling_mean_14', 'rolling_std_14',
'rolling_mean_30', 'rolling_std_30', 'rolling_mean_60',
'rolling_std_60', 'rolling_mean_180', 'rolling_std_180']
mean_enc_colnm = [
'enc_item_id_store_id_mean', 'enc_item_id_store_id_std'
]
# -
########################### Make grid
#################################################################################
def prepare_data(store, state):
grid_1 = pd.read_pickle(processed_data_dir+"grid_part_1.pkl")
grid_2 = pd.read_pickle(processed_data_dir+"grid_part_2.pkl")[grid2_colnm]
grid_3 = pd.read_pickle(processed_data_dir+"grid_part_3.pkl")[grid3_colnm]
grid_df = pd.concat([grid_1, grid_2, grid_3], axis=1)
del grid_1, grid_2, grid_3; gc.collect()
grid_df = grid_df[(grid_df['store_id'] == store) & (grid_df['dept_id'] == state)]
grid_df = grid_df[grid_df['d'] >= FIRST_DAY]
lag = pd.read_pickle(processed_data_dir+"lags_df_28.pkl")[lag_colnm]
lag = lag[lag.index.isin(grid_df.index)]
grid_df = pd.concat([grid_df,
lag],
axis=1)
del lag; gc.collect()
mean_enc = pd.read_pickle(processed_data_dir+"mean_encoding_df.pkl")[mean_enc_colnm]
mean_enc = mean_enc[mean_enc.index.isin(grid_df.index)]
grid_df = pd.concat([grid_df,
mean_enc],
axis=1)
del mean_enc; gc.collect()
grid_df = reduce_mem_usage(grid_df)
return grid_df
validation = {
'cv1' : [1551, 1610],
'cv2' : [1829,1857],
'cv3' : [1857, 1885],
'cv4' : [1885,1913],
'public' : [1913, 1941],
'private' : [1941, 1969]
}
# ### cv1 : 2015-04-28 ~ 2015-06-26
#
# ### cv2 : 2016-02-01 ~ 2016-02-28
#
# ### cv3 : 2016-02-29 ~ 2016-03-27
#
# ### cv4 : 2016-03-28 ~ 2016-04-24
########################### Model params
#################################################################################
lgb_params = {
'boosting_type': 'gbdt',
'objective': 'tweedie',
'tweedie_variance_power': 1.1,
'metric': 'rmse',
'subsample': 0.5,
'subsample_freq': 1,
'learning_rate': 0.015,
'num_leaves': 2**8-1,
'min_data_in_leaf': 2**8-1,
'feature_fraction': 0.5,
'max_bin': 100,
'n_estimators': 3000,
'boost_from_average': False,
'verbose': -1,
'seed' : 1995
}
def pred_q(quantile):
print(quantile)
rmsse_bycv = dict()
for cv in cvs:
print('cv : day', validation[cv])
pred_list = []
for store in STORES:
for state in DEPTS:
print(store,state, 'start')
grid_df = prepare_data(store, state)
model_var = grid_df.columns[~grid_df.columns.isin(remove_feature)]
tr_mask = (grid_df['d'] <= validation[cv][0]) & (grid_df['d'] >= FIRST_DAY)
vl_mask = (grid_df['d'] > validation[cv][0]) & (grid_df['d'] <= validation[cv][1])
model_path = model_dir+'non_recur_model_'+store+'_'+state+'.bin'
m_lgb = pickle.load(open(model_path, 'rb'))
indice = grid_df[vl_mask].index.tolist()
print('starting to predict')
prediction = pd.DataFrame({'y_pred' : m_lgb.predict(grid_df[vl_mask][model_var], float(quantile))})
print('done predicting')
prediction.index = indice
del grid_df, m_lgb, tr_mask, vl_mask; gc.collect()
grid_1 = pd.read_pickle(processed_data_dir+"grid_part_1.pkl")
pd.concat([grid_1.iloc[indice], prediction], axis=1)\
.pivot(index='id', columns='d', values='y_pred')\
.reset_index()\
.set_index('id')\
.to_csv(log_dir+f'submission_storeanddept_{store}_{state}_{cv}.csv')
del grid_1; gc.collect()
########################### Make submissions
#################################################################################
os.chdir(log_dir)
pri = [a for a in os.listdir() if 'storeanddept' in a]
submission = pd.read_csv(raw_data_dir+'sample_submission.csv').set_index('id').iloc[30490:]
sub_id = pd.DataFrame({'id':submission.index.tolist()})
fcol = [f'F{i}' for i in range(1,29)]
sub_copy = submission.copy()
for file in pri:
temp = pd.read_csv(log_dir+file)
temp.columns = ['id']+fcol
sub_copy += sub_id.merge(temp, how='left', on='id').set_index('id').fillna(0)
sub_copy.columns = fcol
sub_copy.to_csv(submission_dir+f'before_ensemble/submission_kaggle_nonrecursive_store_dept_{quantile}.csv')
import concurrent.futures
for quantile in ['0.005', '0.025', '0.165', '0.250', '0.500', '0.750', '0.835', '0.975', '0.995']:
with concurrent.futures.ThreadPoolExecutor(
) as executor:
executor.submit(
pred_q, quantile
)
|
src/gluonts/nursery/QRX-Wrapped-M5-Accuracy-Solution/3. code/3. predict/2-3. nonrecursive_store_dept_PREDICT.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from molmap import model as molmodel
import molmap
import matplotlib.pyplot as plt
import pandas as pd
from tqdm import tqdm
from joblib import load, dump
tqdm.pandas(ascii=True)
import numpy as np
import tensorflow as tf
import os
os.environ["CUDA_VISIBLE_DEVICES"]="0"
np.random.seed(123)
tf.compat.v1.set_random_seed(123)
tmp_feature_dir = './tmpignore'
if not os.path.exists(tmp_feature_dir):
os.makedirs(tmp_feature_dir)
# -
mp1 = molmap.loadmap('../descriptor.mp')
mp2 = molmap.loadmap('../fingerprint.mp')
task_name = 'BACE'
from chembench import load_data
df, induces = load_data(task_name)
# +
smiles_col = df.columns[0]
values_col = df.columns[1:]
Y = df[values_col].astype('float').values
Y = Y.reshape(-1, 1)
X1_name = os.path.join(tmp_feature_dir, 'X1_%s.data' % task_name)
X2_name = os.path.join(tmp_feature_dir, 'X2_%s.data' % task_name)
if not os.path.exists(X1_name):
X1 = mp1.batch_transform(df.smiles, n_jobs = 8)
dump(X1, X1_name)
else:
X1 = load(X1_name)
if not os.path.exists(X2_name):
X2 = mp2.batch_transform(df.smiles, n_jobs = 8)
dump(X2, X2_name)
else:
X2 = load(X2_name)
molmap1_size = X1.shape[1:]
molmap2_size = X2.shape[1:]
# +
def get_pos_weights(trainY):
"""pos_weights: neg_n / pos_n """
dfY = pd.DataFrame(trainY)
pos = dfY == 1
pos_n = pos.sum(axis=0)
neg = dfY == 0
neg_n = neg.sum(axis=0)
pos_weights = (neg_n / pos_n).values
neg_weights = (pos_n / neg_n).values
return pos_weights, neg_weights
prcs_metrics = ['MUV', 'PCBA']
# +
epochs = 800
patience = 50 #early stopping
dense_layers = [256, 128, 32]
batch_size = 128
lr = 1e-4
weight_decay = 0
monitor = 'val_loss'
dense_avf = 'relu'
last_avf = None #sigmoid in loss
if task_name in prcs_metrics:
metric = 'PRC'
else:
metric = 'ROC'
# -
results = []
for i, split_idxs in enumerate(induces):
train_idx, valid_idx, test_idx = split_idxs
print(len(train_idx), len(valid_idx), len(test_idx))
trainX = (X1[train_idx], X2[train_idx])
trainY = Y[train_idx]
validX = (X1[valid_idx], X2[valid_idx])
validY = Y[valid_idx]
testX = (X1[test_idx], X2[test_idx])
testY = Y[test_idx]
pos_weights, neg_weights = get_pos_weights(trainY)
loss = lambda y_true, y_pred: molmodel.loss.weighted_cross_entropy(y_true,y_pred, pos_weights, MASK = -1)
model = molmodel.net.DoublePathNet(molmap1_size, molmap2_size,
n_outputs=Y.shape[-1],
dense_layers=dense_layers,
dense_avf = dense_avf,
last_avf=last_avf)
opt = tf.keras.optimizers.Adam(lr=lr, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) #
#import tensorflow_addons as tfa
#opt = tfa.optimizers.AdamW(weight_decay = 0.1,learning_rate=0.001,beta1=0.9,beta2=0.999, epsilon=1e-08)
model.compile(optimizer = opt, loss = loss)
if i == 0:
performance = molmodel.cbks.CLA_EarlyStoppingAndPerformance((trainX, trainY),
(validX, validY),
patience = patience,
criteria = monitor,
metric = metric,
)
model.fit(trainX, trainY, batch_size=batch_size,
epochs=epochs, verbose= 0, shuffle = True,
validation_data = (validX, validY),
callbacks=[performance])
else:
model.fit(trainX, trainY, batch_size=batch_size,
epochs = performance.best_epoch + 1, verbose = 1, shuffle = True,
validation_data = (validX, validY))
performance.model.set_weights(model.get_weights())
best_epoch = performance.best_epoch
trainable_params = model.count_params()
train_aucs = performance.evaluate(trainX, trainY)
valid_aucs = performance.evaluate(validX, validY)
test_aucs = performance.evaluate(testX, testY)
final_res = {
'task_name':task_name,
'train_auc':np.nanmean(train_aucs),
'valid_auc':np.nanmean(valid_aucs),
'test_auc':np.nanmean(test_aucs),
'metric':metric,
'# trainable params': trainable_params,
'best_epoch': best_epoch,
'batch_size':batch_size,
'lr': lr,
'weight_decay':weight_decay
}
results.append(final_res)
pd.DataFrame(performance.history)[['loss', 'val_loss']].plot()
pd.DataFrame(results).test_auc.mean()
pd.DataFrame(results).test_auc.std()
pd.DataFrame(results)
pd.DataFrame(results).to_csv('./results/%s.csv' % task_name)
|
paper/02_OutofTheBox_benchmark_comparison_DMPNN/run_10_classification_BACE.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Exercise 5.01: Predicting sales from advertising spend using Linear Regression
import numpy as np, pandas as pd
import matplotlib.pyplot as plt, seaborn as sns
advertising = pd.read_csv("advertising.csv")
advertising.head()
plt.scatter(advertising.TV, advertising.Sales, \
marker="+", color='gray')
plt.xlabel("TV")
plt.ylabel("Sales")
plt.show()
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(advertising[['TV']], advertising[['Sales']])
# #### Plotting the relationship
sales_pred = lr.predict(advertising[['TV']])
plt.plot(advertising.TV, sales_pred,"k--")
plt.scatter(advertising.TV, advertising.Sales, \
marker='+', color='gray')
plt.xlabel("TV")
plt.ylabel('Sales')
plt.show()
# ## Exercise 5.02: Creating Features for customer revenue prediction
import pandas as pd
import datetime as dt
df = pd.read_csv('azra_retail_transactions.csv')
df.head()
df['InvoiceDate'] = pd.to_datetime(df['InvoiceDate'])
df['revenue'] = df['UnitPrice']*df['Quantity']
df.head()
operations = {'revenue':'sum',\
'InvoiceDate':'first',\
'CustomerID':'first'}
df = df.groupby('InvoiceNo').agg(operations)
df.head()
df['year'] = df['InvoiceDate'].dt.year
df['days_since'] = (dt.datetime(year=2019, month=12, day=31) \
- df['InvoiceDate']).apply(lambda x: x.days)
# +
operations = {'revenue':'sum',\
'days_since':['max','min','nunique']}
X = df[df['year'] == 2019].groupby('CustomerID').agg(operations)
X.head()
# -
X.columns = [' '.join(col).strip() for col in X.columns.values]
X.head()
X['avg_order_cost'] = X['revenue sum']/X['days_since nunique']
y = df[df['year'] == 2020].groupby('CustomerID')['revenue'].sum()
# +
wrangled_df = pd.concat([X,y], axis=1)
wrangled_df.columns = ['revenue_2019',\
'days_since_first_purchase',\
'days_since_last_purchase',\
'number_of_purchases',\
'avg_order_cost',\
'revenue_2020']
wrangled_df.head()
# -
wrangled_df = wrangled_df[~wrangled_df.revenue_2019.isnull()]
wrangled_df = wrangled_df[~wrangled_df.revenue_2020.isnull()]
wrangled_df = wrangled_df[wrangled_df.revenue_2020 \
< ((wrangled_df.revenue_2020.median()) \
+ wrangled_df.revenue_2020.std()*3)]
wrangled_df = wrangled_df[wrangled_df.revenue_2019 \
< ((wrangled_df.revenue_2019.median()) \
+ wrangled_df.revenue_2019.std()*3)]
wrangled_df.to_csv('wrangled_transactions.csv')
wrangled_df.head()
# ## Exercise 5.03: Examining Relationships between Predictors and Outcome
df = pd.read_csv('wrangled_transactions.csv', \
index_col='CustomerID')
df.plot.scatter(x="days_since_first_purchase", \
y="revenue_2020", \
figsize=[6,6], color='gray')
plt.show()
import seaborn as sns
sns.set_palette('Greys_r')
sns.pairplot(df)
plt.show()
sns.pairplot(df, x_vars=df.columns, y_vars="revenue_2020")
plt.show()
df.corr()
# ## Exercise 5.04: Building a Linear Model Predicting Customer Spend
df = pd.read_csv('wrangled_transactions.csv', \
index_col='CustomerID')
df.corr()
# +
X = df[['revenue_2019',\
'days_since_last_purchase',\
'number_of_purchases',\
'avg_order_cost']]
y = df['revenue_2020']
# +
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 100)
# +
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train,y_train)
# -
model.coef_
model.intercept_
# +
single_customer = pd.DataFrame({
'revenue_2019': [1000],
'days_since_last_purchase': [20],
'number_of_purchases': [2],
'avg_order_cost': [500]
})
model.predict(single_customer)
# +
import matplotlib.pyplot as plt
# %matplotlib inline
plt.scatter(model.predict(X_test), y_test, color='gray')
plt.xlim(0,10000)
plt.ylim(0,10000)
plt.plot([0, 10000], [0, 10000], 'k-')
plt.xlabel('Model Predictions')
plt.ylabel('True Value')
plt.show()
# -
np.corrcoef(model.predict(X_test), y_test)
|
Chapter05/Exercise5.01-5.04.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Demonstration of Mlflow via energy forecasting.
#
# ML flow is a ML lifecycle management tool and is ideal for logging and the analysis of model results.
#
# This is a showcase for ML Flow capabilities, based on the article
# http://the-odd-dataguy.com/be-more-efficient-to-produce-ml-models-with-mlflow
# and a github https://github.com/jeanmidevacc/mlflow-energyforecast
#
# NOTE: It requires the storage account name AccountName and key AccountKey to be set further below.
# !pip install pandas --upgrade --user
# !pip install mlflow --upgrade --user
# !pip install joblib --upgrade --user
# !pip install numpy --upgrade --user
# !pip install scipy --upgrade --user
# !pip install scikit-learn --upgrade --user
# !pip install boto3 --upgrade --user
# +
import time
import json
import os
from joblib import Parallel, delayed
import pandas as pd
import numpy as np
import scipy
from sklearn.model_selection import train_test_split, KFold
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, explained_variance_score
from sklearn.exceptions import ConvergenceWarning
import mlflow
import mlflow.sklearn
from mlflow.tracking import MlflowClient
from warnings import simplefilter
simplefilter(action='ignore', category = FutureWarning)
simplefilter(action='ignore', category = ConvergenceWarning)
# -
# Ensure Minio access
os.environ['MLFLOW_S3_ENDPOINT_URL'] = 'http://minio-service.kubeflow.svc.cluster.local:9000'
os.environ['AWS_ACCESS_KEY_ID'] = 'minio'
os.environ['AWS_SECRET_ACCESS_KEY'] = 'XXXXXX'
# # Data preparation
# Collect the data
df_nationalconsumption_electricity_daily = pd.read_csv("https://raw.githubusercontent.com/jeanmidevacc/mlflow-energyforecast/master/data/rtu_data.csv")
df_nationalconsumption_electricity_daily.set_index(["day"], inplace = True)
# +
# Prepare the training set and the testing set
df_trainvalidate_energyconsumption = df_nationalconsumption_electricity_daily[df_nationalconsumption_electricity_daily["datastatus"] == "Définitif"]
del df_trainvalidate_energyconsumption["datastatus"]
df_test_energyconsumption = df_nationalconsumption_electricity_daily[df_nationalconsumption_electricity_daily["datastatus"] == "Consolidé"]
del df_test_energyconsumption["datastatus"]
print("Size of the training set : ",len(df_trainvalidate_energyconsumption))
print("Size of the testing set : ",len(df_test_energyconsumption))
# +
# Define the inputs and the output
output = "dailyconsumption"
allinputs = list(df_trainvalidate_energyconsumption.columns)
allinputs.remove(output)
print("Output to predict : ", output)
print("Inputs for the prediction : ", allinputs)
# -
# Build different set of featurws for the model
possible_inputs = {
"all" : allinputs,
"only_allday_inputs" : ["weekday", "month", "is_holiday", "week"],
"only_allweatheravg_inputs" : ["avg_min_temperature", "avg_max_temperature", "avg_mean_temperature","wavg_min_temperature", "wavg_max_temperature", "wavg_mean_temperature"],
"only_meanweather_inputs_avg" : ["avg_mean_temperature"],
"only_meanweather_inputs_wavg" : ["wavg_mean_temperature"],
}
# Prepare the output of the model
array_output_train = np.array(df_trainvalidate_energyconsumption[output])
array_output_test = np.array(df_test_energyconsumption[output])
# connect to remote server
remote_server_uri = "http://mlflow.mlflow.svc.cluster.local:5000"
mlflow.set_tracking_uri(remote_server_uri)
# Launch the experiment on mlflow
experiment_name = "electricityconsumption-forecast"
mlflow.set_experiment(experiment_name)
# Define the evaluation function that will do the computation of the different metrics of accuracy (RMSE,MAE,R2)
def evaluation_model(y_test, y_pred):
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
metrics = {
"rmse" : rmse,
"r2" : r2,
"mae" : mae,
}
return metrics
# # KNN regressor
# +
from sklearn.neighbors import KNeighborsRegressor
def train_knnmodel(parameters, inputs, tags, log = False):
with mlflow.start_run(nested = True):
# Prepare the data
array_inputs_train = np.array(df_trainvalidate_energyconsumption[inputs])
array_inputs_test = np.array(df_test_energyconsumption[inputs])
# Build the model
tic = time.time()
model = KNeighborsRegressor(parameters["nbr_neighbors"], weights = parameters["weight_method"])
model.fit(array_inputs_train, array_output_train)
duration_training = time.time() - tic
# Make the prediction
tic1 = time.time()
prediction = model.predict(array_inputs_test)
duration_prediction = time.time() - tic1
# Evaluate the model prediction
metrics = evaluation_model(array_output_test, prediction)
# Log in the console
if log:
print(f"KNN regressor:")
print(parameters)
print(metrics)
# Log in mlflow (parameter)
mlflow.log_params(parameters)
# Log in mlflow (metrics)
metrics["duration_training"] = duration_training
metrics["duration_prediction"] = duration_prediction
mlflow.log_metrics(metrics)
# log in mlflow (model)
mlflow.sklearn.log_model(model, f"model")
# Tag the model
mlflow.set_tags(tags)
# -
AccountName='XXXXXXX'
AccountKey='XXXXXXX'
# Test the different combinations
os.environ["AZURE_STORAGE_CONNECTION_STRING"] = "DefaultEndpointsProtocol=https;AccountName="+AccountName+";AccountKey="+AccountKey+";EndpointSuffix=core.windows.net"
configurations = []
for nbr_neighbors in [1,2,5,10]:
for weight_method in ['uniform','distance']:
for field in possible_inputs:
parameters = {
"nbr_neighbors" : nbr_neighbors,
"weight_method" : weight_method
}
tags = {
"model" : "knn",
"inputs" : field
}
configurations.append([parameters, tags])
train_knnmodel(parameters, possible_inputs[field], tags)
# # MLP regressor
# +
from sklearn.neural_network import MLPRegressor
def train_mlpmodel(parameters, inputs, tags, log = False):
with mlflow.start_run(nested = True):
# Prepare the data
array_inputs_train = np.array(df_trainvalidate_energyconsumption[inputs])
array_inputs_test = np.array(df_test_energyconsumption[inputs])
# Build the model
tic = time.time()
model = MLPRegressor(
hidden_layer_sizes = parameters["hidden_layers"],
activation = parameters["activation"],
solver = parameters["solver"],
max_iter = parameters["nbr_iteration"],
random_state = 0)
model.fit(array_inputs_train, array_output_train)
duration_training = time.time() - tic
# Make the prediction
tic1 = time.time()
prediction = model.predict(array_inputs_test)
duration_prediction = time.time() - tic1
# Evaluate the model prediction
metrics = evaluation_model(array_output_test, prediction)
# Log in the console
if log:
print(f"Random forest regressor:")
print(parameters)
print(metrics)
# Log in mlflow (parameter)
mlflow.log_params(parameters)
# Log in mlflow (metrics)
metrics["duration_training"] = duration_training
metrics["duration_prediction"] = duration_prediction
mlflow.log_metrics(metrics)
# log in mlflow (model)
mlflow.sklearn.log_model(model, f"model")
# Tag the model
mlflow.set_tags(tags)
# -
for hiddenlayers in [4,8,16]:
for activation in ["identity","logistic",]:
for solver in ["lbfgs"]:
for nbriteration in [10,100,1000]:
for field in possible_inputs:
parameters = {
"hidden_layers" : hiddenlayers,
"activation" : activation,
"solver" : solver,
"nbr_iteration" : nbriteration
}
tags = {
"model" : "mlp",
"inputs" : field
}
train_mlpmodel(parameters, possible_inputs[field], tags)
# # Use a handmade model (scipy approach)
# +
class PTG:
def __init__(self, thresholds_x0, thresholds_a, thresholds_b):
self.thresholds_x0 = thresholds_x0
self.thresholds_a = thresholds_a
self.thresholds_b = thresholds_b
def get_ptgmodel(self, x, a, b, x0):
return np.piecewise(x, [x < x0, x >= x0], [lambda x: a*x + b , lambda x : a*x0 + b])
def fit(self, dfx, y):
x = np.array(dfx)
# Define the bounds
bounds_min = [thresholds_a[0], thresholds_b[0], thresholds_x0[0]]
bounds_max = [thresholds_a[1], thresholds_b[1], thresholds_x0[1]]
bounds = (bounds_min, bounds_max)
# Fit a model
popt, pcov = scipy.optimize.curve_fit(self.get_ptgmodel, x, y, bounds = bounds)
# Get the parameter of the model
a = popt[0]
b = popt[1]
x0 = popt[2]
self.coefficients = [a, b, x0]
def predict(self,dfx):
x = np.array(dfx)
predictions = []
for elt in x:
forecast = self.get_ptgmodel(elt, self.coefficients[0], self.coefficients[1], self.coefficients[2])
predictions.append(forecast)
return np.array(predictions)
def train_ptgmodel(parameters, inputs, tags, log = False):
with mlflow.start_run(nested = True):
# Prepare the data
df_inputs_train = df_trainvalidate_energyconsumption[inputs[0]]
df_inputs_test = df_test_energyconsumption[inputs[0]]
# Build the model
tic = time.time()
model = PTG(parameters["thresholds_x0"], parameters["thresholds_a"], parameters["thresholds_b"])
model.fit(df_inputs_train, array_output_train)
duration_training = time.time() - tic
# Make the prediction
tic1 = time.time()
prediction = model.predict(df_inputs_test)
duration_prediction = time.time() - tic1
# Evaluate the model prediction
metrics = evaluation_model(array_output_test, prediction)
# Log in the console
if log:
print(f"PTG:")
print(parameters)
print(metrics)
# Log in mlflow (parameter)
mlflow.log_params(parameters)
# Log in mlflow (metrics)
metrics["duration_training"] = duration_training
metrics["duration_prediction"] = duration_prediction
mlflow.log_metrics(metrics)
# log in mlflow (model)
mlflow.sklearn.log_model(model, f"model")
# Tag the model
mlflow.set_tags(tags)
# +
# Define the parameters of the model
thresholds_x0 = [0, 20]
thresholds_a = [-200000, -50000]
thresholds_b = [1000000, 3000000]
parameters = {
"thresholds_x0" : thresholds_x0,
"thresholds_a" : thresholds_a,
"thresholds_b" : thresholds_b
}
for field in ["only_meanweather_inputs_avg", "only_meanweather_inputs_wavg"]:
tags = {
"model" : "ptg",
"inputs" : field
}
train_ptgmodel(parameters, possible_inputs[field], tags, log = False)
# -
# # Evaluate mlflow results
# Select the run of the experiment
df_runs = mlflow.search_runs(experiment_ids="1")
print("Number of runs done : ", len(df_runs))
# Quick sorting to get the best models based on the RMSE metric
df_runs.sort_values(["metrics.rmse"], ascending = True, inplace = True)
df_runs.head()
# Get the best one
runid_selected = df_runs.head(1)["run_id"].values[0]
runid_selected
|
mlflow/01-MLflow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="2tr1DfOiz9cb" colab_type="text"
# # 20 Newsgroups data import script for *Google Cloud AutoML Natural Language*
#
# This notebook downloads the [20 newsgroups dataset](https://scikit-learn.org/0.19/datasets/twenty_newsgroups.html) using scikit-learn. This dataset contains about 18000 posts from 20 newsgroups, and is useful for text classification. The script transforms the data into a pandas dataframe and finally into a CSV file readable by [Google Cloud AutoML Natural Language](https://cloud.google.com/natural-language/automl).
# + [markdown] id="K65WZ6bMz9cc" colab_type="text"
# ## Imports
# + id="OZDimb-5z9cd" colab_type="code" colab={}
import numpy as np
import pandas as pd
import csv
from sklearn.datasets import fetch_20newsgroups
# + [markdown] id="zYxeG10oz9cg" colab_type="text"
# ## Fetch data
# + id="mV7b2hHfz9ch" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 257} outputId="d3c53e19-eb23-4f2c-a9e4-b607ba0de044"
newsgroups = fetch_20newsgroups(subset='all')
df = pd.DataFrame(newsgroups.data, columns=['text'])
df['categories'] = [newsgroups.target_names[index] for index in newsgroups.target]
df.head()
# + [markdown] id="RMJqpjZwz9cl" colab_type="text"
# ## Clean data
# + id="K6yd6XSLz9cl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 202} outputId="d6328a82-551a-44f2-b286-cdfa923ef2f8"
# Convert multiple whitespace characters into a space
df['text'] = df['text'].str.replace('\s+',' ')
# Trim leading and tailing whitespace
df['text'] = df['text'].str.strip()
# Truncate all fields to the maximum field length of 128kB
df['text'] = df['text'].str.slice(0,131072)
# Remove any rows with empty fields
df = df.replace('', np.NaN).dropna()
# Drop duplicates
df = df.drop_duplicates(subset='text')
# Limit rows to maximum of 100,000
df = df.sample(min(100000, len(df)))
df.head()
# + [markdown] id="exFdr6wVz9co" colab_type="text"
# ## Export to CSV
# + id="pYUzEq-oz9cp" colab_type="code" colab={}
csv_str = df.to_csv(index=False, header=False)
with open("20-newsgroups-dataset.csv", "w") as text_file:
print(csv_str, file=text_file)
# + [markdown] id="1kJX0DKHz9cr" colab_type="text"
# You're all set! Download `20-newsgroups-dataset.csv` and import it into [Google Cloud AutoML Natural Language](https://cloud.google.com/natural-language/automl).
#
# If you are using [Google Colab](https://colab.research.google.com), you will find the file in the left navbar:
#
#
# * From the menu, select **View > Table of Contents**
# * Navigate to the **Files** tab
# * Find the file in `/content` directory.
#
#
#
|
20_newsgroups_automl.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.6 64-bit
# name: python3
# ---
# + pycharm={"name": "#%%\n"}
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 11 11:02:03 2021
@author: Christian
"""
from mip import Model, xsum, maximize, BINARY
from Co2_price import df_data
from electricity_demand import electricity_demand
from Electricity_Price0 import Electricity_price_pivot0
from Electricity_Price1 import Electricity_price_pivot1
from gas_price import gas_p
from heat_demand import heat_demand_pivot
from heat_price import heat_p
from elec_effciency import elec_eff
from electricity_capacity import elec_capacity
from heat_capacity import heat_capacity
elec_demand = electricity_demand.values.tolist()
elec_price_wholesale = Electricity_price_pivot0
elec_price_household_32_05 = Electricity_price_pivot1
co2_price = df_data
gas_price = gas_p
heat_demand_1 = heat_demand_pivot
heat_price_1 = heat_p
el_price = elec_price_wholesale.values.tolist() # Electricity price
del_t = .25 # duration of time step
el_demand = electricity_demand.values.tolist() # Electicity demand
gas_pp = gas_price["Preis"].values.tolist() # Gas price for different plants
em_fc = 0.2 # emission factor
co2_p = co2_price["mean_CO2_tax"].values.tolist() # CO2 Price
capacity_el = elec_capacity.values.tolist() # maximum capacity of electricity for the power plants
capacity_ht = heat_capacity.values.tolist() # maximum capacity of heat for the power plants
heat_demand = heat_demand_1.values.tolist() # heat demand
heat_price = heat_price_1.values.tolist() # heat price
heat_ratio = 400/385 # heat ratio
eff_plants = elec_eff.values.tolist() # the efficiency of the power plants
T = range(len(el_price))
I = range(len(gas_pp))
m = Model("Maximizing profit", sense=maximize)
#variable
y_t = [[m.add_var(lb = 0) for i in I] for t in T] # Electricity generation
el_sold = [[m.add_var(lb = 0) for i in I] for t in T] # electricity sold
# el_sold = [m.add_var(lb = 0) for t in T] # electricity sold
x_t = [[m.add_var(lb = 0) for i in I] for t in T] # Fuel consumption
z_t = [[m.add_var(lb = 0) for i in I] for t in T] # Heat generation
# objective function
# Revenue = Electricity price * demand/generation
# Cost = Fuel price = gas price + emission_factor * co2 price
# Max Proft = Revenue - Cost
m.objective = xsum((el_price[t] * del_t * el_sold[t]) - ( x_t[t][i] * ( gas_p[i] * del_t + (em_fc * co2_p[t]*del_t))) for t in T for i in I) + ((heat_demand[t] * heat_price[t]) for t in T)
m.objective = xsum((el_price[t][i] * del_t * el_sold[t][i]) - (x_t[t][i] * ( gas_p[i] * del_t + (em_fc * co2_p[t]*del_t))) for t in T for i in I) + ((heat_demand[t][i] * heat_price[t][i]) for t in T for i in I)
m.objective = xsum((el_price[t] * del_t * el_sold[t]) - ( x_t[t][i] * ( gas_p[i] * del_t + (em_fc * co2_p[t]*del_t))) for t in T for i in I) + ((heat_demand[t] * heat_price[t]) for t in T)
# constraints
for t in T:
m += xsum(y_t[t][i] for i in I) == el_demand[t]
for i in I:
m += y_t[t][i] <= capacity_el[i] # electricity generation <= maximum capacity of electricity of the plant
m += z_t[t][i] <= capacity_ht[i] # heat generation <= maximum capacity of heat of the plant
m += x_t[t][i] == y_t[t][i]/eff_plants[i] # fuel consumption = Electricity generation / efficiency of the plants
m += heat_demand[t] <= z_t[t][i] # heat demand >= Heat generation
m += y_t[t][i] == heat_ratio * z_t[t][i] # electricity generation >= heat ratio * heat generation
m += y_t[t][i] == el_sold[t] + el_demand[t]
status = m.optimize()
obj= m.objective_value
status
|
Optimization_new2_electricity_households.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
from sklearn import svm
import numpy as np
from matplotlib import pyplot as plt
X = np.arange(-5.,9.,0.1)
X=np.random.permutation(X)
X_=[[i] for i in X]
#print X
b=5.
y=0.5 * X ** 2.0 +3. * X + b + np.random.random(X.shape)* 10.
y_=[i for i in y]
rbf1=svm.SVR(kernel='rbf',C=1, )#degree=2,,gamma=, coef0=
rbf2=svm.SVR(kernel='rbf',C=20, )#degree=2,,gamma=, coef0=
poly=svm.SVR(kernel='poly',C=1,degree=2)
rbf1.fit(X_,y_)
rbf2.fit(X_,y_)
poly.fit(X_,y_)
result1 = rbf1.predict(X_)
result2 = rbf2.predict(X_)
result3 = poly.predict(X_)
plt.hold(True)
plt.plot(X,y,'bo',fillstyle='none')
plt.plot(X,result1,'r.')
plt.plot(X,result2,'g.')
plt.plot(X,result3,'c.')
plt.show()
# -
|
libsvm-learning/SVR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd, numpy as np, requests
# %matplotlib inline
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
import mpld3
mpld3.enable_notebook()
data3=pd.read_excel('export3.xlsx')
data3
from mpl_toolkits.mplot3d import axes3d
x=list(data3['Hosszúság'].values)
y=list(data3['Szélesség'].values)
s=data3['2017.2'].values
formfactor=0.68
s=list((s*1000)**formfactor)
cs={"Élelmiszer":"#543005",
"Ásványvíz":"#9e0142",
"Mezőgazdaság":"#d53e4f",
"Kereskedelem":"#f46d43",
"Szolgáltatás":"#fdae61",
"Vendéglátó":"#fee08b",
"Szállítás":"#ffffbf",
"Textil":"#e6f598",
"Gyógyszer, vegyipar":"#abdda4",
"Építkezés":"#66c2a5",
"Fa, bútor":"#3288bd",
"Kisipar, műanyag":"#5e4fa2",
"Nehézipar, bányászat":"#40004b",
"Energia":"#762a83"}
sectors2=list(cs.keys())
c=[cs[data3['Iparág'].values[k]] for k in range(len(data3['Iparág'].values))]
# +
fig=plt.figure(figsize=(14,14))
ax=axes3d.Axes3D(fig,azim=-70,elev=55)
ax._axis3don = False
scale=1
xlim=np.array([24.25,26.5])
ylim=np.array([45.57,48.00])
points=[]
for j in range(len(x)):
index=j
hindex=0
r=(s[index]/100000000)**0.25
for p in range(len(points)):
if (np.sqrt((points[p][0]-x[index])**2+(points[p][1]-y[index])**2)<((abs(r-points[p][2]))*1.3)):
hindex+=1
points.append([x[index],y[index],r])
# Cylindrical shell
phi = np.linspace(0, 2 * np.pi, 100)
r1 = np.ones(100)
h1 = np.linspace(hindex, hindex+1, 100)
x1 = r * np.outer(np.cos(phi), r1) + x[index]
y1 = r * np.outer(np.sin(phi), r1) + y[index]
z1 = 1 * np.outer(np.ones(np.size(r1)), h1)
# Top cover
phi_a = np.linspace(0, 2 * np.pi, 100)
h2 = np.ones(100)
r2 = np.linspace(0, 1, 100)
phi_grid, r_grid = np.meshgrid(phi_a, r2)
x2 = r * np.cos(phi_grid) * r_grid + x[index]
y2 = r * np.sin(phi_grid) * r_grid + y[index]
z2 = (hindex+1) * np.ones([100,100])
#walls
ax.plot_surface(x1*scale, y1*scale, z1, rstride=5, cstride=100, linewidth=0.1, alpha=1, shade=False,color=c[index])
#top cyl
ax.plot_surface(x2*scale, y2*scale, z2, rstride=100, cstride=34, linewidth=0.1, alpha=1, shade=False,color=c[index])
for w in range(len(sectors2)):
r=0.033
# Cylindrical shell
phi = np.linspace(0, 2 * np.pi, 100)
r1 = np.ones(100)
h1 = np.linspace(w, w+1, 100)
x1 = r * np.outer(np.cos(phi), r1) + 26.05-0.02*w
y1 = r * np.outer(np.sin(phi), r1) + 47.34+0.03*w
z1 = 1 * np.outer(np.ones(np.size(r1)), h1)
# Top cover
phi_a = np.linspace(0, 2 * np.pi, 100)
h2 = np.ones(100)
r2 = np.linspace(0, 1, 100)
phi_grid, r_grid = np.meshgrid(phi_a, r2)
x2 = r * np.cos(phi_grid) * r_grid + 26.05-0.02*w
y2 = r * np.sin(phi_grid) * r_grid + 47.34+0.03*w
z2 = (w+1) * np.ones([100,100])
ax.plot_surface(x1*scale, y1*scale, z1, rstride=5, cstride=100, linewidth=0.1, alpha=1, shade=False,color=colors[w])
ax.plot_surface(x2*scale, y2*scale, z2, rstride=100, cstride=34, linewidth=0.1, alpha=1, shade=False,color=colors[w])
ax.text2D(0.71-w*0.0023, 0.41+w*0.011,sectors2[w], transform=ax.transAxes)
ax.set_zlim([0,70])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.show()
# -
fig.savefig('3d.svg')
|
gazdasag/2019/.ipynb_checkpoints/plotter-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# # A Basic Schedule Analysis Example
# For this example, we will use staffing requirements from a post-anesthesia care unit (PACU). Let's assume that staffing level targets by half-hour for each day of the week have already been set from some previous analysis. As you can see from the following plot, PACU staffing targets exhibit signfificant time of day and day of week effects.
# !mwts demo_d02_t1_a01_ptub_moderate ./inputs/ex_dat/demo_d02_t1_a01_ptub_moderate.dat -s gurobi -p ./outputs/ -t 1200 -g 0.02
# !mwts demo_d02_t12_a01_ptub_moderate ./inputs/ex_dat/demo_d02_t12_a01_ptub_moderate.dat -s gurobi -p ./outputs/ -t 1200 -g 0.02
# !mwts demo_d02_t123_a01_ptub_moderate ./inputs/ex_dat/demo_d02_t123_a01_ptub_moderate.dat -s gurobi -p ./outputs/ -t 1200 -g 0.02
# !mwts demo_d02_t13_a01_ptub_moderate ./inputs/ex_dat/demo_d02_t13_a01_ptub_moderate.dat -s gurobi -p ./outputs/ -t 1200 -g 0.02
colnames = ['tournum', 'tourtype', 'week', 'period', 'day', 'shiftlength', 'startwin']
# +
tur_t1 = pd.read_csv('outputs/demo_d02_t1_a01_ptub_moderate.tur',
skiprows=3,
names=colnames,
sep='\s+',
dtype={'tournum': np.int32,
'tourtype': np.int32,
'week': np.int32,
'period': np.int32,
'day': np.int32,
'shiftlength': np.int32,
'startwin': np.int32})
tur_t12 = pd.read_csv('outputs/demo_d02_t12_a01_ptub_moderate.tur',
skiprows=3,
names=colnames,
sep='\s+',
dtype={'tournum': np.int32,
'tourtype': np.int32,
'week': np.int32,
'period': np.int32,
'day': np.int32,
'shiftlength': np.int32,
'startwin': np.int32})
tur_t13 = pd.read_csv('outputs/demo_d02_t13_a01_ptub_moderate.tur',
skiprows=3,
names=colnames,
sep='\s+',
dtype={'tournum': np.int32,
'tourtype': np.int32,
'week': np.int32,
'period': np.int32,
'day': np.int32,
'shiftlength': np.int32,
'startwin': np.int32})
tur_t123 = pd.read_csv('outputs/demo_d02_t123_a01_ptub_moderate.tur',
skiprows=3,
names=colnames,
sep='\s+',
dtype={'tournum': np.int32,
'tourtype': np.int32,
'week': np.int32,
'period': np.int32,
'day': np.int32,
'shiftlength': np.int32,
'startwin': np.int32})
# -
def make_tours(tur_df, prds_per_fte, nweeks):
tour_df = tur_df.groupby('tournum').agg(tourtype=('tourtype', 'min'),
tot_shifts=('tourtype', 'size'), tot_periods=('shiftlength', 'sum'),
start_win=('startwin', 'min'))
tour_df['tot_hours'] = tour_df['tot_periods'] * 40.0 / prds_per_fte
tour_df['tot_ftes'] = tour_df['tot_periods'] / nweeks / prds_per_fte
return tour_df
# +
tours_t1 = make_tours(tur_t1, 80.0, 4)
tours_t12 = make_tours(tur_t12, 80.0, 4)
tours_t13 = make_tours(tur_t13, 80.0, 4)
tours_t123 = make_tours(tur_t123, 80.0, 4)
# -
tours_t1
def make_tourtype_summary(tour_df):
ttype_sum_df = tour_df.groupby('tourtype').agg(num_tours=('tourtype', 'count'),
tot_periods=('tot_periods', 'sum'),
tot_shifts=('tot_shifts', 'sum'),
tot_hours=('tot_hours', 'sum'),
tot_ftes=('tot_ftes', 'sum'),)
return ttype_sum_df
ttype_sum_t1 = make_tourtype_summary(tours_t1)
ttype_sum_t12 = make_tourtype_summary(tours_t12)
ttype_sum_t13 = make_tourtype_summary(tours_t13)
ttype_sum_t123 = make_tourtype_summary(tours_t123)
ttype_sum_t123
ttype_sum_t13.reset_index()
ttype_sum_t13.to_string(index=False)
ttype_sum_t12
18/46
def make_summary(tours_df, prds_per_fte, nweeks):
# get_fte = lambda x: x.sum() / prds_per_fte / nweeks
# https://stackoverflow.com/questions/38179212/custom-describe-or-aggregate-without-groupby/41363399
summary_df = tours_df.groupby(lambda _: 0).agg(num_tours=('tourtype', 'count'),
tot_periods=('tot_periods', 'sum'),
tot_shifts=('tot_shifts', 'sum'),
tot_hours=('tot_hours', 'sum'),
tot_ftes=('tot_ftes', 'sum'))
return summary_df
summary_t1 = make_summary(tours_t1, 80, 4)
summary_t12 = make_summary(tours_t12, 80, 4)
summary_t13 = make_summary(tours_t13, 80, 4)
summary_t123 = make_summary(tours_t123, 80, 4)
print(summary_t1)
print(summary_t12)
print(summary_t13)
print(summary_t123)
|
tests/.ipynb_checkpoints/scheduling_analysis_example-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
for i in range(2):
for j in range(3):
print(i, j)
break
else:
print('222')
class Solution:
def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:
n1, n2 = len(arr1), len(arr2)
cnt = 0
for i in range(n1):
v1 = arr1[i]
for j in range(n2):
v2 = arr2[j]
if abs(v1-v2) <= d:
break
else:
cnt += 1
return cnt
|
Math/1226/1385. Find the Distance Value Between Two Arrays.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import cfbd
import datetime
import numpy as np
import pandas as pd
# +
# configure API key
configuration = cfbd.Configuration()
configuration.api_key['Authorization'] = 'YOUR_API_KEY_HERE'
configuration.api_key_prefix['Authorization'] = 'Bearer'
# instantiate a games API instance
api_config = cfbd.ApiClient(configuration)
games_api = cfbd.GamesApi(cfbd.ApiClient(configuration))
# +
def date_sort(game):
game_date = datetime.datetime.strptime(game['start_date'], "%Y-%m-%dT%H:%M:%S.000Z")
return game_date
def elo_sort(team):
return team['elo']
def get_expected_score(rating, opp_rating):
exp = (opp_rating - rating) / 400
return 1 / (1 + 10**exp)
def get_new_elos(home_rating, away_rating, margin):
k = 25
# score of 0.5 for a tie
home_score = 0.5
if margin > 0:
# score of 1 for a win
home_score = 1
elif margin < 0:
#score of 0 for a loss
home_score = 0
# get expected home score
expected_home_score = get_expected_score(home_rating, away_rating)
# multiply difference of actual and expected score by k value and adjust home rating
new_home_score = home_rating + k * (home_score - expected_home_score)
# repeat these steps for the away team
# away score is inverse of home score
away_score = 1 - home_score
expected_away_score = get_expected_score(away_rating, home_rating)
new_away_score = away_rating + k * (away_score - expected_away_score)
# return a tuple
return (round(new_home_score), round(new_away_score))
# -
print(get_expected_score(1500, 1500))
print(get_expected_score(1400, 1500))
print(get_expected_score(2000, 1500))
# +
games = []
for year in range(2000, 2022):
response = games_api.get_games(year=year)
games = [*games, *response]
games = [dict(
start_date=g.start_date,
home_team=g.home_team,
home_conference=g.home_conference,
home_points=g.home_points,
away_team=g.away_team,
away_conference=g.away_conference,
away_points=g.away_points
) for g in games if g.home_points is not None and g.away_points is not None]
games.sort(key=date_sort)
# +
# dict object to hold current Elo rating for each team
teams = dict()
# loop through games in order
for game in games:
# get current rating for home team
if game['home_team'] in teams:
home_elo = teams[game['home_team']]
elif game['home_conference'] is not None:
# if no rating, set initial rating to 1500 for FBS teams
home_elo = 1500
else:
# otherwise, set initial rating to 1200 for non-FBS teams
home_elo = 1200
# get current rating for away team
if game['away_team'] in teams:
away_elo = teams[game['away_team']]
elif game['away_conference'] is not None:
# if no rating, set initial rating to 1500 for FBS teams
away_elo = 1500
else:
# otherwise, set initial rating to 1200 for non-FBS teams
away_elo = 1200
# calculate score margin from game
margin = game['home_points'] - game['away_points']
# get new elo ratings
new_elos = get_new_elos(home_elo, away_elo, margin)
# set pregame elos on game dict
game['pregame_home_elo'] = home_elo
game['pregame_away_elo'] = away_elo
# set postgame elos on game dict
game['postgame_home_elo'] = new_elos[0]
game['postgame_away_elo'] = new_elos[1]
# set current elo values in teams dict
teams[game['home_team']] = new_elos[0]
teams[game['away_team']] = new_elos[1]
# +
end_elos = [dict(team=key, elo=teams[key]) for key in teams]
end_elos.sort(key=elo_sort, reverse=True)
end_elos
# +
import matplotlib.pyplot as plt
# This is the styling I use. Check out other themes here: https://matplotlib.org/3.2.1/gallery/style_sheets/style_sheets_reference.html
plt.style.use('fivethirtyeight')
# Graph sizing
plt.rcParams["figure.figsize"] = [20,10]
# -
def generate_chart(team):
team_games = []
for game in games:
if game['home_team'] == team:
team_games.append(dict(start_date=game['start_date'], elo=game['postgame_home_elo']))
if game['away_team'] == team:
team_games.append(dict(start_date=game['start_date'], elo=game['postgame_away_elo']))
df = pd.DataFrame.from_records(team_games)
fig, ax = plt.subplots()
#plt.ylim([0, 2500])
ax.plot(df.index, df['elo'])
ax.set(xlabel='Game No.', ylabel='Elo Rating',
title="Historical Elo Rating - {0}".format(team))
plt.show()
generate_chart('Auburn')
generate_chart('USC')
|
Talking Tech/EloRatings.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.7 64-bit
# language: python
# name: python3
# ---
# # Tweets Analysis
# ## 1. Import Libraries
import numpy as np
import pandas as pd
from time import time
import warnings
from sklearn.svm import SVC
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV
from sklearn.metrics import classification_report, fbeta_score, accuracy_score, confusion_matrix, plot_roc_curve, ConfusionMatrixDisplay, make_scorer
from sklearn.feature_extraction.text import TfidfVectorizer
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from imblearn.over_sampling import RandomOverSampler
# ## 2. Read the Data
tweets = pd.read_csv('Tweets\\final_tweets_classified.csv')
tweets = tweets.drop(['Column1', 'index'], axis=1)
tweets = tweets.reset_index(drop=True)
tweets.head()
tweets.info()
tweets.columns
# ## 3. Predective Statistics
# ### Data Preprocessing & Feature Extraction
tweets.head()
# Drop the neutral class
tweets = tweets[tweets.Class != 'neutral']
tweets = tweets.reset_index(drop=True)
# Convert the classes negative and positive to 0 and 1 respectively
tweets['Class'] = tweets['Class'].map({'negative': 0, 'positive': 1})
display(tweets.tail(10))
X = tweets['Tweet'] # features
y = tweets['Class'] # classes
# Convert to a vector representation
unsampled_tfidf = TfidfVectorizer()
unsampled_X = unsampled_tfidf.fit_transform(X)
unsampled_X
# ### Split the Data
X_train_unsampled, X_test_unsampled, y_train_unsampled, y_test_unsampled = train_test_split(unsampled_X, y, test_size=0.3, random_state=27)
print("Training set has {} samples.".format(X_train_unsampled.shape[0]))
print("Testing set has {} samples.".format(X_test_unsampled.shape[0]))
upsampled_tfidf = TfidfVectorizer()
upsampled_tfidf.fit(X)
X_train_upsampled, X_test_upsampled, y_train_upsampled, y_test_upsampled = train_test_split(X, y, test_size=0.3, random_state=27)
print("Training set has {} samples.".format(X_train_upsampled.shape[0]))
print("Testing set has {} samples.".format(X_test_upsampled.shape[0]))
X_train_upsampled = upsampled_tfidf.transform(X_train_upsampled)
X_test_upsampled = upsampled_tfidf.transform(X_test_upsampled)
upsampled_X = upsampled_tfidf.transform(X)
X_train_upsampled
# +
ros = RandomOverSampler(random_state=27)
X_train_upsampled, y_train_upsampled = ros.fit_resample(X_train_upsampled, y_train_upsampled)
# -
print("Data before upsampling: {} samples.".format(y_train_unsampled.value_counts()[0]))
print("Data before upsampling: {} samples.".format(y_train_unsampled.value_counts()[1]))
print("Data after upsampling: {} samples.".format(y_train_upsampled.value_counts()[0]))
print("Data after upsampling: {} samples.".format(y_train_upsampled.value_counts()[1]))
# ### Training Pipeline
# The goal is to create a function that trains, scores and predicts any model. This will allow for efficient model selection since we can supply the function with multiple models and compare the results to select the most appropriate one.
#
# #### Function Inputs
# > model: the classifier to be trained
# > X_train y_train X_test y_test, X and y
# >
#
# #### Function Output
# - result which is an array of the prediction time and scores respectively
def train_predict_pipeline(model, X_train, y_train, X_test, y_test, X, y):
print(" {} Training ".format(model.__class__.__name__))
results = {}
start = time() # Training start
model = model.fit(X_train, y_train) # Train the model
end = time() # Training end
results['training_time'] = end - start # Store the time
start = time() # Prediction start
predictions_test = model.predict(X_test) # Predict
predictions_train = model.predict(X_train)
end = time() # Prediction end
results['prediction_time'] = end - start # Store the time
results['model_accuracy'] = model.score(X_train, y_train) # Overall accuracy
# Cross validation score
cross_validation_scores = cross_val_score(model,X, y, cv=10)
results['model_cross_validation'] = np.mean(cross_validation_scores)
# Accuracy scores - for plotting
results['accuracy_train'] = accuracy_score(y_train, predictions_train)
results['accuracy_test'] = accuracy_score(y_test, predictions_test)
# F-scores
results['fbeta_train'] = fbeta_score(y_train, predictions_train, beta=0.5)
results['fbeta_test'] = fbeta_score(y_test, predictions_test, beta=0.5)
# Print the report
print(' Accuracy Report ')
print('Model Accuracy: %.2f' % results['model_accuracy'])
print('10-Fold Cross Validation: %.2f' % results['model_cross_validation'])
print('F-beta Score (Training): %.2f' % results['fbeta_train'])
print('F-beta Score (Testing): %.2f' % results['fbeta_test'])
print(' Confusion Matrix ')
print(confusion_matrix(y_test, predictions_test))
print(classification_report(y_test, predictions_test))
display = ConfusionMatrixDisplay.from_estimator(model, X_test, y_test, display_labels=['negative', 'positive'], cmap=plt.cm.Blues)
display.ax_.set_title('Confusion Matrix Display')
plt.show()
# Return the results and the classifier
return results, model
SVC_classifier = SVC(random_state=0,probability=True)
AdaBoost_classifier = AdaBoostClassifier(random_state=0)
Naivebayes_classifier = MultinomialNB()
# +
results_raw = {}
for classifier in [SVC_classifier, AdaBoost_classifier, Naivebayes_classifier]:
classifier_name = classifier.__class__.__name__
results_raw[classifier_name] = {}
results_raw[classifier_name], classifier = train_predict_pipeline(
classifier, X_train_unsampled, y_train_unsampled, X_test_unsampled, y_test_unsampled, unsampled_X, y)
# -
SVC_classifier = SVC(random_state=0, probability=True)
AdaBoost_classifier = AdaBoostClassifier(random_state=0)
Naivebayes_classifier = MultinomialNB()
# +
results = {}
for classifier in [SVC_classifier, AdaBoost_classifier, Naivebayes_classifier]:
classifier_name = classifier.__class__.__name__
results[classifier_name] = {}
results[classifier_name], classifier = train_predict_pipeline(
classifier, X_train_upsampled, y_train_upsampled, X_test_upsampled, y_test_upsampled, upsampled_X, y)
# -
# ### Model Evaluation
results
def evaluate(results, accuracy, f1):
"""
Visualization code to display results of various learners.
inputs:
- learners: a list of supervised learners
- stats: a list of dictionaries of the statistic results from 'train_predict()'
- accuracy: The score for the naive predictor
- f1: The score for the naive predictor
"""
# Create figure
fig, ax = plt.subplots(2, 3, figsize=(15, 10))
# Constants
bar_width = 0.3
colors = ['#083471', '#1F6EB3', '#56A0CE']
for k, learner in enumerate(results.keys()):
for j, metric in enumerate(['training_time', 'accuracy_train', 'fbeta_train', 'prediction_time', 'accuracy_test', 'fbeta_test']):
ax[j//3, j % 3].bar(k*bar_width, results[learner]
[metric], width=bar_width, color=colors[k])
# Add unique y-labels
ax[0, 0].set_ylabel("Time (in seconds)")
ax[0, 1].set_ylabel("Accuracy Score")
ax[0, 2].set_ylabel("F-score")
ax[1, 0].set_ylabel("Time (in seconds)")
ax[1, 1].set_ylabel("Accuracy Score")
ax[1, 2].set_ylabel("Fbeta-score")
# Add titles
ax[0, 0].set_title("Model Training")
ax[0, 1].set_title("Accuracy Score on Training Subset")
ax[0, 2].set_title("F-score on Training Subset")
ax[1, 0].set_title("Model Predicting")
ax[1, 1].set_title("Accuracy Score on Testing Set")
ax[1, 2].set_title("Fbeta-score on Testing Set")
# Add horizontal lines for naive predictors
ax[0, 1].axhline(y=accuracy, xmin=-0.1, xmax=3.0,
linewidth=1, color='k', linestyle='dashed')
ax[1, 1].axhline(y=accuracy, xmin=-0.1, xmax=3.0,
linewidth=1, color='k', linestyle='dashed')
ax[0, 2].axhline(y=f1, xmin=-0.1, xmax=3.0, linewidth=1,
color='k', linestyle='dashed')
ax[1, 2].axhline(y=f1, xmin=-0.1, xmax=3.0, linewidth=1,
color='k', linestyle='dashed')
# Set y-limits for score panels
ax[0, 1].set_ylim((0, 1))
ax[0, 2].set_ylim((0, 1))
ax[1, 1].set_ylim((0, 1))
ax[1, 2].set_ylim((0, 1))
# Create patches for the legend
patches = []
for i, learner in enumerate(results.keys()):
patches.append(mpatches.Patch(color=colors[i], label=learner))
plt.legend(handles=patches, bbox_to_anchor=(-.80, 2.53),
loc='upper center', borderaxespad=0., ncol=3, fontsize='x-large')
# Aesthetics
plt.suptitle(
"Performance Metrics for Three Supervised Learning Models", fontsize=16, y=1.10)
plt.show()
evaluate(results, 0.5, 0.5)
# +
svc_display = plot_roc_curve(SVC_classifier, X_test_upsampled, y_test_upsampled)
ada_display = plot_roc_curve(AdaBoost_classifier, X_test_upsampled, y_test_upsampled, ax=svc_display.ax_)
naive_display = plot_roc_curve(Naivebayes_classifier, X_test_upsampled, y_test_upsampled, ax=ada_display.ax_)
naive_display.figure_.suptitle("ROC curve comparison")
with warnings.catch_warnings():
warnings.simplefilter("ignore")
plt.show()
# -
# ### Fine Tuning
parameters = {'C': [0.1, 1, 1.1, 2, 10, 100],
'kernel': ['linear']}
scorer = make_scorer(fbeta_score, beta=0.5)
grid = GridSearchCV(SVC(random_state=0), param_grid=parameters, scoring=scorer, refit=True, cv=10, verbose=3)
gridSVC = grid.fit(X_train_upsampled, y_train_upsampled)
gridSVC.best_estimator_
# Original SVC accuracy
results['SVC']['accuracy_test']
# Original SVC fbeta score
results['SVC']['fbeta_test']
# Fine tuned SVC accuracy
accuracy_score(y_test_upsampled, gridSVC.predict(X_test_upsampled))
# Fine tuned SVC fbeta score
fbeta_score(y_test_upsampled, gridSVC.predict(X_test_upsampled), beta=0.5)
train_predict_pipeline(SVC(C=1, kernel='linear', random_state=0), X_train_upsampled, y_train_upsampled, X_test_upsampled, y_test_upsampled, upsampled_X, y)
|
tweets-analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Python packages
from itertools import chain
import matplotlib.pyplot as plt
import pickle
import numpy as np
import sys
import os
import pickle
import signal
import argparse
import traceback
import json
import torch
import torch.nn as nn
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from scipy.spatial import distance_matrix
import pandas as pd
# +
# sys.path.insert(1, "/home/ubuntu/pidgin-rl/model")
sys.path.insert(1, '../model')
from datasets import *
from decoder import *
from encoder_v2 import *
from train_encoder_v2 import *
# -
# # Load Data
LANG = "en"
# LANG = "fr"
BATCH_SIZE = 32
DATASET_PATH = '../generate-data/data_final/train/{}.csv'.format(LANG)
INDEXED_DATA_PATH = '../tokenizer/data_final/indexed_data_words.json' # dataset indexed
# TOKENIZED_DATA_PATH = "../tokenizer/data_final/tokens_words.json"
VOCAB_PATH = "../tokenizer/data_final/vocab_words.json"
dataset = pd.read_csv(DATASET_PATH).drop(columns=["Unnamed: 0"])
dataset.head()
with open(VOCAB_PATH) as f:
words = json.load(f)
words = pd.DataFrame.from_dict(words, orient='index', columns=["idx"]).reset_index()
words.drop(columns=["idx"], inplace=True)
words.rename(columns={"index":"label"}, inplace=True)
words.head()
IX_TO_WORD = create_ix_to_vocab_map(VOCAB_PATH)
VOCAB_SIZE = len(words)
en_idx = [0, 1, 2, 6, 18, 19] + list(range(37, VOCAB_SIZE))
fr_idx = list(range(37))
{"<pad>": 0, "<cls>": 1, "<eos>": 2, "allez": 3, "de": 4, "cinquante": 5, "-": 6, "huit": 7, "\u00e0": 8, "droite": 9, "soixante": 10, "et": 11, "onze": 12, "gauche": 13, "puis": 14, "descendez": 15, "quatre": 16, "vingt": 17, "six": 18, ",": 19, "montez": 20, "quinze": 21, "trente": 22, "un": 23, "douze": 24, "neuf": 25, "quarante": 26, "dix": 27, "deux": 28, "sept": 29, "quatorze": 30, "vingts": 31, "cinq": 32, "trois": 33, "treize": 34, "seize": 35, "cent": 36, "move": 37, "forty": 38, "eight": 39, "to": 40, "the": 41, "left": 42, "then": 43, "go": 44, "down": 45, "ten": 46, "up": 47, "eleven": 48, "seventy": 49, "right": 50, "and": 51, "twenty": 52, "thirty": 53, "seven": 54, "sixty": 55, "five": 56, "nineteen": 57, "one": 58, "twelve": 59, "fifty": 60, "nine": 61, "eighty": 62, "three": 63, "ninety": 64, "two": 65, "seventeen": 66, "sixteen": 67, "four": 68, "fourteen": 69, "eighteen": 70, "fifteen": 71, "hundred": 72, "thirteen": 73}
# # Load Model
# Specifies the device, language, model type, and number of epochs, then loads in each checkpoint.
device = torch.device("cpu") if not torch.cuda.is_available() else torch.device("cuda:0")
# Decoder or encoder
model_type = "encoder"
# model_type = "encoder"
N = 9 # last epoch we want
# N is the last epoch we want
MODEL_CHECKPOINTS = ["../model/saved_models/{}_{}/model_epoch_{}.pt".format(
LANG, model_type, i) for i in range(1, N)]
MODELS = [torch.load(checkpoint, map_location=device) for checkpoint in MODEL_CHECKPOINTS]
EMBEDS = [list(model.children())[:-1][0] for model in MODELS]
embed = EMBEDS[-1]
to_embed = torch.tensor(range(VOCAB_SIZE), dtype=torch.long, device=device)
embeddings = embed(to_embed).cpu().detach().numpy()
pd.DataFrame(embeddings)
words = pd.concat([words, pd.DataFrame(embeddings)], axis=1)
words
# # Dimension reduction and Plotting
def PCA_(n, df):
"""
PCAs df into n-dimensional df. Centers data automatically
"""
pca = PCA(n_components=n)
pca_df = pd.DataFrame(pca.fit_transform(np.array(df)))
print('PCAed into shape: ', pca_df.shape)
return pca_df
def tSNE(df):
"""
t-SNEs df into 2 dimensions for visualization
"""
X_embed = TSNE(n_components=2).fit_transform(df)
print('t-SNEd into shape:', X_embed.shape)
return X_embed
def plot_embeds(embeds, names, title='tSNE Visualization of Embeddings'):
"""
Plots embeddings with their corresponding names.
embeds: N x 2 df where N[i] is a point to plot and names[i] is the corresponding label
"""
embeds = np.array(embeds)
for i, embed in enumerate(embeds):
plt.scatter(embed[0], embed[1])
plt.text(embed[0] + 0.05, embed[1] - 0.07, names[i], fontsize=9)
plt.title(title)
plt.show()
# +
# SPLIT DATASET INTO ENGLISH/FRENCH
to_pca = words[words.columns.tolist()[1:]]
to_pca_en = to_pca.iloc[en_idx, :]
to_pca_fr = to_pca.iloc[fr_idx, :]
to_pca.head()
# -
# PCA
pcaed_en = PCA_(2, to_pca_en)
pcaed_fr = PCA_(2, to_pca_fr)
plot_embeds(pcaed_en, list(words.iloc[en_idx,:]['label']), title="PCA Embeddings English")
plot_embeds(pcaed_fr, words.iloc[fr_idx,:]['label'], title="PCA Embeddings French")
# TSNE
tsed_en = tSNE(to_pca_en)
tsned_fr = tSNE(to_pca_fr)
plot_embeds(tsed_en, list(words.iloc[en_idx,:]['label']), title="tSNE Embeddings English")
plot_embeds(tsned_fr, words.iloc[fr_idx,:]['label'], title="tSNE Embeddings French")
# # Distance matrix
# +
def plot_matrix(mat, classes, title):
fig, ax = plt.subplots()
im = ax.imshow(mat)
plt.title(title)
# We want to show all ticks...
ax.set_xticks(np.arange(len(classes)))
ax.set_yticks(np.arange(len(classes)))
# ... and label them with the respective list entries
ax.set_xticklabels(classes, {'fontsize': 7})
ax.set_yticklabels(classes, {'fontsize': 7})
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
fig.colorbar(im)
plt.show()
def vis_distance_matrix(df, classes, title, cos=True):
"""
Visualize pairwise cosine distances between rows of the df.
df should be a pandas dataframe of embedding vectors.
"""
embeds = np.array(df)
if cos:
embeds = normalize(embeds, norm='l2', axis=1, copy=True, return_norm=False)
dists = distance_matrix(embeds, embeds, p=2)
plot_matrix(dists, classes, title)
return dists
# -
# # Sentence Generation (run only if encoder)
def get_perplexity(loss):
"""
loss: per-word loss from evaluation
A perplexity of random guessing is vocab size = 74. Anything lower is extremely good.
"""
return math.exp(loss)
LANG
# +
# Load english data set
iters = load_data(DATASET_PATH, INDEXED_DATA_PATH, LANG, BATCH_SIZE, device)
_, _, en_test_iter = iters
print('Finished loading english data')
# Load french dataset
iters = load_data('../generate-data/data_final/train/fr.csv', INDEXED_DATA_PATH, 'fr', BATCH_SIZE, device)
X_str, train_iter, fr_test_iter = iters
print('Finished loading data')
# -
from train_jointly import evaluate as joint_eval
# Load in models over time
def get_checkpoints(model_dir = '../model/saved_models/en'):
'''
Load in all model checkpoints, save as dict
'''
checkpoints = {}
for file in os.listdir(model_dir):
epoch_num = int(file.split('_')[-1][0])
model_path = os.path.join(model_dir, file)
checkpoints[epoch_num] = torch.load(model_path)
return checkpoints
# + jupyter={"outputs_hidden": true}
# Get english and french checkpoints
en_checkpoints = get_checkpoints()
fr_checkpoints = get_checkpoints('../model/saved_models/fr')
# -
# Get loss afer
def eval_checkpoints(checkpoints, data, device):
'''
Evaluate model checkpoints using provide data
'''
LOSSES = []
for c_ix in range(1, len(checkpoints)+1):
model = checkpoints[c_ix]
dec_criterion = nn.MSELoss()
enc_criterion = nn.CrossEntropyLoss(ignore_index=0, reduction='sum')
loss = joint_eval(model, data, enc_criterion, dec_criterion, device, args=None, type='Test')
LOSSES.append(loss)
print(f"Loss for epoch {c_ix}: {loss}",flush=True,end='\r')
return LOSSES
en_losses_on_english = eval
# +
# Plot encoder loss
import seaborn as sns
enc_perp = [get_perplexity(l[0]/(32*24)) for l in LOSSES]
fig, axs = plt.subplots(1, figsize=(5,5))
sns.scatterplot(range(1,10), enc_perp, ax=axs)
axs.set_title('English MonolingualEncoder Validation Perplexity per word\nusing English dataset')
axs.set(xlabel='Epoch', ylabel='Perplexity');
# -
dec_loss = [l[1]*100**2/32 for l in LOSSES]
fig, axs = plt.subplots(1, figsize=(5,5))
sns.scatterplot(range(1,10), dec_loss, ax=axs)
axs.set_title('Decoder validation loss per sentence\nEnglish Monolingual')
axs.set(xlabel='Epoch', ylabel='MSE Loss');
|
analysis/.ipynb_checkpoints/Analysis-Copy1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import folium
from folium.plugins import HeatMap
df = pd.read_csv("countries-aggregated_csv.csv")
m = folium.Map(tiles = 'Stamen Terrain',min_zoom = 1.5)
display(m)
# -
url = 'https://raw.githubusercontent.com/python-visualization/folium/master/examples/data'
country_shapef = f'{url}/world-countries.json'
folium.Choropleth(
geo_data = country_shapes,
min_zoom=27,
name='Covid-19',
data=df,
columns=['Country', 'Confirmed'],
key_on='feature.properties.name',
fill_color='OrRd',
nan_fill_color='black',
legend_name = 'Total Confirmed COVID cases',
).add_to(m)
m
|
covid _19 analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:research]
# language: python
# name: conda-env-research-py
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/st3107/20210818_iucr_diffpy_talk/blob/main/notebooks/03_example_script_for_colab_final_version.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="a166aa01"
# # Prepare the conda environment
# + [markdown] id="6825c6f9"
# ## Install the mini-conda and use it to install diffpy-cmi
# + colab={"base_uri": "https://localhost:8080/"} id="389bbcac" outputId="504feec5-4971-40bc-a5eb-78801d6df73e"
# !echo $PYTHONPATH
# + colab={"base_uri": "https://localhost:8080/"} id="5d97dea8" outputId="c27bab79-38b3-4875-aac4-1fd72d766d98"
# %env PYTHONPATH=
# + colab={"base_uri": "https://localhost:8080/"} id="4107d153" outputId="a3b8ded1-a504-46ba-fb7f-95fc17cd981e" language="bash"
# MINICONDA_INSTALLER_SCRIPT=Miniconda3-latest-Linux-x86_64.sh
# MINICONDA_PREFIX=/usr/local
# wget https://repo.continuum.io/miniconda/$MINICONDA_INSTALLER_SCRIPT
# chmod +x $MINICONDA_INSTALLER_SCRIPT
# ./$MINICONDA_INSTALLER_SCRIPT -b -f -p $MINICONDA_PREFIX
# + colab={"base_uri": "https://localhost:8080/"} id="b1f9462c" outputId="ae3caeaa-5067-4db2-c5fe-41cd50e9eacf"
# !which conda
# + colab={"base_uri": "https://localhost:8080/"} id="c0ce6b08" outputId="e62ad186-c811-432e-92a6-1607edb0b799"
# !conda --version
# + colab={"base_uri": "https://localhost:8080/"} id="86afa7ec" outputId="86837eb4-b4c7-46a1-8c3e-2d4a6da34cac"
# !conda create -n diffpy -c defaults -c diffpy python=3.7 diffpy-cmi pandas --yes
# + colab={"base_uri": "https://localhost:8080/"} id="819d14e8" outputId="131c3e73-99f6-476d-a4fd-f64dd89986ac"
# !conda env list
# + [markdown] id="226efd77"
# ## Configure the python to recognize the diffpy library
# + colab={"base_uri": "https://localhost:8080/"} id="9cd4710d" outputId="13d1bb51-2470-4c8c-ec2a-4e96b064875d"
# !ls /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy*
# + id="9e2c1c53"
# !cp -r /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy.srfit-3.0.0-py3.7.egg/diffpy/* /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy/
# + id="9b5f9508"
# !cp -r /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy.structure-3.0.1-py3.7.egg/diffpy/* /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy/
# + id="b8c41850"
# !cp -r /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy.utils-3.0.0-py3.7.egg/diffpy/* /usr/local/envs/diffpy/lib/python3.7/site-packages/diffpy/
# + id="24ed2d4c"
import sys
# + id="46822139"
sys.path.insert(1, "/usr/local/envs/diffpy/lib/python3.7/site-packages")
# + [markdown] id="6c9de328"
# ## Test if we can import diffpy
# + id="639e78f5"
import diffpy.srfit
import diffpy.srreal
import diffpy.structure
import diffpy.utils
# + [markdown] id="289d8be6"
# ## Download the example data from github
# + colab={"base_uri": "https://localhost:8080/"} id="88702595" outputId="dbc68ba8-6a1f-4aa4-be68-13ce9f229411"
# !git clone https://github.com/st3107/20210818_iucr_diffpy_talk.git
# + id="2d0cb765"
# !cp -r ./20210818_iucr_diffpy_talk/notebooks/colab_data ./data
# + colab={"base_uri": "https://localhost:8080/"} id="fe65d61d" outputId="50814b88-555f-4226-aa9e-d2f14cdcc287"
# !ls ./data
# + [markdown] id="151bedf9"
# # Customized PDF fitting based on the APIs in diffpy-cmi
# + [markdown] id="17dd4f71"
# In this notebook, we will show an example how to use the APIs in the diffpy-cmi to create your own tools of PDF fitting.
# + id="0cc3754f"
# %matplotlib inline
# + [markdown] id="2737b9f8"
# ## Import the modules
# + [markdown] id="757d919a"
# Below are modules we used to create our tools. We also define a variable "F" which contains a collection of predefined characteristic functions from diffpy-cmi that we will use later.
# + id="e33fe006"
import typing
import matplotlib.pyplot as plt
import numpy as np
from pathlib import Path
from scipy.optimize import least_squares
from diffpy.utils.parsers.loaddata import loadData
from diffpy.srfit.fitbase import FitRecipe, FitContribution, Profile, FitResults
from diffpy.srfit.pdf import PDFGenerator, PDFParser
from diffpy.srfit.fitbase.parameterset import ParameterSet
from pyobjcryst import loadCrystal
from pyobjcryst.crystal import Crystal
import diffpy.srfit.pdf.characteristicfunctions
F = diffpy.srfit.pdf.characteristicfunctions
# + [markdown] id="0338cac2"
# ## Introduction to the basic classes in diffpy-cmi
# + [markdown] id="dffa11d5"
# ### Profile
# + [markdown] id="e017da6f"
# The `Profile` is an object to hold data and metadata. For example, in this example we have a simulated dataset that is a linear line with noise.
#
# `Profile` is a general container for any profile. We make a particular instance of it called `noisy_linear` that contains our particular profile.
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="90a6a4c8" outputId="c2cbbbcf-7083-41ad-f2bb-b890cb91a590"
x = np.arange(0., 10, 0.01)
y = 0.5 * x + 2.0 + np.random.normal(scale=0.5, size=x.shape[0])
noisy_linear = Profile()
noisy_linear.setObservedProfile(x, y)
plt.plot(noisy_linear.x, noisy_linear.y)
# + [markdown] id="e8bb8f6b"
# ### FitContribution
# + [markdown] id="325af62a"
# Now we want to fit something to our profile. We use a `FitContribution` object to hold all the info about each contribution in the fit (e.g., a phase in a multi-phase fit and the model to fit to it). So we create a particular instance of `FitContribution` for this noisy linear data and give it a short and memorable name, `nlc`. Diffpy-cmi also allows you to give this a name attribute that we set to `noisy_linear`. Then we give it our `noisy_linear` `Profile`.
# + id="51f1d460"
nlc = FitContribution("noisy_linear")
nlc.setProfile(noisy_linear)
# + [markdown] id="c435f972"
# `nlc` should also contain the model to fit to the data. The model can be defined by a string equation. For example, our data is a straight line, we may want to use "a * x + b" as the model. Here, the "a", "b" are two scalar parameters and "x" is a the independent variable, this is the most direct way to use diffpy-cmi.
# + id="95160275"
nlc.setEquation("a * x + b")
# + [markdown] id="cd9cb76c"
# ### FitRecipe
# + [markdown] id="c45adc46"
# In general, a fit may contain multiple components (multiple phases, etc. but also the constraints and variables that affect th fit). The object to contain the complex fit is the `FitRecipe` and we need to create a particular instance of this for our (single component) linear fit. Let's call it `nlr` for noisy-linear-recipe. After instantiating it, we add our contribution.
# + id="93ca836e"
nlr = FitRecipe()
nlr.addContribution(nlc)
# + [markdown] id="ed2c75e3"
# After it is added, the `FitContribution` will be an attribute of `FitRecipe` and user can access it.
# + colab={"base_uri": "https://localhost:8080/"} id="45f52ee8" outputId="1431158d-43c1-461c-cef0-e3c6cea8839a"
nlr.noisy_linear
# + [markdown] id="e498ec5f"
# There is a default `FitHook` for printing which is not always useful. We will clear it for this tutorial.
# + id="c6a409f8"
nlr.fithooks.clear()
# + [markdown] id="18a69219"
# We can add the parameters from the model in the `FitContribution` into the `FitRecipe` as variables to vary in the fit.
# + colab={"base_uri": "https://localhost:8080/"} id="528d5143" outputId="7db81371-db1b-4eeb-db55-d7fd403a38d2"
nlr.addVar(nlc.a)
nlr.addVar(nlc.b)
# + [markdown] id="9f8fb4de"
# After it is added, we can set an initial value for it.
# + colab={"base_uri": "https://localhost:8080/"} id="46c28e5e" outputId="b41c3386-7b3a-4f95-9a17-e0109b194310"
nlr.a.setValue(1.)
nlr.b.setValue(1.)
# + [markdown] id="a08810b3"
# ### Optimization
# + [markdown] id="aa5f1828"
# The `FitRecipe` is not in charge of the optimization of parameters. It is only a interface to manage parameters and generate the residual. We need to use optimization tools outside the diffpy-cmi, for example `scipy.optimize.least_squares` that was imported above with its name shortened to `least_squares`. To run it needs the computed residual (sum of squares of difference between the model and the data in this case) and the variables that it will vary, which are returned by the `getValues()` method in `FitRecipe`. After it runs it will update the values to new, refined, values which are the result of the fit.
# + colab={"base_uri": "https://localhost:8080/"} id="1ddde18e" outputId="67f97f35-135f-4b27-9249-dbe170c2c4b8"
least_squares(nlr.residual, nlr.getValues(), verbose=1);
# + [markdown] id="740c32c5"
# Now, we successfully used the diffpy-cmi to do a linear regression. We can do things like plot the results and output a table of the refined parameters
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="08a1a3fc" outputId="4bae8585-9a2c-4a37-ef03-5bc12e1a5c6c"
plt.plot(noisy_linear.x, noisy_linear.y, label="data")
plt.plot(noisy_linear.x, noisy_linear.ycalc, label="fit")
plt.legend()
# + colab={"base_uri": "https://localhost:8080/"} id="426bdeb9" outputId="8ccce42d-49f5-48e8-b629-0844b664b692"
nlr.show()
# + [markdown] id="ab78790c"
# ### Use python function in the equation
# + [markdown] id="79565750"
# What if we cannot write out the equation using the a simple hand-written function? For example, our data is a stretched and scaled zero order Bessel function.
# + id="64f8d80a"
import scipy.special as special
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="98494b9e" outputId="5b46e716-3116-41dd-bf19-5c2805e3a249"
x = np.arange(0., 10, 0.01)
y = 10 * special.besselpoly(x / 0.5, 1, 0) + np.random.normal(scale=0.1, size=x.shape[0])
noisy_bessel = Profile()
noisy_bessel.setObservedProfile(x, y)
plt.plot(noisy_bessel.x, noisy_bessel.y)
# + id="4b43e8de"
nbc = FitContribution("noisy_bessel")
nbc.setProfile(noisy_bessel)
# + [markdown] id="6f90e647"
# In this case, we need to define a Bessel function and register it in the equation using `registerFunction`. Here, the equation "f" is not a scalar parameter "f" but a symbol representing the registered function so the actual model is "y = bessel(x, a, b)"
# + id="17679578"
def bessel(x, a, b):
return a * special.besselpoly(x / b, 1, 0)
# + id="86248115"
nbc.registerFunction(bessel, name="f")
nbc.setEquation("f")
# + colab={"base_uri": "https://localhost:8080/"} id="50efb654" outputId="a04a4bbe-5ea6-457a-b161-a1957f451423"
nbr = FitRecipe()
nbr.clearFitHooks()
nbr.addContribution(nbc)
nbr.addVar(nbc.a)
nbr.addVar(nbc.b)
nbr.a.setValue(0.5)
nbr.b.setValue(0.5)
# + colab={"base_uri": "https://localhost:8080/"} id="6b28af19" outputId="153ba3d1-3952-4cbd-b7b6-2757379605ba"
least_squares(nbr.residual, nbr.getValues(), verbose=1);
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="8272cf5f" outputId="d2c85c46-86bb-40df-b1cb-e8fed76eed0e"
plt.plot(noisy_bessel.x, noisy_bessel.y, label="data")
plt.plot(noisy_bessel.x, noisy_bessel.ycalc, label="fit")
plt.legend()
# + colab={"base_uri": "https://localhost:8080/"} id="1ec8373e" outputId="534baaae-65b1-4702-d009-9267f214236d"
nbr.show()
# + [markdown] id="72e1dab9"
# ### Use PDFGenerator in the equation
# + [markdown] id="cd0a6019"
# Now, what if our data is a PDF data? Our model will include structures with parameters like lattice constants and ADPs. We can define our python function for the calculation of the PDF and add it to `FitContribution`. However, every time there is a new structure, we need to define a function and this is inefficient. We would like a python class that loads a structure inside, calculates PDF when called and contains the parameters of the structure in its attributes.
#
# diffpy-cmi can also accept the python class but it must be the child class of the `ProfileGenerator`. Usually, users don't need to define it because diffpy-cmi provides the predefined `PDFGenerator` for the users, but if you wanted to add a new profile generator, like for a Raman or NMR spectrum, this is how you would do it. For this example of just PDF we just need to use `addProfileGenerator` to add it in the `FitContribution`.
# + id="a01f411c"
crystal = loadCrystal("./data/TiO2_bronze.cif")
pg = PDFGenerator("TiO2")
pg.setStructure(crystal, periodic=True)
# + id="dee933d2"
fc = FitContribution("PDF")
fc.addProfileGenerator(pg)
fc.setEquation("TiO2")
# + [markdown] id="08a171ed"
# After it is added, it is an attribute of `FitContribution`.
# + colab={"base_uri": "https://localhost:8080/"} id="04b03381" outputId="6dc0c61b-626c-4e43-fafa-a21f9b96361d"
fc.TiO2
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="6aaf96a6" outputId="0c502d24-dbbd-4507-cfeb-5610ec6cd3f4"
x = np.arange(0., 10., 0.01)
y = fc.TiO2(x)
plt.plot(x, y)
# + [markdown] id="e9f6f49c"
# ### diffpy-cmi = modeling interface + PDF library
# + [markdown] id="6452a548"
# In a nutshell, diffpy-cmi is a modeling interface together with a library of PDF calculators and characteristic functions. The interface for users to manage the variables and the calculators are separated. Users need to combine them when using the diffpy-cmi. This seems to produce a bit more work but it gives opportunities to developers in the open source world to further develop diffpy-cmi to do more and more things. They can add new calculators in the library keeping the interface untouched, use the calculators in another place or develop their own interface based on diffpy-cmi. They can also build gui's and other user-interfaces to hide some of this complexity from non-programmer users!
#
# In the next section, we will show a simple example how to use diffpy-cmi to fit the PDF.
# + [markdown] id="bb411a4d"
# ## Fit the data of TiO2 nanoparticles with TiO2 bronze phase
# + [markdown] id="470f9842"
# In this section, we will create tools and use them in the fitting of the data from the TiO2 nanoparticles.
# + [markdown] id="Rmk_rMbjV3FD"
# ## The data file of G(r)
# + id="0719b5f8"
GR_FILE = "./data/TiO2_np_ligand.gr"
# + [markdown] id="f22c21a8"
# To create a FitRecipe, we need data and a model. The data is a two column file where the first column is the value of distance `r` and the second column is the value of PDF `G`. The file may also contain the headers where the metadata is written in the "key = value" format. Below shows the first several rows of the data file that we will use in the fitting that was obtiained from the `PDFgetX3` program.
# + colab={"base_uri": "https://localhost:8080/"} id="8e5d88b4" outputId="1db0d43a-5c00-4038-c8d6-b38c0a86e9d9"
# !head -40 "./data/TiO2_np_ligand.gr"
# + [markdown] id="71a4c12d"
# ### Initial guess of the structure
# + [markdown] id="0a99ddcb"
# By uploading the file to the structureMining App in the [PDFitc](https://pdfitc.org/) website we can automatically get good starting models to save us some time. The result is sorted from the best to the worst in the table. We find the best candidate to start with is the bronze phase structure (space group "C2/m") in the Materials Project Database.
# + id="c234f6e1"
DATA_MINING_FILE = "./data/pdfitc_search_results_data.csv"
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="9a69dc92" outputId="7c62f182-4a9e-4e23-f64f-063a6e28855f"
import pandas as pd
df = pd.read_csv(DATA_MINING_FILE, index_col=0)
df[["rw", "formula", "space_group", "db", "db_id"]].head(10)
# + [markdown] id="7824327c"
# We download the cif file from the database and put it to the place shown below.
# + id="b8249e42"
CIF_FILE_B = "./data/TiO2_bronze.cif"
# + [markdown] id="fa0c11b5"
# ### Create our first FitRecipe
#
# In this section, we will create our first FitRecipe. A FitRecipe is the interface that user to interact with in the fitting. It contains FitContribution, which is a fit of anything. Here, we will make a helper function `create_recipe_from_files` that creates a single-FitContribution and FitRecipe from the data and structure files in one step. We can reuse this function so do fits many times over with little typing. This step is not required, but it makes things easier, and these helper functions can be shared to speed things up for everyone.
# + id="90cd1964"
def _create_recipe(
equation: str,
crystals: typing.Dict[str, Crystal],
functions: typing.Dict[str, typing.Tuple[typing.Callable, typing.List[str]]],
profile: Profile,
fc_name: str = "PDF"
) -> FitRecipe:
"""Create the FitRecipe object.
Parameters
----------
equation :
The equation of G(r).
crystals :
A mapping from the name of variable in the equation to the crystal structure for PDF calculation.
functions :
A mapping from the name of variable in the equation to the python function for PDF calculation.
The first argument of the function is the array of r, the other arguments are the parameters.
profile :
The data profile that contains both the metadata and the data.
fc_name :
The name of the FitContribution in the FitRecipe. Default "PDF".
Returns
-------
A FitRecipe object.
"""
fr = FitRecipe()
fc = FitContribution(fc_name)
for name, crystal in crystals.items():
pg = PDFGenerator(name)
pg.setStructure(crystal, periodic=True)
fc.addProfileGenerator(pg)
for name, (f, argnames) in functions.items():
fc.registerFunction(f, name=name, argnames=argnames)
fc.setEquation(equation)
fc.setProfile(profile, xname="r", yname="G", dyname="dG")
fr.addContribution(fc)
return fr
def _get_tags(phase: str, param: str) -> typing.List[str]:
"""Get the tag names.
Parameters
----------
phase
param
Returns
-------
"""
return [param, phase, "{}_{}".format(phase, param)]
def _get_name(*args: str) -> str:
"""Get the name of the variable.
Parameters
----------
args
Returns
-------
"""
return "_".join(args)
def _rename_par(name: str, atoms: list) -> str:
"""Rename of the name of a parameter by replacing the index of the atom in the name by the label of
the atom and revert the order of coordinates and atom name.
Used for the space group constrained parameters. For example, "x_0" where atom index 0 is Ni will become
"Ni0_x" after renamed. If the name can not renamed, return the original name.
Parameters
----------
name
atoms
Returns
-------
"""
parts = name.split("_")
np = len(parts)
na = len(atoms)
if np > 1 and parts[1].isdigit() and -1 < int(parts[1]) < na:
parts[1] = atoms[int(parts[1])].name
parts = parts[::-1]
return "_".join(parts)
def _add_params_in_pg(recipe: FitRecipe, pg: PDFGenerator) -> None:
"""Add parameters in the PDFGenerator.
Parameters
----------
recipe
pg
Returns
-------
"""
name: str = pg.name
recipe.addVar(
pg.scale,
name=_get_name(name, "scale"),
value=0.,
fixed=True,
tags=_get_tags(name, "scale")
).boundRange(0.)
recipe.addVar(
pg.delta2,
name=_get_name(name, "delta2"),
value=0.,
fixed=True,
tags=_get_tags(name, "delta2")
).boundRange(0.)
latpars = pg.phase.sgpars.latpars
for par in latpars:
recipe.addVar(
par,
name=_get_name(name, par.name),
fixed=True,
tags=_get_tags(name, "lat")
).boundRange(0.)
atoms: typing.List[ParameterSet] = pg.phase.getScatterers()
for atom in atoms:
par = atom.Biso
recipe.addVar(
par,
name=_get_name(name, atom.name, "Biso"),
value=0.02,
fixed=True,
tags=_get_tags(name, "adp")
).boundRange(0.)
xyzpars = pg.phase.sgpars.xyzpars
for par in xyzpars:
par_name = _rename_par(par.name, atoms)
recipe.addVar(
par,
name=_get_name(name, par_name),
fixed=True,
tags=_get_tags(name, "xyz")
)
return
def _add_params_in_fc(
recipe: FitRecipe,
fc: FitContribution,
names: typing.List[str],
tags: typing.List[str]
) -> None:
"""Add parameters in the FitContribution.
Parameters
----------
recipe
fc
names
tags
Returns
-------
"""
for name in names:
par = getattr(fc, name)
recipe.addVar(
par,
value=100.,
fixed=True,
tags=tags
)
return
def _initialize_recipe(
recipe: FitRecipe,
functions: typing.Dict[str, typing.Tuple[typing.Callable, typing.List[str]]],
crystals: typing.Dict[str, Crystal],
fc_name: str = "PDF"
) -> None:
"""Initialize the FitRecipe object with variables.
The parameters are the scale of the PDF, the delta2 parameter in the correction of correlated motions,
the atomic displacement parameters (ADPs) of the symmetric unique atoms, the x, y, z positions of the
symmetric unique atoms under the constraint of the symmetry and the parameters in the functions registered
in the FitContribution.
Parameters
----------
recipe
functions
crystals
fc_name
Returns
-------
"""
fc: FitContribution = getattr(recipe, fc_name)
for name, (_, argnames) in functions.items():
_add_params_in_fc(recipe, fc, argnames[1:], tags=[name])
for name in crystals.keys():
pg: PDFGenerator = getattr(fc, name)
_add_params_in_pg(recipe, pg)
recipe.clearFitHooks()
return
def create_recipe_from_files(
equation: str,
cif_files: typing.Dict[str, str],
functions: typing.Dict[str, typing.Tuple[typing.Callable, typing.List[str]]],
data_file: typing.Dict[str, str],
meta_data: typing.Dict[str, typing.Union[str, int, float]] = None,
fc_name: str = "PDF"
) -> FitRecipe:
"""Create the FitRecipe object.
Parameters
----------
equation :
The equation of G(r).
cif_files :
A mapping from the name of variable in the equation to cif files of the crystal structure for PDF
calculation.
functions :
A mapping from the name of variable in the equation to the python function for PDF calculation.
The first argument of the function is the array of r, the other arguments are the parameters.
data_file :
The data file that be loaded into the data profile that contains both the metadata and the data.
meta_data :
Additional metadata to add into the data profile.
fc_name :
The name of the FitContribution in the FitRecipe. Default "PDF".
Returns
-------
A FitRecipe object.
"""
if meta_data is None:
meta_data = {}
crystals = {n: loadCrystal(f) for n, f in cif_files.items()}
pp = PDFParser()
pp.parseFile(data_file)
profile = Profile()
profile.loadParsedData(pp)
profile.meta.update(meta_data)
recipe = _create_recipe(equation, crystals, functions, profile, fc_name=fc_name)
_initialize_recipe(recipe, functions, crystals, fc_name=fc_name)
return recipe
# + [markdown] id="9c045e0e"
# We use the tool to create a recipe. The model is "sphere * bronze", where "sphere" is a spherical characteristic function and the "bronze" is the PDF from the bronze phase TiO2 crystal, whose structure is from the cif file we found in the former sections. The data is loaded from the data file. Besides the metadata in the data file, we also add the "qdamp" and "qbroad" parameters from the calibration.
# + id="ae339254"
recipe = create_recipe_from_files(
"sphere * bronze",
cif_files={"bronze": CIF_FILE_B},
functions={"sphere": (F.sphericalCF, ["r", "bronze_size"])},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + [markdown] id="1b7129cb"
# Here, we show the status of the FitRecipe. The first section in the printed text is the parameters to refine and their current value. As defined in the `_initialize_recipe`, the name will start with the name of the PDFGenerator, where is "bronze" here, and then will be followed by the name of the parameter in that PDFGenerator.
#
# The next section in the printed text is the data and parameter at the FitContribution level and the following sections will be all the parameters in the PDFGenerators.
# + colab={"base_uri": "https://localhost:8080/"} id="99a43ff6" outputId="6d69e60b-4d0e-4a9d-eb88-56d391ba3cb0"
recipe.show()
# + [markdown] id="bca3f606"
# ### Optimize the parameters
# + [markdown] id="1626d182"
# In the last section, we defined our FitRecipe. In this section, we will optimize the parameters in the FitRecipe using the least square regression. The tool is defined as below. Again, we define a helper function for doing this repeatedly with minimal typing. Feel free to reuse these helper functions (we will publish them somewhere soon).
# + id="6ef55d5e"
def optimize_params(
recipe: FitRecipe,
steps: typing.List[typing.List[str]],
rmin: float = None,
rmax: float = None,
rstep: float = None,
print_step: bool = True,
fc_name: str = "PDF",
**kwargs
) -> None:
"""Optimize the parameters in the FitRecipe object using least square regression.
Parameters
----------
recipe :
The FitRecipe object.
steps :
A list of lists of parameter names in the recipe. They will be free and refined one batch after another.
Usually, the scale, lattice should be refined before the APD and XYZ.
rmin :
The minimum r in the range for refinement. If None, use the minimum r in the data.
rmax :
The maximum r in the range for refinement. If None, use the maximum r in the data.
rstep :
The step of r in the range for refinement. If None, use the step of r in the data.
print_step :
If True, print out the refinement step. Default True.
fc_name :
The name of the FitContribution in the FitRecipe. Default "PDF".
kwargs :
The kwargs for the `scipy.optimize.least_square`.
Returns
-------
None.
"""
n = len(steps)
fc: FitContribution = getattr(recipe, fc_name)
p: Profile = fc.profile
p.setCalculationRange(xmin=rmin, xmax=rmax, dx=rstep)
for step in steps:
recipe.fix(*step)
for i, step in enumerate(steps):
recipe.free(*step)
if print_step:
print(
"Step {} / {}: refine {}".format(
i + 1, n, ", ".join(recipe.getNames())
),
end="\r"
)
least_squares(recipe.residual, recipe.getValues(), bounds=recipe.getBounds2(), **kwargs)
return
# + [markdown] id="7eaf73f4"
# We use it to do our first refinement. Usually, we free the parameters one batch after another instead of refining them all at once. The order is usually the scale and lattice constants, the ADPs and $\delta_2$, the positions of atoms and the parameters in the characteristic functions for the first fit.
#
# To begin with, we only refine the data in a small range and we will increase it to the whole range after we find a reasonably good starting model for the small range of the data so that we can save computation time.
# + colab={"base_uri": "https://localhost:8080/"} id="fca93a93" outputId="d361fa4b-cb46-4823-8eab-cdcfa9d8d501"
optimize_params(
recipe,
[
["bronze_scale", "bronze_lat"],
["bronze_adp", "bronze_delta2"],
["bronze_xyz"],
["bronze_size"]
],
rmin=1.6,
rmax=20.0,
rstep=0.02,
ftol=1e-4
)
# + [markdown] id="ff29c7c6"
# ### Visualize the fits
# + [markdown] id="10df0c68"
# In the last section, we refined our FitRecipe. In this section, we will look at the fits. We realize it using `matplotlib.pyplot`.
# + id="1482393e"
def visualize_fits(recipe: FitRecipe, xlim: typing.Tuple = None, fc_name: str = "PDF") -> None:
"""Visualize the fits in the FitRecipe object.
Parameters
----------
recipe :
The FitRecipe object.
xlim :
The boundary of the x to show in the plot.
fc_name :
The name of the FitContribution in the FitRecipe. Default "PDF".
Returns
-------
None.
"""
# get data
fc = getattr(recipe, fc_name)
r = fc.profile.x
g = fc.profile.y
gcalc = fc.profile.ycalc
if xlim is not None:
sel = np.logical_and(r >= xlim[0], r <= xlim[1])
r = r[sel]
g = g[sel]
gcalc = gcalc[sel]
gdiff = g - gcalc
diffzero = -0.8 * np.max(g) * np.ones_like(g)
# plot figure
_, ax = plt.subplots()
ax.plot(r, g, 'bo', label="G(r) Data")
ax.plot(r, gcalc, 'r-', label="G(r) Fit")
ax.plot(r, gdiff + diffzero, 'g-', label="G(r) Diff")
ax.plot(r, diffzero, 'k-')
ax.set_xlabel(r"$r (\AA)$")
ax.set_ylabel(r"$G (\AA^{-2})$")
ax.legend(loc=1)
plt.show()
return
# + [markdown] id="75939957"
# Here, we visualize the fits. It looks fine in general. We find the correct major phase for our sample, which is the TiO2 bronze phase.
# + colab={"base_uri": "https://localhost:8080/", "height": 285} id="418e0f12" outputId="8fc2ddb8-21aa-4b47-aa3a-ca5ba1cc1850"
visualize_fits(recipe)
# + [markdown] id="34114d81"
# ### Save the results in files
# + [markdown] id="31718c6e"
# In the last section, we saw our fits and were satisfied with the fits. In this section, we will save the results from the `FitRecipe`. We create the tool below to export the optimized values of the parameters, the data of the fits and the refined crystal structure in the files in a directory.
# + id="2dbe9dd1"
def save_results(
recipe: FitRecipe,
directory: str,
file_stem: str,
pg_names: typing.List[str] = None,
fc_name: str = "PDF"
) -> None:
"""Save the parameters, fits and structures in the FitRecipe object.
Parameters
----------
recipe :
The FitRecipe object.
directory :
The directory to output the files.
file_stem :
The stem of the filename.
pg_names :
The name of the PDFGenerators (it will also be the name of the structures) to save. If None, not to save.
fc_name
The name of the FitContribution in the FitRecipe. Default "PDF".
Returns
-------
None.
"""
d_path = Path(directory)
d_path.mkdir(parents=True, exist_ok=True)
f_path = d_path.joinpath(file_stem)
fr = FitResults(recipe)
fr.saveResults(str(f_path.with_suffix(".res")))
fc: FitContribution = getattr(recipe, fc_name)
profile: Profile = fc.profile
profile.savetxt(str(f_path.with_suffix(".fgr")))
if pg_names is not None:
for pg_name in pg_names:
pg: PDFGenerator = getattr(fc, pg_name)
stru: Crystal = pg.stru
cif_path = f_path.with_name(
"{}_{}".format(f_path.stem, pg_name)
).with_suffix(".cif")
with cif_path.open("w") as f:
stru.CIFOutput(f)
return
# + [markdown] id="9ca5ec01"
# We save the results in a folder "data/bronze".
# + id="82091cda"
save_results(recipe, "data/bronze", "bronze", ["bronze"])
# + [markdown] id="4a1a867a"
# Here, we show what files are saved.
# + colab={"base_uri": "https://localhost:8080/"} id="877560e7" outputId="b36da7ba-3c8b-4c48-947f-c4795bbb0478"
# !ls "./data/bronze"
# + [markdown] id="4fff7e54"
# The "bronze.res" is a file of optimized parameters.
# + colab={"base_uri": "https://localhost:8080/"} id="5cf16fcf" outputId="dfec3d71-89e4-4039-bfa8-8a661df64529"
# !cat "./data/bronze/bronze.res"
# + [markdown] id="4e82e3a3"
# The "bronze.fgr" is a four-column data file.
# + colab={"base_uri": "https://localhost:8080/"} id="e52cc227" outputId="4048d48f-d5c0-48ea-e307-a2b412b688d5"
# !head -10 "./data/bronze/bronze.fgr"
# + [markdown] id="2c825d30"
# The "bronze_bronze.cif" is a CIF file of the refined bronze phase structure.
# + colab={"base_uri": "https://localhost:8080/"} id="ac66b3e1" outputId="e89d7593-f037-44ef-f799-6825227709c7"
# !cat "./data/bronze/bronze_bronze.cif"
# + [markdown] id="8c002232"
# ## Use PDFitc to find the secondary phase
# + [markdown] id="9cc1ee2a"
# There are still some residuals in the fits. It is likely that there is a secondary phase in the sample that produces a smaller PDF signal and it is hidden in the residuals. We would like to find what this phase could be and thus we output the residuals in a data file alone and submit it to the PDFitc.
# + id="cff1b562"
def export_diff_from_fgr(fgr_file: str, dst_file: str) -> None:
"""Export the difference curve in another file from a file containing x, ycalc, y, dy.
Parameters
----------
fgr_file :
The input file containing four columns x, ycalc, y, dy.
dst_file :
The output file containing two columns x, y.
Returns
-------
None.s
"""
x, ycalc, y, _ = loadData(fgr_file).T
diff = y - ycalc
data = np.column_stack([x, diff])
np.savetxt(dst_file, data, header="x y")
return
# + id="51270e5d"
export_diff_from_fgr("./data/bronze/bronze.fgr", "./data/TiO2_residuals.gr")
# + [markdown] id="203dfb1a"
# We find the secondary phase may be the anatase phase (space group: "$I4_1amd$")
# + colab={"base_uri": "https://localhost:8080/", "height": 359} id="23a20b08" outputId="b4b0ce79-e92d-4b04-91e8-4381137d4a49"
df = pd.read_csv("./data/pdfitc_search_residuals.csv")
df[["rw", "formula", "space_group", "db", "db_id"]].head(10)
# + [markdown] id="3404a13e"
# ## Fit the data with the bronze phase and anatase phase
# + [markdown] id="d9a5ca02"
# We found that the secondary phase might be an anatase phase in the last section. We download its CIF file from the database and use it in our next fitting.
# + id="d796d082"
CIF_FILE_A = "./data/TiO2_anatase.cif"
# + [markdown] id="37ebc383"
# We create a model of mixture of bronze and anatase phase. The PDF is the linear combination of two PDFs.
# + id="f38b14f5"
recipe = create_recipe_from_files(
"sphere1 * bronze + sphere2 * anatase",
cif_files={"bronze": CIF_FILE_B, "anatase": CIF_FILE_A},
functions={
"sphere1": (F.sphericalCF, ["r", "bronze_size"]),
"sphere2": (F.sphericalCF, ["r", "anatase_size"])
},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + [markdown] id="2f6a0c9e"
# Since we have refined the bronze phase, we can use `initializeRecipe` to load the refined parameter values in the recipe for the bronze phase so that we can have a better starting point in the parameter space.
# + id="e7bf3f2b"
from diffpy.srfit.fitbase.fitresults import initializeRecipe
initializeRecipe(recipe, "./data/bronze/bronze.res")
# + [markdown] id="6d932d9d"
# We refined the parameters. This time, we use the tag "scale", "lat", "adp", "delta2" and "xyz" without specifying the name of the phases. It means the free the parameters in that catalog in all phases. It can save us from tedious typing.
# + colab={"base_uri": "https://localhost:8080/"} id="6a4d5be9" outputId="a742c763-1783-4323-f6de-27a80904a53d"
optimize_params(
recipe,
[
["scale", "lat"],
["adp", "delta2"],
["xyz"],
["bronze_size", "anatase_size"]
],
rmin=1.6,
rmax=20.0,
rstep=0.02,
ftol=1e-4
)
# + [markdown] id="72270812"
# The fits look better.
# + colab={"base_uri": "https://localhost:8080/", "height": 284} id="a7b7538d" outputId="ed9019a3-2cd1-4603-fa01-f7f156025767"
visualize_fits(recipe)
# + [markdown] id="58f6da76"
# We save the results in another folder.
# + id="f5b4ed2f"
save_results(recipe, "./data/bronze_anatase", "two_phase", ["bronze", "anatase"])
# + [markdown] id="0c9b22cb"
# ## Fit the data with bronze, anatase and ligand
# + [markdown] id="1341ca98"
# We know that the sample contains ligands. These ligands will produce a low frequency signal in the PDF because the standard deviation of the inter-molecular distances is much larger than the distances of atoms in a crystalline nanoparticle. The slow varying trend in the residuals from our last fit look like the signal from the ligands. We would like to include the PDF of the ligand in our model so that we can have a more accurate fits but at the same time, we don't want to deal with the complicated simulation of a bunch of molecules. Thus, we decide to use a analytic function to simulate the ligand PDF. It is a Gaussian damping sinusoidal wave defined in the function below.
# + id="e6939c70"
def ligand_pdf(r: np.ndarray, a: float, s: float, k: float, r0: float) -> np.ndarray:
"""The Gaussian damping cosine function. Simulate the PDF of the ligand.
Parameters
----------
r :
The array of r.
a :
The amplitude of the function.
s :
The decay rate.
k :
The wave vector.
r0 :
The zero phase r value.
Returns
-------
A data array of function values.
"""
return a * np.exp(-np.square(s * r)) * np.cos(k * (r - r0))
# + [markdown] id="83239761"
# We add this function into our model.
# + id="aee6ab9d"
recipe = create_recipe_from_files(
"sphere1 * bronze + sphere2 * anatase + ligand",
cif_files={"bronze": CIF_FILE_B, "anatase": CIF_FILE_A},
functions={
"sphere1": (F.sphericalCF, ["r", "bronze_size"]),
"sphere2": (F.sphericalCF, ["r", "anatase_size"]),
"ligand": (ligand_pdf, ["r", "ligand_a", "ligand_s", "ligand_k", "ligand_r0"])
},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + [markdown] id="8b708223"
# Like last time, we will use the parameter values from the two phase fit in the last section as the starting point.
# + id="65e635c2"
initializeRecipe(recipe, "./data/bronze_anatase/two_phase.res")
# + [markdown] id="174ee462"
# We set the parameters in our analytic function to be a reasonable value. Below shows the way to do that. All the parameters in the FitRecipe can be set in this way.
# + id="45521a86"
# set the values for the ligand PDF parameters
recipe.ligand_a.setValue(-0.01)
recipe.ligand_s.setValue(0.1)
recipe.ligand_k.setValue(1.5)
recipe.ligand_r0.setValue(3.5);
# + [markdown] id="6f7f0001"
# Here is the starting point of our fitting.
# + [markdown] id="5eb97e4e"
# We refine the FitRecipe starting from the ligand because the parameters in the bronze and anatase are loaded from the last refinement and there probably won't be large changes in them.
# + colab={"base_uri": "https://localhost:8080/"} id="c26a23ea" outputId="0dc7ecc6-bd30-42b7-a1cf-c3e3fe67f04a"
optimize_params(
recipe,
[
["ligand"],
["scale", "lat"],
["adp", "delta2"],
["xyz"],
["bronze_size", "anatase_size"]
],
rmin=1.6,
rmax=20.0,
rstep=0.02,
ftol=1e-4
)
# + [markdown] id="a5c9081c"
# Now, our fits look even better.
# + colab={"base_uri": "https://localhost:8080/", "height": 284} id="1c3775b2" outputId="5e53f43c-aa1a-4275-fd3c-cb7c72d155b1"
visualize_fits(recipe)
# + [markdown] id="5f79b78a"
# We save the results in another folder.
# + id="8cdae7a0"
save_results(recipe, "./data/bronze_anatase_ligand", "three_phase", ["bronze", "anatase"])
# + [markdown] id="666791ae"
# ## Fit the data up to 50 Å
# + [markdown] id="ea5f87d3"
# We have achieved a good fit and we think that the bronze, anatase, ligand mixture is our answer for what are inside our samples. We need to finally confirm it and obtain the structure parameters from the fitting of the whole range of PDF.
# + id="5d842828"
recipe = create_recipe_from_files(
"sphere1 * bronze + sphere2 * anatase + ligand",
cif_files={"bronze": CIF_FILE_B, "anatase": CIF_FILE_A},
functions={
"sphere1": (F.sphericalCF, ["r", "bronze_size"]),
"sphere2": (F.sphericalCF, ["r", "anatase_size"]),
"ligand": (ligand_pdf, ["r", "ligand_a", "ligand_s", "ligand_k", "ligand_r0"])
},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + id="91404d12"
initializeRecipe(recipe, "./data/bronze_anatase_ligand/three_phase.res")
# + colab={"base_uri": "https://localhost:8080/"} id="b76154a3" outputId="103780be-5bb5-46fb-e39c-c1450468ba9d"
optimize_params(
recipe,
[
["scale", "bronze_size", "anatase_size"],
["lat"],
["adp", "delta2"],
["xyz"],
["ligand"],
],
rmin=1.6,
rmax=50.0,
rstep=0.02,
ftol=1e-4
)
# + [markdown] id="b9bcf68d"
# The fits look good. However, if we look carefully at the high-$r$ range. The calculated PDF is over-damped. It is likely that the spherical characteristic function doesn't represent the real case of particle size.
# + id="663f68c2" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="8937a518-77cc-45a2-94c5-3dd4cf49d4f5"
visualize_fits(recipe)
# + id="db50b674" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="5a6cb2c5-dc11-4eb3-8bae-4b3921061b1b"
visualize_fits(recipe, xlim=(30, 50))
# + [markdown] id="773ee8e1"
# We save the results in another folder.
# + id="10e813c2"
save_results(recipe, "./data/bronze_anatase_ligand_50A", "three_phase_50A", ["bronze", "anatase"])
# + [markdown] id="f6f77914"
# ## Fit the data with a core-shell model
# + [markdown] id="85b495c9"
# Maybe the nanoparticle has a core-shell structure where the bronze phase core is wrapped in the anatase phase shell. In this section, we will try the core-shell model.
# + id="17cea174"
recipe = create_recipe_from_files(
"core * bronze + shell * anatase + ligand",
cif_files={"bronze": CIF_FILE_B, "anatase": CIF_FILE_A},
functions={
"core": (F.sphericalCF, ["r", "bronze_diameter"]),
"shell": (F.shellCF, ["r", "bronze_radius", "anatase_thickness"]),
"ligand": (ligand_pdf, ["r", "ligand_a", "ligand_s", "ligand_k", "ligand_r0"])
},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + id="e271771f"
initializeRecipe(recipe, "./data/bronze_anatase_ligand_50A/three_phase_50A.res")
# + id="17b3d17f"
recipe.bronze_diameter.setValue(40.)
recipe.bronze_radius.setValue(20.)
recipe.anatase_thickness.setValue(20.);
# + [markdown] id="c830f515"
# Here, we constrain the "bronze_diameter" by the "2 * bronze_radius" so that the diameter of the bronze phase in the spherical characteristic function will always be determined by the double of inner radius in the shell characteristic function.
# + id="1a997726"
recipe.constrain("bronze_diameter", "2 * bronze_radius")
# + id="e2d6786e" colab={"base_uri": "https://localhost:8080/"} outputId="4819c6a2-00d1-4136-9cd3-6a3c51022ea7"
optimize_params(
recipe,
[
["scale", "core", "shell"],
["lat"],
["adp", "delta2"],
["xyz"],
["ligand"],
],
rmin=1.6,
rmax=50.0,
rstep=0.02,
ftol=1e-4
)
# + id="da8ab926" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="bc7d2483-330d-4f05-a3ff-d506529f3988"
visualize_fits(recipe)
# + id="63987e84"
save_results(recipe, "./data/bronze_anatase_ligand_50A_coreshell", "three_phase_50A_coreshell", ["bronze", "anatase"])
# + [markdown] id="163613e4"
# Let's compare the results from the two fits.
# + id="50e9335a"
def visualize_grs_from_files(
fgr_files: typing.List[str],
xlim: typing.Tuple = None,
ax: plt.Axes = None,
labels: typing.List[str] = None
) -> None:
"""Visualize the G(r) in multiple files.
Parameters
----------
fgr_files :
A list of files containing the r, g data.
xlim :
The boundary of the x to show in the plot.
ax :
The Axes to show the plot.
labels :
The lables of the curves.
Returns
-------
None.
"""
if labels is None:
labels = []
if ax is None:
_, ax = plt.subplots()
for fgr_file in fgr_files:
r, g = loadData(fgr_file).T[:2]
if xlim is not None:
sel = np.logical_and(r >= xlim[0], r <= xlim[1])
r = r[sel]
g = g[sel]
# plot figure
ax.plot(r, g, '-')
ax.set_xlabel(r"$r (\AA)$")
ax.set_ylabel(r"$G (\AA^{-2})$")
if labels is not None:
ax.legend(labels, loc=1)
return
# + [markdown] id="2552e07b"
# It seems that there is no improvement to the fits at the high-$r$.
# + id="7ce7e64e"
SPHERICAL_FILE = "./data/bronze_anatase_ligand_50A/three_phase_50A.fgr"
CORESHELL_FILE = "./data/bronze_anatase_ligand_50A_coreshell/three_phase_50A_coreshell.fgr"
# + id="618159db" colab={"base_uri": "https://localhost:8080/", "height": 393} outputId="6d6740d2-58b4-46d4-b5ee-0c4872335b9e"
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
visualize_grs_from_files(
[GR_FILE, SPHERICAL_FILE, CORESHELL_FILE],
xlim=(30, 50),
ax=ax,
labels=["Data", "Spherical", "Core Shell"]
)
plt.show()
# + [markdown] id="529fc977"
# ## Use a spheroidal characteristic function
# + [markdown] id="2839810c"
# Maybe the particle shape is not a sphere but a spheroid. We will test this possibility by using the spheroidal characteristic function.
# + id="ff80fa9c"
recipe = create_recipe_from_files(
"spheroidal * bronze + sphere * anatase + ligand",
cif_files={"bronze": CIF_FILE_B, "anatase": CIF_FILE_A},
functions={
"spheroidal": (F.spheroidalCF, ["r", "bronze_erad", "bronze_prad"]),
"sphere": (F.sphericalCF, ["r", "anatase_size"]),
"ligand": (ligand_pdf, ["r", "ligand_a", "ligand_s", "ligand_k", "ligand_r0"])
},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + id="02dd5407"
initializeRecipe(recipe, "./data/bronze_anatase_ligand_50A/three_phase_50A.res")
# + id="332f927f"
recipe.bronze_erad.setValue(40.0)
recipe.bronze_prad.setValue(40.0);
# + id="22b49f5d" colab={"base_uri": "https://localhost:8080/"} outputId="e9ab62a6-dab1-4ba2-819a-16e0f627ef49"
optimize_params(
recipe,
[
["scale", "spheroidal", "sphere"],
["lat"],
["adp", "delta2"],
["xyz"],
["ligand"],
],
rmin=1.6,
rmax=50.0,
rstep=0.02,
ftol=1e-4
)
# + id="15e83665" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="a4e9aa73-d0be-4dd4-f259-3c49a90e461b"
visualize_fits(recipe)
# + id="0dce02d3"
save_results(recipe, "./data/bronze_anatase_ligand_50A_spheroidal", "three_phase_50A_spheroidal", ["bronze", "anatase"])
# + [markdown] id="7fef89e0"
# There is a improvement of the quality of the fits at the high-$r$. Maybe the shape of the particle is a spheroid.
# + id="a0e7db73"
SPHEROIDAL_FILE = "./data/bronze_anatase_ligand_50A_spheroidal/three_phase_50A_spheroidal.fgr"
# + id="5c9c4be4" colab={"base_uri": "https://localhost:8080/", "height": 393} outputId="ff29fa86-d98d-4bdb-b8ad-7d8d4e585d95"
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
visualize_grs_from_files(
[GR_FILE, SPHERICAL_FILE, CORESHELL_FILE, SPHEROIDAL_FILE],
xlim=(30, 50),
ax=ax,
labels=["Data", "Spherical", "Core Shell", "Spheroidal"]
)
plt.show()
# + [markdown] id="c1b6710b"
# ## Use a lognormal spherical characteristic function
# + [markdown] id="12142c1d"
# Maybe the particle sizes of the bronze phase nanoparticles are not uniform. They have a distribution. It is likely to be approximated by a lognormal distribution. In this section, we will try the lognormal distribution.
# + id="55f20d2d"
recipe = create_recipe_from_files(
"lognormal * bronze + sphere * anatase + ligand",
cif_files={"bronze": CIF_FILE_B, "anatase": CIF_FILE_A},
functions={
"lognormal": (F.lognormalSphericalCF, ["r", "bronze_size_mean", "bronze_size_std"]),
"sphere": (F.sphericalCF, ["r", "anatase_size"]),
"ligand": (ligand_pdf, ["r", "ligand_a", "ligand_s", "ligand_k", "ligand_r0"])
},
data_file=GR_FILE,
meta_data={"qdamp": 0.04, "qbroad": 0.02}
)
# + id="02ba2490"
initializeRecipe(recipe, "./data/bronze_anatase_ligand_50A/three_phase_50A.res")
# + id="47ff9f33"
recipe.bronze_size_mean.setValue(40.0)
recipe.bronze_size_std.setValue(5.0);
# + id="2426c84a" colab={"base_uri": "https://localhost:8080/"} outputId="43a4cc71-cc94-41be-8a57-c9f0a5980b64"
optimize_params(
recipe,
[
["scale", "sphere", "lognormal"],
["lat"],
["adp", "delta2"],
["xyz"],
["ligand"],
],
rmin=1.6,
rmax=50.0,
rstep=0.02,
ftol=1e-4
)
# + id="74f7db78" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="74d79317-9ddb-43dc-c438-0481d2cfb490"
visualize_fits(recipe)
# + id="87373dc7"
save_results(recipe, "./data/bronze_anatase_ligand_50A_lognormal", "three_phase_50A_lognormal", ["bronze", "anatase"])
# + [markdown] id="0d2f86c1"
# The lognormal spherical distribution function improve the quality of fits at the high-$r$ is slightly better than the spheroid characteristic function. May the size of the particles are not the same value but follows a distribution.
# + id="acc6b394"
LOGNORMAL_FILE = "./data/bronze_anatase_ligand_50A_lognormal/three_phase_50A_lognormal.fgr"
# + id="ede809c2" colab={"base_uri": "https://localhost:8080/", "height": 393} outputId="39212b95-de98-463b-c559-df286a4e1d40"
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
visualize_grs_from_files(
[GR_FILE, SPHERICAL_FILE, CORESHELL_FILE, SPHEROIDAL_FILE, LOGNORMAL_FILE],
xlim=(30, 50),
ax=ax,
labels=["Data", "Spherical", "Core Shell", "Spheroidal", "Lognormal Spherical"]
)
plt.show()
# + [markdown] id="f2414e24"
# ## Particle size
# + [markdown] id="bb8f5387"
# Below shows the TEM image of the sample taken before the ligand was added. The particles are not in the same size while at the same time not perfectly spherical.
#
# 
# + [markdown] id="7bf930a1"
# The TEM results show that the particles size in average is 75 Å while result from the PDF fitting using the spherical characteristic function is 50 Å. This is normal because the particle size in the characteristic function is the size of the domain of structural order, which cannot be larger than the physical size of the particle but in general is smaller due to disorder. This value thus may be smaller than what we saw in the TEM.
# + [markdown] id="29c47315"
# ## Summary
# + [markdown] id="fd96b1d0"
# We reveals that the sample consists of bronze TiO2 nanoparticles and anatase TiO2 nanoparticles and ligands. The bronze TiO2 nanoparticle is the majority as our collaborators expect and the anatase an impurity phase. Its proportion is about 9 %.
# + id="b5c8d283" colab={"base_uri": "https://localhost:8080/"} outputId="0ee74084-9a8a-4a2f-e602-cc92d4e8e3ca"
3.56452857e-02 / (3.44354912e-01 + 3.56452857e-02) * 100
# + [markdown] id="5d7d274a"
# The particle size of bronze phase is about 50 Å while the particle size of anatase phase is about 70 Å. The structure parameters of them are shown below.
# + id="9c8914a2" colab={"base_uri": "https://localhost:8080/"} outputId="318c1640-59c6-4be0-90e3-44437b1ea868"
# !cat "./data/bronze_anatase_ligand_50A/three_phase_50A.res"
# + [markdown] id="3d070d14"
# In this tutorial, we have introduced an universal way to build models to fit the PDF data using diffpy-cmi. The users can not only use any characteristic functions and structures in their models but also define their own calculators as python functions and refine the parameters in it. It offers the users the freedom to create and refine models beyond the traditional ways of multi-phase modeling where the PDF can only be calculated by the structures and a limited number of predefined characteristic functions.
|
notebooks/03_example_script_for_colab_final_version.ipynb
|
# # [FMA: A Dataset For Music Analysis](https://github.com/mdeff/fma)
#
# <NAME>, <NAME>, <NAME>, <NAME>, EPFL LTS2.
#
# ## Free Music Archive web API
#
# All the data in the `raw_*.csv` tables was collected from the Free Music Archive [public API](https://freemusicarchive.org/api). With this notebook, you can:
# * reconstruct the original data,
# * update some fields, e.g. the `track listens` (play count),
# * augment the data with newer fields wich may have been introduced in their API,
# * update the dataset with new songs added to the archive.
#
# Notes:
# * You need a key to access the API, which you can [request online](https://freemusicarchive.org/api/agreement) and write into your `.env` file as a new line reading `FMA_KEY=MYPERSONALKEY`.
# * Requests take some hunderd milliseconds to complete.
import os
import IPython.display as ipd
import utils
fma = utils.FreeMusicArchive(os.environ.get('FMA_KEY'))
# ## 1 Get recently added tracks
#
# * `track_id` are assigned in monotonically increasing order.
# * Tracks can be removed, so that number does not indicate the number of available tracks.
for track_id, artist_name, date_created in zip(*fma.get_recent_tracks()):
print(track_id, date_created, artist_name)
# ## 2 Get metadata about tracks, albums and artists
#
# Given IDs, we can get information about tracks, albums and artists. See the available fields in the [API documentation](https://freemusicarchive.org/api).
fma.get_track(track_id=2, fields=['track_title', 'track_date_created',
'track_duration', 'track_bit_rate',
'track_listens', 'track_interest', 'track_comments', 'track_favorites',
'artist_id', 'album_id'])
fma.get_track_genres(track_id=20)
fma.get_album(album_id=1, fields=['album_title', 'album_tracks',
'album_listens', 'album_comments', 'album_favorites',
'album_date_created', 'album_date_released'])
fma.get_artist(artist_id=1, fields=['artist_name', 'artist_location',
'artist_comments', 'artist_favorites'])
# ## 3 Get data, i.e. raw audio
#
# We can download the original audio as well. Tracks are provided by the archive as MP3 with various bit and sample rates.
track_file = fma.get_track(2, 'track_file')
fma.download_track(track_file, path='track.mp3')
# ## 4 Get genres
#
# Instead of compiling the genres of each track, we can get all the genres present on the archive with some API calls.
genres = fma.get_all_genres()
print('{} genres'.format(genres.shape[0]))
genres[10:25]
# And look for genres related to Rock.
genres[['Rock' in title for title in genres['genre_title']]]
genres[genres['genre_parent_id'] == '12']
|
webapi.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import json
import requests
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.grid'] = True
import pandas as pd
import seaborn as sns
import itertools
import collections
import random
import time
data_dir = 'results'
before = 'pangaea_20200804.json'
def read_results(data):
final = []
for data_dict in data:
results = {}
results['identifier'] = data_dict['identifier']
dd = data_dict['result'] # list of dict
for d in dd:
metric_identifier = d.get('metric_identifier')
sub_principle = metric_identifier.split('-')[1]
principle = sub_principle[0]+'_earned'
principle_total = sub_principle[0]+'_total'
if not sub_principle in results:
results[sub_principle] = d['score']['earned']
else:
results[sub_principle] += d['score']['earned']
if not principle in results:
results[principle] = d['score']['earned']
else:
results[principle] += d['score']['earned']
if not principle_total in results:
results[principle_total] = d['score']['total']
else:
results[principle_total] += d['score']['total']
final.append(results)
df_results = pd.DataFrame.from_dict(final)
cols = ['identifier','F1','F2','F3','F4','A1','A1','I1','I3','R1','R1.1','R1.2','R1.3','F_earned','F_total','A_earned','A_total','I_earned','I_total','R_earned','R_total']
df_results = df_results[cols]
df_results ['F_Principle'] = (df_results ['F_earned'] / df_results ['F_total'] ).round(2)
df_results ['A_Principle'] = (df_results ['A_earned'] / df_results ['A_total'] ).round(2)
df_results ['I_Principle'] = (df_results ['I_earned'] / df_results ['I_total'] ).round(2)
df_results ['R_Principle' ]= (df_results ['R_earned'] / df_results ['R_total'] ).round(2)
df_results = df_results[['identifier','F_Principle','A_Principle','I_Principle','R_Principle']]
return df_results
def histograms_plot(dataframe, features, rows, cols, figname, title):
fig=plt.figure(figsize=(20,4))
# set palette
palette = itertools.cycle(sns.color_palette())
for i, feature in enumerate(features):
c = next(palette)
ax=fig.add_subplot(rows,cols,i+1)
dataframe[feature].plot.hist(bins=20, ax=ax, color=c, range=(0, 1.0), align="left")
ax.set_title(principles.get(feature))
ax.set(xlabel="Score", ylabel="Frequency")
fig.subplots_adjust(top=0.8)
plt.savefig(figname)
plt.suptitle(title,fontsize=15)
plt.show()
# +
principles = {}
principles['F_Principle'] = 'Findability'
principles['A_Principle'] = 'Accessibility'
principles['I_Principle'] = 'Interoperability'
principles['R_Principle'] = 'Reusability'
timestr = time.strftime("%Y%m%d")
# -
# visualize score before improvement
with open(data_dir+'/'+before) as json_file:
before_data = json.load(json_file)
df_before = read_results(before_data)
df_before.head()
fig_name_before = data_dir+'/'+'sub_pangaea_before_'+timestr+'.png'
title_before = 'FAIR Scores of PANGAEA Datasets By Principle (Before Improvement,'+ ' n=' + str(len(df_before))+')'
histograms_plot(df_before, df_before.columns[1:], 1, 4, fig_name_before, title_before)
# Assess previous datasets
datasets = df_before['identifier'].tolist()
# %%time
fuji_service = 'http://localhost:1071/fuji/api/v1/evaluate'
after_data = []
for d in datasets:
req = {'object_identifier':d, 'test_debug':True}
r = requests.post(fuji_service, data=json.dumps(req), headers={'Content-Type': 'application/json'}, auth=('username', 'password'))
json_data = r.json()
records = {}
records['identifier'] = d
records['result'] = json_data
after_data.append(records)
file_name = data_dir+'/'+'pangaea_'+timestr+'.json'
with open(file_name, 'w') as f:
json.dump(after_data, f)
file_name ='results/pangaea_20200807.json'
with open(file_name) as json_file:
after_data = json.load(json_file)
df_after = read_results(after_data)
df_after.head()
# +
b = df_before['identifier'].tolist()
a = df_after['identifier'].tolist()
if set(a) == set(b):
print('same')
# -
df_after.head()
df_after[df_after.F_Principle<0.8]
df_before[df_before.identifier=='https://doi.org/10.1594/PANGAEA.398005']
# visualize score after improvement
# +
with open(file_name) as json_file:
data = json.load(json_file)
df_after = read_results(data)
df_after.head()
# -
fig_name_after = data_dir+'/'+'sub_pangaea_after_'+timestr+'.png'
title_after = 'FAIR Scores of PANGAEA Datasets By Principle (After Improvement,'+ ' n=' + str(len(df_after))+')'
histograms_plot(df_after, df_after.columns[1:], 1, 4, fig_name_after, title_after)
|
notebooks/.ipynb_checkpoints/Test PANGAEA Datasets - Results (Before,After)-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Numba parallel
import numpy as np
from numba import prange, njit, guvectorize
# Lets first get some test resources. The names and the structure from the examples are taken from the calculation of the expected value function in [respy](https://respy.readthedocs.io/en/latest/). The original function can be found [here](https://github.com/OpenSourceEconomics/respy/blob/master/respy/shared.py).
wages = np.ones((100, 4))
nonpecs = np.ones((100, 4))
continuation_values = np.ones((100, 4))
period_draws_emax_risk = np.ones((50, 4))
delta = 0.95
# ## Parallelization of `@jit` functions
#
# ``numba`` offers automatic parallelization of jit functions. This can either happen implicit on array operations or explicit with the keyword statement `parallel=True` and e.g. parralel loops with `prange`.
# The resources for this can be found [here](https://numba.pydata.org/numba-doc/latest/user/parallel.html).
#
@njit(parallel=True)
def parralel_loop(wages, nonpecs, continuation_values, draws, delta):
num_states, n_ch = wages.shape
n_draws, n_choices = draws.shape
out = 0
for k in prange(num_states):
for i in prange(n_draws):
for j in prange(n_choices):
out += (
wages[k, j] * draws[i, j]
+ nonpecs[k, j]
+ delta * continuation_values[k, j]
)
return out
# ## Diagnostics
#
# When calling an explicit parallelized function, ``numba`` tries to create separate calculations to run multiple kernels or threads. The optimization behavior can be inspected by using
# `func.parallel_diagnostics(level=4)`.
#
# The levels can vary from one to four. The resources to this can be found [here](https://numba.pydata.org/numba-doc/latest/user/parallel.html#diagnostics).
#
# An example of the two things above:
parralel_loop(
wages, nonpecs, continuation_values, period_draws_emax_risk, delta
)
parralel_loop.parallel_diagnostics(level=4)
# ## Parallelization of `@guvectorize` functions
#
# When using `@guvectorize`, you can define functions on multiple arrays, which then can be parallelized across the entries of the arrays with `target=”parallel”`. Details to `@guvectorize` can be found [here](https://numba.pydata.org/numba-doc/latest/reference/jit-compilation.html#numba.guvectorize).
@guvectorize(
["f8[:], f8[:], f8[:], f8[:, :], f8, f8[:]"],
"(n_choices), (n_choices), (n_choices), (n_draws, n_choices), () -> ()",
nopython=True,
target="parallel",
)
def calculate_expected_value_functions(
wages, nonpecs, continuation_values, draws, delta, expected_value_functions
):
n_draws, n_choices = draws.shape
expected_value_functions[0] = 0
for i in range(n_draws):
max_value_functions = 0
for j in range(n_choices):
value_function = (
wages[j] * draws[i, j]
+ nonpecs[j]
+ delta * continuation_values[j]
)
if value_function > max_value_functions:
max_value_functions = value_function
expected_value_functions[0] += max_value_functions
expected_value_functions[0] /= n_draws
# The statement `target=”parallel”` does not explicitly state that the code inside the `@guvectorize` function is parallelized itself. However, one can rule out this possibility, if the function diagnosed with the tools described above does not offer any parallelization. Thus, to my knowledge, there is no explicit possibility to fix a parallelization structure. One can only design the code, such that the intended parallelization happens when the `@guvectorized` function is called.
|
templates/02_numba_parallel/02_numba_parallel.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="AYV_dMVDxyc2"
# [](https://github.com/lab-ml/nn)
# [](https://colab.research.google.com/github/lab-ml/nn/blob/master/labml_nn/normalization/group_norm/experiment.ipynb)
#
# ## Weight Standardization & Batch-Channel Normalization - CIFAR 10
#
# This is an experiment training a model with Weight Standardization & Batch-Channel Normalization to classify CIFAR-10 dataset.
# + [markdown] id="AahG_i2y5tY9"
# Install the `labml-nn` package. Optionally `wandb` package for experiment stats.
# + id="ZCzmCrAIVg0L" colab={"base_uri": "https://localhost:8080/"} outputId="8332d030-2fab-4a24-876f-152b7f99a226"
# !pip install labml-nn wandb
# + [markdown] id="SE2VUQ6L5zxI"
# Imports
# + id="0hJXx_g0wS2C"
import torch
import torch.nn as nn
from labml import experiment
from labml_nn.normalization.weight_standardization.experiment import CIFAR10Configs as Configs
# + [markdown] id="Lpggo0wM6qb-"
# Create an experiment
# + id="bFcr9k-l4cAg"
experiment.create(name="cifar10", comment="WS + BCN")
# + [markdown] id="-OnHLi626tJt"
# Initialize configurations
# + id="Piz0c5f44hRo"
conf = Configs()
# + [markdown] id="wwMzCqpD6vkL"
# Set experiment configurations and assign a configurations dictionary to override configurations
# + colab={"base_uri": "https://localhost:8080/", "height": 17} id="e6hmQhTw4nks" outputId="33a5979f-70eb-4d19-e82a-a6b113316cca"
experiment.configs(conf, {
'optimizer.optimizer': 'Adam',
'optimizer.learning_rate': 2.5e-4,
'train_batch_size': 64,
})
# + [markdown] id="KJZRf8527GxL"
# Start the experiment and run the training loop.
# + colab={"base_uri": "https://localhost:8080/", "height": 933, "referenced_widgets": ["1dacd9c82caf40c8b2def0c5fe4f7643", "67e37901c44b4bde9062014542cae018", "9d57be286b7244ca9a5f74cff6c3cf4e", "9e511aaba1204ea9985fb6f55e024039", "61849c45ed0c4436995bb81d7efdac7e", "7ed3376588734d64a229fd8dd6bfe06e", "afd6865a483f4273addb343059632961", "7b765f7623474999a8c9815e02c1cc6b"]} id="aIAWo7Fw5DR8" outputId="cf3d16aa-a9a1-4fd4-cfb4-23e8ea5ea940"
with experiment.start():
conf.run()
# + id="oBXXlP2b7XZO"
|
labml_nn/normalization/weight_standardization/experiment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (Data Science)
# language: python
# name: python3__SAGEMAKER_INTERNAL__arn:aws:sagemaker:us-east-1:081325390199:image/datascience-1.0
# ---
# # Part 2: Train, Check Bias, Tune, Record Lineage, and Register a Model
# <a id='aud-overview'> </a>
#
# ## [Overview](./0-AutoClaimFraudDetection.ipynb)
# * [Notebook 0 : Overview, Architecture and Data Exploration](./0-AutoClaimFraudDetection.ipynb)
# * [Notebook 1: Data Prep, Process, Store Features](./1-data-prep-e2e.ipynb)
# * **[Notebook 2: Train, Check Bias, Tune, Record Lineage, and Register a Model](./2-lineage-train-assess-bias-tune-registry-e2e.ipynb)**
# * **[Architecture](#train)**
# * **[Train a model using XGBoost](#aud-train-model)**
# * **[Model lineage with artifacts and associations](#model-lineage)**
# * **[Evaluate the model for bias with Clarify](#check-bias)**
# * **[Deposit Model and Lineage in SageMaker Model Registry](#model-registry)**
# * [Notebook 3: Mitigate Bias, Train New Model, Store in Registry](./3-mitigate-bias-train-model2-registry-e2e.ipynb)
# * [Notebook 4: Deploy Model, Run Predictions](./4-deploy-run-inference-e2e.ipynb)
# * [Notebook 5 : Create and Run an End-to-End Pipeline to Deploy the Model](./5-pipeline-e2e.ipynb)
# In this section we will show how you can assess pre-training and post-training bias with SageMaker Clarify, Train the Model using XGBoost on SageMaker, and then finally deposit it in the Model Registry, along with the Lineage of Artifacts that were created along the way: data, code and model metadata.
#
# In this second model, you will fix the gender imbalance in the dataset using SMOTE and train another model using XGBoost. This model will also be saved to our registry and eventually approved for deployment.
# <a id ='train'> </a>
# ## Architecture for the ML Lifecycle Stage: Train, Check Bias, Tune, Record Lineage, Register Model
# [overview](#overview)
# ___
#
# 
# ### Install required and/or update libraries
# !python -m pip install -Uq pip
# !python -m pip install -q awswrangler==2.2.0 imbalanced-learn==0.7.0 sagemaker==2.23.1 boto3==1.16.48
# To apply the update to the current kernel, run the following code to refresh the kernel.
import IPython
IPython.Application.instance().kernel.do_shutdown(True)
# ### Load stored variables
# Run the cell below to load any prevously created variables. You should see a print-out of the existing variables. If you don't see anything you may need to create them again or it may be your first time running this notebook.
# %store -r
# %store
# **<font color='red'>Important</font>: You must have run the previous sequancial notebooks to retrieve variables using the StoreMagic command.**
# ### Import libraries
# +
import json
import time
import boto3
import sagemaker
import numpy as np
import pandas as pd
import awswrangler as wr
from sagemaker.inputs import TrainingInput
from sagemaker.xgboost.estimator import XGBoost
from model_package_src.inference_specification import InferenceSpecification
# -
# ### Set region, boto3 and SageMaker SDK variables
#You can change this to a region of your choice
import sagemaker
region = sagemaker.Session().boto_region_name
print("Using AWS Region: {}".format(region))
# +
boto3.setup_default_session(region_name=region)
boto_session = boto3.Session(region_name=region)
s3_client = boto3.client('s3', region_name=region)
sagemaker_boto_client = boto_session.client('sagemaker')
sagemaker_session = sagemaker.session.Session(
boto_session=boto_session,
sagemaker_client=sagemaker_boto_client)
sagemaker_role = sagemaker.get_execution_role()
account_id = boto3.client('sts').get_caller_identity()["Account"]
# +
# variables used for parameterizing the notebook run
estimator_output_path = f's3://{bucket}/{prefix}/training_jobs'
train_instance_count = 1
train_instance_type = "ml.m4.xlarge"
bias_report_1_output_path = f's3://{bucket}/{prefix}/clarify-output/bias_1'
xgb_model_name = 'xgb-insurance-claims-fraud-model'
train_instance_count = 1
train_instance_type = "ml.m5.large"
predictor_instance_count = 1
predictor_instance_type = "ml.c5.large"
batch_transform_instance_count = 1
batch_transform_instance_type = "ml.c5.large"
claify_instance_count = 1
clairfy_instance_type = 'ml.c5.large'
# -
# <a id='aud-train-model'></a>
# ## Train a model using XGBoost
#
# [overview](#overview)
# ___
# Once the training and test datasets have been persisted in S3, you can start training a model by defining which SageMaker Estimator you'd like to use. For this guide, you will use the [XGBoost Open Source Framework](https://sagemaker.readthedocs.io/en/stable/frameworks/xgboost/xgboost.html) to train your model. This estimator is accessed via the SageMaker SDK, but mirrors the open source version of the [XGBoost Python package](https://xgboost.readthedocs.io/en/latest/python/index.html). Any functioanlity provided by the XGBoost Python package can be implemented in your training script.
# ### Set the hyperparameters
# These are the parameters which will be sent to our training script in order to train the model. Although they are all defined as "hyperparameters" here, they can encompass XGBoost's [Learning Task Parameters](https://xgboost.readthedocs.io/en/latest/parameter.html#learning-task-parameters), [Tree Booster Parameters](https://xgboost.readthedocs.io/en/latest/parameter.html#parameters-for-tree-booster), or any other parameters you'd like to configure for XGBoost.
hyperparameters = {
"max_depth": "3",
"eta": "0.2",
"objective": "binary:logistic",
"num_round": "100",
}
# %store hyperparameters
# ### Create and fit the estimator
# If you want to explore the breadth of functionailty offered by the SageMaker XGBoost Framework you can read about all the configuration parameters by referencing the inhereting classes. The XGBoost class inherets from the Framework class and Framework inherets from the EstimatorBase class:
# * [XGBoost Estimator documentation](https://sagemaker.readthedocs.io/en/stable/frameworks/xgboost/xgboost.html#sagemaker.xgboost.estimator.XGBoost)
# * [Framework documentation](https://sagemaker.readthedocs.io/en/stable/api/training/estimators.html#sagemaker.estimator.Framework)
# * [EstimatorBase documentation](https://sagemaker.readthedocs.io/en/stable/api/training/estimators.html#sagemaker.estimator.EstimatorBase)
# +
xgboost_container = sagemaker.image_uris.retrieve("xgboost", region, "1.2-1")
xgb_estimator = sagemaker.estimator.Estimator(image_uri=xgboost_container,
output_path = estimator_output_path,
hyperparameters = hyperparameters,
role = sagemaker_role,
instance_count = train_instance_count,
instance_type = train_instance_type,
framework_version = "1.0-1")
# +
if 'training_job_1_name' not in locals():
train_input = TrainingInput(train_data_uri, content_type='csv')
xgb_estimator.fit(inputs = {'train': train_input})
training_job_1_name = xgb_estimator.latest_training_job.job_name
# %store training_job_1_name
else:
print(f'Using previous training job: {training_job_1_name}')
# +
train_input = TrainingInput(train_data_uri, content_type='csv')
xgb_estimator.fit(inputs = {'train': train_input})
# -
# <a id='model-lineage'></a>
# ## Model lineage with artifacts and associations
#
# [Overview](#aud-overview)
# ___
# Amazon SageMaker ML Lineage Tracking creates and stores information about the steps of a machine learning (ML) workflow from data preparation to model deployment. With the tracking information you can reproduce the workflow steps, track model and dataset lineage, and establish model governance and audit standards. With SageMaker Lineage Tracking data scientists and model builders can do the following:
# * Keep a running history of model discovery experiments.
# * Establish model governance by tracking model lineage artifacts for auditing and compliance verification.
# * Clone and rerun workflows to experiment with what-if scenarios while developing models.
# * Share a workflow that colleagues can reproduce and enhance (for example, while collaborating on solving a business problem).
# * Clone and rerun workflows with additional debugging or logging routines, or new input variations for troubleshooting issues in production models.
#
#
# <a id='register-artifacts'></a>
# ### Register artifacts
# Although the `xgb_estimator` object retains much the data we need to learn about how the model was trained, it is, in fact, an ephermeral object which SageMaker does not persist and cannot be re-instantiated at a later time. Although we lose some of its convieneces once it is gone, we can still get back all the data we need by accessing the training jobs it once created.
training_job_1_info = sagemaker_boto_client.describe_training_job(TrainingJobName=training_job_1_name)
# #### Code artifact
# +
# return any existing artifact which match the our training job's code arn
# ====>
# extract the training code uri and check if it's an exisiting artifact
code_s3_uri = training_job_2_info['AlgorithmSpecification']['TrainingImage']
matching_artifacts = list(sagemaker.lineage.artifact.Artifact.list(
source_uri=code_s3_uri,
sagemaker_session=sagemaker_session))
# use existing arifact if it's already been created, otherwise create a new artifact
if matching_artifacts:
code_artifact = matching_artifacts[0]
print(f'Using existing artifact: {code_artifact.artifact_arn}')
else:
code_artifact = sagemaker.lineage.artifact.Artifact.create(
artifact_name='TrainingScript',
source_uri=code_s3_uri,
artifact_type='Code',
sagemaker_session=sagemaker_session)
print(f'Create artifact {code_artifact.artifact_arn}: SUCCESSFUL')
# -
# #### Training data artifact
# +
training_data_s3_uri = training_job_1_info['InputDataConfig'][0]['DataSource']['S3DataSource']['S3Uri']
matching_artifacts = list(sagemaker.lineage.artifact.Artifact.list(
source_uri=training_data_s3_uri,
sagemaker_session=sagemaker_session))
if matching_artifacts:
training_data_artifact = matching_artifacts[0]
print(f'Using existing artifact: {training_data_artifact.artifact_arn}')
else:
training_data_artifact = sagemaker.lineage.artifact.Artifact.create(
artifact_name='TrainingData',
source_uri=training_data_s3_uri,
artifact_type='Dataset',
sagemaker_session=sagemaker_session)
print(f'Create artifact {training_data_artifact.artifact_arn}: SUCCESSFUL')
# -
# #### Model artifact
# +
trained_model_s3_uri = training_job_1_info['ModelArtifacts']['S3ModelArtifacts']
matching_artifacts = list(sagemaker.lineage.artifact.Artifact.list(
source_uri=trained_model_s3_uri,
sagemaker_session=sagemaker_session))
if matching_artifacts:
model_artifact = matching_artifacts[0]
print(f'Using existing artifact: {model_artifact.artifact_arn}')
else:
model_artifact = sagemaker.lineage.artifact.Artifact.create(
artifact_name='TrainedModel',
source_uri=trained_model_s3_uri,
artifact_type='Model',
sagemaker_session=sagemaker_session)
print(f'Create artifact {model_artifact.artifact_arn}: SUCCESSFUL')
# -
# <a id='Set-artifact-associations'></a>
# ### Set artifact associations
trial_component = sagemaker_boto_client.describe_trial_component(TrialComponentName=training_job_1_name+'-aws-training-job')
trial_component_arn = trial_component['TrialComponentArn']
# #### Input artifacts
# +
input_artifacts = [code_artifact, training_data_artifact]
for a in input_artifacts:
try:
sagemaker.lineage.association.Association.create(
source_arn=a.artifact_arn,
destination_arn=trial_component_arn,
association_type='ContributedTo',
sagemaker_session=sagemaker_session)
print(f"Association with {a.artifact_type}: SUCCEESFUL")
except:
print(f"Association already exists with {a.artifact_type}")
# -
# #### Output artifacts
# +
output_artifacts = [model_artifact]
for a in output_artifacts:
try:
sagemaker.lineage.association.Association.create(
source_arn=a.artifact_arn,
destination_arn=trial_component_arn,
association_type='Produced',
sagemaker_session=sagemaker_session)
print(f"Association with {a.artifact_type}: SUCCESSFUL")
except:
print(f"Association already exists with {a.artifact_type}")
# -
# <a id='check-bias'></a>
# ## Evaluate model for bias with Clarify
#
# [overview](#aud-overview)
# ___
# Amazon SageMaker Clarify helps improve your machine learning (ML) models by detecting potential bias and helping explain the predictions that models make. It helps you identify various types of bias in pretraining data and in posttraining that can emerge during model training or when the model is in production. SageMaker Clarify helps explain how these models make predictions using a feature attribution approach. It also monitors inferences models make in production for bias or feature attribution drift. The fairness and explainability functionality provided by SageMaker Clarify provides components that help AWS customers build less biased and more understandable machine learning models. It also provides tools to help you generate model governance reports which you can use to inform risk and compliance teams, and external regulators.
#
# You can reference the [SageMaker Developer Guide](https://docs.aws.amazon.com/sagemaker/latest/dg/clarify-fairness-and-explainability.html) for more information about SageMaker Clarify.
# ### Create model from estimator
# +
model_1_name = f'{prefix}-xgboost-pre-smote'
# %store model_1_name
model_matches = sagemaker_boto_client.list_models(NameContains=model_1_name)['Models']
if not model_matches:
model_1 = sagemaker_session.create_model_from_job(
name=model_1_name,
training_job_name=training_job_1_info['TrainingJobName'],
role=sagemaker_role,
image_uri=training_job_1_info['AlgorithmSpecification']['TrainingImage'])
else:
print(f"Model {model_1_name} already exists.")
# -
# <a id='bias-v1'></a>
# ### Check for data set bias and model bias
#
# With SageMaker, we can check for pre-training and post-training bias. Pre-training metrics show pre-existing bias in that data, while post-training metrics show bias in the predictions from the model. Using the SageMaker SDK, we can specify which groups we want to check bias across and which metrics we'd like to show.
#
# To run the full Clarify job, you must un-comment the code in the cell below. Running the job will take ~15 minutes. If you wish to save time, you can view the results in the next cell after which loads a pre-generated output if no bias job was run.
# +
train_cols = wr.s3.read_csv(training_data_s3_uri).columns.to_list()
clarify_processor = sagemaker.clarify.SageMakerClarifyProcessor(
role=sagemaker_role,
instance_count=1,
instance_type='ml.c4.xlarge',
sagemaker_session=sagemaker_session)
bias_data_config = sagemaker.clarify.DataConfig(
s3_data_input_path=train_data_uri,
s3_output_path=bias_report_1_output_path,
label='fraud',
headers=train_cols,
dataset_type='text/csv')
model_config = sagemaker.clarify.ModelConfig(
model_name=model_1_name,
instance_type=train_instance_type,
instance_count=1,
accept_type='text/csv')
predictions_config = sagemaker.clarify.ModelPredictedLabelConfig(probability_threshold=0.5)
bias_config = sagemaker.clarify.BiasConfig(
label_values_or_threshold=[0],
facet_name='customer_gender_female',
facet_values_or_threshold=[1])
# un-comment the code below to run the whole job
# if 'clarify_bias_job_1_name' not in locals():
# clarify_processor.run_bias(
# data_config=bias_data_config,
# bias_config=bias_config,
# model_config=model_config,
# model_predicted_label_config=predictions_config,
# pre_training_methods='all',
# post_training_methods='all')
# clarify_bias_job_1_name = clarify_processor.latest_job.name
# %store clarify_bias_job_1_name
# else:
# print(f'Clarify job {clarify_bias_job_name} has already run successfully.')
# -
# Results will be stored in `/opt/ml/processing/output/report.pdf`
# Training to achieve over 90 percent classification accuracy, may be easily possible on an imbalanced classification problem.
#
# Thus, expectations developed regarding classification accuracy that are in reality contingent on balanced class distributions will lead to wrong, misleading assumptions and conclusions : misleading the data scientist and viewers into believing that a model has extremely performance when , actually, it does not.
# ### View results of Clarify job (shortcut)
# Running Clarify on your dataset or model can take ~15 minutes. If you don't have time to run the job, you can view the pre-generated results included with this demo. Otherwise, you can run the job by un-commenting the code in the cell above.
# +
if 'clarify_bias_job_name' in locals():
s3_client.download_file(Bucket=bucket, Key=f'{prefix}/clarify-output/bias-1/analysis.json', Filename='clarify_output/bias_1/analysis.json')
print(f'Downloaded analysis from previous Clarify job: {clarify_bias_job_name}')
else:
print(f'Loading pre-generated analysis file...')
with open('clarify_output/bias_1/analysis.json', 'r') as f:
bias_analysis = json.load(f)
results = bias_analysis['pre_training_bias_metrics']['facets']['customer_gender_female'][0]['metrics'][1]
print(json.dumps(results, indent=4))
# -
# In this example dataset, the data is biased against females with only 38.9% of the data samples from female customers. We will address this in the next notebook where we show how we mitigate this class imbalance bias. Although we are only addressing Class Imbalance as an exemplar of bias statistics, you can also take into consideration many other factors of bias. For more detail, see : [Fairness Measures for Machine Learning in Finance](https://pages.awscloud.com/rs/112-TZM-766/images/Fairness.Measures.for.Machine.Learning.in.Finance.pdf)
#
# for a more detailed example look at [this](https://github.com/aws/amazon-sagemaker-examples/blob/master/sagemaker_processing/fairness_and_explainability/fairness_and_explainability.ipynb) github example.
# For more detailed resulst let's look at the generated report, that can be found here: `s3://{bucket}/e2e-fraud-detect/clarify/bias-2/report.pdf`
# +
# #uncomment to copy report and view
# # !aws s3 cp s3://{bucket}/fraud-detect-demo/clarify-output/bias_1/report.pdf ./clarify_output
# -
# <a id='model-registry'></a>
# ## Deposit Model and Lineage in SageMaker Model Registry
#
# [overview](#aud-overview)
# ____
# Once a useful model has been trained and its artifacts properly associated, the next step is to save the model in a registry for future reference and possible deployment.
#
# ### Create Model Package Group
# A Model Package Groups holds multiple versions or iterations of a model. Though it is not required to create them for every model in the registry, they help organize various models which all have the same purpose and provide autiomatic versioning.
if 'mpg_name' not in locals():
mpg_name = prefix
# %store mpg_name
print(f'Model Package Group name: {mpg_name}')
mpg_input_dict = {
'ModelPackageGroupName': mpg_name,
'ModelPackageGroupDescription': 'Insurance claim fraud detection'
}
# +
matching_mpg = sagemaker_boto_client.list_model_package_groups(NameContains=mpg_name)['ModelPackageGroupSummaryList']
if matching_mpg:
print(f'Using existing Model Package Group: {mpg_name}')
else:
mpg_response = sagemaker_boto_client.create_model_package_group(**mpg_input_dict)
print(f'Create Model Package Group {mpg_name}: SUCCESSFUL')
# %store mpg_name
# -
# ### Create Model Package for trained model
# #### Create and upload a metrics report
# +
model_metrics_report = {'classification_metrics': {}}
for metric in training_job_1_info['FinalMetricDataList']:
stat = {metric['MetricName']: {'value': metric['Value']}}
model_metrics_report['classification_metrics'].update(stat)
with open('training_metrics.json', 'w') as f:
json.dump(model_metrics_report, f)
metrics_s3_key = f"{prefix}/training_jobs/{training_job_1_info['TrainingJobName']}/training_metrics.json"
s3_client.upload_file(Filename='training_metrics.json', Bucket=bucket, Key=metrics_s3_key)
# -
# #### Define the inference spec
# +
mp_inference_spec = InferenceSpecification().get_inference_specification_dict(
ecr_image=training_job_1_info['AlgorithmSpecification']['TrainingImage'],
supports_gpu=False,
supported_content_types=['text/csv'],
supported_mime_types=['text/csv'])
mp_inference_spec['InferenceSpecification']['Containers'][0]['ModelDataUrl'] = training_job_1_info['ModelArtifacts']['S3ModelArtifacts']
# -
# #### Define model metrics
# Metrics other than model quality and bias can be defined. See the Boto3 documentation for [creating a model package](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/sagemaker.html#SageMaker.Client.create_model_package).
model_metrics = {
'ModelQuality': {
'Statistics': {
'ContentType': 'application/json',
'S3Uri': f's3://{bucket}/{prefix}/{metrics_s3_key}'
}
},
'Bias': {
'Report': {
'ContentType': 'application/json',
'S3Uri': f'{bias_report_1_output_path}/analysis.json'
}
}
}
# +
mp_input_dict = {
'ModelPackageGroupName': mpg_name,
'ModelPackageDescription': 'XGBoost classifier to detect insurance fraud.',
'ModelApprovalStatus': 'PendingManualApproval',
'ModelMetrics': model_metrics
}
mp_input_dict.update(mp_inference_spec)
mp1_response = sagemaker_boto_client.create_model_package(**mp_input_dict)
# -
# ### Wait until model package is completed
# +
mp_info = sagemaker_boto_client.describe_model_package(ModelPackageName=mp1_response['ModelPackageArn'])
mp_status = mp_info['ModelPackageStatus']
while mp_status not in ['Completed', 'Failed']:
time.sleep(5)
mp_info = sagemaker_boto_client.describe_model_package(ModelPackageName=mp1_response['ModelPackageArn'])
mp_status = mp_info['ModelPackageStatus']
print(f'model package status: {mp_status}')
print(f'model package status: {mp_status}')
# -
# ### View model package in registry
sagemaker_boto_client.list_model_packages(ModelPackageGroupName=mpg_name)['ModelPackageSummaryList']
# ___
#
# ### Next Notebook: [Mitigate Bias, Train New Model, Store in Registry](./3-mitigate-bias-train-model2-registry-e2e.ipynb)
# To handle the imbalance, in the next notebook, we over-sample (i.e. upsample) the minority class using [SMOTE (Synthetic Minority Over-sampling Technique)](https://imbalanced-learn.readthedocs.io/en/stable/generated/imblearn.over_sampling.SMOTE.html).
|
2-lineage-train-assess-bias-tune-registry-e2e.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
from os import path
from PIL import Image
from wordcloud import WordCloud, STOPWORDS, ImageColorGenerator
import matplotlib.pyplot as plt
# -
# %matplotlib inline
pip install docx2txt
pip install wordcloud
df = pd.read_csv("https://usc-bootcamp-yelpreview-text-analysis.s3.us-east-2.amazonaws.com/reviews.csv", encoding ="latin-1")
df.head()
print(comment_words[0])
comment_words = " "
stop_words =set(STOPWORDS)
stop_words.update([" "])
for i in df.head().reviews:
#print(i)
i = str(i)
separate = i.split(" ")
#print(separate)
for word in separate:
if word not in stop_words:
comment_words += " " + word.lower()
#path = "./map.png"
#mask = np.array(Image.open(path))
final_wordcloud = WordCloud(width = 800, height = 800,
background_color ='pink', #mask = mask,
stopwords = stop_words,
min_font_size = 10).generate(comment_words)
from PIL import Image
import numpy as np
# +
plt.figure(figsize=[10, 10])
plt.imshow(final_wordcloud, interpolation='bilinear')
plt.axis("off")
plt.tight_layout(pad = 0)
plt.show()
WordCloud.to_file("./wordcloud.png")
# -
|
WorldCloud.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import scanpy as sc
import perturbseq as perturb
sc.logging.print_versions()
# +
datapath='/ahg/regevdata/projects/Cell2CellCommunication/perturbseq_benchmarks/data/2018-11-09'
dataset='dc_3hr'
gsm_number='GSM2396856'
anno=datapath+'/'+dataset+'/'+gsm_number+'_'+dataset+'_cbc_gbc_dict_lenient.csv.gz' #also experiment with the strict
pref=datapath+'/'+dataset+'/'+dataset
cells2guide_file=pref+'.cell2guide.csv.gz'
guide2gene_file=pref+'.guide2gene.csv.gz'
# -
adata=sc.read(pref+'.perturb.analysis.h5ad')
adata
perturb.io.read_perturbations_csv(adata,
cell2guide_csv=cells2guide_file,
guide2gene_csv=guide2gene_file,pref='')
adata
# +
import matplotlib.pyplot as plt
# %matplotlib inline
sc.pl.umap(adata,color=['louvain'])
# -
# QC
# ==
perturb.tl.bulk(adata,'guide.compact')
corr=perturb.util.corr_mat(adata.uns['bulk.guide.compact'])
import seaborn as sns
sns.clustermap(corr,vmin=-1,vmax=1,
xticklabels=True,yticklabels=True,
figsize=(20,20),
cmap='bwr')
# Linear model
# ==
adata=adata[adata.obs['guide.compact']!='multiple',:]
adata
#set random generator we will use throughout, so we can have reproducible results
my_rng=np.random.RandomState(1234)
perturbations=list(set(adata.obs['guide.compact']))
print(perturbations)
#run on a smaller subset for fast runtime
perturbations=[x for x in perturbations if ('Stat1' in x) or ('Stat2' in x) or ('Nfkb' in x)]
print(perturbations)
X=pd.DataFrame(adata.obs.loc[:,perturbations],
index=adata.obs_names,
columns=perturbations)
X.sum(axis=1).max() #######
y=pd.DataFrame(adata.X,
index=adata.obs_names,
columns=adata.var_names)
y.shape
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn import linear_model
reg=linear_model.ElasticNet(l1_ratio=0.5,alpha=0.0005,max_iter=10000,
random_state=my_rng)
reg.fit(X,y)
beta=pd.DataFrame(reg.coef_,
index=y.columns,
columns=X.columns,
)
beta.shape
x=0.25
sns.clustermap(beta,vmin=-x,vmax=x,cmap='bwr',
xticklabels=True,figsize=(20,10),
)
# Adjust X
# ==
import sys
sys.path.append("/ahg/regevdata/projects/Cell2CellCommunication/code/MIMOSCA")
import mimosca
# +
#adjust for cases where the guide didn't work
adjust_vars_idx=perturbations
X_adjust=pd.DataFrame(np.array(mimosca.bayes_cov_col(y,
pd.DataFrame(X,
index=X.index),
adjust_vars_idx,
reg)),
index=X.index,
columns=X.columns)
# -
a=plt.hist(np.array(X_adjust).flatten(),100)
plt.ylim(0,100)
plt.xlabel('adjusted x')
plt.scatter(np.array(X).flatten(),
np.array(X_adjust).flatten(),
alpha=0.05,color='black'
)
plt.xlabel('original X')
plt.ylabel('adjusted X')
#re-train model with adjusted X
reg2=linear_model.ElasticNet(l1_ratio=0.5,alpha=0.0005,max_iter=10000,
random_state=my_rng)
reg2.fit(X_adjust,y)
beta2=pd.DataFrame(reg2.coef_,
index=y.columns,
columns=X.columns,
)
x=0.5
sns.clustermap(beta2,vmin=-x,vmax=x,cmap='bwr',
xticklabels=True,figsize=(20,20),
)
|
examples/2021-05-12.Perturbseq_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.11 64-bit (''ml_env'': conda)'
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NoahHA/msci-project/blob/master/RNN_multiclass_classifier.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="5IUMIQDx2Pfh" outputId="07bbee69-7190-4a64-836c-ec3187cb490f"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from sklearn.utils import class_weight
from keras.models import Sequential
from keras.layers import Dense, LSTM, Concatenate, BatchNormalization
from keras.regularizers import l2
from keras import Model
from sklearn.metrics import confusion_matrix
import seaborn as sns
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
import warnings
import tensorflow as tf
from sklearn.preprocessing import StandardScaler
from keras.preprocessing import sequence
warnings.filterwarnings("ignore")
# %matplotlib inline
# + [markdown] id="rl9aky6WApO8"
# # Loads in the Dataframes
# + id="TLrYWwz6ArO9"
# loads the dataframes
higgs_df = pd.read_hdf('/content/drive/MyDrive/Colab Notebooks/ttH.hd5')
semi_leptonic_df = pd.read_hdf('/content/drive/MyDrive/Colab Notebooks/ttsemileptonic.hd5')
fully_leptonic_df = pd.read_hdf('/content/drive/MyDrive/Colab Notebooks/fully_leptonic.hd5')
fully_hadronic_df = pd.read_hdf('/content/drive/MyDrive/Colab Notebooks/fully_hadronic.hd5')
# labels signal vs background
higgs_df["signal"] = 0
semi_leptonic_df["signal"] = 1
fully_hadronic_df["signal"] = 2
fully_leptonic_df["signal"] = 3
# combines the dataframes and randomly shuffles the rows
full_df = higgs_df.append(semi_leptonic_df, ignore_index=True)
full_df = full_df.append(fully_leptonic_df, ignore_index=True)
full_df = full_df.append(fully_hadronic_df, ignore_index=True)
full_df = shuffle(full_df)
event_cols = [
"BiasedDPhi",
"DiJet_mass",
"HT",
"InputMet_InputJet_mindPhi",
"InputMet_pt",
"MHT_pt",
"MinChi",
"MinOmegaHat",
"MinOmegaTilde",
"ncleanedBJet",
"ncleanedJet",
]
object_cols = [
"cleanedJet_pt",
"cleanedJet_area",
"cleanedJet_btagDeepB",
"cleanedJet_chHEF",
"cleanedJet_eta",
"cleanedJet_mass",
"cleanedJet_neHEF",
"cleanedJet_phi",
]
# removes useless columns
df = full_df[event_cols + object_cols + ["signal", "xs_weight"]]
# + [markdown] id="sBZXFYBHA3ec"
# # Splits data into event / object dataframes and train / test dataframes
# + colab={"base_uri": "https://localhost:8080/", "height": 600} id="M6hY56mgA3tN" outputId="014f4afe-29d1-4d28-f40e-cf36586ed810"
scaler = StandardScaler()
# columns that should not be transformed
untransformed_cols = ["ncleanedBJet", "ncleanedJet", "BiasedDP hi", "signal"]
transformed_cols = list(set(event_cols) - set(untransformed_cols))
# takes the log of each column to remove skewness
for col_name in event_cols:
if col_name in transformed_cols:
df[col_name] = np.log(df[col_name])
# splits data into training and validation
num_classes = 4
X, y = df.drop("signal", axis=1), df["signal"]
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=1)
# divides training data into object level and event level features
event_X_train, event_X_test = X_train[event_cols], X_test[event_cols]
object_X_train, object_X_test = X_train[object_cols], X_test[object_cols]
# scales features so they all have the same mean and variance
event_X_train[event_cols] = scaler.fit_transform(event_X_train[event_cols].values)
event_X_test[event_cols] = scaler.transform(event_X_test[event_cols].values)
max_jets = df["ncleanedJet"].max()
# pads input sequences with zeroes so they're all the same length
for col in object_cols:
object_X_train[col] = sequence.pad_sequences(
object_X_train[col].values, padding="post", dtype="float32"
).tolist()
object_X_test[col] = sequence.pad_sequences(
object_X_test[col].values, padding="post", dtype="float32"
).tolist()
# one-hot encodes the label data
y_train = tf.keras.utils.to_categorical(y_train, num_classes=num_classes)
y_test = tf.keras.utils.to_categorical(y_test, num_classes=num_classes)
print(
"Removed Columns:",
[col for col in full_df.columns if col not in set(event_cols + object_cols)],
)
X_train.head()
# + [markdown] id="ZZH_t5B-MKE3"
# # Loads data
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="j_6xk5LXLrri" outputId="60db103b-8dd2-4811-936f-a5baa6ed6fde"
# object data
object_X_train = np.load('/content/drive/MyDrive/RNN_classifier/object_X_train_multiclass.npy')
object_X_test = np.load('/content/drive/MyDrive/RNN_classifier/object_X_test_multiclass.npy')
plt.scatter(object_X_train[:, :, 7], object_X_train[:, :, 4], s=0.1) # plots (eta, phi) for all jets
# + [markdown] id="c-r3qlxjirKc"
# # Hyperparameters
# + id="LF6k4uMKirKc"
# hyperparameters
lr = 0.001
activation = "relu"
batch_size = 32
num_classes = 4
lstm_l2 = 0 #1e-6
mlp_l2 = 0 #1e-4
optimizer = keras.optimizers.Adam(
learning_rate=lr,
)
METRICS = [
keras.metrics.CategoricalAccuracy(name="accuracy"),
keras.metrics.Precision(name="precision"),
keras.metrics.Recall(name="recall"),
keras.metrics.AUC(name='AUC'),
]
y_integers = np.argmax(y_train, axis=1)
class_weights = class_weight.compute_class_weight(
class_weight='balanced', classes=np.unique(y_integers), y=y_integers
)
class_weights = {l: c for l, c in zip(np.unique(y_integers), class_weights)}
# + [markdown] id="zowVOAG4IqhW"
# # Callbacks
# + id="Y0YJf6YIIsTk"
monitor = 'val_loss'
mode = 'auto'
# stops training early if score doesn't improve
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor=monitor,
verbose=1,
patience=6,
mode=mode,
restore_best_weights=True,
)
# saves the network at regular intervals so you can pick the best version
checkpoint = tf.keras.callbacks.ModelCheckpoint(
filepath="/content/drive/MyDrive/RNN_classifier/best_model_multiclass_v2.h5",
monitor=monitor,
verbose=1,
save_best_only=True,
save_weights_only=False,
mode=mode,
save_freq="epoch",
)
# reduces the lr whenever training plateaus
reduce_lr = keras.callbacks.ReduceLROnPlateau(
monitor=monitor,
factor=0.1,
patience=3,
mode=mode,
)
# + [markdown] id="Iz7N3I9kirKc"
# # Defines and compiles the model
# + id="wmHapChZZNms"
DNN_model = Sequential([
Dense(40, input_shape=(event_X_train.shape[1],), activation=activation, kernel_regularizer=l2(mlp_l2)),
BatchNormalization()])
RNN_model = Sequential([
LSTM(
200,
input_shape=(object_X_train.shape[1], object_X_train.shape[2]),
activation="tanh",
unroll=False,
recurrent_dropout=0.0,
kernel_regularizer=l2(lstm_l2)),
BatchNormalization()])
merged = Concatenate()([DNN_model.output, RNN_model.output])
merged = BatchNormalization()(merged)
merged = Dense(40, activation=activation, kernel_regularizer=l2(mlp_l2))(merged)
merged = Dense(num_classes, activation="softmax")(merged)
model = Model(inputs=[DNN_model.input, RNN_model.input], outputs=merged)
model.compile(optimizer=optimizer, loss="categorical_crossentropy", metrics=METRICS)
# plots the model as a graph
#keras.utils.plot_model(model, "RNN_multiclass_model_diagram.png", show_shapes=True, show_layer_names=False)
# + [markdown] id="mCXQcBsrMYKU"
# # Loads pre-trained model
# + id="nFaiJG_4M739"
model = keras.models.load_model('/content/drive/MyDrive/RNN_classifier/best_model_multiclass_v2.h5')
# + [markdown] id="wdXMt--3irKd"
# # Trains the model
# + colab={"base_uri": "https://localhost:8080/", "height": 712} id="GlZaG4tRxmjm" outputId="624ad58c-6b12-455a-9362-60eb4264cf08"
history = model.fit(
[event_X_train, object_X_train],
y_train,
batch_size=32,
class_weight=class_weights,
epochs=6,
callbacks=[early_stopping, checkpoint],
validation_data=([event_X_test, object_X_test], y_test),
verbose=1,
)
# 0.8604
# + [markdown] id="dYsZoohm73aT"
# # Evaluates the model
# + id="7avvPpySKxjM"
y_pred_test = model.predict([event_X_test, object_X_test])
# + id="kHp6wfDaKlpp"
def plot_metrics(history):
metrics = ['loss', 'accuracy', 'precision', 'recall', 'AUC']
fig = plt.figure(figsize=(14, 14))
for n, metric in enumerate(metrics):
name = metric.replace("_"," ")
plt.subplot(3,2,n+1)
plt.plot(history.epoch, history.history[metric], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
plt.legend()
plot_metrics(history)
# + id="YASZc7P8sBmb"
def compare_models(history, history2):
metrics = ['loss', 'accuracy', 'precision', 'recall', 'AUC']
fig = plt.figure(figsize=(14, 14))
for n, metric in enumerate(metrics):
name = metric.replace("_"," ")
plt.subplot(3,2,n+1)
plt.plot(history.epoch, history.history[metric], label='Model 1 Train')
plt.plot(history.epoch, history.history['val_'+metric],
linestyle="--", label='Model 1 Val')
plt.plot(history2.epoch, history2.history[metric], label='Model 2 Train')
plt.plot(history2.epoch, history2.history['val_'+metric],
linestyle="--", label='Model 2 Val')
plt.xlabel('Epoch')
plt.ylabel(name)
plt.legend()
compare_models(history, history2)
# + colab={"base_uri": "https://localhost:8080/", "height": 458} id="l3ziarNa8oev" outputId="4b1a752c-2ba2-4ada-c722-aa80ee89be6e"
def plot_cm(labels, predictions, p=0.5):
signal_types = ['ttH', 'semi leptonic', 'fully hadronic', 'fully leptonic']
cm = confusion_matrix(labels, predictions, normalize='true')
plt.figure(figsize=(7, 7))
sns.heatmap(cm, annot=True, xticklabels=signal_types, yticklabels=signal_types, vmin=0, vmax=1)
plt.title(f'Confusion matrix')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
plot_cm(y_test.argmax(axis=1), y_pred_test.argmax(axis=1))
# + [markdown] id="2FDC_nPX_uBi"
# # Significance as a Function of Threshold
# + id="wVRXpIflsPCg"
preds = model.predict([event_X_test, object_X_test])
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="Pjv6qVX-xR_6" outputId="bab40760-7403-460f-eefc-d9a7917bb890"
test_weight = X_test["xs_weight"].values
test_frac = len(y_test) / len(y_train)
thresholds = np.linspace(0, 1, 50)
significance = np.zeros(len(thresholds), dtype=float)
lum = 140e3
epsilon = 1e-5
sg = np.zeros(len(thresholds))
bg = np.zeros(len(thresholds))
labels = [y.argmax() for y in y_test]
for i, threshold in enumerate(thresholds):
sg[i] = sum([test_weight[j] for j, (pred, label) in enumerate(zip(preds, labels)) if (pred[0] >= threshold and label == 0)]) * lum / test_frac
bg[i] = sum([test_weight[j] for j, (pred, label) in enumerate(zip(preds, labels)) if (pred[0] >= threshold and label != 0)]) * lum / test_frac
significance = sg / np.sqrt(bg + epsilon)
index = significance.argmax()
print(thresholds[index])
plt.plot(thresholds, significance)
plt.show()
# + [markdown] id="Cwd1C5dZo4IJ"
# # Discriminator Plots
# + colab={"base_uri": "https://localhost:8080/", "height": 540} id="fAZPMM-Ro6Af" outputId="66968107-f48d-4610-96e2-35161faeb74a"
test_weight = X_test["xs_weight"].values
labels = [y.argmax() for y in y_test]
signals = [pred[0] for label, pred in zip(labels, preds) if label == 0]
backgrounds = [pred[0] for label, pred in zip(labels, preds) if label != 0]
n_bins = 75
alpha = 0.6
fig, (ax1, ax2) = plt.subplots(2, figsize=(8, 8))
fig.suptitle('Discriminator Plots')
ax1.hist(signals, density=True, bins=n_bins, alpha=alpha)
ax1.hist(backgrounds, density=True, bins=n_bins, alpha=alpha)
ax2.hist(signals, density=False, bins=n_bins, alpha=alpha)
ax2.hist(backgrounds, density=False, bins=n_bins, alpha=alpha)
plt.show()
|
notebooks/RNN_models/RNN_multiclass_1234.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# + [markdown] origin_pos=0
# # 异步计算
# :label:`sec_async`
#
# 今天的计算机是高度并行的系统,由多个CPU核、多个GPU、多个处理单元组成。通常每个CPU核有多个线程,每个设备通常有多个GPU,每个GPU有多个处理单元。总之,我们可以同时处理许多不同的事情,并且通常是在不同的设备上。不幸的是,Python并不善于编写并行和异步代码,至少在没有额外帮助的情况下不是好选择。归根结底,Python是单线程的,将来也是不太可能改变的。因此在诸多的深度学习框架中,MXNet和TensorFlow之类则采用了一种*异步编程*(asynchronous programming)模型来提高性能,而PyTorch则使用了Python自己的调度器来实现不同的性能权衡。对于PyTorch来说GPU操作在默认情况下是异步的。当你调用一个使用GPU的函数时,操作会排队到特定的设备上,但不一定要等到以后才执行。这允许我们并行执行更多的计算,包括在CPU或其他GPU上的操作。
#
# 因此,了解异步编程是如何工作的,通过主动地减少计算需求和相互依赖,有助于我们开发更高效的程序。这使我们能够减少内存开销并提高处理器利用率。
#
# + origin_pos=2 tab=["pytorch"]
import os
import subprocess
import numpy
import torch
from torch import nn
from d2l import torch as d2l
# + [markdown] origin_pos=3
# ## 通过后端异步处理
#
# + [markdown] origin_pos=5 tab=["pytorch"]
# 作为热身,考虑一个简单问题:我们要生成一个随机矩阵并将其相乘。让我们在NumPy和PyTorch张量中都这样做,看看它们的区别。请注意,PyTorch的`tensor`是在GPU上定义的。
#
# + origin_pos=7 tab=["pytorch"]
# GPU计算热身
device = d2l.try_gpu()
a = torch.randn(size=(1000, 1000), device=device)
b = torch.mm(a, a)
with d2l.Benchmark('numpy'):
for _ in range(10):
a = numpy.random.normal(size=(1000, 1000))
b = numpy.dot(a, a)
with d2l.Benchmark('torch'):
for _ in range(10):
a = torch.randn(size=(1000, 1000), device=device)
b = torch.mm(a, a)
# + [markdown] origin_pos=9 tab=["pytorch"]
# 通过PyTorch的基准输出比较快了几个数量级。NumPy点积是在CPU上执行的,而PyTorch矩阵乘法是在GPU上执行的,后者的速度要快得多。但巨大的时间差距表明一定还有其他原因。默认情况下,GPU操作在PyTorch中是异步的。强制PyTorch在返回之前完成所有计算,这种强制说明了之前发生的情况:计算是由后端执行,而前端将控制权返回给了Python。
#
# + origin_pos=11 tab=["pytorch"]
with d2l.Benchmark():
for _ in range(10):
a = torch.randn(size=(1000, 1000), device=device)
b = torch.mm(a, a)
torch.cuda.synchronize(device)
# + [markdown] origin_pos=13 tab=["pytorch"]
# 广义上说,PyTorch有一个用于与用户直接交互的前端(例如通过Python),还有一个由系统用来执行计算的后端。如 :numref:`fig_frontends`所示,用户可以用各种前端语言编写PyTorch程序,如Python和C++。不管使用的前端编程语言是什么,PyTorch程序的执行主要发生在C++实现的后端。由前端语言发出的操作被传递到后端执行。后端管理自己的线程,这些线程不断收集和执行排队的任务。请注意,要使其工作,后端必须能够跟踪计算图中各个步骤之间的依赖关系。因此,不可能并行化相互依赖的操作。
#
# + [markdown] origin_pos=14
# 
# :width:`300px`
# :label:`fig_frontends`
#
# 让我们看另一个简单例子,以便更好地理解依赖关系图。
#
# + origin_pos=16 tab=["pytorch"]
x = torch.ones((1, 2), device=device)
y = torch.ones((1, 2), device=device)
z = x * y + 2
z
# + [markdown] origin_pos=17
# 
# :label:`fig_asyncgraph`
#
# 上面的代码片段在 :numref:`fig_asyncgraph`中进行了说明。每当Python前端线程执行前三条语句中的一条语句时,它只是将任务返回到后端队列。当最后一个语句的结果需要被打印出来时,Python前端线程将等待C++后端线程完成变量`z`的结果计算。这种设计的一个好处是Python前端线程不需要执行实际的计算。因此,不管Python的性能如何,对程序的整体性能几乎没有影响。 :numref:`fig_threading`演示了前端和后端如何交互。
#
# 
# :label:`fig_threading`
#
# ## 障碍器与阻塞器
#
# + [markdown] origin_pos=22
# ## 改进计算
#
# + [markdown] origin_pos=26
# ## 小结
#
# * 深度学习框架可以将Python前端的控制与后端的执行解耦,使得命令可以快速地异步插入后端、并行执行。
# * 异步产生了一个相当灵活的前端,但请注意:过度填充任务队列可能会导致内存消耗过多。建议对每个小批量进行同步,以保持前端和后端大致同步。
# * 芯片供应商提供了复杂的性能分析工具,以获得对深度学习效率更精确的洞察。
#
# + [markdown] origin_pos=28
# ## 练习
#
# + [markdown] origin_pos=30 tab=["pytorch"]
# 1. 在CPU上,对本节中相同的矩阵乘法操作进行基准测试。你仍然可以通过后端观察异步吗?
#
# + [markdown] origin_pos=32 tab=["pytorch"]
# [Discussions](https://discuss.d2l.ai/t/2791)
#
|
submodules/resource/d2l-zh/pytorch/chapter_computational-performance/async-computation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="jYOS34CbTGyp"
# # Comparing the predictive performance of Deepred-Mt
#
#
# + [markdown] id="gESQ0jraTMxm"
# ## Environment
# + id="fFfFHpENpbJa"
import numpy as np
import sklearn.metrics
import matplotlib.pyplot as plt
import sklearn.metrics as metrics
# + [markdown] id="Kcz6jgHPTQM1"
# ### Deepred-Mt installation
# + colab={"base_uri": "https://localhost:8080/"} id="ZD-2nT2rqdwL" outputId="8277dcc5-a568-4fcd-bf73-9c46deb7596f"
# !pip install -U "deepredmt @ git+https://github.com/aedera/deepredmt.git" > /dev/null
# + [markdown] id="jlSV5kcQTbDN"
# ## Make predictions
# + [markdown] id="WnqJ_RjbTcYz"
# To predict C-to-U editing sites, we will download data that include nucleotide windows extracted from mitochondrial protein-coding genes of diverse plants.
# + colab={"base_uri": "https://localhost:8080/"} id="Xz0OQHrvqfXC" outputId="fd47810f-de9e-4355-b854-e3357b59d861"
# !wget https://raw.githubusercontent.com/aedera/deepredmt/main/data/training-data.tsv.gz
# + [markdown] id="c8Nt2sH2TnIr"
# As it is explained [here](https://github.com/aedera/deepredmt/blob/main/data/README.md), this data is composed of eleven fields, where nucleotide windows are stored in the fields #4, #5, and #6.
# + colab={"base_uri": "https://localhost:8080/"} id="kbdaFkJlcqne" outputId="aefbafd3-0c43-4a00-bd6f-7d1308c1802b"
# !zcat training-data.tsv.gz | \
# cut -f4,5,6 | \
# tr -d '\t' > wins.tsv
# !shuf wins.tsv | head -10 | column -t
# + [markdown] id="dFsOTB7WUCYE"
# Now, we will use Deepred-Mt to predict which of the central positions of these nucleotide windows are edited.
# + id="dXXNeUaDMpYB" colab={"base_uri": "https://localhost:8080/"} outputId="ba72174c-6dcc-4f22-93de-e3c98f4103cc"
# !deepredmt wins.tsv > deepredmt-pred.tsv
# + [markdown] id="vNPyaOsDUofg"
# ## Comparing the predictive performance of Deepred-Mt
# + [markdown] id="oAHzVrniU4sT"
# Next, we will compare Deepred-Mt predictions with the C-to-U editing sites previously identified for the downloaded sequences, which are stored in the field #9. In addition, we will also include in this comparison the predictive performance of two state-of-the-art methods to predict editing sites:
#
# * [PREPACT](http://www.prepact.de/prepact-main.php)
# * [PREP-Mt](http://prep.unl.edu/)
#
# The predictions of both methods are already available in the fields #10 and #11.
#
# + id="BVjqOO3SrzW6"
# !paste <(zcat training-data.tsv.gz | cut -f9,10,11) deepredmt-pred.tsv > predictions.tsv
# + [markdown] id="TPUo1VGZePMz"
#
# To measure the predictive performance, we can use precision and recall, which are standard metrics often used in practice. You can find more information regarding these metrics in this [notebook](https://colab.research.google.com/github/aedera/deepredmt/blob/main/notebooks/01_prediction_from_fasta.ipynb).
# + id="BoP-chxQUyfo"
# Read predictions
preds = np.loadtxt('predictions.tsv')
y_true, y_prepact, y_prepmt, y_deepredmt = preds[:,0], preds[:,1], preds[:,2], preds[:,3]
# evaluate performance
prepact_pre, prepact_rec, _ = metrics.precision_recall_curve(y_true, y_prepact)
prepmt_pre, prepmt_rec, _ = metrics.precision_recall_curve(y_true, y_prepmt)
deepredmt_pre, deepredmt_rec, _ = metrics.precision_recall_curve(y_true, y_deepredmt)
# + [markdown] id="gFsuvskwtJEh"
# Now, we can compare the precision and recall obtained for each method.
# + colab={"base_uri": "https://localhost:8080/", "height": 501} id="Bhdl0PjHU2Ct" outputId="997491d4-2ef0-451b-b949-2b8114d3cb3e"
# Plot results
fig, ax = plt.subplots(figsize=(8, 8))
# draw curves
plt.plot(prepact_rec, prepact_pre, c='tab:blue', label='PREPACT')
plt.plot(prepmt_rec, prepmt_pre, c='tab:red', label='PREP-Mt')
plt.plot(deepredmt_rec, deepredmt_pre, c='black', label='Deepred-Mt')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.legend()
ax.set_xlim([0.5, 1])
ax.set_ylim([0.5, 1])
plt.grid(True)
plt.show()
|
notebooks/02_reproduce_comparative_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: dev
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Update sklearn to prevent version mismatches
# !pip install sklearn --upgrade
# install joblib. This will be used to save your model.
# Restart your kernel after installing
# !pip install joblib
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
import pandas as pd
import numpy as np
import os
# # Read the CSV and Perform Basic Data Cleaning
df = pd.read_csv("exoplanet_data.csv")
# Drop the null columns where all values are null
df = df.dropna(axis='columns', how='all')
# Drop the null rows
df = df.dropna()
df.head()
df = pd.get_dummies(df)
df.head()
# # Select your features (columns)
# Set features. This will also be used as your x values.
selected_features = df[['koi_period', 'koi_time0bk', 'koi_slogg', 'koi_srad', 'ra','dec','koi_kepmag']]
df["koi_disposition_CANDIDATE"]
# # Create a Train Test Split
#
# Use `koi_disposition` for the y values
#X = df.drop("koi_disposition", axis=1)
X = selected_features
y = df["koi_disposition_CANDIDATE"].values.reshape(-1, 1)
target_names=["negative", "positive"]
print(X.shape, y.shape)
print(X)
# +
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
from tensorflow.keras.utils import to_categorical
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# -
X_train.head()
# # Pre-processing
#
# Scale the data using the MinMaxScaler and perform some feature selection
# +
# Scale your data
from sklearn.preprocessing import MinMaxScaler
X_minmax = MinMaxScaler().fit(X_train)
y_minmax = MinMaxScaler().fit(y_train)
X_train_minmax = X_minmax.transform(X_train)
X_test_minmax = X_minmax.transform(X_test)
y_train_minmax = y_minmax.transform(y_train)
y_test_minmax = y_minmax.transform(y_test)
# -
# # Train the Model
#
#
from sklearn.svm import SVC
model = SVC(kernel='linear')
model.fit(X_train, y_train.ravel())
print('Test Acc: %.3f' % model.score(X_test, y_test))
# Calculate classification report
from sklearn.metrics import classification_report
predictions = model.predict(X_test)
print(classification_report(y_test, predictions,
target_names=target_names))
# # Save the Model
# save your model by updating "your_name" with your name
# and "your_model" with your model variable
# be sure to turn this in to BCS
# if joblib fails to import, try running the command to install in terminal/git-bash
import joblib
filename = 'grid_search3.sav'
joblib.dump(model, filename)
|
starter_code/model_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (system-wide)
# language: python
# metadata:
# cocalc:
# description: Python 3 programming language
# priority: 100
# url: https://www.python.org/
# name: python3
# resource_dir: /ext/jupyter/kernels/python3
# ---
# decorators allow extra functionality to an already existing function using the @ operator and are then placed on top of the original function
#
#
def func():
return 1
func()
def hello():
return 'Hello!'
greet = hello
greet()# created a copy of its own function hello()
del hello
hello() # hello is deleted
greet() # greet() still carries that original hello()
#functions and objects can be passed to other objects
def hello(name = 'Jose'):
print('The hello() has been executed')
hello()
# +
# define a function in the function
def hello(name='Jose'):
print('The hello() has been executed:')
# functions are only defined inside the hello function
# scope is limited
def greet():
return '\t This is the greet() function inside hello()'
def welcome():
return '\t This is the welcome() function inside hello'
print('I am going to return a function')
if name == 'Jose': # return a function with in a function
return greet
else:
return welcome
my_new_func = hello('Jose')
# -
print(my_new_func())
# +
def cool():
def super_cool():
return 'I am very coo1'
return super_cool
some_func = cool()
# -
some_func()
# +
# passing a function as an argument
def hello():
return 'Hi Jose'
def other(some_define_func):
print('Other code runs here!')
print(some_define_func())
# -
other(hello) # passing raw function of hello
# +
# create a decorator
def new_decorator(original_func):
def wrap_func():
print('Some extra code, before the original function')
original_func()
print('Some extra code, after original function')
return wrap_func
def func_needs_decorator():
print('I want to be decorated!!')
# -
func_needs_decorator()
decorated_func = new_decorator(func_needs_decorator)
decorated_func()
@new_decorator # using @ to create decorator
def func_needs_decorator():
print('I want to be decorated!!')
func_needs_decorator()
|
Decorators.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial 6 (:-})
# ## Constructing Basic Shapes in OpenCV
import cv2
import numpy as np
import matplotlib.pyplot as plt
# +
colors = {'red': (255, 0, 0),
'green': (0, 255, 0),
'blue': (0, 0, 255),
'yellow': (0, 255, 255),
'magenta': (255, 0, 255),
'light_gray': (220, 220, 220)}
image=np.zeros((400,400,3),np.uint8)
image[:]=colors['light_gray']
plt.figure(figsize=(10,6))
plt.imshow(image)
# -
cv2.line(image,(0,0),(400,400),colors["green"],3)
cv2.line(image,(0,400),(400,0),colors['red'],10)
cv2.line(image,(200,0),(200,400),colors["blue"],3)
cv2.line(image,(0,200),(400,200),colors['yellow'],10)
plt.figure(figsize=(10,6))
plt.imshow(image)
image=np.zeros((400,400,3),np.uint8)
image[:]=colors['light_gray']
cv2.rectangle(image,(10,50),(45,320),colors["green"],3)
cv2.rectangle(image,(60,200),(300,120),colors["red"],-1)
plt.figure(figsize=(10,6))
plt.imshow(image)
image=np.zeros((400,400,3),np.uint8)
image[:]=colors['light_gray']
cv2.circle(image,(200,300),25,colors["red"],-1)
plt.figure(figsize=(10,6))
plt.imshow(image)
|
Constructing basic shapes in opencv/Constructing Basic Shapes in OpenCV.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 6.4 컨브넷을 사용한 시퀀스 처리
# 이 노트북은 [케라스 창시자에게 배우는 딥러닝](https://tensorflow.blog/deep-learning-with-python/) 책의 6장 4절의 코드 예제입니다. 책에는 더 많은 내용과 그림이 있습니다. 이 노트북에는 소스 코드에 관련된 설명만 포함합니다. 이 노트북의 설명은 케라스 버전 2.2.2에 맞추어져 있습니다. 케라스 최신 버전이 릴리스되면 노트북을 다시 테스트하기 때문에 설명과 코드의 결과가 조금 다를 수 있습니다.
#
# ---
import keras
keras.__version__
# 5장에서 합성곱 신경망(컨브넷)이 무엇인지 그리고 컴퓨터 비전 문제에 어떻게 잘 맞는지 배웠습니다. 입력의 부분 패치에서 특성을 뽑아내어 구조적인 표현을 만들고 데이터를 효율적으로 사용하는 합성곱 연산의 능력 때문입니다. 컴퓨터 비전에서 뛰어난 컨브넷의 특징이 시퀀스 처리와도 깊게 관련되어 있습니다. 시간을 2D 이미지의 높이와 너비 같은 공간의 차원으로 다룰 수 있습니다.
#
# 1D 컨브넷(1D Convnet)은 특정 시퀀스 처리 문제에서 RNN과 견줄 만합니다. 일반적으로 계산 비용이 훨씬 쌉니다. 1D 컨브넷은 전형적으로 팽창된 커널(dilated kernel)과 함께 사용됩니다.[45](Section0605.html#footnote-06-45) 최근에 오디오 생성과 기계 번역 분야에서 큰 성공을 거두었습니다. 이런 특정 분야의 성공 이외에도 텍스트 분류나 시계열 예측 같은 간단한 문제에서 작은 1D 컨브넷이 RNN을 대신하여 빠르게 처리할 수 있다고 알려져 있습니다.
# ## 6.4.1 시퀀스 데이터를 위한 1D 합성곱 이해하기
#
# 앞서 소개한 합성곱 층은 2D 합성곱입니다. 이미지 텐서에서 2D 패치를 추출하고 모든 패치에 동일한 변환을 적용합니다. 같은 방식으로 시퀀스에서 1D 패치(부분 시퀀스)를 추출하여 1D 합성곱을 적용합니다(그림 6-26 참고).
#
# 
# _그림 6-26. 1D 합성곱 작동 방식: 입력 시퀀스에서 시간 축으로 패치를 추출하여 출력 타임스텝을 만든다_
#
# 이런 1D 합성곱 층은 시퀀스에 있는 지역 패턴을 인식할 수 있습니다. 동일한 변환이 시퀀스에 있는 모든 패치에 적용되기 때문에 특정 위치에서 학습한 패턴을 나중에 다른 위치에서 인식할 수 있습니다. 이는 1D 컨브넷에 (시간의 이동에 대한) 이동 불변성(translation invariant)을 제공합니다. 예를 들어 크기 5인 윈도우를 사용하여 문자 시퀀스를 처리하는 1D 컨브넷은 5개 이하의 단어나 단어의 부분을 학습합니다. 이 컨브넷은 이 단어가 입력 시퀀스의 어느 문장에 있더라도 인식할 수 있습니다. 따라서 문자 수준의 1D 컨브넷은 단어 형태학(word morphology)에 관해 학습할 수 있습니다.[46](Section0605.html#footnote-06-46)
# ## 6.4.2 시퀀스 데이터를 위한 1D 풀링
#
# 컨브넷에서 이미지 텐서의 크기를 다운샘플링하기 위해 사용하는 평균 풀링이나 맥스 풀링 같은 2D 풀링 연산을 배웠습니다. 1D 풀링 연산은 2D 풀링 연산과 동일합니다. 입력에서 1D 패치(부분 시퀀스)를 추출하고 최댓값(최대 풀링)을 출력하거나 평균값(평균 풀링)을 출력합니다. 2D 컨브넷과 마찬가지로 1D 입력의 길이를 줄이기 위해 사용합니다(서브샘플링(subsampling)).
#
# ## 6.4.3 1D 컨브넷 구현
#
# 케라스에서 1D 컨브넷은 `Conv1D` 층을 사용하여 구현합니다. `Conv1D`는 `Conv2D`와 인터페이스가 비슷합니다. `(samples, time, features)` 크기의 3D 텐서를 입력받고 비슷한 형태의 3D 텐서를 반환합니다. 합성곱 윈도우는 시간 축의 1D 윈도우입니다. 즉, 입력 텐서의 두 번째 축입니다.
#
# 간단한 두 개 층으로 된 1D 컨브넷을 만들어 익숙한 IMDB 감성 분류 문제에 적용해 보죠.
#
# 기억을 되살리기 위해 데이터를 로드하고 전처리하는 코드를 다시 보겠습니다.
# +
# 코드 6-45. IMDB 데이터 전처리하기
from keras.datasets import imdb
from keras.preprocessing import sequence
max_features = 10000 # 특성으로 사용할 단어의 수
max_len = 500 # 사용할 텍스트의 길이(가장 빈번한 max_features 개의 단어만 사용합니다)
print('데이터 로드...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), '훈련 시퀀스')
print(len(x_test), '테스트 시퀀스')
print('시퀀스 패딩 (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=max_len)
x_test = sequence.pad_sequences(x_test, maxlen=max_len)
print('x_train 크기:', x_train.shape)
print('x_test 크기:', x_test.shape)
# -
# 1D 컨브넷은 5장에서 사용한 2D 컨브넷과 비슷한 방식으로 구성합니다. `Conv1D`와 `MaxPooling1D` 층을 쌓고 전역 풀링 층이나 `Flatten` 층으로 마칩니다. 이 구조는 3D 입력을 2D 출력으로 바꾸므로 분류나 회귀를 위해 모델에 하나 이상의 `Dense` 층을 추가할 수 있습니다.
#
# 한 가지 다른 점은 1D 컨브넷에 큰 합성곱 윈도우를 사용할 수 있다는 것입니다. 2D 합성곱 층에서 3 × 3 합성곱 윈도우는 3 × 3 = 9 특성을 고려합니다. 하지만 1D 합성곱 층에서 크기 3인 합성곱 윈도우는 3개의 특성만 고려합니다. 그래서 1D 합성곱에 크기 7이나 9의 윈도우를 사용할 수 있습니다.
#
# 다음은 IMDB 데이터셋을 위한 1D 컨브넷의 예입니다:
# +
# 코드 6-46. IMDB 데이터에 1D 컨브넷을 훈련하고 평가하기
from keras.models import Sequential
from keras import layers
from keras.optimizers import RMSprop
model = Sequential()
model.add(layers.Embedding(max_features, 128, input_length=max_len))
model.add(layers.Conv1D(32, 7, activation='relu'))
model.add(layers.MaxPooling1D(5))
model.add(layers.Conv1D(32, 7, activation='relu'))
model.add(layers.GlobalMaxPooling1D())
model.add(layers.Dense(1))
model.summary()
model.compile(optimizer=RMSprop(lr=1e-4),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(x_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
# -
# 그림 6-27과 6-28은 훈련과 검증 결과를 보여줍니다. 검증 정확도는 LSTM보다 조금 낮지만 CPU나 GPU에서 더 빠르게 실행됩니다(속도 향상은 환경에 따라 많이 다릅니다). 여기에서 적절한 에포크 수(4개)로 모델을 다시 훈련하고 테스트 세트에서 확인할 수 있습니다. 이 예는 단어 수준의 감성 분류 작업에 순환 네트워크를 대신하여 빠르고 경제적인 1D 컨브넷을 사용할 수 있음을 보여줍니다.
# +
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.show()
# -
# _그림 6-27. 1D 컨브넷을 사용한 IMDB 문제의 훈련 손실과 검증 손실_
# +
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
# -
# _그림 6-28. 1D 컨브넷을 사용한 IMDB 문제의 훈련 정확도와 검증 정확도_
# ## 6.4.4 CNN과 RNN을 연결하여 긴 시퀀스를 처리하기
#
# 1D 컨브넷이 입력 패치를 독립적으로 처리하기 때문에 RNN과 달리 (합성곱 윈도우 크기의 범위를 넘어선) 타임스텝의 순서에 민감하지 않습니다. 물론 장기간 패턴을 인식하기 위해 많은 합성곱 층과 풀링 층을 쌓을 수 있습니다. 상위 층은 원본 입력에서 긴 범위를 보게 될 것입니다. 이런 방법은 순서를 감지하기엔 부족합니다. 온도 예측 문제에 1D 컨브넷을 적용하여 이를 확인해 보겠습니다. 이 문제는 순서를 감지해야 좋은 예측을 만들어 낼 수 있습니다. 다음은 이전에 정의한 `float_data`, `train_gen`, `val_gen`, `val_steps`를 다시 사용합니다.
# +
import os
import numpy as np
data_dir = './datasets/jena_climate/'
fname = os.path.join(data_dir, 'jena_climate_2009_2016.csv')
f = open(fname)
data = f.read()
f.close()
lines = data.split('\n')
header = lines[0].split(',')
lines = lines[1:]
float_data = np.zeros((len(lines), len(header) - 1))
for i, line in enumerate(lines):
values = [float(x) for x in line.split(',')[1:]]
float_data[i, :] = values
mean = float_data[:200000].mean(axis=0)
float_data -= mean
std = float_data[:200000].std(axis=0)
float_data /= std
def generator(data, lookback, delay, min_index, max_index,
shuffle=False, batch_size=128, step=6):
if max_index is None:
max_index = len(data) - delay - 1
i = min_index + lookback
while 1:
if shuffle:
rows = np.random.randint(
min_index + lookback, max_index, size=batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows),
lookback // step,
data.shape[-1]))
targets = np.zeros((len(rows),))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples, targets
lookback = 1440
step = 6
delay = 144
batch_size = 128
train_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=0,
max_index=200000,
shuffle=True,
step=step,
batch_size=batch_size)
val_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=200001,
max_index=300000,
step=step,
batch_size=batch_size)
test_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=300001,
max_index=None,
step=step,
batch_size=batch_size)
# 전체 검증 세트를 순회하기 위해 val_gen에서 추출할 횟수
val_steps = (300000 - 200001 - lookback) // batch_size
# 전체 테스트 세트를 순회하기 위해 test_gen에서 추출할 횟수
test_steps = (len(float_data) - 300001 - lookback) // batch_size
# +
# 코드 6-47. 예나 데이터에서 1D 컨브넷을 훈련하고 평가하기
from keras.models import Sequential
from keras import layers
from keras.optimizers import RMSprop
model = Sequential()
model.add(layers.Conv1D(32, 5, activation='relu',
input_shape=(None, float_data.shape[-1])))
model.add(layers.MaxPooling1D(3))
model.add(layers.Conv1D(32, 5, activation='relu'))
model.add(layers.MaxPooling1D(3))
model.add(layers.Conv1D(32, 5, activation='relu'))
model.add(layers.GlobalMaxPooling1D())
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=20,
validation_data=val_gen,
validation_steps=val_steps)
# -
# 다음은 훈련 MAE와 검증 MAE입니다.
# +
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
# -
# _그림 6-29. 1D 컨브넷을 사용한 예나 온도 예측 문제의 훈련 손실과 검증 손실_
# 검증 MAE는 0.40 대에 머물러 있습니다. 작은 컨브넷을 사용해서 상식 수준의 기준점을 넘지 못 했습니다. 이는 컨브넷이 입력 시계열에 있는 패턴을 보고 이 패턴의 시간 축의 위치(시작인지 끝 부분인지 등)를 고려하지 않기 때문입니다. 최근 데이터 포인트일수록 오래된 데이터 포인트와는 다르게 해석해야 하기 때문에 컨브넷이 의미 있는 결과를 만들지 못합니다. 이런 컨브넷의 한계는 IMDB 데이터에서는 문제가 되지 않습니다. 긍정 또는 부정적인 감성과 연관된 키워드 패턴의 중요성은 입력 시퀀스에 나타난 위치와 무관하기 때문입니다.
#
# 컨브넷의 속도와 경량함을 RNN의 순서 감지 능력과 결합하는 한가지 전략은 1D 컨브넷을 RNN 이전에 전처리 단계로 사용하는 것입니다(그림 6-30 참고). 수천 개의 스텝을 가진 시퀀스 같이 RNN으로 처리하기엔 현실적으로 너무 긴 시퀀스를 다룰 때 특별히 도움이 됩니다. 컨브넷이 긴 입력 시퀀스를 더 짧은 고수준 특성의 (다운 샘플된) 시퀀스로 변환합니다. 추출된 특성의 시퀀스는 RNN 파트의 입력이 됩니다.
#
# 
# _그림 6-30. 긴 시퀀스를 처리하기 위해 1D 컨브넷과 RNN 결합하기_
# 이 기법이 연구 논문이나 실전 애플리케이션에 자주 등장하지는 않습니다. 아마도 널리 알려지지 않았기 때문일 것입니다. 이 방법은 효과적이므로 많이 사용되기를 바랍니다. 온도 예측 문제에 적용해 보죠. 이 전략은 훨씬 긴 시퀀스를 다룰 수 있으므로 더 오래전 데이터를 바라보거나(데이터 제너레이터의 `lookback` 매개변수를 증가시킵니다), 시계열 데이터를 더 촘촘히 바라볼 수 있습니다(제너레이터의 `step` 매개변수를 감소시킵니다). 여기서는 그냥 `step`을 절반으로 줄여서 사용하겠습니다. 온도 데이터가 30분마다 1 포인트씩 샘플링되기 때문에 결과 시계열 데이터는 두 배로 길어집니다. 앞서 정의한 제너레이터 함수를 다시 사용합니다.
# +
# 코드 6-48. 고밀도 데이터 제너레이터로 예나 데이터셋 준비하기
# 이전에는 6이었습니다(시간마다 1 포인트); 이제는 3 입니다(30분마다 1 포인트)
step = 3
lookback = 1440 # 변경 안 됨
delay = 144 # 변경 안 됨
train_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=0,
max_index=200000,
shuffle=True,
step=step)
val_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=200001,
max_index=300000,
step=step)
test_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=300001,
max_index=None,
step=step)
val_steps = (300000 - 200001 - lookback) // 128
test_steps = (len(float_data) - 300001 - lookback) // 128
# -
# 이 모델은 두 개의 `Conv1D` 층 다음에 `GRU` 층을 놓았습니다.
# +
# 코드 6-49. 1D 합성곱과 GRU 층을 연결한 모델
model = Sequential()
model.add(layers.Conv1D(32, 5, activation='relu',
input_shape=(None, float_data.shape[-1])))
model.add(layers.MaxPooling1D(3))
model.add(layers.Conv1D(32, 5, activation='relu'))
model.add(layers.GRU(32, dropout=0.1, recurrent_dropout=0.5))
model.add(layers.Dense(1))
model.summary()
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=20,
validation_data=val_gen,
validation_steps=val_steps)
# +
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
# -
# _그림 6-31. 1D 컨브넷과 GRU를 사용한 예나 온도 예측 문제의 훈련 손실과 검증 손실_
# 검증 손실로 비교해 보면 이 설정은 규제가 있는 GRU 모델만큼 좋지는 않습니다. 하지만 훨씬 빠르기 때문에 데이터를 두 배 더 많이 처리할 수 있습니다. 여기서는 큰 도움이 안 되었지만 다른 데이터셋에서는 중요할 수 있습니다.
# ## 6.4.5 정리
#
# 다음은 이번 절에서 배운 것들입니다.
#
# - 2D 컨브넷이 2D 공간의 시각적 패턴을 잘 처리하는 것과 같이 1D 컨브넷은 시간에 따른 패턴을 잘 처리합니다. 1D 컨브넷은 특정 자연어 처리 같은 일부 문제에 RNN을 대신할 수 있는 빠른 모델입니다.
# - 전형적으로 1D 컨브넷은 컴퓨터 비전 분야의 2D 컨브넷과 비슷하게 구성합니다. `Conv1D` 층과 `Max-Pooling1D` 층을 쌓고 마지막에 전역 풀링 연산이나 `Flatten` 층을 둡니다.
# - RNN으로 아주 긴 시퀀스를 처리하려면 계산 비용이 많이 듭니다. 1D 컨브넷은 비용이 적게 듭니다. 따라서 1D 컨브넷을 RNN 이전의 전처리 단계로 사용하는 것은 좋은 생각입니다. 시퀀스 길이를 줄이고 RNN이 처리할 유용한 표현을 추출해 줄 것입니다.
#
# 유용하고 중요한 개념이지만 여기서 다루지 않은 것은 팽창 커널을 사용한 1D 합성곱입니다.
|
_books/DeepLearningFromKeras/Part2/Chapter6/6.4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# This file is part of the pyMOR project (http://www.pymor.org).
# Copyright 2013-2020 pyMOR developers and contributors. All rights reserved.
# License: BSD 2-Clause License (http://opensource.org/licenses/BSD-2-Clause)
# -
# %matplotlib notebook
# +
import numpy as np
import scipy.linalg as spla
import matplotlib.pyplot as plt
import matplotlib as mpl
from pymor.basic import *
from pymor.core.config import config
from pymor.core.logger import set_log_levels
set_log_levels({'pymor.algorithms.gram_schmidt.gram_schmidt': 'WARNING'})
set_defaults({'pymor.discretizers.builtin.gui.jupyter.get_visualizer.backend': 'not pythreejs'})
# -
# # Model
# +
p = InstationaryProblem(
StationaryProblem(
domain=LineDomain([0.,1.], left='robin', right='robin'),
diffusion=LincombFunction([ExpressionFunction('(x[...,0] <= 0.5) * 1.', 1),
ExpressionFunction('(0.5 < x[...,0]) * 1.', 1)],
[1,
ProjectionParameterFunctional('diffusion')]),
robin_data=(ConstantFunction(1., 1), ExpressionFunction('(x[...,0] < 1e-10) * 1.', 1)),
outputs=(('l2_boundary', ExpressionFunction('(x[...,0] > (1 - 1e-10)) * 1.', 1)),),
),
ConstantFunction(0., 1),
T=3.
)
fom, _ = discretize_instationary_cg(p, diameter=1/100, nt=100)
# -
fom.visualize(fom.solve(mu=0.1))
fom.visualize(fom.solve(mu=1))
fom.visualize(fom.solve(mu=10))
lti = fom.to_lti()
# # System analysis
print(f'order of the model = {lti.order}')
print(f'number of inputs = {lti.input_dim}')
print(f'number of outputs = {lti.output_dim}')
# +
mu_list = [0.1, 1, 10]
fig, ax = plt.subplots(len(mu_list), 1, sharex=True, sharey=True)
for i, mu in enumerate(mu_list):
poles = lti.poles(mu=mu)
ax[i].plot(poles.real, poles.imag, '.')
ax[i].set_xscale('symlog')
ax[i].set_title(fr'$\mu = {mu}$')
fig.suptitle('System poles')
fig.subplots_adjust(hspace=0.5)
plt.show()
# +
mu_list = [0.1, 1, 10]
fig, ax = plt.subplots()
w = np.logspace(-1, 3, 100)
for mu in mu_list:
lti.mag_plot(w, ax=ax, mu=mu, label=fr'$\mu = {mu}$')
ax.legend()
plt.show()
# +
w_list = np.logspace(-1, 3, 100)
mu_list = np.logspace(-1, 1, 20)
lti_w_mu = np.zeros((len(w_list), len(mu_list)))
for i, mu in enumerate(mu_list):
lti_w_mu[:, i] = spla.norm(lti.freq_resp(w, mu=mu), axis=(1, 2))
# -
fig, ax = plt.subplots()
out = ax.contourf(w_list, mu_list, lti_w_mu.T,
norm=mpl.colors.LogNorm(),
levels=np.logspace(-16, np.log10(lti_w_mu.max()), 100))
ax.set_xlabel(r'Frequency $\omega$')
ax.set_ylabel(r'Parameter $\mu$')
ax.set_xscale('log')
ax.set_yscale('log')
fig.colorbar(out, ticks=np.logspace(-16, 0, 17))
plt.show()
# +
mu_list = [0.1, 1, 10]
fig, ax = plt.subplots()
for mu in mu_list:
hsv = lti.hsv(mu=mu)
ax.semilogy(range(1, len(hsv) + 1), hsv, label=fr'$\mu = {mu}$')
ax.set_title('Hankel singular values')
ax.legend()
plt.show()
# +
fig, ax = plt.subplots()
mu_fine = np.logspace(-1, 1, 20)
h2_norm_mu = [lti.h2_norm(mu=mu) for mu in mu_fine]
ax.plot(mu_fine, h2_norm_mu, label=r'$\mathcal{H}_2$-norm')
if config.HAVE_SLYCOT:
hinf_norm_mu = [lti.hinf_norm(mu=mu) for mu in mu_fine]
ax.plot(mu_fine, hinf_norm_mu, label=r'$\mathcal{H}_\infty$-norm')
hankel_norm_mu = [lti.hankel_norm(mu=mu) for mu in mu_fine]
ax.plot(mu_fine, hankel_norm_mu, label='Hankel norm')
ax.set_xlabel(r'$\mu$')
ax.set_title('System norms')
ax.legend()
plt.show()
# -
# # Balanced truncation
def reduction_errors(lti, r, mu_fine, reductor, **kwargs):
h2_err_mu = []
hinf_err_mu = []
hankel_err_mu = []
for mu in mu_fine:
rom_mu = reductor(lti, mu=mu, **kwargs).reduce(r)
h2_err_mu.append((lti - rom_mu).h2_norm(mu=mu) / lti.h2_norm(mu=mu))
if config.HAVE_SLYCOT:
hinf_err_mu.append((lti - rom_mu).hinf_norm(mu=mu) / lti.hinf_norm(mu=mu))
hankel_err_mu.append((lti - rom_mu).hankel_norm(mu=mu) / lti.hankel_norm(mu=mu))
return h2_err_mu, hinf_err_mu, hankel_err_mu
r = 5
mu_fine = np.logspace(-1, 1, 10)
h2_bt_err_mu, hinf_bt_err_mu, hankel_bt_err_mu = reduction_errors(lti, r, mu_fine, BTReductor)
# +
fig, ax = plt.subplots()
ax.semilogy(mu_fine, h2_bt_err_mu, '.-', label=r'$\mathcal{H}_2$')
if config.HAVE_SLYCOT:
ax.semilogy(mu_fine, hinf_bt_err_mu, '.-', label=r'$\mathcal{H}_\infty$')
ax.semilogy(mu_fine, hankel_bt_err_mu, '.-', label='Hankel')
ax.set_xlabel(r'$\mu$')
ax.set_title('Balanced truncation errors')
ax.legend()
plt.show()
# -
# # Iterative Rational Krylov Algorithm (IRKA)
h2_irka_err_mu, hinf_irka_err_mu, hankel_irka_err_mu = reduction_errors(lti, r, mu_fine, IRKAReductor)
# +
fig, ax = plt.subplots()
ax.semilogy(mu_fine, h2_irka_err_mu, '.-', label=r'$\mathcal{H}_2$')
if config.HAVE_SLYCOT:
ax.semilogy(mu_fine, hinf_irka_err_mu, '.-', label=r'$\mathcal{H}_\infty$')
ax.semilogy(mu_fine, hankel_irka_err_mu, '.-', label='Hankel')
ax.set_xlabel(r'$\mu$')
ax.set_title('IRKA errors')
ax.legend()
plt.show()
# -
# # Two-Sided Iteration Algorithm (TSIA)
h2_tsia_err_mu, hinf_tsia_err_mu, hankel_tsia_err_mu = reduction_errors(lti, r, mu_fine, TSIAReductor)
# +
fig, ax = plt.subplots()
ax.semilogy(mu_fine, h2_tsia_err_mu, '.-', label=r'$\mathcal{H}_2$')
if config.HAVE_SLYCOT:
ax.semilogy(mu_fine, hinf_tsia_err_mu, '.-', label=r'$\mathcal{H}_\infty$')
ax.semilogy(mu_fine, hankel_tsia_err_mu, '.-', label='Hankel')
ax.set_xlabel(r'$\mu$')
ax.set_title('TSIA errors')
ax.legend()
plt.show()
# -
# # One-sided IRKA
h2_osirka_err_mu, hinf_osirka_err_mu, hankel_osirka_err_mu = reduction_errors(
lti, r, mu_fine, OneSidedIRKAReductor, version='V'
)
# +
fig, ax = plt.subplots()
ax.semilogy(mu_fine, h2_osirka_err_mu, '.-', label=r'$\mathcal{H}_2$')
if config.HAVE_SLYCOT:
ax.semilogy(mu_fine, hinf_osirka_err_mu, '.-', label=r'$\mathcal{H}_\infty$')
ax.semilogy(mu_fine, hankel_osirka_err_mu, '.-', label='Hankel')
ax.set_xlabel(r'$\mu$')
ax.set_title('One-sided IRKA errors')
ax.legend()
plt.show()
|
notebooks/parametric_heat.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 27-Jan-2020
# 1. Load Train and Test datasets in Python
# 2. Reduce their sizes by changing data types
# 3. Drop the simulated kinematic states from both datasets
# 4. Extract the 300 satellites from Train that are in Test
# 5. Offset to positive values for each of the 300 satellites
# 6. Export to csv for forecasting in R
import os
import numpy as np
import pandas as pd
import seaborn as sns
import datetime as dt
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.holtwinters import ExponentialSmoothing
sns.set_style('whitegrid')
sns.set(rc={'figure.figsize':(16, 4)})
plt.rc('figure',figsize=(16,12))
plt.rc('font',size=13)
train = pd.read_pickle('train.pkl')
test = pd.read_pickle('test.pkl')
# make original
train_original = train.copy()
test_original = test.copy()
# cell for resetting to original
train = train_original.copy()
test = test_original.copy()
# +
#train.index = train['epoch']
#test.index = test['epoch']
# -
tr = train.drop(train.columns[9:], axis=1)
te = test.drop(test.columns[3:], axis=1)
sat_ids = te['sat_id'].unique()
boolean = [sat_no in sat_ids for sat_no in tr['sat_id']]
tr_300 = tr[boolean]
sum(tr_300['sat_id'].unique() != te['sat_id'].unique())
tr_300.columns[4]
tr_300.shape
tr_300.columns[[0,1,2,4]]
def xport(df, col_no):
df = df[df.columns[[0,1,2,col_no]]]
# this should always be the 4th column because from the above code, df now has 4 columns
k = df.columns[3]
sat = list()
# For each satellite number n from the 300 unique satellite IDs in the Test dataset,
for n in sat_ids:
# grab the data corresponding to satellite n and assign it to a variable satdata_n,
satdata_n = df[df['sat_id'] == n]
# calculate offset_n for that satellite's kinematic state,
offset_n = max(satdata_n[k]) - min(satdata_n[k])
# shift the kinematic state by the amount given by offset_n,
satdata_n.loc[:,k] += offset_n
# put the offsetted data into a list
sat.append(satdata_n)
# concatenate all the dataframes in the list into the now offsetted dataframe,
df = pd.concat(sat)
# export the offsetted dataframe to csv for later analysis
df.to_csv(f'train_{col_no-2}.csv')
# return the offsetted dataframe for further inspection
return df
# %%time
trx_off = xport(df=tr_300, col_no=3)
tr_300.columns
# do the same for y, z, Vx, Vy, Vz
offsetted_dfs = list()
for col in range(4,9):
df_off = xport(df=tr_300, col_no=col)
offsetted_dfs.append(df_off)
print(f'State {col-2} has been exported.')
for i in range(0,len(offsetted_dfs)):
print((offsetted_dfs[0].iloc[:,3] <= 0).sum())
# All offsetted data are now strictly positive.
(trx_off['x'] <= 0).any()
trx.columns[3]
te.to_csv('test_forR.csv')
trx.shape
trx.head()
trx_copy = trx.copy()
# to reset
trx = trx_copy.copy()
sat = list()
# For each satellite number n from the 300 unique satellite IDs in the Test dataset,
for n in range(1,3):
#for sat_no in sat_ids:
# grab the data corresponding to satellite n and assign it to a variable satdata_n,
satdata_n = trx[trx['sat_id'] == n]
# calculate offset_n for that satellite's kinematic state,
offset_n = max(satdata_n['x']) - min(satdata_n['x'])
# shift the kinematic state by the amount given by offset_n,
satdata_n.loc[:,'x'] += offset_n
# put the offsetted data into a list
sat.append(satdata_n)
# and concatenate all the dataframes in the list into the new offsetted dataframe
trx_off = pd.concat(sat)
trx_copy = trx.copy()
# Cannot calculate delta_t by directly taking the difference between two successive epochs because epochs reset to 2014-01-01 at the starting row of each satellite.
# insert r and V
#train.insert(3, 'delta_t', train['epoch'].diff())
train.insert(3, 'r', np.sqrt(train['x']**2 + train['y']**2 + train['z']**2))
train.insert(4, 'V', np.sqrt(train['Vx']**2 + train['Vy']**2 + train['Vz']**2))
# convert timedelta to minutes
train['delta_t'] = train['delta_t'].apply(lambda x: round(x.total_seconds() / 60, 1))
# Classifications for geocentric (earth-centred) orbits:
# - Low Earth Orbit (LEO)..............radius < 2000 km, velocity ~ 7.8 km/s
# - Medium Earth Orbit (MEO).......radius < 35786 km, most commonly around 20200 km
# - Geosynchronous Orbit (GSO)..radius = 35786 km
# - High Earth Orbit (HEO)............radius > 35786 km
gso = 35786
mean_kinem = train.groupby('sat_id')[['r','V']].agg([np.mean, np.min, np.max])
mean_kinem.head()
mean_kinem['r']['mean'][0]
highest = '372 186 429 321 529 470 535 323 272 588'.split()
# mean_kinem['r']['mean'][372] -> 10248
mean_kinem['r']['mean'][429] #-> 10438
#mean_kinem['r']['amax'][429] - mean_kinem['r']['amin'][429]
#plt.plot(mean_kinem['r']['amin'], 'g.', label='min altitude')
#plt.plot(mean_kinem['r']['amax'], 'r.', label='max altitude')
plt.plot(mean_kinem['r']['amax'] - mean_kinem['r']['amin'], 'r.', label='delta altitude')
#plt.plot(mean_kinem['r']['mean'], 'b.', label='mean altitude')
plt.axhline(y=gso, color='r', linestyle='-', label='GSO')
plt.axhline(y=2000, color='black', linestyle='-', label='LEO')
#for k in range(250,271):
plt.axvline(x=429, color='r', linestyle='-', alpha=1, linewidth=1)
plt.xlabel('Satellite ID')
plt.ylabel('Altitude (km)')
plt.legend(loc='best')
#plt.plot(mean_kinem['r']['amin'], 'g.', label='min altitude')
#plt.plot(mean_kinem['r']['amax'], 'r.', label='max altitude')
plt.plot(mean_kinem['r']['mean'], 'b.', label='mean altitude')
plt.axhline(y=gso, color='r', linestyle='-', label='GSO')
plt.axhline(y=2000, color='black', linestyle='-', label='LEO')
#for k in range(250,271):
# plt.axvline(x=k, color='r', linestyle='-', alpha=1, linewidth=0.1)
plt.xlabel('Satellite ID')
plt.ylabel('Altitude (km)')
plt.legend(loc='best')
# None of the satellites are at LEO. Most are at HEO (those above the red line), a few are at GSO (those lying on the red line) and the remaining are at MEO (those below the red line but above the black line).
plt.plot(mean_kinem['V'], '.')
round(train['delta_t'][4].total_seconds() / 60, 1)
train['delta_t'].to_datetime()
train.groupby(by='sat_id')['delta_t'].mean()
train.head()
# +
# index of first observation of satellite
first_indices_train = list()
for sat_no in train['sat_id'].unique():
first_id = train['sat_id'].searchsorted(sat_no)
first_indices_train.append(first_id[0])
first_indices_test = list()
for sat_no in test['sat_id'].unique():
first_id = test['sat_id'].searchsorted(sat_no)
first_indices_test.append(first_id[0])
# -
# Create a function that, for a given satellite ID, extracts the data for that one satellite only.
def one_satdata(sat_id):
return train[train['sat_id'] == sat_id]
# Create a function that, for a given iterable of satellite IDs, extracts all the data for that collection of satellites.
def plot_satdata(sat_id):
plt.plot(train[train['sat_id'] == sat_id]['x'])
plt.show()
for k in range(11,14):
plot_satdata(sat_id=k)
sat = list()
for k in range(1,4):
sat.append(one_satdata(sat_id=k))
sat[1].head()
sat[1].tail()
|
4.a Preparation on the entire dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="qN8P0AnTnAhh"
# ##### Copyright 2020 The TensorFlow Authors.
# + [markdown] colab_type="text" id="MnUwFbCAKB2r"
# ## Before we start
# To edit the colab notebook, please go to "File" -> "Save a copy in Drive" and make any edits on your copy.
#
# Before we start, please run the following to make sure that your environment is
# correctly setup. If you don't see a greeting, please refer to the
# [Installation](../install.md) guide for instructions.
# + cellView="both" colab={} colab_type="code" id="ZrGitA_KnRO0"
#@title Upgrade tensorflow_federated and load TensorBoard
#@test {"skip": true}
# !pip install --quiet --upgrade tensorflow-federated-nightly
# !pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
# %load_ext tensorboard
import sys
if not sys.warnoptions:
import warnings
warnings.simplefilter("ignore")
# + cellView="both" colab={} colab_type="code" id="8BKyHkMxKHfV"
#@title
import collections
from matplotlib import pyplot as plt
from IPython.display import display, HTML, IFrame
import numpy as np
import tensorflow as tf
import tensorflow_federated as tff
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)
np.random.seed(0)
def greetings():
display(HTML('<b><font size="6" color="#ff00f4">Greetings, virtual tutorial participants!</font></b>'))
return True
l = tff.federated_computation(greetings)()
# + [markdown] colab_type="text" id="AftvNA5VMemJ"
# # TensorFlow Federated for Image Classification
# + [markdown] colab_type="text" id="coAumH42q9nz"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/federated/tutorials/federated_learning_for_image_classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/federated/blob/v0.14.0/docs/tutorials/federated_learning_for_image_classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/federated/blob/v0.14.0/docs/tutorials/federated_learning_for_image_classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="Zs2LgZBOMt4M"
# Let's experiment with federated learning in simulation. In this tutorial, we use the classic MNIST training example to introduce the
# Federated Learning (FL) API layer of TFF, `tff.learning` - a set of
# higher-level interfaces that can be used to perform common types of federated
# learning tasks, such as federated training, against user-supplied models
# implemented in TensorFlow.
#
# + [markdown] colab_type="text" id="dN7n8RS7-rLR"
# # Tutorial Outline
# We'll be training a model to perform image classification using the classic MNIST dataset, with the neural net learning to classify digit from image. In this case, we'll be simulating federated learning, with the training data distributed on different devices.
#
# <p><b>Sections</b></p>
#
#
# 1. Load TFF Libraries.
# 2. Explore/preprocess federated EMNIST dataset.
# 3. Create a model.
# 4. Set up federated averaging process for training.
# 5. Analyze training metrics.
# 6. Set up federated evaluation computation.
# 7. Analyze evaluation metrics.
#
#
# + [markdown] colab_type="text" id="5Cyy2AWbLMKj"
# ## Preparing the input data
#
# Let's start with the data. Federated learning requires a federated data set,
# i.e., a collection of data from multiple users. Federated data is typically
# non-[i.i.d.](https://en.wikipedia.org/wiki/Independent_and_identically_distributed_random_variables),
# which poses a unique set of challenges. Users typically have different distributions of data depending on usage patterns.
#
# In order to facilitate experimentation, we seeded the TFF repository with a few
# datasets.
#
# Here's how we can load our sample dataset.
# + colab={} colab_type="code" id="bP6WDENHSSZ9"
# Code for loading federated data from TFF repository
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data()
# + [markdown] colab_type="text" id="yeX8BKgPfeFw"
# The data sets returned by `load_data()` are instances of
# `tff.simulation.ClientData`, an interface that allows you to enumerate the set
# of users, to construct a `tf.data.Dataset` that represents the data of a
# particular user, and to query the structure of individual elements.
#
# Let's explore the dataset.
# + colab={} colab_type="code" id="kN4-U5nJgKig"
len(emnist_train.client_ids)
# + colab={} colab_type="code" id="ZyCzIrSegT62"
# Let's look at the shape of our data
example_dataset = emnist_train.create_tf_dataset_for_client(
emnist_train.client_ids[0])
example_dataset.element_spec
# + colab={} colab_type="code" id="EsvSXGEMgd9G"
# Let's select an example dataset from one of our simulated clients
example_dataset = emnist_train.create_tf_dataset_for_client(
emnist_train.client_ids[0])
# Your code to get an example element from one client:
example_element = next(iter(example_dataset))
example_element['label'].numpy()
# + colab={} colab_type="code" id="OmLV0nfMg98V"
plt.imshow(example_element['pixels'].numpy(), cmap='gray', aspect='equal')
plt.grid(False)
_ = plt.show()
# + [markdown] colab_type="text" id="y-3KUf0kC8TN"
# **Exploring non-iid data**
# + colab={} colab_type="code" id="veWNAxdQfrgZ"
## Example MNIST digits for one client
f = plt.figure(figsize=(20,4))
j = 0
for e in example_dataset.take(40):
plt.subplot(4, 10, j+1)
plt.imshow(e['pixels'].numpy(), cmap='gray', aspect='equal')
plt.axis('off')
j += 1
# + colab={} colab_type="code" id="_XJRWDFWniik"
# Number of examples per layer for a sample of clients
f = plt.figure(figsize=(12,7))
f.suptitle("Label Counts for a Sample of Clients")
for i in range(6):
ds = emnist_train.create_tf_dataset_for_client(emnist_train.client_ids[i])
k = collections.defaultdict(list)
for e in ds:
k[e['label'].numpy()].append(e['label'].numpy())
plt.subplot(2, 3, i+1)
plt.title("Client {}".format(i))
for j in range(10):
plt.hist(k[j], density=False, bins=[0,1,2,3,4,5,6,7,8,9,10])
# + colab={} colab_type="code" id="JOUI4zW9LQNH"
# Let's play around with the emnist_train dataset.
# Let's explore the non-iid charateristic of the example data.
for i in range(5):
ds = emnist_train.create_tf_dataset_for_client(emnist_train.client_ids[i])
k = collections.defaultdict(list)
for e in ds:
k[e['label'].numpy()].append(e['pixels'].numpy())
f = plt.figure(i, figsize=(12,5))
f.suptitle("Client #{}'s Mean Image Per Label".format(i))
for j in range(10):
mn_img = np.mean(k[j],0)
plt.subplot(2, 5, j+1)
plt.imshow(mn_img.reshape((28,28)))#,cmap='gray')
plt.axis('off')
# Each client has different mean images -- each client will be nudging the model
# in their own directions.
# + [markdown] colab_type="text" id="lMd01egqy9we"
# ### Preprocessing the data
#
# Since the data is already a `tf.data.Dataset`, preprocessing can be accomplished using Dataset transformations. [See here](https://www.tensorflow.org/guide/data) for more detail on these transformations.
# + colab={} colab_type="code" id="cyG_BMraSuu_"
NUM_CLIENTS = 10
NUM_EPOCHS = 5
BATCH_SIZE = 20
SHUFFLE_BUFFER = 100
PREFETCH_BUFFER=10
def preprocess(dataset):
def batch_format_fn(element):
"""Flatten a batch `pixels` and return the features as an `OrderedDict`."""
return collections.OrderedDict(
x=tf.reshape(element['pixels'], [-1, 784]),
y=tf.reshape(element['label'], [-1, 1]))
return dataset.repeat(NUM_EPOCHS).shuffle(SHUFFLE_BUFFER).batch(
BATCH_SIZE).map(batch_format_fn).prefetch(PREFETCH_BUFFER)
# + [markdown] colab_type="text" id="m9LXykN_jlJw"
# Let's verify this worked.
# + colab={} colab_type="code" id="VChB7LMQjkYz"
preprocessed_example_dataset = preprocess(example_dataset)
sample_batch = tf.nest.map_structure(lambda x: x.numpy(),
next(iter(preprocessed_example_dataset)))
sample_batch
# + [markdown] colab_type="text" id="JGsMvRQt9Agl"
# Here's a simple helper function that will construct a list of datasets from the
# given set of users as an input to a round of training or evaluation.
# + colab={} colab_type="code" id="_PHMvHAI9xVc"
def make_federated_data(client_data, client_ids):
return [
preprocess(client_data.create_tf_dataset_for_client(x))
for x in client_ids
]
# + [markdown] colab_type="text" id="0M9PfjOtAVqw"
# Now, how do we choose clients?
# + colab={} colab_type="code" id="GZ6NYHxB8xer"
sample_clients = emnist_train.client_ids[0:NUM_CLIENTS]
# Your code to get the federated dataset here for the sampled clients:
federated_train_data = make_federated_data(emnist_train, sample_clients)
print('Number of client datasets: {l}'.format(l=len(federated_train_data)))
print('First dataset: {d}'.format(d=federated_train_data[0]))
# + [markdown] colab_type="text" id="HOxq4tbi9m8-"
# ## Creating a model with Keras
#
# If you are using Keras, you likely already have code that constructs a Keras
# model. Here's an example of a simple model that will suffice for our needs.
# + colab={} colab_type="code" id="LYCsJGJFWbqt"
def create_keras_model():
return tf.keras.models.Sequential([
tf.keras.layers.Input(shape=(784,)),
tf.keras.layers.Dense(10, kernel_initializer='zeros'),
tf.keras.layers.Softmax(),
])
# + [markdown] colab_type="text" id="A0214iKjCTyX"
# **Centralized training with Keras**
# + colab={} colab_type="code" id="g5XW_p4iLlJ2"
## Centralized training with keras ---------------------------------------------
# This is separate from the TFF tutorial, and demonstrates how to train a
# Keras model in a centralized fashion (contrasting training in a federated env)
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Preprocess the data (these are NumPy arrays)
x_train = x_train.reshape(60000, 784).astype("float32") / 255
y_train = y_train.astype("float32")
mod = create_keras_model()
mod.compile(
optimizer=tf.keras.optimizers.RMSprop(),
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()]
)
h = mod.fit(
x_train,
y_train,
batch_size=64,
epochs=2
)
# ------------------------------------------------------------------------------
# + [markdown] colab_type="text" id="l6pzsjoJQ2_D"
# **Federated training using a Keras model**
# + [markdown] colab_type="text" id="NHdraKFH4OU2"
#
#
# In order to use any model with TFF, it needs to be wrapped in an instance of the
# `tff.learning.Model` interface.
# + [markdown] colab_type="text" id="mA8cJoGE3Rh_"
# More keras metrics you can add are [found here](https://www.tensorflow.org/api_docs/python/tf/keras/metrics).
# + colab={} colab_type="code" id="Q3ynrxd53HzY"
def model_fn():
# We _must_ create a new model here, and _not_ capture it from an external
# scope. TFF will call this within different graph contexts.
keras_model = create_keras_model()
return tff.learning.from_keras_model(
keras_model,
input_spec=preprocessed_example_dataset.element_spec,
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
# + [markdown] colab_type="text" id="XJ5E3O18_JZ6"
# ## Training the model on federated data
#
# Now that we have a model wrapped as `tff.learning.Model` for use with TFF, we
# can let TFF construct a Federated Averaging algorithm by invoking the helper
# function `tff.learning.build_federated_averaging_process`, as follows.
# + colab={} colab_type="code" id="sk6mjOfycX5N"
iterative_process = tff.learning.build_federated_averaging_process(
model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(learning_rate=0.02),
# Add server optimizer here!
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(learning_rate=1.0))
# + [markdown] colab_type="text" id="f8FpvN2n67sm"
# What just happened? TFF has constructed a pair of *federated computations* and
# packaged them into a `tff.templates.IterativeProcess` in which these computations
# are available as a pair of properties `initialize` and `next`.
#
# An iterative process will usually be driven by a control loop like:
# ```
# def initialize():
# ...
#
# def next(state):
# ...
#
# iterative_process = IterativeProcess(initialize, next)
# state = iterative_process.initialize()
# for round in range(num_rounds):
# state = iterative_process.next(state)
# ```
#
#
# + [markdown] colab_type="text" id="v1gbHQ_7BiyT"
# Let's invoke the `initialize` computation to construct the server state.
# + colab={} colab_type="code" id="6cagCWlZmcch"
state = iterative_process.initialize()
# + [markdown] colab_type="text" id="TjjxTx9e_rMd"
# The second of the pair of federated computations, `next`, represents a single
# round of Federated Averaging, which consists of pushing the server state
# (including the model parameters) to the clients, on-device training on their
# local data, collecting and averaging model updates, and producing a new updated
# model at the server.
#
# Let's run a single round of training and visualize the results. We can use the
# federated data we've already generated above for a sample of users.
# + colab={} colab_type="code" id="F3M_W9dDE6Tm"
# Run one single round of training.
state, metrics = iterative_process.next(state, federated_train_data)
print('round 1, metrics={}'.format(metrics['train']))
# + [markdown] colab_type="text" id="UmhReXt9G4A5"
# Let's run a few more rounds. As noted earlier, typically at this point you would
# pick a subset of your simulation data from a new randomly selected sample of
# users for each round in order to simulate a realistic deployment in which users
# continuously come and go, but in this interactive notebook, for the sake of
# demonstration we'll just reuse the same users, so that the system converges
# quickly.
# + colab={} colab_type="code" id="qrJkQuCRJP9C"
NUM_ROUNDS = 11
for round_num in range(2, NUM_ROUNDS):
state, metrics = iterative_process.next(state, federated_train_data)
print('round {:2d}, metrics={}'.format(round_num, metrics['train']))
# + [markdown] colab_type="text" id="joHYzn9jcs0Y"
# Training loss is decreasing after each round of federated training, indicating
# the model is converging. There are some important caveats with these training
# metrics, however, see the section on *Evaluation* later in this tutorial.
# + [markdown] colab_type="text" id="ruSHJl1IjhNf"
# ##Displaying model metrics in TensorBoard
# Next, let's visualize the metrics from these federated computations using Tensorboard.
#
# Let's start by creating the directory and the corresponding summary writer to write the metrics to.
#
#
#
# + colab={} colab_type="code" id="E3QUBK41lWDW"
#@test {"skip": true}
import os
import shutil
logdir = "/tmp/logs/scalars/training/"
if os.path.exists(logdir):
shutil.rmtree(logdir)
# Your code to create a summary writer:
summary_writer = tf.summary.create_file_writer(logdir)
state = iterative_process.initialize()
# + [markdown] colab_type="text" id="w-2aGxUlzS_J"
# Plot the relevant scalar metrics with the same summary writer.
# + colab={} colab_type="code" id="JZtr4_8lzN-V"
#@test {"skip": true}
with summary_writer.as_default():
for round_num in range(1, NUM_ROUNDS):
state, metrics = iterative_process.next(state, federated_train_data)
for name, value in metrics['train'].items():
tf.summary.scalar(name, value, step=round_num)
# + [markdown] colab_type="text" id="iUouyAHG0Mk8"
# Start TensorBoard with the root log directory specified above. It can take a few seconds for the data to load.
# + colab={} colab_type="code" id="urYYcmA9089p"
#@test {"skip": true}
# %tensorboard --logdir /tmp/logs/scalars/ --port=0
# + [markdown] colab_type="text" id="jejrFEVP1EDs"
# In order to view evaluation metrics the same way, you can create a separate eval folder, like "logs/scalars/eval", to write to TensorBoard.
# + [markdown] colab_type="text" id="m7lz59lMJ0kj"
# ## Evaluation
# To perform evaluation on federated data, you can construct another *federated
# computation* designed for just this purpose, using the
# `tff.learning.build_federated_evaluation` function, and passing in your model
# constructor as an argument.
# + colab={} colab_type="code" id="nRiXyqnXM2VO"
# Construct federated evaluation computation here:
evaluation = tff.learning.build_federated_evaluation(model_fn)
# + [markdown] colab_type="text" id="SpfgdNDoRjPy"
# Now, let's compile a test sample of federated data and rerun evaluation on the
# test data. The data will come from a different sample of users, but from a
# distinct held-out data set.
# + colab={} colab_type="code" id="in8vProVNc04"
import random
shuffled_ids = emnist_test.client_ids.copy()
random.shuffle(shuffled_ids)
sample_clients = shuffled_ids[0:NUM_CLIENTS]
federated_test_data = make_federated_data(emnist_test, sample_clients)
len(federated_test_data), federated_test_data[0]
# + colab={} colab_type="code" id="ty-ZwfE0NJfV"
# Run evaluation on the test data here, using the federated model produced from
# training:
test_metrics = evaluation(state.model, federated_test_data)
# + colab={} colab_type="code" id="e5fGtIJYNqYH"
str(test_metrics)
# + [markdown] colab_type="text" id="67vYxrDWzRcj"
# This concludes the tutorial. We encourage you to play with the
# parameters (e.g., batch sizes, number of users, epochs, learning rates, etc.), to modify the code above to simulate training on random samples of users in
# each round, and to explore the other tutorials we've developed.
# + [markdown] colab_type="text" id="4Zv28F7QLo8O"
# # Build your own FL algorithms
#
# In the previous tutorials, we learned how to set up model and data pipelines, and use these to perform federated training using the `tff.learning` API.
#
# Of course, this is only the tip of the iceberg when it comes to FL research. In this tutorial, we are going to discuss how to implement federated learning algorithms *without* deferring to the `tff.learning` API. We aim to accomplish the following:
#
# **Goals:**
#
#
# * Understand the general structure of federated learning algorithms.
# * Explore the *Federated Core* of TFF.
# * Use the Federated Core to implement Federated Averaging directly.
#
#
#
# + [markdown] colab_type="text" id="hQ_N9XbULo8P"
# ## Preparing the input data
# We first load and preprocess the EMNIST dataset included in TFF. We essentially use the same code as in the first tutorial.
# + colab={} colab_type="code" id="-WdnFluLLo8P"
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data()
# + colab={} colab_type="code" id="Blrh8zJgLo8R"
NUM_CLIENTS = 10
BATCH_SIZE = 20
def preprocess(dataset):
def batch_format_fn(element):
"""Flatten a batch of EMNIST data and return a (features, label) tuple."""
return (tf.reshape(element['pixels'], [-1, 784]),
tf.reshape(element['label'], [-1, 1]))
return dataset.batch(BATCH_SIZE).map(batch_format_fn)
# + colab={} colab_type="code" id="-vYM_IT7Lo8W"
client_ids = np.random.choice(emnist_train.client_ids, size=NUM_CLIENTS, replace=False)
federated_train_data = [preprocess(emnist_train.create_tf_dataset_for_client(x))
for x in client_ids
]
# + [markdown] colab_type="text" id="gNO_Y9j_Lo8X"
# ## Preparing the model
# + [markdown] colab_type="text" id="LJ0I89ixz8yV"
# We use the same model as the first tutorial, which has a single hidden layer, followed by a softmax layer.
# + colab={} colab_type="code" id="Yfld4oFNLo8Y"
def create_keras_model():
return tf.keras.models.Sequential([
tf.keras.layers.Input(shape=(784,)),
tf.keras.layers.Dense(10, kernel_initializer='zeros'),
tf.keras.layers.Softmax(),
])
# + [markdown] colab_type="text" id="vLln0Q8G0Bky"
# We wrap this Keras model as a `tff.learning.Model`.
# + colab={} colab_type="code" id="SPwbipTNLo8a"
def model_fn():
keras_model = create_keras_model()
return tff.learning.from_keras_model(
keras_model,
input_spec=federated_train_data[0].element_spec,
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
# + [markdown] colab_type="text" id="fPOWP2JjsfTk"
# # Cutomizing FL Algorithm
#
# While the `tff.learning` API encompasses many variants of Federated Averaging, there are many other algorithms that do not fit neatly into this framework. For example, you may want to add regularization, clipping, or more complicated algorithms such as [federated GAN training](https://github.com/google-research/federated/blob/master/gans). You may also be instead be interested in [federated analytics](https://ai.googleblog.com/2020/05/federated-analytics-collaborative-data.html).
# + [markdown] colab_type="text" id="50N36Zz8qyY-"
# For these more advanced algorithms, we'll have to write our own custom FL algorithm.
#
# In general, FL algorithms have 4 main components:
#
# 1. A server-to-client broadcast step.
# 2. A local client update step.
# 3. A client-to-server upload step.
# 4. A server update step.
# + [markdown] colab_type="text" id="jH8s0GRdQt3b"
# In TFF, we generally represent federated algorithms as an `IterativeProcess`. This is simply a class that contains an `initialize_fn` and a `next_fn`. The `initialize_fn` will be used to initialize the server, and the `next_fn` will perform one communication round of federated averaging. Let's write a skeleton of what our iterative process for FedAvg should look like.
#
# First, we have an initialize function that simply creates a `tff.learning.Model`, and returns its trainable weights.
# + colab={} colab_type="code" id="ylLpRa7T5DDh"
def initialize_fn():
model = model_fn()
return model.weights.trainable
# + [markdown] colab_type="text" id="nb1-XAK8fB2A"
# This function looks good, but as we will see later, we will need to make a small modification to make it a TFF computation.
#
# We also want to sketch the `next_fn`.
# + colab={} colab_type="code" id="IeHN-XLZfMso"
def next_fn(server_weights, federated_dataset):
# Broadcast the server weights to the clients.
server_weights_at_client = broadcast(server_weights)
# Each client computes their updated weights.
client_weights = client_update(federated_dataset, server_weights_at_client)
# The server averages these updates.
mean_client_weights = mean(client_weights)
# The server updates its model.
server_weights = server_update(mean_client_weights)
return server_weights
# + [markdown] colab_type="text" id="uWXvjXPWeujU"
# We'll focus on implementing these four components separately. We'll first focus on the parts that can be implemented in pure TensorFlow, namely the client and server update steps.
#
# + [markdown] colab_type="text" id="3yKS4VkALo8g"
# ## TensorFlow Blocks
# + [markdown] colab_type="text" id="bxpNYucgLo8g"
# ### Client update
#
# We will use our `tff.learning.Model` to do client training in essentially the same way you would train a TF model. In particular, we will use `tf.GradientTape` to compute the gradient on batches of data, then apply these gradient using a `client_optimizer`.
#
# Note that each `tff.learning.Model` instance has a `weights` attribute with two sub-attributes:
#
#
# * `trainable`: A list of the tensors corresponding to trainable layers.
# * `non_trainable`: A list of the tensors corresponding to non-trainable layers.
#
# For our purposes, we will only use the trainable weights (as our model only has those!).
#
#
# + colab={} colab_type="code" id="c5rHPKreLo8g"
@tf.function
def client_update(model, dataset, server_weights, client_optimizer):
"""Performs training (using the server model weights) on the client's dataset."""
# Initialize the client model with the current server weights.
client_weights = model.weights.trainable
# Assign the server weights to the client model.
tf.nest.map_structure(lambda x, y: x.assign(y),
client_weights, server_weights)
# Use the client_optimizer to update the local model.
for batch in dataset:
with tf.GradientTape() as tape:
# Compute a forward pass on the batch of data
outputs = model.forward_pass(batch)
# Compute the corresponding gradient
grads = tape.gradient(outputs.loss, client_weights)
grads_and_vars = zip(grads, client_weights)
# Apply the gradient using a client optimizer.
client_optimizer.apply_gradients(grads_and_vars)
return client_weights
# + [markdown] colab_type="text" id="pP0D9XtoLo8i"
# ### Server Update
#
# The server update will require even less effort. We will implement vanilla federated averaging, in which we simply replace the server model weights by the average of the client model weights. Again, we will only focus on the trainable weights.
# + colab={} colab_type="code" id="rYxErLvHLo8i"
@tf.function
def server_update(model, mean_client_weights):
"""Updates the server model weights as the average of the client model weights."""
model_weights = model.weights.trainable
# Assign the mean client weights to the server model.
tf.nest.map_structure(lambda x, y: x.assign(y),
model_weights, mean_client_weights)
return model_weights
# + [markdown] colab_type="text" id="ddCklfWlVr1U"
# Note that the code snippet above is clearly overkill, as we could simply return `mean_client_weights`. However, more advanced implementations of Federated Averaging could use `mean_client_weights` with more sophisticated techniques, such as momentum or adaptivity.
# + [markdown] colab_type="text" id="KuP9g6RFLo8k"
# So far, we've only written pure TensorFlow code. This is by design, as TFF allows you to use much of the TensorFlow code you're already familiar with. However, now we have to specify the *orchestration logic*, that is, the logic that dictates what the server broadcasts to the client, and what the client uploads to the server.
#
# This will require the "Federated Core" of TFF.
# + [markdown] colab_type="text" id="0CgFLVPgLo8l"
# # Introduction to the Federated Core
#
# The Federated Core (FC) is a set of lower-level interfaces that serve as the foundation for the `tff.learning` API. However, these interfaces are not limited to learning. In fact, they can be used for analytics and many other computations over distributed data.
#
# At a high-level, the federated core is a development environment that enables compactly expressed program logic to combine TensorFlow code with distributed communication operators (such as distributed sums and broadcasts). The goal is to give researchers and practitioners expliict control over the distributed communication in their systems, without requiring system implementation details (such as specifying point-to-point network message exchanges).
#
# One key point is that TFF is designed for privacy-preservation. Therefore, it allows explicit control over where data resides, to prevent unwanted accumulation of data at the centralized server location.
# + [markdown] colab_type="text" id="EYinjNqZLo8l"
# ## Federated data
#
# Similar to "Tensor" concept in TensorFlow, which is one of the fundamental concepts, a key concept in TFF is "federated data", which refers to a collection of data items hosted across a group of devices in a distributed system (eg. client datasets, or the server model weights). We model the entire collection of data items across all devices as a single *federated value*.
#
# For example, suppose we have client devices that each have a float representing the temperature of a sensor. We could represent it as a *federated float* by
# + colab={} colab_type="code" id="7EJY0MHpLo8l"
federated_float_on_clients = tff.type_at_clients(tf.float32)
# + [markdown] colab_type="text" id="JSQAXD0FLo8n"
# Federated types are specified by a type `T` of its member constituents (eg. `tf.float32`) and a group `G` of devices. We will focus on the cases where `G` is either `tff.CLIENTS` or `tff.SERVER`. Such a federated type is represented as `{T}@G`, as shown below.
# + colab={} colab_type="code" id="6mlPgubJLo8n"
str(federated_float_on_clients)
# + [markdown] colab_type="text" id="pjAQytkeLo8o"
# Why do we care so much about placements? A key goal of TFF is to enable writing code that could be deployed on a real distributed system. This means that it is vital to reason about which subsets of devices execute which code, and where different pieces of data reside.
#
# TFF focuses on three things: *data*, where the data is *placed*, and how the data is being *transformed*. The first two are encapsulated in federated types, while the last is encapsulated in *federated computations*.
# + [markdown] colab_type="text" id="ZLT2FmVMLo8p"
# ## Federated computations
# + [markdown] colab_type="text" id="-XwDC1vTLo8p"
# TFF is a strongly-typed functional programming environment whose basic units are *federated computations*. These are pieces of logic that accept federated values as input, and return federated values as output.
#
# For example, suppose we wanted to average the temperatures on our client sensors. We could define the following (using our federated float):
# + colab={} colab_type="code" id="IfwXDNR1Lo8p"
@tff.federated_computation(tff.type_at_clients(tf.float32))
def get_average_temperature(client_temperatures):
return tff.federated_mean(client_temperatures)
# + [markdown] colab_type="text" id="iSgs6Te5Lo8r"
# You might ask, how is this different from the `tf.function` decorator in TensorFlow? The key answer is that the code generated by `tff.federated_computation` is neither TensorFlow nor Python code; It is a specification of a distributed system in an internal platform-independent *glue language*.
#
# While this may sound complicated, you can think of TFF computations as functions with well-defined type signatures. These type signatures can be directly queried.
# + colab={} colab_type="code" id="wAG1eDlULo8r"
str(get_average_temperature.type_signature)
# + [markdown] colab_type="text" id="TveOYFfuLo8s"
# This `tff.federated_computation` accepts arguments of federated type `{float32}@CLIENTS`, and returns values of federated type `{float32}@SERVER`. Federated computations may also go from server to client, from client to client, or from server to server. Federated computations can also be composed like normal functions, as long as their type signatures match up.
#
# To support development, TFF allows you to invoke a `tff.federated_computation` as a Python function. For example, we can call
# + colab={} colab_type="code" id="eFoqtuOTLo8t"
get_average_temperature([68.5, 70.3, 69.8])
# + [markdown] colab_type="text" id="ZXn-yje9RJ6H"
# ## Non-eager computations and TensorFlow
# + [markdown] colab_type="text" id="nwyj8f3HLo8w"
# There are two key restrictions to be aware of. First, when the Python interpreter encounters a `tff.federated_computation` decorator, the function is traced once and serialized for future use. Therefore, TFF computations are fundamentally *non-eager*. This behavior is somewhat analogous to that of the [`tf.function`](https://www.tensorflow.org/api_docs/python/tf/function) decorator in TensorFlow.
#
# Second, a federated computation can only consist of federated operators (such as `tff.federated_mean`), they cannot contain TensorFlow operations. TensorFlow code must be confined to blocks decorated with `tff.tf_computation`. Most ordinary TensorFlow code can be directly decotrated, such as the following function that takes a number and adds `0.5` to it.
# + colab={} colab_type="code" id="huz3mNmMLo8w"
@tff.tf_computation(tf.float32)
def add_half(x):
return tf.add(x, 0.5)
# + [markdown] colab_type="text" id="5ptjWALDLo8y"
# These also have type signatures, but *without placements*. For example, we can call
# + colab={} colab_type="code" id="xfAb0vG2Lo8y"
str(add_half.type_signature)
# + [markdown] colab_type="text" id="WNjwrNMjLo8z"
# Here we see an important difference between `tff.federated_computation` and `tff.tf_computation`. The former has explicit placements, while the latter does not.
#
# We can use `tff.tf_computation` blocks in federated computations by specifying placements. Let's create a function that adds half, but only to federated floats at the clients. We can do this by using `tff.federated_map`, which applies a given `tff.tf_computation`, while preserving the placement.
# + colab={} colab_type="code" id="pG6nw3wiLo80"
@tff.federated_computation(tff.type_at_clients(tf.float32))
def add_half_on_clients(x):
return tff.federated_map(add_half, x)
# + [markdown] colab_type="text" id="h4msKRKJLo81"
# This function is almost identical to `add_half`, except that it only accepts values with placement at `tff.CLIENTS`, and returns values with the same placement. We can see this in its type signature:
# + colab={} colab_type="code" id="_C2hDiz0Lo82"
str(add_half_on_clients.type_signature)
# + [markdown] colab_type="text" id="3JxQ0DeiLo83"
# In summary:
#
# * TFF operates on federated values.
# * Each federated value has a *federated type*, with a *type* (eg. `tf.float32`) and a *placement* (eg. `tff.CLIENTS`).
# * Federated values can be transformed using *federated computations*, which must be decorated with `tff.federated_computation` and a federated type signature.
# * TensorFlow code must be contained in blocks with `tff.tf_computation` decorators.
# * These blocks can then be incorporated into federated computations.
#
#
# + [markdown] colab_type="text" id="PvyFWox3Lo83"
# # Building your own FL Algorithm (Part 2)
#
# Now that we've peeked at the Federated Core, we can build our own federated learning algorithm. Remember that above, we defined an `initialize_fn` and `next_fn` for our algorithm. The `next_fn` will make use of the `client_update` and `server_update` we defined using pure TensorFlow code.
#
# However, in order to make our algorithm a federated computation, we will need both the `next_fn` and `initialize_fn` to be `tff.federated_computations`.
# + [markdown] colab_type="text" id="CvY8fh1cLo84"
# ## TensorFlow Federated blocks
# + [markdown] colab_type="text" id="g0zNTO7LLo84"
# ### Creating the initialization computation
#
# The initialize function will be quite simple: We will create a model using `model_fn`. However, remember that we must separate out our TensorFlow code using `tff.tf_computation`.
# + colab={} colab_type="code" id="jJY9xUBZLo84"
@tff.tf_computation
def server_init():
model = model_fn()
return model.weights.trainable
# + [markdown] colab_type="text" id="SGlv8LLgLo85"
# We can then pass this directly into a federated computation using `tff.federated_value`.
# + colab={} colab_type="code" id="m2hinzuRLo86"
@tff.federated_computation
def initialize_fn():
return tff.federated_value(server_init(), tff.SERVER)
# + [markdown] colab_type="text" id="NFBghOgxLo88"
# ### Creating the `next_fn`
#
# We now use our client and server update code to write the actual algorithm. We will first turn our `client_update` into a `tff.tf_computation` that accepts a client datasets and server weights, and outputs an updated client weights tensor.
#
# We will need the corresponding types to properly decorate our function. Luckily, the type of the server weights can be extracted directly from our model.
# + colab={} colab_type="code" id="ph_noHN2Lo88"
dummy_model = model_fn()
tf_dataset_type = tff.SequenceType(dummy_model.input_spec)
# + [markdown] colab_type="text" id="WMPgpTaW66qx"
# Let's look at the dataset type signature. Remember that we took 28 by 28 images (with integer labels) and flattened them.
# + colab={} colab_type="code" id="Ju91izuz64wD"
str(tf_dataset_type)
# + [markdown] colab_type="text" id="kuS8d0BHLo8-"
# We can also extract the model weights type by using our `server_init` function above.
# + colab={} colab_type="code" id="4yx6CExMLo8-"
model_weights_type = server_init.type_signature.result
# + [markdown] colab_type="text" id="mS-Eh6Xj7J15"
# Examining the type signature, we'll be able to see the architecture of our model!
# + colab={} colab_type="code" id="nPdhhM1O7IIL"
str(model_weights_type)
# + [markdown] colab_type="text" id="g1U1wTGRLo8_"
# We can now create our `tff.tf_computation` for the client update.
# + colab={} colab_type="code" id="Q0W05pMWLo9A"
@tff.tf_computation(tf_dataset_type, model_weights_type)
def client_update_fn(tf_dataset, server_weights):
model = model_fn()
client_optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
return client_update(model, tf_dataset, server_weights, client_optimizer)
# + [markdown] colab_type="text" id="uP5quaAuLo9B"
# The `tff.tf_computation` version of the server update can be defined in a similar way, using types we've already extracted.
# + colab={} colab_type="code" id="F4WvQtVzLo9B"
@tff.tf_computation(model_weights_type)
def server_update_fn(mean_client_weights):
model = model_fn()
return server_update(model, mean_client_weights)
# + [markdown] colab_type="text" id="SImhLbu4Lo9D"
# Last, but not least, we need to create the `tff.federated_computation` that brings this all together. This function will accept two *federated values*, one corresponding to the server weights (with placement `tff.SERVER`), and the other corresponding to the client datasets (with placement `tff.CLIENTS`).
#
# Note that both these types were defined above! We simply need to give them the proper placement using `tff.type_at_{server/clients}``.
# + colab={} colab_type="code" id="ekPsA8AsLo9D"
federated_server_type = tff.type_at_server(model_weights_type)
federated_dataset_type = tff.type_at_clients(tf_dataset_type)
# + [markdown] colab_type="text" id="7FXAX7vGLo9G"
# Remember the 4 elements of an FL algorithm?
#
# 1. A server-to-client broadcast step.
# 2. A local client update step.
# 3. A client-to-server upload step.
# 4. A server update step.
#
# Now that we've built up the above, each part can be compactly represented as a single line of TFF code. This simplicity is why we had to take extra care to specify things such as federated types!
# + colab={} colab_type="code" id="Epc7MwfELo9G"
@tff.federated_computation(federated_server_type, federated_dataset_type)
def next_fn(server_weights, federated_dataset):
# Broadcast the server weights to the clients.
server_weights_at_client = tff.federated_broadcast(server_weights)
# Each client computes their updated weights.
client_weights = tff.federated_map(
client_update_fn, (federated_dataset, server_weights_at_client))
# The server averages these updates.
mean_client_weights = tff.federated_mean(client_weights)
# The server updates its model.
server_weights = tff.federated_map(server_update_fn, mean_client_weights)
return server_weights
# + [markdown] colab_type="text" id="kWomG3TtLo9I"
# We now have a `tff.federated_computation` for both the algorithm initialization, and for running one step of the algorithm. To finish our algorithm, we pass these into `tff.templates.IterativeProcess`.
# + colab={} colab_type="code" id="GxdWgEddLo9I"
federated_algorithm = tff.templates.IterativeProcess(
initialize_fn=initialize_fn,
next_fn=next_fn
)
# + [markdown] colab_type="text" id="7Z__9k-Dc1I3"
# Let's look at the *type signature* of the `initialize` and `next` functions of our iterative process.
# + colab={} colab_type="code" id="kyRLXDj-Lo9J"
str(federated_algorithm.initialize.type_signature)
# + [markdown] colab_type="text" id="UyyEi5Kec90_"
# This reflects the fact that `federated_algorithm.initialize` is a no-arg function that returns a single-layer model (with a 784-by-10 weight matrix, and 10 bias units).
# + colab={} colab_type="code" id="mx6yuIKtLo9M"
str(federated_algorithm.next.type_signature)
# + [markdown] colab_type="text" id="efpdHodmdU_6"
# Here, we see that `federated_algorithm.next` accepts a server model and client data, and returns an updated server model.
# + [markdown] colab_type="text" id="4UYZ3qeMLo9N"
# ## Evaluating the algorithm
# + [markdown] colab_type="text" id="jwd9Gs0ULo9O"
# Let's run a few rounds, and see how the loss changes. First, we will define an evaluation function using the *centralized* approach discussed in the second tutorial.
#
# We first create a centralized evaluation dataset, and then apply the same preprocessing we used for the training data.
#
# Note that we only `take` the first 1000 elements for reasons of computational efficiency, but typically we'd use the entire test dataset.
# + colab={} colab_type="code" id="EdNgYoIwLo9P"
central_emnist_test = emnist_test.create_tf_dataset_from_all_clients().take(1000)
central_emnist_test = preprocess(central_emnist_test)
# + [markdown] colab_type="text" id="7R50NZ35dphE"
# Next, we write a function that accepts a server state, and uses Keras to evaluate on the test dataset. If you're familiar with `tf.Keras`, this will all look familiar, though note the use of `set_weights`!
# + colab={} colab_type="code" id="I5UEX4EWLo9Q"
def evaluate(server_state):
keras_model = create_keras_model()
keras_model.compile(
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()]
)
keras_model.set_weights(server_state)
keras_model.evaluate(central_emnist_test)
# + [markdown] colab_type="text" id="hygoBACkLo9S"
# Now, let's initialize our algorithm and evaluate on the test set.
# + colab={} colab_type="code" id="JC6zMDTTLo9S"
server_state = federated_algorithm.initialize()
evaluate(server_state)
# + [markdown] colab_type="text" id="2knqix2cLo9U"
# Let's train for a few rounds and see if anything changes.
# + colab={} colab_type="code" id="v1zBlzFILo9U"
for round in range(15):
server_state = federated_algorithm.next(server_state, federated_train_data)
# + colab={} colab_type="code" id="q91Vjyc_jumU"
evaluate(server_state)
# + [markdown] colab_type="text" id="XM34ammUW-T3"
# We see a slight decrease in the loss function. While the jump is small, note that we've only performed 10 training rounds, and on a small subset of clients. To see better results, we may have to do hundreds if not thousands of rounds.
# + [markdown] colab_type="text" id="o13H5dDFXRFn"
# ## Modifying our algorithm
# + [markdown] colab_type="text" id="Qt4jVD21XTL-"
# At this point, let's stop and think about what we've accomplished. We've implemented Federated Averaging directly by combining pure TensorFlow code (for the client and server updates) with federated computations from the Federated Core of TFF.
#
# To perform more sophisticted learning, we can simply alter what we have above. In particular, by editing the pure TF code above, we can change how the client performs training, or how the server updates its model.
#
# **Challenge:** Add [gradient clipping](https://towardsdatascience.com/what-is-gradient-clipping-b8e815cdfb48) to the `client_update` function.
#
#
#
#
|
docs/openmined2020/openmined_conference_2020.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Setup
# +
# Some code taken from https://github.com/ageron/handson-ml2
import sys
assert sys.version_info >= (3, 8)
import os
import sklearn
from sklearn.preprocessing import PowerTransformer
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
assert sklearn.__version__ >= "0.23.1"
import numpy as np
assert np.__version__ >= "1.19.1"
import seaborn as sns
assert sns.__version__ >= "0.10.1"
# To plot pretty figures
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "end_to_end_project"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
# -
# # Load data
do_standardize = True
pt_method = 'box-cox'
# +
import pandas as pd
assert pd.__version__ >= "1.1.0"
# Model will be trained using this data.
def load_training_data():
data = pd.read_csv('../data/titanic/train.csv')
return data
# This data will only be used when submitting the final analysis.
# It also doesn't contain the Survived column.
def load_testing_data():
data = pd.read_csv('../data/titanic/test.csv')
return data
# -
train_df = load_training_data()
train_df.head()
# original_df is being used to look at the effects of individual transformations
original_df = train_df.copy()
sns.distplot(train_df.Fare, kde=False)
# Divide the Fare to be per person
train_df['Fare'] = train_df.groupby('Ticket')['Fare'].transform(lambda x: x / x.size)
pd.DataFrame(train_df.groupby('Ticket')['Fare'].transform(lambda x: x / x.size))
train_df.compare(original_df)
original_df = train_df.copy()
si = SimpleImputer(missing_values=0.0, strategy='median')
train_df['Fare'] = si.fit_transform(train_df[['Fare']])
train_df.compare(original_df)
sns.distplot(train_df.Fare, kde=False)
original_df = train_df.copy()
pt = PowerTransformer(method=pt_method, standardize=do_standardize)
pt.fit(train_df[['Fare']])
train_df['Fare'] = pt.transform(train_df[['Fare']])
sns.distplot(train_df.Fare, kde=False)
original_df = train_df.copy()
sns.distplot(train_df.Age, kde=False)
si = SimpleImputer(strategy='median')
train_df['Age'] = si.fit_transform(train_df[['Age']])
sns.distplot(train_df.Age, kde=False)
train_df.compare(original_df)
pt = PowerTransformer(method=pt_method, standardize=do_standardize)
pt.fit(train_df[['Age']])
train_df['Age'] = pt.transform(train_df[['Age']])
sns.distplot(train_df.Age, kde=False)
train_df.info()
train_df.Pclass.value_counts()
train_df.Sex.value_counts()
train_df.Cabin.value_counts()
train_df.Embarked.value_counts()
train_df.describe()
# %matplotlib inline
import matplotlib.pyplot as plt
train_df.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots")
plt.show()
# to make this notebook's output identical at every run
np.random.seed(42)
train_set, test_set = train_test_split(train_df, test_size=0.2, random_state=42)
# This will be used the train and validate the model using cross-validation
len(train_set)
# This will only be used after training to see if the resulting model is any good
len(test_set)
# Make a copy of the training set so we can go back if we accidentally change it
passengers_df = train_set.copy()
corr_matrix = passengers_df.corr()
corr_matrix
corr_matrix["Survived"].sort_values(ascending=False)
# +
# Fare has a rather large positive correlation
# Pclass has a rather large negative correlation
# Parch and Age also
# -
g = sns.catplot(x="Survived", hue="Sex",
data=passengers_df, kind="count",
height=4, aspect=.7);
g = sns.catplot(x="Sex", data=passengers_df, kind="count",
height=4, aspect=.7);
g = sns.catplot(x="Survived", col="Embarked",
data=passengers_df, kind="count",
height=4, aspect=.7);
# +
# Ready to use attributes at this time
# Pclass
# Fare
# Age
# -
|
p-titanic/new_titanic_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # import modules
import requests
from bs4 import BeautifulSoup
import csv
from urllib.request import urlopen, Request
# # 견종 A - Z name 추출
dognamelist = []
for i in range(1,24):
BASE_URL = 'https://www.akc.org/dog-breeds/page/'+str(i)+'/'
response = requests.get(BASE_URL)
#print(response.status_code)
dom = BeautifulSoup(response.content, "html.parser")
post_elements = dom.select('h3.breed-type-card__title')
for j in post_elements :
dognamelist.append(j.get_text())
print(j.get_text())
# # 견종 이름으로 반복문 이용해 웹사이트에 접근 시,
# # 404 error 가 뜨는 것들을 추출해 수작업으로 고침.
#
# #### 404 error가 뜨는 것의 사례로는
# #### 견종 이름은 Saint 라고 되어 있으나 웹주소에는 st로 줄여 쓰여진 경우,
# #### 견종 이름에 é, ö, ’, ( 등 특수문자가 포함된 경우 등이 있다.
# +
dogurllist = []
err = []
for i in range(len(dognamelist)):
dog = dognamelist[i].replace(' ', '-')
BASE_URL = 'https://www.akc.org/dog-breeds/'+dog+'/'
response = requests.get(BASE_URL)
if(response.status_code == 200):
dogurllist.append(dog)
print(200, dog)
elif(response.status_code == 404):
dogurllist.append('')
err.append(i)
print(404, dog)
for i in err:
print(i,dognamelist[i])
# -
# 13 <NAME>
dogurllist[err[0]] = 'appenzeller-sennenhunde'
# 17 Australian Stumpy Tail Cattle Dog
dogurllist[err[1]] = 'australian-stump-tail-cattle-dog'
# 77 Cirneco dell’Etna
dogurllist[err[2]] = 'cirneco-delletna'
# 120 <NAME>
dogurllist[err[3]] = 'grand-basset-griffon-vendeen'
# 157 Löwchen
dogurllist[err[4]] = 'lowchen'
# 186 <NAME>
dogurllist[err[5]] = 'petit-basset-griffon-vendeen'
# 192 Poodle (Miniature / Standard)
dogurllist[err[6]] = 'poodle-miniature-standard'
# 193 Poodle (Toy)
dogurllist[193] = 'poodle-toy'
# 215 S<NAME>
dogurllist[err[7]] = 'st-bernard'
for i in err:
print(i,dogurllist[i])
# # Care 의 column names 얻기
# ## NUTRITION, GROOMING, EXERCISE, TRAINING, HEALTH
# +
BASE_URL = 'https://www.akc.org/dog-breeds/' + dogurllist[0] +'/'
response = requests.get(BASE_URL)
print(response.status_code)
dom = BeautifulSoup(response.content, "html.parser")
post_elements = dom.select('div.tabs__inner-content')
print(post_elements)
care_col = []
for i in post_elements :
# text만 추출한 뒤 앞뒤 공백 제거
care_col.append(i.get_text().strip())
# 최종으로 추출해낸 컬럼네임들
print('\n\n\nCARE COLUMN NAMES : \n',care_col)
# -
# # care_col 을 csv 파일에 저장
# newline = ''으로 함으로써 empty line 이 사라진다.
with open('dog_cares.csv', 'w', newline='') as outfile:
writer = csv.writer(outfile)
try :
writer.writerow(('Breed Name', care_col[0], care_col[1], care_col[2], care_col[3], care_col[4]))
finally :
outfile.close()
# # 각 컬럼에 들어갈 값을 크롤링 test
# +
BASE_URL = 'https://www.akc.org/dog-breeds/' + dogurllist[0] +'/'
response = requests.get(BASE_URL)
print(response.status_code)
soup = BeautifulSoup(response.content, "html.parser")
divTag = soup.find_all("div", {"class": "tabs__tab-panel-content"})
index = 0
for tag in divTag:
pTags = tag.find_all("p")
for tag in pTags:
print(index)
print (tag.text)
print('\n')
index += 1
# 출력 결과 index 1, 2, 3, 4, 5 가 각 care_col에 들어갈 텍스트임을 확인함.
# -
# # 반복문을 사용해 272종의 견종 care 정보를 크롤링
# +
c = []
for i in range(len(dogurllist)):
BASE_URL = 'https://www.akc.org/dog-breeds/' + dogurllist[i] +'/'
response = requests.get(BASE_URL)
print(response.status_code)
soup = BeautifulSoup(response.content, "html.parser")
divTag = soup.find_all("div", {"class": "tabs__tab-panel-content"})
index = 0
t = []
for tag in divTag:
pTags = tag.find_all("p")
for tag in pTags:
#print(index)
#print (tag.text)
#print('\n')
index += 1
t.append(tag.text)
c.append(t[1:6])
print(c)
# -
dog_cares = c
for j in range(5) :
print((dognamelist[j], dog_cares[j][0], dog_cares[j][1], dog_cares[j][2], dog_cares[j][3], dog_cares[j][4]))
print(len(dognamelist))
# # 272종의 견종 care 정보를 csv 파일에 저장
with open('dog_cares.csv', 'w', newline='', encoding='UTF8') as outfile:
writer = csv.writer(outfile)
print(writer)
try :
# writer.writerow(('Breed Name',care_col[0], care_col[1], care_col[2], care_col[3], care_col[4]))
for j in range(len(dognamelist)) :
writer.writerow((dognamelist[j], dog_cares[j][0], dog_cares[j][1], dog_cares[j][2],
dog_cares[j][3], dog_cares[j][4]))
print((dognamelist[j], dog_cares[j][0], dog_cares[j][1], dog_cares[j][2],
dog_cares[j][3], dog_cares[j][4]))
finally :
outfile.close()
|
src/dog_cares.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="QUVT0_NQGkyF" colab_type="code" colab={}
# + id="HWJ6_8enGwjP" colab_type="code" outputId="16f3726a-17e9-4d42-a6e7-9282c733a4af" executionInfo={"status": "ok", "timestamp": 1556122875900, "user_tz": -330, "elapsed": 5658, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "16523095505741898105"}} colab={"base_uri": "https://localhost:8080/", "height": 306}
# !nvidia-smi
# + id="gGH9GRXAJUbB" colab_type="code" colab={}
|
GPU_version.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import cv2
import numpy as np
aruco = cv2.aruco
dictionary = aruco.getPredefinedDictionary(aruco.DICT_6X6_100)
marker = aruco.drawMarker(dictionary, 4, 64)
type(marker)
markerLength = 3.6 # Here, our measurement unit is centimetre.
markerSeparation = 1 # Here, our measurement unit is centimetre.
board = aruco.GridBoard_create(4, 6, markerLength, markerSeparation, dictionary)
type(board[0])
img = cv2.imread('../../images/image.png')
img = cv2.resize(img, None, fx=0.5, fy=0.5)
cv2.imshow('test', img)
cv2.waitKey(0)
|
aruco/script/.ipynb_checkpoints/Untitled-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Changing colors of lines intersecting a box
#
#
# The lines intersecting the rectangle are colored in red, while the others
# are left as blue lines. This example showcases the `.intersects_bbox` function.
#
# +
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.transforms import Bbox
from matplotlib.path import Path
# Fixing random state for reproducibility
np.random.seed(19680801)
left, bottom, width, height = (-1, -1, 2, 2)
rect = plt.Rectangle((left, bottom), width, height,
facecolor="black", alpha=0.1)
fig, ax = plt.subplots()
ax.add_patch(rect)
bbox = Bbox.from_bounds(left, bottom, width, height)
for i in range(12):
vertices = (np.random.random((2, 2)) - 0.5) * 6.0
path = Path(vertices)
if path.intersects_bbox(bbox):
color = 'r'
else:
color = 'b'
ax.plot(vertices[:, 0], vertices[:, 1], color=color)
plt.show()
|
matplotlib/gallery_jupyter/misc/bbox_intersect.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import csv
import time
import numpy as np
import copy
import math
from math import inf
import matplotlib.pyplot as plt
# +
# reference: https://www.geeksforgeeks.org/python-program-to-get-all-subsets-of-given-size-of-a-set/
# find all subsets of a given set
import itertools
def findsubsets(s, n):
return [set(i) for i in itertools.combinations(s, n)]
# -
def graph_from_coord(d):
'''
This functions creats and array for distance between the cities given
a list of list contains coordinates of all cities
Inputs:
d: list of lists contains coordinates of all cities
Outputs:
c: a 2D arraay where c[i-1,j-1] is distance between cities i, j (length of edges)
'''
n = len(d)
c = np.empty([n,n])
for i in range(0,n): # for all
i_x = d[i][0]
i_y = d[i][1]
for j in range(0,n):
j_x = d[j][0]
j_y = d[j][1]
c[i,j] = math.sqrt((i_x-j_x)**2 + (i_y-j_y)**2)
return c
# +
def create_bitset(n, S):
'''
This function creates a list with size n as bits (0/1) for given set S. The elements
in the list are 1 for memeber of S and 0 everywhere else.
Inputs:
n: size of the list
S: a set that givens the positions where bits are 1
Outputs:
bitset: a list with size n with 1 for elements in S and 0 everywhere else.
'''
bitset = [0] * n
for i in S:
bitset[i-1] = 1 # -1 beacuse of python indexing
return bitset
# +
def TSP(c):
'''
This function finds the length of shortest path in Travel Salesman Path (TSP) problem.
Inputs:
c: a 2D arraay where c[i-1,j-1] is distance between cities i, j (length of edges)
Outputs:
A: the hashtable (array) in the TSP algorithm. e.g. A[1,0,1,1,0,0,0,1,0,0...,0,8] represents
the length of the shortest path from vortex 1 to vortex 8 by viinting vortecies 1,3,4, and 8 only onces.
min_value: the shortest tour in Travel Salesman Path problem (length of
shortest path to visit all cities only once)
'''
n = c.shape[0]
one_to_n = set(i for i in range(1,n+1)) # a set of all numbers from 1 to n
two_to_n = set(i for i in range(2,n+1)) # a set of all numbers from 2 to n
# A is a (n+1)D array the first n axes are size 2 and (n+1)th axis is size n
# the first n axes represents the set S
# the (n+1)th axis reperesent the distination vortex number
# for example A[1,0,1,1,0,0,0,1,0,0...,0,8] represents the shortest path from vortex 1 to
# vortex 8 by visiting vortecies 1,3,4, and 8 only onces.
x = [2]*n
x.append(n)
A = np.empty(x)
# Base case
S = {1}
bitset = create_bitset(n, S) # bitset for members in S (S={1} here)
bitset.append(1-1) # adding the distenistion (destionation vortex is 1 here), -1 because of pythpon indexing
A[tuple([i for i in bitset])] = 0 # zero for S={1} and destination 1
for m in range(2,n+1): # m is subproblem size
all_S_from_two = findsubsets(two_to_n, m-1) # all subset two_to_n with size m-1
all_S = [{1}|i for i in all_S_from_two] # add one to all elements of all_S_from_two
for S in all_S:
bitset = create_bitset(n, S)
bitset.append(1-1) # adding the distenistion (destionation vortex is 1 here), -1 because of pythpon indexing
A[tuple([i for i in bitset])] = inf # inf for all S except S={1} and destination 1
for m in range(2,n+1): # m is subproblem size
all_S_from_two = findsubsets(two_to_n, m-1) # all subset two_to_n with size m-1
all_S = [{1}|i for i in all_S_from_two] # add one to all elements of all_S_from_two
for S in all_S:
S = set(sorted(S)) # sort S
for j in S:
min_value = inf
if j != 1:
for k in S:
if k != j:
S_minus_j = S - {j}
bitset = create_bitset(n, S_minus_j) # bitset for members in S_minus_j
bitset.append(k-1) # adding the distenistion (destionation vortex is k here), -1 because of pythpon indexing
current_value = A[tuple([i for i in bitset])] + c[k-1,j-1]
if current_value < min_value:
bitset = create_bitset(n, S) # bitset for members in S
bitset.append(j-1) # adding the distenistion (destionation vortex is j here), -1 because of pythpon indexing
A[tuple([i for i in bitset])] = current_value
min_value = A[tuple([i for i in bitset])]
# finding shortest path
min_value = inf
for j in range(2,n+1):
bitset = create_bitset(n, one_to_n) # bitset for members in one_to_n
bitset.append(j-1) # adding the distenistion (destionation vortex is j here), -1 because of pythpon indexing
current_value = A[tuple([i for i in bitset])] + c[j-1,0]
if current_value < min_value:
min_value = current_value
return A, min_value
# +
# plotting the points
def TSP_path(n, A, c):
'''
This function finds all cities visited in orders in TSP problem
Inputs:
A: the hashtable (array) in the TSP algorithm. e.g. A[1,0,1,1,0,0,0,1,0,0...,0,8] represents
the length of the shortest path from vortex 1 to vortex 8 by visiting vortecies 1,3,4, and 8 only onces.
Outputs:
Cities: a list of all cities ordered from last to 1 which are visited.
'''
Cities = []
S = set(i for i in range(1,n+1)) # a set of all numbers from 1 to n
prev_last_index = 1 # previous step last vortex
while len(S) > 1:
min_value = inf
for j in range(2,n+1):
if not j in Cities:
bitset = create_bitset(n, S)
bitset.append(j-1)
if A[tuple([i for i in bitset])] + c[j-1,prev_last_index-1] < min_value:
min_value = A[tuple([i for i in bitset])] + c[j-1,prev_last_index-1]
last_index = j
Cities.append(last_index)
prev_last_index = last_index # updating previous step last vortex
S = S - {last_index}
Cities.append(1)
return Cities
def plot_TSP(Cities,G):
'''
This function plots all cities visited in orders in TSP problem and reports the total distance
of the tour in TSP problem
Inputs:
Cities: a list of all cities ordered from last to 1 which are visited.
Outputs:
a plot of the path traveled between cities with the length of each edge.
tot_dist: the total distance of the tour in TSP problem.
'''
tot_dist = 0
plt.figure(figsize=(15,10))
for i in range(len(Cities)-1):
first_point = Cities[i]
second_point = Cities[i+1]
first_point_x = G[first_point-1][0]
first_point_y = G[first_point-1][1]
second_point_x = G[second_point-1][0]
second_point_y = G[second_point-1][1]
x_values = [first_point_x, second_point_x]
y_values = [first_point_y, second_point_y]
plt.plot(x_values, y_values)
plt.text(first_point_x, first_point_y, str(first_point))
# distance between first_point and second_point
dist = math.sqrt((first_point_x-second_point_x)**2 + (first_point_y-second_point_y)**2)
# puting distance as a text on the middle of the edge
mid_x = 0.5 * (first_point_x+second_point_x)
mid_y = 0.5 * (first_point_y+second_point_y)
plt.text(mid_x, mid_y, str(round(dist,2)), color='green')
tot_dist += dist # to check total travel distance
# to draw last edge (from last vortex to 1)
first_point = Cities[-1]
second_point = Cities[0]
first_point_x = G[first_point-1][0]
first_point_y = G[first_point-1][1]
second_point_x = G[second_point-1][0]
second_point_y = G[second_point-1][1]
x_values = [first_point_x, second_point_x]
y_values = [first_point_y, second_point_y]
plt.plot(x_values, y_values)
plt.text(first_point_x, first_point_y, str(first_point))
# distance between first_point and second_point
dist = math.sqrt((first_point_x-second_point_x)**2 + (first_point_y-second_point_y)**2)
# puting distance as a text on the middle of the edge
mid_x = 0.5 * (first_point_x+second_point_x)
mid_y = 0.5 * (first_point_y+second_point_y)
plt.text(mid_x, mid_y, str(round(dist,2)), color='green')
tot_dist += dist # to check total travel distance
return tot_dist
# -
# ## Examples
# +
# reading the input file as a list
with open('Test_01_12.36.txt') as f:
reader = csv.reader(f, delimiter=" ")
d = list(reader)
n = int(d[0][0]) # n is number of cities
d.pop(0)
d = [[float(i[0]),float(i[1])] for i in d] # convert d into integers
c = graph_from_coord(d) # array of cities distances
start_time = time.time()
A, shortest_path = TSP(c)
print('\n ______The shortest tour to travel has length of:_________')
print(round(shortest_path,2))
Cities = TSP_path(n, A, c)
print('\n ______The cities to visit:_________')
print(Cities)
tot_dist = plot_TSP(Cities,d)
print('\n ______The shortest tour to travel has length of (from the figure to double check):_________')
print(tot_dist)
print("\n --- %s seconds ---" % (time.time() - start_time))
# +
# reading the input file as a list
with open('Test_02_14.00.txt') as f:
reader = csv.reader(f, delimiter=" ")
d = list(reader)
n = int(d[0][0]) # n is number of cities
d.pop(0)
d = [[float(i[0]),float(i[1])] for i in d] # convert d into integers
c = graph_from_coord(d) # array of cities distances
start_time = time.time()
A, shortest_path = TSP(c)
print('\n ______The shortest tour to travel has length of:_________')
print(round(shortest_path,2))
Cities = TSP_path(n, A, c)
print('\n ______The cities to visit:_________')
print(Cities)
tot_dist = plot_TSP(Cities,d)
print('\n ______The shortest tour to travel has length of (from the figure to double check):_________')
print(tot_dist)
print("\n --- %s seconds ---" % (time.time() - start_time))
# +
# reading the input file as a list
with open('Test_03_4.41.txt') as f:
reader = csv.reader(f, delimiter=" ")
d = list(reader)
n = int(d[0][0]) # n is number of cities
d.pop(0)
d = [[float(i[0]),float(i[1])] for i in d] # convert d into integers
c = graph_from_coord(d) # array of cities distances
start_time = time.time()
A, shortest_path = TSP(c)
print('\n ______The shortest tour to travel has length of:_________')
print(round(shortest_path,2))
Cities = TSP_path(n, A, c)
print('\n ______The cities to visit:_________')
print(Cities)
tot_dist = plot_TSP(Cities,d)
print('\n ______The shortest tour to travel has length of (from the figure to double check):_________')
print(tot_dist)
print("\n --- %s seconds ---" % (time.time() - start_time))
# +
# reading the input file as a list
with open('tsp_1to13.txt') as f:
reader = csv.reader(f, delimiter=" ")
d = list(reader)
n = int(d[0][0]) # n is number of cities
d.pop(0)
d = [[float(i[0]),float(i[1])] for i in d] # convert d into integers
c = graph_from_coord(d) # array of cities distances
start_time = time.time()
A, shortest_path = TSP(c)
print('\n ______The shortest tour to travel has length of:_________')
print(round(shortest_path,2))
Cities = TSP_path(n, A, c)
print('\n ______The cities to visit:_________')
print(Cities)
tot_dist = plot_TSP(Cities,d)
print('\n ______The shortest tour to travel has length of (from the figure to double check):_________')
print(tot_dist)
print("\n --- %s seconds ---" % (time.time() - start_time))
# +
# reading the input file as a list
with open('tsp_12to25.txt') as f:
reader = csv.reader(f, delimiter=" ")
d = list(reader)
n = int(d[0][0]) # n is number of cities
d.pop(0)
d = [[float(i[0]),float(i[1])] for i in d] # convert d into integers
c = graph_from_coord(d) # array of cities distances
start_time = time.time()
A, shortest_path = TSP(c)
print('\n ______The shortest tour to travel has length of:_________')
print(round(shortest_path,2))
Cities = TSP_path(n, A, c)
# Cities = [i+11 for i in Cities] # adding 11 to node numbers (because the file is edites) to keep to vortex numbers consistent
print('\n ______The cities to visit:_________')
print(Cities)
tot_dist = plot_TSP(Cities,d)
print('\n ______The shortest tour to travel has length of (from the figure to double check):_________')
print(tot_dist)
print("\n --- %s seconds ---" % (time.time() - start_time))
# -
# The full TSP is combination two simpler above TSPs where edge 12 t o13 is excessive
# TSP(1 to 13) + TSP (12 to 25) - 2 * edge (12 to 13)
# 14662.0046407879 + 14409.202165641733 - 2 * 1314.24
round(14662.0046407879 + 14409.202165641733 - 2 * 1314.2382487374398 , 2)
# +
# # reading the input file as a list
# with open('tsp.txt') as f:
# reader = csv.reader(f, delimiter=" ")
# d = list(reader)
# n = int(d[0][0]) # n is number of cities
# d.pop(0)
# d = [[float(i[0]),float(i[1])] for i in d] # convert d into integers
# c = graph_from_coord(d) # array of cities distances
# start_time = time.time()
# A, shortest_path = TSP(c)
# print('\n ______The shortest tour to travel has length of:_________')
# print(round(shortest_path,2))
# Cities = TSP_path(n, A, c)
# print('\n ______The cities to visit:_________')
# print(Cities)
# tot_dist = plot_TSP(Cities,d)
# print('\n ______The shortest tour to travel has length of (from the figure to double check):_________')
# print(tot_dist)
# print("\n --- %s seconds ---" % (time.time() - start_time))
|
tsp_exact/tsp_bitset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: graphs
# language: python
# name: graphs
# ---
# # Chapter 2 - Random Graph Models
#
# In the first part of this notebook, we provide the code required to generate the Figures in Chapter 2 of the textbook.
#
# In the second part, we consider the GitHub ml developers graph that we introduced in Chapter 1, and compare various statistics for this graph with the values we get for the random graphs models introduced in Chapter 2.
#
# ### Requirements
#
# We use one new package in this notebook called ```plfit``` which can be installed via ```pip install plfit```.
# In case of error when pip installing, you can copy the code from the GitHub repository: https://github.com/keflavich/plfit
#
# As with the previous notebook, make sure to set the data directory properly in the next cell.
#
datadir='../Datasets/'
import igraph as ig
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from collections import Counter
import plfit
from scipy.stats import poisson
# # Part 1 - Generating Figures for Chapter 2
# ## Figure 2.1: size of the giant component
#
# We generate several binomial random graphs with $n$ nodes, where we vary the average node degree (thus, the number of edges). We consider $n=100$ below, and you can try for different $n$. Un-comment the second line to run with $n=10000$ nodes as in the book (this will be much slower).
#
# We plot the theoretical giant component size (black line) and the 90% confidence interval from empirical data in grey, both as a function of the average degree; we see good agreement and we observe the various phases as described in the book.
# +
n = 100
# n=10000
gc_avg = []
gc_std = []
REP = 1000 ## repeats
ad = np.arange(.1,10.1,.1)
for d in ad:
x = []
p = d/(n-1)
for rep in range(REP):
g = ig.Graph.Erdos_Renyi(n=n, p=p)
x.append(g.clusters().giant().vcount())
gc_avg.append(np.mean(x))
gc_std.append(np.std(x))
## theoretical
th = [np.log(n) for i in np.arange(.1,1.1,.1)]
from scipy.optimize import fsolve
def fn(x,d):
return x+np.exp(-x*d)-1
for i in np.arange(1.1,10.1,.1):
th.append(n*fsolve(fn,1,args=(i))[0])
plt.fill_between(ad,[x[0]-1.654*x[1] for x in zip(gc_avg,gc_std)],
[x[0]+1.645*x[1] for x in zip(gc_avg,gc_std)],color='lightgray')
plt.plot(ad,th,color='black')
plt.title('Theoretical predictions (black) vs empirical results (grey)')
plt.xlabel('average degree',fontsize=14)
plt.ylabel('giant component size',fontsize=14);
## un-comment to save plot in a file
#plt.savefig('giant_100.eps');
# -
# ## Figure 2.2: probability that the graph is connected
#
# This is a similar experiment as above, but this time we look at the probability that the random graph is connected.
# We vary some constant $c$ introduced in the book such that edge probability for the binomial graphs is given by $(\log(n)+c)/n$. Once again we compare theory (black line) and experimental results (in grey), with $n=100$ nodes and you can try for different $n$. Un-comment the second line to run with $n=10000$ nodes as in the book (this will be much slower).
#
# In the cell below, the grey area corresponds to a 90% confidence interval for proportions; for empirical proportion $x$ obtained from sample of size $n$, the formula is given by $x \pm 1.645 \sqrt{x(1-x)/n}$.
#
# Here also we see good agreement between theory and experimental results.
# +
n = 100
#n = 10000
REP = 1000 ## repeats
lo = -int(np.floor(np.log(n)*10))/10
if lo<-10:
lo = -10
C = np.arange(lo,10.1,.1)
ic_avg=[]
for c in C:
x = []
p = (c+np.log(n))/n
for rep in range(REP):
g = ig.Graph.Erdos_Renyi(n=n, p=p)
x.append(int(g.is_connected()))
ic_avg.append(np.mean(x))
## theoretical
th = [np.exp(-np.exp(-c)) for c in C]
## plot
plt.fill_between(C,[x-1.654*np.sqrt(x*(1-x)/n) for x in ic_avg],
[x+1.645*np.sqrt(x*(1-x)/n) for x in ic_avg],color='lightgray')
plt.plot(C,th,color='black')
plt.title('Theoretical predictions (black) vs empirical results (grey)')
plt.xlabel(r'constant $c$',fontsize=14)
plt.ylabel('P(graph is connected)',fontsize=14);
## un-comment to save plot in a file
#plt.savefig('connected_100.eps');
# -
# ## Figure 2.4: Distribution of shortest path lengths
#
# We consider a series of binomial random graphs with expected average degree 5, where we vary the number of nodes from $n=50$ to $n=3200$.
#
# We see that as we double the number of nodes, the average shortest path lengths increases slowly.
#
sp = []
N = [50,100,200,400,800,1600,3200]
for n in N:
p = 5/(n-1)
## keep giant component
g = ig.Graph.Erdos_Renyi(n=n, p=p).clusters().giant()
z = g.shortest_paths()
sp.append([x for y in z for x in y])
## plot
plt.boxplot(sp, labels=N, sym='.',whis=5)
plt.ylabel('shortest path length')
plt.xlabel('number of nodes');
## un-comment to save plot in a file
# plt.savefig('path_len.eps')
# ## Figure 2.5 Poisson vs degree distributions
#
# We plot the degree distribution for binomial random graphs with expected average degree 10, and $n=100$ nodes (the black dots), and we compare with the corresponding Poisson distributed (dashed line).
#
# Try increasing $n$; the dots should get closer to the Poisson distribution, with more stable results if you try multiple runs.
#
# Un-comment line 2 to run with $n=10000$ as in the book.
#
n = 100
#n = 10000
p = 10/(n-1)
g = ig.Graph.Erdos_Renyi(n=n, p=p)
x = [x[0] for x in sorted(Counter(g.degree()).items())]
pmf = [poisson.pmf(k,10) for k in x]
frq = [x[1]/n for x in sorted(Counter(g.degree()).items())]
plt.plot(x,frq,'o',color='black')
plt.plot(x,pmf,':',color='black')
plt.xlabel('degree',fontsize=14)
plt.ylabel('frequency/pmf',fontsize=14);
# ## Figure 2.6 -- Power law graphs
#
# We generate a random graph with $n=10,000$ nodes following power law degree distribution with exponent $\gamma=2.5$.
# We do so using the Chung-Lu models described in section 2.5 of the book, and we discard 0-degree nodes.
#
# We then fit and plot the degree distribution of the obtained graph using the ```plfit``` package https://pypi.org/project/plfit/
#
## fast Chung-Lu: generate m edges w.r.t. distribution d
def fastCL(d, m):
n = len(d)
s = np.sum(d)
p = [i/s for i in d]
target = m
tples = []
## generate edges (tuples), drop collisions, until m edges are obtained.
while len(tples) < target:
s = target - len(tples)
e0 = np.random.choice(n, size=s, replace=True, p=p)
e1 = np.random.choice(n, size=s, replace=True, p=p)
tples.extend([(min(e0[i],e1[i]),max(e0[i],e1[i])) for i in range(len(e0)) if e0[i]!=e1[i]]) ## ignore loops
tples = list(set(tples)) ## drop collisions
return tples
# +
## power law graph
gamma = 2.5
n = 10000
## min and max degrees
delta = 1
Delta = np.sqrt(n)
## generate degrees
W = []
for i in np.arange(1,n+1):
W.append(delta * (n/(i-1+n/(Delta/delta)**(gamma-1)))**(1/(gamma-1)))
# deg = [int(np.round(w)) for w in W] ## to enforce integer weights, not an obligation
deg = W
## generate graph with Chung-Lu model
m = int(np.mean(deg)*n/2)
tpl = fastCL(deg,m)
g1 = ig.Graph.TupleList(tpl)
## number of isolated nodes (no edges)
iso = n-g1.vcount()
print('isolates:',iso)
# +
## run plfit and compute K-S statistic (details in the book)
d = g1.degree()
X = plfit.plfit(d)
## those are gamma' and l' minimizing divergence from the tail of the power law distribution
print(X.plfit())
## plot K-S statistics vs. cutoff value l
ax = plt.figure(1)
ax = X.xminvsks()
ax.set_xlabel(r'$\ell$',fontsize=14)
ax.set_ylabel('Kolmogorov-Smirnov statistic',fontsize=12);
# -
## K-S test - this can take a few minutes
# Monte-Carlo test to determine whether distribution is consistent with a power law
KS_tst = X.test_pl(niter=100)
## plot K-S statistics vs. exponent (alpha here, gamma' in the book)
ax = plt.figure(1)
ax = X.alphavsks()
## inverse cdf along with fitted line (as with Figure 2.6 in the book)
X.plotcdf(pointcolor='grey', pointmarker='.',zoom=False)
# ## Figure 2.7: simple d-regular graphs
#
# We generate several $d$-regular graphs and count how many are simple graphs.
# We consider $d=2$ to $d=10$, with $n=100$ nodes. You can try for different $n$. Un-comment the second line to run with $n=10000$ nodes as in the book (this will be much slower).
#
# We plot the empirical proportion of simple graphs below (black dots), and we compare with the theoretical values (dashed line). We see good agreement even for small value $n=100$.
#
n = 100
# n = 10000
REP = 100
D = np.arange(2,11)
simple = []
for d in D:
x = 0
for rep in range(REP):
g = ig.Graph.Degree_Sequence([d for i in range(n)])
x += int(g.is_simple())
simple.append(x/REP)
th = [np.exp(-(d*d-1)/4) for d in D]
plt.plot(D,simple,'o',color='black')
plt.plot(D,th,':',color='black')
plt.xlabel('degree',fontsize=14)
plt.ylabel('P(graph is simple)',fontsize=14);
# # Part 2 -- Experiments section
#
# We use the giant component of the GitHub machine learning (ml) developers subgraph that we introduced in Chapter 1. Recall this graph has 7,083 nodes and 19,491 edges.
#
# We compute several graphs statistics for this "base graph", as reported in the first column of Table 2.8 from the book.
#
# We then generate random graphs with the same number of nodes and edges using 4 different models:
# * binomial (only average degree)
# * Chung-Lu (expected degree distribution)
# * Configuration (exact degree distribution)
# * Configuration with Viger method (connected, simple graph is obtained)
#
# See section 2.8 of the book for a discussion of the results bit as a general observation, more complex models (such as the configuration model with Viger method) tend to preserve more characteristics of the reference graph.
#
# +
## read the GitHub edge list into a graph (gh)
D = pd.read_csv(datadir+'GitHubDevelopers/musae_git_edges.csv')
tuples = [tuple(x) for x in D.values]
gh = ig.Graph.TupleList(tuples, directed = False)
## Add some node features;
## There are 2 class of nodes
## 0: web developer (red), 1: ml developer (blue)
X = pd.read_csv(datadir+'GitHubDevelopers/musae_git_target.csv')
idx = [int(i) for i in gh.vs['name']]
sorterIndex = dict(zip(idx,range(len(idx))))
X['Rank'] = X['id'].map(sorterIndex)
X.sort_values(['Rank'], ascending=[True],inplace=True)
X.dropna(inplace=True)
gh.vs['target'] = list(X['ml_target'])
cls = ['grey','black']
gh.vs['color'] = [cls[i] for i in list(X['ml_target'])]
gh.es['color'] = 'grey'
## for github, 9739 are ml developers, build the subgraph
gh_ml = gh.subgraph([v for v in gh.vs() if v['color']=='black'])
## keep the giant component
sg = gh_ml.clusters().giant()
print(sg.vcount(),'nodes and',sg.ecount(),'edges')
# -
## return statistics from Table 2.8 for graph G
def baseStats(G):
deg = G.degree()
return [G.vcount(),G.ecount(),np.min(deg),np.mean(deg),np.median(deg),np.max(deg),G.diameter(),
np.max(G.clusters().membership)+1,G.clusters().giant().vcount(),sum([x==0 for x in G.degree()]),
G.transitivity_undirected(),G.transitivity_avglocal_undirected()]
## statistice for Base and random graphs
S = []
S.append(['Base Graph'] + baseStats(sg))
## Random (Erdos-Renyi) graph with same number of nodes and edges
er = ig.Graph.Erdos_Renyi(n=sg.vcount(), m=sg.ecount())
S.append(['Erdos-Renyi'] + baseStats(er))
## Random (Chung-Lu) graph with same degree distribution
tpl = fastCL(sg.degree(),sg.ecount())
cl = ig.Graph.Erdos_Renyi(n=sg.vcount(),m=0)
cl.add_edges(tpl)
S.append(['Chung-Lu'] + baseStats(cl))
## Random (configuration model) graph with same degree distribution
cm = ig.Graph.Degree_Sequence(sg.degree(),method='simple')
S.append(['Configuration'] + baseStats(cm))
## Random graph with same degree distribution using the
## configuration model with VL method, which yield a simple graph
cmvl = ig.Graph.Degree_Sequence(sg.degree(),method='vl')
S.append(['Configuration (VL)'] + baseStats(cmvl))
## Store in dataframe and show results
D = pd.DataFrame(S,columns=['graph','nodes','edges',r'$d_{min}$',r'$d_{mean}$',
r'$d_{median}$',r'$d_{max}$','diameter','components','largest','isolates',
r'$C_{glob}$',r'$C_{loc}$'])
D = D.transpose()
D
# ### shortest path length distribution
#
# We compute and compare the minimum path length distribution for several node pairs and for the 5 graphs we have (reference and 4 random ones). Sampling can be used to speed-up the process.
#
# We consider the giant component for disconnected graphs.
#
# We see a reasonably high similarity for all graphs, with the binomial random graph having slightly longer path lengths due to the absence of high degree (hub) nodes in that model.
#
# +
## sampling -- doing all vertices is slower
size = 1000
## using the giant component for disconnected graphs
er_g = er.clusters().giant()
cl_g = cl.clusters().giant()
cm_g = cm.clusters().giant()
## to consider all vertices, replace the code below with:
# sp_sg = [i for v in sg.shortest_paths(source=None) for i in v]
# sp_er = [i for v in er_g.shortest_paths(source=None) for i in v]
# sp_cl = [i for v in cl_g.shortest_paths(source=None) for i in v]
# sp_cm = [i for v in cm_g.shortest_paths(source=None) for i in v]
# sp_cmvl = [i for v in cmvl.shortest_paths(source=None) for i in v]
# to use sampling:
## NB: we sample separately since we use the giant components and graphs may
## have a different number of nodes (except the first and last one)
sp_sg = []
for v in np.random.choice(sg.vcount(),size=size,replace=False):
sp_sg.extend(sg.shortest_paths(source=v)[0])
sp_er = []
for v in np.random.choice(er_g.vcount(),size=size,replace=False):
sp_er.extend(er_g.shortest_paths(source=v)[0])
sp_cl = []
for v in np.random.choice(cl_g.vcount(),size=size,replace=False):
sp_cl.extend(cl_g.shortest_paths(source=v)[0])
sp_cm = []
for v in np.random.choice(cm_g.vcount(),size=size,replace=False):
sp_cm.extend(cm_g.shortest_paths(source=v)[0])
sp_cmvl = []
for v in np.random.choice(cmvl.vcount(),size=size,replace=False):
sp_cmvl.extend(cmvl.shortest_paths(source=v)[0])
## generate boxplots
plt.boxplot([sp_sg,sp_er,sp_cl,sp_cm,sp_cmvl],labels=['Base','Bin','CL','CM','CM(V)'],
sym='.',whis=10, medianprops = dict(linestyle='-', linewidth=2.5,color='black'))
plt.ylabel('shortest path length',fontsize=14);
## save plot to file
#plt.savefig('pathlen_box.eps');
# -
# # Extra material
# ## More power law tests - GitHub subgraphs and Grid graph
#
# We try to fit power law for degree distribution as we did before, this time for 3 real graphs:
# * GitHub ml developers (giant component)
# * GitHub web developers (giant component)
# * Grid (Europe power grid graph, giant component)
#
# While the first two exhibit power law degree distribution, this is clearly not the case for the Grid graph.
#
# ### GitHub ml subgraph
# +
## for github, 9739 are ml developers, build the subgraph
gh_ml = gh.subgraph([v for v in gh.vs() if v['color']=='black'])
## keep the giant component
sg = gh_ml.clusters().giant()
## estimates for xmin and gamma
d = sg.degree()
X = plfit.plfit(d)
print(X.plfit())
ax = plt.figure(1)
ax = X.xminvsks()
ax.set_xlabel(r'$\ell$',fontsize=14)
ax.set_ylabel('Kolmogorov-Smirnov statistic',fontsize=12);
# -
## K-S test -- very good fit here
KS_tst = X.test_pl(niter=100)
# ### GitHub web subgraph
# +
## github web developers subgraph
gh_web = gh.subgraph([v for v in gh.vs() if v['color']!='black'])
## keep the giant component
sg = gh_web.clusters().giant()
## estimates for xmin and gamma
d = sg.degree()
X = plfit.plfit(d)
print(X.plfit())
ax = plt.figure(1)
ax = X.xminvsks()
ax.set_xlabel(r'$\ell$',fontsize=14)
ax.set_ylabel('Kolmogorov-Smirnov statistic',fontsize=12);
# -
## KS test -- not as good as previous graph, but still consistent with power law
## (if p<.1, the data may be inconsistent with a powerlaw.)
KS_tst = X.test_pl(niter=100)
# ### Grid graph
# +
gr = ig.Graph.Read_Ncol(datadir+'GridEurope/gridkit_europe-highvoltage.edges', directed=False)
gr = gr.simplify()
## keep the giant component
sg = gr.clusters().giant()
## estimates for xmin and gamma
d = sg.degree()
X = plfit.plfit(d)
print(X.plfit())
ax = plt.figure(1)
ax = X.xminvsks()
ax.set_xlabel(r'$\ell$',fontsize=14)
ax.set_ylabel('Kolmogorov-Smirnov statistic',fontsize=12);
# -
## we get xmin=15 ... how many nodes does this cover? --> just a few!
sum([x>=15 for x in sg.degree()])
## let's fix xmin=4 to cover more nodes!
d = sg.degree()
X = plfit.plfit(d)
print(X.plfit(xmin=4))
## K-S test -- highly likely not power law
KS_tst = X.test_pl(niter=100)
# ## Independent sets
#
# Illustrating a few functions to find independent sets.
## generate random graph with (at least one) independent set
## n: nodes, s: independent set size, d: avg degree
def indepSet(n,s,d):
N = n-s
di = n*d//2-s*d
## random graph with N nodes
g = ig.Graph.Erdos_Renyi(n=N,m=di)
## extra nodes
g.add_vertices(s)
## assign remaining degree to extra nodes
z = np.random.choice(np.arange(N,n),size=s*d)
deg = [x[1] for x in sorted(Counter(z).items())]
for i in range(len(deg)):
e = np.random.choice(N,deg[i],replace=False)
for j in e:
g.add_edge(j,i+N)
p = list(np.random.permutation(n))
G = g.permute_vertices(p)
return G
# +
g = indepSet(50, 10, 20)
## every set of size min or mode
#ivs = g.independent_vertex_sets(min=9)
## largest set(s) only
ivs = g.largest_independent_vertex_sets()
## maximal sets (that can't be extended)
#ivs = g.maximal_independent_vertex_sets()
print(g.independence_number())
ivs
|
Python_Notebooks/Chapter_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: PythonData
# language: python
# name: pythondata
# ---
# # Analysis with Thomas High School 9th Grade Test Scores Removed
# ## Import and Clean DataFrames
# +
# Dependencies and Setup
import pandas as pd
import pathlib
# File to Load (Remember to change the path if needed.)
school_data_to_load = pathlib.Path("resources/schools_complete.csv")
student_data_to_load = pathlib.Path("resources/students_complete.csv")
# File to write DataFrames to. Will be used to create images for the README.md file.
THS_9th_removed_file_path = pathlib.Path("resources/dataframes_THS_9th_removed.xlsx")
# Read the School Data and Student Data and store into a Pandas DataFrame
school_data_df = pd.read_csv(school_data_to_load)
student_data_df = pd.read_csv(student_data_to_load)
# Cleaning Student Names and Replacing Substrings in a Python String
# Add each prefix and suffix to remove to a list.
prefixes_suffixes = ["Dr. ", "Mr. ","Ms. ", "Mrs. ", "Miss ", " MD", " DDS", " DVM", " PhD"]
# Iterate through the words in the "prefixes_suffixes" list and replace them with an empty space, "".
for word in prefixes_suffixes:
student_data_df["student_name"] = student_data_df["student_name"].str.replace(word, "", regex=False)
# Check names.
student_data_df.head(10)
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## Deliverable 1: Replace the reading and math scores.
#
# ### Replace the 9th grade reading and math scores at Thomas High School with NaN.
# + tags=[]
# Install numpy using conda install numpy or pip install numpy.
# Step 1. Import numpy as np.
import numpy as np
# + tags=[]
# Step 2. Use the loc method on the student_data_df to select all the reading scores from the 9th grade at Thomas High
# School and replace them with NaN.
student_data_df.loc[(student_data_df["school_name"] == "Thomas High School")
& (student_data_df["grade"] == "9th"), "reading_score"] = np.nan
# + tags=[]
# Step 3. Refactor the code in Step 2 to replace the math scores with NaN.
student_data_df.loc[(student_data_df["school_name"] == "<NAME> School")
& (student_data_df["grade"] == "9th"), "math_score"] = np.nan
# +
# Step 4. Check the student data for NaN's.
# print(student_data_df[(student_data_df["school_name"] == "Thomas High School")
# & (student_data_df["grade"] == "9th")].count())
student_data_df.tail(10)
# + [markdown] jp-MarkdownHeadingCollapsed=true tags=[]
# <hr />
#
# ## Deliverable 2 : Repeat the school district analysis
# + [markdown] tags=[] toc-hr-collapsed=true
# ## District Summary
# ### Merge DataFrames
# + tags=[]
# Combine the data into a single dataset
school_data_complete_df = pd.merge(student_data_df, school_data_df, how="left", on=["school_name", "school_name"])
# school_data_complete_df.head()
# -
# ### Student and School Counts, Total Budget
# +
# Calculate the Totals (Schools and Students)
school_count = len(school_data_complete_df["school_name"].unique())
student_count = school_data_complete_df["Student ID"].count()
# Calculate the Total Budget
total_budget = school_data_df["budget"].sum()
# -
# ### Average Scores
# Calculate the Average Scores using the "clean_student_data".
average_reading_score = school_data_complete_df["reading_score"].mean()
average_math_score = school_data_complete_df["math_score"].mean()
# ### Percentage of Students Passing
# #### Reduced Student Count
# + tags=[]
# Step 1. Get the number of students that are in ninth grade at Thomas High School (THS).
# These students have no grades.
THS_9th_count = school_data_complete_df.loc[(school_data_complete_df["school_name"] == "Thomas High School")
& (school_data_complete_df["grade"] == "9th")]["Student ID"].count()
# Step 2. Subtract the number of students that are in ninth grade at Thomas High School
# from the total student count to get the new total student count.
reduced_student_count = student_count - THS_9th_count
# -
# #### Passing Math, Passing Reading
# +
# Get all the students who are passing math in a new DataFrame
passing_math_df = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)]
# Get all the students who are passing reading in a new DataFrame
passing_reading_df = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)]
# Find the number of students passing math and reading individually
passing_math_count = passing_math_df["student_name"].count()
passing_reading_count = passing_reading_df["student_name"].count()
# Step 3. Calculate the passing percentages with the new total student count.
passing_math_percentage = (passing_math_count / float(reduced_student_count)) * 100
passing_reading_percentage = (passing_reading_count / float(reduced_student_count)) * 100
# -
# #### Overall Passing
# +
# Get all the students who passed both reading and math in a new DataFrame
passing_math_reading_df = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)
& (school_data_complete_df["reading_score"] >= 70)]
# Find the number of students who passed both math and reading
overall_passing_math_reading_count = passing_math_reading_df["student_name"].count()
# Step 4.Calculate the overall passing percentage with new total student count.
overall_passing_percentage = (overall_passing_math_reading_count / float(reduced_student_count)) * 100
# -
# ### Create and Format the District Summary
# + tags=[]
# Create a DataFrame
district_summary_df = pd.DataFrame([{
"Total Schools": school_count,
"Total Students": student_count,
"Total Budget": total_budget,
"Average Math Score": average_math_score,
"Average Reading Score": average_reading_score,
"% Passing Math": passing_math_percentage,
"% Passing Reading": passing_reading_percentage,
"% Overall Passing": overall_passing_percentage
}])
# Format the "Total Students" to have the comma for a thousands separator.
district_summary_df["Total Students"] = district_summary_df["Total Students"].map("{:,}".format)
# Format the "Total Budget" to have the comma for a thousands separator, a decimal separator and a "$".
district_summary_df["Total Budget"] = district_summary_df["Total Budget"].map("${:,.2f}".format)
# Format the average score columns
district_summary_df["Average Math Score"] = district_summary_df["Average Math Score"].map("{:.1f}".format)
district_summary_df["Average Reading Score"] = district_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format the percentage columns
district_summary_df["% Passing Math"] = district_summary_df["% Passing Math"].map("{:.1f}".format)
district_summary_df["% Passing Reading"] = district_summary_df["% Passing Reading"].map("{:.1f}".format)
district_summary_df["% Overall Passing"] = district_summary_df["% Overall Passing"].map("{:.1f}".format)
# Display the data frame
district_summary_df
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## School Summary
# ### School Types
# -
# Determine the School Type
per_school_types = school_data_df.set_index(["school_name"])["type"]
# ### Student Counts, School Budgets, Per Student Budgets
# +
# Calculate the total student count.
per_school_counts = school_data_complete_df["school_name"].value_counts()
# Calculate the total school budget and per capita spending
per_school_budget = school_data_complete_df.groupby(["school_name"]).mean()["budget"]
# Calculate the per capita spending.
per_school_capita = per_school_budget / per_school_counts
# -
# ### Average Scores
# Calculate the average test scores.
per_school_math = school_data_complete_df.groupby(["school_name"]).mean()["math_score"]
per_school_reading = school_data_complete_df.groupby(["school_name"]).mean()["reading_score"]
# ### Percentage of Students Passing
# #### Passing Math, Passing Reading
# +
# Get the students passing math per school, and students passing reading per school by creating a
# filtered DataFrame
per_school_passing_math = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)]
per_school_passing_reading = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)]
# Find the number of students passing math and passing reading (individually) per school
per_school_passing_math = per_school_passing_math.groupby(["school_name"]).count()["student_name"]
per_school_passing_reading = per_school_passing_reading.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of students passing math and reading (individually) per school
per_school_passing_math = per_school_passing_math / per_school_counts * 100
per_school_passing_reading = per_school_passing_reading / per_school_counts * 100
# -
# #### Overall Passing
# +
# Get the students passing both math and reading per school by filtering the DataFrame
per_passing_math_reading = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)
& (school_data_complete_df["math_score"] >= 70)]
# Find the number of students passing both math and reading per school
per_passing_math_reading = per_passing_math_reading.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of students passing both math and reading per school
per_overall_passing_percentage = per_passing_math_reading / per_school_counts * 100
# -
# ### Create and Format the School Summary
# +
# Create the DataFrame
per_school_summary_df = pd.DataFrame({
"School Type": per_school_types,
"Total Students": per_school_counts,
"Total School Budget": per_school_budget,
"Per Student Budget": per_school_capita,
"Average Math Score": per_school_math,
"Average Reading Score": per_school_reading,
"% Passing Math": per_school_passing_math,
"% Passing Reading": per_school_passing_reading,
"% Overall Passing": per_overall_passing_percentage
})
# Format the Total School Budget and the Per Student Budget
per_school_summary_df["Total School Budget"] = per_school_summary_df["Total School Budget"].map("${:,.2f}".format)
per_school_summary_df["Per Student Budget"] = per_school_summary_df["Per Student Budget"].map("${:,.2f}".format)
# Display the data frame
per_school_summary_df
# -
# ### Correcting the Thomas High School (THS) Passing Percentages
# #### THS 10th-12th Grade Student Count
# Step 5. Get the number of 10th-12th graders from Thomas High School (THS).
THS_10th_12th_count = (
school_data_complete_df[school_data_complete_df["school_name"] == "Thomas High School"]["reading_score"].count()
)
# #### THS Passing DataFrames
# +
# Step 6. Get all the students passing math from THS
THS_passing_math_df = school_data_complete_df.loc[(school_data_complete_df["school_name"] == "Thomas High School")
& (school_data_complete_df["math_score"] >= 70)]
# Step 7. Get all the students passing reading from THS
THS_passing_reading_df = school_data_complete_df.loc[(school_data_complete_df["school_name"] == "Thomas High School")
& (school_data_complete_df["reading_score"] >= 70)]
# Step 8. Get all the students passing math and reading from THS
THS_overall_passing_df = school_data_complete_df.loc[(school_data_complete_df["school_name"] == "Thomas High School")
& (school_data_complete_df["math_score"] >= 70)
& (school_data_complete_df["reading_score"] >= 70)]
# -
# #### Corrected THS Percentages
# + tags=[]
# Step 9. Calculate the percentage of 10th-12th grade students passing math from Thomas High School.
THS_passing_math = (THS_passing_math_df["Student ID"].count() / THS_10th_12th_count) * 100
# Step 10. Calculate the percentage of 10th-12th grade students passing reading from Thomas High School.
THS_passing_reading = (THS_passing_reading_df["Student ID"].count() / THS_10th_12th_count) * 100
# Step 11. Calculate the overall passing percentage of 10th-12th grade from Thomas High School.
THS_overall_passing = (THS_overall_passing_df["Student ID"].count() / THS_10th_12th_count) * 100
# -
# #### Assign Corrected Data to the School Summary
# +
# Step 12. Replace the passing math percent for Thomas High School in the per_school_summary_df.
per_school_summary_df.loc["Thomas High School", "% Passing Math"] = THS_passing_math
# Step 13. Replace the passing reading percentage for Thomas High School in the per_school_summary_df.
per_school_summary_df.loc["Thomas High School", "% Passing Reading"] = THS_passing_reading
# Step 14. Replace the overall passing percentage for Thomas High School in the per_school_summary_df.
per_school_summary_df.loc["Thomas High School", "% Overall Passing"] = THS_overall_passing
# Show the corrected DataFrame
per_school_summary_df
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## High and Low Performing Schools
# ### High Performers
# + tags=[]
# Sort and show top five schools.
top_schools_df = per_school_summary_df.sort_values(["% Overall Passing"], ascending=False)
top_schools_df.head()
# -
# ### Low Performers
# + tags=[]
# Sort and show bottom five schools.
bottom_schools_df = per_school_summary_df.sort_values(["% Overall Passing"], ascending=True)
bottom_schools_df.head()
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## Average Math and Reading Scores by Grade
# ### Filter by Grade
# + tags=[]
# Create a Series of scores by grade levels using conditionals.
ninth_graders_df = school_data_complete_df[school_data_complete_df["grade"] == "9th"]
tenth_graders_df = school_data_complete_df[school_data_complete_df["grade"] == "10th"]
eleventh_graders_df = school_data_complete_df[school_data_complete_df["grade"] == "11th"]
twelfth_graders_df = school_data_complete_df[school_data_complete_df["grade"] == "12th"]
# -
# ### Average Scores
# + tags=[]
# Group each school Series by the school name for the average math score.
ninth_grade_math_scores = ninth_graders_df.groupby(["school_name"]).mean()["math_score"]
tenth_grade_math_scores = tenth_graders_df.groupby(["school_name"]).mean()["math_score"]
eleventh_grade_math_scores = eleventh_graders_df.groupby(["school_name"]).mean()["math_score"]
twelfth_grade_math_scores = twelfth_graders_df.groupby(["school_name"]).mean()["math_score"]
# Group each school Series by the school name for the average reading score.
ninth_grade_reading_scores = ninth_graders_df.groupby(["school_name"]).mean()["reading_score"]
tenth_grade_reading_scores = tenth_graders_df.groupby(["school_name"]).mean()["reading_score"]
eleventh_grade_reading_scores = eleventh_graders_df.groupby(["school_name"]).mean()["reading_score"]
twelfth_grade_reading_scores = twelfth_graders_df.groupby(["school_name"]).mean()["reading_score"]
# -
# ### Create and Format the Average Scores by Grade DataFrames
# + tags=[]
# Combine each Series for average math scores by school into single data frame.
math_scores_by_grade_df = pd.DataFrame({
"9th": ninth_grade_math_scores,
"10th": tenth_grade_math_scores,
"11th": eleventh_grade_math_scores,
"12th": twelfth_grade_math_scores,
})
# Combine each Series for average reading scores by school into single data frame.
reading_scores_by_grade_df = pd.DataFrame({
"9th": ninth_grade_reading_scores,
"10th": tenth_grade_reading_scores,
"11th": eleventh_grade_reading_scores,
"12th": twelfth_grade_reading_scores,
})
# Format each grade column for the math scores by grade
math_scores_by_grade_df["9th"] = math_scores_by_grade_df["9th"].map("{:.1f}".format)
math_scores_by_grade_df["10th"] = math_scores_by_grade_df["10th"].map("{:.1f}".format)
math_scores_by_grade_df["11th"] = math_scores_by_grade_df["11th"].map("{:.1f}".format)
math_scores_by_grade_df["12th"] = math_scores_by_grade_df["12th"].map("{:.1f}".format)
# Format each grade column for the reading scores by grade
reading_scores_by_grade_df["9th"] = reading_scores_by_grade_df["9th"].map("{:.1f}".format)
reading_scores_by_grade_df["10th"] = reading_scores_by_grade_df["10th"].map("{:.1f}".format)
reading_scores_by_grade_df["11th"] = reading_scores_by_grade_df["11th"].map("{:.1f}".format)
reading_scores_by_grade_df["12th"] = reading_scores_by_grade_df["12th"].map("{:.1f}".format)
# -
# ### Average Math Scores by Grade
# +
# Remove the index.
math_scores_by_grade_df.index.name = None
# Display the data frame
math_scores_by_grade_df
# -
# ### Average Reading Scores by Grade
# +
## Remove the index.
reading_scores_by_grade_df.index.name = None
# Display the data frame
reading_scores_by_grade_df
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## Scores by School Spending
# ### Assign Spending Ranges
# + tags=[]
# Establish the spending bins and group names.
spending_bins = [0, 585, 630, 645, 675]
group_names = ["<=$585", "$585-630", "$630-645", "$645-675"]
# Categorize spending based on the bins.
per_school_summary_df["Spending Ranges (Per Student)"] = pd.cut(per_school_capita, spending_bins, labels=group_names)
# -
# ### Group by Spending Ranges
# +
# Calculate averages for the desired columns.
spending_math_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Math Score"]
spending_reading_scores = (
per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Reading Score"]
)
# Calculate percentages for the desired columns.
spending_passing_math = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Math"]
spending_passing_reading = (
per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Reading"]
)
spending_passing_both = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Overall Passing"]
# -
# ### Create and Format Scores by School Spending DataFrame
# +
# Create the DataFrame
spending_summary_df = pd.DataFrame({
"Average Math Score": spending_math_scores,
"Average Reading Score": spending_reading_scores,
"% Passing Math": spending_passing_math,
"% Passing Reading": spending_passing_reading,
"% Overall Passing": spending_passing_both,
})
# Format the DataFrame
# Format average columns
spending_summary_df["Average Math Score"] = spending_summary_df["Average Math Score"].map("{:.1f}".format)
spending_summary_df["Average Reading Score"] = spending_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format percentage columns
spending_summary_df["% Passing Math"] = spending_summary_df["% Passing Math"].map("{:.1f}".format)
spending_summary_df["% Passing Reading"] = spending_summary_df["% Passing Reading"].map("{:.1f}".format)
spending_summary_df["% Overall Passing"] = spending_summary_df["% Overall Passing"].map("{:.1f}".format)
spending_summary_df
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## Scores by School Size
# ### Assign School Size Ranges
# +
# Establish the bins.
size_bins = [0, 1000, 2000, 5000]
group_names = ["Small (<1000)", "Medium (1000-2000)", "Large (2000-5000)"]
# Categorize spending based on the bins.
per_school_summary_df["School Size"] = pd.cut(per_school_summary_df["Total Students"], size_bins, labels=group_names)
# -
# ### Group by School Size Ranges
# +
# Calculate averages for the desired columns.
size_math_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Math Score"]
size_reading_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Reading Score"]
# Calculate percentages for the desired columns.
size_passing_math = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Math"]
size_passing_reading = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Reading"]
size_passing_both = per_school_summary_df.groupby(["School Size"]).mean()["% Overall Passing"]
# -
# ### Create and Format Scores by School Size DataFrame
# + tags=[]
# Assemble into DataFrame.
size_summary_df = pd.DataFrame({
"Average Math Score": size_math_scores,
"Average Reading Score": size_reading_scores,
"% Passing Math": size_passing_math,
"% Passing Reading": size_passing_reading,
"% Overall Passing": size_passing_both,
})
# Format the DataFrame
# Format average columns
size_summary_df["Average Math Score"] = size_summary_df["Average Math Score"].map("{:.1f}".format)
size_summary_df["Average Reading Score"] = size_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format percentage columns
size_summary_df["% Passing Math"] = size_summary_df["% Passing Math"].map("{:.1f}".format)
size_summary_df["% Passing Reading"] = size_summary_df["% Passing Reading"].map("{:.1f}".format)
size_summary_df["% Overall Passing"] = size_summary_df["% Overall Passing"].map("{:.1f}".format)
size_summary_df
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## Scores by School Type
# ### Group by School Type
# +
# Calculate averages for the desired columns.
type_math_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Math Score"]
type_reading_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Reading Score"]
# Calculate percentages for the desired columns.
type_passing_math = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Math"]
type_passing_reading = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Reading"]
type_passing_both = per_school_summary_df.groupby(["School Type"]).mean()["% Overall Passing"]
# -
# ### Create and Format Scores by School Size DataFrame
# +
# Assemble into DataFrame.
type_summary_df = pd.DataFrame({
"Average Math Score": type_math_scores,
"Average Reading Score": type_reading_scores,
"% Passing Math": type_passing_math,
"% Passing Reading": type_passing_reading,
"% Overall Passing": type_passing_both,
})
# Format the DataFrame
# Format average columns
type_summary_df["Average Math Score"] = type_summary_df["Average Math Score"].map("{:.1f}".format)
type_summary_df["Average Reading Score"] = type_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format percentage columns
type_summary_df["% Passing Math"] = type_summary_df["% Passing Math"].map("{:.1f}".format)
type_summary_df["% Passing Reading"] = type_summary_df["% Passing Reading"].map("{:.1f}".format)
type_summary_df["% Overall Passing"] = type_summary_df["% Overall Passing"].map("{:.1f}".format)
type_summary_df
# -
# <hr />
#
# ## Write DataFrames of Interest to Excel
# + tags=[]
with pd.ExcelWriter(THS_9th_removed_file_path, mode="w") as writer:
student_data_df.tail(10).to_excel(writer, sheet_name="T9 Scores Removed", na_rep="NaN")
district_summary_df.to_excel(writer, sheet_name="T9 District Summary", na_rep="NaN")
per_school_summary_df.to_excel(writer, sheet_name="T9 School Summary", na_rep="NaN")
top_schools_df.head().to_excel(writer, sheet_name="T9 High Performers", na_rep="NaN")
bottom_schools_df.head().to_excel(writer, sheet_name="T9 Low Performers", na_rep="NaN")
math_scores_by_grade_df.to_excel(writer, sheet_name="T9 Math Scores by Grade", na_rep="NaN")
reading_scores_by_grade_df.to_excel(writer, sheet_name="T9 Reading Scores by Grade", na_rep="NaN")
spending_summary_df.to_excel(writer, sheet_name="T9 Scores by Spending", na_rep="NaN")
size_summary_df.to_excel(writer, sheet_name="T9 Scores by Size", na_rep="NaN")
type_summary_df.to_excel(writer, sheet_name="T9 Scores by Type", na_rep="NaN")
# -
# <br />
# <br />
# <br />
# <hr style="height: 7px" />
# <br />
#
# # Analysis with Entire Student List
# ## Import and Clean DataFrames
# + tags=[]
# Files to load
school_data_filepath = pathlib.Path("resources/schools_complete.csv")
student_data_filepath = pathlib.Path("resources/students_complete.csv")
# File to write DataFrames to. Will be used to create images for the README.md file.
all_students_file_path = pathlib.Path("resources/dataframes_all_students.xlsx")
# Read the data files and create the DataFrames
schools_df = pd.read_csv(school_data_filepath)
students_df = pd.read_csv(student_data_filepath)
# Check for missing data (commented out to reduce unnecessary output)
# Determine if there is any missing data in schools
# schools_df.count()
# Determine if there is any missing data in students
# students_df.count()
# Confirming the number of null values in each column is zero
# schools_df.isnull().sum()
# Confirming the number of null values in each column is zero
# students_df.isnull().sum()
# Data types (commented out to reduce unnecessary output)
# Determine data types for the school DataFrame
# schools_df.dtypes
# Determine data types for the student DataFrame
# students_df.dtypes
# Clean student names
# Add each prefix and suffix to remove to a list
prefixes_suffixes = ["Dr. ", "Mr. ","Ms. ", "Mrs. ", "Miss ", " MD", " DDS", " DVM", " PhD"]
# Iterate through the words in the "prefixes_suffixes" list and replace them with an empty space, ""
for word in prefixes_suffixes:
students_df["student_name"] = students_df["student_name"].str.replace(word, "", regex=False)
# Write Cleaned Student Data to CSV (commented out because unused)
# students_df.to_csv(pathlib.Path("resources/clean_students_complete.csv"))
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## District Summary
# ### Merge DataFrames
# -
# Combine the data into a single dataset
school_complete_df = pd.merge(students_df, schools_df, on=["school_name", "school_name"])
# ### Student and School Counts, Total Budget
# +
# Total number of students and schools
student_count = school_complete_df["Student ID"].count()
school_count = len(school_complete_df["school_name"].unique())
# Calculate total budget
total_budget = schools_df["budget"].sum()
# -
# ### Average Scores
# Calculate the average math and reading scores
average_math_score = school_complete_df["math_score"].mean()
average_reading_score = school_complete_df["reading_score"].mean()
# ### Percentage of Students Passing
# #### Passing Math, Passing Reading
# + tags=[]
# Get all the students who are passing math in a new DataFrame
passing_math_df = school_complete_df[school_complete_df["math_score"] >= 70]
# Get all the students who are passing reading in a new DataFrame
passing_reading_df = school_complete_df[school_complete_df["reading_score"] >= 70]
# Find the number of students passing math and reading individually
passing_math_count = passing_math_df["student_name"].count()
passing_reading_count = passing_reading_df["student_name"].count()
# Calculate the percent that passed math and reading individually
passing_math_percentage = (passing_math_count / float(student_count)) * 100
passing_reading_percentage = (passing_reading_count / float(student_count)) * 100
# -
# #### Overall Passing
# +
# Get all the students who passed both reading and math in a new DataFrame
passing_both_df = school_complete_df[(school_complete_df["math_score"] >= 70)
& (school_complete_df["reading_score"] >= 70)]
# Find the number of students who passed both math and reading
passing_both_count = passing_both_df["student_name"].count()
# Calculate the overall passing percentage
passing_both_percentage = (passing_both_count / float(student_count)) * 100
# -
# ### Create and Format the District Summary
# +
# Adding a list of values with keys to create a new DataFrame
district_summary_df = pd.DataFrame([{
"Total Schools": school_count,
"Total Students": student_count,
"Total Budget": total_budget,
"Average Math Score": average_math_score,
"Average Reading Score": average_reading_score,
"% Passing Math": passing_math_percentage,
"% Passing Reading": passing_reading_percentage,
"% Overall Passing": passing_both_percentage
}])
# Format the "Total Students" to have the comma for a thousands separator
district_summary_df["Total Students"] = district_summary_df["Total Students"].map("{:,}".format)
# Format "Total Budget" to have the comma for a thousands separator, a decimal separator, and a "$"
district_summary_df["Total Budget"] = district_summary_df["Total Budget"].map("${:,.2f}".format)
# Format the average score columns
district_summary_df["Average Math Score"] = district_summary_df["Average Math Score"].map("{:.1f}".format)
district_summary_df["Average Reading Score"] = district_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format the percentage columns
district_summary_df["% Passing Math"] = district_summary_df["% Passing Math"].map("{:.1f}".format)
district_summary_df["% Passing Reading"] = district_summary_df["% Passing Reading"].map("{:.1f}".format)
district_summary_df["% Overall Passing"] = district_summary_df["% Overall Passing"].map("{:.1f}".format)
district_summary_df
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## School Summary
# ### School Types
# + tags=[]
# Determine the school type
per_school_types = schools_df.set_index(["school_name"])["type"]
# -
# ### Student Counts, School Budgets, Per Student Budgets
# + tags=[]
# Find the total student count using schools_compelete_df
# per_school_counts = schools_df.set_index(["school_name"])["size"]
per_school_counts = school_complete_df["school_name"].value_counts()
# Find the total school budget
per_school_budget = schools_df.set_index(["school_name"])["budget"]
# Calculate the per capita spending
per_school_capita = per_school_budget / per_school_counts
# -
# ### Average Scores
# Calculate the average math and reading test scores by school
per_school_math = school_complete_df.groupby(["school_name"]).mean()["math_score"]
per_school_reading = school_complete_df.groupby(["school_name"]).mean()["reading_score"]
# ### Percentage of Students Passing
# #### Passing Math, Passing Reading
# +
# Get the students passing math per school, and students passing reading per school by creating a
# filtered DataFrame
per_school_passing_math_df = school_complete_df[school_complete_df["math_score"] >= 70]
per_school_passing_reading_df = school_complete_df[school_complete_df["reading_score"] >= 70]
# Find the number of students passing math and passing reading (individually) per school
per_school_passing_math = per_school_passing_math_df.groupby(["school_name"]).count()["student_name"]
per_school_passing_reading = per_school_passing_reading_df.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of students passing math and reading (individually) per school
per_school_passing_math = (per_school_passing_math / per_school_counts) * 100
per_school_passing_reading = (per_school_passing_reading / per_school_counts) * 100
# -
# #### Overall Passing
# +
# Get the students passing both math and reading per school by filtering the DataFrame
per_school_passing_both_df = school_complete_df[(school_complete_df["math_score"] >= 70)
& (school_complete_df["reading_score"] >= 70)]
# Find the number of students passing both math and reading per school
per_school_passing_both = per_school_passing_both_df.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of students passing both math and reading per school
per_school_passing_both = (per_school_passing_both / per_school_counts) * 100
# -
# ### Create and Format the School Summary
# +
# Adding a list of values with keys to create a new DataFrame
per_school_summary_df = pd.DataFrame({
"School Type": per_school_types,
"Total Students": per_school_counts,
"Total School Budget": per_school_budget,
"Per Student Budget": per_school_capita,
"Average Math Score": per_school_math,
"Average Reading Score": per_school_reading,
"% Passing Math": per_school_passing_math,
"% Passing Reading": per_school_passing_reading,
"% Overall Passing": per_school_passing_both
})
# Format the "Total Students" to have the comma for a thousands separator
# per_school_summary_df["Total Students"] = per_school_summary_df["Total Students"].map("{:,}".format)
# Format the Total School Budget and the Per Student Budget columns
per_school_summary_df["Total School Budget"] = per_school_summary_df["Total School Budget"].map("${:,.2f}".format)
per_school_summary_df["Per Student Budget"] = per_school_summary_df["Per Student Budget"].map("${:,.2f}".format)
# Format the average score columns
# per_school_summary_df["Average Math Score"] = per_school_summary_df["Average Math Score"].map("{:.1f}".format)
# per_school_summary_df["Average Reading Score"] = per_school_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format the percentage columns
# per_school_summary_df["% Passing Math"] = per_school_summary_df["% Passing Math"].map("{:.0f}".format)
# per_school_summary_df["% Passing Reading"] = per_school_summary_df["% Passing Reading"].map("{:.0f}".format)
# per_school_summary_df["% Overall Passing"] = per_school_summary_df["% Overall Passing"].map("{:.0f}".format)
per_school_summary_df
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## High and Low Performing Schools
# ### High Performers
# -
# Sort and show top five schools.
top_schools_df = per_school_summary_df.sort_values(["% Overall Passing"], ascending=False)
top_schools_df.head()
# ### Low Performers
# Sort and show bottom five schools
bottom_schools_df = per_school_summary_df.sort_values(["% Overall Passing"], ascending=True)
bottom_schools_df.head()
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## Average Math and Reading Scores by Grade
# ### Filter by Grade
# + tags=[]
# Create a grade level DataFrames
ninth_graders_df = school_complete_df[school_complete_df["grade"] == "9th"]
tenth_graders_df = school_complete_df[school_complete_df["grade"] == "10th"]
eleventh_graders_df = school_complete_df[school_complete_df["grade"] == "11th"]
twelfth_graders_df = school_complete_df[school_complete_df["grade"] == "12th"]
# -
# ### Average Scores
# + tags=[]
# Group each grade level DataFrame by the school name for the average math score
ninth_grade_math_scores = ninth_graders_df.groupby(["school_name"]).mean()["math_score"]
tenth_grade_math_scores = tenth_graders_df.groupby(["school_name"]).mean()["math_score"]
eleventh_grade_math_scores = eleventh_graders_df.groupby(["school_name"]).mean()["math_score"]
twelfth_grade_math_scores = twelfth_graders_df.groupby(["school_name"]).mean()["math_score"]
# Group each grade level DataFrame by the school name for the average reading score
ninth_grade_reading_scores = ninth_graders_df.groupby(["school_name"]).mean()["reading_score"]
tenth_grade_reading_scores = tenth_graders_df.groupby(["school_name"]).mean()["reading_score"]
eleventh_grade_reading_scores = eleventh_graders_df.groupby(["school_name"]).mean()["reading_score"]
twelfth_grade_reading_scores = twelfth_graders_df.groupby(["school_name"]).mean()["reading_score"]
# -
# ### Create and Format the Average Scores by Grade DataFrames
# +
# Combine each grade level Series for average math scores by school into a single DataFrame
math_scores_by_grade_df = pd.DataFrame({
"9th": ninth_grade_math_scores,
"10th": tenth_grade_math_scores,
"11th": eleventh_grade_math_scores,
"12th": twelfth_grade_math_scores,
})
# Combine each grade level Series for average reading scores by school into a single DataFrame
reading_scores_by_grade_df = pd.DataFrame({
"9th": ninth_grade_reading_scores,
"10th": tenth_grade_reading_scores,
"11th": eleventh_grade_reading_scores,
"12th": twelfth_grade_reading_scores,
})
# Format each grade column of math_scores_by_grade_df
math_scores_by_grade_df["9th"] = math_scores_by_grade_df["9th"].map("{:.1f}".format)
math_scores_by_grade_df["10th"] = math_scores_by_grade_df["10th"].map("{:.1f}".format)
math_scores_by_grade_df["11th"] = math_scores_by_grade_df["11th"].map("{:.1f}".format)
math_scores_by_grade_df["12th"] = math_scores_by_grade_df["12th"].map("{:.1f}".format)
# Format each grade column of reading_scores_by_grade_df
reading_scores_by_grade_df["9th"] = reading_scores_by_grade_df["9th"].map("{:.1f}".format)
reading_scores_by_grade_df["10th"] = reading_scores_by_grade_df["10th"].map("{:.1f}".format)
reading_scores_by_grade_df["11th"] = reading_scores_by_grade_df["11th"].map("{:.1f}".format)
reading_scores_by_grade_df["12th"] = reading_scores_by_grade_df["12th"].map("{:.1f}".format)
# -
# ### Average Math Scores by Grade
# +
# Remove the index name
math_scores_by_grade_df.index.name = None
math_scores_by_grade_df
# -
# ### Average Reading Scores by Grade
# +
# Remove the index name
reading_scores_by_grade_df.index.name = None
reading_scores_by_grade_df
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## Scores by School Spending
# ### Assign Spending Ranges
# +
# Establish the spending bins and group names
spending_bins = [0, 585, 630, 645, 675]
group_names = ["<=$585", "$585-630", "$630-645", "$645-675"]
# Categorize spending based on the bins. Use the "Per Student Budget" column (per_school_capita)
per_school_summary_df["Spending Ranges (Per Student)"] = pd.cut(per_school_capita, spending_bins, labels=group_names)
# -
# ### Group by Spending Ranges
# +
# Calculate averages by spending ranges
spending_math_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Math Score"]
spending_reading_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Reading Score"]
# Calculate percentages by spending ranges
spending_passing_math = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Math"]
spending_passing_reading = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Reading"]
spending_passing_both = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Overall Passing"]
# -
# ### Create and Format Scores by School Spending DataFrame
# +
# Assemble into DataFrame
spending_summary_df = pd.DataFrame({
"Average Math Score": spending_math_scores,
"Average Reading Score": spending_reading_scores,
"% Passing Math": spending_passing_math,
"% Passing Reading": spending_passing_reading,
"% Overall Passing": spending_passing_both,
})
# Format average columns
spending_summary_df["Average Math Score"] = spending_summary_df["Average Math Score"].map("{:.1f}".format)
spending_summary_df["Average Reading Score"] = spending_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format percentage columns
spending_summary_df["% Passing Math"] = spending_summary_df["% Passing Math"].map("{:.1f}".format)
spending_summary_df["% Passing Reading"] = spending_summary_df["% Passing Reading"].map("{:.1f}".format)
spending_summary_df["% Overall Passing"] = spending_summary_df["% Overall Passing"].map("{:.1f}".format)
spending_summary_df
# + [markdown] toc-hr-collapsed=true
# <hr />
#
# ## Scores by School Size
# ### Assign School Size Ranges
# +
# Establish the size bins and group names
size_bins = [0, 1000, 2000, 5000]
group_names = ["Small (<1000)", "Medium (1000-2000)", "Large (2000-5000)"]
# Categorize school size based on the bins. Use the "Total Students" column
per_school_summary_df["School Size"] = pd.cut(per_school_summary_df["Total Students"], size_bins, labels=group_names)
# -
# ### Group by School Size Ranges
# +
# Calculate averages by school size
size_math_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Math Score"]
size_reading_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Reading Score"]
# Calculate percentages by school size
size_passing_math = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Math"]
size_passing_reading = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Reading"]
size_passing_both = per_school_summary_df.groupby(["School Size"]).mean()["% Overall Passing"]
# -
# ### Create and Format Scores by School Size DataFrame
# +
size_summary_df = pd.DataFrame({
"Average Math Score": size_math_scores,
"Average Reading Score": size_reading_scores,
"% Passing Math": size_passing_math,
"% Passing Reading": size_passing_reading,
"% Overall Passing": size_passing_both,
})
# Format average columns
size_summary_df["Average Math Score"] = size_summary_df["Average Math Score"].map("{:.1f}".format)
size_summary_df["Average Reading Score"] = size_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format percentage columns
size_summary_df["% Passing Math"] = size_summary_df["% Passing Math"].map("{:.1f}".format)
size_summary_df["% Passing Reading"] = size_summary_df["% Passing Reading"].map("{:.1f}".format)
size_summary_df["% Overall Passing"] = size_summary_df["% Overall Passing"].map("{:.1f}".format)
size_summary_df
# + [markdown] tags=[] toc-hr-collapsed=true
# <hr />
#
# ## Scores by School Type
# ### Group by School Type
# +
# Calculate averages by school type
type_math_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Math Score"]
type_reading_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Reading Score"]
# Calculate percentages by school type
type_passing_math = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Math"]
type_passing_reading = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Reading"]
type_passing_both = per_school_summary_df.groupby(["School Type"]).mean()["% Overall Passing"]
# -
# ### Create and Format Scores by School Type DataFrame
# +
# Assemble into DataFrame
type_summary_df = pd.DataFrame({
"Average Math Score": type_math_scores,
"Average Reading Score": type_reading_scores,
"% Passing Math": type_passing_math,
"% Passing Reading": type_passing_reading,
"% Overall Passing": type_passing_both,
})
# Format average columns
type_summary_df["Average Math Score"] = type_summary_df["Average Math Score"].map("{:.1f}".format)
type_summary_df["Average Reading Score"] = type_summary_df["Average Reading Score"].map("{:.1f}".format)
# Format percentage columns
type_summary_df["% Passing Math"] = type_summary_df["% Passing Math"].map("{:.1f}".format)
type_summary_df["% Passing Reading"] = type_summary_df["% Passing Reading"].map("{:.1f}".format)
type_summary_df["% Overall Passing"] = type_summary_df["% Overall Passing"].map("{:.1f}".format)
type_summary_df
# -
# <hr />
#
# ## Write DataFrames of Interest to Excel
# + tags=[]
with pd.ExcelWriter(all_students_file_path, mode="w") as writer:
district_summary_df.to_excel(writer, sheet_name="District Summary", na_rep="NaN")
per_school_summary_df.to_excel(writer, sheet_name="School Summary", na_rep="NaN")
top_schools_df.head().to_excel(writer, sheet_name="High Performers", na_rep="NaN")
bottom_schools_df.head().to_excel(writer, sheet_name="Low Performers", na_rep="NaN")
math_scores_by_grade_df.to_excel(writer, sheet_name="Math Scores by Grade", na_rep="NaN")
reading_scores_by_grade_df.to_excel(writer, sheet_name="Reading Scores by Grade", na_rep="NaN")
spending_summary_df.to_excel(writer, sheet_name="Scores by Spending", na_rep="NaN")
size_summary_df.to_excel(writer, sheet_name="Scores by Size", na_rep="NaN")
type_summary_df.to_excel(writer, sheet_name="Scores by Type", na_rep="NaN")
|
PyCitySchools_Challenge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# ## How does concentration change near the head?
# +
import cmocean as cmo
from netCDF4 import Dataset
import matplotlib.pyplot as plt
import matplotlib as mpl
# %matplotlib inline
import matplotlib.gridspec as gspec
import numpy as np
import seaborn as sns
import scipy.stats
import pandas as pd
import canyon_tools.readout_tools as rout
import canyon_tools.savitzky_golay as sg
import os
import sys
import warnings
warnings.filterwarnings("ignore")
# +
grid_file1 = '/data/kramosmu/results/TracerExperiments/3DVISC_REALISTIC/run01/gridGlob.nc'
state_file2 = '/data/kramosmu/results/TracerExperiments/3DVISC_REALISTIC/run01/stateGlob.nc'
with Dataset(grid_file1, 'r') as nbl:
Z1 = nbl.variables['RC'][:]
hfac = nbl.variables['HFacC'][:,:,:]
X = nbl.variables['X'][:]
Y = nbl.variables['Y'][:]
with Dataset(state_file2,'r') as stfl:
time = stfl.variables['T'][:]
mask = rout.getMask(grid_file1,'HFacC')
nx = 616
ny = 360
nz = 90
# +
# Information for all runs is stored in canyon_records.py
lib_path = os.path.abspath('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/PythonScripts/Paper1Figures/') # Add absolute path to my python scripts
sys.path.append(lib_path)
import canyon_records
records = canyon_records.main()
# +
# Indices of all runs that will be consdered for paper 1
select_rec = [0,1,2,3,4,5,6,7,8,9,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,31,32,
33,34,37,38,40,41,42,43,44,45,46,47,48]
# records_dyn has all the runs without the ones where K_bg changes. Use these ones for fitting the data HA2013
ind = [0,3,4,5,6,7,8,9,16,17,18,19,20,21]
records_dyn = []
for ii in ind:
records_dyn.append(records[ii])
# records_step has all the runs in records_dyn plus the step runs (use these to fit Phi with Nmean)
ind = [0,3,4,5,6,7,8,9,16,17,18,19,20,21,37,38,44,45,46,47,48]
records_step = []
for ii in ind:
records_step.append(records[ii])
# records_epsilon has all the runs in records_step plus the epsilon runs (use these to fit Nmax+Nmin)
ind = [0,3,4,5,6,7,8,9,16,17,18,19,20,21,28,29,30,31,32,
33,34,37,38,40,41,42,43,44,45,46,47,48]
records_epsilon = []
for ii in ind:
records_epsilon.append(records[ii])
# records_diffusivity has all the runs with step and epsilon kv profiles; it does not have the dynamics runs
ind = [28,29,30,31,32,33,34,37,38,40,41,42,43,44,45,46,47,48]
records_diffusivity = []
for ii in ind:
records_diffusivity.append(records[ii])
# records_kv has the runs with step kv profile
ind = [28,32,37,38,44,45,46,47,48]
records_kv = []
for ii in ind:
records_kv.append(records[ii])
# records_nokv has the runs without step kv profile
ind = [0,1,2,3,4,5,6,7,8,9,16,17,18,19,20,21,22,23,24,25,26,27,29,30,31,33,34,40,41,42,43]
records_nokv = []
for ii in ind:
records_nokv.append(records[ii])
# records3 has all the runs without the ones where K_bg changes and run with low U high N.
ind = [0,3,4,5,6,7,8,9,16,17,18,19,21]
records3 = []
for ii in ind:
records3.append(records[ii])
# +
keys2 = ['<KEY> <KEY>']
stname = 'UwH' # Station at downstream head side of canyon
for ind in select_rec:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/dTr1dz_%s_%s.csv' %
(records[ind].name,stname))
df = pd.read_csv(filename1)
Nab = 0
Nbe = 0
Nrim = 0
Nmean = 0
for key,ii in zip(keys2, range(len(keys2))):
Nab = Nab + np.min(df[keys2[ii]][0:20]) #0:20
Nbe = Nbe + np.max(df[keys2[ii]][20:24]) #20:24
Nmean = Nmean + np.mean(df[keys2[ii]][20:24])
Nrim = Nrim + df[keys2[ii]][24]
records[ind].dTr_ab = Nab/ len(keys2)
records[ind].dTr_be = Nbe/ len(keys2)
records[ind].dTr0 = df['dTrdz_tt00'][15]
# +
keys2 = ['Tr_profile_tt16','Tr_profile_tt18']
stname = 'UwH' # Station at downstream head side of canyon
for ind in select_rec:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/Tr1_profile_%s_%s.csv' %
(records[ind].name,stname))
df = pd.read_csv(filename1)
Nab = 0
for key,ii in zip(keys2, range(len(keys2))):
Nab = Nab + np.mean(df[keys2[ii]][12:24]) #0:20
records[ind].Tr = Nab / len(keys2)
stname = 'DnC'
for ind in select_rec:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/Tr1_profile_%s_%s.csv' %
(records[ind].name,stname))
df = pd.read_csv(filename1)
records[ind].Tr0 = df['Tr_profile_tt00'][29]
# -
# ### Tracer gradient and concentration
# +
# Tracer gradient
keys = ['<KEY>','<KEY>','<KEY>','<KEY>','dTrdz_tt18']
days = ['1','3','5','7','9']
sns.set_style('darkgrid')
stname = 'UwH' # Station at downstream side of canyon
fig, ax = plt.subplots(1,len(keys),figsize=(15,7), sharey = True, sharex = True)
for rec in records_diffusivity[::2]:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/dTr1dz_%s_%s_%s.csv' %
(rec.exp_code,rec.run_num,stname))
df = pd.read_csv(filename1)
for key,ii,day in zip(keys, range(len(keys)), days):
ax[ii].plot(df[keys[ii]][:],Z1[1:-1],'-o' ,color= sns.xkcd_rgb[rec.color2], label = rec.label)
ax[ii].set_title('day %s' %day)
for ii in range(len(keys)):
ax[ii].set_xlabel('$\partial_zC$ / $\mu$M$m^{-1}$')
ax[ii].axhline(Z1[20],color = '0.5', linestyle = '--') # rim depth
ax[ii].axhline(Z1[24],color = '0.5', linestyle = '--') # rim depth
ax[ii].axhline(Z1[29],color = '0.5', linestyle = '--') # rim depth
ax[0].set_ylabel('depth / m')
ax[len(keys)-1].legend(bbox_to_anchor=(1,1))
# +
# Tracer gradient
keys = ['<KEY>']
days = ['1','3','5','7','9']
sns.set_style('darkgrid')
stname = 'UwH' # Station at downstream side of canyon
fig, ax = plt.subplots(1,len(keys),figsize=(15,7), sharey = True, sharex = True)
for rec in records_epsilon:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/dTr1dz_%s_%s_%s.csv' %
(rec.exp_code,rec.run_num,stname))
df = pd.read_csv(filename1)
for key,ii,day in zip(keys, range(len(keys)), days):
ax[ii].plot(df[keys[ii]][20:32],Z1[21:33], color= sns.xkcd_rgb[rec.color2], label = rec.label)
ax[ii].set_title('day %s' %day)
for ii in range(len(keys)):
ax[ii].set_xlabel('$\partial_zC$ / $\mu$M$m^{-1}$')
ax[0].set_ylabel('depth / m')
ax[len(keys)-1].legend(bbox_to_anchor=(1,1))
# +
# Tracer profile
sns.set_style('darkgrid')
keys = ['Tr_profile_tt02','Tr_profile_tt06','Tr_profile_tt10','Tr_profile_tt14','Tr_profile_tt18']
days = ['1','3','5','7','9']
stname = 'UwH' # Station at downstream side of canyon
fig, ax = plt.subplots(1,len(keys),figsize=(15,7), sharey = True, sharex = True)
for rec in records_diffusivity[::2]:
filename1 = ('/ocean/kramosmu/OutputAnalysis/outputanalysisnotebooks/results/metricsDataFrames/Tr1_profile_%s_%s_%s.csv' %
(rec.exp_code,rec.run_num,stname))
df = pd.read_csv(filename1)
Crim = 0
for key,ii,day in zip(keys, range(len(keys)), days):
ax[ii].plot(df[keys[ii]][:]-df['Tr_profile_tt00'][:],Z1[:],'o-', color= sns.xkcd_rgb[rec.color2], label = rec.label)
ax[ii].set_title('day %s' %day)
Crim = Crim + df[keys[ii]][26]
rec.Crim = Crim / len(keys)
for ii in range(len(keys)):
ax[ii].set_xlabel('$C$ / $\mu$M')
ax[ii].axhline(Z1[12],color = '0.5', linestyle = '--') # rim depth
ax[ii].axhline(Z1[24],color = '0.5', linestyle = '--') # rim depth
ax[0].set_ylabel('depth / m')
ax[len(keys)-1].legend(bbox_to_anchor=(1,1))
#plt.savefig('tracerprofile_comparison_realisticKv.eps', format='eps', frameon=False, bbox='tight')
# -
|
RealisticKvMaps/Concentration_near_head.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
#before running the notebook, download yelp dataset from https://www.yelp.com/dataset/challenge
#untar the dataset with the following command tar -xvf yelp_dataset_challenge_round9.tgz
#in the same directory as this notebook.
import copy
import numpy as np
import sys
import os
import re
from collections import Counter
from datetime import datetime
import json
from text import Tokenizer
import mxnet as mx
from matplotlib import pyplot
from six.moves.urllib.request import urlopen
from sequence import pad_sequences
from IPython.display import display
from IPython.html import widgets
# Enable logging so we will see output during the training
import logging
logger = logging.getLogger()
logger.setLevel(logging.DEBUG)
# -
# Load the reviews and parse JSON
t1 = datetime.now()
with open("yelp_academic_dataset_review.json") as f:
reviews = f.read().strip().split("\n")
reviews = [json.loads(review) for review in reviews]
print(datetime.now() - t1)
# +
texts = [review['text'] for review in reviews]
# Convert our 5 classes into 2 (negative or positive)
binstars = [0 if review['stars'] <= 3 else 1 for review in reviews]
balanced_texts = []
balanced_labels = []
balanced_texts_test = []
balanced_labels_test = []
limit = 50000 # Change this to grow/shrink the dataset
neg_pos_counts_train = [0, 0]
neg_pos_counts_test = [0, 0]
for i in range(len(texts)):
polarity = binstars[i]
text = texts[i].encode('utf-8')
if neg_pos_counts_train[polarity] < limit:
balanced_texts.append(text)
balanced_labels.append(binstars[i])
neg_pos_counts_train[polarity] += 1
elif neg_pos_counts_test[polarity] < limit:
balanced_texts_test.append(text)
balanced_labels_test.append(binstars[i])
neg_pos_counts_test[polarity] += 1
# -
Counter(balanced_labels)
Counter(balanced_labels_test)
# >>> Counter({0: 100000, 1: 100000})
# +
num_words=10000
tokenizer = Tokenizer(num_words)
tokenizer.fit_on_texts(balanced_texts)
balanced_texts = tokenizer.texts_to_sequences(balanced_texts)
balanced_texts_test = tokenizer.texts_to_sequences(balanced_texts_test)
vocabsize = num_words
X = np.concatenate((balanced_texts, balanced_texts_test), axis=0)
# Specify the maximum length of the reviews we want to process and pad the training and test data
maxtextlen = 500
X_train = pad_sequences(balanced_texts, maxlen=maxtextlen)
X_test = pad_sequences(balanced_texts_test, maxlen=maxtextlen)
# convert list to nd array type as mx.io.NDArrayIter takes nd array data type
y_train = np.asarray(balanced_labels)
y_test = np.asarray(balanced_labels_test)
# Create MXNet NDArray Iterators from the numpy training set and labels. A batch size specified and the data will
# be shffled. The iterators will be used as input to train and measure the model performance later.
Batch_Size = 250
train_iter = mx.io.NDArrayIter(X_train, y_train, Batch_Size, shuffle=True)
test_iter = mx.io.NDArrayIter(X_test, y_test, Batch_Size, shuffle=True)
# +
# Let's do some analysis of the data
# Summarize review length
print("Number of unique words : %i" % len(np.unique(np.hstack(X))))
print ('')
print ("Label value")
print (np.unique(y_train))
print ('')
print("Review length: ")
result = [len(x) for x in X]
print("Mean %.2f words (%f)" % (np.mean(result), np.std(result)))
# plot review length distribution
pyplot.boxplot(result)
pyplot.show()
# -
# Let's also take a look at 1 row of the training data
# The integers represent a word in the original text
print ('Review Example - Coded with word index')
print (X[0:1, ])
# +
# create MLP network using MXNet Symbol API
# Create the input layer and place holder for the label
inputdata = mx.sym.Variable('data')
input_y = mx.sym.Variable('softmax_label') # placeholder for label
# We embed the integer representation for each word into a vector of size 32. Embedding is a technique that help
# place related words close together. This helps improve the accuracy of model
# input_dim is the size of the vocabulary. output_dim is the dimension of the output embedded vector.
Embeddata = mx.sym.Embedding(data = inputdata, input_dim=vocabsize, output_dim=32, name='embed')
# The output from the embedding layer will be dimensional matrix, since MLP only accepts 1 dimensional vector,
# we need to flatten it back to one dimension vector
data1 = mx.sym.Flatten(data = Embeddata, name='flatten')
# We create a fully connected layer with 250 neurons. This layer will take the flattened input and
# perform a linear calculation on the input data f(x) = ⟨w, x⟩ + b
fc1 = mx.sym.FullyConnected(data=data1, num_hidden=250)
# We add some nonlearity (Activation) into the network, so we can model non linear data patterns as not problem is linear problem
# Some of the common activations functions are 'relu', 'tanh', sigmoid.
act1 = mx.sym.Activation(data=fc1, act_type="relu")
# We create anothe hidden layer with 2 hidden units as we have 2 desired output (1, 0)
fc2 = mx.sym.FullyConnected(data=act1, num_hidden=2)
# Softmax is a classifier, and cross-entropy loss is used as the loss function by default.
mlp = mx.sym.SoftmaxOutput(data=fc2, label=input_y, name='softmax')
# Now we have completed building the network, let's see what it looks like
#mx.viz.plot_network(mlp)
# -
X_train[0].shape
# +
# Set the number of epochs to run
num_epoch = 10
# Assign the network symbol(mlp) to the module class and we will use gpu here. If cpu is used, then change it
ctx = mx.gpu(0)
mlp_model = mx.mod.Module(symbol=mlp, context=ctx)
# Start training by calling the fit function
mlp_model.fit(train_iter, # training data
eval_data=test_iter, # validation data
optimizer="adam", # use adam optimizer to train
optimizer_params={'learning_rate':0.01}, # set learning rate for adam
eval_metric='acc', # report accuracy during training
batch_end_callback = mx.callback.Speedometer(Batch_Size, 100), # output progress for each 100 data batches
num_epoch=num_epoch) # train data passes indicatd by num_epoch
# -
test_iter.reset()
print test_iter.next()
test_iter.reset()
metric = mx.metric.Accuracy()
mlp_model.score(test_iter, metric)
mlp_model.score(test_iter, ['mse', 'acc'])
# Save the model
prefix = "sentiment_mlp"
mlp_model.save_checkpoint (prefix, num_epoch)
# +
# Let's make some prediction using the saved model
# First load the model
prefix = "sentiment_mlp"
model = mx.mod.Module.load(prefix, num_epoch, False)
# Now we need to bind the model with a datashape that represents the input, which will be 1xmaxtextlen
model.bind(for_training=False, data_shapes=[('data', (1,maxtextlen))])
# +
# Some helper function for making the prediction
# This function takes a text string and return a nd array with word indexes
def prepare_imdb_list(text, maxlen=500, vocabsize=10000):
imdb_word_index = tokenizer.word_index
sentence = []
sentence.append(str(text))
#tokenize the input sentence
tokens = Tokenizer()
tokens.fit_on_texts(sentence)
# get a list of words from the encoding
words = []
for iter in range(len(tokens.word_index)):
words += [key for key,value in tokens.word_index.items() if value==iter+1]
# create a imdb based sequence from the words and specified vocab size
imdb_seq = []
for w in words:
idx = imdb_word_index[w]
if idx < vocabsize:
imdb_seq.append(idx)
# next we need to create a list of list so we can use pad_sequence to pad the inputs
new_list = []
new_list.append(imdb_seq)
new_list = pad_sequences(new_list, maxlen=maxlen)
return new_list
def predict_sentiment(model, text_nd):
sentence_Iter = mx.io.NDArrayIter(text_nd, batch_size=1)
pred = model.predict(sentence_Iter)
return pred
def handle_submit(sender):
text_nd = prepare_imdb_list(inputtext.value)
pred = predict_sentiment(model, text_nd)
outputlabel_0.value = 'Probability for negative sentiment (0): %0.4f ' % pred.asnumpy()[0:1,0]
outputlabel_1.value = 'Probability for positive sentiment (1): %0.4f ' % pred.asnumpy()[0:1,1]
# +
inputtext = widgets.Textarea()
display(inputtext)
inputbutton = widgets.Button(description='Predict Sentiment')
display(inputbutton)
outputlabel_0 = widgets.HTML()
outputlabel_1 = widgets.HTML()
display(outputlabel_0)
display(outputlabel_1)
inputbutton.on_click(handle_submit)
|
yelp_reviewset_mxnet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# # Data Bootcamp: Code Practice A (answerkey)
#
# Optional Code Practice A: Jupyter basics and Python's **[graphics tools](https://davebackus.gitbooks.io/test/content/graphs1.html)** (the Matplotlib package). The goals are to become familiar with Jupyter and Matplotlib and to explore some datasets.
#
# **The data management part of this goes beyond what we've done in class to date.** We recommend you just run the code provided and focus on the graphs for now.
#
# This notebook written by <NAME> for the NYU Stern course [Data Bootcamp](https://nyu.data-bootcamp.com/).
#
# **Check Jupyter before we start.** Run the code below and make sure it works.
# to make sure things are working, run this
import pandas as pd
print('Pandas version: ', pd.__version__)
# If you get something like "Pandas version: 0.17.1" you're fine. If you get an error, bring your computer by and ask for help. If you're unusually brave, go to [StackOverflow](http://stackoverflow.com/a/19961403/804513) and read the instructions. Then come ask for help. (This has to do with how your computer processes unicode. When you hear that word -- unicode -- you should run away at high speed.)
# ## Question 1. Setup
#
# Import packages, arrange for graphs to display in the notebook.
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
# %matplotlib inline
# **Remind yourself:**
#
# * What does the `pandas` package do? [data management]
# * What does the `matplotlib` package do? [graphics]
# * What does `%matplotlib inline` do? [displays plots in the notebook]
# ## Question 2. Jupyter basics
#
# * We refer to the cell that's highlighted as the **current cell**.
# * Clicking once on any cell makes it the current cell. Clicking again allows you to edit it.
# * The + in the toolbar at the top creates a new cell below the current cell.
# * Change a cell from Code to Markdown (in other words, text) with the dropdown menu in the toolbar.
# * To run a cell, hit shift-enter or click on the run-cell icon in the tooolbar (sideways triangle and vertical line).
# * For more information, click on Help at the top. User Interface Tour is a good place to start.
#
# Practice with the following:
#
# * Make this cell the current cell.
# * Add an empty cell below it.
# * Add text to the new cell: your name and the date, for example.
# * *Optional:* Add a link to your LinkedIn or Facebook page. *Hint:* Look at the text in the top cell to find an example of a link.
# * Run the cell.
# ## Question 3. Winner take all and the long tail in the US beer industry
#
# The internet has produced some interesting market behavior, music being a great example. Among them:
#
# * Winner take all. The large producers (Beyonce, for example) take larger shares of the market than they had in the past.
# * The long tail. At the same time, small producers in aggregate increase their share.
#
# Curiously enough, we see the same thing in the US beer industry:
#
# * Scale economies and a reduction in transportation costs (the interstate highway system was built in the 1950s and 60s) led to consolidation, with the large firms getting larger, and the small ones either sellingout or going bankrupt. (How many beer brands can you think of that no longer exist?)
# * Starting in the 1980s, we saw a significant increase in the market share of small firms ("craft brewers") overall, even though each of them remains small.
#
# We illustrate this with data from Victor and <NAME> that describe the output of the top 100 US beer producers from 1947 to 2004. This is background data from their book, [The US Brewing Industry](http://www.amazon.com/The-US-Brewing-Industry-Economic/dp/0262512637), MIT Press, 2004. See [here](http://people.oregonstate.edu/~tremblac/pdf/Appendix%20A%20Weinberg%20Data.pdf) for the names of the brewers. Output is measured in thousands of 31-gallon barrels.
# **Data manipulation.** The data manipulation goes beyond what we've done in class. You're free to ignore it, but here's the idea.
#
# * The spreadsheet contains output by firms ranked 1 to 100 in size. Each row refers to a specific year and includes the outputs of firms in order of size. We don't have their names.
# * We transpose this so that the columns are years and include output for the top-100 firms. The row labels are the size rank of the firm.
# * We then plot the size against the rank for four years to see how it has changed.
# +
url = 'http://pages.stern.nyu.edu/~dbackus/Data/beer_production_1947-2004.xlsx'
beer = pd.read_excel(url, skiprows=12, index_col=0)
print('Dimensions:', beer.shape)
beer[list(range(1,11))].head(3)
# -
vars = list(range(1,101)) # extract top 100 firms
pdf = beer[vars].T # transpose (flip rows and columns)
pdf[[1947, 1967, 1987, 2004]].head()
# **Question.** Can you see consolidation here?
# +
# a basic plot
fig, ax = plt.subplots()
pdf[1947].plot(ax=ax, logy=True)
pdf[1967].plot(ax=ax, logy=True)
pdf[1987].plot(ax=ax, logy=True)
pdf[2004].plot(ax=ax, logy=True)
ax.legend()
# -
# **Answer these questions below.** Code is sufficient, but it's often helpful to add comments to remind yourself what you did, and why.
#
# * Get help for the `set.title` method by typing `ax.set_title?` in a new cell and running it. Note that you can open the documentation this produces in a separate tab with the icon in the upper right (hover text = "Open the pager in an external window").
# * Add a title with `ax.set_title('Your title')`.
# * Change the fontsize of the title to 14.
# * What happens if we add the argument/parameter `lw=2` to the `ax.plot()` statements?
# * Add a label to the x axis with `ax.set_xlabel()`.
# * Add a label to the y axis.
# * Why did we use a log scale (`logy=True`)? What happens if we don't?
# * Use the `color` argument/parameter to choose a more effective set of colors.
# * In what sense do you see "winner takes all"? A "long tail"?
#
# Put each answer in a separate code cell.
# +
# for help
# ax.set_title?
# -
# this is easier if we put the basic plot in a function
def make_plot():
fig, ax = plt.subplots()
pdf[1947].plot(ax=ax, logy=True)
pdf[1967].plot(ax=ax, logy=True)
pdf[1987].plot(ax=ax, logy=True)
pdf[2004].plot(ax=ax, logy=True)
ax.legend()
return ax
ax = make_plot()
ax.set_title('Beer sales by industry rank', fontsize=14)
# +
# line width: put lw=2 in each of the plot statements
# -
ax = make_plot()
ax.set_xlabel('Industry Rank')
ax.set_ylabel('Sales (log scale)')
# +
# log scale: otherwise the differences are too large
# we can't show the alternative because some of the numbers are zero
# +
# color: we add color='somecolor' in each of the plot statements
# -
# ## Question 4. Japan's aging population
#
# Populations are getting older throughout the world, but Japan is a striking example. One of our favorite quotes:
#
# > Last year, for the first time, sales of adult diapers in Japan exceeded those for babies.
#
# Let's see what the numbers look like using projections fron the [United Nations' Population Division](http://esa.un.org/unpd/wpp/Download/Standard/Population/). They have several projections; we use what they call the "medium variant."
#
# We have a similar issue with the data: population by age for a given country and date goes across rows, not down columns. So we choose the ones we want and transpose them. Again, more than we've done so far.
# +
# data input (takes about 20 seconds on a wireless network)
url1 = 'http://esa.un.org/unpd/wpp/DVD/Files/'
url2 = '1_Indicators%20(Standard)/EXCEL_FILES/1_Population/'
url3 = 'WPP2017_POP_F07_1_POPULATION_BY_AGE_BOTH_SEXES.XLSX'
url = url1 + url2 + url3
cols = [2, 4, 5] + list(range(6,28))
prj = pd.read_excel(url, sheetname=1, skiprows=16, parse_cols=cols, na_values=['…'])
print('Dimensions: ', prj.shape)
print('Column labels: ', prj.columns)
# -
# rename some variables
pop = prj
pop = pop.rename(columns={'Reference date (as of 1 July)': 'Year',
'Region, subregion, country or area *': 'Country',
'Country code': 'Code'})
# select countries and years
countries = ['Japan']
years = [2015, 2035, 2055, 2075, 2095]
pop = pop[pop['Country'].isin(countries) & pop['Year'].isin(years)]
pop = pop.drop(['Country', 'Code'], axis=1)
pop = pop.set_index('Year').T
pop = pop/1000 # convert population from thousands to millions
pop.head()
pop.tail()
# **Comment.** Now we have the number of people in any five-year age group running down columns. The column labels are the years.
# With the dataframe `df`:
#
# * Plot the current age distribution with `pop[[2015]].plot()`. Note that `2015` here does not have quotes around it: it's an unusual case of integer column labels.
# * Plot the current age distribution as a bar chart. Which do you think looks better?
# * Create figure and axis objects
# * Use the axis object to plot the age distribution for all the years in the dataframe.
# * Add titles and axis labels.
# * Plot the age distribution for each date in a separate subplot. What argument parameter does this? *Bonus points:* Change the size of the figure to accomodate the subplots.
pop[[2015]].plot()
pop[[2015]].plot(kind='bar')
# my fav
pop[[2015]].plot(kind='barh')
fig, ax = plt.subplots(figsize=(10,6))
pop.plot(ax=ax)
ax.set_title('Population by age')
ax.set_xlabel('Population (millions)')
ax.set_ylabel('Age Range')
pop.plot(kind='bar', subplots=True, figsize=(6,8), sharey=True)
# ## Question 5. Dynamics of the yield curve
#
# One of our favorite topics is the yield curve: a plot of the yield to maturity on a bond against the bond's maturity. The foundation here is yields on zero coupon bonds, which are simpler objects than yields on coupon bonds.
#
# We often refer to bond yields rising or falling, but in fact the yield curve often does different things at different maturities. We will see that here. For several years, short yields have been stuck at zero, yet yields for bond with maturities of two years and above have varied quite a bit.
#
# We use the Fed's well-known [Gurkaynak, Sack, and Wright data](http://www.federalreserve.gov/pubs/feds/2006/200628/200628abs.html), which provides daily data on US Treasury yields from 1961 to the present. The Fed posts the data, but it's in an unfriendly format. So we saved it as a csv file, which we read in below. The variables are yields: `SVENYnn` is the yield for maturity `nn` years.
# data input (takes about 20 seconds on a wireless network)
url = 'http://pages.stern.nyu.edu/~dbackus/Data/feds200628.csv'
gsw = pd.read_csv(url, skiprows=9, index_col=0, usecols=list(range(11)), parse_dates=True)
print('Dimensions: ', gsw.shape)
print('Column labels: ', gsw.columns)
print('Row labels: ', gsw.index)
# grab recent data
df = gsw[gsw.index >= dt.datetime(2010,1,1)]
# convert to annual, last day of year
df = df.resample('A', how='last').sort_index()
df.head()
df.columns = list(range(1,11))
ylds = df.T
ylds.head(3)
# With the dataframe `ylds`:
#
# * Create figure and axis objects
# * Use the axis object to plot the yield curve for all the years in the dataframe.
# * Add a title and axis labels.
# * Explain what you see: What happened to the yield curve over the past six years?
# * **Challenging.** Compute the mean yield for each maturity. Plot them on the same graph in black.
# +
fig, ax = plt.subplots()
ylds.plot(ax=ax)
ax.set_title('US Treasury Yields')
ax.set_ylabel('Yield')
ax.set_xlabel('Maturity in Years')
ybar = ylds.mean(axis=1)
ybar.plot(ax=ax, color='black', linewidth=3, linestyle='dashed')
# -
|
Code/notebooks/bootcamp_practice_a_answerkey.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import nltk
from nltk.tokenize import RegexpTokenizer
from nltk.stem import WordNetLemmatizer
from nltk.corpus import stopwords
from math import log10, sqrt,log
from tqdm import tqdm
WikiHow_sample_all = pd.read_csv('WikiHow_sample_all_withsummary.csv')
def preprocess(documents):
tokenizer = RegexpTokenizer(r'\w+')
tokens = tokenizer.tokenize(documents)
tokens = [token.lower() for token in tokens if token.isalpha()]
tokens = remove_stopwords(tokens)
lemmatizer = WordNetLemmatizer()
tokens = [lemmatizer.lemmatize(token, pos='v') for token in tokens]
return tokens
def remove_stopwords(tokens):
new_tokens = []
stop_words = set(stopwords.words("english"))
for token in tokens:
if token not in stop_words:
new_tokens.append(token)
return new_tokens
def get_inverted_index(data):
n = len(data[data['summary']!='empty'])
df = data.loc[:n,:]
inverted_index = {}
for i in range(len(df)):
tokens = preprocess(df.loc[i,'summary'])
tokens_dist = nltk.FreqDist(tokens)
for voc in tokens_dist.keys():
if voc not in inverted_index.keys():
inverted_index[voc] = [1, tokens_dist[voc]]
else:
inverted_index[voc][0] += 1
inverted_index[voc][1] += tokens_dist[voc]
return inverted_index
inverted_index = get_inverted_index(WikiHow_sample_all)
# +
def length(data):
total_len = 0
for i in range(len(data)):
passage_len = len(preprocess(data.loc[i,'summary']))
total_len += passage_len
total_pa = len(data)
return total_len/total_pa, total_pa
avdl, N = length(WikiHow_sample_all)
# -
def BM25(data, inverted_index,avdl,N, k1 = 1.2, k2 = 100,b = 0.75):
scores = np.zeros((len(data),3))
for i in tqdm(range(len(data))):
tokens_p = preprocess(data.loc[i,'summary'])
tokens_q = preprocess(data.loc[i,'title'])
f_p = nltk.FreqDist(tokens_p)
f_q = nltk.FreqDist(tokens_q)
dl = len(tokens_p)
K = k1*((1-b)+b*(dl/avdl))
bm25 = 0
for token in f_q.keys():
if token in inverted_index.keys():
term1 = log((N-inverted_index[token][0]+0.5)/(inverted_index[token][0]+0.5))
term2 = (k1+1)*f_p[token]/(K+f_p[token])
term3 = (k2+1)*f_q[token]/(k2+f_q[token])
bm25 += term1 *term2 *term3
data.loc[i,'bm25'] = bm25
return data
WikiHow_sample_all = BM25(WikiHow_sample_all, inverted_index,avdl,N, k1 = 1.2, k2 = 100,b = 0.75)
WikiHow_sample_all.to_csv('WikiHow_sample_all_withsummary.csv')
|
Code/Experiment_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:root] *
# language: python
# name: conda-root-py
# ---
# # Classification de documents : prise en main des outils
#
# Le but de ce TP est de classer des documents textuels... Dans un premier temps, nous allons vérifier le bon fonctionnement des outils sur des données jouets puis appliquer les concepts sur des données réelles.
#
#
# ## Conception de la chaine de traitement
# Pour rappel, une chaine de traitement de documents classique est composée des étapes suivantes:
# 1. Lecture des données et importation
# - Dans le cadre de nos TP, nous faisons l'hypothèse que le corpus tient en mémoire... Si ce n'est pas le cas, il faut alors ajouter des structures de données avec des buffers (*data-reader*), bien plus complexes à mettre en place.
# - Le plus grand piège concerne l'encodage des données. Dans le TP... Pas (ou peu) de problème. Dans la vraie vie: il faut faire attention à toujours maitriser les formats d'entrée et de sortie.
# 1. Traitement des données brutes paramétrique. Chaque traitement doit être activable ou desactivable + paramétrable si besoin.
# - Enlever les informations *inutiles* : chiffre, ponctuations, majuscules, etc... <BR>
# **L'utilité dépend de l'application!**
# - Segmenter en mots (=*Tokenization*)
# - Elimination des stop-words
# - Stemming/lemmatisation (racinisation)
# - Byte-pair encoding pour trouver les mots composés (e.g. Sorbonne Université, Ville de Paris, Premier Ministre, etc...)
# 1. Traitement des données numériques
# - Normalisation *term-frequency* / binarisation
# - Normalisation *inverse document frequency*
# - Elimination des mots rares, des mots trop fréquents
# - Construction de critère de séparabilité pour éliminer des mots etc...
# 1. Apprentissage d'un classifieur
# - Choix du type de classifieur
# - Réglage des paramètres du classifieur (régularisation, etc...)
#
# ## Exploitation de la chaine de traitement
#
# On appelle cette étape la réalisation d'une campagne d'expériences: c'est le point clé que nous voulons traviller en TAL cette année.
# 1. Il est impossible de tester toutes les combinaisons par rapport aux propositions ci-dessus... Il faut donc en éliminer un certain nombre.
# - En discutant avec les experts métiers
# - En faisant des tests préliminaires
# 1. Après ce premier filtrage, il faut:
# - Choisir une évaluation fiable et pas trop lente (validation croisée, leave-one-out, split apprentissage/test simple)
# - Lancer des expériences en grand
# - = *grid-search*
# - parallèliser sur plusieurs machines
# - savoir lancer sur un serveur et se déconnecter
# 1. Collecter et analyser les résultats
#
#
# ## Inférence
#
# L'inférence est ensuite très classique: la chaine de traitement optimale est apte à traiter de nouveaux documents
#
# # Etape 1: charger les données
# +
# # !pip install ipython
# # !pip install nbconvert
# # !jupyter nbconvert --to python classifDoc_2021.ipynb
# +
import numpy as np
import matplotlib.pyplot as plt
import codecs
import re
import os.path
# -
# Chargement des données:
def load_pres(fname):
alltxts = []
alllabs = []
s=codecs.open(fname, 'r','utf-8') # pour régler le codage
while True:
txt = s.readline()
if(len(txt))<5:
break
lab = re.sub(r"<[0-9]*:[0-9]*:(.)>.*","\\1",txt)
txt = re.sub(r"<[0-9]*:[0-9]*:.>(.*)","\\1",txt)
if lab.count('M') >0:
alllabs.append(-1)
else:
alllabs.append(1)
alltxts.append(txt)
return alltxts,alllabs
# +
fname = "data/corpus.tache1.learn.utf8"
alltxts, alllabs = load_pres(fname)
# -
print(len(alltxts),len(alllabs))
print(alltxts[0])
print(alllabs[0])
print(alltxts[-1])
print(alllabs[-1])
# +
# def load_movies(path2data): # 1 classe par répertoire
# alltxts = [] # init vide
# labs = []
# cpt = 0
# for cl in os.listdir(path2data): # parcours des fichiers d'un répertoire
# for f in os.listdir(path2data+cl):
# txt = open(path2data+cl+'/'+f).read()
# alltxts.append(txt)
# labs.append(cpt)
# cpt+=1 # chg répertoire = cht classe
# return alltxts,labs
# +
# path = "movies1000/"
# alltxts,alllabs = load_movies(path)
# +
# print(len(alltxts),len(alllabs))
# print(alltxts[0])
# print(alllabs[0])
# print(alltxts[-1])
# print(alllabs[-1])
# -
# # Transformation paramétrique du texte
#
# Vous devez tester, par exemple, les cas suivants:
# - transformation en minuscule ou pas
# - suppression de la ponctuation
# - transformation des mots entièrement en majuscule en marqueurs spécifiques
# - suppression des chiffres ou pas
# - conservation d'une partie du texte seulement (seulement la première ligne = titre, seulement la dernière ligne = résumé, ...)
# - stemming
# - ...
#
#
# Vérifier systématiquement sur un exemple ou deux le bon fonctionnement des méthodes sur deux documents (au moins un de chaque classe).
# +
import string
import re
import unicodedata
import nltk
from nltk.corpus import stopwords
from nltk.stem import *
from nltk.stem.snowball import SnowballStemmer
def preprocessing(X):
res = []
for doc in X:
punc = string.punctuation # recupération de la ponctuation
punc += '\n\r\t'
doc = doc.translate(str.maketrans(punc, ' ' * len(punc)))
doc = unicodedata.normalize('NFD', doc).encode('ascii', 'ignore').decode("utf-8")
doc = doc.lower()
doc = re.sub('[0-9]+', '', doc)
res.append(doc)
return np.array(res)
def formal(X):
stemmer = SnowballStemmer(language='french')
# nltk.download('stopwords')
res = []
stop = stopwords.words('french')
for doc in X:
new_doc = ""
for w in doc.split():
if w not in stop:
new_doc += w + " "
new_doc = [stemmer.stem(X) for X in new_doc.split()]
new_doc = " ".join(new_doc)
res.append(new_doc)
return res
# +
X = np.array(alltxts[:1000])
Y = np.array(alllabs[:1000])
print(X[0])
X_preprocess = preprocessing(X)
print(X_preprocess[0])
X_train = formal(X_preprocess)
print("\n",X_train[0])
# -
# # Extraction du vocabulaire
#
# Exploration préliminaire des jeux de données.
#
# - Quelle est la taille d'origine du vocabulaire?
# - Que reste-t-il si on ne garde que les 100 mots les plus fréquents? [word cloud]
# - Quels sont les 100 mots dont la fréquence documentaire est la plus grande? [word cloud]
# - Quels sont les 100 mots les plus discriminants au sens de odds ratio? [word cloud]
# - Quelle est la distribution d'apparition des mots (Zipf)
# - Quels sont les 100 bigrammes/trigrammes les plus fréquents?
#
# +
from wordcloud import WordCloud
from sklearn.feature_extraction.text import CountVectorizer
print(X.shape)
print(Y.shape)
def flatten(A):
rt = []
for i in A:
if isinstance(i,list):
rt.extend(flatten(i))
else:
rt.append(i)
return rt
words = "".join(flatten(X))
print(words[:200])
wordcloud = WordCloud(background_color='white', max_words=100).generate(words)
plt.imshow(wordcloud)
plt.axis("off")
plt.show()
# vectorizer = CountVectorizer()
# vector = vectorizer.fit_transform(X).toarray()
# names = vectorizer.get_feature_names()
# print(vector.shape)
# n, m = vector.shape
# vector = np.where(vector == 0, 0, 1)
# sums = vector.sum(axis=0)
# res = np.sort(sums)[sums.size-100:]
# print(res)
# words = "".join(flatten(X))
# wordcloud = WordCloud(background_color='white', max_words=100).generate(words)
# plt.imshow(wordcloud)
# plt.axis("off")
# plt.show()
# -
words = "".join(flatten(X_preprocess[:1000]))
unique_words, count = np.unique(words.split(), return_counts=True)
# count = np.where(count > 100, 100, count)
count = np.log(count)
# +
unique_words, count = np.unique(words.split(), return_counts=True)
count_sort_ind = np.argsort(count)
unique_words = unique_words[count_sort_ind]
count = np.sort(count)
print(count)
print(unique_words)
fig = plt.figure(figsize=(8,8))
ax = fig.add_axes([0,0,1,1])
ax.bar(np.arange(len(count)),np.log(count))
plt.title("Log du nombre d'apparition / mot")
plt.show()
# +
unique_words, count = np.unique(words.split(), return_counts=True)
count_sort_ind = np.argsort(count)
unique_words = unique_words[count_sort_ind]
count = np.sort(count)
print(count)
print(unique_words)
fig = plt.figure(figsize=(10,10))
ax = fig.add_axes([0,0,1,1])
ax.bar(unique_words[len(count)-25:],count[len(count)-25:])
plt.title("Nombre d'apparition / mot les plus frequent")
plt.show()
# -
# Question qui devient de plus en plus intéressante avec les approches modernes:
# est-il possible d'extraire des tri-grammes de lettres pour représenter nos documents?
#
# Quelle performances attendrent? Quels sont les avantages et les inconvénients d'une telle approche?
# +
# On peut le faire assez facilemment avec sklearn
# Cela donne plus de contexte a nos mots mais les probabilites de tri-grammes vont etre tres faible
# -
# # Modèles de Machine Learning
#
# Avant de lancer de grandes expériences, il faut se construire une base de travail solide en étudiant les questions suivantes:
#
# - Combien de temps ça prend d'apprendre un classifieur NB/SVM/RegLog sur ces données en fonction de la taille du vocabulaire?
# - La validation croisée est-elle nécessaire? Est ce qu'on obtient les mêmes résultats avec un simple *split*?
# - La validation croisée est-elle stable? A partir de combien de fold (travailler avec différentes graines aléatoires et faire des statistiques basiques)?
# +
# Cela prend beaucoup de temps avec des donnees textuels car nous avons un grand nombre de variables
# Cela depend fortement de la taille du vocabulaire
# La validation est tres pratique car on train nos modeles sur toutes les donnes contrairement au split
# Ici on utlise le split car bien plus rapide, on pourra envisager la validation croisee quand on aura deja fait un choix au niveau des modeles
# -
# ## Première campagne d'expériences
#
# Les techniques sur lesquelles nous travaillons étant sujettes au sur-apprentissage: trouver le paramètre de régularisation dans la documentation et optimiser ce paramètre au sens de la métrique qui vous semble la plus appropriée (cf question précédente).
# - IL FAUT FAIRE PLEIN DE VARIABLE X_train1 X_train2 ... AVEC DES DONNES EN UTILISANT CountVectorizer() (ngram, preprocess, mindf, maxdf etc...)
# - COMPRENDRE LESQUELS SONT LES PLUS IMPORTANTS (mindf, maxdf)
# - PUIS APRES IL FAUT EQUILIBRER LES CLASSES
# - PUIS OPTIMISER LES MODELES
# - PUIS TESTER LES MODELES ET LES COMPARER
# - FAIRE DES COURBES PLT POUR MONTRER QU'ON A TROUVER LE MODEL OPTIMAL (mindf/test_acc)
import sklearn.naive_bayes as nb
from sklearn import svm
from sklearn import linear_model as lin
from sklearn.model_selection import train_test_split
import string
import re
import unicodedata
import nltk
from nltk.corpus import stopwords
from nltk.stem.snowball import SnowballStemmer
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
# ## Fonction pour le traitement de donnees
# +
def preprocessing(X):
res = []
punc = string.punctuation
punc += '\n\r\t'
for doc in X:
doc = doc.translate(str.maketrans(punc, ' ' * len(punc)))
doc = unicodedata.normalize('NFD', doc).encode('ascii', 'ignore').decode("utf-8")
doc = doc.lower()
doc = re.sub('[0-9]+', '', doc)
res.append(doc)
return np.array(res)
def formal(X):
stemmer = SnowballStemmer(language='french')
# nltk.download('stopwords')
res = []
stop = stopwords.words('french')
for doc in X:
new_doc = ""
for w in doc.split():
if w not in stop:
new_doc += w + " "
new_doc = [stemmer.stem(X) for X in new_doc.split()]
new_doc = " ".join(new_doc)
res.append(new_doc)
return res
# -
# ## Importation des deux fichiers contenant les donnees
fname = "data/corpus.tache1.learn.utf8"
alltxts_test, alllabs_test = load_pres(fname)
X = np.array(alltxts)
Y = np.array(alllabs)
# ## Fonctions permettant de faire notre selection de modele suivant les données
# +
model_names = ["SVC1", "SVC0.8", "SVC0.6", "NB", "LR"]
def train_models_and_get_acc(X_train, X_test, Y_train, Y_test, display):
print("--> SVC reg=1.0 :")
clf = svm.LinearSVC(class_weight="balanced", C=1.0)
clf.fit(X_train, Y_train)
acc1 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc1, " %")
if display : display_infos(clf, X_test, Y_test)
print("--> SVC reg=0.8 :")
clf = svm.LinearSVC(class_weight="balanced", C=0.8)
clf.fit(X_train, Y_train)
acc2 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc2, " %")
if display : display_infos(clf, X_test, Y_test)
print("--> SVC reg=0.6 :")
clf = svm.LinearSVC(class_weight="balanced", C=0.6)
clf.fit(X_train, Y_train)
acc3 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc3, " %")
if display : display_infos(clf, X_test, Y_test)
print("--> NB :")
clf = nb.MultinomialNB()
clf.fit(X_train, Y_train)
acc4 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc4, " %")
if display : display_infos(clf, X_test, Y_test)
print("--> LR :")
clf = lin.LogisticRegression(class_weight="balanced")
clf.fit(X_train, Y_train)
acc5 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc5, " %")
if display : display_infos(clf, X_test, Y_test)
return [acc1, acc2, acc3, acc4, acc5]
# -
def display_infos(clf, X_test, Y_test):
# Check le nombre de predictions pour chaque label
predictions = clf.predict(X_test)
unique, counts = np.unique(predictions, return_counts=True)
print("/!\ Prediction counts for label ", unique, " --> ", counts)
# Check le nombre de predictions pour chaque label
unique, counts = np.unique(Y_test, return_counts=True)
print("/!\ Ground truth counts for label ", unique, " --> ", counts)
# Check la precision du label en inferiorite
acc = get_inf_acc(predictions, Y_test)
print("/!\ Accuracy of inferior label :", acc, "%")
# Check la precision du label en superiorite
acc = get_sup_acc(predictions, Y_test)
print("/!\ Accuracy of superior label :", acc, "%\n")
# +
def get_inf_acc(predictions, Y_test):
idx_inf = np.where(predictions==-1, True, False)
tmp_pred = predictions[idx_inf]
tmp_real = Y_test[idx_inf]
cpt = 0
for i in range(len(tmp_pred)):
if tmp_pred[i] == tmp_real[i]:
cpt += 1
return np.round((cpt/len(tmp_pred))*100, 2)
def get_sup_acc(predictions, Y_test):
idx_inf = np.where(predictions==1, True, False)
tmp_pred = predictions[idx_inf]
tmp_real = Y_test[idx_inf]
cpt = 0
for i in range(len(tmp_pred)):
if tmp_pred[i] == tmp_real[i]:
cpt += 1
return np.round((cpt/len(tmp_pred))*100, 2)
# -
def get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer, transformer=None):
X_vector = vectorizer.fit_transform(X)
if transformer is not None:
transformer = transformer.fit(X_vector)
X_final = transformer.transform(X_vector)
else:
X_final = X_vector
X_test_vector = vectorizer.transform(X_test)
return X_final, X_test_vector, Y, Y_test
database_models_name = ["vanilla", "ngram22", "maxfeat500", "stopwords", "min2", "min3", "min4", "max0.9", "max0.8", "max0.7", "min3_max0.7", "ngram22_maxfeat500", "tfidfvectorizer"]
def build_database(X, X_test, Y, Y_test):
database = []
vectorizer = CountVectorizer()
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(ngram_range=(2, 2))
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(max_features=500)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
stop = stopwords.words('french')
vectorizer = CountVectorizer(stop_words=stop)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(min_df=2)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(min_df=3)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(min_df=4)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(max_df=0.9)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(max_df=0.8)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(max_df=0.7)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(max_df=0.7, min_df=3)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = CountVectorizer(ngram_range=(2, 2), max_features=500)
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
vectorizer = TfidfVectorizer()
X_train_vector, Y_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
database.append([X_train_vector, Y_test_vector, Y_train, Y_test])
return np.array(database)
def simulation(db, display=False):
metrics = []
for cpt, element in enumerate(db):
print("---------------- Testing model : ", database_models_name[cpt], " ----------------")
X_train, X_test, Y_train, Y_test = element
metrics.append(train_models_and_get_acc(X_train, X_test, Y_train, Y_test, display))
return metrics
# ## Model selection manuel
import warnings
warnings.filterwarnings('ignore')
# +
# X, X_test, Y, Y_test = train_test_split((X_Y), test_size=0.2)
# db = build_database(X, X_test, Y, Y_test)
# +
# metrics = simulation(db, display=True)
# +
# metrics = np.array(metrics)
# n_data, n_model = metrics.shape
# print("--> Simulation done on", n_data, "different data processing and", n_model, "different models")
# print("--> Metrics :\n", metrics)
# print("--> Best accuracy :", metrics.max(), "from data model : '", database_models_name[metrics.argmax()//n_model], "' and model :'", model_names[metrics.argmax()%n_model], "'")
# -
# ## Model selection avec sklearn
from sklearn import svm, datasets
from sklearn.model_selection import GridSearchCV
# +
model_names = ["SVC", "NB", "LR"]
def train_models_and_get_acc_sklearn(X_train, X_test, Y_train, Y_test, display):
print("--> SVC :")
svc = svm.SVC()
parameters = {'kernel':(['linear']),
'C':[0.5, 1, 2, 5],
'class_weight':(['balanced'])}
clf = GridSearchCV(svc, parameters, cv=5, verbose=True, n_jobs=-1)
best_clf = clf.fit(X_train, Y_train)
acc1 = np.round(best_clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc1, " %")
if display :
display_infos(clf, X_test, Y_test)
performance(best_clf)
print("--> NB :")
clf = nb.MultinomialNB()
clf.fit(X_train, Y_train)
acc2 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc2, " %")
if display : display_infos(clf, X_test, Y_test)
print("--> LR :")
lr = LogisticRegression()
parameters = {'max_iter' : [2000],
'penalty' : ['l1', 'l2'],
'C' : np.logspace(-4, 4, 20),
'solver' : ['liblinear'],
'class_weight':(['balanced'])}
clf = GridSearchCV(lr, parameters, cv=5, verbose=True, n_jobs=-1)
best_clf = clf.fit(X_train,Y_train)
acc3 = np.round(clf.score(X_test, Y_test)*100, 2)
print("Acc : ", acc3, " %")
if display :
display_infos(clf, X_test, Y_test)
performance(best_clf)
return [acc1, acc2, acc3]
# -
def simulation_sklearn(db, display=False):
metrics = []
for cpt, element in enumerate(db):
print("---------------- Testing model : ", database_models_name[cpt], " ----------------")
X_train, X_test, Y_train, Y_test = element
metrics.append(train_models_and_get_acc_sklearn(X_train, X_test, Y_train, Y_test, display))
return metrics
def get_performance(clf):
print('Best Score: ' + str(clf.best_score_))
print('Best Parameters: ' + str(clf.best_params_))
# +
# db = build_database(X, X_test, Y, Y_test)
# +
# metrics = simulation_sklearn(db, display=True)
# -
# ## Model selection + data selection avec sklearn
test_size = 10_000 # Taille des data pour le grid search (MAX = 57400)
# ### --> Selection de data
# +
from sklearn.pipeline import Pipeline
from sklearn.feature_extraction.text import TfidfTransformer
pipeline = Pipeline(
[
("vect", CountVectorizer()),
("tfidf", TfidfTransformer()),
("clf", svm.SVC()),
]
)
parameters = {
"vect__min_df": (0, 1, 2, 3),
"vect__max_df": (0.5, 0.75, 1.0),
'vect__max_features': (None, 1000, 2000, 3000),
"vect__ngram_range": ((1, 1), (1, 2), (1,3)),
'tfidf__use_idf': (True, False),
'tfidf__norm': (None, 'l1', 'l2'),
'clf__class_weight':(['balanced']),
'clf__C': (np.arange(0, 1, 0.1)),
'clf__kernel':(['linear'])
# "clf__max_iter": (20,)
# "clf__alpha": (0.00001, 0.000001),
# "clf__penalty": ("l2", "elasticnet"),
# 'clf__max_iter': (10, 50, 80),
}
# +
# grid_search = GridSearchCV(pipeline, parameters, n_jobs=8, verbose=3, cv=5)
# -
X_select, Y_select = X[:test_size], Y[:test_size]
# +
# from time import time
# t0 = time()
# grid_search.fit(list(X_select), list(Y_select))
# print("done in %0.3fs" % (time() - t0))
# -
# - 4320 fits et n_jobs=8:
# - Temps pour size=2_000 -> 159s
# - Temps pour size=10_000 -> 11075s (184 minutes)
# - Temps pour size=20_000 ->
# ### --> Affichage meilleur paramètres pour la data
# +
# best_parameters = grid_search.best_estimator_.get_params()
# for param_name in sorted(parameters.keys()):
# print("--->%s: %r" % (param_name, best_parameters[param_name]))
# -
# ### --> Creation du dataset optimal
fname = "data/corpus.tache1.learn.utf8"
alltxts_test, alllabs_test = load_pres(fname)
X = np.array(alltxts)
Y = np.array(alllabs)
X, X_test, Y, Y_test = train_test_split(X, Y, test_size=0.2)
# +
transformer = TfidfTransformer(use_idf=True,
norm="l2")
vectorizer = CountVectorizer(max_df=0.75,
min_df=3,
max_features=None,
ngram_range=(1,2)
)
X_train_vector, X_test_vector, Y_train, Y_test = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer, transformer)
# -
# ### --> Verification perte trop grande de mots dans le vocabulaire
# +
print("Avec parametres : ", X_train_vector.shape[1])
vectorizer = CountVectorizer()
test, _, _, _ = get_all_data_vectorized(X, X_test, Y, Y_test, vectorizer)
print("Sans parametres :", test.shape[1])
# -
# ### --> Selection de model en partant d'un dataset optimal
# +
# En fait le premier grid search le fait deja (je crois)
# +
# X_select, Y_select = X_train_vector[:test_size], Y_train[:test_size]
# +
# svc = svm.SVC()
# parameters = {'kernel':(['linear']),
# 'C':np.arange(0, 1, 0.1),
# 'class_weight':(['balanced'])}
# +
# t0 = time()
# clf = GridSearchCV(svc, parameters, n_jobs=8, cv=5, verbose=3)
# best_clf = clf.fit(X_select, Y_select)
# print("done in %0.3fs" % (time() - t0))
# +
# best_parameters = clf.best_estimator_.get_params()
# for param_name in sorted(parameters.keys()):
# print("--->%s: %r" % (param_name, best_parameters[param_name]))
# -
# - 50 fits, njobs=8:
# - size=10_000 --> 88s
# ### --> Entrainement final après avoir selectionner les data et le modele
# +
# test_size = 10_000
# X_select, Y_select = X_train_vector[:test_size], Y_train[:test_size]
# +
# optimal_model = svm.SVC(C=0.3,
# class_weight="balanced",
# kernel="linear")
# optimal_model.fit(X_select, Y_select)
# +
# test_size = 10_000
# X_select, Y_select = X_test_vector[:test_size], Y_test[:test_size]
# +
# acc = np.round(optimal_model.score(X_select, Y_select)*100, 2)
# +
# print("Acc : ", acc, " %")
# display_infos(optimal_model, X_select, Y_select)
# +
# Mauvais résultat car il faut faire tt l'entrainement après avoir balance le dataset.
# Si on ne fait pas ca dans ce sens, les gridsearch qui
# -
# ## Equilibrage des données
#
# Un problème reconnu comme dur dans la communauté est celui de l'équilibrage des classes (*balance* en anglais). Que faire si les données sont à 80, 90 ou 99% dans une des classes?
# Le problème est dur mais fréquent; les solutions sont multiples mais on peut isoler 3 grandes familles de solution.
#
# 1. Ré-équilibrer le jeu de données: supprimer des données dans la classe majoritaire et/ou sur-échantilloner la classe minoritaire.<BR>
# $\Rightarrow$ A vous de jouer pour cette technique
# 1. Changer la formulation de la fonction de coût pour pénaliser plus les erreurs dans la classe minoritaire:
# soit une fonction $\Delta$ mesurant les écarts entre $f(x_i)$ et $y_i$
# $$C = \sum_i \alpha_i \Delta(f(x_i),y_i), \qquad \alpha_i = \left\{
# \begin{array}{ll}
# 1 & \mbox{si } y_i \in \mbox{classe majoritaire}\\
# B>1 & \mbox{si } y_i \in \mbox{classe minoritaire}\\
# \end{array} \right.$$
# <BR>
# $\Rightarrow$ Les SVM et d'autres approches sklearn possèdent des arguments pour régler $B$ ou $1/B$... Ces arguments sont utiles mais pas toujours suffisant.
# 1. Courbe ROC et modification du biais. Une fois la fonction $\hat y = f(x)$ apprise, il est possible de la *bidouiller* a posteriori: si toutes les prédictions $\hat y$ sont dans une classe, on va introduire $b$ dans $\hat y = f(x) + b$ et le faire varier jusqu'à ce qu'un des points change de classe. On peut ensuite aller de plus en plus loin.
# Le calcul de l'ensemble des scores associés à cette approche mène directement à la courbe ROC.
#
# **Note:** certains classifieurs sont intrinsèquement plus résistante au problème d'équilibrage, c'est par exemple le cas des techniques de gradient boosting que vous verrez l'an prochain.
# +
import random
def naive_balancing(X, Y):
label, count = np.unique(Y, return_counts=True)
idx_pos = np.where(Y == 1, True, False)
Y_pos = Y[idx_pos]
Y_pos = Y_pos[:count.min()]
idx_neg = np.where(Y == -1, True, False)
Y_neg = Y[idx_neg]
new_Y = np.concatenate((Y_pos, Y_neg))
new_X = np.concatenate((X[:count.min()], X[idx_neg]))
tmp = list(zip(new_X, new_Y))
random.shuffle(tmp)
new_X, new_Y = zip(*tmp)
label, count = np.unique(new_Y, return_counts=True)
print(label, count)
return new_X, new_Y
# -
# ### --> Selection de data et model avec gridsearch apres balancing
fname = "data/corpus.tache1.learn.utf8"
alltxts, alllabs = load_pres(fname)
X = np.array(alltxts)
Y = np.array(alllabs)
new_X, new_Y = naive_balancing(X,Y)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2) # Test avec new_X, new_Y
# +
# import snowballstemmer
# print(len(X_train))
# stemmer = snowballstemmer.stemmer('french');
# for i in range(len(X_train)):
# stemmer.stemWords(X_train[i].split()[j] for j in range(len(X_train[i].split())))
# print(np.array(X_train).shape)
# for i in range(len(X_test)):
# stemmer.stemWords(X_test[i].split()[j] for j in range(len(X_test[i].split())))
# -
train_size = len(X_train)
test_size = len(X_test)
search = False
print(train_size)
print(test_size)
# +
from sklearn.pipeline import Pipeline
from sklearn.feature_extraction.text import TfidfTransformer
from time import time
from nltk.stem.snowball import SnowballStemmer
sw = stopwords.words('french')
if search :
# Search with booleans
pipeline1 = Pipeline(
[
("vect", TfidfVectorizer()),
("clf", svm.SVC()),
]
)
parameters1 = {
"vect__lowercase": (True, False),
"vect__stop_words": (None, sw),
"vect__strip_accents": (None, "ascii"),
"vect__use_idf": (True, False),
"vect__smooth_idf": (True, False),
"vect__use_idf": (True, False),
"vect__sublinear_tf": (True, False),
"vect__min_df": (1,),
"vect__max_df": (0.1,),
"vect__ngram_range": [(1, 2),],
'vect__max_features': (None,),
"clf__C": (10,100),
'clf__class_weight':(["balanced"]),
'clf__kernel':(['linear']),
"clf__max_iter": (1000,)
}
# Search with numerical values
pipeline2 = Pipeline(
[
("vect", TfidfVectorizer()),
("clf", svm.SVC()),
]
)
parameters2 = {
# "vect__lowercase": (False,),
# "vect__stop_words": (None,),
# "vect__strip_accents": ('ascii',),
# "vect__use_idf": (True,),
# "vect__smooth_idf": (False,),
# "vect__sublinear_tf": (False,),
"vect__min_df": (1,),
"vect__max_df": (0.001,),
"vect__ngram_range": [(1, 2),],
'vect__max_features': (None,),
"clf__C": (10000,),
'clf__class_weight':(["balanced"]),
'clf__kernel':(['linear']),
"clf__max_iter": (1000,)
}
# Search with everything
pipeline3 = Pipeline(
[
("vect", TfidfVectorizer()),
("clf", svm.SVC()),
]
)
parameters3 = {
"vect__lowercase": (False,True),
"vect__stop_words": (None,sw),
"vect__strip_accents": (None, 'ascii'),
# "vect__use_idf": (True,False),
# "vect__smooth_idf": (False,True),
# "vect__sublinear_tf": (False,True),
"vect__min_df": (1, 3, 10, 25),
"vect__max_df": (0.05,0.1,0.5,0.9),
"vect__ngram_range": [(1, 1),(1, 2)],
'vect__max_features': (None,),
"clf__C": (200, 500),
'clf__class_weight':(["balanced"]),
'clf__kernel':(['linear']),
"clf__max_iter": (1000,)
}
grid_search_parameters = GridSearchCV(pipeline3,
parameters3,
scoring="f1", # test "rog_auc"
n_jobs=8,
verbose=3,
cv=3,
refit=True
)
t0 = time()
grid_search_parameters.fit(X_train, Y_train) # Essayer de fit en utilisant les pipelines dans l'autre sens et comparer f1 score
print("done in %0.3fs" % (time() - t0))
# -
# - size=10_000
# - 900 fits, njob=8: 2568s (42 minutes)
# - 135 fits, njob=8: 220s
# - 720 fits, njob=8, scoring="f1", data=naive_balanced : 234s
# - 720 fits, njob=8, scoring="f1", data=not_balanced : 287s
# - size=FULL
# - 900 fits, njob=8, scoring="f1", data=not_balanced : 12_000s
# - 540 fits, njob=8, scoring="f1", data=not_balanced : 2_631s
# - 720 fits, njob=10, scoring="f1", data=not_balanced : 1_719s
# - 1536 fits, njob=8, scoring="f1", data=not_balanced : ????s
def display_model_scores(model, X_test, Y_test):
best_parameters = model.get_params()
for param_name in sorted(best_parameters.keys()):
print("--->%s: %r" % (param_name, best_parameters[param_name]))
grid_predictions = model.predict(X_test)
print(confusion_matrix(Y_test, grid_predictions))
print(classification_report(Y_test, grid_predictions))
# +
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score, f1_score, roc_auc_score
if search :
# display_model_scores(grid_search_parameters, X_train, Y_train)
display_model_scores(grid_search_parameters, X_test, Y_test)
# -
# ### --> Construction dataset optimal
def stemm(X):
stemmer = SnowballStemmer("french")
stem = stemmer.stem(X)
return X
# +
vectorizer = TfidfVectorizer(lowercase=False,
stop_words=None,
strip_accents=None,
use_idf=True,
smooth_idf=True,
sublinear_tf=False,
min_df=1,
max_df=0.05,
ngram_range=(1,2),
)
# Decommenter pour stemming
# print(len(X_train))
# stemmer = snowballstemmer.stemmer('french');
# for i in range(len(X_train)):
# stemmer.stemWords(X_train[i].split()[j] for j in range(len(X_train[i].split())))
# print(np.array(X_train).shape)
X_train_vector, X_test_vector, Y_train, Y_test = get_all_data_vectorized(X_train, X_test, Y_train, Y_test, vectorizer, transformer)
print(X_train_vector.shape)
# -
# ### --> Test model selection avec donnees optimales
if search:
parameters = {
'C': ([200]),
'gamma': (["scale"]),
'class_weight':(["balanced"]),
'kernel':(['linear'])
# "max_iter": (1000,)
}
optimal_model = GridSearchCV(svm.SVC(),
parameters,
scoring="f1", # test "rog_auc"
n_jobs=8,
verbose=3,
cv=3,
refit=True
)
t0 = time()
optimal_model.fit(X_train_vector[:train_size], Y_train[:train_size])
print("done in %0.3fs" % (time() - t0))
if search:
# display_model_scores(optimal_model, X_train_vector, Y_train)
display_model_scores(optimal_model, X_test_vector, Y_test)
# ### --> Entrainement avec model et data optimal sur le TRAIN entier sans max_iter
# +
# fname = "data/corpus.tache1.learn.utf8"
# alltxts_train_final, alllabs_train_final = load_pres(fname)
# X_train_final = np.array(alltxts_train_final)
# Y_train_final = np.array(alllabs_train_final)
fname = "data/corpus.tache1.learn.utf8"
alltxts, alllabs = load_pres(fname)
X = np.array(alltxts)
Y = np.array(alllabs)
X_train_final, X_test, Y_train_final, Y_test = train_test_split(X, Y, test_size=0.2)
# +
final_vectorizer = TfidfVectorizer(lowercase=False,
stop_words=None,
strip_accents=None,
use_idf=True,
smooth_idf=True,
sublinear_tf=False,
min_df=1,
max_df=0.05,
ngram_range=(1,2),
)
X_final_vector = final_vectorizer.fit_transform(X_train_final)
X_test_vector = final_vectorizer.transform(X_test)
# -
final_model = svm.SVC(C=200,
gamma="scale",
class_weight="balanced",
kernel="linear",
verbose=3,
)
print(X_final_vector.shape)
print(Y_train_final.shape)
from time import time
t0 = time()
final_model.fit(X_final_vector, Y_train_final)
print("done in %0.3fs" % (time() - t0))
display_model_scores(final_model, X_final_vector, Y_train_final)
display_model_scores(final_model, X_test_vector, Y_test)
# ### --> Calcul des predictions pour envoie
fname = "data/corpus.tache1.test.utf8"
alltxts_test_final, alllabs_test_final = load_pres(fname)
X_test_final = np.array(alltxts_test)
Y_test_final = np.array(alllabs_test)
X_test_vector = final_vectorizer.transform(X_test_final)
final_pred = final_model.predict(X_test_vector)
print(final_pred.shape)
f = open("output/preds_line.txt", "a")
preds = ""
for i in range(len(final_pred)):
preds += str(final_pred[i]) + "\n"
# print(preds)
f.write(preds)
f.close()
# ### --> Test avec post processing
|
S2/RITAL/TAL/TME/TME1/.ipynb_checkpoints/BenchmarkClassif-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 10 Dimension reduction
#
# Part of ["Introduction to Data Science" course](https://github.com/kupav/data-sc-intro) by <NAME>, [<EMAIL>](mailto:<EMAIL>)
#
# Recommended reading for this section:
#
# 1. <NAME>. (2019). Data Science From Scratch: First Principles with Python (Vol. Second edition). Sebastopol, CA: O’Reilly Media
# 1. <NAME> and <NAME> (2017). Introduction to Machine Learning with Python. O'Reilly
# 1. A beginner’s guide to dimensionality reduction in Machine Learning. https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
#
# The following Python modules will be required. Make sure that you have them installed.
# - `matplotlib`
# - `requests`
# - `numpy`
# - `sklearn`
# ## Lesson 1
# ### Principal components
#
# Before start we define the function the downloads CSV file from the repository.
# +
import csv
import numpy as np
import requests
def load_csv_dataset(file_name, dtype=float):
"""Downloads csv numeric dataset from repo to numpy array."""
base_url = "https://raw.githubusercontent.com/kupav/data-sc-intro/main/data/"
web_data = requests.get(base_url + file_name)
assert web_data.status_code == 200
reader = csv.reader(web_data.text.splitlines(), delimiter=',')
data = []
for row in reader:
try:
# Try to parse as a row of floats
float_row = [dtype(x) for x in row]
data.append(float_row)
except ValueError:
# If parsing as floats failed - this is header
print(row)
return np.array(data)
# -
# Sometimes multidimensional data contain redundant information.
#
# Consider a two dimensional dataset.
data = load_csv_dataset('pca1.csv')
print(data.shape)
# This file contains two columns. Let us plot its separated histograms first
# +
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axs[0].hist(data[:, 0], bins=50)
axs[1].hist(data[:, 1], bins=50);
# -
# We see random normally distributed data.
#
# But their scatter plot looks like this:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(data[:, 0], data[:, 1])
ax.grid()
# It means that the two columns depends on each other: It is easy to notice that they obey the equation
# $$
# y = -2x
# $$
# We can check it:
# +
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(data[:, 0], data[:, 1])
vx = np.linspace(-4, 4, 100)
vy = -2 * vx
ax.plot(vx, vy, color='red')
ax.grid()
# -
# Given a dataset like this we do not need to analyze both of its columns.
#
# Only one contains en essential information.
# More often such strong dependence is absent.
#
# But we see that the data columns are not totally independent:
# +
import matplotlib.pyplot as plt
data = load_csv_dataset('pca2.csv')
fig, ax = plt.subplots()
ax.scatter(data[:, 0], data[:, 1])
ax.grid()
# -
# We observe a cloud of points highly stretched along a curtain direction.
#
# Obviously that variations along this direction are more essential than the perpendicular ones.
#
# Probably the true underlying process that generated these data had string dependence between
# columns
# $$
# y=kx
# $$
# and deviations from it appeared due to noise.
#
# Direction of the most intensive variations is called principal component.
#
# The idea of its finding is as follows.
#
# 
#
# We draw a line and compute distances $d_i$ between it and the data points. Then we rotate the line
# to make the sum of the distances as small as possible.
#
# This line or a unit vector along it is called the first principal component.
#
# The vector perpendicular to the first principal component is called the second principal component.
#
# In the examples above we considered two dimensional data so that the cloud of points could
# be stretched along a single direction.
#
# If data are multidimensional, i.e., there are more then two columns, the number of principal
# components equals to the number of columns.
#
# The first one is the directions where the cloud is the most stretched.
#
# The second one shows the most stretched direction among all perpendicular to the first one.
#
# The third is the most stretched direction that is perpendicular to the first two. And so on.
#
# Data analysis via the principal components is called PCA, Principal Components Analysis.
# ### Computation of the principal components
#
# Mathematically computation of principal components involves the following steps.
#
# First we must compute mean values along each data column and subtract them so that
# the data cloud becomes centered near the origin.
# $$
# \tilde x_i = x_i - \mu
# $$
#
# This is absolutely important step. Omitting it results in incorrect results.
#
# Also it is often recommended to rescale the data columns by dividing by the standard deviation. Together with the shifting means to the origin this is called data standardizing.
# $$
# z_i = \frac{x_i - \mu}{\sigma}
# $$
#
# As we already discussed preliminary standardizing is very important when we have different
# data units in different columns.
#
# If the units are the same (e.g., all columns are in meters) it may be reasonable to left the data not rescaled.
#
# However the shift to the origin must be done in any case.
# The next step is computing variances and covariances.
#
# Let us remember that the variance is the mean squared deviation from the mean value:
# $$
# \overline x = \frac{1}{N}\sum_{i=1}^N x_i.
# $$
# $$
# \text{Var}=\frac{1}{N-1}\sum_{i=1}^N (x_i - \overline x)^2.
# $$
#
# Since we have shifted the data to the origin the mean is zero, so that
# $$
# \text{Var}=\frac{1}{N-1}\sum_{i=1}^N z_i^2.
# $$
#
# Let us denote our multidimensional standardized data as $z_{i,j}$.
#
# Here $i$ is a number of a row. Usually we have many rows. The number of rows is the size of the dataset.
#
# Index $j$ is a number of a column. The number of columns means the dimension of the dataset. Given two columns we have two dimensional dataset.
#
# Covariance is computed like this (provided that the data have zero mean values along $i$):
# $$
# \text{Cov}(j,k)=\frac{1}{N-1}\sum_{i=1}^N z_{i,j} z_{i,k}.
# $$
# Here the summation runs along rows for two columns $j$ and $k$.
#
# If $j=k$ we merely have the variance of the column $j$. And $\text{Cov}(j,k)=\text{Cov}(k,j)$
#
# The matrix collecting covariances for all pairs of the columns is called covariance matrix:
# $$
# C =
# \begin{pmatrix}
# \text{Cov}(0,0) & \text{Cov}(0,1) & \text{Cov}(0,2) & \ldots \\
# \text{Cov}(1,0) & \text{Cov}(1,1) & \text{Cov}(1,2) & \ldots \\
# \ldots & \ldots & \ldots & \ldots
# \end{pmatrix}
# $$
#
# The next step is to compute eigenvalues and eigenvectors of the covariance matrix $C$.
#
# Let us remember: we can multiply a matrix by a vector to obtain a new vector:
# $$
# A v_1 = v_2
# $$
# In general case $v_1$ and $v_2$ are different. They have different lengths and directions.
#
# Each square matrix $N\times N$ has $N$ special vectors such that
# $$
# A u = \lambda u
# $$
# Here $\lambda$ is scalar (i.e., just a number). It means that when we multiply the matrix $A$ by the vector $u$
# we obtain a vector that points the same direction that $u$ but stretched or shrined by $\lambda$.
#
# Scalars $\lambda$ are called eigenvalues of the matrix $A$ and $u$ are its eigenvectors.
#
# Eigenvectors of the covariance matrix $C$ are principal components of our dataset and the corresponding eigenvalues $\lambda$ indicate the range of variations along this components.
#
# For the covariance matrix $C$ the eigenvalues are always real positive numbers (this is because $C$ is symmetric).
#
# The first principal component corresponds to the largest eigenvalue. The second one corresponds to the second largest $\lambda$ and so on.
#
# The eigenvalues indicate how the cloud of points is stretched along the corresponding principal component.
#
# For example if the cloud almost exactly fits a line the first $\lambda_1$ is the largest and all others are close to zero.
#
# If the cloud of multidimensional data is spread along a plane two first eigenvalues $\lambda_1$ and $\lambda_2$ will be large, while all others small. And so on.
#
# Here the function that implements the steps above:
# +
def standardize(data):
"""Standartize data"""
return (data - np.mean(data, axis=0)) / np.std(data, axis=0)
def prin_comp(data):
"""Computes principal components for a multidimensional data
Returns a list of eigenvalues and eigenvectors of the covariance matrix.
Columns of the matrix vec are the principal components. Corresponding
lam indicate their importance. Lamdas are always returned in
the ascending order.
"""
# Covariance matrix
cov = np.cov(data, rowvar=False)
# Eigenvalues and eigenvectors of a symmetric matrix
lam, vec = np.linalg.eigh(cov)
return lam, vec
# -
# We read the dataset and standardize it at once
data = standardize(load_csv_dataset("pca3.csv"))
print(data.shape)
# Before computing the principal components let us visualize the data using histograms and pairwise scatter
# plots.
# +
import matplotlib.pyplot as plt
N = data.shape[1]
fig, axs = plt.subplots(nrows=N, ncols=N, figsize=(10, 10))
for i in range(N):
for j in range(N):
if i == j:
axs[i, i].hist(data[:, i], bins=300, color='C1')
else:
axs[i, j].scatter(data[:, i], data[:, j], s=1)
# Requred to avoid overlapping of the subplots
fig.tight_layout()
# -
# Visual inspection revels that columns 1, 2, and 4 are correlated. (Observe stretched clouds in panels 1-2, and 1-4).
#
# Also the correlated columns are 3 and 5. (Stretched clouds in the panels 3-5.
#
# And these two sets of columns are not correlated at all. (Circular clouds, e.g. in panels 1-3 and 1-5)
#
# These two groups of the correlated columns indicate that in the full 5th dimensional space there are tho
# main independent directions, i.e., the cloud of points is highly stretched along a plane while variations along
# the three other dimensions are small.
#
# Now we compute the principal components.
with np.printoptions(precision=2):
pc_lam, pc_vec = prin_comp(data)
print("pc_lam=\n", pc_lam)
print("pc_vec=\n", pc_vec)
# ### Essential and non-essential principal components
#
# We indeed observe that two principal components are the most essential.
#
# It means altogether that our 5th dimensional dataset is essentially 2 dimensional and
# three dimensions can be dropped out.
#
# This is called dimension reduction.
#
# Since PCA can see only a linear dependencies this is also called a linear dimension reduction.
#
# All criteria for choosing the essential and non essential principal components are based on values of the eigenvalues
# $\lambda_i$.
#
# Sometimes it is obvious, like in our example, which components can be removed.
#
# But if $\lambda_i$ are not so different, various approaches are used. All of them are heuristic, i.e, are based on some intuition.
#
# - Keep components whose eigenvalues are greater than 1.
# - Plot the scatter plot of $i$ against $\lambda_i$ and see if the points can be visually
# separated into two clusters of high and small values.
# - Compute the explained variances: $\tilde\lambda_i = \lambda_i / \sum_{i=1}^N \lambda_i$ (each eigenvalue is divided by the sum of all of them). Then keep those components that explain 95\% of variance.
#
# Let us apply these approaches to our data.
#
# Two the most essential components are indeed grater then 1 while others are less.
#
# The visualization confirms that we have to keep only two components:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
nums = list(range(len(pc_lam)))
ax.scatter(nums, pc_lam);
# The explained variances are:
# Each eigenvalue is divided by their sum and np.flip reverses the order
expl_var = np.flip(pc_lam / np.sum(pc_lam))
print(expl_var)
# Now we apply the cumulative sum to see what components explain 95% of variance
np.cumsum(expl_var)
# We see that this criterion of 95% explained variance is not fulfilled exactly.
#
# The explained variance above 95% includes three components.
#
# But since the sum of the first two gives 94% while the next one bring only 1% it looks reasonable again
# to keep only two components.
# ### Linear dimension reduction using principal components
#
# When we have a matrix whose columns are the principal components and have made a decision which will be kept we compose
# a matrix of this components.
#
# Let us denote the result as $W$. This matrix is also called a projection matrix because we will find projection
# of the original data onto its columns.
#
# The Columns of this matrix are the essential principal components, i.e., the eigenvectors of
# the covariance matrix that correspond to the essential eigenvalues.
#
# The number of the essential components will be the reduced dimension of our data set.
#
# In our example it will be 2, since we have decided to keep only two components.
#
# To perform the reduction we have to take rows of the initial dataset (of course, the one that we obtained after the standardizing)
# and multiply them by the matrix $W$:
# $$
# Z_{\text{red}} = Z w
# $$
# Here $Z$ is standardized dataset whose rows are one by one multiplied by $W$.
#
# The result is $Z_{\text{red}}$, the reduced dataset.
print(pc_vec)
print()
proj_w = pc_vec[:,-2:]
print(proj_w)
# The reduced dataset is:
red_data = data @ proj_w
print(red_data.shape)
# Let us see its scatter plot:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(5,5))
ax.scatter(red_data[:, 0], red_data[:, 1]);
# The circular cloud indicates that there are no more dependencies in our reduced data.
#
# It means that each column is contains an essential information.
# ### Non-Negative Matrix Factorization
#
# Dimension reduction is required to extract essential features from the dataset.
#
# The problem with PCA is that the extracted features can not be treated qualitatively.
#
# We can not say what exactly features are extracted by PCA, what they tell about the original data.
#
# Another approach widely used for feature extraction is named Non-Negative Matrix Factorization (NMF).
#
# NMF can extract easily interpretable features.
#
# For example, in the case of facial images, the features such as eyes, noses, moustaches, and lips.
#
# The important requirement is that the processed data must be non-negative.
#
# Assume there is a data matrix $X$ whose entries are non negative.
#
# Its columns are features and the number of columns $N$.
#
# NMF is representation of this matrix as a product of two non-negative matrices
# $$
# Z \approx W H
# $$
#
# The reduced data are in $W$. Its columns are new features. Their number is $R\leq N$ and the number of rows in $W$ is the same as in $Z$.
#
# The matrix $H$ gives weights of the reduced features in the original features. The most essential reduced features have the largest weights.
#
# This decomposition unlike PCA is approximate and not unique.
#
# The algorithm of NMF is rather complicated and we will use its implementation from the library `sklearn`.
#
# Consider how NMF works: we take two signals and mix them with together and add noise. Then apply NMF to extract the original signals.
#
# First we create the signals:
# +
import csv
import numpy as np
rng = np.random.default_rng()
# Dataset size
size = 1000
# Two original signals
tt = np.linspace(0, 9*np.pi, size)
s0 = 2 - np.fmod(-tt, np.pi) + np.fmod(2*tt, 3*np.pi)
s1 = np.abs(np.cos(tt*2)) + np.sin(0.5*tt)**2
s0 /= s0.max()
s1 /= s1.max()
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=2, ncols=1, figsize=(10, 4), sharex=True)
axs[0].plot(tt, s0)
axs[1].plot(tt, s1);
# -
# Now we create the dataset: we mix two signals with random weights and with noise. Repeat it $N$ times.
# +
# Number of features in the dataset that will be processed
N = 100
# Empty array
data = np.zeros((size, N))
# Weights for the signals in the range [1, 4]
wts0 = 1 + 3 * rng.uniform(size=(size,))
wts1 = 1 + 3 * rng.uniform(size=(size,))
# Mix signals
for i in range(N):
data[:, i] = wts0[i] * s0 + wts1[i] * s1 + 2 * rng.uniform(size=(size,))
# -
# Let us see what we have
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=5, ncols=1, figsize=(10, 10), sharex=True)
for i in range(5):
axs[i].plot(tt, data[:, i])
# Now we apply NMF.
#
# We export the class `NMF` from `sklearn` and specify the we want to get 2 components.
from sklearn.decomposition import NMF
nmf = NMF(n_components=2, init='random', random_state=0, max_iter=10000)
W = nmf.fit_transform(data)
# This is the plot of the extracted features.
#
# Observe that we rescale them by maximum.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(2, 1, figsize=(10, 4), sharex=True)
axs[0].plot(tt, W[:, 0] / np.max(W[:, 0]))
axs[0].plot(tt, s1)
axs[1].plot(tt, W[:, 1] / np.max(W[:, 1]))
axs[1].plot(tt, s0);
# We created the dataset of 100 columns where only two features were essential.
#
# NMF has successfully extracted them.
# ### Nonlinear dimension reduction
#
# PCA and NMF can reveal linear dependencies between data columns, i.e.,
# $$
# y = k x
# $$
#
# If columns depend on each other nonlinearly, for example like
# $$
# y = x^2
# $$
# these methods fail to extract lower dimensional set of features.
#
# To extract nonlinear dependencies one can use various special methods.
#
# The algorithms are rather complicated and we will use their implementation from `sklearn` library.
#
# To test these methods we create a three dimensional dataset whose points lays on a curved smooth surface.
#
# This surface is called manifold.
#
# This dataset will be processed using different methods that tries to find lower dimensional manifolds in high dimensional data.
#
# Descriptions of the methods are taken from the review paper "A beginner’s guide to dimensionality reduction in Machine Learning" by
# <NAME> https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
#
# First we define several useful functions.
# +
def standardize(data):
"""Standartize data"""
return (data - np.mean(data, axis=0)) / np.std(data, axis=0)
def cos_sin(deg):
"""Given an nagles in degrees computes cos and sin"""
rad = deg * np.pi / 180
return np.cos(rad), np.sin(rad)
def rotate(v, ax, ay, az):
"""Rotate a vector v around axis x, y, and z"""
cx, sx = cos_sin(ax)
cy, sy = cos_sin(ay)
cz, sz = cos_sin(az)
Mx = np.array([[1,0,0], [0, cx, -sx], [0, sx, cx]])
My = np.array([[cy, 0, sy], [0, 1, 0], [-sy, 0, cy]])
Mz = np.array([[cz, -sz, 0], [sz, cz, 0], [0, 0, 1]])
return Mz @ (My @ (Mx @ v))
def colorize(row):
"""Given the data row takes its first and second elemends and assingn color codes"""
x, y = row[:2]
if x > 0 and y > 0:
return 0
if x > 0 and y < 0:
return 1
if x < 0 and y > 0:
return 2
if x < 0 and y < 0:
return 3
# -
# Now we create three dimensional dataset.
#
# It will be 3D function
# $$
# z=x^3 - y^2
# $$
# We add a noise to it and rotate to complicate the task.
#
# After that we have to standardize the data.
#
# Manifold searching methods are based on a nearest-neighbor search.
#
# It means that data from different columns are compared.
#
# For the proper work the data must have the same units and moreover they must have same scales.
# +
import csv
import numpy as np
rng = np.random.default_rng()
# Size of the dataset
size = 1000
# There will be three columns
N = 3
# Empty storage
data = np.zeros((size, N))
# Uniform random numbers between -1 and 1
data[:, 0] = 2*rng.uniform(size=(size,))-1
data[:, 1] = 2*rng.uniform(size=(size,))-1
# Function x^3 - x^2 plus noise
data[:, 2] = data[:, 0]**3 - data[:,1]**2 + 0.25 * (2*rng.uniform(size=(size,))-1)
# Different colors in different
clrs = [colorize(row) for row in data]
# Angles of rotation around axes
ax, ay, az = 10, 15, 34
# Perform rotation
for i in range(size):
data[i] = rotate(data[i], ax, ay, az)
data = standardize(data)
# -
# Uncomment the next line to plot figure in a separate interactive window
# # %matplotlib qt
import matplotlib.pyplot as plt
fig, ax = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(8,8))
im = ax.scatter(data[:, 0], data[:, 1], data[:, 2], c=clrs)
# Now we apply different nonlinear methods to represent our three dimensional data on the plane.
# "t-distributed Stochastic Neighbor Embedding (t-SNE): Computes the probability that pairs of data points in the high-dimensional space are related and then chooses a low-dimensional embedding which produce a similar distribution." https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
#
# This method is probabilistic and different runs result in different results.
#
# To freeze a curtain plot we can specify parameters `random_state` that seed the random number generator.
# +
# %matplotlib inline
from sklearn.manifold import TSNE
proj = TSNE() # add here random_state=0 to keep the plot unchanged
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# "Multi-dimensional scaling (MDS): A technique used for analyzing similarity or dissimilarity of data as distances in a geometric spaces. Projects data to a lower dimension such that data points that are close to each other (in terms if Euclidean distance) in the higher dimension are close in the lower dimension as well." https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
# +
from sklearn.manifold import MDS
proj = MDS()
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# "Isometric Feature Mapping (Isomap): Projects data to a lower dimension while preserving the geodesic distance (rather than Euclidean distance as in MDS). Geodesic distance is the shortest distance between two points on a curve." https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
# +
from sklearn.manifold import Isomap
proj = Isomap()
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# "Locally Linear Embedding (LLE): Recovers global non-linear structure from linear fits. Each local patch of the manifold can be written as a linear, weighted sum of its neighbours given enough data." https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
# +
from sklearn.manifold import LocallyLinearEmbedding
proj = LocallyLinearEmbedding()
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# "Hessian Eigenmapping (HLLE): Projects data to a lower dimension while preserving the local neighbourhood like LLE but uses the Hessian operator to better achieve this result and hence the name." https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
# +
from sklearn.manifold import LocallyLinearEmbedding
proj = LocallyLinearEmbedding(method='hessian', n_neighbors=11, eigen_solver='dense')
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# Another improved version of the Locally Linear Embedding.
# +
from sklearn.manifold import LocallyLinearEmbedding
proj = LocallyLinearEmbedding(method='modified')
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# "Spectral Embedding (Laplacian Eigenmaps): Uses spectral techniques to perform dimensionality reduction by mapping nearby inputs to nearby outputs. It preserves locality rather than local linearity" https://towardsdatascience.com/dimensionality-reduction-for-machine-learning-80a46c2ebb7e
# +
from sklearn.manifold import SpectralEmbedding
proj = SpectralEmbedding()
W = proj.fit_transform(data)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(W[:, 0], W[:, 1], c=clrs);
# -
# ### Exercises
#
# 1\. Download the file ""redundant1.csv"" from the repository "https://raw.githubusercontent.com/kupav/data-sc-intro/main/data/".
# Apply PCA to reveal its number of essential features. Compute the reduced dataset and create a scatter plot for it.
#
# 2\. Download the file ""redundant2.csv"" from the repository "https://raw.githubusercontent.com/kupav/data-sc-intro/main/data/".
# Apply NMF and extract two its main features. Plot scatter plot for them.
|
10_Dimension_reduction.ipynb
|