code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ## **Setup**
# +
# Import the necesary packages
import os
import gc
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
import tensorflow as tf
import tensorflow_addons as tfa
# -
config = {
# Basic information
"AUTHOR": "Kiernan",
# Data information
"IMAGE_SIZE": 28,
# Training params
"LR_STYLE": "REDUCE", #['REDUCE', 'SCHEDULE']
"LR": 0.001, #0.000001,
"BATCH_SIZE": 50,
"EPOCHS": 30,
# Loss parameters
"LOSS": "SEMI_HARD", #['HARD', 'SEMI_HARD']
"MARGIN": 0.5,
"SOFT": False,
"DIST_METRIC": "L2", #['L2','squared-L2','angular']
# Model params
# "RUN_FOR_BASE": "3cmjv1lo",
# "FREEZE": "ALL", #['ALL', 'BN', 'None'] which layers to freeze in the body model
# Model params
"FIRST_FILTERS": 16,
"CONV_LAYERS": 4,
"N_FILTERS": 8,
"KERNEL_SIZE": (3,3),
"EMBEDDING_SIZE": 16,
"VECTOR_SIZE": 16,
"DROPOUT": 0.2
}
# ## **Initialize WANDB**
import wandb
from wandb.keras import WandbCallback
from secrets import WANDB
wandb.login(key=WANDB)
run = wandb.init(project="deep-clustering-evaluation", entity="kmcguigan", group="triplet-model", config=config, job_type="train")
# ## **Loading Data**
#
# ### **Load the presplit data**
# +
with open('data/train.npy', mode='rb') as infile:
X_train = np.load(infile, allow_pickle=True)
y_train = np.load(infile, allow_pickle=True)
with open('data/val.npy', mode='rb') as infile:
X_val = np.load(infile, allow_pickle=True)
y_val = np.load(infile, allow_pickle=True)
with open('data/test.npy', mode='rb') as infile:
X_test = np.load(infile, allow_pickle=True)
y_test = np.load(infile, allow_pickle=True)
print(f"Train data shape: {X_train.shape} Val data shape: {X_val.shape} Test data shape: {X_test.shape}")
# -
# ### **Create a data generator**
class CustomDataset(tf.keras.utils.Sequence):
def __init__(self, X, y, classes):
self.X = X
self.y = y
# image meta
self.dims = (config["IMAGE_SIZE"], config["IMAGE_SIZE"])
self.channels = 1
# save the meta on what we will be choosing
self.batch_size = config["BATCH_SIZE"]
self.samples_per_class = self.batch_size // len(classes)
assert(self.batch_size % self.samples_per_class == 0)
# create the image loader
self.indexer = {}
# min_samples = None
for cls in classes:
self.indexer[cls] = np.where(y==cls)[0]
# save the size of a single epoch of data
self.batches_per_epoch = (self.X.shape[0] // self.batch_size) + 1
super(CustomDataset, self).__init__()
def __len__(self):
return self.batches_per_epoch
def on_epoch_end(self):
gc.collect()
return
def __getitem__(self, idx):
X = np.empty((self.batch_size, *self.dims, self.channels))
y = np.empty((self.batch_size), dtype=int)
batch_idx = 0
for cls in self.indexer.keys():
samples = np.random.choice(self.indexer[cls], size=self.samples_per_class, replace=False)
X[batch_idx:batch_idx+self.samples_per_class, :, :, :] = self.X[samples, :, :, :]
y[batch_idx:batch_idx+self.samples_per_class] = self.y[samples]
batch_idx = batch_idx+self.samples_per_class
return X,y
train_ds = CustomDataset(X_train, y_train, [i for i in range(10)])
val_ds = CustomDataset(X_val, y_val, [i for i in range(10)])
test_ds = CustomDataset(X_test, y_test, [i for i in range(10)])
# + [markdown] tags=[]
# ## **Define Metrics**
# + tags=[]
def pairwise_distance(embeddings, squared=False):
dot = tf.matmul(embeddings, tf.transpose(embeddings))
square_norm = tf.linalg.diag_part(dot)
distances = tf.expand_dims(square_norm, 1) - 2.0 * dot + tf.expand_dims(square_norm, 0)
distances = tf.maximum(distances, 0.0)
if(not squared):
mask = tf.cast(tf.equal(distances, 0.0), tf.float32)
distances = distances + mask * 1e-16
distances = tf.sqrt(distances)
distances = distances * (1.0 - mask)
return distances
def angular_distances(embeddings):
embeddings = tf.math.l2_normalize(embeddings, axis=-1)
angular_distances = 1 - tf.matmul(embeddings, tf.transpose(embeddings))
angular_distances = tf.maximum(angular_distances, 0.0)
mask_offdiag = tf.ones_like(angular_distances) - tf.linalg.diag(tf.ones([tf.shape(angular_distances)[0]]))
angular_distances = tf.math.multiply(angular_distances, mask_offdiag)
return angular_distances
def apply_metric(embeddings, labels, metric):
adj = tf.equal(labels, tf.transpose(labels))
adj_not = tf.math.logical_not(adj)
adj = tf.cast(adj, tf.float32) - tf.linalg.diag(tf.ones([tf.shape(labels)[0]]))
adj_not = tf.cast(adj_not, tf.float32)
distances = metric(embeddings)
pos_dist = tf.math.multiply(distances, adj)
neg_dist = tf.math.multiply(distances, adj_not)
pos_dist_mean = tf.reduce_mean(tf.ragged.boolean_mask(pos_dist, mask=tf.math.equal(adj, 1.0)))
neg_dist_mean = tf.reduce_mean(tf.ragged.boolean_mask(neg_dist, mask=tf.math.equal(adj_not, 1.0)))
return pos_dist_mean, neg_dist_mean
# + tags=[]
def positive_distance(labels, embeddings):
adj = tf.equal(labels, tf.transpose(labels))
adj = tf.cast(adj, tf.float32) - tf.linalg.diag(tf.ones([tf.shape(labels)[0]]))
distances = pairwise_distance(embeddings)
pos_dist = tf.math.multiply(distances, adj)
pos_dist_mean = tf.reduce_mean(tf.ragged.boolean_mask(pos_dist, mask=tf.math.equal(adj, 1.0)))
return pos_dist_mean
def negative_distance(labels, embeddings):
adj = tf.math.logical_not(tf.equal(labels, tf.transpose(labels)))
adj = tf.cast(adj, tf.float32)
distances = pairwise_distance(embeddings)
neg_dist = tf.math.multiply(distances, adj)
neg_dist_mean = tf.reduce_mean(tf.ragged.boolean_mask(neg_dist, mask=tf.math.equal(adj, 1.0)))
return neg_dist_mean
def positive_angular(labels, embeddings):
adj = tf.equal(labels, tf.transpose(labels))
adj = tf.cast(adj, tf.float32) - tf.linalg.diag(tf.ones([tf.shape(labels)[0]]))
distances = angular_distances(embeddings)
pos_dist = tf.math.multiply(distances, adj)
pos_dist_mean = tf.reduce_mean(tf.ragged.boolean_mask(pos_dist, mask=tf.math.equal(adj, 1.0)))
return pos_dist_mean
def negative_angular(labels, embeddings):
adj = tf.math.logical_not(tf.equal(labels, tf.transpose(labels)))
adj = tf.cast(adj, tf.float32)
distances = angular_distances(embeddings)
neg_dist = tf.math.multiply(distances, adj)
neg_dist_mean = tf.reduce_mean(tf.ragged.boolean_mask(neg_dist, mask=tf.math.equal(adj, 1.0)))
return neg_dist_mean
# + jupyter={"source_hidden": true} tags=[]
class MetricHandler:
def __init__(self, metric):
self.has_read = {0: False, 1: False}
self.metric = metric
self.results = {0: None, 1: None}
def read_metric(self, reader, embeddings, labels):
if(self.has_read[reader]):
raise Excpetion(f'{reader} reader re-reading data it already has')
other = 1 - reader
if(self.has_read[other]):
value = self.results[reader]
self.results[0] = None
self.results[1] = None
return value
metric_results = apply_metric(embeddings, labels, self.metric)
self.results[0] = metric_results[0]
self.results[1] = metric_results[1]
return self.results[reader]
distance_handler = MetricHandler(pairwise_distance)
angular_handler = MetricHandler(angular_distances)
def pos_distance(labels, embeddings):
return distance_handler.read_metric(0, embeddings, labels)
def neg_distance(labels, embeddings):
return distance_handler.read_metric(1, embeddings, labels)
def pos_angle(labels, embeddings):
return angular_handler.read_metric(0, embeddings, labels)
def neg_angle(labels, embeddings):
return angular_handler.read_metric(1, embeddings, labels)
# + tags=[]
def get_lr_callback(plot=False, batch_size=config['BATCH_SIZE'], epochs=config['EPOCHS']):
lr_start = config['LR']
lr_max = config['LR'] * 5 * batch_size
lr_min = config['LR']
lr_ramp_ep = 4
lr_sus_ep = 0
lr_decay = 0.9
def lrfn(epoch):
if epoch < lr_ramp_ep:
lr = (lr_max - lr_start) / lr_ramp_ep * epoch + lr_start
elif epoch < lr_ramp_ep + lr_sus_ep:
lr = lr_max
else:
lr = (lr_max - lr_min) * lr_decay**(epoch - lr_ramp_ep - lr_sus_ep) + lr_min
return lr
if(plot):
epochs = list(range(epochs))
learning_rates = [lrfn(x) for x in epochs]
plt.scatter(epochs,learning_rates)
ax = plt.gca()
ax.get_yaxis().get_major_formatter().set_scientific(False)
plt.show()
lr_callback = tf.keras.callbacks.LearningRateScheduler(lrfn, verbose=False)
return lr_callback
if(config["LR_STYLE"] == "SCHEDULE"):
lr_callback = get_lr_callback(plot=True)
elif(config["LR_STYLE"] == "REDUCE"):
lr_callback = tf.keras.callbacks.ReduceLROnPlateau(monitor='val_loss', factor=0.9, patience=2)
else:
raise Exception(f"config LR_STYLE {config['LR_STYLE']} is not understood")
# -
# ## **Create Model**
#
# ### **Load the pretrained body model**
# +
def freeze_all(model):
for layer in model.layers:
layer.trainable=False
def freeze_BN(model):
# Unfreeze layers while leaving BatchNorm layers frozen
for layer in model.layers:
if not isinstance(layer, tf.keras.layers.BatchNormalization):
layer.trainable = True
else:
layer.trainable = False
def freeze_none(model):
for layer in model.layers:
layer.trainable = True
# +
# body_file = wandb.restore('body.h5', run_path=f"kmcguigan/deep-clustering-evaluation/{config['RUN_FOR_BASE']}")
# body = tf.keras.models.load_model(body_file.name)
# body_output_shape = body.layers[-1].output_shape[-1]
# config['EMBEDDING_SIZE'] = body_output_shape
# if(config["FREEZE"] == "ALL"):
# freeze_all(body)
# elif(config["FREEZE"] == "BN"):
# freeze_BN(body)
# elif(config["FREEZE"] == "None"):
# freeze_none(body)
# else:
# raise Excpetion(f"config FREEZE is set to {config['FREEZE']} but this freeze method is not understood")
# body.summary()
# +
def create_body(image_shape):
inputs = tf.keras.layers.Input(shape=image_shape)
def conv_block(layer_inputs, n_filters, kernel_size, **kwargs):
x = tf.keras.layers.Conv2D(n_filters, kernel_size, padding="same", **kwargs)(layer_inputs)
x = tf.keras.layers.BatchNormalization()(x)
x = tf.keras.layers.ReLU()(x)
return x
x = conv_block(inputs, config["FIRST_FILTERS"], config["KERNEL_SIZE"], strides=2)
for _ in range(config["CONV_LAYERS"]):
x = conv_block(x, config["N_FILTERS"], config["KERNEL_SIZE"])
x = tf.keras.layers.Conv2D(config["EMBEDDING_SIZE"], (1,1), padding="same")(x)
outputs = tf.keras.layers.GlobalAveragePooling2D()(x)
return tf.keras.models.Model(inputs=inputs, outputs=outputs, name="body")
body = create_body(X_train.shape[1:])
body.summary()
# -
# ### **Create the head**
# +
def create_head(input_shape):
inputs = tf.keras.layers.Input(shape=(input_shape,))
x = tf.keras.layers.Dropout(config["DROPOUT"])(inputs)
x = tf.keras.layers.Dense(config['VECTOR_SIZE'])(x)
outputs = tf.keras.layers.Lambda(lambda x: tf.math.l2_normalize(x, axis=-1))(x)
return tf.keras.models.Model(inputs=inputs, outputs=outputs, name="head")
head = create_head(input_shape=config['EMBEDDING_SIZE'])
head.summary()
# -
# ### **Create the full model**
# +
model = tf.keras.models.Sequential([
body,
head
],
name="combinedModel"
)
if(config["LOSS"] == "HARD"):
loss = tfa.losses.TripletHardLoss(margin=config["MARGIN"], distance_metric=config["DIST_METRIC"], soft=config["SOFT"])
elif(config["LOSS"] == "SEMI_HARD"):
loss = tfa.losses.TripletSemiHardLoss(margin=config["MARGIN"], distance_metric=config["DIST_METRIC"], soft=config["SOFT"])
else:
raise Exception(f"config LOSS of {config['LOSS']} is not understood")
optimizer = tf.keras.optimizers.Adam(learning_rate=config['LR'])
metrics = [
positive_distance,
negative_distance,
positive_angular,
negative_angular
]
model.compile(loss=loss, optimizer=optimizer, metrics=metrics)
model.summary()
# -
# ## **Evaluate Models Initial Performance**
def kmeans_cluster_accuracy(X, y):
embeddings = model.predict(X)
kmeans = KMeans(n_clusters=10, random_state=123)
labels = kmeans.fit_predict(embeddings)
label_mappings = {}
for label in np.unique(labels):
values, counts = np.unique(y[np.where(labels==label)], return_counts=True)
label_mappings[label] = values[np.argmax(counts)]
print(label_mappings)
map_labels = np.vectorize(lambda x: label_mappings[x])
mapped_labels = map_labels(labels)
return accuracy_score(y.reshape((-1,1)), mapped_labels.reshape((-1,1)))
acc = kmeans_cluster_accuracy(X_test, y_test)
print(acc)
run.log({'test/init-test-clustering-accuracy': acc})
acc = kmeans_cluster_accuracy(X_val, y_val)
print(acc)
run.log({'test/init-val-clustering-accuracy': acc})
# ## **Train the Model**
stopper = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=4, restore_best_weights=True)
hist = model.fit(train_ds,
validation_data=val_ds,
epochs=config["EPOCHS"],
callbacks=[stopper, lr_callback, WandbCallback()])
ev = model.evaluate(test_ds, return_dict=True)
log_dict = {f'test/{met}': val for met, val in ev.items()}
run.log(log_dict)
acc = kmeans_cluster_accuracy(X_test, y_test)
print(acc)
run.log({'test/test-clustering-accuracy': acc})
acc = kmeans_cluster_accuracy(X_val, y_val)
print(acc)
run.log({'test/val-clustering-accuracy': acc})
run.finish()
|
4-Triplet-loss-model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# This restacks data after having been scraped from Robospect, such that the
# final table has rows of spectra, and cols of absorption lines (among other things)
# Created 2021 Feb. 10 by E.S.
# +
import pandas as pd
#from astropy.io import fits
from astropy.io.fits import getdata
import matplotlib.pyplot as plt
import numpy as np
# %matplotlib qt
# +
# name of csv file with EWs as produced by pipeline
ew_data_file_name = "/Users/bandari/Documents/git.repos/rrlyrae_metallicity/rrlyrae_metallicity/ew_products/20210225_restacked_ew_info_good_only.csv"
# read in
df_prestack = pd.read_csv(ew_data_file_name)
# -
# stem of names of FITS files with needed data in header
fits_stem = "/Users/bandari/Documents/git.repos/rrlyrae_metallicity/rrlyrae_metallicity/realizations_output/"
# +
# make list of individual spectra for which we have EW data, and
# initialize DataFrame to hold the re-cast data
list_indiv_spectra = list(df_prestack["realization_spec_file_name"].drop_duplicates())
num_indiv_spectra = len(list_indiv_spectra)
df_poststack = pd.DataFrame(columns=["realization_spec_file_name",
"original_spec_file_name",
"FeH", "err_FeH",
"logg", "alpha","Teff",
"EW_Hbeta", "err_EW_Hbeta",
"EW_Hdelta", "err_EW_Hdelta",
"EW_Hgamma", "err_EW_Hgamma",
"EW_Heps", "err_EW_Heps",
"EW_CaIIK", "err_EW_CaIIK"], index=range(num_indiv_spectra)) # initialize
for t in range(0,num_indiv_spectra):
# loop over all spectra realizations we have measured EWs from to populate the dataframe
this_spectrum = list_indiv_spectra[t]
# read in intermediary FITS file to extract values from header
image, hdr = getdata(fits_stem + this_spectrum.split(".")[0] + ".fits", header=True, ignore_missing_end=True)
logg = hdr["LOGG"]
teff = hdr["TEFF"]
alpha = hdr["ALPHA"]
feh = hdr["FEH"]
err_feh = 0.15
# select data from table relevant to this spectrum
data_this_spectrum = df_prestack.where(df_prestack["realization_spec_file_name"] == this_spectrum).dropna().reset_index()
# extract original file name (the one from which realizations are made)
orig_name = data_this_spectrum["original_spec_file_name"].drop_duplicates().values[0]
# extract Balmer lines from the table of data from all the spectra
Hbeta = data_this_spectrum["EQW"].where(data_this_spectrum["line_name"] == "Hbet").dropna().values[0]
err_Hbeta = data_this_spectrum["uncertaintyEQW"].where(data_this_spectrum["line_name"] == "Hbet").dropna().values[0]
Hgamma = data_this_spectrum["EQW"].where(data_this_spectrum["line_name"] == "Hgam").dropna().values[0]
err_Hgamma = data_this_spectrum["uncertaintyEQW"].where(data_this_spectrum["line_name"] == "Hgam").dropna().values[0]
Hdelta = data_this_spectrum["EQW"].where(data_this_spectrum["line_name"] == "Hdel").dropna().values[0]
err_Hdelta = data_this_spectrum["uncertaintyEQW"].where(data_this_spectrum["line_name"] == "Hdel").dropna().values[0]
Heps = data_this_spectrum["EQW"].where(data_this_spectrum["line_name"] == "Heps").dropna().values[0]
err_Heps = data_this_spectrum["uncertaintyEQW"].where(data_this_spectrum["line_name"] == "Heps").dropna().values[0]
CaIIK = data_this_spectrum["EQW"].where(data_this_spectrum["line_name"] == "CaIIK").dropna().values[0]
err_CaIIK = data_this_spectrum["uncertaintyEQW"].where(data_this_spectrum["line_name"] == "CaIIK").dropna().values[0]
# fill in that row in the dataframe
df_poststack.iloc[t]["realization_spec_file_name"] = this_spectrum
df_poststack.iloc[t]["original_spec_file_name"] = orig_name
df_poststack.iloc[t]["logg"] = logg
df_poststack.iloc[t]["Teff"] = teff
df_poststack.iloc[t]["alpha"] = alpha
df_poststack.iloc[t]["FeH"] = feh
df_poststack.iloc[t]["err_FeH"] = err_feh
df_poststack.iloc[t]["EW_Hbeta"] = Hbeta
df_poststack.iloc[t]["err_EW_Hbeta"] = err_Hbeta
df_poststack.iloc[t]["EW_Hdelta"] = Hdelta
df_poststack.iloc[t]["err_EW_Hdelta"] = err_Hdelta
df_poststack.iloc[t]["EW_Hgamma"] = Hgamma
df_poststack.iloc[t]["err_EW_Hgamma"] = err_Hgamma
df_poststack.iloc[t]["EW_Heps"] = Heps
df_poststack.iloc[t]["err_EW_Heps"] = err_Heps
df_poststack.iloc[t]["EW_CaIIK"] = CaIIK
df_poststack.iloc[t]["err_EW_CaIIK"] = err_CaIIK
# +
# to generate a net Balmer line, make a rescaling of Hgamma
# based on Hdelta
# fit a straight line to Hgam vs Hdel
x_data = df_poststack["EW_Hdelta"].values.astype(float) # Hdel
y_data = df_poststack["EW_Hgamma"].values.astype(float) # Hgam
Hgam = np.copy(y_data)
coeff, cov = np.polyfit(x_data, y_data, 1, full=False, cov=True)
m = coeff[0]
b = coeff[1]
err_m = np.sqrt(np.diag(cov))[0]
err_b = np.sqrt(np.diag(cov))[1]
print("m:")
print(m)
print("b:")
print(b)
# generate a rescaled Hgam, call it rHgam
rHgam = np.divide(np.subtract(Hgam, b), m)
# -
## BEGIN TEST TO SEE IF RESCALING IS RIGHT
'''
x_data = df_poststack["EW_Hdelta"].values.astype(float) # Hdel
y_data = rHgam # Hgam
Hgam = np.copy(y_data)
coeff, cov = np.polyfit(x_data, y_data, 1, full=False, cov=True)
m = coeff[0]
b = coeff[1]
err_m = np.sqrt(np.diag(cov))[0]
err_b = np.sqrt(np.diag(cov))[1]
print("m:")
print(m)
print("b:")
print(b)
'''
## END TEST TO SEE IF RESCALING IS RIGHT
# +
# add column of rescaled Hgamma to DataFrame
df_poststack["EW_resc_Hgamma"] = rHgam
# +
# ... or read in text file of ready-made restacked EW data
df_poststack = pd.read_csv(ew_data_file_name)
# +
# plot: how do Balmer lines scale with each other?
plt.clf()
plt.title("Scaling of lines with Hdelta")
plt.scatter(df_poststack["EW_Hdelta"],df_poststack["EW_Hbeta"], s=3, label="Hbeta")
plt.scatter(df_poststack["EW_Hdelta"],np.add(df_poststack["EW_Hgamma"],4), s=3, label="Hgamma+4")
plt.scatter(df_poststack["EW_Hdelta"],np.add(df_poststack["EW_Heps"],8), s=3, label="Heps+8")
#plt.ylim([0,15])
plt.xlabel("EW, Hdelta (Angstr)")
plt.ylabel("EW, non-Hdelta (Angstr)")
plt.legend()
plt.show()
#plt.savefig("junk_balmer_rescalings.pdf")
# +
# plot: how do Balmer lines scale with Teff?
plt.clf()
plt.title("Scaling of lines with Hdelta")
plt.scatter(df_poststack["Teff"],df_poststack["EW_Hbeta"], s=3, label="Hbeta")
plt.scatter(df_poststack["Teff"],np.add(df_poststack["EW_Hgamma"],6), s=3, label="Hgamma+6")
plt.scatter(df_poststack["Teff"],np.add(df_poststack["EW_Hdelta"],12), s=3, label="Hdel+12")
plt.scatter(df_poststack["Teff"],np.add(df_poststack["EW_Balmer"],18), s=3, label="Net Balmer+18")
plt.scatter(df_poststack["Teff"],np.add(df_poststack["EW_Heps"],24), s=3, label="Heps+24")
#plt.ylim([0,70])
plt.xlabel("Teff (K)")
plt.ylabel("EW (Angstr)")
plt.title("Balmer EW trend with Teff")
plt.legend(ncol=5)
plt.show()
#plt.savefig("junk_balmer_rescalings.pdf")
# +
# find linear trend of net Balmer EW with Teff
# fit a straight line to Hgam vs Hdel
y_data = df_poststack["Teff"].values.astype(float) # Hdel
x_data = df_poststack["EW_Balmer"].values.astype(float) # Hgam
coeff, cov = np.polyfit(x_data, y_data, 1, full=False, cov=True)
m = coeff[0]
b = coeff[1]
err_m = np.sqrt(np.diag(cov))[0]
err_b = np.sqrt(np.diag(cov))[1]
print("m:")
print(m)
print("err_m:")
print(err_m)
print("b:")
print(b)
print("err_b:")
print(err_b)
# +
def pred_teff(EW_pass):
teff_pass = np.add(np.multiply(EW_pass,m),b)
return teff_pass
Teff_model = pred_teff(df_poststack["EW_Balmer"])
# +
# make plot of predicted and retrieved Teff
plt.clf()
#plt.scatter(df_poststack["Teff"],np.subtract(Teff_model,df_poststack["Teff"]))
plt.scatter(df_poststack["Teff"],Teff_model)
plt.plot(df_poststack["Teff"],df_poststack["Teff"],"--",color="k")
plt.title("Teff based on Balmer EW")
plt.xlabel("Injected Teff")
plt.ylabel("Retrieved Teff")
plt.show()
# +
# make plot of predicted Teff residuals given Balmer EW
plt.clf()
#plt.scatter(df_poststack["Teff"],np.subtract(Teff_model,df_poststack["Teff"]))
plt.scatter(df_poststack["EW_Balmer"],np.subtract(Teff_model,df_poststack["Teff"]))
#plt.plot(df_poststack["Teff"],np.zeros(len(df_poststack["Teff"])),"--",color="k")
plt.plot(df_poststack["EW_Balmer"],np.zeros(len(df_poststack["Teff"])),"--",color="k")
#plt.title("Teff based on Balmer EW")
plt.title("Teff residuals")
#plt.xlabel("Injected Teff")
plt.xlabel("Balmer EW")
#plt.ylabel("Retrieved Teff")
plt.ylabel("Retrieved Teff")
plt.show()
# +
# plot: KH plot
plt.clf()
plt.title("KH plot")
plt.errorbar(df_poststack["EW_resc_Hgamma"],df_poststack["EW_CaIIK"],
yerr=df_poststack["err_EW_CaIIK"],
marker="o", markersize=2, mfc="k", mec="k", ecolor="gray", linestyle="")
plt.ylim([0,30])
plt.xlabel("EW, net Balmer (Angstr)")
plt.ylabel("EW, CaIIK (Angstr)")
plt.savefig("junk_KH_plot.pdf")
# +
# write out data
#df_poststack.to_csv("junk_ew_data_20200216.csv")
|
notebooks_for_development/restacking_scraped_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="EC1C_OYjCXeE" colab_type="code" colab={}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.decomposition import PCA
# + id="o-h3aT4KCsOa" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 821} outputId="ff60b3dd-b004-4340-fe8a-0896d80e4b50"
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features.
y = iris.target
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
plt.figure(2, figsize=(8, 6))
plt.clf()
# Plot the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1,
edgecolor='k')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
# To getter a better understanding of interaction of the dimensions
# plot the first three PCA dimensions
fig = plt.figure(1, figsize=(8, 6))
ax = Axes3D(fig, elev=-150, azim=110)
X_reduced = PCA(n_components=3).fit_transform(iris.data)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], X_reduced[:, 2], c=y,
cmap=plt.cm.Set1, edgecolor='k', s=40)
ax.set_title("First three PCA directions")
ax.set_xlabel("1st eigenvector")
ax.w_xaxis.set_ticklabels([])
ax.set_ylabel("2nd eigenvector")
ax.w_yaxis.set_ticklabels([])
ax.set_zlabel("3rd eigenvector")
ax.w_zaxis.set_ticklabels([])
plt.show()
# + id="Kqq1AxrOCs1P" colab_type="code" colab={}
X=iris.data
# + id="QxvhApJbC0N2" colab_type="code" colab={}
import torch.nn.functional as F
# + id="YVvJwICwGPGN" colab_type="code" colab={}
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.fc1=nn.Linear(4,200)
self.fc2=nn.Linear(200,24)
self.fc3=nn.Linear(24,1)
def forward(self,x):
h1 =F.relu(self.fc1(x))
h2 =F.relu(self.fc2(h1))
h3 =self.fc3(h2)
return h3
# + id="JauwcMWhDXYa" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="a0eb14cb-3b75-4eb9-90d3-837afedb73be"
network=Net()
network
# + id="qy66ohawFv4z" colab_type="code" colab={}
loss_fn=torch.nn.MSELoss(reduction='mean')
optimizer=torch.optim.SGD(network.parameters(),lr=1e-4)
# + id="l4VhwHEgHlP5" colab_type="code" colab={}
X=X.astype('float64')
y=y.astype('float64')
X=torch.from_numpy(X)
y=torch.from_numpy(y)
# + id="PQGctQoWIuMT" colab_type="code" colab={}
X=X.float()
y=y.float()
ls=[]
# + id="NZDYIPICHpQf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="7521996c-ea6c-4f6c-e695-78bcd8ef5c6e"
for x in range(5000):
y_pred=network(X)
loss=loss_fn(y_pred,y)
ls.append(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# + id="J3uB78l1H09_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="38cd8977-4455-4121-9af3-683a0bab8d7c"
plt.plot(np.linspace(0,100, len(ls)), ls)
plt.show()
# + id="oefzf_24II7B" colab_type="code" colab={}
|
fully connected network/fully connected neural network.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#hide
from tanhNorm.core import *
# # A Variation of Batchnorm without the mean and variance parameters
#
# > This project explores the different possibilities that can lead to elimination of the mean and variance parameters in a Batchnorm layer and still give comparable results. The hypothesis is that this will lead to models that will be more robust to distribution changes in the incoming data.
# <br>
#
# Remark: I will keep updating this website with more notebooks as I perform more and more experiments. I'm still in college and am not working on this full time, so you may not see these notebooks being frequently updated if you've been following them recently.
# ## Install
# > TODO
# ## How to use
# > TODO
|
index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Generate Deep Matches
#
# Pre-compute deep matches for faster computation
# +
import json
from pprint import pprint
import numpy as np
Settings = json.load(open('settings.txt'))
root = Settings['data_root']
from math import ceil, floor
pprint(Settings)
print("")
from pak.datasets.MOT import MOT16
import subprocess
from os import makedirs, listdir
from os.path import join, isfile, isdir, exists, splitext
deepmatch_loc = Settings['deepmatch']
assert(isfile(deepmatch_loc))
root = Settings['data_root']
mot16 = MOT16(root)
# +
# ---------------------
VIDEO = "MOT16-11"
delta_max = 100
# --- start process ---
img_loc = mot16.get_test_imgfolder(VIDEO)
frames = sorted([join(img_loc, f) for f in listdir(img_loc) \
if f.endswith('.jpg')])
def deepmatch(img1, img2):
args = (deepmatch_loc, img1, img2, '-downscale', '3', '-nt', '16')
popen = subprocess.Popen(args, stdout=subprocess.PIPE)
popen.wait()
B = np.fromstring(popen.stdout.read(), sep=' ')
n = B.shape[0]
assert(floor(n) == ceil(n))
assert(floor(n/6) == ceil(n/6))
B = B.reshape((int(n/6), 6))
return B
# check if folder exists
folder_name = join(root, 'DM_' + VIDEO)
if isdir(folder_name):
# recover from previous state!
already_calc = [f for f in listdir(folder_name) if f.endswith('.npy')]
start_i = len(already_calc)
else:
makedirs(folder_name)
start_i = 0
#TOTAL = []
for i in range(start_i, len(frames)):
curr_frame = []
for j in range(i, min(i+delta_max+1, len(frames))):
print("solve " + str(i) + " -> " + str(j))
M = deepmatch(frames[i], frames[j])
curr_frame.append(M)
fname = "f" + "%06d" % (i+1,) + '.npy'
np.save(join(folder_name, fname), np.array(curr_frame))
# #TOTAL.append(curr_frame)
# TOTALnp = np.array(TOTAL)
# np.save('MOT16_11.npy', TOTALnp)
|
prototyping/generate_deep_matches.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + editable=true
# %load_ext sql
# + editable=true
# %sql postgresql://student:student@127.0.0.1/sparkifydb
# + editable=true
# %sql SELECT * FROM songplays LIMIT 5;
# + editable=true
# %sql SELECT * FROM users LIMIT 5;
# + editable=true
# %sql SELECT * FROM songs LIMIT 5;
# + editable=true
# %sql SELECT * FROM artists LIMIT 5;
# + editable=true
# %sql SELECT * FROM time LIMIT 5;
# + [markdown] editable=true
# ## REMEMBER: Restart this notebook to close connection to `sparkifydb`
# Each time you run the cells above, remember to restart this notebook to close the connection to your database. Otherwise, you won't be able to run your code in `create_tables.py`, `etl.py`, or `etl.ipynb` files since you can't make multiple connections to the same database (in this case, sparkifydb).
# + editable=true
# %sql SELECT count(users.user_id), users.level, users.gender FROM users GROUP BY users.level, users.gender
# + editable=true
|
test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/hvarS/CS60075-Team28-Task-1/blob/main/baselines_and_with_features.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Aw13Jr9RdCrS"
# **Imports**
# + colab={"base_uri": "https://localhost:8080/"} id="AZpllGi738qY" outputId="9923627e-5796-4868-da13-0f7dee2ce731"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="QkQkKVA35L-3" outputId="f62abbe7-1516-4d4e-c906-06df6ae06ddb"
# !wget http://nlp.stanford.edu/data/glove.6B.zip
# !unzip glove.6B.zip -d embeddings
# + id="i0IfcPd_6GR4"
import os
import pandas as pd
import numpy as np
import xgboost as xgb
from sklearn.svm import SVR
from sklearn import preprocessing
from sklearn.neural_network import MLPRegressor
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor, AdaBoostRegressor
# + id="Vr3O0KwxUfLR"
FOLDER_PATH = "/content/drive/MyDrive/CS60075-Team28-Task-1"
DATA_FOLDER = os.path.join(FOLDER_PATH,"data/preprocessed")
# + id="rbKLlGrPKfTu"
# import evaluate function
import sys
sys.path.append(FOLDER_PATH)
from eval import evaluate
# + colab={"base_uri": "https://localhost:8080/", "height": 235} id="LeyCMxKPtcOv" outputId="508c6077-927d-43aa-e3cf-84bc92560374"
data = pd.read_csv(os.path.join(DATA_FOLDER, "lcp_single_train_preprocessed.csv"), index_col=0)
data['token'] = data['token'].astype(str)
data['sentence'] = data['sentence'].astype(str)
data.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 235} id="yQ_QxnnMp6eV" outputId="3c0e22fe-2a5a-4324-dad5-5fcabebca4bf"
data_multi = pd.read_csv(os.path.join(DATA_FOLDER, "lcp_multi_train_preprocessed.csv"), index_col=0)
data_multi['token'] = data_multi['token'].astype(str)
data_multi['sentence'] = data_multi['sentence'].astype(str)
data_multi.head()
# + id="6iuUvPq0_4Ob"
# # use if model is to be trained on both data together
# data = pd.concat([data, data_multi])
# + id="shXwG0Yj-VQV" colab={"base_uri": "https://localhost:8080/"} outputId="afcdd3d0-3e56-4c5c-9f93-3f759511d094"
def read_glove_vector(glove_vec):
with open(glove_vec, 'r', encoding='UTF-8') as f:
words = set()
word_to_vec_map = {}
for line in f:
w_line = line.split()
curr_word = w_line[0]
word_to_vec_map[curr_word] = np.array(w_line[1:], dtype=np.float64)
return word_to_vec_map
word_to_vec_map = read_glove_vector('embeddings/glove.6B.300d.txt')
print(len(word_to_vec_map)," words loaded!")
# + id="XwutHald-WLn"
def get_embeddings(sentences, tokens):
token_emb = []
for s,t in zip(sentences, tokens):
# fill unk by nan
# calculate mean over non nan embeddings
# fill unk by the mean embedding of sentence
# pad 0 vectors till max_len
temp_emb = [ word_to_vec_map[x] if x in word_to_vec_map else np.full((300,), np.nan) for x in t.split() ]
# calculate mean for filling null values <unk>
temp_sent_emb = [ word_to_vec_map[x] if x in word_to_vec_map else np.full((300,), np.nan) for x in s.split() ]
mean_emb = np.nanmean(np.array(temp_sent_emb), axis=0)
# single or multi - will be converted to (1,300)
temp_emb = np.mean(np.array([ mean_emb if np.isnan(x[0]) else x for x in temp_emb ]), axis=0)
token_emb.append(temp_emb)
return np.array(token_emb)
# + [markdown] id="XDM8FtGrv3Cu"
# ## CNN Regression Testing
# + id="HUc4c5H8wWiz"
from sklearn.model_selection import train_test_split
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
# + id="EEOeEAEfwAJj"
sentences_train_list = list(data['sentence'])
complexity_train_list = list(data['complexity'])
sentences_train,sentences_test,y_train,y_test = train_test_split(
sentences_train_list, complexity_train_list,
test_size=0.25,
random_state=1000)
# + id="nHsiKksPwilG"
tokenizer = Tokenizer(num_words=5000)
tokenizer.fit_on_texts(sentences_train)
X_train = tokenizer.texts_to_sequences(sentences_train)
X_test = tokenizer.texts_to_sequences(sentences_test)
# Adding 1 because of reserved 0 index
vocab_size = len(tokenizer.word_index) + 1
maxlen = 128
X_train = pad_sequences(X_train, padding='post', maxlen=maxlen)
X_test = pad_sequences(X_test, padding='post', maxlen=maxlen)
# + id="4zo9sbagw1vW"
import numpy as np
def create_embedding_matrix(filepath, word_index, embedding_dim):
vocab_size = len(word_index) + 1
embedding_matrix = np.zeros((vocab_size, embedding_dim))
with open(filepath) as f:
for line in f:
word, *vector = line.split()
if word in word_index:
idx = word_index[word]
embedding_matrix[idx] = np.array(vector, dtype=np.float32)[:embedding_dim]
return embedding_matrix
# + id="Yf3JmHZHxSgc"
embedding_dim = 300
embedding_matrix = create_embedding_matrix('embeddings/glove.6B.300d.txt ,tokenizer.word_index,
embedding_dim' )
# + [markdown] id="fH-qxn1zojp2"
# ## **Test Single Word**
#
#
# + id="cJzy1Juz_gqx"
SUBMISSION_FOLDER = os.path.join(FOLDER_PATH,"predictions/baselines_ankit/single")
if( not os.path.exists(SUBMISSION_FOLDER)):
os.makedirs(SUBMISSION_FOLDER)
# + colab={"base_uri": "https://localhost:8080/"} id="k3iXv8sIXSyR" outputId="35bbc659-c9ab-4195-a35b-3d4665e7b1d3"
sentences_train_list = list(data['sentence'])
complexity_train_list = list(data['complexity'])
tokens_train_list = list(data['token'])
vectors = get_embeddings(sentences_train_list, tokens_train_list)
print(vectors.shape)
# + id="DXS52dlZhyXt"
test_df = pd.read_csv(os.path.join(DATA_FOLDER, "lcp_single_test_preprocessed.csv"), index_col=0)
# + id="G3FLUZ7NdmHW" colab={"base_uri": "https://localhost:8080/"} outputId="087b8f43-9b45-47dc-8ad0-be5afbbf5ba5"
test_df['token'] = test_df['token'].astype(str)
test_df['sentence'] = test_df['sentence'].astype(str)
sentences_test_list = list(test_df['sentence'])
test_tokens_list = list(test_df['token'])
testdf_vectors = get_embeddings(sentences_test_list, test_tokens_list)
testdf_vectors.shape
# + id="FXHiacxNifhJ"
# Linear Regression
reg = LinearRegression().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/linear_regression_baseline.csv", index=False, header=False)
# Gradient Boosting
reg = GradientBoostingRegressor().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/gradient_boosting_baseline.csv", index=False, header=False)
# AdaBoost
reg = AdaBoostRegressor().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/ada_boost_baseline.csv", index=False, header=False)
# SVM regressor
reg = SVR().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/SVM_baseline.csv", index=False, header=False)
# MLP Regressor
reg = MLPRegressor(hidden_layer_sizes=(150)).fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/MLP_baseline.csv", index=False, header=False)
# + colab={"base_uri": "https://localhost:8080/"} id="K6VHoYyIin98" outputId="09d596c4-3e71-4a2b-e7d8-6c9576218336"
evaluate(SUBMISSION_FOLDER, FOLDER_PATH+"/references/lcp_single_test_labelled_preprocessed.csv")
# + id="qcbIxJtE_wrW"
For file gradient_boosting_baseline.csv
pearson : 0.7214444729661804
spearman : 0.6954546622318855
mae : 0.06718193713274725
mse : 0.00777120977316972
r2 : 0.5198533483837506
# + [markdown] id="Svgv6n9e-Q7I"
# ## **Multi Word**
#
# + id="1_Z8spmk_cCb"
SUBMISSION_FOLDER = os.path.join(FOLDER_PATH,"predictions/baselines_ankit/multi")
if( not os.path.exists(SUBMISSION_FOLDER)):
os.makedirs(SUBMISSION_FOLDER)
# + id="CQDHP9vr-jlz"
# DO NOT run if both is being trained together
sentences_train_list = list(data_multi['sentence'])
complexity_train_list = list(data_multi['complexity'])
tokens_train_list = list(data_multi['token'])
# + colab={"base_uri": "https://localhost:8080/"} id="ccLbHMyM-jl1" outputId="889e0cb2-1efd-452a-f756-acebfca756c8"
# DO NOT run if both is being trained together
vectors = get_embeddings(sentences_train_list, tokens_train_list)
print(vectors.shape)
# + id="hYtjY-_T9VNG"
test_df = pd.read_csv(os.path.join(DATA_FOLDER, "lcp_multi_test_preprocessed.csv"), index_col=0)
# + id="R2UTW87W9VNG"
test_df['token'] = test_df['token'].astype(str)
test_df['sentence'] = test_df['sentence'].astype(str)
sentences_test_list = list(test_df['sentence'])
test_tokens_list = list(test_df['token'])
# + colab={"base_uri": "https://localhost:8080/"} id="GiM-EnF79VNH" outputId="5381a7b5-a232-4d29-92a7-ac45c34bf554"
testdf_vectors = get_embeddings(sentences_test_list, test_tokens_list)
testdf_vectors.shape
# + id="Pv8DXM5X9VNH"
# Linear Regression
reg = LinearRegression().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/linear_regression_baseline.csv", index=False, header=False)
# Gradient Boosting
reg = GradientBoostingRegressor().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/gradient_boosting_baseline.csv", index=False, header=False)
# AdaBoost
reg = AdaBoostRegressor().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/ada_boost_baseline.csv", index=False, header=False)
# SVM regressor
reg = SVR().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/SVM_baseline.csv", index=False, header=False)
# MLP Regressor
reg = MLPRegressor(hidden_layer_sizes=(150)).fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(testdf_vectors)
pred = pd.DataFrame({"ID":test_df.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/MLP_baseline.csv", index=False, header=False)
# + colab={"base_uri": "https://localhost:8080/"} id="NvkkKdbS9VNJ" outputId="17382fc5-09ab-49a2-8a1a-ae106597b39a"
evaluate(SUBMISSION_FOLDER, FOLDER_PATH+"/references/lcp_multi_test_labelled_preprocessed.csv")
# + id="PnBDIaZS08B_"
For file linear_regression_baseline.csv
pearson : 0.7384735689252496
spearman : 0.7096751511559939
mae : 0.08420414291697727
mse : 0.011177467719053704
r2 : 0.5369181534723191
For file gradient_boosting_baseline.csv
pearson : 0.7870767227623038
spearman : 0.7664566772179571
mae : 0.07831874126395687
mse : 0.009391251928283358
r2 : 0.6109209712372773
For file SVM_baseline.csv
pearson : 0.7747686594582374
spearman : 0.7563503882622532
mae : 0.07906457106883466
mse : 0.009776174954316456
r2 : 0.5949736323456092
# + id="JCS9A2TN1IcT"
# + [markdown] id="_1wXzYgmV2Mx"
# ## Features - load data
# + colab={"base_uri": "https://localhost:8080/"} id="TmAPF6kVbdX8" outputId="<PASSWORD>"
f1 = pd.read_csv(os.path.join(FOLDER_PATH, "data/extra_features/lcp_single_train_features.csv"), index_col=0)
f1['token'] = f1['token'].astype(str)
f1['sentence'] = f1['sentence'].astype(str)
f1.set_index("id", inplace=True)
# drop unwanted features
f1.drop(['parse', 'lemma'], axis=1, inplace=True)
print(f1.columns)
f2 = pd.read_csv(os.path.join(FOLDER_PATH, "data/added_corpus_presence/lcp_single_train_preprocessed.csv"), index_col=0)
f2['token'] = f2['token'].astype(str)
f2['sentence'] = f2['sentence'].astype(str)
print(f2.columns)
features = f1.merge(f2, on=['id','sentence', 'corpus', 'token', 'complexity'])
# + colab={"base_uri": "https://localhost:8080/", "height": 595} id="-G3zFmbnhPqB" outputId="c5a10a5d-601a-412a-db7e-b58611c36890"
# fill pos nan by NN, as they are in majority
features['pos'] = features['pos'].fillna('NN')
features['token_length'] = features['token_length'].fillna(0)
# categorical encoding
labels = dict(features['pos'].value_counts())
labels = { k:i for i,k in enumerate(labels)}
labels['POS'] = len(labels)
print(labels)
def get_vowels(word):
val = 0
for w in word:
if(w in ['A', 'a', 'E', 'e', 'I', 'i', 'O', 'o', 'U','u']):
val+=1
return val
features['token_vowels'] = features['token'].apply(lambda x: get_vowels(x) )
features['pos'] = features['pos'].apply((lambda x: labels[x]))
# scaler = preprocessing.StandardScaler()
# features[['token_length', 'syllables', 'pos', 'dep num', 'synonyms', 'hypernyms', 'hyponyms', 'google frequency', 'familarity', 'token_vowels']] = \
# scaler.fit_transform(features[['token_length', 'syllables', 'pos', 'dep num', 'synonyms', 'hypernyms', 'hyponyms', 'google frequency', 'familarity', 'token_vowels']])
features.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 349} id="ocBaxNJ1uPD-" outputId="2e9d04ce-f680-48b5-87c6-56e406ae831c"
multi_f1 = pd.read_csv(os.path.join(FOLDER_PATH, "data/extra_features/lcp_multi_train_split_features.csv"), index_col=0)
multi_f1['token'] = multi_f1['token'].astype(str)
multi_f1['sentence'] = multi_f1['sentence'].astype(str)
multi_f1.set_index("id", inplace=True)
# drop unwanted features
multi_f1.drop(['parse', 'token1', 'token2', 'lemma1', 'lemma2', 'Unnamed: 0.1'], axis=1, inplace=True)
multi_f2 = pd.read_csv(os.path.join(FOLDER_PATH, "data/added_corpus_presence/lcp_multi_train_preprocessed.csv"), index_col=0)
multi_f2['token'] = multi_f2['token'].astype(str)
multi_f2['sentence'] = multi_f2['sentence'].astype(str)
multi_features = multi_f1.merge(multi_f2, on=['id','sentence', 'corpus', 'token', 'complexity'])
multi_features.head(2)
# + colab={"base_uri": "https://localhost:8080/", "height": 578} id="6oRx6fW5uxx1" outputId="a2b50257-da5f-4f30-897b-87dd82ae6bdc"
# fill pos nan by NN, as they are in majority
multi_features['pos2'] = multi_features['pos2'].fillna('NN')
multi_features['pos1'] = multi_features['pos1'].apply((lambda x: labels[x]))
multi_features['pos2'] = multi_features['pos2'].apply((lambda x: labels[x]))
# scaler = preprocessing.StandardScaler()
# multi_features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']] = \
# scaler.fit_transform(multi_features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']])
multi_features.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 595} id="-rS4FNqV5vp1" outputId="e51af03f-2af6-41cb-e774-b7b196076fde"
# merge both single and multi features
features['pos1'] = features['pos'].copy()
features['pos2'] = features['pos']
features['dep num1'] = features['dep num']
features['dep num2'] = features['dep num']
features['synonyms1'] = features['synonyms']
features['synonyms2'] = features['synonyms']
features['hypernyms1'] = features['hypernyms']
features['hypernyms2'] = features['hypernyms']
features['hyponyms1'] = features['hyponyms']
features['hyponyms2'] = features['hyponyms']
features['google frequency1'] = features['google frequency']
features['google frequency2'] = features['google frequency1']
features.drop(['pos','dep num', 'synonyms', 'hyponyms', 'hypernyms', 'google frequency'], axis=1, inplace=True)
features = features.append( multi_features)
print(len(features))
scaler = preprocessing.StandardScaler()
features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']] = \
scaler.fit_transform(features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']])
features.head()
# + [markdown] id="7TIJwE4UsGOg"
# ## Test with features - single
# + colab={"base_uri": "https://localhost:8080/"} id="uLEjoKSBwkS0" outputId="d5b8f067-62b6-49a4-f6b0-88b71e79ee97"
sentences_train_list = list(features['sentence'])
complexity_train_list = list(features['complexity'])
tokens_train_list = list(features['token'])
vectors = get_embeddings(sentences_train_list, tokens_train_list)
print(vectors.shape)
# f_vectors = features[['token_length', 'token_vowels', 'syllables', 'pos', 'dep num', 'synonyms', 'hypernyms', 'hyponyms', 'google frequency', 'biomedical', 'bible', 'subtitles', 'wiki', 'familarity']].values
# or
f_vectors = features[['token_length', 'token_vowels', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2',
'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2',
'google frequency1', 'google frequency2',
'biomedical', 'bible', 'subtitles', 'wiki', 'familarity']].values
print(f_vectors.shape)
vectors = np.concatenate((vectors, f_vectors), axis=1)
# + id="38GMvczOV4ES"
SUBMISSION_FOLDER = os.path.join(FOLDER_PATH,"predictions/baselines_ankit/features/single")
if( not os.path.exists(SUBMISSION_FOLDER)):
os.makedirs(SUBMISSION_FOLDER)
# + colab={"base_uri": "https://localhost:8080/", "height": 714} id="_LPMEPl1ioxd" outputId="aa959aa7-0f25-47d5-821a-09b9ea438e2a"
test_f1 = pd.read_csv(os.path.join(FOLDER_PATH, "data/extra_features/lcp_single_test_features.csv"), index_col=0)
test_f1['token'] = test_f1['token'].astype(str)
test_f1['sentence'] = test_f1['sentence'].astype(str)
test_f1.set_index("id", inplace=True)
# drop unwanted features
test_f1.drop(['parse', 'lemma'], axis=1, inplace=True)
test_f2 = pd.read_csv(os.path.join(FOLDER_PATH, "data/added_corpus_presence/lcp_single_test_preprocessed.csv"), index_col=0)
test_f2['token'] = test_f2['token'].astype(str)
test_f2['sentence'] = test_f2['sentence'].astype(str)
test_features = test_f1.merge(test_f2, on=['id','sentence', 'corpus', 'token'])
test_features.head()
# + id="cJTjX8NBioyV" colab={"base_uri": "https://localhost:8080/", "height": 714} outputId="182ab7fa-f2ad-47dc-a941-712d2bac933a"
# # fill pos nan by NN, as they are in majority
# test_features['pos'] = test_features['pos'].fillna('NN')
# # categorical encoding
# test_features['pos'] = test_features['pos'].apply((lambda x: labels[x]))
# def get_vowels(word):
# val = 0
# for w in word:
# if(w in ['A', 'a', 'E', 'e', 'I', 'i', 'O', 'o', 'U','u']):
# val+=1
# return val
# test_features['token_vowels'] = test_features['token'].apply(lambda x: get_vowels(x) )
# test_features[['token_length', 'syllables', 'pos', 'dep num', 'synonyms', 'hypernyms', 'hyponyms', 'google frequency', 'familarity', 'token_vowels']] = \
# scaler.transform(test_features[['token_length', 'syllables', 'pos', 'dep num', 'synonyms', 'hypernyms', 'hyponyms', 'google frequency', 'familarity', 'token_vowels']])
# ########## for all features
# fill pos nan by NN, as they are in majority
test_features['pos'] = test_features['pos'].fillna('NN')
test_features['token_length'] = test_features['token_length'].fillna(0)
test_features['pos'] = test_features['pos'].apply((lambda x: labels[x]))
def get_vowels(word):
val = 0
for w in word:
if(w in ['A', 'a', 'E', 'e', 'I', 'i', 'O', 'o', 'U','u']):
val+=1
return val
test_features['token_vowels'] = test_features['token'].apply(lambda x: get_vowels(x) )
test_features['pos1'] = test_features['pos'].copy()
test_features['pos2'] = test_features['pos']
test_features['dep num1'] = test_features['dep num']
test_features['dep num2'] = test_features['dep num']
test_features['synonyms1'] = test_features['synonyms']
test_features['synonyms2'] = test_features['synonyms']
test_features['hypernyms1'] = test_features['hypernyms']
test_features['hypernyms2'] = test_features['hypernyms']
test_features['hyponyms1'] = test_features['hyponyms']
test_features['hyponyms2'] = test_features['hyponyms']
test_features['google frequency1'] = test_features['google frequency']
test_features['google frequency2'] = test_features['google frequency']
test_features.drop(['pos','dep num', 'synonyms', 'hyponyms', 'hypernyms', 'google frequency'], axis=1, inplace=True)
test_features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']] = \
scaler.transform(test_features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']])
test_features.head()
# + colab={"base_uri": "https://localhost:8080/"} id="7RV33imHjy2j" outputId="7c48f35d-24ef-4581-f6b1-9bba9d73d032"
sentences_test_list = list(test_features['sentence'])
test_tokens_list = list(test_features['token'])
test_vectors = get_embeddings(sentences_test_list, test_tokens_list)
print(test_vectors.shape)
# test_f_vectors = test_features[['token_length', 'token_vowels', 'syllables', 'pos', 'dep num', 'synonyms', 'hypernyms', 'hyponyms', 'google frequency', 'biomedical', 'bible', 'subtitles', 'wiki', 'familarity']].values
test_f_vectors = test_features[['token_length', 'token_vowels', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2',
'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2',
'google frequency1', 'google frequency2',
'biomedical', 'bible', 'subtitles', 'wiki', 'familarity']].values
test_vectors = np.concatenate((test_vectors, test_f_vectors), axis=1)
print(test_vectors.shape)
# + id="HvPffbjPjIBi"
# # # Gradient Boosting
reg = GradientBoostingRegressor(n_estimators=250).fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/gradient_boosting_baseline.csv", index=False, header=False)
# Linear Regression
reg = LinearRegression().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/linear_regression_baseline.csv", index=False, header=False)
# # xgb Regression
# from xgboost import XGBRegressor
# reg = XGBRegressor(objective ='reg:squarederror', n_estimators=250).fit(vectors, np.array(complexity_train_list))
# y_pred = reg.predict(test_vectors)
# pred = pd.DataFrame({"ID":test_features.index, "complexity":y_pred})
# pred.to_csv(SUBMISSION_FOLDER+"/xgb_regression_baseline.csv", index=False, header=False)
# # AdaBoost
reg = AdaBoostRegressor().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/ada_boost_baseline.csv", index=False, header=False)
# SVM regressor
reg = SVR().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/SVM_baseline.csv", index=False, header=False)
# MLP Regressor
reg = MLPRegressor(hidden_layer_sizes=(150)).fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/MLP_baseline.csv", index=False, header=False)
# + colab={"base_uri": "https://localhost:8080/"} id="KzQ_4UNLjVJB" outputId="24c58eeb-a0a9-4820-b83a-3260a2a74023"
evaluate(SUBMISSION_FOLDER, FOLDER_PATH+"/references/lcp_single_test_labelled_preprocessed.csv")
# + id="z_RqzVW85_Hd"
pearson : 0.7420614648980268
spearman : 0.7104726955580672
mae : 0.06555679719442302
mse : 0.007306746999771031
r2 : 0.5485503276131269
pearson : 0.7401818712131418
spearman : 0.7073212533102632
mae : 0.06548487250652647
mse : 0.007338576693601775
r2 : 0.5465837199212888
# + [markdown] id="vYQs4natxevq"
# ## Test with features - multi
# + colab={"base_uri": "https://localhost:8080/"} id="M9LuuTs3xevr" outputId="c9abfa98-2078-451e-f0df-25d99f20b9ed"
sentences_train_list = list(multi_features['sentence'])
complexity_train_list = list(multi_features['complexity'])
tokens_train_list = list(multi_features['token'])
vectors = get_embeddings(sentences_train_list, tokens_train_list)
print(vectors.shape)
f_vectors = multi_features[['token_length', 'token_vowels', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2',
'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2',
'google frequency1', 'google frequency2',
'biomedical', 'bible', 'subtitles', 'wiki', 'familarity']].values
print(f_vectors.shape)
vectors = np.concatenate((vectors, f_vectors), axis=1)
# + id="WTgM0RNsxevu"
SUBMISSION_FOLDER = os.path.join(FOLDER_PATH,"predictions/baselines_ankit/features/multi")
if( not os.path.exists(SUBMISSION_FOLDER)):
os.makedirs(SUBMISSION_FOLDER)
# + colab={"base_uri": "https://localhost:8080/", "height": 332} id="yTAotilTxevv" outputId="15a41e7a-d30c-42d0-9bc8-21581daf1a1e"
test_multi_f1 = pd.read_csv(os.path.join(FOLDER_PATH, "data/extra_features/lcp_multi_test_split_features.csv"), index_col=0)
test_multi_f1['token'] = test_multi_f1['token'].astype(str)
test_multi_f1['sentence'] = test_multi_f1['sentence'].astype(str)
test_multi_f1.set_index("id", inplace=True)
# drop unwanted features
test_multi_f1.drop(['parse', 'token1', 'token2', 'lemma1', 'lemma2', 'Unnamed: 0.1'], axis=1, inplace=True)
test_multi_f2 = pd.read_csv(os.path.join(FOLDER_PATH, "data/added_corpus_presence/lcp_multi_test_preprocessed.csv"), index_col=0)
test_multi_f2['token'] = test_multi_f2['token'].astype(str)
test_multi_f2['sentence'] = test_multi_f2['sentence'].astype(str)
test_multi_features = test_multi_f1.merge(test_multi_f2, on=['id','sentence', 'corpus', 'token'])
test_multi_features['token'] = test_multi_f2['token'].astype(str)
test_multi_features.head(2)
# + id="Gi5GeQE0xevx" colab={"base_uri": "https://localhost:8080/", "height": 680} outputId="d46b1621-d411-4435-e6e8-3cda9cdb1b23"
# fill pos nan by NN, as they are in majority
test_multi_features['pos2'] = test_multi_features['pos2'].fillna('NN')
test_multi_features['pos1'] = test_multi_features['pos1'].apply((lambda x: labels[x]))
test_multi_features['pos2'] = test_multi_features['pos2'].apply((lambda x: labels[x]))
test_multi_features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']] = \
scaler.transform(test_multi_features[['token_length', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2', 'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2', 'google frequency1', 'google frequency2', 'familarity', 'token_vowels']])
test_multi_features.head()
# + colab={"base_uri": "https://localhost:8080/"} id="j18I8X1fxevy" outputId="86cdd2a1-9da7-488d-f9e1-c796df18754a"
sentences_test_list = list(test_multi_features['sentence'])
test_tokens_list = list(test_multi_features['token'])
test_vectors = get_embeddings(sentences_test_list, test_tokens_list)
print(test_vectors.shape)
test_f_vectors = test_multi_features[['token_length', 'token_vowels', 'syllables', 'pos1', 'pos2', 'dep num1', 'dep num2',
'synonyms1', 'synonyms2', 'hypernyms1', 'hypernyms2', 'hyponyms1', 'hyponyms2',
'google frequency1', 'google frequency2',
'biomedical', 'bible', 'subtitles', 'wiki', 'familarity']].values
test_vectors = np.concatenate((test_vectors, test_f_vectors), axis=1)
print(test_vectors.shape)
# + id="qTMHt6NNxev2"
# Linear Regression
reg = LinearRegression().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_multi_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/linear_regression_baseline.csv", index=False, header=False)
# Gradient Boosting
reg = GradientBoostingRegressor(n_estimators=100).fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_multi_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/gradient_boosting_baseline.csv", index=False, header=False)
# AdaBoost
reg = AdaBoostRegressor().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_multi_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/ada_boost_baseline.csv", index=False, header=False)
# SVM regressor
reg = SVR().fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_multi_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/SVM_baseline.csv", index=False, header=False)
# MLP Regressor
reg = MLPRegressor(hidden_layer_sizes=(150)).fit(vectors, np.array(complexity_train_list))
y_pred = reg.predict(test_vectors)
pred = pd.DataFrame({"ID":test_multi_features.index, "complexity":y_pred})
pred.to_csv(SUBMISSION_FOLDER+"/MLP_baseline.csv", index=False, header=False)
# + id="V-K2hsDwxev3" colab={"base_uri": "https://localhost:8080/"} outputId="8738d7c6-0001-4b71-b485-4f7a697fcdfd"
evaluate(SUBMISSION_FOLDER, FOLDER_PATH+"/references/lcp_multi_test_labelled_preprocessed.csv")
|
baselines_and_with_features.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from nltk.corpus import stopwords
import string
# load doc into memory
def load_doc(filename):
# open the file as read only
file = open(filename, 'r')
# read all text
text = file.read()
# close the file
file.close()
return text
# turn a doc into clean tokens
def clean_doc(doc):
# split into tokens by white space
tokens = doc.split()
# remove punctuation from each token
table = str.maketrans('', '', string.punctuation)
tokens = [w.translate(table) for w in tokens]
# remove remaining tokens that are not alphabetic
tokens = [word for word in tokens if word.isalpha()]
# filter out stop words
stop_words = set(stopwords.words('english'))
tokens = [w for w in tokens if not w in stop_words]
# filter out short tokens
tokens = [word for word in tokens if len(word) > 1]
return tokens
# load the document
filename = 'txt_sentoken/pos/cv000_29590.txt'
text = load_doc(filename)
tokens = clean_doc(text)
print(tokens)
|
Python/NLP/.ipynb_checkpoints/Word_embeddings-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="tDMT16v1L5Oq"
# # importing packages
# + id="_A00JHpk0h9P" executionInfo={"status": "ok", "timestamp": 1613497784020, "user_tz": -210, "elapsed": 1314, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
# pip install --upgrade torch torchvision
# use this for training
# + colab={"base_uri": "https://localhost:8080/"} id="dfklmwfuAm4V" executionInfo={"status": "ok", "timestamp": 1613497813328, "user_tz": -210, "elapsed": 30615, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}} outputId="4e947eb9-f752-429b-9152-51408ceddf1d"
# !pip install -qU sentence-transformers
# !pip install -qU wikipedia-api
# !pip install -qU clean-text[gpl]
# !mkdir resources
# !wget -q "https://github.com/sobhe/hazm/releases/download/v0.5/resources-0.5.zip" -P resources
# !unzip -qq resources/resources-0.5.zip -d resources
# !rm -rf /content/4ccae468eb73bf6c4f4de3075ddb5336
# !rm -rf /content/preproc
# !rm preprocessing.py utils.py
# !mkdir -p /content/preproc
# !git clone https://gist.github.com/4ccae468eb73bf6c4f4de3075ddb5336.git /content/preproc/
# !mv /content/preproc/* /content/
# !rm -rf /content/preproc
# !pip install faiss-cpu
# !pip install hazm
# + id="py-1EqOz1S20" executionInfo={"status": "ok", "timestamp": 1613497819496, "user_tz": -210, "elapsed": 12344, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
import numpy as np
import pandas as pd
import re
import os
import faiss
import hazm
from hazm import stopwords_list
import pickle
import requests
from termcolor import colored
from torch.utils.data import DataLoader
from sentence_transformers import InputExample, losses
import torch
import tensorflow as tf
from sentence_transformers import models, SentenceTransformer, util
SentenceTransformer_TrainedOnFarsTail_Path = 'm3hrdadfi/bert-fa-base-uncased-farstail-mean-tokens'
SentenceTransformer_TrainedOn_wikinli_Path = 'm3hrdadfi/bert-fa-base-uncased-wikinli-mean-tokens'
SentenceTransformer_TrainedOn_wikitriplet_Path = 'm3hrdadfi/bert-fa-base-uncased-wikitriplet-mean-tokens'
# + [markdown] id="iOYGIxDN39r-"
# # Helpers
# + id="cXNgHhY239E2" executionInfo={"status": "ok", "timestamp": 1613497821559, "user_tz": -210, "elapsed": 2053, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
# phrases that need to be removed from titles
corona_phrases = ['کرونایی', 'کروناست' ,'کرونا', 'شیوع', 'بحران', 'ویروس',
'ویروس جدید', 'coronavirus', 'corona', 'کووید-19 ',
'کووید', 'بیماری', 'بیمارانی', 'بیماران', '-۱۹', ' وی ', '19', '۱۹',
' بیمار ', 'كرونا', 'كوويد', 'ويروس', r'(\s+)',]
normalizer = hazm.Normalizer()
def clean(text):
"""Cleans the titles for the semantic models"""
for pattern in corona_phrases:
text = re.sub(pattern, " ", text)
text = re.sub(' +[\w] +', " ", text)
text = normalizer.normalize(text)
return text
#---------------------------------- get the results for this model-----------------------#
def get_resutls(questions, top_n):
results = []
for question in questions:
print(question)
# print('question type', type(question))
# we give the cleaned question to the semantic model
question_cleaned = clean(question)
question_emb = sentence_bert_embedder.encode(question_cleaned,
convert_to_tensor=False,
show_progress_bar = False)
emb_que = np.array([question_emb])
faiss.normalize_L2(emb_que)
top_k = index.search(emb_que, top_n)
indices = []
scores = []
# saving all the reults in a dictionary
for score, idx in zip(top_k[0][0], top_k[1][0]):
indices.append(idx)
scores.append(score)
results.append({'question':question,
'index':indices})
return results
# + [markdown] id="E2p2ddkYBAbm"
# # The Dataset
# + id="LNooGa4u03wy" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1613497856251, "user_tz": -210, "elapsed": 23126, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}} outputId="043bef4e-e1f4-49de-bac6-ef4db9947c78"
from google.colab import drive
drive.mount('/content/drive')
# + id="oEd6VWIkAzLJ" executionInfo={"status": "ok", "timestamp": 1613497860472, "user_tz": -210, "elapsed": 2997, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
data_address = '/content/drive/MyDrive/COVID-PSS.xls'
keys_address = '/content/drive/MyDrive/keywords_final_distilled_NE (1).pickle'
cleaned_titles_address = '/content/drive/MyDrive/title_cleaned_without_corona_2.pkl'
annotations_address = '/content/drive/MyDrive/all_annotations.csv'
df = pd.read_csv(data_address)
list_t = pd.read_pickle(cleaned_titles_address)
keywords = pd.read_pickle(keys_address)
keywords = [v for k,v in keywords.items()]
assert len(keywords) == len(df)
df['keywords'] = keywords
df.drop(columns=['img', 'link'], inplace=True)
# + id="UBnP1NlQxkax" executionInfo={"status": "ok", "timestamp": 1613497864536, "user_tz": -210, "elapsed": 1007, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
corpora = []
for i in range(len(list_t)):
keys = '[SEP]'.join(keywords[i])
corpora.append(' '.join([list_t[i], keys]))
# + [markdown] id="w5U7ymXEBJK9"
# # The model
#
# + id="g43lSM6mBCdf" colab={"base_uri": "https://localhost:8080/", "height": 285, "referenced_widgets": ["ffdedc39c2d3475e81067a7ee7df83d5", "c85dc009a4c948cea75509d453c394de", "5fa08d88de9c4c768499c5f82e208258", "6129bb7964d844ea92c00538d902e805", "5b8169c35a4e476c985fc6ceb91adffc", "<KEY>", "018572fd240e465ab54889ea548de1fd", "<KEY>", "686ff1473a944c99adf6c5308f25c10f", "<KEY>", "5731d297ccdc49659d084baa40ee30c6", "0e8a3698adb144a6bbac5e7e652f0aca", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "c6a07cece0c44d17a55e518a61a84d7f", "<KEY>", "f14379ac658548328f2a0e629de44f08", "ace68d148ed848cda1a99d03e66eec14", "88a2c2be0d33417ebd4268981bdf7cde", "7cbe0a9791b248599a7d720f688c358a", "e3ee26d46d834098926a4157ef1e3eaa", "<KEY>", "<KEY>", "e9d629a1042f4ea8a69cad7be9b90373", "<KEY>", "cee1b63a208647c79da61fc3e39f8166", "<KEY>", "99f2e43a027547dcb2274eb39b8cafa5", "632e6cde3c77478395dd66e74d36286a", "8e5f8ff870a842419760b483279ea91c", "<KEY>", "4ca16ba316554e4aae510aff92d396d5", "<KEY>", "fb83d7560d3c440ea3239dbd3c879199", "<KEY>", "4adddebac8174e5395f4e32fb6db5590", "<KEY>", "7f810f70c2f24997b4f1ced648213af9"]} executionInfo={"status": "ok", "timestamp": 1613497883765, "user_tz": -210, "elapsed": 13776, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}} outputId="280bf700-68b6-470e-f2f5-8544b023a6f6"
# preparing the model
def load_sentence_transformer(path):
bert_model_s = models.Transformer(path, max_seq_length=512)
pooling_model = models. Pooling(
bert_model_s.get_word_embedding_dimension(),
pooling_mode_mean_tokens = True,
pooling_mode_cls_token = False,
pooling_mode_max_tokens = False,
)
model = SentenceTransformer(modules= [bert_model_s, pooling_model])
return model
sentence_bert_embedder = load_sentence_transformer(SentenceTransformer_TrainedOn_wikinli_Path)
# + [markdown] id="3f9i46PbyQ8v"
# # Creating Embeddings
# + id="piPvQZIPB75f" colab={"base_uri": "https://localhost:8080/", "height": 114, "referenced_widgets": ["357adf5f37ad404caac2f5622e66a9e0", "20ba6d68ad0f42e59c57e3938977c83b", "364cbb8f0d71455fbc66b72e79f632a6", "95ec09c98e56453b8dd1693df6934027", "ce90d649aabf49448516ab9759a69b6a", "5f8042ec67e84ed29bd11f3804ebe0ad", "abebe021e2434582992b3edd859c81af", "0a891c17504e4d1da7182ad793d3fdbc"]} executionInfo={"status": "ok", "timestamp": 1613497935389, "user_tz": -210, "elapsed": 63136, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}} outputId="4a7a0569-2479-4fb6-d0c8-26f64e930912"
# %%time
# creating corpus embeddings
corpus_embeddings = sentence_bert_embedder.encode(corpora,
convert_to_tensor=True,
show_progress_bar=True,
batch_size = 256)
# + [markdown] id="DWdYqZOX6be1"
# # Sample Qustions
# + id="9H-huK8RoUPn" executionInfo={"status": "ok", "timestamp": 1613498056245, "user_tz": -210, "elapsed": 943, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
# creating sample question embeddings
question = str(questions[1:2])
question_emb = sentence_bert_embedder.encode(question,
convert_to_tensor=False,
show_progress_bar = False)
# + [markdown] id="8XGChoVayhXx"
# Searching with FAISS
# + id="xhivbgmaoUM1" executionInfo={"status": "ok", "timestamp": 1613498059942, "user_tz": -210, "elapsed": 1118, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
## Similarity Scores with FAISS
index = faiss.index_factory(768, "Flat", faiss.METRIC_INNER_PRODUCT)
# corpus
emb_cor = np.array(corpus_embeddings)
faiss.normalize_L2(emb_cor)
# query
index.add(emb_cor)
emb_que = np.array([question_emb])
faiss.normalize_L2(emb_que)
top_k = index.search(emb_que, 100)
# + colab={"base_uri": "https://localhost:8080/"} id="DJsNcofzylI5" executionInfo={"status": "ok", "timestamp": 1613498059942, "user_tz": -210, "elapsed": 1107, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}} outputId="af0abcd4-65c2-4060-e53a-033e80557cd2"
sentence_bert_WikiNli_indices = []
sentence_bert_WikiNli_scores = []
print(question)
print('Top results!')
for score, idx in zip(top_k[0][0], top_k[1][0]):
print(colored(f'{idx}th', 'blue'),' corpus with score', colored( f'{score:.2f}:\n', 'blue'), corpora[idx])
sentence_bert_WikiNli_indices.append(idx)
sentence_bert_WikiNli_scores.append(score)
# + id="rdZQKPgLylGZ"
# + id="YHLh2O-LoUKZ" colab={"base_uri": "https://localhost:8080/", "height": 38} executionInfo={"status": "ok", "timestamp": 1613197381100, "user_tz": -210, "elapsed": 1165, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhP2HqWFQ3YcETBmyXzYJ4aUF6yxEtBp1xeKRYw9g=s64", "userId": "00863812916379381327"}} outputId="973d0805-6f57-4445-e39c-9ab00d5baeff"
question
# + [markdown] id="5bpbRZn46Sud"
# # Sampling in Batches
# + id="j0AqEcA66XLE" executionInfo={"status": "ok", "timestamp": 1613497935996, "user_tz": -210, "elapsed": 56587, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}}
questions = pd.read_pickle('/content/drive/MyDrive/CoPer paper-Models/Sample Queries/Titles_with_Corona.pkl')
# + [markdown] id="gMx8CKYHNkUL"
# Don't put faiss itself in the function it'll give wrong results and indices
# + id="RIIarLBBCKuW"
# create the basic faiss for corpus embeddings
index = faiss.index_factory(768, "Flat", faiss.METRIC_INNER_PRODUCT)
emb_cor = np.array([i.numpy() for i in corpus_embeddings])
faiss.normalize_L2(emb_cor)
index.add(emb_cor)
# + id="wfpuuSInDOhK" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1613454825923, "user_tz": -210, "elapsed": 45647, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09581726699480431020"}} outputId="388bc5f4-3717-43f1-eca6-ad454e9b54b4"
results = get_resutls(questions, top_n = 50)
# + [markdown] id="elrQyo8jyY1h"
# # Saving all in a pickle
# + id="F63zyc_SQ4fg"
with open('/content/drive/MyDrive/CoPer paper-Models/Results/sbert-WikiNli.pkl', 'wb') as f:
pickle.dump(results, f)
# + id="m2-Qyc6EQ9cO"
|
Models/Semantic Models/Sentence BERTs/Sentence BERT- Wikinli.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Imports
import warnings
warnings.simplefilter('ignore')
# For reading data sets from the web.
import pandas
# For lots of great things.
import numpy as np
# To make our plots.
import matplotlib.pyplot as plt
# %matplotlib inline
# Because sympy and LaTeX make
# everything look wonderful!
from sympy import *
init_printing(use_latex=True)
from IPython.display import display
# We will use this to check our implementation...
from sklearn.decomposition import PCA
# We will grab another data set using Keras
# after we finish up with Iris...
import keras
from keras_tqdm import TQDMNotebookCallback
import nilearn
from nilearn import plotting
from nilearn import image
from nilearn import datasets
from nilearn.decomposition import CanICA
from nilearn.input_data import NiftiMasker
from nilearn import image
from nilearn.plotting import plot_stat_map, show
# -
# Load Dataset
dataset = nilearn.datasets.fetch_cobre(n_subjects=146, data_dir="/Users/KJP/Desktop/neural nets/Cobre Dataset2", url=None, verbose=1)
file_paths = dataset["func"]
confounds = dataset["confounds"]
file_paths.sort() #sort file names by alphabetical order, which will result in sorting by patient number
confounds.sort()
del file_paths[74] # number 74 is misisng samples so it needs to be removed
del confounds[74]
# +
#This cell performs group spatial ica decomposition on the dataset. It narrows it down to the top
#100 components.
from nilearn.decomposition import CanICA
canica = CanICA(n_components=100, smoothing_fwhm=10.,
threshold=3., verbose=10, random_state=0)
canica.fit(file_paths)
# Retrieve the independent components in brain space. Directly
# accesible through attribute `components_img_`. Note that this
# attribute is implemented from version 0.4.1. For older versions,
# see note section above for details.
components_img = canica.components_img_
# components_img is a Nifti Image object, and can be saved to a file with
# the following line:
#components_img.to_filename('canica_resting_state.nii.gz')
# +
#Visualize the ica spatial components
from nilearn.plotting import plot_prob_atlas
# Plot all ICA components together
plot_prob_atlas(components_img, title='All ICA components')
# -
# Transform files to their ica components
component_files = canica.transform(file_paths)
# Convert from list to np array
component_files = np.array(component_files)
# Make training and testing input vectors
XData = component_files
YData = np.load('/Users/KJP/Desktop/neural nets/Codes/YData.npy')
XData -= XData.mean()
XData /= XData.max()
x_train = XData[:115] #[1:143:2] these commented out are other options to split data 50 50
x_test = XData[115:] #[0:144:2]
y_train = YData[:115] #[1:143:2]
y_test = YData[115:] #[0:144:2]
x_train = x_train.reshape(x_train.shape[0], x_train.shape[1]*x_train.shape[2])
x_test = x_test.reshape(x_test.shape[0], x_test.shape[1]*x_test.shape[2])
display(x_train.shape)
display(y_train.shape)
display(x_test.shape)
display(y_test.shape)
# +
input_dim=15000
output_dim=2
# Multi-layer net with ReLU hidden layer
model = keras.models.Sequential()
# Here we make the hidden layer (size 2) with a ReL
# activation function, but also initialize the bias
# weights in the network to a constant 0.1
model.add(keras.layers.Dropout(0.2, input_shape=(input_dim,)))
model.add(keras.layers.Dense(1000,activation='relu',
bias_initializer=keras.initializers.Constant(0.1)))
model.add(keras.layers.Dropout(0.1))
model.add(keras.layers.Dense(500,input_dim=input_dim,activation='relu',
bias_initializer=keras.initializers.Constant(0.1)))
model.add(keras.layers.Dropout(0.1))
model.add(keras.layers.Dense(100,activation='relu', bias_initializer=keras.initializers.Constant(0.1)))
# Output layer (size 1), sigmoid activation function
model.add(keras.layers.Dense(output_dim,activation='softmax'))
# Compile as above (default learning rate and other
# hyperparameters for the Adam optimizer).
model.compile(loss='categorical_crossentropy',optimizer=keras.optimizers.Adam(lr=0.00002), metrics=['accuracy'])
# Display the model
print(model.summary())
# -
batch_size = 100
epochs = 150
history = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=0,
validation_split=0.2,
callbacks=[TQDMNotebookCallback()])
plt.figure()
# summarize history for accuracy
plt.subplot(211)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# summarize history for loss
plt.subplot(212)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.tight_layout()
plt.show()
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
|
FMRI Preprocessing/ICA Multilayer Net.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Utilities
# ## Configuring Logging
#
# EvalML uses [the standard python logging package](https://docs.python.org/3/library/logging.html). By default, EvalML will log `INFO`-level logs and higher (warnings, errors and critical) to stdout, and will log everything to `evalml_debug.log` in the current working directory.
#
# If you want to change the location of the logfile, before import, set the `EVALML_LOG_FILE` environment variable to specify a filename within an existing directory in which you have write permission. If you want to disable logging to the logfile, set `EVALML_LOG_FILE` to be empty. If the environment variable is set to an invalid location, EvalML will print a warning message to stdout and will not create a log file.
# ## System Information
#
# EvalML provides a command-line interface (CLI) tool prints the version of EvalML and core dependencies installed, as well as some basic system information. To use this tool, just run `evalml info` in your shell or terminal. This could be useful for debugging purposes or tracking down any version-related issues.
# !evalml info
|
docs/source/user_guide/utilities.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="T87YHLE8d3r3"
# # CSE474/574 - Programming Assignment 1
#
# For grading, we will execute the submitted notebook as follows:
#
# ```shell
# jupyter nbconvert --to python PA1Script.ipynb
# python PA1Script.py
# ```
# + colab={} colab_type="code" id="U_qKlf1hd3r4"
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import pickle
# + [markdown] colab_type="text" id="Fd7C_HpOd3r7"
# ## Part 1 - Linear Regression
# + [markdown] colab_type="text" id="_bihsXKzd3r8"
# ### Problem 1 - Linear Regression with Direct Minimization
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="dpdE0bZ5d3r9" outputId="a255dddc-ae96-4ccf-892b-d6998a9639bd"
print('PROBLEM 1')
print('----------')
# + colab={} colab_type="code" id="Cz4P_wk8d3r_"
def learnOLERegression(X,y):
# Inputs:
# X = N x d
# y = N x 1
# Output:
# w = d x 1
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
b = np.dot(np.transpose(X),y)
a = np.linalg.inv(np.dot(np.transpose(X),X))
w = np.dot(a,b)
return w
# + colab={} colab_type="code" id="oohFdFfPd3sC"
def testOLERegression(w,Xtest,ytest):
# Inputs:
# w = d x 1
# Xtest = N x d
# ytest = N x 1
# Output:
# rmse = scalar value
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
N = np.shape(Xtest)[0]
subtr_ = ytest - np.dot(Xtest,w)
rmse = np.sqrt((1/N) * np.dot(np.transpose(subtr_),subtr_))
return rmse
# + colab={"base_uri": "https://localhost:8080/", "height": 85} colab_type="code" id="XS2_8D5Wd3sE" outputId="642233f5-4d98-4b77-cfa8-7cdb4cd2b785"
Xtrain,ytrain,Xtest,ytest = pickle.load(open('diabetes.pickle','rb'),encoding='latin1')
# add intercept
x1 = np.ones((len(Xtrain),1))
x2 = np.ones((len(Xtest),1))
Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)
Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)
w = learnOLERegression(Xtrain,ytrain)
w_i = learnOLERegression(Xtrain_i,ytrain)
rmse = testOLERegression(w,Xtrain,ytrain)
rmse_i = testOLERegression(w_i,Xtrain_i,ytrain)
print('RMSE without intercept on train data - %.2f'%rmse)
print('RMSE with intercept on train data - %.2f'%rmse_i)
rmse = testOLERegression(w,Xtest,ytest)
rmse_i = testOLERegression(w_i,Xtest_i,ytest)
print('RMSE without intercept on test data - %.2f'%rmse)
print('RMSE with intercept on test data - %.2f'%rmse_i)
# + [markdown] colab_type="text" id="MDRnl7ffd3sH"
# ### Problem 2 - Linear Regression with Gradient Descent
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="whwFznrsd3sH" outputId="9ed5ea9d-eeb8-4738-8bf8-f2590e426c35"
print('PROBLEM 2')
print('----------')
# + colab={} colab_type="code" id="oMpVOeTad3sK"
def regressionObjVal(w, X, y):
# compute squared error (scalar) with respect
# to w (vector) for the given data X and y
#
# Inputs:
# w = d x 1
# X = N x d
# y = N x 1
# Output:
# error = scalar value
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
w = w.reshape(-1,1)
subtr_ = y - np.dot(X,w)
error = 0.5 * np.dot(np.transpose(subtr_),subtr_)
return error
# + colab={} colab_type="code" id="xCzh6MCUd3sM"
def regressionGradient(w, X, y):
# compute gradient of squared error (scalar) with respect
# to w (vector) for the given data X and y
# Inputs:
# w = d x 1
# X = N x d
# y = N x 1
# Output:
# gradient = d length vector (not a d x 1 matrix)
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
w = w.reshape(-1,1)
a_1 = np.dot(np.transpose(X),X)
a_2 = np.dot(a_1,w)
b_1 = np.dot(np.transpose(X),y)
error_grad = a_2 - b_1
return error_grad.flatten()
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="NuLAD7htd3sQ" outputId="72aa0e9b-d15a-4094-c96b-bd05df184880"
Xtrain,ytrain,Xtest,ytest = pickle.load(open('diabetes.pickle','rb'),encoding='latin1')
# add intercept
Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)
Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)
args = (Xtrain_i,ytrain)
opts = {'maxiter' : 50} # Preferred value.
w_init = np.zeros((Xtrain_i.shape[1],1))
soln = minimize(regressionObjVal, w_init, jac=regressionGradient, args=args,method='CG', options=opts)
w = np.transpose(np.array(soln.x))
w = w[:,np.newaxis]
rmse = testOLERegression(w,Xtrain_i,ytrain)
print('Gradient Descent Linear Regression RMSE on train data - %.2f'%rmse)
rmse = testOLERegression(w,Xtest_i,ytest)
print('Gradient Descent Linear Regression RMSE on test data - %.2f'%rmse)
# + [markdown] colab_type="text" id="uzXP3HkNd3sS"
# ## Part 2 - Linear Classification
# + [markdown] colab_type="text" id="ia8ZUHCed3sT"
# ### Problem 3 - Perceptron using Gradient Descent
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="1fT6DsSLd3sT" outputId="20213b9b-04e6-46e9-c450-d6f9a4c45238"
print('PROBLEM 3')
print('----------')
# + colab={} colab_type="code" id="jRt5FDFld3sV"
def predictLinearModel(w,Xtest):
# Inputs:
# w = d x 1
# Xtest = N x d
# Output:
# ypred = N x 1 vector of predictions
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
ypred = np.dot(Xtest,w)
for x in range(len(Xtest)):
if ypred[x] > 0:
ypred[x] = 1
else:
ypred[x] = -1
return ypred
# + colab={} colab_type="code" id="PLgUE_LTd3sX"
def evaluateLinearModel(w,Xtest,ytest):
# Inputs:
# w = d x 1
# Xtest = N x d
# ytest = N x 1
# Output:
# acc = scalar values
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
ypred = np.dot(Xtest,w)
for x in range(len(Xtest)):
if ypred[x] > 0:
ypred[x] = 1
else:
ypred[x] = -1
count_wrong = 0
count_right = 0
for y in range(0,len(Xtest)):
if ypred[y] != ytest[y]:
count_wrong = count_wrong + 1
acc = (len(Xtest) - count_wrong)/(len(Xtest)) * 100
return acc
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="Qav7u3LUd3sZ" outputId="95c2853d-c6be-4082-99d8-464c42a70c9e"
Xtrain,ytrain, Xtest, ytest = pickle.load(open('sample.pickle','rb'))
# add intercept
Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)
Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)
args = (Xtrain_i,ytrain)
opts = {'maxiter' : 50} # Preferred value.
w_init = np.zeros((Xtrain_i.shape[1],1))
soln = minimize(regressionObjVal, w_init, jac=regressionGradient, args=args,method='CG', options=opts)
w = np.transpose(np.array(soln.x))
w = w[:,np.newaxis]
acc = evaluateLinearModel(w,Xtrain_i,ytrain)
print('Perceptron Accuracy on train data - %.2f'%acc)
acc = evaluateLinearModel(w,Xtest_i,ytest)
print('Perceptron Accuracy on test data - %.2f'%acc)
# + [markdown] colab_type="text" id="9xMJ52XDd3sc"
# ### Problem 4 - Logistic Regression Using Newton's Method
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="NhGAfb3Qd3sd" outputId="e82dcbe1-c6b3-4535-b1d9-45704689d0c8"
print('PROBLEM 4')
print('----------')
# + colab={} colab_type="code" id="OAwWVwBbd3sf"
def logisticObjVal(w, X, y):
# compute log-loss error (scalar) with respect
# to w (vector) for the given data X and y
# Inputs:
# w = d x 1
# X = N x d
# y = N x 1
# Output:
# error = scalar
if len(w.shape) == 1:
w = w[:,np.newaxis]
# IMPLEMENT THIS METHOD - REMOVE THE NEXT
N, j = np.shape(X)[0], 0
for i in range(N):
theta_den = np.exp(-y[i,] * (np.dot(np.transpose(w.reshape(-1,1)),X[i,:])))
j = j + np.log(1 + np.exp(theta_den))
error = (1/N)*j
return error
# + colab={} colab_type="code" id="biWcUjrDd3sh"
def logisticGradient(w, X, y):
# compute the gradient of the log-loss error (vector) with respect
# to w (vector) for the given data X and y
#
# Inputs:
# w = d x 1
# X = N x d
# y = N x 1
# Output:
# error = d length gradient vector (not a d x 1 matrix)
if len(w.shape) == 1:
w = w[:,np.newaxis]
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
N, j = np.shape(X)[0], 0
for i in range(N):
theta_den = np.exp(y[i,]*(np.dot(np.transpose(w.reshape(-1,1)),X[i,:])))
j = j + (y[i,]/(1+theta_den))*np.transpose(X[i,:])
gradient = (-1)/N * j
return gradient
# + colab={} colab_type="code" id="tq7TJQAzd3si"
def logisticHessian(w, X, y):
# compute the Hessian of the log-loss error (matrix) with respect
# to w (vector) for the given data X and y
#
# Inputs:
# w = d x 1
# X = N x d
# y = N x 1
# Output:
# Hessian = d x d matrix
if len(w.shape) == 1:
w = w[:,np.newaxis]
# IMPLEMENT THIS METHOD - REMOVE THE NEXT LINE
N, d = np.shape(X)[0], np.shape(X)[1]
j = np.zeros((d,d))
for i in range(N):
theta_den = np.exp(y[i,]*(np.dot(np.transpose(w.reshape(-1,1)),X[i,:])))
j = j + ((theta_den)/(1+theta_den)**2)*np.matmul(np.transpose(X[i,:]),X[i,:])
hessian = (-1)/N * j
return hessian
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="DD-GO3Ybd3sk" outputId="30ffd910-baa7-43de-e49a-f660eaff04f2"
Xtrain,ytrain, Xtest, ytest = pickle.load(open('sample.pickle','rb'))
# add intercept
Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)
Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)
args = (Xtrain_i,ytrain)
opts = {'maxiter' : 50} # Preferred value.
w_init = np.zeros((Xtrain_i.shape[1],1))
soln = minimize(logisticObjVal, w_init, jac=logisticGradient, hess=logisticHessian, args=args,method='Newton-CG', options=opts)
w = np.transpose(np.array(soln.x))
w = np.reshape(w,[len(w),1])
acc = evaluateLinearModel(w,Xtrain_i,ytrain)
print('Logistic Regression Accuracy on train data - %.2f'%acc)
acc = evaluateLinearModel(w,Xtest_i,ytest)
print('Logistic Regression Accuracy on test data - %.2f'%acc)
# + [markdown] colab_type="text" id="gQo-bWUNd3sn"
# ### Problem 5 - Support Vector Machines Using Gradient Descent
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="0x87KGACd3sn" outputId="b7e50c64-979f-4ab1-eea5-9308f39628a8"
print('PROBLEM 5')
print('----------')
# + colab={} colab_type="code" id="Rb60uf3dd3sp"
def trainSGDSVM(X,y,T,eta=0.01):
# learn a linear SVM by implementing the SGD algorithm
#
# Inputs:
# X = N x d
# y = N x 1
# T = number of iterations
# eta = learning rate
# Output:
# weight vector, w = d x 1
# IMPLEMENT THIS METHOD
w = np.zeros([X.shape[1],1])
for iter in range(T):
i = np.random.randint(X.shape[0],size =(1))
if y[i,] * np.dot(X[i,:],w)<1:
w += eta * y[i] * np.transpose(X[i,:])
return w
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="mBorCZ11d3sr" outputId="194dd605-8143-4863-9391-03e04c66bb74"
Xtrain,ytrain, Xtest, ytest = pickle.load(open('sample.pickle','rb'))
# add intercept
Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)
Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)
args = (Xtrain_i,ytrain)
w = trainSGDSVM(Xtrain_i,ytrain,200,0.01)
acc = evaluateLinearModel(w,Xtrain_i,ytrain)
print('SVM Accuracy on train data - %.2f'%acc)
acc = evaluateLinearModel(w,Xtest_i,ytest)
print('SVM Accuracy on test data - %.2f'%acc)
# + [markdown] colab_type="text" id="MEL2ho0Dd3st"
# ### Problem 6 - Plotting decision boundaries
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="1xWQ818md3su" outputId="2e138234-5bf6-42a7-8a19-0e077e0ce6c8"
print('Problem 6')
print('---------')
# + colab={} colab_type="code" id="ewFl6a8ad3sw"
def plotBoundaries(w,X,y):
# plotting boundaries
mn = np.min(X,axis=0)
mx = np.max(X,axis=0)
x1 = np.linspace(mn[1],mx[1],100)
x2 = np.linspace(mn[2],mx[2],100)
xx1,xx2 = np.meshgrid(x1,x2)
xx = np.zeros((x1.shape[0]*x2.shape[0],2))
xx[:,0] = xx1.ravel()
xx[:,1] = xx2.ravel()
xx_i = np.concatenate((np.ones((xx.shape[0],1)), xx), axis=1)
ypred = predictLinearModel(w,xx_i)
ax.contourf(x1,x2,ypred.reshape((x1.shape[0],x2.shape[0])),alpha=0.3,cmap='cool')
ax.scatter(X[:,1],X[:,2],c=y.flatten())
# + colab={"base_uri": "https://localhost:8080/", "height": 427} colab_type="code" id="XPC5I3cGd3sy" outputId="0efd715f-c75b-4e2a-ba66-8bd81cca2ba2"
Xtrain,ytrain, Xtest, ytest = pickle.load(open('sample.pickle','rb'))
# add intercept
Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)
Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)
w_init = np.zeros((Xtrain_i.shape[1],1))
args = (Xtrain_i, ytrain)
opts = {'maxiter' : 50}
# Replace next three lines with code for learning w using the three methods
# Perceptron
soln = minimize(regressionObjVal, w_init, jac=regressionGradient, args=args,method='CG', options=opts)
w_perceptron = np.transpose(np.array(soln.x))
w_perceptron = w_perceptron[:,np.newaxis]
# Logistic
soln = minimize(logisticObjVal, w_init, jac=logisticGradient, hess=logisticHessian, args=args,method='Newton-CG', options=opts)
w_logistic = np.transpose(np.array(soln.x))
w_logistic = np.reshape(w_logistic,[len(w_logistic),1])
# SVM
w_svm = trainSGDSVM(Xtrain_i, ytrain, 200, 0.01)
fig = plt.figure(figsize=(20,6))
ax = plt.subplot(1,3,1)
plotBoundaries(w_perceptron,Xtrain_i,ytrain)
ax.set_title('Perceptron')
ax = plt.subplot(1,3,2)
plotBoundaries(w_logistic,Xtrain_i,ytrain)
ax.set_title('Logistic Regression')
ax = plt.subplot(1,3,3)
plotBoundaries(w_svm,Xtrain_i,ytrain)
ax.set_title('SVM')
# + colab={} colab_type="code" id="fJCesp8GkvQQ"
|
Project-1/PA1Script .ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python2
# ---
# My training of AB emus isn't working... going to explore
import matplotlib
#matplotlib.use('Agg')
from matplotlib import pyplot as plt
# %matplotlib inline
import seaborn as sns
sns.set()
import numpy as np
from pearce.mocks.kittens import TrainingBox, MDHR
cat = TrainingBox(boxno=0, system = 'ki-ls')
cat.load(1.0, HOD = 'corrZheng07', biased_satellites = True, hod_kwargs={'sec_haloprop_key': 'halo_local_density_10'})
cat.halocat.halo_table.colnames
cat.model.param_dict
# + active=""
# cat.halocat.halo_table['halo_local_density_10'].mean()
# -
print cat.model.param_dict.keys()
default_params = cat.model.param_dict
default_params['mean_occupation_centrals_assembias_corr1'] = 0.0
default_params['mean_occupation_satellites_assembias_corr1'] = 0.0
#default_params['mean_occupation_centrals_assembias_split1'] = 0.5
#default_params['mean_occupation_satellites_assembias_split1'] = 0.5
default_params['sigma_logM'] = 0.5
default_params['logMmin'] = 13.5
cat.model.model_dictionary['centrals_occupation'].sec_haloprop_key
r_bins = np.logspace(-1.1, 1.6, 19)
rbc = (r_bins[1:]+r_bins[:-1])/2.0
#default_y = np.zeros((18,))
#for i in xrange(N):
# print i,
cat.populate(default_params)
default_y= cat.calc_xi(r_bins)
#default_y/=N
N = 10
cmap = sns.color_palette("GnBu_d", N)
# +
pname = 'conc_gal_bias'
l, h = -2, 2
#l, h = 0.0, 1.0
d = default_params.copy()
for v, c in zip(np.logspace(l,h,N), cmap):
d[pname] = v
#y = np.zeros((18,))
#for i in xrange(N):
# print i,
cat.populate(d)
y= cat.calc_xi(r_bins)
print v, (y/default_y)[0]
#y/=N
plt.plot(rbc, y/default_y, label = v, c = c)
plt.xscale('log')
#plt.loglog()
plt.legend(loc = 'best')
plt.show();
# -
d['conc_gal_bias'] = 50.0
cat.populate(d)
sat_cut = cat.model.mock.galaxy_table['gal_type'] == 'satellites'
cat.model.mock.galaxy_table.colnames
plt.hist(cat.model.mock.galaxy_table[sat_cut]['conc_galaxy']*1.0/cat.model.mock.galaxy_table[sat_cut]['conc_NFWmodel'])
plt.yscale('log')
set(cat.model.mock.galaxy_table['gal_type'])
cat.model._input_model_dictionary['satellites_profile']._conc_NFWmodel_lookup_table_min,\
cat.model._input_model_dictionary['satellites_profile']._conc_NFWmodel_lookup_table_max
plt.hist(cat.halocat.halo_table['halo_nfw_conc'][np.isfinite(cat.halocat.halo_table['halo_nfw_conc'])][:1000])
plt.yscale('log')
finite_idxs = np.isfinite(cat.halocat.halo_table['halo_nfw_conc'])
np.sum(cat.halocat.halo_table[finite_idxs]['halo_nfw_conc']>100)*1.0/finite_idxs.shape[0]
plt.hist(cat.model.mock.galaxy_table['conc_galaxy'])
plt.yscale('log')
|
notebooks/Test NFW Pop.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/sergio-cabrales/python/blob/main/MoneyFlowIndex.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="ilCCMQZjWSBy"
# Import libraries
import warnings
import numpy as np
import pandas as pd
import pandas_datareader as web
import matplotlib.pyplot as plt
# Set the graph style
plt.style.use('fast')
# Ignore warnings
warnings.filterwarnings('ignore')
# + colab={"base_uri": "https://localhost:8080/", "height": 450} id="PNcDZjVjWaKd" outputId="4a867544-26b9-4274-b180-29f58aee8b3e"
# Get the stock quote
df = web.DataReader('AAPL', data_source='yahoo',start='2019-01-01', end='2021-03-01')
df
# + colab={"base_uri": "https://localhost:8080/", "height": 323} id="sEijg180WfM-" outputId="8988a25f-e3ee-4970-ccf6-a222a277fe66"
# Visualize the data
plt.figure(figsize=(12.2, 4.5))
plt.plot(df['Close'], label='Close Price')
plt.title('Close Price')
plt.xlabel('Date')
plt.ylabel('Close Price USD ($)')
plt.legend(df.columns.values, loc='upper left')
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="J16e_x8ZWg5Y" outputId="6cb629b7-739f-4791-f02d-62777a2035af"
# Calculate the typical price
typical_price = (df['Close'] + df['High'] + df['Low']) / 3
typical_price
# + colab={"base_uri": "https://localhost:8080/"} id="fMNBDXBwWlxQ" outputId="ca50060a-1639-4b71-884f-851d0d0519b0"
# Initialize the period for later
period = 14
# Calculate the money flow
money_flow = typical_price * df['Volume']
money_flow
# + id="sRlYIhh0Wo57"
# Get all of the positive and negative money flow
positive_flow = []
negative_flow = []
# Loop through typical price calculations
for i in range(1, len(typical_price)):
if typical_price[i] > typical_price[i-1]:
positive_flow.append(money_flow[i-1])
negative_flow.append(0)
elif typical_price[i] < typical_price[i-1]:
negative_flow.append(money_flow[i-1])
positive_flow.append(0)
else:
positive_flow.append(0)
negative_flow.append(0)
# + id="6DWT1w62Wreo"
# Storage for the last 14 days
positive_mf = []
negative_mf = []
for i in range(period-1, len(positive_flow)):
positive_mf.append(sum(positive_flow[i+1-period:i+1]))
for i in range(period-1, len(negative_flow)):
negative_mf.append(sum(negative_flow[i+1-period:i+1]))
# + colab={"base_uri": "https://localhost:8080/"} id="Tinx6g86Wuj1" outputId="f7b883cf-3502-4d21-b860-dbb0f943085e"
# Calculate the money flow index
mfi = 100 * (np.array(positive_mf) / (np.array(positive_mf) + np.array(negative_mf)))
# Print the MFI values
mfi
# + colab={"base_uri": "https://localhost:8080/", "height": 585} id="gMzlX7TWWw-K" outputId="eabf3afd-c89c-408c-8dde-12f9b7265c28"
# Create a data frame and put the MFI in
df2 = pd.DataFrame()
df2['MFI'] = mfi
# Create a plot for the MFI values
plt.figure(figsize=(12.2, 4.5))
plt.plot(df2['MFI'], label='MFI')
plt.axhline(10, linestyle='--', color='orange')
# Show the MFI
df2 = pd.DataFrame()
df2['MFI'] = mfi
# Create a plot
plt.figure(figsize=(12.2, 4.5))
plt.plot(df2['MFI'], label = 'MFI')
plt.axhline(10, linestyle='--', color='orange')
plt.axhline(20, linestyle='--', color='blue')
plt.axhline(80, linestyle='--', color='blue')
plt.axhline(90, linestyle='--', color='orange')
plt.title('MFI')
plt.ylabel('MFI Values')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 450} id="Sg_PHJExWy6s" outputId="81dbb3f4-ef13-4321-dcb6-5b6a746bb030"
# Create a data frame to store the additional buy sell signals
limited_df = pd.DataFrame()
limited_df = df[period:]
limited_df['MFI'] = mfi
# Print the limited data frame for debugging
limited_df
# + colab={"base_uri": "https://localhost:8080/", "height": 450} id="k--3xq-zW1A2" outputId="8de44578-2ab8-4dce-fcdb-6e58772c3b6d"
# Automate the buy and sell signals
def get_signal(data, high, low):
buy_signal = []
sell_signal = []
for i in range(len(data['MFI'])):
if data['MFI'][i] > high:
buy_signal.append(np.nan)
sell_signal.append(data['Close'][i])
elif data['MFI'][i] < low:
buy_signal.append(data['Close'][i])
sell_signal.append(np.nan)
else:
sell_signal.append(np.nan)
buy_signal.append(np.nan)
return (buy_signal, sell_signal)
# Add new columns for Buy and Sell
limited_df['Buy'] = get_signal(limited_df, 80, 20)[0]
limited_df['Sell'] = get_signal(limited_df, 80, 20)[1]
# Show the data
limited_df
# + colab={"base_uri": "https://localhost:8080/", "height": 615} id="7T2piA3jW39p" outputId="91b0f414-8047-42cb-ed90-c4375fd6d0fb"
# Plot the data
plt.figure(figsize=(12.2, 4.5))
plt.plot(df['Close'], label = 'Close Price', alpha = 0.5)
plt.scatter(limited_df.index, limited_df['Buy'], color='green', label='Buy Signal', marker='^', alpha = 1)
plt.scatter(limited_df.index, limited_df['Sell'], color='red', label='Sell Signal', marker='v', alpha = 1)
plt.title('Close Price')
plt.xlabel('Date')
plt.ylabel('Close Price USD ($)')
plt.legend(loc='upper left')
plt.show()
# Create a plot
plt.figure(figsize=(12.2, 4.5))
plt.plot(df2['MFI'], label = 'MFI')
plt.axhline(10, linestyle='--', color='orange')
plt.axhline(20, linestyle='--', color='blue')
plt.axhline(80, linestyle='--', color='blue')
plt.axhline(90, linestyle='--', color='orange')
plt.title('MFI')
plt.ylabel('MFI Values')
plt.show()
|
MoneyFlowIndex.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Creates a stp file and then loads up the stp file and then facets the wires
# (edges) of the geometry and plots the faceted eges along with the vertices
# within the stp file.
# +
import paramak
"""Creates an example stp file for plotting html point graphs"""
# this creates a Shape object
example_shape = paramak.ExtrudeMixedShape(
distance=1,
points=[
(100, 0, "straight"),
(200, 0, "circle"),
(250, 50, "circle"),
(200, 100, "straight"),
(150, 100, "spline"),
(140, 75, "spline"),
(110, 45, "spline"),
]
)
# this exports the shape as a html image with a few different view planes
example_shape.export_html("example_shape_RZ.html")
example_shape.export_html("example_shape_XYZ.html", view_plane='XYZ')
example_shape.export_html("example_shape_XZ.html", view_plane='XZ')
# This exports the Shape object as an stp file that will be imported later
example_shape.export_stp("example_shape.stp")
# +
"""Loads an stp file and plots html point graphs"""
# loads the stp file and obtains the solid shape and list of wires / edges
solid, wires = paramak.utils.load_stp_file(
filename="example_shape.stp",
)
# produces a plot on the R (radius) Z axis and saves the html file
paramak.utils.export_wire_to_html(
wires=wires,
tolerance=0.1,
view_plane="RZ",
facet_splines=True,
facet_circles=True,
filename="example_shape_from_stp_RZ.html",
)
# produces a plot on the XZ axis and saves the html file
paramak.utils.export_wire_to_html(
wires=wires,
tolerance=0.1,
view_plane="XZ",
facet_splines=True,
facet_circles=True,
filename="example_shape_from_stp_XZ.html",
)
# produces a 3D plot with XYZ axis and saves the html file
paramak.utils.export_wire_to_html(
wires=wires,
tolerance=0.1,
view_plane="XYZ",
facet_splines=True,
facet_circles=True,
filename="example_shape_from_stp_XYZ.html",
)
# -
|
examples/example_parametric_shapes/make_html_diagram_from_stp_file.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] colab_type="text" id="OlDwW4HY8MoU"
# # Introduction
#
# + [markdown] colab_type="text" id="2pFlZCUv7hM-"
#
# In this notebook, we will
# - Learn how to use BoostedTrees Classifier for training and evaluating
# - Explore how training can be speeded up for small datasets
# - Will develop intuition for how some of the hyperparameters affect the performance of boosted trees.
#
# + colab={} colab_type="code" id="QGP_iZh-1SX3"
# We will use some np and pandas for dealing with input data.
import numpy as np
import pandas as pd
# And of course, we need tensorflow.
import tensorflow as tf
from distutils.version import StrictVersion
# -
tf.__version__
# + [markdown] colab_type="text" id="vfxkZE-MaY0h"
# # Load dataset
# We will be using the titanic dataset, where the goal is to predict passenger survival given characteristiscs such as gender, age, class, etc.
# + colab={} colab_type="code" id="gd995mWZzOTz"
tf.logging.set_verbosity(tf.logging.INFO)
tf.set_random_seed(123)
# Load dataset.
dftrain = pd.read_csv('https://storage.googleapis.com/tf-datasets/titanic/train.csv')
dfeval = pd.read_csv('https://storage.googleapis.com/tf-datasets/titanic/eval.csv')
y_train = dftrain.pop('survived')
y_eval = dfeval.pop('survived')
# + colab={} colab_type="code" id="HPs8YoHMkB7_"
fcol = tf.feature_column
CATEGORICAL_COLUMNS = ['sex', 'n_siblings_spouses', 'parch', 'class', 'deck',
'embark_town', 'alone']
NUMERIC_COLUMNS = ['age', 'fare']
def one_hot_cat_column(feature_name, vocab):
return fcol.indicator_column(
fcol.categorical_column_with_vocabulary_list(feature_name,
vocab))
fc = []
for feature_name in CATEGORICAL_COLUMNS:
# Need to one-hot encode categorical features.
vocabulary = dftrain[feature_name].unique()
fc.append(one_hot_cat_column(feature_name, vocabulary))
for feature_name in NUMERIC_COLUMNS:
fc.append(fcol.numeric_column(feature_name,
dtype=tf.float32))
# + colab={} colab_type="code" id="R_51OufwaY0o"
# Prepare the input fn. Use the entire dataset for a batch since this is such a small dataset.
def make_input_fn(X, y, n_epochs=None, do_batching=True):
def input_fn():
BATCH_SIZE = len(y) # Use entire dataset.
dataset = tf.data.Dataset.from_tensor_slices((X.to_dict(orient='list'), y))
# For training, cycle thru dataset as many times as need (n_epochs=None).
dataset = dataset.repeat(n_epochs)
if do_batching:
dataset = dataset.batch(BATCH_SIZE)
return dataset
return input_fn
# + [markdown] colab_type="text" id="DMwL7qlrAdWk"
# # Training and Evaluating Classifiers
# + colab={} colab_type="code" id="pBhdfNzXjAsT"
TRAIN_SIZE = len(dftrain)
params = {
'n_trees':10,
'center_bias':False,
'l2_regularization':1./TRAIN_SIZE # regularization is per instance, so if you are familiar with XGBoost, you need to divide these values by the num of examples per layer
}
# -
# Exercise: Train a Boosted Trees model using tf.estimator. What are the best results you can get?
# + [markdown] colab_type="text" id="hw4avA1R23dL"
# Train and evaluate the model. We will look at accuracy first.
#
# + colab={"base_uri": "https://localhost:8080/", "height": 852} colab_type="code" id="GsMoeNiEHlox" outputId="ac640831-a46a-4c6a-b901-6663aa9f2ee9"
# Training and evaluation input functions.
n_batches_per_layer = 1 # Use one batch, consisting of the entire dataset to build each layer in the tree.
DO_BATCHING = True
train_input_fn = make_input_fn(dftrain, y_train, n_epochs=None, do_batching=DO_BATCHING)
eval_input_fn = make_input_fn(dfeval, y_eval, n_epochs=1, do_batching=DO_BATCHING)
est = # TODO
est.train(train_input_fn)
# Eval.
pd.Series(est.evaluate(eval_input_fn))
# + [markdown] colab_type="text" id="eE1xyZrt285E"
# Exercise #2: Can you get better performance out of the classifier? How do the results compare to using a DNN? Accuracy and AUC?
# + [markdown] colab_type="text" id="fDNzuC0xUstP"
# # Results
# + [markdown] colab_type="text" id="d_iUYaTq2ZgL"
# Let's understand how our model is performing.
# + colab={"height": 289} colab_type="code" id="kgds_rmq2_2t" outputId="931df046-e7fe-4e7e-9680-5106a40265ad"
pred_dicts = list(est.predict(eval_input_fn))
probs = pd.Series([pred['probabilities'][1] for pred in pred_dicts])
probs.plot(kind='hist', bins=20, title='predicted probabilities');
# + [markdown] colab_type="text" id="jq-CPquY-bG3"
# **???** Why are the probabilities right skewed?
# + [markdown] colab_type="text" id="qrvEyh4Q3YgC"
# Let's plot an ROC curve to understand model performance for various predicition probabilities.
# + colab={"height": 307} colab_type="code" id="ByhMg-_a3K_q" outputId="f02d1b06-cc0a-43ac-b95e-3e9192a59099"
from sklearn.metrics import roc_curve
from matplotlib import pyplot as plt
fpr, tpr, _ = roc_curve(y_eval, probs)
plt.plot(fpr, tpr)
plt.title('ROC curve')
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.xlim(0,)
plt.ylim(0,);
# + [markdown] colab_type="text" id="9HKAt75V3O8E"
# **???** What does true positive rate and false positive rate refer to for this dataset?
# -
# Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
courses/machine_learning/deepdive/supplemental_gradient_boosting/labs/b_boosted_trees_estimator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python38-azureml
# kernelspec:
# display_name: 'Python 3.8.8 64-bit (''anaconda3'': virtualenv)'
# name: python388jvsc74a57bd0dce69896fdb445434427c12e791455610f9ef8e6bb07ea975426634cd43b3db3
# ---
# + gather={"logged": 1620059809458}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import re
# preproccess
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_selection import GenericUnivariateSelect, chi2
# utils
from sklearn.model_selection import cross_validate
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import confusion_matrix
from sklearn.metrics import plot_confusion_matrix
# ML model
from sklearn.dummy import DummyClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import LinearSVC
# -
# load raw data csv files
"""
attributes: name, n_steps, n_ingredients, steps, ingredients
"""
df_train = pd.read_csv("datasets/recipe_train.csv")
df_test = pd.read_csv("datasets/recipe_test.csv")
def preprocess(df):
arr_ingr = df['ingredients'].copy().to_numpy()
arr_steps = df['steps'].copy().to_numpy()
arr_name = df['name'].copy().to_numpy()
_RE_COMBINE_WHITESPACE = re.compile(r"\s+")
## remove all puntuation
for i in range(len(arr_steps)):
arr_steps[i] = re.sub(r'[^\w\s]', '', str(arr_steps[i]))
arr_steps[i] = _RE_COMBINE_WHITESPACE.sub(" ", arr_steps[i]).strip() + ' '
arr_ingr[i] = re.sub(r'[^\w\s]', '', str(arr_ingr[i]))
arr_ingr[i] = _RE_COMBINE_WHITESPACE.sub(" ", arr_ingr[i]).strip() + ' '
arr_name[i] = re.sub(r'[^\w\s]', '', str(arr_name[i]))
arr_name[i] = _RE_COMBINE_WHITESPACE.sub(" ", arr_name[i]).strip()
# combined all three features
X = arr_steps + arr_ingr + arr_name
return X
# Preprocessing:
# 1) Load the raw data
# 2) Transform them to 'trainable' data
# 3) Feature selection
# +
X = preprocess(df_train)
y = df_train['duration_label']
# include both uni-grams and bi-grams
# exclude stop words
vectorizer = TfidfVectorizer(sublinear_tf=True, ngram_range=(1,2), analyzer='word', stop_words= 'english')
X = vectorizer.fit_transform(X)
print("Shape of X (nrow, ncol):", X.shape)
# +
# plot p-values before feature selection
chi_square, p_values = chi2(X, y)
plt.hist(p_values, edgecolor = 'black', bins=100)
plt.xlabel('p-value')
plt.ylabel('frequency')
plt.title("p-values of features (before selection)")
plt.xticks(np.arange(0,1.1,0.1))
plt.show()
# plot p-values after feature selection
fselect = GenericUnivariateSelect(chi2, mode='percentile', param=20)
X_new = fselect.fit_transform(X, y)
chi_square, p_values = chi2(X_new, y)
plt.hist(p_values, edgecolor = 'black', bins=100)
plt.xlabel('p-value')
plt.ylabel('frequency')
plt.title("p-values of features (after selection)")
plt.xticks(np.arange(0,1.1,0.1))
plt.show()
print("Shape of X_new (nrow, ncol):", X_new.shape)
# -
# Hyperparameter tuning
def hyperparameter_tuning(grid, model, X, y):
# define grid search
grid_search = GridSearchCV(estimator=model, param_grid=grid, n_jobs=-1, return_train_score=True)
grid_result = grid_search.fit(X, y)
# summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
train_means = grid_result.cv_results_['mean_train_score']
test_means = grid_result.cv_results_['mean_test_score']
test_stdvs = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
train_results = []
test_results = []
test_vars = []
for train_mean, test_mean, test_stdv, param in zip(train_means, test_means, test_stdvs, params):
if train_mean != 0 and test_mean != 0:
train_results.append(train_mean)
test_results.append(test_mean)
test_vars.append(test_stdv**2)
#print("%f (%f) with: %r" % (mean, stdev, param))
return train_results, test_results, test_vars
dc = DummyClassifier()
baseline = sum(cross_validate(dc, X_new, y, cv=5)['test_score'])/5
print("Baseline accuracy:", baseline)
# +
# Logistic Regression
lg = LogisticRegression(max_iter=1000)
c_values = [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1.0, 5.0, 10.0, 15.0, 20.0]
grid = dict(C=c_values)
train_results_lg, test_results_lg, test_vars_lg = hyperparameter_tuning(grid, lg, X_new, y)
plt.grid()
plt.plot(c_values, train_results_lg, label='Train', marker='o')
plt.plot(c_values, test_results_lg, label='Test', marker='o')
plt.axhline(y=baseline, color='r', linestyle='--', label='zero-r baseline')
plt.title('Logistic regression')
plt.xlabel('Inverse of regularization strength')
plt.ylabel('Accuracy mean')
plt.legend()
plt.plot()
print("Train accuracy:", train_results_lg)
print("Test accuracy:", test_results_lg)
print("Test variance:", test_vars_lg)
# +
# Decision Tree
dt = DecisionTreeClassifier()
max_depths = [1, 5, 10, 15, 20, 25, 50, 100, 200]
grid = dict(max_depth=max_depths)
train_results_dt, test_results_dt, test_vars_dt = hyperparameter_tuning(grid, dt, X_new, y)
plt.grid()
plt.plot(max_depths, train_results_dt, label='Train', marker='o')
plt.plot(max_depths, test_results_dt, label='Test', marker='o')
plt.axhline(y=baseline, color='r', linestyle='--', label='zero-r baseline')
plt.title('Decision Tree')
plt.xlabel('Max depth of tree')
plt.ylabel('Accuracy mean')
plt.legend()
plt.plot()
print("Train accuracy:", train_results_dt)
print("Test accuracy:", test_results_dt)
print("Test variance:", test_vars_dt)
# +
# Linear SVM
lsvm = LinearSVC()
c_values = [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1.0, 5.0, 10.0, 15.0, 20.0]
grid = dict(C = c_values)
train_results_lsvm, test_results_lsvm, test_vars_lsvm = hyperparameter_tuning(grid, lsvm, X_new, y)
plt.grid()
plt.plot(c_values, train_results_lsvm, label='Train', marker='o')
plt.plot(c_values, test_results_lsvm, label='Test', marker='o')
plt.axhline(y=baseline, color='r', linestyle='--', label='zero-r baseline')
plt.xlabel('Regularization parameter')
plt.ylabel('Accuracy mean')
plt.title('Linear SVC')
plt.legend()
plt.plot()
print("Train accuracy:", train_results_lsvm)
print("Test accuracy:", test_results_lsvm)
print("Test variance:", test_vars_lsvm)
# -
# Evaluation: Confusion matrix
X_train, X_test, y_train, y_test = train_test_split(X_new, y, random_state=42)
lg = LogisticRegression(max_iter=1000, C=15.0)
lg.fit(X_train, y_train)
plot_confusion_matrix(lg, X_test, y_test)
plt.title('Logistic Regression')
plt.show()
dt = DecisionTreeClassifier(max_depth=10)
dt.fit(X_train, y_train)
plot_confusion_matrix(dt, X_test, y_test)
plt.title('Decision Tree')
plt.show()
lsvm = LinearSVC(C=1.0)
lsvm.fit(X_train, y_train)
plot_confusion_matrix(lsvm, X_test, y_test)
plt.title('Linear SVM')
plt.show()
# Output results
# +
X_train = preprocess(df_train)
X_test = preprocess(df_test)
y_train = df_train['duration_label']
X = np.concatenate((X_train, X_test), axis=0)
# transform into sparse
vectorizer = TfidfVectorizer(sublinear_tf=True, ngram_range=(1,2))
vectorizer.fit(X)
X_train = vectorizer.transform(X_train)
X_test = vectorizer.transform(X_test)
# feature selection
fselect = GenericUnivariateSelect(chi2, mode='percentile', param=20)
fselect.fit(X_train, y_train)
X_train_new = fselect.transform(X_train)
X_test_new = fselect.transform(X_test)
# +
# logistic regression
lg = LogisticRegression(max_iter=1000, C=15.0)
lg.fit(X_train_new, y_train)
predicts = lg.predict(X_test_new)
ids = np.array(range(len(predicts))) + 1
output = pd.DataFrame({'id': ids, 'duration_label': predicts})
output.to_csv('output/output_lg.csv', index=False)
# +
# decision tree
dt = DecisionTreeClassifier(max_depth=10)
dt.fit(X_train_new, y_train)
predicts = dt.predict(X_test_new)
ids = np.array(range(len(predicts))) + 1
output = pd.DataFrame({'id': ids, 'duration_label': predicts})
output.to_csv('output/output_dt.csv', index=False)
# +
# linear svm
lsvm = LinearSVC(C=1.0)
lsvm.fit(X_train_new, y_train)
predicts = lsvm.predict(X_test_new)
ids = np.array(range(len(predicts))) + 1
output = pd.DataFrame({'id': ids, 'duration_label': predicts})
output.to_csv('output/output_lsvm.csv', index=False)
# -
|
project-2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Build an autoencoder for dimensionaltiy reduction
#
# Model attributes: use dataset API to avoid feed dict
import tensorflow as tf
from tensorflow.data import Dataset as Ds
import pandas as pd
import numpy as np
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
data = pd.read_csv('/Users/dawnstear/desktop/chop_cellpred/data.csv')
print(np.shape(data))
# +
np.random.seed(42)
data = shuffle(data)
celltypes = data['TYPE'] # save cell type vector in case we need it later
labels = data['Labels'] # save labels
data_ = data.drop(['Labels','TYPE'],axis=1) # Take off types & labels for input (AE is unsupervised)
cellcount, genecount = np.shape(data_)
BUFFER = 55 # .shuffle(BUFFER), already shuffled
BATCH_SIZE = 50
X_train, X_test, y_train, y_test = train_test_split(data_.values,labels.values,test_size=0.2,random_state=144)
# Create dataset to avoid using feed_dict() (its very slow)
train_dataset = Ds.from_tensor_slices((X_train)).repeat().batch(BATCH_SIZE)
test_dataset = Ds.from_tensor_slices((X_test)).repeat().batch(BATCH_SIZE)
# Create general iterator, seamlessly switch bt train data and test data sets
iterator = tf.data.Iterator.from_structure(train_dataset.output_types,train_dataset.output_shapes)
# This will return a tuple where next_element[0] = data, if we have labels [via .zip], next_element[1] = labels
next_element = iterator.get_next()
# Make datasets that we can initialize separately, but using the same structure via the common iterator
training_init_op = iterator.make_initializer(train_dataset)
testing_init_op = iterator.make_initializer(test_dataset)
# do we need to normalize/regularize or do batch correction ?
# +
# Vanilla AUTOENCODER model adapted from:
# Author: <NAME>
# Project: https://github.com/aymericdamien/TensorFlow-Examples/
# Training Parameters
learning_rate = 0.01
num_steps = 30000
batch_size = 256
display_step = 1000
examples_to_show = 10
# Network Parameters
num_hidden_1 = 256 # 1st layer num features
num_hidden_2 = 128 # 2nd layer num features (the latent space aka # of dimensions we've reduced to)
num_input = genecount # number of features per cell sample
# Define weights & biases
weights = {
'encoder_h1': tf.Variable(tf.random_normal([num_input, num_hidden_1])),
'encoder_h2': tf.Variable(tf.random_normal([num_hidden_1, num_hidden_2])),
'decoder_h1': tf.Variable(tf.random_normal([num_hidden_2, num_hidden_1])),
'decoder_h2': tf.Variable(tf.random_normal([num_hidden_1, num_input])),
}
biases = {
'encoder_b1': tf.Variable(tf.random_normal([num_hidden_1])),
'encoder_b2': tf.Variable(tf.random_normal([num_hidden_2])),
'decoder_b1': tf.Variable(tf.random_normal([num_hidden_1])),
'decoder_b2': tf.Variable(tf.random_normal([num_input])),
}
# +
# Building the encoder
def encoder(expression_matrix): # what to add to this fcn?
# Perform "exponential linear unit" activation fcn on X*W + b
layer_1 = tf.nn.elu(tf.add(tf.matmul(expression_matrix, weights['encoder_h1']), biases['encoder_b1']))
layer_2 = tf.nn.elu(tf.add(tf.matmul(layer_1, weights['encoder_h2']),biases['encoder_b2']))
return layer_2
# Building the decoder
def decoder(latent_space):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(latent_space, weights['decoder_h1']),biases['decoder_b1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h2']),biases['decoder_b2']))
return layer_2
# Construct model
encoder_op = encoder(tf.cast(next_element,tf.float32)) # cast expression matrix to float32
decoder_op = decoder(encoder_op)
# +
# Prediction
y_pred = decoder_op
# Targets (Labels) are the input data.
y_true = tf.cast(next_element,tf.float32)
# Define loss and optimizer, minimize the mean squared error
loss = tf.reduce_mean(tf.pow(y_true - y_pred, 2))
optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(loss)
# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()
# -
# Start Training
with tf.Session() as sess:
# Run the initializer
sess.run(init)
# Run Data.dataset iterator initializer
sess.run(training_init_op) # reset weights each time ? if train flag == 1
# Training
for i in range(1, num_steps+1):
# Prepare Data
# Get the next batch of MNIST data (only images are needed, not labels)
# batch_x, _ = mnist.train.next_batch(batch_size)
# Run optimization op (backprop) and cost op (to get loss value)
_, l = sess.run([optimizer, loss], feed_dict={X: batch_x})
# Display logs per step
if i % display_step == 0 or i == 1:
print('Step %i: Minibatch Loss: %f' % (i, l))
|
Autoencoder_v2.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.3.0
# language: julia
# name: julia-1.3
# ---
# +
function parse_map(input)
H = length(input)
W = length(input[1])
map = zeros(Bool, (H,W))
asteroids = []
for j = 1:H
for k = 1:W
if input[j][k] == '#'
map[j,k] = true
push!(asteroids, (k,j))
end
end
end
return map, asteroids
end
function parse_map_X(input)
H = length(input)
W = length(input[1])
println(H, W)
map = zeros(Bool, (H,W))
asteroids = []
xpos = (0,0)
for j = 1:H
for k = 1:W
if input[j][k] == '#'
map[j,k] = true
push!(asteroids, (k,j))
end
if input[j][k] == 'X'
print("found")
xpos = (k,j)
end
end
end
return map, asteroids, xpos
end
function count_map(asteroids, counts, map)
cmap = zeros(Int, size(map))
for (j,a) = enumerate(asteroids)
cmap[a[2],a[1]] = counts[j]
end
return cmap
end
function count_visible(asteroids)
N = length(asteroids)
θs = []
for j = 1:N
xc, yc = asteroids[j]
θ = []
for a = asteroids[1:N .!= j]
x,y = a
push!(θ, atan(y-yc,x-xc))
end
push!(θs, θ)
end
return [length(Set(x)) for x in θs]
end
function get_best(asteroids, count)
best = maximum(count)
pos = asteroids[argmax(count)]
return best, (pos[1]-1, pos[2]-1)
end
# -
input = """.#..#
.....
#####
....#
...##"""
map, asteroids = parse_map(split(input, '\n'))
cnt = count_visible(asteroids)
count_map(asteroids, cnt, map)
input = """......#.#.
#..#.#....
..#######.
.#.#.###..
.#..#.....
..#....#.#
#..#....#.
.##.#..###
##...#..#.
.#....####"""
map, asteroids = parse_map(split(input, '\n'))
cnt = count_visible(asteroids)
count_map(asteroids, cnt, map)
get_best(asteroids, cnt)
input = """#.#...#.#.
.###....#.
.#....#...
##.#.#.#.#
....#.#.#.
.##..###.#
..#...##..
..##....##
......#...
.####.###."""
map, asteroids = parse_map(split(input, '\n'))
cnt = count_visible(asteroids)
count_map(asteroids, cnt, map)
get_best(asteroids, cnt)
input = """.#..#..###
####.###.#
....###.#.
..###.##.#
##.##.#.#.
....###..#
..#.#..#.#
#..#.#.###
.##...##.#
.....#.#.."""
map, asteroids = parse_map(split(input, '\n'))
cnt = count_visible(asteroids)
count_map(asteroids, cnt, map)
get_best(asteroids, cnt)
convert(a) = (a[1]-1, a[2]-1)
input = """.#..##.###...#######
##.############..##.
.#.######.########.#
.###.#######.####.#.
#####.##.#.##.###.##
..#####..#.#########
####################
#.####....###.#.#.##
##.#################
#####.##.###..####..
..######..##.#######
####.##.####...##..#
.#####..#.######.###
##...#.##########...
#.##########.#######
.####.#.###.###.#.##
....##.##.###..#####
.#.#.###########.###
#.#.#.#####.####.###
###.##.####.##.#..##"""
map, asteroids = parse_map(split(input, '\n'))
cnt = count_visible(asteroids)
count_map(asteroids, cnt, map)
max, pos = get_best(asteroids, cnt)
print("Best $(max) at $(pos)")
c = (pos[1]+1, pos[2]+1)
v = vaporize(asteroids, c);
v[200]
input = readlines("./inputs/day10.txt")
map, asteroids = parse_map(input);
cnt = count_visible(asteroids)
count_map(asteroids, cnt, map)
best_visible, pos = get_best(asteroids, cnt)
c = (pos[1]+1, pos[2]+1)
v = vaporize(asteroids, c);
v[200][1]*100 + v[200][2]
# +
struct Asteroid
angle::Float64
distance::Float64
start::Tuple{Int,Int}
pos::Tuple{Int,Int}
end
function Asteroid(a::Tuple{Int,Int}, c::Tuple{Int,Int})
θ = mod2pi(pi/2 + atan(a[2]-c[2],a[1]-c[1]))
d = sqrt((a[1]-c[1])^2 + (a[2]-c[2])^2)
return Asteroid(θ, d, c, a)
end
function vaporize(asteroids, c)
N = length(asteroids)
aa = [Asteroid(a, c) for a in asteroids if a != c]
sort!(aa)
for a in aa
#println(a)
end
used_angles = []
vo = []
for a in aa
if a.angle in used_angles
continue
else
push!(used_angles, a.angle)
push!(vo, convert(a.pos))
end
end
return vo
end
# -
import Base: isless
function isless(a::Asteroid, b::Asteroid)
if a.angle == b.angle
return isless(a.distance, b.distance)
else
return isless(a.angle, b.angle)
end
end
input = """
.#....#####...#..
##...##.#####..##
##...#...#.#####.
..#.....X...###..
..#.#.....#....##"""
map, asteroids,xpos = parse_map_X(split(input, '\n'))
vaporize(asteroids, xpos)
|
Day10.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Final Project DL model Notebook - sinple CNN model with two convolutional layers - v02 - load from existing weights
#
# using this notebook to validate performance of the model
# #### imports, settings and constants
# run log:
#
# - local
# - sample data set
# - using trained network
# +
import sys
from keras.models import load_model
import numpy as np
from pathlib import Path
sys.path.append(str(Path.cwd().parent))
from utils import *
current_dir = Path.cwd()
HOME_DIR = current_dir.parent
DATA_DIR = HOME_DIR.joinpath('data')
MODEL_PATH = HOME_DIR.joinpath('savedModels/30122017/CNN_two_convs_30122017_1700.h5')
# comment out one of the two path options to toggle between sample directory and all data
# path = DATA_DIR
path = DATA_DIR.joinpath('sample')
val_path = path.joinpath('valid')
test_path = path.joinpath('test')
# general variables
batch_size = 64
# make sure that plotted images show up in the notebook
# %matplotlib inline
# -
# #### defining CNN model
model = load_model(MODEL_PATH)
model.summary()
# #### test performance and plot confusion matrix on one sample batch of 200 images
val_batches = get_in_batches(val_path, shuffle=False, class_mode=None, batch_size=200)
pred_classes = model.predict_generator(val_batches, 1)
pred_classes = np.argmax(pred_classes, axis=1)
act_classes = val_batches.classes
cm = confusion_matrix(act_classes, pred_classes)
plot_confusion_matrix(cm, val_batches.class_indices)
plt.figure()
plt.show()
# #### validating the model performance on the val set
#
# Running the evaluate generator returns the cost and accuracy of the model. Doing it in a loop allows us to confirm that the performance is stable. Results should be very similar for all runs. Fixed issue that was causing slow performance by changing second parameter of evaluate_generator to 1.
rnd_batches = get_in_batches(val_path, batch_size=batch_size, shuffle=True)
val_res = [model.evaluate_generator(rnd_batches, 1) for i in range(10)]
np.round(val_res, 3)
# #### now we manually load a handful of images from the test set and output the prediction on them
test_batches = get_in_batches(test_path, batch_size=4, class_mode=None)
imgs = test_batches.next()
plots(imgs)
prediction = model.predict(imgs)
np.round(prediction, 3)
|
nbs/finalProjectModelNotebook_CNN_two_convs_validate.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _uuid="0726e5c87066fe363f995135fead5f8dcff3522f"
#
# It is the kernel that I have tried and compiled from the courses of [DATAI Team](https://www.udemy.com/user/datai-team/) (Language of the courses is Turkish: [Python: Sıfırdan Uzmanlığa Programlama (1)](https://www.udemy.com/python-sfrdan-uzmanlga-programlama-1/)), which is [Grandmaster on Kaggle](https://www.kaggle.com/kanncaa1) and has more than 15 courses on Udemy.
#
#
# # **Content**
#
#
# 1. [Python Basics](#1.)
# * [variable](#2.)
# * [user defined functions](#3.)
# * [default ve flexible functions](#4.)
# * [lambda function](#5.)
# * [nested function](#6.)
# * [anonymous function](#7.)
# * [list](#8.)
# * [tuple](#9.)
# * [dictionary](#10.)
# * [conditionals](#11.)
# * [loops](#12.)
# 1. [Object Oriented Programming](#13.)
# * [class](#14.)
# 1. [Numpy](#15.)
# * [basic operations](#16.)
# * [indexing and slicing](#17.)
# * [shape manipulation](#18.)
# * [convert and copy](#19.)
# 1. [Pandas](#20.)
# * [indexing and slicing](#21.)
# * [filtering](#22.)
# * [list comprehension](#23.)
# * [drop and concatenating](#24.)
# * [transforming data](#25.)
# * [iteration example](#26.)
# * [zip example](#27.)
# * [example of list comprehension](#28.)
# 1. [Visualization with Matplotlib](#29.)
# * [line Plot example](#30.)
# * [scatter plot](#31.)
# * [histogram](#32.)
# * [bar plot](#33.)
# * [subplots](#34.)
#
#
#
# + [markdown] _uuid="1cfe3918efa29ed5e7a24f0bc0b798ecfb153908"
#
# <a class="anchor" id="1."></a>
# # 1.Python Basics
# -
# <a class="anchor" id="2."></a>
# ## variable
# + _uuid="da84d0f4479714306fd089d16c2c3220866634b3"
var1 = 10 # integer = int
ay = "temmuz"
var3 = 10.3 # double (float)
s = "<NAME>"
variable_type = type(s) # str = string
print(variable_type)
# -
#
# <a class="anchor" id="3."></a>
# ## user defined functions
# + _uuid="6c6305e553e4c0eb6fee26c421b6148e22a9233b"
def benim_ilk_func(a,b):
"""
bu benim ilk denemem
parametre:
return:
"""
output = (((a+b)*50)/100.0)*a/b
return output
print(benim_ilk_func(20,50))
# -
#
#
# <a class="anchor" id="4."></a>
# ## default ve flexible functions
# + _uuid="a2cc21033e5f0fa81fc4ae493b05ff8bd32456c1"
# %%
# default f: cemberin cevre uzunlugu = 2*pi*r
def cember_cevresi_hesapla(r,pi=3.14):
"""
cember cevresi hesapla
input(parametre): r,pi
output = cemberin cevresi
"""
output = 2*pi*r
return output
# flexible
def hesapla(boy,kilo,*args):
print(args)
output = (boy+kilo)*args[0]
return output
print(cember_cevresi_hesapla(5))
print(hesapla(5,5,10,20,30,40))
# -
#
# <a class="anchor" id="5."></a>
# ## lambda function
# + _uuid="1963a06e2cb324ccfe683e6a0227f62edc1fa982"
def hesapla(x):
return x*x
print(hesapla(3))
sonuc2 = lambda x: x*x
print(sonuc2(3))
# -
# <a class="anchor" id="6."></a>
# ## nested function
# + _uuid="e929a47c4cf672cabd0de094428d0fc7e8e717eb"
def square():
""" return square of value """
def add():
""" add two local variable """
x = 2
y = 3
z = x + y
return z
return add()**2
print(square())
# -
#
# <a class="anchor" id="7."></a>
# ## anonymous function
# + _uuid="2ef03fd0e106debfe79ae63614b7726c5f25129e"
number_list = [1,2,3]
y = map(lambda x:x**2,number_list)
print(list(y))
# -
#
# <a class="anchor" id="8."></a>
# ## list
# + _uuid="5f315d09290b9b09f6012bde9d2e5a8e99c8350d"
liste = [1,2,3,4,5,6]
print(type(liste))
liste_str = ["ptesi","sali","cars"]
print(type(liste_str))
print(liste[1])
print(liste[-1])
print(liste[0:3])
liste.append(7)
print(liste)
liste.remove(7)
print(liste)
liste.reverse()
print(liste)
liste2 = [1,5,4,3,6,7,2]
liste2.sort()
print(liste2)
string_int_liste = [1,2,3,"aa","bb"]
# -
#
# <a class="anchor" id="9."></a>
# ## tuple
# + _uuid="e70c8899488e4d9d9c1a7858d92d75710724bdb5"
t = (1,2,3,3,4,5,6)
print(t.count(5))
print(t.index(3))
# -
#
# <a class="anchor" id="10."></a>
# ## dictionary
# + _uuid="00d89b391f1587392774aa0043ca8f6b26e9cbfd"
def deneme():
dictionary = {"ali":32,"veli":45,"ayse":13}
# ali ,veli ,ayse = keys
# 32,45,13 = values
return dictionary
dic = deneme()
print(dic)
dictionary = {'spain' : 'madrid','usa' : 'vegas'}
print(dictionary.keys())
print(dictionary.values())
dictionary['spain'] = "barcelona" # update existing entry
print(dictionary)
dictionary['france'] = "paris" # Add new entry
print(dictionary)
del dictionary['spain'] # remove entry with key 'spain'
print(dictionary)
print('france' in dictionary) # check include or not
dictionary.clear() # remove all entries in dict
print(dictionary)
# -
#
# <a class="anchor" id="11."></a>
# ## conditionals
# + _uuid="cb5c75dfa001889eec612343e4e3da4c208215b5"
# if else statement
var1 = 10
var2 = 20
if(var1 > var2):
print("var1 buyuktur var2")
elif(var1 == var2):
print("var and var2 esitler")
else:
print("var1 kucuktur var2")
liste = [1,2,3,4,5]
value = 3
if value in liste:
print("evet {} degeri listenin icinde".format(value))
else:
print("hayir")
dictionary = {"ali":32,"veli":45,"ayse":13}
keys = dictionary.keys()
if "veli" in keys:
print("evet")
else:
print("hayir")
# -
#
# <a class="anchor" id="12."></a>
# ## loops
# + _uuid="513cb111770a99cc966e434a2df1a71fef9b0669"
# for loop
for each in range(1,3):
print(each)
for each in "ank ist":
print(each)
for each in "ank ist".split():
print(each)
liste = [1,4,5,6,8,3,3,4,67]
print(sum(liste))
count = 0
for each in liste:
count = count + each
print(count)
# while loop
i = 0
while(i <4):
print(i)
i = i + 1
# + [markdown] _uuid="c1efd8997599b1d3a2d0a374b60acd98df69c486"
#
# <a class="anchor" id="13."></a>
# # 2.Object Oriented Programming
# -
#
# <a class="anchor" id="14."></a>
# ## class
# + _uuid="56247293c183c8d3f93f9375fc952bfce5e4058b"
class Calisan:
zam_orani = 1.8
counter = 0
def __init__(self,isim,soyisim,maas): # constructor
self.isim = isim
self.soyisim = soyisim
self.maas = maas
self.email = isim+soyisim+"@asd.<EMAIL>"
Calisan.counter = Calisan.counter + 1
def giveNameSurname(self):
return self.isim +" " +self.soyisim
def zam_yap(self):
self.maas = self.maas + self.maas*self.zam_orani
# class variable
calisan1 = Calisan("ali", "veli",100)
print("giveNameSurname: ",calisan1.giveNameSurname())
print("maas: ",calisan1.maas)
calisan1.zam_yap()
print("yeni maas: ",calisan1.maas)
# class example
calisan2 = Calisan("ayse", "hatice",200)
calisan3 = Calisan("ayse", "yelda",600)
liste = [calisan1,calisan2,calisan3]
maxi_maas = -1
index = -1
for each in liste:
if(each.maas>maxi_maas):
maxi_maas = each.maas
index = each
print(maxi_maas)
print(index.giveNameSurname())
# + [markdown] _uuid="0ab73690a51b50488b6e2923257c4d4f50736fb6"
#
# <a class="anchor" id="15."></a>
# # 3.Numpy
# + _uuid="3c79ef6f1ae2d9dbdc409723ba06af91ab741fbc"
# importing
import numpy as np
# numpy basics
array = np.array([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]) # 1*15 vector
print(array.shape)
a = array.reshape(-1,1)
print("shape: ",a.shape)
print("dimension: ", a.ndim)
print("data type: ",a.dtype.name)
print("size: ",a.size)
print("type: ",type(a))
array1 = np.array([[1,2,3,4],[5,6,7,8],[9,8,7,5]])
print(array1)
zeros = np.zeros((3,4))
zeros[0,0] = 5
print(zeros)
print(np.ones((3,4)))
print(np.empty((2,3)))
a = np.arange(10,50,5) # 10 dan 50 ye 5er 5 er artır
print(a)
a = np.linspace(10,50,5) #10 50 ye 5 tane yerleştir
print(a)
# -
#
#
# <a class="anchor" id="16."></a>
# ## basic operations
# + _uuid="092d482355b4507b48f04a51f76c7c6ddc2c889b"
a = np.array([1,2,3])
b = np.array([4,5,6])
print(a+b)
print(a-b)
print(a**2)
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[1,2,3],[4,5,6]])
# element wise prodcut
print(a*b)
# matrix prodcut
print(a.dot(b.T))
a = np.random.random((2,2)) # 2 2 lık 0-1 arasında sayı uretiyor
print(a.sum())
print(a.max())
print(a.min())
print(a.sum(axis=0)) # sutunları topla
print(a.sum(axis=1)) # satırları topla
print(np.sqrt(a))
print(np.square(a)) # a**2
print(np.add(a,a))
# -
#
# <a class="anchor" id="17."></a>
# ## indexing and slicing
# + _uuid="6d25f2b499560986d82e12ac1fe4431e497bcade"
import numpy as np
array = np.array([1,2,3,4,5,6,7]) # vector dimension = 1
print(array[0])
print(array[0:4])
reverse_array = array[::-1]
print(reverse_array)
array1 = np.array([[1,2,3,4,5],[6,7,8,9,10]])
print(array1[1,1]) # 1 satır 1 sutun 7
print(array1[:,1]) # tum satır 1 sutun 2,7
print(array1[1,1:4]) # 1 satır 1-4 sutun 7-8-9
print(array1[-1,:]) #son satırın tum sutunları
print(array1[:,-1]) # tum satırların son sutunu 5,10
# -
#
# <a class="anchor" id="18."></a>
# ## shape manipulation
# + _uuid="1f32a201c7f1ccb512fae53289b9b198e37ef105"
array = np.array([[1,2,3],[4,5,6],[7,8,9]])
# flatten
array1 = array.ravel() # duz hale getırıldı
print(array1)
array2 = array1.reshape(3,3) # matrıse cevır
print(array2)
# %% stacking arrays
array1 = np.array([[1,2],[3,4]])
array2 = np.array([[-1,-2],[-3,-4]])
# veritical
#array([[1, 2],
# [3, 4]])
#array([[-1, -2],
# [-3, -4]])
array3 = np.vstack((array1,array2))
print(array3)
# horizontal
#array([[1, 2],[-1, -2],
# [3, 4]],[-3, -4]]
array4 = np.hstack((array1,array2))
print(array4)
# -
#
# <a class="anchor" id="19."></a>
# ## convert and copy
# + _uuid="e5c51e86355b8155f8455a2cac4a2ae3fb67a07b"
liste = [1,2,3,4] # list
array = np.array(liste) #np.array
liste2 = list(array) # list
a = np.array([1,2,3])
b = a
b[0] = 5
print(b[0])
print(a[0]) # a da degıstı
d = np.array([1,2,3])
e = d.copy()
d[0] = 5
print(d[0])
print(e[0]) # e da degısmedi
# + [markdown] _uuid="27ea0c3c2dc2bdde3d24c1a25c9740d07b1eacb5"
#
# <a class="anchor" id="20."></a>
# # 4.Pandas
# + _uuid="cde13ac6290d7a4349b7006b78afe23f434740db"
import pandas as pd
dictionary = {"NAME":["ali","veli","kenan","hilal","ayse","evren","isim1","isim2","isim3"],
"AGE":[15,16,17,33,45,66,70,70,70],
"MAAS": [100,150,240,350,110,220,300,300,300]}
dataFrame1 = pd.DataFrame(dictionary)
print(dataFrame1.head()) # ilk 5 kısım, içerindeki görmek için
print(dataFrame1.tail()) # sondaki 5 tane
# + _uuid="808748687e9dbd5df59942ce93f847053ff6e5d5"
# pandas basic method
print(dataFrame1.columns)
print("------")
print(dataFrame1.info())
print("------")
print(dataFrame1.dtypes)
print("------")
print(dataFrame1.describe()) # numeric feature = columns (age,maas)
# -
#
# <a class="anchor" id="21."></a>
# ## indexing and slicing
# + _uuid="f1f3602dd3c895e42b132fa98ce115c41c931010"
print(dataFrame1["AGE"])
print(dataFrame1.AGE)
dictionary = {"NAME":["ali","veli","kenan",],
"AGE":[15,16,17,],
"MAAS": [100,150,240]}
dataFrame1 = pd.DataFrame(dictionary)
dataFrame1["yeni_feature"] = [-1,-2,-3]
print("---1---")
print(dataFrame1.loc[:, "AGE"])
print("---2---")
print(dataFrame1.loc[:1, "AGE"])
print("---3---")
print(dataFrame1.loc[:1, "AGE":"NAME"])
print("---4---")
print(dataFrame1.loc[:1, ["AGE","NAME"]])
print("---5---")
print(dataFrame1.loc[::-1,:]) #ters yazdı
print("---6---")
print(dataFrame1.loc[:,:"NAME"])
print("---7---")
print(dataFrame1.loc[:,"NAME"])
print("---8---")
print(dataFrame1.iloc[:,2]) #i integer location name yerıne sutun ındexı verdık
# -
#
# <a class="anchor" id="22."></a>
# ## filtering
# + _uuid="349b2efb9a38b68f05f0a3667dd99cc3eb04d7b4"
dictionary = {"NAME":["ali","veli","kenan","hilal","ayse","evren"],
"AGE":[15,16,17,33,45,66],
"MAAS": [100,150,240,350,110,220]}
dataFrame1 = pd.DataFrame(dictionary)
filtre1 = dataFrame1.MAAS > 200
print(filtre1)
filtrelenmis_data = dataFrame1[filtre1]
print(filtrelenmis_data)
filtre2 = dataFrame1.AGE <20
dataFrame1[filtre1 & filtre2]
print(dataFrame1[dataFrame1.AGE > 60])
# -
#
# <a class="anchor" id="23."></a>
# ## list comprehension
# + _uuid="547721af11c24798a31f3b851879a1d035bea167"
import numpy as np
dataFrame1 = pd.DataFrame(dictionary)
ortalama_maas = dataFrame1.MAAS.mean()
# ortalama_maas_np = np.mean(dataFrame1.MAAS)
dataFrame1["maas_seviyesi"] = ["dusuk" if ortalama_maas > each else "yuksek" for each in dataFrame1.MAAS]
print(dataFrame1)
print(dataFrame1.columns)
dataFrame1.columns = [ each.lower() for each in dataFrame1.columns]
print(dataFrame1.columns)
dataFrame1.columns = [each.split()[0]+"_"+each.split()[1] if(len(each.split())>1) else each for each in dataFrame1.columns]
print(dataFrame1) # bosluklu sutun adı varsa _ ekledı ama bızım verıler zaten bosluksuz
# -
#
# <a class="anchor" id="24."></a>
# ## drop and concatenating
# + _uuid="9a36d4d2063ed86983a48b9933763a05c76d7f09"
dataFrame1["yeni_feature"] = [-1,-2,-3,-4,-5,-6]
dataFrame1.drop(["yeni_feature"],axis=1,inplace = True)
# dataFrame1 = dataFrame1.drop(["yeni_feature"],axis=1)
data1 = dataFrame1.head()
print(data1)
data2 = dataFrame1.tail()
print(data2)
# vertical
data_concat = pd.concat([data1,data2],axis=0) #dusey bırlestırdı yanı ust uste
print(data_concat)
# horizontal
maas = dataFrame1.maas
age = dataFrame1.age
data_h_concat = pd.concat([maas,age],axis=1) #yatay bırlestırdı yanı yanyana
print(data_h_concat)
# -
#
# <a class="anchor" id="25."></a>
# ## transforming data
# + _uuid="8dfdfc99525c62b3219467cd6199063368a379a9"
def multiply(age):
return age*2
dataFrame1["apply_metodu"] = dataFrame1.age.apply(multiply)
dataFrame1["list_comp"] = [ each*2 for each in dataFrame1.age]
print(dataFrame1)
# -
#
# <a class="anchor" id="26."></a>
# ## iteration example
# + _uuid="793a4edc49e0f8da8ab4b87808dc0bc74e413ed6"
name = "ronaldo"
it = iter(name)
print(next(it)) # print next iteration
print(*it) # print remaining iteration
# -
#
# <a class="anchor" id="27."></a>
# ## zip example
# + _uuid="c67a856e50020bcf76c46641158269b20abefe7d"
list1 = [1,2,3,4]
list2 = [5,6,7,8]
z = zip(list1,list2)
print(z)
z_list = list(z)
print(z_list)
print("-----")
un_zip = zip(*z_list)
un_list1,un_list2 = list(un_zip) # unzip returns tuble
print(un_list1)
print(un_list2)
print(type(un_list2))
# -
#
#
# <a class="anchor" id="28."></a>
# ## example of list comprehension
# + _uuid="b043f9a779b251c5ebdabece0e3e2c50b6cdef7e"
num1 = [1,2,3]
num2 = [i + 1 for i in num1 ]
print(num2)
# Conditionals on iterable
num1 = [5,10,15]
num2 = [i**2 if i == 10 else i-5 if i < 7 else i+5 for i in num1]
print(num2)
# + [markdown] _uuid="12cc13c9c94d044af4a43b73ef6e88d9c8b8e997"
#
# <a class="anchor" id="29."></a>
# # 5.Visualization with Matplotlib
# + _uuid="b1e8f0ec920434a3085efc3dd1964cd2842f85ad"
import pandas as pd
data = pd.read_csv("../input/Iris.csv")
print(data.columns)
# + _uuid="0876fef0405c953e7013f8120ede8fef5ea6dd53"
print(data.Species.unique())
# + _uuid="d6bd22f365ff765d75c5dba3f1d2609bfbe09523"
data.info()
# + _uuid="75859b43e3c96aa3908db8aff61d20c3091b23f4"
data.describe()
# + _uuid="5acceff465c1b5c2b27a5c40f5b2356f20cfbe94"
df1 = data.drop(["Id"],axis=1)
df1.corr()
# + _uuid="808ae3fb573c385295bcd15d9a533a45ecb31043"
setosa = data[data.Species == "Iris-setosa"]
versicolor = data[data.Species == "Iris-versicolor"]
print(setosa.describe())
print(versicolor.describe())
# + _uuid="432d8e2c3bb84bd9d7dcc084bd18347e816445b7"
import matplotlib.pyplot as plt
setosa = data[data.Species == "Iris-setosa"]
versicolor = data[data.Species == "Iris-versicolor"]
virginica = data[data.Species == "Iris-virginica"]
plt.plot(setosa.Id,setosa.PetalLengthCm,color="red",label= "setosa")
plt.plot(versicolor.Id,versicolor.PetalLengthCm,color="green",label= "versicolor")
plt.plot(virginica.Id,virginica.PetalLengthCm,color="blue",label= "virginica")
plt.legend()
plt.xlabel("Id")
plt.ylabel("PetalLengthCm")
plt.show()
# clf() = cleans it up again you can start a fresh
#plt.clf()
# -
#
#
# <a class="anchor" id="30."></a>
# ## line Plot example
# + _uuid="0ffe93b66174e50a54b722f9500f53041a355601"
# color = color, label = label, linewidth = width of line, alpha = opacity, grid = grid, linestyle = sytle of line
data.SepalLengthCm.plot(kind = 'line', color = 'g',label = 'SepalLengthCm',linewidth=1,alpha = 0.5,grid = True,linestyle = ':')
data.PetalLengthCm.plot(color = 'r',label = 'PetalLengthCm',linewidth=1, alpha = 0.5,grid = True,linestyle = '-.')
plt.legend(loc='upper right') # legend = puts label into plot
plt.xlabel('x axis') # label = name of label
plt.ylabel('y axis')
plt.title('Line Plot') # title = title of plot
plt.show()
# -
#
# <a class="anchor" id="31."></a>
# ## scatter plot
# + _uuid="96399300317ddd073d22011e230f3aade5b5f23f"
setosa = data[data.Species == "Iris-setosa"]
versicolor = data[data.Species == "Iris-versicolor"]
virginica = data[data.Species == "Iris-virginica"]
plt.scatter(setosa.PetalLengthCm,setosa.PetalWidthCm,color="red",label="setosa")
plt.scatter(versicolor.PetalLengthCm,versicolor.PetalWidthCm,color="green",label="versicolor")
plt.scatter(virginica.PetalLengthCm,virginica.PetalWidthCm,color="blue",label="virginica")
plt.legend()
plt.xlabel("PetalLengthCm")
plt.ylabel("PetalWidthCm")
plt.title("scatter plot")
plt.show()
# -
#
#
# <a class="anchor" id="32."></a>
# ## histogram
# + _uuid="3c06cf8beb0415b422b1d398b0e1400cba83c749"
plt.hist(setosa.PetalLengthCm,bins= 10)
plt.xlabel("PetalLengthCm values")
plt.ylabel("frekans")
plt.title("hist")
plt.show()
# -
#
# <a class="anchor" id="33."></a>
# ## bar plot
# + _uuid="031b747e37242b1e328833051b5b7c356f96baf8"
import numpy as np
x = np.array([1,2,3,4,5,6,7])
a = ["turkey","usa","a","b","v","d","s"]
y = x*2+5
plt.bar(a,y)
plt.title("bar plot")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
# -
#
# <a class="anchor" id="34."></a>
# ## subplots
# + _uuid="6a7dd2ac850611be29f9b5d96d8529344c23d086"
df1 = data.drop(["Id"],axis=1)
df1.plot(grid=True,alpha= 0.9,subplots = True)
plt.show()
setosa = data[data.Species == "Iris-setosa"]
versicolor = data[data.Species == "Iris-versicolor"]
virginica = data[data.Species == "Iris-virginica"]
plt.subplot(2,1,1)
plt.plot(setosa.Id,setosa.PetalLengthCm,color="red",label= "setosa")
plt.ylabel("setosa -PetalLengthCm")
plt.subplot(2,1,2)
plt.plot(versicolor.Id,versicolor.PetalLengthCm,color="green",label= "versicolor")
plt.ylabel("versicolor -PetalLengthCm")
plt.show()
|
Python/python-exercise.ipynb
|
# ---
# jupyter:
# jupytext:
# formats: ipynb,md:myst
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="oDP4nK_Zgyg-"
# # MAML Tutorial with JAX
#
# <NAME>
#
# Blog post: https://blog.evjang.com/2019/02/maml-jax.html
#
#
# 21 Feb 2019
#
# Pedagogical tutorial for implementing Model-Agnostic Meta-Learning with JAX's awesome `grad` and `vmap` and `jit` operators.
#
# ## Overview
#
# In this notebook we'll go through:
#
# - how to take gradients, gradients of gradients.
# - how to fit a sinusoid function with a neural network (and do auto-batching with vmap)
# - how to implement MAML and check its numerics
# - how to implement MAML for sinusoid task (single-task objective, batching task instances).
# - extending MAML to handle batching at the task-level
# + colab={} colab_type="code" id="zKVdo3FtgyhE"
### import jax.numpy (almost-drop-in for numpy) and gradient operators.
import jax.numpy as jnp
from jax import grad
# + [markdown] colab_type="text" id="gMgclHhxgyhI"
# ## Gradients of Gradients
#
# JAX makes it easy to compute gradients of python functions. Here, we thrice-differentiate $e^x$ and $x^2$
# + colab={"base_uri": "https://localhost:8080/", "height": 123} colab_type="code" id="Mt-uRwBGgyhJ" outputId="db7f718c-c2fb-4f7e-f31c-39a0d36c7051"
f = lambda x : jnp.exp(x)
g = lambda x : jnp.square(x)
print(grad(f)(1.)) # = e^{1}
print(grad(grad(f))(1.))
print(grad(grad(grad(f)))(1.))
print(grad(g)(2.)) # 2x = 4
print(grad(grad(g))(2.)) # x = 2
print(grad(grad(grad(g)))(2.)) # x = 0
# + [markdown] colab_type="text" id="7mAd3We_gyhP"
# ## Sinusoid Regression and vmap
#
# To get you familiar with JAX syntax first, we'll optimize neural network params with fixed inputs on a mean-squared error loss to $f_\theta(x) = sin(x)$.
# + colab={} colab_type="code" id="JN9KA1PvgyhQ"
from jax import vmap # for auto-vectorizing functions
from functools import partial # for use with vmap
from jax import jit # for compiling functions for speedup
from jax import random # stax initialization uses jax.random
from jax.experimental import stax # neural network library
from jax.experimental.stax import Conv, Dense, MaxPool, Relu, Flatten, LogSoftmax # neural network layers
import matplotlib.pyplot as plt # visualization
# + colab={} colab_type="code" id="DeEALFIHgyhU"
# Use stax to set up network initialization and evaluation functions
net_init, net_apply = stax.serial(
Dense(40), Relu,
Dense(40), Relu,
Dense(1)
)
rng = random.PRNGKey(0)
in_shape = (-1, 1,)
out_shape, net_params = net_init(rng, in_shape)
# + colab={} colab_type="code" id="izIi-P1agyhY"
def loss(params, inputs, targets):
# Computes average loss for the batch
predictions = net_apply(params, inputs)
return jnp.mean((targets - predictions)**2)
# + colab={"base_uri": "https://localhost:8080/", "height": 287} colab_type="code" id="sROmpDEmgyhb" outputId="d1bf00d7-99e7-445e-b439-ea2fabd7a646"
# batch the inference across K=100
xrange_inputs = jnp.linspace(-5,5,100).reshape((100, 1)) # (k, 1)
targets = jnp.sin(xrange_inputs)
predictions = vmap(partial(net_apply, net_params))(xrange_inputs)
losses = vmap(partial(loss, net_params))(xrange_inputs, targets) # per-input loss
plt.plot(xrange_inputs, predictions, label='prediction')
plt.plot(xrange_inputs, losses, label='loss')
plt.plot(xrange_inputs, targets, label='target')
plt.legend()
# + colab={} colab_type="code" id="PxAEhrPGgyhh"
import numpy as np
from jax.experimental import optimizers
from jax.tree_util import tree_multimap # Element-wise manipulation of collections of numpy arrays
# + colab={} colab_type="code" id="iZtAZfEZgyhk"
opt_init, opt_update, get_params = optimizers.adam(step_size=1e-2)
opt_state = opt_init(net_params)
# Define a compiled update step
@jit
def step(i, opt_state, x1, y1):
p = get_params(opt_state)
g = grad(loss)(p, x1, y1)
return opt_update(i, g, opt_state)
for i in range(100):
opt_state = step(i, opt_state, xrange_inputs, targets)
net_params = get_params(opt_state)
# + colab={"base_uri": "https://localhost:8080/", "height": 287} colab_type="code" id="Rm9WIz2egyho" outputId="183de82d-fdf0-4b81-9b14-01a85e6b8839"
# batch the inference across K=100
targets = jnp.sin(xrange_inputs)
predictions = vmap(partial(net_apply, net_params))(xrange_inputs)
losses = vmap(partial(loss, net_params))(xrange_inputs, targets) # per-input loss
plt.plot(xrange_inputs, predictions, label='prediction')
plt.plot(xrange_inputs, losses, label='loss')
plt.plot(xrange_inputs, targets, label='target')
plt.legend()
# + [markdown] colab_type="text" id="7E8gAJBzgyhs"
# ## MAML: Optimizing for Generalization
#
# Suppose task loss function $\mathcal{L}$ is defined with respect to model parameters $\theta$, input features $X$, input labels $Y$. MAML optimizes the following:
#
# $\mathcal{L}(\theta - \nabla \mathcal{L}(\theta, x_1, y_1), x_2, y_2)$
#
# $x_1, y_2$ and $x_2, y_2$ are identically distributed from $X, Y$. Therefore, MAML objective can be thought of as a differentiable cross-validation error (w.r.t. $x_2, y_2$) for a model that learns (via a single gradient descent step) from $x_1, y_1$. Minimizing cross-validation error provides an inductive bias on generalization.
#
# The following toy example checks MAML numerics via parameter $x$ and input $y$.
# + colab={"base_uri": "https://localhost:8080/", "height": 88} colab_type="code" id="2YBFsM2dgyht" outputId="46160194-04b7-46c9-897d-ecb11e9738be"
# gradients of gradients test for MAML
# check numerics
g = lambda x, y : jnp.square(x) + y
x0 = 2.
y0 = 1.
print('grad(g)(x0) = {}'.format(grad(g)(x0, y0))) # 2x = 4
print('x0 - grad(g)(x0) = {}'.format(x0 - grad(g)(x0, y0))) # x - 2x = -2
def maml_objective(x, y):
return g(x - grad(g)(x, y), y)
print('maml_objective(x,y)={}'.format(maml_objective(x0, y0))) # x**2 + 1 = 5
print('x0 - maml_objective(x,y) = {}'.format(x0 - grad(maml_objective)(x0, y0))) # x - (2x)
# + [markdown] colab_type="text" id="V9G-PMxygyhx"
# ## Sinusoid Task + MAML
#
#
# Now let's re-implement the Sinusoidal regression task from Chel<NAME>'s [MAML paper](https://arxiv.org/abs/1703.03400).
# + colab={} colab_type="code" id="s1v5VABkgyhy"
alpha = .1
def inner_update(p, x1, y1):
grads = grad(loss)(p, x1, y1)
inner_sgd_fn = lambda g, state: (state - alpha*g)
return tree_multimap(inner_sgd_fn, grads, p)
def maml_loss(p, x1, y1, x2, y2):
p2 = inner_update(p, x1, y1)
return loss(p2, x2, y2)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="bQvg749Xgyh2" outputId="5043f859-c537-41b8-c390-23670795d57b"
x1 = xrange_inputs
y1 = targets
x2 = jnp.array([0.])
y2 = jnp.array([0.])
maml_loss(net_params, x1, y1, x2, y2)
# + [markdown] colab_type="text" id="zMB6BwPogyh6"
# Let's try minimizing the MAML loss (without batching across multiple tasks, which we will do in the next section)
# + colab={"base_uri": "https://localhost:8080/", "height": 371} colab_type="code" id="pB5ldBO-gyh7" outputId="b2365aa4-d7b8-40a0-d759-8257d3e4d768"
opt_init, opt_update, get_params = optimizers.adam(step_size=1e-3) # this LR seems to be better than 1e-2 and 1e-4
out_shape, net_params = net_init(rng, in_shape)
opt_state = opt_init(net_params)
@jit
def step(i, opt_state, x1, y1, x2, y2):
p = get_params(opt_state)
g = grad(maml_loss)(p, x1, y1, x2, y2)
l = maml_loss(p, x1, y1, x2, y2)
return opt_update(i, g, opt_state), l
K=20
np_maml_loss = []
# Adam optimization
for i in range(20000):
# define the task
A = np.random.uniform(low=0.1, high=.5)
phase = np.random.uniform(low=0., high=jnp.pi)
# meta-training inner split (K examples)
x1 = np.random.uniform(low=-5., high=5., size=(K,1))
y1 = A * np.sin(x1 + phase)
# meta-training outer split (1 example). Like cross-validating with respect to one example.
x2 = np.random.uniform(low=-5., high=5.)
y2 = A * np.sin(x2 + phase)
opt_state, l = step(i, opt_state, x1, y1, x2, y2)
np_maml_loss.append(l)
if i % 1000 == 0:
print(i)
net_params = get_params(opt_state)
# + colab={"base_uri": "https://localhost:8080/", "height": 287} colab_type="code" id="ogcpFdJ9gyh_" outputId="856924a3-ede5-44ba-ba3c-381673713fad"
# batch the inference across K=100
targets = jnp.sin(xrange_inputs)
predictions = vmap(partial(net_apply, net_params))(xrange_inputs)
plt.plot(xrange_inputs, predictions, label='pre-update predictions')
plt.plot(xrange_inputs, targets, label='target')
x1 = np.random.uniform(low=-5., high=5., size=(K,1))
y1 = 1. * np.sin(x1 + 0.)
for i in range(1,5):
net_params = inner_update(net_params, x1, y1)
predictions = vmap(partial(net_apply, net_params))(xrange_inputs)
plt.plot(xrange_inputs, predictions, label='{}-shot predictions'.format(i))
plt.legend()
# + [markdown] colab_type="text" id="7TMYcZKVgyiD"
# ## Batching Meta-Gradient Across Tasks
#
# Kind of does the job but not that great. Let's reduce the variance of gradients in outer loop by averaging across a batch of tasks (not just one task at a time).
#
# vmap is awesome it enables nice handling of batching at two levels: inner-level "intra-task" batching, and outer level batching across tasks.
#
# From a software engineering perspective, it is nice because the "task-batched" MAML implementation simply re-uses code from the non-task batched MAML algorithm, without losing any vectorization benefits.
# + colab={} colab_type="code" id="9Pj04Z7MgyiF"
def sample_tasks(outer_batch_size, inner_batch_size):
# Select amplitude and phase for the task
As = []
phases = []
for _ in range(outer_batch_size):
As.append(np.random.uniform(low=0.1, high=.5))
phases.append(np.random.uniform(low=0., high=jnp.pi))
def get_batch():
xs, ys = [], []
for A, phase in zip(As, phases):
x = np.random.uniform(low=-5., high=5., size=(inner_batch_size, 1))
y = A * np.sin(x + phase)
xs.append(x)
ys.append(y)
return jnp.stack(xs), jnp.stack(ys)
x1, y1 = get_batch()
x2, y2 = get_batch()
return x1, y1, x2, y2
# + colab={"base_uri": "https://localhost:8080/", "height": 287} colab_type="code" id="7dCIGObKgyiJ" outputId="c169b529-0f16-4f20-d20e-d802765e4068"
outer_batch_size = 2
x1, y1, x2, y2 = sample_tasks(outer_batch_size, 50)
for i in range(outer_batch_size):
plt.scatter(x1[i], y1[i], label='task{}-train'.format(i))
for i in range(outer_batch_size):
plt.scatter(x2[i], y2[i], label='task{}-val'.format(i))
plt.legend()
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="BrSX--wpgyiP" outputId="6d81e7ff-7cd9-4aef-c665-952d442369d5"
x2.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 371} colab_type="code" id="P3WQ8_k2gyiU" outputId="fed1b78b-7910-4e44-a80b-18f447379022"
opt_init, opt_update, get_params = optimizers.adam(step_size=1e-3)
out_shape, net_params = net_init(rng, in_shape)
opt_state = opt_init(net_params)
# vmapped version of maml loss.
# returns scalar for all tasks.
def batch_maml_loss(p, x1_b, y1_b, x2_b, y2_b):
task_losses = vmap(partial(maml_loss, p))(x1_b, y1_b, x2_b, y2_b)
return jnp.mean(task_losses)
@jit
def step(i, opt_state, x1, y1, x2, y2):
p = get_params(opt_state)
g = grad(batch_maml_loss)(p, x1, y1, x2, y2)
l = batch_maml_loss(p, x1, y1, x2, y2)
return opt_update(i, g, opt_state), l
np_batched_maml_loss = []
K=20
for i in range(20000):
x1_b, y1_b, x2_b, y2_b = sample_tasks(4, K)
opt_state, l = step(i, opt_state, x1_b, y1_b, x2_b, y2_b)
np_batched_maml_loss.append(l)
if i % 1000 == 0:
print(i)
net_params = get_params(opt_state)
# + colab={"base_uri": "https://localhost:8080/", "height": 287} colab_type="code" id="PmxHLrhYgyiX" outputId="33ac699e-c66d-46e2-affa-98ae948d52e8"
# batch the inference across K=100
targets = jnp.sin(xrange_inputs)
predictions = vmap(partial(net_apply, net_params))(xrange_inputs)
plt.plot(xrange_inputs, predictions, label='pre-update predictions')
plt.plot(xrange_inputs, targets, label='target')
x1 = np.random.uniform(low=-5., high=5., size=(10,1))
y1 = 1. * np.sin(x1 + 0.)
for i in range(1,3):
net_params = inner_update(net_params, x1, y1)
predictions = vmap(partial(net_apply, net_params))(xrange_inputs)
plt.plot(xrange_inputs, predictions, label='{}-shot predictions'.format(i))
plt.legend()
# + colab={"base_uri": "https://localhost:8080/", "height": 287} colab_type="code" id="cQf2BeDjgyib" outputId="fc52caf6-1379-4d60-fe44-99f4e4518698"
# Comparison of maml_loss for task batch size = 1 vs. task batch size = 8
plt.plot(np.convolve(np_maml_loss, [.05]*20), label='task_batch=1')
plt.plot(np.convolve(np_batched_maml_loss, [.05]*20), label='task_batch=4')
plt.ylim(0., 1e-1)
plt.legend()
# + colab={} colab_type="code" id="vCHCvXh-mm1v"
|
docs/notebooks/maml.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
#
# <h1 class="text-center">Méthodes de Monte-Carlo</h1>
#
# - [I. Calcul du volume d'une sphère par la méthode de Riemann](#RIEMANN)
# - [II. Introduction à la méthode de Monte-Carlo : le cas IID](#MC)
# - [III. Eléments de simulation stochastique et méthode du rejet](#SIMUSTO)
# - [IV. Méthodes de réduction de variance](#IS)
# - [V. Introduction aux chaînes de Markov](#INTROMARKOV)
# - [VI. Méthodes de Monte-Carlo à base de chaînes de Markov](#MCMC)
# - [VII. Chemins auto-évitants](#SAW)
#
# <br>
#
# +
# %matplotlib inline
import numpy as np
import sys
from scipy import special, stats
from scipy.optimize import minimize, fminbound
import random
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import pickle
matplotlib.rcParams['figure.figsize'] = (20,10)
matplotlib.rcParams['font.size'] = 22
matplotlib.rcParams['legend.handlelength'] = 2
matplotlib.rcParams['lines.linewidth'] = 3
def grille_Riemann(dim, taille_echantillon):
"""
renvoie les centres d'hypercubes d'une grille multidimensionnelle
"""
N = int(taille_echantillon**(1.0/dim)) # nb de boites par cote, eventuellement arrondi
delta=2.0/N
allG = [np.linspace(-1+delta/2,1-delta/2,num=N) for G in range(dim)]
mesh = np.meshgrid(*allG)
ans = list(zip(*(d.flat for d in mesh)))
if len(ans) != taille_echantillon:
print '> Taille dechantillon ajustee pour la methode de Riemann:', len(ans), 'au lieu de', taille_echantillon,'(dimension =',dim,')'
return np.array(ans)
def N_effectif(dim, taille_echantillon):
"""
renvoie le nombre d'hypercubes utilisés lors de la discrétisation
donne le même résultat que len(grille_Riemann(dim, taille_echantillon))
mais sans générer la grille
"""
return (int(taille_echantillon**(1.0/dim)))**dim
def estimation_Riemann(dim, grille):
"""
calcule l'approximation du volume de la sphére en dimension
dim à l'aide de sommes de Riemann sur la grille fournie
"""
N = len(grille)
estimation = ((2.0**dim) / N) * np.sum(np.linalg.norm(grille,2,axis=1) <= 1.0)
V_theorique = (np.pi**(dim / 2.0)) / special.gamma((dim / 2.0) + 1.0)
ecart_relatif = (estimation - V_theorique) / V_theorique
return [estimation, ecart_relatif]
def estimation_Riemann_coin(dim, grille):
"""
calcule l'approximation du volume de la sphére en dimension
dim à l'aide de sommes de Riemann sur une grille obtenue avec un
déplacement de delta/2 de la grille fournie. Au lieu de travailer avec des centres
des hypercubes, on travail avec des coins.
"""
N = len(grille)
delta = 2.0 / (N**(1.0 / dim))
grille = grille + (delta / 2.0)
estimation = ((2.0**dim) / N) * np.sum(np.linalg.norm(grille,2,axis=1) <= 1.0)
V_theorique = (np.pi**(dim / 2.0)) / special.gamma((dim / 2.0) + 1.0)
ecart_relatif = (estimation - V_theorique) / V_theorique
return [estimation, ecart_relatif]
def estimationp(dim, taille_echantillon, t):
grille = np.random.uniform(-1, 1, size=(taille_echantillon, dim))
estimation = (1.0 / taille_echantillon) * np.sum(np.linalg.norm(grille,2,axis=1) < t)
return estimation
def estimation_IIDMC(dim, taille_echantillon):
"""
calcule l'approximation du volume de la sphére en dimension
dim à l'aide de la méthode de Monte-Carlo
"""
grille = np.random.uniform(-1, 1, size=(taille_echantillon, dim))
V_theorique = (np.pi**(dim / 2.0)) / special.gamma((dim / 2.0) + 1.0)
estimation = ((2.0**dim) / taille_echantillon) * np.sum(np.linalg.norm(grille,2,axis=1) <= 1.0)
ecart_relatif = (estimation - V_theorique) / V_theorique
erreur_relative = ((((2.0**dim) / V_theorique) - 1.0) / taille_echantillon)**(.5)
return [estimation, ecart_relatif, erreur_relative]
# -
#
# <br>
#
# <br>
#
# <a id="RIEMANN"></a><h1 style="border: 5px solid; text-align: center; padding: 10px"> I. Calcul du volume d'une sphère par la méthode de Riemann</h1>
#
# <div class="alert alert-success" style="text-align: center;">On montre dans cette partie les limitations des techniques d'intégration en grande dimension. L'exemple de l'estimation du volume d'une sphère sera le fil rouge du cours.</div>
#
# Le volume $V_d$ délimité par la sphère de rayon $1$ en dimension $d$ est donné par l'expression suivante:
# $$ V_d = \frac{\pi^\frac{d}{2}}{\Gamma(d/2+1)} \mathop{\sim}_{d \to \infty} \frac{1}{\sqrt{\pi d}} \left( \frac{2e\pi}{d} \right)^{d/2}
# $$
#
# où $\Gamma$ correspond à la fonction Gamma. Réexprimant $V_d$ sous forme intégrale :
# $$ V_d = \int_{[-1,1]^d} f(x) dx \ \text{ avec } \ f(x) = {\bf 1}(\lVert x \rVert \leq 1) $$
# on souhaite retrouver la valeur de $V_d$ en estimant l'intégrale ci-dessus à l'aide de sommes de Riemann. Si l'on divise $[-1,1]^d$ en hypercubes de côté $\delta$, on obtient alors l'approximation
# $$ \int_{[-1,1]^d} f \approx \widehat V^{\text{R}}_d \ \text{ avec } \ \widehat V^{\text{R}}_d = \sum_{k=1}^N \delta^d f(x_k) = \frac{2^d}{N} \sum_{k=1}^N f(x_k) $$
# où les $x_k$ sont les centres des hypercubes et $N = (2/\delta)^d$ est le nombre d'hypercubes. Puisque $f$ est continue par morceaux, on a bien $\widehat V^{\text{R}}_d \to V_d$ lorsque le nombre $N$ d'hypercubes utilisés tend vers $+\infty$, i.e., lorsque le pas $\delta$ de la discrétisation tend vers $0$.
#
# <div class="alert alert-success">On définit **l'écart relatif** comme la différence entre l'estimateur et sa valeur théorique, normalisée par la valeur théorique :
# $$ \text{écart relatif } = \frac{ \widehat V - V }{V} $$
# Ici, on connaît la valeur théorique et on peut donc calculer cet écart relatif, mais en pratique la valeur théorique, et donc l'écart relatif, est inconnue.</div>
#
# <p class="bg-primary" style="padding:1em">**QUESTION I.1.** Complétez la fonction `estimation_Riemann` dans le fichier `fonctions_estimation`, puis utilisez le script suivant pour tracer sur une même courbe $\widehat V^{\text{R}}_d$ et sa valeur théorique lorsque $d$ varie entre $2$ et $13$, puis tracez l'évolution de l'écart relatif. Commentez les résultats obtenus et notamment l'influence de $N$ et de la dimension $d$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION I.1.**
#
# Ce que j'ai pu constater c'est que pour une taille d'échantillon (N) fixe, à chaque fois que l'on augmente le nombre de dimensions (d), la méthode de Riemann devient de plus en plus moins précis e plus instable. Pour N supérieur et d fixe, la méthode nous permet de nous approcher les valeurs théoriques, mais le temps de calcul est beaucoup plus long.
#
# </div>
N = 10**6
dimensions = range(2,14)
nb_dimensions = len(dimensions)
from fonctions_auxiliaires import grille_Riemann, N_effectif
from fonctions_estimation import estimation_Riemann, estimation_Riemann_coin, estimation_IIDMC, estimationp
est_Riemann = np.zeros([nb_dimensions,2])
val_th = np.zeros(nb_dimensions)
for i in range(nb_dimensions):
dim = dimensions[i]
print '\n> Estimation par la methode de Riemann en dimension', dim, ': '
grille = grille_Riemann(dim, N)
est_Riemann[i,:] = estimation_Riemann(dim, grille)
print '> [Estimation, Écart Relatif] = ', est_Riemann[i,:]
val_th[i] = (np.pi**(dim / 2.0))/special.gamma(dim / 2.0 + 1)
# +
fig = plt.figure()
plt.plot(dimensions, est_Riemann[:,0], label="Riemann")
plt.plot(dimensions, val_th, 'r--', label="Theorie")
plt.legend(["Riemann", "Theorie"])
fig.suptitle("Riemann vs. Theorie")
plt.xlabel("Nombre de Dimensions")
fig = plt.figure()
plt.plot(dimensions, est_Riemann[:,1])
fig.suptitle("Ecart Relatif")
plt.xlabel("Nombre de Dimensions")
# -
#
# <p class="bg-primary" style="padding:1em">**QUESTION I.2.** Que calcule le code suivant ? Commentez la courbe obtenue.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION I.2.**
# Le code suivante nous donne une idée de la vitesse à laquelle l'estimation de Riemann s'approche de la valeur théorique, i.e., $-log(|(V_{estimee} - V_{theorique}|)$.
#
# Comme pour dimensions différentes le nombre d'hypercubes utilisés varie (au lieu de N, nous avons $N_{effectif}$), il a fallu diviser par $log(N_{effectif})$ pour eliminer cette dépendance.
#
# La vitesse de convergence commence à 0.6 pour $dim = 2$ et sa valeur chute à chaque fois que dim augmente (sauf de $dim = 9$ jusqu'à $dim = 10$). Notre estimation avec la méthode de Riemann devient donc pire, pour les dimensions de plus en plus hautes. En effet, dès que l'on a $dim > 10$, $-log(|(V_{estimee} - V_{theorique}|) \approx 0$, ce que signifie que la valeur estimée est vraiment loin de la théorique.
#
# </div>
vitesse_R = np.zeros(nb_dimensions)
for i in range(nb_dimensions):
dim = dimensions[i]
vitesse_R[i] = -np.log(np.absolute(est_Riemann[i,0] - val_th[i])) / np.log(N_effectif(dim, N))
plt.plot(dimensions, vitesse_R)
plt.xlabel("Nombre de Dimensions")
plt.suptitle("Vitesse de Convergence")
# On s'intéresse à la robustesse de l'estimation précédente. Pour cela, on considère
# $$ \widehat V^{\text{Rc}}_d = \frac{2^d}{N} \sum_{k=1}^N f(c_k) $$
# où $c_k$ est le coin de l'hypercube $k$, i.e., $c_k = x_k + \frac{\delta}{2} {\bf 1}$ avec ${\bf 1} = (1, \ldots, 1) \in R^n$.
#
# <p class="bg-primary" style="padding:1em">**QUESTION I.3.** Définissez la fonction `estimation_Riemann_coin` (toujours dans le fichier `fonctions_estimation`) afin qu'elle renvoie l'estimation et l'écart correspondant à cette nouvelle approximation. Rajoutez sur les courbes précédentes les résultats liés à cette estimation et commentez les résultats obtenus.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION I.3.**
# On trouve pas une amélioration des résultats avec Riemann coin. En effet, la seule chose qui l'on a changé était décaller les points dans la grille. Mais ils restent toujours y placés de façon homogène.
# </div>
est_Riemann = np.zeros([nb_dimensions,2])
est_Riemann_coin = np.zeros([nb_dimensions,2])
for i in range(nb_dimensions):
dim = dimensions[i]
grille = grille_Riemann(dim, N)
print '\n> Estimation par la methode de Riemann (coin) en dimension ' ,dim
est_Riemann[i,:] = estimation_Riemann(dim, grille)
est_Riemann_coin[i,:] = estimation_Riemann_coin(dim, grille)
print '> [Estimation (coin), Écart Relatif] = ', est_Riemann_coin[i,:]
# +
fig = plt.figure()
plt.plot(dimensions, est_Riemann[:,0], label="Methode de Riemann")
plt.plot(dimensions, est_Riemann_coin[:,0], label="Methode de Riemann (coin)")
plt.plot(dimensions, val_th, 'r--', label="Volume theorique")
plt.legend()
plt.xlabel("Nombre de Dimensions")
fig.suptitle("Estimation vs. Valeur theorique")
fig = plt.figure()
plt.plot(dimensions, est_Riemann[:,1], label="Methode de Riemann")
plt.plot(dimensions, est_Riemann_coin[:,1], label="Methode de Riemann (coin)")
plt.legend()
plt.xlabel("Nombre de Dimensions")
fig.suptitle("Ecart Relatif")
# -
# <p class="bg-primary" style="padding:1em">**QUESTION I.4.** Soit $V^-_d$ le volume de la sphère de rayon $1 - K/d$ en dimension $d$ : montrez théoriquement que $V_d - V^-_d \sim (1-e^{-K}) V_d$ lorsque $d \to \infty$, et utilisez ce résultat pour interpréter les résultats précédents.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION I.4.**
# Le volume de la sphère de rayon R = 1-K/d est donné par le volume de la sphère unitaire multiplié par le rayon puissance d. Donc:
#
# $$V_d = \frac{\pi^\frac{d}{2}}{\Gamma(d/2-1)}$$
# $$ $$
# $$V_d^{-} = V_dR^{d} = V_d\bigg(1-\frac{K}{d}\bigg)^{d}$$
#
# La différence entre eux est donnée par:
#
# $$V_{d} - V_{d}^{-} = V_{d} - V_d\bigg(1-\frac{K}{d}\bigg)^{d} = V_d\bigg[1-\bigg(1-\frac{K}{d}\bigg)^{d}\bigg]$$
#
# Le limite lorsque $d \rightarrow +\infty$ est calculé comme ci-dessous:
# $$ $$
# $$ \lim_{d\to\infty} V_d\bigg[1-\bigg(1-\frac{K}{d}\bigg)^{d}\bigg] = \lim_{d\to\infty} V_d \times \bigg[1 - \lim_{d\to\infty}\bigg(1-\frac{K}{D}\bigg)^d\bigg] = \lim_{d\to\infty} V_d \times \bigg[1 - \lim_{d\to\infty}\bigg(\bigg(1+\frac{1}{-d/K}\bigg)^{-d/K}\bigg)^{-K}\bigg] $$
# $$ $$
# $$ = \lim_{d\to\infty} V_d (1 - e^{-K}) = V_d (1 - e^{-K})$$
#
# Q.E.D.
# $$ $$
# Pour l'interprétation: en faisant augmenter le rayon de la deuxième sphère (R = 1-K/d) vers l'infini, il va converger vers 1. Toutefois son volume ne converge pas vers le volume de la sphère de rayon 1. En effet, à l'infini:
#
# $$V_{d}^{-} = V_d\big(1 - (1-e^{-K})\big) = e^{-K} V_d $$
#
# c'est-à-dire, pour d suffisament grande, la deuxième sphère aura un volume égal à $e^{-K}$ fois du volume de la sphère de rayon 1. Les sphères auront donc des rayons égales et des volumes toutefois différents. Une fois que K peut prendre n'import quelle valeur, $V_{d}^{-}$ peut être infiniment petit. Le conclusion est donc que le volume d'une hypersphère en dimension $d \rightarrow \infty$ doit être concentré dans sa surface. Le volume d'une sphère dans un nombre infini de dimensions est zero. Si on reprend le fait que la méthode des sommes de Riemann utilise une grille avec des points disposés de façon homogène, elle ne prend pas en compte cette distribuition de volume, ce qu'explique les erreurs trouvés pour un grand nombre de dimensions.
# </div>
#
#
#
#
# <p class="bg-primary" style="padding:1em"> **$\star$ QUESTION I.5 $\star$.** Quel bilan tirez-vous de l'estimation d'intégrales par somme de Riemann? </p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION I.5.**
# Pour conclure, si l'on travail avec un nombre petit de dimensions, la méthode de Riemann nous permet d'arriver au résultat. L'estimation sera meilleure pour des échantillons plus grands, mais cela nous êmpechera de faire des calcules rapides. En outre, si l'on considère un grand nombre de dimensions (avec N fixe), la méthod échouera. Ce qui se passe c'est qu'en grandes dimensions le nombre de points (hypercubes) necessaires pour le calcule est aussi plus grand. En plus, la somme de Riemann utilise toujours des points disposés géometriquement dans une grille, et cela n'est pas la meilleure façon d'estimer l'integrale. Dans le cas précedent de la sphère, par exemple, nous avons vu que lorsque $d \rightarrow +\infty$, la sphère de rayon 1 avait sont volume concentré dans sa surface. Donc ce serait mieux d'y placer plus de points. Il se passe la même chose avec n'importe quelle fonction. Dans les régions où l'integrale est plus grande, il faudra y ajouter plus de points. La faiblesse de la méthode de Riemann s'agit donc du placement des points dans une grille.
#
#
# </div>
#
# <br>
#
# <br>
#
# <br>
#
# <br>
#
#
#
#
# <a id="MC"></a><h1 style="border: 5px solid; text-align: center; padding: 10px">II. Introduction à la méthode de Monte-Carlo : le cas IID</h1>
#
# <div class="alert alert-success" style="text-align: center;">On introduit maintenant la méthode de Monte-Carlo sur le même problème d'estimation du volume de la sphére et on discute sa vitesse de convergence.</div>
#
# <div class="alert alert-success">**Rappel**. i.i.d. = indépendantes et identiquement distribuées</div>
#
# <h2>II.1. Méthode de Monte-Carlo</h2>
#
# Soit $(X_k, k \geq 1)$ des variables i.i.d. uniformément réparties sur $[-1,1]^d$ et
# $$ \widehat V^{\text{MC}}_d = \frac{2^d}{N} \sum_{k=1}^N f(X_k). $$
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.1.1.** Donnez la densité de $X_1$ et justifiez que $\widehat V^{\text{MC}}_d \to V_d$ lorsque $N \to \infty$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.1.1.**
# Soit $g_X(x)$ la fonction densité de probabilité des variables aleatoires i.i.d $X_k$:
# $$ $$
# $$g_{X_K}(x) = \frac{1}{2^d}\mathbb{1}_{[-1,1]^d}$$
#
# $$ $$
#
#
# $$V_d = \int \mathbb{1}(\lvert X \rvert \leq 1) dx = \int \frac{\mathbb{1}(\lVert X \rVert \leq 1)}{2^d} 2^d dx = E[\mathbb{1}(\lVert X \rVert \leq 1)\times2^d]$$
#
# $$ $$
#
# Un estimator de $V_d$ peut être donc donné par:
#
# $$ \frac{1}{N} \sum_{k=1}^N \mathbb{1}(\lVert X_k \rVert \leq 1)\times2^d = \frac{2^d}{N} \sum_{k=1}^N f(X_k) = \widehat V^{\text{MC}}_d $$
#
# Avec $f(X_k) = \mathbb{1}(\lVert X_k \rVert \leq 1)$. Selon la loi des grands nombres on arrive finalement à:
# $$ $$
#
# $$ \lim_{N\to\infty} \widehat V^{\text{MC}}_d = V_d$$
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.1.2.** Complétez la fonction `estimation_IIDMC` afin d'ajouter aux courbes précédentes l'évolution de $\widehat V^{\text{MC}}_d$ ainsi que l'écart relatif correspondant. Commentez les courbes obtenues.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.1.2.**
# Comme l'on peut constater, les valeurs estimées en utilisant l'estimator naïf de Monte-Carlo ne sont pas autant eloignées des valeurs théoriques comme ceux estimées avec les sommes de Riemann (pour la même taille d'échantillon). En effet, l'écart relative plus grand atteint était de 10.4% par rapport à la valeur théorique (à 11 dimensions). Pour comparer, les sommes de Riemann restaient proches de la valeur théorique jusqu'à $d=6$. On peut supposer que si au lieu d'utiliser la taille de l'échantillon effectif, on avait utilisé la vraie taille, les valeurs avec Monte-Carlo seraient encore meilleures.
#
# </div>
from fonctions_estimation import estimation_IIDMC
est_IIDMC = np.zeros([nb_dimensions,3])
for i in range(nb_dimensions):
dim = dimensions[i]
print '\n> Estimation par Monte Carlo en dimension:', dim
# pour une comparaison juste, on prend la même taille d'échantillon que pour Riemann
est_IIDMC[i,:] = estimation_IIDMC(dim, N_effectif(dim, N))
print '> [Estimation, Écart Relatif] = [', est_IIDMC[i,0], ",", est_IIDMC[i,1], "]"
# +
fig = plt.figure()
plt.plot(dimensions, est_IIDMC[:,0], label="IIDMC")
plt.plot(dimensions, est_Riemann[:,0], label="Riemann")
plt.plot(dimensions, est_Riemann_coin[:,0], label="Riemann coin")
th, = plt.plot(dimensions, val_th, 'r--', label="Theorie")
plt.legend()
plt.xlabel("Dimensions")
fig.suptitle("Volume Sphere")
fig = plt.figure()
plt.plot(dimensions, est_IIDMC[:,1], label="IIDMC")
plt.plot(dimensions, est_Riemann[:,1], label="Riemann")
plt.plot(dimensions, est_Riemann_coin[:,1], label="Riemann coin")
plt.legend()
plt.xlabel("Dimensions")
fig.suptitle("Ecart relatif")
# -
# <p class="bg-primary" style="padding:1em">**QUESTION II.1.3.** Faites tourner le script suivant et commentez les résultats obtenus.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.1.3.**
# Les courbes representées à vert et bleu correspondent à la vitesse de convergence de la méthode des sommes de Riemann et celle de Monte-Carlo.
# On constante que tandis que la vitesse de convergence des sommes de Riemann diminue jusqu'à approximativement zero avant $d=10$, la méthode IIDMC à une vitesse non nulle, même pour $d>10$. C'est-à-dire, les estimations selon Riemann s'eloignent de la valeur théorique, tandis que celles selon IIDMC ont un petit érreur en comparaison. Cependant les oscillations, même pour IIDMC la vitesse à une tendence à décroître avec le nombre de dimensions.
# </div>
vitesse_IIDMC = np.zeros(nb_dimensions)
for i in range(nb_dimensions):
dim = dimensions[i]
vitesse_IIDMC[i] = -np.log(np.absolute(est_IIDMC[i,0] - val_th[i])) / np.log(N_effectif(dim, N))
fig = plt.figure()
plt.plot(dimensions, vitesse_R, label="Riemann")
plt.plot(dimensions, vitesse_IIDMC, label="IIDMC")
plt.legend()
plt.xlabel("Nombre de Dimensions")
fig.suptitle("Vitesse de convergence")
# <p class="bg-primary" style="padding:1em">**QUESTION II.1.4.** Quelle est la vitesse de convergence théorique de l'estimateur $\widehat V^{MC}_d$? Cette vitesse dépend-elle de la dimension ? Commentez par rapport aux résultats numériques précédents.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.1.4.**
#
# Une fois que l'estimateur de Monte-Carlo est basé sur le théorème central limite, en faisant les définitions suivantes, on a:
# $$ $$
#
# $$ V_d = 2^dE[\mathbb{1}(\lVert X\rVert \leq 1)]$$
# $$\sigma^2 = 2^{2d}Var[\mathbb{1}(\lVert X \rVert \leq 1)]$$
#
# $$ $$
# $$ \frac{\frac{2^d\mathbb{1}(\lVert X_1 \rVert \leq 1) \space + ... + \space 2^d\mathbb{1}(\lVert X_N \rVert \leq 1)}{N}- V_d}{\sigma/\sqrt{N}} \sim N(0,1)$$
#
# lorsque $N \rightarrow \infty$. Donc:
# $$ \frac{2^d\mathbb{1}(\lVert X_1 \rVert \leq 1) \space + ... + \space 2^d\mathbb{1}(\lVert X_N \rVert \leq 1)}{N} - V_d = \widehat V^{\text{MC}}_d - V_d \sim N\bigg(0,\bigg(\frac{\sigma}{\sqrt{N}}\bigg)^2\bigg)$$
#
# La vitesse théorique de la méthode de Monte Carlo est par conséquence donnée par $\sqrt{N}$. En faisant augmenter la taille de l'echantillon, la vitesse de convergence augmente. Toutefois, si l'on fait augmenter le nombre de dimensions, la variance $\sigma^2 = 2^{2d}Var[\mathbb{1}(\lVert X \rVert \leq 1)]$, elle augmente aussi, et par conséquence, la vitesse de convergence diminue. Les résultats numériques montrent une diminuition de la vitesse de convergence avec beaucoup d'oscillations. Toutefois les calculs pour Monte-Carlo ont été fait avec des tailles d'échantillon variables pour garder la même taille pour Riemann et IIDMC, donc cela peut expliquer les oscillations que l'on peut regarder dans le graphique.
#
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.1.5.** On fixe la dimension $d = 15$. Répétez l'expérience plusieurs fois : l'estimation donnée par $\widehat V^{\text{MC}}_d$ est-elle stable ? et la vitesse de convergence ? Commentez les résultats obtenus et notamment l'influence de $N$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.1.5.**
# Tout d'abord, pour correctement étudier l'influence de la taille de l'echantillon, dans le calculs j'ai utilisé N et pas le N effectif que j'avais utilisé précédemment pour comparer avec les sommes de Riemann. Pour 15 dimensions et en faisant varier la taille de l'echantillon, on constante que l'estimation IIMC s'approche de la valeur théorique pour N croissant comme prévu théoriquement. J'ai fait des calculs pour un N maximal de $10^6$. Au delà de cette valeur, l'estimation prend beaucoup longtemps. À chaque fois que l'on repete le calcul, on obtient des valeurs différentes, ce qu'était pŕevu une fois que l'estimator est il-même une variable aleatoire. Toutefois l'estimation est stable et bornée. La vitesse de convergence est aussi stable, étant toujours bornée pendant les 100 répétitions. Elle augmente lorsque l'on augmente la taille de l'echantillon, comme prevue théoriquement. Les valeurs estimées trouvées oscillent autour de la valeur théorique. Ces oscillations ont une amplitude qui decroître pour N croissant.
# </div>
nb_repet = 10**2
N = 10**6
dim = 15
estim = np.zeros(nb_repet)
vitesse = np.zeros(nb_repet)
val_th = np.zeros(nb_repet) + np.pi**(dim / 2.0) / special.gamma(dim/2.0 + 1.0)
for i in range(nb_repet):
estim[i] = estimation_IIDMC(dim, N)[0]
vitesse[i] = -np.log(np.absolute(estim[i] - val_th[i])) / np.log(N)
print 'Ready!'
plt.plot(range(nb_repet), estim, label = "Estimation IIMC")
plt.plot(range(nb_repet), vitesse, label = "Vitesse")
plt.plot(range(nb_repet), val_th, 'r--', label = "Theorie")
plt.xlabel("#Repetition")
plt.legend()
plt.suptitle("IIMC pour 15 dimensions et plusieures repetitions")
# <h2>II.2. Précision d'un estimateur</h2>
#
# Le but de cette partie est de montrer que la variance n'est toujours pas une mesure satisfaisante pour mesurer la précision d'un estimateur. On considère pour cela la fonction $p(t) = P(\lVert X \rVert \leq t)$ où $X$ est uniformément répartie sur $[-1,1]^d$.
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.2.1** Donnez l'estimateur de Monte-Carlo de $p(t)$, que l'on notera $\widehat p(t)$, ainsi que son espérance et sa variance. En déduire que $\frac{1}{N} (\widehat p(t) - \widehat p(t)^2)$ est un estimateur de la variance de $\widehat p(t)$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.2.1.**
# La probabilité que l'on souhaite calculer est donnée par:
#
# $$ $$
# $$ p(t) = P(\lVert X \rVert \leq t) = \int_{\lVert X \rVert \leq t} f_X(x)dx = \int_{[-1,1]^d}\mathbb{1}(\lVert x\rVert \leq t)\frac{1}{2^d}dx=E[\mathbb{1}(\lVert X\rVert \leq t)] $$
# $$ $$
# Où $X \sim U[-1,1]^d$. Donc, un estimateur pour la calculer (celui de Monte-Carlo) est:
# $$ $$
# $$\widehat{p(t)}^{MC} = \frac{1}{N}\sum_{k=1}^N\mathbb{1}(\lVert X_k \rVert \leq t)$$
# où $X_k$ sont $i.i.d$ et avec une densité donnée par $1/2^d$. Son esperance est calculé ci-dessous:
# $$ $$
# $$E[\widehat{p(t)}^{MC}] = \frac{1}{N}E\bigg[\sum_{k=1}^N\mathbb{1}(\lVert X_k \rVert \leq t)\bigg]$$
# $$ $$
# $$= \frac{1}{N}\sum_{k=1}^N E\bigg[\mathbb{1}(\lVert X_k \rVert \leq t)\bigg] = \frac{N}{N} E\big[\mathbb{1}(\lVert X \rVert \leq t)\big] = P(\lVert X \rVert \leq t) = p(t)$$
# $$ $$
# L'estimateur est donc centré. Pour la variance, on a:
# $$ $$
# $$Var[\widehat{p(t)}^{MC}] = \frac{1}{N^2}Var\bigg[\sum_{k=1}^N\mathbb{1}(\lVert X_k \rVert \leq t)\bigg] =
# \frac{1}{N^2}\sum_{k=1}^N Var\bigg[\mathbb{1}(\lVert X_k \rVert \leq t)\bigg]$$
# $$ $$
# $$=\frac{1}{N^2}\sum_{k=1}^N\bigg(E[\mathbb{1}(\lVert X_k \rVert \leq t)^2]-E[\mathbb{1}(\lVert X_k \rVert \leq t)]^2\bigg)$$
# $$ $$
# $$=\frac{1}{N^2}\sum_{k=1}^N\bigg(E[\mathbb{1}(\lVert X_k \rVert \leq t)]-E[\mathbb{1}(\lVert X_k \rVert \leq t)]^2\bigg) = \frac{1}{N^2}\times N (p(t)-p(t)^2) = \frac{p(t)-p(t)^2}{N}$$
# $$ $$
# Donc son estimateur est:
# $$ $$
# $$\frac{\widehat p(t)- \widehat p(t)^2}{N}$$
#
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.2.2.** Complétez le script suivant afin de tracer $t \mapsto \widehat p(t) - \widehat p(t)^2$. Pour quelle valeur de $t$ l'estimateur vous semble-t-il être le moins précis ?</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.2.2.**
# Selon le graphique on peut être emmené a penser que pour la valeur maximale de la variance estimée l'estimateur est moin précis, i.e. pour $t$ tel que la courbe de la variance à bleu atteint son maximum (approximativement $t=2.25$). Toutefois, on a pas pris en compte le fait que lorsque les valeurs estimés sont petites, la variance est aussi inférieure. Par conséquence, l'estimation de la variance seule n'est pas un bon critère pour déterminer la précision de l'estimateur.
# </div>
# +
taille_echantillon = 10**4
dim = 15
valeurs_t = np.arange(0,3,.01)
estimation_p = np.zeros((len(valeurs_t),1))
for i in range(len(valeurs_t)):
estimation_p[i] = estimationp(dim, taille_echantillon, valeurs_t[i])
plt.xlabel("t")
plt.plot(valeurs_t, estimation_p - np.power(estimation_p,2), label="Estimation de la variance")
plt.plot(valeurs_t, estimation_p, label="Estimation p")
plt.legend()
plt.xlabel("t")
plt.suptitle("Estimation p = P(|X| <= t)")
# -
# <p class="bg-primary" style="padding:1em">**QUESTION II.2.3.** Justifiez le choix de
# $$ \frac{\sqrt{\widehat p(t) - \widehat p(t)^2}}{\widehat p(t)} $$
# pour évaluer la précision de $\widehat p(t)$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.2.3.**
# Comme remarqué dans la question précédent, l'estimation de la variance seule ne doit être le meilleur critère pour étudier la précision de l'estimateur de Monte-Carlo. Il faudra tenir en compte l'ordre de grandeur des valeurs estimées aussi. Ce nouveau estimateur permet de faire exactement cela en prennant l'estimation de l'écart type et en le divisant par la valeur estimée.
# </div>
#
# <div class="alert alert-success center;">On définit **l'erreur relative** comme le rapport entre l'écart-type de l'estimateur et sa moyenne :
# $$ \text{erreur relative } = \frac{\sqrt{\text{Var}(\widehat V)}}{E (\widehat V)} $$
# En pratique, ces valeurs sont inconnues mais on peut les estimer par Monte-Carlo.</div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.2.4.** Reprenez et complétez le script précédent afin de tracer, sur une autre figure, la courbe $t \mapsto \sqrt{1/\widehat p(t) - 1}$. Pour quelles valeurs de $t$ l'estimateur vous semble-t-il être le moins précis ?</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.2.4.**
# On peut regarder dans le graphique que l'erreur relative diminue lorsque t augmente. Lorsque t tend vers 1, l'estimateur devient imprécis. On trouve donc que l'étude de la précision avec l'estimation de la variance, comme fait dans la question précédente, était faux. En effet, en reprennat ce que l'on avait vu dans le cas de la sphère, pour un nombre élevé de dimensions, les points dans le volume d'une sphère de rayon t, $\{X : \lVert X \rVert \leq t\}$, sont concentrés près de sa surface. Comme les variables aleatoires utilisées par Monte-Carlo sont distribuées uniformement dans l'hypercube $[-1, 1]^d$, pour t petit il y'aura beaucoup des points dans l'hypercube que ne sont pas dans le volume de la sphère. En augmentant t, plus de points y tombent dedans et ceci rend par conséquence l'estimation plus précise.
#
# </div>
plt.xlabel("t")
plt.plot(valeurs_t, np.power(1.0 / estimation_p - 1.0 , .5), label="Erreur Relative")
plt.suptitle("Erreur relative en fonction de t")
# On revient maintenant au cas de la sphère.
#
# <p class="bg-primary" style="padding:1em">**$\star$ QUESTION II.2.5. $\star$** Montrez que dans ce cas, l'erreur relative de l'estimateur de Monte-Carlo est donnée par
# $$ \frac{\sqrt{\text{Var}(\widehat V^{\text{MC}}_d)}}{E(\widehat V^{\text{MC}}_d)} = \frac{c_d}{\sqrt N} \ \text{ avec } \ c_d = \sqrt{\frac{2^d}{V_d}-1}. $$</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.2.5.**
# Comme calculé dans la question précédente:
#
# $$Var\big[\widehat p(t)\big] = \frac{1}{N^2}(p(t)-p(t)^2)$$
#
# Une fois que l'on a $\widehat V_d^{MC} = 2^d \widehat p(1)$:
#
# $$Var\big[\widehat V_d^{MC}\big] = Var\big[2^d \widehat p(1)\big] = \frac{4^d}{N}(p(1) - p(1)^2) = \frac{1}{N}(2^dV_d - V_d^2)$$
# $$ $$
# $$E[\widehat V_d^{MC}] = V_d$$
#
# $$ $$
#
# $$\frac{\sqrt{Var[\widehat V_d^{MC}]}}{E[\widehat V_d^{MC}]} = \frac{1}{\sqrt{N}}\sqrt{\frac{2^d(V_d-V_d^2)}{V_d^2}} = \frac{1}{\sqrt{N}}\sqrt{\frac{2^d}{V_d}-1}$$
#
# Q.E.D.
#
#
# </div>
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.2.6.** Modifiez la fonction `estimation_IIDMC` de telle sorte à ce qu'elle calcule également l'erreur relative d'estimation du volume de la sphère. Tracez la courbe correspondante et commentez les résultats obtenus.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.2.6.**
# Ce que l'on constate d'abord c'est que l'estimation IIDMC suive approximativement la valeur théorique lorsque l'on augmente le nombre de dimensions. Les méthodes de sommes de Riemann présentent des oscillations pour les nombres de dimensions plus élevés, comme on l'avait déjà vu. L'écart relative de IIDMC oscille autour de zero tandis que Riemann présent des valeurs beaucoup plus hautes. Finalement, en augmentant le nombre de dimensions, l'erreur relative (la meilleure façon utilisé ici pour étudier la précision des méthodes), augmente de façon exponencielle (pour une taille d'échantillon fixée).
# </div>
from fonctions_estimation import estimation_IIDMC
est_IIDMC = np.zeros([nb_dimensions,3])
val_th = np.zeros(nb_dimensions)
for i in range(nb_dimensions):
dim = dimensions[i]
val_th[i] = np.pi**(dim / 2.0) / special.gamma(dim / 2.0 + 1.0)
print '> Estimation par Monte Carlo en dimension:', dim
# pour une comparaison juste, on prend la même taille d'échantillon que pour Riemann
est_IIDMC[i,:] = estimation_IIDMC(dim, N)
# +
fig = plt.figure()
plt.plot(dimensions, est_IIDMC[:,0], label="IIDMC")
plt.plot(dimensions, est_Riemann[:,0], label="Riemann")
plt.plot(dimensions, est_Riemann_coin[:,0], label="Riemann (coin)")
plt.plot(dimensions, val_th, 'r--', label="Theorie")
plt.legend()
plt.xlabel("Nombre de dimensions")
fig.suptitle("Comparaison entre methodes")
fig = plt.figure()
plt.plot(dimensions, est_IIDMC[:,1], label="IIDMC")
plt.plot(dimensions, est_Riemann[:,1], label="Riemann")
plt.plot(dimensions, est_Riemann[:,1], label="Riemann coin")
plt.legend()
plt.xlabel("Nombre de dimensions")
fig.suptitle("Ecart Relative")
fig = plt.figure()
errel_IIDMC, = plt.plot(dimensions, est_IIDMC[:,2], label="IIDMC")
plt.legend()
plt.xlabel("Nombre de dimensions")
fig.suptitle("Erreur Relative")
# -
# <h2>II.3. Limitations de la méthode IIDMC</h2>
#
#
# On conclut cette partie par une limitation évidente de la méthode de Monte-Carlo.
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION II.3.1.** Que vaut $\widehat V^{\text{MC}}_{30}$ pour $N = 10^6$? Faites un calcul d'ordre de grandeur pour déterminer le nombre d'échantillons qu'il faudrait pour avoir une erreur relative $\leq 10^{-2}$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.3.1.**
# Le calcul est presenté dans le ci-dessous:
# $$ $$
# $$\frac{\text{erreur relative}_{N=10^6}}{\text{erreur relative}_{N}} = \frac{1/\sqrt{10^6}}{1/\sqrt{N}}$$
# $$ $$
# $$ N = 10^6\bigg(\frac{\text{erreur relative}_{N=10^6}}{0.01}\bigg)^2$$
#
# L'ordre de grandeur est de $10^{+17}$. Donc pour 30 dimensions, obtenir une erreur inférieure à 0.01 avec la méthode de Monte-Carlo naïf n'est pas faisable.
# </div>
dim = 30
N = 10**6
print(N)
print 'Pour N=10^6 et dim = 30: ', estimation_IIDMC(dim, N)
nouvelle_erreur = 0.01
nouveau_n = N*((estimation_IIDMC(dim, N)[2])/(nouvelle_erreur))**2
print 'Pour une erreur relative < 0.01 => N >', nouveau_n
# <p class="bg-primary" style="padding:1em"> **$\star$ QUESTION II.3.2. $\star$** Quel bilan tirez-vous de l'estimation d'intégrales par méthode de Monte-Carlo? </p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION II.3.2.**
# Pour conclure, si d'un côté les méthodes de Riemann permettaient d'estimer l'integral à petits nombres de dimensions, une fois que ce nombre croise un certain seuil, la méthode n'est plus utilisable. On a vu que l'une des raisons était le fait que les méthodes de Riemann utilisent des points distribuées géometriquement dans une grille, ne prennant pas en compte la fonction qu'elles souhaitent estimer. Par contre, la méthode de Monte Carlo utilise des points aleatoires. On n'a que utilisé des distribuitions uniformes pour cela (donc on a pas pris en compte le fonction à intégrer non plus), mais on a déjà trouvé des résultats satisfatoires pour valeurs de dim supérieures. Pour dim fixée, cette méthode converge avec une vitesse de $1/\sqrt{N}$, supérieur à celle des sommes de Riemann. Toutefois, utiliser toujours des distribuitions uniformes n'est pas la meilleure solution comme on a pu constater. Il faudra trouver une meilleure façon d'utiliser les méthodes de Monte Carlo, surtout pour des valeurs de dim élevées.
# </div>
#
# <div class="alert alert-danger"><b>On a illustré ci-dessus la méthode de Monte-Carlo sur l'exemple du calcul de l'intégrale
# $$ \int_{[-1,1]^d} \phi(x) d x \ {\bf {\text{ avec }}} \ \phi(x) = {\bf 1}(\lVert x \rVert \leq 1). $$
# L'idée a été d'interpréter l'intégrale comme une espérance et d'utiliser la loi forte des grands nombres pour approcher cette espérance. Cette idée se généralise aisément au calcul de l'intégrale
# $$ \int \phi(x) f(x) d x $$
# où $f$ est une densité, en réécrivant cette intégrale comme l'espérance de la variable aléatoire $\phi(X)$ où $X$ est de densité $f$. Par ailleurs, contrairement au cas déterministe, la vitesse de convergence de cette méthode est indépendante de la dimension du problème!</b></div>
#
#
#
# <a id="SIMUSTO"></a><h1 style="border: 5px solid; text-align: center; padding: 10px"> III. Eléments de simulation stochastique et méthode du rejet</h1>
#
#
# <div class="alert alert-success"> On présente ici des éléments de simulation stochastique. On discute d'abord de méthodes pour vérifier qu'une variable aléatoire suit une loi donnée, puis on présente la méthode du rejet, qui permet de générer une variable aléatoire avec une loi donnée. Une autre méthode classique et très importante est la méthode de la fonction de répartition inverse qui fait l'objet du DM.</div>
#
#
# <div class="alert alert-success">Nous verrons dans la suite du cours que la méthode du rejet est à la base de la technique d'échantillonnage préférentiel et des méthodes de Monte-Carlo à base de chaînes de Markov.</div>
#
#
# <div class="alert alert-success">**Rappel**. La fonction de répartition d'une variable aléatoire $X$, notée $F_X$, est la fonction $F_X(x) = P(X \leq x)$.</div>
#
#
#
# <h2> III.1. Histogramme et densité </h2>
#
# Soit $X$ une variable aléatoire absolument continue que l'on sait générer mais dont on ne connaît pas la densité. Pour vérifier qu'une densité candidate $g$ est proche de la vraie densité, une manière très visuelle est de générer un échantillon $(X_1, X_2, \ldots)$ de variables i.i.d. distribuées comme $X$ et de comparer un histogramme associé à cet échantillon à $g$.
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.1.1.** Soit $(Y_k)$ i.i.d. qui suivent une loi exponentielle de paramètre $1/2$. Le théorème central limite prédit que
# $$ X = \sum_{k=1}^{100} Y_k $$
# suit approximativement une loi normale : quels sont les paramètres de cette loi ?</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.1.1.**
# D'abord, j'ai consideré que le paramètre de l'exponencielle donné était son espérance selon conseil du professeur. Ainsi, on a:
#
# $$ Y_k \sim exp(1/2)$$
# $$ $$
# Donc, $\mu = 1/2$ et $\sigma^{2} = (1/2)^{2} = 1/4$.
#
# D'après le théorème central limite on sait que:
# $$ $$
#
# $$ \lim_{N\to\infty} \frac{\frac{1}{N} \big(\sum_{k=1}^N Y_k \big)- \mu}{\sqrt{\sigma^2 /N}} \sim N(0, 1)$$
#
# Donc:
#
# $$ \lim_{N\to\infty} \frac{\sum_{k=1}^N Y_k - N\mu}{\sqrt{\sigma^2 N}} \sim N(0, 1)$$
#
# $$ $$
# $$ \lim_{N\to\infty} \sum_{k=1}^N Y_k \sim N(N\mu, N\sigma^2)$$
# $$ $$
# Pour N = 100, on a que la somme de 100 variables aleatories $Y_k$ suive approximativement une distribuition normal comme ci-dessous:
# $$ $$
# $$\sum_{k=1}^{100} Y_k \space\dot\sim\space N(50,25)$$
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.1.2.** Vérifiez votre réponse en complétant le script suivant, et commentez les résultats obtenus.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.1.2.**
# En traçant l'histogramme e la fonction densité de la distribuition normal dont la somme suive approximativement, on constante une correspondance entre les deux, comme l'on savait déjà, d'après le théorème central limite.
# </div>
taille_echantillon = 10**5
nb_termes = 100
parametre_exp = .5
exp = np.zeros((nb_termes, taille_echantillon))
for i in range (nb_termes):
exp[i] = np.random.exponential(parametre_exp, taille_echantillon)
echantillon = np.sum(exp, axis = 0)
count, bins, ignored = plt.hist(echantillon, np.arange(np.min(echantillon)-0.5, np.max(echantillon)+1.5), normed=True)
mu = 100*parametre_exp
sigma = (parametre_exp)*nb_termes**0.5
plt.plot(bins, stats.norm.pdf(bins, loc=mu, scale=sigma), linewidth=2, color='r')
# <p class="bg-primary" style="padding:1em">**QUESTION III.1.3.** Discutez des limitations potentielles de cette méthode.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.1.3.** </div>
#
# <h2> III.2. Fonction de répartition empirique </h2>
#
# Nous présentons maintenant une méthode plus rigoureuse. On considère un échantillon $(X_1, X_2, \ldots)$ de variables i.i.d. distribuées comme $X$ à valeurs dans $R$ et on s'intéresse à la fonction
# $$ \widehat F_N: x \in R \mapsto \frac{1}{N} \sum_{k=1}^N {\bf 1}(X_k \leq x). $$
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.2.1.** Montrez que $\widehat F_N(x) \to F_X(x)$ pour tout $x \in R$ fixé.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.2.1.**
# $$E[\widehat F_N] = E\bigg[\frac{1}{N}\sum_{k=1}^N \mathbb{1}(X_k \leq x)\bigg] = \frac{1}{N}\sum_{k=1}^N E[\mathbb{1}(X_k \leq x)]$$
# $$ $$
# Comme $X_k$ sont i.i.d., on appele $X$ une variable aleatoire i.i.d. avec $X_k$. Une fois que pour l'indicatrice on sait que $E[\mathbb{1}(X \leq x)] = P(X \leq x)$, alors:
# $$ $$
# $$E[\widehat F_N] = \frac{1}{N} NP(X\leq x) = F_X$$
#
# D'après le théorème central limite:
# $$\lim_{N\to\infty} \widehat F_N(x) = F_X(x) $$
# </div>
#
#
# Ce résultat justifie donc d'appeler $\widehat F_N$ **fonction de répartition empirique** de $X$. Pour vérifier qu'une variable aléatoire suit une loi de fonction de répartition $F$, on peut donc superposer $\widehat F_N$ et $F$ et accepter que $F = F_X$ si les deux courbes sont proches pour $n$ suffisamment grands.
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.2.2.** Complétez le script suivant pour vérifier que les fonctions ``stats.expon.rvs``, ``stats.gamma.rvs``, ``stats.uniform.rvs`` et ``stats.expon.rvs`` renvoient bien des variables aléatoires qui suivent la loi uniforme, la loi exponentielle, la loi de Poisson et la loi gamma, respectivement. Utilisez pour cela la fonction ``ecdf``. A partir de quelle taille d'échantillon les approximations vous semblent-elles valides ?</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.2.2.**
# On constate que les fonctions de distribuition empiriques s'approchent des valeurs théoriques lorsque la taille de l'échantillon est suffisamment grande. C'est difficile de definir un seuil dès lequel les approximations semblent valides, car cela depende du niveau de précision que l'on souhaite atteindre. Toutefois, pour N>100, les fontions empiriques sont déjà assez proches des théoriques, permettant de conclure que les variables aleatoires suivent en effet les distribuitions que l'on avait comme hypothèse au début.
#
# </div>
def ecdf(echantillon):
"""
Cette fonction prend en entrée un échantillon
et renvoie le couple (sorted_, yvals) qui est tel que
np.step(sorted_, yvals) trace la fonction de répartition empirique
"""
sorted_ = np.sort(echantillon)
yvals = np.arange(len(sorted_))/float(len(sorted_))
sorted_ = np.append(sorted_, np.amax(echantillon))
sorted_ = np.append(sorted_, np.amax(echantillon)+1)
sorted_ = np.insert(sorted_, 0, np.amin(echantillon)-1)
yvals = np.append(yvals, 1)
yvals = np.append(yvals, 1)
yvals = np.insert(yvals, 0, 0)
return (sorted_, yvals)
# +
taille = 10**2
f, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, sharex='col', sharey='row')
t = ["Exponentielle", "Gamma", "Uniforme", "Poisson"]
for i in range(4):
if i==0: # exponentielle
echantillon = stats.expon.rvs(loc=0, scale=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax1
a.plot(x, stats.expon.cdf(x, loc=0, scale=1))
if i==1: # gamma
echantillon = stats.gamma.rvs(a=2, loc=0, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax2
a.plot(x, stats.gamma.cdf(x, a=2, loc=0, scale=1))
if i==2: # uniforme
echantillon = stats.uniform.rvs(loc=0, scale=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax3
a.plot(x, stats.uniform.cdf(x, loc=0, scale=1))
if i==3: # poisson
echantillon = stats.poisson.rvs(mu=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax4
a.step(x, stats.poisson.cdf(x, mu=1))
s, y = ecdf(echantillon)
a.step(s, y)
a.set_title(t[i])
a.set_xlim([np.min(echantillon)-1, np.max(echantillon)+1])
# -
# <p class="bg-primary" style="padding:1em">**QUESTION III.2.3.** Soient $U_1$, $U_2$ indépendantes et uniformément réparties sur $[0,1]$ et $Z = \sqrt{- 2 \ln U_1} \cos(2 \pi U_2)$. Vous pouvez générer au plus 200 variables aléatoires. Parmi les choix suivants, quelle est selon vous la loi de $Z$?
# <br>
#
# ● Cauchy, i.e., $f_Z(z) \propto 1/(1+z^2)$ (cf. ``stats.cauchy``)
#
# <br>
#
# ● Laplace, i.e., $f_Z(z) \propto e^{-\lvert z \rvert}$ (cf. ``stats.laplace``)
#
# <br>
#
# ● Gauss, i.e., $f_Z(z) \propto e^{-z^2/2}$ (cf. ``stats.norm``)</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.2.3.**
# On a une variable aleatoire Z dont la loi on ne connait pas. On utilise la méthode de la fonction de repartition empirique pour la trouver. La démarche était de générer des échantillons de valeurs aleatoires sélon $U_1$ et $U_2$, puis générer un échantillon de valeurs $Z$ selon la formule. Après il a fallu tracer la fonction de repartition empirique de Z e la comparer avec celles de Gauss, Cauchy et Laplace. Les résultats, en utilisant une taille maximale de 200 variables aleatoires, permettent de conclure que Z suive une loi de Gauss.
# </div>
# +
taille_echantillon = 200
u1 = stats.uniform.rvs(loc=0, scale=1, size=taille_echantillon)
u2 = stats.uniform.rvs(loc=0, scale=1, size=taille_echantillon)
z = ((-2*np.log(u1))**.5)*np.cos(2*np.pi*u2)
s,y = ecdf(z)
plt.step(s,y, label="Empirique")
plt.plot(s, stats.norm.cdf(s, loc=0, scale=1), linewidth=2, label="Gauss")
plt.plot(s, stats.cauchy.cdf(s, loc=0, scale=1), linewidth=2, label="Cauchy")
plt.plot(s, stats.laplace.cdf(s, loc=0, scale=1), linewidth=2, label="Laplace")
plt.legend()
plt.suptitle("Determination de la loi de Z")
# -
# Jusqu'à présent, la méthode proposée n'est pas beaucoup plus rigoureuse que l'utilisation des histogrammes, à la différence qu'il n'y a pas besoin de faire de choix pour les urnes. Un autre avantage est que la vitesse de convergence $\widehat F_N \to F_X$ peut être quantifiée comme on le voit maintenant.
#
# <p class="bg-primary" style="padding:1em">**$\star$ QUESTION III.2.4. $\star$** Quel résultat contrôle les fluctuations de $\widehat F_N(x)$ autour de $F_X(x)$? Montrez que
# $$ P \left( \widehat F_N(x) - \varepsilon_N(x) \leq F_X(x) \leq \widehat F_N(x) + \varepsilon_N(x) \right) \mathop{\longrightarrow}_{n \to \infty} 0{,}95 \ \text{ où } \ \varepsilon_N(x) = \frac{\sigma(x) F^{-1}(0{,}975)}{\sqrt N} $$
# avec $\sigma(x)^2 = F_X(x) (1-F_X(x))$, $F$ la fonction de répartition de la loi normale centrée réduite et $F^{-1}$ son inverse.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.2.4.**
#
# La variable aleatoire $\mathbb{1}(X_k \leq x)$ a pour esperance $E[\mathbb{1}(X_k \leq x)] = P(X_k \leq x) = F_X(x)$. Sa variance est donnée par $\sigma^2(x)$. On sait d'après le théorème central limite que, lorsque $N \rightarrow \infty$:
#
# $$ $$
#
# $$\frac{\frac{1}{N}\sum_{k=1}^N\mathbb{1}(X_k \leq x) - F_X(x)}{\sigma(x) \big/ \sqrt{N}} = \frac{\widehat F_N(x) - F_X(x)}{\sigma(x) \big/ \sqrt{N}} \sim N(0,1)$$
# $$ $$
# Si l'on reécrit maintenant la probabilité qui l'on souhaite calculer comme ci-dessous:
# $$ $$
# $$P \left(- \varepsilon_N(x) \leq F_X(x) - \widehat F_N(x) \leq \varepsilon_N(x) \right)$$
# $$ $$
# $$= P \bigg(-F^{-1}(0.975) \leq \frac{F_X(x) - \widehat F_N(x)}{\sigma(x)\big/\sqrt{N}} \leq F^{-1}(0.975)\bigg)$$
# $$ $$
# Ainsi:
#
# $$\lim_{N\to\infty} P \bigg(-F^{-1}(0.975) \leq \frac{F_X(x) - \widehat F_N(x)}{\sigma(x)\big/\sqrt{N}} \leq F^{-1}(0.975)\bigg) = F(F^{-1}(0.975)) - F(-F^{-1}(0.975))$$
# $$ $$
# $$= 0.975 - (1-0.975) = 0.975 - 0.025 = 0.95 $$
#
# Q.E.D.
# $$ $$
# Les fluctuations varient avec $1\sqrt{N}$. Une vitesse de convergence égale à celle de Monte-Carlo.
# </div>
#
#
# <p class="bg-primary" style="padding:1em">**$\star$ QUESTION III.2.5. $\star$** Quel est le problème de la fonction $\varepsilon_N$? Proposez une fonction $\widehat \varepsilon_N$ sans ce problème et qui satisfait aussi
# $$ P \left( \widehat F_N(x) - \widehat \varepsilon_N(x) \leq F_X(x) \leq \widehat F_N(x) + \widehat \varepsilon_N(x) \right) \mathop{\longrightarrow}_{n \to \infty} 0{,}95. $$</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.2.5.**
# Une fois que l'on utilise la méthode de la fonction de repartition lorsque on ne connait pas la distribuition d'une variable aleatoire, on ne connait non plus sa variance $\sigma^2(x)$ (ou l'écart-type). Cependant, on peut utiliser son estimateur au lieu d'elle-même, i.e. $\widehat{\sigma^2}(x)$.
# $$ $$
# $$\widehat{\sigma^2}(x) = \widehat F_X(x) (1-\widehat F_X(x))$$
#
# On voit facilement que:
#
# $$E[\widehat{\sigma^2}(x)] = F_X(x) (1-F_X(x)) = \sigma^2(x)$$
# $$ $$
# Comme le résultat de la question précédent a été obtenu en faisant $N \rightarrow \infty$, et une fois que $\lim_{N\to\infty} \widehat{\sigma^2}(x) = \sigma^2(x)$, le résultat est encore valable si on changue la variance pour son estimateur, c'est-à-dire:
# $$ $$
# $$\widehat\varepsilon_N(x) = \frac{\sqrt{\widehat{\sigma^2}(x)} F^{-1}(0{,}975)}{\sqrt N}$$
#
#
# </div>
#
#
#
# On remarquera en particulier que $[\widehat F_N(x) - \widehat \varepsilon_N(x), \widehat F_N(x) + \widehat \varepsilon_N(x)]$ est l'**intervalle de confiance bilatéral symétrique** de $F_X(x)$ au niveau asymptotique $95\%$.
#
# <p class="bg-primary" style="padding:1em">**$\star$ QUESTION III.2.6. $\star$** Reprenez et complétez le script précédent pour ajouter les deux enveloppes $\widehat F_{100} \pm \widehat \varepsilon_{100}$. Utilisez pour cela les fonctions ``np.std`` et ``stats.norm.ppf``.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.2.6.**
# À rouge on peut regarder les deux courbes que definent l'interval de confiance bilatéral symétrique de $F_X(x)$ à $95\%$. Elles signifient que on a $95\%$ de chance que la vraie fonction de distribuition y tombe dedans. Si l'on fait diminuer la taille de l'échantillon, l'écart entre ces deux lignes augment car $\widehat\varepsilon_N(x)$ augmente aussi (selon $1/\sqrt{N}$, comme l'on avait vu). Pour $N=10^3$, elles sont déjà vraiment proches l'une de l'autre et des distribuitions théoriques, que dans ce cas on connait.
# </div>
# +
taille = 10**2
f, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, sharex='col', sharey='row')
t = ["Exponentielle", "Gamma", "Uniforme", "Poisson"]
for i in range(4):
if i==0:
echantillon = stats.expon.rvs(loc=0, scale=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax1
a.plot(x, stats.expon.cdf(x, loc=0, scale=1))
if i==1:
echantillon = stats.gamma.rvs(a=2, loc=0, scale=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax2
a.plot(x, stats.gamma.cdf(x, a=2, loc=0, scale=1))
if i==2:
echantillon = stats.uniform.rvs(loc=0, scale=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax3
a.plot(x, stats.uniform.cdf(x, loc=0, scale=1))
if i==3:
echantillon = stats.poisson.rvs(mu=1, size=taille)
x = np.arange(np.min(echantillon)-1, np.max(echantillon)+1, .1)
a = ax4
a.step(x, stats.poisson.cdf(x, mu=1))
s, y = ecdf(echantillon)
ecart_type = np.std(y)
a.step(s, y)
a.set_title(t[i])
epsilon = (ecart_type*stats.norm.ppf(0.975,loc=0, scale=1)) / ((taille**.5))
a.step(s,y + epsilon, 'r', linewidth=1.0)
a.step(s,y - epsilon, 'r', linewidth=1.0)
a.set_xlim([np.min(echantillon)-1, np.max(echantillon)+1])
# -
# <h2> III.3. Méthode du rejet </h2>
#
# Soit $Y$ une variable aléatoire absolument continue admettant pour densité $f$ satisfaisant $f(x) = 0$ si $\lvert x \rvert \geq 1$ et $\sup f < \infty$. On génère itérativement des points uniformément répartis sur $[-1,1] \times [0,K]$ avec $K \geq 2\sup f$ jusqu'à avoir généré un point sous la courbe $f$. Sur la figure ci-dessous, on a généré les quatre croix avant de générer le point noir.
#
# 
#
#
#
# On considère alors l'abscisse du premier point sous la courbe, que l'on note $Z$. Dans le premier devoir maison, on vous demande de démontrer que
# $$ \tag{1} P(Z \leq z) = P(X \leq z \mid U \leq f(X)), \ z \in R, $$
# avec $(X, U)$ uniformément réparti sur $[-1,1] \times [0,K]$.
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.3.1.** Donnez la densité de $(X, U)$ et déduisez de (1) que $Z$ admet $f$ pour densité.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.3.1.**
# Les calculs suivants ont été fait en prennant en compte que U et X sont i.i.d.:
# $$ $$
# $$f_{XU}(x,u) = \frac{1}{2K}\mathbb{1}(|X| \leq 1, 0 \leq U \leq K) = \frac{1}{2K}\mathbb{1}(|X| \leq 1)\mathbb{1}(0 \leq U \leq K)$$
# $$ $$
# $$ P(X \leq z \mid U \leq f(X)) = \frac{\int\int f_{XU}(x,u) dudx}{\int f_U(u) du} = \frac{\frac{1}{2K}\int_{-\infty}^{z}\mathbb{1}(|x| \leq 1)dx \int_{-\infty}^{f(X)} \mathbb{1}(0 \leq u \leq K) du}{\int_{-\infty}^{f(X)} \frac{1}{K}\mathbb{1}(0 \leq u \leq K) du} = F_X(z) $$
#
# $$ $$
# Donc:
# $$P(Z \leq z) = F_Z(z) = F_X(z)$$
# $$ $$
# $$f_Z(z) = \frac{dF_Z(z)}{dz} = \frac{dF_X(z)}{dz} = f_X(z)$$
#
# Q.E.D.
# </div>
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.3.2.** Quelle est la loi du nombre de points rejetés avant d'en accepter un ? En déduire le nombre moyen de simulations nécessaires afin de simuler $Y$ selon cette méthode.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.3.2.**
# La loi est géometrique. Soit p la probabilité d'accepter un point, i.e. $p = P(U \leq f_X(x))$ et W la variable aleatoire correspondent au nombre de points rejectés avant accepter un.
# $$ $$
#
# $$P(W = w) = (1-p)^{w-1}p$$
#
# $$ $$
# Le nombre moyen de simulations necessaire pour accepter un point (i.e. pour simuler Y) est donné par l'ésperance de la loi géometrique, i.e. $1/p$.
#
# </div>
#
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION III.3.3.** Ecrivez un script qui implante cette méthode dans le cas où $f$ est la densité normale tronquée, i.e.,
# $$ f(x) \propto \exp\left( -\frac{x^2}{2} \right) {\bf 1}(-1 \leq x \leq 1). $$
# Vous vérifierez bien que la sortie de votre script admet la bonne loi.
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.3.3.**
# Le graphique montre que les fonctions de repartition théorique et empirique sont proches l'une de l'autre. Comme vu précédemment, on pouvait diminuer encore plus l'écart entre elles en augmentant N.
# </div>
# +
taille_echantillon = 10**4
Z1 = stats.norm.cdf(np.arange(-1, 1, .0001), loc=0, scale=1)
Z = ((2*np.pi)**.5) * (Z1[len(Z1)-1]-Z1[0])
K = 2/Z
x = stats.uniform.rvs(loc=-1, scale=2, size=taille_echantillon)
u = stats.uniform.rvs(loc=0, scale=K, size=taille_echantillon)
echantillon = []
for i in range(taille_echantillon):
fx = np.exp(-(x[i])**2/2)
if (u[i] < fx):
echantillon.append(x[i])
s, y = ecdf(echantillon)
s = s[1:-1]
y = y[1:-1]
plt.step(s, y, label="Fonction de repartition empirique")
plt.plot(s, (stats.norm.cdf(s)-stats.norm.cdf(-1))/(stats.norm.cdf(1)-stats.norm.cdf(-1)), label= "Fonction de repartition theorique")
plt.legend()
# -
# <p class="bg-primary" style="padding:1em">**QUESTION III.3.4.** A l'aide de la méthode du rejet, écrivez un code qui permet de générer une variable aléatoire de densité $\displaystyle f(x) \propto \lvert x \rvert \exp(\lvert x \rvert^\pi) {\bf 1}(\lvert x \rvert < 1)$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION III.3.4.**
# J'ai utilisé la même procedure qu'avant. En plus j'ai intégré numériquement la densité donné pour comparer les fonctions de repartition théorique et empirique. Elles ne diffèrent que par une constante multiplicative.
# </div>
# +
from scipy.integrate import quad
def integrand(x):
return np.absolute(x)*np.exp(np.absolute(x)**np.pi)*np.sign(x-1)*np.sign(-x-1)
taille_echantillon = 10**4
K = 2*np.exp(1)
x = stats.uniform.rvs(loc=-1, scale=2, size=taille_echantillon)
u = stats.uniform.rvs(loc=0, scale=K, size=taille_echantillon)
echantillon = []
for i in range(taille_echantillon):
fx = np.absolute(x[i])*np.exp((np.absolute(x[i]))**np.pi)
if (u[i] < fx):
echantillon.append(x[i])
s, y = ecdf(echantillon)
s = s[1:-1]
theorie = []
for j in range(len(s)):
I = quad(integrand, -1, s[j])
theorie.append(I[0])
y = y[1:-1]
plt.step(s, y, label="Fonction de repartition empirique")
plt.step(s, theorie, label="Fonction de repartition theorique")
plt.legend()
# -
#
#
#
#
# <a id="IS"></a><h1 style="border: 5px solid; text-align: center; padding: 10px">IV. Méthodes de réduction de variance</h1>
#
#
# <div class="alert alert-success"> Pour améliorer l'estimation de $I = \int \phi f$, l'idée des méthodes de réduction de variance (aussi appelées échantillonnage préférentiel) est d'utiliser une représentation différente de l'intégrale :
# $$ I = \int \phi f = \int \widetilde{\phi} g \ \text{ avec } \widetilde \phi = \frac{\phi f}{g} $$
# puis d'utiliser l'estimateur IIDMC
# $$ \frac{1}{N} \sum_{k=1}^N \widetilde \phi(Y_k) $$
# où les $(Y_k)$ sont i.i.d. de densité $g$. Vous verrez dans le DM2 que cette méthode a des liens profonds avec la méthode du rejet.</div>
#
# <h2> IV.1. Exemple de la loi de Cauchy </h2>
#
# On cherche dans cette partie à estimer la probabilité $p=P(X>2)$ où $X$ suit une loi de Cauchy, i.e., $X$ est une variable aléatoire absolument continue de densité
# $$ f(x) = \frac{1}{\pi (1+x^2)}, \ x \in R. $$
# Pour cela, on va considérer $4$ estimateurs de Monte-Carlo:
# $$ \widehat p^i_N = \frac{1}{N} \sum_{k=1}^N Y^i_k $$
# où pour chaque $i=1,\dots,4$ les $(Y^i_k, k \in N)$ sont i.i.d.. Ces 4 estimateurs correspondent aux différentes écritures suivantes de $p$ :
# \begin{align*}
# p & = \int {\bf 1}(x > 2) f(x) d x \tag{1}\\
# & = \frac{1}{2} \int {\bf 1}(\lvert x \rvert > 2) f(x) d x \tag{2}\\
# & = \frac{1}{2} - \int f(x){\bf 1}(0 \leq x \leq 2) d x \tag{3}\\
# & = \int_0^{1/2} \frac{y^{-2}}{\pi (1 + y^{-2})} d y\tag{4}
# \end{align*}
# (1) vient de la définition de $p$, (2) de la parité de $f$, (3) du fait que $f$ s'intègre à $1$ et est paire, et (4) vient de (1) et du changement de variable $y = 1/x$.
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.1.1.** Justifiez que le meilleur estimateur soit celui qui corresponde à la variable aléatoire $Y^i_1$ de variance minimale.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.1.1.**
# <p>Tous les 4 estimateurs ont la même esperance. En effet, pour i = 1, ..., 4, on a:</p>
#
# $$ $$
# $$E[\widehat p_N^i] = p$$
# $$ $$
# Selon le théorème central limite on sait que l'écart entre la valeur estimée et la probabilité souhaitée suive approximativement (pour N suffisament grand), une loi normale:
# $$ $$
# $$ \widehat p_N^i - p \space\dot\sim\space N\bigg(0,\frac{\sigma^2_i}{N}\bigg)$$
# où $\sigma^2_i$ est la variance de $\widehat p_N^i$.
# $$ $$
# Donc pour la même taille d'échantillon, la variance minimale de la différence $\widehat p_N^i - p$ est obtenue pour l'estimateur dont la variance est minimale. Une fois que pour $\frac{\sigma^2_i}{N}$ minimale la différence $\widehat p_N^i - p$ a une probabilité plus grande d'être proche de zero, le meilleur estimateur est celui dont la variance est minimale.
# Comme $\sigma_{Y_1^i}^2 = \frac{\sigma_i^2}{N^2}$, pour N fixe, si la variance de l'estimateur est minimale, la variance de $Y_1$ l'est aussi (comme $Y_k$ sont i.i.d., les variances de $Y_k$ sont égales pour $k=1,...,N$).
#
#
# </div>
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.1.2.** $\widehat p^1$ correspond à l'estimateur naïf de Monte-Carlo : écrivez $Y^1_1 = \varphi_1(X)$ et estimez numériquement $\text{Var}(Y^1_1)$ dans ce cas.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.1.2.**
# $$ p = \int\mathbb{1}(x > 2)f(x)dx = E[\mathbb{1}(X>2)]$$
# où X sont tirés selon f. L'estimateur est donc donné par:
# $$ $$
# $$ \widehat p_N^1 = \frac{1}{N}\sum_{k=1}^N\mathbb{1}(X_k>2) $$
# Dans ce cas:
# $$Y^1_1 = \mathbb{1}(X_1>2)$$
#
# </div>
def methode1(N):
taille_echantillon = N
x = np.random.standard_cauchy(taille_echantillon)
y = []
for i in range(taille_echantillon):
if x[i] > 2:
y.append(1.0)
else:
y.append(0.0)
estimation = (1.0 / taille_echantillon) * np.sum(y)
variance_y = np.var(y, ddof=0)
return [estimation, variance_y]
methode1(10**3)
# <p class="bg-primary" style="padding:1em">**QUESTION IV.1.3.** Utilisez la représentation (2) pour construire $Y^2_1 = \varphi_2(\lvert X \rvert)$. Estimez numériquement $\text{Var}(Y^2_1)$ dans ce cas et justifiez théoriquement la réduction de variance.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.1.3.**
# $$ p = \frac{1}{2}\int\mathbb{1}(|x| > 2)f(x)dx = E[\mathbb{1}(X>2)]$$
# $$ $$
# où X sont tirés selon f. L'estimateur est donc donné par:
# $$ $$
# $$ \widehat p_N^2 = \frac{1}{N}\sum_{k=1}^N\frac{\mathbb{1}(|X_k|>2)}{2} $$
# $$ $$
# Dans ce cas:
# $$ Y_1^2 = \frac{\mathbb{1}(|X_1|>2)}{2} $$
#
# </div>
def methode2(N):
taille_echantillon = N
x = np.random.standard_cauchy(taille_echantillon)
y = []
for i in range(taille_echantillon):
if np.absolute(x[i]) > 2.0:
y.append(0.5)
else:
y.append(0.0)
estimation = np.mean(y)
variance_y = np.var(y, ddof=0)
return [estimation, variance_y]
methode2(10**3)
# <p class="bg-primary" style="padding:1em">**QUESTION IV.1.4.** Utilisez la représentation (3) pour construire $Y^3_1 = \varphi_3(U)$ où $U$ est uniformément répartie, et estimez numériquement $\text{Var}(Y^3_1)$ dans ce cas.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.1.4.**
# $$ p = \frac{1}{2} - \int\mathbb{1}(0 \leq x \leq 2)f(x)dx = \frac{1}{2} - 2\int\frac{\mathbb{1}(0 \leq x \leq 2)}{2}f(x)dx $$
#
# $$ $$
# $$= E\bigg[\frac{1}{2}-2f(X)\mathbb{1}(0 \leq X \leq 2)\bigg]$$
# $$ $$
# où $X$ est uniformement répartie dans $[0, 2]$. L'estimateur est donc donné par:
# $$ $$
# $$ \widehat p_N^3 = \frac{1}{N}\sum_{k=1}^N\bigg(\frac{1}{2} - 2f(X_k)\mathbb{1}(0 \leq X_k \leq 2)\bigg) = \frac{1}{N}\sum_{k=1}^N\bigg(\frac{1}{2} - 2f(X_k)\bigg) $$
# Dans ce cas:
# $$Y^3_1 = \frac{1}{2} - 2f(X_1)$$
# </div>
def methode3(N):
taille_echantillon = N
x = np.random.uniform(0, 2, taille_echantillon)
y = []
for j in range(taille_echantillon):
y.append(.5 - 2/(np.pi*(1+x[j]**2)))
estimation = np.mean(y)
variance_y = np.var(y, ddof=0)
return [estimation, variance_y]
methode3(10**3)
# <p class="bg-primary" style="padding:1em">**QUESTION IV.1.5.** Utilisez la représentation (4) pour construire $Y^4_1 = \varphi_4(U)$ où $U$ est uniformément répartie, et estimez numériquement $\text{Var}(Y^4_1)$ dans ce cas.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.1.5.**
#
# $$ p = \int_0^{\frac{1}{2}}\frac{x^{-2}}{\pi(1+x^{-2})}dx = \int\frac{x^{-2}}{\pi(1+x^{-2})}\mathbb{1}\bigg(0 \leq x\leq \frac{1}{2}\bigg)dx = \frac{1}{2}\int\frac{x^{-2}}{\pi(1+x^{-2})}\frac{\mathbb{1}\big(0 \leq x \leq \frac{1}{2}\big)}{1/2}dx $$
#
# $$ $$
# $$= E\bigg[\frac{X^{-2}}{2\pi(1+X^{-2})}\mathbb{1}(0 \leq X \leq 1/2)\bigg]$$
# où $X \sim U[0, 1/2]$. L'estimateur est donc donné par:
# $$ $$
# $$ \widehat p_N^4 = \frac{1}{N}\sum_{k=1}^N\frac{X_k^{-2}}{2\pi(1+X_k^{-2})}$$
# Dans ce cas:
# $$Y^4_1 = \frac{X_1^{-2}}{2\pi(1+X_1^{-2})}$$
#
# </div>
def methode4(N):
taille_echantillon = N
x = np.random.uniform(0.0, 0.5, taille_echantillon)
y = []
for i in range(taille_echantillon):
y.append((np.power(1.0/x[i], 2.0))/(2.0 * np.pi*(1+np.power(1.0/x[i], 2.0))))
estimation = np.mean(y)
variance_y = np.var(y, ddof=0)
return [estimation, variance_y]
methode4(10**3)
# #### <p class="bg-primary" style="padding:1em">**QUESTION IV.1.6.** En reprenant les codes ci-dessus, calculez pour chacun de ces 4 estimateurs la taille de l'échantillon minimale qui permet d'estimer $p$ avec une erreur relative inférieure à $10^{-2}$ et commentez les résultats obtenus.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.1.6.**
# $$\text{erreur relative} = \frac{\sqrt{Var\big[\widehat p_N^i\big]}}{E\big[\widehat p_N^i\big]} = \frac{\sqrt{\frac{1}{N^2}Var\big[\widehat Y^i\big]}}{E\big[Y^i\big]}$$
# $$ $$
# $$ \text{erreur relative} < 10^{-2} \Leftrightarrow \frac{\sqrt{\frac{1}{N}Var\big[\widehat Y^i\big]}}{E\big[Y^i\big]} < 10^{-2} $$
# $$ $$
# Donc on calcul la taille minimale de l'échantillon comme suit:
# $$ $$
# $$ N > \frac{1}{10^4}\frac{Var\big[Y^i\big]}{E\big[Y^i\big]^2} $$
# </div>
taille_echantillon = 10**5
for j in range(4):
if j == 0:
data = methode1(taille_echantillon)
elif j == 1:
data = methode2(taille_echantillon)
elif j == 2:
data = methode3(taille_echantillon)
elif j == 3:
data = methode4(taille_echantillon)
nb_echa = int(np.power(10.0, 4)*np.power(data[1]/data[0]**2, 1))
print "> Pour l'estimateur", j+1,', il faut un échantillon de taille', nb_echa
# <h2> IV.2. Echantillonnage préférentiel </h2>
#
#
# Soit $g$ une densité de probabilité, appelée, comme pour le rejet, densité auxiliaire dans le cadre de l'échantillonnage préférentiel, telle que $g(x) = 0 \Rightarrow f(x) = 0$ si bien que le rapport $f(x) / g(x)$, et donc l'intégrale
# $$ \int \phi \frac{f}{g} g, $$
# sont bien définis si l'on adopte la convention $0/x = 0$ pour tout $x \in R$. Soit $(Y_k, k \in N)$ des variables i.i.d. de densité $g$ et
# $$ \widehat I^g_N = \frac{1}{N} \sum_{k=1}^N \phi(Y_k) \frac{f(Y_k)}{g(Y_k)} $$
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.1.** Montrez que $\widehat I^g_N$ est un estimateur sans biais et convergent de $I$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.1.**
# $$E\bigg[\frac{1}{N}\sum_{k=1}^N\phi(Y_k)\frac{f(Y_k)}{g(Y_k)}\bigg] = \int\phi(y)\frac{f(y)}{g(y)}g(y)dy = \int\phi(y)f(y)dy = I$$
# $$ $$
# J'ai utilisé juste la définiton d'ésperance et le fait que $Y_k$ sont tirées selon $g$. L'estimateur est donc centré Q.E.D., et selon la loi des grands nombres, il converge vers $I$ lorsque $N\rightarrow \infty$.
#
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.2.** On suppose que $\phi \geq 0$ et l'on considère $g_{\text{opt}} = \phi f / I$. Montrez que $g_{\text{opt}}$ est une densité de probabilité lorsque $\phi \geq 0$, et montrez sans calcul que $\widehat I^{g_{\text{opt}}}_N$ est de variance nulle.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.2.**
# Une fois que $f$ est une densité de probabilité: $f(x) \geq 0$ pour tout $x$ réel. On suppose $\phi(x) \geq 0$ pour tout $x$ réel aussi. Donc $I = \int \phi f \geq 0$ et:
#
# $$ $$
# $$ \int g_{opt} = \int \frac{\phi f}{I} = \frac{1}{I} \int\phi f = 1 $$
#
# $$ $$
# Comme $g_{opt} \geq 0$ et son integral est égal à 1, $g_{opt}$ peut être vue comme une densité de probabilité Q.E.D.
# Intuitivement, en utilisant cette fonction $g$, les valeurs dans notre somme ne sont plus aleatoires mais tous égales à $I$. L'estimateur n'est non plus une variable aleatoire et par conséquence sa variance est nulle.
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.3.** Que vaut $g_{\text{opt}}$ dans le cas de la sphère ? Peut-on l'utiliser ?</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.3.**
# Dans le cas de la sphère, on a:
# $$ $$
# $$V_d = \int_{[-1, 1]^d}\mathbb{1}(\lVert x \rVert \leq 1)dx = \int_{[-1, 1]^d}\frac{\mathbb{1}(\lVert x \rVert \leq 1)}{g_{opt}(x)}g_{opt}(x)dx$$
#
# $$ $$
# Avec $g_{opt}(x) = \frac{f(x)}{V_d}$. Si l'on connaît auparavant le volume que l'on souhaite estimer, alors on peut calculer $V_d$ et utiliser $g_{opt}(x)$.
#
# </div>
#
#
#
#
#
#
# <div class="alert alert-success"> Le problème de $g_{\text{opt}}$ est qu'elle dépend de la quantité $I$ que l'on cherche à estimer : **elle n'est donc pas utilisable en pratique mais cela suggère de chercher une densité auxiliaire qui lui soit proche.** En pratique, on se donne une famille paramétrique $\{g_\theta, \theta \in \Theta\}$ et on va chercher la "meilleure" fonction $g$ au sein de cette famille.</div>
#
#
#
# Pour illustrer cette démarche, on reprend le problème d'estimation du volume de la sphère en dimension $30$. A la fin du BE précédent, nous avons en effet vu que l'estimateur naïf de Monte-Carlo n'était pas efficace dans ce cas. Pour cela, on considère la famille paramétrique $\{g_\theta, \theta > 0\}$ sur $R^d$ où
# $$ g_\theta(x) = \prod_{k=1}^d h_\theta(x_k) \ \text{ avec } \ h_\theta(x_1) \propto (1-x_1^2)^{\theta-1} {\bf 1}(x_1 \in [-1,1]), \ x = (x_1, \ldots, x_d) \in R^d. $$
#
# On notera $\widehat V^{\text{IS}(\theta)}_d$ l'estimation de $V_d$ obtenue par échantillonnage préférentiel en utilisant $g_\theta$ comme fonction auxiliaire.
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.4.** Utilisez le script suivant pour tracer en dimension $d = 2$ la surface $g_\theta$ pour différentes valeurs de $\theta$, et expliquez intuitivement pourquoi, en grande dimension, il devrait être plus efficace de générer selon $g_\theta$ que selon $f$ lorsque $\theta > 1$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.4.**
# On avait vu que lorsque le nombre dimensions tendait vers l'infini, le volume de la sphère se concentré dans sa surface. Pour une grande dimension ce serait donc plus utile d'y placer plus de points qu'ailleurs. La fonction densité de probabilité $g_{opt}^{\theta}$ permet de faire cela tandis que en utilisant $f$ on placerait des points uniformement dans $[-1, 1]^d$.
#
# </div>
def g(x, theta):
'''
x est une matrice avec N lignes et d colonnes
d est la dimension de l'espace
N est la taille de l'echantillon
la fonction renvoie un vecteur de longueur N où la kième entrée correspond à la fonction g
appliquée à la kième ligne
'''
dimension = x.shape[1]
taille_echantillon = x.shape[0]
c =(2 * special.gamma(2*theta) )/ (4**np.float64(theta) * special.gamma(theta)**2)
return c**dimension * np.power(np.prod(1 - np.power(np.float64(x), 2), 1), (np.float64(theta) - 1))
theta = 0.5
x = np.arange(-.99,.99,.01)
y = np.arange(-.99,.99,.01)
X, Y = np.meshgrid(x, y, indexing='ij')
Z = np.zeros(X.shape)
for i in range(len(x)):
for j in range(len(y)):
Z[i,j] = g(np.array([[x[i], y[j]]]), theta)
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=False)
fig.colorbar(surf, shrink=0.5, aspect=5)
fig.suptitle("Fonction auxiliaire g")
plt.show()
# On admet par la suite que si les $(Y_k)$ sont i.i.d. et suivent une loi beta de paramètre $(\theta, \theta)$, alors $g_\theta$ est la densité de $(2Y_k-1, k = 1,\ldots, d)$. Ainsi, pour générer une variable aléatoire de densité $g_\theta$, il suffit de savoir générer des variables aléatoires suivant la loi beta, ce que fait la fonction ``np.random.beta``.
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.5.** Complétez le script suivant puis utilisez-le pour tracer la performance (estimation, écart relatif et erreur relative) de l'estimateur par échantillonnage préférentiel pour $N = 10^5$, $d \in [2,20]$ et $\theta = 7,5$. Comparez avec IIDMC. Que pensez-vous des résultats obtenus ? Analysez notamment l'influence du paramètre $\theta$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.5.**
# Lorsque l'on augmente le $\theta$ dès 1.0 à 7.5, les résultats, plutôt pour dimensions plus grandes, deviennet plus satisfactoires. Tandis que l'estimateur naïf n'est pas utilisable pour dimensions supérieurs à 10, l'échantillonage préferentielle permet d'aller jusqu'à 20. Toutefois l'erreur relative devient pire pour les dimensions plus baisses, comme l'on peut constater d'après le graphique. Si $\theta$ dépasse 7.5, l'erreur à baisses dimensions augmente encore plus.
# </div>
def estimation_IS(dimension, taille_echantillon, theta):
echantillon = 2*np.random.beta(theta, theta, size=(taille_echantillon, dimension)) - 1
fonction_g = g(echantillon, theta)
y = []
for i in range(taille_echantillon):
if (np.linalg.norm(echantillon[i,:],2) <= 1.0):
y.append(1.0 / fonction_g[i])
else:
y.append(0.0)
estimation = np.mean(y)
V_theorique = (np.pi**(dimension / 2.0)) / special.gamma((dimension / 2.0) + 1.0)
ecart_relatif = (estimation - V_theorique) / V_theorique
erreur_relative = np.power((1.0/taille_echantillon)*np.var(y), .5) / np.mean(y)
return [estimation, ecart_relatif, erreur_relative]
N = 10**5
dimensions = range(2,21)
est_IS = np.zeros([len(dimensions),3])
theta = 7.5
val_th = np.zeros([len(dimensions),1])
for i in range(len(dimensions)):
print '> Estimation par échantillonnage préférentiel en dimension ', dimensions[i]
est_IS[i,:] = estimation_IS(dimensions[i], N, theta)
val_th[i] = np.pi**(dimensions[i]/2.0) / special.gamma(dimensions[i]/2.0+1.0)
# +
fig = plt.figure()
plt.plot(dimensions, est_IS[:,0], label="IS")
plt.plot(dimensions, val_th, 'r--', label="Theorie")
plt.legend()
plt.xlabel("Dimension")
fig.suptitle("Estimation")
fig = plt.figure()
plt.plot(dimensions, est_IS[:,1], label="IS")
plt.legend()
plt.xlabel("Dimension")
fig.suptitle("Ecart relatif")
fig = plt.figure()
plt.plot(dimensions, est_IS[:,2], label="IS")
plt.legend()
plt.xlabel("Dimension")
fig.suptitle("Erreur relative")
# -
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.6.** On cherche maintenant à comprendre l'influence de $\theta$. On fixe $N = 10^5$ et $d = 30$: tracez l'évolution de $\widehat V^{\text{IS}(\theta)}_d$, de l'écart relatif et de l'erreur relative correspondant pour $\theta \in [1,30]$ et discutez les résultats.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.6.**
# On constate que l'erreur relative et l'écart relative chutent lorsque $\theta$ dépasse 5. Pour $10 < \theta < 20$, l'erreur relative est même inférieur à 2%, ce qu'était impensable pour l'estimateur naïf à 30 dimensions. Si on l'augmente encore, l'erreur relative commence à monter et la valeur estimée devient moins stable (avec beaucoup plus de fluctuations).
# </div>
N = 10**5
d = 30
theta = np.arange(5,30,1)
est_IS = np.zeros([len(theta),3])
for i in range(len(theta)):
est_IS[i,:] = estimation_IS(d, N, theta[i])
print 'Ready!'
# +
fig = plt.figure()
th = np.zeros([len(theta),1]) + np.pi**(d/2) / special.gamma(d/2+1)
plt.plot(theta, th, 'r--', label="Theorie")
plt.plot(theta, est_IS[:,0], label="IS")
plt.legend()
plt.xlabel("Theta")
fig.suptitle("Estimation")
fig = plt.figure()
plt.plot(theta, est_IS[:,1])
plt.xlabel("Theta")
fig.suptitle("Ecart relatif")
fig = plt.figure()
plt.plot(theta, est_IS[:,2])
plt.xlabel("Theta")
fig.suptitle("Erreur relative")
# -
# <p class="bg-primary" style="padding:1em">**QUESTION IV.2.7.** Pour $N = 10^5$ et $d = 30$, déterminez numériquement le paramètre $\theta_{\text{opt}}$ qui minimise l'erreur relative de $\widehat V_d^{\text{IS}(\theta)}$. Estimez l'erreur relative de $\widehat V_d^{\text{IS}(\theta_{\text{opt}})}$ et estimez le budget de simulation nécessaire pour déterminer $\theta_{\text{opt}}$. Evaluez le nombre d'échantillons nécessaires pour obtenir la même erreur relative que $\widehat V_d^{\text{IS}(\theta_{\text{opt}})}$ par IIDMC. Enfin, étudiez également l'influence de $N$ sur la procédure d'optimisation. </p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION IV.2.7.**
# Soit N la taille d'echantillon telle que IIMDC a la même erreur relative que IS. On sait que l'erreur relative de IIMDC varie selon $1/\sqrt{N}$, donc on peut calculer la taille necessaire comme ci-dessous:
# $$ $$
# $$\frac{\text{erreur relative}_{N=10^5}^{IIDMC}}{\text{erreur relative}_{IS}} = \frac{1/\sqrt{10^5}}{1/\sqrt{N}}$$
# $$ $$
# $$ N = 10^5\bigg(\frac{\text{erreur relative}_{N=10^5}^{IIDMC}}{\text{erreur relative}_{IS}}\bigg)^2$$
# $$ $$
# Les calculs numeriques montrent que c'est physiquement impossible de faire l'estimation avec IIDMC si l'on souhaite la même erreur relative. La taille de l'échantillon pour IIDMC est toujours de l'order de $10^{+18}$.
# Pour $N=10^3$, $\theta = 14.8125$, avec un erreur relative de 0.00621. Pour $N=10^5$, $\theta = 14.8749$, avec un erreur relative de 0.006183. Toutefois, pour $N=10^7$, $\theta = 15.25$ mais l'erreur relative est de 0.006226. Le $\theta_{optimale}$ augmente lorsque $N$ augmente, mais l'erreur relative après $N^6$ n'a pas diminué.
# </div>
#
#
# +
from fonctions_estimation import estimation_IIDMC
def optim_var_IS(theta):
vol_estim = estimation_IS(30, 10**5, theta)
return vol_estim[2]
N = 10**5
d=30
x0 = 5
res_optim = minimize(optim_var_IS, x0, method='nelder-mead',options={'xtol': 1e-5, 'disp': True})
N_tot_IS = res_optim.nit*N
vol_estim = estimation_IS(30, 10**5, res_optim.x)
print '> Volume estime par echantillonnage preferentiel optimise:',vol_estim[0]
print '> avec un theta optimisé de',res_optim.x,'erreur relative de ',res_optim.fun,' pour un budget de simulations de',N_tot_IS+10**5
th = np.pi**(d/2) / special.gamma(d/2+1)
taille_MC = N*((estimation_IIDMC(d, N)[2])/(res_optim.fun))**2
print '> Nombre dechantillons Monte-Carlo necessaires pour obtenir une precision equivalente a IS:',taille_MC
# -
#
#
#
#
# <a id="INTROMARKOV"></a><h1 style="border: 5px solid; text-align: center; padding: 10px">V. Introduction aux chaînes de Markov</h1>
#
# <h2> V.1. Vitesse(s) de convergence(s)</h2>
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.1.** Le script suivant génère une suite $(X_t)$ : quelles sont les valeurs prises par cette suite ? Expliquez simplement sa dynamique.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.1.**
# Le premier élément de la chaîne est $init$. L'élément $X_{k+1}$ va être égale à $X_{k}$ avec une probabilité de $p$, ou égale à $1-X_{k}$ avec une probabilité de $1-p$. Donc, chaque valeur suivante est calculée de forme aleatoire mais elle ne dépende que de la valeur actuelle. La suite va être une chaîne de Markov.
# </div>
#
#
def Markov_intro(t_max, p, init):
X = np.zeros(t_max)
X[0] = init
for time in range(1, t_max):
if (np.random.random() < p):
X[time] = X[time-1];
else:
X[time] = 1 - X[time-1];
return X
#
#
# <div class="alert alert-success" style="text-align: center;"> On dit qu'une suite $(Y_n)$ satisfait le **théorème ergodique** si la suite $(\bar Y_N)$ des moyennes empirique converge presque sûrement vers une constante, i.e., s'il existe une constante $\mu$ telle que $\displaystyle \bar Y_N = \frac{1}{N} \sum_{k=1}^N Y_k \stackrel{\text{p.s.}}{\to} \mu. $ </div>
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.2.** Une suite i.i.d. satisfait-elle le théorème ergodique ? Justifiez votre réponse.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.2.**
# Soit $Y_k$ une suite de variables aleatoires i.i.d., avec $\mu$ son ésperance et $\sigma^2$ sa variance. D'après le théorème central limite, on a:
# $$ $$
# $$ \lim_{N\to\infty} \frac{\sum_{k=1}^N Y_k - \mu}{\sqrt{\sigma^2/N}} \sim N(0, 1)$$
# $$ $$
# Donc,
# $$ \lim_{N\to\infty} \sum_{k=1}^N Y_k \sim N\bigg(\mu, \frac{\sigma^2}{N}\bigg)$$
# $$ $$
# Pour N suffisamment grand, la variance s'approche de zero et donc la somme aleatoire va prend une valeur presque constante égale à $\mu$. Donc une suite de variables aleatoires i.i.d satisfait le théorème ergodique.
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.3.** Utilisez le script suivant pour vérifier que $(X_t)$ satisfait le théorème ergodique. Pour quelles valeurs de $p$ la convergence est-elle la plus rapide ? La condition initiale joue-t-elle un rôle ? Expliquez pourquoi.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.3.**
# $$ $$
# La convergence est plus rapide pour $p$ inférieure. En effet, la courbe à bleu ($p=0.1$) est celle que converge plus vite, et la courbe violet ($p=0.9$) celle que converge plus lentement. La condition initiale ne change ceci, mais augmente le temps de convergence pour toutes les $p$ (parce que si l'on prend $init=1$ on va osciller entre 0 et 1, tandis que si l'on prend par exemple $init = 40$, on oscille entre 40 et -39, donc la moyenne prends plus longtemps pour stabiliser).
# $$ $$
# Pour l'influence de p: intuitivement, pour $p$ plus petite, il y'aura plus de chance que la valeur prochaine de la chaîne soit égale à la valeur actuelle et donc, la chaîne converge plus vite. Si $p$ tend vers 1, on change presque toujours d'état, donc elle prends plus longtemps pour stabiliser autour de la valeur constante.
# </div>
#
#
# +
t_max = 10**2
val_p = np.arange(.1,1,.2)
nb_p = len(val_p)
fig, ax = plt.subplots()
for i in range(nb_p):
p = val_p[i]
traj = Markov_intro(t_max, p, 0)
ax.plot(range(t_max), np.divide(np.cumsum(traj), range(1,1+len(traj))), label="p="+str(p))
plt.legend()
plt.suptitle("Verification du theoreme ergodique")
plt.xlabel("Temps")
plt.ylabel("Moyenne empirique")
# -
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.4.** Pour quelle(s) valeur(s) de $p$ la suite $(X_t)$ est-elle i.i.d.? Concluez.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.4.**
# $$ $$
# On considère comme hypothèse que $init = X_0 = x$, et que la suite $X_t$ est i.i.d.:
# $$ $$
# Pour $k>0$ et en utilisant le fait que $X_k$ et $X_{k-1}$ sont indépendants:
# $$ $$
# $$ P(X_k = x) = p(X_k = x \space\big\vert\space X_{k-1} = x) = p$$
# $$ $$
# $$ P(X_k = x) = p(X_k = x \space\big\vert\space X_{k-1} = 1-x) = 1-p$$
# $$ $$
# Pour vérifier l'égalité, on a besoin que:
# $$ $$
# $$ p = 1 - p $$
# $$ $$
# D'où sort que $p=0.5$. Pour cette valeur de p la suite sera donc i.i.d.
#
# </div>
#
#
#
#
# <div class="alert alert-success" style="text-align: center;"> On rappelle qu'une suite $(Y_n)$ de variables aléatoires à valeurs entières converge en loi vers une variable aléatoire $Y_\infty$, ce que l'on note $Y_n \stackrel{\text{d}}{\to} Y_\infty$, si $P(Y_n = k) \to P(Y_\infty = k)$ pour tout $k \in N$. </div>
#
#
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.5.** Proposez une méthode numérique pour vérifier que $X_n \stackrel{\text{L}}{\to} X_\infty$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.5.**
# $$ $$
# Soit $Y_n$ notre suite (chaîne de Markov). Si l'on génére plusieures chaînes ($N$ chaînes), on peut calculer empiriquement $P(Y_n = k)$. Pour faire cela, je vais considérer $Y_n^i$ le n'ième élement de la i-ième chaîne.
# $$ $$
# $$ P(Y_n = k) = \frac{1}{N}\sum_{i=1}^N\mathbb{1}(Y_n^i = 1)$$
# $$ $$
# Il faut maintenant faire ce calcul pour chaque élement de la chaîne, et pour n élevé, les valeurs doivent converger.
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.6.** Complétez le script suivant pour vérifier numériquement que $X_n \stackrel{\text{L}}{\to} X_\infty$: quelle est la limite ? dépend-elle de $p$? Expliquez comment jouer sur la condition initiale pour que la chaîne de Markov démarre directement à l'équilibre.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.6.**
# $$ $$
# Cependent les différents $p$ utilisées pour générer les chaînes, les probabilités $P(Y_n = 1)$ convergent toutes vers 0.5 lorsque n s'approche de l'infini (pour une chaîne initialisée à 1). Pour $10^4$ chaînes chacune avec une longueur de 50 élements la convergence est bien visible. La limite ne depend donc de $p$ utilisé lors de la creation de la chaîne.
# </div>
#
#
# +
t_max = 5*10**1
taille_echantillon = 10**4
val_p = np.arange(.1,1,.2)
nb_p = len(val_p)
fig, ax = plt.subplots()
for i in range(nb_p):
p = val_p[i]
echantillon = np.zeros((taille_echantillon, t_max))
for j in range(taille_echantillon):
echantillon[j,:] = Markov_intro(t_max, p, 1)
estimation_loi = np.zeros(t_max)
for t in range(t_max):
estimation_loi[t] = (1.0/taille_echantillon)*np.sum(echantillon[:,t] == 1)
ax.plot(range(t_max), estimation_loi, label="p="+str(p))
plt.legend()
plt.suptitle("Verification de la convergence en loi")
plt.xlabel("Temps")
plt.ylabel("Estimation de la loi")
# -
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.7.** Pour quelles valeurs de $p$ la convergence est-elle la plus rapide ? Comparez à la réponse de la question V.1.3 et commentez.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.7.**
# La convergence est maintenant plus rapide pour $p=0.5$, tandis qu'avant elle l'était pour $p=0.1$. On avait vu lors de l'étude du théorème ergodique que la moyenne de toutes les chaînes convergé vers 0.5, donc il était déjà attendu que la chaîne avec $p=0.5$ convergeait plus rapidement vers une variable aleatoire.
# </div>
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION V.1.8.** Vérifiez numériquement que $\displaystyle \sqrt N \left( \bar X_N - \frac{1}{2} \right)$ suit approximativement une loi normale pour $N$ grand et faites le lien avec le théorème central limite</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION V.1.8.**
# Le resultat vient du théorème central limite et de la loi des grands nombres. Une fois que ici $\mu = 1/2$, donc la loi normal a une esperance nulle comme on constate d'après les résultats numériques.
# </div>
#
#
t_max = 10**3
taille_echantillon = 10**4
p = .2
echantillon_markov = np.zeros((taille_echantillon, t_max))
echantillon = np.zeros(taille_echantillon)
x = np.zeros(taille_echantillon)
for j in range(taille_echantillon):
echantillon_markov[j,:] = Markov_intro(t_max, p, 1)
echantillon[j] = (np.mean(echantillon_markov[j,:])-.5)*taille_echantillon**.5
print '> Ready!'
binwidth = 100.0/taille_echantillon
#count, bins, ignored = plt.hist(echantillon, normed=True)
count, bins, ignored = plt.hist(echantillon, normed=True, bins=np.arange(min(echantillon), max(echantillon) + binwidth, binwidth))
sigma = np.std(echantillon)
mu = np.mean(echantillon)
fig, ax = plt.subplots()
ax.plot(bins, 1.0/(sigma * np.sqrt(2.0 * np.pi)) * np.exp( - (bins - mu)**2.0 / (2.0 * sigma**2.0) ), linewidth=2, color='r')
ax.plot(bins, stats.norm.pdf(bins, loc=mu, scale=sigma), linewidth=2, color='r')
plt.suptitle("Verification du theoreme central limite")
# <br>
#
# <br>
#
# <br>
#
# <br>
#
# <br>
#
#
# <br>
#
# <br>
#
# <br>
#
# <br>
#
# <br>
#
#
#
#
#
# <a id="MCMC"></a><h1 style="border: 5px solid; text-align: center; padding: 10px">VI. Méthodes de Monte-Carlo à base de chaînes de Markov</h1>
#
#
#
#
#
#
# <div class="alert alert-success"> Si $(X_n)$ est une chaîne de Markov de mesure stationnaire $f$, alors le théorème ergodique pour les chaînes de Markov garantit que
# $$ \displaystyle \widehat I^{\text{MCMC}} = \frac{1}{N} \sum_{k=1}^N \phi(X_k) $$
# est un estimateur convergent de $\int \phi f$: on a remplacé un échantillon i.i.d. par la trajectoire d'un processus de Markov, on parle alors de méthode **MCMC** (par opposition à IIDMC). Cette méthode n'a d'intérêt que si l'on sait générer une chaîne de Markov avec une probabilité stationnaire donnée : l'**algorithme de Metropolis-Hastings** fait précisément cela, il s'agit de la pierre angulaire des méthodes MCMC.</div>
#
#
#
# <h2> VI.1. Algorithme de Metropolis–Hastings</h2>
#
# L'algorithme de Metropolis--Hastings est un algorithme général qui permet de générer une chaîne de Markov avec une distribution invariante donnée. Soit $\pi$ une mesure de probabilité sur un ensemble dénombrable $\mathfrak{X}$ et $K: \mathfrak{X} \times \mathfrak{X} \to [0,1]$ un noyau de transition, i.e., pour tout $x \in \mathfrak{X}$ la famille $K(x, \cdot) = (K(x,y), y \in \mathfrak{X})$ définit une mesure de probabilité sur $\mathfrak{X}$. L'algorithme de Metropolis-Hastings construit la chaîne de Markov suivante :
# 1. Tirer $Y_t$ selon la loi $K(X_t, \, \cdot)$;
# 2. Calculer
# $$ \displaystyle \varrho(X_t, Y_t) = \min \left( 1, \frac{\pi(Y_t)}{\pi(X_t)} \frac{K(Y_t, X_t)}{K(X_t, Y_t)} \right); $$
# 3. Choisir $\displaystyle X_{t+1} = \begin{cases}
# Y_t & \text{ avec probabilité } \varrho(X_t, Y_t),\\
# X_t & \text{ avec probabilité } 1 - \varrho(X_t, Y_t).
# \end{cases} $
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.1.1.** Calculez $p_{xy} = P(X_2 = y \mid X_1 = x)$ puis montrez que $\pi_x p_{xy} = \pi_y p_{yx}$. Déduisez-en que $X$ admet $\pi$ comme probabilité stationnaire.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.1.1.**
# $$ \displaystyle P(tirer \space y)P(accepter \space y \space | \space tirer \space y) = K(x,y)\rho(x,y)=K(x,y)min\bigg(1, \frac{\pi_y K(y,x)}{\pi_x K(x,y)}\bigg) = K(x,y)$$
#
# $$P_{yx} = K(y,x)\frac{\pi_x K(x,y)}{\pi_y K(y,x)} = \frac{\pi_x}{\pi_y}K(x,y) = \frac{\pi_x}{\pi_y}p_{xy}$$
# </div>
#
#
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.1.2.** Décrivez simplement cet algorithme lorsque le noyau de transition ne dépend pas de l'état de départ, i.e., $K(x, \cdot \,) = k$ pour une certaine mesure de probabilité $k$, et tout $x \in \mathfrak{X}$. Faites le lien avec la méthode du rejet.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.1.2.**
# Dans se cas on fait:
# $$ $$
# 1) Tirer $Y_t$ selon K;
# $$ $$
# 2) Calculer de $\rho = min(1, \frac{\pi(Y_t)}{\pi(X_t)})$;
# $$ $$
# 3) Tirer U selon $U_{[0,1]}$;
# $$ $$
# 4) Accepter $Y_t$ si $U < \rho$. Sinon garder $X_t$.
#
# Dans la méthode du rejet on accepté une valeur si $U \leq f(X)$, avec U uniformement repartie dans $[0,K], (K\geq 2sup(f))$ et où $f(X)$ était la densité que l'on souhaité simuler. Dans la méthode de Metropolis, on souhaite de générer une chaîne telle que les valeurs soient convergents vers une distribuition $\pi$. Si on suppose que $\frac{\pi(Y_t)}{\pi(X_t)}$ est inférieur à l'unité on peut reécrire le critère d'acceptation comme suit:
# $$ $$
# $$ U \leq \pi(Y_t), \text{ où } U \sim U[0, \pi(X_t)]$$
# $$ $$
# Cela ressemble à la méthode du rejet.
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.1.3.** Décrivez simplement $Y_t$ lorsque le noyau de transition est de la forme $K(x, y) = k(y-x)$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.1.3.** </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.1.4.** Discutez des utilisations et avantages potentiels de l'algorithme de Metropolis-Hastings.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.1.4.**
# D'abord, cette méthode ne necessite que la connaissance de la distribuition $\pi$ à une constante près. Cela est très important une fois que la plupart du temps on ne connait les fonctions densités qu'à une constante près (car les constantes de normalization sont difficiles à calculer). En plus, cet algorithme lié à Monter-Carlo (MCMC) permet de resoudre de problèmes complexes en plusieurs dimensions où les autres méthodes échouent.
# </div>
#
#
#
#
# <div class="alert alert-success"> Dans le cas à densité, l'algorithme de Metropolis--Hastings est le même : un noyau de transition est une application $K: R^d \times R^d \to [0,1]$ telle que $K(x, \cdot \,)$ est une densité sur $R^d$ pour chaque $x \in R^d$, et $\pi$ est remplacée par une densité $f$ sur $R^d$. </div>
#
#
#
#
# <h2> VI.2. Vitesse de convergence de la méthode MCMC</h2>
#
#
# La méthode MCMC consiste donc à générer à l'aide de l'algorithme de Metropolis-Hastings une chaîne de Markov ayant une densité cible $f$ comme distribution stationnaire, puis de considérer l'estimateur
# $$ \widehat I^{\text{MCMC}} = \frac{1}{N} \sum_{k=1}^N \phi(X_k) $$
# qui est convergent par le théorème ergodique pour les chaînes de Markov.
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.2.1.** A-t-on comme dans le cas IIDMC $\displaystyle \text{Var}(\widehat I^{\text{MCMC}}) = \frac{\text{Var}(\phi(X_1))}{\sqrt{N}}$? Pourquoi?</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.2.1.**
#
# $$ $$
# $$Var[\widehat{I}^{MCMC}] = \frac{1}{N^2}Var\bigg[\sum_{k=1}^N\phi(X_k)\bigg] =
# \frac{1}{N^2}\sum_{k=1}^N Var\bigg[\phi(X_k)\bigg]$$
# $$ $$
# $$= \frac{1}{N}Var\big[\phi(X_1)\big] \space\text{ (si les variables } \space X_k\space \text{ sont i.i.d)}$$
# $$ $$
# Donc la formule n'est pas applicable si les variables aleatoires de la chaîne de Markov ne sont pas i.i.d.
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.2.2.** Proposez une méthode numérique pour estimer $\text{Var}(\widehat I^{\text{MCMC}})$.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.2.2.**
# D'abord, générer N chaînes de Markov de taille M, ayant pour densité cible $f$, en utilisant l'algorithme de Metropolis-Hashtings. Puis générer N échantillons $\phi(x_k)$, où k varie de 0 à M. Comme cela, on peut estimer la variance de chaque élement des chaînes en utilisant numpy.var. Après on somme toutes les variances et on divise par le nombre de chaînes générées. Sauf si on sait d'abord que les variables aleatoires de la chaîne de Markov sont i.i.d. Dans ce cas, on pourrait utiliser le fait que la variance est égale à $\frac{\text{Var}(\phi(X_1))}{N}$
# </div>
#
#
#
# <h2> VI.3. Méthode MCMC pour l’estimation du volume de la sphère</h2>
#
#
# On retourne à l'exemple de la sphère. On propose quatre noyaux de transition :
# * **Noyau uniforme - indépendant:** $K(x, \cdot \,)$ est la mesure uniforme sur $[-1,1]^d$;
# * **Noyau uniforme - marche aléatoire:** $K(x, y) \propto {\bf 1}(\lVert y - x \rVert \leq \delta)$;
# * **Noyau beta - indépendant:** $K(x, \cdot \,) = g_\theta$ avec $g_\theta$ introduit dans le BE sur l'échantillonnage préférentiel;
# * **No<NAME>sien - marche aléatoire:** $K(x, y) \propto \exp \left( -\lVert y - x \rVert^2 / (2 \sigma^2) \right)$.
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.3.1.** Décrivez par écrit l'algorithme de Metropolis-Hastings dans chacun des ces cas.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.3.1.**
# $$ $$
# On prend la dernière valeur de la chaîne ($X_t$) et après:
# $$ $$
# 1) On tire Y selon K, où K est une des distribuitions mentionnées.
# $$ $$
# 2) On calcule $K(X_t, Y)$, et $K(X_t, Y)$, en utilisant les fonction densité $K$ à une constante multiplicative près.
# $$ $$
# 3) On calcule $\pi(X_t)$ et $\pi(Y)$. Dans notre cas, la distribuition stationnaire était uniforme, donc ces valeurs sont toujours égales à l'unité (car $X_t$ et $Y$ sont dedans $[-1, 1]^d$.
# $$ $$
# 4) On calcule $\rho$ selon la formule specifiée
# $$ $$
# 5) On tire U uniformement dans $[0,1]$.
# $$ $$
# 6) On accepte le $Y$ comme le prochaine valeur de la chaîne si $U \leq \rho$. Sinon la prochaine valeur est la même que la valeur actuelle.
# </div>
#
#
#
# <p class="bg-primary" style="padding:1em">**QUESTION VI.3.2.** Complétez les fonctions ``estimation_MCMC_XXX`` qui implantent ces algorithmes. Pour vérifier votre code, vous vérifierez numériquement et en petite dimension que ces quatre chaînes de Markov ont bien comme distribution stationnaire la mesure uniforme sur la sphère.</p>
#
# <div class="alert alert-warning">**REPONSE A LA QUESTION VI.3.2.**
# J'ai généré des châines de Markov avec plusieurs noyaux et avec la distribuition uniforme comme distribuition stationnaire des chaînes. Après j'ai utilisé la méthode de Monte Carlo avec elles pour estimer le volume d'une sphère.
# </div>
#
#
# +
def markov_chain(chain_size, noyau, dim):
x = np.zeros((chain_size, dim))
y = np.zeros((chain_size, dim))
x[0,:] = 0.0
for i in range (chain_size-1):
if noyau == "uniform_ind":
y = np.random.uniform(-1, 1, size=dim)
K_num = 1
K_den = 1
pi_num = 1
pi_den = 1
elif noyau == "uniform_ma":
y = np.random.uniform(-1, 1, size=dim)
if (np.linalg.norm(y - x[i,:]) <= 2**dim):
K_num = 1.0
else:
K_num = 0
if (np.linalg.norm(x[i,:]-y) <= 2**dim):
K_den = 1
else:
K_den = 0
pi_num = 1
pi_den = 1
elif noyau == "gaussien":
y = np.random.normal(0, 1, size=dim)
K_num = np.exp(-((np.linalg.norm((y-x[i,:]), 2)**2)/2))
K_den = np.exp(-((np.linalg.norm((-y+x[i,:]),2)**2)/2))
pi_num = 1
pi_den = 1
num = pi_num*K_num
den = pi_den*K_den
accept_probability = np.minimum(1, num/den)
if (np.random.uniform(0, 1) <= accept_probability):
x[i+1,:] = y
else:
x[i+1,:] = x[i+1,:]
return x
def estimation_MCMC_unif_ind():
sample = markov_chain(10**4, "uniform_ind", 2)
dim = np.size(sample, 1)
N = np.size(sample, 0)
estimation = ((2.0**dim) / N) * np.sum(np.linalg.norm(sample,2,axis=1) <= 1.0)
return estimation
def estimation_MCMC_unif_MA():
sample = markov_chain(10**4, "uniform_ma", 2)
dim = np.size(sample, 1)
N = np.size(sample, 0)
estimation = ((2.0**dim) / N) * np.sum(np.linalg.norm(sample,2,axis=1) <= 1.0)
return estimation
def estimation_MCMC_gaussien():
sample = markov_chain(10**4, "gaussien", 2)
dim = np.size(sample, 1)
N = np.size(sample, 0)
estimation = ((2.0**dim) / N) * np.sum(np.linalg.norm(sample,2,axis=1) <= 1.0)
return estimation
#def estimation_MCMC_beta():
# -
print 'Volume (uniforme ind): ', estimation_MCMC_unif_ind()
print 'Volume (uniforme): ', estimation_MCMC_unif_MA()
print 'Volume (gaussien): ', estimation_MCMC_gaussien()
|
monte_carlo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from openpyxl import Workbook
from openpyxl import load_workbook
import pandas as pd
import numpy as np
import os
import sys
import copy
import json
import sys
# +
#Outputs all of the Stages, Counts, & Countries (Ex. Engage->Qualify)
if __name__ == "__main__":
output_df = pd.DataFrame()
directory = os.getcwd() + "/data"
files = []
for i in sorted(os.listdir(directory)):
if os.path.isfile(os.path.join(directory,i)) and ('Product_Pipe' in i) and ('~' not in i):
files.append(i)
print(files)
# if put in two excel sheets in commandline
# if(len(sys.argv)>1):
# #files = [sys.argv[1], sys.argv[2], sys.argv[3]]
# files = sys.argv[1:]
# else:
# files = sorted(os.listdir(directory))
# print(files)
#first sheet we do value counts
#prev = first sheet dataframe
filename = files[0]
f = os.path.join(directory, filename)
print(f)
df_prev = pd.read_excel(f, sheet_name='Sheet1')
df_prev = pd.DataFrame(df_prev, columns=['Opp No', 'Sales Stage Name', 'Country', 'Opportunity Source', 'LIO Channel', 'Sector'])
df_prev = df_prev.drop_duplicates(subset=["Opp No"], keep="last")
filename = filename.split(".")[0][-5:]
for i in range(1, len(files)):
filename = files[i]
f = os.path.join(directory, filename)
df_current = pd.read_excel(f, sheet_name='Sheet1')
df_current = pd.DataFrame(df_current, columns=['Opp No', 'Sales Stage Name', 'Country', 'Opportunity Source', 'LIO Channel', 'Sector'])
print(df_current.head(3))
df_current = df_current.drop_duplicates(subset=["Opp No"], keep="last")
temp = df_current["Sales Stage Name"].value_counts()
df_current = df_current.rename(columns= {'Opp No': "Opp No Cur", 'Sales Stage Name': "Sales Stage Name Cur", 'Country': "Country Cur", 'Opportunity Source': "Opp Source Cur", 'LIO Channel': "LIO Channel Cur", 'Sector': "Sector Cur"})
df_compare = pd.merge(df_prev, df_current, how = "outer", left_on=df_prev["Opp No"], right_on = df_current["Opp No Cur"])
df_compare = df_compare.fillna(0)
df_compare.to_excel("test.xlsx")
df_temp = pd.read_excel('engage.xlsx')
temp2 = pd.DataFrame(df_temp)
temp2.to_excel('temp2.xlsx')
L = []
newOpp_list = pd.DataFrame(columns=['Sales Stage Name'])
#outputName = "compare" + str(i) + ".xlsx"
#df_compare.to_excel(outputName)
for index, row in df_compare.iterrows():
Opp_No_prev = row["Opp No"]
Opp_No_cur = row["Opp No Cur"]
Country = row["Country Cur"]
Country_prev = row["Country"]
Opp_Source_prev = row["Opportunity Source"]
Sector_prev = row["Sector"]
LIO_Channel_prev = row["LIO Channel"]
Opp_Source = row["Opp Source Cur"]
Sector = row["Sector Cur"]
LIO_Channel = row["LIO Channel Cur"]
Sales_Stage_Name_prev = row["Sales Stage Name"]
Sales_Stage_Name_cur = row["Sales Stage Name Cur"]
if(Sales_Stage_Name_prev == "Engage" and Sales_Stage_Name_cur==0):
#loss
key1 = "Loss"
key2 = "Engage->Loss"
file = filename.split(".")[0][-5:]
dat= [{'Date': file, 'Changes': key2, 'Changes_Cond': key1, 'Location': Country_prev, 'Source': Opp_Source_prev, 'Owner': LIO_Channel_prev, 'Sector': Sector_prev, 'Count': '1'}]
dd = pd.DataFrame(dat)
L.append(dd)
elif(Sales_Stage_Name_prev == "Engage" and Sales_Stage_Name_cur!=0):
key1 = Sales_Stage_Name_cur
key2 = "Engage->" + Sales_Stage_Name_cur
file = filename.split(".")[0][-5:]
dat= [{'Date': file, 'Changes': key2, 'Changes_Cond': key1, 'Location': Country, 'Source': Opp_Source, 'Owner': LIO_Channel, 'Sector': Sector, 'Count': '1'}]
dd = pd.DataFrame(dat)
L.append(dd)
#outside of loop
df = pd.concat(L)
df_temp = pd.read_excel('engage.xlsx', index_col=[0])
df_temp = pd.DataFrame(df_temp)
frames = [df_temp, df]
df_output = pd.concat(frames, ignore_index=True)
df_output.to_excel('engage.xlsx')
df_current = df_current.rename(columns= {'Opp No Cur': "Opp No", 'Sales Stage Name Cur': "Sales Stage Name", 'Country Cur': "Country", 'Opp Source Cur': "Opportunity Source", 'LIO Channel Cur': "LIO Channel", 'Sector Cur': "Sector"})
df_prev = df_current
# +
#Engage Stats
df2 = pd.read_excel('engage.xlsx', index_col=False)
df2 = pd.DataFrame(df2)
print(df2.head(5))
df2 = df2.drop(columns=['Unnamed: 0', 'Source', 'Owner', 'Sector', 'Date'])
df2 = df2["Changes"].value_counts()
df2 = pd.DataFrame(df2)
df2 = df2.rename(columns={"Changes": "Count"})
df2.to_excel('engage_stats.xlsx')
df2 = pd.read_excel('engage_stats.xlsx', index_col=False)
df2 = pd.DataFrame(df2)
df2 = df2.rename(columns={'Unnamed: 0': "Changes"})
df2.to_excel('engage_stats.xlsx')
# -
#Engage by Location
df2 = pd.read_excel('engage.xlsx', index_col=False)
df2 = pd.DataFrame(df2)
df2 = df2.drop(columns=['Unnamed: 0', 'Source', 'Owner', 'Sector', 'Date'])
# df2.Location = df2.Location.str.strip()
df2 = df2.groupby(['Location', 'Changes'], as_index=False)["Count"].sum()
df2.to_excel('engage_location.xlsx')
#Engage by Owner
df2 = pd.read_excel('engage.xlsx', index_col=False)
df2 = pd.DataFrame(df2)
df2 = df2.drop(columns=['Unnamed: 0', 'Location', 'Source', 'Sector', 'Date'])
df2.Owner = df2.Owner.str.strip()
df2 = df2.groupby(['Owner', 'Changes'], as_index=False)["Count"].sum()
df2.to_excel('engage_owner.xlsx')
#Engage by Sector
df2 = pd.read_excel('engage.xlsx', index_col=False)
df2 = pd.DataFrame(df2)
df2 = df2.drop(columns=['Unnamed: 0', 'Location', 'Source', 'Owner', 'Date'])
df2.Sector = df2.Sector.str.strip()
df2 = df2.groupby(['Sector', 'Changes'], as_index=False)["Count"].sum()
df2.to_excel('engage_sector.xlsx')
|
Jupyter Notebooks/R2M_Engage->.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Rectangle Mania
# [link](https://www.algoexpert.io/questions/Rectangle%20Mania)
# ## My Solution
# O(n^2) time | O(n) space
def rectangleMania(coords):
# Write your code here.
coords = [tuple(coord) for coord in coords]
rows, cols = {}, {}
for coord in coords:
if coord[1] not in rows:
rows[coord[1]] = {coord: True}
else:
rows[coord[1]][coord] = True
for coord in coords:
if coord[0] not in cols:
cols[coord[0]] = {coord: True}
else:
cols[coord[0]][coord] = True
# O(n^2) time
count = 0
for bottomLeft in coords:
leftColLineNum = bottomLeft[0]
leftColLineCollection = cols[leftColLineNum]
for topLeft in leftColLineCollection:
if topLeft[1] > bottomLeft[1]:
topRowLineNum = topLeft[1]
topRowLineCollection = rows[topRowLineNum]
for topRight in topRowLineCollection:
if topRight[0] > topLeft[0]:
rightColLineNum = topRight[0]
rightColLineCollection = cols[rightColLineNum]
for bottomRight in rightColLineCollection:
if bottomRight[1] == bottomLeft[1]:
count += 1
return count
# +
# O(n^2) time | O(n) space
def rectangleMania(coords):
# Write your code here.
coords = [tuple(coord) for coord in coords]
rows, cols = getRowsAndColsCollection(coords)
count = 0
for bottomLeft in coords:
count += getRectanglesCountClockwise(bottomLeft, coords, rows, cols, "UP", bottomLeft[1])
return count
def getRowsAndColsCollection(coords):
rows, cols = {}, {}
for coord in coords:
if coord[1] not in rows:
rows[coord[1]] = {coord: True}
else:
rows[coord[1]][coord] = True
for coord in coords:
if coord[0] not in cols:
cols[coord[0]] = {coord: True}
else:
cols[coord[0]][coord] = True
return rows, cols
def getRectanglesCountClockwise(coord, coords, rows, cols, direction, lowerLeftY):
count = 0
if direction == "UP":
leftColLineNum = coord[0]
leftColLineCollection = cols[leftColLineNum]
for topLeft in leftColLineCollection:
if topLeft[1] > coord[1]:
count += getRectanglesCountClockwise(topLeft, coords, rows, cols, "RIGHT", lowerLeftY)
elif direction == "RIGHT":
topRowLineNum = coord[1]
topRowLineCollection = rows[topRowLineNum]
for topRight in topRowLineCollection:
if topRight[0] > coord[0]:
count += getRectanglesCountClockwise(topRight, coords, rows, cols, "DOWN", lowerLeftY)
elif direction == "DOWN":
rightColLineNum = coord[0]
rightColLineCollection = cols[rightColLineNum]
for bottomRight in rightColLineCollection:
if bottomRight[1] == lowerLeftY:
return 1
return count
# -
# O(n^2) time | O(n) space
def rectangleMania(coords):
# Write your code here.
coordsDict = {tuple(coord): True for coord in coords}
count = 0
for bottomLeft in coords:
for topRight in coords:
if topRight[0] > bottomLeft[0] and topRight[1] > bottomLeft[1]:
topLeft = (bottomLeft[0], topRight[1])
bottomRight = (topRight[0], bottomLeft[1])
if topLeft in coordsDict and bottomRight in coordsDict:
count += 1
return count
# ## Expert Solution
# +
# O(n^2) time | O(n) space - where n is the number of coordinates
def rectangleMania(coords):
coordsTable = getCoordsTable(coords)
return getRectangleCount(coords, coordsTable)
def getCoordsTable(coords):
coordsTable = {}
for coord1 in coords:
coord1Directions = {UP: [], RIGHT: [], DOWN:[], LEFT: []}
for coord2 in coords:
coord2Direction = getCoordDirection(coord1, coord2)
if coord2Direction in coord1Directions:
coord1Directions[coord2Direction].append(coord2)
coord1String = coordToString(coord1)
coordsTable[coord1String] = coord1Directions
return coordsTable
def getCoordDirection(coord1, coord2):
x1, y1 = coord1
x2, y2 = coord2
if y2 == y1:
if x2 > x1:
return RIGHT
elif x2 < x1:
return LEFT
elif x2 == x1:
if y2 > y1:
return UP
elif y2 < y1:
return DOWN
return ""
def getRectangleCount(coords, coordsTable):
rectangleCount = 0
for coord in coords:
rectangleCount += clockwiseCountRectangles(coord, coordsTable, UP, coord)
return rectangleCount
def clockwiseCountRectangles(coord, coordsTable, direction, origin):
coordString = coordToString(coord)
if direction == LEFT:
rectangleFound = origin in coordsTable[coordString][LEFT]
return 1 if rectangleFound else 0
else:
rectangleCount = 0
nextDirection = getNextClockwiseDirection(direction)
for nextCoord in coordsTable[coordString][direction]:
rectangleCount += clockwiseCountRectangles(nextCoord, coordsTable, nextDirection, origin)
return rectangleCount
def getNextClockwiseDirection(direction):
if direction == UP:
return RIGHT
if direction == RIGHT:
return DOWN
if direction == DOWN:
return LEFT
return ""
def coordToString(coord):
x, y = coord
return str(x) + "-" + str(y)
UP = "up"
RIGHT = "right"
DOWN = "down"
LEFT = "left"
# +
# O(n^2) time | O(n) space - where n is the number of coordinates
def rectangleMania(coords):
coordsTable = getCoordsTable(coords)
return getRectangleCount(coords, coordsTable)
def getCoordsTable(coords):
coordsTable = {"x": {}, "y": {}}
for coord in coords:
x, y = coord
if x not in coordsTable["x"]:
coordsTable["x"][x] = []
coordsTable["x"][x].append(coord)
if y not in coordsTable["y"]:
coordsTable["y"][y] = []
coordsTable["y"][y].append(coord)
return coordsTable
def getRectangleCount(coords, coordsTable):
rectangleCount = 0
for coord in coords:
lowerLeftY = coord[1]
rectangleCount += clockwiseCountRectangles(coord, coordsTable, UP, lowerLeftY)
return rectangleCount
def clockwiseCountRectangles(coord1, coordsTable, direction, lowerLeftY):
x1, y1 = coord1
if direction == DOWN:
relevantCoords = coordsTable["x"][x1]
for coord2 in relevantCoords:
lowerRightY = coord2[1]
if lowerRightY == lowerLeftY:
return 1
return 0
else:
rectangleCount = 0
if direction == UP:
relevantCoords = coordsTable["x"][x1]
for coord2 in relevantCoords:
y2 = coord2[1]
isAbove = y2 > y1
if isAbove:
rectangleCount += clockwiseCountRectangles(coord2, coordsTable, RIGHT, lowerLeftY)
elif direction == RIGHT:
relevantCoords = coordsTable["y"][y1]
for coord2 in relevantCoords:
x2 = coord2[0]
isRight = x2 > x1
if isRight:
rectangleCount += clockwiseCountRectangles(coord2, coordsTable, DOWN, lowerLeftY)
return rectangleCount
UP = "up"
RIGHT = "right"
DOWN = "down"
# +
# O(n^2) time | O(n) space - where n is the number of coordinates
def rectangleMania(coords):
coordsTable = getCoordTable(coords)
return getRectangleCount(coords, coordsTable)
def getCoordTable(coords):
coordsTable = {}
for coord in coords:
coordString = coordToString(coord)
coordsTable[coordString] = True
return coordsTable
def getRectangleCount(coords, coordsTable):
rectangleCount = 0
for x1, y1 in coords:
for x2, y2 in coords:
if not isInUpperRight([x1, y1], [x2, y2]):
continue
upperCoordString = coordToString([x1, y2])
rightCoordString = coordToString([x2, y1])
if upperCoordString in coordsTable and rightCoordString in coordsTable:
rectangleCount += 1
return rectangleCount
def isInUpperRight(coord1, coord2):
x1, y1 = coord1
x2, y2 = coord2
return x2 > x1 and y2 > y1
def coordToString(coord):
x, y = coord
return str(x) + "-" + str(y)
# -
# ## Thoughts
# ### Question
# - why the "clockwise" method need O(n^2) time?
|
algoExpert/rectangle_mania/solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.1 64-bit (''deep_learning'': conda)'
# name: python371jvsc74a57bd0c850e6f77ff7c9cbece5364f8526ec42dd183cf59251b1cfd7b71a0467b242c1
# ---
# + [markdown] id="Ng63tDwZSSm5"
# # Using Our IDCM Checkpoint
#
# We provide a fully retrieval trained DistilBert-based instance of the IDCM model on the HuggingFace model hub here: https://huggingface.co/sebastian-hofstaetter/idcm-distilbert-msmarco_doc
#
# This instance can be used to **re-rank a candidate set** of long documents.
#
# If you want to know more about our intra document cascading, check out our paper: https://arxiv.org/abs/2105.09816 🎉
#
# This notebook gives you a minimal usage example of downloading our IDCM checkpoint to encode documents and queries to create a score of their relevance.
#
#
# ---
#
#
# Let's get started by installing the awesome *transformers* library from HuggingFace:
#
# + id="r2WyNOE2R2rW"
pip install transformers
# + [markdown] id="YqkWDa_jWu7c"
# The next step is to download our checkpoint and initialize the tokenizer and models:
#
# + id="oTYEtziISSDl"
from typing import Dict, Union
import torch
from torch import nn as nn
from transformers import AutoTokenizer, AutoModel
from transformers import PreTrainedModel,PretrainedConfig
pre_trained_model_name = "sebastian-hofstaetter/idcm-distilbert-msmarco_doc"
class IDCM_Config(PretrainedConfig):
bert_model:str
# how many passages get scored by BERT
sample_n:int
# type of fast module
sample_context:str
# how many passages to take from bert to create the final score (usually the same as sample_n, but could be set to 1 for max-p)
top_k_chunks:int
# window size
chunk_size:int
# left and right overlap (added to each window)
overlap:int
padding_idx:int = 0
class IDCM_InferenceOnly(PreTrainedModel):
'''
IDCM is a neural re-ranking model for long documents, it creates an intra-document cascade between a fast (CK) and a slow module (BERT_Cat)
This code is only usable for inference (we removed the training mechanism for simplicity)
'''
config_class = IDCM_Config
base_model_prefix = "bert_model"
def __init__(self,
cfg) -> None:
super().__init__(cfg)
#
# bert - scoring
#
if isinstance(cfg.bert_model, str):
self.bert_model = AutoModel.from_pretrained(cfg.bert_model)
else:
self.bert_model = cfg.bert_model
#
# final scoring (combination of bert scores)
#
self._classification_layer = torch.nn.Linear(self.bert_model.config.hidden_size, 1)
self.top_k_chunks = cfg.top_k_chunks
self.top_k_scoring = nn.Parameter(torch.full([1,self.top_k_chunks], 1, dtype=torch.float32, requires_grad=True))
#
# local self attention
#
self.padding_idx= cfg.padding_idx
self.chunk_size = cfg.chunk_size
self.overlap = cfg.overlap
self.extended_chunk_size = self.chunk_size + 2 * self.overlap
#
# sampling stuff
#
self.sample_n = cfg.sample_n
self.sample_context = cfg.sample_context
if self.sample_context == "ck":
i = 3
self.sample_cnn3 = nn.Sequential(
nn.ConstantPad1d((0,i - 1), 0),
nn.Conv1d(kernel_size=i, in_channels=self.bert_model.config.dim, out_channels=self.bert_model.config.dim),
nn.ReLU()
)
elif self.sample_context == "ck-small":
i = 3
self.sample_projector = nn.Linear(self.bert_model.config.dim,384)
self.sample_cnn3 = nn.Sequential(
nn.ConstantPad1d((0,i - 1), 0),
nn.Conv1d(kernel_size=i, in_channels=384, out_channels=128),
nn.ReLU()
)
self.sampling_binweights = nn.Linear(11, 1, bias=True)
torch.nn.init.uniform_(self.sampling_binweights.weight, -0.01, 0.01)
self.kernel_alpha_scaler = nn.Parameter(torch.full([1,1,11], 1, dtype=torch.float32, requires_grad=True))
self.register_buffer("mu",nn.Parameter(torch.tensor([1.0, 0.9, 0.7, 0.5, 0.3, 0.1, -0.1, -0.3, -0.5, -0.7, -0.9]), requires_grad=False).view(1, 1, 1, -1))
self.register_buffer("sigma", nn.Parameter(torch.tensor([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]), requires_grad=False).view(1, 1, 1, -1))
def forward(self,
query: Dict[str, torch.LongTensor],
document: Dict[str, torch.LongTensor],
use_fp16:bool = True,
output_secondary_output: bool = False):
#
# patch up documents - local self attention
#
document_ids = document["input_ids"][:,1:]
if document_ids.shape[1] > self.overlap:
needed_padding = self.extended_chunk_size - (((document_ids.shape[1]) % self.chunk_size) - self.overlap)
else:
needed_padding = self.extended_chunk_size - self.overlap - document_ids.shape[1]
orig_doc_len = document_ids.shape[1]
document_ids = nn.functional.pad(document_ids,(self.overlap, needed_padding),value=self.padding_idx)
chunked_ids = document_ids.unfold(1,self.extended_chunk_size,self.chunk_size)
batch_size = chunked_ids.shape[0]
chunk_pieces = chunked_ids.shape[1]
chunked_ids_unrolled=chunked_ids.reshape(-1,self.extended_chunk_size)
packed_indices = (chunked_ids_unrolled[:,self.overlap:-self.overlap] != self.padding_idx).any(-1)
orig_packed_indices = packed_indices.clone()
ids_packed = chunked_ids_unrolled[packed_indices]
mask_packed = (ids_packed != self.padding_idx)
total_chunks=chunked_ids_unrolled.shape[0]
packed_query_ids = query["input_ids"].unsqueeze(1).expand(-1,chunk_pieces,-1).reshape(-1,query["input_ids"].shape[1])[packed_indices]
packed_query_mask = query["attention_mask"].unsqueeze(1).expand(-1,chunk_pieces,-1).reshape(-1,query["attention_mask"].shape[1])[packed_indices]
#
# sampling
#
if self.sample_n > -1:
#
# ck learned matches
#
if self.sample_context == "ck-small":
query_ctx = torch.nn.functional.normalize(self.sample_cnn3(self.sample_projector(self.bert_model.embeddings(packed_query_ids).detach()).transpose(1,2)).transpose(1, 2),p=2,dim=-1)
document_ctx = torch.nn.functional.normalize(self.sample_cnn3(self.sample_projector(self.bert_model.embeddings(ids_packed).detach()).transpose(1,2)).transpose(1, 2),p=2,dim=-1)
elif self.sample_context == "ck":
query_ctx = torch.nn.functional.normalize(self.sample_cnn3((self.bert_model.embeddings(packed_query_ids).detach()).transpose(1,2)).transpose(1, 2),p=2,dim=-1)
document_ctx = torch.nn.functional.normalize(self.sample_cnn3((self.bert_model.embeddings(ids_packed).detach()).transpose(1,2)).transpose(1, 2),p=2,dim=-1)
else:
qe = self.tk_projector(self.bert_model.embeddings(packed_query_ids).detach())
de = self.tk_projector(self.bert_model.embeddings(ids_packed).detach())
query_ctx = self.tk_contextualizer(qe.transpose(1,0),src_key_padding_mask=~packed_query_mask.bool()).transpose(1,0)
document_ctx = self.tk_contextualizer(de.transpose(1,0),src_key_padding_mask=~mask_packed.bool()).transpose(1,0)
query_ctx = torch.nn.functional.normalize(query_ctx,p=2,dim=-1)
document_ctx= torch.nn.functional.normalize(document_ctx,p=2,dim=-1)
cosine_matrix = torch.bmm(query_ctx,document_ctx.transpose(-1, -2)).unsqueeze(-1)
kernel_activations = torch.exp(- torch.pow(cosine_matrix - self.mu, 2) / (2 * torch.pow(self.sigma, 2))) * mask_packed.unsqueeze(-1).unsqueeze(1)
kernel_res = torch.log(torch.clamp(torch.sum(kernel_activations, 2) * self.kernel_alpha_scaler, min=1e-4)) * packed_query_mask.unsqueeze(-1)
packed_patch_scores = self.sampling_binweights(torch.sum(kernel_res, 1))
sampling_scores_per_doc = torch.zeros((total_chunks,1), dtype=packed_patch_scores.dtype, layout=packed_patch_scores.layout, device=packed_patch_scores.device)
sampling_scores_per_doc[packed_indices] = packed_patch_scores
sampling_scores_per_doc = sampling_scores_per_doc.reshape(batch_size,-1,)
sampling_scores_per_doc_orig = sampling_scores_per_doc.clone()
sampling_scores_per_doc[sampling_scores_per_doc == 0] = -9000
sampling_sorted = sampling_scores_per_doc.sort(descending=True)
sampled_indices = sampling_sorted.indices + torch.arange(0,sampling_scores_per_doc.shape[0]*sampling_scores_per_doc.shape[1],sampling_scores_per_doc.shape[1],device=sampling_scores_per_doc.device).unsqueeze(-1)
sampled_indices = sampled_indices[:,:self.sample_n]
sampled_indices_mask = torch.zeros_like(packed_indices).scatter(0, sampled_indices.reshape(-1), 1)
# pack indices
packed_indices = sampled_indices_mask * packed_indices
packed_query_ids = query["input_ids"].unsqueeze(1).expand(-1,chunk_pieces,-1).reshape(-1,query["input_ids"].shape[1])[packed_indices]
packed_query_mask = query["attention_mask"].unsqueeze(1).expand(-1,chunk_pieces,-1).reshape(-1,query["attention_mask"].shape[1])[packed_indices]
ids_packed = chunked_ids_unrolled[packed_indices]
mask_packed = (ids_packed != self.padding_idx)
#
# expensive bert scores
#
bert_vecs = self.forward_representation(torch.cat([packed_query_ids,ids_packed],dim=1),torch.cat([packed_query_mask,mask_packed],dim=1))
packed_patch_scores = self._classification_layer(bert_vecs)
scores_per_doc = torch.zeros((total_chunks,1), dtype=packed_patch_scores.dtype, layout=packed_patch_scores.layout, device=packed_patch_scores.device)
scores_per_doc[packed_indices] = packed_patch_scores
scores_per_doc = scores_per_doc.reshape(batch_size,-1,)
scores_per_doc_orig = scores_per_doc.clone()
scores_per_doc_orig_sorter = scores_per_doc.clone()
if self.sample_n > -1:
scores_per_doc = scores_per_doc * sampled_indices_mask.view(batch_size,-1)
#
# aggregate bert scores
#
if scores_per_doc.shape[1] < self.top_k_chunks:
scores_per_doc = nn.functional.pad(scores_per_doc,(0, self.top_k_chunks - scores_per_doc.shape[1]))
scores_per_doc[scores_per_doc == 0] = -9000
scores_per_doc_orig_sorter[scores_per_doc_orig_sorter == 0] = -9000
score = torch.sort(scores_per_doc,descending=True,dim=-1).values
score[score <= -8900] = 0
score = (score[:,:self.top_k_chunks] * self.top_k_scoring).sum(dim=1)
if self.sample_n == -1:
if output_secondary_output:
return score,{
"packed_indices": orig_packed_indices.view(batch_size,-1),
"bert_scores":scores_per_doc_orig
}
else:
return score,scores_per_doc_orig
else:
if output_secondary_output:
return score,scores_per_doc_orig,{
"score": score,
"packed_indices": orig_packed_indices.view(batch_size,-1),
"sampling_scores":sampling_scores_per_doc_orig,
"bert_scores":scores_per_doc_orig
}
return score
def forward_representation(self, ids,mask,type_ids=None) -> Dict[str, torch.Tensor]:
if self.bert_model.base_model_prefix == 'distilbert': # diff input / output
pooled = self.bert_model(input_ids=ids,
attention_mask=mask)[0][:,0,:]
elif self.bert_model.base_model_prefix == 'longformer':
_, pooled = self.bert_model(input_ids=ids,
attention_mask=mask.long(),
global_attention_mask = ((1-ids)*mask).long())
elif self.bert_model.base_model_prefix == 'roberta': # no token type ids
_, pooled = self.bert_model(input_ids=ids,
attention_mask=mask)
else:
_, pooled = self.bert_model(input_ids=ids,
token_type_ids=type_ids,
attention_mask=mask)
return pooled
tokenizer = AutoTokenizer.from_pretrained("distilbert-base-uncased") # honestly not sure if that is the best way to go, but it works :)
idcm_model = IDCM_InferenceOnly.from_pretrained(pre_trained_model_name)
# + [markdown] id="EOGT8YQQX1Ot"
# Now we are ready to use the model to encode two sample passages and a query:
# + colab={"base_uri": "https://localhost:8080/"} id="Rzt9Ix9UYMLy" outputId="529e338e-b4e7-4251-cf9b-4363ac8a3ed8"
# our relevant example
passage1_input = tokenizer("We are very happy to show you the 🤗 Transformers library for pre-trained language models. We are helping the community work together towards the goal of advancing NLP 🔥.The easiest way to use a pretrained model on a given task is to use pipeline(). 🤗 Transformers provides the following tasks out of the box: Sentiment analysis: is a text positive or negative? Text generation (in English): provide a prompt and the model will generate what follows. Name entity recognition (NER): in an input sentence, label each word with the entity it represents (person, place, etc.) Question answering: provide the model with some context and a question, extract the answer from the context. Filling masked text: given a text with masked words (e.g., replaced by [MASK]), fill the blanks. Summarization: generate a summary of a long text. Translation: translate a text in another language. Feature extraction: return a tensor representation of the text. Let’s see how this work for sentiment analysis (the other tasks are all covered in the task summary): We are very happy to show you the 🤗 Transformers library for pre-trained language models. We are helping the community work together towards the goal of advancing NLP 🔥.The easiest way to use a pretrained model on a given task is to use pipeline(). 🤗 Transformers provides the following tasks out of the box: Sentiment analysis: is a text positive or negative? Text generation (in English): provide a prompt and the model will generate what follows. Name entity recognition (NER): in an input sentence, label each word with the entity it represents (person, place, etc.) Question answering: provide the model with some context and a question, extract the answer from the context. Filling masked text: given a text with masked words (e.g., replaced by [MASK]), fill the blanks. Summarization: generate a summary of a long text. Translation: translate a text in another language. Feature extraction: return a tensor representation of the text. Let’s see how this work for sentiment analysis (the other tasks are all covered in the task summary): We are very happy to show you the 🤗 Transformers library for pre-trained language models. We are helping the community work together towards the goal of advancing NLP 🔥.The easiest way to use a pretrained model on a given task is to use pipeline(). 🤗 Transformers provides the following tasks out of the box: Sentiment analysis: is a text positive or negative? Text generation (in English): provide a prompt and the model will generate what follows. Name entity recognition (NER): in an input sentence, label each word with the entity it represents (person, place, etc.) Question answering: provide the model with some context and a question, extract the answer from the context. Filling masked text: given a text with masked words (e.g., replaced by [MASK]), fill the blanks. Summarization: generate a summary of a long text. Translation: translate a text in another language. Feature extraction: return a tensor representation of the text. Let’s see how this work for sentiment analysis (the other tasks are all covered in the task summary): We are very happy to show you the 🤗 Transformers library for pre-trained language models. We are helping the community work together towards the goal of advancing NLP 🔥.The easiest way to use a pretrained model on a given task is to use pipeline(). 🤗 Transformers provides the following tasks out of the box: Sentiment analysis: is a text positive or negative? Text generation (in English): provide a prompt and the model will generate what follows. Name entity recognition (NER): in an input sentence, label each word with the entity it represents (person, place, etc.) Question answering: provide the model with some context and a question, extract the answer from the context. Filling masked text: given a text with masked words (e.g., replaced by [MASK]), fill the blanks. Summarization: generate a summary of a long text. Translation: translate a text in another language. Feature extraction: return a tensor representation of the text. Let’s see how this work for sentiment analysis (the other tasks are all covered in the task summary):",return_tensors="pt",max_length=2000,truncation=True)
# a non-relevant example
passage2_input = tokenizer("Most machine learning workflows involve working with data, creating models, optimizing model parameters, and saving the trained models. This tutorial introduces you to a complete ML workflow implemented in PyTorch, with links to learn more about each of these concepts. We’ll use the FashionMNIST dataset to train a neural network that predicts if an input image belongs to one of the following classes: T-shirt/top, Trouser, Pullover, Dress, Coat, Sandal, Shirt, Sneaker, Bag, or Ankle boot. This tutorial assumes a basic familiarity with Python and Deep Learning concepts. Running the Tutorial CodeYou can run this tutorial in a couple of ways: In the cloud: This is the easiest way to get started! Each section has a “Run in Microsoft Learn” link at the top, which opens an integrated notebook in Microsoft Learn with the code in a fully-hosted environment. Locally: This option requires you to setup PyTorch and TorchVision first on your local machine (installation instructions). Download the notebook or copy the code into your favorite IDE.",return_tensors="pt",max_length=2000)
# the user query -> which should give us a better score for the first passage
query_input = tokenizer("what is the transformers library",return_tensors="pt",max_length=30,truncation=True)
print("Passage 1 Tokenized:",len(passage1_input["input_ids"][0]),tokenizer.convert_ids_to_tokens(passage1_input["input_ids"][0]),"\n")
print("Passage 2 Tokenized:",len(passage2_input["input_ids"][0]),tokenizer.convert_ids_to_tokens(passage2_input["input_ids"][0]),"\n")
print("Query Tokenized:",tokenizer.convert_ids_to_tokens(query_input["input_ids"][0]))
score1 = idcm_model(query_input, passage1_input).squeeze(0)
score2 = idcm_model(query_input, passage2_input).squeeze(0)
print("---")
print("score1:",score1)
print("score2",score2)
# + [markdown] id="_1bY5qB9b-AI"
# As we see the model gives the first passage a higher score than the second - yeah!
#
# - If you use our model checkpoint please cite our work as:
#
# ```
# @inproceedings{Hofstaetter2021_idcm,
# author = {<NAME> and <NAME> and <NAME> and <NAME> and <NAME>},
# title = {{Intra-Document Cascading: Learning to Select Passages for Neural Document Ranking}},
# booktitle = {Proc. of SIGIR},
# year = {2021},
# }
# ```
#
# Thank You 😊 If you have any questions feel free to reach out to Sebastian via mail (email in the paper).
#
|
minimal_idcm_usage_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="LuJi8nfc0Z7u"
# # Spark Preparation
# We check if we are in Google Colab. If this is the case, install all necessary packages.
#
# To run spark in Colab, we need to first install all the dependencies in Colab environment i.e. Apache Spark 3.2.1 with hadoop 3.2, Java 8 and Findspark to locate the spark in the system. The tools installation can be carried out inside the Jupyter Notebook of the Colab.
# Learn more from [A Must-Read Guide on How to Work with PySpark on Google Colab for Data Scientists!](https://www.analyticsvidhya.com/blog/2020/11/a-must-read-guide-on-how-to-work-with-pyspark-on-google-colab-for-data-scientists/)
#
# credit: <NAME>
# + id="ULwfUd7MSoCQ"
try:
import google.colab
IN_COLAB = True
except:
IN_COLAB = False
# + id="BGR_RJK5SpPa"
if IN_COLAB:
# !apt-get install openjdk-8-jdk-headless -qq > /dev/null
# !wget -q https://dlcdn.apache.org/spark/spark-3.2.1/spark-3.2.1-bin-hadoop3.2.tgz
# !tar xf spark-3.2.1-bin-hadoop3.2.tgz
# !mv spark-3.2.1-bin-hadoop3.2 spark
# !pip install -q findspark
# + id="DMyX10Mm0eCL"
if IN_COLAB:
import os
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ["SPARK_HOME"] = "/content/spark"
# + id="jSBEhn3A0flq"
import findspark
findspark.init()
# + [markdown] id="_hlLTtzDSllE"
# # Pyspark_Classification_Pipeline_Churn
# + id="eJ_YECvqSllF"
#1 - import module
from pyspark import SparkContext
from pyspark.sql import SparkSession
from pyspark.conf import SparkConf
from pyspark.ml import Pipeline, PipelineModel
from pyspark.ml.classification import DecisionTreeClassifier, DecisionTreeClassificationModel
from pyspark.ml.feature import StringIndexer, IndexToString, VectorAssembler
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.ml.tuning import CrossValidator, ParamGridBuilder
# + id="jN89pzgtSllK"
#2 - Create spark context
sc = SparkContext.getOrCreate()
# + colab={"base_uri": "https://localhost:8080/", "height": 198} id="9s0CkRFRSllM" outputId="8420cfb6-ec76-443b-f118-159eb1ee9dce"
sc
# + colab={"base_uri": "https://localhost:8080/"} id="Iu6ptd5CSllZ" outputId="b2721610-6c5b-48d7-9bae-4c028de01954"
sc._conf.getAll()
# + colab={"base_uri": "https://localhost:8080/"} id="xmHT5L7wSlld" outputId="0c130353-311c-48e9-99fd-ad0a50d965d1"
print (sc.getConf().toDebugString())
# + colab={"base_uri": "https://localhost:8080/"} id="BYQFI_84Sllm" outputId="f39ad495-5127-4a44-edb5-e64895ed3295"
#3 - Setup SparkSession(SparkSQL)
spark = (SparkSession
.builder
.appName("Pyspark_Classification_Pipeline_Churn")
.getOrCreate())
print (spark)
# + colab={"base_uri": "https://localhost:8080/"} id="ocrVwkag0i5c" outputId="4cfafdba-3c33-4bbf-dcca-92efe7da211c"
# !wget https://github.com/kaopanboonyuen/GISTDA2022/raw/main/dataset/churn.csv
# + colab={"base_uri": "https://localhost:8080/"} id="PcDQl2u7Sllu" outputId="805379b2-d22a-4061-a15b-99607858b416"
#4 - Read file to spark DataFrame
data = (spark
.read
.option("header","true")
.option("inferSchema", "true")
.csv("churn.csv"))
data.cache()
print ("finish caching data")
# + colab={"base_uri": "https://localhost:8080/"} id="V8__xrPqSllz" outputId="4700975d-ef72-4f74-e00a-9cbea43bf712"
#5 - Understand data and problems
category = ['International plan','Voice mail plan']
continuous = ['Number vmail messages','Total day minutes','Total day calls','Total day charge','Total eve minutes','Total eve calls','Total eve charge','Total night minutes','Total night calls','Total night charge','Total intl minutes','Total intl calls','Total intl charge','Customer service calls']
label = 'churn'
unique_features = ['State','Account length','Area code']
unused_features = ['Total day charge','Total eve charge','Total night charge','Total intl charge']
#bcz charges computed from minutes / 22.2252
print (len(category) + len(continuous))
# + colab={"base_uri": "https://localhost:8080/", "height": 305} id="AUEpCLX0Sll3" outputId="4ad1b150-ad6a-40ad-e68b-4424086814a0"
data.describe().toPandas()
# + colab={"base_uri": "https://localhost:8080/"} id="U_s9t_YkSll7" outputId="e65643a8-c421-4a45-98a2-ac8d39bc3692"
data.printSchema()
# + colab={"base_uri": "https://localhost:8080/", "height": 285} id="5TP6d6f5SlmG" outputId="a2121952-ab5f-4b1a-dd0c-07beb8de1f4f"
data.sample(False, 0.001, 1234).toPandas()
# + colab={"base_uri": "https://localhost:8080/", "height": 112} id="W7roK5KvSlmL" outputId="e125c9f2-0b22-41ad-dc1a-29c35d8bd2b8"
data.groupBy(label).count().toPandas()
# + colab={"base_uri": "https://localhost:8080/"} id="KZon6uJfSlmO" outputId="14e2b750-ed23-4659-a288-41bbf10ccdec"
#6 - Change column type from boolean to string
data.select(label).printSchema()
data = data.withColumn(label, data[label].cast("string"))
data.select(label).printSchema()
# + colab={"base_uri": "https://localhost:8080/"} id="dE6z_JmpSlma" outputId="9f403187-4223-45c1-fa94-5966fe1c3e25"
#8 - Remove unused variables
print ("number of features : " + str(len(data.drop(label).head())))
for unused_feature in unique_features + unused_features:
print (unused_feature)
data = data.drop(unused_feature)
print ("\nnumber of features remain : " + str(len(data.drop(label).head())))
category = [feature for feature in category if feature not in (unique_features + unused_features)]
continuous = [feature for feature in continuous if feature not in (unique_features + unused_features)]
print ("\nnumber of features remain : " + str(len(category) + len(continuous)))
# + colab={"base_uri": "https://localhost:8080/"} id="EmU9qCllSlmh" outputId="e08a864b-d876-4862-861a-4c0ccbfd0c19"
#9 - split Train and Test data
data = data.sort(label)
(trainingData, testData) = data.randomSplit([0.7, 0.3],seed = 50)
print(type(data))
print(type(trainingData))
print(type(testData))
print ("data count : " + str(data.count()))
print ("trainingData count : " + str(trainingData.count()))
print ("testData count : " + str(testData.count()))
data.groupBy(label).count().show()
trainingData.groupBy(label).count().show()
testData.groupBy(label).count().show()
# + colab={"base_uri": "https://localhost:8080/"} id="dRS4BS7kSlmp" outputId="830b7386-e71f-4a1e-ad47-65208b583867"
#10 - String indexer
featureidx_list = [StringIndexer(inputCol = label, outputCol='label')]
featureidx_list += [StringIndexer(inputCol = c, outputCol=c + 'idx') for c in category]
print (featureidx_list)
# + colab={"base_uri": "https://localhost:8080/"} id="KUCtS0BXSlmt" outputId="8e542b93-30ec-4a31-fff0-4ce0985df72b"
#11 - Create Vector
features = continuous + [c + 'idx' for c in category]
assem = VectorAssembler(inputCols = features ,outputCol="features")
print (type(assem))
# + colab={"base_uri": "https://localhost:8080/"} id="eVdQG9FaSlm5" outputId="1ae3a617-4d43-4ec3-b3c6-245169094ecc"
#12 - Create model
dt = DecisionTreeClassifier(labelCol="label", featuresCol="features")
print (dt)
# + colab={"base_uri": "https://localhost:8080/"} id="QcgxquKDSlm_" outputId="85844042-9943-4c8e-d326-efbdfbe9620e"
#13 - Set ML pipeline
print (featureidx_list)
print (assem)
print (dt)
print ("\n")
all_process_list = featureidx_list + [assem,dt]
print (all_process_list)
pipeline = Pipeline(stages=all_process_list)
print ("\n")
print (pipeline)
# + id="hK5egbhaSlnF"
#14 - Train model
model = pipeline.fit(trainingData)
#predictions.cache()
# + colab={"base_uri": "https://localhost:8080/"} id="sjVh6tJtSlnP" outputId="ecd000c0-d971-423f-ebc1-07b000f72cbf"
#15 - (Optional) Assign multiple parameter lists used to train multiple models
paramGrid = (ParamGridBuilder()
.addGrid(dt.maxDepth, [4,5,6])
.addGrid(dt.minInstancesPerNode, [1,10])
.addGrid(dt.impurity, ["gini","entropy"])
.build())
for param in paramGrid:
print (param)
print ("\n\n")
# + id="qzY0BaQOSlna"
# #16 - (Optional) Train multiple models with multiple parameters
# crossval = CrossValidator(estimator=pipeline,
# estimatorParamMaps=paramGrid,
# evaluator=MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="f1"),
# numFolds=3)
# cvModel = crossval.fit(trainingData)
# model = cvModel.bestModel
# print (model)
# + id="pW-vfaP7Slnf"
#17 - Make predictions
predictions = model.transform(testData)
# + colab={"base_uri": "https://localhost:8080/", "height": 849} id="sDW7coJRSlnj" outputId="64305ef2-aed8-48fc-a714-8e8b4789fc4b"
# Print sample result
predictions.toPandas()
# + colab={"base_uri": "https://localhost:8080/", "height": 424} id="yVutOfTBSlnt" outputId="c178c25b-cf6d-4d6d-864b-d2faef7b0937"
# Print sample result
predictions.select("prediction", "rawPrediction", "probability", "label", "features").toPandas()
# + colab={"base_uri": "https://localhost:8080/"} id="ARvn3Zq6Slny" outputId="ace3160d-6b88-4d69-e6a2-6018aa971c06"
#18 - Evaluate model
for metricName in ['accuracy','weightedPrecision','weightedRecall','f1']:
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName=metricName)
result = evaluator.evaluate(predictions)
print ('%s = %g' % (metricName,result))
if(metricName == 'accuracy') :
print("error = %g " % (1.0 - result))
# + colab={"base_uri": "https://localhost:8080/"} id="nDRit9dySln1" outputId="552d6526-d6e4-47e8-c21f-9243dbd899e9"
#19 - Show tree diagram
treeModel = model.stages[-1]
treeModel_debug_str = treeModel.toDebugString
print (treeModel_debug_str)
# + colab={"base_uri": "https://localhost:8080/"} id="2BQD-3TsSln8" outputId="d9b6bd19-d3bd-4d8c-f5e0-04fe6b210738"
#20 - Save model
model_dir = "/user/admin/"
modelFile = "dt_churn"
#Save model as Pipeline model format
model.write().overwrite().save(model_dir + modelFile +".plmodel")
#Save model as DecisionTree model format
treeModel.write().overwrite().save(model_dir + modelFile +".model")
print ("finish save model")
# + colab={"base_uri": "https://localhost:8080/"} id="esK5X6JgSloB" outputId="afc392bf-befa-42e4-b0b3-bd0540dc0409"
#21 - Load Pipeline model
read_plmodel = PipelineModel.read().load(model_dir + modelFile + ".plmodel")
print (read_plmodel.stages)
# + colab={"base_uri": "https://localhost:8080/"} id="YK0BPBiRSloE" outputId="7eb924d3-51ec-40dc-973f-32e04506c9cb"
#22 - Load DecisionTree model
read_model = DecisionTreeClassificationModel.read().load(model_dir + modelFile + ".model")
print ("depth : " + str(read_model.depth))
print ("numNodes : " + str(read_model.numNodes))
print ("featureImportances : " + str(read_model.featureImportances))
#these lines avaiable for Spark2.1 or above
#print readed_model.numClasses
#print readed_model.numFeatures
# + id="aZHSBSCTSloI"
|
code/5_Pyspark_Classification_Pipeline_Churn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Applying the Expected Context Framework to the Switchboard Corpus
#
# ### Using `DualContextWrapper`
#
# This notebook demonstrates how our implementation of the Expected Context Framework can be applied to the Switchboard dataset. See [this dissertation](https://tisjune.github.io/research/dissertation) for more details about the framework, and more comments on the below analyses.
#
# This notebook will show how to apply `DualContextWrapper`, a wrapper transformer that keeps track of two instances of `ExpectedContextModelTransformer`. For a version of this demo that initializes two separate instances of `ExpectedContextModelTransformer` instead, and that more explicitly demonstrates that functionality, see [this notebook](https://github.com/CornellNLP/Cornell-Conversational-Analysis-Toolkit/blob/ecf/convokit/expected_context_framework/demos/switchboard_exploration_demo.ipynb).
#
#
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import math
import os
# ## 1. Loading and preprocessing the dataset
#
# For this demo, we'll use the Switchboard corpus---a collection of telephone conversations which have been annotated with various dialog acts. More information on the dataset, as it exists in ConvoKit format, can be found [here](https://convokit.cornell.edu/documentation/switchboard.html); the original data is described [here](https://web.stanford.edu/~jurafsky/ws97/CL-dialog.pdf).
#
# We will actually use a preprocessed version of the Switchboard corpus, which we can access below. Since Switchboard consists of transcribed telephone conversations, there are many disfluencies and backchannels, that make utterances messier, and that make it hard to identify what counts as an actual turn. In the version of the corpus we consider, for the purpose of demonstration, we remove the disfluencies and backchannels (acknowledging that we're discarding important parts of the conversations).
from convokit import Corpus
from convokit import download
# +
# OPTION 1: DOWNLOAD CORPUS
# UNCOMMENT THESE LINES TO DOWNLOAD CORPUS
# DATA_DIR = '<YOUR DIRECTORY>'
# SW_CORPUS_PATH = download('switchboard-processed-corpus', data_dir=DATA_DIR)
# OPTION 2: READ PREVIOUSLY-DOWNLOADED CORPUS FROM DISK
# UNCOMMENT THIS LINE AND REPLACE WITH THE DIRECTORY WHERE THE TENNIS-CORPUS IS LOCATED
# SW_CORPUS_PATH = '<YOUR DIRECTORY>'
# -
sw_corpus = Corpus(SW_CORPUS_PATH)
sw_corpus.print_summary_stats()
utt_eg_id = '3496-79'
# as input, we use a preprocessed version of the utterance that only contains alphabetical words, found in the `alpha_text` metadata field.
sw_corpus.get_utterance(utt_eg_id).meta['alpha_text']
# In order to avoid capturing topic-specific information, we restrict our analyses to a vocabulary of unigrams that occurs across many topics, and across many conversations:
from collections import defaultdict
# +
topic_counts = defaultdict(set)
for ut in sw_corpus.iter_utterances():
topic = sw_corpus.get_conversation(ut.conversation_id).meta['topic']
for x in set(ut.meta['alpha_text'].lower().split()):
topic_counts[x].add(topic)
topic_counts = {x: len(y) for x, y in topic_counts.items()}
word_convo_counts = defaultdict(set)
for ut in sw_corpus.iter_utterances():
for x in set(ut.meta['alpha_text'].lower().split()):
word_convo_counts[x].add(ut.conversation_id)
word_convo_counts = {x: len(y) for x, y in word_convo_counts.items()}
min_topic_words = set(x for x,y in topic_counts.items() if y >= 33)
min_convo_words = set(x for x,y in word_convo_counts.items() if y >= 200)
vocab = sorted(min_topic_words.intersection(min_convo_words))
# -
len(vocab)
from convokit.expected_context_framework import ColNormedTfidfTransformer, DualContextWrapper
# ## 2. Applying the Expected Context Framework
#
# To apply the Expected Context Framework, we start by converting the input utterance text to an input vector representation. Here, we represent utterances in a term-document matrix that's _normalized by columns_ (empirically, we found that this ensures that the representations derived by the framework aren't skewed by the relative frequency of utterances). We use `ColNormedTfidfTransformer` transformer to do this:
tfidf_obj = ColNormedTfidfTransformer(input_field='alpha_text', output_field='col_normed_tfidf', binary=True, vocabulary=vocab)
_ = tfidf_obj.fit(sw_corpus)
_ = tfidf_obj.transform(sw_corpus)
# We now use the Expected Context Framework. In short, the framework derives vector representations, and other characterizations, of terms and utterances that are based on their _expected conversational context_---i.e., the replies we expect will follow a term or utterance, or the preceding utterances that we expect the term/utterance will reply to.
#
# We are going to derive characterizations based both on the _forwards_ context, i.e., the expected replies, and the _backwards_ context, i.e., the expected predecessors. We'll apply the framework in each direction, and then compare the characterizations that result. To take care of both interlocked models, we use the `DualContextWrapper` transformer, which will keep track of two `ExpectedContextModelTransformer`s: one that relates utterances to predecessors (`reply_to`), and that outputs utterance-level attributes with the prefix `bk`; the other that relates utterances to replies (`next_id`) and outputs utterance-level attributes with the prefix `fw`. These parameters are specified via the `context_fields` and `output_prefixes` arguments.
#
# Other arguments passed:
# * `vect_field` and `context_vect_field` respectively denote the input vector representations of utterances and context utterances that `ec_fw` will work with. Here, we'll use the same tf-idf representations that we just computed above.
# * `n_svd_dims` denotes the dimensionality of the vector representations that `ec_fw` will output. This is something that you can play around with---for this dataset, we found that more dimensions resulted in messier output, and a coarser, lower-dimensional representation was slightly more interpretable. (Technical note: technically, `ec_fw` produces vector representations of dimension `n_svd_dims`-1, since by default, it removes the first latent dimension, which we find tends to strongly reflect term frequency.)
# * `n_clusters` denotes the number of utterance types that `ec_fw` will infer, given the representations it computes. Note that this is an interpretative step: looking at clusters of utterances helps us get a sense of what information the representations are capturing; this value does not actually impact the representations and other characterizations we derive.
# * `random_state` and `cluster_random_state` are fixed for this demo, so we produce deterministic output.
dual_context_model = DualContextWrapper(context_fields=['reply_to','next_id'], output_prefixes=['bk','fw'],
vect_field='col_normed_tfidf', context_vect_field='col_normed_tfidf',
n_svd_dims=15, n_clusters=2,
random_state=1000, cluster_random_state=1000)
# We'll fit the transformer on the subset of utterances and replies that have at least 5 unigrams from our vocabulary.
dual_context_model.fit(sw_corpus,selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5,
context_selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>= 5)
# ### Interpreting derived representations
#
# Before applying the two transformers, `ec_fw` and `ec_bk` to transform the corpus, we can examine the representations and characterizations it's derived over the training data (note that in this case, the training data is also the corpus that we analyze, but this needn't be the case in general---see [this demo](https://github.com/CornellNLP/Cornell-Conversational-Analysis-Toolkit/blob/master/convokit/expected_context_framework/demos/wiki_awry_demo.ipynb) for an example).
# First, to interpret the representations derived by each model, we can inspect the clusters of representations that we've inferred, for both the forwards and backwards direction. We can access the forwards and backwards models as elements of the `ec_models` attribute. The following function calls print out representative terms and utterances, as well as context terms and utterances, per cluster (next two cells; note that the output is quite long).
dual_context_model.ec_models[0].print_clusters(corpus=sw_corpus)
dual_context_model.ec_models[1].print_clusters(corpus=sw_corpus)
# demo continues below
# We can see that in each case, two clusters emerge that roughly correspond to utterances recounting personal experiences, and those providing commentary, generally not about personal matters. We'll label them as such, noting that there's a roughly 50-50 split with slightly more "personal" utterances than "commentary" ones:
dual_context_model.ec_models[0].set_cluster_names(['personal', 'commentary'])
dual_context_model.ec_models[1].set_cluster_names(['commentary', 'personal'])
# ### Interpreting derived characterizations
#
# The transformer also computes some term-level statistics, which we can return as a Pandas dataframe:
# * forwards and backwards ranges (`fw_range` and `bk_range` respectively): we roughly interpret these as modeling the strengths of our forwards expectations of the replies that a term tends to get, or the backwards expectations of the predecessors that the term tends to follow.
# * shift: this statistic corresponds to the distance between the backwards and forwards representations for each term; we interpret it as the extent to which a term shifts the focus of a conversation.
# * orientation (`orn`): this statistic compares the relative magnitude of forwards and backwards ranges. In a [counseling conversation setting](https://www.cs.cornell.edu/~cristian/Orientation_files/orientation-forwards-backwards.pdf) we interpreted orientation as a measure of the relative extent to which an interlocutor aims to advance the conversation forwards with a term, versus address existing content.
term_df = dual_context_model.get_term_df()
term_df.head()
k=10
print('low orientation')
display(term_df.sort_values('orn').head(k)[['orn']])
print('high orientation')
display(term_df.sort_values('orn').tail(k)[['orn']])
print('\nlow shift')
display(term_df.sort_values('shift').head(k)[['shift']])
print('high shift')
display(term_df.sort_values('shift').tail(k)[['shift']])
# ### Deriving utterance-level representations
#
# We now use the transformer to derive utterance-level characterizations, by transforming the corpus with it. Again, we focus on utterances that are sufficiently long:
_ = dual_context_model.transform(sw_corpus, selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5)
# The `transform` function does the following.
#
# First, it (or rather, its constituent `ExpectedContextModelTransformer`s) derives vector representations of utterances, stored as `fw_repr` and `bk_repr`:
sw_corpus.vectors
# Next, it derives ranges of utterances, stored in the metadata as `fw_range` and `bk_range`:
eg_ut = sw_corpus.get_utterance(utt_eg_id)
print('Forwards range:', eg_ut.meta['fw_range'])
print('Backwards range:', eg_ut.meta['bk_range'])
# It also assigns utterances to inferred types:
print('Forwards cluster:', eg_ut.meta['fw_clustering.cluster'])
print('Backwards cluster:', eg_ut.meta['bk_clustering.cluster'])
# And computes orientations and shifts:
print('shift:', eg_ut.meta['shift'])
print('orientation:', eg_ut.meta['orn'])
# ## 3. Analysis: correspondence to discourse act labels
#
# We explore the relation between the characterizations we've derived, and the various annotations that the utterances are labeled with (for more information on the annotation scheme, see the [manual here](https://web.stanford.edu/~jurafsky/ws97/manual.august1.html)). See [this dissertation](https://tisjune.github.io/research/dissertation) for further explanation of the analyses and findings below. A high-level comment is that this is a tough dataset for the framework to work with, given the relative lack of structure---something future work could think more carefully about.
#
# To facilitate the analysis, we extract relevant utterance attributes into a Pandas dataframe:
df = sw_corpus.get_attribute_table('utterance',
['bk_clustering.cluster', 'fw_clustering.cluster',
'orn', 'shift', 'tags'])
df = df[df['bk_clustering.cluster'].notnull()]
# We will stick to examining the 9 most common tags in the data:
tag_subset = ['aa', 'b', 'ba', 'h', 'ny', 'qw', 'qy', 'sd', 'sv']
for tag in tag_subset:
df['has_' + tag] = df.tags.apply(lambda x: tag in x.split())
# To start, we explore how the forwards and backwards vector representations correspond to these labels. To do this, we will compute log-odds ratios between the inferred utterance clusters and these labels:
def compute_log_odds(col, bool_col, val_subset=None):
if val_subset is not None:
col_vals = val_subset
else:
col_vals = col.unique()
log_odds_entries = []
for val in col_vals:
val_true = sum((col == val) & bool_col)
val_false = sum((col == val) & ~bool_col)
nval_true = sum((col != val) & bool_col)
nval_false = sum((col != val) & ~bool_col)
log_odds_entries.append({'val': val, 'log_odds': np.log((val_true/val_false)/(nval_true/nval_false))})
return log_odds_entries
bk_log_odds = []
for tag in tag_subset:
entry = compute_log_odds(df['bk_clustering.cluster'],df['has_' + tag], ['commentary'])[0]
entry['tag'] = tag
bk_log_odds.append(entry)
bk_log_odds_df = pd.DataFrame(bk_log_odds).set_index('tag').sort_values('log_odds')[['log_odds']]
fw_log_odds = []
for tag in tag_subset:
entry = compute_log_odds(df['fw_clustering.cluster'],df['has_' + tag], ['commentary'])[0]
entry['tag'] = tag
fw_log_odds.append(entry)
fw_log_odds_df = pd.DataFrame(fw_log_odds).set_index('tag').sort_values('log_odds')[['log_odds']]
print('forwards types vs labels')
display(fw_log_odds_df.T)
print('--------------------------')
print('backwards types vs labels')
display(bk_log_odds_df.T)
# Tags further towards the right of the above tables (more positive log-odds) are those that co-occur more with the `commentary` than the `personal` utterance type. We briefly note that both forwards and backwards representations seem to draw a distinction between `sv` (opinion statements) and `sd` (non-opinion statements).
# Next, we explore how the orientation and shift statistics relate to these labels. To do this, we compare statistics for utterances with a particular label, to statistics for utterances without that label.
from scipy import stats
def cohend(d1, d2):
n1, n2 = len(d1), len(d2)
s1, s2 = np.var(d1, ddof=1), np.var(d2, ddof=1)
s = np.sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
u1, u2 = np.mean(d1), np.mean(d2)
return (u1 - u2) / s
def get_pstars(p):
if p < 0.001:
return '***'
elif p < 0.01:
return '**'
elif p < 0.05:
return '*'
else: return ''
stat_col = 'orn'
entries = []
for tag in tag_subset:
has = df[df['has_' + tag]][stat_col]
hasnt = df[~df['has_' + tag]][stat_col]
entry = {'tag': tag, 'pval': stats.mannwhitneyu(has, hasnt)[1],
'cd': cohend(has, hasnt)}
entry['ps'] = get_pstars(entry['pval'] * len(tag_subset))
entries.append(entry)
orn_stat_df = pd.DataFrame(entries).set_index('tag').sort_values('cd')
orn_stat_df = orn_stat_df[np.abs(orn_stat_df.cd) >= .1]
stat_col = 'shift'
entries = []
for tag in tag_subset:
has = df[df['has_' + tag]][stat_col]
hasnt = df[~df['has_' + tag]][stat_col]
entry = {'tag': tag, 'pval': stats.mannwhitneyu(has, hasnt)[1],
'cd': cohend(has, hasnt)}
entry['ps'] = get_pstars(entry['pval'] * len(tag_subset))
entries.append(entry)
shift_stat_df = pd.DataFrame(entries).set_index('tag').sort_values('cd')
shift_stat_df = shift_stat_df[np.abs(shift_stat_df.cd) >= .1]
# (We'll only show labels for which there's a sufficiently large difference, in cohen's delta, between utterances with and without the label)
print('orientation vs labels')
display(orn_stat_df.T)
print('--------------------------')
print('shift vs labels')
display(shift_stat_df.T)
# We note that utterances containing questions (`qw`, `qy`) have higher shifts than utterances which do not. If you're familiar with the DAMSL designations for forwards and backwards looking communicative functions, the output for orientation might look a little puzzling/informative that our view of what counts as forwards/backwards is different from the view espoused by the annotation scheme. We discuss this further in [this dissertation](https://tisjune.github.io/research/dissertation).
# ## 4. Model persistence
#
# Finally, we briefly demonstrate how the model can be saved and loaded for later use
DUAL_MODEL_PATH = os.path.join(SW_CORPUS_PATH, 'dual_model')
dual_context_model.dump(DUAL_MODEL_PATH)
# We dump latent context representations, clustering information, and various input parameters, for each constituent `ExpectedContextModelTransformer`, in separate directories under `DUAL_MODEL_PATH`:
# ls $DUAL_MODEL_PATH
# To load the learned model, we start by initializing a new model:
dual_model_new = DualContextWrapper(context_fields=['reply_to','next_id'], output_prefixes=['bk_new','fw_new'],
vect_field='col_normed_tfidf', context_vect_field='col_normed_tfidf',
wrapper_output_prefix='new',
n_svd_dims=15, n_clusters=2,
random_state=1000, cluster_random_state=1000)
dual_model_new.load(DUAL_MODEL_PATH, model_dirs=['bk','fw'])
# We see that using the re-loaded model to transform the corpus results in the same representations and characterizations as the original one:
_ = dual_model_new.transform(sw_corpus, selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5)
sw_corpus.vectors
np.allclose(sw_corpus.get_vectors('bk_new_repr'), sw_corpus.get_vectors('bk_repr'))
np.allclose(sw_corpus.get_vectors('fw_new_repr'), sw_corpus.get_vectors('fw_repr'))
for ut in sw_corpus.iter_utterances(selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5):
assert ut.meta['orn'] == ut.meta['new_orn']
assert ut.meta['shift'] == ut.meta['new_shift']
# ## 5. Pipeline usage
#
# We also implement a pipeline that handles the following:
# * processes text (via a pipeline supplied by the user)
# * transforms text to input representation (via `ColNormedTfidfTransformer`)
# * derives framework output (via `DualContextWrapper`)
from convokit.expected_context_framework import DualContextPipeline
# see `demo_text_pipelines.py` in this demo's directory for details
# in short, this pipeline will either output the `alpha_text` metadata field
# of an utterance, or write the utterance's `text` attribute into the `alpha_text`
# metadata field
from demo_text_pipelines import switchboard_text_pipeline
# We initialize the pipeline with the following arguments:
# * `text_field` specifies which utterance metadata field to use as text input
# * `text_pipe` specifies the pipeline used to compute the contents of `text_field`
# * `tfidf_params` specifies the parameters to be passed into the underlying `ColNormedTfidfTransformer` object
# * `min_terms` specifies the minimum number of terms in the vocabulary that an utterance must contain for it to be considered in fitting and transforming the underlying `DualContextWrapper` object (see the `selector` argument passed into `dual_context_model.fit` above)
#
# All other arguments are inherited from `DualContextWrapper`.
pipe_obj = DualContextPipeline(context_fields=['reply_to','next_id'],
output_prefixes=['bk','fw'],
text_field='alpha_text', text_pipe=switchboard_text_pipeline(),
tfidf_params={'binary': True, 'vocabulary': vocab},
min_terms=5,
n_svd_dims=15, n_clusters=2,
random_state=1000, cluster_random_state=1000)
# note this might output a warning that `col_normed_tfidf` already exists;
# that's okay: the pipeline is just recomputing this matrix
pipe_obj.fit(sw_corpus)
# Note that the pipeline enables us to transform ad-hoc string input:
eg_ut_new = pipe_obj.transform_utterance('How old were you when you left ?')
# note these attributes have the exact same values as those of eg_ut, computed above
print('shift:', eg_ut_new.meta['shift'])
print('orientation:', eg_ut_new.meta['orn'])
|
convokit/expected_context_framework/demos/switchboard_exploration_dual_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hello Treebeard!
#
# Thanks for trying out Treebeard's cloud deploy and scheduling service.
#
#
# 1. [Requirements](#Requirements)
# 2. [Outputs](#Outputs)
# 3. [Examples](#Examples)
# - [Call an API](#Call-an-API)
# - [Check a hosted file](#Check-a-hosted-file)
# ## Requirements
import treebeard
# This notebook does not depend on the treebeard library, but it should be present in your requirements file.
# The underlying build service sends this notebook to a cloud server which uses the papermill library to run
# the notebook. Having treebeard as a dependency ensure this functions correctly.
# There must be a dependencies file alongside this notebook, either requirements.txt, a pipenv Pipfile, or a Conda environment.yml file.
# Setup
import os
import matplotlib.pyplot as plt
import requests
import json
import pandas as pd
import numpy as np
import seaborn as sns
# %matplotlib inline
# ## Output
# **Output** from your notebooks should be saved in an `output` directory.
# If so, they will be saved on the cloud build server, versioned, and made available via URL endpoints.
# They can be listed on the Treebeard admin page that you can find after running a build.
# create an outputs directory if it does not exist
if 'output' not in os.listdir(): os.mkdir('output')
# # Examples
#
# Here are a few simple examples of data that might be interesting to check over time.
#
# ## Call an API
# What's the current price of BitCoin?
r = requests.get('https://api.coindesk.com/v1/bpi/currentprice.json').json()
print(f"At {r['time']['updateduk']}, the price of Bitcoin is £{r['bpi']['GBP']['rate']}")
# This data was produced from the CoinDesk Bitcoin Price Index (USD). Non-USD currency data converted using hourly conversion rate from openexchangerates.org
# See the last 30 days of the price of Bitcoin, thanks to CoinDesk's API
# +
r = requests.get('https://api.coindesk.com/v1/bpi/historical/close.json').json()
fig, ax = plt.subplots()
ax.plot(pd.DataFrame.from_dict(r)['bpi'][:-2], color='red', linestyle='--')
ax.set_ylabel('Bitcoin Price (£)')
fig.suptitle('Last 30 Days of Bitcoin Price', size=16)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
ax.xaxis.set_major_locator(plt.MaxNLocator(4))
im = plt.imread('https://emojipedia-us.s3.dualstack.us-west-1.amazonaws.com/thumbs/320/apple/237/money-with-wings_1f4b8.png')
newax = fig.add_axes([0.8, 0.8, 0.2, 0.2], anchor='NE')
newax.imshow(im)
newax.axis('off')
plt.savefig('output/bitcoin_price.png', dpi=150, bbox_inches='tight')
# -
# ## Check a hosted file
#
# The [Mauna Loa Observatory](https://www.esrl.noaa.gov/gmd/obop/mlo/) is a USA NOAA Earth System Research Laboratory.
# It publishes measurements of **atmospheric CO2 concentration** regularly.
# The Observatory publishes its own charts [here](https://www.esrl.noaa.gov/gmd/ccgg/trends/mlo.html), but we can recreate them.
# Weekly CO2 data is published here, there are also other datafeeds available
url = "ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_weekly_mlo.txt"
# Pandas can read remote URL file contents
# Skip the first 49 rows as they are explanatory text
# Reading them is helpful though as they define the column names and missing number fills
df = pd.read_table(url, skiprows=49, header=None)
df[0].head()
# Use a regex to turn the variable whitespace between columns into commas
df[0] = df[0].str.strip().str.replace("(\s{1,})", ",")
# Split the column by commas and expand into columns
df = df[0].str.split(',', expand=True)
# Set the column headers
columns = ["yr", "mon", "day", "decimal", "ppm", "days", "1_yr_ago", "10_yr_ago", "since_1800"]
df.columns=columns
# Replace -999.99 with NAs
df = df.replace('-999.99', np.nan)
# Create datetime column
df['date'] = pd.to_datetime(dict(year=df['yr'], month=df['mon'], day=df['day']))
# Set types
df['ppm'] = df['ppm'].apply(pd.to_numeric)
df.tail()
sns.set()
fig, ax = plt.subplots(figsize=(8,8))
sns.lineplot(x='date', y='ppm', data=df)
plt.title("Weekly Atmospheric CO2 concentration at Mauna Loa Observatory")
plt.savefig('output/co2_concentration.png', dpi=150, bbox_inches='tight')
# This is my change
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
from decimal import *
import matplotlib.pyplot as plt
a = [Decimal(3)]
b = [2*Decimal(3).sqrt()]
n = [6]
n_digits_list = [0]
getcontext().prec = 2000
for k in range(1, 2000):
n.append(6*2**k)
b.append(2/(1/a[k-1] + 1/b[k-1]))
a.append((a[k-1]*b[k]).sqrt())
for n_digits, (digit_a, digit_b) in enumerate(zip(a[k].as_tuple()[1], b[k].as_tuple()[1])):
if digit_a != digit_b:
n_digits -= 1
break
n_digits_list.append(n_digits)
plt.figure(figsize = (15, 10))
plt.plot(n_digits_list)
|
pi_calculations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#importing all the imprtant libraries
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
plt.style.use('ggplot')
import tensorflow as tf
import re
from tensorflow.keras.preprocessing.text import Tokenizer
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score
# -
# ### Reading Data
#reading data
fake = pd.read_csv('Fake.csv')
real = pd.read_csv('True.csv')
# ### Understanding Data
# displaying dataframe of fake news
fake.head()
#displaying dataframe of real news
real.head()
fake.isnull().sum()
real.isnull().sum()
# #### we can see that there is no missing data in the datasets
#checking for unique subjects in real dataframe
fake.subject.unique()
#checking for unique subjects in fake dataframe
real.subject.unique()
# ### subject coulmn is unevenly distributed and hence will hamper our classification also the date colums is not useful we can remove that aswell
# dropping redundant columns
fake.drop(['date', 'subject'], axis=1, inplace=True)
real.drop(['date', 'subject'], axis=1, inplace=True)
# ### Labelling fake and real news [ fake = 0, real = 1]
#labelling data
fake['class'] = 0
real['class'] = 1
# ### Visualising the distribution of fake and real news
plt.figure(figsize=(10, 5))
plt.bar('Fake News', len(fake), color='orange')
plt.bar('Real News', len(real), color='green')
plt.title('Distribution of Fake News and Real News', size=15)
plt.xlabel('News Type', size=15)
plt.ylabel('# of News Articles', size=15)
# Difference between number of fake news and real news
print('Difference in news articles:',len(fake)-len(real))
# combining the the fake and real dataset
news = pd.concat([fake, real], ignore_index=True, sort=False)
news
# combining the text and title for simplification
news['text'] = news['title'] + news['text']
news.drop('title', axis=1, inplace=True)
# ### Data PreProcessing
# +
## splitting the data into test and train
features = news['text']
targets = news['class']
X_train, X_test, y_train, y_test = train_test_split(features, targets, test_size=0.30, random_state=18)
# +
## Normalising the data removing url's, blank spaces,symbols etc.
def normalize(data):
normalized = []
for i in data:
i = i.lower()
# get rid of urls
i = re.sub('https?://\S+|www\.\S+', '', i)
# get rid of non words and extra spaces
i = re.sub('\\W', ' ', i)
i = re.sub('\n', '', i)
i = re.sub(' +', ' ', i)
i = re.sub('^ ', '', i)
i = re.sub(' $', '', i)
normalized.append(i)
return normalized
X_train = normalize(X_train)
X_test = normalize(X_test)
# +
max_vocab = 10000
tokenizer = Tokenizer(num_words=max_vocab)
tokenizer.fit_on_texts(X_train)
# -
#converting txt to vector
X_train = tokenizer.texts_to_sequences(X_train)
X_test = tokenizer.texts_to_sequences(X_test)
# padding so that all articles have same length
X_train = tf.keras.preprocessing.sequence.pad_sequences(X_train, padding='post', maxlen=256)
X_test = tf.keras.preprocessing.sequence.pad_sequences(X_test, padding='post', maxlen=256)
# ### Building model
# +
model = tf.keras.Sequential([
tf.keras.layers.Embedding(max_vocab, 32),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(16)),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(1)
])
model.summary()
# +
# early stop to stop training if validation loss stops improving
early_stop = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=2, restore_best_weights=True)
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(1e-4),
metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=10,validation_split=0.1, batch_size=30, shuffle=True, callbacks=[early_stop])
# +
# Visualising Training and validation loss
history_dict = history.history
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = history.epoch
plt.figure(figsize=(12,9))
plt.plot(epochs, loss, 'r', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss', size=20)
plt.xlabel('Epochs', size=20)
plt.ylabel('Loss', size=20)
plt.legend(prop={'size': 20})
plt.show()
plt.figure(figsize=(12,9))
plt.plot(epochs, acc, 'g', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy', size=20)
plt.xlabel('Epochs', size=20)
plt.ylabel('Accuracy', size=20)
plt.legend(prop={'size': 20})
plt.ylim((0.5,1))
plt.show()
# -
# ### Evaluating the model
# model evaluation
model.evaluate(X_test, y_test)
# +
pred = model.predict(X_test)
binary_predictions = []
for i in pred:
if i >= 0.5:
binary_predictions.append(1)
else:
binary_predictions.append(0)
# -
print('Accuracy on testing set:', accuracy_score(binary_predictions, y_test))
print('Precision on testing set:', precision_score(binary_predictions, y_test))
print('Recall on testing set:', recall_score(binary_predictions, y_test))
# +
## Visualising confusion matrix
matrix = confusion_matrix(binary_predictions, y_test, normalize='all')
plt.figure(figsize=(16, 9))
ax= plt.subplot()
sns.heatmap(matrix, annot=True, ax = ax)
# labels, title and ticks
ax.set_xlabel('Predicted Labels', size=20)
ax.set_ylabel('True Labels', size=20)
ax.set_title('Confusion Matrix', size=20)
ax.xaxis.set_ticklabels([0,1], size=15)
ax.yaxis.set_ticklabels([0,1], size=15)
|
RNN.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.3
# language: julia
# name: julia-1.5
# ---
# # MOwNiT
# ## Laboratorium 1
# ### Arytmetyka komputerowa
#
#
# IEEE-754 Analysis http://babbage.cs.qc.cuny.edu/IEEE-754/
bitstring(Float32(1.0))
bitstring(Float64(1.0))
# domyślnie Float64
bitstring(1.0)
# Float16
bitstring(Float16(1.0))
# znak, cecha, mantysa
# uwaga - w Julii tablice indeksujemy od 1
# uwaga: ukryta jedynka nie jest pamiętana
# uwaga: cecha jest pamiętana w kodzie z nadmiarem (tutaj BIAS=127)
decode(x::Float32) = (b=bitstring(x); (b[1], b[2:9], b[10:32]))
decode(Float32(1.0))
println(significand(Float32(1.0)), "*2^", exponent(Float32(1.0)))
# co ile liczby sa reprezentowane
c=Float32[]
a=Float32(1.0)
r=1:10
for i=r
push!(c, a)
a=nextfloat(a)
end
map(x-> bitstring(x),c)
# Maszynowe epsilon mówi, jaki jest odstęp między kolejnymi liczbami zmiennoprzecinkowymi reprezentowanymi w komputerze
eps(Float32(1))
eps(Float32)
# + nbgrader={"grade": true, "grade_id": "cell-510e2987d5b4ebfc", "locked": false, "points": 2, "schema_version": 1, "solution": true}
# Badanie postaci zdenormalizowanej. Co się dzieje, jak liczby są coraz mniejsze?
a=Float32(1.1)
for i=1:149
a=a/Float32(2.0)
println(decode(a), " ", issubnormal(a))
end
# -
# Rysowanie wykresów
#using Pkg
#Pkg.add("Plots")
# http://docs.juliaplots.org/latest/tutorial/
using Plots
scatter(1:1:5, [2,2,3,3,5])
# <b> Zadanie 1 </b> Porównać w języku Julia reprezentację bitową liczby 1/3 dla Float16, Float32, Float64 oraz liczby,
# która jest inicjalizowana jako Float16, a potem rzutowana na Float64.
# <b>Zadanie 2</b> Zbadać, jak zmienia się odległość między kolejnymi liczbami zminnoprzecinkowymi
# reprezentowanymi w komputerze za pomocą języka Julia.
# Narysować wykres używając Plots zależności odległości od wartości liczby dla zakresu od 1.0 do 1000000.0.
# <b>Zadanie 3</b> Jedną z bibliotek numerycznych, jaką będziemy używać na zajęciach jest <a href="http://home.agh.edu.pl/~kzajac/dydakt/mownit/lab1/gsl.html">GSL</a> (język C). Korzystając ze <a href="https://www.gnu.org/software/gsl/doc/html/ieee754.html"> wsparcia dla wyświetlania reprezentacji liczb zmiennoprzecinkowych</a> zobaczyć jak zmienia się cecha i mantysa dla coraz mniejszych liczb. Zaobserwować, kiedy matysa przestaje być znormalizowana i dlaczego?
# <b>Zadanie 4</b> Na przykładzie wybranego algorytmu niestabilnego numerycznie:
# 1. Pokazać, że działa źle.
# 2. Pokazać które konkretnie działania powodują zwiększenie błędu (np. dzielenie przez małą liczbę, cancellation).
# 3. Zademonstować wersję stabilną.
#
# Wszystkie punkty przedstawić w postaci notatnika Julii.
|
Mownit_Lab1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Flights example
# + pycharm={"name": "#%%\n"}
import numpy as np
import pandas
from IPython.core.display import display
import raha
# -
# ## Run error detection and repair 30 times
#
# We use ground truth to label 20 tuples in each run.
# + pycharm={"name": "#%%\n"}
datasets = []
for i in range(30):
from raha import analysis_utilities
app_1 = raha.Detection()
app_2 = raha.Correction()
# How many tuples would you label?
app_1.LABELING_BUDGET = 20
app_2.LABELING_BUDGET = 0
# Would you like to see the logs?
app_1.VERBOSE = False
app_2.VERBOSE = False
dataset_dictionary = {
"name": "flights",
"path": "datasets/flights/dirty.csv",
"clean_path": "datasets/flights/clean.csv"
}
d = app_1.initialize_dataset(dataset_dictionary)
app_1.run_strategies(d)
app_1.generate_features(d)
app_1.build_clusters(d)
while len(d.labeled_tuples) < app_1.LABELING_BUDGET:
app_1.sample_tuple(d)
if d.has_ground_truth:
app_1.label_with_ground_truth(d)
app_1.propagate_labels(d)
app_1.predict_labels(d)
app_2.initialize_models(d)
app_2.initialize_dataset(d)
for si in d.labeled_tuples:
d.sampled_tuple = si
app_2.update_models(d)
app_2.generate_features(d)
app_2.predict_corrections(d)
print(f"Run {i} done")
datasets.append(d)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Evaluation
# +
evaluation_df = pandas.DataFrame(columns=["Task", "Precision", "Recall", "F1 Score"])
for d in datasets:
edp, edr, edf = d.get_data_cleaning_evaluation(d.detected_cells)[:3]
ecp, ecr, ecf = d.get_data_cleaning_evaluation(d.corrected_cells)[-3:]
evaluation_df = evaluation_df.append({"Task": "Error Detection (Raha)", "Precision": edp,
"Recall": edr, "F1 Score": edf}, ignore_index=True)
evaluation_df = evaluation_df.append({"Task": "Error Correction (Baran)", "Precision": ecp,
"Recall": ecr, "F1 Score": ecf}, ignore_index=True)
display(evaluation_df)
evaluation_df.groupby("Task").agg(["mean", "std", "min", "max"])
# -
# ## Analyze the alternative repairs
# + pycharm={"name": "#%%\n"}
alternative_count_list = []
for d in datasets:
number_of_repairs = len(d.correction_collection)
number_of_repairs_hist = dict()
for cell_repairs in d.correction_collection.values():
num = len(cell_repairs)
number_of_repairs_hist[num] = number_of_repairs_hist.get(num, 0) + 1
hist = [0] * (max(number_of_repairs_hist.keys()) + 1)
for num, count in number_of_repairs_hist.items():
hist[num] = count
alternative_count_list.append(number_of_repairs_hist)
#print(f"Histogram of the number of alternative repairs: {list(enumerate(hist))}")
max_alternatives = max(max(h.keys()) for h in alternative_count_list)
alternative_count_df = pandas.DataFrame(columns=list(range(max_alternatives + 1)))
for hist in alternative_count_list:
alternative_count_df = alternative_count_df.append(hist, ignore_index=True)
alternative_count_df.drop(0,axis=1,inplace=True)
alternative_count_df = alternative_count_df.fillna(0)
alternative_count_df
# + pycharm={"name": "#%%\n"}
mean_number_of_repairs = (alternative_count_df * np.arange(1,max_alternatives+1,1)).sum(axis=1) / alternative_count_df.sum(axis=1)
mean_number_of_repairs.agg(["mean", "std", "min", "max"])
# + pycharm={"name": "#%%\n"}
more_than_one = alternative_count_df.loc[:, alternative_count_df.columns[1:]].sum(axis=1) / alternative_count_df.sum(axis=1)
more_than_one.agg(["mean", "std", "min", "max"])
# + pycharm={"name": "#%%\n"}
print("Mean number of cells with x predicted alternatives in 10 runs")
mean_count_series = alternative_count_df.mean()
mean_count_series
# + pycharm={"name": "#%%\n"}
correct_repairs = datasets[0].get_actual_errors_dictionary()
collection = []
correct_repair_probs = []
incorrect_repair_probs = []
other_repair_probs = []
for d in datasets:
wrong_detection = 0
alt_available_all = 0
for cell, repairs in d.correction_collection.items():
if cell in correct_repairs:
if len(repairs) > 1:
alt_available_all += 1
else:
wrong_detection += 1
alt_rate = alt_available_all / len(d.correction_collection)
error_repaired_cells = [cell for cell, correction in d.corrected_cells.items() if cell in correct_repairs and correction != correct_repairs[cell]]
#print(f"Number of incorrectly repaired cells: {len(error_repaired_cells)}")
error_rate = len(error_repaired_cells) / len(d.corrected_cells)
alt_available = 0
correct_repair_available = 0
correct_repair_only = 0
correct_repair_highest = 0
correct_repair_better_chosen = 0
for cell in error_repaired_cells:
assert len(d.correction_collection[cell]) > 0
if len(d.correction_collection[cell]) > 1:
alt_available += 1
if correct_repairs[cell] in d.correction_collection[cell].keys():
correct_repair_available += 1
other_repairs = d.correction_collection[cell].copy()
other_repairs.pop(d.corrected_cells[cell], None)
other_repairs.pop(correct_repairs[cell], None)
if len(other_repairs) == 0:
correct_repair_only += 1
if d.correction_collection[cell][correct_repairs[cell]] > max(list(other_repairs.values()) + [0]):
correct_repair_highest += 1
if d.correction_collection[cell][correct_repairs[cell]] > d.correction_collection[cell][d.corrected_cells[cell]]:
correct_repair_better_chosen += 1
#print(f"Number of incorrectly repaired cells, where the correct repair is among the alternative repairs: {correct_repair_available}")
collection.append((len(d.correction_collection),
alt_available_all,
alt_rate,
len(error_repaired_cells),
error_rate,
wrong_detection,
alt_available,
correct_repair_available,
correct_repair_highest,
correct_repair_only,
correct_repair_better_chosen))
for cell in error_repaired_cells:
if correct_repairs[cell] in d.correction_collection[cell]:
correct_repair_probs.append(d.correction_collection[cell][correct_repairs[cell]])
incorrect_repair_probs.append(d.correction_confidences[cell])
other_repair_probs.append([prob for val, prob in d.correction_collection[cell].items()
if val not in [correct_repairs[cell], d.corrected_cells[cell]]])
repairable_df = pandas.DataFrame(collection, columns=["repairs",
"alt_all",
"alt_rate",
"errors",
"error_rate",
"wrong_detection",
"alt_if_error",
"correct_in_alt",
"highest_alternative",
"only_alternative",
"higher_chosen"])
repairable_df["error_alt_avail"] = repairable_df["alt_if_error"] / repairable_df["errors"]
repairable_df["correct_alt_avail"] = repairable_df["correct_in_alt"] / repairable_df["errors"]
repairable_df["highest_if_avail"] = repairable_df["highest_alternative"] / repairable_df["correct_in_alt"]
repairable_df["only_if_avail"] = repairable_df["only_alternative"] / repairable_df["correct_in_alt"]
repairable_df["highest_if_error"] = repairable_df["highest_alternative"] / repairable_df["errors"]
repairable_df["highest_is_correct"] = repairable_df["highest_alternative"] / repairable_df["alt_all"]
repairable_df["higher_percentage"] = repairable_df["higher_chosen"] / repairable_df["errors"]
repairable_df.describe(percentiles=[0.25, 0.5, 0.75])
# + pycharm={"name": "#%%\n"}
repairable_df
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Analyze detection confidence vs error probability
# + pycharm={"name": "#%%\n"}
import importlib
from raha import analysis_utilities
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.ion()
# + pycharm={"name": "#%%\n"}
importlib.reload(analysis_utilities)
# + pycharm={"name": "#%%\n"}
evaluation_dfs = []
for d in datasets:
df = analysis_utilities.get_detection_evaluation_df(d)
evaluation_dfs.append(df)
#display(df)
#display(df.value_counts(subset=["detected", "truth"]))
#display(analysis_utilities.detection_evaluation(df))
#display(analysis_utilities.detection_correctness_by_confidence(df,number_of_bins=10))
df = pandas.concat(evaluation_dfs)
# + pycharm={"name": "#%%\n"}
analysis_utilities.detection_evaluation(df, sharey="all", number_of_bins=100)
# + pycharm={"name": "#%%\n"}
1 - ((df["p"] < 0.01) | (df["p"] > 0.99)).sum() / len(df.index)
# + pycharm={"name": "#%%\n"}
1 - ((df["p"] < 0.05) | (df["p"] > 0.95)).sum() / len(df.index)
# + pycharm={"name": "#%%\n"}
analysis_utilities.detection_evaluation(df, sharey="row",number_of_bins=100).savefig("flights_detection_split.pdf", dpi=600)
# + pycharm={"name": "#%%\n"}
analysis_utilities.detection_evaluation_without_grouping(df,number_of_bins=100).savefig("flights_detection_overview.pdf", dpi=600)
# + pycharm={"name": "#%%\n"}
(df["p"] >= 0.99).sum() / (df["p"] >= 0.5).sum()
# + pycharm={"name": "#%%\n"}
(df["detected"] & ~df["truth"] & df["p"] >= 0.99).sum() / (df["detected"] & df["p"] >= 0.99).sum()
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Analyze confidence vs error probability
# + pycharm={"name": "#%%\n"}
r_p_dfs = []
for d in datasets:
r_p_dfs.append(analysis_utilities.get_correction_confidence_df(d))
r_p_df = pandas.concat(r_p_dfs)
# + pycharm={"name": "#%%\n"}
analysis_utilities.correction_confidence_distribution(r_p_df, number_of_bins=100)
# + pycharm={"name": "#%%\n"}
(r_p_df["confidence"] >= 0.99).sum() / len(r_p_df.index)
# + pycharm={"name": "#%%\n"}
(r_p_df["confidence"] >= 0.95).sum() / len(r_p_df.index)
# + pycharm={"name": "#%%\n"}
((r_p_df["confidence"] >= 0.99) & (r_p_df["detection_correct"] == False)).sum() / (r_p_df["confidence"] >= 0.99).sum()
# + pycharm={"name": "#%%\n"}
((r_p_df["confidence"] >= 0.99) & (r_p_df["detection_correct"] == False)).sum() / (r_p_df["detection_correct"] == False).sum()
# + pycharm={"name": "#%%\n"}
((r_p_df["confidence"] >= 0.99) & (r_p_df["detection_correct"] == True)).sum() / (r_p_df["detection_correct"] == True).sum()
# + pycharm={"name": "#%%\n"}
analysis_utilities.correction_confidence_distributions(r_p_df, number_of_bins=100)
# + pycharm={"name": "#%%\n"}
analysis_utilities.correction_confidence_distribution(r_p_df, number_of_bins=100).savefig("flights_correction_overview.pdf")
analysis_utilities.correction_confidence_distributions(r_p_df, number_of_bins=100).savefig("flights_correction_split.pdf")
# + pycharm={"name": "#%%"}
|
flights_evaluation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (pit10K)
# language: python
# name: pit10k
# ---
# +
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
REPO_DIR = os.path.dirname(os.getcwd())
sys.path.append(os.path.join(REPO_DIR, 'lib'))
DATA_PATH = os.path.join(REPO_DIR, 'data')
from population import location
COORDINATES_CSV = os.path.join(DATA_PATH, 'city', 'population', 'coordinates_leeds.csv')
#location.request_coords_to_csv(COORDINATES_CSV)
# -
# Collect coords into list
coords_types = location.get_coords(COORDINATES_CSV)
coords = list(zip(*coords_types))
# Convert coordinates into numpy array
X = np.array(list(zip(*coords[:2])))
X
plt.plot(X[:, 0], X[:, 1], 'o')
plt.title('Accommodations in Leeds')
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.axis('equal')
plt.show()
|
notebooks/households.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (pytorch)
# language: python
# name: pytorch
# ---
# # Federated learning: random seed
# This notebook is a copy of the notebook [Federated learning basic concepts](./federated_learning_basic_concepts.ipynb). The difference is that, here, we set a seed using [Reproducibility](https://github.com/sherpaai/Sherpa.ai-Federated-Learning-Framework/blob/master/shfl/private/reproducibility.py) Singleton Class, in order to ensure the reproducibility of the experiment. If you execute this experiment many times, you should always obtain the same results.
# However, apart from that, the structure is identical so the text has been removed for clearness. Please refer to the original notebook for the detailed description of the experiment.
# +
from shfl.private.reproducibility import Reproducibility
# Server
Reproducibility(1234)
# In case of client
# Reproducibility.get_instance().set_seed(ID)
# + [markdown] pycharm={"is_executing": false}
# ## The data
# + pycharm={"is_executing": false}
import matplotlib.pyplot as plt
import shfl
database = shfl.data_base.Emnist()
train_data, train_labels, test_data, test_labels = database.load_data()
print(len(train_data))
print(len(test_data))
print(type(train_data[0]))
train_data[0].shape
plt.imshow(train_data[0])
iid_distribution = shfl.data_distribution.IidDataDistribution(database)
federated_data, test_data, test_labels = iid_distribution.get_federated_data(num_nodes=20, percent=10)
print(type(federated_data))
print(federated_data.num_nodes())
federated_data[0].private_data
# -
# ## The model
# + pycharm={"is_executing": false}
import tensorflow as tf
def model_builder():
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3), padding='same', activation='relu', strides=1, input_shape=(28, 28, 1)))
model.add(tf.keras.layers.MaxPooling2D(pool_size=2, strides=2, padding='valid'))
model.add(tf.keras.layers.Dropout(0.4))
model.add(tf.keras.layers.Conv2D(32, kernel_size=(3, 3), padding='same', activation='relu', strides=1))
model.add(tf.keras.layers.MaxPooling2D(pool_size=2, strides=2, padding='valid'))
model.add(tf.keras.layers.Dropout(0.3))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(128, activation='relu'))
model.add(tf.keras.layers.Dropout(0.1))
model.add(tf.keras.layers.Dense(64, activation='relu'))
model.add(tf.keras.layers.Dense(10, activation='softmax'))
criterion = tf.keras.losses.CategoricalCrossentropy()
optimizer = tf.keras.optimizers.RMSprop()
metrics = [tf.keras.metrics.categorical_accuracy]
return shfl.model.DeepLearningModel(model=model, criterion=criterion, optimizer=optimizer, metrics=metrics)
# + pycharm={"is_executing": false}
aggregator = shfl.federated_aggregator.FedAvgAggregator()
federated_government = shfl.federated_government.FederatedGovernment(model_builder, federated_data, aggregator)
# + pycharm={"is_executing": false}
import numpy as np
class Reshape(shfl.private.FederatedTransformation):
def apply(self, labeled_data):
labeled_data.data = np.reshape(labeled_data.data, (labeled_data.data.shape[0], labeled_data.data.shape[1], labeled_data.data.shape[2],1))
shfl.private.federated_operation.apply_federated_transformation(federated_data, Reshape())
# + pycharm={"is_executing": false, "name": "#%%\n"}
import numpy as np
class Normalize(shfl.private.FederatedTransformation):
def __init__(self, mean, std):
self.__mean = mean
self.__std = std
def apply(self, labeled_data):
labeled_data.data = (labeled_data.data - self.__mean)/self.__std
mean = np.mean(train_data.data)
std = np.std(train_data.data)
shfl.private.federated_operation.apply_federated_transformation(federated_data, Normalize(mean, std))
# -
# ## Run the federated learning experiment
# + pycharm={"is_executing": true}
test_data = np.reshape(test_data, (test_data.shape[0], test_data.shape[1], test_data.shape[2],1))
federated_government.run_rounds(3, test_data, test_labels)
|
notebooks/federated_learning/federated_learning_basic_concepts_random_seed.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/chathumal93/ADB-Palu/blob/main/1_PSBAS_Result.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="UshkTxDRZjDt"
# # Environment Setup
#
# Install the necessary packages and import the already installed Python packages.
# + id="lATIVR5dZ2tN"
# Uncomment for the first Runtime
# !pip install geopandas
# + id="FTsn4_XtYzwA"
import numpy as np
import pandas as pd
from shapely.geometry import Point
from geopandas import GeoDataFrame
# + [markdown] id="ON0Axgq7Z1YV"
# # Data Access
#
# Run the below code to mount google drive with this notebook and access the files inside.
# + id="U7dcFNSAaRYu" colab={"base_uri": "https://localhost:8080/"} outputId="9992423d-6f3c-42d4-b629-c9073061b69d"
from google.colab import drive
drive.mount('/content/drive/')
# + [markdown] id="V8WZ8L9b-0ZG"
# Define the input and output file paths according to the mounted google drive directory
# + id="NA52pAwaYzwE"
# PSBAS CSV file Path
PSBAS = '/content/drive/MyDrive/EARR/1_Data/2_P-SBAS/DTSLOS_ait_20181109_20211105_ASC.csv'
# Output Shape file Path
Out = '/content/drive/MyDrive/EARR/2_Results/2_P-SBAS/DTSLOS_ait_20181109_20211105_ASC.shp'
# + [markdown] id="CIJzdjqlz9Bb"
# # Dataframe creation
# Run below code to read the PSBAS csv file into a dataframe and arrange the infomation with the relevant columns.
# + id="a3lXRM8eYzwF"
# Read PSBAS data in csv format
data = pd.read_csv(PSBAS,skiprows=43)
# Re-arranging the column names (This is based on the geo-portal visualization requirement)
column_names_01 = ['ID','Lat','Lon','Topo','V_LOS','COH','cosN','cosE','cosU','TS']
# Getting the image list (Frist image as the Refernce Image)
img_list = list(pd.read_csv(PSBAS, nrows=1, skiprows=39))
# Getting the slave image name list
slv_img_list = img_list[1:]
# Slave image name list re-arrange
column_names_02 = []
# Getting the data tag of slave images
for datetime_tag in range(len(slv_img_list)):
date_tag = slv_img_list[datetime_tag].split('T')[0].split(' ')[1]
column_names_02.append('DL'+ date_tag.split('-')[0]+''+date_tag.split('-')[1]+''+date_tag.split('-')[2])
# Define the dataframe with re-arranged columns
column_all = column_names_01 + column_names_02
data.columns = column_all
# + [markdown] id="4fxMgHHg0JJD"
# # Parameter Conversion
# Run below code to convert all the **Velocity** and **Displacement** information into milimeter (mm) scale.
#
# + id="X4pJqD9sYzwF"
#Conversion of parameters in to mm scale
#Conversion of Velocity into mm scale
data['V_LOS'] = np.array(data['V_LOS'])*10
#Conversion of Displacement into mm scale
for col in column_names_02:
data[col] = np.array(data[col])*10
# + [markdown] id="JIWBbvto0S0D"
# # Final Product
# Run the below code to convert the geodataframe into a shapefile for further analysis.
# + id="VlTgMoaOYzwG"
# Accessing the Lat and Long from dataframe for geometry conversion
geometry = [Point(xy) for xy in zip(data.Lon, data.Lat)]
# Creating a Geodataframe - "EPSG:4326"
gdf = GeoDataFrame(data, crs="EPSG:4326", geometry=geometry)
# Exporting the Geodataframe as a shape file
gdf.to_file(Out)
|
1_PSBAS_Result.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
music_data = pd.read_csv('music.csv')
#input set
X = music_data.drop(columns='genre')
#output set
y = music_data['genre']
#split the train , test data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
#build model, train model, make prediction
model = DecisionTreeClassifier()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
#checking accuracy
accuracy_score(y_test, predictions)
|
Music_Predictions_Project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
#
# <a href='http://www.pieriandata.com'> <img src='../Pierian_Data_Logo.png' /></a>
# ___
# # NumPy Exercises - Solutions
#
# Now that we've learned about NumPy let's test your knowledge. We'll start off with a few simple tasks and then you'll be asked some more complicated questions.
# #### Import NumPy as np
import numpy as np
# #### Create an array of 10 zeros
np.zeros(10)
# #### Create an array of 10 ones
np.ones(10)
# #### Create an array of 10 fives
np.ones(10) * 5
# #### Create an array of the integers from 10 to 50
np.arange(10,51)
# #### Create an array of all the even integers from 10 to 50
np.arange(10,51,2)
# #### Create a 3x3 matrix with values ranging from 0 to 8
np.arange(9).reshape(3,3)
# #### Create a 3x3 identity matrix
np.eye(3)
# #### Use NumPy to generate a random number between 0 and 1
np.random.rand(1)
# #### Use NumPy to generate an array of 25 random numbers sampled from a standard normal distribution
np.random.randn(25)
# #### Create the following matrix:
np.arange(1,101).reshape(10,10) / 100
# #### Create an array of 20 linearly spaced points between 0 and 1:
np.linspace(0,1,20)
# ## Numpy Indexing and Selection
#
# Now you will be given a few matrices, and be asked to replicate the resulting matrix outputs:
mat = np.arange(1,26).reshape(5,5)
mat
# +
# WRITE CODE HERE THAT REPRODUCES THE OUTPUT OF THE CELL BELOW
# BE CAREFUL NOT TO RUN THE CELL BELOW, OTHERWISE YOU WON'T
# BE ABLE TO SEE THE OUTPUT ANY MORE
# -
mat[2:,1:]
# +
# WRITE CODE HERE THAT REPRODUCES THE OUTPUT OF THE CELL BELOW
# BE CAREFUL NOT TO RUN THE CELL BELOW, OTHERWISE YOU WON'T
# BE ABLE TO SEE THE OUTPUT ANY MORE
# -
mat[3,4]
# +
# WRITE CODE HERE THAT REPRODUCES THE OUTPUT OF THE CELL BELOW
# BE CAREFUL NOT TO RUN THE CELL BELOW, OTHERWISE YOU WON'T
# BE ABLE TO SEE THE OUTPUT ANY MORE
# -
mat[:3,1:2]
# +
# WRITE CODE HERE THAT REPRODUCES THE OUTPUT OF THE CELL BELOW
# BE CAREFUL NOT TO RUN THE CELL BELOW, OTHERWISE YOU WON'T
# BE ABLE TO SEE THE OUTPUT ANY MORE
# -
mat[4,:]
# +
# WRITE CODE HERE THAT REPRODUCES THE OUTPUT OF THE CELL BELOW
# BE CAREFUL NOT TO RUN THE CELL BELOW, OTHERWISE YOU WON'T
# BE ABLE TO SEE THE OUTPUT ANY MORE
# -
mat[3:5,:]
# ### Now do the following
# #### Get the sum of all the values in mat
mat.sum()
# #### Get the standard deviation of the values in mat
mat.std()
# #### Get the sum of all the columns in mat
mat.sum(axis=0)
# # Great Job!
|
Udemy/Refactored_Py_DS_ML_Bootcamp-master/02-Python-for-Data-Analysis-NumPy/05-Numpy Exercises - Solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Abstimmungsfaktor Agglomerationen
# ### Vorbereitung und Datenimport
# +
# import libraries
import pandas as pd
import numpy as np
from pyaxis import pyaxis
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import altair as alt
# from datetime import datetime
# import re
# import os
# import json
# import requests
pd.options.display.max_colwidth = 200
# -
# import vote data
Abstimmungsresultate_URL = 'https://www.bfs.admin.ch/bfsstatic/dam/assets/12567434/master'
px = pyaxis.parse(Abstimmungsresultate_URL, encoding='ISO-8859-2')
# import settlement types
agglomerationen = pd.read_excel("input/Raumgliederungen.xlsx", skiprows=1)[1:]
# import additional information for municipalities
kennzahlen = pd.read_excel("input/je-d-21.03.01.xlsx", skiprows=5)[3:2205]
kennzahlen.Gemeindecode = kennzahlen.Gemeindecode.astype(int)
# Vorlagen, die am Ständemehr gescheitert sind
staendemehr = ['2013-03-03 Bundesbeschluss über die Familienpolitik',
'1994-06-12 Bundesbeschluss über einen Kulturförderungsartikel in der Bundesverfassung (Art. 27septies BV)',
'1994-06-12 Bundesbeschluss über die Revision der Bürgerrechtsregelung in der Bundesverfassung (Erleichterte Einbürgerung für junge Ausländer)',
'1983-02-27 Bundesbeschluss über den Energieartikel in der Bundesverfassung']
# ---
# ### Daten aufbereiten
# extract relevant data
data = px['DATA'].set_index(["Datum und Vorlage", "Kanton (-) / Bezirk (>>) / Gemeinde (......)", "Ergebnis"]).unstack(level=-1).reset_index()
data.columns = ['Datum und Vorlage', 'Regionsbezeichnung', 'Abgegebene Stimmen', 'Beteiligung in %', 'Gültige Stimmzettel', 'Ja','Ja in %', 'Nein','Stimmberechtigte']
data = data.replace('"..."', np.nan)
lookup_table = pd.DataFrame.from_dict({"code": px['METADATA']['CODES(Kanton (-) / Bezirk (>>) / Gemeinde (......))'], "description" : px['METADATA']['VALUES(Kanton (-) / Bezirk (>>) / Gemeinde (......))']})
data['Code'] = data['Regionsbezeichnung'].map(lookup_table.set_index('description').code)
# subset municipal and national data
data_gdes = data[(data.Code.str.len() == 4)]
data_ch = data[data['Regionsbezeichnung'] == 'Schweiz']
# merge settlement types
data_gdes.Code = data_gdes.Code.astype(int)
agglomerationen['BFS Gde-nummer'] = agglomerationen['BFS Gde-nummer'].astype(int)
data_gdes = data_gdes.merge(agglomerationen, left_on="Code", right_on="BFS Gde-nummer", how="left")
data_gdes = data_gdes[~pd.isnull(data_gdes['BFS Gde-nummer'])]
# extract date
data_gdes['Datum'] = pd.to_datetime(data_gdes['Datum und Vorlage'].str[0:10])
data_gdes_valid = data_gdes[data_gdes.Datum > "1981-04-05"]
# fix data types
data_gdes_valid['Ja'] = data_gdes_valid['Ja'].astype(float)
data_gdes_valid['Nein'] = data_gdes_valid['Nein'].astype(float)
data_gdes_valid['Stimmberechtigte'] = data_gdes_valid['Stimmberechtigte'].astype(float)
# ---
# ### Kodierung der Siedlungstypen
# Agglomerationen:
# - Städtische Arbeitsplatzgemeinde einer grossen Agglomeration (112)
# - Städtische Wohngemeinde einer grossen Agglomeration (113)
# - Städtische Arbeitsplatzgemeinde einer mittelgrossen Agglomeration (122)
# - Städtische Wohngemeinde einer mittelgrossen Agglomeration (123)
#
# Städte
# - Kernstadt einer grossen Agglomeration (111)
# - Kernstadt einer mittelgrossen Agglomeration (121)
#
# Land
# - restliche Gemeinden
#
# https://www.atlas.bfs.admin.ch/maps/13/de/12359_12482_3191_227/20387.html
data_gdes_valid["municipality_type"] = 0
# Agglomerationen als Typ 1 codieren
data_gdes_valid.loc[data_gdes["Gemeindetypologie 2012 (25 Typen)"].astype(int).isin([112, 113, 122, 123]), "municipality_type"] = 1
# Städte als Typ 2 codieren
data_gdes_valid.loc[data_gdes["Gemeindetypologie 2012 (25 Typen)"].astype(int).isin([111, 121]), "municipality_type"] = 2
# ---
# ## Auswertung nach Gemeindetyp
#
# - Agglomeration: municipality_type = 1
# - Städte: municipality_type = 2
# - Land: municipality_type = 0
# ### Gewinnrate der Agglomerationen
# + tags=[]
results_agglos = []
for Vorlage in data_gdes_valid['Datum und Vorlage'].unique():
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 1)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 1)].Nein.astype(float).sum()
results_agglos.append([Vorlage, 100 /(yes + no)*yes])
results_agglos = pd.DataFrame(results_agglos)
# -
results_agglos = results_agglos.merge(data_ch[['Datum und Vorlage', 'Ja in %']], left_on=0, right_on="Datum und Vorlage", how="left")
results_agglos['angenommen_ch'] = results_agglos['Ja in %'].astype(float) > 50
results_agglos['angenommen_agglo'] = results_agglos[1].astype(float) > 50
results_agglos['quota_agglo'] = results_agglos.angenommen_agglo == results_agglos.angenommen_ch
# #### Gewinnrate ohne Ständemehr
# + tags=[]
results_agglos['quota_agglo'].value_counts(normalize=True)
# -
# #### Gewinnrate mit Ständemehr
results_agglos.loc[results_agglos['Datum und Vorlage'].isin(staendemehr), 'angenommen_ch'] = False
results_agglos['quota_agglo'] = results_agglos.angenommen_agglo == results_agglos.angenommen_ch
results_agglos['quota_agglo'].value_counts(normalize=True)
# ### Gewinnrate der Städte
results_cities = []
for Vorlage in data_gdes_valid['Datum und Vorlage'].unique():
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 2)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 2)].Nein.astype(float).sum()
results_cities.append([Vorlage, 100 /(yes + no)*yes])
results_cities = pd.DataFrame(results_cities)
results_cities = results_cities.merge(data_ch[['Datum und Vorlage', 'Ja in %']], left_on=0, right_on="Datum und Vorlage", how="left")
results_cities['angenommen_ch'] = results_cities['Ja in %'].astype(float) > 50
results_cities['angenommen_city'] = results_cities[1].astype(float) > 50
results_cities['quota_city'] = results_cities.angenommen_city == results_cities.angenommen_ch
# #### Gewinnrate ohne Ständemehr
results_cities['quota_city'].value_counts(normalize=True)
results_cities.loc[results_cities['Datum und Vorlage'].isin(staendemehr), 'angenommen_ch'] = False
results_cities['quota_city'] = results_cities.angenommen_city == results_cities.angenommen_ch
# #### Gewinnrate mit Ständemehr
results_cities['quota_city'].value_counts(normalize=True)
# ### Gewinnrate der Landgemeinden
results_rural = []
for Vorlage in data_gdes_valid['Datum und Vorlage'].unique():
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 0)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 0)].Nein.astype(float).sum()
results_rural.append([Vorlage, 100 /(yes + no)*yes])
results_rural = pd.DataFrame(results_rural)
results_rural = results_rural.merge(data_ch[['Datum und Vorlage', 'Ja in %']], left_on=0, right_on="Datum und Vorlage", how="left")
results_rural['angenommen_ch'] = results_rural['Ja in %'].astype(float) > 50
results_rural['angenommen_rural'] = results_rural[1].astype(float) > 50
results_rural['quota_rural'] = results_rural.angenommen_rural== results_rural.angenommen_ch
# +
#### Gewinnrate ohne Ständemehr
# -
results_rural['quota_rural'].value_counts(normalize=True)
results_rural.loc[results_rural['Datum und Vorlage'].isin(staendemehr), 'angenommen_ch'] = False
results_rural['quota_rural'] = results_rural.angenommen_rural == results_rural.angenommen_ch
# +
#### Gewinnrate mit Ständemehr
# -
results_rural['quota_rural'].value_counts(normalize=True)
## Visualize data
bar_data = pd.DataFrame({
'groups': pd.DataFrame(results_rural['quota_rural'].value_counts(normalize=True)).join(pd.DataFrame(results_cities['quota_city'].value_counts(normalize=True))).join(pd.DataFrame(results_agglos['quota_agglo'].value_counts(normalize=True))).columns,
'pct': pd.DataFrame(results_rural['quota_rural'].value_counts(normalize=True)).join(pd.DataFrame(results_cities['quota_city'].value_counts(normalize=True))).join(pd.DataFrame(results_agglos['quota_agglo'].value_counts(normalize=True))).iloc[0,:].values
})
alt.Chart(bar_data, width=650, height=500).mark_bar().encode(
x='groups',
y='pct'
)
# ---
# ### Einwohner nach Gemeindetyp 2018
# merge and subset data
data_einwohner = data_gdes_valid[['Code', 'Gemeindename', 'Kanton', 'municipality_type']].drop_duplicates().merge(kennzahlen[['Gemeindecode', 'Einwohner']], how="left", left_on="Code", right_on="Gemeindecode")
data_einwohner[['municipality_type', 'Einwohner']].groupby('municipality_type').sum()
# ### Wähler nach Jahr und Gemeindetyp
# #### 1981
voters1981 = data_gdes_valid[data_gdes_valid['Datum und Vorlage'] == '1981-06-14 Bundesbeschluss über die Volksinitiative ŤGleiche Rechte für Mann und Frauť'][['municipality_type', 'Ja', 'Nein', 'Stimmberechtigte']].groupby('municipality_type').sum()
voters1981['Stimmende'] = voters1981[['Ja', 'Nein']].sum(axis=1)
voters1981['Stimmende_Anteile'] = 100 / voters1981['Stimmende'].sum() * voters1981['Stimmende']
voters1981['Stimmberechtigte_Anteile'] = 100 / voters1981['Stimmberechtigte'].sum() * voters1981['Stimmberechtigte']
voters1981[['Stimmberechtigte', 'Stimmende', 'Stimmende_Anteile', 'Stimmberechtigte_Anteile']]
# #### 1995
voters1995 = data_gdes_valid[(data_gdes_valid.Datum.dt.year == 1995) & (data_gdes_valid['Datum und Vorlage'] == '1995-03-12 Bundesbeschluss über eine Ausgabenbremse')][['municipality_type', 'Ja', 'Nein', 'Stimmberechtigte']].groupby('municipality_type').sum()
voters1995['Stimmende'] = voters1995[['Ja', 'Nein']].sum(axis=1)
voters1995['Stimmende_Anteile'] = 100 / voters1995['Stimmende'].sum() * voters1995['Stimmende']
voters1995['Stimmberechtigte_Anteile'] = 100 / voters1995['Stimmberechtigte'].sum() * voters1995['Stimmberechtigte']
voters1995[['Stimmberechtigte', 'Stimmende', 'Stimmende_Anteile', 'Stimmberechtigte_Anteile']]
# #### 2020
voters2020 = data_gdes_valid[data_gdes_valid['Datum und Vorlage'] == '2020-02-09 Änderung vom 14. Dezember 2018 des Strafgesetzbuches und des Militärstrafgesetzes (Diskriminierung und Aufruf zu Hass aufgrund der sexuellen Orientierung)'][['municipality_type', 'Ja', 'Nein', 'Stimmberechtigte']].groupby('municipality_type').sum()
voters2020['Stimmende'] = voters2020[['Ja', 'Nein']].sum(axis=1)
voters2020['Stimmende_Anteile'] = 100 / voters2020['Stimmende'].sum() * voters2020['Stimmende']
voters2020['Stimmberechtigte_Anteile'] = 100 / voters2020['Stimmberechtigte'].sum() * voters2020['Stimmberechtigte']
voters2020[['Stimmberechtigte', 'Stimmende', 'Stimmende_Anteile', 'Stimmberechtigte_Anteile']]
# #### Jährlich Durchschnittswerte der Stimmberechtigtenanteile nach Region visualisieren
voters = data_gdes_valid[['Datum und Vorlage', 'municipality_type', 'Ja', 'Nein', 'Stimmberechtigte']].groupby(['Datum und Vorlage', 'municipality_type']).sum().reset_index()
voters['Stimmende'] = voters[['Ja', 'Nein']].sum(axis=1)
voters_berechtigt = voters[['Datum und Vorlage', 'municipality_type', 'Stimmberechtigte']].pivot(index='Datum und Vorlage', columns='municipality_type', values='Stimmberechtigte').reset_index()
voters_berechtigt['Anteil_Land'] = 100 / voters_berechtigt[[0, 1, 2]].sum(axis=1) * voters_berechtigt[0]
voters_berechtigt['Anteil_Agglo'] = 100 / voters_berechtigt[[0, 1, 2]].sum(axis=1) * voters_berechtigt[1]
voters_berechtigt['Anteil_Stadt'] = 100 / voters_berechtigt[[0, 1, 2]].sum(axis=1) * voters_berechtigt[2]
voters_berechtigt['Datum'] = pd.to_datetime(voters_berechtigt['Datum und Vorlage'].str[0:10])
voters_berechtigt['Jahr'] = voters_berechtigt['Datum'].dt.year
alt.Chart(pd.melt(voters_berechtigt[['Jahr', 'Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']].groupby('Jahr').mean().reset_index(), id_vars=['Jahr'], value_vars=['Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']), width=650, height=500, title="Stimmberechtigte nach Region").mark_line().encode(
x='Jahr',
y='value',
color='municipality_type'
)
# #### Jährlich Durchschnittswerte der Wähleranteile nach Region visualisieren
voters_actual = voters[['Datum und Vorlage', 'municipality_type', 'Stimmende']].pivot(index='Datum und Vorlage', columns='municipality_type', values='Stimmende').reset_index()
voters_actual['Anteil_Land'] = 100 / voters_actual[[0, 1, 2]].sum(axis=1) * voters_actual[0]
voters_actual['Anteil_Agglo'] = 100 / voters_actual[[0, 1, 2]].sum(axis=1) * voters_actual[1]
voters_actual['Anteil_Stadt'] = 100 / voters_actual[[0, 1, 2]].sum(axis=1) * voters_actual[2]
voters_actual['Datum'] = pd.to_datetime(voters_actual['Datum und Vorlage'].str[0:10])
voters_actual['Jahr'] = voters_actual['Datum'].dt.year
alt.Chart(pd.melt(voters_actual[['Jahr', 'Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']].groupby('Jahr').mean().reset_index(), id_vars=['Jahr'], value_vars=['Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']), width=650, height=500, title="Stimmbürgeranteile nach Region und Jahr").mark_line().encode(
x='Jahr',
y='value',
color='municipality_type'
)
# #### Werte der Wähleranteile für alle einzelnen Abstimmungen nach Region visualisieren
alt.Chart(pd.melt(voters_actual[['Jahr', 'Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']].reset_index(), id_vars=['index'], value_vars=['Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']), width=650, height=500, title="Stimmbürgeranteile nach Region").mark_line().encode(
x='index',
y='value',
color='municipality_type'
)
# #### Gesamte Stimmbeteiligung für alle einzelnen Abstimmungen visualisieren
voters_beteiligung = voters[['Datum und Vorlage', 'Stimmberechtigte', 'Stimmende']].groupby('Datum und Vorlage').sum().reset_index()
voters_beteiligung['Stimmbeteiligung'] = 100 / voters_beteiligung.Stimmberechtigte * voters_beteiligung.Stimmende
alt.Chart(voters_beteiligung[['Stimmbeteiligung']].reset_index(), width=650, height=500, title="Stimmbeteiligung").mark_line().encode(
x='index',
y='Stimmbeteiligung'
)
# ### Stimmbeteligung nach Abstimmung und Region visualisieren
voters_beteiligung_region = voters[['Datum und Vorlage', 'Stimmberechtigte', 'Stimmende', 'municipality_type']].groupby(['Datum und Vorlage', 'municipality_type']).sum().reset_index()
voters_beteiligung_region['Stimmbeteiligung'] = 100 / voters_beteiligung_region.Stimmberechtigte * voters_beteiligung_region.Stimmende
voters_beteiligung_region.loc[voters_beteiligung_region.municipality_type == 1, "municipality_type"] = 'agglo'
voters_beteiligung_region.loc[voters_beteiligung_region.municipality_type == 2, "municipality_type"] = 'urban'
voters_beteiligung_region.loc[voters_beteiligung_region.municipality_type == 0, "municipality_type"] = 'rural'
alt.Chart(voters_beteiligung_region[['municipality_type', 'Stimmbeteiligung']].reset_index(), width=650, height=500, title="Stimmbeteiligung nach Region").mark_line().encode(
x='index',
y='Stimmbeteiligung',
color='municipality_type',
tooltip='Stimmbeteiligung'
)
# ---
# ## Knappe Abstimmungen ermitteln
data_ch[(data['Ja in %'].astype(float) > 49) & (data['Ja in %'].astype(float) < 51)]
# ### Wie haben die Agglomerationen dabei abgestimmt?
#
# Nur Werte ab 1981 haben Aussagekraft
close_votes = []
for Vorlage in data_ch[(data['Ja in %'].astype(float) > 49) & (data['Ja in %'].astype(float) < 51)]['Datum und Vorlage']:
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 1)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 1)].Nein.astype(float).sum()
close_votes.append([Vorlage, 100 /(yes + no)*yes, data_ch[data_ch['Datum und Vorlage'] == Vorlage]['Ja in %'].values[0]])
pd.DataFrame(close_votes, columns=['Vorlage', 'Resultat Agglos', 'Resultat CH'])
# - 17 knappe (50% (+/- 1 Prozentpunkt)) Abstimmungen seit 1981
# - dabei haben die Agglomerationen in 13 Fällen wie die Schweiz abgestimmt (4 Abweichungen)
# - Abweichungen ausgerechnet bei:
# - 1982: **Ausländergesetz**
# - 1992: **Bundesbeschluss über den Europäischen Wirtschaftsraum (EWR)**
# - 2014: **Volksinitiative Gegen Masseneinwanderung**
# - 2015: Bundesgesetz über Radio und Fernsehen
# ---
# ## In welchen Abstimmungen findet man Abweichungen? (umstrittene Abstimmungen)
# create comparison table
comparison_table = []
for Vorlage in data_gdes_valid['Datum und Vorlage'].unique():
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 1)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 1)].Nein.astype(float).sum()
pct_agglo = 100 /(yes + no)*yes
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 2)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 2)].Nein.astype(float).sum()
pct_city = 100 /(yes + no)*yes
yes = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 0)].Ja.astype(float).sum()
no = data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid.municipality_type == 0)].Nein.astype(float).sum()
pct_rural = 100 /(yes + no)*yes
pct_ch = float(data_ch[data_ch['Datum und Vorlage'] == Vorlage]['Ja in %'].values[0])
comparison_table.append([Vorlage, pct_agglo, pct_city, pct_rural, pct_ch])
comparison_table = pd.DataFrame(comparison_table, columns = ["Vorlage", "pct_agglo", "pct_city", "pct_rural", "pct_ch"])
comparison_table['Datum'] = pd.to_datetime(comparison_table['Vorlage'].str[0:10])
comparison_table['Vorlage'] = comparison_table['Vorlage'].str[11:]
# subset "controversial" votes
comparison_table = comparison_table.query('~(pct_agglo > 50 & pct_city > 50 & pct_rural > 50 & pct_ch > 50) & ~(pct_agglo < 50 & pct_city < 50 & pct_rural < 50 & pct_ch < 50)')
# calculate alliances
comparison_table['alliance'] = np.nan
comparison_table.loc[((comparison_table.pct_agglo > 50) & (comparison_table.pct_city > 50)) | ((comparison_table.pct_agglo < 50) & (comparison_table.pct_city < 50)), 'alliance'] = 'city'
comparison_table.loc[((comparison_table.pct_agglo > 50) & (comparison_table.pct_rural > 50)) | ((comparison_table.pct_agglo < 50) & (comparison_table.pct_rural < 50)), 'alliance'] = 'rural'
# #### Wie oft geht die Agglomeration mit welchen Regionen Allianzen ein?
comparison_table.alliance.value_counts()
# #### Wo finden sich "unheilige" Allienazen?
comparison_table[pd.isnull(comparison_table.alliance)]
# ---
# ### Welche Agglomerations-Gemeinde stimmt am meisten mit der CH?
# (wird nicht in Artikel verwendet)
gde_rank = []
for bfsid in data_gdes_valid[data_gdes_valid.municipality_type == 1]['Code'].unique():
win = 0
loss = 0
for Vorlage in data_gdes_valid['Datum und Vorlage'].unique():
res_ch = float(data_ch[data_ch['Datum und Vorlage'] == Vorlage]['Ja in %'].values[0])
res_gde = float(data_gdes_valid[(data_gdes_valid['Datum und Vorlage'] == Vorlage) & (data_gdes_valid['Code'] == bfsid)]['Ja in %'].values[0])
if (((res_ch - 50 ) * (res_gde - 50)) > 0):
win += 1
else:
loss += 1
gde_name = data_gdes_valid[(data_gdes_valid['Code'] == bfsid)]['Gemeindename'].values[0]
gde_rank.append([gde_name, (100 / (win + loss)) * win])
pd.DataFrame(gde_rank).sort_values(by=1, ascending=False)
# ---
# ## PCA-Analyse
# (wird nicht in Artikel verwendet)
data_pca = data_gdes_valid[['Datum und Vorlage', 'Code', 'Ja in %']].pivot(index="Code", columns="Datum und Vorlage", values='Ja in %')
X_std = StandardScaler().fit_transform(data_pca.dropna())
# Create a PCA instance: pca
pca = PCA(n_components=20)
principalComponents = pca.fit(X_std)
# Plot the explained variances
features = range(pca.n_components_)
bar_data = pd.DataFrame({
'PCA features': features,
'Variance %': pca.explained_variance_ratio_
})
alt.Chart(bar_data, width=650, height=500).mark_bar().encode(
x='PCA features',
y='Variance %'
)
pca = PCA(n_components=2)
pca.fit(X_std)
principalComponents = pca.transform(X_std)
pca_result = pd.DataFrame()
pca_result["comp1"] = principalComponents[:,0]
pca_result["comp2"] = principalComponents[:,1]
pca_result["id"] = data_pca.dropna().index
pca_result = pca_result.merge(data_gdes_valid[['Code', 'Gemeindename', 'Kanton', 'municipality_type']].drop_duplicates(), how='left', left_on='id', right_on='Code')
pca_result.loc[pca_result.municipality_type == 1, "municipality_type"] = 'agglo'
pca_result.loc[pca_result.municipality_type == 2, "municipality_type"] = 'urban'
pca_result.loc[pca_result.municipality_type == 0, "municipality_type"] = 'rural'
# + tags=[]
# load a simple dataset as a pandas DataFrame
alt.Chart(pca_result, width=650, height=500, title="PCA Gemeinden").mark_point().encode(
x='comp1',
y='comp2',
tooltip='Gemeindename',
color='municipality_type'
).interactive()
# -
alt.Chart(pca_result[pca_result.municipality_type == "agglo"], width=650, height=500, title="PCA Agglomerationen").mark_point().encode(
x='comp1',
y='comp2',
tooltip='Gemeindename',
color='Kanton'
).interactive()
# ## Test & Datenüberprüfung
# #### Fallen einzelne Gemeinden aus dem Raster? (ok)
list1 = data_gdes['Code'].unique().astype(int).tolist()
list2 = agglomerationen['BFS Gde-nummer'].unique().astype(int).tolist()
missing_gdes = (list(list(set(list1)-set(list2)) + list(set(list2)-set(list1))))
data_gdes[data_gdes['Code'].isin(missing_gdes)].Regionsbezeichnung.unique()
# #### Ist die Summe der Gemeinde resultate identisch zur CH-Resultat? (für knappe Abstimmungen) (ok)
calc_check = []
for Vorlage in data_ch[(data['Ja in %'].astype(float) > 49) & (data['Ja in %'].astype(float) < 51)]['Datum und Vorlage']:
yes = data[(data['Datum und Vorlage'] == Vorlage) & (data.Code.str.len() == 4)].Ja.astype(float).sum()
no = data[(data['Datum und Vorlage'] == Vorlage) & (data.Code.str.len() == 4)].Nein.astype(float).sum()
calc_check.append([Vorlage, 100 /(yes + no)*yes, data_ch[data_ch['Datum und Vorlage'] == Vorlage]['Ja in %'].values[0]])
calc_check = pd.DataFrame(calc_check)
# + tags=[]
calc_check
# -
# #### Blick in ausgewälte Abstimmungen
results_agglos[results_agglos[0].str.contains("Waffenrichtlinie")]
results_agglos[results_agglos[0].str.contains("Durchsetzungs")]
# ---
# ## Daten für Visualisierung exportieren
comparison_table.to_excel('output/allianzen.xlsx', index=False)
voters_actual[['Jahr', 'Anteil_Agglo', 'Anteil_Land', 'Anteil_Stadt']].groupby('Jahr').mean().reset_index().to_csv("output/waehleranteile.csv", index=False)
# +
data_map = data_gdes_valid[['Code', 'Gemeindename', 'Kanton', 'municipality_type']].drop_duplicates()
data_map['Gemeindename'] = data_map['Gemeindename'].apply(lambda x: x if "(" not in x else x[0:x.find("(")-1])
data_map.loc[data_map.municipality_type == 1, "municipality_type"] = 'Agglomeration'
data_map.loc[data_map.municipality_type == 2, "municipality_type"] = 'Stadt'
data_map.loc[data_map.municipality_type == 0, "municipality_type"] = 'Land'
data_map.to_csv("output/municipality_map.csv", index=False)
# -
# ---
# ### Notebook als HTML exportieren
# + tags=[]
alt.renderers.enable('html')
# !jupyter nbconvert abstimmungsfaktor_agglomerationen.ipynb
# -
|
abstimmungsfaktor_agglomerationen.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import itertools
import matplotlib.pyplot as plt
import matplotlib as mpl
import pymc3 as pm
from theano import as_op
import theano.tensor as tt
import numpy as np
from scipy import stats
import tqdm
import pandas as pd
from scipy import stats
import seaborn as sns
import DeadTime
sns.set(font_scale=1.6)
# %matplotlib inline
# %load_ext version_information
# %version_information pymc3, scipy
# -
DT = DeadTime.TimeStamps(size=1000000)
DT.apply_nonpar_deadtime(1e-1)
TS = DeadTime.TimeSeries(DT)
fig, ax = plt.subplots(1,1, figsize=(8,4))
sns.distplot(TS.timeseries, 15, label=('Deadtime 1e-1'));
XX = np.arange(60, 151)
plt.plot(XX, stats.poisson(100).pmf(XX), 'r', label='Poisson 100')
plt.legend()
plt.xlabel('Reported rate')
kde = stats.gaussian_kde(TS.timeseries)
# plt.plot(XX, kde.evaluate(XX), 'g')
def dist_from_hist(param, kde, xlim=(50,150), N=100):
width = xlim[1] - xlim[0]
x = np.linspace(xlim[0], xlim[1], N)
y = kde.evaluate(x)
# what was never sampled should have a small probability but not 0,
# so we'll extend the domain and use linear approximation of density on it
x = np.concatenate([[x[0] - 3 * width], x, [x[-1] + 3 * width]])
y = np.concatenate([[0], y, [0]])
return pm.distributions.Interpolated(param, x, y)
with pm.Model() as model:
# Priors are posteriors from previous iteration
dat = dist_from_hist('dat', kde)
# draw 10000 posterior samples
trace = pm.sample(10000)
pm.traceplot(trace)
pm.traceplot(trace, combined=True)
# +
fig, ax = plt.subplots(1,1, figsize=(8,4))
sns.distplot(TS.timeseries, 15, label=('Deadtime 1e-1'));
XX = np.arange(60, 151)
plt.plot(XX, stats.poisson(100).pmf(XX), 'r', label='Poisson 100')
plt.xlabel('Reported rate')
kde = stats.gaussian_kde(TS.timeseries)
sns.distplot(trace['dat'], 15, label='mcmc')
plt.legend()
# -
|
Counting/Dead Time Empirical.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Review test
#
# ## Review exercise 1
# menti.com 52 00 21
# ## Review exercise 2
# menti.com 74 95 17
# ## Review exercise 3
def squared(x):
return x**2
# Write a function
# ```python
# derivative(x, h, f)
# ```
# which calculates the first numerical derivative of an arbitrary function $f(x)$. Use the formula $\frac{f(x + h) -f(x - h)}{2 h}$.
#
# Note: in Python you can pass a function as an argument of another function!
#
#
# Test it using parameters $x = 4$, $h = 0.0001$ and the function
# ```
# squared
# ```
# defined above.
# # Lecture 3 - continuing the introduction to Python
# ## Data types in Python
type(1)
type(1.1)
type(1 + 2j)
type(True)
type("Hello World")
a = 1
type(a)
b = 1.1
type(b)
c = a + b
# What is the type of c?
type(c)
d = 2
type(d)
e = a + d
# What is the type of e?
type(e)
f = a / d
# _Warning: Python 2 behaves differently here, but Python 2 is not relevant anylonger (unsupported since 1.1.2020)._
# What is the type of f?
type(f)
# #### Hints
#
# ##### Integer overflows
# Integer variables cannot overflow in Python, i.e. you can have an arbitrarily high Integer number. This is different to other programming languages such as C, where the size of an Integer number is fixed. If you do not know, what any of this means, it will be explained later when talking about numpy as numpy integers can overflow.
# ##### Floating point precision
#
# Floating point numbers have limited precision (53 bits or 16 digits). A number can become arbitrarily high, but it has limited precisions. This is due to how internally, floating points are stored in memory. More details on [wikipedia](https://en.wikipedia.org/wiki/Floating-point_arithmetic) and a tutorial can be found [here](http://cstl-csm.semo.edu/xzhang/Class%20Folder/CS280/Workbook_HTML/FLOATING_tut.htm)
#
# 
# Attribution: Joeleoj123 / CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0)
# Why is this relevant?
# +
a_large_number = 10**12 + 0.1
a_large_number
# +
a_small_number = 0.0000001
many_times = 10000000
for i in range(0, many_times):
a_large_number = a_large_number + a_small_number
a_large_number
# +
a_large_number = a_large_number + often * a_small_number
a_large_number
# -
# Whaaaaaaaaat?
#
# Well - limited precisions.
# ```python
# a_large_number + a_small_number
# ```
#
# is, due to limited precision, calculated to be
# ```python
# a_large_number + a_small_number
# ```
#
# ### String operations
# String is text. A new string is simply started by enclosing text in "
'This is a string'
# Double quotes " and single quotes ' are equivalent Python, there is no syntactic difference. [A very popular convention](https://stackoverflow.com/a/56190/859591) is to use single quotes for constants and double quotes for human readable text or sentances. A different popular convention is to use only [only double quotes](https://black.readthedocs.io/en/stable/the_black_code_style.html#strings).
# +
x = 7
f'The value of x is {x}'
# +
import math
y = 6.589309493
f'The value of y is {round(y)}'
# +
a_lot_of_text = (
'line1'
'line2'
'line3')
a_lot_of_text
# -
# But...
# +
a_lot_of_text = """
line1
line2
line3"""
a_lot_of_text
# -
# Why is there a \n?
# #### Exercise 1
#
# Write code which shows the following text 'PI is <...>'. Substitute <...> by the value of PI. Hint:
# ```Python
# math.pi
# ```
# returns pi
import math
f'PI is {math.pi}'
# ## Multiple assignments and return values
a, b = 1, 2
a
b
# #### Functions with multiple return values
#
# +
import math
def calculate_growth_doubling_time(value_t1, value_t2, time_diff):
growth_rate = (value_t2 / value_t1)**(1 / time_diff) - 1
doubling_time = math.log(2) / math.log(growth_rate + 1)
return growth_rate, doubling_time
# +
growth_rate, doubling_time = calculate_growth_doubling_time(1, 1.2, 1)
print(growth_rate)
print(doubling_time)
# -
# #### Exercise 2
#
# Write a function that calculates the growth_rate, the doubling time, and the relative growth_rate given by $\frac{\textrm{value_t2} - \textrm{value_t1}}{\textrm{value_t1}}$. Use the upper function calculate_growth_doubling_time for that purpose. Return all three values. The function should be called
#
# ```python
# growth_parameters(value_t1, value_t2, time_diff)
# ```
# ## Some basic data structures in Python
# ### Lists
#
l = [1, 2, 3]
l
l[1]
# Important: different to R, an index in Python starts with 0, not with 1. So the first element of a list is 0!
l[0]
# What will happen here?
l[3]
l[0:2]
l = [1, 2, 3, 4, 5, 6]
l[1:5]
len(l)
l[-1]
# #### Exercise 3
#
# Write a function named
# ```python
# list_info(l)
# ```
# that takes a list and returns the length of the list, the first element and the last element. Test the code with the list
#
# ```python
# [7, 14, 21, 43]
# ```
#
#
# #### Operators on lists
[1, 2] * 2
[1, 2] + [2]
[1, 2] + 2
# ## Control structures: loops
#
# Loops allow to repeat things. We will see that they become obsolete in many cases, when working with the scientific packages in Python (such as numpy), but we still introduce them.
for x in range(3):
print(x)
for x in range(17, 19):
print(x)
# What will happen here?
for x in range(19, 17):
print(x)
# +
l = [1, 2, 3]
for v in l:
print(v)
# -
# other programing languages do it like this, in Python you never need this!
for k in range(0, len(l)):
print(l[k])
# #### Pro: this may become important - if you do not understand it now, don't worry.
#
# Lists are passed by reference - whatever you do to a list in function, will also affect the list outside of the function. Watch!
def change_list(l):
l1 = l
l1[0] = 43
return l1
l = [1, 2, 3]
result = change_list(l)
print(l)
print(result)
def do_not_change_list(l):
l1 = l.copy()
l1[0] = 43
return l1
l = [1, 2, 3]
result = do_not_change_list(l)
print(l)
print(result)
# ### List comprehensions
#
# To work with lists and for loops is not very Pythonic. In many cases list comprehensions are much more convenient:
# +
l = [1, 10, 100]
# Take log10 of all list elements:
[math.log(i, 10) for i in l]
# -
# #### Exercise 4
#
# Write a function
#
# ```python
# log10_list(l)
# ```
#
# which calculates the logarithmus with basis 10 of all elements in that list and returns the resulting list. Test it on the list
#
# ```python
# l = [1, 10, 100, 1000]
# ```
#
# Print
#
# ```python
# l
# ```
#
# before and after calling your function.
# ## Reading data
#
# We will read data from disk. This is just to make things more interesting. Do not worry about the details now.
# +
import csv
with open('austria_covid_19_data.csv', 'r') as read_obj:
# pass the file object to reader() to get the reader object
csv_reader = csv.reader(read_obj)
# Pass reader object to list() to get a list of lists
list_of_rows = list(csv_reader)
list_of_rows
# +
### get second column
infected_cases = [i[1] for i in list_of_rows]
infected_cases
# +
### remove first line, as it contains header
infected_cases = infected_cases[1:]
infected_cases
# +
### convert to integer, as it is string
infected_cases = [int(i) for i in infected_cases]
infected_cases
# -
# ## Plotting data with matplotlib
# +
import math
import matplotlib.pyplot as plt
plt.plot(infected_cases, label = 'infections')
plt.plot([math.log(i, 10) for i in infected_cases], label = 'log(infections)')
plt.plot([infected_cases[0] * 1.28**i for i in range(len(infected_cases))], label = 'exponential with growth rate 28%')
plt.xlabel('Time')
plt.ylabel('Infections')
plt.title('Infections')
plt.legend()
plt.show()
# +
import matplotlib.pyplot as plt
import math
plt.plot([math.log(i, 10) for i in infected_cases], label = 'log(infections)')
plt.xlabel('Time')
plt.ylabel('log(infections)')
plt.title('Log(infections)')
plt.legend()
plt.show()
# -
# #### Exercise 5
#
# Calculate the daily growth rate for all time steps and the doubling time for all time steps and plot both in one extra figure, i.e. one figure showing the growth rate, the other one showing the doubling time. For that purpose you can use the function
#
# ```
# calculate_growth_doubling_time(value_t1, value_t2, time_diff)
# ```
#
# defined above.
#
# Note: A very Pythonic way to achieve this involes zusing `zip()` and parameter unpacking using `*`. This a bit beyond scope of this excercise, a non-Pythonic way is perfectly fine for now.
# #### Exercise 6
#
# Write a function which calculates the growth rate and doubling time for all time steps, i.e. similar to the code in Exercise 5. The function is defined as
#
# ```
# growth_rate_doubling_time(l, interval)
# ```
#
# Interval defines how many days are between the start and the end value (i.e. value_t1 and value_t2 in calculate_growth_doubling_time). Test the function by applying it to the infection data with an interval time of 7 and plotting the growth rate and the doubling time.
#
#
|
lecture03-python-introduction/lecture03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
data = pd.read_csv("BIPMetadata.csv")
created = data["created"]
updated = data["updated"]
updated[500]
def format_date(date_column):
new_dates = []
for date in date_column:
month = date[0:date.find('/')]
date = date[date.find('/')+1:]
day = date[0:date.find('/')]
year = date[date.find('/')+1:]
if (len(month) == 1):
month = "0" + month
if (len(day) == 1):
day = "0" + day
newDate = year + "-" + month + "-" + day
new_dates.append(newDate)
return new_dates
new_created = format_date(created)
new_updated = format_date(updated)
new_query = []
for query in data["sql_query"]:
if (len(query) > 5000):
query = query[0:5000]
new_query.append(query)
new_d = []
for d in data.description:
if (len(d) > 200):
d = d[0:200]
new_d.append(d)
data["updated"] = new_updated
data["created"] = new_created
data["sql_query"] = new_query
data["description"] = new_d
data
data.to_csv("BIPMetadata_cleaned.csv")
|
server/db/Data/.ipynb_checkpoints/BIPMetadata_Cleaner-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### Introduction
# [Jupyter](http://jupyter.org/) has a beautiful notebook that lets you write and execute code, analyze data, embed content, and share reproducible work. Jupyter Notebook (previously referred to as IPython Notebook) allows you to easily share your code, data, plots, and explanation in a sinle notebook. Publishing is flexible: PDF, HTML, ipynb, dashboards, slides, and more. Code cells are based on an input and output format. For example:
print "hello world"
# #### Installation
# There are a few ways to use a Jupyter Notebook:
#
# * Install with [```pip```](https://pypi.python.org/pypi/pip). Open a terminal and type: ```$ pip install jupyter```.
# * Windows users can install with [```setuptools```](http://ipython.org/ipython-doc/2/install/install.html#windows).
# * [Anaconda](https://store.continuum.io/cshop/anaconda/) and [Enthought](https://store.enthought.com/downloads/#default) allow you to download a desktop version of Jupyter Notebook.
# * [nteract](https://nteract.io/) allows users to work in a notebook enviornment via a desktop application.
# * [Microsoft Azure](https://notebooks.azure.com/) provides hosted access to Jupyter Notebooks.
# * [Domino Data Lab](http://support.dominodatalab.com/hc/en-us/articles/204856585-Jupyter-Notebooks) offers web-based Notebooks.
# * [tmpnb](https://github.com/jupyter/tmpnb) launches a temporary online Notebook for individual users.
# #### Getting Started
# Once you've installed the Notebook, you start from your terminal by calling ```$ jupyter notebook```. This will open a browser on a [localhost](https://en.wikipedia.org/wiki/Localhost) to the URL of your Notebooks, by default http://127.0.0.1:8888. Windows users need to open up their Command Prompt. You'll see a dashboard with all your Notebooks. You can launch your Notebooks from there. The Notebook has the advantage of looking the same when you're coding and publishing. You just have all the options to move code, run cells, change kernels, and [use Markdown](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet) when you're running a NB.
# #### Helpful Commands
# **- Tab Completion:** Jupyter supports tab completion! You can type ```object_name.<TAB>``` to view an object’s attributes. For tips on cell magics, running Notebooks, and exploring objects, check out the [Jupyter docs](https://ipython.org/ipython-doc/dev/interactive/tutorial.html#introducing-ipython).
# <br>**- Help:** provides an introduction and overview of features.
help
# **- Quick Reference:** open quick reference by running:
quickref
# **- Keyboard Shortcuts:** ```Shift-Enter``` will run a cell, ```Ctrl-Enter``` will run a cell in-place, ```Alt-Enter``` will run a cell and insert another below. See more shortcuts [here](https://ipython.org/ipython-doc/1/interactive/notebook.html#keyboard-shortcuts).
# #### Languages
# The bulk of this tutorial discusses executing python code in Jupyter notebooks. You can also use Jupyter notebooks to execute R code. Skip down to the [R section] for more information on using IRkernel with Jupyter notebooks and graphing examples.
# #### Package Management
# When installing packages in Jupyter, you either need to install the package in your actual shell, or run the ```!``` prefix, e.g.:
#
# # !pip install packagename
#
# You may want to [reload submodules](http://stackoverflow.com/questions/5364050/reloading-submodules-in-ipython) if you've edited the code in one. IPython comes with automatic reloading magic. You can reload all changed modules before executing a new line.
#
# # %load_ext autoreload
# # %autoreload 2
# Some useful packages that we'll use in this tutorial include:
# * [Pandas](https://plot.ly/pandas/): import data via a url and create a dataframe to easily handle data for analysis and graphing. See examples of using Pandas here: https://plot.ly/pandas/.
# * [NumPy](https://plot.ly/numpy/): a package for scientific computing with tools for algebra, random number generation, integrating with databases, and managing data. See examples of using NumPy here: https://plot.ly/numpy/.
# * [SciPy](http://www.scipy.org/): a Python-based ecosystem of packages for math, science, and engineering.
# * [Plotly](https://plot.ly/python/getting-started): a graphing library for making interactive, publication-quality graphs. See examples of statistic, scientific, 3D charts, and more here: https://plot.ly/python.
import pandas as pd
import numpy as np
import scipy as sp
import plotly.plotly as py
# #### Import Data
# You can use pandas `read_csv()` function to import data. In the example below, we import a csv [hosted on github](https://github.com/plotly/datasets/) and display it in a [table using Plotly](https://plot.ly/python/table/):
# +
import plotly.plotly as py
import plotly.figure_factory as ff
import pandas as pd
df = pd.read_csv("https://raw.githubusercontent.com/plotly/datasets/master/school_earnings.csv")
table = ff.create_table(df)
py.iplot(table, filename='jupyter-table1')
# -
# Use `dataframe.column_title` to index the dataframe:
schools = df.School
schools[0]
# Most pandas functions also work on an entire dataframe. For example, calling ```std()``` calculates the standard deviation for each column.
df.std()
# #### Plotting Inline
# You can use [Plotly's python API](https://plot.ly/python) to plot inside your Jupyter Notebook by calling ```plotly.plotly.iplot()``` or ```plotly.offline.iplot()``` if working offline. Plotting in the notebook gives you the advantage of keeping your data analysis and plots in one place. Now we can do a bit of interactive plotting. Head to the [Plotly getting started](https://plot.ly/python/) page to learn how to set your credentials. Calling the plot with ```iplot``` automaticallly generates an interactive version of the plot inside the Notebook in an iframe. See below:
# +
import plotly.plotly as py
import plotly.graph_objs as go
data = [go.Bar(x=df.School,
y=df.Gap)]
py.iplot(data, filename='jupyter-basic_bar')
# -
# Plotting multiple traces and styling the chart with custom colors and titles is simple with Plotly syntax. Additionally, you can control the privacy with [```sharing```](https://plot.ly/python/privacy/) set to ```public```, ```private```, or ```secret```.
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace_women = go.Bar(x=df.School,
y=df.Women,
name='Women',
marker=dict(color='#ffcdd2'))
trace_men = go.Bar(x=df.School,
y=df.Men,
name='Men',
marker=dict(color='#A2D5F2'))
trace_gap = go.Bar(x=df.School,
y=df.Gap,
name='Gap',
marker=dict(color='#59606D'))
data = [trace_women, trace_men, trace_gap]
layout = go.Layout(title="Average Earnings for Graduates",
xaxis=dict(title='School'),
yaxis=dict(title='Salary (in thousands)'))
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, sharing='private', filename='jupyter-styled_bar')
# -
# Now we have interactive charts displayed in our notebook. Hover on the chart to see the values for each bar, click and drag to zoom into a specific section or click on the legend to hide/show a trace.
# #### Plotting Interactive Maps
# Plotly is now integrated with [Mapbox](https://www.mapbox.com/). In this example we'll plot lattitude and longitude data of nuclear waste sites. To plot on Mapbox maps with Plotly you'll need a Mapbox account and a [Mapbox Access Token](https://www.mapbox.com/studio/signin/) which you can add to your [Plotly settings]().
# +
import plotly.plotly as py
import plotly.graph_objs as go
import pandas as pd
# mapbox_access_token = 'ADD YOUR TOKEN HERE'
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/Nuclear%20Waste%20Sites%20on%20American%20Campuses.csv')
site_lat = df.lat
site_lon = df.lon
locations_name = df.text
data = [
go.Scattermapbox(
lat=site_lat,
lon=site_lon,
mode='markers',
marker=dict(
size=17,
color='rgb(255, 0, 0)',
opacity=0.7
),
text=locations_name,
hoverinfo='text'
),
go.Scattermapbox(
lat=site_lat,
lon=site_lon,
mode='markers',
marker=dict(
size=8,
color='rgb(242, 177, 172)',
opacity=0.7
),
hoverinfo='none'
)]
layout = go.Layout(
title='Nuclear Waste Sites on Campus',
autosize=True,
hovermode='closest',
showlegend=False,
mapbox=dict(
accesstoken=mapbox_access_token,
bearing=0,
center=dict(
lat=38,
lon=-94
),
pitch=0,
zoom=3,
style='light'
),
)
fig = dict(data=data, layout=layout)
py.iplot(fig, filename='jupyter-Nuclear Waste Sites on American Campuses')
# -
# #### 3D Plotting
# Using Numpy and Plotly, we can make interactive [3D plots](https://plot.ly/python/#3d) in the Notebook as well.
# +
import plotly.plotly as py
import plotly.graph_objs as go
import numpy as np
s = np.linspace(0, 2 * np.pi, 240)
t = np.linspace(0, np.pi, 240)
tGrid, sGrid = np.meshgrid(s, t)
r = 2 + np.sin(7 * sGrid + 5 * tGrid) # r = 2 + sin(7s+5t)
x = r * np.cos(sGrid) * np.sin(tGrid) # x = r*cos(s)*sin(t)
y = r * np.sin(sGrid) * np.sin(tGrid) # y = r*sin(s)*sin(t)
z = r * np.cos(tGrid) # z = r*cos(t)
surface = go.Surface(x=x, y=y, z=z)
data = [surface]
layout = go.Layout(
title='Parametric Plot',
scene=dict(
xaxis=dict(
gridcolor='rgb(255, 255, 255)',
zerolinecolor='rgb(255, 255, 255)',
showbackground=True,
backgroundcolor='rgb(230, 230,230)'
),
yaxis=dict(
gridcolor='rgb(255, 255, 255)',
zerolinecolor='rgb(255, 255, 255)',
showbackground=True,
backgroundcolor='rgb(230, 230,230)'
),
zaxis=dict(
gridcolor='rgb(255, 255, 255)',
zerolinecolor='rgb(255, 255, 255)',
showbackground=True,
backgroundcolor='rgb(230, 230,230)'
)
)
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='jupyter-parametric_plot')
# -
# #### Animated Plots
# Checkout Plotly's [animation documentation](https://plot.ly/python/#animations) to see how to create animated plots inline in Jupyter notebooks like the Gapminder plot displayed below:
# 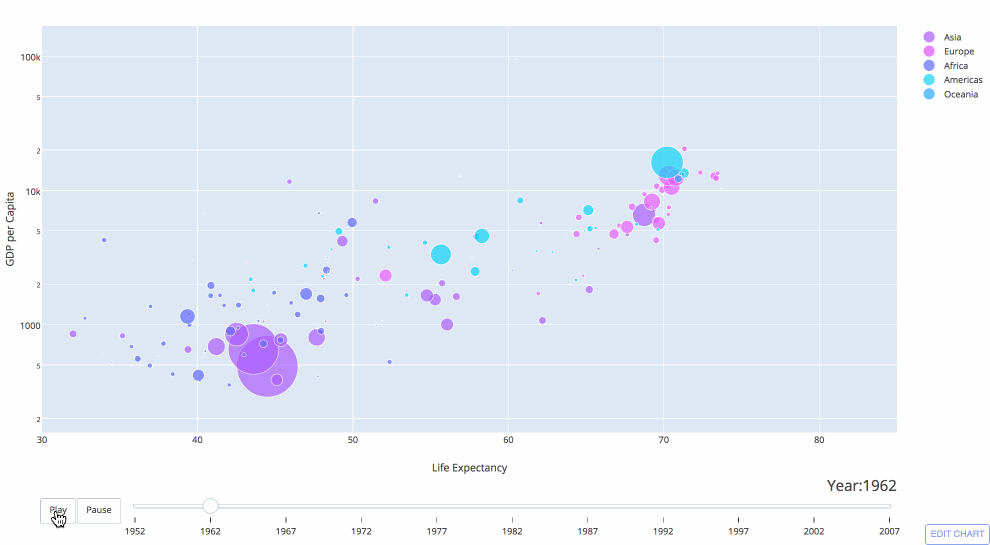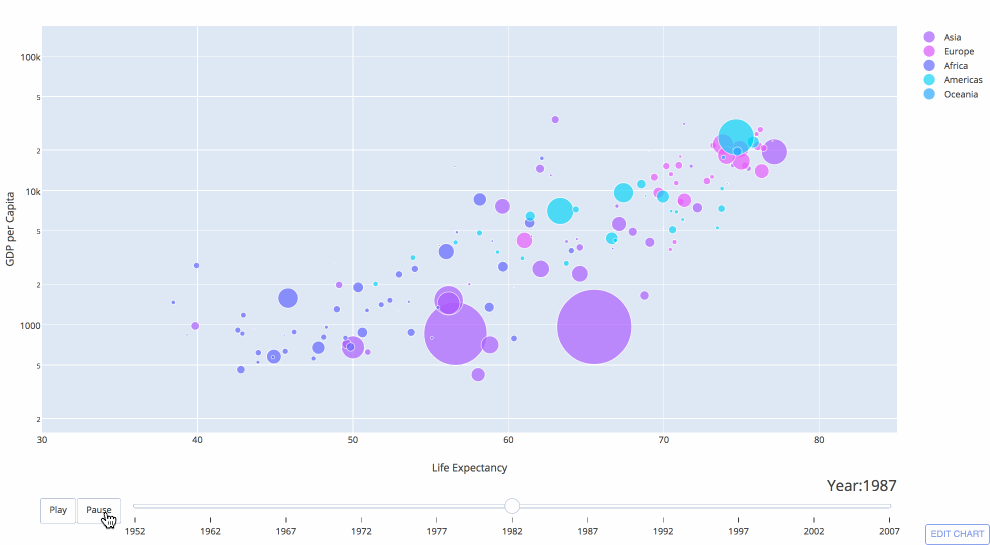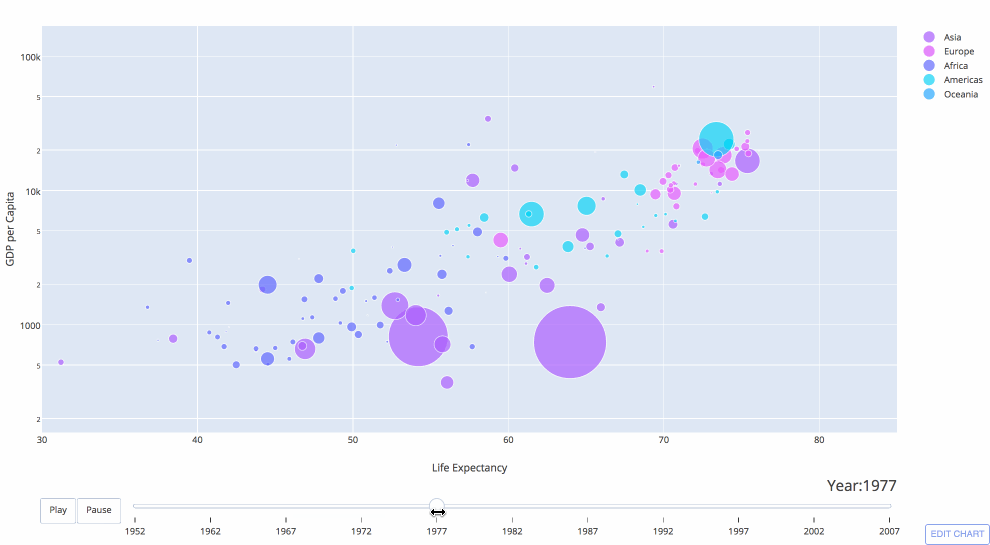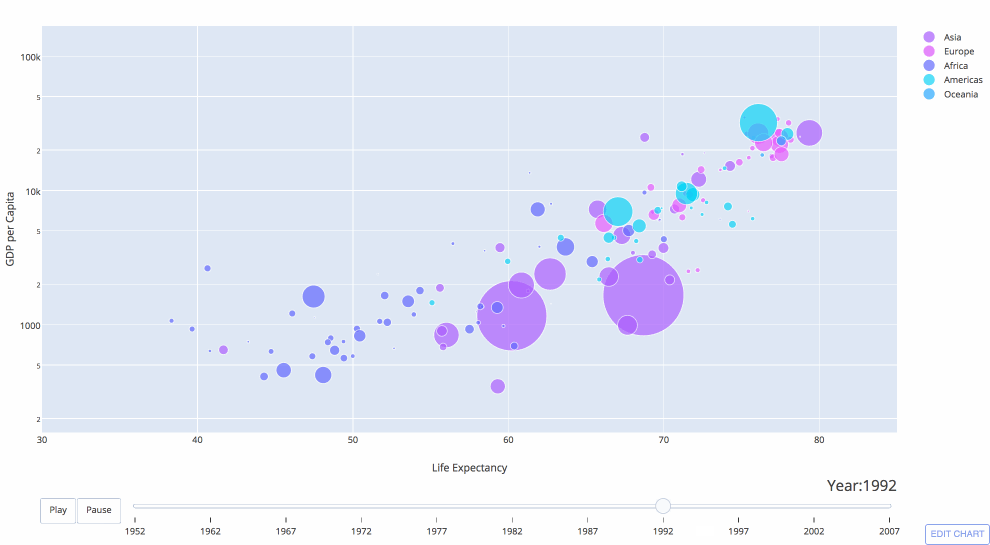
# #### Plot Controls & IPython widgets
# Add sliders, buttons, and dropdowns to your inline chart:
# +
import plotly.plotly as py
import numpy as np
data = [dict(
visible = False,
line=dict(color='00CED1', width=6),
name = '𝜈 = '+str(step),
x = np.arange(0,10,0.01),
y = np.sin(step*np.arange(0,10,0.01))) for step in np.arange(0,5,0.1)]
data[10]['visible'] = True
steps = []
for i in range(len(data)):
step = dict(
method = 'restyle',
args = ['visible', [False] * len(data)],
)
step['args'][1][i] = True # Toggle i'th trace to "visible"
steps.append(step)
sliders = [dict(
active = 10,
currentvalue = {"prefix": "Frequency: "},
pad = {"t": 50},
steps = steps
)]
layout = dict(sliders=sliders)
fig = dict(data=data, layout=layout)
py.iplot(fig, filename='Sine Wave Slider')
# -
# Additionally, [IPython widgets](http://moderndata.plot.ly/widgets-in-ipython-notebook-and-plotly/) allow you to add sliders, widgets, search boxes, and more to your Notebook. See the [widget docs](https://ipython.org/ipython-doc/3/api/generated/IPython.html.widgets.interaction.html) for more information. For others to be able to access your work, they'll need IPython. Or, you can use a cloud-based NB option so others can run your work.
# <br>
# <img src="http://moderndata.plot.ly/wp-content/uploads/2015/01/best_gif_ever.gif"/>
# #### Executing R Code
# IRkernel, an R kernel for Jupyter, allows you to write and execute R code in a Jupyter notebook. Checkout the [IRkernel documentation](https://irkernel.github.io/installation/) for some simple installation instructions. Once IRkernel is installed, open a Jupyter Notebook by calling `$ jupyter notebook` and use the New dropdown to select an R notebook.
#
# 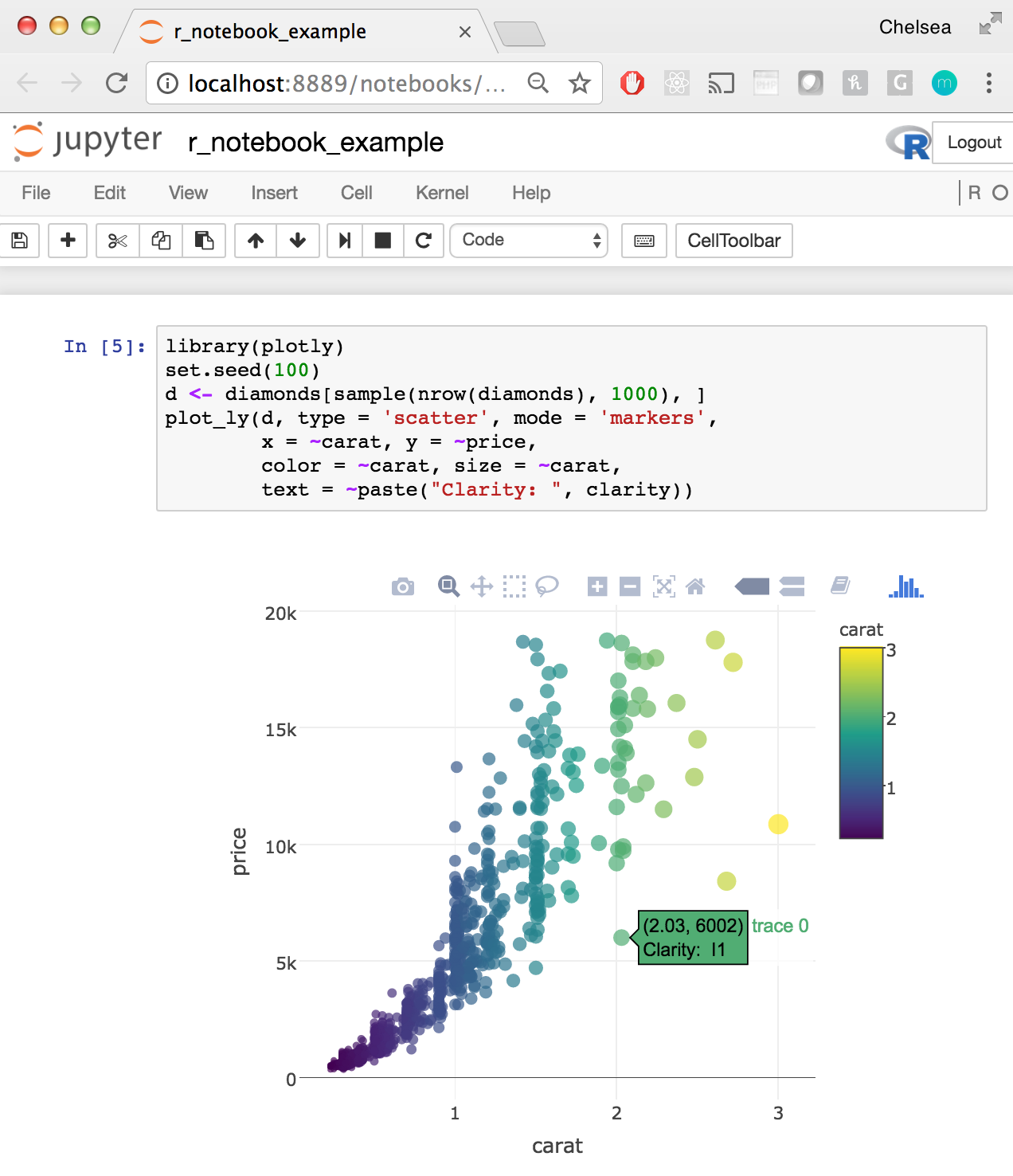
#
# See a full R example Jupyter Notebook here: https://plot.ly/~chelsea_lyn/14069
# #### Additional Embed Features
# We've seen how to embed Plotly tables and charts as iframes in the notebook, with `IPython.display` we can embed additional features, such a videos. For example, from YouTube:
from IPython.display import YouTubeVideo
YouTubeVideo("wupToqz1e2g")
# #### LaTeX
# We can embed LaTeX inside a Notebook by putting a ```$$``` around our math, then run the cell as a Markdown cell. For example, the cell below is ```$$c = \sqrt{a^2 + b^2}$$```, but the Notebook renders the expression.
# $$c = \sqrt{a^2 + b^2}$$
# Or, you can display output from Python, as seen [here](http://stackoverflow.com/questions/13208286/how-to-write-latex-in-ipython-notebook).
# +
from IPython.display import display, Math, Latex
display(Math(r'F(k) = \int_{-\infty}^{\infty} f(x) e^{2\pi i k} dx'))
# -
# #### Exporting & Publishing Notebooks
# We can export the Notebook as an HTML, PDF, .py, .ipynb, Markdown, and reST file. You can also turn your NB [into a slideshow](http://ipython.org/ipython-doc/2/notebook/nbconvert.html). You can publish Jupyter Notebooks on Plotly. Simply visit [plot.ly](https://plot.ly/organize/home?create=notebook) and select the `+ Create` button in the upper right hand corner. Select Notebook and upload your Jupyter notebook (.ipynb) file!
# The notebooks that you upload will be stored in your [Plotly organize folder](https://plot.ly/organize) and hosted at a unique link to make sharing quick and easy.
# See some example notebooks:
# - https://plot.ly/~chelsea_lyn/14066
# - https://plot.ly/~notebook_demo/35
# - https://plot.ly/~notebook_demo/85
# - https://plot.ly/~notebook_demo/128
# #### Publishing Dashboards
# Users publishing interactive graphs can also use [Plotly's dashboarding tool](https://plot.ly/dashboard/create) to arrange plots with a drag and drop interface. These dashboards can be published, embedded, and shared. <img src="http://i.imgur.com/hz0eNpH.png" />
# ### Publishing Dash Apps
# For users looking to ship and productionize Python apps, [dash](https://github.com/plotly/dash) is an assemblage of Flask, Socketio, Jinja, Plotly and boiler plate CSS and JS for easily creating data visualization web-apps with your Python data analysis backend.
# <br>
# <img src="https://camo.githubusercontent.com/a38f9ed71170e3112dd3e4af1d11d4b081fe2e25/687474703a2f2f692e696d6775722e636f6d2f643379346e776d2e676966"/>
# <br>
# ### Jupyter Gallery
# For more Jupyter tutorials, checkout [Plotly's python documentation](https://plot.ly/python/): all documentation is written in jupyter notebooks that you can download and run yourself or checkout these [user submitted examples](https://plot.ly/ipython-notebooks/)!
#
# [](https://plot.ly/ipython-notebooks/)
# +
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
# !pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'jupyter_tutorial.ipynb', 'python/ipython-notebook-tutorial/', 'Jupyter Notebook Tutorial',
'Jupyter notebook tutorial on how to install, run, and use Jupyter for interactive matplotlib plotting, data analysis, and publishing code',
title = 'Jupyter Notebook Tutorial | plotly',
name = 'Jupyter Notebook Tutorial',
thumbnail='thumbnail/ipythonnb.jpg', language='python',
page_type='example_index', has_thumbnail='true', display_as='file_settings', order=11,
ipynb='~chelsea_lyn/14070')
# -
|
_posts/python/fundamentals/ipython-notebooks/jupyter_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Says One Neuron To Another
# ## Neural network architectures
# 1. Set up a new git repository in your GitHub account
# 2. Pick two datasets from
# https://en.wikipedia.org/wiki/List_of_datasets_for_machine-learning_research
# 3. Choose a programming language (Python, C/C++, Java)
# 4. Formulate ideas on how neural networks can be used to accomplish the task for the specific dataset
# 5. Build a neural network to model the prediction process programmatically
# 6. Document your process and results
# 7. Commit your source code, documentation and other supporting files to the git repository in GitHub
#
# # Dataset:
#
# `tf.keras.datasets.mnist.load_data(path="mnist.npz")`
#
# - This is a dataset of 60,000 28x28 grayscale images of the 10 digits, along with a test set of 10,000 images.
# - x_train, x_test: uint8 arrays of grayscale image data with shapes (num_samples, 28, 28).
# - y_train, y_test: uint8 arrays of digit labels (integers in range 0-9) with shapes (num_samples,).
# - License: <NAME> and <NAME> hold the copyright of MNIST dataset, which is a derivative work from original NIST datasets. MNIST dataset is made available under the terms of the Creative Commons Attribution-Share Alike 3.0 license.
#
# - The data files train.csv and test.csv contain gray-scale images of hand-drawn digits, from zero through nine.
#
# - Each image is 28 pixels in height and 28 pixels in width, for a total of 784 pixels in total. Each pixel has a single pixel-value associated with it, indicating the lightness or darkness of that pixel, with higher numbers meaning darker. This pixel-value is an integer between 0 and 255, inclusive.
#
# # Step-1
# ## Preparing Environment
import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
# ## Importing data
(x_train,y_train),(x_test,y_test) = mnist.load_data()
print(x_train.shape)
print(x_test.shape)
# ## Normalizing data
x_train = x_train.reshape(60000,784)/255
x_test = x_test.reshape(10000,784)/255
# # Step 2: Initializing Parameters
# ## Weights and Bias
#
# ### Structure of Neural Network
#
# - Input Layer has 784 neurons(28 x 28)
# - Hidden Layer has 15 neurons
# - Output Layer has 10 neurons(10 classes)
#
# - `bias0` and `bias1` are used for forward propagation
# - `re_bias0` and `re_bias1` are used for backward propagation
#
#
# - `weight0` and `weight1` are used for forward propagation
# - `re_weight0` and `re_weight1` are used for backward propagation
#
#
# +
bias0 = [0]*15
bias1 = [0]*10
re_bias0 = [0]*15
re_bias1 = [0]*10
weight0 = [[0 for i in range(784)]for i in range(15)]
weight1 = [[0 for i in range(15)]for i in range(10)]
re_weight0 = [[0 for i in range(784)]for i in range(15)]
re_weight1 = [[0 for i in range(15)]for i in range(10)]
for i in range(15):
bias0[i] = np.random.rand()*0.1
for i in range(10):
bias1[i] = np.random.rand()*0.1
for i in range(15):
for j in range(784):
weight0[i][j] = np.random.randn()*0.1
for i in range(10):
for j in range(15):
weight1[i][j] = np.random.randn()*0.1
# -
# ## Input and Output layers
#
# - `Input0` are the values that are given to hidden layer along with weight and bias
# - `Output0` are the output of hidden layer from our activation function sigmoid.
#
# - `Input1` are the values given to output layer
# - `Output1` is the prediction using softmax function.
#
# +
Input0 = [0]*15
Input1 = [0]*10
Output0 = [0]*15
Output1 = [0]*10
Input0_test = [0]*15
Input1_test = [0]*10
Output0_test = [0]*15
Output1_test = [0]*10
# -
# # Step 3: Defining all Methods
# ## Sigmoid function
# 
def sigmoid(x):
return 1/(1+np.exp(-x))
# ## Derivative of Sigmoid function
# - The derivative of the sigmoid function sigm at any x∈R is implemented as dsigm(x)dx:=sigm(x)(1−sigm(x))
# 
def dsigm(x):
return sigmoid(x)*(1-sigmoid(x))
# ## Softmax function
#
# 
def softmax(x_array):
a = np.max(x_array)
exp_x = np.exp(x_array-a)
sum_exp_x = np.sum(exp_x)
y_array = exp_x/sum_exp_x
return y_array
# ## Delta Function, Sum of Squares Error and Back Propagation Function
# +
def delta(num,t_n,Op1,Ip1,we1):
sum_1 = 0
for i in range(10):
sum_1 += (Op1[i]-t_n[i])*we1[i][num]*dsigm(Ip1[i])
return sum_1
def sum_of_squares_error(y,t):
return 0.5*np.sum((y-t)**2)
def back_propagation(Out0,Out1,In0,In1,t_num,x_t,l_rate):
global weight0
global weight1
global bias0
global bias1
for i in range(10):
for j in range(15):
re_weight1[i][j] = (Out1[i]-t_num[i])*dsigm(In1[i])
weight1[i][j] -= l_rate*re_weight1[i][j]*Out0[j]
for i in range(15):
for j in range(784):
re_weight0[i][j] = delta(i,t_num,Out1,In1,weight1)*dsigm(In0[i])
weight0[i][j] -= l_rate*re_weight0[i][j]*x_t[j]
for i in range(10):
re_bias1[i] = (Out1[i]-t_num[i])*dsigm(In1[i])
bias1[i] -= l_rate*re_bias1[i]
for i in range(15):
re_bias0[i] = delta(i,t_num,Out1,In1,weight1)*dsigm(In0[i])
bias0[i] -= l_rate*re_bias0[i]
# -
# ## Accuracy Function
def accuracy(y_list,t_list,switch):
max_y = np.argmax(y_list,axis=1)
max_t = np.argmax(t_list,axis=1)
if switch == "train":
return np.sum(max_y == max_t)/100
elif switch == "test":
return np.sum(max_y == max_t)/ 10000
# ## Function to visualize
def plot_figure(acc, loss, num, name):
x = list(range(num))
y = acc
z = loss
plt.plot(x, y, label = "accuracy")
plt.plot(x, z, label = "loss")
plt.legend(loc = "lower right")
plt.savefig("../reports/"+name+"_acc_loss.jpg")
# # Step 4: Hyperparameters
#
# - After changing the values of these hypermaters, I found that these had a decent performance.
learning_rate = 0.1
epochs = 12
input_words = 3
# # Step 5: Training the model
# +
all_train_accuracy = []
all_train_loss = []
for l in range(epochs):
print("Epoch :"+str(l))
for k in range(input_words):
train_prediction = []
train_answer = []
print("Iteration "+str(l*input_words+k)+": ", end="")
for j in range(100):
for i in range(15):
Input0[i] = np.dot(x_train[k*100+j],weight0[i])+bias0[i]
Output0[i] = sigmoid(Input0[i])
for i in range(10):
Input1[i] = np.dot(Output0,weight1[i])+bias1[i]
Output1 = softmax(Input1)
train_num = [0]*10
train_num[y_train[k*100+j]] = train_num[y_train[k*100+j]]+1
train_prediction.append(Output1)
train_answer.append(train_num)
back_propagation(Output0,Output1,Input0,Input1,train_num,x_train[k*100+j],learning_rate)
train_acc = accuracy(train_prediction,train_answer,"train")
train_loss = sum_of_squares_error(Output1,train_num)
print(" train_accuracy = "+str(train_acc), end="\t")
print(" train_loss = "+str(train_loss))
all_train_accuracy.append(train_acc)
all_train_loss.append(train_loss)
number = epochs*input_words
plot_figure(all_train_accuracy, all_train_loss,number,"train")
# -
# # Step 6: Testing the model
# +
test_prediction = []
test_answer = []
for j in range(10000):
for i in range(15):
Input0_test[i] = np.dot(x_test[j],weight0[i])+bias0[i]
Output0_test[i] = sigmoid(Input0_test[i])
for i in range(10):
Input1_test[i] = np.dot(Output0_test,weight1[i])+bias1[i]
Output1_test = softmax(Input1_test)
test_num = [0]*10
test_num[y_test[j]] = test_num[y_test[j]]+1
test_prediction.append(Output1_test)
test_answer.append(test_num)
test_acc = accuracy(test_prediction,test_answer,"test")
test_loss = sum_of_squares_error(Output1_test,test_num)
print("test_accuracy = "+str(test_acc), end="\t")
print("test_loss = "+str(test_loss))
# -
# # Step 7: Visualizing the performance of our model
# +
X_train__ = x_test.reshape(x_test.shape[0], 28, 28)
fig, axis = plt.subplots(4, 3, figsize=(15, 5))
for i, ax in enumerate(axis.flat):
randomindex=int(np.random.rand()*1000)
ax.imshow(X_train__[randomindex], cmap='binary')
digit = y_test[randomindex]
prediction=test_prediction[randomindex].argmax()
ax.axis(False)
ax.set(title = f"[Label: {digit}| Prediction: {prediction}]");
# -
# # Results and Future Developments:
#
# - For training accuracy, we reached a Global Maxima of 97%.
# - For testing, we had an accuracy of 77.79%.
#
# - Our model trained pretty well but we could not obtain similar train and test accuracies this might be because of overfitting or not enough data to train our model or a shallow network with only one hidden layer.
# - In future we can try to implement a deeper network with more hidden layers and also instead of initializing weights and biases with random values we can use some standard weights which are trained on more powerful machines.
|
notebooks/Digit Recognizer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: dp_tf1.8
# language: python
# name: dp_tf1.8
# ---
# ### DeepPavlov sequence-to-sequence tutorial
# In this tutorial we are going to implement sequence-to-sequence [[original paper]](https://arxiv.org/abs/1409.3215) model in DeepPavlov.
#
# Sequence-to-sequence is the concept of mapping input sequence to target sequence. Sequence-to-sequence models consist of two main components: encoder and decoder. Encoder is used to encode the input sequence to dense representation and decoder uses this dense representation to generate target sequence.
#
# 
#
# Here, input sequence is ABC, special token <EOS\> (end of sequence) is used as indicator to start decoding target sequence WXYZ.
#
# To implement this model in DeepPavlov we have to code some DeepPavlov abstractions:
# * **DatasetReader** to read the data
# * **DatasetIterator** to generate batches
# * **Vocabulary** to convert words to indexes
# * **Model** to train it and then use it
# * and some other components for pre- and postprocessing
# +
# %load_ext autoreload
# %autoreload 2
import deeppavlov
import json
import numpy as np
import tensorflow as tf
from itertools import chain
from pathlib import Path
# -
# ### Download & extract dataset
from deeppavlov.core.data.utils import download_decompress
download_decompress('http://files.deeppavlov.ai/datasets/personachat_v2.tar.gz', './personachat')
# ### DatasetReader
# DatasetReader is used to read and parse data from files. Here, we define new PersonaChatDatasetReader which reads [PersonaChat dataset](https://arxiv.org/abs/1801.07243). PersonaChat dataset consists of dialogs and user personalities.
#
# User personality is described by four sentences, e.g.:
#
# i like to remodel homes.
# i like to go hunting.
# i like to shoot a bow.
# my favorite holiday is halloween.
# +
from deeppavlov.core.commands.train import build_model_from_config
from deeppavlov.core.data.dataset_reader import DatasetReader
from deeppavlov.core.data.utils import download_decompress
from deeppavlov.core.common.registry import register
@register('personachat_dataset_reader')
class PersonaChatDatasetReader(DatasetReader):
"""
PersonaChat dataset from
<NAME>. et al. Personalizing Dialogue Agents: I have a dog, do you have pets too?
https://arxiv.org/abs/1801.07243
Also, this dataset is used in ConvAI2 http://convai.io/
This class reads dataset to the following format:
[{
'persona': [list of persona sentences],
'x': input utterance,
'y': output utterance,
'dialog_history': list of previous utterances
'candidates': [list of candidate utterances]
'y_idx': index of y utt in candidates list
},
...
]
"""
def read(self, dir_path: str, mode='self_original'):
dir_path = Path(dir_path)
dataset = {}
for dt in ['train', 'valid', 'test']:
dataset[dt] = self._parse_data(dir_path / '{}_{}.txt'.format(dt, mode))
return dataset
@staticmethod
def _parse_data(filename):
examples = []
print(filename)
curr_persona = []
curr_dialog_history = []
persona_done = False
with filename.open('r') as fin:
for line in fin:
line = ' '.join(line.strip().split(' ')[1:])
your_persona_pref = 'your persona: '
if line[:len(your_persona_pref)] == your_persona_pref and persona_done:
curr_persona = [line[len(your_persona_pref):]]
curr_dialog_history = []
persona_done = False
elif line[:len(your_persona_pref)] == your_persona_pref:
curr_persona.append(line[len(your_persona_pref):])
else:
persona_done = True
x, y, _, candidates = line.split('\t')
candidates = candidates.split('|')
example = {
'persona': curr_persona,
'x': x,
'y': y,
'dialog_history': curr_dialog_history[:],
'candidates': candidates,
'y_idx': candidates.index(y)
}
curr_dialog_history.extend([x, y])
examples.append(example)
return examples
# -
data = PersonaChatDatasetReader().read('./personachat')
# #### Let's check dataset size
for k in data:
print(k, len(data[k]))
data['train'][0]
# ### Dataset iterator
# Dataset iterator is used to generate batches from parsed dataset (DatasetReader). Let's extract only *x* and *y* from parsed dataset and use them to predict sentence *y* by sentence *x*.
# +
from deeppavlov.core.data.data_learning_iterator import DataLearningIterator
@register('personachat_iterator')
class PersonaChatIterator(DataLearningIterator):
def split(self, *args, **kwargs):
for dt in ['train', 'valid', 'test']:
setattr(self, dt, self._to_tuple(getattr(self, dt)))
@staticmethod
def _to_tuple(data):
"""
Returns:
list of (x, y)
"""
return list(map(lambda x: (x['x'], x['y']), data))
# -
# Let's look on data in batches:
iterator = PersonaChatIterator(data)
batch = [el for el in iterator.gen_batches(5, 'train')][0]
for x, y in zip(*batch):
print('x:', x)
print('y:', y)
print('----------')
# ### Tokenizer
# Tokenizer is used to extract tokens from utterance.
from deeppavlov.models.tokenizers.lazy_tokenizer import LazyTokenizer
tokenizer = LazyTokenizer()
tokenizer(['Hello my friend'])
# ### Vocabulary
# Vocabulary prepares mapping from tokens to token indexes. It uses train data to build this mapping.
#
# We will implement DialogVocab (inherited from SimpleVocabulary) wich adds all tokens from *x* and *y* utterances to vocabulary.
# +
from deeppavlov.core.data.simple_vocab import SimpleVocabulary
@register('dialog_vocab')
class DialogVocab(SimpleVocabulary):
def fit(self, *args):
tokens = chain(*args)
super().fit(tokens)
def __call__(self, batch, **kwargs):
indices_batch = []
for utt in batch:
tokens = [self[token] for token in utt]
indices_batch.append(tokens)
return indices_batch
# -
# Let's create instance of DialogVocab. We define save and load paths, minimal frequence of tokens which are added to vocabulary and set of special tokens.
#
# Special tokens are:
# * <PAD\> - padding
# * <BOS\> - begin of sequence
# * <EOS\> - end of sequence
# * <UNK\> - unknown token - token which is not presented in vocabulary
#
# And fit it on tokens from *x* and *y*.
# +
vocab = DialogVocab(
save_path='./vocab.dict',
load_path='./vocab.dict',
min_freq=2,
special_tokens=('<PAD>','<BOS>', '<EOS>', '<UNK>',),
unk_token='<UNK>'
)
vocab.fit(tokenizer(iterator.get_instances(data_type='train')[0]), tokenizer(iterator.get_instances(data_type='train')[1]))
vocab.save()
# -
# Top 10 most frequent tokens in train dataset:
vocab.freqs.most_common(10)
# Number of tokens in vocabulary:
len(vocab)
# Let's use built vocabulary to encode some tokenized sentence.
vocab([['<BOS>', 'hello', 'my', 'friend', 'there_is_no_such_word_in_dataset', 'and_this', '<EOS>', '<PAD>']])
# ### Padding
# To feed sequences of token indexes to neural model we should make their lengths equal. If sequence is too short we add <PAD\> symbols to the end of sequence. If sequence is too long we just cut it.
#
# SentencePadder implements such behavior, it also adds <BOS\> and <EOS\> tokens.
# +
from deeppavlov.core.models.component import Component
@register('sentence_padder')
class SentencePadder(Component):
def __init__(self, length_limit, pad_token_id=0, start_token_id=1, end_token_id=2, *args, **kwargs):
self.length_limit = length_limit
self.pad_token_id = pad_token_id
self.start_token_id = start_token_id
self.end_token_id = end_token_id
def __call__(self, batch):
for i in range(len(batch)):
batch[i] = batch[i][:self.length_limit]
batch[i] = [self.start_token_id] + batch[i] + [self.end_token_id]
batch[i] += [self.pad_token_id] * (self.length_limit + 2 - len(batch[i]))
return batch
# -
padder = SentencePadder(length_limit=6)
vocab(padder(vocab([['hello', 'my', 'friend', 'there_is_no_such_word_in_dataset', 'and_this']])))
# ### Seq2Seq Model
# Model consists of two main components: encoder and decoder. We can implement them independently and then put them together in one Seq2Seq model.
# #### Encoder
# Encoder builds hidden representation of input sequence.
def encoder(inputs, inputs_len, embedding_matrix, cell_size, keep_prob=1.0):
# inputs: tf.int32 tensor with shape bs x seq_len with token ids
# inputs_len: tf.int32 tensor with shape bs
# embedding_matrix: tf.float32 tensor with shape vocab_size x vocab_dim
# cell_size: hidden size of recurrent cell
# keep_prob: dropout keep probability
with tf.variable_scope('encoder'):
# first of all we should embed every token in input sequence (use tf.nn.embedding_lookup, don't forget about dropout)
x_emb = tf.nn.dropout(tf.nn.embedding_lookup(embedding_matrix, inputs), keep_prob=keep_prob)
# define recurrent cell (LSTM or GRU)
encoder_cell = tf.nn.rnn_cell.GRUCell(
num_units=cell_size,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name='encoder_cell')
# use tf.nn.dynamic_rnn to encode input sequence, use actual length of input sequence
encoder_outputs, encoder_state = tf.nn.dynamic_rnn(cell=encoder_cell, inputs=x_emb, sequence_length=inputs_len, dtype=tf.float32)
return encoder_outputs, encoder_state
# Check your encoder implementation:
#
# next cell output shapes are
#
# 32 x 10 x 100 and 32 x 100
# +
tf.reset_default_graph()
vocab_size = 100
hidden_dim = 100
inputs = tf.cast(tf.random_uniform(shape=[32, 10]) * vocab_size, tf.int32) # bs x seq_len
mask = tf.cast(tf.random_uniform(shape=[32, 10]) * 2, tf.int32) # bs x seq_len
inputs_len = tf.reduce_sum(mask, axis=1)
embedding_matrix = tf.random_uniform(shape=[vocab_size, hidden_dim])
encoder(inputs, inputs_len, embedding_matrix, hidden_dim)
# -
# #### Decoder
# Decoder uses encoder outputs and encoder state to produce output sequence.
#
# Here, you should:
# * define your decoder_cell (GRU or LSTM)
#
# it will be your baseline seq2seq model.
#
#
# And, to improve the model:
# * add Teacher Forcing
# * add Attention Mechanism
def decoder(encoder_outputs, encoder_state, embedding_matrix, mask,
cell_size, max_length, y_ph,
start_token_id=1, keep_prob=1.0,
teacher_forcing_rate_ph=None,
use_attention=False, is_train=True):
# decoder
# encoder_outputs: tf.float32 tensor with shape bs x seq_len x encoder_cell_size
# encoder_state: tf.float32 tensor with shape bs x encoder_cell_size
# embedding_matrix: tf.float32 tensor with shape vocab_size x vocab_dim
# mask: tf.int32 tensor with shape bs x seq_len with zeros for masked sequence elements
# cell_size: hidden size of recurrent cell
# max_length: max length of output sequence
# start_token_id: id of <BOS> token in vocabulary
# keep_prob: dropout keep probability
# teacher_forcing_rate_ph: rate of using teacher forcing on each decoding step
# use_attention: use attention on encoder outputs or use only encoder_state
# is_train: is it training or inference? at inference time we can't use teacher forcing
with tf.variable_scope('decoder'):
# define decoder recurrent cell
decoder_cell = tf.nn.rnn_cell.GRUCell(
num_units=cell_size,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name='decoder_cell')
# initial value of output_token on previsous step is start_token
output_token = tf.ones(shape=(tf.shape(encoder_outputs)[0],), dtype=tf.int32) * start_token_id
# let's define initial value of decoder state with encoder_state
decoder_state = encoder_state
pred_tokens = []
logits = []
# use for loop to sequentially call recurrent cell
for i in range(max_length):
"""
TEACHER FORCING
# here you can try to implement teacher forcing for your model
# details about teacher forcing are explained further in tutorial
# pseudo code:
NOTE THAT FOLLOWING CONDITIONS SHOULD BE EVALUATED AT GRAPH RUNTIME
use tf.cond and tf.logical operations instead of python if
if i > 0 and is_train and random_value < teacher_forcing_rate_ph:
input_token = y_ph[:, i-1]
else:
input_token = output_token
input_token_emb = tf.nn.embedding_lookup(embedding_matrix, input_token)
"""
if i > 0:
input_token_emb = tf.cond(
tf.logical_and(
is_train,
tf.random_uniform(shape=(), maxval=1) <= teacher_forcing_rate_ph
),
lambda: tf.nn.embedding_lookup(embedding_matrix, y_ph[:, i-1]), # teacher forcing
lambda: tf.nn.embedding_lookup(embedding_matrix, output_token)
)
else:
input_token_emb = tf.nn.embedding_lookup(embedding_matrix, output_token)
"""
ATTENTION MECHANISM
# here you can add attention to your model
# you can find details about attention further in tutorial
"""
if use_attention:
# compute attention and concat attention vector to input_token_emb
att = dot_attention(encoder_outputs, decoder_state, mask, scope='att')
input_token_emb = tf.concat([input_token_emb, att], axis=-1)
input_token_emb = tf.nn.dropout(input_token_emb, keep_prob=keep_prob)
# call recurrent cell
decoder_outputs, decoder_state = decoder_cell(input_token_emb, decoder_state)
decoder_outputs = tf.nn.dropout(decoder_outputs, keep_prob=keep_prob)
# project decoder output to embeddings dimension
embeddings_dim = embedding_matrix.get_shape()[1]
output_proj = tf.layers.dense(decoder_outputs, embeddings_dim, activation=tf.nn.tanh,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name='proj', reuse=tf.AUTO_REUSE)
# compute logits
output_logits = tf.matmul(output_proj, embedding_matrix, transpose_b=True)
logits.append(output_logits)
output_probs = tf.nn.softmax(output_logits)
output_token = tf.argmax(output_probs, axis=-1)
pred_tokens.append(output_token)
y_pred_tokens = tf.transpose(tf.stack(pred_tokens, axis=0), [1, 0])
y_logits = tf.transpose(tf.stack(logits, axis=0), [1, 0, 2])
return y_pred_tokens, y_logits
# Output of next cell should be with shapes:
#
# 32 x 10
# 32 x 10 x 100
# +
tf.reset_default_graph()
vocab_size = 100
hidden_dim = 100
inputs = tf.cast(tf.random_uniform(shape=[32, 10]) * vocab_size, tf.int32) # bs x seq_len
mask = tf.cast(tf.random_uniform(shape=[32, 10]) * 2, tf.int32) # bs x seq_len
inputs_len = tf.reduce_sum(mask, axis=1)
embedding_matrix = tf.random_uniform(shape=[vocab_size, hidden_dim])
teacher_forcing_rate = tf.random_uniform(shape=())
y = tf.cast(tf.random_uniform(shape=[32, 10]) * vocab_size, tf.int32)
encoder_outputs, encoder_state = encoder(inputs, inputs_len, embedding_matrix, hidden_dim)
decoder(encoder_outputs, encoder_state, embedding_matrix, mask, hidden_dim, max_length=10,
y_ph=y, teacher_forcing_rate_ph=teacher_forcing_rate)
# -
# #### Model
# Seq2Seq model should be inherited from TFModel class and implement following methods:
# * train_on_batch - this method is called in training phase
# * \_\_call\_\_ - this method is called to make predictions
# +
from deeppavlov.core.models.tf_model import TFModel
@register('seq2seq')
class Seq2Seq(TFModel):
def __init__(self, **kwargs):
# hyperparameters
# dimension of word embeddings
self.embeddings_dim = kwargs.get('embeddings_dim', 100)
# size of recurrent cell in encoder and decoder
self.cell_size = kwargs.get('cell_size', 200)
# dropout keep_probability
self.keep_prob = kwargs.get('keep_prob', 0.8)
# learning rate
self.learning_rate = kwargs.get('learning_rate', 3e-04)
# max length of output sequence
self.max_length = kwargs.get('max_length', 20)
self.grad_clip = kwargs.get('grad_clip', 5.0)
self.start_token_id = kwargs.get('start_token_id', 1)
self.vocab_size = kwargs.get('vocab_size', 11595)
self.teacher_forcing_rate = kwargs.get('teacher_forcing_rate', 0.0)
self.use_attention = kwargs.get('use_attention', False)
# create tensorflow session to run computational graph in it
self.sess_config = tf.ConfigProto(allow_soft_placement=True)
self.sess_config.gpu_options.allow_growth = True
self.sess = tf.Session(config=self.sess_config)
self.init_graph()
# define train op
self.train_op = self.get_train_op(self.loss, self.lr_ph,
optimizer=tf.train.AdamOptimizer,
clip_norm=self.grad_clip)
# initialize graph variables
self.sess.run(tf.global_variables_initializer())
super().__init__(**kwargs)
# load saved model if there is one
if self.load_path is not None:
self.load()
def init_graph(self):
# create placeholders
self.init_placeholders()
self.x_mask = tf.cast(self.x_ph, tf.int32)
self.y_mask = tf.cast(self.y_ph, tf.int32)
self.x_len = tf.reduce_sum(self.x_mask, axis=1)
# create embeddings matrix for tokens
self.embeddings = tf.Variable(tf.random_uniform((self.vocab_size, self.embeddings_dim), -0.1, 0.1, name='embeddings'), dtype=tf.float32)
# encoder
encoder_outputs, encoder_state = encoder(self.x_ph, self.x_len, self.embeddings, self.cell_size, self.keep_prob_ph)
# decoder
self.y_pred_tokens, y_logits = decoder(encoder_outputs, encoder_state, self.embeddings, self.x_mask,
self.cell_size, self.max_length,
self.y_ph, self.start_token_id, self.keep_prob_ph,
self.teacher_forcing_rate_ph, self.use_attention, self.is_train_ph)
# loss
self.y_ohe = tf.one_hot(self.y_ph, depth=self.vocab_size)
self.y_mask = tf.cast(self.y_mask, tf.float32)
self.loss = tf.nn.softmax_cross_entropy_with_logits(labels=self.y_ohe, logits=y_logits) * self.y_mask
self.loss = tf.reduce_sum(self.loss) / tf.reduce_sum(self.y_mask)
def init_placeholders(self):
# placeholders for inputs
self.x_ph = tf.placeholder(shape=(None, None), dtype=tf.int32, name='x_ph')
# at inference time y_ph is used (y_ph exists in computational graph) when teacher forcing is activated, so we add dummy default value
# this dummy value is not actually used at inference
self.y_ph = tf.placeholder_with_default(tf.zeros_like(self.x_ph), shape=(None,None), name='y_ph')
# placeholders for model parameters
self.lr_ph = tf.placeholder(dtype=tf.float32, shape=[], name='lr_ph')
self.keep_prob_ph = tf.placeholder_with_default(1.0, shape=[], name='keep_prob_ph')
self.is_train_ph = tf.placeholder_with_default(False, shape=[], name='is_train_ph')
self.teacher_forcing_rate_ph = tf.placeholder_with_default(0.0, shape=[], name='teacher_forcing_rate_ph')
def _build_feed_dict(self, x, y=None):
feed_dict = {
self.x_ph: x,
}
if y is not None:
feed_dict.update({
self.y_ph: y,
self.lr_ph: self.learning_rate,
self.keep_prob_ph: self.keep_prob,
self.is_train_ph: True,
self.teacher_forcing_rate_ph: self.teacher_forcing_rate,
})
return feed_dict
def train_on_batch(self, x, y):
feed_dict = self._build_feed_dict(x, y)
loss, _ = self.sess.run([self.loss, self.train_op], feed_dict=feed_dict)
return loss
def __call__(self, x):
feed_dict = self._build_feed_dict(x)
y_pred = self.sess.run(self.y_pred_tokens, feed_dict=feed_dict)
return y_pred
# -
# Let's create model with random weights and default parameters, change path to model, otherwise it will be stored in deeppavlov/download folder:
s2s = Seq2Seq(
save_path='PATH_TO_YOUR_WORKING_DIR/model',
load_path='PATH_TO_YOUR_WORKING_DIR/model'
)
# Here, we firstly run all preprocessing steps and call seq2seq model, and then convert token indexes to tokens. As result we should get some random sequence of words.
vocab(s2s(padder(vocab([['hello', 'my', 'friend', 'there_is_no_such_word_in_dataset', 'and_this']]))))
# #### Attention mechanism
# Attention mechanism [[paper](https://arxiv.org/abs/1409.0473)] allows to aggregate information from "memory" according to current state. By aggregating we suppose weighted sum of "memory" items. Weight of each memory item depends on current state.
#
# Without attention decoder could use only last hidden state of encoder. Attention mechanism gives access to all encoder states during decoding.
#
# 
#
# One of the simpliest ways to compute attention weights (*a_ij*) is to compute them by dot product between memory items and state and then apply softmax function. Other ways of computing *multiplicative* attention could be found in this [paper](https://arxiv.org/abs/1508.04025).
#
# We also need a mask to skip some sequence elements like <PAD\>. To make weight of undesired memory items close to zero we can add big negative value to logits (result of dot product) before applying softmax.
def softmax_mask(values, mask):
# adds big negative to masked values
INF = 1e30
return -INF * (1 - tf.cast(mask, tf.float32)) + values
def dot_attention(memory, state, mask, scope="dot_attention"):
# inputs: bs x seq_len x hidden_dim
# state: bs x hidden_dim
# mask: bs x seq_len
with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
# dot product between each item in memory and state
logits = tf.matmul(memory, tf.expand_dims(state, axis=1), transpose_b=True)
logits = tf.squeeze(logits, [2])
# apply mask to logits
logits = softmax_mask(logits, mask)
# apply softmax to logits
att_weights = tf.expand_dims(tf.nn.softmax(logits), axis=2)
# compute weighted sum of items in memory
att = tf.reduce_sum(att_weights * memory, axis=1)
return att
# Check your implementation:
#
# outputs should be with shapes 32 x 100
tf.reset_default_graph()
memory = tf.random_normal(shape=[32, 10, 100]) # bs x seq_len x hidden_dim
state = tf.random_normal(shape=[32, 100]) # bs x hidden_dim
mask = tf.cast(tf.random_normal(shape=[32, 10]), tf.int32) # bs x seq_len
dot_attention(memory, state, mask)
# #### Teacher forcing
#
# We have implemented decoder, which takes as input it's own output during training and inference time. But, at early stages of training it could be hard for model to produce long sequences depending on it's own close to random output. Teacher forcing can help with this: instead of feeding model's output we can feed ground truth tokens. It helps model on training time, but on inference we still can rely only on it's own output.
#
#
# Using model's output:
#
# <img src="img/sampling.png" alt="sampling" width=50%/>
#
# Teacher forcing:
#
# <img src="img/teacher_forcing.png" alt="teacher_forcing" width=50%/>
#
# It is not necessary to feed ground truth tokens on each time step - we can randomly choose with some rate if we want ground truth input or predicted by model.
# *teacher_forcing_rate* parameter of seq2seq model can control such behavior.
#
# More details about teacher forcing could be found in DeepLearningBook [Chapter 10.2.1](http://www.deeplearningbook.org/contents/rnn.html)
# Let's create model with random weights and default parameters:
# Here, we firstly run all preprocessing steps and call seq2seq model, and then convert token indexes to tokens. As result we should get some random sequence of words.
# ### Postprocessing
# In postprocessing step we are going to remove all <PAD\>, <BOS\>, <EOS\> tokens.
@register('postprocessing')
class SentencePostprocessor(Component):
def __init__(self, pad_token='<PAD>', start_token='<BOS>', end_token='<EOS>', *args, **kwargs):
self.pad_token = pad_token
self.start_token = start_token
self.end_token = end_token
def __call__(self, batch):
for i in range(len(batch)):
batch[i] = ' '.join(self._postproc(batch[i]))
return batch
def _postproc(self, utt):
if self.end_token in utt:
utt = utt[:utt.index(self.end_token)]
return utt
postprocess = SentencePostprocessor()
postprocess(vocab(s2s(padder(vocab([['hello', 'my', 'friend', 'there_is_no_such_word_in_dataset', 'and_this']])))))
# ### Create config file
# Let's put is all together in one config file.
config = {
"dataset_reader": {
"name": "personachat_dataset_reader",
"data_path": "YOUR_PATH_TO_FOLDER_WITH_PERSONACHAT_DATASET"
},
"dataset_iterator": {
"name": "personachat_iterator",
"seed": 1337,
"shuffle": True
},
"chainer": {
"in": ["x"],
"in_y": ["y"],
"pipe": [
{
"name": "lazy_tokenizer",
"id": "tokenizer",
"in": ["x"],
"out": ["x_tokens"]
},
{
"name": "lazy_tokenizer",
"id": "tokenizer",
"in": ["y"],
"out": ["y_tokens"]
},
{
"name": "dialog_vocab",
"id": "vocab",
"save_path": "YOUR_PATH_TO_WORKING_DIR/vocab.dict",
"load_path": "YOUR_PATH_TO_WORKING_DIR/vocab.dict",
"min_freq": 2,
"special_tokens": ["<PAD>","<BOS>", "<EOS>", "<UNK>"],
"unk_token": "<UNK>",
"fit_on": ["x_tokens", "y_tokens"],
"in": ["x_tokens"],
"out": ["x_tokens_ids"]
},
{
"ref": "vocab",
"in": ["y_tokens"],
"out": ["y_tokens_ids"]
},
{
"name": "sentence_padder",
"id": "padder",
"length_limit": 20,
"in": ["x_tokens_ids"],
"out": ["x_tokens_ids"]
},
{
"ref": "padder",
"in": ["y_tokens_ids"],
"out": ["y_tokens_ids"]
},
{
"name": "seq2seq",
"id": "s2s",
"max_length": "#padder.length_limit+2",
"cell_size": 250,
"embeddings_dim": 50,
"vocab_size": 11595,
"keep_prob": 0.8,
"learning_rate": 3e-04,
"teacher_forcing_rate": 0.0,
"use_attention": False,
"save_path": "YOUR_PATH_TO_WORKING_DIR/model",
"load_path": "YOUR_PATH_TO_WORKING_DIR/model",
"in": ["x_tokens_ids"],
"in_y": ["y_tokens_ids"],
"out": ["y_predicted_tokens_ids"],
},
{
"ref": "vocab",
"in": ["y_predicted_tokens_ids"],
"out": ["y_predicted_tokens"]
},
{
"name": "postprocessing",
"in": ["y_predicted_tokens"],
"out": ["y_predicted_tokens"]
}
],
"out": ["y_predicted_tokens"]
},
"train": {
"log_every_n_batches": 100,
"val_every_n_epochs":0,
"batch_size": 64,
"validation_patience": 0,
"epochs": 20,
"metrics": ["bleu"],
}
}
# ### Interact with model using config
from deeppavlov.core.commands.infer import build_model_from_config
model = build_model_from_config(config)
model(['Hi, how are you?', 'Any ideas my dear friend?'])
# ### Train model
#
# Run experiments with and without attention, with teacher forcing and without.
from deeppavlov.core.commands.train import train_evaluate_model_from_config
json.dump(config, open('seq2seq.json', 'w'))
train_evaluate_model_from_config('seq2seq.json')
model = build_model_from_config(config)
model(['hi, how are you?', 'any ideas my dear friend?', 'okay, i agree with you', 'good bye!'])
# To improve the model you can try to use multilayer (use MultiRNNCell) encoder and decoder, try to use attention with trainable parameters (not dot product scoring function).
|
examples/tutorials/04_deeppavlov_chitchat.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1> Using Machine Learning APIs </h1>
#
# First, visit <a href="http://console.cloud.google.com/apis">API console</a>, choose "Credentials" on the left-hand menu. Choose "Create Credentials" and generate an API key for your application. You should probably restrict it by IP address to prevent abuse, but for now, just leave that field blank and delete the API key after trying out this demo.
#
# Copy-paste your API Key here:
APIKEY="CHANGE-THIS-KEY" # Replace with your API key
# <b> Note: Make sure you generate an API Key and replace the value above. The sample key will not work.</b>
#
# From the same API console, choose "Dashboard" on the left-hand menu and "Enable API".
#
# Enable the following APIs for your project (search for them) if they are not already enabled:
# <ol>
# <li> Google Translate API </li>
# <li> Google Cloud Vision API </li>
# <li> Google Natural Language API </li>
# <li> Google Cloud Speech API </li>
# </ol>
#
# Finally, because we are calling the APIs from Python (clients in many other languages are available), let's install the Python package (it's not installed by default on Datalab)
# !pip install --upgrade google-api-python-client
# <h2> Invoke Translate API </h2>
# +
# running Translate API
from googleapiclient.discovery import build
service = build('translate', 'v2', developerKey=APIKEY)
# use the service
inputs = ['is it really this easy?', 'amazing technology', 'wow']
outputs = service.translations().list(source='en', target='fr', q=inputs).execute()
# print outputs
for input, output in zip(inputs, outputs['translations']):
print("{0} -> {1}".format(input, output['translatedText']))
# -
# <h2> Invoke Vision API </h2>
#
# The Vision API can work off an image in Cloud Storage or embedded directly into a POST message. I'll use Cloud Storage and do OCR on this image: <img src="https://storage.googleapis.com/cloud-training-demos/vision/sign2.jpg" width="200" />. That photograph is from http://www.publicdomainpictures.net/view-image.php?image=15842
#
# Running Vision API
import base64
IMAGE="gs://cloud-training-demos/vision/sign2.jpg"
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
'source': {
'gcs_image_uri': IMAGE
}
},
'features': [{
'type': 'TEXT_DETECTION',
'maxResults': 3,
}]
}],
})
responses = request.execute(num_retries=3)
print(responses)
foreigntext = responses['responses'][0]['textAnnotations'][0]['description']
foreignlang = responses['responses'][0]['textAnnotations'][0]['locale']
print(foreignlang, foreigntext)
# <h2> Translate sign </h2>
inputs=[foreigntext]
outputs = service.translations().list(source=foreignlang, target='en', q=inputs).execute()
# print(outputs)
for input, output in zip(inputs, outputs['translations']):
print("{0} -> {1}".format(input, output['translatedText']))
# <h2> Sentiment analysis with Language API </h2>
#
# Let's evaluate the sentiment of some famous quotes using Google Cloud Natural Language API.
lservice = build('language', 'v1beta1', developerKey=APIKEY)
quotes = [
'To succeed, you must have tremendous perseverance, tremendous will.',
'It’s not that I’m so smart, it’s just that I stay with problems longer.',
'Love is quivering happiness.',
'Love is of all passions the strongest, for it attacks simultaneously the head, the heart, and the senses.',
'What difference does it make to the dead, the orphans and the homeless, whether the mad destruction is wrought under the name of totalitarianism or in the holy name of liberty or democracy?',
'When someone you love dies, and you’re not expecting it, you don’t lose her all at once; you lose her in pieces over a long time — the way the mail stops coming, and her scent fades from the pillows and even from the clothes in her closet and drawers. '
]
for quote in quotes:
response = lservice.documents().analyzeSentiment(
body={
'document': {
'type': 'PLAIN_TEXT',
'content': quote
}
}).execute()
polarity = response['documentSentiment']['polarity']
magnitude = response['documentSentiment']['magnitude']
print('POLARITY=%s MAGNITUDE=%s for %s' % (polarity, magnitude, quote))
# <h2> Speech API </h2>
#
# The Speech API can work on streaming data, audio content encoded and embedded directly into the POST message, or on a file on Cloud Storage. Here I'll pass in this <a href="https://storage.googleapis.com/cloud-training-demos/vision/audio.raw">audio file</a> in Cloud Storage.
sservice = build('speech', 'v1', developerKey=APIKEY)
response = sservice.speech().recognize(
body={
'config': {
'languageCode' : 'en-US',
'encoding': 'LINEAR16',
'sampleRateHertz': 16000
},
'audio': {
'uri': 'gs://cloud-training-demos/vision/audio.raw'
}
}).execute()
print(response)
print(response['results'][0]['alternatives'][0]['transcript'])
print('Confidence=%f' % response['results'][0]['alternatives'][0]['confidence'])
# <h2> Clean up </h2>
#
# Remember to delete the API key by visiting <a href="http://console.cloud.google.com/apis">API console</a>.
#
# If necessary, commit all your notebooks to git.
#
# If you are running Datalab on a Compute Engine VM or delegating to one, remember to stop or shut it down so that you are not charged.
#
# ## Challenge Exercise
#
# Here are a few portraits from the Metropolitan Museum of Art, New York (they are part of a [BigQuery public dataset](https://bigquery.cloud.google.com/dataset/bigquery-public-data:the_met) ):
#
# * gs://cloud-training-demos/images/met/APS6880.jpg
# * gs://cloud-training-demos/images/met/DP205018.jpg
# * gs://cloud-training-demos/images/met/DP290402.jpg
# * gs://cloud-training-demos/images/met/DP700302.jpg
#
# Use the Vision API to identify which of these images depict happy people and which ones depict unhappy people.
#
# Hint (highlight to see): <p style="color:white">You will need to look for joyLikelihood and/or sorrowLikelihood from the response.</p>
# Copyright 2018 Google Inc.
# Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
CPB100/lab4c/mlapis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# In google colab, for master version of catalyst, uncomment this:
# master version should be fully compatible with this notebook
# # ! pip install git+git://github.com/catalyst-team/catalyst.git
# For last release version of catalyst, uncomment this:
# # ! pip install catalyst
# -
# # Segmentation
# If you have Unet, all CV is segmentation now.
# ## Goals
#
# - train Unet on isbi dataset
# - visualize the predictions
# # Preparation
# Get the data:
# ! wget -P ./data/ https://www.dropbox.com/s/0rvuae4mj6jn922/isbi.tar.gz
# ! tar -xf ./data/isbi.tar.gz -C ./data/
# Final folder structure with training data:
# ```bash
# catalyst-examples/
# data/
# isbi/
# train-volume.tif
# train-labels.tif
# ```
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
# # Data
# +
# # ! pip install tifffile
# +
import tifffile as tiff
images = tiff.imread('./data/isbi/train-volume.tif')
masks = tiff.imread('./data/isbi/train-labels.tif')
data = list(zip(images, masks))
train_data = data[:-4]
valid_data = data[-4:]
# +
import collections
import numpy as np
import torch
import torchvision
import torchvision.transforms as transforms
from catalyst.data.augmentor import Augmentor
from catalyst.dl.utils import UtilsFactory
bs = 4
num_workers = 4
data_transform = transforms.Compose([
Augmentor(
dict_key="features",
augment_fn=lambda x: \
torch.from_numpy(x.copy().astype(np.float32) / 255.).unsqueeze_(0)),
Augmentor(
dict_key="features",
augment_fn=transforms.Normalize(
(0.5, ),
(0.5, ))),
Augmentor(
dict_key="targets",
augment_fn=lambda x: \
torch.from_numpy(x.copy().astype(np.float32) / 255.).unsqueeze_(0))
])
open_fn = lambda x: {"features": x[0], "targets": x[1]}
loaders = collections.OrderedDict()
train_loader = UtilsFactory.create_loader(
train_data,
open_fn=open_fn,
dict_transform=data_transform,
batch_size=bs,
num_workers=num_workers,
shuffle=True)
valid_loader = UtilsFactory.create_loader(
valid_data,
open_fn=open_fn,
dict_transform=data_transform,
batch_size=bs,
num_workers=num_workers,
shuffle=False)
loaders["train"] = train_loader
loaders["valid"] = valid_loader
# -
# # Model
from catalyst.contrib.models.segmentation import UNet
# # Train
# +
import torch
import torch.nn as nn
from catalyst.dl.experiments import SupervisedRunner
# experiment setup
num_epochs = 10
logdir = "./logs/segmentation_notebook"
# model, criterion, optimizer
model = UNet(num_classes=1, in_channels=1, num_filters=64, num_blocks=4)
criterion = nn.BCEWithLogitsLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[10, 20, 40], gamma=0.3)
# model runner
runner = SupervisedRunner()
# model training
runner.train(
model=model,
criterion=criterion,
optimizer=optimizer,
loaders=loaders,
logdir=logdir,
num_epochs=num_epochs,
verbose=True
)
# -
# # Inference
from catalyst.dl.callbacks import InferCallback, CheckpointCallback
loaders = collections.OrderedDict([("infer", loaders["valid"])])
runner.infer(
model=model,
loaders=loaders,
callbacks=[
CheckpointCallback(
resume=f"{logdir}/checkpoints/best.pth"),
InferCallback()
],
)
# # Predictions visualization
import matplotlib.pyplot as plt
plt.style.use("ggplot")
# %matplotlib inline
# +
sigmoid = lambda x: 1/(1 + np.exp(-x))
for i, (input, output) in enumerate(zip(
valid_data, runner.callbacks[1].predictions["logits"])):
image, mask = input
threshold = 0.5
plt.figure(figsize=(10,8))
plt.subplot(1, 3, 1)
plt.imshow(image, 'gray')
plt.subplot(1, 3, 2)
output = sigmoid(output[0].copy())
output = (output > threshold).astype(np.uint8)
plt.imshow(output, 'gray')
plt.subplot(1, 3, 3)
plt.imshow(mask, 'gray')
plt.show()
# -
|
examples/segmentation-example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Parameters and Hyperparameters of Fitted Models
# Load previously fitted models, and save their fitted parameters and used hyperparameters (default values or optimized via grid search) to CSV files for easy inspection!
# +
from pathlib import Path
import pickle
import pandas as pd
# -
# Directory conteining all results of "Molecular Similarity Survey".
dir_results = Path.cwd()
dir_models = Path(dir_results, "models_2D_3D")
dir_models_analysis = Path(dir_models, "analysis")
# ## Single Feature Models
# +
dir_single_feature_models = Path(dir_models, "single_feature_models")
names_single_feature_models = ["tanimoto_cdk_Extended", "TanimotoCombo"]
df_params_single_feature = []
for name in names_single_feature_models:
file_model = Path(dir_single_feature_models, f"{name}.pickle")
model = pickle.load(open(file_model, "rb"))
logreg = model.named_steps["logisticregression"]
params = {"model": name,
"coef": logreg.coef_[0, 0],
"intercept": logreg.intercept_[0]
}
df_params_single_feature.append(params)
df_params_single_feature = pd.DataFrame(df_params_single_feature)
df_params_single_feature
# -
file_params_single_feature = Path(dir_models_analysis,
"params_single_feature_models.csv")
df_params_single_feature.to_csv(file_params_single_feature, index=False)
# ## Double Feature Default Models
# +
dir_double_feature_default_models = Path(dir_models, "double_feature_default_models")
names_double_feature_default_models = ["noreg", "l1", "l2", "enet"]
n_features = 2
df_params_double_feature_default = []
for name in names_double_feature_default_models:
file_model = Path(dir_double_feature_default_models, f"{name}.pickle")
logreg = pickle.load(open(file_model, "rb"))
params = {"model": name}
params.update({f"coef{i}": logreg.coef_[0, i]
for i in range(n_features)})
params["intercept"] = logreg.intercept_[0]
params["C"] = logreg.C
params["l1_ratio"] = logreg.l1_ratio
df_params_double_feature_default.append(params)
df_params_double_feature_default = pd.DataFrame(df_params_double_feature_default)
df_params_double_feature_default
# -
file_params_double_feature_default = Path(dir_models_analysis,
"params_double_feature_default_models.csv")
df_params_double_feature_default.to_csv(file_params_double_feature_default, index=False)
# ## Double Feature Optimized Models
# +
dir_double_feature_optimized_models = Path(dir_models, "double_feature_optimized_models")
names_double_feature_optimized_models = ["l1", "l2", "enet"]
n_features = 2
df_params_double_feature_optimized = []
for name in names_double_feature_optimized_models:
file_model = Path(dir_double_feature_optimized_models, f"{name}.pickle")
logreg = pickle.load(open(file_model, "rb"))
params = {"model": name}
params.update({f"coef{i}": logreg.coef_[0, i]
for i in range(n_features)})
params["intercept"] = logreg.intercept_[0]
params["C"] = logreg.C
params["l1_ratio"] = logreg.l1_ratio
df_params_double_feature_optimized.append(params)
df_params_double_feature_optimized = pd.DataFrame(df_params_double_feature_optimized)
df_params_double_feature_optimized
# -
file_params_double_feature_optimized = Path(dir_models_analysis,
"params_double_feature_optimized_models.csv")
df_params_double_feature_optimized.to_csv(file_params_double_feature_optimized, index=False)
|
webapp/results_survey_molecular_similarity/.ipynb_checkpoints/analyze_parameters_models_2D_3D_01-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Lists
example1 = [1,2,3,4,]
example2 = ['a','b','c']
example3 = [1 , 'a', True]
x = ['M', 'O','N','T','Y',' ','P','Y','T','H','O','N']
print(x)
type(x)
x[0]
print(x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7], x[8], x[9], x[10], x[11])
x = [12, 43, 4, 1, 6, 343, 10]
x[0]
x[1]
x = [1.1, 3.5, 4.2, 9.4]
x[0]
x = ['himanshu', 'aggarwal', 'ironhack', 'data analysis']
x[0]
x = [1 , 'himanshu', 2.0, True]
x[0]
x[1]
x[3]
x = ['a', 'b', 'c', 'd', 'e', 'f', 'g']
x[:]
x[:3]
x[3:]
x[3:5]
x = [12, 43, 4, 1, 6, 343, 10]
len(x)
x[6]
x[len(x)-1]
x = [1, 1.1, 23, 5.3, 5, 8.3, 'hello', True]
len(x)
x = [1, 1.1, 23, 5.3, 5, 8.3, 'hello', True]
x.index('hello')
x.index(8.3)
print(x)
x.append('hello')
print(x)
x.append('there')
print(x)
print(x)
x.pop()
print(x)
x.pop()
print(x)
# # Exercises
# # 1.1
lst = [1,2,34,5,3,12,9, 8, 67, 89, 98, 90, 39, 21, 45, 46, 23, 13]
len(lst)
lst[0]
lst[17]
lst.index(90)
lst[0:8]
|
Jupyter/.ipynb_checkpoints/Python Data Structures - Lists-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#export
from nb_006b import *
from concurrent.futures import ProcessPoolExecutor
# # Camvid
# ## Setup
# +
PATH = Path('data/camvid')
PATH_X = PATH/'701_StillsRaw_full'
PATH_Y = PATH/'LabeledApproved_full'
PATH_Y_PROCESSED = PATH/'LabelProcessed'
label_csv = PATH/'label_colors.txt'
PATH_Y_PROCESSED.mkdir(exist_ok=True)
# -
list(PATH_Y.iterdir())[0]
def get_y_fn(x_fn): return PATH_Y/f'{x_fn.name[:-4]}_L.png'
def get_y_proc_fn(y_fn): return PATH_Y_PROCESSED/f'{y_fn.name[:-6]}_P.png'
x_fns = get_image_files(PATH_X)
y_fns = [get_y_fn(o) for o in x_fns]
y_proc_fns = [get_y_proc_fn(o) for o in y_fns]
x_fns[:3],y_fns[:3],y_proc_fns[:3]
def parse_code(l):
a,b = [c for c in l.strip().split("\t") if c]
return tuple(int(o) for o in a.split(' ')), b
label_codes,label_names = zip(*[parse_code(l) for l in open(PATH/"label_colors.txt")])
label_t = tensor(label_codes)
n_labels = len(label_codes)
label_codes[:5],label_names[:5], n_labels
# +
name2code = dict(zip(label_names, label_codes))
name2id = {v:k for k,v in enumerate(label_names)}
void_code = name2id['Void']
code2id = ByteTensor(255,255,255).zero_()+void_code
for i,code in enumerate(label_codes):
if not code == void_code: code2id[code]=i
# -
def colors_to_codes(color_data):
n = len(color_data)
idxs = tuple(color_data.reshape(n,-1).long())
return code2id[idxs].view(color_data.shape[1:])
i = 0
x_img = open_image(x_fns[i])
y_img_mask = open_mask(y_fns[i])
y_img = Image(y_img_mask.data.int())
y_code = colors_to_codes(y_img.data)
def codes_to_colors(label_data):
h,w = label_data.shape
idxs = label_data.flatten().long()
return Image(label_t.index_select(0, idxs).reshape(h,w,3).permute(2,0,1))
y_img2 = codes_to_colors(y_code)
y_img.show(), y_img2.show()
# +
def process_file(fns):
yfn, pfn = fns
if not pfn.exists():
y_data = open_mask(yfn).px.long()
proc_data = colors_to_codes(y_data)
img = PIL.Image.fromarray(proc_data.numpy())
img.save(pfn)
return pfn
def process_label_files(y_fns, y_proc_fns):
ex = ProcessPoolExecutor(16)
for pfn in ex.map(process_file, zip(y_fns, y_proc_fns)):
pass
# -
# %time process_label_files(y_fns, y_proc_fns)
def get_datasets(path, valid_pct=0.2):
x_fns = get_image_files(path)
y_fns = [get_y_fn(o) for o in x_fns]
y_proc_fns = [get_y_proc_fn(o) for o in y_fns]
total = len(x_fns)
train, valid = random_split(valid_pct, x_fns, y_proc_fns)
return (MatchedImageDataset(*train), MatchedImageDataset(*valid))
def get_tfm_datasets(size):
datasets = get_datasets(PATH_X)
tfms = get_transforms(do_flip=True, max_rotate=4, max_lighting=0.2)
return transform_datasets(*datasets, tfms=tfms, tfm_y=True, size=size)
default_norm,default_denorm = normalize_funcs(*imagenet_stats)
bs = 8
size = 512
tfms = get_transforms(do_flip=True, max_rotate=4, max_lighting=0.2)
def get_data(size, bs):
return DataBunch.create(*get_tfm_datasets(size), bs=bs, tfms=default_norm)
data = get_data(size, bs)
x, y = data.train_ds[0]
x.shape, y.shape, y.data.dtype
# ## Unet
def accuracy_no_void(input, target):
target = target.squeeze()
mask = target != void_code
return (input.argmax(dim=1)[mask]==target[mask]).float().mean()
accuracy_no_void(p,y)
metrics=[accuracy_no_void]
lr = 1e-3
body = create_body(tvm.resnet34(True), 2)
model = DynamicUnet(body, n_classes=len(label_codes)).cuda()
learn = Learner(data, model, metrics=metrics, loss_fn=CrossEntropyFlat())
learn.split([model[0][6], model[1]])
learn.freeze()
lr_find(learn)
learn.recorder.plot()
lr = 1e-2
learn.fit_one_cycle(6, slice(lr), pct_start=0.05)
learn.save('u0')
learn.load('u0')
x,y = next(iter(learn.data.valid_dl))
py = learn.model(x).detach()
py = py.softmax(dim=1).max(dim=1, keepdim=True)[1]
x,y,py = x.cpu(),y.cpu(),py.cpu()
x = default_denorm(x)
n = 4
fig, axs = plt.subplots(n,3,figsize=(10,10), sharey=True)
for i in range(n):
Image(x[i]).show(ax=axs[i][0])
codes_to_image(y[i].numpy()).show(ax=axs[i][1])
codes_to_image(py[i].numpy()).show(ax=axs[i][2])
learn.unfreeze()
lr=1e-2
learn.fit_one_cycle(6, slice(lr/100,lr), pct_start=0.05)
size=640
bs = 4
learn.data = get_data(size, bs)
# +
#learn.freeze()
# -
learn.fit_one_cycle(6, slice(lr), pct_start=0.05)
id2code
# ## Fin
|
dev_nb/006c_camvid.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# # T81-558: Applications of Deep Neural Networks
# **Class 12: Deep Learning Applications**
# * Instructor: [<NAME>](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
# * For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Tonight we will see how to apply deep learning networks to data science. There are many applications of deep learning. However, we will focus primarily upon data science. For this class we will go beyond simple academic examples and see how to construct an ensemble that could potentially lead to a high score on a Kaggle competition. We will see how to evaluate the importance of features and several ways to combine models.
#
# Tonights topics include:
#
# * Log Loss Error
# * Evaluating Feature Importance
# * The Biological Response Data Set
# * Neural Network Bagging
# * Nueral Network Ensemble
# # Helpful Functions from Previous Classes
#
# The following are utility functions from previous classes.
# +
from sklearn import preprocessing
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shutil
import os
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df,name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = "{}-{}".format(name,x)
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the origional column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df,name,target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x)==str(tv) else 0 for x in l]
name2 = "{}-{}".format(name,tv)
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df,name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df,name,mean=None,sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name]-mean)/sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df,target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
return df.as_matrix(result).astype(np.float32),df.as_matrix([target]).astype(np.int32)
else:
# Regression
return df.as_matrix(result).astype(np.float32),df.as_matrix([target]).astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return "{}:{:>02}:{:>05.2f}".format(h, m, s)
# Regression chart, we will see more of this chart in the next class.
def chart_regression(pred,y):
t = pd.DataFrame({'pred' : pred, 'y' : y_test.flatten()})
t.sort_values(by=['y'],inplace=True)
a = plt.plot(t['y'].tolist(),label='expected')
b = plt.plot(t['pred'].tolist(),label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Get a new directory to hold checkpoints from a neural network. This allows the neural network to be
# loaded later. If the erase param is set to true, the contents of the directory will be cleared.
def get_model_dir(name,erase):
base_path = os.path.join(".","dnn")
model_dir = os.path.join(base_path,name)
os.makedirs(model_dir,exist_ok=True)
if erase and len(model_dir)>4 and os.path.isdir(model_dir):
shutil.rmtree(model_dir,ignore_errors=True) # be careful, this deletes everything below the specified path
return model_dir
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name]-df[name].mean())>=(sd*df[name].std()))]
df.drop(drop_rows,axis=0,inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low =-1, normalized_high =1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# -
# # LogLoss Error
#
# Log loss is an error metric that is often used in place of accuracy for classification. Log loss allows for "partial credit" when a miss classification occurs. For example, a model might be used to classify A, B and C. The correct answer might be A, however if the classification network chose B as having the highest probability, then accuracy gives the neural network no credit for this classification.
#
# However, with log loss, the probability of the correct answer is added to the score. For example, the correct answer might be A, but if the neural network only predicted .8 probability of A being correct, then the value -log(.8) is added.
#
# $$ logloss = -\frac{1}{N}\sum^N_{i=1}\sum^M_{j=1}y_{ij} \log(\hat{y}_{ij}) $$
#
# The following table shows the logloss scores that correspond to the average predicted accuracy for the correct item. The **pred** column specifies the average probability for the correct class. The **logloss** column specifies the log loss for that probability.
#
# +
import numpy as np
import pandas as pd
from IPython.display import display, HTML
loss = [1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.075, 0.05, 0.025, 1e-8 ]
df = pd.DataFrame({'pred':loss, 'logloss': -np.log(loss)},columns=['pred','logloss'])
display(df)
# -
# The table below shows the opposit. For a given logloss, what is the average probability for the correct class.
# +
import numpy as np
import pandas as pd
from IPython.display import display, HTML
loss = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.5, 2, 2.5, 3, 3.5, 4 ]
df = pd.DataFrame({'logloss':loss, 'pred': np.exp(np.negative(loss))},
columns=['logloss','pred'])
display(df)
# -
# # Evaluating Feature Importance
#
# Feature importance tells us how important each of the features (from the feature/import vector are to the prediction of a neural network, or other model. There are many different ways to evaluate feature importance for neural networks. The following paper presents a very good (and readable) overview of the various means of evaluating the importance of neural network inputs/features.
#
# <NAME>., <NAME>., & <NAME>. (2004). [An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data](http://depts.washington.edu/oldenlab/wordpress/wp-content/uploads/2013/03/EcologicalModelling_2004.pdf). *Ecological Modelling*, 178(3), 389-397.
#
# In summary, the following methods are available to neural networks:
#
# * Connection Weights Algorithm
# * Partial Derivatives
# * Input Perturbation
# * Sensitivity Analysis
# * Forward Stepwise Addition
# * Improved Stepwise Selection 1
# * Backward Stepwise Elimination
# * Improved Stepwise Selection
#
# For this class we will use the **Input Perturbation** feature ranking algorithm. This algorithm will work with any regression or classification network. implementation of the input perturbation algorithm for scikit-learn is given in the next section. This algorithm is implemented in a function below that will work with any scikit-learn model.
#
# This algorithm was introduced by [Breiman](https://en.wikipedia.org/wiki/Leo_Breiman) in his seminal paper on random forests. Although he presented this algorithm in conjunction with random forests, it is model-independent and appropriate for any supervised learning model. This algorithm, known as the input perturbation algorithm, works by evaluating a trained model’s accuracy with each of the inputs individually shuffled from a data set. Shuffling an input causes it to become useless—effectively removing it from the model. More important inputs will produce a less accurate score when they are removed by shuffling them. This process makes sense, because important features will contribute to the accuracy of the model.
#
# The provided algorithm will use logloss to evaluate a classification problem and RMSE for regression.
# +
from sklearn import metrics
import scipy as sp
import numpy as np
import math
def mlogloss(y_test, preds):
epsilon = 1e-15
sum = 0
for row in zip(preds,y_test):
x = row[0][row[1]]
x = max(epsilon,x)
x = min(1-epsilon,x)
sum+=math.log(x)
return( (-1/len(preds))*sum)
def perturbation_rank(model, x, y, names, regression):
errors = []
for i in range(x.shape[1]):
hold = np.array(x[:, i])
np.random.shuffle(x[:, i])
if regression:
# The following code is only needed until Google fixes SKCOMPAT
# pred = model.predict(x)
pred = list(model.predict(x_test, as_iterable=True))
error = metrics.mean_squared_error(y, pred)
else:
# The following code is only needed until Google fixes SKCOMPAT
# pred = model.predict_proba(x)
pred = list(model.predict_proba(x_test, as_iterable=True))
error = mlogloss(y, pred)
errors.append(error)
x[:, i] = hold
max_error = np.max(errors)
importance = [e/max_error for e in errors]
data = {'name':names,'error':errors,'importance':importance}
result = pd.DataFrame(data, columns = ['name','error','importance'])
result.sort_values(by=['importance'], ascending=[0], inplace=True)
return result
# -
# ### Classification Input Perturbation Ranking
# +
# Classification ranking
import os
import pandas as pd
from sklearn.model_selection import train_test_split
import tensorflow as tf
import tensorflow.contrib.learn as learn
import numpy as np
from tensorflow.contrib.learn.python.learn.metric_spec import MetricSpec
# Set the desired TensorFlow output level for this example
tf.logging.set_verbosity(tf.logging.INFO)
path = "./data/"
filename = os.path.join(path,"iris.csv")
df = pd.read_csv(filename,na_values=['NA','?'])
# Encode feature vector
encode_numeric_zscore(df,'petal_w')
encode_numeric_zscore(df,'petal_l')
encode_numeric_zscore(df,'sepal_w')
encode_numeric_zscore(df,'sepal_l')
species = encode_text_index(df,"species")
num_classes = len(species)
# Create x & y for training
# Create the x-side (feature vectors) of the training
x, y = to_xy(df,'species')
# Split into train/test
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.25, random_state=45)
# Get/clear a directory to store the neural network to
model_dir = get_model_dir('iris',True)
# Create a deep neural network with 3 hidden layers of 10, 20, 5
feature_columns = [tf.contrib.layers.real_valued_column("", dimension=x.shape[1])]
classifier = learn.DNNClassifier(
model_dir= model_dir,
config=tf.contrib.learn.RunConfig(save_checkpoints_secs=1),
hidden_units=[10, 20, 5], n_classes=num_classes, feature_columns=feature_columns)
# Might be needed in future versions of "TensorFlow Learn"
#classifier = learn.SKCompat(classifier) # For Sklearn compatibility
# Early stopping
validation_monitor = tf.contrib.learn.monitors.ValidationMonitor(
x_test,
y_test,
every_n_steps=500,
#metrics=validation_metrics,
early_stopping_metric="loss",
early_stopping_metric_minimize=True,
early_stopping_rounds=50)
# Fit/train neural network
classifier.fit(x_train, y_train,monitors=[validation_monitor],steps=10000)
# +
# Set the desired TensorFlow output level for this example
tf.logging.set_verbosity(tf.logging.ERROR)
# Rank the features
from IPython.display import display, HTML
names = df.columns.values[0:-1] # x column names
rank = perturbation_rank(classifier, x_test, y_test, names, False)
display(rank)
# -
# ### Regression Input Perturbation Ranking
# +
import tensorflow as tf
import tensorflow.contrib.learn as learn
from sklearn.model_selection import train_test_split
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from scipy.stats import zscore
path = "./data/"
# Set the desired TensorFlow output level for this example
tf.logging.set_verbosity(tf.logging.INFO)
filename_read = os.path.join(path,"auto-mpg.csv")
df = pd.read_csv(filename_read,na_values=['NA','?'])
# create feature vector
missing_median(df, 'horsepower')
df.drop('name',1,inplace=True)
encode_numeric_zscore(df, 'horsepower')
encode_numeric_zscore(df, 'weight')
encode_numeric_zscore(df, 'cylinders')
encode_numeric_zscore(df, 'displacement')
encode_numeric_zscore(df, 'acceleration')
encode_text_dummy(df, 'origin')
# Encode to a 2D matrix for training
x,y = to_xy(df,'mpg')
# Split into train/test
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.20, random_state=42)
# Get/clear a directory to store the neural network to
model_dir = get_model_dir('mpg',True)
# Create a deep neural network with 3 hidden layers of 50, 25, 10
feature_columns = [tf.contrib.layers.real_valued_column("", dimension=x.shape[1])]
regressor = learn.DNNRegressor(
model_dir= model_dir,
config=tf.contrib.learn.RunConfig(save_checkpoints_secs=1),
feature_columns=feature_columns,
hidden_units=[50, 25, 10])
# Might be needed in future versions of "TensorFlow Learn"
#classifier = learn.SKCompat(classifier) # For Sklearn compatibility
# Early stopping
validation_monitor = tf.contrib.learn.monitors.ValidationMonitor(
x_test,
y_test,
every_n_steps=500,
early_stopping_metric="loss",
early_stopping_metric_minimize=True,
early_stopping_rounds=50)
# Fit/train neural network
regressor.fit(x_train, y_train,monitors=[validation_monitor],steps=10000)
# +
# Set the desired TensorFlow output level for this example
tf.logging.set_verbosity(tf.logging.ERROR)
# Rank the features
from IPython.display import display, HTML
names = df.columns.values[1:] # x column names
rank = perturbation_rank(regressor, x_test, y_test, names, True)
display(rank)
# -
# # The Biological Response Data Set
#
# * [Biological Response Dataset at Kaggle](https://www.kaggle.com/c/bioresponse)
# * [1st place interview for Boehringer Ingelheim Biological Response](http://blog.kaggle.com/2012/07/05/1st-place-interview-for-boehringer-ingelheim-biological-response/)
# +
import tensorflow.contrib.learn as skflow
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from scipy.stats import zscore
from sklearn.model_selection import KFold
from IPython.display import HTML, display
path = "./data/"
filename_train = os.path.join(path,"bio_train.csv")
filename_test = os.path.join(path,"bio_test.csv")
filename_submit = os.path.join(path,"bio_submit.csv")
df_train = pd.read_csv(filename_train,na_values=['NA','?'])
df_test = pd.read_csv(filename_test,na_values=['NA','?'])
activity_classes = encode_text_index(df_train,'Activity')
#display(df_train)
# -
# ### Biological Response with Neural Network
# +
import os
import pandas as pd
import tensorflow as tf
import tensorflow.contrib.learn as learn
from sklearn.model_selection import train_test_split
import tensorflow.contrib.learn as skflow
import numpy as np
import sklearn
# Set the desired TensorFlow output level for this example
tf.logging.set_verbosity(tf.logging.ERROR)
# Encode feature vector
x, y = to_xy(df_train,'Activity')
x_submit = df_test.as_matrix().astype(np.float32)
num_classes = len(activity_classes)
# Split into train/test
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.25, random_state=42)
# Get/clear a directory to store the neural network to
model_dir = get_model_dir('bio',True)
# Create a deep neural network with 4 hidden layers of [500, 250, 100, 50]
feature_columns = [tf.contrib.layers.real_valued_column("", dimension=x.shape[1])]
classifier = learn.DNNClassifier(
model_dir= model_dir,
config=tf.contrib.learn.RunConfig(save_checkpoints_secs=60),
hidden_units=[500, 250, 100, 50], n_classes=num_classes, feature_columns=feature_columns)
# Might be needed in future versions of "TensorFlow Learn"
#classifier = learn.SKCompat(classifier) # For Sklearn compatibility
# Early stopping
validation_monitor = tf.contrib.learn.monitors.ValidationMonitor(
x_test,
y_test,
every_n_steps=500,
#metrics=validation_metrics,
early_stopping_metric="loss",
early_stopping_metric_minimize=True,
early_stopping_rounds=50)
# Fit/train neural network
print("Fitting/Training...")
classifier.fit(x_train, y_train,monitors=[validation_monitor],steps=10000)
print("Fitting done...")
# Give logloss error
pred = np.array(list(classifier.predict_proba(x_test, as_iterable=True)))
pred = pred[:,1]
# Clip so that min is never exactly 0, max never 1
pred = np.clip(pred,a_min=1e-6,a_max=(1-1e-6))
print("Validation logloss: {}".format(sklearn.metrics.log_loss(y_test,pred)))
# Evaluate success using accuracy
pred = list(classifier.predict(x_test, as_iterable=True))
score = metrics.accuracy_score(y_test, pred)
print("Validation accuracy score: {}".format(score))
# Build a submission file
pred_submit = np.array(list(classifier.predict_proba(x_submit, as_iterable=True)))
pred_submit = pred_submit[:,1]
# Clip so that min is never exactly 0, max never 1
pred = np.clip(pred,a_min=1e-6,a_max=(1-1e-6))
submit_df = pd.DataFrame({'MoleculeId':[x+1 for x in range(len(pred_submit))],'PredictedProbability':pred_submit})
submit_df.to_csv(filename_submit, index=False)
# -
pred = np.array(list(classifier.predict_proba(x_test, as_iterable=True)))
pred = pred[:,1]
print(np.array(list(zip(pred,y_test))))
# # What Features/Columns are Important
#
# The following uses perturbation ranking to evaluate the neural network.
# +
# Set the desired TensorFlow output level for this example
tf.logging.set_verbosity(tf.logging.ERROR)
# Rank the features
from IPython.display import display, HTML
names = df_train.columns.values[0:-1] # x column names
rank = perturbation_rank(classifier, x_test, y_test, names, False)
display(rank)
# -
# ### Biological Response with Random Forest
# +
# Random Forest
from sklearn.ensemble import RandomForestClassifier
import sklearn
x, y = to_xy(df_train,'Activity')
y = y.ravel() # Make y just a 1D array, as required by random forest
x_test = df_test.as_matrix().astype(np.float32)
rf = RandomForestClassifier(n_estimators=100)
rf.fit(x, y)
pred = rf.predict_proba(x_test)
pred = pred[:,1]
pred_insample = rf.predict_proba(x)
pred_insample = pred_insample[:,1]
submit_df = pd.DataFrame({'MoleculeId':[x+1 for x in range(len(pred))],'PredictedProbability':pred})
submit_df.to_csv(filename_submit, index=False)
print("Insample logloss: {}".format(sklearn.metrics.log_loss(y,pred_insample)))
#display(submit_df)
# -
# # Neural Network Bagging
#
# Neural networks will typically achieve better results when they are bagged. Bagging a neural network is a process where the same neural network is trained over and over and the results are averaged together.
# +
import numpy as np
import os
import pandas as pd
import math
from sklearn.neighbors import KNeighborsClassifier
from sklearn.cross_validation import StratifiedKFold
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
import tensorflow.contrib.learn as learn
PATH = "./data/"
SHUFFLE = False
FOLDS = 10
def mlogloss(y_test, preds):
epsilon = 1e-15
sum = 0
for row in zip(preds,y_test):
x = row[0][row[1]]
x = max(epsilon,x)
x = min(1-epsilon,x)
sum+=math.log(x)
return( (-1/len(preds))*sum)
def stretch(y):
return (y - y.min()) / (y.max() - y.min())
def blend_ensemble(x, y, x_submit):
folds = list(StratifiedKFold(y, FOLDS))
feature_columns = [tf.contrib.layers.real_valued_column("", dimension=x.shape[0])]
models = [
learn.DNNClassifier(hidden_units=[100, 50, 25, 5], n_classes=2, feature_columns=feature_columns), # steps=1000
learn.DNNClassifier(hidden_units=[100, 50, 25, 5], n_classes=2, feature_columns=feature_columns), # steps=500
learn.DNNClassifier(hidden_units=[200, 100, 50, 25], n_classes=2, feature_columns=feature_columns), # steps=1000
learn.DNNClassifier(hidden_units=[200, 100, 50, 25], n_classes=2, feature_columns=feature_columns), # steps=500
learn.DNNClassifier(hidden_units=[50, 25, 5], n_classes=2, feature_columns=feature_columns)] #steps=500
dataset_blend_train = np.zeros((x.shape[0], len(models)))
dataset_blend_test = np.zeros((x_submit.shape[0], len(models)))
for j, model in enumerate(models):
print("Model: {} : {}".format(j, model) )
fold_sums = np.zeros((x_submit.shape[0], len(folds)))
total_loss = 0
for i, (train, test) in enumerate(folds):
x_train = x[train]
y_train = y[train]
x_test = x[test]
y_test = y[test]
model.fit(x_train, y_train,steps=10)
pred = np.array(list(classifier.predict_proba(x_test, as_iterable=True)))
# pred = model.predict_proba(x_test)
dataset_blend_train[test, j] = pred[:, 1]
pred2 = np.array(list(classifier.predict_proba(x_submit, as_iterable=True)))
#fold_sums[:, i] = model.predict_proba(x_submit)[:, 1]
fold_sums[:, i] = pred2[:, 1]
loss = mlogloss(y_test, pred)
total_loss+=loss
print("Fold #{}: loss={}".format(i,loss))
print("{}: Mean loss={}".format(model.__class__.__name__,total_loss/len(folds)))
dataset_blend_test[:, j] = fold_sums.mean(1)
print()
print("Blending models.")
blend = LogisticRegression()
blend.fit(dataset_blend_train, y)
return blend.predict_proba(dataset_blend_test)
if __name__ == '__main__':
np.random.seed(42) # seed to shuffle the train set
print("Loading data...")
filename_train = os.path.join(PATH, "bio_train.csv")
df_train = pd.read_csv(filename_train, na_values=['NA', '?'])
filename_submit = os.path.join(PATH, "bio_test.csv")
df_submit = pd.read_csv(filename_submit, na_values=['NA', '?'])
predictors = list(df_train.columns.values)
predictors.remove('Activity')
x = df_train.as_matrix(predictors)
y = df_train['Activity']
x_submit = df_submit.as_matrix()
if SHUFFLE:
idx = np.random.permutation(y.size)
x = x[idx]
y = y[idx]
submit_data = blend_ensemble(x, y, x_submit)
submit_data = stretch(submit_data)
####################
# Build submit file
####################
ids = [id+1 for id in range(submit_data.shape[0])]
submit_filename = os.path.join(PATH, "bio_submit.csv")
submit_df = pd.DataFrame({'MoleculeId': ids, 'PredictedProbability': submit_data[:, 1]},
columns=['MoleculeId','PredictedProbability'])
submit_df.to_csv(submit_filename, index=False)
# -
# # Neural Network Ensemble
#
# A neural network ensemble combines neural network predictions with other models. The exact blend of all of these models is determined by logistic regression. The following code performs this blend for a classification.
# +
import numpy as np
import os
import pandas as pd
import math
from sklearn.neighbors import KNeighborsClassifier
from sklearn.cross_validation import StratifiedKFold
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
import tensorflow.contrib.learn as learn
import tensorflow as tf
PATH = "./data/"
SHUFFLE = False
FOLDS = 10
def mlogloss(y_test, preds):
epsilon = 1e-15
sum = 0
for row in zip(preds,y_test):
x = row[0][row[1]]
x = max(epsilon,x)
x = min(1-epsilon,x)
sum+=math.log(x)
return( (-1/len(preds))*sum)
def stretch(y):
return (y - y.min()) / (y.max() - y.min())
def blend_ensemble(x, y, x_submit):
folds = list(StratifiedKFold(y, FOLDS))
feature_columns = [tf.contrib.layers.real_valued_column("", dimension=x.shape[1])]
models = [
learn.DNNClassifier(hidden_units=[100, 50, 25, 5], n_classes=2, feature_columns=feature_columns),
KNeighborsClassifier(n_neighbors=3),
RandomForestClassifier(n_estimators=100, n_jobs=-1, criterion='gini'),
RandomForestClassifier(n_estimators=100, n_jobs=-1, criterion='entropy'),
ExtraTreesClassifier(n_estimators=100, n_jobs=-1, criterion='gini'),
ExtraTreesClassifier(n_estimators=100, n_jobs=-1, criterion='entropy'),
GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=50)]
dataset_blend_train = np.zeros((x.shape[0], len(models)))
dataset_blend_test = np.zeros((x_submit.shape[0], len(models)))
for j, model in enumerate(models):
print("Model: {} : {}".format(j, model) )
fold_sums = np.zeros((x_submit.shape[0], len(folds)))
total_loss = 0
for i, (train, test) in enumerate(folds):
x_train = x[train]
y_train = y[train]
x_test = x[test]
y_test = y[test]
if type(model) == tf.contrib.learn.python.learn.estimators.dnn.DNNClassifier:
model.fit(x_train, y_train,steps=10)
pred = np.array(list(classifier.predict_proba(x_test, as_iterable=True)))
pred2 = np.array(list(classifier.predict_proba(x_submit, as_iterable=True)))
else:
model.fit(x_train, y_train)
pred = model.predict_proba(x_test)
pred2 = model.predict_proba(x_submit)
dataset_blend_train[test, j] = pred[:, 1]
fold_sums[:, i] = pred2[:, 1]
loss = mlogloss(y_test, pred)
total_loss+=loss
print("Fold #{}: loss={}".format(i,loss))
print("{}: Mean loss={}".format(model.__class__.__name__,total_loss/len(folds)))
dataset_blend_test[:, j] = fold_sums.mean(1)
print()
print("Blending models.")
blend = LogisticRegression()
blend.fit(dataset_blend_train, y)
return blend.predict_proba(dataset_blend_test)
if __name__ == '__main__':
np.random.seed(42) # seed to shuffle the train set
print("Loading data...")
filename_train = os.path.join(PATH, "bio_train.csv")
df_train = pd.read_csv(filename_train, na_values=['NA', '?'])
filename_submit = os.path.join(PATH, "bio_test.csv")
df_submit = pd.read_csv(filename_submit, na_values=['NA', '?'])
predictors = list(df_train.columns.values)
predictors.remove('Activity')
x = df_train.as_matrix(predictors)
y = df_train['Activity']
x_submit = df_submit.as_matrix()
if SHUFFLE:
idx = np.random.permutation(y.size)
x = x[idx]
y = y[idx]
submit_data = blend_ensemble(x, y, x_submit)
submit_data = stretch(submit_data)
####################
# Build submit file
####################
ids = [id+1 for id in range(submit_data.shape[0])]
submit_filename = os.path.join(PATH, "bio_submit.csv")
submit_df = pd.DataFrame({'MoleculeId': ids, 'PredictedProbability': submit_data[:, 1]},
columns=['MoleculeId','PredictedProbability'])
submit_df.to_csv(submit_filename, index=False)
# -
|
t81_558_class12_app.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Time: O(n)
# Space: O(1)
def find_unique_element(arr):
unique = arr[0]
for i in range(1, len(arr)):
unique ^= arr[i]
return unique
if __name__=='__main__':
tc = [[6,2,4,3,4,2,3],
[-1,2,-1,3,2],
[9,4,9,6,4]]
for t in tc:
print(find_unique_element(t))
# -
|
assignments/array/Xor method to find the element that occurs one.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Market implied price surfaces: v1
#
# What combination of varibles does a current price imply?
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
import xlwings as xw
from tqdm import tqdm
import dtale
plt.rcParams["figure.figsize"] = (15, 10)
plt.style.use("seaborn-deep")
# -
wb = xw.Book('data/SPValueCorona.xlsx')
sht = wb.sheets["Valuing the Index"]
# +
curr_level_cell = sht.range("C4")
cash_ret_cell = sht.range("C6")
earn_drop_cell = sht.range("C7")
earn_growth_cell = sht.range("C8")
risk_free_cell = sht.range("C9")
value_cell = sht.range("C16")
# -
# Set inputs
risk_free_cell.value = 0.015
curr_level_cell.value = 2475.56
earn_growth.value = 0.048
# Partial derivatives
# Three variables that probably matter:
cash_ret_init = cash_ret_cell.value
earn_drop_init = earn_drop_cell.value
earn_growth_init = earn_growth_cell.value
# to reset
cash_ret_cell.value = cash_ret_init
earn_drop_cell.value = earn_drop_init
earn_growth_cell.value = earn_growth_init
# +
# Value vs earnings drop
earn_drop_range = np.linspace(-0.5, 0, 50)
values_earn_drop = []
for drop in tqdm(earn_drop_range):
earn_drop_cell.value = drop
values_earn_drop.append(value_cell.value)
earn_drop_cell.value = earn_drop_init
# -
plt.plot(earn_drop_range, values_earn_drop)
# Change per % drop in earnings
grad_earn_drop = np.polyfit(earn_drop_range, np.array(values_earn_drop), 1)[0]/100
print(grad_earn_drop)
# Value vs y2-5 growth
earn_growth_range = np.linspace(0, 0.05, 50)
values_earn_growth = []
for growth in tqdm(earn_growth_range):
earn_growth_cell.value = growth
values_earn_growth.append(value_cell.value)
plt.plot(earn_growth_range, values_earn_growth)
grad = np.polyfit(earn_growth_range, np.array(values_earn_growth), 1)[0]/100
print(grad)
# Generate data
wb.app.calculation = "manual"
results = []
n_res = 50
counter = 0
for drop in np.linspace(-0.5, 0, n_res):
counter +=1
if counter % 5 == 0:
print(".")
for growth in (np.linspace(0, 0.25, n_res)):
earn_growth_cell.value = growth
earn_drop_cell.value = drop
wb.app.calculate()
results.append([growth, drop, value_cell.value])
print("Done")
df = pd.DataFrame(results, columns=["earn_growth", "earn_drop", "value"])
df.head()
df.to_csv("excel/mc_value_vs_growth_drop.csv", index=None)
mesh = pd.pivot_table(df, values="value", index="earn_drop", columns="earn_growth")
mesh.head()
plt.figure(facecolor="w")
sns.heatmap(data=mesh,
xticklabels=mesh.columns.values.round(3),
yticklabels=mesh.index.values.round(3))
# +
# Get projection line
# currprice = mesh[(mesh < 2500) & (mesh > 2450)]
# currprice
# price_implied_drops = []
# for col in currprice.columns:
# try:
# price_implied_drops.append(currprice.index[currprice[col].notnull()].values.mean())
# except:
# price_implied_drops.append(price_implied_drops[-1])
# -
plt.figure()
plt.plot(currprice.columns.values, np.array(price_implied_drops))
plt.xlabel("y2-5 growth")
plt.ylabel("Earnings drop")
plt.title("Contour for S&P = 2475")
plt.show()
# +
plt.rcParams.update({'font.size': 18})
fig, ax = plt.subplots(facecolor="w")
# levels = list(range(1500, 2301, 250)) + list(range(2350, 2551, 50)) + list(range(2600, 4501, 500))
levels = [1500, 1750] + list(range(2000, 3000, 150)) + [3100, 3400] + list(range(3750, 6000, 500))
CS = ax.contour(mesh.columns, mesh.index, mesh.values.round(2), levels=levels, linewidths=6)
clabel_pos = []
for x in [0.01, 0.2, 0.04, 0.06, 0.07, 0.08, 0.09, 0.1, 0.11, 0.12, 0.13, 0.14, 0.16, 0.18]:
clabel_pos.append((x, 2*x -0.5))
plt.clabel(CS,fmt="%1.0f", fontsize=22, manual=clabel_pos)
ax.set_ylabel("FY2020 Earnings", labelpad=20)
ax.set_xlabel("FY2021-2024 growth", labelpad=20)
ax.set_yticklabels([f"{100*y:.0f}%" for y in ax.get_yticks()])
ax.set_xticklabels([f"{100*x:.0f}%" for x in ax.get_xticks()])
ax.set_title("Intrinsic value of the S&P500", pad=20)
plt.savefig("spy_earnings_growth_contour.png", bbox_inches='tight', dpi=600)
plt.show()
# -
# %matplotlib notebook
fig = plt.figure()
ax = Axes3D(fig)
# ax.trisurf(mesh.index, mesh.columns, mesh.values)
ax.plot_trisurf(df.earn_drop, df.earn_growth, df.value, cmap="viridis")
ax.set_title('Surface plot')
ax.set_xlabel('Drop in 2020 earnings')
ax.set_ylabel('y2-5 earnings growth')
ax.set_zlabel('S&P value')
plt.show()
# ## Contours
#
# What combinations of earnings growth and drop explain the current market price? This is represented by a contour in drop/growth space.
|
MarketImpliedSurfaces/SPY_Corona_v1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # PSE disclosures
from fastquant import DisclosuresPSE
# ## fetching company disclosures
dpse = DisclosuresPSE(symbol='JFC',
start_date='1-1-2020',
end_date='5-1-2020'
)
dpse
# summary of each disclosure
dpse.company_disclosures.head()
# includes details
dpse.disclosures_combined.head()
#get details in each disclosure given edge_no
dpse.disclosure_tables['a5df62b1a9558fe60de8473cebbd6407'].shape
dpse.disclosures_combined['Subject of the Disclosure']
dpse.disclosures_combined['Background/Description of the Disclosure']
# ## visualization
dpse.disclosure_types
#all disclosures superposed with percent change
fig = dpse.plot_disclosures()
#all disclosures superposed with close price
fig = dpse.plot_disclosures(indicator='close', diff=False, percent=False)
# ## filtering disclosures
#disclosures co-incident with max percent change
maximum = dpse.filter_disclosures()
maximum
#disclosures co-incident with min percent change
minimum = dpse.filter_disclosures(operation='min')
minimum
#what happened then?
maximum['Background/Description of the Disclosure'].values
#details
maximum['Subject of the Disclosure'].values
#get url
maximum['url'].values
#what happened during minimum?
minimum['Background/Description of the Disclosure'].values
#details
minimum['Subject of the Disclosure'].values
#get url
minimum['url'].values
# # Investagrams disclosures
from fastquant import DisclosuresInvestagrams
dinv = DisclosuresInvestagrams(symbol='JFC', from_date='2018-01-01', to_date='2020-04-01')
dinv.dividends
dinv.earnings
# # disclosures-based strategy (under development)
# + active=""
# !pip install backtrader[plotting]
# + active=""
# import pandas as pd
# from fastquant import backtest
#
# df = pd.read_csv("../data/JFC_20180101_20190110_DCV.csv")
#
# backtest('smac', df, fast_period=15, slow_period=40)
# +
from fastquant import BaseStrategy, DisclosuresPSE
class DisclosuresStrategy(BaseStrategy):
"""
Disclosure-based trading strategy
Parameters
----------
"""
params = (
("fast_period", 10), # period for the fast moving average
("slow_period", 30),
)
def __init__(self):
# Initialize global variables
super().__init__()
# Strategy level variables
self.fast_period = self.params.fast_period
self.slow_period = self.params.slow_period
print("===Strategy level arguments===")
print("fast_period :", self.fast_period)
print("slow_period :", self.slow_period)
sma_fast = bt.ind.SMA(period=self.fast_period) # fast moving average
sma_slow = bt.ind.SMA(period=self.slow_period) # slow moving average
self.crossover = bt.ind.CrossOver(
sma_fast, sma_slow
) # crossover signal
def buy_signal(self):
return self.crossover > 0
def sell_signal(self):
return self.crossover < 0
# + active=""
# cols = "datetime open high low close volume openinterest".split()
#
# def parse_data_format(format):
# data_format = {}
# for n,col in enumerate(cols):
# for f in format:
# if col[0]==f:
# data_format[col] = n
# else:
# data_format[col] = None
# return data_format
# -
DATA_FORMAT_MAPPING= {"dcv": {
"datetime": 0,
"open": None,
"high": None,
"low": None,
"close": 1,
"volume": 2,
"openinterest": None},
"dohlc": {
"datetime": 0,
"open": 1,
"high": 2,
"low": 3,
"close": 4,
"volume": None,
"openinterest": None
}
}
# +
from fastquant import get_stock_data
data = get_stock_data("JFC",
start_date="2019-01-01",
end_date="2020-01-01",
format="dohlc"
)
data.head()
# + active=""
# from datetime import datetime
# import pandas as pd
# import backtrader as bt
# import backtrader.feeds as btfeed
#
# from fastquant import DATA_FILE, COMMISSION_PER_TRANSACTION, INIT_CASH
# from fastquant import STRATEGY_MAPPING
#
# cerebro = bt.Cerebro(stdstats=False)
# # cerebro.addobserver(bt.observers.Broker)
# # cerebro.addobserver(bt.observers.Trades)
# # cerebro.addobserver(bt.observers.BuySell)
#
# cerebro.addstrategy(DisclosuresStrategy,
# #STRATEGY_MAPPING["rsi"],
# init_cash=INIT_CASH)
#
# cerebro.broker.setcommission(commission=COMMISSION_PER_TRANSACTION)
#
# pd_data = bt.feeds.PandasData(dataname=data,
# fromdate=datetime(2019, 1, 1),
# todate=datetime(2020, 1, 1),
# **DATA_FORMAT_MAPPING["dohlc"]
#
# )
#
# cerebro.adddata(pd_data)
# cerebro.broker.setcash(INIT_CASH)
# # Allows us to set buy price based on next day closing
# # (technically impossible, but reasonable assuming you use all your money to buy market at the end of the next day)
# cerebro.broker.set_coc(True)
# print("Starting Portfolio Value: %.2f" % cerebro.broker.getvalue())
# cerebro.run()
# print("Final Portfolio Value: %.2f" % cerebro.broker.getvalue())
#
# # fig = pl.figure(figsize=(20, 10))
# # cerebro.plot()
# -
|
examples/disclosures.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Timeline
#
# [![open_in_colab][colab_badge]][colab_notebook_link]
# [![open_in_binder][binder_badge]][binder_notebook_link]
#
# [colab_badge]: https://colab.research.google.com/assets/colab-badge.svg
# [colab_notebook_link]: https://colab.research.google.com/github/UnfoldedInc/examples/blob/master/notebooks/06%20-%20Timeline.ipynb
# [binder_badge]: https://mybinder.org/badge_logo.svg
# [binder_notebook_link]: https://mybinder.org/v2/gh/UnfoldedInc/examples/master?urlpath=lab/tree/notebooks/06%20-%20Timeline.ipynb
# Unfolded Studio supports [time playback for temporal analytics](https://docs.unfolded.ai/studio/map-guide/playback). If you have a column in your dataset with temporal data, you can add a filter to it and it will be displayed as an interactive timeline over the map. Unfolded Map SDK makes it possible to control this filter remotely.
# ## Dependencies
#
# This notebook requires the following Python dependencies:
#
# - `unfolded.map-sdk`: The Unfolded Map SDK
# - `pandas`: DataFrame library
#
# If running this notebook in Binder, these dependencies should already be installed. If running in Colab, the next cell will install these dependencies.
# If in Colab, install this notebook's required dependencies
import sys
if "google.colab" in sys.modules:
# !pip install 'unfolded.map_sdk>=0.6.0' pandas
# ## Imports
from unfolded.map_sdk import UnfoldedMap
from datetime import datetime
import pandas as pd
# ## Using Map Timelines
# First, create a map and add data to it:
unfolded_map = UnfoldedMap(height=600)
unfolded_map
url = 'https://raw.githubusercontent.com/UnfoldedInc/examples/master/notebooks/data/earthquakes.csv'
df = pd.read_csv(url)
unfolded_map.add_dataset({
'label': 'Earthquakes',
'data': df
})
# ## Updating timeline range
# First, let's convert the `DateTime` column to [`datetime`](https://docs.python.org/3/library/datetime.html):
df['DateTime']= pd.to_datetime(df['DateTime'])
# Now we can calculate the time extent:
time_extent = [df['DateTime'].min(), df['DateTime'].max()]
time_extent
# Here we add a `DateTime` filter to the map:
unfolded_map.set_filter({
'id': 'time-filter',
'field': 'DateTime',
'value': [
time_extent[0].timestamp() * 1000,
time_extent[1].timestamp() * 1000,
]
})
# Once you execute the above, you should see the timeline appear in the map.
# ## Controlling the timeline
# Once we have added the timeline filter we can use [`set_timeline_config()`](https://docs.unfolded.ai/map-sdk/api/set-timeline-config) which offers more possibilities to control the timeline:
# + tags=[]
unfolded_map.set_timeline_config({
'idx': 0,
'current_time_interval': {
'start_time': time_extent[0].timestamp() * 1000,
'end_time': time_extent[1].timestamp() * 1000
},
'is_visible': True
})
# -
# This function [offers more possibilities](https://docs.unfolded.ai/map-sdk/api/set-timeline-config) to control the timeline.
# ## Animating the timeline
# Let's first set the timeline to a narrower range:
# + tags=[]
unfolded_map.set_timeline_config({
'idx': 0,
'current_time_interval': {
'start_time': datetime(1967,1,1).timestamp() * 1000,
'end_time': datetime(1968,1,1).timestamp() * 1000
},
'is_visible': True
})
# -
# Now we can start the animation:
unfolded_map.set_timeline_config({
'idx': 0,
'is_animating': True,
'speed': 1
})
# We can also hide the timeline:
unfolded_map.set_timeline_config({
'idx': 0,
'is_visible': False
})
# Now let's stop the animation and display the timeline back:
unfolded_map.set_timeline_config({
'idx': 0,
'is_animating': False,
'is_visible': True
})
|
notebooks/06 - Timeline.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction to Data Science
# In this project, you will be applying to CRISP-DM (Cross-industry Process for Data Mining) methodology to solve data science problem. The methodology has six steps:
# 1. Business understanding
# 2. Data understanding
# 3. Data preparation
# 4. Modeling
# 5. Evaluation
# 6. Deployment
#
# #### 1. Business Understanding
# While various digital marketing tools make it easier to track online behavior, consumers' offline behavior is hard to collect and even harder to draw insights from. However, abundance of geospatial data from mobile devices can help us determining consumers' offline behavior. The insights draw from the analysis can help brands to strategize their marketing plan for Out-of-Home (OOH) marketing and advertising. Questions that we're trying to answer are listed below:
# 1. Which billboards have the highest potential reach i.e. number of unique audiences?
# 2. When (time of the day) are the audiences most likely to see the advertisement?
# 3. Where should I build my next billboard?
#
# #### 2. Data Understanding
# There are three data sources:
# 1. Consumer Data: Data originated from consumers' devices which provide coordinates and the timestamp
# 2. Survey Data: Data i.e. map of subdistricts surveyed by city officials or government
# 3. Billboard Locations: Coordinates for billboards
# This project focuses on spatiotemporal analysis, and will ignore categorical variables that are present in consumer data.
#
# **Note:** Due to large volume of consumer data, a sample data file is uploaded.
#
|
Project_1/.ipynb_checkpoints/README.md-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Get the HPS model to run
# - get the inputs correct
# - run through all steps
# - get an accuracy estimate
# %matplotlib inline
# +
import os
import sys
sys.path.append('/home/surchs/git/Proteus/')
from proteus.predic import high_confidence
#from proteus.predic import prediction
import numpy as np
import pandas as pd
import nibabel as nib
import sklearn as skl
import seaborn as sbn
import scipy.io as sio
from matplotlib import pyplot as plt
from sklearn.model_selection import StratifiedKFold
# -
import warnings
#warnings.filterwarnings('ignore')
# Paths
root_p = '/home/surchs/sim_big/PROJECT/abide_hps/'
# Pheno
sample_p = os.path.join(root_p, 'pheno', 'psm_abide1.csv')
# Data
resid_ct_p = os.path.join(root_p, 'residual', 'ct_30mm_residual_psm.npy')
resid_fc_p = os.path.join(root_p, 'residual', 'sd_30mm_residual_psm.npy')
mask_p = os.path.join(root_p, 'mask', 'MIST_mask.nii.gz')
subtype_fc_p = os.path.join(root_p, 'subtypes', 'subtypes_fc.npz')
subtype_ct_p = os.path.join(root_p, 'subtypes', 'subtypes_ct.npz')
# Load data
sample = pd.read_csv(sample_p)
sample['DX_CODE'] = sample['DX_GROUP'].replace({'Autism':1, 'Control':0})
s_fc = np.load(subtype_fc_p)
s_ct = np.load(subtype_ct_p)
# Reshape FC to add to the table
fc_weights = np.reshape(s_fc['weights'], (370, 5*20))
fc_cols = ['fc_n{}_s{}'.format(nid+1, sid+1) for sid in range(5) for nid in range(20)]
# Same for CT
ct_weights = s_ct['weights']
ct_cols = ['ct_s{}'.format(sid+1) for sid in range(5)]
# Combine both
weights = np.concatenate((ct_weights, fc_weights),1)
cols = ct_cols + fc_cols
# Into a pandas DF
w_data = pd.DataFrame(data=weights, columns=cols)
# Combine both for the full dataset
dataset = sample.join(w_data)
# +
# Select the features
scaler = skl.preprocessing.StandardScaler()
# Add BV to the subtype weights
col_features = ['BV'] + cols
# Build features
x_ = dataset.loc[:, col_features]
# Take the numeric diagnosis code
y_ = dataset.loc[:, ['DX_CODE']].values.squeeze()
# Normalize
x_ = scaler.fit_transform(x_)
# +
# Prep store
store = {key:list() for key in ['accuracy_overall',
'accuracy_asd',
'precision_asd',
'precision_tdc',
'recall_asd',
'recall_tdc',
'f1_asd',
'f1_tdc'
]}
# Run the model and see where that gets us
skf = StratifiedKFold(n_splits=3)
for train_index, val_index in skf.split(x_,y_):
X_training, X_val = x_[train_index], x_[val_index]
y_training, y_val = y_[train_index], y_[val_index]
hpc = high_confidence.TwoStagesPrediction(
n_iter=500,
shuffle_test_split=0.5,
min_gamma=.90,
gamma=0.95,
thresh_ratio=0.1,
verbose=False)
hpc.fit(X_training, X_training, y_training)
_, dic_results = hpc.predict(X_val, X_val)
acc = skl.metrics.accuracy_score(y_val, (dic_results['s1df'][:,0]>0).astype(float))
store['accuracy_overall'].append(acc)
# Get the guys we think are ASD
pos_mask = (dic_results['s2df'][:,1]>0)
acc_s2 = skl.metrics.accuracy_score(y_val[pos_mask], (dic_results['s1df'][:,0]>0).astype(float)[pos_mask])
store['accuracy_asd'].append(acc_s2)
print('Classifying TDC vs ASD...')
print((dic_results['s1df'][:,0]>0).astype(float))
y_pred = (dic_results['s1df'][:,0]>0).astype(float)
# Compute precision of the classifier for ASD
asd_p = skl.metrics.precision_score(y_val, y_pred, pos_label=1)
store['precision_asd'].append(asd_p)
# Compute precision of the classifier for TDC
tdc_p = skl.metrics.precision_score(y_val, y_pred, pos_label=0)
store['precision_tdc'].append(tdc_p)
# Recall Ratio of ASD label
asd_r = skl.metrics.recall_score(y_val, y_pred, pos_label=1)
store['recall_asd'].append(asd_r)
# Recall Ratio of TDC label
tdc_r = skl.metrics.recall_score(y_val, y_pred, pos_label=0)
store['recall_tdc'].append(tdc_r)
# F1 Ratio of ASD label
asd_f = skl.metrics.f1_score(y_val, y_pred, pos_label=1)
store['f1_asd'].append(asd_f)
# Recall Ratio of TDC label
tdc_f = skl.metrics.f1_score(y_val, y_pred, pos_label=0)
store['f1_tdc'].append(tdc_f)
# -
#print(scores_ad_cn)
print('Mean stage 1 validation accuracy: ',np.mean(store['accuracy_overall']))
#print(scores_s2)
print('Mean stage 2 accuracy: ', np.mean(store['accuracy_asd']))
#print(ad_precision)
print('Mean precision for ASD: ',np.mean(store['precision_asd']))
#print(cn_precision)
print('Mean precision for TDC: ',np.mean(store['precision_tdc']))
#print(ad_recall)
print('Mean recall for ASD: ',np.mean(store['recall_asd']))
#print(cn_recall)
print('Mean recall for TDC: ',np.mean(store['recall_tdc']))
#print(ad_f1_score)
print('Mean f1 score for ASD: ',np.mean(store['f1_asd']))
#print(cn_f1_score)
print('Mean f1 score for TDC: ',np.mean(store['f1_tdc']))
# Run the model and see where that gets us
skf = StratifiedKFold(n_splits=3)
for train_index, val_index in skf.split(x_,y_):
X_training, X_val = x_[train_index], x_[val_index]
y_training, y_val = y_[train_index], y_[val_index]
hpc = high_confidence.TwoStagesPrediction(
n_iter=500,
shuffle_test_split=0.5,
min_gamma=.90,
gamma=0.95,
thresh_ratio=0.1,
verbose=False)
hpc.fit(X_training, X_training, y_training)
_, dic_results = hpc.predict(X_val, X_val)
acc = skl.metrics.accuracy_score(y_val, (dic_results['s1df'][:,0]>0).astype(float))
store['accuracy_overall'].append(acc)
# Get the guys we think are ASD
pos_mask = (dic_results['s2df'][:,1]>0)
acc_s2 = skl.metrics.accuracy_score(y_val[pos_mask], (dic_results['s1df'][:,0]>0).astype(float)[pos_mask])
store['accuracy_asd'].append(acc_s2)
print('Classifying TDC vs ASD...')
print((dic_results['s1df'][:,0]>0).astype(float))
array_results, dic_results = hpc.predict(X_val, X_val)
y_pred = (dic_results['s1df'][:,0]>0).astype(float)
lr_decision = dic_results['s2df'][:,1]
predic_stats(y_val, y_pred, lr_decision)
# # Do it without crossvalidation
# +
#reload(high_confidence)
hpc = high_confidence.TwoStagesPrediction(
n_iter=500,
shuffle_test_split=0.5,
min_gamma=.9,
thresh_ratio=0.1, gamma=0.9)
hpc.fit(x_, x_, y_)
# -
hpc.gamma
array_results, dic_results = hpc.predict(x_, x_)
y_pred = (dic_results['s1df'][:,0]>0).astype(float)
lr_decision = dic_results['s2df'][:,1]
predic_stats(y_, y_pred, lr_decision)
sample.shape
sample['DX_GROUP'].value_counts()
array_results.shape
def predic_stats(y_, y_pred, lr_decision):
# number of AD subjects
n_ad = sum(y_)
print('Total number of TARGET subjects: ', n_ad)
# number of CN subjects
n_cn = len(y_) - sum(y_)
print('Total number of NON-TARGET subjects: ', n_cn)
# number of subjects predicted as AD at stage 1
n_pos = sum(y_pred)
print('Stage 1 number of hits (true and false positives): ', n_pos)
# true positives at stage 1
n_pos_ad = sum(y_pred[y_.astype(bool)])
print('Stage 1 TRUE positives: ', n_pos_ad)
# false positives at stage 1
n_pos_cn = n_pos - n_pos_ad
print('Stage 1 FALSE positives: ', n_pos_cn)
# number of CN subjects not identified as positive (true negatives)
n_neg1_cn = n_cn - n_pos_cn
print('Stage 1 TRUE negatives: ', n_neg1_cn)
# number of all flagged HPC-AD subjects
n_flag = sum(y_pred[lr_decision>0])
print('Total number of flagged HPC-AD subjects: ', n_flag)
# number of flagged HPC-AD subjects who are actually AD (true positives)
n_flag_ad = sum(y_[lr_decision>0])
print('Number of flagged HPC-AD subjects that are TRUE positives: ', n_flag_ad)
# number of flagged HPC-AD subjects that are actually CN (false positives)
n_flag_cn = n_flag - n_flag_ad
print('Number of flagged HPC-AD subjects that are FALSE positives: ', n_flag_cn)
# number of CN subjects that were not flagged (true negatives)
n_neg_cn = n_cn - n_flag_cn
print('Number of true negatives: ', n_neg_cn)
print('#############################')
print('Stage 1 stats for TARGET vs NON-TARGET')
print('Precision for AD: ', n_pos_ad/(n_pos_ad + n_pos_cn))
print('Recall (or sensitivity) for AD: ', n_pos_ad/n_ad)
sens = n_pos_ad/n_ad
print('Specificity: ', n_neg1_cn/n_cn)
spec = n_neg1_cn/n_cn
fp = (1-spec)*664
tp = sens*336
adj_prec = tp/(tp+fp)
print('Adjusted precision for 33.6% baseline rate: ', adj_prec)
print('Accuracy: ', (n_pos_ad + n_neg1_cn)/(n_ad + n_cn))
print('#############################')
print('Stage 2 stats for TARGET vs NON-TARGET')
print('Precision for HPC-AD: ', n_flag_ad/n_flag)
print('Recall (or sensitivity) for HPC-AD: ', n_flag_ad/n_ad)
sens_2 = n_flag_ad/n_ad
print('Specificity: ', n_neg_cn/n_cn)
spec_2 = n_neg_cn/n_cn
fp_2 = (1-spec_2)*664
tp_2 = sens_2*336
adj_prec_2 = tp_2/(tp_2 + fp_2)
print('Adjusted precision for 33.6% baseline rate: ', adj_prec_2)
print('Accuracy: ', (n_flag_ad + n_neg_cn)/(n_ad + n_cn))
plt.hist(hpc.training_hit_probability,20)
plt.ylim(0,300)
plt.rcParams.update({'font.size': 18})
# Make some figures
predic_stats()
dic_results.keys()
def stats_mask(y_true, y_pred, mask_selected=None):
if mask_selected is None:
mask_selected = np.ones(y_pred.shape).astype(bool)
print('------------------------')
print('Ratio:', y_true[mask_selected].sum()/y_true.sum())
print('# : ', y_true[mask_selected].sum())
print('# true values: ',mask_selected.sum())
print('ACC : ', np.mean((y_true == y_pred)[mask_selected]))
print('Level 1')
stats_mask(y_, (dic_results['s1df'][:,0]>0).astype(float))
pos_mask = (dic_results['s2df'][:,1]>0)
acc_s2 = metrics.accuracy_score(y_val[tmp_mask], (dic_results['s1df'][:,0]>0).astype(float)[pos_mask])
|
Analysis/hps_v1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import os
import tensorflow.compat.v1 as tf
import math
import numpy as np
import itertools
print((tf.__version__))
tf.enable_eager_execution()
# tf.compat.v1.enable_eager_execution()
from waymo_open_dataset.utils import range_image_utils
from waymo_open_dataset.utils import transform_utils
from waymo_open_dataset.utils import frame_utils
from waymo_open_dataset import dataset_pb2 as open_dataset
waymo_to_labels = {
0 : 'UNKNOWN',
1 : 'VEHICLE',
2 : 'PEDESTRIAN',
3 : 'SIGN',
4 : 'CYCLIST'
}
# PATH = '/MyTeams/YonohubBlocksRadwan/WaymoDataset/training_0000/segment-10017090168044687777_6380_000_6400_000_with_camera_labels.tfrecord'
# path = '/MyTeams/YonohubBlocksRadwan/WaymoDataset/training_0000/'
# files = []
# # r=root, d=directories, f = files
# for r, d, f in os.walk(path):
# for file in f:
# if '.tfrecord' in file:
# files.append(os.path.join(r, file))
# break
# print(files)
# counter = 0
file = "/MyTeams/YonohubBlocksRadwan/WaymoDataset/training_0000/segment-10391312872392849784_4099_400_4119_400_with_camera_labels.tfrecord"
frames = []
# for file in files:
dataset = tf.data.TFRecordDataset(file, compression_type='')
for data in dataset:
# counter += 1
frame = open_dataset.Frame()
frame.ParseFromString(bytearray(data.numpy()))
frames.append(frame)
# +
import tensorflow
laser_labels = []
timestamps = []
FImages = []
for i in range(0, len(frames)):
frame_images = []
for index, image in enumerate(frames[i].images):
frame_images.append(tensorflow.image.decode_jpeg(image.image).numpy())
FImages.append(frame_images[0])
# laser labels (3d bounding boxes)
laser_labels.append(frames[i].laser_labels)
timestamps.append(frames[i].timestamp_micros)
# -
print(frames[1].context)
# +
# !pip install openpyxl
from openpyxl import Workbook
from openpyxl import load_workbook
headers = ['timestamp_us' ,'frame no', 'tracking ID', 'label', 'x', 'y', 'z',
'width', 'length', 'height', 'heading', 'speedx', 'speedy', 'accx', 'accy']
workbook_name = 'sample.xlsx'
wb = Workbook()
page = wb.active
page.append(headers)
# +
for i in range(0, len(laser_labels)):
for x in range(0, len(laser_labels[i])):
if laser_labels[i][x].type != 3:
new_row = [timestamps[i],
i,
laser_labels[i][x].id,
waymo_to_labels[laser_labels[i][x].type],
laser_labels[i][x].box.center_x,
laser_labels[i][x].box.center_y,
laser_labels[i][x].box.center_z,
laser_labels[i][x].box.width,
laser_labels[i][x].box.length,
laser_labels[i][x].box.height,
laser_labels[i][x].box.heading,
laser_labels[i][x].metadata.speed_x,
laser_labels[i][x].metadata.speed_y,
laser_labels[i][x].metadata.accel_x,
laser_labels[i][x].metadata.accel_y]
page.append(new_row)
# -
wb.save(filename = workbook_name)
# +
import cv2
import numpy as np
import glob
height, width, layers = FImages[0].shape
size = (width,height)
out = cv2.VideoWriter('project.avi',cv2.VideoWriter_fourcc(*'DIVX'), 10, size)
for i in range(len(FImages)):
out.write(FImages[i])
out.release()
# -
|
waymo_ros/scripts/.ipynb_checkpoints/DataAnalysis-Copy1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="hXjzLejG9p7T"
# ## Setting the environment for Colab
# + id="73w3sNFb1iLX"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="H7dGde5z1iA-" executionInfo={"status": "ok", "timestamp": 1605996502398, "user_tz": 360, "elapsed": 787, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="b7c69239-244e-48a6-e2b7-64533612b252"
# %cd "/content/drive/My Drive/Colab Notebooks/w266_final/project_re"
# + colab={"base_uri": "https://localhost:8080/"} id="Ku2Ukkc99v_v" executionInfo={"status": "ok", "timestamp": 1605996510151, "user_tz": 360, "elapsed": 5021, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="6048d39b-3033-4319-c64e-0eb5ca81ab80"
#pip installations for colab
# !pip install transformers
# !pip install pytorch_pretrained_bert
# + id="zQ8s9u1X02SE" executionInfo={"status": "ok", "timestamp": 1605996518860, "user_tz": 360, "elapsed": 3077, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}}
# %load_ext autoreload
# #%autoreload
import os, json
from types import SimpleNamespace
from experiment import run_model
from eval import calculate_stats
import pickle
from datetime import datetime
import torch
# + id="ZA70W8Z202SF" executionInfo={"status": "ok", "timestamp": 1605996522129, "user_tz": 360, "elapsed": 729, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}}
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# device = "cpu"
# + id="NMGWLjZx02SF" executionInfo={"status": "ok", "timestamp": 1605996527666, "user_tz": 360, "elapsed": 664, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}}
config_folder = "config/"
class obj(object):
def __init__(self, d):
for a, b in d.items():
if isinstance(b, (list, tuple)):
setattr(self, a, [obj(x) if isinstance(x, dict) else x for x in b])
else:
setattr(self, a, obj(b) if isinstance(b, dict) else b)
with open(os.path.join(config_folder, "config.json")) as f:
config = obj(json.load(f))
# + id="ZfGSxKv102SF" colab={"base_uri": "https://localhost:8080/", "height": 703, "referenced_widgets": ["17d87c6749b4493598cab2516e9720d4", "bf661495b0cc49b59a835482239a21b3", "73be5e7ea5104cb1ab86c132a6a2fca1", "4f9141feded249d7a64c32d1bc3cea05", "54f89d4e09fc4a3e9ba6cabfb7bed49a", "dba355926c8b41bb93376aaabcc6bb09", "d60943d0e2ef41ae89afa0fc01f38b74", "d6b9ddb34a8149dd88ef6950aec96fcb", "9a28d9a006e146459a87daf7e7992345", "<KEY>", "41c7eedf0c54402c8181a4a8f710a157", "<KEY>", "<KEY>", "1ea639eba7144c8eb700b295df4ce7d3", "<KEY>", "<KEY>", "f1887c46e7cc4999a6b32a494b4a50bc", "f456a4c61a7f47d2ac6f8e562306d602", "<KEY>", "<KEY>", "<KEY>", "7d04c3a0b3524955b50722f23eee3d13", "<KEY>", "a557b43a4c754a2d9453a7f5ca7b205b", "<KEY>", "<KEY>", "d2b84b62ec074ee0931d4912aa0ecdbd", "<KEY>", "bb98a69c5c684a37b63757dcc2ef9c6f", "5c68a91762ce40d1b07ba4423fc93152", "a7fc86d815e842c2add0eac1be77877f", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "13413e89d4114cc6ab6d91bbbc23a4f3", "948fa8b0e86343c39129314228beac6e", "<KEY>", "0b00cd62400943e5a6cc104a5e566774", "6b55d1f35a2940d6b31b800b07751af5", "<KEY>", "f685d3f3169a4183ac06c853c3e1206e", "5a4ec52e4c3f45149485ac307504ae22", "5babe66da9df442b945d0b846333d3f6", "093d4c2a95d24fc3811aaee4ec82c9d0", "2462a3408d1948ca910ba09196be8bea", "e412fd873e6d426aaca15a26773beb79", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "1a34debf193f4e0691d9a65ea0fbe980", "<KEY>", "b941424c666a491ea0c4540341ee5f98", "<KEY>"]} executionInfo={"status": "ok", "timestamp": 1606002078278, "user_tz": 360, "elapsed": 5547577, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="c8f37c4d-b5d4-497b-e84f-8067c39c3124"
train_inputs, train_labels, train_preds, train_loss, dev_inputs, dev_labels, dev_loss, dev_preds = run_model(config, device)
# + id="Is0w7Th602SG" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606002078654, "user_tz": 360, "elapsed": 2981237, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="b946cc24-e51d-42e8-cd2a-a8795f9d9b24"
train_inputs, train_labels, train_preds, train_loss, dev_inputs, dev_labels, dev_loss, dev_preds
# + id="-h3t9sM-02SG" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606002078655, "user_tz": 360, "elapsed": 2978964, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="9725dec5-6a37-42fb-93a4-98988441340f"
import numpy as np
np.array(dev_labels).shape, np.array(dev_preds).shape, np.array(train_preds).shape, np.array(train_labels).shape
# + id="lvicXaF502SG" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606002080267, "user_tz": 360, "elapsed": 2978525, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="a46ab07b-0d15-4f03-a963-d0c629465edc"
# %autoreload
train_mcc, train_f1_score, train_df_results, train_label_matches_df = calculate_stats(train_labels,train_preds )
dev_mcc, dev_f1_score, dev_df_results, dev_label_matches_df = calculate_stats(dev_labels,dev_preds )
# + id="3-nz5WrV02SG" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606002080268, "user_tz": 360, "elapsed": 2975717, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="414fef2e-39bf-4b47-d452-5240c5a6e635"
all_experiment_results = []
all_experiment_results.append([str(config), train_loss, dev_loss, train_mcc, train_f1_score,dev_mcc,dev_f1_score,
dev_labels, dev_preds,train_labels,train_preds, train_inputs, dev_inputs])
len(all_experiment_results[0])
# + id="3C5UH_ok02SG" colab={"base_uri": "https://localhost:8080/", "height": 638} executionInfo={"status": "ok", "timestamp": 1606002080268, "user_tz": 360, "elapsed": 2973003, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="237650e2-f8c7-4ade-bbe6-36bdbc048a8f"
dev_label_matches_df
# + id="9luAAfJvdb_e" executionInfo={"status": "ok", "timestamp": 1606002080503, "user_tz": 360, "elapsed": 2966621, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}}
all_model_results_pickle_file = config.programsettings.REPORTS_DIR + "multi_model_experiment_results_" + str(datetime.now()).replace(":", "_").replace(".", "_") + ".pkl"
with open(all_model_results_pickle_file, "wb") as f:
pickle.dump(all_experiment_results, f)
# + colab={"base_uri": "https://localhost:8080/"} id="rCGxo2lTdjIu" executionInfo={"status": "ok", "timestamp": 1606002422604, "user_tz": 360, "elapsed": 712, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="5922d73e-9ad0-47b8-d572-2ec09206ed5b"
from sklearn.metrics import classification_report
print(classification_report(dev_labels,dev_preds ))
# + [markdown] id="Dwg2UDtD1o1n"
# ## Analyzing results
# + id="315O8vk11m7B"
with open("reports/re/multi_model_experiment_results_2020-11-19 20_25_02_351087.pkl", "rb") as f:
all_model_results_pickle_file = pickle.load(f)
# + colab={"base_uri": "https://localhost:8080/"} id="vMXMTssY17pF" executionInfo={"status": "ok", "timestamp": 1605846412231, "user_tz": 360, "elapsed": 386, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="e0877b90-ebd2-4776-d37a-b360faffbb96"
all_model_results_pickle_file
# + colab={"base_uri": "https://localhost:8080/"} id="lRksPTUW4-qa" executionInfo={"status": "ok", "timestamp": 1605846450241, "user_tz": 360, "elapsed": 432, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="ca56c38b-fe14-4b56-9ec8-c10b94fa91fb"
len(all_model_results_pickle_file[0])
# + id="oL579jiQKz8z"
str_config = all_model_results_pickle_file[0][0]
train_loss = all_model_results_pickle_file[0][1]
dev_loss = all_model_results_pickle_file[0][2]
train_mcc = all_model_results_pickle_file[0][3]
train_f1_score = all_model_results_pickle_file[0][4]
dev_mcc = all_model_results_pickle_file[0][5]
dev_f1_score = all_model_results_pickle_file[0][6]
all_dev_label_ids = all_model_results_pickle_file[0][7]
dev_preds = all_model_results_pickle_file[0][8]
train_label_ids = all_model_results_pickle_file[0][9]
train_preds = all_model_results_pickle_file[0][10]
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="bntviS5yOVGC" executionInfo={"status": "ok", "timestamp": 1605851885234, "user_tz": 360, "elapsed": 825, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="28269da8-27c6-4e3f-b3da-44389fce676d"
str_config
# + colab={"base_uri": "https://localhost:8080/"} id="KK2qIfr0G1Vf" executionInfo={"status": "ok", "timestamp": 1605851202469, "user_tz": 360, "elapsed": 2372, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="587fd5ba-9eaa-4855-d768-0889cd5f3425"
# %autoreload
train_mcc, train_f1_score, train_df_results, train_label_matches_df = calculate_stats(train_label_ids,train_preds )
dev_mcc, dev_f1_score, dev_df_results, dev_label_matches_df = calculate_stats(all_dev_label_ids,dev_preds )
# + colab={"base_uri": "https://localhost:8080/", "height": 669} id="bupVhN18G1mq" executionInfo={"status": "ok", "timestamp": 1605855623817, "user_tz": 360, "elapsed": 634, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="35ca48c0-8675-43fe-8c9c-58f1378f0b69"
dev_df_results[(dev_df_results['matched'] == False) & (dev_df_results['labels']=='ADE-Drug')]
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="10xyba0UG1J3" executionInfo={"status": "ok", "timestamp": 1605856216508, "user_tz": 360, "elapsed": 531, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="f1e766ac-ab79-46c0-d5bd-5fbc81fa4f02"
dev_df[dev_df['relation_code'] == 7].iloc[0:20, :]
# + id="IyKeGE8C4--l"
# + colab={"base_uri": "https://localhost:8080/"} id="kUtWoVOv6FJL" executionInfo={"status": "ok", "timestamp": 1605848937737, "user_tz": 360, "elapsed": 367, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="59f0b8be-1a69-48e1-8e20-125561ccb7df"
print(len(dev_preds))
print(len(dev_preds) == len(all_dev_label_ids))
# + id="Itoo5Txf6FVG"
#import numpy as np
#missed_outputs = np.where((dev_preds) != (all_dev_label_ids))[0]
# + colab={"base_uri": "https://localhost:8080/"} id="tYzNA_zC6E-k" executionInfo={"status": "ok", "timestamp": 1605847769225, "user_tz": 360, "elapsed": 420, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="fc85086c-01a4-45c9-f140-3a87d7300c53"
#len(missed_outputs)
# + id="q-Px_AeO4-e5"
import pandas as pd
dev_df = pd.read_csv("data_divided/dev.tsv", sep = "\t", header=None)
dev_df = dev_df.rename(columns={0: "id", 1: "relation_code", 2: "alpha", 3:"string"})
# + colab={"base_uri": "https://localhost:8080/"} id="tfCW1I21_vvV" executionInfo={"status": "ok", "timestamp": 1605848154374, "user_tz": 360, "elapsed": 497, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="4cb753be-d27e-4750-a83c-1b54aa3a1181"
len(dev_df)
# + id="nUsrWw_R_viE"
dev_df['dev_preds'] = pd.Series(dev_preds)
dev_df['dev_true_ids'] = pd.Series(all_dev_label_ids)
# + colab={"base_uri": "https://localhost:8080/", "height": 530} id="twaxxgTsAmVy" executionInfo={"status": "ok", "timestamp": 1605849356763, "user_tz": 360, "elapsed": 580, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="48445da2-5771-4ce3-d1d5-d1b32ce1816a"
pd.set_option('display.max_colwidth', -1)
dev_df[(dev_df['dev_preds'] != dev_df['dev_true_ids']) & (dev_df['relation_code']==7)]
# + colab={"base_uri": "https://localhost:8080/"} id="F4xItyS1AmJy" executionInfo={"status": "ok", "timestamp": 1605849196587, "user_tz": 360, "elapsed": 507, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="f45c3272-12e2-4e57-d22a-ee178355c7b2"
dev_df['dev_preds'].value_counts()
# + colab={"base_uri": "https://localhost:8080/"} id="lIGd_fNX__Ja" executionInfo={"status": "ok", "timestamp": 1605849560945, "user_tz": 360, "elapsed": 516, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEI3USGoSv9o6JShJGhR2V47o7KYZh-Ya1FgZ6=s64", "userId": "13066601150058162597"}} outputId="d1350f49-22e4-4e2f-ca4f-4fe13617a1bf"
dev_df['dev_true_ids'].value_counts()
# + [markdown] id="LvRHdAoG02SG"
# ## Try with different configuration
# + [markdown] id="sVmcapNS02SG"
# ### Just change model from BIOR to BERT Sequence
# + id="Hm9uV-Fn02SG"
config.programsettings.MODEL_NAME = "BERT_Sequence"
config.programsettings.DEBUG_PRINT = 0
# + id="55NyNInK02SG" colab={"referenced_widgets": ["c24ac2854e2a42f5b047c4404ae6b887", "2b55719d740c4f829dc70df549e54481", "3d513c0b236e45a1adf7c94a990f395d", "afc5661d218f4aacaa7ef4deca7c3c40", "47677d823eb24af7aad9ec2a95e28795", "<KEY>", "1ba869dcd74a4c58a0743665390f1586", "5a91e8f749ae4d98bd237a78e3a1539b", "a09871f45dec408e9664800de5a8e3b9", "c1264800a6c74436a2b7d53215160e51", "d942588f56da46549d08e5a531a076f9", "80e23c8267d14ceab9a9a5eef620fda0"]} outputId="930f77d7-41f6-4b6a-9cbc-0d935cd90592"
train_label_ids, train_preds, train_loss, all_dev_label_ids, dev_loss, dev_preds = run_model(config, device)
# + id="CYcXWc3602SG" outputId="e0668e47-2a60-4baf-fadd-7b5ae8b05894"
train_mcc, train_f1_score, train_df_results, train_label_matches_df = calculate_stats(train_label_ids,train_preds )
dev_mcc, dev_f1_score, dev_df_results, dev_label_matches_df = calculate_stats(all_dev_label_ids,dev_preds)
# + id="XcTOGfVG02SG" outputId="40a52852-8811-4a76-9d22-aec27730d2fa"
all_experiment_results.append([str(config), train_loss, dev_loss, train_mcc, train_f1_score,dev_mcc,dev_f1_score,
all_dev_label_ids, dev_preds,train_label_ids,train_preds ])
all_experiment_results
# + id="WA50tSDT02SG" outputId="ca1b42aa-c7a7-4698-dd04-e3a6e60d3ab1"
dev_label_matches_df
# + id="7_eKql-o02SG"
all_model_results_pickle_file = config.programsettings.REPORTS_DIR + "multi_model_experiment_results_" + str(datetime.now()).replace(":", "_").replace(".", "_") + ".pkl"
with open(all_model_results_pickle_file, "wb") as f:
pickle.dump(all_experiment_results, f)
# + id="S-cwMQQp02SG" outputId="88e2686a-62c4-4a11-98ac-026a622193f9"
for i in range(0,50):
print (all_dev_label_ids[i], dev_preds[i])
# + id="WHfbRkjj02SH" outputId="bd267f74-562f-46ca-e3e8-1de614183950"
from sklearn.metrics import classification_report
print(classification_report(all_dev_label_ids,dev_preds ))
# + id="dfgd6M8Z02SH"
# + id="ZWvzCvFH3Eey"
|
project_re/val_experiments/Experiments_Val_epochs5_256_weights.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/bala-codes/Natural-Language-Processing-NLP/blob/master/Neural%20Machine%20Translation/1.%20Seq2Seq%20%5BEnc%20%2B%20Dec%5D%20Model%20for%20Neural%20Machine%20Translation%20(Without%20Attention%20Mechanism).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="hxGjrP6hWeB9" colab_type="text"
# # A Comprehensive Guide to Neural Machine Translation using Seq2Seq Modelling using PyTorch
#
# In this post, we will be building a sequence to sequence deep learning model using PyTorch and TorchText. Here I am doing an German to English neural machine translation. But the same concept can be extended to other problems such as Named Entity Recognition (NER), Text Summarization etc,.
# + [markdown] id="9Rr5xoWgk4Lb" colab_type="text"
# # Table of Contents:
# ## 1. Introduction
# ## 2. Data Preparation and Pre-processing
# ## 3. Long Short Term Memory (LSTM) - Under the Hood
# ## 4. Encoder Model Architecture (Seq2Seq)¶
# ## 5. Encoder Code Implementation (Seq2Seq)
# ## 6. Decoder Model Architecture (Seq2Seq)
# ## 7. Decoder Code Implementation (Seq2Seq)
# ## 8. Seq2Seq (Encoder + Decoder) Interface
# ## 9. Seq2Seq (Encoder + Decoder) Code Implementation
# ## 10. Seq2Seq Model Training
# ## 11. Seq2Seq Model Inference
# + [markdown] id="2pSOAqoHlD3y" colab_type="text"
# # 1. Introduction
# + [markdown] id="M2fGJ_1qXRxu" colab_type="text"
# Here I am doing a German to English neural machine translation. But the same concept can be extended to other problems such as Named Entity Recognition (NER), Text Summarization, etc,.
#
# So the Sequence to Sequence (seq2seq) model in this post uses an encoder-decoder architecture, which uses a type of RNN called LSTM (Long Short Term Memory), where the encoder neural network encodes the input german sequence into a single vector, also called as a Context Vector.
# This Context Vector is said to contain the abstract representation of the input german sequence.
#
# This vector is then passed into the decoder neural network, which is used to output the corresponding English translation sentence, one word at a time.
# + [markdown] id="PSuJ-9X_qk1b" colab_type="text"
# # Necessary Imports
# + id="S-Ycz13hbUbC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 86} outputId="a7de9cd3-87c1-44fe-a086-8e561932435c"
# !pip install torchtext==0.6.0 --quiet
import torch
import torch.nn as nn
import torch.optim as optim
from torchtext.datasets import Multi30k
from torchtext.data import Field, BucketIterator
import numpy as np
import pandas as pd
import spacy
import random
from torchtext.data.metrics import bleu_score
from pprint import pprint
from torch.utils.tensorboard import SummaryWriter
from torchsummary import summary
'''
# Seeding for reproducible results everytime
SEED = 777
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True'''
# + [markdown] id="42fLcaN_kPxf" colab_type="text"
# # 2. Data Preparation & Pre-processing
# + [markdown] id="-FHjZ6RnqoNJ" colab_type="text"
# Loading the SpaCy's vocabulary for our desired languages. SpaCy also supports many languages like french, german etc,.
#
#
# + id="GrNraUABrDq2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 255} outputId="5961207b-7121-488f-af92-e17b9ac73c1f"
# !python -m spacy download en --quiet
# !python -m spacy download de --quiet
# + id="N7Da1d8Pb-p4" colab_type="code" colab={}
spacy_german = spacy.load("de")
spacy_english = spacy.load("en")
# + [markdown] id="Xu2SLNiZrd0Q" colab_type="text"
# Now let's create custom tokenization methods for the languages. Tokenization is a process of breaking the sentence into a list of individual tokens (words).
#
# We can make use of PyTorch's TorchText library for data pre-processing and SpaCy for vocabulary building (English and German) & tokenization of our data.
# + id="leVROD_6qz16" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="940587fb-fa3c-4b0d-a7b9-cf5003d6709a"
def tokenize_german(text):
return [token.text for token in spacy_german.tokenizer(text)]
def tokenize_english(text):
return [token.text for token in spacy_english.tokenizer(text)]
### Sample Run ###
sample_text = "I love machine learning"
print(tokenize_english(sample_text))
# + [markdown] id="CfbseIvPUuFz" colab_type="text"
# Torch text is a powerful library for making the text data ready for variety of NLP tasks. It has all the tools to perform preprocessing on the textual data.
#
# Let's see some of the process it can do,
#
# 1. Train/ Valid/ Test Split: partition your data into a specified train/ valid/ test set.
#
# 2. File Loading: load the text corpus of various formats (.txt,.json,.csv).
# 3. Tokenization: breaking sentences into list of words.
# 4. Vocab: Generate a list of vocabulary from the text corpus.
# 5. Words to Integer Mapper: Map words into integer numbers for the entire corpus and vice versa.
# 6. Word Vector: Convert a word from higher dimension to lower dimension (Word Embedding).
# 7. Batching: Generate batches of sample.
# + [markdown] id="fRa1BNkOU3nK" colab_type="text"
# So once we get to understand what can be done in torch text, let's talk about how it can be implemented in the torch text module. Here we are going to make use of 3 classes under torch text.
#
# 1. Fields :
# > This is a class under the torch text, where we specify how the preprocessing should be done on our data corpus.
# 2. TabularDataset :
# > Using this class, we can actually define the Dataset of columns stored in CSV, TSV, or JSON format and also map them into integers.
# 3. BucketIterator :
# > Using this class, we can perform padding our data for approximation and make batches with our data for model training.
#
# Here our source language (SRC - Input) is German and target language (TRG - Output) is English. We also add 2 extra tokens "start of sequence" <sos> and "end of sequence" <EOS> for effective model training.
# + id="yn8CDZ1ssIju" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 119} outputId="89a750dc-cffe-4316-ba57-155f67ed7675"
german = Field(tokenize=tokenize_german,
lower=True,
init_token="<sos>",
eos_token="<eos>")
english = Field(tokenize=tokenize_english,
lower=True,
init_token="<sos>",
eos_token="<eos>")
train_data, valid_data, test_data = Multi30k.splits(exts = (".de", ".en"),
fields=(german, english))
german.build_vocab(train_data, max_size=10000, min_freq=3)
english.build_vocab(train_data, max_size=10000, min_freq=3)
# + id="ILXUMSRVLhb-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="e55efed2-501e-4f25-fdb1-5a1fe816f739"
print(f"Unique tokens in source (de) vocabulary: {len(german.vocab)}")
print(f"Unique tokens in target (en) vocabulary: {len(english.vocab)}")
# + id="yiRsZjvEME18" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="73256f46-cc6d-4526-f0a0-1e34008a5be0"
# dir(english.vocab)
print(english.vocab.__dict__.keys())
print(list(english.vocab.__dict__.values()))
e = list(english.vocab.__dict__.values())
for i in e:
print(i)
# + id="IhhJy36TM4SV" colab_type="code" colab={}
word_2_idx = dict(e[3])
idx_2_word = {}
for k,v in word_2_idx.items():
idx_2_word[v] = k
# + [markdown] id="Xb-ecGHHxQCS" colab_type="text"
# # Dataset sneek peek
# + id="yvt8AUrWvbA_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 122} outputId="e9c3c5bb-6960-4e51-c1de-3a0ea96bb6a4"
print(f"Number of training examples: {len(train_data.examples)}")
print(f"Number of validation examples: {len(valid_data.examples)}")
print(f"Number of testing examples: {len(test_data.examples)}")
print(train_data[5].__dict__.keys())
pprint(train_data[5].__dict__.values())
# + [markdown] id="A5CbOTA-nCMF" colab_type="text"
# After setting the language pre-processing criteria, the next step is to create batches of training, testing and validation data using iterators.
#
# Creating batches is an exhaustive process, luckily we can make use of TorchText's iterator libraries.
#
# Here we are using BucketIterator for effective padding of source and target sentences. We can access the source (german) batch of data using .src attribute and it's correspondign (english) batch of data using .trg attribute.
# + id="9Gmz5adIwbwF" colab_type="code" colab={}
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
BATCH_SIZE = 32
train_iterator, valid_iterator, test_iterator = BucketIterator.splits((train_data, valid_data, test_data),
batch_size = BATCH_SIZE,
sort_within_batch=True,
sort_key=lambda x: len(x.src),
device = device)
# + [markdown] id="xvYIL8X1-LAP" colab_type="text"
# ## Actual text data before tokenized
# + id="4vWNHTlL8nSg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 561} outputId="c50535ec-de6b-4a9f-9815-3d810ed9899b"
count = 0
max_len_eng = []
max_len_ger = []
for data in train_data:
max_len_ger.append(len(data.src))
max_len_eng.append(len(data.trg))
if count < 10 :
print("German - ",*data.src, " Length - ", len(data.src))
print("English - ",*data.trg, " Length - ", len(data.trg))
print()
count += 1
print("Maximum Length of English sentence {} and German sentence {} in the dataset".format(max(max_len_eng),max(max_len_ger)))
print("Minimum Length of English sentence {} and German sentence {} in the dataset".format(min(max_len_eng),min(max_len_ger)))
# + id="PYL8BmZI0Bzh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="6e4665c5-de0f-43c9-fb8d-ccccad7a1f7e"
count = 0
for data in train_iterator:
if count < 1 :
print("Shapes", data.src.shape, data.trg.shape)
print()
print("German - ",*data.src, " Length - ", len(data.src))
print()
print("English - ",*data.trg, " Length - ", len(data.trg))
temp_ger = data.src
temp_eng = data.trg
count += 1
# + id="kr7ue9mDRNLp" colab_type="code" colab={}
temp_eng_idx = (temp_eng).cpu().detach().numpy()
temp_ger_idx = (temp_ger).cpu().detach().numpy()
# + [markdown] id="27RquKagotom" colab_type="text"
# I just experimented with a batch size of 32 and a sample target batch is shown below. The sentences are tokenized into list of words and indexed according to the vocabulary. The "pad" token gets an index of 1.
#
# Each column corresponds to a sentence indexed into numbers and we have 32 such sentences in a single target batch and the number of rows corresponds to the maximum length of that sentence. Short sentences are padded with 1 to compensate.
# The table (Idx.csv) contains the numerical indices of the words, which is later fed into the word embedding and converted into dense representation for Seq2Seq processing.
# + id="4dg028v3Ru7c" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="e92672e6-4f1b-420b-f971-bd5dda9ce405"
df_eng_idx = pd.DataFrame(data = temp_eng_idx, columns = [str("S_")+str(x) for x in np.arange(1, 33)])
df_eng_idx.index.name = 'Time Steps'
df_eng_idx.index = df_eng_idx.index + 1
# df_eng_idx.to_csv('/content/idx.csv')
df_eng_idx
# + id="HtkVuHkaT7ba" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="8db50740-9917-4c37-ecfc-9415c29e1a5c"
df_eng_word = pd.DataFrame(columns = [str("S_")+str(x) for x in np.arange(1, 33)])
df_eng_word = df_eng_idx.replace(idx_2_word)
# df_eng_word.to_csv('/content/Words.csv')
df_eng_word
# + [markdown] id="N0sxi0e0lkvK" colab_type="text"
# # 3. Long Short Term Memory (LSTM) - Under the Hood
# + [markdown] id="OL7l0Fj-lcng" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/2560/1*sQBwBtwCwqqXY0k5O0ZvMg.png">
#
# The above picture shows the units present under a single LSTM Cell. I will add some references to learn more about LSTM in the last and why it works well for long sequences.
#
# But to simply put, Vanilla RNN, Gated Recurrent Unit (GRU) is not able to capture the long term dependencies due to its nature of design and suffers heavily by the Vanishing Gradient problem, which makes the rate of change in weights and bias values negligible, resulting in poor generalization.
#
# But LSTM has some special units called gates (Remember gate, Forget gate, Update gate), which helps to overcome the problems stated before.
#
# Inside the LSTM cell, we have a bunch of mini neural networks with sigmoid and TanH activations at the final layer and few vector adder, Concat, multiplications operations.
#
# 1. Sigmoid NN → Squishes the values between 0 and 1. Say a value closer to 0 means to forget and a value closer to 1 means to remember.
#
# 2. Embedding NN → Converts the input word indices into word embedding.
#
# 3. TanH NN → Squishes the values between -1 and 1. Helps to regulate the vector values from either getting exploded to the maximum or shrank to the minimum.
#
# 4. The hidden state and the cell state are referred to here as the context vector, which are the outputs from the LSTM cell. The input is the sentence's numerical indexes fed into the embedding NN.
#
# + [markdown] id="7ef7R9ZGy7Ca" colab_type="text"
# # 4. Encoder Model Architecture (Seq2Seq)
# + [markdown] id="HFPrrZlAp-8o" colab_type="text"
# Before moving to seq2seq model, we need to create Encoder ,Decoder and create a interface between them in the seq2seq model.
#
# Let's pass the german input sequence "Ich liebe tief lernen" which translates to "I love deep learning" in english.
#
#
#
# + [markdown] id="mMvkk_AM1orm" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/1200/1*aNcybCTdPlrXsCwIo1OfTg.png">
# + [markdown] id="wj94RR0ZYizi" colab_type="text"
# For a lighter note, let's explain the process happening in the above image. The Encoder of the Seq2Seq model takes one input at a time. Our input German word sequence is "ich Liebe Tief Lernen".
#
# Also, we append the start of sequence "SOS" and the end of sentence "EOS" tokens in the starting and in the ending of the input sentence.
#
# Therefore at
# At time step-0, the "SOS" token is sent,
# At time step-1 the token "ich" is sent,
# At time step-2 the token "Liebe" is sent,
# At time step-3 the token "Tief" is sent,
# At time step-4 the token "Lernen" is sent,
# At time step-4 the token "EOS" is sent.
#
# And the first block in the Encoder architecture is the word embedding layer [shown in green block], which converts the input indexed word into a dense vector representation called word embedding (sizes - 100/200/300).
#
# Then our word embedding vector is sent to the LSTM cell, where it is combined with the hidden state (hs), and the cell state (cs) of the previous time step and the encoder block outputs a new hs and a cs which is passed to the next LSTM cell.
#
# It is understood that the hs and cs captured some vector representation of the sentence so far.
#
# At time step-0, the hidden state and cell state are either initialized fully of zeros or random numbers.
#
# Then after we sent pass all our input german word sequence, a context vector [shown in yellow block] (hs, cs) is finally obtained, which is a dense representation of the word sequence and can be sent to the decoder's first LSTM (hs, cs) for the corresponding English translation.
#
# In the above figure, we use 2 layer LSTM architecture, where we connect the first LSTM to the second LSTM and we then we obtain 2 context vectors stacked on top as the final output.
#
# It is a must that we design identical encoder and decoder blocks in the seq2seq model.
#
# The above visualization is applicable for a single sentence from a batch. Say we have a batch size of 5 (Experimental), then we pass 5 sentences at a time to the Encoder, which looks like the below figure.
# + [markdown] id="7wDhJhtXd1zL" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/1200/1*xP8MgIfKwjStFDUo0_W3QA.png">
#
# ## The same concept is extended to a batch size of 5 (experimental), where we consider 5 input sentences and the first token from each sentences is sent to the encoder at a time. Each sequences in the batch is maintained to have the same length using the padding token.
# + [markdown] id="Cbfs74GwmKcq" colab_type="text"
# # 5. Encoder Code Implementation (Seq2Seq)
# + id="-vlOtY31y40q" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="58a0f92e-7d38-43ee-9d10-b8eb06f62ffe"
class EncoderLSTM(nn.Module):
def __init__(self, input_size, embedding_size, hidden_size, num_layers, p):
super(EncoderLSTM, self).__init__()
# Size of the one hot vectors that will be the input to the encoder
#self.input_size = input_size
# Output size of the word embedding NN
#self.embedding_size = embedding_size
# Dimension of the NN's inside the lstm cell/ (hs,cs)'s dimension.
self.hidden_size = hidden_size
# Number of layers in the lstm
self.num_layers = num_layers
# Regularization parameter
self.dropout = nn.Dropout(p)
self.tag = True
# Shape --------------------> (5376, 300) [input size, embedding dims]
self.embedding = nn.Embedding(input_size, embedding_size)
# Shape -----------> (300, 2, 1024) [embedding dims, hidden size, num layers]
self.LSTM = nn.LSTM(embedding_size, hidden_size, num_layers, dropout = p)
# Shape of x (26, 32) [Sequence_length, batch_size]
def forward(self, x):
# Shape -----------> (26, 32, 300) [Sequence_length , batch_size , embedding dims]
embedding = self.dropout(self.embedding(x))
# Shape --> outputs (26, 32, 1024) [Sequence_length , batch_size , hidden_size]
# Shape --> (hs, cs) (2, 32, 1024) , (2, 32, 1024) [num_layers, batch_size size, hidden_size]
outputs, (hidden_state, cell_state) = self.LSTM(embedding)
return hidden_state, cell_state
input_size_encoder = len(german.vocab)
encoder_embedding_size = 300
hidden_size = 1024
num_layers = 2
encoder_dropout = 0.5
encoder_lstm = EncoderLSTM(input_size_encoder, encoder_embedding_size,
hidden_size, num_layers, encoder_dropout).to(device)
print(encoder_lstm)
# + [markdown] id="6Bm8AObR4U9X" colab_type="text"
# # 6. Decoder Model Architecture (Seq2Seq)
# + [markdown] id="FDSnNEG6iAO3" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/800/1*FtDDCniBMb8HXYEM6PRohQ.png">
#
# The decoder also does a single step at a time.
#
# The Context Vector from the Encoder block is provided as the hidden state (hs) and cell state (cs) for the decoder's first LSTM block.
#
# The start of the sentence "SOS" token is passed to the embedding NN, then passed to the first LSTM cell of the decoder, and finally, it is passed through a linear layer [Shown in Pink color], which provides an output English token prediction probabilities (4556 Probabilities), hidden state (hs), Cell State (cs).
#
# The output word with the highest probability is chosen, hidden state (hs), Cell State (cs) is passed as the inputs to the next LSTM cell and this process is executed until it reaches the end of sentences "EOS".
#
# The subsequent layers will use the hidden and cell state from the previous time steps.
#
# The above visualization is applicable for a single sentence from a batch. Say we have a batch size of 5 (Experimental), then we pass 5 sentences at a time to the Encoder, which provide 5 sets of Context Vectors, and they all are passed into the Decoder, which looks like the below figure.
# + [markdown] id="Vp04ma6hyz_A" colab_type="text"
# ## Teach Force Ratio:
#
# In addition to other blocks, you will also see the block shown below in the Decoder of the Seq2Seq architecture.
#
# While model training, we send the inputs (German Sequence) and targets (English Sequence). After the context vector is obtained from the Encoder, we send them Vector and the target to the Decoder for translation.
#
# But during model Inference, the target is generated from the decoder based on the generalization of the training data. So the output predicted words are sent as the next input word to the decoder until a <SOS> token is obtained.
#
# So in model training itself, we can use the teach force ratio (tfr), where we can actually control the flow of input words to the decoder.
#
# <img src="https://cdn-images-1.medium.com/max/600/1*YJpyqouvpmu4_Ej9ockl4A.png">
#
# Teach Force Ratio methodWe can send the actual target words to the decoder part while training (Shown in Green Color).
#
# We can also send the predicted target word, as the input to the decoder (Shown in Red Color).
#
# Whether sending either of the words (actual target or predicted target) can be regulated with a probability of 50% so at any time step one of them is passed during the training.
#
# This method is like a Regularization so that the model trains efficiently during the process.
#
# The above visualization is applicable for a single sentence from a batch. Say we have a batch size of 5 (Experimental), then we pass 5 sentences at a time to the Encoder, which provide 5 sets of Context Vectors, and they all are passed into the Decoder, which looks like the below figure.
# + [markdown] id="2V1yo6_tkL_o" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/2560/1*UPyGSZSuIQ52IjyFdPpm6A.png">
#
# The same concept is extended to a batch size of 5 (experimental), where we consider 5 input encoder's context vectors and the first token <"sos"> is sent to the decoder at a time.
# + [markdown] id="UtjW6kjByunW" colab_type="text"
#
# + [markdown] id="cIhD2-OBmVnS" colab_type="text"
# # 7. Decoder Code Implementation (Seq2Seq)
# + id="dnGwwU6p2Zfh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 119} outputId="0b6caa95-b495-4ca5-8075-7f86fd9ef1a6"
class DecoderLSTM(nn.Module):
def __init__(self, input_size, embedding_size, hidden_size, num_layers, p, output_size):
super(DecoderLSTM, self).__init__()
# Size of the one hot vectors that will be the input to the encoder
#self.input_size = input_size
# Output size of the word embedding NN
#self.embedding_size = embedding_size
# Dimension of the NN's inside the lstm cell/ (hs,cs)'s dimension.
self.hidden_size = hidden_size
# Number of layers in the lstm
self.num_layers = num_layers
# Size of the one hot vectors that will be the output to the encoder (English Vocab Size)
self.output_size = output_size
# Regularization parameter
self.dropout = nn.Dropout(p)
# Shape --------------------> (5376, 300) [input size, embedding dims]
self.embedding = nn.Embedding(input_size, embedding_size)
# Shape -----------> (300, 2, 1024) [embedding dims, hidden size, num layers]
self.LSTM = nn.LSTM(embedding_size, hidden_size, num_layers, dropout = p)
# Shape -----------> (1024, 4556) [embedding dims, hidden size, num layers]
self.fc = nn.Linear(hidden_size, output_size)
# Shape of x (32) [batch_size]
def forward(self, x, hidden_state, cell_state):
# Shape of x (1, 32) [1, batch_size]
x = x.unsqueeze(0)
# Shape -----------> (1, 32, 300) [1, batch_size, embedding dims]
embedding = self.dropout(self.embedding(x))
# Shape --> outputs (1, 32, 1024) [1, batch_size , hidden_size]
# Shape --> (hs, cs) (2, 32, 1024) , (2, 32, 1024) [num_layers, batch_size size, hidden_size] (passing encoder's hs, cs - context vectors)
outputs, (hidden_state, cell_state) = self.LSTM(embedding, (hidden_state, cell_state))
# Shape --> predictions (1, 32, 4556) [ 1, batch_size , output_size]
predictions = self.fc(outputs)
# Shape --> predictions (32, 4556) [batch_size , output_size]
predictions = predictions.squeeze(0)
return predictions, hidden_state, cell_state
input_size_decoder = len(english.vocab)
decoder_embedding_size = 300
hidden_size = 1024
num_layers = 2
decoder_dropout = 0.5
output_size = len(english.vocab)
decoder_lstm = DecoderLSTM(input_size_decoder, decoder_embedding_size,
hidden_size, num_layers, decoder_dropout, output_size).to(device)
print(decoder_lstm)
# + [markdown] id="Sok8t_j76Ozp" colab_type="text"
# # 8. Seq2Seq (Encoder + Decoder) Interface
# + [markdown] id="5ZcNPOpB_DeW" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/1200/1*d9kP4XoWGnIcmyhX-g4Xvw.png">
# + [markdown] id="GYYkTeNokhRu" colab_type="text"
# ## The final seq2seq implementation looks like the figure above.
#
# ## 1. Provide both input (German) and output (English) sentences.
# ## 2. Pass the input sequence to the encoder and extract context vectors.
# ## 3. Pass the output sequence to the decoder, context vecotr from encoder to produce the predicted output sequence.
#
# + [markdown] id="uhJZFJxG_HbA" colab_type="text"
# <img src="https://cdn-images-1.medium.com/max/1200/1*7SVU_REkIUALmegTbFI9Fw.png">
# + id="t0rHNbZe7ALr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="182d7e9d-f29a-4741-8aec-1653bfb4173d"
for batch in train_iterator:
print(batch.src.shape)
print(batch.trg.shape)
break
x = batch.trg[1]
print(x)
# + [markdown] id="3al--sEzmfmU" colab_type="text"
# # 9. Seq2Seq (Encoder + Decoder) Code Implementation
# + id="UuHGodQe4r9v" colab_type="code" colab={}
class Seq2Seq(nn.Module):
def __init__(self, Encoder_LSTM, Decoder_LSTM):
super(Seq2Seq, self).__init__()
self.Encoder_LSTM = Encoder_LSTM
self.Decoder_LSTM = Decoder_LSTM
def forward(self, source, target, tfr=0.5):
# Shape - Source : (10, 32) [(Sentence length German + some padding), Number of Sentences]
batch_size = source.shape[1]
# Shape - Source : (14, 32) [(Sentence length English + some padding), Number of Sentences]
target_len = target.shape[0]
target_vocab_size = len(english.vocab)
# Shape --> outputs (14, 32, 5766)
outputs = torch.zeros(target_len, batch_size, target_vocab_size).to(device)
# Shape --> (hs, cs) (2, 32, 1024) ,(2, 32, 1024) [num_layers, batch_size size, hidden_size] (contains encoder's hs, cs - context vectors)
hidden_state, cell_state = self.Encoder_LSTM(source)
# Shape of x (32 elements)
x = target[0] # Trigger token <SOS>
for i in range(1, target_len):
# Shape --> output (32, 5766)
output, hidden_state, cell_state = self.Decoder_LSTM(x, hidden_state, cell_state)
outputs[i] = output
best_guess = output.argmax(1) # 0th dimension is batch size, 1st dimension is word embedding
x = target[i] if random.random() < tfr else best_guess # Either pass the next word correctly from the dataset or use the earlier predicted word
# Shape --> outputs (14, 32, 5766)
return outputs
# + id="mOQL9vk49H2U" colab_type="code" colab={}
# Hyperparameters
learning_rate = 0.001
writer = SummaryWriter(f"runs/loss_plot")
step = 0
model = Seq2Seq(encoder_lstm, decoder_lstm).to(device)
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
pad_idx = english.vocab.stoi["<pad>"]
criterion = nn.CrossEntropyLoss(ignore_index=pad_idx)
# + id="OpsjQCsZ_srZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 238} outputId="e12c9dd4-f0d2-4138-9eaf-2b6595deb101"
model
# + id="UtH0Bnq3qFmd" colab_type="code" colab={}
def translate_sentence(model, sentence, german, english, device, max_length=50):
spacy_ger = spacy.load("de")
if type(sentence) == str:
tokens = [token.text.lower() for token in spacy_ger(sentence)]
else:
tokens = [token.lower() for token in sentence]
tokens.insert(0, german.init_token)
tokens.append(german.eos_token)
text_to_indices = [german.vocab.stoi[token] for token in tokens]
sentence_tensor = torch.LongTensor(text_to_indices).unsqueeze(1).to(device)
# Build encoder hidden, cell state
with torch.no_grad():
hidden, cell = model.Encoder_LSTM(sentence_tensor)
outputs = [english.vocab.stoi["<sos>"]]
for _ in range(max_length):
previous_word = torch.LongTensor([outputs[-1]]).to(device)
with torch.no_grad():
output, hidden, cell = model.Decoder_LSTM(previous_word, hidden, cell)
best_guess = output.argmax(1).item()
outputs.append(best_guess)
# Model predicts it's the end of the sentence
if output.argmax(1).item() == english.vocab.stoi["<eos>"]:
break
translated_sentence = [english.vocab.itos[idx] for idx in outputs]
return translated_sentence[1:]
def bleu(data, model, german, english, device):
targets = []
outputs = []
for example in data:
src = vars(example)["src"]
trg = vars(example)["trg"]
prediction = translate_sentence(model, src, german, english, device)
prediction = prediction[:-1] # remove <eos> token
targets.append([trg])
outputs.append(prediction)
return bleu_score(outputs, targets)
def checkpoint_and_save(model, best_loss, epoch, optimizer, epoch_loss):
print('saving')
print()
state = {'model': model,'best_loss': best_loss,'epoch': epoch,'rng_state': torch.get_rng_state(), 'optimizer': optimizer.state_dict(),}
torch.save(state, '/content/checkpoint-NMT')
torch.save(model.state_dict(),'/content/checkpoint-NMT-SD')
# + [markdown] id="W6VnFyCnNlTz" colab_type="text"
# # 10. Seq2Seq Model Training
# + id="T4jLBPRD9osT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="3a9baa27-1492-4cae-b2a7-f42b0e2e316d"
|epoch_loss = 0.0
num_epochs = 100
best_loss = 999999
best_epoch = -1
sentence1 = "ein mann in einem blauen hemd steht auf einer leiter und putzt ein fenster"
ts1 = []
for epoch in range(num_epochs):
print("Epoch - {} / {}".format(epoch+1, num_epochs))
model.eval()
translated_sentence1 = translate_sentence(model, sentence1, german, english, device, max_length=50)
print(f"Translated example sentence 1: \n {translated_sentence1}")
ts1.append(translated_sentence1)
model.train(True)
for batch_idx, batch in enumerate(train_iterator):
input = batch.src.to(device)
target = batch.trg.to(device)
# Pass the input and target for model's forward method
output = model(input, target)
output = output[1:].reshape(-1, output.shape[2])
target = target[1:].reshape(-1)
# Clear the accumulating gradients
optimizer.zero_grad()
# Calculate the loss value for every epoch
loss = criterion(output, target)
# Calculate the gradients for weights & biases using back-propagation
loss.backward()
# Clip the gradient value is it exceeds > 1
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1)
# Update the weights values using the gradients we calculated using bp
optimizer.step()
step += 1
epoch_loss += loss.item()
writer.add_scalar("Training loss", loss, global_step=step)
if epoch_loss < best_loss:
best_loss = epoch_loss
best_epoch = epoch
checkpoint_and_save(model, best_loss, epoch, optimizer, epoch_loss)
if ((epoch - best_epoch) >= 10):
print("no improvement in 10 epochs, break")
break
print("Epoch_Loss - {}".format(loss.item()))
print()
print(epoch_loss / len(train_iterator))
score = bleu(test_data[1:100], model, german, english, device)
print(f"Bleu score {score*100:.2f}")
# + id="AqylUksMJtVo" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b85f51ef-9dc9-4524-b8c8-fa2758012bde"
# #%load_ext tensorboard
# %tensorboard --logdir runs/
# + [markdown] id="-yyYsPQ2ml7Y" colab_type="text"
# # 11. Seq2Seq Model Inference
# + id="s8seg8haidFT" colab_type="code" colab={}
progress = []
import nltk
from nltk.tokenize.treebank import TreebankWordDetokenizer
for i, sen in enumerate(ts1):
progress.append(TreebankWordDetokenizer().detokenize(sen))
print(progress)
# + id="VH2U-LbhH1dw" colab_type="code" colab={}
progress_df = pd.DataFrame(data = progress, columns=['Predicted Sentence'])
progress_df.index.name = "Epochs"
progress_df.to_csv('/content/predicted_sentence.csv')
progress_df.head()
# + [markdown] id="TAUieohaNpvd" colab_type="text"
# # Model Inference
# + id="BxcYB6cRJKIZ" colab_type="code" colab={}
model.eval()
test_sentences = ["Zwei Männer gehen die Straße entlang", "Kinder spielen im Park.", "Diese Stadt verdient eine bessere Klasse von Verbrechern. Der Spaßvogel"]
actual_sentences = ["Two men are walking down the street", "Children play in the park", "This city deserves a better class of criminals. The joker"]
pred_sentences = []
for idx, i in enumerate(test_sentences):
model.eval()
translated_sentence = translate_sentence(model, i, german, english, device, max_length=50)
progress.append(TreebankWordDetokenizer().detokenize(translated_sentence))
print("German : {}".format(i))
print("Actual Sentence in English : {}".format(actual_sentences[idx]))
print("Predicted Sentence in English : {}".format(progress[-1]))
print()
|
Neural Machine Translation/1. Seq2Seq [Enc + Dec] Model for Neural Machine Translation (Without Attention Mechanism).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
from synthetic import standardise
np.random.seed(4)
T = 200
GC1 = np.array([[1,0,1],[1,1,1],[0,0,0]])
GC2 = np.array([[1,0,1],[0,1,0],[0,0,0]])
GC_l = np.zeros([T,3,3])
GC_l[0] = GC1
alpha = 0.5
alpha_l = np.zeros(T)
X = np.zeros([T,3])
X[:,2] = np.random.randint(-1,2,size=T)
alpha_l[T//4:3*T//4] = alpha
for i in range(1,T):
X[i,0] = X[i-1,0] + X[i-1,2]
X[i,1] = alpha_l[i] * X[i-1,2] * X[i-1,0]
if alpha_l[i] == 0:
GC_l[i] = GC2
else:
GC_l[i] = GC1
plt.plot(X)
|
generator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Observations and Insights
#
# 1. Only Capomulin produced a marked decrease in tumor volume (≈20%), while other treatments saw similarly paced tumor growth (≈50%) throughout treatment.
# 2. All drug samples saw increases in metastatic sites throughout treatment, however both the Capomulin and Infubinol samples increased less quickly.
# 3. The Capomulin sample ended treatment with a survival rate over 80%, while the other samples ended their treatments with a survival rate under 50%.
# ## Dependencies and starter code
# +
# Dependencies
import matplotlib.pyplot as plt
import pandas as pd
import scipy.stats as st
from scipy.stats import linregress
import numpy as np
# Study data files
mouse_metadata = "data/Mouse_metadata.csv"
study_results = "data/Study_results.csv"
# Read the mouse data and the study results
mouse_metadata = pd.read_csv(mouse_metadata)
study_results = pd.read_csv(study_results)
# Combine the data into a single dataset
merge_data = pd.merge(mouse_metadata, study_results, on = "Mouse ID", how = "outer")
# merge_data.head()
# Sort merged dataset by Tumor Volume to allow for median values to be correct
merge_data_sort = merge_data.sort_values(["Tumor Volume (mm3)"], ascending = True)
# merge_data_sort.head()
# -
# ## Summary statistics
# +
# Generate a summary statistics table of mean, median, variance, standard deviation, and SEM of the tumor volume for each regimen
# Identify the diferrent Drug Regimen along with the total Tumor Volume for each using .groupby
regimen_grouped = merge_data_sort.groupby(["Drug Regimen"])
# regimen_grouped
# Create computation for the mean of each regimen
regimen_mean = regimen_grouped["Tumor Volume (mm3)"].mean()
# Create computation for the median of each regimen
regimen_median = regimen_grouped["Tumor Volume (mm3)"].median()
# Create computation for the variance of each regimen
regimen_variance = regimen_grouped["Tumor Volume (mm3)"].var()
# Create computation for the standard deviation of each regimen
regimen_std = regimen_grouped["Tumor Volume (mm3)"].std()
# Create computation for the SEM
regimen_sem = regimen_grouped["Tumor Volume (mm3)"].sem()
summary_stats = pd.DataFrame({"Mean": regimen_mean, "Median":regimen_median, "Variance":regimen_variance, "Standard Deviation": regimen_std, "SEM": regimen_sem})
summary_stats
# -
# ## Bar plots
# +
# .groupby Drug Regimen with .count and Mouse ID to determine the data points
regimen_data_points = merge_data.groupby(["Drug Regimen"]).count()["Mouse ID"]
# regimen_data_points
# Generate a bar plot showing number of data points for each treatment regimen using pandas
regimen_data_points.sort_values(ascending = False).plot(kind = "bar", figsize = (6,4))
# Set the box chart labels
plt.title("Data Points Visual")
plt.xlabel("Drug Regimen")
plt.ylabel("Data Points")
# Show the chart and format layout
plt.show()
# +
# Generate a bar plot showing number of data points for each treatment regimen using pyplot
# Create an array with the datapoints
users = [230, 178, 178, 188, 186, 181, 161, 228, 181, 182]
# Sort in descending order
users.sort(reverse = True)
# Set the x-axis to be the amount of the Drug Regimen
x_axis = np.arange(len(regimen_data_points))
plt.bar(x_axis, users, color = 'b', alpha = 0.75, align = 'center')
tick_locations = [value for value in x_axis]
plt.xticks(tick_locations, ['Capomulin', 'Ceftamin',
'Infubinol', 'Ketapril',
'Naftisol', 'Placebo',
'Propriva', 'Ramicane',
'Stelasyn', 'Zoniferol'], rotation = 'vertical')
plt.xlim(-0.75, len(x_axis) - 0.25)
plt.ylim(0, max(users) + 10)
# Set chart labels
plt.title("Data Points Visual")
plt.xlabel("Drug Regimen")
plt.ylabel("Data Points")
# Show chart and format layout
plt.show()
plt.tight_layout()
# -
# ## Pie plots
# +
# .groupby Mouse ID and Sex to find the unique number of male VS female
groupby_gender = merge_data.groupby(["Mouse ID","Sex"])
# groupby_gender
mouse_gender_df = pd.DataFrame(groupby_gender.size())
# Create the dataframe with total count of Female and Male mice
mouse_gender = pd.DataFrame(mouse_gender_df.groupby(["Sex"]).count())
mouse_gender.columns = ["Total Count"]
# Create and format the percentage of female VS male
mouse_gender["Percentage of Sex"] = (100 * (mouse_gender["Total Count"] / mouse_gender["Total Count"].sum()))
# Format the "Percentage of Sex" column
mouse_gender["Percentage of Sex"] = mouse_gender["Percentage of Sex"]
# mouse_gender
# Generate a pie plot showing the distribution of female VS male mice using pandas
colors = ['blue', 'red']
explode = (0.1, 0)
plot = mouse_gender.plot.pie(y = 'Total Count',figsize = (5,5), colors = colors, startangle = 140, explode = explode, shadow = True, autopct = "%1.1f%%")
# +
# Generate a pie plot showing the distribution of female VS male mice using pyplot
# Create Labels for the sections of the pie
labels = ["Female","Male"]
# List the values of each section of the pie chart
sizes = [49.799197,50.200803]
# Set colors for each section of the pie
colors = ['blue', 'red']
# Determine which section of the circle to explode
explode = (0.1, 0)
# Create the pie chart based upon the values
plt.pie(sizes, explode = explode, labels = labels, colors = colors, autopct = "%1.1f%%", shadow = True, startangle = 140)
# Set equal axis
plt.axis("equal")
# -
# ## Quartiles, outliers and boxplots
# +
# Calculate the final tumor volume of each mouse across four of the most promising treatment regimens. Calculate the IQR and quantitatively determine if there are any potential outliers.
best_regimens = merge_data[merge_data["Drug Regimen"].isin(["Capomulin", "Ramicane", "Infubinol", "Ceftamin"])]
best_regimens = best_regimens.sort_values(["Drug Regimen", "Mouse ID", "Timepoint"], ascending = True)
# best_regimes
best_regimens_data = best_regimens[["Drug Regimen", "Mouse ID", "Timepoint", "Tumor Volume (mm3)"]]
best_regimens_data
# +
# .groupby Drug Regimen and Mouse ID to capture Last Tumor Measurement
best_regimens_sort = best_regimens_data.groupby(['Drug Regimen', 'Mouse ID']).last()['Tumor Volume (mm3)']
# best_regimens_sort.head()
# Turn retrieved data into dataframe
best_regimen_df = best_regimens_sort.to_frame()
# best_regimen_df
# Create a list to use as labels
top_4 = ['Capomulin', 'Ramicane', 'Infubinol','Ceftamin']
# Generate a box plot of the final Tumor Volume of each mouse across four regimens of interest
final_df = best_regimen_df.reset_index()
tumor_lists = final_df.groupby('Drug Regimen')['Tumor Volume (mm3)'].apply(list)
tumor_list_df = pd.DataFrame(tumor_lists)
tumor_list_df = tumor_list_df.reindex(top_4)
tumor_vols = [vol for vol in tumor_list_df['Tumor Volume (mm3)']]
flierprops = dict(marker = 'o', markerfacecolor = 'r', markersize = 10)
plt.boxplot(tumor_vols, flierprops = flierprops, patch_artist = True, labels = top_4)
plt.ylim(10, 80)
plt.show()
# -
# ## Line and scatter plots
# +
# Generate a line plot of time point versus tumor volume for a mouse treated with Capomulin
time_vs_tumer = merge_data[merge_data["Mouse ID"].isin(["j119"])]
# time_vs_tumer
time_vs_tumer_data = time_vs_tumer[["Mouse ID", "Timepoint", "Tumor Volume (mm3)"]]
# time_vs_tumer_data
line_plot_df = time_vs_tumer_data.reset_index()
# line_plot_df
line_plot_final = line_plot_df[["Mouse ID", "Timepoint", "Tumor Volume (mm3)"]]
line_plot_final
lines = line_plot_final.plot.line()
tumorvolume_list = line_plot_final['Tumor Volume (mm3)'].tolist()
timepoint_list = line_plot_final['Timepoint'].tolist()
# +
# Generate a scatter plot of mouse weight versus average tumor volume for the Capomulin regimen
capomulin_scatter = merge_data[merge_data["Drug Regimen"].isin(["Capomulin"])]
capomulin_scatter_df = best_regimens[["Mouse ID","Weight (g)", "Tumor Volume (mm3)"]]
capomulin_scatter_plot = capomulin_scatter.reset_index()
capomulin_sorted = capomulin_scatter_plot.sort_values(["Weight (g)"], ascending = True)
capomulin_grouped_weight = capomulin_scatter_plot.groupby("Weight (g)")["Tumor Volume (mm3)"].mean()
capo_grouped_plot = pd.DataFrame(capomulin_grouped_weight).reset_index()
#capomulin_scatter = capomulin_grouped_weight.plot.scatter(x='Weight (g)', y='Tumor Volume (mm3)')
#
capomulin_scatter = capo_grouped_plot.plot(kind = 'scatter', x = 'Weight (g)', y = 'Tumor Volume (mm3)', grid = True, figsize= (8,8))
#capomulin_scatter
# -
# Calculate the correlation coefficient and linear regression model for mouse weight and average tumor volume for the Capomulin regimen
x_values = capo_grouped_plot["Weight (g)"]
y_values = capo_grouped_plot["Tumor Volume (mm3)"]
(slope, intercept, rvalue, pvalue, stderr) = linregress(x_values, y_values)
regress_values = x_values * slope + intercept
line_eq = "y =" + str(round(slope, 2)) + "x + " + str(round(intercept, 2))
plt.scatter(x_values, y_values)
plt.plot(x_values, regress_values, "r-")
plt.annotate(line_eq, (6, 10),fontsize = 10, color = "red")
plt.xlabel("Weight")
plt.ylabel("Tumor Volume")
plt.title("Weight Vs. Avg Tumor Vol")
plt.show()
|
Pymaceuticals/pymaceuticals_Final.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # CoReference Network -- Richards
#
# Notes
# * Notebook currently treats the letter author and recipient as co-references. A strict author-recipient network at the moment (2021-09-27) would only have two nodes (<NAME> and <NAME>).
# +
import re, json, glob, csv, sys, os, warnings
import pandas as pd
import numpy as np
import itertools as iter
import networkx as nx
import xml.etree.ElementTree as ET
import seaborn as sns
import matplotlib.pyplot as plt
from networkx.algorithms import community
from networkx.readwrite import json_graph
from json import JSONEncoder
from operator import itemgetter
from collections import Counter
# Ignore warnings related to deprecated functions.
warnings.filterwarnings('ignore')
# Import project-specific functions.
# Python files (.py) have to be in same folder to work.
lib_path = os.path.abspath(os.path.join(os.path.dirname('Correspondence_XML_parser.py'), '../Scripts'))
sys.path.append(lib_path)
from Correspondence_XML_parser import *
# # Read in config.py (git ignored file) for API username and pw.
# config_path = os.path.abspath(os.path.join(os.path.dirname('config.py'), '../Scripts'))
# sys.path.append(config_path)
# import config
# url = 'https://dsg.xmldb-dev.northeastern.edu/BaseX964/rest/psc/'
# user = config.username
# pw = config.password
# -
# ## Gather XML Files
# +
# Declare directory location to shorten filepaths later.
abs_dir = "/Users/quinn.wi/Documents/"
input_directory = "Data/PSC/Richards/ESR-XML-Files-MHS/*.xml"
# Gather all .xml files using glob.
files = glob.glob(abs_dir + input_directory)
# +
# # %%time
# # Must be connected to Northeastern's VPN.
# r = requests.get(url,
# auth = (user, pw),
# headers = {'Content-Type': 'application/xml'}
# )
# # Read in contents of pipeline.
# soup = BeautifulSoup(r.content, 'html.parser')
# # Split soup's content by \n (each line is a file path to an XML doc).
# # Use filter() to remove empty strings ('').
# # Convert back to list using list().
# files = list(filter(None, soup.text.split('\n')))
# # Filter list and retrieve only jqa/ files.
# files = [i for i in files if 'esr/' in i]
# len(files)
# -
# ## Build Dataframe
# +
# %%time
# Build dataframe from XML files.
# build_dataframe() called from Correspondence_XML_parser
# df = build_dataframe(files, url, user, pw)
df = build_dataframe(files)
# Lowercase values in source, target, and reference columns.
df['source'] = df['source'].str.lower()
df['target'] = df['target'].str.lower()
df['references'] = df['references'].str.lower()
# Split references into list objects.
df['references'] = df['references'].str.split(r',|;')
df.head(3)
# -
# ## Reshape Dataframe for Network
# +
# %%time
# Explode list so that each list value becomes a row.
refs = df.explode('references')
# Create file-person matrix.
refs = pd.crosstab(refs['file'], refs['references'])
# Repeat with correspondence (source + target)
source = pd.crosstab(df['file'], df['source'])
target = pd.crosstab(df['file'], df['target'])
# Sum values of sources to refs or create new column with sources' values.
for col in source:
if col in refs:
refs[str(col)] = refs[str(col)] + source[str(col)]
else:
refs[str(col)] = source[str(col)]
# Repeat for targets.
for col in target:
if col in refs:
refs[str(col)] = refs[str(col)] + target[str(col)]
else:
refs[str(col)] = target[str(col)]
# Convert entry-person matrix into an adjacency matrix of persons.
refs = refs.T.dot(refs)
# # Change diagonal values to zero. That is, a person cannot co-occur with themself.
# np.fill_diagonal(refs.values, 0)
# Create new 'source' column that corresponds to index (person).
refs['source'] = refs.index
# # Reshape dataframe to focus on source, target, and weight.
# # Rename 'people' column name to 'target'.
df_graph = pd.melt(refs, id_vars = ['source'], var_name = 'target', value_name = 'weight') \
.rename(columns = {'references':'target'}) \
.query('(source != "u") & (target != "u")') \
.query('(source != target) & (weight >= 1)')
# Remove rows with empty source or target.
df_graph['source'].replace('', np.nan, inplace=True)
df_graph['target'].replace('', np.nan, inplace=True)
df_graph.dropna(subset=['source', 'target'], inplace=True)
# Chart distribution of weights.
sns.histplot(data = df_graph, x = 'weight')
plt.show()
df_graph.head(3)
# -
# ## Build Graph Object
# +
# %%time
# %%time
# Initialize graph object.
G = nx.from_pandas_edgelist(df, 'source', 'target', 'weight')
# Add nodes.
nodes = list( dict.fromkeys( df['source'].values.tolist() + df['target'].values.tolist() ))
G.add_nodes_from(nodes)
print (nx.info(G))
# Set degree attributes.
nx.set_node_attributes(G, dict(G.degree(G.nodes())), 'degree')
# Sort nodes by degree and print top results.
sorted_degree = sorted(dict(G.degree(G.nodes())).items(),
key = itemgetter(1), reverse = True)
print ("Top 10 nodes by degree:")
for d in sorted_degree[:10]:
print (f'\t{d}')
# Measure network density.
density = nx.density(G)
print (f"Network density: {density:.3f}")
# Related to diameter, check if network is connected and, therefore, can have a diameter.
print (f"Is the network connected? {nx.is_connected(G)}")
# Get a list of network components (communities).
# Find the largest component.
components = nx.connected_components(G)
largest_component = max(components, key = len)
# Create a subgraph of the largest component and measure its diameter.
subgraph = G.subgraph(largest_component)
diameter = nx.diameter(subgraph)
print (f"Network diameter of the largest component: {diameter:.3f}")
# Find triadic closure (similar to density).
triadic_closure = nx.transitivity(G)
print (f"Triadic closure: {triadic_closure:.3f}\n")
# Find centrality measures.
betweenness_dict = nx.betweenness_centrality(G) # Run betweenness centrality
eigenvector_dict = nx.eigenvector_centrality(G) # Run eigenvector centrality
degree_cent_dict = nx.degree_centrality(G)
# Assign each centrality measure to an attribute.
nx.set_node_attributes(G, betweenness_dict, 'betweenness')
nx.set_node_attributes(G, eigenvector_dict, 'eigenvector')
nx.set_node_attributes(G, degree_cent_dict, 'degree_cent')
# Find communities.
communities = community.naive_greedy_modularity_communities(subgraph)
# communities = community.k_clique_communities(subgraph, 5)
# communities = community.greedy_modularity_communities(subgraph)
# communities = community.kernighan_lin_bisection(subgraph)
# Create a dictionary that maps nodes to their community.
modularity_dict = {}
for i, c in enumerate(communities):
for name in c:
modularity_dict[name] = i
# Add modularity information to graph object.
nx.set_node_attributes(subgraph, modularity_dict, 'modularity')
# -
# ## Write as Graph Object
# +
# %%time
# Convert graph object into a dictionary.
data = json_graph.node_link_data(G)
data_json = json.dumps(data)
with open(abs_dir + "GitHub/dsg-mhs/lab_space/projects/richards/coref/data/Richards_coRef-network.json", "w") as f:
f.write(data_json)
# -
|
Jupyter_Notebooks/Networks/Richards_coRef.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example Capacity Test using Captest
#
# The captest module of the Captest package contains the `CapData` class and a few functions top level functions. `CapData` objects hold simulated data from PVsyst (or other simulation) and measured data from a DAS or SCADA system and provide methods to load, filter, and visualize the data and methods for performing regressions on the filtered data.
#
# This example goes through typical steps of performing a capacity test following the ASTM E2848 standard using the Captest package.
#
# ## Imports
# +
# %matplotlib inline
import pandas as pd
# import captest as pvc
from captest import capdata as pvc
from bokeh.io import output_notebook, show
# uncomment below two lines to use cptest.scatter_hv in notebook
import holoviews as hv
hv.extension('bokeh')
#if working offline with the CapData.plot() method may fail
#run 'export BOKEH_RESOURCES=inline' at the command line before
#running the jupyter notebook
output_notebook()
# -
# ## Load and Plot Measured Data
#
# We begin by instantiating a `CapData` object, which we will use to load and store the measured data. In this example we will calculate reporting conditions from the measured data, so we load and filter the measured data first.
das = pvc.CapData('das')
# The `load_data` method by default will look for and attempt to load all csvs in a 'data' folder. In this case we have a single file and provide the filename, so only the file specified is loaded.
das.load_data(fname='example_meas_data.csv', source='AlsoEnergy')
# The `load_data` method assigns the data to the dataframe attribute `df` of the `CapData` object.
das.df.head(3)
# The `load_data` method by default attempts to infer the type of measurement and the type of sensor in each column of the dataframe. For example, a measurement from a ambient temperature sensor would be categorized as 'temp-amb-'. A python dictionary which translates from the column titles in the input file and the inferred type is created and saved to the `trans` attribute. This translation dictionary is used in the `view` and `rview` methods to easily access columns of data of a certain type without renaming columns or typing long column names. This dictionary also enables much of the functionality of the `CapData` class methods to perform common capacity testing tasks, like generating scatter plots and performing regressions, with minimal user input.
das.review_trans()
# User input is required to set which inferred measurement type is the correct one for the regression variables. The `set_reg_trans` method is used to set this relationship.
das.set_reg_trans(power='-mtr-', poa='irr-poa-', t_amb='temp-amb-', w_vel='wind--')
# The `plot` method creates a group of time series plots that are useful for performing an initial visual inspection of the imported data.
#
# The plots are structured around the translation dictionary groupings. A single plot is generated for each different type of data (translation dictionary keys) and each column within that measurement type (translation dictionary values) is plotted as a separate series on the plot. In this example there are two different weather stations, which each have pyranometers measuring plane of array and global horizontal irradiance. This arrangement of sensors results in two plots which each have two lines.
das.agg_sensors(agg_map={'-inv-':'sum', 'irr-poa-':'mean', 'temp-amb-':'mean', 'wind--':'mean'})
das.plot(marker='line', width=900, height=250, ncols=1)
# ## Filtering Measured Data
# The `CapData` class provides a number of convience methods to apply filtering steps as defined in ASTM E2848. The following section demonstrates the use of the more commonly used filtering steps to remove measured data points.
# Uncomment and run to copy over the filtered dataset with the unfiltered data.
das.reset_flt()
# A common first step is to review the scatter plot of the POA irradiance against the power production. The `scatter` method returns a basic non-interactive version of this plot as shown below.
#
# If you have the optional dependency Holoviews installed, `scatter_hv` will return an interactive scatter plot. Additionally, `scatter_hv` includes an option to return a timeseries plot of power that is linked to the scatter plot, so points selected in the scatter plot will be highlighted in the time series.
# Uncomment the below line to use scatter_hv with linked time series
das.scatter_hv(timeseries=True)
# +
# das.scatter()
# -
# In this example, we have multiple measurements of the same value from different sensors. In this case a common first step is to compare measurements from the different sensors and remove data for timestamps where the measurements differ above some acceptable threshold. The `filter_sensors` method provides a convient method to accomplish this taks for the groups of measurements identified as regression values.
das.filter_sensors()
# The `get_summary` method will return a dataframe summarizing the filtering steps that have been applied, the agruments passed to them, the number of points prior to filtering, and the number of points after filtering.
das.get_summary()
# The `custom_filter` method provides a means to update the summary data when using filtering functions not defined as `CapData` methods. The `custom_filter` method allows passing any function or method that takes a DataFrame as the first argument and returns the filtered dataframe with rows removed. Passed methods can be user-defined or Pandas DataFrame methods.
#
# Below, we use the `custom_filter` method with the pandas DataFrame `dropna` method to removing missing data and update the summary data.
das.custom_filter(pd.DataFrame.dropna)
# The `filter_irr` method provides a convient way to remove remove data based on the irradiance measurments. Here we use it to simply remove periods of low irradiance.
das.get_summary()
das.filter_irr(200, 2000)
# We can re-run the `scatter` method to see the results of the filtering steps.
das.scatter()
# The `filter_outliers` method uses scikit-learn's elliptic envelope to remove outlier points. A future release will include a way to interactively select points to be removed.
das.filter_outliers()
das.scatter()
# The `reg_cpt` method performs a regression on the data stored in df_flt using the regression equation specified by the standard. The regression equation is stored in the `reg_fml` attribute as shown below. Regressions are performed using the statsmodels package.
#
# The `reg_cpt` method has an option to filter data based on the regression results as specified in the standard, as demonstrated below.
das.reg_fml
das.reg_cpt(filter=True, summary=False)
das.get_summary()
# ____
# #### Calculation of Reporting Conditions
#
# The `rep_cond` method provide a variety of ways to calculate reporting conditions. Using `rep_cond` the reporting conditions are always calculated from the data store in the df_flt attribute. Refer to the example notebook "Reporting Conditions Examples" for a thourough explanation of the `rep_cond` functionality. By default the reporting conditions are calcualted following the guidance of ASTM E2939-13.
das.rep_cond()
# ----
# Previously we used the irradiance filter to filter out data below 200 W/m<sup>2</sup>. The irradiance filter can also be used to filter irradiance based on a percentage band around a reference value. This approach is shown here to remove data where the irradiance is outside of +/- 50% of the reporting irradiance.
das.filter_irr(0.5, 1.5, ref_val=das.rc['poa'][0])
das.scatter()
# The regression method is used again without the filter option to perform the final regression of the measured data. The result of the regression is statsmodels object containing the regression coefficients and other information generated when performing the regression. This object is stored in the CapData `ols_model` attribute.
das.reg_cpt()
das.ols_model.params
das.ols_model.pvalues
# ## Load and Filter PVsyst Data
#
# To load and filter the modeled data, typically from PVsyst, we simply create a new CapData object, load the PVsyst data, and apply the filtering methods as appropriate.
sim = pvc.CapData('sim')
# To load pvsyst data we use the load_data method with the load_pvsyst option set to True. By default the `load_data` method will search for a csv file that includes 'pvsyst' in the filename in a 'data' directory in the same directory as this file. If you have saved the pvsyst file in a different location, you can use the path and fname arguments to load it.
sim.load_data(load_pvsyst=True)
sim.trans
sim.set_reg_trans(power='real_pwr--', poa='irr-poa-', t_amb='temp-amb-', w_vel='wind--')
# +
# sim.plot()
# -
# Write over cptest.flt_sim dataframe with a copy of the original unfiltered dataframe
sim.reset_flt()
# As a first step we use the `filter_time` method to select a 60 day period of data centered around the measured data.
sim.filter_time(test_date='10/11/1990', days=60)
sim.scatter()
sim.filter_irr(200, 930)
sim.scatter()
sim.get_summary()
# The `filter_pvsyt` method removes data for times when shade is present or the 'IL Pmin', IL Vmin', 'IL Pmax', 'IL Vmax' output values are greater than 0.
sim.filter_pvsyst()
sim.filter_irr(0.5, 1.5, ref_val=das.rc['poa'][0])
sim.reg_cpt()
# ## Results
#
# The `get_summary` and `res_summary` functions display the results of filtering on simulated and measured data and the final capacity test results comparing measured capacity to expected capacity, respectively.
pvc.get_summary(das, sim)
pvc.res_summary(sim, das, 6000, '+/- 7', print_res=True)
# Uncomment and run the below lines to produce a scatter plot overlaying the final measured and PVsyst data.
# %%opts Scatter (alpha=0.3)
# %%opts Scatter [width=600]
das.scatter_hv().relabel('Measured') * sim.scatter_hv().relabel('PVsyst')
|
docs/examples/complete_capacity_test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
train.head()
test.head()
df = pd.DataFrame(train)
# counting words in anchor column
wordcount_anchor = df['anchor'].str.split().str.len()
wordcount_anchor
wordcount_anchor.max()
# using the maximum number of words in 'anchor' plus one for the number of columns so each word in a row gets its own column
split_anchor = df['anchor'].str.rsplit(' ', 6, expand=True)
split_anchor
# counting words in target column
wordcount_target = df['target'].str.split().str.len()
wordcount_target
wordcount_target.max()
# doing the same as we did for anchor
split_target = df['target'].str.rsplit(' ', 16, expand=True)
split_target
from collections import Counter
def dupe_wc(x):
x = str(x).split()
d = 0
for key, val in Counter(x).items():
d = d + (val > 1)
return d
train['anchor_target'] = train['anchor'] + ' ' + train['target']
#Each row would represent each patent case, showing all words in anchor and target.
train['anchor_target']
train['dupecount'] = train['anchor_target'].apply(dupe_wc)
#This shows the number of words that appear in both anchor and target
train['dupecount']
import matplotlib.pyplot as plt
df1=train['dupecount']
#Most cases (18,246) have no exact words that appear both in anchor and target.
#However 13,701 cases have 1 word duplicated in both anchor and target
# in 4 cases, 5 words are duplicated. Considering the max word count in anchor is 5, the sets of words would be
# identical between anchor and target.
df1.value_counts()
df1.value_counts().plot(kind= 'barh')
plt.xlabel("Number of cases")
plt.ylabel("Number of words duplicated in both anchor and target")
#Now we divide the number of duplicated words by 5, which is the maximum number of words duplicated,
# to achieve the scores for each cases between 0 and 1.
#i.e. for the 4 cases where all 5 words are duplicated, the score would be 1.
train['dupecount']/5
df2=train['dupecount']/5
df2.value_counts().plot(kind= 'barh')
plt.xlabel("Number of cases")
plt.ylabel("Semantic Similiary Scores")
avg = sum(df2) / len(df2)
round(avg, 4)
train_avg = sum(train['score']) / len(train['score'])
round(train_avg, 4)
import statistics
statistics.median(df2)
statistics.median(train['score'])
# Based on the simple comparison of average and medians, we can conclude that calculating the semantic scores
# using the number of exact words duplicated in anchor and target is not a good approach, since such method yields
# significantly different results from actual scores given in the training data.
|
source/Attempt 1 - Patent Semantics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # Powerful digit counts
#
# The 5-digit number, $16807=7^5$, is also a fifth power. Similarly, the 9-digit number, $134217728=8^9$, is a ninth power.
#
# How many n-digit positive integers exist which are also an nth power?
# + [markdown] deletable=true editable=true
# ## Solution note:
#
# The base may not be larger than 9, as $10^n$ has $n+1$ digits.
#
# Observation: If $a^n$ does not have $n$ digits, then neither does $a^m$ for any $m>n$.
# + deletable=true editable=true
from itertools import count
s = 0
for base in range(1, 10):
for exp in count(1):
if len(str(base**exp)) == exp:
s += 1
print(base, exp, base**exp)
else: break
print(s)
# -
|
063/63.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tetrahedron
from crossproduct import Point, Triangle, Tetrahedron
import matplotlib.pyplot as plt
# ## \__init__
triangles=(Triangle(Point(0,0,0),Point(1,1,0),Point(0,1,0)),
Triangle(Point(0,0,0),Point(1,1,0),Point(0,1,1)),
Triangle(Point(1,1,0),Point(0,1,0),Point(0,1,1)),
Triangle(Point(0,1,0),Point(0,0,0),Point(0,1,1)),
)
th=Tetrahedron(*triangles)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
th.plot(ax)
th
|
notebooks/dev/Tetrahedron.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# # Guide for Authors
# -
print('Welcome to "The Fuzzing Book"!')
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# This notebook compiles the most important conventions for all chapters (notebooks) of "The Fuzzing Book".
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Organization of this Book
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Chapters as Notebooks
#
# Each chapter comes in its own _Jupyter notebook_. A single notebook (= a chapter) should cover the material (text and code, possibly slides) for a 90-minute lecture.
#
# A chapter notebook should be named `Topic.ipynb`, where `Topic` is the topic. `Topic` must be usable as a Python module and should characterize the main contribution. If the main contribution of your chapter is a class `FooFuzzer`, for instance, then your topic (and notebook name) should be `FooFuzzer`, such that users can state
#
# ```python
# from FooFuzzer import FooFuzzer
# ```
#
# Since class and module names should start with uppercase letters, all non-notebook files and folders start with lowercase letters. this may make it easier to differentiate them. The special notebook `index.ipynb` gets converted into the home pages `index.html` (on fuzzingbook.org) and `README.md` (on GitHub).
#
# Notebooks are stored in the `notebooks` folder.
# -
# ### DebuggingBook and FuzzingBook
#
# This project shares some infrastructure (and even chapters) with "The Fuzzing Book". Everything in `shared/` is maintained in "The Debugging Book" and only copied over to "The Fuzzing Book". If you want to edit or change any of the files in `shared/`, do so in "The Debugging Book".
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Output Formats
#
# The notebooks by themselves can be used by instructors and students to toy around with. They can edit code (and text) as they like and even run them as a slide show.
#
# The notebook can be _exported_ to multiple (non-interactive) formats:
#
# * HTML – for placing this material online.
# * PDF – for printing
# * Python – for coding
# * Slides – for presenting
#
# The included Makefile can generate all of these automatically (and a few more).
#
# At this point, we mostly focus on HTML and Python, as we want to get these out quickly; but you should also occasionally ensure that your notebooks can (still) be exported into PDF. Other formats (Word, Markdown) are experimental.
# -
# ## Sites
#
# All sources for the book end up on the [Github project page](https://github.com/uds-se/fuzzingbook). This holds the sources (notebooks), utilities (Makefiles), as well as an issue tracker.
#
# The derived material for the book ends up in the `docs/` folder, from where it is eventually pushed to the [fuzzingbook website](http://www.fuzzingbook.org/). This site allows to read the chapters online, can launch Jupyter notebooks using the binder service, and provides access to code and slide formats. Use `make publish` to create and update the site.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### The Book PDF
#
# The book PDF is compiled automatically from the individual notebooks. Each notebook becomes a chapter; references are compiled in the final chapter. Use `make book` to create the book.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ## Creating and Building
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Tools you will need
#
# To work on the notebook files, you need the following:
#
# 1. Jupyter notebook. The easiest way to install this is via the [Anaconda distribution](https://www.anaconda.com/download/).
#
# 2. Once you have the Jupyter notebook installed, you can start editing and coding right away by starting `jupyter notebook` (or `jupyter lab`) in the topmost project folder.
#
# 3. If (like me) you don't like the Jupyter Notebook interface, I recommend [Jupyter Lab](https://jupyterlab.readthedocs.io/en/stable/), the designated successor to Jupyter Notebook. Invoke it as `jupyter lab`. It comes with a much more modern interface, but misses autocompletion and a couple of extensions. I am running it [as a Desktop application](http://christopherroach.com/articles/jupyterlab-desktop-app/) which gets rid of all the browser toolbars.
#
# 4. To create the entire book (with citations, references, and all), you also need the [ipybublish](https://github.com/chrisjsewell/ipypublish) package. This allows you to create the HTML files, merge multiple chapters into a single PDF or HTML file, create slides, and more. The Makefile provides the essential tools for creation.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Version Control
#
# We use git in a single strand of revisions. Feel free branch for features, but eventually merge back into the main "master" branch. Sync early; sync often. Only push if everything ("make all") builds and passes.
#
# The Github repo thus will typically reflect work in progress. If you reach a stable milestone, you can push things on the fuzzingbook.org web site, using `make publish`.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### nbdime
#
# The [nbdime](https://github.com/jupyter/nbdime) package gives you tools such as `nbdiff` (and even better, `nbdiff-web`) to compare notebooks against each other; this ensures that cell _contents_ are compared rather than the binary format.
#
# `nbdime config-git --enable` integrates nbdime with git such that `git diff` runs the above tools; merging should also be notebook-specific.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### nbstripout
#
# Notebooks in version control _should not contain output cells,_ as these tend to change a lot. (Hey, we're talking random output generation here!) To have output cells automatically stripped during commit, install the [nbstripout](https://github.com/kynan/nbstripout) package and use
#
# ```
# nbstripout --install
# ```
#
# to set it up as a git filter. The `notebooks/` folder comes with a `.gitattributes` file already set up for `nbstripout`, so you should be all set.
#
# Note that _published_ notebooks (in short, anything under the `docs/` tree _should_ have their output cells included, such that users can download and edit notebooks with pre-rendered output. This folder contains a `.gitattributes` file that should explicitly disable `nbstripout`, but it can't hurt to check.
#
# As an example, the following cell
#
# 1. _should_ have its output included in the [HTML version of this guide](https://www.fuzzingbook.org/beta/html/Guide_for_Authors.html);
# 2. _should not_ have its output included in [the git repo](https://github.com/uds-se/fuzzingbook/blob/master/notebooks/Guide_for_Authors.ipynb) (`notebooks/`);
# 3. _should_ have its output included in [downloadable and editable notebooks](https://github.com/uds-se/fuzzingbook/blob/master/docs/beta/notebooks/Guide_for_Authors.ipynb) (`docs/notebooks/` and `docs/beta/notebooks/`).
# -
import random
random.random()
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Inkscape and GraphViz
#
# Creating derived files uses [Inkscape](https://inkscape.org/en/) and [Graphviz](https://www.graphviz.org/) – through its [Python wrapper](https://pypi.org/project/graphviz/) – to process SVG images. These tools are not automatically installed, but are available on pip, _brew_ and _apt-get_ for all major distributions.
# -
# ### LaTeX Fonts
#
# By default, creating PDF uses XeLaTeX with a couple of special fonts, which you can find in the `fonts/` folder; install these fonts system-wide to make them accessible to XeLaTeX.
#
# You can also run `make LATEX=pdflatex` to use `pdflatex` and standard LaTeX fonts instead.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Creating Derived Formats (HTML, PDF, code, ...)
#
# The [Makefile](../Makefile) provides rules for all targets. Type `make help` for instructions.
#
# The Makefile should work with GNU make and a standard Jupyter Notebook installation. To create the multi-chapter book and BibTeX citation support, you need to install the [iPyPublish](https://github.com/chrisjsewell/ipypublish) package (which includes the `nbpublish` command).
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Creating a New Chapter
#
# To create a new chapter for the book,
#
# 1. Set up a new `.ipynb` notebook file as copy of [Template.ipynb](Template.ipynb).
# 2. Include it in the `CHAPTERS` list in the `Makefile`.
# 3. Add it to the git repository.
# -
# ## Teaching a Topic
#
# Each chapter should be devoted to a central concept and a small set of lessons to be learned. I recommend the following structure:
#
# * Introduce the problem ("We want to parse inputs")
# * Illustrate it with some code examples ("Here's some input I'd like to parse")
# * Develop a first (possibly quick and dirty) solution ("A PEG parser is short and often does the job"_
# * Show that it works and how it works ("Here's a neat derivation tree. Look how we can use this to mutate and combine expressions!")
# * Develop a second, more elaborated solution, which should then become the main contribution. ("Here's a general LR(1) parser that does not require a special grammar format. (You can skip it if you're not interested)")
# * Offload non-essential extensions to later sections or to exercises. ("Implement a universal parser, using the Dragon Book")
#
# The key idea is that readers should be able to grasp the essentials of the problem and the solution in the beginning of the chapter, and get further into details as they progress through it. Make it easy for readers to be drawn in, providing insights of value quickly. If they are interested to understand how things work, they will get deeper into the topic. If they just want to use the technique (because they may be more interested in later chapters), having them read only the first few examples should be fine for them, too.
#
# Whatever you introduce should be motivated first, and illustrated after. Motivate the code you'll be writing, and use plenty of examples to show what the code just introduced is doing. Remember that readers should have fun interacting with your code and your examples. Show and tell again and again and again.
# ### Special Sections
# #### Quizzes
# You can have _quizzes_ as part of the notebook. These are created using the `quiz()` function. Its arguments are
#
# * The question
# * A list of options
# * The correct answer(s) - either
# * the single number of the one single correct answer (starting with 1)
# * a list of numbers of correct answers (multiple choices)
#
# To make the answer less obvious, you can specify it as a string containing an arithmetic expression evaluating to the desired number(s). The expression will remain in the code (and possibly be shown as hint in the quiz).
from bookutils import quiz
# A single-choice quiz
quiz("The color of the sky is", ['blue', 'red', 'black'], '5 - 4')
# A multiple-choice quiz
quiz("What is this book?", ['Novel', 'Friendly', 'Useful'], ['5 - 4', '1 + 1', '27 / 9'])
# Cells that contain only the `quiz()` call will not be rendered (but the quiz will).
# #### Synopsis
# Each chapter should have a section named "Synopsis" at the very end:
#
# ```markdown
# ## Synopsis
#
# This is the text of the synopsis.
# ```
# This section is evaluated at the very end of the notebook. It should summarize the most important functionality (classes, methods, etc.) together with examples. In the derived HTML and PDF files, it is rendered at the beginning, such that it can serve as a quick reference
# #### Excursions
# There may be longer stretches of text (and code!) that are too special, too boring, or too repetitve to read. You can mark such stretches as "Excursions" by enclosing them in MarkDown cells that state:
#
# ```markdown
# #### Excursion: TITLE
# ```
#
# and
#
# ```markdown
# #### End of Excursion
# ```
# Stretches between these two markers get special treatment when rendering:
#
# * In the resulting HTML output, these blocks are set up such that they are shown on demand only.
# * In printed (PDF) versions, they will be replaced by a pointer to the online version.
# * In the resulting slides, they will be omitted right away.
# Here is an example of an excursion:
# #### Excursion: Fine points on Excursion Cells
# Note that the `Excursion` and `End of Excursion` cells must be separate cells; they cannot be merged with others.
# #### End of Excursion
# ### Ignored Code
#
# If a code cell starts with
# ```python
# # ignore
# ```
# then the code will not show up in rendered input. Its _output_ will, however.
# This is useful for cells that create drawings, for instance - the focus should be on the result, not the code.
#
# This also applies to cells that start with a call to `display()` or `quiz()`.
# ### Ignored Cells
#
# You can have _any_ cell not show up at all (including its output) in any rendered input by adding the following meta-data to the cell:
# ```json
# {
# "ipub": {
# "ignore": true
# }
# ```
#
# + [markdown] ipub={"ignore": true}
# *This* text, for instance, does not show up in the rendered version.
# -
# ### Documentation Assertions
#
# If a code cell starts with
# ```python
# # docassert
# ```
# then the code will not show up in rendered input (like `# ignore`), but also not in exported code.
# This is useful for inserting _assertions_ that encode assumptions made in the (following) documentation. Having this assertion fail means that the documentation no longer applies.
#
# Since the documentation is not part of exported code, and since code may behave differently in standalone Python, these assertions are not exported.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Coding
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ### Set up
#
# The first code block in each notebook should be
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
import bookutils
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# This sets up stuff such that notebooks can import each other's code (see below). This import statement is removed in the exported Python code, as the .py files would import each other directly.
# -
# Importing `bookutils` also sets a fixed _seed_ for random number generation. This way, whenever you execute a notebook from scratch (restarting the kernel), you get the exact same results; these results will also end up in the derived HTML and PDF files. (If you run a notebook or a cell for the second time, you will get more random results.)
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Coding Style and Consistency
#
# Here's a few rules regarding coding style.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Use Python 3
#
# We use Python 3 (specifically, Python 3.9.7) for all code. As of 2021, there is no need anymore to include compatibility hacks for earlier Python versions.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Follow Python Coding Conventions
#
# We use _standard Python coding conventions_ according to [PEP 8](https://www.python.org/dev/peps/pep-0008/).
#
# Your code must pass the `pycodestyle` style checks which you get by invoking `make style`. A very easy way to meet this goal is to invoke `make reformat`, which reformats all code accordingly. The `code prettify` notebook extension also allows you to automatically make your code (mostly) adhere to PEP 8.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### One Cell per Definition
#
# Use one cell for each definition or example. During importing, this makes it easier to decide which cells to import (see below).
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Identifiers
#
# In the book, this is how we denote `variables`, `functions()` and `methods()`, `Classes`, `Notebooks`, `variables_and_constants`, `EXPORTED_CONSTANTS`, `files`, `folders/`, and `<grammar-elements>`.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Quotes
#
# If you have the choice between quoting styles, prefer
# * double quotes (`"strings"`) around strings that are used for interpolation or that are natural language messages, and
# * single quotes (`'characters'`) for single characters and formal language symbols that a end user would not see.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Read More
#
# Beyond simple syntactical things, here's a [very nice guide](https://docs.python-guide.org/writing/style/) to get you started writing "pythonic" code.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ### Importing Code from Notebooks
#
# To import the code of individual notebooks, you can import directly from .ipynb notebook files.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
from Fuzzer import fuzzer
# + button=false new_sheet=false run_control={"read_only": false}
fuzzer(100, ord('0'), 10)
# -
# **Important**: When importing a notebook, the module loader will **only** load cells that start with
#
# * a function definition (`def`)
# * a class definition (`class`)
# * a variable definition if all uppercase (`ABC = 123`)
# * `import` and `from` statements
#
# All other cells are _ignored_ to avoid recomputation of notebooks and clutter of `print()` output.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# Exported Python code will import from the respective .py file instead. The exported Python code is set up such that only the above items will be imported.
# -
# If importing a module prints out something (or has other side effects), that is an error. Use `make check-imports` to check whether your modules import without output.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# Import modules only as you need them, such that you can motivate them well in the text.
# -
# ### Imports and Dependencies
#
# Try to depend on as few other notebooks as possible. This will not only ease construction and reconstruction of the code, but also reduce requirements for readers, giving then more flexibility in navigating through the book.
#
# When you import a notebook, this will show up as a dependency in the [Sitemap](00_Table_of_Contents.ipynb). If the imported module is not critical for understanding, and thus should not appear as a dependency in the sitemap, mark the import as "minor dependency" as follows:
from Reducer import DeltaDebuggingReducer # minor dependency
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Design and Architecture
#
# Stick to simple functions and data types. We want our readers to focus on functionality, not Python. You are encouraged to write in a "pythonic" style, making use of elegant Python features such as list comprehensions, sets, and more; however, if you do so, be sure to explain the code such that readers familiar with, say, C or Java can still understand things.
# -
# ### Incomplete Examples
#
# When introducing examples for students to complete, use the ellipsis `...` to indicate where students should add code, as in here:
def student_example():
x = some_value()
# Now, do something with x
...
# The ellipsis is legal code in Python 3. (Actually, it is an `Ellipsis` object.)
# ### Introducing Classes
#
# Defining _classes_ can be a bit tricky, since all of a class must fit into a single cell. This defeats the incremental style preferred for notebooks. By defining a class _as a subclass of itself_, though, you can avoid this problem.
# Here's an example. We introduce a class `Foo`:
class Foo:
def __init__(self):
pass
def bar(self):
pass
# Now we could discuss what `__init__()` and `bar()` do, or give an example of how to use them:
f = Foo()
f.bar()
# We now can introduce a new `Foo` method by subclassing from `Foo` into a class which is _also_ called `Foo`:
class Foo(Foo):
def baz(self):
pass
# This is the same as if we had subclassed `Foo` into `Foo_1` with `Foo` then becoming an alias for `Foo_1`. The original `Foo` class is overshadowed by the new one:
new_f = Foo()
new_f.baz()
# Note, though, that _existing_ objects keep their original class:
from ExpectError import ExpectError
with ExpectError(AttributeError):
f.baz()
# ## Helpers
#
# There's a couple of notebooks with helpful functions, including [Timer](Timer.ipynb), [ExpectError and ExpectTimeout](ExpectError.ipynb). Also check out the [Coverage](Coverage.ipynb) class.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Quality Assurance
#
# In your code, make use of plenty of assertions that allow to catch errors quickly. These assertions also help your readers understand the code.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Issue Tracker
#
# The [Github project page](https://github.com/uds-se/fuzzingbook) allows to enter and track issues.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"} toc-hr-collapsed=false
# ## Writing Text
#
# Text blocks use Markdown syntax. [Here is a handy guide](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet).
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Sections
#
# Any chapter notebook must begin with `# TITLE`, and sections and subsections should then follow by `## SECTION` and `### SUBSECTION`.
#
# Sections should start with their own block, to facilitate cross-referencing.
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Highlighting
#
# Use
#
# * _emphasis_ (`_emphasis_`) for highlighting,
# * *emphasis* (`*emphasis*`) for highlighting terms that will go into the index,
# * `backticks` for code and other verbatim elements.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Hyphens and Dashes
#
# Use "–" for em-dashes, "-" for hyphens, and "$-$" for minus.
# -
# ### Quotes
#
# Use standard typewriter quotes (`"quoted string"`) for quoted text. The PDF version will automatically convert these to "smart" (e.g. left and right) quotes.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Lists and Enumerations
#
# You can use bulleted lists:
#
# * Item A
# * Item B
#
# and enumerations:
#
# 1. item 1
# 1. item 2
#
# For description lists, use a combination of bulleted lists and highlights:
#
# * **PDF** is great for reading offline
# * **HTML** is great for reading online
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
#
# ### Math
#
# LaTeX math formatting works, too.
#
# `$x = \sum_{n = 1}^{\infty}\frac{1}{n}$` gets you
# $x = \sum_{n = 1}^{\infty}\frac{1}{n}$.
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Inline Code
#
# Python code normally goes into its own cells, but you can also have it in the text:
#
# ```python
# s = "Python syntax highlighting"
# print(s)
# ```
# + [markdown] button=false ipub={"figure": {"caption": "Figure caption.", "height": 0.4, "label": "fig:flabel", "placement": "H", "widefigure": false}} new_sheet=false run_control={"read_only": false}
# ### Images
#
# To insert images, use Markdown syntax `{width=100%}` inserts a picture from the `PICS` folder.
# + [markdown] button=false ipub={"figure": {"caption": "This is <NAME>", "label": "fig:zeller", "placement": "H", "widefigure": false, "width": 1}} new_sheet=false run_control={"read_only": false}
# {width=100%}
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# All pictures go to `PICS/`, both in source as well as derived formats; both are stored in git, too. (Not all of us have all tools to recreate diagrams, etc.)
# -
# ### Footnotes
#
# Markdown supports footnotes, as in [^footnote]. These are rendered as footnotes in HTML and PDF, _but not within Jupyter_; hence, readers may find them confusing. So far, the book makes no use of footnotes, and uses parenthesized text instead.
#
# [^footnote]: Test, [Link](https://www.fuzzingbook.org).
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Floating Elements and References
#
# \todo[inline]{I haven't gotten this to work yet -- AZ}
#
# To produce floating elements in LaTeX and PDF, edit the metadata of the cell which contains it. (In the Jupyter Notebook Toolbar go to View -> Cell Toolbar -> Edit Metadata and a button will appear above each cell.) This allows you to control placement and create labels.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Floating Figures
#
# Edit metadata as follows:
#
# ```json
# {
# "ipub": {
# "figure": {
# "caption": "Figure caption.",
# "label": "fig:flabel",
# "placement": "H",
# "height":0.4,
# "widefigure": false,
# }
# }
# }
# ```
#
# - all tags are optional
# - height/width correspond to the fraction of the page height/width, only one should be used (aspect ratio will be maintained automatically)
# - `placement` is optional and constitutes using a placement arguments for the figure (e.g. \begin{figure}[H]). See [Positioning_images_and_tables](https://www.sharelatex.com/learn/Positioning_images_and_tables).
# - `widefigure` is optional and constitutes expanding the figure to the page width (i.e. \begin{figure*}) (placement arguments will then be ignored)
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# #### Floating Tables
#
# For **tables** (e.g. those output by `pandas`), enter in cell metadata:
#
# ```json
# {
# "ipub": {
# "table": {
# "caption": "Table caption.",
# "label": "tbl:tlabel",
# "placement": "H",
# "alternate": "gray!20"
# }
# }
# }
# ```
#
# - `caption` and `label` are optional
# - `placement` is optional and constitutes using a placement arguments for the table (e.g. \begin{table}[H]). See [Positioning_images_and_tables](https://www.sharelatex.com/learn/Positioning_images_and_tables).
# - `alternate` is optional and constitutes using alternating colors for the table rows (e.g. \rowcolors{2}{gray!25}{white}). See (https://tex.stackexchange.com/a/5365/107738)[https://tex.stackexchange.com/a/5365/107738].
# - if tables exceed the text width, in latex, they will be shrunk to fit
#
#
# #### Floating Equations
#
# For **equations** (e.g. those output by `sympy`), enter in cell metadata:
#
# ```json
# {
# "ipub": {
# "equation": {
# "environment": "equation",
# "label": "eqn:elabel"
# }
# }
# }
# ```
#
# - environment is optional and can be 'none' or any of those available in [amsmath](https://www.sharelatex.com/learn/Aligning_equations_with_amsmath); 'equation', 'align','multline','gather', or their \* variants. Additionally, 'breqn' or 'breqn\*' will select the experimental [breqn](https://ctan.org/pkg/breqn) environment to *smart* wrap long equations.
# - label is optional and will only be used if the equation is in an environment
#
#
# #### References
#
# To reference a floating object, use `\cref`, e.g. \cref{eq:texdemo}
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Cross-Referencing
#
# #### Section References
#
# * To refer to sections in the same notebook, use the header name as anchor, e.g.
# `[Code](#Code)` gives you [Code](#Code). For multi-word titles, replace spaces by hyphens (`-`), as in [Using Notebooks as Modules](#Using-Notebooks-as-Modules).
#
# * To refer to cells (e.g. equations or figures), you can define a label as cell metadata. See [Floating Elements and References](#Floating-Elements-and-References) for details.
#
# * To refer to other notebooks, use a Markdown cross-reference to the notebook file, e.g. [the "Fuzzing" chapter](Fuzzer.ipynb). A special script will be run to take care of these links. Reference chapters by name, not by number.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Citations
#
# To cite papers, cite in LaTeX style. The text
# -
print(r"\cite{Purdom1972}")
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# is expanded to \cite{Purdom1972}, which in HTML and PDF should be a nice reference.
# The keys refer to BibTeX entries in [fuzzingbook.bib](fuzzingbook.bib).
# * LaTeX/PDF output will have a "References" section appended.
# * HTML output will link to the URL field from the BibTeX entry. Be sure it points to the DOI.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Todo's
#
# * To mark todo's, use `\todo{Thing to be done}.` \todo{Expand this}
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ### Tables
#
# Tables with fixed contents can be produced using Markdown syntax:
#
# | Tables | Are | Cool |
# | ------ | ---:| ----:|
# | Zebra | 2 | 30 |
# | Gnu | 20 | 400 |
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# If you want to produce tables from Python data, the `PrettyTable` package (included in the book) allows to [produce tables with LaTeX-style formatting.](http://blog.juliusschulz.de/blog/ultimate-ipython-notebook)
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
from bookutils import PrettyTable as pt
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
import numpy as np
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
data = np.array([[1, 2, 30], [2, 3, 400]])
pt.PrettyTable(data, [r"$\frac{a}{b}$", r"$b$",
r"$c$"], print_latex_longtable=False)
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ### Plots and Data
#
# It is possible to include plots in notebooks. Here is an example of plotting a function:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# %matplotlib inline
import matplotlib.pyplot as plt
x = np.linspace(0, 3 * np.pi, 500)
plt.plot(x, np.sin(x ** 2))
plt.title('A simple chirp');
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# And here's an example of plotting data:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# %matplotlib inline
import matplotlib.pyplot as plt
data = [25, 36, 57]
plt.plot(data)
plt.title('Increase in data');
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# Plots are available in all derived versions (HTML, PDF, etc.) Plots with `plotly` are even nicer (and interactive, even in HTML), However, at this point, we cannot export them to PDF, so `matplotlib` it is.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Slides
#
# You can set up the notebooks such that they also can be presented as slides. In the browser, select View -> Cell Toolbar -> Slideshow. You can then select a slide type for each cell:
#
# * `New slide` starts a new slide with the cell (typically, every `## SECTION` in the chapter)
# * `Sub-slide` starts a new sub-slide which you navigate "down" to (anything in the section)
# * `Fragment` is a cell that gets revealed after a click (on the same slide)
# * `Skip` is skipped during the slide show (e.g. `import` statements; navigation guides)
# * `Notes` goes into presenter notes
#
# To create slides, do `make slides`; to view them, change into the `slides/` folder and open the created HTML files. (The `reveal.js` package has to be in the same folder as the slide to be presented.)
#
# The ability to use slide shows is a compelling argument for teachers and instructors in our audience.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "notes"}
# (Hint: In a slide presentation, type `s` to see presenter notes.)
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Writing Tools
#
# When you're editing in the browser, you may find these extensions helpful:
#
# ### Jupyter Notebook
#
# [Jupyter Notebook Extensions](https://github.com/ipython-contrib/jupyter_contrib_nbextensions) is a collection of productivity-enhancing tools (including spellcheckers).
#
# I found these extensions to be particularly useful:
#
# * Spell Checker (while you're editing)
# * Table of contents (for quick navigation)
# * Code prettify (to produce "nice" syntax)
# * Codefolding
# * Live Markdown Preview (while you're editing)
#
# ### Jupyter Lab
#
# Extensions for _Jupyter Lab_ are much less varied and less supported, but things get better. I am running
#
# * [Spell Checker](https://github.com/ijmbarr/jupyterlab_spellchecker)
#
# * [Table of Contents](https://github.com/jupyterlab/jupyterlab-toc)
#
# * [JupyterLab-LSP](https://towardsdatascience.com/jupyterlab-2-0-edd4155ab897) providing code completion, signatures, style checkers, and more.
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Interaction
#
# It is possible to include interactive elements in a notebook, as in the following example:
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# ```python
# try:
# from ipywidgets import interact, interactive, fixed, interact_manual
#
# x = interact(fuzzer, char_start=(32, 128), char_range=(0, 96))
# except ImportError:
# pass
# ```
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# Note that such elements will be present in the notebook versions only, but not in the HTML and PDF versions, so use them sparingly (if at all). To avoid errors during production of derived files, protect against `ImportError` exceptions as in the above example.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Read More
#
# Here is some documentation on the tools we use:
#
# 1. [Markdown Cheatsheet](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet) - general introduction to Markdown
#
# 1. [iPyPublish](https://github.com/chrisjsewell/ipypublish) - rich set of tools to create documents with citations and references
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
#
#
# ## Alternative Tool Sets
#
# We don't currently use these, but they are worth learning:
#
# 1. [Making Publication-Ready Python Notebooks](http://blog.juliusschulz.de/blog/ultimate-ipython-notebook) - Another tool set on how to produce book chapters from notebooks
#
# 1. [Writing academic papers in plain text with Markdown and Jupyter notebook](https://sylvaindeville.net/2015/07/17/writing-academic-papers-in-plain-text-with-markdown-and-jupyter-notebook/) - Alternate ways on how to generate citations
#
# 1. [A Jupyter LaTeX template](https://gist.github.com/goerz/d5019bedacf5956bcf03ca8683dc5217#file-revtex-tplx) - How to define a LaTeX template
#
# 1. [Boost Your Jupyter Notebook Productivity](https://towardsdatascience.com/jupyter-notebook-hints-1f26b08429ad) - a collection of hints for debugging and profiling Jupyter notebooks
#
#
|
notebooks/Guide_for_Authors.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # First Example using QuantLib
# *Copyright (c) 2015 <NAME>*
#
#
# Redistribution and use in source and binary forms, with or without
# modification, are permitted provided that the following conditions are met:
#
# - Redistributions of source code must retain the above copyright notice,
# this list of conditions and the following disclaimer.
#
# THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
# AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
# IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
# DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDERS OR CONTRIBUTORS BE LIABLE
# FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL
# DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR
# SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
# CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY,
# OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE
# OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
#
# This disclaimer is taken from the QuantLib license
import QuantLib as ql
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# Set Evaluation Date
today = ql.Date(31,3,2015)
ql.Settings.instance().setEvaluationDate(today)
# +
# Pricing a plain vanilla interest rate swap
# -
# Flat yield curve
rate = ql.SimpleQuote(0.03)
rate_handle = ql.QuoteHandle(rate)
dc = ql.Actual365Fixed()
disc_curve = ql.FlatForward(today, rate_handle, dc)
disc_curve.enableExtrapolation()
hyts = ql.YieldTermStructureHandle(disc_curve)
# ## Plot the yield curve
discount = np.vectorize(hyts.discount)
tg = np.arange(0,10,1./12.)
plt.plot(tg, discount(tg))
plt.xlabel("time")
plt.ylabel("discount factor")
plt.title("Flat Forward Curve")
# ##Setup the swap
# +
start = ql.TARGET().advance(today, ql.Period("2D"))
end = ql.TARGET().advance(start, ql.Period("10Y"))
nominal = 1e7
typ = ql.VanillaSwap.Payer
fixRate = 0.03
fixedLegTenor = ql.Period("1y")
fixedLegBDC = ql.ModifiedFollowing
fixedLegDC = ql.Thirty360(ql.Thirty360.BondBasis)
index = ql.Euribor6M(ql.YieldTermStructureHandle(disc_curve))
spread = 0.0
fixedSchedule = ql.Schedule(start,
end,
fixedLegTenor,
index.fixingCalendar(),
fixedLegBDC,
fixedLegBDC,
ql.DateGeneration.Backward,
False)
floatSchedule = ql.Schedule(start,
end,
index.tenor(),
index.fixingCalendar(),
index.businessDayConvention(),
index.businessDayConvention(),
ql.DateGeneration.Backward,
False)
swap = ql.VanillaSwap(typ,
nominal,
fixedSchedule,
fixRate,
fixedLegDC,
floatSchedule,
index,
spread,
index.dayCounter())
# -
# ##Setup pricing engine
engine = ql.DiscountingSwapEngine(ql.YieldTermStructureHandle(disc_curve))
swap.setPricingEngine(engine)
# ## Calculate NPV and fair rate
swap.NPV()
swap.fairRate()
|
First_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
# This notebook is a simple monthly sales analysis using SQL from scratch. The notebook uses various SQL statements, to perform different data science data processing analysis.
# +
import pandas as pd
import numpy as np
# -
import pymysql
#Establishing db connection with notebook
conn=pymysql.connect(host='localhost',port=int(3306),user='root',passwd='',db='officesupplies')
#Let's retrive the records in our table
sales = pd.read_sql("SELECT * FROM p6_officesupplies;", conn)
sales.head()
#Checking the duplicates
sales = pd.read_sql('SELECT Region, Rep, Item, Units FROM p6_officesupplies GROUP BY Region, Rep, Item, Units HAVING count(*) > 1;', conn)
sales
#Now we can delete the duplicates in dataset
sales = ('DELETE FROM p6_officesupplies WHERE field in (SELECT Region, Rep, Item, Units FROM p6_officesupplies GROUP BY Region, Rep, Item, Units HAVING count(*) > 1);', conn)
sales
#Let's group our customer regionally
regions = pd.read_sql("SELECT * FROM p6_officesupplies ORDER BY Region;", conn)
regions
#Let's print the Easter customers only
EastClients = pd.read_sql("SELECT Region, Item, Units FROM p6_officesupplies WHERE Region = 'East';", conn)
EastClients
#Let's print our Central customers alone
CentralClients = pd.read_sql("SELECT OrderDate, Region, Rep, Item, Units FROM p6_officesupplies WHERE Region = 'Central';", conn)
CentralClients
dateconv= ('SELECT * FROM p6_officesupplies WHERE OrderDate(NOW()) between 1-Feb-2015 and 26-Feb-2015);', conn)
dateconv
|
SQLnotebook (1).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example of DenseCRF with non-RGB data
# This notebook goes through an example of how to use DenseCRFs on non-RGB data.
# At the same time, it will explain basic concepts and walk through an example, so it could be useful even if you're dealing with RGB data, though do have a look at [PyDenseCRF's README](https://github.com/lucasb-eyer/pydensecrf#pydensecrf) too!
# # Basic setup
# It is highly recommended you install PyDenseCRF through pip, for example `pip install git+https://github.com/lucasb-eyer/pydensecrf.git`, but if for some reason you couldn't, you can always use it like so after compiling it:
# + deletable=true editable=true
#import sys
#sys.path.insert(0,'/path/to/pydensecrf/')
import pydensecrf.densecrf as dcrf
from pydensecrf.utils import unary_from_softmax, create_pairwise_bilateral
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# -
# # Unary Potential
# The unary potential consists of per-pixel class-probabilities. This could come from any kind of model such as a random-forest or the softmax of a deep neural network.
# + [markdown] deletable=true editable=true
# ## Create unary potential
# + deletable=true editable=true
from scipy.stats import multivariate_normal
H, W, NLABELS = 400, 512, 2
# This creates a gaussian blob...
pos = np.stack(np.mgrid[0:H, 0:W], axis=2)
rv = multivariate_normal([H//2, W//2], (H//4)*(W//4))
probs = rv.pdf(pos)
# ...which we project into the range [0.4, 0.6]
probs = (probs-probs.min()) / (probs.max()-probs.min())
probs = 0.5 + 0.2 * (probs-0.5)
# The first dimension needs to be equal to the number of classes.
# Let's have one "foreground" and one "background" class.
# So replicate the gaussian blob but invert it to create the probability
# of the "background" class to be the opposite of "foreground".
probs = np.tile(probs[np.newaxis,:,:],(2,1,1))
probs[1,:,:] = 1 - probs[0,:,:]
# Let's have a look:
plt.figure(figsize=(15,5))
plt.subplot(1,2,1); plt.imshow(probs[0,:,:]); plt.title('Foreground probability'); plt.axis('off'); plt.colorbar();
plt.subplot(1,2,2); plt.imshow(probs[1,:,:]); plt.title('Background probability'); plt.axis('off'); plt.colorbar();
# -
# ## Run inference with unary potential
# We can already run a DenseCRF with only a unary potential.
# This doesn't account for neighborhoods at all, so it's not the greatest idea, but we can do it:
# +
# Inference without pair-wise terms
U = unary_from_softmax(probs) # note: num classes is first dim
d = dcrf.DenseCRF2D(W, H, NLABELS)
d.setUnaryEnergy(U)
# Run inference for 10 iterations
Q_unary = d.inference(10)
# The Q is now the approximate posterior, we can get a MAP estimate using argmax.
map_soln_unary = np.argmax(Q_unary, axis=0)
# Unfortunately, the DenseCRF flattens everything, so get it back into picture form.
map_soln_unary = map_soln_unary.reshape((H,W))
# And let's have a look.
plt.imshow(map_soln_unary); plt.axis('off'); plt.title('MAP Solution without pairwise terms');
# -
# # Pairwise terms
# The whole point of DenseCRFs is to use some form of content to smooth out predictions. This is done via "pairwise" terms, which encode relationships between elements.
# ## Add (non-RGB) pairwise term
# For example, in image processing, a popular pairwise relationship is the "bilateral" one, which roughly says that pixels with either a similar color or a similar location are likely to belong to the same class.
# +
NCHAN=1
# Create simple image which will serve as bilateral.
# Note that we put the channel dimension last here,
# but we could also have it be the first dimension and
# just change the `chdim` parameter to `0` further down.
img = np.zeros((H,W,NCHAN), np.uint8)
img[H//3:2*H//3,W//4:3*W//4,:] = 1
plt.imshow(img[:,:,0]); plt.title('Bilateral image'); plt.axis('off'); plt.colorbar();
# +
# Create the pairwise bilateral term from the above image.
# The two `s{dims,chan}` parameters are model hyper-parameters defining
# the strength of the location and image content bilaterals, respectively.
pairwise_energy = create_pairwise_bilateral(sdims=(10,10), schan=(0.01,), img=img, chdim=2)
# pairwise_energy now contains as many dimensions as the DenseCRF has features,
# which in this case is 3: (x,y,channel1)
img_en = pairwise_energy.reshape((-1, H, W)) # Reshape just for plotting
plt.figure(figsize=(15,5))
plt.subplot(1,3,1); plt.imshow(img_en[0]); plt.title('Pairwise bilateral [x]'); plt.axis('off'); plt.colorbar();
plt.subplot(1,3,2); plt.imshow(img_en[1]); plt.title('Pairwise bilateral [y]'); plt.axis('off'); plt.colorbar();
plt.subplot(1,3,3); plt.imshow(img_en[2]); plt.title('Pairwise bilateral [c]'); plt.axis('off'); plt.colorbar();
# + [markdown] deletable=true editable=true
# ## Run inference of complete DenseCRF
# -
# Now we can create a dense CRF with both unary and pairwise potentials and run inference on it to get our final result.
# + deletable=true editable=true
d = dcrf.DenseCRF2D(W, H, NLABELS)
d.setUnaryEnergy(U)
d.addPairwiseEnergy(pairwise_energy, compat=10) # `compat` is the "strength" of this potential.
# This time, let's do inference in steps ourselves
# so that we can look at intermediate solutions
# as well as monitor KL-divergence, which indicates
# how well we have converged.
# PyDenseCRF also requires us to keep track of two
# temporary buffers it needs for computations.
Q, tmp1, tmp2 = d.startInference()
for _ in range(5):
d.stepInference(Q, tmp1, tmp2)
kl1 = d.klDivergence(Q) / (H*W)
map_soln1 = np.argmax(Q, axis=0).reshape((H,W))
for _ in range(20):
d.stepInference(Q, tmp1, tmp2)
kl2 = d.klDivergence(Q) / (H*W)
map_soln2 = np.argmax(Q, axis=0).reshape((H,W))
for _ in range(50):
d.stepInference(Q, tmp1, tmp2)
kl3 = d.klDivergence(Q) / (H*W)
map_soln3 = np.argmax(Q, axis=0).reshape((H,W))
img_en = pairwise_energy.reshape((-1, H, W)) # Reshape just for plotting
plt.figure(figsize=(15,5))
plt.subplot(1,3,1); plt.imshow(map_soln1);
plt.title('MAP Solution with DenseCRF\n(5 steps, KL={:.2f})'.format(kl1)); plt.axis('off');
plt.subplot(1,3,2); plt.imshow(map_soln2);
plt.title('MAP Solution with DenseCRF\n(20 steps, KL={:.2f})'.format(kl2)); plt.axis('off');
plt.subplot(1,3,3); plt.imshow(map_soln3);
plt.title('MAP Solution with DenseCRF\n(75 steps, KL={:.2f})'.format(kl3)); plt.axis('off');
|
examples/Non RGB Example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Follow-Me Project
# Congratulations on reaching the final project of the Robotics Nanodegree!
#
# Previously, you worked on the Semantic Segmentation lab where you built a deep learning network that locates a particular human target within an image. For this project, you will utilize what you implemented and learned from that lab and extend it to train a deep learning model that will allow a simulated quadcopter to follow around the person that it detects!
#
# Most of the code below is similar to the lab with some minor modifications. You can start with your existing solution, and modify and improve upon it to train the best possible model for this task.
#
# You can click on any of the following to quickly jump to that part of this notebook:
# 1. [Data Collection](#data)
# 2. [FCN Layers](#fcn)
# 3. [Build the Model](#build)
# 4. [Training](#training)
# 5. [Prediction](#prediction)
# 6. [Evaluation](#evaluation)
# ## Data Collection<a id='data'></a>
# We have provided you with a starting dataset for this project. Download instructions can be found in the README for this project's repo.
# Alternatively, you can collect additional data of your own to improve your model. Check out the "Collecting Data" section in the Project Lesson in the Classroom for more details!
# +
import os
import glob
import sys
import tensorflow as tf
from scipy import misc
import numpy as np
from tensorflow.contrib.keras.python import keras
from tensorflow.contrib.keras.python.keras import layers, models
from tensorflow import image
from utils import scoring_utils
from utils.separable_conv2d import SeparableConv2DKeras, BilinearUpSampling2D
from utils import data_iterator
from utils import plotting_tools
from utils import model_tools
# -
# ## FCN Layers <a id='fcn'></a>
# In the Classroom, we discussed the different layers that constitute a fully convolutional network (FCN). The following code will introduce you to the functions that you need to build your semantic segmentation model.
# ### Separable Convolutions
# The Encoder for your FCN will essentially require separable convolution layers, due to their advantages as explained in the classroom. The 1x1 convolution layer in the FCN, however, is a regular convolution. Implementations for both are provided below for your use. Each includes batch normalization with the ReLU activation function applied to the layers.
# +
def separable_conv2d_batchnorm(input_layer, filters, strides=1):
output_layer = SeparableConv2DKeras(filters=filters,kernel_size=3, strides=strides,
padding='same', activation='relu')(input_layer)
output_layer = layers.BatchNormalization()(output_layer)
return output_layer
def conv2d_batchnorm(input_layer, filters, kernel_size=3, strides=1):
output_layer = layers.Conv2D(filters=filters, kernel_size=kernel_size, strides=strides,
padding='same', activation='relu')(input_layer)
output_layer = layers.BatchNormalization()(output_layer)
return output_layer
# -
# ### Bilinear Upsampling
# The following helper function implements the bilinear upsampling layer. Upsampling by a factor of 2 is generally recommended, but you can try out different factors as well. Upsampling is used in the decoder block of the FCN.
def bilinear_upsample(input_layer):
output_layer = BilinearUpSampling2D((2,2))(input_layer)
return output_layer
# ## Build the Model <a id='build'></a>
# In the following cells, you will build an FCN to train a model to detect and locate the hero target within an image. The steps are:
# - Create an `encoder_block`
# - Create a `decoder_block`
# - Build the FCN consisting of encoder block(s), a 1x1 convolution, and decoder block(s). This step requires experimentation with different numbers of layers and filter sizes to build your model.
# ### Encoder Block
# Create an encoder block that includes a separable convolution layer using the `separable_conv2d_batchnorm()` function. The `filters` parameter defines the size or depth of the output layer. For example, 32 or 64.
def encoder_block(input_layer, filters, strides):
# TODO Create a separable convolution layer using the separable_conv2d_batchnorm() function.
output_layer = separable_conv2d_batchnorm(input_layer, filters, strides)
return output_layer
# ### Decoder Block
# The decoder block is comprised of three parts:
# - A bilinear upsampling layer using the upsample_bilinear() function. The current recommended factor for upsampling is set to 2.
# - A layer concatenation step. This step is similar to skip connections. You will concatenate the upsampled small_ip_layer and the large_ip_layer.
# - Some (one or two) additional separable convolution layers to extract some more spatial information from prior layers.
def decoder_block(small_ip_layer, large_ip_layer, filters):
# TODO Upsample the small input layer using the bilinear_upsample() function.
upsampled = bilinear_upsample(small_ip_layer)
# TODO Concatenate the upsampled and large input layers using layers.concatenate
concat_layer = layers.concatenate([upsampled, large_ip_layer])
# TODO Add some number of separable convolution layers
output_layer = separable_conv2d_batchnorm(concat_layer, filters)
output_layer1 = separable_conv2d_batchnorm(output_layer, filters)
return output_layer1
# ### Model
#
# Now that you have the encoder and decoder blocks ready, go ahead and build your FCN architecture!
#
# There are three steps:
# - Add encoder blocks to build the encoder layers. This is similar to how you added regular convolutional layers in your CNN lab.
# - Add a 1x1 Convolution layer using the conv2d_batchnorm() function. Remember that 1x1 Convolutions require a kernel and stride of 1.
# - Add decoder blocks for the decoder layers.
def fcn_model(inputs, num_classes):
# TODO Add Encoder Blocks.
# Remember that with each encoder layer, the depth of your model (the number of filters) increases.
block_1 = encoder_block(inputs, 64, 2)
block_2 = encoder_block(block_1, 128, 2)
# TODO Add 1x1 Convolution layer using conv2d_batchnorm().
block_3 = conv2d_batchnorm(block_2, 256, kernel_size=1, strides=1)
# TODO: Add the same number of Decoder Blocks as the number of Encoder Blocks
block_4 = decoder_block(block_3, block_1, 128)
block_5 = decoder_block(block_4, inputs, 64)
# The function returns the output layer of your model. "x" is the final layer obtained from the last decoder_block()
return layers.Conv2D(num_classes, 3, activation='softmax', padding='same')(block_5)
# ## Training <a id='training'></a>
# The following cells will use the FCN you created and define an ouput layer based on the size of the processed image and the number of classes recognized. You will define the hyperparameters to compile and train your model.
#
# Please Note: For this project, the helper code in `data_iterator.py` will resize the copter images to 160x160x3 to speed up training.
# +
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
image_hw = 160
image_shape = (image_hw, image_hw, 3)
inputs = layers.Input(image_shape)
num_classes = 3
# Call fcn_model()
output_layer = fcn_model(inputs, num_classes)
# -
# ### Hyperparameters
# Define and tune your hyperparameters.
# - **batch_size**: number of training samples/images that get propagated through the network in a single pass.
# - **num_epochs**: number of times the entire training dataset gets propagated through the network.
# - **steps_per_epoch**: number of batches of training images that go through the network in 1 epoch. We have provided you with a default value. One recommended value to try would be based on the total number of images in training dataset divided by the batch_size.
# - **validation_steps**: number of batches of validation images that go through the network in 1 epoch. This is similar to steps_per_epoch, except validation_steps is for the validation dataset. We have provided you with a default value for this as well.
# - **workers**: maximum number of processes to spin up. This can affect your training speed and is dependent on your hardware. We have provided a recommended value to work with.
learning_rate = 0.001
batch_size = 30
num_epochs = 12
steps_per_epoch = 250
validation_steps = 39
workers = 4
print("here")
# +
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# Define the Keras model and compile it for training
model = models.Model(inputs=inputs, outputs=output_layer)
model.compile(optimizer=keras.optimizers.Adam(learning_rate), loss='categorical_crossentropy')
# Data iterators for loading the training and validation data
train_iter = data_iterator.BatchIteratorSimple(batch_size=batch_size,
data_folder=os.path.join('..', 'data', 'train'),
image_shape=image_shape,
shift_aug=True)
val_iter = data_iterator.BatchIteratorSimple(batch_size=batch_size,
data_folder=os.path.join('..', 'data', 'validation'),
image_shape=image_shape)
logger_cb = plotting_tools.LoggerPlotter()
callbacks = [logger_cb]
model.fit_generator(train_iter,
steps_per_epoch = steps_per_epoch, # the number of batches per epoch,
epochs = num_epochs, # the number of epochs to train for,
validation_data = val_iter, # validation iterator
validation_steps = validation_steps, # the number of batches to validate on
callbacks=callbacks,
workers = workers)
print("Here")
# -
# Save your trained model weights
weight_file_name = 'model_weights'
model_tools.save_network(model, weight_file_name)
print("Here")
# ## Prediction <a id='prediction'></a>
#
# Now that you have your model trained and saved, you can make predictions on your validation dataset. These predictions can be compared to the mask images, which are the ground truth labels, to evaluate how well your model is doing under different conditions.
#
# There are three different predictions available from the helper code provided:
# - **patrol_with_targ**: Test how well the network can detect the hero from a distance.
# - **patrol_non_targ**: Test how often the network makes a mistake and identifies the wrong person as the target.
# - **following_images**: Test how well the network can identify the target while following them.
# +
# If you need to load a model which you previously trained you can uncomment the codeline that calls the function below.
# weight_file_name = 'model_weights'
# restored_model = model_tools.load_network(weight_file_name)
# -
# The following cell will write predictions to files and return paths to the appropriate directories.
# The `run_num` parameter is used to define or group all the data for a particular model run. You can change it for different runs. For example, 'run_1', 'run_2' etc.
# +
run_num = 'run_1'
val_with_targ, pred_with_targ = model_tools.write_predictions_grade_set(model,
run_num,'patrol_with_targ', 'sample_evaluation_data')
val_no_targ, pred_no_targ = model_tools.write_predictions_grade_set(model,
run_num,'patrol_non_targ', 'sample_evaluation_data')
val_following, pred_following = model_tools.write_predictions_grade_set(model,
run_num,'following_images', 'sample_evaluation_data')
print("Here")
# -
# Now lets look at your predictions, and compare them to the ground truth labels and original images.
# Run each of the following cells to visualize some sample images from the predictions in the validation set.
# images while following the target
im_files = plotting_tools.get_im_file_sample('sample_evaluation_data','following_images', run_num)
for i in range(3):
im_tuple = plotting_tools.load_images(im_files[i])
plotting_tools.show_images(im_tuple)
print("Here")
# images while at patrol without target
im_files = plotting_tools.get_im_file_sample('sample_evaluation_data','patrol_non_targ', run_num)
for i in range(3):
im_tuple = plotting_tools.load_images(im_files[i])
plotting_tools.show_images(im_tuple)
print("Here")
# +
# images while at patrol with target
im_files = plotting_tools.get_im_file_sample('sample_evaluation_data','patrol_with_targ', run_num)
for i in range(3):
im_tuple = plotting_tools.load_images(im_files[i])
plotting_tools.show_images(im_tuple)
print("Here")
# -
# ## Evaluation <a id='evaluation'></a>
# Evaluate your model! The following cells include several different scores to help you evaluate your model under the different conditions discussed during the Prediction step.
# Scores for while the quad is following behind the target.
true_pos1, false_pos1, false_neg1, iou1 = scoring_utils.score_run_iou(val_following, pred_following)
print("Here")
# Scores for images while the quad is on patrol and the target is not visable
true_pos2, false_pos2, false_neg2, iou2 = scoring_utils.score_run_iou(val_no_targ, pred_no_targ)
print("Here")
# This score measures how well the neural network can detect the target from far away
true_pos3, false_pos3, false_neg3, iou3 = scoring_utils.score_run_iou(val_with_targ, pred_with_targ)
print("Here")
# +
# Sum all the true positives, etc from the three datasets to get a weight for the score
true_pos = true_pos1 + true_pos2 + true_pos3
false_pos = false_pos1 + false_pos2 + false_pos3
false_neg = false_neg1 + false_neg2 + false_neg3
weight = true_pos/(true_pos+false_neg+false_pos)
print(weight)
# -
# The IoU for the dataset that never includes the hero is excluded from grading
final_IoU = (iou1 + iou3)/2
print(final_IoU)
# And the final grade score is
final_score = final_IoU * weight
print(final_score)
|
models/model_b/model_training.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # WordNet
# + [markdown] slideshow={"slide_type": "fragment"}
# **WordNet :** base de données lexicales pour l’anglais.
#
# NLTK fournit une interface d’interrogation.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Les Synsets de WordNet
#
# Liste de *Synsets* pour un terme donné.
#
# **Synsets** : ensembles de synonymes pour chaque acception.
#
# Souvent, un seul *Synset*.
# + slideshow={"slide_type": "-"}
# Import Wordnet
import nltk
from nltk.corpus import wordnet
# -
# Synsets of the word "Duck"
syn = wordnet.synsets('duck')
print(syn)
# + [markdown] slideshow={"slide_type": "subslide"}
# Pour chaque *synset* d’un terme, on peut obtenir :
# - sa définition
# - des exemples d’utilisation
# - son étiquette grammaticale (*n*, *a*, *r* ou *v*)
# - la liste de ses hyponymes et de ses hyperonymes
# - les plus proches hyperonymes communs avec un autre *synset*
# - ses lemmes
# + slideshow={"slide_type": "-"}
definition = syn[0].definition()
examples = syn[4].examples()
tag = syn[0].pos()
hypernyms = syn[0].hypernyms()
hyponyms = syn[0].hyponyms()
lemmas = syn[7].lemmas()
related = syn[0].lowest_common_hypernyms(wordnet.synset('boat.n.01'))
# + [markdown] slideshow={"slide_type": "slide"}
# ### Rechercher les synonymes
#
# Les lemmes d’un *Synset* se concevant comme des synonymes, l’une des finalités envisageables serait par exemple d’en obtenir la liste pour une certaine catégorie grammaticale :
# + slideshow={"slide_type": "-"}
def get_synonyms(word, pos=None):
"""Lists all possible synonyms of a word, except the word itself.
Keyword arguments:
word -- the word to look up
pos -- POS-tagging
"""
synonyms = set()
synsets = wordnet.synsets(word, pos=pos)
for synset in synsets:
[synonyms.add(lemma.name()) for lemma in synset.lemmas()]
synonyms.remove(word)
return synonyms
synonyms = get_synonyms('duck', 'v')
print(synonyms)
# + [markdown] slideshow={"slide_type": "slide"}
# ### Rechercher les antonymes
#
# À l’inverse, on peut aussi bien lister les antonymes d’un *Synset* particulier :
# + slideshow={"slide_type": "-"}
def get_antonyms(synset):
"""Lists the antonyms of all the possible synonyms of a
particular Synset.
Keyword argument:
synset -- the given synset
"""
antonyms = set()
for lemma in synset.lemmas():
[antonyms.add(antonym.name()) for antonym in lemma.antonyms()]
return antonyms
kind = wordnet.synset('kind.a.01')
antonyms = get_antonyms(kind)
# + [markdown] slideshow={"slide_type": "slide"}
# ### Comparer des *synsets*
#
# L’accès aux hyperonymes et aux hyponymes d’un *synset* permet de :
# - remonter jusqu’à l’hyperonyme racine
# - obtenir la liste des *synsets* voisins
# - calculer la similarité lexicale entre deux *synsets*
# + slideshow={"slide_type": "-"}
# Start synset
duck = wordnet.synset('duck.n.01')
# + [markdown] slideshow={"slide_type": "subslide"}
# Comment obtenir la liste des *synsets* voisins ?
# + slideshow={"slide_type": "-"}
duck_hypernym = duck.hypernyms()[0]
duck_related = duck_hypernym.hyponyms()
print(duck_related)
# + [markdown] slideshow={"slide_type": "fragment"}
# Comment remonter jusqu’à l’hyperonyme racine ?
# + slideshow={"slide_type": "-"}
path_to_duck = duck.hypernym_paths()
print(path_to_duck)
# + [markdown] slideshow={"slide_type": "subslide"}
# Comment calculer la similitude entre deux *synsets* ?
# + slideshow={"slide_type": "-"}
duck = wordnet.synset('duck.n.01')
goose = wordnet.synset('goose.n.01')
whale = wordnet.synset('whale.n.01')
boat = wordnet.synset('boat.n.01')
# + [markdown] slideshow={"slide_type": "fragment"}
# Les différents calculs de similarité lexicale se basent sur la plus courte distance entre les *synsets* et un hyperonyme commun :
# + slideshow={"slide_type": "-"}
goose.shortest_path_distance(duck)
# + [markdown] slideshow={"slide_type": "subslide"}
# Quelques calculs de similarité lexicale :
# + slideshow={"slide_type": "-"}
# Based on the path
path_sim = duck.path_similarity(goose)
# Leacock-Chordorow similarity
lch_sim = duck.lch_similarity(goose)
# Wu-Palmer similarity
wu_sim = duck.wup_similarity(goose)
# + [markdown] slideshow={"slide_type": "subslide"}
# Les scores peuvent fortement varier selon la méthode utilisée :
# + [markdown] slideshow={"slide_type": "fragment"}
# - **Leacock-Chordorow :** renvoie un score de similarité lexicale entre deux mots, basé d’une part sur le plus court chemin qui connecte leurs sens et d’autre part sur la profondeur maximale de ces sens dans la taxonomie.
# + [markdown] slideshow={"slide_type": "fragment"}
# - **Wu-Palmer :** renvoie un score de similarité lexicale entre les sens de deux mots, basé sur leur profondeur dans la taxonomie ainsi que sur celle de leur ancêtre le plus spécifique (*Least Common Subsumer*).
# + [markdown] slideshow={"slide_type": "subslide"}
# Comme ces calculs reposent sur des hyperonymes communs, ils ne sont pas opportuns :
# - pour des termes employés dans des contextes grammaticaux différents (*duck*/nom, *duck*/verbe)
# - pour la similarité entre deux verbes (peu ont un hyperonyme commun)
# + [markdown] slideshow={"slide_type": "fragment"}
# La réponse renvoyée sera de type `None`
# + [markdown] slideshow={"slide_type": "slide"}
# ## Un WordNet pour le français ?
#
# **WOLF :** Wordnet Libre du Français
# - depuis 2008
# - licence libre CeCILL
# - développé à l’Inria
# - basé sur la traduction du WordNet de Princeton
# + [markdown] slideshow={"slide_type": "subslide"}
# WOLF est intégré à WordNet :
# + slideshow={"slide_type": "-"}
import nltk
from nltk.corpus import wordnet
synsets = wordnet.synsets('canard', lang='fra')
print(synsets)
# + [markdown] slideshow={"slide_type": "fragment"}
# Comme d’autres langues dans le cadre du projet *Open Multilingual WordNet* :
# + slideshow={"slide_type": "-"}
print(wordnet.langs())
# + [markdown] slideshow={"slide_type": "subslide"}
# Le paramètre `lang` s’emploie avec les méthodes :
# - `synsets()` : obtenir la liste des *synsets* d’une langue
# - `lemma_names()` : obtenir la liste des lemmes pour un *synset*
# - `lemma()` : construire une instance `Lemma`
# - `words()` : obtenir une liste des mots du WordNet
# + slideshow={"slide_type": "-"}
duck_lemmas = wordnet.synset('duck.n.01').lemma_names('fra')
lemma = wordnet.lemma('duck.n.01.canard', lang='fra').name()
words_fr = wordnet.words('fra')
# + [markdown] slideshow={"slide_type": "subslide"}
# Quelques ajustements permettent de soutenir une recherche de synonymes multilingue :
# + slideshow={"slide_type": "-"}
def get_synonyms(word, pos=None, lang='eng'):
"""Lists all possible synonyms of a word, except the word itself
for a given language.
Keyword arguments:
word -- the word to look up
pos -- POS-tagging
lang -- language parameter to translate
"""
synonyms = set()
synsets = wordnet.synsets(word, pos=pos, lang=lang)
for synset in synsets:
[synonyms.add(lemma.name()) for lemma in synset.lemmas(lang)]
try:
synonyms.remove(word)
return synonyms
except KeyError:
postags = {"n": "noun", "a": "adjective", "v":"verb", "r": "adverb"}
return f'There is no match for "{word}" as {postags[pos]} in "{lang}" WordNet version.'
synonyms = get_synonyms('barca', 'n', 'ita')
|
4.text-processing/4.wordnet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Navigator254/-to-do-list/blob/master/L2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="Qhh_nLT-dGwI"
import numpy as np
import math
# + colab={"base_uri": "https://localhost:8080/"} id="ZhqK9XSmdU78" outputId="fc35ddbb-26b7-4d11-83b9-1afc9d66b4c6"
# L2 loss function
def L2(y_hat,y):
s = np.dot(y - y_hat, y - y_hat)
return s
y_hat = np.array([.9,0.2,0.1,.4,.9])
y= np.array([.9,0.1,0.1,.4,.9])
print("L2 = " + str(L2(y_hat,y)))
|
L2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 第三章 PyTorch基础:Tensor和Autograd
#
# ## 3.1 Tensor
#
# Tensor,又名张量,读者可能对这个名词似曾相识,因它不仅在PyTorch中出现过,它也是Theano、TensorFlow、
# Torch和MxNet中重要的数据结构。关于张量的本质不乏深度的剖析,但从工程角度来讲,可简单地认为它就是一个数组,且支持高效的科学计算。它可以是一个数(标量)、一维数组(向量)、二维数组(矩阵)和更高维的数组(高阶数据)。Tensor和Numpy的ndarrays类似,但PyTorch的tensor支持GPU加速。
#
# 本节将系统讲解tensor的使用,力求面面俱到,但不会涉及每个函数。对于更多函数及其用法,读者可通过在IPython/Notebook中使用函数名加`?`查看帮助文档,或查阅PyTorch官方文档[^1]。
#
# [^1]: http://docs.pytorch.org
# Let's begin
from __future__ import print_function
import torch as t
t.__version__
# ### 3.1.1 基础操作
#
# 学习过Numpy的读者会对本节内容感到非常熟悉,因tensor的接口有意设计成与Numpy类似,以方便用户使用。但不熟悉Numpy也没关系,本节内容并不要求先掌握Numpy。
#
# 从接口的角度来讲,对tensor的操作可分为两类:
#
# 1. `torch.function`,如`torch.save`等。
# 2. 另一类是`tensor.function`,如`tensor.view`等。
#
# 为方便使用,对tensor的大部分操作同时支持这两类接口,在本书中不做具体区分,如`torch.sum (torch.sum(a, b))`与`tensor.sum (a.sum(b))`功能等价。
#
# 而从存储的角度来讲,对tensor的操作又可分为两类:
#
# 1. 不会修改自身的数据,如 `a.add(b)`, 加法的结果会返回一个新的tensor。
# 2. 会修改自身的数据,如 `a.add_(b)`, 加法的结果仍存储在a中,a被修改了。
#
# 函数名以`_`结尾的都是inplace方式, 即会修改调用者自己的数据,在实际应用中需加以区分。
#
# #### 创建Tensor
#
# 在PyTorch中新建tensor的方法有很多,具体如表3-1所示。
#
# 表3-1: 常见新建tensor的方法
#
# |函数|功能|
# |:---:|:---:|
# |Tensor(\*sizes)|基础构造函数|
# |tensor(data,)|类似np.array的构造函数|
# |ones(\*sizes)|全1Tensor|
# |zeros(\*sizes)|全0Tensor|
# |eye(\*sizes)|对角线为1,其他为0|
# |arange(s,e,step|从s到e,步长为step|
# |linspace(s,e,steps)|从s到e,均匀切分成steps份|
# |rand/randn(\*sizes)|均匀/标准分布|
# |normal(mean,std)/uniform(from,to)|正态分布/均匀分布|
# |randperm(m)|随机排列|
#
# 这些创建方法都可以在创建的时候指定数据类型dtype和存放device(cpu/gpu).
#
#
# 其中使用`Tensor`函数新建tensor是最复杂多变的方式,它既可以接收一个list,并根据list的数据新建tensor,也能根据指定的形状新建tensor,还能传入其他的tensor,下面举几个例子。
# 指定tensor的形状
a = t.Tensor(2, 3)
a # 数值取决于内存空间的状态,print时候可能overflow
# 用list的数据创建tensor
b = t.Tensor([[1,2,3],[4,5,6]])
b
b.tolist() # 把tensor转为list
# `tensor.size()`返回`torch.Size`对象,它是tuple的子类,但其使用方式与tuple略有区别
b_size = b.size()
b_size
b.numel() # b中元素总个数,2*3,等价于b.nelement()
# 创建一个和b形状一样的tensor
c = t.Tensor(b_size)
# 创建一个元素为2和3的tensor
d = t.Tensor((2, 3))
c, d
# 除了`tensor.size()`,还可以利用`tensor.shape`直接查看tensor的形状,`tensor.shape`等价于`tensor.size()`
c.shape
# 需要注意的是,`t.Tensor(*sizes)`创建tensor时,系统不会马上分配空间,只是会计算剩余的内存是否足够使用,使用到tensor时才会分配,而其它操作都是在创建完tensor之后马上进行空间分配。其它常用的创建tensor的方法举例如下。
t.ones(2, 3)
t.zeros(2, 3)
t.arange(1, 6, 2)
t.linspace(1, 10, 3)
t.randn(2, 3, device=t.device('cpu'))
t.randperm(5) # 长度为5的随机排列
t.eye(2, 3, dtype=t.int) # 对角线为1, 不要求行列数一致
# `torch.tensor`是在0.4版本新增加的一个新版本的创建tensor方法,使用的方法,和参数几乎和`np.array`完全一致
scalar = t.tensor(3.14159)
print('scalar: %s, shape of sclar: %s' %(scalar, scalar.shape))
vector = t.tensor([1, 2])
print('vector: %s, shape of vector: %s' %(vector, vector.shape))
tensor = t.Tensor(1,2) # 注意和t.tensor([1, 2])的区别
tensor.shape
matrix = t.tensor([[0.1, 1.2], [2.2, 3.1], [4.9, 5.2]])
matrix,matrix.shape
t.tensor([[0.11111, 0.222222, 0.3333333]],
dtype=t.float64,
device=t.device('cpu'))
empty_tensor = t.tensor([])
empty_tensor.shape
# #### 常用Tensor操作
# 通过`tensor.view`方法可以调整tensor的形状,但必须保证调整前后元素总数一致。`view`不会修改自身的数据,返回的新tensor与源tensor共享内存,也即更改其中的一个,另外一个也会跟着改变。在实际应用中可能经常需要添加或减少某一维度,这时候`squeeze`和`unsqueeze`两个函数就派上用场了。
a = t.arange(0, 6)
a.view(2, 3)
b = a.view(-1, 3) # 当某一维为-1的时候,会自动计算它的大小
b.shape
b.unsqueeze(1) # 注意形状,在第1维(下标从0开始)上增加“1”
#等价于 b[:,None]
b[:, None].shape
b.unsqueeze(-2) # -2表示倒数第二个维度
c = b.view(1, 1, 1, 2, 3)
c.squeeze(0) # 压缩第0维的“1”
c.squeeze() # 把所有维度为“1”的压缩
a[1] = 100
b # a修改,b作为view之后的,也会跟着修改
# `resize`是另一种可用来调整`size`的方法,但与`view`不同,它可以修改tensor的大小。如果新大小超过了原大小,会自动分配新的内存空间,而如果新大小小于原大小,则之前的数据依旧会被保存,看一个例子。
b.resize_(1, 3)
b
b.resize_(3, 3) # 旧的数据依旧保存着,多出的大小会分配新空间
b
# #### 索引操作
#
# Tensor支持与numpy.ndarray类似的索引操作,语法上也类似,下面通过一些例子,讲解常用的索引操作。如无特殊说明,索引出来的结果与原tensor共享内存,也即修改一个,另一个会跟着修改。
a = t.randn(3, 4)
a
a[0] # 第0行(下标从0开始)
a[:, 0] # 第0列
a[0][2] # 第0行第2个元素,等价于a[0, 2]
a[0, -1] # 第0行最后一个元素
a[:2] # 前两行
a[:2, 0:2] # 前两行,第0,1列
print(a[0:1, :2]) # 第0行,前两列
print(a[0, :2]) # 注意两者的区别:形状不同
# None类似于np.newaxis, 为a新增了一个轴
# 等价于a.view(1, a.shape[0], a.shape[1])
a[None].shape
a[None].shape # 等价于a[None,:,:]
a[:,None,:].shape
a[:,None,:,None,None].shape
a > 1 # 返回一个ByteTensor
a[a>1] # 等价于a.masked_select(a>1)
# 选择结果与原tensor不共享内存空间
a[t.LongTensor([0,1])] # 第0行和第1行
# 其它常用的选择函数如表3-2所示。
#
# 表3-2常用的选择函数
#
# 函数|功能|
# :---:|:---:|
# index_select(input, dim, index)|在指定维度dim上选取,比如选取某些行、某些列
# masked_select(input, mask)|例子如上,a[a>0],使用ByteTensor进行选取
# non_zero(input)|非0元素的下标
# gather(input, dim, index)|根据index,在dim维度上选取数据,输出的size与index一样
#
#
# `gather`是一个比较复杂的操作,对一个2维tensor,输出的每个元素如下:
#
# ```python
# out[i][j] = input[index[i][j]][j] # dim=0
# out[i][j] = input[i][index[i][j]] # dim=1
# ```
# 三维tensor的`gather`操作同理,下面举几个例子。
a = t.arange(0, 16).view(4, 4)
a
# 选取对角线的元素
index = t.LongTensor([[0,1,2,3]])
a.gather(0, index)
# 选取反对角线上的元素
index = t.LongTensor([[3,2,1,0]]).t()
a.gather(1, index)
# 选取反对角线上的元素,注意与上面的不同
index = t.LongTensor([[3,2,1,0]])
a.gather(0, index)
# 选取两个对角线上的元素
index = t.LongTensor([[0,1,2,3],[3,2,1,0]]).t()
b = a.gather(1, index)
b
# 与`gather`相对应的逆操作是`scatter_`,`gather`把数据从input中按index取出,而`scatter_`是把取出的数据再放回去。注意`scatter_`函数是inplace操作。
#
# ```python
# out = input.gather(dim, index)
# -->近似逆操作
# out = Tensor()
# out.scatter_(dim, index)
# ```
# 把两个对角线元素放回去到指定位置
c = t.zeros(4,4)
c.scatter_(1, index, b)
# 对tensor的任何索引操作仍是一个tensor,想要获取标准的python对象数值,需要调用`tensor.item()`, 这个方法只对包含一个元素的tensor适用
a[0,0] #依旧是tensor)
a[0,0].item() # python float
d = a[0:1, 0:1, None]
print(d.shape)
d.item() # 只包含一个元素的tensor即可调用tensor.item,与形状无关
# +
# a[0].item() ->
# raise ValueError: only one element tensors can be converted to Python scalars
# -
# #### 高级索引
# PyTorch在0.2版本中完善了索引操作,目前已经支持绝大多数numpy的高级索引[^10]。高级索引可以看成是普通索引操作的扩展,但是高级索引操作的结果一般不和原始的Tensor贡献内出。
# [^10]: https://docs.scipy.org/doc/numpy/reference/arrays.indexing.html#advanced-indexing
x = t.arange(0,27).view(3,3,3)
x
x[[1, 2], [1, 2], [2, 0]] # x[1,1,2]和x[2,2,0]
x[[2, 1, 0], [0], [1]] # x[2,0,1],x[1,0,1],x[0,0,1]
x[[0, 2], ...] # x[0] 和 x[2]
# #### Tensor类型
#
# Tensor有不同的数据类型,如表3-3所示,每种类型分别对应有CPU和GPU版本(HalfTensor除外)。默认的tensor是FloatTensor,可通过`t.set_default_tensor_type` 来修改默认tensor类型(如果默认类型为GPU tensor,则所有操作都将在GPU上进行)。Tensor的类型对分析内存占用很有帮助。例如对于一个size为(1000, 1000, 1000)的FloatTensor,它有`1000*1000*1000=10^9`个元素,每个元素占32bit/8 = 4Byte内存,所以共占大约4GB内存/显存。HalfTensor是专门为GPU版本设计的,同样的元素个数,显存占用只有FloatTensor的一半,所以可以极大缓解GPU显存不足的问题,但由于HalfTensor所能表示的数值大小和精度有限[^2],所以可能出现溢出等问题。
#
# [^2]: https://stackoverflow.com/questions/872544/what-range-of-numbers-can-be-represented-in-a-16-32-and-64-bit-ieee-754-syste
#
# 表3-3: tensor数据类型
#
# | Data type | dtype | CPU tensor | GPU tensor |
# | ------------------------ | --------------------------------- | ------------------------------------------------------------ | ------------------------- |
# | 32-bit floating point | `torch.float32` or `torch.float` | `torch.FloatTensor` | `torch.cuda.FloatTensor` |
# | 64-bit floating point | `torch.float64` or `torch.double` | `torch.DoubleTensor` | `torch.cuda.DoubleTensor` |
# | 16-bit floating point | `torch.float16` or `torch.half` | `torch.HalfTensor` | `torch.cuda.HalfTensor` |
# | 8-bit integer (unsigned) | `torch.uint8` | [`torch.ByteTensor`](https://pytorch.org/docs/stable/tensors.html#torch.ByteTensor) | `torch.cuda.ByteTensor` |
# | 8-bit integer (signed) | `torch.int8` | `torch.CharTensor` | `torch.cuda.CharTensor` |
# | 16-bit integer (signed) | `torch.int16` or `torch.short` | `torch.ShortTensor` | `torch.cuda.ShortTensor` |
# | 32-bit integer (signed) | `torch.int32` or `torch.int` | `torch.IntTensor` | `torch.cuda.IntTensor` |
# | 64-bit integer (signed) | `torch.int64` or `torch.long` | `torch.LongTensor` | `torch.cuda.LongTensor` |
#
#
#
# 各数据类型之间可以互相转换,`type(new_type)`是通用的做法,同时还有`float`、`long`、`half`等快捷方法。CPU tensor与GPU tensor之间的互相转换通过`tensor.cuda`和`tensor.cpu`方法实现,此外还可以使用`tensor.to(device)`。Tensor还有一个`new`方法,用法与`t.Tensor`一样,会调用该tensor对应类型的构造函数,生成与当前tensor类型一致的tensor。`torch.*_like(tensora)` 可以生成和`tensora`拥有同样属性(类型,形状,cpu/gpu)的新tensor。 `tensor.new_*(new_shape)` 新建一个不同形状的tensor。
# 设置默认tensor,注意参数是字符串
t.set_default_tensor_type('torch.DoubleTensor')
a = t.Tensor(2,3)
a.dtype # 现在a是DoubleTensor,dtype是float64
# 恢复之前的默认设置
t.set_default_tensor_type('torch.FloatTensor')
# 把a转成FloatTensor,等价于b=a.type(t.FloatTensor)
b = a.float()
b.dtype
c = a.type_as(b)
c
a.new(2,3) # 等价于torch.DoubleTensor(2,3),建议使用a.new_tensor
t.zeros_like(a) #等价于t.zeros(a.shape,dtype=a.dtype,device=a.device)
t.zeros_like(a, dtype=t.int16) #可以修改某些属性
t.rand_like(a)
a.new_ones(4,5, dtype=t.int)
a.new_tensor([3,4]) #
# #### 逐元素操作
#
# 这部分操作会对tensor的每一个元素(point-wise,又名element-wise)进行操作,此类操作的输入与输出形状一致。常用的操作如表3-4所示。
#
# 表3-4: 常见的逐元素操作
#
# |函数|功能|
# |:--:|:--:|
# |abs/sqrt/div/exp/fmod/log/pow..|绝对值/平方根/除法/指数/求余/求幂..|
# |cos/sin/asin/atan2/cosh..|相关三角函数|
# |ceil/round/floor/trunc| 上取整/四舍五入/下取整/只保留整数部分|
# |clamp(input, min, max)|超过min和max部分截断|
# |sigmod/tanh..|激活函数
#
# 对于很多操作,例如div、mul、pow、fmod等,PyTorch都实现了运算符重载,所以可以直接使用运算符。如`a ** 2` 等价于`torch.pow(a,2)`, `a * 2`等价于`torch.mul(a,2)`。
#
# 其中`clamp(x, min, max)`的输出满足以下公式:
# $$
# y_i =
# \begin{cases}
# min, & \text{if } x_i \lt min \\
# x_i, & \text{if } min \le x_i \le max \\
# max, & \text{if } x_i \gt max\\
# \end{cases}
# $$
# `clamp`常用在某些需要比较大小的地方,如取一个tensor的每个元素与另一个数的较大值。
a = t.arange(0, 6).view(2, 3)
t.cos(a)
a % 3 # 等价于t.fmod(a, 3)
a ** 2 # 等价于t.pow(a, 2)
# 取a中的每一个元素与3相比较大的一个 (小于3的截断成3)
print(a)
t.clamp(a, min=3)
b = a.sin_() # 效果同 a = a.sin();b=a ,但是更高效节省显存
a
# #### 归并操作
# 此类操作会使输出形状小于输入形状,并可以沿着某一维度进行指定操作。如加法`sum`,既可以计算整个tensor的和,也可以计算tensor中每一行或每一列的和。常用的归并操作如表3-5所示。
#
# 表3-5: 常用归并操作
#
# |函数|功能|
# |:---:|:---:|
# |mean/sum/median/mode|均值/和/中位数/众数|
# |norm/dist|范数/距离|
# |std/var|标准差/方差|
# |cumsum/cumprod|累加/累乘|
#
# 以上大多数函数都有一个参数**`dim`**,用来指定这些操作是在哪个维度上执行的。关于dim(对应于Numpy中的axis)的解释众说纷纭,这里提供一个简单的记忆方式:
#
# 假设输入的形状是(m, n, k)
#
# - 如果指定dim=0,输出的形状就是(1, n, k)或者(n, k)
# - 如果指定dim=1,输出的形状就是(m, 1, k)或者(m, k)
# - 如果指定dim=2,输出的形状就是(m, n, 1)或者(m, n)
#
# size中是否有"1",取决于参数`keepdim`,`keepdim=True`会保留维度`1`。注意,以上只是经验总结,并非所有函数都符合这种形状变化方式,如`cumsum`。
b = t.ones(2, 3)
b.sum(dim = 0, keepdim=True)
# keepdim=False,不保留维度"1",注意形状
b.sum(dim=0, keepdim=False)
b.sum(dim=1)
a = t.arange(0, 6).view(2, 3)
print(a)
a.cumsum(dim=1) # 沿着行累加
# #### 比较
# 比较函数中有一些是逐元素比较,操作类似于逐元素操作,还有一些则类似于归并操作。常用比较函数如表3-6所示。
#
# 表3-6: 常用比较函数
#
# |函数|功能|
# |:--:|:--:|
# |gt/lt/ge/le/eq/ne|大于/小于/大于等于/小于等于/等于/不等|
# |topk|最大的k个数|
# |sort|排序|
# |max/min|比较两个tensor最大最小值|
#
# 表中第一行的比较操作已经实现了运算符重载,因此可以使用`a>=b`、`a>b`、`a!=b`、`a==b`,其返回结果是一个`ByteTensor`,可用来选取元素。max/min这两个操作比较特殊,以max来说,它有以下三种使用情况:
# - t.max(tensor):返回tensor中最大的一个数
# - t.max(tensor,dim):指定维上最大的数,返回tensor和下标
# - t.max(tensor1, tensor2): 比较两个tensor相比较大的元素
#
# 至于比较一个tensor和一个数,可以使用clamp函数。下面举例说明。
a = t.linspace(0, 15, 6).view(2, 3)
a
b = t.linspace(15, 0, 6).view(2, 3)
b
a>b
a[a>b] # a中大于b的元素
t.max(a)
t.max(b, dim=1)
# 第一个返回值的15和6分别表示第0行和第1行最大的元素
# 第二个返回值的0和0表示上述最大的数是该行第0个元素
t.max(a,b)
# 比较a和10较大的元素
t.clamp(a, min=10)
# #### 线性代数
#
# PyTorch的线性函数主要封装了Blas和Lapack,其用法和接口都与之类似。常用的线性代数函数如表3-7所示。
#
# 表3-7: 常用的线性代数函数
#
# |函数|功能|
# |:---:|:---:|
# |trace|对角线元素之和(矩阵的迹)|
# |diag|对角线元素|
# |triu/tril|矩阵的上三角/下三角,可指定偏移量|
# |mm/bmm|矩阵乘法,batch的矩阵乘法|
# |addmm/addbmm/addmv/addr/badbmm..|矩阵运算
# |t|转置|
# |dot/cross|内积/外积
# |inverse|求逆矩阵
# |svd|奇异值分解
#
# 具体使用说明请参见官方文档[^3],需要注意的是,矩阵的转置会导致存储空间不连续,需调用它的`.contiguous`方法将其转为连续。
# [^3]: http://pytorch.org/docs/torch.html#blas-and-lapack-operations
b = a.t()
b.is_contiguous()
b.contiguous()
# ### 3.1.2 Tensor和Numpy
#
# Tensor和Numpy数组之间具有很高的相似性,彼此之间的互操作也非常简单高效。需要注意的是,Numpy和Tensor共享内存。由于Numpy历史悠久,支持丰富的操作,所以当遇到Tensor不支持的操作时,可先转成Numpy数组,处理后再转回tensor,其转换开销很小。
import numpy as np
a = np.ones([2, 3],dtype=np.float32)
a
b = t.from_numpy(a)
b
b = t.Tensor(a) # 也可以直接将numpy对象传入Tensor
b
a[0, 1]=100
b
c = b.numpy() # a, b, c三个对象共享内存
c
# **注意**: 当numpy的数据类型和Tensor的类型不一样的时候,数据会被复制,不会共享内存。
a = np.ones([2, 3])
# 注意和上面的a的区别(dtype不是float32)
a.dtype
b = t.Tensor(a) # 此处进行拷贝,不共享内存
b.dtype
c = t.from_numpy(a) # 注意c的类型(DoubleTensor)
c
a[0, 1] = 100
b # b与a不共享内存,所以即使a改变了,b也不变
c # c与a共享内存
# **注意:** 不论输入的类型是什么,t.tensor都会进行数据拷贝,不会共享内存
tensor = t.tensor(a)
tensor[0,0]=0
a
# 广播法则(broadcast)是科学运算中经常使用的一个技巧,它在快速执行向量化的同时不会占用额外的内存/显存。
# Numpy的广播法则定义如下:
#
# - 让所有输入数组都向其中shape最长的数组看齐,shape中不足的部分通过在前面加1补齐
# - 两个数组要么在某一个维度的长度一致,要么其中一个为1,否则不能计算
# - 当输入数组的某个维度的长度为1时,计算时沿此维度复制扩充成一样的形状
#
# PyTorch当前已经支持了自动广播法则,但是笔者还是建议读者通过以下两个函数的组合手动实现广播法则,这样更直观,更不易出错:
#
# - `unsqueeze`或者`view`,或者tensor[None],:为数据某一维的形状补1,实现法则1
# - `expand`或者`expand_as`,重复数组,实现法则3;该操作不会复制数组,所以不会占用额外的空间。
#
# 注意,repeat实现与expand相类似的功能,但是repeat会把相同数据复制多份,因此会占用额外的空间。
a = t.ones(3, 2)
b = t.zeros(2, 3,1)
# 自动广播法则
# 第一步:a是2维,b是3维,所以先在较小的a前面补1 ,
# 即:a.unsqueeze(0),a的形状变成(1,3,2),b的形状是(2,3,1),
# 第二步: a和b在第一维和第三维形状不一样,其中一个为1 ,
# 可以利用广播法则扩展,两个形状都变成了(2,3,2)
a+b
# 手动广播法则
# 或者 a.view(1,3,2).expand(2,3,2)+b.expand(2,3,2)
a[None].expand(2, 3, 2) + b.expand(2,3,2)
# expand不会占用额外空间,只会在需要的时候才扩充,可极大节省内存
e = a.unsqueeze(0).expand(10000000000000, 3,2)
# ### 3.1.3 内部结构
#
# tensor的数据结构如图3-1所示。tensor分为头信息区(Tensor)和存储区(Storage),信息区主要保存着tensor的形状(size)、步长(stride)、数据类型(type)等信息,而真正的数据则保存成连续数组。由于数据动辄成千上万,因此信息区元素占用内存较少,主要内存占用则取决于tensor中元素的数目,也即存储区的大小。
#
# 一般来说一个tensor有着与之相对应的storage, storage是在data之上封装的接口,便于使用,而不同tensor的头信息一般不同,但却可能使用相同的数据。下面看两个例子。
#
# 
a = t.arange(0, 6)
a.storage()
b = a.view(2, 3)
b.storage()
# 一个对象的id值可以看作它在内存中的地址
# storage的内存地址一样,即是同一个storage
id(b.storage()) == id(a.storage())
# a改变,b也随之改变,因为他们共享storage
a[1] = 100
b
c = a[2:]
c.storage()
c.data_ptr(), a.data_ptr() # data_ptr返回tensor首元素的内存地址
# 可以看出相差8,这是因为2*4=8--相差两个元素,每个元素占4个字节(float)
c[0] = -100 # c[0]的内存地址对应a[2]的内存地址
a
d = t.Tensor(c.storage())
d[0] = 6666
b
# 下面4个tensor共享storage
id(a.storage()) == id(b.storage()) == id(c.storage()) == id(d.storage())
a.storage_offset(), c.storage_offset(), d.storage_offset()
e = b[::2, ::2] # 隔2行/列取一个元素
id(e.storage()) == id(a.storage())
b.stride(), e.stride()
e.is_contiguous()
# 可见绝大多数操作并不修改tensor的数据,而只是修改了tensor的头信息。这种做法更节省内存,同时提升了处理速度。在使用中需要注意。
# 此外有些操作会导致tensor不连续,这时需调用`tensor.contiguous`方法将它们变成连续的数据,该方法会使数据复制一份,不再与原来的数据共享storage。
# 另外读者可以思考一下,之前说过的高级索引一般不共享stroage,而普通索引共享storage,这是为什么?(提示:普通索引可以通过只修改tensor的offset,stride和size,而不修改storage来实现)。
# ### 3.1.4 其它有关Tensor的话题
# 这部分的内容不好专门划分一小节,但是笔者认为仍值得读者注意,故而将其放在这一小节。
# #### GPU/CPU
# tensor可以很随意的在gpu/cpu上传输。使用`tensor.cuda(device_id)`或者`tensor.cpu()`。另外一个更通用的方法是`tensor.to(device)`。
a = t.randn(3, 4)
a.device
if t.cuda.is_available():
a = t.randn(3,4, device=t.device('cuda:1'))
# 等价于
# a.t.randn(3,4).cuda(1)
# 但是前者更快
a.device
device = t.device('cpu')
a.to(device)
# **注意**
# - 尽量使用`tensor.to(device)`, 将`device`设为一个可配置的参数,这样可以很轻松的使程序同时兼容GPU和CPU
# - 数据在GPU之中传输的速度要远快于内存(CPU)到显存(GPU), 所以尽量避免频繁的在内存和显存中传输数据。
# #### 持久化
# Tensor的保存和加载十分的简单,使用t.save和t.load即可完成相应的功能。在save/load时可指定使用的`pickle`模块,在load时还可将GPU tensor映射到CPU或其它GPU上。
if t.cuda.is_available():
a = a.cuda(1) # 把a转为GPU1上的tensor,
t.save(a,'a.pth')
# 加载为b, 存储于GPU1上(因为保存时tensor就在GPU1上)
b = t.load('a.pth')
# 加载为c, 存储于CPU
c = t.load('a.pth', map_location=lambda storage, loc: storage)
# 加载为d, 存储于GPU0上
d = t.load('a.pth', map_location={'cuda:1':'cuda:0'})
# #### 向量化
# 向量化计算是一种特殊的并行计算方式,相对于一般程序在同一时间只执行一个操作的方式,它可在同一时间执行多个操作,通常是对不同的数据执行同样的一个或一批指令,或者说把指令应用于一个数组/向量上。向量化可极大提高科学运算的效率,Python本身是一门高级语言,使用很方便,但这也意味着很多操作很低效,尤其是`for`循环。在科学计算程序中应当极力避免使用Python原生的`for循环`。
def for_loop_add(x, y):
result = []
for i,j in zip(x, y):
result.append(i + j)
return t.Tensor(result)
x = t.zeros(100)
y = t.ones(100)
# %timeit -n 10 for_loop_add(x, y)
# %timeit -n 10 x + y
# 可见二者有超过几十倍的速度差距,因此在实际使用中应尽量调用内建函数(buildin-function),这些函数底层由C/C++实现,能通过执行底层优化实现高效计算。因此在平时写代码时,就应养成向量化的思维习惯,千万避免对较大的tensor进行逐元素遍历。
# 此外还有以下几点需要注意:
# - 大多数`t.function`都有一个参数`out`,这时候产生的结果将保存在out指定tensor之中。
# - `t.set_num_threads`可以设置PyTorch进行CPU多线程并行计算时候所占用的线程数,这个可以用来限制PyTorch所占用的CPU数目。
# - `t.set_printoptions`可以用来设置打印tensor时的数值精度和格式。
# 下面举例说明。
a = t.arange(0, 20000000)
print(a[-1], a[-2]) # 32bit的IntTensor精度有限导致溢出
b = t.LongTensor()
t.arange(0, 20000000, out=b) # 64bit的LongTensor不会溢出
b[-1],b[-2]
a = t.randn(2,3)
a
t.set_printoptions(precision=10)
a
# ### 3.1.5 小试牛刀:线性回归
# 线性回归是机器学习入门知识,应用十分广泛。线性回归利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的,其表达形式为$y = wx+b+e$,$e$为误差服从均值为0的正态分布。首先让我们来确认线性回归的损失函数:
# $$
# loss = \sum_i^N \frac 1 2 ({y_i-(wx_i+b)})^2
# $$
# 然后利用随机梯度下降法更新参数$\textbf{w}$和$\textbf{b}$来最小化损失函数,最终学得$\textbf{w}$和$\textbf{b}$的数值。
# +
import torch as t
# %matplotlib inline
from matplotlib import pyplot as plt
from IPython import display
device = t.device('cpu') #如果你想用gpu,改成t.device('cuda:0')
# +
# 设置随机数种子,保证在不同电脑上运行时下面的输出一致
t.manual_seed(1000)
def get_fake_data(batch_size=8):
''' 产生随机数据:y=x*2+3,加上了一些噪声'''
x = t.rand(batch_size, 1, device=device) * 5
y = x * 2 + 3 + t.randn(batch_size, 1, device=device)
return x, y
# -
# 来看看产生的x-y分布
x, y = get_fake_data(batch_size=16)
plt.scatter(x.squeeze().cpu().numpy(), y.squeeze().cpu().numpy())
# +
# 随机初始化参数
w = t.rand(1, 1).to(device)
b = t.zeros(1, 1).to(device)
lr =0.02 # 学习率
for ii in range(500):
x, y = get_fake_data(batch_size=4)
# forward:计算loss
y_pred = x.mm(w) + b.expand_as(y) # x@W等价于x.mm(w);for python3 only
loss = 0.5 * (y_pred - y) ** 2 # 均方误差
loss = loss.mean()
# backward:手动计算梯度
dloss = 1
dy_pred = dloss * (y_pred - y)
dw = x.t().mm(dy_pred)
db = dy_pred.sum()
# 更新参数
w.sub_(lr * dw)
b.sub_(lr * db)
if ii%50 ==0:
# 画图
display.clear_output(wait=True)
x = t.arange(0, 6).view(-1, 1)
y = x.mm(w) + b.expand_as(x)
plt.plot(x.cpu().numpy(), y.cpu().numpy()) # predicted
x2, y2 = get_fake_data(batch_size=32)
plt.scatter(x2.numpy(), y2.numpy()) # true data
plt.xlim(0, 5)
plt.ylim(0, 13)
plt.show()
plt.pause(0.5)
print('w: ', w.item(), 'b: ', b.item())
# -
# 可见程序已经基本学出w=2、b=3,并且图中直线和数据已经实现较好的拟合。
# 虽然上面提到了许多操作,但是只要掌握了这个例子基本上就可以了,其他的知识,读者日后遇到的时候,可以再看看这部份的内容或者查找对应文档。
#
|
chapter3/Tensor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ethereum Price
# by: <NAME>
# ### 1. Read Dataset
import csv
import pandas as pd
import numpy as np
df = pd.read_csv('../data/raw/bitcoin/ethereum_price.csv', parse_dates = ['Date'])
df.tail()
# ### 2. Data Investigation
df.columns
df.count()
df.dtypes
# #### There is a missing data here and there are several data which have different format. Some of the data do not use number format
# Change object to format number, and replace '-' to 'NaN'
df['Volume'] = df['Volume'].apply(lambda x: float(str(x).replace(',','')))
df['Market Cap'] = df['Market Cap'].replace('-', 'NaN')
df['Market Cap'] = df['Market Cap'].apply(lambda x: float(str(x).replace(',','')))
df.tail()
df.count()
df.info()
missingdf = pd.DataFrame(df.isna().sum()).rename(columns = {0: 'total'})
missingdf['percent'] = missingdf['total'] / len(df)
missingdf
# Lets see the correlation between each column
correlation = df.corr(method="pearson")
correlation['Market Cap']
# +
#Plot data to see the relation between each column
import matplotlib.pyplot as plt
plt.figure(figsize=(25, 25))
O = df['Open']
MC = df['Market Cap']
plt.subplot(5,5,5)
plt.scatter(MC, O)
plt.title('Open vs Market Cap')
plt.show
# -
# To fill the NaN value I try to interpolate the data using linear method using value from Open column. Because from the information above we can see that Market Cap has the closest correlation with Open.
# To fill the NaN value I try to interpolate the data using linear method using value from Open column. Because from the figure above we can see that Market Cap has linear condition with Open
# +
from sklearn import linear_model
model = linear_model.LinearRegression()
Open = df[['Open']].iloc[0:759]
Market_Cap = df['Market Cap'].iloc[0:759]
# -
#Train model
model.fit(Open, Market_Cap)
#The model score almost 1 so that indicate the model is near to the truth
model.score(Open, Market_Cap)
# Here I make a new column Market Cap Predict which contains Market Cap with no NaN value
#Add a new column which is filled the missing data from model fit
open = df[['Open']]
Market_Cap_Predict = model.predict(open)
df['Market Cap Predict'] = Market_Cap_Predict
df.tail()
df.count()
df.describe()
# #### Now the data is clean, no null value and has same format
# ### 3. Data Visualization
# Set Date as it's index
df.set_index('Date', inplace = True )
# +
# Visualization the average of Open based on time (Week)
# %matplotlib inline
plt.figure(figsize=(25, 25))
plt.subplot(3,3,1)
plt.ylabel('Open')
df.Open.plot()
plt.title('Date vs Open')
plt.subplot(3,3,2)
plt.ylabel('Low')
df.Low.plot()
plt.title('Date vs Low')
plt.subplot(3,3,3)
plt.ylabel('High')
df.High.plot()
plt.title('Date vs High')
plt.subplot(3,3,4)
plt.ylabel('Close')
df.Close.plot()
plt.title('Date vs Close')
plt.subplot(3,3,5)
plt.ylabel('Volume')
df.Volume.plot()
plt.title('Date vs Volume')
plt.subplot(3,3,6)
plt.ylabel('Market Cap Predict')
df['Market Cap Predict'].plot()
plt.title('Date vs Market Cap Predict')
# -
|
notebooks/14. ethereum_price.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Testing MPI version for Imaging and deconvolution demonstration
# This script makes a fake data set and then deconvolves it. Finally the full and residual visibility are plotted.
# %lsmagic
# +
from mpi4py import MPI
print(MPI.COMM_WORLD.size)
# +
# %matplotlib inline
import os
import sys
sys.path.append(os.path.join('..', '..'))
from data_models.parameters import arl_path
results_dir = arl_path('test_results')
from matplotlib import pylab
pylab.rcParams['figure.figsize'] = (8.0, 8.0)
pylab.rcParams['image.cmap'] = 'rainbow'
import numpy
from astropy.coordinates import SkyCoord
from astropy import units as u
from astropy.wcs.utils import pixel_to_skycoord
from matplotlib import pyplot as plt
from processing_components.image.iterators import image_raster_iter
from wrappers.serial.visibility.base import create_visibility
from wrappers.serial.skycomponent.operations import create_skycomponent
from wrappers.serial.image.operations import show_image, export_image_to_fits
from wrappers.serial.image.deconvolution import deconvolve_cube, restore_cube
from wrappers.serial.visibility.iterators import vis_timeslice_iter
from wrappers.serial.simulation.testing_support import create_test_image
from wrappers.serial.simulation.configurations import create_named_configuration
from wrappers.serial.imaging.base import create_image_from_visibility
from workflows.mpi.imaging.imaging_mpi import predict_list_mpi_workflow, invert_list_mpi_workflow, deconvolve_list_mpi_workflow,weight_list_mpi_workflow
from data_models.polarisation import PolarisationFrame
import logging
log = logging.getLogger()
log.setLevel(logging.DEBUG)
log.addHandler(logging.StreamHandler(sys.stdout))
# -
pylab.rcParams['figure.figsize'] = (12.0, 12.0)
pylab.rcParams['image.cmap'] = 'rainbow'
# Construct LOW core configuration
lowcore = create_named_configuration('LOWBD2', rmax=400.0)
print(lowcore.xyz)
# We create the visibility. This just makes the uvw, time, antenna1, antenna2, weight columns in a table
times = numpy.zeros([1])
frequency = numpy.array([1e8])
channel_bandwidth = numpy.array([1e6])
phasecentre = SkyCoord(ra=+15.0 * u.deg, dec=-45.0 * u.deg, frame='icrs', equinox='J2000')
vt = create_visibility(lowcore, times, frequency, channel_bandwidth=channel_bandwidth,
weight=1.0, phasecentre=phasecentre, polarisation_frame=PolarisationFrame('stokesI'))
print(vt)
# Plot the synthesized uv coverage.
plt.clf()
plt.plot(vt.data['uvw'][:,0], vt.data['uvw'][:,1], '.', color='b')
plt.plot(-vt.data['uvw'][:,0], -vt.data['uvw'][:,1], '.', color='b')
plt.show()
# Read the venerable test image, constructing an image
m31image = create_test_image(frequency=frequency, cellsize=0.0005)
nchan, npol, ny, nx = m31image.data.shape
m31image.wcs.wcs.crval[0] = vt.phasecentre.ra.deg
m31image.wcs.wcs.crval[1] = vt.phasecentre.dec.deg
m31image.wcs.wcs.crpix[0] = float(nx // 2)
m31image.wcs.wcs.crpix[1] = float(ny // 2)
print("My image:")
print(m31image)
print(m31image.data)
#print(m31image.wcs)
#print(m31image.polarisation_frame)
sumwt = numpy.zeros([m31image.nchan, m31image.npol])
fig=show_image(m31image)
vt = predict_list_mpi_workflow([vt], [m31image], context='2d',use_serial_predict=True)
print(vt)
# To check that we got the prediction right, plot the amplitude of the visibility.
vt=vt[0]
uvdist=numpy.sqrt(vt.data['uvw'][:,0]**2+vt.data['uvw'][:,1]**2)
plt.clf()
plt.plot(uvdist, numpy.abs(vt.data['vis']), '.')
plt.xlabel('uvdist')
plt.ylabel('Amp Visibility')
plt.show()
# Make the dirty image and point spread function
# +
model = create_image_from_visibility(vt, cellsize=0.001, npixel=256)
dirty, sumwt = invert_list_mpi_workflow([vt], [model], context='2d')[0]
psf, sumwt = invert_list_mpi_workflow([vt], [model], context='2d', dopsf=True)[0]
show_image(dirty)
show_image(psf)
print("Max, min in dirty image = %.6f, %.6f, sumwt = %f" % (dirty.data.max(), dirty.data.min(), sumwt))
print("Max, min in PSF = %.6f, %.6f, sumwt = %f" % (psf.data.max(), psf.data.min(), sumwt))
export_image_to_fits(dirty, '%s/imaging_dirty.fits'%(results_dir))
export_image_to_fits(psf, '%s/imaging_psf.fits'%(results_dir))
# -
# Deconvolve using clean
result=deconvolve_list_mpi_workflow([(dirty,sumwt)], [(psf,sumwt)], [model])
# +
comp, residual = deconvolve_cube(dirty, psf, niter=1000, threshold=0.001, fracthresh=0.01, window_shape='quarter',
gain=0.7, scales=[0, 3, 10, 30])
restored = restore_cube(comp, psf, residual)
# Show the results
fig=show_image(comp)
plt.title('Solution')
fig=show_image(residual)
plt.title('Residual')
fig=show_image(restored)
plt.title('Restored')
# -
# Predict the visibility of the model
vtmodel = create_visibility(lowcore, times, frequency, channel_bandwidth=channel_bandwidth,
weight=1.0, phasecentre=phasecentre,
polarisation_frame=PolarisationFrame('stokesI'))
vtmodel=predict_list_serial_workflow([vtmodel], [comp], context='2d')[0]
# Now we will plot the original visibility and the residual visibility.
# +
uvdist=numpy.sqrt(vt.data['uvw'][:,0]**2+vt.data['uvw'][:,1]**2)
plt.clf()
plt.plot(uvdist, numpy.abs(vt.data['vis'][:]-vtmodel.data['vis'][:]), '.', color='r',
label='Residual')
plt.plot(uvdist, numpy.abs(vt.data['vis'][:]), '.', color='b', label='Original')
plt.xlabel('uvdist')
plt.ylabel('Amp Visibility')
plt.legend()
plt.show()
# -
|
deprecated_code/workflows/mpi/imaging_mpi.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Entropy
#
# **Entropy** - measurment of the uncertainty of the information
#
# First, let's create our first decision tree classifier.
# +
from sklearn import tree # Importing sklearn library, which has module "tree", which has DecisionTreeClassifier class.
import pandas as pd
import numpy as np
data = pd.DataFrame({'X_0': [1, 1, 1, 0, 0, 0, 0, 1], 'X_1': [0, 0, 0, 1, 0, 0, 0, 1], 'Y': [1, 1, 1, 1, 0, 0, 0, 0]})
data.head(8) # Creating smaple dataset
clf = tree.DecisionTreeClassifier(criterion = 'entropy') # Creating Decision Tree with Entropy
X = data[['X_0', 'X_1']] # Creating input dataset
y = data.Y # Creating output dataset
clf.fit(X, y) # Training Decision Tree
tree.plot_tree(clf) # Plotting Decision Tree
clf.predict(X) # Predicting Y's based on our input dataset
# -
# ## Formulas
#
# Entropy is usually mentioned as E or H. To calculate the entropy of the current set of data, we should use following formula:
#
# $$E=\ -\sum{(\ p}_{i\ }\ast\ \log_2{p_i})$$
#
# Where pi is a probabylity to clasiffy some object as a class i.
#
# To know how much information we got, we should calculate **Information Gain (IG)** using follwoing formula:
#
# $$IG=E\ \left(Y\right)-E\ (Y/X)$$
#
# Where E(Y) - initial entropy and E(Y|X):
#
# $$E\left(Y/X\right)=\ \frac{n_1}{N}\ast\ E_1+\ \frac{n_2}{N}\ast\ E_2$$
# Video about Informational Entropy on Khan Academy:
# https://www.khanacademy.org/computing/computer-science/informationtheory/moderninfotheory/v/information-entropy
#
# Link to the white board with the material: https://miro.com/welcomeonboard/sEwevZ1KZxpytAkx0qJ3mKbMS4NlD2GjtvcI2VpztAMQvmM34EKeuxW14VacrnPN
|
Basics of ML/(Entropy)_21_10_2020.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# PyTorch: 새 autograd Function 정의하기
# ----------------------------------------
#
# $y=\sin(x)$ 을 예측할 수 있도록, $-\pi$ 부터 $\pi$ 까지
# 유클리드 거리(Euclidean distance)를 최소화하도록 3차 다항식을 학습합니다.
# 다항식을 $y=a+bx+cx^2+dx^3$ 라고 쓰는 대신 $y=a+b P_3(c+dx)$ 로 다항식을 적겠습니다.
# 여기서 $P_3(x)=
# rac{1}{2}\left(5x^3-3x
# ight)$ 은 3차
# `르장드르 다항식(Legendre polynomial)`_ 입니다.
#
# https://en.wikipedia.org/wiki/Legendre_polynomials
#
# 이 구현은 PyTorch 텐서 연산을 사용하여 순전파 단계를 계산하고, PyTorch autograd를 사용하여
# 변화도(gradient)를 계산합니다.
#
# 아래 구현에서는 $P_3'(x)$ 을 수행하기 위해 사용자 정의 autograd Function를 구현합니다.
# 수학적으로는 $P_3'(x)=
# rac{3}{2}\left(5x^2-1
# ight)$ 입니다.
#
# +
import torch
import math
class LegendrePolynomial3(torch.autograd.Function):
"""
torch.autograd.Function을 상속받아 사용자 정의 autograd Function을 구현하고,
텐서 연산을 하는 순전파 단계와 역전파 단계를 구현해보겠습니다.
"""
@staticmethod
def forward(ctx, input):
"""
순전파 단계에서는 입력을 갖는 텐서를 받아 출력을 갖는 텐서를 반환합니다.
ctx는 컨텍스트 객체(context object)로 역전파 연산을 위한 정보 저장에 사용합니다.
ctx.save_for_backward 메소드를 사용하여 역전파 단계에서 사용할 어떤 객체도
저장(cache)해 둘 수 있습니다.
"""
ctx.save_for_backward(input)
return 0.5 * (5 * input ** 3 - 3 * input)
@staticmethod
def backward(ctx, grad_output):
"""
역전파 단계에서는 출력에 대한 손실(loss)의 변화도(gradient)를 갖는 텐서를 받고,
입력에 대한 손실의 변화도를 계산해야 합니다.
"""
input, = ctx.saved_tensors
return grad_output * 1.5 * (5 * input ** 2 - 1)
dtype = torch.float
device = torch.device("cpu")
# device = torch.device("cuda:0") # GPU에서 실행하려면 이 주석을 제거하세요
# 입력값과 출력값을 갖는 텐서들을 생성합니다.
# requires_grad=False가 기본값으로 설정되어 역전파 단계 중에 이 텐서들에 대한 변화도를 계산할
# 필요가 없음을 나타냅니다.
x = torch.linspace(-math.pi, math.pi, 2000, device=device, dtype=dtype)
y = torch.sin(x)
# 가중치를 갖는 임의의 텐서를 생성합니다. 3차 다항식이므로 4개의 가중치가 필요합니다:
# y = a + b * P3(c + d * x)
# 이 가중치들이 수렴(convergence)하기 위해서는 정답으로부터 너무 멀리 떨어지지 않은 값으로
# 초기화가 되어야 합니다.
# requires_grad=True로 설정하여 역전파 단계 중에 이 텐서들에 대한 변화도를 계산할 필요가
# 있음을 나타냅니다.
a = torch.full((), 0.0, device=device, dtype=dtype, requires_grad=True)
b = torch.full((), -1.0, device=device, dtype=dtype, requires_grad=True)
c = torch.full((), 0.0, device=device, dtype=dtype, requires_grad=True)
d = torch.full((), 0.3, device=device, dtype=dtype, requires_grad=True)
learning_rate = 5e-6
for t in range(2000):
# 사용자 정의 Function을 적용하기 위해 Function.apply 메소드를 사용합니다.
# 여기에 'P3'라고 이름을 붙였습니다.
P3 = LegendrePolynomial3.apply
# 순전파 단계: 연산을 하여 예측값 y를 계산합니다;
# 사용자 정의 autograd 연산을 사용하여 P3를 계산합니다.
y_pred = a + b * P3(c + d * x)
# 손실을 계산하고 출력합니다.
loss = (y_pred - y).pow(2).sum()
if t % 100 == 99:
print(t, loss.item())
# autograd를 사용하여 역전파 단계를 계산합니다.
loss.backward()
# 경사하강법(gradient descent)을 사용하여 가중치를 갱신합니다.
with torch.no_grad():
a -= learning_rate * a.grad
b -= learning_rate * b.grad
c -= learning_rate * c.grad
d -= learning_rate * d.grad
# 가중치 갱신 후에는 변화도를 직접 0으로 만듭니다.
a.grad = None
b.grad = None
c.grad = None
d.grad = None
print(f'Result: y = {a.item()} + {b.item()} * P3({c.item()} + {d.item()} x)')
|
docs/_downloads/0b586e23ee09407ff674ff01b010923c/polynomial_custom_function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import gym
import tensorflow as tf
import itertools
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import importlib
# import IPython
# # %autosave 240
import sys
sys.path.append('../../embodied_arch/')
import embodied_AC as emg
from embodied_misc import ActionPolicyNetwork, ValueNetwork, SensoriumNetworkTemplate
sys.path.append('../../minoritygame/') #
from minority_env import MinorityGame1vN_env as minority_agent
# ## Minority Game Benchmark Setup
actor = lambda s: ActionPolicyNetwork(s, hSeq=(12,), gamma_reg=1.)
value = lambda s: ValueNetwork(s, hSeq=(8,), gamma_reg=1.)
sensor = lambda st, out_dim: SensoriumNetworkTemplate(st, hSeq=(16,8,16,), out_dim=out_dim, gamma_reg=5.)
num_episodes = 100
n_epochs = 1001
importlib.reload(emg)
# +
tf.reset_default_graph()
menv = minority_agent(33, 4, 4, 0.5)
embrf = emg.EmbodiedAgentAC(
name="mingame-AC",
env_=menv,
alpha_p=5., alpha_v=1.e-1,
actorNN=actor, sensorium=sensor, valueNN=value
)
# alpha_p=45., alpha_v=150,
embrf.max_episode_length = 30 #101 # dangerous... may incentivize finite n behavior
# +
print(menv.state_space_size, menv.action_space_size)
print(embrf, embrf.s_size, embrf.a_size)
sess = tf.InteractiveSession()
embrf.init_graph(sess) # note tboard log dir
# +
## Verify step + play set up
state = embrf.env.reset()
print(state, embrf.act(state, sess))
embrf.env.step(embrf.act(state, sess))
embrf.play(sess)
embrf.last_total_return
# -
# ### Pre-test Agent
print('Baselining untrained pnet...')
rwd_mg0 = []
for k in range(num_episodes):
embrf.play(sess)
rwd_mg0.append(embrf.last_total_return)
if k%int(num_episodes/5) == 0: print("\rEpisode {}/{}".format(k, num_episodes),end="")
base_perf_mg = np.mean(np.array(rwd_mg0)/float(embrf.max_episode_length))
print("\nAgent wins an average of {} pct".format(100.0*base_perf_mg))
# ### Train Agent w/ Algo on Experience Tuples
# +
obs = []
for ct in range(750):
embrf.play(sess)
tmp = embrf.pretrainV(sess)
obs.append(tmp)
print('\r\tIteration {}: Value loss({})'.format(ct, tmp), end="")
plt.plot(obs)
# from collections import Counter
# # ?Counter
# -
sns.violinplot(obs)
# Train pnet on mingame episodes
print('Training...')
saver = tf.train.Saver(max_to_keep=1)
hist = embrf.work(sess, saver, num_epochs = n_epochs)
sns.violinplot(hist)
# ### Post-test Agent
# Test pnet!
print('Testing...')
rwd_mg = []
for k in range(num_episodes):
embrf.play(sess)
rwd_mg.append(embrf.last_total_return)
if k%int(num_episodes/5) == 0: print("\rEpisode {}/{}".format(k, num_episodes),end="")
trained_perf_mg = np.mean(np.array(rwd_mg)/float(embrf.max_episode_length))
print("\nAgent wins an average of {} pct compared to baseline of {} pct".format(
100*trained_perf_mg, 100*base_perf_mg) )
# +
fig, axs = plt.subplots(2, 1, sharex=True)
sns.violinplot(rwd_mg0, ax = axs[0])
axs[0].set_title('Baseline Mean Success Percentage')
sns.violinplot(rwd_mg, ax = axs[1])
axs[1].set_title('Trained Mean Success Percentage')
print("\nAgent wins an average of {} pct \ncompared to baseline of {} pct".format(
100*trained_perf_mg, 100*base_perf_mg) )
# +
# sess.close()
|
embodied_arch/unit-tests/.ipynb_checkpoints/certify-MG-AC-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
from IPython.core.debugger import Tracer
from keras.datasets import mnist
from keras.layers import Input, Dense, Reshape, Flatten, Dropout
from keras.layers import BatchNormalization
from keras.layers import LeakyReLU
from keras.models import Sequential
from keras.optimizers import Adam
import matplotlib.pyplot as plt
plt.switch_backend('agg')
# +
class GAN(object):
""" Generative Adversarial Network class """
def __init__(self, width=28, height=28, channels=1):
self.width = width
self.height = height
self.channels = channels
self.shape = (self.width, self.height, self.channels)
self.optimizer = Adam(lr=0.01, beta_1=0.4, decay=8e-8)
self.G = self.__generator()
self.G.compile(loss='binary_crossentropy', optimizer=self.optimizer)
self.D = self.__discriminator()
self.D.compile(loss='binary_crossentropy', optimizer=self.optimizer, metrics=['accuracy'])
self.stacked_generator_discriminator = self.__stacked_generator_discriminator()
self.stacked_generator_discriminator.compile(loss='binary_crossentropy', optimizer=self.optimize
def __generator(self):
""" Declare generator """
model = Sequential()
model.add(Dense(256, input_shape=(100,)))
model.add(LeakyReLU(alpha=0.2))
model.add(BatchNormalization(momentum=0.7))
model.add(Dense(512))
model.add(LeakyReLU(alpha=0.2))
model.add(BatchNormalization(momentum=0.7))
model.add(Dense(1024))
model.add(LeakyReLU(alpha=0.2))
model.add(BatchNormalization(momentum=0.7))
model.add(Dense(self.width * self.height * self.channels, activation='tanh'))
model.add(Reshape((self.width, self.height, self.channels)))
return model
def __discriminator(self):
""" Declare discriminator """
model = Sequential()
model.add(Flatten(input_shape=self.shape))
model.add(Dense((self.width * self.height * self.channels), input_shape=self.shape))
model.add(LeakyReLU(alpha=0.2))
model.add(Dense((self.width * self.height * self.channels)/2))
model.add(LeakyReLU(alpha=0.2))
model.add(Dense(1, activation='sigmoid'))
model.summary()
return model
def __stacked_generator_discriminator(self):
self.D.trainable = False
model = Sequential()
model.add(self.G)
model.add(self.D)
return model
def train(self, X_train, epochs=20000, batch = 32, save_interval = 100):
for cnt in range(epochs):
## train discriminator
random_index = np.random.randint(0, len(X_train) - batch/2)
legit_images = X_train[random_index : random_index + batch/2].reshape(batch/2, self.width, self.height, self.channels)
gen_noise = np.random.normal(0, 1, (batch/2, 100))
syntetic_images = self.G.predict(gen_noise)
x_combined_batch = np.concatenate((legit_images, syntetic_images))
y_combined_batch = np.concatenate((np.ones((batch/2, 1)), np.zeros((batch/2, 1))))
d_loss = self.D.train_on_batch(x_combined_batch, y_combined_batch)
# train generator
noise = np.random.normal(0, 1, (batch, 100))
y_mislabled = np.ones((batch, 1))
g_loss = self.stacked_generator_discriminator.train_on_batch(noise, y_mislabled)
print ('epoch: %d, [Discriminator :: d_loss: %f], [ Generator :: loss: %f]' % (cnt, d_loss[0], g_loss))
if cnt % save_interval == 0:
self.plot_images(save2file=True, step=cnt)
def plot_images(self, save2file=False, samples=16, step=0):
''' Plot and generated images '''
filename = "./images/mnist_%d.png" % step
noise = np.random.normal(0, 1, (samples, 100))
images = self.G.predict(noise)
plt.figure(figsize=(10, 10))
for i in range(images.shape[0]):
plt.subplot(4, 4, i+1)
image = images[i, :, :, :]
image = np.reshape(image, [self.height, self.width])
plt.imshow(image, cmap='gray')
plt.axis('off')
plt.tight_layout()
if save2file:
plt.savefig(filename)
plt.close('all')
else:
plt.show()
|
Chapter09/.ipynb_checkpoints/GAN-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## LSTM AE based clusteing
# +
from time import time
from keras.datasets import mnist
import numpy as np
np.random.seed(10)
import numpy as np
import keras.backend as K
from keras.engine.topology import Layer, InputSpec
from keras.layers import Dense, Input
from keras.models import Model
from keras.optimizers import SGD
from keras import callbacks
from keras.initializers import VarianceScaling
from sklearn.cluster import KMeans
import metrics
from keras.models import Model
from keras import backend as K
from keras import layers
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D, Flatten, Reshape, Conv2DTranspose
from keras.models import Model
import numpy as np
import os
from keras.preprocessing.image import load_img
from skimage import transform
import _pickle as cPickle
import _pickle
import seaborn as sns
import sklearn.metrics
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
# %matplotlib inline
import gzip
from skimage import transform
import numpy as np
from PIL import Image
import matplotlib
import os
# For plotting graphs via ssh with no display
# Ref: https://stackoverflow.com/questions/2801882/generating-a-png-with-matplotlib-when-display-is-undefined
matplotlib.use('Agg')
from keras.preprocessing.image import load_img
from matplotlib import pyplot as plt
from numpy import float32
from sklearn import metrics
from sklearn.cluster.k_means_ import KMeans
from sklearn import manifold
from sklearn.utils.linear_assignment_ import linear_assignment
from sklearn import preprocessing
from sklearn.utils import shuffle
# -
# ### Load breast biohistology images for convolutional input
def loadDataset():
data= []
labels =[]
root ='/home/rkarim/Training_data/'
for rootName,dirName,fileNames in os.walk(root):
if(not rootName == root):
for fileName in fileNames:
imgGray = load_img(rootName+'/'+fileName,color_mode='grayscale')
if rootName.split('/')[1] == 'Benign':
labels+=[0]
elif rootName.split('/')[1]== 'InSitu':
labels+=[1]
elif rootName.split('/')[1] == 'Invasive':
labels+=[2]
else:
labels+=[3]
transformed=transform.resize(np.array(imgGray),(508,508))
data += [transformed.reshape((transformed.shape[0],transformed.shape[1],1))]
data = np.stack(data)
labels = np.stack(labels)
#data,labels = shuffle(data,labels,random_state = 0)
return [data,labels]
x, y = loadDataset()
# +
y = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3]
y = np.array(y)
# -
data = x.astype('float32') / 255.
#x = np.reshape(x, (len(x), 508, 508)) # adapt this if using `channels_first` image data format
data.shape
data = np.reshape(data, (len(data), 508, 508))
# +
n_clusters = len(np.unique(y))
print("Number of cluster: " + str(n_clusters))
print("Input shape: " + str(data.shape))
print("Timestep: " + str(data.shape[0]))
print("Data dimension: " + str(data.shape[1]))
# +
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28)) # adapt this if using `channels_first` image data format
x_test = np.reshape(x_test, (len(x_test), 28, 28)) # adapt this if using `channels_first` image data format
x = np.concatenate((x_train, x_test))
y = np.concatenate((y_train, y_test))
# +
n_clusters = len(np.unique(y))
print("Number of cluster: " + str(n_clusters))
print("Input shape: " + str(x.shape))
print("Timestep: " + str(x.shape[0]))
print("Data dimension: " + str(x.shape[1]))
# +
init = VarianceScaling(scale=1. / 3., mode='fan_in', distribution='uniform')
import keras
from keras import backend as K
from keras.models import Sequential, Model
from keras.layers import Input, LSTM, RepeatVector
from keras.layers.core import Flatten, Dense, Dropout, Lambda
from keras.optimizers import SGD, RMSprop, Adam
from keras import objectives
from keras.models import Sequential
from keras.layers import LSTM
from keras.layers import Dense
from keras.layers import RepeatVector
from keras.layers import TimeDistributed
def LSTM_AE(timesteps, n_features):
"""
Creates an LSTM Autoencoder (VAE). Returns Autoencoder, Encoder, Generator.
(All code by fchollet - see reference.)
# Arguments
input_dim: int.
timesteps: int, input timestep dimension.
latent_dim: int, latent z-layer shape.
# References
- [Building Autoencoders in Keras](https://blog.keras.io/building-autoencoders-in-keras.html)
"""
inputs = Input(shape=(timesteps, n_features))
encoded = LSTM(128, activation='relu',return_sequences=True)(inputs)
encoded = LSTM(64, activation='relu',return_sequences=False)(encoded)
decoded = RepeatVector(timesteps)(encoded)
decoded = LSTM(64, activation='relu', return_sequences=True)(decoded)
decoded = LSTM(128, activation='relu', return_sequences=True)(decoded)
decoded = TimeDistributed(Dense(n_features))(decoded)
return Model(inputs=inputs, outputs=decoded, name='LSTM_AE'), Model(inputs=inputs, outputs=encoded, name='encoder')
# +
timesteps = data.shape[1] # equal to the lookback
n_features = data.shape[2] # 59
autoencoder, encoder = LSTM_AE(timesteps, n_features)
autoencoder.summary()
# -
# ### Pretrain LSTM autoencoder
pretrain_epochs = 100
batch_size = 128
save_dir = 'results/'
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(data, data, batch_size=batch_size, epochs=pretrain_epochs)
autoencoder.save_weights(save_dir+'/conv_ae_weights.h5')
autoencoder.load_weights(save_dir+'/conv_ae_weights.h5')
# ### Build clustering model with convolutional autoencoder
class ClusteringLayer(Layer):
"""
Clustering layer converts input sample (feature) to soft label, i.e. a vector that represents the probability of the
sample belonging to each cluster. The probability is calculated with student's t-distribution.
# Example
```
model.add(ClusteringLayer(n_clusters=10))
```
# Arguments
n_clusters: number of clusters.
weights: list of Numpy array with shape `(n_clusters, n_features)` witch represents the initial cluster centers.
alpha: degrees of freedom parameter in Student's t-distribution. Default to 1.0.
# Input shape
2D tensor with shape: `(n_samples, n_features)`.
# Output shape
2D tensor with shape: `(n_samples, n_clusters)`.
"""
def __init__(self, n_clusters, weights=None, alpha=1.0, **kwargs):
if 'input_shape' not in kwargs and 'input_dim' in kwargs:
kwargs['input_shape'] = (kwargs.pop('input_dim'),)
super(ClusteringLayer, self).__init__(**kwargs)
self.n_clusters = n_clusters
self.alpha = alpha
self.initial_weights = weights
self.input_spec = InputSpec(ndim=2)
def build(self, input_shape):
assert len(input_shape) == 2
input_dim = input_shape[1]
self.input_spec = InputSpec(dtype=K.floatx(), shape=(None, input_dim))
self.clusters = self.add_weight((self.n_clusters, input_dim), initializer='glorot_uniform', name='clusters')
if self.initial_weights is not None:
self.set_weights(self.initial_weights)
del self.initial_weights
self.built = True
def call(self, inputs, **kwargs):
""" student t-distribution, as same as used in t-SNE algorithm.
Measure the similarity between embedded point z_i and centroid µ_j.
q_ij = 1/(1+dist(x_i, µ_j)^2), then normalize it.
q_ij can be interpreted as the probability of assigning sample i to cluster j.
(i.e., a soft assignment)
Arguments:
inputs: the variable containing data, shape=(n_samples, n_features)
Return:
q: student's t-distribution, or soft labels for each sample. shape=(n_samples, n_clusters)
"""
q = 1.0 / (1.0 + (K.sum(K.square(K.expand_dims(inputs, axis=1) - self.clusters), axis=2) / self.alpha))
q **= (self.alpha + 1.0) / 2.0
q = K.transpose(K.transpose(q) / K.sum(q, axis=1)) # Make sure each sample's 10 values add up to 1.
return q
def compute_output_shape(self, input_shape):
assert input_shape and len(input_shape) == 2
return input_shape[0], self.n_clusters
def get_config(self):
config = {'n_clusters': self.n_clusters}
base_config = super(ClusteringLayer, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
clustering_layer = ClusteringLayer(n_clusters, name='clustering')(encoder.output)
model = Model(inputs=encoder.input, outputs=clustering_layer)
model.compile(optimizer='adam', loss='kld')
# ### Step 1: initialize cluster centers using k-means
kmeans = KMeans(n_clusters=n_clusters, n_init=5)
y_pred_kmeans = kmeans.fit_predict(encoder.predict(data))
metrics.accuracy_score(y, y_pred_kmeans)
y_pred_last = np.copy(y_pred_kmeans)
model.get_layer(name='clustering').set_weights([kmeans.cluster_centers_])
# ### Step 2: deep clustering
#computing an auxiliary target distribution
def target_distribution(q):
weight = q ** 2 / q.sum(0)
return (weight.T / weight.sum(1)).T
loss = 0
index = 0
maxiter = 10000
update_interval = 10
index_array = np.arange(data.shape[0])
tol = 0.01 # tolerance threshold to stop training
# ### Start training
# +
for ite in range(int(maxiter)):
if ite % update_interval == 0:
q = model.predict(data, verbose=0)
p = target_distribution(q) # update the auxiliary target distribution p
# evaluate the clustering performance
y_pred = q.argmax(1)
if y is not None:
acc = np.round(metrics.accuracy_score(y, y_pred), 5)
nmi = np.round(metrics.mutual_info_score(y, y_pred), 5)
ari = np.round(metrics.adjusted_rand_score(y, y_pred), 5)
loss = np.round(loss, 5)
print('Iter %d: acc = %.5f, nmi = %.5f, ari = %.5f' % (ite, acc, nmi, ari), ' ; loss=', loss)
# check stop criterion
delta_label = np.sum(y_pred != y_pred_last).astype(np.float32) / y_pred.shape[0]
y_pred_last = np.copy(y_pred)
if ite > 0 and delta_label < tol:
print('delta_label ', delta_label, '< tol ', tol)
print('Reached tolerance threshold. Stopping training.')
break
idx = index_array[index * batch_size: min((index+1) * batch_size, data.shape[0])]
loss = model.train_on_batch(x=data[idx], y=p[idx])
index = index + 1 if (index + 1) * batch_size <= data.shape[0] else 0
model.save_weights(save_dir + '/conv_DEC_model_final.h5')
# -
# ### Load the clustering model trained weights
model.load_weights(save_dir + '/conv_DEC_model_final.h5')
# ### Final Evaluation
# +
#Eval.
q = model.predict(data, verbose=0)
p = target_distribution(q) # update the auxiliary target distribution p
# evaluate the clustering performance
y_pred = q.argmax(1)
if y is not None:
acc = np.round(metrics.accuracy_score(y, y_pred), 2)
nmi = np.round(metrics.mutual_info_score(y, y_pred), 2)
ari = np.round(metrics.adjusted_rand_score(y, y_pred), 2)
loss = np.round(loss, 5)
print('Acc = %.5f, nmi = %.5f, ari = %.5f' % (acc, nmi, ari), ' ; loss=', loss)
# +
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
# %matplotlib inline
sns.set(font_scale=3)
confusion_matrix = sklearn.metrics.confusion_matrix(y, y_pred)
plt.figure(figsize=(14, 10))
sns.heatmap(confusion_matrix, annot=True, fmt="d", annot_kws={"size": 20});
plt.title("Confusion matrix", fontsize=30)
plt.ylabel('True label', fontsize=25)
plt.xlabel('Clustering label', fontsize=25)
plt.show()
# -
def vis_data(x_train_encoded, y_train, vis_dim, n_predict, n_train, build_anim):
cmap = plt.get_cmap('rainbow', 10)
# 3-dim vis: show one view, then compile animated .gif of many angled views
if vis_dim == 3:
# Simple static figure
fig = plt.figure()
ax = plt.axes(projection='3d')
p = ax.scatter3D(x_train_encoded[:,0], x_train_encoded[:,1], x_train_encoded[:,2],
c=y_train[:n_predict], cmap=cmap, edgecolor='black')
fig.colorbar(p, drawedges=True)
plt.show()
# Build animation from many static figures
if build_anim:
angles = np.linspace(180, 360, 20)
i = 0
for angle in angles:
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.view_init(10, angle)
p = ax.scatter3D(x_train_encoded[:,0], x_train_encoded[:,1], x_train_encoded[:,2],
c=y_train[:n_predict], cmap=cmap, edgecolor='black')
fig.colorbar(p, drawedges=True)
outfile = 'anim/3dplot_step_' + chr(i + 97) + '.png'
plt.savefig(outfile, dpi=96)
i += 1
call(['convert', '-delay', '50', 'anim/3dplot*', 'anim/3dplot_anim_' + str(n_train) + '.gif'])
# 2-dim vis: plot and colorbar.
elif vis_dim == 2:
plt.scatter(x_train_encoded[:,0], x_train_encoded[:,1],
c=y_train[:n_predict], edgecolor='black', cmap=cmap)
plt.colorbar(drawedges=True)
plt.show()
# +
# Encode a number of MNIST digits, then perform t-SNE dim-reduction.
x_train_predict = encoder.predict(data)
#print "Performing t-SNE dimensionality reduction..."
x_train_encoded = TSNE(n_components=2).fit_transform(x_train_predict)
#np.save('%sx_%sdim_tnse_%s.npy' % (266, 2, 266), x_train_encoded)
#x_train_encoded = np.load(str(n_predict) + 'x_' + str(vis_dim) + 'dim_tnse_' + str(n_train) + '.npy')
# +
# Visualize result.
train_new = False
n_train = 70000
predict_new = False
n_predict = 70000
vis_dim = 2
build_anim = False
vis_data(x_train_encoded, y, vis_dim, n_predict, n_train, build_anim)
# -
import sklearn
sklearn.__version__
|
Notebooks/Keras-LSTM_AE-Biohistology.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Convexity of the ohmic model
#
# (see also handwritten notes)
#
# PH, July 2020
import numpy as np
import matplotlib.pyplot as plt
import sympy
from sympy import symbols, simplify, sqrt, lambdify
e, y, R, v0 = symbols('e y R v0', positive=True)
p, x = symbols('p x')
# ## Convexity in the power
# Correction factor c(i)
c = 2/(1+sqrt(1+4*p*R/v0**2))
c
c.subs({R:1, v0:1, p:0}), c.subs({R:1, v0:1, p:-1/4}), c.subs({R:1, v0:1, p:+1/4})
i = p/v0*c
i
# Normarlized current, with $x = 4p$ (so $x > -1 $)
i_n = i.subs({R:1, v0:1, p:x/4})*2
i_n
# Joule losses
pJ = R*i**2
pJ
# normalized Joule losses
pJn = i_n**2
pJn
# First derivative
pJn.diff(x,1)
# second derivative: difficult to proove it is ≥ 0!
d2pJn = pJn.diff(x,2)
d2pJn
# Focus on numerator:
denom = (sqrt(x + 1) + 1)**4 * 2 * (x+1)**2 # always >0
simplify(d2pJn*denom )
# Comment : proof of positivity is _yet to be done_, but seems achievable!
# ### Plots: current, Joule losses, 2nd derivative
#
# Note: the normalized plots here do not use the same normalization as in the sympy expression. In the plots, normalization is such that:
#
# - $p$ is defined as $>-1$ (like $x$ above)
# - $i \approx p$ around 0 (while $i\approx p/2$ above)
# - $p_J \approx p^2$ around 0 (while $p_J \approx p^2/4$ above)
# +
x_vec = np.linspace(-0.9999, 2, 300)
i_vec = x_vec * 2/(1+np.sqrt(1+x_vec))
fig, ax = plt.subplots()
ax.axvline(0, color='k', lw=1)
ax.axhline(0, color='k', lw=1)
ax.axvline(-1, color='tab:red', lw=2, ls=':', label='discharge limit')
ax.plot(x_vec, i_vec)
ax.plot(x_vec, x_vec, 'C0:', label='$v=v_0$ approx.')
ax.legend()
ax.set(
title = 'Current i(p), normalized',
xlabel = 'p (normalized)'
)
ax.grid()
# +
pJ_vec = i_vec**2
fig, ax = plt.subplots()
ax.axvline(0, color='k', lw=1)
ax.axhline(0, color='k', lw=1)
ax.axvline(-1, color='tab:red', lw=2, ls=':', label='discharge limit')
ax.plot(x_vec, pJ_vec)
ax.plot(x_vec, x_vec**2, 'C0:', label='$v=v_0$ approx.')
ax.legend()
ax.set(
title = 'Joule losses pJ(p)',
xlabel = 'p',
ylim = (-0.5, 4.1)
)
ax.grid()
fig.savefig('Joule losses pJ(p).png', dpi=200, bbox_inches='tight')
# -
d2pJ_fun(0)
# +
d2pJ_fun = lambdify(x, 4*d2pJn, modules=np)
fig, ax = plt.subplots()
ax.axvline(0, color='k', lw=1)
ax.axhline(0, color='k', lw=1)
ax.axvline(-1, color='tab:red', lw=2, ls=':', label='discharge limit')
ax.plot(x_vec, d2pJ_fun(x_vec))
ax.legend()
ax.set(
title = 'Second derivative of pJ(p)',
xlabel = 'p',
ylim=(-1,10)
)
ax.grid()
# -
# ## Effect of $v_0$ variation with SoE
#
# Two classical options:
#
# - $v_0 = \sqrt{2E/C}$ (Super caps)
# - $v_0 = v_{00} + a.E$ (affine approximation for battery OCV)
#
# TO BE STUDIED... 21/07/20
# ### Supercaps
pJnSC = pJ.subs({R:1, p:x/4, v0:sqrt(y)})*4
pJnSC
pJnSC.diff(y,2)
|
Convexity Ohmic model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext sparkmagic.magics
# %manage_spark
# %spark?
# + language="spark"
#
# import pyspark
# import random
#
# num_samples = 100000000
#
# def inside(p):
# x, y = random.random(), random.random()
# return x*x + y*y < 1
#
# count = sc.parallelize(range(0, num_samples)).filter(inside).count()
#
# pi = 4 * count / num_samples
# print(pi)
#
# sc.stop()
# + language="spark"
#
# import pyspark
# -
|
notebooks/1-data_acquisition/1.2-check_environment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import re
from datetime import datetime
import warnings
warnings.filterwarnings("ignore")
# ### Online and Offline Training data
df_on = pd.read_csv('DataSets/ccf_online_stage1_train.csv')
df_off = pd.read_csv('DataSets/ccf_offline_stage1_train.csv')
print("Online Training Data Sample\nShape:"+str(df_on.shape))
df_on.head()
print("Offline Training Data Sample\nShape:"+str(df_off.shape))
df_off.head()
# ### Test Data (Offline)
df_test = pd.read_csv('DataSets/ccf_offline_stage1_test_revised.csv')
print("Testing Data(Offline) Sample\nShape:"+str(df_test.shape))
df_test.head()
# ### Converting Coupon to String Type
print('Data type of coupon in different datasets\nOnline: '+str(df_on['Coupon_id'].dtypes)+'\nOffline: '+
str(df_off['Coupon_id'].dtypes)+'\nTest: '+str(df_test['Coupon_id'].dtypes))
df_off['Coupon_id'] = [int(i) if i==i else i for i in df_off['Coupon_id']]
df_off['Coupon_id'] = df_off['Coupon_id'].apply(lambda x: "{:.0f}".
format(x) if not pd.isnull(x) else x)
df_test['Coupon_id'] = df_test['Coupon_id'].apply(lambda x: "{:.0f}".
format(x) if not pd.isnull(x) else x)
print('After conversion, data type of coupon in different datasets\nOnline: '+str(df_on['Coupon_id'].dtypes)+'\nOffline: '+
str(df_off['Coupon_id'].dtypes)+'\nTest: '+str(df_test['Coupon_id'].dtypes))
print('Data type of coupon in different datasets\nOnline: '+str(df_on['Coupon_id'].dtypes)+'\nOffline: '+
str(df_off['Coupon_id'].dtypes)+'\nTest: '+str(df_test['Coupon_id'].dtypes))
# #### Converting Date to DateTime format
# +
#Online Training Data
df_on['Date'] = pd.to_datetime(df_on["Date"],format='%Y%m%d')
df_on['Date_received'] = pd.to_datetime(df_on["Date_received"],format='%Y%m%d')
#Offline Training Data
df_off['Date'] = pd.to_datetime(df_off["Date"],format='%Y%m%d')
df_off['Date_received'] = pd.to_datetime(df_off["Date_received"],format='%Y%m%d')
# -
# ### Removing Duplicates from Online and Offline Training Data
# +
#Removing duplicates and giving frequency counts(Count) to each row
#Online
x = 'g8h.|$hTdo+jC9^@'
df_on_unique = (df_on.fillna(x).groupby(['User_id', 'Merchant_id', 'Action', 'Coupon_id', 'Discount_rate',
'Date_received', 'Date']).size().reset_index()
.rename(columns={0 : 'Count'}).replace(x,np.NaN))
df_on_unique["Date_received"]=pd.to_datetime(df_on_unique["Date_received"])
df_on_unique["Date"]=pd.to_datetime(df_on_unique["Date"])
print("Online Training Data Shape:"+str(df_on_unique.shape))
# +
#Offline
x = 'g8h.|$hTdo+jC9^@' #garbage value for nan values
df_off_unique = (df_off.fillna(x).groupby(['User_id', 'Merchant_id', 'Coupon_id', 'Discount_rate', 'Distance',
'Date_received', 'Date']).size().reset_index()
.rename(columns={0 : 'Count'}).replace(x,np.NaN))
df_off_unique["Date_received"]=pd.to_datetime(df_off_unique["Date_received"])
df_off_unique["Date"]=pd.to_datetime(df_off_unique["Date"])
print("Offline Training Data Shape:"+str(df_off_unique.shape))
# -
# #### Filling Nan for Distance (OFFLINE)
df_off_unique['Distance'].fillna(df_off_unique['Distance'].mean(), inplace=True)
df_off_unique['Distance'] = df_off_unique.Distance.astype(int)
# ### Converting Discount Ratio to Rate
# +
#Funtion to convert discount ratio to discount rate
def convert_discount(discount):
values = []
for i in discount:
if ':' in i:
i = i.split(':')
rate = round((int(i[0]) - int(i[1]))/int(i[0]),3)
values.append([int(i[0]),int(i[1]),rate])
elif '.' in i:
i = float(i)
x = 100*i
values.append([100,int(100-x),i])
discounts = dict(zip(discount,values))
return discounts
# convert_discount(list(df_of['Discount_rate']))
# -
#ONLINE DATA
df_on_coupon = df_on_unique[(df_on_unique['Coupon_id'].isna()==False) & (df_on_unique['Coupon_id']!='fixed')]
discounts_online = list(df_on_coupon['Discount_rate'].unique())
df_on_coupon.loc[:,('Discount')] = df_on_coupon.loc[:,('Discount_rate')]
df_on_coupon.loc[:,('Discount_rate')] = df_on_coupon[df_on_coupon['Coupon_id']!='fixed'].loc[:,('Discount')].map(convert_discount(discounts_online))
df_on_coupon[['Original_price','Discounted_price','Rate']] = pd.DataFrame(df_on_coupon['Discount_rate'].values.tolist(), index= df_on_coupon.index)
df_on_coupon.head()
df_on_coupon = df_on_coupon.append(df_on_unique[df_on_unique['Coupon_id']=='fixed'], sort=False)
df_on_coupon.shape, df_on_unique[df_on_unique['Coupon_id'].isna()==False].shape
#OFFLINE DATA
df_off_coupon = df_off_unique[(df_off_unique['Coupon_id'].isna()==False)].copy()
discounts_offline = list(df_off_coupon['Discount_rate'].unique())
df_off_coupon.loc[:,('Discount')] = df_off_coupon.loc[:,('Discount_rate')]
df_off_coupon['Discount_rate'] = df_off_coupon['Discount'].map(convert_discount(discounts_offline))
df_off_coupon[['Original_price','Discounted_price','Rate']] = pd.DataFrame(df_off_coupon.Discount_rate.values.tolist(), index= df_off_coupon.index)
df_off_coupon.head()
# ### Training Data (Online + Offline)
df_train = df_on_unique.append(df_off_unique, sort=False)
df_train = df_train.sort_values(by = ['User_id'] )
df_train = df_train.reset_index()
del df_train['index']
print("Training Data(Offline+Online) \nShape:"+str(df_train.shape))
df_train.head()
# ## User Anlaysis
# ## User distribution: Online, Offline and Test Data
users_on = set(df_on_unique['User_id'])
users_off = set(df_off_unique['User_id'])
users_test = set(df_test['User_id'])
len(users_on),len(users_off),len(users_test)
all_three = (users_on.intersection(users_off)).intersection(users_test)
len(all_three)
off_test_only = users_test.intersection(users_off) - all_three
off_on_only = users_on.intersection(users_off) - all_three
on_test_only = users_on.intersection(users_test) - all_three
len(off_test_only ),len(off_on_only),len(on_test_only)
only_test = users_test - (off_test_only.union(on_test_only)).union(all_three)
only_offline = users_off - (off_test_only.union(off_on_only)).union(all_three)
only_online = users_on - (off_on_only.union(on_test_only)).union(all_three)
len(only_test ),len(only_offline),len(only_online)
all_users = (users_on.union(users_off)).union(users_test)
len(all_users)
# <img src ="imgs/UserDistribution.png" width="60%">
# ### Distributing users into three categores:
# 1. users getting coupon
# 2. users making purchases without coupon
# 3. users making purchases with coupon
# +
#Online
df_on_get_coupon = df_on_unique[df_on_unique['Action']==2]
df_on_no_coupon = df_on_unique[df_on_unique['Coupon_id'].isna()]
df_on_redeem_coupon = df_on_unique[(df_on_unique['Date'].isna()==False) & (df_on_unique['Coupon_id'].isna()==False)]
print('ONLINE: Shape of Get Coupon'+ str(df_on_get_coupon.shape))
print('ONLINE: Shape of No Coupon'+ str(df_on_no_coupon.shape))
print('ONLINE: Shape of Redeem Coupon'+ str(df_on_redeem_coupon.shape))
#Offline
df_off_get_coupon = df_off_unique[(df_off_unique['Date'].isna()) & (df_off_unique['Coupon_id'].isna()==False)]
df_off_no_coupon = df_off_unique[df_off_unique['Coupon_id'].isna()]
df_off_redeem_coupon = df_off_unique[(df_off_unique['Date'].isna()==False) & (df_off_unique['Coupon_id'].isna()==False)]
print('\nOFFLINE: Shape of Get Coupon'+ str(df_off_get_coupon.shape))
print('OFFLINE: Shape of No Coupon'+ str(df_off_no_coupon.shape))
print('OFFLINE: Shape of Redeem Coupon'+ str(df_off_redeem_coupon.shape))
#Complete Traininig Data
df_train_get_coupon = df_train[(df_train['Date'].isna()) & (df_train['Coupon_id'].isna()==False)]
df_train_no_coupon = df_train[df_train['Coupon_id'].isna()]
df_train_redeem_coupon = df_train[(df_train['Date'].isna()==False) & (df_train['Coupon_id'].isna()==False)]
print('\nONLINE+OFFLINE: Shape of Get Coupon'+ str(df_train_get_coupon.shape))
print('ONLINE+OFFLINE: Shape of No Coupon'+ str(df_train_no_coupon.shape))
print('ONLINE+OFFLINE: Shape of Redeem Coupon'+ str(df_train_redeem_coupon.shape))
df_train_coupon = df_on_coupon.append(df_off_coupon, sort=False)
# -
# ### User : Online, Offline or Common(Online+Offline) Tag
# 0: Common User
# 1: Only Offline
# 2: Only Online
users_on = set(df_on["User_id"].unique()) #number of users in online data
users_off = set(df_off["User_id"].unique()) #number of users in offline data
users_test = set(df_test["User_id"].unique()) #number of users in test data
common_users = set(users_off.intersection(users_on)) #number of users having both online and offline presence
online_users = list(users_on - common_users)
offline_users = list(users_off - common_users)
common_users = list(common_users)
print('Count of only Online Users: '+ str(len(online_users)))
print('Count of only Offline Users: '+ str(len(offline_users)))
print('Count of Common Users: '+ str(len(common_users)))
# +
common_tags = [0 for _ in range(len(common_users))]
offline_tags = [1 for _ in range(len(offline_users))]
online_tags = [2 for _ in range(len(online_users))]
#Common Users DataFrame
tag_0 = pd.DataFrame(
{'Users': common_users,
'Tag': common_tags
})
#Offline Users DataFrame
tag_1 = pd.DataFrame(
{'Users': offline_users,
'Tag': offline_tags
})
#Online Users DataFrame
tag_2 = pd.DataFrame(
{'Users': online_users,
'Tag': online_tags
})
user_tag = tag_0.append(tag_1, sort=False)
user_tag = user_tag.append(tag_2, sort=False)
user_tag.sample(5)
# -
# ### User Redemption Score
#Users in training Dataset
user_redemption_train = pd.DataFrame(df_train_coupon.groupby(['User_id'])['Coupon_id','Date'].count()).reset_index()
user_redemption_train.columns = ['User_id','User_Released', 'User_Redeemed']
user_redemption_train['User_Ratio'] = round(user_redemption_train['User_Redeemed']/user_redemption_train['User_Released'],2)
# user_redemption_train[user_redemption_train['User_Ratio']!=0].head()
user_redemption_train.sample(4)
# +
plt.figure(figsize=(8,5))
sns.distplot(user_redemption_train[user_redemption_train['User_Ratio']!=0]['User_Ratio'],kde=False,bins=26)
# sns.distplot(user_redemption_train['User_Ratio'],kde=False,bins=26)
plt.xlabel('User Redemption Ratio')
plt.ylabel('Count of Users')
plt.title('User Redemption Score Distribution')
plt.show()
# -
# ### Users and their Merchant Preferences
visits= pd.DataFrame(df_train.groupby(['User_id','Merchant_id']).size()).reset_index()
visits.columns = ['User_id','Merchant_id','Visits']
visits.head()
plt.figure(figsize=(15,10))
ax = sns.countplot(visits['Visits'])
ax.set_xticklabels(ax.get_xticklabels(),rotation=90)
i = 4
for p in ax.patches:
ax.annotate('{:.0f}'.format(p.get_height()), (p.get_x()+0.1, p.get_height()+50))
i-=1
if i <0:
break
plt.xlabel('Number of User-Merchant Visits')
plt.ylabel('Count')
plt.title('Plot for frequency of user-merchant visits (OFFLINE)')
plt.show()
# #### For offline:
# Around 69% of times the frequency of user-merchant pair is 1.<br>
# #### For online:
# Around 79.4% of times the frequency of user-merchant pair is 1.<br>
# So, users don't prefer any certain set of merchants.
# ### Users as Purchasers and Non-Purchasers
# Purchasers (Number of buys >= 5)<br>
# Non Purchasers (Number of buys < 5)
user_purchasers = pd.DataFrame(df_train.groupby(['User_id'])['Date'].count())
user_purchasers.columns = ['User_Buys']
user_purchasers['User_Buys'].describe()
user_purchasers['Purchaser'] = [1 if x>=5 else 0 for x in user_purchasers['User_Buys']]
user_purchasers.sample(5)
# ### For any user-merchant pair, the distance should remain constant (Offline)
user_merchant_distance = pd.DataFrame(df_off_unique.groupby(['User_id','Merchant_id'])['Distance'].nunique()).reset_index()
user_merchant_distance['Distance'].unique()
# Unique distance values for a user-merchant pair are 0 (for nan distance value) and 1.<br>
# This shows for any user-merchant pair, the distance value remains constant.
# ### Users: Recent (Active during last month) or Not Recent
users_purchase = df_train[df_train['Date'].isna()==False]
recent_users = pd.DataFrame(users_purchase.groupby(['User_id'])['Date'].agg(['max'])).reset_index()
recent_users.columns = ['User_id', 'LastActivityDate']
recent_users['LastDate'] = pd.to_datetime('20160701',format='%Y%m%d')
recent_users.head()
recent_users['RecentDuration'] = recent_users['LastDate'] - recent_users['LastActivityDate']
recent_users['RecentDuration'] = recent_users['RecentDuration'].dt.days.astype('str')
recent_users['RecentDuration'] = pd.to_numeric(recent_users['RecentDuration'],errors="coerce")
recent_users['RecentDuration'].describe()
recent_users['User_Recent'] = [1 if x<=31 else 0 for x in recent_users['RecentDuration']]
recent_users.head()
bins = [0,10,20,30,40,50,60,70,80,90,182,200]
labels =[10,9,8,7,6,5,4,3,2,1,0]
recent_users['User_Recency_bucket'] = pd.cut(recent_users['RecentDuration'], bins,labels=labels)
recent_users.head()
# ### Common Users: Online and Offline visits
df_train = df_train.merge(user_tag['Tag'],how='outer', left_on='User_id', right_on=user_tag['Users'])
common_users = df_train[df_train['Tag']==0]
common_users_activity = common_users.groupby(['User_id'])['Action','Distance'].count()
common_users_activity.columns = ['Online_Activity','Offline_Activity']
common_users_activity.sample(2)
# ### User tracking (Online click to Offline buy)
common_users['Action'].fillna(3, inplace=True)
common_users.loc[:,('Action')] = [4 if (x==3) & (y==y) else x for (x,y) in zip(common_users['Action'],common_users['Date'])]
common_users.head()
common_users.loc[:,('DateTrack')] = common_users.loc[:,('Date')]
common_users.DateTrack.fillna(common_users.Date_received, inplace=True)
common_users.loc[:,('Action')] = common_users.loc[:,('Action')].astype(int)
common_users.loc[:,('Action')] = common_users.loc[:,('Action')].astype(str)
common_users.head()
common_users = common_users.sort_values(by=['User_id','DateTrack'])
common_users.head()
common_user_activity = common_users.groupby(['User_id'])['Action'].apply(list).reset_index(name='ActivityList')
common_user_activity.head()
common_user_activity.loc[:,('ActivityList')] = common_user_activity.loc[:,('ActivityList')] .apply(lambda x: ''.join(x))
common_user_activity.loc[:,('OnlineToOffline')] = [1 if re.search('\d*0\d*4\d*',a) else 0 for a in common_user_activity['ActivityList']]
common_user_activity.head(20)
common_user_activity[common_user_activity['OnlineToOffline']==1].shape[0]/common_user_activity.shape[0]
# ## User not redeeming coupons (Journey Tracking)
redemption_tracking = df_train[(df_train['Date'].isna()) | (df_train['Coupon_id'].isna())]
redemption_tracking.loc[:,('DateTrack')] = redemption_tracking.loc[:,('Date')]
redemption_tracking['DateTrack'].fillna(redemption_tracking['Date_received'],inplace=True)
redemption_tracking.loc[:,('Purchasing')] = [1 if x==x else 0 for x in redemption_tracking['Date']]
redemption_tracking.head()
users_redemption_tracking = pd.DataFrame(redemption_tracking.groupby(['User_id','Merchant_id'])['Purchasing'].nunique()).reset_index()
notredeeming = users_redemption_tracking[users_redemption_tracking['Purchasing']==2].reset_index(drop=True)
notredeeming.columns = ['User_id','Merchant_id','Purchase_unique']
notredeeming.head(5)
tracking_noredeem = pd.merge(redemption_tracking,notredeeming)
tracking_noredeem = tracking_noredeem.drop(['Purchase_unique','Distance','Count','Discount_rate'],axis=1)
tracking_noredeem = tracking_noredeem.sort_values(by=['User_id','Merchant_id','DateTrack'])
tracking_noredeem.head(10)
tracking_noredeem['Purchase_difference'] = tracking_noredeem.groupby(['User_id','Merchant_id'])['Purchasing'].apply(lambda x: x - x.shift(1))
tracking_noredeem['Date_difference'] = tracking_noredeem.groupby(['User_id','Merchant_id'])['DateTrack'].apply(lambda x: x - x.shift(1))
tracking_noredeem.head()
tracking_noredeem['Date_difference'] = tracking_noredeem['Date_difference'].dt.days.astype('str')
tracking_noredeem['Date_difference'] = pd.to_numeric(tracking_noredeem['Date_difference'],errors="coerce")
tracking_noredeem.head(10)
# ## User and number of unique merchants
user_merchant_count = pd.DataFrame(df_train.groupby(['User_id'])['Merchant_id'].nunique().reset_index(name='UserMerchantCount'))
user_merchant_count.head()
# ## User Recency list
user_dates = df_train[df_train['Date'].isna()==False]
user_dates['First_day'] = pd.to_datetime('20160101',format='%Y%m%d')
user_dates['DayNum'] = user_dates['Date'] - user_dates['First_day']
user_dates['DayNum'] = user_dates['DayNum'].dt.days.astype('str')
user_dates['DayNum'] = pd.to_numeric(user_dates['DayNum'],errors="coerce") + 1
user_dates
user_days = pd.DataFrame(user_dates.groupby(['User_id'])['DayNum'].apply(list).reset_index(name='DayList'))
user_days['DayList'] = user_days['DayList'].apply(lambda x : sorted(set(x)))
user_days
# ## USER LEVEL FEATURES
users_level_data = pd.DataFrame(df_train['User_id'].unique()).reset_index(drop=True)
users_level_data.columns = ['User_id']
users_level_data.shape
# +
#Adding Offline(1) or Online+Offline (Common User : 0) Tag of the user
users_level_data = users_level_data.merge(user_tag['Tag'],how='left', left_on='User_id', right_on=user_tag['Users'])
#Adding Number of coupons redeemed by each user and its redemption score
users_level_data = pd.merge(users_level_data, user_redemption_train, how='left', on='User_id')
# users_level_data = pd.merge(users_level_data, user_redemption_train['User_Ratio'], how='left', left_on='User_id', right_on=user_redemption_train['User_id'])
#Adding number of Buys of each User and Purchaser(Buys>=5) or NotPurchaser
users_level_data = pd.merge(users_level_data,user_purchasers['User_Buys'], how='left', left_on='User_id', right_on=user_purchasers.index)
users_level_data = pd.merge(users_level_data,user_purchasers['Purchaser'], how='left', left_on='User_id', right_on=user_purchasers.index)
#Recent users (active during last month) or not
# users_level_data = pd.merge(users_level_data,recent_users['User_Recent'], how='left', left_on='User_id', right_on=recent_users.index)
# users_level_data['User_Recent'].fillna(0, inplace=True)
#User and number of unique merchants
users_level_data = pd.merge(users_level_data,user_merchant_count,how='left',on='User_id')
#User purchases day list
users_level_data = pd.merge(users_level_data,user_days,how='left',on='User_id')
# users_level_data = pd.merge(users_level_data,recent_users['User_Recency_bucket'], how='left', left_on='User_id', right_on=recent_users.index)
# users_level_data['User_Recency_bucket'].fillna(0, inplace=True)
# -
for row in users_level_data.loc[users_level_data.DayList.isnull(), 'DayList'].index:
users_level_data.at[row, 'DayList'] = []
users_level_data.fillna(0, inplace=True)
users_level_data.isna().sum()
users_level_data
users_level_data.to_csv('DataSets/DatasetsCreated/user_level.csv',index=False)
len(users_on.union(users_off))
|
Approach2/UserLevelAnalysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="/assets/tutorial03_code.ipynb" class="link-button">Download</a>
# <a href="https://colab.research.google.com/github/technion046195/technion046195/blob/master/content/tutorial03/code.ipynb" target="_blank">
# <img src="../assets/colab-badge.svg" style="display:inline"/>
# </a>
#
# <center><h1>
# תרגול 3 - Overfitting and generalization
# </h1></center>
# ## Setup
# +
## Importing packages
import os # A build in package for interacting with the OS. For example to create a folder.
import numpy as np # Numerical package (mainly multi-dimensional arrays and linear algebra)
import pandas as pd # A package for working with data frames
import matplotlib.pyplot as plt # A plotting package
import imageio # A package to read and write image (is used here to save gif images)
## Setup matplotlib to output figures into the notebook
## - To make the figures interactive (zoomable, tooltip, etc.) use ""%matplotlib notebook" instead
# %matplotlib inline
## Setting some nice matplotlib defaults
plt.rcParams['figure.figsize'] = (4.5, 4.5) # Set default plot's sizes
plt.rcParams['figure.dpi'] = 120 # Set default plot's dpi (increase fonts' size)
plt.rcParams['axes.grid'] = True # Show grid by default in figures
## Auxiliary function for prining equations, pandas tables and images in cells output
from IPython.core.display import display, HTML, Latex, Markdown
## Create output folder
if not os.path.isdir('./output'):
os.mkdir('./output')
# -
# ## Ex. 3.3
# +
x = np.array([6, 1, 4, 5])
y = np.array([4, 2, 5, 2])
x_grid = np.arange(0, 8, 0.1)
# -
## Ploting
fig, ax = plt.subplots(figsize=(4.5, 3))
ax.plot(x, y, 'x', ms=10, mew=3, label=f'Dataset')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='upper left')
ax.set_xlim(0, 8)
ax.set_ylim(0, 8)
plt.tight_layout()
fig.savefig('./output/ex_3_3_dataset.png')
# ### Section 1
# +
x_train = x[:3]
y_train = y[:3]
x_test = x[3:]
y_test = y[3:]
# -
## Defining augmentation
aug_func = lambda x, k: x[:, None] ** np.arange(0, k + 1)[None, :]
for k in np.arange(2):
## Augment the dataset
x_aug = aug_func(x_train, k)
## Calcualting theta
theta = np.linalg.inv(x_aug.T @ x_aug) @ (x_aug.T @ y_train)
denom = np.linalg.det(x_aug.T @ x_aug).round()
## Defineing the predictor
h1 = lambda x: aug_func(x, k) @ theta
## Ploting
fig, ax = plt.subplots(figsize=(4.5, 3))
ax.plot(x_train, y_train, 'x', ms=10, mew=3, label=f'Train set')
ax.plot(x_test, y_test, 'xr', ms=10, mew=3, label=f'Test set')
ax.plot(x_grid, h1(x_grid), label=f'Liner model')
ax.set_title(f'K={k}')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='upper left')
ax.set_xlim(0, 8)
ax.set_ylim(0, 8)
plt.tight_layout()
fig.savefig(f'./output/ex_3_3_1_order_{k}.png')
## Test cost
test_score = ((h1(x_test) - y_test) ** 2).mean() ** 0.5
display(Markdown(f'K={k}: '
+ r'$\boldsymbol{\theta}^*_{\mathcal{D}}=\frac{1}{' + f'{denom}}}${theta * denom}={theta}, '
+ f'Test score = {test_score:.3f}'
))
# ## Section 3
# +
x_train2 = x_train[:2]
y_train2 = y_train[:2]
x_val = x_train[2:]
y_val = y_train[2:]
val_scores = {}
for k in np.arange(2):
## Augment the dataset
x_aug = aug_func(x_train2, k)
## Calcualting theta
theta = np.linalg.inv(x_aug.T @ x_aug) @ (x_aug.T @ y_train2)
denom = np.linalg.det(x_aug.T @ x_aug).round()
## Defineing the predictor
h1 = lambda x: aug_func(x, k) @ theta
## Ploting
fig, ax = plt.subplots(figsize=(4.5, 3))
ax.plot(x_train2, y_train2, 'x', ms=10, mew=3, label=f'Train set')
ax.plot(x_val, y_val, 'xg', ms=10, mew=3, label=f'Validation set')
ax.plot(x_test, y_test, 'xr', ms=10, mew=3, label=f'Test set')
ax.plot(x_grid, h1(x_grid), label=f'Liner model')
ax.set_title(f'K={k}')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='upper left')
ax.set_xlim(0, 8)
ax.set_ylim(0, 8)
plt.tight_layout()
fig.savefig(f'./output/ex_3_3_3_order_{k}.png')
## Validataion score
val_score = ((h1(x_val) - y_val) ** 2).mean() ** 0.5
val_scores[k] = val_score
display(Markdown(f'K={k}: '
+ r'$\boldsymbol{\theta}^*_{\mathcal{D}}=\frac{1}{' + f'{denom}}}${theta * denom}={theta}, '
+ f'Validataion score = {val_score:.3f}'
))
display(Markdown(f'#### Best K'))
best_k = min(val_scores, key=val_scores.get)
display(Markdown(f'best K={best_k}'))
# -
# ## Section 4
val_scores = {}
for k in np.arange(2):
val_scores_cross = []
for i in range(x_train.shape[0]):
x_train2 = np.concatenate((x_train[:i], x_train[(i+1):]), axis=0)
y_train2 = np.concatenate((y_train[:i], y_train[(i+1):]), axis=0)
x_val = x[i:(i+1)]
y_val = y[i:(i+1)]
## Augment the dataset
x_aug = aug_func(x_train2, k)
## Calcualting theta
theta = np.linalg.inv(x_aug.T @ x_aug) @ (x_aug.T @ y_train2)
denom = np.linalg.det(x_aug.T @ x_aug).round()
## Defineing the predictor
h1 = lambda x: aug_func(x, k) @ theta
## Ploting
fig, ax = plt.subplots(figsize=(4.5, 3))
ax.plot(x_train2, y_train2, 'x', ms=10, mew=3, label=f'Train set')
ax.plot(x_val, y_val, 'xg', ms=10, mew=3, label=f'Validation set')
ax.plot(x_test, y_test, 'xr', ms=10, mew=3, label=f'Test set')
ax.plot(x_grid, h1(x_grid), label=f'Liner model')
ax.set_title(f'K={k}, fold={i}')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='upper left')
ax.set_xlim(0, 8)
ax.set_ylim(0, 8)
plt.tight_layout()
fig.savefig(f'./output/ex_4_3_4_order_{k}_fold_{i}.png')
## Validataion score
val_score = ((h1(x_val) - y_val) ** 2).mean() ** 0.5
display(Markdown(f'K={k}: '
+ r'$\boldsymbol{\theta}^*_{\mathcal{D}}=\frac{1}{' + f'{denom}}}${theta * denom}={theta}, '
+ f'Validataion score = {val_score:.3f}'
))
val_scores_cross.append(val_score)
val_scores[k] = np.mean(val_scores_cross)
display(Markdown(f'-> K={k}: Mean validataion score = {val_scores[k]:.3f}'))
display(Markdown(f'#### Best K'))
best_k = max(val_scores, key=val_scores.get)
display(Markdown(f'best K={k}'))
|
content/tutorial03/code.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# instala o pacote sqldf
# INSTALLING FROM CRAN
# Executar apenas na primeira vez
install.packages("sqldf")
# +
install.packages("data.table")
install.packages("DataExplorer")
library(data.table)
library(DataExplorer)
# -
source("https://raw.githubusercontent.com/claudioteix/RLibrary/master/MyLibrary.R")
library(sqldf)
# Carrega o dataset criado no RStudio no servidor CEFET
# já com todas as cláusulas de data cleaning
load("flights.Rda")
nrow(df10)
head(df10)
str(df10)
# Transforma o formato POSIXlt em chr
# para que possa ser trabalhado em conjunto com o sqldf
df10$depart_expect <- as.character(df10$depart_expect)
df10$depart <- as.character(df10$depart)
df10$arrival_expect <- as.character(df10$arrival_expect)
df10$arrival <- as.character(df10$arrival)
str(df10)
query<-"select destiny, origin, airline, flight, depart, arrival, departure_delay, arrival_delay,"
query<-paste(query,"depart_temperature, depart_dew_point, depart_humidity, depart_pressure, depart_visibility, depart_conditions,", sep=" ")
query<-paste(query,"arrival_temperature, arrival_dew_point, arrival_humidity, arrival_pressure, arrival_visibility, arrival_conditions", sep=" ")
query<-paste(query, "from df10", sep=" ")
print(query)
train_set<-sqldf(query)
str(train_set)
# Carrega as bibliotecas necessárias para trabalhar com as transações e os algoritmos
library("arules")
library("arulesSequences")
library("arulesViz")
# Remove as características que não serão analisadas
train_set$depart_temperature <- NULL
train_set$depart_dew_point <- NULL
train_set$depart_humidity <- NULL
train_set$depart_pressure <- NULL
train_set$depart_visibility <- NULL
train_set$arrival_temperature <- NULL
train_set$arrival_dew_point <- NULL
train_set$arrival_humidity <- NULL
train_set$arrival_pressure <- NULL
train_set$arrival_visibility <- NULL
str(train_set)
# +
# cria duas listas com todos os valores da coluna depart (index column=5)
# já separados nos formatos YYYY-MM-DD e HH:MM:SS respectivamente
depart_d<-sapply(strsplit(train_set[,5], " ", fixed = TRUE), "[", 1)
depart_h<-sapply(strsplit(train_set[,5], " ", fixed = TRUE), "[", 2)
# cria duas listas com todos os valores da coluna arrival (index column=6)
# já separados nos formatos YYYY-MM-DD e HH:MM:SS respectivamente
arrival_d<-sapply(strsplit(train_set[,6], " ", fixed = TRUE), "[", 1)
arrival_h<-sapply(strsplit(train_set[,6], " ", fixed = TRUE), "[", 2)
# cria um novo dataframe com essas duas novas colunas
x <- data.frame("depart_date" = depart_d, "depart_time" = depart_h, "arrival_date" = arrival_d, "arrival_time" = arrival_h)
# cria um novo dataframe com a combinação do dataframe train_set e x
flights <- cbind(train_set,x)
# -
str(flights)
head(flights)
# Remove as características que não serão analisadas
flights$depart <- NULL
flights$arrival <- NULL
str(flights)
introduce(flights)
PlotMissing(flights)
BarDiscrete(flights$origin)
counts <- table(flights$depart_time)
barplot(counts, main="Flights Distribution by Departure Time",
xlab="Departure Time")
HistogramContinuous(flights)
CorrelationDiscrete(flights)
CorrelationContinuous(flights)
counts <- table(flights$departure_delay)
barplot(counts, main="Flights Distribution by Departure Delay",
xlab="Departure Delay")
# Sum the flights delayed by departure time (HH)
query<-"select depart_time_HH, count(flight) as total_flights
from (select substr(depart_time,1,2) as depart_time_HH, flight
from flights)
group by depart_time_HH
order by total_flights"
print(query)
result<-sqldf(query)
result
# Analisa a estatística descritiva das características departure_delay e arrival_delay que serão categorizadas
summary(flights$departure_delay)
summary(flights$arrival_delay)
flights$depart_conditions <- as.factor(flights$depart_conditions)
flights$arrival_conditions <- as.factor(flights$arrival_conditions)
str(flights)
# **Departure Time** is a key factor that we are going to examine.<br>
# We want to know which time is the best time for flight.
# +
## Categoriza as variáveis departure_delay e arrival_delay
flights$departure_delay <- ordered(cut(flights$departure_delay, c(60,75,125,240)),
labels = c("None", "Low", "High"))
flights$arrival_delay <- ordered(cut(flights$arrival_delay, c(60,75,125,240)),
labels = c("None", "Low", "High"))
# -
## Categoriza a variável depart_time
flights$depart_time <- ordered(cut(as.integer(substr(flights$depart_time,1,2)), c(00,06,12,18,23)),
labels = c("Overnight", "Morning", "Afternoon", "Evening"))
head(flights)
# Sum the flights delayed during Overnight
query<-"select count(flight) from flights where depart_time='Overnight'"
print(query)
result<-sqldf(query)
result
# Sum the flights delayed during Overnight and departure_delay='None'
query<-"select count(flight) from flights where depart_time='Overnight' and departure_delay='None'"
print(query)
result_2<-sqldf(query)
result_2
# Confidence = 0,1918 ou 19,18%
# Sum the flights delayed during Morning
query<-"select count(flight) from flights where depart_time='Morning'"
result_3<-sqldf(query)
result_3
# Sum the flights delayed during Morning and departure_delay='None'
query<-"select count(flight) from flights where depart_time='Morning' and departure_delay='None'"
result_4<-sqldf(query)
result_4
# Confidence = 0,2363 ou 23,63%
# Sum the flights delayed during Afternoon
query<-"select count(flight) from flights where depart_time='Afternoon'"
result_5<-sqldf(query)
result_5
# Sum the flights delayed during Afternoon and departure_delay='None'
query<-"select count(flight) from flights where depart_time='Afternoon' and departure_delay='None'"
result_6<-sqldf(query)
result_6
# Confidence = 0,2531 ou 25,31%
# Sum the flights delayed during Evening
query<-"select count(flight) from flights where depart_time='Evening'"
result_7<-sqldf(query)
result_7
# Sum the flights delayed during Evening and departure_delay='None'
query<-"select count(flight) from flights where depart_time='Evening' and departure_delay='None'"
result_8<-sqldf(query)
result_8
# Confidence = 0,2749 ou 27,49%
# **Flights Departed Without Delay**<br>
# **Period of Time** **(%)**<br>
# Overnight
#
#
# 19,18%<br>
# Morning
#
#
# 23,63%<br>
# Afternoon
#
#
# 25,31%<br>
# <span style="color:blue">
# Evening
#
#
# 27,49%</span><br>
# <br><br>
# **Conclusion:** The best time period to flight is from 19H to 23H (Evening)
# Creating the transactions and running the Apriori Algorithm,
# we have the same results.
## Cria as transações
train_set_transactions <- as(flights, "transactions")
train_set_transactions
str(train_set_transactions)
head(train_set_transactions@data)
head(train_set_transactions@itemInfo)
head(train_set_transactions@itemsetInfo)
# Nesta parte do trabalho, executar-se-á o algoritmo APRIORI
# para gerar regras com a seguinte especificcação:
#
# 1. com suporte de 0,5, confiança de 0,9 e tamanho minimo = 2
# 2. com um atributo do lado esquerdo e um do lado direito e tamanho maximo=3
# 3. com lado direito limitado ao valor do atributo arrival_delay=None Arrival Delay
# 4. e lado esquerdo livre.
#
# Isso significa que estamos interessados em qualquer causa que provoque
# a consequência arrival_delay=High Arrival Delay.
#rules <- apriori(train_set_transactions, parameter=list(supp = 0.01, conf = 0.8, minlen=1, maxlen= 10, target = "rules"), appearance=list(rhs = c("arrival_delay=High"),default="lhs"),control=NULL)
#rules <- apriori(train_set_transactions, parameter=list(conf = 0.9, minlen=1, maxlen= 10, target = "rules"), appearance=list(rhs = c("arrival_delay=None"),default="lhs"),control=NULL)
#rules <- apriori(train_set_transactions, parameter = list(supp = 0.9, conf = 0.9, target = "rules"), appearance=list(rhs = c("arrival_delay=High"),default="lhs"),control=NULL)
rules <- apriori(train_set_transactions, parameter = list(supp = 0.01, conf = 0.1, target = "rules"), appearance=list(lhs = c("depart_time=Evening"), rhs = c("departure_delay=None")),control=NULL)
rules_a <- as(rules, "data.frame")
head(rules_a)
irules <- inspect(rules)
rules.sorted <- sort(rules, by="lift")
inspect(rules.sorted)
# Interpretando o resultado da primeira regra, temos:
# SUPPORT = 0,015 significa que 1,5% das 53.705 transações, representam o padrão {airline=WEB, departure_delay=High}
# CONFIDENCE = 0,92 significa que 92% das 53.705 transações que contém o padrão {airline=WEB, departure_delay=High} também contém o padrão {arrival_delay=High}
# O lift de uma regra de associação A Þ B indica o quanto
# mais freqüente torna-se B, quando A ocorre.
# Esta medida é computada por:
# Lift(A Þ B) = Conf(A Þ B) ÷ Sup(B).
# Indica que quando ocorre um voo com o padrão {airline=WEB, departure_delay=High} existe chance 4(quatro) vezes maior de ocorrer o padrão {arrival_delay=High}
# {arrival_delay=High} significa um atraso entre 2 até 4 horas.
|
CLAUDIO_TEIXEIRA_TRAB_DM_v3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.5 64-bit (''.venv'': venv)'
# language: python
# name: python3
# ---
# # Trees 🌲
#
# Trees are a hierarchical data structure with nodes having parent-child relationships between them.
class TreeNode:
def __init__(self, val = 0, left = None, right = None) -> None:
self.val = val
self.left = left
self.right = right
# A node can have **n** children.
#
# In binary trees a node has two children.
#
#
|
Data Structures/Trees.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + slideshow={"slide_type": "skip"}
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
from numpy import *
from IPython.html.widgets import *
from IPython.display import display
import matplotlib.pyplot as plt
from IPython.core.display import clear_output
# + slideshow={"slide_type": "skip"} language="javascript"
# /*
# Install with
# sudo ipython install-nbextension https://bitbucket.org/ipre/calico/downloads/calico-document-tools-1.0.zip
#
# and do citations like
#
# [CITE](#cite-PER-GRA:2007)
# */
# IPython.load_extensions('calico-document-tools');
# + [markdown] slideshow={"slide_type": "slide"}
# <!--bibtex
#
# @incollection{LeCun:2012vf,
# author = {LeCun, <NAME> and Bottou, <NAME> Orr, <NAME> and Muller, Klaus-Robert},
# title = {{Efficient backprop}},
# booktitle = {Neural Networks: tricks of the trade},
# year = {2012},
# pages = {9--48},
# publisher = {Springer}
# }
#
# -->
# -
# # Neural Network Tricks
# In this notebook, I'll show the effects of various techniques ("tricks") used to improve the performance of neural networks. Most of them come from the <a name="ref-1"/>[(LeCun, Bottou, Orr and Muller, 2012)](#cite-LeCun:2012vf) paper.
# + [markdown] slideshow={"slide_type": "subslide"}
# Previously, we built a basic neural network in the "Backprop Exercise" notebook. Here, I'll use a slightly refactored version of the `NeuralNetwork` class:
# -
# %pycat neural_network.py
# +
from sklearn.decomposition import PCA
from sklearn.cross_validation import train_test_split, ShuffleSplit
from sklearn.preprocessing import OneHotEncoder
from neural_network import NeuralNetwork
# The classifier network
class ClassifierNetwork(NeuralNetwork):
"""Neural network with classification error plots."""
def errors_for(self, t, x):
x, t = self.preprocessed(x, t)
y = self.predictions_for(x)
mse = multiply(y-t,y-t).mean()
mce = (y.argmax(axis=1) != t.argmax(axis=1)).mean()
return mse, mce
def train_classifier(self, dataset, fig=None, ax=None, epochs=1000):
"""Perform the classification task for the data using the given network, without using train-test split."""
X, T = dataset.data, dataset.target
_X, _T = self.preprocessed(X, T)
errors=[]
for epoch in range(epochs):
self.update_weights(_T, _X)
errors.append(self.errors_for(T, X))
if fig is not None and mod(epoch+1, 100) == 0:
aerrors=array(errors).T
self.plot_errors(ax, aerrors.T, epoch, epochs, ylabel='Errors', ylim=3.0)
ax.legend(['RMSE', 'RMCE'], loc='ba')
clear_output(wait=True)
display(fig)
ax.cla()
if errors[-1][1] == 0: # Perfect classification
break
plt.close()
return errors[-1]
def plot_errors(self, ax, errors, epoch, epochs, ylabel, ylim=1.0):
"""Plots the error graph."""
ax.plot(arange(epoch), errors[:epoch])
ax.set_xlim([0, epochs])
ax.set_ylim([0, ylim])
ax.set_xlabel("Training epoch")
ax.set_ylabel(ylabel)
ax.set_title(ylabel)
ax.grid()
ax.legend(['Training', 'Test'], loc="best")
class ClassifierNetworkWithOneHot(ClassifierNetwork):
"""Encodes target values using one-hot encoding."""
def preprocessed(self, X, T=None):
if T is not None:
if not hasattr(self, 'encoder'):
self.encoder = OneHotEncoder(sparse=False).fit(T[:,newaxis])
T = self.encoder.transform(T[:,newaxis])*2 - 1
return super(ClassifierNetworkWithOneHot, self).preprocessed(X, T)
# Classifier with PCA preprocessing
class ClassifierNetworkForImages(ClassifierNetworkWithOneHot):
"""Applies PCA to the input data."""
def preprocessed(self, X, T=None):
if not hasattr(self, 'pca'):
self.pca = PCA(n_components = self.num_nodes[0], whiten=True, copy=True).fit(X)
return super(ClassifierNetworkForImages, self).preprocessed(self.pca.transform(X),T)
def train_classifier(self, dataset, fig=None, axs=None, epochs=1000, batch_size=0.1, test_size=0.2):
"""Perform the classification task for the data using the given network."""
# Split to training and test
X_train, X_test, T_train, T_test = train_test_split(dataset.data, dataset.target, test_size=test_size)
errors=[]
for epoch, epochs in self.train(X_train, T_train, epochs=epochs, batch_size=batch_size):
errors.append(self.errors_for(T_train, X_train) + self.errors_for(T_test, X_test))
if fig is not None and mod(epoch+1, 100) == 0:
aerrors=array(errors).T
self.plot_errors(axs[0], aerrors[::2].T, epoch, epochs, ylabel='RMSE', ylim=3.0)
self.plot_errors(axs[1], aerrors[1::2].T,epoch, epochs, ylabel='Classification Error', ylim=1.0)
clear_output(wait=True)
display(fig)
[ax.cla() for ax in axs]
plt.close()
train_rmse, train_rce, test_rmse, test_rce = errors[-1]
return train_rmse, test_rmse, train_rce, test_rce
# + [markdown] slideshow={"slide_type": "subslide"}
# Here are some datasets we'll be using:
# +
from sklearn.datasets.base import Bunch
from sklearn.datasets import load_digits
# The XOR dataset
dataset_xor = Bunch()
dataset_xor['data'] = array([
[ 1,-1],
[-1, 1],
[ 1, 1],
[-1,-1]], dtype=float)
dataset_xor['target'] = array([
1,
1,
0,
0], dtype=float)
dataset_digits=load_digits()
# + [markdown] slideshow={"slide_type": "slide"}
# Now let's see how the "basic" network does for these tasks.
# + slideshow={"slide_type": "subslide"}
base_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2])
print(base_xor_net.train_classifier(dataset_xor, *plt.subplots(figsize=(5,5)), epochs=500))
# -
# Note that the network often gets stuck in a local minimum.
# + slideshow={"slide_type": "subslide"}
base_digits_net = ClassifierNetworkForImages(num_nodes=[20, 20, 10])
print(base_digits_net.train_classifier(dataset_digits, *plt.subplots(1, 2, figsize=(10,5)), epochs=1000))
# + [markdown] slideshow={"slide_type": "slide"}
# # Activation function
#
# Let's try the "funny tanh" as the activation function. For the XOR dataset, this ameliorates the problem of the network getting stuck in the local minimum.
# +
from neural_network import ActivationFunction
class FunnyTanh(ActivationFunction):
def apply(self, x):
return 1.7159 * tanh(x*2/3) + 0.001 * x
funnytanh_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2], activation_function=FunnyTanh())
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=300
for result in results:
Ws = base_xor_net.initial_weights() # keep the same initial weights
base_xor_net.Ws = Ws
funnytanh_xor_net.Ws = Ws
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=funnytanh_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'funnytanh'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None
# + [markdown] slideshow={"slide_type": "slide"}
# # Better initial weights
#
# Let's change the initial random weights to have standard deviation of $1/\sqrt m$, where $m$ is the number of connection feeding *into* the node.
# +
def better_initial_weights(self):
return [standard_normal((n + 1, m)) / sqrt(n + 1) for n, m in zip(self.num_nodes[:-1], self.num_nodes[1:])]
better_weight_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2])
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=300
for result in results:
base_xor_net.Ws = base_xor_net.initial_weights()
better_weight_xor_net.Ws = better_initial_weights(better_weight_xor_net)
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=better_weight_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'better_weight'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None
# + [markdown] slideshow={"slide_type": "slide"}
# # Momentum
#
# Let's add the momentum to the stochastic gradient update. Now, instead of updating the weights as
#
# $$
# W \leftarrow W - \eta \frac{\partial E}{\partial W}
# $$
#
# We will keep the *previous weight update* $V$ and *momentum* $\mu$ so that:
#
# $$
# \begin{align*}
# V &\leftarrow \mu V - \eta \frac{\partial E}{\partial W} \\
# W &\leftarrow W + V
# \end{align*}
# $$
#
# The *momentum* $\mu$ modulates how much of the previous weight update is reflected in the current update.
# +
from neural_network import _with_bias
class ClassifierNetworkWithMomentum(ClassifierNetworkWithOneHot):
def __init__(self, *args, **kwargs):
super(ClassifierNetworkWithMomentum, self).__init__(*args, **kwargs)
self.momentum = kwargs['momentum'] if kwargs.has_key('momentum') else 0.9
self.Vs = [zeros(W.shape) for W in self.Ws]
def gradient_descent(self, deltas, zs):
N = zs[0].shape[0]
Js= [self.eta * dot(_with_bias(z).T, delta) / N for W, z, delta in zip(self.Ws, zs[:-1], deltas)]
self.Vs = [self.momentum * V - J for V, J in zip(self.Vs, Js)]
return [W + V for W, V in zip(self.Vs, self.Ws)]
momentum_xor_net = ClassifierNetworkWithMomentum(num_nodes=[2, 2, 2], eta=0.05)
#print(momentum_xor_net.train_classifier(dataset_xor, *plt.subplots(figsize=(5,5)), epochs=500))
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=600
for result in results:
Ws = base_xor_net.initial_weights()
base_xor_net.Ws = Ws
momentum_xor_net.Ws = Ws
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=momentum_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'momentum'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None
# + [markdown] slideshow={"slide_type": "slide"}
# # Pre-train using autoencoder
#
# We'll first perform an "unsupervised learning" using an auto-encoder: instead of predicting the target values, we'll train it to predict the input values.
# +
class AutoEncoderNetwork(ClassifierNetwork):
def train_unsupervised(self, dataset, fig=None, ax=None, epochs=1000):
"""Perform unsupervised learning from the data."""
X = self.preprocessed(dataset.data)
T = X.copy()
errors=[]
for epoch in range(epochs):
self.update_weights(T, X)
errors.append(self.errors_for(T, X))
if fig is not None and mod(epoch+1, 100) == 0:
aerrors=array(errors).T
self.plot_errors(ax, aerrors.T, epoch, epochs, ylabel='Errors', ylim=3.0)
ax.legend(['RMSE', '(Ignore this)'], loc='ba')
clear_output(wait=True)
display(fig)
ax.cla()
plt.close()
return errors[-1]
ae_xor_net = AutoEncoderNetwork(num_nodes=[2, 2, 2])
print(ae_xor_net.train_unsupervised(dataset_xor, *plt.subplots(figsize=(5,5)), epochs=500))
# + [markdown] slideshow={"slide_type": "subslide"}
# Then, we'd train the classifier network starting from the hidden weights that was learned.
# + slideshow={"slide_type": "-"}
ae_xor_net = AutoEncoderNetwork(num_nodes=[2, 2, 2])
aeweight_xor_net = ClassifierNetworkWithOneHot(num_nodes=[2, 2, 2], activation_function=FunnyTanh())
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=300
for result in results:
Ws = base_xor_net.initial_weights()
base_xor_net.Ws = Ws
ae_xor_net.Ws = ae_xor_net.initial_weights()
ae_xor_net.train_unsupervised(dataset_xor, epochs=100) # Only train for a short amount
Wh = ae_xor_net.Ws[0]
aeweight_xor_net.Ws = [W.copy() for W in Ws]
aeweight_xor_net.Ws[0] = Wh
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=aeweight_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'autoencoder'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None
# + [markdown] slideshow={"slide_type": "slide"}
# # Putting everything together
#
# Now we'll combine all of the techniques above. We'll also run it longer (1000 epochs) to see if
# +
class ClassifierNetwork2(ClassifierNetworkWithMomentum):
def __init__(self, *args, **kwargs):
if not kwargs.has_key('activation_function'):
kwargs['activation_function'] = FunnyTanh()
super(ClassifierNetwork2, self).__init__(*args, **kwargs)
def initial_weights(self):
Ws0 = [standard_normal((n + 1, m)) / sqrt(n + 1) for n, m in zip(self.num_nodes[:-1], self.num_nodes[1:])]
ae_network = AutoEncoderNetwork(num_nodes=[self.num_nodes[0], self.num_nodes[1], self.num_nodes[0]],Ws = Ws0)
ae_network.train_unsupervised(dataset_xor, epochs=100) # Only train for a short amount
Ws0[0] = ae_network.Ws[0]
return Ws0
improved_xor_net = ClassifierNetwork2(num_nodes=[2, 2, 2], eta=0.05)
# Train 10 times and see how many times it gets stuck
results=zeros((10,2))
epochs=600
for result in results:
base_xor_net.Ws = base_xor_net.initial_weights()
improved_xor_net.Ws = improved_xor_net.initial_weights()
result[0]=base_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
result[1]=improved_xor_net.train_classifier(dataset_xor, epochs=epochs)[1]
plt.bar(arange(2), (results<1e-8).mean(axis=0) * 100.0)
plt.xticks(arange(2)+.5, ['base', 'improved'])
plt.xlim([-.25, 2.25])
plt.ylim([0, 100.0])
plt.grid()
plt.title('Pct successful training by %d epochs (out of %d trials)'% (epochs, results.shape[0]))
None
# + [markdown] slideshow={"slide_type": "slide"}
# #References
#
# <a name="cite-LeCun:2012vf"/><sup>[^](#ref-1) </sup>LeCun, <NAME> <NAME> Orr, <NAME> and <NAME>. 2012. _Efficient backprop_.
#
#
|
notebooks/NeuralNetworkTricks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/alex000kim/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/module1-join-and-reshape-data/LS_DSPT3_121_Join_and_Reshape_Data.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="pmU5YUal1eTZ"
# _Lambda School Data Science_
#
# # Join and Reshape datasets
#
# Objectives
# - concatenate data with pandas
# - merge data with pandas
# - understand tidy data formatting
# - melt and pivot data with pandas
#
# Links
# - [Pandas Cheat Sheet](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf)
# - [Tidy Data](https://en.wikipedia.org/wiki/Tidy_data)
# - Combine Data Sets: Standard Joins
# - Tidy Data
# - Reshaping Data
# - Python Data Science Handbook
# - [Chapter 3.6](https://jakevdp.github.io/PythonDataScienceHandbook/03.06-concat-and-append.html), Combining Datasets: Concat and Append
# - [Chapter 3.7](https://jakevdp.github.io/PythonDataScienceHandbook/03.07-merge-and-join.html), Combining Datasets: Merge and Join
# - [Chapter 3.8](https://jakevdp.github.io/PythonDataScienceHandbook/03.08-aggregation-and-grouping.html), Aggregation and Grouping
# - [Chapter 3.9](https://jakevdp.github.io/PythonDataScienceHandbook/03.09-pivot-tables.html), Pivot Tables
#
# Reference
# - Pandas Documentation: [Reshaping and Pivot Tables](https://pandas.pydata.org/pandas-docs/stable/reshaping.html)
# - Modern Pandas, Part 5: [Tidy Data](https://tomaugspurger.github.io/modern-5-tidy.html)
# - [<NAME>'s famous paper](http://vita.had.co.nz/papers/tidy-data.html) on Tidy Data
# + [markdown] colab_type="text" id="Mmi3J5fXrwZ3"
# ## Download data
#
# We’ll work with a dataset of [3 Million Instacart Orders, Open Sourced](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2)!
# + colab_type="code" id="K2kcrJVybjrW" outputId="f491bab7-818d-48db-b6e1-f414c3a8a69d" colab={"base_uri": "https://localhost:8080/", "height": 221}
# !wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
# + colab_type="code" id="kqX40b2kdgAb" outputId="db398609-f6dd-4b26-930f-3c8d993bf870" colab={"base_uri": "https://localhost:8080/", "height": 258}
# !tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
# + id="qer8GlIyKR-a" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="0630bcd1-fc77-4eac-d5bb-d07ff0f3b1d5"
# %cd /content/
# + id="u-PxGzHXKUev" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="1740007e-6f11-4b98-e2f5-befb06553b51"
# !ls -lh *.csv
# + colab_type="code" id="YbCvZZCBfHCI" outputId="52af85bf-44db-485c-fa5d-a9f5a7a73dde" colab={"base_uri": "https://localhost:8080/", "height": 36}
# %cd instacart_2017_05_01
# + id="etshR5kpvWOj" colab_type="code" outputId="96432d60-4326-491b-9d74-057961061aee" colab={"base_uri": "https://localhost:8080/", "height": 128}
# !ls -lh *.csv
# + id="bCqqDA8eLeEg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="c508c0de-3d91-4c7e-8cdf-04c516e7bcfe"
# %cd /content/
# + id="L5ClXQ9wLhs1" colab_type="code" colab={}
# !rm -rf instacart_2017_05_01/
# + id="wWHEE1KPLpow" colab_type="code" colab={}
# !rm instacart_online_grocery_shopping_2017_05_01.tar.gz
# + [markdown] id="4xfByfuSKipi" colab_type="text"
# ## Download with Python
# + id="y24ozoEaLv3f" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="f48f80a5-da4c-4880-d2cb-adab9ac3a8ec"
# %cd /content/
# + id="ieeRnlqFKhwm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="5582959f-a758-48a3-8c75-16bfe907513d"
import urllib.request
url = 'https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz'
file_name = 'instacart_online_grocery_shopping_2017_05_01.tar.gz'
urllib.request.urlretrieve(url, file_name)
# + id="-WDWwt2IKh8p" colab_type="code" colab={}
import tarfile
tar = tarfile.open(file_name, "r:gz")
tar.extractall()
tar.close()
# + id="LXFXBFFtKiAE" colab_type="code" colab={}
import os
# + id="ZTvsZnx_KiDf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="dde63cfb-c736-4fba-a2aa-9ba25c3ecf9f"
print(os.getcwd())
# + id="N6MptFSIMVZw" colab_type="code" colab={}
os.chdir('/content/instacart_2017_05_01/')
# + id="6EkUvAHsMVc_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="fe472379-a672-493c-dcbf-42871254680c"
print(os.getcwd())
# + id="5x4pC2ygMVmn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 128} outputId="36a90e53-d62f-4ea6-e6a1-cea2b50a8117"
import glob
glob.glob("/content/instacart_2017_05_01/*.csv")
# + [markdown] id="RcCu3Tlgv6J2" colab_type="text"
# # Join Datasets
# + [markdown] colab_type="text" id="RsA14wiKr03j"
# ## Goal: Reproduce this example
#
# The first two orders for user id 1:
# + colab_type="code" id="vLqOTMcfjprg" outputId="ccb20543-bb7d-47e0-b15e-db3140af5a93" colab={"base_uri": "https://localhost:8080/", "height": 312}
from IPython.display import display, Image
url = 'https://cdn-images-1.medium.com/max/1600/1*vYGFQCafJtGBBX5mbl0xyw.png'
example = Image(url=url, width=600)
display(example)
# + [markdown] colab_type="text" id="nPwG8aM_txl4"
# ## Load data
#
# Here's a list of all six CSV filenames
# + colab_type="code" id="Ksah0cOrfdJQ" outputId="d0cedb00-b1ee-4a41-a8ea-73c1eb108bc3" colab={"base_uri": "https://localhost:8080/", "height": 128}
# !ls -lh *.csv
# + [markdown] colab_type="text" id="AHT7fKuxvPgV"
# For each CSV
# - Load it with pandas
# - Look at the dataframe's shape
# - Look at its head (first rows)
# - `display(example)`
# - Which columns does it have in common with the example we want to reproduce?
# + id="aCACQqqPNGZf" colab_type="code" colab={}
import pandas as pd
# + [markdown] colab_type="text" id="cB_5T6TprcUH"
# ### aisles
# + colab_type="code" id="JB3bvwSDK6v3" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="25a9691a-639b-4e29-989a-1651c96e36c3"
aisles = pd.read_csv("aisles.csv")
aisles.head()
# + id="q4kTfGuLNWs0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="3cdf203f-c3bf-4c46-e5a3-2c85f5517008"
aisles.shape
# + id="XkOTetwpNdu3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="5c568580-9040-4152-e9df-a3358c60c382"
display(example)
# + id="wzf3bBHxOGAR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 300} outputId="36a1a0cc-4332-4cbf-9eff-52aa371e4372"
aisles.describe()
# + id="RoF10d3GOfL8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 175} outputId="663f009f-54b9-4b1e-d7a8-a91d402a1de4"
aisles.describe(exclude='number')
# + [markdown] colab_type="text" id="9-GrkqM6rfXr"
# ### departments
# + id="yxFd5n20yOVn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="0933ab66-6a00-4d12-fb78-f3ae22d0c77a"
departments = pd.read_csv('departments.csv')
departments.head()
# + id="nVT7Lu8eNkhi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="cf2eabb8-70ca-42da-cfca-dd86a6a5e91f"
departments.shape
# + id="jpaszZKhNklL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="be9cc3ff-3f5f-48b7-c190-cee0e2685c8c"
display(example)
# + [markdown] colab_type="text" id="VhhVcn9kK-nG"
# ### order_products__prior
# + id="86rIMNFSzKaG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="0de830c8-2269-46a6-d891-24216dea9db2"
order_products__prior = pd.read_csv('order_products__prior.csv')
order_products__prior.head()
# + id="JycLr2VRQBQZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="8b63c697-04d1-4033-d061-69710d800556"
order_products__prior.shape
# + [markdown] id="4iIBYxC4PXds" colab_type="text"
# We need:
# - order_id
# - product_id
# - add_to_cart_order
# + [markdown] colab_type="text" id="HVYJEKJcLBut"
# ### order_products__train
# + id="xgwSUCBk6Ciy" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="5966f3a8-c231-46f6-a0ca-100dbbf1bf0f"
order_products__train = pd.read_csv('order_products__train.csv')
order_products__train.head()
# + id="YuN-0yviQHnl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="17a368d4-8ae8-469a-eb3c-1bcbfd3e9db9"
order_products__train.shape
# + [markdown] colab_type="text" id="LYPrWUJnrp7G"
# ### orders
# + id="UfPRTW5w128P" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="5859d3db-9a9c-4529-8cdd-c1ed60a492da"
orders = pd.read_csv('orders.csv')
orders.head()
# + id="sUN5UM0_Qacn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="fee9ef54-1a87-495a-eee8-374d573b68a1"
display(example)
# + [markdown] id="aCxwysS_QhTz" colab_type="text"
# ### We need:
# - order_id
# - user_id
# - order_number
# - order_dow
# - order_hour_of_day
# + [markdown] colab_type="text" id="nIX3SYXersao"
# ### products
# + id="3BKG5dxy2IOA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="a57d94b0-6ccf-4fbc-8d58-52c6578561bb"
products = pd.read_csv('products.csv')
products.head()
# + id="OlSRNK9CQvj1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="27748a37-4794-4a8b-8b9a-7e53208056ad"
products.shape
# + [markdown] colab_type="text" id="cbHumXOiJfy2"
# ## Concatenate order_products__prior and order_products__train
# + colab_type="code" id="TJ23kqpAY8Vv" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="b94018cf-1843-4054-fe25-50e02cc4e615"
order_products = pd.concat([order_products__prior, order_products__train])
order_products.shape
# + id="hseH2LmjRQ7y" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="98df1706-1c74-4f65-b096-d439b2466507"
print(order_products__prior.shape, order_products__train.shape, order_products.shape)
# + id="V0qh7a-wRRIw" colab_type="code" colab={}
assert len(order_products__prior) + len(order_products__train) == len(order_products)
# + id="EkjEck5-SE6w" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="58c6d4b3-ed31-4190-c139-525203c354dc"
display(example)
# + [markdown] id="ozUmNU-PSFSG" colab_type="text"
# # Short `groupby` example
# + id="oeaSes8vSMhF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="18e0b8d3-70a2-4763-f2e2-253207a1a697"
order_products.groupby('order_id')['product_id'].count().mean()
# + id="32ohHNV4SMk1" colab_type="code" colab={}
grouped_orders = order_products.groupby('order_id')
# + id="-8SYBpjdSMrw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="a01cb588-b41c-4fe7-96ff-ca39863ce674"
grouped_orders.get_group(2539329)
# + id="DLEbSnClS6Kf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="1709f304-5e90-4bfa-c247-420a1f203ffd"
order_products[order_products['order_id'] == 2539329]
# + id="do3FGmpFTFh_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="71895286-ad2f-4c15-8ef6-6f7936083247"
grouped_orders['product_id'].count()
# + id="QYeXNrG9TX-w" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 288} outputId="748247ff-291d-4cfa-dda7-cb2d59369389"
grouped_orders['product_id'].count().hist()
# + id="nOHhZMv1TpeS" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 288} outputId="43509f5c-3444-4b76-b88f-044dc80510b4"
grouped_orders['product_id'].count().hist(bins=50)
# + [markdown] colab_type="text" id="Z1YRw5ypJuv2"
# ## Get a subset of orders — the first two orders for user id 1
# + [markdown] id="eJ9EixWs6K64" colab_type="text"
# From `orders` dataframe:
# - user_id
# - order_id
# - order_number
# - order_dow
# - order_hour_of_day
# + id="BWA1re37V0Yn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="4f10cabd-6de1-4423-d050-8f0a7b6ec403"
orders.head()
# + id="K8ydBRgLWENC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="1654cd0a-be1e-4f26-ce49-d2176b375640"
orders.shape
# + id="YsmO7D3WWIt0" colab_type="code" colab={}
condition = (orders['user_id'] == 1) & (orders['order_number'] <= 2)
columns = ['order_id','user_id', 'order_number', 'order_dow', 'order_hour_of_day']
subset = orders[condition][columns]
# + id="kNIXF3RdYMe8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 112} outputId="0a57b358-5dda-4079-c193-d0e2d2e3342b"
subset.head()
# + [markdown] colab_type="text" id="3K1p0QHuKPnt"
# ## Merge dataframes
# + [markdown] id="4MVZ9vb1BuO0" colab_type="text"
# Merge the subset from `orders` with columns from `order_products`
# + id="3lajwEE86iKc" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="51ae07f3-b558-4d29-b95b-cc836d3fd33d"
columns = ['order_id','product_id','add_to_cart_order']
merged = pd.merge(subset, order_products[columns])
merged.head()
# + id="bqCv43Dkabm8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="8a804921-25c2-4e0f-de9e-a3b787b45df6"
display(example)
# + [markdown] id="i1uLO1bxByfz" colab_type="text"
# Merge with columns from `products`
# + id="D3Hfo2dkJlmh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="bb45440f-1363-41f7-c455-8baf3d40c6ad"
final = pd.merge(merged, products[['product_id', 'product_name']])
final.head()
# + id="Jj7ahpTMa7zU" colab_type="code" colab={}
columns = ['user_id', 'order_id', 'order_number','order_dow','order_hour_of_day','add_to_cart_order', 'product_id','product_name']
final = final[columns]
# + id="eD08ERH_bVvO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 394} outputId="367c928d-ddbf-414f-8a4a-b5b587c5fbb6"
final
# + id="lSMh9NBObe-b" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 394} outputId="015a8388-a069-49d9-8323-3197adbd33f2"
final = final.sort_values(by=['order_number', 'add_to_cart_order'])
final
# + id="S8DA1bFsb3-o" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 165} outputId="4c08f904-f41a-4e7e-d3a7-ae5cbef981f3"
columns = [col.replace('_', ' ') for col in final.columns]
columns
# + id="Y4FHXWLqcGx4" colab_type="code" colab={}
final.columns = columns
# + id="71lmRNw6cJfk" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 394} outputId="003edaf7-035e-4060-9099-c65be1bce8f9"
final
# + id="amLO_qIKcNt1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="324d8b0b-845f-45ff-8e72-b193ca46ed63"
display(example)
# + [markdown] id="dDfzKXJdwApV" colab_type="text"
# # Reshape Datasets
# + [markdown] id="4stCppWhwIx0" colab_type="text"
# ## Why reshape data?
#
# #### Some libraries prefer data in different formats
#
# For example, the Seaborn data visualization library prefers data in "Tidy" format often (but not always).
#
# > "[Seaborn will be most powerful when your datasets have a particular organization.](https://seaborn.pydata.org/introduction.html#organizing-datasets) This format ia alternately called “long-form” or “tidy” data and is described in detail by <NAME>. The rules can be simply stated:
#
# > - Each variable is a column
# - Each observation is a row
#
# > A helpful mindset for determining whether your data are tidy is to think backwards from the plot you want to draw. From this perspective, a “variable” is something that will be assigned a role in the plot."
#
# #### Data science is often about putting square pegs in round holes
#
# Here's an inspiring [video clip from _Apollo 13_](https://www.youtube.com/watch?v=ry55--J4_VQ): “Invent a way to put a square peg in a round hole.” It's a good metaphor for data wrangling!
# + [markdown] id="79KITszBwXp7" colab_type="text"
# ## <NAME>'s Examples
#
# From his paper, [Tidy Data](http://vita.had.co.nz/papers/tidy-data.html)
# + id="Jna5sk5FwYHr" colab_type="code" colab={}
# %matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
table1 = pd.DataFrame(
[[np.nan, 2],
[16, 11],
[3, 1]],
index=['<NAME>', '<NAME>', '<NAME>'],
columns=['treatmenta', 'treatmentb'])
table2 = table1.T
# + [markdown] id="eWe5rpI9wdvT" colab_type="text"
# "Table 1 provides some data about an imaginary experiment in a format commonly seen in the wild.
#
# The table has two columns and three rows, and both rows and columns are labelled."
# + id="SdUp5LbcwgNK" colab_type="code" outputId="376f9e07-bf3e-4d27-b892-2c97f3090084" colab={"base_uri": "https://localhost:8080/", "height": 143}
table1
# + [markdown] id="SaEcDmZhwmon" colab_type="text"
# "There are many ways to structure the same underlying data.
#
# Table 2 shows the same data as Table 1, but the rows and columns have been transposed. The data is the same, but the layout is different."
# + id="SwDVoCj5woAn" colab_type="code" outputId="a3e422a5-bc56-494f-fb12-7ca35946ecf3" colab={"base_uri": "https://localhost:8080/", "height": 112}
table2
# + [markdown] id="k3ratDNbwsyN" colab_type="text"
# "Table 3 reorganises Table 1 to make the values, variables and obserations more clear.
#
# Table 3 is the tidy version of Table 1. Each row represents an observation, the result of one treatment on one person, and each column is a variable."
#
# | name | trt | result |
# |--------------|-----|--------|
# | <NAME> | a | - |
# | <NAME> | a | 16 |
# | <NAME> | a | 3 |
# | <NAME> | b | 2 |
# | <NAME> | b | 11 |
# | <NAME> | b | 1 |
# + [markdown] id="WsvD1I3TwwnI" colab_type="text"
# ## Table 1 --> Tidy
#
# We can use the pandas `melt` function to reshape Table 1 into Tidy format.
# + id="S48tKmC46veF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 143} outputId="d7166c72-5531-4243-a055-e8a404203b87"
table1
# + id="H7HNzovLdaC9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="77d7153a-148e-4c19-bc23-05469b61af59"
table1.index
# + id="0Ow4YrVJddyW" colab_type="code" colab={}
table1 = table1.reset_index()
# + id="hHdzTOO_dxWE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 143} outputId="057a2bdb-115f-43e1-8249-49540571ed53"
table1
# + id="pIDvJSCfdlGT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 238} outputId="49afdb4c-a910-4f93-9b70-b2fe1b5c463a"
tidy = table1.melt(id_vars='index')
tidy
# + id="3WLrOgF3d1Ik" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 238} outputId="7a14945e-9a8f-4d45-e61d-5e61e45452d8"
tidy.columns = ['name', 'trt', 'result']
tidy
# + [markdown] id="Ck15sXaJxPrd" colab_type="text"
# ## Table 2 --> Tidy
# + id="k2Qn94RIxQhV" colab_type="code" colab={}
##### LEAVE BLANK --an assignment exercise #####
# + [markdown] id="As0W7PWLxea3" colab_type="text"
# ## Tidy --> Table 1
#
# The `pivot_table` function is the inverse of `melt`.
# + id="rVA_RFAgeXjV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 143} outputId="8c292ad2-a5ea-4699-8e43-e8feec32eeb4"
table1
# + id="CdZZiLYoxfJC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 175} outputId="32fc06dc-a081-4f35-8ba1-f42a59f5c5e6"
tidy.pivot_table(index='name', columns='trt', values='result')
# + [markdown] id="3GeAKoSZxoPS" colab_type="text"
# ## Tidy --> Table 2
# + id="W2jjciN2xk9r" colab_type="code" colab={}
##### LEAVE BLANK --an assignment exercise #####
# + [markdown] id="jr0jQy6Oxqi7" colab_type="text"
# # Seaborn example
#
# The rules can be simply stated:
#
# - Each variable is a column
# - Each observation is a row
#
# A helpful mindset for determining whether your data are tidy is to think backwards from the plot you want to draw. From this perspective, a “variable” is something that will be assigned a role in the plot."
# + id="-tf_9JBKev4M" colab_type="code" colab={}
import seaborn as sns
# + id="kWo3FIP9xuKo" colab_type="code" outputId="45635d8d-24df-4cac-ab7a-a393fa5449ed" colab={"base_uri": "https://localhost:8080/", "height": 225}
sns.catplot(x='trt', y='result', col='name',
kind='bar', data=tidy, height=3);
# + [markdown] id="cIgT41Rxx4oj" colab_type="text"
# ## Now with Instacart data
# + id="Oydw0VvGxyDJ" colab_type="code" colab={}
products = pd.read_csv('products.csv')
order_products = pd.concat([pd.read_csv('order_products__prior.csv'),
pd.read_csv('order_products__train.csv')])
orders = pd.read_csv('orders.csv')
# + id="Lw8vKCkRiHmM" colab_type="code" colab={}
# + [markdown] id="6p-IsG0jyXQj" colab_type="text"
# ## Goal: Reproduce part of this example
#
# Instead of a plot with 50 products, we'll just do two — the first products from each list
# - Half And Half Ultra Pasteurized
# - Half Baked Frozen Yogurt
# + id="Rs-_n9yjyZ15" colab_type="code" outputId="ecb84887-c304-4986-a8a5-fe5bd3eb4bc8" colab={"base_uri": "https://localhost:8080/", "height": 383}
from IPython.display import display, Image
url = 'https://cdn-images-1.medium.com/max/1600/1*wKfV6OV-_1Ipwrl7AjjSuw.png'
example = Image(url=url, width=600)
display(example)
# + [markdown] id="Vj5GR7I4ydBg" colab_type="text"
# So, given a `product_name` we need to calculate its `order_hour_of_day` pattern.
# + [markdown] id="Vc9_s7-LyhBI" colab_type="text"
# ## Subset and Merge
#
# One challenge of performing a merge on this data is that the `products` and `orders` datasets do not have any common columns that we can merge on. Due to this we will have to use the `order_products` dataset to provide the columns that we will use to perform the merge.
# + id="W1yHMS-OyUTH" colab_type="code" colab={}
product_names = ['Half And Half Ultra Pasteurized', 'Half Baked Frozen Yogurt']
# + id="OPHtnODdgFsv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="cc6e27f5-6b45-4b5c-ca5c-b6c2e624e3e4"
products.columns
# + id="Qe2XFEd_gF5F" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 73} outputId="e956ee18-3609-4be1-a0b2-abbd075f0484"
orders.columns
# + id="rcJ2VwUMgF07" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="c79ecfd7-e88a-42fc-e503-0589fb8d7434"
order_products.columns
# + id="4SLQ7R0JgFxL" colab_type="code" colab={}
merged = (products[['product_id', 'product_name']]
.merge(order_products[['order_id', 'product_id']])
.merge(orders[['order_id', 'order_hour_of_day']]))
# + id="Iz5cXZdbgFpE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="d25b73c8-b0b1-43dc-e6e3-a1af47e5f73f"
merged.head()
# + id="FvWrPhCCiUeS" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="344bb069-5ee8-40ce-8e9c-872526de8390"
condition = merged['product_name'].isin(product_names)
subset = merged[condition]
subset.head()
# + id="2ncTVF_SiyuO" colab_type="code" colab={}
assert sorted(list(subset['product_name'].unique())) == sorted(product_names)
# + [markdown] id="UvhcadjFzx0Q" colab_type="text"
# ## 4 ways to reshape and plot
# + [markdown] id="aEE_nCWjzz7f" colab_type="text"
# ### 1. value_counts
# + id="vTL3Cko87VL-" colab_type="code" colab={}
froyo = subset[subset['product_name'] == 'Half Baked Frozen Yogurt']
cream = subset[subset['product_name'] == 'Half And Half Ultra Pasteurized']
# + id="8Ew5Jn7Rj2Ei" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="1841ca3b-aeff-40b0-98c5-04b5484007f0"
cream.head()
# + id="kasfKrUzjtq1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="0a3ab671-de38-4c34-d88a-6692c08624cb"
cream['order_hour_of_day'].value_counts(normalize=True).sort_index().plot()
froyo['order_hour_of_day'].value_counts(normalize=True).sort_index().plot();
# + id="xog-OdvsjtyD" colab_type="code" colab={}
# + [markdown] id="tMSd6YDj0BjE" colab_type="text"
# ### 2. crosstab
# + id="Slu2bWYK0CZD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 303} outputId="0a19b8f2-e501-4bff-e3a8-93b6417fb3d4"
pd.crosstab(subset['order_hour_of_day'], subset['product_name'], normalize='columns').plot()
# + [markdown] id="ICjPVqO70Hv8" colab_type="text"
# ### 3. Pivot Table
# + id="LQtMNVa10I_S" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 303} outputId="b10edcf8-f768-4942-db30-ecc00e45b574"
subset.pivot_table(index='order_hour_of_day', columns='product_name', values='order_id', aggfunc=len).plot()
# + [markdown] id="7A9jfBVv0M7e" colab_type="text"
# ### 4. melt
# + id="2mwa2KZ2lNa2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 238} outputId="90d3a54c-895f-4461-8db7-b60d870f232c"
table = pd.crosstab(subset['order_hour_of_day'],
subset['product_name'],
normalize=True)
table.head()
# + id="liJMF_1alRZL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="b596b525-745c-42af-985d-7a2c55d86099"
melted = (table
.reset_index()
.melt(id_vars='order_hour_of_day')
.rename(columns={
'order_hour_of_day': 'Hour of Day Ordered',
'product_name': 'Product',
'value': 'Percent of Orders by Product'
}))
melted
# + id="HxYfO5Oulka5" colab_type="code" colab={}
import seaborn as sns
# + id="2AmbAKm20PAg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 369} outputId="a49f7473-48ce-4fff-c81f-a0bfb5e21f86"
sns.relplot(x='Hour of Day Ordered',
y='Percent of Orders by Product',
hue='Product',
data=melted,
kind='line');
# + id="D7UAb4c7ljRS" colab_type="code" colab={}
|
module1-join-and-reshape-data/LS_DSPT3_121_Join_and_Reshape_Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # k-MEANS CHALLENGE
#
# **File:** kMeansChallenge.ipynb
#
# **Course:** Data Science Foundations: Data Mining in Python
# # CHALLENGE
#
# For this challenge, I invite you to to the following:
#
# 1. Import and prepare the `iris` dataset.
# 1. Conduct a k-means cluster analysis.
# 1. Visualize the clusters.
# # IMPORT LIBRARIES
import pandas as pd # For dataframes
import matplotlib.pyplot as plt # For plotting data
import seaborn as sns # For plotting data
from sklearn.cluster import KMeans # For k-Means
from sklearn.model_selection import GridSearchCV # For grid search
from sklearn.metrics import silhouette_score # For metrics and scores
from sklearn.preprocessing import StandardScaler # For standardizing data
# # LOAD DATA
# Read the `iris` from "iris.csv" in the data folder and save in `df`.
# +
# Reads the .csv file into variable df
df = pd.read_csv('data/iris.csv')
# Displays the first 5 rows of df
df.head()
# +
# Separate the class variable in y
y = df.species
# Remove the y column from df
X = df.drop('species', axis=1)
# Standardize df
X = pd.DataFrame(
StandardScaler().fit_transform(X),
columns=X.columns)
# Display the first 5 rows of X
X.head()
# +
# Set up the kMeans object
km = KMeans(
n_clusters=3,
random_state=1,
init='k-means++',
n_init=10)
# Fit the model to the data
km.fit(X)
# Display the parameters of the fitted model
km.get_params()
# +
# Create a scatter plot
sns.scatterplot(
x='sepal_length',
y='sepal_width',
data=X,
hue=y,
style=km.labels_,
palette=["orange", "green", "blue"])
# Add cluster centers to the same plot
plt.scatter(
km.cluster_centers_[:,0],
km.cluster_centers_[:,1],
marker='x',
s=200,
c='red')
# -
# # CLEAN UP
#
# - If desired, clear the results with Cell > All Output > Clear.
# - Save your work by selecting File > Save and Checkpoint.
# - Shut down the Python kernel and close the file by selecting File > Close and Halt.
|
BE_kMeansChallenge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 20180429
#
# urllib 라이브러리를 활용해 간단한 웹 브라우저를 만들어보자.
import urllib.request, urllib.parse, urllib.error
fhand = urllib.request.urlopen('http://data.pr4e.org/romeo.txt')
for line in fhand:
print(line.decode().strip())
# +
fhand = urllib.request.urlopen('http://data.pr4e.org/romeo.txt')
counts = dict()
for line in fhand:
words = line.decode().split()
for word in words:
counts[word] = counts.get(word, 0) + 1
print(counts)
# -
fhand = urllib.request.urlopen('http://www.dr-chuck.com/page1.htm')
for line in fhand:
print(line.decode().strip())
|
web crawling/20180429.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.7 (''venv'': venv)'
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
weather = pd.read_csv("./data/weather.csv", index_col="DATE")
weather
weather['NAME'].value_counts()
weather_CDMX = weather[weather['NAME'] == 'MEXICO CITY, MX'].copy()
weather_CDMX
weather_Tuxtla = weather[weather['NAME'] == 'TUXTLA GUTIERREZ DGE, MX']
sns.displot(
data = weather_Tuxtla.isna().melt(value_name="Missing"),
y = "variable",
hue="Missing",
multiple = "fill",
aspect=1.25
)
plt.ylabel("")
plt.xlabel("")
plt.title("Missing values")
core_weather = weather_Tuxtla[["PRCP", "TMAX", "TMIN"]].copy()
core_weather.columns = ["precip", "temp_max", "temp_min"]
core_weather.apply(pd.isnull).sum()/core_weather.shape[0]
core_weather.apply(pd.isnull).sum()
core_weather["precip"].value_counts() / core_weather.shape[0]
np.mean(core_weather['precip'])
core_weather['precip'].plot()
core_weather['precip'] = core_weather['precip'].fillna(value=np.mean(core_weather['precip']))
core_weather.apply(pd.isnull).sum()/core_weather.shape[0]
core_weather = core_weather.fillna(method="ffill")
sns.displot(
data = core_weather.isna().melt(value_name="Missing"),
y = "variable",
hue="Missing",
multiple = "fill",
aspect=1.25
)
plt.ylabel("")
plt.xlabel("")
plt.title("Missing values")
core_weather.dtypes
core_weather.index
core_weather.index = pd.to_datetime(core_weather.index)
core_weather[["temp_max", "temp_min"]].plot()
core_weather.index.year.value_counts().sort_index()
core_weather.groupby(core_weather.index.year).apply(lambda x: x["precip"].sum()).plot()
core_weather["target"] = core_weather.shift(-1)["temp_max"]
core_weather
core_weather = core_weather.iloc[:-1,:].copy()
core_weather
# +
from sklearn.linear_model import Ridge
reg = Ridge(alpha=.1)
# -
predictors = ["precip", "temp_max", "temp_min"]
train = core_weather.loc[:"2009-12-31"]
test = core_weather.loc["2010-01-01":]
train
test
reg.fit(train[predictors], train["target"])
predictions = reg.predict(test[predictors])
from sklearn.metrics import mean_squared_error
mean_squared_error(test["target"], predictions)
combined = pd.concat([test["target"], pd.Series(predictions, index=test.index)], axis=1)
combined.columns = ["actual", "predictions"]
combined
|
Weather_Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Write an informative test failure message
# The test result reports become a lot easier to read when you make good use of the optional message argument of the assert statement.
#
# In a previous exercise, you wrote a test for the convert_to_int() function. The function takes an integer valued string with commas as thousand separators e.g. "2,081" as argument and should return the integer 2081.
#
# In this exercise, you will rewrite the test called test_on_string_with_one_comma() so that it prints an informative message if the test fails.
# +
import pytest
from preprocessing_helpers import convert_to_int
def test_on_string_with_one_comma():
test_argument = "2,081"
expected = 2081
actual = convert_to_int(test_argument)
# Format the string with the actual return value
message = "convert_to_int('2,081') should return the int 2081, but it actually returned {0}".format(actual)
# +
import pytest
from preprocessing_helpers import convert_to_int
def test_on_string_with_one_comma():
test_argument = "2,081"
expected = 2081
actual = convert_to_int(test_argument)
# Format the string with the actual return value
message = "convert_to_int('2,081') should return the int 2081, but it actually returned {0}".format(actual)
# Write the assert statement which prints message on failure
assert (actual == expected), message
# -
# # Testing float return values
# The get_data_as_numpy_array() function (which was called mystery_function() in one of the previous exercises) takes two arguments: the path to a clean data file and the number of data columns in the file . An example file has been printed out in the IPython console. It contains three rows.
#
# The function converts the data into a 3x2 NumPy array with dtype=float64. The expected return value has been stored in a variable called expected. Print it out to see it.
#
# The housing areas are in the first column and the housing prices are in the second column. This array will be the features that will be fed to the linear regression model for learning.
#
# The return value contains floats. Therefore you have to be especially careful when writing unit tests for this function.
# +
import numpy as np
import pytest
from as_numpy import get_data_as_numpy_array
def test_on_clean_file():
expected = np.array([[2081.0, 314942.0],
[1059.0, 186606.0],
[1148.0, 206186.0]
]
)
actual = get_data_as_numpy_array("example_clean_data.txt", num_columns=2)
message = "Expected return value: {0}, Actual return value: {1}".format(expected, actual)
# Complete the assert statement
assert actual == pytest.approx(expected), message
# -
# # Testing with multiple assert statements
# You're now going to test the function split_into_training_and_testing_sets() from the models module.
#
# It takes a n x 2 NumPy array containing housing area and prices as argument. To see an example argument, print the variable example_argument in the IPython console.
#
# The function returns a 2-tuple of NumPy arrays (training_set, testing_set). The training set contains int(0.75 * n) (approx. 75%) randomly selected rows of the argument array. The testing set contains the remaining rows.
#
# Print the variable expected_return_value in the IPython console. example_argument had 6 rows. Therefore the training array has int(0.75 * 6) = 4 of its rows and the testing array has the remaining 2 rows.
#
# numpy as np, pytest and split_into_training_and_testing_sets have been imported for you.
def test_on_six_rows():
example_argument = np.array([[2081.0, 314942.0], [1059.0, 186606.0],
[1148.0, 206186.0], [1506.0, 248419.0],
[1210.0, 214114.0], [1697.0, 277794.0]]
)
# Fill in with training array's expected number of rows
expected_training_array_num_rows = 4
def test_on_six_rows():
example_argument = np.array([[2081.0, 314942.0], [1059.0, 186606.0],
[1148.0, 206186.0], [1506.0, 248419.0],
[1210.0, 214114.0], [1697.0, 277794.0]]
)
# Fill in with training array's expected number of rows
expected_training_array_num_rows = 4
# Fill in with testing array's expected number of rows
expected_testing_array_num_rows = 2
def test_on_six_rows():
example_argument = np.array([[2081.0, 314942.0], [1059.0, 186606.0],
[1148.0, 206186.0], [1506.0, 248419.0],
[1210.0, 214114.0], [1697.0, 277794.0]]
)
# Fill in with training array's expected number of rows
expected_training_array_num_rows = 4
# Fill in with testing array's expected number of rows
expected_testing_array_num_rows = 2
actual = split_into_training_and_testing_sets(example_argument)
# Write the assert statement checking training array's number of rows
assert actual[0].shape[0] == expected_training_array_num_rows, "The actual number of rows in the training array is not {}".format(expected_training_array_num_rows)
def test_on_six_rows():
example_argument = np.array([[2081.0, 314942.0], [1059.0, 186606.0],
[1148.0, 206186.0], [1506.0, 248419.0],
[1210.0, 214114.0], [1697.0, 277794.0]]
)
# Fill in with training array's expected number of rows
expected_training_array_num_rows = 4
# Fill in with testing array's expected number of rows
expected_testing_array_num_rows = 2
actual = split_into_training_and_testing_sets(example_argument)
# Write the assert statement checking training array's number of rows
assert actual[0].shape[0] == expected_training_array_num_rows, "The actual number of rows in the training array is not {}".format(expected_training_array_num_rows)
# Write the assert statement checking testing array's number of rows
assert actual[0].shape[1] == expected_testing_array_num_rows, "The actual number of rows in the testing array is not {}".format(expected_testing_array_num_rows)
# # Practice the context manager
# In pytest, you can test whether a function raises an exception by using a context manager. Let's practice your understanding of this important context manager, the with statement and the as clause.
#
# At any step, feel free to run the code by pressing the "Run Code" button and check if the output matches your expectations.
# +
import pytest
# Fill in with a context manager that will silence the ValueError
with pytest.raises(ValueError):
raise ValueError
# +
import pytest
try:
# Fill in with a context manager that raises Failed if no OSError is raised
with pytest.raises(OSError):
raise ValueError
except:
print("pytest raised an exception because no OSError was raised in the context.")
# +
import pytest
# Store the raised ValueError in the variable exc_info
with pytest.raises(ValueError) as exc_info:
raise ValueError("Silence me!")
# +
import pytest
with pytest.raises(ValueError) as exc_info:
raise ValueError("Silence me!")
# Check if the raised ValueError contains the correct message
assert exc_info.match("Silence me!")
# -
# # Unit test a ValueError
# Sometimes, you want a function to raise an exception when called on bad arguments. This prevents the function from returning nonsense results or hard-to-interpret exceptions. This is an important behavior which should be unit tested.
#
# Remember the function split_into_training_and_testing_sets()? It takes a NumPy array containing housing area and prices as argument. The function randomly splits the array row wise into training and testing arrays in the ratio 3:1, and returns the resulting arrays in a tuple.
#
# If the argument array has only 1 row, the testing array will be empty. To avoid this situation, you want the function to not return anything, but raise a ValueError with the message
#
# "Argument data_array must have at least 2 rows, it actually has just 1".
# +
import numpy as np
import pytest
from train import split_into_training_and_testing_sets
def test_on_one_row():
test_argument = np.array([[1382.0, 390167.0]])
# Fill in with a context manager for checking ValueError
with pytest.raises(ValueError):
split_into_training_and_testing_sets(test_argument)
# +
import numpy as np
import pytest
from train import split_into_training_and_testing_sets
def test_on_one_row():
test_argument = np.array([[1382.0, 390167.0]])
# Store information about raised ValueError in exc_info
with pytest.raises(ValueError) as exc_info:
split_into_training_and_testing_sets(test_argument)
# -
# # Testing well: Boundary values
# Remember row_to_list()? It takes a row containing housing area and prices e.g. ```"2,041\t123,781\n"``` and returns the data as a list e.g. ```["2,041", "123,781"]```.
#
# A row can be mapped to a 2-tuple (m, n), where m is the number of tab separators. n is 1 if the row has any missing values, and 0 otherwise.
#
# For example,
#
# - "123\t456\n" (1, 0).
# - "\t456\n" (1, 1).
# - "\t456\t\n" (2, 1).
#
# The function only returns a list for arguments mapping to (1, 0). All other tuples correspond to invalid rows, with either more than one tab or missing values. The function returns None in all these cases. See the plot.
#
# This mapping shows that the function has normal behavior at (1, 0), and special behavior everywhere else.
# +
import pytest
from preprocessing_helpers import row_to_list
def test_on_no_tab_no_missing_value(): # (0, 0) boundary value
# Assign actual to the return value for the argument "123\n"
actual = row_to_list("123\n")
assert actual is None, "Expected: None, Actual: {0}".format(actual)
# +
import pytest
from preprocessing_helpers import row_to_list
def test_on_no_tab_no_missing_value(): # (0, 0) boundary value
# Assign actual to the return value for the argument "123\n"
actual = row_to_list("123\n")
assert actual is None, "Expected: None, Actual: {0}".format(actual)
def test_on_two_tabs_no_missing_value(): # (2, 0) boundary value
actual = row_to_list("123\t4,567\t89\n")
# Complete the assert statement
assert actual is None, "Expected: None, Actual: {0}".format(actual)
# +
import pytest
from preprocessing_helpers import row_to_list
def test_on_no_tab_no_missing_value(): # (0, 0) boundary value
# Assign actual to the return value for the argument "123\n"
actual = row_to_list("123\n")
assert actual is None, "Expected: None, Actual: {0}".format(actual)
def test_on_two_tabs_no_missing_value(): # (2, 0) boundary value
actual = row_to_list("123\t4,567\t89\n")
# Complete the assert statement
assert actual is None, "Expected: None, Actual: {0}".format(actual)
def test_on_one_tab_with_missing_value(): # (1, 1) boundary value
actual = row_to_list("\t4,567\n")
# Format the failure message
assert actual is None, "Expected: None, Actual: {0}".format(actual)
# -
# # Testing well: Values triggering special logic
# Look at the plot. The boundary values of row_to_list() are now marked in orange. The normal argument is marked in green and the values triggering special behavior are marked in blue.
#
# In the last exercise, you wrote tests for boundary values. In this exercise, you are going to write tests for values triggering special behavior, in particular, (0, 1) and (2, 1). These are values triggering special logic since the function returns None instead of a list.
# +
import pytest
from preprocessing_helpers import row_to_list
def test_on_no_tab_with_missing_value(): # (0, 1) case
# Assign to the actual return value for the argument "\n"
actual = row_to_list("\n")
# Write the assert statement with a failure message
assert actual is None, "Expected: None, Actual: {0}".format(actual)
def test_on_two_tabs_with_missing_value(): # (2, 1) case
# Assign to the actual return value for the argument "123\t\t89\n"
actual = row_to_list("123\t\t89\n")
# Write the assert statement with a failure message
assert actual is None, "Expected: None, Actual: {0}".format(actual)
# -
# # Testing well: Normal arguments
# This time, you will test row_to_list() with normal arguments i.e. arguments mapping to the tuple (1, 0). The plot is provided to you for reference.
#
# Remembering that the best practice is to test for two to three normal arguments, you will write two tests in this exercise.
# +
import pytest
from preprocessing_helpers import row_to_list
def test_on_normal_argument_1():
actual = row_to_list("123\t4,567\n")
# Fill in with the expected return value for the argument "123\t4,567\n"
expected = row_to_list("123\t4,567\n")
assert actual == expected, "Expected: {0}, Actual: {1}".format(expected, actual)
# +
import pytest
from preprocessing_helpers import row_to_list
def test_on_normal_argument_1():
actual = row_to_list("123\t4,567\n")
# Fill in with the expected return value for the argument "123\t4,567\n"
expected = ["123", "4,567"]
assert actual == expected, "Expected: {0}, Actual: {1}".format(expected, actual)
def test_on_normal_argument_2():
actual = row_to_list("1,059\t186,606\n")
expected = ["1,059", "186,606"]
# Write the assert statement along with a failure message
assert actual == expected, "Expected: {0}, Actual: {1}".format(actual, expected)
# -
# # TDD: Tests for normal arguments
# In this and the following exercises, you will implement the function convert_to_int() using Test Driven Development (TDD). In TDD, you write the tests first and implement the function later.
#
# Normal arguments for convert_to_int() are integer strings with comma as thousand separators. Since the best practice is to test a function for two to three normal arguments, here are three examples with no comma, one comma and two commas respectively.
#
# |Argument value |Expected return value|
# |---------------|---------------------|
# |"756" |756|
# |"2,081" |2081|
# |"1,034,891" |1034891|
# Since the convert_to_int() function does not exist yet, you won't be able to import it. But you will use it in the tests anyway. That's how TDD works.
#
# pytest has already been imported for you.
# +
def test_with_no_comma():
actual = convert_to_int("756")
# Complete the assert statement
assert actual == 756, "Expected: 756, Actual: {0}".format(actual)
def test_with_one_comma():
actual = convert_to_int("2,081")
# Complete the assert statement
assert actual == 2081, "Expected: 2081, Actual: {0}".format(actual)
def test_with_two_commas():
actual = convert_to_int("1,034,891")
# Complete the assert statement
assert actual == 1034891, "Expected: 1034891, Actual: {0}".format(actual)
# -
# # TDD: Requirement collection
# What should convert_to_int() do if the arguments are not normal? In particular, there are three special argument types:
#
# 1. Arguments that are missing a comma e.g. "178100,301".
# 2. Arguments that have the comma in the wrong place e.g. "12,72,891".
# 3. Float valued strings e.g. "23,816.92".
#
# Also, should convert_to_int() raise an exception for specific argument values?
#
# When your boss asked you to implement the function, she didn't say anything about these cases! But since you want to write tests for special and bad arguments as a part of TDD, you go and ask your boss.
#
# She says that convert_to_int() should return None for every special argument and there are no bad arguments for this function.
#
# pytest has been imported for you.
# +
# Give a name to the test for an argument with missing comma
def test_on_string_with_missing_comma():
actual = convert_to_int("178100,301")
assert actual is None, "Expected: None, Actual: {0}".format(actual)
def test_on_string_with_incorrectly_placed_comma():
# Assign to the actual return value for the argument "12,72,891"
actual = convert_to_int("12,72,891")
assert actual is None, "Expected: None, Actual: {0}".format(actual)
def test_on_float_valued_string():
actual = convert_to_int("23,816.92")
# Complete the assert statement
assert actual is None, "Expected: None, Actual: {0}".format(actual)
# -
# # TDD: Implement the function
# convert_to_int() returns None for the following:
#
# 1. Arguments with missing thousands comma e.g. ```"178100,301"```. If you split the string at the comma using ```"178100,301".split(",")```, then the resulting list ```["178100", "301"]``` will have at least one entry with length greater than 3 e.g. "178100".
#
# 2. Arguments with incorrectly placed comma e.g. "12,72,891". If you split this at the comma, then the resulting list is ```["12", "72", "891"]```. Note that the first entry is allowed to have any length between 1 and 3. But if any other entry has a length other than 3, like "72", then there's an incorrectly placed comma.
#
# 3. Float valued strings e.g. ```"23,816.92"```. If you remove the commas and call int() on this string i.e. ```int("23816.92")```, you will get a ValueError.
def convert_to_int(integer_string_with_commas):
comma_separated_parts = integer_string_with_commas.split(",")
for i in range(len(comma_separated_parts)):
# Write an if statement for checking missing commas
if len(comma_separated_parts[i]) > 3:
return None
def convert_to_int(integer_string_with_commas):
comma_separated_parts = integer_string_with_commas.split(",")
for i in range(len(comma_separated_parts)):
# Write an if statement for checking missing commas
if len(comma_separated_parts[i]) > 3:
return None
# Write the if statement for incorrectly placed commas
if i != 0 and len(comma_separated_parts[i]) != 3:
return None
|
unit-testing-for-data-science-in-python/2. Intermediate unit testing/notebook_section_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.6.4
# language: julia
# name: julia-0.6
# ---
include("trajViz.jl")
trajViz(x0=0.0,
y0=0.0,
x_dest=2500.0,
y_dest=-400.0,
CASType=:correctedSector,
policyFile="LOWFI_mid3_maxdist_2km_nmac_150m_Discount_0.95_ActWeight_0.5_IfSample_false_PenAction_3.0_PenConflict_50.0_PenCloseness_500.0_PenNmac_7000.0_Sigma_v_5.0_alert_5.0_theta_3.0_phi_7.0_coc_3.0_2018-11-13T18\:55\:43.491",
intTrajFile="intTraj.csv",
figName="")
trajViz(x0=0.0,
y0=0.0,
x_dest=2500.0,
y_dest=-400.0,
CASType=:correctedClosest,
policyFile="LOWFI_mid3_maxdist_2km_nmac_150m_Discount_0.95_ActWeight_0.5_IfSample_false_PenAction_3.0_PenConflict_50.0_PenCloseness_500.0_PenNmac_7000.0_Sigma_v_5.0_alert_5.0_theta_3.0_phi_7.0_coc_3.0_2018-11-13T18\:55\:43.491",
intTrajFile="intTraj.csv",
figName="")
trajViz(x0=0.0,
y0=0.0,
x_dest=2500.0,
y_dest=-400.0,
CASType=:VICASMulti,
policyFile="LOWFI_mid3_maxdist_2km_nmac_150m_Discount_0.95_ActWeight_0.5_IfSample_false_PenAction_3.0_PenConflict_50.0_PenCloseness_500.0_PenNmac_7000.0_Sigma_v_5.0_alert_5.0_theta_3.0_phi_7.0_coc_3.0_2018-11-13T18\:55\:43.491",
intTrajFile="intTraj.csv",
figName="")
trajViz(x0=0.0,
y0=0.0,
x_dest=2500.0,
y_dest=-400.0,
CASType=:VICASClosest,
policyFile="LOWFI_mid3_maxdist_2km_nmac_150m_Discount_0.95_ActWeight_0.5_IfSample_false_PenAction_3.0_PenConflict_50.0_PenCloseness_500.0_PenNmac_7000.0_Sigma_v_5.0_alert_5.0_theta_3.0_phi_7.0_coc_3.0_2018-11-13T18\:55\:43.491",
intTrajFile="intTraj.csv",
figName="")
trajViz(x0=0.0,
y0=0.0,
x_dest=2500.0,
y_dest=-400.0,
CASType=:NOCAS,
policyFile="LOWFI_mid3_maxdist_2km_nmac_150m_Discount_0.95_ActWeight_0.5_IfSample_false_PenAction_3.0_PenConflict_50.0_PenCloseness_500.0_PenNmac_7000.0_Sigma_v_5.0_alert_5.0_theta_3.0_phi_7.0_coc_3.0_2018-11-13T18\:55\:43.491",
intTrajFile="intTraj.csv",
figName="")
|
Evaluation/TrajectoryViz/Non-Interactive Trajectory Visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Best Coding Practices in Jupyterlab
# * El código se ejecuta secuencialmente
# * Guarda resultados para no tener que volver a calcularlos
# * El código debería ser legible
# * Crea celdas pequeñas, funciones
# * El código debe ser reusable
# * No copy/paste, importar código
# * Mantén el código ordenado
# * Documentar
# * versiones mínimas
# * usar entornos virtuales
# * Reproducible
# * Docker, Binder...
|
EuroSciPy-2019/4 - Wednesday/Best Coding Practices in Jupyterlab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="oRgpqL0KVO43"
# # CIS6930 Week 2: Autoencoders
#
# ---
#
# Preparation: Go to `Runtime > Change runtime type` and choose `GPU` for the hardware accelerator.
#
#
# + [markdown] id="WNf7qUvYDCeD"
#
# + [markdown] id="b1dpc5PwIghS"
# ## A magic command to check your assigned GPU
# + id="uayE3ioc3k_h"
# gpu_info = !nvidia-smi -L
gpu_info = "\n".join(gpu_info)
if gpu_info.find("failed") >= 0:
print("Not connected to a GPU")
else:
print(gpu_info)
# + [markdown] id="_Jpe1bw6ImPn"
# ## Libraries
# + id="a7h-6LpjVDHW"
import copy
import random
from time import time
from typing import Any, Dict
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim
from torch.utils.data import Dataset, TensorDataset, DataLoader
# + [markdown] id="RZLilYXAI7Cr"
# ## MNIST dataset from Torchvision
# + id="T9sBXgBsV6dI"
import torchvision
train_dataset = torchvision.datasets.MNIST("./data", train=True, download=True,
transform=torchvision.transforms.Compose(
[torchvision.transforms.ToTensor(),
# For standardization: 0.1307 (mean), 0.3081 (var)
torchvision.transforms.Normalize((0.1307,), (0.3081,))]))
train_dataset, valid_dataset = torch.utils.data.random_split(train_dataset, [50000, 10000],
generator=torch.Generator().manual_seed(5))
test_dataset = torchvision.datasets.MNIST("/data", train=False, download=True,
transform=torchvision.transforms.Compose(
[torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.1307,), (0.3081,))]))
# + id="mcnUXJ-uWC5f"
from matplotlib import pyplot as plt
plt.imshow(train_dataset[0][0].squeeze(0), cmap="gray", interpolation="none")
# + id="-stPdW6xs-nl"
train_dataset[0][0].view(-1).shape
# + [markdown] id="2-_kIWnkdbxO"
# ## Training framework
#
# It must have been cumbersome to copy and paste the training code to run experiments with different configurations.
#
# TBD in a little bit more organized manner.
#
# + id="Tjf9SlQi5DeA"
def train(model: nn.Module,
train_dataset: Dataset,
valid_dataset: Dataset,
config: Dict[str, Any],
random_seed: int = 0):
# Random Seeds ===============
torch.manual_seed(random_seed)
random.seed(random_seed)
np.random.seed(random_seed)
# Random Seeds ===============
# GPU configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
#device = torch.device("tpu" if torch.cuda.is_available() else "cpu")
dl_train = DataLoader(train_dataset,
batch_size=config["batch_size"])
dl_valid = DataLoader(valid_dataset)
# Model, Optimzier, Loss function
model = model.to(device)
# Optimizer
optimizer = config["optimizer_cls"](model.parameters(), lr=config["lr"])
loss_fn = nn.MSELoss()
# For each epoch
eval_list = []
t0 = time()
best_val = None
best_model = None
for n in range(config["n_epochs"]):
t1 = time()
print("Epoch {}".format(n))
# Training
train_loss = 0.
train_pred_list = []
train_true_list = []
model.train() # Switch to the training mode
# For each batch
for batch in dl_train:
optimizer.zero_grad() # Initialize gradient information
X, y = batch
X = X.view(X.size(0), -1).to(device) # (batch_size, 1, 28, 28) -> (batch_size, 768)
out = model(X) # Call `forward()` function of the model
loss = loss_fn(out, X) # Calculate loss
loss.backward() # Backpropagate the loss value
optimizer.step() # Update the parameters
train_loss += loss.data.item() * config["batch_size"]
train_loss /= (len(dl_train) * config["batch_size"])
print(" Training loss: {:.4f}".format(train_loss))
# Validation
valid_loss = 0.
valid_pred_list = []
valid_true_list = []
model.eval() # Switch to the evaluation mode
for i, batch in enumerate(dl_valid):
X, y = batch
X = X.view(X.size(0), -1).to(device) # (batch_size, 1, 28, 28) -> (batch_size, 768)
out = model(X)
loss = loss_fn(out, X.to(device))
valid_loss += loss.data.item()
valid_loss /= len(dl_valid)
print(" Validation loss: {:.4f}".format(valid_loss))
# Model selection
if best_val is None or valid_loss < best_val:
best_model = copy.deepcopy(model)
best_val = valid_loss
# Orig/generated image pair
x_pair = torch.cat([X[0].reshape(28, 28), torch.zeros(28, 1).to(device), model(X[0]).reshape(28, 28)], axis=1)
plt.imshow(x_pair.detach().cpu().numpy(),
cmap="gray", interpolation="none")
plt.show()
t2 = time()
print(" Elapsed time: {:.1f} [sec]".format(t2 - t1))
# Store train/validation loss values
eval_list.append([n, train_loss, valid_loss, t2 - t1])
eval_df = pd.DataFrame(eval_list, columns=["epoch", "train_loss", "valid_loss", "time"])
eval_df.set_index("epoch")
print("Total time: {:.1f} [sec]".format(t2 - t0))
# Return the best model and trainining/validation information
return {"model": best_model,
"best_val": best_val,
"eval_df": eval_df}
# + [markdown] id="xdMZBvboJIHm"
# # DO NOT EDIT THE CODE UNTIL HERE
# + [markdown] id="I0L_hTepIpvk"
# ## Models (In-class exercise)
# + [markdown] id="Bn5P7EweIwIo"
# ### Exercise 1: Autoencoder
# + id="Ld4cjWy80pj6"
## Complete the code ##
class AutoEncoder(nn.Module):
def __init__(self,
hidden_dim: int = 64):
super().__init__()
self.encoder = nn.Sequential(nn.Linear(784, hidden_dim),
nn.ReLU())
self.decoder = nn.Sequential(nn.Linear(hidden_dim, 784))
def encode(self, x):
return self.encoder(x)
def decode(self, x):
return self.decoder(x)
def forward(self, x):
out = self.encode(x)
out = self.decode(out)
return out
# + [markdown] id="zo-wbm7LI0Cx"
# ### Exercise 2: Denoising Autoencoder
# + id="lH-kSfXv7hN8"
## Complete the code ##
class DenoisingAutoEncoder(nn.Module):
def __init__(self,
hidden_dim: int = 64,
noise_factor: float = 0.01):
super().__init__()
#
#
#
def encode(self, x):
return self.encoder(x)
def decode(self, x):
return self.decoder(x)
def forward(self, x):
if self.training: # True if model.train(); False if model.eval()
# Add noise
# COMPLETE CODE (3-5 LINES)
# + id="YikkRUN27pX6"
class DenoisingAutoEncoder(nn.Module):
def __init__(self,
hidden_dim: int = 64,
noise_factor: float = 0.01):
super().__init__()
self.noise_factor = noise_factor
self.encoder = nn.Sequential(nn.Linear(28 * 28, hidden_dim),
nn.ReLU())
self.decoder = nn.Sequential(nn.Linear(hidden_dim, 28 * 28))
def encode(self, x):
return self.encoder(x)
def decode(self, x):
return self.decoder(x)
def forward(self, x):
if self.training: # True if model.train(); False if model.eval()
# Add random noise for training
x += torch.randn_like(x) * self.noise_factor
embedding = self.encoder(x)
out = self.decoder(embedding)
return out
# + id="KeCY3o1f8Clk"
# torch.randn_like(torch.Tensor([1,2,3]))
# + [markdown] id="63J0pvJEJgwk"
# ## Experiment: Original Image Reconstruction
#
#
# + id="75vip-Mb6pds"
# Change the learning rate and run the same experiment
config = {"optimizer_cls": optim.Adam,
"lr": 0.0001, # lr = {0.01, 0.001, 0.0001}
"batch_size": 16,
"n_epochs": 5}
model = AutoEncoder()
output = train(model, train_dataset, valid_dataset, config)
# + [markdown] id="Tece4BZBOiN4"
# ### Generating images
#
# After training, you can generate images from latent vectors
# + id="-EcgQRylOk1v"
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
plt.imshow(test_dataset[0][0].squeeze(0),
cmap="gray",
interpolation="none")
plt.show()
# Use the first data
X, y = test_dataset[0]
z = model.encode(X.view(-1).to(device))
out0 = model.decode(z)
out1 = model.decode(z + (torch.randn_like(z) * 0.1)) # Add small noise
out2 = model.decode(z + (torch.randn_like(z) * 0.5)) # Add medium noise
out3 = model.decode(z + (torch.randn_like(z) * 1.0)) # Add large noise
plt.imshow(out0.view(28, 28).detach().cpu(),
cmap="gray",
interpolation="none")
plt.show()
plt.imshow(out1.view(28, 28).detach().cpu(),
cmap="gray",
interpolation="none")
plt.show()
plt.imshow(out2.view(28, 28).detach().cpu(),
cmap="gray",
interpolation="none")
plt.show()
plt.imshow(out3.view(28, 28).detach().cpu(),
cmap="gray",
interpolation="none")
plt.show()
# + id="WbiXkpCdaugc"
# Generating images from random noise
for i in range(6):
plt.imshow(
model(torch.randn_like(X.view(-1)).to(device)).detach().cpu().view(28, 28),
cmap="gray",
interpolation="none")
plt.show()
|
notebooks/cis6930_week2_autoencoders.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Improving Word2vec Algorithms
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
# %matplotlib inline
##from __future__ import print_function
import collections
import math
import numpy as np
import os
import random
import tensorflow as tf
import bz2
from matplotlib import pylab
from six.moves import range
from six.moves.urllib.request import urlretrieve
from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
import nltk # standard preprocessing
##import operator # sorting items in dictionary by value
#nltk.download() #tokenizers/punkt/PY3/english.pickle
from math import ceil
import csv
# ## Dataset
# This code downloads a [dataset](http://www.evanjones.ca/software/wikipedia2text.html) consisting of several Wikipedia articles totaling up to roughly 61 megabytes. Additionally the code makes sure the file has the correct size after downloading it.
# +
url = 'http://www.evanjones.ca/software/'
def maybe_download(filename, expected_bytes):
"""Download a file if not present, and make sure it's the right size."""
if not os.path.exists(filename):
filename, _ = urlretrieve(url + filename, filename)
statinfo = os.stat(filename)
if statinfo.st_size == expected_bytes:
print('Found and verified %s' % filename)
else:
print(statinfo.st_size)
raise Exception(
'Failed to verify ' + filename + '. Can you get to it with a browser?')
return filename
filename = maybe_download('wikipedia2text-extracted.txt.bz2', 18377035)
# -
# ## Read Data with Preprocessing with NLTK
# Reads data as it is to a string, convert to lower-case and tokenize it using the nltk library. This code reads data in 1MB portions as processing the full text at once slows down the task and returns a list of words.
# +
def read_data(filename):
"""
Extract the first file enclosed in a zip file as a list of words
and pre-processes it using the nltk python library
"""
with bz2.BZ2File(filename) as f:
data = []
file_size = os.stat(filename).st_size
chunk_size = 1024 * 1024 # reading 1 MB at a time as the dataset is moderately large
print('Reading data...')
for i in range(ceil(file_size//chunk_size)+1):
bytes_to_read = min(chunk_size,file_size-(i*chunk_size))
file_string = f.read(bytes_to_read).decode('utf-8')
file_string = file_string.lower()
# tokenizes a string to words residing in a list
file_string = nltk.word_tokenize(file_string)
data.extend(file_string)
return data
words = read_data(filename)
print('Data size %d' % len(words))
token_count = len(words)
print('Example words (start): ',words[:10])
print('Example words (end): ',words[-10:])
# -
# ## Building the Dictionaries
# Builds the following. To understand each of these elements, let us also assume the text "I like to go to school"
#
# * `dictionary`: maps a string word to an ID (e.g. {I:0, like:1, to:2, go:3, school:4})
# * `reverse_dictionary`: maps an ID to a string word (e.g. {0:I, 1:like, 2:to, 3:go, 4:school}
# * `count`: List of list of (word, frequency) elements (e.g. [(I,1),(like,1),(to,2),(go,1),(school,1)]
# * `data` : Contain the string of text we read, where string words are replaced with word IDs (e.g. [0, 1, 2, 3, 2, 4])
#
# It also introduces an additional special token `UNK` to denote rare words to are too rare to make use of.
# +
# we restrict our vocabulary size to 50000
vocabulary_size = 50000
def build_dataset(words):
count = [['UNK', -1]]
# Gets only the vocabulary_size most common words as the vocabulary
# All the other words will be replaced with UNK token
count.extend(collections.Counter(words).most_common(vocabulary_size - 1))
dictionary = dict()
# Create an ID for each word by giving the current length of the dictionary
# And adding that item to the dictionary
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
# Traverse through all the text we have and produce a list
# where each element corresponds to the ID of the word found at that index
for word in words:
# If word is in the dictionary use the word ID,
# else use the ID of the special token "UNK"
if word in dictionary:
index = dictionary[word]
else:
index = 0 # dictionary['UNK']
unk_count = unk_count + 1
data.append(index)
# update the count variable with the number of UNK occurences
count[0][1] = unk_count
reverse_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
# Make sure the dictionary is of size of the vocabulary
assert len(dictionary) == vocabulary_size
return data, count, dictionary, reverse_dictionary
data, count, dictionary, reverse_dictionary = build_dataset(words)
print('Most common words (+UNK)', count[:5])
print('Sample data', data[:10])
del words # Hint to reduce memory.
# -
# ## Generating Batches of Data for Skip-Gram
# Generates a batch or target words (`batch`) and a batch of corresponding context words (`labels`). It reads `2*window_size+1` words at a time (called a `span`) and create `2*window_size` datapoints in a single span. The function continue in this manner until `batch_size` datapoints are created. Everytime we reach the end of the word sequence, we start from beginning.
# +
data_index = 0
def generate_batch_skip_gram(batch_size, window_size):
# data_index is updated by 1 everytime we read a data point
global data_index
# two numpy arras to hold target words (batch)
# and context words (labels)
batch = np.ndarray(shape=(batch_size), dtype=np.int32)
labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
# span defines the total window size, where
# data we consider at an instance looks as follows.
# [ skip_window target skip_window ]
span = 2 * window_size + 1
# The buffer holds the data contained within the span
buffer = collections.deque(maxlen=span)
# Fill the buffer and update the data_index
for _ in range(span):
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
# This is the number of context words we sample for a single target word
num_samples = 2*window_size
# We break the batch reading into two for loops
# The inner for loop fills in the batch and labels with
# num_samples data points using data contained withing the span
# The outper for loop repeat this for batch_size//num_samples times
# to produce a full batch
for i in range(batch_size // num_samples):
k=0
# avoid the target word itself as a prediction
# fill in batch and label numpy arrays
for j in list(range(window_size))+list(range(window_size+1,2*window_size+1)):
batch[i * num_samples + k] = buffer[window_size]
labels[i * num_samples + k, 0] = buffer[j]
k += 1
# Everytime we read num_samples data points,
# we have created the maximum number of datapoints possible
# withing a single span, so we need to move the span by 1
# to create a fresh new span
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
return batch, labels
print('data:', [reverse_dictionary[di] for di in data[:8]])
for window_size in [1, 2]:
data_index = 0
batch, labels = generate_batch_skip_gram(batch_size=8, window_size=window_size)
print('\nwith window_size = %d:' % window_size)
print(' batch:', [reverse_dictionary[bi] for bi in batch])
print(' labels:', [reverse_dictionary[li] for li in labels.reshape(8)])
# -
# ## Original Skip-Gram Algorithm
# The original skip-gram algorithm did not have a hidden layer but calculated the loss from the embeddings themselves. Therefore, skip-gram algorithm had two different embedding layers one for inputs and one for outputs.
# ### Defining Hyperparameters
#
# Here we define several hyperparameters including `batch_size` (amount of samples in a single batch) `embedding_size` (size of embedding vectors) `window_size` (context window size).
# +
batch_size = 128 # Data points in a single batch
embedding_size = 128 # Dimension of the embedding vector.
window_size = 4 # How many words to consider left and right.
# We pick a random validation set to sample nearest neighbors
valid_size = 16 # Random set of words to evaluate similarity on.
# We sample valid datapoints randomly from a large window without always being deterministic
valid_window = 50
# When selecting valid examples, we select some of the most frequent words as well as
# some moderately rare words as well
valid_examples = np.array(random.sample(range(valid_window), valid_size))
valid_examples = np.append(valid_examples,random.sample(range(1000, 1000+valid_window), valid_size),axis=0)
num_sampled = 32 # Number of negative examples to sample.
# -
# ### Defining Inputs and Outputs
#
# Here we define placeholders for feeding in training inputs and outputs (each of size `batch_size`) and a constant tensor to contain validation examples.
# +
tf.reset_default_graph()
# Training input data (target word IDs).
train_dataset = tf.placeholder(tf.int32, shape=[batch_size])
# Training input label data (context word IDs)
train_labels = tf.placeholder(tf.int64, shape=[batch_size, 1])
# Validation input data, we don't need a placeholder
# as we have already defined the IDs of the words selected
# as validation data
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
# -
# ### Defining Model Parameters and Other Variables
# We now define two TensorFlow variables as embedding layers(`in_embeddings` and `out_embeddings`). Note that we do not have any neural network parameters (`softmax_weights` and `softmax_biases`) as we had in the skip-gram algorithm code.
# +
# Variables
# Embedding layers, contains the word embeddings
# We define two embedding layers
# in_embeddings is used to lookup embeddings corresponding to target words (inputs)
in_embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)
)
# out_embeddings is used to lookup embeddings corresponding to contect words (labels)
out_embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)
)
# -
# ### Defining the Model Computations
#
# Here we define several TensorFlow opeartions required for computing loss and predictions. We first defing an opeartion to fetch negative samples for a given batch of data. Next we define embedding lookup functions for both true (`in_embed` and `out_embed`) and negative (`negative_embed`) data where these opeartions fetch the corresponding embedding vectors for a set of given inputs. With that, we define negative sampling loss manually using the embeddings returned by the lookups.
# +
# 1. Compute negative sampels for a given batch of data
# Returns a [num_sampled] size Tensor
negative_samples, _, _ = tf.nn.log_uniform_candidate_sampler(train_labels, num_true=1, num_sampled=num_sampled,
unique=True, range_max=vocabulary_size)
# 2. Look up embeddings for inputs, outputs and negative samples.
in_embed = tf.nn.embedding_lookup(in_embeddings, train_dataset)
out_embed = tf.nn.embedding_lookup(out_embeddings, tf.reshape(train_labels,[-1]))
negative_embed = tf.nn.embedding_lookup(out_embeddings, negative_samples)
# 3. Manually defining negative sample loss
# As Tensorflow have a limited amount of flexibility in the built-in sampled_softmax_loss function,
# we have to manually define the loss fuction.
# 3.1. Computing the loss for the positive sample
# Exactly we compute log(sigma(v_o * v_i^T)) with this equation
loss = tf.reduce_mean(
tf.log(
tf.nn.sigmoid(
tf.reduce_sum(
tf.diag([1.0 for _ in range(batch_size)])*
tf.matmul(out_embed,tf.transpose(in_embed)),
axis=0)
)
)
)
# 3.2. Computing loss for the negative samples
# We compute sum(log(sigma(-v_no * v_i^T))) with the following
# Note: The exact way this part is computed in TensorFlow library appears to be
# by taking only the weights corresponding to true samples and negative samples
# and then computing the softmax_cross_entropy_with_logits for that subset of weights.
# More infor at: https://github.com/tensorflow/tensorflow/blob/r1.8/tensorflow/python/ops/nn_impl.py
# Though the approach is different, the idea remains the same
loss += tf.reduce_mean(
tf.reduce_sum(
tf.log(tf.nn.sigmoid(-tf.matmul(negative_embed,tf.transpose(in_embed)))),
axis=0
)
)
# The above is the log likelihood.
# We would like to transform this to the negative log likelihood
# to convert this to a loss. This provides us with
# L = - (log(sigma(v_o * v_i^T))+sum(log(sigma(-v_no * v_i^T))))
loss *= -1.0
# -
# ### Calculating Word Similarities
# We calculate the similarity between two given words in terms of the cosine distance. To do this efficiently we use matrix operations to do so, as shown below.
# Compute the similarity between minibatch examples and all embeddings.
# We use the cosine distance:
norm = tf.sqrt(tf.reduce_sum(tf.square((in_embeddings+out_embeddings)/2.0), 1, keepdims=True))
normalized_embeddings = out_embeddings / norm
valid_embeddings = tf.nn.embedding_lookup(
normalized_embeddings, valid_dataset)
similarity = tf.matmul(valid_embeddings, tf.transpose(normalized_embeddings))
# ### Model Parameter Optimizer
#
# We then define a constant learning rate and an optimizer which uses the Adagrad method. Feel free to experiment with other optimizers listed [here](https://www.tensorflow.org/api_guides/python/train).
# Optimizer.
optimizer = tf.train.AdagradOptimizer(1.0).minimize(loss)
# ## Running the Original Skip-gram Algorithm
#
# Here we run the original skip-gram algorithm we defined above. Specifically, we first initialize variables, and then train the algorithm for many steps (`num_steps`). And every few steps we evaluate the algorithm on a fixed validation set and print out the words that appear to be closest for a given set of words.
# +
num_steps = 100001
skip_gram_loss_original = [] # Collect the sequential loss values for plotting purposes
# ConfigProto is a way of providing various configuration settings
# required to execute the graph
with tf.Session(config=tf.ConfigProto(allow_soft_placement=True)) as session:
# Initialize the variables in the graph
tf.global_variables_initializer().run()
print('Initialized')
average_loss = 0
# Train the Word2vec model for num_step iterations
for step in range(num_steps):
# Generate a single batch of data
batch_data, batch_labels = generate_batch_skip_gram(
batch_size, window_size)
# Populate the feed_dict and run the optimizer (minimize loss)
# and compute the loss
feed_dict = {train_dataset : batch_data, train_labels : batch_labels}
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
# Update the average loss variable
average_loss += l
if (step+1) % 2000 == 0:
if step > 0:
average_loss = average_loss / 2000
# The average loss is an estimate of the loss over the last 2000 batches.
print('Average loss at step %d: %f' % (step+1, average_loss))
skip_gram_loss_original.append(average_loss)
average_loss = 0
# Here we compute the top_k closest words for a given validation word
# in terms of the cosine distance
# We do this for all the words in the validation set
# Note: This is an expensive step
if (step+1) % 10000 == 0:
sim = similarity.eval()
for i in range(valid_size):
valid_word = reverse_dictionary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log = 'Nearest to %s:' % valid_word
for k in range(top_k):
close_word = reverse_dictionary[nearest[k]]
log = '%s %s,' % (log, close_word)
print(log)
skip_gram_original_final_embeddings = normalized_embeddings.eval()
np.save('skip_original_embeddings',skip_gram_original_final_embeddings)
with open('skip_original_losses.csv', 'wt') as f:
writer = csv.writer(f, delimiter=',')
writer.writerow(skip_gram_loss_original)
# -
# ## Plotting Skip Gram Loss vs Original Skip Gram Loss
# Here we plot skip gram loss we got from chapter 3 with the original skip gram loss we just ran to see which one performs better.
# +
# Load the skip-gram losses from the calculations we did in Chapter 3
# So you need to make sure you have this csv file before running the code below
skip_loss_path = os.path.join('..','ch3','skip_losses.csv')
with open(skip_loss_path, 'rt') as f:
reader = csv.reader(f,delimiter=',')
for r_i,row in enumerate(reader):
if r_i == 0:
skip_gram_loss = [float(s) for s in row]
pylab.figure(figsize=(15,5)) # figure in inches
# Define the x axis
x = np.arange(len(skip_gram_loss))*2000
# Plot the skip_gram_loss (loaded from chapter 3)
pylab.plot(x, skip_gram_loss, label="Skip-Gram (Improved)",linestyle='--',linewidth=2)
# Plot the original skip gram loss from what we just ran
pylab.plot(x, skip_gram_loss_original, label="Skip-Gram (Original)",linewidth=2)
# Set some text around the plot
pylab.title('Original vs Improved Skip-Gram Loss Decrease Over Time',fontsize=24)
pylab.xlabel('Iterations',fontsize=22)
pylab.ylabel('Loss',fontsize=22)
pylab.legend(loc=1,fontsize=22)
# use for saving the figure if needed
pylab.savefig('loss_skipgram_original_vs_impr.jpg')
pylab.show()
# -
# ## Plotting Skip-Gram Loss vs CBOW Loss
#
# Here we compare the skip-gram loss and CBOW loss to compare which loss decreases quicker. Refer the text for an analysis of the results.
# +
# Load the skip-gram losses from the calculations we did in Chapter 3
# So you need to make sure you have this csv file before running the code below
cbow_loss_path = os.path.join('..','ch3','cbow_losses.csv')
with open(cbow_loss_path, 'rt') as f:
reader = csv.reader(f,delimiter=',')
for r_i,row in enumerate(reader):
if r_i == 0:
cbow_loss = [float(s) for s in row]
pylab.figure(figsize=(15,5)) # in inches
# Define the x axis
x = np.arange(len(skip_gram_loss))*2000
# Plot the skip_gram_loss (loaded from chapter 3)
pylab.plot(x, skip_gram_loss, label="Skip-Gram",linestyle='--',linewidth=2)
# Plot the cbow_loss (loaded from chapter 3)
pylab.plot(x, cbow_loss, label="CBOW",linewidth=2)
# Set some text around the plot
pylab.title('Skip-Gram vs CBOW Loss Decrease Over Time',fontsize=24)
pylab.xlabel('Iterations',fontsize=22)
pylab.ylabel('Loss',fontsize=22)
pylab.legend(loc=1,fontsize=22)
# use for saving the figure if needed
pylab.savefig('loss_skipgram_vs_cbow.png')
pylab.show()
# -
# ## Plotting TSNE Embeddings for Skip-Gram and CBOW Side by Side
#
# Loss itself is not an adequate measure of performance. Therefore we visualize the learned embeddings by projecting the embeddings to a two dimensional canvas with a technique known as t-SNE.
def find_clustered_embeddings(embeddings,distance_threshold,sample_threshold):
'''
Find only the closely clustered embeddings.
This gets rid of more sparsly distributed word embeddings and make the visualization clearer
This is useful for t-SNE visualization
distance_threshold: maximum distance between two points to qualify as neighbors
sample_threshold: number of neighbors required to be considered a cluster
'''
# calculate cosine similarity
cosine_sim = np.dot(embeddings,np.transpose(embeddings))
norm = np.dot(np.sum(embeddings**2,axis=1).reshape(-1,1),np.sum(np.transpose(embeddings)**2,axis=0).reshape(1,-1))
assert cosine_sim.shape == norm.shape
cosine_sim /= norm
# make all the diagonal entries zero otherwise this will be picked as highest
np.fill_diagonal(cosine_sim, -1.0)
argmax_cos_sim = np.argmax(cosine_sim, axis=1)
mod_cos_sim = cosine_sim
# find the maximums in a loop to count if there are more than n items above threshold
for _ in range(sample_threshold-1):
argmax_cos_sim = np.argmax(cosine_sim, axis=1)
mod_cos_sim[np.arange(mod_cos_sim.shape[0]),argmax_cos_sim] = -1
max_cosine_sim = np.max(mod_cos_sim,axis=1)
return np.where(max_cosine_sim>distance_threshold)[0]
# ### Fitting the skip-gram and CBOW embeddings to a t-SNE
# We fit skip-gram and CBOW embeddings to a t-SNE to get their mapping on a two dimensional surface. We only visualize densely clustered data points to avoid clutter in the visualization. This is achieved with the above function `find_clustered_embeddings`.
# +
# Load the previously saved embeddings from Chapter 3 exercise
skip_emb_path = os.path.join('..','ch3','skip_embeddings.npy')
cbow_emb_path = os.path.join('..','ch3','cbow_embeddings.npy')
skip_gram_final_embeddings = np.load(skip_emb_path)
cbow_final_embeddings = np.load(cbow_emb_path)
num_points = 1000 # we will use a large sample space to build the T-SNE manifold and then prune it using cosine similarity
# Create a t-SNE object from scikit-learn
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)
print('Fitting embeddings to T-SNE (skip-gram and CBOW)')
# Get the T-SNE manifold for skip-gram embeddings
print('\tSkip-gram')
sg_selected_embeddings = skip_gram_final_embeddings[:num_points, :]
sg_two_d_embeddings = tsne.fit_transform(sg_selected_embeddings)
# Get the T-SNE manifold for CBOW embeddings
print('\tCBOW')
cbow_selected_embeddings = cbow_final_embeddings[:num_points, :]
cbow_two_d_embeddings = tsne.fit_transform(cbow_selected_embeddings)
print('Pruning the T-SNE embeddings (skip-gram and CBOW)')
# Prune the embeddings by getting ones only more than n-many sample above the similarity threshold
# this unclutters the visualization
# Prune skip-gram
print('\tSkip-gram')
sg_selected_ids = find_clustered_embeddings(sg_selected_embeddings,.3,10)
sg_two_d_embeddings = sg_two_d_embeddings[sg_selected_ids,:]
# Prune CBOW
print('\tCBOW')
cbow_selected_ids = find_clustered_embeddings(cbow_selected_embeddings,.3,10)
cbow_two_d_embeddings = cbow_two_d_embeddings[cbow_selected_ids,:]
# Some stats about pruning
print('Out of ',num_points,' samples (skip-gram), ', sg_selected_ids.shape[0],' samples were selected by pruning')
print('Out of ',num_points,' samples (CBOW), ', cbow_selected_ids.shape[0],' samples were selected by pruning')
# -
# ### Plotting the Embeddings
# Here we plot the embeddings side by side, each embedding layer on its own subplot. We also use different colors for data points to improve clarity.
# +
def plot_embeddings_side_by_side(sg_embeddings, cbow_embeddings, sg_labels, cbow_labels):
''' Plots word embeddings of skip-gram and CBOW side by side as subplots
'''
# number of clusters for each word embedding
# clustering is used to assign different colors as a visual aid
n_clusters = 20
# automatically build a discrete set of colors, each for cluster
print('Define Label colors for %d',n_clusters)
label_colors = [pylab.cm.spectral(float(i) /n_clusters) for i in range(n_clusters)]
# Make sure number of embeddings and their labels are the same
assert sg_embeddings.shape[0] >= len(sg_labels), 'More labels than embeddings'
assert cbow_embeddings.shape[0] >= len(cbow_labels), 'More labels than embeddings'
print('Running K-Means for skip-gram')
# Define K-Means
sg_kmeans = KMeans(n_clusters=n_clusters, init='k-means++', random_state=0).fit(sg_embeddings)
sg_kmeans_labels = sg_kmeans.labels_
sg_cluster_centroids = sg_kmeans.cluster_centers_
print('Running K-Means for CBOW')
cbow_kmeans = KMeans(n_clusters=n_clusters, init='k-means++', random_state=0).fit(cbow_embeddings)
cbow_kmeans_labels = cbow_kmeans.labels_
cbow_cluster_centroids = cbow_kmeans.cluster_centers_
print('K-Means ran successfully')
print('Plotting results')
pylab.figure(figsize=(25,20)) # in inches
# Get the first subplot
pylab.subplot(1, 2, 1)
# Plot all the embeddings and their corresponding words for skip-gram
for i, (label,klabel) in enumerate(zip(sg_labels,sg_kmeans_labels)):
center = sg_cluster_centroids[klabel,:]
x, y = cbow_embeddings[i,:]
# This is just to spread the data points around a bit
# So that the labels are clearer
# We repel datapoints from the cluster centroid
if x < center[0]:
x += -abs(np.random.normal(scale=2.0))
else:
x += abs(np.random.normal(scale=2.0))
if y < center[1]:
y += -abs(np.random.normal(scale=2.0))
else:
y += abs(np.random.normal(scale=2.0))
pylab.scatter(x, y, c=label_colors[klabel])
x = x if np.random.random()<0.5 else x + 10
y = y if np.random.random()<0.5 else y - 10
pylab.annotate(label, xy=(x, y), xytext=(0, 0), textcoords='offset points',
ha='right', va='bottom',fontsize=16)
pylab.title('t-SNE for Skip-Gram',fontsize=24)
# Get the second subplot
pylab.subplot(1, 2, 2)
# Plot all the embeddings and their corresponding words for CBOW
for i, (label,klabel) in enumerate(zip(cbow_labels,cbow_kmeans_labels)):
center = cbow_cluster_centroids[klabel,:]
x, y = cbow_embeddings[i,:]
# This is just to spread the data points around a bit
# So that the labels are clearer
# We repel datapoints from the cluster centroid
if x < center[0]:
x += -abs(np.random.normal(scale=2.0))
else:
x += abs(np.random.normal(scale=2.0))
if y < center[1]:
y += -abs(np.random.normal(scale=2.0))
else:
y += abs(np.random.normal(scale=2.0))
pylab.scatter(x, y, c=label_colors[klabel])
x = x if np.random.random()<0.5 else x + np.random.randint(0,10)
y = y + np.random.randint(0,5) if np.random.random()<0.5 else y - np.random.randint(0,5)
pylab.annotate(label, xy=(x, y), xytext=(0, 0), textcoords='offset points',
ha='right', va='bottom',fontsize=16)
pylab.title('t-SNE for CBOW',fontsize=24)
# use for saving the figure if needed
pylab.savefig('tsne_skip_vs_cbow.png')
pylab.show()
# Run the function
sg_words = [reverse_dictionary[i] for i in sg_selected_ids]
cbow_words = [reverse_dictionary[i] for i in cbow_selected_ids]
plot_embeddings_side_by_side(sg_two_d_embeddings, cbow_two_d_embeddings, sg_words,cbow_words)
# -
# # CBOW Algorithm
# ## Changing the data generation process
# We need to define a new data generator for CBOW. Shape of the new input array is (batch_size, context_window*2). That is, a batch in CBOW captures all the words in the context of a given word.
# +
data_index = 0
def generate_batch_cbow(batch_size, window_size):
# window_size is the amount of words we're looking at from each side of a given word
# creates a single batch
# data_index is updated by 1 everytime we read a set of data point
global data_index
# span defines the total window size, where
# data we consider at an instance looks as follows.
# [ skip_window target skip_window ]
# e.g if skip_window = 2 then span = 5
span = 2 * window_size + 1 # [ skip_window target skip_window ]
# two numpy arras to hold target words (batch)
# and context words (labels)
# Note that batch has span-1=2*window_size columns
batch = np.ndarray(shape=(batch_size,span-1), dtype=np.int32)
labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
# The buffer holds the data contained within the span
buffer = collections.deque(maxlen=span)
# Fill the buffer and update the data_index
for _ in range(span):
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
# Here we do the batch reading
# We iterate through each batch index
# For each batch index, we iterate through span elements
# to fill in the columns of batch array
for i in range(batch_size):
target = window_size # target label at the center of the buffer
target_to_avoid = [ window_size ] # we only need to know the words around a given word, not the word itself
# add selected target to avoid_list for next time
col_idx = 0
for j in range(span):
# ignore the target word when creating the batch
if j==span//2:
continue
batch[i,col_idx] = buffer[j]
col_idx += 1
labels[i, 0] = buffer[target]
# Everytime we read a data point,
# we need to move the span by 1
# to create a fresh new span
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
return batch, labels
for window_size in [1,2]:
data_index = 0
batch, labels = generate_batch_cbow(batch_size=8, window_size=window_size)
print('\nwith window_size = %d:' % (window_size))
print(' batch:', [[reverse_dictionary[bii] for bii in bi] for bi in batch])
print(' labels:', [reverse_dictionary[li] for li in labels.reshape(8)])
# -
# # Using Candidate Sampling with the Unigram Distribution for Negative Sampling
# ## Unigram distribution
# The unigram distribution $U(w_i)$ for a given word $w_i$ is given by,
#
# $ P(w_i|w_1,...,w_{i-1}) \simeq P(w_i) = \frac{count(w_i)}{\sum_{w_j \in corpus}count(w_j)} = U(w_i) $
#
# The original paper found that if words are sampled the noise for the negative sampling with a particular distribution gives the best results. And the distribution is given by,
#
# $ U(w)^{3/4} / Z $ where $Z$ is a constant.
# +
# Creating vocabulary file and unigram counts
# Requried by the tf.nn.fixed_unigram_candidate_sampler
# vocabulary file: Each valid line in this file (which should have a CSV-like format) corresponds to a valid word ID. IDs are in sequential order.
# unigrams: A list of unigram counts or probabilities, one per ID in sequential order. Exactly one of vocab_file and unigrams should be passed to this operation.
word_count_dictionary = {}
unigrams = [0 for _ in range(vocabulary_size)]
for word,w_count in count:
w_idx = dictionary[word]
unigrams[w_idx] = w_count*1.0/token_count
word_count_dictionary[w_idx] = w_count
print('First 10 Unigram probabilities')
print(unigrams[:10])
# -
# ### Defining Hyperparameters
#
# Here we define several hyperparameters including `batch_size` (amount of samples in a single batch) `embedding_size` (size of embedding vectors) `window_size` (context window size).
# +
batch_size = 128 # Data points in a single batch
embedding_size = 128 # Dimension of the embedding vector.
# How many words to consider left and right.
# Skip gram by design does not require to have all the context words in a given step
# However, for CBOW that's a requirement, so we limit the window size
window_size = 2
# We pick a random validation set to sample nearest neighbors
valid_size = 16 # Random set of words to evaluate similarity on.
# We sample valid datapoints randomly from a large window without always being deterministic
valid_window = 50
# When selecting valid examples, we select some of the most frequent words as well as
# some moderately rare words as well
valid_examples = np.array(random.sample(range(valid_window), valid_size))
valid_examples = np.append(valid_examples,random.sample(range(1000, 1000+valid_window), valid_size),axis=0)
num_sampled = 32 # Number of negative examples to sample.
# -
# ### Defining Inputs and Outputs
#
# Here we define placeholders for feeding in training inputs and outputs (each of size `batch_size`) and a constant tensor to contain validation examples.
# +
tf.reset_default_graph()
# Training input data (target word IDs). Note that it has 2*window_size columns
train_dataset = tf.placeholder(tf.int32, shape=[batch_size,2*window_size])
# Training input label data (context word IDs)
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
# Validation input data, we don't need a placeholder
# as we have already defined the IDs of the words selected
# as validation data
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
# -
# ### Defining Model Parameters and Other Variables
# We now define several TensorFlow variables such as an embedding layer (`embeddings`) and neural network parameters (`softmax_weights` and `softmax_biases`)
# +
# Variables.
# Embedding layer, contains the word embeddings
embeddings = tf.Variable(tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0,dtype=tf.float32))
# Softmax Weights and Biases
softmax_weights = tf.Variable(tf.truncated_normal([vocabulary_size, embedding_size],
stddev=0.5 / math.sqrt(embedding_size),dtype=tf.float32))
softmax_biases = tf.Variable(tf.random_uniform([vocabulary_size],0.0,0.01))
# -
# ### Defining the Model Computations
#
# We first defing a lookup function to fetch the corresponding embedding vectors for a set of given inputs. Concretely, we define $2\times$`window_size` embedding lookups. We then concatenate all these looked up embedding vectors to form a matrix of size `[batch_size, embedding_size, 2*window_size]`. Thereafter, we average these embedding lookups to produce an average embeddings of size `[batch_size, embedding_size]`. With that, we define negative sampling loss function `tf.nn.sampled_softmax_loss` which takes in the embedding vectors and previously defined neural network parameters.
# +
# Model.
# Look up embeddings for a batch of inputs.
# Here we do embedding lookups for each column in the input placeholder
# and then average them to produce an embedding_size word vector
stacked_embedings = None
print('Defining %d embedding lookups representing each word in the context'%(2*window_size))
for i in range(2*window_size):
embedding_i = tf.nn.embedding_lookup(embeddings, train_dataset[:,i])
x_size,y_size = embedding_i.get_shape().as_list()
if stacked_embedings is None:
stacked_embedings = tf.reshape(embedding_i,[x_size,y_size,1])
else:
stacked_embedings = tf.concat(axis=2,values=[stacked_embedings,tf.reshape(embedding_i,[x_size,y_size,1])])
assert stacked_embedings.get_shape().as_list()[2]==2*window_size
print("Stacked embedding size: %s"%stacked_embedings.get_shape().as_list())
mean_embeddings = tf.reduce_mean(stacked_embedings,2,keepdims=False)
print("Reduced mean embedding size: %s"%mean_embeddings.get_shape().as_list())
# Compute the softmax loss, using a sample of the negative labels each time.
# inputs are embeddings of the train words
# with this loss we optimize weights, biases, embeddings
# However, unlike at the previous instance (Chapter 3) we use a different sample to sampel negative classes
# Particularly we use a unigram candidate sampler, to which we provide
# the unigram probabilities we computed earlier. For details about the passed arguments
# Refer the text in Chapter 4
candidate_sampler = tf.nn.fixed_unigram_candidate_sampler(true_classes = tf.cast(train_labels,dtype=tf.int64), num_true = 1,
num_sampled = num_sampled,
unique = True, range_max = vocabulary_size,
distortion=0.75,
num_reserved_ids=0,
unigrams=unigrams, name='unigram_sampler')
# The loss is very similar to what we defined in Chapter 3, except for
# passing the above defined sampler to the function.
loss = tf.reduce_mean(
tf.nn.sampled_softmax_loss(weights=softmax_weights, biases=softmax_biases, inputs=mean_embeddings,
labels=train_labels, num_sampled=num_sampled, num_classes=vocabulary_size,
sampled_values=candidate_sampler))
# -
# ### Model Parameter Optimizer
#
# We then define a learning rate as a constant and an optimizer which uses the Adagrad method. Feel free to experiment with other optimizers listed [here](https://www.tensorflow.org/api_guides/python/train).
optimizer = tf.train.AdagradOptimizer(1.0).minimize(loss)
# ### Calculating Word Similarities
# We calculate the similarity between two given words in terms of the cosine distance. To do this efficiently we use matrix operations to do so, as shown below.
# +
# Compute the similarity between minibatch examples and all embeddings.
# We use the cosine distance:
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keepdims=True))
normalized_embeddings = embeddings / norm
valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings, valid_dataset)
similarity = tf.matmul(valid_embeddings, tf.transpose(normalized_embeddings))
# -
# ## Running CBOW with Unigram Candidate Sampling
#
# Here we run the CBOW algorithm with unigram based candidate sampling, we defined above. Specifically, we first initialize variables, and then train the algorithm for many steps (`num_steps`). And every few steps we evaluate the algorithm on a fixed validation set and print out the words that appear to be closest for a given set of words.
# +
num_steps = 100001
cbow_loss_unigram = []
# ConfigProto is a way of providing various configuration settings
# required to execute the graph
with tf.Session(config=tf.ConfigProto(allow_soft_placement=True)) as session:
# Initialize the variables in the graph
tf.global_variables_initializer().run()
print('Initialized')
average_loss = 0
# Train the Word2vec model for num_step iterations
for step in range(num_steps):
# Generate a single batch of data
batch_data, batch_labels = generate_batch_cbow(batch_size, window_size)
# Populate the feed_dict and run the optimizer (minimize loss)
# and compute the loss
feed_dict = {train_dataset : batch_data, train_labels : batch_labels}
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
# Update the average loss variable
average_loss += l
if (step+1) % 2000 == 0:
if step > 0:
average_loss = average_loss / 2000
# The average loss is an estimate of the loss over the last 2000 batches.
cbow_loss_unigram.append(average_loss)
print('Average loss at step %d: %f' % (step+1, average_loss))
average_loss = 0
# Evaluating validation set word similarities
if (step+1) % 10000 == 0:
sim = similarity.eval()
# Here we compute the top_k closest words for a given validation word
# in terms of the cosine distance
# We do this for all the words in the validation set
# Note: This is an expensive step
for i in range(valid_size):
valid_word = reverse_dictionary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log = 'Nearest to %s:' % valid_word
for k in range(top_k):
close_word = reverse_dictionary[nearest[k]]
log = '%s %s,' % (log, close_word)
print(log)
cbow_final_embeddings = normalized_embeddings.eval()
with open('cbow_unigram_losses.csv', 'wt') as f:
writer = csv.writer(f, delimiter=',')
writer.writerow(cbow_loss_unigram)
# -
# # Subsampling the Frequent words
#
# This is important as the most-frequent words such as "in", "a", "the" do not add a significant value to word embeddings. For example, a training input output tuple (France, Paris) has more information than (France, The). So if we can avoid such frequent words, it can help to boost the quality of word vectors.
#
# Therefore we sample each word $w_i$ with a probability $P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}}$
# ## Generating Word Sequence with Subsampling
# +
subsampled_data = []
drop_count = 0
drop_examples = []
# Here we traverse through the data and drop irrelavent words
# according to the subsampling probability
for w_i in data:
# Note that the paper uses t=1e-5
# This is fine when using a normalized frequency of words
# But we are using raw frequencies so we set t=1e5
p_w_i = 1 - np.sqrt(1e5/word_count_dictionary[w_i])
if np.random.random() < p_w_i:
drop_count += 1
drop_examples.append(reverse_dictionary[w_i])
else:
subsampled_data.append(w_i)
# Print some statistics
print('Dropped %d%% words (%d words) in total...'%(drop_count*100.0/len(data),drop_count))
print('Dropped Examples: ', drop_examples[:20])
print('\nOriginal data: ',[reverse_dictionary[w_i] for w_i in data[:20]])
print('\nSubsampled data: ',[reverse_dictionary[w_i] for w_i in subsampled_data[:20]])
# -
# ## Running CBOW with Unigram Sampling + Subsampling
#
# Here we run the CBOW with unigram sampling and subsampling which we defined above. Specifically, we first initialize variables, and then train the algorithm for many steps (`num_steps`). And every few steps we evaluate the algorithm on a fixed validation set and print out the words that appear to be closest for a given set of words.
# +
num_steps = 100001
cbow_loss_unigram_subsampled = []
# ConfigProto is a way of providing various configuration settings
# required to execute the graph
with tf.Session(config=tf.ConfigProto(allow_soft_placement=True)) as session:
# Initialize the variables in the graph
tf.global_variables_initializer().run()
print('Initialized')
average_loss = 0
# Train the Word2vec model for num_step iterations
for step in range(num_steps):
# Generate a single batch of data
batch_data, batch_labels = generate_batch_cbow(batch_size, window_size)
# Populate the feed_dict and run the optimizer (minimize loss)
# and compute the loss
feed_dict = {train_dataset : batch_data, train_labels : batch_labels}
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
# Update the average loss variable
average_loss += l
if (step+1) % 2000 == 0:
if step > 0:
average_loss = average_loss / 2000
# The average loss is an estimate of the loss over the last 2000 batches.
cbow_loss_unigram_subsampled.append(average_loss)
print('Average loss at step %d: %f' % (step+1, average_loss))
average_loss = 0
# Evaluating validation set word similarities
if (step+1) % 10000 == 0:
sim = similarity.eval()
# Here we compute the top_k closest words for a given validation word
# in terms of the cosine distance
# We do this for all the words in the validation set
# Note: This is an expensive step
for i in range(valid_size):
valid_word = reverse_dictionary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log = 'Nearest to %s:' % valid_word
for k in range(top_k):
close_word = reverse_dictionary[nearest[k]]
log = '%s %s,' % (log, close_word)
print(log)
cbow_final_embeddings = normalized_embeddings.eval()
with open('cbow_unigram_subsampled_losses.csv', 'wt') as f:
writer = csv.writer(f, delimiter=',')
writer.writerow(cbow_loss_unigram_subsampled)
# -
# ## Plotting CBOW (Original), Unigram based Negative Sampling and Subsampling Losses
#
# Here we plot the losses obtained over time for all the CBOW based algorithms to see which one performs better. We provide a detailed analysis of the observations in the Chapter 4 text.
# +
pylab.figure(figsize=(15,5)) # in inches
# Define the x axis
x = np.arange(len(skip_gram_loss))*2000
# Plotting standard CBOW loss, CBOW loss with unigram sampling and
# CBOW loss with unigram sampling + subsampling here in one plot
pylab.plot(x, cbow_loss, label="CBOW",linestyle='--',linewidth=2)
pylab.plot(x, cbow_loss_unigram, label="CBOW (Unigram)",linestyle='-.',linewidth=2,marker='^',markersize=5)
pylab.plot(x, cbow_loss_unigram_subsampled, label="CBOW (Unigram+Subsampling)",linewidth=2)
# Some text around the plots
pylab.title('Original CBOW vs Various Improvements Loss Decrease Over-Time',fontsize=24)
pylab.xlabel('Iterations',fontsize=22)
pylab.ylabel('Loss',fontsize=22)
pylab.legend(loc=1,fontsize=22)
# Use for saving the figure if needed
pylab.savefig('loss_cbow_vs_all_improvements.png')
pylab.show()
# -
|
ch4/ch4_word2vec_improvements.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.3
# language: julia
# name: julia-1.6
# ---
# +
function makef(a)
f(x) = a = x
f
end
f = makef(3)
dump(f)
# +
function makef(a)
A = Ref(a)
f(x) = A[] = x
f
end
f = makef(3)
dump(f)
# +
function makef(a)
A = fill(a)
f(x) = A[] = x
f
end
f = makef(3)
dump(f)
# -
|
0022/remove Core.Box.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
name = 'Corey'
name.lower()
name.capitalize()
name.upper()
name.find("o")
# +
#Exercise 11, Casting (putting something forcefully together)
number ="5"
second_number="7"
type(number)
int("5") + int("7")
# -
#Exercise no. 12, the input() Function
print("programmers name")
name= input()
print("hello programmer "+ name+".")
|
01_Workshop-master/Chapter01/Exercise10/Exercise10.ipynb
|