code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Programming with Python
#
# ## Episode 1 - Introduction - Analyzing Patient Data
#
# Teaching: 60 min,
# Exercises: 30 min
#
# Objectives
#
# - Assign values to variables.
#
# - Explain what a library is and what libraries are used for.
#
# - Import a Python library and use the functions it contains.
#
# - Read tabular data from a file into a program.
#
# - Select individual values and subsections from data.
#
# - Perform operations on arrays of data.
#
# - Plot simple graphs from data.
# ## Our Dataset
# In this episode we will learn how to work with CSV files in Python. Our dataset contains patient inflammation data - where each row represents a different patient and the column represent inflammation data over a series of days.
#
# 
#
#
# However, before we discuss how to deal with many data points, letâs learn how to work with single data values.
#
#
# ## Variables
# Any Python interpreter can be used as a calculator:
#
# ```
# 3 + 5 * 4
# ```
3 + 5 * 4
# This is great but not very interesting. To do anything useful with data, we need to assign its value to a variable. In Python, we can assign a value to a variable, using the equals sign =. For example, to assign value 60 to a variable weight_kg, we would execute:
#
# ```
# weight_kg = 60
# ```
weight_kg = 60
# From now on, whenever we use weight_kg, Python will substitute the value we assigned to it. In essence, a variable is just a name for a value.
#
# ```
# weight_kg + 5
# ```
weight_kg + 5
# In Python, variable names:
#
# - can include letters, digits, and underscores - `A-z, a-z, _`
# - cannot start with a digit
# - are case sensitive.
#
# This means that, for example:
#
# `weight0` is a valid variable name, whereas `0weight` is not
# `weight` and `Weight` are different variables
#
# #### Types of data
# Python knows various types of data. Three common ones are:
#
# - integer numbers (whole numbers)
# - floating point numbers (numbers with a decimal point)
# - and strings (of characters).
#
# In the example above, variable `weight_kg` has an integer value of `60`. To create a variable with a floating point value, we can execute:
#
# ```
# weight_kg = 60.0
# ```
weight_kg = 60.0
print(type(weight_kg))
# And to create a string we simply have to add single or double quotes around some text, for example:
#
# ```
# weight_kg_text = 'weight in kilograms:'
# ```
#
# To display the value of a variable to the screen in Python, we can use the print function:
#
# ```
# print(weight_kg)
# ```
weight_kg_text = "weight in kilograms"
# We can display multiple things at once using only one print command:
#
# ```
# print(weight_kg_text, weight_kg)
# ```
print(weight_kg_text, weight_kg)
# Moreover, we can do arithmetic with variables right inside the print function:
#
# ```
# print('weight in pounds:', 2.2 * weight_kg)
# ```
print('weight in pounds:', 2.2 * weight_kg)
# The above command, however, did not change the value of weight_kg:
#
# ```
# print(weight_kg)
# ```
print(weight_kg)
weight_kg = 65.0
# To change the value of the ``weight_kg variable, we have to assign `weight_kg` a new value using the equals `=` sign:
#
# ```
# weight_kg = 65.0
# print('weight in kilograms is now:', weight_kg)
# ```
print('weight in kilograms is now:', weight_kg)
# #### Variables as Sticky Notes
#
# A variable is analogous to a sticky note with a name written on it: assigning a value to a variable is like writing a value on the sticky note with a particular name.
#
# This means that assigning a value to one variable does not change values of other variables (or sticky notes). For example, letâs store the subjectâs weight in pounds in its own variable:
#
# ```
# # There are 2.2 pounds per kilogram
# weight_lb = 2.2 * weight_kg
# print(weight_kg_text, weight_kg, 'and in pounds:', weight_lb)
# ```
weight_lb = 2.2 * weight_kg
print(weight_kg_text, weight_kg, 'and in pounds:', weight_lb)
# #### Updating a Variable
#
# Variables calculated from other variables do not change value just because the orignal variable change value (unlike cells in Excel):
#
# ```
# weight_kg = 100.0
# print('weight in kilograms is now:', weight_kg, 'and weight in pounds is still:', weight_lb)
# ```
weight_kg = 93.0
print("weight_kg", weight_kg)
weight_lb = weight_kg*2.2
print("weight_lb", weight_lb)
print('weight in kilograms is now:', weight_kg, 'and weight in pounds is now:', weight_lb)
# Since `weight_lb` doesnât *remember* where its value comes from, so it is not updated when we change `weight_kg`.
# ## Libraries
#
# Words are useful, but whatâs more useful are the sentences and stories we build with them (or indeed entire books or whole libraries). Similarly, while a lot of powerful, general tools are built into Python, specialized tools built up from these basic units live in *libraries* that can be called upon when needed.
# ### Loading data into Python
#
# In order to load our inflammation dataset into Python, we need to access (import in Python terminology) a library called `NumPy` (which stands for Numerical Python).
#
# In general you should use this library if you want to do fancy things with numbers, especially if you have matrices or arrays. We can import `NumPy` using:
#
# ```
# import numpy
# ```
import numpy
# Importing a library is like getting a piece of lab equipment out of a storage locker and setting it up on the bench. Libraries provide additional functionality to the basic Python package, much like a new piece of equipment adds functionality to a lab space. Just like in the lab, importing too many libraries can sometimes complicate and slow down your programs - so we only import what we need for each program. Once weâve imported the library, we can ask the library to read our data file for us:
#
# ```
# numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
# ```
numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
# The expression `numpy.loadtxt(...)` is a function call that asks Python to run the function `loadtxt` which belongs to the `numpy` library. This dot `.` notation is used everywhere in Python: the thing that appears before the dot contains the thing that appears after.
#
# As an example, <NAME> is the John that belongs to the Smith family. We could use the dot notation to write his name smith.john, just as `loadtxt` is a function that belongs to the `numpy` library.
#
# `numpy.loadtxt` has two parameters: the name of the file we want to read and the delimiter that separates values on a line. These both need to be character strings (or strings for short), so we put them in quotes.
#
# Since we havenât told it to do anything else with the functionâs output, the notebook displays it. In this case, that output is the data we just loaded. By default, only a few rows and columns are shown (with ... to omit elements when displaying big arrays). To save space, Python displays numbers as 1. instead of 1.0 when thereâs nothing interesting after the decimal point.
#
# Our call to `numpy.loadtxt` read our file but didnât save the data in memory. To do that, we need to assign the array to a variable. Just as we can assign a single value to a variable, we can also assign an array of values to a variable using the same syntax. Letâs re-run `numpy.loadtxt` and save the returned data:
#
# ```
# data = numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
# ```
data = numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
# This statement doesnât produce any output because weâve assigned the output to the variable `data`. If we want to check that the data has been loaded, we can print the variableâs value:
#
# ```
# print(data)
# ```
print(data)
# Now that the data is in memory, we can manipulate it. First, letâs ask Python what type of thing `data` refers to:
#
# ```
# print(type(data))
# ```
print(type(data))
# The output tells us that data currently refers to an N-dimensional array, the functionality for which is provided by the `NumPy` library. This data correspond to arthritis patientsâ inflammation. The rows are the individual patients, and the columns are their daily inflammation measurements.
#
# #### Data Type
#
# A NumPy array contains one or more elements of the same type. The type function will only tell you that a variable is a NumPy array but wonât tell you the type of thing inside the array. We can find out the type of the data contained in the NumPy array.
#
# ```
# print(data.dtype)
# ```
print(data.dtype)
# This tells us that the NumPy arrayâs elements are floating-point numbers.
#
# With the following command, we can see the arrayâs shape:
#
# ```
# print(data.shape)
# ```
print(data.shape)
# The output tells us that the data array variable contains 60 rows and 40 columns. When we created the variable data to store our arthritis data, we didnât just create the array; we also created information about the array, called members or attributes. This extra information describes data in the same way an adjective describes a noun. data.shape is an attribute of data which describes the dimensions of data. We use the same dotted notation for the attributes of variables that we use for the functions in libraries because they have the same part-and-whole relationship.
#
# If we want to get a single number from the array, we must provide an index in square brackets after the variable name, just as we do in math when referring to an element of a matrix. Our inflammation data has two dimensions, so we will need to use two indices to refer to one specific value:
#
# ```
# print('first value in data:', data[0, 0])
# print('middle value in data:', data[30, 20])
# ```
print('first value in data:', data[0, 0])
print('middle value in data:', data[30, 20])
# The expression `data[30, 20]` accesses the element at row 30, column 20. While this expression may not surprise you, `data[0, 0]` might.
#
# #### Zero Indexing
#
# Programming languages like Fortran, MATLAB and R start counting at 1 because thatâs what human beings have done for thousands of years. Languages in the C family (including C++, Java, Perl, and Python) count from 0 because it represents an offset from the first value in the array (the second value is offset by one index from the first value). This is closer to the way that computers represent arrays (if you are interested in the historical reasons behind counting indices from zero, you can read <NAME>âs blog post).
#
# As a result, if we have an MÃN array in Python, its indices go from 0 to M-1 on the first axis and 0 to N-1 on the second. It takes a bit of getting used to, but one way to remember the rule is that the index is how many steps we have to take from the start to get the item we want.
# #### In the Corner
#
# What may also surprise you is that when Python displays an array, it shows the element with index `[0, 0]` in the upper left corner rather than the lower left. This is consistent with the way mathematicians draw matrices but different from the Cartesian coordinates. The indices are (row, column) instead of (column, row) for the same reason, which can be confusing when plotting data.
# #### Slicing data
#
# An index like `[30, 20]` selects a single element of an array, but we can select whole sections as well. For example, we can select the first ten days (columns) of values for the first four patients (rows) like this:
#
# ```
# print(data[0:4, 0:10])
# ```
print(data[0:4, 0:10])
# The slice `[0:4]` means, *Start at index 0 and go up to, but not including, index 4*.
#
# Again, the up-to-but-not-including takes a bit of getting used to, but the rule is that the difference between the upper and lower bounds is the number of values in the slice.
#
# Also, we donât have to start slices at `0`:
#
# ```
# print(data[5:10, 0:10])
# ```
print(data[5:10, 0:10])
# and we donât have to include the upper or lower bound on the slice.
#
# If we donât include the lower bound, Python uses 0 by default; if we donât include the upper, the slice runs to the end of the axis, and if we donât include either (i.e., if we just use `:` on its own), the slice includes everything:
#
# ```
# small = data[:3, 36:]
# print('small is:')
# print(small)
# ```
small = data[:3, 36:]
print("small is:")
print(small)
# The above example selects rows 0 through 2 and columns 36 through to the end of the array.
#
# thus small is:
# ```
# [[ 2. 3. 0. 0.]
# [ 1. 1. 0. 1.]
# [ 2. 2. 1. 1.]]
# ```
#
# Arrays also know how to perform common mathematical operations on their values. The simplest operations with data are arithmetic: addition, subtraction, multiplication, and division. When you do such operations on arrays, the operation is done element-by-element. Thus:
#
# ```
# doubledata = data * 2.0
# ```
doubledata = data * 2.0
# will create a new array doubledata each element of which is twice the value of the corresponding element in data:
#
# ```
# print('original:')
# print(data[:3, 36:])
# print('doubledata:')
# print(doubledata[:3, 36:])
# ```
print("original:")
print(data[:3, 36:])
print("doubledata:")
print(doubledata[:3, 36:])
# If, instead of taking an array and doing arithmetic with a single value (as above), you did the arithmetic operation with another array of the same shape, the operation will be done on corresponding elements of the two arrays. Thus:
#
# ```
# tripledata = doubledata + data
# ```
tripledata = doubledata + data
# will give you an array where `tripledata[0,0]` will equal `doubledata[0,0]` plus `data[0,0]`, and so on for all other elements of the arrays.
#
# ```
# print('tripledata:')
# print(tripledata[:3, 36:])
# ```
print("tripledata:")
print(tripledata[:3, 36:])
# Often, we want to do more than add, subtract, multiply, and divide array elements. NumPy knows how to do more complex operations, too. If we want to find the average inflammation for all patients on all days, for example, we can ask NumPy to compute dataâs mean value:
#
# ```
#
# ```
print(numpy.mean(data))
# `mean()` is a function that takes an array as an argument.
#
# However, not all functions have input.
#
# Generally, a function uses inputs to produce outputs. However, some functions produce outputs without needing any input. For example, checking the current time doesnât require any input.
#
# ```
# import time
# print(time.ctime())
# ```
import time
print(time.ctime())
# For functions that donât take in any arguments, we still need parentheses `()` to tell Python to go and do something for us.
#
# NumPy has lots of useful functions that take an array as input. Letâs use three of those functions to get some descriptive values about the dataset. Weâll also use *multiple assignment*, a convenient Python feature that will enable us to do this all in one line.
#
# ```
# maxval, minval, stdval = numpy.max(data), numpy.min(data), numpy.std(data)
# ```
maxval, minval, stdval = numpy.max(data), numpy.min(data), numpy.std(data)
# Here weâve assigned the return value from `numpy.max(data)` to the variable `maxval`, the return value from `numpy.min(data)` to `minval`, and so on.
#
# Let'a have a look at the results:
#
# ```
# print('maximum inflammation:', maxval)
# print('minimum inflammation:', minval)
# print('standard deviation:', stdval)
# ```
print('maximum inflammation:', maxval)
print('minimum inflammation:', minval)
print('standard deviation:', stdval)
# #### Mystery Functions in IPython
#
# How did we know what functions NumPy has and how to use them?
#
# If you are working in IPython or in a Jupyter Notebook (which we are), there is an easy way to find out. If you type the name of something followed by a dot `.`, then you can use `Tab` completion (e.g. type `numpy.` and then press `tab`) to see a list of all functions and attributes that you can use.
# +
# numpy.cumprod?
# -
# After selecting one, you can also add a question mark `?` (e.g. `numpy.cumprod?`), and IPython will return an explanation of the method!
#
# This is the same as running `help(numpy.cumprod)`.
# When analyzing data, though, we often want to look at variations in statistical values, such as the maximum inflammation per patient or the average inflammation per day. One way to do this is to create a new temporary array of the data we want, then ask it to do the calculation:
#
# ```
# patient_0 = data[0, :] # Comment: 0 on the first axis (rows), everything on the second (columns)
# print('maximum inflammation for patient 0:', numpy.max(patient_0))
# ```
patient_0 = data[0, :] # Comment: 0 on the first axis (rows), everything on the second (columns)
print('maximum inflammation for patient 0:', numpy.max(patient_0))
# Everything in a line of code following the `#` symbol is a comment that is ignored by Python. Comments allow programmers to leave explanatory notes for other programmers or their future selves.
# +
#this is a developer note
# -
# We donât actually need to store the row in a variable of its own. Instead, we can combine the selection and the function call:
#
# ```
# print('maximum inflammation for patient 2:', numpy.max(data[2, :]))
# ```
print("maximum inflammation for patient 2:", numpy.max(data[2, :]))
# Operations Across Axes
#
# What if we need the maximum inflammation for each patient over all days or the average for each day ? In other words want to perform the operation across a different axis.
#
# To support this functionality, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
#
# ```
# print(numpy.mean(data, axis=0))
# ```
print(numpy.mean(data, axis=0))
# As a quick check, we can ask this array what its shape is:
#
# ```
# print(numpy.mean(data, axis=0).shape)
# ```
print(numpy.mean(data, axis=0).shape)
# The results (40,) tells us we have an NÃ1 vector, so this is the average inflammation per day for all 40 patients. If we average across axis 1 (columns in our example), we use:
#
# ```
# print(numpy.mean(data, axis=1))
# ```
print(numpy.mean(data, axis=1))
print(numpy.mean(data, axis=1).shape)
# which is the average inflammation per patient across all days.
#
# And if you are now confused, here's a simpler example:
#
# ```
# tiny = [[ 1, 2, 3],
# [ 10, 20, 30],
# [ 100, 200, 300]]
#
# print(tiny)
# print('Sum the entire matrix: ', numpy.sum(tiny))
# ```
# +
tiny = [[ 1, 2, 3],
[ 10, 20, 30],
[ 100, 200, 300]]
print(tiny)
print('Sum the entire matrix: ', numpy.sum(tiny))
# -
# Now let's add the rows (first axis, ie zeroth)
#
# ```
# print('Sum the columns (ie add the rows): ', numpy.sum(tiny, axis=0))
# ```
print('Sum the columns (ie add the rows): ', numpy.sum(tiny, axis=0))
print('Sum the columns (ie add the rows): ', numpy.mean(tiny, axis=0))
# and now on the other dimension (axis=1, ie the second dimension)
#
# ```
# print('Sum the rows (ie add the columns): ', numpy.sum(tiny, axis=1))
# ```
print('Sum the rows (ie add the columns): ', numpy.sum(tiny, axis=1))
print('Sum the rows (ie add the columns): ', numpy.mean(tiny, axis=1))
# ### Visualising data
#
# The mathematician <NAME> once said, âThe purpose of computing is insight, not numbers,â and the best way to develop insight is often to visualize data.
#
# Visualization deserves an entire workshop of its own, but we can explore a few features of Pythonâs `matplotlib` library here. While there is no official plotting library, `matplotlib` is the de facto standard. First, we will import the `pyplo` module from `matplotlib` and use two of its functions to create and display a heat map of our data:
#
# ```
# import matplotlib.pyplot
# plot = matplotlib.pyplot.imshow(data)
# ```
import matplotlib.pyplot
plot = matplotlib.pyplot.imshow(data)
# #### Heatmap of the Data
#
# Blue pixels in this heat map represent low values, while yellow pixels represent high values. As we can see, inflammation rises and falls over a 40-day period.
#
# #### Some IPython Magic
#
# If youâre using a Jupyter notebook, youâll need to execute the following command in order for your matplotlib images to appear in the notebook when show() is called:
#
# ```
# # %matplotlib inline
# ```
# %matplotlib inline
# The `%` indicates an IPython magic function - a function that is only valid within the notebook environment. Note that you only have to execute this function once per notebook.
# Letâs take a look at the average inflammation over time:
#
# ```
# ave_inflammation = numpy.mean(data, axis=0)
# ave_plot = matplotlib.pyplot.plot(ave_inflammation)
# ```
ave_inflammation = numpy.mean(data, axis=0)
ave_plot = matplotlib.pyplot.plot(ave_inflammation)
# Here, we have put the average per day across all patients in the variable `ave_inflammation`, then asked `matplotlib.pyplot` to create and display a line graph of those values. The result is a roughly linear rise and fall, which is suspicious: we might instead expect a sharper rise and slower fall.
#
# Letâs have a look at two other statistics, the maximum inflamation of all the patients each day:
# ```
# max_plot = matplotlib.pyplot.plot(numpy.max(data, axis=0))
# ```
max_plot = matplotlib.pyplot.plot(numpy.max(data, axis=0))
# ... and the minimum inflamation across all patient each day ...
# ```
# min_plot = matplotlib.pyplot.plot(numpy.min(data, axis=0))
# matplotlib.pyplot.show()
# ```
min_plot = matplotlib.pyplot.plot(numpy.min(data, axis=0))
matplotlib.pyplot.show()
# The maximum value rises and falls smoothly, while the minimum seems to be a step function. Neither trend seems particularly likely, so either thereâs a mistake in our calculations or something is wrong with our data. This insight would have been difficult to reach by examining the numbers themselves without visualization tools.
# ### Grouping plots
#
# You can group similar plots in a single figure using subplots. This script below uses a number of new commands. The function `matplotlib.pyplot.figure()` creates a space into which we will place all of our plots. The parameter `figsize` tells Python how big to make this space.
#
# Each subplot is placed into the figure using its `add_subplot` method. The `add_subplot` method takes 3 parameters. The first denotes how many total rows of subplots there are, the second parameter refers to the total number of subplot columns, and the final parameter denotes which subplot your variable is referencing (left-to-right, top-to-bottom). Each subplot is stored in a different variable (`axes1`, `axes2`, `axes3`).
#
# Once a subplot is created, the axes can be labeled using the `set_xlabel()` command (or `set_ylabel()`). Here are our three plots side by side:
#
# +
import numpy
import matplotlib.pyplot
data = numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
fig = matplotlib.pyplot.figure(figsize=(15.0, 15.0))
axes1 = fig.add_subplot(3, 3, 1)
axes2 = fig.add_subplot(3, 3, 5)
axes3 = fig.add_subplot(3, 3, 9)
axes1.set_ylabel('average')
axes1.set_xlabel('days')
axes1.plot(numpy.mean(data, axis=0))
axes2.set_ylabel('max')
axes2.set_xlabel('days')
axes2.plot(numpy.max(data, axis=0))
axes3.set_ylabel('min')
axes3.set_xlabel('days')
axes3.plot(numpy.min(data, axis=0))
fig.tight_layout()
# -
# ##### The Previous Plots as Subplots
#
# The call to `loadtxt` reads our data, and the rest of the program tells the plotting library how large we want the figure to be, that weâre creating three subplots, what to draw for each one, and that we want a tight layout. (If we leave out that call to fig.tight_layout()`, the graphs will actually be squeezed together more closely.)
# Exercise: See if you add the label `Days` to the X-Axis of each subplot
# ##### Scientists Dislike Typing.
# We will always use the syntax `import numpy` to import NumPy. However, in order to save typing, it is often suggested to make a shortcut like so: `import numpy as np`. If you ever see Python code online using a NumPy function with np (for example, `np.loadtxt(...))`, itâs because theyâve used this shortcut. When working with other people, it is important to agree on a convention of how common libraries are imported.
#
# In other words:
#
# ```
# import numpy
# numpy.random.rand()
# ```
#
# is the same as:
#
# ```
# import numpy as np
# np.random.rand()
# ```
#
#
# ## Exercises
# ### Variables
#
# What values do the variables mass and age have after each statement in the following program?
# ```
# mass = 47.5
# age = 122
# mass = mass * 2.0a
# age = age - 20
# print(mass, age)
# ```
# Test your answers by executing the commands.
mass = 47.5
age = 122
mass = mass * 2.0
age = age - 20
print(mass, age)
# Solution: Mass = 95, Age = 102
# ### Sorting Out References
#
# What does the following program print out?
# ```
# first, second = 'Grace', 'Hopper'
# third, fourth = second, first
# print(third, fourth)
# ```
first, second = 'Grace', 'Hopper'
third, fourth = second, first
print(third, fourth)
# Solution: Hopper, Grace
# ### Slicing Strings
# A section of an array is called a slice. We can take slices of character strings as well:
# ```
# element = 'oxygen'
# print('first three characters:', element[0:3])
# print('last three characters:', element[3:6])
# ```
#
# What is the value of `element[:4]` ? What about `element[4:]`? Or `element[:]` ?
#
# What about `element[-1]` and `element[-2]` ?
element = 'oxygen'
print('first three characters:', element[0:3])
print('last three characters:', element[3:6])
print('first 4 characters', element[:4])
print('letters after the 4th character', element[4:])
print('all letters in string', element[:])
print('last character in string', element[-1])
print('second last character in string', element[-2])
print(element[1:-1])
# Solution:
# Given those answers, explain what `element[1:-1]` does.
print(element[1:-1])
# Solution: prints string without the first and last characters
# ### Thin Slices
#
# The expression `element[3:3]` produces an empty string, i.e., a string that contains no characters. If data holds our array of patient data, what does `data[3:3, 4:4]` produce? What about `data[3:3, :]` ?
print(data[3:3, :])
print(data[3:3, 4:4])
#
# ### Plot Scaling
# Why do all of our plots stop just short of the upper end of our graph?
# Solution:
# If we want to change this, we can use the `set_ylim(min, max)` method of each âaxesâ, for example:
# ```
# axes3.set_ylim(0,6)
# ```
# Update your plotting code to automatically set a more appropriate scale. (Hint: you can make use of the max and min methods to help.)
# +
import numpy
import matplotlib.pyplot
data = numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
fig = matplotlib.pyplot.figure(figsize=(15.0, 15.0))
axes1 = fig.add_subplot(3, 3, 1)
axes2 = fig.add_subplot(3, 3, 2)
axes3 = fig.add_subplot(3, 3, 3)
axes1.set_ylabel('average')
axes1.set_xlabel("days")
axes1.plot(numpy.mean(data, axis=0))
axes2.set_ylabel('max')
axes2.set_xlabel('days')
axes2.set_ylabel('average')
axes2.plot(numpy.mean(data, axis=0), drawstyle='steps-mid')
axes3.set_ylabel('min')
axes3.set_xlabel('days')
axes3.plot(numpy.min(data, axis=0))
fig.tight_layout()
# -
# ### Drawing Straight Lines
# In the center and right subplots above, we expect all lines to look like step functions because non-integer value are not realistic for the minimum and maximum values. However, you can see that the lines are not always vertical or horizontal, and in particular the step function in the subplot on the right looks slanted. Why is this?
#
# Try adding a `drawstyle` parameter to your plotting:
# ```
# axes2.set_ylabel('average')
# axes2.plot(numpy.mean(data, axis=0), drawstyle='steps-mid')
# ```
# Solution:
# ### Make Your Own Plot
# Create a plot showing the standard deviation (using `numpy.std`) of the inflammation data for each day across all patients.
std_plot = matplotlib.pyplot.plot(numpy.std(data, axis=0))
matplotlib.pyplot.show()
# +
import numpy
import matplotlib.pyplot
data = numpy.loadtxt(fname='data/inflammation-01.csv', delimiter=',')
fig = matplotlib.pyplot.figure(figsize=(15.0, 15.0))
axes1 = fig.add_subplot(3, 3, 1)
axes2 = fig.add_subplot(3, 3, 4)
axes3 = fig.add_subplot(3, 3, 7)
axes1.set_ylabel('average')
axes1.set_xlabel("days")
axes1.set_xlim(0, 39)
axes1.set_ylim(0, 14)
axes1.plot(numpy.mean(data, axis=0))
axes2.set_xlim(0, 39)
axes2.set_ylim(0, 14)
axes2.set_xlabel('days')
axes2.set_ylabel('average')
axes2.plot(numpy.mean(data, axis=0), drawstyle='steps-mid')
axes3.set_ylabel('min')
axes3.set_ylim(0,6)
axes3.set_xlim(0, 39)
axes3.set_xlabel('days')
axes3.plot(numpy.min(data, axis=0))
fig.tight_layout()
# -
# ### Moving Plots Around
# Modify the program to display the three plots vertically rather than side by side.
# ### Stacking Arrays
# Arrays can be concatenated and stacked on top of one another, using NumPyâs `vstack` and `hstack` functions for vertical and horizontal stacking, respectively.
#
# Run the following code to view `A`, `B` and `C`
#
# +
import numpy
A = numpy.array([[1,2,3], [4,5,6], [7, 8, 9]])
print('A = ')
print(A)
B = numpy.hstack([A, A])
print('B = ')
print(B)
C = numpy.vstack([A, A])
print('C = ')
print(C)
# -
# Write some additional code that slices the first and last columns of `A`,
# and stacks them into a 3x2 array. Make sure to print the results to verify your solution.
D = A[:, 2:]
print(D)
E = A[1, 2:]
# ### Change In Inflammation
# This patient data is longitudinal in the sense that each row represents a series of observations relating to one individual. This means that the change in inflammation over time is a meaningful concept.
#
# The `numpy.diff()` function takes a NumPy array and returns the differences between two successive values along a specified axis. For example, with the following `numpy.array`:
#
# ```
# npdiff = numpy.array([ 0, 2, 5, 9, 14])
# ```
#
# Calling `numpy.diff(npdiff)` would do the following calculations
#
# `2 - 0`, `5 - 2`, `9 - 5`, `14 - 9`
#
# and produce the following array.
#
# `[2, 3, 4, 5]`
npdiff = numpy.array([ 0, 2, 5, 9, 14])
numpy.diff(npdiff)
# In our `data` Which axis would it make sense to use this function along?
# Solution
datadiff = numpy.diff(data, axis=0)
print((datadiff).shape)
datachange = numpy.absolute(data, axis=0)
print(datachange)
std_plot = matplotlib.pyplot.plot(numpy.diff(data, axis=1))
matplotlib.pyplot.show()
# If the shape of an individual data file is (60, 40) (60 rows and 40 columns), what would the shape of the array be after you run the diff() function and why?
# Solution
# How would you find the largest change in inflammation for each patient? Does it matter if the change in inflammation is an increase or a decrease? Hint: NumPy has a function called `numpy.absolute()`,
# Solution:
# ## Key Points
# Import a library into a program using import library_name.
#
# Use the numpy library to work with arrays in Python.
#
# Use `variable` `=` `value` to assign a value to a variable in order to record it in memory.
#
# Variables are created on demand whenever a value is assigned to them.
#
# Use `print(something)` to display the value of something.
#
# The expression `array.shape` gives the shape of an array.
#
# Use `array[x, y]` to select a single element from a 2D array.
#
# Array indices start at 0, not 1.
#
# Use `low:high` to specify a slice that includes the indices from low to high-1.
#
# All the indexing and slicing that works on arrays also works on strings.
#
# Use `#` and some kind of explanation to add comments to programs.
#
# Use `numpy.mean(array)`, `numpy.max(array)`, and `numpy.min(array)` to calculate simple statistics.
#
# Use `numpy.mean(array, axis=0)` or `numpy.mean(array, axis=1)` to calculate statistics across the specified axis.
#
# Use the `pyplot` library from `matplotlib` for creating simple visualizations.
# ### Save, and version control your changes
#
# - save your work: `File -> Save`
# - add all your changes to your local repository: `Terminal -> git add .`
# - commit your updates a new Git version: `Terminal -> git commit -m "End of Episode 2"`
# - push your lastest commits to GitHub: `Terminal -> git push`
|
lessons/python/ep1-introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Introduction: How can you use leaf indexes from a tree ensemble?
#
# Supose we have fitted tree ensemble of size $T$. Then calculation of a predict on a new object can be viewed as follows. First original features of the sample are transformed to a sequence of $T$ categorical features indicating at which leaf of each tree the object gets. Then that sequence of categorical features is one-hot encoded. And finally predict calculated as a scalar product of one-hot encoding and vector of all leaf values of the ensemble.
#
# So a tree ensemble can be viewed as linear model over transformed features. Ultimately, one can say that boosting on trees is a linear model with a generator of tree-transformed features. And in process of training it generates new features and fits coefficients for them in a greedy way.
#
# This decomposition of a tree ensemble on a feature transformation and a linear model suggests several tricks:
# 1. We can tune leaf values alltogether (not greedily) with the help of all techiques for linear models.
# 2. Transfer learning: we can take feature transformation from one model and apply it to other dataset with same features (e.g. to predict other target or fit new model on a fresh data).
# 3. Online learning: we can keep feature transformation (i. e. tree-structures) constant and perform online updates on leaf values (viewed as a coefficients of the linear model). See real world example in this paper [Practical Lessons from Predicting Clicks on Ads at Facebook](https://research.fb.com/wp-content/uploads/2016/11/practical-lessons-from-predicting-clicks-on-ads-at-facebook.pdf).
#
# ## In this tutorial we will:
#
# 1. See how to get feature transformation from a catboost model (i. e. calculate at which leafs of model trees objects get).
# 2. Perform a sanity check for the first use case of leaf indexes calculation mentioned above on the california housing dataset.
# +
from __future__ import print_function
import numpy as np
from scipy.stats import ttest_rel
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics import mean_squared_error
from catboost import CatBoostRegressor
seed = 42
# -
# ### Download and split data
# Since it's a demo let's leave major part of the data to test.
data = fetch_california_housing(return_X_y=True)
splitted_data = train_test_split(*data, test_size = 0.9, random_state=seed)
X_train, X_test, y_train, y_test = splitted_data
X_train, X_validate, y_train, y_validate = train_test_split(X_train, y_train, test_size=0.2, random_state=seed)
print("{:<20} {}".format("train size:", X_train.shape[0]))
print("{:<20} {}".format("validation size:", X_validate.shape[0]))
print("{:<20} {}".format("test size:", X_test.shape[0]))
# ### Fit catboost
# I've put very large learning rate in order to get small model (and fast tutorial).
#
# Decreasing of learning rate yields better but larger ensemble. The effect of leaf values tuning deteriorates in that case but remains statistically significant. Iterestingly that trick still works for ensemble of size $\approx 500$ (learning_rate 0.1-0.2) when number of features in linear model exceeds number of training objects five times.
#
#
catboost_params = {
"iterations": 500,
"learning_rate": 0.6,
"depth": 4,
"loss_function": "RMSE",
"verbose": False,
"random_seed": seed
}
cb_regressor = CatBoostRegressor(**catboost_params)
cb_regressor.fit(X_train, y_train, eval_set=(X_validate, y_validate), plot=True)
print("tree count: {}".format(cb_regressor.tree_count_))
print("best rmse: {:.5}".format(cb_regressor.best_score_['validation_0']["RMSE"]))
# ### Transform train data
# +
class LeafIndexTransformer(object):
def __init__(self, model):
self.model = model
self.transformer = OneHotEncoder(handle_unknown="ignore")
def fit(self, X):
leaf_indexes = self.model.calc_leaf_indexes(X)
self.transformer.fit(leaf_indexes)
def transform(self, X):
leaf_indexes = self.model.calc_leaf_indexes(X)
return self.transformer.transform(leaf_indexes)
transformer = LeafIndexTransformer(cb_regressor)
transformer.fit(X_train)
train_embedding = transformer.transform(X_train)
validate_embedding = transformer.transform(X_validate)
# -
# ### Fit linear model
# +
lin_reg = ElasticNet(warm_start=True)
alpha_range = np.round(np.exp(np.linspace(np.log(0.001), np.log(0.01), 5)), decimals=5)
best_alpha = None
best_loss = None
for curr_alpha in alpha_range:
lin_reg.set_params(alpha=curr_alpha)
lin_reg.fit(train_embedding, y_train)
validate_predict = lin_reg.predict(validate_embedding)
validate_loss = mean_squared_error(y_validate, validate_predict)
if best_alpha is None or best_loss > validate_loss:
best_alpha = curr_alpha
best_loss = validate_loss
print("best alpha: {}".format(best_alpha))
print("best rmse: {}".format(np.sqrt(best_loss)))
# -
lin_reg.set_params(alpha=best_alpha)
lin_reg.fit(train_embedding, y_train)
# ### Evaluate on test data
# +
test_embedding = transformer.transform(X_test)
tuned_predict = lin_reg.predict(test_embedding)
untuned_predict = cb_regressor.predict(X_test)
tuned_rmse = np.sqrt(np.mean((tuned_predict - y_test)**2))
untuned_rmse = np.sqrt(np.mean((untuned_predict - y_test)**2))
percent_delta = 100. * (untuned_rmse / tuned_rmse - 1)
print("Tuned model test rmse: {:.5}".format(tuned_rmse))
print("Untuned model test rmse: {:.5} (+{:.2}%)".format(untuned_rmse, percent_delta))
pvalue = ttest_rel((tuned_predict - y_test)**2, (untuned_predict - y_test)**2).pvalue
print("pvalue: {:.5}".format(pvalue))
# -
|
catboost/tutorials/leaf_indexes_calculation/leaf_indexes_calculation_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="7bU3Tqu6XiSM"
import pandas as pd
import numpy as np
from keras.models import Sequential, load_model
from keras.layers import Dense, Dropout, Activation, Flatten, LSTM, TimeDistributed, RepeatVector
from keras.optimizers import adam_v2
from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau, Callback
from sklearn.preprocessing import StandardScaler, MinMaxScaler
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, mean_absolute_error, median_absolute_error, r2_score, explained_variance_score
from scipy import stats, arange
from matplotlib.pyplot import MultipleLocator
from sklearn import tree
# + id="7hHH7assXrSQ"
### Import data & dropna
df = pd.read_excel('d1.xlsx')
df = df.dropna()
### Data selection(date)
data = df[df.Date < '20151231']
# data = df
data = data.drop(["Date"], axis=1)
### Average hour data
d1 = data.values
n = d1.shape[0]%4
m = int((d1.shape[0] - n)/4)
avg = np.zeros((m, d1.shape[1]))
for i in range(d1.shape[1]):
di = d1[:,i].tolist()
x = len(di)%4
while x:
di.pop()
x -= 1
arr = np.array(di).reshape(m, 4)
temp = np.mean(arr, axis = 1)
avg[:, i] = temp
# + colab={"base_uri": "https://localhost:8080/", "height": 482} id="wNGH5S9kXtrg" outputId="9cc06019-9b85-4b28-a16e-2e032dbf073e"
### All data
groups = [0]
i = 1
# plot each column
plt.figure(figsize = (10, 8))
for group in groups:
plt.subplot(len(groups), 1, i)
plt.plot(avg[:, group])
plt.title(df.columns[group+1], y=0.5, loc='right')
i += 1
plt.show()
# + id="GxioP53HXwlK"
### Data normalization
scaler = MinMaxScaler(feature_range=(0, 1))
data = scaler.fit_transform(avg)
# + colab={"base_uri": "https://localhost:8080/", "height": 273} id="vdC2OSJFXy6d" outputId="2872675c-e2f2-4dc2-86af-8bc17d0c0bd7"
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = pd.DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = pd.concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
n_lag = 168
n_out = 72
n_features = 1
reframed = series_to_supervised(data, n_lag, n_out)
#reframed.drop(reframed.columns[[46,47,48,49,50,51,52,53]], axis=1, inplace=True)
reframed.head()
# + colab={"base_uri": "https://localhost:8080/"} id="VHZZXwobX1oi" outputId="43e3f417-3e17-422f-c14b-72568cf17f7c"
values = reframed.values
n_val_hours = 3*24
train = values[:-n_out-n_lag+1, :]
test = values[-1:,:]
train_X, train_y = train[:, :-n_out], train[:, -n_out:]
test_X, test_y = test[:, :-n_out], test[:, -n_out:]
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="Sb-jz7wrX4DJ" outputId="75599e94-39a3-4956-e6b7-8da80028661e"
# design dtree model
clf = tree.DecisionTreeRegressor()
# fit model
clf.fit(train_X,train_y)
# + id="7LzxZNlBX6MY"
# make a prediction
predict_y = clf.predict(test_X)
# yhat = predict_y.reshape(predict_y.shape[0],1)
# test_X = test_X.reshape((test_X.shape[0],n_lag*n_features))
# # invert scaling for forecast
# inv_yhat = np.concatenate((yhat, test_X[:, -8:]), axis=1)
inv_yhat = scaler.inverse_transform(predict_y)
inv_yhat = inv_yhat.reshape(inv_yhat.shape[1], inv_yhat.shape[0])
Prediction = inv_yhat
# + id="8os_o4KMX8Rb"
# invert scaling for actual
test_y = test_y.reshape(test_y.shape[1], test_y.shape[0])
# inv_y = np.concatenate((test_y, test_X[:, -8:]), axis=1)
inv_y = scaler.inverse_transform(test_y)
# inv_y = inv_y.reshape(inv_y.shape[1], inv_y.shape[0])
Truth = inv_y
# + colab={"base_uri": "https://localhost:8080/", "height": 266} id="EWyFd_dUX_uG" outputId="fe32eead-ea23-42a6-c120-98b6e1141500"
### Visualization
x = [x for x in range(n_val_hours)]
fig, ax = plt.subplots(figsize=(15,5), dpi = 300)
ax.plot(x, Prediction, linewidth=2.0, label = "Prediction")
ax.plot(x, Truth, linewidth=2.0, label = "Truth")
x_major_locator=MultipleLocator(24)
ax=plt.gca()
ax.xaxis.set_major_locator(x_major_locator)
ax.legend(loc=2);
plt.grid(linestyle='-.')
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="r4ZpR4dkYAj_" outputId="40db8939-a6ee-4110-8c3f-4f6b481caea8"
### Analysis
MSE = mean_squared_error(Truth, Prediction)
RMSE = np.sqrt(MSE)
print('RMSE: %.3f' %RMSE)
MAE = mean_absolute_error(Truth, Prediction)
print('MAE: %.3f' %MAE)
MAPE = np.mean(np.abs((Truth - Prediction) / Truth)) * 100
print('MAPE: %.3f' %MAPE)
MedAE = median_absolute_error(Truth, Prediction)
print('MedAE: %.3f' %MedAE)
r2_score = r2_score(Truth, Prediction)
print('r2_score: %.3f' %r2_score)
explained_variance_score = explained_variance_score(Truth, Prediction)
print('explained_variance_score: %.3f' %explained_variance_score)
|
Reference/DecisionTree.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pytorch_maskrcnn
# language: python
# name: pt_mask_rcnn_env
# ---
# # Nuclei Detect demo
#
# This notebook can be used to predict cells and nuclei given one has the sufficient model and data
import matplotlib.pyplot as plt
import matplotlib.pylab as pylab
import random
#import requests
from io import BytesIO
from PIL import Image
import numpy as np
import os
import cv2
from matplotlib.image import imread
# Those are the relevant imports for the detection model
# +
from maskrcnn_benchmark.config import cfg
pylab.rcParams['figure.figsize'] = 20, 12
# importing the prediction class
from predictor import NUCLEIdemo
# -
# The NUCLEIdemo class can load the config file and does the image prediction.
# +
configuration_file = "../configs/nuclei_1gpu_nonorm_offline.yaml"
#configuration_file = "/home/max/github/nuclei_cell_detect/configs/nuclei_1gpu_nonorm_offline.yaml"
# update the config options with the config file
cfg.merge_from_file(configuration_file)
# manual override some options
cfg.merge_from_list(["MODEL.DEVICE", "cpu"])
# change dimensions of test images
cfg.merge_from_list(['INPUT.MAX_SIZE_TEST','2049'])
# change number of classes
cfg.merge_from_list(['MODEL.ROI_BOX_HEAD.NUM_CLASSES','4'])
# change normalization, here model was not normalized
cfg.merge_from_list(['INPUT.PIXEL_MEAN', [0., 0., 0.]])
# define model to use here
cfg.merge_from_list(['MODEL.WEIGHT', '/home/maxsen/DEEPL/models_new/20190313_offline_augment/model_final.pth'])
# define how many objects can be identified per image
cfg.merge_from_list(['TEST.DETECTIONS_PER_IMG', '120'])
# show the configuration
#print(cfg)
# -
# Change the confidence threshold.
# +
# load image
def load(path):
pil_image = Image.open(path).convert("RGB")
#print(pil_image)
# convert to BGR format
image = np.array(pil_image)[:, :, [2, 1, 0]]
return image
def load_matplot(path):
img = imread(path)
return img
def load_cv2(path):
img = cv2.imread(path,cv2.IMREAD_ANYDEPTH)
img = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)
img = cv2.normalize(img, img, 0, 255, cv2.NORM_MINMAX)
img = np.uint8(img)
#img = cv2.convertScaleAbs(img)
return img
'''
>>> img = np.empty((100,100,1),dtype = np.uint16)
>>> image = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)
>>> cvuint8 = cv2.convertScaleAbs(image)
>>> cvuint8.dtype
dtype('uint8')
'''
# show image alongside the result and save if necessary
def imshow(img, result, save_path=None):
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
ax1.imshow(img)
plt.axis('off')
ax2 = fig.add_subplot(1,2,2)
ax2.imshow(result)
plt.axis('off')
if save_path:
plt.savefig(save_path, bbox_inches = 'tight')
plt.show()
else:
plt.show()
def imshow_single(result, save_path=None):
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.imshow(result)
plt.axis('off')
if save_path:
plt.savefig(save_path, bbox_inches='tight')
plt.close()
else:
plt.show()
# -
# Let's define a few helper functions for loading images from a URL
nuclei_detect = NUCLEIdemo(
cfg,
min_image_size=1024,
confidence_threshold=0.7,
)
# ### Define the image paths and show the results
# +
img_path = '../../ms2/ssss/'
#img_path = '/data/proj/smFISH/Students/Max_Senftleben/files/data/20190309_aug_pop/ss/'
img_path = '/data/proj/smFISH/Simone/test_intron/AMEXP20181106/AMEXP20181106_hyb1/test_run_20181123_AMEXP20181106_hyb1_filtered_png/test_run_20181123_AMEXP20181106_hyb1_DAPI_filtered_png/'
# random image is taken from the image path
random_img = random.choice(os.listdir(img_path))
image = load(img_path + random_img)
image_matplot = load_matplot(img_path + random_img)
image_cv2 = load_cv2(img_path + random_img)
print(type(image_cv2))
print(image_cv2.shape)
print(image_cv2.dtype)
result, prediction = nuclei_detect.run_on_opencv_image(image_cv2)
imshow(image_cv2, result)
print(vars(prediction))
# -
def make_numpy(prediction, image, path):
list_masks = vars(prediction)['extra_fields']['mask']
masks_to_save = []
img = np.squeeze(np.dsplit(image,3)[0], axis=2)
masks_to_save.append(img)
# iterate through the list of masks
for i, label in enumerate(vars(prediction)['extra_fields']['labels']):
numpy_mask = list_masks[i].numpy().transpose(1,2,0)
numpy_mask = np.squeeze(numpy_mask, axis=2)
numpy_mask[numpy_mask > 0] = label
masks_to_save.append(numpy_mask)
np.save(path, np.dstack(masks_to_save))
# +
# predict for a folder of images
img_path = '/data/proj/smFISH/Simone/test_intron/AMEXP20181106/AMEXP20181106_hyb1/test_run_20181123_AMEXP20181106_hyb1_filtered_png/test_run_20181123_AMEXP20181106_hyb1_DAPI_filtered_png/'
save_results = '/data/proj/smFISH/Students/Max_Senftleben/files/results/'
save_independently = save_results + '20190329_test_run_20181123_AMEXP20181106_hyb1_DAPI_filtered_png/'
save_npy = save_results + '20190329_test_run_20181123_AMEXP20181106_hyb1_DAPI_filtered_npy/'
# done on cpu to check if there is a difference in prediction
save_independently_cpu = '/data/proj/smFISH/Students/Max_Senftleben/files/results/20190331_AMEXP20181106_DAPI_filtered_predicted_with_cpu/'
def save_pred_as_numpy():
for one_image in os.listdir(img_path):
print("Image {} is handled.".format(one_image))
image = load_cv2(img_path + one_image)
# normalization ca be applied
result, prediction = nuclei_detect.run_on_opencv_image(image)
img = Image.fromarray(result)
img.save(save_independently + one_image[:-4] + '_pred.png')
make_numpy(prediction, image, save_npy + one_image[:-4] + '_pred.npy')
#imshow(image, result)
#main()
# +
#make_numpy(prediction, image_cv2, 'test.npy')
# check numpy files
save_npy = '/data/proj/smFISH/Students/Max_Senftleben/files/results/20190329_test_run_20181123_AMEXP20181106_hyb1_DAPI_filtered_npy/'
random_img = random.choice(os.listdir(save_npy))
mask = np.load(save_npy+random_img)
mask_list = np.dsplit(mask, mask.shape[2])
for i in mask_list:
plt.imshow(np.squeeze(i, axis=2)*100)
plt.show()
print(np.unique(i)
# -
|
parsing/old_scripts/.ipynb_checkpoints/whole_folder-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: aind
# kernelspec:
# display_name: Python (aind)
# language: python
# name: aind
# ---
# + outputHidden=false inputHidden=false
import os
import cv2
import numpy as np
from matplotlib import pyplot as plt
# %matplotlib inline
# + outputHidden=false inputHidden=false
os.getcwd()
# + outputHidden=false inputHidden=false
image = cv2.cvtColor(cv2.imread('thumbs-up-down.jpg'), cv2.COLOR_BGR2RGB)
plt.imshow(image)
# + outputHidden=false inputHidden=false
gray = np.average(image, axis=-1).astype(np.uint8)
plt.imshow(gray, cmap='gray')
# + outputHidden=false inputHidden=false
retval, binarized = cv2.threshold(gray, 225, 255, cv2.THRESH_BINARY_INV)
# + outputHidden=false inputHidden=false
plt.imshow(binarized)
# + outputHidden=false inputHidden=false
retval, contours, hierarchy = cv2.findContours(binarized, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
# + outputHidden=false inputHidden=false
plt.imshow(all_contours)
# + outputHidden=false inputHidden=false
for contour in contours:
print(len(contour))
#get ellipse
(x,y), (MA,ma), angle = cv2.fitEllipse(contour)
x, y, MA, ma = [int(x) for x in [x, y, MA, ma]]
#draw contour
s_contours = cv2.drawContours(np.copy(image), contours, -1, (0,255,2), 2)
#draw ellipse
s_contours = cv2.ellipse(np.copy(s_contours), (x,y), (MA,ma), angle, 0, 360, (255,0,0), 2)
plt.imshow(s_contours)
plt.show()
# + outputHidden=false inputHidden=false
def left_hand_crop(image, selected_contour):
"""
Left hand crop
:param image: the original image
:param contours: the contour that will be used for cropping
:return: the cropped image around the left hand
"""
## TODO: Detect the bounding rectangle of the left hand contour
## TODO: Crop the image using the dimensions of the bounding rectangle
# Make a copy of the image to crop
cropped_image = np.copy(image)
(x,y), (MA,ma), angle = cv2.fitEllipse(selected_contour)
x, y, MA, ma = [int(x) for x in [x, y, MA, ma]]
s_contour = cv2.drawContours(np.copy(image), selected_contour, -1, (0,255,2), 2)
x,y,w,h = cv2.boundingRect(selected_contour)
box_image = cv2.rectangle(s_contour, (x,y), (x+w,y+h), (200,0,200),2)
cropped_image = image[y: y + h, x: x + w]
return cropped_image
## TODO: Select the left hand contour from the list
## Replace this value
selected_contour = contours[1]
# If you've selected a contour
if(selected_contour is not None):
# Call the crop function with that contour passed in as a parameter
cropped_image = left_hand_crop(image, selected_contour)
# Display the cropped image side-by-side with the original
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
f.tight_layout()
ax1.imshow(image)
ax1.set_title('Original Image')
ax2.imshow(cropped_image)
ax2.set_title('Cropped Image')
# + outputHidden=false inputHidden=false
|
notebook experiments/contour.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: welly
# language: python
# name: welly
# ---
# ## Well
#
# Some preliminaries...
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import welly
welly.__version__
import os
# env = %env
# ## Make an 'empty' well
w = welly.Well()
w.header.uwi = 'foo'
w.header
w.uwi
# Or, instantiate with some basic data:
w = welly.Well(params={'header': {'name': 'foo', 'uwi':'05045123450000'}})
w.header
w.header['uwi']
# The well name and UWI are also provided at the well level for convenience:
w.name, w.uwi
# ## Load a well from LAS
#
# Use the `from_las()` method to load a well by passing a filename as a `str`.
#
# This is really just a wrapper for `lasio` but instantiates a `Header`, `Curve`s, etc.
from welly import Well
w = Well.from_las('P-129_out.LAS')
w.data['GR'].null = -111.11
w.las.well["NULL"].value = -111.11
w.header
l = w.to_lasio()
l.well['NULL']
w.to_las('x.las', null_value=-111.111)
# !ls -l x.las
# !head -100 x.las
w.las.params['UWID'].value
tracks = ['MD', 'GR', 'RHOB', ['DT', 'DTS'], 'MD']
w.plot(tracks=tracks)
# ## Aliases and curve quality
#
# We can define aliases for curves, and check the quality of curves with a dictionary of tests:
alias = {
"Gamma": ["GR", "GAM", "GRC", "SGR", "NGT"],
"Density": ["RHOZ", "RHOB", "DEN", "RHOZ"],
"Sonic": ["DT", "AC", "DTP", "DT4P"],
"Caliper": ["CAL", "CALI", "CALS", "C1"],
'Porosity SS': ['NPSS', 'DPSS'],
}
# +
import welly.quality as q
tests = {
'Each': [
q.no_flat,
q.no_monotonic,
q.no_gaps,
],
'Gamma': [
q.all_positive,
q.all_below(450),
q.check_units(['API', 'GAPI']),
],
'DT': [
q.all_positive,
],
'Sonic': [
q.all_between(1, 10000), # 1333 to 5000 m/s
q.no_spikes(10), # 10 spikes allowed
],
}
# -
w = Well.from_las('P-129_out.LAS')
r = w.qc_data(tests, alias=alias)
# This returns a dictionary of curves in which the values are dictionaries of **test name: test result** pairs.
r
# There's also an HTML table for rendering in Notebooks:
from IPython.display import HTML
html = w.qc_table_html(tests, alias=alias)
HTML(html)
# ## Add a striplog
from striplog import Legend, Striplog
legend = Legend.builtin('NSDOE')
strip = Striplog.from_image('P-129_280_1935.png', 280, 1935, legend=legend)
strip.plot()
w.data['strip'] = strip
tracks = ['MD', 'strip', 'GR', 'RHOB', ['DT', 'DTS'], 'MD']
w.plot(tracks=tracks)
plt.ylim(1000, 1200)
# ## Header
#
# Maybe should be called 'meta' as it's not really a header...
w.header
w.header.name
w.uwi # Fails because not present in this file. See one way to add it in a minute.
# ## Location and CRS
w.location
from welly import CRS
w.location.crs = CRS.from_epsg(2038)
w.location.crs
# Right now there's no position log â we need to load a deviation survey.
w.location.position
# ## Add deviation data to a well
# +
import numpy as np
from welly import Well
p = Well.from_las('P-130_out.LAS')
# -
dev = np.loadtxt('P-130_deviation_survey.csv', delimiter=',', skiprows=1)
# The columns are MD, inclination, azimuth, and TVD.
dev[:5]
# `add_deviation` assumes those are the columns, and computes a position log.
p.location.add_deviation(dev[:, :3], td=2618.3)
# The columns in the position log are _x_ offset, _y_ offset, and TVD.
p.location.position[:5]
p.location.trajectory()
p.location.plot_plan()
p.location.plot_3d()
# ## Export curves to data matrix
#
# Make a NumPy array:
w.data_as_matrix()
# ## Export curves to pandas
#
# Pandas is an optional dependency. You'll need it to make this work.
df = w.df()
df.head()
df.GR.plot()
# This also gives us another path to getting a matrix:
w.df().values
# You'll have to get depth separately:
w.df().index.values
# To get the UWI of the well as well, e.g. if you want to combine multiple wells (maybe using `welly.Project.df()`):
df = w.df(uwi=True)
df.head()
# ### Pandas with an alias dictionary
alias
keys = ['CALI', 'Gamma', 'Density', 'Sonic', 'RLA1']
w.df(keys=keys, alias=alias, rename_aliased=True).head()
|
tutorial/Well.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + pycharm={"is_executing": false, "name": "#%%\n"}
import pandas as pd
from src.features.utils import read_processed_data
import os
os.chdir('..')
from src.features.feature_class import FeatureEngineering
# + pycharm={"is_executing": false, "name": "#%%\n"}
df_bitcoin, df, df_test = read_processed_data()
# + pycharm={"is_executing": false, "name": "#%%\n"}
fe = FeatureEngineering(df, df_bitcoin, df_test)
# + pycharm={"is_executing": false, "name": "#%%\n"}
df = fe.df
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.shape
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.links_blockchain_site.head()
# -
df.links_blockchain_site
df.links_blockchain_site[df.links_blockchain_site != '0'] = 1
df.links_blockchain_site.unique()
df.links_blockchain_site.iloc[-3] == '0'
# + pycharm={"is_executing": false, "name": "#%%\n"}
df = fe._fill_na(df, 'links_blockchain_site', 'set:0')
# -
df.links_blockchain_site.isna().sum()
df.links_blockchain_site
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.links_blockchain_site.head()
# -
df.links_blockchain_site.apply(lambda x: True if not False else False).unique()
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.links_blockchain_site.unique()
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.links_blockchain_site = df.links_blockchain_site.astype(int)
# + pycharm={"is_executing": false, "name": "#%%\n"}
import numpy as np
np.array(df.ico_data_kyc_required.unique()).all(np.array([0,1]))
# + pycharm={"is_executing": false, "name": "#%%\n"}
assert list(df.ico_data_kyc_required.unique()) == [0,1], "Just 0 and 1 in binary feature allowed!"
|
notebooks/1.2_AV_construct_binary_feature.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={} tags=[]
# <img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# + [markdown] papermill={} tags=[]
# # LinkedIn - Send likes from post to gsheet
# <a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/LinkedIn/LinkedIn_Send_likes_from_post_to_gsheet.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
# + [markdown] papermill={} tags=[]
# **Tags:** #linkedin #post #likes #gsheet #naas_drivers #content #snippet #googlesheets
# + [markdown] papermill={} tags=[]
# **Author:** [<NAME>](https://www.linkedin.com/in/florent-ravenel/)
# + [markdown] papermill={} tags=[]
# In this template, you will extract likes from post and divide them in 2 categories :
# - People in your network
# - People not in your network
#
# Then, data will be sent in 3 sheets to trigger specific actions:
# - POST_LIKES : total of likes from post
# - MY_NETWORK : People in your network
# - NOT_MY_NETWORK : People not in your network
#
# Check the other templates to create a full workflow
# + [markdown] papermill={} tags=[]
# ## Input
# + [markdown] papermill={} tags=[]
# ### Import libraries
# + papermill={} tags=[]
from naas_drivers import linkedin, gsheet
import random
import time
import pandas as pd
from datetime import datetime
# + [markdown] papermill={} tags=[]
# ### Setup LinkedIn
# ð <a href='https://www.notion.so/LinkedIn-driver-Get-your-cookies-d20a8e7e508e42af8a5b52e33f3dba75'>How to get your cookies ?</a>
# + papermill={} tags=[]
# Lindekin cookies
LI_AT = "AQEDARCNSioDe6wmAAABfqF-HR4AAAF-xYqhHlYAtSu7EZZEpFer0UZF-GLuz2DNSz4asOOyCRxPGFjenv37irMObYYgxxxxxxx"
JSESSIONID = "ajax:12XXXXXXXXXXXXXXXXX"
# Post url
POST_URL = "POST_URL"
# + [markdown] papermill={} tags=[]
# ### Setup your Google Sheet
# ð Get your spreadsheet id => it is located in your gsheet url after "https://docs.google.com/spreadsheets/d/" and before "/edit"<br>
# ð Share your gsheet with our service account to connect : <EMAIL><br>
# ð Create your sheet before sending data into it
# + papermill={} tags=[]
# Spreadsheet id
SPREADSHEET_ID = "SPREADSHEET_ID"
# Sheet names
SHEET_POST_LIKES = "POST_LIKES"
SHEET_MY_NETWORK = "MY_NETWORK"
SHEET_NOT_MY_NETWORK = "NOT_MY_NETWORK"
# + [markdown] papermill={} tags=[]
# ### Constant
# + papermill={} tags=[]
DATETIME_FORMAT = "%Y-%m-%d %H:%M:%S"
# + [markdown] papermill={} tags=[]
# ## Model
# + [markdown] papermill={} tags=[]
# ### Get likes from post
# + papermill={} tags=[]
df_posts = linkedin.connect(LI_AT, JSESSIONID).post.get_likes(POST_URL)
df_posts["DATE_EXTRACT"] = datetime.now().strftime(DATETIME_FORMAT)
# + [markdown] papermill={} tags=[]
# ### Get network for profiles
# + papermill={} tags=[]
df_network = pd.DataFrame()
for _, row in df_posts.iterrows():
profile_id = row.PROFILE_ID
# Get network information to know distance between you and people who likes the post
tmp_network = linkedin.connect(LI_AT, JSESSIONID).profile.get_network(profile_id)
# Concat dataframe
df_network = pd.concat([df_network, tmp_network], axis=0)
# Time sleep in made to mimic human behavior, here it is randomly done between 2 and 5 seconds
time.sleep(random.randint(2, 5))
df_network.head(5)
# + [markdown] papermill={} tags=[]
# ### Merge posts likes and network data
# + papermill={} tags=[]
df_all = pd.merge(df_posts, df_network, on=["PROFILE_URN", "PROFILE_ID"], how="left")
df_all = df_all.sort_values(by=["FOLLOWERS_COUNT"], ascending=False)
df_all = df_all[df_all["DISTANCE"] != "SELF"].reset_index(drop=True)
df_all.head(5)
# + [markdown] papermill={} tags=[]
# ### Split my network or not
# + papermill={} tags=[]
# My network
my_network = df_all[df_all["DISTANCE"] == "DISTANCE_1"].reset_index(drop=True)
my_network["DATE_EXTRACT"] = datetime.now().strftime(DATETIME_FORMAT)
my_network.head(5)
# + papermill={} tags=[]
# Not in my network
not_my_network = df_all[df_all["DISTANCE"] != "DISTANCE_1"].reset_index(drop=True)
not_my_network["DATE_EXTRACT"] = datetime.now().strftime(DATETIME_FORMAT)
not_my_network.head(5)
# + [markdown] papermill={} tags=[]
# ## Output
# + [markdown] papermill={} tags=[]
# ### Save post likes in gsheet
# + papermill={} tags=[]
gsheet.connect(SPREADSHEET_ID).send(df_posts, sheet_name=SHEET_POST_LIKES, append=False)
# + [markdown] papermill={} tags=[]
# ### Save people from my network in gsheet
# + papermill={} tags=[]
gsheet.connect(SPREADSHEET_ID).send(my_network, sheet_name=SHEET_MY_NETWORK, append=False)
# + [markdown] papermill={} tags=[]
# ### Save people not in my network in gsheet
# + papermill={} tags=[]
gsheet.connect(SPREADSHEET_ID).send(not_my_network, sheet_name=SHEET_NOT_MY_NETWORK, append=False)
|
LinkedIn/LinkedIn_Send_likes_from_post_to_gsheet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Simple Classifier / Logistic Regression
# This notebook will demosntrate a simple logistic regression model predicting whether a house is ```low-priced``` or ```expensive```. Similar to our linear model in ```1_linear_regression.ipynb```, we feed features from the HousingPrice dataset into the classifier model. However, now, we expect our model to output a score that determines in which category the considered house is.
# 
# $ $ Let $\mathbf{X} \in \mathbb{R}^{N\times (D+1)}$ denote our data with $N$ samples and $D$ feature dimensions. Our targets, the binary labels, are given by $\mathbf{y} \in \mathbb{R}^{N\times 1}$. We want to estimate them with a simple classifier of the form
#
# $$ \mathbf{y} = \sigma \left( \mathbf{X} \mathbf{w} \right), $$
#
# $ $ where $\mathbf{w}\in \mathbb{R}^{(D+1) \times 1}$ is the weight of our classifier. The sigmoid function $\sigma: \mathbb{R} \to [0, 1]$, defined by
#
# $$ \sigma(t) = \frac{1}{1+\mathrm{exp}(-t)}, $$
#
# is used to squeeze the ouputs of the linear layer into the range $[0, 1]$. This provides us with a probabilistic interpretation of the ouput of the neural network and we can compute the label predictions by rounding the output.
# <img src="https://miro.medium.com/max/2400/1*RqXFpiNGwdiKBWyLJc_E7g.png" width="800">
# +
from exercise_code.data.csv_dataset import CSVDataset
from exercise_code.data.csv_dataset import FeatureSelectorAndNormalizationTransform
from exercise_code.data.dataloader import DataLoader
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import seaborn as sns
pd.options.mode.chained_assignment = None # default='warn'
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
# -
# ## 1. Load your data
# We apply the same dataloading and preprocessing steps as in the notebook ```1_linear_regression.ipynb```.
# +
target_column = 'SalePrice'
i2dl_exercises_path = os.path.dirname(os.path.abspath(os.getcwd()))
root_path = os.path.join(i2dl_exercises_path, "datasets", 'housing')
housing_file_path = os.path.join(root_path, "housing_train.csv")
download_url = 'https://cdn3.vision.in.tum.de/~dl4cv/housing_train.zip'
# Always make sure this line was run at least once before trying to
# access the data manually, as the data is downloaded in the
# constructor of CSVDataset.
train_dataset = CSVDataset(target_column=target_column, root=root_path, download_url=download_url, mode="train")
# -
# For the data transformations, compute min, max and mean for each feature column. We perform the same transformation on the training, validation, and test data.
# +
df = train_dataset.df
# Select only 2 features to keep plus the target column.
#selected_columns = ['OverallQual', 'GrLivArea', target_column]
selected_columns = ['GrLivArea', target_column]
mn, mx, mean = df.min(), df.max(), df.mean()
column_stats = {}
for column in selected_columns:
crt_col_stats = {'min' : mn[column],
'max' : mx[column],
'mean': mean[column]}
column_stats[column] = crt_col_stats
transform = FeatureSelectorAndNormalizationTransform(column_stats, target_column)
def rescale(data, key = "SalePrice", column_stats = column_stats):
""" Rescales input series y"""
mx = column_stats[key]["max"]
mn = column_stats[key]["min"]
return data * (mx - mn) + mn
# +
# Always make sure this line was run at least once before trying to
# access the data manually, as the data is downloaded in the
# constructor of CSVDataset.
train_dataset = CSVDataset(mode="train", target_column=target_column, root=root_path, download_url=download_url, transform=transform)
val_dataset = CSVDataset(mode="val", target_column=target_column, root=root_path, download_url=download_url, transform=transform)
test_dataset = CSVDataset(mode="test", target_column=target_column, root=root_path, download_url=download_url, transform=transform)
print("Number of training samples:", len(train_dataset))
print("Number of validation samples:", len(val_dataset))
print("Number of test samples:", len(test_dataset))
# +
# load training data into a matrix of shape (N, D), same for targets resulting in the shape (N, 1)
X_train = [train_dataset[i]['features'] for i in range((len(train_dataset)))]
X_train = np.stack(X_train, axis=0)
y_train = [train_dataset[i]['target'] for i in range((len(train_dataset)))]
y_train = np.stack(y_train, axis=0)
print("train data shape:", X_train.shape)
print("train targets shape:", y_train.shape)
# load validation data
X_val = [val_dataset[i]['features'] for i in range((len(val_dataset)))]
X_val = np.stack(X_val, axis=0)
y_val = [val_dataset[i]['target'] for i in range((len(val_dataset)))]
y_val = np.stack(y_val, axis=0)
print("val data shape:", X_val.shape)
print("val targets shape:", y_val.shape)
# load train data
X_test = [test_dataset[i]['features'] for i in range((len(test_dataset)))]
X_test = np.stack(X_test, axis=0)
y_test = [test_dataset[i]['target'] for i in range((len(test_dataset)))]
y_test = np.stack(y_test, axis=0)
print("test data shape:", X_val.shape)
print("test targets shape:", y_val.shape)
# 0 encodes small prices, 1 encodes large prices.
# -
# In the following, we model the regression task as a binary classification problem in the categories ```low-priced```and ```expensive``` by labeling the 30% of the houses that are sold with the lowest price with ```0``` and, accordingly, the 30% of the houses with the highest price with ```1```.
# +
from exercise_code.networks.utils import binarize
y_all = np.concatenate([y_train, y_val, y_test])
thirty_percentile = np.percentile(y_all, 30)
seventy_percentile = np.percentile(y_all, 70)
# Prepare the labels for classification.
X_train, y_train = binarize(X_train, y_train, thirty_percentile, seventy_percentile )
X_val, y_val = binarize(X_val, y_val, thirty_percentile, seventy_percentile)
X_test, y_test = binarize(X_test, y_test, thirty_percentile, seventy_percentile)
# -
# ## 1. Set up a classfier model
# We define a simple classifier in ```exercise_code/networks/classifier.py```. Implement the forward pass in method ```forward()``` and the backward pass in ```backward()``` in the Network class ```Classifier```. This time, you also need to implement the function ```sigmoid()```.
# +
from exercise_code.networks.classifier import Classifier
model = Classifier(num_features=1)
model.initialize_weights()
y_out, _ = model(X_train)
# plot the prediction
plt.scatter(X_train, y_train)
plt.plot(X_train, y_out, color='r')
# -
# ## 2. Implement the Loss Function: Binary Cross Entropy
#
#
# In this part, you will implement a binary cross entropy (BCE) loss function. Open the file `exercise_code/networks/loss.py` and implement the forward and backward pass of BCE loss into the `forward` and `backward` function.
#
# Remember the BCE loss function is:
# $$ bce = -\hat y log(y) - (1- \hat y) log(1-y)$$
#
# $ $ where $y$ is the output of your model, and $\hat y$ is the ground truth of the data
# +
from exercise_code.networks.loss import BCE
bce_loss = BCE()
# -
# ## Forward and Backward Check
#
# Once you have finished implementation of BCE loss class, you can run the following code to check whether your forward result and backward gradient are correct. You should expect your relative error to be lower than 1e-8.
#
# Here we will use a numeric gradient check to debug the backward pass:
#
# $$ \frac {df(x)}{dx} = \frac{f(x+h) - f(x-h)}{2h} $$
#
# where $h$ is a very small number, in practice approximately 1e-5 or so.
from exercise_code.tests.loss_tests import *
print (BCETest(bce_loss)())
# ## 3. Run Solver
#
# You have successfully implement a solver in the last task, now we will use that solver to solve this logistic regression problem.
# +
from exercise_code.solver import Solver
from exercise_code.networks.utils import test_accuracy
from exercise_code.networks.classifier import Classifier
# Select the number of features, you want your task to train on.
# Feel free to play with the sizes.
num_features = 1
# initialize model and weights
model = Classifier(num_features=num_features)
model.initialize_weights()
y_out, _ = model(X_test)
accuracy = test_accuracy(y_out, y_test)
print("Accuracy BEFORE training {:.1f}%".format(accuracy*100))
if np.shape(X_val)[1]==1:
plt.scatter(X_val, y_val, label = "Ground Truth")
inds = X_test.flatten().argsort(0)
plt.plot(X_test[inds], y_out[inds], color='r', label = "Prediction")
plt.legend()
plt.show()
data = {'X_train': X_train, 'y_train': y_train,
'X_val': X_val, 'y_val': y_val}
# We are going to use the BCE loss for this task.
loss = BCE()
# Please use these hyperparmeter as we also use them later in the evaluation
learning_rate = 1e-1
epochs = 25000
# Setup for the actual solver that's going to do the job of training
# the model on the given data. set 'verbose=True' to see real time
# progress of the training.
solver = Solver(model,
data,
loss,
learning_rate,
verbose=True,
print_every = 1000)
# Train the model, and look at the results.
solver.train(epochs)
plt.plot(solver.val_loss_history, label = "Validation Loss")
plt.plot(solver.train_loss_history, label = "Train Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.show()
# Test final performance
y_out, _ = model(X_test)
accuracy = test_accuracy(y_out, y_test)
print("Accuracy AFTER training {:.1f}%".format(accuracy*100))
if np.shape(X_test)[1]==1:
plt.scatter(X_test, y_test, label = "Ground Truth")
inds = X_test.argsort(0).flatten()
plt.plot(X_test[inds], y_out[inds], color='r', label = "Prediction")
plt.legend()
plt.show()
# -
# ### Save your BCELoss, Classifier and Solver for Submission
# Simply save your objects using the following cell. This will save them to a pickle file `models/logistic_regression.p`.
# +
from exercise_code.tests import save_pickle
save_pickle(
data_dict={
"BCE_class": BCE,
"Classifier_class": Classifier,
"Solver_class": Solver
},
file_name="logistic_regression.p"
)
# -
# # Submission Instructions
#
# Now, that you have completed the neccessary parts in the notebook, you can go on and submit your files.
#
# 1. Go on [our submission page](https://dvl.in.tum.de/teaching/submission/), register for an account and login. We use your matriculation number and send an email with the login details to the mail account associated. When in doubt, login into tum online and check your mails there. You will get an id which we need in the next step.
# 2. Navigate to `exercise_code` directory and run the `create_submission.sh` file to create the zip file of your model. This will create a single `zip` file that you need to upload. Otherwise, you can also zip it manually if you don't want to use the bash script.
# 3. Log into [our submission page](https://dvl.in.tum.de/teaching/submission/) with your account details and upload the `zip` file. Once successfully uploaded, you should be able to see the submitted "dummy_model.p" file selectable on the top.
# 4. Click on this file and run the submission script. You will get an email with your score as well as a message if you have surpassed the threshold.
# # Submission Goals
#
# - Goal: Successfully implement a classifier, a BCE loss function and a solver that can perform gradient descent and finally the model can predict the given dataset with an accuracy higher than 85%.
# - Test cases:
# 1. Does `forward()` and `backward()` of your classifier return the correct value and data type?
# 2. Does `forward()` and `backward()` of your BCE loss return the correct value and data type?
# 3. Does your `solver.train()` train the model that it achieves a prediction accuracy of your model beyond the given threshold accuracy of 85%? We train your classifier model with new initialised weights, lr = 0.1 and 25000 epochs on a 1-D classification problem.
# - Reachable points [0, 100]: 0 if not implemented, 100 if all tests passed, 33.3 per passed test
# - Threshold to clear exercise: 80
# - Submission start: __May 14, 2020 12.00__
# - Submission deadline : __May 20, 2020 23.59__
# - You can make multiple submission uptil the deadline. Your __best submission__ will be considered for bonus
#
|
exercise_04/.ipynb_checkpoints/2_logistic_regression-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/KSY1526/myblog/blob/master/_notebooks/2022-03-07-dacon_hands.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="BOHiVh7CjMwr"
# # "[DACON] ìëì ë¶ë¥ 겜ì§ëí with Pytorch"
# - author: <NAME>
# - categories: [jupyter, book, Deep Learning, Pytorch, DACON, Classifier]
# - image: images/220307.png
# + [markdown] id="JN62i9OOjMzH"
# # ë°ìŽí° ë¶ë¬ì€êž°
# + colab={"base_uri": "https://localhost:8080/"} id="V0lYI233jFd4" outputId="5dfd0036-8021-4748-8f9b-9be07a54c9fe"
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] id="-PkU7rLoRmtB"
# ë°ìŽí°ë¥Œ êµ¬êž ëëŒìŽëžì ì¬ë €ëê³ , ìœë©ê³Œ ì°ëí©ëë€.
# + colab={"base_uri": "https://localhost:8080/", "height": 299} id="C8SQLp5NjsrU" outputId="4589af9e-f96f-40af-b038-9f486f64987c"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
path = '/content/drive/MyDrive/hand_classification/'
train = pd.read_csv(path + 'train.csv')
test = pd.read_csv(path + 'test.csv')
sample_submission = pd.read_csv(path + 'sample_submission.csv')
train.head()
# + [markdown] id="ZhENqqX3RsXD"
# ë°ìŽí°ë¥Œ íë€ì€ë¡ ìœê³ ì ìœíëì§ íìží©ëë€. pathë ë°ìŽí° íìŒìŽ ì ì¥ëìŽìë 겜ë¡ë¥Œ ì믞í©ëë€.
# + [markdown] id="lodAPamOR3dA"
# # ë°ìŽí° ìŽíŽë³Žêž°
# + colab={"base_uri": "https://localhost:8080/"} id="irH1M_CSPcs6" outputId="92a18744-a5f0-4f96-d804-866b92dcafe0"
print(train.shape)
print(test.shape)
# + [markdown] id="LKj_XMFLR5Tm"
# ë°ìŽí°ì 칌ëŒìë íê² ìŽ ì ìžíê³ 33ê°ìŽê³ ížë ìž ë°ìŽí° 2335ê°. í
ì€íž ë°ìŽí° 9343ê° ì
ëë€.
#
# ë°ìŽí° ê°ìê° 2335ê°ë©Ž íëŒë¯ží°ê° ë§ì 몚ëžì ì¬ì©íêž° ì¡°êž ì ì ë°ìŽí°ìŽê³ , í
ì€íž ë°ìŽí°ê° íšì¬ ë§ì ê²ë í¹ì§ì
ëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="7-9FxUYSQI27" outputId="68f021c4-32be-4f87-b68c-1c177fbf8e69"
train.info()
# + [markdown] id="pjSVDMTFSYgd"
# ë°ìŽí° 칌ëŒëª
곌 ê²°ìž¡ì¹ë¥Œ íìžíêž° ìí íšìì
ëë€. ê²°ìž¡ì¹ë ìë ê²ìŒë¡ íìžë©ëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="w2ZKgWftPq41" outputId="b0090652-4754-40d3-9f82-67afbbee6aa9"
train['target'].value_counts()
# + [markdown] id="WfE0e0tASfIH"
# ì°ëŠ¬ê° ë§ì¶°ìŒ íë íê² ê°ì ë¶í¬ì
ëë€. ìë¹í ê³šê³ ë£š ë¶í¬ëìŽìë 걞 ì ì ììµëë€.
#
# ë¶ê· ííê² ë¶í¬ëìŽìë€ë©Ž ë³ëì ì¡°ì ìŽ íìí©ëë€ë§ ê·žëŽ íìë ììŽë³Žì
ëë€.
# + colab={"base_uri": "https://localhost:8080/", "height": 498} id="CteOqxPBPeqx" outputId="e242c478-255b-4429-b60e-7db34db911ef"
plt.figure(figsize=[12,8])
plt.text(s="Target variables",x=0,y=1.3, va='bottom',ha='center',color='#189AB4',fontsize=25)
plt.pie(train['target'].value_counts(),autopct='%1.1f%%', pctdistance=1.1)
plt.legend(['3', '2', '1', '0'], loc = "upper right",title="Programming Languages", prop={'size': 15})
plt.show()
# + [markdown] id="4XgccUMuS-nR"
# ë°©êž ìŽíŽë³ž ëŽì©ì íìŽ ê·žëí륌 íµíŽ ìê°í íììµëë€.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="ZW9-bXS-j_Ml" outputId="eeb534b2-2e60-4be1-b284-daa6068a326b"
train.describe().T
# + [markdown] id="Bc50mG2WTFfF"
# ë°ìŽí°ì ë¶í¬ë¥Œ ë³Žë€ ììží ìŽíŽë³Žêž° ìíŽ describe íšì륌 ì¬ì©íìµëë€. 칌ëŒìê° ë€ì ë§êž° ë묞ì 볎Ʞ ížíêž° ìíŽ T íšì륌 ì¬ì©íìµëë€.
#
# ë³ìë€ì ìŽëŠìŽ 몚ë sensor_ ííë¡ êµ¬ì±ëìŽ ììµëë€. ë íê· ê°ìŽ 몚ë 0 ê·Œì²ì ìêµ°ì.
#
# ë³ìë€ë§ë€ ì¡°êžì© ì°šìŽë ìì§ë§ ëì²Žë¡ ìµìê°ì -130 ë°ìŒë¡ë ìëšìŽì§ê³ ìµëê°ë +130 ìë¡ë ì¬ëŒê°ì§ ììµëë€.
#
# ë³ìë€ì ë¶í¬ê° ìë¹í ì ì¬íŽ 볎ìŽëë°ì. ìŽë¯žì§ì íëì íœì
ê° ê°ìŽ íëì ë°ìŽí°ë¥Œ 32ë¶í í ë°ìŽí°ë¡ ì¶ìž¡ë©ëë€.
#
# ìŽë° ë°ìŽí°ë ë³ìê° ìŒêŽì±ìŽ ìêž° ë묞ì ë¥ë¬ë êž°ë° ëªšëžìŽ íšìšì ìŒ ê²ìŒë¡ íëšë©ëë€.
# + [markdown] id="40c6hCE7UxQi"
# # ë°ìŽí° ì€ìŒìŒë§
# + colab={"base_uri": "https://localhost:8080/"} id="IJDSXbnJkFLn" outputId="d80c28ef-60af-4914-e614-34b9268ddfb7"
train_x = train.drop(['id', 'target'], axis = 1)
test_x = test.drop(['id'], axis = 1)
mins = train_x.min()
maxs = train_x.max()
mins[:5]
# + [markdown] id="Hb3bB9RXbBdx"
# ë°ìŽí° ëŽ ì¹ŒëŒë³ë¡ ìµìê°, ìµëê°ì ì¶ì¶íìµëë€. ë°ìŽí°ë€ì ì€ìŒìŒë§ íêž° ìí 목ì ì
ëë€.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="RcARdOtnUoNy" outputId="5b59a98d-3619-4e66-8f03-e0ed9ecc4f14"
train_x = (train_x - mins) / (maxs - mins)
test_x = (test_x - mins) / (maxs - mins)
train_x.describe().T[['min', 'max']]
# + [markdown] id="27vHXOuXbUz1"
# (ë°ìŽí° - ìµìê°) / (ìµëê° - ìµìê°) ì°ì°ì ê±°ì¹ê² ëë©Ž ë°ìŽí° ê°ë€ìŽ 몚ë 0~1 ì¬ìŽë¡ ê°ì§ê² ë©ëë€.
#
# ë¥ë¬ëìì ì
ë ¥ê°ì íì€í ìí€ë ê²ìŽ ìë¹í ì€ìí©ëë€.
# + [markdown] id="8aVHkX2HWheR"
# # ë°ìŽí° ë¡ë ë§ë€êž°
# + colab={"base_uri": "https://localhost:8080/"} id="dbD8xgrZV2Sh" outputId="22f5282d-6c5b-48aa-e514-3cff4368ece7"
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import random
random.seed(42)
torch.manual_seed(42)
# + [markdown] id="JSSCVqsUbwR-"
# ë¥ë¬ëì íìí íìŽí ì¹ êŽë š íší€ì§ë€ì ì€ì¹í©ëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="bt4rz3boU1ta" outputId="6bbad156-0177-466f-f697-be55b64f3642"
train_x = torch.from_numpy(train_x.to_numpy()).float()
train_y = torch.tensor(train['target'].to_numpy(), dtype = torch.int64)
test_x = torch.from_numpy(test_x.to_numpy()).float()
train_x
# + [markdown] id="8y8lriPUb3g6"
# ë°ìŽí°ê° íë€ì€ì ë°ìŽí° íë ì íììŒë¡ ì ì¥ëìŽ ììµëë€. ë°ìŽí° íë ìì ëíìŽë¡, ë€ì ëíìŽë¥Œ í
ì ííë¡ ë°êŸŒ 몚ìµì
ëë€.
#
# íìŽí ì¹ ëªšëžì ìŽì©íêž° ìíŽì ë°ìŽí°ë í
ìííë¡ ë³ííŽì£ŒìŽìŒ í©ëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="14fN49_qZHnV" outputId="546621b5-57f0-450d-903c-d96cd8329a1a"
train_dataset = TensorDataset(train_x, train_y)
print(train_dataset.__len__())
print(train_dataset.__getitem__(1))
# + [markdown] id="mXHzj7cvcarP"
# ì
ë ¥í ë°ìŽí°ë¥Œ íìŽí ì¹ìì ì§ìíë TensorDataset íšì륌 ì¬ì©íŽ ë°ìŽí° ì
ííë¡ ë§ë€ììµëë€.
#
# ë°ìŽí°ê° ë°ìŽí° ì
ëŽ ì ì
ë ¥ ë¬ëì§ len, getitem íšì륌 íµíŽ íìžíë€ì.
#
# ë°ë¡ ë€ì ëì€ë ë°ìŽí° ë¡ë륌 ì¬ì©íêž° ìíŽì ë°ìŽí° ì
ííë¡ ë°ìŽí°ë¥Œ ë§ë€ìŽìŒ í©ëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="-RzF6FLzaYBt" outputId="36650272-8af8-482f-efaa-a2b1cecae8ff"
train_dataloader = DataLoader(train_dataset, batch_size = 16, shuffle = True)
for batch_idx, samples in enumerate(train_dataloader):
if batch_idx > 0:
break
print(samples[0].shape)
print(samples[1])
# + [markdown] id="1wz9Bk42c0k1"
# ë°ìŽí° ì
ì íìŽí ì¹ ëŽ DataLoader íšìì ë£ìŽ ë°ìŽí° ë¡ë륌 ë§ë€ììµëë€.
#
# ë°ìŽí° ë¡ë íìì ìŽì©íë©Ž ë°°ì¹ëšìë¡ ë°ìŽí°ë¥Œ 몚ëžì ë£ì ì ìê³ shuffle ìžì륌 ì¬ì©íŽ ë°ìŽí°ë¥Œ ìœê² ìì ìë ììµëë€.
# + [markdown] id="7hFFow4DcvLC"
# # ëªšëž ì í©íêž°
# + colab={"base_uri": "https://localhost:8080/"} id="LIYCcEByarKS" outputId="2084acdf-e352-4d05-d7ff-e0dde0937113"
class Models(nn.Module):
def __init__(self):
super().__init__()
self.linear_relu_stack = nn.Sequential(
nn.Linear(32, 64),
nn.BatchNorm1d(64),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(64, 128),
nn.BatchNorm1d(128),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(128, 4),
)
def forward(self, x):
x = self.linear_relu_stack(x)
return x
model = Models()
print(model)
# + [markdown] id="nSn4HNMEdPGy"
# ê°ëší ë¥ë¬ë 몚ëžì ì§ì ì ìíìµëë€. íìŽí ì¹ ëŽ nn.Module íŽëì€ë¥Œ ììë°ììµëë€.
#
# 32ê°ì ì
ë ¥ ë°ìŽí°ë¥Œ ë°ì 64ê°, 128ê°ë¡ ìë ìžµ ëŽ ë
žë ê°ì륌 ë늬ë€ê° ììž¡ ê°ìŽ 4ê°ìŽêž° ë묞ì ìµì¢
ì¶ë ¥ ë
žëë 4ê°ë¡ 구ì±íìµëë€.
#
# BatchNorm1dì Dropoutì ìŽì©íŽ ë°°ì¹ ì ê·íì ëë¡ìì êž°ë¥ì ì¬ì©íìŒë©° íì±í íšìë¡ë Relu륌 ì¬ì©íìµëë€.
#
# ë°ìŽí°ê° ì êž° ë묞ì íëŒë¯ží°ìê° ë§ìŒë©Ž ìë ê² ê°ìì ìžµì ì ê² ìììµëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="U5CVDmNveAEY" outputId="cf29285b-a0d7-4eaa-c9e6-7b81db69d132"
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
for epoch in range(20):
running_loss = 0.0
accuracy = 0
for i, data in enumerate(train_dataloader, 0):
inputs, labels = data
optimizer.zero_grad() # 맀ê°ë³ì륌 0ìŒë¡ ë§ëëë€. 맀 íìµì ìŽêž°ííŽì€ìŒí©ëë€.
outputs = model(inputs) # ì
ë ¥ê°ì ë£ìŽ ìì í륌 ì§íìíµëë€.
loss = criterion(outputs, labels) # ëªšëž ì¶ë ¥ê°ì ì€ì ê°ì ìì€íšìì ëì
í©ëë€.
loss.backward() # ìì€íšììì ìì í ìíí©ëë€.
optimizer.step() # ìµí°ë§ìŽì 륌 ì¬ì©íŽ 맀ê°ë³ì륌 ìµì íí©ëë€.
running_loss += loss.item()
_, predictions = torch.max(outputs, 1)
for label, prediction in zip(labels, predictions):
if label == prediction:
accuracy = accuracy + 1
print(f'{epoch + 1} ìí¬í¬ loss: {running_loss / i:.3f}')
print(f'{epoch + 1} ìí¬í¬ ì íë: {accuracy / (i * 16):.3f}')
# + [markdown] id="FpxJxRoeempy"
# 20 ìí¬í¬ë¥Œ ì§ííìŒë©° ìí¬í¬ë§ë€ íìµìŽ ì ëìŽê°ëì§ë¥Œ íê°íìµëë€. ìµí°ë§ìŽì ë¡ ë¬Žëí Adamì ì¬ì©íìµëë€.
#
# ìì€íšìë CrossEntropyLossì ì¬ì©íëë°, íê²ê°ì ì-í« ìžìœë© íì§ ììë ììì ì ì©ììŒì£Œë©° ìíížë§¥ì€íšìê¹ì§ ììì ì ì©íŽì€ì ìì€ê°ì 구íŽì£Œë ížëŠ¬í íšì ì
ëë€.
# + [markdown] id="tVhDMfx5fgnk"
# # ëªšëž íê°
# + colab={"base_uri": "https://localhost:8080/"} id="n89V4yHNShPS" outputId="ef345fc6-c16f-4652-9503-2b2a29d0be1a"
model.eval() # 몚ëžì íê°ëªšëë¡ ë°ê¿ëë€. dropoutìŽ ìŒìŽëì§ ììµëë€.
with torch.no_grad(): # ìŽ ìì ìœëë ê°ì€ì¹ ì
ë°ìŽížê° ìŒìŽëì§ ììµëë€.
outputs = model(test_x)
_, pred = torch.max(outputs, 1)
pred
# + [markdown] id="X0ZTNfqvfrcL"
# ìì 구í 몚ëžì í
ì€íž ë°ìŽí°ë¥Œ ë£ìŽì 결곌륌 ì¶ë ¥í©ëë€. torch.max íšìê° ë§€ì° ížëŠ¬í©ëë€.
# + colab={"base_uri": "https://localhost:8080/"} id="3fN9eTUuVygL" outputId="0add9d68-c390-4457-c4cc-f17e4af0a780"
sample_submission['target'] = pred.numpy()
sample_submission['target'].value_counts()
# + [markdown] id="bx6MQzlKf-VU"
# í
ì€íž ë°ìŽí°ì íê² ììž¡ ê° ë¶í¬ ì
ëë€. ë€ì ë¶ê· íìŽ ìì§ë§ ê·žëë 몚ëžìŽ ìŽëì ë êž°ë¥ì íë ê² ê°ìµëë€.
# + id="ohnQMw3bUhCM"
sample_submission.to_csv('dacon_hands_4.csv',index=False)
# + [markdown] id="TqpEf6_1gKa1"
# ìµì¢
결곌륌 csv ííë¡ ì ì¥í©ëë€.
# + [markdown] id="6sLv3tc0gRc-"
# # ëëì
# + [markdown] id="TVwfye__gTdA"
# ìì ê°ê°í ì§ííì§ ììŒë©Ž ì€ë ¥ìŽ êžë°© ë
¹ì°ë ê² ê°ìµëë€. ê°ëší ë¥ë¬ë ìœë륌 ì°ë ê²ë ìœì§ ìë€ì.
#
# 몚ëžì ë ìµì í ìí¬ì ìì ê² ê°ìµëë€. ìžµ ê°ì ì¡°ì , íë ìžµ ë
žë ì ë³ê²œ ë± ì¬ë¬ê°ì§ë¥Œ ìëí ì ìê² ë€ì.
#
# ë°ìŽí°ê° ì ìŽì ë¥ë¬ë 몚ëžìŽ ì ì±ë¥ì ë°íí ê¹ ìì¬ìŽ ììëë° êœ€ êŽì°®ì 몚ìµì ë³Žìž ê² ê°ìµëë€.
#
# ë¥ë¬ë ìœëë ì¬êž°ì ë§ìŽ ì°žê³ íìµëë€. ê°ì¬í©ëë€.
#
# (http://www.gisdeveloper.co.kr/?p=8443)
|
_notebooks/2022-03-07-dacon_hands.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: bmcs_env
# language: python
# name: bmcs_env
# ---
# # Time dependent tensile response
# %matplotlib widget
import matplotlib.pylab as plt
from bmcs_beam.tension.time_dependent_cracking import TimeDependentCracking
import sympy as sp
sp.init_printing()
import numpy as np
# # Single material point
# ## Time dependent function
TimeDependentCracking(T_prime_0 = 100).interact()
# ### Time-dependent temperature evolution function
#
# Find a suitable continuous function that can represent the temperature evolution during the hydration. Currently the a function of a Weibull type has been chosen and transformed such that the peak value and the corresponding time can be specified as a parameter.
t = sp.symbols('t', nonnegative=True)
T_m = sp.Symbol("T_m", positive = True)
T_s = sp.Symbol("T_s", positive = True)
omega_fn = 1 - sp.exp(-(t/T_s)**T_m)
T_prime_0 = sp.Symbol("T_prime_0", positive = True)
T_t = (1 - omega_fn) * T_prime_0 * t
# **Shape functions for temperature evolution**
T_t
T_prime_t = sp.simplify(T_t.diff(t))
T_prime_t
# **Transform the shape function**
# to be able to explicitly specify the maximum temperature and corresponding time
t_argmax_T = sp.Symbol("t_argmax_T")
T_s_sol = sp.solve( sp.Eq( sp.solve(T_prime_t,t)[0], t_argmax_T ), T_s)[0]
T_max = sp.Symbol("T_max", positive=True)
T_prime_0_sol = sp.solve(sp.Eq(T_t.subs(T_s, T_s_sol).subs(t, t_argmax_T), T_max),
T_prime_0)[0]
T_max_t = sp.simplify( T_t.subs({T_s: T_s_sol, T_prime_0: T_prime_0_sol}) )
T_max_t
get_T_t = sp.lambdify((t, T_prime_0, T_m, T_s), T_t)
get_T_max_t = sp.lambdify((t, T_max, t_argmax_T, T_m), T_max_t)
data = dict(T_prime_0=100, T_m=1, T_s=1)
_, ax = plt.subplots(1,1)
t_range = np.linspace(0,10,100)
plt.plot(t_range, get_T_t(t_range, **data));
plt.plot(t_range, get_T_max_t(t_range, 37, 1., 2));
# ### Time dependent compressive strength
# **From Eurocode 2:**
# $s$ captures the effect of cement type on the time evolution of the compressive strength
# it ranges from $s = 0.2$ for class R (rapid), $s = 0.25$ for class N (normal), and $s = 0.38$ for class S (slow).
s = sp.Symbol("s", positive=True)
beta_cc = sp.exp( s * (1 - sp.sqrt(28/t)))
beta_cc
get_beta_cc = sp.lambdify((t, s), beta_cc )
_, ax = plt.subplots(1,1)
plt.plot(t_range, get_beta_cc(t_range, 0.2))
# ### Compressive strength
f_cm_28 = sp.Symbol("f_cm28", positive=True)
f_cm_28
f_cm_t = beta_cc * f_cm_28
f_cm_t
get_f_cm_t = sp.lambdify((t, f_cm_28, s), f_cm_t)
# ### Tensile strength
f_ctm = sp.Symbol("f_ctm", positive=True)
alpha_f = sp.Symbol("alpha_f", positive=True)
f_ctm_t = beta_cc * f_ctm
f_ctm_t
get_f_ctm_t = sp.lambdify((t, f_ctm, s), f_ctm_t)
# ### Elastic modulus
E_cm_28 = sp.Symbol("E_cm28", positive=True)
E_cm_t = (f_cm_t / f_cm_28)**0.3 * E_cm_28
E_cm_t
get_E_cm_t = sp.lambdify((t, E_cm_28, s), E_cm_t)
# ## Uncracked state
# - Specimen is clamped at both sides. Then $\varepsilon_\mathrm{app} = 0, \forall x \in \Omega$
# - Then the matrix stress is given as
# \begin{align}
# \sigma^\mathrm{m}(x,t) = - E^\mathrm{m}(t)
# \cdot \alpha \int_0^t T^\prime(x,\theta)\, \mathrm{d}\theta
# \end{align}
alpha = sp.Symbol("alpha", positive=True )
eps_eff = alpha * T_max_t
dot_T_max_t = sp.simplify(T_max_t.diff(t))
dot_eps_eff = alpha * dot_T_max_t
dot_E_cm_t = E_cm_t.diff(t)
sig_t = E_cm_t * eps_eff
dot_sig_t = E_cm_t * dot_eps_eff + dot_E_cm_t * eps_eff
sp.simplify(dot_sig_t)
# Integral cannot be resolved algebraically - numerical integration is used
# +
#sig2_t = sp.integrate(dot_sig_t, (t,0,t))
# -
# # Single crack state
# ## Time-dependent debonding process
# ### Fibers
# - If there is a crack at $x_I$, then there can be non-zero apparent strains within the debonded zone - measurable using local strain sensors, i.e.
# \begin{align}
# \exists x \in (L_I^{(-)},L_I^{(+)}), \; \varepsilon_\mathrm{app}^\mathrm{f}(x,t) \neq 0.
# \end{align}
# - However, the integral of apparent strain in the fibers must disappear within the debonded zone, i.e.
# \begin{align}
# \int_{L^{(-)}}^{L^{(+)}}\varepsilon^\mathrm{f}_\mathrm{app}(x,t)\, \mathrm{d}x = 0
# \end{align}
# - Crack bridging fiber stress is given as
# \begin{align}
# \sigma^{\mathrm{f}}(x=0, t) = E^{\mathrm{f}} \varepsilon^{\mathrm{f}}_\mathrm{eff}(x=0, t)
# \end{align}
# ### Matrix
# - The integrated apparent strain in the matrix must be equal to crack opening $w_I$, i.e.
# \begin{align}
# \int_{L_I^{(-)}}^{L_I^{(+)}}\varepsilon^\mathrm{m}_\mathrm{app}(x,t)\, \mathrm{d}x + w_I = 0
# \end{align}
# - Considering symmetry, we can write
# \begin{align}
# \int_{0}^{L_I^{(+)}}\varepsilon^\mathrm{m}_\mathrm{app}(x,t)\, \mathrm{d}x
# + \frac{1}{2} w_I(t) = 0
# \end{align}
# This relation holds for a homogeneous strain distribution along the bar specimen.
# Considering a non reinforced concrete bar, it is possible to detect the time of
# a crack occurrence by requiring setting:
# \begin{align}
# f_\mathrm{ct}(t) = \sigma_\mathrm{c}(t)
# \end{align}
# # Multiple cracks
# The temperature development during the hydration process follows the relation
# \begin{align}
# T(t,x)
# \end{align}
# At the same time, the material parameters of the concrete matrix and of bond are
# defined as time functions
# \begin{align}
# E(t), f_\mathrm{ct}(t), \tau(t)
# \end{align}
# Temperature-induced concrete strain in a point $x$ at time $t$ is expressed as
# \begin{align}
# \bar{\varepsilon}_{T}(t,x) = \alpha \int_0^t \frac{\mathrm{d} T(t,x)}{\mathrm{d} t} {\mathrm{d} t}
# \end{align}
# \begin{align}
# \bar{\varepsilon}_\mathrm{app} = \bar{\varepsilon}_\mathrm{eff} + \bar{\varepsilon}_\mathrm{\Delta T}
# \end{align}
# If the apparent strain is suppressed, i.e. $\bar{\varepsilon}_\mathrm{app} = 0$, the effective stress is given as
# \begin{align}
# 0 = \bar{\varepsilon}_\mathrm{eff} +
# \bar{\varepsilon}_{\Delta T} \implies
# \bar{\varepsilon}_\mathrm{eff} = - \alpha \Delta T
# \end{align}
# More precisely, this equation reads
# \begin{align}
# \bar{\varepsilon}_\mathrm{eff}(t) = - \alpha \, \int_0^t \frac{\mathrm{d}T}{ \mathrm{d}t} \, \mathrm{d} t
# \end{align}
# Current force at the boundary of the specimen is then given as
# \begin{align}
# \sigma = E(t) \, \varepsilon_{\mathrm{eff}}(t)
# \end{align}
# \begin{align}
# \sigma = E(t) \left(\varepsilon_{\mathrm{app}}(x,t) - \alpha \int_0^t T^\prime(x,\theta) \, \mathrm{d}\theta \right)
# \end{align}
# **Salient features of the algorithm**
#
# Non-linearity included by cracking stress
#
# - find the time and location of the next crack occurrence
# - provide a local, crack-centered solution of the cracking problem
|
bmcs_beam/tension/time_dependent_cracking.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="Sblxia5TgLd3"
# ### **Import Google Drive**
# + colab_type="code" id="XoRXn_JGbXXF" outputId="cc54aeb8-921a-4e75-96cd-e96315a43fda" colab={"base_uri": "https://localhost:8080/", "height": 34}
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] colab_type="text" id="jkKqS3sugTfv"
# ### **Import Library**
# + colab_type="code" id="Sq0-DSkQb1QL" outputId="e1f56ec9-d7aa-4c10-f1bc-f2a460de8240" colab={"base_uri": "https://localhost:8080/", "height": 88}
import glob
import numpy as np
import os
import shutil
np.random.seed(42)
from sklearn.preprocessing import LabelEncoder
import cv2
import tensorflow as tf
import keras
import shutil
import random
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.utils import class_weight
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, cohen_kappa_score
# + [markdown] colab_type="text" id="2hoyY92GgqLN"
# ### **Load Data**
# + colab_type="code" id="5YBUfq-TRS5g" colab={}
os.chdir('/content/drive/My Drive/Colab Notebooks/DATA RD/')
Train = glob.glob('/content/drive/My Drive/Colab Notebooks/DATA RD/DATASETS/Data Split/Train/*')
Val=glob.glob('/content/drive/My Drive/Colab Notebooks/DATA RD/DATASETS/Data Split/Validation/*')
Test=glob.glob('/content/drive/My Drive/Colab Notebooks/DATA RD/DATASETS/Data Split/Test/*')
# + colab_type="code" id="VwWB-ob7cR0c" outputId="468e254a-1018-4f15-8000-ace8aeb9d0b8" colab={"base_uri": "https://localhost:8080/", "height": 269}
import matplotlib.image as mpimg
for ima in Train[600:601]:
img=mpimg.imread(ima)
imgplot = plt.imshow(img)
plt.show()
# + [markdown] colab_type="text" id="f7VYJa04g1oz"
# ### **Data Preparation**
# + colab_type="code" id="TfB7k95fcYy_" colab={}
nrows = 224
ncolumns = 224
channels = 3
def read_and_process_image(list_of_images):
X = [] # images
y = [] # labels
for image in list_of_images:
X.append(cv2.resize(cv2.imread(image, cv2.IMREAD_COLOR), (nrows,ncolumns), interpolation=cv2.INTER_CUBIC)) #Read the image
#get the labels
if 'Normal' in image:
y.append(0)
elif 'Mild' in image:
y.append(1)
elif 'Moderate' in image:
y.append(2)
elif 'Severe' in image:
y.append(3)
return X, y
# + colab_type="code" id="reNQR9Z5c0cK" colab={}
X_train, y_train = read_and_process_image(Train)
X_val, y_val = read_and_process_image(Val)
X_test, y_test = read_and_process_image(Test)
# + colab_type="code" id="T0wReCythoBX" outputId="1e38a33f-2260-4ca9-e29f-b9f1e616062e" colab={"base_uri": "https://localhost:8080/", "height": 68}
import seaborn as sns
import gc
gc.collect()
#Convert list to numpy array
X_train = np.array(X_train)
y_train= np.array(y_train)
X_val = np.array(X_val)
y_val= np.array(y_val)
X_test = np.array(X_test)
y_test= np.array(y_test)
print('Train:',X_train.shape,y_train.shape)
print('Val:',X_val.shape,y_val.shape)
print('Test',X_test.shape,y_test.shape)
# + colab_type="code" id="blCi7eQauK9m" outputId="76cd5b08-bd85-48c7-f0f4-33c6d737b688" colab={"base_uri": "https://localhost:8080/", "height": 298}
sns.countplot(y_train)
plt.title('Total Data Training')
# + colab_type="code" id="J7zQR5AxuPzF" outputId="1be54816-69fa-4a6e-e5f3-cab9026da34b" colab={"base_uri": "https://localhost:8080/", "height": 298}
sns.countplot(y_val)
plt.title('Total Data Validasi')
# + colab_type="code" id="02Z9N2vXuSBh" outputId="77dc7618-59ed-488a-aaab-44e2bc1c6ebe" colab={"base_uri": "https://localhost:8080/", "height": 298}
sns.countplot(y_test)
plt.title('Total Data Test')
# + colab_type="code" id="EqPK3IPxo95J" outputId="7a40cb13-83e5-4364-fc23-a70b0bf3e305" colab={"base_uri": "https://localhost:8080/", "height": 34}
y_train_ohe = pd.get_dummies(y_train)
y_val_ohe=pd.get_dummies(y_val)
y_test_ohe=pd.get_dummies(y_test)
y_train_ohe.shape,y_val_ohe.shape,y_test_ohe.shape
# + [markdown] colab_type="text" id="4iJYJgisg8dH"
# ### **Model Parameters**
# + colab_type="code" id="ytNo2TStiKeq" colab={}
batch_size = 16
EPOCHS = 100
WARMUP_EPOCHS = 2
LEARNING_RATE = 0.001
WARMUP_LEARNING_RATE = 1e-3
HEIGHT = 224
WIDTH = 224
CANAL = 3
N_CLASSES = 4
ES_PATIENCE = 5
RLROP_PATIENCE = 3
DECAY_DROP = 0.5
# + [markdown] colab_type="text" id="2SMJXHEXhQIN"
# ### **Data Generator**
# + colab_type="code" id="hYQ9Kosh3IE4" colab={}
train_datagen =tf.keras.preprocessing.image.ImageDataGenerator(
rotation_range=360,
horizontal_flip=True,
vertical_flip=True)
test_datagen=tf.keras.preprocessing.image.ImageDataGenerator()
# + colab_type="code" id="A2RgBtZ6gQQ-" colab={}
train_generator = train_datagen.flow(X_train, y_train_ohe, batch_size=batch_size)
val_generator = test_datagen.flow(X_val, y_val_ohe, batch_size=batch_size)
test_generator = test_datagen.flow(X_test, y_test_ohe, batch_size=batch_size)
# + [markdown] colab_type="text" id="2pL98gvOhA8H"
# ### **Define Model**
# + colab_type="code" id="d5DMG4bLpybJ" colab={}
IMG_SHAPE = (224, 224, 3)
base_model =tf.keras.applications.InceptionV3(weights='imagenet',
include_top=False,
input_shape=IMG_SHAPE)
x =tf.keras.layers.GlobalAveragePooling2D()(base_model.output)
x =tf.keras.layers.Dropout(0.5)(x)
x =tf.keras.layers.Dense(128, activation='relu')(x)
x =tf.keras.layers.Dropout(0.5)(x)
final_output =tf.keras.layers.Dense(N_CLASSES, activation='softmax', name='final_output')(x)
model =tf.keras.models.Model(inputs=base_model.inputs,outputs=final_output)
# + [markdown] colab_type="text" id="91aZG6YAhKWd"
# ### **Train Top Layers**
# + colab_type="code" id="rTCGYgB4bPZu" outputId="d22133f6-13d8-4128-b564-149e1eeab6d8" colab={"base_uri": "https://localhost:8080/", "height": 1000}
for layer in model.layers:
layer.trainable = False
for i in range(-5, 0):
model.layers[i].trainable = True
metric_list = ["accuracy"]
optimizer =tf.keras.optimizers.Adam(lr=WARMUP_LEARNING_RATE)
model.compile(optimizer=optimizer, loss="categorical_crossentropy", metrics=metric_list)
model.summary()
# + colab_type="code" id="k0bm5xjY3VFo" outputId="72a6e8e0-2ee6-4ca4-b797-57b4a42c7932" colab={"base_uri": "https://localhost:8080/", "height": 173}
import time
start = time.time()
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = val_generator.n//val_generator.batch_size
history_warmup = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=val_generator,
validation_steps=STEP_SIZE_VALID,
epochs=WARMUP_EPOCHS,
verbose=1).history
end = time.time()
print('Waktu Training:', end - start)
# + [markdown] id="xGyydfKvPmKJ" colab_type="text"
# ### **Train Fine Tuning**
# + id="VIbkVHPKPUt_" colab_type="code" outputId="917f2d01-3bbb-4b49-f998-d5cdf4c60607" colab={"base_uri": "https://localhost:8080/", "height": 1000}
for layer in model.layers:
layer.trainable = True
es =tf.keras.callbacks.EarlyStopping(monitor='val_loss', mode='min', patience=ES_PATIENCE, restore_best_weights=True, verbose=1)
rlrop =tf.keras.callbacks.ReduceLROnPlateau(monitor='val_loss', mode='min', patience=RLROP_PATIENCE, factor=DECAY_DROP, min_lr=1e-6, verbose=1)
callback_list = [es]
optimizer =tf.keras.optimizers.Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer, loss="categorical_crossentropy", metrics=metric_list)
model.summary()
# + id="LVulv235PjBY" colab_type="code" outputId="c26dd0ab-4411-4e78-a160-181bcf1012b6" colab={"base_uri": "https://localhost:8080/", "height": 867}
history_finetunning = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=val_generator,
validation_steps=STEP_SIZE_VALID,
epochs=EPOCHS,
callbacks=callback_list,
verbose=1).history
# + [markdown] colab_type="text" id="AwoapwzXhsW6"
# ### **Model Graph**
# + colab_type="code" id="KRcO67Vicu1O" outputId="90a93983-150d-4a83-b420-c42c982b914c" colab={"base_uri": "https://localhost:8080/", "height": 1000}
history = {'loss': history_warmup['loss'] + history_finetunning['loss'],
'val_loss': history_warmup['val_loss'] + history_finetunning['val_loss'],
'acc': history_warmup['accuracy'] + history_finetunning['accuracy'],
'val_acc': history_warmup['val_accuracy'] + history_finetunning['val_accuracy']}
sns.set_style("whitegrid")
fig, (ax1, ax2) = plt.subplots(2, 1, sharex='col', figsize=(20, 18))
ax1.plot(history['loss'], label='Train loss')
ax1.plot(history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history['acc'], label='Train accuracy')
ax2.plot(history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
plt.xlabel('Epochs')
sns.despine()
plt.show()
# + [markdown] colab_type="text" id="_h4374OuiJMn"
# ### **Evaluate Model**
# + colab_type="code" id="t4erNAeF1pkZ" outputId="9946a1da-0ea0-42a6-d9df-bbb594a123df" colab={"base_uri": "https://localhost:8080/", "height": 51}
loss_Val, acc_Val = model.evaluate(X_val, y_val_ohe,batch_size=1, verbose=1)
print("Validation: accuracy = %f ; loss_v = %f" % (acc_Val, loss_Val))
# + colab_type="code" id="bMS3Sz5Wak24" colab={}
lastFullTrainPred = np.empty((0, N_CLASSES))
lastFullTrainLabels = np.empty((0, N_CLASSES))
lastFullValPred = np.empty((0, N_CLASSES))
lastFullValLabels = np.empty((0, N_CLASSES))
for i in range(STEP_SIZE_TRAIN+1):
im, lbl = next(train_generator)
scores = model.predict(im, batch_size=train_generator.batch_size)
lastFullTrainPred = np.append(lastFullTrainPred, scores, axis=0)
lastFullTrainLabels = np.append(lastFullTrainLabels, lbl, axis=0)
for i in range(STEP_SIZE_VALID+1):
im, lbl = next(val_generator)
scores = model.predict(im, batch_size=val_generator.batch_size)
lastFullValPred = np.append(lastFullValPred, scores, axis=0)
lastFullValLabels = np.append(lastFullValLabels, lbl, axis=0)
# + colab_type="code" id="4lyPRBembKGQ" colab={}
lastFullComPred = np.concatenate((lastFullTrainPred, lastFullValPred))
lastFullComLabels = np.concatenate((lastFullTrainLabels, lastFullValLabels))
complete_labels = [np.argmax(label) for label in lastFullComLabels]
train_preds = [np.argmax(pred) for pred in lastFullTrainPred]
train_labels = [np.argmax(label) for label in lastFullTrainLabels]
validation_preds = [np.argmax(pred) for pred in lastFullValPred]
validation_labels = [np.argmax(label) for label in lastFullValLabels]
# + colab_type="code" id="vH0NTCX8awLW" outputId="39343bb7-2dba-4259-f7ce-20f962aaa69e" colab={"base_uri": "https://localhost:8080/", "height": 419}
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
labels = ['0 - No DR', '1 - Mild', '2 - Moderate', '3 - Severe']
train_cnf_matrix = confusion_matrix(train_labels, train_preds)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation')
plt.show()
|
Trainer-Collaboratories/Fine_Tuning/InceptionV3/Fine_tuning_InceptionV3(GAP_128_0,5).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Policy Evaluation & Iteration on a GridWorld example
import numpy as np
from gridworld import GridworldEnv
import copy
env = GridworldEnv()
# #### Args of environment:
# policy: [S, A] shaped matrix representing the policy.
# env: OpenAI env. env.P represents the transition probabilities (system probability) of the environment.
# env.P[s][a] is a list of transition tuples (prob, next_state, reward, done).
# env.nS is a number of states in the environment.
# env.nA is a number of actions in the environment.
# theta: We stop evaluation once our value function change is less than theta for all states.
# discount_factor: Gamma discount factor.
env.nA
env.P
# ### Policy Evaluation (Sutton & Barto book) -
#
# <img src="./images/sutton_barto_policy_evaluation.png">
#
#
# ### Implementation -
# <img src="./images/policy_eval.jpg">
def policy_eval(policy, env, discount_factor, theta):
V = np.zeros(env.nS)
k=0
while True:
V_old = copy.deepcopy(V)
for state in range(env.nS):
agg_value = 0
for action in range(env.nA):
for prob_system,next_state,reward,done in env.P[state][action]:
agg_value += (V[next_state]*discount_factor + reward)*prob_system*policy[state][action]
V[state] = agg_value
change = np.linalg.norm(np.abs(V - V_old))
if change<theta:
break
return np.array(V)
given_policy = np.ones([env.nS, env.nA]) / env.nA
# 16 states, 4 actions - 16*4 matrix
given_policy
policy_eval(given_policy,env,1,0.00001)
#from dennybritz repo
expected_v = np.array([0, -14, -20, -22, -14, -18, -20, -20, -20, -20, -18, -14, -22, -20, -14, 0])
# ### Policy Iteration
#
# <img src="./images/policy_iteration.png">
#
#
# 1)Randomly initialize a policy
# 2)Evaluate the policy
# 3)Select the best action according to current policy (present_best_action in code)
# 4)Evaluate expected
#
# value of each action by doing one-step lookahed (action_expected_value_vector in code) as -
#
# <img src="./images/action_value.gif">
# ### .
#
# 5)Select the best action from one step lookahed action_expected_value_vector - improved_best_action
# 6)Change the policy
# 7)if present_best_action=improved_best_action exit(); else Go to step 2
#
# *NOTE - terminating condition I have used in policy evaluation: L2-norm(|V_new - V_old|)< theta
# +
def action_value_vector(env,present_state,V,discount_factor):
action_expected_value_vector = np.zeros(env.nA)
for action in range(env.nA):
for prob_system,next_state,reward,done in env.P[present_state][action]:
action_expected_value_vector[action] += prob_system*(reward + discount_factor*V[next_state])
return action_expected_value_vector
def policy_iter(env):
#random initialization of policy
policy = np.ones([env.nS, env.nA]) / env.nA
theta = 0.001
discount_factor = 1
while True:
#evaluate policy
V = policy_eval(policy,env,discount_factor,theta)
print(V)
print(policy)
policy_change = False
for state in range(env.nS):
present_best_action = np.argmax(policy[state])
#one step lookahead to calculate expected value of actions at current policy and its value function V
action_values = action_value_vector(env,state,V,discount_factor)
#select the improved best action
improved_best_action = np.argmax(action_values)
#CHANGE POLICY
action_switch = [0,0,0,0]
action_switch[improved_best_action] = 1
action_switch = np.array(action_switch)
policy[state] = action_switch
#flag for optimality
if present_best_action != improved_best_action:
policy_change=True
if policy_change==False:
return policy,V
# -
policy_iter(env)
#from dennybritz repo
expected_v = np.array([ 0, -1, -2, -3, -1, -2, -3, -2, -2, -3, -2, -1, -3, -2, -1, 0])
expected_v
# ### Value Iteration
# <img src="./images/value_iteration.png">
# +
def value_iter(env):
#random initialization of policy & value function
policy = np.zeros([env.nS, env.nA])
V = np.zeros(env.nS)
theta = 0.001
discount_factor = 1
while True:
V_old = copy.deepcopy(V)
for state in range(env.nS):
#print(V)
#print(policy)
#one step lookahead to calculate expected value of actions at current policy and its value function V
action_values = action_value_vector(env,state,V,discount_factor)
#Note - we are taking max here not argmax hence we are updating value function that comes by taking best action!
#update value function
V[state] = np.max(action_values)
#update policy
best_action = np.argmax(action_values)
switch = np.zeros(env.nA)
switch[best_action] = 1
policy[state] = switch
change = np.linalg.norm(abs(V - V_old))
if change<theta:
break
#last updated policy will be optimal policy and similarly value function will be optimal as well
return policy,V
# -
value_iter(env)
|
Dynamic Programming/Dynamic-Programming-methods .ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root
# +
## constant
hbar = 6.63e-34;
me = 1.6e-31;
print(hbar**2/(me*(1e-9)**2))
# +
P = 2e3*(3*np.pi/2); # larger P gives us more solution...
KA_scan = np.linspace(-4*np.pi, 4*np.pi, 4000);
plt.figure();
plt.plot(KA_scan, np.cos(KA_scan)+(P/(KA_scan))*np.sin(KA_scan), '.b')
plt.axhline(1);
plt.axhline(-1);
plt.axvline(np.pi)
plt.xlabel('Ka');
plt.ylabel('RHS')
plt.title('$mV_0a/\hbar^2 = 6\pi$')
plt.savefig('solving_kp_transcendental.png', dpi = 300)
plt.show();
def RHS(x):
return np.cos(x)+(P/(x))*np.sin(x);
## roots at pi
print(RHS(np.pi)+1)
# -
# ## Notes on the Transcendental Eq.
# The solutions are values for which the value of the root func is less than 1. Cuz then we can solve the left hand side.
def RHS(x):
return np.cos(x)+(P/(x))*np.sin(x);
# +
## do a scan of K...
Kguesses = np.linspace(1e-3,4*np.pi, 10000);
band_structure = [];
for kguess in Kguesses:
val = RHS(kguess);
if(abs(val) <1):
q = np.arccos(val);
E = kguess**2;
band_structure.append([q,E]);
band_structure = np.array(band_structure);
plt.figure(figsize = (5,5))
alpha = 0.1;
plt.plot(band_structure[:,0], alpha*band_structure[:,1], '.b', markersize = 1);
plt.plot(-band_structure[:,0], alpha*band_structure[:,1], '.b', markersize = 1);
# plt.plot(Kguesses, alpha*Kguesses**2, '.c', markersize = 0.1);
# plt.plot(-Kguesses, alpha*Kguesses**2, '.c', markersize = 0.1);
# plt.axvline(np.pi, linestyle = '--')
# plt.axvline(-np.pi, linestyle = '--')
plt.xlabel('qa', fontsize = 16);
plt.ylabel('Energy', fontsize = 16)
plt.xlim((-np.pi, np.pi))
plt.savefig('Konig_Penny_bands.png', dpi = 300)
plt.show();
# -
# ## wave function solutions
# When we force the determinant of the matrix to be 0, then the rows of the matrix are linearly independent with respect to each other. In that regards, once we figure out the matrix equation, we cannot resolve any further relations on the four coefficients (A,B,C,D)
# +
## do a scan of K...
plt.figure(figsize = (5,10));
Kguesses = np.linspace(1e-3,4*np.pi, 8);
for kguess in Kguesses:
val = RHS(kguess);
if(abs(val) <1):
q = np.arccos(val);
E = kguess**2;
x2 = np.linspace(0,1, 100); #a has been 1 in everything we've done
x1 = np.linspace(-1, 0, 100);
xtot = np.linspace(-1, 1, 100);
C = 1; D = 0;
print(np.cos(q) - RHS(kguess))
A = C*np.exp(1j*q)*np.exp(1j*kguess);
B = D*np.exp(1j*q)*np.exp(-1j*kguess);
## true wavefunction reconstruction
psi1 = A*np.exp(1j*kguess*(x1)) + B*np.exp(-1j*kguess*(x1))
psi2 = C*np.exp(1j*kguess*x2) + D*np.exp(-1j*kguess*x2)
## check that the bloch boundary is satisfied
psi_check = A*np.exp(1j*kguess*(x1-1)) + B*np.exp(-1j*kguess*(x1-1))
psi_check_2 = ( C*np.exp(1j*kguess*x1) + D*np.exp(-1j*kguess*x1))*np.exp(1j*q)
## we should not be able to do this..
psi_test = A*np.exp(1j*kguess*(xtot)) + B*np.exp(-1j*kguess*(xtot))
psi_test2 = C*np.exp(1j*kguess*xtot) + D*np.exp(-1j*kguess*xtot)
plt.subplot(211);
plt.plot(x1, psi1, '.-r');
plt.plot(x2, psi2, '.-b');
#plt.plot(xtot, psi_test, '.-b')
#plt.plot(xtot, psi_test2, '.-r')
plt.axvline(0, linestyle = '--')
plt.subplot(212)
plt.plot(x1, psi_check, '.y')
plt.plot(x1, psi_check_2, '.r', markersize = 0.9)
plt.show();
# -
# ## negative sign of the potential
# +
def RHS_flip(x):
P = 10*np.pi;
return np.cos(x)+(P/(x))*np.sin(x);
## do a scan of K...
Kguesses = np.linspace(1e-3,4*np.pi, 10000);
band_structure = [];
for kguess in Kguesses:
val = RHS_flip(kguess);
if(abs(val) <1):
q = np.arccos(val);
E = kguess**2;
band_structure.append([q,E]);
band_structure = np.array(band_structure);
plt.figure(figsize = (5,5))
alpha = 0.1;
plt.plot(band_structure[:,0], alpha*band_structure[:,1], '.g', markersize = 1);
plt.plot(-band_structure[:,0], alpha*band_structure[:,1], '.g', markersize = 1);
# plt.plot(Kguesses, alpha*Kguesses**2, '.c', markersize = 0.1);
# plt.plot(-Kguesses, alpha*Kguesses**2, '.c', markersize = 0.1);
# plt.axvline(np.pi, linestyle = '--')
# plt.axvline(-np.pi, linestyle = '--')
plt.xlabel('qa', fontsize = 16);
plt.ylabel('Energy', fontsize = 16)
plt.xlim((-np.pi, np.pi))
plt.savefig('Konig_Penny_well_bands.png', dpi = 300)
plt.show();
# -
|
notebooks/Analytic Theories/Konig Penny Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/dataqueenpend/-Assignments_fsDS_OneNeuron/blob/main/Programming_Assignment_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="0MWHC9QMQ72i"
# Write a Python program to print "Hello Python"?
#
#
# + id="3bPdP78fQ3-2"
def hello():
print('Hello Python')
# + colab={"base_uri": "https://localhost:8080/"} id="IwqtVc4DRLFY" outputId="13a2a9b5-5ce6-43b2-8b4b-45678967bbf8"
hello()
# + [markdown] id="E9DsP5S8Q-IG"
# Write a Python program to do arithmetical operations addition and division.?
#
# + id="ZCeCB73CREA-"
def add_div():
typ = input('Addition or division? (Type a or d): ')
num1 = int(input('Type first number: '))
num2 = int(input('Type second number: '))
if typ == 'a':
addition = num1+num2
print('Your result is: {}'.format(addition))
else:
division = num1/num2
print('Your result is: {}'.format(division))
# + colab={"base_uri": "https://localhost:8080/"} id="lkNNVZcOTBYj" outputId="ca03340a-6628-4844-9ac9-bdc580cca4f5"
add_div()
# + [markdown] id="VVoeKzSdQ_JG"
# Write a Python program to find the area of a triangle?
#
# + id="pW7cPrJxREi3"
def triangle_area():
side = int(input('Type length of the side of the triangle: '))
height = int(input('Type height of the triangle: '))
area = (1/2 * side) * height
print('Area of your triangle is: {}'.format(area))
# + colab={"base_uri": "https://localhost:8080/"} id="vjg3BU8sUhcZ" outputId="87d77a92-8ce8-417b-8b16-49c181590d01"
triangle_area()
# + [markdown] id="tzKLNhq7Q_9F"
# Write a Python program to swap two variables?
#
# + id="v5NxXDCARE_-"
def swap_vars(x,y):
x,y = y, x
return x, y
# + id="5QZq55XrVBjQ"
x = 1
y = 2
# + colab={"base_uri": "https://localhost:8080/"} id="RJpS7IcQVDk3" outputId="fecfc638-bfbd-44e8-9a19-348e705a1c6f"
swap_vars(x,y)
# + [markdown] id="AV-V2Vt9RDJu"
# Write a Python program to generate a random number?
# + id="c1enztUcRFfk"
def random_generator():
from random import random
number = random()
return number
# + colab={"base_uri": "https://localhost:8080/"} id="_1-Uzp8ha_jy" outputId="2b84d432-c31f-4e83-eb95-53de26c3bad4"
random_generator()
|
Python Assignments/Programming_Assignment_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1><center>Udemy Courses Analysis<center>
# <center>Analysis of data gathered from Udemy Courses. Link is available at https://www.kaggle.com/andrewmvd/udemy-courses?select=udemy_courses.csv<center>
# ### I. Importing modules and libraries
#
# For this step, I imported numpy, and matplotlib modules. After setting up the modules, the csv file was also imported.
import numpy as np
import pandas as pd
# +
import os
import csv
os.chdir("C:\\Users\\maegr\Documents\Maymay\DataScience\modules")
#Opens the data file as df
with open("udemy_courses.csv", "r") as courses_df:
courses_df = pd.read_csv('udemy_courses.csv')
# -
# ### II. Describing the Courses
#
# Instead of getting the statistical values separately, the **describe** syntax was used so that it would be easier to analyze the data.
courses_df.describe()
# #### Conclusions:
# 1. If someone is planning to take a Udemy course, it must be noted that the average price of Udemy Courses is **66.049 USD**. Some of the courses are entirely **free**, while others could go as high as **200 USD**
# 2. The average number of subcsribers per course is **3197**
# 3. Some courses could have as high as **27455** reviews while some courses don't have any review at all.
# 3. In order to finish a course, one must spend an average of **4.09 hours**.
# ### III. Amount of Courses by Subject
#
# The pie chart below describes the distribution of the amount of courses per subject
courses_df['subject'].value_counts() / courses_df['subject'].value_counts().sum()
# #### Conclusions:
# 1. About 32.6% of lessons from Udemy is about Web Development, which makes it the most popular subject in the site.
# 2. The Web Development course is followed closely by Business Finance with around 32.5%.
# 3. Musical Instruments is at third, while Graphic Design is placed at last.
# ### IV. Standard Deviation and Mean
# Part III already discussed the following details but this is another way of getting the standard deviation
# +
print("Mean Values")
print( "Price: " + str(courses_df["price"].mean()) )
print( "Number of subscribers: "+ str(courses_df["num_subscribers"].mean()) )
print( "Number of reviews: "+ str(courses_df["num_reviews"].mean()) )
print( "Number of lectures: "+ str(courses_df["num_lectures"].mean()) )
print( "Content Duration: "+ str(courses_df["content_duration"].mean()) )
print("\nStandard Deviation")
print( "Price: " + str(courses_df["price"].std()) )
print( "Number of subscribers: "+ str(courses_df["num_subscribers"].std()) )
print( "Number of reviews: "+ str(courses_df["num_reviews"].std()) )
print( "Number of lectures: "+ str(courses_df["num_lectures"].std()) )
print( "Content Duration: "+ str(courses_df["content_duration"].std()) )
# -
# #### Conclusions:
# 1. Based from the table above, we can infer that the there the standard deviation between the price and the number of lectures is small hence, they are more closely distributed around the mean value gathered earlier.
# ### V. Maximum and Minimum Values
# Below are the maximum and minimum values of the given data
# +
print( "Maximum Course Price: " + str(courses_df["price"].max()) )
print( "Minimum Course Price: " + str(courses_df["price"].min()) )
print( "\nMaximum Number of subscribers: "+ str(courses_df["num_subscribers"].max()) )
print( "Minimum Number of subscribers: "+ str(courses_df["num_subscribers"].min()) )
print( "\nMaximum Number of reviews: "+ str(courses_df["num_reviews"].max()) )
print( "Minimum Number of reviews: "+ str(courses_df["num_reviews"].min()) )
print( "\nMaximum Number of lectures: "+ str(courses_df["num_lectures"].max()) )
print( "Minimum Number of lectures: "+ str(courses_df["num_lectures"].min()) )
print( "\nMaximum Content Duration: "+ str(courses_df["content_duration"].max()) )
print( "Minimum Content Duration: "+ str(courses_df["content_duration"].min()) )
# -
# Conclusions:
# 1. The most expensive course costs 200USD while there are courses that are free.
# 2. The most subscribed course has 268923 subscribers
# 3. The most reviewed course has 27445 reviews
# 4. The most number of lectures in a course is 779. Surprisingly, there are courses that do not have any lectures at all.
# 5. The maximum content duration of a course is 78.5 hours, while again, there are courses that have 0 content duration.
# ### VI. Most Popular Paid Courses
# The table below shows the most popular paid courses in Udemy based on the number of subscribers
# +
paid_courses_df = courses_df.query("price != 0")
top25_paid = paid_courses_df.sort_values("num_subscribers", ascending=False)[0:25].sort_values("num_subscribers", ascending=False)
top25_paid
# -
# #### Conclusions:
# 1. The most popular paid course is "The Web Developer Bootcamp".
# 2. 21 out of 25 most popular paid courses is about Web Development. From this and the conclusion made earlier, it is possible that many udemy users are interested in learning about Web Development.
# 3. Those most popular paid course in musical instruments is about learning to play piano and guitar.
# ### VII Most Popular Free Courses
# +
free_courses_df = courses_df.query("price == 0")
top25_free = free_courses_df.sort_values("num_subscribers", ascending=False)[0:25].sort_values("num_subscribers", ascending=False)
top25_free
# -
# #### Conclusions:
# 1. The most popular free course is "Learn HTML5 Programming from scratch".
# 2. 21 out of 25 most popular free courses is about Web Development.
# 3. Those most popular free course in musical instruments is about learning to play electric guitar, titled "Free Beginner Electric Guitar Lessons"
# ### VIII. Highest reviewed course
num_reviews_df = courses_df.query("num_reviews != 0")
top25_reviewed = num_reviews_df.sort_values("num_reviews", ascending=False)[0:25].sort_values("num_reviews", ascending=True).reset_index(drop=True).reset_index()
top25_reviewed.max()
# #### Conclusions:
# 1. The highest reviewed course is about Web Designing under the subject Web Development.
# 2. At the time of the csv file upload, the title of the course is "Web Design for Web Developers" but currently, it is titled as "Ultimate Web Designer & Web Developer Course for 2021"
# 3. It takes 43 hours to finish the course.
# 4. It costs around 200 USD before but currently, it is priced at 89.99 USD.
# 5. The course is good for Intermediate Level learners
#
# To check the course, visit the link https://www.udemy.com/web-developer-course/
# ## General Conclusions
#
# IF someone is interested in learning about Web Development, Business Finance, Musical Instruments, and Graphics Design, it is recommended that they visit Udemy since there's a variety of courses they could try from the website. There are also free courses available. Meanwhile, if they don't mind paying for the contents, they should know that the average price per course is 66 USD and could possibly go as high as 200 USD.
|
Udemy_Courses_Analysis_Baybay1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import json
import string
import numpy as np
from tensorflow.keras.models import load_model
from tensorflow.keras.preprocessing.sequence import pad_sequences
# -
buck_t1=8 #threshold bucket1
max_out_len=12
# +
#upload dictionaries
with open('dict_w2i_chatbot.json') as json_file:
dict_w2i = json.load(json_file)
with open('dict_i2w_chatbot.json') as json_file:
dict_i2w = json.load(json_file)
with open('contractions_dict.json') as json_file:
contractions_dict = json.load(json_file)
# -
one_hot_len=len(dict_w2i)
# +
#upload models
encoder_model= load_model('models/encoder_inf_b1_nobucket_noval.h5')
decoder_model= load_model('models/decoder_inf_b1_nobucket_noval.h5')
# -
#preprocessing input string
def exp_remPunt(sent):
'''
clean the input sentence
- set to lower
- remove contract form
- remove punctuation
'''
clean_sent=[]
table = str.maketrans(dict.fromkeys(string.punctuation))
remove_digits = str.maketrans('', '', string.digits)
sent=sent.lower()
for word in sent.split():
if word in contractions_dict:
sent = sent.replace(word, contractions_dict[word]) #expand
sent = sent.translate(remove_digits)
clean_sent.append(sent.translate(table).lower()) #remove punt and set to lower
return clean_sent
def string_to_seq(l_sent):
'''
input list string
'''
emb_str=[]
for l in l_sent:
for word in l.split():
if (word in dict_w2i):
emb_str.append(dict_w2i[word])
emb_str = pad_sequences([emb_str],8, padding='post')
return np.flip(emb_str) #reverse and return
# +
def chat_loop(sentence):
stop_model=False #iteration condition
sentence=exp_remPunt(sentence)
if sentence=='quitbot':
stop_model=True
sentence=string_to_seq(sentence)
#define init variables
target_seq=np.zeros((1,1))
target_seq[0,0]=dict_w2i['<sos>'] #target seq must be init with start word
answer_seq=[] #the final answer will be a sequence of numbers
#encode the input
states_= encoder_model.predict(sentence)
while not stop_model:
decoder_output,state_h,state_c=decoder_model.predict([target_seq]+states_)
#get sampled word
sampled_word=np.argmax(decoder_output[0,-1,:])
#check iteration condition: stop model if eos or len>output len
if sampled_word==dict_w2i['<eos>'] or len(answer_seq)>=max_out_len:
stop_model=True
continue
else:
answer_seq.append(sampled_word)
#update target seq for next iteration
target_seq=np.zeros((1,1))
target_seq[0,0]=sampled_word #last word
#update states
states_=[state_h,state_c]
#print(answer_seq)
#answer_seq
mm="BOT:"
for i in answer_seq:
mm=mm+" " +dict_i2w[str(i)]
print(mm)
#print(f'You entered {sentence}')
# +
print("Type \"quitbot\" to exit. Let\'s start! \n \n")
stop_condition=False
while not stop_condition:
sentence = input("YOU: ")
if sentence=='quitbot':
print("good bye")
stop_condition=True
continue
chat_loop(sentence)
# -
|
NLP/Chatbot/chatbot_main_no_attention.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Jupyter Notebooksä»ç»
#
# ## åèš
#     æ¬Notebookäž»èŠé对PYNQ对Jupyter Notebooksè¿è¡ä»ç»ïŒä»ç»ç倧纲åéŽäºJupyter Notebookså®æ¹çNotebook ExamplesïŒäž»èŠå
æ¬ä»¥äžå䞪æ¹é¢çå
容ïŒ
# 1. ä»ä¹æ¯Jupyter Notebook
# 2. Jupyter Notebookçåºæ¬éšä»¶ååèœ
# 3. åŠäœåšJupyter Notebookäžè¿è¡ä»£ç
# 4. åŠäœåšJupyter NotebookäžçŒåMarkdownææ¡£
# 5. åšPYNQäžïŒJupyter Notebookèœåä»ä¹
#
# å
³äºJupyter Notebookså®æ¹çæŽå€å
容ïŒå¯ä»¥åèïŒ[Jupyter å®æ¹ææ¡£](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/examples_index.html).
# ## 第äžéšåïŒä»ä¹æ¯Jupyter Notebook?
# Jupyter Notebookæ¯äžäžª**亀äºåŒçç¬è®°æ¬**ïŒæ¬èŽšæ¯äžäžªWebåºçšçšåºïŒå¯ä»¥åšäžäžªææ¡£äžå
å«ä»¥äžçåèœïŒ
#
# * åšæ代ç (çŒå代ç åè¿è¡ä»£ç )
# * æå
¥äº€äºåŒçå°æ§ä»¶
# * ç»åŸ(æ°æ®å¯è§å)
# * æå
¥æ³šéææ¡£(Markdownæ ŒåŒ)
# * åŸçåè§é¢çæŸç€º
# * å
¬åŒççŒå
#
# è¿ç§ææ¡£æäŸäº**äžç§å®æŽåç¬ç«ç计ç®è®°åœæ¹åŒ**ïŒå¹¶äžå¯ä»¥èœ¬æ¢æåç§æ ŒåŒä»¥çµåçç圢åŒäžä»äººå
±äº«ã
# ### Jupyter Notebookå
å«ä»¥äžäžäžªç»ä»¶ïŒ
# * WebåºçšçšåºïŒäžäžªçšäºçŒååè¿è¡ä»£ç ååäœç¬è®°æ¬ææ¡£ç亀äºåŒWebåºçšçšåºã
# * å
æ ž(Kernels)ïŒåœç»å®çŒçšè¯èšç代ç è¿è¡æ¶ïŒå
æ žäŒè°çšäžäžªåç¬çè¿çšå¯åšå¹¶çšæ¥èŸåºç»æ并è¿åç»æç»Webåºçšçšåºãåæ¶å
æ žä¹å€ç诞åŠäº€äºåŒå°éšä»¶ãé项å¡åå
ççåèœã
# * ç¬è®°æ¬ææ¡£ïŒç¬è®°æ¬ææ¡£å
å«äºWebåºçšçšåºçææå
容ïŒå
æ¬ïŒèŸå
¥åèŸåºã泚éææ¡£ãæ¹çšåŒãåŸçå对äžäžªå¯¹è±¡çå¯åªäœè¡šç°åœ¢åŒãåæ¶ïŒæ¯äžäžªç¬è®°æ¬ææ¡£æèªå·±çå
æ žã
# #### 1.Webåºçšçšåº<br>
# Webåºçšå±åºå¯ä»¥å®æ以äžå ç§åºçšïŒ
# * åšæµè§åšå
**çŒå代ç **ïŒåæ¶å
·æè¯æ³èªåšé«äº®ãTabè¡¥å
šåæ£æ¥
# * åšæµè§åšäž**è¿è¡ä»£ç **ïŒåæ¶çŽæ¥åšæµè§åšäžèŸåºè¿è¡ç»æ
# * æ¥ç垊æ**å¯åªäœ**ç计ç®ç»æïŒæ¯åŠïŒHTML,LaTeX,PNG,SVG,PDFç
# * æå
¥å䜿çš**亀äºåŒJavaScriptçå°æ§ä»¶**ïŒå¯ä»¥çšæ¥æ建亀äºåŒçšæ·çé¢å¹¶äžå¯è§åå
æ žè®¡ç®ç»æã
# * 䜿çšMarkdownæ ŒåŒçŒå泚éææ¡£
# * éè¿äžå级å«çæ é¢æ建åå±çæ件管çæš¡åŒ
# * åšææ¡£äžä»¥Markdownç圢åŒäœ¿çšLaTeXè¯æ³çŒåæ°åŠå
¬åŒ
# #### 2.å
æ ž
#     Jupyter Notebookæ¯æäžç³»åäžåççŒçšè¯èšãæ¯åœæåŒäžäžªNotebook,Webåºçšçšåºå°±åŒå¯äžäžªå
æ žæ¥è¿è¡ä»£ç ãæ¯äžªå
æ žè¿è¡åšåç¬çäžäžªçŒçšè¯èšäžãå
æ žæ¯æ以äžçŒçšè¯èš:
# * [Python](https://github.com/ipython/ipython)
# * [Julia](https://github.com/JuliaLang/IJulia.jl)
# * [R](https://github.com/takluyver/IRkernel)
# * [Ruby](https://github.com/minrk/iruby)
# * [Haskell](https://github.com/gibiansky/IHaskell)
# * [Scala](https://github.com/Bridgewater/scala-notebook)
# * [node.js](https://gist.github.com/Carreau/4279371)
# * [Go](https://github.com/takluyver/igo)<br>
#
#     PythonäœäžºJupyter Notebookçéçšå
æ žæ¯æè¯èšïŒå¯ä»¥çšæ¥å¯¹PYNQè¿è¡çŒçšïŒåæ¶åšPYNQäžæ建çJupyter Notebookä¹åªå®è£
äºPythonçå
æ žã<br>
#     Webæµè§åšéè¿JSONãoverZeroMQ/WebSocketsçä¿¡æ¯çåè®®ïŒæ¥äœ¿å
æ žåNotebookçWebåºçšçšåºè¿è¡äº€äºïŒå€§éšåçšæ·äžéèŠäºè§£è¿äºç»èïŒäœæ¯éèŠå»ç解å
æ žæ¯è¿è¡åšZYNQäžçèWebæµè§åšåæäŸäºäžäºæ¥å£ç»è¿äžªå
æ žãå
³äºäžè¿°çç»èå
容ïŒå¯ä»¥åèïŒ[ç¹å»æ¥çæŽå€ç»èä¿¡æ¯](http://ipython.org/ipython-doc/dev/development/messaging.html)
# #### 3.Notebookææ¡£
#     Notebookææ¡£å
å«äº€äºç**èŸå
¥åèŸåº**åé代ç éšåç**解éæ§æå**ïŒè¿è¡ä»£ç æ产çç**åç§èŸåº**,å
æ¬HTMLãåŸçãè§é¢ãåå¹³é¢åŸ,éœå¯ä»¥è¢«åµå
¥åšç¬è®°æ¬äž,è¿äœ¿åŸå®å¯ä»¥è¿è¡å®æŽåç¬ç«çè®°åœè®¡ç®ãåœåšçµèäžè¿è¡è¿äžªç¬è®°æ¬webåºçšçšåºæ¶,ç¬è®°æ¬æ件åªæ¯äžäžªåçŒäžº**ipynb**çæ¬å°æ件ãè¿å³å®äºå®èœå€åŸæ¹äŸ¿å°è¢«ç»ç»å°æ件倹äžå¹¶äžåäžä»äººå享ã
# Noteboook äžçCellæ以äžåç§ç±»åïŒ
#
# * **Code cells:** çšäºèŸå
¥åèŸåºè¿è¡åšå
æ žäžç代ç
# * **Markdown cells:** çšMarkdownæ ŒåŒçŒèŸé代ç ææ¬å¹¶äžå¯ä»¥åµå
¥LaTeXæ ŒåŒçæ¹çšs
# * **Heading cells:** çŒèŸæ é¢ïŒäžå»ºè®®äœ¿çšïŒå 䞺åšMarkdown celläžå¯ä»¥è¿è¡æ é¢ççŒåïŒ
# * **Raw cells:** æ æ ŒåŒææ¬ïŒå¯ä»¥äœ¿çšåœä»€è¡å°ç¬è®°æ¬èœ¬å䞺åŠäžç§æ ŒåŒïŒåŠHTML
#
#     åšNotebookææ¡£å
éšïŒéçšäºbase64çŒç çJsonæ ŒåŒæ°æ®ïŒè¿è®©ä»»äœäžç§çŒçšè¯èšéœå¯¹å®ä»¬è¿è¡æäœïŒè¿æ¯ç±äºJSONéçšå®å
šç¬ç«äºçŒçšè¯èšçææ¬æ ŒåŒæ¥ååšå衚瀺æ°æ®,并äžNotebookæ档对äºçæ¬æ§å¶ä¹ååå奜ã
#     Notebookä¹å¯ä»¥å¯Œåºäžºäžåçéææ ŒåŒïŒæ¯åŠHTMLãreStructeredTextãLaTeX, PDFïŒæè
䜿çšJupyterç`nbconvert`åèœå°å®èœ¬äžºå¹»ç¯ç圢åŒïŒå¯¹äºPYNQçäžäºææ¡£ïŒå
æ¬è¿ç¯ïŒéœæ¯äœ¿çšNotebookè¿è¡çŒåçã<br>
#     æ€å€,ä»»äœä»**å
Œ
±URLæå¯ä»¥å
±äº«çGitHub**è·åçNotebookéœå¯ä»¥éè¿[nbviewer](http://nbviewer.ipython.org) çŽæ¥è¿è¡æ¥çè**äžéèŠå®è£
Jupyter**ã
# ## 第äºéšåïŒJupyter Notebookçåºæ¬éšä»¶ååèœ
# ### Notebookçäž»æ§é¢æ¿(Dashboard)
#     åšPYNQéïŒNotebookçæå¡åšè¿è¡åšARM®å€çåšäžãåœäœ çæ¿å¡é
眮奜çœç»åïŒäœ å¯ä»¥éè¿æµè§åšèŸå
¥[pynq:9090](pynq:9090)æ¥è¿å
¥äž»çé¢ãäž»æ§é¢æ¿æ¯Notebookç䞻页ãå®çäž»èŠç®çæ¯æŸç€ºNotebookååšåœåç®åœäžçæ件ã䞟äŸæ¥è¯Ž,è¿æ¯äžäžªæ件ç®åœçæªåŸ:
# 
#     åœåçæ件路åŸäŒæŸç€ºåšæ¹(åŠäžåŸ **/example**)ãå¯ä»¥éè¿ç¹å»è¿äžªè·¯åŸæè
äžé¢åç®åœåè¡šæ¥å¯»æŸèªå·±çæ件ã
# 
#     åŠäžåŸæ瀺ïŒåŠææ³èŠå建äžäžªæ°çNotebookïŒå¯ä»¥éè¿åå»äž»çé¢ç"New"æé®ïŒå¯ä»¥å建äžäžªæ°çPython3 NotebookãåŠææ³èŠäžäŒ äžäžªNotebookïŒå¯ä»¥ç¹å»Newæ蟹çUploadæ¥äžäŒ å·²æçNotebookã
# 
# 
#     æåŒäžäžªNotebookåïŒåšäž»çé¢çNotebookäžäŒæŸç€º"Running"è¿äžªç¶æïŒèåšRunningçé项å¡äžä¹äŒå°å·²ç»æåŒçNotebookæŸç€ºåšäžé¢ïŒä»£è¡šNotebookæ£åšè¿è¡ãèŠæ³šæïŒå
³éNotebookç页é¢å¹¶äžèœå®å
šéåºNotebookïŒåªæéè¿Shutdownæé®æèœå€çæ£çå
³éNotebookã
# 
#     ç¹å»æ件åæ¹çå°æ¹æ ŒåïŒåšé¡µé¢é¡¶éšå·Šäžè§å°äŒæŸç€ºå¯¹æ件çäžäºæäœïŒå
æ¬éåœåãå€å¶ãå
³éè¿äžªNotebookè¿çš(åšNotebook Runningçæ
åµäž)ã
# ### Notebookççšæ·çé¢è§åŸ
#     åœæåå建äºäžäžªæ°çNotebook以åïŒäŒè¿å
¥Notebookççšæ·çé¢(user interface)ïŒè¿äžªçé¢å¯ä»¥è¿è¡ä»£ç ççŒåãè¿è¡çæäœã并äžæŽäžªçšæ·çé¢å¯ä»¥äž»èŠå䞺äžäžªéšåïŒ
# * èåæ
# * å·¥å
·æ
# * å(Notebookå
·äœçå
容)<br>
#
#     æ³èŠå¯¹äžè¿°çåèœè¿è¡æŽå€çäºè§£ïŒå¯ä»¥éè¿åå»èåæ äž"Help"é项å¡äžç"User Interface Tour"(åŠäžåŸæ瀺)
# 
#     Notebookäžçåç±äž€ç§æš¡åŒæææïŒåå«äžº**çŒèŸæš¡åŒ**å**åœä»€æš¡åŒ**
# #### çŒèŸæš¡åŒ
# 
#     åœåå€äºçŒèŸæš¡åŒæ¶ïŒåšåŽæ¯äžäžªç»¿è²çæ¡ãåšè¿ç§æ
åµäžïŒä»£ç åå
å¯ä»¥åäžäžªæ®éçææ¬çŒèŸåšäžæ ·çŒèŸææ¬ã
# <div class="alert alert-success">
# å¯ä»¥éè¿æäž`Enter`é®æè
åå»åè¿å
¥çŒèŸæš¡åŒ
# </div>
# #### åœä»€æš¡åŒ
# 
#     åœåå€äºåœä»€æš¡åŒäžæ¶ïŒäžèœå¯¹åå
éšè¿è¡çŒèŸïŒäœæ¯å¯ä»¥å°åäœäžºäžäžªæŽäœè¿è¡æäœãæŽéèŠçæ¯ïŒåšåœä»€æš¡åŒäžå¯ä»¥çµæŽ»å°äœ¿çšé®çè¿è¡å¿«æ·é®æäœïŒå æ€åšåœä»€æš¡åŒäž**äžèŠ**è¿è¡çŒèŸæäœ **!** (åŸå¯èœè§Šåäžäºå¿«æ·é®æäœé æäžå¿
èŠç圱å)
# <div class="alert alert-success">
# å¯ä»¥éè¿æäž`Esc`é®æè
åå»ç©ºçœå€è¿å
¥åœä»€æš¡åŒ
# </div>
# ### éŒ æ æäœå¯Œèª
#     éŒ æ å¯ä»¥åå»åæ¥éæ©åïŒåŠæç¹å»çæ¯åçå
éšåäŒè¿å
¥çŒèŸæš¡åŒïŒåŠæç¹å»çæ¯ç©ºçœå€åäŒè¿å
¥åœä»€æš¡åŒã
# 
#     åŠææ³èŠéè¿éŒ æ åšåäžè¿è¡ä»£ç ïŒå¯ä»¥éè¿éæ©åå并äžåšå·¥å
·æ äžéæ©"Cell:Run"æ¥æ§è¡ä»£ç ïŒåŠææ³èŠå€å¶åïŒå¯ä»¥åšå·¥å
·æ äžéæ©"Edit:Copy"ã<br>
#     åœåäžæ¯ä»¥Markdownæ ŒåŒæè
æ é¢æ ŒåŒæ¶ïŒåäŒåç°äž€ç§æ
åµïŒ**é¢è§æš¡åŒ**æè
**çŒèŸæš¡åŒ(æºç æš¡åŒ)** ïŒé¢è§æš¡åŒäžäŒçå°ææ¬æŸç€ºææïŒåœåšçŒèŸæš¡åŒäžïŒå¯ä»¥çå°çŒèŸææ¬çæºç ãåŠææ³èŠéè¿éŒ æ å°æºç æš¡åŒèœ¬å䞺é¢è§æš¡åŒïŒå¯ä»¥éè¿éæ©åå并äžåšå·¥å
·æ äžéæ©"Cell:Run"æ¥æ§è¡ä»£ç ïŒåŠææ³èŠå°é¢è§æš¡åŒèœ¬äžºçŒèŸæš¡åŒïŒååå»åå³å¯ã
# ### é®çæäœå¯Œèª
#     对äºé®ççé®çé®ïŒåæ ·ç±äž€ç§äžåçå¿«æ·é®æ¹åŒïŒåå«äžºåšçŒèŸæš¡åŒæ žåœä»€æš¡åŒäžçå¿«æ·é®ãæéèŠçå¿«æ·é®æ¯`Enter`é®ïŒçšæ¥è¿å
¥çŒèŸæš¡åŒïŒåŠäžäžªæ¯`Esc`é®ïŒçšäºéåºçŒèŸæš¡åŒè¿å
¥åœä»€æš¡åŒã<br>
#     åšçŒèŸæš¡åŒäžïŒç±äºå€§éšåçé®çéœçšäºææ¬ççŒèŸæ以快æ·é®åŸå°ïŒèåšåœä»€æš¡åŒäžïŒæŽäžªé®çéœå¯ä»¥åœäœå¿«æ·é®äœ¿çšïŒå æ€æåŸå€å¿«æ·é®ã
#     äžé¢äžºäžäºåžžçšçå¿«æ·é®ç»åïŒ
# 
# 
# ## 第äžéšåïŒåŠäœåšJupyter Notebookäžè¿è¡ä»£ç
#     Jupyter Notebookæ¯äžäžªäº€äºåŒçŒå并è¿è¡ä»£ç çç¯å¢ã并äžæ¯æå€ç§çŒçšè¯èšãäœæ¯,æ¯äžªNotebookäžäžäžªåç¬çå
æ žçžäºè¿æ¥ãåšPynqäžïŒNotebookäžIPythonå
æ žçžè¿å¹¶äžè¿è¡Python代ç ã
# #### 䜿çšä»£ç åèŸå
¥åè¿è¡ä»£ç
#     建ç«äžäžªåçå±æ§äžºä»£ç åïŒåšçŒèŸæš¡åŒäžåšåäžèŸå
¥ä»£ç å³å¯äœ¿çš`Shift+Enter`(é®çå¿«æ·é®)æéŒ æ ç¹å»`Cell-Run Cells`æ¥è¿è¡ä»£ç ãæ¯åŠå®ä¹äžäžªåé并äžèŸåºå®ïŒ
a = 10
print(a)
#     åšé®çå¿«æ·é®äžïŒæ䞀ç§è¿è¡ä»£ç çæ¹åŒïŒ
# * `Alt+Enter`çšäºè¿è¡åœåå并äžåšäžæ¹æ°æå
¥äžäžªå
# * `Ctrl+Enter`çšäºè¿è¡åœååç¶åè¿å
¥åœä»€æš¡åŒ
# #### æ§å¶å
æ ž
#     åšNotebookäžïŒä»£ç è¿è¡åšäžäžªç§°äœâå
æ žâçåç¬è¿çšäžïŒå
æ žå¯ä»¥è¢«äžæåéæ°å¯åšãæ¯åŠå¯ä»¥å¯Œå
¥äžäžªè®¡æ¶æš¡åïŒç¶ååšå
æ žè¿è¡äžçæ
åµäžäžæå
æ žåéæ°å¯åšå
æ žãäžæåéæ°å¯åšå
æ žçæ¹åŒåŠäžåŸæ瀺ïŒ
# 
import time
time.sleep(10)
# #### åçèåæ
#     åçèåæ äžæå€ç§è¿è¡ä»£ç çæ¹åŒïŒå
æ¬ïŒ
# * Run and Select Below (è¿è¡æéçå并äžéäžäžäžäžª)
# * Run and Insert Below (è¿è¡æéçå并äžåšäžé¢å建äžäžªæ°çå)
# * Run All (è¿è¡ææçå)
# * Run All Above (è¿è¡æéååçææå)
# * Run All Below (è¿è¡æéååçå)
# #### sys.stdout
# èŸå
¥åèŸåºæµéœå¯ä»¥äœäžºææ¬åšèŸåºç空çœå€æŸç€º
print("Hello from Pynq!")
# #### åŒæ¥çèŸåºæš¡åŒ
#     åšNotebookäžïŒåšå
æ žäžçæçææèŸåºéœæ¯åŒæ¥æŸç€ºçïŒæ¯åŠäžé¢ç代ç ïŒæ¯0.5ç§äŒèŸåºäžæ¬¡ç»æïŒèäžæ¯å
šéšåšæåèŸåºã
import time,sys
for i in range(8):
print(i)
time.sleep(0.5)
# #### 对倧éæ°æ®èŸåºçæ¯æ
#     䞺äºæŽå¥œå°å€ç倧éå°æ°æ®èŸåºïŒåœéèŠèŸåºå€§éæ°æ®çæ¶åïŒèŸåºæ¡å¯ä»¥è¢«æå ãåŠäžé¢ç代ç æ瀺ïŒåå»ç»ææ 巊䟧å¯ä»¥äœ¿æ°æ®æå æå±åŒã
for i in range(50):
print(i)
# ## 第åéšåïŒåŠäœåšJupyter NotebookäžçŒåMarkdownææ¡£
#     åšJupyter NotebookäžïŒå¯ä»¥åšåçéæ©äžéæ©Markdownæ ŒåŒçåæ¥è¿è¡Markdownæ ŒåŒææ¡£ççŒåãMarkdownæ¯äžç§å¯ä»¥äœ¿çšæ®éææ¬çŒèŸåšçŒåçæ è®°è¯èšïŒéè¿ç®åçæ è®°è¯æ³ïŒå®å¯ä»¥äœ¿æ®éææ¬å
容å
·æäžå®çæ ŒåŒãæŽå€å
·äœçæè¿°å¯ä»¥åèïŒ[Markdown诊ç»ä»ç»](http://daringfireball.net/projects/markdown/)
# ### Markdownåºæ¬è¯æ³
#     åšMarkdownäžïŒå¯ä»¥å¯¹æå®å
容䞀端添å `* *`å`** **`å°å
容*æ¹äžºæäœ*å**åäœå ç²**
#     建ç«äžäºåå±åè¡šïŒåŠïŒ
# * 第1æ¥
# - 1.1
# - 1.1.1
# - 1.1.2
# - 1.1.3
# * 第2æ¥
# - 2.1
# * 第3æ¥
# - 3.1
# <br>
#
#
#     æè
ïŒ
# 1. 第1æ¥
# 1. 1.1
# 2. 1.2
# 2. 第äºæ¥
# 3. 第äžæ¥
# æ·»å æ°Žå¹³åå²çº¿:
#
# ---
# è¿è¡åŒçšïŒ
# > Beautiful is better than ugly.
# > Explicit is better than implicit.
# > Simple is better than complex.
# > Complex is better than complicated.
# > Flat is better than nested.
# > Sparse is better than dense.
# > Readability counts.
# > Special cases aren't special enough to break the rules.
# > Although practicality beats purity.
# > Errors should never pass silently.
# > Unless explicitly silenced.
# > In the face of ambiguity, refuse the temptation to guess.
# > There should be one-- and preferably only one --obvious way to do it.
# > Although that way may not be obvious at first unless you're Dutch.
# > Now is better than never.
# > Although never is often better than *right* now.
# > If the implementation is hard to explain, it's a bad idea.
# > If the implementation is easy to explain, it may be a good idea.
# > Namespaces are one honking great idea -- let's do more of those!
# å°æåäžçœç«è¿è¡éŸæ¥ïŒ
#
# [Jupyterå®çœ](http://jupyter.org)
# #### 1.æ é¢ç®¡ç
#     åšMarkdownçŒèŸæš¡åŒäžïŒåšæ³èŠè®Ÿçœ®äžºæ é¢çæååé¢å `#+ç©ºæ Œ`æ¥è¡šç€ºèœ¬å䞺æ é¢ïŒäžäžª#æ¯äžçº§æ é¢ïŒäž€äžª#æ¯äºçº§æ é¢ïŒä»¥æ€ç±»æšïŒæå€æ¯æå
级æ é¢ãåŠïŒ
# ```
# # è¿æ¯äžçº§æ é¢
# ## è¿æ¯äºçº§æ é¢
# ### è¿æ¯äžçº§æ é¢
# #### è¿æ¯å级æ é¢
# ##### è¿æ¯äºçº§æ é¢
# ###### è¿æ¯å
级æ é¢
# ```
# #### 2.åµå
¥ä»£ç
# åšMarkdownçŒèŸæš¡åŒäžïŒå¯ä»¥åµå
¥è¯Žææ§ç代ç èäžåPyhtonäžæ§è¡å®ïŒåŠïŒ
#
# def f(x):
# """çšäºè®¡ç®å¹³æ¹çåœæ°"""
# return x**2
# 以åå
¶ä»çŒçšè¯èšïŒåŠïŒ
#
# if (i=0; i<n; i++) {
# printf("hello %d\n", i);
# x += 4;
# }
# #### 3.åšMarkdownçŒèŸæš¡åŒäžäœ¿çšLaTeXè¿è¡å
¬åŒççŒå
# åå©äºMarkdownåLaTexïŒå¯ä»¥åšNotebookäžçŒåæ°åŠè¡šèŸŸåŒå¹¶äžæŸç€ºåšåå
ã
# åšlatex代ç çéŠå°Ÿå äž`$`å³å¯åšåäž**åµå
¥**éèŠè¡šèŸŸçå
¬åŒïŒåŠïŒ
#
# ```
# Inline example: $e^{i\pi} + 1 = 0$
# ```
# åšé¢è§æš¡åŒäžïŒå
¬åŒäŒè¢«æž²æ并äžæŸç€ºåŠäžïŒ<br>
#
# $e^{i\pi} + 1 = 0$
#
# ---
# åšlatex代ç çéŠå°Ÿå äž`$$`å¯åšåäžåªæŸç€ºéèŠè¡šèŸŸçå
¬åŒïŒåŠïŒ
#
# ```latex
# $$e^x=\sum_{i=0}^\infty \frac{1}{i!}x^i$$
# ```
# åšé¢è§æš¡åŒäžïŒå
¬åŒäŒè¢«æž²æ并äžæŸç€ºåŠäžïŒ
# $$e^x=\sum_{i=0}^\infty \frac{1}{i!}x^i$$
# #### 4.GitHubé£æ ŒçMarkdown
#
# Notebookåæ¶æ¯æGitHubé£æ ŒçMarkdwonïŒå æ€å¯ä»¥äœ¿çšäžäžªéé³ç¬Šæ¥æŸç€ºä»£ç åãåŠïŒ
#
# <pre>
# ```python
# print "Hello World"
# ```
# </pre>
#
# <pre>
# ```javascript
# console.log("Hello World")
# ```
# </pre>
# èŸåºçç»æïŒ
# ```python
# print "Hello World"
# ```
#
# ```javascript
# console.log("Hello World")
# ```
# 以åäžäžªè¡šæ ŒïŒåŠïŒ
#
# <pre>
# ```
#
# | This | is |
# |------|------|
# | a | table|
#
# ```
# </pre>
# èŸåºçç»æïŒ
#
# | This | is |
# |------|------|
# | a | table|
# #### 5.çæHTML
# å 䞺Markdownå
åµäºHTMLïŒå æ€ä¹å¯ä»¥å¢å 诞åŠHTMLè¡šæ ŒçæåïŒ
# <table>
# <tr>
# <th>Header 1</th>
# <th>Header 2</th>
# </tr>
# <tr>
# <td>row 1, cell 1</td>
# <td>row 1, cell 2</td>
# </tr>
# <tr>
# <td>row 2, cell 1</td>
# <td>row 2, cell 2</td>
# </tr>
# </table>
# #### 6.æ¬å°æ件å 蜜
# åŠæåšNotebookçæ件倹äžææ¬å°æ件ïŒå¯ä»¥çŽæ¥åšMarkdownåäžè¿è¡çŽ¢åŒ,åŒçšæ ŒåŒåŠäžïŒ
#
#
# [æ件ç®åœ](æ件å称)
# #### 7.æ¬å°æ件çå®å
šåéç§æ§
# éèŠæ³šæïŒJupyter Notebookåæ¶æ¯å¯ä»¥äœäžºäžäžªéçšçæ件æå¡åšè䜿çšïŒå æ€æªåšNotebookæ件倹å
çæ件æ¯æ²¡æ访é®æéçïŒå æ€å¯ä»¥äž¥æ Œæ§å¶Notebookæ件倹äžçæ件ãä¹å 䞺è¿äžªåå ãæ以区ç建议äžèŠåšéèŠçç®åœäžäœ¿çšJupyter Notebookæå¡åš(æ¯åŠ homeæ件倹)ã
#
# åœä»¥åå¯ç ä¿æ€çæ¹åŒè¿è¡äžäžªNotebookæ¶ïŒæ¬å°æ件çæéåªéäºåªè¯»æ件ïŒåŠåéèŠç»è¿èº«ä»œéªè¯ãæå
³è¿æ¹é¢çæŽå€ä¿¡æ¯ïŒå¯ä»¥åé
Jupyteræå
³è¿è¡Notebookæå¡åšçææ¡£ïŒ[ç¹å»æ€å€](http://jupyter-notebook.readthedocs.io/en/latest/public_server.html).
# ## åšPYNQäžïŒJupyter Notebookèœé¢å€åä»ä¹
# #### 1.å 蜜æ¯ç¹æµæ件
# åšJupyter NotebookäžïŒå¯ä»¥çŽæ¥éè¿äžºPYNQç¹å«å®å¶çåºå»å 蜜æ¯ç¹æµæ件æ¥å 蜜硬件端çæ¶æ
# +
from pynq.overlays.base import BaseOverlay
base = BaseOverlay("base.bit")
# -
# æ§è¡äžè¿°ä»£ç ä¹åïŒå¯ä»¥åšåŒåæ¿äžçå°æ瀺ç¯"Done"éªçäºäžäžïŒå³ç¡¬ä»¶ç«¯å·²ç»å 蜜äºç¡¬ä»¶ç»æïŒä¹åå°±å¯ä»¥å¯¹æ¿èœœèµæºè¿è¡è®¿é®ïŒåŠæ§å¶çæç4é¢LEDç¯
for led in base.leds:
led.on()#åŒå¯LEDç¯
for led in base.leds:
led.off()#å
³éLEDç¯
# #### 2.ç»åJupyter Notebook Widgetsåšå端æ§å¶æ¿èœœç¡¬ä»¶è®Ÿæœ
# åšæåŒå§äžæ¶åå°Jupyter Notebookäžæ亀äºåŒçå°æ§ä»¶ïŒå æ€å¯ä»¥éè¿å°æ§ä»¶æ建äžäžªç®åçå端ç»ææ¥èŸå¥œçæ§å¶æ¿èœœç¡¬ä»¶è®Ÿæœ
# %gui asyncio
import asyncio
def wait_for_change(widget, value):
future = asyncio.Future()
def getvalue(change):
# make the new value available
future.set_result(change.new)
widget.unobserve(getvalue, value)
widget.observe(getvalue, value)
return future
# +
from pynq.overlays.base import BaseOverlay
import ipywidgets as widgets
base = BaseOverlay("base.bit")
for led in base.leds:
led.on()
# +
from ipywidgets import IntSlider
slider = IntSlider(min = 0,max = 7)
rgbled_position = [4,5]
async def f():
while(1):
x = await wait_for_change(slider, 'value')
for led in rgbled_position:
base.rgbleds[led].write(x)
base.rgbleds[led].write(x)
asyncio.ensure_future(f())
slider
# -
# éè¿ç§»åšäžé¢çæ¡åïŒå¯ä»¥æ§å¶æ¿èœœäžçRGB-LEDçé¢è²æŸç€º
# #### 3.éè¿Pythonäžçæ°æ®å€çåºå€çäžæŸç€ºæ°æ®
#     å 䞺Pythonäžå
眮äºè®žå€æ°æ®å€çåºïŒå¯ä»¥å°æ°æ®åŸå¥œå°å¯è§ååšçé¢äžãæ以è¿çšPythonïŒå¯ä»¥å°åšåŒåæ¿äžè·åçä¿¡æ¯åŸå¥œå°è¡šç°åºæ¥ïŒäŸåŠçŽè§å°æŸç€ºäžäºæ°æ®ïŒåŠèŸåºDAC-ADC_Pmodåè·¯æµé误差.ïŒ
# +
# %matplotlib inline
from math import ceil
from time import sleep
import numpy as np
import matplotlib.pyplot as plt
from pynq.lib import Pmod_ADC, Pmod_DAC
from pynq.overlays.base import BaseOverlay
ol = BaseOverlay("base.bit")
dac = Pmod_DAC(ol.PMODB)
adc = Pmod_ADC(ol.PMODA)
delay = 0.0
values = np.linspace(0, 2, 20)
samples = []
for value in values:
dac.write(value)
sleep(delay)
sample = adc.read()
samples.append(sample[0])
# print('Value written: {:4.2f}\tSample read: {:4.2f}\tError: {:+4.4f}'.
# format(value, sample[0], sample[0]-value))
X = np.arange(len(values))
plt.bar(X + 0.0, values, facecolor='blue',
edgecolor='white', width=0.5, label="Written_to_DAC")
plt.bar(X + 0.25, samples, facecolor='red',
edgecolor='white', width=0.5, label="Read_from_ADC")
plt.title('DAC-ADC Linearity')
plt.xlabel('Sample_number')
plt.ylabel('Volts')
plt.legend(loc='upper left', frameon=False)
plt.show()
# -
# #### 4.çŽæ¥æ§è¡Linux Shellæ什
# åšJupyter NotebookäžïŒå¯ä»¥åšä»£ç ååé¢å äžäžª"!"åå¯ä»¥çŽæ¥æ·»å shellæ什æ¥æ§è¡shellæ什<br>
# åŠïŒæ¥çç³»ç»ä¿¡æ¯ç
# æ¥çç³»ç»ä¿¡æ¯
# !cat /proc/cpuinfo
# æ¥çLinuxçæ¬
# !cat /etc/os-release | grep VERSION
# éè¿å
æ žè®¡ç®CPUé床
# !head -5 /proc/cpuinfo | grep "BogoMIPS"
|
Jupyter/Xupsh-jupyter_notebooks-Introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Daniel-ASG/Aulas_de_cursos/blob/main/An%C3%A1lise_de_Dados_em_Python_Aula_03.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="QIQ_e6dLrHVB"
# # Análise dos dados de reembolso dos senadores - 2020
#
# https://www12.senado.leg.br/dados-abertos
#
# https://www12.senado.leg.br/dados-abertos/conjuntos?grupo=senadores&portal=administrativo
#
#
# + id="fZzA5wZarA41"
import pandas as pd
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="zTcuv2ejrqL1" outputId="dc2aa77b-faf5-44e4-f28b-c1dd8278135e"
df = pd.read_csv('http://www.senado.gov.br/transparencia/LAI/verba/2020.csv',
sep=';',
encoding='latin1',
skiprows=1,
decimal=',')
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="L3nZkIQdsZmU" outputId="de9a7e47-41da-43e8-ef03-1eb1c26b8e72"
df.info()
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="lurL0-iRtMft" outputId="66420f28-fffc-4c54-be5c-552535791cb8"
df.describe().round(2)
# + colab={"base_uri": "https://localhost:8080/"} id="ujbQ3BV-uGfG" outputId="423b4f3e-65b0-4122-f698-dbbbc3570b32"
df['VALOR_REEMBOLSADO'].sum()
# + colab={"base_uri": "https://localhost:8080/"} id="Kge6btIUuhod" outputId="31ee9e9b-2ef7-4c97-d8b9-8d81a2257f21"
df['SENADOR'].value_counts()
# + colab={"base_uri": "https://localhost:8080/"} id="PPZDyfEzuuIG" outputId="b9094dd3-cdf1-462c-a9d2-77a3640f1999"
df.groupby(by='SENADOR')['VALOR_REEMBOLSADO'].sum().sort_values(ascending=False)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="9NzDFpdDvMJP" outputId="e5a8e84d-3794-4d17-82bf-8292b046da28"
df.nlargest(5, 'VALOR_REEMBOLSADO').T
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="A7B228gBvqg9" outputId="aeec11c8-f57c-44d3-84f5-4ce6ea97bf89"
df.nsmallest(5, 'VALOR_REEMBOLSADO').T
# + colab={"base_uri": "https://localhost:8080/"} id="peMwfqX7v-Vz" outputId="8024a47b-076d-4569-bb3d-c08dd49e232c"
df['TIPO_DESPESA'].value_counts()
# + colab={"base_uri": "https://localhost:8080/"} id="HWfT_Dt7wWkd" outputId="d44a9b12-895f-4533-e465-0078e826f532"
df.groupby('TIPO_DESPESA')['VALOR_REEMBOLSADO'].sum().sort_values(ascending=False)
# + [markdown] id="-Kfr6IdYxDil"
# # Análise do eleitorado brasileiro
#
# https://www.tse.jus.br/eleicoes/estatisticas/estatisticas-eleitorais
#
# Eleições 2018 -> https://cdn.tse.jus.br/estatistica/sead/eleitorado/eleitorado_municipio_2018.csv
#
# Eleições 2020 -> https://cdn.tse.jus.br/estatistica/sead/eleitorado/eleitorado_municipio_2020.csv
# + id="jkfEOoMNwzAy"
import pandas as pd
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="ECD7nzl5yPaM" outputId="d9835e40-65ab-49f4-fbf3-2bda6442be3a"
df = pd.read_csv('https://cdn.tse.jus.br/estatistica/sead/eleitorado/eleitorado_municipio_2018.csv',
sep=';',
encoding='latin1')
df.head().T
# + colab={"base_uri": "https://localhost:8080/"} id="YoFjuM-WyeaD" outputId="a576cd08-d78e-45a1-ef16-467c9cac5072"
df.info()
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="qbudSus7zHhM" outputId="8e41c906-9be1-4067-c9b6-d03834ff07ac"
df.nlargest(5, 'QTD_ELEITORES_DEFICIENTE')
# + colab={"base_uri": "https://localhost:8080/"} id="68tiQWU8zk7Y" outputId="9a625f62-7804-46f1-ab3e-52854e6da2d4"
print(f'Eleitoras: {df["QTD_ELEITORES_FEMININO"].sum()}')
print(f'Eleitores: {df["QTD_ELEITORES_MASCULINO"].sum()}')
print(f'Não informado: {df["QTD_ELEITORES_NAOINFORMADO"].sum()}')
# + id="9l44Cvbm0TUj"
tot_eleitores = df['QTD_ELEITORES'].sum()
tot_fem = df['QTD_ELEITORES_FEMININO'].sum()
tot_mas = df['QTD_ELEITORES_MASCULINO'].sum()
tot_nao = df['QTD_ELEITORES_NAOINFORMADO'].sum()
# + colab={"base_uri": "https://localhost:8080/"} id="fQfMp1pu0eV5" outputId="0b1f09d9-5c0b-41c6-9ab8-adbf9ac51209"
print(f'Eleitoras: {tot_fem/tot_eleitores*100:.2f}%')
print(f'Eleitores: {tot_mas/tot_eleitores*100:.2f}%')
print(f'Não informado: {tot_nao/tot_eleitores*100:.2f}%')
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="3pYYCG_W1lSZ" outputId="9834829a-cd60-4363-c916-4a4fdd7fd6f5"
df[df['QTD_ELEITORES_MASCULINO'] > df['QTD_ELEITORES_FEMININO']]
# + id="7jAmj6OO2RLE"
df['RELACAO_FM'] = df['QTD_ELEITORES_FEMININO'] / df['QTD_ELEITORES_MASCULINO']
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="AuQKJzKB2yl_" outputId="28a6653e-c7e1-4a43-fc63-85a75d545752"
df.nlargest(5, 'RELACAO_FM').T
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="FQ9F56aE27sa" outputId="87df642a-a001-4145-c53e-29013dd43220"
df.nsmallest(5, 'RELACAO_FM').T
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="8vlQ66nk3os9" outputId="cfde0f88-836f-44dd-dd63-8f05845c9d9c"
df_Brasil = df[df['CD_PAIS'] == 1].copy()
df_Brasil
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="-Qzn1teO4TQP" outputId="39bfe23c-556d-48bc-9a47-e491baf05e68"
df_exterior = df[df['CD_PAIS'] != 1].copy()
df_exterior
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="MwJ2jPwb5FGN" outputId="d99efe0c-86a7-4865-bc52-0bb09df3c45e"
df_Brasil.nlargest(5, 'RELACAO_FM').T
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="cfNfUqV46FCm" outputId="879f0bdd-8ffd-4eb5-ec05-88bc8eaf5d0c"
df_Brasil.nsmallest(5, 'RELACAO_FM').T
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="AiXWi_fC6NLW" outputId="a0392ea5-d3f9-437e-c167-582a6f1f8195"
df_Brasil['RELACAO_FM'].plot.hist(bins=100);
# + id="krPFNJQq6uXI"
import seaborn as sns
import matplotlib.pyplot as plt
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="yQcVTu9Z7GMZ" outputId="feb10e56-246a-4d11-b25b-2bdff92d7a20"
sns.histplot(df_Brasil['RELACAO_FM'], bins=100, color='red');
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="fZvRfLUh7nvT" outputId="9b00b8e9-4e53-4b87-b62b-ec840fa5e1d7"
sns.histplot(df_Brasil['RELACAO_FM'], bins=100, color='red')
plt.title('Relação Eleitoras/Eleitores', fontsize=18)
plt.xlabel('Eleitoras/Eleitores', fontsize=14)
plt.ylabel('Frequência', fontsize=14)
plt.axvline(1, color='black', linestyle='--');
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="rLh5BUaE8G3I" outputId="a2260344-d87d-4145-b968-7d52ace836ab"
sns.swarmplot(data=df_Brasil, x='NM_REGIAO', y='RELACAO_FM')
plt.axhline(1, color='black', linestyle='--')
# + colab={"base_uri": "https://localhost:8080/"} id="Rns9nCy-83xf" outputId="64c9aa97-3ab4-44e1-e8c8-e6978195f599"
lista = ['QTD_ELEITORES_16', 'QTD_ELEITORES_17', 'QTD_ELEITORES_18',
'QTD_ELEITORES_19', 'QTD_ELEITORES_20']
tot_idade = df[lista].sum()
tot_idade
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="CR6hwAOi_dIA" outputId="61d334da-e8a4-4b14-fc94-335550932554"
tot_idade.plot.barh();
# + [markdown] id="b7NlUnPr_yO-"
# # Mapa das escolas do RS por taxa de distorção de série
# + id="zldeeGLh_o5I"
import pandas as pd
import folium
# + colab={"base_uri": "https://localhost:8080/", "height": 229} id="eUzgC5lJBehL" outputId="09b920b6-ed49-4199-e7b8-31f56a34f4f3"
df = pd.read_csv('http://dados.fee.tche.br/ckan-download/fee-2013-mun-taxa-de-distorcao-idade-serie-total-102524.csv',
encoding='latin1',
skiprows=1)
df.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 195} id="FKVZ6asECix3" outputId="54e77bf7-d86c-40cd-fbd0-7f39f545a5db"
df = df.rename(columns={'/Educação/Ens...de Série/Total 2013 (-)': 'tx_distorcao'})
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="njkkSlhJDFF6" outputId="ecc9da0e-e86d-45ac-9b9d-c4d3d780196b"
df.info()
# + colab={"base_uri": "https://localhost:8080/"} id="ZuBZ76BSDdFp" outputId="b5b81fab-cb48-4763-e307-a1c4339b47ed"
df['tx_distorcao'] = df['tx_distorcao'].str.replace(',','.').astype(float)
df.info()
# + colab={"base_uri": "https://localhost:8080/", "height": 343} id="KuoZMe1AGZQ2" outputId="fab0c2c2-196c-42b0-91d7-ccfb7ff8e2f8"
df.nsmallest(10, 'tx_distorcao')
# + colab={"base_uri": "https://localhost:8080/", "height": 343} id="qXn6qkZmGpVw" outputId="b45c5709-031e-48cd-a011-0b0926584f96"
df.nlargest(10, 'tx_distorcao')
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="Zkh2nBTpGt2l" outputId="60fb1e0c-91d3-4c6f-f256-10a0f2939e7f"
df['tx_distorcao'].plot.hist(bins=100);
# + colab={"base_uri": "https://localhost:8080/"} id="3lkxAa__HAPB" outputId="a6e49401-2469-445b-fb34-b538ae898fa5"
df[df['tx_distorcao'] <= 10].count()
# + colab={"base_uri": "https://localhost:8080/"} id="hkjhhbFWHPNa" outputId="1daf38f7-fd8d-430b-947b-f6d9e01623c8"
df[df['tx_distorcao'] >= 45].count()
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="Uy-UyzDrHZty" outputId="de78ae58-58f7-41ae-cc0f-9c54061da649"
brasil = folium.Map(location=[-13.6603615, -69.6775883],
zoom_start=4)
brasil
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="KwEm8OPcHxbf" outputId="51ebf2a0-376e-418e-9dc6-0890316d587f"
rs = folium.Map(location=[-30.3918717, -55.9134377],
zoom_start=7)
rs
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="z0VLHGdiIRtv" outputId="d64fb20e-858a-434d-d425-668ccca3c625"
for indice, municipio in df[df['tx_distorcao'] <= 10].iterrows():
folium.Marker(
location=[municipio['latitude'], municipio['longitude']],
popup=municipio['MunicÃpio'],
icon=folium.map.Icon(color='green')
).add_to(rs)
rs
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="74iUXp8paKu1" outputId="97d7b8c2-1afa-4487-c86e-6589e34bbe25"
for indice, municipio in df[df['tx_distorcao'] >= 45].iterrows():
folium.Marker(
location=[municipio['latitude'], municipio['longitude']],
popup=municipio['MunicÃpio'],
icon=folium.map.Icon(color='red')
).add_to(rs)
rs
# + colab={"base_uri": "https://localhost:8080/"} id="__kBlgUhbFB2" outputId="a250ec69-c853-4186-87a5-deb95f9fa2d5"
df[df['MunicÃpio'] == 'Porto Alegre']['tx_distorcao']
|
Análise_de_Dados_em_Python_Aula_03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Neural Network Classifier
# ---
# # Imports
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
from sklearn import metrics
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, GRU
from tensorflow.keras.layers import Dropout
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from imblearn.under_sampling import NearMiss, RandomUnderSampler
from imblearn.over_sampling import SMOTE, RandomOverSampler
from collections import Counter
import pickle
# +
from numpy.random import seed
seed(1)
# Set random seed
tf.random.set_seed(42)
# -
# # Read in Data
#
# Import data and observe the basics
csv_file = "../data/drugs_2020_simply_imputed.csv"
df = pd.read_csv(csv_file)
print(df.shape)
df.head()
# > **16829 rows and 67 columns**
# >> **However some of these columns are dropped and one is our target columns, PRISDUM**
df.columns
# - Drop the index columns created from saving a DataFrame to a csv.
# - Also drop the columns we have identified as either too correlated or not useful for our model.
features = ['accgdln', 'casetype', 'combdrg2', 'crimhist', 'disposit',
'district', 'drugmin', 'dsplea', 'intdum', 'methmin', 'mweight','nodrug',
'offguide', 'quarter', 'reas1', 'reas2', 'reas3', 'sources', 'statmax', 'statmin',
'age', 'newrace', 'monsex', 'monrace', 'neweduc', 'newcnvtn', 'citwhere', 'newcit'
]
# ## Train Test Split
# Set our X and Y
X = df[features]
y = df['prisdum']
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y)
X_no = X.drop(columns=['age', 'newrace', 'monsex', 'monrace', 'neweduc', 'newcnvtn', 'citwhere', 'newcit'])
X_no_train, X_no_test, y_no_train, y_no_test = train_test_split(X_no, y, stratify=y)
# # Scale Data for Neural Network Classifier
sc = StandardScaler()
X_train_sc = sc.fit_transform(X_train)
X_test_sc = sc.transform(X_test)
sc = StandardScaler()
X_no_train_sc = sc.fit_transform(X_no_train)
X_no_test_sc = sc.transform(X_no_test)
# ### Null Model
y.value_counts(normalize=True)
# > We see that we have a very imblanced dataset.
y_test.value_counts()
# ## Model on Imblanced Data
# +
model = Sequential()
model.add(Dense(64, input_shape=(X_train_sc.shape[1],), activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='bce',
optimizer='adam',
metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', patience=10, verbose=1)
history = model.fit(
X_train_sc,
y_train,
validation_data=(X_test_sc, y_test),
epochs=200,
callbacks=[early_stop]
)
# +
preds = np.round(model.predict(X_test_sc),0)
tn, fp, fn, tp = metrics.confusion_matrix(y_test, preds).ravel()
cm = pd.DataFrame(metrics.confusion_matrix(y_test, preds),
columns=['predicted_no_prison', 'predicted_prison'],
index=['actual_no_prison', 'actual_prison']
)
cm
# -
misclass1 = []
for row_index, (input, prediction, label) in enumerate(zip (X_test_sc, preds, y_test)):
if prediction != label:
misclass1.append(row_index)
print(len(misclass1))
# #### Analysis:
#
# >loss: 0.1126 - accuracy: 0.9609 - val_loss: 0.1429 - val_accuracy: 0.9587
#
# As expected, a very accurate model. However, likely suffering because of the test-set class imbalance as it hardly beats our Null Model of about 95.5%
#
# This very high accuracy leads to only 174 misclassifications, 26 of which are in the position we are most interested in; predicted no-prison, actual prison.
# ### Without Demographic information
# +
model = Sequential()
model.add(Dense(64, input_shape=(X_no_train_sc.shape[1],), activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='bce',
optimizer='adam',
metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', patience=10, verbose=1)
history = model.fit(
X_no_train_sc,
y_no_train,
validation_data=(X_no_test_sc, y_no_test),
epochs=200,
callbacks=[early_stop]
)
# +
preds = np.round(model.predict(X_no_test_sc),0)
tn, fp, fn, tp = metrics.confusion_matrix(y_no_test, preds).ravel()
cm = pd.DataFrame(metrics.confusion_matrix(y_no_test, preds),
columns=['predicted_no_prison', 'predicted_prison'],
index=['actual_no_prison', 'actual_prison']
)
cm
# -
misclass1_no = []
for row_index, (input, prediction, label) in enumerate(zip (X_no_test_sc, preds, y_no_test)):
if prediction != label:
misclass1_no.append(row_index)
print(len(misclass1_no))
# #### Analysis:
# >loss: 0.1251 - accuracy: 0.9608 - val_loss: 0.1591 - val_accuracy: 0.9587
#
# As expected, we again have a very accurate model. However, likely suffering because of the test-set class imbalance as it barely beats our null model.
#
# This very high accuracy leads to only 174 misclassifications, 18 of which are in the position we are most interested in; predicted no-prison, actual prison.
# ---
#
# # Balance Imbalanced Data
#
# ---
# ## Under Sample Majority
nm = RandomUnderSampler()
X_train_under, y_train_under = nm.fit_resample(X_train_sc, y_train)
y_train_under.value_counts(normalize=True)
# +
model = Sequential()
model.add(Dense(64, input_shape=(X_train_under.shape[1],), activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='bce',
optimizer='adam',
metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', patience=10, verbose=1)
history = model.fit(
X_train_under,
y_train_under,
validation_data=(X_test_sc, y_test),
epochs=200,
callbacks=[early_stop]
)
# +
preds = np.round(model.predict(X_test_sc),0)
tn, fp, fn, tp = metrics.confusion_matrix(y_test, preds).ravel()
cm = pd.DataFrame(metrics.confusion_matrix(y_test, preds),
columns=['predicted_no_prison', 'predicted_prison'],
index=['actual_no_prison', 'actual_prison']
)
cm
# -
misclass2 = []
for row_index, (input, prediction, label) in enumerate(zip (X_test_sc, preds, y_test)):
if prediction != label:
misclass2.append(row_index)
print(len(misclass2))
# #### Analysis
#
# >loss: 0.3535 - accuracy: 0.8451 - val_loss: 0.5578 - val_accuracy: 0.7322
#
# After balancing, we have a much more reasonable model. There is evidence of overfitting when looking at the train accuracy of 84.51% versus a test accuracy of 73.22%, but we are more concerned with what was misclassified.
#
# We see a large relative increase in misclassifications, as expected with such a large loss in accuracy, with a total of 1127 misclassifications, 1098 of which are in the position we are most interested in; predicted no-prison, actual prison.
# ### Without Demographic information
nm = RandomUnderSampler()
X_no_train_under, y_no_train_under = nm.fit_resample(X_no_train_sc, y_no_train)
# +
model = Sequential()
model.add(Dense(64, input_shape=(X_no_train_under.shape[1],), activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='bce',
optimizer='adam',
metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', patience=10, verbose=1)
history = model.fit(
X_no_train_under,
y_no_train_under,
validation_data=(X_no_test_sc, y_no_test),
epochs=200,
callbacks=[early_stop]
)
# +
preds = np.round(model.predict(X_no_test_sc),0)
tn, fp, fn, tp = metrics.confusion_matrix(y_no_test, preds).ravel()
cm = pd.DataFrame(metrics.confusion_matrix(y_no_test, preds),
columns=['predicted_no_prison', 'predicted_prison'],
index=['actual_no_prison', 'actual_prison']
)
cm
# -
misclass2_no = []
for row_index, (input, prediction, label) in enumerate(zip (X_no_test_sc, preds, y_no_test)):
if prediction != label:
misclass2_no.append(row_index)
print(len(misclass2_no))
# #### Analysis
#
# > loss: 0.4105 - accuracy: 0.8265 - val_loss: 0.5280 - val_accuracy: 0.7184
#
# After removing demographics, we see a small drop in accuracy, however this can be attributed to simple a loss of features.
#
# We do see a small relative increase in misclassifications from the similar model that included demographics, a total of 1185 misclassifications, 1161 of which are in the position we are most interested in; predicted no-prison, actual prison.
# #### Save model for Application
model.save('NN_under_nodem')
# ## SMOTE
# +
smo = SMOTE()
X_train_smote, y_train_smote = smo.fit_resample(X_train_sc, y_train)
# +
model = Sequential()
model.add(Dense(64, input_shape=(X_train_smote.shape[1],), activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='bce',
optimizer='adam',
metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', patience=10, verbose=1)
history = model.fit(
X_train_smote,
y_train_smote,
validation_data=(X_test_sc, y_test),
epochs=200,
callbacks=[early_stop]
)
# +
preds = np.round(model.predict(X_test_sc),0)
tn, fp, fn, tp = metrics.confusion_matrix(y_test, preds).ravel()
cm = pd.DataFrame(metrics.confusion_matrix(y_test, preds),
columns=['predicted_no_prison', 'predicted_prison'],
index=['actual_no_prison', 'actual_prison']
)
cm
# -
misclass3 = []
for row_index, (input, prediction, label) in enumerate(zip (X_test_sc, preds, y_test)):
if prediction != label:
misclass3.append(row_index)
print(len(misclass3))
# #### Analysis
#
# > loss: 0.1826 - accuracy: 0.9312 - val_loss: 0.3377 - val_accuracy: 0.8893
#
# SMOTE produced a much stronger model, with higher accuracy for both train and test sets as well as a smaller difference between the two accuracies.
#
# Due to this higher accuracy, we have a lower misclassification rate with a total of 466, 396 of which are in the position we are most interested in; predicted no-prison, actual prison.
# ### Without Demographic information
nm = RandomUnderSampler()
X_no_train_under, y_no_train_under = nm.fit_resample(X_no_train_sc, y_no_train)
# +
model = Sequential()
model.add(Dense(64, input_shape=(X_no_train_under.shape[1],), activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='bce',
optimizer='adam',
metrics=['accuracy'])
early_stop = EarlyStopping(monitor='val_loss', patience=10, verbose=1)
history = model.fit(
X_no_train_under,
y_no_train_under,
validation_data=(X_no_test_sc, y_no_test),
epochs=200,
callbacks=[early_stop]
)
# +
preds = np.round(model.predict(X_no_test_sc),0)
tn, fp, fn, tp = metrics.confusion_matrix(y_no_test, preds).ravel()
cm = pd.DataFrame(metrics.confusion_matrix(y_no_test, preds),
columns=['predicted_no_prison', 'predicted_prison'],
index=['actual_no_prison', 'actual_prison']
)
cm
# -
misclass3_no = []
for row_index, (input, prediction, label) in enumerate(zip (X_no_test_sc, preds, y_no_test)):
if prediction != label:
misclass3_no.append(row_index)
print(len(misclass3_no))
# #### Analysis
#
# > loss: 0.3958 - accuracy: 0.8292 - val_loss: 0.5057 - val_accuracy: 0.7410
#
# Now we start to see some interesting comparisons. When removing demographics, we see a significant loss in accuracy; part of which can be explained by the removal of features in general. We also see evidence of overfitting, but not to the level of the UnderSample balancing technique.
#
# We do see a large relative increase in misclassifications from the similar model that included demographics, a total of 1090 misclassifications, 1060 of which are in the position we are most interested in; predicted no-prison, actual prison.
# #### Save model for Application
model.save('NN_smote_nodem')
# ---
# # Misclassifications
import warnings
warnings.filterwarnings("ignore")
# +
tar_misclass_set = [misclass3_no]
tar_misclass_ids = {}
for misclass in tar_misclass_set:
for ids in misclass:
if ids in tar_misclass_ids.keys():
tar_misclass_ids[ids] += 1
else:
tar_misclass_ids[ids] = 1
tar_misclass_df = df.iloc[[item for sublist in tar_misclass_set for item in sublist]]
tar_misclass_df['no_of_misclass'] = 0
for ids in tar_misclass_df.index:
tar_misclass_df['no_of_misclass'].loc[ids] = tar_misclass_ids[ids]
# -
print(tar_misclass_df.shape)
tar_misclass_df.head()
# ---
# ## Save Desired Model's Misclassifications to CSV
#
# We will save the misclassifications from our saved models, SMOTE and Undersample Majority, to a CSV for EDA purposes.
tar_misclass_df.to_csv('NN_misclass_df.csv')
|
code/03_Modeling_NN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Rizwan-Ahmed-Surhio/Accountants/blob/main/6_OtherOperators.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="UaVe3TYoRUJ2"
# # Logical Operators
# + [markdown] id="YPcPtWvFm4vK"
# ### Buy if
# #### 1 - Sales Grwoth is 15% and above
# #### 2 - Net Profit Margin is 4% and above
# + [markdown] id="h61JjPGbooL4"
# ## AND
# + id="_CIjV-PARIva"
ABC_sales_growth = 0.18
ABC_net_margin = 0.05
# + id="eO5mutRSZqpX"
buy_decision = ABC_sales_growth >= 0.15 and ABC_net_margin >= 0.04
# + id="l8KDHOCsaU5Q"
print(buy_decision)
# + id="nuFqb6DWaZmK"
XYZ_sales_growth = 0.11
XYZ_net_margin = 0.09
# + id="npe0MXg4oROW"
buy_decision = XYZ_sales_growth >= 0.15 and XYZ_net_margin >= 0.04
# + id="UeqVcHLYoRyX"
print(buy_decision)
# + [markdown] id="weL2YOGIorY1"
# ## OR
# + id="fSxuBwOBokro"
buy_decision = XYZ_sales_growth >= 0.15 or XYZ_net_margin >= 0.04
# + id="FnXLWzCSok8N"
print(buy_decision)
# + [markdown] id="a9TRezpko29E"
# ## NOT
# + id="FiZ2q6pfo44c"
buy_decision = not(XYZ_sales_growth >= 0.15 or XYZ_net_margin >= 0.04 )
# + id="mGnaQI0SpRYa"
print(buy_decision)
# + id="MrGxQYpmRh34"
|
6_OtherOperators.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Machine Learning for Engineers: [StochasticGradientDescent](https://www.apmonitor.com/pds/index.php/Main/StochasticGradientDescent)
# - [Stochastic Gradient Descent](https://www.apmonitor.com/pds/index.php/Main/StochasticGradientDescent)
# - Source Blocks: 2
# - Description: Introduction to Stochastic Gradient Descent
# - [Course Overview](https://apmonitor.com/pds)
# - [Course Schedule](https://apmonitor.com/pds/index.php/Main/CourseSchedule)
#
from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss='modified_huber',shuffle=True,random_state=101)
sgd.fit(XA,yA)
yP = sgd.predict(XB)
# +
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import SGDClassifier
classifier = SGDClassifier(loss='modified_huber',shuffle=True,random_state=101)
# The digits dataset
digits = datasets.load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
# Split into train and test subsets (50% each)
X_train, X_test, y_train, y_test = train_test_split(
data, digits.target, test_size=0.5, shuffle=False)
# Learn the digits on the first half of the digits
classifier.fit(X_train, y_train)
# Test on second half of data
n = np.random.randint(int(n_samples/2),n_samples)
print('Predicted: ' + str(classifier.predict(digits.data[n:n+1])[0]))
# Show number
plt.imshow(digits.images[n], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
|
All_Source_Code/StochasticGradientDescent/StochasticGradientDescent.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: clean_country
# language: python
# name: clean_country
# ---
# # `clean_country()`: Clean and validate countries and regions
# ## Introduction
#
# The function `clean_country()` cleans a column containing country names and/or [ISO 3166](https://en.wikipedia.org/wiki/List_of_ISO_3166_country_codes) country codes, and standardizes them in a desired format. The function `validate_country()` validates either a single country or a column of countries, returning True if the value is valid, and False otherwise. The countries/regions supported and the regular expressions used can be found on [github](https://github.com/sfu-db/dataprep/blob/develop/dataprep/clean/country_data.tsv).
#
# Countries can be converted to and from the following formats via the `input_format` and `output_format` parameters:
#
# * Short country name (name): "United States"
# * Official state name (official): "United States of America"
# * ISO 3166-1 alpha-2 (alpha-2): "US"
# * ISO 3166-1 alpha-3 (alpha-3): "USA"
# * ISO 3166-1 numeric (numeric): "840"
#
# `input_format` can also be set to "auto" which automatically infers the input format.
#
# The `strict` parameter allows for control over the type of matching used for the "name" and "official" input formats.
#
# * False (default for `clean_country()`), search the input for a regex match
# * True (default for `validate_country()`), look for a direct match with a country value in the same format
#
# The `fuzzy_dist` parameter sets the maximum edit distance (number of single character insertions, deletions or substitutions required to change one word into the other) allowed between the input and a country regex.
#
# * 0 (default), countries at most 0 edits from matching a regex are successfully cleaned
# * 1, countries at most 1 edit from matching a regex are successfully cleaned
# * n, countries at most n edits from matching a regex are successfully cleaned
#
# Invalid parsing is handled with the `errors` parameter:
#
# * "coerce" (default), invalid parsing will be set as NaN
# * "ignore", then invalid parsing will return the input
# * "raise", then invalid parsing will raise an exception
#
#
# After cleaning, a **report** is printed that provides the following information:
#
# * How many values were cleaned (the value must be transformed)
# * How many values could not be parsed
# * And the data summary: how many values in the correct format, and how many values are null
#
# The following sections demonstrate the functionality of `clean_country()` and `validate_country()`.
# ### An example dirty dataset
import pandas as pd
import numpy as np
df = pd.DataFrame({"messy_country":
["Canada", "foo canada bar", "cnada", "northern ireland",
" ireland ", "congo, kinshasa", "congo, brazzaville",
304, "233", " tr ", "ARG", "hello", np.nan, "NULL"]
})
df
# ## 1. Default `clean_country()`
# By default, the `input_format` parameter is set to "auto" (automatically determines the input format), the `output_format` parameter is set to "name". The `fuzzy_dist` parameter is set to 0 and `strict` is False. The `errors` parameter is set to "coerce" (set NaN when parsing is invalid).
from dataprep.clean import clean_country
clean_country(df, "messy_country")
# Note "Canada" is considered not cleaned in the report since it's cleaned value is the same as the input. Also, "northern ireland" is invalid because it is part of the United Kingdom. Kinshasa and Brazzaville are the capital cities of their respective countries.
# ## 2. Input formats
#
# This section demonstrates the supported country input formats.
#
# ### name
#
# If the input contains a match with one of the country regexes then it is successfully converted.
clean_country(df, "messy_country", input_format="name")
# ### official
#
# Does the same thing as `input_format = "name"`.
clean_country(df, "messy_country", input_format="official")
# ### alpha-2
#
# Looks for a direct match with a ISO 3166-1 alpha-2 country code, case insensitive and ignoring leading and trailing whitespace.
clean_country(df, "messy_country", input_format="alpha-2")
# ### alpha-3
#
# Looks for a direct match with a ISO 3166-1 alpha-3 country code, case insensitive and ignoring leading and trailing whitespace.
clean_country(df, "messy_country", input_format="alpha-3")
# ### numeric
#
# Looks for a direct match with a ISO 3166-1 numeric country code, case insensitive and ignoring leading and trailing whitespace. Works on integers and strings.
clean_country(df, "messy_country", input_format="numeric")
# ## 3. Output formats
#
# This section demonstrates the supported output country formats.
#
# ### official
clean_country(df, "messy_country", output_format="official")
# ### alpha-2
clean_country(df, "messy_country", output_format="alpha-2")
# ### alpha-3
clean_country(df, "messy_country", output_format="alpha-3")
# ### numeric
clean_country(df, "messy_country", output_format="numeric")
# ### Any combination of input and output formats may be used.
clean_country(df, "messy_country", input_format="alpha-2", output_format="official")
# ## 4. `strict` parameter
#
# This parameter allows for control over the type of matching used for "name" and "official" input formats. When False, the input is searched for a regex match. When True, matching is done by looking for a direct match with a country in the same format.
clean_country(df, "messy_country", strict=True)
# "foo canada bar", "congo kinshasa" and "congo brazzaville" are now invalid because they are not a direct match with a country in the "name" or "official" formats.
# ## 5. Fuzzy Matching
#
# The `fuzzy_dist` parameter sets the maximum edit distance (number of single character insertions, deletions or substitutions required to change one word into the other) allowed between the input and a country regex. If an input is successfully cleaned by `clean_country()` with `fuzzy_dist = 0` then that input with one character inserted, deleted or substituted will match with `fuzzy_dist = 1`. This parameter only applies to the "name" and "official" input formats.
# ### `fuzzy_dist = 1`
#
# Countries at most one edit away from matching a regex are successfully cleaned.
df = pd.DataFrame({"messy_country":
["canada", "cnada", "australa", "xntarctica", "koreea", "cxnda",
"afghnitan", "country: cnada", "foo indnesia bar"]
})
clean_country(df, "messy_country", fuzzy_dist=1)
# ### `fuzzy_dist = 2`
#
# Countries at most two edits away from matching a regex are successfully cleaned.
clean_country(df, "messy_country", fuzzy_dist=2)
# ## 6. `inplace` parameter
# This just deletes the given column from the returned dataframe.
# A new column containing cleaned coordinates is added with a title in the format `"{original title}_clean"`.
clean_country(df, "messy_country", fuzzy_dist=2, inplace=True)
# ## 7. `validate_country()`
#
# `validate_lat_long()` returns True when the input is a valid country value otherwise it returns False. Valid types are the same as `clean_country()`. By default `strict = True`, as opposed to `clean_country()` which has `strict` set to False by default. The default `input_type` is "auto".
# +
from dataprep.clean import validate_country
print(validate_country("switzerland"))
print(validate_country("country = united states"))
print(validate_country("country = united states", strict=False))
print(validate_country("ca"))
print(validate_country(800))
# -
# ### `validate_country()` on a pandas series
#
# Since `strict = True` by default, the inputs "foo canada bar", "congo, kinshasa" and "congo, brazzaville" are invalid since they don't directly match a country in the "name" or "official" formats.
# +
df = pd.DataFrame({"messy_country":
["Canada", "foo canada bar", "cnada", "northern ireland",
" ireland ", "congo, kinshasa", "congo, brazzaville",
304, "233", " tr ", "ARG", "hello", np.nan, "NULL"]
})
df["valid"] = validate_country(df["messy_country"])
df
# -
# ### `strict = False`
# For "name" and "official" input types the input is searched for a regex match.
df["valid"] = validate_country(df["messy_country"], strict=False)
df
# ### Specifying `input_format`
df["valid"] = validate_country(df["messy_country"], input_format="numeric")
df
# ## Credit
#
# The country data and regular expressions used are based on the [country_converter](https://github.com/konstantinstadler/country_converter) project.
|
docs/source/user_guide/clean/clean_country.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SIkR and SEkIkR Models
#
# In order to model the delayed nature of both incubation and recovery, we can add additional compartments representing disease progression. In the SIkR model we add addiional stages to the infectious state, say $I_i^{\alpha}$ which transition to each other in equal rates
#
# $$
# \dot{I}^{\alpha}_i (t) = \gamma_I k \left(I_i^{{\alpha}-1} - I_{i}^{\alpha}\right)
# $$
#
# with a total of $\alpha=1,2,\dots k$ stages. In the SEkIkR model, we also add additional exposed stages which model the virus incubation period
#
# $$
# \dot{E}^{\alpha}_i (t) = \gamma_E k \left(E_i^{{\alpha}-1} - E_{i}^{\alpha}\right)
# $$
#
# with a total of $k$ stages.
#
# The multiplication of the intrisic rates by $k$ preserves the mean transition time regardless of the number of stages, $\langle T \rangle = \gamma^{-1}$. However, increasing the number of stages reduces the uncertainty of the transition time, such that $\sigma_T = \gamma^{-1}/\sqrt{k}$.
# %%capture
## compile PyRoss for this notebook
import os
owd = os.getcwd()
os.chdir('../../')
# %run setup.py install
os.chdir(owd)
# %matplotlib inline
import numpy as np
import pyross
import matplotlib.pyplot as plt
#from matplotlib import rc; rc('text', usetex=True)
from scipy import optimize
# ## SIkR Model
# We now initial an SIkR model with one infected individual, assuming an average incubation and recovery time of three weeks $\pm$10%.
# +
beta = 0.
gIs = 1.0 / 21 # Assume combined incubation and recovery time of three weeks
M = 4; Ni = np.ones(M) * 1e3;
N = np.sum(Ni);
IdM = np.eye(M);
def contactMatrix(t) :
return IdM;
K = 100; # so stddev of recovery time is 10% of mean
I0 = np.zeros((K,M));
I0[0,:]= 1;
S0 = np.zeros(M)
for i in range(M) :
S0[i] = Ni[i] - np.sum(I0[:,i])
I0 = np.reshape(I0, K*M);
Tf=35; Nf = 10*Tf+1
parameters = {'beta':beta, 'gI':gIs, 'k':K}
model = pyross.deterministic.SIkR(parameters, M, Ni)
data=model.simulate(S0, I0, contactMatrix, Tf, Nf)
# +
S = data['X'][:, 0];
Is1 = np.transpose(data['X'][:, (M)::M])
t = data['t'];
fig = plt.figure(num=None, figsize=(10, 8), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 22})
for i in range(K) :
plt.plot(t, Is1[i], lw = 2, color = np.array([1 - i/K,0,i/K]), alpha = 0.5)
plt.plot(t[0:-1], np.diff(1 - (np.sum(Is1,0))/np.diff(t)[0]), lw = 4, color = 'dimgrey')
plt.fill_between(t[0:-1], np.diff(1 - (np.sum(Is1,0))/np.diff(t)[0]), lw = 4, color = 'dimgrey', alpha = 0.25)
plt.grid()
plt.ylim(0, 1.2 * np.max(np.diff(1 - (np.sum(Is1,0))/np.diff(t)[0] ) ))
plt.title("Distribution of recovery times in SIkR Model");
# -
# ## SEkIkR Model
# We now refine the model by using two separate stages for the incubation and recovery. We now take an incubation period of two weeks $\pm$25%, and a recovery time of one week $\pm$10%, and initialize the model with a single exposed, incubating case. We find that the mean time to recovery from the moment of exposure is still three weeks. However, the variance is now larger because of the elavated uncertainty in the incubation period
# +
beta = 0.
gIs = 1.0 / 7 # Recovery rate of a week
gE = 1.0 / 14; # Incubation period of two weeks
M = 4; Ni = np.ones(M) * 1e3;
N = np.sum(Ni);
IdM = np.eye(M);
def contactMatrix(t) :
return IdM;
K = 100; # So stddiv in recovery time is 10% of mean
KE = 16; # So stddiv in recovery time is 25% of mean
S0 = np.zeros(M)
I0 = np.zeros((K,M));
E0 = np.zeros((KE,M));
# I0[0,:]= 1;
E0[0,:]= 1;
for i in range(M) :
S0[i] = Ni[i] - np.sum(I0[:,i]) - np.sum(E0[:,i])
I0 = np.reshape(I0, K*M);
E0 = np.reshape(E0, KE*M);
Tf=35; Nf = 10*Tf+1
parameters = {'beta':beta, 'gE':gE, 'gI':gIs, 'kI':K, 'kE' : KE}
model = pyross.deterministic.SEkIkR(parameters, M, Ni)
data=model.simulate(S0, E0, I0, contactMatrix, Tf, Nf)
# +
S = data['X'][:, 0];
Is1 = np.transpose(data['X'][:, (M + KE*M)::M])
Es1 = np.transpose(data['X'][:, (M):(M + KE*M):M])
t = data['t'];
fig = plt.figure(num=None, figsize=(10, 8), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 22})
for i in range(KE) :
plt.plot(t, Es1[i], lw = 2, color = np.array([1 - i/KE,0,i/KE]), alpha = 0.5)
plt.plot(t[0:-1], np.diff(1 - (np.sum(Es1,0))/np.diff(t)[0]), lw = 4, color = 'dimgrey')
plt.fill_between(t[0:-1], np.diff(1 - (np.sum(Es1,0))/np.diff(t)[0]), lw = 4, color = 'dimgrey', alpha = 0.25)
plt.grid();
plt.ylim(0, 1.2 * np.max(np.diff(1 - (np.sum(Es1,0))/np.diff(t)[0] ) ))
plt.title("Distribution of incubation times in SEkIkR Model");
fig = plt.figure(num=None, figsize=(10, 8), dpi=80, facecolor='w', edgecolor='k')
for i in range(K) :
plt.plot(t, Is1[i], lw = 2, color = np.array([1 - i/K,0,i/K]), alpha = 0.5)
plt.plot(t[0:-1], np.diff(1 - (np.sum(Is1,0) + np.sum(Es1,0))/np.diff(t)[0]), lw = 4, color = 'dimgrey')
plt.fill_between(t[0:-1], np.diff(1 - (np.sum(Is1,0)+np.sum(Es1,0))/np.diff(t)[0]), lw = 4, color = 'dimgrey', alpha = 0.25)
plt.grid()
plt.ylim(0, 1.2 * np.max(np.diff(1 - (np.sum(Es1,0) + np.sum(Is1,0))/np.diff(t)[0] ) ))
plt.title("Distribution of total recovery times in SEkIkR Model");
|
examples/deterministic/ex06b-SIkR-and-SEkIkR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_pytorch_p36
# language: python
# name: conda_pytorch_p36
# ---
# ## Training Amazon SageMaker models by using the Deep Graph Library with PyTorch backend
# The **Amazon SageMaker Python SDK** makes it easy to train Deep Graph Library (DGL) models. In this example, you train a simple graph neural network using the [DMLC DGL API](https://github.com/dmlc/dgl.git) and the [Cora dataset](https://relational.fit.cvut.cz/dataset/CORA). The Cora dataset describes a citation network. The Cora dataset consists of 2,708 scientific publications classified into one of seven classes. The citation network consists of 5,429 links. The task is to train a node classification model using Cora dataset.
# ### Setup
# Define a few variables that are needed later in the example.
# +
import sagemaker
from sagemaker import get_execution_role
from sagemaker.session import Session
# Setup session
sess = sagemaker.Session()
# S3 bucket for saving code and model artifacts.
# Feel free to specify a different bucket here.
bucket = sess.default_bucket()
# Location to put your custom code.
custom_code_upload_location = 'customcode'
# IAM execution role that gives Amazon SageMaker access to resources in your AWS account.
# You can use the Amazon SageMaker Python SDK to get the role from the notebook environment.
role = get_execution_role()
# -
# ### The training script
# The pytorch_gcn.py script provides all the code you need for training an Amazon SageMaker model.
# !cat pytorch_gcn.py
# ### SageMaker's estimator class
# The Amazon SageMaker Estimator allows you to run single machine in Amazon SageMaker, using CPU or GPU-based instances.
#
# When you create the estimator, pass in the filename of the training script and the name of the IAM execution role. You can also provide a few other parameters. train_instance_count and train_instance_type determine the number and type of Amazon SageMaker instances that are used for the training job. The hyperparameters parameter is a dictionary of values that is passed to your training script as parameters so that you can use argparse to parse them. You can see how to access these values in the pytorch_gcn.py script above.
#
# Here, you can directly use the DL Container provided by Amazon SageMaker for training DGL models by specifying the PyTorch framework version (>= 1.3.1) and the python version (only py3). You can also add a task_tag with value 'DGL' to help tracking the task.
#
# For this example, choose one ml.p3.2xlarge instance. You can also use a CPU instance such as ml.c4.2xlarge for the CPU image.
# +
from sagemaker.pytorch import PyTorch
CODE_PATH = 'pytorch_gcn.py'
account = sess.boto_session.client('sts').get_caller_identity()['Account']
region = sess.boto_session.region_name
params = {}
params['dataset'] = 'cora'
task_tags = [{'Key':'ML Task', 'Value':'DGL'}]
estimator = PyTorch(entry_point=CODE_PATH,
role=role,
train_instance_count=1,
train_instance_type='ml.p3.2xlarge', # 'ml.c4.2xlarge '
framework_version="1.3.1",
py_version='py3',
debugger_hook_config=False,
tags=task_tags,
hyperparameters=params,
sagemaker_session=sess)
# -
# ### Running the Training Job
# After you construct the Estimator object, fit it by using Amazon SageMaker. The dataset is automatically downloaded.
estimator.fit()
# ## Output
# You can get the model training output from the Amazon Sagemaker console by searching for the training task named pytorch-gcn and looking for the address of 'S3 model artifact'
|
sagemaker-python-sdk/dgl_gcn/pytorch_gcn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1> OpenSees Examples Manual Examples for OpenSeesPy</h1>
# <h2>OpenSees Example 1a. 2D Elastic Cantilever Column -- Static Pushover</h2>
# <p>
#
# You can find the original Examples:<br>
# https://opensees.berkeley.edu/wiki/index.php/Examples_Manual<br>
# Original Examples by By <NAME> & <NAME>, 2006, in Tcl<br>
# Converted to OpenSeesPy by SilviaMazzoni, 2020<br>
# <p>
#
# <h2> Simulation Process</h2>
#
# Each example script does the following:
# <h3>A. Build the model</h3>
# <ol>
# <li>model dimensions and degrees-of-freedom</li>
# <li>nodal coordinates</li>
# <li>nodal constraints -- boundary conditions</li>
# <li>nodal masses</li>
# <li>elements and element connectivity</li>
# <li>recorders for output</li>
# </ol>
# <h3>B. Define & apply gravity load</h3>
# <ol>
# <li>nodal or element load</li>
# <li>static-analysis parameters (tolerances & load increments)</li>
# <li>analyze</li>
# <li>hold gravity loads constant</li>
# <li>reset time to zero</li>
# </ol>
# <h3>C. Define and apply lateral load</h3>
# <dl>
# <li>Time Series and Load Pattern (nodal loads for static analysis, support ground motion for earthquake)</li>
# <li>lateral-analysis parameters (tolerances and displacement/time increments)</li>
# <b>Static Lateral-Load Analysis</b>
# <li>define the displacement increments and displacement path</li>
# <b>Dynamic Lateral-Load Analysis</b>
# <li>define the input motion and all associated parameters, such as scaling and input type</li>
# <li>define analysis duration and time increment</li>
# <li>define damping</li>
# <li>analyze</li>
# <p>
#
# <b>Introductory Examples</b>
# The objective of Example 1a and Example 1b is to give an overview of input-file format in OpenSees using simple scripts.
# These scripts do not take advantage of the Tcl scripting capabilities shown in the later examples. However, they do provide starting a place where the input file is similar to that of more familiar Finite-Element Analysis software. Subsequent examples should be used as the basis for user input files.
#
# <h1> OpenSees Example 1a. 2D Elastic Cantilever Column -- Static Pushover</h1>
# Introduction
# Example 1a is a simple model of an elastic cantilever column.
# <b> Objectives of Example 1b </b>
# - overview of basic OpenSees input structure<br>
# - coordinates, boundary conditions, element connectivity, nodal masses, nodal loads, etc.<br>
# - two-node, one element
# <img src="https://opensees.berkeley.edu/wiki/images/e/ec/Example1a_Push.GIF">
#
# +
############################################################
# EXAMPLE:
# pyEx1a.Canti2D.Push.tcl.py
# for OpenSeesPy
# --------------------------------------------------------#
# by: <NAME>, 2020
# <EMAIL>
############################################################
# This file was obtained from a conversion of the updated Tcl script
############################################################
# configure Python workspace
import openseespy.opensees as ops
import eSEESminiPy
import os
import math
import numpy as numpy
import matplotlib.pyplot as plt
ops.wipe()
# --------------------------------------------------------------------------------------------------
# Example 1. cantilever 2D
# static pushover analysis with gravity.
# all units are in kip, inch, second
# elasticBeamColumn ELEMENT
# <NAME> and <NAME>, 2006
#
# ^Y
# or
# 2 __
# or |
# or |
# or |
# (1) 36'
# or |
# or |
# or |
# =1= ---- -------->X
#
# SET UP ----------------------------------------------------------------------------
ops.wipe() # clear opensees model
ops.model('basic','-ndm',2,'-ndf',3) # 2 dimensions, 3 dof per node
if not os.path.exists('Data'):
os.mkdir('Data')
# define GEOMETRY -------------------------------------------------------------
# nodal coordinates:
ops.node(1,0,0) # node , X Y
ops.node(2,0,432)
# Single point constraints -- Boundary Conditions
ops.fix(1,1,1,1) # node DX DY RZ
# nodal masses:
ops.mass(2,5.18,0.,0.) # node , Mx My Mz, Mass=Weight/g.
# Define ELEMENTS -------------------------------------------------------------
# define geometric transformation: performs a linear geometric transformation of beam stiffness
# and resisting force from the basic system to the global-coordinate system
ops.geomTransf('Linear',1) # associate a tag to transformation
# connectivity: (make A very large, 10e6 times its actual value)
# element elasticBeamColumn eleTag iNode jNode A E Iz transfTag
ops.element('elasticBeamColumn',1,1,2,3600000000,4227,1080000,1) # element elasticBeamColumn 1 1 2 3600000000 4227 1080000 1;
# Define RECORDERS -------------------------------------------------------------
ops.recorder('Node','-file','Data/DFreeEx1aPush.out','-time','-node',2,'-dof',1,2,3,'disp') # displacements of free nodes
ops.recorder('Node','-file','Data/DBaseEx1aPush.out','-time','-node',1,'-dof',1,2,3,'disp') # displacements of support nodes
ops.recorder('Node','-file','Data/RBaseEx1aPush.out','-time','-node',1,'-dof',1,2,3,'reaction') # support reaction
ops.recorder('Element','-file','Data/FColEx1aPush.out','-time','-ele',1,'globalForce') # element forces -- column
ops.recorder('Element','-file','Data/DColEx1aPush.out','-time','-ele',1,'deformation') # element deformations -- column
# define GRAVITY -------------------------------------------------------------
ops.timeSeries('Linear',1) # timeSeries Linear 1;
# define Load Pattern
ops.pattern('Plain',1,1) #
ops.load(2,0.,-2000.,0.) # node , FX FY MZ -- superstructure-weight
ops.wipeAnalysis() # adding this to clear Analysis module
ops.constraints('Plain') # how it handles boundary conditions
ops.numberer('Plain') # renumber dofs to minimize band-width (optimization), if you want to
ops.system('BandGeneral') # how to store and solve the system of equations in the analysis
ops.test('NormDispIncr',1.0e-8,6) # determine if convergence has been achieved at the end of an iteration step
ops.algorithm('Newton') # use Newtons solution algorithm: updates tangent stiffness at every iteration
ops.integrator('LoadControl',0.1) # determine the next time step for an analysis, apply gravity in 10 steps
ops.analysis('Static') # define type of analysis static or transient
ops.analyze(10) # perform gravity analysis
ops.loadConst('-time',0.0) # hold gravity constant and restart time
# define LATERAL load -------------------------------------------------------------
# Lateral load pattern
ops.timeSeries('Linear',2) # timeSeries Linear 2;
# define Load Pattern
ops.pattern('Plain',2,2) #
ops.load(2,2000.,0.0,0.0) # node , FX FY MZ -- representative lateral load at top node
# pushover: diplacement controlled static analysis
ops.integrator('DisplacementControl',2,1,0.1) # switch to displacement control, for node 11, dof 1, 0.1 increment
ops.analyze(1000) # apply 100 steps of pushover analysis to a displacement of 10
print('Done!')
# -
eSEESminiPy.drawModel()
# plot deformed shape at end of analysis (it may have returned to rest)
# amplify the deformtions by 5
eSEESminiPy.drawDeformedShape(5)
ops.wipe() # the wipe command here closes all recorder files
plt.close('all')
fname3 = 'Data/DFreeEx1aPush.out'
dataDFree = numpy.loadtxt(fname3)
plt.subplot(211)
plt.title('Ex1a.Canti2D.Push.tcl')
plt.grid(True)
plt.plot(dataDFree[:,1])
plt.xlabel('Step Number')
plt.ylabel('Free-Node Displacement')
plt.subplot(212)
plt.grid(True)
plt.plot(dataDFree[:,1],dataDFree[:,0])
plt.xlabel('Free-Node Disp.')
plt.ylabel('Pseudo-Time (~Force)')
plt.show()
print('End of Run: pyEx1a.Canti2D.Push.tcl.py')
|
BraineryBytes_OpenSees_Examples_Manual_Example_1a_Elastic_Cantilever_Column_Pushover.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, IBMQ
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from ibm_quantum_widgets import *
# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()
# +
import qiskit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute
from qiskit import Aer
from qiskit import IBMQ
from qiskit.compiler import transpile
from time import perf_counter
from qiskit.tools.visualization import plot_histogram
import numpy as np
import math
'''
params
---------------
picture: square 2d array of integers representing grayscale values
assume the length (n) is some power of 2
return
---------------
a flattened representation of picture using bitstrings (boolean arrays)
'''
def convert_to_bits (picture):
n = len(picture)
ret = []
for i in range(n):
for j in range(n):
value = picture[i][j]
bitstring = bin(value)[2:]
ret.append([0 for i in range(8 - len(bitstring))] + [1 if c=='1' else 0 for c in bitstring])
return ret
'''
params
----------------
bitStr: a representation of an image using bitstrings to represent grayscale values
return
----------------
A quantum circuit containing the NEQR representation of the image
'''
def neqr(bitStr):
newBitStr = bitStr
#print(newBitStr)
#print("\n")
# Pixel position
idx = QuantumRegister(math.ceil(math.log2(len(newBitStr))), 'idx')
# Pixel intensity values
intensity = QuantumRegister(8, 'intensity')
# Classical Register
creg = ClassicalRegister(10, 'creg')
# Quantum Image Representation as a quantum circuit
# with Pixel Position and Intensity registers
quantumImage = QuantumCircuit(intensity, idx, creg)
numOfQubits = quantumImage.num_qubits
print("\n>> Initial Number of Qubits:", numOfQubits)
# -----------------------------------
# Drawing the Quantum Circuit
# -----------------------------------
lengthIntensity = intensity.size
lengthIdx = idx.size
start = perf_counter()
quantumImage.i([intensity[lengthIntensity-1-i] for i in range(lengthIntensity)])
quantumImage.h([idx[lengthIdx-1-i] for i in range(lengthIdx)])
numOfPixels = len(newBitStr)
for i in range(numOfPixels):
bin_ind = bin(i)[2:]
bin_ind = (lengthIdx - len(bin_ind)) * '0' + bin_ind
bin_ind = bin_ind[::-1]
# X-gate (enabling zero-controlled nature)
for j in range(len(bin_ind)):
if bin_ind[j] == '0':
quantumImage.x(idx[j])
# Configuring Multi-Qubit Controlled-NOT (mcx) gates with control and target qubits
for j in range(len(newBitStr[i])):
if newBitStr[i][j] == 1:
quantumImage.mcx(idx, intensity[lengthIntensity-1-j])
# X-gate (reversing the Negated state of the qubits)
for j in range(len(bin_ind)):
if bin_ind[j] == '0':
quantumImage.x(idx[j])
quantumImage.barrier()
quantumImage.measure(range(10), range(10))
end = perf_counter()
print(f">> Circuit construction took {(end-start)} seconds.")
return (quantumImage, intensity)
if __name__ == '__main__':
test_picture_2x2 = [[0, 100], [200, 255]]
test_picture_3x3 = [[25, 50, 75], [100, 125, 150], [175, 200, 225]]
test_picture_4x4 = [[0, 100, 143, 83], [200, 255, 43, 22], [12, 234, 23, 5], [112, 113, 117, 125]]
test_picture_5x5 = [[0, 100, 212, 12, 32], [0, 100, 212, 12, 32], [0, 100, 212, 12, 32], [0, 100, 212, 12, 32], [0, 100, 212, 12, 32]]
arr = convert_to_bits(test_picture_2x2)
arr1 = convert_to_bits(test_picture_3x3)
arr2 = convert_to_bits(test_picture_4x4)
arr3 = convert_to_bits(test_picture_5x5)
print("2x2: ", arr, "\n")
#print("3x3: ", arr1, "\n")
#print("4x4: ", arr2, "\n")
#print("5x5: ", arr3, "\n")
qc_image, _ = neqr(arr)
# -
qc_image.draw()
# +
# Circuit Dimensions
print('>> Circuit dimensions')
print('>> Circuit depth (length of critical path): ', qc_image.depth())
print('>> Total Number of Gate Operations: ', qc_image.size())
# Get the number of qubits needed to run the circuit
active_qubits = {}
for op in qc_image.data:
if op[0].name != "barrier" and op[0].name != "snapshot":
for qubit in op[1]:
active_qubits[qubit.index] = True
print(f">> Width: {len(active_qubits)} qubits")
print(f">> Width (total number of qubits and clbits): {qc_image.width()} qubits")
print(f">> Gates used: {qc_image.count_ops()}")
print(f">> Fundamental Gates: {qc_image.decompose().count_ops()}")
# Testing qc_image circuit using Fake Simulator
# to simulate the error in a real quantum computer
from qiskit.providers.aer import AerSimulator
from qiskit.test.mock import FakeMontreal
device_backend = FakeMontreal()
sim_montreal = AerSimulator.from_backend(device_backend)
#### TRANSPILING
start_transpile = perf_counter()
tcirc = transpile(qc_image, sim_montreal, optimization_level=1) # Optimization Level = 1 (default)
end_transpile = perf_counter()
print(f"\n>> Circuit transpilation took {(end_transpile-start_transpile)} seconds.")
#### SIMULATING
start_sim = perf_counter()
# Run transpiled circuit on FakeMontreal
result_noise = sim_montreal.run(tcirc).result()
# Get counts for each possible result
counts_noise = result_noise.get_counts()
end_sim = perf_counter()
print(f"\n>> Circuit simulation took {(end_sim-start_sim)} seconds.")
# +
#plot_histogram(counts_noise, figsize=(30, 15))
#print(counts_noise)
# +
from qiskit.compiler import assemble
aer_sim = Aer.get_backend('aer_simulator')
t_qc_image = transpile(qc_image, aer_sim)
shots = 1024
qobj = assemble(t_qc_image, shots=shots)
job_neqr = aer_sim.run(qobj)
result_neqr = job_neqr.result()
counts_neqr = result_neqr.get_counts()
print('Encoded: 00 = ', arr[0])
print('Encoded: 01 = ', arr[1])
print('Encoded: 10 = ', arr[2])
print('Encoded: 11 = ', arr[3])
print("\nExpected Counts per pixel = ", shots/len(arr))
print("Experimental Counts", counts_neqr)
print("\nExpected probability for each pixel = ", 1.0/(len(arr)))
plot_histogram(counts_neqr)
# -
machine = "ibmq_santiago"
backend = provider.get_backend(machine)
santiago_sim = AerSimulator.from_backend(backend)
start_sim = perf_counter()
result = santiago_sim.run(qc_image).result()
counts = result.get_counts(qc_image)
end_sim = perf_counter()
print("\n", end_sim-start_sim)
print("\nExpected Counts per pixel = ", shots/len(arr), "\n")
for(measured_state, count) in counts.items():
big_endian_state = measured_state[::-1]
print(f"Measured {big_endian_state} {count} times.")
machine = "ibmq_belem"
backend = provider.get_backend(machine)
santiago_sim = AerSimulator.from_backend(backend)
start_sim = perf_counter()
result = santiago_sim.run(qc_image).result()
counts = result.get_counts(qc_image)
end_sim = perf_counter()
print(end_sim-start_sim)
print("\nExpected Counts per pixel = ", shots/len(arr), "\n")
for(measured_state, count) in counts.items():
big_endian_state = measured_state[::-1]
print(f"Measured {big_endian_state} {count} times.")
# +
# Testing qc_image circuit using Fake Simulator
# to simulate the error in a real quantum computer
from qiskit.providers.aer import AerSimulator
from qiskit.test.mock import FakeMumbai
device_backend = FakeMumbai()
sim_brooklyn = AerSimulator.from_backend(device_backend)
#### TRANSPILING
start_transpile = perf_counter()
tcirc = transpile(qc_image, sim_brooklyn, optimization_level=1) # Optimization Level = 1 (default)
end_transpile = perf_counter()
print(f"\n>> Circuit transpilation took {(end_transpile-start_transpile)} seconds.")
#### SIMULATING
start_sim = perf_counter()
# Run transpiled circuit on FakeMontreal
result_noise = sim_brooklyn.run(tcirc).result()
# Get counts for each possible result
counts_noise = result_noise.get_counts()
end_sim = perf_counter()
print(f"\n>> Circuit simulation took {(end_sim-start_sim)} seconds.")
# -
from qiskit.test.mock import FakeMontreal
fake_athens = FakeMontreal()
t_qc = transpile(qc_image, fake_athens, optimization_level=3)
qobj = assemble(t_qc, shots=4096)
result = fake_athens.run(qobj).result()
counts = result.get_counts(qc_image)
print(counts)
plot_histogram(counts)
plot_histogram(counts, figsize=(30, 15))
|
REPA_NEQR_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: DESI 19.12
# language: python
# name: desi-19.12
# ---
# # Getting started on jupyter.nersc.gov
# Lets first setup the DESI environment and install the DESI-specific kernel
# ```bash
# source /global/common/software/desi/desi_environment.sh 19.12
# ${DESIMODULES}/install_jupyter_kernel.sh 19.12
# ```
# See [https://desi.lbl.gov/trac/wiki/Computing/JupyterAtNERSC](https://desi.lbl.gov/trac/wiki/Computing/JupyterAtNERSC) for more details.
#
# Now we can import DESI-specific python packages from [desihub](https://github.com/desihub/).
#
#
# # Reading DESI spectra
# For instance we can use `desispec` to read in some DESI BGS coadded spectra from Comissioning that I've included in the repo
from desispec.io import read_spectra
# -- plotting --
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['font.family'] = 'serif'
mpl.rcParams['axes.linewidth'] = 1.5
mpl.rcParams['axes.xmargin'] = 1
mpl.rcParams['xtick.labelsize'] = 'x-large'
mpl.rcParams['xtick.major.size'] = 5
mpl.rcParams['xtick.major.width'] = 1.5
mpl.rcParams['ytick.labelsize'] = 'x-large'
mpl.rcParams['ytick.major.size'] = 5
mpl.rcParams['ytick.major.width'] = 1.5
mpl.rcParams['legend.frameon'] = False
spectra = read_spectra('coadd-66003-20200315-1-00055654.few.fits') # handful of BGS galaxies from Tile 66003 observed on 03/15/2020, Petal #1, Exposure #00055654
# +
fig = plt.figure(figsize=(15,10))
sub = fig.add_subplot(211)
sub.plot(spectra.wave['brz'], spectra.flux['brz'][2])
sub.set_xlim(3.6e3, 9.8e3)
sub.set_ylabel('flux ($10^{-17} erg/s/\AA/s/cm^2$)', fontsize=25)
sub.set_ylim(-5, 20)
sub = fig.add_subplot(212)
sub.plot(spectra.wave['brz'], spectra.flux['brz'][6])
sub.set_xlabel('wavelength ($\AA$)', fontsize=25)
sub.set_xlim(3.6e3, 9.8e3)
#sub.set_ylabel('flux ($10^{-17} erg/s/\AA/s/cm^2$)', fontsize=25)
sub.set_ylim(-5, 20)
# -
# # Fitting Redshifts using `redrock`
# The main goal of DESI is to measure the redshifts of millions of galaxies. Redshifts will be measured for galaxy spectra, like the ones above using `redrock`: https://github.com/desihub/redrock
#
# `redrock` can be easily run on DESI spectra on the command line
f_spec = 'coadd-66003-20200315-1-00055654.few.fits'
f_rr_h5 = 'redrock.coadd.h5'
f_rr = 'zbest.coadd.fits'
print(f_rr)
# !rrdesi -o $f_rr_h5 -z $f_rr $f_spec
# # `redrock` outputs
# Lets take a look at what `redrock` outputs
from astropy.table import Table
zbest = Table.read('zbest.coadd.fits', hdu=1)
zbest
import redrock.templates
templates = dict()
for filename in redrock.templates.find_templates():
t = redrock.templates.Template(filename)
templates[(t.template_type, t.sub_type)] = t
# ## `redrock` galaxy templates
# `redrock` fits galaxy spectra with a linear combination of PCA templates. Here's what the galaxy templates look like:
fig = plt.figure(figsize=(15,5))
sub = fig.add_subplot(111)
for i in range(templates[('GALAXY', '')].flux.shape[0]):
sub.plot(templates[('GALAXY', '')].wave, templates[('GALAXY', '')].flux[i])
sub.set_xlim(templates[('GALAXY', '')].wave.min(), templates[('GALAXY', '')].wave.max())
sub.set_ylim(-0.02, 0.02)
# Since the `redrock` output file contains the coefficients of the PCA templates, we can use these templates to reconstruct the best-fit `redrock` fit
i = 2
z = zbest['Z'][i]
targetid = zbest['TARGETID'][i]
ncoeff = templates[(zbest['SPECTYPE'][i].strip(), zbest['SUBTYPE'][i].strip())].flux.shape[0]
coeff = zbest['COEFF'][i][0:ncoeff]
print('z_redrock = %.3f' % z)
tflux = templates[(zbest['SPECTYPE'][i].strip(), zbest['SUBTYPE'][i].strip())].flux.T.dot(coeff)
twave = templates[(zbest['SPECTYPE'][i].strip(), zbest['SUBTYPE'][i].strip())].wave * (1+z)
# +
fig = plt.figure(figsize=(15,10))
sub = fig.add_subplot(211)
for band in spectra.bands:
sub.plot(spectra.wave[band], spectra.flux[band][i], 'C0', alpha=0.5)
for icoeff in range(ncoeff):
sub.plot(twave, templates[(zbest['SPECTYPE'][i].strip(), zbest['SUBTYPE'][i].strip())].flux[icoeff] * coeff[icoeff], ls=':', lw=0.5)
sub.plot(twave, tflux, 'r-')
sub.set_ylim(-5, 40)
sub.set_xlim(3500, 10000)
# -
# For more details on the redrock output check out the following tutorials:
# - https://github.com/desihub/tutorials/blob/master/redrock/RedrockOutputs.ipynb
# - https://github.com/desihub/tutorials/blob/master/redrock/RedrockPlotSpec.md
|
Dec2020/galaxies/fitting_redshifts.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/gr8nishan/Fast-Ai-Course/blob/master/Tabular_Data_Lesson_4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="ljvInO4vf5VM" colab_type="code" colab={}
from fastai import *
from fastai.tabular import *
# + id="3YyFCCaXgAjg" colab_type="code" colab={}
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
# + id="ri2BDl8hgR9Q" colab_type="code" colab={}
dep_var = 'salary'
cat_names = ['workclass','education','marital-status','occupation','relationship','race']
cont_names =['age','fnlwgt','education-num']
procs = [FillMissing,Categorify,Normalize]
# + id="QTENjnirhNtG" colab_type="code" colab={}
test = TabularList.from_df(df.iloc[800:1000].copy(),path=path,cat_names = cat_names,cont_names=cont_names)
# + id="vo7RgQt7hlSP" colab_type="code" colab={}
data = (TabularList.from_df(df,path=path,cat_names = cat_names,cont_names=cont_names,procs=procs)
.split_by_idx(list(range(800,1000)))
.label_from_df(cols=dep_var)
.add_test(test,label=0)
.databunch())
# + id="qvkvU33MifWs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 352} outputId="e979db74-6a44-4ee1-ce98-1f2df50b5907"
data.show_batch(rows=10)
# + id="PsuLAh3Wi8kX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 94} outputId="badd449c-58b0-4074-f5b1-1ed776dd4854"
learn=tabular_learner(data,layers=[200,100],metrics=accuracy)
learn.fit(1,1e-2)
# + id="olSCBFioj_LD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 306} outputId="498b4632-f930-42d2-fe48-2378d5ef638b"
df=pd.read_csv(path/'adult.csv')
df.head()
# + id="5CDfM1Y4wd6c" colab_type="code" colab={}
|
Lesson 4 - Tabular Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Chapter 6 â Decision Trees**
# _This notebook contains all the sample code and solutions to the exercises in chapter 6._
# # Setup
# First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
# +
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
# %matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "decision_trees"
def image_path(fig_id):
return os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id)
def save_fig(fig_id, tight_layout=True):
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(image_path(fig_id) + ".png", format='png', dpi=300)
# -
# # Training and visualizing
# +
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
# +
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file=image_path("iris_tree.dot"),
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
# +
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
if plot_training:
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
plt.axis(axes)
if iris:
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
if legend:
plt.legend(loc="lower right", fontsize=14)
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
save_fig("decision_tree_decision_boundaries_plot")
plt.show()
# -
# # Predicting classes and class probabilities
tree_clf.predict_proba([[5, 1.5]])
tree_clf.predict([[5, 1.5]])
# # Sensitivity to training set details
X[(X[:, 1]==X[:, 1][y==1].max()) & (y==1)] # widest Iris-Versicolor flower
# +
not_widest_versicolor = (X[:, 1]!=1.8) | (y==2)
X_tweaked = X[not_widest_versicolor]
y_tweaked = y[not_widest_versicolor]
tree_clf_tweaked = DecisionTreeClassifier(max_depth=2, random_state=40)
tree_clf_tweaked.fit(X_tweaked, y_tweaked)
# +
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf_tweaked, X_tweaked, y_tweaked, legend=False)
plt.plot([0, 7.5], [0.8, 0.8], "k-", linewidth=2)
plt.plot([0, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.text(1.0, 0.9, "Depth=0", fontsize=15)
plt.text(1.0, 1.80, "Depth=1", fontsize=13)
save_fig("decision_tree_instability_plot")
plt.show()
# +
from sklearn.datasets import make_moons
Xm, ym = make_moons(n_samples=100, noise=0.25, random_state=53)
deep_tree_clf1 = DecisionTreeClassifier(random_state=42)
deep_tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)
deep_tree_clf1.fit(Xm, ym)
deep_tree_clf2.fit(Xm, ym)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(deep_tree_clf1, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("No restrictions", fontsize=16)
plt.subplot(122)
plot_decision_boundary(deep_tree_clf2, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("min_samples_leaf = {}".format(deep_tree_clf2.min_samples_leaf), fontsize=14)
save_fig("min_samples_leaf_plot")
plt.show()
# +
angle = np.pi / 180 * 20
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xr = X.dot(rotation_matrix)
tree_clf_r = DecisionTreeClassifier(random_state=42)
tree_clf_r.fit(Xr, y)
plt.figure(figsize=(8, 3))
plot_decision_boundary(tree_clf_r, Xr, y, axes=[0.5, 7.5, -1.0, 1], iris=False)
plt.show()
# +
np.random.seed(6)
Xs = np.random.rand(100, 2) - 0.5
ys = (Xs[:, 0] > 0).astype(np.float32) * 2
angle = np.pi / 4
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xsr = Xs.dot(rotation_matrix)
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(tree_clf_s, Xs, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.subplot(122)
plot_decision_boundary(tree_clf_sr, Xsr, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
save_fig("sensitivity_to_rotation_plot")
plt.show()
# -
# # Regression trees
# Quadratic training set + noise
np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10
# +
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X, y)
# +
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
y_pred = tree_reg.predict(x1)
plt.axis(axes)
plt.xlabel("$x_1$", fontsize=18)
if ylabel:
plt.ylabel(ylabel, fontsize=18, rotation=0)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)
plt.subplot(122)
plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "Depth=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)
save_fig("tree_regression_plot")
plt.show()
# -
export_graphviz(
tree_reg1,
out_file=image_path("regression_tree.dot"),
feature_names=["x1"],
rounded=True,
filled=True
)
# +
tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)
plt.subplot(122)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf={}".format(tree_reg2.min_samples_leaf), fontsize=14)
save_fig("tree_regression_regularization_plot")
plt.show()
# -
# # Exercise solutions
# ## 1. to 6.
# See appendix A.
# ## 7.
# _Exercise: train and fine-tune a Decision Tree for the moons dataset._
# a. Generate a moons dataset using `make_moons(n_samples=10000, noise=0.4)`.
# Adding `random_state=42` to make this notebook's output constant:
# +
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=10000, noise=0.4, random_state=42)
# -
# b. Split it into a training set and a test set using `train_test_split()`.
# +
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# -
# c. Use grid search with cross-validation (with the help of the `GridSearchCV` class) to find good hyperparameter values for a `DecisionTreeClassifier`. Hint: try various values for `max_leaf_nodes`.
# +
from sklearn.model_selection import GridSearchCV
params = {'max_leaf_nodes': list(range(2, 100)), 'min_samples_split': [2, 3, 4]}
grid_search_cv = GridSearchCV(DecisionTreeClassifier(random_state=42), params, n_jobs=-1, verbose=1)
grid_search_cv.fit(X_train, y_train)
# -
grid_search_cv.best_estimator_
# d. Train it on the full training set using these hyperparameters, and measure your model's performance on the test set. You should get roughly 85% to 87% accuracy.
# By default, `GridSearchCV` trains the best model found on the whole training set (you can change this by setting `refit=False`), so we don't need to do it again. We can simply evaluate the model's accuracy:
# +
from sklearn.metrics import accuracy_score
y_pred = grid_search_cv.predict(X_test)
accuracy_score(y_test, y_pred)
# -
# ## 8.
# _Exercise: Grow a forest._
# a. Continuing the previous exercise, generate 1,000 subsets of the training set, each containing 100 instances selected randomly. Hint: you can use Scikit-Learn's `ShuffleSplit` class for this.
# +
from sklearn.model_selection import ShuffleSplit
n_trees = 1000
n_instances = 100
mini_sets = []
rs = ShuffleSplit(n_splits=n_trees, test_size=len(X_train) - n_instances, random_state=42)
for mini_train_index, mini_test_index in rs.split(X_train):
X_mini_train = X_train[mini_train_index]
y_mini_train = y_train[mini_train_index]
mini_sets.append((X_mini_train, y_mini_train))
# -
# b. Train one Decision Tree on each subset, using the best hyperparameter values found above. Evaluate these 1,000 Decision Trees on the test set. Since they were trained on smaller sets, these Decision Trees will likely perform worse than the first Decision Tree, achieving only about 80% accuracy.
# +
from sklearn.base import clone
forest = [clone(grid_search_cv.best_estimator_) for _ in range(n_trees)]
accuracy_scores = []
for tree, (X_mini_train, y_mini_train) in zip(forest, mini_sets):
tree.fit(X_mini_train, y_mini_train)
y_pred = tree.predict(X_test)
accuracy_scores.append(accuracy_score(y_test, y_pred))
np.mean(accuracy_scores)
# -
# c. Now comes the magic. For each test set instance, generate the predictions of the 1,000 Decision Trees, and keep only the most frequent prediction (you can use SciPy's `mode()` function for this). This gives you _majority-vote predictions_ over the test set.
# +
Y_pred = np.empty([n_trees, len(X_test)], dtype=np.uint8)
for tree_index, tree in enumerate(forest):
Y_pred[tree_index] = tree.predict(X_test)
# +
from scipy.stats import mode
y_pred_majority_votes, n_votes = mode(Y_pred, axis=0)
# -
# d. Evaluate these predictions on the test set: you should obtain a slightly higher accuracy than your first model (about 0.5 to 1.5% higher). Congratulations, you have trained a Random Forest classifier!
accuracy_score(y_test, y_pred_majority_votes.reshape([-1]))
|
06_decision_trees.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# #### **Title**: Bars Element
#
# **Dependencies**: Bokeh
#
# **Backends**: [Bokeh](./Bars.ipynb), [Matplotlib](../matplotlib/Bars.ipynb), [Plotly](../plotly/Bars.ipynb)
import numpy as np
import pandas as pd
import holoviews as hv
hv.extension('bokeh')
# The ``Bars`` Element uses bars to show discrete, numerical comparisons across categories. One axis of the chart shows the specific categories being compared and the other axis represents a continuous value.
#
# Bars may also be grouped or stacked by supplying a second key dimension representing sub-categories. Therefore the ``Bars`` Element expects a tabular data format with one or two key dimensions (``kdims``) and one or more value dimensions (``vdims``). See the [Tabular Datasets](../../../user_guide/08-Tabular_Datasets.ipynb) user guide for supported data formats, which include arrays, pandas dataframes and dictionaries of arrays.
# +
data = [('one',8),('two', 10), ('three', 16), ('four', 8), ('five', 4), ('six', 1)]
bars = hv.Bars(data, hv.Dimension('Car occupants'), 'Count')
bars
# -
# We can achieve the same plot using a Pandas DataFrame:
# ```
# hv.Bars(pd.DataFrame(data, columns=['Car occupants','Count']))
# ```
# A ``Bars`` element can be sliced and selecting on like any other element:
bars[['one', 'two', 'three']] + bars[['four', 'five', 'six']]
# It is possible to define an explicit ordering for a set of Bars by explicit declaring `Dimension.values` either in the Dimension constructor or using the `.redim.values()` approach:
# +
occupants = hv.Dimension('Car occupants', values=['three', 'two', 'four', 'one', 'five', 'six'])
# or using .redim.values(**{'Car Occupants': ['three', 'two', 'four', 'one', 'five', 'six']})
hv.Bars(data, occupants, 'Count')
# -
# ``Bars`` also supports nested categorical groupings. Next we'll use a Pandas DataFrame to construct a random sample of pets sub-divided by male and female:
# +
samples = 100
pets = ['Cat', 'Dog', 'Hamster', 'Rabbit']
genders = ['Female', 'Male']
pets_sample = np.random.choice(pets, samples)
gender_sample = np.random.choice(genders, samples)
count = np.random.randint(1, 5, size=samples)
df = pd.DataFrame({'Pets': pets_sample, 'Gender': gender_sample, 'Count': count})
df.head(2)
# +
bars = hv.Bars(df, kdims=['Pets', 'Gender']).aggregate(function=np.sum)
bars.opts(width=500)
# -
#
# Just as before we can provide an explicit ordering by declaring the `Dimension.values`. Alternatively we can also make use of the `.sort` method, internally `Bars` will use topological sorting to ensure consistent ordering.
bars.redim.values(Pets=pets, Gender=genders) + bars.sort()
# To drop the second level of tick labels we can set `multi_level=False`, which will indicate the groupings using a legend instead:
bars.sort() + bars.clone().opts(multi_level=False)
# Lastly, Bars can be also be stacked by setting `stacked=True`:
bars.opts(stacked=True)
# For full documentation and the available style and plot options, use ``hv.help(hv.Bars)``.
|
examples/reference/elements/bokeh/Bars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pvfactors_py3
# language: python
# name: pvfactors_py3
# ---
# pvfactors: Jupyter notebook guide
# ============================
# This Jupyter notebook demonstrates how to use the package for irradiance calculations.
# <h3>Imports and settings</h3>
# +
# Import external libraries
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
import pandas as pd
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
# Settings
# %matplotlib inline
np.set_printoptions(precision=3, linewidth=300)
# -
# ## TL;DR
# Given some timeseries inputs:
df_inputs = pd.DataFrame(
{'solar_zenith': [20., 50.],
'solar_azimuth': [110., 250.],
'surface_tilt': [10., 20.],
'surface_azimuth': [90., 270.],
'dni': [1000., 900.],
'dhi': [50., 100.],
'albedo': [0.2, 0.2]},
index=[datetime(2017, 8, 31, 11), datetime(2017, 8, 31, 15)]
)
df_inputs
# And some PV array parameters:
pvarray_parameters = {
'n_pvrows': 3, # number of pv rows
'pvrow_height': 1, # height of pvrows (measured at center / torque tube)
'pvrow_width': 1, # width of pvrows
'axis_azimuth': 0., # azimuth angle of rotation axis
'gcr': 0.4, # ground coverage ratio
}
# The user can quickly create a PV array with ``pvfactors``, and manipulate it with the engine
from pvfactors.geometry import OrderedPVArray
# Create PV array
pvarray = OrderedPVArray.init_from_dict(pvarray_parameters)
from pvfactors.engine import PVEngine
# Create engine
engine = PVEngine(pvarray)
# Fit engine to data
engine.fit(df_inputs.index, df_inputs.dni, df_inputs.dhi,
df_inputs.solar_zenith, df_inputs.solar_azimuth,
df_inputs.surface_tilt, df_inputs.surface_azimuth,
df_inputs.albedo)
# The user can then plot the PV array geometry at any given time of the simulation:
# Plot pvarray shapely geometries
f, ax = plt.subplots(figsize=(10, 5))
pvarray.plot_at_idx(1, ax)
plt.show()
# It is then very easy to run simulations using the defined engine:
pvarray = engine.run_full_mode(fn_build_report=lambda pvarray: pvarray)
# And inspect the results thanks to the simple geometry API
print("Incident irradiance on front surface of middle pv row: {} W/m2"
.format(pvarray.ts_pvrows[1].front.get_param_weighted('qinc')))
print("Reflected irradiance on back surface of left pv row: {} W/m2"
.format(pvarray.ts_pvrows[0].back.get_param_weighted('reflection')))
print("Isotropic irradiance on back surface of right pv row: {} W/m2"
.format(pvarray.ts_pvrows[2].back.get_param_weighted('isotropic')))
# The users can also create a "report" while running the simulations that will rely on the simple API shown above, and which will look like whatever the users want.
# +
# Create a function that will build a report
def fn_report(pvarray): return {'total_incident_back': pvarray.ts_pvrows[1].back.get_param_weighted('qinc'),
'total_absorbed_back': pvarray.ts_pvrows[1].back.get_param_weighted('qabs')}
# Run full mode simulation
report = engine.run_full_mode(fn_build_report=fn_report)
# Print results (report is defined by report function passed by user)
df_report = pd.DataFrame(report, index=df_inputs.index)
df_report
|
docs/tutorials/pvfactors_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# Monte Carlo integration
# =======================
#
# Imagine that we want to measure the area of a pond with arbitrary shape.
# Suppose that this pond is in the middle of a field with known area $A$.
# If we throw $N$ stones randomly, such that they land within the
# boundaries of the field, and we count the number of stones that fall in
# the pond $N_{in}$, the area of the pond will be approximately
# proportional to the fraction of stones that make a splash, multiplied by
# $A$: $$A_{pond}=\frac{N_{in}}{N}A.$$ This simple procedure is an example
# of the âMonte Carloâ method.
#
# Simple Monte Carlo integration
# ------------------------------
#
# More generaly, imagine a rectangle of height $H$ in the integration
# interval $[a,b]$, such that the function $f(x)$ is within its
# boundaries. Compute $n$ pairs of random numbers $(x_i,y_i)$ such that
# they are uniformly distributed inside this rectangle. The fraction of
# points that fall within the area contained below $f(x)$, <span>*i.
# e.*</span>, that satisfy $y_i \leq f(x_i)$ is an estimate of the ratio o
# fthe integral of $f(x)$ and the area of the rectangle. Hence, the
# estimate of the integral will be given by:
# $$\int _a^b{f(x)dx} \simeq I(N) = \frac{N_{in}}{N}H(b-a).
# $$
#
# Another Monte Carlo procedure is based on the definition:
# $$\langle g \rangle=\frac{1}{(b-a)} \int _a^b{f(x)dx}.
# $$ In order to determine this average, we sample the
# value of $f(x)$:
# $$\langle f \rangle \simeq \frac{1}{N}\sum_{i=1}^{N}f(x_i),$$ where the
# $N$ values $x_i$ are distributed unformly in the interval $[a,b]$. The
# integral will be given by $$I(N)=(b-a) \langle f \rangle .$$
# Monte Carlo error analysis
# --------------------------
#
# The Monte Carlo method clearly yields approximate results. The accuracy
# deppends on the number of values $N$ that we use for the average. A
# possible measure of the error is the âvarianceâ $\sigma^2$ defined by:
# $$\sigma ^2=\langle f^2 \rangle - \langle f \rangle ^2,
# $$ where
# $$\langle f \rangle = \frac{1}{N} \sum_{i=1}^N f(x_i)$$ and
# $$\langle f^2 \rangle = \frac{1}{N} \sum_{i=1}^{N} f(x_i)^2.$$ The
# âstandard deviationâ is $\sigma$. However, we should expect that the
# error decreases with the number of points $N$, and the quantity $\sigma$
# defines by (\[mc\_sigma\]) does not. Hence, this cannot be a good
# measure of the error.
#
# Imagine that we perform several measurements of the integral, each of
# them yielding a result $I_n$. These values have been obtained with
# different sequences of $N$ random numbers. According to the central
# limit theorem, these values whould be normally dstributed around a mean
# $\langle I
# \rangle$. Suppouse that we have a set of $M$ of such measurements
# ${I_n}$. A convenient measure of the differences of these measurements
# is the âstandard deviation of the meansâ $\sigma_M$:
# $$\sigma_M ^2=\langle I^2 \rangle - \langle I \rangle ^2,
# $$ where
# $$\langle I \rangle = \frac{1}{M} \sum_{n=1}^M I_n$$ and
# $$\langle I^2 \rangle = \frac{1}{M} \sum_{n=1}^{M} I_n^2.$$
# It can be proven that
# $$\sigma_M \approx \sigma/\sqrt{N}.
# $$ This relation becomes exact in the limit of a very
# large number of measurements. Note that this expression implies that the
# error decreases with the squere root of the number of trials, meaning
# that if we want to reduce the error by a factor 10, we need 100 times
# more points for the average.
#
# ### Exercise 10.1: One dimensional integration
#
# 1. Write a program that implements the âhit and missâ Monte Carlo
# integration algorithm. Find the estimate $I(N)$ for the integral of
# $$f(x)=4\sqrt{1-x^2}$$ as a function of $N$, in the interval
# $(0,1)$. Choose $H=1$, and sample only the $x$-dependent part
# $\sqrt{1-x^2}$, and multiply the result by 4. Calculate the
# difference between $I(N)$ and the exact result $\pi$. This
# difference is a measure of the error associated with the Monte
# Carlo estimate. Make a log-log plot of the error as a function of
# $N$. What is the approximate functional deppendece of the error on
# $N$ for large $N$?
#
# 2. Estimate the integral of $f(x)$ using the simple Monte Carlo
# integration by averaging over $N$ points, using (\[mc\_integral2\]),
# and compute the error as a function of $N$, for $N$ upt to 10,000.
# Determine the approximate functional deppendence of the error on $N$
# for large $N$. How many trials are necessary to determine $I_N$ to
# two decimal places?
#
# 3. Perform 10 measurements $I_n(N)$, with $N=10,000$ using different
# random sequences. Show in a table the values of $I_n$ and $\sigma$
# according to (\[mc\_integral2\]) and (\[mc\_sigma\]).
# Use (\[mc\_sigmam\]) to estimate the standard deviation of the
# means, and compare to the values obtained from (\[mc\_sigma2\])
# using the 100,000 values.
#
# 4. To verify that your result for the error is independent of the
# number of sets you used to divide your data, repeat the previous
# item grouping your results in 20 groups of 5,000 points each.
#
# ### Exercise 10.2: Importance of randomness
#
# To examine the effects of a poor random number generator, modify your
# program to use the linear congruential random number generator using the
# perameters $a=5$, $c=0$ and the seed $x_1=1$. Repeat the integral of the
# previous exercise and compare your results.
#
# #### Challenge 10.1:
#
# Exercise 10.2
#
#
#
# +
# %matplotlib inline
import numpy as np
from matplotlib import pyplot
# Hit and miss Monte Carlo integration
ngroups = 16
I = np.zeros(ngroups)
N = np.zeros(ngroups)
E = np.zeros(ngroups)
n0 = 100
for i in range(ngroups):
N[i] = n0
x = np.random.random(n0)
y = np.random.random(n0)
I[i] = 0.
Nin = 0
for j in range(n0):
if(y[j] < np.sqrt(1-x[j]**2)):
Nin += 1
I[i] = 4.*float(Nin)/float(n0)
E[i] = abs(I[i]-np.pi)
print n0,Nin,I[i],E[i]
n0 *= 2
pyplot.plot(N,E,ls='-',c='red',lw=3);
pyplot.plot(N,0.8/np.sqrt(N),ls='-',c='blue',lw=3);
pyplot.xscale('log')
pyplot.yscale('log')
# +
# Simple Monte Carlo Integration
ngroups = 16
I = np.zeros(ngroups)
N = np.zeros(ngroups)
E = np.zeros(ngroups)
n0 = 100
for i in range(ngroups):
N[i] = n0
r = np.random.random(n0)
I[i] = 0.
for j in range(n0):
x = r[j]
I[i] += np.sqrt(1-x**2)
I[i] *= 4./float(n0)
E[i] = abs(I[i]-np.pi)
print n0,I[i],E[i]
n0 *= 2
pyplot.plot(N,E,ls='-',c='red',lw=3);
pyplot.plot(N,0.8/np.sqrt(N),ls='-',c='blue',lw=3);
pyplot.xscale('log')
pyplot.yscale('log')
# +
n0 = 100000
I = np.zeros(n0)
r = np.random.random(n0)
for j in range(n0):
x = r[j]
I[j] = 4*np.sqrt(1-x**2)
def group_measurements(ngroups):
global I,n0
nmeasurements = n0/ngroups
for n in range(ngroups):
Ig = 0.
Ig2 = 0.
for i in range(n*nmeasurements,(n+1)*nmeasurements):
Ig += I[i]
Ig2 += I[i]**2
Ig /= nmeasurements
Ig2 /= nmeasurements
sigma = Ig2-Ig**2
print Ig,Ig2,sigma
group_measurements(10)
print "============================="
group_measurements(20)
print "============================="
group_measurements(1)
# -
# Variance reduction
# ------------------
#
# If the function being integrated does not fluctuate too much in the
# interval of integration, and does not differ much from the average
# value, then the standard Monte Carlo mean-value method should work well
# with a reasonable number of points. Otherwise, we will find that the
# variance is very large, meaning that some points will make small
# contributions, while others will make large contributions to the
# integral. If this is the case, the algorithm will be very inefficient.
# The method can be improved by splitting the function $f(x)$ in two
# $f(x)=f_1(x)+f_2(x)$, such that the integral of $f_1(x)$ is known, and
# $f_2(x)$ as a small variance. The âvariance reductionâ technique,
# consists then in evaluating the integral of $f_2(x)$ to obtain:
# $$\int _a^b{f(x)dx}=\int _a^b {f_1(x)dx} + \int _a^b{f_2(x)dx} = \int
# _a^b{f_1(x)dx}+J.$$
#
# Importance Sampling
# -------------------
#
# Imagine that we want to sample the function $f(x)=e^{-x^2}$ in the
# interval $[0,1]$. It is evident that most of our points will fall in the
# region where the value of $f(x)$ is very small, and therefore we will
# need a large number of values to achieve a decent accuracy. A way to
# improve the measurement by reducing the variance is obtained by
# âimportance samplingâ. As the name says, the idea is to sample the
# regions with larger contributions to the integral. For this goal, we
# introduce a probability distribution $P(x)$ normalized in the interval
# of integration $$\int _a^b{P(x)dx} = 1.$$ Then, we can rewrite the
# integral of $f(x)$ as $$I=\int _a^b{\frac{f(x)}{P(x)}P(x)dx}
# $$ We can evaluate this integral, by sampling
# according to the probability distribution $P(x)$ and evaluating the sum
# $$I(N)=\frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{P(x_i)}.
# $$ Note that for the uniform case $P(x)=1/(b-a)$, the
# expression reduces to the simple Monte Carlo integral.
#
# We are free to choose $P(x)$ now. We wish to do it in a way to reduce
# and minimize the variance of the integrand $f(x)/P(x)$. The way to to
# this is picking a $P(x)$ that mimics $f(x)$ where $f(x)$ is large. if we
# are able to determine an apropiate $P(x)$, the integrand will be slowly
# varying, and hence the variance will be reduced. Another consideration
# is that the generation of points according to the distribution $P(x)$
# should be a simple task. As an example, let us consider again the
# integral $$I=\int _0^1 {e^{-x^2}dx}.$$ A reasonable choice for a weigh
# function is $P(x)=Ae^{-x}$, where $A$ is a normalization constant.
#
# Notice that for $P(x)=f(x)$ the variance is zero! This is known as the
# zero variance property. There is a catch, though: The probability function
# $P(x)$ needs to be normalized, implying that in reality, $P(x)=f(x)/\int f(x)dx$, which
# assumes that we know in advance precisely the integral that we are trying to calculate!
#
# ### Exercise 10.3: Importance sampling
#
# 1. Choose the weight function $P(x)=e^{-x}$ and evaluate the integral:
# $$\int _0^{\infty} {x^{3/2}e^{-x}dx}.$$
#
# 2. Choose $P(x)=e^{-ax}$ and estimate the integral
# $$\int _0^{\pi} \frac{dx}{x^2+\cos ^2{x}}.$$ Determine the value of
# $a$ that minimizes the variance of the integral.
#
#
# +
# Trapezoidal integration
def trapezoids(func, xmin, xmax, nmax):
Isim = func(xmin)+func(xmax)
h = (xmax-xmin)/nmax
for i in range(1,nmax):
x = xmin+i*h
Isim += 2*func(x)
Isim *= h/2
return Isim
def f(x):
return x**1.5*np.exp(-x)
print "Trapezoids: ", trapezoids(f, 0., 20., 100000)
# Simple Monte Carlo integration
n0 = 1000000
r = np.random.random(n0)
x = -np.log(r)
Itot = np.sum(x**1.5)
print "Simple Monte Carlo: ", Itot/n0
# +
# Trapezoidal integration
def g(x):
return 1./(x**2+np.cos(x)**2)
print "Trapezoids: ", trapezoids(g, 0., np.pi, 1000000)
# Simple Monte Carlo integration
n0 = 100000
a = np.arange(0.1,2.1,0.1)
I = np.arange(0.1,2.1,0.1)
r = np.random.random(n0)
I0 = np.sum(1./((r*np.pi)**2+np.cos(r*np.pi)**2))
print "Simple Monte Carlo: ", I0/n0*np.pi
# Importance Sampling
print "Importance Sampling:"
x = -np.log(r)
i = 0
for ai in a:
norm = (1.-np.exp(-ai*np.pi))/ai
x1 = norm*x/ai
Itot = 0.
Nin = 0
for xi in x1:
if(xi <= np.pi):
Nin += 1
Itot += g(xi)*np.exp(xi*ai)
Itot *= norm
I[i] = Itot/Nin
i += 1
print ai,Itot/Nin
pyplot.plot(a,I,ls='-',marker='o',c='red',lw=3);
# -
# ### Exercise 10.4: The Metropolis algorithm
#
# Use the Metropolis algorithm to sample points according to a ditribution
# and estimate the integral $$\int _0^4 {x^2e^{-x}dx},$$ with
# $P(x)=e^{-x}$ for $0 \leq x \leq 4$. Plot the number of times the
# walker is at points $x_0$, $x_1$, $x_2$, ... Is the integrand sampled
# uniformly? If not, what is the approximate region of $x$ where the
# integrand is sampled more often?
# +
delta = 2
xmin = 0.
xmax = 4.
def f(x):
return x**2*np.exp(-x)
def P(x):
global xmin, xmax
if(x < xmin or x > xmax):
return 0.
return np.exp(-x)
def metropolis(xold):
global delta
xtrial = np.random.random()
xtrial = xold+(2*xtrial-1)*delta
weight = P(xtrial)/P(xold)
xnew = xold
if(weight >= 1): #Accept
xnew = xtrial
elif(weight != 0):
r = np.random.random()
if(r <= weight): #Accept
xnew = xtrial
return xnew
xwalker = (xmax+xmin)/2.
for i in range(100000):
xwalker = metropolis(xwalker)
I0 = 0.
N = 300000
x = np.zeros(N)
x[0] = xwalker
for i in range(1,N):
x[i] = metropolis(x[i-1])
I0 += x[i]**2
binwidth=0.1
pyplot.hist(x,bins=np.arange(xmin-1, xmax+1, 0.1),normed=True);
print "Trapezoids: ", trapezoids(f,xmin,xmax,10000)
print "Metropolis: ", I0/(1.-np.exp(-4.))/N
# -
# #### Challenge 10.1
#
# - Calculate the integral $\int_0^1 x^2 dx=1/3$ using simple MC integration and importance sampling with $P(x)=x$.
#
# - Calculate the integral $\int_0^1 \sqrt{x}dx=2/3$ using simple MC integration and $P(x)=1-e^{-ax}$. Find the values of $a$ that minimizes the variance.
|
10_01_montecarlo_integration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Quantitative QC by CV calculation
# The data used in this notebook is lymphocyte data for one patient's B cells and T cells. We use this data to show the proteome variation between the cell types. Here, we calculate CVs to show the quality of the data.
#
# After calculating CVs, we calculate Spearman correlation among replicates.
#
# First, we import our loader module. This brings the functions defined there (in our repository at ~/load_data.py) into scope so we can use them in this script. Then we can load our data and store it as <code>data</code>.
#
# Calling <code>head</code> shows the first several lines of the dataframe, which provides an idea of the type of data present and the structure of the dataframe.
import load_data
#data_raw = load_data.load_FragPipe()
data_raw=load_data.load_max_quant()
data_raw.head()
# Now we normalize across runs. Note that following median normalization, we reverse the log2, leaving the data aligned between runs but allowing the most typical coefficient variation calculation.
import data_utils
data_log2_normalized = data_utils.normalize(data_raw)
data_normalized = data_log2_normalized.apply(lambda series: 2**series)
# Next, we select the proteins that are measured in at least three samples from each group, allowing the calculations to proceed without imputed zero-handling.
import data_utils
cell_types = [' B_', ' T_']
indecies = data_normalized.apply(data_utils.check_three_of_each_type, axis=1,
cell_types = cell_types)
data = data_normalized[indecies]
data.head()
# Finally, we will calculate the coeffients of variation for each protein within each of the two cell types.
from scipy.stats import variation
from statistics import mean
import pandas as pd
from numpy import isnan
# +
CVs = {}
for population in cell_types:
cells_in_population = list(s for s in data.columns.values.tolist() if population in s)
data_by_type = data[cells_in_population]
#now we have a dataframe with just one subpopulation
#Call variation function
var = data_by_type.apply(variation, axis=1, nan_policy='omit')
CVs[population] = var
#Here we report an overview
print (population)
print ('Mean CV:\t',mean(var))
print ('Min CV: \t',min(var))
print ('Max CV: \t',max(var))
print ('nan: \t',len([i for i in var if isnan(i)]))
print ('Zero: \t',len([i for i in var if i==0]))
var_under_20 = len([i for i in var if i < .2])
var_under_10 = len([i for i in var if i < .1])
count = len(var)#len([i for i in var if i!=0])
print ('Under 10%:\t',var_under_10,'\t{0:.2f}'.format(var_under_10/count))
print ('Under 20%:\t',var_under_20,'\t{0:.2f}'.format(var_under_20/count))
print (count)
print ()
CVs = pd.DataFrame.from_dict(CVs)
# -
# Next, we will visualize the data, which shows that the majority of proteins have small coefficients of variation.
# +
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(font_scale=1.5)
sns.set_style("white")
figure = sns.violinplot(data=CVs, width=.5)
figure.set_ylabel("Coefficient of Variation")
figure.set_xticklabels(['B cells', 'T cells'])
#plt.savefig("data/figures/CV.png", dpi=300)
plt.show()
# +
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(font_scale=1.5)
sns.set_style("white")
figure = sns.distplot(CVs[' B_'], hist = False, label='B cells')#, width=.5)
figure = sns.distplot(CVs[' T_'], hist = False, label='T cells')#, width=.5)
figure.set_ylabel("Relative Frequency")
figure.set_xlabel("Coefficient of Variation")
figure.legend(['B cells', 'T cells'])
plt.show()
# -
# Here we summarize the CVs overall. Note that the CVs were calculated within types and so still represent technical variability, not variation between cell types.
# +
var = CVs.values.flatten()
print ('Mean CV:\t',mean(var))
print ('Min CV: \t',min(var))
print ('Max CV: \t',max(var))
print ('nan: \t',len([i for i in var if isnan(i)]))
print ('Zero: \t',len([i for i in var if i==0]))
var_under_20 = len([i for i in var if i < .2])
var_under_10 = len([i for i in var if i < .1])
count = len(var)#len([i for i in var if i!=0])
print ('Under 10%:\t',var_under_10,'\t{0:.2f}'.format(var_under_10/count))
print ('Under 20%:\t',var_under_20,'\t{0:.2f}'.format(var_under_20/count))
# -
# This shows accuracy in repeatedly characterizing each cell type.
# ### Correlation coefficient
# Next, we show reproducibility of the replicates by Spearman correlation coefficient.
# +
correlations = data.corr(method="spearman")
labels=['B cells - C10','B cells - C11',
'B cells - C12','B cells - C13',
'B cells - C9 ','T cells - D10',
'T cells - D11','T cells - D12',
'T cells - D13','T cells - D9 ']
correlations.index=labels
correlations.columns=labels
import numpy as np
mask = np.zeros(correlations.shape, dtype=bool)
mask[np.triu_indices(len(mask))] = True
sns.heatmap(correlations, cmap = 'coolwarm', mask = mask)
plt.savefig("data/correlations_heatmap_FragPipe.png", dpi=300,
bbox_inches='tight')
# +
from numpy import nan
#drop self-correlations of 1
for sample in correlations.columns:
correlations[sample][sample]=nan
correlations
# -
# Here we split the dataset by cell type and perform the same correlation test. We then take the average correlation between replicates.
# +
from numpy import nan
corr_type = {}
corr_summary={}
for cell_type in cell_types:
cells_of_type = list(s for s in data.columns.values.tolist() if cell_type in s)
data_by_type = data[cells_of_type]
corr_of_type = data_by_type.corr(method='spearman')
#drop self-correlations of 1
for sample in corr_of_type.columns:
corr_of_type[sample][sample]=nan
corr_type[cell_type] = corr_of_type
#take the average of the correlations between a sample and
# the other samples of the same type
summary = corr_of_type.apply(lambda x: mean(x.dropna()))
corr_summary[cell_type] = mean(summary)
print (cell_type,"average correlation:\t",mean(summary))
# -
# With the average correlation between each set of replicates, we now average them to get the overall average.
mean(corr_summary.values())
# Now, we calculate the average correlation when comparing a B cell replicate to a T cell replicate. We expect this to be lower than either of the two above numbers comparing replicates within a cell type.
# +
B_cells = list(s for s in correlations.index if 'B cells' in s)
T_cells = list(s for s in correlations.index if 'T cells' in s)
corr_cross_types = []
for B in B_cells:
for T in T_cells:
c = correlations[B][T]
corr_cross_types.append(c)
print("Mean cross-type correlations:")
mean(corr_cross_types)
# -
|
Quantitative_QC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# _Lambda School Data Science_
# # XGBoost examples
#
# ## 1. Scikit-Learn API, Missing Values
# - [XGBoost FAQ: How to deal with missing values](https://xgboost.readthedocs.io/en/latest/faq.html?highlight=missing#how-to-deal-with-missing-value)
# - [XGBoost Python API Reference: Scikit-Learn API](https://xgboost.readthedocs.io/en/latest/python/python_api.html#module-xgboost.sklearn) (`XGBRegressor` and `XGBClassifier`)
# In this example, we load Titanic data and encode categoricals as ordinals, but do _not_ impute missing values:
# +
import category_encoders as ce
import pandas as pd
import seaborn as sns
titanic = sns.load_dataset('titanic')
X = titanic[['age', 'class', 'deck', 'embarked', 'fare', 'sex']]
y = titanic['survived']
encoder = ce.OrdinalEncoder(handle_unknown='ignore',
cols=['class', 'deck', 'embarked', 'sex'])
X_transformed = encoder.fit_transform(X)
X_transformed.head(10)
# -
X_transformed.isnull().sum()
# `XGBClassifier` can be used like a scikit-learn estimator, but it works with missing values!
# +
from sklearn.model_selection import cross_val_score
from xgboost import XGBClassifier
from sklearn.ensemble import RandomForestClassifier
model = XGBClassifier()
cross_val_score(model, X_transformed, y,
scoring='accuracy', cv=5, n_jobs=-1)
# -
# ## 2. Learning API, early stopping, monotonic constraints
# ### Monotonic constraints
#
# _From [**Ideas on interpreting machine learning**](https://www.oreilly.com/ideas/ideas-on-interpreting-machine-learning) by <NAME>, <NAME>, and <NAME>_
#
# 
#
# > **Monotonicity is often expected by regulators:** no matter what a training data sample says, regulators may still want to see monotonic behavior. Consider savings account balances in credit scoring. A high savings account balance should be an indication of creditworthiness, whereas a low savings account balance should be an indicator of potential default risk. If a certain batch of training data contains many examples of individuals with high savings account balances defaulting on loans or individuals with low savings account balances paying off loans, of course a machine-learned response function trained on this data would be non-monotonic with respect to savings account balance. This type of predictive function could be unsatisfactory to regulators because it defies decades of accumulated domain expertise and thus decreases trust in the model or sample data.
#
#
# > **Monotonicity enables consistent reason code generation:** consistent reason code generation is generally considered a gold standard of model interpretability. If monotonicity is guaranteed by a credit scoring model, reasoning about credit applications is straightforward and automatic. If someone's savings account balance is low, their credit worthiness is also low. Once monotonicity is assured, reasons for credit decisions can then be reliably ranked...
# ### More about monotonic constraints and interpretability
# - [XGBoost Tutorials â Monotonic Constraints](https://xgboost.readthedocs.io/en/latest/tutorials/monotonic.html)
# - [A Tutorial of Model Monotonicity Constraint Using Xgboost](https://xiaoxiaowang87.github.io/monotonicity_constraint/)
# - [Monotonicity constraints in LightGBM](https://blog.datadive.net/monotonicity-constraints-in-machine-learning/)
# - [TensorFlow Lattice](https://github.com/tensorflow/lattice): "an implementation of Monotonic Calibrated Interpolated Look-Up Tables in TensorFlow."
# - [A curated list of awesome machine learning interpretability resources](https://github.com/jphall663/awesome-machine-learning-interpretability)
# ***This example is adapted from [A Tutorial of Model Monotonicity Constraint Using Xgboost](https://xiaoxiaowang87.github.io/monotonicity_constraint/)***
#
# > For a tree-based model, if for each split of a particular variable we require the right daughter nodeâs average value to be higher than the left daughter node (otherwise the split will not be made), then approximately this predictorâs relationship with the dependent variable is monotonically increasing; and vise versa.
#
# > Iâm going to use the California Housing dataset for this tutorial. This dataset consists of 20,460 observations. Each observation represents a neighborhood in California. The response variable is the median house value of a neighborhood. Predictors include median income, average house occupancy, and location etc. of that neighborhood.
# +
from sklearn.datasets.california_housing import fetch_california_housing
from sklearn.model_selection import train_test_split
california_housing = fetch_california_housing()
columns = ['Median Income', 'House Age', 'Average Rooms',
'Average Bedrooms', 'Population', 'Average Occupancy',
'Latitude', 'Longitude']
X = pd.DataFrame(california_housing.data, columns=columns)
X['Median Income'] = X['Median Income'] * 10000
y = pd.Series(california_housing.target * 100000,
name='Median House Value')
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=123)
print(california_housing.DESCR)
# -
# > To start, we use a single feature âthe median incomeâ to predict the house value. We first split the data into training and testing datasets. Then We use a 5-fold cross-validation and early-stopping on the training dataset to determine the best number of trees. Last, we use the entire training set to train my model and evaluate its performance on the testset.
#
# > Notice the model parameter `'monotone_constraints'`. This is where the monotonicity constraints are set in Xgboost. For now I set `'monotone_constraints': '(0)'`, which means a single feature without constraint.
# [XGBoost Data Interface](https://xgboost.readthedocs.io/en/latest/python/python_intro.html#data-interface)
# +
import xgboost as xgb
features = ['Median Income']
dtrain = xgb.DMatrix(X_train[features], label=y_train)
dtest = xgb.DMatrix(X_test[features], label=y_test)
# -
# - [Enforcing Monotonic Constraints in XGBoost](https://xgboost.readthedocs.io/en/latest/tutorials/monotonic.html#enforcing-monotonic-constraints-in-xgboost)
# - [XGBoost Tutorials: Notes on Parameter Tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html)
# - [XGBoost Python API Reference: Learning API](https://xgboost.readthedocs.io/en/latest/python/python_api.html#module-xgboost.training)
# - [xgboost.cv](https://xgboost.readthedocs.io/en/latest/python/python_api.html#xgboost.cv) parameters
# - params (dict) â Booster params.
# - dtrain (DMatrix) â Data to be trained.
# - num_boost_round (int) â Number of boosting iterations.
# - nfold (int) â Number of folds in CV.
# - early_stopping_rounds (int) â Activates early stopping. CV error needs to decrease at least every <early_stopping_rounds> round(s) to continue. Last entry in evaluation history is the one from best iteration.
# - as_pandas (bool, default True) â Return pd.DataFrame when pandas is installed. If False or pandas is not installed, return np.ndarray
# +
params = {'monotone_constraints': '(0)', # no constraint
'max_depth': 2,
'eta': 0.1,
'silent': 1,
'n_jobs': -1,
'seed': 0,
'eval_metric': 'rmse'}
# Without early stopping
bst_cv = xgb.cv(params, dtrain, num_boost_round=1000, nfold=5,
early_stopping_rounds=None, as_pandas=True)
# -
bst_cv.tail()
bst_cv[['train-rmse-mean', 'test-rmse-mean']].plot();
# With early stopping. Use CV to find the best number of trees
bst_cv = xgb.cv(params, dtrain, num_boost_round=1000, nfold=5,
early_stopping_rounds=10, as_pandas=True)
bst_cv[['train-rmse-mean', 'test-rmse-mean']].plot();
bst = xgb.train(params, dtrain, num_boost_round=60)
print(bst.eval(dtest))
# > We can also check the relationship between the feature (median income) and the dependent variable (median house value)
#
# **Bad News:** [PDPbox](https://github.com/SauceCat/PDPbox) works with scikit-learn, but not xgboost :-(
#
# **Good News:** [The tutorial](https://xiaoxiaowang87.github.io/monotonicity_constraint/) has a custom partial dependency function. We can adapt it and get a better understanding [how partial dependence plots work](https://twitter.com/ChristophMolnar/status/1066398522608635904)!
#
# > Here I wrote a helper function partial_dependency to calculate the variable dependency or partial dependency for an arbitrary model. The partial dependency describes that when other variables fixed, how the average response depends on a predictor.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def partial_dependency(bst, X, y, feature):
"""
Calculate the dependency (or partial dependency) of a response
variable on a predictor (or multiple predictors)
1. Sample a grid of values of a predictor.
2. For each value, replace every row of that predictor with
this value, calculate the average prediction.
"""
X_temp = X.copy()
grid = np.linspace(start=np.percentile(X_temp[feature], 0.1),
stop=np.percentile(X_temp[feature], 99.5),
num=50)
y_pred = np.zeros(len(grid))
for i, value in enumerate(grid):
X_temp[feature] = value
data = xgb.DMatrix(X_temp)
y_pred[i] = np.average(
bst.predict(data, ntree_limit=bst.best_ntree_limit))
plt.plot(grid, y_pred, '-', color='red', linewidth=2.5)
plt.plot(X, y, 'o', color='grey', alpha=0.01)
plt.xlim(min(grid), max(grid))
plt.xlabel(feature)
plt.ylabel(y.name)
plt.show()
# -
# > Without any monotonicity constraint, the relationship between the median income and median house value looks like this:
# +
print(params['monotone_constraints'])
partial_dependency(bst, X_train[features], y_train,
feature='Median Income')
# -
# > One can see that at very low income and income around 10 (times its unit), the relationship between median income and median house value is not strictly monotonic.
#
# > You may be able to find some explanations for this non-monotonic behavior (e.g. feature interactions). In some cases, it may even be a real effect which still holds true after more features are fitted. If you are very convinced about that, I suggest you not enforce any monotonic constraint on the variable, otherwise important relationships may be ignored. But when the non-monotonic behavior is purely because of noise, setting monotonic constraints can reduce overfitting.
#
# > For this example, it is hard to justify that neighborhoods with a low median income have a high median house value. Therefore we will try enforcing the monotonicity on the median income:
params['monotone_constraints'] = '(1)'
# > We then ... refit the model and evaluate it on the testset. Below is the result:
bst = xgb.train(params, dtrain, num_boost_round=60)
print(bst.eval(dtest))
# > We may have reduced overfitting and improved our performance on the testset. However, given that statistical uncertainties on these numbers are probably just as big as the differences, it is just a hypothesis. For this example, the bottom line is that adding monotonicity constraint does not significantly hurt the performance.
#
# > Now we can check the variable dependency again:
partial_dependency(bst, X_train[features], y_train,
feature='Median Income')
# > Great! Now the response is monotonically increasing with the predictor. This model has also become a bit easier to explain.
#
# > We can also enforce monotonicity constraints while fitting multiple features. For example:
# +
features = ['Median Income', 'Average Occupancy', 'House Age']
params['monotone_constraints'] = '(1, -1, 1)'
dtrain = xgb.DMatrix(X_train[features], label=y_train)
dtest = xgb.DMatrix(X_test[features], label=y_test)
bst = xgb.train(params, dtrain, num_boost_round=60)
print(bst.eval(dtest))
for feature in features:
partial_dependency(bst, X_train[features], y_train, feature=feature)
# -
# > We assume that median house value is positively correlated with median income and house age, but negatively correlated with average house occupancy.
#
# > Is it a good idea to enforce monotonicity constraints on features? It depends. For the example here, I didnât see a significant performance decrease, and I think the directions of these variables make intuitive sense. For other cases, especially when the number of variables is large, it may be difficult and even dangerous to do so. It certainly relies on a lot of domain expertise and exploratory analysis to fit a model that is âas simple as possible, but no simplerâ.
|
module3-permutation-boosting/BONUS_xgboost_missing_values_monotonic_constraints.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, MinMaxScaler, OneHotEncoder
from xgboost import XGBClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB, CategoricalNB
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from xgboost import plot_importance
# -
df = pd.read_csv('features.csv')
# ## EDA
df.head()
df.shape
df.columns.values
df.info()
df.describe(include='all')
# +
#Histogram to check distribution and skewness
l= ['Zero_Crossings', 'Duration', 'Amp_range', 'Avg_amp', 'Freq_range',
'Pulses_per_Sec', 'Partials', 'MFCC', 'Spectral Rolloff']
plt.figure(figsize=(15,20))
for i in range(len(l)):
plt.subplot(5,2,i+1)
sns.histplot(df[l[i]],kde=True)
plt.show()
# +
#Boxplot to check for outliers
l= ['Zero_Crossings', 'Duration', 'Amp_range', 'Avg_amp', 'Freq_range',
'Pulses_per_Sec', 'Partials', 'MFCC', 'Spectral Rolloff']
plt.figure(figsize=(20,25))
for i in range(0,len(l)):
plt.subplot(5,2,i+1)
sns.set_style('whitegrid')
sns.boxplot(df[l[i]],color='green',orient='h')
plt.tight_layout()
plt.show()
# -
#Quality correlation matrix
k = 9 #number of variables for heatmap
cols = df.corr().nlargest(k, 'Amp_range')['Amp_range'].index
cm = df[cols].corr()
plt.figure(figsize=(10,6))
sns.heatmap(cm, annot=True, cmap = 'coolwarm')
df['Call'].value_counts()
df['Species'].value_counts()
# ## Data Cleansing
df['Call'].unique()
clean = {'unknown':np.NaN, 'growl?': 'growl','Growl':'growl', 'growl ':'growl', 'hiss?':'hiss', 'Hiss':'hiss',
'Sharp Hiss':'hiss', 'purr sequence': 'purr', 'Loud rumble/roar':'roar', 'call?':'call', 'main call':'call',
'call sequence':'call', 'roar or call':'roar', 'roar?':'roar', 'purr sequence':'purr', ' roar':'roar', 'hiss ':'hiss',
'mew?':'mew', 'Call sequence(possible mew)':'call', 'call sequence?':'call', 'single call?':'call',
'grow/hiss':'growl/hiss'}
df.replace(clean, inplace = True)
df['Call'].unique()
df['Age'].unique()
# +
clean2 = {'A':'Adult','Adult ':'Adult', 'Juvenile ':'Juvenile', 'juvenile':'Juvenile'}
df.replace(clean2, inplace = True)
df['Age'].fillna('Unknown', inplace = True)
df['Age'].unique()
# -
df['Sex'].unique()
# +
clean3 = {'Female ':'Female','F':'Female', 'M':'Male','male ':'Male', 'P':'Pair', 'Pair (Unknown)':'Pair', 'G':'Group', 'G (1 M and 2F)':'Group'}
df.replace(clean3, inplace = True)
df['Sex'].fillna('Unknown', inplace = True)
df['Sex'].unique()
# -
df.describe(include='object')
# ## Standardize Continuous Features
# +
continuous = ['Zero_Crossings', 'Duration', 'Amp_range', 'Avg_amp', 'Freq_range',
'Pulses_per_Sec', 'Partials', 'MFCC', 'Spectral Rolloff']
scaler = StandardScaler()
for var in continuous:
df[var] = df[var].astype('float64')
df[var] = scaler.fit_transform(df[var].values.reshape(-1, 1))
# -
df.describe(include='float64')
#Save new clean data to new CSV
df.to_csv('features_cleaned.csv', index=False)
# ## Convert categorical variables into dummy/indicator variables
# +
categorical = ['Sex', 'Age', 'Species']
for var in categorical:
df = pd.concat([df, pd.get_dummies(df[var], prefix=var)], axis=1)
del df[var]
df.info()
# -
# # Vocalization Classification
# ## Splitting data
X = df[pd.notnull(df['Call'])].drop(['Call'], axis=1)
y = df[pd.notnull(df['Call'])]['Call']
print(X.shape)
print(y.shape)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.30)
print(X_train.shape)
print(X_test.shape)
print('Call values for Data')
print(df['Call'].value_counts())
print('\n')
print('Call values for Training')
print(y_train.value_counts())
print('\n')
print('Call values for Testing')
print(y_test.value_counts())
print('Calls trained for but not tested for')
print(set(np.unique(y_train))-set(np.unique(y_test)))
print('Calls test for but not trained for')
print(set(np.unique(y_test))-set(np.unique(y_train)))
# ## XGBoost
# +
parameters = dict(
objective='multi:softprob',
random_state = 30,
max_depth=9,
learning_rate=0.01,
subsample=0.8,
colsample_bytree=0.4,
tree_method='gpu_hist')
#eval_metric='mlogloss'
clf = XGBClassifier(**parameters, n_estimators=1200)
# -
clf.fit(X_train, y_train)
clf.score(X_train, y_train)
clf.score(X_test,y_test)
y_pred = clf.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred)))
# +
names = sorted(list(set(np.unique(y_test)).union(set(y_pred))))
cnf = confusion_matrix(y_test, y_pred)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names, yticklabels=names,cmap= "YlOrBr")
plt.title('XGBoost')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',clf.score(X_test, y_test))
# -
plot_importance(clf)
figsize=(5,10)
# ## SVM
clf_svc = SVC()
clf_svc.fit(X_train, y_train)
clf_svc.score(X_train, y_train)
clf_svc.score(X_test, y_test)
y_pred_svc=clf_svc.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred_svc))
print('3. False Positive')
print(set(np.unique(y_pred_svc))-set(np.unique(y_test)))
print('4. False Negative')
print(set(np.unique(y_test))-set(np.unique(y_pred_svc)))
# +
names_svc = sorted(list(set(np.unique(y_test)).union(set(y_pred_svc))))
cnf = confusion_matrix(y_test, y_pred_svc)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_svc, yticklabels=names_svc,cmap= "YlOrBr")
plt.title('SVM Confusion Matrix')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',clf_svc.score(X_test, y_test))
# -
# ## Naive Bayes
gnb = GaussianNB()
gnb.fit(X_train, y_train)
gnb.score(X_train, y_train)
gnb.score(X_test, y_test)
y_pred_nb = gnb.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred_nb))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_nb))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_nb)))
# +
names_nb = sorted(list(set(np.unique(y_test)).union(set(y_pred_nb))))
cnf = confusion_matrix(y_test, y_pred_nb)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_nb, yticklabels=names_nb,cmap= "YlOrBr")
plt.title('Naive Bayes Confusion Matrix')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',gnb.score(X_test, y_test))
# -
# ## Logistic Regression
lr = LogisticRegression(solver='liblinear', multi_class='ovr')
lr.fit(X_train,y_train)
lr.score(X_train, y_train)
lr.score(X_test, y_test)
y_pred_lr = lr.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred_lr))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_lr))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_lr)))
# +
names_lr = sorted(list(set(np.unique(y_test)).union(set(y_pred_lr))))
cnf = confusion_matrix(y_test, y_pred_lr)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_lr, yticklabels=names_lr,cmap= "YlOrBr")
plt.title('Logistic Regression')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',lr.score(X_test, y_test))
# -
# ## KNN
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
knn.score(X_train, y_train)
knn.score(X_test, y_test)
y_pred_knn = knn.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred_knn))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_knn))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_knn)))
# +
names_knn = sorted(list(set(np.unique(y_test)).union(set(y_pred_knn))))
cnf = confusion_matrix(y_test, y_pred_knn)
fig, ax = plt.subplots(figsize=(8,4))
#Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_knn, yticklabels=names_knn,cmap= "YlOrBr")
plt.title('KNN')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',knn.score(X_test, y_test))
# -
# ## Decision Tree Classifier
cart = DecisionTreeClassifier()
cart.fit(X_train, y_train)
cart.score(X_train, y_train)
cart.score(X_test, y_test)
y_pred_cart = cart.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred_cart))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_cart))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_cart)))
# +
names_cart = sorted(list(set(np.unique(y_test)).union(set(y_pred_cart))))
cnf = confusion_matrix(y_test, y_pred_cart)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_cart, yticklabels=names_cart,cmap= "YlOrBr")
plt.title('Decision Tree Classifier')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',cart.score(X_test, y_test))
# -
# ## Random Forest Classifier
rf = RandomForestClassifier()
rf.fit(X_train, y_train)
rf.score(X_train, y_train)
rf.score(X_test, y_test)
y_pred_rf = cart.predict(X_test)
print('1. Tested Calls')
print(np.unique(y_test))
print('2. Predicted Calls')
print(np.unique(y_pred_rf))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_rf))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_rf)))
# +
names_rf = sorted(list(set(np.unique(y_test)).union(set(y_pred_rf))))
cnf = confusion_matrix(y_test, y_pred_rf)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_rf, yticklabels=names_rf,cmap= "YlOrBr")
plt.title('Random Forest')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',rf.score(X_test, y_test))
# -
#The data is unbalanced, this could be fixed by updating the class weights
#Or getting more varied data
df['Call'].value_counts()
# # Species Classification
df2= pd.read_csv('features_cleaned.csv')
df2.head()
df2.info()
# ## Convert categorical variables into dummy/indicator variables
# +
categorical = ['Sex', 'Age', 'Call']
for var in categorical:
df2 = pd.concat([df2, pd.get_dummies(df2[var], prefix=var)], axis=1)
del df2[var]
df2.info()
# -
# ## Splitting data
X = df2[pd.notnull(df2['Species'])].drop(['Species'], axis=1)
y = df2[pd.notnull(df2['Species'])]['Species']
print(X.shape)
print(y.shape)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.30)
print(X_train.shape)
print(X_test.shape)
print('Species values for Data')
print(df2['Species'].value_counts())
print('\n')
print('Species values for Training')
print(y_train.value_counts())
print('\n')
print('Species values for Testing')
print(y_test.value_counts())
print('Species trained for but not tested for')
print(set(np.unique(y_train))-set(np.unique(y_test)))
print('Species test for but not trained for')
print(set(np.unique(y_test))-set(np.unique(y_train)))
# ## XGBoost
# +
parameters = dict(
objective='multi:softprob',
random_state = 30,
max_depth=9,
learning_rate=0.01,
subsample=0.8,
colsample_bytree=0.4,
tree_method='gpu_hist')
#eval_metric='mlogloss'
clf = XGBClassifier(**parameters, n_estimators=1200)
# -
clf.fit(X_train, y_train)
clf.score(X_train, y_train)
clf.score(X_test,y_test)
y_pred = clf.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred)))
# +
names = sorted(list(set(np.unique(y_test)).union(set(y_pred))))
cnf = confusion_matrix(y_test, y_pred)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names, yticklabels=names,cmap= "YlOrBr")
plt.title('XGBoost')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',clf.score(X_test, y_test))
# -
plot_importance(clf)
figsize=(8,4)
# ## SVM
clf_svc = SVC()
clf_svc.fit(X_train, y_train)
clf_svc.score(X_train, y_train)
clf_svc.score(X_test, y_test)
y_pred_svc=clf_svc.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred_svc))
print('3. False Positive')
print(set(np.unique(y_pred_svc))-set(np.unique(y_test)))
print('4. False Negative')
print(set(np.unique(y_test))-set(np.unique(y_pred_svc)))
# +
names_svc = sorted(list(set(np.unique(y_test)).union(set(y_pred_svc))))
cnf = confusion_matrix(y_test, y_pred_svc)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_svc, yticklabels=names_svc,cmap= "YlOrBr")
plt.title('SVM Confusion Matrix')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',clf_svc.score(X_test, y_test))
# -
# ## Naive Bayes
gnb = GaussianNB()
gnb.fit(X_train, y_train)
gnb.score(X_train, y_train)
gnb.score(X_test, y_test)
y_pred_nb = gnb.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred_nb))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_nb))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_nb)))
# +
names_nb = sorted(list(set(np.unique(y_test)).union(set(y_pred_nb))))
cnf = confusion_matrix(y_test, y_pred_nb)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_nb, yticklabels=names_nb,cmap= "YlOrBr")
plt.title('Naive Bayes Confusion Matrix')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',gnb.score(X_test, y_test))
# -
# ## Logistic Regression
lr = LogisticRegression(solver='liblinear', multi_class='ovr')
lr.fit(X_train,y_train)
lr.score(X_train, y_train)
lr.score(X_test, y_test)
y_pred_lr = lr.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred_lr))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_lr))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_lr)))
# +
names_lr = sorted(list(set(np.unique(y_test)).union(set(y_pred_lr))))
cnf = confusion_matrix(y_test, y_pred_lr)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_lr, yticklabels=names_lr,cmap= "YlOrBr")
plt.title('Logistic Regression')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',lr.score(X_test, y_test))
# -
# ## KNN
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
knn.score(X_train, y_train)
knn.score(X_test, y_test)
y_pred_knn = knn.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred_knn))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_knn))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_knn)))
# +
names_knn = sorted(list(set(np.unique(y_test)).union(set(y_pred_knn))))
cnf = confusion_matrix(y_test, y_pred_knn)
fig, ax = plt.subplots(figsize=(8,4))
#Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_knn, yticklabels=names_knn,cmap= "YlOrBr")
plt.title('KNN')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',knn.score(X_test, y_test))
# -
# ## Decision Tree Classifier
cart = DecisionTreeClassifier()
cart.fit(X_train, y_train)
cart.score(X_train, y_train)
cart.score(X_test, y_test)
y_pred_cart = cart.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred_cart))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_cart))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_cart)))
# +
names_cart = sorted(list(set(np.unique(y_test)).union(set(y_pred_cart))))
cnf = confusion_matrix(y_test, y_pred_cart)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_cart, yticklabels=names_cart,cmap= "YlOrBr")
plt.title('Decision Tree Classifier')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',cart.score(X_test, y_test))
# -
# ## Random Forest Classifier
rf = RandomForestClassifier()
rf.fit(X_train, y_train)
rf.score(X_train, y_train)
rf.score(X_test, y_test)
y_pred_rf = cart.predict(X_test)
print('1. Tested Species')
print(np.unique(y_test))
print('2. Predicted Species')
print(np.unique(y_pred_rf))
print('3. Not tested for but predicted')
print(set(np.unique(y_pred_rf))-set(np.unique(y_test)))
print('4. Tested for but not predicted')
print(set(np.unique(y_test))-set(np.unique(y_pred_rf)))
# +
names_rf = sorted(list(set(np.unique(y_test)).union(set(y_pred_rf))))
cnf = confusion_matrix(y_test, y_pred_rf)
fig, ax = plt.subplots(figsize=(8,4))
# Normalise
cnf = cnf.astype('float')/cnf.sum(axis=1)[:, np.newaxis]
sns.heatmap(cnf, annot=True, fmt='.1%', xticklabels=names_rf, yticklabels=names_rf,cmap= "YlOrBr")
plt.title('Random Forest')
ax.xaxis.set_label_position('top')
plt.ylabel('Actual')
plt.xlabel('Predicted')
plt.show(block=False)
print('Accuracy',rf.score(X_test, y_test))
# -
# #The data is unbalanced, this could be fixed by updating the class weights
# #Or getting more varied data
# df2['Species'].value_counts()
|
Feature Cleaning and First Models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/pcsilcan/dm/blob/master/20202/dm_20202_0601_overfitting.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="f2D1TwvrQXm0" colab_type="code" colab={}
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# + id="ew1cCEPRQ15x" colab_type="code" colab={}
np.random.seed(1981)
n_samples = 30
degrees = [1, 15, 3, 5]
true_fun = lambda X: np.cos(1.5 * np.pi * X)
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples)*0.1
# + id="8F959IkqRjtB" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 822} outputId="9e569e6b-25e8-4743-9e07-f8be8583f382"
plt.figure(figsize=(14, 14))
for i in range(len(degrees)):
ax = plt.subplot(2, 2, i + 1)
plt.setp(ax, xticks=(), yticks=())
polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X[:, np.newaxis], y)
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="Real Function")
plt.scatter(X, y, label="Training points")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc="best")
plt.title("Degrees %d"%(degrees[i]))
plt.show()
# + id="WxMSRfgbSnW_" colab_type="code" colab={}
|
20202/dm_20202_0601_overfitting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Extract Time Series Data
#
# With this notebook the TimeSeries for predefined FIBER Conditions can be extracted.
#
#
# +
from typing import Optional
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import venn
from fiber import Cohort
from fiber.condition import MRNs
from fiber.config import OCCURRENCE_INDEX, VERBOSE
from fiber.dataframe import (
column_threshold_clip,
create_id_column,
merge_to_base,
time_window_clip
)
from fiber.plots.distributions import bars
from fiberutils.time_series_utils import ssr_transform
from fiber.condition import Patient, MRNs
from fiber.condition import Diagnosis
from fiber.condition import Measurement, Encounter, Drug, TobaccoUse,LabValue, VitalSign, Procedure
from fiber.storage import yaml as fiberyaml
#from fiberutils.cohort_utils import get_time_series, pivot_time_series
import pandas as pd
import pyarrow.parquet as pq
import numpy as np
import os
import matplotlib.pyplot as plt
from functools import reduce
import json
import math
import inspect
import json
import sys
from pydoc import locate
import requests
##### REQUIRES THE DATAFRAME FOLDER TO BE NAMED 'Cohorts', WHICH INCLUDES ALL PRECOMPUTED DATAFRAMES #####
from typing import Optional
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import venn
from fiber import Cohort
from fiber.condition import MRNs
from fiber.config import OCCURRENCE_INDEX, VERBOSE
from fiber.dataframe import (
column_threshold_clip,
create_id_column,
merge_to_base,
time_window_clip
)
from fiber.plots.distributions import bars
from fiberutils.time_series_utils import ssr_transform
from fiber.condition import Patient, MRNs
from fiber.condition import Diagnosis
from fiber.condition import Measurement, Encounter, Drug, TobaccoUse,LabValue, VitalSign, Procedure
from fiber.storage import yaml as fiberyaml
#from fiberutils.cohort_utils import get_time_series, pivot_time_series
import pandas as pd
import pyarrow.parquet as pq
import numpy as np
import os
import matplotlib.pyplot as plt
from functools import reduce
import json
import math
import inspect
import json
import sys
from pydoc import locate
#import request
# -
#generic function get cohort from mrns
def df_to_cohort(df):
#mrns = list(df.index.values)
#mrns = list(map(str, mrns))
p_condition = MRNs(df)
print(MRNs(df))
cohort = Cohort(p_condition)
#print(mrns)
return cohort
#MRN Data frame :
sample = pq.read_table('Cohort/Feature_Extraction/ALL_HF_cohort_unsupervised_only_all_count_all_mean_preprocessed.parquet').to_pandas()
sample['medical_record_number']=sample.index
# Saving Hf_Onset as age_in_days for PIVOT config necessary and for the function time series for
sample = sample["HF_Onset_age_in_days"]
sample = sample.to_frame()
sample.reset_index(level=0, inplace=True)
sample.rename(columns = {"HF_Onset_age_in_days": "age_in_days"}, inplace = True)
#create a small sample
#sample = sample.head(10) #to try with small sample
sample
#convert df to fiber cohort
cohort_EF_Baseline = df_to_cohort(sample)
cohort_EF_Baseline
# +
#Functions to get detailed information of the FIBER Conditiond to be able to extract the right data
def rename_columns( df,col_ignore):
replacements = {}
for column in df.columns:
replacements[column] = get(column,col_ignore)
return replacements
def get(feature,col_ignor):
#context first empty :
context=""
code=""
# does not support time window information inside feature name yet
if feature.startswith(col_ignor):
return feature.replace('_', ' ').replace('.', '|')
split_name = feature.split('__')
if split_name[1] in [
i[0]
for i in inspect.getmembers(
sys.modules['fiber.condition'],
inspect.isclass
)
]:
aggregation = split_name[0]
split_name = split_name[1:]
else:
aggregation = "time series"
if len(split_name) == 3:
class_name, context, code = split_name
condition_class = locate(f'fiber.condition.{class_name}')
description = get_description(condition_class, code, context)
else:
class_name, description = split_name
return f'{class_name} | {code }|{description.capitalize()} ({aggregation}) | {context}'
def get_description( condition_class, code, context):
return condition_class(
code=code,
context=context
).patients_per(
condition_class.description_column
)[
condition_class.description_column.name.lower()
].iloc[0]
#columns that should be ignored for the timeseries extraction
col_ignore=('age_in_days', 'gender', 'religion', 'race','medical_record_number','HF_Onset_age_in_days','patient_ethnic_group','deceased_indicator','mother_account_number','address_zip','marital_status_code')
col_ignore
# -
# # Create Feature look up table with human readable names
col=['original_feature_name','human_readable']
feature_look_up=pd.DataFrame(columns=col)
feature_look_up
# ### Drug Dictionary
#non drug columns:
col_for_dropping=['age_in_days',
'gender',
'religion',
'race',
'medical_record_number',
'patient_ethnic_group',
'deceased_indicator',
'mother_account_number',
'address_zip',
'date_of_birth',
'month_of_birth',
'marital_status_code']
# load drug dataframe:
#get Medical Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/Drug_after_onset_HF_ALL_mmm_0_2'
drug = pq.read_table(df_path).to_pandas()
#print(drug)
drug=drug.drop(col_for_dropping,axis=1)
drug_renamed_column=rename_columns(drug,col_ignore)
for n in drug_renamed_column.items():
parts=n[1].split('|')
original_feature_name=n[0]
human_readable=str(parts[2].replace(' (time series) ','')).strip()
feature_look_up=feature_look_up.append({'original_feature_name':original_feature_name,'human_readable':human_readable},ignore_index=True)
feature_look_up
# ### Diagnosis Dictionary
# load Diagnosis dataframe:
#get Medical Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/Diagnosis_after_onset_HF_ALL_mmm_0_2_cleaned'
diagnosis = pq.read_table(df_path).to_pandas()
diagnosis=diagnosis.drop(col_for_dropping,axis=1)
#create diagnosis dictionary
diagnosis_renamed_column=rename_columns(diagnosis,col_ignore)
for n in diagnosis_renamed_column.items():
parts=n[1].split('|')
original_feature_name=n[0]
human_readable=str(parts[2].replace(' (time series) ','')).strip()
feature_look_up=feature_look_up.append({'original_feature_name':original_feature_name,'human_readable':human_readable},ignore_index=True)
feature_look_up
# ### Procedures Dictionary
# load Procedure dataframe:
#get Procedure Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/Procedure_after_onset_HF_ALL_mmm_0_6'
procedures = pq.read_table(df_path).to_pandas()
procedures=procedures.drop(col_for_dropping,axis=1)
procedures_renamed_column=rename_columns(procedures,col_ignore)
for n in procedures_renamed_column.items():
parts=n[1].split('|')
original_feature_name=n[0]
human_readable=str(parts[2].replace(' (time series) ','')).strip()
feature_look_up=feature_look_up.append({'original_feature_name':original_feature_name,'human_readable':human_readable},ignore_index=True)
feature_look_up
# ### Vital Sign
col_for_dropping=[]
# load Vital Sign dataframe:
#get Vital Sign Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/VitalSign_after_onset_HF_ALL_mmm_0_6_cleaned'
vital = pq.read_table(df_path).to_pandas()
vital=vital.drop(col_for_dropping,axis=1)
#create Vital Signs dictionary
vital_renamed_column=rename_columns(vital,col_ignore)
vital_renamed_column
for n in vital_renamed_column.items():
parts=n[1].split('|')
original_feature_name=n[0]
if original_feature_name !='medical_record_number':
human_readable=str(parts[2].replace(' (time series) ','')).strip()
feature_look_up=feature_look_up.append({'original_feature_name':original_feature_name,'human_readable':human_readable},ignore_index=True)
feature_look_up
# ### Lab Values
# load Lab Values dataframe:
#get Lab Values Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/LabValue_after_onset_HF_ALL_mmm_0_8_cleaned'
lab = pq.read_table(df_path).to_pandas()
lab=lab.drop(col_for_dropping,axis=1)
#create lab values dictionary
lab_renamed_column=rename_columns(lab,col_ignore)
for n in lab_renamed_column.items():
parts=n[1].split('|')
original_feature_name=n[0]
if original_feature_name !='medical_record_number':
human_readable=str(parts[2].replace(' (time series) ','')).strip()
feature_look_up=feature_look_up.append({'original_feature_name':original_feature_name,'human_readable':human_readable},ignore_index=True)
feature_look_up
feature_look_up.to_parquet('Cohort/feature_look_up.parquet')
vital
# # Inpatient
#non drug columns:
col_for_dropping=['age_in_days',
'gender',
'religion',
'race',
'medical_record_number',
'patient_ethnic_group',
'deceased_indicator',
'mother_account_number',
'address_zip',
'date_of_birth',
'month_of_birth',
'marital_status_code']
conditions=Encounter(description='%Inpatient%')
inpatient_time_series=cohort_EF_Baseline.get(conditions)
inpatient_time_series
inpatient_time_series.to_parquet('Cohort/Time_Series/Inpatient_Events_raw.parquet')
# # Ejection Fraction
#Define ejection fraction condition:
conditions=(LabValue('%ejection%'))
ej_time_series=cohort_EF_Baseline.time_series_for(
conditions
)
ej_time_series
ej_time_series.to_parquet('Cohort/Time_Series/Ejection_Fraction_raw.parquet')
# # Drugs
#non drug columns:
col_for_dropping=['age_in_days',
'gender',
'religion',
'race',
'medical_record_number',
'patient_ethnic_group',
'deceased_indicator',
'mother_account_number',
'address_zip',
'date_of_birth',
'month_of_birth',
'marital_status_code']
# load drug dataframe:
#get Medical Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/Drug_after_onset_HF_ALL_mmm_0_2'
drug = pq.read_table(df_path).to_pandas()
#print(drug)
drug=drug.drop(col_for_dropping,axis=1)
drug
#create drug dictionary
drug_renamed_column=rename_columns(drug,col_ignore)
#get Drug Features for Time series
'''structure for drug time series feature:
conditions=(Drug(context='TDS',
code='01060-ACETAMINOPHEN TABS',
description='Acetaminophen tabs',
data_columns=['medical_record_number','age_in_days', 'context_name',
'MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|)
'''
for n in drug_renamed_column.items():
parts=n[1].split('|')
drug_statement='Drug(context=\''+str(parts[3]).strip()+'\',code=\''+str(parts[1]).strip()+'\',description=\''+str(parts[2].replace(' (time series) ','')).strip()+'\',data_columns=[\'medical_record_number\',\'age_in_days\', \'context_name\',\'MATERIAL_NAME\',\'GENERIC_NAME\',\'BRAND1\',\'numeric_value\'])|'
#drug_statement='a'+n[1]
print(drug_statement)
#print(parts[3])
# +
#final Format Drugs Copied from the output above
conditions=(Drug(context='COMPURECORD',code='Cefazolin',description='Cefazolin',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='COMPURECORD',code='Fentanyl',description='Fentanyl',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='COMPURECORD',code='Midazolam',description='Midazolam',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='COMPURECORD',code='Propofol',description='Propofol',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='Cardiac Cath',code='Antiplatelets+Aspirin',description='Aspirin',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='Cardiac Cath',code='Diuretic+Lasix',description='Lasix',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC IMMUNIZATION',code='51',description='Influenza vaccine',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='10113',description='Potassium chloride 10 meq/100 ml intravenous piggyback',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='10168',description='Potassium chloride er 20 meq tablet,extended release(part/cryst)',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='10196',description='Famotidine 20 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='10292',description='Magnesium oxide 400 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='12097',description='Bisacodyl 10 mg rectal suppository',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='12204',description='Pantoprazole 40 mg tablet,delayed release',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='12421',description='Ferrous sulfate 325 mg (65 mg iron) tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='1311',description='Sennosides 8.6 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='13116',description='Lisinopril 10 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='13136',description='Insulin regular human 100 unit/ml injection solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='13455',description='Warfarin 5 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='14455',description='Fentanyl (pf) 50 mcg/ml injection solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='1451',description='Acetaminophen 325 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='1454',description='Carvedilol 6.25 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='14861',description='Glucagon (human recombinant) 1 mg solution for injection',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='14951',description='Docusate sodium 100 mg capsule',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='15419',description='Aspirin 81 mg chewable tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='16470',description='Lisinopril 5 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='16639',description='Furosemide 20 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='16822',description='Sodium chloride 0.9 % intravenous solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='16843',description='Metoprolol succinate er 25 mg tablet,extended release 24 hr',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='17270',description='Insulin lispro 100 unit/ml subcutaneous solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='19073',description='Heparin (porcine) 5,000 unit/ml injection solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='19767',description='Electrolyte-a intravenous solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='19813',description='Ipratropium bromide 0.02 % solution for inhalation',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='2063',description='Insulin glargine 100 unit/ml subcutaneous solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='21305',description='Famotidine (pf) 20 mg/50 ml in 0.9 % nacl (iso) intravenous piggyback',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='2424',description='Albuterol sulfate 2.5 mg/3 ml (0.083 %) solution for nebulization',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='25410',description='Dextrose 50 % in water (d50w) intravenous solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='25735',description='Morphine 2 mg/ml injection syringe',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='2767',description='Polyethylene glycol 3350 17 gram oral powder packet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='31504',description='Metoprolol tartrate 25 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='37111',description='Vancomycin 1 gram/200 ml in dextrose 5 % intravenous piggyback',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='400001',description='Zz ims template',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='400284',description='Sodium chloride 0.9 % iv bolus',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='421',description='Furosemide 40 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='5171',description='Dextrose 40 % oral gel',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='5511',description='Sodium chloride 0.45 % intravenous solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='65572',description='Heparin (porcine) 25,000 unit/250 ml (100 unit/ml) in dextrose 5 % iv',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='689',description='Furosemide 10 mg/ml injection solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='7045',description='Clopidogrel 75 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='7307',description='Amlodipine 5 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='74103',description='Ondansetron hcl (pf) 4 mg/2 ml injection solution',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='76121',description='Magnesium sulfate 1 gram/50 ml in 0.9 % sodium chloride iv piggyback',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='7735',description='Aspirin 81 mg tablet,delayed release',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='7769',description='Perflutren lipid microspheres 1.1 mg/ml intravenous suspension',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='8098',description='Spironolactone 25 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='8267',description='Carvedilol 3.125 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='9554',description='Oxycodone-acetaminophen 5 mg-325 mg tablet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='95567',description='Glucagon (human recombinant) 1 mg/ml solution for injection',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='EPIC MEDICATION',code='9940',description='Potassium chloride 20 meq oral packet',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='TDS ALLERGY',code='12336-MEDS',description='Meds',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value'])|
Drug(context='TDS',code='01060-ACETAMINOPHEN TABS',description='Acetaminophen tabs',data_columns=['medical_record_number','age_in_days', 'context_name','MATERIAL_NAME','GENERIC_NAME','BRAND1','numeric_value']))
# -
#extract the time series data
drug_time_series=cohort_EF_Baseline.time_series_for(
conditions
)
# unique values and feature names:
drug_time_series['material_name'].unique()
drug_time_series.to_parquet('Cohort/Time_Series/Drug_02.parquet')
# # Diagnosis
#non drug columns:
col_for_dropping=['age_in_days',
'gender',
'religion',
'race',
'medical_record_number',
'patient_ethnic_group',
'deceased_indicator',
'mother_account_number',
'address_zip',
'date_of_birth',
'month_of_birth',
'marital_status_code']
# load Diagnosis dataframe:
#get Medical Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/Diagnosis_after_onset_HF_ALL_mmm_0_2_cleaned'
diagnosis = pq.read_table(df_path).to_pandas()
diagnosis=diagnosis.drop(col_for_dropping,axis=1)
diagnosis
#create diagnosis dictionary
diagnosis_renamed_column=rename_columns(diagnosis,col_ignore)
diagnosis_renamed_column
#get Drug Features for Time series
'''structure for diagnosis time series feature:
conditions=(Diagnosis(context='ICD-10',
code='D64.9',
data_columns=['medical_record_number','description','age_in_days',
'context_name', 'context_diagnosis_code', 'numeric_value'])|)
'''
for n in diagnosis_renamed_column.items():
parts=n[1].split('|')
diagnosis_statement='Diagnosis(context=\''+str(parts[3]).strip()+'\',code=\''+str(parts[1]).strip()+'\',description=\''+str(parts[2].replace(' (time series) ','')).strip()+'\',data_columns=[\'medical_record_number\',\'age_in_days\',\'description\', \'context_name\',\'context_diagnosis_code\',\'numeric_value\'])|'
#drug_statement='a'+n[1]
print(diagnosis_statement)
#print(parts[3])
#final Format Diagnosis Copied from the output above
conditions=(Diagnosis(context='APRDRG MDC',code='005',description='Circulatory system diseases',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='D64.9',description='Anemia, unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='E11.9',description='Type 2 diabetes mellitus without complications',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='E78.5',description='Hyperlipidemia, unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='I10',description='Essential (primary) hypertension',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='I25.10',description='Atherosclerotic heart disease of native coronary artery without angina pectoris',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='I48.91',description='Unspecified atrial fibrillation',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='I50.20',description='Unspecified systolic (congestive) heart failure',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='I50.22',description='Chronic systolic (congestive) heart failure',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='I50.9',description='Heart failure, unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='N17.9',description='Acute kidney failure, unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='R06.02',description='Shortness of breath',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='R07.9',description='Chest pain, unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='R69',description='Illness, unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-10',code='Z23',description='Encounter for immunization',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='250.00',description='Diabetes mellitus without mention of complication type ii or unspecified type not stated as uncontrolled',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='272.0',description='Pure hypercholesterolemia',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='272.4',description='Other and unspecified hyperlipidemia',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='285.9',description='Anemia unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='401.9',description='Unspecified essential hypertension',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='403.90',description='Hypertensive chronic kidney disease unspecified with chronic kidney disease stage i through stage iv or unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='414.00',description='Coronary atherosclerosis of unspecified type of vessel native or graft',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='414.01',description='Coronary atherosclerosis of native coronary artery',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='416.8',description='Other chronic pulmonary heart diseases',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='424.0',description='Mitral valve disorders',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='425.4',description='Other primary cardiomyopathies',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='427.31',description='Atrial fibrillation',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='428.0',description='Congestive heart failure unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='428.20',description='Unspecified systolic heart failure',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='428.22',description='Chronic systolic heart failure',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='486',description='Pneumonia organism unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='584.9',description='Acute kidney failure unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='585.9',description='Chronic kidney disease unspecified',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='780.79',description='Other malaise and fatigue',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='786.05',description='Shortness of breath',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='786.50',description='Unspecified chest pain',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='I10',description='Not available',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='V04.81',description='Need for prophylactic vaccination and inoculation against influenza',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='V14',description='Personal history of allergy to medicinal agents',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='ICD-9',code='V15.82',description='Personal history of tobacco use',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='10026',description='Shortness of breath',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='113033',description='Chf (congestive heart failure)',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='114039',description='Hyperlipidemia',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='144791',description='Essential hypertension',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='154288',description='Htn (hypertension)',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='154321',description='Cad (coronary artery disease)',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='158530',description='Hypertension',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='163845',description='Essential (primary) hypertension',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='5107',description='Atrial fibrillation',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value'])|
Diagnosis(context='IMO',code='94485',description='Diabetes mellitus',data_columns=['medical_record_number','age_in_days','description', 'context_name','context_diagnosis_code','numeric_value']))
#extract the time series data
diagnosis_time_series=cohort_EF_Baseline.time_series_for(
conditions
)
diagnosis_time_series
# unique values and feature names:
diagnosis_time_series['description'].unique()
diagnosis_time_series.to_parquet('Cohort/Time_Series/Diagnosis_02.parquet')
# # Procedures
#non Procedure columns:
col_for_dropping=['age_in_days',
'gender',
'religion',
'race',
'medical_record_number',
'patient_ethnic_group',
'deceased_indicator',
'mother_account_number',
'address_zip',
'date_of_birth',
'month_of_birth',
'marital_status_code']
# load Procedure dataframe:
#get Procedure Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/Procedure_after_onset_HF_ALL_mmm_0_6'
procedures = pq.read_table(df_path).to_pandas()
procedures=procedures.drop(col_for_dropping,axis=1)
procedures
#create procedure dictionary
procedures_renamed_column=rename_columns(procedures,col_ignore)
procedures_renamed_column
#get Drug Features for Time series
'''structure for diagnosis time series feature:
conditions=(Diagnosis(context='ICD-10',
code='D64.9',
data_columns=['medical_record_number','description','age_in_days',
'context_name', 'context_diagnosis_code', 'numeric_value'])|)
'''
for n in procedures_renamed_column.items():
parts=n[1].split('|')
procedures_statement='Procedure(context=\''+str(parts[3]).strip()+'\',code=\''+str(parts[1]).strip()+'\',description=\''+str(parts[2].replace(' (time series) ','')).strip()+'\',data_columns=[\'medical_record_number\',\'age_in_days\', \'context_name\',\'PROCEDURE_DESCRIPTION\',\'numeric_value\'])|'
#drug_statement='a'+n[1]
print(procedures_statement)
#print(parts[3])
#Final Procedure Format, copied from above
conditions=(Procedure(context='CAREFUSION LAB',code='AMY',description='Hemoglobin a1c',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='BMP',description='Basic metabolic panel',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='C&P',description='Cbc+platelet',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='CMP',description='Comprehensive metabolic panel',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='CPD',description='Cbc+plt+diff',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='CTP',description='Cbc+platelet',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='PO4',description='Phosphorus-blood',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='PRO',description='Prothrombin time',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='PT',description='Prothrombin time',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='PTPTT',description='Pt and aptt',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='TROI',description='Troponin i',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='TS-G',description='Type and screen',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CAREFUSION LAB',code='UCHEM',description='Urinalysis, routine',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='71010',description='Radiologic examination, chest; single view, frontal',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='71020',description='Radiologic examination, chest, 2 views, frontal and lateral;',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='80048',description='Basic metabolic panel (calcium, total) this panel must include the following: calcium, total (82310), carbon dioxide (82374), chloride (82435), creatinine (82565), glucose (82947), potassium (84132), sodium (84295), urea nitrogen (bun) (84520)',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='80053',description='Comprehensive metabolic panel this panel must include the following: albumin (82040), bilirubin, total (82247), calcium, total (82310), carbon dioxide (bicarbonate) (82374), chloride (82435), creatinine (82565), glucose (82947), phosphatase, alkaline (84075), potassium (84132), protein, total (84155), sodium (84295), transferase, alanine amino (alt) (sgpt) (84460), transferase, aspartate amino (ast) (sgot) (84450), urea nitrogen (bun) (84520)',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='81003',description='Urinalysis, by dip stick or tablet reagent for bilirubin, glucose, hemoglobin, ketones, leukocytes, nitrite, ph, protein, specific gravity, urobilinogen, any number of these constituents; automated, without microscopy',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='83735',description='Magnesium',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='84100',description='Phosphorus inorganic (phosphate);',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='84484',description='Troponin, quantitative',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='85025',description='Blood count; complete (cbc), automated (hgb, hct, rbc, wbc and platelet count) and automated differential wbc count',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='85027',description='Blood count; complete (cbc), automated (hgb, hct, rbc, wbc and platelet count)',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='85610',description='Prothrombin time;',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='85730',description='Thromboplastin time, partial (ptt); plasma or whole blood',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='CPT-4',code='93000',description='Electrocardiogram, routine ecg with at least 12 leads; with interpretation and report',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EKG',code='93000-ELECTROCARDIOGRAM, COMPLETE',description='Electrocardiogram, complete',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC CPT-4',code='100516',description='Type and screen',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='(RESP)',description='Respirations',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='(T-O)',description='Temperature, oral',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='(T-T)',description='Temperature, tympanic',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='119049',description='Type and screen',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6029',description='Basic metabolic panel',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6032',description='Comprehensive metabolic panel',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6104',description='Urinalysis, routine',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='64302',description='Pt and aptt',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6432',description='Phosphorus-blood',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='64914',description='X-ray chest 1 view portable',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='64924',description='X-ray chest pa and lateral only',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6509',description='Troponin i',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6550',description='Cbc+plt+diff',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6551',description='Cbc+platelet',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='6624',description='Prothrombin time',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='7509',description='Electrocardiogram, complete',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='BP SITE',description='Bp site',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='DBP',description='Diastolic blood pressure',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='HEIGHT',description='Height',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='PAIN SCALE',description='Pain scale',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='PULSE',description='Pulse',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='PULSE OXIMETRY',description='O2 saturation',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='R APACHE TEMPERATURE',description='R apache temperature',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='R IP PAIN SCALE ADULT',description='R ip pain scale adult',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='SBP',description='Systolic blood pressure',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='TEMPERATURE',description='Temperature',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])|
Procedure(context='EPIC',code='WEIGHT',description='Weight',data_columns=['medical_record_number','age_in_days', 'context_name','PROCEDURE_DESCRIPTION','numeric_value'])
)
#extract the time series data
procedures_time_series=cohort_EF_Baseline.time_series_for(
conditions
)
procedures_time_series
procedures_time_series['procedure_description'].unique()
procedures_time_series.to_parquet('Cohort/Time_Series/Procedures_06.parquet')
# # Vital Signs
#non vital signs columns:
col_for_dropping=[
'medical_record_number',
'median__VitalSign__EPIC__(RESP)',
'median__VitalSign__EPIC__(T-O)',
'median__VitalSign__EPIC__(T-T)',
'median__VitalSign__EPIC__DBP',
'median__VitalSign__EPIC__PULSE',
'median__VitalSign__EPIC__PULSE OXIMETRY',
'median__VitalSign__EPIC__SBP',
'median__VitalSign__EPIC__TEMPERATURE',
'min__VitalSign__EPIC__(RESP)',
'min__VitalSign__EPIC__(T-O)',
'min__VitalSign__EPIC__(T-T)',
'min__VitalSign__EPIC__DBP',
'min__VitalSign__EPIC__PULSE',
'min__VitalSign__EPIC__PULSE OXIMETRY',
'min__VitalSign__EPIC__SBP',
'min__VitalSign__EPIC__TEMPERATURE'
]
# load Vital Sign dataframe:
#get Vital Sign Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/VitalSign_after_onset_HF_ALL_mmm_0_6_cleaned'
vital = pq.read_table(df_path).to_pandas()
vital=vital.drop(col_for_dropping,axis=1)
vital
further_col_drop=[]
for c in vital.columns:
if ('max' not in c) :
print(c)
further_col_drop.append(c)
further_col_drop
#create Vital Signs dictionary
vital_renamed_column=rename_columns(vital,col_ignore)
vital_renamed_column
#get Vital Signs Features for Time series
'''structure for diagnosis time series feature:
conditions=(Diagnosis(context='ICD-10',
code='D64.9',
data_columns=['medical_record_number','description','age_in_days',
'context_name', 'context_diagnosis_code', 'numeric_value'])|)
'''
for n in vital_renamed_column.items():
parts=n[1].split('|')
vital_statement='VitalSign(context=\''+str(parts[3]).strip()+'\',code=\''+str(parts[1]).strip()+'\',description=\''+str(parts[2].replace(' (max) ','')).strip()+'\')|'
#drug_statement='a'+n[1]
print(vital_statement)
#print(parts[3])
#Final Vital Signs Format copied from above
conditions=(
VitalSign(context='EPIC',code='(RESP)',description='Respirations')|
VitalSign(context='EPIC',code='(T-O)',description='Temperature, oral')|
VitalSign(context='EPIC',code='(T-T)',description='Temperature, tympanic')|
VitalSign(context='EPIC',code='DBP',description='Diastolic blood pressure')|
VitalSign(context='EPIC',code='PULSE',description='Pulse')|
VitalSign(context='EPIC',code='PULSE OXIMETRY',description='O2 saturation')|
VitalSign(context='EPIC',code='SBP',description='Systolic blood pressure')|
VitalSign(context='EPIC',code='TEMPERATURE',description='Temperature') )
#extract the time series data
vital_time_series=cohort_EF_Baseline.time_series_for(
conditions
)
vital_time_series
# unique values and feature names:
vital_time_series['context_procedure_code'].unique()
vital_time_series.loc[vital_time_series['medical_record_number']=='1000133708']
vital_time_series.to_parquet('Cohort/Time_Series/VitalSign_06.parquet')
# # LabValues
#non LabValues columns:
col_for_dropping=[
'median__LabValue__ALBUMIN, BLD',
'median__LabValue__ALK PHOSPHATASE, BLD',
'median__LabValue__ALT(SGPT)',
'median__LabValue__APTT',
'median__LabValue__AST (SGOT)',
'median__LabValue__ATRIAL RATE',
'median__LabValue__BASOPHIL %',
'median__LabValue__BILIRUBIN TOTAL',
'median__LabValue__CALCIUM, BLD',
'median__LabValue__CARBON DIOXIDE-BLD',
'median__LabValue__CHLORIDE-BLD',
'median__LabValue__CREATININE-SERUM',
'median__LabValue__EOSINOPHIL #',
'median__LabValue__EOSINOPHIL %',
'median__LabValue__GLUCOSE',
'median__LabValue__HEMATOCRIT',
'median__LabValue__HEMOGLOBIN',
'median__LabValue__INR',
'median__LabValue__LYMPHOCYTE #',
'median__LabValue__LYMPHOCYTE %',
'median__LabValue__MAGNESIUM-BLD',
'median__LabValue__MEAN CORP. HGB',
'median__LabValue__MEAN CORP. HGB CONC.',
'median__LabValue__MEAN CORP. VOLUME',
'median__LabValue__MEAN PLT VOLUME',
'median__LabValue__MONOCYTE #',
'median__LabValue__MONOCYTE %',
'median__LabValue__NEUTROPHIL #',
'median__LabValue__NEUTROPHIL %',
'median__LabValue__P AXIS',
'median__LabValue__P-R INTERVAL',
'median__LabValue__PLATELET',
'median__LabValue__POTASSIUMBLD',
'median__LabValue__PRO TIME',
'median__LabValue__PROTEIN TOTAL-BLD',
'median__LabValue__QRS DURATION',
'median__LabValue__QT',
'median__LabValue__QTC',
'median__LabValue__R AXIS',
'median__LabValue__RBC BLOOD CELL',
'median__LabValue__RED DISTRIB. WIDTH',
'median__LabValue__SODIUM-BLD',
'median__LabValue__T AXIS',
'median__LabValue__UREA NITROGEN-BLD',
'median__LabValue__VENTRICULAR RATE',
'median__LabValue__WHITE BLOOD CELL',
'min__LabValue__ALBUMIN, BLD',
'min__LabValue__ALK PHOSPHATASE, BLD',
'min__LabValue__ALT(SGPT)',
'min__LabValue__APTT',
'min__LabValue__AST (SGOT)',
'min__LabValue__ATRIAL RATE',
'min__LabValue__BILIRUBIN TOTAL',
'min__LabValue__CALCIUM, BLD',
'min__LabValue__CARBON DIOXIDE-BLD',
'min__LabValue__CHLORIDE-BLD',
'min__LabValue__CREATININE-SERUM',
'min__LabValue__GLUCOSE',
'min__LabValue__HEMATOCRIT',
'min__LabValue__HEMOGLOBIN',
'min__LabValue__INR',
'min__LabValue__LYMPHOCYTE #',
'min__LabValue__LYMPHOCYTE %',
'min__LabValue__MAGNESIUM-BLD',
'min__LabValue__MEAN CORP. HGB',
'min__LabValue__MEAN CORP. HGB CONC.',
'min__LabValue__MEAN CORP. VOLUME',
'min__LabValue__MEAN PLT VOLUME',
'min__LabValue__MONOCYTE #',
'min__LabValue__MONOCYTE %',
'min__LabValue__NEUTROPHIL #',
'min__LabValue__NEUTROPHIL %',
'min__LabValue__P AXIS',
'min__LabValue__P-R INTERVAL',
'min__LabValue__PLATELET',
'min__LabValue__POTASSIUMBLD',
'min__LabValue__PRO TIME',
'min__LabValue__PROTEIN TOTAL-BLD',
'min__LabValue__QRS DURATION',
'min__LabValue__QT',
'min__LabValue__QTC',
'min__LabValue__R AXIS',
'min__LabValue__RBC BLOOD CELL',
'min__LabValue__RED DISTRIB. WIDTH',
'min__LabValue__SODIUM-BLD',
'min__LabValue__T AXIS',
'min__LabValue__UREA NITROGEN-BLD',
'min__LabValue__VENTRICULAR RATE',
'min__LabValue__WHITE BLOOD CELL',
'medical_record_number'
]
# load Lab Values dataframe:
#get Lab Values Features for Timeseries Extraction:
df_path='Cohort/Feature_Extraction/Unsupervised_ALL_HF/LabValue_after_onset_HF_ALL_mmm_0_8_cleaned'
lab = pq.read_table(df_path).to_pandas()
lab=lab.drop(col_for_dropping,axis=1)
lab
further_col_drop=[]
for c in lab.columns:
if ('max' not in c) :
print(c)
further_col_drop.append(c)
further_col_drop
#create lab values dictionary
lab_renamed_column=rename_columns(lab,col_ignore)
lab_renamed_column
#get lab Values Features for Time series
'''structure for diagnosis time series feature:
conditions=(Diagnosis(context='ICD-10',
code='D64.9',
data_columns=['medical_record_number','description','age_in_days',
'context_name', 'context_diagnosis_code', 'numeric_value'])|)
'''
for n in lab_renamed_column.items():
parts=n[1].split('|')
lab_statement='LabValue(\''+str(parts[2].replace(' (max) ','')).strip()+'\')|'
#drug_statement='a'+n[1]
print(lab_statement)
#print(parts[3])
#Final Format for LabValues Copied from output above
conditions=(LabValue('Albumin, bld')|
LabValue('Alk phosphatase, bld')|
LabValue('Alt(sgpt)')|
LabValue('Aptt')|
LabValue('Ast (sgot)')|
LabValue('Atrial rate')|
LabValue('Basophil #')|
LabValue('Basophil %')|
LabValue('Bilirubin total')|
LabValue('Calcium, bld')|
LabValue('Carbon dioxide-bld')|
LabValue('Chloride-bld')|
LabValue('Creatinine-serum')|
LabValue('Eosinophil #')|
LabValue('Eosinophil %')|
LabValue('Glucose')|
LabValue('Hematocrit')|
LabValue('Hemoglobin')|
LabValue('Inr')|
LabValue('Lymphocyte #')|
LabValue('Lymphocyte %')|
LabValue('Magnesium-bld')|
LabValue('Mean corp. hgb')|
LabValue('Mean corp. hgb conc.')|
LabValue('Mean corp. volume')|
LabValue('Mean plt volume')|
LabValue('Monocyte #')|
LabValue('Monocyte %')|
LabValue('Neutrophil #')|
LabValue('Neutrophil %')|
LabValue('P axis')|
LabValue('P-r interval')|
LabValue('Platelet')|
LabValue('Potassiumbld')|
LabValue('Pro time')|
LabValue('Protein total-bld')|
LabValue('Qrs duration')|
LabValue('Qt')|
LabValue('Qtc')|
LabValue('R axis')|
LabValue('Rbc blood cell')|
LabValue('Red distrib. width')|
LabValue('Sodium-bld')|
LabValue('T axis')|
LabValue('Urea nitrogen-bld')|
LabValue('Ventricular rate')|
LabValue('White blood cell'))
# +
#conditions=(LabValue('White blood cell'))
# -
#extract the time series data
lab_time_series=cohort_EF_Baseline.time_series_for(
conditions
)
lab_time_series
for n in lab_time_series['test_name'].unique():
print(n)
lab_time_series.to_parquet('Cohort/Time_Series/LabValues_08.parquet')
# unique values and feature names:
t=lab_time_series['test_name'].unique()
for n in t :
print(n)
# # Snips
# +
import math
import os
import sys
import fiber
import numpy as np
import pandas as pd
import pyarrow.parquet as pq
# from fiber import fiber
from fiber.cohort import Cohort
from fiber.condition import (
Diagnosis,
Drug,
Encounter,
LabValue,
Measurement,
MRNs,
Patient,
Procedure,
TobaccoUse,
VitalSign,
)
from fiber.storage import yaml as fiberyaml
from fiber.utils import Timer
from fiberutils import cohort_utils
from typing import Optional
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import venn
from fiber import Cohort
from fiber.condition import MRNs
from fiber.config import OCCURRENCE_INDEX, VERBOSE
from fiber.dataframe import (
column_threshold_clip,
create_id_column,
merge_to_base,
time_window_clip
)
from fiber.plots.distributions import bars
from fiberutils.time_series_utils import ssr_transform
from fiber.condition import Patient, MRNs
from fiber.condition import Diagnosis
from fiber.condition import Measurement, Encounter, Drug, TobaccoUse,LabValue, VitalSign, Procedure
from fiber.storage import yaml as fiberyaml
#from fiberutils.cohort_utils import get_time_series, pivot_time_series
import pandas as pd
import pyarrow.parquet as pq
import numpy as np
import os
import matplotlib.pyplot as plt
from functools import reduce
import json
import math
import inspect
import json
import sys
from pydoc import locate
import requests
# -
#read dataframe
mrn_table = pq.read_table(
"Cohort/Feature_Extraction/ALL_HF_cohort_unsupervised_only_after_onset_HF_ALL_all_any_all_mean_small_cleaned.parquet").to_pandas()
mrn_table.reset_index(level=0, inplace=True)
mrn = mrn_table[["medical_record_number", "HF_Onset_age_in_days"]]
# mrn_cond = MRNs(mrns=(mrn))
# cohort = Cohort(mrn_cond)
mrn=mrn.head(10000)
mrn
|
Feature_Extraction/Time_Series/Extract_Time_Series_Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6.4 64-bit
# language: python
# name: python36464bitc2077ed07ea84d23aa5b518d224882ab
# ---
@nombre_decorador
def function():
print("1")
# + tags=[]
# defining a decorator
def hello_decorator(func):
def inner1():
print("Hello, this is before function execution")
func()
print("This is after function execution")
return inner1
# defining a function, to be called inside wrapper
def function_to_be_used():
print("This is inside the function !!")
# passing 'function_to_be_used' inside the
# decorator to control its behavior
function_to_be_used = hello_decorator(func=function_to_be_used)
# calling the function
function_to_be_used()
# -
5!
5*4*3*2*1
# #### One example
# + tags=[]
# importing libraries
import time
import math
def calculate_time(func):
def inner1(*args, **kwargs):
print("Anterior")
begin = time.time()
time.sleep(1)
func(*args, **kwargs)
end = time.time()
print("Total time", end - begin, " seconds")
return inner1
@calculate_time
def factorial(num):
#time.sleep(2)
print(math.factorial(num))
factorial(num=2)
# + tags=[]
@calculate_time
def x():
print("2")
x()
# + tags=[]
def ar(*args):
print(args)
ar(1,5,7,3,"g")
# + tags=[]
def kwar(**kwargs):
print(kwargs)
kwar(x=1, y=5, z=7, h=3, m="g")
# -
# #### One example
# +
def decorator(*args, **kwargs):
print("Inside decorator")
def inner(func):
print("Inside inner function")
print("I like", kwargs['like'])
return func
return inner
@decorator(like="geeksforgeeks")
def func():
print("Inside actual function")
func()
# + tags=[]
from functools import wraps
from datetime import datetime
import math
import time
def decorator_v2(timed):
def real_decorator(function):
@wraps(function)
def wrapper(*args, **kwargs):
if timed:
begin_2 = datetime.now()
print("begin_2:", begin_2)
retval = function(*args, **kwargs)
if timed:
end_2 = datetime.now()
print("end_2:", end_2)
print("--------------")
print("With datetime:")
print("Total datetime: ", end_2 - begin_2, " seconds")
return retval
return wrapper
return real_decorator
@decorator_v2(timed=True)
def fact(a):
return math.factorial(a)
fact(100000)
# + tags=[]
@decorator_v2(timed=True)
def fact(a):
time.sleep(2)
return math.factorial(a)
fact(6)
# +
from functools import wraps
from datetime import datetime
import math
import time
def nombre_decorador(*args, **kwargs):
def inner(function):
@wraps(function)
def wrapper(*a, **k):
# antes
retval = function(*a, **k)
# después
return retval
return wrapper
return inner
@nombre_decorador(timed=True)
def fact(a):
return math.factorial(a)
fact(a=1000)
# -
|
week8_ML_lr_knn_encoder/day1_ci-cd_decorators/theory/python/decorators.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Convolutional Neural Network Example
#
# Build a convolutional neural network with TensorFlow v2.
#
# This example is using a low-level approach to better understand all mechanics behind building convolutional neural networks and the training process.
#
# - Author: <NAME>
# - Project: https://github.com/aymericdamien/TensorFlow-Examples/
# ## CNN Overview
#
# 
#
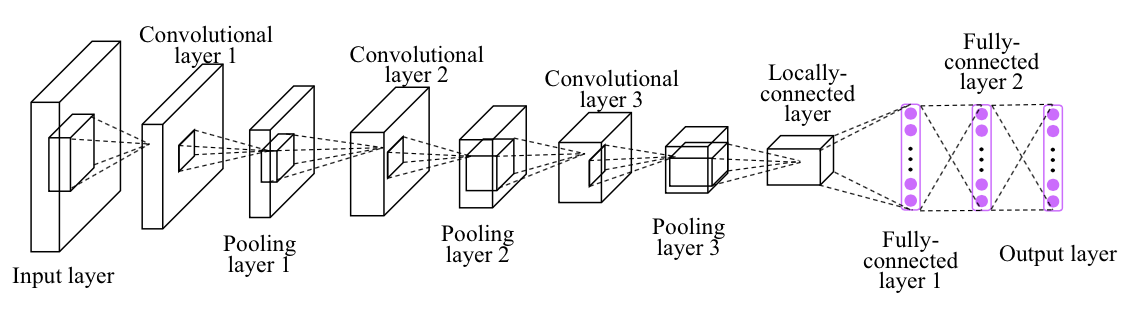
# ## MNIST Dataset Overview
#
# This example is using MNIST handwritten digits. The dataset contains 60,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 255.
#
# In this example, each image will be converted to float32 and normalized to [0, 1].
#
# 
#
# More info: http://yann.lecun.com/exdb/mnist/
# +
from __future__ import absolute_import, division, print_function
import tensorflow as tf
import numpy as np
# +
# MNIST dataset parameters.
num_classes = 10 # total classes (0-9 digits).
# Training parameters.
learning_rate = 0.001
training_steps = 200
batch_size = 128
display_step = 10
# Network parameters.
conv1_filters = 32 # number of filters for 1st conv layer.
conv2_filters = 64 # number of filters for 2nd conv layer.
fc1_units = 1024 # number of neurons for 1st fully-connected layer.
# -
# Prepare MNIST data.
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Convert to float32.
x_train, x_test = np.array(x_train, np.float32), np.array(x_test, np.float32)
# Normalize images value from [0, 255] to [0, 1].
x_train, x_test = x_train / 255., x_test / 255.
# Use tf.data API to shuffle and batch data.
train_data = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_data = train_data.repeat().shuffle(5000).batch(batch_size).prefetch(1)
# +
# Create some wrappers for simplicity.
def conv2d(x, W, b, strides=1):
# Conv2D wrapper, with bias and relu activation.
x = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='SAME')
x = tf.nn.bias_add(x, b)
return tf.nn.relu(x)
def maxpool2d(x, k=2):
# MaxPool2D wrapper.
return tf.nn.max_pool(x, ksize=[1, k, k, 1], strides=[1, k, k, 1], padding='SAME')
# +
# Store layers weight & bias
# A random value generator to initialize weights.
random_normal = tf.initializers.RandomNormal()
weights = {
# Conv Layer 1: 5x5 conv, 1 input, 32 filters (MNIST has 1 color channel only).
'wc1': tf.Variable(random_normal([5, 5, 1, conv1_filters])),
# Conv Layer 2: 5x5 conv, 32 inputs, 64 filters.
'wc2': tf.Variable(random_normal([5, 5, conv1_filters, conv2_filters])),
# FC Layer 1: 7*7*64 inputs, 1024 units.
'wd1': tf.Variable(random_normal([7*7*64, fc1_units])),
# FC Out Layer: 1024 inputs, 10 units (total number of classes)
'out': tf.Variable(random_normal([fc1_units, num_classes]))
}
biases = {
'bc1': tf.Variable(tf.zeros([conv1_filters])),
'bc2': tf.Variable(tf.zeros([conv2_filters])),
'bd1': tf.Variable(tf.zeros([fc1_units])),
'out': tf.Variable(tf.zeros([num_classes]))
}
# -
# Create model
def conv_net(x):
# Input shape: [-1, 28, 28, 1]. A batch of 28x28x1 (grayscale) images.
x = tf.reshape(x, [-1, 28, 28, 1])
# Convolution Layer. Output shape: [-1, 28, 28, 32].
conv1 = conv2d(x, weights['wc1'], biases['bc1'])
# Max Pooling (down-sampling). Output shape: [-1, 14, 14, 32].
conv1 = maxpool2d(conv1, k=2)
# Convolution Layer. Output shape: [-1, 14, 14, 64].
conv2 = conv2d(conv1, weights['wc2'], biases['bc2'])
# Max Pooling (down-sampling). Output shape: [-1, 7, 7, 64].
conv2 = maxpool2d(conv2, k=2)
# Reshape conv2 output to fit fully connected layer input, Output shape: [-1, 7*7*64].
fc1 = tf.reshape(conv2, [-1, weights['wd1'].get_shape().as_list()[0]])
# Fully connected layer, Output shape: [-1, 1024].
fc1 = tf.add(tf.matmul(fc1, weights['wd1']), biases['bd1'])
# Apply ReLU to fc1 output for non-linearity.
fc1 = tf.nn.relu(fc1)
# Fully connected layer, Output shape: [-1, 10].
out = tf.add(tf.matmul(fc1, weights['out']), biases['out'])
# Apply softmax to normalize the logits to a probability distribution.
return tf.nn.softmax(out)
# +
# Cross-Entropy loss function.
def cross_entropy(y_pred, y_true):
# Encode label to a one hot vector.
y_true = tf.one_hot(y_true, depth=num_classes)
# Clip prediction values to avoid log(0) error.
y_pred = tf.clip_by_value(y_pred, 1e-9, 1.)
# Compute cross-entropy.
return tf.reduce_mean(-tf.reduce_sum(y_true * tf.math.log(y_pred)))
# Accuracy metric.
def accuracy(y_pred, y_true):
# Predicted class is the index of highest score in prediction vector (i.e. argmax).
correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64))
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis=-1)
# ADAM optimizer.
optimizer = tf.optimizers.Adam(learning_rate)
# -
# Optimization process.
def run_optimization(x, y):
# Wrap computation inside a GradientTape for automatic differentiation.
with tf.GradientTape() as g:
pred = conv_net(x)
loss = cross_entropy(pred, y)
# Variables to update, i.e. trainable variables.
trainable_variables = list(weights.values()) + list(biases.values())
# Compute gradients.
gradients = g.gradient(loss, trainable_variables)
# Update W and b following gradients.
optimizer.apply_gradients(zip(gradients, trainable_variables))
# Run training for the given number of steps.
for step, (batch_x, batch_y) in enumerate(train_data.take(training_steps), 1):
# Run the optimization to update W and b values.
run_optimization(batch_x, batch_y)
if step % display_step == 0:
pred = conv_net(batch_x)
loss = cross_entropy(pred, batch_y)
acc = accuracy(pred, batch_y)
print("step: %i, loss: %f, accuracy: %f" % (step, loss, acc))
# Test model on validation set.
pred = conv_net(x_test)
print("Test Accuracy: %f" % accuracy(pred, y_test))
# Visualize predictions.
import matplotlib.pyplot as plt
# +
# Predict 5 images from validation set.
n_images = 5
test_images = x_test[:n_images]
predictions = conv_net(test_images)
# Display image and model prediction.
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction: %i" % np.argmax(predictions.numpy()[i]))
|
More-DL/pure_Tensorflow_2.0/tensorflow_v2/notebooks/3_NeuralNetworks/convolutional_network_raw.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## First Assignment
# #### 1) Apply the appropriate string methods to the **x** variable (as '.upper') to change it exactly to: "$Dichlorodiphenyltrichloroethane$".
import numpy as np
import pandas as pd
x = "DiClOrod IFeNi lTRicLOr oETaNo DiChlorod iPHeny lTrichL oroEThaNe"
print(x[34:-1].capitalize().replace(' ', ''))
# #### 2) Assign respectively the values: 'word', 15, 3.14 and 'list' to variables A, B, C and D in a single line of code. Then, print them in that same order on a single line separated by a space, using only one print statement.
A,B,C,D = 'word', 15, 3.14, 'list'
print(A,B,C,D)
# #### 3) Use the **input()** function to receive an input in the form **'68.4 1.71'**, that is, two floating point numbers in a line separated by space. Then, assign these numbers to the variables **w** and **h** respectively, which represent an individual's weight and height (hint: take a look at the '.split()' method). With this data, calculate the individual's Body Mass Index (BMI) from the following relationship:
#
# \begin{equation}
# BMI = \dfrac{weight}{height^2}
# \end{equation}
# +
w,h = input("Enter your weight and height").split(' ',-1)
print(f"Your weight is {w} your height is {h} ")
BMI = float(w)/(float(h)**2)
print('Your body mass index (BMI) is {}'.format(BMI))
# -
# #### This value can also be classified according to ranges of values, following to the table below. Use conditional structures to classify and print the classification assigned to the individual.
#
# <center><img src="https://healthtravelguide.com/wp-content/uploads/2020/06/Body-mass-index-table.png" width="30%"><\center>
#
#
# (source: https://healthtravelguide.com/bmi-calculator/)
if BMI < 18.5:
print('Underweight')
elif BMI >=18.5 and BMI <25.0:
print('Normal weight')
elif BMI >=25.0 and BMI <=29.9:
print('Pre-obesity')
elif BMI > 29.9:
print('Obese')
else:
print(f'BMI {BMI} not valid')
# #### 4) Receive an integer as an input and, using a loop, calculate the factorial of this number, that is, the product of all the integers from one to the number provided.
number = int(input("Write an integer: "))
fac = 1
n=1
while n <= number:
fac = fac * n
n=n+1
print(fac)
#alternative
number = int(input("Write an integer: "))
fac = 1
for n in range(1,number+1):
fac =fac * n #das gleiche wie 'fac *= n'
print(fac)
# #### 5) Using a while loop and the input function, read an indefinite number of integers until the number read is -1. Present the sum of all these numbers in the form of a print, excluding the -1 read at the end.
n=0
summe=0
while n != -1:
n = int(input("Write a number: "))
summe = n + summe
summe+=1
print(summe)
# #### 6) Read the **first name** of an employee, his **amount of hours worked** and the **salary per hour** in a single line separated by commas. Next, calculate the **total salary** for this employee and show it to two decimal places.
name,hours,salary_hour=input('Write your name, whole hours worked and salary per hour, separated by ","').split(',')
total_salary = int(hours) * float(salary_hour)
print(f"{name}'s total salary with {int(hours)} hours is {total_salary:.2f} Euros")
# #### 7) Read three floating point values **A**, **B** and **C** respectively. Then calculate itens a, b, c, d and e:
A,B,C = input('Enter A,B,C: ').split(',')
A=float(A)
B=float(B)
C=float(C)
# a) the area of the triangle rectangle with A as the base and C as the height.
area_triangle = 1/2 * A * C
print(area_triangle)
# b) the area of the circle of radius C. (pi = 3.14159)
area_circle = C**2 * np.pi
print(area_circle)
# c) the area of the trapezoid that has A and B for bases and C for height.
area_trapezoid = (A+B)/2 * C
print(area_trapezoid)
# d) the area of the square that has side B.
area_square = B**2
print(area_square)
# e) the area of the rectangle that has sides A and B.
area_rectangle = A * B
print(area_rectangle)
# #### 8) Read **the values a, b and c** and calculate the **roots of the second degree equation** $ax^{2}+bx+c=0$ using [this formula](https://en.wikipedia.org/wiki/Quadratic_equation). If it is not possible to calculate the roots, display the message **âThere are no real rootsâ**.
def quad_roots(a,b,c):
N1=0
N2=0
w=b**2-4*a*c
if w>=0:
N1=(-b+np.sqrt(w))/(2*a)
N2=(-b-np.sqrt(w))/(2*a)
print(f"Roots are {N1} and {N2}")
roots=True
else:
print("There are no real roots.")
roots=False
return N1,N2,roots
a,b,c = input('Enter a,b,c: ').split(',')
a=float(a);b=float(b);c=float(c)
quad_roots(a,b,c)
# #### 9) Read four floating point numerical values corresponding to the coordinates of two geographical coordinates in the cartesian plane. Each point will come in a line with its coordinates separated by space. Then calculate and show the distance between these two points.
#
# (obs: $d=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$)
point_1 = input('Enter the coordinates of point 1 x y: ').split(' ')
x1 = float(point_1[0])
y1 = float(point_1[1])
point_2 = input('Enter the coordinates of point 2 x y: ').split(' ')
x2 = float(point_2[0])
y2 = float(point_2[1])
d = np.sqrt((x2-x1)**2+(y2-y1)**2)
print(f'The distance is {d:.2f}')
# #### 10) Read **two floating point numbers** on a line that represent **coordinates of a cartesian point**. With this, use **conditional structures** to determine if you are at the origin, printing the message **'origin'**; in one of the axes, printing **'x axis'** or **'y axis'**; or in one of the four quadrants, printing **'q1'**, **'q2**', **'q3'** or **'q4'**.
# +
def read_node():
point = input('Enter the coordinates of point x y: ').split(' ')
x = float(point[0])
y = float(point[1])
return x,y
def check_location(x,y):
if x==0 and y==0:
loc='Origin'
elif x==0 and y!=0:
loc='y axis'
elif x!=0 and y==0:
loc='x axis'
elif x>0 and y>0:
loc='q1'
elif x<0 and y>0:
loc='q2'
elif x<0 and y<0:
loc='q3'
elif x>0 and y<0:
loc='q4'
return loc
# -
x,y = read_node()
loc=check_location(x,y)
print(loc)
# #### 11) Read an integer that represents a phone code for international dialing.
# #### Then, inform to which country the code belongs to, considering the generated table below:
# (You just need to consider the first 10 entries)
import pandas as pd
df = pd.read_html('https://en.wikipedia.org/wiki/Telephone_numbers_in_Europe')[1]
df = df.iloc[:,:2]
df.head(20)
code=int(input('Enter an integer: '))
country=df[df["Country calling code"]==str(code)]["Country"].item()
print(country)
# #### 12) Write a piece of code that reads 6 numbers in a row. Next, show the number of positive values entered. On the next line, print the average of the values to one decimal place.
a = input("Write 6 numbers: ").split(',')
positive=0
summe=0
for number in a:
if int(number)>0:
positive=positive+1
summe=summe+int(number)
print(f'The count of positive numbers is {positive}')
average=summe/positive
print(round(average,1))
# #### 13) Read an integer **N**. Then print the **square of each of the even values**, from 1 to N, including N, if applicable, arranged one per line.
N = input('Write a number: ')
for x in range(1,int(N)+1):
if x %2==0:
x=x**2
print(x)
# #### 14) Using **input()**, read an integer and print its classification as **'even / odd'** and **'positive / negative'** . The two classes for the number must be printed on the same line separated by a space. In the case of zero, print only **'null'**.
L = int(input('Write a number: '))
if L==0:
print('null')
else:
if L %2==0:
print('even')
else:
print('odd')
#------
if L<0:
print('negative')
else:
print('positive')
# ## Challenge
# #### 15) Ordering problems are recurrent in the history of programming. Over time, several algorithms have been developed to fulfill this function. The simplest of these algorithms is the [**Bubble Sort**](https://en.wikipedia.org/wiki/Bubble_sort), which is based on comparisons of elements two by two in a loop of passes through the elements. Your mission, if you decide to accept it, will be to input six whole numbers ramdonly ordered. Then implement the **Bubble Sort** principle to order these six numbers **using only loops and conditionals**.
# #### At the end, print the six numbers in ascending order on a single line separated by spaces.
liste=input('Write six whole numbers: ').split(',')
test=1
while test>0:
test=0
for i in range(len(liste)-1):
a=int(liste[i])
b=int(liste[i+1])
if a>b:
liste[i]=b
liste[i+1]=a
test=test+1
print(liste)
|
Assignments/Assignment_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Let's kill off `Runner`
# +
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# -
#export
from exp.nb_09 import *
AvgStats
# ## Imagenette data
path = datasets.untar_data(datasets.URLs.IMAGENETTE_160)
# +
tfms = [make_rgb, ResizeFixed(128), to_byte_tensor, to_float_tensor]
bs=64
il = ImageList.from_files(path, tfms=tfms)
sd = SplitData.split_by_func(il, partial(grandparent_splitter, valid_name='val'))
ll = label_by_func(sd, parent_labeler, proc_y=CategoryProcessor())
data = ll.to_databunch(bs, c_in=3, c_out=10, num_workers=4)
# -
cbfs = [partial(AvgStatsCallback,accuracy),
CudaCallback,
partial(BatchTransformXCallback, norm_imagenette)]
nfs = [32]*4
# Having a Runner is great but not essential when the `Learner` already has everything needed in its state. We implement everything inside it directly instead of building a second object.
# +
#export
def param_getter(m): return m.parameters()
class Learner():
def __init__(self, model, data, loss_func, opt_func=sgd_opt, lr=1e-2, splitter=param_getter,
cbs=None, cb_funcs=None):
self.model,self.data,self.loss_func,self.opt_func,self.lr,self.splitter = model,data,loss_func,opt_func,lr,splitter
self.in_train,self.logger,self.opt = False,print,None
# NB: Things marked "NEW" are covered in lesson 12
# NEW: avoid need for set_runner
self.cbs = []
self.add_cb(TrainEvalCallback())
self.add_cbs(cbs)
self.add_cbs(cbf() for cbf in listify(cb_funcs))
def add_cbs(self, cbs):
for cb in listify(cbs): self.add_cb(cb)
def add_cb(self, cb):
cb.set_runner(self)
setattr(self, cb.name, cb)
self.cbs.append(cb)
def remove_cbs(self, cbs):
for cb in listify(cbs): self.cbs.remove(cb)
def one_batch(self, i, xb, yb):
try:
self.iter = i
self.xb,self.yb = xb,yb; self('begin_batch')
self.pred = self.model(self.xb); self('after_pred')
self.loss = self.loss_func(self.pred, self.yb); self('after_loss')
if not self.in_train: return
self.loss.backward(); self('after_backward')
self.opt.step(); self('after_step')
self.opt.zero_grad()
except CancelBatchException: self('after_cancel_batch')
finally: self('after_batch')
def all_batches(self):
self.iters = len(self.dl)
try:
for i,(xb,yb) in enumerate(self.dl): self.one_batch(i, xb, yb)
except CancelEpochException: self('after_cancel_epoch')
def do_begin_fit(self, epochs):
self.epochs,self.loss = epochs,tensor(0.)
self('begin_fit')
def do_begin_epoch(self, epoch):
self.epoch,self.dl = epoch,self.data.train_dl
return self('begin_epoch')
def fit(self, epochs, cbs=None, reset_opt=False):
# NEW: pass callbacks to fit() and have them removed when done
self.add_cbs(cbs)
# NEW: create optimizer on fit(), optionally replacing existing
if reset_opt or not self.opt: self.opt = self.opt_func(self.splitter(self.model), lr=self.lr)
try:
self.do_begin_fit(epochs)
for epoch in range(epochs):
self.do_begin_epoch(epoch)
if not self('begin_epoch'): self.all_batches()
with torch.no_grad():
self.dl = self.data.valid_dl
if not self('begin_validate'): self.all_batches()
self('after_epoch')
except CancelTrainException: self('after_cancel_train')
finally:
self('after_fit')
self.remove_cbs(cbs)
ALL_CBS = {'begin_batch', 'after_pred', 'after_loss', 'after_backward', 'after_step',
'after_cancel_batch', 'after_batch', 'after_cancel_epoch', 'begin_fit',
'begin_epoch', 'begin_epoch', 'begin_validate', 'after_epoch',
'after_cancel_train', 'after_fit'}
def __call__(self, cb_name):
res = False
assert cb_name in self.ALL_CBS
for cb in sorted(self.cbs, key=lambda x: x._order): res = cb(cb_name) and res
return res
# -
#export
class AvgStatsCallback(Callback):
def __init__(self, metrics):
self.train_stats,self.valid_stats = AvgStats(metrics,True),AvgStats(metrics,False)
def begin_epoch(self):
self.train_stats.reset()
self.valid_stats.reset()
def after_loss(self):
stats = self.train_stats if self.in_train else self.valid_stats
with torch.no_grad(): stats.accumulate(self.run)
def after_epoch(self):
#We use the logger function of the `Learner` here, it can be customized to write in a file or in a progress bar
self.logger(self.train_stats)
self.logger(self.valid_stats)
cbfs = [partial(AvgStatsCallback,accuracy),
CudaCallback,
partial(BatchTransformXCallback, norm_imagenette)]
#export
def get_learner(nfs, data, lr, layer, loss_func=F.cross_entropy,
cb_funcs=None, opt_func=sgd_opt, **kwargs):
model = get_cnn_model(data, nfs, layer, **kwargs)
init_cnn(model)
return Learner(model, data, loss_func, lr=lr, cb_funcs=cb_funcs, opt_func=opt_func)
learn = get_learner(nfs, data, 0.4, conv_layer, cb_funcs=cbfs)
# %time learn.fit(1)
# ## Check everything works
# Let's check our previous callbacks still work.
cbfs += [Recorder]
learn = get_learner(nfs, data, 0.4, conv_layer, cb_funcs=cbfs)
phases = combine_scheds([0.3, 0.7], cos_1cycle_anneal(0.2, 0.6, 0.2))
sched = ParamScheduler('lr', phases)
learn.fit(1, sched)
learn.recorder.plot_lr()
learn.recorder.plot_loss()
# ## Export
# !./notebook2script.py 09b_learner.ipynb
|
nbs/dl2/09b_learner.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="../../../img/logo-bdc.png" align="right" width="64"/>
#
# # <span style="color:#336699">Web Time Series Service (WTSS) - Examples</span>
# <hr style="border:2px solid #0077b9;">
#
# <div style="text-align: left;">
# <a href="https://nbviewer.jupyter.org/github/brazil-data-cube/code-gallery/blob/master/jupyter/Python/wtss/wtss-examples.ipynb"><img src="https://raw.githubusercontent.com/jupyter/design/master/logos/Badges/nbviewer_badge.svg" align="center"/></a>
# </div>
#
# <br/>
#
# <div style="text-align: center;font-size: 90%;">
# <NAME><sup><a href="https://orcid.org/0000-0002-0082-9498"><i class="fab fa-lg fa-orcid" style="color: #a6ce39"></i></a></sup>, <NAME><sup><a href="https://orcid.org/0000-0001-6181-2158"><i class="fab fa-lg fa-orcid" style="color: #a6ce39"></i></a></sup>, <NAME><sup><a href="https://orcid.org/0000-0001-7534-0219"><i class="fab fa-lg fa-orcid" style="color: #a6ce39"></i></a></sup>
# <br/><br/>
# Earth Observation and Geoinformatics Division, National Institute for Space Research (INPE)
# <br/>
# Avenida dos Astronautas, 1758, Jardim da Granja, São José dos Campos, SP 12227-010, Brazil
# <br/><br/>
# Contact: <a href="mailto:<EMAIL>"><EMAIL></a>
# <br/><br/>
# Last Update: March 12, 2021
# </div>
#
# <br/>
#
# <div style="text-align: justify; margin-left: 25%; margin-right: 25%;">
# <b>Abstract.</b> This Jupyter Notebook gives shows how to use the WTSS service to extract time series from <em>Brazil Data Cube</em>' service and how to perform a basic time series manipulation.
# </div>
#
# <br/>
# <div style="text-align: justify; margin-left: 25%; margin-right: 25%;font-size: 75%; border-style: solid; border-color: #0077b9; border-width: 1px; padding: 5px;">
# <b>This Jupyter Notebook is a supplement to the following paper:</b>
# <div style="margin-left: 10px; margin-right: 10px">
# <NAME>.; <NAME>.; <NAME>. <a href="http://www.seer.ufu.br/index.php/revistabrasileiracartografia/article/view/44004" target="_blank">Web Services for Big Earth Observation Data</a>. Revista Brasileira de Cartografia, v. 69, n. 5, 18 maio 2017.
# </div>
# </div>
# # Python Client API
# <hr style="border:1px solid #0077b9;">
# If you haven't installed the [WTSS client for Python](https://github.com/brazil-data-cube/wtss.py), install it with `pip`:
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
# #!pip install wtss[matplotlib]
# -
# For more information on [WTSS client for Python](https://github.com/brazil-data-cube/wtss.py), see the introductory Jupyter Notebook about [Web Time Series Service (WTSS)](./wtss-introduction.ipynb) Introduction notebook.
# # Set the service and Search for time series
# <hr style="border:1px solid #0077b9;">
# Import the WTSS client library:
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
from wtss import WTSS
# -
# Define the service to be used:
service = WTSS('https://brazildatacube.dpi.inpe.br/', access_token='<PASSWORD>')
service.coverages
# Let's access the CBERS-4/AWFI coverage using the `CB4_64_16D_STK-1` product:
cbers4_coverage = service['CB4_64_16D_STK-1']
cbers4_coverage
# CBERS-4/AWFI spectral bands 15 and 16 correspond to the red and near-infrared (NIR) wavelength regions, respectivelly:
red_band = 'BAND15'
nir_band = 'BAND16'
# Let's retrieve the time series for data product `CB4_64_16D_STK-1`, in the location of `latitude -16.817` and `longitude -52.079` from January 1st, 2017 to December 31st, 2019, using the `ts` method:
time_series = cbers4_coverage.ts(attributes=(red_band, nir_band),
latitude=-16.817, longitude=-52.079,
start_date="2017-01-01", end_date="2019-12-31")
# # Plot the Time Series
# <hr style="border:1px solid #0077b9;">
time_series.plot()
# # Scatter Plot
# <hr style="border:1px solid #0077b9;">
# Let's see the time series values:
print(time_series.values(red_band))
print()
print(time_series.values(nir_band))
# Performing a scatterplot between `red` and `NIR` Time Series we can see the correlation of theese bands through the time for the selected pixel:
import matplotlib.pyplot as plt
plt.scatter(time_series.values(red_band), time_series.values(nir_band), alpha=0.5)
plt.title('Scatter plot')
plt.xlabel('Red')
plt.ylabel('NIR')
plt.show()
# Time series of spatially-close points are likely to be similar. We can verify this by comparing our first time series to a time series extracted from `latitude -16.819` and `longitude -52.079` (also ranging from January 1st, 2017 to December 31st, 2019):
time_series2 = cbers4_coverage.ts(attributes=(red_band, nir_band),
latitude=-16.819, longitude=-52.079,
start_date="2017-01-01", end_date="2019-12-31")
plt.scatter(time_series.values(nir_band), time_series2.values(nir_band), alpha=0.5)
ident = [0.0, max(time_series.values(nir_band))] # Reference Line
plt.plot(ident,ident, color='red', ls='--')
plt.title('Scatter plot')
plt.xlabel('NIR TS1')
plt.ylabel('NIR TS2')
plt.show()
# If all points were positioned on the red line, the time series would be equal. However, since they are similar, the points are located close to the red line, meaning they present close values.
# # Calculate Median Time Series
# <hr style="border:1px solid #0077b9;">
# Another application would be: given a set of Time Series we may want to extract the median time series, which normally is the one with less noise.
#
# Let's start by acquiring a few time series from an agricultural region, in this case a fixed `longitude -53.989` but a variable `latitude` ranging from `-16.905` until `-16.955` by a rate of `-0.01`, considering images from January 1st, 2017 to December 31st, 2019.
import numpy
agriculture_time_series = []
for latitude in numpy.arange(-16.905,-16.955,-0.01):
time_series = cbers4_coverage.ts(attributes=(nir_band),
latitude=float(latitude), longitude=-53.989,
start_date="2017-01-01", end_date="2019-12-31")
agriculture_time_series.append(time_series.values(nir_band))
# This loop provides a total of five time series:
len(agriculture_time_series)
# The `Numpy` library provides the `median()` method, which calculates the median value of an array, and since we want to obtain the median value among the different time series, we can use the parameter `axis=0`:
median = numpy.median(agriculture_time_series, axis=0)
median
# Now let's plot the original time series, in `grey` and the median time series, in `blue`:
for i in range(len(agriculture_time_series)):
plt.plot(agriculture_time_series[i], color='grey', alpha=0.5)
plt.plot(median, color='blue', linewidth=2)
plt.show()
# We can visually note that the `blue` time series is centered in comparison to the `grey` ones.
# # Time Series Smoothing
# <hr style="border:1px solid #0077b9;">
# Smoothing Algorithms are helpful to reduce time series noise, one of the most used smoothing algorithm is <NAME>, which has an implementation on the `scipy` library:
from scipy.signal import savgol_filter
median_smoothed = savgol_filter(median, window_length = 9, polyorder = 2)
# <div style="text-align: center; margin-left: 25%; margin-right: 25%; border-style: solid; border-color: #0077b9; border-width: 1px; padding: 5px;">
# <b>Note:</b> The <em>Savitz Golay</em> algorithm uses a window_length and a polynomial order as parameters. You can change these values to see the impacts on the smoothed time series.
# </div>
# Now let's see the difference between the original time series and the smoothed one:
plt.plot(median, color='blue')
plt.plot(median_smoothed, color='red')
plt.show()
# We can observe that the smoothed time series (red) has less spikes than the original one (blue).
# # References
# <hr style="border:1px solid #0077b9;">
#
# - [Python Client Library for Web Time Series Service - User Guide](https://wtss.readthedocs.io/en/latest/index.html)
#
#
# - [Python Client Library for Web Time Series Service - GitHub Repository](https://github.com/brazil-data-cube/wtss.py)
#
#
# - [WTSS OpenAPI 3 Specification](https://github.com/brazil-data-cube/wtss-spec)
#
#
# - <NAME>.; <NAME>.; <NAME>.; <NAME>. [Web Services for Big Earth Observation Data](http://www.seer.ufu.br/index.php/revistabrasileiracartografia/article/view/44004). Revista Brasileira de Cartografia, v. 69, n. 5, 18 maio 2017.
# # See also the following Jupyter Notebooks
# <hr style="border:1px solid #0077b9;">
#
# * [Introduction to the Web Time Series Service (WTSS)](./wtss-introduction.ipynb)
|
jupyter/Python/wtss/wtss-examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# Copyright (c) Microsoft Corporation. All rights reserved.
# Licensed under the MIT License.
# # Azure Machine Learning Pipelines: Getting Started
#
# ## Overview
#
# Read [Azure Machine Learning Pipelines](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-ml-pipelines) overview, or the [readme article](../README.md) on Azure Machine Learning Pipelines to get more information.
#
#
# This Notebook shows basic construction of a **pipeline** that runs jobs unattended in different compute clusters.
# ## Prerequisites and Azure Machine Learning Basics
# Make sure you go through the configuration Notebook located at https://github.com/Azure/MachineLearningNotebooks first if you haven't. This sets you up with a working config file that has information on your workspace, subscription id, etc.
#
# ### Azure Machine Learning Imports
#
# In this first code cell, we import key Azure Machine Learning modules that we will use below.
# +
import azureml.core
from azureml.core import Workspace, Experiment, Datastore
from azureml.core.compute import AmlCompute
from azureml.core.compute import ComputeTarget
from azureml.widgets import RunDetails
# Check core SDK version number
print("SDK version:", azureml.core.VERSION)
# -
# ### Pipeline-specific SDK imports
#
# Here, we import key pipeline modules, whose use will be illustrated in the examples below.
# +
from azureml.pipeline.core import Pipeline
from azureml.pipeline.steps import PythonScriptStep
print("Pipeline SDK-specific imports completed")
# -
# ### Initialize Workspace
#
# Initialize a [workspace](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.workspace(class%29) object from persisted configuration.
# + tags=["create workspace"]
ws = Workspace.from_config()
print(ws.name, ws.resource_group, ws.location, ws.subscription_id, sep = '\n')
# Default datastore (Azure file storage)
def_file_store = ws.get_default_datastore()
# The above call is equivalent to Datastore(ws, "workspacefilestore") or simply Datastore(ws)
print("Default datastore's name: {}".format(def_file_store.name))
# Blob storage associated with the workspace
# The following call GETS the Azure Blob Store associated with your workspace.
# Note that workspaceblobstore is **the name of this store and CANNOT BE CHANGED and must be used as is**
def_blob_store = Datastore(ws, "workspaceblobstore")
print("Blobstore's name: {}".format(def_blob_store.name))
# +
# project folder
project_folder = '.'
print('Sample projects will be created in {}.'.format(project_folder))
# -
# ### Required data and script files for the the tutorial
# Sample files required to finish this tutorial are already copied to the project folder specified above. Even though the .py provided in the samples don't have much "ML work," as a data scientist, you will work on this extensively as part of your work. To complete this tutorial, the contents of these files are not very important. The one-line files are for demostration purpose only.
# ### Datastore concepts
# A [Datastore](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.datastore(class) is a place where data can be stored that is then made accessible to a compute either by means of mounting or copying the data to the compute target.
#
# A Datastore can either be backed by an Azure File Storage (default) or by an Azure Blob Storage.
#
# In this next step, we will upload the training and test set into the workspace's default storage (File storage), and another piece of data to Azure Blob Storage. When to use [Azure Blobs](https://docs.microsoft.com/en-us/azure/storage/blobs/storage-blobs-introduction), [Azure Files](https://docs.microsoft.com/en-us/azure/storage/files/storage-files-introduction), or [Azure Disks](https://docs.microsoft.com/en-us/azure/virtual-machines/linux/managed-disks-overview) is [detailed here](https://docs.microsoft.com/en-us/azure/storage/common/storage-decide-blobs-files-disks).
#
# **Please take good note of the concept of the datastore.**
# #### Upload data to default datastore
# Default datastore on workspace is the Azure File storage. The workspace has a Blob storage associated with it as well. Let's upload a file to each of these storages.
# +
# get_default_datastore() gets the default Azure File Store associated with your workspace.
# Here we are reusing the def_file_store object we obtained earlier
# target_path is the directory at the destination
def_file_store.upload_files(['./20news.pkl'],
target_path = '20newsgroups',
overwrite = True,
show_progress = True)
# Here we are reusing the def_blob_store we created earlier
def_blob_store.upload_files(["./20news.pkl"], target_path="20newsgroups", overwrite=True)
print("Upload calls completed")
# -
# #### (Optional) See your files using Azure Portal
# Once you successfully uploaded the files, you can browse to them (or upload more files) using [Azure Portal](https://portal.azure.com). At the portal, make sure you have selected **AzureML Nursery** as your subscription (click *Resource Groups* and then select the subscription). Then look for your **Machine Learning Workspace** (it has your *alias* as the name). It has a link to your storage. Click on the storage link. It will take you to a page where you can see [Blobs](https://docs.microsoft.com/en-us/azure/storage/blobs/storage-blobs-introduction), [Files](https://docs.microsoft.com/en-us/azure/storage/files/storage-files-introduction), [Tables](https://docs.microsoft.com/en-us/azure/storage/tables/table-storage-overview), and [Queues](https://docs.microsoft.com/en-us/azure/storage/queues/storage-queues-introduction). We have just uploaded a file to the Blob storage and another one to the File storage. You should be able to see both of these files in their respective locations.
# ### Compute Targets
# A compute target specifies where to execute your program such as a remote Docker on a VM, or a cluster. A compute target needs to be addressable and accessible by you.
#
# **You need at least one compute target to send your payload to. We are planning to use Azure Machine Learning Compute exclusively for this tutorial for all steps. However in some cases you may require multiple compute targets as some steps may run in one compute target like Azure Machine Learning Compute, and some other steps in the same pipeline could run in a different compute target.**
#
# *The example belows show creating/retrieving/attaching to an Azure Machine Learning Compute instance.*
# #### List of Compute Targets on the workspace
cts = ws.compute_targets
for ct in cts:
print(ct)
# #### Retrieve or create a Azure Machine Learning compute
# Azure Machine Learning Compute is a service for provisioning and managing clusters of Azure virtual machines for running machine learning workloads. Let's create a new Azure Machine Learning Compute in the current workspace, if it doesn't already exist. We will then run the training script on this compute target.
#
# If we could not find the compute with the given name in the previous cell, then we will create a new compute here. We will create an Azure Machine Learning Compute containing **STANDARD_D2_V2 CPU VMs**. This process is broken down into the following steps:
#
# 1. Create the configuration
# 2. Create the Azure Machine Learning compute
#
# **This process will take about 3 minutes and is providing only sparse output in the process. Please make sure to wait until the call returns before moving to the next cell.**
# +
from azureml.core.compute_target import ComputeTargetException
aml_compute_target = "aml-compute"
try:
aml_compute = AmlCompute(ws, aml_compute_target)
print("found existing compute target.")
except ComputeTargetException:
print("creating new compute target")
provisioning_config = AmlCompute.provisioning_configuration(vm_size = "STANDARD_D2_V2",
min_nodes = 1,
max_nodes = 4)
aml_compute = ComputeTarget.create(ws, aml_compute_target, provisioning_config)
aml_compute.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
print("Azure Machine Learning Compute attached")
# +
# For a more detailed view of current Azure Machine Learning Compute status, use get_status()
# example: un-comment the following line.
# print(aml_compute.get_status().serialize())
# -
# **Wait for this call to finish before proceeding (you will see the asterisk turning to a number).**
#
# Now that you have created the compute target, let's see what the workspace's compute_targets() function returns. You should now see one entry named 'amlcompute' of type AmlCompute.
# **Now that we have completed learning the basics of Azure Machine Learning (AML), let's go ahead and start understanding the Pipeline concepts.**
# ## Creating a Step in a Pipeline
# A Step is a unit of execution. Step typically needs a target of execution (compute target), a script to execute, and may require script arguments and inputs, and can produce outputs. The step also could take a number of other parameters. Azure Machine Learning Pipelines provides the following built-in Steps:
#
# - [**PythonScriptStep**](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-steps/azureml.pipeline.steps.python_script_step.pythonscriptstep?view=azure-ml-py): Add a step to run a Python script in a Pipeline.
# - [**AdlaStep**](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-steps/azureml.pipeline.steps.adla_step.adlastep?view=azure-ml-py): Adds a step to run U-SQL script using Azure Data Lake Analytics.
# - [**DataTransferStep**](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-steps/azureml.pipeline.steps.data_transfer_step.datatransferstep?view=azure-ml-py): Transfers data between Azure Blob and Data Lake accounts.
# - [**DatabricksStep**](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-steps/azureml.pipeline.steps.databricks_step.databricksstep?view=azure-ml-py): Adds a DataBricks notebook as a step in a Pipeline.
# - [**HyperDriveStep**](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-steps/azureml.pipeline.steps.hyper_drive_step.hyperdrivestep?view=azure-ml-py): Creates a Hyper Drive step for Hyper Parameter Tuning in a Pipeline.
#
# The following code will create a PythonScriptStep to be executed in the Azure Machine Learning Compute we created above using train.py, one of the files already made available in the project folder.
#
# A **PythonScriptStep** is a basic, built-in step to run a Python Script on a compute target. It takes a script name and optionally other parameters like arguments for the script, compute target, inputs and outputs. If no compute target is specified, default compute target for the workspace is used.
# +
# Uses default values for PythonScriptStep construct.
# Syntax
# PythonScriptStep(
# script_name,
# name=None,
# arguments=None,
# compute_target=None,
# runconfig=None,
# inputs=None,
# outputs=None,
# params=None,
# source_directory=None,
# allow_reuse=True,
# version=None,
# hash_paths=None)
# This returns a Step
step1 = PythonScriptStep(name="train_step",
script_name="train.py",
compute_target=aml_compute,
source_directory=project_folder,
allow_reuse=False)
print("Step1 created")
# -
# **Note:** In the above call to PythonScriptStep(), the flag *allow_reuse* determines whether the step should reuse previous results when run with the same settings/inputs. This flag's default value is *True*; the default is set to *True* because, when inputs and parameters have not changed, we typically do not want to re-run a given pipeline step.
#
# If *allow_reuse* is set to *False*, a new run will always be generated for this step during pipeline execution. The *allow_reuse* flag can come in handy in situations where you do *not* want to re-run a pipeline step.
# ## Running a few steps in parallel
# Here we are looking at a simple scenario where we are running a few steps (all involving PythonScriptStep) in parallel. Running nodes in **parallel** is the default behavior for steps in a pipeline.
#
# We already have one step defined earlier. Let's define few more steps.
# +
# All steps use files already available in the project_folder
# All steps use the same Azure Machine Learning compute target as well
step2 = PythonScriptStep(name="compare_step",
script_name="compare.py",
compute_target=aml_compute,
source_directory=project_folder)
step3 = PythonScriptStep(name="extract_step",
script_name="extract.py",
compute_target=aml_compute,
source_directory=project_folder)
# list of steps to run
steps = [step1, step2, step3]
print("Step lists created")
# -
# ### Build the pipeline
# Once we have the steps (or steps collection), we can build the [pipeline](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-core/azureml.pipeline.core.pipeline.pipeline?view=azure-ml-py). By deafult, all these steps will run in **parallel** once we submit the pipeline for run.
#
# A pipeline is created with a list of steps and a workspace. Submit a pipeline using [submit](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.experiment%28class%29?view=azure-ml-py#submit). When submit is called, a [PipelineRun](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-core/azureml.pipeline.core.pipelinerun?view=azure-ml-py) is created which in turn creates [StepRun](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-core/azureml.pipeline.core.steprun?view=azure-ml-py) objects for each step in the workflow.
# +
# Syntax
# Pipeline(workspace,
# steps,
# description=None,
# default_datastore_name=None,
# default_source_directory=None,
# resolve_closure=True,
# _workflow_provider=None,
# _service_endpoint=None)
pipeline1 = Pipeline(workspace=ws, steps=steps)
print ("Pipeline is built")
# -
# ### Validate the pipeline
# You have the option to [validate](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-core/azureml.pipeline.core.pipeline.pipeline?view=azure-ml-py#validate) the pipeline prior to submitting for run. The platform runs validation steps such as checking for circular dependencies and parameter checks etc. even if you do not explicitly call validate method.
pipeline1.validate()
print("Pipeline validation complete")
# ### Submit the pipeline
# [Submitting](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-core/azureml.pipeline.core.pipeline.pipeline?view=azure-ml-py#submit) the pipeline involves creating an [Experiment](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.experiment?view=azure-ml-py) object and providing the built pipeline for submission.
# +
# Submit syntax
# submit(experiment_name,
# pipeline_parameters=None,
# continue_on_node_failure=False,
# regenerate_outputs=False)
pipeline_run1 = Experiment(ws, 'Hello_World1').submit(pipeline1, regenerate_outputs=True)
print("Pipeline is submitted for execution")
# -
# **Note:** If regenerate_outputs is set to True, a new submit will always force generation of all step outputs, and disallow data reuse for any step of this run. Once this run is complete, however, subsequent runs may reuse the results of this run.
#
# ### Examine the pipeline run
#
# #### Use RunDetails Widget
# We are going to use the RunDetails widget to examine the run of the pipeline. You can click each row below to get more details on the step runs.
RunDetails(pipeline_run1).show()
# #### Use Pipeline SDK objects
# You can cycle through the node_run objects and examine job logs, stdout, and stderr of each of the steps.
step_runs = pipeline_run1.get_children()
for step_run in step_runs:
status = step_run.get_status()
print('Script:', step_run.name, 'status:', status)
# Change this if you want to see details even if the Step has succeeded.
if status == "Failed":
joblog = step_run.get_job_log()
print('job log:', joblog)
# #### Get additonal run details
# If you wait until the pipeline_run is finished, you may be able to get additional details on the run. **Since this is a blocking call, the following code is commented out.**
# +
#pipeline_run1.wait_for_completion()
#for step_run in pipeline_run1.get_children():
# print("{}: {}".format(step_run.name, step_run.get_metrics()))
# -
# ## Running a few steps in sequence
# Now let's see how we run a few steps in sequence. We already have three steps defined earlier. Let's *reuse* those steps for this part.
#
# We will reuse step1, step2, step3, but build the pipeline in such a way that we chain step3 after step2 and step2 after step1. Note that there is no explicit data dependency between these steps, but still steps can be made dependent by using the [run_after](https://docs.microsoft.com/en-us/python/api/azureml-pipeline-core/azureml.pipeline.core.builder.pipelinestep?view=azure-ml-py#run-after) construct.
# +
step2.run_after(step1)
step3.run_after(step2)
# Try a loop
#step2.run_after(step3)
# Now, construct the pipeline using the steps.
# We can specify the "final step" in the chain,
# Pipeline will take care of "transitive closure" and
# figure out the implicit or explicit dependencies
# https://www.geeksforgeeks.org/transitive-closure-of-a-graph/
pipeline2 = Pipeline(workspace=ws, steps=[step3])
print ("Pipeline is built")
pipeline2.validate()
print("Simple validation complete")
# -
pipeline_run2 = Experiment(ws, 'Hello_World2').submit(pipeline2)
print("Pipeline is submitted for execution")
RunDetails(pipeline_run2).show()
# # Next: Pipelines with data dependency
# The next [notebook](./aml-pipelines-with-data-dependency-steps.ipynb) demostrates how to construct a pipeline with data dependency.
|
how-to-use-azureml/machine-learning-pipelines/intro-to-pipelines/aml-pipelines-getting-started.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Liner Regression Model Tutorial
#
# ***
#
# ## Introduction:
#
# Since the early years of humanity, there has always been a desire to predict future outcomes before they happened. The Ancient Greeks used Oracles, or divine priestesses, to predict the future by listening to their supposed messages from the Gods. The Ancient Chinese would engrave messages on bones, mashup and heat the bones, and then use the priest to interpret the answers returned by divine entities. While their approaches may have been different, the goal was the same: **predict an outcome before it happened.**
#
# As time went on, humanity developed and invented new fields of study related to mathematics and statistics. These topics would help scientist and mathematicians develop new ways to explore their world and devise more realistic means of prediction that were grounded in observations and data.
#
# **However, all these models required data that could be measured and manipulated, something that was challenging to obtain before the advent of the computer.** Enter the age of the modern computer, and data went from a scarce asset to an overly abundant commodity that required new technologies to handle and analyzes.
#
# The combination of a large amount of data & powerful computers that could compute more numbers in a few minutes than a single person could in their entire life, meant we could make models more accurate and dynamic than ever before. Soon, the field of machine learning would take off as individuals realized they could create computer programs that could learn from all of this data. New models were developed to handle different types of data and problems, and a repository of new techniques could be referenced to devise new solutions to old problems.
#
# One of the models we will discuss in this series is the Linear Regression Model. **The Linear Regression Model attempts to model the relationship between two variables by fitting a linear equation (a line) to observed data**. In the model, one variable is considered to be an **explanatory variable** (X Variable), and the other is considered to be a **dependent variable** (Y Variable).
# ## Background:
#
# In our example, we are going to try an model the relationships between two financial assets, the price of a single share of Exxon Mobile stock and the price of a barrel of oil. **The question we are trying to answer is, does the explanatory variable (Oil) do a good job at predicting the dependent variable (a single share of Exxon Mobile stock.)**
#
# ### Why a linear regression model?
# There are so many models to choose from, why this one? Well there can be many reasons why we would choose a given model, but there were a few key reasons why a linear regression model is being selected for this example
#
# > - We want to know whether one measurement variable is associated with another measurement variable.
# > - We want to measure the strength of the association (r2).
# > - We want an equation that describes the relationship and can be used to predict unknown values.
# ***
# The linear model will take the following form:
#
# $y = \beta_0 + \beta_1x$
#
# Where each term represents:
#
# - $y$ is the response
# - $x$ is the feature
# - $\beta_0$ is the intercept
# - $\beta_1$ is the coefficient for x
# ## Step One: Import our libraries
# To build our model, we will need some tools at our disposal to make the process as seamless as possible. We will not go through all the libraries but will take the time to explain a few.
#
# 1. **Pandas** - This will make grabbing and transforming the data quick.
# 2. **Sklearn** - We can leverage the built-in machine learning models they have.
# 3. **Scipy** - This will make interpreting our output much more comfortable.
# 4. **Matplotlib** - Visuals are critical to analysis, and this library will help us build those visuals.
# +
#https://matplotlib.org/gallery/color/named_colors.html
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
import math
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
from scipy import stats
from scipy.stats import kurtosis, skew
# %matplotlib inline
# -
# ***
# ## Step Two: Load the Data
# We want our data in a DataFrame as this will give it the proper structure need to analyze the data. Once we load the data into a DataFrame, we need an index so we will set that equal to our date column. Finally, it is good to check the data looks correct before moving on, so let us print out the first five rows using the `head()` method.
# +
# load the data
#path =r"C:\Users\305197\OneDrive - Petco Animal Supplies\OneDrive-2019-03-29\oil_exxon.xlsx"
path =r"C:\Users\Alex\OneDrive\Growth - Tutorial Videos\Lessons - Python\Python For Finance\oil_exxon.xlsx"
price_data = pd.read_excel(path)
# set the index equal to the date column & then drop the old date column
price_data.index = pd.to_datetime(price_data['date'])
price_data = price_data.drop(['date'], axis = 1)
# print the first five rows
price_data.head()
# -
# ***
# ## Step Three: Clean the data
# The chances of getting a perfectly cleaned dataset that meets all of the requirements is slim to none, so to make this tutorial more realistic we will clean the data. Here is the checklist when it comes to cleaning the data:
#
# > 1. Check the data types, to make sure they are correct. For example, it usually does not make sense for a number to be a string.
# > 2. Make sure the column names are correct. Having the correct column names makes the process of selecting data easier.
# > 3. Check for and drop/fill missing values. Dropping errors helps to control for errors when running.
# check the data types, in this case everything looks fine no changes need to be made.
price_data.dtypes
# While looking at the data, we can see one of the columns is misspelled, so let us fix that by creating a dictionary object where the old name is the key, and the new name is the value for that key. Once we do that, we can call the `rename()` method on the DataFrame and pass through the `new_column_names` dictionary through the `columns` parameter.
# +
# define the new name.
new_column_names = {'exon_price':'exxon_price'}
# rename the column
price_data = price_data.rename(columns = new_column_names)
price_data.head()
# -
# Missing values, they can be a problem because they can create errors when running calcs. The first thing is we should always check to see if there are any missing values. If we use the `.isna().any()` method on the DataFrame it will return each column with a boolean, where `True` means it has missing values and `False` means it does not have any missing values. Once, we know the data has missing values we can use the `dropna()` method to drop any rows that have a missing value.
# +
# check for missing values
display(price_data.isna().any())
# drop any missing values
price_data = price_data.dropna()
# let's check to make sure they've all been removed.
price_data.isna().any()
# -
# ***
# ## Section Four: Explore the Data
# Okay, now that we have a clean dataset let us explore it a little. Again, this is a critical step as it helps us understand some of the following questions:
#
# 1. How is the data distributed?
# 2. Does there appear to be a relationship between the two variables?
# 3. Are there any outliers?
# 4. Is the data skewed?
#
# By better understanding the answers to these questions we can validate whether we need to do further transformations or if we need to change the model we picked.
# ***
# ### Build a Scatter Plot
# Scatter plots help us visualize the relationship between our data, so let us plot our data using the graph so we can explore the relationship. We need to define the x-coordinate and the y-coordinate, and then plot them using the `plot()` method. Now, we did a few formatting steps, so our graph comes out logically.
# +
# define the x & y data.
x = price_data['exxon_price']
y = price_data['oil_price']
# create the scatter plot.
plt.plot(x, y, 'o', color ='cadetblue', label = 'Daily Price')
# make sure it's formatted.
plt.title("Exxon Vs. Oil")
plt.xlabel("Exxon Mobile")
plt.ylabel("Oil")
plt.legend()
plt.show()
# -
# ***
# ### Measure the Correlation
# At first glance, we can tell there is some relationship here because they seem to be moving in tandem. The relationship means if one goes up the other appears to go up as well and also tells us it appears to be a positive relationship because they both move up. However, if we would like to attach a number to this relationship so we can quantify it. Well, in this case, let us measure the correlation between the two variables. We will take the DataFrame and call the `corr()` method to return a DataFrame with the metrics.
# let's measure that correlation
price_data.corr()
# Okay, so there is a correlation and a strong one at that. Generally speaking, this is how we measure the strength of correlations.
#
# - Very strong relationship **(|r|>0.8 =>)**
# - Strong relationship **(0.6â€|r|)**
# - Moderate relationship **(0.4â€|r|)**
# - Weak relationship **(0.2â€|r|)**
# - Very weak relationship **(|r|)**
#
# ***
# ### Create a Statistical Summary
# Okay, so we see there is a correlation let us create a statistical summary to help describe the dataset. We will use the `describe()` method to output a DataFrame with all this info.
# let's take a look at a statistical summary.
price_data.describe()
# Nothing stands out as a concern at this point, our range is healthy, and all the data falls within 3 Standard deviations of the mean. In other words, we do not seem to have any outliers that we need to worry with. They both have the same count so we look good there and we get a good idea of the min and max. Overall, we should be happy with the output.
# ***
# ### Checking for Outliers and Skewness
# We do not want outliers, and we want to make sure our data does not have skew because this could impact results in specific models. The first thing we will do is a plot a histogram for each column of data. The data will help us get a good idea of the distribution. Once, we have done that we will do some hard measurements to validate our visuals.
price_data.hist(grid = False, color = 'cadetblue')
# Okay, so some of the data does appear to be skewed but not too much. However, we probably should verify this by taking some measurements. Two good metrics we can use are the kurtosis and skew, where kurtosis measure the height of our distribution and skew measures whether it is positively or negatively skewed. We will use the `scipy.stats` module to do the measurements.
# +
# calculate the excess kurtosis using the fisher method. The alternative is Pearson which calculates regular kurtosis.
exxon_kurtosis = kurtosis(price_data['exxon_price'], fisher = True)
oil_kurtosis = kurtosis(price_data['oil_price'], fisher = True)
# calculate the skewness
exxon_skew = skew(price_data['exxon_price'])
oil_skew = skew(price_data['oil_price'])
display("Exxon Excess Kurtosis: {:.2}".format(exxon_kurtosis)) # this looks fine
display("Oil Excess Kurtosis: {:.2}".format(oil_kurtosis)) # this looks fine
display("Exxon Skew: {:.2}".format(exxon_skew)) # moderately skewed
display("Oil Skew: {:.2}".format(oil_skew)) # moderately skewed, it's a little high but we will accept it.
# -
# We can also perform a `kurtosistest()` and `skewtest()` on our data to test whether the data is normally distributed. With these two functions we test the null hypothesis that the kurtosis of the population from which the sample was drawn is that of the normal distribution: kurtosis = 3(n-1)/(n+1) & the null hypothesis that the skewness of the population that the sample was drawn from is the same as that of a corresponding normal distribution, respectively.
#
# However, there is a **big caveat** to this. As our dataset grows larger, the chances of us rejecting the null hypothesis increases even if there is only slight kurtosis or skew. In other words, even if our dataset is slightly non-normal, we will reject the null hypothesis. These results are unrealistic because the chances of us having a perfectly normal dataset are very very slim, so we have to take these results with a grain of salt.
# +
# perform a kurtosis test
display('Exxon')
display(stats.kurtosistest(price_data['exxon_price']))
display('Oil')
display(stats.kurtosistest(price_data['oil_price']))
# perform a skew test
display('Exxon')
display(stats.skewtest(price_data['exxon_price']))
display('Oil')
display(stats.skewtest(price_data['oil_price']))
# -
# If we look at the results above, we will reject the null hypothesis 3 out of 4 times, even with the data being slightly skewed or having mild kurtosis. This is why we always need to visualize the data and calculate the metrics before running these test.
# ***
#
# **Kurtosis**
# - Any distribution with **kurtosis â3 (excess â0)** is called mesokurtic. This is a normal distribution
# - Any distribution with **kurtosis <3 (excess kurtosis <0)** is called platykurtic. Tails are shorter and thinner, and often its central peak is lower and broader.
# - Any distribution with **kurtosis >3 (excess kurtosis >0)** is called leptokurtic. Tails are longer and fatter, and often its central peak is higher and sharper.
#
# ***
#
# **Skewness**
# - If skewness is **less than â1 or greater than +1**, the distribution is highly skewed.
# - If skewness is **between â1 and âÂœ or between +Âœ and +1**, the distribution is moderately skewed.
# - If skewness is **between âÂœ and +Âœ**, the distribution is approximately symmetric.
# ## Section Five: Build the Model
# At this point, we feel comfortable moving forward other than the data being slightly skewed nothing else is stopping us from going with the linear regression model.
#
# ***
# ### Split the Data
# The first thing we need to do is split the data into a training set and a test set. The training set is what we will train the model on and the test set is what we will test it on. The convention is to have 20% dedicated to testing and the remaining 80% to training, but these are not hard limits.
# +
# define our input variable (X) & output variable.
Y = price_data.drop('oil_price', axis = 1)
X = price_data[['oil_price']]
# Split X and y into X_
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.30, random_state=1)
# -
# ***
# ### Create & Fit the model
# Making the model surprises many people of how easy this step is. All we do is create an instance of the linear regression model from Sklearn and then call the `fit()` method to train the model on our training data.
# +
# create a Linear Regression model object.
regression_model = LinearRegression()
# pass through the X_train & y_train data set.
regression_model.fit(X_train, y_train)
# -
# ***
# ### Explore the output
# Let us see what got sent back to us. First, we can check the coefficient of each independent variable in our model. In this case, it is just the oil price. After that let us take a look at the intercept of our regression formula.
# +
# let's grab the coefficient of our model and the intercept.
intercept = regression_model.intercept_[0]
coefficient = regression_model.coef_[0][0]
print("The Coefficient for our model is {:.2}".format(coefficient))
print("The intercept for our model is {:.4}".format(intercept))
# -
# Interpreting the coefficient, we would say that a single unit increase in oil **is associated with a 0.24** increase in the price of Exxon Mobile stock. **We are NOT CLAIMING CAUSATION, just association.**
# ***
# ### Taking a Single Prediction
# Now that we understand what the model looks like and how to interpret the output let us make some predictions. If we want we can make a single prediction by passing through a price in a list of list. Once we have an output, we slice it to get the value.
# let's test a prediction
prediction = regression_model.predict([[67.33]])
predicted_value = prediction[0][0]
print("The predicted value is {:.4}".format(predicted_value))
# To interpret the output, we would say that given a barrel of oil for 67.33 we would predict Exxon Mobile to be trading for 85.95.
# ***
# ### Making Multiple Predictions at Once
# Great, so we have a good working model let us test it on the data we set aside. We will call the `predict()` method and pass through our `X_test` dataset at which point a list of predictions will be returned to us.
# +
# Get multiple predictions.
y_predict = regression_model.predict(X_test)
# Show the first 5 predictions
y_predict[:5]
# -
# ## Section Six: Evaluating the Model
# Once we have a functioning model that we can use to make predictions we need to evaluate how useful our model is. There is no sense of using a model that makes horrible predictions, so we should look at different metrics to see how it did.
#
# Now to make this process easier on ourselves, we are going to recreate our same model using the `statsmodel.api` library. The reason why is that they have numerous built-in functions that make calculating metrics like confidence intervals and p-values a breeze. The output from the `statsmodel.api` will not be identical to our `sklearn` library but it will be very close.
# +
# define our intput
X2 = sm.add_constant(X)
# create a OLS model.
model = sm.OLS(Y, X2)
# fit the data
est = model.fit()
# -
# ***
# ### Confidence Intervals
# First, let us calculate confidence intervals. Keep in mind that by default that the calculated using 95% intervals. We interpret this by saying if the population from which this sample was drawn was sampled 100 times. Approximately 95 of those confidence intervals would contain the "true" coefficient.
#
# Why do we provide a confidence range? Well, it comes from the fact that we only have a sample of the population, not the entire population itself. Because of this concept, means that the "true" coefficient could exist in the interval below or it couldn't, but we cannot say for sure. We provide some uncertainty by providing a range, usually 95% interval, where the coefficient is probably in.
# make some confidence intervals, 95% by default.
est.conf_int()
# Interpreting the output above, we would say that with 95% confidence the `oil_price` coefficient **exists between 0.214 & 0.248**.
# > - Want a narrower range? Decrease your confidence.
# > - Want a wider range? Increase your confidence.
# ***
# ### Hypothesis Testing
#
# - **Null Hypothesis:** There is no relationship between the price of oil and the price of Exxon.
# - The coefficient equals 0.
# - **Alternative Hypothesis:** There is a relationship between the price of oil and the price of Exxon.
# - The coefficient does not equal to 0.
#
# - If we reject the null, we are saying there is a relationship, and the coefficient does not equal 0.
# - If we fail to reject the null, we are saying there is no relationship, and the coefficient does equal 0.
# estimate the p-values.
est.pvalues
# The p-value represents the probability that the coefficient equals 0. We want a p-value that is less than 0.05 if it is we can reject the null hypothesis. In this case, the p-value for the oil_price coefficient is much lower than 0.05, so we can reject the null hypothesis and say that there is a relationship and that we believe it to be between oil and the price of Exxon.
# ## Section Seven: Model Fit
# We can examine how well our data fit the model, so we will take `y_predictions` and compare them to our `y_actuals` these will be our residuals. From here we can calculate a few metrics to help quantify how well our model fits the data. Here are a few popular metrics:
#
# - **Mean Absolute Error (MAE):** Is the mean of the absolute value of the errors. This metric gives an idea of magnitude but no idea of direction (too high or too low).
#
# - **Mean Squared Error (MSE):** Is the mean of the squared errors.MSE is more popular than MAE because MSE "punishes" more significant errors.
#
# - **Root Mean Squared Error (RMSE):** Is the square root of the mean of the squared errors. RMSE is even more favored because it allows us to interpret the output in y-units.
#
# Luckily for us, `sklearn` and `statsmodel` both contain functions that will calculate these metrics for us.
#
# +
# calculate the mean squared error.
model_mse = mean_squared_error(y_test, y_predict)
# calculate the mean absolute error.
model_mae = mean_absolute_error(y_test, y_predict)
# calulcate the root mean squared error
model_rmse = math.sqrt(model_mse)
# display the output
print("MSE {:.3}".format(model_mse))
print("MAE {:.3}".format(model_mae))
print("RMSE {:.3}".format(model_rmse))
# -
# ***
# ## R-Squared
# The R-Squared metric provides us a way to measure the goodness of fit or how well our data fits the model. The higher the R-Squared metric, the better the data fit our model. However, we have to know the limitations of R-Square. One limitation is that R-Square increases as the number of feature increases in our model, so it does not pay to select the model with the highest R-Square. A more popular metric is the adjusted R-Square which penalizes more complex models. Let us calculate both.
model_r2 = r2_score(y_test, y_predict)
print("R2: {:.2}".format(model_r2))
# With R-Square & adjusted R-Square, we have to be careful when interpreting the output because it depends on what our the goal is. The R-squared is generally of secondary importance unless the main concern is using the regression equation to make accurate predictions. It boils down to the domain-specific problem, and many people would argue an R-Square of .36 is great for stocks because it is hard to control for all the external factors, while others may not agree.
# ***
# ### Create a Summary of the Model Output
# Let us create a summary of some of our keep metrics, Sklearn does not have a good way of creating this output so we would have to calculate all the metrics ourselves. Let us avoid this and use the `statsmodel.api` library as we can create the same model we did up above, but we can also leverage the `summary()` method to create an output for us. Some of the metrics might differ slightly, but they generally should be the same
# print out a summary
print(est.summary())
# Now looking at the table above, we get a good overview of how our model performed and provides some of the key metrics we discussed up above. The only additional metric we will describe here is the t-value which is the coefficient divided by the standard error. The higher the t-value, the more evidence we have to reject the null hypothesis.
# ### Plot the Residuals
# It's good to see how the residulas are distributed because they should be normally distributed.
# Grab the residuals & then call the hist() method
(y_test - y_predict).hist(grid = False, color = 'royalblue')
plt.title("Model Residuals")
plt.show()
# ***
# ### Plotting our Line
# We have this beautiful model, but we cannot see it. Let us create a graph where we have our data and our linear regression line on our graph. We should also highlight some of our key metrics below so we should also add them below.
# +
# Plot outputs
plt.scatter(X_test, y_test, color='gainsboro', label = 'Price')
plt.plot(X_test, y_predict, color='royalblue', linewidth = 3, linestyle= '-',label ='Regression Line')
plt.title("Linear Regression Exxon Mobile Vs. Oil")
plt.xlabel("Oil")
plt.ylabel("Exxon Mobile")
plt.legend()
plt.show()
# The coefficients
print('Oil coefficient:' + '\033[1m' + '{:.2}''\033[0m'.format(regression_model.coef_[0][0]))
# The mean squared error
print('Mean squared error: ' + '\033[1m' + '{:.4}''\033[0m'.format(model_mse))
# The mean squared error
print('Root Mean squared error: ' + '\033[1m' + '{:.4}''\033[0m'.format(math.sqrt(model_mse)))
# Explained variance score: 1 is perfect prediction
print('R2 score: '+ '\033[1m' + '{:.2}''\033[0m'.format(r2_score(y_test,y_predict)))
# -
# ## Step Six: Save the Model for future use
# We will probably want to use this model in the future, so let us save our work so we can use it later. Saving the model can be achieved by storing our model in a pickle which is storing a python object as a character stream in a file which can be reloaded later to use.
# +
import pickle
# pickle the model.
with open('my_linear_regression.sav','wb') as f:
pickle.dump(regression_model,f)
# load it back in.
with open('my_linear_regression.sav', 'rb') as pickle_file:
regression_model_2 = pickle.load(pickle_file)
# make a new prediction.
regression_model_2.predict([[67.33]])
|
python/python-data-science/machine-learning/simple-linear-regression/Linear Regression Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # [NTDS'19] assignment 1: network science
# [ntds'19]: https://github.com/mdeff/ntds_2019
#
# [<NAME>](https://lts4.epfl.ch/bayram), [EPFL LTS4](https://lts4.epfl.ch) and
# [<NAME>](https://people.epfl.ch/nikolaos.karalias), [EPFL LTS2](https://lts2.epfl.ch).
# ## Students
#
# * Team: `<your team number>`
# * Students: `<your name`> (for the indivudual submission) or `<the name of all students in the team>` (for the team submission)
# ## Rules
#
# Grading:
# * The first deadline is for individual submissions. The second deadline is for the team submission.
# * All team members will receive the same grade based on the team solution submitted on the second deadline.
# * As a fallback, a team can ask for individual grading. In that case, solutions submitted on the first deadline are graded.
# * Collaboration between team members is encouraged. No collaboration between teams is allowed.
#
# Submission:
# * Textual answers shall be short. Typically one to two sentences.
# * Code has to be clean.
# * You cannot import any other library than we imported.
# Note that Networkx is imported in the second section and cannot be used in the first.
# * When submitting, the notebook is executed and the results are stored. I.e., if you open the notebook again it should show numerical results and plots. We won't be able to execute your notebooks.
# * The notebook is re-executed from a blank state before submission. That is to be sure it is reproducible. You can click "Kernel" then "Restart Kernel and Run All Cells" in Jupyter.
# ## Objective
#
# The purpose of this milestone is to explore a given dataset, represent it by network by constructing different graphs. In the first section, you will analyze the network properties. In the second section, you will explore various network models and find out the network model fitting the ones you construct from the dataset.
# ## Cora Dataset
#
# The [Cora dataset](https://linqs.soe.ucsc.edu/node/236) consists of scientific publications classified into one of seven research fields.
#
# * **Citation graph:** the citation network can be constructed from the connections given in the `cora.cites` file.
# * **Feature graph:** each publication in the dataset is described by a 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary and its research field, given in the `cora.content` file. The dictionary consists of 1433 unique words. A feature graph can be constructed using the Euclidean distance between the feature vector of the publications.
#
# The [`README`](data/cora/README) provides details about the content of [`cora.cites`](data/cora/cora.cites) and [`cora.content`](data/cora/cora.content).
# ## Section 1: Network Properties
# +
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
# %matplotlib inline
# -
# ### Question 1: Construct a Citation Graph and a Feature Graph
# Read the `cora.content` file into a Pandas DataFrame by setting a header for the column names. Check the `README` file.
column_list = # Your code here.
pd_content = pd.read_csv('data/cora/cora.content', delimiter='\t', names=column_list)
pd_content.head()
# Print out the number of papers contained in each of the reasearch fields.
#
# **Hint:** You can use the `value_counts()` function.
# +
# Your code here.
# -
# Select all papers from a field of your choice and store their feature vectors into a NumPy array.
# Check its shape.
my_field = # Your code here.
features = # Your code here.
features.shape
# Let $D$ be the Euclidean distance matrix whose $(i,j)$ entry corresponds to the Euclidean distance between feature vectors $i$ and $j$.
# Using the feature vectors of the papers from the field which you have selected, construct $D$ as a Numpy array.
distance = # Your code here.
distance.shape
# Check the mean pairwise distance $\mathbb{E}[D]$.
mean_distance = distance.mean()
mean_distance
# Plot an histogram of the euclidean distances.
plt.figure(1, figsize=(8, 4))
plt.title("Histogram of Euclidean distances between papers")
plt.hist(distance.flatten());
# Now create an adjacency matrix for the papers by thresholding the Euclidean distance matrix.
# The resulting (unweighted) adjacency matrix should have entries
# $$ A_{ij} = \begin{cases} 1, \; \text{if} \; d(i,j)< \mathbb{E}[D], \; i \neq j, \\ 0, \; \text{otherwise.} \end{cases} $$
#
# First, let us choose the mean distance as the threshold.
threshold = mean_distance
A_feature = # Your code here.
# Now read the `cora.cites` file and construct the citation graph by converting the given citation connections into an adjacency matrix.
# +
cora_cites = np.genfromtxt('data/cora/cora.cites', delimiter='\t')
A_citation = # Your code here.
A_citation.shape
# -
# Get the adjacency matrix of the citation graph for the field that you chose.
# You have to appropriately reduce the adjacency matrix of the citation graph.
# +
# Your code here.
# -
# Check if your adjacency matrix is symmetric. Symmetrize your final adjacency matrix if it's not already symmetric.
# Your code here.
np.count_nonzero(A_citation - A_citation.transpose())
# Check the shape of your adjacency matrix again.
A_citation.shape
# ### Question 2: Degree Distribution and Moments
# What is the total number of edges in each graph?
num_edges_feature = # Your code here.
num_edges_citation = # Your code here.
print(f"Number of edges in the feature graph: {num_edges_feature}")
print(f"Number of edges in the citation graph: {num_edges_citation}")
# Plot the degree distribution histogram for each of the graphs.
# +
degrees_citation = # Your code here.
degrees_feature = # Your code here.
deg_hist_normalization = np.ones(degrees_citation.shape[0]) / degrees_citation.shape[0]
fig, axes = plt.subplots(1, 2, figsize=(16, 4))
axes[0].set_title('Citation graph degree distribution')
axes[0].hist(degrees_citation, weights=deg_hist_normalization);
axes[1].set_title('Feature graph degree distribution')
axes[1].hist(degrees_feature, weights=deg_hist_normalization);
# -
# Calculate the first and second moments of the degree distribution of each graph.
# +
cit_moment_1 = # Your code here.
cit_moment_2 = # Your code here.
feat_moment_1 = # Your code here.
feat_moment_2 = # Your code here.
print(f"1st moment of citation graph: {cit_moment_1}")
print(f"2nd moment of citation graph: {cit_moment_2}")
print(f"1st moment of feature graph: {feat_moment_1}")
print(f"2nd moment of feature graph: {feat_moment_2}")
# -
# What information do the moments provide you about the graphs?
# Explain the differences in moments between graphs by comparing their degree distributions.
# **Your answer here:**
# Select the 20 largest hubs for each of the graphs and remove them. Observe the sparsity pattern of the adjacency matrices of the citation and feature graphs before and after such a reduction.
# +
reduced_A_feature = # Your code here
reduced_A_citation = # Your code here
fig, axes = plt.subplots(2, 2, figsize=(16, 16))
axes[0, 0].set_title('Feature graph: adjacency matrix sparsity pattern')
axes[0, 0].spy(A_feature);
axes[0, 1].set_title('Feature graph without top 20 hubs: adjacency matrix sparsity pattern')
axes[0, 1].spy(reduced_A_feature);
axes[1, 0].set_title('Citation graph: adjacency matrix sparsity pattern')
axes[1, 0].spy(A_citation);
axes[1, 1].set_title('Citation graph without top 20 hubs: adjacency matrix sparsity pattern')
axes[1, 1].spy(reduced_A_citation);
# -
# Plot the new degree distribution histograms.
# +
reduced_degrees_feat = # Your code here.
reduced_degrees_cit = # Your code here.
deg_hist_normalization = np.ones(reduced_degrees_feat.shape[0])/reduced_degrees_feat.shape[0]
fig, axes = plt.subplots(1, 2, figsize=(16, 4))
axes[0].set_title('Citation graph degree distribution')
axes[0].hist(reduced_degrees_cit, weights=deg_hist_normalization);
axes[1].set_title('Feature graph degree distribution')
axes[1].hist(reduced_degrees_feat, weights=deg_hist_normalization);
# -
# Compute the first and second moments for the new graphs.
# +
reduced_cit_moment_1 = # Your code here.
reduced_cit_moment_2 = # Your code here.
reduced_feat_moment_1 = # Your code here.
reduced_feat_moment_2 = # Your code here.
print("Citation graph first moment:", reduced_cit_moment_1)
print("Citation graph second moment:", reduced_cit_moment_2)
print("Feature graph first moment: ", reduced_feat_moment_1)
print("Feature graph second moment: ", reduced_feat_moment_2)
# -
# Print the number of edges in the reduced graphs.
# +
# Your code here
# -
# Is the effect of removing the hubs the same for both networks? Look at the percentage changes for each moment. Which of the moments is affected the most and in which graph? Explain why.
#
# **Hint:** Examine the degree distributions.
# **Your answer here:**
# ### Question 3: Pruning, sparsity, paths
# By adjusting the threshold of the euclidean distance matrix, prune the feature graph so that its number of edges is roughly close (within a hundred edges) to the number of edges in the citation graph.
# +
threshold = # Your code here.
A_feature_pruned = # Your code here
num_edges_feature_pruned = # Your code here.
print(f"Number of edges in the feature graph: {num_edges_feature}")
print(f"Number of edges in the feature graph after pruning: {num_edges_feature_pruned}")
print(f"Number of edges in the citation graph: {num_edges_citation}")
# -
# Check your results by comparing the sparsity patterns and total number of edges between the graphs.
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].set_title('Citation graph sparsity')
axes[0].spy(A_citation);
axes[1].set_title('Feature graph sparsity')
axes[1].spy(A_feature_pruned);
# Let $C_{k}(i,j)$ denote the number of paths of length $k$ from node $i$ to node $j$.
#
# We define the path matrix $P$, with entries
# $ P_{ij} = \displaystyle\sum_{k=0}^{N}C_{k}(i,j). $
# Calculate the path matrices for both the citation and the unpruned feature graphs for $N =10$.
#
# **Hint:** Use [powers of the adjacency matrix](https://en.wikipedia.org/wiki/Adjacency_matrix#Matrix_powers).
path_matrix_citation = # Your code here.
path_matrix_feature = # Your code here.
# Check the sparsity pattern for both of path matrices.
fig, axes = plt.subplots(1, 2, figsize=(16, 9))
axes[0].set_title('Citation Path matrix sparsity')
axes[0].spy(path_matrix_citation);
axes[1].set_title('Feature Path matrix sparsity')
axes[1].spy(path_matrix_feature);
# Now calculate the path matrix of the pruned feature graph for $N=10$. Plot the corresponding sparsity pattern. Is there any difference?
# +
path_matrix_pruned = # Your code here.
plt.figure(figsize=(12, 6))
plt.title('Feature Path matrix sparsity')
plt.spy(path_matrix_pruned);
# -
# **Your answer here:**
# Describe how you can use the above process of counting paths to determine whether a graph is connected or not. Is the original (unpruned) feature graph connected?
# **Your answer here:**
# If the graph is connected, how can you guess its diameter using the path matrix?
# **Your answer here:**
# If any of your graphs is connected, calculate the diameter using that process.
diameter = # Your code here.
print(f"The diameter is: {diameter}")
# Check if your guess was correct using [NetworkX](https://networkx.github.io/documentation/stable/reference/algorithms/generated/networkx.algorithms.distance_measures.diameter.html).
# Note: usage of NetworkX is only allowed in this part of Section 1.
import networkx as nx
feature_graph = nx.from_numpy_matrix(A_feature)
print(f"Diameter according to networkx: {nx.diameter(feature_graph)}")
# ## Section 2: Network Models
# In this section, you will analyze the feature and citation graphs you constructed in the previous section in terms of the network model types.
# For this purpose, you can use the NetworkX libary imported below.
import networkx as nx
# Let us create NetworkX graph objects from the adjacency matrices computed in the previous section.
G_citation = nx.from_numpy_matrix(A_citation)
print('Number of nodes: {}, Number of edges: {}'. format(G_citation.number_of_nodes(), G_citation.number_of_edges()))
print('Number of self-loops: {}, Number of connected components: {}'. format(G_citation.number_of_selfloops(), nx.number_connected_components(G_citation)))
# In the rest of this assignment, we will consider the pruned feature graph as the feature network.
G_feature = nx.from_numpy_matrix(A_feature_pruned)
print('Number of nodes: {}, Number of edges: {}'. format(G_feature.number_of_nodes(), G_feature.number_of_edges()))
print('Number of self-loops: {}, Number of connected components: {}'. format(G_feature.number_of_selfloops(), nx.number_connected_components(G_feature)))
# ### Question 4: Simulation with ErdÅsâRényi and BarabásiâAlbert models
# Create an ErdÅsâRényi and a BarabásiâAlbert graph using NetworkX to simulate the citation graph and the feature graph you have. When choosing parameters for the networks, take into account the number of vertices and edges of the original networks.
# The number of nodes should exactly match the number of nodes in the original citation and feature graphs.
assert len(G_citation.nodes()) == len(G_feature.nodes())
n = len(G_citation.nodes())
n
# The number of match shall fit the average of the number of edges in the citation and the feature graph.
m = np.round((G_citation.size() + G_feature.size()) / 2)
m
# How do you determine the probability parameter for the ErdÅsâRényi graph?
# **Your answer here:**
p = # Your code here.
G_er = nx.erdos_renyi_graph(n, p)
# Check the number of edges in the ErdÅsâRényi graph.
print('My Erdos-Rényi network that simulates the citation graph has {} edges.'.format(G_er.size()))
# How do you determine the preferential attachment parameter for BarabásiâAlbert graphs?
# **Your answer here:**
q = # Your code here.
G_ba = nx.barabasi_albert_graph(n, q)
# Check the number of edges in the BarabásiâAlbert graph.
print('My Barabási-Albert network that simulates the citation graph has {} edges.'.format(G_ba.size()))
# ### Question 5: Giant Component
# Check the size of the largest connected component in the citation and feature graphs.
giant_citation = # Your code here.
print('The giant component of the citation graph has {} nodes and {} edges.'.format(giant_citation.number_of_nodes(), giant_citation.size()))
giant_feature = # Your code here.
print('The giant component of the feature graph has {} nodes and {} edges.'.format(giant_feature.number_of_nodes(), giant_feature.size()))
# Check the size of the giant components in the generated ErdÅsâRényi graph.
giant_er = # Your code here.
print('The giant component of the Erdos-Rényi network has {} nodes and {} edges.'.format(giant_er.number_of_nodes(), giant_er.size()))
# Let us match the number of nodes in the giant component of the feature graph by simulating a new ErdÅsâRényi network.
# How do you choose the probability parameter this time?
#
# **Hint:** Recall the expected giant component size from the lectures.
# **Your answer here:**
p_new = # Your code here.
G_er_new = nx.erdos_renyi_graph(n, p_new)
# Check the size of the new ErdÅsâRényi network and its giant component.
print('My new Erdos Renyi network that simulates the citation graph has {} edges.'.format(G_er_new.size()))
giant_er_new = # Your code here.
print('The giant component of the new Erdos-Rényi network has {} nodes and {} edges.'.format(giant_er_new.number_of_nodes(), giant_er_new.size()))
# ### Question 6: Degree Distributions
# Recall the degree distribution of the citation and the feature graph.
fig, axes = plt.subplots(1, 2, figsize=(15, 6))
axes[0].set_title('Citation graph')
citation_degrees = # Your code here.
axes[0].hist(citation_degrees);
axes[1].set_title('Feature graph')
feature_degrees = # Your code here.
axes[1].hist(feature_degrees);
# What does the degree distribution tell us about a network? Can you make a prediction on the network model type of the citation and the feature graph by looking at their degree distributions?
# **Your answer here:**
# Now, plot the degree distribution historgrams for the simulated networks.
fig, axes = plt.subplots(1, 3, figsize=(20, 6))
axes[0].set_title('Erdos-Rényi network')
er_degrees = # Your code here.
axes[0].hist(er_degrees);
axes[1].set_title('Barabási-Albert network')
ba_degrees = # Your code here.
axes[1].hist(ba_degrees);
axes[2].set_title('new Erdos-Rényi network')
er_new_degrees = # Your code here.
axes[2].hist(er_new_degrees);
# In terms of the degree distribution, is there a good match between the citation and feature graphs and the simulated networks?
# For the citation graph, choose one of the simulated networks above that match its degree distribution best. Indicate your preference below.
# **Your answer here:**
# You can also simulate a network using the configuration model to match its degree disctribution exactly. Refer to [Configuration model](https://networkx.github.io/documentation/stable/reference/generated/networkx.generators.degree_seq.configuration_model.html#networkx.generators.degree_seq.configuration_model).
#
# Let us create another network to match the degree distribution of the feature graph.
G_config = nx.configuration_model(feature_degrees)
print('Configuration model has {} nodes and {} edges.'.format(G_config.number_of_nodes(), G_config.size()))
# Does it mean that we create the same graph with the feature graph by the configuration model? If not, how do you understand that they are not the same?
# **Your answer here:**
# ### Question 7: Clustering Coefficient
# Let us check the average clustering coefficient of the original citation and feature graphs.
nx.average_clustering(G_citation)
nx.average_clustering(G_feature)
# What does the clustering coefficient tell us about a network? Comment on the values you obtain for the citation and feature graph.
# **Your answer here:**
# Now, let us check the average clustering coefficient for the simulated networks.
nx.average_clustering(G_er)
nx.average_clustering(G_ba)
nx.average_clustering(nx.Graph(G_config))
# Comment on the values you obtain for the simulated networks. Is there any good match to the citation or feature graph in terms of clustering coefficient?
# **Your answer here:**
# Check the other [network model generators](https://networkx.github.io/documentation/networkx-1.10/reference/generators.html) provided by NetworkX. Which one do you predict to have a better match to the citation graph or the feature graph in terms of degree distribution and clustering coefficient at the same time? Justify your answer.
# **Your answer here:**
# If you find a better fit, create a graph object below for that network model. Print the number of edges and the average clustering coefficient. Plot the histogram of the degree distribution.
# +
# Your code here.
# -
# Comment on the similarities of your match.
# **Your answer here:**
|
assignments/.ipynb_checkpoints/1_network_science-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Aligning MRS voxels with the anatomy
#
# Several steps in the analysis and interpertation of the MRS data require knowledge of the anatomical location of the volume from which MRS data was acquired. In particular, we would like to know how much of the volume contains gray matter, relative to other tissue components, such as white matter, CSF, etc. In order to infer this, we need to acquire a T1-weighted MRI scan in the same session, and (assuming the subject hasn't moved too much), use the segmentation of the T1w image into different tissue types (e.g. using [Freesurfer](http://surfer.nmr.mgh.harvard.edu)).
#
# However, in order to do that, we first need to align the MRS voxel with the T1w data, so that we can extract these quantities.
# +
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# %matplotlib inline
import os.path as op
import nibabel as nib
import MRS.data as mrd
import IPython.html.widgets as wdg
import IPython.display as display
# -
mrs_nifti = nib.load(op.join(mrd.data_folder, '12_1_PROBE_MEGA_L_Occ.nii.gz'))
t1_nifti = nib.load(op.join(mrd.data_folder, '5062_2_1.nii.gz'))
# In order to be able to align the files with regard to each other, they need to both encode an affine transformation relative to the scanner space. For a very thorough introduction to these transformations and their utility, see [this tutorial](http://nipy.bic.berkeley.edu/nightly/nibabel/doc/coordinate_systems.html)
mrs_aff = mrs_nifti.get_affine()
t1_aff = t1_nifti.get_affine()
print("The affine transform for the MRS data is:")
print(mrs_aff)
print("The affine transform for the T1 data is:")
print(t1_aff)
# If you read the aformentioned [tutorial](http://nipy.bic.berkeley.edu/nightly/nibabel/doc/coordinate_systems.html), this will make sense. The diagonal of the top ledt 3 x 3 matrix encodes the resolution of the voxels used in each of the acquisitions (in mm). The MRS data has a single 2.5 x 2.5 x 2.5 cm$^2$ isotropic voxel, and the T1 has (approximately) 0.9 x 0.9 x 0.9 mm$^2$ isotropic voxels. They were both acquired without any rotation relative to the scanner coordinate system, which is why the off-diagonal terms of the top left 3 x 3 matrix is all zeros. The 4th column of each of these matrices encodes the xyz shift (again, in mm) relative to the scanner isocenter.
# Composing these two transformations together tells us how to align the two volumes relative to each other. In particular, we might ask where in the t1 coordinate system the center of the MRS voxel is. Since we are multiplying
composed_affine = np.dot(np.linalg.pinv(t1_aff), mrs_aff)
# This allows us to compute the location of the center of the MRS voxel in the T1 volume coordinates, and the locations of the corners of the voxel:
# +
mrs_center = [0,0,0,1]
t1_center = np.round(np.dot(composed_affine, mrs_center)).astype(int)
mrs_corners = [[-0.5, -0.5, -0.5, 1],
[-0.5, -0.5, 0.5, 1],
[-0.5, 0.5, -0.5, 1],
[-0.5, 0.5, 0.5, 1],
[ 0.5, -0.5, -0.5, 1],
[ 0.5, -0.5, 0.5, 1],
[ 0.5, 0.5, -0.5, 1],
[ 0.5, 0.5, 0.5, 1]]
t1_corners = [np.round(np.dot(composed_affine, c)).astype(int) for c in mrs_corners]
# -
t1_corners
# Using this information, we can manually create a volume that only contains the T1-weighted data in the MRS ROI:
t1_data = t1_nifti.get_data().squeeze()
mrs_roi = np.ones_like(t1_data) * np.nan
mrs_roi[144:172, 176:204, 78:106] = t1_data[144:172, 176:204, 78:106]
# To view this, we will create a rather rough orthographic viewer of the T1 data, using IPython's interactive widget system. We add the data int the MRS ROI using a different color map, so that we can see where it is in the context of the anatomy
def show_voxel(x=t1_center[0], y=t1_center[1], z=t1_center[2]):
fig = plt.figure()
ax = fig.add_subplot(221)
ax.axis('off')
ax.imshow(np.rot90(t1_data[:, :, z]), matplotlib.cm.bone)
ax.imshow(np.rot90(mrs_roi[:, :, z]), matplotlib.cm.jet)
ax.plot([x, x], [0, t1_data.shape[0]], color='w')
ax.plot([0, t1_data.shape[1]], [y, y], color='w')
ax.set_ylim([0, t1_data.shape[0]])
ax.set_xlim([0, t1_data.shape[1]])
ax = fig.add_subplot(222)
ax.axis('off')
ax.imshow(np.rot90(t1_data[:, -y, :]), matplotlib.cm.bone)
ax.imshow(np.rot90(mrs_roi[:, -y, :]), matplotlib.cm.jet)
ax.plot([x, x], [0, t1_data.shape[1]], color='w')
ax.plot([0, t1_data.shape[1]], [z, z], color='w')
ax.set_xlim([0, t1_data.shape[0]])
ax.set_ylim([t1_data.shape[2], 0])
ax = fig.add_subplot(223)
ax.axis('off')
ax.imshow(np.rot90(t1_data[x, :, :]), matplotlib.cm.bone)
ax.imshow(np.rot90(mrs_roi[x, :, :]), matplotlib.cm.jet)
ax.plot([t1_data.shape[1]-y, t1_data.shape[1]-y], [0, t1_data.shape[1]], color='w')
ax.plot([0, t1_data.shape[1]], [z, z], color='w')
ax.set_xlim([0, t1_data.shape[1]])
ax.set_ylim([t1_data.shape[2], 0])
fig.set_size_inches(10, 10)
return fig
def voxel_viewer(t1_data, mrs_roi):
pb_widget = wdg.interactive(show_voxel,
t1_data = wdg.fixed(t1_data),
mrs_roi = wdg.fixed(mrs_roi),
x=wdg.IntSliderWidget(min=0, max=t1_data.shape[0]-1, value=155),
y=wdg.IntSliderWidget(min=0, max=t1_data.shape[1]-1, value=65),
z=wdg.IntSliderWidget(min=0, max=t1_data.shape[2]-1, value=92)
)
display.display(pb_widget)
voxel_viewer(t1_data, mrs_roi)
# Note that SMAL contains a module that will use the T1 information to extract the voxel statistics, based on a Freesurfer segmentation. This is the `MRS.freesurfer` module. See the module documentation for more details
# # Caveat
#
# Finally, an important caveat: the MRS voxel is a large voxel and its edges are not as sharp as you might want them to be. Many scan sequences will apply suppression bands of out-of-volume information, but even so, there is a fall-off of information around the edges of the nominal MRS voxel. There, you might want to consider your alignment and segmentation to be rough estimates.
|
ipynb/003-aligning-with-anatomy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import numpy, scipy, matplotlib.pyplot as plt, librosa, IPython.display, mir_eval, urllib
# [← Back to Index](index.html)
# # Exercise: Understanding Audio Features through Sonification
# This is an *exercise* notebook. It's a playground for your Python code. Feel free to write and execute your code without fear.
#
# When you see a cell that looks like this:
# +
# plt.plot?
# -
# that is a cue to use a particular command, in this case, `plot`. Run the cell to see documentation for that command. (To quickly close the Help window, press `q`.)
#
# For more documentation, visit the links in the Help menu above. Also see the other notebooks; all the exercises here are covered somewhere else in separate notebooks.
# This exercise is loosely based upon "Lab 1" from previous MIR workshops ([2010](https://ccrma.stanford.edu/workshops/mir2010/Lab1_2010.pdf)).
# ## Goals
# In this exercise, you will segment, feature extract, and analyze audio files.
# 1. Detect onsets in an audio signal.
# 2. Segment the audio signal at each onset.
# 3. Compute features for each segment.
# 4. Gain intuition into the features by listening to each segment separately.
# ## Step 1: Retrieve Audio
# Download the file `simpleLoop.wav` onto your local machine.
# +
filename = '125_bounce.wav'
#filename = 'conga_groove.wav'
#filename = '58bpm.wav'
url = 'http://audio.musicinformationretrieval.com/' + filename
# urllib.urlretrieve?
# -
# Make sure the download worked:
# %ls
# Save the audio signal into an array.
# +
# librosa.load?
# -
# Show the sample rate:
print fs
# Listen to the audio signal.
# +
# IPython.display.Audio?
# -
# Display the audio signal.
# +
# librosa.display.waveplot?
# -
# Compute the short-time Fourier transform:
# +
# librosa.stft?
# -
# For display purposes, compute the log amplitude of the STFT:
# +
# librosa.logamplitude?
# -
# Display the spectrogram.
# +
# Play with the parameters, including x_axis and y_axis
# librosa.display.specshow?
# -
# ## Step 2: Detect Onsets
# Find the times, in seconds, when onsets occur in the audio signal.
# +
# librosa.onset.onset_detect?
# +
# librosa.frames_to_time?
# -
# Convert the onset times into sample indices.
# +
# librosa.frames_to_samples?
# -
# Play a "beep" at each onset.
# +
# Use the `length` parameter so the click track is the same length as the original signal
# mir_eval.sonify.clicks?
# +
# Play the click track "added to" the original signal
# IPython.display.Audio?
# -
# ## Step 3: Segment the Audio
# Save into an array, `segments`, 100-ms segments beginning at each onset.
# Assuming these variables exist:
# x: array containing the audio signal
# fs: corresponding sampling frequency
# onset_samples: array of onsets in units of samples
frame_sz = int(0.100*fs)
segments = numpy.array([x[i:i+frame_sz] for i in onset_samples])
# Here is a function that adds 300 ms of silence onto the end of each segment and concatenates them into one signal.
#
# Later, we will use this function to listen to each segment, perhaps sorted in a different order.
def concatenate_segments(segments, fs=44100, pad_time=0.300):
padded_segments = [numpy.concatenate([segment, numpy.zeros(int(pad_time*fs))]) for segment in segments]
return numpy.concatenate(padded_segments)
concatenated_signal = concatenate_segments(segments, fs)
# Listen to the newly concatenated signal.
# +
# IPython.display.Audio?
# -
# ## Step 4: Extract Features
# For each segment, compute the zero crossing rate.
# +
# returns a boolean array
# librosa.core.zero_crossings?
# +
# you'll need this to actually count the number of zero crossings per segment
# sum?
# -
# Use `argsort` to find an index array, `ind`, such that `segments[ind]` is sorted by zero crossing rate.
# zcrs: array, number of zero crossings in each frame
ind = numpy.argsort(zcrs)
print ind
# Sort the segments by zero crossing rate, and concatenate the sorted segments.
concatenated_signal = concatenate_segments(segments[ind], fs)
# ## Step 5: Listen to Segments
# Listen to the sorted segments. What do you hear?
# +
# IPython.display.Audio?
# -
# ## More Exercises
# Repeat the steps above for the following audio files:
# +
#url = 'http://audio.musicinformationretrieval.com/conga_groove.wav'
#url = 'http://audio.musicinformationretrieval.com/58bpm.wav'
# -
# [← Back to Index](index.html)
|
feature_sonification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Microestructura y Sistemas de Trading
# ## Notas de Administracion Activa
# +
# Remover todos los objetos del "Environment"
rm(list = ls())
# los 0s aceptados antes de expresas una cifra en notaci?n cient?fica
options("scipen"=100, "digits"=4)
# Cargas librer?as a utilizar
#suppressMessages(library(Quandl)) # Descargar Precios
#suppressMessages(library(ROI)) # Optimizacion para portafolio
#suppressMessages(library(knitr)) # Opciones de documentaci?n + c?digo
#suppressMessages(library(xlsx)) # Leer archivos XLSx
#suppressMessages(library(kableExtra)) # Tablas en HTML
#suppressMessages(library(PortfolioAnalytics)) # Teor?a Moderna de Portafolios
options(knitr.table.format = "html")
# -
tk <- as.data.frame(read.csv(file = "IAK_holdings.csv",header = FALSE, sep = ","))
cs <- c("date", "adj_close")
class(tk)
tk
|
Notas_R/Notas_AdminActiva/Notas_AdministracionActiva.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from IPython.display import display
import os, sys, itertools, csv
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
from mutil.alemutdf import get_all_sample_mut_df, get_gene_mut_count_mat, get_multi_exp_max_freq_mut_df, get_mut_type_avg_frac_across_class_df
from mutil.metadata import get_condition_val_dict, get_condition_field_val_set
from mutil.genome import get_K12_pos_from_BOP27, NON_K12_EXP_L
from mutil.params import ASSOC_ALPHA, MULTI_HYP_CORR_METHOD
pd.options.display.max_columns = 100
# starting efforts for refactoring of assoc NBs.
FEAT_ANNOT = "operons"
LINK_ANNOT = "operon links"
all_muts_df = pd.read_pickle("./data/4_6_df.pkl")
display(all_muts_df.shape, all_muts_df.head())
# +
from mutil.metadata import get_all_exp_cond_d
all_exp_cond_d = get_all_exp_cond_d("./data/metadata/")
all_exp_cond_d["TOL_2,3-butanediol"] = all_exp_cond_d.pop("TOL_2 3-butanediol") # TODO: workaround for bug of missing comma. Fix root bug
all_exp_cond_d
# -
# So that rows will always contain the same amount of things
all_muts_df = all_muts_df.replace('', "None")
display(all_muts_df.shape, all_muts_df.head())
# +
from mutil.metadata_categories_for_associations import METADATA_CATEGORIES_FOR_ASSOCIATIONS
for condition in METADATA_CATEGORIES_FOR_ASSOCIATIONS:
all_muts_df[condition] = all_muts_df["exp"].apply(lambda exp: all_exp_cond_d[exp][condition])
# -
all_muts_df = all_muts_df.reset_index(drop=True)
# The below is the necessary logic without this filtering.
exp_target_cond_df = all_muts_df.copy()
display(exp_target_cond_df.shape, exp_target_cond_df.head())
# +
from mutil.metadata_categories_for_associations import METADATA_CATEGORIES_FOR_ASSOCIATIONS
for condition in METADATA_CATEGORIES_FOR_ASSOCIATIONS:
all_muts_df[condition] = all_muts_df["exp"].apply(lambda exp: all_exp_cond_d[exp][condition])
# -
unique_condition_set = set()
for cond_cat in METADATA_CATEGORIES_FOR_ASSOCIATIONS:
unique_condition_set |= set(exp_target_cond_df[cond_cat].unique())
unique_condition_set
# +
from mutil.feature import get_feat_d
feat_cond_df = pd.DataFrame()
for _, r in exp_target_cond_df.iterrows():
if r["exp"] not in NON_K12_EXP_L:
for op_ID, links in r[LINK_ANNOT].items():
if op_ID != "unknown":
for cond_col in METADATA_CATEGORIES_FOR_ASSOCIATIONS:
if r[cond_col] in unique_condition_set: # I'm not quite sure why I had to check this in the legacy code.
try:
op_feat_d = get_feat_d(RegulonDB_ID=op_ID, json=r[FEAT_ANNOT])
df = pd.DataFrame([{"feature": op_feat_d["name"], "condition": r[cond_col]} for _ in range(0, len(links))])
feat_cond_df = feat_cond_df.append(df, ignore_index=True)
except:
display(r, op_ID, r[FEAT_ANNOT], op_feat_d)
display(len(feat_cond_df), feat_cond_df.head())
# +
from statsmodels.stats import multitest
import scipy
def get_contingency_table(count_mat, row_name, col_name):
# count of feature and condition match
row_col_count = count_mat.loc[row_name, col_name]
# count of feature and NOT condition match
row_not_col_sum_count = count_mat.loc[row_name].sum() - row_col_count
not_row_col_sum_count = count_mat.T.loc[col_name].sum() - row_col_count
all_mat_sum_count = count_mat.sum(axis=1).sum()
not_row_not_col_sum_count = all_mat_sum_count - \
row_col_count - row_not_col_sum_count - not_row_col_sum_count
contingency_table = [
[row_col_count, row_not_col_sum_count],
[not_row_col_sum_count, not_row_not_col_sum_count]
]
return contingency_table
test_df = pd.DataFrame([[1, 2, 3],
[4, 5, 6]],
index=["y1", "y2"],
columns=["x1", "x2", "x3"])
contingency_table = get_contingency_table(test_df, "y2", "x3")
expected_contingency_table = [[6, 9], [3, 3]]
assert(contingency_table == expected_contingency_table)
def get_multiple_hypothesis_correction(pval_df):
# Dataframe seemed to be designed to iterate by column more easily than row (see df.iteritems())
# Have to combine all p-value columns because multitest.multipletests only takes 1D array inputs.
pval_l = []
for col in list(pval_df.columns.values):
pval_l += list(pval_df[col])
corrected_pval_result = multitest.multipletests(
pvals=pval_l,
alpha=ASSOC_ALPHA,
method=MULTI_HYP_CORR_METHOD)
# The following splits the multitest.multipletests 1D array output into the same shape, though transposed.
corrected_pval_l = corrected_pval_result[1]
df_col_len = pval_df.shape[0]
corrected_pval_mat = [corrected_pval_l[i:i+df_col_len]
for i in range(0, len(corrected_pval_l), df_col_len)]
# building df with new p-values
corrected_pval_df = pval_df.copy()
for outer_l_idx in range(0, len(corrected_pval_df.columns)):
for inner_l_idx in range(0, len(corrected_pval_df)):
corrected_pval = corrected_pval_mat[outer_l_idx][inner_l_idx]
corrected_pval_df.iloc[inner_l_idx, outer_l_idx] = corrected_pval
return corrected_pval_df
# def get_enrich_genetic_target_df(cond_col, mut_df):
def get_enrich_genetic_target_df(feat_cond_df):
# Creates tables of counts between each mutation and unique condition.
cross_counts_df = pd.crosstab(
feat_cond_df["feature"], feat_cond_df["condition"]
)
# To reuse the same DF indeces without having to remake it.
enrich_odds_ratio_df = cross_counts_df.copy()
enrich_pvals_df = cross_counts_df.copy()
for cond in cross_counts_df.columns.values:
for feat in cross_counts_df.index:
contingency_table = get_contingency_table(cross_counts_df, feat, cond)
odds_ratio, p_val = scipy.stats.fisher_exact(contingency_table, alternative="greater")
enrich_odds_ratio_df.loc[feat, cond] = odds_ratio
enrich_pvals_df.loc[feat, cond] = p_val
enriched_pvals_df = get_multiple_hypothesis_correction(enrich_pvals_df)
return enrich_odds_ratio_df, enrich_pvals_df, cross_counts_df
# -
enrich_odds_ratio_df, enrich_pvals_df, cross_counts_df = get_enrich_genetic_target_df(feat_cond_df)
signif_genomic_feat_cond_json = []
mut_feat_cond_assoc_json = []
for (mut_serial, row) in enrich_pvals_df.iterrows():
for cond in row.index:
p_val = enrich_pvals_df.at[mut_serial, cond]
odds_ratio = enrich_odds_ratio_df.at[mut_serial, cond]
mut_feat_cond_assoc_json.append({"mutated features": mut_serial, "condition": cond, "odd ratio": odds_ratio, "p value":p_val})
if odds_ratio > 1 and p_val < ASSOC_ALPHA:
signif_genomic_feat_cond_json.append({"mutated features": mut_serial, "condition": cond, "odd ratio": odds_ratio, "p value":p_val})
assoc_df = pd.DataFrame()
for d in mut_feat_cond_assoc_json:
assoc_df = assoc_df.append(d, ignore_index=True)
assoc_df = assoc_df.set_index("mutated features")
assoc_df.to_csv("./data/supp/mut_op_cond_assocs.csv")
import pickle
f = open("./data/signif_operon_cond_json.pkl", 'wb')
pickle.dump(signif_genomic_feat_cond_json, f)
signf_assoc_feat_cond_d = {d["mutated features"]:set() for d in signif_genomic_feat_cond_json}
for d in signif_genomic_feat_cond_json:
target = d["mutated features"]
condition = d["condition"]
if target in signf_assoc_feat_cond_d.keys():
signf_assoc_feat_cond_d[target].add(condition)
else:
signf_assoc_feat_cond_d[target] = {condition}
# signf_assoc_feat_cond_d
# +
def _get_feat_signf_assoc_cond_set(feat_d, mut_conds):
feat_signf_assoc_cond_set = set()
if feat_d["name"] in signf_assoc_feat_cond_d.keys():
# Only includes conditions from exp mut comes from, therefore may be subset of signf assoc cond.
for c in signf_assoc_feat_cond_d[feat_d["name"]]:
if c in mut_conds:
feat_signf_assoc_cond_set.add(c)
return feat_signf_assoc_cond_set
def get_feat_signf_assoc_cond_set_json(mut_df_row, feat_annot_name):
feat_json = []
for d in mut_df_row[feat_annot_name]:
feat_d = d.copy()
mut_conds = list(mut_df_row[METADATA_CATEGORIES_FOR_ASSOCIATIONS])
feat_d["significantly associated conditions"] = _get_feat_signf_assoc_cond_set(d, mut_conds)
feat_json.append(feat_d)
return feat_json
exp_target_cond_df[FEAT_ANNOT] = exp_target_cond_df.apply(lambda r: get_feat_signf_assoc_cond_set_json(r, FEAT_ANNOT), axis=1)
# -
exp_target_cond_df.to_pickle("./data/4_7_df.pkl")
exp_target_cond_df.shape
|
4_7_assoc_operon_to_conds.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import nltk
nltk.download_shell()
messages=[line.strip() for line in open("SMSSpamCollection")]
messages[3]
for i,v in enumerate(messages[:50]):
print(i,v)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
messages=pd.read_csv("SMSSpamCollection",sep="\t",names=["Label","Messages"])
messages
messages.describe()
messages.groupby("Label").describe()
messages["Length"]=messages["Messages"].apply(len)
import string
string.punctuation
from nltk.corpus import stopwords
# +
def text_processing(mess):
"""
1.remove punc
2.remove stopwards
3.return
"""
nopunc=[word for word in mess if word is not string.punctuation]
nopunc="".join(nopunc)
w=[word for word in nopunc.split() if word is not stopwords.word("english") ]
return w
# -
# Check to make sure its working
messages['Messages'].head(5).apply(text_process)
def text_process(mess):
"""
Takes in a string of text, then performs the following:
1. Remove all punctuation
2. Remove all stopwords
3. Returns a list of the cleaned text
"""
# Check characters to see if they are in punctuation
nopunc = [char for char in mess if char not in string.punctuation]
# Join the characters again to form the string.
nopunc = ''.join(nopunc)
# Now just remove any stopwords
return [word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer()
X = cv.fit_transform(text_process(messages['Messages'])).toarray()
y=messages["Label"]
from sklearn.preprocessing import LabelEncoder
l=LabelEncoder()
y=l.fit(y)
y
labelEncoder_y=LabelEncoder()
y=labelEncoder_y.fit_transform(y)
y.shape
X.shape
# +
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 0)
# -
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
import re
corpus = []
for i in range(0, len(messages)):
review = re.sub('[^a-zA-Z]', ' ', messages['Messages'][i])
review = review.lower()
review = review.split()
ps = PorterStemmer()
review = [ps.stem(word) for word in review if not word in set(stopwords.words('english'))]
review = ' '.join(review)
corpus.append(review)
corpus
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer()
X = cv.fit_transform(corpus).toarray()
len(X)
y
y=np.reshape(y,(len(y),1))
X.shape
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 0)
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
word=messages["Messages"][4]
y_pred1=classifier.predict(word)
word
cm
print(classification_report(y_pred,y_test))
|
nlp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/pachterlab/BLCSBGLKP_2020/blob/master/notebooks/.ipynb_checkpoints/lampseq-checkpoint.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="MbCBRM_pQnQJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="9b3ff28e-fe3e-44cd-85b9-a18be1196a45"
# !date
# + id="GeTyr26NQnQV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 136} outputId="a9ac93d8-2964-4cc2-e784-7d06fc3d0055"
# !git clone https://github.com/pachterlab/BLCSBGLKP_2020.git
# !mkdir temporary
# + id="sRf4twTIQnQd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 326} outputId="b19430cf-23a7-4026-9731-6f64752361ab"
# !pip install anndata
# + [markdown] id="LANmmWFvQnQk" colab_type="text"
# # LampSeq
# + [markdown] id="gs7hKEDsQnQk" colab_type="raw"
# Forward primer -- Viral genome sequence -- FIP primer -- Barcode -- FIP Primer
# >A_F3
# TCCAGATGAGGATGAAGAAGA
# >B_F3
# TGGCTACTACCGAAGAGCT
# >C_F3
# AACACAAGCTTTCGGCAG
#
# >A_B3
# AGTCTGAACAACTGGTGTAAG
# >B_B3
# TGCAGCATTGTTAGCAGGAT
# >C_B3
# GAAATTTGGATCTTTGTCATCC
#
# A-FIP-Barcode AGAGCAGCAGAAGTGGCACNNNNNNNNNNAGGTGATTGTGAAGAAGAAGAG
# B-FIP-Barcode TCTGGCCCAGTTCCTAGGTAGTNNNNNNNNNNCCAGACGAATTCGTGGTGG
# C-FIP-Barcode TGCGGCCAATGTTTGTAATCAGNNNNNNNNNNCCAAGGAAATTTTGGGGAC
#
#
#
#
# >B_B3
# TGCAGCATTGTTAGCAGGAT
#
# Read will look like
# B_B3 - B-FIP-Barcode
# read: TGCAGCATTGTTAGCAGGAT TCTGGCCCAGTTCCTAGGTAGT NNNNNNNNNN CCAGACGAATTCGTGGTGG
# biological: 0, 20
# FIP : 20, 42
# Barcode: 42, 52
# FIP:: 52, end
# + id="PW4sD9t3QnQl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="146b89e6-0b61-4eda-9d00-8feffc58e01d"
# We need cmake to install kallisto and bustools from source
# !apt update
# !apt-get install autoconf
# !apt install -y cmake
# + id="Lp16UNmwQnQq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="6e623902-5b54-4d72-d555-dce27c5d81c4"
# !git clone https://github.com/pachterlab/kallisto.git
# !mv kallisto/ temporary/
# !cd temporary/kallisto && git checkout covid && mkdir build && cd build && cmake .. && make
# !chmod +x temporary/kallisto/build/src/kallisto
# !mv temporary/kallisto/build/src/kallisto /usr/local/bin/
# + id="Sb7r9CgUQnQu" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="cf2a7f9b-a1e0-460d-93be-aa309cfa41b6"
# !git clone https://github.com/BUStools/bustools.git
# !mv bustools/ temporary/
# !cd temporary/bustools && git checkout covid && mkdir build && cd build && cmake .. && make
# !chmod +x temporary/bustools/build/src/bustools
# !mv temporary/bustools/build/src/bustools /usr/local/bin/
# + id="Na0EbE6KQnQz" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="60a29c24-c601-4997-b5dd-5ab9cdbec010"
# !kallisto version
# !bustools version
# + id="U66PHITPQnQ4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 153} outputId="abefc194-8f6d-4693-af08-15f9b2151753"
# !kallisto index -i ./temporary/lamp_index.idx -k 9 BLCSBGLKP_2020/data/lampseq/transcriptome.fa
# + id="JTdfIl0sQnRA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 170} outputId="e105b77d-7633-405b-c1b2-a73416a789f1"
# !kallisto bus -x LAMPSeq -t 2 -o ./temporary/out_lamp -i ./temporary/lamp_index.idx BLCSBGLKP_2020/data/lampseq/R1.fastq.gz
# + id="Ky7zP-OfQnRD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="fc8dc3de-0ce0-4e1e-c587-99209a717b9d"
# sort the BUS file by barcode
# !bustools sort -t 2 -m 1G -o temporary/out_lamp/sort.bus temporary/out_lamp/output.bus
# Correct to the barcodes in the whitelist (obtained from the SampleSheet)
# !bustools correct -d temporary/out_lamp/dump.txt -w BLCSBGLKP_2020/data/lampseq/whitelist.txt -o temporary/out_lamp/sort.correct.bus temporary/out_lamp/sort.bus
# Sort again to sum the Amplicon counts
# !bustools sort -t 2 -m 1G -o temporary/out_lamp/sort.correct.sort.bus temporary/out_lamp/sort.correct.bus
# write busfile to text output
# !bustools text -p temporary/out_lamp/sort.correct.sort.bus > temporary/out_lamp/data.txt
# Write the sorted bus file out for barcode QC
# !bustools text -p temporary/out_lamp/sort.bus > temporary/out_lamp/sort.txt
# + id="Y7zpvvrfQnRI" colab_type="code" colab={}
# + id="gc7b6zq1QnRN" colab_type="code" colab={}
# + id="lmgkbp-FQnRS" colab_type="code" colab={}
# + id="j9m_hgLXQnRV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="2b801cfe-ebf7-495e-ac83-c86acd72f5aa"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import string
import anndata
from collections import defaultdict
from collections import OrderedDict
from mpl_toolkits.axes_grid1 import make_axes_locatable
import matplotlib as mpl
import matplotlib.patches as mpatches
from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
from sklearn.preprocessing import scale
from sklearn.preprocessing import normalize
from sklearn.decomposition import TruncatedSVD
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
from scipy.special import expit as sigmoid
def nd(arr):
return np.asarray(arr).reshape(-1)
def yex(ax):
lims = [
np.min([ax.get_xlim(), ax.get_ylim()]), # min of both axes
np.max([ax.get_xlim(), ax.get_ylim()]), # max of both axes
]
# now plot both limits against eachother
ax.plot(lims, lims, 'k-', alpha=0.75, zorder=0)
ax.set_aspect('equal')
ax.set_xlim(lims)
ax.set_ylim(lims)
return ax
cm = {1:"#D43F3A", 0:"#3182bd"}
fsize=20
plt.rcParams.update({'font.size': fsize})
# %config InlineBackend.figure_format = 'retina'
# + id="2wGDaF9wQnRb" colab_type="code" colab={}
df = pd.read_csv("temporary/out_lamp/data.txt", sep="\t", header=None, names=["bcs", "umi", "ecs", "cnt"])
# + id="Yma3PerBQnRm" colab_type="code" colab={}
s = df.groupby("bcs")[["cnt"]].sum()
# + id="wqv2o9mYQnRs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 235} outputId="c2d76c75-d99e-4867-d6cf-6c6849f4e3eb"
s.head()
# + id="qrB8cfmbQnR1" colab_type="code" colab={}
# + [markdown] id="eYkK4IbGQnR5" colab_type="text"
# # Load map between
# + id="lEppPCFfQnR8" colab_type="code" colab={}
m = pd.read_csv( "BLCSBGLKP_2020/data/lampseq/ss2lamp.txt", sep="\t", header=None, names=["ss_bcs", "lamp_bcs"])
# + id="uiFgIfwPQnR_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="ecbe65f1-0fd1-4055-af71-b6363616b7da"
m.head()
# + id="yqz5PzrEQnSD" colab_type="code" colab={}
kb_raw = anndata.read_h5ad("BLCSBGLKP_2020/data/kb/adata.h5ad")
kb_raw.obs.index = kb_raw.obs.bcs.values
# + id="XHOLj4pwQnSG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="ea7b81f0-5cc7-4ebc-85df-5ff798c7c70c"
kb_raw
# + id="l5k1M6WZQnSK" colab_type="code" colab={}
a = np.logical_and((kb_raw.obs.plate=="Plate1").values, (kb_raw.obs.lysate=="HEK293").values)
b = np.logical_and(a, kb_raw.obs.ATCC_RNA.values==0)
c = np.logical_and(b, kb_raw.obs.ATCC_viral.values==0)
kb = kb_raw[b]
# + id="vodX_CfNQnSN" colab_type="code" colab={}
s = s.loc[m.lamp_bcs]
# + id="TP6nBbMBQnSQ" colab_type="code" colab={}
kb = kb[kb.obs.loc[m.ss_bcs].index]
# + id="Oss4ZqsmQnSW" colab_type="code" colab={}
g = "N1"
a = nd(s.cnt.values)
b = nd(kb.layers['raw'][:,kb.var.gene==g])
# + id="1w4vqlDCQnSZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 406} outputId="1e300dd9-94e3-4563-b609-fab6c5708e8e"
fig, ax = plt.subplots(figsize=(5,5))
x = a
y = b
ax.scatter(x, y, color="k")
yex(ax)
ax.set_xlabel("LAMP-seq {} counts".format("B_B3"))
ax.set_ylabel("SwabSeq {} counts".format(g[0]))
ax.xaxis.set_major_formatter(mpl.ticker.StrMethodFormatter('{x:,.0f}'))
ax.yaxis.set_major_formatter(mpl.ticker.StrMethodFormatter('{x:,.0f}'))
for label in ax.get_xticklabels():
label.set_ha("right")
label.set_rotation(45)
#plt.savefig("./figs/ss_v_lamp.png",bbox_inches='tight', dpi=300)
plt.show()
|
notebooks/.ipynb_checkpoints/lampseq-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import pandas as pd
#name columns
giss = pd.read_csv('giss_landocean.csv', names = ['year','2','3','4','5','6','7','8','9','10','11','12','13','14','15','16','17','18','19','20'])
#giss=giss.truncate(before=71, after=100, copy=True)
x = input('Enter Year between 1951 and 1980: ')
#user input year
#locate corresponding row and adjacent rows
row = giss.loc[giss['year']==x].index[0]
row_previous = giss.loc[giss['year']==x-1].index[0]
row_after = giss.loc[giss['year']==x+1].index[0]
#locate column 14 value
#locate previous year and subsequent year value in column 14
T = giss.iloc[row,13]
T_previous = giss.iloc[row_previous,13]
T_after = giss.iloc[row_after,13]
#equation
T2 = ((T/100.000) - .375) * .080
dT = ((abs(T_previous - T)/1.000 + abs(T_after - T)/1.000)/2.000)*2.500
dH = T2 + dT
print("The annual rate of SLR is: {}".format(dH))
|
SLR Equation.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Outlier Detection
# (anomaly detection, noise detection, deviation detection, or exception mining)
#
# ## Definition Outlier
# - An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs. (Grubbs, 1969)
#
# - An observation which appears to be inconsistent with the remainder of that set of data. (Barnett and Lewis, 1994)
#
# ## Objective
# ... to learn what "normal" data look like, and then use this view to detect abnormal instances or new trends in time series.
#
#
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.ticker import StrMethodFormatter
sns.set()
tesla = pd.read_csv('../dataset/TSLA.csv')
tesla['Date'] = pd.to_datetime(tesla['Date'])
tesla.head()
tesla.tail()
# Now we will plot the histogram and check the distribution of the Close Price.
#
# A histogram divides the values within a numerical variable into âbinsâ, and counts the number of observations that fall into each bin. By visualizing these binned counts in a columnar fashion, we can obtain a very immediate and intuitive sense of the distribution of values within a variable.
#
#axs = df_crosscorrelated[['Close', 'ma7', 'ma14', 'ma25']].hist(bins=25, grid=False, figsize=(12,8), color='#86bf91', zorder=2, rwidth=0.9)
ax = tesla.hist(column='Close',bins=25, grid=False, figsize=(12,8), color='#86bf91', zorder=2, rwidth=0.9)
ax = ax[0]
for x in ax:
# Despine
x.spines['right'].set_visible(False)
x.spines['top'].set_visible(False)
x.spines['left'].set_visible(False)
# Switch off ticks
x.tick_params(axis="both", which="both", bottom="off", top="off", labelbottom="on", left="off", right="off", labelleft="on")
# Draw horizontal axis lines
vals = x.get_yticks()
for tick in vals:
x.axhline(y=tick, linestyle='dashed', alpha=0.4, color='#eeeeee', zorder=1)
# Remove title
x.set_title("")
# Set x-axis label
x.set_xlabel("Close Price (USD)", labelpad=20, weight='bold', size=12)
# Set y-axis label
x.set_ylabel("Frequency", labelpad=20, weight='bold', size=12)
# Format y-axis label
x.yaxis.set_major_formatter(StrMethodFormatter('{x:,g}'))
# From the above graph, we can see that data is not centred towards the mean. The value going towards the left to the mean is decreasing whereas it is increasing towards the right.
#
# Let us see the descriptive statistics of this column like mean, standard deviation, min, and maximum values. Use the below code for the same.
tesla['Close'].describe()
# Now we will use 3 standard deviations and everything lying away from this will be treated as an outlier. We will see an upper limit and lower limit using 3 standard deviations. Every data point that lies beyond the upper limit and lower limit will be an outlier. Use the below code for the same.
upper = tesla['Close'].mean() + 3*tesla['Close'].std()
lower = tesla['Close'].mean() - 3*tesla['Close'].std()
print('upper bound: {}'.format(upper))
print('lower bound: {}'.format(lower))
print('{} of {} datapointa are outside 3 standard deviations.'.format(
tesla['Close'].shape[0]-tesla[(tesla['Close']<upper) & (tesla['Close']>lower)].shape[0],
tesla['Close'].shape[0]))
# ## Z-score
#
# Simple, we can use Z-score to detect outliers, which timestamps gave very uncertain high and low value. (to define outliers for a single numeric variable)
#
# It tells us about how far data is away from standard deviation. It is calculated by subtracting the mean from the data point and dividing it by the standard deviation.
#
# The Z-score formula for a sample would be as follows:
#
# $$z=\frac{x-\mu}{\sigma}$$
#
# where:
# - $x$ = score,
# - $\mu$ = mean of the population,
# - $\sigma$ = Population Standard deviation
#
# Let us see practically how this is done.
zscore_close = (tesla['Close'] - tesla['Close'].mean()) / tesla['Close'].std()
# We can see for each row the z score is computed.
#
# Now we will detect only those rows that have z score greater than 3 or less than -3.
#
# Use the function below.
def detect(signal, treshold = 3.0):
detected = []
for i in range(len(signal)):
if np.abs(signal[i]) > treshold:
detected.append(i)
return detected
# Based on z-score table, 3.0 already positioned at 99.73% of the population.
# 
# https://ai-ml-analytics.com/z-scores-in-statistics/
outliers = detect(zscore_close)
print (print('{} of {} datapointa are outside 3 standard deviations.'.format(
np.array(outliers).shape[0],
tesla['Close'].shape[0])))
fig, ax = plt.subplots(figsize=(10,4))
tesla.plot(x='Date',y='Close',ax=ax)
ax.plot(tesla['Date'], tesla['Close'], 'x', markevery=outliers, label="outliers")
ax.hlines(upper, tesla['Date'].min(), tesla['Date'].max(), colors='r', linestyles='dotted', label='upper limit')
plt.legend()
plt.show()
# We can see that, we have outliers but not very usefull.
# ## Lag Correlation and Moving Average
#
# We can create features with lag and moving average to performa a [outliers detection in multivariate data](https://towardsdatascience.com/multivariate-outlier-detection-in-python-e946cfc843b3).
#
# There are various distance metrics, scores, and techniques to detect outliers:
#
# - **Euclidean Distance (ED):** to identify outliers based on their distance to the center point
# - **Mahalanobis Distance (MD):** to identify outliers based on their scaled distance to the center point. It is scaled in such a way, that the principle component axis have unit variance. ([see also](https://en.wikipedia.org/wiki/Mahalanobis_distance))
def df_shift(df,lag=0, start=1, skip=1, rejected_columns = []):
df = df.copy()
if not lag:
return df
cols ={}
for i in range(start,lag+1,skip):
for x in list(df.columns):
if x not in rejected_columns:
if not x in cols:
cols[x] = ['{}_{}'.format(x, i)]
else:
cols[x].append('{}_{}'.format(x, i))
for k,v in cols.items():
columns = v
dfn = pd.DataFrame(data=None, columns=columns, index=df.index)
i = (skip - 1)
for c in columns:
dfn[c] = df[k].shift(periods=i)
i+=skip
df = pd.concat([df, dfn], axis = 1).reindex(df.index)
return df
tesla = tesla[['Date','Close']]
tesla.head(1)
df_crosscorrelated = df_shift(tesla, lag = 10, start = 1, skip = 2,rejected_columns=['Date'])
df_crosscorrelated['ma7'] = df_crosscorrelated['Close'].rolling(7).mean()
df_crosscorrelated['ma14'] = df_crosscorrelated['Close'].rolling(14).mean()
df_crosscorrelated['ma25'] = df_crosscorrelated['Close'].rolling(25).mean()
df_crosscorrelated.head(10)
plt.figure(figsize=(15, 4))
plt.subplot(1,3,1)
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_5'])
plt.title('close vs shifted 5')
plt.subplot(1,3,2)
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_7'])
plt.title('close vs shifted 7')
plt.subplot(1,3,3)
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_9'])
plt.title('close vs shifted 9')
plt.show()
plt.figure(figsize=(10,5))
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_1'],label='close vs shifted 1')
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_3'],label='close vs shifted 3')
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_5'],label='close vs shifted 5')
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_7'],label='close vs shifted 7')
plt.scatter(df_crosscorrelated['Close'],df_crosscorrelated['Close_9'],label='close vs shifted 9')
plt.legend()
plt.show()
fig, ax = plt.subplots(figsize=(10,4))
df_crosscorrelated.plot(x='Date',y=['Close','ma7','ma14','ma25'],ax=ax)
plt.show()
# ### distance between center and point
#
# - center point
# - covariance matrix
# +
selected_column = ['Close','Close_1','Close_3','Close_5','Close_7','Close_9','ma7','ma14','ma25']
crosscorrelated = df_crosscorrelated[selected_column].dropna().to_numpy()
print ('degrees of freedom: {}'.format(crosscorrelated.shape[1]))
# Covariance matrix
covariance = np.cov(crosscorrelated , rowvar=False)
# Covariance matrix power of -1
covariance_pm1 = np.linalg.matrix_power(covariance, -1)
# Center point
centerpoint = np.mean(crosscorrelated , axis=0)
# -
# We are ready to find the distance between the center point and each observation (point) in the data-set. We also need to find a cutoff value from the Chi-Square distribution. The reason why Chi-Square is used to find cutoff value is, Mahalanobis Distance returns the distance as squared ($D^2$). We should also take the quantile value as 0.95 while finding cutoff because the points outside the 0.95 (two-tailed) will be considered as an outlier. Less quantile means less cutoff value. We also need a degree of freedom value for Chi-Square, and it is equal to the number of variables in our data-set, so 9.
# +
from scipy.stats import chi2
# Distances between center point and
distances = []
for i, val in enumerate(crosscorrelated):
p1 = val
p2 = centerpoint
distance = (p1-p2).T.dot(covariance_pm1).dot(p1-p2)
distances.append(distance)
distances = np.array(distances)
# Cutoff (threshold) value from Chi-Sqaure Distribution for detecting outliers
cutoff = chi2.ppf(0.95, crosscorrelated.shape[1])
# Index of outliers
outlierIndexes = np.where(distances > cutoff )
print('--- Index of Outliers ----')
print(outlierIndexes[0])
#print('--- Observations found as outlier -----')
#print(crosscorrelated[ distances > cutoff , :])
# -
fig, ax = plt.subplots(figsize=(10,4))
tesla.plot(x='Date',y='Close',ax=ax)
ax.plot(tesla['Date'], tesla['Close'], 'x', markevery=outlierIndexes[0]+df_crosscorrelated.shape[0]-crosscorrelated.shape[0], label="outliers")
plt.legend()
plt.show()
# +
colormap = plt.cm.RdBu
plt.figure(figsize=(10, 5))
ax=plt.subplot(111)
plt.title('cross correlation', y=1.05, size=16)
selected_column = ['Close','Close_1','Close_3','Close_5','Close_7','Close_9','ma7','ma14','ma25']
sns.heatmap(df_crosscorrelated[selected_column].corr(), ax=ax, linewidths=0.1,vmax=1.0,
square=True, cmap=colormap, linecolor='white', annot=True, fmt='.3f', annot_kws={"fontsize":10})
plt.show()
# -
# ## Clustering
#
# Any instance that has low affinity to all the clusters is likely to be an outier.
#
# ### K-Mean
#
# K-Mean is an algorithm that can cluster datasets with known number of clusters $k$ very efficiently.
#
# Lets train a K-Means cluster on the dataset from above and plot the score as a function of $k$:
# +
from sklearn.cluster import KMeans
n_cluster = range(1, 20)
data = df_crosscorrelated.iloc[:,1:].dropna().values
kmeans = [KMeans(n_clusters=i).fit(data) for i in n_cluster]
scores = [kmeans[i].score(data) for i in range(len(kmeans))]
inertia = [kmeans[i].inertia_ for i in range(len(kmeans))]
fig, ax = plt.subplots(sharex="all",figsize=(10,6))
plt.subplot(2, 1, 1)
plt.plot(n_cluster, scores,'o-')
plt.ylabel('Score')
plt.title('Elbow Curve')
plt.xticks(n_cluster)
plt.subplot(2, 1, 2)
plt.plot(n_cluster, inertia,'o-')
plt.xlabel('Number of Clusters')
plt.ylabel('Inertia')
plt.xticks(n_cluster)
plt.show()
# -
# **Inertia**: Sum of squared distances of samples to their closest cluster center.
#
# **Score**: Opposite of the value of X on the K-means objective.
#
# We can see that after 4 Cluster we are not seeing any more variance so we can train model with 4 Cluster now
# +
from mpl_toolkits.mplot3d import Axes3D
X = df_crosscorrelated[['Close','ma14','ma25']].dropna()
X = X.reset_index(drop=True)
km = KMeans(n_clusters=4)
km.fit(X)
km.predict(X)
labels = km.labels_
fig = plt.figure(1, figsize=(7,7))
ax = Axes3D(fig)
ax.scatter(X.iloc[:,0], X.iloc[:,1], X.iloc[:,2],
c=labels.astype(np.float), edgecolor="k")
ax.set_xlabel("Close")
ax.set_ylabel("ma14")
ax.set_zlabel("ma25")
plt.title("K Means", fontsize=14)
plt.show()
from sklearn.decomposition import PCA
# +
from sklearn.preprocessing import StandardScaler
X = df_crosscorrelated.iloc[:,1:].dropna().values
X_std = StandardScaler().fit_transform(X)
mean_vec = np.mean(X_std, axis=0)
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
eig_pairs = [(np.abs(eig_vals[i]),eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs.sort(key = lambda x: x[0], reverse= True)
tot = sum(eig_vals)
var_exp = [(i/tot)*100 for i in sorted(eig_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.figure(figsize=(10, 5))
plt.bar(range(len(var_exp)), var_exp, alpha=0.3, align='center', label='individual explained variance', color = 'g')
plt.step(range(len(cum_var_exp)), cum_var_exp, where='mid',label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.show();
# -
# You can see that the first component contain 99% Explained variance
# Take useful feature and standardize them
X = df_crosscorrelated.iloc[:,1:].dropna().values
X_std = StandardScaler().fit_transform(X)
data = pd.DataFrame(X_std)
# reduce to 2 important features
pca = PCA(n_components=2)
data = pca.fit_transform(data)
# standardize these 2 new features
scaler = StandardScaler()
np_scaled = scaler.fit_transform(data)
data = pd.DataFrame(np_scaled)
data.tail()
df = df_crosscorrelated.dropna().copy()
kmeans = [KMeans(n_clusters=i).fit(data) for i in n_cluster]
df['cluster'] = kmeans[3].predict(data)
df.index = data.index
df['principal_feature1'] = data[0]
df['principal_feature2'] = data[1]
df['cluster'].value_counts()
df.head()
# plot the different clusters with the 2 main features
fig, ax = plt.subplots(figsize=(10,6))
colors = {0:'red', 1:'blue', 2:'green', 3:'pink', 4:'black', 5:'orange', 6:'cyan', 7:'yellow', 8:'brown', 9:'purple', 10:'white', 11: 'grey'}
ax.scatter(df['principal_feature1'], df['principal_feature2'], c=df["cluster"].apply(lambda x: colors[x]))
plt.show();
# +
# return Series of distance between each point and its distance with the closest centroid
def getDistanceByPoint(data, model):
distance = pd.Series(dtype="float64")
for i in range(0,len(data)):
Xa = np.array(data.loc[i])
Xb = model.cluster_centers_[model.labels_[i]-1]
#distance.set_value(i, np.linalg.norm(Xa-Xb))
distance.at[i]=np.linalg.norm(Xa-Xb)
return distance
outliers_fraction = 0.01
# get the distance between each point and its nearest centroid. The biggest distances are considered as anomaly
distance = getDistanceByPoint(data, kmeans[3])
number_of_outliers = int(outliers_fraction*len(distance))
threshold = distance.nlargest(number_of_outliers).min()
# anomaly1 contain the anomaly result of the above method Cluster (0:normal, 1:anomaly)
df['anomaly1'] = (distance >= threshold).astype(int)
# -
fig, ax = plt.subplots(figsize=(10,6))
colors = {0:'blue', 1:'red'}
ax.scatter(df['principal_feature1'], df['principal_feature2'], c=df["anomaly1"].apply(lambda x: colors[x]))
plt.xlabel('principal feature1')
plt.ylabel('principal feature2')
plt.show()
df.anomaly1.value_counts()
plt.figure(figsize=(15, 6))
plt.plot(df['Close'], label='close',c='b')
plt.plot(df['Close'], 'o', label='outliers',markevery=df.loc[df['anomaly1'] == 1].index.tolist(),c='r')
plt.xticks(np.arange(df.shape[0])[::15],df['Date'][::15],rotation='-45')
plt.legend()
plt.show()
# +
a = df.loc[df['anomaly1'] == 0, 'Close']
b = df.loc[df['anomaly1'] == 1, 'Close']
fig, axs = plt.subplots(figsize=(10,6))
axs.hist([a,b], bins=32, stacked=True, color=['blue', 'red'])
plt.show()
# -
ori_len = df_crosscorrelated.shape[0] - X.shape[0]
ori_len
# +
#np.where(outliers==-1)[0] + ori_len
# -
# ## IsolationForest
#
# I will use IsolationForest from sklearn library. When defining the algorithm there is an important parameter called contamination. It is the percentage of observations that the algorithm will expect as outliers. We fit the X (2 features HP and Speed) to the algorithm and use fit_predict to use it also on X. This produces plain outliers (-1 is outlier, 1 is inlier). We can also use the function decision_function to get the scores Isolation Forest gave to each sample.
# +
from sklearn.ensemble import IsolationForest
X = df_crosscorrelated.iloc[:,1:].dropna().values
np_scaled = StandardScaler().fit_transform(X)
data = pd.DataFrame(np_scaled)
# train isolation forest
model = IsolationForest(contamination=outliers_fraction)
model.fit(data)
df['anomaly2'] = pd.Series(model.predict(np_scaled))
fig, ax = plt.subplots(figsize=(20,10))
a = df.loc[df['anomaly2'] == -1, ['Date', 'Close']] #anomaly
ax.plot(df['Date'], df['Close'], color='blue', label = 'Normal',linewidth=0.7)
ax.scatter(a['Date'],a['Close'], color='red', label = 'Anomaly', s = 200)
plt.legend()
plt.show();
# +
# visualisation of anomaly with avg price repartition
a = df.loc[df['anomaly2'] == 1, 'Close']
b = df.loc[df['anomaly2'] == -1, 'Close']
fig, axs = plt.subplots(figsize=(20,8))
axs.hist([a,b], bins=32, stacked=True, color=['blue', 'red'])
plt.show();
# -
# ## Support Vector Machine (SVM)
#
# A support vector machine is another effective technique for detecting anomalies. A SVM is typically associated with supervised learning, but OneClassSVM can be used to identify anomalies as an unsupervised problems.
#
# ### One class SVM
#
# According to the paper: Support Vector Method for Novelty Detection. SVMs are max-margin methods, i.e. they do not model a probability distribution. The idea of SVM for anomaly detection is to **find a function that is positive for regions with high density of points, and negative for small densities**.
#
# - Unsupervised Outlier Detection.
# - Estimate the support of a high-dimensional distribution.
# - The implementation is based on [libsvm](https://www.csie.ntu.edu.tw/~cjlin/libsvm/).
# +
from sklearn.svm import OneClassSVM
X = df_crosscorrelated.iloc[:,1:].dropna().values
np_scaled = StandardScaler().fit_transform(X)
data = pd.DataFrame(np_scaled)
# train oneclassSVM
model = OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.01)
model.fit(data)
df['anomaly3'] = pd.Series(model.predict(np_scaled))
fig, ax = plt.subplots(figsize=(20,6))
a = df.loc[df['anomaly3'] == -1, ['Date', 'Close']] #anomaly
ax.plot(df['Date'], df['Close'], color='blue', label ='Normal', linewidth = 0.7)
ax.scatter(a['Date'],a['Close'], color='red', label = 'Anomaly', s = 100)
plt.legend()
plt.show();
# +
a = df.loc[df['anomaly3'] == 1, 'Close']
b = df.loc[df['anomaly3'] == -1, 'Close']
fig, axs = plt.subplots(figsize=(20,6))
axs.hist([a,b], bins=32, stacked=True, color=['blue', 'red'])
plt.show();
# -
# ## Gaussian Distribution
#
# We will be using the Gaussian distribution (normal distribution) to develop an anomaly detection algorithm, that is, weâll assume that our data are normally distributed. This is an assumption that cannot hold true for all data sets, yet when it does, it proves an effective method for spotting outliers.
#
# Scikit-Learnâs `covariance.EllipticEnvelope` is a function that tries to figure out the key parameters of our dataâs general distribution by assuming that our entire data is an expression of an underlying multivariate Gaussian distribution.
# +
from sklearn.covariance import EllipticEnvelope
envelope = EllipticEnvelope(contamination = outliers_fraction)
X = df_crosscorrelated.iloc[:,1:].dropna().values
np_scaled = StandardScaler().fit_transform(X)
envelope.fit(np_scaled)
outliers = envelope.predict(np_scaled)
plt.figure(figsize=(15, 6))
plt.plot(df_crosscorrelated['Close'], label='close',c='b')
plt.plot(df_crosscorrelated['Close'], 'o', label='outliers',
markevery=(np.where(outliers==-1)[0] + ori_len).tolist(),c='r')
plt.xticks(np.arange(df_crosscorrelated.shape[0])[::15],df_crosscorrelated['Date'][::15],rotation='-45')
plt.legend()
plt.show()
# +
close = df_crosscorrelated['Close'].values
a = close[np.where(outliers==1)[0]]
b = close[np.where(outliers==-1)[0]]
fig, axs = plt.subplots(figsize=(10,6))
axs.hist([a,b], bins=32, stacked=True, color=['blue', 'red'])
plt.show()
# -
|
misc/outliers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Edge effect jitter in BLS which leads to additional noise
#
# This tutorial shows the effect, as described in our paper ([Hippke & Heller 2019, appendix B](https://arxiv.org/pdf/1901.02015.pdf)).
#
# The original BLS implementation did not account for transit events occurring to be divided between the first and the last bin of the folded light curve. This was noted by <NAME> in 2002, and an updated version of BLS was made (ee-bls.f) to account for this edge effect. The patch is commonly realized by extending the phase array through appending the first bin once again at the end, so that a split transit is stitched together, and
# present once in full length. The disadvantage of this approach has apparently been ignored: The test statistic is affected by a small amount of additional noise. Depending on the trial period, a transit signal (if present) is sometimes partly located in the first and the second bin. The lower (in-transit) flux values from the first bin are appended at the end of the data, resulting in a change of the ratio between out-of-transit and in-transit flux.
# There are phase-folded periods with one, two, or more than two bins which contain the in-transit flux. This causes a variation (over periods) of the summed noise floor, resulting in additional jitter in the test statistic. For typical Kepler light curves, the reduction in detection efficiency is comparable to a reduction in transit depth of ⌠0.1 â 1 %. TLS corrects this effect by subtracting the difference of the summed residuals between the patched
# and the non-patched phased data. A visualization of this effect on the statistic is shown in Fig. B.1, using synthetic data. In real data, the effect is usually overpowered by noise, and was thus ignored, but is nonetheless present.
# We start by creating synthetic test data:
# +
import numpy
import batman
from transitleastsquares import transitleastsquares, period_grid
from astropy.stats import BoxLeastSquares
# Create empty time series to inject transits and noise
numpy.random.seed(seed=0) # reproducibility
start = 12
days = 365.25 * 3
samples_per_day = 12
samples = int(days * samples_per_day)
t = numpy.linspace(start, start + days, samples)
# Use batman to create transits
ma = batman.TransitParams()
ma.t0 = start + 20 # time of inferior conjunction; first transit is X days after start
ma.per = 365.25 # orbital period
ma.rp = 6371 / 696342 # 6371 planet radius (in units of stellar radii)
ma.a = 217 # semi-major axis (in units of stellar radii)
ma.inc = 90 # orbital inclination (in degrees)
ma.ecc = 0 # eccentricity
ma.w = 90 # longitude of periastron (in degrees)
ma.u = [0.5, 0.5] # limb darkening coefficients
ma.limb_dark = "quadratic" # limb darkening model
m = batman.TransitModel(ma, t) # initializes model
original_flux = m.light_curve(ma) # calculates light curve
# Create noise and merge with flux
ppm = 5
stdev = 10**-6 * ppm
noise = numpy.random.normal(0, stdev, int(samples))
y = original_flux + noise
y_box = numpy.copy(y)
t_box = numpy.copy(t)
# -
# Now, we search these data with TLS and BLS:
# +
# Search with TLS
model = transitleastsquares(t, y)
results = model.power(
period_min=360,
period_max=370,
transit_depth_min=ppm*10**-6,
oversampling_factor=10,
duration_grid_step=1.02,
u=[0.4, 0.4],
limb_dark='quadratic',
M_star = 1,
M_star_max=1.1
)
# Search with BLS
periods = period_grid(
R_star=1,
M_star=1,
time_span=(max(t) - min(t)),
period_min=360, # 10.04
period_max=370, # 10.05
oversampling_factor=10)
durations = numpy.linspace(0.2, 0.7, 50)
model = BoxLeastSquares(t_box, y_box)
results_bls = model.power(periods, durations)
# Flatten the BLS periodogram for comparability
chi2 = 1 / results_bls.power
SR = min(chi2) / chi2
SDE = (1 - numpy.mean(SR)) / numpy.std(SR)
SDE_power = SR - numpy.min(SR) # shift down to touch 0
scale = SDE / numpy.max(SDE_power) # scale factor to touch max=SDE
SDE_power = SDE_power * scale
# -
# Finally, we plot the result:
# +
import matplotlib.pyplot as plt
from matplotlib import rcParams; rcParams["figure.dpi"] = 150
fig, axes = plt.subplots(1, 2, sharey=True, figsize=(5, 3))
# TLS
axes[0].plot(
results.periods,
results.power - numpy.median(results.power),
color='black', lw=0.5)
axes[0].set_ylabel(r'SDE')
axes[0].set_xlabel('Period (days)')
axes[0].set_xlim(min(results.periods), max(results.periods))
# BLS
axes[1].plot(
results_bls.period,
SDE_power - numpy.median(SDE_power),
color='black', lw=0.5)
axes[1].set_xlabel('Period (days)')
axes[1].set_xlim(min(periods), max(periods))
# Pretty plotting
plt.subplots_adjust(hspace=0)
plt.subplots_adjust(wspace=0)
axes[1].tick_params("y", left=False)
axes[0].set_xticks([360, 362.5, 365, 367.5])
axes[1].set_xticks([362.5, 365, 367.5, 370])
axes[0].text(361, 0.3, 'TLS')
axes[1].text(361, 0.3, 'BLS jitter');
|
tutorials/08 Edge effect jitter correction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
from copy import deepcopy
import itertools
import jsonlines
from pathlib import Path
from sklearn.metrics import classification_report
from sklearn.metrics import cohen_kappa_score
from tasks.pattern_matching import WinomtPatternMatchingTask
from tasks.pattern_matching.winomt_utils.language_predictors.util import WB_GENDER_TYPES, GENDER
from tasks.contrastive_conditioning import WinomtContrastiveConditioningTask
from translation_models.fairseq_models import load_sota_evaluator
from translation_models.testing_models import DictTranslationModel
# + pycharm={"name": "#%%\n"}
# Define data paths
data_path = Path(".") / "data"
winomt_enru_translations_path = data_path / "google.ru.full.txt"
winomt_enru_annotator1_path = data_path / "en-ru.annotator1.jsonl"
winomt_enru_annotator2_path = data_path / "en-ru.annotator2.jsonl"
# + pycharm={"name": "#%%\n"}
# Load annotations
with jsonlines.open(winomt_enru_annotator1_path) as f:
annotations1 = {line["Sample ID"]: line for line in f}
with jsonlines.open(winomt_enru_annotator2_path) as f:
annotations2 = {line["Sample ID"]: line for line in f}
# Flatten labels
for key in annotations1:
annotations1[key]["label"] = annotations1[key]["label"][0]
for key in annotations2:
annotations2[key]["label"] = annotations2[key]["label"][0]
# + pycharm={"name": "#%%\n"}
# Remove samples that were only partially annotated
for key in list(annotations1.keys()):
if key not in annotations2:
del annotations1[key]
for key in list(annotations2.keys()):
if key not in annotations1:
del annotations2[key]
# + pycharm={"name": "#%%\n"}
# Inter-annotator agreement before data cleaning
keys = list(annotations1.keys())
labels1 = [annotations1[key]["label"] for key in keys]
labels2 = [annotations2[key]["label"] for key in keys]
kappa = cohen_kappa_score(labels1, labels2)
print(kappa)
# + pycharm={"name": "#%%\n"}
# Clean data
for annotations in [annotations1, annotations2]:
for key in keys:
# Treat neutral as correct
if annotations[key]["label"] == "Both / Neutral / Ambiguous":
annotations[key]["label"] = annotations[key]["Gold Gender"].title()
# Treat bad as wrong
if annotations[key]["label"] == "Translation too bad to tell":
annotations[key]["label"] = "Male" if annotations[key]["Gold Gender"] == "female" else "Female"
# + pycharm={"name": "#%%\n"}
# Inter-annotator agreement after data cleaning
keys = list(annotations1.keys())
labels1 = [annotations1[key]["label"] for key in keys]
labels2 = [annotations2[key]["label"] for key in keys]
kappa = cohen_kappa_score(labels1, labels2)
print(kappa)
# + pycharm={"name": "#%%\n"}
# Merge annotations
annotations = list(itertools.chain(annotations1.values(), annotations2.values()))
# + pycharm={"name": "#%%\n"}
# Load translations
with open(winomt_enru_translations_path) as f:
translations = {line.split(" ||| ")[0].strip(): line.split(" ||| ")[1].strip() for line in f}
# + pycharm={"name": "#%%\n"}
# Run classic (pattern-matching) WinoMT
winomt_pattern_matching = WinomtPatternMatchingTask(
tgt_language="ru",
skip_neutral_gold=False,
verbose=True,
)
pattern_matching_evaluated_samples = winomt_pattern_matching.evaluate(DictTranslationModel(translations)).samples
# + pycharm={"name": "#%%\n"}
# Run contrastive conditioning
evaluator_model = load_sota_evaluator("ru")
winomt_contrastive_conditioning = WinomtContrastiveConditioningTask(
evaluator_model=evaluator_model,
skip_neutral_gold=False,
category_wise_weighting=True,
)
contrastive_conditioning_weighted_evaluated_samples = winomt_contrastive_conditioning.evaluate(DictTranslationModel(translations)).samples
# + pycharm={"name": "#%%\n"}
# Create unweighted contrastive conditioning samples
contrastive_conditioning_unweighted_evaluated_samples = deepcopy(contrastive_conditioning_weighted_evaluated_samples)
for sample in contrastive_conditioning_unweighted_evaluated_samples:
sample.weight = 1
# + pycharm={"name": "#%%\n"}
# Evaluate
for evaluated_samples in [
pattern_matching_evaluated_samples,
contrastive_conditioning_unweighted_evaluated_samples,
contrastive_conditioning_weighted_evaluated_samples,
]:
predicted_labels = []
gold_labels = []
weights = []
for annotation in annotations:
gold_labels.append(WB_GENDER_TYPES[annotation["label"].lower()].value)
sample_index = int(annotation["Index"])
evaluated_sample = evaluated_samples[sample_index]
assert evaluated_sample.sentence == annotation["Source Sentence"]
if hasattr(evaluated_sample, "predicted_gender"):
predicted_gender = evaluated_sample.predicted_gender.value
# Convert neutral or unknown to gold in order to treat classic WinoMT as fairly as possible
if predicted_gender in {GENDER.neutral.value, GENDER.unknown.value}:
predicted_gender = evaluated_sample.gold_gender.value
else:
if evaluated_sample.is_correct:
predicted_gender = WB_GENDER_TYPES[evaluated_sample.gold_gender].value
else:
predicted_gender = int(not WB_GENDER_TYPES[evaluated_sample.gold_gender].value)
predicted_labels.append(predicted_gender)
weights.append(getattr(evaluated_sample, "weight", 1))
class_labels = [gender.value for gender in GENDER][:2]
target_names = [gender.name for gender in GENDER][:2]
print(classification_report(
y_true=gold_labels,
y_pred=predicted_labels,
labels=class_labels,
target_names=target_names,
sample_weight=weights,
zero_division=True,
digits=3,
))
# -
|
human_validation/winomt/human_validation_winomt_enru.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # k-Nearest Neighbor (kNN) exercise
#
# *Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the [assignments page](http://vision.stanford.edu/teaching/cs231n/assignments.html) on the course website.*
#
# The kNN classifier consists of two stages:
#
# - During training, the classifier takes the training data and simply remembers it
# - During testing, kNN classifies every test image by comparing to all training images and transfering the labels of the k most similar training examples
# - The value of k is cross-validated
#
# In this exercise you will implement these steps and understand the basic Image Classification pipeline, cross-validation, and gain proficiency in writing efficient, vectorized code.
# +
# Run some setup code for this notebook.
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
# %matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
# %load_ext autoreload
# %autoreload 2
# +
# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print 'Training data shape: ', X_train.shape
print 'Training labels shape: ', y_train.shape
print 'Test data shape: ', X_test.shape
print 'Test labels shape: ', y_test.shape
# -
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
# +
# Subsample the data for more efficient code execution in this exercise
num_training = 5000
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
# -
# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print X_train.shape, X_test.shape
# +
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
# -
# We would now like to classify the test data with the kNN classifier. Recall that we can break down this process into two steps:
#
# 1. First we must compute the distances between all test examples and all train examples.
# 2. Given these distances, for each test example we find the k nearest examples and have them vote for the label
#
# Lets begin with computing the distance matrix between all training and test examples. For example, if there are **Ntr** training examples and **Nte** test examples, this stage should result in a **Nte x Ntr** matrix where each element (i,j) is the distance between the i-th test and j-th train example.
#
# First, open `cs231n/classifiers/k_nearest_neighbor.py` and implement the function `compute_distances_two_loops` that uses a (very inefficient) double loop over all pairs of (test, train) examples and computes the distance matrix one element at a time.
# +
# Open cs231n/classifiers/k_nearest_neighbor.py and implement
# compute_distances_two_loops.
# Test your implementation:
dists = classifier.compute_distances_two_loops(X_test)
print dists.shape
# -
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()
# **Inline Question #1:** Notice the structured patterns in the distance matrix, where some rows or columns are visible brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)
#
# - What in the data is the cause behind the distinctly bright rows?
# - What causes the columns?
# **Your Answer**: *fill this in.*
#
#
# +
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)
# -
# You should expect to see approximately `27%` accuracy. Now lets try out a larger `k`, say `k = 5`:
y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)
# You should expect to see a slightly better performance than with `k = 1`.
# +
# Now lets speed up distance matrix computation by using partial vectorization
# with one loop. Implement the function compute_distances_one_loop and run the
# code below:
dists_one = classifier.compute_distances_one_loop(X_test)
# To ensure that our vectorized implementation is correct, we make sure that it
# agrees with the naive implementation. There are many ways to decide whether
# two matrices are similar; one of the simplest is the Frobenius norm. In case
# you haven't seen it before, the Frobenius norm of two matrices is the square
# root of the squared sum of differences of all elements; in other words, reshape
# the matrices into vectors and compute the Euclidean distance between them.
difference = np.linalg.norm(dists - dists_one, ord='fro')
print 'Difference was: %f' % (difference, )
if difference < 0.001:
print 'Good! The distance matrices are the same'
else:
print 'Uh-oh! The distance matrices are different'
# +
# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print 'Difference was: %f' % (difference, )
if difference < 0.001:
print 'Good! The distance matrices are the same'
else:
print 'Uh-oh! The distance matrices are different'
# +
# Let's compare how fast the implementations are
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print 'Two loop version took %f seconds' % two_loop_time
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print 'One loop version took %f seconds' % one_loop_time
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print 'No loop version took %f seconds' % no_loop_time
# you should see significantly faster performance with the fully vectorized implementation
# -
# ### Cross-validation
#
# We have implemented the k-Nearest Neighbor classifier but we set the value k = 5 arbitrarily. We will now determine the best value of this hyperparameter with cross-validation.
# +
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
pass
################################################################################
# END OF YOUR CODE #
################################################################################
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
pass
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print 'k = %d, accuracy = %f' % (k, accuracy)
# +
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
# +
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 1
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)
|
assignment1/.ipynb_checkpoints/knn-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Demo notebook
# We can also create parts of our Jupyter Book based on Jupyter Notebooks.
# Let's simulate data for two conditions and print their first ten rows:
# +
import numpy as np
cond_1 = np.random.rand(100)
print(f'Condition 1 = {cond_1[:10]}')
cond_2 = cond_1 + (np.random.rand(100))
print(f'Condition 2 = {cond_2[:10]}')
# -
# We can also display in our Jupyter Book more complex datastructures, like pandas dataframes:
# +
import pandas as pd
df = pd.DataFrame(
{'condition_1': cond_1, 'condition_2': cond_2},
index=np.arange(100)
)
df[:10]
# -
# And of course, we can display plots as well!
# +
import matplotlib.pyplot as plt
plt.scatter(cond_1, cond_2, alpha=.6)
plt.xlabel('condition 1')
plt.ylabel('condition 2')
plt.title('Scatterplot')
plt.show()
|
content/demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
prostade_dataframe = pd.read_csv('modeled_metastatic_prostate_cancer_incidence.csv')
prostade_dataframe
continued = prostade_dataframe[prostade_dataframe['Runtype'] == 'continued']
continued.head(5)
continued.plot(x ='Year', y='FHCRC')
continued.plot(x ='Year', y='UMICH')
discontinued = prostade_dataframe[prostade_dataframe['Runtype'] == 'discontinued']
descontinued.head(5)
|
EDA-Havard.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Name
# Data preparation using PySpark on Cloud Dataproc
#
#
# # Label
# Cloud Dataproc, GCP, Cloud Storage,PySpark, Kubeflow, pipelines, components
#
#
# # Summary
# A Kubeflow Pipeline component to prepare data by submitting a PySpark job to Cloud Dataproc.
#
#
# # Details
# ## Intended use
# Use the component to run an Apache PySpark job as one preprocessing step in a Kubeflow Pipeline.
#
#
# ## Runtime arguments
# | Argument | Description | Optional | Data type | Accepted values | Default |
# |----------------------|------------|----------|--------------|-----------------|---------|
# | project_id | The ID of the Google Cloud Platform (GCP) project that the cluster belongs to. | No | GCPProjectID | | |
# | region | The Cloud Dataproc region to handle the request. | No | GCPRegion | | |
# | cluster_name | The name of the cluster to run the job. | No | String | | |
# | main_python_file_uri | The HCFS URI of the Python file to use as the driver. This must be a .py file. | No | GCSPath | | |
# | args | The arguments to pass to the driver. Do not include arguments, such as --conf, that can be set as job properties, since a collision may occur that causes an incorrect job submission. | Yes | List | | None |
# | pyspark_job | The payload of a [PySparkJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/PySparkJob). | Yes | Dict | | None |
# | job | The payload of a [Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs). | Yes | Dict | | None |
#
# ## Output
# Name | Description | Type
# :--- | :---------- | :---
# job_id | The ID of the created job. | String
#
# ## Cautions & requirements
#
# To use the component, you must:
# * Set up a GCP project by following this [guide](https://cloud.google.com/dataproc/docs/guides/setup-project).
# * [Create a new cluster](https://cloud.google.com/dataproc/docs/guides/create-cluster).
# * Run the component under a secret [Kubeflow user service account](https://www.kubeflow.org/docs/started/getting-started-gke/#gcp-service-accounts) in a Kubeflow cluster. For example:
#
# ```
# component_op(...).apply(gcp.use_gcp_secret('user-gcp-sa'))
# ```
# * Grant the Kubeflow user service account the role `roles/dataproc.editor` on the project.
#
# ## Detailed description
#
# This component creates a PySpark job from the [Dataproc submit job REST API](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs/submit).
#
# Follow these steps to use the component in a pipeline:
#
# 1. Install the Kubeflow Pipeline SDK:
# +
# %%capture --no-stderr
KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.14/kfp.tar.gz'
# !pip3 install $KFP_PACKAGE --upgrade
# -
# 2. Load the component using KFP SDK
# +
import kfp.components as comp
dataproc_submit_pyspark_job_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/a97f1d0ad0e7b92203f35c5b0b9af3a314952e05/components/gcp/dataproc/submit_pyspark_job/component.yaml')
help(dataproc_submit_pyspark_job_op)
# -
# ### Sample
#
# Note: The following sample code works in an IPython notebook or directly in Python code. See the sample code below to learn how to execute the template.
#
#
# #### Setup a Dataproc cluster
#
# [Create a new Dataproc cluster](https://cloud.google.com/dataproc/docs/guides/create-cluster) (or reuse an existing one) before running the sample code.
#
#
# #### Prepare a PySpark job
#
# Upload your PySpark code file to a Cloud Storage bucket. For example, this is a publicly accessible `hello-world.py` in Cloud Storage:
# !gsutil cat gs://dataproc-examples-2f10d78d114f6aaec76462e3c310f31f/src/pyspark/hello-world/hello-world.py
# #### Set sample parameters
# + tags=["parameters"]
PROJECT_ID = '<Please put your project ID here>'
CLUSTER_NAME = '<Please put your existing cluster name here>'
REGION = 'us-central1'
PYSPARK_FILE_URI = 'gs://dataproc-examples-2f10d78d114f6aaec76462e3c310f31f/src/pyspark/hello-world/hello-world.py'
ARGS = ''
EXPERIMENT_NAME = 'Dataproc - Submit PySpark Job'
# -
# #### Example pipeline that uses the component
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='Dataproc submit PySpark job pipeline',
description='Dataproc submit PySpark job pipeline'
)
def dataproc_submit_pyspark_job_pipeline(
project_id = PROJECT_ID,
region = REGION,
cluster_name = CLUSTER_NAME,
main_python_file_uri = PYSPARK_FILE_URI,
args = ARGS,
pyspark_job='{}',
job='{}',
wait_interval='30'
):
dataproc_submit_pyspark_job_op(
project_id=project_id,
region=region,
cluster_name=cluster_name,
main_python_file_uri=main_python_file_uri,
args=args,
pyspark_job=pyspark_job,
job=job,
wait_interval=wait_interval).apply(gcp.use_gcp_secret('user-gcp-sa'))
# #### Compile the pipeline
pipeline_func = dataproc_submit_pyspark_job_pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
# #### Submit the pipeline for execution
# +
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
# -
# ## References
#
# * [Create a new Dataproc cluster](https://cloud.google.com/dataproc/docs/guides/create-cluster)
# * [PySparkJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/PySparkJob)
# * [Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs)
#
# ## License
# By deploying or using this software you agree to comply with the [AI Hub Terms of Service](https://aihub.cloud.google.com/u/0/aihub-tos) and the [Google APIs Terms of Service](https://developers.google.com/terms/). To the extent of a direct conflict of terms, the AI Hub Terms of Service will control.
|
components/gcp/dataproc/submit_pyspark_job/sample.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
############## PLEASE RUN THIS CELL FIRST! ###################
# import everything and define a test runner function
from importlib import reload
from helper import run
import ecc, helper
# -
# Verify curve Example
prime = 137
x, y = 73, 128
print(y**2 % prime == (x**3 + 7) % prime)
# ### Exercise 1
# Find out which points are valid on the curve \\( y^2 = x^3 + 7: F_{223} \\)
# ```
# (192,105), (17,56), (200,119), (1,193), (42,99)
# ```
#
# +
# Exercise 1
from ecc import FieldElement, Point
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
points = ((192,105), (17,56), (200,119), (1,193), (42,99))
# iterate over points
# Initialize points this way:
# x = FieldElement(x_raw, prime)
# y = FieldElement(y_raw, prime)
# try initializing, ValueError means not on curve
# p = Point(x, y, a, b)
# print whether it's on the curve or not
# -
# ### Exercise 2
#
#
#
#
# #### Make [this test](/edit/session2/ecc.py) pass: `ecc.py:ECCTest:test_on_curve`
# +
# Exercise 2
reload(ecc)
run(ecc.ECCTest('test_on_curve'))
# -
from ecc import FieldElement, Point
# Example where x1 != x2
prime = 137
a = FieldElement(0, prime)
b = FieldElement(7, prime)
p1 = Point(FieldElement(73, prime), FieldElement(128, prime), a, b)
p2 = Point(FieldElement(46, prime), FieldElement(22, prime), a, b)
print(p1+p2)
# ### Exercise 3
# Find the following point additions on the curve \\( y^2 = x^3 + 7: F_{223} \\)
# ```
# (192,105) + (17,56), (47,71) + (117,141), (143,98) + (76,66)
# ```
#
# +
# Exercise 3
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
additions = ((192, 105, 17, 56), (47, 71, 117, 141), (143, 98, 76, 66))
# iterate over the additions to be done
# Initialize points this way:
# x1 = FieldElement(x1_raw, prime)
# y1 = FieldElement(y1_raw, prime)
# p1 = Point(x1, y1, a, b)
# x2 = FieldElement(x2_raw, prime)
# y2 = FieldElement(y2_raw, prime)
# p2 = Point(x2, y2, a, b)
# print p1+p2
# -
# ### Exercise 4
#
#
#
#
# #### Make [this test](/edit/session2/ecc.py) pass: `ecc.py:ECCTest:test_add`
# +
# Exercise 4
reload(ecc)
run(ecc.ECCTest('test_add'))
# -
from ecc import FieldElement, Point
# Example where x1 != x2
prime = 137
a = FieldElement(0, prime)
b = FieldElement(7, prime)
p = Point(FieldElement(73, prime), FieldElement(128, prime), a, b)
print(p+p)
# ### Exercise 5
# Find the following scalar multiplications on the curve \\( y^2 = x^3 + 7: F_{223} \\)
#
# * 2*(192,105)
# * 2*(143,98)
# * 2*(47,71)
# * 4*(47,71)
# * 8*(47,71)
# * 21*(47,71)
#
# #### Hint: add the point to itself n times
#
# +
# Exercise 5
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
multiplications = ((2, 192, 105), (2, 143, 98), (2, 47, 71), (4, 47, 71), (8, 47, 71), (21, 47, 71))
# iterate over the multiplications
# Initialize points this way:
# x = FieldElement(x_raw, prime)
# y = FieldElement(y_raw, prime)
# p = Point(x, y, a, b)
# start product at 0 (point at infinity)
# loop over n times (n is 2, 4, 8 or 21 in the above examples)
# add the point to the product
# print product
# -
from ecc import FieldElement, Point
# Group Example
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
g = Point(FieldElement(47, prime), FieldElement(71, prime), a, b)
inf = Point(None, None, a, b)
total = g
count = 1
while total != inf:
print('{}:{}'.format(count, total))
total += g
count += 1
print('{}:{}'.format(count, total))
# ### Exercise 6
# Find out what the order of the group generated by (15, 86) is on \\( y^2 = x^3 + 7: F_{223} \\)
#
# #### Hint: add the point to itself until you get the point at infinity
#
# +
# Exercise 6
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
x = FieldElement(15, prime)
y = FieldElement(86, prime)
p = Point(x, y, a, b)
inf = Point(None, None, a, b)
# start product at point
# start counter at 1
# loop until you get point at infinity (0)
# add the point to the product
# increment counter
# print counter
# -
# ### Exercise 7
#
#
#
#
# #### Make [this test](/edit/session2/ecc.py) pass: `ecc.py:ECCTest:test_rmul`
# +
# Exercise 7
reload(ecc)
run(ecc.ECCTest('test_rmul'))
# -
# Confirgming G is on the curve
p = 2**256 - 2**32 - 977
x = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
y = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
print(y**2 % p == (x**3 + 7) % p)
# Confirming order of G is n
from ecc import G
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
print(n*G)
# Getting the public point from a secret
from ecc import G
secret = 999
point = secret*G
print(point)
# ### Exercise 8
# Get the public point where the scalar is the following:
#
# * 7
# * 1485
# * \\(2^{128}\\)
# * \\(2^{240}+2^{31}\\)
#
# +
# Exercise 8
secrets = (7, 1485, 2**128, 2**240+2**31)
# iterate over secrets
# get the public point
# -
# ### Exercise 9
#
#
#
#
# #### Make [this test](/edit/session2/ecc.py) pass: `ecc.py:S256Test:test_pubpoint`
# +
# Exercise 9
reload(ecc)
run(ecc.S256Test('test_pubpoint'))
# -
# SEC Example
from ecc import S256Point
point = S256Point(0x5CBDF0646E5DB4EAA398F365F2EA7A0E3D419B7E0330E39CE92BDDEDCAC4F9BC, 0x6AEBCA40BA255960A3178D6D861A54DBA813D0B813FDE7B5A5082628087264DA)
uncompressed = b'\x04' + point.x.num.to_bytes(32, 'big') + point.y.num.to_bytes(32, 'big')
print(uncompressed.hex())
if point.y.num % 2 == 1:
compressed = b'\x03' + point.x.num.to_bytes(32, 'big')
else:
compressed = b'\x02' + point.x.num.to_bytes(32, 'big')
print(compressed.hex())
# ### Exercise 10
# Find the compressed and uncompressed SEC format for pub keys where the private keys are:
# ```
# 999**3, 123, 42424242
# ```
#
# +
# Exercise 10
secrets = (999**3, 123, 42424242)
# iterate through secrets
# get public point
# uncompressed - b'\x04' followed by x coord, then y coord
# here's how you express a coordinate in bytes: some_integer.to_bytes(32, 'big')
# compressed - b'\x02'/b'\x03' follewed by x coord. 02 if y is even, 03 otherwise
# print the .hex() of both
# -
# ### Exercise 11
#
#
#
#
# #### Make [this test](/edit/session2/ecc.py) pass: `ecc.py:S256Test:test_sec`
# +
# Exercise 11
reload(ecc)
run(ecc.S256Test('test_sec'))
# -
# Address Example
from helper import encode_base58, hash160, hash256
sec = bytes.fromhex('025CBDF0646E5DB4EAA398F365F2EA7A0E3D419B7E0330E39CE92BDDEDCAC4F9BC')
h160 = hash160(sec)
raw = b'\x00' + h160
raw = raw + hash256(raw)[:4]
addr = encode_base58(raw)
print(addr)
# ### Exercise 12
# Find the mainnet and testnet addresses corresponding to the private keys:
#
# * \\(888^3\\), compressed
# * 321, uncompressed
# * 4242424242, uncompressed
#
# +
# Exercise 12
from ecc import G
components = (
# (secret, compressed)
(888**3, True),
(321, False),
(4242424242, False),
)
# iterate through components
# get the public point
# get the sec format
# hash160 the result
# prepend b'\x00' for mainnet b'\x6f' for testnet
# raw is the prefix + h160
# get the hash256 of the raw, first 4 bytes are the checksum
# append checksum
# encode_base58 the whole thing
# -
# ### Exercise 13
#
#
#
#
# #### Make [this test](/edit/session2/helper.py) pass: `helper.py:HelperTest:test_encode_base58_checksum`
# +
# Exercise 13
reload(helper)
run(helper.HelperTest('test_encode_base58_checksum'))
# -
# ### Exercise 14
#
#
#
#
# #### Make [this test](/edit/session2/ecc.py) pass: `ecc.py:S256Test:test_address`
# +
# Exercise 14
reload(ecc)
run(ecc.S256Test('test_address'))
# -
# ### Exercise 15
# Create a testnet address using your own secret key (use your name and email as the password if you can't think of anything). Record this secret key for tomorrow!
#
# +
# Exercise 15
from ecc import G
from helper import little_endian_to_int, hash256
# use a passphrase
passphrase = b'<<PASSWORD> with your <PASSWORD> and email>'
secret = little_endian_to_int(hash256(passphrase))
# get the public point
# if you completed 7.2, just do the .address(testnet=True) method on the public point
|
session2/session2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Read the dataset
# +
import pandas as pd
df = pd.read_csv('b.csv')
# -
df.info()
# Clean the data
categoryCol=['substrict','type','direction']
for i in categoryCol:
df[i]=df[i].astype("category")
# +
df['time'] = pd.to_datetime(df['time'], format='%Y.%m.%d')
for i in range(len(df)):
if df.loc[i,'time'] < pd.Timestamp(2011, 1, 1):
df.loc[i,'time']=pd.Timestamp(2011, 1, 1)
# -
def cleanMinus(data):
data=str(data)
if data.find('-')==-1:
return data
data=data.split('-')
return data[0]
def cleanColMinus(df,colName):
for i in range(len(df)):
df.loc[i,colName]=cleanMinus(df.loc[i,colName])
minusCols=['price','price per m2']
for i in minusCols:
cleanColMinus(df,i)
df[i]=df[i].astype('float64')
# Finish the data cleaning
df.info()
df.index = df['time']
df.price.plot(figsize=(15,8), title= 'house price trend', fontsize=14)
df['price per m2'].plot(figsize=(15,8), title= 'average price per m2', fontsize=14)
from sklearn.tree import DecisionTreeClassifier
df
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit(df['substrict'])
print(le.transform(df['substrict']))
list(le.classes_)
# +
typeEncoder=preprocessing.LabelEncoder().fit(df['type'])
directionEncoder=preprocessing.LabelEncoder().fit(df['direction'])
df['type']=typeEncoder.transform(df['type'])
df['direction']=directionEncoder.transform(df['direction'])
# -
df
# +
clf = DecisionTreeClassifier()
X_train=df[['X','Y','time','type','direction','square']]
X_train=df[['X','Y','type','direction','square']]
y_train=df['price']
clf = clf.fit(X_train,y_train)
# -
y_pred = clf.predict(X_train)
# Now, we calculate the RMSE value.
((y_pred - y_train) ** 2).mean() ** .5
from sklearn.linear_model import LinearRegression
linearclf=LinearRegression()
linearclf = linearclf.fit(X_train,y_train)
linear_pred = linearclf.predict(X_train)
linearRMSE=((linear_pred - y_train) ** 2).mean() ** .5
print(linearRMSE)
print(y_pred)
from sklearn.neighbors import KNeighborsClassifier
knnclf = KNeighborsClassifier()
knnclf = knnclf.fit(X_train,y_train)
knn_pred = knnclf.predict(X_train)
knnRMSE=((knn_pred - y_train) ** 2).mean() ** .5
print(knnRMSE)
from sklearn.neural_network import MLPClassifier
mlpclf = MLPClassifier(random_state=0, max_iter=800,alpha = 1e-4,hidden_layer_sizes = (50,50),verbose = True)
mlpclf = mlpclf.fit(X_train,y_train)
mlp_pred = mlpclf.predict(X_train)
mlpRMSE=((mlp_pred - y_train) ** 2).mean() ** .5
print(mlpRMSE)
# +
df.price.plot(figsize=(15,8), title= 'house price trend', fontsize=14)
# +
import matplotlib.pylab as plt
plt.plot(forecast_trend)
# +
from statsmodels.tsa.arima_model import ARMA
if __name__ == '__main__':
mpl.rcParams['font.sans-serif'] = 'SimHei'
mpl.rcParams['axes.unicode_minus'] = False
data=pd.read_csv('AirPassengers.csv',header=0,names=['date','peo_num'])
data = pd.Series(data["peo_num"].values, \
index=pd.DatetimeIndex(data["date"].values, freq='MS'))
decomposition=seasonal_decompose(data,model='additive')
trend=decomposition.trend
seasonal=decomposition.seasonal
residual=decomposition.resid
#对äžéšååå«è¿è¡æå
trend.dropna(inplace=True)
trend_diff=trend.diff(periods=2)
trend_diff.dropna(inplace=True)
#åå«å¯¹äžéšåè¿è¡æåz
order_trend=sm.tsa.stattools.arma_order_select_ic(trend_diff)['bic_min_order']
#order_trend=(3,2)
model_trend=ARMA(trend_diff,order_trend)
result_trend=model_trend.fit()
predict_trend=result_trend.predict()+trend.shift(2)
forecast_trend,_,_=result_trend.forecast(11)
forecast_trend=pd.Series(forecast_trend, index=pd.DatetimeIndex(start='1960-07-01',end='1961-05-01',freq='MS'))
trend_predict=pd.concat([predict_trend,forecast_trend],axis=0)
for i in range(11,0,-1):
trend_predict.values[-i]+=trend_predict[-i-2]
value_seasonal=[]
for i in range(5):
value_seasonal.append(seasonal.values[i])
forecast_seasonal=pd.Series(value_seasonal,\
index=pd.DatetimeIndex(start='1961-01-01',end='1961-05-01',freq='MS'))
seasonal_predict=pd.concat([seasonal,forecast_seasonal],axis=0)
residual.dropna(inplace=True)
order_residual=sm.tsa.stattools.arma_order_select_ic(residual)['bic_min_order']
model_residual=ARMA(residual,order_residual)
result_residual=model_residual.fit()
predict_residual=result_residual.predict()
forecast_residual,_,_=result_residual.forecast(11)
forecast_residual=pd.Series(forecast_residual,\
index=pd.DatetimeIndex(start='1960-07-01',end='1961-05-01',freq='MS'))
residual_predict=pd.concat([predict_residual,forecast_residual],axis=0)
test_data=trend_predict+seasonal_predict+residual_predict
print(test_data)
data.plot(label='train_data',legend=True)
test_data.plot(label='forecast_data',legend=True)
|
ml/demo/myhouse.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Ea9Dg91MUTCS"
# **CS3753-Data Science Project by <NAME>**
# + id="yO12UHBqUdEN"
#imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#ML model imports
from sklearn.preprocessing import LabelEncoder
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# + [markdown] id="tICx7vaS7a7S"
# **Load and Prepare data**
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="tpwinbiRVnPH" outputId="8b38adf0-c328-4937-fca6-28d3a056a102"
#Load the data
data = pd.read_csv('train.csv')
#Print some rows
data.head()
# + colab={"base_uri": "https://localhost:8080/"} id="m5QUjRsirEgV" outputId="5b9eec40-0dcd-480d-85e9-729dccda573f"
#get the original shape
print('Shape of the original data (rows,columns) = ' + str(np.array(data).shape))
# + [markdown] id="YDNNC3ks70JE"
# **Data pre-processing to clean**
# + colab={"base_uri": "https://localhost:8080/"} id="Rkdsur8_8DOq" outputId="4f3dbcb8-7749-42d1-dc90-4397eeae7616"
#Get empty values
data.isna().sum()
# + id="4HDxzoZ48wcZ"
#drop empty vaues
data = data.drop(["Cabin", "Name","Ticket","PassengerId"], axis=1)
data = data.dropna(subset=['Embarked', 'Age'])
# + colab={"base_uri": "https://localhost:8080/"} id="Dsk9Zlej9Wc9" outputId="2df45235-7a06-4c69-c616-d5a3a5b09093"
#check the data for no empety values
data.isna().sum()
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="k025AY1apKIt" outputId="2dc50b3c-4789-4a33-e3e4-b2e806315e41"
#Print the table after preprocesisng
data.head()
# + colab={"base_uri": "https://localhost:8080/"} id="7dqcbzI_WF9M" outputId="bb120b20-8f86-4a37-c07f-998bd60273eb"
#Get the shape of the data
print('Shape of the data (rows,columns) = ' + str(np.array(data).shape))
# + [markdown] id="uc3fYHMF75QT"
# **Data analysis and plots**
# + colab={"base_uri": "https://localhost:8080/", "height": 287} id="9Acnh23RWKmb" outputId="3d449b12-88b1-458f-e960-51311c8c9fa0"
#Summary Statistics
data.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 316} id="zGzaXAx1Wjge" outputId="79deb3ac-eb32-4f8d-87a1-48e3dc23c05f"
#Count number of survivors and casualties
survive = data['Survived'].value_counts()
print('Number of people that did not survive = ' + str(survive[0]))
print('Number of people that survived = ' + str(survive[1]))
plt.figure()
bars = plt.bar([0,1],survive)
bars[0].set_color('orange')
plt.xticks([0,1], ['Died', 'Survived'])
plt.ylabel("Count")
plt.title("Casualties and Survivor amount in Titanic")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 574} id="xawlscQwXI_M" outputId="bfc081bc-15e7-4335-a775-c098095ff5dd"
#Plot of survivors for columns sex, pclass, sibsp, parch, and embarked
cols = ['Sex', 'Pclass','SibSp','Parch','Embarked']
plt.figure(figsize = (15,30))
for i in enumerate(cols):
plt.subplot(6,3,i[0]+1)
sns.countplot(x=i[1], hue='Survived',data=data)
# + colab={"base_uri": "https://localhost:8080/", "height": 137} id="1sTSecr248gm" outputId="9f32ca87-a510-4aa0-a808-6658c64b940b"
#Survival rate by Sex
data.groupby('Sex')[['Survived']].mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 167} id="UoOgaEQN5ppV" outputId="768a277c-c32b-45dd-d434-2ae13306ce48"
#Survival rate by Pclass
data.groupby('Pclass')[['Survived']].mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 257} id="21PsNOVE5vhT" outputId="74cac98e-d305-4090-c93d-dc09f8f52d79"
#Survival rate by SibSp
data.groupby('SibSp')[['Survived']].mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 287} id="c5QkdFr_5zZa" outputId="a2f300e6-467d-419f-9c8e-e750353b5d38"
#Survival rate by Parch
data.groupby('Parch')[['Survived']].mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 167} id="nxdpTC-A56nN" outputId="99791387-e9cd-4701-a452-3e5e3f2bb8b0"
#Survival rate by Embarked
data.groupby('Embarked')[['Survived']].mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 137} id="g4uODo8q5HaW" outputId="7a8073dc-257a-4963-cd75-4c2025dd675b"
#Survival rate by Sex and Class
data.pivot_table('Survived', index='Sex', columns='Pclass')
# + colab={"base_uri": "https://localhost:8080/", "height": 137} id="xSGQU3DT6D13" outputId="a67ca84a-4946-4449-91e2-aa7742486c35"
#Survival rate by Sex and Port
data.pivot_table('Survived', index='Sex', columns='Embarked')
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="h6_o4Xho54fo" outputId="19ca2c94-aad1-420c-ed09-81fea37206b0"
#Survival rate of each class
sns.barplot(x='Pclass', y='Survived',data=data);
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="zrIwiSRz6WOk" outputId="3e0c38d7-26a9-48a2-d649-c9b8288469c5"
#Survival rate by sex,age,and class
age = pd.cut(data['Age'], [0,18,80])
data.pivot_table('Survived',['Sex',age],'Pclass')
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="1B4vnRWK690m" outputId="bceeb000-67fa-4a72-c422-b606d3840702"
#plot the prices paid by each class
plt.scatter(data['Fare'],data['Pclass'],color='purple',label='Passenger Paid')
plt.ylabel("Class")
plt.xlabel("Price (Fare)")
plt.title("Price by Class")
plt.yticks([1,2,3],['First','Second','Third'])
plt.legend()
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 375} id="_Vt1-y2b9xJD" outputId="2d8347c1-ff40-418f-9b5a-813d388ad8c7"
#plot correlations
cols2 = ['Survived','Age','SibSp','Parch','Fare']
df_num = data[cols2]
print(df_num.corr())
sns.heatmap(df_num.corr(),annot=True,square=True);
# + [markdown] id="oMCG3m4l7-PN"
# **Prepare data for ML**
# + colab={"base_uri": "https://localhost:8080/"} id="LM48P45w_0i2" outputId="67a2c941-7058-4c8b-904c-8a84f3582337"
#check datatypes
data.dtypes
# + colab={"base_uri": "https://localhost:8080/"} id="iT0sxBij_oQT" outputId="824c01fc-c837-4812-b34d-96cc50968726"
#Unique values in columns
print(data['Sex'].unique())
print(data['Embarked'].unique())
# + id="SIJzpRYoASV6"
#Encode columns
label = LabelEncoder()
#sex column
data.iloc[:, 2] = label.fit_transform(data.iloc[:, 2].values)
#embarked column
data.iloc[:, 7] = label.fit_transform(data.iloc[:, 7].values)
# + colab={"base_uri": "https://localhost:8080/"} id="fRE4E6Ng8sJS" outputId="83d298d0-6400-429f-e949-7767be17c087"
#Unique values in columns after encoding
print(data['Sex'].unique())
print(data['Embarked'].unique())
# + colab={"base_uri": "https://localhost:8080/"} id="10jX1tGq_3aT" outputId="56c5f80d-b29f-460f-d94f-4b27c63f9264"
#check data types after encoding
data.dtypes
# + id="gKiLNAQyxl3l" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="15db2ac9-c88a-4c16-81de-b98768b66000"
#Final dataframe used in ML
data.head()
# + [markdown] id="6tYhQhh98C2V"
# **Create ML models and train them with training data and target**
# + id="XTo9t3p-AmFI"
#Split the data into independent 'X' & dependent 'Y' variables
x = data.iloc[:, 1:8].values
#target data
y = data.iloc[:, 0].values
# + id="4WNC6rujBeXx"
#Get our test data from the training data
xTrain, xTest, yTrain, yTest = train_test_split(x,y,test_size=0.2, random_state=0)
# + id="WK06lqN6AxJ_"
#Create function with ML models
def models(xTrain, yTrain):
#logisitic regression
log = LogisticRegression(random_state=0)
log.fit(xTrain,yTrain)
#Kneighbors
knn = KNeighborsClassifier(n_neighbors=5, metric='minkowski', p=2)
knn.fit(xTrain,yTrain)
#SVC linear kernel
svc_linear = SVC(kernel='linear', random_state=0)
svc_linear.fit(xTrain,yTrain)
#SVC RBF kernel
svc_rbf = SVC(kernel='rbf', random_state=0)
svc_rbf.fit(xTrain,yTrain)
#GaussianNB
gauss = GaussianNB()
gauss.fit(xTrain,yTrain)
#Decision Tree
tree = DecisionTreeClassifier(criterion='entropy', random_state=0)
tree.fit(xTrain,yTrain)
#Random Forest Classifier
forest = RandomForestClassifier(n_estimators=10, criterion='entropy', random_state=0)
forest.fit(xTrain,yTrain)
#Print accuracy of each model
print('Logisitic Regression Training Accuracy: ', log.score(xTrain,yTrain))
print('K Neighbors Training Accuracy: ', knn.score(xTrain,yTrain))
print('SVC linear Training Accuracy: ', svc_linear.score(xTrain,yTrain))
print('SVC RBF Training Accuracy: ', svc_rbf.score(xTrain,yTrain))
print('Gaussian NB Training Accuracy: ', gauss.score(xTrain,yTrain))
print('Decision Tree Training Accuracy: ', tree.score(xTrain,yTrain))
print('Random Forest Training Accuracy: ', forest.score(xTrain,yTrain))
return log,knn,svc_linear,svc_rbf,gauss,tree,forest
# + colab={"base_uri": "https://localhost:8080/"} id="dfRGbnq3D_2w" outputId="fd87fd26-c4c3-40e0-9d41-f6a1c470ce60"
#Train the models
model = models(xTrain, yTrain)
# + colab={"base_uri": "https://localhost:8080/"} id="qGXj-w8HE8pO" outputId="a6c642eb-bcdb-46d7-c35e-f37b32b74df8"
#Confusion matrix & accuracy for models in test data
modelNames = ['Logistic Regression' , 'K Neighbors', 'SVC Linear', 'SVC RBF',
'Gaussian NB', 'Decision Tree', 'Random Forest']
for i in range(len(model)):
matrix = confusion_matrix(yTest,model[i].predict(xTest))
#Get the true negative, false positive, false negative, & true positive
TN, FP, FN, TP = confusion_matrix(yTest,model[i].predict(xTest)).ravel()
#Accuracy
acc = (TP + TN) / (TP + TN + FN + FP)
#Print the info
print(matrix)
print('{} Testing Accuracy = {}'.format(modelNames[i],acc))
print()
# + colab={"base_uri": "https://localhost:8080/", "height": 287} id="K6EN7SgcGKU_" outputId="1adbbaf4-bf2f-40ec-f58f-c6ef28ad01ed"
#Get priority of features
forest = model[6]
priorities = pd.DataFrame({'Feature':data.iloc[:, 1:8].columns, 'Priority': np.round(forest.feature_importances_,3)})
priorities = priorities.sort_values('Priority', ascending=False).set_index('Feature')
priorities
# + colab={"base_uri": "https://localhost:8080/", "height": 320} id="IYl1FE2BIDNY" outputId="c5c47ca3-8301-4688-97bb-dabc036ade0b"
#plot the features
priorities.plot.bar()
plt.ylabel("Value");
# + [markdown] id="xMNzOYuy8Kz4"
# **ML model of choice results**
# + colab={"base_uri": "https://localhost:8080/"} id="_57RUQmWJNPh" outputId="552b74b1-89b1-40de-ad01-1e74d8c24072"
#Predict using Random Forest Classifier
pred = model[6].predict(xTest)
print(pred)
print()
#Print raw values
print(yTest)
# + id="fjyekmtpLILZ"
#Test the test file
test = pd.read_csv('test.csv')
#Drop same columns
test = test.drop(["Cabin", "Name","Ticket","PassengerId"], axis=1)
# + colab={"base_uri": "https://localhost:8080/"} id="s0rDolhwVNWz" outputId="dd84618c-f048-4174-efb0-ccbe0e9ba53e"
#Check for Nanvalues
test.isna().sum()
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="4Zu5XywmVVSf" outputId="e54f7786-57c2-491b-aa0e-df8810c4ae54"
#Drop na values
test = test.dropna(subset=['Age','Fare'])
#Encode columns
#sex column
test.iloc[:, 1] = label.fit_transform(test.iloc[:, 1].values)
#embarked column
test.iloc[:, 6] = label.fit_transform(test.iloc[:, 6].values)
test.head()
# + id="bHHQ-iWyOljE"
#Convert to numpy array
testArray = np.array(test)
#Create empty array to store survival
Survival = []
#Test the survival of each person
for person in testArray:
person = person.reshape(1,-1)
pred = model[6].predict(person)
Survival.append(pred[0])
# + id="Dzq3cqQTSHTo"
#Read the data again and add the surival column
testResult = pd.read_csv('test.csv')
testResult = testResult.dropna(subset=['Age','Fare'])
testResult['Survived'] = Survival
# + colab={"base_uri": "https://localhost:8080/", "height": 647} id="YSFpUjl5SW3n" outputId="e315e3d3-5691-4423-ff79-9a34472a6c07"
#print a couple rows from the new table
testResult.head(20)
# + [markdown] id="N0yjRt1Y8RpJ"
# **Custom test**
# + colab={"base_uri": "https://localhost:8080/"} id="IDiIpxP0UENd" outputId="f8bede2c-6708-40df-95b4-0c9d135b4481"
#Test my own survival
mySurival = [[1,0,16,0,0,100,2]]
#Print my prediction using Random Forest Classifier
pred = model[6].predict(mySurival)
print("My prediction: " + str(pred[0]))
if pred[0] == 0:
print("I did not survive!")
else:
print("I survived the Titanic!")
|
Titanic-Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="h0Rz-yvlfNLs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 513} outputId="36358188-c13d-4afd-9325-dc0a7b20f17b" executionInfo={"status": "ok", "timestamp": 1583391550318, "user_tz": -60, "elapsed": 14038, "user": {"displayName": "Pawe\u01<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
# !pip install --upgrade tables
# !pip install eli5
# !pip install xgboost
# + id="xUETFnpqfXQE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 168} outputId="c4b7f2e7-3781-40fc-d648-15e7a0b11645" executionInfo={"status": "ok", "timestamp": 1583391649332, "user_tz": -60, "elapsed": 2346, "user": {"displayName": "Pawe\u01<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.dummy import DummyRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
import xgboost as xgb
from sklearn.metrics import mean_absolute_error as mae
from sklearn.model_selection import cross_val_score, KFold
import eli5
from eli5.sklearn import PermutationImportance
# + id="FjdL98QkfySh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="d7e3294d-34a9-493a-895a-6baae29ee189" executionInfo={"status": "ok", "timestamp": 1583391692330, "user_tz": -60, "elapsed": 488, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
# cd "/content/drive/My Drive/Colab Notebooks/matrix_two/dw_matrix_car"
# + id="vGq05Jpqf9Pd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="d1481eee-7207-413d-edc5-f75ec88c38f1" executionInfo={"status": "ok", "timestamp": 1583391704308, "user_tz": -60, "elapsed": 4372, "user": {"displayName": "Pawe\u01<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
df = pd.read_hdf('data/car.h5')
df.shape
# + id="bAdtzUkVf_Ne" colab_type="code" colab={}
df = df[ df['price_currency'] != 'EUR' ]
# + [markdown] id="CdidutLPgMdR" colab_type="text"
# ## Feature engineering
# + id="tyStH02_gHJc" colab_type="code" colab={}
SUFFIX_CAT = '__cat'
for feat in df.columns:
if isinstance(df[feat][0], list): continue
if SUFFIX_CAT in feat: continue
df[feat + SUFFIX_CAT] = df[feat].factorize()[0]
# + id="icwpFs7ygP2O" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e2b5c194-2e4a-4400-cb22-35a07b71e751" executionInfo={"status": "ok", "timestamp": 1583391796304, "user_tz": -60, "elapsed": 586, "user": {"displayName": "Pawe\u<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
cat_feats = [x for x in df.columns if SUFFIX_CAT in x ]
# remove price related features
cat_feats = [x for x in cat_feats if 'price' not in x ]
len(cat_feats)
# + id="Ja7ZIqoVgWml" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="cbb3fa6e-c0aa-461c-aae1-81f11439bca5" executionInfo={"status": "ok", "timestamp": 1583391817795, "user_tz": -60, "elapsed": 5150, "user": {"displayName": "Pawe\u014<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
X = df[ cat_feats ].values
y = df['price_value'].values
model = DecisionTreeRegressor(max_depth=5)
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
np.mean(scores)
# + id="yxuFTMGigau9" colab_type="code" colab={}
def run_model(model, feats):
X = df[ feats ].values
y = df['price_value'].values
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
# + [markdown] id="_lONrDnWhFKr" colab_type="text"
# ## Decision Tree
# + id="O0in0UFwgwkU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="9be8e21a-f6c0-43c6-f978-1f8d4109155b" executionInfo={"status": "ok", "timestamp": 1583391951590, "user_tz": -60, "elapsed": 4501, "user": {"displayName": "Pawe\u0142 Dulak", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
run_model( DecisionTreeRegressor(max_depth=5), cat_feats )
# + [markdown] id="hvl4GYRVhH7Q" colab_type="text"
# ## Random Forest
# + id="cubQ8Uymg7jt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="dc8fb6ac-f95e-4e30-c442-7231880906f3" executionInfo={"status": "ok", "timestamp": 1583392276976, "user_tz": -60, "elapsed": 255929, "user": {"displayName": "Pawe\u0142 Dulak", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
model = RandomForestRegressor(max_depth=5, n_estimators=50, random_state=0)
run_model( model, cat_feats )
# + [markdown] id="JjAbhnwFhgyF" colab_type="text"
# ## XGBoost
# + id="2Jx5MUL8hiD3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="d69641ca-f0bd-4b42-9e87-90e1bf6c240a" executionInfo={"status": "ok", "timestamp": 1583392369984, "user_tz": -60, "elapsed": 61100, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
xgb_params = {
'max_depth': 5,
'n_estimators': 50,
'seed': 0,
'learning_rate': 0.1
}
model = xgb.XGBRegressor (**xgb_params)
run_model( model, cat_feats )
# + id="sFbXBo4yhL1a" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 408} outputId="a8a14625-0ccf-4744-e9c9-d5dda3ea3303" executionInfo={"status": "ok", "timestamp": 1583392749801, "user_tz": -60, "elapsed": 360157, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
m = xgb.XGBRegressor(**xgb_params)
m.fit(X, y)
imp = PermutationImportance(m, random_state=0).fit(X, y)
eli5.show_weights(imp, feature_names=cat_feats)
# + id="k4OHLHqDinln" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="4674d5b1-29f7-477a-fd12-2b788199ae62" executionInfo={"status": "ok", "timestamp": 1583392786627, "user_tz": -60, "elapsed": 499, "user": {"displayName": "Pawe\u014<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
feats = ['param_napÄd__cat', 'param_rok-produkcji__cat', 'param_stan__cat', 'param_skrzynia-biegów__cat', 'param_faktura-vat__cat', 'param_moc__cat', 'param_marka-pojazdu__cat', 'param_typ__cat', 'feature_kamera-cofania__cat', 'param_pojemnoÅÄ-skokowa__cat', 'seller_name__cat', 'param_kod-silnika__cat', 'param_model-pojazdu__cat', 'feature_wspomaganie-kierownicy__cat', 'param_wersja__cat', 'feature_czujniki-parkowania-przednie__cat', 'feature_asystent-pasa-ruchu__cat', 'feature_regulowane-zawieszenie__cat', 'feature_system-start-stop__cat', 'feature_ÅwiatÅa-led__cat']
len(feats)
# + id="31arP-nnkIYM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="105be597-bd86-410d-b8c9-22cd665f5631" executionInfo={"status": "ok", "timestamp": 1583392826691, "user_tz": -60, "elapsed": 13592, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
xgb_params = {
'max_depth': 5,
'n_estimators': 50,
'seed': 0,
'learning_rate': 0.1
}
model = xgb.XGBRegressor (**xgb_params)
run_model( model, feats )
# + id="e4jiLVX7kO-_" colab_type="code" colab={}
df['param_rok-produkcji'] = df['param_rok-produkcji'].map(lambda x: -1 if str(x) == 'None' else int(x))
# + id="sq9nchKwkx6y" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="af7b24e2-d95f-464f-ff5c-f338fdf1d270" executionInfo={"status": "ok", "timestamp": 1583392991529, "user_tz": -60, "elapsed": 13794, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
feats = ['param_napÄd__cat', 'param_rok-produkcji', 'param_stan__cat', 'param_skrzynia-biegów__cat', 'param_faktura-vat__cat', 'param_moc__cat', 'param_marka-pojazdu__cat', 'param_typ__cat', 'feature_kamera-cofania__cat', 'param_pojemnoÅÄ-skokowa__cat', 'seller_name__cat', 'param_kod-silnika__cat', 'param_model-pojazdu__cat', 'feature_wspomaganie-kierownicy__cat', 'param_wersja__cat', 'feature_czujniki-parkowania-przednie__cat', 'feature_asystent-pasa-ruchu__cat', 'feature_regulowane-zawieszenie__cat', 'feature_system-start-stop__cat', 'feature_ÅwiatÅa-led__cat']
model = xgb.XGBRegressor (**xgb_params)
run_model( model, feats )
# + id="tUv_cTPgk3Lp" colab_type="code" colab={}
df['param_moc'] = df['param_moc'].map(lambda x: -1 if str(x) == 'None' else int(x.split(' ')[0]) )
# + id="e1h2HiTRlWdb" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="27655cee-baeb-4f4b-e284-dd4cb51b1706" executionInfo={"status": "ok", "timestamp": 1583393179845, "user_tz": -60, "elapsed": 13720, "user": {"displayName": "Pawe\u0142 Dulak", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
feats = ['param_napÄd__cat', 'param_rok-produkcji', 'param_stan__cat', 'param_skrzynia-biegów__cat', 'param_faktura-vat__cat',
'param_moc', 'param_marka-pojazdu__cat', 'param_typ__cat', 'feature_kamera-cofania__cat', 'param_pojemnoÅÄ-skokowa__cat',
'seller_name__cat', 'param_kod-silnika__cat', 'param_model-pojazdu__cat', 'feature_wspomaganie-kierownicy__cat', 'param_wersja__cat',
'feature_czujniki-parkowania-przednie__cat', 'feature_asystent-pasa-ruchu__cat', 'feature_regulowane-zawieszenie__cat',
'feature_system-start-stop__cat', 'feature_ÅwiatÅa-led__cat']
model = xgb.XGBRegressor (**xgb_params)
run_model( model, feats )
# + id="pZZUGrVellLE" colab_type="code" colab={}
df['param_pojemnoÅÄ-skokowa'] = df['param_pojemnoÅÄ-skokowa'].map(lambda x: -1 if str(x) == 'None' else int(x.split('cm')[0].replace(' ', '')) )
# + id="9tU-ETmgmMF9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="581cc899-077f-4c5a-a986-587bb4acb315" executionInfo={"status": "ok", "timestamp": 1583393397959, "user_tz": -60, "elapsed": 13291, "user": {"displayName": "Pawe\u0142 Dulak", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhPGyDfshns1R1nSgOCeFI5QxlaXlERiLn_gcOEJQ=s64", "userId": "16380328722087813309"}}
feats = ['param_napÄd__cat', 'param_rok-produkcji', 'param_stan__cat', 'param_skrzynia-biegów__cat', 'param_faktura-vat__cat',
'param_moc', 'param_marka-pojazdu__cat', 'param_typ__cat', 'feature_kamera-cofania__cat', 'param_pojemnoÅÄ-skokowa',
'seller_name__cat', 'param_kod-silnika__cat', 'param_model-pojazdu__cat', 'feature_wspomaganie-kierownicy__cat', 'param_wersja__cat',
'feature_czujniki-parkowania-przednie__cat', 'feature_asystent-pasa-ruchu__cat', 'feature_regulowane-zawieszenie__cat',
'feature_system-start-stop__cat', 'feature_ÅwiatÅa-led__cat']
model = xgb.XGBRegressor (**xgb_params)
run_model( model, feats )
# + id="m7z9Rt0ImahJ" colab_type="code" colab={}
|
day4_XGBoost.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#hide
# %load_ext autoreload
# %autoreload 2
# +
# default_exp data
# -
# # data
#
# > Handle data loading and manipulation
#hide
from nbdev.showdoc import *
#export
import pandas as pd
import numpy as np
from pathlib2 import Path
from datetime import timedelta, datetime as dt
# ## Initial data load
#export
DEFAULT_PI_PATH=Path('/home/pi/get_temp_C.out')
FALLBACK_PATH=Path('webapp3/data/get_temp_C.out')
#export
def convert_time(s):
return s[0:5]
#export
def load_data():
path=DEFAULT_PI_PATH
if not path.is_file():
path=FALLBACK_PATH
df=pd.read_csv(path, sep=' ', header=None, names=['dev_sn', 'date', 'time', 'temp_raw', 'temp_C'])
# keep only values of the last 7 days
now = dt.now()
now = dt(now.year, now.month, now.day, now.hour, now.minute) # date, hours and minutes only
td7 = timedelta(days=7)
one_week_ago = now - td7
df = df[df.date >= one_week_ago.strftime('%Y-%m-%d')]
# remove rows with nan entries
df = df[~df.isna().any(axis=1)]
# keep hour and minute from time only
df['time'] = df['time'].apply(convert_time)
# add a datetime column from date and time columns, drop the later ones
df['date_time']=pd.to_datetime(df['date']+df['time'], format='%Y-%m-%d%H:%M')
df = df.drop(['date', 'time'], axis=1)
dfs = {}
idx = pd.date_range(start = one_week_ago, end = now, freq = 'T')
for sn in df[df.temp_raw.notna()].dev_sn.unique():
# create a copy for each device / serial number
dfd = df[df.dev_sn == sn].copy()
# reset index due to skipped rows (different serial number)
dfd = dfd.reset_index(drop = True)
# remov duplicate rows for the same time stamp
dfd = dfd[~dfd.date_time.duplicated(keep='first')]
# fill gaps in case of missing measured data points, use df to do ut everywhere the same way
dfd = dfd.set_index('date_time').reindex(idx).rename_axis('date_time').reset_index()
# add a timestamp column
dfd['timestamp'] = (dfd.date_time.values.astype(np.int64) // 10 ** 9).tolist()
# store within dictionary
dfs.update({sn: dfd})
return dfs
df = load_data()
df['28-032197791b3c'].head()
|
01_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # a2 - Python Basics
# Fill in the below code cells as specified. Note that cells may utilize variables and functions defined in previous cells; we should be able to use the `Kernal > Restart & Clear All` menu item followed by `Cell > Run All` to execute your entire notebook and see the correct output.
# ## Part 1. Introductions
# Create a variable **`my_name`** that stores your name (a string).
my_name = "Emily"
print(my_name)
# Create a variable **`my_age`** that stores your age (a number).
my_age = 28
print(my_age)
# Define a function **`make_introduction()`** that takes in two arguments: a name and an age. The function should _return_ a string of the format `"Hello, my name is {NAME} and I'm {AGE} years old."` (replacing `{NAME}` and `{AGE}` with the arguments).
# - Note that you can turn a number into a string using the built-in `str()` function.
# +
def make_introduction(my_name, my_age)
introduction = "Hello, my name is " + NAME + "and I'm "" + str(AGE) "years old.")
print(make_introduction)
def make_introduction(my_name, my_age):
Introduction = "Hello, my name is " + NAME + "and I'm " + str(AGE) "years old."
def make_introduction(my_args):
#body: statements (code)
greeting = "Hello " + name
print(greeting)
say_hello("Matt")
name - "<NAME>"
print(name)
say_hello("dr. <NAME>")
print (name)
# -
# Create a variable **`my_intro`** by passing your variables `my_name` and `my_age` into your `make_introduction()` function. Print the variable after you create it.
# Create a variable **`loud_intro`**, which is your `my_intro` variable with all of the letters capitalized (use the `upper()` string method). Print the variable after you create it.
# Create a variable **`casual_intro`** by using the `replace()` string function to replace (substitute) "Hello, my name is", with "Hey, I'm" in your `my_intro` variable. You may need to look up the arguments for this function! Print the variable after you create it.
# Create a variable `intro_e_count` that stores the number of times the letter `'e'` (lower-case only) appears in the `my_intro` variable. Find a [string method](https://docs.python.org/3.6/library/stdtypes.html#string-methods) that will "count" the occurences. Print the variable after you create it.
# ## Part 2. Money
# Define a function **`compound_interest()`** that takes three arguments: an initial bank balance (principle, in dollars), an annual interest rate, and a number of years. The function should calculate the [continuous compound interest](https://en.wikipedia.org/wiki/Compound_interest#Continuous_compounding) and _return_ the resulting total balance after that many number of years.
# - See [here](http://www.mathwarehouse.com/calculators/continuous-compound-interest-calculator.php) for an example of the formula and a calculator you can use to check your work.
# - Be sure and call your function with some testing numbers: \$1000 at 6% for 5 years should lead to a balance of \$1349.86.
# - You will need to import the `math` module for mathematical functions.
# Define a function **`print_earnings()`** that takes three numbers as arguments: an initial principle, an annual interest rate, and a number of years. This function should _print out_ the earnings over this period in the following format:
#
# ```
# Initial principle: $1000
# Annual interest rate: %6.0
# Interest earned in 5 years: $349.86
# Total value after 5 years: $1349.86
# ```
#
# Note that interest rate should be printed as a percentage, monetary values should have a leading `$`, and you should round monetary values to the nearest penny. Don't worry about extra or missing trailing 0s (in values like `%6.0` or `$101.5`).
# Define a function **`value_of_change()`** that takes in **named** arguments representing amounts of different US coins (`quarters`, `dimes`, `nickels`, and `pennies`)--each of the arguments should have a default value of `0`. The function should _return_ the total value in dollars of those coins. For example, 5 quarters, 4 dimes, 3, nickels, and 2 pennies have a value of `1.82` dollars.
# Define a function **`consolidate_change`** that takes as arguments counts of different US coins (similar to the previous function) and prints out the _simplest_ number of bills and coins needed to make that amount.
#
# For example, when called with arguments of 10 quarters, 9 dimes, 8 nickels, and 7 pennies, the function should print:
#
# ```
# Number of dollars: 3
# Number of quarters: 3
# Number of dimes: 1
# Number of nickels: 0
# Number of pennies: 2
# Total amount: $3.87
# ```
#
# You _must_ use your previous `value_of_change()` method in this calculation. _Hint:_ think about converting the coins to a giant pile of pennies, and then determining how many (whole number) dollars you can divide them into. Then put those pennies aside, and determine how many (whole number) quarters you can make with the rest, etc.
# ## Part 3. Time
# Use the [date()](https://docs.python.org/3/library/datetime.html#datetime.date) function from the `datetime` module to create a variable **`summer_break`** that represents the first day of Summer break (June 9, 2018). Note that this function will return a value of type `date`.
# Create a variable **`days_to_break`** that is how many days from the _current date_ (today--look for a method of the [date class](https://docs.python.org/3/library/datetime.html#date-objects)) to Summer break. _Hint:_ variables of the `date` type support the subtraction operator! Print the variable after you create it; it's fine if the printed result includes a `00:00:00` timestamp.
# Define a function **`can_drink_us()`** that takes as an argument a birth date (as a `date` value). This function should _return_ the `date` in which a person born on that day can legally purchase alcohol in the US (i.e., when they turn 21 years old).
#
# In order to calculate this date, you should use the [dateutil.relativedelta](https://dateutil.readthedocs.io/en/stable/relativedelta.html) library, which is included with Anaconda. You will need to import the `relativedelta` function from this library, which will let you specify a "time change" in terms of years that can then be added to a date. See [the examples](https://dateutil.readthedocs.io/en/stable/examples.html#relativedelta-examples) for details.
#
# Demonstrate your function works by printing out when someone born _today_ will be able to legally drink.
# Define a function **`make_birthday_intro()`** that takes in two arguments: a name (`string`), and a birth date (`date`). This function should _return_ a string of the format `"Hello, my name is {NAME} and I'm {AGE} years old. In {N} days I'll be {NEW_AGE}"` (replacing `{NAME}`, `{AGE}`, `{N}`, and `{NEW_AGE}` with appropriate values).
#
# - You should utilize your **`make_introduction()`** function from Part 1! You may need to calculate a variable to pass into that function call.
# - _Hint_: use the `relativedelta()` function to calculate the person's current age, as well as when they will turn 1 year older. You can get the number of days or years from a `relativedelta` value (e.g., `time_difference`) by accessing the `.days` or `.years` properties (e.g., `time_difference.years`).
# Create a variable **`my_bday_intro`** by calling your `make_birthday_intro()` function and passing in your name (already a variable!) and your birthdate. Print the variable after you create it.
|
exercise-3/python-basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "notes"}
# [](https://mybinder.org/v2/gh/eth-cscs/abcpy/master?filepath=examples%2FRejection_ABC_closer_look.ipynb)
#
# # A closer look to Rejection ABC
#
# In this notebook, we give some insights on how Rejection ABC (and ABC in general) works, using `ABCpy`.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Approximate Bayesian Computation (ABC)
# + [markdown] slideshow={"slide_type": "-"}
# Approximate Bayesian Computation is a set of methods that allow to find the 'best' parameters of a scientific model with respect to observations from the real world. More specifically, ABC sits in the set of Bayesian inference methods; therefore, it provides the user not only with a point estimate of parameter values, but with a _posterior_ distribution quantifying uncertainty.
#
#
# To infer the parameters of a model using ABC, three basic ingredients are required:
# - A model is required that, given some input parameters, can generate synthetic observations
# - Some prior knowledge about the input parameters is required (a Uniform distribution over the parameters space is always possible)
# - A discrepancy function is required that quantifies how similar two sets of observations (real and synthetic) are. Here, we will use the simple Euclidean distance between observations.
#
# **Note: we do not need the likelihood function of the bi-variate normal distribution!**
#
# In this model, we will consider a setup in which a scientist measures height and weigth of a set of people and wants to use a statistical model to describe them; moreover, she also wants to find the posterior distributon over parameters.
# + slideshow={"slide_type": "skip"}
from math import cos, sin, pi
import matplotlib.mlab as mlab
import numpy as np
import scipy
from matplotlib import gridspec, pyplot as plt
from numpy.linalg import inv
from scipy.stats import multivariate_normal
from abcpy.probabilisticmodels import ProbabilisticModel, Continuous, InputConnector
from abcpy.continuousmodels import Uniform
from abcpy.statistics import Identity
from abcpy.distances import Euclidean
from abcpy.inferences import RejectionABC
from abcpy.backends import BackendDummy as Backend
# %matplotlib inline
# -
# Let us define the model we will consider; this is specifically a bivariate normal model, in which the covariance matrix is defined in the following way (method `get_cov`):
#
# - the standard deviations s1 and s2 are used to define a diagonal covariance matrix
# - then, a rotation matrix corresponding to angle alpha is used to rotate that to a correlated covariance matrix.
#
# Essentially, then, s1 and s2 are the standard deviation of the final bivariate normal along the directions in which the two components are uncorrelated. This is related to eigendecomposition, but this is not the main point here.
#
# We use `ABCpy` API to define the model:
class BivariateNormal(ProbabilisticModel, Continuous):
def __init__(self, parameters, name='BivariateNormal'):
# We expect input of type parameters = [m1, m2, s1, s2, alpha]
if not isinstance(parameters, list):
raise TypeError('Input of Normal model is of type list')
if len(parameters) != 5:
raise RuntimeError('Input list must be of length 5, containing [m1, m2, s1, s2, alpha].')
input_connector = InputConnector.from_list(parameters)
super().__init__(input_connector, name)
def _check_input(self, input_values):
# Check whether input has correct type or format
if len(input_values) != 5:
raise ValueError('Number of parameters of BivariateNormal model must be 5.')
# Check whether input is from correct domain
m1 = input_values[0]
m2 = input_values[1]
s1 = input_values[2]
s2 = input_values[3]
alpha = input_values[4]
if s1 < 0 or s2 < 0:
return False
return True
def _check_output(self, values):
if not isinstance(values, np.array):
raise ValueError('This returns a bivariate array')
if values.shape[0] != 2:
raise RuntimeError('The size of the output has to be 2.')
return True
def get_output_dimension(self):
return 2
def forward_simulate(self, input_values, k, rng=np.random.RandomState()):
# Extract the input parameters
m1 = input_values[0]
m2 = input_values[1]
s1 = input_values[2]
s2 = input_values[3]
alpha = input_values[4]
mean = np.array([m1, m2])
cov = self.get_cov(s1, s2, alpha)
obs_pd = multivariate_normal(mean=mean, cov=cov)
vector_of_k_samples = obs_pd.rvs(k)
# Format the output to obey API
result = [np.array([x]) for x in vector_of_k_samples]
return result
def get_cov(self, s1, s2, alpha):
"""Function to generate a covariance bivariate covariance matrix; it starts from considering a
diagonal covariance matrix with standard deviations s1, s2 and then applies the rotation matrix with
angle alpha. """
r = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]]) # Rotation matrix
e = np.array([[s1, 0], [0, s2]]) # Eigenvalue matrix
rde = np.dot(r, e)
rt = np.transpose(r)
cov = np.dot(rde, rt)
return cov
# Next, we define some help functions for plots:
# + slideshow={"slide_type": "skip"}
def plot_dspace(ax, sl, marker, color):
"""Plot the data in 'sl' on 'ax';"""
ax.set_xlim(100,220)
ax.set_ylim(30,150)
ax.set_xlabel('Height in cm')
ax.set_ylabel('Weigth in kg')
for samples in sl:
ax.plot(samples[:,0], samples[:,1], marker, c=color)
# + slideshow={"slide_type": "skip"}
def plot_pspace(ax_means, ax_vars, ax_angle, m1, m2, s1, s2, alpha, color):
"""Plot parameter space. m1 and m2 are the means of the height and weight respectively, while s1, s2 are
two standard deviations for the eigenvalue normal components. Finally, alpha is the angle that determines the
amount of rotation applied to the two independent components to get the covariance matrix."""
ax_means.set_xlabel('Mean of height')
ax_means.set_ylabel('Mean of weight')
ax_means.set_xlim(120,200)
ax_means.set_ylim(50,150)
ax_means.plot(m1, m2, 'o', c=color)
ax_vars.set_xlabel('Standard deviation 1')
ax_vars.set_ylabel('Standard deviation 2')
ax_vars.set_xlim(0,100)
ax_vars.set_ylim(0,100)
ax_vars.plot(s1, s2, 'o', c=color)
ax_angle.set_xlabel('Rotation angle')
ax_angle.set_xlim(0, pi/2)
ax_angle.set_yticks([])
ax_angle.plot(np.linspace(0, pi, 10), [0]*10, c='black', linewidth=0.2)
ax_angle.plot(alpha, 0, 'o', c=color)
# + slideshow={"slide_type": "skip"}
def plot_all(axs, m1, m2, s1, s2, alpha, color, marker, model, k):
"""Function plotting pameters, generating data from them and plotting data too. It uses the model
to generate k samples from the provided set of parameters.
m1 and m2 are the means of the height and weight respectively, while s1, s2 are
two standard deviations for the eigenvalue normal components. Finally, alpha is the angle that determines the
amount of rotation applied to the two independent components to get the covariance matrix.
"""
ax_pspace_means, ax_pspace_vars, ax_pspace_angle, ax_dspace = axs
plot_pspace(ax_pspace_means, ax_pspace_vars, ax_pspace_angle, m1, m2, s1, s2, alpha, color)
samples = model.forward_simulate([m1, m2, s1, s2, alpha], k)
plot_dspace(ax_dspace, samples, marker, color)
# -
# Define now the probabilistic model; we put uniform priors on the parameters:
# +
m1 = Uniform([[120], [200]], name="Mean_height")
m2 = Uniform([[50], [150]], name="Mean_weigth")
s1 = Uniform([[0], [100]], name="sd_1")
s2 = Uniform([[0], [100]], name="sd_2")
alpha = Uniform([[0], [pi/2]], name="alpha")
bivariate_normal = BivariateNormal([m1, m2, s1, s2, alpha])
# -
# Assume now that the scientist obtained an observation, from field data, that was generated by the model with a specific set of parameters `obs_par`; this is of course fictitious, but we take this assumption in order to check whether we are able to recover decently the actual model parameters we used.
# + pycharm={"name": "#%%\n"}
obs_par = np.array([175, 75, 90, 35, pi/4.])
obs = bivariate_normal.forward_simulate(obs_par, 100)
# + slideshow={"slide_type": "subslide"}
fig_obs = plt.figure(dpi=300)
fig_obs.set_size_inches(9,9)
ax_obs = fig_obs.add_subplot(111)
ax_obs.set_title('Observations')
plot_dspace(ax_obs, obs, 'x', 'C0')
# + [markdown] slideshow={"slide_type": "slide"}
# ## Rejection ABC
# This is the most fundamental algorithm for ABC; it works in four steps:
#
# Repeat:
# 1. draw a parameter sample theta from the prior
# 2. generate synthetic observations from the model using theta
# 3. compute the distance between observed and synthetic data
# 4. if the distance is smaller than a threshold, add theta to accepted parameters
#
# And the loop continues until enough parameter values are accepted. The output is a set of accepted parameters, that resembles the parameters 'true' (posterior) distribution.
#
#
# 
# + [markdown] slideshow={"slide_type": "slide"}
# ### RejectionABC in Figures
# We will now display the observations generated from the model for a set of parameter values; specifically, we consider 4 different sets of parameter values (corresponding to the four different colors) which are displayed in the left hand side set of plot; the corresponding observations are of the same color in the right plot; in the latter, we also show the observation (blue).
#
# + slideshow={"slide_type": "skip"}
np.random.seed(0)
fig_sim = plt.figure(dpi=150)
fig_sim.set_size_inches(19, 9)
gs = gridspec.GridSpec(1, 2, width_ratios=[1,1], height_ratios=[1])
gs_pspace = gridspec.GridSpecFromSubplotSpec(2, 2, subplot_spec=gs[0,0], width_ratios=[1, 1], height_ratios=[4,1])
ax_pspace_means = plt.subplot(gs_pspace[0,0])
ax_pspace_vars = plt.subplot(gs_pspace[0,1])
ax_pspace_angle = plt.subplot(gs_pspace[1,:])
ax_dspace = plt.subplot(gs[0,1])
axs = (ax_pspace_means, ax_pspace_vars, ax_pspace_angle, ax_dspace)
#plot_dspace(ax_dspace, [obs], 'x', 'C0')
plot_all(axs, 130,110,95,50,pi/5, 'C1', 'x', bivariate_normal, 100)
plot_all(axs, 170,80,60,5,0.3, 'C2', 'x', bivariate_normal, 100)
plot_all(axs, 135,55,10,70,1.3, 'C3', 'x', bivariate_normal, 100)
plot_all(axs, 190,120,21,21,pi/3., 'C4', 'x', bivariate_normal, 100)
plot_dspace(ax_dspace, obs, 'X', 'C0')
# -
# The idea of ABC is the following: similar data sets come from similar sets of parameters. For this reason, to obtain the best parameter values which fit the observation, we will compare the observation with the synthetic data for different choices of parameters, for instance, above you can see that the green dataset is a better match for the observation than the others.
# + [markdown] slideshow={"slide_type": "skip"}
# Let us now generate some samples from the prior and see how well they fit the observation:
# +
n_prior_samples = 100
params_prior = np.zeros((n_prior_samples,5))
for i in range(n_prior_samples):
m1_val = m1.forward_simulate([[120], [200]], k=1)
m2_val = m2.forward_simulate([[50], [150]], k=1)
s1_val = s1.forward_simulate([[0], [100]], k=1)
s2_val = s2.forward_simulate([[0], [100]], k=1)
alpha_val = alpha.forward_simulate([[0], [pi / 2]], k=1)
params_prior[i] = np.array([m1_val, m2_val, s1_val, s2_val, alpha_val]).squeeze()
# + slideshow={"slide_type": "subslide"}
np.random.seed(0)
fig_abc1 = plt.figure(dpi=150)
fig_abc1.set_size_inches(19, 9)
gs = gridspec.GridSpec(1, 2, width_ratios=[1,1], height_ratios=[1])
gs_pspace = gridspec.GridSpecFromSubplotSpec(2, 2, subplot_spec=gs[0,0], width_ratios=[1, 1], height_ratios=[4,1])
ax_pspace_means = plt.subplot(gs_pspace[0,0])
ax_pspace_vars = plt.subplot(gs_pspace[0,1])
ax_pspace_angle = plt.subplot(gs_pspace[1,:])
ax_dspace = plt.subplot(gs[0,1])
axs = (ax_pspace_means, ax_pspace_vars, ax_pspace_angle, ax_dspace)
for i in range(0, n_prior_samples):
plot_all(axs, params_prior[i,0], params_prior[i,1], params_prior[i,2], params_prior[i,3], params_prior[i,4],
'C1', '.', bivariate_normal, k=100)
plot_pspace(ax_pspace_means, ax_pspace_vars, ax_pspace_angle, *obs_par, color="C0")
plot_dspace(ax_dspace, obs, 'X', 'C0')
# -
# Above, the blue dot represent the parameter values which originated the observation, while the orange parameter values are the ones sampled from the prior; the corresponding synthetic datasets are shown as orange clouds of dots, while the observation is shown as blue crosses.
# ### Inference
# Now, let's perform inference with Rejection ABC to get some approximate posterior samples:
# +
statistics_calculator = Identity()
distance_calculator = Euclidean(statistics_calculator)
backend = Backend()
sampler = RejectionABC([bivariate_normal], [distance_calculator], backend, seed=1)
# -
# Sampling may take a while. It will take longer the more you decrease the threshold epsilon or increase the number of samples.
n_samples = 100 # number of posterior samples we aim for
n_samples_per_param = 100 # number of simulations for each set of parameter values
journal = sampler.sample([obs], n_samples, n_samples_per_param, epsilon=15)
print(journal.number_of_simulations)
# Now, we will produce a plot similar to the above one for the prior but starting from the posterior samples.
posterior_samples = np.array(journal.get_accepted_parameters()).squeeze()
# +
np.random.seed(0)
fig_abc1 = plt.figure(dpi=150)
fig_abc1.set_size_inches(19, 9)
gs = gridspec.GridSpec(1, 2, width_ratios=[1,1], height_ratios=[1])
gs_pspace = gridspec.GridSpecFromSubplotSpec(2, 2, subplot_spec=gs[0,0], width_ratios=[1, 1], height_ratios=[4,1])
ax_pspace_means = plt.subplot(gs_pspace[0,0])
ax_pspace_vars = plt.subplot(gs_pspace[0,1])
ax_pspace_angle = plt.subplot(gs_pspace[1,:])
ax_dspace = plt.subplot(gs[0,1])
axs = (ax_pspace_means, ax_pspace_vars, ax_pspace_angle, ax_dspace)
for i in range(0, n_samples):
plot_all(axs, posterior_samples[i,0], posterior_samples[i,1], posterior_samples[i,2], posterior_samples[i,3],
posterior_samples[i,4], 'C1', '.', bivariate_normal, k=100)
plot_pspace(ax_pspace_means, ax_pspace_vars, ax_pspace_angle, *obs_par, color="C0")
plot_dspace(ax_dspace, obs, 'X', 'C0')
# -
# Now, you can see that the sythetic datasets are much closer to the observation. Also, the parameter values which generated those are not anymore evenly spread on the parameter space.
#
# The mean parameters are very much concentrated close to the exact parameter value; with regards to the other ones, they are a bit more spread out.
|
examples/2_Rejection_ABC_closer_look.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
% matplotlib inline
import numpy as np
import math
import matplotlib.pyplot as plt
import sys
import time
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from skimage import measure
from skimage.draw import ellipsoid
from numpy import linalg, random, ones, zeros, eye, dot
from numpy.linalg import norm, inv, cholesky
from scipy.linalg import solve_triangular
from scipy.sparse.linalg import spilu
from sklearn.cross_validation import train_test_split
from mpl_toolkits.mplot3d import Axes3D
from collections import namedtuple
from multiprocessing import Pool
initial_rho = 1.0
max_iter = 15
max_coord_iter = 35
initial_step_size = .1
timer_thresh = .5
def kernel(x1, x2):
return math.exp(-1 * math.pow(norm(x1 - x2), 2
) / (2 * math.pow(sigma, 2)))
def kernel_vect(x_list, x2):
return np.exp(-1 * np.power(norm(x_list - x2, axis=1), 2) / (2 * math.pow(sigma, 2)))
def loss_vect(t, rho):
return np.power(np.maximum(np.zeros(t.shape), np.absolute(rho - t) - delta), 2)
def f(args):
return f_expand(*args)
def f_expand(x_data, x_test, beta, rho):
start = time.time()
w = np.dot(beta, kernel_vect(x_data, x_test)) - rho
end = time.time()
if end - start > timer_thresh:
print 'f:', end - start, 'sec'
return w
def f_vect(slabSVM, x_test_matrix, beta, rho):
start = time.time()
w = np.empty(x_test_matrix.shape[0])
for i in range(x_test_matrix.shape[0]):
w[i] = np.dot(kernel_vect(slabSVM.x_data, x_test_matrix[i, :]), beta) - rho
end = time.time()
if end - start > timer_thresh:
print 'f_vect:', end - start, 'sec'
return w
def step(element, step_size, resid):
return element - (step_size * resid)
def incomplete_cholesky_decomp4(K):
start = time.time()
assert K.shape[0] == K.shape[1]
n = K.shape[0]
K_prime = K.copy()
G = np.zeros(K.shape)
P = np.identity(K.shape[0])
for j in range(n):
G[j, j] = K[j, j]
max_num = 0
while np.sum(np.diagonal(G[i:n, i:n])) > .0001:
max_num += 1
j = np.argmax(np.diagonal(G[i:n, i:n])) + i
P[i, i] = 0
P[j, j] = 0
P[i, j] = 1
P[j, i] = 1
# K_prime[0:n,i] <-> K_prime[0:n,j]
temp = K_prime[0:n, i].copy()
K_prime[0:n, i] = K_prime[0:n, j]
K_prime[0:n, j] = temp
# K_prime[i,0:n] <-> K_prime[j,0:n]
temp = K_prime[i, 0:n].copy()
K_prime[i, 0:n] = K_prime[j, 0:n]
K_prime[j, 0:n] = temp
# G[i,0:i+1] <-> G[j,0:i+1]
temp = G[i, 0:i + 1].copy()
G[i, 0:i + 1] = G[j, 0:i + 1]
G[j, 0:i + 1] = temp
G[i, i] = math.sqrt(K_prime[i, i])
G[i + 1: n, i] = K_prime[i + 1: n, i]
a_sum = np.zeros(G[i + 1: n, 0].shape)
for k in range(i):
a_sum += G[i + 1: n, k] * G[i, k]
G[i + 1: n, i] -= a_sum
assert G[i, i] != 0
G[i + 1: n, i] = G[i + 1: n, i] / G[i, i]
for t in range(i + 1, n):
G[t, t] = K_prime[t, t]
a_sum = 0
for k in range(i + 1):
a_sum += G[t, k] ** 2
G[t, t] -= a_sum
end = time.time()
if end - start > timer_thresh:
print 'incomplete_cholesky_decomp4:', end - start, 'sec'
return G, P, max_num
class Slab_SVM:
def get_H(self, opt_on):
start = time.time()
if opt_on == 'b':
start1 = time.time()
ret = gamma * 2 * self.K
end1 = time.time()
if end1 - start1 > timer_thresh:
print 'get_H - part I:', end1 - start1, 'sec'
start1 = time.time()
ret += 2 / (v) * self.K_K
end1 = time.time()
if end1 - start1 > timer_thresh:
print 'get_H - part II:', end1 - start1, 'sec'
elif opt_on == 'rho':
ret = 2 / (v * self.m)
end = time.time()
if end - start > timer_thresh:
print 'get_H:', end - start, 'sec'
return ret
def loss_der_der(self, t, rho):
if abs(rho - t) < delta:
return 0
else:
return 2
def loss_der(self, grad, t, rho, opt_on):
grad = 0
if opt_on == 'b':
if rho - t > delta:
grad = -2.0 * (rho - t - delta)
if -rho + t > delta:
grad = 2.0 * (-rho + t - delta)
return grad
if opt_on == 'rho':
if rho - t > delta:
grad = 2.0 * (rho - t - delta)
if -rho + t > delta:
grad = -2.0 * (-rho + t - delta)
return grad
raise Exception(grad, g_loss_type, t, rho, delta)
def loss_der_vect(self, t, rho, opt_on):
grad = np.zeros(t.shape)
if opt_on == 'b':
grad[rho - t > delta] = -2.0 * (rho - t[rho - t > delta] - delta)
grad[-rho + t > delta] = 2.0 * (-rho + t[-rho + t > delta] - delta)
return grad
if opt_on == 'rho':
grad[rho - t > delta] = 2 * (rho - t[rho - t > delta] - delta)
grad[-rho + t > delta] = -2 * (-rho + t[-rho + t > delta] - delta)
return grad
raise Exception(grad, g_loss_type, t, rho, delta)
def z(self, x1, w, b):
# w = random.normal(0, 1.0/sigma, size=(D,len(x1)))
# b = random.uniform(0,2*np.pi,size=D)
return math.sqrt(2.0 / D) * np.cos(np.dot(w, x1) + b)
def obj_funct(self, beta, rho):
start = time.time()
# if gamma * np.dot(beta, np.dot(self.K, beta)) < 0:
# raise Exception(gamma * np.dot(beta, np.dot(self.K, beta)))
# if gamma * np.dot( np.dot(beta, self.K_ilu.L.A), np.dot( self.K_ilu.U.A, beta) ) < 0:
# raise Exception(gamma * np.dot( np.dot(beta, self.K_ilu.L.A), np.dot( self.K_ilu.U.A, beta) ))
obj = gamma * np.dot(beta, np.dot(self.K, beta)) + \
1.0 / (v * self.m) * np.sum(loss_vect(np.dot(self.K, beta), rho)) - rho
end = time.time()
if end - start > timer_thresh:
print 'obj_funct:', end - start, 'sec'
return obj
def backtrack_step_size(self, step_size, obj, resid, grad, beta, rho, opt_on):
start = time.time()
min_step_size = sys.float_info.epsilon
if step_size == min_step_size:
step_size = initial_step_size
else:
step_size = step_size * (2 ** 20)
iters = 0
# c = .000001
# (c*step_size*np.dot(grad, resid)) + \
while obj <= (self.obj_funct(step(beta, step_size, resid), rho) if opt_on == 'b' \
else self.obj_funct(beta, step(rho, step_size, resid))):
iters += 1
step_size = step_size * 0.7
assert not math.isnan(step_size)
if step_size < min_step_size:
step_size = min_step_size
end = time.time()
# if end - start > timer_thresh:
print 'backtrack_step_size:', end - start, 'sec iters', iters, \
'opt_on', opt_on, \
' WARNING: step size not found'
return step_size
assert obj > (self.obj_funct(step(beta, step_size, resid), rho) if opt_on == 'b' \
else self.obj_funct(beta, step(rho, step_size, resid)))
end = time.time()
if end - start > timer_thresh:
print 'backtrack_step_size:', end - start, 'sec, iters', iters, 'opt_on', opt_on
return step_size
def get_resid(self, beta, rho, grad, loss_vect_list, opt_on):
start = time.time()
# self.H = self.get_H(beta,rho,loss_vect_list,opt_on)
if opt_on == 'b':
if is_approx:
resid = self.H_ilu.solve(grad)
# resid = np.dot(self.incomplete_cholesky_T_inv,
# np.dot(self.incomplete_cholesky_inv, grad))
# resid = self.incomplete_cholesky.solve(grad)
else:
if Use_Cholesky:
# resid = linalg.solve(self.L.T.conj(), linalg.solve(self.L,grad))
resid = np.dot(self.L_T_inv, np.dot(self.L_inv, grad))
# resid = spilu(self.H, drop_tol=0, fill_factor=250).solve(grad)
else:
resid = np.dot(self.H_inv, grad)
else:
resid = grad # /self.H
end = time.time()
if end - start > timer_thresh:
print 'get_resid:', end - start, 'sec'
return resid
def obj_grad(self, opt_on):
start = time.time()
if opt_on == 'b':
grad = gamma * 2.0 * np.dot(self.K, self.beta)
for i in range(self.m):
grad += 1.0 / (v * self.m) * (self.K[i] * self.loss_der(0,
np.dot(self.K[i],
self.beta),
self.rho,
opt_on))
elif opt_on == 'rho':
grad = 1 / (v * self.m) * np.sum(self.loss_der_vect(np.dot(self.K, self.beta),
self.rho,
opt_on)) - 1
else:
print '[obj_grad] Error'
end = time.time()
if end - start > timer_thresh:
print 'obj_grad:', end - start, 'sec'
return grad
def grad_des_iterate(self, opt_on='b'):
start = time.time()
loss_vect_list = np.where(np.absolute(self.rho - np.dot(self.K,
self.beta)) >= delta)[0]
end = time.time()
if end - start > timer_thresh:
print 'find sv:', end - start, 'sec'
obj = self.obj_funct(self.beta, self.rho)
if obj < -self.rho:
raise Exception(obj)
# self.obj_array[self.iterations]=(obj)
self.grad = self.obj_grad(opt_on)
# self.obj_grad_array[self.iterations]=norm(self.grad)
if norm(self.grad) < (min_grad_rho if opt_on == 'rho' else min_grad_beta):
print 'Stopping crit: norm(grad) small', norm(self.grad), 'opt_on', opt_on
return True
resid = self.get_resid(self.beta, self.rho, self.grad, loss_vect_list, opt_on)
if opt_on == 'rho':
self.step_size_rho = self.backtrack_step_size(self.step_size_rho, obj, resid,
self.grad, self.beta,
self.rho, opt_on)
self.rho = max(0, step(self.rho, self.step_size_rho, resid)) # Update
else:
self.step_size_beta = self.backtrack_step_size(self.step_size_beta, obj, resid,
self.grad, self.beta,
self.rho, opt_on)
self.beta = step(self.beta, self.step_size_beta, resid) # Update
end = time.time()
if end - start > timer_thresh:
print 'grad_des_iterate:', end - start, 'sec'
return False
def grad_des_coord(self, opt_on=''):
start = time.time()
for j in range(max_coord_iter): # max_iter if i<max_iter-1 else 2*max_iter):
self.iterations += 1
converged = self.grad_des_iterate(opt_on=opt_on)
if converged:
break
end = time.time()
if end - start > timer_thresh:
print 'grad_des_coord:', end - start, 'sec'
def grad_des(self):
start = time.time()
self.obj_array = -1 * np.ones(max_iter)
self.obj_grad_array = np.zeros((max_iter))
self.obj_grad_check_array = np.zeros(max_iter)
self.beta = zeros(self.m)
self.rho = initial_rho
self.grad_buffer = zeros(self.beta.shape)
self.step_size_beta = initial_step_size
self.step_size_rho = initial_step_size
self.iterations = 0
print 'obj', self.obj_funct(self.beta, self.rho)
for i in range(max_iter):
self.grad_des_coord(opt_on='b')
self.grad_des_coord(opt_on='rho')
if i == max_iter - 1:
converged_b = self.grad_des_coord(opt_on='b')
converged_b = self.grad_des_coord(opt_on='b')
print 'obj', self.obj_funct(self.beta, self.rho)
print 'grad b', norm(self.obj_grad('b')), 'grad rho', norm(self.obj_grad('rho'))
print 'b', norm(self.beta), 'rho', self.rho
print 'self.iterations', self.iterations
if norm(self.obj_grad('b')) < min_grad_beta and \
norm(self.obj_grad('rho')) < min_grad_rho:
print 'Stopping crit: norm(grad) small, opt_on b and rho'
return True
if i == max_iter - 1:
print 'WARNING: Did not converge'
end = time.time()
# if end - start > timer_thresh:
print 'grad_des:', ((str(end - start) + ' sec') if end - start < 60 \
else (str((end - start) / 60.) + ' min'))
def pop_K(self):
start = time.time()
self.K = np.zeros((self.m, self.m))
if Fourier_Feature:
z_cache = np.zeros((self.m, D))
w = random.normal(0, 1.0 / sigma, size=(self.m * D, len(self.x_data[0])))
b = random.uniform(0, 2 * np.pi, size=self.m * D)
for i in range(self.m):
z_cache[i] = self.z(self.x_data[i], w[i:i + D, :], b[i:i + D])
end = time.time()
if end - start > timer_thresh:
print 'z_cache:', end - start, 'sec'
for i in range(self.m):
self.K[i, :] = np.dot(z_cache, z_cache[i])
# for j in range(self.m):
# self.z(self.x_data[i]),self.z(self.x_data[j]))
else:
for i in range(self.m):
self.K[i, :] = kernel_vect(self.x_data, self.x_data[i])
if Fourier_Feature:
K_test = np.zeros((self.m, self.m))
for i in range(self.m):
K_test[i, :] = kernel_vect(self.x_data, self.x_data[i])
print 'Fourier norm diff', norm(K_test - self.K)
self.K_K = np.dot(self.K, self.K)
self.H = self.get_H('b')
if is_approx:
# incomplete_cholesky, P, k = incomplete_cholesky_decomp4(self.H.copy())
# self.K_ilu = spilu(self.K,drop_tol=drop_tol, fill_factor=250)
# self.K = np.dot(self.K_ilu.L.A,self.K_ilu.U.A)
# self.K_K = np.dot(self.K, self.K)
# self.K_K = np.dot(np.dot(self.K_ilu.L.A, self.K_ilu.U.A),
# np.dot(self.K_ilu.L.A,self.K_ilu.U.A))
# self.H = self.get_H('b')
self.H_ilu = spilu(self.H, drop_tol=drop_tol, fill_factor=250)
else:
if Use_Cholesky:
self.L = cholesky(self.H)
self.L_inv = linalg.solve(self.L, np.identity(self.L.shape[0]))
self.L_T_inv = linalg.solve(self.L.T, np.identity(self.L.shape[0]))
else:
self.H_inv = inv(self.H)
end = time.time()
if end - start > timer_thresh:
print 'pop_K:', end - start, 'sec'
def get_K_inv(K):
start = time.time()
K_inv = inv(K)
end = time.time()
if end - start > timer_thresh:
print 'get_K_inv:', end - start, 'sec'
return K_inv
def get_K_cond(K):
start = time.time()
K_cond = linalg.cond(K)
end = time.time()
if end - start > timer_thresh:
print 'get_K_cond:', end - start, 'sec'
return K_cond
def pre_comp_K():
start = time.time()
K = get_K()
end = time.time()
if end - start > timer_thresh:
print 'pre_comp_K:', end - start, 'sec'
return K # , K_inv
def __init__(self, x_data):
start = time.time()
self.x_data = x_data
self.m = len(self.x_data)
self.pop_K()
if np.min(linalg.eigvals(self.K)) < 0:
raise Exception(linalg.eigvals(self.K))
if np.min(linalg.eigvalsh(self.K)) < 0:
raise Exception(linalg.eigvalsh(self.K))
self.grad_des()
end = time.time()
if end - start > timer_thresh:
print '__init__:', ((str(end - start) + ' sec') if end - start < 60 \
else (str((end - start) / 60.) + ' min'))
def get_data_points(data_ratio):
start = time.time()
x = []
f = open('bunny.obj.txt')
for line in f:
line = line.strip()
if line != '' and line[0] != '#':
line_split = line.split()
if len(line_split) == 4 and line_split[0] == 'v':
x.append(line_split[1:])
x = np.array(x)
x = x.astype(np.float)
x = sorted(x, key=lambda a_entry: a_entry[0])
x = np.array(x)
x = x[data_ratio * x.shape[0] / 10:, :]
print 'points:', len(x)
end = time.time()
if end - start > timer_thresh:
print 'get_data_points:', end - start, 'sec'
return x
grid_steps = 100
def proc_data(beta, rho, data):
start = time.time()
print 'delta', delta
print 'rho', rho
print 'np.abs(data - delta) < .1 -> ', (np.where(np.abs(data - delta) < .1)[0].shape)
print 'np.abs(data - delta) < .01 -> ', (np.where(np.abs(data - delta) < .01)[0].shape)
print 'np.abs(data - delta) < .001 -> ', (np.where(np.abs(data - delta) < .001)[0].shape)
print 'np.abs(data - delta) < .0001 -> ', (np.where(np.abs(data - delta) < .0001)[0].shape)
print 'data < delta -> ', (np.where(data < delta)[0].shape)
print 'data > delta -> ', (np.where(data > delta)[0].shape)
print 'data < 0 -> ', (np.where(data < 0)[0].shape)
print 'data == 0 -> ', (np.where(data == 0)[0].shape)
print 'data > 0 -> ', (np.where(data > 0)[0].shape)
print 'min -> ', (np.amin(data))
print 'max -> ', (np.amax(data))
end = time.time()
if end - start > timer_thresh:
print 'proc_results:', ((str(end - start) + ' sec') if end - start < 60 \
else (str((end - start) / 60.) + ' min'))
def pop_data_grid(slabSVM, beta, rho, x0_max, x1_max, x2_max, x0_min, x1_min, x2_min):
start = time.time()
data = np.zeros((grid_steps, grid_steps, grid_steps))
x0_range = np.linspace(x0_min, x0_max, grid_steps)
x1_range = np.linspace(x1_min, x1_max, grid_steps)
x2_range = np.linspace(x2_min, x2_max, grid_steps)
end = time.time()
if end - start > timer_thresh:
print 'alloc mem:', end - start
pool = Pool(processes=4)
args = []
for i in range(grid_steps):
for j in range(grid_steps):
for k in range(grid_steps):
args.append((slabSVM.x_data,
np.asarray([x0_range[i],
x1_range[j],
x2_range[k]]),
slabSVM.beta,
slabSVM.rho,))
end = time.time()
if end - start > timer_thresh:
print 'pop_data_grid args:', end - start, 'sec'
eval_map = pool.map(f, args)
end = time.time()
if end - start > timer_thresh:
print 'pop_data_grid pool map:', ((str(end - start) + ' sec') \
if end - start < 60 \
else (str((end - start) / 60.) + ' min'))
counter = 0
for i in range(grid_steps):
for j in range(grid_steps):
for k in range(grid_steps):
data[i, j, k] = eval_map[counter]
counter += 1
end = time.time()
if end - start > timer_thresh:
print 'pop_data_grid:', ((str(end - start) + ' sec') \
if end - start < 60 \
else (str((end - start) / 60.) + ' min'))
return data
# +
g_loss_type = 'square-hinge'
g_method = 'Newton'
g_Desc = {}
g_counter=0
approx_avg = []
true_avg = []
approx_iterations = []
true_iterations = []
D = 1000
v = .0001
sigma = .0084
gamma = 1.
delta = 0.0
is_approx = True
Use_Cholesky = True
Fourier_Feature = False
data_ratio = 0
min_grad_beta = 0.00001
min_grad_rho = 0.00001
g_x = get_data_points(data_ratio)
x0_max = np.amax(g_x[:,0])
x0_min = np.amin(g_x[:,0])
x1_max = np.amax(g_x[:,1])
x1_min = np.amin(g_x[:,1])
x2_max = np.amax(g_x[:,2])
x2_min = np.amin(g_x[:,2])
start = time.time()
fig = plt.figure(figsize=(10, 12))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(g_x[:,0],g_x[:,2],g_x[:,1])
ax.view_init(elev=20., azim=240)
plt.show()
end = time.time()
if end - start > timer_thresh:
print 'scatter:',end - start,'sec'
drop_tol=0
for drop_tol in [0, 10**-10, 5*10**-10, 10**-9, 10**-8, 10**-6, 10**-4, 10**-2, 1, 2]:
g_counter += 1
print '-----------------------------------'
print 'drop_tol',drop_tol
print 'v',v
print 'sigma',sigma
print 'gamma',gamma
g_Desc[g_counter] = Slab_SVM(g_x)
g_Desc[g_counter].end_obj = g_Desc[g_counter].obj_funct(g_Desc[g_counter].beta,
g_Desc[g_counter].rho)
print 'obj',g_Desc[g_counter].obj_funct(g_Desc[g_counter].beta,g_Desc[g_counter].rho)
print 'norm(grad)',norm(g_Desc[g_counter].obj_grad('b'))
print 'Desc iterations',g_Desc[g_counter].iterations
print 'Desc rho',g_Desc[g_counter].rho
print '-----------------------------------'
print
data = pop_data_grid(g_Desc[g_counter], g_Desc[g_counter].beta,g_Desc[g_counter].rho,
x0_max,x1_max,x2_max,x0_min,x1_min,x2_min)
verts, faces = measure.marching_cubes(data, 0)
for elev in [180,120,60,90]:
for azim in [30,90,180,240]:
fig = plt.figure(figsize=(10, 12))
ax = fig.add_subplot(111, projection='3d')
mesh = Poly3DCollection(verts[faces])
ax.add_collection3d(mesh)
ax.view_init(elev=elev, azim=azim)
ax.set_xlim(0,grid_steps)
ax.set_ylim(0,grid_steps)
ax.set_zlim(0,grid_steps)
plt.show()
break
break
# +
g_m = len(g_x)
start = time.time()
losses = []
for i in range(g_m):
losses.append(f((g_Desc[g_counter].x_data, g_x[i], g_Desc[g_counter].beta,
g_Desc[g_counter].rho)))
losses = np.asarray(losses)
end = time.time()
if end - start > timer_thresh:
print 'losses = []:',end - start,'sec'
if is_approx:
approx_avg.append(np.average( losses ))
approx_iterations.append(g_Desc[g_counter].iterations)
else:
true_avg.append(np.average( losses ))
true_iterations.append(g_Desc[g_counter].iterations)
print 'losses min -> ',(np.amin( losses ))
print 'losses argmin -> ',(np.argmin( losses ))
print 'losses x[min] -> ',g_x[(np.argmin( losses ))]
print 'losses max -> ',(np.amax( losses ))
print 'losses argmax -> ',(np.argmax( losses ))
print 'losses x[max] -> ',g_x[(np.argmax( losses ))]
print 'v',v
print 'sigma',sigma
data = pop_data_grid(g_Desc[g_counter], g_Desc[g_counter].beta,g_Desc[g_counter].rho,
x0_max,x1_max,x2_max,x0_min,x1_min,x2_min)
proc_data(g_Desc[g_counter].beta,g_Desc[g_counter].rho,data)
# +
# Use marching cubes to obtain the surface mesh of these ellipsoids
verts, faces = measure.marching_cubes(data, 0)
for elev in [180,120,60,90]:
for azim in [30,90,180,240]:
# Display resulting triangular mesh using Matplotlib. This can also be done
# with mayavi (see skimage.measure.marching_cubes docstring).
fig = plt.figure(figsize=(10, 12))
ax = fig.add_subplot(111, projection='3d')
# Fancy indexing: `verts[faces]` to generate a collection of triangles
mesh = Poly3DCollection(verts[faces])
ax.add_collection3d(mesh)
ax.view_init(elev=elev, azim=azim)
ax.set_xlim(0,grid_steps)
ax.set_ylim(0,grid_steps)
ax.set_zlim(0,grid_steps)
plt.show()
# break
# break
# +
surface_data = []
for i in range(grid_steps):
for j in range(grid_steps):
for k in range(grid_steps):
if abs(data[i,j,k]) < .001:
surface_data.append([i,j,k])
surface_data = np.asarray(surface_data)
print surface_data.shape
fig1 = plt.figure(figsize=(10, 12))
ax1 = fig1.add_subplot(111, projection='3d')
ax1.scatter(surface_data[:,0],surface_data[:,1],surface_data[:,2])
ax1.view_init(elev=180., azim=240)
plt.show()
fig2 = plt.figure(figsize=(10, 12))
ax2 = fig2.add_subplot(111, projection='3d')
ax2.scatter(surface_data[:,0],surface_data[:,1],surface_data[:,2])
ax2.view_init(elev=90., azim=240)
plt.show()
fig3 = plt.figure(figsize=(10, 12))
ax3 = fig3.add_subplot(111, projection='3d')
ax3.scatter(surface_data[:,0],surface_data[:,1],surface_data[:,2])
ax3.view_init(elev=100., azim=240)
plt.show()
# +
# +
# %matplotlib nbagg
plt.clf()
plt.cla()
ax = plt.subplot(1,1,1)
print approx_avg
print true_avg
# approx_iterations = []
# true_iterations = []
ax.scatter(range(1,len(approx_avg)+1),
approx_avg,marker='^',
label='Approximate Low Rank Kernel')
ax.scatter(range(1,len(true_avg)+1),
true_avg,marker='*',
label='Exact Kernel')
handles, labels = ax.get_legend_handles_labels()
plt.legend(handles, labels)
plt.title('Average Error vs Data Size')
plt.ylabel('Average Error')
plt.xlabel('Data Size')
# +
# %matplotlib nbagg
plt.clf()
plt.cla()
ax = plt.subplot(1,1,1)
print approx_iterations
print true_iterations
ax.scatter(range(1,len(approx_iterations)+1),
approx_iterations,marker='^',
label='Approximate Low Rank Kernel')
ax.scatter(range(1,len(true_iterations)+1),
true_iterations,marker='*',
label='Exact Kernel')
handles, labels = ax.get_legend_handles_labels()
plt.legend(handles, labels)
plt.title('Descent Iterations vs Data Size')
plt.ylabel('Descent Iterations')
plt.xlabel('Data Size')
# -
fig = plt.figure(figsize=(10, 12))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(g_x[:,0],g_x[:,2],g_x[:,1])
ax.view_init(elev=20., azim=240)
plt.show()
# +
# Use marching cubes to obtain the surface mesh of these ellipsoids
verts, faces = measure.marching_cubes(data, 0)
# Display resulting triangular mesh using Matplotlib. This can also be done
# with mayavi (see skimage.measure.marching_cubes docstring).
fig = plt.figure(figsize=(10, 12))
ax = fig.add_subplot(111, projection='3d')
# Fancy indexing: `verts[faces]` to generate a collection of triangles
mesh = Poly3DCollection(verts[faces])
ax.add_collection3d(mesh)
ax.set_xlabel("x-axis")
ax.set_ylabel("y-axis")
ax.set_zlabel("z-axis")
ax.set_xlim(-1, 30)
ax.set_ylim(-1, 30)
ax.set_zlim(-1, 30)
ax.view_init(elev=20., azim=240)
plt.show()
# -
|
Primal-Slab-SVM-Rabbit.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="X6aRomqiGdP3"
# #INFO
# experiments that can take place :
#
#
#
#
#
# 1. changing BERT from pretrained from base-uncased to bertweet
# 2. keeping or omitting verified
# 3. trainig pairs of (source , reply) , (source-tag)
# 4. add source aggregated (known stance)
#
# source_reply_*.json format last used
#
#
#
# + [markdown] id="2T38W5nfg0Gh"
# ##setup
#
# + id="aSiJXX_0SDdY" colab={"base_uri": "https://localhost:8080/"} outputId="46d44fc3-a1c0-488d-ddc6-320e62ce3389"
import tensorflow as tf
import torch
import os
import pandas as pd
# !pip install transformers
from transformers import BertTokenizer
from torch.utils.data import TensorDataset, random_split
from torch.utils.data import DataLoader, RandomSampler, SequentialSampler
from transformers import BertForSequenceClassification, AdamW, BertConfig
from transformers import get_linear_schedule_with_warmup
import numpy as np
import time
import datetime
import random
import matplotlib.pyplot as plt
% matplotlib inline
import json
import seaborn as sns
from sklearn.metrics import matthews_corrcoef
# + id="ErfLSv-oUQYU" colab={"base_uri": "https://localhost:8080/"} outputId="62adf3f2-2617-4d8c-925d-ce91a4641578"
import tensorflow as tf
# Get the GPU device name.
device_name = tf.test.gpu_device_name()
# The device name should look like the following:
if device_name == '/device:GPU:0':
print('Found GPU at: {}'.format(device_name))
else:
raise SystemError('GPU device not found')
# + id="-VXvVRsXrURK"
import time
import datetime
def format_time(elapsed):
'''
Takes a time in seconds and returns a string hh:mm:ss
'''
# Round to the nearest second.
elapsed_rounded = int(round((elapsed)))
# Format as hh:mm:ss
return str(datetime.timedelta(seconds=elapsed_rounded))
# + id="UYjuJgINUZnl" colab={"base_uri": "https://localhost:8080/"} outputId="12166a20-0ed2-476b-f427-1507d6b288c1"
import torch
# If there's a GPU available...
if torch.cuda.is_available():
# Tell PyTorch to use the GPU.
device = torch.device("cuda")
print('There are %d GPU(s) available.' % torch.cuda.device_count())
print('We will use the GPU:', torch.cuda.get_device_name(0))
# If not...
else:
print('No GPU available, using the CPU instead.')
device = torch.device("cpu")
# + id="dc3Jg9qbUuQP" colab={"base_uri": "https://localhost:8080/"} outputId="e0dc1c6d-a290-428d-c649-c72c169d8fc7"
# !pip3 install emoji
# + colab={"base_uri": "https://localhost:8080/"} id="bNMCGuZHVrSP" outputId="1f5a7254-9ad2-4e26-f0f0-bfda1edf2c6f"
a=np.array([[[1,2],[1,2]],[[1,2],[1,2]],[[1,2],[1,2]]])
flat_predictions = np.concatenate(a, axis=0)
flat_predictions.shape
# + [markdown] id="X3WECWiuhA83"
# ## loading data
#
# + id="gAj46f1PbZPq" colab={"base_uri": "https://localhost:8080/"} outputId="9d784e59-73e2-4491-c704-58c41a44c00d"
# !git clone "https://github.com/parsafarinnia/rumoureval2019"
# + [markdown] id="Dc6qxJ2RBb7M"
# ### Loading source - aggregated stance(from key)
# format is {sourceId : [s,d,q,c]}
# + id="sbysBQjFBxsz"
import pickle
source_stance_train = pickle.load(open ("/content/rumoureval2019/source_stance_train.p","rb"))
source_stance_dev = pickle.load(open ("/content/rumoureval2019/source_stance_dev.p","rb"))
source_stance_test = pickle.load(open ("/content/rumoureval2019/source_stance_test.p","rb"))
# + [markdown] id="lUsElwTc07GB"
# ### preprocessed clean data (Sardar's)
# + colab={"base_uri": "https://localhost:8080/", "height": 222} id="TPNivOxqVY9D" outputId="937002d3-6b92-4f00-dbc7-126ab94ba99a"
with open('/content/rumoureval2019/rum_ver_stance_dev') as f:
data = json.load(f)
dev_cleaned=pd.DataFrame.from_dict(data)
dev_cleaned
# + id="DKCOjXwFV0ab"
with open('/content/rumoureval2019/rum_ver_stance_train') as f:
data = json.load(f)
train_cleaned=pd.DataFrame.from_dict(data)
train_cleaned.veracitytag.unique()
# + id="78NKwjXRjola"
map= {"Rum":1,"unverified":2,"na":0}
train_parent_child = train_cleaned[['text','parent_body','rum_tag']]
dev_parent_child = dev_cleaned[['text','parent_body','rum_tag']]
train_parent_child=train_parent_child.replace({"rum_tag":map})
dev_parent_child = dev_parent_child.replace({"rum_tag":map})
dev_parent_child
# + [markdown] id="TmYvAQUmyDH2"
# ### parsa preprocessing
# + id="7qpnfKHByMNn"
with open('/content/rumoureval2019/source_reply_dev.json') as f:
data = json.load(f)
dev_cleaned=pd.DataFrame.from_dict(data)
with open('/content/rumoureval2019/source_reply_test.json') as f1:
data = json.load(f1)
test_cleaned=pd.DataFrame.from_dict(data)
with open('/content/rumoureval2019/source_reply_train.json') as f2:
data = json.load(f2)
train_cleaned=pd.DataFrame.from_dict(data)
map= {'unverified':1, 'true':2, 'false':0}
train_parent_child=train_cleaned.replace({"class":map})
dev_parent_child = dev_cleaned.replace({"class":map})
test_parent_child = test_cleaned.replace({"class":map})
test_parent_child.groupby(['source_text']).mean().shape
# + [markdown] id="0SSlbY_P1LNH"
# ### normal not preprocessed data(only sources work now)
# + id="67gB5K4kblDK" colab={"base_uri": "https://localhost:8080/", "height": 406} outputId="ce1a033e-1c57-4017-b433-8d69d2a19717"
train = pd.read_json("/content/rumoureval2019/train.json")
# train = train.drop(train[train['class']=='unverified'].index)
train
# + id="5u-pmvrOb9Lj" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="c5f2fe04-48fe-4875-f267-3bfb56833b43"
dev = pd.read_json("/content/rumoureval2019/dev.json")
# dev = dev.drop(dev[dev['class']=='unverified'].index)
dev
# + id="STgF7ojDcQuJ" colab={"base_uri": "https://localhost:8080/", "height": 406} outputId="1257dbe8-9675-4d04-ae0a-b59dfad9046e"
test = pd.read_json("/content/rumoureval2019/test.json")
test
# + id="ZGBcDnTac0dL" colab={"base_uri": "https://localhost:8080/", "height": 406} outputId="e2fb70e6-87bb-4c2a-dde2-983223e0025b"
# mapping categorical to numerical
map= {"true":1,"unverified":2,"false":0}
train=train.replace({"class":map})
train
# + id="762FLlX0dvRG"
test=test.replace({"class":map})
dev=dev.replace({"class":map})
# + [markdown] id="r6RP4whLVEDS"
# ### importing saved vectorized data
# + id="iKsHsxXAVJb6"
import pickle
bert_tweet_vecs = pickle.load( open( "/content/rumoureval2019/bert_tweet_vecs.p", "rb" ) )
train_features=bert_tweet_vecs['train']
dev_features=bert_tweet_vecs['dev']
test_features=bert_tweet_vecs['test']
# + [markdown] id="KkfH0sdU1nZg"
# ### final data for train dev test
# + [markdown] id="jXfN299e3ew1"
# #### parsa cleaned data
#
# + id="PIsFQgEV4oOw" colab={"base_uri": "https://localhost:8080/", "height": 240} outputId="e8c7cac3-7628-4502-f6ac-0122caf4b415"
'''
if preprocessed by parsa
'''
train_sources=train_parent_child.source_text.values
train_comments=train_parent_child.reply_text.values
train_labels=train_parent_child['class'].values
dev_sources = dev_parent_child.source_text.values
dev_comments = dev_parent_child.reply_text.values
dev_labels = dev_parent_child['class'].values
test_sources = test_parent_child.source_text.values
test_comments = test_parent_child.reply_text.values
test_labels = test_parent_child['class'].values
# + id="VEvA3ryq7DxA"
train_sources=np.reshape(train_sources,(len(train_sources),1))
train_comments=np.reshape(train_comments,(len(train_comments),1))
train_data=np.concatenate([train_sources,train_comments],axis=1)
dev_sources=np.reshape(dev_sources,(len(dev_sources),1))
dev_comments=np.reshape(dev_comments,(len(dev_comments),1))
dev_data=np.concatenate([dev_sources,dev_comments],axis=1)
test_sources=np.reshape(test_sources,(len(test_sources),1))
test_comments=np.reshape(test_comments,(len(test_comments),1))
test_data=np.concatenate([test_sources,test_comments],axis=1)
# + [markdown] id="VPETM7YX7AdV"
# #### by others
# sardars and source only tweet
# + id="yHLMtzcKhrQj" colab={"base_uri": "https://localhost:8080/"} outputId="3d3d66e6-1b4e-4617-dac6-46f4d4529e51"
'''
if not preprocessed
'''
train_sentences=train.text.values
train_labels = train["class"].values
test_sentences=test.text.values
test_labels = test["class"].values
dev_sentences=dev.text.values
dev_labels = dev["class"].values
'''
if preprocessed by sardar
'''
# train_sources=train_parent_child.parent_body.values
# train_comments=train_parent_child.text.values
# train_labels=train_parent_child.rum_tag.values
# dev_sources = dev_parent_child.parent_body.values
# dev_comments = dev_parent_child.text.values
# dev_labels = dev_parent_child.rum_tag.values
'''
from sklearn.model_selection import train_test_split
train_sources=np.reshape(train_sources,(len(train_sources),1))
train_comments=np.reshape(train_comments,(len(train_comments),1))
train_data=np.concatenate([train_sources,train_comments],axis=1)
train_data, val_data, train_labels, val_labels = train_test_split(train_data, train_labels, test_size=0.2)
dev_sources=np.reshape(dev_sources,(len(dev_sources),1))
dev_comments=np.reshape(dev_comments,(len(dev_comments),1))
test_data=np.concatenate([dev_sources,dev_comments],axis=1)
'''
# + id="<KEY>"
train_ids=train.index.values
dev_ids=dev.index.values
test_ids=test.index.values
# + id="ky02kEOgQxMg"
#rearrange train stance
rearranged_list_train=[]
for train_id in train_ids:
rearranged_list_train.append(source_stance_train[train_id])
rearranged_list_dev=[]
for train_id in dev_ids:
rearranged_list_dev.append(source_stance_dev[train_id])
rearranged_list_test=[]
for train_id in test_ids:
rearranged_list_test.append(source_stance_test[train_id])
# + id="n0HMu_LsI_12"
train_labels_hv=[]
for label in train['class'].values:
dummy=[0,0,0]
dummy[label]=1
train_labels_hv.append(dummy)
test_labels_hv=[]
for label in test['class'].values:
dummy=[0,0,0]
dummy[label]=1
test_labels_hv.append(dummy)
dev_labels_hv=[]
for label in dev['class'].values:
dummy=[0,0,0]
dummy[label]=1
dev_labels_hv.append(dummy)
# + id="gPUp7OXcTXp3" colab={"base_uri": "https://localhost:8080/"} outputId="44e1a0eb-cdc0-4e15-d748-aac8fe8d5a66"
stance_train=np.array(rearranged_list_train)
stance_dev=np.array(rearranged_list_dev)
stance_test=np.array(rearranged_list_test)
train_labels_hv=np.array(train_labels_hv)
dev_labels_hv=np.array(dev_labels_hv)
test_labels_hv=np.array(test_labels_hv)
print(stance_train.shape)
print(train_labels_hv.shape)
print(stance_dev.shape)
print(dev_labels_hv.shape)
print(stance_test.shape)
print(test_labels_hv.shape)
# + [markdown] id="XIwoQjKLhKrw"
# ## loading berts
#
#
#
# + id="b8VmLiL7VHj5" colab={"base_uri": "https://localhost:8080/", "height": 233, "referenced_widgets": ["aa0a80fdc4ad4186899ef6bfff31a55f", "<KEY>", "<KEY>", "<KEY>", "64d9868eeb274938abc34f5b9547e78c", "<KEY>", "<KEY>", "<KEY>", "1cc8270f69e3471da460253421c97d8c", "<KEY>", "<KEY>", "<KEY>", "c16b16e3fbb447408c49c8804e49c1f8", "94743e57d2624fd99993c565e2317d5a", "79d9eaa7c825463089846af8aef43a56", "<KEY>", "2f2091ea64be4842bddf02035935a966", "<KEY>", "<KEY>", "443c960c190848a9a1a5d8d8d5d8756e", "c2db17b28e4549358713454d42691758", "6f6fa748ae904ad1bc5072458aba210d", "40f26f125a2f4a31984f5798a9d8a8c6", "d01fb150b0094457a9f2015fefdd84c0", "b88109de7be3483a9d8d1a325350d238", "<KEY>", "7dc5e304d2e5461693b3158e2dd7dd67", "<KEY>", "<KEY>", "ed2ee9c7a5154200a3ecbad519b51112", "<KEY>", "<KEY>"]} outputId="d658f70a-8a9a-460e-ef30-6528b9b23c98"
from transformers import AutoModel, AutoTokenizer
# Load BERT TWEET tokenizer and model
bert_tweet = AutoModel.from_pretrained("vinai/bertweet-base")
tokenizer_tweet = AutoTokenizer.from_pretrained("vinai/bertweet-base",normalization=True)
# bert_tweet = AutoModel.from_pretrained("bert-base-uncased")
# tokenizer_tweet = AutoTokenizer.from_pretrained("bert-base-uncased",normalization=True)
# + [markdown] id="2lkzEiD5El_z"
# #Training
# + [markdown] id="ieRgqaXUT-Tm"
# ## Naive bayes
# + colab={"base_uri": "https://localhost:8080/"} id="oFef1EAnUEFW" outputId="65af6f4c-9345-4383-9c04-a7b662de948d"
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
x=np.concatenate([train_features,dev_features])
x_stance=np.concatenate([stance_train,stance_dev])
x=np.concatenate([x,x_stance],axis=1)
y=np.concatenate([train_labels,dev_labels])
x_test=np.concatenate([test_features,stance_test],axis=1)
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(x)
x=scaler.transform(x)
x_test=scaler.transform(x_test)
clf = MultinomialNB()
clf.fit(x, y)
y_pred=clf.predict(x_test)
print(classification_report(test_labels, y_pred, labels=[0,1,2]))
# + [markdown] id="6-CloMPJISQM"
# ## random forest
# + colab={"base_uri": "https://localhost:8080/"} id="XJpVQLSHIWR8" outputId="741d3a3c-32ae-4580-9319-d4258d723ea7"
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.metrics import classification_report
clf = RandomForestClassifier( random_state=0)
x=np.concatenate([train_features,dev_features])
x_stance=np.concatenate([stance_train,stance_dev])
x=np.concatenate([x,x_stance],axis=1)
y=np.concatenate([train_labels,dev_labels])
x_test=np.concatenate([test_features,stance_test],axis=1)
clf.fit(x, y)
y_pred=clf.predict(x_test)
print(classification_report(test_labels, y_pred, labels=[0,1,2]))
# + [markdown] id="Ou84ofGp9d_3"
# ## SVM
# + colab={"base_uri": "https://localhost:8080/"} id="wa_ShLjl9dJ3" outputId="b62cc274-0883-40d2-ae2c-001359766601"
from sklearn import svm
from sklearn.metrics import classification_report
clf = svm.SVC()
x=np.concatenate([train_features,dev_features])
x_stance=np.concatenate([stance_train,stance_dev])
x=np.concatenate([x,x_stance],axis=1)
y=np.concatenate([train_labels,dev_labels])
x_test=np.concatenate([test_features,stance_test],axis=1)
clf.fit(x,y)
y_pred=clf.predict(x_test)
print(classification_report(test_labels, y_pred, labels=[0,1,2]))
# + colab={"base_uri": "https://localhost:8080/"} id="QTRzjFXoevh5" outputId="06245b47-ebef-402d-ca88-7591fceff97b"
clf = BaggingClassifier(base_estimator=svm.SVC(),n_estimators=15, random_state=0)
clf.fit(x,y)
y_pred=clf.predict(x_test)
print(classification_report(test_labels, y_pred, labels=[0,1,2]))
# + [markdown] id="0uxW2Fd9ZxAn"
# ### knn bagging
# + colab={"base_uri": "https://localhost:8080/"} id="g5FRjcEoZNko" outputId="86985c52-41c5-43d7-cd54-9c2f897e0601"
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
clf = BaggingClassifier(KNeighborsClassifier(3),max_samples=0.5, max_features=0.5)
x=np.concatenate([train_features,dev_features])
x_stance=np.concatenate([stance_train,stance_dev])
x=np.concatenate([x,x_stance],axis=1)
y=np.concatenate([train_labels,dev_labels])
x_test=np.concatenate([test_features,stance_test],axis=1)
clf.fit(x,y)
y_pred=clf.predict(x_test)
print(classification_report(test_labels, y_pred, labels=[0,1,2]))
# + [markdown] id="L0Gj7hYYpy4L"
# ### tokenizer
# + [markdown] id="qavGT1ZL8VG_"
# #### source - comment bert
# + id="W_rfdgQPqp20"
#tokenizer for 2 sentence input
def two_sentence_tokenizer_func(tokenizer_kind,sentences,labels):
'''
inputs:
tokenizer_kind: is the the tokenizer of choice (normal bert, tweet bert)
sentences: train , dev, test
outputs:
torchs of
ids
attention_mask
labels
'''
input_ids = []
attention_masks = []
# For every sentence...
for pair in sentences:
# `encode_plus` will:
# (1) Tokenize the sentence.
# (2) Prepend the `[CLS]` token to the start.
# (3) Append the `[SEP]` token to the end.
# (4) Map tokens to their IDs.
# (5) Pad or truncate the sentence to `max_length`
# (6) Create attention masks for [PAD] tokens.
encoded_dict = tokenizer_kind(
pair[0],pair[1], # Sentence to encode.
return_tensors = 'pt', # Return pytorch tensors.
padding='max_length',
truncation=True
)
# Add the encoded sentence to the list.
input_ids.append(encoded_dict['input_ids'])
# And its attention mask (simply differentiates padding from non-padding).
attention_masks.append(encoded_dict['attention_mask'])
# Convert the lists into tensors.
# input_ids = torch.FloatTensor(input_ids)
# print(input_ids[0].shape)
# attention_masks = torch.FloatTensor(attention_masks)
# print(attention_masks)
# labels = torch.tensor(labels)
input_ids = torch.cat(input_ids, dim=0)
attention_masks = torch.cat(attention_masks, dim=0)
labels = torch.tensor(labels)
return input_ids, attention_masks ,labels
# + [markdown] id="udJyf5aO8ame"
# #### source only bert
# + id="0KRoiEfKhnEA"
# Tokenize all of the sentences and map the tokens to thier word IDs.
def tokenizer_func(tokenizer_kind,sentences,labels):
'''
inputs:
tokenizer_kind: is the the tokenizer of choice (normal bert, tweet bert)
sentences: train , dev, test
outputs:
torchs of
ids
attention_mask
labels
'''
input_ids = []
attention_masks = []
# For every sentence...
for sent in sentences:
# `encode_plus` will:
# (1) Tokenize the sentence.
# (2) Prepend the `[CLS]` token to the start.
# (3) Append the `[SEP]` token to the end.
# (4) Map tokens to their IDs.
# (5) Pad or truncate the sentence to `max_length`
# (6) Create attention masks for [PAD] tokens.
encoded_dict = tokenizer_kind.encode_plus(
sent, # Sentence to encode.
add_special_tokens = True, # Add '[CLS]' and '[SEP]'
max_length = 128, # Pad & truncate all sentences.
pad_to_max_length = True,
return_attention_mask = True, # Construct attn. masks.
return_tensors = 'pt', # Return pytorch tensors.
truncation=True,
)
# Add the encoded sentence to the list.
input_ids.append(encoded_dict['input_ids'])
# And its attention mask (simply differentiates padding from non-padding).
attention_masks.append(encoded_dict['attention_mask'])
# Convert the lists into tensors.
input_ids = torch.cat(input_ids, dim=0)
attention_masks = torch.cat(attention_masks, dim=0)
labels = torch.tensor(labels)
return input_ids, attention_masks ,labels
# Print sentence 0, now as a list of IDs.
# + [markdown] id="FYG0q9cKFaAH"
# #### data loader
#
# + id="LADqlLr3nV9F" colab={"base_uri": "https://localhost:8080/"} outputId="d2dd5542-62d4-4166-8691-4f61bb991679"
#two sentence source comment
# train_input_ids,train_attention_masks,train_labels=two_sentence_tokenizer_func(tokenizer_tweet,train_data,train_labels)
# val_input_ids,val_attention_masks,val_labels=two_sentence_tokenizer_func(tokenizer_tweet,dev_data,dev_labels)
#source only
train_input_ids,train_attention_masks,train_labels=tokenizer_func(tokenizer_tweet,train_sentences,train_labels)
dev_input_ids,dev_attention_masks,dev_labels=tokenizer_func(tokenizer_tweet,dev_sentences,dev_labels)
test_input_ids,test_attention_masks,test_labels=tokenizer_func(tokenizer_tweet,test_sentences,test_labels)
# + id="eGF8ODFgoyMY"
from torch.utils.data import DataLoader, RandomSampler, SequentialSampler
from torch.utils.data import TensorDataset
train_dataset = TensorDataset(train_input_ids, train_attention_masks, train_labels)
val_dataset = TensorDataset(train_input_ids, train_attention_masks, train_labels)
# The DataLoader needs to know our batch size for training, so we specify it
# here. For fine-tuning BERT on a specific task, the authors recommend a batch
# size of 16 or 32.
batch_size = 16
# Create the DataLoaders for our training and validation sets.
# We'll take training samples in random order.
train_dataloader = DataLoader(
train_dataset, # The training samples.
sampler = RandomSampler(train_dataset), # Select batches randomly
batch_size = batch_size # Trains with this batch size.
)
# For validation the order doesn't matter, so we'll just read them sequentially.
validation_dataloader = DataLoader(
val_dataset, # The validation samples.
sampler = SequentialSampler(val_dataset), # Pull out batches sequentially.
batch_size = batch_size # Evaluate with this batch size.
)
# test_dataloader=DataLoader(
# test_dataset,
# sampler = SequentialSampler(test_dataset),
# batch_size = batch_size
# )
# + id="4bedl6U89XjQ"
# + [markdown] id="57bR57PBFZIo"
# ##stance aggregated source , merge model
# + colab={"base_uri": "https://localhost:8080/"} id="3RsIHAQtXu-N" outputId="514c05f2-f260-4c39-fec6-311aaaeff3bb"
train_input_ids,train_attention_masks,train_labels=tokenizer_func(tokenizer_tweet,train_sentences,train_labels)
dev_input_ids,dev_attention_masks,dev_labels=tokenizer_func(tokenizer_tweet,dev_sentences,dev_labels)
test_input_ids,test_attention_masks,test_labels=tokenizer_func(tokenizer_tweet,test_sentences,test_labels)
# + [markdown] id="s2Q29pDkl6hc"
# ### Vectorizing train test dev
# + colab={"base_uri": "https://localhost:8080/", "height": 275} id="1zohI7yMeFzb" outputId="4ba10fdd-7825-4350-a85a-381c8844832b"
t0 = time.time()
# bert_tweet.cuda()
bert_tweet.eval()
with torch.no_grad():
# batch = tuple(t.to(device) for t in batch)
last_hidden_states_train = bert_tweet(train_input_ids, attention_mask=train_attention_masks)
train_features = last_hidden_states_train[0][:,0,:].numpy()
print('train done')
last_hidden_states_dev = bert_tweet(dev_input_ids, attention_mask=dev_attention_masks)
dev_features = last_hidden_states_dev[0][:,0,:].numpy()
print('dev done')
last_hidden_states_test = bert_tweet(test_input_ids, attention_mask=test_attention_masks)
test_features = last_hidden_states_test[0][:,0,:].numpy()
print('test done')
elapsed = format_time(time.time() - t0)
print(elapsed)
# + id="2aG6Xd4G7HpM"
bert_tweet_vecs={"train":train_features,"dev":dev_features,"test":test_features}
pickle.dump( bert_tweet_vecs, open( "bert_tweet_vecs.p", "wb" ) )
# + [markdown] id="eEP_0foNpotU"
# ### defining architucture
# + id="6Vlvwv4XFb_k"
from sklearn.metrics import f1_score
def f1_h(y_true,y_pred):
y_true_int=np.argmax(y_true,axis=1)
y_pred_int=np.argmax(y_pred,axis=1)
macro=f1_score(y_true_int, y_pred_int, average='macro')
return macro
# + colab={"base_uri": "https://localhost:8080/", "height": 533} id="iNoS9oqap-0M" outputId="c0ba7280-902c-42e3-c48c-ca9bf6e2f344"
from tensorflow import keras
from tensorflow.keras import layers
from keras.layers.normalization import BatchNormalization
source_input = keras.Input(shape=(768,),name="source")
source_input1=BatchNormalization()(source_input)
source_dense = layers.Dense(16,activation="tanh")
source_out = source_dense(source_input1)
# source_output = source_dense(source_dropped_out)
DO_layer_stance = tf.keras.layers.Dropout(.4, input_shape=(8,))
stance_input = keras.Input(shape=(4,),name="stance")
stance_dense = layers.Dense(8,activation="linear")
stance_output1= stance_dense(stance_input)
stance_output = DO_layer_stance(stance_output1)
concated_input1 = layers.concatenate([stance_output,source_out])
label=layers.Dense(3,activation="softmax",name="label")
verification_prediction=label(concated_input1)
combined_model=keras.Model(inputs=[source_input,stance_input],outputs=[verification_prediction])
keras.utils.plot_model(combined_model, "multi_input_and_output_model.png", show_shapes=True)
# + colab={"base_uri": "https://localhost:8080/"} id="HIfLeOPx0-H7" outputId="f654d78b-22ee-43fa-a549-527de3081e11"
from keras.callbacks import ModelCheckpoint
my_callbacks = [
tf.keras.callbacks.EarlyStopping(patience=10),
tf.keras.callbacks.ModelCheckpoint(filepath='model.{epoch:02d}-{val_loss:.2f}.h5'),
tf.keras.callbacks.TensorBoard(log_dir='./logs'),
]
combined_model.compile(
loss=keras.losses.CategoricalCrossentropy(from_logits=False),
optimizer=keras.optimizers.Adam(lr=0.0001),
metrics=["accuracy"],
)
# checkpoint = ModelCheckpoint('model-{epoch:03d}-{accuracy:03f}-{val_acc:03f}.h5', verbose=1, monitor='val_loss',save_best_only=True, mode='auto')
history = combined_model.fit({"source":train_features,"stance":stance_train},train_labels_hv, batch_size=16, epochs=500, validation_data=({"source":dev_features,"stance":stance_dev},dev_labels_hv), callbacks=my_callbacks)
# test_scores = combined_model.evaluate({"source":test_features,"stance":stance_test},test_labels_hv, verbose=2)
y_pred_test=combined_model.predict({"source":test_features,"stance":stance_test})
y_pred_dev=combined_model.predict({"source":dev_features,"stance":stance_dev})
print("f1 score dev:" ,f1_h(dev_labels_hv,y_pred_dev))
print("f1 score test:" ,f1_h(test_labels_hv,y_pred_test))
# + colab={"base_uri": "https://localhost:8080/"} id="lfEqOYHhzb1z" outputId="fd58f54c-aa35-4403-edcc-ad51b9155e3b"
combined_model.summary()
# + [markdown] id="IeA21Taj73GX"
#
# + [markdown] id="b6Fs50yehFUw"
# ## source and source-reply only
# no meta-dataa
# no stance
#
# + [markdown] id="iC00H6Tip6SR"
# ### training
#
# + id="hd3A_KHkp9B6" colab={"base_uri": "https://localhost:8080/"} outputId="5fd3e1cb-a1f1-4e35-8e0b-e1b395e8badf"
from transformers import BertForSequenceClassification, AdamW, BertConfig
from transformers import BertTokenizer,AutoModelForSequenceClassification
# Load BertForSequenceClassification, the pretrained BERT model with a single
# linear classification layer on top.
model = AutoModelForSequenceClassification.from_pretrained(
"vinai/bertweet-base", # Use the 12-layer BERT model, with an uncased vocab.
num_labels = 3, # The number of output labels--2 for binary classification.
# You can increase this for multi-class tasks.
output_attentions = False, # Whether the model returns attentions weights.
output_hidden_states = False, # Whether the model returns all hidden-states.
)
# Tell pytorch to run this model on the GPU.
model.cuda()
# + id="tyZq-8aaqjIC"
optimizer = AdamW(model.parameters(),
lr = 2e-5, # args.learning_rate - default is 5e-5, our notebook had 2e-5
eps = 1e-8 # args.adam_epsilon - default is 1e-8.
)
# + id="lxDgEkg2q2hC" colab={"base_uri": "https://localhost:8080/"} outputId="bec33b77-dedb-454f-bebe-e37fbdbe63fb"
from transformers import get_linear_schedule_with_warmup
# Number of training epochs. The BERT authors recommend between 2 and 4.
epochs = 20
total_steps = len(train_dataloader) * epochs
# Create the learning rate scheduler.
scheduler = get_linear_schedule_with_warmup(optimizer,
num_warmup_steps = 0, # Default value in run_glue.py
num_training_steps = total_steps)
print(total_steps)
# + id="20T95KmZrTv7"
import numpy as np
# Function to calculate the accuracy of our predictions vs labels
def flat_accuracy(preds, labels):
pred_flat = np.argmax(preds, axis=1).flatten()
labels_flat = labels.flatten()
return np.sum(pred_flat == labels_flat) / len(labels_flat)
# + id="5s04Gok2rXTj" colab={"base_uri": "https://localhost:8080/"} outputId="233cd4af-ff3a-4178-f910-03ddb058eb33"
import random
import numpy as np
# This training code is based on the `run_glue.py` script here:
# https://github.com/huggingface/transformers/blob/5bfcd0485ece086ebcbed2d008813037968a9e58/examples/run_glue.py#L128
# Set the seed value all over the place to make this reproducible.
seed_val = 42
random.seed(seed_val)
np.random.seed(seed_val)
torch.manual_seed(seed_val)
torch.cuda.manual_seed_all(seed_val)
# We'll store a number of quantities such as training and validation loss,
# validation accuracy, and timings.
training_stats = []
# Measure the total training time for the whole run.
total_t0 = time.time()
# For each epoch...
for epoch_i in range(0, epochs):
# ========================================
# Training
# ========================================
# Perform one full pass over the training set.
print("")
print('======== Epoch {:} / {:} ========'.format(epoch_i + 1, epochs))
print('Training...')
# Measure how long the training epoch takes.
# Reset the total loss for this epoch.
total_train_loss = 0
# Put the model into training mode. Don't be mislead--the call to
# `train` just changes the *mode*, it doesn't *perform* the training.
# `dropout` and `batchnorm` layers behave differently during training
# vs. test (source: https://stackoverflow.com/questions/51433378/what-does-model-train-do-in-pytorch)
model.train()
# For each batch of training data...
for step, batch in enumerate(train_dataloader):
# Progress update every 40 batches.
if step % 40 == 0 and not step == 0:
# Calculate elapsed time in minutes.
elapsed = format_time(time.time() - t0)
# Report progress.
print(' Batch {:>5,} of {:>5,}. Elapsed: {:}.'.format(step, len(train_dataloader), elapsed))
# Unpack this training batch from our dataloader.
#
# As we unpack the batch, we'll also copy each tensor to the GPU using the
# `to` method.
#
# `batch` contains three pytorch tensors:
# [0]: input ids
# [1]: attention masks
# [2]: labels
b_input_ids = batch[0].to(device)
b_input_mask = batch[1].to(device)
b_labels = batch[2].to(device)
# Always clear any previously calculated gradients before performing a
# backward pass. PyTorch doesn't do this automatically because
# accumulating the gradients is "convenient while training RNNs".
# (source: https://stackoverflow.com/questions/48001598/why-do-we-need-to-call-zero-grad-in-pytorch)
model.zero_grad()
# Perform a forward pass (evaluate the model on this training batch).
# The documentation for this `model` function is here:
# https://huggingface.co/transformers/v2.2.0/model_doc/bert.html#transformers.BertForSequenceClassification
# It returns different numbers of parameters depending on what arguments
# arge given and what flags are set. For our useage here, it returns
# the loss (because we provided labels) and the "logits"--the model
# outputs prior to activation.
loss, logits = model(b_input_ids,
token_type_ids=None,
attention_mask=b_input_mask,
labels=b_labels)
# Accumulate the training loss over all of the batches so that we can
# calculate the average loss at the end. `loss` is a Tensor containing a
# single value; the `.item()` function just returns the Python value
# from the tensor.
total_train_loss += loss.item()
# Perform a backward pass to calculate the gradients.
loss.backward()
# Clip the norm of the gradients to 1.0.
# This is to help prevent the "exploding gradients" problem.
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
# Update parameters and take a step using the computed gradient.
# The optimizer dictates the "update rule"--how the parameters are
# modified based on their gradients, the learning rate, etc.
optimizer.step()
# Update the learning rate.
scheduler.step()
# Calculate the average loss over all of the batches.
avg_train_loss = total_train_loss / len(train_dataloader)
# Measure how long this epoch took.
training_time = format_time(time.time() - t0)
print("")
print(" Average training loss: {0:.2f}".format(avg_train_loss))
print(" Training epcoh took: {:}".format(training_time))
# ========================================
# Validation
# ========================================
# After the completion of each training epoch, measure our performance on
# our validation set.
print("")
print("Running Validation...")
t0 = time.time()
# Put the model in evaluation mode--the dropout layers behave differently
# during evaluation.
model.eval()
# Tracking variables
total_eval_accuracy = 0
total_eval_loss = 0
nb_eval_steps = 0
# Evaluate data for one epoch
for batch in validation_dataloader:
# Unpack this training batch from our dataloader.
#
# As we unpack the batch, we'll also copy each tensor to the GPU using
# the `to` method.
#
# `batch` contains three pytorch tensors:
# [0]: input ids
# [1]: attention masks
# [2]: labels
b_input_ids = batch[0].to(device)
b_input_mask = batch[1].to(device)
b_labels = batch[2].to(device)
# Tell pytorch not to bother with constructing the compute graph during
# the forward pass, since this is only needed for backprop (training).
with torch.no_grad():
# Forward pass, calculate logit predictions.
# token_type_ids is the same as the "segment ids", which
# differentiates sentence 1 and 2 in 2-sentence tasks.
# The documentation for this `model` function is here:
# https://huggingface.co/transformers/v2.2.0/model_doc/bert.html#transformers.BertForSequenceClassification
# Get the "logits" output by the model. The "logits" are the output
# values prior to applying an activation function like the softmax.
(loss, logits) = model(b_input_ids,
token_type_ids=None,
attention_mask=b_input_mask,
labels=b_labels)
# Accumulate the validation loss.
total_eval_loss += loss.item()
# Move logits and labels to CPU
logits = logits.detach().cpu().numpy()
label_ids = b_labels.to('cpu').numpy()
# Calculate the accuracy for this batch of test sentences, and
# accumulate it over all batches.
total_eval_accuracy += flat_accuracy(logits, label_ids)
# Report the final accuracy for this validation run.
avg_val_accuracy = total_eval_accuracy / len(validation_dataloader)
print(" Accuracy: {0:.2f}".format(avg_val_accuracy))
# Calculate the average loss over all of the batches.
avg_val_loss = total_eval_loss / len(validation_dataloader)
# Measure how long the validation run took.
validation_time = format_time(time.time() - t0)
print(" Validation Loss: {0:.2f}".format(avg_val_loss))
print(" Validation took: {:}".format(validation_time))
# Record all statistics from this epoch.
training_stats.append(
{
'epoch': epoch_i + 1,
'Training Loss': avg_train_loss,
'Valid. Loss': avg_val_loss,
'Valid. Accur.': avg_val_accuracy,
'Training Time': training_time,
'Validation Time': validation_time
}
)
print("")
print("Training complete!")
print("Total training took {:} (h:mm:ss)".format(format_time(time.time()-total_t0)))
# + id="7J7hAD67uhaF" colab={"base_uri": "https://localhost:8080/", "height": 677} outputId="8e32f066-293c-4c8f-8613-b36298812a1b"
import pandas as pd
# Display floats with two decimal places.
pd.set_option('precision', 2)
# Create a DataFrame from our training statistics.
df_stats = pd.DataFrame(data=training_stats)
# Use the 'epoch' as the row index.
df_stats = df_stats.set_index('epoch')
# A hack to force the column headers to wrap.
#df = df.style.set_table_styles([dict(selector="th",props=[('max-width', '70px')])])
# Display the table.
df_stats
# + id="6vyPYgL8ulrG" colab={"base_uri": "https://localhost:8080/", "height": 426} outputId="25aa5748-9413-4085-f938-5a2f5236b460"
import matplotlib.pyplot as plt
% matplotlib inline
import seaborn as sns
# Use plot styling from seaborn.
sns.set(style='darkgrid')
# Increase the plot size and font size.
sns.set(font_scale=1.5)
plt.rcParams["figure.figsize"] = (12,6)
# Plot the learning curve.
plt.plot(df_stats['Training Loss'], 'b-o', label="Training")
plt.plot(df_stats['Valid. Loss'], 'g-o', label="Validation")
# Label the plot.
plt.title("Training & Validation Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.xticks(range(0,epochs))
plt.show()
# + id="cL-4lX8fEyuT"
# + [markdown] id="Xglvux0FxmSL"
# ## testing on test set
# + id="FndGf73WwojH" colab={"base_uri": "https://localhost:8080/"} outputId="951059c0-d4b9-4e85-b52c-069ff3057493"
batch_size=16
#source comment
# test_input_ids,test_attention_masks,test_labels=two_sentence_tokenizer_func(tokenizer_tweet,test_data,test_labels)
# source only
test_input_ids,test_attention_masks,test_labels=tokenizer_func(tokenizer_tweet,test_sentences,test_labels)
prediction_data = TensorDataset(test_input_ids, test_attention_masks, test_labels)
prediction_sampler = SequentialSampler(prediction_data)
prediction_dataloader = DataLoader(prediction_data, sampler=prediction_sampler, batch_size=batch_size)
# + id="FUgB_jnEx9k_" colab={"base_uri": "https://localhost:8080/"} outputId="5ee59a13-f79e-4f64-8589-d4baf0a62024"
# %time
# Prediction on test set
print('Predicting labels for {:,} test sentences...'.format(len(test_input_ids)))
# Put model in evaluation mode
model.eval()
print('Predicting labels for {:,} test batches...'.format(len(prediction_dataloader)))
# Tracking variables
predictions , true_labels = [], []
# Predict
for batch in prediction_dataloader:
# Add batch to GPU
batch = tuple(t.to(device) for t in batch)
# Unpack the inputs from our dataloader
b_input_ids, b_input_mask, b_labels = batch
# Telling the model not to compute or store gradients, saving memory and
# speeding up prediction
with torch.no_grad():
# Forward pass, calculate logit predictions
outputs = model(b_input_ids, token_type_ids=None,
attention_mask=b_input_mask)
logits = outputs[0]
# Move logits and labels to CPU
logits = logits.detach().cpu().numpy()
label_ids = b_labels.to('cpu').numpy()
# Store predictions and true labels
predictions.append(logits)
true_labels.append(label_ids)
# + colab={"base_uri": "https://localhost:8080/"} id="L8lzdvme-5dA" outputId="8f522638-253b-4353-a3a5-0a6de3899aaf"
len(true_labels)
# + [markdown] id="ZLJ1dr0r-EaH"
# ### results and metrics
# + [markdown] id="u4H7eI8bIH-v"
# #### f1 and accuracy
# + id="ZJlBenj3-KfY"
from sklearn.metrics import plot_confusion_matrix
# + id="ET2w4UXlzEjd"
flat_predictions = np.concatenate(predictions, axis=0)
# For each sample, pick the label (0 or 1) with the higher score.
flat_predictions = np.argmax(flat_predictions, axis=1).flatten()
# Combine the correct labels for each batch into a single list.
flat_true_labels = np.concatenate(true_labels, axis=0)
# + colab={"base_uri": "https://localhost:8080/"} id="dziE8cXWFPd1" outputId="2e4e1eaf-d74d-4873-9ed0-20c52be11c0b"
flat_predictions
# + id="pSBYmTG75TAs" colab={"base_uri": "https://localhost:8080/"} outputId="c96437f4-acd9-4f31-e3a8-7dac633914af"
# with dropping unverified from train and val
from sklearn.metrics import f1_score
macro=f1_score(flat_true_labels, flat_predictions, average='macro')
micro=f1_score(flat_true_labels, flat_predictions, average='micro')
weighted=f1_score(flat_true_labels, flat_predictions, average='weighted')
print('macro f1 score: %.3f' %macro)
print('micro f1 score: %.3f' %micro)
print('weighted f1 score: %.3f' %weighted)
# + [markdown] id="2F3TJ-NXVig2"
# #### confusion matrix
# + id="5MSDhhFIVgzS"
import numpy as np
def plot_confusion_matrix(cm,
target_names,
title='Confusion matrix',
cmap=None,
normalize=True):
import matplotlib.pyplot as plt
import numpy as np
import itertools
accuracy = np.trace(cm) / float(np.sum(cm))
misclass = 1 - accuracy
if cmap is None:
cmap = plt.get_cmap('Blues')
plt.figure(figsize=(8, 6))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
if target_names is not None:
tick_marks = np.arange(len(target_names))
plt.xticks(tick_marks, target_names, rotation=45)
plt.yticks(tick_marks, target_names)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
thresh = cm.max() / 1.5 if normalize else cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
if normalize:
plt.text(j, i, "{:0.4f}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
else:
plt.text(j, i, "{:,}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label\naccuracy={:0.4f}; misclass={:0.4f}'.format(accuracy, misclass))
plt.show()
# + id="cGjE1L9ZVmbJ" colab={"base_uri": "https://localhost:8080/", "height": 466} outputId="5c473f99-0893-4be9-f1d1-109af926d648"
from sklearn.metrics import confusion_matrix
plot_confusion_matrix(cm = confusion_matrix(test_labels, y_pred),
normalize = False,
target_names = ['0', '1','2'],
title = "Confusion Matrix")
# + [markdown] id="I6zeu_Q4IN3l"
# #### pooling with reply tags for tests
# counting how many reply each source has to do pooling
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="_2j_BYtzIU9y" outputId="7ec4fc13-e6a3-40e2-981e-1791a3719e9e"
test_cleaned.head()
# + id="rZSY7nlzJ8lZ"
def pooling(source_texts,predicted_label):
index=[]
index.append(0)
for i in range(len(source_texts)-1):
if source_texts[i]==source_texts[i+1]:
i+=1
else:
index.append(i+1)
index.append(len(source_texts)-1)
av=[]
pooling_prediction = predicted_label
for i in range(len(index)-1):
sum=0
for k in range(index[i],index[i+1]):
sum+=predicted_label[k]
av.append(sum/(index[i+1]-index[i]))
myList =[0 , 1 ,2]
pred_pooling=[ min(myList, key=lambda x:abs(x-av[i])) for i in range(len(av))]
return pred_pooling
# + colab={"base_uri": "https://localhost:8080/"} id="_GIW9kvMOD1F" outputId="ba872db2-301e-44ef-fce8-a2ed871faaf4"
from sklearn.metrics import f1_score
source_texts_labels=test_cleaned['source_text'].values
test_labels= test_parent_child['class'].values
true_labels= pooling(source_texts_labels,test_labels)
pred= pooling(source_texts_labels,flat_predictions)
macro=f1_score(true_labels, pred, average='macro')
micro=f1_score(true_labels, pred, average='micro')
print('macro f1 score: %.3f' %macro)
print('micro f1 score: %.3f' %micro)
# + id="and6nMDmUQry"
for item in true_labels:
if item ==3:
print(1)
# + [markdown] id="iU6trTiTL6Pd"
# # save model
# + colab={"base_uri": "https://localhost:8080/"} id="EYQ7ncUSL8Kq" outputId="69cfdc4f-9633-4915-aed7-46f6a1f514f5"
import os
# Saving best-practices: if you use defaults names for the model, you can reload it using from_pretrained()
output_dir = './model_save/'
# Create output directory if needed
if not os.path.exists(output_dir):
os.makedirs(output_dir)
print("Saving model to %s" % output_dir)
# Save a trained model, configuration and tokenizer using `save_pretrained()`.
# They can then be reloaded using `from_pretrained()`
model_to_save = model.module if hasattr(model, 'module') else model # Take care of distributed/parallel training
model_to_save.save_pretrained(output_dir)
tokenizer_tweet.save_pretrained(output_dir)
# Good practice: save your training arguments together with the trained model
# torch.save(args, os.path.join(output_dir, 'training_args.bin'))
# + id="MaLQ6fZlMuKx" colab={"base_uri": "https://localhost:8080/"} outputId="fddf4a97-59c0-4a23-aff3-7912461a0cf0"
from google.colab import drive
drive.mount('/content/drive')
# + id="FWIOX-rhMvLE"
# !cp -r ./model_save/ "/content/drive/MyDrive/rumour"
# + [markdown] id="ZLFzXpwoWW5B"
# # Load model
# + id="v-aOKv1kOKco" colab={"base_uri": "https://localhost:8080/"} outputId="ac53bea2-5d36-45fe-a73e-a3542bf7ff1d"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="hGvsolojWoOL" outputId="3cec1792-49cd-4b24-8fcd-4b05e477feaa"
# %time
from transformers import BertConfig, BertModel
from transformers import BertTokenizer,AutoModelForSequenceClassification
input_saved_model_dir="/content/drive/MyDrive/rumour/comment_source"
model=AutoModelForSequenceClassification.from_pretrained(input_saved_model_dir)
# tokenizer_tweet = BertTokenizer.from_pretrained(input_saved_model_dir)
# Copy the model to the GPU.
model.to(device)
# + id="oG-z7lNqbjrr"
|
rumor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import sqlite3
# connect to the dataset
myDB = './data/cephalopod_RnD.db'
connection = sqlite3.connect(myDB)
# read the data into a dataframe
mySQL = "SELECT * FROM spady_defense"
df = pd.read_sql(mySQL, connection)
# -
# how many records?
len(df)
# print the top of the dataframe
df.head(10)
# print the tail
df.tail()
# what are the datatypes?
print(df.dtypes)
# print the a random middlish row
print(df.loc[[44]])
print(df.loc[44])
print(df.loc[44:50])
# An error! Let's force the string: n/a into a NaN
df['TimetoReact'] = pd.to_numeric(df['TimetoReact'], errors='coerce')
print(df.dtypes)
# +
# lets go back to our strings
# Treatment Active ReactionType InkDischarge BodyPattern
# field8 field9 field10 field11 field12
# first lets see if anything exists in the field columns
pd.notna(df['field8'])
# -
# check again, using an aggregate
pd.notna(df['field8']).sum()
# check another way
df['field9'].unique().tolist()
# much more efficent way to check.
df[['field8', 'field9', 'field10', 'field11', 'field12']].drop_duplicates()
# remove the extra columns
# from pandas documentation:
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.drop.html
# -- axis : {0 or âindexâ, 1 or âcolumnsâ}, default 0
# ---- Whether to drop labels from the index (0 or âindexâ) or columns (1 or âcolumnsâ).
df.drop(['field8', 'field9', 'field10', 'field11', 'field12'], axis=1, inplace=True)
# get an overview of our numeric data
df.describe()
# +
na_lc = pd.isna(df['LineCrosses']).sum()
na_rt = pd.isna(df['TimetoReact']).sum()
print("the number of nulls in line crosses: %s" % na_lc)
print("the number of nulls in time to react: %s" % na_rt)
# -
# check the other columns
# Treatment Active ReactionType InkDischarge BodyPattern
for column in df.select_dtypes(include=object).keys():
print("-----")
print("Value counts in: %s" % column)
print(df[column].value_counts())
print("\n")
df.select_dtypes(include=object)
# visualize Line Crosses
df["LineCrosses"].plot.hist()
# visualize Time to React
df["TimetoReact"].plot.hist()
# +
import seaborn as sns
sns.set(rc={'figure.figsize':(9, 7)})
sns.boxplot(
x="LineCrosses",
y="Treatment",
data=df,
palette="vlag")
# -
sns.boxplot(
x="TimetoReact",
y="Treatment",
data=df,
whis="range",
palette="vlag")
sns.countplot(x="Treatment", hue="InkDischarge", data=df)
sns.countplot(x="Treatment", hue="ReactionType", data=df)
sns.countplot(x="Treatment", hue="BodyPattern", data=df)
|
ch4-exploring-data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Vincent-Emma/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/Vincent_Emma_DS_Unit_1_Sprint_Challenge_2_Data_Wrangling_and_Storytelling.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="4yMHi_PX9hEz"
# # Data Science Unit 1 Sprint Challenge 2
#
# ## Data Wrangling and Storytelling
#
# Taming data from its raw form into informative insights and stories.
# + [markdown] id="9wIvtOss9H_i" colab_type="text"
# ## Data Wrangling
#
# In this Sprint Challenge you will first "wrangle" some data from [Gapminder](https://www.gapminder.org/about-gapminder/), a Swedish non-profit co-founded by <NAME>. "Gapminder produces free teaching resources making the world understandable based on reliable statistics."
# - [Cell phones (total), by country and year](https://raw.githubusercontent.com/open-numbers/ddf--gapminder--systema_globalis/master/ddf--datapoints--cell_phones_total--by--geo--time.csv)
# - [Population (total), by country and year](https://raw.githubusercontent.com/open-numbers/ddf--gapminder--systema_globalis/master/ddf--datapoints--population_total--by--geo--time.csv)
# - [Geo country codes](https://github.com/open-numbers/ddf--gapminder--systema_globalis/blob/master/ddf--entities--geo--country.csv)
#
# These two links have everything you need to successfully complete the first part of this sprint challenge.
# - [Pandas documentation: Working with Text Data](https://pandas.pydata.org/pandas-docs/stable/text.html) (one question)
# - [Pandas Cheat Sheet](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf) (everything else)
# + [markdown] colab_type="text" id="wWEU2GemX68A"
# ### Part 0. Load data
#
# You don't need to add or change anything here. Just run this cell and it loads the data for you, into three dataframes.
# + colab_type="code" id="bxKtSi5sRQOl" colab={}
import pandas as pd
cell_phones = pd.read_csv('https://raw.githubusercontent.com/open-numbers/ddf--gapminder--systema_globalis/master/ddf--datapoints--cell_phones_total--by--geo--time.csv')
population = pd.read_csv('https://raw.githubusercontent.com/open-numbers/ddf--gapminder--systema_globalis/master/ddf--datapoints--population_total--by--geo--time.csv')
geo_country_codes = (pd.read_csv('https://raw.githubusercontent.com/open-numbers/ddf--gapminder--systema_globalis/master/ddf--entities--geo--country.csv')
.rename(columns={'country': 'geo', 'name': 'country'}))
# + [markdown] colab_type="text" id="AZmVTeCsX9RC"
# ### Part 1. Join data
# + [markdown] colab_type="text" id="GLzX58u4SfEy"
# First, join the `cell_phones` and `population` dataframes (with an inner join on `geo` and `time`).
#
# The resulting dataframe's shape should be: (8590, 4)
# + colab_type="code" id="GVV7Hnj4SXBa" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="0fb19805-2d66-4f77-fb0c-98ad3202a015"
cp = cell_phones.merge(population, on =['geo', 'time'], how='inner')
cp.shape
# + [markdown] colab_type="text" id="xsXpDbwwW241"
# Then, select the `geo` and `country` columns from the `geo_country_codes` dataframe, and join with your population and cell phone data.
#
# The resulting dataframe's shape should be: (8590, 5)
# + colab_type="code" id="Q2LaZta_W2CE" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="bd91b8cd-f61e-4c1b-ec99-164f04d08bbd"
df = cp.merge(geo_country_codes[['geo', 'country']], how='inner')
df.shape
# + [markdown] colab_type="text" id="oK96Uj7vYjFX"
# ### Part 2. Make features
# + [markdown] colab_type="text" id="AD2fBNrOYzCG"
# Calculate the number of cell phones per person, and add this column onto your dataframe.
#
# (You've calculated correctly if you get 1.220 cell phones per person in the United States in 2017.)
# + colab_type="code" id="wXI9nQthYnFK" colab={"base_uri": "https://localhost:8080/", "height": 195} outputId="86a8e3ec-80d9-42ff-9c28-b1649cfffd0b"
df['phone_per_person'] = df.cell_phones_total/df.population_total
df[df.country == 'United States'].tail()
# + [markdown] colab_type="text" id="S3QFdsnRZMH6"
# Modify the `geo` column to make the geo codes uppercase instead of lowercase.
# + colab_type="code" id="93ADij8_YkOq" colab={"base_uri": "https://localhost:8080/", "height": 195} outputId="3eed0493-0a64-447c-cdce-665fd3d59ee9"
df.geo = df.geo.str.upper()
df.head()
# + [markdown] colab_type="text" id="hlPDAFCfaF6C"
# ### Part 3. Process data
# + [markdown] colab_type="text" id="k-pudNWve2SQ"
# Use the describe function, to describe your dataframe's numeric columns, and then its non-numeric columns.
#
# (You'll see the time period ranges from 1960 to 2017, and there are 195 unique countries represented.)
# + colab_type="code" id="g26yemKre2Cu" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="742f67b3-a442-46cb-aa8e-7d3d01fdbeca"
import numpy as np
df.describe()
# + id="BlRgOZwxY5sV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 166} outputId="91b98d30-a79d-45be-a5ae-9572809f5560"
df.describe(exclude = np.number)
# + [markdown] colab_type="text" id="zALg-RrYaLcI"
# In 2017, what were the top 5 countries with the most cell phones total?
#
# Your list of countries should have these totals:
#
# | country | cell phones total |
# |:-------:|:-----------------:|
# | ? | 1,474,097,000 |
# | ? | 1,168,902,277 |
# | ? | 458,923,202 |
# | ? | 395,881,000 |
# | ? | 236,488,548 |
#
#
# + colab_type="code" id="JdlWvezHaZxD" colab={}
# This optional code formats float numbers with comma separators
pd.options.display.float_format = '{:,}'.format
# + colab_type="code" id="KONQkQZ3haNC" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="39c8882e-2012-4f82-972b-bca8e22612fd"
year = df[df['time'] == 2017]
first = year[['country', 'cell_phones_total']].groupby('country').first()
sort = first.sort_values('cell_phones_total', ascending = False)
sort.head(7)
# + [markdown] colab_type="text" id="03V3Wln_h0dj"
# 2017 was the first year that China had more cell phones than people.
#
# What was the first year that the USA had more cell phones than people?
# + colab_type="code" id="smX8vzu4cyju" colab={"base_uri": "https://localhost:8080/", "height": 77} outputId="dc8d8c02-42da-4a05-c620-b7567baa62c8"
usa = df[df['country']=='United States']
cpt = usa[usa['cell_phones_total']>usa['population_total']]
sort = cpt.sort_values('time', ascending=True)
sort.head(1)
# + [markdown] colab_type="text" id="6J7iwMnTg8KZ"
# ### Part 4. Reshape data
# + [markdown] colab_type="text" id="LP9InazRkUxG"
# *This part is not needed to pass the sprint challenge, only to get a 3! Only work on this after completing the other sections.*
#
# Create a pivot table:
# - Columns: Years 2007â2017
# - Rows: China, India, United States, Indonesia, Brazil (order doesn't matter)
# - Values: Cell Phones Total
#
# The table's shape should be: (5, 11)
# + colab_type="code" id="JD7mXXjLj4Ue" colab={}
years = df[(df['time']>=2007) & (df['time']<+2017)]
years = years.set_index('country')
country_l = ['China', 'India', 'United States', 'Indonesia', 'Brazil']
countries = years.loc[country_l]
# + colab_type="code" id="O4Aecv1fmQlj" colab={"base_uri": "https://localhost:8080/", "height": 262} outputId="a8abfe3d-9674-4546-dad6-881bcc14924f"
pivot = countries.pivot_table(index='country', columns='time', values='cell_phones_total')
pivot
# + [markdown] colab_type="text" id="CNKTu2DCnAo6"
# Sort these 5 countries, by biggest increase in cell phones from 2007 to 2017.
#
# Which country had 935,282,277 more cell phones in 2017 versus 2007?
# + id="Vdgsqiz1yHKJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 690} outputId="4c59e101-88ab-4fdc-ad8d-950f97cab5d3"
#just based on math the country would be India but I dont have a good code to prove that
pivot['difference'] = pivot[2017] - pivot[2007]
pivot.head()
# + [markdown] colab_type="text" id="7iHkMsa3Rorh"
# If you have the time and curiosity, what other questions can you ask and answer with this data?
# + [markdown] id="vtcAJOAV9k3X" colab_type="text"
# ## Data Storytelling
#
# In this part of the sprint challenge you'll work with a dataset from **FiveThirtyEight's article, [Every Guest <NAME> Ever Had On âThe Daily Showâ](https://fivethirtyeight.com/features/every-guest-jon-stewart-ever-had-on-the-daily-show/)**!
# + [markdown] id="UtjoIqvm9yFg" colab_type="text"
# ### Part 0 â Run this starter code
#
# You don't need to add or change anything here. Just run this cell and it loads the data for you, into a dataframe named `df`.
#
# (You can explore the data if you want, but it's not required to pass the Sprint Challenge.)
# + id="tYujbhIz9zKU" colab_type="code" colab={}
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
url = 'https://raw.githubusercontent.com/fivethirtyeight/data/master/daily-show-guests/daily_show_guests.csv'
df = pd.read_csv(url).rename(columns={'YEAR': 'Year', 'Raw_Guest_List': 'Guest'})
def get_occupation(group):
if group in ['Acting', 'Comedy', 'Musician']:
return 'Acting, Comedy & Music'
elif group in ['Media', 'media']:
return 'Media'
elif group in ['Government', 'Politician', 'Political Aide']:
return 'Government and Politics'
else:
return 'Other'
df['Occupation'] = df['Group'].apply(get_occupation)
# + [markdown] id="5hjnMK3j90Rp" colab_type="text"
# ### Part 1 â What's the breakdown of guestsâ occupations per year?
#
# For example, in 1999, what percentage of guests were actors, comedians, or musicians? What percentage were in the media? What percentage were in politics? What percentage were from another occupation?
#
# Then, what about in 2000? In 2001? And so on, up through 2015.
#
# So, **for each year of _The Daily Show_, calculate the percentage of guests from each occupation:**
# - Acting, Comedy & Music
# - Government and Politics
# - Media
# - Other
#
# #### Hints:
# You can make a crosstab. (See pandas documentation for examples, explanation, and parameters.)
#
# You'll know you've calculated correctly when the percentage of "Acting, Comedy & Music" guests is 90.36% in 1999, and 45% in 2015.
# + id="EbobyiHv916F" colab_type="code" colab={}
# + [markdown] id="Kiq56dZb92LY" colab_type="text"
# ### Part 2 â Recreate this explanatory visualization:
# + id="HKLDMWwP98vz" colab_type="code" outputId="0397fcdf-80e5-4072-88f4-af2f14fcf0f2" colab={"base_uri": "https://localhost:8080/", "height": 406}
from IPython.display import display, Image
png = 'https://fivethirtyeight.com/wp-content/uploads/2015/08/hickey-datalab-dailyshow.png'
example = Image(png, width=500)
display(example)
# + [markdown] id="TK5fDIag9-F6" colab_type="text"
# **Hints:**
# - You can choose any Python visualization library you want. I've verified the plot can be reproduced with matplotlib, pandas plot, or seaborn. I assume other libraries like altair or plotly would work too.
# - If you choose to use seaborn, you may want to upgrade the version to 0.9.0.
#
# **Expectations:** Your plot should include:
# - 3 lines visualizing "occupation of guests, by year." The shapes of the lines should look roughly identical to 538's example. Each line should be a different color. (But you don't need to use the _same_ colors as 538.)
# - Legend or labels for the lines. (But you don't need each label positioned next to its line or colored like 538.)
# - Title in the upper left: _"Who Got To Be On 'The Daily Show'?"_ with more visual emphasis than the subtitle. (Bolder and/or larger font.)
# - Subtitle underneath the title: _"Occupation of guests, by year"_
#
# **Optional Bonus Challenge:**
# - Give your plot polished aesthetics, with improved resemblance to the 538 example.
# - Any visual element not specifically mentioned in the expectations is an optional bonus.
# + id="CaB8MMV099Kh" colab_type="code" colab={}
|
Vincent_Emma_DS_Unit_1_Sprint_Challenge_2_Data_Wrangling_and_Storytelling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Doing Geospatial in Python
#
# Version: 1.1, 2021-09-28
#
# <img style="float: left;" src="images/geopython-logo.png">
#
# With a low barrier to entry and large ecosystem of tools and libraries,
# [Python](https://python.org) is the lingua franca for geospatial.
# Whether you are doing data acquisition, processing, publishing, integration,
# analysis or software development, there is no shortage of solid Python tools
# to assist you in your daily workflows.
#
# This workshop will provide an introduction to performing common GIS/geospatial
# tasks using Python geospatial tools such as OWSLib, Shapely, Fiona/Rasterio,
# and common geospatial libraries like GDAL, PROJ, pycsw, as well as other tools
# from the geopython toolchain. Manipulate vector/raster data using Shapely,
# Fiona and Rasterio. Publish data and metadata to OGC APIs using
# pygeoapi, pygeometa, pycsw, and more. Visualize your data on a map using Folium,
# Bokeh and more. Plus a few extras in between!
#
# The workshop is provided using the Jupyter Notebook environment with Python 3.
#
# ## FOSS4G 2021 Workshop team
#
#
# <table>
# <tr>
# <td><a href="https://twitter.com/tomkralidis"><img width="150" src="https://avatars.githubusercontent.com/u/910430?v=4"/></a></td>
# <td><a href="https://twitter.com/justb4"><img width="150" src="https://avatars.githubusercontent.com/u/582630?v=4"/></a></td>
# <td><a href="https://twitter.com/ldesousa"><img width="150" src="https://avatars.githubusercontent.com/u/1137878?v=4"/></a></td>
# <td><a href="https://twitter.com/francbartoli"><img width="150" src="https://avatars.githubusercontent.com/u/560676?v=4"/></a></td>
# <td><a href="https://twitter.com/kalxas"><img width="150" src="https://avatars.githubusercontent.com/u/383944?v=4"/></a></td>
# </tr>
# <tr>
# <td><NAME></td>
# <td><NAME></td>
# <td><NAME></td>
# <td><NAME></td>
# <td><NAME></td>
# </tr>
# </table>
#
# ## Table of contents
#
# 1. [Introduction](01-introduction.ipynb)
# 2. [Geometry](02-geometry.ipynb)
# 3. [Spatial Reference Systems](03-spatial-reference-systems.ipynb)
# 4. [Vector data](04-vector-data.ipynb)
# 5. [Raster data](05-raster-data.ipynb)
# 6. [Data analysis](06-data-analysis.ipynb)
# 7. [Visualization](07-visualization.ipynb)
# 8. [Metadata](08-metadata.ipynb)
# 9. [Publishing](09-publishing.ipynb)
# 10. [Remote Data](10-remote-data.ipynb)
# 11. [Emerging Technology and Trends](11-emerging-technology-trends.ipynb)
# 12. [Conclusion](12-conclusion.ipynb)
#
# ## Workshop setup
#
# Information on setting up the workshop can be found at https://geopython.github.io/geopython-workshop
#
# ## Workshop environment
#
# This workshop is running at http://localhost:8888
#
# The pycsw instance is running at http://localhost:8001
#
# The pygeoapi instance is running at http://localhost:5000
#
# ## Workshop data
#
# The workshop is bundled with sample data to demonstrate and facilitate the
# exercises. Users have the ability to add their own data and update the live
# code examples and/or exercises to learn with local data.
#
# ### Input data
#
# Data are located in each directory, so you should be able to access
# them by using `../data/file.xyz`.
#
# ### Output data
#
# Output data created from live code will be located in `/data/output`.
#
# ## About Jupyter
# This workshop uses [Jupyter](https://jupyter.org) to be able to demonstrate geospatial
# Python functionality in a fun and interactive fashion. Please note that Jupyter is
# not a software development environment and should only be used to provide instructional
# material along with code.
#
# ## Support
# A [Gitter](https://gitter.im/geopython/geopython-workshop) channel exists for
# discussion and live support from the developers of the workshop.
# ## Motivation
#
# Who doesn't like their data on a map right? GIS software comes in many flavours and programming languages such
# as Java, C, JavaScript, Golang and many more. So what's so special about Python for geospatial?
#
# In a nutshell: low barrier and fun!
#
# * Widely available: Python works on Windows, Mac, Linux and more
# * Minimal setup: the standard Python install provides significant packages, libraries and functionality out of the box
# * Fast enough. You can write a faster program in a lower level language but you can write programs faster in Python
# * Easy to read and understand
# ```python
# cities = ['Toronto', 'Amsterdam', 'Athens']
# for city in cities:
# print(city)
# ```
# * Easy to glue to core C/C++ tooling
# * Large ecosystem of supported packages ([Python Package Index [PyPI]](https://pypi.org), [GitHub](https://github.com), etc.)
# * Geospatial aware: Python has the widest and most supported geospatial software presence
# * Python bindings of core tooling (GDAL, PROJ, GEOS)
# * Flexible higher level packages (OWSLib)
# * Servers (pygeoapi, PyWPS, pycsw, etc.)
# * Support in traditional desktop GIS (QGIS, GRASS, Esri)
# * Large ecosystem of packages and projects in big data handling, data science, Earth system data processing/exploitation
# * xarray, Dask, Zarr
# * SciPy
# * NumPy
# * Matplotlib
# * Pandas/GeoPandas
# * PyTroll
# ## License
#
# <img style="float: left;" src="images/cc-by-sa.png">
#
# This material is licensed under a [Creative Commons Attribution-ShareAlike 4.0 International License](https://creativecommons.org/licenses/by-sa/4.0/).
#
# ### Authors
#
# This workshop was originally created by [GISMentors](https://gismentors.cz) (in alphabetical order):
#
# * [<NAME>](https://github.com/jachym)
# * [<NAME>](https://github.com/lucadelu)
# * [<NAME>](https://github.com/landam)
#
# Source: https://github.com/GISMentors/geopython-english
#
# This workshop was later adapted by (in alphabetical order):
#
# * [<NAME>](https://github.com/francbartoli)
# * [<NAME>](https://github.com/justb4)
# * [<NAME>](https://twitter.com/tomkralidis)
# * [<NAME>](https://github.com/ldesousa)
# * [<NAME>](https://github.com/kalxas)
#
# ### Deliveries
#
# This workshop has been delivered at the following conferences/events:
# * [FOSS4G 2019](https://2019.foss4g.org) (version 1.0)
# * [FOSS4G 2021](https://2021.foss4g.org) (version 1.1)
#
# ### Materials
#
# Notebooks, sample data, and all setup/configurations are available at https://github.com/geopython/geopython-workshop
#
# ### Additional sources used in this workshop
#
# - [Introduction to Python GIS](https://automating-gis-processes.github.io/CSC/)
#
#
# Ready, set, here we go!
#
# ---
#
# [Geometry ->](02-geometry.ipynb)
|
workshop/jupyter/content/notebooks/01-introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
#富å
¥äœ¿çšçåº
import numpy as np;from math import *
import matplotlib.pyplot as plt;from matplotlib import ticker
from matplotlib.ticker import MaxNLocator
#å®ä¹ç©åœ¢åºåïŒè®ŸN=5
N = 5;N0 = 51 #åºåé¿åºŠ
rn = np.ones(N);N1 = int((N0-N)/2)
xn = np.append(np.zeros(N1),rn)
xn = np.append(xn,np.zeros(N1))
#对ç©åœ¢åºååDTFT
n = np.arange(N0)-N1
w = (np.arange(501)-int(501/2))*4*pi/500
w = w.reshape(-1,1) #å°w(n)蜬䞺äžå
xe = np.dot(np.exp(-1j*n*w),xn)
#ç»å¶ç©åœ¢åºååå
¶å¹
床谱åœæ°
fig,axs = plt.subplots(2,1,constrained_layout=True)
axs[0].stem(n,xn,basefmt="");axs[1].plot(w/pi,np.abs(xe))
axs[0].set_title('ç©åœ¢åºåçx(n)');axs[0].set_xlabel('n')
axs[1].set_title('ç©åœ¢åºåçå¹
床谱åœæ°');axs[1].grid()
axs[1].set_xlabel(r'$ \omega / \pi $')
axs[1].set_ylabel(r'$ |X( e^{j \omega} )| $')
axs[0].set_ylim([0,1.5]);axs[1].set_ylim([0,5])
axs[1].xaxis.set_major_locator(MaxNLocator(11))
axs[1].yaxis.set_major_locator(MaxNLocator(5))
plt.rcParams['font.sans-serif']=['SimHei'] #çšæ¥æ£åžžæŸç€ºäžææ çŸ
plt.rcParams['axes.unicode_minus'] = False #çšæ¥æŸç€ºèŽå·
plt.show();fig.savefig('./dtft.png',dpi=500)
# -
|
chap2/program_2.6.1/program_2.6.1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="r--_QUPHVc_S" outputId="da90a5b2-7d09-4e38-86f5-af39505294f8"
import sys
# !{sys.executable} -m pip install pycbc ligo-common --no-cache-dir
# + id="WBhFBQsJVv_h"
import numpy as np
import math
import pylab
import matplotlib.pyplot as plt
import random
import pycbc
from pycbc import distributions
from pycbc.waveform import get_td_waveform
from pycbc.detector import Detector
import pycbc.coordinates as co
from pycbc.psd import welch, interpolate
from pycbc.psd import interpolate, inverse_spectrum_truncation
from pycbc.noise.gaussian import noise_from_psd
from pycbc.noise.gaussian import frequency_noise_from_psd
from pycbc.filter import matched_filter
det_l1 = Detector('L1')
apx = 'IMRPhenomD'
N=2048*16 #N is number of samples, N=length/delta_t
fs=2048 #fs is sampling frequnecy
length=16 #duration of segment
delta_f=1.0/16
f_samples = 16385
f_lower=30
delta_t=1.0/2048
# N=2048*16.0 #N is number of samples, N=length/delta_t
# print(N)
# fs=2048.0 #fs is sampling frequnecy
# print(fs)
# length=16 #duration of segment
# print(length)
# delta_f=fs/N
# print(delta_f)
# f_samples = int(N/2+ 1)
# print(f_samples)
# f_lower=40
# print(f_lower)
# delta_t=1.0/2048
# print(delta_t)
# + id="IUMSOsmSVwcI"
from pycbc.psd.analytical import AdVDesignSensitivityP1200087
def get_psd(f_samples, delta_f, low_freq_cutoff):
psd=AdVDesignSensitivityP1200087(f_samples, delta_f, low_freq_cutoff)
return psd
from pycbc.noise.gaussian import frequency_noise_from_psd
def get_noise(psd, seed=None):
noise=frequency_noise_from_psd(psd, seed=seed)
noise_time = noise.to_timeseries()
return noise_time
def add_noise_signal(noise, signal):
length_signal = len(signal)
signal_plus_noise=noise
signal_plus_noise[0:length_signal]=np.add(noise[0:length_signal], signal)
return signal_plus_noise
from pycbc.psd import welch, interpolate
def get_whiten(signal_plus_noise):
signal_freq_series=signal_plus_noise.to_frequencyseries()
numerator = signal_freq_series
psd_to_whiten = interpolate(welch(signal_plus_noise), 1.0 / signal_plus_noise.duration)
denominator=np.sqrt(psd_to_whiten)
whiten_freq = (numerator / denominator)
whiten=whiten_freq.to_timeseries().highpass_fir(30., 512).lowpass_fir(300.0, 512)
return whiten
def get_8s(whiten, signal_peak_index=None):
whiten.start_time = 0
cropped = whiten.time_slice(0,8)
return cropped
psd=get_psd(f_samples, delta_f, f_lower)
def DISTRIBUTIONS(low, high, samples):
var_dist = distributions.Uniform(var = (low, high))
return var_dist.rvs(size = samples)
def SPIN_DISTRIBUTIONS(samples):
theta_low = 0.
theta_high = 1.
phi_low = 0.
phi_high = 2.
uniform_solid_angle_distribution = distributions.UniformSolidAngle(polar_bounds=(theta_low,theta_high),
azimuthal_bounds=(phi_low,phi_high))
solid_angle_samples = uniform_solid_angle_distribution.rvs(size=samples)
spin_mag = np.ndarray(shape=(samples), dtype=float)
for i in range(0,samples):
spin_mag[i] = 1.
spinx, spiny, spinz = co.spherical_to_cartesian(spin_mag,solid_angle_samples['phi'],solid_angle_samples['theta'])
return spinz
# + id="tIsrMOcxwg8w"
def get_params(samples):
mass1_samples = DISTRIBUTIONS(10, 80, samples)
mass2_samples = DISTRIBUTIONS(10, 80, samples)
right_ascension_samples = DISTRIBUTIONS(0 , 2*math.pi, samples)
polarization_samples = DISTRIBUTIONS(0 , 2*math.pi, samples)
declination_samples = DISTRIBUTIONS((-math.pi/2)+0.0001, (math.pi/2)-0.0001, samples)
spinz1 = SPIN_DISTRIBUTIONS(samples)
spinz2 = SPIN_DISTRIBUTIONS(samples)
snr_req = DISTRIBUTIONS(2, 17, samples)
DIST = DISTRIBUTIONS(2500, 3000, samples)
return mass1_samples, mass2_samples, right_ascension_samples, polarization_samples, declination_samples, spinz1, spinz2, snr_req, DIST
# + id="Bg1EFOuoVwyJ"
def DATA_GENERATION(samples):
mass1_samples, mass2_samples, right_ascension_samples, polarization_samples, declination_samples, spinz1, spinz2, snr_req, DIST = get_params(samples)
for i in range(0,samples):
seed = random.randint(1, 256)
# NOTE: Inclination runs from 0 to pi, with poles at 0 and pi
# coa_phase runs from 0 to 2 pi.
try:
hp, hc = get_td_waveform(approximant=apx,
mass1=mass1_samples[i][0],
mass2=mass2_samples[i][0],
spin1z=spinz1[i],
spin2z=spinz2[i],
delta_t=delta_t,
distance = DIST[i][0],
f_lower=40)
except:
try:
hp, hc = get_td_waveform(approximant=apx,
mass1=mass1_samples[i][0],
mass2=mass2_samples[i][0],
spin1z=spinz1[i],
spin2z=spinz2[i],
delta_t=delta_t,
distance = DIST[i][0],
f_lower=50)
except RuntimeError:
hp, hc = get_td_waveform(approximant=apx,
mass1=mass1_samples[i][0],
mass2=mass2_samples[i][0],
spin1z=spinz1[i],
spin2z=spinz2[i],
delta_t=delta_t*2,
distance = DIST[i][0],
f_lower=40)
signal_l1 = det_l1.project_wave(hp, hc, right_ascension_samples[i][0], declination_samples[i][0], polarization_samples[i][0])
signal_l1.append_zeros(10*2048)
signal_l1 = signal_l1.cyclic_time_shift(5)
signal_l1.start_time = 0
noise=get_noise(psd)
final = add_noise_signal(noise, signal_l1)
hps=signal_l1
conditioned=final
hps.resize(len(conditioned))
template = hps.cyclic_time_shift(hps.start_time)
psd_whiten=interpolate(welch(conditioned), 1.0 / conditioned.duration)
snr = matched_filter(template, conditioned, psd=psd_whiten, low_frequency_cutoff=40, sigmasq = 1)
peak = abs(snr).numpy().argmax()
snrp = snr[peak]
time = snr.sample_times[peak]
signal_l1_scaled = signal_l1*snr_req[i][0] / abs(snrp)
final_scaled = add_noise_signal(noise, signal_l1_scaled)
whiten = get_whiten (final_scaled)
data = get_8s(whiten)
my_dir = '/content/Positive Test DATA/' # write the file name in which you need to put the data
name = 111000000+i+1
np.save(my_dir + str(name), data)
# + id="wFeaqXT7VxD3"
DATA_GENERATION(12288)
# + id="aySSSNmZVxd4" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="b69a534a-ab7a-4c8e-b5b1-ab24489dd091"
import shutil
shutil.make_archive('/content/Positive_Test_DATA', 'zip', 'Positive Test DATA')
# + colab={"base_uri": "https://localhost:8080/"} id="0TDqXOjn3h5T" outputId="42f6acc5-a05d-42a4-f693-0a1fd6daec3a"
from google.colab import drive
drive.mount('/content/gdrive',force_remount=True)
# + colab={"base_uri": "https://localhost:8080/"} id="lrrRPRwv3jTQ" outputId="8e88e89f-4b56-457d-f426-039cda579b97"
# !cp Positive_Test_DATA.zip '/content/gdrive/My Drive/'
# !ls -lt '/content/gdrive/My Drive/'
# + colab={"base_uri": "https://localhost:8080/"} id="oPmBpV8VYD0P" outputId="864b0ad8-03a0-4453-92af-82aad3bda6c8"
# N=2048*16 #N is number of samples, N=length/delta_t
# print(N)
# fs=2048.0 #fs is sampling frequnecy
# print(fs)
# length=16 #duration of segment
# print(length)
# delta_f=fs/N
# print(delta_f)
# f_samples = int(N/2+ 1)
# print(f_samples)
# f_lower=30
# print(f_lower)
# delta_t=1.0/2048
# print(delta_t)
|
GWS_DATA_GENERATION_Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Stroke prediction
# ## P2: EDA
# + pycharm={"is_executing": false, "name": "#%%\n"}
import jenkspy as jenkspy
import pandas as pd
import numpy as np
import seaborn as sns
# + pycharm={"is_executing": false, "name": "#%%\n"}
df= pd.read_csv('healthcare-dataset-stroke-data.csv')
df
# + pycharm={"is_executing": false, "name": "#%%\n"}
corrtable = df.corr()
corrtable
# + pycharm={"is_executing": false, "name": "#%%\n"}
sns.heatmap(corrtable)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Summery of dataset when stroke is 0
# + pycharm={"is_executing": false, "name": "#%%\n"}
df[df['stroke'] == 0].describe()
# -
# ## Summery of dataset when stroke is 1
# + pycharm={"is_executing": false, "name": "#%%\n"}
df[df['stroke'] == 1].describe()
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Categories of **work_type**
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.work_type.unique()
# -
# ## Categories of **smoking_status**
# + pycharm={"is_executing": false, "name": "#%%\n"}
df.smoking_status.unique()
# + [markdown] pycharm={"name": "#%% md\n"}
# ## heart disease and stroke
# + pycharm={"is_executing": false, "name": "#%% \n"}
cross_tab_heart_disease = pd.crosstab(df['heart_disease'],df['stroke'])
cross_tab_heart_disease
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_heart_disease.plot(kind='bar',stacked = True)
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_heart_disease_norm = cross_tab_heart_disease.div(cross_tab_heart_disease.sum(1),axis=0)
cross_tab_heart_disease_norm.plot(kind='bar',stacked = True)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## smoking_state and stroke
# + pycharm={"is_executing": false, "name": "#%% \n"}
cross_tab_smoking = pd.crosstab(df['smoking_status'],df['stroke'])
cross_tab_smoking
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_smoking_norm = cross_tab_smoking.div(cross_tab_smoking.sum(1),axis=0)
cross_tab_smoking_norm.plot(kind='bar',stacked = True)
# -
# ## gender and stroke
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_gender = pd.crosstab(df['stroke'],df['gender'])
cross_tab_gender
# + pycharm={"is_executing": false, "name": "#%%\n"}
round(cross_tab_gender.div(cross_tab_gender.sum(0),axis=1)*100,1)
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_gender.plot(kind='bar',stacked = True)
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_gender_norm = cross_tab_gender.div(cross_tab_gender.sum(1),axis=0)
cross_tab_gender_norm.plot(kind='bar',stacked = True)
# + [markdown] pycharm={"is_executing": false, "name": "#%% md\n"}
# ## age and stroke
# + pycharm={"is_executing": false, "name": "#%%\n"}
breaks = jenkspy.jenks_breaks(df['age'], nb_class=10)
print(breaks)
df['age jenkspy'] = pd.cut(df['age'], bins=breaks, labels=["1", "2", "3", "4", "5","6","7","8","9","10"])
cross_tab1 = pd.crosstab(df['age jenkspy'], df['stroke'])
cross_tab1_normal = cross_tab1.div(cross_tab1.sum(1), axis=0)
cross_tab1_normal.plot(kind='bar', stacked=True)
# -
# ## ever_married and stroke
# + pycharm={"is_executing": false, "name": "#%% \n"}
cross_tab_married = pd.crosstab(df['ever_married'],df['stroke'])
cross_tab_married
# + pycharm={"is_executing": false, "name": "#%%\n"}
cross_tab_married_norm = cross_tab_married.div(cross_tab_married.sum(1),axis=0)
cross_tab_married_norm.plot(kind='bar',stacked = True)
# -
# ## avg_glucose_level and stroke
# + pycharm={"is_executing": false, "name": "#%%\n"}
breaks = jenkspy.jenks_breaks(df['avg_glucose_level'], nb_class=6)
print(breaks)
df['avg_glucose_level jenkspy'] = pd.cut(df['avg_glucose_level'], bins=breaks, labels=["1", "2", "3", "4", "5", "6"])
cross_tab2 = pd.crosstab(df['avg_glucose_level jenkspy'], df['stroke'])
cross_tab2_normal = cross_tab2.div(cross_tab2.sum(1), axis=0)
cross_tab2_normal.plot(kind='bar', stacked=True)
# -
# ## bmi and stroke
# + pycharm={"is_executing": false, "name": "#%%\n"}
breaks = jenkspy.jenks_breaks(df['bmi'], nb_class=5)
print(breaks)
df['bmi jenkspy'] = pd.cut(df['bmi'], bins=breaks, labels=["1", "2", "3", "4", "5"])
cross_tab2 = pd.crosstab(df['bmi jenkspy'], df['stroke'])
cross_tab2_normal = cross_tab2.div(cross_tab2.sum(1), axis=0)
cross_tab2_normal.plot(kind='bar', stacked=True)
# + pycharm={"is_executing": false, "name": "#%%\n"}
df=df.drop(columns=['bmi jenkspy','avg_glucose_level jenkspy','age jenkspy'])
df
# + [markdown] pycharm={"name": "#%% md\n"}
# ## pairplot of dataset
# + pycharm={"is_executing": false, "name": "#%%\n"}
sns.pairplot(df)
|
P2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:python3]
# language: python
# name: conda-env-python3-py
# ---
# +
import pickle
filename = "../../outputs/captions_tokens/2/bigram_overlap.pickle"
with open(filename, "rb") as file:
captions = pickle.load(file)
# -
# %load_ext autoreload
from self_bleu import self_bleu
# %autoreload 2
test_captions = captions[:1000]
# %%time
self_bleu(captions)
{
100: 1.21,
1000: 129
|
evaluation/ACL 2019 - self_BLEU.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Self Organizing Map (SOM)
# Realizaremos un ejercicio que consiste en un formulario de un banco rellenado por clientes que quieren acceder a una tarjeta de crédito. Nuestro objetivo es determinar la gente que ha mentido en dicho formulario.
#
# Para ello vamos a tener una serie de puntos en el espacio 15 dimensiones que se corresponden al número de variables que vamos a utilizar (ver tabla abajo), y nosotros vamos a tener que fabricar una serie de nodos en ese espacio dimensional que serán la salida de la red neuronal. Se inicializará con una salida de pesos aleatorios del mismo tamaño o dimensión que el vector de datos y localizaremos la neurona que está más cerca de cada uno de los clientes y la actualizaremos para que esté todavÃa más cerca de ese cliente. Para ello aplicaremos una función de distancia o cercanÃa para actualizar dichos nodos. Al aplicar esto varias veces el espacio de salida irá perdiendo dimensiones hasta que la distancia entre las observaciones dejará de disminuir. La columna Class indica si la solicitud fue aprobada (1) o no (0)
# ### Recordemos los pasos para entrenar un SOM:
#
# - <span style='color:#288c17'> <b>PASO 1:</span> Empezamos con un dataset compuesto de *n_features* variables independientes.
#
# - <span style='color:#288c17'> <b>PASO 2:</span> Preparamos una parrilla compuesta de nodos, cada uno con un vector de pesos de *n_features* elementos.
#
# - <span style='color:#288c17'> <b>PASO 3:</span> Aleatoriamente inicializamos valores del vector de pesos a números pequeños cercanos a $0$ (pero no $0$).
#
# - <span style='color:#288c17'> <b>PASO 4:</span> Seleccionar una observación aleatoria del dataser.
#
# - <span style='color:#288c17'> <b>PASO 5:</span> Calcular la distancia EuclÃdea desde dicho puntos a las diferentes neuronas de la red.
#
# - <span style='color:#288c17'> <b>PASO 6:</span> Seleccionar la neurona con la menor distancia al punto. Dicha neurona es el nodo ganador.
#
# - <span style='color:#288c17'> <b>PASO 7:</span> Actualizar lso epsos del nodo ganador para moverlo más cerca dle punto.
#
# - <span style='color:#288c17'> <b>PASO 8:</span> Utilizar una función Gaussiana al vecindario del punto de medie el nodo ganador y actualizar los pesos de los vecinos para moverlos más cerca del punto. El radio de los vecinos afectados es la desviación tÃpica de la Gaussiana.
#
# - <span style='color:#288c17'> <b>PASO 9:</span> Repetir los pasos <span style='color:#288c17'> <b>1</span> a <span style='color:#288c17'> <b>5</span> y actualizar los pesos después de cada observación (*Reinforcement Learning*) o después de un conjunto de observaciones (*Batch Learning*), hasta que la red neuronal converja en un punto donde los vecindarios no cambien.
# Importar las librerÃas
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importar el dataset
dataset = pd.read_csv("Credit_Card_Applications.csv")
X = dataset.iloc[:, :-1].values #datos que usaremos para las variables
y = dataset.iloc[:, -1].values # metemos la columna Class en el vector y, que serÃa como la predicción
dataset
# Escalado de caracterÃsticas. Estandarizamos las varibales entre 0 y 1 (normalizamos)
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler(feature_range = (0, 1))
X = sc.fit_transform(X)
X
# +
# Entrenar el SOM
#Para ello importamos minisom que se encuentra en nuestra carpeta.
# Es un algoritmo pillado de internet para usar y mostrar SOMs.
# En el archivo se indica qué es cada variable
from minisom import MiniSom
# - x,y son los cuadrados del SOM
# - input_len es la longitud de la entrada, en qué espacio vectorial empezamos a establecer als proyercciones
# - sigma es el radio incial
# - learning_rate es la capacidad de ir adaptando la capacidad de los pesos
som = MiniSom(x = 10, y = 10, input_len = 15, sigma = 1.0, learning_rate = 0.5)
som.random_weights_init(X) #inicializamos los pesos aleatorios dandole los datos para entrenar (X)
som.train_random(data = X, num_iteration = 100)
# +
# Visualizar los resultados
from pylab import bone, pcolor, colorbar, plot, show
bone() #con bone establecemos la ventana de dibujo
# con pcolor() establecemos un gradiente que nos permita agregar los colores
# de las distancias medias entre nuestras neuronas de forma automática (distance_map())
# esta función nos devuelve todas las distancias medias en forma matricial, la cual trasponemos
# con .T ya que vienen por fila y las queremos por columna
pcolor(som.distance_map().T)
colorbar() #una leyenda de barra que nos indique la distancia media a los vecinos
markers = ['o', 's']
colors = ['r', 'g']
for i, x in enumerate(X): #i para la posicion y la x para los valores especÃficos de cada cliente
w = som.winner(x) #nos dice dónde está los nodos ganadores
plot(w[0]+0.5, w[1]+0.5, # posiciones x,y (el 0,0 está abajo la izquierda, por eso lo de +0.5 para que empiece en medio del tablero)
markers[y[i]], markeredgecolor = colors[y[i]], markerfacecolor = 'None',
markersize = 10, markeredgewidth = 2)
show()
# -
# Si nos fijamos en el mapa de arriba podemos detectar los fraudes que son los valores atipicos que no siguen las reglas generales, que serÃan los nodos que están más alejados del resto (celdas blancas).
#
# Los circulos rojos son los clientes que no han obtenido aprobación y los cuadrados rojos los que no.
# +
# Encontrar los fraudes
mappings = som.win_map(X) #nos devuelve los nodos ganadores de cada observación
#marcamos las coordenadas de las celdas blancas, si hubiera celdas blancas o muy blancas se podrÃan
#concatenar(este no es el caso pero lo hacemos para ver como se harÃa).
frauds = sc.inverse_transform(frauds)
frauds = np.concatenate( (mappings[(4,4)], mappings[(7,8)]), axis = 0 )
#en fradus nos sale una lista con los clientes que están en ese nodo(o nodos) que supuestamente han
#cometido fraude.
# -
|
datasets/Part_4_Self_Organizing_Maps_SOM/som.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# name: conda_python3
# ---
# # Segment Real Time Data + Personalize
#
# In this module you are going to be adding the ability to maintain a real-time dataset that represents the latest user behavior for users of the Retail Demo Store. You will then connect that dataset to the Personalize dataset groups that you built in the first part of the workshop. This will enable your Personalize models to be kept up to date with the latest events your users are performing.
#
# This workshop will use the Segment analytics.js library to collect real-time data from the Retail Demo Store, and then feed that event data into the Segment platform, where it can be routed directly to a Personalize Tracker, and then used to maintain the latest behavioral data for your personalization user-item interaction data.
#
# Recommended Time: 45 Minutes
#
# ## Prerequisites
#
# In order to complete this workshop, you will need to complete the 1.1-Personalize workbook in this directory. You will also need a Segment workspace. If you are doing this workshop as part of a live workshop event, ask your moderator how to set up a Segment workspace. If you are running this workshop on your own, you can *click here* to create a Segment account. We do not recommend using your production Segment workspace for this workshop.
#
# ## Segment Platform Overview
# Segment is a customer data platform (CDP) that helps you collect, clean, and control your customer data. Segment provides several types of Sources which you can use to collect your data, and which you can choose from based on the needs of your app or site. For websites, you can use a javascript library to collect data. If you have a mobile app, you can embed one of Segmentâs Mobile SDKs, and if youâd like to create messages directly on a server (if you have, for example a dedicated .NET server that processes payments), Segment has several server-based libraries that you can embed directly into your backend code. With Segment, you can also use cloud-sources to import data about your app or site from other tools like Zendesk or Salesforce, to enrich the data sent through Segment. By using Segment to decouple data collection from data use, you can create a centralized data supply chain based on organized and modular data.
#
# 
# ## Setup
#
# Segment uses *sources* as a way to organize data inputs into the platform. Configuring a source will allow you to collect real-time event data from the Retail Demo Store user interface, and pass that information to Segment. You need to be signed into your Segment workspace to begin this process. Once you are signed in to the Segment console (https://app.segment.com), click on your workspace, and then âConnectionsâ in the upper left hand corner of the screen. Then, click âAdd Sourceâ.
#
# 
#
# Select the âjavascriptâ source type.
#
# 
#
# And click âAdd Sourceâ.
#
# 
#
# Give your source a name. We recommend âretail-demo-store.â
#
# 
#
# The next screen confirms that your source was successfully created.
#
# 
#
# Now that you are here, set the write key for your new source in the environment variable below.
#
# Copy the string in the `analytics.load(â...â)` section shown above, and paste it into the variable in the cell below.
#
# You will need this in a few minutes, when you enable Segment events collection in the Retail Demo Store.
#
# Make sure you run the cell after you paste the key.
# +
import boto3
# Enter your Segment write key here, from the above step
segment_write_key = "YOUR_SEGMENT_WRITE_KEY_GOES_HERE"
# -
# Now that you have a working source, letâs wire up our event data to Amazon Personalize.
#
# ## Configure the Segment Personalize Destination
#
# Segment uses Destinations to route real-time event data to a data consumer application. In this case, you will be using the Segment Personalize destination. This destination will take real-time events from Segment, pass them through an AWS Lambda function, and then into the user-item interactions dataset in your Retail Demo Store.
#
# Click âConnectionsâ in the upper left corner of the screen, and then the âAdd Destinationâ button.
#
# 
#
# In the Segment destinations catalog, type âpersonalizeâ into the search text box in the upper left corner of the screen. You will see the Amazon Personalize destination appear in the search results. Click the tile for the destination.
#
# 
#
# Then, click the âConfigure Amazon Personalizeâ button.
#
# 
#
# Select your source from the earlier part of this process; this screen should show the source you created in the steps above.
#
# 
#
# Then, click the âConfirm Sourceâ button.
#
# 
#
# At this point, you are ready to configure the AWS Lambda function that the destination will need to process events from the Retail Demo Store.
#
# 
#
# The Retail Demo Store deployment in your AWS account will have a pre-configured Lambda function that you can use to configure the destination. This function is deployed to the Retail Demo store during the environment setup steps at the beginning of the workshop.
#
# Segment uses a Lambda function as a way to allow you to customize the event names and properties that are sent to Personalize for training purposes. The Cloud Formation Template and code for this Lambda is available for your use, if you would like to use this pattern in your own applications.
#
# Log in to your AWS Console, and select Lambda under the Services finder in the top left corner of the screen. You will see a screen that looks like this:
#
# 
#
# Find the SegmentPersonalizeEventsDestination and click on it. Keep this tab or window open as you will need it in a few steps when you configure Amazon Personalize.
#
# 
#
# At the top of the screen, you will see the ARN for the Lambda function. Click the copy link shown above to copy the ARN to the clipboard, then go back to the Segment console for your Personalize destination, and click on Lambda **.
#
# 
#
# On the next screen, paste in the ARN for the Lambda. And click the Save button.
#
# 
#
# Next, you will give Segment permission to call your Lambda from their AWS account. Click the Role Address** link.
#
# 
#
# Next, go to your AWS Console tab or window, and select IAM from Services, and then click on Roles. In the search text box, search for Segment.
#
# 
#
# Select the SegmentCrossAccountLambda role, and copy the Role ARN. You can easily copy the whole string by clicking the copy button to the right of the ARN as shown in the screen shot.
#
# 
#
# Go back to the Segment console destination configuration tab or window, and paste in the ARN you just copied and click Save.
#
# 
#
# Next, click the âExternal IDâ link.
#
# 
#
# NOTE: This is not a security best practice, but for the workshop we are forced to hard-code an external ID into the role deployment. Please do not use this pattern in a production application.
#
# Segmentâs integration supports using the write key for the source that is sending data to this destination as the External ID, and you should use this feature instead of a hard-coded external ID.
#
# Enter '123456789' in the External ID field, and click Save.
#
# 
#
# Next, you need to set the region for the Lambda that is deployed in your account.
#
# If you are running this in an AWS managed workshop, ask your event admins for the region in which you are running the workshop. If you are running the workshop in us-west-2, there is no need to change this setting. Otherwise, use the region in which the workshop is deployed, otherwise Segment will not be able to invoke your Lambda.
#
# 
#
#
# 
#
# Finally, click the slider button at the top of the screen to enable the destination. You must enable the destination or events will not be sent to Personalize in the following steps.
#
# 
# ## Configure Lambda Parameters and Review Code
#
# Before the destination can send events to your Amazon Personalize events tracker, you will need to tell the destination lambda where to send the events. It looks for an environment variable called 'personalize_tracking_id'.
#
# Let's set that. Run the following cell to look up the relevant Amazon Personalize tracker from the Personalize workbook.
#
# We can then set the appropriate value in the destination Lambda.
# +
ssm = boto3.client('ssm')
# First, let's look up the appropriate tracking string
response = ssm.get_parameter(
Name='retaildemostore-personalize-event-tracker-id'
)
tracking_id = response['Parameter']['Value']
print(tracking_id)
# -
# Go to your AWS console tab or window, and select Lambda from the Services menu.
#
# Find the SegmentPersonalizeEventsDestination, and click on it in the list.
#
# 
#
# 
#
# Then, scroll down to the parameters section.
#
# 
#
# The tracking parameter should be set to the tracker from the first workbook.
#
# Click the edit button, then paste in the tracking ID from the cell above, and click the Redeploy button at the top of the screen.
#
# Take some time to look at the code that this Lambda uses to send events to Personalize. You can use this code in your own deployment, however you may need to change the event parameters sent to Amazon Personalize depending on the dataset you set up.
#
# ```python
# def lambda_handler(event, context):
# # In high volume applications, remove this code.
# logger.debug("Got event: " + json.dumps(event))
#
# # Segment will invoke your function once per event type you have configured
# # in the Personalize destination in Segment.
# try:
# if ('anonymousId' in event or 'userId' in event and 'properties' in event):
# # Make sure this event contains an itemId since this is required for the Retail Demo Store
# # dataset - you can also check for specific event names here if needed, and only pass the ones
# # that you want to use in the training dataset
# if (not 'productId' in event['properties']):
# logger.debug("Got event with no productId, discarding.")
# return
#
# logger.debug("Calling putEvents()")
# # Function parameters for put_events call.
# params = {
# 'trackingId': personalize_tracking_id,
# 'sessionId': event['anonymousId']
# }
#
# # If a user is signed in, we'll get a userId. Otherwise for anonymous
# # sessions, we will not have a userId. We still want to call put_events
# # in both cases. Once the user identifies themsevles for the session,
# # subsequent events will have the userId for the same session and
# # Personalize will be able to connect prior anonymous to that user.
# if event.get('userId'):
# params['userId'] = event['userId']
#
# # YOU WILL NEED TO MODIFY THIS PART TO MATCH THE EVENT PROPS
# # THAT COME FROM YOUR EVENTS
# #
# # Personalize needs the event identifier
# # that was used to train the model. In this case, we're using the
# # product's productId passed through Segment to represent the itemId.
# #
# properties = { 'itemId': event['properties']['productId'] }
#
# # Build the event that we're sending to Personalize. Note that Personalize
# # expects a specific event format
# personalize_event = {
# 'eventId': event['messageId'],
# 'sentAt': int(dp.parse(event['timestamp']).strftime('%s')),
# 'eventType': event['event'],
# 'properties': json.dumps(properties)
# }
#
# params['eventList'] = [ personalize_event ]
#
# logger.debug('put_events parameters: {}'.format(json.dumps(params, indent = 2)))
# # Call put_events
# response = personalize_events.put_events(**params)
# else:
# logger.debug("Segment event does not contain required fields (anonymousId and sku)")
# ```
#
# ## Validate that Real-Time Events are Flowing from the Retail Demo Store
#
# You are now ready to send live events to Personalize from the Retail Demo Store. In order to do this, you will need to enable the Segment client side integration with the Retail Demo Store. Segment provides a variety of ways to collect real time events, and a full discussion of how this works is beyond the scope of this document, however the Retail Demo Store represents a fairly typical deployment for most web applications, in that it uses the Segment analytics.js library, loaded via the Segment CDN, to inject their code into the web application.
#
# Because the Retail Demo Store is a Vue.js application, this code is loaded in the head tag of index.html file:
# ```html
# <head>
# <meta charset="utf-8">
# <meta http-equiv="X-UA-Compatible" content="IE=edge">
# <meta name="viewport" content="width=device-width, initial-scale=1, shrink-to-fit=no">
# <link rel="apple-touch-icon" sizes="180x180" href="<%= BASE_URL %>apple-touch-icon.png">
# <link rel="icon" type="image/png" sizes="32x32" href="<%= BASE_URL %>favicon-32x32.png">
# <link rel="icon" type="image/png" sizes="16x16" href="<%= BASE_URL %>favicon-16x16.png">
# <link rel="manifest" href="<%= BASE_URL %>site.webmanifest">
# <link rel="stylesheet" href="https://stackpath.bootstrapcdn.com/bootstrap/4.3.1/css/bootstrap.min.css" integrity="<KEY>" crossorigin="anonymous">
# <link rel="stylesheet" href="https://use.fontawesome.com/releases/v5.3.1/css/all.css" integrity="<KEY>" crossorigin="anonymous">
# <title>Retail Demo Store</title>
# <!-- This code is for the Segment integration - DO NOT REMOVE -->
# <%= VUE_APP_SEGMENT_WRITE_KEY === 'NONE' ? '' : `<script>\r\n !function(){var analytics=window.analytics=window.analytics||[];if(!analytics.initialize)if(analytics.invoked)window.console&&console.error&&console.error(\"Segment snippet included twice.\");else{analytics.invoked=!0;analytics.methods=[\"trackSubmit\",\"trackClick\",\"trackLink\",\"trackForm\",\"pageview\",\"identify\",\"reset\",\"group\",\"track\",\"ready\",\"alias\",\"debug\",\"page\",\"once\",\"off\",\"on\",\"addSourceMiddleware\",\"addIntegrationMiddleware\",\"setAnonymousId\",\"addDestinationMiddleware\"];analytics.factory=function(e){return function(){var t=Array.prototype.slice.call(arguments);t.unshift(e);analytics.push(t);return analytics}};for(var e=0;e<analytics.methods.length;e++){var key=analytics.methods[e];analytics[key]=analytics.factory(key)}analytics.load=function(key,e){var t=document.createElement(\"script\");t.type=\"text\/javascript\";t.async=!0;t.src=\"https:\/\/cdn.segment.com\/analytics.js\/v1\/\" + key + \"\/analytics.min.js\";var n=document.getElementsByTagName(\"script\")[0];n.parentNode.insertBefore(t,n);analytics._loadOptions=e};analytics.SNIPPET_VERSION=\"4.13.1\";\r\n analytics.load(\"${VUE_APP_SEGMENT_WRITE_KEY}\");\r\n analytics.page();\r\n }}();\r\n<\/script>` %>
# </head>
# ```
# This ensures that the Segment library is available at all times for each user action in the user interface of the Retail Demo Store. Each time a user performs an action in the Retail Demo Store user interface (such as viewing a product, adding a product to a cart, searching, etc.) an event is sent to Segment with the properties associated with that userâs action. Note that this code is only loaded if an environment variable is set to define the write key for the Segment source which will accept events from the Retail Demo Store. This will become important in a moment.
# ```javascript
# let eventProperties = {
# productId: product.id,
# name: product.name,
# category: product.category,
# image: product.image,
# feature: feature,
# experimentCorrelationId: experimentCorrelationId,
# price: +product.price.toFixed(2)
# };
#
# if (this.segmentEnabled()) {
# window.analytics.track('ProductLiked', eventProperties);
# }
# ```
# This allows you to collect data that is relevant to any tool that might need to be kept updated with the latest user behavior.
#
# ## Sending Real-Time Events
#
# Since you have already connected Segment to Personalize, letâs test this data path by triggering events from the Retail Demo Store user interface which is deployed in your AWS account.
#
# Run the following code to set the SSM parameter that holds the Segment write key.
# +
# Set the Segment write key in the string below, and run this cell.
# THIS IS ONLY REQUIRED IF YOU DID NOT SET THE SEGMENT WRITE KEY IN YOUR ORIGINAL DEPLOYMENT
import boto3
ssm = boto3.client('ssm')
if segment_write_key:
response = ssm.put_parameter(
Name='retaildemostore-segment-write-key',
Value='{}'.format(segment_write_key),
Type='String',
Overwrite=True
)
print(segment_write_key)
# -
# You now have an environment variable that will enable the Segment data collection library in the code in `index.html`. All we need to do now, is force a re-deploy of the Retail Demo Store.
#
# To do that, go back to your AWS Console tab or window, and select Code Pipeline from the Services search. Then, find the pipeline name that contains `WebUIPipeline` and click that link.
#
# 
#
# Then, select the âRelease Changeâ button, and confirm the release once the popup shows up. You will see a confirmation that the pipeline is re-deploying the web ui for the Retail Demo Store.
#
# 
#
# This process should complete in a few minutes. Once this is done, you will see the bottom tile confirm that your deployment has completed:
#
# 
#
# ## Log in as a Retail Demo Store User
#
# **IMPORTANT**
#
# Once this is confirmed, tab back to the Retail Demo Store web UI, and refresh the screen to reload the user interface. This will load the libraries you just deployed, and will allow your instance of the Retail Demo Store to send events to Segment.
#
# In the Personalize workshop, you created an account for the Retail Demo Store. If you are not logged in as that account, log in now.
#
# Then, open another tab to the Segment console, and select âretail-demo-storeâ under the Sources tab:
#
# 
#
# And then click on the Debugger tab.
#
# 
#
# Here you will be able to see live events coming from the Retail Demo Store this:
#
# 
#
# Go back to the Retail Demo Store web app tab, and click on some categories of products. You should start to see events appear in the Segment debugger at this point. This means that the actions you are performing as a user are now being sent to the training datasets in Personalize.
#
# Now that you have events flowing from your web application to Personalize, you can keep the Personalize data sets up to date, and re-train them as required by your application use cases.
#
# You can finish the workshop here, or learn more about what you can do with Segmentâs Customer Data Platform (Personas) and Amazon Personalize in the next workbook:
#
# [Segment CDP Workbook](../6-CustomerDataPlatforms/6.1-Segment.ipynb)
|
workshop/1-Personalization/1.2-Real-Time-Events-Segment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using PyMC3
# In this assignment, we will learn how to use a library for probabilistic programming and inference called <a href="http://docs.pymc.io/">PyMC3</a>.
# ### Installation
# Libraries that are required for this tasks can be installed with the following command (if you use PyPI):
#
# ```bash
# pip install pymc3 pandas numpy matplotlib seaborn
# ```
#
# You can also install pymc3 from source using <a href="https://github.com/pymc-devs/pymc3#installation">the instruction</a>.
# +
# #! pip install pymc3 pandas numpy matplotlib seaborn
# +
# #! conda install pyqt=4 -y
# -
import numpy as np
import pandas as pd
import numpy.random as rnd
import seaborn as sns
from matplotlib import animation
import pymc3 as pm
from grader import Grader
# %pylab inline
# ### Grading
# We will create a grader instance below and use it to collect your answers. Note that these outputs will be stored locally inside grader and will be uploaded to the platform only after running submitting function in the last part of this assignment. If you want to make a partial submission, you can run that cell anytime you want.
grader = Grader()
# ## Task 1. Alice and Bob
#
# Alice and Bob are trading on the market. Both of them are selling the Thing and want to get as high profit as possible.
# Every hour they check out with each other's prices and adjust their prices to compete on the market. Although they have different strategies for price setting.
#
# **Alice**: takes Bob's price during the **previous** hour, multiply by 0.6, add 90\$, add Gaussian noise from $N(0, 20^2)$.
#
# **Bob**: takes Alice's price during the **current** hour, multiply by 1.2 and subtract 20\$, add Gaussian noise from $N(0, 10^2)$.
#
# The problem is to find the joint distribution of Alice and Bob's prices after many hours of such an experiment.
# ### Task 1.1
#
# Implement the `run_simulation` function according to the description above.
def run_simulation(alice_start_price=300.0, bob_start_price=300.0, seed=42, num_hours=10000, burnin=1000):
"""Simulates an evolution of prices set by Bob and Alice.
The function should simulate Alice and Bob behavior for `burnin' hours, then ignore the obtained
simulation results, and then simulate it for `num_hours' more.
The initial burnin (also sometimes called warmup) is done to make sure that the distribution stabilized.
Please don't change the signature of the function.
Returns:
two lists, with Alice and with Bob prices. Both lists should be of length num_hours.
"""
np.random.seed(seed)
alice_prices = [alice_start_price]
bob_prices = [bob_start_price]
#### YOUR CODE HERE ####
for i in range(num_hours):
alice_price = bob_prices[-1]*0.6 + 90 + np.random.normal(loc=0, scale=20)
bob_price = alice_price*1.2 - 20 + np.random.normal(loc=0, scale=10)
alice_prices.append(alice_price)
bob_prices.append(bob_price)
### END OF YOUR CODE ###
return alice_prices[burnin:], bob_prices[burnin:]
alice_prices, bob_prices = run_simulation(alice_start_price=300, bob_start_price=300, seed=42, num_hours=3, burnin=1)
if len(alice_prices) != 3:
raise RuntimeError('Make sure that the function returns `num_hours` data points.')
grader.submit_simulation_trajectory(alice_prices, bob_prices)
# ### Task 1.2
# What is the average prices for Alice and Bob after the burnin period? Whose prices are higher?
#### YOUR CODE HERE ####
alice_prices, bob_prices = run_simulation()
average_alice_price = np.mean(alice_prices)
average_bob_price = np.mean(bob_prices)
### END OF YOUR CODE ###
grader.submit_simulation_mean(average_alice_price, average_bob_price)
# ### Task 1.3
#
# Let's look at the 2-d histogram of prices, computed using kernel density estimation.
data = np.array(run_simulation())
sns.jointplot(data[0, :], data[1, :], stat_func=None, kind='kde')
# Clearly, the prices of Bob and Alce are highly correlated. What is the Pearson correlation coefficient of Alice and Bob prices?
#### YOUR CODE HERE ####
correlation = np.corrcoef(data[0, :], data[1, :])[0][1]
### END OF YOUR CODE ###
grader.submit_simulation_correlation(correlation)
# ### Task 1.4
# We observe an interesting effect here: seems like the bivariate distribution of Alice and Bob prices converges to a correlated bivariate Gaussian distribution.
#
# Let's check, whether the results change if we use different random seed and starting points.
for (ap, bp) in ((1, 10,), (10, 100), (100, 1000)):
data_tmp = np.array(run_simulation(alice_start_price=ap, bob_start_price=bp))
print(np.corrcoef(data_tmp[0, :], data[1, :]))
for s in (1, 10, 100):
data_tmp = np.array(run_simulation(seed=s))
print(np.corrcoef(data_tmp[0, :], data[1, :]))
# +
# Pick different starting prices, e.g 10, 1000, 10000 for Bob and Alice.
# Does the joint distribution of the two prices depend on these parameters?
POSSIBLE_ANSWERS = {
0: 'Depends on random seed and starting prices',
1: 'Depends only on random seed',
2: 'Depends only on starting prices',
3: 'Does not depend on random seed and starting prices'
}
idx = 3 ### TYPE THE INDEX OF THE CORRECT ANSWER HERE ###
answer = POSSIBLE_ANSWERS[idx]
grader.submit_simulation_depends(answer)
# -
# ## Task 2. Logistic regression with PyMC3
#
# Logistic regression is a powerful model that allows you to analyze how a set of features affects some binary target label. Posterior distribution over the weights gives us an estimation of the influence of each particular feature on the probability of the target being equal to one. But most importantly, posterior distribution gives us the interval estimates for each weight of the model. This is very important for data analysis when you want to not only provide a good model but also estimate the uncertainty of your conclusions.
#
# In this task, we will learn how to use PyMC3 library to perform approximate Bayesian inference for logistic regression.
#
# This part of the assignment is based on the logistic regression tutorial by <NAME> and <NAME>.
# ### Logistic regression.
#
# The problem here is to model how the probability that a person has salary $\geq$ \$50K is affected by his/her age, education, sex and other features.
#
# Let $y_i = 1$ if i-th person's salary is $\geq$ \$50K and $y_i = 0$ otherwise. Let $x_{ij}$ be $j$-th feature of $i$-th person.
#
# Logistic regression models this probabilty in the following way:
#
# $$p(y_i = 1 \mid \beta) = \sigma (\beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik} ), $$
#
# where $\sigma(t) = \frac1{1 + e^{-t}}$
# #### Odds ratio.
# Let's try to answer the following question: does a gender of a person affects his or her salary? To do it we will use the concept of *odds*.
#
# If we have a binary random variable $y$ (which may indicate whether a person makes \$50K) and if the probabilty of the positive outcome $p(y = 1)$ is for example 0.8, we will say that the *odds* are 4 to 1 (or just 4 for short), because succeding is 4 time more likely than failing $\frac{p(y = 1)}{p(y = 0)} = \frac{0.8}{0.2} = 4$.
#
# Now, let's return to the effect of gender on the salary. Let's compute the **ratio** between the odds of a male having salary $\geq $ \$50K and the odds of a female (with the same level of education, experience and everything else) having salary $\geq$ \$50K. The first feature of each person in the dataset is the gender. Specifically, $x_{i1} = 0$ if the person is female and $x_{i1} = 1$ otherwise. Consider two people $i$ and $j$ having all but one features the same with the only difference in $x_{i1} \neq x_{j1}$.
#
# If the logistic regression model above estimates the probabilities exactly, the odds for a male will be (check it!):
# $$
# \frac{p(y_i = 1 \mid x_{i1}=1, x_{i2}, \ldots, x_{ik})}{p(y_i = 0 \mid x_{i1}=1, x_{i2}, \ldots, x_{ik})} = \frac{\sigma(\beta_1 + \beta_2 x_{i2} + \ldots)}{1 - \sigma(\beta_1 + \beta_2 x_{i2} + \ldots)} = \exp(\beta_1 + \beta_2 x_{i2} + \ldots)
# $$
#
# Now the ratio of the male and female odds will be:
# $$
# \frac{\exp(\beta_1 \cdot 1 + \beta_2 x_{i2} + \ldots)}{\exp(\beta_1 \cdot 0 + \beta_2 x_{i2} + \ldots)} = \exp(\beta_1)
# $$
#
# So given the correct logistic regression model, we can estimate odds ratio for some feature (gender in this example) by just looking at the corresponding coefficient. But of course, even if all the logistic regression assumptions are met we cannot estimate the coefficient exactly from real-world data, it's just too noisy. So it would be really nice to build an interval estimate, which would tell us something along the lines "with probability 0.95 the odds ratio is greater than 0.8 and less than 1.2, so we cannot conclude that there is any gender discrimination in the salaries" (or vice versa, that "with probability 0.95 the odds ratio is greater than 1.5 and less than 1.9 and the discrimination takes place because a male has at least 1.5 higher probability to get >$50k than a female with the same level of education, age, etc."). In Bayesian statistics, this interval estimate is called *credible interval*.
#
# Unfortunately, it's impossible to compute this credible interval analytically. So let's use MCMC for that!
#
# #### Credible interval
# A credible interval for the value of $\exp(\beta_1)$ is an interval $[a, b]$ such that $p(a \leq \exp(\beta_1) \leq b \mid X_{\text{train}}, y_{\text{train}})$ is $0.95$ (or some other predefined value). To compute the interval, we need access to the posterior distribution $p(\exp(\beta_1) \mid X_{\text{train}}, y_{\text{train}})$.
#
# Lets for simplicity focus on the posterior on the parameters $p(\beta_1 \mid X_{\text{train}}, y_{\text{train}})$ since if we compute it, we can always find $[a, b]$ such that $p(\log a \leq \beta_1 \leq \log b \mid X_{\text{train}}, y_{\text{train}}) = p(a \leq \exp(\beta_1) \leq b \mid X_{\text{train}}, y_{\text{train}}) = 0.95$
#
# ### Task 2.1 MAP inference
# Let's read the dataset. This is a post-processed version of the [UCI Adult dataset](http://archive.ics.uci.edu/ml/datasets/Adult).
data = pd.read_csv("adult_us_postprocessed.csv")
data.head()
# Each row of the dataset is a person with his (her) features. The last column is the target variable $y$. 1 indicates that this person's annual salary is more than $50K.
#
# First of all let's set up a Bayesian logistic regression model (i.e. define priors on the parameters $\alpha$ and $\beta$ of the model) that predicts the value of "income_more_50K" based on person's age and education:
#
# $$
# p(y = 1 \mid \alpha, \beta_1, \beta_2) = \sigma(\alpha + \beta_1 x_1 + \beta_2 x_2) \\
# \alpha \sim N(0, 100^2) \\
# \beta_1 \sim N(0, 100^2) \\
# \beta_2 \sim N(0, 100^2), \\
# $$
#
# where $x_1$ is a person's age, $x_2$ is his/her level of education, y indicates his/her level of income, $\alpha$, $\beta_1$ and $\beta_2$ are paramters of the model.
# +
with pm.Model() as manual_logistic_model:
# Declare pymc random variables for logistic regression coefficients with uninformative
# prior distributions N(0, 100^2) on each weight using pm.Normal.
# Don't forget to give each variable a unique name.
#### YOUR CODE HERE ####
alpha = pm.Normal('alpha', mu=0, sd=100)
beta_age_coefficient = pm.Normal('beta_age_coefficient', mu=0, sd=100)
beta_education_coefficient = pm.Normal('beta_education_coefficient', mu=0, sd=100)
### END OF YOUR CODE ###
# Thansform these random variables into vector of probabilities p(y_i=1) using logistic regression model specified
# above. PyMC random variables are theano shared variables and support simple mathematical operations.
# For example:
# z = pm.Normal('x', 0, 1) * np.array([1, 2, 3]) + pm.Normal('y', 0, 1) * np.array([4, 5, 6])`
# is a correct PyMC expression.
# Use pm.invlogit for the sigmoid function.
#### YOUR CODE HERE ####
z = alpha + beta_age_coefficient*np.array(data['age']) + beta_education_coefficient*np.array(data['educ'])
a = pm.invlogit(z)
### END OF YOUR CODE ###
# Declare PyMC Bernoulli random vector with probability of success equal to the corresponding value
# given by the sigmoid function.
# Supply target vector using "observed" argument in the constructor.
#### YOUR CODE HERE ####
y_obs = pm.Bernoulli('y_obs', p=a, observed=data['income_more_50K'])
### END OF YOUR CODE ###
# Use pm.find_MAP() to find the maximum a-posteriori estimate for the vector of logistic regression weights.
map_estimate = pm.find_MAP()
print(map_estimate)
# -
# Sumbit MAP estimations of corresponding coefficients:
with pm.Model() as logistic_model:
# There's a simpler interface for generalized linear models in pymc3.
# Try to train the same model using pm.glm.GLM.from_formula.
# Do not forget to specify that the target variable is binary (and hence follows Binomial distribution).
#### YOUR CODE HERE ####
pm.glm.GLM.from_formula('income_more_50K ~ age + educ', data, family=pm.glm.families.Binomial())
### END OF YOUR CODE ###
map_estimate = pm.find_MAP()
print(map_estimate)
beta_age_coefficient = 0.043483 ### TYPE MAP ESTIMATE OF THE AGE COEFFICIENT HERE ###
beta_education_coefficient = 0.3621089 ### TYPE MAP ESTIMATE OF THE EDUCATION COEFFICIENT HERE ###
grader.submit_pymc_map_estimates(beta_age_coefficient, beta_education_coefficient)
# ### Task 2.2 MCMC
# To find credible regions let's perform MCMC inference.
# You will need the following function to visualize the sampling process.
# You don't need to change it.
def plot_traces(traces, burnin=2000):
'''
Convenience function:
Plot traces with overlaid means and values
'''
ax = pm.traceplot(traces[burnin:], figsize=(12,len(traces.varnames)*1.5),
lines={k: v['mean'] for k, v in pm.summary(traces[burnin:]).iterrows()})
for i, mn in enumerate(pm.summary(traces[burnin:])['mean']):
ax[i,0].annotate('{:.2f}'.format(mn), xy=(mn,0), xycoords='data'
,xytext=(5,10), textcoords='offset points', rotation=90
,va='bottom', fontsize='large', color='#AA0022')
# #### Metropolis-Hastings
# Let's use Metropolis-Hastings algorithm for finding the samples from the posterior distribution.
#
# Once you wrote the code, explore the hyperparameters of Metropolis-Hastings such as the proposal distribution variance to speed up the convergence. You can use `plot_traces` function in the next cell to visually inspect the convergence.
#
# You may also use MAP-estimate to initialize the sampling scheme to speed things up. This will make the warmup (burnin) period shorter since you will start from a probable point.
data['agesq'] = data['age'] ** 2
data.head()
with pm.Model() as logistic_model:
# Since it is unlikely that the dependency between the age and salary is linear, we will include age squared
# into features so that we can model dependency that favors certain ages.
# Train Bayesian logistic regression model on the following features: sex, age, age^2, educ, hours
# Use pm.sample to run MCMC to train this model.
# To specify the particular sampler method (Metropolis-Hastings) to pm.sample,
# use `pm.Metropolis`.
# Train your model for 400 samples.
# Save the output of pm.sample to a variable: this is the trace of the sampling procedure and will be used
# to estimate the statistics of the posterior distribution.
#### YOUR CODE HERE ####
pm.glm.GLM.from_formula('income_more_50K ~ sex + age + agesq + educ + hours', data, family=pm.glm.families.Binomial())
with logistic_model:
trace = pm.sample(400, step=pm.Metropolis())
### END OF YOUR CODE ###
plot_traces(trace, burnin=200)
# #### NUTS sampler
# Use pm.sample without specifying a particular sampling method (pymc3 will choose it automatically).
# The sampling algorithm that will be used in this case is NUTS, which is a form of Hamiltonian Monte Carlo, in which parameters are tuned automatically. This is an advanced method that we hadn't cover in the lectures, but it usually converges faster and gives less correlated samples compared to vanilla Metropolis-Hastings.
#
# Since the NUTS sampler doesn't require to tune hyperparameters, let's run it for 10 times more iterations than Metropolis-Hastings.
with pm.Model() as logistic_model:
# Train Bayesian logistic regression model on the following features: sex, age, age_squared, educ, hours
# Use pm.sample to run MCMC to train this model.
# Train your model for *4000* samples (ten times more than before).
# Training can take a while, so relax and wait :)
#### YOUR CODE HERE ####
pm.glm.GLM.from_formula('income_more_50K ~ sex + age + agesq + educ + hours', data, family=pm.glm.families.Binomial())
with logistic_model:
trace = pm.sample(4000, step=pm.NUTS())
### END OF YOUR CODE ###
plot_traces(trace)
# #### Estimating the odds ratio
# Now, let's build the posterior distribution on the odds ratio given the dataset (approximated by MCMC).
# We don't need to use a large burn-in here, since we initialize sampling
# from a good point (from our approximation of the most probable
# point (MAP) to be more precise).
burnin = 100
b = trace['sex[T. Male]'][burnin:]
plt.hist(np.exp(b), bins=20, normed=True)
plt.xlabel("Odds Ratio")
plt.show()
#
# Finally, we can find a credible interval (recall that credible intervals are Bayesian and confidence intervals are frequentist) for this quantity. This may be the best part about Bayesian statistics: we get to interpret credibility intervals the way we've always wanted to interpret them. We are 95% confident that the odds ratio lies within our interval!
lb, ub = np.percentile(b, 2.5), np.percentile(b, 97.5)
print("P(%.3f < Odds Ratio < %.3f) = 0.95" % (np.exp(lb), np.exp(ub)))
# Submit the obtained credible interval.
grader.submit_pymc_odds_ratio_interval(np.exp(lb), np.exp(ub))
# ### Task 2.3 interpreting the results
# +
# Does the gender affects salary in the provided dataset?
# (Note that the data is from 1996 and maybe not representative
# of the current situation in the world.)
POSSIBLE_ANSWERS = {
0: 'No, there is certainly no discrimination',
1: 'We cannot say for sure',
2: 'Yes, we are 95% sure that a female is *less* likely to get >$50K than a male with the same age, level of education, etc.',
3: 'Yes, we are 95% sure that a female is *more* likely to get >$50K than a male with the same age, level of education, etc.',
}
idx = 2 ### TYPE THE INDEX OF THE CORRECT ANSWER HERE ###
answer = POSSIBLE_ANSWERS[idx]
grader.submit_is_there_discrimination(answer)
# -
# # Authorization & Submission
# To submit assignment parts to Cousera platform, please, enter your e-mail and token into variables below. You can generate token on this programming assignment page. <b>Note:</b> Token expires 30 minutes after generation.
STUDENT_EMAIL = ''
STUDENT_TOKEN = ''
grader.status()
# If you want to submit these answers, run cell below
# +
#grader.submit(STUDENT_EMAIL, STUDENT_TOKEN)
# -
# # (Optional) generating videos of sampling process
# For this (optional) part you will need to install ffmpeg, e.g. by the following command on linux
#
# apt-get install ffmpeg
#
# or the following command on Mac
#
# brew install ffmpeg
# ## Setting things up
# You don't need to modify the code below, it sets up the plotting functions. The code is based on [MCMC visualization tutorial](https://twiecki.github.io/blog/2014/01/02/visualizing-mcmc/).
# +
from IPython.display import HTML
# Number of MCMC iteration to animate.
samples = 400
figsize(6, 6)
fig = plt.figure()
s_width = (0.81, 1.29)
a_width = (0.11, 0.39)
samples_width = (0, samples)
ax1 = fig.add_subplot(221, xlim=s_width, ylim=samples_width)
ax2 = fig.add_subplot(224, xlim=samples_width, ylim=a_width)
ax3 = fig.add_subplot(223, xlim=s_width, ylim=a_width,
xlabel='male coef',
ylabel='educ coef')
fig.subplots_adjust(wspace=0.0, hspace=0.0)
line1, = ax1.plot([], [], lw=1)
line2, = ax2.plot([], [], lw=1)
line3, = ax3.plot([], [], 'o', lw=2, alpha=.1)
line4, = ax3.plot([], [], lw=1, alpha=.3)
line5, = ax3.plot([], [], 'k', lw=1)
line6, = ax3.plot([], [], 'k', lw=1)
ax1.set_xticklabels([])
ax2.set_yticklabels([])
lines = [line1, line2, line3, line4, line5, line6]
def init():
for line in lines:
line.set_data([], [])
return lines
def animate(i):
with logistic_model:
if i == 0:
# Burnin
for j in range(samples): iter_sample.__next__()
trace = iter_sample.__next__()
# import pdb; pdb.set_trace()
line1.set_data(trace['sex[T. Male]'][::-1], range(len(trace['sex[T. Male]'])))
line2.set_data(range(len(trace['educ'])), trace['educ'][::-1])
line3.set_data(trace['sex[T. Male]'], trace['educ'])
line4.set_data(trace['sex[T. Male]'], trace['educ'])
male = trace['sex[T. Male]'][-1]
educ = trace['educ'][-1]
line5.set_data([male, male], [educ, a_width[1]])
line6.set_data([male, s_width[1]], [educ, educ])
return lines
# -
# ## Animating Metropolis-Hastings
with pm.Model() as logistic_model:
# Again define Bayesian logistic regression model on the following features: sex, age, age_squared, educ, hours
#### YOUR CODE HERE ####
pm.glm.GLM.from_formula('income_more_50K ~ sex + age + agesq + educ + hours', data, family=pm.glm.families.Binomial())
### END OF YOUR CODE ###
step = pm.Metropolis()
iter_sample = pm.iter_sample(2 * samples, step, start=map_estimate)
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=samples, interval=5, blit=True)
HTML(anim.to_html5_video())
# Note that generating the video may take a while.
# ## Animating NUTS
# Now rerun the animation providing the NUTS sampling method as the step argument.
|
Bayesian Methods for Machine Learning/Week4/Week4. Practical Assignment. MCMC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.6.0
# language: julia
# name: julia-0.6
# ---
# # DiscreteDP Example: Bioeconomic Model
# ** <NAME> **
#
# *Department of Economics, University of Tokyo*
# From Miranda and Fackler, Applied Computational Economics and Finance, 2002, Section 7.6.6
# `Julia` translation of the [python version](http://nbviewer.jupyter.org/github/QuantEcon/QuantEcon.notebooks/blob/master/ddp_ex_MF_7_6_6_py.ipynb)
using QuantEcon
using Plots
pyplot()
# +
emax = 8 # Energy carrying capacity
n = emax + 1 # Number of states, 0, ..., emax
m = 3 # Number of areas (actions), 0, ..., m-1
e = [2, 4, 5] # Energy offerings
p = [1.0, 0.7, 0.8] # Survival probabilities
q = [0.5, 0.8, 0.7] # Success probabilities
T = 10 # Time horizon
# Terminal values
v_term = ones(n)
v_term[1]= 0;
# -
# We follow the state-action pairs formulation approach.
# +
L = n * m # Number of feasible state-action pairs
s_indices = Vector{Int}(L)
for i in 1:n
s_indices[(i-1) * m + 1 : i * m] = i
end
a_indices = Vector{Int}(L)
for i in 1:n
a_indices[(i-1) * m + 1 : i * m] = 1:m
end
# -
# Reward vector
R = zeros(L);
# Transition probability array
Q = zeros(L, n)
for (i, s) in enumerate(s_indices)
k = a_indices[i]
if s == 1
Q[i, 1] = 1
elseif s == 2
Q[i, minimum([emax+1, s-1+e[k]])] = p[k] * q[k]
Q[i, 1] = 1 - p[k] * q[k]
else
Q[i, minimum([emax+1, s-1+e[k]])] = p[k] * q[k]
Q[i, s-1] = p[k] * (1 - q[k])
Q[i, 1] = 1 - p[k]
end
end
# The current version of `DiscreteDP` does not accept $\beta = 1$.
# So I use a value very close to 1.
# Discount factor
beta = 0.99999999;
# Create a DiscreteDP
ddp = DiscreteDP(R, Q, beta, s_indices, a_indices);
# `backward_induction` used in the python version does not exist in `QuantEcon.jl`.
# So I simply repeat `bellman_operator`.
vs = Matrix(T+1, n)
vs[T+1, :] = v_term
for t in T+1:-1:2
vs[t-1, :] = bellman_operator(ddp, vs[t, :])
end
p1 = bar(0:8, vs[1, :], xlabel="Stock of Energy", xticks=0:1:8,
ylabel="Probability", yticks=0:0.2:1, ylims=(0,1), label="",
title="Survivial Probability, Period 0", )
p2 = bar(0:8, vs[6, :], xlabel="Stock of Energy", xticks=0:1:8,
ylabel="Probability", yticks=0:0.2:1, ylims=(0,1), label="",
title="Survivial Probability, Period 5", )
plot(p1, p2, layout=(1,2), size=(700,230))
|
quanteconomics/ddp_ex_MF_7_6_6_jl.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Day 2: I Was Told There Would Be No Math
# The elves are running low on wrapping paper, and so they need to submit an order for more. They have a list of the dimensions (length l, width w, and height h) of each present, and only want to order exactly as much as they need.
#
# Fortunately, every present is a box (a perfect right rectangular prism), which makes calculating the required wrapping paper for each gift a little easier: find the surface area of the box, which is 2*l*w + 2*w*h + 2*h*l. The elves also need a little extra paper for each present: the area of the smallest side.
#
# For example:
#
# * A present with dimensions 2x3x4 requires 2*6 + 2*12 + 2*8 = 52 square feet of wrapping paper plus 6 square feet of slack, for a total of 58 square feet.
# * A present with dimensions 1x1x10 requires 2*1 + 2*10 + 2*10 = 42 square feet of wrapping paper plus 1 square foot of slack, for a total of 43 square feet.
#
# All numbers in the elves' list are in feet. How many total square feet of wrapping paper should they order?
#
#
with open("input.txt","r") as f:
input_data = [[int(x0) for x0 in x.split("x")] for x in f.read().split("\n")]
def area(whl):
result = 0
surface_small = None
for i in range(2):
for j in range(i+1, 3):
surface = whl[i] * whl[j]
if (surface_small is None) or (surface < surface_small):
surface_small = surface
result = result + surface * 2
result = result + surface_small
return result
def all_area(input_data):
return sum([area(whl) for whl in input_data])
all_area(input_data)
# # Part Two
# The elves are also running low on ribbon. Ribbon is all the same width, so they only have to worry about the length they need to order, which they would again like to be exact.
#
# The ribbon required to wrap a present is the shortest distance around its sides, or the smallest perimeter of any one face. Each present also requires a bow made out of ribbon as well; the feet of ribbon required for the perfect bow is equal to the cubic feet of volume of the present. Don't ask how they tie the bow, though; they'll never tell.
#
# For example:
#
# * A present with dimensions 2x3x4 requires 2+2+3+3 = 10 feet of ribbon to wrap the present plus 2*3*4 = 24 feet of ribbon for the bow, for a total of 34 feet.
# * A present with dimensions 1x1x10 requires 1+1+1+1 = 4 feet of ribbon to wrap the present plus 1*1*10 = 10 feet of ribbon for the bow, for a total of 14 feet.
#
# How many total feet of ribbon should they order?
def length(whl):
whl_sort =sorted(whl)
return (whl_sort[0]+whl_sort[1]) * 2 + whl_sort[0] * whl_sort[1] * whl_sort[2]
def all_length(input_data):
return sum([length(whl) for whl in input_data])
all_length(input_data)
|
2015/Day02/Day2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # RWET Programming Exercise B: Lists and list operations
#
# To do this exercise, download this notebook and open it on your own computer. There are several tasks described below. Your job is to change the code in the cells so that the output from running the cell matches the expected output indicated above the cell.
# ## Task 1: Simple indexing and list functions
#
# There is a list of numbers assigned to a variable `number_list` in the code below that has been assigned a list of numbers. Run this cell before filling in the answers below.
number_list = [-2, -58, 4, 36, -6, 60, -57]
# Write another expression in the cell below, using square bracket index notation, that causes the 4th element of `number_list` (i.e., the number `36`) to be displayed when running the code in the cell.
#
# Expected output: `36`
# Now write an expression that evaluates to the number of items in the list (i.e., `7`), using the `len()` function.
#
# Expected output: `7`
# The following expression:
#
# print max(number_list)
#
# ... will print the largest value in `number_list` (i.e., `60`). Change the variable `x` in the code below so that the expression
#
# print sorted(number_list)[x]
#
# ... does the same thing. (i.e., when you run the cell, it should display `60`.)
#
# Expected output: `20`
x = 0
sorted(number_list)[x]
# ## Task 2: List slices
#
# Write an expression below that evaluates to a slice of `number_list` starting with its second element and ending with its fifth element (exclusive).
#
# Expected output: `[-2, -58, 4, 36, -6, 60, -57]`
# Now, write an expression below that evaluates to a slice of `number_list` starting with its third element and ending at the end of the list.
#
# Expected output: `[4, 36, -6, 60, -57]`
# Finally, fill in a value for the variable `x` below so that the expression below it evaluates to a slice of `number_list` starting at the second-to-last element of the list and ending at the end of the list. (Hint: `x` should be a negative integer.)
#
# Expected output: `[60, -57]`
x = 0
number_list[x:]
# ## Task 3: List comprehensions
#
# For this problem set, I'm introducing a new Python operator: the modulo operator, `%`. This operator returns the *remainder* of dividing one integer by another. For example:
22 % 3
# This expression evaluates to `1` because the remainder of dividing `22` by `3` is `1`. We can use the modulo operator to test whether or not a number is even (i.e., divisible by 2), by using the number `2` on the right side of the operator:
100 % 2
101 % 2
# Given the above information, write a list comprehension that evaluates to a list containing *only* the members of `number_list` that are *divisible by three*. Use the modulo operator in the membership expression of the list comprehension.
#
# Expected output: `[36, -6, 60, -57]`
# ## Task 4: Splitting strings
#
# In the cell below, a variable `float_str` is set to a string containing a list of floating-point numbers, separated by semicolons (`;`). (Make sure to run this cell before you proceed, so that the variable will be available in subsequent cells.)
float_str = "5.8;6.9;3.1;5.9;6.6;6.5;6.5;5.6;6;6.4;3.32;6.0;6.0;6.3;6.6;6.6"
# Write an expression below that converts this string into a list of floating-point numbers. The type of the expression should be `list` and the type of individual elements in the list should be `float`. Hint: You'll need to use the `float()` function, the `.split()` method, and a list comprehension.
#
# Expected output:
#
# [5.8, 6.9, 3.1, 5.9, 6.6, 6.5, 6.5, 5.6, 6.0, 6.4, 3.32, 6.0, 6.0, 6.3, 6.6, 6.6]
# Using the expression you wrote above as a starting point, write an expression below that evaluates to the *sum* of the numbers in the list.
#
# Expected output: `94.11999999999999` (or close to that)
# ## Task 5: Strings in list comprehensions
#
# In the cell below, I've defined a list of strings and assigned it to a variable called `greek`. Make sure to run this cell before you continue.
greek = ["alpha", "beta", "gamma", "delta", "epsilon"]
# Okay. Your job in the next cell is to write an expression that evaluates to a list of strings in `greek` that contain *exactly five letters*.
#
# Expected output: `["alpha", "gamma", "delta"]`
# In the cell below, write an expression that evaluates to a string containing each of the *first letters* of each string in `greek`. Hint: You'll need to use a list comprehension and the `.join()` method.
#
# Expected output: `'abgde'`
# ## Task 6: For loops
#
# The cell below has the skeleton of the `for` loop written for you. Replace the string `"blip"` with an expression such that the cell, when executed, outputs the first ten multiples of five.
#
# Expected output:
#
# 0
# 5
# 10
# 15
# 20
# 25
# 30
# 35
# 40
# 45
#
for i in range(10):
print("blip")
# Using the variable `greek` that was defined earlier, write a `for` loop in the cell below so that when the cell is executed it outputs, on separate lines, each of the elements of the list in upper case.
#
# Expected output:
#
# ALPHA
# BETA
# GAMMA
# DELTA
# EPSILON
# You're done! Good job.
|
programming-exercise-b.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Naturalcolors tutorial
import numpy as np
import importlib
import matplotlib as mpl
import naturalcolors.colorpalette as ncp
# ### Documentation
# Documentation on how to create a colormap from a list of colors (a **listed colormap**) or by specifying anchor points between which the RGB(A) colors are interpolated (a **linear segmented colormap**) can be found here:
#
# https://matplotlib.org/3.1.0/tutorials/colors/colormap-manipulation.html
# ### The *naturalcolors* colormap
# *Naturalcolors* provides wrapper functions to create a colormap from a list of colors in a json file. The colormap is generated by calling the `naturalcolors()` function from the `colorpalette` submodule.
natcmap_list,natcmap_linseg = ncp.naturalcolors()
# The resulting listed and linear segmented colormaps can be visualized either by a **colorbar** or a **color circle**
ncp.drawColorBar(natcmap_linseg)
# Draw a color circle with the naturalcolors colormap
ncp.drawColorCircle(natcmap_linseg, 15, 2000)
# ### Custom colormaps
# You can create your own custom colormaps directly from a **list of colors** or by loading them from a json file using the `load_colors` function from the colorpalette submodule.
#
# The json file should be structures as a list of rgb(a) colors:
# ```
# [[234,33,59],
# [237,65,55],
# [239,102,58],
# ...]
# ```
colors = [[0.31, 0.45, 0.56],[0.9,0.9,0.9], [0.75, 0.51, 0.38]]
cmap_list,cmap_linseg = ncp.make_colormap(colors, 'BlueWhiteOrange')
ncp.drawColorCircle(cmap_linseg, area=500)
# ### Registered colormaps
# Registered colormaps can also be called directly from their name
nc.colorpalette.drawColorCircle('Blues', area=500)
# A registered colormap can be accessed from its name by the following equivalent commands:
# +
# from the cmap submodule
mpl.cm.get_cmap('Blues')
# from the pyplot submodule
mpl.pyplot.get_cmap('Blues')
# -
# A list of *n* colors can be extracted from a colormap using the `get_colors` function of the colorpalette submodule (calls `cmap(np.linspace(0,1,n)` internally). Using the flag `scramble=True` (default=False) rearranges the color array as `[[first rgb],[last rgb],[second rgb],...]]`
ncp.get_colors('Blues', 5, scramble=True)
|
tutorial/naturalcolors_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/marprezd/datasc-python-lab/blob/main/lab/bollywood.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Uou6YUre_VJk"
# # Descriptive Analytics in the Bollywood Dataset.
# The data file `bollywood.csv` contains box office collection and social media promotion information about movies released in 2013â2015 period.
#
# + id="FDtvlWufCSCE"
# Import Pandas and Plotly libraries
import pandas as pd
import plotly.graph_objects as go
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="99_koQuwJcxL" outputId="50958702-2851-4c51-f178-7a7a6e494fbf"
# We will use the pd.read.csv method to read the bollywood.csv dataset and load it into a DataFrame.
df = pd.read_csv('drive/MyDrive/Colab Notebooks/data/bollywood.csv')
# Let's see the first few records of the DataFrame
df.head(5)
# + [markdown] id="p48kRJ1vNXNt"
# ## Structure of the Bollywood DataFrame.
# + [markdown] id="GQ8Av4vlyZZx"
# This DataFrame has got the following columns:
#
# - SlNo â Release Date
# - MovieName â Name of the movie
# - ReleaseTime â Mentions special time of release. **LW (Long weekend), FS (Festive Season), HS (Holiday Season), N (Normal)**
# - Genre â Genre of the film such as **Romance, Thriller, Action, Comedy**, etc.
# - Budget â Movie creation budget
# - BoxOfficeCollection â Box office collection
# - YoutubeViews â Number of views of the YouTube trailers
# - YoutubeLikes â Number of likes of the YouTube trailers
# - YoutubeDislikes â Number of dislikes of the YouTube trailers
#
# We will use the `info()` method to explore the **metadata information** of the dataset.
# + colab={"base_uri": "https://localhost:8080/"} id="3kiYgUs3PAGb" outputId="58f3a681-8a03-460c-f033-f66b3d6e775a"
# Print the metadata information of the dataset
df.info()
# + [markdown] id="cKWaid-PpeJI"
# In this dataset there are a total of 149 records in 10 columns, there are no lost values; 1 Column is floating type, 5 columns are integer type and 4 columns are of objects type. The memory consumption of the dataset is 11.8 kb.
# + [markdown] id="8IG_LTcu3HUM"
# ## Let's start with the descriptive analysis.
# + [markdown] id="fMtT1NYN3MCj"
# ### How many movies got released in each genre?
#
# Since gender is a column with categorical variables we will use the value_counts() method that allows us to know the number of occurrences of a unique value in each of the columns.
# + colab={"base_uri": "https://localhost:8080/"} id="xROsOL9d8vpw" outputId="df120772-77c5-4208-f9f4-dd60cc24eaab"
# Print how many movies got released in each genre
df.Genre.value_counts()
# + [markdown] id="M-y3Zq5TAIfD"
# As you can see at the output, the Comedy genre has got the largest number of releases followed very closely by the Drama genre. On the other hand, the Action and Thriller genres are those that have got a smaller number of releases.
# + [markdown] id="c4gGdKjVEUY5"
# ### How many movies in each genre has got released in different release times like long weekend, festive season, etc?
#
# To find the answer to this question we will use the crosstab() method that allows us to perform a cross-tabulation between the Genre and ReleaseTime columns.
# + colab={"base_uri": "https://localhost:8080/", "height": 300} id="-WqJ-efuEh46" outputId="ed3ca80a-b6d9-48a2-ea51-8db4a44d7cfd"
# Find how many movies in each genre got released in different release times
pd.crosstab(df['Genre'], df['ReleaseTime'])
# + [markdown] id="rHzpr8UeatCG"
# As shown in the output, most of the genres throw their movies in the **normal season (N)**. The **Drama** genre is the one that has got the most releases in **Holiday Season (HS)** and **normal season (N)**.
|
lab/bollywood.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Apartado 6 - Import
# - Import modulos
# - Abrir ficheros
# ------------------------------------------------------------------
# ## Import modulos
# [HELP](https://realpython.com/python-modules-packages/)
# +
import mi_modulo
suma = mi_modulo.suma_2(a=2, b=6)
print(suma)
# -
resta = mi_modulo.resta_2(a=7, b=6)
resta
# +
from mi_modulo import resta_2
resta2 = resta_2(a=5, b=3)
resta2
# +
import mi_modulo as mm
mm.resta_2()
# -
# --------------------------------------------------------------------------
# ## Abrir ficheros
with open('file_to_save.txt', 'a') as open_file:
open_file.write('A string to write\n')
with open('file_to_save.txt', 'a') as open_file:
for i in range(3):
open_file.write('A string to write ' + str(i) + '\n')
with open('file_to_save.txt', 'a') as open_file:
open_file.write("\n------\n Last Line.\n ")
with open('file_to_save.txt', 'r') as open_file:
all_text = open_file.read()
print(all_text)
with open('file_to_save.txt', 'r') as open_file:
line = open_file.readline()
print(type(line))
print(line)
l = "\n"
with open('file_to_save.txt', 'r') as open_file:
line = open_file.readline()
count = 1
while line:
if count == 2:
pass
print(line)
line = open_file.readline()
count += 1
line = open_file.readline()
print("- linea:", line)
with open("new_file.gh", "a") as new_file:
new_file.write("Primera\n")
new_file.write("Segunda\n")
new_file.write("Tercera\n")
print("Se ha escrito")
with open("new_file.gh", "r") as new_file:
linea = new_file.readline()
print(linea)
print(new_file.readline())
print(new_file.readline())
with open('file_to_save.txt', 'r') as open_file:
line = open_file.readline()
while line:
if "1" in line:
print(line)
break
print(line)
line = open_file.readline()
with open('file_to_save.txt', 'r') as open_file:
line = open_file.readline()
while line:
if "|" in line:
lista_strings = line.split("|")
nombre = lista_strings[0]
dinero = lista_strings[1]
print("Nombre: ", nombre)
print("Dinero: ", dinero)
print("----------")
line = open_file.readline()
# +
l = ["a", "b", "c"]
if "a" in l:
print("YES")
# +
s = "A string to write 1"
for elem in s:
if elem == "1":
break
print(elem)
# -
# `split`
# +
txt = "hello, my name is Peter, I am 26 years old"
x = txt.split(", ")
print(x)
# -
|
others/resources/python/precurse_python/6_import/6_import.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#import Turtle, random, numpy
import ##Fill
# Set up the screen
screen = ##Fill
#set up the screen title & bgcolor or use your own background
##Fill
# Draw Border
border = #Fill
# set initial score
score = #Fill
# Draw Score
score_pen = #Fill
score_pen.speed(0)
score_pen.color(#Fill)
score_pen.penup()
score_pen.setposition(#Fill, #Fill)
scorestring = "Score: %s" %#Fill
score_pen.write(scorestring, False, align="left", font=("Arial", 14, "normal"))
score_pen.hideturtle()
# Create player turtle set up the player color, shape, and starting position
player = #Fill
##Fill
player.speed(0)
player.setposition(#Fill, #Fill)
player.setheading(90)
playerspeed = 15
# choose a number of enemies
number_of_enemies = #Fill
# Create an empty list of enemies
enemies = #Fill
#Add enemies to the list
for i in range(#Fill):
#Create the enemy
enemies.append(#Fill)
for enemy in enemies:
enemy.color(#Fill)
enemy.shape(#Fill)
enemy.penup()
enemy.speed(0)
x = random.randint(#Fill, #Fill)
y = random.randint(#Fill, #Fill)
enemy.setposition(#Fill, #Fill)
enemyspeed = 2
#Create the playerâs bullet
bullet = #Fill
#Give bullet a color and a shape
#Fill
bullet.penup()
bullet.speed(0)
bullet.setheading(90)
bullet.shapesize(0.5, 0.5)
bullet.hideturtle()
bulletspeed = 20
##Define bullet state
##ready â ready to fire
##fire â bullet is firing
bulletstate = "ready"
#Move the player left and right
def move_left():
x = #Fill
x = x - #Fill
if x < #Fill :
x =
player.setx(#Fill)
def move_right():
x = #Fill
x = x+ #Fill
if x > #Fill
x =
player.setx(#Fill)
#fire bullet function
def fire_bullet():
global bulletstate
if bulletstate == "ready":
bulletstate = "fire"
x = #Fill
y = #Fill
bullet.setposition(x,y)
bullet.showturtle()
def isCollision(t1,t2):
distance = #Fill
if distance < #Fill:
return #Fill
else:
return #Fill
#Keyboard Binding
#move left when pressing left arrow
#Fill
#Move to the right when pressing right arrow
#Fill
#fire bullet when pressing space
#Fill
#Main game loop
while True:
for enemy in enemies:
#move the enemy
x = #Fill
x = x + #Fill
enemy.setx(#Fill)
#Move the enemy back and down
if enemy.xcor()> #Fill:
#move all the enemy down
for e in enemies:
y = #Fill
y = y - #Fill
e.sety(#Fill)
#Change enemy Direction
enemyspeed = enemyspeed * #Fill
if enemy.xcor()< #Fill:
#Move all enemies down
##FILL, Similar as above
#Change enemy direction
##FILL
#Check for a collison between the bullet and the enemy
if isCollision(#Fill, #Fill):
#Reset the bullet
bullet.hideturtle()
bulletstate = "ready"
bullet.setposition(0,-400)
# Reset the enemy
x = random.randint(#Fill)
y = #Fill
enemy.setposition(#Fill , #Fill)
#Update the score
score = score + #Fill
scorestring = "Score:%s"%score
score_pen.clear()
score_pen.write(scorestring, False, align="left"
, font=("Arial", 14, "normal"))
#check if the enemy hit the player
if isCollision(#Fill , #Fill ):
#Hide player
player.#Fill
#Hide enemy
enemy.#Fill
print(#Fill)
#break (uncomment this when you done coding)
#Move the bullet
if bulletstate == #Fill:
y = #Fill
y = y + #Fill
bullet.sety(#Fill)
#Check to see if the bullet has gone to the tip
if bullet.ycor()>#Fill:
bullet.#Fill
bulletstate = #Fill
|
Python_Class/.ipynb_checkpoints/Space_war Frame-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: EDC-GPU 0.24.5 (Python3)
# language: python
# name: edc-gpu
# ---
# + papermill={"duration": 0.110831, "end_time": "2021-08-16T08:44:37.664968", "exception": false, "start_time": "2021-08-16T08:44:37.554137", "status": "completed"} tags=[]
from edc import check_compatibility
check_compatibility("user-0.24.5", dependencies=["SH"])
# + jupyter={"outputs_hidden": true} papermill={"duration": 10.83097, "end_time": "2021-08-16T08:44:48.527411", "exception": false, "start_time": "2021-08-16T08:44:37.696441", "status": "completed"} tags=[]
# !python3 -m pip install git+https://github.com/aireo-project/aireo_lib
# + jupyter={"outputs_hidden": true} papermill={"duration": 2.476669, "end_time": "2021-08-16T08:44:51.051895", "exception": false, "start_time": "2021-08-16T08:44:48.575226", "status": "completed"} tags=[]
# !python3 -m pip install shapely geopandas
# + [markdown] papermill={"duration": 0.045916, "end_time": "2021-08-16T08:44:51.148191", "exception": false, "start_time": "2021-08-16T08:44:51.102275", "status": "completed"} tags=[]
# ## Introduction ##
#
# The notebook demonstrates the use of aireo_lib , a python library created as a part of the AIREO (Artificial Intelligence Ready Earth Observation training datasets) project. The project aims to make EO datasets easily accessible for the ML (Machine Learning) community. As such, AIREO specifications (shorthand specs) which define metadata elements to be included with the training dataset are proposed, supplemented by a best-practices document which suggests how to fill those metadata elements. Finally, the library takes all into account and implements specs, best-practices and offers an easy-to-use pythonic interface bridging the gap between EO and ML community.
#
# Therefore, this notebook is divided into two sections, one for the training dataset creator (usually from the EO community) and the other for its user (usually from the ML community). The structure of the notebook is the following:
#
# 1) For Creator
#
# - Create a [STAC](https://stacspec.org/) catalog object using the library
#
# - Populate metadata elements prescribed by the AIREO specs
#
# - Generate a STAC metadata directory using the library
#
# - Check AIREO compliance level and metadata completeness
#
#
# 2) For User
#
# - Create a training dataset object as defined in the library using only the STAC metadata
#
# - Get example instances from the object and other dataset variables like the number of instances, etc.
#
# - Use library's functions to plot the data
#
# - Investigate statistics using the library
# + [markdown] papermill={"duration": 0.044659, "end_time": "2021-08-16T08:44:51.239197", "exception": false, "start_time": "2021-08-16T08:44:51.194538", "status": "completed"} tags=[]
# #### About the training dataset
# SpaceNet7 is a collection of satellite image time series covering 100 different locations in a diverse range of environments. It also includes a set of polygons for each image marking out the building footprints. The image data was collected by Planet satellites at an interval of roughly one month for each location for a period of two years. This is not compeltely consistent across different locations. The data was then manually annotated by a team at SpaceNet to produce the building footprint polygons. The full data from 60 areas was released as a public dataset.
#
# We have simplified the dataset slightly for the purpose of creating a pilot AIREO dataset. We have converted all building polygons to boolean raster masks, and have stored these and the images in netcdf files as time series of raster data, one for each location. We have also standardized image resolution across all locations. This notebook only makes use of 5 AOIs out of 60 for demonstration purposes.
#
# This dataset can be used to train ML models for the task of automatic building detection in satellite images, and for the tracking of building development over time.
# + [markdown] papermill={"duration": 0.044969, "end_time": "2021-08-16T08:44:51.330457", "exception": false, "start_time": "2021-08-16T08:44:51.285488", "status": "completed"} tags=[]
# ## AIREO STAC Catalog basics
# + [markdown] papermill={"duration": 0.044839, "end_time": "2021-08-16T08:44:51.420129", "exception": false, "start_time": "2021-08-16T08:44:51.375290", "status": "completed"} tags=[]
#
# The AIREO specs propose a hierarchical structure for STAC metadata. It is a two level structure where the dataset is represented by a collection of AOIs (Area Of Interests), hence, the dataset and AOI being the two levels.
#
# 1. At the dataset level we have a dataset catalog whose metadata elements are the core elements proposed in the AIREO spec. In addition to it, the common metadata elements across each AOI are also at the dataset level, which we shall call root level henceforth. Here, for each data variable there is a separate json which is a STAC Item by definition and is named using the field_schema metadata element. Additionally, there is also a datasheet file in markdown format at the root level which contains human readable information about the key elements of the dataset.
#
# 2. Each AOI has a separate folder within the root level. And in each AOI folder there is a STAC collection representing that AOI and additional json files for each data variable. The additional json files here too, are STAC Items and follow a similar naming convention to the ones at the root level. The assets for each AOI, i.e. the files containing actual data are also in the folder.
#
# The diagram below summarises this hierarchical structure:
#
#
# ```
# Root level (dataset)
# â
# â DatasetCatalog.json
# â datasheet.md
# â references_output1.json
# â features_input1.json
# â ...
# â
# â
# ââââAOI 1
# â 1.json (AOI Collection)
# â feature_input1.json
# â reference_output1.json
# â <reference_asset>
# â <feature_asseet>
# â
# â
# ââââAOI 2
# â ...
# â
# â
# ââââAOI 3
# â ...
# â
# ...
# ```
# + [markdown] papermill={"duration": 0.047798, "end_time": "2021-08-16T08:44:51.512806", "exception": false, "start_time": "2021-08-16T08:44:51.465008", "status": "completed"} tags=[]
# ## Creating a STAC catalog with aireo_lib
#
# The aireo_lib library makes it easier to generate the STAC metadata directory as defined above. Some of the useful functionalities in the library are:
# - Define python dictionaries for metadata at the root level and use a simple function to add it to the STAC catalog. The library validates the data automatically when it is added.
#
# - Similarly, python dictionaries can be defined for each AOI and are also validated automatically.
#
# - Links and assets for all the json files are automatically generated.
#
# - Datasheet is also generated automatically.
#
# - The directory structure is created by the library and assets copied to their respective locations in the hierarchy.
#
# - Evaluating metadata completeness and compliance level.
#
#
# Follow the code and comments below to understand the steps needed to generate STAC metadata with the library.
# + papermill={"duration": 1.671065, "end_time": "2021-08-16T08:44:53.229408", "exception": false, "start_time": "2021-08-16T08:44:51.558343", "status": "completed"} tags=[]
import aireo_lib.core
import os
import json
import numpy as np
from tqdm.notebook import tqdm
from shapely import geometry
import shutil
import xarray as xr
from pathlib import Path
import geopandas as gpd
# + papermill={"duration": 0.052751, "end_time": "2021-08-16T08:44:53.327747", "exception": false, "start_time": "2021-08-16T08:44:53.274996", "status": "completed"} tags=[]
# Path to write the STAC root metadata file too
catalog_fn_w_path = os.environ['EDC_PATH']+'/data/SpaceNet7/sp7_stac/TDS.json'
# Creating an empty STAC Catalog object
new_tds_ctl_o = aireo_lib.core.tds_stac_io.DatasetSTACCatalog()
# + papermill={"duration": 2.974131, "end_time": "2021-08-16T08:44:56.346564", "exception": false, "start_time": "2021-08-16T08:44:53.372433", "status": "completed"} tags=[]
# AOI list int the TDS
dataset_path = os.environ['EDC_PATH']+'/data/SpaceNet7/Data/sp7_sample'
aoi_ids = [aoi_id for aoi_id in os.listdir(dataset_path) if aoi_id[0]!='.'][0:3]
# + papermill={"duration": 0.058143, "end_time": "2021-08-16T08:44:56.448641", "exception": false, "start_time": "2021-08-16T08:44:56.390498", "status": "completed"} tags=[]
# Creating root metadata dictionary
tds_root_core_metadata_d = {}
tds_root_core_metadata_d['aireo_version'] = "0.0.1-alpha.1"
tds_root_core_metadata_d['title'] = "Images with buildings labelled covering short range of time for each AOI"
tds_root_core_metadata_d['description'] = "Covers 60 areas of interest at 4m resolution with images at monthly intervals. Each image is annotated with polygons labelling buildings. Dataset allows for the monitioring and prediction of building development over time."
tds_root_core_metadata_d['created'] = '2020-07-13'
tds_root_core_metadata_d['license_url_list'] = 'https://creativecommons.org/licenses/by-sa/4.0/'
tds_root_core_metadata_d['license'] = "CC-BY-SA-4.0"
tds_root_core_metadata_d["providers_name"]= "[SpaceNet LLC]"
tds_root_core_metadata_d["providers_description"] = "Data gathered by Planet satellites, dataset then created by Spacenet "
tds_root_core_metadata_d["providers_roles"] = {"SpaceNet":["processor","host","licensor","producer"], 'AIREO':["producer", "processor" , "host"]}
tds_root_core_metadata_d["providers_url"]= {"Spacenet":"https://spacenet.ai/",
'AIREO': 'https://aireo.net/'}
tds_root_core_metadata_d['id'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
tds_root_core_metadata_d['type'] = "Collection"
tds_root_core_metadata_d['stac_version'] = '1.0.0-beta.2'
tds_root_core_metadata_d['provenance'] = 'Data gathered from Planet satellites and annotatations produced by SpaceNet LLC'
tds_root_core_metadata_d['purpose'] = "Using semantic segmentation track buidling development over time. Segment individual images from each timestep then use this knowledge to track development over time for one AOI."
tds_root_core_metadata_d['tasks'] = ['Semantic Segmentation']
tds_root_core_metadata_d['data_preprocessing'] = {'type':'free-text', 'recipe':'Original dataset included images from one AOI as seperate tiff files. We have combined these into one netcdf datacube for each AOI. The building labels were stored as polygons in the original dataset. We have converted to raster masks and have stored them in netcdf datacubes, one for each AOI.'}
tds_root_core_metadata_d['funding_info'] = "The AIREO project is funded by ESA. The underlying data was gathered by Planet, then annotated and released by SpaceNet for free use."
tds_root_core_metadata_d['field_schema'] = {'features': {'input1': ['georeferenced_eo_data','georeferenced_eo_datacube']}, 'references': {'output1': ['reference_data']}}
tds_root_core_metadata_d['example_definition'] = "An individual example consists of a single image, and a raster mask representing the buildings visible in the image."
tds_root_core_metadata_d['data_completeness'] = "Dataset is sufficent for task and requires no external sources."
tds_root_core_metadata_d['data_split'] = "Recommend train/test/validation split of 40 AOIs in train, 10 in test and 10 in validation. Should ensure the density of buildings in images is roughly equal for these splits ie. not training on sparsely populated areas then testing on densely populated areas."
tds_root_core_metadata_d['data_sharing'] = "The dataset will be shared on Euro Data Cube (EDC) and can be accessed through jupyter notebooks on EDC."
tds_root_core_metadata_d['compliance_level'] = 'level 1'
tds_root_core_metadata_d['example_window_size'] = 100
tds_root_core_metadata_d['example_stride'] = 80
tds_root_core_metadata_d['data_completeness'] = "The data spans a large geographic range. There are some unusable sections of the images due to cloud cover and instrument malfunction."
tds_root_core_metadata_d['data_split'] = "It is important when splitting data for testing, training and validation, that the density of buildings is similar in each split. For example if we train on sparsely developed areas then our model's performance will likely suffer when tested on highly developed areas."
tds_root_core_metadata_d['data_sharing'] = "The dataset will be shared on Euro Data Cube (EDC) and can be accessed through jupyter notebooks on EDC."
tds_root_core_metadata_d['compliance_level'] = 'level 1'
tds_root_core_metadata_d['links'] = []
# + papermill={"duration": 0.062471, "end_time": "2021-08-16T08:44:56.556249", "exception": false, "start_time": "2021-08-16T08:44:56.493778", "status": "completed"} tags=[]
# Make root level feature metadata
g_feature_metadata_d = {}
g_feature_metadata_d['type'] = "Feature"
g_feature_metadata_d['stac_version'] = "1.0.0-beta.2"
g_feature_metadata_d['stac_extensions'] = ["georeferenced_eo_data","georeferenced_eo_datacube"]
g_feature_metadata_d['id'] = "common_feature_metadata"
g_feature_metadata_d['collection'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
g_feature_metadata_d["properties"] = {}
# add metadata from georeferencedeodata profile first
g_feature_metadata_d["properties"]['parent_identifier'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
g_feature_metadata_d["properties"]['identifier'] = "Null"
g_feature_metadata_d["properties"]['composed_of'] = "Null"
g_feature_metadata_d["properties"]['linked_with'] = "Null"
g_feature_metadata_d['properties']['product_type'] = "Time series of monthly images for one AOI. Each image shares geometry and bounding box."
g_feature_metadata_d["properties"]["native_product_format"] = "netcdf"
g_feature_metadata_d["properties"]['processing_level'] = "Null"
g_feature_metadata_d["properties"]['auxiliary_dataset_filename'] = "Null"
g_feature_metadata_d['properties']['CRS'] = 'EPSG:3857'
# dimensions of the whole dataset
x_min = -13545862.01592866
y_min = -4510398.55370881
x_max = 16133718.82286585
y_max = 6887891.10417667
g_feature_metadata_d['bbox'] = [x_min,y_min,x_max,y_max]
g_feature_metadata_d['geometry'] = geometry.mapping(geometry.box(x_min,y_min,x_max,y_max,ccw=True))
# now add data for georeferencedeodatacube profile
g_feature_metadata_d["properties"]["dimensions"] = {}
g_feature_metadata_d["properties"]["dimensions"]["x"] = {
"type": "spatial",
"axis": "x",
"extent": [
x_min,
x_max
],
"reference_system": 3857
}
g_feature_metadata_d["properties"]["dimensions"]["y"] = {
"type": "spatial",
"axis": "y",
"extent": [
y_min,
y_max
],
"reference_system": 3857
}
g_feature_metadata_d["properties"]["dimensions"]["temporal"] = {
"type": "temporal",
"extent": [
"2017-07-01T00:00:00.000000000",
"2020-01-01T00:00:00.000000000"
]
}
g_feature_metadata_d["properties"]["dimensions"]["spectral"] = {
"type": "bands",
"values": [
"red",
"green",
"blue"
]
}
g_feature_metadata_d["properties"]['datetime'] = "2019"
g_feature_metadata_d['links'] = []
g_feature_metadata_d["assets"] = {}
# make feature metadata dictionary
feature_metadata_d = {}
feature_metadata_d['input1'] = g_feature_metadata_d
# + papermill={"duration": 0.064373, "end_time": "2021-08-16T08:44:56.664682", "exception": false, "start_time": "2021-08-16T08:44:56.600309", "status": "completed"} tags=[]
# create common reference data
g_ref_data_metadata_d = {}
g_ref_data_metadata_d['id'] = f'common_reference_metadata'
g_ref_data_metadata_d['type'] = "Feature"
g_ref_data_metadata_d['stac_version'] = "1.0.0-beta.2"
g_ref_data_metadata_d['stac_extensions'] = ["reference_data"]
g_ref_data_metadata_d['collection'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
g_ref_data_metadata_d['properties'] = {}
g_ref_data_metadata_d['properties']['name'] = 'Reference Metadata'
g_ref_data_metadata_d['properties']['description'] = "The reference data consists of datacubes of raster masks representing the building outlines in the training images. One datacube corresponds to one AOI."
g_ref_data_metadata_d['properties']['type'] = "annotated"
g_ref_data_metadata_d['properties']['task'] = "Semantic Segmentation"
g_ref_data_metadata_d['properties']['classes'] = [[{'BUILDING':255,'NOT_BUILDING':0}]]
g_ref_data_metadata_d['properties']['overviews'] = ["The are dataset covers roughly 40000 square kilometers. 6.94% of this is labelled by this reference data as containing buildings."]
g_ref_data_metadata_d['properties']['collection_method'] = "The reference data was produced by manual annotation of the original satellite images."
g_ref_data_metadata_d['properties']['data_preprocessing'] = {'type': 'free-text', 'recipe':"The polygons in the original reference data were converted into rasters with the same dimensions and coordinates as the relevant feature data."}
g_ref_data_metadata_d['properties']['CRS'] = 'EPSG:3857'
g_ref_data_metadata_d["properties"]['value'] = 0.
g_ref_data_metadata_d['properties']["orientation"]= "Null"
g_ref_data_metadata_d["properties"]['time_range'] = "2021"
g_ref_data_metadata_d["properties"]['datetime'] = "2019"
g_ref_data_metadata_d['bbox'] = [x_min,y_min, x_max, y_max]
g_ref_data_metadata_d['geometry'] = geometry.mapping(geometry.box(x_min,y_min,x_max,y_max,ccw=True))
g_ref_data_metadata_d['links'] = []
g_ref_data_metadata_d["assets"] = {}
ref_metadata_d = {}
ref_metadata_d['output1'] = g_ref_data_metadata_d
# + papermill={"duration": 0.068539, "end_time": "2021-08-16T08:44:56.777075", "exception": false, "start_time": "2021-08-16T08:44:56.708536", "status": "completed"} tags=[]
# Check if feature data is compliant
aireo_lib.tds_stac_io.validate_item(feature_metadata_d['input1'])
# + papermill={"duration": 0.089913, "end_time": "2021-08-16T08:44:56.922842", "exception": false, "start_time": "2021-08-16T08:44:56.832929", "status": "completed"} tags=[]
# Add TDS global core elements metadata, and add global level profile metadata to the catalog object.
new_tds_ctl_o.add_tds_root_metadata(tds_root_core_metadata_d, feature_metadata_d, ref_metadata_d)
# + papermill={"duration": 0.052464, "end_time": "2021-08-16T08:44:57.024174", "exception": false, "start_time": "2021-08-16T08:44:56.971710", "status": "completed"} tags=[]
new_tds_ctl_o.valid_tds_root
# + papermill={"duration": 82.782083, "end_time": "2021-08-16T08:46:19.851258", "exception": false, "start_time": "2021-08-16T08:44:57.069175", "status": "completed"} tags=[]
# Adding metadata for each AOI
for aoi_id in tqdm(aoi_ids):
# Dictionary for each AOI collection metadata
aoi_metadata_d = {}
aoi_metadata_d['type'] = "Collection"
aoi_metadata_d["id"] = f"{aoi_id}"
aoi_metadata_d['stac_version'] = '1.0.0-beta.2'
aoi_metadata_d['title'] = f"{aoi_id} Collection"
aoi_metadata_d['description'] = "Datacube of Satellite images for one AOI and datacube of corresponding building masks."
aoi_metadata_d["license"] = "Various (CC-BY-4.0, Creative Commons CC BY-SA 3.0 IGO)"
masks_path = dataset_path + '/' + aoi_id + '/building_masks.nc'
with xr.open_dataarray(masks_path) as masks:
minx = masks.coords['x'].values[0]
maxx = masks.coords['x'].values[-1]
miny = masks.coords['y'].values[0]
maxy = masks.coords['y'].values[-1]
start_time = str(min(masks['date'].values))
end_time = str(max(masks['date'].values))
unique, counts = np.unique(masks.values,return_counts=True)
# calculate percentage of images taken up by buildings
building_percent = 100*(counts[1]/counts[0])
bbox = [minx,miny,maxx,maxy]
geo = geometry.mapping(geometry.box(minx,miny,maxx,maxy))
aoi_metadata_d["bbox"]= bbox
aoi_metadata_d['geometry'] = geo
aoi_metadata_d["extent"] = {"spatial" : {"bbox":[bbox]},
"temporal": {"interval":[[start_time,end_time]]}}
aoi_metadata_d['time_range'] = start_time+' to '+end_time
aoi_metadata_d['links'] = []
aoi_metadata_d["assets"] = {}
# Dictionary for each AOI's reference metadata
aoi_reference_metadata_d = {}
aoi_reference_metadata_d['id'] = f'reference_metadata_AOI_{aoi_id}'
aoi_reference_metadata_d['type'] = "Feature"
aoi_reference_metadata_d['stac_version'] = "1.0.0-beta.2"
aoi_reference_metadata_d['stac_extensions'] = ["reference_data"]
aoi_reference_metadata_d['collection'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
aoi_reference_metadata_d['bbox'] = bbox
aoi_reference_metadata_d['geometry'] = geo
aoi_reference_metadata_d['properties'] = {}
aoi_reference_metadata_d["properties"]['name'] = str(aoi_id)+ " Reference metadata"
aoi_reference_metadata_d['properties']['description'] = "The reference data consists of time series of raster masks stored in datacubes. These masks cover the buildings present in the corresponding satellite images."
aoi_reference_metadata_d['properties']['type'] = "Raster"
aoi_reference_metadata_d['properties']['task'] = "Semantic Segmentation"
aoi_reference_metadata_d['properties']['classes'] = [[{'BUILDING':255,'NOT_BUILDING':0}]]
aoi_reference_metadata_d['properties']['overviews'] = [str(building_percent)+"% of this AOI is covered by buildings"]
aoi_reference_metadata_d['properties']['collection_method'] = "Building polygons were manually created by a team at SpaceNet."
aoi_reference_metadata_d['properties']['data_preprocessing'] = "The polygons in the original reference data were converted into rasters."
aoi_reference_metadata_d['properties']['CRS'] = 'EPSG:3857'
aoi_reference_metadata_d['time_range'] = start_time+' to '+end_time
aoi_reference_metadata_d["properties"]['value'] = 0
aoi_reference_metadata_d['properties']["orientation"]= "null"
aoi_reference_metadata_d["properties"]['datetime'] = start_time
aoi_reference_metadata_d['links'] = []
aoi_reference_metadata_d["assets"] = {}
aoi_reference_d = {}
aoi_reference_d['output1'] = aoi_reference_metadata_d
# Dictionary for each AOI's feature metadata
aoi_feature_data_metadata_d = {}
aoi_feature_data_metadata_d['type'] = "Feature"
aoi_feature_data_metadata_d['stac_version'] = "1.0.0-beta.2"
aoi_feature_data_metadata_d['stac_extensions'] = ["georeferenced_eo_datacube","georeferenced_eo_data"]
aoi_feature_data_metadata_d['id'] = f'predictive_feature_metadata_AOI_{aoi_id}'
aoi_feature_data_metadata_d['collection'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
aoi_feature_data_metadata_d["bbox"]= bbox
aoi_feature_data_metadata_d['geometry'] = geo
# first add data from Georeferenced data profile
aoi_feature_data_metadata_d["properties"] = {}
aoi_feature_data_metadata_d["properties"]['parent_identifier'] = "706cf9e2-bd46-11eb-8529-0242ac130003"
aoi_feature_data_metadata_d["properties"]['identifier'] = aoi_id
aoi_feature_data_metadata_d["properties"]['composed_of'] = "Null"
aoi_feature_data_metadata_d["properties"]['linked_with'] = "Null"
aoi_feature_data_metadata_d['properties']['product_type'] = "Time series of monthly images for one AOI. Each image shares geometry and bounding box."
aoi_feature_data_metadata_d["properties"]["native_product_format"] = "netcdf"
aoi_feature_data_metadata_d["properties"]['processing_level'] = "Null"
aoi_feature_data_metadata_d["properties"]['auxiliary_dataset_filename'] = "Null"
aoi_feature_data_metadata_d["properties"]['identifier'] = str(aoi_id)
aoi_feature_data_metadata_d["properties"]['datetime'] = start_time
# add dimension object for datacube profile
aoi_feature_data_metadata_d["properties"]["dimensions"] = {}
aoi_feature_data_metadata_d["properties"]["dimensions"]["x"] = {
"type": "spatial",
"axis": "x",
"extent": [
minx,
maxx
],
"reference_system": 3857
}
aoi_feature_data_metadata_d["properties"]["dimensions"]["y"] = {
"type": "spatial",
"axis": "y",
"extent": [
miny,
maxy
],
"reference_system": 3857
}
aoi_feature_data_metadata_d["properties"]["dimensions"]["temporal"] = {
"type": "temporal",
"extent": [
start_time,
end_time
]
}
aoi_feature_data_metadata_d["properties"]["dimensions"]["spectral"] = {
"type": "bands",
"values": [
"red",
"green",
"blue"
]
}
aoi_feature_data_metadata_d['links'] = []
aoi_feature_data_metadata_d["assets"] = {}
aoi_feature_d = {}
aoi_feature_d['input1'] = aoi_feature_data_metadata_d
aoi_ref_data_asset_path_d = {'output1':dataset_path+'/'+aoi_id+'/building_masks.nc'}
aoi_feature_asset_path_d = {'input1':dataset_path+'/'+aoi_id+'/images_masked.nc'}
print(new_tds_ctl_o.add_aoi_metadata(aoi_metadata_d=aoi_metadata_d,
aoi_feature_metadata_d=aoi_feature_d,
aoi_ref_data_metadata_d=aoi_reference_d,
aoi_feature_asset_path_d=aoi_feature_asset_path_d,
aoi_ref_data_asset_path_d=aoi_ref_data_asset_path_d))
# + [markdown] papermill={"duration": 0.050775, "end_time": "2021-08-16T08:46:19.948724", "exception": false, "start_time": "2021-08-16T08:46:19.897949", "status": "completed"} tags=[]
# #### stac_generated folder creation
# + [markdown] papermill={"duration": 0.052099, "end_time": "2021-08-16T08:46:20.047177", "exception": false, "start_time": "2021-08-16T08:46:19.995078", "status": "completed"} tags=[]
# Prior to this step, you will need to create a folder called 'biomass_stac_generated' in your environment and leave it empty
# + papermill={"duration": 152.430542, "end_time": "2021-08-16T08:48:52.533588", "exception": false, "start_time": "2021-08-16T08:46:20.103046", "status": "completed"} tags=[]
catalog_fn_w_path = './sp7_stac/TDS.json'
if os.path.exists('./sp7_stac'):
shutil.rmtree(catalog_fn_w_path.replace('/TDS.json',''))
# Write catalog to json
new_tds_ctl_o.write_TDS_STAC_Catalog(catalog_fn_w_path)
# + [markdown] papermill={"duration": 0.04568, "end_time": "2021-08-16T08:48:52.626081", "exception": false, "start_time": "2021-08-16T08:48:52.580401", "status": "completed"} tags=[]
# ##### Checking AIREO compiance level
# + papermill={"duration": 0.05908, "end_time": "2021-08-16T08:48:52.734215", "exception": false, "start_time": "2021-08-16T08:48:52.675135", "status": "completed"} tags=[]
new_tds_ctl_o = aireo_lib.core.tds_stac_io.DatasetSTACCatalog.from_TDSCatalog(catalog_fn_w_path)
new_tds_ctl_o.compute_compliance_level()
# + [markdown] papermill={"duration": 0.046834, "end_time": "2021-08-16T08:48:52.827759", "exception": false, "start_time": "2021-08-16T08:48:52.780925", "status": "completed"} tags=[]
# ##### Checking metadata completeness
# + papermill={"duration": 0.057673, "end_time": "2021-08-16T08:48:52.933737", "exception": false, "start_time": "2021-08-16T08:48:52.876064", "status": "completed"} tags=[]
new_tds_ctl_o.report_metadata_completeness()
# + [markdown] papermill={"duration": 0.060458, "end_time": "2021-08-16T08:48:53.040550", "exception": false, "start_time": "2021-08-16T08:48:52.980092", "status": "completed"} tags=[]
# #### Defining AOI class
# + papermill={"duration": 0.069431, "end_time": "2021-08-16T08:48:53.156828", "exception": false, "start_time": "2021-08-16T08:48:53.087397", "status": "completed"} tags=[]
class AOIDatasetSpaceNet:
"""
This class is to load and to store all data (input features/ reference data) for one area of interest. An area of interest is defined by its bounding box, its geometry, and its time interval. For each specific EO TDS the user needs to create a subclass of AOIDataset and implements its abstract methods.
"""
def __init__(self, AOI_STAC_collection, TDS_STAC_catalog):
self.AOI_STAC_collection = AOI_STAC_collection
self.TDS_STAC_catalog = TDS_STAC_catalog
self.stride = self.TDS_STAC_catalog.tds_ctl_root_info.tds_root_metadata_d['example_stride']
self.window_size = self.TDS_STAC_catalog.tds_ctl_root_info.tds_root_metadata_d['example_window_size']
for eo_feature in self.AOI_STAC_collection.aoi_all_field_metadata.features:
aoi_feature_asset_path_d = self.AOI_STAC_collection.aoi_all_field_metadata.features[eo_feature].data_asset_w_path
self.feature_var_name = 'features_'+eo_feature
self.feature_data = xr.open_dataarray(aoi_feature_asset_path_d)
for reference_data in self.AOI_STAC_collection.aoi_all_field_metadata.references:
aoi_ref_data_asset_path_d = self.AOI_STAC_collection.aoi_all_field_metadata.references[reference_data].data_asset_w_path
self.ref_var_name = 'references_'+reference_data
self.reference_data = xr.open_dataarray(aoi_ref_data_asset_path_d)
self.timesteps = self.feature_data['date'].values
self.data = self.feature_data.to_dataset(name=self.feature_var_name)
# Add second DataArray to existing dataset
self.data[self.ref_var_name] = self.reference_data
def __getitem__(self, index):
if index >= len(self):
sys.exit('index out of range')
# Return examples based on window size and stride metadata
sample_image = self.feature_data[0]
x1_ceiling = int((sample_image.shape[1]-self.window_size)/self.stride) +1
y1_ceiling = int((sample_image.shape[2]-self.window_size)/self.stride) +1
single_image_examples = x1_ceiling*y1_ceiling
timestep = int(index/single_image_examples)
image = self.feature_data[timestep]
image_index = index - timestep*single_image_examples
x1 = self.stride*(image_index%x1_ceiling)
y1 = self.stride*(int(image_index/x1_ceiling))
x2 = x1+self.window_size
y2 = y1+self.window_size
date = self.timesteps[timestep]
image = image[:,x1:x2,y1:y2]
building_mask = self.reference_data[timestep,x1:x2,y1:y2]
ds = self.data.isel(date=[timestep],band=[0,1,2,3],x=slice(x1,x2),y=slice(y1,y2)).squeeze()
return ds
# return the number of timesteps multiplied by number of examples in a single timestep
def __len__(self):
sample_image = self.feature_data[0]
x1_ceiling = int((sample_image.shape[1]-self.window_size)/self.stride) +1
y1_ceiling = int((sample_image.shape[2]-self.window_size)/self.stride) +1
single_image_examples = int(x1_ceiling)*int(y1_ceiling)
return len(self.timesteps)*single_image_examples
def get_length(self):
return len(self)
# + [markdown] papermill={"duration": 0.055276, "end_time": "2021-08-16T08:48:53.259491", "exception": false, "start_time": "2021-08-16T08:48:53.204215", "status": "completed"} tags=[]
# ## Dataset user
# + [markdown] papermill={"duration": 0.051176, "end_time": "2021-08-16T08:48:53.358825", "exception": false, "start_time": "2021-08-16T08:48:53.307649", "status": "completed"} tags=[]
# The user of the dataset can access most of what is offered by the dataset using just its STAC catalog. All he/she needs to do is create a dataset object by passing to it the path to the STAC catalog at the root level. The library automatically reads in all the metadata and loads the assets into the dataset object. Some of the functionalities that a dataset object offers through aireo_lib are:
#
# - Can access an example instance from the dataset which serves as an input-output pair for a Machine Learning algorithm.
#
# - Xarrays are used to store data and give examples.
#
# - Dataset can also return each AOI independently
#
# - Offer basic plotting functions for each variable in the dataset and AOI.
#
# - Some statistics can also be calculated at both the AOI level and whole dataset level.
#
# + [markdown] papermill={"duration": 0.048299, "end_time": "2021-08-16T08:48:53.453719", "exception": false, "start_time": "2021-08-16T08:48:53.405420", "status": "completed"} tags=[]
# ### Parsing TDS
# + papermill={"duration": 157.255008, "end_time": "2021-08-16T08:51:30.754927", "exception": false, "start_time": "2021-08-16T08:48:53.499919", "status": "completed"} tags=[]
from aireo_lib.core import EOTrainingDataset
sp7_tds_ctl_fn = Path(os.environ['EDC_PATH']+'/data/SpaceNet7/sp7_stac/TDS.json')
eo_tds_obj = EOTrainingDataset(sp7_tds_ctl_fn, AOIDatasetSpaceNet)
# + papermill={"duration": 0.097771, "end_time": "2021-08-16T08:51:30.899237", "exception": false, "start_time": "2021-08-16T08:51:30.801466", "status": "completed"} tags=[]
len(eo_tds_obj)
# + papermill={"duration": 0.096538, "end_time": "2021-08-16T08:51:31.043129", "exception": false, "start_time": "2021-08-16T08:51:30.946591", "status": "completed"} tags=[]
eo_tds_obj[4204]
# + papermill={"duration": 0.05616, "end_time": "2021-08-16T08:51:31.147461", "exception": false, "start_time": "2021-08-16T08:51:31.091301", "status": "completed"} tags=[]
help(eo_tds_obj.get_subset)
# + papermill={"duration": 0.07034, "end_time": "2021-08-16T08:51:31.266363", "exception": false, "start_time": "2021-08-16T08:51:31.196023", "status": "completed"} tags=[]
eo_tds_obj.get_subset([19,1121])
# + papermill={"duration": 0.059268, "end_time": "2021-08-16T08:51:31.373782", "exception": false, "start_time": "2021-08-16T08:51:31.314514", "status": "completed"} tags=[]
aoi_objs = eo_tds_obj.get_aoi_datasets()
len(aoi_objs[1])
# + [markdown] papermill={"duration": 0.049489, "end_time": "2021-08-16T08:51:31.476505", "exception": false, "start_time": "2021-08-16T08:51:31.427016", "status": "completed"} tags=[]
# ### Plotting functions in aireo_lib
# + papermill={"duration": 2.699753, "end_time": "2021-08-16T08:51:34.226114", "exception": false, "start_time": "2021-08-16T08:51:31.526361", "status": "completed"} tags=[]
from importlib import reload
from aireo_lib.plotting import EOTDSPlot as aireo_viz
reload(aireo_lib.plotting)
plot_d = aireo_viz.plot_example(EOTDS=eo_tds_obj,
ex_index=128,
field_names=['features_input1', 'references_output1'])
# + papermill={"duration": 36.001783, "end_time": "2021-08-16T08:52:10.278664", "exception": false, "start_time": "2021-08-16T08:51:34.276881", "status": "completed"} tags=[]
aoi_obj = eo_tds_obj.get_aoi_dataset(2)
# Basic plot of all the variables in an AOI, returns a dict of matplotlib figures
aoi_plots_d = aireo_viz.plot_aoi_dataset(aoi_obj)
aoi_plots_d
# + papermill={"duration": 0.739061, "end_time": "2021-08-16T08:52:11.098896", "exception": false, "start_time": "2021-08-16T08:52:10.359835", "status": "completed"} tags=[]
aireo_viz.map_aois(eo_tds_obj)
# + [markdown] papermill={"duration": 0.054692, "end_time": "2021-08-16T08:52:11.208813", "exception": false, "start_time": "2021-08-16T08:52:11.154121", "status": "completed"} tags=[]
# ### Statistics functions in aireo_lib
#
# + papermill={"duration": 0.093199, "end_time": "2021-08-16T08:52:11.355274", "exception": false, "start_time": "2021-08-16T08:52:11.262075", "status": "completed"} tags=[]
import aireo_lib.statistics
# + papermill={"duration": 33.18652, "end_time": "2021-08-16T08:52:44.592406", "exception": false, "start_time": "2021-08-16T08:52:11.405886", "status": "completed"} tags=[]
aireo_lib.statistics.EOTDSStatistics.reference_data_statistics(eo_tds_obj)
# + papermill={"duration": 0.059996, "end_time": "2021-08-16T08:52:44.707693", "exception": false, "start_time": "2021-08-16T08:52:44.647697", "status": "completed"} tags=[]
aireo_lib.statistics.EOTDSStatistics.metadata_statistics(eo_tds_obj)
|
notebooks/contributions/AIREO_pilot_dataset_-_SpaceNet7.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import os
gpus = len(tf.config.list_physical_devices('GPU'))
assert gpus > 0
# -
data_dir = '../data/dogs_vs_cats'
print(os.listdir(data_dir))
IMG_SIZE = 224
BATCH_SIZE = 64
# +
train_ds = tf.keras.preprocessing.image_dataset_from_directory(
data_dir + '/train',
validation_split=0.2,
subset="training",
seed=123,
image_size=(IMG_SIZE, IMG_SIZE),
batch_size=BATCH_SIZE)
valid_ds = tf.keras.preprocessing.image_dataset_from_directory(
data_dir + '/train',
validation_split=0.2,
subset="validation",
seed=123,
image_size=(IMG_SIZE, IMG_SIZE),
batch_size=BATCH_SIZE)
# -
class_names = train_ds.class_names
print(class_names)
# +
# def format_label(label):
# string_label = label_info.int2str(label)
# return string_label.split("-")[1]
plt.figure(figsize=(10, 10))
for images, labels in train_ds.take(1):
for i in range(9):
ax = plt.subplot(3, 3, i + 1)
plt.imshow(images[i].numpy().astype("uint8"))
plt.title(class_names[labels[i]])
plt.axis("off")
# -
for image_batch, labels_batch in train_ds:
print(image_batch.shape)
print(labels_batch.shape)
break
# +
from tensorflow.keras.applications import EfficientNetB0
from tensorflow.keras import layers
def build_model(num_classes):
inputs = layers.Input(shape=(IMG_SIZE, IMG_SIZE, 3))
x = inputs
model = EfficientNetB0(include_top=False, input_tensor=x, weights='imagenet')
model.trainable = False
x = layers.GlobalAveragePooling2D(name="avg_pool")(model.output)
x = layers.BatchNormalization()(x)
top_dropout_rate = 0.2
x = layers.Dropout(top_dropout_rate, name="top_dropout")(x)
outputs = layers.Dense(num_classes, activation="softmax", name="pred")(x)
model = tf.keras.Model(inputs, outputs, name="EfficientNet")
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-2)
model.compile(
optimizer=optimizer, loss="sparse_categorical_crossentropy", metrics=["accuracy"]
)
return model
# -
model = build_model(len(class_names))
model.summary()
epochs = 5
hist = model.fit(train_ds, epochs=epochs, validation_data=valid_ds, verbose=2)
# +
def plot_hist(hist):
plt.plot(hist.history["accuracy"])
plt.plot(hist.history["val_accuracy"])
plt.title("model accuracy")
plt.ylabel("accuracy")
plt.xlabel("epoch")
plt.legend(["train", "validation"], loc="upper left")
plt.show()
plot_hist(hist)
# +
def unfreeze_model(model):
# We unfreeze the top 20 layers while leaving BatchNorm layers frozen
for layer in model.layers[-20:]:
if not isinstance(layer, layers.BatchNormalization):
layer.trainable = True
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
model.compile(
optimizer=optimizer, loss="sparse_categorical_crossentropy", metrics=["accuracy"]
)
unfreeze_model(model)
# -
epochs = 5
hist = model.fit(train_ds, epochs=epochs, validation_data=valid_ds, verbose=2)
plot_hist(hist)
test_filenames = os.listdir(data_dir + '/test1')
test_df = pd.DataFrame({
'filename': test_filenames
})
nb_samples = test_df.shape[0]
print(nb_samples)
test_df.head()
# +
from tensorflow.keras.preprocessing.image import ImageDataGenerator
test_gen = ImageDataGenerator()
test_generator = test_gen.flow_from_dataframe(
test_df,
data_dir + '/test1',
x_col='filename',
y_col=None,
class_mode=None,
batch_size=BATCH_SIZE,
target_size=(IMG_SIZE, IMG_SIZE),
shuffle=False,
)
# -
predictions = model.predict(test_generator)
test_df['category'] = np.argmax(predictions, axis=-1)
test_df.head()
submission_df = test_df.copy()
submission_df['id'] = submission_df['filename'].str.split('.').str[0]
submission_df['label'] = submission_df['category']
submission_df.drop(['filename', 'category'], axis=1, inplace=True)
submission_df.to_csv('submission.csv', index=False)
|
dogs_vs_cats.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import time
from glob import glob
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from tqdm import tqdm
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
from torchvision.utils import make_grid
from torchvision import datasets, transforms
from torchvision.datasets import ImageFolder
# -
DATA_PATH = '/media/xiaolong/9bbdf31a-3238-4691-845c-7f9126769abe/Dataset/fruits-360'
files_training = glob(os.path.join(DATA_PATH,'Training', '*/*.jpg'))
files_testing = glob(os.path.join(DATA_PATH, 'Test', '*/*.jpg'))
num_images = len(files_training)
print('Number of images in Training file:', num_images)
print(len(files_testing))
# +
min_images = 1000
im_cnt = []
class_names = []
print('{:20s}'.format('class'), end='')
print('Count')
print('-' * 24)
for folder in os.listdir(os.path.join(DATA_PATH, 'Training')):
folder_num = len(os.listdir(os.path.join(DATA_PATH,'Training',folder)))
im_cnt.append(folder_num)
class_names.append(folder)
print('{:20s}'.format(folder), end=' ')
print(folder_num)
if (folder_num < min_images):
min_images = folder_num
folder_name = folder
num_classes = len(class_names)
print("\nMinumum imgages per category:", min_images, 'Category:', folder)
print('Average number of Images per Category: {:.0f}'.format(np.array(im_cnt).mean()))
print('Total number of classes: {}'.format(num_classes))
# -
tensor_transform = transforms.Compose([transforms.ToTensor()])
all_data = ImageFolder(os.path.join(DATA_PATH, 'Training'), tensor_transform)
data_loader = torch.utils.data.DataLoader(all_data, batch_size=512, shuffle=True)
# +
pop_mean = []
pop_std = []
for i, data in enumerate(data_loader, 0):
numpy_image = data[0].numpy()
batch_mean = np.mean(numpy_image, axis=(0,2,3))
batch_std = np.std(numpy_image, axis=(0,2,3))
pop_mean.append(batch_mean)
pop_std.append(batch_std)
pop_mean = np.array(pop_mean).mean(axis=0)
pop_std = np.array(pop_std).mean(axis=0)
# -
print(pop_mean)
print(pop_std)
np.random.seed(123)
shuffle = np.random.permutation(num_images)
print(shuffle, len(shuffle))
split_val = int(num_images * 0.2)
print('Total number of images:', num_images)
print('Number of valid images after split:',len(shuffle[:split_val]))
print('Number of train images after split:',len(shuffle[split_val:]))
# +
from torch.utils.data import Dataset
class FruitTrainDataset(Dataset):
def __init__(self, files, shuffle, split_val, class_names, transform=transforms.ToTensor()):
self.shuffle = shuffle
self.class_names = class_names
self.split_val = split_val
self.data = np.array([files[i] for i in shuffle[split_val:]])
self.transform=transform
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
img = Image.open(self.data[idx])
name = self.data[idx].split('/')[-2]
y = self.class_names.index(name)
img = self.transform(img)
return img, y
class FruitValidDataset(Dataset):
def __init__(self, files, shuffle, split_val, class_names, transform=transforms.ToTensor()):
self.shuffle = shuffle
self.class_names = class_names
self.split_val = split_val
self.data = np.array([files[i] for i in shuffle[:split_val]])
self.transform=transform
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
img = Image.open(self.data[idx])
name = self.data[idx].split('/')[-2]
y = self.class_names.index(name)
img = self.transform(img)
return img, y
class FruitTestDataset(Dataset):
def __init__(self, path, class_names, transform=transforms.ToTensor()):
self.class_names = class_names
self.data = np.array(glob(os.path.join(path, '*/*.jpg')))
self.transform=transform
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
img = Image.open(self.data[idx])
name = self.data[idx].split('/')[-2]
y = self.class_names.index(name)
img = self.transform(img)
return img, y
# +
data_transforms = {
'train': transforms.Compose([
transforms.RandomHorizontalFlip(),
transforms.RandomVerticalFlip(),
transforms.ToTensor(),
transforms.Normalize(pop_mean, pop_std) # These were the mean and standard deviations that we calculated earlier.
]),
'Test': transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(pop_mean, pop_std) # These were the mean and standard deviations that we calculated earlier.
]),
'valid': transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(pop_mean, pop_std) # These were the mean and standard deviations that we calculated earlier.
])
}
train_dataset = FruitTrainDataset(files_training, shuffle, split_val, class_names, data_transforms['train'])
valid_dataset = FruitValidDataset(files_training, shuffle, split_val, class_names, data_transforms['valid'])
test_dataset = FruitTestDataset(os.path.join(DATA_PATH, 'Test'), class_names, transform=data_transforms['Test'])
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=64, shuffle=True)
# +
dataloaders = {'train': train_loader,
'valid': valid_loader,
'Test': test_loader}
dataset_sizes = {
'train': len(train_dataset),
'valid': len(valid_dataset),
'Test': len(test_dataset)
}
dataset_sizes
# -
def imshow(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0))
inp = pop_std * inp + pop_mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.001)
# +
inputs, classes = next(iter(train_loader))
out = make_grid(inputs)
fruits = ['' for x in range(len(classes))]
for i in range(len(classes)):
fruits[i] = class_names[classes[i].item()]
imshow(out)
print(fruits)
# -
class Net(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.conv1 = nn.Conv2d(3, 16, kernel_size=5)
self.conv1_bn = nn.BatchNorm2d(16)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(16, 32, kernel_size=3)
self.conv2_bn = nn.BatchNorm2d(32)
self.conv3 = nn.Conv2d(32, 64, kernel_size=3)
self.conv3_bn = nn.BatchNorm2d(64)
self.fc1 = nn.Linear(64 * 10 * 10, 250)
self.fc2 = nn.Linear(250, num_classes)
def forward(self, x):
x = self.pool(F.relu(self.conv1_bn(self.conv1(x))))
x = self.pool(F.relu(self.conv2_bn(self.conv2(x))))
x = self.pool(F.relu(self.conv3_bn(self.conv3(x))))
x = x.view(-1, 64 * 10 * 10)
x = F.dropout(F.relu(self.fc1(x)), training=self.training, p=0.4)
x = self.fc2(x)
return F.log_softmax(x, dim=1)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device
from torchsummary import summary
model = Net(num_classes)
model.to(device)
summary(model, (3, 100, 100))
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), 0.01, momentum=0.9)
from torch.optim.lr_scheduler import *
scheduler=StepLR(optimizer,step_size=3)
def train(model,device, train_loader, epoch):
model.train()
for data in tqdm(train_loader):
x, y = data
x = x.to(device)
y = y.to(device)
optimizer.zero_grad()
y_hat = model(x)
loss = criterion(y_hat, y)
loss.backward()
optimizer.step()
print ('Train Epoch: {}\t Loss: {:.6f}'.format(epoch, loss.item()))
def valid(model, device, valid_loader):
model.eval()
valid_loss = 0
correct = 0
with torch.no_grad():
for data in tqdm(valid_loader):
x, y = data
x = x.to(device)
y = y.to(device)
optimizer.zero_grad()
y_hat = model(x)
valid_loss += criterion(y_hat, y).item() # sum up batch loss
pred = y_hat.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(y.view_as(pred)).sum().item()
valid_loss /= len(valid_loader.dataset)
print('\nValid set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
valid_loss, correct, len(valid_dataset),
100. * correct / len(valid_dataset)))
for epoch in range(1, 10):
train(model=model, device=device, train_loader=train_loader, epoch=epoch)
valid(model=model, device=device, valid_loader=valid_loader)
|
fruits-360/build_model_from_scrach.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # <NAME>
# https://www.investopedia.com/trading/heikin-ashi-better-candlestick/
# + outputHidden=false inputHidden=false
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
# fix_yahoo_finance is used to fetch data
import fix_yahoo_finance as yf
yf.pdr_override()
# + outputHidden=false inputHidden=false
# input
symbol = 'AAPL'
start = '2018-10-01'
end = '2019-01-01'
# Read data
df = yf.download(symbol,start,end)
# View Columns
df.head()
# + outputHidden=false inputHidden=false
def Heiken_Ashi(df):
df['HA_Close']=(df['Open']+ df['High']+ df['Low']+ df['Close'])/4
df['HA_Open']=(df['Open']+df['Close'])/2
for i in range(1, len(df)):
df['HA_Open'][i]=(df['HA_Open'][i-1]+df['HA_Close'][i-1])/2
df['HA_High']=df[['HA_Open','HA_Close','High']].max(axis=1)
df['HA_Low']=df[['HA_Open','HA_Close','Low']].min(axis=1)
return
Heiken_Ashi(df)
# + outputHidden=false inputHidden=false
df.head()
# + outputHidden=false inputHidden=false
HA = df[['HA_Open','HA_High','HA_Low','HA_Close', 'Volume']]
# + outputHidden=false inputHidden=false
HA.head()
# + outputHidden=false inputHidden=false
from matplotlib import dates as mdates
import datetime as dt
dfc = HA.reset_index()
dfc['Date'] = mdates.date2num(dfc['Date'].astype(dt.date))
dfc.head()
# + outputHidden=false inputHidden=false
from mpl_finance import candlestick_ohlc
fig = plt.figure(figsize=(14,10))
ax1 = plt.subplot(2, 1, 1)
candlestick_ohlc(ax1,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax1.xaxis_date()
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax1.grid(True, which='both')
ax1.minorticks_on()
ax1v = ax1.twinx()
dfc['VolumePositive'] = dfc['HA_Open'] < dfc['HA_Close']
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
ax1v.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
ax1v.axes.yaxis.set_ticklabels([])
ax1v.set_ylim(0, 3*df.Volume.max())
ax1.set_title('Stock '+ symbol +' Closing Price (Heiken Ashi)')
ax1.set_ylabel('Price')
ax2 = plt.subplot(2, 1, 2)
ax2.bar(dfc.index, dfc['Volume'], color=dfc.VolumePositive.map({True: 'g', False: 'r'}))
ax2.grid()
ax2.set_ylabel('Volume')
ax2.set_xlabel('Date')
# -
# ## Compare Heiken Ashi and Candlesticks
# + outputHidden=false inputHidden=false
from matplotlib import dates as mdates
import datetime as dt
cs = df.reset_index()
cs['Date'] = mdates.date2num(cs['Date'].astype(dt.date))
cs.head()
# + outputHidden=false inputHidden=false
cs = cs[['Date', 'Open', 'High', 'Low', 'Close', 'Volume']]
# + outputHidden=false inputHidden=false
fig = plt.figure(figsize=(14,10))
ax1 = plt.subplot(2, 1, 1)
candlestick_ohlc(ax1,cs.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax1.xaxis_date()
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax1.grid(True, which='both')
ax1.minorticks_on()
ax1v = ax1.twinx()
cs['VolumePositive'] = cs['Open'] < cs['Close']
colors = cs.VolumePositive.map({True: 'g', False: 'r'})
ax1v.bar(cs.Date, cs['Volume'], color=colors, alpha=0.4)
ax1v.axes.yaxis.set_ticklabels([])
ax1v.set_ylim(0, 3*cs.Volume.max())
ax1.set_title('Stock '+ symbol +' Closing Price (Candlestick)')
ax1.set_ylabel('Price')
ax2 = plt.subplot(2, 1, 2)
ax2.bar(cs.index, cs['Volume'], color=cs.VolumePositive.map({True: 'g', False: 'r'}))
ax2.grid()
ax2.set_ylabel('Volume')
ax2.set_xlabel('Date')
# + outputHidden=false inputHidden=false
fig = plt.figure(figsize=(30,14))
ax1 = plt.subplot(2, 2, 1)
candlestick_ohlc(ax1,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax1.xaxis_date()
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax1.grid(True, which='both')
ax1.minorticks_on()
ax1v = ax1.twinx()
dfc['VolumePositive'] = dfc['HA_Open'] < dfc['HA_Close']
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
ax1v.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
ax1v.axes.yaxis.set_ticklabels([])
ax1v.set_ylim(0, 3*df.Volume.max())
ax1.set_title('Stock '+ symbol +' Closing Price (Heiken Ashi)', fontweight="bold", fontsize=18)
ax1.set_ylabel('Price')
ax1.set_xlabel('Date')
ax2 = plt.subplot(2, 2, 2)
candlestick_ohlc(ax2,cs.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax2.xaxis_date()
ax2.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax2.grid(True, which='both')
ax2.minorticks_on()
ax2v = ax2.twinx()
cs['VolumePositive'] = cs['Open'] < cs['Close']
colors = cs.VolumePositive.map({True: 'g', False: 'r'})
ax2v.bar(cs.Date, cs['Volume'], color=colors, alpha=0.4)
ax2v.axes.yaxis.set_ticklabels([])
ax2v.set_ylim(0, 3*cs.Volume.max())
ax2.set_title('Stock '+ symbol +' Closing Price (Candlestick)', fontweight="bold", fontsize=18)
ax2.set_ylabel('Price')
ax2.set_xlabel('Date')
|
Python_Stock/Technical_Indicators/Heiken_Ashi.ipynb
|
// -*- coding: utf-8 -*-
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .js
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Javascript (Node.js)
// language: javascript
// name: javascript
// ---
// Axios is a promise-based HTTP client which is written in JavaScript to perform HTTP communications. It has one powerful feature called Interceptors. Axios interceptors allow you to run your code or modify the request and/or response before the request and/or response reaches their destination.
// ## Axios Interceptors
// Axios interceptors allow you to run your code or modify the request and/or response before the request and/or response is started.
// In simple words,
// - It allows you to write or execute a piece of your code before the request gets sent.
// - It allows you to write or execute a piece of your code before response reaches the calling end.
// Before we implement interceptors, I have created one LocalStorageService.js. It is one service which allows us to store our data to LocalStorage. Whenever we need LocalStorageService, we just simple Inject it and use it.
// LocalStorageService.js
const LocalStorageService = (function(){
var _service;
function _getService() {
if(!_service) {
_service = this;
return _service
}
return _service
}
function _setToken(tokenObj) {
localStorage.setItem('access_token', tokenObj.access_token);
localStorage.setItem('refresh_token', tokenObj.refresh_token);
}
function _getAccessToken() {
return localStorage.getItem('access_token');
}
function _getRefreshToken() {
return localStorage.getItem('refresh_token');
}
function _clearToken() {
localStorage.removeItem('access_token');
localStorage.removeItem('refresh_token');
}
return {
getService : _getService,
setToken : _setToken,
getAccessToken : _getAccessToken,
getRefreshToken : _getRefreshToken,
clearToken : _clearToken
}
})();
//export default LocalStorageService;
//import axios from "axios";
const axios=require('axios');
const localStorageService = LocalStorageService.getService();
// ## Add a request Interceptor
// I will try to modify each request header to set access token in the Authorization HTTP header.
// So we have two callbacks in request interceptor one with parameter config object and another one with the error object.
// Config is the object of AxiosRequestConfig which contains URL, base URL, headers request, body data, response type, timeout, etc.
// ### In short, it contains all of the information about your request.
// I am getting an Access token using localStorageService and modifying the Config objectâs headers. I am setting access token in the Authorization HTTP header and also setting Content-type as âapplication/jsonâ. After my these modifications, I am returning the config object.
// Add a request interceptor
axios.interceptors.request.use(
config => {
const token = localStorageService.getAccessToken();
if (token) {
config.headers['Authorization'] = 'Bearer ' + token;
}
// config.headers['Content-Type'] = 'application/json';
return config;
},
error => {
Promise.reject(error)
});
// ## Add a response Interceptor
// We also have two callbacks in response interceptors. One gets executed when we have a response from the Http call and another one gets executed when we have an error.
// We will simply return our response when there is no error. Weâll handle the error if there is any.
// As you can see in the following condition I am checking âIs Request has a 401 status code?â and âIs it failed again?â
// if (error.response.status === 401 && !originalRequest._retry) {...}
// If the request failed again then return Error object with Promise
// return Promise.reject(error);
// I have one endpoint(/v1/Auth/token) where If I provide a valid refresh token then It will return new Access token and Refresh token either It will fail with 401 status code.
// 1. I will put an Access token and Refresh token to LocalStorage using localStorageService.
// 2. Change Authorization header with the new Access token in originalRequest which is failed cause of not valid access token
// 3. return originalRequest object with Axios.
axios.interceptors.response.use(response => {
return response
},
function (error) {
const originalRequest = error.config;
if (error.response.status === 401 && !originalRequest._retry) {
originalRequest._retry = true;
return axios.post('/auth/token',
{
"refresh_token": localStorageService.getRefreshToken()
})
.then(res => {
if (res.status === 201) {
// 1) put token to LocalStorage
localStorageService.setToken(res.data);
// 2) Change Authorization header
axios.defaults.headers.common['Authorization'] = 'Bearer ' + localStorageService.getAccessToken();
// 3) return originalRequest object with Axios.
return axios(originalRequest);
}
})
}
// return Error object with Promise
return Promise.reject(error);
}
);
// If my refresh token is not valid then my endpoint(/v1/Auth/token) will come with 401 status code and If we do not handle it then it will go in an infinite loop.
// So above is my condition to stop going in an infinite loop, If the condition is true I just simple redirect to the Login page.
|
notebooks/Front End Web Security/Handling Access and Refresh Tokens using Axios Interceptors.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="NSv6p5YZ5PUh"
# #Step-1: Import the packages & Dataset
# + id="Y3pfNCRUA1U5" colab={"base_uri": "https://localhost:8080/"} outputId="dc799ae9-1efc-4771-9d46-50b2411b4b48"
# Let's import the packages required for the analysis
import pandas as pd # Pandas used for Data analysis, Data importing, exporting etc
import numpy as np # NumPy is used for mathematical operatons
import seaborn as sns
# !pip install inventorize3 # Install this package since it is not available in colab
import inventorize3 as inv # import the inventorize3
#Dataset link: kaggle datasets download -d carrie1/ecommerce-data
# + id="8AJi9FuTA1U5"
# import the data
raw_data= pd.read_csv("/content/drive/MyDrive/archive.zip",encoding='unicode_escape')
# Please change the path of the file while exeuting in your system
# encoding is used to ingonre the special charecters in the data
# + [markdown] id="DNhOxR-H_2kN"
# # Step2: Data Cleaning & Preprocessing
# + colab={"base_uri": "https://localhost:8080/", "height": 201} id="WkhxKvagA1VG" outputId="ed11579b-ac4e-45e7-f5c1-da4606fe6959"
# Will check how data looks like
raw_data.head()
# + colab={"base_uri": "https://localhost:8080/"} id="s-6yPyFYA1VH" outputId="86d8f064-12a1-47ae-f387-e5a3f9f586ef"
# Dimesnsion of the data
raw_data.shape
# + colab={"base_uri": "https://localhost:8080/"} id="IWTf56c4l1pE" outputId="ac9a5c49-f3da-48a2-d83b-a841c9baf71b"
# Let us check the types of the columns
raw_data.dtypes
# + colab={"base_uri": "https://localhost:8080/"} id="Wg7zO4CqA1VH" outputId="a7389b74-cc63-4f9e-8749-09cfae553aee"
# Minimum & Max date in dataset
raw_data['InvoiceDate']= pd.to_datetime(raw_data['InvoiceDate'])
print(raw_data['InvoiceDate'].min(), raw_data['InvoiceDate'].max())
# + id="ug6bE-BSA1VH"
# Lets clean the data
data= raw_data.drop_duplicates() # drop all the duplicate line items
data= data.dropna() # drop all null value rows
data= data[data['Quantity']>0] # Filter out rows where quantity sold is less than or equal to zero
# + colab={"base_uri": "https://localhost:8080/"} id="zQb8IAdgA1VH" outputId="8a6db7ea-58f4-4319-a048-fcf485e0157e"
# lets check dimension
data.shape
# + id="061uKJPQA1VI"
# Lets consider only required columns
data1= data[['StockCode','Description','Quantity','UnitPrice']]
# + colab={"base_uri": "https://localhost:8080/"} id="Ksmjh169A1VI" outputId="268bc68b-6093-47c9-891b-1aa05f7db875"
# Add new column as revenue
data1['revenue']=data1['Quantity']*data1['UnitPrice']
# + colab={"base_uri": "https://localhost:8080/", "height": 201} id="zG2U7YBkLNGC" outputId="fa8b5d14-c675-406c-e69b-e1b7b250858a"
data1.head()
# + id="WMBsir7VA1VJ"
# Lets summarize the data for SKU's ( Per SKU Total Quantity & Total Revenue)
data2= data1.groupby(['StockCode','Description']).agg(Volume=('Quantity',np.sum),Revenue=('revenue',np.sum)).reset_index()
# + colab={"base_uri": "https://localhost:8080/", "height": 201} id="kldUAudfLk-i" outputId="2aae6400-3a04-4860-e1b0-b898af8542b1"
data2.head()
# + [markdown] id="y3AMty3pMYBo"
# #Step-3: Inventory classifcation bassis Sales Volume
# + id="1lqx8p7iA1VJ"
# Lets classify the products to A B & C categories
data_abc= inv.ABC(data2[['StockCode','Volume']])
# + id="em9QIDlhA1VJ" colab={"base_uri": "https://localhost:8080/", "height": 201} outputId="d771ead8-6f0a-43a5-f5ad-058c37063752"
# Lets check the classification
data_abc.tail()
# + colab={"base_uri": "https://localhost:8080/"} id="aGV2Ki8LA1VK" outputId="03a6b3f3-ef25-4023-b19e-76fca14b2f1e"
# let us check the count of Categories
data_abc.Category.value_counts()
# + id="9D_h9DXjA1VK" colab={"base_uri": "https://localhost:8080/", "height": 140} outputId="c4187eee-b5a4-4521-9a24-a8c8936a3170"
# What is the Sales volume share of A, B & C class products
data_summary= data_abc.groupby('Category').agg(Count=('Category',np.count_nonzero),Volume_share=('Percentage',np.sum)).reset_index()
data_summary['Volume_share']= data_summary['Volume_share']*100
data_summary
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="r65us_nsA1VL" outputId="4235d735-dbc0-42f6-c01d-5527997a3514"
# Lets plot the graph for count of Categories A, B, C
sns.countplot(x='Category',data=data_abc, label=True )
# + id="oVm3Tb9BHbu5"
# Lets export the classified inventory data to the CSV
data_abc.to_csv('/content/drive/MyDrive/classified_data.csv')
# + id="lJ6P0mPnNqwy"
|
_notebooks/2020-02-25-Inventory-Classification-in-3-Steps.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import json
def read_json(path):
with open(path, "r") as stream:
foo = json.load(stream)
return foo
imdb_path = "../data/imdb_crop/meta-data.json"
wiki_path = "../data/wiki_crop/meta-data.json"
adience_path = "../data/Adience/meta-data-aligned.json"
imdb_stats = read_json(imdb_path)
wiki_stats = read_json(wiki_path)
adience_stats = read_json(adience_path)
# +
possible_ages = sorted(
list(set(list(imdb_stats["ages"].keys()) + list(wiki_stats["ages"].keys())))
)
ages = {}
for age in possible_ages:
try:
count_imdb = imdb_stats["ages"][age]
except Exception as e:
print("imdb", e)
count_imdb = 0
try:
count_wiki = wiki_stats["ages"][age]
except Exception as e:
print("wiki", e)
count_wiki = 0
ages[int(age)] = count_imdb + count_wiki
# -
sum(list(ages.values())) - (
sum(list(imdb_stats["ages"].values())) + sum(list(wiki_stats["ages"].values()))
)
ages = {age: ages[age] for age in sorted(list(ages.keys()))}
import matplotlib.pyplot as plt
# +
a_dictionary = ages
keys = a_dictionary.keys()
values = a_dictionary.values()
plt.figure(figsize=(10, 10))
plt.bar(keys, values)
plt.xlabel("age", fontsize=15)
plt.ylabel("count", fontsize=15)
plt.savefig("imdb-wiki-ages.pdf")
# -
ages = {
age: adience_stats["ages"][str(age)]
for age in sorted([float(foo) for foo in list(adience_stats["ages"].keys())])
}
# +
a_dictionary = ages
keys = a_dictionary.keys()
values = a_dictionary.values()
plt.figure(figsize=(10, 10))
plt.bar(keys, values)
plt.xlabel("age", fontsize=15)
plt.ylabel("count", fontsize=15)
plt.savefig("adience-ages.pdf")
|
notebooks/imdb-wiki-metadata.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Real World Tutorial 1: Translating Poetry
# =========================================
#
# First example
# -------------
#
# We build workflows by calling functions. The simplest example of this
# is the "diamond workflow":
# +
from noodles import run_single
from noodles.tutorial import (add, sub, mul)
u = add(5, 4)
v = sub(u, 3)
w = sub(u, 2)
x = mul(v, w)
answer = run_single(x)
print("The answer is {0}.".format(answer))
# -
# That looks like any other Python code! But this example is a bit silly.
# How do we leverage Noodles to earn an honest living? Here's a slightly less
# silly example (but only just!). We will build a small translation engine
# that translates sentences by submitting each word to an online dictionary
# over a Rest API. To do this we make loops ("For thou shalt make loops of
# blue"). First we build the program as you would do in Python, then we
# sprinkle some Noodles magic and make it work parallel! Furthermore, we'll
# see how to:
#
# * make more loops
# * cache results for reuse
# ## Making loops
#
# Thats all swell, but how do we make a parallel loop? Let's look at a `map` operation; in Python there are several ways to perform a function on all elements in an array. For this example, we will translate some words using the Glosbe service, which has a nice REST interface. We first build some functionality to use this interface.
# +
import urllib.request
import json
import re
class Translate:
"""Translate words and sentences in the worst possible way. The Glosbe dictionary
has a nice REST interface that we query for a phrase. We then take the first result.
To translate a sentence, we cut it in pieces, translate it and paste it back into
a Frankenstein monster."""
def __init__(self, src_lang='en', tgt_lang='fy'):
self.src = src_lang
self.tgt = tgt_lang
self.url = 'https://glosbe.com/gapi/translate?' \
'from={src}&dest={tgt}&' \
'phrase={{phrase}}&format=json'.format(
src=src_lang, tgt=tgt_lang)
def query_phrase(self, phrase):
with urllib.request.urlopen(self.url.format(phrase=phrase.lower())) as response:
translation = json.loads(response.read().decode())
return translation
def word(self, phrase):
translation = self.query_phrase(phrase)
#translation = {'tuc': [{'phrase': {'text': phrase.lower()[::-1]}}]}
if len(translation['tuc']) > 0 and 'phrase' in translation['tuc'][0]:
result = translation['tuc'][0]['phrase']['text']
if phrase[0].isupper():
return result.title()
else:
return result
else:
return "<" + phrase + ">"
def sentence(self, phrase):
words = re.sub("[^\w]", " ", phrase).split()
space = re.sub("[\w]+", "{}", phrase)
return space.format(*map(self.word, words))
# -
# We start with a list of strings that desparately need translation. And add a little
# routine to print it in a gracious manner.
# +
shakespeare = [
"If music be the food of love, play on,",
"Give me excess of it; that surfeiting,",
"The appetite may sicken, and so die."]
def print_poem(intro, poem):
print(intro)
for line in poem:
print(" ", line)
print()
print_poem("Original:", shakespeare)
# -
# Beginning Python programmers like to append things; this is not how you are
# supposed to program in Python; if you do, please go and read <NAME>'s *Writing Idiomatic Python*.
shakespeare_auf_deutsch = []
for line in shakespeare:
shakespeare_auf_deutsch.append(
Translate('en', 'de').sentence(line))
print_poem("Auf Deutsch:", shakespeare_auf_deutsch)
# Rather use a comprehension like so:
shakespeare_ynt_frysk = \
(Translate('en', 'fy').sentence(line) for line in shakespeare)
print_poem("Yn it Frysk:", shakespeare_ynt_frysk)
# Or use `map`:
shakespeare_pa_dansk = \
map(Translate('en', 'da').sentence, shakespeare)
print_poem("PÃ¥ Dansk:", shakespeare_pa_dansk)
# ## Noodlify!
# If your connection is a bit slow, you may find that the translations take a while to process. Wouldn't it be nice to do it in parallel? How much code would we have to change to get there in Noodles? Let's take the slow part of the program and add a `@schedule` decorator, and run! Sadly, it is not that simple. We can add `@schedule` to the `word` method. This means that it will return a promise.
#
# * Rule: *Functions that take promises need to be scheduled functions, or refer to a scheduled function at some level.*
#
# We could write
#
# return schedule(space.format)(*(self.word(w) for w in words))
#
# in the last line of the `sentence` method, but the string format method doesn't support wrapping. We rely on getting the signature of a function by calling `inspect.signature`. In some cases of build-in function this raises an exception. We may find a work around for these cases in future versions of Noodles. For the moment we'll have to define a little wrapper function.
# +
from noodles import schedule
@schedule
def format_string(s, *args, **kwargs):
return s.format(*args, **kwargs)
import urllib.request
import json
import re
class Translate:
"""Translate words and sentences in the worst possible way. The Glosbe dictionary
has a nice REST interface that we query for a phrase. We then take the first result.
To translate a sentence, we cut it in pieces, translate it and paste it back into
a Frankenstein monster."""
def __init__(self, src_lang='en', tgt_lang='fy'):
self.src = src_lang
self.tgt = tgt_lang
self.url = 'https://glosbe.com/gapi/translate?' \
'from={src}&dest={tgt}&' \
'phrase={{phrase}}&format=json'.format(
src=src_lang, tgt=tgt_lang)
def query_phrase(self, phrase):
with urllib.request.urlopen(self.url.format(phrase=phrase.lower())) as response:
translation = json.loads(response.read().decode())
return translation
@schedule
def word(self, phrase):
#translation = {'tuc': [{'phrase': {'text': phrase.lower()[::-1]}}]}
translation = self.query_phrase(phrase)
if len(translation['tuc']) > 0 and 'phrase' in translation['tuc'][0]:
result = translation['tuc'][0]['phrase']['text']
if phrase[0].isupper():
return result.title()
else:
return result
else:
return "<" + phrase + ">"
def sentence(self, phrase):
words = re.sub("[^\w]", " ", phrase).split()
space = re.sub("[\w]+", "{}", phrase)
return format_string(space, *map(self.word, words))
def __str__(self):
return "[{} -> {}]".format(self.src, self.tgt)
def __serialize__(self, pack):
return pack({'src_lang': self.src,
'tgt_lang': self.tgt})
@classmethod
def __construct__(cls, msg):
return cls(**msg)
# -
# Let's take stock of the mutations to the original. We've added a `@schedule` decorator to `word`, and changed a function call in `sentence`. Also we added the `__str__` method; this is only needed to plot the workflow graph. Let's run the new script.
# +
from noodles import gather, run_parallel
from noodles.tutorial import get_workflow_graph
shakespeare_en_esperanto = \
map(Translate('en', 'eo').sentence, shakespeare)
wf = gather(*shakespeare_en_esperanto)
workflow_graph = get_workflow_graph(wf._workflow)
result = run_parallel(wf, n_threads=8)
print_poem("Shakespeare en Esperanto:", result)
# -
# The last peculiar thing that you may notice, is the `gather` function. It collects the promises that `map` generates and creates a single new promise. The definition of `gather` is very simple:
#
# @schedule
# def gather(*lst):
# return lst
#
# The workflow graph of the Esperanto translator script looks like this:
workflow_graph.attr(size='10')
workflow_graph
# ## Dealing with repetition
# In the following example we have a line with some repetition.
# +
from noodles import (schedule, gather_all)
import re
@schedule
def word_size(word):
return len(word)
@schedule
def format_string(s, *args, **kwargs):
return s.format(*args, **kwargs)
def word_size_phrase(phrase):
words = re.sub("[^\w]", " ", phrase).split()
space = re.sub("[\w]+", "{}", phrase)
word_lengths = map(word_size, words)
return format_string(space, *word_lengths)
# +
from noodles.tutorial import display_workflows, run_and_print_log
display_workflows(
prefix='poetry',
sizes=word_size_phrase("Oote oote oote, Boe"))
# -
# Let's run the example workflows now, but focus on the actions taken, looking at the logs. The function ``run_and_print_log`` in the tutorial module runs our workflow with four parallel threads and caches results in a Sqlite3 database.
#
# To see how this program is being run, we monitor the job submission, retrieval and result storage. First, should you have run this tutorial before, remove the database file.
# remove the database if it already exists
# !rm -f tutorial.db
# Running the workflow, we can now see that at the second occurence of the word 'oote', the function call is attached to the first job that asked for the same result. The job `word_size('oote')` is run only once.
run_and_print_log(word_size_phrase("Oote oote oote, Boe"), highlight=range(4, 8))
# Now, running a similar workflow again, notice that previous results are retrieved from the database.
run_and_print_log(word_size_phrase("Oe oe oote oote oote"), highlight=range(5, 10))
# Although the result of every single job is retrieved we still had to go through the trouble of looking up the results of `word_size('Oote')`, `word_size('oote')`, and `word_size('Boe')` to find out that we wanted the result from the `format_string`. If you want to cache the result of an entire workflow, pack the workflow in another scheduled function!
# ## Versioning
# We may add a version string to a function. This version is taken into account when looking up results in the database.
# +
@schedule(version='1.0')
def word_size_phrase(phrase):
words = re.sub("[^\w]", " ", phrase).split()
space = re.sub("[\w]+", "{}", phrase)
word_lengths = map(word_size, words)
return format_string(space, *word_lengths)
run_and_print_log(
word_size_phrase("Kneu kneu kneu kneu ote kneu eur"),
highlight=[1, 17])
# -
# See how the first job is evaluated to return a new workflow. Note that if the version is omitted, it is automatically generated from the source of the function. For example, let's say we decided the function `word_size_phrase` should return a dictionary of all word sizes in stead of a string. Here we use the function called `lift` to transform a dictionary containing promises to a promise of a dictionary. `lift` can handle lists, dictionaries, sets, tuples and objects that are constructable from their `__dict__` member.
# +
from noodles import lift
def word_size_phrase(phrase):
words = re.sub("[^\w]", " ", phrase).split()
return lift({word: word_size(word) for word in words})
display_workflows(prefix='poetry', lift=word_size_phrase("Kneu kneu kneu kneu ote kneu eur"))
# -
run_and_print_log(word_size_phrase("Kneu kneu kneu kneu ote kneu eur"))
# **Be careful with versions!** Noodles will believe you upon your word! If we lie about the version, it will go ahead and retrieve the result belonging to the old function:
# +
@schedule(version='1.0')
def word_size_phrase(phrase):
words = re.sub("[^\w]", " ", phrase).split()
return lift({word: word_size(word) for word in words})
run_and_print_log(
word_size_phrase("Kneu kneu kneu kneu ote kneu eur"),
highlight=[1])
|
doc/source/poetry_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="QhKseqmTp42i"
# # Sparse PCA with Normalize
# + [markdown] id="qYaaIKnwp42k"
# This code template is for Sparse Principal Component Analysis(SparsePCA) along with Standard Scaler in python for dimensionality reduction technique and Data Rescaling using Normalize. It is used to decompose a multivariate dataset into a set of successive orthogonal components that explain a maximum amount of the variance, keeping only the most significant singular vectors to project the data to a lower dimensional space.
# + [markdown] id="RDr-Ht80p42l"
# ### Required Packages
# + id="TS_Vylujp42l"
import warnings
import itertools
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
from sklearn.preprocessing import LabelEncoder
from sklearn import preprocessing
from sklearn.decomposition import SparsePCA
from numpy.linalg import eigh
warnings.filterwarnings('ignore')
# + [markdown] id="J-ci_3myp42m"
# ### Initialization
#
# Filepath of CSV file
# + id="FtRICDAMp42m"
#filepath
file_path= ""
# + [markdown] id="hnoL8olHp42n"
# List of features which are required for model training .
# + id="CCsCXBc2p42o"
#x_values
features=[]
# + [markdown] id="7etfIseNp42o"
# Target feature for prediction.
# + id="Mz_HRahNp42p"
#y_value
target=''
# + [markdown] id="GCjQKr5lp42p"
# ### Data Fetching
#
# Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
#
# We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="7f2Gs0mJp42q" outputId="b462c734-adf4-4363-8b17-0d6309f99d77"
df=pd.read_csv(file_path)
df.head()
# + [markdown] id="BJN9EFiOp42q"
# ### Feature Selections
#
# It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
#
# We will assign all the required input features to X and target/outcome to Y.
# + id="OAk6wQ3yp42r"
X = df[features]
Y = df[target]
# + [markdown] id="U0FCmwVsp42r"
# ### Data Preprocessing
#
# Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
#
# + id="ha_2HZlZp42r"
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
# + colab={"base_uri": "https://localhost:8080/", "height": 240} id="oQ4uwJVTp42r" outputId="ad0ecec1-197b-4891-de8c-b36eebf72608"
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
# + [markdown] id="b102g7XVp42s"
# #### Correlation Map
#
# In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="QriWBYRap42s" outputId="33cde261-18e4-499d-8504-649595fd32cd"
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
# + [markdown] id="EdNMBeTBp42s"
# ### Data Rescaling
#
# For rescaling the data normalize function of Sklearn is used.
#
# Normalization is the process of scaling individual samples to have unit norm. This process can be useful if you plan to use a quadratic form such as the dot-product or any other kernel to quantify the similarity of any pair of samples.
#
# The function normalize provides a quick and easy way to scale input vectors individually to unit norm (vector length).
#
# <a href="https://scikit-learn.org/stable/modules/preprocessing.html">More about Normalize</a>
# + colab={"base_uri": "https://localhost:8080/", "height": 178} id="jUU3y7z0p42s" outputId="d9afd8ec-9d14-46ea-e53c-92af84c5010a"
X_Norm = preprocessing.normalize(X)
X=pd.DataFrame(X_Norm,columns=X.columns)
X.head(3)
# + [markdown] id="WKffbayip42t"
# ### Choosing the number of components
#
# A vital part of using Sparse PCA in practice is the ability to estimate how many components are needed to describe the data. This can be determined by looking at the cumulative explained variance ratio as a function of the number of components.
#
# This curve quantifies how much of the total, dimensional variance is contained within the first N components.
# + [markdown] id="8iFgDbLgp42t"
# ### Explained Variance
# + [markdown] id="YYaYX67Sp42t"
# Explained variance refers to the variance explained by each of the principal components (eigenvectors). It can be represented as a function of ratio of related eigenvalue and sum of eigenvalues of all eigenvectors.
# + [markdown] id="4px36pADp42t"
# The function below returns a list with the values of explained variance and also plots cumulative explained variance
# + id="xURRsYUwp42t"
def explained_variance_plot(X):
cov_matrix = np.cov(X, rowvar=False) #this function returns the co-variance matrix for the features
egnvalues, egnvectors = eigh(cov_matrix) #eigen decomposition is done here to fetch eigen-values and eigen-vectos
total_egnvalues = sum(egnvalues)
var_exp = [(i/total_egnvalues) for i in sorted(egnvalues, reverse=True)]
plt.plot(np.cumsum(var_exp))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
return var_exp
# + colab={"base_uri": "https://localhost:8080/", "height": 279} id="EaLuCmJip42u" outputId="f4d15f7a-4352-4fb2-c4b5-ef8b471f85fd"
var_exp=explained_variance_plot(X)
# + [markdown] id="Ou8nkR6xp42u"
# #### Scree plot
# The scree plot helps you to determine the optimal number of components. The eigenvalue of each component in the initial solution is plotted. Generally, you want to extract the components on the steep slope. The components on the shallow slope contribute little to the solution.
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="HhaPQpyVp42u" outputId="a324956a-6b55-4ffb-c7cf-0c100eab0551"
plt.plot(var_exp, 'ro-', linewidth=2)
plt.title('Scree Plot')
plt.xlabel('Principal Component')
plt.ylabel('Proportion of Variance Explained')
plt.show()
# + [markdown] id="D037_5Hsp42u"
# # Model
#
# Sparse PCA is used to decompose a multivariate dataset in a set of successive orthogonal components that explain a maximum amount of the variance. In scikit-learn, Sparse PCA finds the set of sparse components that can optimally reconstruct the data. The amount of sparseness is controllable by the coefficient of the L1 penalty, given by the parameter alpha.
#
# #### Tunning parameters reference :
# [API](https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.SparsePCA.html)
# + id="ceokHiPrp42u"
spca = SparsePCA(n_components=4)
spcaX = pd.DataFrame(data = spca.fit_transform(X))
# + [markdown] id="8RLKlxLmp42v"
# #### Output Dataframe
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="ieD7nR1xp42v" outputId="cbbb4c70-2ebe-4c20-e989-c33aaf1cb893"
finalDf = pd.concat([spcaX, Y], axis = 1)
finalDf.head()
# + [markdown] id="DFcUtcFxZiSM"
# #### Creator: <NAME> , Github: [Profile - Iamgrootsh7](https://github.com/iamgrootsh7)
|
Dimensionality Reduction/PCA/SparsePCA_Normalize.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Episode 18: Parsing with PyParsing
#
# Battered by Imperial Algebraic Formalisms, we now seek shelter in the caves of declarative code using the PyParsing library (https://github.com/pyparsing/pyparsing/).
#
# Having already struggled with parsing by hand, and the soon to be infamous SLY tooling, perhaps our rag-tag band will find some relief in recognizing the calculator language using expressions instead of imperative code or grammar definitions!
# !pip install pyparsing
# Once more `conda install pyparsing` would also work...
import nbimport
import Episode17
# ## Step 1: Lexical Analysis
import pyparsing
from pyparsing import Word, LineEnd, alphas, nums
pyparsing.ParserElement.setDefaultWhitespaceChars(' \t')
ID = pyparsing.Combine(pyparsing.Char(alphas) + pyparsing.ZeroOrMore(pyparsing.Char(pyparsing.alphanums)))
ID.parseString('ABC123 1234')
NUM = Word(nums)
NUM.parseString('1234')
atom = ID ^ NUM
atom.parseString('1234'), atom.parseString('abC33')
op = pyparsing.Char('+-')
op.parseString('+-+-'), op.parseString('- 42')
token_test = (LineEnd() ^ atom ^ op ^ '=')[...]
test_src = '1 + 2 - 3\nA = 42\n'
token_test.parseString(test_src)
token_test2 = (LineEnd() | atom | op | '=')[...]
token_test2.parseString(test_src)
# ## Step 2: Syntactic Analysis
expression = pyparsing.Forward()
expression <<= atom + pyparsing.Optional(op + expression)
assign = ID + '=' + expression
statement = (assign | expression) + LineEnd()
statements = statement[...]
# ## Step 3: There is NO Step 3...
#
# Or is there?
statements.parseString(test_src)
statements.parseString(test_src, parseAll=True)
statement2 = pyparsing.Group((assign ^ expression) + LineEnd())
statements2 = statement2[...]
statements2.setDebug()
statements2.parseString(test_src, parseAll=True)
# ### Cruft...
#
# ...from an abortive attempt to use `setDefaultWhitespaceChars()` after the fact.
statements.setDebug()
statements.parseString(test_src, parseAll=True)
statements.setDefaultWhitespaceChars = pyparsing.ParserElement.setDefaultWhitespaceChars
statements.setDefaultWhitespaceChars(' \t')
statements.parseString(test_src, parseAll=True)
pyparsing.ParserElement.setDefaultWhitespaceChars(' \t')
ID = Word(alphas)
atom = ID | Word(nums)
expression = pyparsing.Forward()
expression <<= atom + pyparsing.Optional(op + expression)
assign = ID + '=' + expression
statement = (assign | expression) + LineEnd()
statements = statement[...]
statements.parseString(test_src, parseAll=True)
|
ohop/Episode18.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.7 ('food')
# language: python
# name: python3
# ---
from food.tools import *
from food.paths import *
from food.psql import *
import numpy as np
import torch
from torch.nn import CosineSimilarity
import requests
from food.qdrant import *
cos = CosineSimilarity(dim=1, eps=1e-08)
import pandas as pd
collection_name = 'food'
table = 'foods'
foods = read_sql(table)
# foods = foods.set_index('id')
foods = foods.drop(columns = ['clip'])
foods['text'] = ('the food is ' +
foods['category'] + ' .'
' It has a little bit of ' +
foods['description'].str.split(',').apply(lambda l:' '.join(list(reversed(l))))
).str.lower().str.replace(':','')
foods.to_sql(schema = 'food',name = 'foods_prompted',if_exists = 'append',con=engine,index=False)
foods
pd.read_sql('select * from food.foods_prompted where clip is not null limit 5',engine)
engine.execute("truncate table food.indexed")
|
archive/foods_prompted_tosql.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + deletable=true editable=true
# ls \
# + deletable=true editable=true
#富å
¥çžå
³åº
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# + deletable=true editable=true
#读åæ°æ®
evaluation=pd.read_csv('submit.txt')
product_info=pd.read_csv('product_info.txt')
product_quantity=pd.read_csv('product_quantity.txt')
# + deletable=true editable=true
#æŸç€ºæ°æ®å°ºå¯ž
print(evaluation.shape)
print(product_info.shape)
print(product_quantity.shape)
# + deletable=true editable=true
#æŸç€ºproduct_infoæ°æ®æ ŒåŒ
evaluation.head()
# + deletable=true editable=true
#æŸç€ºproduct_infoæ°æ®æ ŒåŒ
product_info.head()
# + deletable=true editable=true
#æŸç€ºproduct_quantityæ°æ®æ ŒåŒ
product_quantity.head()
# + [markdown] deletable=true editable=true
# # 以äžæ°æ®å¯Œå
¥å®æ
# # ââââââââââââââââââââââââââââââââââââ
# + deletable=true editable=true
train_day=product_quantity.groupby(['product_id','product_date']).sum()['ciiquantity'].unstack()#.mean(axis=1)
train_day.head()
# + deletable=true editable=true
train_day.sum().plot(figsize=(15,6))
# + deletable=true editable=true
for i in range(2):
train_day[train_day.index==i+1].sum().plot(figsize=(15,6))
# + deletable=true editable=true
product_quantity['product_month']=product_quantity['product_date'].apply(lambda x: x[0:7])
train_month=product_quantity.groupby(['product_id','product_month']).sum()['ciiquantity'].unstack()
train_month.ix[:,0:12]
# + deletable=true editable=true
train_month.sum().plot(figsize=(15,6))
# + deletable=true editable=true
for i in range(1):
train_month[train_month.index==i+1].sum().plot(figsize=(15,6))
# + deletable=true editable=true
def produce2015(index):
product_id=evaluation['product_id'][index]
product_month=evaluation['product_month'][index]
try:
return train_month['2015-'+product_month[5:7]][product_id]*1.1
except Exception as err:
return 0
evaluation.ciiquantity_month=evaluation.index.map(produce2015)
def produce2014(index):
product_id=evaluation['product_id'][index]
product_month=evaluation['product_month'][index]
try:
return train_month['2014-'+product_month[5:7]][product_id]*1.2
except Exception as err:
return 0
evaluation[0:4000].ciiquantity_month=evaluation[0:4000].index.map(produce2014)
evaluation.to_csv('my_ansower.csv',index=False)
evaluation.head()
# + deletable=true editable=true
evaluation
# + [markdown] deletable=true editable=true
# # 以äžéè¿æ仜ç®åé¢æµ
# # ââââââââââââââââââââââââââââââââââââ
# + deletable=true editable=true
#train_day=product_quantity
train_day=pd.DataFrame({'product_id':product_quantity.product_id,'ciiquantity':product_quantity.ciiquantity,'product_date':product_quantity.product_date,})
train_day=train_day.sort_values(by =['product_id','product_date'])
train_day[0:10]
# + deletable=true editable=true
for i in range(2):
train_day[train_day['product_id']==i+1].plot(x='product_date', y='ciiquantity',figsize=(15,6))
# + deletable=true editable=true
Ttrain_day=train_day[0:5]
Ttrain_day
# + deletable=true editable=true
from datetime import datetime
pd.options.mode.chained_assignment = None #çŠæ¢SettingWithCopyWarning èŠå
Ttrain_day=train_day[0:5]
def getweek(product_date):
yyyy=int(product_date[0:4])
mm=int(product_date[5:7])
dd=int(product_date[8:10])
return datetime(yyyy,mm,dd).weekday()+1
def addweekday(table):
table['week']=table['product_date'].apply(getweek)
dummies = pd.get_dummies(Ttrain_day['week'], prefix='week', drop_first=False)
table = pd.concat([Ttrain_day, dummies], axis=1)
table = table.drop('week', axis=1)
return table
Ttrain_day=addweekday(Ttrain_day)
Ttrain_day
# + deletable=true editable=true
Ttrain_day=train_day[0:5]
Ttrain_day=addweekday(Ttrain_day)
def addfeature(table,features):
for feature in features:
table[feature]=table['product_id'].apply(lambda x: product_info[product_info.product_id==x][feature])
table=table.drop('product_id', 1)
return table
features=['eval','eval2','eval3','eval4','voters','maxstock']
Ttrain_day=addfeature(Ttrain_day,features)
Ttrain_day
# + deletable=true editable=true
Ttrain_day=train_day[0:5]
Ttrain_day=addweekday(Ttrain_day)
Ttrain_day=addfeature(Ttrain_day,features)
def Scalingfeature(table,features):
for feature in features:
mean, std = product_info[feature].mean(), product_info[feature].std()
table.loc[:, feature] = (table[feature] - mean)/std
return table
features=['eval','eval2','eval3','eval4','voters','maxstock']
Ttrain_day=Scalingfeature(Ttrain_day,features)
Ttrain_day
# + deletable=true editable=true
features=['eval','eval2','eval3','eval4','voters','maxstock']
Ttrain_day=train_day[0:500]
Ttrain_day=addweekday(Ttrain_day)
Ttrain_day=addfeature(Ttrain_day,features)
Ttrain_day=Scalingfeature(Ttrain_day,features)
Ttrain_day.head()
# + deletable=true editable=true
|
ctrip.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ããã§ãéåç·åœ¢ã·ã¹ãã åé¡ã«ãŸã€ããå°ãçºå±çãªè©±é¡ã玹ä»ããããããã®ã³ã©ã ã®å
容ã¯æ¬ç·šã®ç解ã«å¿
é ã§ã¯ãªãã®ã§ãé£ãããŠåãããªãå Žåã¯é©å®é£ã°ããŠæ¬¡ã®ç« ã«é²ãã§ã»ããã
#
# ## ã³ã©ã ïŒäœã©ã³ã¯è¡åã«å¯Ÿããé«éãªç¹ç°å€å解ãšãµã³ããªã³ã°ïŒéå-inspiredã¢ã«ãŽãªãºã ïŒ
# +
import sys
import time
from collections import Counter
import numpy as np
import sklearn
from sklearn.decomposition import TruncatedSVD
import matplotlib
import matplotlib.pyplot as plt
print("python: %s"%sys.version)
print("numpy: %s"%np.version.version)
print("matplotlib: %s"%matplotlib.__version__)
print("scikit-learn: %s"%sklearn.__version__)
# -
# ### æŠèŠ
# äœã©ã³ã¯ãªããã«ããã¢ã³ $H$ ã«ãããã€ããã¯ã¹ $e^{-iHt}$ ã¯éåèšç®æ©ã§å¹ççã«ã·ãã¥ã¬ãŒãããããšãã§ããã
# ããã«ããã¢ã³ã®å¹ççãªã·ãã¥ã¬ãŒãã¯éåäœçžæšå®ã¢ã«ãŽãªãºã ãHHLã¢ã«ãŽãªãºã ãè¡ãããã®åææ¡ä»¶ã§ãããããéåèšç®æ©ã¯äœã©ã³ã¯ãªè¡åã«å¯ŸããŠçš®ã
ã®é«éãªã¢ã«ãŽãªãºã ãèªç¶ã«å®è¡ã§ããã
# éåæšèŠã·ã¹ãã (Quantum recommendation system) ã¯ãã®ãããªå¿çšã®äžã€ã§ãéåèšç®æ©ã¯äœã©ã³ã¯ãªè¡åã®ä»»æã®è¡ãã¯ãã«ã«å¯ŸããTop-$k$ç¹ç°å€ç©ºéãžå°åœ±ãããã¯ãã«ããã®L2ãµã³ããªã³ã°ãè¡ãããšãããã®ã§ããããã®ãµã³ããªã³ã°æäœã¯ãäŸãã°WebãµãŒãã¹ã«ããã賌買履æŽã«åºã¥ããŠãŒã¶ãžã®ã¢ã€ãã æšèŠã®æäœã«å¯Ÿå¿ããŠããããéåèšç®æ©ã¯é«éãªæšèŠã·ã¹ãã ãšããŠæŽ»çšããããšãã§ããã
# ïŒæ³šïŒãŠãŒã¶ãžã®æšèŠã¯ãè¡ããŠãŒã¶ã»åãã¢ã€ãã ã»èŠçŽ ãæå®ãŠãŒã¶ãæå®ã¢ã€ãã ã奜ããã©ããããšããå奜è¡åïŒéåžžã¯äœã©ã³ã¯ã ãšä»®å®ãããïŒã«åºã¥ããŠè¡ãããïŒ
#
# ããããäžè¬ã«åé¡ã«äœã©ã³ã¯è¿äŒŒå¯èœæ§ãªã©ã®åŒ·ãè¿äŒŒãå ãã£ãå Žåãéåžžã®å€å
žèšç®æ©ã§ã®èšç®ãé«éã«ãªãç¹ã«æ³šæããªããã°ãªããªããè¿å¹Žãäžèšã®éåæšèŠã·ã¹ãã ãè¡ãæäœã¯ãçš®ã
ã®ããŒã¿æ§é ãã¢ã«ãŽãªãºã ãçšããããšã§éåžžã®èšç®æ©ã§ãå€é
åŒæéã§å®çŸå¯èœã ãšããããšãããã£ãã
# ãã®ã³ã©ã ã§ã¯ãäœã©ã³ã¯ãªè¡åã«å¯Ÿããæã¡åãç¹ç°å€å解ãããã³ç¹ç°å€ç©ºéã«å°åœ±ããããã¯ãã«ããã®ãµã³ããªã³ã°ããéåžžã®èšç®æ©ã ãã§ãè¡åã®ãµã€ãºã«å¯ŸããŠåŸæ¥ããææ°çã«é«éã«ãªããšããç¹ã«ã€ããŠè§£èª¬ããã
#
# ãã®äžé£ã®ç 究ã¯äž»ã«Ewin Tangã«ãã£ãŠè¡ããããã®ã§ãã[1][2][3]ã
# ãã®ç 究ã¯ä»¥äžã®åå¥ã®äž»èŠèŠçŽ ãã€ãªãããã®ã§ããã
#
# 1. ã»ã°ã¡ã³ãæš
# 2. 確ççæäœãçšããæã¡åãç¹ç°å€å解
# 3. æ£åŽãµã³ããªã³ã°
# 4. å
ç©ã®æšå®
#
# ãŸããåé¡èšå®ãæ瀺ãããã®ã®ã¡äžèšã®äžã€ã«ã€ããŠãããã解説ãããããçµã¿ããããŠäœã©ã³ã¯è¿äŒŒããç¹åŸŽéããã®ãµã³ããªã³ã°ãå¯èœã§ããããšãã³ãŒããå®è¡ããªããæŠèŠ³ããã
# ### åé¡èšå®
#
# äœã©ã³ã¯è¿äŒŒããã®ç¹ç°å€ç©ºéã®å°åœ±ãµã³ããªã³ã°ã¯ä»¥äžã®ãããªåé¡ãšããŠå®çŸ©ãããã
#
# åæç¶æ
ãšããŠã$2^n, 2^m$ã®å€§ããã®è¡å$A$ãèãããè¡å$A$ã¯å
šãŠã®èŠçŽ ã0ã§ããã
# ãã®æã以äžã®äºã€ã®æäœãã©ã³ãã ãªé åºã§$q$åèŠæ±ãããã
#
# 1. å€ã®æŽæ°
# $A$ã®$i$è¡$j$åã®èŠçŽ ã$v$ã«æŽæ°ããã
#
# 2. å°åœ±ãµã³ããªã³ã°
# $A$ã®$i$è¡ç®ã®æåã$A$ã®Top-$k$ç¹ç°å€ç©ºéã«å°åœ±ãããã¯ãã«$v$ãåŸãã
# ãã¯ãã«$v$ã®$j$çªç®ã®èŠçŽ ã$\frac{v_j^2}{\sum_l v_l^2}$ã®ç¢ºçã§åºåããã
# ãã ãã$k$ã¯é«ã
$O(n,m)$ã§ããã
#
# äžèšã«$\epsilon$ã®èª€å·®ã蚱容ããæãé«éã«åŠçãè¡ãããã
# èªæãªäžèšã®ã¢ã«ãŽãªãºã ã¯$2^n, 2^m$ã®é
åãã¹ããŒã¹åœ¢åŒã§ç¢ºä¿ããæ¿å
¥ã$O(n,m)$ã§è¡ããå°åœ±ãµã³ããªã³ã°ã¯ç¹ç°å€å解ãéããŠ${\rm poly}(2^n,2^m)$ã§è¡ãæ¹æ³ã§ããã
# ãããæ¹åãã${\rm poly}(q,n,m,\epsilon^{-1})$ã®èšç®éã§è¡ãããã
#
# éåèšç®æ©ãçšãããšãäžèšã®èšç®ã${\rm poly}(q,n,m,\epsilon^{-1})$ã§è¡ãããšãã§ããã
# ããã¯ãHHLã¢ã«ãŽãªãºã ã®äžéšãå€æŽããQuantum projectionãšãããããã³ã«ãå®æœããããšã§å¯èœãšãªãã
# è¿å¹Žã®Ewin Tangã«ããè«æã¯ããã®èšç®ãå€å
žèšç®æ©ã§ãåãã${\rm poly}(q,n,m,\epsilon^{-1})$ã§å¯èœã§ãããšãããã®ã§ããã
#
# ### åã®ã»ã°ã¡ã³ãæš
#
# éåžžãæã
ãããã°ã©ã ã§é
åã確ä¿ãããšãã¡ã¢ãªäžã®é£ç¶çãªã¢ãã¬ã¹ã«æå®ãã容éã®æ°åã確ä¿ãããã
# ã©ã³ãã ã¢ã¯ã»ã¹ã¡ã¢ãªã§ã¯èªã¿åºããšæžã蟌ã¿ã¯O(1)ã§å®äºã§ãããããéåžžã¯ãã®æ¹æ³ã§ç¢ºä¿ãããã
# äžæ¹ãé
åã«å¯ŸããèŠæ±ãèªã¿åºããšæžã蟌ã¿ã ãã§ã¯ãªãæ¿å
¥ãåé€ããµã³ããªã³ã°ãªã©ãããå Žåã
# ããããããŒã¿ã®ä¿æã®ä»æ¹ã¯å¿
ãããé«éãšã¯éããªãã
# åŸã£ãŠãããŒã¿ã«å¯ŸããèŠæ±ãåãªãèªã¿åºããšæžã蟌ã¿ã«éããªãå Žåããã®ç®çã«é©ããç¹æ®ãªããŒã¿ã®ä¿ææ¹æ³ãçšããããããããããŒã¿æ§é ãšåŒã¶ã
# åã«é¢ããã»ã°ã¡ã³ãæšã¯ããŒã¿æ§é ã®äžçš®ã§ãããããŒã¿ã®æŽæ°ãåºéåã®èšç®ããµã³ããªã³ã°ãé«éã«è¡ãããšãã§ããã
#
# 察象ãšãªãããŒã¿ã®å€§ããã$N=2^n$ãšãããïŒã®çŽ¯ä¹ã§ãªãå Žåã¯ã环ä¹ã«ãªããŸã§æ«å°Ÿã0ã§åãããã
# ãŸãã$2N$ã®é·ãã®é
åã確ä¿ãããæåã¯$2N$åã®èŠçŽ ã¯0ã§åãŸã£ãŠããã
# åã®ã»ã°ã¡ã³ãæšã§ã¯ä»¥äžã®4ã€ã®æäœãè¡ããã
#
# 1. å€ã®æŽæ°: $i$çªç®ã®ããŒã¿ã«å€$v$ãæžã蟌ãã
#
# 2. å€ã®ååŸ: $i$çªç®ã®ããŒã¿ãåãåºãã
#
# 3. ç·åã®ååŸ: å
šããŒã¿ã®åãåãåºãã
#
# 4. ãµã³ããªã³ã°: $i$çªç®ã®ããŒã¿ã$\frac{a_i}{\sum_j a_j}$ã®ç¢ºçã§åãåºãã
#
# äžèšãéåžžã®é
åã§æçŽã«è¡ããšä»¥äžã®ãããªã³ãŒãã«ãªãã
class VectorSampler():
def __init__(self,size):
self.size = size
self.array = np.zeros(size)
self.sum = 0
self.index_list = np.arange(self.size)
def update(self,index,value):
self.sum += value - self.array[index]
self.array[index] = value
def get_element(self,index):
return self.array[index]
def get_sum(self):
return self.sum
def sampling(self):
normalized_array = self.array / self.sum
result = np.random.choice(self.index_list, p = normalized_array)
return result
# ã©ã³ãã ãªèªã¿åºã/æžã蟌ã¿çãè¡ã£ãŠãäžèšã®é¢æ°ããã³ãããŒã¯ããŠã¿ããã
# +
n_list_vec = [10**2,10**3,10**4,10**5,10**6,10**7,10**8]
update_time_vec = []
get_element_time_vec = []
get_sum_time_vec = []
sampling_time_vec = []
for n in n_list_vec:
data_structure = VectorSampler(n)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
index = np.random.randint(n)
value = np.random.rand()
data_structure.update(index,value)
rep+=1
elapsed = (time.time()-start_time)/rep
update_time_vec.append(elapsed)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
index = np.random.randint(n)
data_structure.get_element(index)
rep+=1
elapsed = (time.time()-start_time)/rep
get_element_time_vec.append(elapsed)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
data_structure.get_sum()
rep+=1
elapsed = (time.time()-start_time)/rep
get_sum_time_vec.append(elapsed)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
data_structure.sampling()
rep+=1
elapsed = (time.time()-start_time)/rep
sampling_time_vec.append(elapsed)
plt.plot(n_list_vec, update_time_vec,label="update")
plt.plot(n_list_vec, get_element_time_vec,label="get_element")
plt.plot(n_list_vec, get_sum_time_vec,label="get_sum")
plt.plot(n_list_vec, sampling_time_vec,label="sampling")
plt.xlabel("size")
plt.ylabel("time (sec)")
plt.xscale("log")
plt.yscale("log")
plt.legend()
plt.show()
# -
# ä»ã®é¢æ°ã®æéãå®æ°ã§ã¹ã±ãŒã«ããäžãsamplingã ããç·åœ¢ã«æéãããã£ãŠããããšããããã
# ã»ã°ã¡ã³ãæšã§ã¯ïŒã€ã®åœä»€ã以äžã®ããã«å®è£
ãããïŒå³ã§ã€ã¡ãŒãžãããšããããããïŒäŸãã°ãã®[ããã°](https://proc-cpuinfo.fixstars.com/2017/07/optimize-segment-tree/)ãåç
§ïŒ
#
# 1. $i$çªç®ã®å€ã®æŽæ°
# $a_{2^n + i}=v$ãšæŽæ°ããäžã§ïŒ$N=2^n$ã§é
åã®é·ãã¯$2N$ïŒãããã«å
šãŠã®$j=1,2,\ldots$ã«ã€ã㊠$k = \lfloor \frac{2^n + i}{2^j} \rfloor, \: a_k \leftarrow a_k-a_i+v$ ãšããæŽæ°ãè¡ãã
# ãã®åŠçã¯$O(n)$ã§çµããã
#
# 2. $i$çªç®ã®å€ã®ååŸ
# $a_{2^n + i}$ãè¿ãã
# ãã®åŠçã¯$O(1)$ã§çµããã
#
# 3. ç·åã®ååŸ
# $a_0$ãè¿ãã
# ãã®åŠçã¯$O(1)$ã§çµããã
#
# 4. ãµã³ããªã³ã°
# $i=1$ãšããã$b=0$ã$\frac{a_i}{a_i + a_{i+1}}$ã$b=1$ã$\frac{a_{i+1}}{a_i+a_{i+1}}$ã®ç¢ºçã§åŸããããµã³ããªã³ã°ãè¡ãã
# $b=0$ãšãªã£ãå Žåã$i \leftarrow i+2^k$ãšæŽæ°ããã
# $b=1$ãšãªã£ãå Žåã$i \leftarrow i+2^{k+1}$ãšæŽæ°ããã
# $k \leftarrow k+1$ãšããã
# $i\geq 2^n$ãšãªã£ããçµäºãã$i-2^n$ãè¿ãã
# ãã®åŠçã¯$O(n)$ã§çµããã
#
# åŸã£ãŠãé·ã$n$ã®ãã¯ãã«ã«é¢ããäžèšåçš®ã®åœä»€ã$q$åäžããããå Žåããã®å®æœãé«ã
$O(q \log N)$ã§è¡ãããšãã§ããã
#
# å®è£
ã¯ä»¥äžã®ããã«ãªãã
class SegmentTree(object):
def __init__(self, size):
_size = 1
while _size<size:
_size*=2
self.size = _size*2
self.array = np.zeros(_size*2)
def update(self,index, value):
position = self.size//2 + index
difference = value - self.array[position]
while position>0:
self.array[position]+=difference
position //= 2
def get_element(self,index):
return self.array[self.size//2 + index]
def get_sum(self):
return self.array[1]
def sampling(self):
current_node = 1
while current_node<self.size//2:
left_children = self.array[current_node*2]
right_children = self.array[current_node*2+1]
left_weight = left_children / (left_children + right_children)
if np.random.rand() < left_weight:
current_node = current_node*2
else:
current_node = current_node*2+1
return current_node - self.size//2
# ã»ã°ã¡ã³ãæšããã³ãããŒã¯ããŠã¿ããã
# +
n_list_seg = [10**2,10**3,10**4,10**5,10**6,10**7,10**8]
update_time_seg = []
get_element_time_seg = []
get_sum_time_seg = []
sampling_time_seg = []
for n in n_list_seg:
data_structure = SegmentTree(n)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
index = np.random.randint(n)
value = np.random.rand()
data_structure.update(index,value)
rep+=1
elapsed = (time.time()-start_time)/rep
update_time_seg.append(elapsed)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
index = np.random.randint(n)
data_structure.get_element(index)
rep+=1
elapsed = (time.time()-start_time)/rep
get_element_time_seg.append(elapsed)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
data_structure.get_sum()
rep+=1
elapsed = (time.time()-start_time)/rep
get_sum_time_seg.append(elapsed)
start_time = time.time()
rep = 0
while time.time()-start_time<0.1:
data_structure.sampling()
rep+=1
elapsed = (time.time()-start_time)/rep
sampling_time_seg.append(elapsed)
plt.plot(n_list_seg, update_time_seg,label="update")
plt.plot(n_list_seg, get_element_time_seg,label="get_element")
plt.plot(n_list_seg, get_sum_time_seg,label="get_sum")
plt.plot(n_list_seg, sampling_time_seg,label="sampling")
plt.xlabel("size")
plt.ylabel("time (sec)")
plt.xscale("log")
plt.yscale("log")
plt.legend()
plt.show()
# -
# å
ã»ã©ã®çŽ æŽãªããŒã¿æ§é ã®æéãšæ¯èŒããŠã¿ããã
cmap = plt.get_cmap("tab10")
plt.plot(n_list_vec, update_time_vec,label="vector update",color=cmap(0),linestyle="--")
plt.plot(n_list_seg, update_time_seg,label="segtree update",color=cmap(0))
plt.plot(n_list_vec, get_element_time_vec,label="vector get_element",color=cmap(1),linestyle="--")
plt.plot(n_list_seg, get_element_time_seg,label="segtree get_element",color=cmap(1))
plt.plot(n_list_vec, get_sum_time_vec,label="vector get_sum",color=cmap(2),linestyle="--")
plt.plot(n_list_seg, get_sum_time_seg,label="segtree get_sum",color=cmap(2))
plt.plot(n_list_vec, sampling_time_vec,label="vector sampling",color=cmap(3),linestyle="--")
plt.plot(n_list_seg, sampling_time_seg,label="segtree sampling",color=cmap(3))
plt.xlabel("size")
plt.ylabel("time (sec)")
plt.xscale("log")
plt.yscale("log")
plt.legend()
plt.show()
# updateã®é¢æ°ã¯segtreeã®æ¹ãå€å°é
ããã®ã®ãsamplingã®ã³ã¹ããå§åçã«æžã£ãŠããããšããããã
#
# ãªããæ¬çš¿ã§ã¯ç»å Žããªãããåã®ã»ã°ã¡ã³ãæšã¯äžããããåºéã«é¢ããåãæ±ããæäœã$O(\log N)$ã§è¡ãããšãã§ãããããã¯éåžžã®ãã¯ãã«ã§ã¯ææªã§$O(N)$ãããã
# ãŸããã»ã°ã¡ã³ãæšã¯äºã€ã®èŠçŽ éã®æŒç®ãã¢ãã€ããããªãã¡ãŒãå
ãæã¡çµååãæãç«ãŠã°æ§ã
ãªå¯Ÿè±¡ã«å¯Ÿãé©çšããããšãã§ãããäŸãã°$f(a,b)=\min(a,b)$ãšããããšã§åºéæå°å€ãæ±ããã»ã°ã¡ã³ãæšãæ§ç¯ã§ããã
#
# ã»ã°ã¡ã³ãæšã¯ãã¯ãã«ã«å¯ŸããããŒã¿æ§é ã ããå€å°ã®æ¡åŒµãããããšã§è¡åãã»ã°ã¡ã³ãæšã®éåãšããŠè¡šãããšãã§ãããäžèšã®ãããª$m \times n$è¡åãèãããã
#
# - $i$è¡ç®ã®é·ã$n$ã®ãã¯ãã«$T_i$ãã»ã°ã¡ã³ãæš$S_i$ãšããŠä¿æããã
# - $i$è¡ç®ã®ãã¯ãã«ã®ç·åã$|T_i|$ã䞊ã¹ãé·ã$m$ã®ãã¯ãã«$C = \{|T_i|\}$ãã»ã°ã¡ã³ãæš$S'$ãšããŠä¿æããã
#
# äžèšã®ãããªããŒã¿æ§é ã¯ã以äžã®æäœãå
šãŠ${\rm poly}(\log n, \log m)$ã§è¡ãã
#
# 1. å€ã®æŽæ°: $(i,j)$èŠçŽ ã$v$ã«æŽæ°ããã
# 2. å€ã®ååŸ: $(i,j)$èŠçŽ ãååŸããã
# 3. è¡ãã«ã ã®ååŸ: äžããããè¡æ·»ãå$i$ã«å¯Ÿãã$i$è¡ç®ã®ãã«ã $|T_i|$ãååŸããã
# 4. è¡ãã¯ãã«ã®ãµã³ããªã³ã°: äžããããè¡æ·»ãå$i$ã«å¯Ÿããåæ·»ãå$j$ã$\frac{T_{ij}}{\sum_j{ T_{ij}}}$ã®ç¢ºçã§åŸãã
# 5. ç·åã®ååŸ: è¡åã®å
šèŠçŽ ã®å$\sum_{ij} T_{ij}$ãååŸããã
# 6. è¡ãã«ã ã®ãµã³ããªã³ã°: è¡æ·»ãå$i$ã$\frac{|T_i|}{\sum_i |T_i|}$ã®ç¢ºçã§åŸãã
#
# å®è£
ã¯ä»¥äžã®ããã«ãªãã
class SegmentTreeMatrix(object):
def __init__(self, height, width):
_height = 1
while _height<height:
_height*=2
_width = 1
while _width<width:
_width*=2
self.width = _width
self.height = _height
self.column_norm_segtree = SegmentTree(self.height)
self.row_segtree_list = []
for row_index in range(self.height):
self.row_segtree_list.append(SegmentTree(self.width))
def update(self,i,j, value):
self.row_segtree_list[i].update(j,value)
self.column_norm_segtree.update(i, self.row_segtree_list[i].get_sum())
def get_element(self,i,j):
return self.row_segtree_list[i].get_element(j)
def get_row_norm(self,i):
return self.row_segtree_list[i].get_sum()
def sampling_column_in_row(self,i):
return self.row_segtree_list[i].sampling()
def get_sum(self):
return self.column_norm_segtree.get_sum()
def sampling_row(self):
return self.column_norm_segtree.sampling()
# ### 確ççãªæã¡åãç¹ç°å€å解
#
# ç¹ç°å€å解ãšã¯ãæ£æ¹è¡åãšã¯éããªãè¡å$A$ã«ã€ããŠã$A=UDV^{\dagger}$ãšããå解ãè¡ãè¡åæäœã§ããã
# ãã®æã$U,V$ ã¯ãŠãã¿ãªè¡åã§ããã$D$ã¯å®å¯Ÿè§è¡åã§ããããŸãã$\dagger$ã¯ãšã«ããŒãå
±åœ¹(転眮ã®è€çŽ å
±åœ¹)ãè¡šãã
# $D$ã®å¯Ÿè§èŠçŽ ã$A$ã®ç¹ç°å€ãšåŒã¶ãè¡å$A$ã®å¹
ãšé«ãã®å°ããã»ãã®å€ã$n$ã§ããå Žåãç¹ç°å€ã¯$n$åãããå解ã®èšç®éã¯$O(n^3)$ã§ããã$U$ãš$V$ã®$i$çªç®ã®åãã¯ãã«ãã$A$ã®$i$çªç®ã®ç¹ç°å€ã®å·Šç¹ç°å€ãã¯ãã«ãå³ç¹ç°å€ãã¯ãã«ãšåŒã¶ã
#
# ç¹ç°å€å解ã¯numpyã«æšæºã§æèŒãããŠããã
n = 3
m = 4
A = np.random.rand(n,m)
U,singular_value_list,Vd = np.linalg.svd(A)
D = np.zeros( (n,m) )
np.fill_diagonal(D,singular_value_list)
print("A=\n{}\n".format(A))
print("U=\n{}\n".format(U))
print("D=\n{}\n".format(D))
print("V^d=\n{}\n".format(Vd))
print("UDV^d=\n{}\n".format(U@D@Vd))
# èšç®ã³ã¹ãã¯ä»¥äžã®ããã«ãªãã
# +
n_list = np.arange(100,1500,100)
elapsed_times_svd = []
for n in n_list:
matrix = np.random.rand(n,n)
start_time = time.time()
s,d,v = np.linalg.svd(matrix)
elapsed = time.time()-start_time
elapsed_times_svd.append(elapsed)
plt.plot(n_list,elapsed_times_svd)
plt.xlabel("size")
plt.ylabel("time (sec)")
plt.show()
# -
# æã¡åãç¹ç°å€å解ãšã¯ãå®æ°$k$ã«ã€ããŠãç¹ç°å€ã®éåã®ãã¡å€§ãããã®ãã$k$åã®ç¹ç°å€ãšç¹ç°å€ãã¯ãã«ãåãåºãæäœã§ããã
# å®æ°$k=n$ã§ããå Žåã¯éåžžã®ç¹ç°å€å解ãšäžèŽãããããéåžžã¯$k$ã$n$ããã¯ããã«å°ããå Žåããã°ãã°èããã
#
# æãçŽ æŽãªæã¡åãç¹ç°å€å解ã¯ãäžèšã®$O(n^2 k)$ã®ã¢ã«ãŽãªãºã ã§ããã
#
# 1. åèŠçŽ ã $N(0,1)$ ã®ç¬ç«ãªæ£èŠååžã«åŸã$n \times k$ã®è¡å$B$ãäœæãããèšç®ã³ã¹ãã¯$O(nk)$ã
# 2. $C = AB$ãèšç®ãããèšç®ã³ã¹ãã¯$O(n^2 k)$ã
# 3. $C$ã®è¡ãã¯ãã«ãçŽäº€åããè¡å$D$ãåŸããèšç®ã³ã¹ãã¯$O(n^2 k)$ã
# 4. $E=DA$ãèšç®ãããèšç®ã³ã¹ãã¯$O(n^2 k)$ã
# 5. $E$ãç¹ç°å€å解ãã$E=U'DV^{\dagger}$ãåŸããèšç®ã³ã¹ãã¯$O(n^2 k)$ã
# 6. $U = D^{\rm T}U'$ãèšç®ãããèšç®ã³ã¹ãã¯$O(n^2 k)$ã
#
# çµæãšããŠåŸãããU,D,Vã¯é«ã確çã§$A$ã®ç¹ç°å€å解ãšäžèŽããã
# ããããç¹ç°å€å解ã¯scikit-learnã«å®è£
ãããŠããã
# +
k = 10
n_list_tsvd = np.arange(100,5000,100)
elapsed_times_tsvd = []
for n in n_list_tsvd:
matrix = np.random.rand(n,n)
tsvd = TruncatedSVD(n_components=k)
start_time = time.time()
tsvd.fit(matrix)
elapsed = time.time()-start_time
elapsed_times_tsvd.append(elapsed)
plt.plot(n_list,elapsed_times_svd,label="SVD")
plt.plot(n_list_tsvd,elapsed_times_tsvd,label="truncated SVD")
plt.legend()
plt.xlabel("size")
plt.ylabel("time (sec)")
plt.show()
# -
# å
šãŠã®ç¹ç°å€ãåŸãFull SVDã«æ¯ã¹ãå§åçã«é«éã§ããããšããããã
#
# ããã«ãFKVã¢ã«ãŽãªãºã ãšãããã®ãååšããããã€ãã®æ¡ä»¶ãæºãããããšãTruncated SVDãããããªãé«éåãå¯èœã«ãªããæé ã¯ä»¥äžã®éãã§ããã
#
# 1. è¡å$A$ããè¡ãã«ã ãéã¿ãšããŠ$p$åã®è¡ããµã³ããªã³ã°ãã$B$ãäœæãããè¡æ·»ãå$i$ãè¡ãã«ã ã®éã¿ã¥ãã§åŸããµã³ããªã³ã°ã®ã³ã¹ãã$S_1(A)$ãšããŠãèšç®ã³ã¹ãã¯$O(S_1(A) p)$ã
# 2. è¡å$B$ãããã©ã³ãã ã«è¡ãéžã³ãéžã°ããè¡ããèŠçŽ ãéã¿ãšããŠåããµã³ããªã³ã°ãããæäœã$p$åè¡ã$C$ãäœæãããè¡ãã¯ãã«ããã®èŠçŽ ã®ãµã³ããªã³ã°ã³ã¹ãã$S_2(A)$ãšããŠãèšç®ã³ã¹ãã¯$O(S_2(A)p)$ã
# 3. $C$ãç¹ç°å€å解ããŠ$C=U'DV'^{\dagger}$ãåŸããèšç®ã³ã¹ãã¯$O(p^3)$ã
# 4. $V = B^T U' D^+$ãèšç®ãããèšç®ã³ã¹ãã¯$O(np^2)$ã
# 5. $V = V^{\dagger}D^+A$ãèšç®ãããèšç®ã³ã¹ãã¯$O(n^2 p)$ã
#
# $p$ã$\log n$ã®å€é
åŒãšããŠããçµæãšããŠåŸããã$U,D,V$ã¯é«ã確çã§$A$ã®ç¹ç°å€å解ã®è¯ãè¿äŒŒãšãªããæé 3. ãŸã§ã§åŸããããç©ãåãã°$U$ãåŸããã$(B,V',D)$ã®ã»ããã®ããšã$V$ã®ç°¡æœè¡šçŸãšåŒã¶ãåŸã£ãŠã$V$ã®ç°¡æœè¡šçŸãåŸãããã®èšç®éã¯${\rm poly}(S_1(A), S_2(A), \log n)$ã§ããã
#
# è¡åã®è¡šçŸãšããŠã»ã°ã¡ã³ãæšè¡åãçšãããšã$S_1(A), S_2(A)$ã¯ã©ã¡ãã${\rm poly}(\log n)$ã§ãããåŸã£ãŠãFKVã¢ã«ãŽãªãºã ã¯è¡åãã»ã°ã¡ã³ãæšã®åœ¢åŒã§ä¿æãããŠããå Žåã¯å¹ççã«è¡ãããšãã§ããã
#
# FKVã¢ã«ãŽãªãºã ã®å®è£
ã¯ä»¥äžã®ããã«ãªãã
def singular_value_decomposition_FKV(segtree_matrix, k, subsample_count):
# row sampling
## sampled row index list
row_index_list = []
## normalization factor for each sampled row index
row_norm_list = []
matrix_sum = segtree_matrix.get_sum()
for _ in range(subsample_count):
# choose row indices, where its weight is norm of row
row_index = segtree_matrix.sampling_row()
row_index_list.append(row_index)
row_chosen_prob = segtree_matrix.get_row_norm(row_index) / matrix_sum
row_norm_list.append(subsample_count * row_chosen_prob)
# column sampling
## sampled column index list
col_index_list = []
## normalization factor for each sampled column index
col_norm_list = []
## uniformly choose row index from sampled index for sampling column
col_sample_row = np.random.choice(row_index_list,size=subsample_count)
for row_index in col_sample_row:
# choose column indices, where its weight is element at chosen row/column.
col_index = segtree_matrix.sampling_column_in_row(row_index)
col_index_list.append(col_index)
col_chosen_prob = 0.
# compute sum of element in chosen column in row-sampled matrix
for row_index_for_ave in row_index_list:
col_chosen_prob += segtree_matrix.get_element(row_index_for_ave, col_index) / segtree_matrix.get_row_norm(row_index_for_ave)
col_norm_list.append(col_chosen_prob)
# pick normalized element from original matrix
subsample_matrix = np.zeros( (subsample_count, subsample_count) )
for sub_row in range(subsample_count):
for sub_col in range(subsample_count):
org_row = row_index_list[sub_row]
org_col = col_index_list[sub_col]
element = segtree_matrix.get_element(org_row, org_col)
norm_factor = row_norm_list[sub_row] * col_norm_list[sub_col]
subsample_matrix[sub_row,sub_col] = element / norm_factor
# perform SVD for sampled matrix
## since segtree matrix contains squared values as elements, take sqrt for svd
u,d,_ = np.linalg.svd(np.sqrt(subsample_matrix))
# take top-k matrix
d = d[:k]
u = u[:,:k]
return (row_index_list, d, u)
# äžã®ã³ãŒãã§ç€ºãããã«ãéåç¶æ
ã®ãã«ã³ã®èŠåãšåããããããéåç¶æ
ã®å€ã¯L2-normã§ãµã³ããªã³ã°ããããã»ã°ã¡ã³ãæšã¯åã«å¯ŸããŠå®çŸ©ããããããç·åãL2-normã®äºä¹ãšãªããããã»ã°ã¡ã³ãæšè¡åã®èŠçŽ ã«ã¯å奜è¡åã®èŠçŽ ã®äºæ
ã®å€ãæ ŒçŽããããåŸã£ãŠããµãè¡åãäœæããåŸã«ç¹ç°å€å解ããéã«ã¯ãå
šèŠçŽ ã®sqrtãåãå¿
èŠãããã
#
# ãã®ããšãèžãŸããæ©éFKV algorithmãè©ŠããŠã¿ããã
# +
n = m = 200
k = 10
p = 50
dense_matrix = np.zeros( (m,n) )
seg_tree = SegmentTreeMatrix(height = m, width = n)
for y in range(m):
for x in range(n):
val = np.random.rand()
seg_tree.update(y,x,val**2)
dense_matrix[y,x] = val
sampled_row_index_list, d, u = singular_value_decomposition_FKV(seg_tree, k, p)
print("FKV SVD\n",d)
_, d , _ = np.linalg.svd(dense_matrix)
print("Full SVD\n",d[:k])
tsvd = TruncatedSVD(n_components=k, n_iter=1)
tsvd.fit(dense_matrix)
print("Trunc SVD\n",tsvd.singular_values_)
# -
# ç°¡åãªæ€èšŒã®ããã$200 \times 200$ã®è¡åãã$50 \times 50$ã®ãµãè¡åãäœæããTop-10ã®ç¹ç°å€ã衚瀺ããŠãããæ倧ç¹ç°å€ã¯ãããããã£ãŠãããã®ã®ã以éã®ç¹ç°å€ã§ãããã²ã©ãããšãåããã
#
# 次ã«$200 \times 200$ã®è¡åãã$1000 \times 1000$ã®ãµãè¡å(ãšããã®ãåãããªãã)ãäœæããTop-10ã®ç¹ç°å€ã衚瀺ããŠãããåœããåã ãããã®èšç®èªäœã¯å
ã®è¡åãã倧ããªè¡åããµã³ããªã³ã°ããŠããããæçšã§ã¯ãªãæäœã§ããã
# +
n = m = 200
k = 10
p = 1000
dense_matrix = np.zeros( (m,n) )
seg_tree = SegmentTreeMatrix(height = m, width = n)
for y in range(m):
for x in range(n):
val = np.random.rand()
seg_tree.update(y,x,val**2)
dense_matrix[y,x] = val
sampled_row_index_list, d, u = singular_value_decomposition_FKV(seg_tree, k, p)
print("FKV SVD\n",d)
_, d , _ = np.linalg.svd(dense_matrix)
print("Full SVD\n",d[:k])
tsvd = TruncatedSVD(n_components=k, n_iter=1)
tsvd.fit(dense_matrix)
print("Trunc SVD\n",tsvd.singular_values_)
# -
# ãŸã ååãšã¯èšããªãããæ£ããå€ã«æŒžè¿çã«è¿ã¥ããŠããããšãåãããå®ã¯ãFKVã§å¿
èŠãšãªããµã³ããªã³ã°æ°$p$ã¯$10^7 \times \max \left(\frac{k^{5.5}}{\epsilon^{17}}, \frac{k^4}{\epsilon^{24}} \right)$ãšãããšãã§ããªãå€é
åŒã«ãªã£ãŠãããåŸã£ãŠã$k=10, \epsilon=0.1$ã«å¯ŸããŠçè«çãªç²ŸåºŠä¿èšŒãåŸãããã«ã¯ã$p=10^{29.5}$ãšãããšãã§ããªãæ°ã®ãµã€ãºã®è¡åãèŠè«ãããããããæäœãšããŠæå³ãæã€ã«ã¯$n,m > p$ã§ããå¿
èŠãããããã®è¡åã®ãµã€ãºã¯åèŠçŽ ã1bitã ãšããŠã$10^{59}$byteãšãªããè¡ã§ãã$10^{14}$PBãšããå°åºä¿æã§ããªããµã€ãºãšãªãããã¡ãããäžèšã®å€é
åŒãä¿æ°ã¯çè«çãªèšŒæã®ããã®ãªãŒããŒããããå«ããããå®éã«ã¯ããã»ã©å€§ããããªããšãããããã®çµæã¯åŸããããšæããããããããã«ãã**ç¡æ¡ä»¶ã«å€é
åŒã ããæçšã ãšèšããææ³ã§ã¯ãªã**ããšã¯å¿µé ã«å
¥ããŠããããã
# ### æ£åŽãµã³ããªã³ã°
# äžè¬ã«ç¢ºçååžã¯é«éã«ãµã³ããªã³ã°å¯èœãšã¯éããªãã
# äŸãã°$2^n$åã®èŠçŽ ã®ãã¡$i$çªç®ã®èŠçŽ ã$p_i$ã®ç¢ºçã§åŸãããååžã§ã$i$ã«å¯ŸããŠ$p_i$ãå¹ççã«èšç®ã§ãããšããŠãããµã³ããªã³ã°ã«ã¯äžè¬ã«ææ°çãªæéãèŠããã
#
# æ£åŽãµã³ããªã³ã°ã¯äžèšã®ãããªå¹ççã«ãµã³ããªã³ã°ã§ãããšã¯éããªãååž$P$ããããšãã
# $P$ãšé¡äŒŒããŠããå¹ççã«ãµã³ããªã³ã°å¯èœãªååž$Q$ãçšããŠ$P$ããã®ãµã³ããªã³ã°ãå¹ççã«è¡ãææ³ã§ããããã®æãæçµçã«ãµã³ããªã³ã°ãããååž$P$ãç®çååžãç®çååžã«è¿ããšæåŸ
ãããå¹ççã«ãµã³ããªã³ã°å¯èœãªååž$Q$ãææ¡ååžãšåŒã¶ã
#
# å
·äœçãªæç¶ãã¯ä»¥äžã§ããã
#
# 1. $M \geq \max_i \left( \frac{p_i}{q_i} \right)$ãšãªã$M$ãæ±ããã
# 2. $Q$ãããµã³ããªã³ã°ãè¡ãã$i$ãåŸãã
# 3. $t = \frac{p_i}{Mq_i}$ãèšç®ããã
# 4. [0,1]ã®åºéã®äžæ§ä¹±æ° $r$ ãåŸãã$r<t$ãªã$i$ãåºåãããããã§ãªããã°1.ããããçŽãã
#
# äžèšã®æç¶ãã§åŸããããµã³ããªã³ã°æäœã¯$Q$ããã®ãµã³ããªã³ã°æäœãšäžèŽããã
# äžèšã®æäœã«å¿
èŠãªèšç®éã¯$Q$ããã®ãµã³ããªã³ã°ã®æäœãå¹ççãªã$O(M)$ã®æåŸ
å€ã§çµäºããã
#
# å¹çã®æè¯ã®ã±ãŒã¹ã¯ç¢ºçååž$P$ãš$Q$ãäžèŽããŠããå Žåã§ããã$M=1$ãšãªãããã ããã®å Žåã¯ããããæ£åŽãµã³ããªã³ã°ãè¡ãæå³ããªããææªã®ã±ãŒã¹ã¯$p_i > 0$ã§ãã€$q_i=0$ãšãªããããª$i$ãååšããå Žåã§ããããã®å Žåã$M = \infty$ãšãªãæ£åŽãµã³ããªã³ã°ã¯ããããå®è¡ã§ããªãã
#
#
# äŸãšããŠãäžæ§ååžã«ååè¿ã$n$åã®ã·ã³ãã«ã«ã€ããŠã®ç¢ºçååž$\{p_i\}$ãèãããããã®ååžã¯å
šãŠã®indexã«ã€ããŠããããã$p_i < 1.1 (1/n)$ã§ããããšãä¿éãããŠãããšããã$\{p_i\}$ãããµã³ããªã³ã°ããã«ã¯ææªã§$O(n)$ãå¿
èŠã«ãªãããäžæ§ååžã¯$\log n$ã®é床ã§é«éã«ãµã³ããªã³ã°ããããšãã§ããã
#
# ãã®ããšãå©çšããŠã$\{p_i\}$ããã®ãµã³ããªã³ã°ãäžæ§ååžã®ãµã³ããªã³ã°ãçšããŠæ£åŽãµã³ããªã³ã°ããŠã¿ããã(以äžã®å®è£
ã§ã¯èŠæ Œåã®ããã«åŸ®åŠã«$M=1.1$ãããããŠãããããããã$M=1.1$ãšãªãã)
# +
def direct_sampling(prob_dist,index_list):
index = np.random.choice(index_list, p = prob_dist)
return index
def rejection_sampling(prob_dist, M, n):
sampling_count = 0
while True:
index = np.random.randint(n)
sampling_count+=1
thr = prob_dist[index]/(M /n)
r = np.random.rand()
if r<thr:
return index, sampling_count
# -
# ãŸããæ£åŽãµã³ããªã³ã°ãããµã³ããªã³ã°ãããååžãããªãªãžãã«ã®ååžãåçŸããŠããããæ€èšŒããŠã¿ããã
# +
n = 10
prob_dist = (1./n) * (1.+ (np.random.rand(n)-0.5)*0.1)
prob_dist /= np.sum(prob_dist)
M = np.max(prob_dist / (1./n))
index_list = np.arange(n)
sample_count = 10**6
sample_rejection = []
for _ in range(sample_count):
sample, _ =rejection_sampling(prob_dist, M, n)
sample_rejection.append(sample)
counter = Counter(sample_rejection)
rejection_probs = []
for i in index_list:
rejection_probs.append(counter[i]/sample_count)
plt.plot(index_list, prob_dist, label="target")
plt.plot(index_list, [1/n]*n, label="uniform",linestyle = "--")
plt.errorbar(index_list, rejection_probs, yerr=1./np.sqrt(sample_count), label="rejection")
plt.legend()
plt.xlabel("synbols")
plt.ylabel("probability")
plt.show()
# -
# 確ãã«æ£åŽãµã³ããªã³ã°ããåŸãããååžãšç®çååžãäžèŽããŠããããšããããã次ã«ãéåžžã®ãµã³ããªã³ã°ãšã®é床æ¯èŒã®ãã³ãããŒã¯ãåã£ãŠã¿ããã
# +
n_list = [10,10**2,10**3,10**4,10**5,10**6,10**7]
direct_sampling_time = []
rejection_sampling_time = []
sampling_count_list = []
M_list = []
for n in n_list:
prob_dist = (1./n) * (1.+ (np.random.rand(n)-0.5)*0.1)
prob_dist /= np.sum(prob_dist)
M = np.max(prob_dist / (1./n))
index_list = np.arange(n)
start_time = time.time()
rep = 0
while time.time()-start_time < 0.1:
index = direct_sampling(prob_dist,index_list)
rep+=1
elapsed_direct = (time.time()-start_time)/rep
start_time = time.time()
rep = 0
sampling_count_average = 0
while time.time()-start_time < 0.1:
index, sampling_count = rejection_sampling(prob_dist, M, n)
sampling_count_average += sampling_count
rep+=1
elapsed_rejection = (time.time()-start_time)/rep
sampling_count_average /= rep
direct_sampling_time.append(elapsed_direct)
rejection_sampling_time.append(elapsed_rejection)
M_list.append(M)
sampling_count_list.append(sampling_count_average)
plt.plot(n_list, direct_sampling_time,label="direct")
plt.plot(n_list, rejection_sampling_time,label="rejection")
plt.legend()
plt.xlabel("size")
plt.ylabel("time (sec)")
plt.xscale("log")
plt.yscale("log")
print("M={}".format(np.mean(M_list)))
print("average repetition in rejection sampling = {}".format(np.mean(sampling_count_list)))
# -
# è¯ããµã³ãã©ãŒãæã£ãŠããå ŽåãçŽæ¥çãªãµã³ããªã³ã°ã«æ¯ã¹ãæ£åŽãµã³ããªã³ã°ã¯å§åçã«é«éã§ããããšããããããŸãã$M$ã®å€ãšãµã³ããªã³ã°åæ°ãããããäžèŽããŠããã
#
# æ£åŽãµã³ããªã³ã°ãè¡ãã«ããã£ãŠæ³šæããªããã°ãªããªãç¹ãäºã€ããã
#
# äžã€ç®ã¯ãæ£åŽãµã³ããªã³ã°ãçšãã代ããã«ãç®çååžã®ç¢ºçãã¯ãã«ã«é¢ãã环ç©åãã»ã°ã¡ã³ãæšãªã©ã®ããŒã¿æ§é ãçšããããšã§ãé«éã«ãµã³ããªã³ã°ãå¯èœã«ãªããšããå¯èœæ§ãååšããç¹ã§ãããäŸãã°ã»ã°ã¡ã³ãæšãäžãããããã¯ãã«ã§åæåããæç¶ãã«ã¯$O(n)$ãå¿
èŠãšãªãããµã³ããªã³ã°ã®åæ°ã$s$ãšããå ŽåãããŒã¿æ§é ãçšããŠä»¥éã®ãµã³ããªã³ã°ãå¹çåããå Žåã®èšç®éã¯$O(n + s \log n)$ã§ãããæ£åŽãµã³ããªã³ã°ãè¡ã£ãå Žåã¯$O(M s \log n)$ã§ãããåŸã£ãŠãæ£åŽãµã³ããªã³ã°ãè¡ãå©ç¹ãããå Žåã¯
#
# $$
# \frac{n}{\log n} > (M-1) s
# $$
#
# ã®å Žåã§ãããåŸã£ãŠã$n$ã«å¯ŸããŠ$M$ã$s$ãéåžžã«å€§ãããããªå Žåã¯æåã«ããŒã¿æ§é ãäœã£ãŠããŸãã¹ãã§ãããäžæ¹ãå°ãã$M$ãä¿éãããŠãããµã³ããªã³ã°ã®åæ°ã倧ãããªãå Žåã¯æ£åŽãµã³ããªã³ã°ã¯æå¹ã§ããã
#
# äºã€ç®ã¯$M$ã®èšç®ã³ã¹ãã§ãããäžèšã§ã¯$M$ã®èšç®ã³ã¹ãã¯ç¡èŠãããããããªãããäžè¬ã«äºã€ã®ååžãäžãããããšãããã®éã®$M$ãã©ã®çšåºŠã«åãŸãããèšç®ããã®ã¯$O(n)$ã®æéãå¿
èŠãšãªãããã$n$ã®æéããããŠ$M$ãèšç®ãããšãããšãæ£åŽãµã³ããªã³ã°ã®ã³ã¹ãã¯$O(n + Ms\log n)$ãšãªãåžžã«ã»ã°ã¡ã³ãæšãçšããã¢ãããŒãããäœéã§ãããåŸã£ãŠãæ£åŽãµã³ããªã³ã°ãæå¹ã«çšããã«ã¯ãç®çååžã®æ¢ç¥ã®æ§è³ªããè¿ããšç¢ºä¿¡ãæãŠãææ¡ååžãæ§æã§ããªããã°ãªããªãã
# ### å
ç©ã®æšå®
#
# äºã€ã®é·ã$n$ã®ãã¯ãã«$x,y$ããããšãããã®äºã€ã®å
ç©$x\cdot y$ãæ±ããèšç®ã¯$O(n)$ãèŠãããäžæ¹ã$x,y$ã«ã€ããŠããã€ãè¿œå ã®æäœãèš±ãããŠãããšãããã誀差ã®ç¯å²å
ã§ããé«éã«å
ç©ã®å€ãæšå®ããããšãã§ããã
#
# ãµã³ããªã³ã°å¯èœã§ãã«ã ãæ¢ç¥ã®ãã¯ãã«$x$ãšãäžè¬ã®ãã¯ãã«$y$ãããå Žåã確ç$p_i = \frac{x_i^2}{\left|x\right|^2}$ã®ç¢ºçã§å€$z_i = \frac{y_i}{x_i}|x|^2$ããšãä¹±æ°$z$ãèããããã®æã$z$ã®æåŸ
å€ã¯$E[z] = \sum_i p_i z_i = \sum_i x_i y_i = x \cdot y$ãšãªãããŸãã$z$ã®åæ£ã¯$V[z]^2 \leq |x|^2|y|^2$ãšãªãã
# +
n = 100
x = np.random.rand(n)
x_square = x**2
x_square_norm = np.sum(x_square)
x_square_normalized = x_square / x_square_norm
y = np.random.rand(n)
inner_product = np.dot(x,y)
index_list = np.arange(n)
avg = 0
sampling_count_list = np.arange(0,1000000,1000)[1:]
estimation_list = []
for sample_index in range(max(sampling_count_list)):
index = np.random.choice(index_list, p = x_square_normalized)
z = y[index]/x[index] * x_square_norm
avg += z
if sample_index+1 in sampling_count_list:
estimation_list.append(avg/(sample_index+1))
plt.plot([min(sampling_count_list), max(sampling_count_list)], [inner_product, inner_product], label = "inner_product")
plt.plot(sampling_count_list, estimation_list,label = "estimation")
plt.legend()
plt.show()
# -
# ä¹±æ°ã®å¹³åãšåæ£ãäžãããããšããmedian-of-meansãšåŒã°ãããã¯ããã¯ã§ç²ŸåºŠãä¿èšŒã§ãããµã³ãã«æ°ãå°ãããšãã§ããã
# å
·äœçã«ã¯ã$\frac{9}{2\epsilon^2}$åã®ãµã³ãã«ã«ã€ããŠã®å¹³åå€$\langle x\cdot y \rangle$ãèšç®ããããã®æäœã$6 \log \delta^{-1}$åè¡ãããã®äžå€®å€ãåãåºãã
# ãã®ãšããåŸãããäžå€®å€ãæ£ããå€ã®$\epsilon |x||y|$以å
ã«ãã確çã¯$1-\delta$以äžã§ããããšãä¿èšŒã§ããã
#
# åŸã£ãŠã$1-\delta$以äžã®ä¿¡é ŒåºŠã§$\epsilon|x||y|$以äžã®èª€å·®ã§$x \cdot y$ãåŸãããã«å¿
èŠãªãµã³ããªã³ã°ã¯$O(\epsilon^{-2} \log \delta^{-1})$ã§ããã
# ### ãããŸã§ã®ãŸãšã
#
# ãããŸã§ã§çŽ¹ä»ããèŠçŽ ããã£ãããŸãšãããã
#
# #### ã»ã°ã¡ã³ãæšè¡å
#
# ã»ã°ã¡ã³ãæšè¡åã¯$m \times n$ã®å®æ°è¡å$T$ã«å¯Ÿãã以äžã®æäœãå
šãŠé«ã
$O(\log nm)$ã®æéã§å®çŸããã
#
# - $i$è¡$j$åèŠçŽ $T_{ij}$ã®èªã¿åºã
# - $i$è¡$j$åèŠçŽ $T_{ij}$ã®æŽæ°
# - $i$è¡ç®ã®L1ãã«ã $|T_i|$ã®èšç®
# - $i$è¡ç®ã«å¯Ÿããåæ·»ãå$j$ã$\frac{T_{ij}}{|T_i|}$ã®ç¢ºçã§åŸããµã³ããªã³ã°
# - è¡åèŠçŽ ã®ç·å$|T|:=\sum_i |T_i|$ã®èšç®
# - è¡æ·»ãå$i$ã$\frac{|T_i|}{\sum_i |T|}$ã®ç¢ºçã§åŸããµã³ããªã³ã°
#
# ãªããè¡å$S$ã«å¯ŸããŠL2-normã«å¯Ÿãããµã³ããªã³ã°ãè¡ãããå Žåã¯ã$T_{ij} = S_{ij}^2$ãšããŠããã°ãäžèšã®ãã«ã ã¯L2-normã®äºä¹ã«ãèŠçŽ ç·åã¯ãããããŠã¹ãã«ã ã®äºä¹ã«ããµã³ããªã³ã°ã¯äºä¹éã¿ã§ã®ãµã³ããªã³ã°ã«ãªãã
#
# #### FKVã¢ã«ãŽãªãºã
# ãã$n \times k$ã®è¡å$V$ãã$p = {\rm poly}(k)$ãæºããæŽæ°$p$ã«ã€ããŠã$n \times p$ã®ã»ã°ã¡ã³ãæšè¡å$A$ãš$p \times k$ã®å¯è¡å$B$ã®ç©ã§$V = AB$ãšè¡šããããšãã$(A,B)$ã$V$ã®ç°¡æœè¡šçŸãšåŒã¶ã
#
# FKVã¢ã«ãŽãªãºã ã¯ã$m \times n$ã®ã»ã°ã¡ã³ãæšè¡å$T$ãšæŽæ°$k$ãšå°ããå®æ°$\epsilon$ã«å¯Ÿãã$T$ã®Top-$k$å³ç¹ç°å€è¡å$V_k$ã
#
# $$
# |T - T^{\rm FKV}|^2_{\rm F} \leq |T - T^{\rm SVD}|^2_{\rm F} + \epsilon |T|^2_{\rm F}
# $$
#
# ãšè¿äŒŒããè¡å $T^{\rm FKV}$ ã®ç°¡æœè¡šçŸ$(A,B)$ã$k,\epsilon^{-1}$ã«å¯ŸããŠå€é
åŒæéã§äžããããã ãã$T^{\rm SVD}$ã¯SVDãçšããŠåŸããã$T$ã«å¯Ÿããæè¯ã®rank-$k$è¿äŒŒã§ããã$|T|_{\rm F}$ã¯è¡åã®ãããããŠã¹ãã«ã ã§ããã
#
# #### æ£åŽãµã³ããªã³ã°
#
# $n$åã®ã·ã³ãã«ã«å¯Ÿããç®çååž$\{p_i\}$ãšææ¡ååž$\{q_i\}$ãèããããããã®ååžã¯ä»¥äžãæºãããšããã
#
# - äžãããã$i$ã«å¯ŸããŠ$p_i$ãš$q_i$ã$O(\log n)$ã§èšç®å¯èœ
# - æ·»ãå$i$ã$q_i$ã®ç¢ºçã§åŸããµã³ããªã³ã°ã$O(\log n)$ã§å¯èœ
# - ä»»æã®$i$ã«ã€ããŠ$M \geq \frac{p_i}{q_i}$ãæºããæŽæ°$M$ãèšç®å¯èœ
#
# ãã®æãæ·»ãå$i$ã$p_i$ã®ç¢ºçã§åŸããµã³ããªã³ã°ã$O(M \log n)$ã§å¯èœã«ãªãã
#
# #### å
ç©ã®æšå®
# é·ã$n$ã®ãã¯ãã«$x,y$ã«ã€ããŠã以äžãæºãããããšããã
#
# - äžããããæ·»ãå$i$ã«ã€ããŠã$x_i,y_i$ãå¹ççã«èšç®ã§ããã
# - ãã«ã $|x|$ãå¹ççã«èšç®ã§ããã
# - æ·»ãå$i$ã$\frac{x_i}{|x|}$ã®ç¢ºçã§åŸããµã³ããªã³ã°ãå¹ççã«è¡ããã
#
# ãã®æã$x\cdot y$ã®å€ã$1-\delta$以äžã®ç¢ºçã§$\epsilon |x||y|$以å
ã®èª€å·®ã§æ±ããèšç®ã${\rm poly}(\epsilon^{-1},\log \delta^{-1})$ã§è¡ãããšãã§ããã
# ### äœã©ã³ã¯è¡åãçšããé«éãªæšèŠ
#
# äžèšãŸã§ã®ãã¯ããã¯ãåãã£ãŠããã°ãåŸã¯çµã¿åãããã ãã§ãããEwin Tangã«ããè«æã®æ®ã©ã¯ãäžèšãçµã¿åãããæã«èŠè«ãããæ¡ä»¶ãæºããããããšã®èšŒæãšã誀差ãèšç®éã®è§£æã§ããã
# 誀差ã®è©äŸ¡ãè¡ããšèšäºãéåžžã«é·ããªããããããã§ã¯è¡åã§ããã°ãããããŠã¹ãã«ã ã®å·®ãã確çååžã§ããã°total variational distanceã®å·®ã$\epsilon$ã®æ¯çã®ãšã©ãŒã§æãããããã€èšç®æéã¯${\rm poly}(\epsilon)$ã«æãããããšããçµæã ãè¿°ã¹ãŠããã
#
# <NAME>angã®è«æã¯çŸæç¹(2019幎3æ)ã§3æ¬[1][2][3]ãããªããããã®èšäºã§ã¯æåã®äºã€ã玹ä»ããããšãã£ãŠããäºæ¬ç®ã®è«æã®çµæã¯äžæ¬ç®ã®è«æã®äžéçµæãšããŠåŸããããã®ãªã®ã§ãå®è³ªäžæ¬ç®ã®çŽ¹ä»ã§ããã
#
# #### äœã©ã³ã¯è¡åã®äž»æååæ
#
# Ewin Tangã®ã¢ã«ãŽãªãºã ã¯å
šäœã®ã¢ã«ãŽãªãºã ã®ååéšåãšããŠ$i$è¡ãã¯ãã«ã®äž»æååæãè¡ãããŸããäž»æååæãšã¯ä»¥äžã®ãããªæç¶ãã§ããã
#
# è¡å$A$ã«å¯ŸããŠç¹ç°å€å解$A = U_k D_k V_k^{\dagger}$ãåŸããããšãã$A$ã®$i$è¡ç®ãã¯ãã«ã®Top-$k$ç¹ç°å€ç©ºéãžæ¬¡å
ãæžããããã¯ãã«$v = A_i V_k$ã®èŠçŽ ã$A_i$ã®Top-$k$äž»æåãšåŒã¶ããã®$k$äž»æåã確ç$1-\delta$以äžã§$\epsilon$以å
ã®èª€å·®ã§æ±ããæäœã${\rm poly}(\log nm, \epsilon^{-1}, \log \delta^{-1} )$ã§è¡ãããã
#
# è¡å$A$ã¯ã»ã°ã¡ã³ãè¡åãçšããè¡åã«æ ŒçŽããããšã§ãFKVã¢ã«ãŽãªãºã ãå®æœã§ãããFKVã¢ã«ãŽãªãºã ãå®æœãããšã$V=A_p^{\rm T}UD^+$ãšãªãç°¡æœè¡šçŸ$(A_p^{\rm T},UD^+)$ãå¹ççã«åŸãããšãã§ããããã®æã$A_p$ã¯$p$åã®è¡ã$A$ãããµã³ããªã³ã°ãããã»ã°ã¡ã³ãæšè¡åè¡šçŸãæã€ãç°¡æœè¡šçŸã®$U,D^+$ã«ã€ããŠãTop-$k$åã®ç¹ç°å€ãšç¹ç°å€ãã¯ãã«ã®ã¿ãåãåºããè¡åããããã$U_k, D_k^+$ãšããŠãæã
ãããã¹ãããšã¯äž»æåãã¯ãã«
#
# $$
# v = A_i V_k =A_i A_p^{\rm T} U_k D_k^+
# $$
#
# ãèšç®ããããšã§ãããäž»æåã®èŠçŽ æ°ã¯$k$åãªã®ã§ã$j$çªç®ã®äž»æå
#
# $$
# v_j = A_i \cdot (A_p^{\rm T} V_k D_k^+)_j
# $$
#
# ãæ±ããæäœã$k$åç¹°ãè¿ãã°ããããã®ãšãã$A_i$ã¯ã»ã°ã¡ã³ãæšã§ããã$(A_p^{\rm T} V_k D_k^+)_{kj}$ã¯${\rm poly}(k)$ã§èšç®å¯èœã§ãããåŸã£ãŠãå
ç©ã®æšå®ãè¡ãæ¡ä»¶ãæºãããŠããã$V_k$ã®åãã¯ãã«ã¯ãŠãã¿ãªè¡åã®åãè¿äŒŒãããã®ã§ããããããã«ã ã¯$O(1)$ã§ããããããã£ãŠã$v_i$ã®èª€å·®ã¯$\epsilon |A_i|$ã§ããã
# #### äœã©ã³ã¯è¡åã®ç¹ç°å€ç©ºéãžã®å°åœ±
# è¡å$A$ã®å³ç¹ç°å€è¡åã®Top-$k$ç¹ç°å€ã«çžåœããè¡ãåãåºãããã®ã$V_k$ãšãããè¡å$A$ã®ããè¡$A_i$ãTop-$k$ç¹ç°å€ç©ºéãžå°åœ±ãããšã¯ã
#
# $$
# A_i' = A_i V_k V_k^{\dagger}
# $$
#
# ãšããèšç®ãè¡ãããšãšçãããæã
ã®ç®çã¯äžããããæ·»ãå$i$ã«ã€ããŠãäžèšã®ããã«æ±ãŸã$A_i'$ãããæåã®L2-normã®éã¿ã§ãµã³ããªã³ã°ãè¡ãããšã§ãããäžã€åã®ç¯ã§$A_i V_k$ã¯åŸãããŠãããããæã
ãããã¹ãããšã¯
#
# $$
# A_i' = v V_k^{\dagger} = v D_k^{+} U_k ^{\dagger} A_p
# $$
#
# ãããµã³ããªã³ã°ããããšã§ããããããæ£åŽãµã³ããªã³ã°ãçšããŠè¡ãã
# èšå·ãç°¡ç¥åããããã$B :=D_k^{+} U_k ^{\dagger}$ã$w = (A_i')^{\rm T}$ãšå®çŸ©ãããšã以äžã®ããã«ãªãã
#
# $$
# w = A_p^{\rm T} B v^{\rm T}
# $$
#
# ãŸãã$A_p^{\rm T} B$ã®ä»»æã®åãã¯ãã«ã¯ãµã³ããªã³ã°å¯èœã§ããããšã瀺ãã$A_p^{\rm T}B$ã®$j$è¡ç®ã¯$B$ã®$j$åç®ã$B^{(j)}$ãšããŠã$A_p^{\rm T} B^{(j)}$ã§ãããåŸã£ãŠãç®çååžã¯
#
# $$
# p_i = \frac{|(A_p^{\rm T})_i B^{(j)}|^2}{|A_p^{\rm T} B^{(j)}|^2}
# $$
#
# ã§ãããããã«å¯Ÿãã
#
# $$
# q_i = \sum_{l=1}^p \frac{|(A_p)_l|^2 (B^{(j)}_l)^2}{\sum_{m=1}^p |(A_p)_m|^2 (B^{(j)}_m)^2} \frac{|(A_p)_{jl}|^2}{|(A_p)_l|^2}
# $$
#
# ãšããææ¡ååžãèãããšãããã¯å¹ççã«ãµã³ããªã³ã°å¯èœã§ããããã€ã³ãŒã·ãŒã·ã¥ã¯ã«ãã®äžçåŒãš$V'$ã®åã¯$V'$ãçé·è¡åã§ããããšããåãã«ã ã1ã§ããããšãçšãããšã$M$ã$k$ã®å€é
åŒã§æããããããšã瀺ãããåŸã£ãŠã$A_p^{\rm T} B$ã®ä»»æã®åãã¯ãã«ã¯ãµã³ããªã³ã°å¯èœã§ããã
#
# æåŸã«$A_p^{\rm T}B v^{\rm T}$ã¯å¹ççã«ãµã³ããªã³ã°å¯èœã§ããããšã瀺ãã$C=A_p^{\rm T}B$ãšçœ®ããšåç¯ãšåã圢åŒã§
#
# $$
# q_i = \sum_{l=1}^p \frac{|C^{(l)}|^2 v_l^2}{\sum_{m=1}^p |C^{(m)}|^2 v_m^2} \frac{|C_{il}|^2}{|C^{(l)}|^2}
# $$
#
# ãææ¡ååžãšããŠçšããããã®ææ¡ååžã®ç©ã®å·Šã¯ã»ã°ã¡ã³ãæšã®æ§è³ªãçšããŠãµã³ããªã³ã°å¯èœã§ãããå³ã¯çŽåã®æ£åŽãµã³ããªã³ã°ã§å¯èœã§ããããã ããå·Šéšã¯ç¹å®ã®$i$ã«ã€ããŠèšç®ããããšãé£ãããããè¿äŒŒçã«ä»¥äžã®å€ãçšããã
#
# $$
# \tilde{q}(i) = \sum_{l=1}^k \frac{|v_l|^2}{|v|^2} \frac{C_{il}^2}{|C^{(l)}|^2}
# $$
#
# ããã«ãããæçµçã«åŸãããååžã«$\epsilon$ã®total variational distanceã®èª€å·®ã¯ä¹ããã®ã®ãå¹ççã«æ£åŽãµã³ããªã³ã°ãå¯èœãšãªãã
# ### åèæç®
# [1] <NAME>, âA quantum-inspired classical algorithm for recommendation systemsâ, STOC 2019 Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, Pages 217-228 , https://arxiv.org/abs/1807.04271
# [2] <NAME>, âQuantum-inspired classical algorithms for principal component analysis and supervised clusteringâ, https://arxiv.org/abs/1811.00414
# [3] <NAME>, <NAME>, and <NAME>, âQuantum-inspired low-rank stochastic regression with logarithmic dependence on the dimensionâ, https://arxiv.org/abs/1811.04909
|
notebooks/7.3c_quantum_inspired_algorithm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# The first section only have exploratory trials...
# +
## This function will use CKAN api to get packages list plus the url for the resources under each entity
## The results are stored in a pandas DF
import pprint
import requests
import pandas as pd
def getPackageList(url_api):
r = requests.get(url_api)
j = r.json()
return(pd.DataFrame({"package_id": j['result']}))
def getResourceUrl(package_id):
url = "https://opendata.porto.hackacity.eu" + "/api/3/action/package_show?id=" + package_id;
r = requests.get(url)
j = r.json()
return(j['result']['resources'][0]['url'])
# +
## Usage
url_api = "https://opendata.porto.hackacity.eu/api/3/action/package_list"
df = getPackageList(url_api)
df["resource_url"] = list(map(getResourceUrl, df["package_id"]))
#print(df)
# +
## Get packageIds as a list
def getPackageIds(url):
r = requests.get(url)
j = r.json()
return(j['result'])
# +
## Usage
url = "https://opendata.porto.hackacity.eu/api/3/action/package_list";
packageIdsList = getPackageIds(url)
#print(packageIdsList)
# +
## For a list of packagesIds extract the available metadata and store the results in a pandas DF
from pandas.io.json import json_normalize
def normalizeJSON(url, package_id):
url = url + package_id;
r = requests.get(url)
j = r.json()
return(json_normalize(j['result']))
def appendRowToDF(df1, df2):
df = pd.DataFrame()
if df1.empty:
df = df1.copy()
else:
df = pd.concat([df1,df2])
return(df)
# +
## Usage
packagesMetadata = pd.DataFrame()
url = "https://opendata.porto.hackacity.eu/api/3/action/package_show?id="
for packageId in packageIdsList:
row = normalizeJSON(url, packageId)
packagesMetadata = appendRowToDF(packagesMetadata, row)
# +
## Request live data and store the result in a panda DF
import requests
import pprint
import pandas
from pandas.io.json import json_normalize
def getLiveData(api_url, package_id = None, device_id = None):
if (package_id is None) and (device_id is not None):
url = api_url + "/v2/entities?id=" + device_id
elif (package_id is not None) and (device_id is None):
url = api_url + "/v2/entities?type=" + package_id
else:
raise Exception("package_id or device_id required or are simultaneous defined!")
print(url)
r = requests.get(url)
j = r.json()
#pprint.pprint(j)
return(json_normalize(j))
# +
## Example with error
#api_url = "https://broker.fiware.urbanplatform.portodigital.pt"
#df = getLiveData(api_url)
# -
## Example without device id
api_url = "https://broker.fiware.urbanplatform.portodigital.pt"
package_id = "AirQualityObserved"
df = getLiveData(api_url, package_id)
## Example with device id
api_url = "https://broker.fiware.urbanplatform.portodigital.pt"
device_id = "urn:ngsi-ld:AirQualityObserved:porto:environment:ubiwhere:5adf39366f555a4514e7ea54"
df = getLiveData(api_url, device_id = device_id)
# +
## Example
## require getHistoricalData function declared below!!!
#resource_list = ['urn:ngsi-ld:AirQualityObserved:porto:environment:ubiwhere:5adf39366f555a4514e7ea54',
# 'urn:ngsi-ld:AirQualityObserved:porto:environment:ubiwhere:5b97a1bde521e3053085c08c',
# 'urn:ngsi-ld:AirQualityObserved:porto:environment:ubiwhere:5b632f2706599b05e998bed8',
# 'urn:ngsi-ld:AirQualityObserved:porto:environment:ubiwhere:5b72dbfa06599b05e9a74f27',
# 'urn:ngsi-ld:AirQualityObserved:porto:environment:ubiwhere:5b97a1a6e521e3053085c067']
#api_url = "http://history-data.urbanplatform.portodigital.pt"
#df = pd.DataFrame()
#for resource in resource_list:
# print(resource)
# df1 = getHistoricalData(api_url, device_id = resource, no=500)
# #print(df1.columns)
# if df.empty:
# df = df1.copy()
# else:
# df = pd.concat([df,df1])
# #print(df.columns)
# -
#
# From this point forward are the sequential steps to get the IOT data...
#
# +
## List IOT entities
import requests
import json
def getListIOTEntities(api_url):
url = api_url + "/v2/types"
r = requests.get(url)
j = r.json()
entity_list = []
for item in j:
#print(item['type'])
entity_list.append(item['type'])
return(entity_list)
# -
api_url = "https://broker.fiware.urbanplatform.portodigital.pt"
entity_list = getListIOTEntities(api_url)
print(entity_list)
# +
## Reduce entity_list to the ones of interest (MANUAL STEP)
#1 entity_list = ['AirQualityObserved']
#2 entity_list = ['NoiseLevelObserved']
#3 entity_list = ['TrafficFlowObserved']
entity_list = ['WeatherObserved']
# +
## Get list of all available resources/devices for an entity
import requests
import pprint
def getResourceList(api_url, entity_name):
# First let's the ID's from the FiWare
url = api_url + "/v2/entities?type=" + entity_name
#print(url)
r = requests.get(url, verify=False)
j = r.json()
#print(j)
resources_list = []
for resource in j:
resources_list.append(resource['id'])
return(resources_list)
# +
api_url = "https://broker.fiware.urbanplatform.portodigital.pt"
resource_list = []
for entity in entity_list:
print(entity)
resource_list.append(getResourceList(api_url, entity))
# +
#print(resource_list)
# -
#Flat resource_list
resource_list_flat = [item for sublist in resource_list for item in sublist]
# +
#Remove stuff that is giving errors
#resource_list_flat.remove('Trindade_1_Rotacao')
# -
print(resource_list_flat)
# +
## Request historical data with resource_id and store the results as a panda DF for a single device
import requests
import pprint
import pandas
from pandas.io.json import json_normalize
def convertJSONHistoricalToDF(j, entity = None):
print(entity)
if (entity is (None or "NoiseLevelObserved" or "AirQualityObserved")):
df = pd.DataFrame()
for i in range(0,len(j['data']['attributes'])):
df[j['data']['attributes'][i]['attrName']] = j['data']['attributes'][i]['values']
## expand location attributes
#for key in df['location'][0].keys():
# df[key] = str(df['location'][0][key])
df['long'] = df['location'][0]['coordinates'][0]
df['lat'] = df['location'][0]['coordinates'][1]
df['device_id'] = j['data']['entityId']
#print(df)
elif (entity is "TrafficFlowObserved"):
df = pd.DataFrame()
#TODO
elif (entity is "WeatherObserved"):
df = pd.DataFrame()
for i in range(0, len(j['data']['attributes'])):
df[j['data']['attributes'][i]['attrName']] = j['data']['attributes'][i]['values']
df['long'] = df['location'][0]['coordinates'][0]
df['lat'] = df['location'][0]['coordinates'][1]
df['device_id'] = j['data']['entityId']
else:
raise Exception("Wrong json template specified")
return(df)
def getHistoricalData(api_url, device_id=None, no=20, output="json"):
if (device_id is not None):
url = api_url + "/v2/entities/" + device_id + "?limit=" + str(no)
else:
raise Exception("device_id is required")
r = requests.get(url)
j = r.json()
if "error" not in j:
if (output is "json"):
return (j)
elif (output is "df"):
return (convertJSONHistoricalToDF(j, entity))
else:
raise Exception("invalid output")
#def getHistoricalData(api_url, device_id = None, no = 20):
# if (device_id is not None):
# url = api_url + "/v2/entities/" + device_id + "?limit=" + str(no)
# else:
# raise Exception("device_id is required")
#
# #print(url)
# r = requests.get(url)
# j = r.json()
# #json_normalize(j['data'], record_path=['attributes']).transpose()
# return(convertJSONHistoricalToDF(j, entity))
# +
import pandas as pd
api_url = "http://history-data.urbanplatform.portodigital.pt"
df = pd.DataFrame()
for resource in resource_list_flat:
print(entity)
print(resource)
df1 = getHistoricalData(api_url, device_id = resource, no=500, output="df")
print(df1)
#print(df1.columns)
if df1 is not None:
if df.empty:
df = df1.copy()
else:
df = pd.concat([df,df1], sort=False)
#print(df.columns)
# +
# DF operations
import time
import datetime
# Convert timestamp to unixtime
def convert_df_to_unix(s):
time_mask = "%Y-%m-%dT%H:%M:%S.%f"
return(time.mktime(datetime.datetime.strptime(s, time_mask).timetuple()))
# -
df['time'] = list(map(convert_df_to_unix, df['dateObserved']))
# +
## Save columns to csv in a custom order
mandatory_column_list = ["time", "lat", "long"]
if (entity is "AirQualityObserved"):
data_column_list = ["CO", "NO2", "O3", "Ox", "PM1", "PM10", "PM25"]
for data_column in data_column_list:
filepath = "./output/" + "IOT_" + "AirQuality_" + data_column + ".csv"
print(filepath)
df.to_csv(filepath, columns = mandatory_column_list + [data_column],
index = False, na_rep = "", header = True)
elif (entity is "NoiseLevelObserved"):
data_column_list = ["LAeq"]
for data_column in data_column_list:
filepath = "./output/" + "IOT_" + "NoiseLevelObserved_" + data_column + ".csv"
print(filepath)
df.to_csv(filepath, columns = mandatory_column_list + [data_column],
index = False, na_rep = "", header = True)
elif (entity is "TrafficFlowObserved"):
data_column_list = ["LAeq"]
for data_column in data_column_list:
filepath = "./output/" + "IOT_" + "TrafficFlowObserved_" + data_column + ".csv"
print(filepath)
df.to_csv(filepath, columns = mandatory_column_list + [data_column],
index = False, na_rep = "", header = True)
elif (entity is "WeatherObserved"):
data_column_list = ['barometricPressure', 'precipitation', 'relativeHumidity',
'solarRadiation', 'temperature', 'windDirection', 'windSpeed']
for data_column in data_column_list:
filepath = "./output/" + "IOT_" + "WeatherObserved_" + data_column + ".csv"
print(filepath)
df.to_csv(filepath, columns = mandatory_column_list + [data_column],
index = False, na_rep = "", header = True)
# -
print(df.columns)
|
get_IOT_data.ipynb
|