problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4. In the stands of the hockey arena, there are several rows with 168 seats in each row. For the final match, 2016 students from several sports schools were invited as spectators, with no more than 40 from each school. Students from any school must be seated in one row. What is the minimum number of rows that must be in the arena to ensure this can always be done?
|
Answer: 15.
Solution. Suppose that 57 schools sent 35 students each to the final match, and one school sent 21 students. Since only four groups of 35 students can fit in one row, the number of rows required to accommodate the students from 57 schools should be no less than $\frac{57}{4}=14 \frac{1}{4}$, which means at least 15 rows are needed.
We will show that 15 rows are sufficient. Assume that there is one large row on the stand, divided by aisles into sectors of 168 seats each. We will seat the students on this large row, ignoring the aisles, starting with the students from the first school, then the second, and so on. As a result, 12 sectors will be fully occupied. With this seating arrangement, students from no more than 11 schools can be seated in two sectors. Since any four schools can fit in one sector, it is sufficient to have three sectors for seating the remaining students.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=9^{n}-1$, where $n$ is a natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 13. Find $x$.
|
Answer: 728.
Solution. Since the number $x$ is even, one of its prime divisors is 2. Therefore, we need to find all $x$ that have exactly two odd prime divisors, one of which is 13. The remainders of the powers of 9 when divided by 13 are $9, 3, 1$ and then repeat cyclically. Thus, the divisibility of $x$ by 13 means that $n$ is a multiple of 3, that is, $x=9^{3m}-1$. From this,
$$
x=p \cdot q, \quad \text{where } p=9^{m}-1, \quad q=9^{2m}+9^{m}+1
$$
Note that the numbers $p$ and $q$ are coprime. Indeed, if a number $r$ divides both $p$ and $q$, then it also divides 3, since
$$
3=q-(9^{2m}-1)-(9^{m}-1)=q-p(9^{m}+2)
$$
But $p$ is not divisible by 3, hence $r=1$.
We will prove that the number $p$ is a power of two only when $m=1$. Indeed, let $m>1$. Write $p=(3^{m}-1)(3^{m}+1)$. In the right-hand side, we have the product of two consecutive even numbers, both greater than 4. Therefore, at least one of them is not divisible by 4 and, thus, is not a power of 2.
If $m=1$, we get $x=9^{3}-1=728=2^{3} \cdot 7 \cdot 13$, which fits our criteria. We will show that there are no solutions when $m>1$. One of the numbers $p$ and $q$ is divisible by 13. Consider two cases.
1) $p$ is divisible by 13. Then $m \vdots 3$, that is, $m=3k$. If $k=1$, then $p$ is divisible by 7 and 13. For $k>1$, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ will be factored into two coprime factors, neither of which is a power of 2. Therefore, $x$ has at least three different odd prime divisors, which is impossible.
2) $q$ is divisible by 13. Note that $p$ has an odd divisor, and $q$ is odd and coprime with $p$. Then $q$ must be a power of 13, that is, $q=13^{s}$ for some natural number $s$. The remainder of $q$ when divided by 8 is 5 for odd $s$ and 1 for even $s$. On the other hand, this remainder must be the same as that of $9^{2m}+9^{m}+1$, which is 3, which is impossible.
|
728
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For what smallest $k$ can $k$ cells be marked on an $8 \times 9$ board such that for any placement of a four-cell figure on the board, it can be rotated and flipped.
|
Answer: 16.
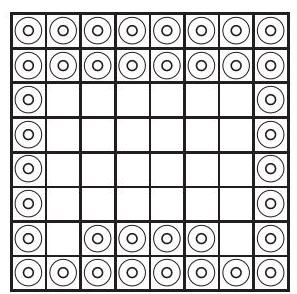
Solution. It is not hard to notice that in any $2 \times 4$ rectangle, there are at least two marked cells. Since from an $8 \times 9$ board, 8 non-overlapping $2 \times 4$ rectangles can be cut out, there must be at least 16 marked cells in it. An example with 16 marked cells is shown in the figure.

|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the stands of the hockey arena, there are several rows with 168 seats in each row. For the final match, 2016 students from several sports schools were invited as spectators, with no more than 45 from each school. Students from any school need to be seated in one row. What is the minimum number of rows that must be in the arena to ensure this can always be done?
|
Answer: 16.
Solution. Suppose that 46 schools sent 43 students each to the final match, and one school sent 34 students. Since only three groups of 43 students can fit in one row, the number of rows required to accommodate the students from 46 schools should be no less than $\frac{46}{3}=15 \frac{1}{3}$, which means at least 16 rows are needed.
We will show that 16 rows are sufficient. Assume that there is one large row on the stand, divided by aisles into sectors of 168 seats each. We will seat the students on this large row, ignoring the aisles, starting with the students from the first school, then the second, and so on. As a result, 12 sectors will be fully occupied. With this seating arrangement, students from no more than 11 schools can be on two sectors. Since any three schools can fit in one sector, four sectors are sufficient for seating the remaining students.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=9^{n}-1$, where $n$ is a natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 7. Find $x$.
|
Answer: 728.
Solution. Since the number $x$ is even, one of its prime divisors is 2. Therefore, we need to find all $x$ that have exactly two odd prime divisors, one of which is 7. The remainders of the powers of 9 when divided by 7 are $2, 4, 1$ and then repeat cyclically. Thus, the divisibility of $x$ by 7 means that $n$ is a multiple of 3, that is, $x=9^{3m}-1$. From this,
$$
x=p \cdot q, \quad \text{where } p=9^{m}-1, \quad q=9^{2m}+9^{m}+1
$$
Note that the numbers $p$ and $q$ are coprime. Indeed, if a number $r$ divides both $p$ and $q$, then it also divides 3, since
$$
3=q-(9^{2m}-1)-(9^{m}-1)=q-p(9^{m}+2)
$$
But $p$ is not divisible by 3, hence $r=1$.
We will prove that the number $p$ is a power of two only when $m=1$. Indeed, let $m>1$. Write $p=(3^{m}-1)(3^{m}+1)$. In the right-hand side, we have the product of two consecutive even numbers, both greater than 4. Therefore, at least one of them is not divisible by 4 and, thus, is not a power of 2.
If $m=1$, we get $x=9^{3}-1=728=2^{3} \cdot 7 \cdot 13$, which fits our criteria. We will show that there are no solutions when $m>1$. One of the numbers $p$ and $q$ is divisible by 7. Consider two cases.
1) $p$ is divisible by 7. Then $m \vdots 3$, that is, $m=3k$. If $k=1$, then $p$ is divisible by 7 and 13. For $k>1$, we can apply the same reasoning to $p$ as we did to $x$. In both cases, $p$ will be factored into two coprime factors, neither of which is a power of 2. Therefore, $x$ has at least three different odd prime divisors, which is impossible.
2) $q$ is divisible by 7. Note that $p$ has an odd divisor, and $q$ is odd and coprime with $p$. Then $q$ must be a power of 7, that is, $q=7^{s}$ for some natural number $s$. Thus, the remainder of $q$ when divided by 8 is 7 for odd $s$ and 1 for even $s$. On the other hand, this remainder must be the same as that of $9^{2m}+9^{m}+1$, which is 3, which is impossible.
|
728
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the cells of a $10 \times 10$ table, the numbers $1,2,3, \ldots, 100$ are arranged such that the sum of the numbers in any $2 \times 2$ square does not exceed $S$. Find the smallest possible value of $S$.
|
Answer: 202.
Solution. Divide the $10 \times 10$ table into 25 squares of $2 \times 2$. Since the sum of the numbers in the entire table is
$$
1+2+\cdots+100=\frac{100 \cdot 101}{2}=5050
$$
the arithmetic mean of the sums of the numbers in these 25 squares is 202. Therefore, in at least one square, the sum of the numbers is not less than 202, that is, $S \geqslant 202$. An example of an arrangement where the value $S=202$ is achieved is shown in the figure.
| 100 | 99 | 98 | 97 | 96 | 95 | 94 | 93 | 92 | 91 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 90 | 89 | 88 | 87 | 86 | 85 | 84 | 83 | 82 | 81 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 80 | 79 | 78 | 77 | 76 | 75 | 74 | 73 | 72 | 71 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 70 | 69 | 68 | 67 | 66 | 65 | 64 | 63 | 62 | 61 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 60 | 59 | 58 | 57 | 56 | 55 | 54 | 53 | 52 | 51 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
|
202
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a school, there are 920 students, and in each class, there are no more than $k$ students. All students need to go on a bus tour. For this, 16 buses, each with 71 seats, have been booked. The students need to be seated on the buses so that students from each class end up in the same bus. For what largest $k$ is this guaranteed to be possible?
|
Answer: 17.
Solution. If $k=18$, then it is not always possible to seat the students in the buses. Indeed, suppose the school has 50 classes of 18 students each and two classes of 10 students each. Only three classes of 18 students can fit in one bus. Therefore, it would require at least 17 buses to transport students from such classes.
We will show that if there are no more than 17 students in each class, it is always possible to seat the students in the buses. Number the seats in the buses consecutively: from 1 to 71 in the first bus, from 72 to 142 in the second, and so on. Seat the students in the order of increasing seat numbers, starting with all students from the first class, then from the second, and so on. As a result, the students will fit into 13 buses, since $13 \cdot 71=923>920$. With this seating arrangement, students from no more than 12 classes can end up in two buses. It is sufficient to use three buses to accommodate these classes, since any four classes can fit in one bus.
|
17
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=5^{n}-1$, where $n-$ is a natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 11. Find $x$.
|
Answer: 3124.
Solution. Since the number $x$ is even, one of its prime divisors is 2. Therefore, we need to find all $x$ that have exactly two odd prime divisors, one of which is 11. The remainders of the powers of 5 when divided by 11 are $5, 3, 4, 9, 1$ and then repeat cyclically. Thus, the divisibility of $x$ by 11 means that $n$ is a multiple of 5, that is, $x = 5^{5m} - 1$. From here, using the formula for the sum of a geometric progression,
$$
x = p \cdot q, \quad \text{where } p = 5^m - 1, \quad q = 1 + 5^m + 5^{2m} + 5^{3m} + 5^{4m}
$$
Note that the numbers $p$ and $q$ are coprime. Indeed, let the number $r$ divide both $p$ and $q$. Then
$$
5 = q - (5^m - 1) - (5^{2m} - 1) - (5^{3m} - 1) - (5^{4m} - 1)
$$
Differences of the form $5^{km} - 1$ are divisible by $p$ and, therefore, by $r$. Thus, $r$ is a divisor of 5. But $p$ is not divisible by 5, hence $r = 1$.
We will prove that the number $p$ is a power of two only when $m = 1$. Indeed, let $m > 1$. If $m = 2k$, then write $p = (5^k - 1)(5^k + 1)$. On the right side, we have the product of two consecutive even numbers. At least one of them is greater than 4 and does not divide by 4, so it is not a power of 2. Now let $m = 2k + 1$. Then
$$
p = 5^m - 5 + 4 = 5 \cdot (5^k - 1)(5^k + 1) + 4.
$$
The right side is not divisible by 8, since $(5^k - 1)(5^k + 1)$ is divisible by 8 as the product of two consecutive even numbers. Since $p > 4$, the number $p$ cannot be a power of two.
When $m = 1$, we get $x = 3124 = 4 \cdot 11 \cdot 71$, which fits. We will show that there are no solutions when $m > 1$. One of the numbers $p$ and $q$ is divisible by 11. Consider two cases.
1) $p$ is divisible by 11. Then $m \vdots 5$, that is, $m = 5k$. If $k = 1$, then $p$ is divisible by 11 and 71. For $k > 1$, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ will decompose into two coprime factors that are not powers of two. Therefore, $x$ has at least three different odd prime divisors, which is impossible.
2) $q$ is divisible by 11. Note that $p$ has an odd divisor, and $q$ is odd and coprime with $p$. Then $q$ must be a power of 11. The remainder of $5^m$ when divided by 8 is 5 for odd $m$ and 1 for even $m$. If $m$ is odd, the remainder of $q$ when divided by 8 is the same as that of $1 + 5 + 1 + 5 + 1 = 13$, which is 5. For even $m$, the remainder of $q$ when divided by 8 is also 5. But the remainders of $11^s$ when divided by 8 are only 3 and 1, so $q$ cannot be a power of 11.
|
3124
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the black cells of an $8 \times 8$ chessboard, the numbers $1,2,3, \ldots, 32$ are placed such that the sum of the numbers in any $2 \times 2$ square does not exceed $S$. Find the smallest possible value of $S$.
|
Answer: 33.
Solution. Divide the chessboard into 16 squares of $2 \times 2$. Since the sum of the numbers in all the black cells is
$$
1+2+\cdots+32=\frac{32 \cdot 33}{2}=16 \cdot 33
$$
the arithmetic mean of the sums of the numbers in these 16 squares is 33. Therefore, in at least one square, the sum of the numbers is not less than 33, i.e., $S \geqslant 33$. An example of an arrangement where $S=33$ is achieved is shown in the figure.
| 32 | | 31 | | 30 | | 29 | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | 1 | | 2 | | 3 | | 4 |
| 28 | | 27 | | 26 | | 25 | |
| | 5 | | 6 | | 7 | | 8 |
| 24 | | 23 | | 22 | | 21 | |
| | 9 | | 10 | | 11 | | 12 |
| 20 | | 19 | | 18 | | 17 | |
| | 13 | | 14 | | 15 | | 16 |
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
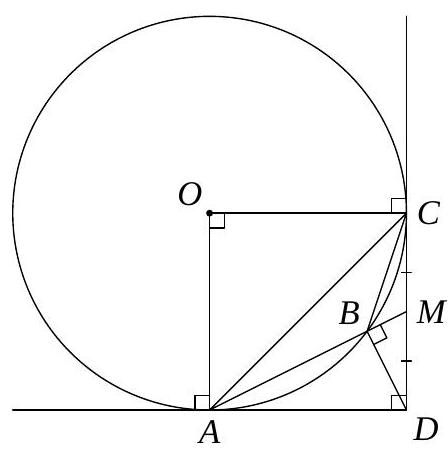
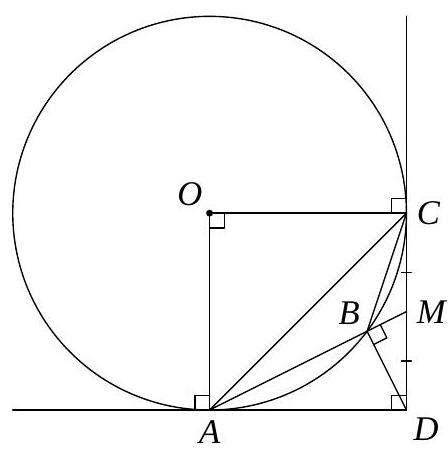
3. Triangle $A B C$ with angle $\angle A B C=135^{\circ}$ is inscribed in circle $\omega$. The lines tangent to $\omega$ at points $A$ and $C$ intersect at point $D$. Find $\angle A B D$, given that $A B$ bisects segment $C D$. Answer: $90^{\circ}$
|
Solution. Let $O$ be the center of $\omega$, $M$ be the intersection point of lines $A B$ and $C D$. Note that
$$
\angle A O C=2\left(180^{\circ}-\angle A B C\right)=2\left(180^{\circ}-135^{\circ}\right)=90^{\circ} .
$$
Then quadrilateral $A O C D$ is a square, and thus $\angle A D C=90^{\circ}$. By the tangent-secant theorem,
$$
D M^{2}=M C^{2}=B M \cdot A M, \quad \text { that is } \quad \frac{D M}{A M}=\frac{B M}{D M} .
$$
Therefore, triangles $D B M$ and $A D M$ are similar, from which
$$
\angle A B D=180^{\circ}-\angle M B D=180^{\circ}-\angle A D M=90^{\circ}
$$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A warehouse stores 1500 tons of various goods in containers. The weight of any container is a multiple of a ton and does not exceed $k$ tons. A train consisting of 25 platforms, each with a load capacity of 80 tons, has been dispatched to the warehouse. For what maximum $k$ can this train guarantee the transportation of all goods?
|
Answer: 26.
Solution. If $k=27$, then it is not always possible to transport all the goods. Indeed, suppose there are 55 containers, each weighing 27 tons, and one weighing 15 tons. Only two containers of 27 tons each can fit on one platform. Therefore, to transport 55 such containers, at least 28 platforms are required.
We will show that if the weight of each container does not exceed 26 tons, then it is always possible to transport them from the warehouse. Imagine that the containers store boxes, each weighing one ton, and the containers themselves are weightless. We will sequentially load the platforms with these boxes: as soon as the current platform is full, we move to the next one. We will load the boxes starting with all the boxes from the first container, then from the second, and so on. As a result, the boxes will fit on 19 platforms, since $19 \cdot 80=1520>1500$. With such placement, boxes from no more than 18 containers can end up on two platforms. To accommodate these containers, 6 platforms are sufficient, since any three containers can fit on one platform.
|
26
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=8^{n}-1$, where $n$ is a natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 31. Find $x$.
|
Answer: 32767.
Solution. One of the simple divisors of $x$ is obviously 7. First, let's prove that a number of the form $y=8^{k}-1$ is a power of 7 only in the case $k=1$. Indeed, for $k>1$, write $y=a b$, where $a=2^{k}-1, b=2^{2 k}+2^{k}+1$. Since
$$
b=2^{2 k}-1+2^{k}-1+3=a\left(2^{k}+2\right)+3
$$
the numbers $a$ and $b$ cannot both be divisible by 7, and $y$ will not be a power of 7.
The remainders of the powers of 8 when divided by 31 are $8,2,16,4,1$ and then repeat cyclically. Therefore, the divisibility of $x$ by 31 means that $n$ is a multiple of 5, i.e., $x=8^{5 m}-1$. Note also that $m$ is not divisible by 4, otherwise the divisors of $x$ will include 3, 5, and 7. For $m=1$, we get $x=32767=7 \cdot 31 \cdot 151$, which fits. Let's show that there are no solutions for $m>1$. By the formula for the sum of a geometric progression,
$$
x=p \cdot q, \quad \text{where } p=8^{m}-1, q=1+8^{m}+8^{2 m}+8^{3 m}+8^{4 m}
$$
Let's prove that the numbers $p$ and $q$ are coprime. Indeed, let the number $r$ divide $p$ and $q$. Then
$$
5=q-\left(8^{m}-1\right)-\left(8^{2 m}-1\right)-\left(8^{3 m}-1\right)-\left(8^{4 m}-1\right)
$$
Differences of the form $8^{k m}-1$ are divisible by $p$ and, therefore, by $r$. Thus, $r$ is a divisor of 5. But the remainders of $8^{m}$ when divided by 5 are $3,4,2,1$ and then repeat cyclically. Since $m$ is not a multiple of 4, the number $p$ is not divisible by 5, hence $r=1$. This means that $q$ is not divisible by 7, since $p \vdots$. Consider two cases.
1) $p$ is a multiple of 31. Then $m \vdots 5$, i.e., $m=5 k$. If $k=1$, then $p$ is divisible by 31 and 151. For $k>1$, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ will decompose into the product of two coprime numbers, neither of which are powers of 7. Taking into account the divisibility of $x$ by 7, we get that $x$ has at least four different prime divisors.
2) $q$ is a multiple of 31. Note that $p$ is divisible by 7, not being a power of 7, and $q$ is coprime with $p$. Then $q$ must be a power of 31, i.e., $q=31^{s}$. Transitioning to remainders when divided by 8, we get $1=(-1)^{s}$, hence $s$ is even. Moreover, the remainders of $31^{s}$ when divided by 7 for even $s$ are $2,4,1$ and then repeat cyclically. But the remainder of $q$ when divided by 7 is 5. Thus, $q$ cannot be a power of 31.
|
32767
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the theater, there are $k$ rows of seats. 770 spectators came to the theater and sat down (possibly not occupying all the seats). After the intermission, all the spectators forgot which seats they had and sat down differently. For what largest $k$ will there definitely be 4 spectators who sat in the same row both before and after the intermission?
|
Answer: 16
Solution. If the audience is seated on 16 rows, then on some row there are no fewer than 49 spectators (otherwise, there would be no more than 48 spectators on each row, and the total would not exceed $16 \cdot 48=7683$, making it impossible to seat the spectators of this row after the intermission such that there are no more than three in each row. Thus, $k=16$ works.
Now, we will show that with 17 rows, the audience can be seated in such a way that the required four spectators do not exist. Let the $n$-th column be the seats in the hall with number $n$, cyclically ordered by rows:
$$
1,2, \ldots, 17,1,2, \ldots, 17, \ldots
$$
A cyclic shift of a column by $m$ rows is a permutation of the column where the new row number of each spectator is obtained from the old one by shifting $m$ positions to the right in the sequence (*). Fill the columns numbered from 1 to 45 with spectators, as well as the first 5 seats of the 46th column. Thus, there will be $17 \cdot 45 + 5 = 770$ people in the hall. After the intermission, we will seat the spectators as follows. The spectators in columns $1,2,3$ sit in their original seats; in columns $4,5,6$, the spectators are cyclically shifted by one row, in columns $7,8,9$ by two rows, and so on. As a result, we will have a situation where there are no four spectators who sat in the same row both before and after the intermission.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=9^{n}-1$, where $n$ is a natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 11. Find $x$.
|
Answer: 59048.
Solution. Since the number $x$ is even, one of its prime divisors is 2. Therefore, we need to find all $x$ that have exactly two odd prime divisors, one of which is 11. First, let's prove that the number $3^{s}+1$ cannot be a power of two when $s>1$, and the number $3^{s}-1$ cannot be a power of two when $s>2$. Indeed, for $s>1$, the number $3^{s}+1$ is greater than 8 and is not divisible by 8, as its remainder when divided by 8 is 4 or 2. Now let $s>2$. If $s$ is odd, the number $3^{s}-1$ is greater than 8 and is not divisible by 8, as its remainder when divided by 8 is 2. If $s=2k$, then $3^{s}-1$ is divisible by the number $3^{k}+1$, which is not a power of two. From the above, it follows, in particular, that $9^{s}-1$ will be a power of two only when $s=1$.
The remainders of the powers of 9 when divided by 11 are $9, 4, 3, 5, 1$ and then repeat cyclically. Therefore, the divisibility of $x$ by 11 means that $n$ is a multiple of 5, i.e., $x=9^{5m}-1$. If $m=1$, we get $x=9^{5}-1=59048=2^{3} \cdot 11^{2} \cdot 61$, which fits our criteria. Let's show that there are no solutions for $m>1$. Consider two cases.
1) $m$ is odd. By the formula for the sum of a geometric progression,
$$
x=p \cdot q, \quad \text{where } p=9^{m}-1, \quad q=1+9^{m}+9^{2m}+9^{3m}+9^{4m}
$$
Let's prove that the numbers $p$ and $q$ are coprime. Indeed, let the number $r$ divide both $p$ and $q$. Then
$$
5=q-(9^{m}-1)-(9^{2m}-1)-(9^{3m}-1)-(9^{4m}-1)
$$
Differences of the form $9^{km}-1$ are divisible by $p$ and, therefore, by $r$. Thus, $r$ is a divisor of 5. But $p$ is not divisible by 5 when $m$ is odd, so $r=1$.
Suppose $p$ is divisible by 11. Then $m \vdots \leq 5$, i.e., $m=5k$. If $k=1$, then $p$ is divisible by 11 and 61. For $k>1$, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ will decompose into two coprime factors that are not powers of two. Therefore, $x$ has at least three different odd prime divisors, which is impossible.
Now suppose $q$ is divisible by 11. Note that $p$ has an odd divisor, and $q$ is odd and coprime with $p$. Then $q$ must be a power of 11, i.e., $q=11^{s}$. But the remainder of $11^{s}$ when divided by 8 is 3 for odd $s$ and 1 for even $s$, while the remainder of $q$ when divided by 8 is 5. Therefore, the number $q$ cannot be a power of 11.
2) $m$ is even. Then $n=2k$ for $k \geq 5$, and
$$
x=(9^{k}-1)(9^{k}+1)=(3^{k}-1)(3^{k}+1)(9^{k}+1)
$$
The factors on the right side are coprime, since the pairs of numbers $3^{k} \pm 1$ and $9^{k} \pm 1$ are odd and differ by 2. Moreover, none of the factors is a power of two. Indeed, we have already proven this for the first two, and $9^{k}+1$ is greater than 8 and gives a remainder of 2 when divided by 8. Thus, $x$ has at least three different odd prime divisors, which is impossible.
|
59048
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=9^{n}-1$, where $n-$ is an odd natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 61. Find $x$.
|
Answer: 59048.
Solution. Since the number $x$ is even, one of its prime divisors is 2. Therefore, we need to find all $x$ that have exactly two odd prime divisors, one of which is 61. The remainders of the powers of 9 when divided by 61 are $9, 20, 58, 34, 1$ and then repeat cyclically. Thus, the divisibility of $x$ by 61 means that $n$ is a multiple of 5, i.e., $x = 9^{5m} - 1$, where $m$ is odd. By the formula for the sum of a geometric progression,
$$
x = p \cdot q, \quad \text{where } p = 9^m - 1, \quad q = 1 + 9^m + 9^{2m} + 9^{3m} + 9^{4m}
$$
We will prove that the numbers $p$ and $q$ are coprime. Indeed, let the number $r$ divide both $p$ and $q$. Then
$$
5 = q - (9^m - 1) - (9^{2m} - 1) - (9^{3m} - 1) - (9^{4m} - 1)
$$
Differences of the form $9^{km} - 1$ are divisible by $p$ and, therefore, by $r$. Hence, $r$ is a divisor of 5. But $p$ is not divisible by 5 when $m$ is odd, so $r = 1$.
We will prove that the number $p$ is a power of two exactly when $m = 1$. Indeed, for $m > 1$, we can write $p = (3^m - 1)(3^m + 1)$. In the right-hand side, we have the product of two consecutive even numbers, both greater than 2. Therefore, at least one of them is not divisible by 4 and, hence, is not a power of 2.
If $m = 1$, we get $x = 9^5 - 1 = 59048 = 2^3 \cdot 11^2 \cdot 61$, which fits our criteria. We will show that there are no solutions for $m > 1$. Consider two cases.
1) $p$ is divisible by 61. Then $m \vdots 5$, i.e., $m = 5k$. If $k = 1$, then $p$ is divisible by 11 and 61. For $k > 1$, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ will decompose into two coprime factors, neither of which is a power of 2. Therefore, $x$ has at least three different odd prime divisors, which is impossible.
2) $q$ is divisible by 61. Note that $p$ has an odd divisor, and $q$ is odd and coprime with $p$. Then $q$ must be a power of 61, i.e., $q = 61^s$. Note that $s \vdots 3$, since $q - 1$ is divisible by 9, and the remainders of $61^s$ when divided by 9 are $7, 4, 1$ and then repeat cyclically. Additionally, when divided by 8, the number $q$ gives a remainder of 5, while the remainder of $61^s$ is 5 for odd $s$ and 1 for even $s$. Therefore, $s$ is odd, so $s$ has the form $6k + 3$ for some natural number $k$.
Now let's compare the remainders of $q$ and $61^s$ when divided by 7. The remainders of $61^s$ are $5, 4, 6, 2, 3, 1$ and then repeat cyclically. For $s = 6k + 3$, all of them coincide with 6. The remainders of $9^m$ are $2, 4, 1$ and then repeat cyclically. Therefore, it is sufficient to find the remainders of $q$ for $m = 1, 2, 3$. They are
$$
\begin{aligned}
& (1 + 2 + 4 + 1 + 2) \bmod 7 = 3, \quad \text{if } m = 1, \\
& (1 + 4 + 1 + 2 + 4) \bmod 7 = 5, \quad \text{if } m = 2, \\
& (1 + 1 + 2 + 4 + 1) \bmod 7 = 2, \quad \text{if } m = 3.
\end{aligned}
$$
Since none of these numbers coincide with 6, $q$ cannot be a power of 61.
|
59048
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle $ABC$, the median $AM$ is drawn. Circle $\alpha$ passes through point $A$, touches line $BC$ at point $M$, and intersects sides $AB$ and $AC$ at points $D$ and $E$ respectively. On the arc $AD$ that does not contain point $E$, a point $F$ is chosen such that $\angle BFE = 72^{\circ}$. It turns out that $\angle DEF = \angle ABC$. Find the angle $\angle CME$.
|
Answer: $36^{\circ}$.
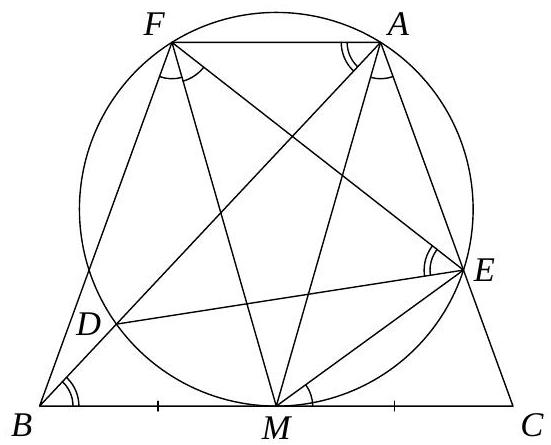
Solution. Inscribed angles $D A F$ and $D E F$ subtend the arc $D F$ and are therefore equal. Given that $\angle F A B = \angle A B C$, it follows that $B C \parallel A F$. Then the line $\ell$, passing through point $M$ and perpendicular to the tangent $B C$, contains the diameter of the circle $\omega$ and is perpendicular to its chord $A F$. Thus, points $A$ and $F$ are symmetric with respect to $\ell$, meaning that $\ell$ is the axis of symmetry of the trapezoid $B C A F$. This implies that $A C = B F$ and $A M = F M$. Therefore, triangles $B F M$ and $C A M$ are congruent by the three sides, so $\angle B F M = \angle E A M$. Additionally, $\angle E F M = \angle E A M$ as inscribed angles subtending the same chord. Thus, $F M$ is the angle bisector of $\angle B F E$, and
$$
\angle E A M = \angle E F M = \frac{1}{2} \angle B F E = 36^{\circ}.
$$
Notice now that the angle between the chord $E M$ and the tangent $B C$ is equal to the inscribed angle subtending $E M$. Therefore, $\angle C M E = \angle E A M = 36^{\circ}$.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=7^{n}+1$, where $n$ is an odd natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 11. Find $x$.
|
Answer: 16808.
Solution. Since the number $x$ is even, one of its prime divisors is 2. Therefore, we need to find all $x$ that have exactly two odd prime divisors, one of which is 11. The divisibility of $x$ by 11 is equivalent to $n$ being an odd multiple of 5, that is, $x=7^{5m}+1$ for some odd $m$. From here, using the formula for the sum of a geometric progression,
$$
x=p \cdot q, \quad \text{where } p=7^{m}+1, q=1-7^{m}+7^{2m}-7^{3m}+7^{4m}
$$
Note that $p$ and $q$ are coprime. Indeed, let the number $r$ divide both $p$ and $q$. Then
$$
5=q-(7^{m}+1)-(7^{2m}-1)-(7^{3m}+1)-(7^{4m}-1)
$$
The expressions in parentheses on the right-hand side are divisible by $p$ and, therefore, by $r$. Thus, $r$ is a divisor of 5. But the remainders of the powers of 7 when divided by 5 are 2, 4, 3, 1, and then they cyclically repeat. Therefore, $p$ is not divisible by 5 for odd $m$, hence $r=1$.
We will prove that the number $p$ is a power of two only when $m=1$. Indeed, let $m>1$ and $7^{m}+1=2^{s}$. Then $s \geqslant 4$ and the number $7^{m}+1$ is divisible by 16. But this is impossible, since the remainders of $7^{m}$ when divided by 16 are only 7 and 1.
If $m=1$, we get $x=16808=2^{3} \cdot 11 \cdot 191$, which fits our criteria. We will show that there are no solutions for $m \geqslant 3$. Consider two cases.
1) $p$ is divisible by 11. Then $m \vdots 5$, that is, $m=5k$. If $k=1$, then $p$ is divisible by 11 and 191. For $k>1$, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ will decompose into two coprime factors that are not powers of two. Therefore, $x$ will have at least three different odd prime divisors, which is impossible.
2) $q$ is divisible by 11. Note that $p$ has an odd divisor, and $q$ is odd and coprime with $p$. Then $q$ must be a power of 11. The remainder of $7^{m}$ when divided by 8 is -1 due to the oddness of $m$. Therefore, the number $q$ gives a remainder of 5 when divided by 8. But the remainders of $11^{s}$ when divided by 8 are only 3 and 1, so $q$ cannot be a power of 11.
|
16808
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A circle $\omega$ is circumscribed around triangle $ABC$. A line tangent to $\omega$ at point $C$ intersects the ray $BA$ at point $P$. On the ray $PC$ beyond point $C$, a point $Q$ is marked such that $PC = QC$. The segment $BQ$ intersects the circle $\omega$ again at point $K$. On the smaller arc $BK$ of the circle $\omega$, a point $L$ is marked such that $\angle LAK = \angle CQB$. Find the angle $\angle PCA$, given that $\angle ALQ = 60^{\circ}$.
|
Answer: $30^{\circ}$.
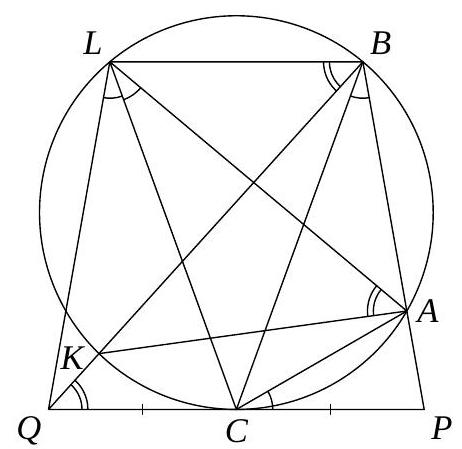
Solution. Inscribed angles $L A K$ and $L B K$ subtend the arc $L K$ and are therefore equal. Given that $\angle L B Q = \angle B Q C$, it follows that $B L \| P Q$. Then the line $\ell$, passing through point $C$ and perpendicular to the tangent $P Q$, contains the diameter of the circle $\omega$ and is perpendicular to its chord $B L$. Therefore, points $B$ and $L$ are symmetric with respect to $\ell$, meaning that $\ell$ is the axis of symmetry of the trapezoid $P Q L B$. From this, it follows that $B P = L Q$ and $B C = L C$. Hence, triangles $Q L C$ and $P B C$ are congruent by the three sides, so $\angle Q L C = \angle A B C$. Additionally, $\angle A L C = \angle A B C$ as inscribed angles subtending the same chord. Therefore, $L C$ is the angle bisector of $\angle A L Q$, and
$$
\angle A B C = \angle A L C = \frac{1}{2} \angle A L Q = 30^{\circ}.
$$
Note that the angle between the chord $A C$ and the tangent $C P$ is equal to the inscribed angle subtending $A C$. Therefore, $\angle P C A = \angle A B C = 30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. What is the maximum number of vertices of a regular 2016-gon that can be marked so that no four marked vertices are the vertices of any rectangle?
|
Answer: 1009.
Solution. Note that an inscribed quadrilateral is a rectangle if and only if its diagonals are diameters of the circumscribed circle. The 2016-gon has exactly 1008 pairs of diametrically opposite vertices. If no rectangle can be formed from the marked vertices, then only in one pair can both vertices be marked. Therefore, no more than \(1007 + 2 = 1009\) vertices can be marked.
On the other hand, number the vertices of the 2016-gon in order from 1 to 2016 and mark the first 1009 vertices. Only the vertices numbered 1 and 1009 will be diametrically opposite. Therefore, 1009 satisfies the condition of the problem.
|
1009
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a natural number $x=6^{n}+1$, where $n-$ is an odd natural number. It is known that $x$ has exactly three distinct prime divisors, one of which is 11. Find $x$.
|
Answer: 7777.
Solution. The divisibility of $x$ by 11 is equivalent to $n$ being an odd multiple of 5, that is, $x=6^{5m}+1$ for some odd $m$. From here, using the formula for the sum of a geometric progression,
$$
x=p \cdot q, \quad \text{where } p=6^{m}+1, q=1-6^{m}+6^{2m}-6^{3m}+6^{4m}
$$
Note that $p$ and $q$ are coprime. Indeed, let the number $r$ divide both $p$ and $q$. Then
$$
5=q-(6^{m}+1)-(6^{2m}-1)-(6^{3m}+1)-(6^{4m}-1)
$$
The expressions in parentheses on the right-hand side are divisible by $p$ and, therefore, by $r$. Thus, $r$ is a divisor of 5. But the remainder of the division of $p$ by 5 is 2 for any $m$. Therefore, $p$ is not divisible by 5, which means $r=1$.
Since the number $m$ is odd, one of the prime divisors of $p$ is 7. We will prove that $p$ is a power of 7 only when $m=1$. Suppose $m \geqslant 3$ and $6^{m}+1=7^{s}$. Then the number $7^{s}-1$ is divisible by $2^{m}$ and, therefore, by 8. This implies that $s$ is even, that is, $s=2k$. Therefore, $2^{m} \cdot 3^{m}=(7^{k}-1)(7^{k}+1)$. Since $7^{k}+1$ is not divisible by 3, the number $7^{k}-1$ is divisible by $3^{m}$ and, therefore, $7^{k}-1 \geqslant 3^{m}$. But then
$$
7^{k}+1 \leqslant 2^{m} \cdot 1
$$
1) $p$ is divisible by 11. If $p$ is not a power of 7, we can apply the same reasoning to $p$ as to $x$. In both cases, $p$ is the product of 7 and two coprime factors that are not powers of 7. Therefore, $x$ has at least four different prime divisors, which is impossible.
2) $q$ is divisible by 11. Note that $p$ is divisible by 7 and is not a power of 7, and $q$ is coprime with $p$. Then $q$ must be a power of 11. The remainder of the division of $6^{m}$ by 7 is -1 due to the oddness of $m$. Therefore, the number $q$ gives a remainder of 5 when divided by 8. But the remainders of the division of $11^{s}$ by 7 can only be 4, 2, and 1, so $q$ cannot be a power of 11.
|
7777
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points) The rules of the game are as follows: from 64 different items, on each turn, the player must form a set of items that has not been mentioned in the game before, with the number of items equal to the player's age in years. Players take turns; either player can start the game; the player who cannot make a move loses. Sets of items are considered different if they differ by at least one item or if they contain a different number of items. In the game, Vasily and Fyodor are participating; each player has the opportunity to make at least one move. It is known that: a) Vasily is 2 years older than Fyodor; b) Fyodor is at least 5 years old; c) Fyodor always wins. What is the minimum number of years Vasily can be?
|
Answer: 34 years
Solution: The game move is the selection of 64 elements from a certain subset, which contains as many elements as the player's age. Thus, the problem requires comparing the number of ways to make such a selection: the player with a greater number of ways to choose their "own" subset, i.e., $C_{64}^{x}$, will always win. Let $V$ be Basil's age in years, and $F$ be Fyodor's age in years. According to the conditions: $5 \leq F, F+2=V, V \leq 64$ (since each player can make a move, i.e., at least one combination can be chosen). It is also known that $C_{64}^{F}>C_{64}^{V}$ always (in the case of equality, Fyodor would lose if he went first). We need to find the minimum $V$ that satisfies all the listed conditions.
Let Fyodor's age be denoted by $x$, and Basil's age by $x+2$. Consider the integer function $x \mapsto C_{64}^{x}$. It increases from 0 to 32 and decreases from 32 to 64. Additionally, $C_{64}^{31}=C_{64}^{33}$. Therefore, the inequality $C_{64}^{x}>C_{64}^{x+2}$ holds if and only if $x \geq 32$. Thus, the minimum value of $x+2$ is 34.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (10 points) Minister K. issued an order that citizens will only be received if the number of ways to choose a group of four people from those who have come is less than the number of ways to choose a group of two people from them. Determine the maximum number of citizens that the minister can receive?
|
Answer: 5.
Solution: The number of ways to choose a group of four people from $n$ people is $C_{n}^{4}$; a group of two people is $C_{n}^{2}$. We are interested in the maximum natural number $n$ such that $C_{n}^{4}<C_{n}^{2}$. Transforming:
$$
\frac{n(n-1)(n-2)(n-3)}{1 \cdot 2 \cdot 3 \cdot 4}<\frac{n(n-1)}{2} \Leftrightarrow \frac{(n-2)(n-3)}{3 \cdot 4}<1
$$
Solving the inequality using the interval method, we get that $-1<n<6$. Therefore, the maximum $n$ is 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) In math class, each dwarf needs to find a three-digit number without zero digits, divisible by 3, such that when 297 is added to it, the result is a number with the same digits but in reverse order. What is the minimum number of dwarfs that should be in the class so that among the numbers they find, there are always at least two identical ones?
|
Answer: 19.
Solution: Let the number of numbers that satisfy the condition of the problem be $N$. Then, by the Pigeonhole Principle, the minimum number of gnomes must be $N+1$.
Let's write a three-digit number as $\overline{x y z}$, where $x$ is the number of hundreds, $y$ is the number of tens, and $z$ is the number of units. Since along with the number $\overline{x y z}$, the number $\overline{z y x}$ is also considered, then $x>0$ and $z>0$. According to the condition, $100 x+10 y+z+297=100 z+10 y+x$. Let's transform this:
$$
99 z-99 x=297 \Leftrightarrow x=z-3
$$
Since $0<x=z-3 \leq 9$ and $z \leq 9$, then $0<x \leq 6$. Thus, we have 6 suitable values for $x$. Each $x$ corresponds to one value of $z$, and $y$ is any number from 1 to 9 for which $\overline{x y z}$ is divisible by 3. Note that
$$
0=(x+y+z) \quad \bmod 3=(2 x+y) \quad \bmod 3
$$
which means any pair $(x, z)$ uniquely determines $y \bmod 3$. Among the numbers from 1 to 9, there are exactly 3 numbers with a given remainder when divided by 3. Therefore, the condition of the problem is satisfied by $6 \cdot 3=18$ numbers, and the minimum number of gnomes is 19.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. (40 points) Find the number of pairs of natural numbers $m$ and $n$, satisfying the equation $\frac{1}{m}+\frac{1}{n}=\frac{1}{2020}$.
|
Answer: 45.
Solution: Transform the given equation
\[
\begin{gathered}
\frac{1}{m}+\frac{1}{n}=\frac{1}{2020} \Leftrightarrow \frac{n+m}{m \cdot n}=\frac{1}{2020} \Leftrightarrow m n=2020(n+m) \Leftrightarrow \\
\Leftrightarrow m n-2020 n-2020 m+2020^{2}-2020^{2}=0 \Leftrightarrow(n-2020)(m-2020)=2020^{2}
\end{gathered}
\]
The solutions to this equation are \( m = d + 2020 \) and \( n = \frac{2020^{2}}{d} + 2020 \), where \( d \) is any divisor of \( 2020^{2} \). It remains to find the number of such divisors. Note that \( 2020^{2} = 2^{4} \cdot 5^{2} \cdot 101^{2} \). If \( d \) is a divisor of \( 2020^{2} \), then 2 can appear in its prime factorization in powers \( 0, \ldots, 4 \), and 5 and 101 can appear in powers \( 0, 1, 2 \). Therefore, the total number of such factorizations is \( 5 \cdot 3 \cdot 3 = 45 \).
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) From village $A$ to village $B$, the Indians take three times as long to travel by canoe as from village $B$ to village $A$. How many times longer than usual can the Indians take to travel from $B$ to $A$ by canoe without paddles?
|
Answer: 3 times.
Solution: It is not hard to see that village V is upstream from village A. Let's denote the speed of the river current as $v_{r}$, and the average speed of the canoe in still water as $v$. If $S$ is the distance along the river from A to V, then from the condition we have
$$
3 \frac{S}{v+v_{r}}=\frac{S}{v-v_{r}}
$$
From this, we get that
$$
v=2 v_{r}
$$
Let the time it takes for the Indians to travel from V to A without paddles (i.e., only by the river current) be $k$ times longer than with paddles. This gives us the equation
$$
k \frac{S}{v+v_{r}}=\frac{S}{v_{r}}
$$
Then, taking into account $(*)$, we find that $k=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) The ballroom in the palace of the thirtieth kingdom is a region on the plane, the coordinates of which satisfy the conditions $|x| \leqslant 4,|y| \leqslant 6$. How many identical parquet tiles, having the shape of a rectangle with sides 1.5 and 2, are needed to tile the floor of the room? Tiling is considered to be laying without gaps, without overlaps, and not extending beyond the boundaries of the area.
|
Answer: 32.
Solution: From the condition, we find that the magic room is a rectangle with sides parallel to the coordinate axes, and the lengths of the sides parallel to the x-axis are 8, while the lengths of the sides parallel to the y-axis are 12. It is not hard to see that a tiling exists (along the side of the room with length 12, an integer number of tiles with side length 1.5 can be placed; and, obviously, along the side of the room with length 8, an integer number of tiles with side length 2 can also be placed). The area of the room is $8 \times 12 = 96$, and the area of one tile is $1.5 \times 2 = 3$. Therefore, we get that a total of $96 \div 3 = 32$ tiles are required.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (40 points) To enter Ali Baba's cave, it is necessary to zero out 28 counters, each set to a natural number in the range from 1 to 2017. Treasure hunters are allowed, in one move, to decrease the values of some of the counters by the same number, which they can change from move to move. Indicate the minimum number of moves in which the treasure hunters can, with certainty, zero out the counters (regardless of the initial values) and enter the cave.
|
Answer: In 11 moves.
## Solution:
Estimation. Suppose the counters are set to all powers of two from 1 to 1024 and some 17 other numbers. Since the order of moves does not matter, we can arrange them in descending order of the numbers being subtracted. We will show by induction that after the $k$-th move, there is a number on the board that is not less than $2^{10-k}$. The base case - 0 moves - is obvious. Suppose after $k$ moves, there is a number on the board that is not less than $2^{10-k}$. If we subtract a number greater than $2^{10-k-1}$ on the $k$-th move, then this and the previous moves have not affected the number $2^{10-k-1}$, and the proof is complete. Otherwise, after the subtraction, there will be a number not less than $2^{10-k-1}$, which is not less than $2^{10-k}$. From the proven statement, it follows that after 10 moves, there will still be a number on the board that is not less than $2^{0}=1$, meaning that at least 11 moves are required.
Example. By subtracting $2^{10}$ from all numbers not less than $2^{10}$, we will make all numbers less than $2^{10}$. The next step will similarly make all numbers less than $2^{9}$, and so on. After the tenth step, all numbers will be less than $2^{0}=1$, that is, they will all be zeros.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an island, there are two tribes: the tribe of knights, who always tell the truth, and the tribe of liars, who always lie. On the main holiday, 2017 islanders sat around a large round table. Each islander said the phrase: "my neighbors are from the same tribe." It turned out that two liars made a mistake and accidentally told the truth. How many liars can sit at this table?
|
Answer: 1344 liars
Solution. Note that no two knights can sit next to each other, meaning the neighbors of each knight are liars. Indeed, consider a chain of knights sitting in a row, surrounded by liars. Suppose there are at least two knights in this chain. The neighbors of the extreme knight are a knight and a liar, but this is impossible since the knight would then be lying. Therefore, no two knights sit next to each other, and the neighbors of each knight are liars.
We will call those liars who did not make a mistake, true liars. According to the condition, the neighbors of each true liar are from different tribes. Therefore, the neighbors of true liars must be a knight and a liar. This means the sequence "LRLRL...LRL" repeats until it encounters a false liar. If a knight sits before him, then a knight also sits after him. If a liar sits before him, then a liar also sits after him. Therefore, the seating arrangement with false liars can be obtained from the seating arrangement "LRLRL...LRL" by either seating a false liar between two liars or by a true liar leaving the table (and then his neighbor liar becomes a false liar). The first action increases the remainder of the total number of people sitting at the table divided by 1, the second decreases it by 1. Since in the seating arrangement "LRLRL...LRL" the number of islanders is divisible by 3, and 2017 gives a remainder of 1 when divided by 3, we need to reduce the remainder 0 by 1 twice. Thus, we need to remove two liars from the seating arrangement of 2019 islanders. Therefore, the number of liars is $2019 \cdot \frac{2}{3}-2=1344$.
|
1344
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In each cell of a $2017 \times 2017$ board, there is a chip. In one operation, you can remove a chip that has a non-zero even number of neighbors (neighbors are chips located in cells that share a side or a corner). What is the minimum number of chips that can be left on the board using such operations?
#
|
# Answer: 2
Solution. If there are only two chips on the board, then each of them has no more than one neighbor, and according to the rules, they cannot be removed. Therefore, at least two chips will remain. We will show how to leave exactly two chips on the board. For this, we will provide an algorithm that allows clearing two adjacent rows (or two adjacent columns) on an $m \times n$ board. Let's assume we want to clear the top two rows. We will number the cells from 1 to $n$. First, we will remove the chip from the 2nd cell of the second row (this can be done because it has 8 neighbors), then we will remove the corner chip (it now has 2 neighbors), then the 3rd chip from the first row (it has 4 neighbors), then the 2nd chip from the first row (it has 2 neighbors), and the 1st chip from the second row (it also has 2 neighbors). Next, moving from left to right, we will sequentially remove all the chips from the first row (each of them will have 4 neighbors at the moment of removal, except for the last one, which will have 2 neighbors), and then similarly remove the chips from the second row. This way, we will clear the two top rows. We will apply these actions sequentially, alternating between rows and columns, until only the chips in a $3 \times 3$ square remain. Dealing with them is quite simple: we remove the central one, then the four corner ones in any order, then the remaining top one, and finally, the remaining bottom one.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an island, there live knights who always tell the truth, and liars who always lie. In a room, 15 islanders gathered. Each of those in the room said two phrases: "Among my acquaintances in this room, there are exactly six liars" and "among my acquaintances in this room, there are no more than seven knights." How many knights can there be in this room?
|
Answer: 9 knights
Solution. If there is a liar in the room, then his statement "among my acquaintances in this room, there are no more than seven knights" is a lie, and there are no fewer than 8 knights in the room. If there is a knight in the room, then his statement "among my acquaintances in this room, there are exactly six liars" is true, and there are no fewer than 6 liars in the room. Therefore, there are both knights and liars in the room, with no fewer than 8 knights and no fewer than 6 liars. This means there are no more than $15-6=9$ knights. Suppose there are exactly 8 knights. Then there are 7 liars in the room, and each of them has more than 7 acquaintances who are knights. Therefore, each of them is acquainted with all the knights in the room. This means that each knight is also acquainted with all the liars in the room, i.e., each knight has 7 acquaintances who are liars. But then he would be lying. Therefore, there cannot be 8 knights. Thus, there are 9 knights in the room. Such a situation is possible if each knight knows each liar, and no one else is acquainted with anyone else.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given various natural numbers $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ and $a_{7}$. Prove that $\left(a_{1}-a_{2}\right)^{4}+\left(a_{2}-a_{3}\right)^{4}+\left(a_{3}-a_{4}\right)^{4}+\left(a_{4}-a_{5}\right)^{4}+\left(a_{5}-a_{6}\right)^{4}+\left(a_{6}-\right.$ $\left.a_{7}\right)^{4}+\left(a_{7}-a_{1}\right)^{4} \geqslant 82$.
|
Solution. Note that all the terms are no less than 1. If one of the brackets is at least 3, then the entire sum is certainly greater than $3^{4}+1=82$. Therefore, we will assume from now on that the absolute value of any bracket does not exceed 2. Mark the numbers $a_{1}, a_{2}, \ldots, a_{7}$ on a line. Let $a_{j}$ be the smallest of them, and $a_{k}$ be the largest. Then $\left|a_{i}-a_{i+1}\right|$ is the length of the segment connecting points $a_{i}$ and $a_{i+1}$. Let's assume for definiteness that $k>j$. Then $\left|a_{k}-a_{j}\right| \leqslant\left|a_{j+1}-a_{j}\right|+\ldots+\left|a_{k}-a_{k-1}\right|$ and $\left|a_{j}-a_{k}\right| \leqslant\left|a_{k+1}-a_{k}\right|+\ldots+\left|a_{7}-a_{6}\right|+\left|a_{1}-a_{7}\right|+\ldots+\left|a_{j}-a_{j-1}\right|$. Adding these inequalities, we get the inequality
$$
\left|a_{1}-a_{2}\right|+\left|a_{2}-a_{3}\right|+\ldots+\left|a_{7}-a_{1}\right| \geqslant 2\left(a_{k}-a_{j}\right) \geqslant 12
$$
Thus, the sum of the absolute values is at least 12, which means we have either at least six twos, or five twos and two ones. The sum of the fourth powers of the differences in both cases is no less than 82.
|
82
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of rooks that can be placed on the cells of a $300 \times 300$ board so that each rook attacks no more than one other rook? (A rook attacks all cells it can reach according to chess rules, without passing through other pieces.)
#
|
# Answer: 400
First solution. We will prove that no more than 400 rooks can be placed on the board. In each row or column, there are no more than two rooks; otherwise, the rook that is not at the edge will attack at least two other rooks. Suppose there are $k$ columns with two rooks each. Consider one such pair. They attack each other, so there are no rooks in the rows where they are located. Thus, rooks can only be in $300-2k$ rows. Since there are no more than two rooks in each of these rows, the total number of rooks is no more than $2(300-2k) + 2k = 600 - 2k$. On the other hand, in $k$ columns, there are two rooks each, and in the remaining $300-k$ columns, there is no more than one rook, so the total number of rooks is no more than $(300-k) + 2k = 300 + k$. Therefore, the total number of rooks is no more than $\frac{1}{3}((600-2k) + 2(300+k)) = 400$.
Next, we will show how to place 400 rooks. On a $3 \times 3$ board, 4 rooks can be placed as shown in the figure, and then 100 such squares can be placed along the diagonal.
Second solution. On the board, there can be rooks that do not attack any other rooks, as well as pairs of rooks that attack each other. Let there be $k$ single rooks and $n$ pairs of rooks that attack each other. Then the total number of rooks on the board is $k + 2n$. We will count the total number of occupied rows and columns (for convenience, we will call them lines). Each single rook occupies its own row and its own column, i.e., two lines. Each pair of rooks occupies three lines. Therefore, the total number of lines occupied is $2k + 3n$. Thus, $2k + 3n \leq 600$. Therefore, $k + 2n = \frac{2}{3}(2k + 3n) - \frac{k}{3} \leq \frac{2}{3}(2k + 3n) \leq \frac{2}{3} \cdot 600 = 400$.
The example of placement is the same as in the first solution.
|
400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of chips that can be placed in the cells of a chessboard (no more than one chip per cell) so that no more than three chips are placed on each diagonal?
|
Answer: 38
Solution. Consider the eight-cell diagonal consisting of black cells, and the parallel diagonals consisting of black cells. These diagonals have $2, 4, 6, 8, 6, 4,$ and 2 cells. On each of the outermost diagonals, no more than two chips can be placed, and on each of the middle diagonals, no more than three. Therefore, a total of no more than $2 \cdot 2 + 5 \cdot 3 = 19$ chips can be placed on the black cells.
chips. Similarly, no more than 19 chips can be placed on the white cells. Therefore, a total of no more than 38 chips can be placed on the board.
An example of placing 38 chips is shown in the figure.
|
38
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an island, there live knights who always tell the truth, and liars who always lie. On the main holiday, 100 islanders sat around a large round table. Half of those present said: "both my neighbors are liars," and the rest said: "one of my neighbors is a liar." What is the maximum number of knights that can sit at this table?
|
# Answer: 67
Solution. Note that three knights cannot sit in a row, since then the middle knight would not be able to utter any of the required phrases. Let $k$ be the number of pairs of neighboring knights. Then each of the knights said the phrase "among my neighbors there is exactly one liar," so $2 k \leqslant 50$. Moreover, to the left of this pair there is definitely a liar, and all these liars are different. Let's call such two knights and a liar a triplet. In triplets, $3 k$ islanders are involved. Consider the remaining $100-3 k$ islanders. No two knights among them sit next to each other, nor next to knights from the triplets (otherwise, three knights in a row would form, which is impossible). Then to the left of each knight, there must be a liar, all these liars are different and distinct from the liars included in the triplets. Thus, the number of knights is no more than $2 k+\frac{1}{2}(100-3 k)=50+\frac{k}{2} \leqslant 50+\frac{25}{2}=67 \frac{1}{2}$. Therefore, the number of knights is no more than 67.
Here is an example showing that 67 knights can be present:
$$
\text { LKL LKL LKL ... LKL LK LK LK ... LK L }
$$
(the block "LKL" is repeated 25 times, the block "LK" - 12 times).
|
67
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) Young marketer Masha was supposed to survey 50 customers in an electronics store throughout the day. However, there were fewer customers in the store that day. What is the maximum number of customers Masha could have surveyed, given that according to her data, 7 of the respondents made an impulse purchase, 75% of the remaining respondents bought the product under the influence of advertising, and the number of customers who chose the product based on the advice of a sales consultant is one-third of the number who chose the product under the influence of advertising.
|
Answer: 47.
Solution: Let the number of customers surveyed be $x$. Then, the number of customers who made a purchase under the influence of advertising is $(x-7) \cdot 3 / 4$, and the number of customers who made a purchase on the advice of a sales consultant is $(x-7)/4$. Since the number of customers can only be an integer, $x-7$ must be divisible by 4. The maximum suitable number $x$, less than 50, is 47.
|
47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) The reception hall in the palace of the tritriandiat kingdom consists of points on the plane whose coordinates satisfy the condition $4|x|+5|y| \leqslant 20$. How many identical two-sided parquet tiles, shaped as right triangles with legs of 1 and 5/4, are needed to tile the floor of the hall? Tiling is considered to be laying without gaps, overlaps, and not exceeding the boundaries of the area.
|
Answer: 64.
Solution: It is not hard to see that the reception hall is a rhombus with vertices at points $(-5,0),(0,4),(5,0)$ and $(0,-4)$, and each quarter of the hall (bounded by the coordinate axes and one of the sides, i.e., forming a right-angled triangle) is similar to one parquet tile with a similarity ratio of 4. Therefore, to tile the hall, $4 \cdot 4^{2}=64$ tiles will be required.
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (40 points) At the "Horizon" base, 175 university students arrived. Some of them are acquainted with each other, while others are not. It is known that any six students can be accommodated in two three-person rooms such that all those in the same room are acquainted with each other. What is the minimum number of pairs of acquainted students that could be among those who arrived at the base?
|
Answer: 15050.
Solution: It is clear that each student has no more than three unfamiliar students. If each student has no more than two unfamiliar students, then each is familiar with at least 172 students, and the total number of pairs of familiar students is no less than $175 \times 172 / 2 = 15050$. Suppose there is a student $A$ who has three unfamiliar students $B_{1}, B_{2}$, and $B_{3}$. Consider the group of six students: $A, B_{1}$, $B_{2}$, $B_{3}$, and two other arbitrary students $C$ and $D$. They can be seated in two three-person rooms, so $A$ must be in the same room with $C$ and $D$, which means $C$ and $D$ are familiar with each other and with $A$. Therefore, any two students, different from $B_{1}$, $B_{2}$, and $B_{3}$, are familiar with each other. In particular, if some student, different from $B_{1}$, $B_{2}$, and $B_{3}$, is unfamiliar with someone, then this someone is one of $B_{1}$, $B_{2}$, and $B_{3}$. But each $B_{i}$ is unfamiliar with no more than three students, so the number of pairs of unfamiliar students is no more than nine. Therefore, in this case, the number of pairs of familiar students is no less than $175 \cdot 174 / 2 - 9 = 15216 > 15050$. We will now show that 15050 pairs of students can exist. Seat all students at a large round table and make everyone familiar except those sitting next to each other. It is not difficult to verify that this construction satisfies the condition of the problem.
|
15050
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) In the Martian calendar, a year consists of 5882 days, and each month has either 100 or 77 days. How many months are there in the Martian calendar?
|
Answer: 74.
Solution: Let $x$ be the number of months with 100 days, and $y$ be the number of months with 77 days. According to the problem, $100 x + 77 y = 5882$. It is obvious that $y \leqslant 66$, otherwise $x < 0$. Notice that
$$
x \bmod 11 = 100 x \quad \bmod 11 = 5882 \quad \bmod 11 = 8
$$
Thus, $x = 11 k + 8$ for some integer $k$, from which we have
$$
(11 k + 8) \cdot 100 + 77 y = 5882 \Longleftrightarrow 1100 k = 5082 - 77 y = 77(66 - y)
$$
The right side is divisible by 100, but 77 and 100 are coprime. Therefore, the number $66 - y$, which lies between 0 and 65, must be divisible by 100. This is only possible when $y = 66$. Therefore, $x = 0.01 \cdot (5882 - 76 \cdot 66) = 8$ and $x + y = 74$.
|
74
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) Professor K., wishing to be known as a wit, plans to tell no fewer than two but no more than three different jokes at each of his lectures. At the same time, the sets of jokes told at different lectures should not coincide. How many lectures in total will Professor K. be able to give if he knows 8 jokes?
|
Answer: 84.
Solution: The professor can use all possible triplets of anecdotes (the number of which is $C_{8}^{3}=56$), as well as all pairs of anecdotes (which is $C_{8}^{2}=28$). Therefore, the maximum number of sets of anecdotes the professor can use in lectures is $56+28=84$.
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (20 points) We will call a word any finite sequence of letters of the Russian alphabet. How many different five-letter words can be formed from the letters of the word САМСА? And from the letters of the word ПАСТА? In your answer, indicate the sum of the found numbers.
|
Answer: 90.
Solution: In the word SAMSA, the letter A appears twice and the letter S appears twice. Therefore, the number of different words will be $\frac{5!}{2!\cdot 2!}=30$. In the word PASTA, only the letter A appears twice. Therefore, the number of different words in this case will be $\frac{5!}{2!}=60$. In total, we get $30+60=90$.
|
90
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (40 points) Let $P(n)$ denote the product of the digits of a natural number $n$. For what largest natural number $k$ does there exist a natural number $n>10$ such that
$$
P(n)<P(2 n)<\ldots<P(k n) ?
$$
|
# Answer: 9.
Solution: First, let's show that $k<10$. Indeed, for $k \geqslant 10$, the set of numbers includes $P(10 n)$. It equals zero because the number $10 n$ ends in 0. Then $P(n)<0$, which is impossible.
Now let's provide an implementation for $k=9$. We can take $n$ as a number of the form $\underbrace{\overline{11 \ldots 1}}_{j}$ for any $j \geqslant 2$. In this case, $P(s n)=s^{j}, s=1, \ldots, k$, and the numbers $s^{j}$ clearly increase.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (40 points) The numbers from 1 to 600 are divided into several groups. It is known that if a group contains more than one number, then the sum of any two numbers in this group is divisible by 6. What is the minimum number of groups that can be formed?
|
Answer: 202.
Solution: For $k=0,1, \ldots, 5$, let $G_{k}$ be the set of numbers from 1 to 600 that give a remainder of $k$ when divided by 6. Suppose a number $a$ from $G_{k}$ is included in some group. If another number $b$ is also in this group, then it belongs to $G_{6-k}$, otherwise $a+b$ is not divisible by 6. Suppose there is a third number $c$ in this group. Then it lies in both $G_{k}$ and $G_{6-k}$. This is possible only for $k=0$ and $k=3$. Numbers not in $G_{0}$ and $G_{3}$ can only be included in two-element groups, and there are 400 such numbers. Therefore, they form at least 200 groups. The sets $G_{0}$ and $G_{3}$ can form groups, but they cannot be combined into one. Thus, at least 202 groups are required in total.
We will provide an implementation of the partition into 202 groups. One of them will be $G_{0}$, another will be $G_{3}$, and we will also choose groups of the form $\{6 n+k, 6 n+6-k\}$, where $n=0,1, \ldots, 99$ and $k=1,2$.
|
202
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. (40 points) Five boys played a word game: each of them wrote down 7 different words. It turned out that each boy had exactly 2 words that were not found in any of the other boys' lists. What is the maximum number of different words that the boys could have written in total?
|
Answer: 22.
Solution: In total, $5 \times 7=35$ words were written. Since each boy wrote exactly 2 words that did not appear in any of the other boys' writings, there were a total of $5 \times 2=10$ such unique words. From the remaining 25 words (repeated), each was written at least twice. Therefore, there are no more than $\left[\frac{25}{2}\right]=12$ of them, and the total number of words does not exceed $10+12=22$.
Example of the distribution of repeated words $\left(s_{i}\right)$ :
| | $s_{1}$ | $s_{2}$ | $s_{3}$ | $s_{4}$ | $s_{5}$ | $s_{6}$ | $s_{7}$ | $s_{8}$ | $s_{9}$ | $s_{10}$ | $s_{11}$ | $s_{12}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $M_{1}$ | + | + | + | + | + | | | | | | | |
| $M_{2}$ | + | | | | + | + | + | + | | | | |
| $M_{3}$ | | + | | | | + | | | + | + | | + |
| $M_{4}$ | | | + | | | | + | | + | | + | + |
| $M_{5}$ | | | | + | | | | + | | + | + | + |
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. (40 points) In a store where all items cost a whole number of rubles, two special offers are in effect:
1) A customer who buys at least three items can choose one item as a gift (free of charge), the cost of which does not exceed the minimum cost of the paid items;
2) A customer who buys exactly one item for no less than $N$ rubles receives a $20\%$ discount on the next purchase (of any number of items).
A customer, visiting the store for the first time, wants to purchase exactly four items with a total cost of 1000 rubles, the cheapest of which costs no less than 99 rubles. Determine the largest $N$, for which the second offer is more beneficial for him.
|
Answer: 504.
Solution: Let $S$ denote the total cost of the four items that interested the customer, and let $X$ be the minimum possible cost of the items. Being interested in exactly four items means that the customer can take advantage of either offer 1 or offer 2, but not both.
Let the items cost $s_{1}, s_{2}, s_{3}, s_{4}$ rubles, where $s_{1} \geqslant s_{2} \geqslant s_{3} \geqslant s_{4} \geqslant X$. In the case of the first special offer, the customer can only receive the item costing $s_{4}$ for free; thus, they will spend $S-s_{4}$ rubles. In the case of the second special offer, the customer will spend
$$
s_{i}+0.8\left(S-s_{i}\right)=0.2 s_{i}+0.8 S
$$
where $s_{i}$ is the minimum of the costs that are not less than $N$ (it exists, otherwise the second offer could not be used).
The second special offer is more beneficial to the customer if
$$
0.2 s_{i}+0.8 S<S-s_{4} \Leftrightarrow 0.2 s_{i}<0.2 S-s_{4} \Leftrightarrow s_{i}<S-5 s_{4}
$$
from which $N \leqslant s_{i}<S-5 s_{4} \leqslant S-5 X$, that is, $N \leqslant S-1-5 X=1000-1-5 \cdot 99=504$.
Let's check that the value 504 is achievable for $N$. Suppose the costs of the items are 99, 198, 199, and 504 rubles. And suppose the customer buys the item costing 504 rubles to use the second special offer. Then they will pay the amount $504+$ $+0.8 \cdot 496=900.8$, which is less than the amount spent in the case of using the first special offer $-1000-99=901$.
|
504
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Triangle $A B C$ with angle $\angle A B C=135^{\circ}$ is inscribed in circle $\omega$. The lines tangent to $\omega$ at points $A$ and $C$ intersect at point $D$. Find $\angle A B D$, given that $A B$ bisects segment $C D$. Answer: $90^{\circ}$
|
Solution. Let $O$ be the center of $\omega$, $M$ be the intersection point of lines $A B$ and $C D$. Note that
$$
\angle A O C=2\left(180^{\circ}-\angle A B C\right)=2\left(180^{\circ}-135^{\circ}\right)=90^{\circ} .
$$
Then quadrilateral $A O C D$ is a square, and thus $\angle A D C=90^{\circ}$. By the tangent-secant theorem,
$$
D M^{2}=M C^{2}=B M \cdot A M, \quad \text { that is } \quad \frac{D M}{A M}=\frac{B M}{D M} .
$$
Therefore, triangles $D B M$ and $A D M$ are similar, from which
$$
\angle A B D=180^{\circ}-\angle M B D=180^{\circ}-\angle A D M=90^{\circ}
$$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) In math class, each dwarf needs to find a three-digit number such that when 198 is added to it, the result is a number with the same digits but in reverse order. For what maximum number of dwarfs could all the numbers they find be different?
|
Answer: 70.
Solution: By the Pigeonhole Principle, the maximum number of gnomes is equal to the number of numbers that satisfy the condition of the problem.
Let the three-digit number be denoted as $\overline{x y z}$, where $x$ is the hundreds digit, $y$ is the tens digit, and $z$ is the units digit. Since the number $\overline{x y z}$ and the number $\overline{z y x}$ are considered together, then $x>0$ and $z>0$. According to the condition, $100 x + 10 y + z + 198 = 100 z + 10 y + x$. Transforming this, we get:
$$
99 z - 99 x = 198 \Leftrightarrow x = z - 2.
$$
Since $0 < x = z - 2 \leq 9$ and $z \leq 9$, then $0 < x \leq 7$. Therefore, there are 7 possible values for $x$. Each $x$ corresponds to one value of $z$, while $y$ can be any digit. Thus, the number of numbers that satisfy the condition of the problem is $7 \cdot 10 = 70$.
|
70
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. (40 points) On an island, there live only 50 knights, who always tell the truth, and 15 commoners, who can either tell the truth or lie. A scatterbrained professor, who came to the island to give a lecture, forgot what color hat he was wearing. How many of the local residents should the professor ask about the color of his hat to be sure of what it is?
|
Answer: 31.
Solution: Since the professor will only ask about the color of the hat, to accurately determine the color of the hat, it is necessary to survey more knights than commoners. In the worst case, among those surveyed, there could be all the commoners on the island, i.e., 15 people; therefore, it is necessary to survey no fewer than 31 people to ensure that the opinion of the knights prevails.
|
31
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (30 points) In the royal dining hall, there are three tables, and three identical pies are served. For lunch, the king invited six princes to his table. At the second table, one can seat from 12 to 18 courtiers, and at the third table, from 10 to 20 knights. Each pie is cut into equal pieces according to the number of people sitting at the table. There is a rule at the court - the lunch of a knight together with the lunch of a courtier equals the lunch of the king. Determine the maximum possible number of knights the king can invite to lunch on this day. How many courtiers will sit at their table in this case?
|
Answer: Both guests and courtiers will be 14 people on that day.
First solution: Let the number of courtiers at the table be $a$, and the number of knights be $-b$, then the dining rule can be written as $\frac{1}{a} + \frac{1}{b} = \frac{1}{7} \Leftrightarrow \frac{1}{b} = \frac{1}{7} - \frac{1}{a}$. Maximizing the value of $b$ is equivalent to minimizing the value of $\frac{1}{b}$, which, from the dining rule, is equivalent to maximizing the value of $\frac{1}{a}$, which is equivalent to minimizing the value of $a$. Therefore, the options should be tried starting with the minimum possible number of courtiers.
$$
\begin{aligned}
& a=12 \Rightarrow b=\frac{7 a}{a-7}=\frac{7 \cdot 12}{5} \notin \mathbb{N} \\
& a=13 \Rightarrow b=\frac{7 a}{a-7}=\frac{7 \cdot 13}{6} \notin \mathbb{N} \\
& a=14 \Rightarrow b=\frac{7 a}{a-7}=\frac{7 \cdot 14}{7}=14
\end{aligned}
$$
Second solution: Let the number of courtiers at the table be $a$, and the number of knights be $-b$, then the dining rule can be written as $\frac{1}{a} + \frac{1}{b} = \frac{1}{7} \Leftrightarrow 7(a+b) = ab$. Thus, the value of $ab$ must be divisible by 7, i.e., one of the numbers $a$ and $b$ must be divisible by 7. If the number of knights is divisible by 7, then it is 14, as among the numbers from 10 to 20, only 14 is divisible by 7. If the number of courtiers is divisible by 7, then it is also 14, as it lies in the range from 12 to 18. Thus, in any case, one of the numbers $a$ and $b$ is 14, and then the other is also 14.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) During the draw before the math marathon, team captains were asked to name the smallest possible sum of the digits in the decimal representation of the number $n+1$, given that the sum of the digits of the number $n$ is 2017. What was the answer given by the captain of the team that won the draw?
|
Answer: 2.
Solution: First, we show that the answer is not less than 2. If the sum of the digits of the number $n+1$ is 1, then $n+1=10 \ldots 0$, and the decimal representation of $n$ consists entirely of nines. Then the number $n$ is divisible by 9, and the sum of its digits, therefore, is also. But this is impossible since 2017 is not divisible by 9.
It remains to provide an example of a number $n+1$ whose sum of digits is 2. Since $2017=224 \cdot 9+1$, we can set $n=19 \ldots 9$, where the digit 9 is repeated 224 times. Indeed, in this case, $n+1=20 \ldots 0$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) Before the math lesson, the teacher wrote nine consecutive numbers on the board, but the duty students accidentally erased one of them. When the lesson began, it turned out that the sum of the remaining eight numbers is 1703. Which number did the duty students erase?
|
Answer: 214.
Solution: Let the average of the original numbers be $a$. Then these numbers can be written in a symmetric form:
$$
a-4, a-3, a-2, a-1, a, a+1, a+2, a+3, a+4
$$
The erased number has the form $a+b$, where $-4 \leqslant b \leqslant 4$, and the sum of the remaining numbers is $9a - (a+b) = 8a - b$. On the other hand, this sum is also equal to $1703 = 8 \cdot 213 - 1$. Therefore,
$$
8 \cdot 213 - 1 = 8a - b, \quad \text{from which} \quad 8(a - 213) = b - 1
$$
Then the number $b-1$ is divisible by 8 and lies in the interval $[-5, 3]$. Thus, $b=1, a=213$, and the number that was erased is $213 + 1 = 214$.
|
214
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) Alexei came up with the following game. First, he chooses a number $x$ such that $2017 \leqslant x \leqslant 2117$. Then he checks if $x$ is divisible by 3, 5, 7, 9, and 11 without a remainder. If $x$ is divisible by 3, Alexei awards the number 3 points, if by 5 - then 5 points, ..., if by 11 - then 11 points. The points earned for the number are summed. Which number should be chosen in this game to score the maximum number of points?
|
Answer: $2079=11 \cdot 9 \cdot 7 \cdot 3$.
Solution: Note that the divisibility of $x$ by 9 immediately gives 12 points, as it also implies divisibility by 3. If the number $x$ is not divisible by 11, it will score no more than $9+7+5+3=24$ points, and if it is not divisible by 9, it will score no more than $11+7+5+3=26$ points. If the number is divisible by both 11 and 9, then it is a multiple of 99. In the given range, the only such number is 2079. Since 2079 is also divisible by 7, it gives $11+9+7+3=30$ points.
It remains to note that more than 30 points cannot be scored. Indeed, such a result can only be achieved by a number that is simultaneously divisible by $3, 5, 7, 9$, and 11. The smallest such number is $11 \cdot 9 \cdot 7 \cdot 5=3465$, but it is greater than 2117.
|
2079
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (30 points) In triangle $K I A$, angles $K$ and $I$ are equal to $30^{\circ}$. On the line passing through point $K$ perpendicular to side $K I$, a point $N$ is marked such that $A N$ is equal to $K I$. Find the measure of angle $KAN$.
|
Answer: $90^{\circ}$ or $30^{\circ}$.
Solution: Let $K I=2 a$, and point $H$ be the foot of the perpendicular from vertex $A$ to the
line $K N$. According to the condition, $\triangle K I A$ is isosceles with base $K I$, hence $A$ lies on the perpendicular bisector of $K I$, from which we have that $A H=a$.
It is easy to notice that $\triangle A H N$ is a right triangle, in which the leg $A H$ is half the hypotenuse $A N$. Therefore, $\angle H A N=60^{\circ}$. Since $A H \| K I$, then $\angle K A H = \angle A K I$. From this, we get that, since point $N$ can be located on different sides of the line $K I$, either $\angle K A N = \angle H A N + \angle H A K = 60^{\circ} + 30^{\circ}$, or $\angle K A N = \angle H A N - \angle H A K = 60^{\circ} - 30^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Inside the circle $\omega$ are located intersecting at points $K$ and $L$ circles $\omega_{1}$ and $\omega_{2}$, touching the circle $\omega$ at points $M$ and $N$. It turned out that points $K, M$, and $N$ lie on the same line. Find the radius of the circle $\omega$, if the radii of the circles $\omega_{1}$ and $\omega_{2}$ are 3 and 5, respectively.
|
Answer: 8.
Solution. Let $O, O_{1}, O_{2}$ be the centers of the circles $\omega, \omega_{1}, \omega_{2}$, respectively. The radii $O M$ and $O_{1} M$ of the circles $\omega$ and $\omega_{1}$ are perpendicular to their common tangent at point $M$. Therefore, they are parallel, which means that point $O_{1}$ lies on the segment $O M$. Similarly, it follows that point $O_{2}$ lies on the segment $O N$ (see the figure). Since triangles $O M N, O_{1} M K$, and $O_{2} K N$ are isosceles,
$$
\angle M K O_{1} = \angle K M O_{1} = \angle K N O_{2} = \angle N K O_{2}
$$
Therefore, $K O_{1} \| N O$ and $K O_{2} \| M O$, which means that $O O_{1} K O_{2}$ is a parallelogram. Then
$$
M O = M O_{1} + O_{1} O = M O_{1} + K O_{2} = 3 + 5 = 8
$$
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the country of Alphia, there are 150 cities, some of which are connected by express trains that do not stop at intermediate stations. It is known that any four cities can be divided into two pairs such that there is an express train running between the cities of each pair. What is the minimum number of pairs of cities connected by express trains?
|
Answer: 11025.
Solution. Suppose that some city (let's call it Alfsk) is connected by express trains to no more than 146 cities. Then a quartet of cities, consisting of Alfsk and any three with which it is not connected, does not satisfy the problem's condition, since Alfsk cannot be paired with any of the three remaining cities. Therefore, each city is connected to at least 147 cities. Consequently, the total number of pairs of cities connected by express trains is no less than $\frac{147 \cdot 150}{2}=11025$.
Now, let's show that there can be exactly 11025 pairs of cities. Number the cities from 1 to 150 and connect by express trains all cities except the first and the 150th, as well as cities whose numbers differ by one. Let's check that this construction satisfies the problem's condition. Since each city is connected by express trains to 147 cities, the total number of connected city pairs is exactly $\frac{147 \cdot 150}{2}=11025$. Now, take any quartet of cities. There are two cases.
1) There is a city not connected to two of the three remaining cities. Let city $A$ not be connected to cities $B$ and $C$, but be connected to city $D$. Then cities $B$ and $C$ must be connected to each other, since the remainders of their numbers when divided by 150 differ by 2. Therefore, the pairs $(A, D)$ and $(B, C)$ are suitable.
2) All cities are connected to at least two of the three remaining cities. Let city $A$ be connected to cities $B$ and $C$. By assumption, city $D$ must be connected to $B$ or $C$. If it is connected to $B$, then the pairs $(A, C)$ and $(B, D)$ are suitable, and if to $C$, then the pairs $(A, B)$ and $(C, D)$.
|
11025
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Inside the circle $\omega$ is a circle $\omega_{1}$ that is tangent to it at point $K$. The circle $\omega_{2}$ is tangent to the circle $\omega_{1}$ at point $L$ and intersects the circle $\omega$ at points $M$ and $N$. It turns out that points $K, L$, and $M$ lie on the same line. Find the radius of the circle $\omega$, if the radii of the circles $\omega_{1}$ and $\omega_{2}$ are 4 and 7, respectively.
|
Answer: 11.
Solution. Let $O, O_{1}, O_{2}$ be the centers of the circles $\omega, \omega_{1}, \omega_{2}$, respectively. The radii $O K$ and $O_{1} K$ of the circles $\omega$ and $\omega_{1}$ are perpendicular to their common tangent at point $K$. Therefore, they are parallel, which means that point $O_{1}$ lies on the segment $O K$ (see the figure). Since triangles $O K M$, $O_{1} K L$, and $O_{2} L M$ are isosceles,
$$
\angle K M O = \angle L K O_{1} = \angle K L O_{1} = \angle M L O_{2} = \angle L M O_{2}
$$
Therefore, $K O \parallel M O_{2}$ and $O_{1} O_{2} \parallel M O$, which means that $O O_{1} O_{2} M$ is a parallelogram. Then
$$
O M = O_{1} O_{2} = O_{1} L + L O_{2} = 4 + 7 = 11
$$
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the country of Betia, there are 125 cities, some of which are connected by express trains that do not stop at intermediate stations. It is known that any four cities can be toured in a circle in some order. What is the minimum number of pairs of cities connected by express trains?
|
Answer: 7688.
Solution. Suppose that some city (let's call it Betsk) is connected by express trains to no more than 122 cities. Take a quartet of cities consisting of Betsk and any three other cities, two of which Betsk is not connected to. This quartet cannot be traveled in a circle, otherwise Betsk must be connected to at least two cities: one to arrive from, and another to depart to. Therefore, each city is connected to at least 123 cities. Consequently, the total number of pairs of cities connected by express trains is no less than $\frac{123 \cdot 125}{2}=7687 \frac{1}{2}$. But the number of pairs must be an integer, so it is at least 7688.
Now, let's show that the number of pairs of cities can be exactly 7688. Number the cities from 1 to 125 and connect by express trains all pairs of cities, except for pairs with numbers $2k-1$ and $2k$ for $k=1,2, \ldots, 62$. Let's verify that this construction satisfies the problem's condition. Since each city is connected by express trains to 123 cities, and the 125th city is connected to 124 cities, the total number of pairs of connected cities is $\frac{1}{2}(124 \cdot 123 + 124) = 7688$. Now, take any quartet of cities $A, B, C, D$. In this quartet, each city is connected to at least two of the others. Suppose that $B$ is connected to $A$ and $C$. If $D$ is also connected to $A$ and $C$, then the route $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ works. Otherwise, $D$ is not connected to exactly one of the cities $A$ and $C$ (let it be $C$). Then $C$ is connected to $A$, and $D$ is connected to $B$, and the cities can be traveled in a circle $A \rightarrow C \rightarrow B \rightarrow D \rightarrow A$.
|
7688
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In an arm wrestling tournament, 510 athletes are participating. 1 point is awarded for a win, and 0 points for a loss. If the winner initially had fewer points than the opponent, the winner additionally receives one point from the loser. In each round, participants with a difference of no more than 1 point in their scores compete. The tournament ends as soon as a sole leader is determined. What is the minimum number of rounds that need to be played?
|
# Answer: 9.
Solution. Let there be $N=2 m+k$ athletes in the leading group before the next round, with $2 m$ of them meeting each other, and $k$ meeting participants who have one point less. Note that if athletes with $n$ and $n+1$ points meet, they will end up with $n$ and $n+2$ points regardless of the outcome. Therefore, after the round, there will be $m+k$ participants in the leading group. The minimum value of this sum is $\frac{N}{2}$ for even $N$ and $\frac{N+1}{2}$ for odd $N$. According to the problem, after the first round, there will be no fewer than 255 leaders, after the second round - no fewer than 128, and after each subsequent round, the number of leaders will decrease by no more than half. Therefore, it will take no fewer than $2+\log _{2} 128=9$ rounds.
We will show that the tournament can be completed in 9 rounds. We will prove two statements.
1) In a tournament with $2^{n}$ participants, the winner can be determined in $n$ rounds. We will use induction on $n$. For $n=1$, this is obvious. Suppose the statement is true for some $n$. Then, in a tournament with $2^{n+1}$ participants, after the first round, $2^{n}$ athletes will have 0 points and $2^{n}$ will have 1 point. We will conduct two independent tournaments in these groups. By the induction hypothesis, both can be completed in $n$ rounds. The winner of the second tournament will become the overall winner, and he will be determined in $n+1$ rounds.
2) For $n \geqslant 3$, in a tournament with $2^{n}-2$ participants, the winner can be determined in $n$ rounds. After the first round, $2^{n-1}-1$ athletes will have 0 points and $2^{n-1}-1$ will have 1 point. If in the second round, only one pair of opponents has a different number of points, then after the round, $2^{n-2}$ participants will have 0 points and 2 points, and $2^{n-1}-2$ participants will have 1 point. We will now use induction on $n$. For $n=3$, we will pair athletes with the same number of points, after which the tournament will end. Suppose $n>3$ and the statement is true for $n-1$. By statement 1) and the induction hypothesis, independent tournaments can be organized in the groups with 0, 1, and 2 points, and the first and third groups will end in $n-2$ rounds, while the second group will end in $n-1$ rounds (but the last round will not be needed). The winner of the third group will win the entire tournament, as he will have $n+1$ points, while participants from other groups will have no more than $n$ points. In total, the tournament will last $n$ rounds.
It remains to apply statement 2) for $n=9$.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the village of Sosnovka, there are 240 residents, some of whom are acquainted with each other, while others are not. It is known that any five residents can be seated at a round table such that each of them is acquainted with both of their neighbors. What is the minimum number of pairs of acquaintances that can exist in Sosnovka?
|
Answer: 28440.
Solution. Suppose that some resident (let's call him Petya) is not acquainted with at least three other residents. Choose the following five people: Petya, the three residents he is not acquainted with, and one more arbitrary person. They cannot be seated around a round table in the required manner, since next to Petya there will inevitably be a person he is not acquainted with. Therefore, each resident of the village cannot have more than two unfamiliar people. Hence, each is acquainted with at least 237 residents, and the total number of pairs of acquaintances is no less than $\frac{240 \cdot 237}{2}=28440$.
Now, let's show that the number of pairs of acquaintances can be exactly 28440. Seat all residents around a large round table and introduce everyone except those sitting next to each other. Verify that this construction satisfies the problem's condition. Since each resident is not acquainted with exactly two others, he is acquainted with exactly 237 people, and the total number of pairs of acquaintances is $\frac{240 \cdot 237}{2}=28440$. Now, take any five residents and seat them in the required manner. Remove all others from the large round table and denote the remaining in cyclic order as $A, B, C, D, E$. Then the seating arrangement $A, C, E, B, D$ will work. Indeed, any two new neighbors did not sit next to each other at the large round table and therefore know each other.
|
28440
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a tennis tournament, 254 schoolchildren are participating. A win earns 1 point, a loss earns 0 points. If the winner initially had fewer points than the opponent, the winner additionally receives one point from the loser. In each round, participants with the same number of points compete, but in one of the pairs, a difference of 1 point between opponents is allowed. The tournament ends as soon as a sole leader is determined. How many schoolchildren will finish the tournament with 5 points?
|
Answer: 56.
Solution. Let $f(m, k)$ denote the number of students who have $k$ points after $m$ rounds. If $f(m, k)$ is even for any $k \in \{0, \ldots, m\}$, then participants with different numbers of points will not meet in the $(m+1)$-th round (otherwise, there would be at least two such meetings). Also, note that if athletes with $n$ and $n+1$ points meet, they will end up with $n$ and $n+2$ points, respectively, regardless of the outcome. We will prove two statements.
1) In a tournament with $2^n$ participants, after $m$ rounds, $2^{n-m} \cdot C_m^k$ athletes will have $k$ points, where $m \leq n$ and $k \in \{0, \ldots, m\}$. Let $f(m, k)$ be the number of participants who have $k$ points after $m$ rounds. We will use induction on $m$. If $m=0$, then $k=0$, and $f(0,0)=2^n$. For the inductive step, assume that the required equality holds for some $m < n$. Then each group with the same number of points contains an even number of participants, so all participants can be paired. After the $(m+1)$-th round, the groups of athletes with no wins and no losses will be halved. Therefore,
$$
f(m+1,0)=\frac{1}{2} f(m, 0)=\frac{1}{2} \cdot 2^{n-m}=2^{n-(m+1)} \cdot C_{m+1}^{0} \quad \text{and} \quad f(m+1, m+1)=\frac{1}{2} f(m, m)=2^{n-(m+1)} \cdot C_{m+1}^{m+1}
$$
Now, let $k \in \{1, \ldots, m\}$. After the $(m+1)$-th round, $k$ points will be held by those who had $k$ points and lost, as well as those who had $k-1$ points and won. Therefore,
$$
f(m+1, k)=\frac{1}{2} \cdot f(m, k)+\frac{1}{2} \cdot f(m, k-1)=2^{n-m-1}\left(C_m^k + C_m^{k-1}\right)=2^{n-(m+1)} \cdot C_{m+1}^k
$$
(in the last transition, we used the main identity of Pascal's triangle). Thus, the inductive step is complete.
2) In a tournament with $2^n - 2$ participants and fewer than $n$ rounds, the numbers $f(2m, k)$ are even for any $k$ from 0 to $n$, and the numbers $f(2m-1, k)$ are odd only for $k=m-1$ and $k=m$. We will use induction on $n$. For $n=2$, everything is obvious. Assume that the statement is true for some $n$. Then, in a tournament with $2^{n+1}$ participants, after the first round, $2^n - 1$ participants will have 0 points and 1 point. After the second round, $2^{n-1}$ participants will have 0 points and 2 points, and $2^n - 2$ participants will have 1 point. For the first two groups, we use 1), and for the third group, we use the inductive hypothesis.
Now, introduce fictitious participants $A$ and $B$. Let them play against each other in odd rounds, with $A$ winning; this does not affect the other participants. Additionally, let $A$ play against some $A'$ and lose, and $B$ win against some $B'$ in the $(2m)$-th round. Then $A'$ must have $m$ points, and $B'$ must have $(m-1)$ points. By 2), the numbers $f(2m-1, m-1)$ and $f(2m-1, m)$ are odd, and by 1), after adding $A$ and $B$, they become even. Therefore, in the absence of $A$ and $B$, participants $A'$ and $B'$ must play against each other; as a result, they will have $m-1$ and $m+1$ points, respectively, just as after playing against $A$ and $B$. Thus, adding $A$ and $B$ does not affect the distribution of points among the other participants.
Now, apply statement 1) for $n=8$. The tournament will end after 8 rounds, and $C_8^5 = \frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} = 56$ participants will have 5 points. Note that $A$ and $B$ will have 4 points each and, therefore, will not be included in this number.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression for $a, b \geqslant 0$
$$
\frac{|a-3 b-2|+|3 a-b|}{\sqrt{a^{2}+(b+1)^{2}}}
$$
|
Answer: 2.
Solution 1. The minimized expression is $d_{1}+d_{2}$, where $d_{1}, d_{2}$ are the distances from points $A(1,3)$ and $B(3,1)$ to the line $\ell$ defined by the equation $a x-(b+1) y+1=0$. It can be rewritten as
$y=\frac{a}{b+1} x+\frac{1}{b+1}$ or $y=p x+q$, where $p \geqslant 0, q \in(0,1]$. We can assume that the line $\ell$ intersects the segment $A B$, otherwise we can rotate it around the point $C(0, q)$ towards $A B$, reducing $d_{1}$ and $d_{2}$. Then $d_{1}+d_{2}=A B \cdot \sin \alpha$, where $\alpha$ is the angle between the lines $\ell$ and $A B$. The right side reaches its minimum when the angle $\alpha$ is the smallest, which is realized when $\alpha=\angle C A B$ or $\alpha=\angle C B A$. Both of these angles are not less than $\frac{\pi}{4}$, and $\angle C B A=\frac{\pi}{4}$ when $a=b=0$. Therefore, the minimum of $d_{1}+d_{2}$ is $A B \cdot \frac{\sqrt{2}}{2}=2$.
Solution 2. Let $A$ be the maximized expression, $c=b+1 \geqslant 1$. Then
$$
A=\frac{|a-3 c+1|+|3 a-c+1|}{\sqrt{a^{2}+c^{2}}}
$$
Consider three cases.
1) Suppose $c \geqslant 3 a+1$. Then
$$
A=\frac{3 c-a-1+c-3 a-1}{\sqrt{a^{2}+c^{2}}}=\frac{4 c-4 a-2}{\sqrt{a^{2}+c^{2}}} \geqslant \frac{8 a+2}{\sqrt{a^{2}+(3 a+1)^{2}}}=\frac{8 a+2}{\sqrt{10 a^{2}+6 a+1}}
$$
and the inequality becomes an equality when $c=3 a+1$. Moreover,
$$
\frac{(8 a+2)^{2}}{10 a^{2}+6 a+1}=\frac{64 a^{2}+32 a+4}{10 a^{2}+6 a+1} \geqslant \frac{40 a^{2}+24 a+4}{10 a^{2}+6 a+1}=4
$$
and equality is achieved when $a=0$. Thus, the minimum of $A$ is realized when $a=0, c=1$ and is equal to 2.
2) Suppose $\frac{a+1}{3} \leqslant c \leqslant 3 a+1$. Then
$$
A=\frac{3 c-a-1+3 a-c+1}{\sqrt{a^{2}+c^{2}}}=\frac{2 c+2 a}{\sqrt{a^{2}+c^{2}}} \geqslant \frac{2 \left(\frac{a+1}{3}\right)+2 a}{\sqrt{a^{2}+\left(\frac{a+1}{3}\right)^{2}}}=\frac{\frac{8}{3} a+\frac{2}{3}}{\sqrt{a^{2}+\left(\frac{a+1}{3}\right)^{2}}}=\frac{8 a+2}{\sqrt{10 a^{2}+2 a+1}} \geqslant \frac{8 a+2}{\sqrt{10 a^{2}+6 a+1}} \geqslant 2
$$
Thus, in this case, the minimum of $A$ is not realized.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Points $K, L$ and $M$ are the midpoints of sides $AB, BC$ and $CD$ of parallelogram $ABCD$. It turned out that quadrilaterals $KBLM$ and $BCDK$ are cyclic. Find the ratio $AC: AD$.
---
The translation is provided as requested, maintaining the original formatting and structure.
|
Answer: 2.
Solution. Let $N$ be the point of intersection of the diagonals of the parallelogram. Quadrilateral $K B L M$ is an inscribed trapezoid, so $K B = L M$. Multiplying this equality by 2, we get $A B = B D$. Then $A K = D N$ and
$$
\angle A K N = 180^{\circ} - \angle K A D = 180^{\circ} - \angle A D N = \angle D N K
$$
Thus, triangles $A K N$ and $D N K$ are equal, from which $D K = A N$. On the other hand, $B C D K$ is also an inscribed trapezoid, so $D K = B C = A D$. Then
$$
\frac{A C}{A D} = \frac{2 A N}{A D} = \frac{2 A N}{D K} = 2
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the village of Beryozovka, there are 200 residents, some of whom are acquainted with each other, while others are not. It is known that any six residents can be seated at a round table such that each of them is acquainted with both of their neighbors. What is the minimum number of pairs of acquainted residents in Beryozovka?
|
Answer: 19600.
Solution. Suppose that some resident (let's call him Vasya) is not acquainted with at least four other residents. We will select the following six people: Vasya, four residents he is not acquainted with, and one more arbitrary person. They cannot be seated around a round table in the required manner, since there will inevitably be an unfamiliar person sitting next to Vasya. Therefore, each resident of the village cannot have more than three unfamiliar people. Hence, each is acquainted with at least 196 residents, and the number of pairs of acquaintances is no less than $\frac{200 \cdot 196}{2}=19600$.
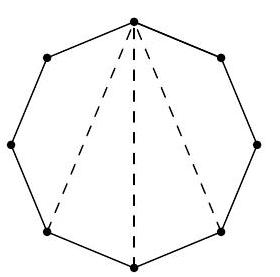
Now, let's show that the number of pairs of acquaintances can be exactly 19600. Seat all residents around a large round table. We will call two people almost opposite if there are at least 98 people sitting between them in both directions. Now, let's make all residents acquainted with each other except those sitting almost opposite. Since each resident is not acquainted with exactly three others, each is acquainted with exactly 196 people, and the total number of pairs of acquaintances is $\frac{200 \cdot 196}{2}=19600$. Now, take any six residents and denote them (in the order of their seating at the table) as $A_{1}, \ldots, A_{6}$. If in this cycle all neighbors are acquainted with each other, the desired seating arrangement is found. Otherwise, there exist two unfamiliar neighbors (let these be $A_{1}$ and $A_{2}$). Number all people at the large table in the same cyclic order from 1 to 200, starting with $A_{1}$. Note that the numbers of two unfamiliar residents can differ only by 99, 100, or 101. Let $N_{1}, \ldots, N_{6}$ be the numbers of $A_{1}, \ldots, A_{6}$, respectively. Then $N_{1}=1$ and $N_{2} \geqslant N_{1}+99=100$. Since the numbers $N_{i}$ are natural and strictly increasing, for $i \geqslant 2$ the inequalities $98+i \leqslant N_{i} \leqslant 194+i$ hold. Let's make two simple observations.
1) Resident $A_{1}$ is acquainted with $A_{5}$ and $A_{6}$. Indeed, for $i=5$ or $i=6$,
$$
N_{i}-N_{1}=N_{i}-1 \geqslant N_{5}-1 \geqslant 103-1=102>101
$$
2) For $2 \leqslant j < i \leqslant 6$, $A_{i}$ is acquainted with $A_{j}$. Indeed, $N_{i} > N_{j}$ and
$$
N_{i}-N_{j} \leqslant 194+i-(98+j)=96+(i-j) \leqslant 98<99
$$
Now, from 1) and 2) it follows that the cyclic seating arrangement $A_{1} \rightarrow A_{5} \rightarrow A_{3} \rightarrow A_{2} \rightarrow A_{4} \rightarrow A_{6} \rightarrow A_{1}$ satisfies the condition of the problem.
|
19600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a tennis tournament, 1152 schoolchildren are participating. 1 point is awarded for a win, and 0 points for a loss. Before each round, pairs are formed by drawing lots among participants with the same number of points (those who do not find a pair are awarded a point without playing). A player is eliminated after the second loss. The tournament continues as long as at least one pair of opponents can be formed. How many rounds will have to be played?
|
Answer: 14.
Solution. Note that $1152=1024+128$. Let's prove two statements first.
1) In a tournament with $2^{n}$ participants, for any $m \in\{1, \ldots, n\}$, after the $m$-th round, there will be $2^{n-m}$ participants without any losses and $m \cdot 2^{n-m}$ participants with one loss. We will use induction on $m$. For $m=1$, everything is obvious. Suppose for some $m<n$ the statement is true. Then before the $(m+1)$-th round, all participants will be divided into pairs. After the round, the number of participants without any losses will be halved, i.e., it will become $2^{n-m-1}$. One loss will be incurred by those who lost in the group of leaders (there are $2^{n-m-1}$ such people), and by those who already had one loss and won (by the induction hypothesis, there are $m \cdot 2^{n-m-1}$ such people). In total, we will get $(m+1) \cdot 2^{n-m-1}$. The rest of the participants will leave the tournament. Thus, the inductive step is completed.
2) We can divide the participants into two groups of 1024 and 128 participants and assume that for the first 10 rounds they play separate tournaments. Indeed, in each round, we will only pair participants from the same group. By 1), all participants in the first group can be paired. Therefore, if someone is left without a pair in the overall tournament, we can assume that this participant is from the second group. After 10 rounds, the results of the two groups are simply combined.
Now let's count the number of rounds. We will record the remaining participants as pairs $(a, b)$, where $b$ is the number of leaders, and $a$ is the number of participants with one loss. By 1), in the first group, after the tenth round, there will be $(10,1)$ participants. In the second group, after the seventh round, there will be $(7,1)$ participants, and their number will change as follows:
$$
(7,1) \rightarrow(4,1) \rightarrow(2,1) \rightarrow(1,1)
$$
In total, after the tenth round, there will be $(11,2)$ participants remaining in the tournament. Their further dynamics up to the fourteenth round are as follows:
$$
(11,2) \rightarrow(7,1) \rightarrow(4,1) \rightarrow(2,1) \rightarrow(1,1)
$$
After this, no more pairs can be formed, and the tournament ends.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Inside triangle $ABC$, a point $P$ is chosen such that $AP=BP$ and $CP=AC$. Find $\angle CBP$, given that $\angle BAC = 2 \angle ABC$.
---
Here is the translation of the provided text, maintaining the original formatting and structure.
|
Answer: $30^{\circ}$.
Solution 1. Draw the perpendicular bisector of side $A B$. Obviously, it will pass through point $P$. Let $C^{\prime}$ be the point symmetric to $C$ with respect to this perpendicular (see the left figure). By symmetry, $\angle C^{\prime} B A = \angle C A B = 2 \angle A B C$, hence $\angle C^{\prime} B C = \angle A B C$. On the other hand, lines $C C^{\prime}$ and $A B$ are parallel, so $\angle A B C = \angle B C C^{\prime}$. Therefore, $\angle B C C^{\prime} = \angle C^{\prime} B C$, triangle $B C^{\prime} C$ is isosceles, and $B C^{\prime} = C^{\prime} C$. By symmetry, $B C^{\prime} = A C$ and $C P = C^{\prime} P$, and by the condition $A C = C P$. Thus,
$$
C^{\prime} P = C P = A C = B C^{\prime} = C^{\prime} C
$$
and triangle $P C C^{\prime}$ is equilateral. Therefore, $\angle C C^{\prime} P = 60^{\circ}$. Note that
$$
180^{\circ} - 2 \angle P B C^{\prime} = \angle P C^{\prime} B = \angle B C^{\prime} C - 60^{\circ} = 120^{\circ} - 2 \angle C B C^{\prime}
$$
Therefore,
$$
\angle C B P = \angle P B C^{\prime} - \angle C B C^{\prime} = \frac{1}{2} \left(180^{\circ} - 120^{\circ}\right) = 30^{\circ}.
$$
Solution 2. Let $\alpha = \angle P A B, \beta = \angle P A C, \gamma = \angle P B C, \varphi = \alpha + \gamma$ (see the right figure). By the condition, $\angle P B A = \alpha, \angle C P A = \beta$, and
$$
\alpha + \beta = 2 \varphi = 2(\alpha + \gamma) \Longleftrightarrow 2 \gamma = \beta - \alpha
$$
By the Law of Sines,
$$
\frac{A C}{\sin \varphi} = \frac{A B}{\sin \left(180^{\circ} - 3 \varphi\right)} \Longleftrightarrow \frac{\sin 3 \varphi}{\sin \varphi} = \frac{A B}{A C}
$$
Note that
$$
A B = 2 A P \cos \alpha = 4 A C \cos \alpha \cos \beta \Longleftrightarrow \frac{A B}{A C} = 2(\cos (\alpha + \beta) + \cos (\beta - \alpha)) = 2 \cos 2 \varphi + 2 \cos 2 \gamma
$$
Moreover,
$$
\frac{\sin 3 \varphi}{\sin \varphi} = 3 - 4 \sin^2 \varphi = 2 \cos 2 \varphi + 1
$$
Therefore,
$$
2 \cos 2 \varphi + 2 \cos 2 \gamma = 2 \cos 2 \varphi + 1 \Longleftrightarrow \cos 2 \gamma = \frac{1}{2} \Longleftrightarrow 2 \gamma = 60^{\circ} \Longleftrightarrow \gamma = 30^{\circ}
$$
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A health camp was visited by 175 schoolchildren. Some of the children know each other, while others do not. It is known that any six schoolchildren can be accommodated in two three-person rooms so that all schoolchildren in the same room know each other. What is the minimum number of pairs of schoolchildren who could have come to the camp knowing each other?
|
Answer: 15050.
Solution. Suppose that some student (let's call him Vasya) is not acquainted with at least four students. We will select the following six children: Vasya, four students he is not acquainted with, and one more arbitrary student. It is impossible to seat them in two rooms, since out of this six, Vasya is acquainted with no more than one person. Therefore, each student has no more than three unknowns. Let's consider two cases.
1) Each student is not acquainted with no more than two children. Then any student has at least 172 acquaintances, and the total number of pairs of acquaintances is no less than $\frac{175 \cdot 172}{2}=15050$.
2) There exists a student who is not acquainted with three children. Let's denote such a student by $A$, and the unknown people by $B_{1}, B_{2}$, and $B_{3}$. We will select the following six children: $A, B_{1}, B_{2}, B_{3}$, and two more arbitrary students $C$ and $D$. Since they can be seated in two three-person rooms, $A$ must end up in a room with $C$ and $D$. But then students $C$ and $D$ must be acquainted with each other and with $A$. Thus, we have established that any students, other than $B_{1}, B_{2}$, and $B_{3}$, are acquainted with each other. In particular, this means that any student, other than $B_{1}, B_{2}$, and $B_{3}$, can be not acquainted only with someone from $B_{i}$. But each $B_{i}$ is not acquainted with no more than three students, so the number of pairs of unknowns does not exceed nine. Therefore, the number of pairs of acquaintances is no less than $\frac{175 \cdot 174}{2}-9=15216>15050$.

Considering 1) and 2), it remains to show that the number of pairs of acquaintances can be exactly 15050. Let's seat all the students at a large round table and make everyone acquainted except those sitting next to each other. Let's check that this construction satisfies the problem's condition. Since each student is acquainted with 172 students, the total number of pairs of acquaintances is exactly $\frac{175 \cdot 172}{2}=15050$. Take any six students and seat them in two rooms. Remove all the others from the large round table and denote the remaining ones in a cyclic order as $A, B, C, D, E, F$. Now seat students $A, C, E$ in one room, and $B, D, F$ in the other. The inhabitants of each room are not sitting next to each other at the table, and, in particular, they were not sitting next to each other at the large table. Therefore, they all know each other.
|
15050
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a qualification arm wrestling tournament, 896 athletes participate. A victory earns 1 point, a defeat earns 0 points. Before each round, pairs are formed by drawing lots among participants with an equal number of points (those who do not find a pair are awarded a point without playing). After the second defeat, an athlete is eliminated from the tournament. As soon as a sole leader is determined, the tournament ends, and all remaining athletes on the tournament are considered to have passed the qualification. Find the number of such athletes.
|
Answer: 10.
Solution. Note that $896=1024-128$. First, let's prove an auxiliary statement.
In a tournament with $2^{n}$ participants, for any $m \in\{1, \ldots, n\}$, after the $m$-th round, there will be $2^{n-m}$ athletes without any losses and $m \cdot 2^{n-m}$ athletes with one loss. We will use induction on $m$. For $m=1$, everything is obvious. Suppose for some $m<n$ the statement is true. Then before the $(m+1)$-th round, all participants will be paired. After the round, the number of athletes without any losses will be halved, i.e., it will become $2^{n-m-1}$. One loss will be incurred by those who lost in the group of leaders (there are $2^{n-m-1}$ such people), and by those who already had one loss and won (by the induction hypothesis, there are $m \cdot 2^{n-m-1}$ such people). In total, we will have $(m+1) \cdot 2^{n-m-1}$. The remaining participants will leave the tournament. Thus, the inductive step is completed.
Suppose that parallel to ours, a second qualifying tournament with 128 participants is held under the same rules. We can treat these two tournaments as parts of one (with 1024 participants) up to the seventh round. We will pair only athletes from their own tournament in each round. This is possible because, by the above, the number of leaders and participants with one loss in the second and overall tournament will be even, and thus in the first one as well. We will record the remaining participants as pairs $(a, b)$, where $b$ is the number of leaders, and $a$ is the number of athletes with one loss. By the auxiliary statement, after the seventh round, in the overall tournament, there will be $(56,8)$ participants, and in the second one - $(7,1)$. Therefore, in our tournament, there will be $(49,7)$ athletes, and their number will change as follows:
$$
(49,7) \rightarrow(28,4) \rightarrow(16,2) \rightarrow(9,1)
$$
Thus, the tournament will end after the tenth round, and 10 athletes will qualify.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a triangle $ABC$ with the largest side $BC$. The bisector of its angle $C$ intersects the altitudes $AA_{1}$ and $BB_{1}$ at points $P$ and $Q$ respectively, and the circumcircle of $ABC$ at point $L$. Find $\angle ACB$, if it is known that $AP=LQ$.
|
Answer: $60^{\circ}$.
Solution. Let $\alpha=\angle B C L, \beta=\angle A L C, \gamma=\angle B L C$ (see the figure). We will prove the equality of triangles $A L P$ and $B L Q$. Note that $A P=L Q$ by the condition and $A L=L B$ as chords corresponding to equal angles. Moreover,
$$
\angle A P L=\angle A_{1} P C=90^{\circ}-\alpha=\angle B_{1} Q C=\angle B Q L
$$
Then, by the Law of Sines,
$$
\frac{A P}{\sin \angle A L P}=\frac{A L}{\sin \angle A P L}=\frac{L B}{\sin \angle B Q L}=\frac{L Q}{\sin \angle L B Q}, \quad \text { hence } \quad \sin \angle A L P=\sin \angle L B Q
$$
But $\angle A L P=\angle A B C<90^{\circ}$ and
$$
\angle L B Q=180^{\circ}-\angle B L C-\angle B Q L=90^{\circ}-\angle B A C+\alpha<90^{\circ}-\angle B A C+\angle A C B \leqslant 90^{\circ}
$$
(the last inequality is true because $B C \geqslant A B$). Therefore, the angles $A L P$ and $L B Q$ are acute, and they are equal due to the equality of their sines. Thus, triangles $A L P$ and $B L Q$ are equal by a side and two angles. Therefore, $\angle L A P=\angle Q L B=\gamma$. Now from triangle $A L P$
$$
\beta+\gamma+90^{\circ}-\alpha=180^{\circ} \Longrightarrow \beta+\gamma=90^{\circ}+\alpha
$$
and from quadrilateral $A L B C$
$$
\beta+\gamma=180^{\circ}-2 \alpha \Longrightarrow 180^{\circ}-2 \alpha=90^{\circ}+\alpha \Longrightarrow \alpha=30^{\circ} \Longrightarrow \angle A C B=60^{\circ}
$$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a health camp, 225 schoolchildren are resting. Some of the children know each other, while others do not. It is known that among any six schoolchildren, there are three non-intersecting pairs who know each other. What is the minimum number of pairs of schoolchildren who could be resting in the camp?
|
Answer: 24750.
Solution. Suppose that some student (let's call him Vasya) is not acquainted with at least five other students. Then Vasya and the five students he is not acquainted with form a group of six that does not satisfy the condition of the problem. Therefore, each student can have no more than four unknowns. Thus, each student is acquainted with at least 220 students, and the number of pairs of acquaintances is no less than $\frac{225 \cdot 220}{2}=24750$.
Now, let's show that the number of pairs of acquaintances can be exactly 24750. Seat all the students around a large round table and introduce everyone except those sitting next to each other and those sitting one apart. Let's check that this construction satisfies the condition of the problem. Since each student is not acquainted with exactly four other students, each student is acquainted with exactly 220 students, and the total number of pairs of acquaintances is $\frac{225 \cdot 220}{2}=24750$.

Now consider any group of six students. Leave only them at the large round table. Notice that each of them is acquainted with the one sitting "opposite" him (i.e., the one sitting two seats away), since at the large table, he could not be either his neighbor or the one sitting one seat away. Thus, we have selected three non-overlapping pairs of acquaintances.
|
24750
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a tennis tournament, 512 schoolchildren are participating. 1 point is awarded for a win, and 0 points for a loss. Before each round, pairs are formed by lottery among participants with the same number of points (those who do not find a pair are awarded a point without playing). The tournament ends as soon as a sole leader is determined. How many schoolchildren will finish the tournament with 6 points?
|
Answer: 84.
Solution. We will show that in a tournament with $2^{n}$ participants, no one will score points without playing, and for any $k \in\{0, \ldots, n\}$, exactly $C_{n}^{k}$ participants will end up with $k$ points. We will use induction on $n$. For $n=1$, this is obvious. Suppose that for some $n$ both statements are true. Then, in a tournament with $2^{n+1}$ participants, after the first round, $2^{n}$ students will have 0 points and $2^{n}$ students will have 1 point. We will continue to conduct the draw so that participants from these groups only meet each other. By the inductive hypothesis, this is always possible, and such an assumption clearly does not affect the distribution of points. In other words, we are conducting two independent tournaments with $2^{n}$ participants each. By the inductive hypothesis, in the first tournament, $C_{n}^{k}$ students will score $k$ points, and in the second tournament, $-C_{n}^{k-1}$ students will score $k$ points, since all participants started with one point. In the end, $C_{n}^{k}+C_{n}^{k-1}=C_{n+1}^{k}$ students will score $k$ points (we used the main identity of Pascal's triangle). Thus, the inductive step is completed. It remains to note that $C_{9}^{6}=\frac{9 \cdot 8 \cdot 7}{1 \cdot 2 \cdot 3}=84$.
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression for $a, b>0$
$$
\frac{(2 a+2 a b-b(b+1))^{2}+\left(b-4 a^{2}+2 a(b+1)\right)^{2}}{4 a^{2}+b^{2}}
$$
|
Answer: 1.
Solution 1. The minimized expression is the sum of the squares of the distances from point $A(1,2 a)$ to the lines $\ell_{1}$ and $\ell_{2}$, given by the equations
$$
\ell_{1}: 2 a x+b y-b(b+1)=0 \quad \text { and } \quad \ell_{2}: b x-2 a y+2 a(b+1)=0
$$
These lines are perpendicular and intersect at point $B(0, b+1)$. Then, by the Pythagorean theorem, we need to find the minimum of $A B^{2}=1+(b+1-2 a)^{2}$, which is 1 and is achieved, for example, when $a=b=1$.
Solution 2. Transform the numerator of the fraction:
$$
\begin{aligned}
& (2 a+2 a b-b(b+1))^{2}+\left(b-4 a^{2}+2 a(b+1)\right)^{2}= \\
& =4 a^{2}+4 a^{2} b^{2}+b^{2}(b+1)^{2}+8 a^{2} b-4 a b(b+1)-4 a b^{2}(b+1)+ \\
& +b^{2}+16 a^{4}+4 a^{2}(b+1)^{2}-8 a^{2} b+4 a b(b+1)-16 a^{3}(b+1)= \\
& \quad=\left(4 a^{2}+b^{2}\right)\left(1+4 a^{2}+(b+1)^{2}-4 a(b+1)\right)=\left(4 a^{2}+b^{2}\right)\left(1+(b+1-2 a)^{2}\right)
\end{aligned}
$$
Thus, we need to find the minimum of the function $(b+1-2 a)^{2}+1$ for positive $a$ and $b$. It is 1 and is achieved, for example, when $a=b=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides $A B$ and $B C$ of an equilateral triangle $A B C$, points $P$ and $Q$ are chosen such that $A P: P B = B Q: Q C = 2: 1$. Find $\angle A K B$, where $K$ is the intersection point of segments $A Q$ and $C P$.
|
Answer: $90^{\circ}$.
Solution 1. Let $B H$ be the height and median of triangle $A B C$. Draw a line through vertex $B$ parallel to $A C$ and denote the point of its intersection with line $C P$ as $D$ (see the left figure). Triangles $B P D$ and $A P C$ are similar with a coefficient of $\frac{1}{2}$, hence $D B = \frac{1}{2} A C = A H$. Therefore, $A D B H$ is a rectangle, which means $\angle A D B = 90^{\circ}$. Note that triangles $A B Q$ and $C A P$ are congruent by two sides and an angle. Then
$$
\angle B D K = \angle D C A = \angle B A K.
$$
Thus, quadrilateral $A D B K$ is cyclic, from which $\angle A K B = 180^{\circ} - \angle A D B = 90^{\circ}$.
Solution 2. Draw the height $C H$ in triangle $A B C$ (see the right figure). Since $B H = \frac{1}{2} A B$, we get $\frac{B P}{B H} = \frac{2}{3} = \frac{B Q}{B C}$. Therefore, triangles $B P Q$ and $B H C$ are similar, from which $\angle B P Q = \angle B H C = 90^{\circ}$. Note now that $B Q = A P$, $A B = C A$, and $\angle A B Q = \angle C A P = 60^{\circ}$. Then triangles $A B Q$ and $C A P$ are congruent by two sides and an angle. Since $\angle A Q B = \angle C P A = 180^{\circ} - \angle C P B$, quadrilateral $B P K Q$ is cyclic, from which
$$
\angle A K B = 180^{\circ} - \angle B K Q = 180^{\circ} - \angle B P Q = 90^{\circ}
$$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The government has decided to privatize civil aviation. For each pair of 202 cities in the country, the airline connecting them is sold to one of the private airlines. The mandatory condition for the sale is as follows: each airline must ensure the possibility of flying from any city to any other (possibly with several layovers). What is the maximum number of companies that can buy the airlines?
|
Answer: 101.
Solution. First, we prove that for $k \in \{1, \ldots, 100\}$, the remainders of the numbers
$$
0, k, 2k, 3k, \ldots, 99k, 100k
$$
when divided by the prime number 101 are distinct. Indeed, if for some $0 \leqslant a < b \leqslant 100$ the numbers $ak$ and $bk$ give the same remainder when divided by 101, then the number $bk - ak = (b-a)k$ is divisible by 101, which is impossible because $1 \leqslant k \leqslant 100$ and $0 < b-a < 101$. Now consider the numerical sequence
$$
\mathcal{P}_{k}: \quad 0, k, 2k, 3k, \ldots, 99k, 100k, 100k+101, 99k+101, \ldots, 3k+101, 2k+101, k+101, 101
$$
Notice that all the remainders of the numbers in $\mathcal{P}_{k}$ when divided by 202 are distinct. Indeed, if two different numbers in $\mathcal{P}_{k}$ give the same remainder when divided by 202, then they also give the same remainder when divided by 101. Then these numbers are of the form $ak$ and $ak + 101$, which is impossible because they have different parities. Since $\mathcal{P}_{k}$ contains exactly 202 numbers, their remainders take all possible values from 0 to 201.
Now let's move on to solving the problem. Since each airline must ensure communication between all cities, it must have at least 201 air routes. The total number of air routes is $\frac{202 \cdot 201}{2}$, so the number of airlines does not exceed 101.
We will now show that the number of airlines participating in the privatization of air routes can be exactly 101. Let's agree to denote the remainder of the division of an integer $a$ by 202 by $\langle a \rangle$. We will number the cities from 0 to 201. For any $k = 1, \ldots, 100$, we will assign to the $k$-th airline the air routes connecting cities with numbers $\langle a \rangle$ and $\langle b \rangle$, where $a$ and $b$ are adjacent numbers in the sequence $\mathcal{P}_{k}$. Since the remainders of the numbers in $\mathcal{P}_{k}$ run through (in a certain order) all values from 0 to 201, the airline can ensure travel from any city to any other. Note also that no air route will be assigned to two airlines at the same time. Indeed, let $k$ and $m$ be different numbers from 1 to 100, and $(a, b)$ and $(c, d)$ be pairs of adjacent numbers from the sequences $\mathcal{P}_{k}$ and $\mathcal{P}_{m}$ respectively, such that $\{\langle a \rangle, \langle b \rangle\} = \{\langle c \rangle, \langle d \rangle\}$. Then, by the above, $\{a, b\} = \{c, d\}$, which is impossible since $b - a = k \neq m = d - c$.
We will sell all the remaining air routes from the first hundred airlines to the 101st airline. We will prove that it can also ensure travel from any city to any other. Obviously, it owns the air route $(0, 101)$, since 0 and 101 do not neighbor in the sequence $\mathcal{P}_{k}$ for any $k$. Now we will show that for any $m \in \{1, \ldots, 100\}$, the air routes $(0, 202 - m)$ and $(101, 101 - m)$ also belong to the 101st airline. Indeed, let the route $(0, 202 - m)$ belong to the airline with number $k \leqslant 100$. Then $202 - m = k$, which is impossible since $k + m \leqslant 200$. The second statement is verified similarly. Thus, the 101st airline connects any two cities via the cities 0 and 101.
|
101
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In an arm wrestling tournament, $2^{n}$ athletes participate, where $n$ is a natural number greater than 7. One point is awarded for a win, and zero points for a loss. Before each round, pairs are formed by drawing lots among participants with the same number of points (those who do not find a pair are simply given a point). After the seventh round, it turned out that exactly 42 participants had 5 points. What is $n$?
|
Answer: 8.
Solution. Let $f(m, k)$ be the number of participants who have scored $k$ points after $m$ rounds. We will prove by induction on $m$ that
$$
f(m, k)=2^{n-m} \cdot C_{m}^{k}, \quad \text { where } 0 \leqslant k \leqslant m \leqslant 2^{n}
$$
If $m=0$, then $k=0$, and $f(0,0)=2^{n}$. We will now perform the inductive step. Suppose that for some $m<n$ the required equality holds. Then each group with the same number of points contains an even number of participants, so all participants can be paired. After the $(m+1)$-th round, the groups of athletes with no wins and no losses will be halved. Therefore,
$$
f(m+1,0)=\frac{1}{2} f(m, 0)=\frac{1}{2} \cdot 2^{n-m}=2^{n-(m+1)} \cdot C_{m+1}^{0} \quad \text { and } \quad f(m+1, m+1)=\frac{1}{2} f(m, m)=2^{n-(m+1)} \cdot C_{m+1}^{m+1}
$$
Now let $k \in\{1, \ldots, m\}$. After the $(m+1)$-th round, $k$ points will be scored by those who had $k$ points and lost, as well as by those who had $k-1$ point and won. Therefore,
$$
f(m+1, k)=\frac{1}{2} \cdot f(m, k)+\frac{1}{2} \cdot f(m, k-1)=2^{n-m-1}\left(C_{m}^{k}+C_{m}^{k-1}\right)=2^{n-(m+1)} \cdot C_{m+1}^{k}
$$
(in the last transition, we used the main identity of Pascal's triangle). Thus, the inductive step is completed. It remains to note that
$$
42=f(7,5)=2^{n-7} \cdot C_{7}^{5}=2^{n-7} \cdot \frac{7 \cdot 6}{2}=42 \cdot 2^{n-8}, \quad \text { that is } n=8 .
$$
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression for $a, b>0$
$$
\frac{(3 a b-6 b+a(1-a))^{2}+\left(9 b^{2}+2 a+3 b(1-a)\right)^{2}}{a^{2}+9 b^{2}}
$$
|
# Answer: 4.
Solution 1. The minimized expression is the sum of the squares of the distances from point $A(3 b,-2)$ to the lines $\ell_{1}$ and $\ell_{2}$, given by the equations
$$
\ell_{1}: a x+3 b y+a(1-a)=0 \quad \text { and } \quad \ell_{2}: 3 b x-a y+3 b(1-a)=0
$$
These lines are perpendicular and intersect at point $B(a-1,0)$. Then, by the Pythagorean theorem, we need to find the minimum of $A B^{2}=(a-1-3 b)^{2}+4$, which is 4 and is achieved, for example, when $a=4$ and $b=1$.
Solution 2. Transform the numerator of the fraction:
$$
\begin{aligned}
& (3 a b-6 b+a(1-a))^{2}+\left(9 b^{2}+2 a+3 b(1-a)\right)^{2}= \\
& =36 b^{2}+9 a^{2} b^{2}+a^{2}(1-a)^{2}-36 a b^{2}-12 a b(1-a)+6 a^{2} b(1-a)+ \\
& +4 a^{2}+81 b^{4}+9 b^{2}(1-a)^{2}+36 a b^{2}+12 a b(1-a)+54 b^{3}(1-a)= \\
& \quad=\left(a^{2}+9 b^{2}\right)\left(4+9 b^{2}+(1-a)^{2}+6 b(1-a)\right)=\left(a^{2}+9 b^{2}\right)\left(4+(1-a+3 b)^{2}\right)
\end{aligned}
$$
Thus, we need to find the minimum of the function $(1-a+3 b)^{2}+1$ for positive $a$ and $b$. It is 4 and is achieved, for example, when $a=4$ and $b=1$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the hypotenuse $A B$ of an isosceles right triangle $A B C$, points $K$ and $L$ are marked such that $A K: K L: L B=1: 2: \sqrt{3}$. Find $\angle K C L$.
|
Answer: $45^{\circ}$.
Solution 1. Let $A K=1$. Then $K L=2$ and $L B=\sqrt{3}$, so $A B=3+\sqrt{3}$ and $A C=B C=\frac{3+\sqrt{3}}{\sqrt{2}}$. Therefore,
$$
A C \cdot B C=6+3 \sqrt{3}=3(2+\sqrt{3})=A L \cdot K B, \quad \text { or } \quad \frac{K B}{B C}=\frac{C A}{A L} .
$$
Since $\angle K B C=45^{\circ}=\angle C A L$, triangles $C B K$ and $L A C$ are similar. Therefore, $\angle B C K=\angle A L C$ and
$$
\angle A L C=\angle B C L+\angle L B C=\angle B C L+45^{\circ}=\angle B C K-\angle K C L+45^{\circ}=\angle A L C-\angle K C L+45^{\circ},
$$
from which $\angle K C L=45^{\circ}$.
Solution 2. Extend triangle $A B C$ to form a square $A B C D$, and let $M$ be the intersection point of lines $B D$ and $C L$ (see the figure). Let $a=A C$. Triangles $A L C$ and $B L M$ are similar with a ratio of $\sqrt{3}$. Therefore,
$$
B M=\frac{a}{\sqrt{3}}, \quad C M=\sqrt{a^{2}+\frac{a^{2}}{3}}=\frac{2 a}{\sqrt{3}}, \quad \frac{A B}{C M}=\sqrt{\frac{3}{2}}
$$
Moreover,
$$
B L=\frac{A B}{\sqrt{3}+1}, \quad C L=\frac{C M \cdot \sqrt{3}}{\sqrt{3}+1}, \quad \frac{C L}{B L}=\sqrt{3} \cdot \frac{C M}{A B}=\sqrt{2}
$$
and also
$$
K L=\frac{2 A B}{\sqrt{3}+3}, \quad M L=\frac{C M}{\sqrt{3}+1}, \quad \frac{K L}{M L}=\frac{2}{\sqrt{3}} \cdot \frac{A B}{C M}=\sqrt{2}
$$
Thus, $\frac{C L}{B L}=\frac{K L}{M L}$, and triangles $B L M$ and $C L K$ are similar. Therefore, $\angle K C L=\angle M B L=45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The government has decided to privatize civil aviation. For each pair of the country's 127 cities, the connecting airline is sold to one of the private airlines. Each airline must make all the purchased air routes one-way, but in such a way as to ensure the possibility of flying from any city to any other (possibly with several layovers). What is the maximum number of companies that can buy the air routes?
|
# Answer: 63.
Solution. For integers $k$ and $n$, let $N_{k, n}$ denote the remainder when $k \cdot n$ is divided by the prime number 127. First, we prove that if $k$ is not divisible by 127, then the numbers $N_{k, 0}, \ldots, N_{k, 126}$ are distinct. Indeed, if for some $0 \leqslant a < b \leqslant 126$ the numbers $a k$ and $b k$ give the same remainder when divided by 127, then the number $b k - a k = (b - a) k$ is divisible by 127, which is impossible since $0 < b - a < 127$. Therefore, the numbers $N_{k, 0}, \ldots, N_{k, 126}$ take all values from 0 to 126, and $N_{k, 127}$ is zero.
Now let's proceed to solving the problem. Take an arbitrary airline participating in the privatization. Since it must ensure communication between all cities on its own, for any city, it must have an airline leading to this city and an airline leading out of it. Thus, each city must be connected by at least two airlines belonging to this company. Therefore, the company must have at least 127 airlines. The total number of airlines is $\frac{127 \cdot 126}{2} = 127 \cdot 63$, so the number of airlines does not exceed 63.
Now we show that exactly 63 airlines could have participated in the privatization. Number the cities from 0 to 126. For any $k = 1, \ldots, 63$, assign to the $k$-th airline the airlines leading from the city with number $N_{k, n}$ to the city with number $N_{k, n+1}$, where $n \in \{0, \ldots, 126\}$. By the above, such airlines, starting and ending in city 0, cyclically pass through (in a certain order) all other cities. Thus, the $k$-th airline can ensure a flight from any city to any other. It remains to check that no airline is assigned to two companies at the same time. Indeed, let $k, m \in \{1, \ldots, 63\}$ and some airline is assigned to both the $k$-th and $m$-th companies. Then there exist $i, j \in \{1, \ldots, 126\}$ such that $N_{k, i} = N_{m, j}$ and $N_{k, i+1} = N_{m, j+1}$. We get $N_{k, i+1} - N_{k, i} = N_{m, j+1} - N_{m, j}$, which implies $k = m$.
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Sasha chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \), while if they are connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
|
Answer: $n=35$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, let $n$ be even. Among seven numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $q$ is a prime divisor of $n$, then among four consecutively connected numbers, there exists a pair of adjacent numbers whose sum is not divisible by $q$. Consider a chain $(a, b, c, d)$ of consecutively connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which does not exist.
From 1) and 3), it follows that the number $n$ has at least two distinct odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from 3. Suppose, for example, that $p=3$. No more than two numbers are divisible by 3 (if there are three, they form a cycle). The remaining numbers can be divided into two groups, giving remainders 1 and 2 when divided by 3. One of these groups is empty, otherwise any number from the smaller group will be connected to at least three numbers from the other group, which is impossible. The sum of the numbers in one group is not divisible by 3. Therefore, there exists a three-link chain in which the sum of any pair of connected numbers is not divisible by 3 and, hence, is divisible by $q$. But this contradicts 2).
Thus, if $n$ has exactly two distinct odd prime divisors, then $n \geqslant 5 \cdot 7=35$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>35$. The arrangement for $n=35$ is shown in the figure.
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y, z \in (0,2]$, find the maximum value of the expression
$$
A=\frac{\left(x^{3}-6\right) \sqrt[3]{x+6}+\left(y^{3}-6\right) \sqrt[3]{y+6}+\left(z^{3}-6\right) \sqrt[3]{z+6}}{x^{2}+y^{2}+z^{2}}
$$
|
Answer: 1.
Solution. For $x \in(0,2]$, the inequalities $\sqrt[3]{x+6} \leqslant 2$ and $x^{3} \leqslant 2 x^{2}$ hold, from which
$$
\left(x^{3}-6\right) \sqrt[3]{x+6} \leqslant 2\left(2 x^{2}-6\right)
$$
Similarly, the other two terms in the numerator of $A$ are estimated. Therefore,
$$
A \leqslant 2 \cdot \frac{2 x^{2}-6+2 y^{2}-6+2 z^{2}-6}{x^{2}+y^{2}+z^{2}}=4-\frac{36}{x^{2}+y^{2}+z^{2}} \leqslant 4-\frac{36}{12}=1
$$
Equality is achieved when $x=y=z=2$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The diagonals of the inscribed quadrilateral $ABCD$ intersect at point $O$. Inside triangle $AOB$, a point $K$ is chosen such that line $KO$ is the bisector of angle $CK$. Ray $DK$ intersects the circumcircle of triangle $COK$ again at point $L$, and ray $CK$ intersects the circumcircle of triangle $DOK$ again at point $M$. Find the ratio of the areas of triangles $ALO$ and $BMO$.
|
Answer: 1.
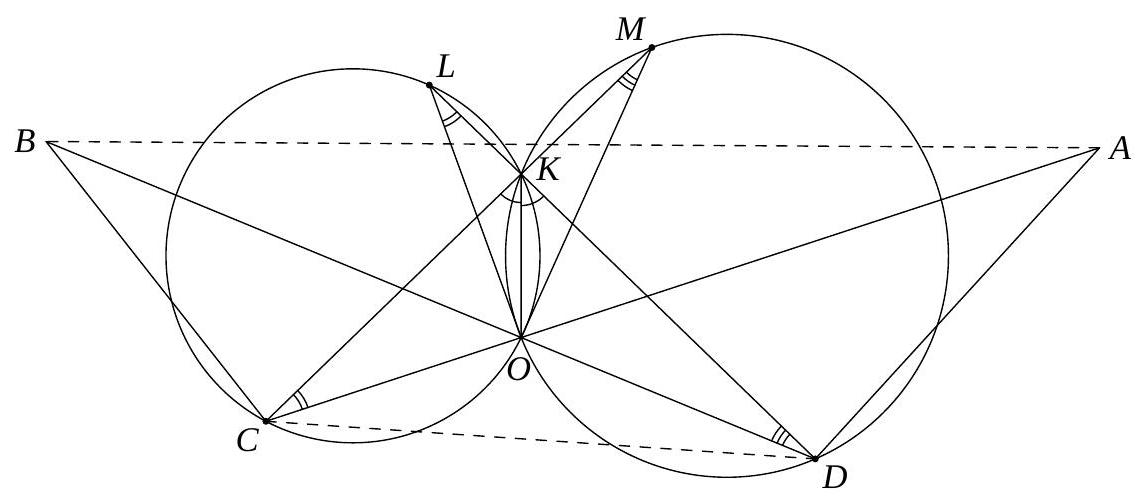
Solution. Let $r_{1}$ and $r_{2}$ be the radii of the circumcircles of triangles $C O K$ and $D O K$, respectively. Note that
$$
\angle L K O=180^{\circ}-\angle D K O=180^{\circ}-\angle C K O=\angle M K O
$$
from which $\frac{L O}{M O}=\frac{r_{1}}{r_{2}}$. Moreover, the inscribed quadrilateral $A B C D$ implies that triangles $A O D$ and $B O C$ are similar by two angles. Then
$$
\frac{A O}{B O}=\frac{O D}{O C}=\frac{r_{2}}{r_{1}}
$$
since the chords $O D$ and $O C$ correspond to equal inscribed angles. Therefore,
$$
\frac{L O}{M O} \cdot \frac{A O}{B O}=1 \Longleftrightarrow L O \cdot A O=M O \cdot B O
$$
Since $\angle K M O=\angle K D O$ and $\angle K L O=\angle K C O$, triangles $M C O$ and $D L O$ are similar, from which
$$
\begin{gathered}
\angle A O L=\angle A O M+\angle L O M=180^{\circ}-\angle C O M+\angle L O M= \\
\quad=180^{\circ}-\angle D O L+\angle L O M=\angle B O L+\angle L O M=\angle B O M
\end{gathered}
$$
Thus,
$$
S_{A O L}=\frac{1}{2} \cdot L O \cdot A O \cdot \sin \angle A O L=\frac{1}{2} \cdot M O \cdot B O \cdot \sin \angle B O M=S_{B O M}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A natural number $x$ in a base $r$ system ( $r \leqslant 36$ ) has the form $\overline{p p q q}$, and $2 q=5 p$. It turns out that the $r$-ary representation of the number $x^{2}$ is a seven-digit palindrome with a zero middle digit. (A palindrome is a number that reads the same from left to right and from right to left). Find the sum of the $r$-ary digits of the number $x^{2}$.
|
Answer: 36.
Solution. Let's agree to write $u \equiv v(\bmod w)$ if $(u-v) \vdots w$. Let $p=2 s, q=5 s$. Then $x=\overline{p p q q}_{r}=\left(p r^{2}+q\right)(r+1)=s\left(2 r^{2}+5\right)(r+1)$. From the condition on $x^{2}$, we get the equality
$$
s^{2}\left(2 r^{2}+5\right)^{2}\left(r^{2}+2 r+1\right)=a\left(1+r^{6}\right)+b\left(r+r^{5}\right)+c\left(r^{2}+r^{4}\right)
$$
where $a, b, c$ are some $r$-ary digits. Let's make two observations.
1) For any natural $n$
$$
r^{n}=(1+r-1)^{n} \equiv(-1)^{n}(1-n(1+r))\left(\bmod (1+r)^{2}\right)
$$
The right side of $(*)$ is divisible by $(1+r)^{2}$, from which
$$
0 \equiv a(2-6(1+r))-b(2-6(1+r))+c(2-6(1+r))=2(1-3(1+r))(a-b+c)\left(\bmod (1+r)^{2}\right)
$$
Since $1-3(1+r)$ is coprime with $(1+r)^{2}$, $2(a-b+c)$ is divisible by $(1+r)^{2}$. But this number lies in the interval $(-2 r, 4 r) \subset\left(-(1+r)^{2},(1+r)^{2}\right)$, hence $b=a+c$.
2) Equate the remainders of the left and right sides of $(*)$ when divided by $1+r^{2}$:
$$
18 s^{2} r \equiv b r\left(1+r^{4}\right) \equiv 2 b r\left(\bmod \left(1+r^{2}\right)\right)
$$
Since $r$ is coprime with $1+r^{2}$, $2\left(9 s^{2}-b\right)$ is divisible by $1+r^{2}$. Note that $4 s^{2} \leqslant r-1$, otherwise the number $x^{2}$ will be eight-digit. In addition, $r \geqslant 5 s+1 \geqslant 6$. Therefore
$$
2\left(9 s^{2}-b\right)-2 r>-1-r^{2}
$$
Thus, $b=9 s^{2}$.
Since $b$ is an $r$-ary digit, from 2) it follows that $9 s^{2} \leqslant r-1$. Since $s>0$, we get $s=1$ and $b=9$. By 1), the sum of the digits of $x^{2}$ is $2(a+b+c)=4 b=36$.
Remark. It can be verified by direct calculation that $2255_{21}^{2}=4950594_{21}$. Thus, the situation described in the problem is realized.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Sasha chooses a natural number $n$ and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers $a$ and $b$ are not connected by a segment, then the sum $a+b$ must be coprime with $n$; if connected, then the numbers $a+b$ and $n$ must have a common natural divisor greater than 1. For what smallest $n$ does such an arrangement exist?
|
Answer: $n=35$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, let $n$ be even. Among eight numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $q$ is a prime divisor of $n$, then among four consecutively connected numbers, there exists a pair of adjacent numbers whose sum is not divisible by $q$. Consider a chain $(a, b, c, d)$ of consecutively connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which does not exist.
From 1) and 3), it follows that the number $n$ has at least two distinct odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from 3. Suppose, for example, that $p=3$. No more than two numbers are divisible by 3 (if there are three, they form a cycle). The remaining numbers (at least 6) can be divided into two groups, giving remainders 1 and 2 when divided by 3. We will show that one of these groups is empty. If this is not the case, then each number from one group is connected to any number from the other. But then in one group there are no more than three numbers, and in the other no more than two, which is impossible. The sum of the numbers in one group is not divisible by 3. Therefore, there exists a three-link chain in which the sum of any pair of connected numbers is not divisible by 3 and, therefore, is divisible by $q$. But this contradicts 2).
Thus, if $n$ has exactly two distinct odd prime divisors, then $n \geqslant 5 \cdot 7=35$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>35$. The arrangement for $n=35$ is shown in the figure.
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $x, y, z \geqslant 3$ find the minimum value of the expression
$$
A=\frac{\left(x^{3}-24\right) \sqrt[3]{x+24}+\left(y^{3}-24\right) \sqrt[3]{y+24}+\left(z^{3}-24\right) \sqrt[3]{z+24}}{x y+y z+z x}
$$
|
Answer: 1.
Solution. For $x \geqslant 3$, the inequalities $\sqrt[3]{x+24} \geqslant 3$ and $x^{3} \geqslant 3 x^{2}$ hold, from which
$$
\left(x^{3}-24\right) \sqrt[3]{x+24} \geqslant 3\left(3 x^{2}-24\right)
$$
Similarly, the other two terms in the numerator of $A$ are estimated. Therefore,
$$
A \geqslant 3 \cdot \frac{3 x^{2}-24+3 y^{2}-24+3 z^{2}-24}{x y+y z+z x}=9\left(\frac{x^{2}+y^{2}+z^{2}}{x y+y z+z x}-\frac{24}{x y+y z+z x}\right) \geqslant 9\left(1-\frac{24}{27}\right)=1
$$
Equality is achieved when $x=y=z=3$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides $AB$ and $AC$ of an acute-angled triangle $ABC$, points $K$ and $L$ are marked such that the quadrilateral $B K L C$ is cyclic. Inside this quadrilateral, a point $M$ is chosen so that the line $AM$ is the bisector of angle $BMC$. The ray $BM$ intersects the circumcircle of triangle $AMC$ again at point $P$, and the ray $CM$ intersects the circumcircle of triangle $AMB$ again at point $Q$. Find the ratio of the areas of triangles $ALP$ and $AKQ$.
|
Answer: 1.

Solution. Let $r_{1}$ and $r_{2}$ be the radii of the circumcircles of triangles $A M B$ and $A M C$, respectively. Since $A M$ is the bisector of angle $B M C$, the following equalities hold:
$$
\angle A M B = \angle A M C \quad \text{and} \quad \angle A M P = \angle A M Q
$$
from which $\frac{A B}{A C} = \frac{r_{1}}{r_{2}} = \frac{A Q}{A P}$. Moreover, from the inscribed quadrilateral $B K L C$, it follows that
$$
\angle A L K = 180^{\circ} - \angle K L C = \angle A B C
$$
Thus, triangles $A L K$ and $A B C$ are similar by two angles. Therefore,
$$
\frac{A L}{A K} = \frac{A B}{A C} = \frac{A Q}{A P} \Longrightarrow A L \cdot A P = A K \cdot A Q
$$
From the equalities $\angle A B M = \angle A Q M$ and $\angle A P M = \angle A C M$, it follows that $\angle B A P = \angle C A Q$, from which
$$
\angle L A P = \angle C A P = \angle B A P - \angle B A C = \angle C A Q - \angle B A C = \angle B A Q = \angle K A Q
$$
Thus,
$$
S_{A L P} = \frac{1}{2} \cdot A L \cdot A P \cdot \sin \angle L A P = \frac{1}{2} \cdot A K \cdot A Q \cdot \sin \angle K A Q = S_{A K Q}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A natural number $x$ in a base $r(r \leqslant 400)$ numeral system has the form $\overline{p p q q}$, and $7 q=17 p$. It turns out that the $r$-ary representation of the number $x^{2}$ is a seven-digit palindrome with a zero middle digit. (A palindrome is a number that reads the same from left to right and from right to left). Find the sum of the $r$-ary digits of the number $x^{2}$.
|
Answer: 400.
Solution. Let's agree to write $u \equiv v(\bmod w)$ if $(u-v) \vdots w$. Let $p=7 s, q=17 s$. Then $x=\overline{p p q q}_{r}=\left(p r^{2}+q\right)(r+1)=s\left(7 r^{2}+17\right)(r+1)$. From the condition on $x^{2}$, we get the equality
$$
s^{2}\left(7 r^{2}+17\right)^{2}\left(r^{2}+2 r+1\right)=a\left(1+r^{6}\right)+b\left(r+r^{5}\right)+c\left(r^{2}+r^{4}\right)
$$
where $a, b, c$ are some $r$-ary digits. Let's make two observations.
1) For any natural $n$
$$
r^{n}=(1+r-1)^{n} \equiv(-1)^{n}(1-n(1+r))\left(\bmod (1+r)^{2}\right)
$$
The right side of $(*)$ is divisible by $(1+r)^{2}$, from which
$$
0 \equiv a(2-6(1+r))-b(2-6(1+r))+c(2-6(1+r))=2(1-3(1+r))(a-b+c)\left(\bmod (1+r)^{2}\right)
$$
Since $1-3(1+r)$ is coprime with $(1+r)^{2}$, $2(a-b+c)$ is divisible by $(1+r)^{2}$. But this number lies in the interval $(-2 r, 4 r) \subset\left(-(1+r)^{2},(1+r)^{2}\right)$, hence $b=a+c$.
2) Equate the remainders of the left and right sides of $(*)$ when divided by $1+r^{2}$:
$$
200 s^{2} r \equiv b r\left(1+r^{4}\right) \equiv 2 b r\left(\bmod \left(1+r^{2}\right)\right)
$$
Since $r$ is coprime with $1+r^{2}$, $2\left(100 s^{2}-b\right)$ is divisible by $1+r^{2}$. Note that $49 s^{2} \leqslant r-1$, otherwise the number $x^{2}$ will be an eight-digit number. In addition, $r \geqslant 17 s+1 \geqslant 18$. Therefore
$$
2\left(100 s^{2}-b\right)-2 r>-1-r^{2}
$$
Thus, $b=100 s^{2}$.
Since $b$ is an $r$-ary digit, from 2) it follows that $100 s^{2}0$, we get $s=1$ and $b=100$. By 1$)$, the sum of the digits of $x^{2}$ is $2(a+b+c)=4 b=100$.
Remark. Direct calculation shows that $(7,7,17,17)_{120}^{2}=(49,100,51,0,51,100,49)_{120}$. Thus, the situation described in the condition is realized.
|
400
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Tanya chooses a natural number n and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers a and b are not connected by a segment, then the sum $a^{2}+b^{2}$ must be coprime with n; if connected, then the numbers $a^{2}+b^{2}$ and n must have a common natural divisor greater than 1. For what smallest n does such an arrangement exist?
|
Answer: $n=65$.
Solution. First, let's make three observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among five numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $d$ is a divisor of $n$, then no more than two numbers are divisible by $d$. Suppose there are three such numbers. Then they must be pairwise connected, and thus form a three-link cycle.
3) If $q$ is a prime divisor of $n$, then among four sequentially connected numbers, there exists a pair of adjacent numbers whose sum of squares is not divisible by $q$. Suppose there is a chain $(a, b, c, d)$ of sequentially connected numbers such that the sum of squares of any pair of adjacent numbers is divisible by $q$. Then
$$
a^{2}+d^{2}=\left(a^{2}+b^{2}\right)-\left(b^{2}+c^{2}\right)+\left(c^{2}+d^{2}\right) \vdots q
$$
This means that the numbers $a$ and $d$ are connected, so there is a cycle of length 4 in the picture, which does not exist.
From 1) and 3), it follows that the number $n$ has at least two different odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from $3, 7, 11$. Suppose, for example, that $p \in \{3, 7, 11\}$. Note that for any natural number $a$
$$
a^{2} \bmod 3 \in \{0,1\}, \quad a^{2} \bmod 7 \in \{0,1,2,4\}, \quad a^{2} \bmod 11 \in \{0,1,3,4,5,9\}
$$
Therefore, $a^{2}+b^{2}$ is divisible by $p$ if and only if $a^{2}$ and $b^{2}$ are divisible by $p$, and thus $a$ and $b$ are divisible by $p$. By 2), this condition can be satisfied by only one pair. From the remaining four pairs of connected numbers, a three-link chain can be formed in which the sum of squares of each pair of adjacent numbers is divisible by $q$. But this contradicts 3).
Thus, if $n$ has exactly two different odd prime divisors, then $n \geqslant 5 \cdot 13=65$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>65$. The arrangement for $n=65$ is shown in the figure.
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $x, y, z \geqslant 1$, find the minimum value of the expression
$$
A=\frac{\sqrt{3 x^{4}+y}+\sqrt{3 y^{4}+z}+\sqrt{3 z^{4}+x}-3}{x y+y z+z x}
$$
|
Answer: 1.
Solution. Note that for $x, y \geqslant 1$
$$
\sqrt{3 x^{4}+y}-1=\sqrt{x^{4}+2 x^{4}+y}-1 \geqslant \sqrt{x^{4}+2 x^{2}+1}-1=x^{2}
$$
Similarly, it can be shown that
$$
\sqrt{3 y^{4}+z}-1 \geqslant y^{2}, \quad \sqrt{3 z^{4}+x}-1 \geqslant z^{2}
$$
Therefore,
$$
A \geqslant \frac{x^{2}+y^{2}+z^{2}}{x y+y z+z x} \geqslant 1
$$
Equality is achieved when $x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a cyclic quadrilateral $A B C D$ with perpendicular diagonals. On the circle circumscribed around it, a point $E$ is marked, diametrically opposite to $D$, and the segments $A B$ and $D E$ do not intersect. Find the ratio of the areas of triangle $B C D$ and quadrilateral $A B E D$.
|
Answer: 1.
Solution. Let $N$ be the intersection point of $A C$ and $B D$, and $H$ be the foot of the perpendicular dropped from point $E$ to line $A C$. By the problem's condition, $D E$ is the diameter of the circle. Therefore, $\angle D B E=90^{\circ}$, which implies $B E \| A C$. Additionally, $\angle D C E=90^{\circ}$ and
$$
\angle C D E=90^{\circ}-\angle D E C=90^{\circ}-\angle D A C=\angle A D B
$$
from which it follows that $C E=A B$. Thus, $A B E C$ is an isosceles trapezoid, and
$$
C N=A C-A N=A C-C H=A H
$$
It remains to note that
$$
2 \cdot S_{A B E D}=B D \cdot A N+B D \cdot B E=B D \cdot A H=B D \cdot C N=2 \cdot S_{B C D}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a square table of size $2021 \times 2021$. Each of its cells is colored in one of $n$ colors. It is known that for any four cells of the same color located in the same column, there are no cells of the same color to the right of the top one and to the left of the bottom one. What is the smallest $n$ for which this is possible?
|
Answer: 506.
Solution. Consider some specific color (say, blue). In each column, mark the three lower blue cells with a cross, and the rest with a zero (if there are fewer than four blue cells in the column, mark all cells with a cross). Note that in any row, there is no more than one blue cell with a zero (otherwise, for the leftmost of them, the condition of the problem is violated). Therefore, there are no more than 2021 blue cells with a zero. In addition, the number of blue cells with a cross does not exceed $3 \cdot 2021$. Thus, the total number of blue cells does not exceed $2021 + 3 \cdot 2021 = 4 \cdot 2021$. These arguments are valid for any color. Therefore, the total number of colors is not less than
$$
\frac{2021^{2}}{4 \cdot 2021} = \frac{2021}{4} = 505.25
$$
Thus, $n \geqslant 506$.
We will show that $n=506$ is achievable. Sequentially number all diagonals from bottom to top, running from northwest to southeast, with numbers from 1 to 4041. Paint the first four diagonals in the first color, the next four in the second color, and so on in a cycle (so after the 506th color, the first color will follow again). We will check that this coloring satisfies the condition of the problem. Note that no color is used more than twice, since $506 \cdot 4 \cdot 2 = 4048 > 4041$. Let the $k$-th color appear twice. In the first block, the topmost cell of this color will be in the row with number $4k$. In the second block, the bottommost cell of this color is in the row with number
$$
4(506+k-1)+1-2020 = 4k+1
$$
Thus, cells of the same color from different blocks cannot be in the same row.
## Variant 4
|
506
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Tanya chooses a natural number $n$ and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers $a$ and $b$ are not connected by a segment, then the sum $a^{2}+b^{2}$ must be coprime with $n$; if $a$ and $b$ are connected, then the numbers $a^{2}+b^{2}$ and $n$ must have a common natural divisor greater than 1. For what smallest $n$ does such an arrangement exist?
|
Answer: $n=65$.
Solution. First, let's make three observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among six numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $d$ is a divisor of $n$, then no more than two numbers are divisible by $d$. Suppose there are three such numbers. Then they must be pairwise connected and, therefore, form a three-link cycle.
3) If $q$ is a prime divisor of $n$, and in the chain $(a, b, c, d)$ of sequentially connected numbers, the sum of the squares of any pair of adjacent numbers is divisible by $q$, then $(a, b, c, d)$ forms a cycle. Indeed,
$$
a^{2}+d^{2}=\left(a^{2}+b^{2}\right)-\left(b^{2}+c^{2}\right)+\left(c^{2}+d^{2}\right) \vdots q
$$
that is, the numbers $a$ and $d$ are also connected.
From 1) and 3), it follows that the number $n$ has at least two distinct odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from $3, 7, 11$. Suppose, for example, that $p \in\{3,7,11\}$. Note that for any natural number $a$
$$
a^{2} \bmod 3 \in\{0,1\}, \quad a^{2} \bmod 7 \in\{0,1,2,4\}, \quad a^{2} \bmod 11 \in\{0,1,3,4,5,9\}
$$
Therefore, $a^{2}+b^{2}$ is divisible by $p$ if and only if $a^{2}$ and $b^{2}$ are divisible by $p$, and hence $a$ and $b$ are divisible by $p$. By 2), this condition can be satisfied by only one pair. From the remaining six pairs of connected numbers, a non-cyclic three-link chain can be formed (for example, passing along the left and top or right and bottom sides of the large rectangle). In this chain, the sum of the squares of each pair of adjacent numbers is divisible by $q$, which contradicts 3).
Thus, if $n$ has exactly two distinct odd prime divisors, then $n \geqslant 5 \cdot 13=65$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>65$. The arrangement for $n=65$ is shown in the figure.
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y, z \in(0,1]$ find the maximum value of the expression
$$
A=\frac{\sqrt{8 x^{4}+y}+\sqrt{8 y^{4}+z}+\sqrt{8 z^{4}+x}-3}{x+y+z}
$$
|
Answer: 2.
Solution. Note that for $x, y \in(0,1]$
$$
\sqrt{8 x^{4}+y}-1=\sqrt{4 x^{4}+4 x^{4}+y}-1 \leqslant \sqrt{4 x^{2}+4 x+1}-1=2 x .
$$
Similarly, it can be shown that
$$
\sqrt{3 y^{4}+z}-1 \leqslant 2 y, \quad \sqrt{3 z^{4}+x}-1 \leqslant 2 z
$$
Therefore,
$$
A \leqslant \frac{2 x+2 y+2 z}{x+y+z}=2
$$
Equality is achieved when $x=y=z=1$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The diagonal $AC$ of the inscribed quadrilateral $ABCD$ is the diameter of the circumscribed circle $\omega$ around it. A line perpendicular to the segment $BC$ was drawn from point $D$, intersecting the circle $\omega$ again at point $E$. Find the ratio of the areas of triangle $BCD$ and quadrilateral $ABEC$.
|
Answer: 1.

Solution. Let $N$ be the intersection point of $B C$ and $D E$, and $H$ be the foot of the perpendicular dropped from point $A$ to line $D E$. By the problem's condition, $A C$ is the diameter of the circle. Therefore, $\angle A B C=90^{\circ}$, which implies $A B \| D E$. Additionally, $\angle A D C=90^{\circ}$ and
$$
\angle A C D=90^{\circ}-\angle D A C=90^{\circ}-\angle D E C=90^{\circ}-\angle N E C=\angle E C B
$$
from which it follows that $A D=B E$. Thus, $D A B E$ is an isosceles trapezoid, and
$$
D N=D E-E N=D E-D H=E H
$$
It remains to note that
$$
2 \cdot S_{A B E C}=B C \cdot E N+B C \cdot A B=B C \cdot E H=B C \cdot D N=2 \cdot S_{B C D}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The board has the number 5555 written in an even base $r$ ($r \geqslant 18$). Petya found out that the $r$-ary representation of $x^2$ is an eight-digit palindrome, where the difference between the fourth and third digits is 2. (A palindrome is a number that reads the same from left to right and from right to left). For which $r$ is this possible?
|
Answer: $r=24$.
Solution. Let's agree to write $u \equiv v(\bmod w)$ if $(u-v) \vdots w$. According to the condition, there exist such $r$-ary digits $a, b, c, d$ that $d-c=2$ and
$$
25(r+1)^{2}\left(r^{2}+1\right)^{2}=a\left(r^{7}+1\right)+b\left(r^{6}+r\right)+c\left(r^{5}+r^{2}\right)+d\left(r^{4}+r^{3}\right)
$$
Let's make some observations.
1) Since $r^{6} \equiv-1\left(\bmod \left(r^{2}+1\right)\right)$, the following equalities hold:
$$
r^{7}+1 \equiv 1-r\left(\bmod \left(r^{2}+1\right)\right) \quad \text { and } \quad r^{6}+r \equiv r-1\left(\bmod \left(r^{2}+1\right)\right)
$$
Moreover, $r^{4} \equiv 1\left(\bmod \left(r^{2}+1\right)\right)$, hence
$$
r^{5}+r^{2} \equiv r-1\left(\bmod \left(r^{2}+1\right)\right) \quad \text { and } \quad r^{4}+r^{3} \equiv 1-r\left(\bmod \left(r^{2}+1\right)\right)
$$
Then, by $(*)$
$$
0 \equiv(a-b-c+d)(1-r)\left(\bmod \left(r^{2}+1\right)\right)
$$
Note that $r^{2}+1+(1-r)(r+1)=2$, and the numbers $1-r$ and $r^{2}+1$ are odd. Therefore, they are coprime, which implies $a-b-c+d \vdots\left(r^{2}+1\right)$. But
$$
|a-b-c+d| \leqslant 2(r-1)<2 r<r^{2}+1
$$
Thus, $b-a=d-c=2$.
2) Since $r^{n} \equiv 1(\bmod (r-1))$ for any natural $n$, from $(*)$ and 1$)$ it follows that
$$
25 \cdot 16 \equiv 2(a+b+c+d)=4(b+c)(\bmod (r-1))
$$
Since $r-1$ is odd, $r-1$ divides the number $100-(b+c)$.
3) For any natural $n$
$$
r^{n}=(r+1-1)^{n} \equiv(-1)^{n}(1-n(r+1))\left(\bmod (r+1)^{2}\right)
$$
The right-hand side of $(*)$ is divisible by $(r+1)^{2}$, hence
$$
0 \equiv(7 a-5 b+3 c-d)(r+1)\left(\bmod (r+1)^{2}\right)
$$
Thus, the number
$$
7 a-5 b+3 c-d=7(b-2)-5 b+3 c-(c+2)=2(b+c)-16
$$
is divisible by $r+1$. Therefore, $b+c-8 \vdots(r+1)$ due to the oddness of $r+1$. Hence, $b+c=8$ or $b+c=8+r+1$. In the second case,
$$
0 \equiv 92-(r+1) \equiv 90(\bmod (r-1))
$$
Since $r$ is even and $r-1 \geqslant 17$, we get $r=46$. Then $a=25$ and $b=27$, which is impossible since $b=50 \bmod 46=4$. Therefore, $b+c=8$. By 2$) 92 \vdots(r-1)$, hence $r=24$.
Remark. If $b+c=8$ and $r=24$, then
$$
a=25 \bmod 24=1, \quad b=a+2=3, \quad c=8-b=5, \quad d=c+2=7
$$
The equality $5555_{24}^{2}=13577531_{24}$ is verified by direct computation.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a square table of size $2023 \times 2023$. Each of its cells is colored in one of $n$ colors. It is known that for any six cells of the same color located in the same row, there are no cells of the same color above the leftmost of them and below the rightmost of them. What is the smallest $n$ for which this is possible?
|
Answer: 338.
Solution. Consider some specific color (say, blue). In each row, mark the five leftmost blue cells with a cross, and the rest with a zero (if there are fewer than six blue cells in the row, mark all cells with a cross). Note that in any column, there is no more than one blue cell with a zero (otherwise, for the topmost one, the condition of the problem is violated). Therefore, there are no more than 2023 blue cells with a zero. In addition, the number of blue cells with a cross does not exceed $5 \cdot 2023$. Thus, the total number of blue cells does not exceed $2023 + 5 \cdot 2023 = 6 \cdot 2023$. These arguments are valid for any color. Therefore, the total number of colors is no less than
$$
\frac{2023^{2}}{6 \cdot 2023} = \frac{2023}{6} = 337 \frac{1}{6}
$$
Thus, $n \geqslant 338$.
We will show that $n=338$ is achievable. Sequentially number all diagonals from top to bottom, running from southwest to northeast, with numbers from 1 to 4045. Paint the first six diagonals in the first color, the next six in the second color, and so on in a cycle (so after the 338th color, the first color will follow again). We will check that this coloring satisfies the condition of the problem. Note that no color is used more than twice, since $338 \cdot 6 \cdot 2 = 4056 > 4045$. Let the $k$-th color appear twice. In the first block, the rightmost cell of this color will be in the column with number $6k$. In the second block, the leftmost cell of this color is in the column with number
$$
6(338+k-1)+1-2022 = 6k+1
$$
Thus, cells of the same color from different blocks cannot be in the same column.
|
338
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Nastya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the difference \( a - b \) must be coprime with \( n \), and if they are connected, then \( a - b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
|
Answer: $n=5 \cdot 7 \cdot 11=385$.
Solution. We will make two observations.
1) $n$ is not divisible by 2 and 3. Among seven numbers, there are always three numbers of the same parity. If $n$ is even, then they must be pairwise connected. Moreover, among seven numbers, there will be three numbers that give the same remainder when divided by 3. If $n$ is divisible by 3, then these numbers also form a three-link cycle. But such cycles do not exist in the picture.
2) If $p$ is a prime divisor of $n$, then among three consecutively connected numbers, there exists a pair of adjacent numbers whose difference is not divisible by $p$. Let $(a, b, c)$ be a chain of consecutively connected numbers where $a-b$ and $b-c$ are divisible by $p$. Then $a-c=(a-b)+(b-c) \vdots p$. This means that $(a, b, c)$ forms a three-link cycle, which is impossible.
We will show that the number $n$ has at least three distinct prime divisors. Let $p$ be a prime divisor of $n$. There are no more than three distinct pairs $(a, b)$ for which $a-b \vdots p$. If there were 4 such pairs, then some two of them would intersect, which contradicts 2). But in total, 7 pairs of numbers are connected by segments, so $n$ has at least three distinct prime divisors. In view of 1), the minimal possible values for them are $5, 7, 11$, that is, $n \geqslant 5 \cdot 7 \cdot 11=385$. The arrangement for $n=385$ is shown in the figure.
|
385
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y \in(0,1]$, find the maximum value of the expression
$$
A=\frac{\left(x^{2}-y\right) \sqrt{y+x^{3}-x y}+\left(y^{2}-x\right) \sqrt{x+y^{3}-x y}+1}{(x-y)^{2}+1}
$$
|
Answer: 1.
Solution. Note that
$$
y+x^{3}-x y-x^{2}=\left(y-x^{2}\right)(1-x)
$$
If $y \geqslant x^{2}$, then
$$
\sqrt{y+x^{3}-x y} \geqslant x \quad \text { and } \quad\left(x^{2}-y\right)\left(\sqrt{y+x^{3}-x y}-x\right) \leqslant 0
$$
and when $y<x^{2}$
$$
\sqrt{y+x^{3}-x y} \leqslant x \quad \text { and } \quad\left(x^{2}-y\right)\left(\sqrt{y+x^{3}-x y}-x\right) \leqslant 0
$$
In both cases, the inequality $\left(x^{2}-y\right) \sqrt{y+x^{3}-x y} \leqslant x^{3}-x y$ holds. Estimating the second term in the numerator of $A$ similarly, we get
$$
A \leqslant \frac{x^{3}+y^{3}-2 x y+1}{(x-y)^{2}+1} \leqslant \frac{x^{2}+y^{2}-2 x y+1}{(x-y)^{2}+1}=1
$$
Equality is achieved when $x=y=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the side $AB$ of an acute-angled triangle $ABC$, a point $M$ is marked. A point $D$ is chosen inside the triangle. Circles $\omega_{A}$ and $\omega_{B}$ are circumscribed around triangles $AMD$ and $BMD$ respectively. The side $AC$ intersects the circle $\omega_{A}$ again at point $P$, and the side $BC$ intersects the circle $\omega_{B}$ again at point $Q$. The ray $PD$ intersects the circle $\omega_{B}$ again at point $R$, and the ray $QD$ intersects the circle $\omega_{A}$ again at point $S$. Find the ratio of the areas of triangles $ACR$ and $BCS$.
|
# Answer: 1.
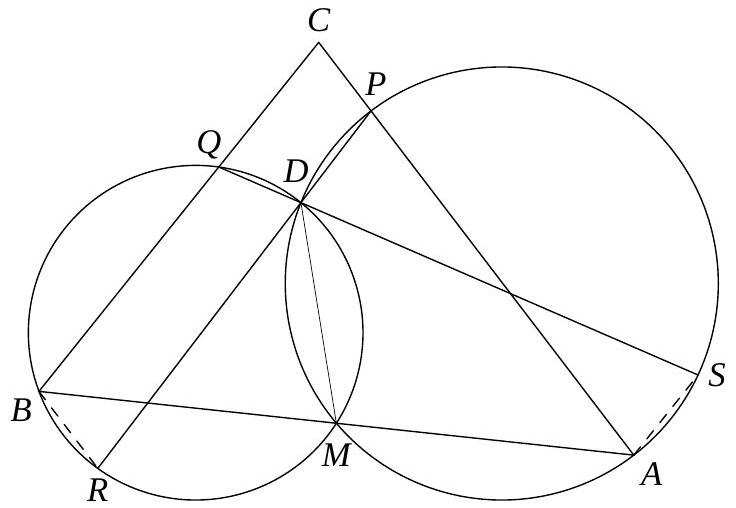
Solution. Notice that
$$
\angle P A M=180^{\circ}-\angle P D M=\angle R D M=\angle R B M
$$
from which it follows that $B R \| A C$. Therefore, the distances from points $B$ and $R$ to the line $A C$ are the same. Thus, triangles $A B C$ and $A C R$ have the same base $A C$ and the same heights dropped to $A C$. Therefore, the areas of these triangles are equal. Additionally,
$$
\angle Q B M=180^{\circ}-\angle Q D M=\angle M D S=180^{\circ}-\angle M A S
$$
from which it follows that $A S \| B C$. Therefore, the distances from points $A$ and $S$ to the line $B C$ are the same. Thus, triangles $A B C$ and $B C S$ have the same base $B C$ and the same heights dropped to $B C$. Therefore, the areas of these triangles are also equal. As a result, we get $S_{A C R}=S_{A B C}=S_{B C S}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y \in[1,3]$ find the minimum value of the expression
$$
A=\frac{\left(3 x y+x^{2}\right) \sqrt{3 x y+x-3 y}+\left(3 x y+y^{2}\right) \sqrt{3 x y+y-3 x}}{x^{2} y+y^{2} x}
$$
|
Answer: 4.
Solution. Note that
$$
3 x y+x-3 y-x^{2}=(3 y-x)(x-1) \geqslant 0
$$
since $x \geqslant 1$ and $x \leqslant 3 \leqslant 3 y$. Then
$$
\left(3 x y+x^{2}\right) \sqrt{3 x y+x-3 y} \geqslant 3 x^{2} y+x^{3} \quad \text { and, similarly, } \quad\left(3 x y+y^{2}\right) \sqrt{3 x y+y-3 x} \geqslant 3 y^{2} x+y^{3} .
$$
Moreover, by the Cauchy inequality
$$
x^{2} y+y^{2} x=x y(x+y) \leqslant \frac{1}{4}(x+y)^{3}
$$
Therefore,
$$
A \geqslant \frac{3 x y(x+y)+x^{3}+y^{3}}{\frac{1}{4}(x+y)^{3}}=4 \cdot \frac{(x+y)^{3}}{(x+y)^{3}}=4
$$
Equality is achieved when $x=y=1$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the side $B C$ of triangle $A B C$ with obtuse angle $C$, a point $M$ is marked. Point $D$ is chosen such that triangle $B C D$ is acute, and points $A$ and $D$ lie on opposite sides of line $B C$. Circles $\omega_{B}$ and $\omega_{C}$ are circumscribed around triangles $B M D$ and $C M D$ respectively. Side $A B$ intersects circle $\omega_{B}$ again at point $P$, and ray $A C$ intersects circle $\omega_{C}$ again at point $Q$. Segment $P D$ intersects circle $\omega_{C}$ again at point $R$, and ray $Q D$ intersects circle $\omega_{B}$ again at point $S$. Find the ratio of the areas of triangles $A B R$ and $A C S$.
|
# Answer: 1.

Solution. Notice that
$$
\angle S B M=180^{\circ}-\angle S D M=\angle M D Q=180^{\circ}-\angle M C Q
$$
from which $S B \| A C$. Therefore, the distances from points $B$ and $S$ to line $A C$ are the same. Thus, triangles $A B C$ and $A S C$ have the same base $A C$ and equal heights dropped to $A C$. Therefore, the areas of these triangles are equal. Additionally,
$$
\angle P B M=\angle P D M=\angle R D M=\angle R C M
$$
from which $B P \| R C$. Therefore, the distances from points $R$ and $C$ to line $A B$ are the same. Thus, triangles $A B C$ and $A B R$ have the same base $A B$ and equal heights dropped to $A B$. Therefore, the areas of these triangles are also equal. As a result, we get $S_{A S C}=S_{A B C}=S_{A B R}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Kostya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \), and if they are connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?

|
Answer: $n=15$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among any five numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) $n$ has at least two distinct prime divisors. Suppose $n$ is a power of a prime number $p$. Take a chain $(a, b, c, d)$ of sequentially connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which is not there.
Thus, the number $n$ has at least two distinct odd prime divisors, hence $n \geqslant 15$. The arrangement for $n=15$ is shown in the figure.
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y, z \in(0,1]$ find the minimum value of the expression
$$
A=\frac{(x+2 y) \sqrt{x+y-x y}+(y+2 z) \sqrt{y+z-y z}+(z+2 x) \sqrt{z+x-z x}}{x y+y z+z x}
$$
|
Answer: 3.
Solution. Note that for $x, y \in(0,1]$
$$
\sqrt{x+y-x y}=\sqrt{x+y(1-x)} \geqslant \sqrt{x} \geqslant x
$$
Then $(x+2 y) \sqrt{x+y-x y} \geqslant x^{2}+2 x y$ and similarly,
$$
(y+2 z) \sqrt{y+z-y z} \geqslant y^{2}+2 y z, \quad(z+2 x) \sqrt{z+x-z x} \geqslant z^{2}+2 z x
$$
Therefore,
$$
A \geqslant \frac{x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x}{x y+y z+z x}=\frac{(x+y+z)^{2}}{x y+y z+z x} \geqslant 3
$$
Equality is achieved when $x=y=z=1$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.