problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4. Given a cube. $A, B$ and $C$ are the midpoints of its edges (see figure). What is the angle $ABC$?
Answer. $120^{\circ}$.
|
Solution. 1st method. Draw diagonals $D E \| B C$ and $E F \| A B$ and let $K$ be the point on the extension of diagonal $D E$ beyond point $E$ (see figure). Then $\angle A B C = \angle F E K$. But triangle $D E F$ is equilateral, so
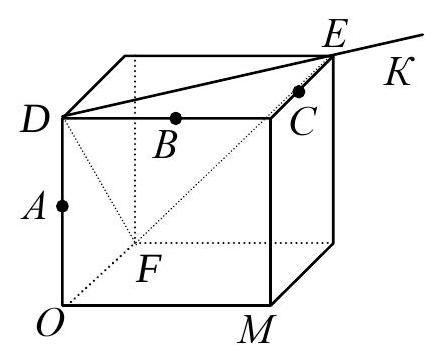
$\angle D E F = 60^{\circ}$, and therefore, $\angle F E K = 120^{\circ}$.
2nd method. Introduce a coordinate system with the origin at point $O$, axes $O x, O y$, and $O z$ directed along vectors $\overrightarrow{\mathrm{OM}}, \overrightarrow{\mathrm{OF}}$, and $\overrightarrow{\mathrm{OD}}$ respectively, and let the edge of the cube be 2. Then $A(0 ; 0 ; 1), B(1 ; 0 ; 2)$, $C(2 ; 1 ; 2)$. Therefore, $\overrightarrow{\mathrm{BA}}(-1 ; 0 ;-1), |\overrightarrow{\mathrm{BA}}| = \sqrt{2}, \overrightarrow{\mathrm{BC}}(1 ; 1 ; 0), |\overrightarrow{\mathrm{BC}}| = \sqrt{2}$. Now we find the scalar product of vectors $\overrightarrow{\mathrm{BA}}$ and $\overrightarrow{\mathrm{BC}}$ in two ways:
$\overrightarrow{\mathrm{BA}} \cdot \overrightarrow{\mathrm{BC}} = (-1) \cdot 1 + 0 \cdot 1 + (-1) \cdot 0 = -1$ and $\overrightarrow{\mathrm{BA}} \cdot \overrightarrow{\mathrm{BC}} = \sqrt{2} \cdot \sqrt{2} \cos A B C$. From these two equations, we get that $\cos A B C = -0.5$, i.e., the angle $A B C$ is $120^{\circ}$.
3rd method. Let the edge of the cube be 1. Then, by the Pythagorean theorem, $A B = B C = \frac{\sqrt{2}}{2} ; D C = \frac{\sqrt{5}}{2}$ and $A C = \sqrt{\mathrm{AD}^{2} + \mathrm{DC}^{2}} = \sqrt{\frac{3}{2}}$. Now, using the cosine rule in triangle $A B C$, we find that $\cos A B C = -0.5$.
Grading criteria.
- Correct answer with all justifications - 7 points.
- Correct solution process, but incorrect answer due to an arithmetic error - 5 points.
- Answer of $60^{\circ} - 4$ points.
- Only the answer (including the correct one) - 0 points.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many natural numbers $n$ exist for which $4^{n}-15$ is a square of an integer?
|
Answer. Two.
Solution. Let $4^{n}-15=x^{2}$, where $x$ is an integer. It is obvious that $x \neq 0$. If $x$ is negative, then $(-x)^{2}$ is also equal to $4^{n}-15$; therefore, we will assume that $4^{n}-15=x^{2}$, where $x$ is a natural number. From the equation $2^{2 n}-15=x^{2}$, we get: $2^{2 n}-x^{2}=15$, and using the formula for factoring the difference of squares: $\left(2^{n}-x\right)\left(2^{n}+x\right)=15$. Since $x$ is a natural number, the second factor on the left in the last equation is positive, and therefore the first factor must also be positive. The number 15 can be factored into natural numbers in two ways: $15=3 \cdot 5=1 \cdot 15$. Since $x>0$, we have $2^{n}+x>2^{n}-x$. Thus, there are only two possible cases:
$\left\{\begin{array}{l}2^{n}-x=1, \\ 2^{n}+x=15\end{array}\right.$ or $\left\{\begin{array}{l}2^{n}-x=3, \\ 2^{n}+x=5 .\end{array}\right.$
Solving the first system of equations (it is most convenient to simply add the equations), we get that $2 \cdot 2^{n}=16$, i.e., $n=3$. Similarly, from the second system, we get that $n=2$.
We could solve without limiting ourselves to natural values of $x$, but then the number of systems to be considered would increase, as the cases $15=(-1) \cdot(-15)=(-3) \cdot(-5)$ would also be possible.
Grading criteria.
- Correct answer with full justification - 7 points.
- Cases of factoring 15 into negative factors not considered without justification, why negative factors can be ignored - 6 points.
- Systems for determining $n$ correctly set up, but not checked for natural solutions - 5 points.
- Only one of the two possible factorizations of the number 15 considered - 5 points.
- Reasonable arguments that did not lead to a solution - 1-2 points.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.1
## Condition:
Grandma is embroidering her grandchildren's names on their towels. She embroidered the name "ANNA" in 20 minutes, and the name "LINA" in 16 minutes. She spends the same amount of time on the same letters, and possibly different times on different letters. How long will it take her to embroider the name "LILI"?
|
Express the answer in minutes.
Answer: 12
Exact match of the answer - 1 point
Solution.
Since the grandmother spends the same amount of time on identical letters, she will spend $20: 2=10$ minutes on the syllable "NA". Then she will spend
$16-10=6$ minutes on the syllable "LI". Therefore, she will spend $6+6=12$ minutes on the name "LILI".
## Condition:
Mashenka is signing gifts beautifully for New Year. She wrote "MAMA" in 12 minutes, and the name "MILA" in 8 minutes. She spends the same amount of time on identical letters, and possibly different amounts of time on different letters. How long will it take her to write the name "LILI"?
Express the answer in minutes.
Answer: 4
Exact match of the answer - 1 point
Solution by analogy with task № 3.1.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.3
## Condition:
Petya is teaching his cat to read and for this, he makes him cards with words, burning them. He burned the word "MAMA" in 20 minutes, and the word "MISKA" in 35 minutes. He spends the same amount of time on identical letters, and possibly different times on different letters. How long will it take him to burn "KIS KIS"?
|
Express the answer in minutes.
Answer: 50
Exact match of the answer - 1 point
Solution by analogy with problem № 3.1.
## Condition:
Grandma is embroidering her grandchildren's names on their towels. She embroidered the name "LANA" in 15 minutes, and the name "ALLA" in 12 minutes. She spends the same amount of time on the same letters, and possibly different times on different letters. How long will it take her to embroider the name "NANA"?
Answer in minutes.
Answer: 18
Exact match of the answer - 1 point
Solution by analogy with problem № 3.1.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 4.1
## Condition:
On an island of knights, who always tell the truth, and liars, who always lie, a five-story building was built. One resident lived on each floor. One day, each of them made the same statement:
"There are more liars above me than knights below me!"
How many liars can live in this building?
|
# Answer: 3
## Exact match of the answer -1 point
## Solution.
Notice that the person living on the 5th floor is definitely lying, as there is no one living above them, including liars. Therefore, there are 0 liars above them, and 0 or more knights below. Now consider the resident on the 1st floor. They definitely told the truth, as there are 0 knights below them, and at least 1 liar living above, specifically the one on the 5th floor.
Now let's focus on the resident on the 4th floor. Above them lives exactly 1 liar, and below - at least 1 knight on the 1st floor. Therefore, their statement is false in any case. This means they are a liar. Then, the resident on the 2nd floor, similar to the reasoning about the one on the 1st floor, is a knight. The only one left to determine is the resident on the 3rd floor. Above them live 2 liars, and below - 2 knights. Therefore, their statement is false. Hence, they are a liar.
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 4.3
## Condition:
On an island of knights, who always tell the truth, and liars, who always lie, a six-story building was built. One resident lived on each floor. One day, each of them made the same statement:
"There are more liars above me than knights below me!" How many liars can live in this building?
|
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with task No. 4.1.
## Condition:
On an island of knights, who always tell the truth, and liars, who always lie, a five-story building was built. One resident lived on each floor. One day, each of them made the same statement:
"There are more liars below me than knights above me!" How many knights can live in this building?
## Answer: 2
Exact match of the answer - 1 point
Solution by analogy with task No. 4.1.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 5.1
## Condition:
In a correct equation, identical digits were replaced with the same letters, and different digits with different letters. The result is
$$
P+\mathrm{P}+\mathrm{A}+3+Д+\mathrm{H}+\mathrm{U}+\mathrm{K}=\mathrm{U} \mathrm{U}
$$
What can U be equal to?
|
# Answer:
$\circ 1$
$\circ 2$
$\checkmark 3$
$\circ 4$
० 5
० 6
○ 7
○ 8
$\circ 9$
$\circ 0$
Exact match of the answer - 1 point
## Solution.
Notice that the expression involves 9 different letters, meaning all digits except one are used. On the left, we have the sum of eight different single-digit numbers. The sum of all single-digit numbers is $0+1+2+3+4+5+6+7+8+9=45$. Let's see which two-digit numbers with identical digits can be obtained by summing eight numbers.
$44=45-1, 33=45-12, 22=45-23, 11=45-34$. The last two are not possible because the maximum sum of two single-digit numbers is $17=8+9$. Also, 44 is not suitable because to get it, we would need to use all numbers except 0 and 1, but then U cannot be 4 because 4 is already used on the left. The variant 33 is quite suitable. $12=3+9$, and we get the equality:
$$
0+1+2+4+5+6+7+8=33
$$
## Condition:
In a correct equality, identical digits were replaced by identical letters, and different digits by different letters. The result is
$$
П+\mathrm{O}+\mathrm{Б}+\mathrm{E}+Д+\mathrm{И}+Ш+\mathrm{b}=\mathrm{AA} .
$$
What can $A$ be equal to?
## Answer:
$\circ 1$
$\circ 2$
$\checkmark 3$
$\circ 4$
$\circ 5$
○ 6
○ 7
○ 8
० 9
$\circ 0$
Exact match of the answer - 1 point
Solution by analogy with problem № 5.1.
## Condition:
In a correct equality, identical digits were replaced by identical letters, and different digits by different letters. The result is
$$
\mathrm{C}+\mathrm{y}+П+\mathrm{E}+\mathrm{P}+\mathrm{K}+Л+\mathrm{A}+Д=\mathrm{AA}
$$
What can $A$ be equal to?
## Answer:
$\circ 1$
$\circ 2$
$\circ 3$
$\checkmark 4$
$\circ 5$
० 6
○ 7
○ 8
० 9
$\circ 0$
Exact match of the answer - 1 point
Solution by analogy with problem № 5.1.
## Condition:
In a correct equality, identical digits were replaced by identical letters, and different digits by different letters. The result is
$$
Г+\mathrm{P}+\mathrm{A}+Д+\mathrm{y}+\mathrm{C}+\mathrm{H}+\mathrm{И}+\mathrm{K}=\text { ИИ. }
$$
What can И be equal to?
## Answer:
$\circ 1$
$\circ 2$
$\circ 3$
$\checkmark 4$
$\circ 5$
० 6
○ 7
○ 8
० 9
○ 0
Exact match of the answer - 1 point
Solution by analogy with problem № 5.1.
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 6.1
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
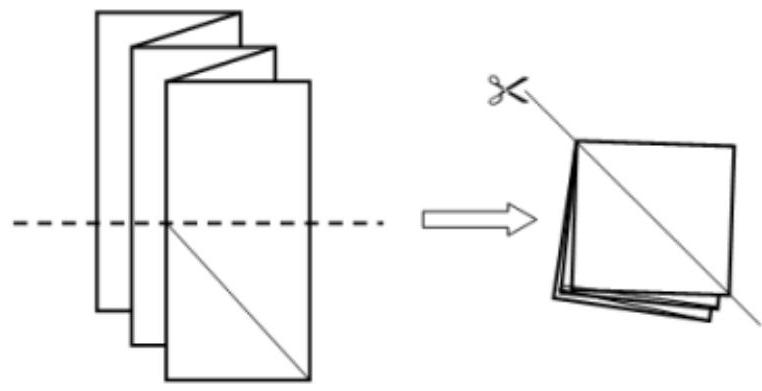
How many pieces of paper were obtained after this?
|
Answer: 9
Exact match of the answer - 1 point
## Solution.
Unfold the paper and mark the lines of the cuts.
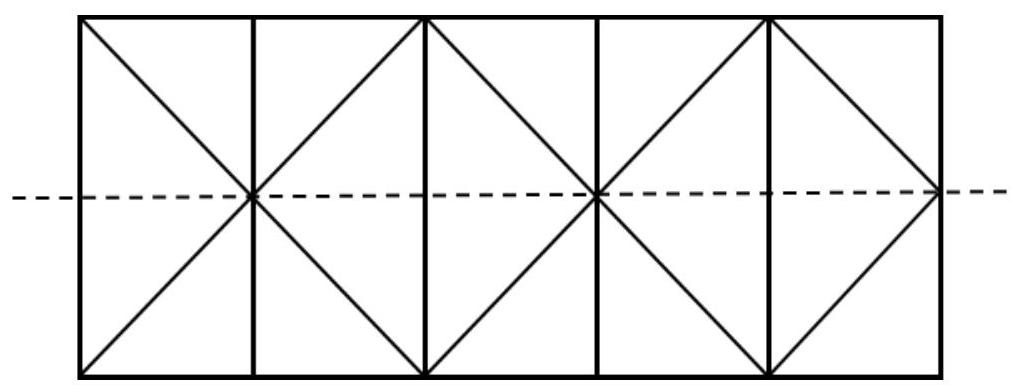
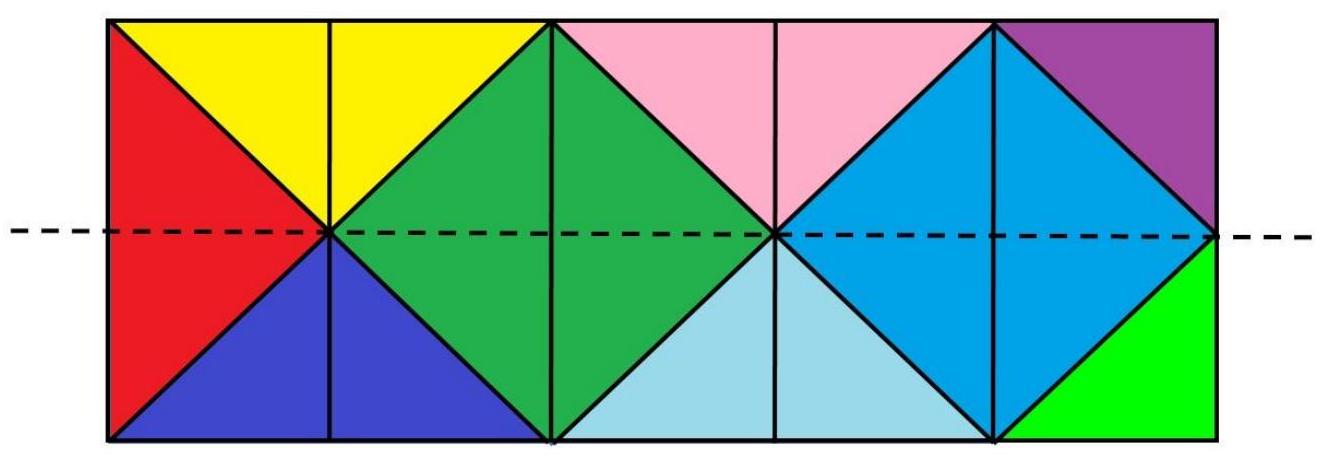
Now it is easy to count the resulting pieces. For convenience, they are highlighted in color.
## Problem:
A sheet of paper was folded like an accordion as shown in the picture, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
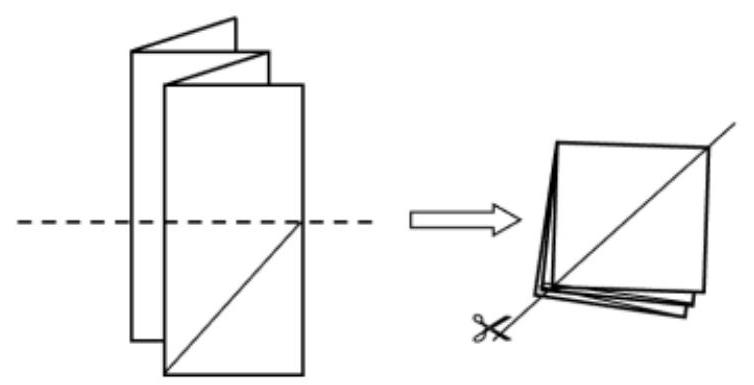
How many pieces of paper were obtained after this?
Answer: 8
Exact match of the answer - 1 point
Solution by analogy with problem № 6.1.
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.1
## Condition:
On the Misty Planet, santiks, kubriks, and tugriks are in circulation. One santik can be exchanged for 1 kubrik or 1 tugrik, 1 kubrik can be exchanged for 3 santiks, and 1 tugrik can be exchanged for 4 santiks. No other exchanges are allowed. Jolly U, initially having 1 santik, made 20 exchanges, and now he has 25 santiks (and no other money). How many times did he exchange kubriks for santiks?
|
# Answer: 6
## Exact match of the answer -1 point
## Solution.
To increase the number of santiks, we need to exchange them for kubriks or tugriks. In essence, we need to perform a double exchange, that is, first convert a santik into a tugrik or kubrik at a 1:1 ratio, and then increase the number of coins. Since the total number of exchanges is 20, 10 "double exchanges" were conducted. When exchanging a kubrik, the number of coins increases by 2, and when exchanging a tugrik, it increases by 3. Starting with 1 coin, it became 25 - the number of coins increased by 24. If all exchanges were made using kubriks, the number of coins would have increased by 20. In our case, it increased by 24, so 4 exchanges were made with tugriks, and 6 with kubriks.
#
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.2
Condition:
In the city of Abracodabra, funtics, tubrics, and santics are in circulation. One funtic can be exchanged for 1 tubric or 1 santic, 1 tubric for 5 funtics, and 1 santic for 2 funtics. No other exchanges are allowed. Lunatic, initially having 1 funtic, made 24 exchanges and now has 40 funtics (and no other money). How many times did he exchange tubrics for funtics?
|
Answer: 9
Exact match of the answer -1 point
Solution by analogy with task No. 7.1.
## Condition:
On the planet Mon Calamari, dataries, flans, and pegats are in circulation. One datary can be exchanged for 1 flan or 1 pegat, 1 flan - for 2 dataries, and 1 pegat - for 4 dataries. No other exchanges are allowed. Meray, initially having 1 datary, made 20 exchanges, and now he has 25 dataries (and no other money). How many times did he exchange flans for dataries?
Answer: 3
Exact match of the answer -1 point
Solution by analogy with task No. 7.1.
## Condition:
In the machine, there are tokens, wrappers, and stamps. The machine can exchange 1 token for 1 wrapper or 1 stamp, 1 stamp for 2 tokens, or 1 wrapper for 3 tokens. No other exchanges can be made by the machine. Nезнайка, initially having 1 token, made 30 exchanges, and now he has 20 tokens (and no more wrappers or stamps). How many times did he exchange wrappers for tokens?
Answer: 4
Exact match of the answer -1 point
Solution by analogy with task No. 7.1.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. $\left(7\right.$ points) Calculate $\frac{(2009 \cdot 2029+100) \cdot(1999 \cdot 2039+400)}{2019^{4}}$.
|
# Solution.
$2009 \cdot 2029+100=(2019-10) \cdot(2019+10)+100=2019^{2}-10^{2}+100=2019^{2}$.
$1999 \cdot 2039+400=(2019-20) \cdot(2019+20)+400=2019^{2}-20^{2}+400=2019^{2}$.
Then $\frac{2019^{2} \cdot 2019^{2}}{2019^{4}}=1$
Answer. 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) Find all natural solutions to the equation $2 n-\frac{1}{n^{5}}=3-\frac{2}{n}$.
#
|
# Solution.
1 method. $2 n-\frac{1}{n^{5}}=3-\frac{2}{n}, 2 n-3=\frac{1}{n^{5}}-\frac{2}{n}, 2 n-3=\frac{1-2 n^{4}}{n^{5}}$.
For $n=1$ the equality is true, for $n>1 \quad 2 n-3>0, \frac{1-2 n^{4}}{n^{5}}<0$.
Answer. $n=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) A traveler was riding in a bus and saw a two-digit number on a kilometer post. He fell asleep and woke up an hour later to see a three-digit number on the kilometer post, where the first digit was the same as the second digit an hour ago, the second digit was zero, and the third digit was the same as the first digit an hour ago. Two hours later, he looked out the window and saw a kilometer post with the same number as two hours ago, except the zero was replaced by another digit. Find the speed of the bus (assuming it moved at a constant speed).
|
Solution. Let the first number the traveler saw be $\overline{x y}=10 x+y$. After an hour, the number became $\overline{y o x}=100 y+x$. After 2 hours, it became $\overline{y z x}=100 x+10 z+x$. Since the bus's speed is constant, $\overline{y o x}-\overline{x y}=\frac{1}{2} \cdot(\overline{y z x}-\overline{y o x})$, that is, $100 y+x-10 x-y=\frac{1}{2} \cdot(100 y+10 z+x-100 y-x), 9 \cdot(11 y-x)=5 z$.
Since the left side is divisible by 9, the right side is also divisible by 9. Therefore, $z=9$, and the speed of the bus is $5 \cdot z$ and equals 45 km/h. Answer. 45 km/h
|
45
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For natural numbers $a$ and $b$, it is known that $5a-1$ is divisible by $b$, $a-10$ is divisible by $b$, but $3a+5$ is not divisible by $b$. What values can the number $b$ take?
|
Answer: 49.
Solution. The number $(5 a-1)-5 \cdot(a-10)=49$ is divisible by $b$, so either $b=1$, or $b=7$, or $b=49$. If the number $(3 a+5)-3 \cdot(a-10)=35$ were divisible by $b$, then $3 a+5$ would be divisible by $b$, which is not the case. Therefore, the options $b=1$ and $b=7$ are impossible. The numbers $a=10$ and $b=49$ show that $b=49$ is achievable.
Comment. (a) Incorrect answer -1 point.
(b) Proven that $b$ is a divisor of $49-3$ points.
(c) Proven that $b$ is not equal to 7 or a stronger statement from which it follows that $b \neq 7-1$ point.
Points for the above items are summed except in the following cases:
Proven items (b) and (c) -6 points.
Correct solution -7 points.
Note. Checking the existence of such numbers $a$ and $b$ is not mandatory, as it is assumed in the problem statement.
|
49
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is an infinite grid plane, none of the points of which are painted blue. For one ruble, you can choose a cell and paint all its sides blue, even if some side was already painted. What is the minimum amount of money you need to pay to get a grid square $1001 \times 1001$, all grid lines inside and on the boundary of which will be painted blue? It is not required that only the grid lines of the square are painted in the end.
|
Answer: 503000 rubles.
Solution: We will call a segment in the solution any segment connecting grid nodes at a distance equal to the side of a cell. Let $s$ be our $1001 \times 1001$ square. Any cell either has two common segments with the perimeter of $s$ (in which case it falls into a corner of $s$), or has no more than one common segment with it. If we take fewer than 4000 cells, they will cover fewer than $2 \cdot 4 + 4000 - 4 = 4004$ segments of the perimeter, and thus will not cover the perimeter, so to cover the perimeter, we need to paint no fewer than 4000 cells.
Consider the $999 \times 999$ square obtained from $s$ by removing a border of width 1. Divide it into $\frac{999 \cdot 999 - 1}{2}$ rectangles of $1 \times 2$ and one cell. In each rectangle, a cell must be painted, otherwise the smaller median line of this rectangle will not be painted (it belongs only to the two cells of this rectangle). Therefore, in such rectangles, no fewer than $\frac{999 \cdot 999 - 1}{2} = 500 \cdot 998 = 499000$ cells must be painted.
Note that no cell inside the $999 \times 999$ square can have common segments with the perimeter of $s$. Therefore, the number of necessary cells is no less than $499000 + 4000 = 503000$. We will construct an example for which exactly 503000 cells need to be painted. Paint each cell from the border of width 1 of our square, which will cost 4000 rubles. Mentally color the previously encountered $999 \times 999$ square in a chessboard pattern with green and red colors, with fewer green cells than red ones. If we pay for each green cell, we will get a properly painted $s$ square and will spend a total of $\frac{999 \cdot 999 - 1}{2} + 4000 = 503000$ rubles.
Comment: Answer -1 point.
Example of coloring - 2 points.
Proved that it is necessary to spend no less than 4000 rubles on the perimeter of $s$ - 1 point.
Proved that it is necessary to spend no less than 499000 rubles on painting the inner $999 \times 999$ square - 3 points.
Points for the above items are cumulative.
If the solution is generally correct but lacks an explanation of why the sets of cells involved in the two estimates do not intersect - 6 points.
|
503000
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers from 1 to 8 are arranged in a circle. A number is called large if it is greater than its neighbors, and small if it is less than its neighbors. Each number in the arrangement is either large or small. What is the greatest possible sum of the small numbers?
|
Answer: 13.
Instructions. Adjacent numbers cannot be of the same type, so large and small numbers alternate, and there are four of each. 8 is large. 7 is also large, since a small number must be less than two numbers, and seven is less than only one. 1 and 2 are small. 6 and 5 cannot both be small, as they are less than only two numbers, and they cannot be adjacent in this case. Therefore, the sum of the two other small numbers (besides 1 and 2) is no more than 10. And the sum of the small numbers is no more than 13. Example: $8,6,7,1,3$, $2,5,4$.
Criteria. Only the correct answer and example: 2 points.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 In Pokémon hunting, 11 adults and $n$ children participated. Together, they caught $n^{2}+3 n-2$ Pokémon, with all adults catching the same number, and all children catching the same number, but each child catching 6 fewer than an adult. How many children participated in the game?
|
Solution: Let each child catch $m$ pokemons. Then $n m+11(m+6)=n^{2}+3 n-2$. From this, $(n+11) m=n^{2}+3 n-68$. Therefore, the right side is divisible by $n+11$. We have $n^{2}+3 n-68=$ $n(n+11)-8(n+11)+20$, so 20 is divisible by $n+11$. The only divisor of 20 greater than 10 is 20 itself, so $n+11=20, n=9$.
## Criteria:
- No points are deducted for the lack of an example for $n=9$.
- It is shown that $n=9$ works, but it is not proven that there are no other options -1 point.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5 What is the largest number of non-overlapping groups into which all integers from 1 to 25 can be divided so that the sum of the numbers in each group is a perfect square?
|
Solution 1: A group consisting of a single number can only be formed by 5 squares. The remaining 20 numbers must be divided into groups of at least two. Therefore, there will be no more than 15 groups in total. Let's check that exactly 15 groups are not possible. Indeed, in such a case, the numbers 1, 4, 9, 16, 25 form separate groups, and the remaining numbers are divided into pairs. The sum of the remaining numbers is 270, and they can give pairwise sums from 5 to 47. Thus, the number 270 must be the sum of 10 numbers, each of which is 9, 16, 25, or 36. Modulo 9, these numbers give remainders of 0 and 7, so the remainder 7 is used either 0 or 9 times. In the first case, the remainder of the sum modulo 27 is 9, not 0, and in the second case, the sum of all numbers is no more than \(25 \cdot 9 + 36 = 261\).
An example with 14 groups: we will separate the numbers 9, 16, and 25 into individual groups, and the rest will be divided into 11 pairs with a sum of 25.
Solution 2: We can explicitly provide 11 numbers that are not perfect squares and such that their pairwise sums are not squares. These numbers are \(2, 8, 10, 11, 13, 18, 19, 20, 21, 22\), and 24 (this requires extensive manual verification). From this, it follows that the situation with 5 single groups and 10 pairs is impossible.
Solution 3: Suppose the squares form separate groups, and the other numbers are divided into pairs. Then, with the number 21 in a group, there can only be 15, but then in the group with 10, there is only the number 6, and then with the number 19, there is only 17, and we get that a pair for the number 8 cannot be found.
## Criteria:
- Only proven that there are no more than 14 groups, no example provided - 4 points;
- Example provided, but not proven that 15 groups are not possible - 2 points.
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. The numbers $415, 43, 7, 8, 74, 3$ are written on cards (see figure). Arrange the cards in a row so that the resulting ten-digit number is the smallest possible.
|
Answer: $\square 3415 \square 43 \square 74 \square 7 \square 8$
The correct answer can simply be recorded as the number 3415437478.
+ correct answer provided
- incorrect answer or no answer provided
|
3415437478
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. One side of a rectangle was increased by 3 times, and the other was reduced by 2 times, resulting in a square. What is the side of the square if the area of the rectangle is $54 \mathrm{m}^{2} ?$
|
Answer: 9 m.
Let's reduce the side of the given rectangle by half (see Fig. 5.3a). Then the area of the resulting rectangle will be 27 m $^{2}$ (see Fig. 5.3b). Next, we will increase the other side by three times, that is, "add" two more rectangles (see Fig. 5.3c). The area of the resulting figure will become $27 \cdot 3=81$ (m ${ }^{2}$ ). Since, by the condition, a square has formed, its area is $81 \mathrm{~m}^{2}$. Therefore, the side of the resulting square is 9 meters.
Fig. 5.3a

Fig. 5.3b
Fig. 5.3c
+ complete justified solution
$\pm$ the area of the square is correctly obtained, but the side is not found or is found incorrectly
Ғ only the correct answer is provided or the correct answer is obtained by considering a specific case (a rectangle with specific sides)
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. The number 61 is written on the board. Every minute, the number is erased from the board and replaced with the product of its digits, increased by 13. That is, after one minute, the number on the board will be $19 (6 \cdot 1 + 13 = 19)$. What number will be on the board after an hour?
|
Answer: 16.
Let's consider the numbers that will be written on the board over the first few minutes:
| After one minute | $6 \cdot 1+13=\mathbf{1 9}$ |
| :---: | :---: |
| After two minutes | $1 \cdot 9+13=\mathbf{2 2}$ |
| After three minutes | $2 \cdot 2+13=\mathbf{1 7}$ |
| After four minutes | $1 \cdot 7+13=\mathbf{2 0}$ |
| After five minutes | $2 \cdot \mathbf{1}+13=\mathbf{1 3}$ |
| After six minutes | $1 \cdot 3+13=\mathbf{1 6}$ |
| After seven minutes | $1 \cdot 6+13=\mathbf{1 9}$ |
Notice that after the sixth minute, the numbers start to repeat. In one hour (60 minutes), exactly 10 cycles of six minutes will pass. Therefore, after one hour, the number that can be read on the board will be 16.
+ complete justified solution
$\pm$ the pattern is correctly identified and the correct answer is given, but the justification is not complete
dry the pattern is correctly identified, but the correct answer is not obtained
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. CONDITION
At the factory, there are exactly 217 women, among whom 17 are brunettes, and the remaining 200 are blondes. Before New Year's, all of them dyed their hair, and each of these women wrote on "VKontakte" the surnames of exactly 200 women from the factory, whom they believed to be definitely blondes. Each of the brunettes correctly identified all the blondes, while each blonde could indicate anyone except herself. Prove that based on this data, it is possible to identify at least 13 blondes.
|
Solution. According to the problem, the correct list of all 200 blondes will be on "Vkontakte" exactly for 17 female workers at the plant: brunettes will write exactly this list, and a blonde will never write it, as otherwise she would have to include herself in it. Therefore, if a certain list appears not 17 times, but any other number, then it is incorrect and was written by a blonde. Remove all lists that appear exactly 17 times. There will be $217-17 \mathrm{n}$ lists left. $217-17 \mathrm{n} \geq 0$, so $\mathrm{n} \leq 12$ (we remember that the number is natural). Then at least $217-12 \cdot 17=13$ lists remain, and we have identified at least 13 of their authors - blondes.
## Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct proof | 7 points |
| It is justified that the correct list of blondes appears exactly 17 times (without further progress) | 4 points |
| It is justified that the correct list of blondes appears at least 17 times (without further progress) | 2 points |
| There is only the idea of identifying blondes as the authors of incorrect lists | 1 point |
| Any ideas that do not lead to proof | not evaluated |
|
13
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7.4 Vanya wrote the numbers $1,2,3, \ldots, 13$ in his notebook. He multiplied five of them by 3, and the rest by 7, then added all the products. Could the result have been 433?
|
Solution. Let's try to figure out the situation. Let A be the sum of the five numbers that need to be multiplied by 3, and B be the sum of the other eight numbers (which need to be multiplied by 7). Consider the sum after multiplication: 3A + 7B. We can write it as (taking into account that the sum of all thirteen numbers is 91):
\[
3(A+B)+4 B=3 \cdot 91+4 B=273+4 B
\]
We would like this sum to be equal to 433:
\[
273+4 B=433, \quad 4 B=160, \quad B=40
\]
Let's select eight numbers with a sum of 40. The sum \(1+2+\ldots+7+12=40\).
The sum of the other five numbers: \(8+9+10+11+13=51\).
We can check:
\[
3(8+9+10+11+13)+7(1+2+\ldots+7+12)=3 \cdot 51+7 \cdot 40=153+280=433
\]
Answer: it could.
|
433
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5 In triangle ABC, the median BM is drawn. It is known that $\angle \mathrm{BAC}=30^{\circ}, \angle \mathrm{BMC}=45^{\circ}$. Find angle BAC.
|
Solution. See fig.
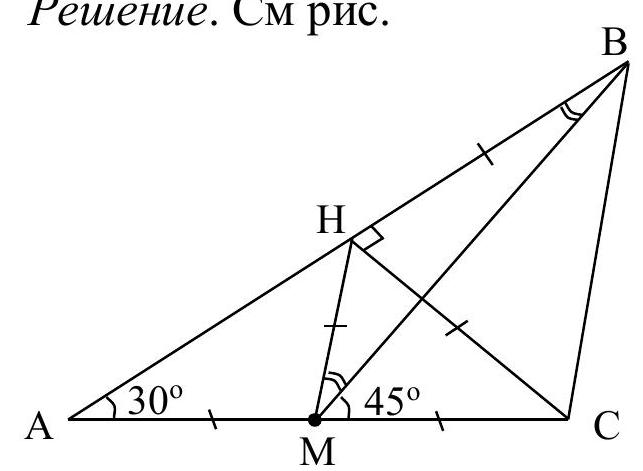
C
$\triangle \mathrm{AMB}: \angle \mathrm{AMB}=135^{\circ} \Rightarrow \angle \mathrm{ABM}=15^{\circ}$
Let $\mathrm{AC}=2 \mathrm{~b}$. Then $\mathrm{AM}=\mathrm{MC}=\mathrm{b}, \mathrm{CH}=\frac{1}{2} \mathrm{AC}=\frac{1}{2} \cdot 2 \mathrm{~b}=\mathrm{b}$ (as the leg opposite the $30^{\circ}$ angle in $\left.\triangle \mathrm{AHC}\right)$.
$\mathrm{MH}=\mathrm{b}$ (as the median from the vertex of the right angle in $\triangle \mathrm{AHC}$).
Thus, $\triangle \mathrm{MHC}$ is equilateral, so
$$
\angle \mathrm{HMC}=60^{\circ} \Rightarrow \angle \mathrm{HMB}=\angle \mathrm{HMC}-\angle \mathrm{BMC}=60^{\circ}-45^{\circ}=15^{\circ} .
$$
Therefore, $\triangle \mathrm{MHB}$ is isosceles: $\mathrm{BH}=\mathrm{MH}=\mathrm{b}$. We get: $\triangle \mathrm{BHC}$ is an isosceles right triangle, $\angle \mathrm{ABC}=\angle \mathrm{HBC}=45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №3
The base and the lateral side of an isosceles triangle are 34 and 49, respectively.
a) Prove that the midline of the triangle, parallel to the base, intersects the inscribed circle of the triangle.
b) Find the length of the segment of this midline that is contained within the circle.
|
# Answer: 8.
## Solution
a) Let $\mathrm{O}$ be the center of the inscribed circle in triangle $ABC$ with sides $AB = AC = 49$, $BC = 34$, and $AH$ be the height of the triangle. Points $M$ and $N$ are the midpoints of sides $AB$ and $AC$, respectively, and $K$ is the intersection point of $AH$ and $MN$. Since $MN$ is the midline of the isosceles triangle, point $K$ is the common midpoint of $MN$ and $AH$.
From the right triangle $ABH$, we find that
$$
A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{49 - 17^{2}} = 8 \sqrt{33},
$$
so, $K H = 4 \sqrt{33}$.
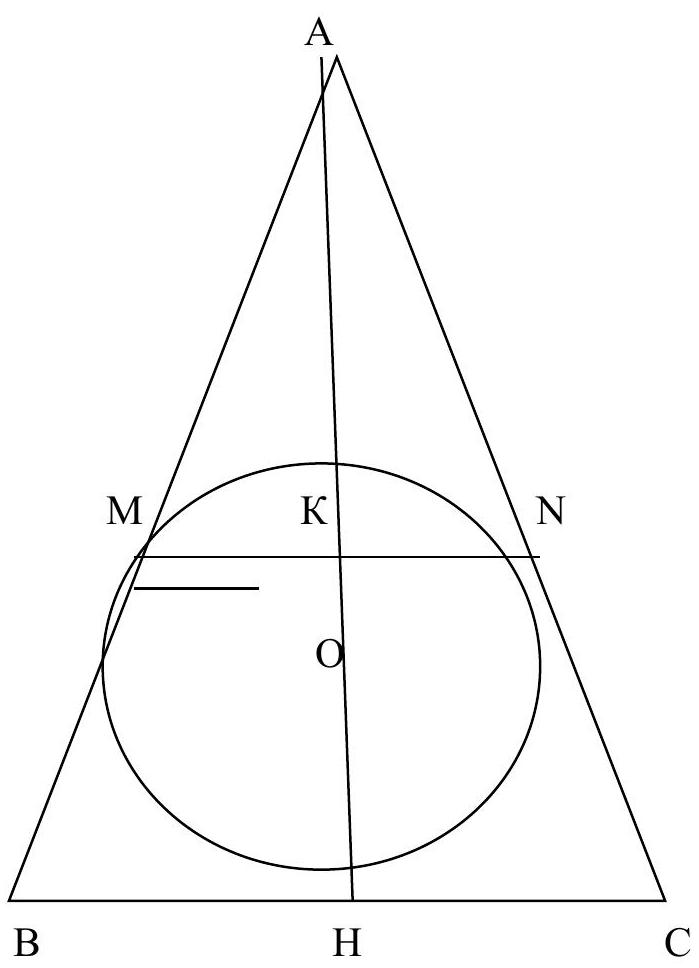
Let $r$ be the radius of the inscribed circle of triangle $ABC$. Then
$$
r = \frac{S_{ABC}}{p} = \frac{\frac{1}{2} BC \cdot AH}{AB + BH} = \frac{17 \cdot 8 \sqrt{33}}{49 + 17} = \frac{68 \sqrt{33}}{33}
$$
and the diameter of the inscribed circle is $2r = \frac{136 \sqrt{33}}{33}$. Clearly, $\frac{136}{33} > 4$, so $2r = \frac{136 \sqrt{33}}{33} > 4 \sqrt{33} = KH$.
Therefore, the inscribed circle intersects the midline $MN$ of the triangle.
b) To calculate the length of the segment of the midline, we introduce a coordinate system on the plane as follows: the $OX$ axis is directed along the base of the triangle, and the $OY$ axis is directed along the height.
Then the inscribed circle in the triangle is given by the equation
$$
x^{2} + \left(y - \frac{68 \sqrt{33}}{33}\right)^{2} = \left(\frac{68 \sqrt{33}}{33}\right)^{2}
$$
and the midline of the triangle is given by the equation
$$
y = 4 \sqrt{33}.
$$
Substituting this value into the equation of the circle, we get the values
$$
x_{1} = -4 \quad \text{and} \quad x_{2} = 4.
$$
Thus, the length of the segment of the midline inside the circle is 8.
|
8
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. An army of mice attacked a grain warehouse. To fight the mice, one cat was released into the warehouse on the first day, a second cat on the next day, and each subsequent day, one more cat was released. A mouse eats 100 grams of grain per day, and a cat eats 10 mice per day. After several days, there were no mice left. After calculating the losses, it was found that the mice had eaten 55 kg of grain over these few days. How many mice were there? (A mouse manages to eat 100 grams of grain even on the day it is caught by a cat.)
|
Solution. Let the entire process last $n$ days, then by its end, there were $n$ cats on the warehouse, with the first cat eating $10 n$ mice, the second cat eating 10( $n-1)$ mice, $\ldots, n$-th cat - 10 mice, meaning there were a total of $10(1+2+\ldots+n)$ mice. Let's calculate how much grain the mice ate.
Ten mice caught by the cat on the first day ate $10 \cdot 0.1=1$ kg of grain. Twenty mice caught on the second day (by two cats) ate $20 \cdot 2 \cdot 0.1=4$ kg of grain over 2 days.
Thirty mice caught on the third day ate $30 \cdot 3 \cdot 0.1=9$ kg of grain over 3 days.
Forty mice caught on the fourth day ate $40 \cdot 4 \cdot 0.1=16$ kg of grain over 4 days.
Fifty mice caught on the fifth day ate $50 \cdot 5 \cdot 0.1=25$ kg of grain over 5 days.
In total, over five days, $1+4+9+16+25=55$ kg of grain was eaten.
Therefore, the process lasted 5 days, and there were 150 mice.
Evaluation criteria. A positive score is allowed if the solution path is correct but not completed to the answer due to arithmetic errors, but no more than 3 points. In particular, if it is correctly established that the process lasted 5 days but the number of mice is calculated incorrectly, -3 points.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.4
## Condition:
Cupcakes are sold in boxes of 2, eclairs - in boxes of 6, and gingerbread - in boxes of 15. You can only buy whole boxes, you cannot open them. Alice bought an equal number of cupcakes, eclairs, and gingerbread. What is the smallest number of boxes she could have taken
|
Answer: 22
Exact match of the answer - 1 point
Solution by analogy with task №3.1
#
|
22
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 5.1
## Condition:
A Dog, a Cat, and a Mouse are running around a circular lake. They all started simultaneously in the same direction from the same point and finished at the same time, each running at a constant speed. The Dog ran 12 laps, the Cat ran 6 laps, and the Mouse ran 4 laps. How many total overtakes were made from the start to the finish?
If two or more overtakes occur simultaneously, each overtake is counted separately. The start and finish moments are not counted as overtakes.
|
# Answer: 13
## Exact match of the answer -1 point
## Solution.
At the moment when the faster runner catches up with the slower one, he is ahead by one lap. The Dog has lapped the Cat by 6 laps, meaning it has caught up with her 6 times, with the last catch-up at the finish line not counting as a lap, so the Dog has lapped the Cat 5 times. The Dog has lapped the Mouse by 8 laps, meaning it has caught up with the Mouse 7 times. The Cat has lapped the Mouse by 2 laps, completing 1 lap. In total, the animals have completed $5+7+1=13$ laps.
#
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 5.3
## Condition:
A Dog, a Cat, and a Mouse are running around a circular lake. They all started in the same direction from the same point and finished at the same time, each running at a constant speed.
The Dog ran 12 laps, the Cat ran 7 laps, and the Mouse ran 3 laps. How many total overtakes were made from the start to the finish?
If two or more overtakes occur simultaneously, each overtake is counted separately. The start and finish moments are not counted as overtakes.
|
# Answer: 15
Exact match of the answer -1 point
Solution by analogy with task №5.1
#
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 5.4
## Condition:
A Dog, a Cat, and a Mouse are running around a circular lake. They started simultaneously in the same direction from the same point and finished simultaneously, all running at constant speeds.
The Dog ran 12 laps, the Cat ran 5 laps, and the Mouse ran 2 laps. How many total overtakes were made from the start to the finish?
If two or more overtakes occur simultaneously, each overtake is counted separately. The start and finish moments are not counted as overtakes.
|
Answer: 17
Exact match of the answer -1 point
Solution by analogy with task №5.1
#
|
17
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
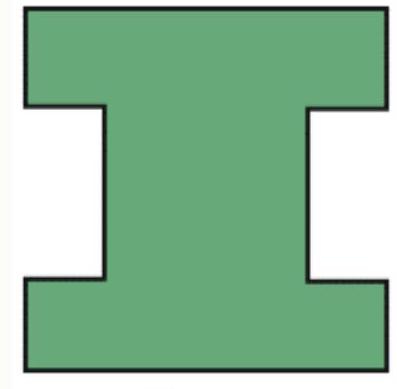
# Task № 6.1
## Condition:
Anya, Tanya, and Vanya had identical cardboard squares with a side of 16 cm. Each of them cut off two rectangles from their square, as shown in the figure, and all 6 rectangles are the same. The perimeter of Anya's figure is 88 cm, and the perimeter of Vanya's figure is 82 cm.

Anya

Vanya

Tanya
Find the perimeter of Tanya's figure. Express your answer in centimeters.
|
Answer: 76
Exact match of the answer - 1 point
## Solution.
The perimeter of the original square is $16 \cdot 4=64 \text{ cm}$. By cutting off 2 rectangles, Anya increased the perimeter of the figure by 4 larger sides of the rectangles, specifically by 88-64=24 cm. The larger side of the rectangle is $24: 4=6$ cm.
Vanya, by cutting off two rectangles, increased the perimeter of the figure by two larger sides of the rectangles and two smaller sides, specifically by 82-64=18 cm, of which 12 cm are the two larger sides, and the remaining 6 cm are the two smaller sides. Thus, the smaller side of the rectangle is 3 cm. Tanya, by cutting off two rectangles, increased the perimeter of the figure by 4 smaller sides of the rectangles, that is, by $3 \cdot 4=12$ cm. The perimeter of the resulting figure is 64+12=76 cm.
|
76
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 6.2
## Condition:
Anya, Tanya, and Vanya had identical cardboard squares with a side of 15 cm. Each of them cut off two rectangles from their square, as shown in the figure, and all 6 rectangles are the same. The perimeter of Anya's figure is 88 cm, and the perimeter of Vanya's figure is 80 cm.

Anya

Vanya

Tanya
Find the perimeter of Tanya's figure. Express your answer in centimeters.
|
Answer: 72
Exact match of the answer -1 point
Solution by analogy with task №6.1
## Condition:
Anya, Tanya, and Vanya had identical cardboard squares with a side of 16 cm. Each of them cut off two rectangles from their square, as shown in the picture, all 6 rectangles are the same. The perimeter of Anya's figure is 92 cm, the perimeter of Vanya's figure is 86 cm.

Anya

Vanya
Tanya
Find the perimeter of Tanya's figure. Express the answer in centimeters.
Answer: 80
Exact match of the answer -1 point
Solution by analogy with task №6.1
## Condition:
Anya, Tanya, and Vanya had identical cardboard squares with a side of 15 cm. Each of them cut off two rectangles from their square, as shown in the picture, all 6 rectangles are the same. The perimeter of Anya's figure is 84 cm, the perimeter of Vanya's figure is 76 cm.

Anya

Vanya

Tanya
Find the perimeter of Tanya's figure. Express the answer in centimeters.
Answer: 68
Exact match of the answer -1 point
Solution by analogy with task №6.1
## Condition:
In the examples, each letter corresponds to a digit from 0 to 9. The same letters correspond to the same digits, different letters correspond to different digits.
$$
\begin{aligned}
& \text { L: E = T+O } \\
& \text { O+C=E } \times \mathbf{H}=\mathrm{b}
\end{aligned}
$$
What number is encoded by the following word?
## zero
Answer: 4368
## Exact match of the answer -1 point
## Solution.
Since $\mathrm{E} \times \mathrm{H}=\mathrm{b}$, then b can only be 8 or 6: 8 = 2 * 4, or 6 = 2 * 3.
If $\mathrm{b}=6$, then $\mathrm{E}$ and $\mathrm{H}$ are 2 and 3 in some order. $\mathrm{O}+\mathrm{C}=6$, this can only be 1 + 5 or 5 + 1 (0 + 6, 2 + 4, and 3 + 3 do not work, as 2, 3, and 6 are already used). Then the sum $\mathrm{T}+\mathrm{O}$ is at least 4 + 1 = 5 (0 + 1 cannot be the result of dividing L by E, and 2 and 3 are already used). But the result of dividing a single-digit number L by 2 or 3 is less than 5, a contradiction.
Then $\mathrm{b}=8$, and $\mathrm{E}$ and $\mathrm{H}$ are 2 and 4 in some order. E cannot be 4, as there is no other digit besides 8 that is divisible by 4, for the letter L. Therefore, $\mathrm{E}=2, \mathrm{H}=4$. The only even digit left for the letter L is 6. We get that $6: 2=\mathrm{T}+\mathrm{O}, \mathrm{O}+\mathrm{C}=2 \times 4=8$ and the unused digits are 0, 1, 3, 5, 7, and 9. Since $\mathrm{T}+\mathrm{O}=3$, this is 3 + 0 or 0 + 3, but if $\mathrm{O}=0$, then $\mathrm{C}=8$, and 8 is already used, so $\mathrm{O}=3, \mathrm{~T}=0$ and $\mathrm{C}=5$.
The word ZERO then corresponds to the number 4368.
## Condition:
In the examples, each letter corresponds to a digit from 0 to 9. The same letters correspond to the same digits, different letters correspond to different digits.
$$
\begin{aligned}
& \text { L: } \mathrm{E}=\mathrm{T}+\mathrm{O} \\
& \mathrm{O}+\mathrm{C}=\mathrm{E} \times \mathrm{H}=\mathrm{b}
\end{aligned}
$$
What number is encoded by the following word?
## ELEPHANT
Answer: 5634
Exact match of the answer -1 point
Solution by analogy with task №7.1
## Condition:
In the examples, each letter corresponds to a digit from 0 to 9. The same letters correspond to the same digits, different letters correspond to different digits.
$$
\begin{aligned}
& \text { L: } \mathrm{E}=\mathrm{T}+\mathrm{O} \\
& \mathrm{O}+\mathrm{C}=\mathrm{E} \times \mathrm{H}=\mathrm{b}
\end{aligned}
$$
What number is encoded by the following word?
## salt
Answer: 5368
Exact match of the answer -1 point
Solution by analogy with task №7.1
## Condition:
In the examples, each letter corresponds to a digit from 0 to 9. The same letters correspond to the same digits, different letters correspond to different digits.
$$
\begin{aligned}
& \text { L: } \mathrm{E}=\mathrm{T}+\mathrm{O} \\
& \mathrm{O}+\mathrm{C}=\mathrm{E} \times \mathrm{H}=\mathrm{b}
\end{aligned}
$$
What number is encoded by the following word?
$$
\text { C ET b }
$$
Answer: 5208
Exact match of the answer -1 point
Solution by analogy with task №7.1
|
68
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 8.1
## Condition:
Zebras Alex, Buffy, Web, and Gunya counted their stripes. During this, they had the following conversation.
Alex: “Gunya, Buffy, and I have 70 stripes together.”
Buffy: “I have twice as many stripes as Gunya.”
Gunya: “I have 2 more stripes than Alex.”
Web: “I have more stripes than Alex and Gunya together, but fewer than Buffy.”
How many stripes does Web have?
|
# Answer: 35
## Exact match of the answer -1 point
## Solution.
Let the number of stripes on the zebras of Alex, Buffy, Webby, and Gunya be A, B, V, and $\Gamma$ respectively. It is known that A+B+$\Gamma=70, B=2\Gamma, \Gamma=\mathrm{A}+2$, from the last two equations we get that $B=2\mathrm{A}+4$. Substituting B and $\Gamma$ into the first equation, we get $\mathrm{A}+2\mathrm{A}+4+\mathrm{A}+2=70$, from which $4\mathrm{A}=64, \mathrm{A}=16, \Gamma=18$ and B=36. Webby has more stripes than $\mathrm{A}+\Gamma=34$, but fewer than $\mathrm{B}=36$, so $\mathrm{B}=35$.
## Condition:
The zebras Alex, Buffy, Webby, and Gunya counted their stripes. In the process, they had the following conversation.
Alex: "I, Gunya, and Buffy together have 74 stripes."
Buffy: "I have twice as many stripes as Gunya."
Gunya: "I have 2 more stripes than Alex."
Webby: "I have more stripes than Alex and Gunya together, but fewer than Buffy."
How many stripes does Webby have?
Answer: 37
Exact match of the answer -1 point
Solution by analogy with problem 8.1
## Condition:
The zebras Alex, Buffy, Webby, and Gunya counted their stripes. In the process, they had the following conversation.
Alex: "I, Gunya, and Buffy together have 78 stripes."
Buffy: "I have twice as many stripes as Gunya."
Gunya: "I have 2 more stripes than Alex."
Webby: "I have more stripes than Alex and Gunya together, but fewer than Buffy."
How many stripes does Webby have?
Answer: 39
Exact match of the answer -1 point
Solution by analogy with problem 8.1
## Condition:
The zebras Alex, Buffy, Webby, and Gunya counted their stripes. In the process, they had the following conversation.
Alex: "I, Gunya, and Buffy together have 82 stripes."
Buffy: "I have twice as many stripes as Gunya."
Gunya: "I have 2 more stripes than Alex."
Webby: "I have more stripes than Alex and Gunya together, but fewer than Buffy."
How many stripes does Webby have?
Answer: 41
Exact match of the answer -1 point
Solution by analogy with problem 8.1
|
41
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Dima wrote a sequence of 0s and 1s in his notebook. Then he noticed that a 1 follows a 0 sixteen times, a 0 follows a 1 fifteen times, and a 0 follows 01 eight times. How many times does a 0 follow 11?
|
# Answer. 7.
Solution. The combination 01 appears 16 times in the tetrad, while the combination 10 appears 15 times. Therefore, the string starts with 0, meaning that before each combination 10 there is either 0 or 1. According to the condition, eight times it is 0, so the combination 110 appears $15-8=7$ times.
Criteria. Full solution - 7 points. Noted that the string starts with 0 without further progress - 2 points. Considered specific cases of concrete sequences and obtained the correct answer - 1 point. Only answer - 0.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Masha drew a rhombus in her notebook and wrote four numbers at the vertices, the sum of which is 2021. Then she wrote the product of the numbers at the ends of each side of the rhombus and calculated the sum of the numbers written on the sides. Katya increased all the numbers written by Masha at the vertices by 1, and then repeated what Masha did and calculated the new sum of the numbers on the sides. By how much is Katya's sum greater than Masha's?
|
Answer: 4046.
Solution. Let Masha write the numbers $a, b, c, d$ at the vertices of the rhombus, then $a+b+c+d=2021$, and she obtained the sum of the products
$$
a b+b c+c d+d a=(a+c)(b+d)
$$
Since Katya increased each number by 1, her sum is
$$
(a+c+2)(b+d+2)=(a+c)(b+d)+2(a+b+c+d)+4
$$
greater than Masha's by $2(a+b+c+d)+4=2 \cdot 2021+4=4046$.
Criteria. Full solution - 7 points. Considered a particular case with the correct answer - 1 point. Only answer - 0 points.
|
4046
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Every second, the computer outputs a number equal to the sum of the digits of the previous number, multiplied by 31. On the first second, the number 2020 was displayed. What number will be displayed on the 2020th second
|
Answer: 310.
Solution: Let's calculate the first few numbers displayed on the screen.
On the first second, the number $a_{1}=2020$ is displayed, then
on the second second, the number $a_{2}=(2+0+2+0) \cdot 31=4 \cdot 31=124$ is displayed;
on the third second, the number $a_{3}=(1+2+4) \cdot 31=7 \cdot 31=217$;
on the 4th second, the number $a_{4}=(2+1+7) \cdot 31=310$;
on the 5th second, the number $a_{5}=(3+1+0) \cdot 31=4 \cdot 31=124=a_{2}$.
Since each subsequent number is calculated using only the previous number, the numbers displayed on the screen will repeat with a period of 3. The number of seconds (2020 - 1) is divisible by 3, so on the 2020th second, the number 310 will be displayed.
# Criteria:
7 points - correct answer and complete justification;
5-6 points - correct answer and generally correct reasoning, with minor gaps or inaccuracies
4 points - correct line of reasoning provided, but a computational error was made;
answer only - 0 points.
|
310
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Two runners, starting simultaneously at constant speeds, run on a circular track in opposite directions. One of them runs the loop in 5 minutes, while the other takes 8 minutes. Find the number of different meeting points of the runners on the track, if they ran for at least an hour.
#
|
# Solution.
Let the length of the track be $\mathrm{S}$ meters. Then the speeds of the runners are $\mathrm{S} / 5$ and $\mathrm{S} / 8$ meters per minute, respectively.
Assume the runners start from the same point. They will meet again after $\mathrm{S} /(\mathrm{S} / 5+\mathrm{S} / 8)=40 / 13$ minutes.
Now, let's determine when they will meet again at the starting point. If the first runner completes the circular track $\mathrm{n}$ times and the second runner completes it $\mathrm{m}$ times, then by comparing the time, we get $5 \mathrm{n}=8 \mathrm{~m}, \mathrm{n}=8 \mathrm{a}, \mathrm{m}=5 \mathrm{~b}$, where $\mathrm{a}, \mathrm{b}$ are natural numbers.
The smallest possible values of $\mathrm{a}$ and $\mathrm{b}$ are 8 and 5, respectively. Therefore, they will both return to the starting point for the first time after $5 \cdot 8=40$ minutes. They meet every $40/13$ minutes on the track. In total, there will be $40 : (40 / 13)=13$ different meeting points.
If they start from different points, they will meet no later than $40/13$ minutes. Subsequently, events will unfold similarly to case 1 with a period of 40 minutes. Since $40 + 40/13$ minutes is less than an hour, there will be exactly 13 meeting points in an hour.
Answer: 13 points.
## Grading Criteria:
7 points - Both cases of the runners' movement are considered and justified.
5 points - Only one case of the runners' movement is considered and justified.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. How much greater is one of two positive numbers than the other if their arithmetic mean is $2 \sqrt{3}$ and the geometric mean is $\sqrt{3}$?
(Hint: the geometric mean of two numbers $m$ and $n$ is the number $p=\sqrt{\mathrm{mn}}$).
|
# Solution.
Let the unknown numbers be denoted by $x$ and $y$. Then, from the problem statement, we get:
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ \frac { x + y } { 2 } = 2 \sqrt { 3 } , } \\
{ \sqrt { x y } = \sqrt { 3 } , }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x+y=4 \sqrt{3}, \\
x y=3 .
\end{array}\right.\right. \\
& \text { Then }|x-y|=\sqrt{(x-y)^{2}}=\sqrt{(x+y)^{2}-4 x y}=\sqrt{4^{2} \cdot 3-4 \cdot 3}=6 .
\end{aligned}
$$
Other methods of solution are possible.
Answer: 6 .
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the record of three two-digit numbers, there are no zeros, and in each of them, both digits are different. Their sum is 40. What could be their sum if the digits in them are swapped?
|
Answer: 103.
Solution. In all numbers, the tens digit is 1. Otherwise, the larger number is at least 21, and the other two are at least 12. Their sum is no less than $12+12+21=44$, which is not equal to 40. The sum of the units digits is 10 (zeros are not allowed). Therefore, the sum of the numbers with swapped digits is 103.
There are only three possible sets of numbers: $12,12,16$ or $12,13,15$, and 13, 13, 14. (This can justify the answer)
Criteria. Answer with one or two examples: 1 point.
Answer with three examples, but without proof that there are no others: 2 points.
Complete solution: 7 points.
|
103
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the largest natural number $\mathrm{n}$, for which the system of inequalities
$1<x<2, 2<x^{2}<3, \ldots, n<x^{n}<n+1$
has a solution. (6 points)
|
Solution. From the condition $: n=4$.
Rewrite the inequalities as:
$\left\{\begin{aligned} & 16^{3} \text{, then for } n=5 \text{ the given system is already inconsistent: the intervals } [\sqrt[3]{3}, \sqrt[4]{4}] \text{ and } [\sqrt[5]{2}, \sqrt[5]{6}] \text{ do not intersect.} \\ & \text{For } n=4 \text{, it is not difficult to find a value of } x \text{ that satisfies all four inequalities (for example, } x=1.45 \text{).} \end{aligned}\right.$
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There is a bag with 16 letters: А, А, А, А, В, В, Д, И, И, М, М, Н, Н, Н, Я, Я. Anna, Vanya, Danya, and Dima each took 4 letters from it, after which the bag was empty. How many of them could have successfully spelled out their names? Explain your answer.
|
2. Answer: 3.
Solution. All of them could not have formed their names, as there were not enough letters D. Anna, Vanya, and Dima could have drawn cards from which they could form their names, while Danya would have been left with the cards: V, I, M, Ya.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Alexei drew 7 lines on a plane, which divided it into several parts. Then he chose two adjacent parts (adjacent parts are those that share a common side), counted how many sides each of them contains, and added these two numbers. What is the largest number he could have obtained? Explain your answer.

|
4. Answer: 10.
Solution. Consider any two adjacent parts. Temporarily remove the line containing their boundary. Then these two parts will become one large part. It has a maximum of 6 sides (each line can contain no more than one side of this part). Return the line we removed. It will be a side for both small parts (+2),

and it intersects a maximum of two sides of the large part, turning one large side into two small sides (+2).
Example. Lines containing the sides of a regular hexagon and a line passing through the midpoints of two of its adjacent sides. The two parts forming the hexagon have a total of 10 sides.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. The numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ form a geometric progression. Among them, there are both rational and irrational numbers. What is the maximum number of terms in this progression that can be rational numbers?
|
Answer: 3.
Example: let $a_{1}=1, q=\sqrt{2}$, we get the geometric progression $1, \sqrt{2}, 2, 2\sqrt{2}, 4$. Evaluation. If there are 4 rational numbers among them, then there will be two consecutive rational members of the geometric progression. This means that the common ratio of the progression (the ratio of the subsequent term to the previous one) is a rational number. But then, with a rational $a_{1}$, all terms of the progression are rational numbers, and with an irrational $a_{1}$, all terms are irrational.
Remarks. An example of a geometric progression with three rational and two irrational numbers is given - 3 points. It is proven that there cannot be more than three rational numbers, but no example is provided - 3 points. If both are present, 7 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A cube of size $n \times n \times n$, where $n$ is a natural number, was cut into 99 smaller cubes, of which exactly one has an edge length different from 1 (each of the others has an edge length of 1). Find the volume of the original cube.
|
Answer: 125.
Let $m$ be the length of the edge of the cube, different from the unit cube. We get the equation $n^{3}-m^{3}=98$ (in natural numbers). Further, $(n-m)\left(n^{2}+n m+m^{2}\right)=98$. The numbers $m$ and $n$ are of the same parity, otherwise $n^{3}-m^{3}$ would be an odd number. Moreover, if $n$ and $m$ are even numbers, then $n^{3}-m^{3}$ would be divisible by 8, but 98 is not divisible by 8. Therefore, $m$ and $n$ are odd, and the first factor of the product $(n-m)\left(n^{2}+n m+m^{2}\right)$ is an even number, while the second is odd. Finally, the second factor is greater than the first: $n^{2}+n m+m^{2}>n>n-m$. From this and the factorization $98=2 \cdot 7 \cdot 7$ into prime factors, we obtain the system of equations $n-m=2, n^{2}+n m+m^{2}=49$. The only solution to this system in natural numbers is the pair $n=5, m=3$.
Remark. The correct answer with verification is worth up to 3 points.
|
125
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a box, there are oranges, pears, and apples, a total of 60 fruits. It is known that there are 3 times more apples than non-apples, and there are 5 times fewer pears than non-pears. How many oranges are in the box?
|
Answer: 5.
Solution. Since there are 3 times more apples than non-apples, apples make up $\frac{3}{4}$ of the total number of fruits, i.e., there are $\frac{3}{4} \cdot 60=45$ apples. Since there are 5 times fewer pears than non-pears, pears make up $\frac{1}{6}$ of the total number of fruits, i.e., there are $\frac{1}{6} \cdot 60=10$ pears. Therefore, the total number of oranges is $60-45-10=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. Oleg bought a chocolate bar for $n$ rubles, and after some time, he sold it for 96 rubles. It turned out that he sold the chocolate bar for exactly $n \%$ more than he bought it for. For how many rubles did Oleg buy the chocolate bar?
|
Answer: 60.
Solution. From the condition of the problem, it follows that $96=n \cdot\left(1+\frac{n}{100}\right)$. Transforming this equation, we get
$$
0=n^{2}+100 n-9600 \quad \Leftrightarrow \quad 0=(n+160)(n-60)
$$
Thus, $n=60$, since the chocolate bar cannot cost a negative number of rubles.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. Masha has three identical dice, on the faces of each of which six different prime numbers are written, with a total sum of 87.
Masha rolled all three dice twice. The first time, the sum of the numbers that came up was 10, and the second time, the sum was 62.
Exactly one of the six numbers did not come up at all. Which one?
|
# Answer: 17.
Solution. Note that the number 10 can be uniquely represented as the sum of three prime numbers: $10=2+3+5$. This means that the numbers $2,3,5$ are on the dice and they came up the first time.
Note that if the even number 62 can be represented as the sum of three prime numbers, then one of them is even and therefore equals 2. Then the sum of the remaining two is 60. Note that among these two numbers, there cannot be the number 2, 3, or 5, and they must be different (since the numbers 58, 57, 55, and 30 are composite). This means that the dice have two different prime numbers with a sum of 60, greater than 5, and they came up the second time (along with 2).
Thus, each die has the numbers $2,3,5$, as well as two other prime numbers with a sum of 60. Since the sum of all six numbers is 87, the sixth number, which never came up, is $87-2-3-5-60=17$.
|
17
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. In the cells of a $2 \times 35$ table (2 rows, 35 columns), non-zero real numbers are placed, and all numbers in the top row are distinct. For any two numbers in the same column, the following condition is satisfied: one number is the square of the other.
(a) (1 point) What is the maximum number of negative numbers that can be in this table?
(b) (3 points) What is the minimum number of distinct numbers that can be in the bottom row?
|
Answer: (a) 35. (b) 12.
Solution. (a) In any column, there can be no more than one negative number, so the total number of negative numbers is no more than 35. There can be exactly 35 if, for example, the top numbers are $-1, -2, -3, \ldots, -35$, and below them are the numbers $1^{2}, 2^{2}, 3^{2}, \ldots, 35^{2}$ respectively.
(b) We will prove that each number in the bottom row appears no more than 3 times.
- Suppose the number $a0$ appears in the bottom row. If the top number in the column with number $a$ is the square of the bottom number, then the number $a^{2}$ is written above it. If the bottom number is the square of the top number, then above it is written $-\sqrt{a}$ or $\sqrt{a}$. Since all the numbers in the top row are distinct, the number $a$ in the bottom row appears no more than 3 times.
Since each number in the bottom row appears no more than 3 times, and there are 35 numbers in total, there are at least $\frac{35}{3} > 11$, i.e., at least 12 different numbers.
It remains to provide an example of how exactly 12 different numbers can appear in the bottom row. Consider the 12 smallest prime numbers: $2 = p_{1} < p_{2} < \ldots < p_{12}$. Let the number $p_{1}^{2}$ be written in the bottom of the first three columns, and the numbers $-p_{1}, p_{1}$, and $p_{1}^{4}$ be written above them. Similarly, in the next three columns, the number $p_{2}^{2}$ is written in the bottom, and the numbers $-p_{2}, p_{2}$, and $p_{2}^{4}$ are written above them, and so on. In the last two columns, the number $p_{12}^{2}$ is written in the bottom, and the numbers $-p_{12}$ and $p_{12}$ are written above them.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. In a convex quadrilateral $A B C D$, the bisectors of angles $A$ and $C$ are parallel, and the bisectors of angles $B$ and $D$ intersect at an angle of $46^{\circ}$, as shown in the figure. How many degrees does the acute angle between the bisectors of angles $A$ and $B$ measure?

|
Answer: 67.
Solution. Let's mark the points of intersection of the angle bisectors $K, L, M, N$ (see Fig. 2). Additionally, let $\angle A=2 \alpha, \angle B=2 \beta, \angle C=2 \gamma, \angle D=2 \delta$. Since the sum of the angles of quadrilateral
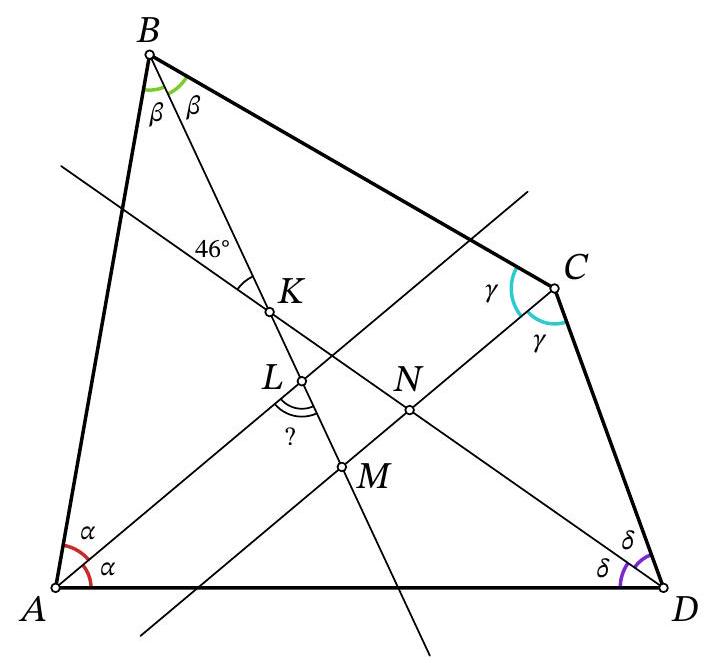
Fig. 2: to the solution of problem 8.5
$ABCD$ is $360^{\circ}$, we have:
$$
\begin{gathered}
2 \alpha+2 \beta+2 \gamma+2 \delta=360^{\circ} \\
\alpha+\beta+\gamma+\delta=180^{\circ}
\end{gathered}
$$
Consider triangle $KMN$. In it:
- $\angle MKN=46^{\circ}$,
- $\angle KMN=\angle ALM=\alpha+\beta$, since $\angle ALM$ is the exterior angle of triangle $ABL$ (this is the angle we need to find in the problem),
- $\angle KNM=\angle CND=180^{\circ}-\gamma-\delta=\alpha+\beta$.
Therefore, triangle $KMN$ is isosceles, and $\angle KMN=\frac{180^{\circ}-46^{\circ}}{2}=67^{\circ}$.
Another solution. Fix angle $A$ and translate angle $C$ parallel so that vertex $C$ lies on the angle bisector of angle $A$. (Or more formally, mark a point $C'$ on the angle bisector of angle $A$ and draw rays from it in the same direction as rays $CB$ and $CD$; the intersections of these rays with rays $AB$ and $AD$ are denoted by $B'$ and $D'$, respectively, as shown in Fig. 3.)
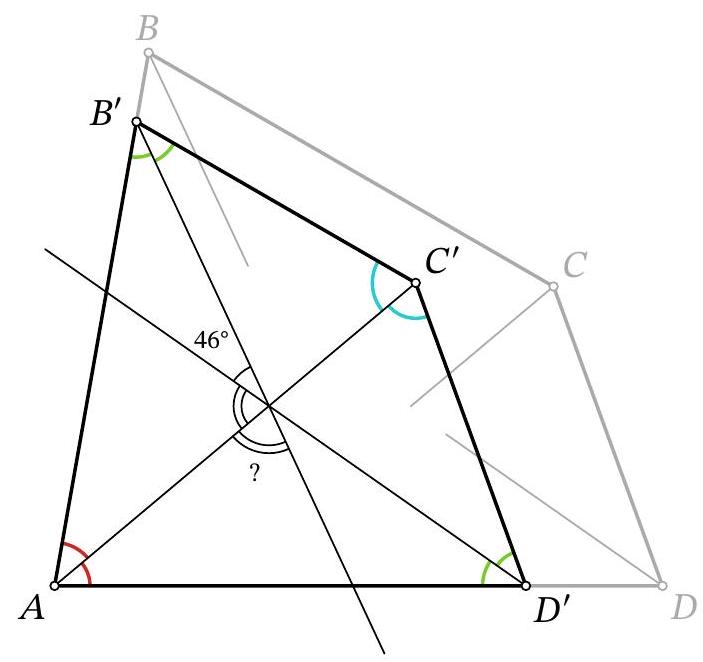
Fig. 3: to the solution of problem 8.5
The sides of the new quadrilateral $AB'C'D'$ are parallel to the sides of the original quadrilateral; thus, the angles between these sides are the same. Consequently, the angle bisectors of the new quadrilateral are parallel to the corresponding angle bisectors of the original, and the angles between them are also preserved.
But this means that the angle bisectors of angles $A$ and $C'$ coincide, so the entire new picture is symmetric with respect to the line $AC'$ (from the congruence of triangles $AB'C'$ and $AD'C'$ by the common side and the adjacent angles).
From the symmetry, it follows that the other two angle bisectors intersect on the line $AC'$ and form equal angles with it. Then the required angle, after doubling, will complement $46^{\circ}$ to a straight angle. Therefore, it is equal to $\frac{1}{2}\left(180^{\circ}-46^{\circ}\right)=67^{\circ}$.
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. How many ways are there to arrange in a row $n$ crosses and 13 zeros so that among any three consecutive symbols there is at least one zero, if
(a) (2 points) $n=27$
(b) (2 points) $n=26$ ?
|
Answer: (a) 14. (b) 105.
Solution. Let's number the zeros from left to right with numbers from 1 to 13. Denote the number of crosses before the first zero by $a_{1}$, between the first and second zero by $a_{2}, \ldots$, after the thirteenth zero by $a_{14}$. We get that $a_{1}+a_{2}+\ldots+a_{14}=n$. The condition that among any three consecutive symbols there is at least one zero is equivalent to the fact that three crosses cannot go in a row, that is, $a_{i} \leqslant 2$ for any $i=1,2, \ldots, 14$. Note that suitable sequences of crosses and zeros are in one-to-one correspondence with sequences $a_{1}, a_{2}, \ldots, a_{14}$ with the specified conditions.
(a) The sum of 14 non-negative integers is 27, and each of them is no more than 2. This means that one of the $a_{i}$ must be equal to 1, and all the others must be equal to 2. Since $i$ can take any value from 1 to 14, we get that there are exactly 14 options.
(b) Now the sum of 14 non-negative integers is 26. This means that either some $a_{i}$ is equal to 0, and all the others are equal to 2, or some $a_{j}$ and $a_{k}$ are equal to 1, and all the others are equal to 2. In the first case, we get 14 options. In the second case, we get $\mathrm{C}_{14}^{2}=\frac{14 \cdot 13}{2}=$ 91 options, since we need to choose 2 indices out of 14 possible ones.
In total, we get exactly $14+91=105$ options.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.8. Given a triangle $A B C$, in which $\angle A=42^{\circ}$ and $A B<A C$. Point $K$ on side $A C$ is such that $A B=C K$. Points $P$ and $Q$ are the midpoints of segments $A K$ and $B C$ respectively. How many degrees does angle $A C B$ measure, if it is known that $\angle P Q C=110^{\circ} ?$
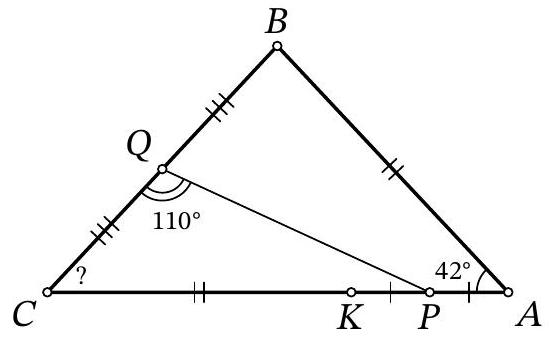
|
Answer: 49.

Fig. 4: to the solution of problem 8.8
Solution. Mark a point $L$ on the extension of side $C A$ beyond point $A$ such that $A L = A B$ (Fig. 4).
Notice that line $P Q$ is parallel to line $B L$ as the midline in triangle $B C L$. Therefore, $\angle L B C = \angle P Q C = 110^{\circ}$.
In the isosceles triangle $B A L$, the external angle at vertex $A$ is $42^{\circ}$, so the angles at the base are $\angle A L B = \angle A B L = \frac{1}{2} \cdot 42^{\circ} = 21^{\circ}$.
From the sum of the angles in triangle $B C L$, we find the required angle:
$$
\angle A C B = 180^{\circ} - \angle C L B - \angle L B C = 180^{\circ} - 110^{\circ} - 21^{\circ} = 49^{\circ}
$$
## 8th grade
|
49
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. What is the greatest number of consecutive natural numbers, each of which has exactly four natural divisors (including 1 and the number itself)?
|
Answer: three numbers.
Solution. Suppose there are four consecutive numbers that satisfy the condition. Note that among four consecutive numbers, one is divisible by 4. Then, in the prime factorization of this number, there are at least two twos. If there is another prime divisor $p$ different from two, then the number of divisors of the number is at least six: $1, 2, 4, p, 2p, 4p$. If the factorization contains only twos, then for the number of divisors to be exactly four ($1, 2, 4, 8$), there must be exactly three twos. Thus, there is only one number divisible by 4 that has exactly four divisors - the number 8. Its neighbors (7 and 9) do not satisfy the condition, so the number of such numbers is no more than three.
Example of three consecutive numbers, each of which has exactly four natural divisors: $33, 34, 35$. There are other examples as well.
## Grading Criteria
+ A complete and well-reasoned solution is provided
± A generally correct but insufficiently justified solution is provided (without containing incorrect statements). For example, the correct answer and example are provided, it is noted that among four consecutive numbers one is divisible by 4, but the case $n=8$ is not mentioned
Ғ The correct answer and example are provided, but there is an error in the reasoning. For example, it is stated that any number divisible by four has more than four divisors
干 Only the correct answer and example are provided
- Only the answer "three numbers" is provided
- The problem is not solved or is solved incorrectly
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Does there exist a natural number such that after increasing it by 18, the sum of its digits decreases by 18?
|
Answer: can
Solution. For example, the number 982 works. $982+18=1000$.
| | |
| :--- | :--- |
| | |
| | |
| ${ }_{15-x}$ | $\times$ |
## Grading Criteria.
Only answer: 0 points.
Correct example provided: 7 points.
|
982
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the Island of Logic, there live 40 knights (who always tell the truth), 25 liars (who always lie), and several sophists. A sophist can only utter phrases that a knight or a liar could not say in their place. For example, standing next to a liar, a sophist can say, "We are both liars" (because if he were a knight, this statement would be false, and if he were a liar, it would be true). One day, a sophist made two statements about the island's inhabitants:
1. "There are exactly ... liars on the island."
2. "There are no more sophists on the island than liars."
Reconstruct the first statement of the sophist. How many sophists are on the island?
|
Answer. 1) There are exactly 26 liars on the island; 2) 27 sophists.
Solution.
1) If a sophist were a liar, he would have to tell the truth, and then he would say that there are $25+1=26$ liars. If he were a knight, there would be 25 liars, and he would lie.
2) Let C be the total number of sophists on the island. If a sophist were a liar, he would have to tell the truth, and then he would say that $\mathrm{C}-1 \leq 25+1$, or $\mathrm{C} \leq 27$. If a sophist were a knight, he would have to lie, and then it would be true that $\mathrm{C}-1>25$, or $\mathrm{C}>26$. The only natural number that satisfies both inequalities is 27.
## Grading Criteria.
Correctly stating the claim about liars without justification: 1 point.
Correctly stating the number of sophists without justification: 2 points.
For justifying each of the claims, an additional 2 points are added.
|
26
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A sequence of 2016 numbers is written. Each one, except the first and the last, is equal to the sum of its neighbors. Find the sum of all 2016 numbers.
|
Answer: the sum of all numbers is zero.
Solution. Let the first number be $a$, and the second $b$. Denote the third as $x$. Then $a+x=b$ and, therefore, $x=b-a$. Now, express the fourth in terms of $a$ and $b$: $b+y=b-a$ and, therefore, $y=-a$. Continuing, we get: $a, b, b-a, -a, -b, a-b, a, b, \ldots$ This means the numbers repeat with a period of 6. Since 2016:6=336, the sum of all numbers is the sum of the first six, multiplied by 336. The sum of the first six is zero, so the sum of all is zero.
## Grading Criteria.
Only the answer: 0 points.
Specific example analysis: 1 point.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a $5 \times 5$ board, a cross consisting of five cells (a cell and all its neighbors) is located. What is the minimum number of detectors needed to place on the board cells to accurately determine the position of the cross? (A detector indicates whether a cell belongs to the cross or not, and the detectors trigger simultaneously.)
|
Answer: 4.
Solution. There are 9 possible positions for the cross on the board, which is the same as the number of positions for the central cell of the cross. A detector has two states, so the total number of possible states for three detectors is $2^{3}=8$, and thus, they cannot distinguish between 9 positions of the cross. Examples of possible arrangements of four detectors are shown in the figures

## Grading Criteria.
Only the answer: 0 points.
Example with 4 detectors: 3 points.
Proof of the insufficiency of three detectors: 4 points.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3.6. Petya can draw only 4 things: the sun, a ball, a tomato, and a banana. But he does it extremely realistically! Today he drew several things, among which there were exactly 15 yellow, 18 round, and 13 edible. What is the maximum number of balls he could have drawn?
Petya believes that all tomatoes are round and red, all balls are round and can be of any color, and all bananas are yellow and not round.
|
Answer: 18.
Solution. Since there are a total of 18 round objects, and all balls are round, there were no more than 18 balls. Note that there could have been exactly 18, if 2 yellow balls, 16 green balls, and 13 bananas were drawn.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3.7. Katya passes the time while her parents are at work. On a piece of paper, she absentmindedly drew Cheburashkas in two rows (at least one Cheburashka was drawn in each row).
Then, after some thought, between every two adjacent Cheburashkas in a row, she drew a Gena the Crocodile. And then to the left of each Cheburashka, she drew a Old Lady Shapoklyak. And finally, between every two characters in a row, she drew a Krakozyabra.
Looking carefully at the drawing, she realized that only the Krakozyabras looked good, and she angrily erased all the others. In the end, her parents saw two rows of Krakozyabras: a total of 29. How many Cheburashkas were erased?
|
Answer: 11.
Solution. The Krokodilofes are drawn exactly in the gaps between the other characters. In each of the two rows of gaps, there is 1 less gap than there are characters, so
There are 2 fewer Krokodilofes than all the other characters. Therefore, Cheburashkas, Crocodile Gens, and Old Ladies Shapoklyak total $29+2=31$. We will now consider only them, forgetting about the Krokodilofes.
Each Cheburashka has one neighboring Old Lady Shapoklyak to the left, so there are an equal number of them. Crocodile Gens are drawn exactly in the gaps between Cheburashkas, so by the previously described principle, there are 2 fewer of them than Cheburashkas.
Let's mentally add 2 Crocodile Gens. Then the total number of characters will be $31+2=33$. In this case, all three characters are now equal, so there were 11 Cheburashkas.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3.8. A small raft was swaying by the riverbank. Five mice weighing 70 g each, three moles weighing 90 g each, and four hamsters weighing 120 g each approached the shore. What is the minimum number of grams the raft must be able to support so that all the animals can cross to the other side, possibly in several trips "back and forth"? The raft cannot move across the river without a rower.
|
Answer: 140.
Solution. If the raft can carry less than two animals, then they will not all be able to cross. Indeed, in this case, one animal would have to row back and forth on the raft, without the possibility of staying on the other side of the river (since the raft cannot return without a rower).
Therefore, the raft must be able to carry at least the two lightest animals, i.e., at least $70 \cdot 2=140$ grams. We will show that if the raft's capacity is 140 grams, then all the animals can cross to the other side of the river.
We will designate two mice as "rowers," and call them $A$ and $B$. The two mouse rowers row to the other side; $B$ stays there, while $A$ returns with the raft. Then, one of the other animals rows to the other side. Mouse $B$ returns the raft.
Thus, one animal has been ferried, and the rest of the animals and the raft are back in the initial position. Therefore, by repeating the same operations, we can ferry the next animal. And so on, until all the animals are ferried.
At the very end, $A$ and $B$ will row to the other side, and all the animals will have crossed.
## 4th grade
|
140
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.1. Assign each letter a digit $1,2,3,4,5$ so that all inequalities are satisfied.
$$
3>\mathrm{A}>\mathrm{M}<\mathrm{E}<\mathrm{H}<\mathrm{A}
$$
Different letters must correspond to different digits. Write the number ZAMENA as your answer.
|
Answer: 541234.
Solution. From the condition, it follows that $\mathrm{M}<\mathrm{E}<\mathrm{H}<\mathrm{A}<3$. The numbers from 1 to 5 are uniquely ordered, so $\mathrm{M}=1, \mathrm{E}=2, \mathrm{H}=3, \mathrm{~A}=4,3=5$. Then ZAMENA $=541234$.
|
541234
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
|
Answer: 24.
Solution. In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.5. Write the largest eight-digit number in which all even digits are present. (Even digits: $0,2,4,6,8$.)
|
Answer: 99986420.
Solution. The number 99986420 meets the condition of the problem. Suppose there exists a larger eight-digit number. It is clear that its first three digits must be nines. Since there are only 5 even digits, the last five digits are $0,2,4,6,8$ in some order. But then such an eight-digit number cannot exceed 99986420, a contradiction.
|
99986420
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.6. Some digits in the rectangle are already placed. Place the remaining digits so that:
- the sum of the digits in each column is the same;
- the sum of the digits in each row is the same;
- the sum of the digits in the red cells is equal to the sum of the digits in any row. Enter the three-digit number $A B C$ as your answer.
| 4 | | 3 |
| :--- | :--- | :--- |
| | $A$ | 1 |
| 1 | | 6 |
| $B$ | 2 | $C$ |
|
Answer: 652.
Solution. If we add 3 to the sum of the two upper red numbers, we get the same number as if we added the sum of the two lower red numbers. Therefore, the unknown lower red number is 2. Then, in each row, the sum is $1+2+6=$ 9. This means that the unknown upper red number complements $4+3$ to 9, i.e., it is also 2. We have found that the sum of the digits in each row is 9. This means that the sum of the numbers in the entire table is 36, and in each column, it is 12. Now, it is not difficult, by sequentially considering columns and rows with one unknown number, to fill in the entire table (for example, we can first determine that $C=2$ and $A=6$, and then $B=5$):
| 4 | 2 | 3 |
| :--- | :--- | :--- |
| 2 | 6 | 1 |
| 1 | 2 | 6 |
| 5 | 2 | 2 |
We get that the number $A B C$ is 652.
|
652
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.8. If in the number 79777 the digit 9 is crossed out, the number 7777 is obtained. How many different five-digit numbers exist from which 7777 can be obtained by crossing out one digit?
|
Answer: 45.
Solution. Note that 77777 is one of such numbers. Next, we will consider five-digit numbers where to get 7777, we need to strike out a digit that is not 7.
If the first digit in the number is struck out, there are 8 options for it: $1,2,3,4,5,6,8,9$. If, however, the second, third, fourth, or fifth digit in the number is struck out, there are 9 options for it: $0,1,2,3,4,5,6,8,9$.
Obviously, all the corresponding numbers are distinct, and there are $1+8+9+9+9+9=45$ of them.
## 5th grade
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. Sasha wrote down on the board all two-digit numbers divisible by 6, and then erased those that do not end in 4. What is the largest number that ended up on the board?
|
Answer: 84.
Solution. Let's take the largest two-digit number divisible by 6, which is 96, and sequentially subtract 6 from it. This way, we will go through all numbers divisible by 6 in descending order. We will stop at the first one that ends in 4, which is what we need.
$$
96 \rightarrow 90 \rightarrow 84
$$
|
84
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
Answer: 43.
Solution. The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. At the end-of-the-year school dance, there were twice as many boys as girls. Masha counted that there were 8 fewer girls, besides herself, than boys. How many boys came to the dance?
|
Answer: 14.
Solution. Let there be $d$ girls at the disco, then there are twice as many boys, i.e., $d+d$. The number of girls, excluding Masha, is $d-1$ (all except herself).
Since there are 8 more boys than the other girls, excluding Masha, then $d+d=(d-1)+8$. From this, it follows that $d=7$, so the total number of boys is $7+7=14$.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. From a $6 \times 6$ grid square, gray triangles have been cut out. What is the area of the remaining figure? The side length of each cell is 1 cm. Give your answer in square centimeters.
|
Answer: 27.
Solution. The area of the entire square is $6 \cdot 6=36$ sq. cm.
Divide the triangle located in the middle of the square into two smaller triangles, as shown in the picture on the left. Then the dark gray triangles can be combined into a rectangle $1 \times 3$, and the light gray triangles into a rectangle $2 \times 3$. Therefore, the area of the figure that remains after cutting out all the triangles is 36-3-6 $=27$ sq. cm.
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.6. A three-digit number and two two-digit numbers are written on the board. The sum of the numbers that contain a seven in their notation is 208. The sum of the numbers that contain a three in their notation is 76. Find the sum of all three numbers.
|
Answer: 247.
Solution. Let the three-digit number be $A$, the two-digit numbers be $-B$ and $C$. Among the numbers whose sum is 76, there cannot be a three-digit number. The sum cannot consist of a single number either, because otherwise that number would be 76, but it does not contain a three. Therefore, 76 is the sum of two two-digit numbers, each of which contains a three:
$$
B+C=76
$$
Among the numbers whose sum is 208, there must be a three-digit number (since the sum of two-digit numbers is only 76). It cannot be the only one, because the number 208 does not contain a seven. Therefore, there is at least one two-digit number in this sum - but not both at the same time (otherwise the three-digit number would be $208-76=132$, but it does not contain a seven).
Without loss of generality, let's assume that the two-digit number in this sum is $B$. Then
$$
A+B=208
$$
and both of these numbers contain a seven.
Therefore, the number $B$ contains both a three and a seven, i.e., $B=37$ or $B=73$.
If $B=73$, then $C=76-B=3$ - not a two-digit number. Therefore, $B=37, C=76-37=39$, $A=208-37=171$.
The sum of all the numbers is $171+37+39=247$.
|
247
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. In the country, there are 100 cities: 30 of them are located in the mountainous part of the country, and 70 are in the plain. Over three years, air routes were established between the cities. Each year, 50 new air routes were opened in the country: all cities were randomly divided into 50 pairs, and a route was opened between the cities in the same pair. After three years, it turned out that out of the 150 routes opened, exactly 21 connect pairs of "mountainous" cities. How many routes connect pairs of "plain" cities?
|
# Answer: 81.
Solution. Each flight has two ends (two cities it connects). Moreover, after three years, each city is the end of exactly three flights.
In the "mountain" cities, flights have a total of $30 \cdot 3=90$ ends. Among these, 21 flights connect two "mountain" cities. Each such flight between "mountain" cities has two ends, so each of these flights is counted twice. The remaining $90-2 \cdot 21=48$ are the ends of flights that start from "mountain" cities and lead to "plain" cities. Therefore, there are exactly 48 flights between "mountain" and "plain" cities.
Now let's consider the ends of flights that start from "plain" cities. There are a total of $70 \cdot 3=$ 210 ends, but as we have already determined, 48 of these are the ends of flights leading to "mountain" cities. Therefore, the flights between two "plain" cities have $210-48=162$ ends. Each such flight has two ends, so the answer to the problem is $162: 2=$ 81.
## 6th grade
|
81
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. Masha placed the numbers from 1 to 16 in the cells of a $4 \times 4$ table so that any two numbers differing by one were in adjacent cells.
And Sasha erased all the numbers except for 1, 4, 9, and 16. What number was in the cell with the question mark?
| | 1 | | $?$ |
| :---: | :---: | :---: | :---: |
| | 4 | | |
| | | 16 | |
| | | 9 | |
|
Answer: 13.
Solution. Since any two numbers that differ by one are in adjacent cells, the number in the upper left corner must be either 2 (neighbor of 1) or a number that has only one neighbor - 1 or 16. The second option does not work for us, so we can write the numbers 2 and 3 in the table.
| 2 | 1 | | $?$ |
| :---: | :---: | :---: | :---: |
| 3 | 4 | | |
| | | 16 | |
| | | 9 | |
If the number 8 is to the right of the number 9, then the placement of the numbers $7,6,5$ is uniquely determined.
| 2 | 1 | | $?$ |
| :---: | :---: | :---: | :---: |
| 3 | 4 | 5 | 6 |
| | | 16 | 7 |
| | | 9 | 8 |
But then we cannot place any number in the upper right corner, so this option does not work. It turns out that to the left of the number 9 is the number 8, and to the right is 10.
| 2 | 1 | | $?$ |
| :---: | :---: | :---: | :---: |
| 3 | 4 | | |
| | | 16 | |
| | 8 | 9 | 10 |
In the left part of the table, the placement of the numbers $7,6,5$ is uniquely determined, and in the right part - 11 and 12.
| 2 | 1 | | $?$ |
| :---: | :---: | :---: | :---: |
| 3 | 4 | | 12 |
| 6 | 5 | 16 | 11 |
| 7 | 8 | 9 | 10 |
Next to the number 16, only the number 15 can stand. Now it only remains to write the numbers 13 and 14 into the table.
| 2 | 1 | 14 | 13 |
| :---: | :---: | :---: | :---: |
| 3 | 4 | 15 | 12 |
| 6 | 5 | 16 | 11 |
| 7 | 8 | 9 | 10 |
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. For preparing one portion of salad, 2 cucumbers, 2 tomatoes, 75 grams of feta cheese, and 1 pepper are required. The restaurant's warehouse has 60 peppers, 4.2 kg of feta cheese, 116 tomatoes, and 117 cucumbers. How many portions can be made?
|
Answer: 56.
Solution. The pepper will last for $60: 1=60$ servings.
The feta cheese will last for $4200: 75=56$ servings (kilograms converted to grams).
The tomatoes will last for $116: 2=58$ servings.
The cucumbers will last for $117: 2=58.5$, i.e., 58 whole servings.
Since all ingredients must be included in each serving, exactly 56 servings can be prepared.
|
56
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.3. Vitya and his mother left home at the same time and walked in opposite directions at the same speed: Vitya - to school, and his mother - to work. After 10 minutes, Vitya realized he didn't have the keys to the house, and he would return from school earlier than his mother, so he started to catch up with her, increasing his speed fivefold. How many minutes after he realized he needed to get the keys will Vitya catch up with his mother?
|
Answer: 5 minutes.
Solution. Let Vitya and his mother initially walk at a speed of $s$ meters per minute. After 10 minutes, when Vitya realized he had forgotten his keys, the distance between him and his mother became $10 s + 10 s = 20 s$. When Vitya started to catch up with his mother, he walked at a speed of $5 s$ meters per minute, so the distance between him and his mother decreased by $4 s$ meters per minute. Therefore, it would take $20 s : 4 s = 5$ minutes for the distance to reduce to zero.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. In the park, paths are laid out as shown in the figure. Two workers started to asphalt them, starting simultaneously from point $A$. They lay asphalt at constant speeds: the first on the section $A-B-C$, the second on the section $A-D-E-F-C$. In the end, they finished the work simultaneously, spending 9 hours on it. It is known that the second works 1.2 times faster than the first. How many minutes did the second spend laying asphalt on the section $D E$?
|
Answer: 45.
Solution. Let the line $A D$ intersect the line $C F$ at point $G$, as shown in the figure below. Since $A B C G$ and $D E F G$ are rectangles, we have $A B=C G, B C=A G, E F=D G$ and $D E=F G$.
The second worker works 1.2 times faster than the first, and the working time was the same, so the second worker laid 1.2 times more asphalt than the first. Let the first worker lay $x=A B+B C$ asphalt on the section $A-B-C$, then the second worker on the section $A-D-E-F-C$ laid
$$
\begin{aligned}
1.2 x & =A D+D E+E F+F G+G C=(A D+E F+C G)+(D E+F G)= \\
& =(B C+A B)+(D E+D E)=x+2 D E
\end{aligned}
$$
From this, we find that $D E=0.1 x$, which is 12 times less than the total amount of asphalt on the second section. Therefore, the second worker spent 12 times less time on the section $D E$ than on his entire path. He worked a total of $9 \cdot 60=540$ minutes, so he spent $\frac{540}{12}=45$ minutes on $D E$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.6. Several oranges (not necessarily of equal weight) were picked from a tree. When they were weighed, it turned out that the weight of any three oranges taken together is less than $5 \%$ of the total weight of the remaining oranges. What is the smallest number of oranges that could have been picked?
|
Answer: 64.
Solution. 64 oranges could have been, for example, if all of them had the same mass $m$, since $\frac{3 m}{61 m}<0.05$.
Suppose there were no more than 63 oranges. Consider the three heaviest oranges with a total mass of $M$. All the other oranges (no more than 60) can be divided into no more than 20 groups, each containing no more than 3 oranges. Obviously, the total mass in each group does not exceed $M$, so the total mass in all groups does not exceed $20 M$. Since $\frac{M}{20 M}=0.05$, the three heaviest oranges account for no less than $5\%$ of the total mass of the other oranges. Contradiction.
|
64
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. There are exactly 120 ways to color five cells in a $5 \times 5$ table so that each column and each row contains exactly one colored cell.
There are exactly 96 ways to color five cells in a $5 \times 5$ table without a corner cell so that each column and each row contains exactly one colored cell.
How many ways are there to color five cells in a $5 \times 5$ table without two corner cells so that each column and each row contains exactly one colored cell?

|
Answer: 78.
Solution. Consider the colorings of a $5 \times 5$ table described in the problem (i.e., such that in each column and each row exactly one cell is colored).
For convenience, let's introduce some notations. The top-left corner cell of the $5 \times 5$ table will be called $A$, and the bottom-right corner cell will be called $B$. Suppose that among the colorings of the first table, exactly $a$ have the cell $A$ colored, and exactly $b$ have the cell $B$ colored. Clearly, $a=b$ due to symmetry.
Notice that the number of colorings of the second table is equal to the number of colorings of the first table where the cell $A$ is not colored. The number of colorings of the third table is equal to the number of colorings of the first table where neither $A$ nor $B$ is colored. To find this, we subtract from 120 the number of colorings of the first table where $A$ or $B$ is colored. To count the number of such colorings, we add $a$ and $b$, and then subtract what has been counted twice - the ways where both $A$ and $B$ are colored.
All colorings of the first table can be divided into two types: those in which the cell $A$ is colored, and those in which it is not. This leads to the equation $120=a+96$, i.e., $a=24$. Then $b=24$ as well.
The number of colorings where both $A$ and $B$ are colored is the same as the number of ways to color the central $3 \times 3$ square. It is easy to see that there are exactly $3!=6$ such ways (to choose the colored cell in its top row, there are 3 ways, in the middle row - 2 ways, and in the bottom row - 1 way).
Thus, the answer to the problem is the number $120-(24+24-6)=78$.
## 7th grade
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2. Three pirates were dividing a treasure. The first one got a third of the initial number of coins and one more coin, the second one got a quarter of the initial number of coins and five more coins, the third one got a fifth of the initial number of coins and twenty more coins (thus all the coins were distributed). How many coins were in the treasure?
|
Answer: 120.
Solution. Let $m$ be the initial total number of coins in the treasure. The pirates collectively took $\left(\frac{m}{3}+1\right)+\left(\frac{m}{4}+5\right)+\left(\frac{m}{5}+20\right)$ coins. Since they divided the entire treasure, this sum equals $m$. Expanding the brackets in the equation
$$
\left(\frac{m}{3}+1\right)+\left(\frac{m}{4}+5\right)+\left(\frac{m}{5}+20\right)=m
$$
and bringing the fractions to a common denominator, we get $\frac{47}{60} m+26=m$, from which $\frac{13}{60} m=26$, that is, $m=120$.
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. If a platoon of soldiers is divided into brigades of 7 people, then 2 people will not fit into any brigade. If the platoon is divided into brigades of 12 people, then again 2 people will not fit into any brigade. What is the minimum number of soldiers that need to be added to the platoon so that it can be completely divided into brigades of 7 people and also into brigades of 12 people?
|
Answer: 82.
Solution. A platoon can be entirely divided into brigades of 7 and brigades of 12 if and only if the number of people in it is divisible by $7 \cdot 12=84$.
Remove two people from the platoon. Then the remaining people can be divided into brigades both ways, meaning their number is divisible by 84. Return the two removed people; to reach the next number divisible by 84, we need to add 82 more people.
|
82
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.

Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are $60^{\circ}$, so it is equilateral, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a $5 \times 5$ square, some cells have been painted black as shown in the figure. Consider all possible squares whose sides lie along the grid lines. In how many of them is the number of black and white cells the same?

|
Answer: 16.
Solution. An equal number of black and white cells can only be in squares $2 \times 2$ or $4 \times 4$ (in all other squares, there is an odd number of cells in total, so there cannot be an equal number of black and white cells). There are only two non-fitting $2 \times 2$ squares (both of which contain the center of the table, but do not contain any cells above the center), so there are exactly $16-2=14$ fitting $2 \times 2$ squares. And among the $4 \times 4$ squares, only the two lower ones fit.
Thus, the total number of squares with an equal number of black and white cells is exactly $14+2=16$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. The arithmetic mean of three two-digit natural numbers $x, y, z$ is 60. What is the maximum value that the expression $\frac{x+y}{z}$ can take?
|
Answer: 17.
Solution. From the condition, it follows that the sum of the numbers $x, y, z$ is $60 \cdot 3=180$. Then
$$
\frac{x+y}{z}=\frac{180-z}{z}=\frac{180}{z}-1 \leqslant \frac{180}{10}-1=17
$$
since $z \geqslant 10$. Note also that when $x=90, y=80, z=10$, the value 17 is achieved.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
|
Answer: 21.
Solution. Since $AC$ is the diameter of the circle, point $O$ is the midpoint of $AC$, and $\angle AKC = 90^{\circ}$.
Then
$$
\angle BAC = \angle BAK + \angle CAK = \angle BCA + \angle CAK = \angle BKA = 90^{\circ}.
$$
The area of the right triangle $ABC$ can be found as $\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 14 = 42$. Since the median $BO$ divides its area in half, the area of triangle $BOC$ is $\frac{42}{2} = 21$.
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Find any solution to the puzzle
$$
\overline{A B C A}=182 \cdot \overline{C D}
$$
where $A, B, C, D$ are four different non-zero digits (the notation $\overline{X Y \ldots Z}$ means the decimal representation of the number).
As an answer, write the four-digit number $\overline{A B C D}$.
|
Answer: 2916.
Solution. $\overline{A B C A}=1001 A+10 \cdot \overline{B C}$. Note that 1001 and 182 are divisible by 91, therefore, $10 \cdot \overline{B C}$ is also divisible by 91, i.e., $\overline{B C}=91$.
Substituting $B=9, C=1$ and dividing by 91, we get the equation $11 A=10+2 D$. On the left side of this equation, we have a number divisible by 11, and on the right side, an even two-digit number less than 30. Therefore, this number is 22, from which $A=2$ and $D=6$.
|
2916
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. In a race, several people participated, including Andrey, Dima, and Lёnya. No two participants of this race arrived at the same time.
- The number of people who arrived before Andrey is 2 times less than the number of people who arrived after him.
- The number of people who arrived before Dima is 3 times less than the number of people who arrived after him.
- The number of people who arrived before Lёnya is 4 times less than the number of people who arrived after him.
What is the smallest number of people that could have participated in the race?
|
Answer: 61.
Solution. Let $x$ be the number of people who ran before Andrey, then $2x$ people ran after him. We get that there were $3x+1$ participants in the race.
Let $y$ be the number of people who ran before Dima, then there were $4y+1$ participants in total.
Finally, let $z$ be the number of people who ran before Lenya, then there were $5z+1$ participants in total.
If we subtract 1 from the total number of runners, the result should be divisible by 3, 4, and 5. The smallest such number is 60, so there were at least 61 participants.
It remains to note that the condition could have been met with 61 participants. For example, if among them Andrey came in 21st, Dima in 16th, and Lenya in 13th.
|
61
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. A natural number is called interesting if all its digits are different, and the sum of any two adjacent digits is a square of a natural number. Find the largest interesting number.
|
Answer: 6310972.
Solution. Mark 10 points on the plane, representing the digits from 0 to 9, and connect those that sum to the square of a natural number.
On such a diagram, we need to find the path of maximum length, as the largest number should have the maximum number of digits. It is easy to notice that this path is $2-7-9-0-1-3-6$. To make the number as large as possible, the first digit should be as large as possible, i.e., the answer is the number 6310972.
|
6310972
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Given an isosceles triangle $A B C$, where $A B=A C$ and $\angle A B C=53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $A K$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $A C$;
- $K M=A B$
- angle $M A K$ is the maximum possible.
How many degrees does angle $B A M$ measure?
|
Answer: 44.
Solution. Let the length of segment $AB$ be $R$. Draw a circle with center $K$ and radius $R$ (on which point $M$ lies), as well as the tangent $AP$ to it such that the point of tangency $P$ lies on the same side of $AC$ as $B$. Since $M$ lies inside the angle $PAK$ or on its boundary, the angle $MAK$ does not exceed the angle $PAK$, and these angles are equal only if points $M$ and $P$ coincide. Therefore, $M$ is this point of tangency.

The radius $KM$ of the circle is perpendicular to the tangent $AM$. Also, in the right triangle $AMK$, the leg $MK$ is half the hypotenuse $AK$, so $\angle MAK=30^{\circ}$. Additionally, from the condition, we get that $\angle BAC=180^{\circ}-2 \cdot 53^{\circ}=74^{\circ}$. Therefore,
$$
\angle BAM=\angle BAC-\angle MAK=74^{\circ}-30^{\circ}=44^{\circ}
$$
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.8. A computer can apply three operations to a number: "increase by 2", "increase by 3", "multiply by 2". The computer was given the number 1 and was made to try all possible combinations of 6 operations (each of these combinations is applied to the initial number 1). After how many of these combinations will the computer end up with an even number?
|
Answer: 486.
Solution. If the number was odd before the last operation, then one of the two operations "increase by 3" or "multiply by 2" will make it even, but the third will not. Similarly, if the number was even before the last operation, then one of the two operations "increase by 2" or "multiply by 2" will make it even, but the third will not.
Thus, the first 5 operations can be performed in any order - this gives $3^{5}$ options. To get an even result on the last operation, there are exactly 2 options, so the total number of combinations is $3^{2} \cdot 2=486$.
## 9th grade
|
486
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. In a $3 \times 3$ table, the digits from 1 to 9 are arranged (each digit is written in exactly one cell). The digits 1, 2, 3, 4 are placed as shown in the figure. It is also known that the sum of the digits in the cells adjacent to the digit 5 is 9. Find the sum of the digits in the cells adjacent to the digit 6.
| 1 | | 3 |
| :--- | :--- | :--- |
| | | |
| 2 | | 4 |
|
Answer: 29.
Solution. Note that the smallest possible sum of the digits around the digit 5 is exactly $1+2+6=9$, and this is only possible when it is below the digit 1 and above the digit 2, with the digit 6 in the center.
Indeed, if 5 is in the center, then the sum of the surrounding digits is $6+7+8+$ $9>9$. And if 5 is not in the center (and the digit in the center is at least 6) and not below 1, then the sum of the surrounding digits is at least $1+3+6>9$.
| 1 | | 3 |
| :--- | :--- | :--- |
| 5 | 6 | |
| 2 | | 4 |
Since 6 is in the center, the sum of the surrounding digits is $5+7+8+9=29$.
|
29
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.2. In the first hour of the shift, the master made 35 parts. Then he realized that, maintaining the current speed, he would have to stay an extra hour to complete the shift's plan. By increasing his speed by 15 parts per hour, he completed the plan half an hour before the end of the shift. How many parts should the master produce during the shift?
|
Answer: 210.
Solution. Let $N$ be the number of parts he still needs to manufacture. If he continued to make 35 parts per hour, he would finish in $\frac{N}{35}$ hours. When he sped up and started producing 50 parts per hour, he completed the work in $\frac{N}{50}$ hours.
From the condition, it follows that $\frac{N}{35}-\frac{N}{50}=1.5$, which means $\frac{3}{350} N=1.5$, from which we find $N=175$. Then the number of parts that need to be manufactured in one shift is $175+35=210$.
|
210
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.3. The farmer said: "I have $N$ rabbits. Long ears are exactly on 13 of them. And exactly 17 of them can jump far."
The traveler rightly noted: "Therefore, among your rabbits, there are at least 3 rabbits that simultaneously have long ears and can jump far."
What is the largest value that the number $N$ can take?
|
Answer: 27.
Solution. If $N \geqslant 28$, then the traveler is wrong: it is possible that the farmer had only 2 long-eared rabbits that can jump far. In addition to them, there were 11 long-eared rabbits that cannot jump far, and 15 rabbits without long ears that can jump far. The remaining $N-28$ rabbits neither have long ears nor can jump far.
If $N=27$, then the traveler is right. Indeed, from the condition, it follows that exactly 10 rabbits cannot jump far. Since 13 rabbits have long ears, at least $13-10=3$ of them both have long ears and can jump far.
|
27
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. At a round table, 40 knights and 10 samurais are sitting. Exactly 7 knights have a samurai as their right neighbor. What is the maximum number of knights that could be sitting next to two knights?
|
# Answer: 32.
Solution. Let's divide the people sitting at the table into alternating groups of consecutive knights and consecutive samurais. From the condition, it follows that there are exactly 14 such groups (7 groups of knights and 7 groups of samurais), since the 7 knights mentioned in the condition are precisely the rightmost knights in the groups of knights.
Note that at least 8 knights do not sit next to two knights: these are the 7 knights mentioned in the condition and at least 1 leftmost knight in a group of more than one knight (such a group exists because there are 7 groups and 40 knights). Therefore, no more than $40-8=32$ knights sit between two knights.
Now let's provide an example. For this, we will take 6 groups of knights consisting of 1 person each and one group of 34, while the samurais can be distributed arbitrarily among 7 groups (not forgetting that the groups of knights and samurais alternate). It is clear that 32 non-edge knights from the "large" group of knights are the ones we are looking for.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. The teacher wrote a number on the board. Sasha decided to divide it by 102 with a remainder, and Masha - by 103. It turned out that the quotient obtained by Sasha and the remainder obtained by Masha add up to 20. What remainder did Sasha get? List all possible options.
|
Answer: 20.
Solution. Let $n$ be the number on the board, divide it by 102 and by 103 with remainders:
$$
n=102 a+b ; \quad n=103 c+(20-a)
$$
Subtract the second equation from the first:
$$
0=103(a-c)+(b-20)
$$
From this, it follows that $b-20$ is divisible by 103. Since $0 \leqslant b \leqslant 101$, we get that $b=20$.
Notice also that, for example, for the number $n=122$, the remainder $b=20$ is indeed possible.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. An equilateral triangle with a side of 10 is divided into 100 small equilateral triangles with a side of 1. Find the number of rhombi consisting of 8 small triangles (such rhombi can be rotated).
|
Answer: 84.
Solution. Rhombuses consisting of eight triangles can be of one of three types:

It is clear that the number of rhombuses of each orientation will be the same, so let's consider only the vertical ones. Each of them is uniquely determined by its top triangle. Now it is easy to count the number of such triangles.

In the first row, there is 1 such triangle, in the second row - 2, in the third row - 3, ..., in the seventh row - 7. In total, there are \(1+2+3+\ldots+7=28\) vertical rhombuses, and therefore, the answer to the problem is \(28 \cdot 3 = 84\).
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. How many real numbers $x$ exist such that the value of the expression $\sqrt{123-\sqrt{x}}$ is an integer?
|
Answer: 12.
Solution. From the condition, it follows that the value $s=123-\sqrt{x} \leqslant 123$ is a square of an integer. Since $11^{2}<123<12^{2}$, this value can take one of 12 values $0^{2}$, $1^{2}, 2^{2}, \ldots, 11^{2}$. And for each of these 12 values of $s$, there is a unique value of $x=(123-s)^{2}$ (obviously, all these values of $x$ are distinct).
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. At exactly noon, a truck left the village and headed for the city, at the same time, a car left the city and headed for the village. If the truck had left 45 minutes earlier, they would have met 18 kilometers closer to the city. And if the car had left 20 minutes earlier, they would have met $k$ kilometers closer to the village. Find $k$.
|
Answer: 8.
Solution. We will express all distances in kilometers, time in hours, and speed in kilometers per hour. Let the distance between the village and the city be $S$, the speed of the truck be $x$, and the speed of the car be $y$. The time until the first meeting is $\frac{S}{x+y}$, so the distance from the village to the actual meeting point is $\frac{S x}{x+y}$.
In the first hypothetical scenario, the truck will travel $0.75 x$ kilometers in 45 minutes, meaning it will take another $\frac{S-0.75 x}{x+y}$ hours to reach the expected first meeting point, and the truck will travel another $\frac{(S-0.75 x) x}{x+y}$ kilometers. According to the problem, we know that
$$
18=0.75 x+\frac{(S-0.75 x) x}{x+y}-\frac{S x}{x+y}=0.75 \frac{x y}{x+y}
$$
from which we find $\frac{x y}{x+y}=18 \cdot \frac{4}{3}=24$.
In the second scenario, the car will travel $y / 3$ kilometers in 20 minutes, meaning it will take another $\frac{S-y / 3}{x+y}$ hours to reach the expected second meeting point, and the truck will travel $\frac{(S-y / 3) x}{x+y}$ kilometers during this time. The value we need to find is
$$
\frac{S x}{x+y}-\frac{(S-y / 3) x}{x+y}=\frac{x y / 3}{x+y}=24 / 3=8
$$
Another solution. Instead of the scenario "the truck left 45 minutes earlier," we will consider the scenario "the car left 45 minutes later" - it is clear that the meeting point will be the same in this case.
We will solve the problem graphically. Along the $O x$ axis, we will plot the coordinates of the vehicles such that the city corresponds to the coordinate 0 and the village to the coordinate $p>0$. Along the $O t$ axis, we will plot time (the common start of movement in the original scenario will correspond to $t=0$). We will represent the car's movement with a red line and the truck's movement with a blue line; in addition, we will mark two alternative graphs of the car's movement (with a start 45 minutes later and 20 minutes earlier). The meeting point in the original scenario (location and time) will be denoted by $A$, and in the alternative scenarios by $B$ and $C$:
By Thales' theorem,
$$
\frac{45}{20}=\frac{A B}{A C}=\frac{\Delta x_{1}}{\Delta x_{2}}
$$
Since $\Delta x_{1}=18$ kilometers according to the problem, then $\Delta x_{2}=8$ kilometers.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.4. Consider the sequence
$$
a_{n}=\cos (\underbrace{100 \ldots 0^{\circ}}_{n-1})
$$
For example, $a_{1}=\cos 1^{\circ}, a_{6}=\cos 100000^{\circ}$.
How many of the numbers $a_{1}, a_{2}, \ldots, a_{100}$ are positive?
|
Answer: 99.
Solution. Note that for an integer $x$ divisible by 40, the cosines of the angles $x^{\circ}$ and $10 x^{\circ}$ coincide, since the difference between these angles $9 x^{\circ}$ is divisible by $360^{\circ}$. Therefore, $\cos \left(\left(10^{k}\right)^{\circ}\right)=$ $\cos \left(\left(10^{k+1}\right)^{\circ}\right)$ for all $k \geqslant 3$.
It is clear that $\cos \left(1^{\circ}\right)>0, \cos \left(10^{\circ}\right)>0, \cos \left(100^{\circ}\right)<0$, and subsequently $0<\cos \left(1000^{\circ}\right)=\cos \left(10000^{\circ}\right)=\ldots=$ $\cos \left(\left(10^{99}\right)^{\circ}\right)$. Thus, among our numbers, exactly 99 are positive.
|
99
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. A circle $\omega$ is inscribed in trapezoid $A B C D$, and $L$ is the point of tangency of $\omega$ and side $C D$. It is known that $C L: L D=1: 4$. Find the area of trapezoid $A B C D$, if $B C=9$, $C D=30$.
|
Answer: 972.
Solution. Let's mark the center of the circle $I$, as well as the points of tangency $P, Q, K$ with the sides $B C$, $A D, A B$ respectively. Note that $I P \perp B C, I Q \perp A D$, i.e., points $P, I, Q$ lie on the same line, and $P Q$ is the height of the given trapezoid, equal to the diameter of its inscribed circle. Also, the segments of tangents $A K=A Q, B K=B P, C P=C L, D L=D Q$ are equal.
From the condition, it follows that $C P=C L=\frac{1}{5} \cdot 30=6, D Q=D L=\frac{4}{5} \cdot 30=24$. Then $B K=B P=$ $B C-C P=9-6=3$.
Since the lines $C I$ and $D I$ are the angle bisectors of angles $C$ and $D$ of the trapezoid, we have $\angle I C D+$ $\angle I D C=\frac{1}{2}(\angle C+\angle D)=\frac{180^{\circ}}{2}=90^{\circ}$, i.e., triangle $C I D$ is a right triangle with a right angle at vertex $I$. Since $I L$ is its height dropped to the hypotenuse, $I L=$ $\sqrt{C L \cdot D L}=12$. This is the radius of the circle.
Similarly, considering the height $I K$ in the right triangle $A I B$, we get $12=$ $I K=\sqrt{A K \cdot B K}$. Using $B K=3$, we extract $A K=A Q=48$.
Thus, the area of the trapezoid is
$$
S_{A B C D}=\frac{B C+A D}{2} \cdot C H=\frac{9+(48+24)}{2} \cdot 24=972
$$
|
972
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. In a grid table with 5 rows and 6 columns, each cell contains either a cross, a zero, or a star. It is known that:
- in each column, the number of zeros is not less than the number of crosses;
- in each column, the number of zeros is not less than the number of stars;
- in each row, the number of crosses is not less than the number of zeros;
- in each row, the number of crosses is not less than the number of stars.
How many stars can be in such a table? List all possible options.
|
Answer: 6.
Solution. Since in each column there are no fewer O's (noughts) than X's (crosses), then in the entire table there are no fewer O's than X's. Similarly, considering the rows, it follows that in the entire table there are no fewer X's than O's. Therefore, there are an equal number of X's and O's in the entire table, and also there are an equal number of them in each row and each column.
From the condition, it also follows that in each column there cannot be 0 or 1 O's, so there are no fewer than 2. Since the number of X's and O's in the column is equal, there cannot be 3 or more, i.e., there are exactly 2. Therefore, in each column there is exactly one star, i.e., there are a total of 6.
It is also worth noting that the described construction indeed exists. For example, in the following table all conditions are met:
| x | $\times$ | $\times$ | | | O |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | O | 0 | $\times$ | $\times$ | $x$ |
| $*$ | * | $\times$ | $\times$ | 0 | O |
| ○ | 0 | * | $*$ | $\times$ | $x$ |
| $\times$ | $x$ | 0 | 0 | $*$ | * |
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. Olya drew $N$ different lines on the plane, any two of which intersect. It turned out that among any 15 lines, there are always two lines such that the angle between them is $60^{\circ}$. What is the largest $N$ for which this is possible?
|
Answer: 42.
Solution. First, we will show that 42 such lines exist. Draw three lines so that the angle between any two of them is $60^{\circ}$, and take 14 such triplets at different angles:
It is clear that when choosing any 15 lines, at least two of them will be in the same triplet, and the angle between them will be $60^{\circ}$. For example, 42 lines passing through one point, with the angle between any two adjacent lines being $\frac{180^{\circ}}{42}$, fit the described construction.
Now we will prove that there cannot be 43 or more lines that meet the condition. Suppose the contrary and consider such 43 lines. Choose an arbitrary point $O$ on the plane; instead of each line, we will consider a line parallel to the given one and passing through $O$ (obviously, the angles between the lines do not change with such parallel translations; since all the lines initially intersected, they cannot coincide after the translation).
Draw an auxiliary line through point $O$ that does not coincide with any of the drawn lines and does not form a $60^{\circ}$ angle with any of them; we will call this line the "horizontal." Choose the "upper" half-plane relative to the horizontal and divide it into three sectors of $60^{\circ}$ each:
It is clear that each of the 43 lines passes through exactly one sector; therefore, by the pigeonhole principle, one of the sectors will contain at least 15 lines. However, all angles between the lines in one sector will be strictly less than $60^{\circ}$, which leads to a contradiction.
|
42
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.