problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. Let's divide the sequence of natural numbers into groups:
$(1),(2,3),(4,5,6)(7,8,9,10), \ldots$
Denote $S_{n}$ as the sum of the $n$-th group of numbers. Find $S_{16}-S_{4}-S_{1}$.
|
Solution. Note that in the $n$-th group there are $n$ terms and the first one is $\frac{n(n-1)}{2}+$ 1. The last term of the $n$-th group is $\frac{n(n-1)}{2}+1+(n-1)=\frac{n^{2}+n}{2}$. Therefore, $S_{n}=\left(\frac{n(n-1)}{2}+1+\frac{n(n+1)}{2}\right) \cdot \frac{n}{2}=\frac{n\left(n^{2}+1\right)}{2}$. Hence, $S_{16}-S_{4}-S_{1}=$ $2056-34-1=2021$
|
2021
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3.1. Condition:
Danil took a white cube and numbered its faces with numbers from 1 to 6, writing each one exactly once. It turned out that the sum of the numbers on one pair of opposite faces is 11. What can the sum of the numbers on none of the remaining pairs of opposite faces NOT be?
## Answer options:
$\square 5$
$\square 6$
$\square 7$
$\square 9$
|
# Solution.
If the sum of the numbers on opposite faces is 11, then the numbers on these faces are 5 and 6. The remaining numbers can be paired in three ways: $(1,2)$ and $(3,4); (1,3)$ and $(2,4); (1,4)$ and $(2,3)$, i.e., the sums that CAN be obtained are: $3,7,4,6$ and 5. Therefore, the sums that CANNOT be obtained are 8, 9, and 10.
|
9
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
# 5.1. Condition:
Polina came to the cafeteria and saw that 2 puff pastries cost 3 times more than 2 pies. Polina didn't have enough money for 2 puff pastries, but she did have enough for 1 pie and 1 puff pastry. After the purchase, she wondered how many times more money she spent buying 1 puff pastry and 1 pie instead of 2 pies. Help Polina answer this question.
|
Answer: 2
## Solution.
2 puff pastries are 3 times more expensive than 2 pies, so one puff pastry is 3 times more expensive than one pie, which means one puff pastry costs as much as 3 pies. Therefore, 1 puff pastry and 1 pie cost as much as 4 pies. Then they are 2 times more expensive than 2 pies.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.1. Condition:
A five-digit number is called a hill if the first three digits are in ascending order and the last three digits are in descending order. For example, 13760 and 28932 are hills, while 78821 and 86521 are not hills. How many hills exist that are greater than the number $77777?$
#
|
# Answer: 36
## Solution.
Suitable slides must start with 7, so the next digit is either 8 or 9. If the second position is occupied by the digit 9, the third digit will not be greater than the second, so the condition is only satisfied by 8. Therefore, the third position is occupied by 9. The last two positions can be occupied by any two different digits from 0 to 8. There are $9 \cdot 8 / 2 = 36$ such pairs of digits, because we first choose a digit for the second-to-last position (from 0 to 8), and then from the remaining eight digits, we choose the one that will go at the end (from 0 to 8, excluding the digit in the second-to-last position). Since the order of the digits matters, we divide the resulting number of ways by two, as the digits are divided into pairs of the form (a, b), (b, a). For example, the combination of digits 2 and 7 can be 27 or 72 (in that order), and in each such pair, only one way is suitable - where the digits are in descending order.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.2. Condition:
A five-digit number is called a pit if the first three digits are in descending order, and the last three digits are in ascending order. For example, 73016 and 98346 are pits, while 88012 and 56821 are not pits. How many pits are there that are less than the number $22222?$
|
Answer: 36
## Solution.
Suitable pits must start with 2, so the next is either 1 or 0. If the second position is occupied by the digit 1, then the third digit will not be greater than the second, so the condition is only satisfied by 0. Therefore, the third position is 0. The last two places can be occupied by any two different digits from 1 to 9. There are $9 \cdot 8 / 2 = 36$ such pairs of digits, because we first choose a digit for the second-to-last place (from 1 to 9), and then from the remaining eight digits we choose the one that will go at the end (from 1 to 9, excluding the digit at the second-to-last position). Since the order of the digits matters, we divide the resulting number of ways by two, as the digits are divided into pairs of the form (a, b), (b, a). For example, the combination of digits 2 and 7 can be 27 or 72 (in exactly that order), and in each such pair, only one way fits - where the digits are in descending order.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. If the discriminant of the quadratic polynomial $f(x)=a x^{2}+2 b x+c$ is subtracted from the discriminant of the quadratic polynomial $g(x)=(a+1) x^{2}+2(b+2) x+c+4$, the result is 24. Find $f(-2)$.
|
Answer: 6.
Solution: We have: $D_{1}-D_{2}=4\left(b^{2}-a c-(b+2)^{2}+(a+1)(c+4)\right)=4(-4 b+4 a+c)=$ $4 f(-2)$.
Comment: Correct answer without justification - 0 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Six people - liars and knights - sat around a table. Liars always lie, while knights always tell the truth. Each of them was given a coin. Then each of them passed their coin to one of their two neighbors. After that, 3 people said: "I have one coin," while the other 3 said: "I have no coins." What is the maximum number of knights that could have been sitting at the table?
|
Answer: 4.
Solution: After passing the coins, each person sitting at the table can have 0, 1, or 2 coins. The total number of coins will be 6. Note that if a person lies, they will state a number of coins that differs from the actual number by 1 or 2. Since the total number of coins based on the answers differs from the actual total by $6-3=3$, at least 2 people must have lied. Therefore, there are no more than 4 knights at the table. Suppose the knights sitting at the table pass the coins as follows (arrows indicate the direction of the coin transfer; the number of coins after the transfer is in parentheses): $\leftrightarrow K(1)-L(0) \rightarrow L(1) \rightarrow L(1) \rightarrow L(1) \rightarrow K(2) \leftrightarrow$. In this case, all knights tell the truth, while the liars lie, saying they have 0 coins.
Comment: It is proven that there are no more than 4 knights at the table - 5 points. It is proven that there can be 4 knights at the table - 2 points.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. On the board, there are $N$ prime numbers (not necessarily distinct). It turns out that the sum of any three numbers on the board is also a prime number. For what largest $N$ is this possible
|
Answer: $N=4$.
Solution. Consider the remainders when the $N$ written numbers are divided by 3. All three remainders cannot occur, because in this case, the sum of three numbers with different remainders will be divisible by 3 (and will be greater than 3), so it will not be a prime number. Therefore, there can be no more than 2 possible remainders. Also, note that there cannot be 3 numbers with the same remainder, because the sum of these three numbers will be divisible by 3 (and will be greater than 3), so it will not be a prime number. Thus, $N$ cannot be greater than $2 \cdot 2=4$.
$N$ can equal 4. For example, if the numbers written on the board are $3,3,5,5$ (sums $11,13)$.
Remark. There are other examples. For instance, $3,3,5,11$ (sums 19, 17, 11). Comment. It is proven that $N$ is not greater than $4-5$ points. An example with 4 numbers is provided - 2 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. The numbers $2^{2019}$ and $5^{2019}$ are written consecutively. How many digits are written in total?
|
Answer: 2020.
Solution. Let the number $2^{2019}$ contain $\mathrm{m}$ digits, and the number $5^{2019}$ contain $\mathrm{n}$ digits. Then the following inequalities hold: $10^{\mathrm{m}-1}<2^{2019}<10^{\mathrm{m}}, 10^{\mathrm{n}-1}<5^{2019}<10^{\mathrm{n}}$ (the inequalities are strict because the power of two or five is not equal to the power of ten). Multiplying these inequalities, we get: $10^{\mathrm{m}+\mathrm{n}-2}<10^{2019}<10^{\mathrm{m}+\mathrm{n}}$. From this, it follows that the exponent 2019 is between $\mathrm{m}+\mathrm{n}-2$ and $\mathrm{m}+\mathrm{n}$, so $2019=\mathrm{m}+\mathrm{n}-1$ and $\mathrm{m}+\mathrm{n}=2020$. This means that a total of 2020 digits have been written.
|
2020
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. Each cell of a $7 \mathrm{x} 8$ table (7 rows and 8 columns) is painted in one of three colors: red, yellow, or green. In each row, the number of red cells is not less than the number of yellow cells and not less than the number of green cells, and in each column, the number of yellow cells is not less than the number of red cells and not less than the number of green cells. How many green cells can there be in such a table?
|
Answer: 8.
Solution. 1) In each row of the table, there are no fewer red cells than yellow ones, so in the entire table, there are no fewer red cells than yellow ones. In each column of the table, there are no fewer yellow cells than red ones, so in the entire table, there are no fewer yellow cells than red ones. Thus, in the table, there is an equal number of red and yellow cells.
2) Suppose that in some column, there are more yellow cells than red ones. Since in each of the other columns, there are no fewer yellow cells than red ones, then in the entire table, there would be more yellow cells than red ones, but this is not the case (see 1). Therefore, in each of the eight columns, there are an equal number of red and yellow cells.
3) Since in each column, there are no fewer yellow cells than green ones, the cases where in each column: a) 1 yellow, 1 red, 5 green cells and b) 2 yellow, 2 red, 3 green cells are excluded. The only remaining case is when in each column there are 3 red, 3 yellow, and 1 green cell. Then, in total, there are 8 green cells in the table. This case is possible. For example, see the table.
| | $\bar{\sim}$ | Y | $\mathbf{R}$ | $\bar{R}$ | $\cdots$ | $j \pi$ | $\mathbf{R}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\bar{\kappa}$ | $\bar{\kappa}$ | | | $\mathbf{R}$ | ऊ | $\mathbf{R}$ | |
| | | | $\vec{x}$ | | | | |
| | | $=$ | | | | | |
| | $\overline{\mathbf{R}}$ | $\mathbf{R}$ | 3 | $\mathbf{R}$ | $\boldsymbol{A}$ | $\kappa$ | |
| | $\mathcal{\Psi}$ | $\mathbb{w}$ | Y | $\mathbf{R}$ | y | | |
| | | | | | | | |
## Grading Criteria
7 points - A complete and well-reasoned solution is provided.
6 points - A generally correct solution is provided, containing minor gaps or inaccuracies.
4 points - It is proven that there can only be 8 green cells, but an example is not provided.
2 points - Only the correct answer and an example are provided.
0 points - Only the answer is provided.
0 points - The problem is not solved or is solved incorrectly.
Internet resources: $\underline{\text { http://www.problems.ru, https://olimpiada.ru. }}$
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
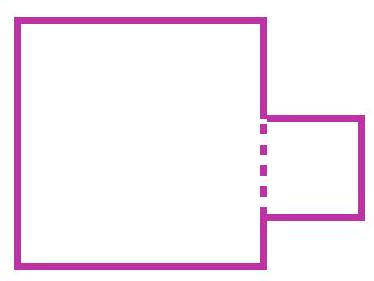
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
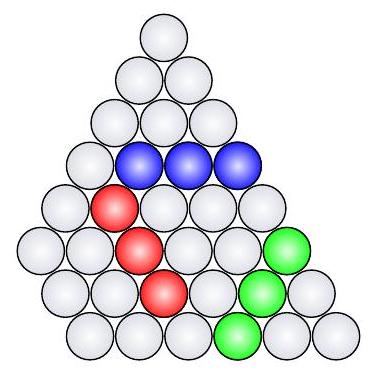
4-5. Given a figure consisting of 33 circles. You need to choose three circles that are consecutive in one of the directions. In how many ways can this be done? The image shows three of the desired ways.
|
Answer: 57.
Solution. The number of options along the long side is $1+2+3+4+5+6=21$. Along each of the other two directions, it is $-4+4+4+3+2+1=18$. The total number of options is $21+18 \cdot 2=57$
|
57
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.

|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
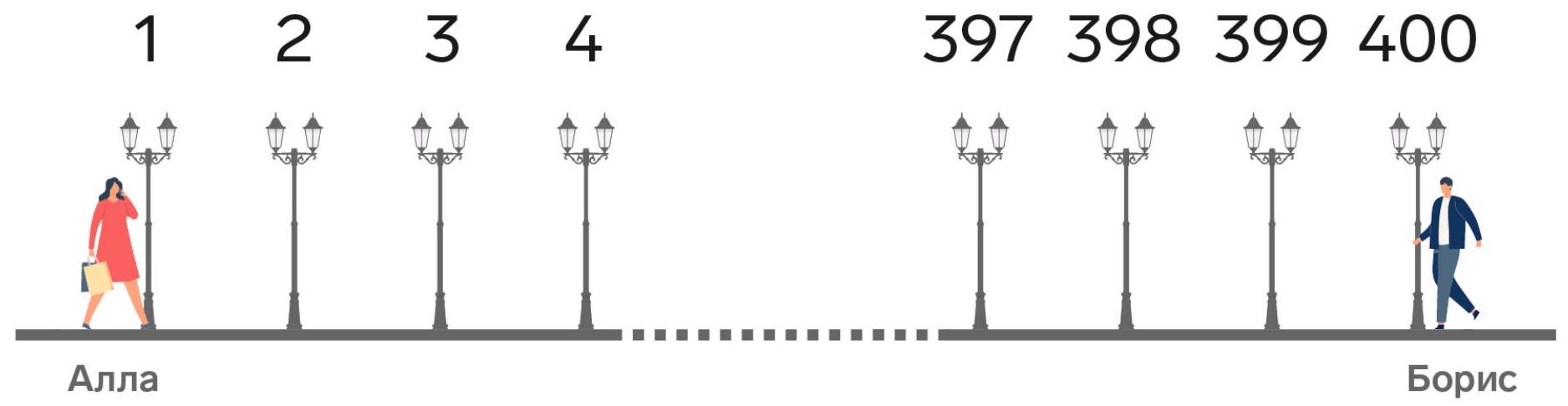
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.
|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
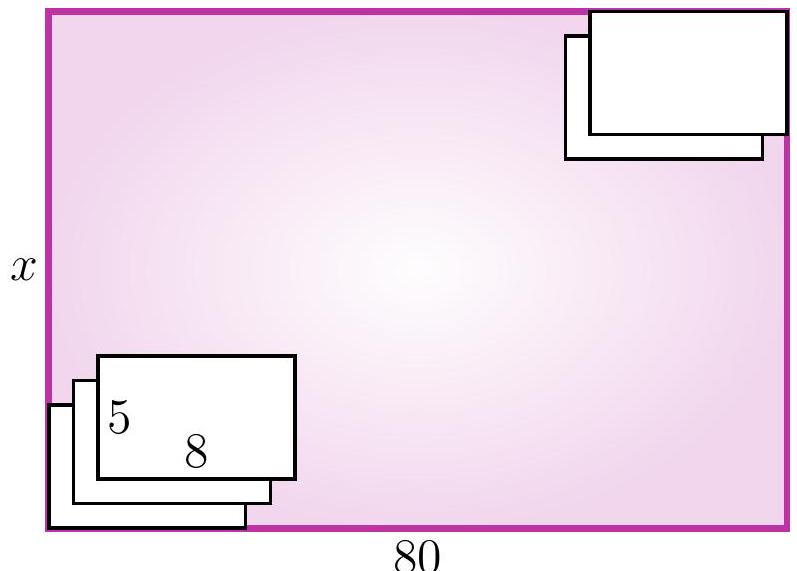
5-6. A rectangular table of size $x$ cm $\times 80$ cm is covered with identical sheets of paper of size 5 cm $\times 8$ cm. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.
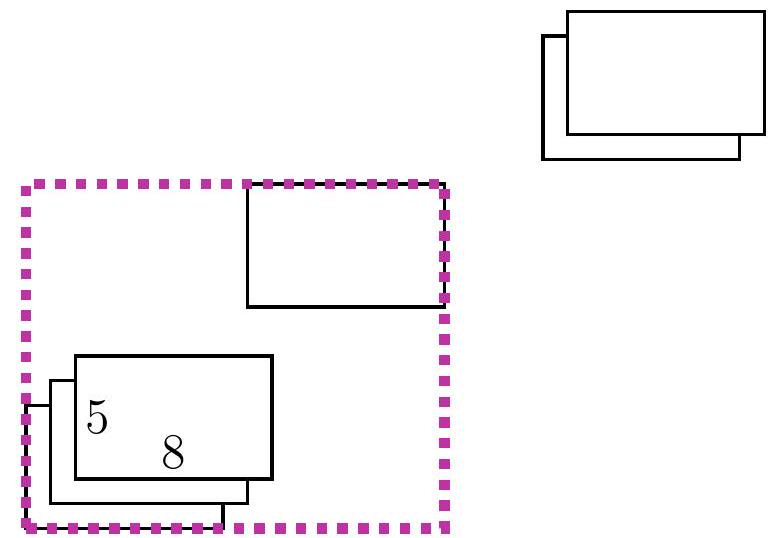
We will call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: specifically, the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-3. A secret object is a rectangle measuring $200 \times 300$ meters. Outside the object, there is a guard at each of the four corners. An intruder approached the perimeter of the secret object from the outside, and all the guards ran to him along the shortest paths along the external perimeter (the intruder remained in place). Three of the guards ran a total of 850 meters to reach the intruder. How many meters did the fourth guard run to reach the intruder?
|
Answer: 150.
Solution. Note that no matter where the violator is, two guards in opposite corners will run a distance equal to half the perimeter in total.

Therefore, all four guards will run a total distance equal to the perimeter (two in diagonally opposite corners will run a total of half the perimeter, and the other two will also run half the perimeter). Therefore, the fourth guard will run a distance that complements 850 to the perimeter, which is 1000, i.e., 150 meters.
|
150
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-4. In a giraffe beauty contest, two giraffes, Tall and Spotted, made it to the final. 135 voters are divided into 5 districts, each district is divided into 9 precincts, and each precinct has 3 voters. The voters choose the winner by majority vote in their precinct; in the district, the giraffe that wins the majority of the precincts wins; finally, the giraffe that wins the majority of the districts is declared the winner of the final. The giraffe Tall won. What is the minimum number of voters who could have voted for him?
|
Answer: 30.
Solution. For High to win the final, he must win in 3 districts. To win in a district, High must win in 5 precincts of that district. In total, he needs to win in at least $3 \cdot 5=15$ precincts. To win in a precinct, at least 2 voters must vote for him. Therefore, at least 30 voters are needed.
Comment. In problems with questions like "what is the greatest" and "what is the least," the solution usually consists of two parts: estimation and example. Estimation is the proof that a greater (or lesser, depending on the question) answer cannot be achieved, and the example is the proof that the given answer can be achieved.
In the solution above, we did not provide an example (i.e., did not prove) that 30 voters are sufficient. For completeness, the solution is missing the phrase: "From the above reasoning, it is clear that 30 voters for High can be sufficient: 2 voters per 5 precincts in any 3 districts."
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
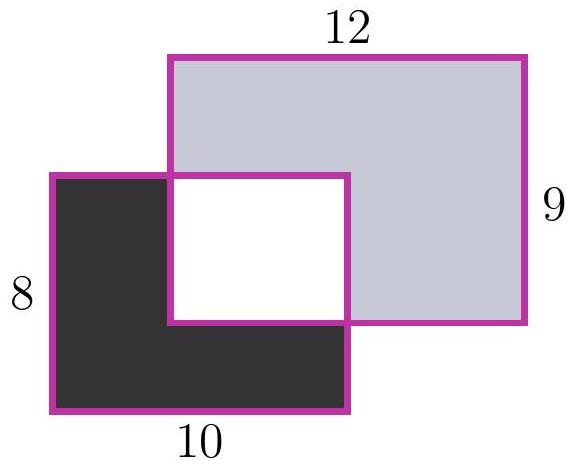
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
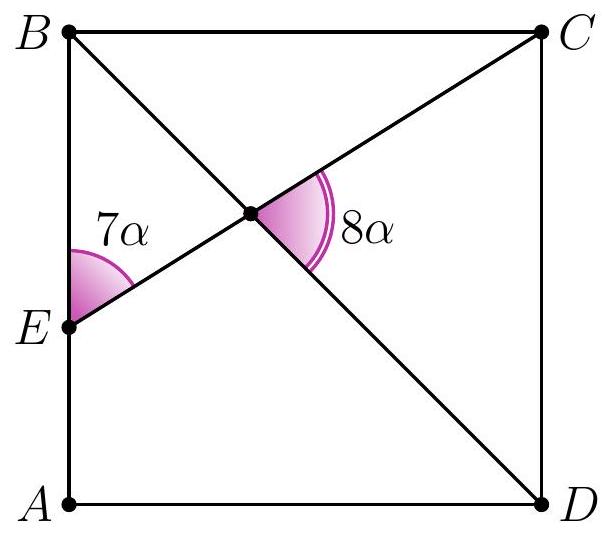
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
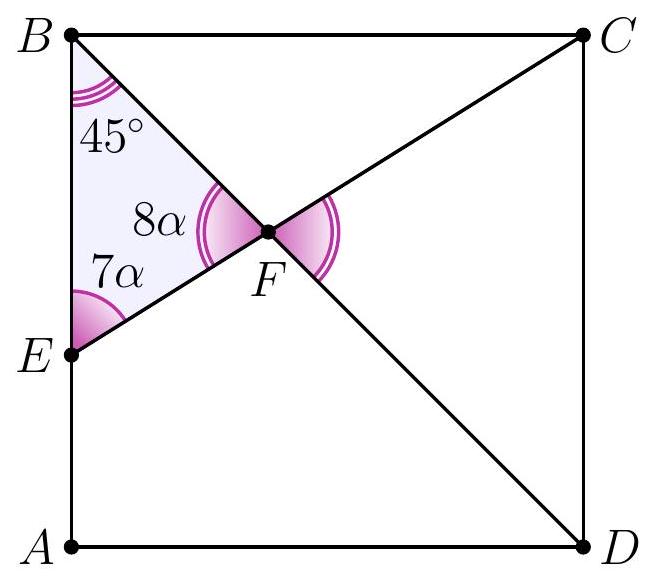
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
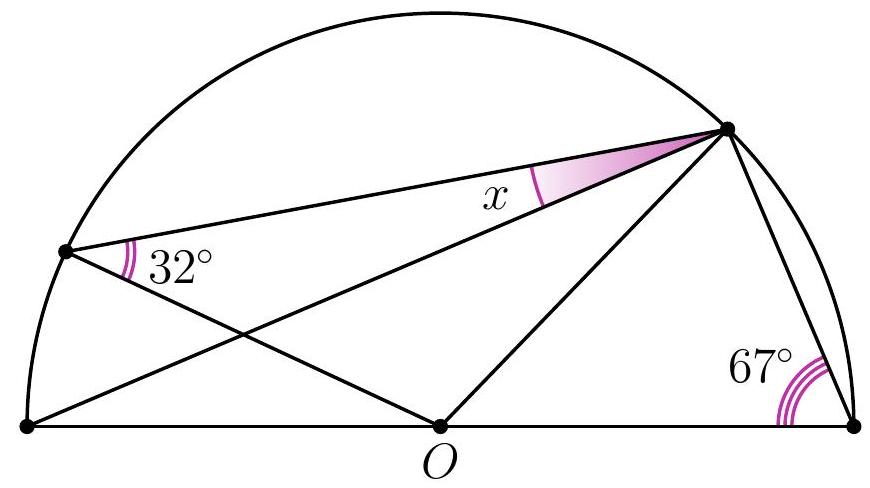
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
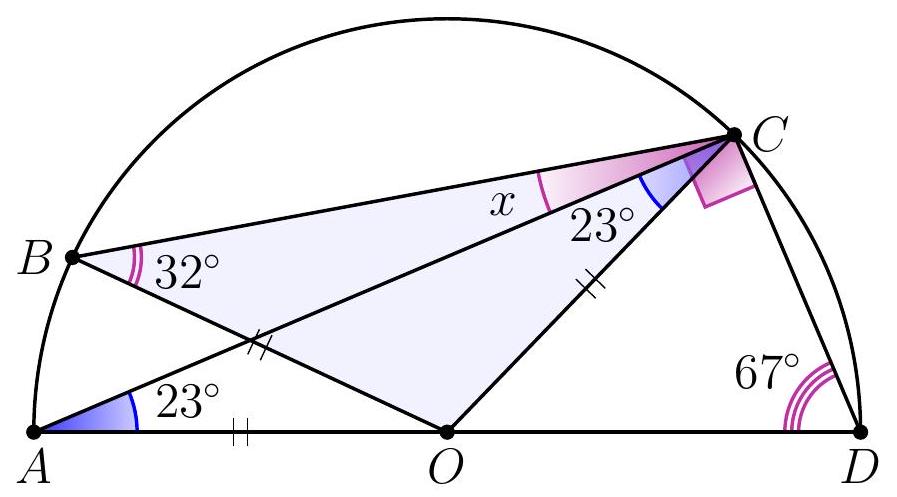
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
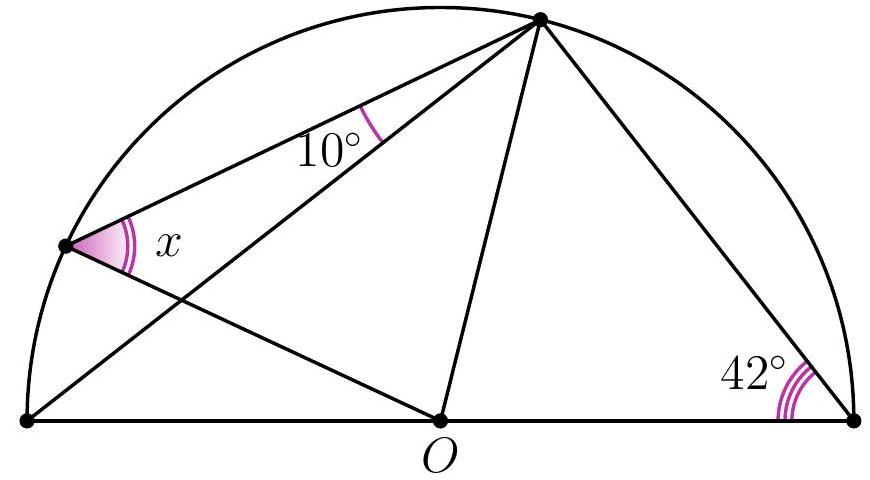
11-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
|
Answer: 58.
Solution. Angle $ACD$ is a right angle since it subtends the diameter of the circle.
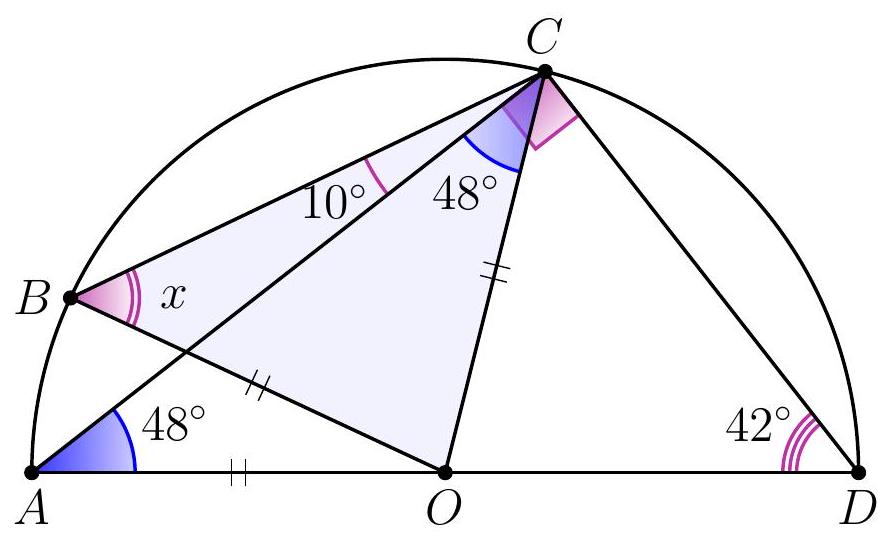
Therefore, $\angle CAD = 90^{\circ} - \angle CDA = 48^{\circ}$. Also, $AO = BO = CO$ as they are radii of the circle, so $\angle OCA = \angle ACO = 48^{\circ}$ and $x = \angle OBC = \angle OCB = 48^{\circ} + 10^{\circ} = 58^{\circ}$.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. What is the minimum number of cells that need to be marked on an $8 \times 9$ board so that among any five consecutive cells in a row, column, or diagonal, there is a marked cell
Fig. 11.4a
|
Answer: 14 cells.
Solution. Example.
See Fig. 11.4a.
Estimate. Let's highlight 14 rectangles of size $\quad 1 \times 5 \quad$ on the board, touching only two central cells (see Fig. 11.4b). In each of them, there must be at least one marked cell, meaning there are at least 14 marked cells.
Examiners are recommended to check the example very carefully, especially all the diagonals.
Grading Criteria.
«+» A complete and well-reasoned solution is provided
«干» The correct answer and correct estimate are provided, but the example is missing or incorrect «干» The correct answer and correct example are provided, but the estimate is missing or incorrect «-» Only the answer is provided
«-» The problem is not solved or is solved incorrectly
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find at least one four-digit number that has the following property: if the sum of all its digits is multiplied by the product of all its digits, the result is 3990. (I. Rubanov)
|
Solution. Note that $3990=2 \cdot 3 \cdot 5 \cdot 7 \cdot 19=1 \cdot 6 \cdot 5 \cdot 7 \cdot 19$ and $6+5+7+1=19$. Therefore, any four-digit number that contains one 1, one 6, one 5, and one 7 will work, for example, 1567.
Comment. To receive full credit, it is sufficient to provide any correct example.
|
1567
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Three motorcyclists start simultaneously from one point on a circular highway in the same direction. The first motorcyclist caught up with the second for the first time after making 4.5 laps from the start, and 30 minutes before that, he caught up with the third motorcyclist for the first time. The second motorcyclist caught up with the third for the first time three hours after the start. How many laps per hour does the first motorcyclist make?
#
|
# Solution
Let $x, y, z$ be the speeds of the first, second, and third motorcyclists in circles per hour, respectively.
Express the time it takes for the first motorcyclist to catch up with the second, the first to catch up with the third, and the second to catch up with the third in different ways.
We obtain the system of equations
$$
\left\{\begin{array}{c}
\frac{1}{x-y}=\frac{4.5}{x} \\
\frac{1}{x-z}=\frac{4.5}{x}-\frac{1}{2} \\
\frac{1}{y-z}=3
\end{array}\right.
$$
Solving the system of equations, we get the answer $x=3$.
## Grading Criteria
Only the correct answer - 0 points.
Individual expressions for the time of individual motorcyclists are obtained - 1 point.
One, two, or three equations of the system are correctly formulated, or if another method was chosen, depending on the progress in the solution - 2-4 points.
The problem is solved, but contains one or two arithmetic errors, resulting in an incorrect answer - 5-6 points.
The correct answer is obtained with justification - 7 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. The hikers had several identical packs of cookies. At the midday break, they opened two packs and divided the cookies equally among all the participants of the hike. One cookie was left over, and the hikers fed it to a squirrel. At the evening break, they opened another three packs and also divided the cookies equally. This time, 13 cookies were left over. How many hikers were on the hike? Justify your answer.
|
Solution: Let there be $n$ tourists in the group, and $m$ cookies in each pack (where $m$ and $n$ are natural numbers, and $n > 13$). According to the problem, the numbers $x = 2m - 1$ and $y = 3m - 13$ are divisible by $n$. Therefore, the number $3x - 2y = 23$ is also divisible by $n$. Since 23 is a prime number and has only two natural divisors, the divisor 1 is not suitable because it is less than 13. Thus, $n = 23$.
We also need to verify that this situation is possible. So, let's assume there are 23 tourists in the group. Then the described situation will occur, for example, if there are 12 cookies in each pack.
Answer: There are 23 tourists in the group.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| It is proven that there could only be 23 tourists, and an example of the number of cookies in a pack that satisfies the condition of the problem is provided | 7 points |
| It is proven that there could only be 23 tourists, but no example of the number of cookies in a pack that satisfies the condition of the problem is provided | 5 points |
| A correct example (with 23 tourists) is provided, but it is not proven that there cannot be a different number of tourists | 2 points |
| The correct answer without justification and an example | 0 points |
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. It is known that $a^{2}+2=b^{4}, b^{2}+2=c^{4}, c^{2}+2=a^{4}$. What is the value of the product $\left(a^{2}-1\right)\left(b^{2}-1\right)\left(c^{2}-1\right)$? Find all possible values and prove that there are no others.
|
Solution: Subtract 1 from both sides of each equation, we get:
$$
\begin{gathered}
a^{2}+1=b^{4}-1=\left(b^{2}-1\right)\left(b^{2}+1\right) \\
b^{2}+1=\left(c^{2}-1\right)\left(c^{2}+1\right), \quad c^{2}+1=\left(a^{2}-1\right)\left(a^{2}+1\right)
\end{gathered}
$$
Multiply the left and right parts of all three equations, and after canceling the positive number $\left(a^{2}+1\right)\left(b^{2}+1\right)\left(c^{2}+1\right)$, we get $\left(a^{2}-1\right)\left(b^{2}-1\right)\left(c^{2}-1\right)=1$. Therefore, the desired product can only be 1. Since the transformations involved an inequivalent step (multiplying the left and right parts of several equations is only a transition to a consequence), it is necessary to show that the number 1 can indeed be obtained. This case will occur, for example, when $a=b=c=\sqrt{2}$.
Answer: 1.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer with a confirming example of numbers $a, b, c$ | 7 points |
| Correct and justified answer without a confirming example of numbers $a, b, c$ | 6 points |
| Example of numbers $a, b, c$ satisfying the condition of the problem, for which the value of the desired expression is 1 | 1 point |
| Algebraic calculations that did not lead to a solution, as well as an answer without justification or an incorrect answer | 0 points |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. When fully fueled, a motorboat can travel exactly 40 km upstream or exactly 60 km downstream. What is the greatest distance the motorboat can travel along the river if the fuel must be enough for the round trip, back to the starting point? Justify your answer.
|
# Solution:
Method 1. Let's launch a raft along with the boat, which will move with the current, and observe the boat from this raft. Then, no matter which direction the boat goes, upstream or downstream, it will be at the same distance from the raft by the time the fuel runs out. This means that the raft will be at the midpoint of the segment between the extreme possible positions of the boat, i.e., (60 - 40) : 2 = 10 km downstream from the starting point. The boat will be 50 km away from it. This means the boat's speed is 50 : 10 = 5 times greater than the speed of the current. This means that downstream, the boat travels at a speed 6 times greater than the current, and upstream at a speed 4 times greater. Thus, downstream the boat travels 1.5 times faster than upstream. To cover the same distance there and back, we need to travel upstream 1.5 times longer than downstream, i.e., 3/5 of the total travel time. During this time, the boat will be 30 km away from the raft, and the raft will be carried 6 km downstream by the river. This means the boat can travel 24 km in one direction.
Method 2. Let the speed of the boat be \( x \) km/h, the current speed be \( -y \) km/h, and the fuel reserve in the boat is enough for \( t \) hours of travel. The problem conditions can be written as the system
\[
\left\{\begin{array}{l}
(x+y) \cdot t=60 \\
(x-y) \cdot t=40
\end{array}\right.
\]
By adding the equations of the system term by term, we get \( x t = 50 \), and by subtracting them term by term, we get \( y t = 10 \). Suppose we now set off upstream and travel for such a time \( T \) that in the remaining time \( t - T \) we return to the starting point. This means that the condition \((x-y) T = (x+y)(t-T)\) must be satisfied. Taking into account the first equation of the system, we get from it that \( x T = 30 \). Since \( x t = 50 \), then \( T = 0.6 t \). Then, during time \( T \), the boat will be at a distance from the starting point equal to \((x-y) \cdot 0.6 t = 0.6 \cdot 40 = 24\) km.
Answer: 24 km.
Grading Recommendations:
| present in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| There is an arithmetic error in the correct solution, possibly leading to an incorrect answer | 6 points |
| The system of equations correctly describing the conditions of the problem is obtained (but not solved) | 1 point |
| Incorrect solution or its absence | 0 points |
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. We took ten consecutive natural numbers greater than 1, multiplied them, found all the prime divisors of the resulting number, and multiplied these prime divisors (taking each exactly once). What is the smallest number that could have resulted? Fully justify your answer.
Solution. We will prove that among ten consecutive numbers, there must be a number that has a prime divisor different from $2, 3, 5, 7$. Let's count how many of the ten consecutive numbers can have the specified four divisors. Out of ten numbers, exactly five are divisible by 2, and at least one of these five numbers is divisible by 3. (This fact can be taken for granted in the work, but let's recall one possible proof. The remainders from dividing six consecutive numbers by 6 form a set from 0 to 5, i.e., there is a number with a remainder of 0, which is divisible by both 2 and 3.) Further, the set of ten numbers contains at least three and no more than four numbers that are divisible by 3. If there are three such numbers, at least one of these three is divisible by 2 and has already been counted. If there are four such numbers, they have the form $3k, 3k+3, 3k+6, 3k+9$. Depending on the parity of $k$, either $3k, 3k+6$ or $3k+3, 3k+9$ are divisible by 2. Thus, when considering numbers divisible by 3, we can add no more than two new numbers to the five even numbers already counted. Ten consecutive numbers contain exactly two numbers that are divisible by 5, one of which is even and has already been counted. Therefore, divisibility by 5 adds no more than one number to the seven already counted. Among ten consecutive numbers, no more than two are divisible by 7, one of which is even and has already been counted. Divisibility by 7 adds no more than one number to the eight already counted. Thus, among ten consecutive numbers, no more than nine have at least one of the divisors $2, 3, 5, 7$, i.e., there is a number with a larger prime divisor and not divisible by any of the first four prime numbers. Therefore, in the product of ten numbers, there will be at least one divisor different from $2, 3, 5, 7$, so the product of all prime divisors will be greater than 210. The smallest possible product is $2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2310$.
|
Answer: 2310.
## Municipal Stage of the All-Russian Mathematics Olympiad 2018-2019 Academic Year
10th Grade
Grading Criteria
| Score | Points for |
| :---: | :---: | :--- |
| 7 | Complete solution, a correct algorithm of actions for Zhenya is provided, and all conditions are verified. |
| 6 | Complete solution, a correct algorithm of actions for Zhenya is provided, but it is not verified that the arrangement obtained by the algorithm satisfies all conditions. |
| 4 | An algorithm of actions for Zhenya is constructed, based on dividing the cells into pairs. Due to an unsuccessful choice of cell placement and (or) the sequence of their filling, the solution is not completed. The correct answer is provided or no answer is given. |
| 2 | An arrangement of numbers is provided that satisfies the condition of the problem, but the sequence of moves by the players is not described. |
| 1 | An algorithm of actions for Zhenya is constructed, based on dividing the cells into pairs. Due to an unsuccessful choice of cell placement and (or) the sequence of their filling, the end of the solution contains an error. An incorrect answer is provided (see 4 points). |
| 0 | Incorrect solution, or only the answer is written without reasoning, or the problem statement is misunderstood. |
| Problem 2 | Score | Points for |
| :---: | :---: | :---: |
| | 7 | Fully correct solution. |
| | 3 | The existence of two different roots is proven, but their location, as stated in the problem, is not indicated or justified. |
| | 0 | Incorrect proof. In particular, an error in the choice of the initial statement and its consequences, or an error in working with inequalities. |
| Problem 3 | Score | Points for |
| :---: | :---: | :---: |
| | 7 | Fully correct solution. Correct answer. |
| | 5 | Correct solution containing an arithmetic error. The answer provided differs from the correct one due to an arithmetic error. |
| | 4 | Generally correct solution containing an error in the application of trigonometric functions. The answer provided differs from the correct one due to an incorrect replacement of a trigonometric function with a cofunction and (or) an incorrect transition to a half-angle. |
| | 3 | It is proven that the segments marked as \(x\) and \(y\) on the diagram are equal. |
| | 0 | Incorrect solution, in particular due to a misunderstanding of the configuration of the tangents. |
| Score | Points for |
| :--- | :--- | :--- |
| Problem 4 | Fully correct solution. |
| 5 | Partially correct proof containing an arithmetic error. |
| 4 | Partially correct proof containing an error in counting the number of terms. |
| | Partially correct proof containing an error in applying the formula for the sum of an arithmetic progression. |
| 1 | It is stated that the expression on the right is the sum of sums of arithmetic progressions. Further progress is absent. |
| 0 | Incorrect solution. |
| | Score | Points for |
| :---: | :---: | :---: |
| | 7 | Fully correct solution. |
| | 6 | It is proven that among ten consecutive numbers, there is always a number that has a prime divisor different from 2, 3, 5, 7. The proven statement is applied to find the answer. The answer provided may be incorrect, differing from the correct one by replacing the divisor 11 with (one) another divisor. |
| Problem 5 | 5 | It is proven that among ten consecutive numbers, there is always a number that has a prime divisor different from 2, 3, 5, 7. It is indicated that this fact must be applied to find the answer. The application of the proven statement is not completed or is incorrect. Or it is proven that the sought number is greater than 210, but no answer is provided. |
| | 3 | It is not proven that among ten consecutive numbers, there is always a number that has a prime divisor different from 2, 3, 5, 7, but it is indicated that this fact must be applied to find the answer. The correct answer may be provided. |
| | 2 | Only divisibility by 2, 3, 5, 7 is considered, the question of the presence or absence of other prime divisors is not taken into account. |
| | 1 | The correct answer is provided without justification. |
| | 0 | Incorrect solution. Incorrect answer (see 6 points). |
|
2310
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many 4-digit numbers exist where the digit in the thousands place is greater than the digit in the hundreds place?
|
Solution. The digit in the thousands place can take one of 9 possible values: $1,2,3, \ldots, 9$ (we cannot take 0, since the number is four-digit). For each of these options, we can specify the corresponding number of options for the hundreds digit: 1, $2,3, \ldots, 9$. That is, there are a total of 45 options. The other two digits are arbitrary (10 options each), so we get the answer: $45 \cdot 10 \cdot 10=4500$ options.
|
4500
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. What is the smallest value that the GCD $(x, y)$ can take, where $x$ and $y$ are natural numbers, if the LCM $(x, y)=(x-y)^{2}$?
|
Solution:
When $x=4$ and $y=2$, LCM $(x, y)=(x-y)^{2}=4$, and GCD $(x, y)=2$. Thus, 2 is achievable.
Assume that GCD $(x, y)=1$ (the numbers are coprime). Then LCM $(x, y)=x y$. From the condition, we get that $x y=x^{2}-2 x y+y^{2}$. We obtain $x^{2}-3 x y+y^{2}=0$. Solving the obtained quadratic equation with respect to $x$, we get the discriminant $5 y^{2}$. The square root of the discriminant $\sqrt{5} \cdot y$ is an irrational number, and for $x$ to be a natural number, it must be rational. This is a contradiction. Therefore, GCD $(x, y) \neq 1$.
Answer: 2.
| Criteria | Points |
| :--- | :---: |
| Complete solution of the problem. | 7 |
| Proved that GCD $(x, y) \neq 1$. Correct answer, but no example of numbers for GCD $(x, y)=2$ provided. | 5 |
| Correct answer with an example. | 2 |
| Only the correct answer, without evaluation and example. | 0 |
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Sasha solved the quadratic equation $3 x^{2}+b x+c=0$ (where $b$ and $c$ are some real numbers). In his answer, he got exactly one root: $x=-4$. Find $b$.
|
Answer: 24
Solution. By Vieta's theorem $x_{1}+x_{2}=-b / 3$. In our case $x_{1}=x_{2}=-4$, hence $-b / 3=-8$ and $b=24$.
Remark. Another solution can be obtained by noticing that the equation should reduce to a perfect square $3(x+4)^{2}=0$.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Find the sum
$$
\sqrt[7]{(-7)^{7}}+\sqrt[8]{(-8)^{8}}+\sqrt[9]{(-9)^{9}}+\ldots+\sqrt[100]{(-100)^{100}}
$$
(Each term is of the form $\left.\sqrt[k]{(-k)^{k}}\right)$
|
Answer: 47
Solution. Note that $\sqrt[k]{(-k)^{k}}$ equals $k$ when $k$ is even, and equals $-k$ when $k$ is odd. Therefore, our sum is $-7+8-9+10-\ldots-99+100=(-7+8)+(-9+10)+\ldots+(-99+100)$. In the last expression, there are 47 parentheses, each of which equals 1.
|
47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. For triangle $A B C$, the following is known: $A B=12, B C=10, \angle A B C=120^{\circ}$. Find $R^{2}$, where $R-$ is the radius of the smallest circle in which this triangle can be placed.
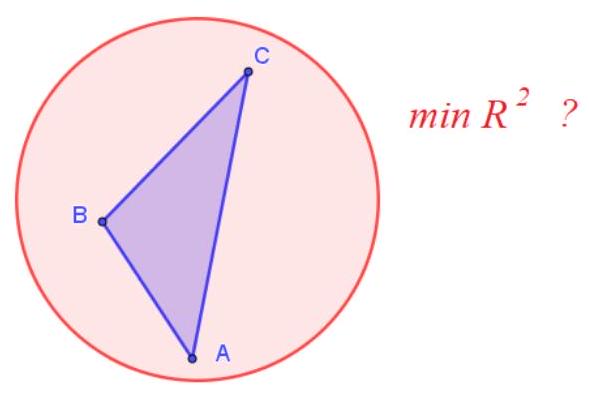
|
Answer: 91
Solution. Since segment $AC$ fits inside the circle, $2R \geqslant AC$. On the other hand, the circle constructed with $AC$ as its diameter covers the triangle $ABC$, since $\angle ABC > 90^{\circ}$. Therefore, the desired value of $R$ is $AC / 2$, and $R^2 = AC^2 / 4$.
Next, by the cosine rule, we have $AC^2 = AB^2 + BC^2 - 2 \cdot AB \cdot BC \cdot \cos 120^{\circ} = 12^2 + 10^2 + 2 \cdot 12 \cdot 10 / 2 = 4(6^2 + 5^2 + 6 \cdot 5) = 4 \cdot 91$
|
91
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Let's consider the number 616. The sum of its digits is 13, and the product of its digits is 36. What is the largest natural number whose sum of digits is 13 and the product of its digits is 36?
|
Answer: 3322111
Solution. In the decimal representation of this number, there cannot be any zeros. Let's list all the digits of this number that are greater than 1; their product is still 36. Since 36 can be factored into prime factors as $36=2 \cdot 2 \cdot 3 \cdot 3$, the possible sets of digits greater than 1 are: $\{2,2,3,3\},\{2,2,9\},\{2,3,6\},\{3,3,4\}$, $\{4,9\},\{6,6\}$. Since the sum of the digits is 13, the number of ones can be uniquely determined in each case, resulting in the possible sets of digits: $\{1,1,1,2,2,3,3\},\{2,2,9\},\{1,1,2,3,6\},\{1,1,1,3,3,4\},\{4,9\}$, $\{1,6,6\}$. We see that the largest number can be a seven-digit number, and this is only possible in the first case. It remains to note that the largest number with the set of digits $\{1,1,1,2,2,3,3\}$ is the number 3322111.
|
3322111
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. On a plane, 55 points are marked - the vertices of a certain regular 54-gon and its center. Petya wants to paint a triplet of the marked points in red so that the painted points are the vertices of some equilateral triangle. In how many ways can Petya do this?
|
Answer: 72
Solution. Assume that our 54-gon is inscribed in a circle, and its vertices divide this circle into 54 arcs of length 1.
If one of the painted points is the center, then the other two painted points must be the ends of an arc of size $54 / 6=9$. There are 54 such possibilities.
Otherwise, all three painted vertices must form an equilateral triangle, the vertices of which divide the circle into 3 arcs of size $54 / 3=18$. There are $-54 / 3=18$ such possibilities.
In total: $54+18=72$ options.
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In a row, the numbers are written: $100^{100}, 101^{101}, 102^{102}, \ldots, 234^{234}$ (i.e., the numbers of the form $n^{n}$ for natural numbers n from 100 to 234). How many of the listed numbers are perfect squares? (A perfect square is the square of an integer.)
|
# Answer: 71
Solution. Consider a number of the form $m^{k}$, where $m$ and $k$ are natural numbers. If $k$ is even, then $m^{k}$ is a perfect square. If $k$ is odd, then $m^{k}$ is a perfect square if and only if $m$ is a perfect square. Thus, the answer to our problem is the total number of even numbers and odd perfect squares in the set of numbers $\{100,101,102, \ldots, 234\}$. The number of even numbers needed is $(234-98) / 2=68$. The number of perfect squares needed is exactly $3: 11^{2}, 13^{2}, 15^{2}$. In total, there are $68+3=71$ numbers that meet the criteria.
|
71
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. On the coordinate plane, a parallelogram $O A B C$ is drawn, with its center located at the point $\left(\frac{19}{2}, \frac{15}{2}\right)$, and points $A, B$, and $C$ have natural coordinates. Find the number of such parallelograms. (Here, $O$ denotes the origin - the point $(0,0)$; two parallelograms with the same set of vertices are considered the same, i.e., $O A B C$ and $O C B A$ are considered the same parallelogram.)
|
Answer: 126.
Solution. Note that $O A B C$ is a parallelogram if and only if the point $E\left(\frac{19}{2}, \frac{15}{2}\right)$ is the midpoint of segments $O B$ and $A C$, and moreover, points $O, A, B, C$ do not lie on the same line.
Point $E$ is the midpoint of segment $O B$, so $B$ is uniquely determined as $(19,15)$. Let $\left(x_{a}, y_{a}\right),\left(x_{c}, y_{c}\right)$ be the coordinates of points $A$ and $C$. Since $E$ is the midpoint of segment $A C$, we have $x_{a}+x_{c}=19, y_{a}+y_{c}=15$. Then for $x_{a}$ there are 18 possible natural values: $1,2, \ldots, 18$, each of which uniquely corresponds to a natural $x_{c}=19-x_{a}$. Similarly, for $y_{a}$ there are 14 possibilities. In total, there are $18 \cdot 14=252$ possibilities for choosing point $A$, and for each of them, a suitable point $C$ is uniquely determined. According to our agreement ($O A B C$ and $O C B A$ are considered the same parallelogram), we have $252 / 2=126$ options.
Note that in all the specified options, point $A$ (and $C$) does not lie on the line $O B$ (otherwise, $\left.y_{a} / x_{a}=15 / 19\right)$, i.e., the parallelogram $O A B C$ does not degenerate. Thus, all the found options indeed fit.
|
126
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In the class, two students sit at each desk. The number of desks where two boys sit is twice the number of desks where two girls sit. And the number of desks where two girls sit is twice the number of desks where a boy and a girl sit. How many boys are there in the class if there are 10 girls?
Answer: there are 18 boys in the class.
|
Solution. Let the number of desks where a boy and a girl sit be $x$. Then the number of desks with two girls is $2x$. Therefore, the total number of girls is $2 \cdot 2x + x = 5x = 10$, from which $x = 2$. Then the number of desks with two boys is $4x = 8$. Therefore, the total number of boys is $2 \cdot 8 + 2 = 18$.
Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used:
3 6. The number of desks with two girls is correctly found, but further reasoning is missing or incorrect.
3 6. The number of desks with a boy and a girl is correctly found, but further reasoning is missing or incorrect.
2 b. The correct answer is provided, but there is no justification.
06 . The problem is not solved or is solved incorrectly.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. A natural number is written on the board. Nikolai noticed that he can append a digit to the right of it in two ways so that the resulting number is divisible by 9. In how many ways can he append a digit to the right of the given number so that the resulting number is divisible by 3?
|
Answer: 4 ways.
Solution. Note that the difference between the two numbers "noticed" by Nikolai is less than 10, but is divisible by 9. Therefore, this difference is 9. This is only possible if the appended digits are 0 and 9. Then it is easy to see that for divisibility by 3, in addition to these two digits, the digits 3 and 6 can also be appended. In total, there are 4 ways.
## Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used
2 6. It is proven that Nikolai could only append 0 or 9 at the beginning.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. An archipelago consists of several small islands and one large island. It was decided to build bridges between the islands so that the large island would be connected to each small island by two bridges, and any two small islands would be connected by one bridge.
By November 1, all the bridges between the small islands and several (at least one) bridges leading to the large island - a total of 28 bridges - had been built. How many islands are there in the archipelago?
Answer: 8 islands
|
Solution. Let's number the small islands of the archipelago. If a bridge connects islands with numbers $a$ and $b$, we write the smaller of these two numbers on this bridge.
Suppose the number of small islands in the archipelago is no more than six. Then there are no more than 5 bridges with the number 1, no more than 4 bridges with the number 2, and so on. No more than 12 bridges lead to the large island. Therefore, the total number of bridges built is no more than
$$
5+4+3+2+1+12=2728
$$
which also contradicts the condition.
Thus, there are 7 small islands in the archipelago, and a total of 8 islands.
## Criteria
4 points. A complete and justified solution is provided.
06 . The problem is not solved or solved incorrectly.
In other cases, sum the following criteria (but do not exceed 4 points):
2 points. It is proven that the number of islands is no more than eight (if there is an arithmetic error in the proof, then 16 .)
2 6. It is proven that the number of islands is no less than eight (if there is an arithmetic error in the proof, then 1 point).
16 . The correct answer is provided.

|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
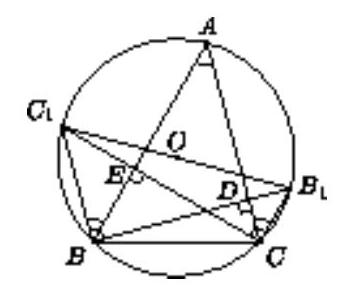
9.7. Given a cyclic quadrilateral $A B C D$. The rays $A B$ and $D C$ intersect at point $K$. It turns out that points $B, D$, as well as the midpoints of segments $A C$ and $K C$, lie on the same circle. What values can the angle $A D C$ take?
(G. Zhukov $)$
|
Answer: $90^{\circ}$.
Solution. Let $N$ and $M$ be the midpoints of segments $K C$ and $A C$, respectively. Then $M N$ is the midline of triangle $A K C$, so $\angle B A C = \angle N M C$. Additionally, $\angle B A C = \angle B D C$, since quadrilateral $A B C D$ is cyclic.
Suppose points $M$ and $N$ lie on the same side of line $B D$. Then $M$ lies inside triangle $B C D$; hence, it lies inside triangle $B N D$, and therefore inside its circumcircle. But then points $B, N, D$, and $M$ cannot lie on the same circle. Therefore, $N$ and $M$ must lie on opposite sides of $B D$, and $\angle B D C = \angle B M N$.
From the parallelism of $M N$ and $A K$, it follows that $\angle B M N = \angle A B M$, hence $\angle B A C = \angle B D C = \angle A B M$. This implies $A M = M B$, meaning that in triangle $A B C$, the median $B M$ is equal to half the side $A C$, from which $\angle A B C = 90^{\circ}$, and therefore $\angle A D C = 90^{\circ}$.
Comment. Points are not deducted for the lack of justification for the placement of points $M$ and $N$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. Given a cyclic quadrilateral $A B C D$. The rays $A B$ and $D C$ intersect at point $K$. It turns out that points $B, D$, as well as the midpoints of segments $A C$ and $K C$, lie on the same circle. What values can the angle $A D C$ take?
(G. Zhukov)
|
Answer: $90^{\circ}$.
Solution. Let $N$ and $M$ be the midpoints of segments $K C$ and $A C$, respectively. Then $M N$ is the midline of triangle $A K C$, so $\angle B A C = \angle N M C$. Additionally, $\angle B A C = \angle B D C$, since quadrilateral $A B C D$ is cyclic.
Suppose points $M$ and $N$ lie on the same side of line $B D$. Then $M$ lies inside triangle $B C D$; hence, it lies inside triangle $B N D$, and therefore inside its circumcircle. But then points $B, N, D$, and $M$ cannot lie on the same circle. Therefore, $N$ and $M$ must lie on opposite sides of $B D$, and $\angle B D C = \angle B M N$.
From the parallelism of $M N$ and $A K$, it follows that $\angle B M N = \angle A B M$, hence $\angle B A C = \angle B D C = \angle A B M$. This implies $A M = M B$, meaning that in triangle $A B C$, the median $B M$ is equal to half the side $A C$, from which $\angle A B C = 90^{\circ}$, and therefore $\angle A D C = 90^{\circ}$.
Comment. Points are not deducted for the lack of justification for the placement of points $M$ and $N$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.7. Given a polynomial
$$
P(x)=a_{2 n} x^{2 n}+a_{2 n-1} x^{2 n-1}+\ldots+a_{1} x+a_{0}
$$
where each coefficient $a_{i}$ belongs to the interval $[100,101]$. For what minimal $n$ can such a polynomial have a real root? (I. Bogdanov, K. Sukhov)
|
Answer. $n=100$.
Solution. Let's call a polynomial that satisfies the condition of the problem beautiful. The polynomial $P(x)=100\left(x^{200}+x^{198}+\ldots+x^{2}+\right.$ $+1)+101\left(x^{199}+x^{197}+\ldots+x\right)$ is beautiful and has a root -1. Therefore, when $n=100$, the required is possible.
It remains to show that for $n<100$, the required is impossible. Indeed, for any beautiful polynomial $P(x)$, the inequality $P(x)>0$ must hold for all $x$. This inequality is obviously satisfied for $x \geqslant 0$; for negative $x=-t$, it follows from the inequality
$$
100\left(t^{2 n}+t^{2 n-2}+\ldots+t^{2}+1\right)>101\left(t^{2 n-1}+t^{2 n-3}+\ldots+t\right)
$$
Thus, it is sufficient to prove this inequality for all $t>0$. Multiplying (*) by $t+1$, we obtain the equivalent inequality $100\left(t^{2 n+1}+t^{2 n}+\ldots+1\right)>101\left(t^{2 n}+t^{2 n-1}+\ldots+t\right)$, or
$$
100\left(t^{2 n+1}+1\right)>t^{2 n}+t^{2 n-1}+\ldots+t
$$
Note that for all $k=1, \ldots, n$, the inequality $\left(t^{k}-1\right)\left(t^{2 n+1-k}-1\right) \geqslant 0$ holds, since both parentheses have the same sign for $t>0$. Expanding the parentheses, we get
$$
t^{2 n+1}+1 \geqslant t^{2 n+1-k}+t^{k}
$$
Adding all such inequalities and considering that $n<100$, we obtain
$$
t^{2 n}+t^{2 n-1}+\ldots+t \leqslant n\left(t^{2 n+1}+1\right)<100\left(t^{2 n+1}+1\right)
$$
which proves $(* *)$.
Comment. Only the answer - 0 points.
An example of a polynomial satisfying the condition of the problem for $n=100$ - 1 point.
It is proven that $n \geqslant 100$ - 4 points.
If this inequality is not proven but reduced to the inequality $(* *)$ - 2 points.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For what values of $a$ do the equations
$$
x^{2}+a x+1=0 \quad \text { and } \quad x^{2}+x+a=0
$$
have at least one common root?
|
Solution. Let $x_{0}$ be the common root of the equations. Substitute into the equations, equate the expressions for $x_{0}^{2}$.
$$
\begin{aligned}
& \left\{\begin{array}{l}
x_{0}^{2} + a x_{0} + 1 = 0, \\
x_{0}^{2} + x_{0} + a = 0
\end{array}\right. \\
& (a-1) x_{0} = a-1 \quad a x_{0} + 1 = x_{0} + a \\
&
\end{aligned}
$$
We get two cases. When $a=1$, the equations coincide, $x^{2} + x + 1 = 0$ has no roots. When $x_{0}=1$, by substitution we get $a=-2$.
Answer. When $a=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let $F(x)$ and $G(x)$ be polynomials of degree 2021. It is known that for all real $x$, $F(F(x)) = G(G(x))$ and there exists a real number $k, k \neq 0$, such that for all real $x$, $F(k F(F(x))) = G(k G(G(x)))$. Find the degree of the polynomial $F(x) - G(x)$.
|
Solution. Since $F(F(x))=G(G(x))$, then $F(k G(G(x)))=G(k G(G(x)))$. This equality holds for all $x$, i.e., for more than 2022 values of the variable (Since the polynomial $G(x)$ takes an infinite number of values). Therefore, the polynomials coincide, their difference has degree 0.
Answer. The degree of $F(x)-G(x)$ is 0, the polynomials coincide.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. "That" and "this", plus half of "that" and "this" - what percentage of three quarters of "that" and "this" would this be?
|
3. "That" and "this", plus half of "that" and "this" - this is one and a half "that" and "this", which is twice as much as three quarters of "that" and "this", i.e., it constitutes $200 \%$ of them.
Answer: $200 \%$.
|
200
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In two groups, there is an equal number of students. Each student studies at least one language: English or French. It is known that 5 people in the first group and 5 in the second group study both languages. The number of students studying French in the first group is three times less than in the second group. The number of students studying English in the second group is four times less than in the first group. What is the minimum possible number of students in one group?
|
4. Let the number of people studying French in the first group be $x$, then in the second group it is $3x$. Let the number of people studying English in the second group be $y$, then in the first group it is $4y$. The total number of people in the first group is $x+4y-5$, and in the second group it is $3x+y-5$. By equating these values, we get $3y=2x$, from which it follows that $y$ is an even number. Note also that $y \leq 5$, since if 5 people study two languages, then at least five people study English. From this, it follows that the minimum value of $y=6$, then $x=9$, and the total number of students in one group is $x+4y-5=9+24-5=28$ students.
Answer: 28 students.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In 8 "Y" grade, there are quite a few underachievers, but Vovochka performs the worst of all. The pedagogical council decided that either Vovochka must correct his failing grades by the end of the quarter, or he will be expelled. If Vovochka corrects his grades, then 24% of the class will be underachievers, but if he is expelled, the percentage of underachievers will be 25%. What is the current percentage of underachievers in 8 "Y"?
#
|
# Solution
Let there be $n$ students in the class now. According to the condition, $0.24 n = 0.25(n-1)$, which means $0.01 n = 0.25$. Therefore, $n = 25$. One person makes up $4 \%$ of 25, so there are now $24 + 4 = 28 \%$ of underachievers.
Answer: $28 \%$.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The heights of an acute-angled triangle $ABC$, drawn from points $B$ and $C$, were extended to intersect the circumscribed circle at points $B_{1}$ and $C_{1}$. It turned out that the segment $B_{1} C_{1}$ passes through the center of the circumscribed circle. Find the angle $BAC$.
|
# Solution
Since $B_{1} C_{1}$ is the diameter of the circle, $\angle B_{1} B C_{1}=\angle B_{1} C C_{1}=90^{\circ}$, therefore, $B C_{1} \| A C$ and $C B_{1} \| A B$ (see figure). Since $B C_{1} \| A C$, then $\angle C_{1} B A=\angle A=\alpha$. Similarly, $\angle B_{1} C A=\angle A=\alpha$. The degree measure of the arc $B_{1} C_{1}$ is $180^{\circ}$, so the sum of the inscribed angles $C_{1} B A$ and $B_{1} C A$ is $90^{\circ}$, which means $\angle A=45^{\circ}$.
Answer: $45^{\circ}$.
Remarks: The answer can also be obtained by proving that triangle $C D B_{1}$ is an isosceles right triangle.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. CONDITION
On an 8x8 chessboard, 64 checkers numbered from 1 to 64 are placed. 64 students take turns approaching the board and flipping only those checkers whose numbers are divisible by the ordinal number of the current student. A "Queen" is a checker that has been flipped an odd number of times. How many "Queens" will be on the board after the last student has stepped away from it?
|
Solution. Obviously, each checker is flipped as many times as its number has divisors. Therefore, the number of "queens" will be the number of numbers from 1 to 64 that have an odd number of divisors, and this property is only possessed by perfect squares. Thus, the numbers of the "queens" remaining on the board will be $1, 4, 9, 16, 25, 36, 49$, and 64, which totals 8.
Answer: 8.
## Grading Criteria for Problem 6.
The answer is correct, but there are remarks on the clarity of its presentation and justification. 5 points.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 8.5
For a triangle, one of whose angles is equal to $120^{\circ}$, it is known that it can be cut into two isosceles triangles. What can the other two angles of the original triangle be?
## Number of points 7
|
Answer:
$40^{\circ}$ and $20^{\circ}$ or $45^{\circ}$ and $15^{\circ}$.
## Solution
Let in triangle $ABC$, $\angle B=120^{\circ}$. The cut specified in the problem must pass through one of the vertices of the triangle (otherwise, two triangles will not be formed upon division). It can pass through vertex $B$ or another vertex. In the first case (where $BD$ is the cut line), at least one of the resulting triangles, for example, triangle $BDC$, will not be acute-angled, so $BC$ is its base. Then $\angle DBC = \angle DCB = \alpha$, and $\angle BDA = 2\alpha$ is the exterior angle of triangle $BDC$. In triangle $ABD$, side $AB$ cannot be the base (otherwise, from the equality $DA = DB = DC$, it would follow that $\angle B = 90^{\circ}$, which contradicts the condition). Therefore, its base is either $AD$ or $BD$.
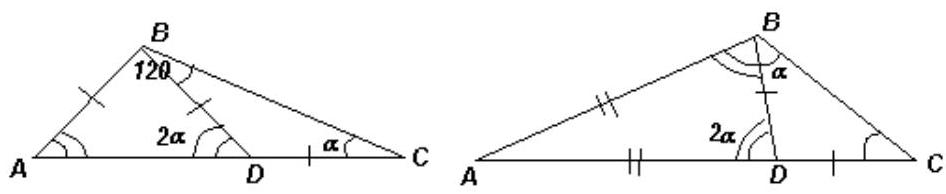
If $AD$ is the base, then $AB = DB$ (left figure). Then $\angle A = \angle BDA = 2\alpha$. From triangle $ABC$, we get $2\alpha + \alpha = 60^{\circ}$, so $\alpha = 20^{\circ}$. Thus, $\angle C = 20^{\circ}$ and $\angle A = 40^{\circ}$. If $BD$ is the base, then $AB = AD$ (right figure). Then $\angle ABD = \angle BDA = 2\alpha$. Therefore, $\angle B = 3\alpha$, so $\alpha = 40^{\circ}$, which means $\angle C = 40^{\circ}$. In the second case, the cut line must pass through the vertex of the larger of the two acute angles (where $AE$ is the cut line, see figure). Then both resulting triangles will be obtuse-angled. In this case, $AB = BE$ and $AE = EC$. Therefore, $\angle BAE = \angle BEA = \frac{1}{2}(180^{\circ} - \angle B) = 30^{\circ}$, and $\angle EAC = \angle ECA = \frac{1}{2} \angle BEA = 15^{\circ}$.
Thus, $\angle C = 15^{\circ}$ and $\angle A = 45^{\circ}$.
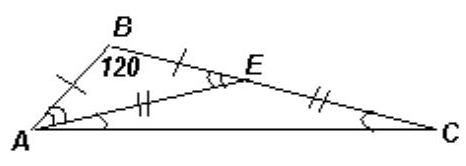
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. What is the largest number of different natural numbers that can be chosen so that the sum of any three of them is a prime number?
|
Solution. One example of four numbers that satisfy the condition of the problem is $1,3,7,9$. Indeed, the numbers $1+3+7=11, 1+3+9=13, 1+7+9=17, 3+7+9=19$ are prime.
Suppose it was possible to choose five numbers. Consider the remainders of these numbers when divided by 3. If there are three identical remainders among them, then the sum of the corresponding numbers is divisible by 3. If there are no three identical remainders, then each of the remainders 0, 1, or 2 must be present. Then the sum of three numbers with different remainders when divided by 3 is divisible by 3. This sum is not equal to 3, since all numbers are different and natural. Therefore, this sum is a composite number.
There are other examples as well, such as $3,7,9,31$, etc.
Answer: 4 numbers
Criteria. 7 points - correct and justified solution; 5 points - correct estimate without example; 2 points - correct answer and example provided; 0 points - only the correct answer provided.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Solve the equation:
$1+\frac{3}{x+3}\left(1+\frac{2}{x+2}\left(1+\frac{1}{x+1}\right)\right)=x$.
#
|
# Solution.
$1+\frac{1}{x+1}=\frac{x+2}{x+1}$, therefore the given equation is equivalent to the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+1}\right)=x$ under the condition that $\mathrm{x} \neq-2$. Proceeding similarly, we get that $1+\frac{3}{x+3}=x$, where $\mathrm{x} \neq-2$ and $\mathrm{x} \neq-3$. The roots of this equation are the numbers 2 and -2, so the only root of the original equation is the number 2.
## Grading Criteria
- Only the correct answer is provided - 1 point.
- The correct solution process, but the extraneous root is not discarded - 3 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. Three families of parallel lines have been drawn, with 10 lines in each. What is the maximum number of triangles they can cut out of the plane?
|
Solution. Consider 100 nodes - the intersection points of lines from the first and second directions. Divide them into 10 sectors: the first sector - nodes lying on the first lines of the first and second directions. The second sector - nodes lying on the second lines (excluding points lying in the first sector) and so on. Triangles with sides parallel to three fixed directions can have two orientations, and each of our 100 nodes can be the vertex of no more than one triangle of each orientation. Therefore, 10 lines of the third direction form no more than 2.25 triangles with the last five sectors, since these five sectors contain only 25 nodes in total.
Furthermore, note that each of the lines of the third direction forms no more than one triangle of each orientation with nodes belonging to one sector. Therefore, the number of triangles with vertices in the nodes of the remaining five sectors will not exceed \(10 \cdot 2 \cdot 5\).
In total, there are no more than \(100 + 50 = 150\) triangles.
An example with 150 triangles is shown in the figure.
Answer: 150 triangles
|
150
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For what smallest natural $k$ does the number 2016 $\cdot$ 20162016 $\cdot$ 201620162016 $\cdot$... 20162016...2016( $k$ factors) divide without remainder by $3^{67}$?
|
Solution.
We will show that in the case of 27 factors, the product is divisible by $3^{67}$, but not by $3^{68}$.
$2016 \cdot 20162016 \cdot \ldots \cdot \underbrace{20162016 . .2016}_{27 \text { times }}=$
$=2016^{27} \cdot(1 \cdot 1001 \cdot 1001001 \cdot \ldots \cdot \underbrace{1001001 \ldots 1001}_{27 \text { times }})=$
$=3^{54} \cdot 244^{27} \cdot(1001 \cdot 1001001 \cdot \ldots \cdot \underbrace{1001001 \ldots 1001}_{27 \text { times }})$.
244 is not divisible by 3.
$\underbrace{1001001 . . .1001}$ is not divisible by 3 if $\overline{k \vdots} 3$. $k$ ones
$\underbrace{1001001 \ldots 1001}: 3$, but not divisible by $9=3^{2}$, if $k$ ones
$k=3,6,12,15,21,24$. Their product is divisible by $3^{6}$.
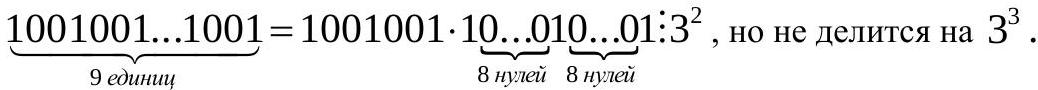
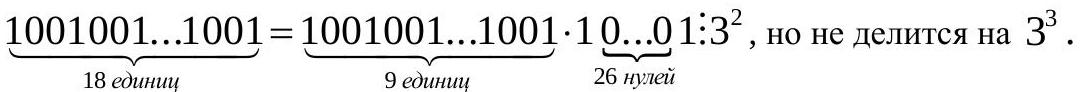
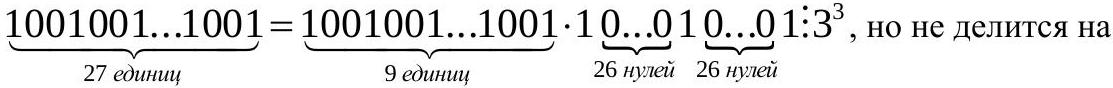
$3^{4}$.
$54+6+2+2+3=67$
$2016 \cdot 20162016 \cdot \ldots \cdot \underbrace{20162016 \ldots 2016}_{27 \text { times }}: 3^{67}$, but not divisible by $3^{68}$.
Answer: 27
## Recommendations for checking.
Answer without proof -0 points.
Proven that, $2016 \cdot 20162016 \cdot \ldots \cdot \underbrace{20162016 \ldots 2016}_{27 \text { times }}: 3^{67}-5$ points.
|
27
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Each of the equations $a x^{2}-b x+c=0$ and $c x^{2}-a x+b=0$ has two distinct real roots. The sum of the roots of the first equation is non-negative, and the product of the roots of the first equation is 9 times the sum of the roots of the second equation. Find the ratio of the sum of the roots of the first equation to the product of the roots of the second equation.
|
# Solution.
From the condition, it follows that the coefficients $a, c \neq 0$.
By Vieta's theorem, from the condition it follows that $\frac{c}{a}=9 \frac{a}{c}$. Hence, $c^{2}=9 a^{2}$, which means $\left[\begin{array}{l}c=3 a, \\ c=-3 a .\end{array}\right.$
1 case.
$c=3 a$.
We get the equations $a x^{2}-b x+3 a=0$ and $3 a x^{2}-a x+b=0$.
By the condition $\frac{b}{a} \geq 0, b^{2}-12 a^{2}>0, a^{2}-12 a b>0$.
That is, $\frac{b}{a} \geq 0, \frac{b^{2}}{a^{2}}>12,1-12 \frac{b}{a}>0$. Making the substitution $\frac{b}{a}=t$, we get the system of inequalities:
$\left\{\begin{array}{l}t \geq 0, \\ t^{2}>12, \\ t0, a^{2}+12 a b>0$.
These inequalities are satisfied for any $a$ and $b$ such that $\frac{b}{a} \geq 0$.
The sum of the roots of the first equation is $\frac{b}{a}$. The product of the roots of the second equation is $-\frac{b}{3 a}$. The ratio is -3.
Answer: -3.
## Recommendations for checking.
Only the value $3-2$ points found.
Values $\pm 3-3$ points found.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A circle is inscribed in triangle $A B C$. Two points $E$ and $F$ are marked on the largest side of the triangle $A C$ such that $A E=A B$, and $C F=C B$. Segment $B E$ intersects the inscribed circle at points $P$ and $Q$, with $B P=1, P Q=8$. What is the length of segment $E F$?
|
Solution.
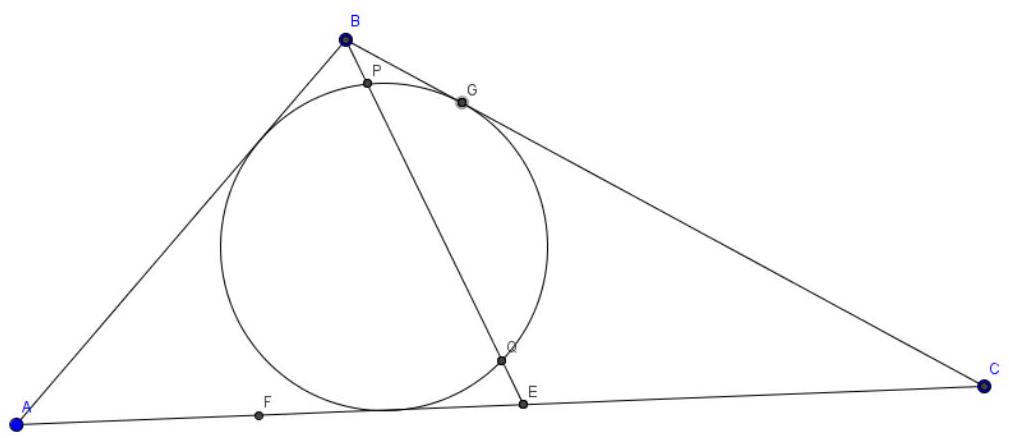
Let the sides of the triangle be $AB=c, AC=b, BC=a$. Then $EF=a+c-b$.
Let $G$ be the point of tangency of the inscribed circle with side $BC$. Then $BG^2 = BQ \cdot BP = 9$. Therefore, $BG = 3$.
Since the segments of tangents drawn from a point to a circle are equal, we have $2BG + 2b = a + b + c$.
Therefore, $a + c - b = 2BG = 6$.
Answer: 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the parliament of a certain state, there are 2016 deputies, who are divided into 3 factions: "blues," "reds," and "greens." Each deputy either always tells the truth or always lies. Each deputy was asked the following three questions:
1) Are you a member of the "blues" faction?
2) Are you a member of the "reds" faction?
3) Are you a member of the "greens" faction?
1208 deputies answered affirmatively to the first question, 908 deputies answered affirmatively to the second question, and 608 deputies answered affirmatively to the third question. In which faction are there more deputies who lie than those who tell the truth, and by how many?
|
# Solution.
Let the number of deputies telling the truth in the "blue," "red," and "green" factions be $r_{1}, r_{2},$ and $r_{3}$ respectively, and the number of deputies lying in the "blue," "red," and "green" factions be $l_{1}, l_{2},$ and $l_{3}$ respectively.
According to the problem:
$\left\{\begin{array}{l}r_{1}+r_{2}+r_{3}+l_{1}+l_{2}+l_{3}=2016, \\ r_{1}+l_{2}+l_{3}=1208, \\ r_{2}+l_{1}+l_{3}=908, \\ r_{3}+l_{1}+l_{2}=608 .\end{array}\right.$
Let $l_{1}-r_{1}=a, l_{2}-r_{2}=b, l_{3}-r_{3}=c$.
Subtracting the third equation from the second, we get $b-a=300$. Or $a=b-300$.
Subtracting the fourth equation from the third, we get $c-b=300$. Or $c=b+300$.
Subtracting the first equation from the sum of the second, third, and fourth equations, we get $l_{1}+l_{2}+l_{3}=708$. Therefore, $r_{1}+r_{2}+r_{3}=1308$.
Then $a+b+c=-600$. Or $3b=-600$.
Thus, $b=-200, a=-500, c=100$. That is, there are 100 more liars in the "green" faction.
Answer: There are 100 more people lying in the "green" faction.
## Recommendations for checking.
The mathematical model of the problem is correctly formulated - 3 points.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Calculate:
$$
\left(\frac{1+2}{3}+\frac{4+5}{6}+\frac{7+8}{9}+\ldots+\frac{2017+2018}{2019}\right)+\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)
$$
|
Answer: 1346.
Solution. We have
$$
\begin{aligned}
& \left(\frac{1+2}{3}+\frac{4+5}{6}+\frac{7+8}{9}+\ldots+\frac{2017+2018}{2019}\right)+\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)= \\
= & \left(\frac{(3-2)+(3-1)}{3}+\frac{(6-2)+(6-1)}{6}+\frac{(9-2)+(9-1)}{9}+\ldots\right. \\
& \left.\ldots+\frac{(2019-2)+(2019-1)}{2019}\right)+\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)= \\
= & \left(\frac{(3+3)-(2+1)}{3}+\frac{(6+6)-(2+1)}{6}+\frac{(9+9)-(2+1)}{9}+\ldots\right. \\
& \left.\ldots+\frac{(2019+2019)-(2+1)}{2019}\right)+\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)= \\
= & \left(2-\frac{3}{3}+2-\frac{3}{6}+2-\frac{3}{9}+\ldots+2-\frac{3}{2019}\right)+\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)= \\
= & 2 \cdot 673-\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)+\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{673}\right)= \\
= & 2 \cdot 673=1346 .
\end{aligned}
$$
## Criteria
1 6. Only the correct answer without proof.
2 b. Using correct algebraic manipulations, the sums with ellipses were eliminated, but an arithmetic error was made.
4 b. Any complete and correct solution.
|
1346
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Square $A B C D$ is inscribed in circle $\omega$. On the smaller arc $C D$ of circle $\omega$, an arbitrary point $M$ is chosen. Inside the square, points $K$ and $L$ are marked such that $K L M D$ is a square. Find $\angle A K D$.
|
Answer: $135^{\circ}$.
Solution.
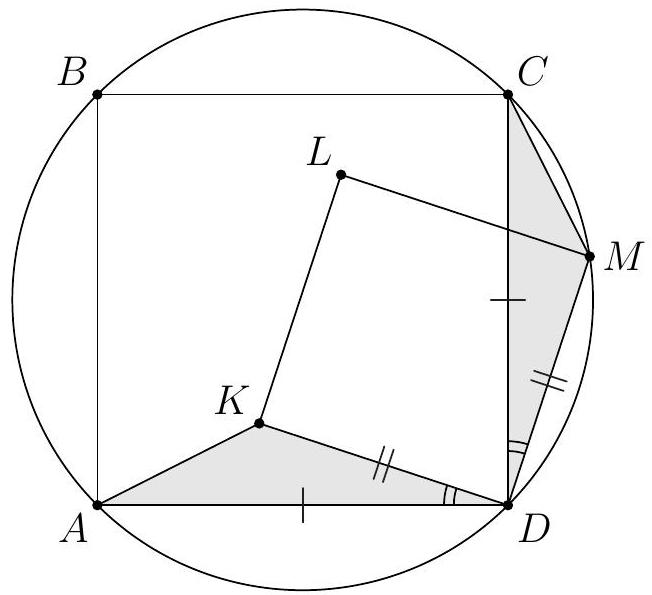
We will prove the equality of triangles $D A K$ and $D C M$. Let's check that the conditions of the first criterion for the equality of triangles are met. Segments $D A$ and $D C$ are equal as sides of the square $A B C D$, and segments $D K$ and $D M$ are equal as sides of the square $K L M D$. Furthermore, since angles $A D C$ and $K D M$ of the original squares are right angles, we can write
$$
\angle A D K=90^{\circ}-\angle K D C=\angle C D M
$$
Thus, triangles $D A K$ and $D C M$ are indeed equal. Therefore, $\angle A K D=\angle C M D$. But $\angle C M D=135^{\circ}$, since it is an inscribed angle subtending the arc $D A B C$ of the circle $\omega$, and the measure of this arc is $270^{\circ}$. Then $\angle A K D=135^{\circ}$, which is what we needed to find.
## Criteria
0 points. Any incomplete or incorrect solution.
1 point. Only the correct answer without proof.
1 point. The possible equality of triangles $D A K$ and $D C M$ is mentioned in the work, but not proven or incorrectly proven; no further progress.
2 points. The possible equality of triangles $D A K$ and $D C M$ is mentioned in the work, but not proven or incorrectly proven; the solution is completed and the correct answer is obtained.
2 points. The equality of triangles $D A K$ and $D C M$ is proven, but the angle $A K D$ is not found or calculated incorrectly.
4 points. Any complete and correct solution.
|
135
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Given a positive number $a$. It is known that the equation $x^{3}+1=a x$ has exactly two positive roots, and the ratio of the larger to the smaller one is 2018. The equation $x^{3}+1=a x^{2}$ also has exactly two positive roots. Prove that the ratio of the larger to the smaller one is also 2018.
|
Solution. Let the positive roots of the equation $x^{3}+1=a x$ be denoted by $x_{1}$ and $x_{2}$ $\left(0<x_{1}<x_{2}, x_{2}: x_{1}=2018\right)$. Substitute them into the equation and divide the two resulting equations by $x_{1}^{3}$ and $x_{2}^{3}$:
\[
\begin{aligned}
& x_{1}^{3}+1=a x_{1} \Longleftrightarrow 1+\left(\frac{1}{x_{1}}\right)^{3}=a\left(\frac{1}{x_{1}}\right)^{2} \\
& x_{2}^{3}+1=a x_{2} \Longleftrightarrow 1+\left(\frac{1}{x_{2}}\right)^{3}=a\left(\frac{1}{x_{2}}\right)^{2}
\end{aligned}
\]
From the formulas, it is clear that $\frac{1}{x_{1}}$ and $\frac{1}{x_{2}}$ are the positive roots of the equation $x^{3}+1=a x^{2}$. According to the condition, there are exactly two such roots, and we need to find the ratio of the larger to the smaller. It is evident that $\frac{1}{x_{2}}<\frac{1}{x_{1}}$. Therefore, $\frac{1}{x_{1}}: \frac{1}{x_{2}}=x_{2}: x_{1}=2018$.
## Criteria
2 6. The work notes that when the first equation from the condition is divided by $x^{3}$ and the substitution $\frac{1}{x} \rightarrow x$ is made, the first equation transforms into the second, but there is no further progress.
3 6. The work proves that the second equation has positive roots $\frac{1}{x_{1}}$ and $\frac{1}{x_{2}}$, but the ratio of the larger to the smaller is found incorrectly (for example, the larger and smaller are swapped).
4 6. Any complete and correct solution.
|
2018
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.2. Petya took half of the candies from the box and put them in two pockets. Deciding that he took too many, Petya took out 6 candies from each pocket and put them back into the box. By how many more candies did the box have than Petya's pockets?
|
Answer: 24.
Solution. Let $x$ be the number of candies in one of Petya's pockets before he returned some of the candies to the box. At that moment, there were $2 x$ candies in the box.
After Petya took out 6 candies from each pocket, he had
$$
(x-6)+(x-6)=2 x-12 \text{ candies }
$$
and there were $2 x+12$ candies in the box.
Thus, there were $(2 x+12)-(2 x-12)=24$ more candies in the box than Petya had.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.5. On the meadow, there were 12 cows. The shepherds brought a flock of sheep. There were more sheep than the cows' ears, but fewer than the cows' legs. How many sheep were there if there were 12 times more sheep than shepherds?
|
Answer: 36 sheep.
Solution. Since there are 12 times more sheep than shepherds, the number of sheep is divisible by 12. In addition, the number of sheep is more than $12 \cdot 2=24$ (the number of ears of cows) and less than $12 \cdot 4=$ 48 (the number of legs of cows). The only number divisible by 12 and between 24 and 48 is 36.
|
36
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. Vanya goes to the swimming pool every Wednesday and Friday. After one of his visits, he noticed that he had already gone 10 times this month. What will be the date of the third visit in the next month if he continues to go on Wednesdays and Fridays?
|
Answer: 12.
Solution. Vanya visited the swimming pool 10 times in a month, which means he visited it 5 times on Wednesdays and 5 times on Fridays.
If the first visit to the swimming pool in this month fell on a Friday, then from the first Friday to the last Friday he visited (including the first and last Friday), 29 days have passed. This means that in this month, there are no more than two days left, so the next Wednesday will fall into the next month.
If the first visit to the swimming pool in this month fell on a Wednesday, then from the first Wednesday to the last Wednesday he visited (including the first and last Wednesday), 29 days have passed. In the month, there are no more than two days left, so the last Friday falls exactly on the 31st of the month.
Thus, the Wednesdays in the next month will fall on the 5th, 12th, 19th, and 26th, and the Fridays on the 7th, 14th, 21st, and 28th. The third visit will be on the 12th.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.4. From sticks of the same length, a row of 700 octagons was laid out as shown in the figure. How many sticks were used in total?

Answer, option 1. 7001.
Answer, option 2. 3501.
Answer, option 3. 5601.
Answer, option 4. 4901.
|
Solution option 1. In the first octagon, there are 8 sticks. Constructing each subsequent octagon adds 7 sticks. In total, it will be $8+7 \cdot 999=7001$ sticks.
|
7001
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
2.4. The standard 12-hour clock face is arranged as shown in the figure. At noon, both the hour and minute hands were vertical, and now the hour hand is exactly pointing to the "18 minutes" mark.
To which mark (in minutes) is the minute hand pointing at this moment?
Answer, option 1. 24.
Answer, option 2. 48.
Answer, option 3. 12.
Answer, option 4. 36.
|
Solution Option 1. From noon to the current moment, the hour hand has traveled a distance 12 times greater than the minute hand. The hour hand has traveled 17 divisions, so the minute hand has traveled \(12 \cdot 17 = 204\) divisions. Subtracting 60 divisions from 204 as many times as possible (considering that the minute hand has completed several full circles), we get \(204 - 3 \cdot 60 = 24\).
|
24
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4.4. In parallelogram $A B C D$, the angle at vertex $A$ is $60^{\circ}$, $A B=73$, and $B C=88$. The bisector of angle $A B C$ intersects segment $A D$ at point $E$, and ray $C D$ at point $F$. Find the length of segment $E F$.
Answer, option 1. 9.
Answer, option 2. 13.
Answer, option 3. 12.
Answer, option 4. 15.
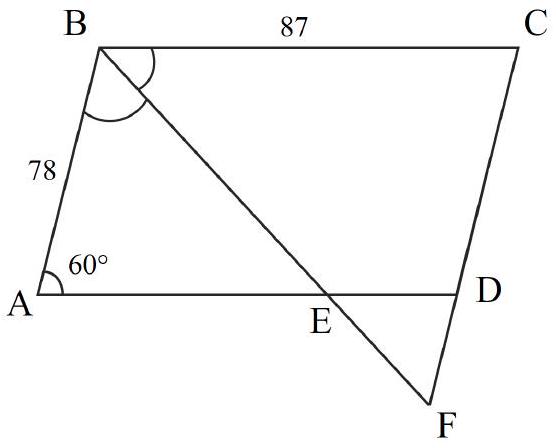
|
Solution 1. Lines $A D$ and $B C$ are parallel, therefore
$$
\angle A B C=180^{\circ}-\angle B A D=120^{\circ}
$$
(angles $A B C$ and $B A D$ are consecutive interior angles). Then $\angle A B E=60^{\circ}$ and $\angle C B E=60^{\circ}$, since $B E$ is the bisector of angle $A B C$. In triangle $A B E$, the angles at vertices $A$ and $B$ are both $60^{\circ}$. Therefore, the angle at vertex $E$ is also $60^{\circ}$, making this triangle equilateral. Thus, $B E=A B=78$. Also, in triangle $B C F$, the angles at vertices $B$ and $C$ are both $60^{\circ}$. Therefore, this triangle is also equilateral, so $B F=B C=87$. Thus, $E F=B F-B E=87-78=9$.
|
9
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
6.4. To be freed from Ivan the Fisherman's net, the Golden Fish gives him a reward: either 4 pearls and 1 diamond; or 2 emeralds and 2 diamonds; or 2 pearls, 1 emerald, and 1 diamond. After several releases of the Golden Fish, Ivan the Fisherman received 1000 pearls, 800 emeralds, and some number of diamonds. How many times did the Golden Fish get caught in Ivan the Fisherman's net?
Answer, option 1. 900.
Answer, option 2. 550.
Answer, option 1. 1400.
Answer, option 2. 650.
|
Solution 1. Let there be $x$ actions of the first type, $y$ actions of the second type, and $z$ actions of the third type. From the problem statement, we get two equations $4 x+2 z=2000, 2 y+z=800$, and we need to find $x+y+z$. By adding the first equation to twice the second, we get $4 x+4 y+4 z=3600$, from which $x+y+z=900$.
Remark. The situation described in the problem is indeed possible, for example, with $x=499, y=399$ and $z=2$. There are many other options.
|
900
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In the Go section, there are 55 boys of different ratings. The boys decided to play a tournament, each with each other in one game. To make it more interesting, some of the boys were allowed to use a computer's help exactly once during the tournament. If in a game, one of the boys uses a computer's help and the other does not, the one using the computer wins; otherwise, the one with the higher rating wins. There are no draws in Go.
By the end of the tournament, two boys were found, each of whom won more games than any of the two boys with the highest ratings. What could be the maximum number of boys who did not use a computer?
Answer, option 1. 45 players.
Answer, option 2. 55 players.
Answer, option 3. 35 players.
Answer, option 4. 50 players.
|
Solution Option 1. Let's number the players in descending order of their strength from first to fiftieth.
We will assume that each won game brings the player one point. Consider two players who ultimately scored more points than the two strongest participants. It is clear that the number of one of them is not less than 4. If he did not use the computer, he could win no more than 46 players. Therefore, even with the help of the computer, he could score no more than 47 points. This means that each of the two strongest players scored no more than 46 points. If no one had used the computer, the two strongest would have scored 49 and 48 points. Thus, due to the computer, they must have lost at least 3 and 2 points, respectively. Therefore, the computer was used no less than \(3+2=5\) times, meaning that no more than 45 boys played without it.
Let's provide an example showing that there could have been 5 boys who used the computer. Suppose players from 3rd to 7th used the computer: three of them won against the 1st player, and two - against the 2nd. The two strongest players will win 46 games each, while the 3rd and 4th players scored 48 and 47 points, respectively.
|
45
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a triangle $A B C$, where $\angle B A C=60^{\circ}$. Point $S$ is the midpoint of the angle bisector $A D$. It is known that $\angle S B A=30^{\circ}$. Find DC/BS.
|
3. Answer: 2. Solution: We have $\mathrm{BS}=\mathrm{AS}=\mathrm{SD}$, therefore, triangle $\mathrm{ABD}$ is a right triangle (in it, the median is equal to half the side), then $\angle A C D=30^{\circ}$, hence $A D=D C$, from which we get that the required ratio is 2.
Criteria: correct solution - 7 points, proved that the triangle is right, but no further progress - 3 points, otherwise -0 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On 52 cards, the numbers from 1 to 52 are written. It is considered that 1 is older than 52, and in all other pairs, the card with the larger number is older. The cards are lying on the table in a random order face down. In one question, Petya can find out which card is older in any pair. Can Petya guarantee to find the card with 52 in no more than 64 questions?
|
6. Answer: it can. We will divide the cards into 13 quartets. In each quartet, we will make the following comparisons: by dividing the quartet into pairs, we will determine the higher cards in the pairs (let $\mathrm{a}>\mathrm{b}$ and $c>d$), then we will determine the higher of the two higher cards (let $a>c$). Card $a$ is higher than two cards, so $\mathrm{a} \neq 1$. Therefore, $\mathrm{b} \neq 52$ and $\mathrm{c} \neq 52$. Compare $a$ and $d$. If $a>d$, then $d \neq 52$, so the number $a$ is the highest in the quartet. Then we move on to the next quartet. If this situation repeats in all quartets, then in $4 \cdot 13=52$ questions we will eliminate 39 cards that are not 52, and among the 13 remaining cards, there will be no card 1. By comparing the remaining cards one by one and discarding the lower one, we will find the card 52 in another 12 questions. Suppose, however, that in some quartet during the fourth comparison it turned out that $\mathrm{a}<c>d>a$. It is clear that this is only possible if the quartet contains the numbers 1 and 52: $\mathrm{c}=1, \mathrm{~d}=52$ or $\mathrm{d}=1, \mathrm{a}=52$. Compare $\mathrm{b}$ and $\mathrm{d}$ ( $b \neq 52$ ). If $b>d$, then $a=52$, and if $b<d$, then $d=52$. Thus, we found the card 52 in no more than 53 questions.
Criteria: An algorithm for finding the required card is presented and justified, which always works - 7 points. In other cases - 0 points. Insufficient justification - minus $1-2$ points.
|
53
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Inside the square $A B C D$, points $K$ and $M$ are marked (point $M$ is inside triangle $A B D$, point $K$ is inside $B M C$) such that triangles $B A M$ and $D K M$ are equal $(A M=K M, B M=M D, A B=K D)$. Find $\angle K C M$, if $\angle A M B=100^{\circ}$
|
Answer: $35^{\circ}$.
Solution. Note that triangles $A B M$ and $A M D$ are also equal by three sides. Thus, point $M$ lies on the diagonal $A C$ of the square, meaning $\angle M C D=\angle M A D=\angle M A B=45^{\circ}($ Fig. 1$)$.
In addition, from the equality of triangles $B A M$ and $D K M$, it follows that $\angle M K D=$ $\angle B A M=45^{\circ}$. Therefore, quadrilateral $M K C D$ is cyclic. Then $\angle K C M=\angle K D M=180^{\circ}-100^{\circ}-45^{\circ}=35^{\circ}$.
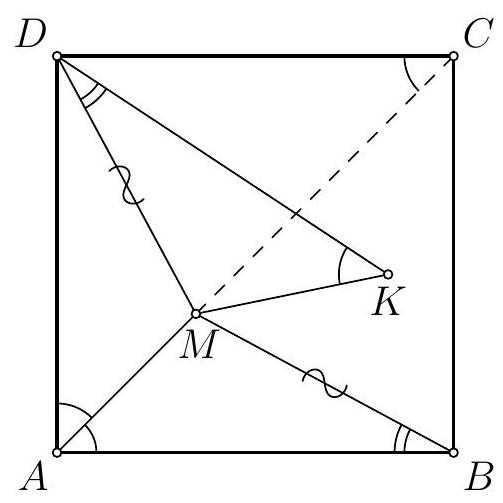
Fig. 1: to the solution of problem 5
## Criteria
4 p. A complete and justified solution is provided.
0 p. The problem is not solved or is solved incorrectly.
In other cases, sum the following criteria:
3 p. The cyclic nature of quadrilateral $M K C D$ is proven.
1 p. It is proven that point $M$ lies on diagonal $A C$.
0 p. The correct answer is provided.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. For what least natural value of \( b \) does the equation
$$
x^{2}+b x+25=0
$$
have at least one root?
|
Answer: 10
Solution. The equation has at least one root if and only if the discriminant $D=b^{2}-4 \cdot 25=$ $=b^{2}-100$ is greater than or equal to 0. For positive $b$, this condition is equivalent to the condition $b \geqslant 10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Every month Ivan pays a fixed amount from his salary for a mortgage, and the remaining part of the salary is spent on current expenses. In December, Ivan paid $40 \%$ of his salary for the mortgage. In January, Ivan's salary increased by $9 \%$. By what percentage did the amount spent on current expenses increase in January (compared to December)?
|
Answer: 15
Solution. Let Ivan's December salary be $100 r$. Then Ivan paid $40 r$ for the mortgage, and in December, he spent $60 r$ on current expenses. In January, Ivan's salary was $109 r$, so he spent $109 r - 40 r = 69 r$ on current expenses. Thus, the amount spent on current expenses increased by $9 r$, which is $\frac{9}{60}$ of the December amount or 15 percent.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. It is known that the area of the shaded region of the figure is $\frac{32}{\pi}$, and the radius of the smaller circle is 3 times smaller than the radius of the larger circle. What is the length of the smaller circle?

|
# Answer: 4
Solution. Let the radius of the smaller circle be $R$, then the radius of the larger circle is $3R$. The area of the smaller circle is $S_{1}=\pi R^{2}$, and the area of the larger circle is $S_{2}=\pi(3R)^{2}=9\pi R^{2}$. Therefore, the area of the shaded part is $S_{2}-S_{1}=8\pi R^{2}$. We have $8\pi R^{2}=\frac{32}{\pi}$, from which $(\pi R)^{2}=4$ and $\pi R=2$. Thus, the length of the smaller circle is $2\pi R=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. In the product
$$
24^{a} \cdot 25^{b} \cdot 26^{c} \cdot 27^{d} \cdot 28^{e} \cdot 29^{f} \cdot 30^{g}
$$
the seven exponents $a, b, c, d, e, f, g$ were replaced by the numbers $1, 2, 3, 5, 8, 10, 11$ in some order. Find the maximum number of zeros that the decimal representation of this product can end with.
|
Answer: 32
Solution. The prime factor 5 enters the factorization of this product with multiplicity $2 b+g$, so there are no more than $2 b+g$ zeros in this product. Since $b \leqslant 11$ (the largest of the given exponents) and $b+g \leqslant 11+10$ (the sum of the two largest of the given exponents), then $2 b+g \leqslant 11+11+10=32$.
On the other hand, for example, the product $24^{8} \cdot 25^{11} \cdot 26^{1} \cdot 27^{2} \cdot 28^{3} \cdot 29^{5} \cdot 30^{10}$ ends with exactly 32 zeros, since the prime number 5 enters the factorization of this product with multiplicity $2 \cdot 11+10=32$, and the prime number 2 enters the factorization of this product with multiplicity $3 \cdot 8+1+3+10>32$.
|
32
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. The geometric progression $b_{1}, b_{2}, \ldots$ is such that $b_{25}=2 \operatorname{tg} \alpha, b_{31}=2 \sin \alpha$ for some acute angle $\alpha$. Find the number $n$ for which $b_{n}=\sin 2 \alpha$.
#
|
# Answer: 37
Solution. Let $q$ be the common ratio of our progression. Using the fact that $b_{31}=b_{25} q^{6}$ and $\sin 2 \alpha=2 \sin \alpha \cos \alpha$. We have $q^{6}=\frac{b_{31}}{b_{25}}=\frac{2 \sin \alpha}{2 \tan \alpha}=\cos \alpha$.
On the other hand, $\frac{\sin 2 \alpha}{2 \sin \alpha}=\cos \alpha$, from which $\sin 2 \alpha=b_{31} \cdot q^{6}=b_{37}$.
We see that $n=37$ fits. No other $n$ fits, since $0<q^{6}<1$, which means $0<|q|<1$, so no two terms of the progression coincide.
|
37
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Given a rectangular parallelepiped $2 \times 3 \times 2 \sqrt{3}$. What is the smallest value that the sum of the distances from an arbitrary point in space to all eight of its vertices can take?
|
Answer: 20
Solution. Let $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ be the given parallelepiped. The sum of the distances from point $X$ to two opposite vertices $A$ and $C^{\prime}$ is not less than the length of $A C^{\prime}$, i.e., the length $d$ of the major diagonal. Summing up similar inequalities, we have $X A+X B+X C+X D+X A^{\prime}+X B^{\prime}+X C^{\prime}+X D^{\prime}=\left(X A+X C^{\prime}\right)+\left(X B+X D^{\prime}\right)+$ $+\left(X C+X A^{\prime}\right)+\left(X D+X B^{\prime}\right) \geqslant A C^{\prime}+B D^{\prime}+C A^{\prime}+D B^{\prime}=4 d$. Equality is achieved when $X$ is the center of the parallelepiped.
It remains to calculate $d=\sqrt{A B^{2}+A D^{2}+A A^{\prime 2}}=5$, and then the answer is $4 d=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Let $n=34000$. Among the vertices of a regular $n$-gon $A_{1} A_{2} \ldots A_{n}$, the vertices $A_{i}$ are painted red for which the number $i$ is a power of two, i.e., $i=1,2,4,8,16, \ldots$ In how many ways can 400 vertices of this $n$-gon be chosen so that they are the vertices of a regular 400-gon and none of them are red?
|
# Answer: 77
Solution. There are $\frac{34000}{400}=85$ ways to choose the correct 400-gon. Consider one of these options, where the vertex numbers of the 400-gon are of the form $a+85 k$ for a fixed $a \in\{1,2, \ldots, 85\}$. Let's see in which options the red vertices will be present.
Consider the powers of two not exceeding 34000: $1,2,4,8,16,32,64,128,256,512, \ldots$. They give remainders when divided by 85: $1,2,4,8,16,32,64,43,1,2, \ldots$ (starting from 1, the remainders repeat, as each subsequent remainder is obtained by multiplying the previous one by 2 and taking the remainder when divided by 85). Thus, red vertices are present in the considered 400-gon if and only if $a=1,2,4,8,16,32,64,43$, i.e., in 8 options. Therefore, the answer is $85-8=77$.
|
77
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many four-digit numbers exist that are divisible by 17 and end in 17?
|
1. Let's denote the four-digit number as $\overline{x y 17}$. Then the number $\overline{x y 17}-17$ is also divisible by 17. But $\overline{x y 17}-17=100 \cdot \overline{x y}+17-17=100 \cdot \overline{x y}$. Since the numbers 100 and 17 are coprime, the two-digit number $\overline{x y}$ is divisible by 17. By enumeration, we find all two-digit numbers divisible by 17: 17, 34, 51, 68, 85. There are five of them. Therefore, there will also be five such numbers: 1717, 3417, 5117, 6817, 8517.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Every day, from Monday to Friday, the old man went to the blue sea and cast his net into the water. Each day, the net caught no more fish than the previous day. In total, over the five days, the old man caught exactly 100 fish. What is the smallest total number of fish he could have caught on the three days - Monday, Wednesday, and Friday?
|
Answer: 50.
Solution. Estimation. On Tuesday and Thursday, the old man caught no more fish than on Monday and Wednesday, so over the specified three days, he caught no less than half of 100, which is no less than 50 fish.
Example. If the old man caught 25 fish each of the first four days and caught nothing on Friday, the conditions of the problem are met, and exactly 50 fish were caught over the specified three days.
|
50
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)

|
Answer: 24.
Solution. In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
Answer: 43.
Solution. The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. From a $6 \times 6$ grid square, gray triangles have been cut out. What is the area of the remaining figure? The side length of each cell is 1 cm. Give your answer in square centimeters.
|
Answer: 27.
Solution. The area of the entire square is $6 \cdot 6=36$ sq. cm.
Divide the triangle located in the middle of the square into two smaller triangles, as shown in the picture on the left. Then the dark gray triangles can be combined into a rectangle $1 \times 3$, and the light gray triangles into a rectangle $2 \times 3$. Therefore, the area of the figure that remains after cutting out all the triangles is 36-3-6 $=27$ sq. cm.
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. In the park, paths are laid out as shown in the figure. Two workers started to asphalt them, starting simultaneously from point $A$. They lay asphalt at constant speeds: the first on the section $A-B-C$, the second on the section $A-D-E-F-C$. In the end, they finished the work simultaneously, spending 9 hours on it. It is known that the second works 1.2 times faster than the first. How many minutes did the second spend laying asphalt on the section $D E$?
|
Answer: 45.
Solution. Let the line $A D$ intersect the line $C F$ at point $G$, as shown in the figure below. Since $A B C G$ and $D E F G$ are rectangles, we have $A B=C G, B C=A G, E F=D G$ and $D E=F G$.
The second worker works 1.2 times faster than the first, and the working time was the same, so the second worker laid 1.2 times more asphalt than the first. Let the first worker lay $x=A B+B C$ asphalt on the section $A-B-C$, then the second worker on the section $A-D-E-F-C$ laid
$$
\begin{aligned}
1.2 x & =A D+D E+E F+F G+G C=(A D+E F+C G)+(D E+F G)= \\
& =(B C+A B)+(D E+D E)=x+2 D E
\end{aligned}
$$
From this, we find that $D E=0.1 x$, which is 12 times less than the total amount of asphalt on the second section. Therefore, the second worker spent 12 times less time on the section $D E$ than on his entire path. He worked a total of $9 \cdot 60=540$ minutes, so he spent $\frac{540}{12}=45$ minutes on $D E$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. There are exactly 120 ways to color five cells in a $5 \times 5$ table so that each column and each row contains exactly one colored cell.
There are exactly 96 ways to color five cells in a $5 \times 5$ table without a corner cell so that each column and each row contains exactly one colored cell.
How many ways are there to color five cells in a $5 \times 5$ table without two corner cells so that each column and each row contains exactly one colored cell?

|
Answer: 78.
Solution. Consider the colorings of a $5 \times 5$ table described in the problem (i.e., such that in each column and each row exactly one cell is colored).
For convenience, let's introduce some notations. Let the top-left corner cell of the $5 \times 5$ table be called $A$, and the bottom-right corner cell be called $B$. Suppose that among the colorings of the first table, exactly $a$ have the cell $A$ colored, and exactly $b$ have the cell $B$ colored. Clearly, $a=b$ due to symmetry.
Notice that the number of colorings of the second table is equal to the number of colorings of the first table where the cell $A$ is not colored. The number of colorings of the third table is equal to the number of colorings of the first table where neither $A$ nor $B$ is colored. To find this, we subtract from 120 the number of colorings of the first table where $A$ or $B$ is colored. To count the number of such colorings, we add $a$ and $b$, and then subtract what has been counted twice - the ways where both $A$ and $B$ are colored.
All colorings of the first table can be divided into two types: those in which the cell $A$ is colored, and those in which it is not. This leads to the equation $120=a+96$, i.e., $a=24$. Then $b=24$ as well.
The number of colorings where both $A$ and $B$ are colored is the same as the number of ways to color the central $3 \times 3$ square. It is easy to see that there are exactly $3!=6$ such ways (to choose the colored cell in its top row, there are 3 ways, in the middle row - 2 ways, and in the bottom row - 1 way).
Thus, the answer to the problem is the number $120-(24+24-6)=78$.
## 7th grade
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are $60^{\circ}$, so it is equilateral, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a $5 \times 5$ square, some cells have been painted black as shown in the figure. Consider all possible squares whose sides lie along the grid lines. In how many of them is the number of black and white cells the same?

|
Answer: 16.
Solution. An equal number of black and white cells can only be in squares $2 \times 2$ or $4 \times 4$ (in all other squares, there is an odd number of cells in total, so there cannot be an equal number of black and white cells). There are only two non-fitting $2 \times 2$ squares (both of which contain the center of the table, but do not contain any cells above the center), so there are exactly $16-2=14$ fitting $2 \times 2$ squares. And among the $4 \times 4$ squares, only the two lower ones fit.
Thus, the total number of squares with an equal number of black and white cells is exactly $14+2=16$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
|
Answer: 21.
Solution. Since $AC$ is the diameter of the circle, point $O$ is the midpoint of $AC$, and $\angle AKC = 90^{\circ}$.
Then
$$
\angle BAC = \angle BAK + \angle CAK = \angle BCA + \angle CAK = \angle BKA = 90^{\circ}.
$$
The area of the right triangle $ABC$ can be found as $\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 14 = 42$. Since the median $BO$ divides its area in half, the area of triangle $BOC$ is $\frac{42}{2} = 21$.
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Given an isosceles triangle $ABC$, where $AB = AC$ and $\angle ABC = 53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $AK$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $AC$;
- $KM = AB$
- angle $MAK$ is the maximum possible.
How many degrees does angle $BAM$ measure?
|
Answer: 44.
Solution. Let the length of segment $AB$ be $R$. Draw a circle with center $K$ and radius $R$ (on which point $M$ lies), as well as the tangent $AP$ to it such that the point of tangency $P$ lies on the same side of $AC$ as $B$. Since $M$ lies inside the angle $PAK$ or on its boundary, the angle $MAK$ does not exceed the angle $PAK$, and these angles are equal only if points $M$ and $P$ coincide. Therefore, $M$ is this point of tangency.
The radius $KM$ of the circle is perpendicular to the tangent $AM$. Also, in the right triangle $AMK$, the leg $MK$ is half the hypotenuse $AK$, so $\angle MAK=30^{\circ}$. Additionally, from the condition, we get that $\angle BAC=180^{\circ}-2 \cdot 53^{\circ}=74^{\circ}$. Therefore,
$$
\angle BAM=\angle BAC-\angle MAK=74^{\circ}-30^{\circ}=44^{\circ}
$$
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. An equilateral triangle with a side of 10 is divided into 100 small equilateral triangles with a side of 1. Find the number of rhombi consisting of 8 small triangles (such rhombi can be rotated).
|
Answer: 84.
Solution. Rhombuses consisting of eight triangles can be of one of three types:

It is clear that the number of rhombuses of each orientation will be the same, so let's consider only the vertical ones. Each of them is uniquely determined by its top triangle. Now it is easy to count the number of such triangles.
In the first row, there is 1 such triangle, in the second - 2, in the third - 3, ..., in the seventh - 7. In total, \(1+2+3+\ldots+7=28\) vertical rhombuses, and therefore, the answer to the problem is \(28 \cdot 3 = 84\).
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. A circle $\omega$ is inscribed in trapezoid $A B C D$, and $L$ is the point of tangency of $\omega$ and side $C D$. It is known that $C L: L D=1: 4$. Find the area of trapezoid $A B C D$, if $B C=9$, $C D=30$.
|
Answer: 972.
Solution. Let's mark the center of the circle $I$, as well as the points of tangency $P, Q, K$ with the sides $B C$, $A D, A B$ respectively. Note that $I P \perp B C, I Q \perp A D$, i.e., points $P, I, Q$ lie on the same line, and $P Q$ is the height of the given trapezoid, equal to the diameter of its inscribed circle. Also, the segments of tangents $A K=A Q, B K=B P, C P=C L, D L=D Q$ are equal.
From the condition, it follows that $C P=C L=\frac{1}{5} \cdot 30=6, D Q=D L=\frac{4}{5} \cdot 30=24$. Then $B K=B P=$ $B C-C P=9-6=3$.
Since the lines $C I$ and $D I$ are the angle bisectors of angles $C$ and $D$ of the trapezoid, we have $\angle I C D+$ $\angle I D C=\frac{1}{2}(\angle C+\angle D)=\frac{180^{\circ}}{2}=90^{\circ}$, i.e., triangle $C I D$ is a right triangle with a right angle at vertex $I$. Since $I L$ is its height dropped to the hypotenuse, $I L=$ $\sqrt{C L \cdot D L}=12$. This is the radius of the circle.
Similarly, considering the height $I K$ in the right triangle $A I B$, we get $12=$ $I K=\sqrt{A K \cdot B K}$. Using $B K=3$, we extract $A K=A Q=48$.
Thus, the area of the trapezoid is
$$
S_{A B C D}=\frac{B C+A D}{2} \cdot C H=\frac{9+(48+24)}{2} \cdot 24=972
$$
|
972
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The teacher drew the graph of the function $y=\frac{k}{x}$ and three lines with a slope of $k$ ( $k$ is not equal to zero). Petya wrote down the abscissas of all six points of intersection and multiplied them. Prove that the result does not depend on the choice of the number $k$.
|
10.1. A line parallel to the line $y=k x$ has the equation $y=k x+b$ The abscissas of its intersection points with the hyperbola are both roots of the equation $\frac{k}{x}=k x+b, \quad$ equivalent to the equation $k x^{2}+b x-k=0$. The product of the roots of this equation is -1. Multiplying three such products, we get the answer: -1.
|
-1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. The plane departed from Perm on September 28 at noon and arrived in Kirov at 11:00 AM (all departure and arrival times mentioned in the problem are local). At 7:00 PM the same day, the plane departed from Kirov to Yakutsk and arrived there at 7:00 AM. Three hours later, it departed from Yakutsk to Perm and returned there at 11:00 AM on September 29. How much time did the plane spend in the air? Answer: 12 hours.
|
# Solution.
The plane was absent in Perm for 23 hours. Out of these, it was stationed in Kirov for 8 hours (from 11 to 19) and for 3 hours in Yakutsk. In total, out of these 23 hours, it was stationed $8+3=11$ (hours), i.e., the plane was in the air for $23-11=12$ (hours).
## Grading Criteria.
- Correct solution -7 points.
- Correct answer without justification -2 points.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On a glade, 25 gnomes gathered. It is known that 1) every gnome who put on a hat also put on shoes; 2) 12 gnomes came without a hat; 3) 5 gnomes came barefoot. Which gnomes are more and by how many: those who came in shoes but without a hat, or those who put on a hat?
|
Answer. There are 6 more gnomes who put on a cap.
## Solution.
From condition 2, it follows that $25-12=13$ gnomes came in a cap.
From condition 1, we get that exactly 13 gnomes came both in a cap and in shoes.
From condition 3, it follows that a total of $25-5=20$ gnomes came in shoes.
Thus, $20-13=7$ gnomes came in shoes but without a cap.
Therefore, those who put on a cap (13 gnomes) are 6 more than those who came in shoes but without a cap (7 gnomes).
## Grading Criteria.
- Correct solution - 7 points.
- Correct answer with incomplete justification - 3-4 points.
- Only the correct answer without justification - 2 points.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The difference of the squares of two numbers is 6, and if each of these numbers is decreased by 2, then the difference of their squares becomes equal to 18. What is the sum of these numbers?
|
Answer: -2.
## Solution.
Given:
\[
\begin{aligned}
& a^{2}-b^{2}=6 \\
& (a-2)^{2}-(b-2)^{2}=18
\end{aligned}
\]
There are different ways to proceed.
## Method 1.
\((a-2)^{2}-(b-2)^{2}=a^{2}-4a+4-b^{2}+4b-4=a^{2}-b^{2}-4(a-b)\). Since from the first condition \(a^{2}-b^{2}=6\), we get \(6-4(a-b)=18\). Hence, \(a-b=-3\), and from the first equation, we get \(a+b=-2\).
## Method 2.
\[
\begin{aligned}
& a^{2}-b^{2}=(a-b)(a+b)=6 \\
& (a-2)^{2}-(b-2)^{2}=(a-b)(a+b-4)=18
\end{aligned}
\]
Clearly, all factors in the given equations are not zero. Dividing the second equation by the first and denoting the desired sum \(a+b=x\), we get \(\frac{x-4}{x}=3\), from which \(x=-2\).
## Grading Criteria.
- Correct solution - 7 points.
- Obtained the equation \(\frac{a+b-4}{a+b}=3\) but made an arithmetic error in further solution - 4 points.
- Correctly found the difference \(a-b\), but no further progress - 3 points.
- Made a sign error in finding \(a+b\) or \(a-b\) - no more than 3 points.
- Only the correct answer without justification - 2 points.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. At the stadium, through the checkpoints numbered 1, 2, 3, and 4, an equal number of fans entered. They then passed through several more checkpoints, moving along the arrows, and at the fork, the fans were evenly distributed. At checkpoint 7, 15 people passed the control.
How many people passed through checkpoint 8?
Checkpoint (control and pass point) - a place where stadium staff check fans for tickets and prohibited items.
|
Answer: 24
Solution. Let $2x$ people pass through each of the first four checkpoints. Then, through checkpoint 7, $2x$ people passed from the first two checkpoints and $x$ from the third, totaling $5x=15$ people, from which $x=3$. Therefore, each of the first four checkpoints had 6 people, and checkpoint 8 was passed by everyone who entered through the first four checkpoints, which is 24 people.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. A gardener grows white and red flowers: peonies and roses. In his garden, there are 301 stems, among which 135 are roses and 182 are red flowers. What is the smallest number of red peonies that can grow in the gardener's garden?
|
Answer: 47
Solution. Estimation: The number of red peonies is the difference between the number of red flowers and the number of red roses. The number of red roses is no more than the total number of roses, i.e., no more than 135. Therefore, the number of red peonies is no less than $182-135=47$.
Let's provide an example where the conditions of the problem are met, and the number of red peonies is exactly 47. Suppose there are 47 red peonies, 135 red roses, 0 white roses, and 119 white peonies.
|
47
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. In February of a non-leap year, Kirill and Vova decided to eat ice cream according to certain rules. If the date was even and the day of the week was Wednesday or Thursday, they each ate seven portions of ice cream. If the day of the week was Monday or Tuesday and the date was odd, they each ate three portions of ice cream. If the day of the week was Friday, the number of portions each ate was equal to the date on the calendar. Ice cream was forbidden on all other days and under other conditions. What is the maximum number of portions of ice cream that Vova could have eaten in February under these conditions?
|
# Answer: 110
Solution. February has 28 days, which is exactly 4 Mondays, 4 Tuesdays, and so on. Moreover, if Monday falls on an even date in one week, the following Monday will fall on an odd date, and vice versa. This means that the same day of the week falls on an even date twice and an odd date twice, regardless of which day of the week the month starts. Therefore, for Mondays, Tuesdays, Wednesdays, and Thursdays, Kirill and Vova will eat $4 \cdot (7+3) = 40$ portions of ice cream. For the four Fridays, the number of portions eaten will be $x, x+7, x+14$, and $x+21$, where $x$ is the date on which the first Friday falls. The maximum number of portions will be eaten when the first Friday is on February 7. Then $x + x + 7 + x + 14 + x + 21 = 42 + 4x = 42 + 28 = 70$, and in total, Vova will eat $70 + 40 = 110$ portions of ice cream.
|
110
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.