problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
9.1. On a circle, 1000 points are marked, each colored in one of $k$ colors. It turns out that among any five pairwise intersecting segments, whose endpoints are 10 different marked points, there will be at least three segments, each of which has endpoints of different colors. For what smallest $k$ is this possible?
(S. Berlov)
|
Answer. For $k=143$.
Solution. Suppose there are 8 points of one color (say, red) on the circle. Add two more marked points to them, forming a decagon $A_{1} A_{2} \ldots A_{5} B_{1} B_{2} \ldots B_{5}$. Then the segments $A_{1} B_{1}, A_{2} B_{2}, \ldots, A_{5} B_{5}$ intersect each other, and among them, there are three segments with all endpoints red. This contradicts the condition. Therefore, there are no more than seven points of each color, so $k \geqslant \frac{1000}{7}$, that is, $k \geqslant 143$.
For $k=143$, mark an additional, 1001st, point and divide all marked points into 143 groups of 7 consecutive points each. Color each group with its own color. Let $A_{1} B_{1}, \ldots$, $A_{5} B_{5}$ be five pairwise intersecting segments with endpoints at the marked points. We can assume that the points $A_{1}, A_{2}, \ldots, A_{5}, B_{1}$, $B_{2}, \ldots, B_{5}$ are located on the circle in this order. Suppose the segment $A_{1} B_{1}$ has endpoints of the same color (say, red). Then either all points $A_{1}, A_{2}, \ldots, A_{5}$, or all points $B_{1}, B_{2}, \ldots, B_{5}$ are red. In the first case, at most two of the points $B_{1}, B_{2}, \ldots, B_{5}$ are red. But then three segments not containing these points will have endpoints of different colors. The second case is analogous.
|
143
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. On the board, the numbers $\sqrt{2}$ and $\sqrt{5}$ are written. It is allowed to add to the board the sum, difference, or product of any two different numbers already written on the board. Prove that it is possible to write the number 1 on the board.
|
Solution: The simplest way is to provide a sequence of numbers that will lead to the number 1. For example, the following sequence works:
$$
\begin{gathered}
\sqrt{2}+\sqrt{5}, \quad 2 \sqrt{2}+\sqrt{5}, \quad 3 \sqrt{2}+\sqrt{5}, \quad \sqrt{2}-\sqrt{5}, \quad 2 \sqrt{2}-\sqrt{5}, \quad 3 \sqrt{2}-\sqrt{5} \\
(\sqrt{2}+\sqrt{5})(\sqrt{2}-\sqrt{5})=-3, \quad(3 \sqrt{2}+\sqrt{5})(3 \sqrt{2}-\sqrt{5})=13 \\
13-3=10, \quad 10-3=7, \quad 7-3=4, \quad 4-3=1
\end{gathered}
$$
Note: The sequence of operations is not unique.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct sequence of listed numbers | 7 points |
| Correct sequence is not present, but a method to obtain an integer is found | 3 points |
| Examples of sequences that do not lead to the answer or examples of impossible sequences | 0 points |
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.5. On a shelf, there are 12 books. In how many ways can 5 of them be chosen if books standing next to each other cannot be chosen? Justify your answer.
|
Solution: Let's place one more, the thirteenth book, on the right side of the shelf. We will mentally glue each selected book to the book to its right. This is possible since we do not select the 13th book and do not select adjacent books. This will result in 5 glued two-volume sets and 3 separate books. Therefore, the number of ways is the same as the number of ways to arrange 5 two-volume sets (considering them identical) and 3 single-volume books (also identical) in a row. This number is equal to the number of combinations of 8 taken 3 at a time, which is $\frac{8!}{3!(8-3)!}=56$.
Note: Other methods of solving are possible (induction by the number of books, direct enumeration, etc.).
Answer: 56 ways.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| A correct approach but an incorrect answer due to arithmetic errors | 6 points |
| The correct idea of "gluing" a book to the one on its right did not lead to the correct answer because the rightmost book was not correctly accounted for | 4 points |
| In solving by complete enumeration, not all cases were considered | 2 points |
| Correct answer without justification | 1 point |
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. Let \(a\) and \(b\) be positive numbers. Find the minimum value of the fraction \(\frac{(a+b)(a+2)(b+2)}{16ab}\). Justify your answer.
|
Solution: By the inequality between the arithmetic mean and the geometric mean of two numbers, the following three inequalities hold:
$$
a+b \geqslant 2 \sqrt{a b}, \quad a+2 \geqslant 2 \sqrt{2 a}, \quad b+2 \geqslant 2 \sqrt{b}
$$
Multiplying the left and right sides of these three inequalities, we get
$$
(a+b)(a+2)(b+2) \geqslant 8 \sqrt{a b \cdot 2 a \cdot 2 b}
$$
which is equivalent to the inequality $\frac{(a+b)(a+2)(b+2)}{16 a b} \geqslant 1$. The value 1 is achieved at the set $a=b=2$.
Note: The fraction given in the problem is a special case of the fraction $\frac{(a+b)(a+c)(b+c)}{8 a b c}$. Its minimum (for positive variables) is also 1 and is achieved when $a=b=c$. The proof of this fact does not differ from the one provided in the solution.
## Answer: 1.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The equation $\frac{(a+b)(a+2)(b+2)}{16 a b}=t$ (or an equivalent one) is investigated as a quadratic (in one of the variables) with parameters, but the investigation is incomplete or incorrect | 4 points |
| The case $a=b$ is correctly investigated, but it is not justified that the minimum of the fraction is achieved precisely under this assumption | 3 points |
| The set at which the minimum value of the fraction is achieved $(a=b=2)$ is indicated, but its optimality is not proven | 1 point |
| Correct answer without justification and/or any calculations from which the solution process is not clear | 0 points |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. The factory paints cubes in 6 colors (each face in its own color, the set of colors is fixed). How many varieties of cubes can be produced?
|
Solution: Suppose the procedure of painting the cube goes as follows: an unpainted cube is placed in a machine in a certain fixed position, and then its faces are painted in a certain order: bottom, top, right, left, front, back. First, let's calculate how many ways such a painting can be done. The bottom face can be painted in any of the six colors. After that, there are only five possibilities for the top face, as one color has already been used. Then the right face can be painted in four ways, the left face in three, the front face in two, and there is no choice for the color of the back face - it must be painted in the remaining unused color. Therefore, the total number of ways to paint is $6 \cdot 5 \cdot 4 \cdot 3 \cdot 2=720$. However, the number of different types of cubes is much less, since the cube can be placed in a fixed position in various ways. How many? The cube can be placed on any of its six faces and then rotated in one of four ways - giving a total of $6 \cdot 4=24$ ways. Therefore, the number of types of cubes is 24 times less than the number of ways to paint, which is 30.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Matvey decided to start eating properly and every day he ate one bun less and one pear more than the previous day. In total, during the time of proper nutrition, he ate 264 buns and 187 pears. How many days was Matvey on a proper diet?
|
Answer: 11 days.
Solution: If we "reverse" the sequence of the number of buns, while leaving the pears unchanged, the total number of buns and pears will not change, and the difference between the number of buns and pears eaten each day will become constant. Since $264-187=77=7 \cdot 11$, the correct diet lasted either 7, 11, or 77 days. Since the number of days is odd, the total number of buns and pears eaten is equal to the product of the number of days and the number of buns and pears eaten on the middle day. But 264 is not divisible by 7, so the number of days cannot be 7 or 77.
Criteria: Full solution - 7 points. If the reason why there cannot be a different number of days is not justified, but the rest is correct - 5 points. Only the answer - 1 point. The problem assumes that the event has already occurred, so the student is not required to provide an example of how Matvey could have eaten this way.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. Option 1.
Find the value of the expression $101+102-103-104+105+106-107-108+\ldots-619$?
|
Answer: 100.
Solution. Subtract and add the number 620 at the end of the expression. Then the numbers from 101 to 620 will be divided into $(620-100): 4=130$ quartets. And in each quartet, the sum of the numbers will be equal to -4. Then the value of the expression will be equal to $(101+102-103-104)+(105+106-107-108)+\ldots-619-620)+620=$ $130(-4)+620=100$.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Option 1
On a sheet, two rectangles are drawn. It is known that both the length and the width of the second rectangle are 3 cm larger than the length and width of the first rectangle, and the area of the second rectangle is 48 cm ${ }^{2}$ larger than the area of the first rectangle. Find the perimeter of the second rectangle.
|
Answer: 38.
Solution: Let the first rectangle have a length of $a$ cm and a width of $b$ cm. Then the length of the second rectangle is $a+3$ cm, and the width is $b+3$ cm. From the condition, it follows that $(a+3)(b+3)-a b=48$, then $3(a+b)=39, a+b=13$ and $(a+3)+(b+3)=19$. Therefore, the perimeter is 38 cm.
## Variant 2
On a sheet, two rectangles are drawn. It is known that both the length and the width of the second rectangle are 4 cm greater than the length and width of the first, and the area of the second rectangle is 56 cm $^{2}$ greater than the area of the first. Find the perimeter of the second rectangle.
Answer: 36.
## Variant 3
On a sheet, two rectangles are drawn. It is known that both the length and the width of the second rectangle are 5 cm greater than the length and width of the first, and the area of the second rectangle is $70 \mathrm{~cm}^{2}$ greater than the area of the first. Find the perimeter of the second rectangle.
Answer: 38.
## Variant 4
On a sheet, two rectangles are drawn. It is known that both the length and the width of the second rectangle are 6 cm greater than the length and width of the first, and the area of the second rectangle is 96 cm $^{2}$ greater than the area of the first. Find the perimeter of the second rectangle.
Answer: 44.
## Variant 5
On a sheet, two rectangles are drawn. It is known that both the length and the width of the second rectangle are 7 cm greater than the length and width of the first, and the area of the second rectangle is 98 cm $^{2}$ greater than the area of the first. Find the perimeter of the second rectangle.
Answer: 42.
|
38
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Option 1.
Along a road, 10 lampposts were placed at equal distances, and the distance between the outermost posts was $k$ meters. Along another road, 100 lampposts were placed at the same distances, and the distance between the outermost posts was $m$ meters. Find the ratio $m: k$.
|
Answer: 11.
Solution: Let the distance between adjacent posts be $x$ meters. Then, in the first case, the distance between the outermost posts is $(10-1) x=9 x=k$ meters. And in the second case, $(100-1) x=99 x=m$ meters. Therefore, the desired ratio is $m: k=(99 x):(9 x)=11$.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Variant 1 Sasha wrote the number 765476547654 on the board. He wants to erase several digits so that the remaining digits form the largest possible number divisible by 9. What is this number?
|
Answer: 7654765464.
Solution: The sum of the digits of the original number is $3 \cdot(7+6+5+4)=66$. According to the divisibility rule for 9, the sum of the erased digits must give a remainder of 3 when divided by 9. It is impossible to select digits with a sum of 3. Digits with a sum of $3+9=12$ can be chosen, and with a sum of $12+9=21$ or more, at least 3 digits can be taken. Among two numbers, the larger one is the one with more digits, so two digits with a sum of $12-7$ and 5 or 6 and 6 should be erased. Among two ten-digit numbers, the larger one is the one with larger digits in the higher positions. Therefore, the last "5" and the last "7" should be erased.
Variant 2 Sasha wrote the number 764576457645 on the board. He wants to erase several digits so that the remaining digits form the largest possible number divisible by 9. What is this number?
Answer: 7647645645.
Variant 3 Sasha wrote the number 674567456745 on the board. He wants to erase several digits so that the remaining digits form the largest possible number divisible by 9. What is this number?
Answer: 7457456745.
Variant 4 Sasha wrote the number 456745674567 on the board. He wants to erase several digits so that the remaining digits form the largest possible number divisible by 9. What is this number?
Answer: 4674567456.
Variant 5 Sasha wrote the number 546754675467 on the board. He wants to erase several digits so that the remaining digits form the largest possible number divisible by 9. What is this number?
Answer: 5475475467.
|
7654765464
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Variant 1
In the garden, there are 26 trees - apple trees and pears. It turned out that among any 18 trees, there is at least one apple tree, and among any 10 trees, there is at least one pear. How many pears are there in the garden?
|
Answer: 17.
Solution: Since among 18 trees there is at least one apple tree, there are no more than 17 pears. And since among any 10 trees there is at least one pear, there are no more than 9 apple trees. There are 26 trees in total, so there are 9 apple trees and 17 pears.
## Variant 2
In the garden, there are 26 trees - apple and pear trees. It turned out that among any 18 trees, there is at least one apple tree, and among any 10 trees, there is at least one pear tree. How many apple trees are there in the garden?
Answer: 9.
## Variant 3
In the garden, there are 27 trees - apple and pear trees. It turned out that among any 19 trees, there is at least one apple tree, and among any 10 trees, there is at least one pear tree. How many pear trees are there in the garden?
Answer: 18.
## Variant 4
In the garden, there are 27 trees - apple and pear trees. It turned out that among any 18 trees, there is at least one apple tree, and among any 11 trees, there is at least one pear tree. How many apple trees are there in the garden?
Answer: 10.
## Variant 5
In the garden, there are 29 trees - apple and pear trees. It turned out that among any 19 trees, there is at least one apple tree, and among any 12 trees, there is at least one pear tree. How many apple trees are there in the garden?
Answer: 11.
|
17
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1
Petya wrote down all positive numbers that divide some natural number $N$. It turned out that the sum of the two largest written numbers is 3333. Find all such $N$. If there are several numbers, write their sum in the answer.
|
Answer: 2222.
Solution: Note that one of the listed numbers will be equal to $N$. Since the sum of the two largest listed numbers is odd, these numbers have different parity. This means that the number 2 is a divisor of $N$, so the second number is $N / 2$. According to the condition, $N + N / 2 = 3333$. Therefore, $N = 2222$.
## Variant 2
Petya listed all positive numbers that divide some natural number $N$ on the board. It turned out that the sum of the two largest listed numbers is 3021. Find all such $N$. If there are several numbers, write their sum in the answer.
Answer: 2014.
## Variant 3
Petya listed all positive numbers that divide some natural number $N$ on the board. It turned out that the sum of the two largest listed numbers is 6663. Find all such $N$. If there are several numbers, write their sum in the answer.
Answer: 4442.
## Variant 4
Petya listed all positive numbers that divide some natural number $N$ on the board. It turned out that the sum of the two largest listed numbers is 3201. Find all such $N$. If there are several numbers, write their sum in the answer.
Answer: 2134.
## Variant 5
Petya listed all positive numbers that divide some natural number $N$ on the board. It turned out that the sum of the two largest listed numbers is 2301. Find all such $N$. If there are several numbers, write their sum in the answer.
Answer: 1534.
|
2222
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
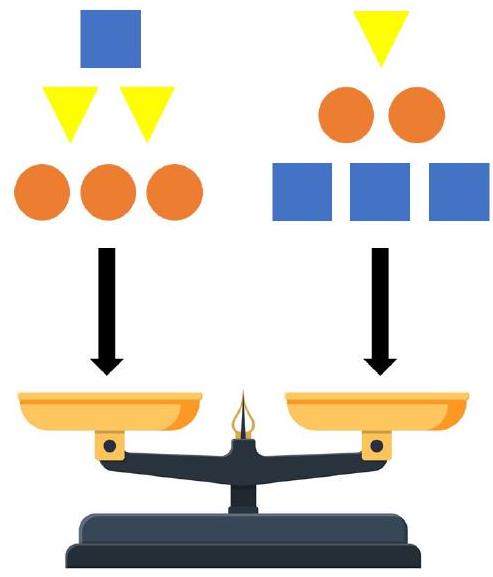
Problem 4.1. Circular weights weigh 200 grams, square ones weigh 300 grams, and triangular ones weigh 150 grams. 12 weights were placed on the pan balance as shown in the figure. Which pan is heavier and by how many grams?
|
Answer: The right side is 250 grams heavier.
Solution. The weight of the left pan in grams is
$$
1 \cdot 300+2 \cdot 150+3 \cdot 200=1200
$$
The weight of the right pan in grams is
$$
1 \cdot 150+2 \cdot 200+3 \cdot 300=1450
$$
Thus, the right pan is 250 grams heavier than the left pan.
|
250
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.2. In class 4A, each child has no fewer than 11 classmates and no fewer than 13 female classmates. What is the smallest number of children that can study in this class?
|
Answer: 26.
Solution. It is not difficult to verify that a class consisting of 12 boys and 14 girls satisfies the condition of the problem. Now let's prove that it cannot be less.
It is clear that there are both boys and girls in the class. Each boy in the class has at least 11 classmates, so there must be at least 12 boys in total. Each girl in the class has at least 13 female classmates, so there must be at least 14 girls in total. Therefore, there are at least $12+14=26$ children in the class.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Sasha had 47 sticks. Using them all, he formed several letters "B" and "V" as shown in the figure. What is the maximum number of letters "B" that Sasha could have formed?

|
Answer: 8.
Solution. To form the letter "Б", 4 sticks are needed, and to form the letter "В", 5 sticks are needed.
- Sasha could not have formed at least 12 letters "Б" because it would require no less than 48 sticks.
- If Sasha had formed 11 letters "Б", he would have $47-11 \cdot 4=3$ sticks left. This would not be enough even for one letter "В".
- If Sasha had formed 10 letters "Б", he would have $47-10 \cdot 4=7$ sticks left. One letter "В" could be formed, but there would be extra sticks left.
- If Sasha had formed 9 letters "Б", he would have $47-9 \cdot 4=11$ sticks left. Two letters "В" could be formed, but there would be one extra stick left.
- If Sasha had formed 8 letters "Б", he would have $47-8 \cdot 4=15$ sticks left. This is exactly enough for 3 letters "В".
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.6. Zhenya took a $3 \times 3$ board and placed a column of blue and red cubes on each cell. Then he drew a diagram of the resulting arrangement: he labeled the number of cubes of both colors in each column (the order of the cubes is unknown).
What is the maximum number of blue cubes Zhenya can see if he looks at the construction from the front? (For example, if a column of 8 cubes is in front of a column of 5, then all 5 cubes of the closer column and only the top 3 cubes of the farther column will be visible.)
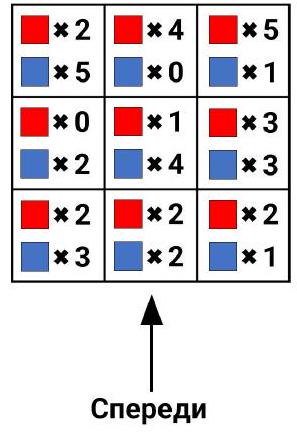
|
Answer: 12.
Solution. Let's understand the maximum number of blue cubes Zhenya can see in each of the three rows: left, middle, and right.
Left row. The first column consists of 5 cubes (2 red and 3 blue), so it completely blocks the second column, as well as 5 out of 7 cubes in the last column.
Thus, Zhenya sees all the cubes in the first column (3 of which are blue), as well as 2 cubes from the last column (both can be blue). That is, in this row, he will see a maximum of $3+2=5$ blue cubes.
Middle row. The first column consists of 4 cubes (2 red and 2 blue), so it completely blocks the last column, as well as 4 out of 5 cubes in the second column.
Thus, Zhenya sees all the cubes in the first column (2 of which are blue), as well as 1 cube from the second column (it can be blue). That is, in this row, he will see a maximum of $2+1=3$ blue cubes.
Right row. The first column consists of 3 cubes (2 red and 1 blue), so it blocks 3 out of 6 cubes in the second column. Meanwhile, the second column completely blocks the last column.
Thus, Zhenya sees all the cubes in the first column (1 of which is blue), as well as 3 cubes from the second column (all three can be blue). That is, in this row, he will see a maximum of $1+3=4$ blue cubes.
In total, Zhenya will see a maximum of $5+3+4=12$ blue cubes.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. On the table, there are 4 stacks of coins. The first stack has 9 coins, the second has 7, the third has 5, and the fourth has 10. In one move, it is allowed to add one coin to three different stacks. What is the minimum number of moves required to make the number of coins in all stacks equal?
|
Answer: 11.
Solution. Suppose $N$ moves were made, after which the number of coins in all stacks became equal.
Let's slightly change the rules. Suppose initially there were not 9, 7, 5, and 10 coins in the stacks, but $N+9, N+7, N+5$, and $N+10$ respectively; and we will perform the moves as follows: instead of adding one coin to three stacks, we will take one coin from a stack (the one into which we did not add a coin during the original move). Note that the final result will not change! (In fact, instead of adding coins to three stacks, we add them to all four and then take one away.)
Under the new rules, answering the question is much easier. In one move, we take one coin from any stack, and our goal is to make the number of coins in all stacks equal as quickly as possible. It is easy to understand that for this, we need to leave $N+5$ coins in each stack. For this, we need to take 4 coins from the first stack, 2 from the second, 0 from the third, and 5 from the fourth. In total, we need to make $4+2+0+5=11$ moves.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. Denis threw darts at four identical dartboards: he threw exactly three darts at each board, where they landed is shown in the figure. On the first board, he scored 30 points, on the second - 38 points, on the third - 41 points. How many points did he score on the fourth board? (For hitting each specific zone - ring or central field - a certain number of points is awarded.)
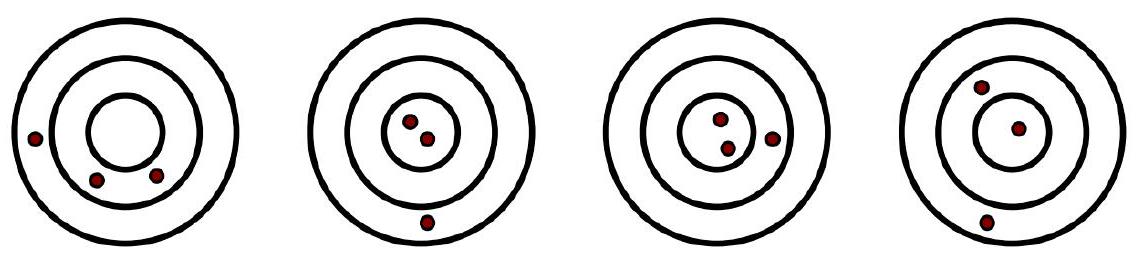
|
Answer: 34.
Solution. "Add" the first two dart fields: we get 2 hits in the central field, 2 hits in the inner ring, 2 hits in the outer ring. Thus, the sum of points on the first and second fields is twice the number of points obtained for the fourth field.
From this, it is not difficult to get the answer
$$
(30+38): 2=34
$$
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
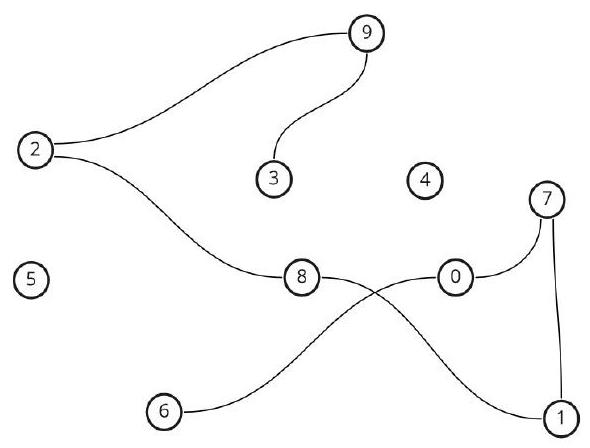
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. The figure shows 4 squares. It is known that the length of segment $A B$ is 11, the length of segment $F E$ is 13, and the length of segment $C D$ is 5. What is the length of segment $G H$?
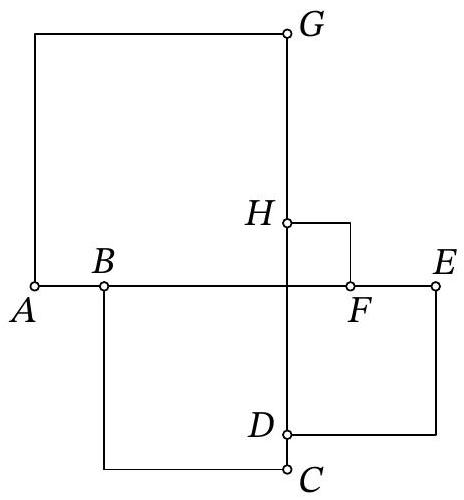
|
Answer: 29.
Solution. The side of the largest square (with vertex $A$) is greater than the side of the second largest square (with vertex $C$) by the length of segment $A B$, which is 11. Similarly, the side of the second largest square is greater than the side of the third largest square (with vertex $E$) by the length of segment $C D$, which is 5. And its side is greater than the side of the smallest square by the length of segment $E F$, which is 13. In total, the side of the largest square is greater than the side of the smallest square by the length of segment $G H$, which is $11+5+13=29$.
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. A rectangle was cut into nine squares, as shown in the figure. The lengths of the sides of the rectangle and all the squares are integers. What is the smallest value that the perimeter of the rectangle can take?
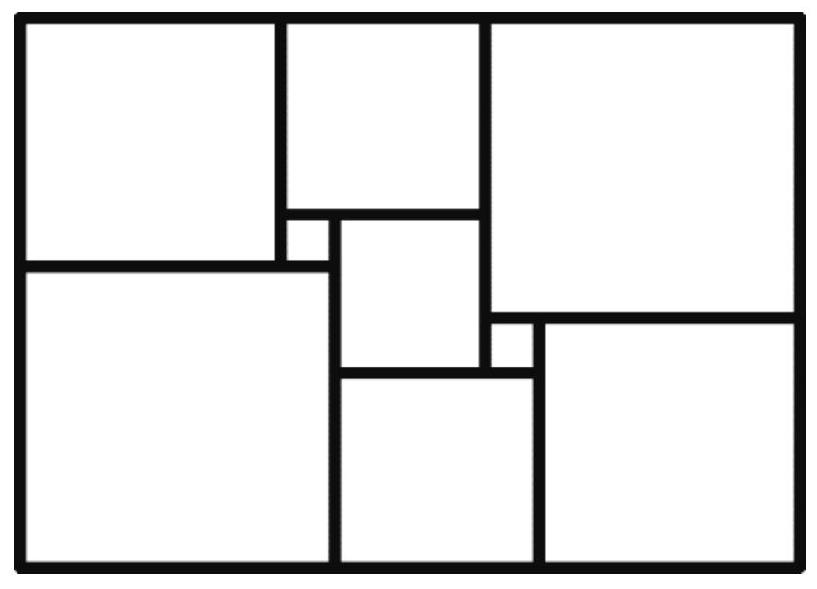
|
Answer: 52.
Solution. Inside the square, we will write the length of its side. Let the sides of the two squares be $a$ and $b$, and we will sequentially calculate the lengths of the sides of the squares.
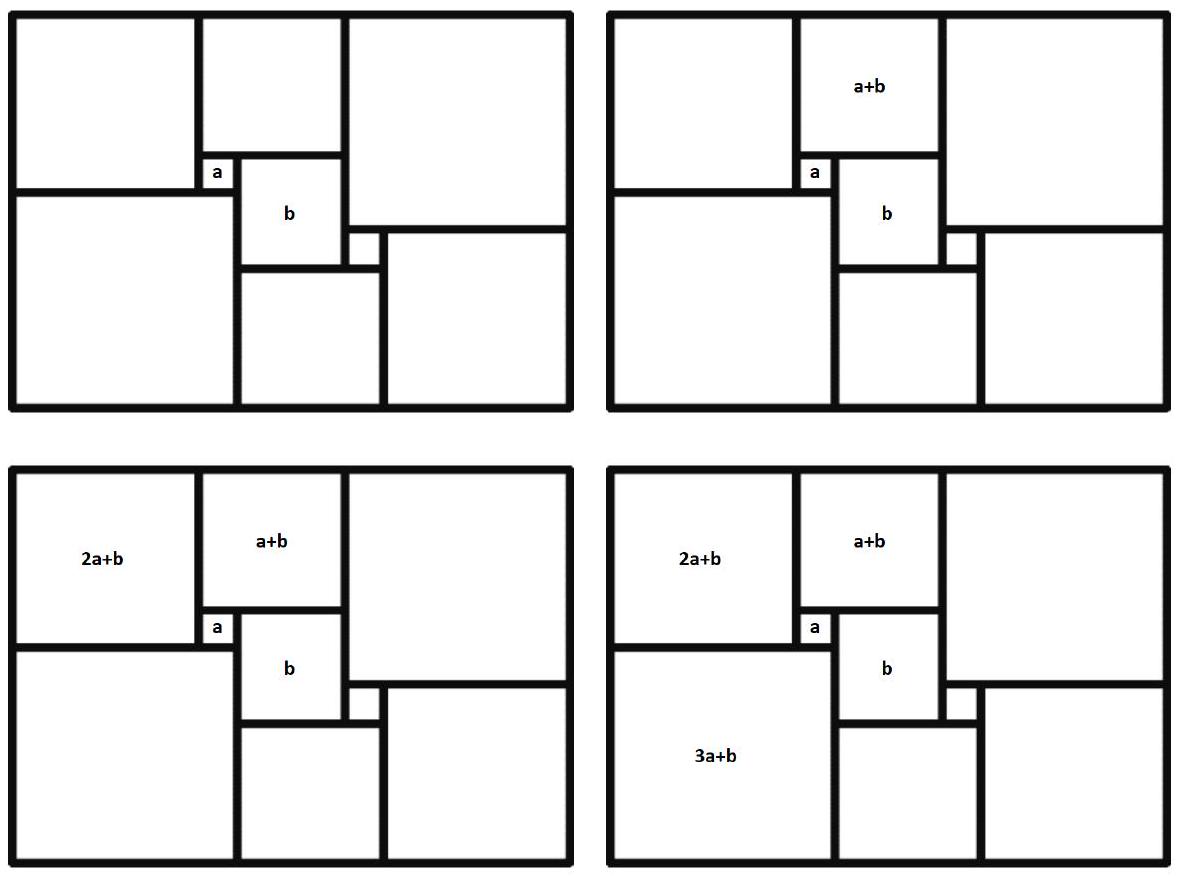
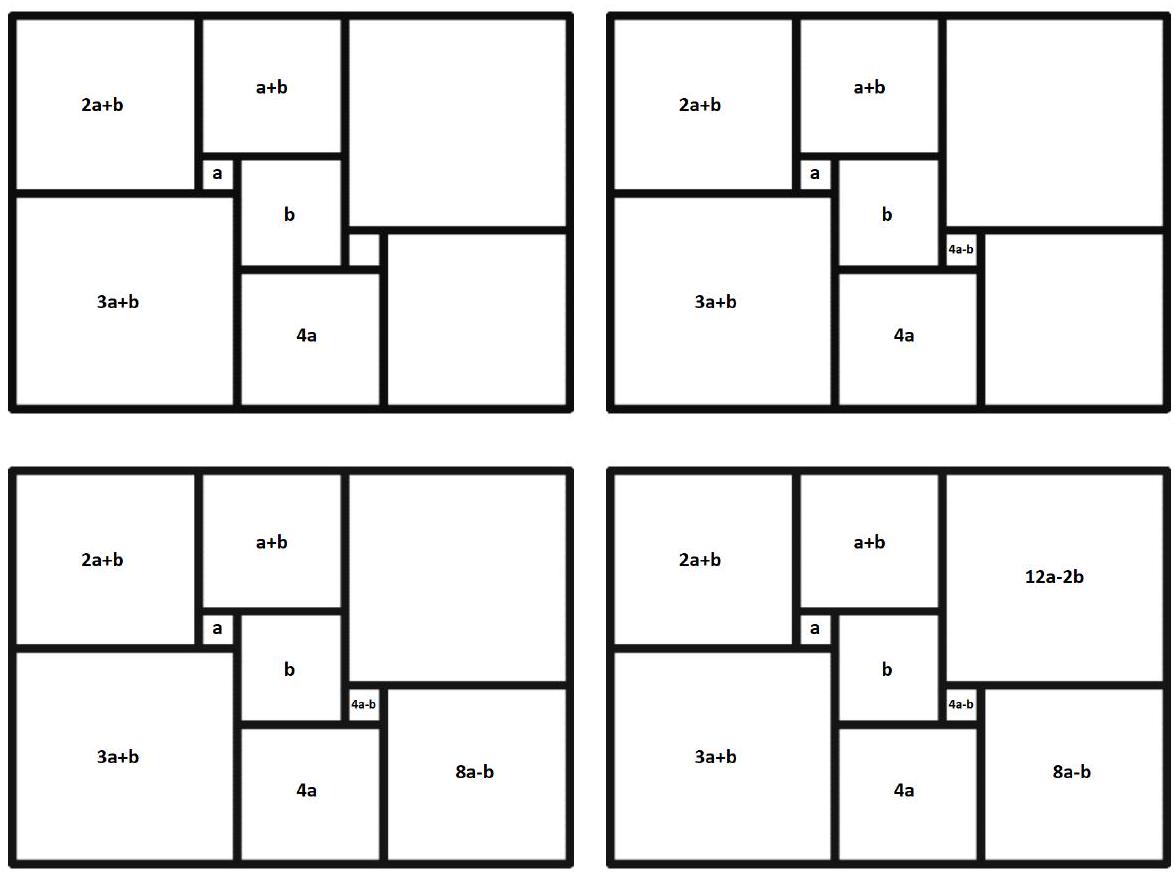
The sum of the lengths of the sides of the two squares adjacent to the left side of the rectangle is equal to the sum of the lengths of the sides of the two squares adjacent to the right side of the rectangle. We get the equation
$$
\begin{aligned}
(2 a+b)+(3 a+b) & =(12 a-2 b)+(8 a-b) \\
5 a+2 b & =20 a-3 b \\
b & =3 a
\end{aligned}
$$
Thus, to minimize the perimeter of the rectangle, we need to choose $a=1$, $b=3$. It is easy to check that with these values, the rectangle will have dimensions $11 \times 15$, and its perimeter will be 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. A square was cut into four equal rectangles, and from them, a large letter P was formed, as shown in the figure, with a perimeter of 56.
What is the perimeter of the original square
|
Answer: 32.
Solution. Let the width of the rectangle be $x$. From the first drawing, we understand that the length of the rectangle is four times its width, that is, it is equal to $4 x$. Now we can calculate the dimensions of the letter P.
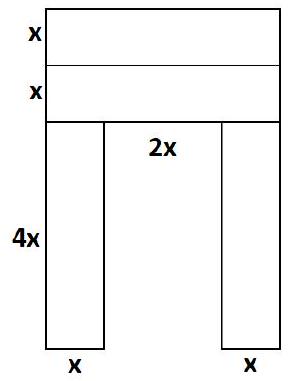
From this, we get the equation
$$
\begin{gathered}
28 x=56 \\
x=2
\end{gathered}
$$
The perimeter of the square is $16 x=32$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other diagonal is 21. What is the sum of the numbers in the five shaded cells?
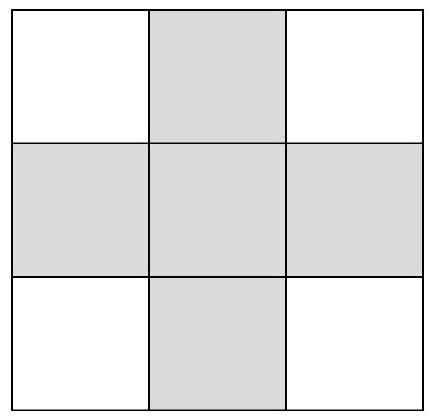
|
Answer: 25.
Solution. Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. For quadrilateral $ABCD$, it is known that $AB=BD, \angle ABD=\angle DBC, \angle BCD=90^{\circ}$. A point $E$ is marked on segment $BC$ such that $AD=DE$. What is the length of segment $BD$, if it is known that $BE=7, EC=5$?
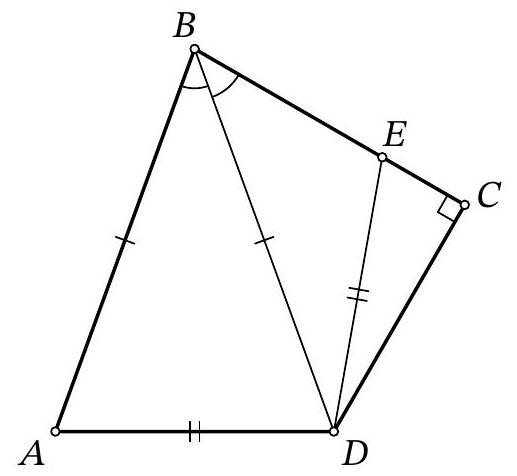
|
Answer: 17.
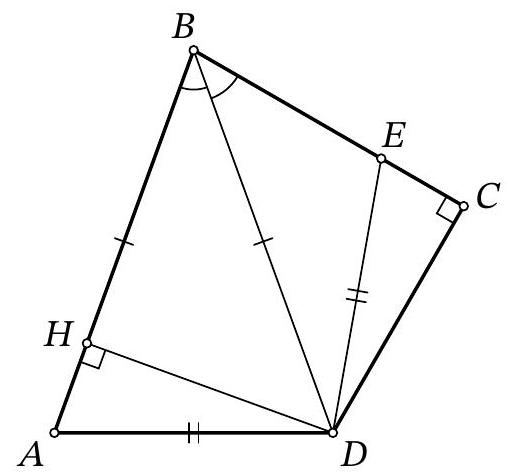
Fig. 3: to the solution of problem 8.6
Solution. In the isosceles triangle $ABD$, drop a perpendicular from point $D$, let $H$ be its foot (Fig. 3). Since this triangle is acute-angled ($\angle ABD = \angle CBD < 90^\circ$, $\left.\angle BAD = \angle ADB = \frac{180^\circ - \angle ABD}{2} < 90^\circ\right)$, point $H$ lies on the segment $AB$.
Notice that the right triangles $BDH$ and $BDC$ are equal by the common hypotenuse $BD$ and the acute angle at vertex $B$. Therefore, $BH = BC$ and $DH = CD$.
Now, notice that the right triangles $ADH$ and $EDC$ are also equal by the hypotenuse $AD = ED$ and the leg $DH = CD$. Therefore, $EC = AH$.
Thus, $BD = BA = BH + AH = BC + EC = (7 + 5) + 5 = 17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. From left to right, intersecting squares with sides $12, 9, 7, 3$ are depicted respectively. By how much is the sum of the black areas greater than the sum of the gray areas?
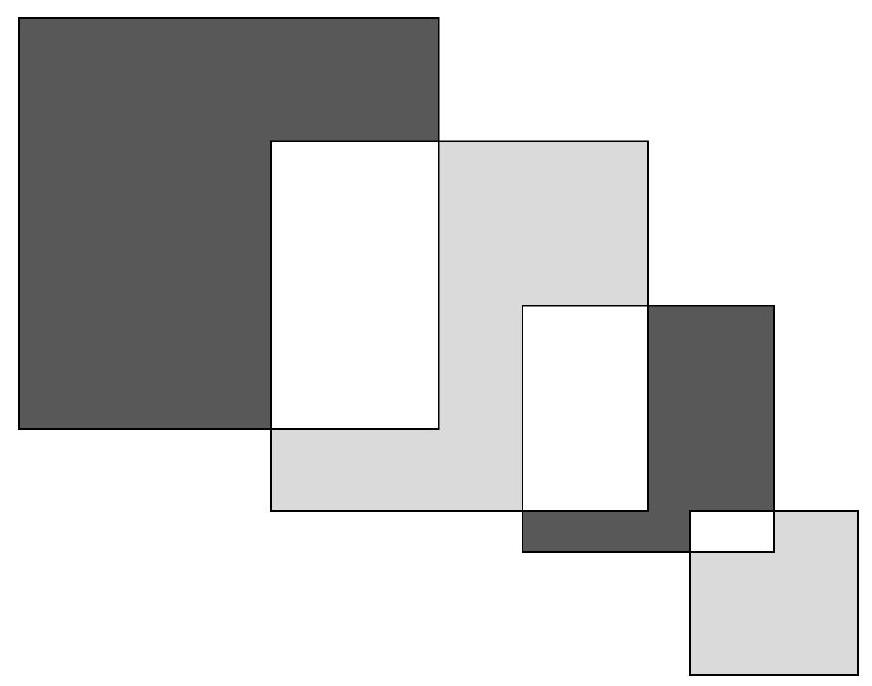
|
Answer: 103.
Solution. Let's denote the areas by $A, B, C, D, E, F, G$.
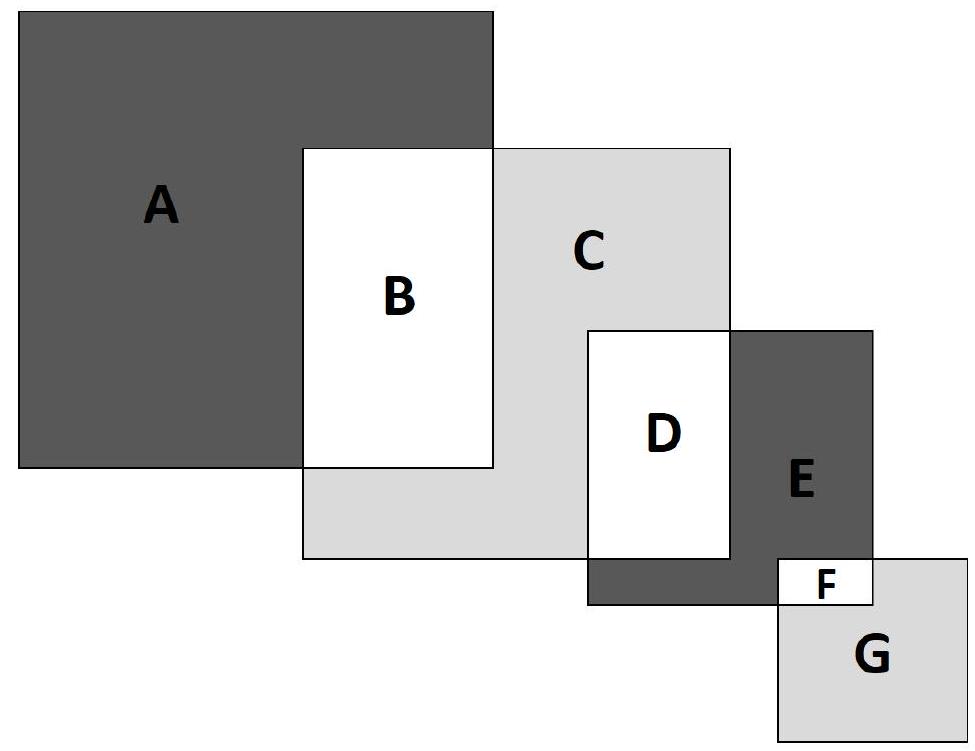
We will compute the desired difference in areas:
$$
\begin{aligned}
A+E-(C+G) & =A-C+E-G=A+B-B-C-D+D+E+F-F-G= \\
& =(A+B)-(B+C+D)+(D+E+F)-(F+G)= \\
& =12^{2}-9^{2}+7^{2}-3^{2}=103
\end{aligned}
$$
|
103
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
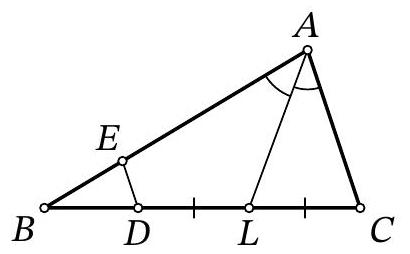
|
Answer: 3.
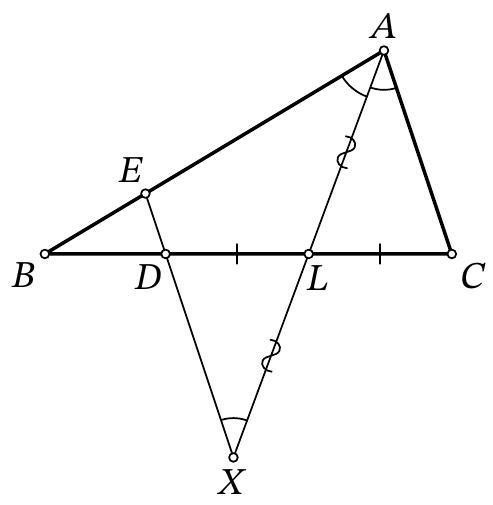
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
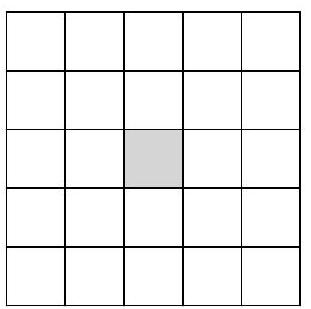
Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers located inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
|
Answer: 16.
Solution. Divide the $5 \times 5$ square without the central cell into four $2 \times 3$ rectangles, and each of these into two $1 \times 3$ rectangles.
We get 8 rectangles of $1 \times 3$, the sum of the numbers in each of which is 23. Since the sum of all the numbers is 200, we find the number in the central cell as $200 - 23 \cdot 8 = 16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. Rectangle $ABCD$ is such that $AD = 2AB$. Point $M$ is the midpoint of side $AD$. Inside the rectangle, there is a point $K$ such that $\angle AMK = 80^{\circ}$ and ray $KD$ is the bisector of angle $MKC$. How many degrees does angle $KDA$ measure?

|
Answer: 35.
Solution. Let's start with the assumption that the quadrilateral KMDС is inscribed (several proofs of this fact will be proposed below).
Using the fact that in the inscribed quadrilateral $K M D C$ the sum of opposite angles is $180^{\circ}$, we get $\angle M K D=\frac{\angle M K C}{2}=\frac{180^{\circ}-\angle M D C}{2}=45^{\circ}$. The angle $A M K$ as an external angle for triangle $K D M$ is equal to the sum of angles $M K D$ and $K D A$, so the required angle КDA is $80^{\circ}-45^{\circ}=35^{\circ}$.
Fig. 8: to the solution of problem 10.8
Let's provide the first possible proof of the inscribed nature of quadrilateral KMDC. Consider triangle $M K C$ and its circumscribed circle. Note that point $D$ lies on the bisector of angle $M K C$, and is equidistant from vertices $M$ and $C$ (Fig. 8). However, the bisector of an angle in a non-isosceles triangle and the perpendicular bisector of its opposite side, as is known, intersect at the midpoint of the "smaller" arc of the circumscribed circle of the triangle. In other words, $D$ is the midpoint of the arc $M C$ of the circumscribed circle of triangle $M K C$, not containing point $K$. It should also be noted that $M K \neq K C$ (otherwise, triangles $K M D$ and $K C D$ would be equal, but $\angle K M D>90^{\circ}>\angle K C D$ ).
Let's provide the second possible proof of the inscribed nature of quadrilateral KMDC. It will use the fourth criterion for the equality of triangles: if two sides and an angle not between them are equal in two triangles, then these triangles are either equal or the sum of the other two angles not between them is $180^{\circ}$. The fourth criterion is satisfied for triangles $M D K$ and $C D K (M D=D C, D K$ - common, $\angle M K D=\angle C K D)$. However, angles $K M D$ and $K C D$ are not equal (again, the first is obtuse, and the second is acute), so their sum is $180^{\circ}$, which are the opposite angles of quadrilateral KMDC. Therefore, it is inscribed.
## 11th grade
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. A natural number $n$ is called interesting if $2 n$ is a perfect square, and $15 n$ is a perfect cube. Find the smallest interesting number.
|
Answer: 1800.
Solution. Factorize the number $n$ into prime factors. For a number to be a square, it is necessary that all prime numbers in this factorization appear in even powers, and for a number to be a cube, it is necessary that all prime numbers appear in powers divisible by 3.
Let's look at the power of two that divides $n$. First, this power is odd, since $2 n$ is a perfect square. Second, this power is divisible by 3, since $15 n$ is a perfect cube. Therefore, the minimum power of two is 3.
Now let's look at the power of three that divides $n$. First, this power is even, since $2 n$ is a perfect square. Second, this power gives a remainder of 2 when divided by 3, since $15 n$ is a perfect cube. Therefore, the minimum power of three is 2.
Similarly, for five, we get that its minimum power is 2.
Therefore, $n$ is divisible by $2^{3} 3^{2} 5^{2}=1800$, i.e., $n \geqslant 1800$. It is not difficult to check that $n=$ 1800 satisfies all the conditions of the problem.
|
1800
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
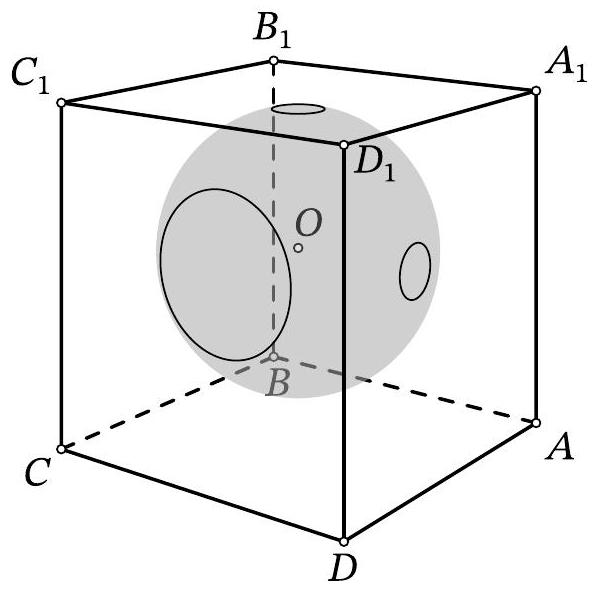
Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
|
Answer: 17.
Solution. Let $\omega$ be the circle that the sphere cuts out on the face $C D D_{1} C_{1}$. From point $O$
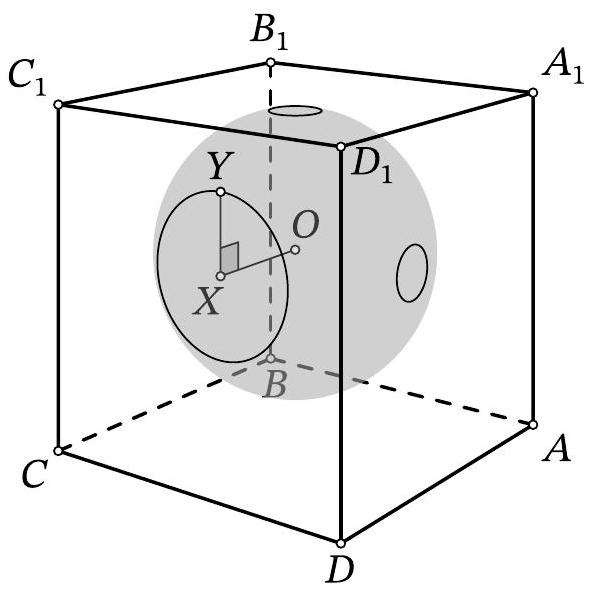
Fig. 10: to the solution of problem 11.6
drop a perpendicular $O X$ to this face, then point $X$ is the center of $\omega$ (point $O$ is equidistant from all points of $\omega$, so the projection of $O$ onto the plane of $\omega$ is also equidistant from them). Let $Y$ be an arbitrary point on $\omega$ (Fig. 10). Triangle $OXY$ is a right triangle; by the problem statement, $X Y=3$ and $O Y=10$. By the Pythagorean theorem, we get $O X^{2}=10^{2}-3^{2}=91$.
Similarly, we find the squares of the distances from point $O$ to the planes $A_{1} B_{1} C_{1} D_{1}$ and $A D D_{1} A_{1}$, which are both equal to $10^{2}-1^{2}=99$.
By the spatial Pythagorean theorem, the square of the length of segment $O D_{1}$ is equal to the sum of the squares of the distances from point $O$ to the three faces containing point $D_{1}$. Therefore, $O D_{1}^{2}=$ $91+99+99=289$, from which $O D_{1}=17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Dad is preparing gifts. He distributed 115 candies into bags, with each bag containing a different number of candies. In the three smallest gifts, there are 20 candies, and in the three largest gifts, there are 50 candies. How many bags are the candies distributed into? How many candies are in the smallest gift?
|
Answer: 10 packages, 5 candies.
Solution. Let's number the gifts from the smallest to the largest, from 1 to $n$. If the third gift has 7 or fewer candies, then the three smallest gifts have no more than $7+6+5=18$ candies. This contradicts the condition. Therefore, the third gift has at least 8 candies. Similarly, the third from the last gift has no more than 15 candies $(16+17+18=51>50)$.
Remove the three largest and the three smallest gifts. In the remaining gifts, there will be $115-20-$ $50=45$ candies, and each has between 9 and 14 candies. Three packages are clearly not enough $(14+13+12=39)$, and five would be too many $(9+10+11+12+13=55)$. Therefore, 45 candies are distributed in 4 packages. This is possible: $47=9+11+12+13$. Note that the fourth package cannot have more than 9 candies: $10+11+12+13=46>45$.
If the fourth package has 9 candies, then the third has no more than 8, the second no more than 7, so the first package has no less than $20-8-7=5$ candies. But no more than that, since $6+7+8=21$.
Criteria. Only the answer - 0 points. Only correct estimates for the third from the beginning and the third from the end package - 3 points. Only a justified answer for the number of packages - 5 points. Full solution - 7 points.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 It is known that $10 \%$ of people own no less than $90 \%$ of all the money in the world. For what minimum percentage of all people can it be guaranteed that these people own $95 \%$ of all the money?
|
Solution. Let $100 S$ be the total amount of money in the world (regardless of the currency), and the total number of people be $100 N$ (where $N$ can be non-integer, which is not important). Then at least $90 S$ of the money is owned by $10 N$ people (let's call this group oligarchs). The remaining $90 N$ people (let's call them commoners) have less than $10 S$ in total. Let's take the poorest half of the commoners. These $45 N$ people have no more than half of the money of all commoners, which is no more than $5 S$. Therefore, if we take all people except these $45 N$, they will have at least $95 S$ in total. There are $55 N$ such people, which is $55 \%$. We have proven that $55 \%$ of the richest people own $95 \%$ or more of all the money.
Let's provide an example showing that less than $55 \%$ may not be possible. Suppose there are 100 people, 10 of whom have 81 million each, and 90 have 1 million each. Then out of the total capital of 900 million, $90 \%$ (810 million) belongs to the first ten people, and the condition of the problem is satisfied. $95 \%$ of the capital is 855 million. To accumulate this amount, it is necessary to have the 55 richest people: $10 \cdot 81 + 45 \cdot 1$.
Answer: $55 \%$.
| IS IN THE SOLUTION | SCORE |
| :--- | :---: |
| Correct and justified answer | 7 points |
| The problem is correctly solved in specific monetary units (for example, assuming the total amount of money is 10000000000 yuan) | points not to be reduced |
| It is proven that $55 \%$ of the richest people own at least $95 \%$ of all the money, but there is no example showing the precision of the estimate, OR an example showing the precision of the estimate $55 \%$, but no proof that the example is optimal | 3 points |
| Examples where the "rich" people are more than $55 \%$ and/or more crude estimates than $55 \%$ are provided | 0 points |
|
55
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 Let $n$ - be a natural number greater than 10. What digit can stand immediately after the decimal point in the decimal representation of the number $\sqrt{n^{2}+n}$? Provide all possible answers and prove that there are no others.
|
Solution. Method 1. $n^{2}+n=(n+0.5)^{2}-0.2510$ ), the digit immediately after the decimal point is no less than 4. That is, it is 4.
Method 2. The required digit is the last digit in the number $\left[10 \sqrt{n^{2}+n}\right]=$ $\left[\sqrt{100 n^{2}+100 n}\right]$. Note that $100 n^{2}+100 n100 n^{2}+80 n+16=(10 n+4)^{2}$. Then $\left[\sqrt{100 n^{2}+100 n}\right]=$ $10 n+4$, and the last digit of this number is 4.
Method 3. We have $n+0.4$ solved incorrectly, which may have led to an incorrect answer | 5 points |
| One of the two statements is proven: a) the required digit is less than 5; b) the required digit is greater than 3; plus an example is provided showing that the digit 4 is possible | 4 points |
| One of the two statements is proven: a) the required digit is less than 5; b) the required digit is greater than 3 | 3 points |
| The problem is correctly reduced to a system of inequalities or to an equation with an integer part | 2 points |
| The correct answer is illustrated with an example showing that the digit 4 is possible | 1 point |
| The correct answer without justification or an incorrect answer | 0 points |
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the island of knights and liars (liars always lie, knights always tell the truth), each resident supports exactly one football team. In a survey, all residents of the island participated. To the question "Do you support 'Rostov'?", 40% of the residents answered "Yes". To a similar question about 'Zенit', 30% answered affirmatively, about 'Locomotive' - 50%, and about CSKA - 0%. What percentage of the island's residents actually support 'Rostov'?
|
Solution. Let $x \%$ of the island's inhabitants be liars. Then $(100-x) \%$ are knights. Since each knight answered affirmatively to exactly one of the questions, and each liar to three, we have $(100-x)+3 x=40+30+50$, from which $x=10$. Since none of the island's inhabitants said they support CSKA, all liars support CSKA. Each of them claimed to support "Rostov," so the actual supporters of "Rostov" are $40 \% - 10 \% = 30 \%$ of the population. Answer: $30 \%$.
|
30
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let quadrilateral $A B C D$ be inscribed. The rays $A B$ and $D C$ intersect at point K. It turns out that points $B, D$, and the midpoints $M$ and $N$ of segments $A C$ and $K C$ lie on the same circle. What values can the angle $A D C$ take?

|
Solution. Note that $MN$ is the midline in triangle $AKC$, so $\angle BAC = \angle NMC$. Moreover, $\angle BAC = \angle BDC$ since quadrilateral $ABCD$ is cyclic. Suppose points $M$ and $N$ lie on the same side of line $BD$. Then $M$ lies inside triangle $BCD$ and, therefore, inside triangle $BND$, and thus inside its circumcircle. However, this means that points $B, N, D$, and $M$ cannot lie on the same circle. Therefore, $N$ and $M$ lie on opposite sides of $BD$, and $\angle BDC = \angle BMN$.
From the parallelism of $MN$ and $AK$, it follows that $\angle BMN = \angle ABM$, hence $\angle BAC = \angle BDC = \angle ABM$. From this, we get $AM = MB$, meaning that in triangle $ABC$, the median $BM$ is equal to half the side $AC$. Therefore, $\angle ABC = 90^\circ$, and thus $\angle ADC = 90^\circ$. Answer: $90^\circ$.
Comment. If the solution is correct but lacks reasoning about the positions of points $N$ and $M$ relative to segment $BD$, deduct 2 points.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A student drew an empty $50 \times 50$ table and wrote a number above each column and to the left of each row. It turned out that all 100 written numbers are distinct, with 50 of them being rational and 50 being irrational. Then, in each cell of the table, he wrote the product of the numbers written next to its row and its column (as in a multiplication table). What is the maximum number of products in this table that could be rational numbers?
|
Solution. We will show that there are no fewer than 1225 irrational numbers in the table. Suppose that among the rational numbers there is zero, and it is written on the upper side of the table.
Let along the left side of the table there be $x$ irrational and $50-x$ rational numbers. Then along the upper side, there are $50-x$ irrational numbers and $x$ rational numbers, including 0. Note that the product of a non-zero rational and an irrational number is always irrational. Therefore, in the table, there are at least $x(x-1)+(50-x)^{2}$ irrational numbers. Consider the function $f(x)=x(x-1)+(50-x)^{2}=2 x^{2}-101 x+2500$. The vertex of the parabola $f(x)$ is at the point with abscissa $\frac{101}{4}=25.25$, so the minimum value of $f(x)$ at an integer point is achieved at $x=25$ and it is equal to $25 \cdot 24+25^{2}=1225$.
If we replace zero with a non-zero rational number, the number of irrational numbers will only increase. Therefore, in the table, there are at least 1225 irrational numbers in any case. This means that in the table there are no more than $2500-1225=1275$ rational numbers.
It remains to provide an example of a table with 1275 rational numbers. If along the left side we write the numbers $1,2, \ldots, 24,25, \sqrt{2}, 2 \sqrt{2}, \ldots, 24 \sqrt{2}, 25 \sqrt{2}$, and along the upper side we write the numbers $0,26,27, \ldots, 49,26 \sqrt{2}, 27 \sqrt{2}, \ldots, 50 \sqrt{2}$, then the only irrational numbers will be $25 \cdot 24+25^{2}=1225$ products of non-zero rational and irrational numbers. Answer: 1275.
|
1275
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the sum $\sin x + \sin y + \sin z$, given that $\sin x = \tan y$, $\sin y = \tan z$, $\sin z = \tan x$.
|
Answer: 0.
First solution. From $\sin x = \tan y$, we get $\sin x \cos y = \sin y$. Therefore, $|\sin x| \cdot |\cos y| = |\sin y|$. This means $|\sin x| \geq |\sin y|$, and the inequality becomes an equality only if either $\sin y = \sin x = 0$, or $|\cos y| = 1$ (which again implies $\sin y = \sin x = 0$). Similarly, from the remaining equations, we obtain the inequalities $|\sin y| \geq |\sin z|$ and $|\sin z| \geq |\sin x|$. Thus, $|\sin x| \geq |\sin y| \geq |\sin z| \geq |\sin x|$. Therefore, $|\sin x| = |\sin y| = |\sin z|$. Since all inequalities have become equalities, we have $\sin x = \sin y = \sin z = 0$, and $\sin x + \sin y + \sin z = 0$.
Second solution. If one of the sines is zero, then the tangent equal to it is also zero, which means the sine in the numerator of the tangent is zero. Consequently, the other sines and tangents are also zero. In this case, $\sin x + \sin y + \sin z = 0$.
Suppose none of the sines are zero. Multiplying all three equations, we get $\sin x \sin y \sin z = \tan y \tan z \tan x = \frac{\sin x \sin y \sin z}{\cos x \cos y \cos z}$. Since $\sin x \sin y \sin z \neq 0$, we have $\cos x \cos y \cos z = 1$. This is only possible if $|\cos x| = |\cos y| = |\cos z| = 1$, which means the sines are zero, and the considered case is impossible.
Comment. A correct answer without justification - 0 points.
An answer obtained by considering an example - 1 point.
At least one case is incorrectly considered (or omitted) - no more than 3 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) An apprentice chef took two buckets of unpeeled potatoes and cleaned everything in an hour. In the process, $25 \%$ of the potatoes went into peels. How long did it take for him to accumulate exactly one bucket of peeled potatoes?
|
Solution. Since a quarter of the potatoes went into peels, then in one hour, three quarters of two buckets of cleaned potatoes were obtained. This means that in one hour, the trainee cook got $\frac{3}{2}$ buckets, and exactly one bucket in 40 minutes.
Answer. 40 minutes.
## Comments on Evaluation.
Correct answer only - 1 point.
Correct reasoning - 2 points.
Correct approach, but an arithmetic error was made (with a reasonable answer) - 5 points.
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) 13 children sat at a round table and agreed that boys would lie to girls, but tell the truth to each other, and girls, on the contrary, would lie to boys, but tell the truth to each other. One of the children said to their right neighbor: "The majority of us are boys." That child said to their right neighbor: "The majority of us are girls," and that one to their right neighbor: "The majority of us are boys," and so on, until the last child said to the first: "The majority of us are boys." How many boys are at the table?
|
Solution. It is clear that there were both boys and girls at the table. Let's see how the children were seated. A group of boys sitting next to each other is followed by a group of girls, then boys again, then girls, and so on (a group can consist of just one person). Groups of boys and girls alternate, so their number is even. Since the statement "most of us are boys" was heard seven times, six of the statements "most of us are girls" were false, and there were six groups.
The alternation of true and false statements means that there were two children in each group. Only the first and last child sitting next to each other said the same thing, so there were three people in their group. These are boys, as they are in the majority. In total, there were $2+2+2=6$ girls and $2+2+3=7$ boys sitting at the table.
The diagram shows exactly how the children were seated at the table. The first speaker is outlined in a frame.
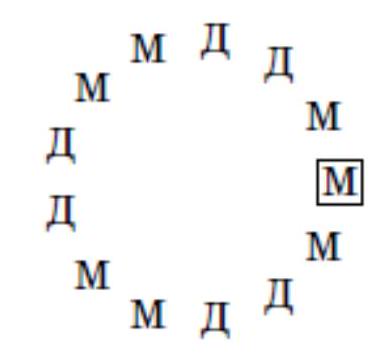
Answer. 7.
Maximum points - 35.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. There are more than 20 but fewer than 30 people in the class, and everyone has a different birthday. Petya said: "There are twice as many people older than me as there are younger than me in the class." Katya said: "There are three times fewer people older than me as there are younger than me in the class." How many people are in the class if Petya and Katya are both correct?
|
Answer: 25.
Solution: From Petya's words, it is clear that without him, the number of students in the class is a multiple of 3 (2 parts + 1 part). That is, together with him, there can be 22, 25, or 28 people in the class. Similarly, from Katya's words, it is clear that without her, the number of students in the class is a multiple of 4. The numbers that fit are 21, 25, 29. Since both statements are true, the number that satisfies both conditions is 25.
Grading criteria: Correct answer with verification - 1 point.
If the solution is by enumeration and one of the cases from 21 to 29 is missed without explanation, then 1 point.
Correct answer with all necessary explanations - 7 points.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Three three-digit numbers, in the notation of which all digits except zero participate, add up to 1665. In each number, the first digit was swapped with the last digit. This resulted in three new three-digit numbers. What is the sum of the new numbers
|
Solution: The sum of the last digits of the three original numbers is 5, 15, or 25. However, 5 and 25 are excluded, as they cannot be represented as the sum of three different digits (from 1 to 9), so 15 remains. Therefore, the sum of the middle digits is also 15, and the sum of the first digits is 15. It then becomes clear that by rearranging the digits, we will again obtain three numbers whose sum is 1665.
Finally, let's present a triplet of numbers (one of the possible ones) that
satisfies the conditions of the problem: $159, 672, 834$.
Answer: 1665.
Grading criteria: Correct answer with all necessary explanations 7 points. Presenting a triplet of numbers that satisfy the conditions of the problem is not mandatory. Their existence follows from the problem's conditions.
|
1665
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Petya cut an $8 \times 8$ square along the cell boundaries into parts of equal perimeter. It turned out that not all parts were equal. What is the maximum number of parts he could have obtained?
#
|
# Answer: 21.
Solution: Let $S$ be the smallest area among the figures obtained by Petya.
If $S=1$, then this figure is a $1 \times 1$ square and its perimeter is 4. Then all of Petya's figures have a perimeter of 4, meaning they are all $1 \times 1$ squares. But this means that all figures are equal, which contradicts the condition.
Similarly, if $S=2$, then this figure is a $2 \times 1$ rectangle and its perimeter is 6. Then all of Petya's figures have a perimeter of 6, meaning they are all $2 \times 1$ rectangles. But this means that all figures are equal, which contradicts the condition.
If $S=3$, then the total number of figures is no more than $64 / 3$, meaning no more than 21. An example with 21 figures is easy to construct - from 10 $2 \times 3$ rectangles, each made of two L-shaped figures of three cells, and one $2 \times 2$ square. Both the L-shaped figure and the square have a perimeter of 8.
Finally, if $S \geq 4$, then the number of figures is no more than $64 / 4 = 16$.
Grading criteria: Correct answer with all necessary explanations 7 points.
If it is proven that there are no more than 21 figures, but no example of cutting is provided - 5 points.
If an example of cutting into 21 parts is provided, but it is not proven that more is impossible - 2 points.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the table, there are 4 stacks of coins. The first stack has 9 coins, the second has 7, the third has 5, and the fourth has 10. In one move, you are allowed to add one coin to three different stacks. What is the minimum number of moves required to make the number of coins in all stacks equal?
#
|
# Answer: in 11 moves.
Solution 1. Consider the differences between the number of coins in each of the other stacks and the number of coins in stack No. 3. In one move, either each of these differences increases by 1 (if all stacks except 3 are chosen for adding coins), or exactly 1 of these differences decreases by 1 (in other cases). Initially, these differences are 4, 2, and 5. Thus, to reduce all these differences to 0, it will take no less than $4+2+5=11$ moves.
11 moves are possible: 4 times we choose all stacks except No. 1, 2 times all stacks except No. 2, and 5 times all stacks except No. 4. In the end, there will be 16 coins in each stack.
Solution 2. Let us say we have made $s$ moves, of which $s_{\mathrm{k}}$ moves involve adding a coin to all stacks except $\mathrm{k}(\mathrm{k} \in\{1,2,3,4\})$. Then, from the condition that the number of coins in all stacks is equal after all moves, we get: $9+\mathrm{s}-\mathrm{s}_{1}=7+\mathrm{s}-\mathrm{s}_{2}=5+\mathrm{s}-\mathrm{s}_{3}=10+\mathrm{s}-\mathrm{s}_{4}$. Therefore, $s_{1}=4+s_{3} \geq 4, s_{2}=2+s_{3} \geq 2$ and $s_{4}=5+s_{3} \geq 5$. Thus, $s \geq s_{1}+s_{2}+s_{4} \geq 4+2+5=11$. An example of 11 moves is the same as in Solution 1.
Criteria. Only the answer - 1 point. Answer with an example - 3 points. Only proof that the number of moves is no less than 11 - 4 points.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Find the largest natural number, all digits of which are different, and the product of these digits is a square of a natural number.
|
Answer: 986431. Solution: Obviously, among these digits there is no zero. Further, we have $1 \cdot 2 \cdot \ldots \cdot 9=2^{7} \cdot 3^{4} \cdot 5^{1} \cdot 7^{1}$. Therefore, we need to remove the digits 5 and 7, and also need to make the odd power of two even. This means we need to remove the digit 2: obviously, we should not remove the digits 6 and 8, as we need the maximum result. Clearly, the remaining digits should be arranged in descending order: 986431. As a result, the product of these digits will be $5184=(72)^{2}$.
|
986431
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the pop ensemble "Sunshine," everyone plays either the violin or the double bass. The average age of those who play the violin is 22 years, and those who play the double bass is 45 years. Igor changed his instrument and started playing the violin instead of the double bass. As a result, the average age of those who play the violin increased by 1 year, and the average age of those who play the double bass also increased by 1 year. How many people are in the ensemble "Sunshine"? Answer: 23.
|
Solution. Let $x$ be the number of people who play the contrabass, excluding Igor, and $y$ be the number of people who play the violin (also excluding Igor).
From the condition, it follows that the total age of those who play the contrabass was initially equal to: $(x+1) \cdot 45$, and when Igor changed the instrument, it became equal to $x \cdot 46$.
Then Igor's age is $(x+1) \cdot 45 - x \cdot 46 = 45 - x$.
Similarly, we get that Igor's age is $23 \cdot (y+1) - 22 \cdot y = y + 23$.
Then $45 - x = y + 23$, from which $x + y = 22$ is the number of pirates without Igor, and with Igor - 23.
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. 3.1. Find the number of four-digit numbers composed of the digits $1,2,3,4,5,6,7$ (each digit is used no more than once) that are divisible by 15.
|
Answer: 36.
Solution.
For a number to be divisible by 15, it must be divisible by 3 and by 5. Therefore, according to the divisibility rule for 5, the last digit can only be 5. The sum of the digits of the number must be divisible by 3. For this, the sum of the first three digits must give a remainder of 1 when divided by 3 (since 5 gives a remainder of 2 when divided by 3). Let's exclude 5 and replace the numbers with their remainders when divided by 3: 1, 2, 0, 1, 0, 1. To get a remainder of 1, we can:
1) choose two ones and a two (3 ways);
2) choose one and two zeros (3 ways).
In total, there are 6 ways. Note that we did not count any of the ways twice. The 3 chosen digits can be arranged in the number in $3 \cdot 2 \cdot 1=6$ ways. Therefore, the total number of such numbers is $6 \cdot 6=36$.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. 4.1. In a right triangle $ABC$ (right angle at $C$), the bisector $BK$ is drawn. Point $L$ on side $BC$ is such that $\angle CKL = \angle ABC / 2$. Find $KB$, if $AB = 18, BL = 8$.
|
Answer: 12.
## Solution.
Note that $\angle L K B=\angle C K B-\angle C K L=\angle C A B+\angle A B K-\angle C K L$ (the last equality holds because $\angle C K B$ is an exterior angle of triangle $A B K$). Since $\angle C K L=\angle A B C / 2=\angle A B K$, we have that $\angle L K B=\angle C A B$. From the fact that $\angle A B K=\angle K B L$, we conclude that triangles $K L B$ and $A K B$ are similar by two angles. We obtain the equality of ratios $\frac{K B}{B L}=\frac{A B}{K B}$. Therefore, $K B=\sqrt{B L \cdot A B}=\sqrt{18 \cdot 8}=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. 5.1. Find the largest natural number in which all digits are different and any two adjacent digits differ by 6 or 7.
|
Answer: 60718293.
## Solution.
We will map each digit from 0 to 9 to a vertex in a graph and connect the vertices with an edge if the corresponding digits differ by 6 or 7.
We see that the vertices corresponding to the digits 4 and 5 are not connected to anything, so the maximum number that can be obtained will be 8 digits long. The vertices corresponding to the digits 3 and 6 can only be the first or last in the number. Since we need to find the maximum number, it is uniquely determined by moving along the edges of the graph and will be equal to 60718293.
|
60718293
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. 6.1. The figure "lame rook" can move to an adjacent cell in one move. On a $20 \times 20$ board, crosses were placed in all cells that the "lame rook" can reach from the top-left corner in exactly 10 moves. How many cells were marked with a cross?
|
Answer: 36.
## Solution.
Let's set up a coordinate system so that the top-left cell has coordinates $(0,0)$. In one move, the sum of the rook's coordinates changes by 1. In 10 moves, the sum of the coordinates cannot exceed 10, and it will become an even number.
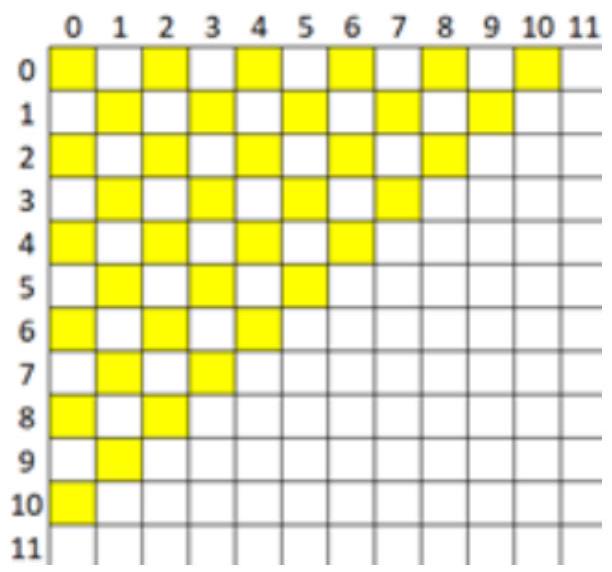
Thus, only the shaded cells on the diagram can be marked with a cross. It is clear that the shaded cells will be marked. Their number is 36. 6.2. The figure "crippled rook" can move to an adjacent cell in one move. On a $20 \times 20$ board, crosses were placed in all cells that the "crippled rook" can reach from the top-left corner in exactly 12 moves. How many cells were marked with a cross?
Answer: 49.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. 7.1. The line $y=M$ intersects the graph of the function $y=x^{3}-84 x$ at points with abscissas $a$, $b$, and $c$ ($a<b<c$, see the figure). It turned out that the distance between $a$ and $b$ is half the distance between $b$ and $c$. Find $M$.
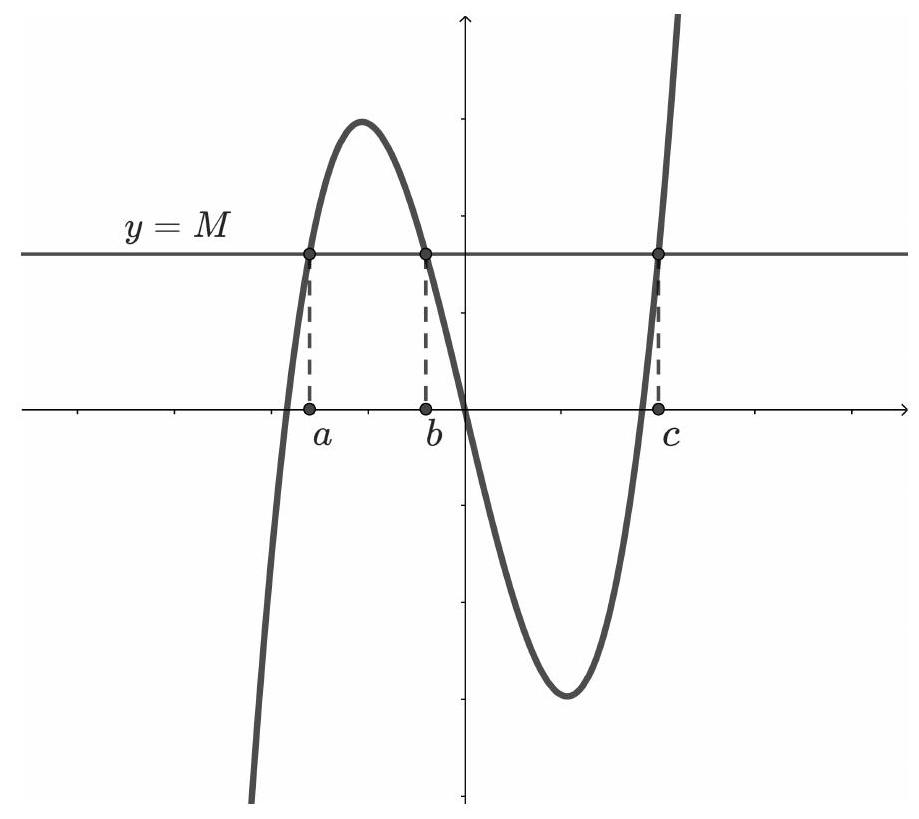
|
Answer: 160.
## Solution.
1st method. Since the coordinates of the intersection points $a, b$, and $c$ satisfy the equation $x^{3}-84 x-M=0$, by Vieta's theorem, we have the following equalities: $a+b+c=0$ (1), $ab+bc+ac=-84$ (2), $abc=M$ (3). According to the condition, $2(b-a)=c-b$ or $3b=c+2a$. Considering (1), $c=-5b, a=4b$. Substituting into (2): $-5b^{2}+4b^{2}-20b^{2}=-84$, from which we find $b^{2}=4$. Considering that $a$ and $b$ are negative, $b=-2, a=-8, c=10$. Substituting into (3) $M=(-2) \cdot(-8) \cdot 10=160$.
2nd method. Substituting $a, b, c$ for $x$ in the cubic polynomial equation, we get $a^{3}-84a=M, b^{3}-84b=M, c^{3}-84c=M(1)$. Subtracting the first equation from the second, the second from the third, and the third from the first, and dividing the resulting equations by $b-a, c-b$, and $a-c$, respectively, we obtain the following equalities: $a^{2}+ab+b^{2}=84, b^{2}+bc+c^{2}=84, a^{2}+ac+c^{2}=84$. Subtracting the first from the second, we get $b^{2}-a^{2}+b(c-a)+c^{2}-b^{2}=0$. After combining like terms and dividing by $c-a$, we obtain the equality $a+b+c=0$ (2).
According to the condition, $2(b-a)=c-b$ or $3b=c+2a$. Considering (2), $a=4b, c=-5b$.
Adding the equations (1) $a^{3}+b^{3}+c^{3}-84(a+b+c)=3M$, and considering (2), we get $a^{3}+b^{3}+c^{3}=3M$. Substituting the previously obtained values for $a$ and $c$, we then have $-125b^{3}+b^{3}+64b^{3}=3M$, from which $M=-20b^{3}$. Substituting the found $M$ into expression (1): $b^{3}-84b=-20b^{3}$. Solving this equation for $b$, considering that $b<0$, we get $b=-2$. Then $M=160$.
|
160
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. 8.1. How many increasing arithmetic progressions of 22 different natural numbers exist, in which all numbers are no greater than 1000?
|
Answer: 23312.
## Solution.
Consider the 22nd term of each such progression, it will have the form $a_{22}=a_{1}+21d$. This means that $a_{1}$ and $a_{22}$ will have the same remainders when divided by 21. Each pair of numbers not exceeding 1000, giving the same remainders when divided by 21, defines one of the required progressions, since to construct a progression it is sufficient to divide the segment between $a_{1}$ and $a_{22}$ on the number line into 21 equal parts. Let's find the number of such pairs. Since $1000=21 \cdot 47+13$, 13 remainders occur 48 times and 8 remainders 47 times. Then the number of the required progressions will be equal to $13 \cdot C_{48}^{2}+8 \cdot C_{47}^{2}=$ $\frac{13 \cdot 48 \cdot 47}{2}+\frac{8 \cdot 47 \cdot 46}{2}=23312$.
|
23312
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Indicate the smallest number ending in 37 with the sum of its digits equal to 37 and divisible by 37.
|
Answer: 99937.
Solution. The number is the smaller, the fewer digits are required to write it. Two digits - these are the last two digits, their sum is 10. Therefore, the sum of the other digits is 27, and there are at least three of them, since the largest digit is 9. Thus, the number 99937 satisfies three of the four requirements. It remains to check that it is divisible by
|
99937
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Cyclists Petya, Vlad, and Timur simultaneously started a warm-up race on a circular cycling track. Their speeds are 27 km/h, 30 km/h, and 32 km/h, respectively. After what shortest time will they all be at the same point on the track again? (The length of the cycling track is 400 meters.)
|
Answer: 24 min.
Solution. Vlad rides 3 km/h faster than Petya. Therefore, he will overtake him by one lap (i.e., ride 400 m more) in $\frac{0.4}{3}$ h $=8$ min. Timur rides 2 km/h faster than Vlad. Therefore, he will overtake him by one lap in $\frac{0.4}{2}$ h $=12$ min. The least common multiple of the numbers 8 and 12 is 24.
Grading. 7 points for the correct solution.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the rebus
$$
\mathbf{K}\mathbf{O}>\mathbf{H}>\mathbf{A}>\mathbf{B}>\mathbf{U}>\mathbf{P}>\mathbf{y}>\mathbf{C}
$$
different letters represent different digits. How many solutions does the rebus have?
|
Answer: 0.
Solution. From the rebus, it follows that $\mathbf{P}>\mathbf{O}>\mathbf{P}$. This cannot be! Evaluation. 7 points for the correct solution.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Karlson counts 1000 buns baked by Fräulein Bock: «one, two, three, ..., nine hundred ninety eight, nine hundred ninety nine, thousand». How many words will he say in total? (Each word is counted as many times as it was said.)
|
Answer: 2611.
Solution. One word will be required to pronounce 37 numbers: $1,2,3,4,5,6,7$, $8,9,10,11,12,13,14,15,16,17,18,19,20,30,40,50,60,70,80,90,100,200,300,400$, $500,600,700,800,900,1000$.
Among the first 99 numbers, the number of those pronounced in two words: $99-27=72$, thus, the number of words required for their pronunciation is $2 \cdot 72=144$.
In each subsequent hundred (there are 9 of them), each number that is pronounced in one word in the first hundred will be pronounced in two, and the number of words is $9 \cdot 2 \cdot 27=486$. The rest are pronounced in three words: $9 \cdot 3 \cdot(99-27)=1944$.
Thus, to count all the cookies, $37+144+486+1944=2611$ words will be needed.
## Criteria.
1 point. The number of numbers pronounced in one word is found and justified.
2 points. The number of words required to pronounce numbers from 1 to 99 is found and justified correctly.
2 points. The number of words required to pronounce numbers in any hundred after 100 is found and justified correctly.
Comment. Points for the criteria above are cumulative.
3 points. The correct answer without justification.
|
2611
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. A semicircle with diameter $A B$ and center at point $O$ is divided by points $C$ and $D$ into three parts such that point $C$ lies on the arc $A D$. Perpendiculars $D E$ and $D F$ are dropped from point $D$ to segments $O C$ and $A B$ respectively. It turns out that $D E$ is the angle bisector of triangle $A D C$, and $D O$ is the angle bisector of triangle $A D F$. Find the angle $C A D$.
|
Answer: $20^{\circ}$.
Solution. Triangle $A O D$ is isosceles ($O D=O A$, as radii), hence, $\angle O A D=\angle O D A$. Since $D O$ is the bisector of angle $A D F$, then $\angle O A D=\angle O D F$. Calculation of angles in the right triangle $A F D$ shows that $\angle O A D=30^{\circ}$. Let $G$ be the point of intersection of segments $A D$ and $O C$. Segment $D E$ is the height and bisector in triangle $D G C$. Therefore, triangle $D G C$ is isosceles with angle $E C D$ at the base. Triangle $O C D$ is also isosceles with angle $E C D$ at the base, hence, the angles at the vertices of these two triangles are also equal, i.e., $\angle C D G=\angle C O D$. Let $\angle C D G=\angle C O D=a$, then $\angle G C D=\angle O D C=30^{\circ}+a$. By calculating the sum of the angles in triangle $C O D$, we get that $a=40^{\circ}$. The required angle $\angle C A D$ is inscribed and subtends the same arc as the central angle $\angle D O C$, therefore, $\angle C A D=20^{\circ}$.
## Criteria.
7 points. A complete and justified solution is provided.
2 points. Only the value of $\angle O A D$ is found.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Seryozha decided to start eating properly and every day he ate one fewer chocolate cookie and one more sugar-free cookie than the previous day. In total, during the time of proper nutrition, he ate 264 chocolate cookies and 187 sugar-free cookies. How many days was Seryozha on a proper diet?
|
Answer: 11 days.
Solution 1. The total number of cookies eaten each day is the same. In total, Seryozha ate $264+187=451=11 \cdot 41$ cookies. Since the proper diet lasted more than one day and he ate more than one cookie each day, either he ate for 11 days, 41 cookies each day, or for 41 days, 11 cookies each day. But since the number of sugar-free cookies increased by 1 each day, in the second case, it would have exceeded 11 on one of the days. Therefore, this case is impossible.
Solution 2. If we "reverse" the sequence of the number of chocolate cookies, while leaving the sugar-free cookies unchanged, the total number of cookies will not change, but the difference between the number of chocolate cookies and sugar-free cookies eaten each day will become constant. Since $264-187=77=7 \cdot 11$, the proper diet lasted either 7, 11, or 77 days. Since the number of days is odd, the total number of cookies eaten is the product of the number of days and the number of cookies eaten on the middle day. But 264 is not divisible by 7, so the number of days cannot be 7 or 77.
Criteria. Full solution - 7 points. Not justified why there cannot be a different number of days, but the rest is correct - 5 points. Only the answer - 1 point. The problem assumes that the event has already occurred, so the student is not required to provide an example of how Seryozha could have eaten this way.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. At the factory, there are exactly 217 women, among whom 17 are brunettes, and the remaining 200 are blondes. Before New Year's, all of them dyed their hair, and each of these women wrote in "VK" the surnames of exactly 200 women from the factory, whom they believed to be definitely blondes. Each of the brunettes correctly identified all the blondes, while each blonde could indicate anyone except herself. Prove that based on these data, it is possible to identify at least 13 blondes.
|
Solution: According to the problem, the correct list of all 200 blondes will be on "Vkontakte" exactly for 17 female workers at the plant: brunettes will write exactly this list, and a blonde will never write it, as otherwise she would have to include herself in it. Therefore, if a certain list appears not 17 times but any other number, it is incorrect and was written by a blonde. Remove all lists that appear exactly 17 times. There will be $217-17n$ lists left. $217-17n \geqslant 0$, so $n \leqslant 12$ (we remember that $n$ is a natural number). Then at least $217-12 \cdot 17=13$ lists remain, and we have identified at least 13 of their authors, who are blondes. Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct proof | 7 points |
| It is justified that the correct list of blondes appears exactly 17 times (without further progress) | 4 points |
| It is justified that the correct list of blondes appears at least 17 times (without further progress) | 2 points |
| There is only the idea of identifying blondes as the authors of incorrect lists | 1 point |
| Any ideas that do not lead to proof | not evaluated |
|
13
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. Three bear cubs were dividing three pieces of cheese weighing 10 g, 12 g, and 15 g. A fox came to help them. She can simultaneously bite and eat 1 g of cheese from any two pieces. Can the fox leave the bear cubs equal pieces of cheese?
|
Answer: She can.
Solution. Let's provide one of the possible examples of how the fox could do it. For convenience, let's record the results of the fox's "work" in a table.
| 10 | 12 | 15 |
| :---: | :---: | :---: |
| 9 | 12 | 14 |
| 8 | 12 | 13 |
| 7 | 12 | 12 |
| 7 | 11 | 11 |
| 7 | 10 | 10 |
| 7 | 9 | 9 |
| 7 | 8 | 8 |
| 7 | 7 | 7 |
How one might guess the solution. First, try to equalize only two pieces of cheese, and then all three.
## Grading Criteria.
- Correct algorithm (regardless of length, written in words or in a table) - 7 points.
- Generally correct algorithm with missing steps - **5** points.
- Shows how to equalize two pieces, but no further progress - 2 points.
- Only the answer "yes" or "she can" - **0** points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the underwater kingdom, there live octopuses with seven and eight legs. Those with 7 legs always lie, while those with 8 legs always tell the truth. One day, a conversation took place between three octopuses.
Green octopus: "We have 21 legs together." Blue octopus (to the green one): "You're lying!" Red octopus: "Both of you are lying!"
1) Could the green octopus have told the truth? Why?
2) How many legs did each octopus have? (Justify your answer.)
|
Answer. 1) Could not.
2) The green octopus has 7 legs, the blue one has 8 legs, and the red one has 7 legs.
Solution.
1) If the green octopus had told the truth, then each octopus would have 7 legs. This means that the green octopus, according to the condition, should have lied. We get a contradiction, so the green octopus lied.
2) Since the green octopus lied, it has 7 legs. The blue octopus told the truth about the green one, so it has 8 legs. The red octopus lied because not both but only one in front of him lied, so the red one has 7 legs.
## Grading Criteria.
- Correct solution for both parts - 7 points.
- Correct solution for the first part + partial solution for the second - 4-5 points.
- Correct solution for the first part - 3 points.
- Partially correct but incomplete reasoning - 1-2 points.
- Only answers for all parts - $\mathbf{0}$ points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Private Petrov took a bucket of unpeeled potatoes and cleaned them in 1 hour. In the process, $25 \%$ of the potatoes went into peels. How long did it take for him to have half a bucket of peeled potatoes?
|
Answer. In 40 minutes.
Solution. Since a quarter of the potatoes went into peels, Petrov received three quarters of a bucket of peeled potatoes in 1 hour. This means that a quarter of a bucket of peeled potatoes Petrov received in 20 minutes, and half a bucket - in 40 minutes.
## Grading Criteria.
- Correct solution - 7 points.
- Correct approach, but an arithmetic error at the end of the solution (the answer should still be reasonable, not 1 hour or 10 minutes) - 5 points.
- Correct reasoning - up to 2 points.
- Only the answer $-\mathbf{1}$ point.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. The figure shown on the right is made of matches (the side of a small square is one match). The area of the entire shaded figure is 300 square centimeters. Find the total length of all the matches used.
|
Answer: 140 cm.
Solution. Let the area of one small square be $a$. Then, the diagram shows 8 small squares with area $a$ and one large square with area $4a$. The total area is $8a + 4a = 300$, from which $a = 25 \text{ cm}^2$. Therefore, the side of a small square is 5 cm.
Notice that the rectangle formed by two adjacent small squares contains 7 matches. There are 4 such non-overlapping rectangles in the diagram, meaning 28 matches were used. Considering that the length of one match is 5 cm, the total length of all matches is 140 cm.
## Criteria
1 p. Only the correct answer without justification.
2 p. The area of the small square is correctly found, but there is no further progress.
3 p. The length of the match is correctly found, but the answer is not obtained.
4 p. The correct answer and justification are provided.
|
140
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Immediately after harvesting, the water content in 1 ton of tomatoes was $99 \%$. By the time of sale, the water share had decreased by $4 \%$ (after drying). What did the total weight of the tomatoes become?
|
Solution. The weight of the dry matter in tomatoes is $1 \%$ of 1 ton - 10 kg. After drying, the weight of the dry matter does not change and constitutes $5 \%(100 \%-$ $(99 \%-4 \%))$ of the total weight of the tomatoes. In other words, the total weight is 200 kg.
Remark. Perhaps, the student can be given 2 - 3 points if, during the solution, they figured out how to calculate the weight of the dry matter but did not use it for further reasoning.
Answer. 200 kg.
|
200
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 11.2. (7 points)
The master makes a whole number of parts in one hour, more than 5, and the apprentice makes 2 parts less. The master completes the order in a whole number of hours, and two apprentices together - one hour faster. How many parts does the order consist of?
|
Answer: 24.
Solution: Let $x$ be the number of parts in the order; $y$ (parts per hour) be the master's productivity $(y>5)$; $y-2$ (parts per hour) be the apprentice's productivity; $2 y$ - 4 (parts per hour) be the productivity of two apprentices.
Then $\frac{x}{y}$ is the time for the master to complete the order, $\frac{x}{2 y-4}$ is the time for the apprentices to complete the order.
According to the condition, $\frac{x}{y}=\frac{x}{2 y-4}+1$.
Expressing $x$ from this equation, we get: $x=\frac{2 y^{2}-4 y}{y-4}, \frac{x}{y}=\frac{2 y-4}{y-4}$.
Consider $2 y-4=2 y-8+4=2(y-4)+4$.
Then $\frac{x}{y}=\frac{2(y-4)+4}{y-4}=2+\frac{4}{y-4}$.
According to the condition $\frac{x}{y} \in Z, 2 \in Z$. Therefore, $\frac{4}{y-4} \in Z$.
$y>5$, then $y-4=2, y=6$ and $y-4=4, y=8$.
Find $x: \frac{x}{6}=4, x=24$ or $\frac{x}{8}=3, x=24$.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 11.3. (7 points)
The base of the pyramid with vertex $P$ is a quadrilateral $A B C D$, where the sum of angles $A$ and $D$ is five times smaller than the sum of angles $B$ and $C$. Find the angle between the planes of the faces $P A B$ and $P C D$, if both are perpendicular to the base.
|
Answer: $60^{\circ}$.
Solution: Let the planes $A P B$ and $C P D$ intersect along the line $P X$ (point $X$ lies in the plane $A B C$, see the figure).
Since $(A P B) \perp(A B C)$ and $(C P D) \perp(A B C)$, then $P X \perp(A B C)$. Therefore, the angle $\angle B X C$ is the linear angle of the dihedral angle with edge $P X$. From the problem statement, it follows that in the quadrilateral $A B C D$, the sum of angles $A$ and $D$ is $60^{\circ}$, hence $\angle B X C = 120^{\circ}$. The obtained angle is obtuse, so the angle between the specified planes is $60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 11.5. (7 points)
At a joint conference of the party of liars and the party of truth-tellers, 32 people were elected to the presidium and seated in four rows of eight. During the break, each member of the presidium claimed that among their neighbors there are representatives of both parties. It is known that liars always lie, and truth-tellers always tell the truth. What is the minimum number of liars in the presidium for the described situation to be possible? (Two members of the presidium are considered neighbors if one of them sits to the left, right, in front, or behind the other).
|
Answer: with eight liars.
Solution: Divide all the seats in the presidium into eight groups as shown in the figure. If there are fewer than eight liars, then in one of these groups, only truth-tellers will be sitting, which is impossible. The contradiction obtained shows that there are no fewer than eight liars. The figure shows how eight liars can be seated in the presidium so that the condition of the problem is satisfied.
Comments. Without an example of seating the liars - 5 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Petya came up with a four-digit number, in which all the digits are different. It is known that the sum of the first three digits of this number is divisible by 9 and the sum of the last three digits of this number is divisible by 9. What values can the sum of all the digits of this number take? Find all possible values and explain why there are no others.
|
2. Answer. The sum of the digits is 18.
According to the condition, the sum of the first three digits is divisible by 9, and the sum of the last three is also divisible by 9. Therefore, the difference between the first and the last digit is divisible by 9. Since all digits are different, the first digit is 9, and the last digit is zero. Since the sum of the last three digits is divisible by 9, and the last digit is 0, the sum of the two middle digits is also divisible by 9. Since the middle digits are both less than 9 and greater than 0, their sum is less than 18 but greater than zero (and divisible by 9). Therefore, the sum of the two middle digits is 9, and the sum of all the digits of this number is 18.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In triangle $ABC$, $AB = 3 \cdot BC$, point $M$ is the midpoint of side $AB$, and $BD$ is the angle bisector. Find the angle $MDB$.
---
Here is the translation of the given text, maintaining the original formatting and structure.
|
4. Answer. $90^{\circ}$.
Let $X$ be the midpoint of segment $M B$, and draw segment $D X$. By the property of the angle bisector, we have
$$
A D: D C = A B: B C = 3: 1
$$
On the other hand, $A X: X B = 3: 1$, so $A D: D C = A X: X B$. Therefore, $X D \parallel B C$. Then $\angle X B D = \angle D B C = \angle X D B$, which means that $X D = X B = X M$. From this, we get that $\angle M D B = 90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. CONDITION
In what minimum number of colors should natural numbers be painted so that any two numbers, the difference between which is 3, 4, or 6, are of different colors?
|
Solution. Let the number $n=1$ be color $A$, then the numbers 4, 5, and 7 must be painted in another color. Let $n=4$ be color $B$, then from $7-4=3$, it follows that the number $n=7$ is of the third color $C$. Therefore, at least 3 colors are required. The coloring $A A A B B B C C C A A A B B B \ldots$ is the desired one.
Answer. 3.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. After watching the movie, viewers rated it one by one with an integer score from 0 to 10. At any given time, the movie's rating was calculated as the sum of all the given scores divided by their number. At some point in time $T$, the rating became an integer, and then with each new voting viewer, it decreased by one. What is the maximum number of viewers who could have voted after moment $T$?
(O. Dmitriev, R. Zhenodarov)
|
Answer: 5.
Solution. Consider a moment when the rating has decreased by 1. Suppose that before this, $n$ people had voted, and the rating was an integer $x$. Thus, the sum of the scores was $n x$. Let the next viewer give $y$ points. Then the sum of the scores becomes $n x + y = (n + 1)(x - 1)$, from which $y = x - n - 1$. The maximum possible value of $x$ is 10, and the minimum possible value of $n$ is 1; therefore, the maximum value of $y$ (on the first such step) is 8.
With each subsequent step, the value of $x$ decreases by 1, and the value of $n$ increases by 1. Consequently, on the second step, the value of $y$ does not exceed 6, on the third step - 4, and so on. Since any rating is not less than 0, the number of steps does not exceed 5.
It remains to show that five steps are possible. Suppose that at moment $T$ the rating is 10 (with 1 voter), then the second viewer gives 8 points, the third - 6, the fourth - 4, the fifth - 2, and the sixth - 0. Then the rating sequentially takes the values $9, 8, 7, 6,$ and 5.
Comment. Only the answer - 0 points.
Only an example is provided where 5 viewers voted - 2 points.
It is proven with full justification that more than 5 viewers could not have voted (but the example is missing or incorrect) - 5 points.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. After watching the movie, viewers rated it one by one with an integer score from 0 to 10. At any given time, the movie's rating was calculated as the sum of all the given scores divided by their number. At some point in time $T$, the rating became an integer, and then with each new voting viewer, it decreased by one. What is the maximum number of viewers who could have voted after moment $T?$
(O. Dmitriev, R. Zhenodarov)
|
# Answer: 5.
Solution. Consider a moment when the rating has decreased by 1. Suppose that before this, $n$ people had voted, and the rating was an integer $x$. This means the sum of the scores was $n x$. Let the next viewer give $y$ points. Then the sum of the scores becomes $n x + y = (n + 1)(x - 1)$, from which $y = x - n - 1$. The maximum possible value of $x$ is 10, and the minimum possible value of $n$ is 1; therefore, the maximum value of $y$ (on the first such step) is 8.
With each subsequent step, the value of $x$ decreases by 1, and the value of $n$ increases by 1. Consequently, on the second step, the value of $y$ does not exceed 6, on the third step - 4, and so on. Since any rating is not less than 0, the number of steps does not exceed 5.
It remains to show that five steps are possible. Suppose the rating at moment $T$ is 10 (with one voter), then the second viewer gives 8 points, the third - 6, the fourth - 4, the fifth - 2, and the sixth - 0. Then the rating sequentially takes the values $9, 8, 7, 6,$ and 5.
Comment. Only the answer - 0 points.
Only an example is provided where 5 viewers voted - 2 points.
It is proven with full justification that more than 5 viewers could not have voted (but the example is missing or incorrect) - 5 points.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For what least natural $n$ do there exist such natural $a$ and $b$ that
$$
\text { GCD }(a, b)=999 \text { and } \text{LCM}(a, b)=n!
$$
(here $n!=1 \cdot 2 \cdot \ldots \cdot n)$ ?
|
2. For what smallest natural $n$ do there exist such natural $a$ and $b$ that
$$
\text { GCD }(a, b)=999 \text { and } \text{LCM}(a, b)=n!
$$
(Here $n!=1 \cdot 2 \cdot \ldots \cdot n) ?$
ANSWER. $n=37$.
SOLUTION. Since $\text{LCM}(a, b)$ is divisible by $\text{GCD}(a, b)=999=27 \cdot 37$, and the number 37 is prime, $n \geqslant 37$. On the other hand, for $n=37$ the numbers $a=37!, b=999$ are suitable.
|
37
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Vova has 19 math grades in his journal, all twos and threes, and the first four grades are twos. It turned out that among the quartets of consecutive grades, all 16 possible combinations of four twos and threes are present. What are Vova's last four grades?
|
5. Vova has 19 math grades in his journal, all twos and threes, and the first four grades are twos. It turned out that among the quartets of consecutive grades, all 16 possible combinations of four twos and threes are present. What are Vova's last four grades?
ANSWER. 3222.
SOLUTION. Note that there are exactly 16 quartets of consecutive grades in a string of 19 grades, meaning each combination appears exactly once. After the first four twos, there must be a three, otherwise the combination of four twos would appear twice. Therefore, after the combination 3222, neither 2 nor 3 can follow, as in both cases, a combination that has already appeared would reappear. Thus, the combination 3222 must be at the end of the string.
|
3222
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The lateral sides $K L$ and $M N$ of trapezoid $K L M N$ are equal to 15 and 12, respectively, and the base $L M=3$. The bisector of angle $N K L$ passes through the midpoint of side $M N$. Find the area of the trapezoid. Answer: 80.
|
# Solution.
Let $Q$ be the midpoint of segment $M N$. Extend the bisector of angle $N K L$ to intersect line $L M$ at point $P$. $\angle N K Q = \angle Q K L$.
$\angle N K Q = \angle K P L$ (alternate interior angles). Then $\angle Q K L = \angle K P L$ and $\triangle K P L$ is isosceles. $K L = L P$. Therefore, $M P = K L - M L = 12$.
$\triangle K Q N = \triangle M P Q (M Q = Q N, \angle K Q N = \angle M Q P, \angle K N Q = \angle Q M P)$.
Then $K N = M P = 12$.
Draw $M R \parallel K L (R \in K N)$. $M R = K L = 15$, $M N = 12$, $R N = K N - M L = 12 - 3 = 9$, $12^2 + 9^2 = 15^2$. Therefore, $\angle M N R = 90^\circ$ and $M N$ is the height of the trapezoid.
$\mathrm{S}_{K L M N} = \frac{1}{2}(K N + M L) \cdot M N = \frac{1}{2}(3 + 12) \cdot 12 = 80$.
Recommendations for checking.
Base $K N$ found: 4 points.
Height of the trapezoid found: 3 points.
Arithmetic error: -1 point.
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The working day at the enterprise lasted 8 hours. During this time, the labor productivity was as planned for the first six hours, and then it decreased by $25 \%$. The director (in agreement with the labor collective) extended the shift by one hour. As a result, it turned out that again the first six hours were worked with planned productivity, and then it decreased by $30 \%$. By what percentage did the overall labor productivity for the shift increase as a result of extending the working day?
|
1. Answer: by 8 percent. Solution. Let's take 1 for the planned labor productivity (the volume of work performed per hour). Then before the shift extension, workers completed $6+1.5=7.5$ units of work per shift. And after the extension, $8+2.1=8.1$ units. Thus, the overall productivity per shift became $8.1: 7.5 \times 100 \% = 108 \%$ of the initial, meaning it increased by $8 \%$. Grading criteria. Correct solution - 7 points. Initial and final productivity per shift correctly expressed in conditional units, but the percentage ratio is expressed incorrectly - 4 points. In all other cases - 0 points.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Each cell of a $5 \times 5$ square contains a number. The numbers in any row and any column form an arithmetic progression. The numbers in the corners of the square are $1, 25, 17, 81$. What number is in the central cell? Don't forget to justify your answer.
| 1 | | | | 25 |
| :--- | :--- | :--- | :--- | :--- |
| | | | | |
| | | $x$ | | |
| | | | | |
| 81 | | | | 17 |
|
2. Answer: 31. Solution. In any arithmetic progression $a_{5}=a_{1}+4 d, a_{3}=a_{1}+2 d \Rightarrow$ $a_{3}=\left(a_{1}+a_{5}\right) / 2$. Therefore, in the third cell of the first column stands the number 41, in the third cell of the last column stands the number 21, and in the middle cell of the second row (i.e., in the central cell of the table) stands the number 31. Grading criteria. Correct solution - 7 points. Numbers in the middle cells are indicated without any justification - 3 points. In all other cases (including one answer without explanation) - 0 points.
|
31
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Triangle $A B C$ is similar to the triangle formed by its altitudes. Two sides of triangle $A B C$ are 4 cm and 9 cm. Find the third side.
|
4. Answer. 6 cm. Solution. Let $A B=9, B C=4, A C=x, S$ - the area of triangle $A B C$. Then the heights of the triangle are $2 S / 4, 2 S / 9, 2 S / x$. By the triangle inequality, side $A C$ can be either the largest or the middle in length. Applying the triangle inequality to the triangle formed by the heights, we see that among the quantities $2 S / 4, 2 S / 9, 2 S / x$, the quantity $2 S / x$ can also be either the largest or the middle. However, the larger the side, the smaller the height drawn to it, and the height to the largest side can only be the smallest. Therefore, the side $x$ (and the height drawn to it) can only be the middle. This allows us to write the proportion $9: x = 2 S / 4: 2 S / x$ and $x=6$. Grading criteria. Full solution - 7 points. The proportion is written correctly, but not justified (in any way) - 4 points. In all other cases (including an answer without a solution) - 0 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest natural number that has exactly 12 different natural divisors, the largest prime divisor of which is the number 101, and the last digit is zero.
|
Solution. Let $n$ be the desired number. According to the condition, $n: 101, n: 2, n: 5$. Consider the number $m=2 \cdot 5 \cdot 101$, note that it has exactly 8 different natural divisors $(1$, $2,5,101,2 \cdot 5, \ldots, 2 \cdot 5 \cdot 101$ ), so $n>m$. Since $n$ is the smallest natural number satisfying the condition of the problem, we will further consider the number $2 \cdot m=2 \cdot 2 \cdot 5 \cdot 101$, obtained from $m$ by multiplying by the smallest of the prime numbers. Note that the number $2 m=2^{2} \cdot 5 \cdot 101$ has exactly 12 different natural divisors $(1,2,4,5,101$, $2 \cdot 5, \ldots, 2 \cdot 2 \cdot 5 \cdot 101$ ), so $n=2^{2} \cdot 5 \cdot 101=2020$. Answer: 2020.
Comment. In the solution, the well-known function $\tau(n)$ - the number of natural divisors of the number $n$ - can be used. Moreover, if the canonical decomposition into prime factors of the number $n$ has the form $n=p_{1}^{\alpha_{1}} \cdot p_{2}^{\alpha_{2}} \cdot p_{3}^{\alpha_{3}} \cdot \ldots \cdot p_{k}^{\alpha_{k}}$, then $\tau(n)=$ $\left(\alpha_{1}+1\right) \cdot\left(\alpha_{2}+1\right) \cdot \ldots \cdot\left(\alpha_{k}+1\right)$. If an olympiad participant uses the last formula without proof, no points are deducted.
|
2020
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many four-digit numbers exist where the digit in the thousands place is greater than the digit in the hundreds place?
|
Solution. The digit in the thousands place can take one of 9 possible values: $1,2,3, \ldots, 9$ (we cannot take 0, since the number is four-digit). For each of these options, we can specify the corresponding number of options for the hundreds digit: $1,2,3$, ..., 9. That is, in total $1+2+\ldots+9=45$ options. The other two digits are arbitrary (10 options each), so we get the answer: $45 \cdot 10 \cdot 10=4500$ options. Answer: 4500.
|
4500
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the minimum number of chips that need to be taken so that in any arrangement of them on the cells of a chessboard, there would necessarily be 4 chips standing in a row horizontally?
|
Solution. Consider one row. To ensure that there are 4 chips in it, there must be no less than 7 chips (6 chips can be placed in two groups of 3 chips). If there are a total of $6 \cdot 8+1=49$ chips, then by the pigeonhole principle, there will definitely be a row with no fewer than 7 chips. On the other hand, it is impossible to get by with fewer chips: 48 chips can be placed in groups of 6 in each row so that the condition is not met. Answer: 49.
Comment. Only the correct answer - 1 point. It is shown that 49 chips are always sufficient - no less than 4 points.
|
49
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. We consider all possible $100-$-digit numbers, where each digit is equal to 1 or 2. For each, the remainder when divided by 1024 is calculated. How many different remainders are there among these?
|
5. Solution: Subtract the number $11 \ldots 1$ (one hundred ones) from all the numbers. The numbers under consideration have turned into numbers consisting of zeros and ones from 0 to $11 \ldots 1$. We will show that if two of these numbers have differences in the last 10 digits, then they have different remainders when divided by 1024. If this is not the case, then consider the difference between these numbers. It should be divisible by 1024, but it ends with fewer than 10 zeros, preceded by a 1 or 9. According to the divisibility rule for powers of two, such a number is not divisible by $2^{10}$.
## Instructions for checking:
Most olympiad participants know the divisibility rule for powers of two:
A number is divisible by $2^{\mathrm{n}}$ if and only if the last $\mathrm{n}$ digits of this number form a number that is divisible by $2^{\text {n }}$.
Proving it is simple, but of course, it is not necessary.
|
1024
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In a supermarket, there are two types of fruit sets for sale. The first type of set consists of 3 apples and 15 oranges and costs 360 rubles. The second type of set consists of 20 apples and 5 oranges and costs 500 rubles. Fruits are sold only in sets, and sets cannot be divided. Seryozha came to the supermarket and wants to buy an equal number of apples and oranges. What is the smallest amount of money he will have to spend, if he cannot leave without buying anything?
|
Solution: Let Sergey buy $x$ sets of the first type and $y$ sets of the second type. Then he bought $3x + 20y$ apples and $15x + 5y$ oranges. From the problem's condition, it follows that these numbers are equal, that is, $15y = 12x$ or $5y = 4x$. The smaller $y$ is, the smaller $x$ is, and the smaller the amount paid. The smallest natural $y$ is 4, then $x = 5$, and the amount spent in rubles is $5 \cdot 360 + 4 \cdot 500 = 3800$.
Answer: 3800 rubles.
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Correct justified answer | 7 points |
| A correct approach but an incorrect answer due to arithmetic errors | 6 points |
| It is shown that 3800 rubles can be spent, but it is not shown that a smaller amount cannot be spent | 2 points |
| Examples of purchases costing more than 3800 rubles | 0 points |
|
3800
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. Six different natural numbers from 6 to 11 are placed on the faces of a cube. The cube was rolled twice. The first time, the sum of the numbers on the four side faces was 36, and the second time it was 33. What number is written on the face opposite the one with the number 10? Justify your answer.
|
Solution: The sum of the numbers on all 6 faces of the die is 51. Therefore, the sum of the numbers on the top and bottom faces during the first roll is 15, and during the second roll, it is 18. The number 15 can be obtained (as the sum of two different integers from the interval [6; 11]) in two ways: 15 = 9 + 6 = 8 + 7. The number 18 also in two ways: 18 = 7 + 11 = 8 + 10. If the numbers 7 and 8 lie on opposite faces, then both of the latter representations are impossible. Therefore, of the two specified representations of the number 15, the first one holds, and in the die, the number 9 lies opposite the number 6. Now, if during the second roll, the numbers on the top and bottom faces were 8 and 10, it is clear that the number 10 lies opposite the number 8. And if during the second roll, the numbers on the top and bottom faces were 7 and 11, then on one pair of opposite side faces are the numbers 6 and 9, and on the other - the remaining 8 and 10, and again, the number 10 lies opposite the number 8.
Answer: 8.
Note: The problem can be easily reduced to a regular die as follows: remove 5 dots from each face. Then the die will become regular, and the condition will read: "The first time, the sum of the numbers on the four side faces was 16, the second time - 13. What number is written on the face opposite the one where the number 5 is written?". Further reasoning does not change fundamentally.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct justified answer | 7 points |
| Correct answer, supported by a correct example of a die (any of the two possible) | 3 points |
| Impossibility of some situations is justified (for example, that 10 cannot lie opposite 11 or that the sum during the first roll cannot be realized as 6 + 9 + 10 + 11), but not all impossible situations are analyzed | 2 points |
| The problem is correctly reduced to a regular die | |
| Answer without justification (or incorrect answer) | 1 point |
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. On a line, several points were marked. Then, between each pair of neighboring points, one more point was marked, and this operation was repeated once more. As a result, 101 points were obtained. How many points were marked initially?
|
9.1. Answer: 26. Solution. Let there initially be $k$ points marked. Then $k-1$ more points were added to them (one between the first and second, second and third, $\ldots, k-1$-th and $k$-th marked points), and then another $(k+(k-1))-1=$ $2 k-2$ points. In total, the number of points became $4 k-3$. Solving the equation $4 k-3=101$, we find the answer.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. The average height of 11 football players on the team is 182 cm. During the match, the referee sent off one player, and the average height of the remaining players became 181 cm. What is the height of the player who was sent off?
|
Answer: 192 cm. Solution. Let $S$ be the sum that results from adding the heights of the 10 remaining football players. Then $\frac{S}{10}=181$ and $\frac{S+x}{11}=182$, where $x$ is the height of the removed football player. From this, $S=1810$ and $x=182 \cdot 11-S=2002-1810=192$.
|
192
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Petya wrote down all natural numbers from 1 to $n$ in a row on the board and counted the total number of digits written. It turned out to be 777. What is $n$?
|
Answer: 295. Solution: Since a total of 777 digits have been written, $n$ must be a three-digit number: indeed, in the case of a two-digit $n$, no more than $9+2 \cdot 90=189$ digits would have been written, and in the case of a four-digit (or more) number, more than $9+2 \cdot 90+3 \cdot 900=2889$ digits would have been written. Let $k$ be the number of three-digit numbers written ($k=n-99$). Then the total number of digits written is $9+2 \cdot 90+3 \cdot k$ $=777$. From this, $k=196$, and $n=k+99=295$.
|
295
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In a bag for a bingo game, there are 90 barrels with numbers from 1 to 90. What is the minimum number of barrels that need to be drawn at random from the bag to guarantee getting a barrel with a number divisible by 3 or 5 (or both 3 and 5)?
|
Answer: 49. Solution. We will call numbers that are divisible by 3 or 5 desirable. The number of numbers from 1 to 90 that are divisible by 3 is 30 ( =90: 3 ), and those divisible by 5 is 18 ( =90:5). If we add $30+18=48$, then all numbers that are divisible only by 3 and only by 5 will be counted once, and numbers that are divisible by both 3 and 5, i.e., divisible by 15, will be counted twice. The number of such (doubly counted) numbers is $6=90: 15$. Therefore, by subtracting $48-6$, we get 42 desirable numbers. The remaining 48 undesirable numbers ( =90 - 42) could have appeared on the first 48 drawn tokens, but then the 49th drawn token will definitely be desirable.
|
49
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. How many six-digit natural numbers exist, each of which has adjacent digits with different parity
|
Answer: 28125. Solution. If the first (most significant) digit is even, then it can be chosen in four ways $(2,4,6,8)$, and all subsequent ones can be chosen in five ways (possible candidates for the second, fourth, and sixth digits are $1,3,5,7,9$, and for the third and fifth - $0,2,4,6,8$). In the end, by the rule of product, we will have a total of $4 \cdot 5^{5}=12500$ numbers with the first even digit. Similarly, in the case of an odd first digit, we get $5 \cdot 5^{5}=15625$ numbers. Thus, the total number of the desired numbers is 28125. Remark. The same result can be obtained if we immediately use the rule of product. The first digit can be chosen in nine ways (taking any digit except 0), after which the second digit can be chosen in five ways (taking any digit with a different parity from the first digit), and so on: the following digits can be chosen in five ways (and the number of ways does not depend on the previous digits). Therefore, by the rule of product, we get the result: $9 \cdot 5^{5}$.
|
28125
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Points $A, B, C, D$ are located at the vertices of rectangle $ABCD$, its sides and diagonals $AC$ and $BD$ are roads. The first car traveled the route $B \rightarrow$ $C \rightarrow A \rightarrow D$ in one hour, and the second car traveled the route $D \rightarrow B \rightarrow C \rightarrow A$ in one hour. After how much time will the cars meet if they simultaneously leave point $C$: the first one on the route $C \rightarrow$ $B \rightarrow D$, and the second one on the route $C \rightarrow A \rightarrow D \rightarrow B$, and the meeting will occur on the road $BD$? (The speeds of both cars are constant).
|
Answer: In 40 minutes.
Solution: The diagonals of a rectangle have the same length and are longer than any of its sides. In one hour, together the two cars would travel three times the length of side $B C$ and three times the diagonal, since one car travels two sides equal to $B C$ and one diagonal in an hour, while the other car travels two diagonals and one side equal to $B C$ in an hour. Therefore, in one-third of an hour, or 20 minutes, the two cars together will travel one side equal to $B C$ and one equal to the diagonal. The entire described route to the meeting point on $B D$ they will cover in twice this time.
Comment: Correct answer without justification - 1 point.
Correct answer obtained by example - 3 points.
Note: It can be proven (but is not required in this problem) that the meeting will definitely occur on the road $B D$.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A straight road passes not far from Mount Fuji. The driver of a car noticed the mountain 60 km to the north, and an hour later - 45 km to the west. What is the shortest distance the car passed from Mount Fuji?
|
Answer: 36 km.
Solution: The mountain and the observation points are at the vertices of a right-angled triangle with legs of 60 and 45. The hypotenuse in this case is 75. By equating the areas of the triangle calculated in different ways, we get that the product of the legs is equal to the product of the hypotenuse and the height, which is the required distance.
Thus, $60 \cdot 45=75 \cdot x \Rightarrow x=36$.
Grading criteria. Only the answer - 1 point. Answer with a diagram of the right-angled triangle and the height - 2 points.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. This year, the son and daughter are so many years old that the product of their ages is 7 times less than the father's age. And in three years, the product of their ages will already be equal to the father's age. Find the father's age.
|
Answer: 21 years
Solution. Let $n$ be the son's age, $m$ be the daughter's age, then the father's age is $7 m n$. In three years, the son's age will be $n+3$, the daughter's age will be $m+3$, and the father's age will be $7 \mathrm{mn}+3$, and according to the condition, the equation $(n+3)(m+3)=7 m n+3$ will be satisfied. After combining like terms and canceling by 3, we get: $2 m n-n-m=2$. Multiply the last equation by 2 and represent it as: $(2 m-1)(2 n-1)=5$.
Thus, $2 m-1=5, 2 n-1=1$ (or vice versa), so $m=3, n=1$ and, therefore, $7 m n=21$. That is, currently the son and daughter are 1 year and 3 years old (or vice versa), and the father is 21 years old.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A right triangle $A B C$ (cathetus $B C$ is greater than cathetus $A C$) is inscribed in a circle. A point $D$ is chosen on side $B C$ such that $B D=A C$, and point $M$ is the midpoint of the arc $A C B$. Find the angle $C D M$.
|
Answer: $45^{\circ}$.
Solution. Note that $A B$ is the diameter of the circumscribed circle. Connect point $M$ with points $A, B, C$, and $D$. Since arcs $A M$ and $B M$ are equal, the chords $A M$ and $B M$ that subtend them are also equal. Segments $B D$ and $A C$ are equal by the condition. Finally, angles $M B C$ and $M A C$ are equal, as inscribed angles subtending the same arc. Thus, triangles $M B D$ and $M A C$ are equal by two sides and the angle between them. This implies the equality of sides $M D$ and $M C$, meaning that triangle $M C D$ is isosceles. It remains to note that $\angle M C D=\angle M C B=\angle M A B=45^{\circ}$, since arc $M B$ is half of the circle. Criteria for evaluation. Proof of the equality of triangles $M B D$ and $M A C$ - 3 points.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. When a certain number is divided by 13 and 15 with a remainder, the same incomplete quotients are obtained. Find the largest such number.
|
Answer: 90. Suppose the number a satisfies the condition of the problem. Then the equalities $a=13 d+b=15 d+c$ hold, where $d$ is the quotient from the condition of the problem. From this, $2 d=b-c \leq 12$, i.e., $d \leq 6$, and the remainder $b$ from dividing the number by 13 is no more than 12. For $d=6$ and $b=12$, we obtain the desired largest number 90. Verification: $90=13 \cdot 6+12, 90=15 \cdot 6+0$.
Comment. The number 90 is provided with verification of this number without justification of its maximality - 1 point. The number 90 is provided with justification of the estimate without verification of this number - 5 points.
|
90
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Oleg drew an empty $50 \times 50$ table and wrote a non-zero number above each column and to the left of each row. It turned out that all 100 written numbers are distinct, with 50 of them being rational and the other 50 being irrational. Then, in each cell of the table, he wrote the product of the numbers written next to its row and its column (a "multiplication table"). What is the maximum number of products in this table that could be rational numbers? (O. Podlipsky)
|
Answer: 1250 works.
Solution. First, we show that there are at least 1250 irrational numbers in the table. Suppose along the left side of the table, there are $x$ irrational and $50-x$ rational numbers. Then along the top side, there are $50-x$ irrational and $x$ rational numbers. Since the product of a non-zero rational and an irrational number is always irrational, there are at least $x^{2}+(50-x)^{2}$ irrational numbers in the table. Here, $x^{2}+(50-x)^{2}=2 x^{2}-100 x+50^{2}=2(x-25)^{2}+2 \cdot 25^{2} \geqslant 2 \cdot 25^{2}=1250$, which is what we needed to show. Therefore, there are at most $2500-1250=1250$ rational numbers in the table.
Exactly 1250 rational numbers in the table can occur, for example, in the following case. Along the left side, the numbers are $1,2, \ldots, 24,25, \sqrt{2}, 2 \sqrt{2}, \ldots, 25 \sqrt{2}$, and along the top side, the numbers are $26,27, \ldots, 49,50,26 \sqrt{2}, 27 \sqrt{2}, \ldots, 50 \sqrt{2}$. Then, the only irrational numbers will be the $2 \cdot 25^{2}=1250$ products of a rational and an irrational number.
Comment. Only the correct answer -0 points.
Proof that there are no more than 1250 rational numbers -4 points.
If the proof is only conducted in a special case where an equal number of rational and irrational numbers are along the left (or top) side, 2 points are given instead of 4 for this part of the solution.
The inequality $x^{2}+(50-x)^{2} \geqslant 1250$ (or an equivalent one) is used without proof - 1 point is deducted.
A correct example showing that there could be exactly 1250 rational numbers -3 points.
The statement that the product of a non-zero rational and an irrational number is irrational can be used without proof.
|
1250
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Does there exist a four-digit natural number with distinct non-zero digits that has the following property: if this number is added to the same number written in reverse order, the result is divisible by $101 ?$
|
Answer. It exists.
Solution. For example, the number 1234 works. Indeed, $1234+4321=5555=101 \cdot 55$.
Remark. A number $\overline{a b c d}$ with distinct non-zero digits satisfies the condition if and only if $a+d=b+c$.
Comment. Any correct example with verification that it fits - 7 points.
Any correct example without verification that it fits - 5 points.
|
1234
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. There are 9 cards with numbers $1,2,3,4,5,6,7,8$ and 9. What is the maximum number of these cards that can be laid out in some order in a row so that on any two adjacent cards, one of the numbers is divisible by the other?
|
Answer: 8.
Solution: Note that it is impossible to lay out all 9 cards in a row as required. This follows from the fact that each of the cards with numbers 5 and 7 can only have one neighbor card with the number 1. Therefore, both cards 5 and 7 must be at the edges, and the card with the number 1 must be adjacent to each of them, which is impossible.
It is possible to select 8 cards and arrange them in a row according to the requirements of the problem, for example: $9,3,6,2,4,8,1,5$.
Comment: Proof that it is impossible to lay out all the cards - 4 points.
Any correct example of arranging 8 cards - 3 points.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Petya bought one cupcake, two muffins, and three bagels, Anya bought three cupcakes and a bagel, and Kolya bought six muffins. They all paid the same amount of money for their purchases. Lena bought two cupcakes and two bagels. How many muffins could she have bought for the same amount she spent?
|
Answer: 5 cupcakes.
Solution: The total cost of Petya and Anya's purchases is equal to the cost of two of Kolya's purchases. If we denote P, K, and B as the costs of a cake, a cupcake, and a bagel, respectively, we get the equation: $(P + 2K + 3L) + (3P + 5) = 12K$, from which it follows that $4P + 4B = 10K$, or $2P + 2B = 5K$.
Remark: From the condition, we can also calculate all the cost ratios, specifically, $P : K : B = 7 : 4 : 3$.
Comment: Only the correct answer without explanation -1 point.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. What is the minimum number of 3-cell corners that need to be painted in a $6 \times 6$ square so that no more corners can be painted? (Painted corners must not overlap.)
|
Answer: 6.
Solution. Let the cells of a $6 \times 6$ square be painted in such a way that no more corners can be painted. Then, in each $2 \times 2$ square, at least 2 cells are painted, otherwise, a corner in this square can still be painted. By dividing the $6 \times 6$ square into 9 $2 \times 2$ squares, we get that at least $9 \cdot 2 = 18$ cells are painted. Therefore, at least 6 corners are painted.
Figure 3 shows how to paint 6 corners so that no more corners can be painted.
Comment. It is proven that the number of painted corners is no less than $6-4$ points.
An example with 6 painted corners is drawn - 3 points.
Figure 3
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the smallest number that contains only the digits 2 and 3 in equal quantities, and is divisible by 2 and 3.
|
Answer: 223332.
Sketch of the solution. If a number is divisible by 3, then the sum of its digits is divisible by 3, which means the number of twos is a multiple of three, and thus, there must be at least three twos. Therefore, the desired number is a six-digit number. Since it is divisible by 2, it ends in 2. The number is smaller the smaller the leading digits are, hence the answer.
Criteria. Correct answer without justification: 2 points.
|
223332
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A rectangle with sides $6 \mathrm{~cm}$ and $3 \mathrm{~cm}$ was cut into three rectangles of equal perimeter. What can the perimeter of these rectangles be? Find all possible answers.
|
Answer: 14 cm, 10 cm, 10.5 cm.
Sketch of the solution.
Let's cut a rectangle with sides $a$ and $b$. Cases 1 and 2. Cut the rectangle into three equal rectangles with two cuts parallel to side $a$.
The perimeter of these rectangles is $\mathrm{P}=2(a+b / 3)$. 1) If $a=3$ cm and $b=6$ cm, then $P=10$ cm. 2) If $a=6$ cm and $b=3 \mathrm{~cm}$, then $P=14 \mathrm{cm}$.
Cases 3 and 4. Cut one rectangle parallel to side $a$, and cut the remaining part into two equal rectangles parallel to side $b$ (see figure). If the perimeters of the rectangles are equal, then their semi-perimeters are also equal, so $\mathrm{a}+\mathrm{x}=\mathrm{b}-\mathrm{x}+\mathrm{a} / 2$, from which $2 \mathrm{x}=\mathrm{b}-\mathrm{a} / 2$ under the condition $\mathrm{b}-\mathrm{a} / 2>0$. The perimeter of these rectangles is $\mathrm{P}=2 \mathrm{a}+\mathrm{b}-\mathrm{a} / 2=3 \mathrm{a} / 2+\mathrm{b}$. 1) If $a=3$ cm and $b=6 \mathrm{cm}$, then $P=10.5$ cm. 4) If $a=6$ cm and $b=3$ cm, then $\mathrm{b}-\mathrm{a} / 2=0$ and the condition for the existence of the rectangle is not satisfied.
Criteria. Correct answer, without explanations: 2 points.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.