problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
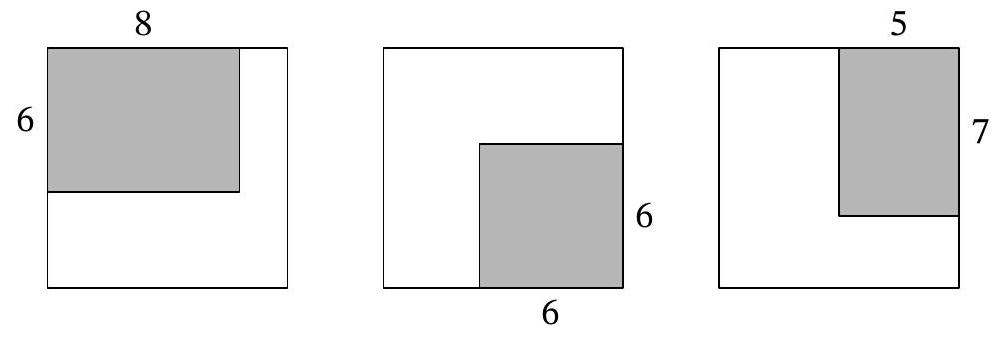
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.

The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, this results in a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
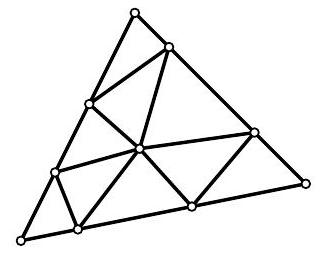
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
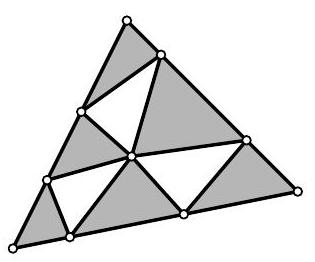
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
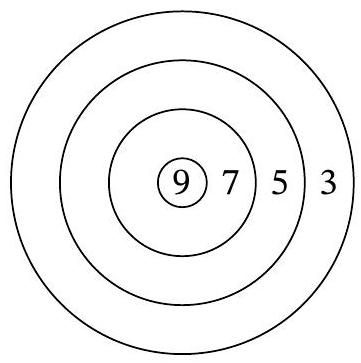
Problem 6.4. Misha made himself a homemade dartboard during the summer at the cottage. The round board is divided by circles into several sectors - darts can be thrown into it. Points are awarded for hitting a sector as indicated on the board.
Misha threw 8 darts 3 times. The second time he scored twice as many points as the first time, and the third time he scored 1.5 times as many points as the second time. How many points did he score the second time?
|
Answer: 48.
Solution. The smallest possible score that can be achieved with eight darts is $3 \cdot 8=24$. Then, the second time, Misha scored no less than $24 \cdot 2=48$ points, and the third time, no less than $48 \cdot 1.5=72$.
On the other hand, $72=9 \cdot 8$ is the highest possible score that can be achieved with eight darts. Therefore, the third time, Misha scored exactly 72 points, and the second time, exactly 48.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
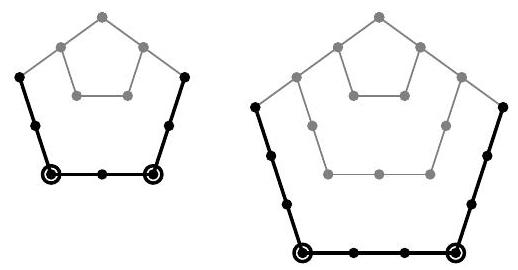
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to form such pictures, how many stones will be on the 10th picture?
-
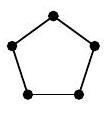
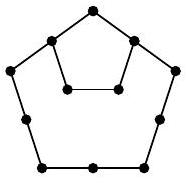
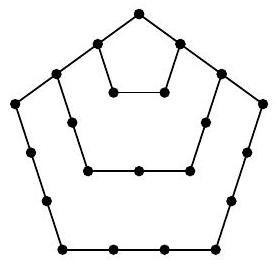
|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we can calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
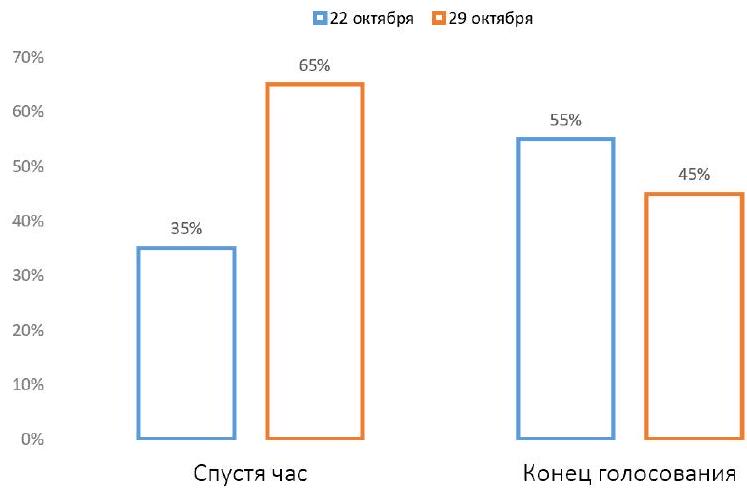
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
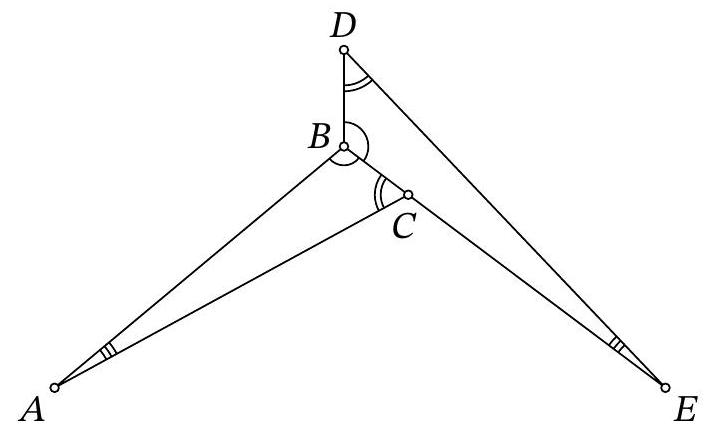
|
Answer: 7.
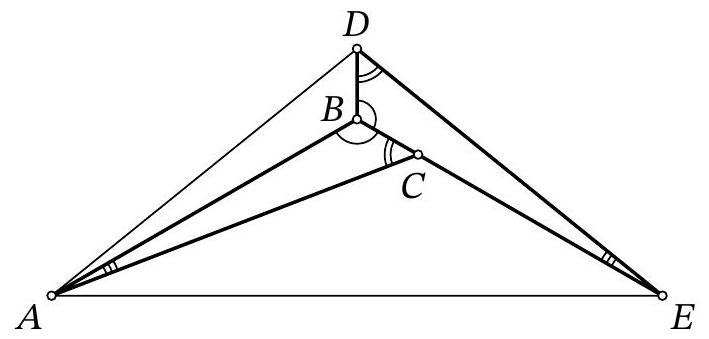
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
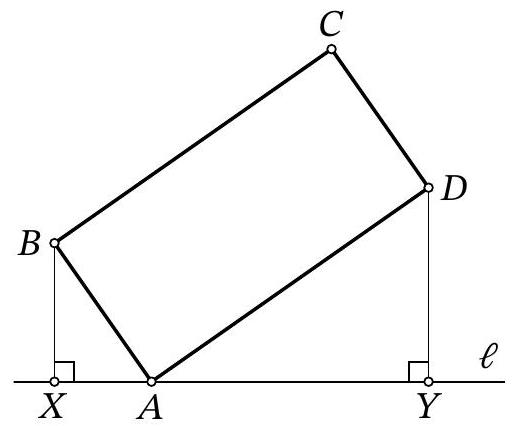
|
Answer: 13.
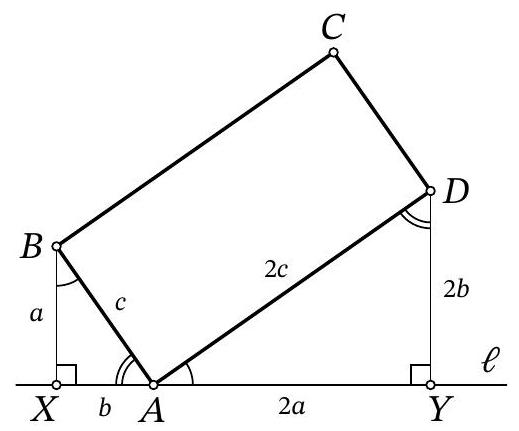
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity coefficient is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
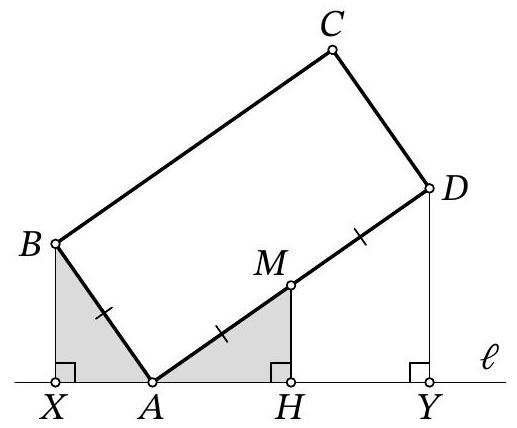
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $A B C$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $A C$, point $K$ is marked, and on side $B C$, points $L$ and $M$ are marked such that $K L=K M$ (point $L$ lies on segment $B M$).
Find the length of segment $L M$, given that $A K=4, B L=31, M C=3$.
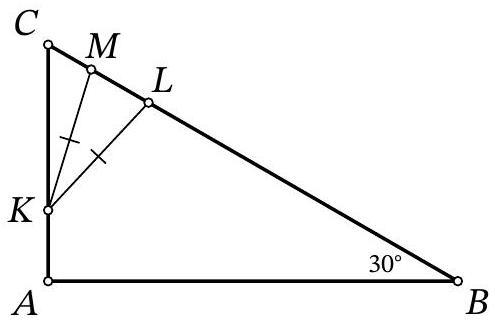
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
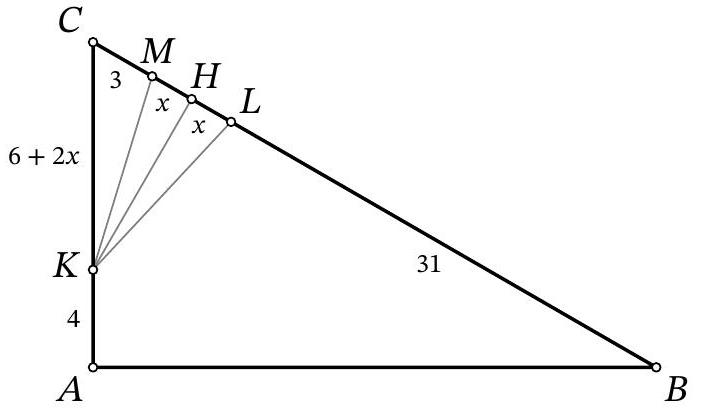
Fig. 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
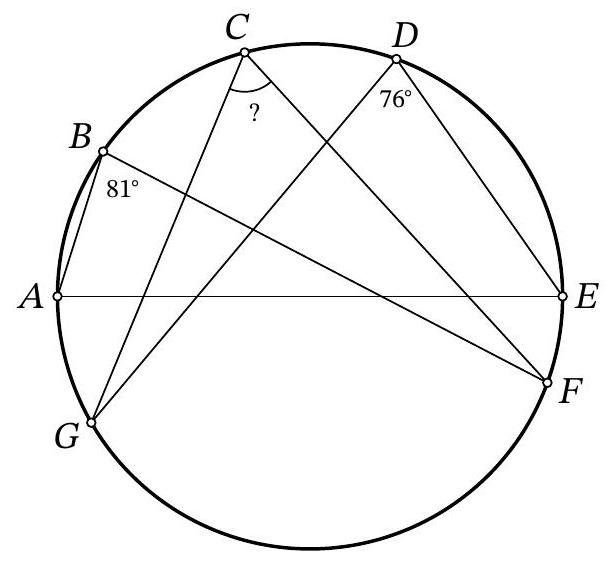
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
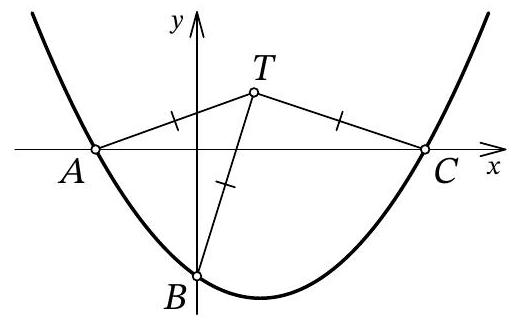
|
Answer: -6.
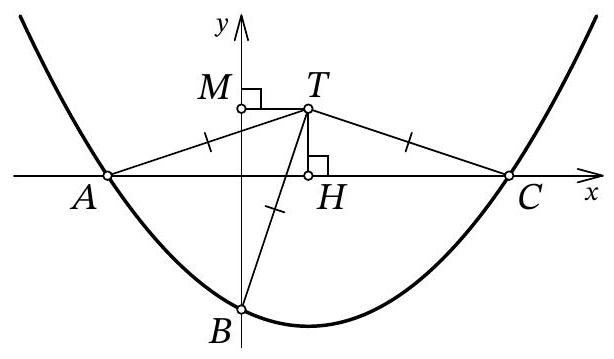
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
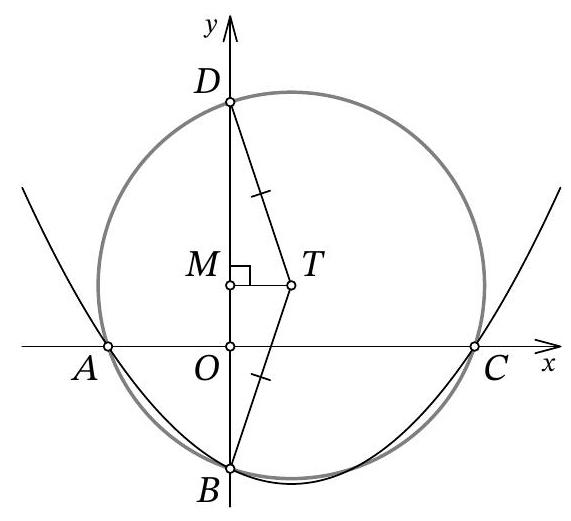
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
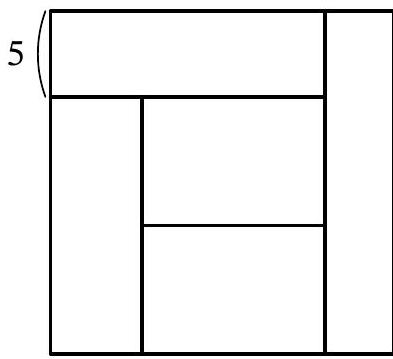
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them by $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side by $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
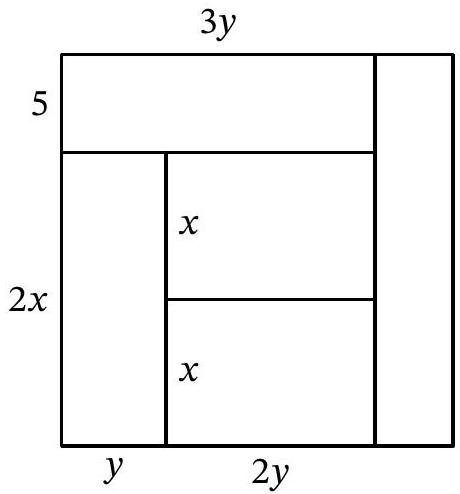
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose the teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.

|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
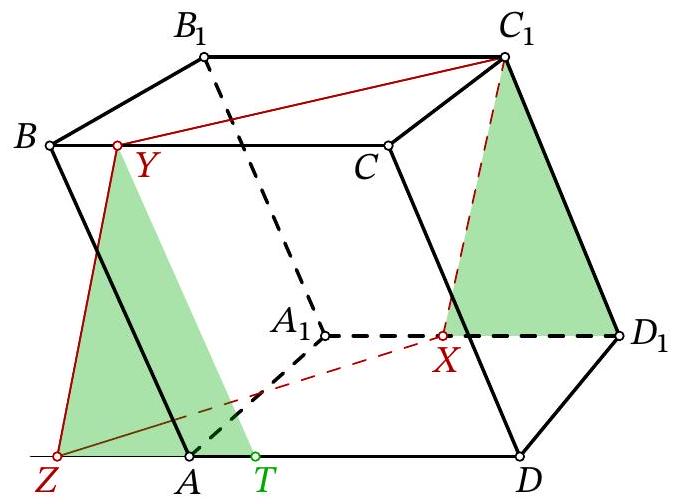
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4 The pirates, led by John Silver on Treasure Island, found Billy Bones' chest, which contained 40 coins worth 1 ducat each and 40 coins worth 5 ducats each. John Silver has not yet decided how to divide this money among all the pirates (he does not want to take anything for himself). For what maximum number of pirates can any of his decisions on dividing the coins be implemented (each pirate must receive a whole number of ducats; it is possible that some pirates will not receive any money at all)? Justify your answer.
|
Solution. We will show that if there are no more than 11 pirates, Silver can divide the coins as he wishes. Indeed, let the $i$-th pirate need to receive $S_{i}$ coins. $S_{i}=5 x_{i}+a_{i}$, for some integers $x_{i}$ and $a_{i}$ (where $a_{i}$ is the remainder of the division of $S_{i}$ by 5). Note that the sum of all $S_{i}$ is 240 ducats, so the sum of all $a_{i}$ is divisible by 5. Each of the numbers $a_{i}$ is no more than 4, so the sum of $a_{i}$ is no more than 44, and being divisible by 5, it is no more than 40. We will give out all $a_{i}$ in one-ducat coins - there will be enough. Now it remains to give each pirate a sum that is a multiple of 5 ducats. This is easily done since the number of one-ducat coins left will be a multiple of 5.
If there are 12 or more pirates, the captain will not be able to pay, for example, such sums: 10 pirates 4 ducats each, one 3 ducats, and one the rest, 197 ducats. Indeed, the first 11 pirates can only be paid with one-ducat coins, and for this, no less than 43 are needed.
Answer: 11 pirates.
| THERE IS IN THE SOLUTION | SCORE |
| :--- | :---: |
| Correct and justified answer | 7 points |
| Correct justification that for any number of pirates less than 12 and any decision by Silver, the distribution is possible plus an example of distribution for 12 people, which is not possible (if its impossibility is not proven) | 4 points |
| Correct justification that for any number of pirates less than 12 and any decision by Silver, the distribution is possible | 3 points |
| Correct example of when it will not be possible to distribute the coins for 12 pirates (with proof of impossibility) | 2 points |
| Correct example of when it will not be possible to distribute the coins for 12 pirates (without proof of impossibility) | 1 point |
| Correct answer without justification or with incorrect justification OR examples of the impossibility of distributing money for a number of pirates greater than 12 | 0 points |
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Uncle Chernomor assigns 9 or 10 of his thirty-three bogatyrs (knights) to duty each evening. What is the smallest number of days after which it can happen that all bogatyrs have been on duty the same number of times?
|
# 10.5. 7.
Let \( m \) and \( n \) be the number of days when 9 and 10 heroes were on duty, respectively. Let \( k \) be the number of days each hero was on duty. Then \( 9m + 10n = 33k \). Note that from this, \( n \) must be divisible by 3.
Firstly, the equation \( 9m + 10n = 33 \) has no solutions. Indeed, \( n \) cannot be greater than 3, so \( n \) is either 0 or 3, but \( 33 - 10n \) is not divisible by 9.
Secondly, the equation \( 9m + 10n = 66 \) has a unique solution in non-negative integers \( m = 3, n = 4 \). This is easy to verify by substituting \( n \) with 0, 3, 6. Note that \( m + n = 7 \).
Furthermore, if \( k \geq 3 \), then from the inequalities \( 10(m + n) \geq 9m + 10n = 33k \geq 99 \) it follows that \( m + n > 8 \).
It remains to provide an example of a duty schedule for 7 days. Assign the heroes numbers from 1 to 33. First day: 1-9; second day: 10-18; third day: 19-27; fourth day: 27-33 and 1-3; in the remaining days, 10 heroes in order.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.7. In a white $2016 \times 2016$ table, some cells are painted black. We will call a natural number $k$ successful if $k \leqslant 2016$, and in each of the grid squares with side $k$ located in the table, exactly $k$ cells are painted. (For example, if all cells are black, then only the number 1 is successful.) What is the maximum number of numbers that can be successful?
( B. Bakayev)
|
Answer: 1008 numbers.
Solution. Consider an arbitrary coloring of the table. Let there be at least two successful numbers, and let $a$ be the smallest of them, and $b$ be the largest.
Divide $b$ by $a$ with a remainder: $b = qa + r$, where $0 \leq r < a$. If $r \neq 0$, then the number $qa$ is also successful, and $a < qa < b$. Since $r < a$, we have $(q+1)a > qa + r = b$; thus, in the square $b \times b$, there will be more than $b$ black cells, which is impossible. Therefore, $q < 2$, which means $b < 2a$.
The total number of successful numbers does not exceed the number of natural numbers from $a$ to $b$, that is, it is no more than $b - a + 1 < b - b/2 + 1 = b/2 + 1 \leq 1009$. Thus, this number is no more than 1008.
It remains to provide an example of a coloring for which there are 1008 successful numbers. Color black all the cells in the 1008th row and only them. Consider an arbitrary square with side $d \geq 1009$. It intersects with the 1008th row, so it contains a whole row of marked cells, which means there are exactly $d$ of them. Thus, all numbers from 1009 to 2016 are successful, and there are exactly 1008 such numbers.
Comment. Only the answer - 0 points.
Provided an example with 1008 successful numbers - 2 points.
Proved only that the number of successful numbers is no more than 1008 - 4 points.
|
1008
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. Ten-digit natural numbers $a, b, c$ are such that $a+b=c$. What is the maximum number of their 30 digits that can be odd?
(I. Bogdanov)
#
|
# Answer. 29.
Solution. Note that if $a+b=c$, then all three numbers $a, b$, $c$ cannot be odd simultaneously. Therefore, among them, there is at least one even number, and the last digit of this number will also be even. Thus, among the 30 digits, there is at least one even digit, and the number of odd digits is no more than 29.
Example $1999999999+1111111111=3111111110$, shows that among the 30 digits, there can be exactly 29 odd digits.
Remark. There are many examples with 29 odd digits, for example, $3999999999+3999999999=7999999998$.
Comment. Only the answer without any correct explanations - 0 points.
Only proof that the number of odd digits is no more than $29-3$ points.
Only a correct example with 29 odd digits - 3 points. 9.7. Vasya wrote natural numbers from 1 to 81 in the cells of a $9 \times 9$ table (each cell contains one number, all numbers are different). It turned out that any two numbers differing by 3 are in adjacent cells. Is it true that there will necessarily be two corner cells, the difference of the numbers in which is divisible by 6?
(O. Podlipsky)
Answer. True.
Solution. Consider the remainders of the numbers in the four corner cells when divided by 3. By the pigeonhole principle, at least two of these numbers, $x$ and $y$, will have the same remainder, meaning the difference $y-x$ is divisible by 3. Without loss of generality, assume $x<y$.
Color the cells of our table in a checkerboard pattern with black and white such that the corner cells are black. Consider the cells with numbers $x, x+3, x+6, \ldots, y-3, y$. Any two of these numbers are in cells with a common side, meaning they are in cells of different colors. Therefore, all numbers in this sequence that have the same parity as $x$ are in black cells, and all others are in white cells. Since the number $y$ is in a black cell, it has the same parity as $x$, meaning $y-x$ is even. Thus, $y-x$ is divisible by 6.
Comment. Only the answer - 0 points;
Considering specific examples of number placement is not evaluated.
(1) It is correctly proven that the difference of some two numbers $x$ and $y$ in the corner cells is divisible by 3 - 2 points.
(2) The checkerboard coloring is considered, and it is noted that numbers differing by 3 are in cells of different colors - 2 points.
(3) It is then noted that all corner cells are of the same color, and it is claimed that the numbers in cells $x$ and $y$ have the same parity - another 2 points.
The points for advancements (1)-(3) are cumulative. Note that the proof of the evenness of the difference $x-y$ can be conducted without using the checkerboard coloring - such a proof should be evaluated accordingly.
Some remarks regarding these points, as well as some errors that may appear in the solutions, are provided below.
(1') After obtaining (1), it is claimed without justification that the numbers $x$ and $y$ have the same parity - no additional points are awarded.
(2') The idea of checkerboard coloring is not evaluated separately.
(3') Even after obtaining (2) and (3), the claim that $x$ and $y$ have the same parity requires some justification. Specifically, it is necessary to mention that there is a path from $x$ to $y$ where the numbers in adjacent cells differ by 3. (This mention can be implicit, for example, in an inductive argument.) If such a mention is absent, the problem is scored no more than 6 points. In particular, criteria (1)-(3) together give a sum of 6.
Some participants may believe that the difference between any two numbers in adjacent cells is 3. This fact is incorrect; any reasoning based on this fact is scored 0 points.
Some participants may conclude from the statement that any numbers differing by 3 are in cells of different colors (in the checkerboard coloring) that any two adjacent numbers have different parities. This conclusion is incorrect! If such an error is present in the solution, the problem is scored no more than 5 points. (5 points are awarded only if this argument is applied only to numbers having the same remainder when divided by 3.)
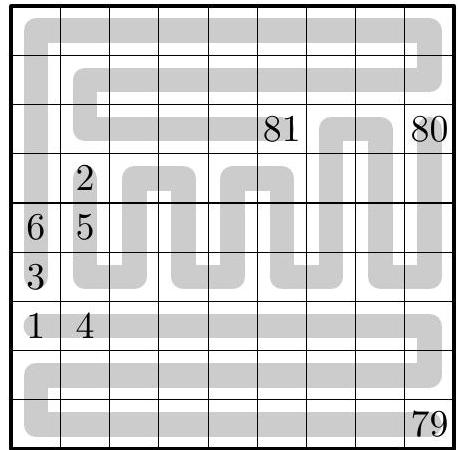
Fig. 1
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.8. Given a $1000 \times 1000$ chessboard. A figure called a cheetah, from any cell $x$, attacks all cells of a $19 \times 19$ square centered at $x$, except for the cells that are in the same row or column as $x$. What is the maximum number of non-attacking cheetahs that can be placed on the board?
(I. Bogdanov)
|
Answer: 100000.
Solution: Divide the board into $100^{2}$ squares of size $10 \times 10$. We will show that in each square, no more than 10 leopards can stand without attacking each other - from this it will follow that the total number of leopards cannot exceed $100^{2} \cdot 10=100000$.
Consider an arbitrary square $Q$ of size $10 \times 10$ and an arbitrary leopard $g$ in it. Leopard $g$ attacks all cells of the square, except for the cells that lie in the same row or column as it. If one of the other leopards $g^{\prime}$ in the square $Q$ stands in the same row as $g$, and another, $g^{\prime \prime}$, stands in the same column as $g$, then $g^{\prime}$ and $g^{\prime \prime}$ stand in different rows and columns and, consequently, attack each other; this is impossible. Otherwise, without loss of generality, all leopards in the square $Q$ stand in the same row as $g$, meaning there are no more than 10 of them.
Thus, we have shown that the total number of leopards cannot exceed 100,000; it remains to provide an example where this estimate is achieved. Number the columns of the board consecutively with the numbers $1,2, \ldots, 1000$. Place leopards on all cells of the columns whose numbers are divisible by 10. There will be $1000 \cdot 100=100000$ of these leopards, and they will not attack each other.
Comment: Only an example of placing 100000 leopards that do not attack each other is given - 2 points.
Examples with fewer leopards are not evaluated.
If only the proof that the number of leopards cannot exceed $100000$ is provided - 5 points.
If this estimate is only reduced to proving that in any $10 \times 10$ square there are no more than 10 leopards - 2 points instead of 5 for this part of the solution.
|
100000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. There are 30 logs, the lengths of which are 3 or 4 meters, and their total length is one hundred meters. How many cuts can be made to saw all these logs into pieces 1 meter long? (Each cut saws exactly one log).
|
Answer: 70.
Solution. First method The total length of the logs is 100 meters. If it were one log, 99 cuts would be needed. Since there are 30 logs, 29 cuts have already been made. Therefore, $99-29=70$ cuts remain to be made.
Second method Let's find the number of logs of each type. If all were 3-meter logs, their total length would be 90 meters. Since the total length is 100 meters, there are 10 logs that are 4 meters long and 20 logs that are 3 meters long. For each 4-meter log, three cuts are required, and for each 3-meter log, two cuts are required. In total: $10 \cdot 3 + 20 \cdot 2 = 70$ cuts.
Grading criteria.
“+” A complete and well-reasoned solution is provided
“±” A generally correct reasoning is provided, but a computational error is made
“±” Only the correct answer is provided or the correct answer is obtained from a specific example
“-” The problem is not solved or is solved incorrectly
|
70
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. All natural numbers from 1 to 1000 inclusive are divided into two groups: even and odd. In which group is the sum of all digits used to write the numbers greater, and by how much?
|
Answer. The sum of the digits of odd numbers is 499 more.
Solution. The sum of the digits of the number 1 is equal to the sum of the digits of the number 1000; the other numbers can be divided into pairs: $2-3,4-5,6-7,8-9, \ldots, 998-999$. In each pair, the unit digit of the odd number is 1 more than that of the even number, while the tens and hundreds are the same. There are 499 such pairs.
|
499
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. In the product of three natural numbers, each factor was decreased by 3. Could the product have increased by exactly 2022 in this case?
|
Answer. Yes, it could.
Solution. The product $1 \cdot 1 \cdot 678$ serves as an example. After the specified operation, it becomes $(-2) \cdot(-2) \cdot 675=2700=678+2022$.
Remark. The given example is the only one. Here is how to come up with it. Suppose two of the factors were 1, and the third was $a$. Their product was $a$, and after the reduction, it became $(-2)^{2}(a-3)=4 a-12$. Therefore, for $4 a-12=a+2022$, the condition is satisfied. Solving this equation, we get $a=678$.
Comment. Only the correct answer - 0 points.
A set of numbers satisfying the condition is presented - 7 points.
In an otherwise correct solution, due to an arithmetic error, the set $1,1, a$ is obtained, where the value of $a$ is incorrect - 5 points.
|
678
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Daisies grew along the path. Between every two daisies, a cornflower grew, and then between each cornflower and daisy - a dandelion. It turned out that now 101 flowers grow along the path. How many daisies grow along the path?
|
Solution. If at some point there are $n$ flowers growing, then there are $n-1$ gaps between them, so $n-1$ flowers grow between them, and the total becomes $2n-1$ flowers. (The absence of this phrase does not result in a score reduction). Let's move to the solution from the end. After the dandelions appear, there are 101 flowers, so before that, there were $(101+1): 2=51$ flowers. This means that the total of cornflowers and daisies was 51. Therefore, the number of daisies is $(51+1): 2=26$.
Answer. 26 daisies.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Let all numbers $x, y, z$ be non-zero. Find all values that the expression
$$
\left(\frac{x}{|y|}-\frac{|x|}{y}\right) \cdot\left(\frac{y}{|z|}-\frac{|y|}{z}\right) \cdot\left(\frac{z}{|x|}-\frac{|z|}{x}\right)
$$
can take.
|
Solution: By the Pigeonhole Principle, among the numbers $x, y$, and $z$, there will be two numbers of the same sign. Then the corresponding bracket will be equal to 0, and the entire product will also be equal to 0.
Answer: Only the number 0.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| correct and justified answer | 7 points |
| some (not all) cases of modulus expansion are correctly analyzed | 3 points |
| an example is provided showing that 0 can be obtained | 1 point |
| correct answer without justification (or with incorrect justification) | 0 points |
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Petya and three of his classmates started a 100-meter race at the same time, and Petya came in first. After 12 seconds from the start of the race, no one had finished yet, and the four participants had run a total of 288 meters. When Petya finished the race, the other three participants had 40 meters left to run in total. How many meters did Petya run in the first 12 seconds? Justify your answer. It is assumed that each participant ran at a constant speed.
|
Solution: The runners were supposed to run a total of 400 meters, and in 12 seconds they ran 288 meters, meaning that in 1 second the runners run $288: 12=$ 24 meters. When Petya finished, the runners had run $400-40=360$ meters, so from the start, $360: 24=15$ seconds had passed. Therefore, Petya runs at a speed of $100 / 15$ meters per second, and in 12 seconds he runs $\frac{100}{15} \cdot 12=80$ meters.
Answer: 80 meters.
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| correct and fully justified answer | 7 points |
| an incorrect answer due solely to arithmetic errors | 6 points |
| the equation (system of equations) is correctly set up but not solved, the solution of which leads to the answer | 4 points |
| only partial cases are considered (e.g., when the speeds of the other three runners are the same) and/or only the sum of the speeds of all 4 runners (24 m/s) is found | 2 points |
| only the correct answer is given without justification (or with incorrect justification) | 1 point |
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. All natural numbers from 1 to 20 were divided into pairs, and the numbers in each pair were added. What is the maximum number of the ten resulting sums that can be divisible by 11? Justify your answer.
|
Solution: The number 11 is the only number in the set that is divisible by 11, so adding it to any other number will disrupt divisibility by 11. Therefore, all 10 sums cannot be divisible by 11. One example where nine sums are divisible by 11 is as follows:
$(1,10),(2,20),(3,19),(4,18),(5,17),(6,16),(7,15),(8,14),(9,13),(11,12)$.
Answer: 9 sums.
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Presence of a correct example and proof of its optimality | 7 points |
| There is a proof that 10 sums cannot be obtained (in the absence of an example with 9 sums) | 3 points |
| An example is provided showing that 9 sums can be obtained (in the absence of a proof of its optimality) | 1 point |
| Correct answer without justification (with incorrect justification) | 0 points |
| Examples of a smaller number of sums (in any quantity) | not evaluated |
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Seven friends entered a cafe and ordered 3 small cups of coffee, 8 medium cups, and 10 large cups. The volume of a small cup is half the volume of a medium cup, and the volume of a large cup is three times the volume of a small cup. How should the friends divide the cups of coffee among themselves so that everyone drinks an equal amount of coffee? Pouring coffee from one cup to another is not allowed.
|
Solution: Let's call the amount of coffee in a small cup a "norm". Then, in total, we have $3+8 \times 2+10 \times 3=49$ norms. Since there are seven friends, each should get 7 norms.
We divide as follows: 1 small + 2 large - 3 people; 2 medium + 1 large - 4 people.
Criteria. A correct example - 7 points. No additional reasoning is required. If the result is obtained that each person needs 7 "norms", but the example is not shown (or the example is incorrect) - $\mathbf{1}$ point.
Incorrect example, lack of example - 0 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a football tournament, 12 teams participated. By September, they had played several games, and no two teams had played each other more than once. It is known that the first team played exactly 11 games. Three teams played 9 games each. One team played 5 games. Four teams played 4 games each. Two teams played only one game each. And
## MATHEMATICS
9th GRADE
the information about the twelfth team was lost. How many games did the 12th team play?
|
Answer: 5 games.
Solution. Let the first team K1 play 11 games - i.e., once with everyone. Teams K2 and K3 played 1 game each - these are games with team K1.
There are 9 teams left (K4-K12). Three of these teams (K4, K5, K6) played 9 games each. One of these games was with K1. And 8 with all teams K4-K12 (except themselves).
Teams K7, K8, K9, K10 played 4 games each. It is clear that these games were with teams K1, K4, K5, K6. (And there were no other games for these teams)
Team K11 played 5 games. 4 of them were with K1, K4, K5, K6. And it is certain that she did not play with teams K2, K3, K7, K8, K9, K10. Thus, she played the fifth game with team K12.
In total, team K12 played 5 games (with K1, K4-6, K11) (and did not play with K2, K3, K7-K10).
Criteria. Correct solution - 7 points.
Fully correctly described who played with whom, but there is no answer to the question of the problem (or it is somehow incorrect) - 6 points.
Noted that the team that played 11 games played with everyone (without further progress) - 0 points. If it is also noted that two teams played only with it - **1** point.
A school student can use graphs for their solution without explaining the terms used.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a convex quadrilateral ABCD. Point $M$ is the midpoint of side BC, and point $N$ is the midpoint of side CD. Segments AM, AN, and $MN$ divide the quadrilateral into four triangles, the areas of which, written in some order, are consecutive natural numbers. What is the maximum possible area of triangle $\mathrm{ABD}$?
|
Answer: 6.
Solution. Estimation. Let $n, n+1, n+2, n+3$ be the areas of the four triangles. Then the area of quadrilateral $ABCD$ is $4n+6$. $MN$ is the midline of triangle $BCD$, so $S_{BCD} = 4S_{MCN}$, but $S_{MCN} \geq n$, hence $S_{BCD} \geq 4n$. Then $S_{ABD} = S_{ABCD} - S_{BCD} \leq 6$.
Example. If $ABCD$ is an isosceles trapezoid with bases $BC=4$ and $AD=6$ and height 2, then $S_{ABD} = 6$. The areas of triangles $CMN$, $ABM$, $AND$, and $AMN$ are 1, 2, 3, and 4, respectively, i.e., they are consecutive natural numbers.
Criteria. A fully correct solution - 7 points.
A correct solution, but the example is not shown to be suitable (the fact that the areas of the four specified triangles are consecutive natural numbers is not justified) - 5 points.
It is proven that the area does not exceed 6, but there is no example where the area is 6 (or it is incorrect) - 4 points.
An example is obtained where the area of triangle $ABD$ is 6 (with justification and verification of calculations), but there is no explanation of why it cannot be more than 6 - **3** points.
The example is correct, but without justification that it fits the conditions of the problem (that the areas of the required triangles are 4 consecutive numbers) - **1** point.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Simplify the expression: $\frac{8}{1+a^{8}}+\frac{4}{1+a^{4}}+\frac{2}{1+a^{2}}+\frac{1}{1+a}+\frac{1}{1-a}$ and find its value at $a=2^{-\frac{1}{16}}$.
|
Solution. Add the last two terms, then add the obtained sum to the third term from the end, and so on. As a result, we get $\frac{16}{1-a^{16}}$. Substituting $a$ with the value $2^{-\frac{1}{16}}$, we get 32.
Answer: 32
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the product of all roots of the equation $x^{4}+4 x^{3}-2015 x^{2}-4038 x+2018=0$.
|
Solution. Transform the equation to the form: $\left(x^{2}+2 x\right)^{2}-2019\left(x^{2}+2 x\right)+2018=0$. Introduce the substitution $\boldsymbol{t}=\boldsymbol{x}^{2}+2 \boldsymbol{x}$, we get the equation: $t^{2}-2019 t+2018=0$, the roots of which are $t_{1}=1, t_{2}=2018$. Then $x^{2}+2 x-1=0$ or $x^{2}+2 x-2018=0$, from which we have $x_{1,2}=-1 \pm \sqrt{2}$, $x_{3,4}=-1 \pm \sqrt{2019}$. Their product is 2018.
Answer: 2018.
|
2018
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Each participant in the school charity event brought either one encyclopedia, or three fiction books, or two reference books. In total, 150 encyclopedias were collected. After the event, two bookshelves in the library were filled, with an equal number of books on each. On the first shelf, there was one fifth of all the reference books, one seventh of all the fiction books, and all the encyclopedias. How many participants were there in the event, and how many books did they bring in total?
|
Solution. Let $x$ be the fifth part of the reference books, $y$ be the seventh part of all fiction books. Then on the first shelf, there are $-x+y+150$ books, and on the second shelf, there are $-4x+6y$ books. From the condition of the problem, the number of books on the shelves is equal, therefore, $x+y+150=4x+6y$, from which $3x+5y=150$. But the number of reference books is a multiple of 2, and the number of fiction books is a multiple of 3, i.e., $x=2k, y=3n$. Then the equation takes the form: $6k+15n=150$. Solving in natural numbers: $n=10-\frac{6}{15}k$, therefore, $k=15, n=4$, from which $x=30, y=12$. Finally, we get that a total of 150 reference books were brought by 75 participants, 84 fiction books were brought by 42 participants. Thus, 267 people participated in the campaign, bringing 384 books.
Answer: 267 people, 384 books.
|
267
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the sides $A B$ and $B C$ of an equilateral triangle $A B C$, points $L$ and $K$ are marked, respectively, and $M$ is the intersection point of segments $A K$ and $C L$. It is known that the area of triangle $A M C$ is equal to the area of quadrilateral $L B K M$. Find the angle $A M C$.
|
Solution. From the equality of the areas of triangle $A M C$ and quadrilateral $L B K M$, it follows that the areas of triangles $A C K$ and $C B L$ are equal (see the figure), because in this case, the same area of triangle $C M K$ is added to the equal areas. We have $S_{A C K}=\frac{1}{2} A C \cdot C K \cdot \sin \angle A C K$, and $S_{C B L}=\frac{1}{2} B C \cdot B L \cdot \sin \angle C B L$, considering the equality of sides and angles in the equilateral triangle, we get that $C K=L B$, i.e., $\triangle A C K=\triangle C B L$ by two sides and the included angle. Therefore, $\angle C K A=\angle B L C$. Considering that $\angle B L C+\angle B C L=180^{\circ}-\angle L B C=120^{\circ}$, we obtain
$$
\angle A M C=\angle M C K+\angle M K C=\angle L C B+\angle B L C=120^{\circ} .
$$
Answer: $120^{\circ}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Clone 1
The teacher wanted to write an example for calculation on the board:
$$
1,05+1,15+1,25+1,4+1,5+1,6+1,75+1,85+1,95=?
$$
but accidentally forgot to write one comma. After this, Kolya went to the board and, correctly performing all the operations, obtained an integer result. What is it?
|
Answer: 27
## Solution
Let's calculate the sum
$$
1.05+1.15+1.25+1.4+1.5+1.6+1.75+1.85+1.95=13.5
$$
Therefore, in order to get an integer, the decimal point should be omitted in the number with the fractional part 0.5. As a result, instead of the number 1.5, the number 15 will appear on the board, and the result will increase by $15-1.5=13.5$ and will be equal to 27. We can also calculate it differently: notice that $1.05+1.95=1.15+1.85=1.25+1.75=1.6+1.4=3$. Then Kolya got the sum $3 \cdot 4+15=27$.
## Clone 2
The teacher wanted to write on the board the following calculation:
$$
2.05+2.15+2.25+2.4+2.5+2.6+2.75+2.85+2.95=?,
$$
but accidentally forgot to write one decimal point. After this, Kolya went to the board and, correctly performing all the operations, got an integer result. What is it?
## Answer: 45
## Clone 3
The teacher wanted to write on the board the following calculation:
$$
3.05+3.15+3.25+3.4+3.5+3.6+3.75+3.85+3.95=?,
$$
but accidentally forgot to write one decimal point. After this, Kolya went to the board and, correctly performing all the operations, got an integer result. What is it?
## Answer: 63
## Clone 4
The teacher wanted to write on the board the following calculation:
$$
4.05+4.15+4.25+4.4+4.5+4.6+4.75+4.85+4.95=?,
$$
but accidentally forgot to write one decimal point. After this, Kolya went to the board and, correctly performing all the operations, got an integer result. What is it?
## Answer: 81
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Clone 1
On an island, there live knights who always tell the truth, and liars who always lie. Before a friendly match, 30 islanders gathered in T-shirts with numbers on them—arbitrary natural numbers. Each of them said: “I have a T-shirt with an odd number.” After that, they exchanged T-shirts, and each said: “I have a T-shirt with an even number.” How many knights participated in the exchange?
|
# Answer: 15
## Solution
Notice that each knight exchanged a shirt with an odd number for a shirt with an even number, while each liar exchanged a shirt with an even number for a shirt with an odd number. This means that each knight exchanged with a liar, so there are no more knights than liars. On the other hand, each liar exchanged with a knight, so there are no more liars than knights. Therefore, the number of knights and liars is the same - half of the total number of islanders.
## Clone 2
On an island, there live knights who always tell the truth and liars who always lie. Before a friendly match, 40 islanders gathered in shirts with numbers - arbitrary natural numbers. Each of them said: "I have a shirt with an odd number." After this, they exchanged shirts, and each said: "I have a shirt with an even number." How many knights participated in the exchange?
## Answer: 20
## Clone 3
On an island, there live knights who always tell the truth and liars who always lie. Before a friendly match, 50 islanders gathered in shirts with numbers - arbitrary natural numbers. Each of them said: "I have a shirt with an odd number." After this, they exchanged shirts, and each said: "I have a shirt with an even number." How many knights participated in the exchange?
## Answer: 25
## Clone 4
On an island, there live knights who always tell the truth and liars who always lie. Before a friendly match, 60 islanders gathered in shirts with numbers - natural numbers. Each of them said: "I have a shirt with an odd number." After this, they exchanged shirts, and each said: "I have a shirt with an even number." How many knights participated in the exchange?
## Answer: 30
#
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
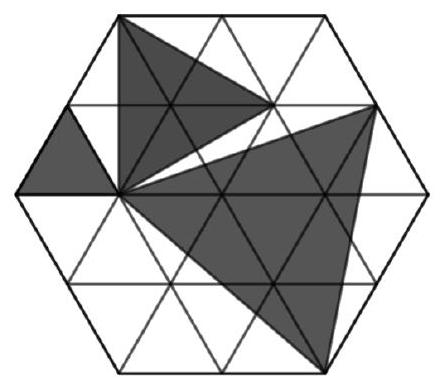
# 6. Clone 1
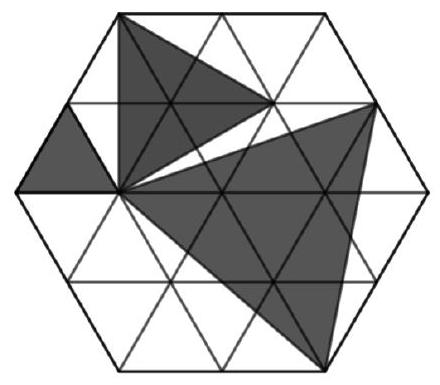
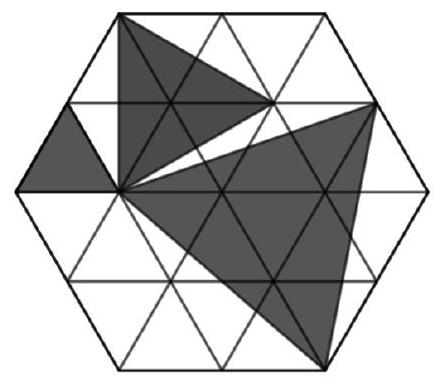
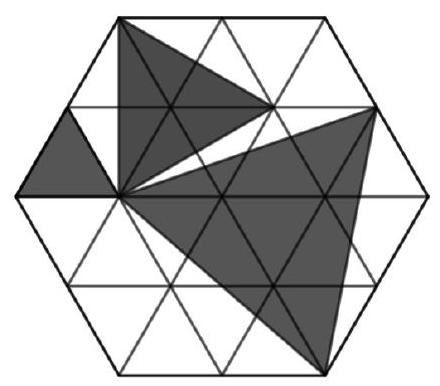
The figure shows a hexagon composed of identical equilateral triangles, each with an area of 10. Find the area of the shaded part.
#
|
# Answer: 110
## Solution
We will call the equilateral triangles that make up the original hexagon unit triangles. Consider each of the highlighted triangles inside the hexagon separately. The smallest one coincides with the unit triangle and has an area of 10. The medium triangle is inscribed in a hexagon made up of six unit equilateral triangles. The diagram shows that this triangle is equal to half the area of the hexagon, as it can be divided into parts equal to the unshaded parts of this hexagon. Thus, its area is equal to three areas of the unit triangles.
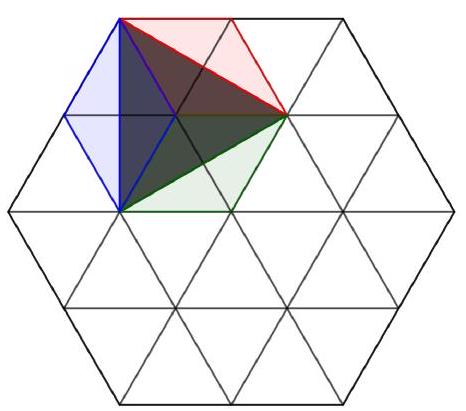
The largest triangle is inscribed in a figure made up of 13 unit triangles. Notice that it is also composed of an integer number of unit triangles. If we do not consider the central triangle, the rest can be divided into fragments equal to the unshaded parts. Then its area is equal to \((13-1) / 2 + 1 = 7\) areas of the unit triangles.
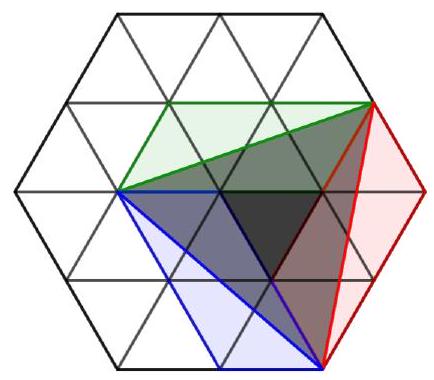
Thus, the total area of the shaded part is \(10 \cdot (1 + 3 + 7) = 110\).
## Clone 2
In the diagram, a hexagon is composed of identical equilateral triangles, each with an area of 2. Find the area of the shaded part.
Answer: 22
## Clone 3
In the diagram, a hexagon is composed of identical equilateral triangles, each with an area of 3. Find the area of the shaded part.
Answer: 33
## Clone 4
In the diagram, a hexagon is composed of identical equilateral triangles, each with an area of 5. Find the area of the shaded part.
Answer: 55
#
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. When the passengers entered the empty tram, half of them took seats. How many passengers entered at the very beginning, if after the first stop their number increased by exactly $8 \%$ and it is known that the tram can accommodate no more than 70 people?
|
Answer: 50. From the condition, it follows that the number of passengers is divisible by 2 (since half took seats) and by 25 (8% is $2/25$ of the total number). Therefore, the initial number of passengers was divisible by 50, but it was less than 70, so it was 50.
Comment. Answer only - 0 points.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. The price of a ticket to the stadium was 25 rubles. After the ticket prices were reduced, the number of spectators at the stadium increased by $50 \%$, and the revenue from ticket sales increased by $14 \%$. What is the new price of a ticket to the stadium after the price reduction?
|
Answer: 19 rubles.
Let's denote: $a$ - the number of spectators coming to the stadium; $x$ - the ratio of the new ticket price to the price of 25 rubles. The new revenue is: on the one hand $(25 \cdot x) \cdot a \cdot 1.5$, on the other hand $25 \cdot 1.14 \cdot a$. From the equality $(25 \cdot x) \cdot a \cdot 1.5 = 25 \cdot 1.14 \cdot a$ we get $x=0.76$ and $25 \cdot 0.76=19$.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In triangle $A B C$, the bisectors $A D$ and $C E$ were drawn. It turned out that $A E + C D = A C$. Find the angle $B$.
---
The text has been translated while preserving the original formatting and line breaks.
|
Answer: angle $B$ is equal to $60^{\circ}$.
Let $\alpha$ and $\gamma$ be the measures of angles $A$ and $C$ of triangle $ABC$. On side $AC$, we mark segment $AF$ equal to $AE$. From the condition, we get the equality of segments $CD$ and $CF$. Let the bisectors $AD$ and $CE$ intersect segments $EF$ and $FD$
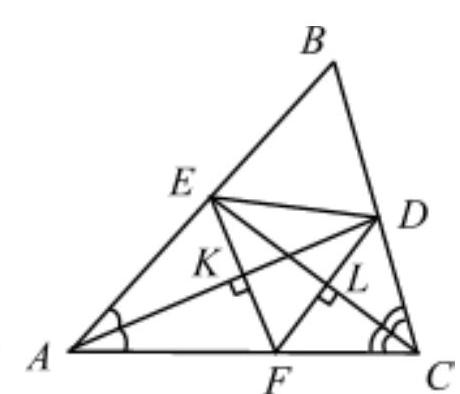
at points $K$ and $L$. In the isosceles triangle $FAE$, segment $AK$ is a bisector, hence a median and an altitude, as is segment $CL$ in $FCD$. In triangle $EFD$, segments $EL$ and $DK$ are medians and altitudes, so it is equilateral. Further, $\angle AFE = 90^{\circ} - \alpha / 2$, $\angle EFD = 60^{\circ}$, and $\angle DFC = 90^{\circ} - \gamma / 2$. Adding these angles and equating to $180^{\circ}$, we get $\alpha + \gamma = 120^{\circ}$. Therefore, angle $B$ is equal to $60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Petya was exchanging stickers. He trades one sticker for 5 others. At first, he had 1 sticker. How many stickers will he have after 30 exchanges?
|
Answer: 121.
Solution: After each exchange, the number of Petya's stickers increases by 4 (one sticker disappears and 5 new ones appear). After 30 exchanges, the number of stickers will increase by $30 * 4 = 120$. Initially, Petya had one sticker, so after 30 exchanges, he will have $1 + 120 = 121$.
|
121
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Three jumps of a two-headed dragon are equal to 5 jumps of a three-headed one. But in the time it takes for the two-headed dragon to make 4 jumps, the three-headed one makes 7 jumps. Which one runs faster? Justify your answer.
#
|
# Answer. Three-headed.
Solution. Consider the time it takes for a two-headed dragon to make 3*4=12 jumps. In this time, a three-headed dragon makes $3 * 7=21$ jumps. Since 12=4*3, 12 jumps of the two-headed dragon are equal to 4*5=20 jumps of the three-headed dragon. Thus, in the same amount of time, the three-headed dragon moves 21 jumps, while the two-headed dragon moves 20 jumps of the three-headed dragon. Therefore, the three-headed dragon runs faster.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.9. On a plane, $N$ points are marked. Any three of them form a triangle, the angles of which in degrees are expressed by natural numbers. For what largest $N$ is this possible
$$
\text { (E. Bakayev) }
$$
|
Answer: 180.

Fig. 1
First Solution. Example. First, we will show that the required is possible when $N=180$. Mark 180 points on the circle, dividing it into 180 equal arcs, each $2^{\circ}$. The measure of any arc with endpoints at two of the marked points is expressed as an even number of degrees, so the measure of any inscribed angle in the circle, formed by three marked points, is a natural number of degrees. Therefore, 180 marked points satisfy the condition of the problem.
Estimate. It remains to prove that $N \leqslant 180$. Any three marked points form a triangle, so they cannot lie on the same line. Assuming the marked points are located on the coordinate plane, let $A$ be any of them with the maximum ordinate. Among the remaining points, choose points $B$ and $C$ such that the angle $B A C$ is maximized.
From the problem's condition, it follows that in triangle $A B C$, the measures of angles $A B C$ and $A C B$ are at least $1^{\circ}$, so the measure of angle $B A C$ is at most $178^{\circ}$. Due to the choice of points $B$ and $C$, the remaining $N-3$ marked points lie strictly inside angle $B A C$, and each ray starting from point $A$ contains no more than one of them. By drawing a ray through each marked point inside angle $B A C$ starting from point $A$, we obtain $N-3$ distinct rays, dividing $\angle B A C$ into $N-2$ angles. If $N-2>178$, then at least one of these angles has a measure less than $1^{\circ}$ and is an angle of some triangle with vertices at three marked points, which contradicts the problem's condition. Therefore, $N-2 \leqslant 178$, that is, $N \leqslant 180$, which was to be proved.
Remark 1. The choice of the point $A$ used in the solution can also be described in the following ways.
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the game "Sportlotto-Shish," the main prize is drawn according to the following rules. Each person in the studio independently writes down any number of different pairs of different integers from the set from 1 to 5. If some participants have written down the same pairs, these participants share the main prize. How many participants should be in the studio to ensure that the prize is definitely awarded?
|
Solution. A total of different pairs can be formed $5 * 4 / 2=10$. It is taken into account that the digits in the pair are different and the order of the digits within the pair does not matter. Each pair can be written down or not written down by the participant. A total of different sets can be formed $2^{10}=1024$. Among them, there is an empty set (no pair is written down). In total, 1023 sets. For someone to have matching sets, the presence of 1024 people is necessary.
Comment. It is essential to exclude the empty set and then add one person (by the pigeonhole principle). A correct answer without excluding the empty set is rated 1 point.
|
1024
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a row, 33 weights are arranged in ascending order. It is known that any four consecutive weights can be distributed on two scales so that equilibrium is achieved. The third weight weighs 9 g, and the ninth weighs 33 g. How much does the 33rd weight weigh?
|
Solution. Let the weights of the weights be $a_{1}<a_{2}<\cdots<a_{33}$. For all $k=1,2, \ldots, 30$ the equalities $a_{k}+a_{k+3}=a_{k+1}+a_{k+2}$, equivalent to $a_{k+3}-a_{k+2}=$ $a_{k+1}-a_{k}$, hold. Let $a_{4}-a_{3}=a_{2}-a_{1}=d$ and $a_{5}-a_{6}=a_{3}-a_{2}=\mathrm{c}$, then $a_{6}-$ $a_{5}=a_{4}-a_{3}=d, a_{7}-a_{6}=a_{5}-a_{4}=$ c and so on. From this, $a_{1}+d+c=$ $a_{3}=9$ and $a_{1}+4 d+4 c=a_{9}=33$. From the difference of the last equalities we get $d+c=8$, and then $a_{1}=1$. We calculate $a_{33}=a_{1}+16(d+c)=129$.
Comment. An incomplete solution, brought to a system of two equations connecting $a_{1}, d, c,-4$ points.
|
129
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The least common multiple of seven natural numbers is 2012. Find the smallest possible sum of these numbers.
|
Solution: Let's factorize the number 2012 into prime factors $2012=2^{2} \cdot 503$.
One of the numbers, the LCM of which is 2012, must be divisible by $2^{2}=4$, and one (possibly the same) - by 503. If the same number is divisible by both 4 and 503, then it is divisible by 2012, and the sum of seven numbers is not less than 2018. If 4 and 503 are divisible by different numbers, then the sum of all seven numbers is not less than $4+503+1+1+1+1+1=512$. Since LCM(4,503,1,1,1,1,1)=2012, then 512 is the smallest possible value of the sum.
## Comments on Checking
The proof of minimality only considers the case where 4 and 503 are divisible by different numbers - 2 points.
An example of numbers with a sum of 512 is provided, but there is no proof of minimality - 3 points.
It is proven that the sum $\geq 512$, but no example of such numbers is given - 4 points.
|
512
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Three lines intersect at one point 0. Outside these lines, a point M is taken and perpendiculars are dropped from it to them. The points $\mathrm{H}_{1}, \mathrm{H}_{2}$ and $\mathrm{H}_{3}$ are the bases of these perpendiculars. Find the ratio of the length of the segment OM to the radius of the circle circumscribed around the triangle $\mathrm{H}_{1} \mathrm{H}_{2} \mathrm{H}_{3}$.
Answer: 2.
|
Solution
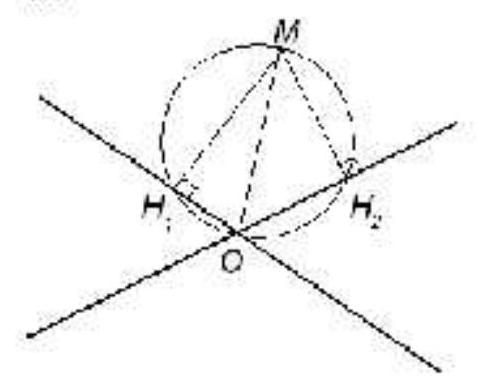
$2, \prime \prime$
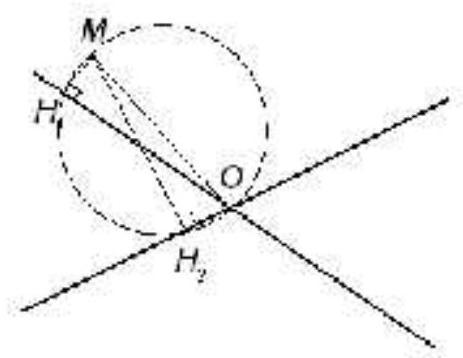
First, consider two intersecting lines and a point $M$ lying outside these lines. $\mathrm{H}_{1}$ and $\mathrm{H}_{2}$ are the feet of the perpendiculars dropped from point $\mathrm{M}$ to these lines. The possible cases are:
1) $\mathrm{H}_{1}$ and $\mathrm{H}_{2}$ lie on opposite sides of the line $0 M$
2) $\mathrm{H}_{1}$ and $\mathrm{H}_{2}$ lie on the same side of the line $0 M$;
3) $\mathrm{H}_{1}$ or $\mathrm{H}_{2}$ coincides with point 0
In the first case, $\angle \mathrm{MH} \mathrm{H}_{1} \mathrm{O} + \angle \mathrm{MH} \mathrm{H}_{2} \mathrm{O} = 90^{\circ} + 90^{\circ} = 180^{\circ}$. The quadrilateral $\mathrm{MH}_{1} \mathrm{OH}_{2}$ is cyclic, i.e., points $\mathrm{M}, \mathrm{H}_{1}, \mathrm{O}$, and $\mathrm{H}_{2}$ lie on the same circle, with the diameter of this circle being segment $OM$. In the second case, the quadrilateral $\mathrm{MH}_{1} \mathrm{H}_{2} \mathrm{O}$ is also cyclic. Points $M, \mathrm{H}_{1}, \mathrm{O}$, and $\mathrm{H}_{2}$ again lie on the same circle with diameter $OM$. In the third case, it is obvious that for points $M, H_{1}, 0$, and $H_{2}$, we get the same result.
Draw a third line and mark point $\mathrm{H}_{3}$. Then, obviously, points $\mathrm{H}_{1}$, $\mathrm{H}_{2}$, and $\mathrm{H}_{3}$ lie on the circle with diameter $OM$, and the desired ratio is 2.
## Comments on Grading
The problem is solved, but in proving that $\mathrm{M}, \mathrm{H}_{1}, \mathrm{O}$, and $\mathrm{H}_{2}$ lie on the same circle, only case 1) or case 2) is considered -5 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
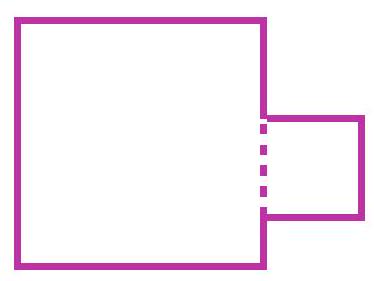
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.
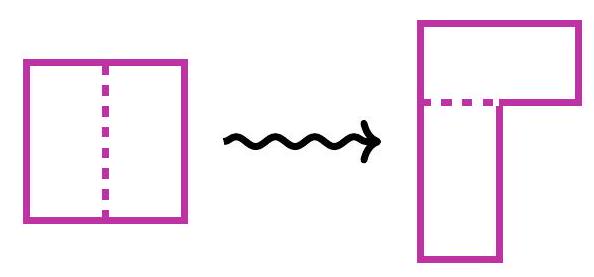
|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.

|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-6. On a rectangular table of size $x$ cm $\times 80$ cm, identical sheets of paper of size 5 cm $\times 8$ cm are placed. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
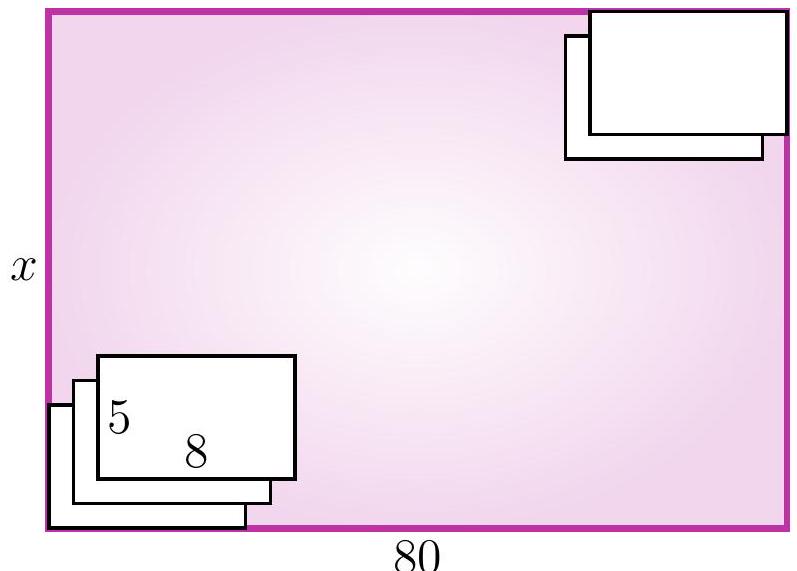
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.
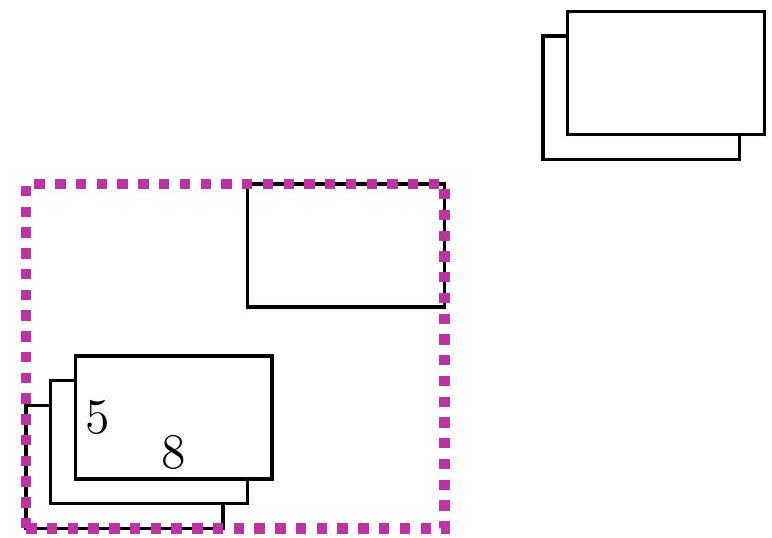
Let's call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5 cm, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
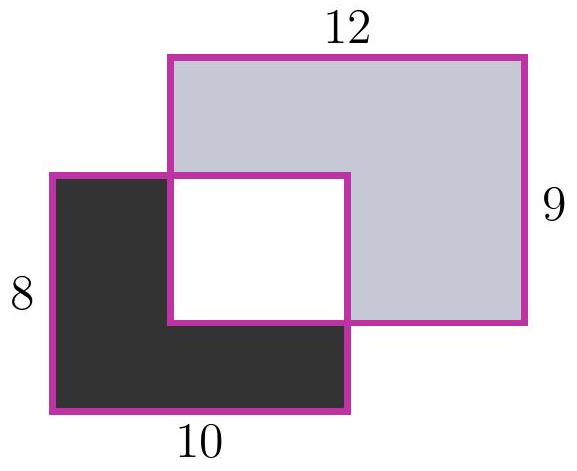
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
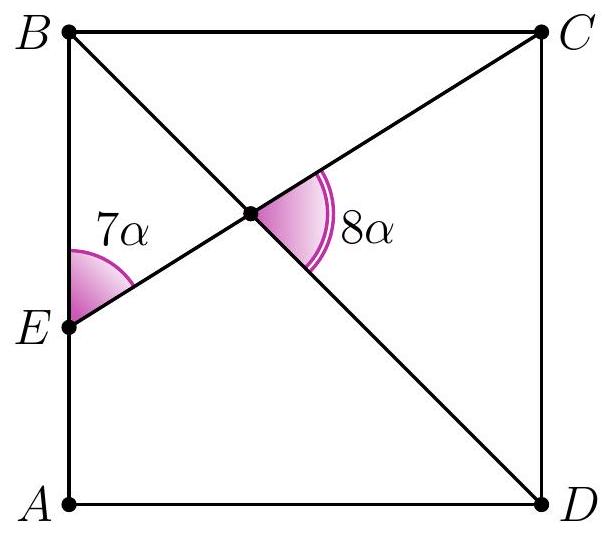
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
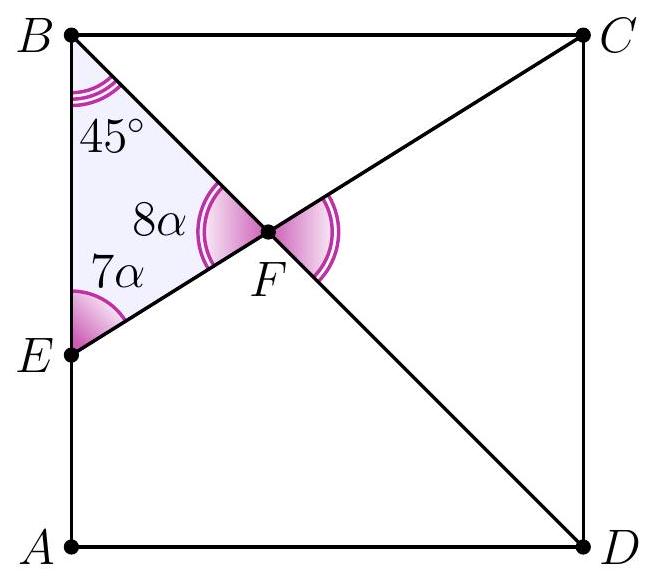
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?

|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
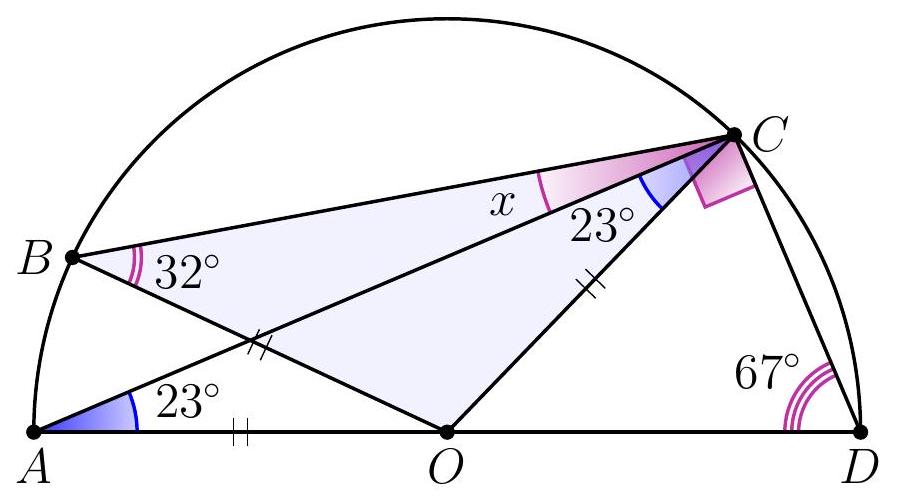
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
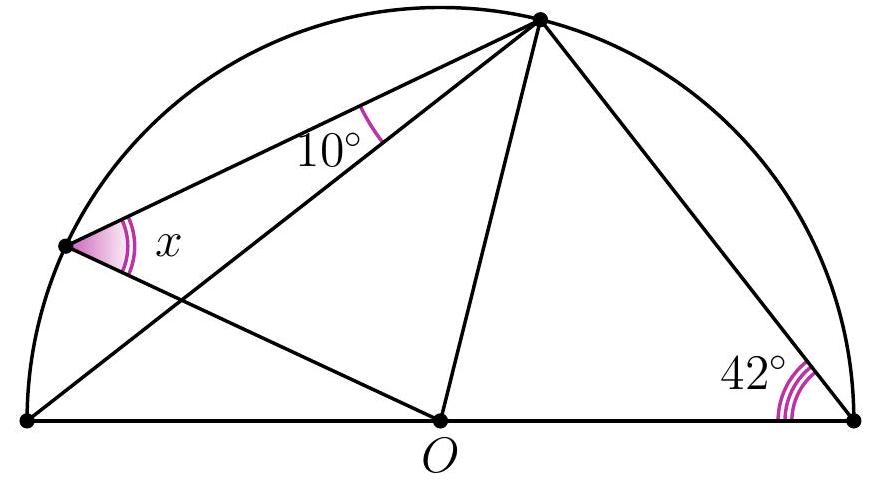
|
Answer: 58.
Solution. Angle $ACD$ is a right angle since it subtends the diameter of the circle.
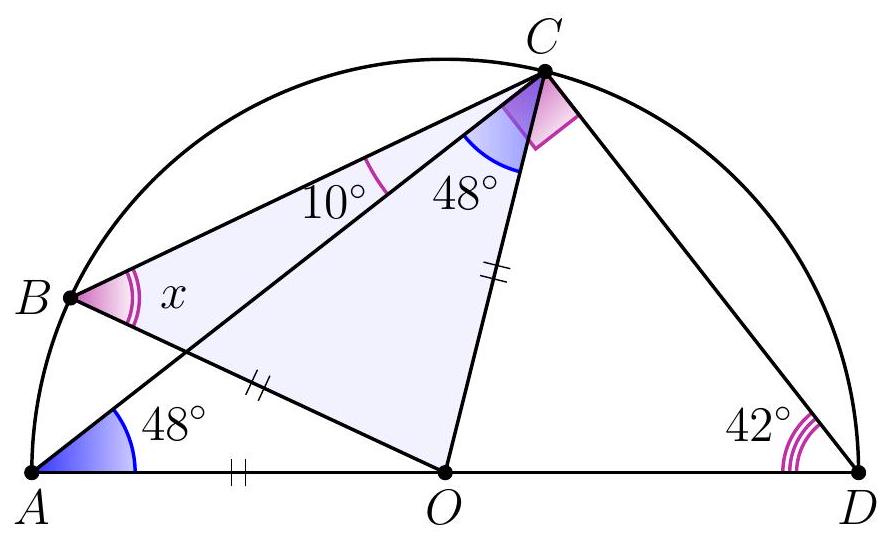
Therefore, $\angle CAD = 90^{\circ} - \angle CDA = 48^{\circ}$. Also, $AO = BO = CO$ as they are radii of the circle, so $\angle OCA = \angle ACO = 48^{\circ}$ and $x = \angle OBC = \angle OCB = 48^{\circ} + 10^{\circ} = 58^{\circ}$.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. On the board, there are 2017 digits. From these, several numbers were formed, the sums of the digits of these numbers were calculated, and then the sum of all the numbers was subtracted by the sum of the sums of their digits. The resulting number was broken down into digits, and the above operation was repeated again. After performing this operation several times, only one digit remained on the board for the first time. What is this digit?
|
Solution. Since the difference between a number and the sum of its digits is divisible by 9, the first operation will result in a number that is a multiple of 9. Moreover, if we take the sum of several numbers and subtract the sum of the digits of these numbers, the result will also be a multiple of 9. Continuing the calculations, we will get numbers that are multiples of 9 but decreasing in absolute value. In the end, the first single-digit number we obtain must be divisible by 9, and that is only 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. The numbers from 1 to 20 are arranged in a circle. We will paint a number blue if it is divisible without a remainder by the number to its left. Otherwise, we will paint it red. What is the maximum number of blue numbers that could be in the circle?
|
# Solution.
Evaluation. It is obvious that numbers cannot be blue if the number to their left is greater than or equal to 11. That is, no more than 10 numbers can be blue.
Example. As an example, both any correct arrangement and a correct algorithm are counted. An example of a correct algorithm.
1) write down the number 20
2) if the last written number $=2 \mathrm{k}$, then write the number $\mathrm{k}$ to its left, otherwise write the largest unused number to its left.
3) while there are unused numbers - repeat step 2.
## Criteria.
7 points for having both the evaluation and a correct example
4 points for only the example
3 points for only the evaluation.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. A dandelion blooms in the morning, remains yellow for this and the next day, turns white on the third morning, and by evening of the third day, it has lost its petals. Yesterday afternoon, there were 20 yellow and 14 white dandelions on the meadow, and today there are 15 yellow and 11 white. How many yellow dandelions were there on the meadow the day before yesterday? Provide all possible answers and prove that there are no others.
|
Solution: All yellow dandelions the day before yesterday are the white dandelions of yesterday and the white dandelions of today. Therefore, the day before yesterday there were $14+11=25$ yellow dandelions.
Answer: 25 dandelions.
Note: The number of yellow dandelions yesterday and today is not needed for solving the problem.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct justified answer | 7 points |
| Answer without justification OR incorrect answer | 0 points |
|
25
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. It is known that $a b c=1$. Calculate the sum
$$
\frac{1}{1+a+a b}+\frac{1}{1+b+b c}+\frac{1}{1+c+c a}
$$
|
Solution: Note that
$$
\frac{1}{1+a+a b}=\frac{1}{a b c+a+a b}=\frac{1}{a(1+b+b c)}=\frac{a b c}{a(1+b+b c)}=\frac{b c}{1+b+b c}
$$
Similarly, by replacing 1 with the number $a b c$, we have
$$
\frac{1}{1+c+c a}=\frac{a b}{1+a+a b}=\frac{a b^{2} c}{1+b+b c}=\frac{b}{1+b+b c} .
$$
Then
$$
\frac{1}{1+a+a b}+\frac{1}{1+b+b c}+\frac{1}{1+c+c a}=\frac{b c}{1+b+b c}+\frac{1}{1+b+b c}+\frac{b}{1+b+b c}=1
$$
Answer: 1.
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Correct justified answer | 7 points |
| Correct answer obtained by considering special cases (in any number) | 1 point |
| Correct answer without justification OR incorrect answer OR algebraic transformations not leading to the answer | 0 points |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. On a certain segment, its endpoints and three internal points were marked. It turned out that all pairwise distances between the five marked points are different and are expressed in whole centimeters. What is the smallest possible length of the segment? Justify your answer.
|
Solution: There are 5 points, so there are 10 pairwise distances. If all of them are expressed as positive whole numbers of centimeters and are distinct, at least one of them is not less than 10. Therefore, the length of the segment is not less than 10. Suppose the length of the segment is exactly 10. Then the pairwise distances are all numbers from 1 to 10. Among them, there is a length of 9. This means that there must be a point that is 1 cm away from one of the segment's ends, let's say from the left end - see the top diagram, marked points are black. Then points that are 1 cm away from the right end and 2 cm away from the left (they are crossed out in the diagram) cannot be marked, otherwise there would be two segments of 1 cm. To achieve a length of 8 cm, a point must be marked 2 cm away from the right end. Now, points that are 1 or 2 cm away from the marked points (white points in the diagram) cannot be marked. Only two points remain, but each of them is the midpoint of a segment between some already marked points, so they cannot be marked either. Therefore, it is impossible to mark 5 points on a segment of length 10 in the required manner, and the length of the segment must be strictly greater than 10 cm.
This length is a whole number of centimeters, as it represents the distance between marked points - the ends of the segment. Therefore, it is not less than 11 cm. We will show the required arrangement of marked points on a segment of length 11. Let the marked points (from left to right) be points \(A, B, C, D\), and \(E\). Let \(AB = 1\), \(BC = 3\), \(CD = 5\), \(DE = 2\) - all distances in centimeters (see the bottom diagram). Then \(AC = 4\), \(AD = 9\), \(AE = 11\), \(BD = 8\), \(BE = 10\), \(CE = 7\) - all 10 distances are different.
Answer: 11 centimeters.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct justified answer | 7 points |
| Proven that marking points in the required manner on a segment of length 10 is impossible, but no example on a segment of length 11 cm | 5 points |
| Provided an example of the correct arrangement of points on a segment of length 11, but not justified that a length of 10 is impossible | 2 points |
| Correct answer without justification | 1 point |
| Incorrect examples of point placement OR correct placement of points on segments longer than 11 cm | 0 points |
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3.1. Condition:
The number 4597 is displayed on the computer screen. In one move, it is allowed to swap any two adjacent digits, but after this, 100 is subtracted from the resulting number. What is the largest number that can be obtained by making no more than two moves?
|
Answer: 8357
## Solution.
The first digit cannot exceed 8, since to obtain the other digits, you need to move the nine forward by two places and subtract one from it. Note that in any other example, the first digit will be less than 8, as we can only get an eight from a nine, and all other digits are less than 9. The only way to get the digit 8 in the first position is to move the 9 forward twice.
#
|
8357
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4.1. Condition:
In front of the elevator stand people weighing 50, 51, 55, 57, 58, 59, 60, 63, 75, and 140 kg. The elevator's load capacity is 180 kg. What is the minimum number of trips needed to get everyone up?
|
Answer: 4 (or 7)
## Solution.
In one trip, the elevator can move no more than three people, as the minimum possible weight of four people will be no less than $50+51+55+57=213>180$. Note that no one will be able to go up with the person weighing 140 kg, so a separate trip will be required for his ascent. For the remaining nine people, at least $\frac{9}{3}=3$ trips will be needed, as no more than 3 people can fit in the elevator. The trips will be as follows: $(50,51,75),(55,57,63),(58,59,60)$ and (140).
In this problem, 7 is also accepted as a correct answer if the solution takes into account not only the elevator's ascents but also its descents to pick up people.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4.2. Condition:
In front of the elevator stand people weighing 150, 60, 70, 71, 72, 100, 101, 102, and 103 kg. The elevator's load capacity is 200 kg. What is the minimum number of trips needed to get everyone up?
|
Answer: 5 (or 9)
## Solution
In one trip, the elevator can move no more than two people, as the minimum possible weight of three people will be no less than $60+70+71=201>200$. Note that no one will be able to go up with the person weighing 150 kg, so a separate trip will be required for his ascent. For the remaining nine people, at least $\frac{8}{2}=4$ trips will be needed, as no more than 2 people can fit in the elevator. Thus, the trips will be: $(60,103),(70,102),(71,101),(72,100)$ and (150).
In this problem, 9 is also considered a correct answer if the solution takes into account not only the elevator's ascents but also its descents to pick up people.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4.3. Condition:
In front of the elevator stand people weighing 150, 62, 63, 66, 70, 75, 79, 84, 95, 96, and 99 kg. The elevator's load capacity is 190 kg. What is the minimum number of trips needed to get everyone up?
|
# Answer: 6 (or 11)
## Solution.
In one trip, the elevator can move no more than two people, as the minimum possible weight of three people will be no less than $62+63+66=191>190$. Note that no one will be able to go up with the person weighing 150 kg, so a separate trip will be required for his ascent. For the remaining ten people, at least $\frac{10}{2}=5$ trips will be needed, as no more than 2 people can fit in the elevator. Thus, the trips will be: (62, 99), $(63,96),(66,95),(70,84),(75,79)$ and (150).
In this problem, 11 is also considered a correct answer if the solution takes into account not only the elevator's ascents but also its descents to pick up people.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4.4. Condition:
In front of the elevator stand people weighing $130,60,61,65,68,70,79,81,83,87,90,91$ and 95 kg. The elevator's load capacity is 175 kg. What is the minimum number of trips needed to get everyone up?
|
# Answer: 7 (or 13)
## Solution.
In one trip, the elevator can move no more than two people, as the minimum possible weight of three people will be no less than $60+61+65=186>175$. Note that no one will be able to go up with the person weighing 135 kg, so a separate trip will be required for his ascent. Six trips will be needed for the remaining ten people, as no more than 2 people can fit in the elevator. The trips will be as follows: $(60,95),(61,91),(65,90),(68,87),(70,83),(79,81)$ and $(130)$.
In this problem, 13 is also considered a correct answer if the solution takes into account not only the elevator's ascents but also its descents to pick up people.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5.1. Condition:
In the warehouse, there are 8 cabinets, each containing 4 boxes, each with 10 mobile phones. The warehouse, each cabinet, and each box are locked. The manager has been tasked with retrieving 52 mobile phones. What is the minimum number of keys the manager should take with them?
|
# Answer: 9
Solution. To retrieve 52 phones, at least 6 boxes need to be opened. To open 6 boxes, no fewer than 2 cabinets need to be opened. Additionally, 1 key to the warehouse is required. In total, $6+2+1=9$ keys need to be taken by the manager.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.2. Condition:
On an island, there are two tribes: knights, who always tell the truth, and liars, who always lie. Four islanders lined up, each 1 meter apart from each other.
- The leftmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
- The rightmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
It is known that there are two knights and two liars in the row. What distances could the second and third islanders from the left have mentioned? List all possible options.
## Options for matching:
Second islander $\quad 1$ m
Third islander $\quad 2$ m
3 m
$4$ m
#
|
# Answer:
The second islander -1 m
The third islander -1 m.
## Solution.
Let's number the islanders from left to right. Suppose the first one is a knight. Then from his statement, it follows that the third one is also a knight; by the principle of exclusion, the second and fourth must be liars. The fourth said that his fellow islander stands two meters away. This is true, but the fourth is a liar, which leads to a contradiction. Therefore, the first one must be a liar.
Notice that a similar situation is created for the fourth and the first: if we look at the line from right to left, the fourth will be the first in it, and the same reasoning will apply to him. That is, the fourth must also be a liar. It follows that the second and third are knights, as the liars are the first and fourth.
From the above, it follows that the second and third are knights, who will say "one meter."
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.3. Condition:
On an island, there are two tribes: knights, who always tell the truth, and liars, who always lie. Four islanders lined up, each 1 meter apart from each other.
- The leftmost in the row said: "My fellow tribesman in this row stands 1 meter away from me."
- The second from the left said: "My fellow tribesman in this row stands 2 meters away from me."
It is known that there are two knights and two liars in the row. What distances could the third and fourth islanders from the left have named? List all possible options.
## Options for matching:
Third islander $\quad 1$ m
Fourth islander $\quad 2$ m
$3 \mathrm{M}$
$4 \mathrm{M}$
#
|
# Answer:
The third islander -1 m; 3 m; 4 m.
The fourth islander -2 m.
## Solution.
Let's number the islanders from right to left. Suppose the first one is a knight. Then, from his statement, it follows that the second one is also a knight. However, the second one said that his fellow tribesman is two meters away from him, which is a lie, since the first one, who should be the fellow tribesman of the second, is standing next to him. Therefore, we conclude:
the first one is a liar.
Now, from the first one's statement, it follows that the second one must be a knight, otherwise he would be a liar and the first one would have told the truth. If the second one is a knight, then from his statement, it follows that the fourth one is also a knight. This leaves the third one to be only a liar.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-1. Postman Pechkin calculated that he walked half the distance (at a speed of 5 km/h) and only a third of the time he was cycling (at a speed of 12 km/h). Did he make a mistake in his calculations?
|
Answer. Mistaken.
Solution. Let's denote the entire distance Pechkin traveled as $2 S$ km. Then, on foot, he covered a distance of $S$ km and spent $S / 5 = 0.2 S$ (hours) on it. According to the problem, this constituted $2 / 3$ of the total time spent, meaning the entire journey took $0.2 S : 2 / 3 = 0.3 S$ (hours), and he cycled for $0.1 S$ hours. Therefore, his speed should be $S / (0.1 S) = 10$ (km/h).
Criteria. Only the answer - 0 points. Complete solution - 7 points.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-2. The school volleyball team played several matches. After they won another match, the share of victories increased by $1 / 6$. To increase the share of victories by another 1/6, the volleyball players had to win two more consecutive matches. What is the minimum number of victories the team needs to achieve to increase the share of wins by another 1/6?
|
Answer: 6.
Solution: Let the team initially play $n$ matches, of which $k$ were won. Then, after the next win, the share of victories increased by $\frac{k+1}{n+1}-\frac{k}{n}=\frac{1}{6}$. Similarly, after two more wins, the increase was $\frac{k+3}{n+3}-\frac{k+1}{n+1}=\frac{1}{6}$. Simplifying each equation, we get the system
$$
\left\{\begin{array}{c}
n-k=\frac{n(n+1)}{6} \\
2(n-k)=\frac{(n+1)(n+3)}{6}
\end{array}\right.
$$
Dividing the second equation by the first, we get that $\frac{n+3}{n}=2$, from which $n=3$. Substituting this value into the first equation, we find that $k=3-3 \cdot 4 / 6=1$. Thus, at the beginning, the share of victories was $1 / 3$, after the next win - 2/4, and after two more wins, the team had $1+1+2=4$ victories in $3+1+2=6$ games. If the team wins $m$ more games, their share of victories will be $\frac{4+m}{6+m}$, which should match $\frac{4}{6}+\frac{1}{6}=\frac{5}{6}$. Solving the corresponding equation, we get that $m=6$.
Criteria: Only the answer - 0 points. The system of equations is set up - 5 points. Complete solution - 7 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-5. Two three-digit numbers are written on the board in a multiplication example. If the multiplication sign is replaced with 0, a seven-digit number is obtained, which is an integer multiple of the product. By what factor exactly
|
Answer: 73.
Solution. Let the original numbers be denoted by $a$ and $b$. Then the specified seven-digit number will have the form $10000a + b$. According to the condition, $10000a + b = nab$, from which we get $b = \frac{10000}{na - 1}$.
Note that the numbers $a$ and $a-1$ do not have common divisors, so $na - 1 = p$ is a divisor of 10000. Moreover, $nab \geq 10000a$, which means $nb \geq 10000$, and $n \geq 10000 / 999 > 10$. Therefore, $n \geq 11$, $p \geq 1099$, so we need to check the values of $p$ equal to $10000, 5000, 2500, 2000, 1250$ and find those for which $p+1$ can be factored into a two-digit ($n$) and a three-digit ($a$) divisor.
Let $p = 10000$, then $10001 = 73 \cdot 137$, so $n = 73$, $a = 137$, $b = 10000 \cdot a / p = a$.
Let $p = 5000$, then $5001 = 3 \cdot 1667$, the number 1667 is prime; there are no three-digit divisors.
Let $p = 2500$, then $2501 = 41 \cdot 61$, there are no three-digit divisors.
Let $p = 2000$, then $2001 = 3 \cdot 23 \cdot 29$. Since $n \geq 11$, the suitable value is at least 23, but then $a \leq 3 \cdot 29 = 87$, which is a two-digit number.
Let $p = 1250$, then $1251 = 3 \cdot 417$, the number 417 is prime. There is no factorization into a two-digit and a three-digit number.
Thus, only the case $n = 73$ remains. Indeed, $1370137 / 73 = 18769 = 137 \cdot 137$.
Criteria. Only the answer - 1 point, the equation is correctly set up - 3 points. The correct answer is derived, but the enumeration is incomplete or unproven - 5 points.
|
73
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. From the digits $1,2,3,4,5,6,7,8,9$, nine (not necessarily distinct) nine-digit numbers are formed; each digit is used exactly once in each number. What is the maximum number of zeros that the sum of these nine numbers can end with?
(N. Agakhanov)
|
Answer: Up to 8 zeros.
Solution: We will show that the sum cannot end with 9 zeros. Each of the numbers formed is divisible by 9, since the sum of its digits is divisible by 9. Therefore, their sum is also divisible by 9. The smallest natural number divisible by 9 and ending with nine zeros is $9 \cdot 10^{9}$, so the sum of our numbers is not less than $9 \cdot 10^{9}$. This means that one of them is not less than $10^{9}$, which is impossible.
It remains to show how to form numbers whose sum ends with eight zeros. For example, we can take eight numbers equal to 987654321, and one number 198765432. Their sum is $81 \cdot 10^{8}$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. Polina has two closed boxes - a square one and a round one. She was told that the round one contains 4 white and 6 black balls, while the square one contains 10 black balls. In one move, Polina can take a ball from any box without looking and either throw it away or move it to the other box. Polina wants to make the contents of the boxes the same. What is the minimum number of moves Polina can guarantee to achieve this?

|
Answer: 15
Solution. Suppose that in the end, both boxes still contain both white and black balls. Then the last action Polina took was to draw a ball of a certain color from one of the boxes, and there were still both black and white balls left. But she could not have done this with certainty, meaning she could have kept drawing balls of the wrong color. Therefore, in the end, there will be balls of only one color left, and the other color must be removed. If we draw a ball from one of the boxes and put it back, the action has no effect, so with each draw, it is necessary to either move or remove the ball.
If we remove the black balls, it will take a minimum of 16 actions, and if we remove the white balls, it will take a minimum of 10 actions, since the white balls can only be found at the bottom of the first box. In this case, there will be between 10 and 16 black balls left in the second box, and to separate them, it will take at least 5 more actions. Example: remove everything from the first box, and then move 5 balls from the second box to the first.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.2. In Olya's black box, there are 5 apples and 7 pears, and in the white box, there are 12 pears. In one move, Olya can blindly take a fruit from any box and either eat it or move it to the other box. Olya wants the contents of the boxes to be the same. What is the minimum number of moves Olya can guarantee to achieve this? The boxes are closed, and the fruits cannot be identified by touch.
|
# Answer: 18
Solution. Suppose that in the end both boxes still contain both apples and pears. Then the last action Olya took was to take some fruit from a box, and there were still both apples and pears left. Because of this, she could not guarantee that she would take the needed fruit, as she might have picked the wrong one. Therefore, at the end, only one fruit should remain in each box, and the other needs to be removed.
If we remove the pears, it would require a minimum of 19 actions, and if we remove the apples, it would require a minimum of 12 actions, as the apples might be at the bottom of the box. In this case, there will be between 12 and 18 pears left in the white box, and it will take at least 6 more actions to sort them. Example: remove everything from the black box, and then transfer 6 pears from the white box to the black box.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.3. Inna has two closed boxes - a square one and a round one. She was told that the round box contains 3 white and 10 black balls, while the square box contains 8 black balls. In one move, Inna can, without looking, take a ball from any box and either throw it away or move it to the other box. Inna wants to make the contents of the boxes the same. What is the minimum number of moves Inna can guarantee to achieve this?
|
Answer: 17
Solution. Suppose that in both boxes, there are both white and black balls left in the end. Then the last action Inna took was to draw a ball of a certain color from one of the boxes, and there were still both black and white balls left. However, she could not have done this with certainty, i.e., she might have kept drawing balls of the wrong color. Therefore, in the end, there will be balls of only one color left, and the other color needs to be removed.
If removing black balls, it would require a minimum of 18 actions, and if removing white balls - a minimum of 13 actions, since white balls can only be found at the bottom of the first box. At this point, there will be from 8 to 28 black balls left in the second box, and to separate them, it will require at least 4 more actions. Example: remove everything from the first box, and then transfer 4 balls from the second box to the first.
|
17
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.4. In Zhenya's black box, there are 8 bananas and 10 mangoes, and in the white box - 12 mangoes. In one move, Zhenya, without looking, can take a fruit from any box and either eat it or move it to the other box. Zhenya wants the contents of the boxes to be the same. What is the minimum number of moves Zhenya can guarantee to achieve this? The boxes are closed, and the fruits cannot be identified by touch.
|
# Answer: 24
Solution. Suppose that in the end, both boxes still contain both bananas and mangoes. Then the last action was Zhenya taking some fruit from a box, and both types of fruit remained. Because of this, she could not guarantee picking the right fruit, as she might have picked the wrong one.
If removing mangoes, it would require a minimum of 22 actions, and if removing bananas - a minimum of 18 actions, since bananas might be at the bottom of the box. In this case, there would be between 12 and 22 mangoes left in the white box, and it would take at least 6 more actions to sort them. Example: remove everything from the black box, and then transfer 6 mangoes from the white box to the black box.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. A chocolate bar weighed 250 g and cost 50 rubles. Recently, to save money, the manufacturer reduced the weight of the bar to 200 g, and increased its price to 52 rubles. By what percentage did the manufacturer's revenue increase?
|
# Answer: 30
Solution. We will calculate by what percentage the cost of one kilogram has increased. Before the increase, 1 kg cost 200 rubles, and after the increase, it costs $52 \cdot 5=260$ rubles. The increase is 60 rubles per kg, which originally cost 200 rubles. This is $\frac{60}{200} \cdot 100 \% = 30 \%$
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.2. A chocolate bar weighed 400 g and cost 150 rubles. Recently, to save money, the manufacturer reduced the weight of the bar to 300 g, and increased its price to 180 rubles. By what percentage did the manufacturer's revenue increase?
|
# Answer: 60
Solution. We will calculate by what percentage the cost of 1 kg 200 g has increased. Before the increase, this amount cost 450 rubles, and after the increase, it costs $180 \cdot 4=720$ rubles. The increase is 270 rubles on 1.2 kg, which originally cost 450 rubles. This is $\frac{270}{450} \cdot 100 \%=$ $60 \%$
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.4. A package of milk with a volume of 1 liter cost 60 rubles. Recently, in order to save money, the manufacturer reduced the volume of the package to 0.9 liters, and increased its price to 81 rubles. By what percentage did the manufacturer's revenue increase?
|
# Answer: 50
Solution. We will calculate by what percentage the cost of 9 liters of milk has increased. Before the increase, 9 liters cost $9 \cdot 60=540$ rubles, and after the increase, $-81 \cdot 10=810$ rubles. The increase amounts to 270 rubles for 9 liters. This amount previously cost 540 rubles. This is $\frac{270}{540} \cdot 100 \% = 50 \%$
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Galia thought of a number, multiplied it by N, then added N to the result, divided the resulting number by N, and subtracted N. In the end, she got a number that is 2021 less than the originally thought number. What is N?
|
Answer: 2022
Solution. Let the number she thought of be $\mathrm{k}$, then after two operations, she will have the number $\mathrm{kN}+\mathrm{N}$, and after division, she will have the number $\mathrm{k}+1$, which is 1 more than the number she thought of. And when she subtracts $\mathrm{N}$, the result will be a number that is $\mathrm{N}-1$ less than the original number.
|
2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. Galia thought of a number, multiplied it by $\mathrm{N}$, then added $\mathrm{N}$ to the result, divided the resulting number by N, and subtracted N. In the end, she got a number that is 7729 less than the originally thought number. What is N?
|
Answer: 7730
Solution. Let the number she thought of be $\mathrm{k}$, then after two operations, she will have the number $\mathrm{kN}+\mathrm{N}$, and after division, she will have the number $\mathrm{k}+1$, which is 1 more than the number she thought of. And when she subtracts $\mathrm{N}$, the result will be a number that is $\mathrm{N}-1$ less than the initial number.
|
7730
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.3. Galia thought of a number, multiplied it by N, then added N to the result, divided the resulting number by N, and subtracted N. In the end, she got a number that is 100 less than the originally thought number. What is N?
|
Answer: 101
Solution. Let the number she thought of be $\mathrm{k}$, then after two operations, she will have the number $\mathrm{kN}+\mathrm{N}$, and after division, she will have the number $\mathrm{k}+1$, which is 1 more than the number she thought of. And when she subtracts $\mathrm{N}$, the result will be a number that is $\mathrm{N}-1$ less than the original number.
|
101
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. For the celebration of the Name Day in the 5th grade parallel, several pizzas were ordered. 14 pizzas were ordered for all the boys, with each boy getting an equal share. Each girl also received an equal share, but half as much as each boy. How many pizzas were ordered if it is known that there are 13 girls in this parallel, and there are more boys than girls? Pizzas can be divided into parts.
|
# Answer: 15
Solution. Let the number of boys be $m$, and the number of pizzas that the girls received be $x$. If each boy had eaten as much as each girl, the boys would have eaten 7 pizzas. Then $m: 13=7: x$, from which $m x=91$. The number 91 has only one divisor greater than 13, which is 91. Therefore, $m=91, x=1$, the answer is $14+1=15$ pizzas (unfortunately, only one pizza was ordered for 13 girls, but this was by their choice).
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. For the celebration of the Name Day in the 5th grade parallel, several pizzas were ordered. 10 pizzas were ordered for all the boys, with each boy getting an equal share. Each girl also received an equal share, but half as much as each boy. How many pizzas were ordered if it is known that there are 11 girls in this parallel, and there are more boys than girls? Pizzas can be divided into parts.
|
# Answer: 11
Solution. Let the number of boys be $m$, and the number of pizzas that the girls received be $x$. If each boy had eaten as much as each girl, the boys would have eaten 5 pizzas. Then $m: 11 = 5: x$, from which we get $m x = 55$. The number 55 has only one divisor greater than 11, which is 55. Therefore, $m = 55, x = 1$, and the answer is $10 + 1 = 11$ pizzas (unfortunately, only one pizza was ordered for 11 girls, but this was by their choice).
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. For the celebration of the Name Day in the 5th grade parallel, several pizzas were ordered. 22 pizzas were ordered for all the boys, with each boy getting an equal share. Each girl also received an equal share, but half as much as each boy. How many pizzas were ordered if it is known that there are 13 girls in this parallel, and there are more boys than girls? Pizzas can be divided into parts.
|
# Answer: 23
Solution. Let the number of boys be $m$, and the number of pizzas that the girls received be $x$. If each boy had eaten as much as each girl, the boys would have eaten 11 pizzas. Then $m: 13 = 11: x$, from which $m x = 143$. The number 143 has only one divisor greater than 13, which is 143. Therefore, $m = 143, x = 1$, the answer is $22 + 1 = 23$ pizzas (alas, only one pizza was ordered for 13 girls, but this was by their choice).
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. For the celebration of the Name Day in the 5th grade parallel, several pizzas were ordered. 10 pizzas were ordered for all the boys, with each boy getting an equal share. Each girl also received an equal share, but half as much as each boy. How many pizzas were ordered if it is known that there are 17 girls in this parallel, and there are more boys than girls? Pizzas can be divided into parts.
|
Answer: 11
Solution. Let the number of boys be $m$, and the number of pizzas that the girls got be $x$. If each boy had eaten as much as each girl, the boys would have eaten 5 pizzas. Then $m: 17 = 5: x$, from which $m x = 85$. The number 85 has only one divisor greater than 17, which is 85. Therefore, $m=85, x=1$, the answer is $10+1=11$ pizzas.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. How many natural numbers $\mathrm{N}$ greater than 900 exist such that among the numbers $3 \mathrm{~N}, \mathrm{~N}-$ $900, N+15,2 N$ exactly two are four-digit numbers?
|
Answer: 5069
Solution. Note that $2 \mathrm{~N}>\mathrm{N}+15$, and if we write the numbers in ascending order, we get $\mathrm{N}-900, \mathrm{~N}+15,2 \mathrm{~N}, 3 \mathrm{~N}$. Four-digit numbers can only be two consecutive ones. If the four-digit numbers are $\mathrm{N}-900$ and $\mathrm{N}+15$, then $2 \mathrm{~N}$ must be a five-digit number, i.e., $\mathrm{N} \geq 5000$. At the same time, $\mathrm{N}$ is less than 9985 (so that $\mathrm{N}+15$ is a four-digit number), i.e., $\mathrm{N}$ is from 5000 to 9984, 4985 options. If $\mathrm{N}+15,2 \mathrm{~N}$ are four-digit numbers, then $\mathrm{N}-900$ is a three-digit number, $\mathrm{N} \leq 999+$ $900=1899$, but then $3 \mathrm{~N}$ cannot be a five-digit number. If the numbers $2 \mathrm{~N}$ and $3 \mathrm{~N}$ are four-digit numbers, then $\mathrm{N} \geq 500$, but according to the condition $\mathrm{N}>900$. At the same time, $\mathrm{N}+15$ must be a three-digit number, hence $N \leq 984$, so $N$ takes values from 901 to 984, another 84 options. In total $4985+84=5069$ options.
|
5069
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. How many natural numbers $\mathrm{N}$ greater than 300 exist such that among the numbers $4 \mathrm{~N}, \mathrm{~N}-$ $300, N+45,2 N$ exactly two are four-digit numbers?
|
Answer: 5410
Solution. Note that $2 \mathrm{~N}>\mathrm{N}+15$, and if we write the numbers in ascending order, we get $\mathrm{N}-300, \mathrm{~N}+45,2 \mathrm{~N}, 4 \mathrm{~N}$. Only two consecutive numbers can be four-digit. If the four-digit numbers are $\mathrm{N}-300$ and $\mathrm{N}+15$, then $2 \mathrm{~N}$ must be a five-digit number, i.e., $\mathrm{N} \geq 5000$. At the same time, N is less than 9955 (so that N + 45 is a four-digit number), i.e., N is from 5000 to 9954, 4955 options. If $\mathrm{N}+45,2 \mathrm{~N}$ are four-digit, then $\mathrm{N}-300$ is a three-digit number, $\mathrm{N} \leq 999+$ $300=1399$, but then $4 \mathrm{~N}$ cannot be a five-digit number. If the numbers $2 \mathrm{~N}$ and $4 \mathrm{~N}$ are four-digit, then $\mathrm{N} \geq 500$. At the same time, $\mathrm{N}+45$ must be a three-digit number, from which $\mathrm{N} \leq 954$, that is, $\mathrm{N}$ takes values from 500 to 954, another 455 options. In total $4955+455=5410$ options.
|
5410
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. How many natural numbers $\mathrm{N}$ greater than 700 exist such that among the numbers $3 \mathrm{~N}, \mathrm{~N}-$ $700, N+35,2 N$ exactly two are four-digit numbers?
|
Answer: 5229
Solution. Note that $2 \mathrm{~N}>\mathrm{N}+35$, and if we write the numbers in ascending order, we get $\mathrm{N}-700, \mathrm{~N}+35,2 \mathrm{~N}, 3 \mathrm{~N}$. Only two consecutive numbers can be four-digit. If the four-digit numbers are $\mathrm{N}-700$ and $\mathrm{N}+35$, then $2 \mathrm{~N}$ must be a five-digit number, i.e., $\mathrm{N} \geq 5000$. At the same time, N is less than 9965 (so that N + 35 is a four-digit number), i.e., N is from 5000 to 9964, 4965 options. If $\mathrm{N}+35,2 \mathrm{~N}$ are four-digit, then $\mathrm{N}-700$ is a three-digit number, $\mathrm{N} \leq 999+$ $700=1699$, but then $3 \mathrm{~N}$ cannot be a five-digit number. If the numbers $2 \mathrm{~N}$ and $3 \mathrm{~N}$ are four-digit, then $\mathrm{N} \geq 500$, but according to the condition $\mathrm{N}>700$. At the same time, $\mathrm{N}+35$ must be a three-digit number, from which $N \leq 964$, so $N$ takes values from 701 to 964, another 264 options. In total $4965+264=5229$ options.
|
5229
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved two seats to the right, Galia had moved one seat to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she got up?
|
# Answer: 2
Solution. Let's see how the seat number of everyone except Anya has changed. Varya's seat number increased by 2, Galia's decreased by 1, and the sum of Diana's and Eli's seat numbers did not change. At the same time, the total sum of the seat numbers did not change, so Anya's seat number must have decreased by 1. But then the seat left for her cannot be seat 5 (since there is no seat 6), so the seat left for her must be seat 1, and initially, she had seat 2.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved three seats to the right, Galia had moved one seat to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she stood up?
|
Answer: 3
Solution. Let's see how the seat number changed for everyone except Anya. Varya's seat number increased by 3, Galia's decreased by 1, and the sum of Diana's and Eli's seat numbers did not change. At the same time, the total sum of the seat numbers did not change, so Anya's seat number must have decreased by 2. But then the seat left for her cannot be seat 5 (since there is no seat 6), so the seat left for her must be seat 1, and initially, she had seat 3.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved one seat to the right, Galia had moved three seats to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she got up?
|
# Answer: 3
Solution. Let's see how the seat number of everyone except Anya has changed. Varya's seat number increased by 1, Galia's decreased by 3, and the sum of Diana's and El's seat numbers did not change. At the same time, the total sum of the seats did not change, so Anya's seat number must have increased by 2. However, the seat left for her cannot be seat 1 (since there is no seat 0 or -1), so the seat left for her must be seat 5, and initially, she had seat 3.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved one seat to the right, Galia had moved two seats to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she got up?
|
# Answer: 4
Solution. Let's see how the seat number of everyone except Anya has changed. Varya's seat number increased by 1, Galia's decreased by 2, and the sum of Diana's and Eli's seat numbers did not change. At the same time, the total sum of the seat numbers did not change, so Anya's seat number must have increased by 1. However, the seat left for her cannot be seat 1 (since there is no seat 0), so the seat left for her must be seat 5, and initially, she had seat 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Misha calculated the products $1 \times 2, 2 \times 3$, $3 \times 4, \ldots, 2017 \times 2018$. For how many of them is the last digit zero?
|
Solution. The last digit of the product depends on the last digits of the factors. In the sequence of natural numbers, the last digits repeat every ten. In each ten, in the sequence of products, four products end in zero: ... $4 \times \ldots 5, \ldots 5 \times \ldots 6, \ldots 9 \times \ldots 0, \ldots 0 \times \ldots 1$. ... There are 201 complete tens. And at the end, there are seven more products, two of which end in zero.
Thus, a total of $4 \times 201 + 2 = 806$ products end in zero.
Criteria. Any correct solution: 7 points.
In the solution, two zeros from the last incomplete ten are lost: 4 points.
Only the correct answer is provided: 1 point.
|
806
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the pantry, Winnie-the-Pooh keeps 11 pots, seven of which contain jam, and four contain honey. All the pots are lined up, and Winnie remembers that the pots with honey are standing together. What is the minimum number of pots Winnie-the-Pooh needs to check to find a pot with honey?
|
Answer: one.
Solution. Let's number the pots from 1 to 11 in the order of their arrangement in a row. Exactly one of the pots numbered 4 and 8 contains honey. Therefore, it is sufficient to check one of them. It is impossible to identify the pot with honey without checking, as any pot may contain either honey or jam.
Criteria. Any correct solution: 7 points.
It is stated that the 4th (8th) pot should be checked, but it is not specified what to do if it contains jam: 3 points.
Only the correct answer is provided: 0 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is a $6 \times 6$ square, all cells of which are white. In one move, it is allowed to change the color of both cells in any domino (a rectangle of two cells) to the opposite. What is the minimum number of moves required to obtain a square with a checkerboard pattern? Don't forget to explain why a smaller number of moves would not be enough.
|
Answer: 18 moves.
Solution. Note that in the chessboard coloring of a $6 \times 6$ square, there are 18 black cells. At the same time, no two of them can be turned black in one move, because they are not covered by one domino. Therefore, at least 18 moves are required (at least one move per cell). This can be done in 18 moves, for example, by dividing the board into 9 squares of $2 \times 2$, and in each square, first recoloring the bottom domino, and then the right one. There are other algorithms as well.
Criteria. Only the answer - 1 point, correctly formulated algorithm - 5 points. Full solution 7 points.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. To the number $A$, consisting of eight non-zero digits, a seven-digit number, consisting of identical digits, was added, and the eight-digit number $B$ was obtained. It turned out that the number $B$ can be obtained from the number $A$ by rearranging some of the digits. What digit can the number $A$ start with if the last digit of the number $B$ is 5?
|
Answer: 5.
Solution: Since the numbers $A$ and $B$ have the same sum of digits, their difference is divisible by 9. Therefore, the added seven-digit number with identical digits is divisible by 9. This means it consists of nines. That is, we can consider that $10^7$ was added to the number $A$ and 1 was subtracted. This means that the number $B$ is obtained from the number $A$ by increasing the first digit by 1 and decreasing the last digit by 1 (since there are no zeros in $A$ and $B$ is eight-digit), while the other digits remain unchanged. Since the number $B$ can be obtained from the number $A$ by permuting some digits, the last digit of the number $B$ coincides with the first digit of the number $A$ (and vice versa). Therefore, the number $A$ can only start with the digit 5.
Comment: It is proven that the added number consists of nines - 2 points.
Answer obtained by considering an example - 1 point.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. On a checkerboard of size $8 \times 8$, 8 checkerboard ships of size $1 \times 3$ are placed such that no two cells occupied by different ships share any points. One shot is allowed to pierce all 8 cells of one row or one column. What is the minimum number of shots needed to guarantee hitting at least one ship?
|
Answer: 2 shots.
Solution. We will make 2 shots as shown in Fig. 5. Suppose we did not hit any ship. Then there are no ships in area 1. In each of areas 2 and 3, there is no more than 1 ship. Therefore, there are at least 6 ships in area 4.
Area 4 is a $5 \times 5$ square. Then in this area, horizontally placed ships cannot lie in adjacent rows, and vertically placed ships cannot lie in adjacent columns. Therefore, in this area, there are 3 "vertical" and 3 "horizontal" ships, and one of them lies
Fig. 5 in the central row, and another in the central column of the area. But then both of these ships contain the central cell of the area. Contradiction. Therefore, at least one ship is hit.
We will show that if only one shot is made, it is possible not to hit any ship. Suppose the shot was made in some row. Note that in one row, two ships can be placed. Then if the shot was made in a row with an odd number, two ships could stand in rows with numbers $2, 4, 6$, and 8. If the shot was made in a row with an even number, two ships could stand in rows with numbers $1, 3, 5$, and 7.
Remark. It can be shown that even 5 ships cannot be placed in area 4.
Comment. Only shown how to wound a ship with 2 shots - 4 points.
Only proven that 1 shot may not be enough - 2 points.
A correct example of two shots is given, but it is not explained why at least one ship will be hit - 1 point (instead of 4 points for the first criterion).
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A tea set consists of six identical cups and six identical saucers. Six different sets were packed into two boxes, all saucers in one box, and all cups in the other. All items are wrapped in opaque paper and are indistinguishable by touch. Find the minimum number of items that need to be taken out of these boxes to guarantee getting at least one pair consisting of a cup and a saucer from the same set. Justify your answer. (You know which box contains the cups and which box contains the saucers.)
|
Solution. Explanation by example. 18 cups and 12 saucers may not be enough. Let's number the sets. By randomly picking 18 cups, we might get all the cups from sets №1, 2, 3.
By randomly picking 12 saucers, we might get all the saucers from sets №5, 6. It is impossible to form a cup-saucer pair. Adding one more saucer to this set, the only way it still cannot form a pair is if the thirteenth saucer belongs to set №4.
General proof. $n$ taken cups and $30-n$ taken saucers can end up from different sets $(n>0)$. Suppose the taken cups completely occupy $k$ sets, and $r$ more cups are taken from some single set. Then $n=6k+r, 30-n=30-6k-r=6(4-k)+(6-r)$, here the saucers also occupy $4-k$ sets completely, and there are $6-r$ saucers left. It can happen that the sets occupied by cups and saucers do not intersect, and such sets sum up to 4. The remaining taken cups and saucers can end up from different sets, the remainders from division by 6 allow this. Further, adding the 31st item may still not allow forming a cup-saucer pair, as the new item belongs to an already encountered incomplete set, or the 30 cups and saucers are grouped by 6 and belong to different sets.
Now we show that 32 items allow forming a pair. Take 31 cups. Since there are more than 30 cups, we have at least one cup from each set. Any taken saucer will allow forming a pair. Answer. 32 items.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From Central Square to the station, there is a straight street divided by 11 intersections into 12 equal blocks. At each intersection, there is a traffic light. All traffic lights simultaneously turn green for 3 minutes, then red for 1 minute. It takes the bus two minutes to travel one block (from intersection to intersection), while a car takes one minute to travel one block. The bus and the car start from the square at the same time, at which moment all traffic lights turn green. Which vehicle will arrive at the station first, and how many minutes earlier?
|
Solution. A car will travel three blocks without obstacles in the first three minutes. Upon approaching the intersection separating the third and fourth blocks, the car will stop at the traffic light for 1 minute. Thus, to travel three blocks and start moving on the fourth block, the car will need four minutes. The car's movement will then repeat, and it will leave the ninth block along with the intersection after 12 minutes. The next three blocks will be traveled in 3 minutes, and since there is no traffic light after the twelfth block, it will arrive at the station 15 minutes after leaving the square.
The bus will travel the first block, the first intersection, and the second block without stopping and will approach the second intersection at the moment when the red light changes to green. Therefore, at the beginning of the third block, the same situation will occur as at the beginning of the first block - the bus starts moving on the third block when the traffic light turns green. It will then pass all intersections without stopping at traffic lights again. The bus's travel time is 24 minutes.
Thus, the car will arrive 9 minutes earlier.
Answer. The car will arrive first, overtaking the bus by 9 minutes.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In quadrilateral $A B C D$, points $X, Y, Z$ are the midpoints of segments $A B, A D, B C$ respectively. It is known that $X Y$ is perpendicular to $A B$, $Y Z$ is perpendicular to $B C$, and the measure of angle $A B C$ is $100^{\circ}$. Find the measure of angle $A C D$.
|
Solution 1. Triangles $A Y B, B Y C, A Y C$ and $C Y D$ are isosceles, as follows from the condition. Let the equal angles be $\angle B A Y=\angle A B Y=x, \angle C B Y=\angle B C Y=y$, $\angle D C Y=\angle C D Y=z, \angle C A Y=\angle A C Y=v$ (see fig.). We are given that $x+y=100^{\circ}$. We need to find $z+v$.
The sum of the angles in quadrilateral $A B C D$ is $x+x+y+y+z+z=360^{\circ}$. From this, $z=80^{\circ}$. Let's calculate the angle at the vertex of the isosceles triangle $C Y D$. $\angle C Y D=180^{\circ}-2 z=20^{\circ}$. This angle is the external angle of triangle $A Y C$, so $\angle C Y D=2 v$, from which $v=10^{\circ}$. Now we can find the measure of angle $A C D$. $\angle A C D=z+v=80^{\circ}+10^{\circ}=90^{\circ}$.
Solution 2. From the condition, it immediately follows that triangles $A Y B$ and $B Y C$ are isosceles, and the lateral sides are equal to each other and equal to segments $A Y$ and $Y D$. We get that point $Y$ is the center of the circle circumscribed around quadrilateral $A B C D$, and $A D$ is the diameter of this circle. Therefore, angle $A C D$ is a right angle. Answer. $\angle A C D=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Three runners - Anton, Seryozha, and Tolya - are participating in a 100 m race. When Anton finished, Seryozha was 10 meters behind him, and when Seryozha finished, Tolya was 10 meters behind him. What distance was Tolya from Anton when Anton finished? (It is assumed that all boys run at constant, but of course, not equal speeds.)
|
Answer: 19 m.
Solution: Since Tolya's speed is $9 / 10$ of Seryozha's speed, by the time Anton finished, Tolya had run $9 / 10$ of the distance covered by Seryozha, which is $90 \cdot 9 / 10=81$ m. Thus, when Anton finished, Tolya and Anton were 19 m apart.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.