problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. Anya and Danya together weigh 82 kg, Danya and Tanya - 74 kg, Tanya and Vanya - 75 kg, Vanya and Manya - 65 kg, Manya and Anya - 62 kg. Who is the heaviest and how much does he/she weigh?
|
Answer. Vanya weighs 43 kg.
Solution. Adding the weights given in the condition: $82+74+75+65+62=358$, we get the doubled weight of all the children. That is, all the children together weigh $358 / 2=179$.
Anya, Danya, Tanya, and Vanya together weigh $82+75=157$, so Manya weighs 179 $157=22$.
Similarly, we find that Anya weighs 179-(74+65)=40, Danya weighs 179$(75+62)=42$, Tanya weighs $179-(82+65)=32$, and Vanya weighs $179-(74+62)=43$. Thus, the heaviest is Vanya, and he weighs 43 kg.
|
43
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A student passed 31 exams over 5 years of study. Each subsequent year, he passed more exams than the previous year, and in the fifth year, he passed three times as many exams as in the first year. How many exams did he pass in the fourth year?
|
# Answer: 8.
Solution: Let $a, b, c, d, e$ be the number of exams taken in each year of study. According to the problem, $a+b+c+d+e=31, a<b<c<d<e$.
Replace the numbers $b, c, d, e$ in the equation with definitely not larger values:
$a+(a+1)+(a+2)+(a+3)+3a \leq 31$. We get $7a \leq 25$. Replacing these numbers with definitely not smaller values, we get $a+(3a-3)+(3a-2)+(3a-1)+3a \geq 31$. We get $13a \geq 37$. Therefore, $a=3$. In this case, $e=9, b+c+d=19$.
If $d<8$, then this sum is no more than $5+6+7=18$. The numbers 5, 6, 8 fit. Evaluation criteria. The answer alone is not scored. An answer with an example of all five numbers - 2 points.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A circle with center at point $O$ is circumscribed around quadrilateral $A B C D$. The diagonals of the quadrilateral are perpendicular. Find the length of side $B C$, if the distance from point $O$ to side $A D$ is 1.
|
Answer: $B C=2$
Solution. Let $O E \perp A D$, then $O E=1$. Draw a line through point $A$ perpendicular to $A D$, which intersects the circle at point $M$. Then $D M$ is a diameter and $D O=O M$. Since $\angle D B A=\angle D M A$ (as inscribed angles subtending the same arc), $\angle M D A=90^{\circ}-\angle D M A$ and $\angle C A B=90^{\circ}-\angle D B A$, then $\angle C A B=\angle M D A$. Therefore, arc $A M$ is equal to arc $B C$ and $B C=A M$. $\triangle M D A$ is similar to $\triangle O D E$ (by two equal angles) with a similarity ratio of $\frac{1}{2}$, so $2 O E=A M=B C=2$.
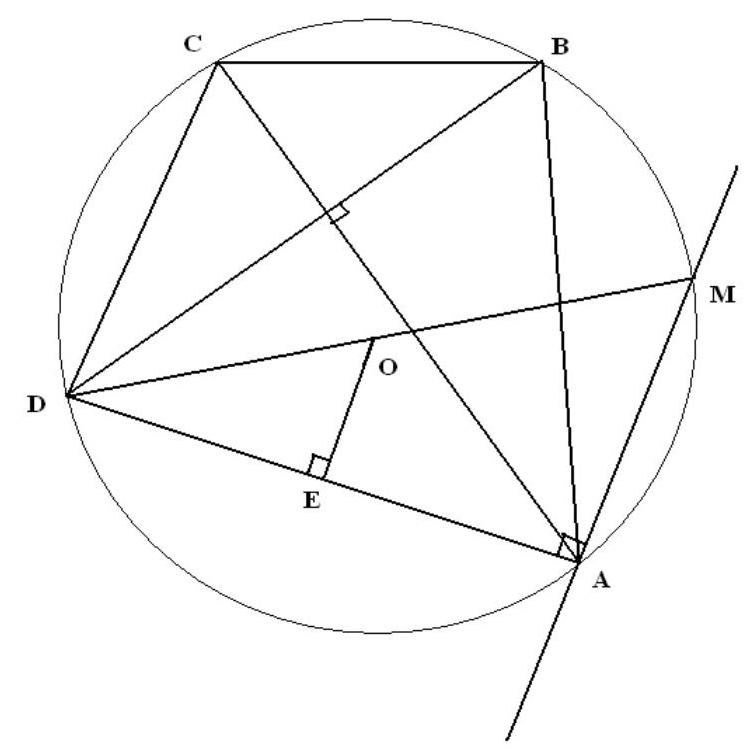
## Grading Criteria.
Similarity of $\triangle O E D$ and $\triangle C B A$ is proven - 2 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.3
In a convex pentagon $P Q R S T$, angle $P R T$ is half the size of angle $Q R S$, and all sides are equal. Find angle $P R T$.
## Number of points 7
|
Answer:
$30^{\circ}$.
Solution. From the condition of the problem, it follows that $\angle P R Q+\angle T R S=\angle P R T(*)$.
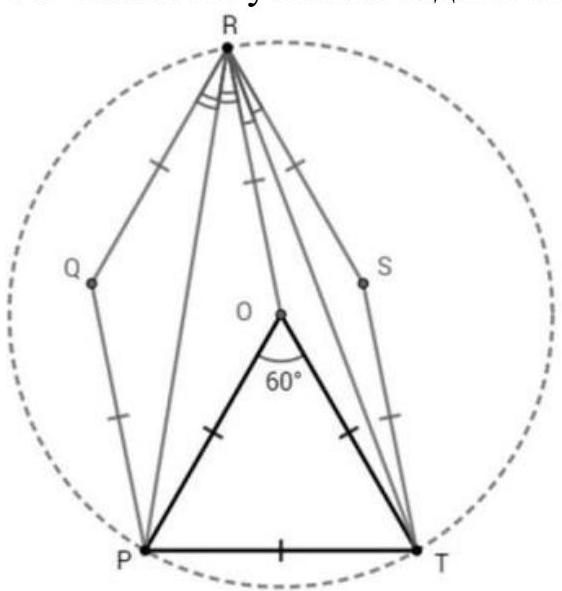
Figure a
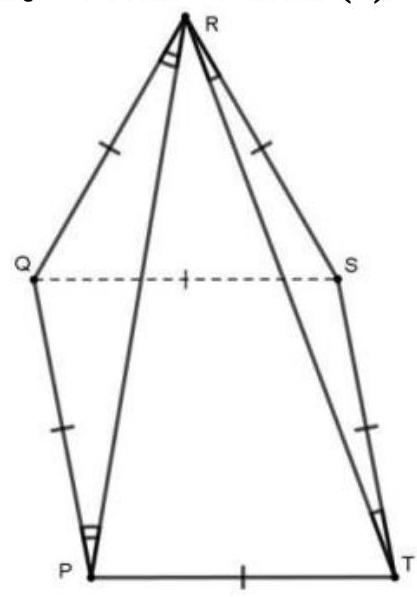
Figure b
First method. We use the "folding" method. Reflect triangle $P Q R$ symmetrically with respect to line $P R$, and triangle $T S R$ with respect to line $T R$ (see Fig. a). From the equality (*) and the equality $R Q=R S$, it follows that the images of points $Q$ and $S$ are the same point $O$.
Note that triangle $T O P$ is equilateral. Moreover, $O R=O P=O T$. Therefore, $O$ is the center of the circumscribed circle of triangle $P R T$. Then $\angle P R T=$ $0.5 \angle P O T=30^{\circ}$.
Second method. We prove that QPTS is a parallelogram (see Fig. b).
Indeed, using the equality of the angles at the bases of the isosceles triangles $P Q R$ and $R S T$ and the equality (*), we get: $\angle Q P T+\angle P T S=\angle Q P R+\angle R P T+$ $\angle R T P+\angle S T R=\angle P R Q+\angle T R S+\left(180^{\circ}-\angle P R T\right)=180^{\circ}$.
Thus, $P Q \| S T$ and $P Q=S T$ (by condition), that is, $Q P T S$ is a parallelogram. Then $Q S=P T$, so triangle $Q R S$ is equilateral.
Therefore, $\angle P R T=0.5 \angle Q R S=30^{\circ}$.
## Additional grading criteria
"7" A complete and justified solution is provided
“4-6" A generally correct solution is provided, containing minor gaps or inaccuracies (for example, the fact that the images of points $\mathrm{Q}$ and $\mathrm{S}$ coincide under the symmetries is used but not justified)
"1-3" The correct answer is obtained, assuming that QPTS is a parallelogram, but this is not proven
"0" Only the answer is provided or the answer is obtained by considering a regular pentagon
" 0 " An incorrect solution is provided or no solution is provided
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 9.5
In the class, there are 30 students: excellent students, average students, and poor students. Excellent students always answer questions correctly, poor students always make mistakes, and average students answer the questions given to them strictly in turn, alternating between correct and incorrect answers. All students were asked three questions: "Are you an excellent student?", "Are you an average student?", and "Are you a poor student?". 19 students answered "Yes" to the first question, 12 to the second, and 9 to the third. How many average students are there in this class?
## Number of points 7
#
|
# Answer:
20 C-students
Solution. Let $\mathrm{a}$ be the number of excellent students, $\mathrm{b}$ be the number of poor students, $\mathrm{c}$ be the number of C-students who answered the first question incorrectly, answered the second question correctly, and answered the third question incorrectly (we will call these C-students of the first type), and $\mathrm{d}$ be the number of C-students who answered the first question correctly, answered the second question incorrectly, and answered the third question correctly (we will call these C-students of the second type).
The first question was answered "Yes" by excellent students, poor students, and C-students of the first type, so $\mathrm{a}+\mathrm{b}+\mathrm{c}=19$. The second question was answered "Yes" by poor students and C-students of the first type, so $\mathrm{b}+\mathrm{c}=12$. The third question was answered "Yes" only by C-students of the first type, so $c=9$. From the second equation, we get that $b=3$, and from the first equation: $\mathrm{a}=7$. There are 30 students in the class, so $\mathrm{d}=30-19=11$, therefore, the total number of C-students is: $9+11=20$.
## Additional criteria for evaluation
- “7" - a complete and justified solution is provided
- “5-6” - a generally correct reasoning is provided, containing minor gaps or inaccuracies
- “1-2" - in the provided reasoning, it is indicated that C-students can be of two types, but there is no further progress or a computational error has been made.
- "0" - the problem is not solved or solved incorrectly
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. In the album, a checkered rectangle $3 \times 7$ is drawn. Igor the robot was asked to trace all the lines with a marker, and it took him 26 minutes (the robot draws lines at a constant speed). How many minutes will it take him to trace all the lines of a checkered square $5 \times 5$?
|
Answer: 30 minutes.
Solution. Note that the grid rectangle $3 \times 7$ consists of four horizontal lines of length 7 and eight vertical lines of length 3. Then the total length of all lines is $4 \cdot 7 + 8 \cdot 3 = 52$. It turns out that Igor spends $26 : 52 = 1 / 2$ minutes on the side of one cell.
The rectangle $5 \times 5$ consists of six vertical and six horizontal lines of length 5. Thus, the total length of the lines is $6 \cdot 5 + 6 \cdot 5 = 60$. Then it will take Igor $60 \cdot 1 / 2 = 30$ minutes to outline it.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. There are 9 cards with numbers $1,2,3,4,5,6,7,8$ and 9. What is the maximum number of these cards that can be laid out in some order in a row so that on any two adjacent cards, one of the numbers is divisible by the other?
|
Answer: 8.
Solution: Note that it is impossible to arrange all 9 cards in a row as required. This follows from the fact that each of the cards with numbers 5 and 7 can only have one neighbor, the card with the number 1. Therefore, both cards 5 and 7 must be at the ends, and the card with the number 1 must be adjacent to each of them, which is impossible.
It is possible to select 8 cards and arrange them in a row according to the requirements of the problem, for example: $9,3,6,2,4,8,1,5$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Karlson counts 200 buns baked by Fräulein Bock: «one, two, three, ..., one hundred and nine, one hundred and ten, two hundred». How many words will he say in total? (Each word is counted as many times as it was said.)
|
Answer. 443 words.
Solution. One word is required to pronounce 29 numbers: $1,2,3,4,5,6,7,8,9,10,11,12$, $13,14,15,16,17,18,19,20,30,40,50,60,70,80,90,100,200$.
Among the first 99 numbers, the number of those pronounced in two words: $99-27=72$, thus, the number of words required for their pronunciation is $2 \cdot 72=144$.
In the next hundred (from 101 to 199), each number that is pronounced in one word in the first hundred will be pronounced in two, and the number of words is: $2 \cdot 27=54$. The rest are pronounced in three words: 3 . $(99-27)=216$.
Thus, to count all the buns, $29+144+54+216=443$ words will be needed.
## Criteria.
1 point. The number of numbers pronounced in one word is found reasonably.
2 points. The number of words required to pronounce numbers from 1 to 99 is found correctly and reasonably.
2 points. The number of words required to pronounce numbers from 100 to 199 or 200 is found correctly and reasonably.
Comment. Points according to the criteria above are summed up.
3 points. The correct answer without reasoning.
|
443
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Ivan and Petr are running in the same direction on circular tracks with a common center, and initially, they are at the minimum distance from each other. Ivan completes one full circle every 20 seconds, while Petr completes one full circle every 28 seconds. After what least amount of time will they be at the maximum distance from each other?
|
Answer: 35 seconds.
Solution. Ivan and Petr will be at the minimum distance from each other at the starting points after the LCM $(20,28)=140$ seconds. In this time, Ivan will complete 7 laps, and Petr will complete 5 laps relative to the starting point. Consider this movement in a reference frame where Petr is stationary, then Ivan will complete 2 laps. Therefore, after 140: $4=35$ seconds, Ivan will run half a lap. At this moment, they will be at the maximum distance from each other for the first time.
Criteria. Only answer: 1 point.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Rational numbers $a, b$ and $с$ are such that $(a+b+c)(a+b-c)=2 c^{2}$. Prove that $c=0$.
---
Translation:
4. Rational numbers $a, b$ and $c$ are such that $(a+b+c)(a+b-c)=2 c^{2}$. Prove that $c=0$.
|
Solution. The initial equality is equivalent to the following $(a+b)^{2}-c^{2}=2 c^{2}$, or $(a+b)^{2}=3 c^{2}$. If $c \neq 0$, we get $((a+b) / c)^{2}=3 .|(a+b) / c|={ }^{-}$. On the left, we have a rational number, since the sum, quotient, and absolute value of rational numbers are rational, while on the right, we have an irrational number, and the equality is impossible. Therefore, $c=0$.
Criteria. The equality $(a+b)^{2}=3 c^{2}$ is obtained, but there is no further progress: 1 point.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Find the number of three-digit numbers for which the second digit is less than the third by 3.
|
7.1. The first digit of the number can be chosen in 9 ways (it can be any digit from 1 to 9), the second digit in 7 ways (it can be any digit from 0 to 6), and the third digit is uniquely determined. We get $9 \cdot 7 \cdot 1=63$ three-digit numbers that satisfy the condition of the problem.
Answer: 63
|
63
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. A plot of $80 \times 50$ meters is allocated for gardens and is fenced on the outside. How should 5 straight fences of the same length be installed inside the plot to divide it into 5 rectangular plots of equal area?
|
7.3. One of the possible solutions is shown in the figure. The fences have a length of 40 m, their ends are marked with bold dots (the horizontal segment is composed of two fences).

|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. The monkey becomes happy when it eats three different fruits. What is the maximum number of monkeys that can be made happy with 20 pears, 30 bananas, 40 peaches, and 50 tangerines?
|
7.4. Let's set the tangerines aside for now. There are $20+30+40=90$ fruits left. Since we feed each monkey no more than one tangerine, each monkey will eat at least two of these 90 fruits. Therefore, there can be no more than $90: 2=45$ monkeys. We will show how to satisfy 45 monkeys:
5 monkeys eat a pear, a banana, and a tangerine;
15 monkeys - a pear, a peach, and a tangerine; 25 monkeys - a peach, a banana, and a tangerine.
Answer: 45 monkeys.
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Zya decided to buy a crumblik. In the store, they also sold kryambliks. Zya bought a kryamblik and received coupons worth $50\%$ of the cost of the purchased kryamblik. With these coupons, he was able to pay $20\%$ of the cost of the crumblik. After paying the remaining amount, he bought the crumblik as well. By what percentage did Zya's expenses on buying the kryamblik and crumblik exceed the originally planned expenses for buying the crumblik?
|
7.5. From the condition of the problem, it follows that $50 \%$ of the cost of a kryamblik is equal to $20 \%$ of the cost of a krumblik. This means that the kryamblik constitutes $40 \%$ of the cost of the krumblik. Zya paid the full cost of the kryamblik and the remaining $80 \%$ of the cost of the krumblik. Thus, he paid $120 \%$ of the cost of the krumblik. Therefore, his expenses exceeded the initially planned expenses by $20 \%$.
Answer: $20 \%$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. What is the sum of the digits of the number $A=100^{40}-100^{30}+100^{20}-100^{10}+1$?
|
# Answer: 361.
Solution. The number is the sum of three numbers: a number composed of 20 nines followed by 60 zeros, a number composed of 20 nines followed by 20 zeros, and finally the number 1. All nines and the one fall on the zeros of the other addends, so there is no carry-over, and the answer is $180+180+1=361$.
Comment. Correct answer without justification -2 points.
|
361
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Given three quadratic trinomials $f(x)=a x^{2}+b x+c, g(x)=b x^{2}+c x+a, h(x)=c x^{2}+$ $a x+b$, where $a, b, c$ are distinct non-zero real numbers. From them, three equations were formed: $f(x)=g(x), f(x)=h(x), g(x)=h(x)$. Find the product of all roots of these three equations, given that each of them has two distinct roots.
|
Answer. 1.
Solution. Since it is known that all equations have roots, we can use Vieta's theorem. Then the product of all roots will be equal to $\frac{c-a}{a-b} \cdot \frac{a-b}{b-c} \cdot \frac{b-c}{c-a}=1$.
Comment. Correct answer without justification - 0 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Toshi is traveling from point A to point B via point C. From A to C, Toshi travels at an average speed of 75 km/h, and from C to B, Toshi travels at an average speed of 145 km/h. The entire journey from A to B took Toshi 4 hours and 48 minutes. The next day, Toshi travels back at an average speed of 100 km/h. The journey from B to C took Toshi 2 hours, and the journey from C to A was completed at an average speed of 70 km/h. Find the distance between B and C.
|
Answer: 290 km.
Solution. Let x km be the distance between B and C, and y km be the distance between A and C. From the system of equations $x / 145 + y / 75 = 24 / 5$ and $(x + y) / 100 = 2 + y / 70$, we find: $x = 290$ and $y = 210$.
Computational error - 5 points.
|
290
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. In a $4 \times 4$ square, each of the 16 cells was painted either black or white. Then, in each of the nine $2 \times 2$ squares that can be identified within this square, the number of black cells was counted. The resulting numbers were 0, 2, 2, 3, 3, 4, 4, 4, 4. How many black cells can there be in the large square? List all possible options.
|
Answer: 11
Solution. Note that squares with 0 white cells and 4 white cells cannot intersect. If a square with 0 white cells is not in a corner, then it does not intersect with more than three other squares (the square can be in the center or adjacent to the middle of a side). Let the white square be in the bottom-left corner, then we have 5 squares suspected of containing 4 black cells, of which 4 are entirely black, and one has 2 or 3 black cells. Note that the squares marked in Figure 1 contain no more than 2 black cells, so exactly 2. Then the three corner squares either all contain 4 cells, but then 5 squares contain 4 black cells; or two corners contain 4, and one contains 3. In total, this results in 11 cells. Figures 2 and 3 show examples of such arrangements.
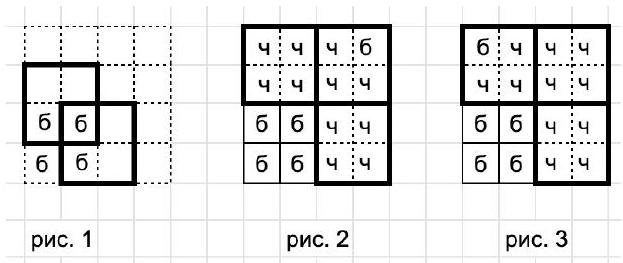
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Mother gives pocket money to her children: 1 ruble to Anya, 2 rubles to Borya, 3 rubles to Vitya, then 4 rubles to Anya, 5 rubles to Borya and so on until she gives 202 rubles to Anya, and 203 rubles to Borya. By how many rubles will Anya receive more than Vitya?
|
# Answer: 68
Solution. Note that Anya will receive money one more time than Vitya. If we remove the first ruble, then each subsequent time Anya receives one more ruble than Vitya. Thus, it remains to determine how many such times there were. Apart from 1 ruble and 2 rubles, all the "moves" by mom break down into triples: $(203-2): 3=67$. Thus, on each round, Anya will receive one more ruble than Vitya, and with the very first move, she received an additional ruble. In total, the answer is 68.
|
68
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In a hotel, rooms are arranged in a row in order from 1 to 10000. Masha and Alina checked into the hotel in two different rooms. The sum of the room numbers they are staying in is 2022, and the sum of the room numbers of all the rooms between them is 3033. In which room is Masha staying, if her room has a lower number than Alina's room?
|
Answer: 1009
Solution. If there is exactly one room between Masha's and Alina's rooms, then it is room number 3033, but then Masha's and Alina's rooms are 3032 and 3034, and their sum is not 2022.
Consider room B, whose number is 1 more than Masha's room. Also consider room V, whose number is 1 less than Alina's room. Note that the sum of the numbers of rooms B and V is also 2022, so there are at least three rooms between Alina and Masha.
If there are at least four rooms, then take rooms Γ and D adjacent to rooms B and V: M, B, Γ, .., D, V, A. The sum of the numbers of Γ and D is also 2022, but then the sum of the numbers between them is at least 4044, which is too many.
Therefore, there are exactly three rooms between Alina and Masha, the sum of the two outermost rooms is 2022, and the middle number is 1011. Then our numbers are: 1009, 1010, 1011, 1012, 1013. Masha's room number is 1009.
|
1009
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In a batch, there are 90000 boxes of vaccine weighing 3300 grams each, and 5000 small boxes weighing 200 grams each. What is the minimum number of temperature-controlled containers needed if, according to the new rules, no more than 100 kilograms can be placed in each?
|
Answer: 3000
Solution. Note that no more than 30 boxes of vaccines can be placed in one container. Thus, less than $90000 / 30=3000$ containers would not be enough. Also, note that if a container holds 30 boxes, there is still room for 5 small boxes, so all these small boxes will fit into the free spaces.
|
3000
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. What is the largest number of different natural numbers that can be chosen so that the sum of any three of them is a prime number?
|
Answer: 4 numbers. Example: $1,3,7,9$. Indeed, the numbers $1+3+7=11, 1+3+9=13$, $1+7+9=17, 3+7+9=19$ are prime. Evaluation. Note that among five natural numbers, it is always possible to choose three whose sum is a composite number. Consider the remainders of these five numbers when divided by 3. If there are three identical remainders, then the sum of the corresponding numbers is divisible by 3. If there are no three identical remainders, then each of the three possible remainders $0,1,2$ must be present. Then the sum of three numbers with different remainders when divided by 3 is divisible by 3. This sum is not equal to 3, since all numbers are different and natural. Therefore, this sum is a composite number.
Remarks. An example of four numbers without evaluation - no more than 3 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Ten guides were leading ten tour groups through the halls of the Hermitage. The groups did not necessarily have equal numbers, but on average, there were 9 people in each group. When one of the groups finished their tour, the average number of tourists per group decreased to 8 people. How many people were in the group that finished the tour?
|
Answer: 18.
Solution: The total number of excursionists initially was $9 \cdot 10=90$. After one of the groups finished the excursion, $8 \cdot 9=72$ excursionists remained. Therefore, the group that finished the excursion had $90-72=18$ excursionists.
Comment: A correct answer without justification - 0 points.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. In the school gym, there is one arm wrestling table. The physical education teacher organized a school tournament. He calls any two participants who have not yet met each other for a match. There are no draws. If a participant loses twice, they are eliminated from the tournament. After 29 matches were held, all participants were eliminated except for two. How many schoolchildren participated in the tournament
|
Answer: 16.
Solution: Each participant is eliminated after exactly two losses. In the situation where two "finalists" remain, the total number of losses is 29. If $n$ people have been eliminated from the tournament, then they have collectively suffered $2 n$ losses, while the "finalists" could have $0(0+0), 1(0+1)$ or $2(1+1)$ losses. Considering that $2 n$ and $2 n+2$ are even numbers, we arrive at the equation $2 n+1=29$, from which $n=14$, and the total number of participants is 16.
Comment: A correct answer without justification - 0 points.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Four pirates divided a treasure of 100 coins. It is known that among them, there are exactly two liars (who always lie) and exactly two knights (who always tell the truth).
They said:
First pirate: “We divided the coins equally.”
Second pirate: “Everyone has a different number of coins, but each got at least 15 coins.”
Third pirate: “Each person’s number of coins is divisible by 5.”
Fourth pirate: “Everyone has a different number of coins, but each got no more than 35 coins.”
What is the maximum number of coins that could have gone to one pirate?
|
Answer: 40 coins
Solution. Note that the first and fourth pirates could not have told the truth simultaneously.
If the first pirate is a knight, then everyone received 25 coins (such a situation is possible). In this case, the maximum number is 25.
If the fourth pirate is a knight, then each received no more than 35 coins. And in this case, the maximum number of coins is no more than 35.
If both the first and fourth pirates are liars, then the second and third pirates told the truth. Then any three pirates received no less than $15+20+25=60$ coins, so the fourth pirate received no more than 40. Such a situation is possible if the pirates received 15, 20, 35, and 40 coins. In this case, the maximum number is 40 (and the answer to the problem is 40).
Comment. The correct answer without justification - 0 points.
Identified pairs of answers that cannot be correct simultaneously - 2 points. Proved that one pirate cannot receive more than 40 coins - 3 points. Provided an example of the distribution of coins - 2 points.
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. One hundred non-zero integers are written in a circle such that each number is greater than the product of the two numbers following it in a clockwise direction. What is the maximum number of positive numbers that can be among these 100 written numbers?
|
Answer: 50.
Solution: Note that two consecutive numbers cannot both be positive (i.e., natural numbers). Suppose the opposite. Then their product is positive, and the number before them (counterclockwise) is also a natural number. Since it is greater than the product of these two natural numbers, it is greater than each of them. Continuing this reasoning, we will conclude that all numbers are natural, and if we move counterclockwise, the numbers will increase. However, when the "circle closes," we will arrive at a contradiction.
Therefore, in any pair of adjacent numbers, there is at least one negative number. Dividing our 100 numbers into 50 pairs, we get that there are no fewer than 50 negative numbers, and thus no more than 50 positive numbers. If we alternate a positive number 2 and a negative number -2, we will get an example of the arrangement of 50 positive and 50 negative numbers that satisfy the problem's condition.
Comment: Correct answer without justification - 0 points.
Proving the impossibility of placing two positive numbers next to each other - 3 points.
Proving that there are no more than 50 positive numbers - 1 point.
Providing an example with 50 positive numbers - 3 points.
|
50
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Sergey wrote down the numbers from 500 to 1499 in a row in some order. Under each number, except the leftmost one, he wrote the GCD of that number and its left neighbor, obtaining a second row of 999 numbers. Then he applied the same rule to get a third row of 998 numbers, from it a fourth row of 997 numbers, and so on. He stopped when all the numbers in the next row were equal to one for the first time. What is the maximum number of rows he could have written by this moment?
|
Answer: 501 (in the second variant 10001).
Let's prove that all numbers in the 501st row are already equal to 1. Indeed, if there is a number $d \neq 1$ in it, then in the 500th row there are 2 numbers divisible by $d$, in the 449th row - 3 such numbers, ..., in the 1st row there are 501 such numbers. But no number $d$ has so many multiples among 1000 consecutive numbers!
Thus, Sergei could not write more than 501 rows. If he arranges the first row with 500 even numbers followed by 500 odd numbers, then in the 500th row an even number will remain, so he will stop only after the 501st row.
|
501
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a regular 20-gon, four consecutive vertices $A, B, C$ and $D$ are marked. Inside it, a point $E$ is chosen such that $A E=D E$ and $\angle B E C=2 \angle C E D$. Find the angle $A E B$.
|
Answer: $39^{\circ}$ (in the $2^{nd}$ variant: $36^{\circ}$).
Note that $ABCD$ is an isosceles trapezoid with angles $\angle ABC = \angle DBC = 180^{\circ} \cdot 18 / 20 = 162^{\circ}$. Point E lies on the perpendicular bisector of the base $AC$, and therefore, triangle $BEC$ is isosceles. Draw the height $EH$ in it, and drop a perpendicular $CK$ from point C to line $ED$. We have: $\angle CEH = \angle BEC / 2 = \angle CED$. Therefore, right triangles $CEH$ and $CEK$ are equal by the acute angle and hypotenuse. In particular, $CK = CH = DC / 2 = CD / 2$, so in the right triangle $CKD$, the angle $KDC$ is $30^{\circ}$. In the quadrilateral $CDEH$, three angles are $30^{\circ}$, $162^{\circ}$, and $90^{\circ}$, so the last angle $HED$ is $78^{\circ}$. Finally, $\angle CEK = \angle HED / 2 = 39^{\circ}$, and $\angle AEB$ is the same.
|
39
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The exam consists of $N \geqslant 3000$ questions. Each of the 31 students has learned exactly 3000 of them, and every question is known by at least 29 students. Before the exam, the teacher openly laid out all the question cards in a circle. He asked the students to point to one of the questions and explained that he would give this question to the first student in alphabetical order, the next question in the clockwise direction to the second student, the next to the third, and so on (one question to each student). However, the students were unable to point to a card such that each of them received a question they knew. For what smallest $N$ could this have happened?
|
Answer: $N=3100$.
Each student does not know $N-3000$ questions and thus can mentally mark exactly that many cards which do not suit them as the initial one. Together, they can indicate no more than $31(N-3000)$ different cards. If $31(N-3000)<N$, then the students can indicate a card that suits everyone. This inequality is equivalent to $30 N<31 \cdot 3000$, i.e., $N<3100$. Therefore, when $N<3100$, the situation described in the problem is impossible.
Let $N=3100$. We describe a situation (one of many) that satisfies the problem's conditions. Number the cards from 1 to 31000. Let the first student know all questions except for the 100 cards whose numbers give a remainder of 1 when divided by 31. The second student knows all cards except those with a remainder of 3, and thus his initial cards are those with a remainder of 2. The third student knows all cards except those with a remainder of 5, and thus forbids initial cards with a remainder of 3. In general, the $k$-th student does not know questions with a remainder of $2 k-1$ and thus forbids initial cards with a remainder of $k$. Thus, all cards are forbidden. Each student knows exactly 3000 questions, and each question is known by everyone except one student.
|
3100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Ten different natural numbers are such that the product of any 5 of them is even, and the sum of all 10 numbers is odd. What is their smallest possible sum
|
Answer: 65.
Solution. The product of 5 odd numbers is odd $\Rightarrow$ among the given ten numbers, there are no more than 4 odd numbers. 4 odd numbers are also impossible, since then the sum of all numbers would be even, while according to the condition, it is odd. Therefore, there are a maximum of 3 odd numbers. If there are exactly 3, then there are 7 even numbers. The sum will be minimal if we take the first, smallest numbers. Among the odd numbers, these are 1, 3, 5; among the even numbers, they are $-2, 4, 6, 8, 10, 12, 14$. Their sum $=65$. If there are fewer odd numbers, then the maximum of 5 is subtracted from the sum, and the minimum of 16 is added, meaning the sum will be larger. Therefore, the found set provides the minimum sum.
Criteria. Answer - 1 point. Indicating the set of numbers - another 1 point. Justification that the number of odd numbers is no more than $4-2$ points. Justification that the number of odd numbers is not 4 (and generally any even number) - 1 point. Justification that if there are fewer than 3 odd numbers, the sum will be larger - 1 point. Justification that exactly this set of numbers gives the minimum sum - 1 point.
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Solve the inequality: $\sqrt{(x-2)^{2}\left(x-x^{2}\right)}<\sqrt{4 x-1-\left(x^{2}-3 x\right)^{2}}$.
|
11.1. Answer: $x=2$.
The left side of the original inequality is defined at $x=2$ and. At the point $x=2$, the inequality is true. We will prove that there are no solutions on the interval $[0 ; 1]$. For this, we will square both sides and bring the inequality to the form $x^{2}(1-x)<-1$. The last inequality is not satisfied for $x \in [0 ; 1]$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
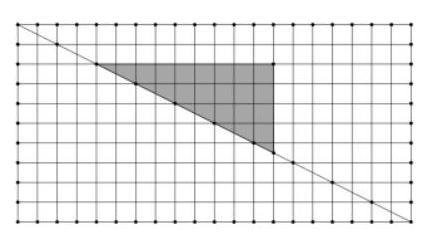
1. All horizontal and vertical distances between adjacent points are equal to 1. What is the area of the triangle with vertices at the black points?
|
Answer. 1.
Solution. The area of the triangle can be found, for example, by subtracting from half the area of the square the area of the square and the areas of two right triangles. We get $S=10-4-2-3=1$. The figure can be divided in other ways.
Comment. An answer without justification - 0 points. A partition that allows finding the area but lacks calculations - 2 points. With the correct method of solution, there are calculation errors - deduct 2 points for each error.
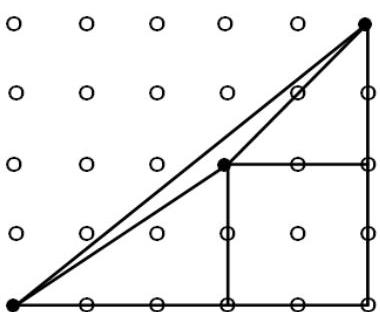
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There were 1009 gnomes with 2017 cards, numbered from 1 to 2017. Ori had one card, and each of the other gnomes had two. All the gnomes knew only the numbers on their own cards. Each gnome, except Ori, said: "I am sure that I cannot give Ori any of my cards so that the sum of the numbers on his two cards would be 2018." What number is on Ori's card?
|
Answer: 1009
Solution: If one of the gnomes has a card with the number 1, then he must be sure that Ori does not have a card with the number 2017. This can only be certain if the card with the number 2017 is also in the hands of this gnome. Similarly, the gnome with the card that has the number 2 has another card with the number 2016, the gnome with the card that has the number 3 has another card with the number 2015, and so on. All the cards in the gnomes' hands will be divided into pairs that sum to 2018. But all the cards except the card with the number 1009 can be divided into such pairs. It is this card that Ori has.
Comment: It is proven that some of the gnomes' cards can be divided into pairs that sum to 2018 - 3 points. It is proven that all the cards in the gnomes' hands can be divided into pairs that sum to 2018, but the answer is not found - 5 points.
|
1009
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Vanya wrote down a four-digit number, subtracted a two-digit number from it, multiplied the result by a two-digit number, divided by the sum of two single-digit numbers, added a single-digit number, and then divided the result by the sum of three single-digit numbers. To write all the numbers, he used only one digit (not 0). Vanya got an integer as the answer. What is this number, and which digit could Vanya have used?
|
Answer: 2017; any digit.
Solution. Let the digit be $a$. We get $\left(\frac{(\overline{a a a a}-\overline{a \bar{a}} \cdot \cdot \overline{a a}}{a+a}+a\right):(a+a+a)$. Then
$$
\overline{a a a a}-\overline{a a}=\overline{a a 00}=a \cdot 1100 \Rightarrow \frac{\bar{a}}{a a}=a \cdot 11
$$
The numerator of the fraction is equal to $a \cdot 1100 \cdot a \cdot 11=a \cdot a \cdot 12100$. The fraction $\frac{(\overline{a a a \bar{a}}-\overline{a a}) \cdot \overline{a \bar{a}}}{a+a}=a \cdot 6050$. Then the expression $\frac{(\overline{a a a \bar{a}}-\overline{a a}) \cdot \overline{a \bar{a}}}{a+a}+a=6051 a$. Dividing by $3 a$, we get 2017, and this is true for any digit $a \neq 0$.
Comment. Finding the number for one specific digit, which is indicated in the answer - 2 points. Finding the number for several (but not all) digits, which are indicated in the answer - 3-4 points. Finding the number for several (but not all) digits, and making, but not proving, the conclusion that the digit can be any - 5 points. Finding the number for any digit (in general form or by complete enumeration) - 7 points. For useful progress without a solution - 1 point.
|
2017
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The giants were prepared 813 burgers, among which are cheeseburgers, hamburgers, fishburgers, and chickenburgers. If three of them start eating cheeseburgers, then in that time two giants will eat all the hamburgers. If five take on eating hamburgers, then in that time six giants will eat all the fishburgers. If seven start eating fishburgers, then in that time one giant can eat all the chickenburgers. How many burgers of each type were prepared for the giants? (The time it takes for one giant to eat one burger does not depend on the type of burger, and all giants eat at the same speed.)
|
Answer: 252 fishburgers, 36 chickenburgers, 210 hamburgers, and 315 cheeseburgers.
Solution: Let $a, b, c$, and $d$ be the quantities of cheeseburgers, hamburgers, fishburgers, and chickenburgers, respectively. According to the problem, $a + b + c + d = 813$. The statement that while three people eat cheeseburgers, two will eat all the hamburgers means that $\frac{a}{3} = \frac{b}{2}$. Similarly, the equalities $\frac{b}{5} = \frac{c}{6}$ and $\frac{c}{7} = d$ hold. Express all unknowns in terms of one, for example, $c$. We have $d = \frac{c}{7}, b = \frac{5c}{6}$, and $a = \frac{3b}{2} = \frac{5c}{4}$. Then $\frac{5c}{4} + \frac{5c}{6} + c + \frac{c}{7} = 813$, from which $c = 252$. Then $d = 36, b = 210$, and $a = 315$.
Comment: The answer is found by trial and error, and it is not shown that there are no other solutions - 3 points. $3$ arithmetic errors with correct reasoning reduce the score by 1-3 points.
|
252
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
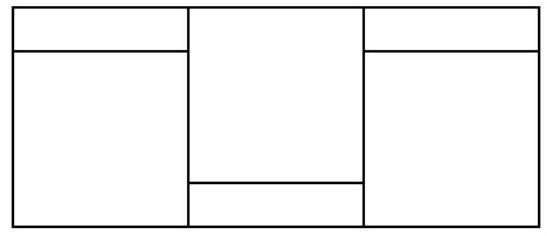
|
Answer: 52.
Solution. All sides of a square are equal, and its perimeter is 24, so each side is $24: 4=6$. The perimeter of the rectangle is 16, and its two largest sides are each 6, so the two smallest sides are each $(16-6 \cdot 2): 2=2$. Then the entire large rectangle has dimensions $8 \times 18$, and its perimeter is $2 \cdot(8+18)=$ 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
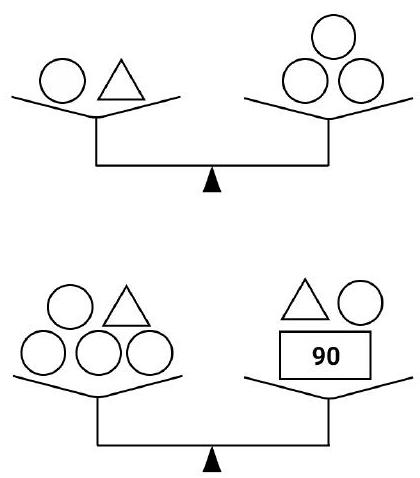
|
Answer: 60.
Solution. From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. In the picture, nine small squares are drawn, with arrows on eight of them. The numbers 1 and 9 are already placed. Replace the letters in the remaining squares with numbers from 2 to 8 so that the arrows from the square with the number 1 point in the direction of the square with the number 2 (the number 2 can be in square $A$ or $B$), the arrows from the square with the number 2 point in the direction of the square with the number 3, and so on, the arrows from the square with the number 8 point in the direction of the square with the number 9.
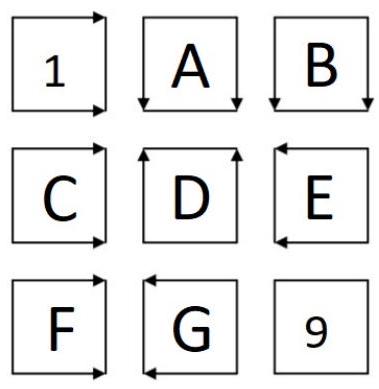
Construct the correspondence.
- In square $A$
- In square $B$
- In square $C$
- In square $D$
- In square $E$
- In square $F$
- In square $G$
- stands the number 2.
- stands the number 3.
- stands the number 4.
- stands the number 5.
- stands the number 6.
- stands the number 7.
- stands the number 8.
|
Answer: In square $A$ there is the number 6, in $B-2$, in $C-4$, in $D-5$, in $E-3$, in $F-8$, in $G-7$.
Solution. Let's order all the squares by the numbers in them. This "increasing chain" contains all nine squares.
Notice that in this chain, immediately before $C$ can only be $E$ (only the arrows from $E$ point to $C$). Similarly, immediately before $E$ can only be $B$ (not $C$, because $C$ is after $E$). Immediately before $B$ can only be 1. Therefore, the numbers in squares $B, E, C$ are $2,3,4$ respectively. Then 5 is definitely in $D$, 6 is definitely in $A$, 7 is definitely in $G$, and 8 is definitely in $F$.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Seven boxes are arranged in a circle, each containing several coins. The diagram shows how many coins are in each box.
In one move, it is allowed to move one coin to a neighboring box. What is the minimum number of moves required to equalize the number of coins in all the boxes?

|
Answer: 22.
Solution. Note that there are a total of 91 coins, so after all the moves, each box should have exactly 13 coins. At least 7 coins need to be moved from the box with 20 coins. Now consider the boxes adjacent to the box with 20 coins. Initially, they have a total of 25 coins, and at least 7 more coins will be transferred from the box with 20 coins. In the end, these two boxes should have a total of 26 coins, so at least \(25 + 7 - 26 = 6\) coins need to be moved from these boxes. Next, consider the boxes with 17 and 18 coins, from which at least 4 and 5 coins need to be moved, respectively. In total, there should be at least \(7 + 6 + 4 + 5 = 22\) moves.
Let's provide an example of how to equalize all the boxes in exactly 22 moves. From the box with 20 coins, we move 3 coins to the box with 10 (which then becomes 13), and 4 coins to the box with 15 (which then becomes 19). From the box that now has 19 coins, we move 6 coins to the box with 5 coins (which then becomes 11). From the box with 17 coins, we move 2 coins to the box with 11, and 2 coins to the box with 6 (which then becomes 8). Finally, we move 5 coins from the box with 18 coins to the box with 8 coins. In the end, each box has exactly 13 coins. It is easy to verify that exactly 22 moves were made.
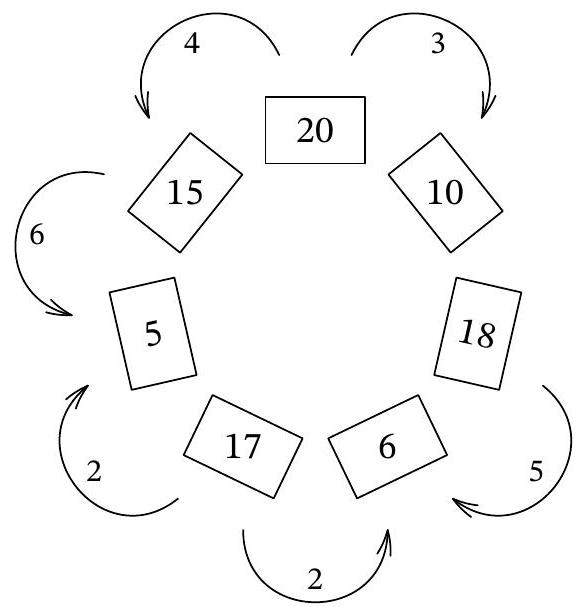
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.

|
Answer: 7.
Solution. Since $ABCD$ is a square, then $AB = BC = CD = AD$.
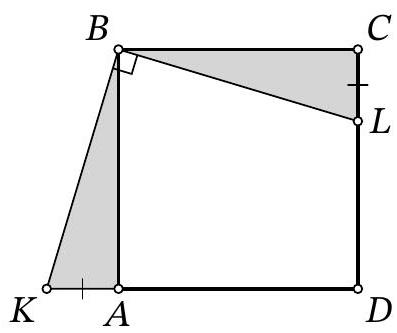
Fig. 1: to the solution of problem 8.4
Notice that $\angle ABK = \angle CBL$, since they both complement $\angle ABL$ to $90^{\circ}$. Therefore, right triangles $ABK$ and $CBL$ are congruent by the acute angle and the leg $AB = BC$ (Fig. 1). Consequently, $AK = CL = 6$. Then
$$
LD = CD - CL = AD - CL = (KD - AK) - CL = KD - 2 \cdot CL = 19 - 2 \cdot 6 = 7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. There are 7 completely identical cubes, each of which has 1 dot marked on one face, 2 dots on another, ..., and 6 dots on the sixth face. Moreover, on any two opposite faces, the total number of dots is 7.
These 7 cubes were used to form the figure shown in the diagram, such that on each pair of glued faces, the same number of dots is marked. All dots were erased from all faces except nine, as shown in the diagram. What is the total number of dots that were initially marked on the surface of the figure?
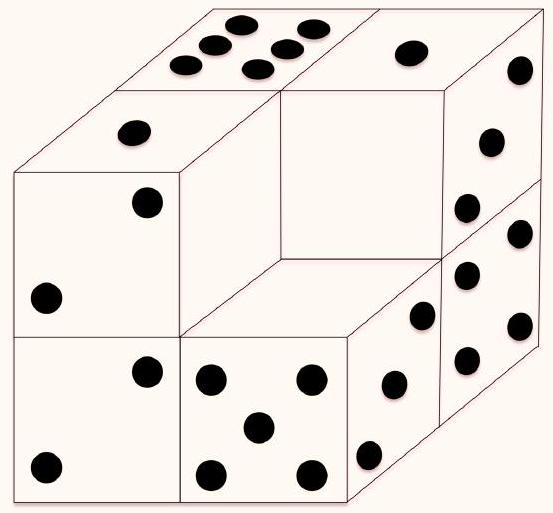
|
Answer: 75.
Solution. There are 9 ways to cut off a "brick" consisting of two $1 \times 1 \times 1$ cubes from our figure. In each such "brick," there are two opposite faces $1 \times 1$, the distance between which is 2. Let's correspond these two faces to each other.
Consider one such pair of faces: on one of them, the dots were not erased, while on the other, they were erased. It is not difficult to understand that originally there were the same number of dots on these faces.
Let's calculate the total number of dots that were originally on all 9 pairs of faces. We get
$$
2 \cdot(1+1+6+2+2+5+3+3+4)=54
$$
There are 6 faces $1 \times 1$ left, about which we still know nothing. However, it can be noticed that they are divided into pairs according to the following principle: in one pair, there will be faces from one $1 \times 1 \times 1$ cube. In each such pair, the sum of the numbers was 7. Then we get that the number of dots on the surface of the figure originally was
$$
54+3 \cdot 7=75
$$
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. For quadrilateral $ABCD$, it is known that $\angle BAC = \angle CAD = 60^{\circ}$, $AB + AD = AC$. It is also known that $\angle ACD = 23^{\circ}$. How many degrees does the angle $ABC$ measure?
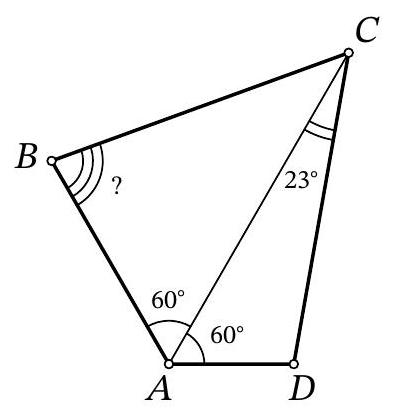
|
Answer: 83.
Solution. Mark a point $K$ on the ray $AB$ such that $AK = AC$. Then the triangle $KAC$ is equilateral; in particular, $\angle AKC = 60^{\circ}$ and $KC = AC$. At the same time, $BK = AK - AB = AC - AB = AD$. This means that triangles $BKC$ and $DAC$ are equal by two sides and the angle $60^{\circ}$ between them (Fig. 2).
It remains to note that the angle $\angle ABC$ - the exterior angle of triangle $BKC$ - is equal to the exterior angle at vertex $D$ of triangle $DAC$, which is calculated as the sum of two interior angles: $60^{\circ} + 23^{\circ} = 83^{\circ}$.
|
83
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. On the base $AC$ of isosceles triangle $ABC (AB = BC)$, a point $M$ is marked. It is known that $AM = 7, MB = 3, \angle BMC = 60^\circ$. Find the length of segment $AC$.
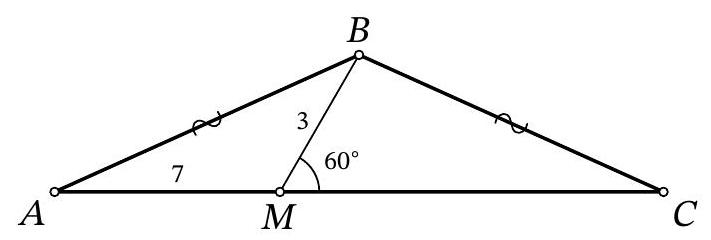
|
Answer: 17.
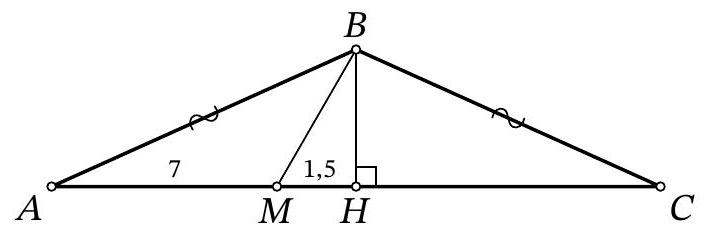
Fig. 3: to the solution of problem 9.5
Solution. In the isosceles triangle \(ABC\), draw the height and median \(BH\) (Fig. 3). Note that in the right triangle \(BHM\), the angle at vertex \(B\) is \(30^\circ\), so \(HM = \frac{1}{2} BM = 1.5\). Then \(AC = 2AH = 2(AM + MH) = 2 \cdot (7 + 1.5) = 17\).
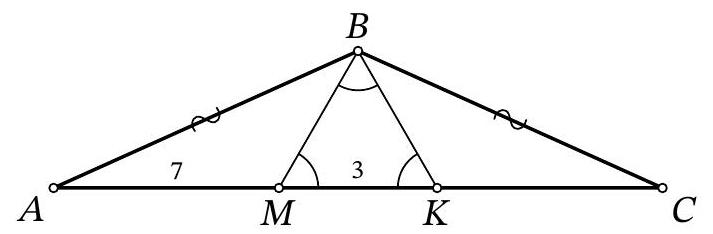
Fig. 4: to the solution of problem 9.5
Another solution. Mark a point \(K\) on \(MC\) such that \(\angle BKM = 60^\circ\) (Fig. 4; such a point lies exactly on the segment \(MC\) because \(\angle BCM = \angle BAM = \angle BMC - \angle ABM < 60^\circ\)). Note that in triangle \(BMK\), two angles are \(60^\circ\), so it is equilateral and \(BK = MK = BM = 3\). Also note that triangles \(ABM\) and \(CBK\) are equal because \(BC = AB\), \(\angle A = \angle C\), \(\angle AMB = \angle CKB = 120^\circ\) (therefore, \(\angle ABM = \angle CBK\)). Then \(CK = AM = 7\) and \(AC = AM + MK + KC = 7 + 3 + 7 = 17\).
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
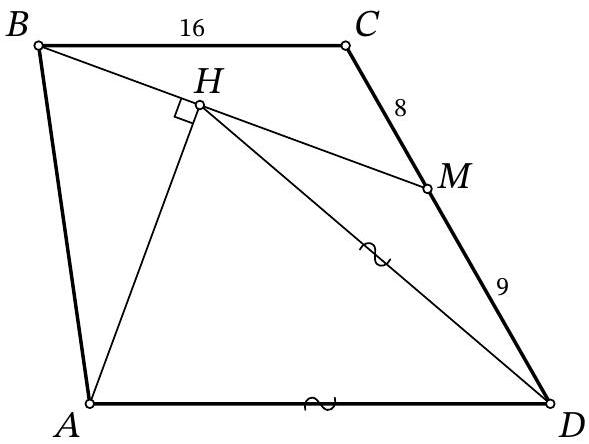
|
Answer: 18.
Solution. Let the lines $B M$ and $A D$ intersect at point $K$ (Fig. 5). Since $B C \| A D$, triangles $B C M$ and $K D M$ are similar by angles, from which we obtain $D K = B C \cdot \frac{D M}{C M} = 16 \cdot \frac{9}{8} = 18$.
Fig. 5: Solution to problem 9.8
In the isosceles triangle $A D H$, draw the altitude and median $D S$. Then, in triangle $A H K$, the segment $D S$ passes through the midpoint of side $A H$ and is parallel to $H K$. Therefore, $D S$ is the midline of this triangle, and $A D = D K = 18$.
Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.
## 10th Grade
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. On the side $AD$ of rectangle $ABCD$, a point $E$ is marked. On the segment $EC$, there is a point $M$ such that $AB = BM, AE = EM$. Find the length of side $BC$, given that $ED = 16, CD = 12$.
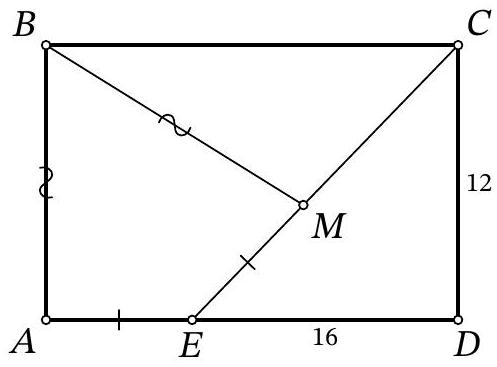
|
Answer: 20.
Solution. Note that triangles $A B E$ and $M B E$ are equal to each other by three sides. Then $\angle B M E=\angle B A E=90^{\circ}$.
Fig. 6: to the solution of problem 10.3
From the parallelism of $A D$ and $B C$, it follows that $\angle B C M=\angle C E D$ (Fig. 6). Therefore, right triangles $B C M$ and $C E D$ are equal by an acute angle and the leg $B M=A B=C D$. Using the Pythagorean theorem for triangle $C D E$, we conclude
$$
B C=C E=\sqrt{C D^{2}+E D^{2}}=\sqrt{12^{2}+16^{2}}=20
$$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. In a convex quadrilateral $A B C D$, the midpoint of side $A D$ is marked as point $M$. Segments $B M$ and $A C$ intersect at point $O$. It is known that $\angle A B M=55^{\circ}, \angle A M B=$ $70^{\circ}, \angle B O C=80^{\circ}, \angle A D C=60^{\circ}$. How many degrees does the angle $B C A$ measure?
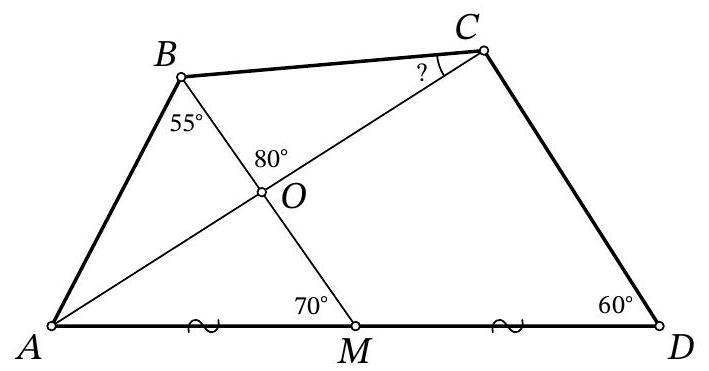
|
Answer: 35.
Solution. Since
$$
\angle B A M=180^{\circ}-\angle A B M-\angle A M B=180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}=\angle A B M
$$
triangle $A B M$ is isosceles, and $A M=B M$.
Notice that $\angle O A M=180^{\circ}-\angle A O M-\angle A M O=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}$, so $\angle A C D=$ $180^{\circ}-\angle C A D-\angle A D C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$.
Fig. 7: to the solution of problem 10.6
Draw segment $C M$ (Fig. 7). Since in a right triangle, the median to the hypotenuse is equal to half of it, we have $C M=D M=A M=B M$. Triangle $M C D$ is isosceles with an angle of $60^{\circ}$ at the base, so it is equilateral, and $\angle C M D=60^{\circ}$. Then $\angle B M C=180^{\circ}-\angle A M B-\angle C M D=180^{\circ}-70^{\circ}-60^{\circ}=50^{\circ}$. Since triangle $B M C$ is isosceles with vertex $M$, we have $\angle C B M=$ $\frac{1}{2}\left(180^{\circ}-\angle B M C\right)=\frac{1}{2}\left(180^{\circ}-50^{\circ}\right)=65^{\circ}$. Finally,
$$
\angle B C A=180^{\circ}-\angle C B M-\angle B O C=180^{\circ}-65^{\circ}-80^{\circ}=35^{\circ} \text {. }
$$
Remark. There are other solutions that use the fact that $A B C D$ is a cyclic quadrilateral with the center of the circumscribed circle $M$.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Quadrilateral $ABCD$ is inscribed in a circle. It is known that $BC=CD, \angle BCA=$ $64^{\circ}, \angle ACD=70^{\circ}$. A point $O$ is marked on segment $AC$ such that $\angle ADO=32^{\circ}$. How many degrees does the angle $BOC$ measure?
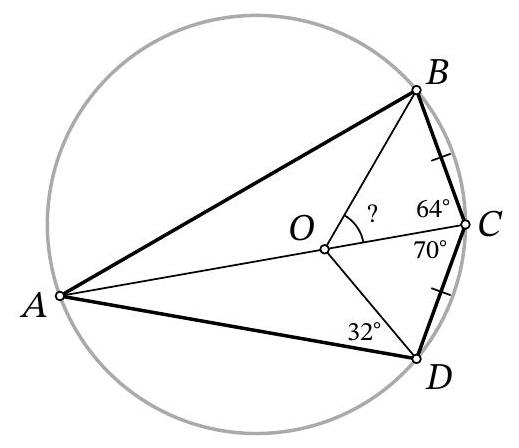
|
Answer: 58.
Solution. As is known, in a circle, inscribed angles subtended by equal chords are either equal or supplementary to $180^{\circ}$. Since $B C=C D$ and $\angle B A D<180^{\circ}$, we get that $\angle B A C=\angle D A C$.
Fig. 9: to the solution of problem 11.5
Since $\angle B D A=\angle B C A=64^{\circ}$, we get that $\angle B D O=\angle A D O=32^{\circ}$. Therefore, point $O$ lies on the two angle bisectors of triangle $A B D$, i.e., it is the point of intersection of the angle bisectors (Fig. 9). Then
$$
\angle B O C=\angle B A O+\angle A B O=\frac{\angle B A D+\angle A B D}{2}=\frac{180^{\circ}-\angle B D A}{2}=\frac{180^{\circ}-64^{\circ}}{2}=58^{\circ}
$$
Remark. The solution could also have been completed differently: since $O$ is the point of intersection of the angle bisectors of triangle $A B D$, by the trident lemma $C D=C B=C O$, from which $\angle C O B$ is easily found.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. Oleg drew an empty $50 \times 50$ table and wrote a number above each column and to the left of each row. It turned out that all 100 written numbers are distinct, with 50 of them being rational and the other 50 being irrational. Then, in each cell of the table, he wrote the product of the numbers written next to its row and its column (a "multiplication table"). What is the maximum number of products in this table that could be rational numbers?
(O. Podlipsky)
|
Answer: 1275 products.
Solution. First, let's show that there are no fewer than 1225 irrational numbers in the table. Suppose that among the rational numbers, there is a zero, and it is written along the top side of the table.
Let $x$ be the number of irrational numbers and $50-x$ the number of rational numbers written along the left side of the table. Then, along the top side, there are $50-x$ irrational and $x$ rational numbers (including zero). Note that the product of a non-zero rational and an irrational number is always irrational. Therefore, there are at least $x(x-1) + (50-x)^2$ irrational numbers in the table. Note that $f(x) = x(x-1) + (50-x)^2 = 2x^2 - 101x + 50^2$. The vertex of the parabola $f(x)$ is at the point $101/4 = 25.25$, so the minimum value of $f(x)$ at an integer point is achieved at $x=25$ and is equal to $25 \cdot 24 + 25^2 = 1225$.
If zero is replaced by a non-zero rational number, the number of irrational numbers can only increase. Therefore, in any case, there are no fewer than 1225 irrational numbers in the table. Thus, there are no more than $2500 - 1225 = 1275$ rational numbers in the table.
Exactly 1275 rational numbers can be in the table, for example, in the following case. Along the left side, the numbers are $1, 2, \ldots, 24, 25, \sqrt{2}, 2\sqrt{2}, \ldots, 25\sqrt{2}$, and along the top side, the numbers are $0, 26, 27, \ldots, 49, 26\sqrt{2}, 27\sqrt{2}, \ldots, 50\sqrt{2}$. Then, the only irrational products will be $25 \cdot 24 + 25^2 = 1225$ products of non-zero rational and irrational numbers.
Comment. Only the correct answer - 0 points.
Proof that there are no more than 1275 rational numbers - 4 points.
If the proof is only conducted in a special case where an equal number of rational and irrational numbers are along the left (or top) side - 1 point is given for this part of the solution instead of 4.
The inequality $x(x-1) + (50-x)^2 \geqslant 1225$ (or an equivalent one) is used without proof - 1 point is deducted.
A correct example showing that there could be exactly 1275 rational numbers - 3 points.
Only an example with non-zero numbers showing that there could be exactly 1250 rational numbers - 1 point.
The statement that the product of a non-zero rational and an irrational number is irrational can be used without proof.
If this statement is significantly used for any (not necessarily non-zero) numbers (i.e., an incorrect statement is used!) - no more than 2 points are given for the problem.
|
1275
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Each of the 10 people is either a knight, who always tells the truth, or a liar, who always lies. Each of them thought of some number (not necessarily an integer). Then the first said: “My number is greater than 1”, the second said: “My number is greater than $2”, \ldots$, the tenth said: “My number is greater than $10”. After that, all ten, speaking in some order, said: “My number is less than 1”, “My number is less than $2”, \ldots$, “My number is less than 10” (each said exactly one of these ten phrases). What is the maximum number of knights that could have been among these 10 people?
(O. Podlipsky)
|
Answer: 9 knights.
Solution. Estimation. Note that none of the knights could have said the phrase "My number is greater than 10," otherwise the number they thought of would indeed be greater than 10. But then he could not have said any of the phrases "My number is less than 1," "My number is less than 2," ..., "My number is less than 10." Therefore, there is at least one liar, and there are no more than 9 knights.
Example. Let's show that there could have been 9 knights. Suppose the first person thought of the number 1.5, the second -2.5, ..., the ninth -9.5, and the tenth person thought of the number 5. Then for $k=1,2, \ldots, 9$, the $k$-th person could have said the true phrases "My number is greater than $k$" and "My number is less than $k+1$" (i.e., he is a knight), while the tenth person is a liar, saying the phrases "My number is greater than 10" and "My number is less than 1."
Remark. The example given above ceases to be valid if the tenth person thinks of a number outside the interval $(0 ; 10)$, as then exactly one of his answers is true.
Comment. It is proven that there are no more than 9 knights (or, equivalently, there is at least one liar) - 3 points.
The example showing that there could have been 9 knights, with the indication of which person said which phrases - 4 points.
If the example provided is not fully described (for example, it is not specified what number the liar thought of, or it is not clearly indicated who said which phrase) - out of 4 points for the example, no more than 2 points are given.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. The cells of a $2 \times 2019$ table must be filled with numbers (exactly one number in each cell) according to the following rules. In the top row, there should be 2019 real numbers, none of which are equal, and in the bottom row, there should be the same 2019 numbers, but in a different order. In each of the 2019 columns, there should be two different numbers, and the sum of these two numbers should be a rational number. What is the maximum number of irrational numbers that could be in the first row of the table?
(S. Kudrya)
|
Answer: 2016.
Solution. Estimation. We will prove that in the first row of the table, where numbers are arranged according to the rules, there are no fewer than three rational numbers (and, accordingly, no more than 2016 irrational numbers). Each number appearing in the table is written in exactly two cells, one of which is in the top row, and the other in the bottom row. Consider some column, let the number in its top cell be \(a_1\), and in the bottom cell \(a_2\) (we will briefly denote such a column as \((a_1, a_2)\)). We will color the column \((a_1, a_2)\). We will find the column where the number \(a_2\) is in the top cell and color it. If this column is \((a_2, a_1)\), we will end the process. Otherwise, if this column is \((a_2, a_3)\), where \(a_3 \neq a_1\), we will continue: we will color the column where the number \(a_3\) is in the top cell, and so on - until we reach the column where \(a_1\) is in the bottom cell (this will definitely happen, since the numbers equal to \(a_2, a_3, \ldots\) are colored in pairs). At the end of the process, we will get a set of colored columns \((a_1, a_2), (a_2, a_3), \ldots, (a_k, a_1)\), which we will call a cycle of length \(k\). If there are still uncolored columns, we will highlight another cycle, and so on. In the end, the set of all columns of the table will be divided into non-intersecting cycles. Since the sum of the lengths of all cycles is 2019, there will be a cycle of odd length.
Consider this cycle: \((a_1, a_2), (a_2, a_3), \ldots, (a_{2t+1}, a_1)\), where \(t \geq 1\). By the condition, \(a_1 + a_2 = b_1, a_2 + a_3 = b_2, \ldots, a_{2t+1} + a_1 = b_{2t+1}\), where all \(b_i\) are rational numbers. Then \(2a_1 = (a_1 + a_2) - (a_2 + a_3) + (a_3 + a_4) - \ldots - (a_{2t} + a_{2t+1}) + (a_{2t+1} + a_1) = b_1 - b_2 + b_3 - \ldots - b_{2t} + b_{2t+1}\) is a rational number, so \(a_1\) is rational. Similarly, all numbers \(a_1, a_2, \ldots, a_{2t+1}\) are rational, and there are no fewer than \(2t+1 \geq 3\).
Example. We will provide an example of a table filled according to the rules, in the top row of which there are 2016 irrational numbers:
\[
\begin{array}{|l|l|l|l|l|l|l|l|l|l|}
\hline 1 & 2 & 3 & 1+\sqrt{2} & 1-\sqrt{2} & 2+\sqrt{2} & 2-\sqrt{2} & \ldots & 1008+\sqrt{2} & 1008-\sqrt{2} \\
\hline 2 & 3 & 1 & 1-\sqrt{2} & 1+\sqrt{2} & 2-\sqrt{2} & 2+\sqrt{2} & \ldots & 1008-\sqrt{2} & 1008+\sqrt{2} \\
\hline
\end{array}
\]
Remark. Note that the condition of the odd length of the row of the table is significant. For an even length of the row, it is not difficult to construct examples of tables in which all numbers are irrational.
The condition that a number does not stand under itself is also important, otherwise a cycle of length 1 could appear, and the answer to the problem would be 2018.
Comment. The correct estimation (no more than 2016 irrational or, equivalently, no fewer than 3 rational numbers) is proven - 5 points.
The statement about the partition of the permutation into independent cycles is accepted without proof.
If the estimation is not proven, it is proven that in the columns forming a cycle of odd length, all numbers are rational - 2 points (out of 5 possible points for the estimation).
A correct example with 2016 irrational numbers is provided - 2 points.
Proof of the irrationality of square roots of natural numbers that are not perfect squares, cube roots of natural numbers that are not perfect cubes, etc., is not required.
|
2016
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Petya was exchanging stickers. He trades one sticker for 5 others. At first, he had 1 sticker. How many stickers will he have after 50 exchanges?
|
Answer: 201.
Solution: After each exchange, the number of Petya's stickers increases by 4 (one sticker disappears and 5 new ones appear). After 50 exchanges, the number of stickers will increase by 50*4=200. Initially, Petya had one sticker, so after 50 exchanges, he will have $1+200=201$.
|
201
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. One day Uncle Fyodor weighed Sharik and Matroskin. It turned out that Sharik is 6 kg heavier than Matroskin, and Matroskin is three times lighter than Sharik. How much did Matroskin weigh?
|
Answer: 3 kg.
Solution: Since Matroskin is three times lighter than Sharik, Matroskin is lighter than Sharik by two of his own weights. According to the condition, this is equal to 6 kg, i.e., Matroskin weighs $6: 2=3$ kg.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Mom bought a box of lump sugar (sugar in cubes). The children first ate the top layer - 77 cubes, then the side layer - 55 cubes, and finally, the front layer. How many sugar cubes are left in the box?
|
Answer: 300 or 0.
Solution. A box has three dimensions: height, width, and depth. To find out how many cubes are in the top layer, you need to multiply the width by the depth, and for the side layer, multiply the height by the depth. After the top layer is eaten, the height decreases by 1, while the depth remains the same. Therefore, 77 and 55 must be divisible by the original depth of the box. Since the common factors of 77 and 55 are only 1 and 11. If the depth is 1, then nothing is left after the front layer is eaten. If we assume that some sugar is still left, then the depth of the box is 11. Then the width is 77:11=7 cubes, and the height after the top layer is eaten is 55:11=5 cubes. After the side layer is eaten, the width decreases by 1 (becoming 7-1=6 cubes), and after the front layer is eaten, the depth decreases by 1 and becomes 11-1=10. Therefore, the remaining height of the sugar in the box is 5, the width is 6, and the depth is 10 cubes. That is, there are $5 * 6 * 10=300$ cubes of sugar left in the box.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Cut a square with a side of 4 into rectangles, the sum of the perimeters of which is 25.
|
For example, two rectangles $2 \times 0.5$ and one rectangle $3.5 \times 4-$ cm. The total perimeter is $2 * 2 * (2 + 0.5) + 2 * (3.5 + 4) = 25$.

|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Someone wrote down two numbers $5^{2020}$ and $2^{2020}$ in a row. How many digits will the resulting number contain?
|
Solution. Let the number $2^{2020}$ contain $m$ digits, and the number $5^{2020}$ contain $n$ digits. Then the following inequalities hold: $10^{m-1}<2^{2020}<10^{m}, 10^{n-1}<5^{2020}<10^{n}$ (the inequalities are strict because the power of two or five is not equal to the power of ten). Multiplying these inequalities, we get $10^{m+n-2}<10^{2020}<10^{m+n}$. From this, it follows that the exponent 2020 is between $m+n-2$ and $m+n$, so $2020=m+n-1$ and $m+n=2021$. This means that a total of 2021 digits have been written.
Answer: 2021.
|
2021
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The older brother noticed that in 10 years, the younger brother will be as old as he is now, and his age will be twice the current age of the younger brother. How old is the younger brother now?
|
Answer: 20 years.
Solution. Let the current age of the younger brother be $x$ years, and the older brother be $y$ years. In 10 years, the younger brother's age will be $y$ years, and the older brother's age will be $2x$ years. Since the age of each has changed by 10 years, we have the equations: $y+10=2x, x+10=y$. By adding and simplifying the equations, we get $x=20$.
Criteria. Any correct solution: 7 points.
Correct answer: 1 point.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A rectangle $10 \times 20$ is divided into unit squares. How many triangles are formed after drawing one diagonal?
|
Answer: 220.
Solution. The figure shows one of the obtainable triangles. All such triangles are right-angled, and the vertex of the right angle can be any lattice node,
except those lying on the diagonal. There are a total of $21 \times 11$ nodes, and 11 of them are on the
diagonal, so the number of triangles is $21 \times 11 - 11 = 220$.
Criteria. Any correct solution: 7 points.
Incorrectly accounting for nodes on the diagonal: 4 points.
Correct answer: 2 points.
|
220
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. (7 points)
Prove that $\sqrt{\frac{11 \ldots 1}{2 n \text { digits }}-\underbrace{22 \ldots .2}_{n \text { digits }}}=\underbrace{33 \ldots 3}_{n \text { digits }}$.
|
# Solution:
$$
\begin{aligned}
& \sqrt{\underbrace{11 \ldots 1}_{2 n \text { digits }}-\underbrace{22 \ldots 2}_{n \text { digits }}}=\sqrt{\frac{1}{9} \cdot \underbrace{99 \ldots 9}_{2 n \text { digits }}-\frac{2}{9} \cdot \underbrace{99 \ldots 9}_{n \text { digits }}}=\frac{1}{3} \sqrt{\left(10^{2 n}-1\right)-2\left(10^{n}-1\right)}=\frac{1}{3} \sqrt{\left(10^{n}-1\right)^{2}}= \\
& =\frac{1}{3}\left(10^{n}-1\right)=\frac{1}{3} \cdot \underbrace{99 \ldots 9}_{n \text { digits }}=\underbrace{33 \ldots 3}_{n \text { digits }} \\
& \text { 10.2. (7 points) }
\end{aligned}
$$
Petya ran down a moving escalator and counted 30 steps. Then he ran up the same escalator with the same speed relative to the escalator and counted 70 steps. How many steps would he have counted if he had gone down a stationary escalator?
Answer: 42.
Solution: Let $S$ be the length of the escalator in steps, $x$ be the speed of the escalator, and $V$ be Petya's own speed.
Petya's movement relative to the ground:
| | $V$ | $t$ | $S$ |
| :--- | :---: | :---: | :---: |
| Movement down | $V+x$ | $t_{1}$ | $(V+x) t_{1}=S$ |
| Movement up | $V-x$ | $t_{2}$ | $(V-x) t_{2}=S$ |
Petya's movement relative to the escalator:
| | $V$ | $t$ | $S$ |
| :--- | :---: | :---: | :---: |
| Movement down | $V$ | $t_{1}$ | 30 |
| Movement up | $V$ | $t_{2}$ | 70 |
We set up the system:
$$
\left\{\begin{array}{l}
(V+x) t_{1}=S \\
(V-x) t_{2}=S \\
V \cdot t_{1}=30 \\
V \cdot t_{2}=70
\end{array}\right.
$$
Express
from
the last
equalities
$t_{1}, t_{2}$ and substitute into the first two equations respectively:
$$
\left\{\begin{array}{l}
(V+x) \cdot \frac{30}{V}=S \\
(V-x) \cdot \frac{70}{V}=S
\end{array}\right.
$$
Solving this system for $S$, we get: $S=42$.
|
42
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# 10.5. (7 points)
At a joint conference of the party of liars and the party of truth-tellers, 32 people were elected to the presidium and seated in four rows of eight. During the break, each member of the presidium claimed that among their neighbors there are representatives of both parties. It is known that liars always lie, and truth-tellers always tell the truth. What is the minimum number of liars in the presidium for the described situation to be possible? (Two members of the presidium are neighbors if one of them sits to the left, right, in front of, or behind the other).
|
Answer: with eight liars.
Solution: Divide all the seats in the presidium into eight groups as shown in the figure. If there are fewer than eight liars, then in one of these groups, only truth-tellers will be sitting, which is impossible. The contradiction obtained shows that there are no fewer than eight liars. The figure shows how eight liars can be seated in the presidium so that the condition of the problem is satisfied.
Comments. Without an example of seating the liars - 5 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Emperor Pea has a worm in one of his rejuvenating apples. He has 13 apples in total, and they are arranged in a circle in a special box for rejuvenating apples. To find the worm, Emperor Pea decided to use a balance scale. He knows that all the apples weigh the same, except for the one with the worm, which is heavier. There is a small problem, however, in that after each weighing, the apples must be returned to the box, each to the exact spot where it was before. After Emperor Pea returns the apples to the box, the worm immediately and unnoticed crawls into one of the two adjacent apples (and stays there until the next weighing). Help Emperor Pea find the wormy apple. (That is, after some weighing, Emperor Pea can accurately determine which apple the worm is currently inside before putting the apples back in the box. Minimizing the number of weighings is not necessary.)
|
# Solution.
Let's number the apples clockwise. The neighboring apples will be numbered 1 and 2, 2 and 3, ..., 12 and 13, 13 and 1.
Weigh apples 1, 2, 3, 4, 5, 6 against 7, 8, 9, 10, 11, 12.
If they are equal, then the worm is in apple 13.
Suppose 1, 2, ..., 6 are heavier.
Then after the apples are put back and the worm crawls somewhere, it can be in one of the apples numbered 13, 1, 2, 3, 4, 5, 6, 7.
Weigh 13, 1, 2, 3 against 4, 5, 6, 7.
Suppose 13, 1, 2, 3 are heavier.
After the worm crawls, it can be in one of the apples: 12, 13, 1, 2, 3, 4.
Weigh 12, 13, 1 against 2, 3, 4.
Suppose 12, 13, 1 are heavier.
After the worm crawls, it can be in one of the apples: 11, 12, 13, 1, 2.
Weigh 11, 12 against 1, 2.
If they are equal, then the worm is in apple 13.
Suppose 11, 12 are heavier. Then after the worm crawls, it is in one of the apples 10, 11, 12, 13.
Weigh 11 and 12.
If they are not equal, the worm is in the heavier one.
Otherwise, it is in 10 or 13 and after crawling in one of 9, 11, 12, 1.
Weigh 9 and 11.
If they are not equal, the worm is in the heavier one. Otherwise, it is in 12 or 1, after crawling in 11, 13, or 2.
Weigh 11 and 13. If they are not equal, the worm is in the heavier one. If they are equal, it is in 1.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In 60 chandeliers (each chandelier has 4 lampshades), lampshades need to be replaced. Each electrician spends 5 minutes replacing one lampshade. A total of 48 electricians will be working. Two lampshades in a chandelier cannot be replaced simultaneously. What is the minimum time required to replace all the lampshades in all the chandeliers?
|
Answer: 25 minutes
Solution. Let's show how to proceed. First, 48 electricians replace one lampshade in 48 chandeliers, which takes 5 minutes, and 48 chandeliers have one lampshade replaced, while 12 have none replaced. Then, 12 electricians replace lampshades in the chandeliers that haven't been replaced yet, while the remaining 36 electricians replace the second lampshades in 36 chandeliers. This again takes 5 minutes, resulting in 36 chandeliers with two new lampshades and 24 with one. Now, 24 electricians replace the second lampshades, and 24 replace the third. Now, 24 chandeliers have three new lampshades and $36-$ have two. Now, 36 electricians replace 36 third lampshades and 12 electricians replace 12 fourth lampshades. Now, 48 chandeliers have three new lampshades and 12 have four. The final stage is 48 electricians replacing the last lampshades in 48 chandeliers. Thus, in 5 stages, i.e., 25 minutes, all lampshades in the chandeliers are replaced. Let's show that it cannot be done in less than 25 minutes. It is necessary to replace 60.4 = 240 lampshades. It takes 5 minutes for each lampshade, so in total, it is no less than $240 \cdot 5=1200$ minutes. But we have 48 electricians, so this can be done in $1200: 48=$ 25 minutes, but no less.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Find the perimeter of a rectangle if the sum of the lengths of two of its sides is 10 dm, and the sum of the lengths of three of its sides is 14 dm.
|
Answer: 18 dm, 19 dm or 20 dm
Solution. If the sum of two adjacent sides is 10 dm, then the perimeter is 20 dm, which does not contradict the condition on the sum of three sides. If the sum of opposite sides is 10 dm, then each of these sides is 5 dm. In this case, the adjacent side to them is 4 dm or 4.5 dm.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-1-1. Select the numbers that serve as counterexamples to the given statement: “If the sum of the digits of a natural number is divisible by 27, then the number itself is divisible by $27$.”
a) 81 ; b) 999 ; c) 9918 ; d) 18 .
|
Answer: only 9918.
Solution option 1. The statements about 81 and 18 are definitely not counterexamples, as for them, the premise "if the sum of the digits of a natural number is divisible by 27" is not satisfied.
The statement about 999 is not a counterexample, as it does not contradict our statement.
Finally, the number 9918 is a counterexample, since for it, the sum of the digits is divisible by 27, but the number itself $9918=9 \cdot 1102$ is not divisible by 27.
|
9918
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
10-2-1. Petya writes down a sequence of numbers: if the current number is equal to $x$, then the next one is $\frac{1}{1-x}$. The first number in the sequence is 2. What is the five hundredth number?
|
Answer: -1.
Solution variant 1. Let's list the first few terms of the obtained sequence:
$$
2,-1,1 / 2,2, \ldots
$$
We see that the sequence has entered a cycle with a period of 3. Since the number 500 when divided by 3 gives a remainder of 2, the 500th term will be the same as the 2nd. That is, the five hundredth number will be equal to -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3-1. Non-negative integers $a, b, c, d$ are such that
$$
a b+b c+c d+d a=707
$$
What is the smallest value that the sum $a+b+c+d$ can take?
|
Answer: 108.
Solution variant 1. The given equality can be rewritten as
\[
(a+c)(b+d)=7 \cdot 101
\]
where the numbers 7 and 101 are prime. Therefore, either one of the expressions in parentheses is 1 and the other is 707, or one of the expressions in parentheses is 7 and the other is 101. In the first case, \(a+b+c+d\) equals 708, and in the second case, it equals 108, and 108 is the smaller of these two numbers.
Comment. It follows from the solution that the equality given in the problem is indeed possible. We can take any non-negative integers with the conditions \(a+c=7\), \(b+d=101\). For example, \(a=1\), \(c=6\), \(b=1\), \(d=100\).
|
108
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-4-1. Anya and Borya are playing rock-paper-scissors. In this game, each player chooses one of the figures: rock, scissors, or paper. Rock beats scissors, scissors beat paper, and paper beats rock. If the players choose the same figure, the game ends in a tie.
Anya and Borya played 25 rounds. Anya chose rock 12 times, scissors 6 times, and paper 7 times. Borya chose rock 13 times, scissors 9 times, and paper 3 times. There were no ties in any of the rounds. How many times could Anya have won? List all possible answers.
|
Answer: 16.
Solution version 1. Note that, since there were no draws, when Anya chose rock, Borya must have chosen scissors or paper. Anya chose rock 12 times. Borya chose scissors or paper a total of $9+3=12$ times. Therefore, all these cases must have occurred in the rounds where Anya chose rock.
This means that in all the other 13 rounds (when Anya chose scissors or paper), Borya chose rock.
From the rounds where Anya chose rock, she won 9 times: when Borya chose scissors. From the rounds where Borya chose rock, Anya won 7 times: when she chose paper. Therefore, Anya won 16 times.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-6-1. In the figure, there are two circles with centers $A$ and $B$. Additionally, points $A, B$, and $C$ lie on the same line, and points $D, B$, and $E$ also lie on the same line. Find the degree measure of the angle marked with a “?”.
|
Answer: $24^{\circ}$.
Solution Variant 1. The inscribed angle $BFE$ is half the central angle $BAE$, so we will find the angle $BAE$. This angle can be found from the isosceles triangle $BAE$ ($AB=AE$ as radii of the circle). Angles $ABE$ and $DBC$ are equal as vertical angles. Note that triangle $DBC$ is isosceles with $BD$ and $BC$ equal as radii. Thus:
$$
\begin{gathered}
\angle ABE = \angle DBC = 180^{\circ} - 57^{\circ} - 57^{\circ} = 66^{\circ} \\
\angle BAE = 180^{\circ} - 66^{\circ} - 66^{\circ} = 48^{\circ} \\
\angle BFE = \frac{1}{2} \angle BAE = \frac{1}{2} \cdot 48^{\circ} = 24^{\circ}
\end{gathered}
$$
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-7-1. At a large round table, 90 people are feasting, facing the center of the table: 40 barons, 30 counts, and 20 marquises. On a signal, exactly those who have both neighbors—left and right—with the same title should stand up. What is the maximum number of people who can stand up?
For example, for a count to stand up, both of his neighbors must have the same title, but it does not necessarily have to be a count.
|
Answer: 86.
Solution Variant 1. We ask half of the revelers, standing every other person, to step forward. Then all the people will be divided into two circles: an inner and an outer one. Note that a person in the inner circle has both neighbors in the outer circle, and they are also neighbors there. Similarly for a person in the outer circle.
Thus, we only need to find the maximum number of neighbors of the same title in the two new circles. Since each of the two new circles has 45 people, none of them can consist entirely of nobles of the same title. Therefore, in each circle, there are at least two pairs of neighbors of different titles (there cannot be just one). Thus, in total, there are at least 4 pairs of neighbors of different titles in both circles. Therefore, out of 90 revelers, 4 definitely will not stand.
In the reasoning above, we proved that more than 86 revelers cannot stand. But does a situation exist where exactly 86 stand? Yes, and an example of such a situation can easily be constructed from our reasoning: place 40 barons and 5 counts in a row in the outer circle, and 25 counts and 20 marquises in a row in the inner circle. Then we will have exactly 4 pairs of neighbors of different titles. In general, any example where there are two types of people in each circle, with people of one type in a row and people of the other type also in a row, will work.
|
86
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-7-3. At a large round table, 55 people are feasting, facing the center of the table: 25 barons, 20 counts, and 10 marquises. On a signal, exactly those who have both neighbors—left and right—with the same title should stand up. What is the maximum number of people who can stand up?
For example, for a count to stand up, both of his neighbors must have the same title, but it does not necessarily have to be a count.
|
Answer: 52.
Solution variant 3. We will place people in a new circle every other person: $1,3,5,7$, $\ldots, 55,2,4,6, \ldots, 54$, back to 1. It is sufficient to find the maximum number of neighbors with the same title in the new circle.
It is clear that there are neighbors of different titles in the new circle. It is also clear that the number of different-title neighbors in the new circle cannot be 1. It cannot be 2 either (then the new circle would be arranged as follows: feasters of one title, then feasters of another title. Where would the third title be then?). But it can be 3: for example, first all the barons, then all the counts, then all the marquises.
Thus, we have shown that at least three out of 55 feasters will not stand up, and we have constructed an example where only three can fail to stand. Therefore, the answer to the problem is 52.
|
52
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-8-1. There is a magical grid sheet of size $2000 \times 70$, initially all cells are gray. The painter stands on a certain cell and paints it red. Every second, the painter takes two steps: one cell to the left and one cell down, and paints the cell red where he ends up after the two steps. If the painter is in the leftmost column and needs to step left, he teleports to the rightmost cell of the same row; if the painter is in the bottom row and needs to step down, he teleports to the top cell of the same column. After several moves, the painter returns to the cell where he started. How many red cells are on the sheet at this moment?
The image below shows an example of the painter's moves: first the painter is in cell 1, then in cell 2, and so on.
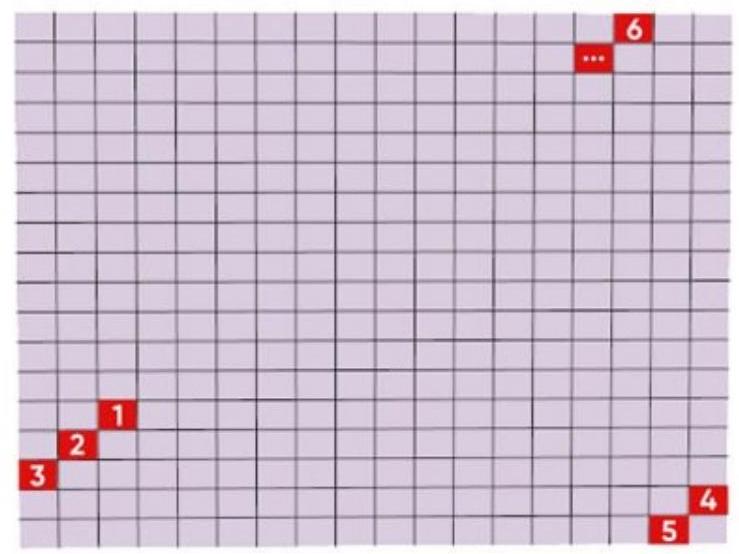
Comment. Let's provide another, equivalent, formulation of this problem. A grid sheet of size $2000 \times 70$ is glued into a torus, as shown in the picture.

The painter walks on the torus "diagonally". After several moves, the painter returns to the cell where he started. How many red cells are on the sheet at this moment?
|
Answer: 14000.
Solution version 1. We need to understand how many cells will be painted by the time the painter returns to the initial cell. Note that after every 2000 moves, the painter returns to the starting column, and after every 140 moves, he returns to the starting row. Therefore, he will return to the initial cell for the first time after $\operatorname{LCM}(2000,140)=14000$ moves. Thus, a total of 14000 cells will be painted red.
Comment. Note that the number of painted cells does not depend on which cell the painter starts from! This may not be obvious in the formulation with a sheet of paper, but it is clearer in the formulation with a torus: see the two paths starting from the red and blue cells in the figure. Intuitively, it is clear that these two paths are obtained from each other by a "shift" on the surface of the torus.
|
14000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Inside parallelogram $A B C D$, a point $E$ is chosen such that $A E=D E$ and $\angle A B E=90^{\circ}$. Point $M$ is the midpoint of segment $B C$. Find the angle $D M E$.
|
Answer: $90^{\circ}$.
First solution. Let $N$ be the midpoint of segment $A D$. Since triangle $A E D$ is isosceles, its median $E N$ is also an altitude, that is, $E N \perp A D$. Therefore, $N E \perp B C$ (see Fig. 2).
Since $A D \| B C$ and $B M = M C = A N = N D = A D / 2$, quadrilaterals $A B M N$ and $B M D N$ are parallelograms, from which $A B \| M N$ and $B N \| D M$. Since $\angle A B E = 90^{\circ}$ and $A B \| M N$, we get $B E \perp M N$. Thus, $E$ is the orthocenter of triangle $B M N$, from which $M E \perp B N$. Finally, from $B N \| D M$, we get $M E \perp D M$, that is, $\angle D M E = 90^{\circ}$.
Fig. 2
Fig. 3
Second solution. On the extension of segment $A B$ beyond point $B$, mark point $F$ such that $A B = B F$ (see Fig. 3). Then $B F = C D$ and $B F \| C D$, so quadrilateral $B D C F$ is a parallelogram. Point $M$ is the midpoint of diagonal $B C$ of this parallelogram, hence $M$ is also the midpoint of its diagonal $D F$.
Line $B E$ is the perpendicular bisector of segment $A F$, from which $A E = F E$. From the condition, we now get that $D E = A E = F E$. Therefore, point $E$ lies on the perpendicular bisector of $D F$. Hence, $\angle E M D = 90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. A confectionery factory produces $N$ types of candies. For New Year, the factory gave each of 1000 school students a gift containing candies of several types (the compositions of the gifts could be different). Each student noticed that for any 11 types of candies, they received a candy of at least one of these types. However, it turned out that for any two types, there is a student who received a candy of exactly one of these two types. Find the largest possible value of $N$.
|
Answer. $N=5501$.
Solution. Let $A_{1}, A_{2}, \ldots, A_{N}$ be the sets of students who did not receive candies of the 1st, 2nd, ..., $N$-th types, respectively. According to the problem, all these sets are distinct; moreover, each student is contained in no more than ten of them. Therefore, the total number of elements in these sets does not exceed $1000 \cdot 10 = 10000$.
Suppose there are exactly $k$ one-element sets among our sets. Then the number of sets containing more than one student does not exceed $\frac{10000-k}{2}$, so the total number of all non-empty sets does not exceed $\frac{10000-k}{2} + k = \frac{10000+k}{2} \leqslant \frac{11000}{2} = 5500$. Taking into account that one of the sets can be empty, we get that $N \leqslant 5501$.
It remains to show how the described situation could arise when $N=5501$. Make the set $A_{5501}$ empty; the distinct sets $A_{4501}, \ldots, A_{5500}$ will each contain one student. It remains to choose distinct two-element sets $A_{1}, \ldots, A_{4500}$ such that each student is in exactly 9 of them. For this, for example, we can divide the students into 100 groups of 10 people and take all pairs of children in the same group (there will be exactly $100 \cdot \frac{10 \cdot 9}{2} = 4500$ such pairs).
Remark. The construction can be completed in different ways. For example, we can arrange the students in a circle and form each two-element set either from a pair of opposite students (there will be 500 such pairs) or from a pair of students with no more than three other students between them.
Comment. Only the correct answer without justification (or with incorrect justification) - 0 points.
Only proof that $N \leqslant 5501$ - 4 points.
Only an example with $N=5501$ types - 3 points.
If the participant did not take into account that one type can be present in all gifts (i.e., the corresponding set $A_{i}$ can be empty) and therefore obtained the answer 5500 - 1 point is deducted.
|
5501
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a coordinate plane with the origin at point $O$, a parabola $y=x^{2}$ is drawn. Points $A, B$ are marked on the parabola such that $\angle A O B$ is a right angle. Find the smallest possible value of the area of triangle $A O B$.
|
5. Answer: 1. Solution. Let $A\left(a, a^{2}\right), B\left(b, b^{2}\right)$ be arbitrary points on the parabola. Then, by the Pythagorean theorem, $a^{2}+a^{4}+b^{2}+b^{4}=(a-b)^{2}+\left(a^{2}-b^{2}\right)^{2} \Leftrightarrow a b=-1$. From this, we find the expression for the area of the triangle: $2 S=\sqrt{a^{2}+a^{4}} \cdot \sqrt{\frac{1}{a^{2}}+\frac{1}{a^{4}}}=\sqrt{2+\left(a^{2}+\frac{1}{a^{2}}\right)} \geq 2$ (the last inequality follows from the inequality between the arithmetic mean and the geometric mean). It is clear that the value 1 is achieved for an isosceles triangle with vertices $O$, $A(1,1), B(-1,1)$.
Grading criteria. Correct solution - 7 points. The necessary inequality is proven, but it is not indicated that there exists a triangle with such an area - 5 points. The relationship between the coordinates of the points on the parabola is obtained, but there is no further progress - 1 point. The relationship between the coordinates is obtained and the formula for the area is written, but the estimate for the area is not made - 2 points. In all other cases - 0 points.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The numbers $1,2, \ldots, 2016$ are written on a board. It is allowed to erase any two numbers and replace them with their arithmetic mean. How should one proceed to ensure that the number 1000 remains on the board?
|
6. Solution. We will first act according to the following scheme: $1,2,3, \ldots, n-3, n-2, n-1, n \rightarrow 1,2,3, \ldots, n-3, n-1, n-1 \rightarrow 1,2,3, \ldots, n-3, n-1$. Acting in this way, we will arrive at the set $1,2,3, \ldots, 1000,1002$. Then we will act according to the same scheme from the other end:
\[
\begin{aligned}
& 1,2,3, \ldots, 1000,1002 \rightarrow 2,2,4, \ldots, 1000,1002 \rightarrow 2,4,5, \ldots, 1000,1002 \rightarrow 3,5, \ldots, 1000,1002 \\
& \rightarrow 4,6, \ldots, 1000,1002 \rightarrow 5,7, \ldots, 1000,1002 \rightarrow \ldots \rightarrow 997,999,1000,1002 \rightarrow 998,1000,1002 \\
& \rightarrow 1000,1000 \rightarrow 1000
\end{aligned}
\]
Grading criteria. Correct algorithm - 7 points. In other cases - 0 points.
|
1000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Karlson counts 200 buns baked by Fräulein Bock: «one, two, three, ..., one hundred and nine, one hundred and ten, ..., one hundred and ninety-eight, one hundred and ninety-nine, two hundred». How many words will he say in total? (Each word is counted as many times as it was said.)
|
Answer: 443 words.
Solution. One word will be required to pronounce 29 numbers: $1,2,3,4,5,6,7$, $8,9,10,11,12,13,14,15,16,17,18,19,20,30,40,50,60,70,80,90,100,200$.
Among the first 99 numbers, the number of those pronounced in two words: $99-27=72$, thus, the number of words required for their pronunciation is $2 \cdot 72=144$.
In the next hundred (from 101 to 199), each number that is pronounced in one word in the first hundred will be pronounced in two, and the number of words is: $2 \cdot 27=54$. The rest are pronounced in three words: $3 \cdot(99-27)=216$.
Thus, to count all the pastries, $29+144+54+216=443$ words will be needed.
## Criteria.
1 point. The number of numbers pronounced in one word is found reasonably.
2 points. The number of words required to pronounce numbers from 1 to 99 is found correctly and reasonably.
2 points. The number of words required to pronounce numbers from 100 to 199 or 200 is found correctly and reasonably.
Comment. Points for the criteria above are cumulative.
3 points. The correct answer without reasoning.
|
443
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In the notebook, all irreducible fractions with the numerator 15 are written down, which are greater than $\frac{1}{16}$ and less than $\frac{1}{15}$. How many such fractions are written down in the notebook?
|
Answer: 8 fractions.
Solution. We look for all suitable irreducible fractions of the form $\frac{n}{15}$. Since $\frac{1}{16}<\frac{15}{n}$, then $\frac{15}{225}>\frac{15}{n}$, and $n>225$. Therefore, $225<n<240$. The fraction $\frac{n}{15}$ is irreducible, meaning $n$ is not divisible by 3 or 5. It is not difficult to verify that out of the range from 226 to 239 (14 numbers), we need to exclude 6 numbers (228, 230, 231, 234, 235, 237). This leaves 8 possible values for $n$.
## Criteria.
1 point. Correct answer without correct justification.
3 points. Correctly obtained range for $n$.
$\mathbf{0}$ points. Not all cases considered when listing fractions.
Comment. It is quite possible that participants will try to list all such fractions and then justify why the denominator cannot be greater or less, carefully watch the accuracy of such justifications.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Lёsha colors cells inside a $6 \times 6$ square drawn on graph paper. Then he marks the nodes (intersections of the grid lines) to which the same number of colored and uncolored squares are adjacent. What is the maximum number of nodes that can be marked?
|
Answer: 45.
## Solution.
Estimation. Each grid node belongs to one, two, or four squares.
The corner vertices of the original square are adjacent to only one small square, so Lёsha will not be able to mark them. Therefore, the maximum number of marked nodes does not exceed $7 \cdot 7-4=45$.
Example.
With a checkerboard coloring, Lёsha will be able to mark all nodes except the points described above.
## Criteria.
2 points. A correct coloring is devised, but the number of nodes is incorrectly counted.
3 points. A correct example is provided.
3 points. The estimation is correctly proven.
7 points. A complete, correct, and justified solution.
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. All natural numbers are written in a row without spaces: 12345678910111213 .... What is the position of the twelfth ninth from the beginning?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
Answer: 174
Solution. The first nine is in the ninth position, the second is in the 29th position (between the first and second nines, we start writing two-digit numbers), the third is in the 49th position, and so on. The ninth nine (from the number 89) is in the $9+2 \cdot 80=$ 169th position (numbers from 1 to 9 occupy one position each, and numbers from 10 to 89 occupy two positions each). Next, 90919293... are written. From this, the twelfth nine is in the 174th position.
|
174
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.1. From a square grid with a side of 40, a rectangle $36 \times 37$ was cut out, adjacent to one of the corners of the square. Grisha wants to color a five-cell cross in the remaining piece. In how many ways can he do this?
|
Answer: 113
Solution 1. If the rectangle had not been cut out, the number of ways to color the cross would be $38 \times 38=1444$ (the cross is determined by its central cell, which cannot be adjacent to the edge). Due to the cut-out, $36 \times 37-1$ ways are lost (the center of the cross cannot be in the cut-out rectangle or adjacent to its side, but it can share a vertex with a vertex of the cut-out rectangle). From this, we get the answer.
Solution 2. Suppose the four first columns and three first rows remain uncut. Then the center of the cross can be placed in the second or third column (but not in the first or last row), or in the second row (excluding the first three columns and the last one), and also at the intersection of the third row and the third column.
|
113
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Every evening, starting from September 1st, little Anton ate one pastry. After eating another pastry, he noticed that during this entire time, he had eaten 10 delicious pastries (the rest seemed tasteless to him). But among any seven consecutive pastries he ate, no fewer than three turned out to be delicious. What is the maximum number of pastries Anton could have eaten?
|
Answer: 26
Solution. We will show that among 27 pastries, there will be no fewer than 11 delicious pastries. Let's number the pastries from 1 to 27. Note that among the first seven pastries, at least three are delicious, among the next seven as well, and among the pastries numbered from 15 to 21, there are at least three more (a total of nine delicious pastries have been found).
Among the pastries numbered from 21 to 27, there are also at least three delicious ones. One of them could have been counted earlier (if the pastry numbered 21 is delicious), but there will be at least two more delicious pastries with numbers from 22 to 27. Thus, there could not have been more than 26 pastries.
Note that there could have been 26 pastries. For example, let the delicious pastries be those with numbers $5, 6, 7, 12, 13, 14, 19, 20, 21, 26$. It is easy to see that the conditions of the problem are satisfied.
|
26
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Find the smallest natural number $n$ such that the natural number $n^{2}+14 n+13$ is divisible by 68.
|
Answer: 21
Solution. Note that $n^{2}+14 n+13=(n+1)(n+13)$, and $68=4 \cdot 17$. Therefore, one of the numbers $n+1$ and $n+13$ must be divisible by 17. Moreover, $n$ must be odd; otherwise, $n+1$ and $n+13$ would both be odd. The smallest such natural number $n$ is $2 \cdot 17-13=21$. Note that it works because $21^{2}+14 \cdot 21+13=$ $(21+1) \cdot(21+13)=22 \cdot 34=11 \cdot 68$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. On September 2nd, Robin Bobin ate 12 chickens, and starting from September 3rd, he ate every day as many as he had already eaten on average in September. On September 15th, Robin Bobin ate 32 chickens. How many chickens did he eat on September 1st?
|
Answer: 52
Solution. Let at the beginning of the $k$-th day he on average ate $x$ chickens. This means that by this point, he had eaten $(k-1) x$ chickens. Then on the $k$-th day, he also ate $x$ chickens, which means that over $k$ days, he ate $k x$ chickens. This means that after the $k$-th day, the average number of chickens eaten did not change, and thus, on the $k+1$-th day, the same number will be eaten. This means that this average number is 32 chickens. Therefore, in the first two days, Robin Bobin ate 64 chickens, i.e., on the first day -52 chickens.
|
52
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In quadrilateral $A B C D$, $A B=B C=C D$. Let $E$ be the intersection point of $A B$ and $C D$ (with $B$ between $A$ and $E$). It turns out that $A C=C E$ and $\angle D B C=15^{\circ}$. Find $\angle A E D$.
|
Answer: $50^{\circ}$
Solution. We will solve the general problem. Let $\angle D B C=\alpha$, and $\angle B E C=\beta$. From the isosceles property of $\triangle D C B$, we get $\angle B D C=\alpha$. From the isosceles property of $\triangle A C E$, we get $\angle B E C=\angle B A C$, and from the isosceles property of $\triangle A B C$, we get $\angle B A C=\angle A C B=\beta$. Then $\angle A C D=2 \beta$ as an exterior angle. Therefore, the sum of the angles in triangle $B C D$ is $2 \alpha+3 \beta=180^{\circ}$. In our problem, $\alpha=15^{\circ}$, then $\beta=\frac{180^{\circ}-2 \cdot 15^{\circ}}{3}=50^{\circ}$.
|
50
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. There are 15 rectangular sheets of paper. In each move, one of the sheets is chosen and divided by a straight cut, not passing through the vertices, into two sheets. After 60 moves, it turned out that all the sheets are either triangles or hexagons. How many hexagons?
|
Answer: 25
Solution. Let after 60 cuts, $x$ hexagons and $75-x$ triangles are formed (there were 15 sheets, and with each cut, the number of sheets increases by 1). Now let's count the number of sides. Initially, there were $15 \cdot 4=60$ sides, and with each cut, the number of sides increases by 4 (the cut divides two sides of the sheet in half, and also counts as a side in the two new sheets). After 60 cuts, we get 300 sides. Knowing how many sides each triangle and hexagon has, we get $300=3(75-x)+6 x$, from which $x=25$.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 2001 coins on the table. Two players play the following game: they take turns, on each turn the first player can take any odd number of coins from 1 to 99, the second player can take any even number of coins from 2 to 100, and so on. The player who cannot make a move loses. Who wins with correct play?
|
5. The first one wins. Winning strategy: the first player should take 81 coins from the table on the first move. On each subsequent move, if the second player takes x coins, then the first player should take (101 - x) coins. He can always do this because if x is an even number from 2 to 100, then (101 - x) is an odd number from 1 to 99. Since 2001 = 101 * 19 + 81 + 1, after 19 such "responses" the first player will leave 1 coin on the table after his move, and the second player will not be able to make a move, i.e., will lose.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.3. Given a convex quadrilateral $ABCD$, $X$ is the midpoint of diagonal $AC$. It turns out that $CD \parallel BX$. Find $AD$, if it is known that $BX=3, BC=7, CD=6$.
|
Answer: 14.
Solution. Double the median $B X$ of triangle $A B C$, to get point $M$. Quadrilateral $A B C M$ is a parallelogram (Fig. 1).
Notice that $B C D M$ is also a parallelogram, since segments $B M$ and $C D$ are equal in length (both 6) and parallel. This means that point $M$ lies on segment $A D$, since $A M \| B C$ and $M D \| B C$.
Fig. 1: to the solution of problem 9.3
Now it is easy to find the desired segment:
$$
A D=A M+M D=B C+B C=14
$$
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. The sides of the square $A B C D$ are parallel to the coordinate axes, with $A B$ lying on the y-axis, and the square is positioned as shown in the figure. The parabola defined by the equation
$$
y=\frac{1}{5} x^{2}+a x+b
$$
passes through points $B$ and $C$. Additionally, the vertex of this parabola (point $E$) lies on the segment $A D$. Find the sum of the roots of the quadratic trinomial whose graph is the parabola.
|
Answer: 20.
Solution. Note that the parabola is symmetric with respect to the vertical axis passing through its vertex, point $E$. Since points $B$ and $C$ are on the same horizontal line, they are symmetric with respect to this axis. This means that this axis passes through the midpoint of $B C$, and therefore, through the midpoint of $A D$.
Now that we have established that $E$ is the midpoint of $A D$, let's find the length of the side of the square $A B C D$. By completing the square in the quadratic polynomial, we get
$$
y=\frac{1}{5}\left(x-x_{E}\right)^{2}+y_{E}
$$
where $\left(x_{E}, y_{E}\right)$ are the coordinates of the vertex of the parabola (we will similarly denote the coordinates of other marked points). Substituting $x=x_{B}, y=y_{B}$ (the equality will hold since $B$ lies on the parabola) and moving $y_{E}$ to the left side, we get:
$$
y_{B}-y_{E}=\frac{1}{5}\left(x_{B}-x_{E}\right)^{2}
$$
If we denote the unknown side length of the square by $L$, then $y_{B}-y_{E}=L$ and $x_{B}-x_{E}=L / 2$. We obtain the relation $L=\frac{1}{5}(L / 2)^{2}$, from which it is not difficult to extract $L=20$.
It remains to recall that the points on the graph corresponding to the roots of the polynomial are also symmetric with respect to the axis of the parabola, which means that the semi-sum of the roots is equal to the abscissa of the vertex $x_{E}=L / 2$. Therefore, the sum of the roots is $L=20$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.4. An isosceles trapezoid $ABCD$ with bases $BC$ and $AD$ is such that $\angle ADC = 2 \angle CAD = 82^{\circ}$. Inside the trapezoid, a point $T$ is chosen such that $CT = CD, AT = TD$. Find $\angle TCD$. Give your answer in degrees.
|
Answer: $38^{\circ}$.
Solution. Let $a$ be the length of the lateral side of the trapezoid. Note that point $T$ lies on the perpendicular bisector of the bases of the trapezoid, that is, on its axis of symmetry. From symmetry, we get that $B T=T C=a$ (Fig. 5).
Fig. 5: to the solution of problem 10.4
Next, note that $\angle B A D=\angle C D A=2 \angle C A D$, so $A C$ is the bisector of angle $B A D$. Since $\angle C A D=\angle A C B$ due to parallelism, triangle $A B C$ is isosceles. Therefore, $B C$ is also equal to $a$.
We have obtained that triangle $B T C$ is equilateral, and its angles are each $60^{\circ}$. Now it is not difficult to calculate the required angle:
$$
\angle T C D=\angle B C D-\angle B C T=\left(180^{\circ}-\angle A D C\right)-60^{\circ}=120^{\circ}-\angle A D C=38^{\circ} .
$$
|
38
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. Given a right triangle $ABC$ with legs $AB=42$ and $BC=56$. A circle passing through point $B$ intersects side $AB$ at point $P$, side $BC$ at point $Q$, and side $AC$ at points $K$ and $L$. It is known that $PK=KQ$ and $QL: PL=3: 4$. Find $PQ^2$.
|
Answer: 1250.
Solution. Since in a cyclic quadrilateral the sum of opposite angles is $180^{\circ}$, then $\angle P K L=\angle P L Q=90^{\circ}$. From the condition, it also follows that right triangles $A B C$ and $Q L P$ are similar (Fig. 6). From this similarity and the cyclic nature of the pentagon
Fig. 6: to the solution of problem 10.7
$B Q L K P$, we get that $\angle C=\angle Q P L=\angle Q K L$, so triangle $C Q K$ is isosceles and $C Q=Q K$. Similarly, $\angle A=\angle P Q L=180^{\circ}-\angle P K L=\angle A K P$, so $A P=P K$. Also, by the condition, $P K=K Q$.
Thus, $C Q=Q K=P K=A P=x$. From the condition, we have
$$
A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{14^{2}\left(3^{2}+4^{2}\right)}=14 \cdot 5=70
$$
and also $\cos A=\frac{3}{5}$ and $\cos C=\frac{4}{5}$. Drop perpendiculars $P P^{\prime}$ and $Q Q^{\prime}$ to the hypotenuse $A C$. Then
$$
70=A C=A K+K C=2 A P^{\prime}+2 C Q^{\prime}=2 x \cos A+2 x \cos C=2 x\left(\frac{3}{5}+\frac{4}{5}\right)=\frac{14}{5} x
$$
from which $x=25$. By the Pythagorean theorem in triangle $P K Q$, we get
$$
P Q^{2}=P K^{2}+Q K^{2}=25^{2}+25^{2}=1250
$$
Another solution. As in the previous solution, by the Pythagorean theorem, we find $A C=70$. Also, from the similarity and the cyclic nature, we get $\angle C=\angle Q P L=\angle Q B L$, so triangle $C L B$ is isosceles and $C L=L B$. Similarly, $\angle A=\angle P Q L=\angle P B L$, so $A L=B L=C L$, i.e., $L$ is the midpoint of the hypotenuse.
Point $K$ is equidistant from points $P$ and $Q$, i.e., it is the midpoint of the arc $P L Q$ of the given circle and lies on the angle bisector of $\angle B$. Then, by the property of the angle bisector, we get $A K: K C=$ $A B: B C=3: 4$, which gives us $A K=\frac{3}{7} A C=30$ and $C K=\frac{4}{7} A C=40$. From the properties of secants to a circle drawn from the same point, we get $A K \cdot A L=A B \cdot A P$ and $C K \cdot C L=C Q \cdot C B$, from which respectively
$$
A P=\frac{A K \cdot A L}{A B}=\frac{30 \cdot 35}{42}=25 \quad \text { and } \quad C Q=\frac{C K \cdot C L}{C B}=\frac{40 \cdot 35}{56}=25
$$
Then $B P=A B-A P=17$ and $B Q=B C-C Q=31$, from which by the Pythagorean theorem in triangle $P B Q$ we get $P Q^{2}=P B^{2}+B Q^{2}=17^{2}+31^{2}=1250$.
|
1250
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. On the side $AC$ of triangle $ABC$, points $M$ and $N$ are marked ($M$ lies on the segment $AN$). It is known that $AB = AN$, $BC = MC$. The circumcircles of triangles $ABM$ and $CBN$ intersect at points $B$ and $K$. How many degrees does the angle $AKC$ measure if $\angle ABC = 68^\circ$?
|
Answer: 124.
Solution. From the given in the problem, it follows that $68^{\circ}+\alpha+\gamma=180^{\circ}$, where $\alpha$ and $\gamma$ denote the measures of angles $A$ and $C$ of the triangle, respectively. Since triangle $BAN$ is isosceles, $\angle BNA=90^{\circ}-\frac{1}{2} \alpha$, so $\angle BNC=90^{\circ}+\frac{1}{2} \alpha$. Similarly, $\angle BMA=90^{\circ}+\frac{1}{2} \gamma$.
From the fact that these angles are inscribed in the corresponding circles, we get $\angle BKA=90^{\circ}+\frac{1}{2} \alpha$ and $\angle BKC=90^{\circ}+\frac{1}{2} \gamma$ (Fig. 7). It remains
$$
\angle AKC=360^{\circ}-\angle BKA-\angle BKC=180^{\circ}-\frac{1}{2}(\alpha+\gamma)=90^{\circ}+\frac{1}{2} \cdot 68^{\circ}=124^{\circ}
$$
Fig. 7: to the solution of problem 11.4
Remark. Point $K$ is the incenter of triangle $ABC$.
|
124
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Inside the tetrahedron $A B C D$, points $X$ and $Y$ are given. The distances from point $X$ to the faces $A B C, A B D, A C D, B C D$ are $14, 11, 29, 8$ respectively. And the distances from point $Y$ to the faces $A B C, A B D, A C D, B C D$ are $15, 13, 25, 11$ respectively. Find the radius of the inscribed sphere of the tetrahedron $A B C D$.
|
Answer: 17.
Solution. Consider a point $Z$ lying on the ray $XY$ such that $XY: YZ = 1: 2$. We will prove that this point is the center of the inscribed sphere of the tetrahedron.
Drop perpendiculars $X_{\alpha}, Y_{\alpha}, Z_{\alpha}$ from points $X, Y, Z$ to the plane $\alpha$ - obviously, they will lie in the same plane perpendicular to $\alpha$ (Fig. 9a). Also, draw a line through $X$ parallel to $X_{\alpha} Y_{\alpha}$, and denote its intersections with the lines $Y Y_{\alpha}$ and $Z Z_{\alpha}$ as $Y^{\prime}$ and $Z^{\prime}$, respectively (Fig. 9b).
Since triangles $X Y Y^{\prime}$ and $X Z Z^{\prime}$ are similar with a ratio of 3, and $Z^{\prime} Z_{\alpha} = Y^{\prime} Y_{\alpha} = X X_{\alpha}$, we have $Z Z_{\alpha} = X X_{\alpha} + 3(Y Y_{\alpha} - X X_{\alpha}) = 3 Y Y_{\alpha} - 2 X X_{\alpha}$. (The difference $Y Y_{\alpha} - X X_{\alpha}$ can be either positive, as shown in the figure, or negative.)
We obtain that the distances from $Z$ to the faces $ABC, ABD, ACD, BCD$ are respectively $3 \cdot 15 - 2 \cdot 14 = 17, 3 \cdot 13 - 2 \cdot 11 = 17, 3 \cdot 25 - 2 \cdot 29 = 17, 3 \cdot 11 - 2 \cdot 8 = 17$. Moreover, it is clear that the point $Z$ is on the same side of each face as points $X$ and $Y$ (otherwise, the formula would give us a negative distance), which means it also lies inside the tetrahedron.
A point inside the tetrahedron, the distances from which to its faces are equal, is unique - it is the center of the inscribed sphere. The radius of the sphere is equal to the distance from the center to the faces, which is 17.
(a) tetrahedron
(b) section $X Y Y_{\alpha} X_{\alpha}$
Fig. 9: to the solution of problem 11.8
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Clone 1
The figure shows a hexagon composed of identical equilateral triangles, each with an area of 10. Find the area of the shaded part.
#
|
# Answer: 110
## Solution
We will call the equilateral triangles that make up the original hexagon unit triangles. Consider each of the highlighted triangles inside the hexagon separately. The smallest one coincides with the unit triangle and has an area of 10. The medium triangle is inscribed in a hexagon made up of six unit equilateral triangles. The diagram shows that this triangle is equal to half the area of the hexagon, as it can be divided into parts equal to the unshaded parts of this hexagon. Thus, its area is equal to three areas of the unit triangles.
The largest triangle is inscribed in a figure made up of 13 unit triangles. Notice that it is also composed of an integer number of unit triangles. If we do not consider the central triangle, the rest can be divided into fragments equal to the unshaded parts. Then its area is equal to \((13-1) / 2 + 1 = 7\) areas of the unit triangles.
Thus, the total area of the shaded part is \(10 \cdot (1 + 3 + 7) = 110\).
## Clone 2
In the diagram, a hexagon is composed of identical equilateral triangles, each with an area of 2. Find the area of the shaded part.
Answer: 22
## Clone 3
In the diagram, a hexagon is composed of identical equilateral triangles, each with an area of 3. Find the area of the shaded part.
Answer: 33
## Clone 4
In the diagram, a hexagon is composed of identical equilateral triangles, each with an area of 5. Find the area of the shaded part.
Answer: 55
#
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In a class, there are 18 children. The parents decided to gift the children from this class a cake. To do this, they first asked each child the area of the piece they wanted to receive. After that, they ordered a square cake, the area of which is exactly equal to the sum of the 18 named numbers. However, upon seeing the cake, the children wanted their pieces to be square as well. The parents can cut the cake with cuts parallel to the sides of the cake (cuts are not required to start or end on the side of the cake). For what largest $k$ can the parents guarantee to cut out $k$ square pieces from the ordered cake, which can be given to $k$ children, so that each of them gets what they want?
(A. Ibragimov, I. Bogdanov)
|
Answer. $k=12$.
Solution. We always assume that the area of the cake is 1. We will show that for some children's requests, the parents will not be able to cut out more than 12 required pieces. Choose a number $1 / 15 > x > 1 / 16$. Suppose that 15 main children ordered a piece of cake with an area of $x$ each (and the other three made arbitrary orders so that the total area of the ordered pieces is equal to 1). Mentally divide the cake into 16 equal squares and mark all 9 vertices of these squares that do not lie on the boundary of the cake (see Fig. 3). Then strictly inside any square piece of area $x$ will lie one of the marked points, that is, no more than nine such pieces can be cut out. Therefore, at least six children will not get their desired pieces.
It remains to prove that 12 children will always be able to get what they want. Let $a_{1} \geqslant a_{2} \geqslant \ldots \geqslant a_{18}$ be the side lengths of the pieces that the children want to get, that is,
$$
a_{1}^{2}+a_{2}^{2}+\ldots+a_{18}^{2}=1
$$
We will show that from a square, pieces with sides $a_{7}, a_{8}, \ldots, a_{18}$ can be cut out.
For this, we need the inequalities
$$
a_{7}+a_{10}+a_{13}+a_{16} \leqslant 1 \quad \text { and } \quad a_{7}+a_{8}+a_{9} \leqslant 1
$$
To prove the first inequality, note that
$$
\begin{aligned}
1 \geqslant & a_{1}^{2}+a_{2}^{2}+\ldots+a_{16}^{2} \geqslant 4 a_{4}^{2}+4 a_{8}^{2}+4 a_{12}^{2}+4 a_{16}^{2} \geqslant \\
& \geqslant 4\left(a_{7}^{2}+a_{10}^{2}+a_{13}^{2}+a_{16}^{2}\right) \geqslant\left(a_{7}+a_{10}+a_{13}+a_{16}\right)^{2}
\end{aligned}
$$
In the last transition, we used the inequality between the quadratic mean and the arithmetic mean. The second inequality is proved similarly:
| $a_{16}$ | $a_{17} \mid a$ | |
| :---: | :---: | :---: |
| $a_{13}$ | $a_{14}$ | $a_{15}$ |
| $a_{10}$ | $a_{11}$ | $a_{12}$ |
| $a_{7}$ | $a_{\S}$ | $a$ |
$1 \geqslant a_{1}^{2}+a_{2}^{2}+\ldots+a_{9}^{2} \geqslant 3 a_{3}^{2}+3 a_{6}^{2}+3 a_{9}^{2} \geqslant$
$\geqslant 3\left(a_{7}^{2}+a_{8}^{2}+a_{9}^{2}\right) \geqslant\left(a_{7}+a_{8}+a_{9}\right)^{2}$.
Fig. 3
Fig. 4
From inequalities $(*)$ it follows that the cake can be cut into horizontal
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.5. Hooligan Dima made a construction in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the figure.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire construction to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).

|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:

From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-
|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a poll was being held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the poll.
Then, 80 more people participated in the poll, voting only for October 22. After that, the poll ended. The final distribution of votes is also shown on the graph.
How many people participated in the poll?
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.