problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
8.5. For a natural number $N$, all its divisors were listed, then the sum of digits for each of these divisors was calculated. It turned out that among these sums, all numbers from 1 to 9 were found. Find the smallest value of $N$.
|
Answer: 288.
Solution. Note that the number 288 has divisors $1,2,3,4,32,6,16,8,9$. Therefore, this number satisfies the condition of the problem. We will prove that there is no smaller number that satisfies the condition.
Indeed, since $N$ must have a divisor with the sum of digits 9, $N$ is divisible by 9. Now consider the divisor $d$ with the sum of digits 8. $d$ is not divisible by 3, so the numbers $d$ and 9 are coprime, which means $N$ is divisible by $9d$. If $d \geq 32$, then $9d \geq 288$, that is,
$N \geq 288$. Therefore, it remains to check $d=26, d=17$, and $d=8$.
If $d=26$, then $9d=234$. This number does not have a divisor with the sum of digits 5, and any number divisible by it is greater than 288.
If $d=17$, then $9d=153$. This number does not have a divisor with the sum of digits 2, and any number divisible by it is greater than 288.
If $d=8$, then $9d=72$. The numbers divisible by it and less than 288 are 144 and 216. But these numbers do not have a divisor with the sum of digits 5.
Grading criteria. “+” A complete and well-reasoned solution is provided “士” A generally correct reasoning is provided, containing minor gaps or inaccuracies
“Ғ” Only the correct answer is provided
“-” The problem is not solved or solved incorrectly
|
288
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. On an $8 \times 8$ chessboard, $k$ rooks and $k$ knights are placed such that no figure attacks any other. What is the largest $k$ for which this is possible?
|
Answer: 5.
Solution: From the condition, it follows that in one row (column) with a rook, no other figure can stand.
Suppose 6 rooks were placed on the board. Then they stand in 6 rows and 6 columns. Therefore, only 4 unpicked cells will remain (located at the intersection of two empty rows and two empty columns). It is impossible to place 6 knights in these cells. Therefore, $k$ is no more than 5.
In Fig. 3, it is shown how to place 5 rooks and 5 knights on the board so that they do not attack each other.
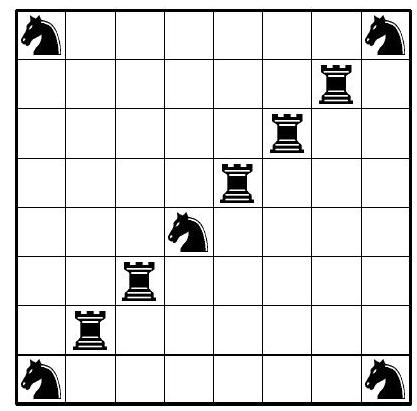
Fig. 3
Remark. There are other examples of placement.
Comment. Only proved that $k$ is no more than $5-4$ points.
Only provided an example of placing 5 knights and 5 rooks - 3 points.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 7.2
There are 30 logs, the lengths of which are 3 or 4 meters, and their total length is one hundred meters. How many cuts are needed to saw all these logs into pieces 1 meter long? (Each cut saws exactly one log).
Points 7
#
|
# Answer:
70
## Solution
## First Method
The total length of the logs is 100 meters. If it were a single log, 99 cuts would be needed. Since there are 30 logs, 29 cuts have already been made. Therefore, another $99-29=70$ cuts are needed.
## Second Method
Let's find the number of logs of each type. If all the logs were 3 meters long, their total length would be 90 meters. Since the total length is 100 meters, there are 10 logs that are 4 meters long and 20 logs that are 3 meters long. For each 4-meter log, three cuts are needed, and for each 3-meter log, two cuts are needed. In total: $10 \times 3 + 20 \times 2 = 70$ cuts.
Additional criteria for evaluation.
"4 or 5 points" A generally correct reasoning is provided, but a computational error is made.
"2 or 3 points" Only the correct answer is provided or the correct answer is obtained from a specific example.
|
70
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. CONDITION
A right triangle $ABC$ with hypotenuse $AB$ is inscribed in a circle. A point $D$ is taken on the larger leg $BC$ such that $AC = BD$, and point $E$ is the midpoint of the arc $AB$ containing point $C$. Find the angle $DEC$.
|
Solution. Point $E$ is the midpoint of arc $AB$, so $AE = BE$. Moreover, inscribed angles $CAE$ and $EBD$, subtending the same arc, are equal. Given that $AC = BD$, triangles $ACE$ and $BDE$ are congruent, which implies that angle $CEA$ is equal to angle $BED$. Therefore, angle $DEC$ is equal to angle $BEA$ and both are $90^{\circ}$, since angle $BEA$ is equal to angle $BCA$.
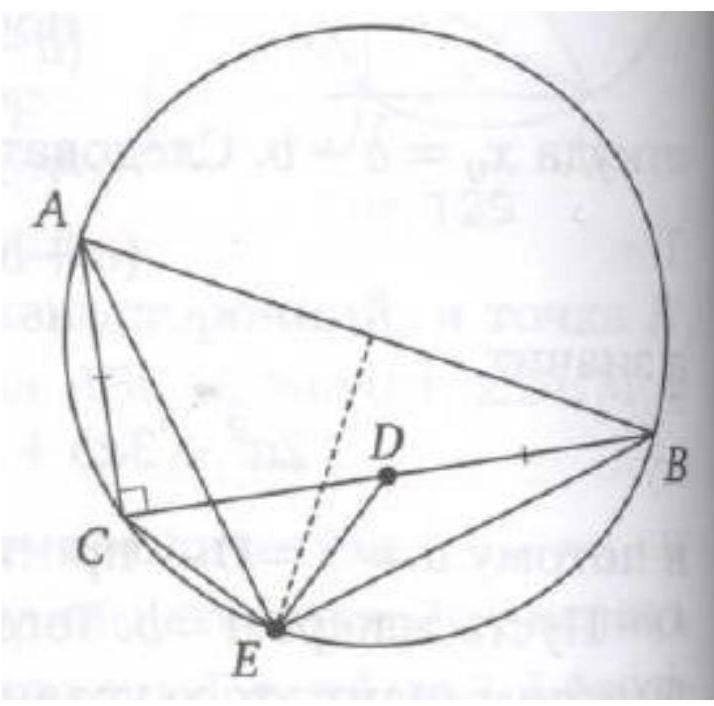
## Answer. $90^{0}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numbers $\sqrt{2}$ and $\sqrt{5}$ are written on the board. You can add to the board the sum, difference, or product of any two different numbers already written on the board. Prove that you can write the number 1 on the board.
|
Solution: For example, we get $\sqrt{5}-\sqrt{2}$, then $\sqrt{5}+\sqrt{2}$ and $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})=5-2=3$, then $\sqrt{2} \cdot \sqrt{5}=\sqrt{10}$, then $\sqrt{10}-3$ and $\sqrt{10}+3$ and finally $(\sqrt{10}-3)(\sqrt{10}+3)=10-9=1$.
Criteria. The goal is achieved if the same numbers are used in some operations (this is prohibited by the condition) - 3 points.
|
1
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. From 80 identical Lego parts, several figures were assembled, with the number of parts used in all figures being different. For the manufacture of the three smallest figures, 14 parts were used, and in the three largest, 43 were used in total. How many figures were assembled? How many parts are in the largest figure?
|
Answer: 8 figurines, 16 parts.
Solution. Let the number of parts in the figurines be denoted by $a_{1}43$, so $a_{n-2} \leqslant 13$.
Remove the three largest and three smallest figurines. In the remaining figurines, there will be $80-14-$ $43=23$ parts, and each will have between 7 and 12 parts. One figurine is clearly insufficient, and three would be too many $(7+8+9=24)$. Therefore, 23 parts form 2 figurines. This is possible, and in only one way: $23=11+12$. We have $43=13+14+16$ - the only decomposition with $a_{6} \geqslant 13$.
Criteria. Only the answer - 0 points. Only correct estimates for $a_{3}$ and $a_{n-2}-3$ points. Only a justified answer for the number of figurines - 5 points. Complete solution - 7 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The diagonals of the circumscribed trapezoid $A B C D$ with bases $A D$ and $B C$ intersect at point O. The radii of the inscribed circles of triangles $A O D, A O B, B O C$ are 6, 2, and $3 / 2$ respectively. Find the radius of the inscribed circle of triangle $C O D$.
|
Answer: 3
Solution. We will prove a more general statement, that $\frac{1}{r_{1}}+\frac{1}{r_{3}}=\frac{1}{r_{2}}+\frac{1}{r_{4}}$, where $r_{1}, r_{2}, r_{3}$ and $r_{4}$ are the radii of the inscribed circles of triangles $A O D, A O B, B O C$ and $C O D$ respectively.
Let $A B=a, B C=b, C D=c, A D=d, O A=x, O D=y, S_{\triangle A O D}=S$. Let $\frac{b}{d}=k$.
Triangle $C O B$ is similar to triangle $A O D$ with a similarity coefficient $k$, so $S_{\triangle C O B}=k^{2} S$, $O B=k y, O C=k x, S_{\triangle A O B}=S_{\triangle C O D}=k S$. Then
$$
r_{1}=\frac{2 S}{x+y+d}, \quad r_{3}=\frac{2 k^{2} S}{k x+k y+b}, \quad r_{2}=\frac{2 k S}{k y+x+a}, \quad r_{4}=\frac{2 k S}{k x+y+c}
$$
Thus,
$$
2\left(\frac{1}{r_{1}}+\frac{1}{r_{3}}\right)=\frac{x+y+d}{S}+\frac{k x+k y+b}{k^{2} S}=\frac{x+y}{S}+\frac{x+y}{k S}+\frac{d k+\frac{b}{k}}{k S}=\frac{x+y}{S}+\frac{x+y}{k S}+\frac{b+d}{k S}
$$
Here we used that $d k=b$ and $\frac{b}{k}=d$ from the similarity of triangles $A O D$ and $B O C$. Further,
$$
2\left(\frac{1}{r_{2}}+\frac{1}{r_{4}}\right)=\frac{k x+y+c}{k S}+\frac{x+k y+a}{k S}=\frac{x+y}{S}+\frac{x+y}{k S}+\frac{a+c}{k S}=\frac{x+y}{S}+\frac{x+y}{k S}+\frac{b+d}{k S}
$$
where $a+c=b+d$, since the trapezoid is circumscribed. Thus, we have proved that $\frac{1}{r_{1}}+\frac{1}{r_{3}}=$ $\frac{1}{r_{2}}+\frac{1}{r_{4}}$.
By the condition, $\frac{1}{6}+\frac{1}{1.5}=\frac{1}{2}+\frac{1}{r_{4}}$, from which $r_{4}=3$.
Criteria. The solution contains a statement that is not common knowledge and which the reader cannot establish on their own in 5 minutes - no more than 3 points.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In the product of three natural numbers, each factor was decreased by 3. Could the product have increased by exactly $2016$?
(N. Agakhanov, I. Bogdanov)
|
Answer. Yes, it could.
Solution. The product $1 \cdot 1 \cdot 676$ serves as an example. After the specified operation, it becomes $(-2) \cdot(-2) \cdot 673 = 2692 = 676 + 2016$.
Remark. The given example is the only one. Here is how to come up with it. Suppose two of the factors were 1, and the third was $-a$. Their product was $a$, and after the reduction, it became $(-2)^2(a-3) = 4a - 12$. Therefore, for $4a - 12 = a + 2016$, the condition is satisfied. Solving this equation, we get $a = 676$.
Comment. Only the correct answer - 0 points,
A set of numbers that satisfies the condition is presented - 7 points.
In an otherwise correct solution, due to an arithmetic error, the answer is the set $1, 1, a$, where the value of $a$ is incorrectly given - 5 points.
|
676
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
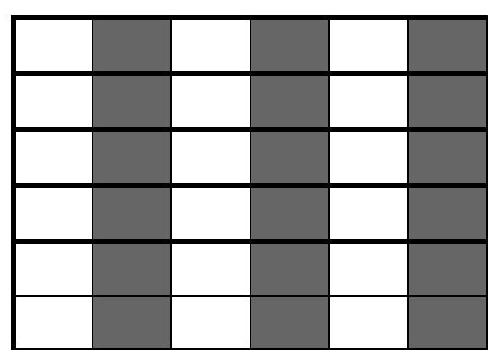
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
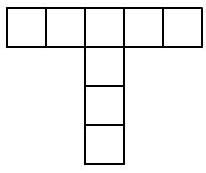
|
Answer: 24.
Solution. In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
Answer: 43.
Solution. The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. From a $6 \times 6$ grid square, gray triangles have been cut out. What is the area of the remaining figure? The side length of each cell is 1 cm. Give your answer in square centimeters.
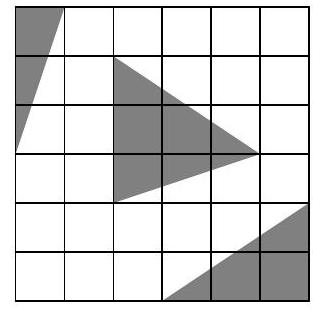
|
Answer: 27.
Solution. The area of the entire square is $6 \cdot 6=36$ sq. cm.
Divide the triangle located in the middle of the square into two smaller triangles, as shown in the picture on the left. Then the dark gray triangles can be combined into a rectangle $1 \times 3$, and the light gray triangles into a rectangle $2 \times 3$. Therefore, the area of the figure that remains after cutting out all the triangles is 36-3-6 $=27$ sq. cm.
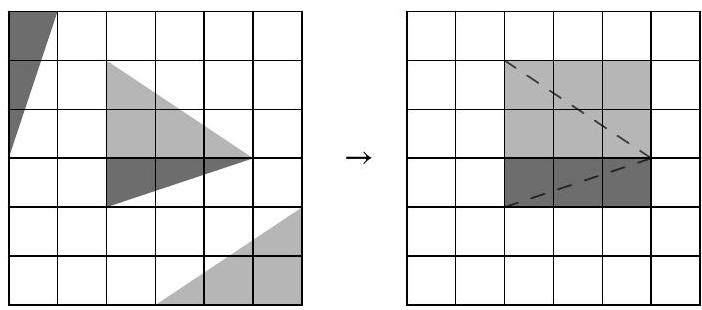
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. In the park, paths are laid out as shown in the figure. Two workers started to asphalt them, starting simultaneously from point $A$. They lay asphalt at constant speeds: the first on the section $A-B-C$, the second on the section $A-D-E-F-C$. In the end, they finished the work simultaneously, spending 9 hours on it. It is known that the second works 1.2 times faster than the first. How many minutes did the second spend laying asphalt on the section $D E$?
|
Answer: 45.
Solution. Let the line $A D$ intersect the line $C F$ at point $G$, as shown in the figure below. Since $A B C G$ and $D E F G$ are rectangles, we have $A B=C G, B C=A G, E F=D G$ and $D E=F G$.
The second worker works 1.2 times faster than the first, and the working time was the same, so the second worker laid 1.2 times more asphalt than the first. Let the first worker lay $x=A B+B C$ asphalt on the section $A-B-C$, then the second worker on the section $A-D-E-F-C$ laid
$$
\begin{aligned}
1.2 x & =A D+D E+E F+F G+G C=(A D+E F+C G)+(D E+F G)= \\
& =(B C+A B)+(D E+D E)=x+2 D E
\end{aligned}
$$
From this, we find that $D E=0.1 x$, which is 12 times less than the total amount of asphalt on the second section. Therefore, the second worker spent 12 times less time on the section $D E$ than on his entire path. He worked a total of $9 \cdot 60=540$ minutes, so he spent $\frac{540}{12}=45$ minutes on $D E$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. There are exactly 120 ways to color five cells in a $5 \times 5$ table so that each column and each row contains exactly one colored cell.
There are exactly 96 ways to color five cells in a $5 \times 5$ table without a corner cell so that each column and each row contains exactly one colored cell.
How many ways are there to color five cells in a $5 \times 5$ table without two corner cells so that each column and each row contains exactly one colored cell?

|
Answer: 78.
Solution. Consider the colorings of a $5 \times 5$ table described in the problem (i.e., such that in each column and each row exactly one cell is colored).
For convenience, let's introduce some notations. Let the top-left corner cell of the $5 \times 5$ table be called $A$, and the bottom-right corner cell be called $B$. Suppose that among the colorings of the first table, exactly $a$ have the cell $A$ colored, and exactly $b$ have the cell $B$ colored. Clearly, $a=b$ due to symmetry.
Notice that the number of colorings of the second table is equal to the number of colorings of the first table where the cell $A$ is not colored. The number of colorings of the third table is equal to the number of colorings of the first table where neither $A$ nor $B$ is colored. To find this, we subtract from 120 the number of colorings of the first table where $A$ or $B$ is colored. To count the number of such colorings, we add $a$ and $b$, and then subtract what has been counted twice - the ways where both $A$ and $B$ are colored.
All colorings of the first table can be divided into two types: those in which the cell $A$ is colored, and those in which it is not. This leads to the equation $120=a+96$, i.e., $a=24$. Then $b=24$ as well.
The number of colorings where both $A$ and $B$ are colored is the same as the number of ways to color the central $3 \times 3$ square. It is easy to see that there are exactly $3!=6$ such ways (to choose the colored cell in its top row, there are 3 ways, in the middle row - 2 ways, and in the bottom row - 1 way).
Thus, the answer to the problem is the number $120-(24+24-6)=78$.
## 7th grade
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
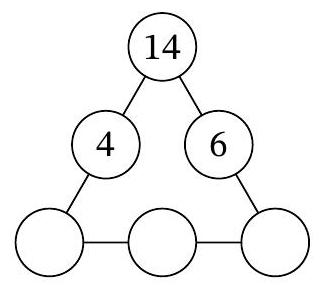
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
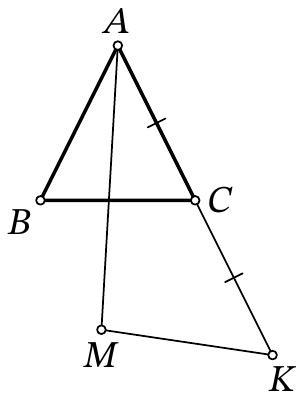
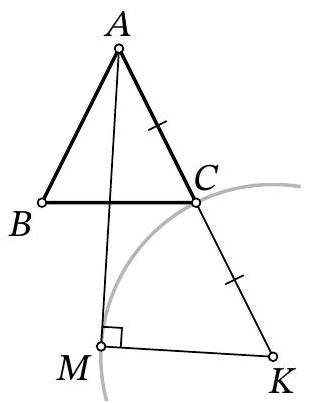
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
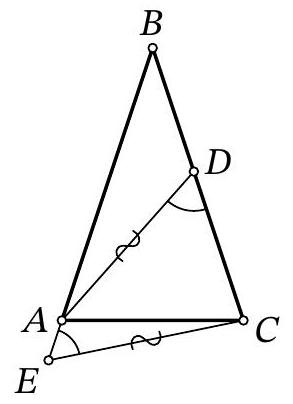
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
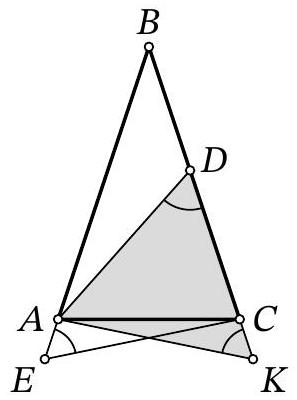
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are both $60^{\circ}$, so it is an equilateral triangle, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a $5 \times 5$ square, some cells have been painted black as shown in the figure. Consider all possible squares whose sides lie along the grid lines. In how many of them is the number of black and white cells the same?

|
Answer: 16.
Solution. An equal number of black and white cells can only be in squares $2 \times 2$ or $4 \times 4$ (in all other squares, there is an odd number of cells in total, so there cannot be an equal number of black and white cells). There are only two non-fitting $2 \times 2$ squares (both of which contain the center of the table, but do not contain any cells above the center), so there are exactly $16-2=14$ fitting $2 \times 2$ squares. And among the $4 \times 4$ squares, only the two lower ones fit.
Thus, the total number of squares with an equal number of black and white cells is exactly $14+2=16$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
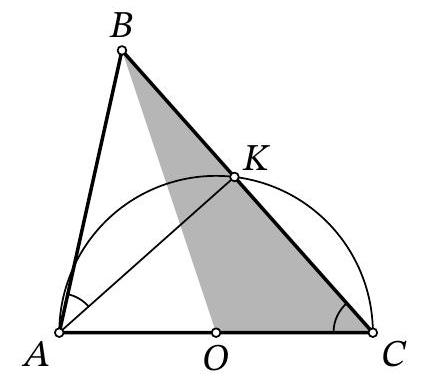
|
Answer: 21.
Solution. Since $AC$ is the diameter of the circle, point $O$ is the midpoint of $AC$, and $\angle AKC = 90^{\circ}$.
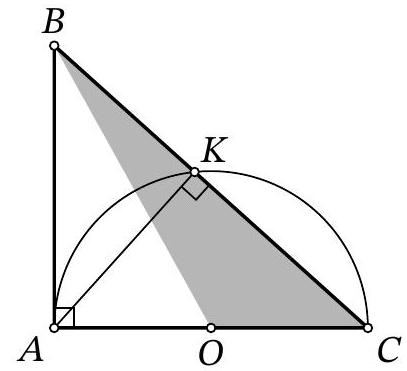
Then,
$$
\angle BAC = \angle BAK + \angle CAK = \angle BCA + \angle CAK = \angle BKA = 90^{\circ}.
$$
The area of the right triangle $ABC$ can be found as $\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 14 = 42$. Since the median $BO$ divides its area in half, the area of triangle $BOC$ is $\frac{42}{2} = 21$.
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Given an isosceles triangle $A B C$, where $A B=A C$ and $\angle A B C=53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $A K$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $A C$;
- $K M=A B$
- angle $M A K$ is the maximum possible.
How many degrees does angle $B A M$ measure?
|
Answer: 44.
Solution. Let the length of segment $AB$ be $R$. Draw a circle with center $K$ and radius $R$ (on which point $M$ lies), as well as the tangent $AP$ to it such that the point of tangency $P$ lies on the same side of $AC$ as $B$. Since $M$ lies inside the angle $PAK$ or on its boundary, the angle $MAK$ does not exceed the angle $PAK$, and these angles are equal only if points $M$ and $P$ coincide. Therefore, $M$ is this point of tangency.
The radius $KM$ of the circle is perpendicular to the tangent $AM$. Also, in the right triangle $AMK$, the leg $MK$ is half the hypotenuse $AK$, so $\angle MAK=30^{\circ}$. Additionally, from the condition, we get that $\angle BAC=180^{\circ}-2 \cdot 53^{\circ}=74^{\circ}$. Therefore,
$$
\angle BAM=\angle BAC-\angle MAK=74^{\circ}-30^{\circ}=44^{\circ}
$$
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. An equilateral triangle with a side of 10 is divided into 100 small equilateral triangles with a side of 1. Find the number of rhombi consisting of 8 small triangles (such rhombi can be rotated).
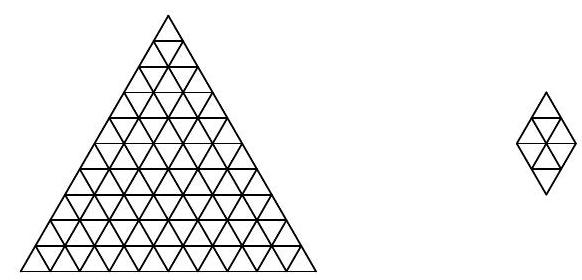
|
Answer: 84.
Solution. Rhombuses consisting of eight triangles can be of one of three types:

It is clear that the number of rhombuses of each orientation will be the same, so let's consider only the vertical ones. Each of them is uniquely determined by its top triangle. Now it is easy to count the number of such triangles.
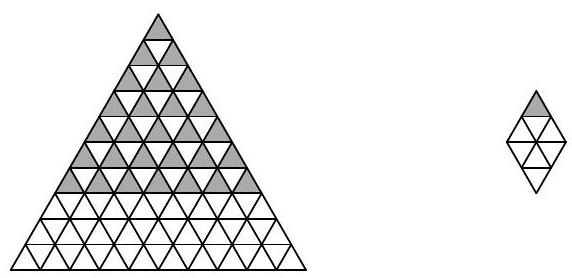
In the first row, there is 1 such triangle, in the second - 2, in the third - 3, ..., in the seventh - 7. In total, \(1+2+3+\ldots+7=28\) vertical rhombuses, and therefore, the answer to the problem is \(28 \cdot 3 = 84\).
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. A circle $\omega$ is inscribed in trapezoid $A B C D$, and $L$ is the point of tangency of $\omega$ and side $C D$. It is known that $C L: L D=1: 4$. Find the area of trapezoid $A B C D$, if $B C=9$, $C D=30$.

|
Answer: 972.
Solution. Let's mark the center of the circle $I$, as well as the points of tangency $P, Q, K$ with the sides $B C$, $A D, A B$ respectively. Note that $I P \perp B C, I Q \perp A D$, i.e., points $P, I, Q$ lie on the same line, and $P Q$ is the height of the given trapezoid, equal to the diameter of its inscribed circle. Also, the segments of tangents $A K=A Q, B K=B P, C P=C L, D L=D Q$ are equal.

From the condition, it follows that $C P=C L=\frac{1}{5} \cdot 30=6, D Q=D L=\frac{4}{5} \cdot 30=24$. Then $B K=B P=$ $B C-C P=9-6=3$.
Since the lines $C I$ and $D I$ are the angle bisectors of angles $C$ and $D$ of the trapezoid, we have $\angle I C D+$ $\angle I D C=\frac{1}{2}(\angle C+\angle D)=\frac{180^{\circ}}{2}=90^{\circ}$, i.e., triangle $C I D$ is a right triangle with a right angle at vertex $I$. Since $I L$ is its height dropped to the hypotenuse, $I L=$ $\sqrt{C L \cdot D L}=12$. This is the radius of the circle.
Similarly, considering the height $I K$ in the right triangle $A I B$, we get $12=$ $I K=\sqrt{A K \cdot B K}$. Using $B K=3$, we extract $A K=A Q=48$.
Thus, the area of the trapezoid is
$$
S_{A B C D}=\frac{B C+A D}{2} \cdot C H=\frac{9+(48+24)}{2} \cdot 24=972
$$
|
972
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. A beginner gardener planted daisies, buttercups, and marguerites on their plot. When they sprouted, it turned out that there were 5 times more daisies than non-daisies, and 5 times fewer buttercups than non-buttercups. What fraction of the sprouted plants are marguerites?
|
Answer. Zero. They did not germinate.
Solution. Daisies make up $5 / 6$ of all the flowers, and dandelions make up $1/6$. Therefore, their total number equals the total number of flowers.
Criteria. Only the answer - 0 points. Complete solution - 7 points.
|
0
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-3. Vika has been recording her grades since the beginning of the year. At the beginning of the second quarter, she received a five, after which the proportion of fives increased by 0.15. After another grade, the proportion of fives increased by another 0.1. How many more fives does she need to get to increase their proportion by another 0.2?
|
Answer: 4.
Solution: Let's say Vika had $n$ grades in the first quarter, of which $k$ were fives. Then, after the first five in the second quarter, the proportion of fives increased by $\frac{k+1}{n+1}-\frac{k}{n}=0.15$. Similarly, after the second five, the increase was $\frac{k+2}{n+2}-\frac{k+1}{n+1}=0.1$. Simplifying each equation, we get the system
$$
\left\{\begin{array}{c}
n-k=0.15 n(n+1) \\
n-k=0.1(n+1)(n+2)
\end{array}\right.
$$
In particular, $0.15 n(n+1)=0.1(n+1)(n+2)$, which means $1.5 n=n+2, n=4$. Substituting this value into the first equation, we find that $k=4-0.15 \cdot 4 \cdot 5=1$. Therefore, after receiving two fives in the second quarter, the proportion of fives became $3 / 6=0.5$. Vika wants the proportion of fives to be $0.5+0.2=0.7$ after receiving another $m$ fives, which means $\frac{3+m}{6+m}=0.7$. Solving this equation, we get $m=4$.
Criteria: Answer without justification - 0 points. System of equations formulated - 2 points. Complete solution - 7 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A new series of "Kinder Surprises" - chocolate eggs, each containing a toy car - was delivered to the store. The seller told Pete that there are only five different types of cars in the new series, and it is impossible to determine which car is inside by the appearance of the egg. What is the minimum number of "Kinder Surprises" Pete should buy to guarantee having three cars of the same type, regardless of which type?
|
Solution. If Petya buys 10 "Kinder Surprises," in the least favorable situation for him, he will get two cars of each type. If he buys 11 "Kinder Surprises," he will get three cars of one type. Let's prove this. Suppose Petya bought 11 "Kinder Surprises" but did not get three cars of one type. This means the number of cars is no more than 10 (two cars of one type, a total of five types). Contradiction.
Answer. Petya should buy no fewer than 11 "Kinder Surprises."
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A $3 \times 3$ table is initially filled with zeros. In one move, any $2 \times 2$ square in the table is selected, and all zeros in it are replaced with crosses, and all crosses with zeros. We will call any arrangement of crosses and zeros in the table a "pattern." How many different patterns can be obtained as a result of such moves? Patterns that can be obtained from each other by rotating $90^{\circ}$ or $180^{\circ}$ are considered different.
|
Solution. First method. Different drawings differ by at least one cell in the table, either plus or minus. The symbol in a given specific cell is determined by the parity (even or odd) of the number of swaps performed in each $2 \times 2$ square containing that cell. Each $2 \times 2$ square contains exactly one corner cell of the table, and each such square has its own unique corner cell. The parity of the number of swaps in each square corresponds to the symbol in its unique corner cell (if there is a cross in the corner cell, the number of swaps was odd; if there is a circle, the number of swaps was even). Therefore, each combination of symbols in the table uniquely corresponds to a combination of circles and crosses in the corner cells of the table. Since the number of different combinations in four cells is $2^{4}=16$, there are 16 drawings in total.
Second method. One can create a transition table and show that when swaps are performed multiple times, cycles arise, and some drawings transition into others. The images below show all possible ways to place crosses and circles, and the number of corresponding drawings in one group. Drawings in the same group differ from each other by rotations of $90^{\circ}$ or $180^{\circ}$. The presence of cycles proves that the number of drawings is limited, and fewer than $2^{9}$.
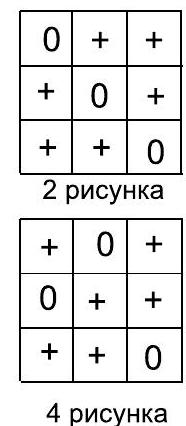
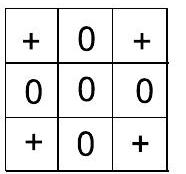
1 drawing
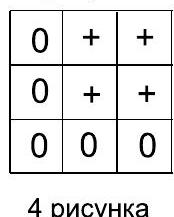

1 drawing
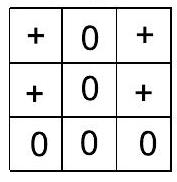
4 drawings
Answer. 16 drawings.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two cyclists are training on a circular stadium. In the first two hours, Ivanov lapped Petrov by 3 laps. Then Ivanov increased his speed by 10 km/h, and as a result, after 3 hours from the start, he lapped Petrov by 7 laps. Find the length of the lap.
|
4. Answer: 4 km. Solution: let I be Ivanov's speed (initial), Π be Petrov's speed, K be the length of the circle. Then 2I - 2Π = 3K and 2I - 2(Ι - Π) = 3K and 3(Ι - Π) = 3K - 10, express Ι - Π from both equations and equate, we get 14K - 20 = 9K, from which K = 4.
Criteria: correct solution - 7 points; the system is set up, but there is no further progress - 2 points; in all other cases - 0 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. How many rectangular trapezoids $A B C D$ exist, where angles $A$ and $B$ are right angles, $A D=2$, $C D=B C$, the sides have integer lengths, and the perimeter is less than 100?
|
Answer: 5.
Solution. Let $C D=B C=a, A B=b$. Drop a perpendicular from point $D$ to $B C$, and apply the Pythagorean theorem: $(a-2)^{2}+b^{2}=a^{2}$. From this, $b^{2}=4(a-1), a=\frac{b^{2}}{4}+1$. Suppose $A D=2$ is the smaller base of the trapezoid. The perimeter $P=2 a+b+2a$, so $b>2$. Considering that $a=\frac{b^{2}}{4}+1$, $b$ must be even, yielding the permissible values of $b: 4,6,8,10,12$.
Suppose $A D=2$ is not the smaller base of the trapezoid. Then $a=1$ or $a=2$. In the first case, there is a contradiction with the relation $a=\frac{b^{2}}{4}+1$. In the second case, the quadrilateral $A B C D$ becomes a square, which is not considered a trapezoid.
Comment. A correct and justified solution - 7 points. Proven that $b \leq 12$ - 4 points. Odd values of $b$ not eliminated - 3 points deducted. The value $b=2$ not eliminated - 1 point deducted. The correct answer obtained by selecting numbers that satisfy the condition, but not shown that other answers are impossible - 3 points, if there is an incomplete justification - 4-5 points. Some answers found by selection - 1-2 points. The problem is not solved or solved incorrectly - 0 points.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
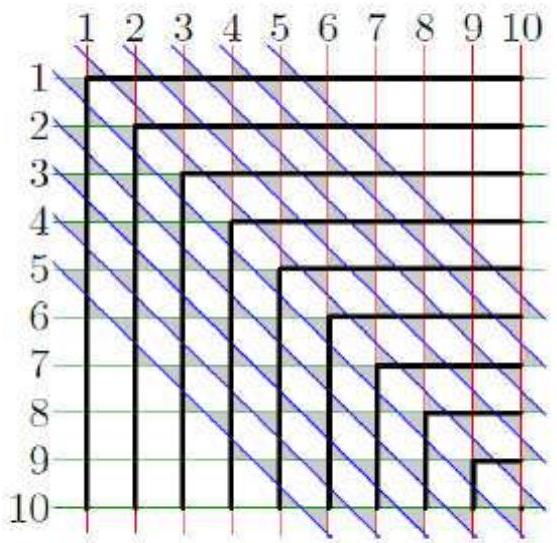
9.5. What is the maximum number of figures consisting of 4 1x1 squares, as shown in the diagram, that can be cut out from a $6 \times 6$ table, if cutting can only be done along the grid lines?
#
|
# Solution:
Example:

The diagram shows that 8 figures can be cut out.
Evaluation:
We will color the even-numbered columns in gray and the odd-numbered columns in white. For each figure cut out, there will be 2 more cells of one color than the other. Therefore, to cut out the entire table, we need the number of figures with three gray cells to be equal to the number of figures with three white cells, which means the number must be even. 36:4=9, which is an odd number, so it is impossible to cut out the entire figure.
Answer: 8 figures.
| Criteria | Points |
| :--- | :---: |
| Complete solution of the problem. | 7 |
| Only the evaluation, without an example. | 5 |
| Correct answer with an example. | 2 |
| Only the correct answer, without evaluation and example. | 0 |
| Incorrect solution. | 0 |
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Point E is the midpoint of side AB of parallelogram ABCD. On segment DE, there is a point F such that $\mathrm{AD}=\mathbf{B F}$. Find the measure of angle CFD.
|
Solution: Extend DE until it intersects line BC at point K (see figure). Since $\mathrm{BK} \| \mathrm{AD}$, then $\angle \mathrm{KBE}=\angle \mathrm{DAE}$. Moreover, $\angle \mathrm{KEB}=\angle \mathrm{DEA}$ and $\mathrm{AE}=\mathrm{BE}$, so triangles $\mathrm{BKE}$ and $\mathrm{ADE}$ are congruent. Therefore, $\mathrm{BK}=\mathrm{AD}=\mathrm{BC}$.
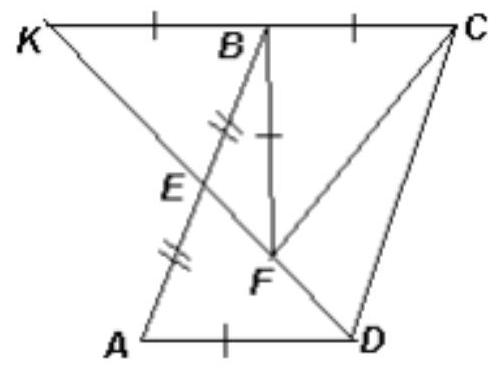
Thus, in triangle $\mathrm{CFK}$, the median FB is equal to half the side to which it is drawn, so this triangle is a right triangle with a right angle at F. Therefore, angle CFD is also a right angle.
Answer: $90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Solve the equation $2 \sin ^{2} x+1=\cos (\sqrt{2} x)$.
|
Answer: $x=0$. Solution. The left side of the equation $\geq 1$, and the right side $\leq 1$. Therefore, the equation is equivalent to the system: $\sin x=0, \cos \sqrt{2} x=1$. We have: $x=\pi n, \sqrt{2} x=2 \pi k$ ( $n, k-$ integers). From this, $n=k \cdot \sqrt{2}$. Since $\sqrt{2}$ is an irrational number, the last equality is possible only when $n=k=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At a round table, 12 people are sitting. Some of them are knights, who always tell the truth, and the rest are liars, who always lie. Each person declared their left neighbor to be a liar. Can we definitely state how many knights and how many liars are at the table?
|
1. Answer: Yes, it is possible.
If a knight is sitting in some place, then he told the truth, and to his left should sit a liar. Conversely, if a liar is sitting in some place, then to his left sits the one who was incorrectly called a liar, that is, a knight. This means that knights and liars alternate around the table, meaning there are 6 of each.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest natural number that ends in 56, is divisible by 56, and has the sum of its digits equal to 56.
|
2. Answer: 29899856.
The number has the form $100 A+56$, where $A$ is divisible by 7 and is even. The sum of the digits of $A$ is 45. It is sufficient to indicate the smallest number with these properties. Clearly, it must be at least six digits. The smallest even number with a digit sum of 45 is 199998, but it is not divisible by 7. The next larger such numbers start with the digit 2, and end with 8, as otherwise the sum of the digits would be less. Then the other digits are one more 8 and the rest are nines. The next two largest options are 289998 and 298998. It is easy to see that the first of these is not divisible by 7, but the second is, so we append 56 to it.
|
29899856
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The student was given an assignment consisting of 20 problems. For each correctly solved problem, they receive 8 points, for each incorrectly solved problem - minus 5 points, and for a problem they did not attempt - 0 points. The student scored a total of 13 points. How many problems did the student attempt?
|
# Solution.
Let $x$ be the number of problems solved correctly, $y$ be the number of problems solved incorrectly. Then we get the equation $8x - 5y = 13$. This equation can be solved in two ways.
1st method. Rewrite the equation as $8(x + y) = 13(1 + y)$. We see that the number $x + y$ is divisible by 13. On the other hand, by the condition, $x + y$ is no more than 20. Therefore, $x + y = 13$ (in this case, $x = 6$, $y = 7$).
One solution to the equation is immediately guessed: $x_0 = 1, y_0 = -1$. For any integer $t$, the pair of numbers $x = 1 + 5t, y = -1 + 8t$ also satisfies this equation.
Answer: 13 problems.
Other methods of solution are possible.
Criteria: only one correct answer is given without justification - 1 point.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. Solve the equation:
$1+\frac{3}{x+3}\left(1+\frac{2}{x+2}\left(1+\frac{1}{x+1}\right)\right)=x$.
|
# Solution.
$1+\frac{1}{x+1}=\frac{x+2}{x+1}$, therefore the given equation is equivalent to the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+1}\right)=x$ under the condition that $\mathrm{x} \neq-2$. Proceeding similarly, we get $1+\frac{3}{x+3}=x$, where $\mathrm{x} \neq-2$ and $\mathrm{x} \neq-3$. The roots of this equation are the numbers 2 and -2, so the only root of the original equation is the number 2.
## Grading Criteria
- Only the correct answer is provided - 1 point.
- The correct solution process, but the extraneous root is not discarded - 3 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Three families of parallel lines have been drawn, with 10 lines in each. What is the maximum number of triangles they can cut out of the plane?
|
Solution. Consider 100 nodes - the intersection points of lines from the first and second directions. Divide them into 10 sectors: the first sector - nodes lying on the first lines of the first and second directions. The second sector - nodes lying on the second lines (excluding points lying in the first sector) and so on. Triangles with sides parallel to three fixed directions can have two orientations, and each of our 100 nodes can be the vertex of no more than one triangle of each orientation. Therefore, 10 lines of the third direction form no more than 2.25 triangles with the last five sectors, since these five sectors contain only 25 nodes in total.
Furthermore, note that each of the lines of the third direction forms no more than one triangle of each orientation with nodes belonging to one sector. Therefore, the number of triangles with vertices in the nodes of the remaining five sectors will not exceed \(10 \cdot 2 \cdot 5\).
In total, there are no more than \(100 + 50 = 150\) triangles.
An example with 150 triangles is shown in the figure.
Answer: 150 triangles
|
150
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Denis housed chameleons that can change color only to two colors: red and brown. Initially, the number of red chameleons was five times the number of brown chameleons. After two brown chameleons turned red, the number of red chameleons became eight times the number of brown chameleons. Find out how many chameleons Denis has.
|
Solution. Let $t$ be the number of brown chameleons Denis had. Then the number of red chameleons was $5t$. From the problem statement, we get the equation $5 t+2=8(t-2)$. Solving this, we find $t=6$. Therefore, the total number of chameleons is $6 t$, which is 36.
Answer. 36
Recommendations for checking. Only the correct answer - 0 points. Answer with verification - 1 point. Correctly formulated equation, but incorrectly solved not due to arithmetic - no more than 4 points. No justification for the formulation of the equation, but it is clear from the context what the author meant - do not deduct.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For various positive numbers $a$ and $b$, it is known that
$$
a^{3}-b^{3}=3\left(2 a^{2} b-3 a b^{2}+b^{3}\right)
$$
By how many times is the larger number greater than the smaller one?
|
Solution. Let's consider and transform the difference:
$$
\begin{aligned}
& 0=a^{3}-b^{3}-3\left(2 a^{2} b-3 a b^{2}+b^{3}\right)= \\
& (a-b)\left(a^{2}+a b+b^{2}\right)-3\left(2 a b(a-b)-b^{2}(a-b)\right)= \\
& (a-b)\left(a^{2}+a b+b^{2}-6 a b+3 b^{2}\right)= \\
& (a-b)\left(a^{2}-5 a b+4 b^{2}\right)=(a-b)(a-4 b)(a-b)
\end{aligned}
$$
By the condition \(a \neq b\), we get \(a = 4b\), which means the larger number is 4 times greater.
Answer: 4.
Recommendations for checking. Only the correct answer - 0 points. Answer with verification - 2 points. One factor \(a-b\) is highlighted - no less than 2 points, two factors \(a-b\) are highlighted - no less than 4 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Next to the number 2022 on the board, an unknown positive number less than 2022 was written. Then one of the numbers on the board was replaced by their arithmetic mean. This replacement was performed 9 more times, and the arithmetic mean was always an integer. Find the smaller of the numbers originally written on the board.
|
Solution. Let at some point the numbers $a$ and $b$ be written on the board, with $a > b$. Then notice that after the specified operation, the difference between the numbers will become twice as small, regardless of which number we erase, since
$$
a - b = 2\left(a - \frac{a + b}{2}\right) = 2\left(\frac{a + b}{2} - b\right)
$$
Then after 10 operations, we have $2022 - x = 2^{10} * \Delta$, where $x$ is the unknown number written, and $\Delta$ is the last difference, so $x = 2022 - 1024 \Delta$,
since $x$ is positive, the only possible natural value for $\Delta$ is 1, hence $x = 998$.
Answer. 998.
Recommendations for checking. Only the correct answer - 1 point. The correct answer with the assumption that the largest or smallest number was erased each time - no more than 2 points. Formula (1) or a proven similar statement - no less than 3 points. Without justification, assume that the last difference is 1, deduct 2 points.
|
998
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers from 1 to 2019 were written in a row. Which digit was written more: ones or twos, and by how many?
|
2. Answer. There are 990 more ones. Solution. From 1 to 999, their quantity is the same. From 1000 to 1999, there are 1000 more ones. From 2000 to 2009, there are 10 more twos. From 2010 to 2019, it is the same again. In total, $1000-10=990$.
Grading criteria. Full solution - 7 points. In other cases $-\mathbf{0}$ points.
|
990
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The length of the road from the Capital to city O is 2020 kilometers. Along the road are kilometer markers. On the first marker, on the front side, 1 is written, and on the back - 2019; on the second - 2 and 2018 ..., on the last - 2019 and 1. A marker is called good if the two written numbers have a common divisor other than 1, otherwise it is called bad. How many bad markers are there along this road?
|
3. Answer: 800. Solution. Note that the sum of two numbers on a pillar is 2020. If both numbers are divisible by some common divisor, then $2020=4 * 5 * 101$ is also divisible by this divisor. All even pillars are good, all divisible by 5 are good, all divisible by 101 are good. In total, there are odd pillars $2020 / 2=1010$. Among them, not divisible by 5 are $1010 * 4 / 5=808$. Among them, not divisible by 101 are $808 * 100 / 101=800$ (this is the number of all bad pillars).
Grading criteria. Full solution - 7 points. It is noted that the divisors of good pillars are the divisors of the number 2020 - $\mathbf{1}$ point. Part of the divisors is correctly excluded, but not all - up to 3 points. Answer without explanation - $\mathbf{0}$ points.
|
800
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On November 15, a tournament of the game of dodgeball was held. In each game, two teams competed. A win was worth 15 points, a draw 11, and a loss earned no points. Each team played against each other once. At the end of the tournament, the total number of points scored was 1151. How many teams were there?
|
6. Answer: 12 teams. Solution. Let there be $\mathrm{N}$ teams. Then the number of games was $\mathrm{N}(\mathrm{N}-1) / 2$. For each game, a total of 15 or 22 points are earned. Therefore, the number of games was no less than $53(1151 / 22)$ and no more than $76(1151 / 15)$.
Note that if there were no more than 10 teams, then the number of games would not exceed 45. And if there were no fewer than 13 teams, then the number of games would be no less than 78. Therefore, the number of teams was 11 (55 games) or 12 (66 games). In each game, teams score exactly 15 points in total! And 7 additional points if there was a draw. Thus, the total number of draws is (1151-55*15)/7 (a non-integer - this could not have been the case) or (1151-66*15)/7=23. Therefore, the only option is that there were 12 teams.
Grading criteria. Full solution - 7 points. Determined that there were 11 or 12 teams, and one of the cases was not eliminated - 3 points. Justified that the number of games was no less than 53 and no more than 76 without further progress - 2 points. Correct answer with a constructed example - 2 points. Only the correct answer without explanation - 0 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many positive numbers are there among the first 100 terms of the sequence: $\sin 1^{\circ}, \sin 10^{\circ}, \sin 100^{\circ}, \sin 1000^{\circ}, \ldots ?$
|
2. Note that all members of the sequence, starting from $\sin 1000^{\circ}$, are equal to each other, since the difference between the numbers $10^{k+1}$ and $10^{k}$ for natural $k>2$ is a multiple of 360. Indeed, $10^{k+1}-10^{k}=10^{k}(10-1)=9 \cdot 10^{k}=$ $9 \cdot 4 \cdot 10 \cdot 25 \cdot 10^{k-3} \vdots 360$. By direct verification, we can see that $\sin 1^{\circ}>0$, $\sin 10^{\circ}>0, \sin 100^{\circ}>0, \sin 1000^{\circ}=\sin \left(360^{\circ} \cdot 3-80^{\circ}\right)=\sin \left(-80^{\circ}\right)<0$. Therefore, the rest of the members of the sequence will also be negative. Thus, among the first 100 members of the sequence, there will be exactly three positive members.
Answer: 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle $A B C \quad A C=18 \text{ cm}, B C=21$ cm. Point $K$ is the midpoint of side $B C$, and point $M$ is the midpoint of side $A B$, point $N$ lies on side $A C$ and $A N=6 \text{ cm}$. Given that $M N=K N$. Find the length of side $A B$.
|
3. Since $M$ and $K$ are midpoints of the sides, we will extend the segments $NM$ and $NK$ beyond the specified points by the same distance and connect the points $L, B, A, N$; as well as $F, B, N, C$. Then the quadrilaterals $ALBN$ and $NBFC$ become parallelograms. Since in a parallelogram the sum of the squares of the diagonals is equal to the sum of the squares of its sides, we have:
$NF^2 + BC^2 = 2NB^2 + 2NC^2$ (for parallelogram $NBFC$) and $AB^2 + NL^2 = 2AN^2 + 2NB^2$ (for parallelogram $ALBN$).
From the first equation, express $NF^2 = 2NB^2 + 288 - 441$ and, considering that $MN = KN$, we get: $AB^2 + 2NB^2 - 153 = 72 + 2NB^2$, from which $AB = 15 \text{ cm}$.
Answer: 15 cm
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. We will call a number greater than 25 semi-prime if it is the sum of some two different prime numbers. What is the maximum number of consecutive semi-prime numbers that can be semi-prime?
|
5. Note that an odd semiprime number can only be the sum of two and an odd prime number.
Let's show that three consecutive odd numbers $2n+1, 2n+3, 2n+5$, greater than 25, cannot all be semiprimes simultaneously. Assume the opposite. Then we get that the numbers $2n-1, 2n+1, 2n+3$ are prime, and all of them are greater than 3. But one of these three numbers is divisible by 3. This leads to a contradiction. Therefore, three consecutive odd numbers $2n+1, 2n+3, 2n+5$, greater than 25, cannot all be semiprimes simultaneously.
Note that among any six consecutive natural numbers, there are three consecutive odd numbers, so there cannot be more than five consecutive semiprime numbers. Five consecutive numbers can be semiprimes; for example, $30=17+13, 31=29+2, 32=19+13, 33=31+2, 34=23+11$. There are other examples as well.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Out of four classes, $28\%$ of the students received a "5" for the final math test, "4" - $35\%$, "3" - $25\%$, and "2" - $12\%$. How many students took the test if there are no more than 30 students in each class?
|
1. Answer: 100.
From the condition, it follows that the number of schoolchildren must be divisible by 25, 20, and 4. The smallest suitable number is 100, the next one is 200, but it would not work for us since, according to the condition, there cannot be more than 120 people in 4 classes.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the office, each computer was connected by wires to exactly 5 other computers. After some computers were infected by a virus, all wires from the infected computers were disconnected (a total of 26 wires were disconnected). Now, each of the uninfected computers is connected by wires to only 3 others. How many computers were infected by the virus?
|
# 5. Answer: 8.
Let $\mathrm{m}$ be the number of infected computers, and $\mathrm{n}$ be the number of uninfected computers. Then, before the infection, there were $5(\mathrm{~m}+\mathrm{n}) / 2$ cables, and after the disconnection, there were $3 \mathrm{n} / 2$ cables (from which it follows that $\mathrm{n}$ is even). The difference between these numbers is 26, leading to the equation $5 \mathrm{~m}+2 \mathrm{n}=52$. This equation has two solutions in natural numbers where $\mathrm{n}$ is even (this can be proven by enumeration): $\mathrm{m}=4, \mathrm{n}=16$ and $\mathrm{m}=8, \mathrm{n}=6$. The first solution does not work: even if all infected computers were connected only to healthy ones, a maximum of $4 \cdot 5=20$ cables would have to be disconnected, not 26.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. Kolya made a figure from four identical blocks as shown in the picture. What is the surface area of this figure? Express your answer in square centimeters.
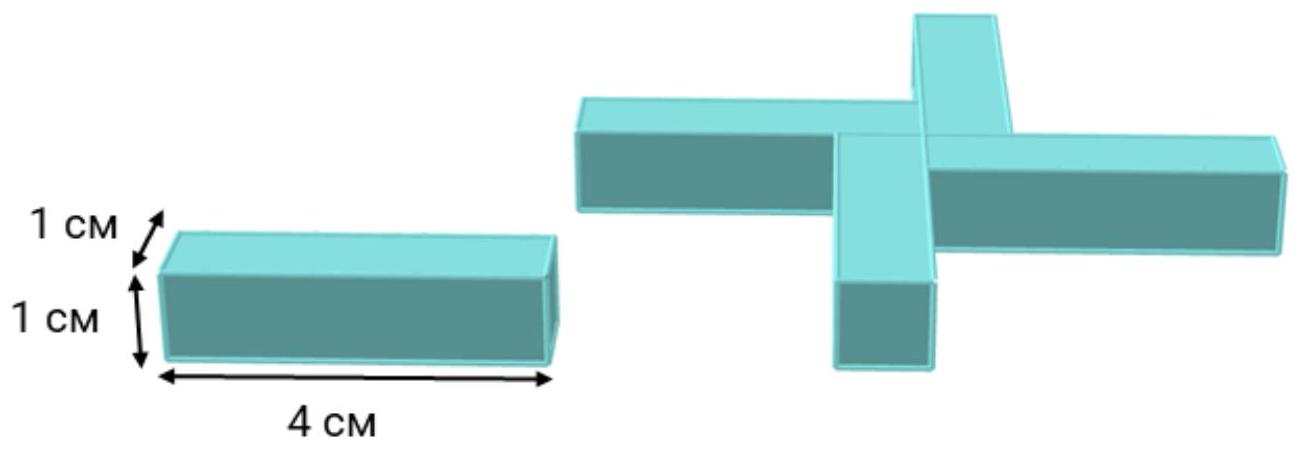
|
Answer: 64.
Solution. The surface area of one block is 18 cm². Out of this area, 2 cm² is "lost" at the joints with other blocks, leaving a total area of $18-2=16$ cm². Since there are 4 blocks, the answer is $4 \cdot 16=64$ cm².
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-3. Olya bought three gifts and packed them in three rectangular boxes: blue, red, and green. She tried to place these gifts in different ways: one on the table, and two on top of each other on the floor. Some distances are given in the diagram. Find the height of the table $h$. Express your answer in centimeters.
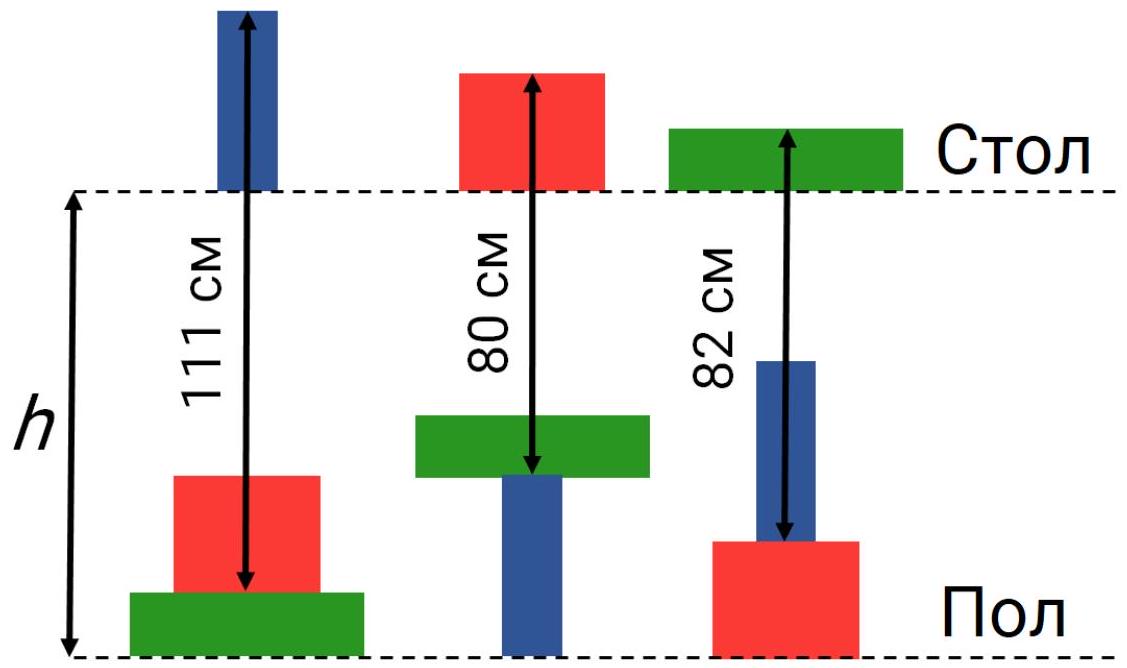
|
Answer: 91.
Solution: Let the height of the blue rectangle be $b$, the height of the red rectangle be $r$, and the height of the green rectangle be $g$. Then, according to the condition, $h+b-g=111, h+r-b=80, h+g-r=82$. Adding all these equations, we get $3h=273$, from which $h=91$.
|
91
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-4. There are 50 parking spaces on a parking lot, numbered from 1 to 50. Currently, all parking spaces are empty. Two cars, a black one and a pink one, have arrived at the parking lot. How many ways are there to park these cars such that there is at least one empty parking space between them?
If the black and pink cars switch places, this is considered a new way.
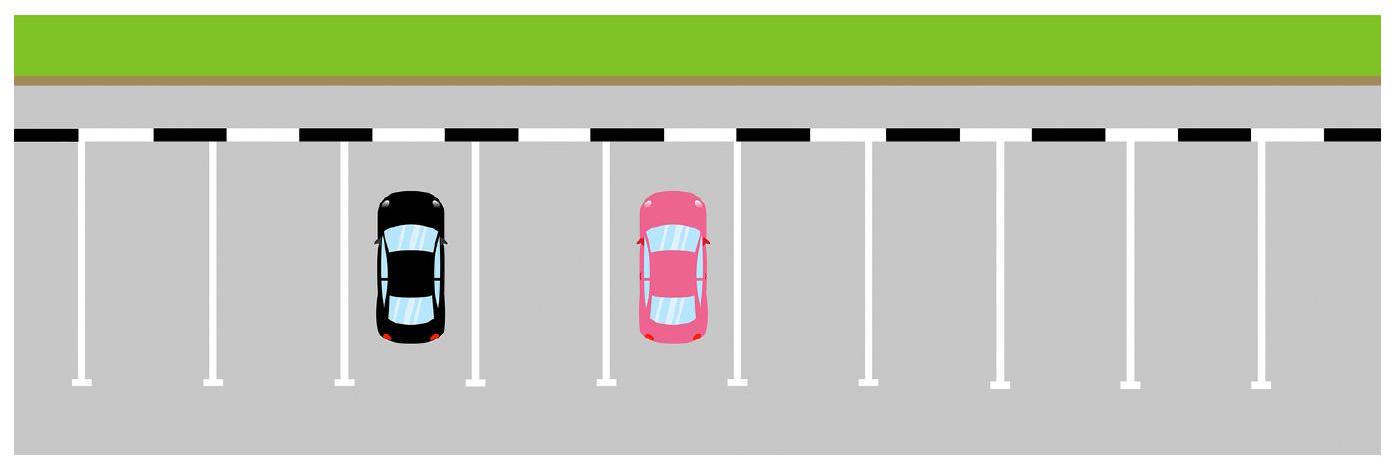
|
Answer: 2352.
Solution I. Carefully consider the cases of the placement of the black car. If it parks in spot number 1 or 50, the pink car can park in any of the 48 spots (numbered from 3 to 50 or from 1 to 48, respectively). If the black car parks in a spot numbered from 2 to 49, the pink car has only 47 options (all except the spot of the black car and the two adjacent spots). In total, there are $2 \cdot 48 + 48 \cdot 47 = 2352$ options.
Solution II. Count the number of options as a difference: from the total number of possible ways to arrange the two cars, subtract the "extra" - the number of ways in which they are adjacent.
In total, we have 50 $\cdot$ 49 options: for each of the 50 ways to choose a spot for the black car, there are 49 ways to choose a spot for the pink car. The number of options where the cars are adjacent is $49 \cdot 2$: for each of the 49 ways to choose two adjacent parking spots, there are 2 ways to park the cars.
Thus, the answer is $50 \cdot 49 - 49 \cdot 2 = 2352$.
|
2352
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the table, there are candies of three types: caramels, toffees, and lollipops. It is known that there are 8 fewer caramels than all the other candies, and there are 14 fewer toffees than all the other candies. How many lollipops are on the table? Be sure to explain your answer.
|
# Solution.
Method 1. Since there are 8 fewer caramels than other candies, there are 4 fewer caramels than half of the candies. Since there are 14 fewer toffees than all other candies, there are 7 fewer toffees than half of the candies. Thus, if we remove all caramels and toffees, 4 + 7 = 11 candies will remain. Since the remaining candies are exactly the lollipops, there are 11 lollipops.
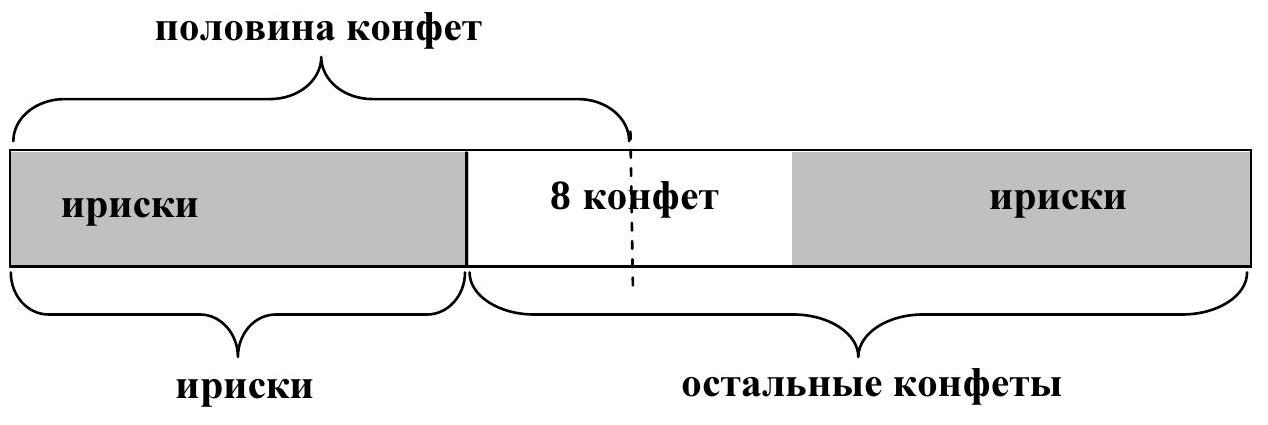
## Method 2.
Let $л, \kappa, u$ be the number of lollipops, caramels, and toffees, respectively.
According to the problem,
$\pi + \kappa = 8 + u$,
$\pi + u = 14 + \kappa$.
Adding these equations, we get: $2 \pi + \kappa + u = 22 + \kappa + u$
Therefore, $2 \pi = 22$, from which $\pi = 11$.
## Grading Criteria.
Complete correct solution - 7 points.
One arithmetic error in solving the system, but the solution method is correct - 4-5 points.
Correct answer and verification that it fits - 3 points.
The problem is solved with a specific example (e.g., "let there be 30 candies in total, then...") - 2 points.
Correct answer without justification - 2 points.
Other cases - 0 points.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a magical coffee shop, 55 creatures met: elves and dwarves. Each ordered either a cup of tea or a cup of coffee. All elves tell the truth when drinking tea and lie when drinking coffee, while all dwarves do the opposite. When asked, "Are you drinking tea?" 44 of those present answered "yes," and when asked, "Are you a dwarf?" 33 answered "yes." In reality - how many of those present were drinking tea and how many were dwarves? Please explain your answer.
|
# Solution.
Let's see how gnomes and elves would answer the questions and create the corresponding table,
| | "Are you drinking tea?" | "Are you a gnome?" |
| :---: | :---: | :---: |
| Elf drinking tea | yes | no |
| Elf drinking coffee | yes | yes |
| Gnome drinking tea | no | no |
| Gnome drinking coffee | no | yes |
From the table, we can see that all elves will answer "Yes" to the first question, while all gnomes will answer "No." Therefore, there are 44 elves, and thus $55 - 44 = 11$ gnomes. On the second question, "Yes" will be answered by those drinking coffee, and "No" by those drinking tea. Therefore, 33 beings drink coffee, and thus $55 - 33 = 22$ beings drink tea.
Answer. In reality, 22 beings drink tea and 11 of the gathered beings are gnomes. Grading criteria.
Full solution - 7 points.
An answer to only one question (i.e., only the number of gnomes or only the number of tea drinkers) with full justification - 3 points.
The number of coffee drinkers and the number of elves were found (with justification), but no further progress was made (i.e., did not subtract the found numbers from 55) - 3 points.
Only the correct answer without justification (possibly with a check on a specific example that everything adds up) - 2 points.
All-Russian School Olympiad in Mathematics 2015-2016 academic year.
School stage. 7th grade
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given an angle of $13^{0}$. How to obtain an angle of $11^{0}$?
|
3. One possible option: lay off the angle of $13^{0}$, 13 times, then the difference between the straight angle and the obtained angle will give the required angle $\left(180^{\circ}-13 \cdot 13^{0}=11^{\circ}\right)$
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. CONDITION
Given a right triangle $A B C$ with legs $A C=3$ and $B C=4$. Construct triangle $A_{1} B_{1} C_{1}$ by sequentially moving point $A$ a certain distance parallel to segment $B C$ (point $A_{1}$ ), then point $B-$ parallel to segment $A_{1} C$ (point $B_{1}$ ), and finally point $C$ - parallel to segment $A_{1} B_{1}$ (point $C_{1}$ ). What is the length of segment $B_{1} C_{1}$, if it turns out that angle $A_{1} B_{1} C_{1}$ is a right angle and $A_{1} B_{1}=1$?
|
Solution. When a vertex of a triangle is moved parallel to its base, the area of the triangle does not change. Therefore, we sequentially obtain the equality of the areas of triangles $A B C, A_{1} B C, A_{1} B_{1} C$, and finally, $A_{1} B_{1} C_{1}$. Thus, $B_{1} C_{1}=2 S / A_{1} B_{1}=12$.
Answer: 12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. CONDITION
Vladislav Vladimirovich, taking less than 100 rubles, went for a walk. Entering any cafe and having at that moment $m$ rubles $n$ kopecks, he spent $n$ rubles $m$ kopecks ( $m$ and $n$ - natural numbers). What is the maximum number of cafes Vladislav Vladimirovich could visit?
|
Solution. Method one. Let Vladislav Vladimirovich have $a$ rubles $b$ kopecks upon entering the first cafe. It is clear that $b \leqslant a$. Then upon exiting, he will have $a-b-1$ rubles and $b-a+100$ kopecks. Let $a-b=t \leqslant 99$. Thus, Vladislav Vladimirovich now has $t-1$ rubles and $100-t$ kopecks. The condition for the possibility of visiting the second cafe is $t-1 \geqslant 100-t$, or (since $t$ is an integer) $t \geqslant 51$. After visiting the second cafe, Vladislav Vladimirovich has $2 t-102$ rubles and $201-2 t$ kopecks. To be able to visit the third cafe, it is necessary and sufficient that $t \geqslant 76$. Similarly, to visit the fourth cafe, it is necessary and sufficient that $t \geqslant 89$, to visit the fifth $-t \geqslant 95$, to visit the sixth $-t \geqslant 98$, and to visit the seventh $-t$ must be greater than 99. The latter is impossible, while the previous inequality is feasible. Therefore, the answer is 6.
Method two. To visit a cafe, it is necessary that the number of rubles in Vladislav Vladimirovich's wallet is not less than the number of kopecks. Let the difference between the number of rubles and kopecks be $p$ $(0 \leqslant p$ (in the absence of an example for 6 cafes) | 4 points |
| an example for 6 cafes is provided, but its optimality is not proven | 3 points |
| any examples for fewer than 6 cafe visits or proof that 8 or more cafes cannot be visited | 0 points |
| answer without justification | 0 points |
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. First solution: Since the Rabbit ran at a speed twice that of Alice, by the time Alice arrived at the Duchess's, the Rabbit was again halfway. Since he was 10 minutes late, Alice spent 20 minutes on half the journey, and 40 minutes on the entire journey.
|
Second solution: Let the time it took for Alice to walk from the Rabbit's house to the Duchess's house be $t$ minutes. The Rabbit walked half the distance with Alice, which took him $\frac{t}{2}$ minutes. Then he ran a distance equal to $\frac{3}{2}$ of the distance from his house to the Duchess's house. Since he ran twice as fast, it took him half the time, i.e., $\frac{3 t}{4}$ minutes. In total, the Rabbit spent $\frac{5 t}{4}$ on the entire journey. The Rabbit was 10 minutes late, so $\frac{5}{4} t - t = 10, t = 40$ minutes.
Answer: The reception was scheduled for 12:40.
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From the sequence of natural numbers, all numbers that are squares or cubes of integers have been erased. Which of the remaining numbers is in the hundredth place?
|
Solution. Consider the first hundred natural numbers. Among these numbers, there are ten squares (from 1 to $10^{2}=100$) and four cubes (from 1 to $4^{3}=64$). Note that two of these numbers, namely, 1 and 64, are both squares and cubes. Thus, from the first hundred, we have crossed out 12 numbers. Among the next twelve numbers, there are neither squares nor cubes ($11^{2}=121,5^{3}=125$), therefore, among the remaining numbers, the hundredth place is occupied by the number 112.
Answer: 112.
|
112
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1.
When multiplying a two-digit and a three-digit number, a four-digit number of the form $A=\overline{a b a b}$ is obtained. Find the largest $A$, given that $A$ is divisible by 14.
|
Answer: 9898.
Solution.
Note that $A=\overline{a b a b}=\overline{a b} \cdot 101$. Since 101 and 14 are coprime, $\overline{a b}$ is divisible by 14. The maximum value of $\overline{a b}=98$.
|
9898
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Variant 1. Find the number of four-digit numbers where the digit in the units place is exactly 1 more than the digit in the tens place (the number cannot start with zero).
|
Answer: 810.
Solution. The leading digit of the number can be chosen in 9 ways (any digit except zero). The digit in the hundreds place can be chosen in 10 ways (any digit will do). The digit in the tens place can be any digit from 0 to 8, and the digit in the units place is uniquely determined by the chosen digit in the tens place. In total, there are $9 \cdot 10 \cdot 9=810$ options.
|
810
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 2.
Find the number of four-digit numbers for which the digit in the units place is exactly 2 more than the digit in the hundreds place (the number cannot start with zero).
|
Answer: 720.
Option 3
Find the number of four-digit numbers where the digit in the hundreds place is exactly 3 more than the digit in the units place (the number cannot start with zero).
Answer: 630.
|
630
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Option 1.
In the Ivanov family, both the mother and the father, and their three children, were born on April 1st. When the first child was born, the parents' combined age was 45 years. The third child in the family was born a year ago, when the sum of the ages of all family members was 70 years. How old is the middle child now, if the sum of the ages of the children is 14 years?
|
Answer: 5.
Solution.
If the first child is older than the second child by $x$ years, and the middle child is older than the third child by $y$ years, then $70-45=3(x+y)+y$, because the age of each parent and the eldest child increased by $(x+y)$ years by the time the third child was born, and the age of the second child increased by $y$ years. Similarly, $(x+y+1)+(y+1)+1=14$. We have the system of equations $3x+4y=25, x+2y=11$, from which we find $x=3, y=4$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Option 1.
In the district, there are three villages A, B, and C connected by dirt roads, with any two villages being connected by several (more than one) roads. Traffic on the roads is two-way. We will call a path from one village to another either a road connecting them or a chain of two roads passing through a third village. It is known that villages A and B are connected by 34 paths, and villages B and C are connected by 29 paths. What is the smallest number of paths that can connect villages A and C?
|
Answer: 26.
Solution.
Let there be $k$ roads between cities A and B, $m$ roads between cities B and V, and $n$ roads between cities A and V. Then the number of paths from A to B is $k + m n$, and the number of paths from B to V is $m + k n$. We have the system of equations $k + m n = 34$, $m + k n = 29$, where the unknowns are natural numbers greater than 1. Subtracting the second equation from the first, we get: $(m - k)(n - 1) = 5$. We need to check all divisors of 5: 1 and 5. Thus, $n = 2$ or $n = 6$. For each $n$, we find $k$ and $m$ by solving the original system of linear equations. If $n = 2$, then $k = 8$ and $m = 13$. If $n = 6$, then $k = 4$ and $m = 5$. The number of paths connecting cities A and B is $n + k m$. In the first case, $n + k m = 2 + 8 \cdot 13 = 106$, and in the second case, $n + k m = 6 + 4 \cdot 5 = 26$. Therefore, the desired answer is 26.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
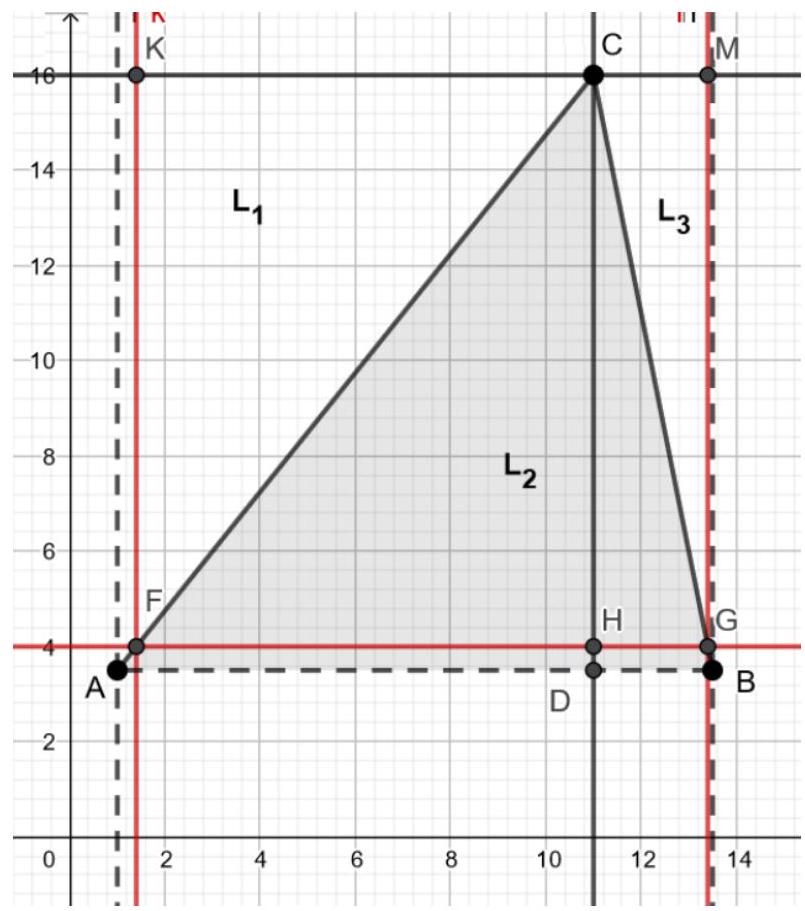
# 6. Variant 1.
The vertices of the triangle have coordinates $A(1 ; 3.5), B(13.5 ; 3.5), C(11 ; 16)$. Consider horizontal lines given by the equations $y=n$, where $n$ is an integer. Find the sum of the lengths of the segments cut off on these lines by the sides of the triangle.
|
Answer: 78.
Solution.
Draw the line $y=4$, and let it intersect the triangle $A B C$ at points $F$ and $G$. Construct a rectangle $F K M G$ such that $K M$ passes through point $C$ parallel to the $O x$ axis. Let $L_{1}, L_{2}, L_{3}$ be the sums of the lengths of the segments cut by the lines $y=n$ in the triangles $F K C$, $F C G$, and $C M G$, respectively. Due to symmetry (equal triangles $K F C = F C H$ and $C H G = C M G$), $L_{1} + L_{3} = L_{2}$. Find the length of $F G$ from the similarity of triangles $A B C$ and $F C G$. Since $\frac{D C}{H C} = \frac{A B}{F G}$, then $F G = 12$, so $L_{2} = L_{1} + L_{3} = 12 \cdot 13 / 2 = 78$.
|
78
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1.
Numbers $x$ and $y$ satisfy the equation $\frac{x}{x+y}+\frac{y}{2(x-y)}=1$. Find all possible values of the expression $\frac{5 x+y}{x-2 y}$, and in the answer, write their sum.
|
Answer: 21.
Solution.
By bringing to a common denominator and combining like terms, we get the equality $3 y^{2}=x y$. If $y=0$, then $x$ is any non-zero number. In this case, the value of the expression is 5. If $x=3 y \neq 0$, then in this case, the value of the expression is 16. The final answer is $5+16=21$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. The children went to the forest to pick mushrooms. If Anya gives half of her mushrooms to Vitya, all the children will have the same number of mushrooms, and if instead Anya gives all her mushrooms to Sasha, Sasha will have as many mushrooms as all the others combined. How many children went to pick mushrooms
|
Answer: 6 children.
Solution: Let Anya give half of her mushrooms to Vitya. Now all the children have the same number of mushrooms (this means that Vitya did not have any mushrooms of his own). For Sanya to now get all of Anya's mushrooms, he needs to take the mushrooms from Vitya and Anya. Then he will have the mushrooms of three children: Vitya, Anya, and his own. The same number will be with the others, which means that besides Vitya, Anya, and Sanya, three more children went to the forest.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
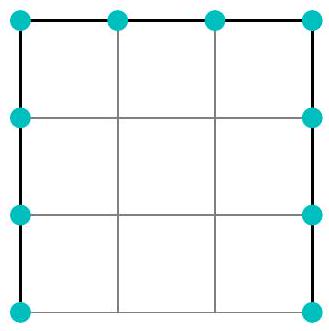
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
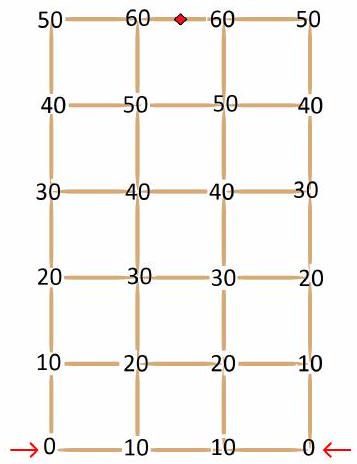
Problem 4.5. Hooligan Dima laid out a structure in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the diagram.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire structure to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
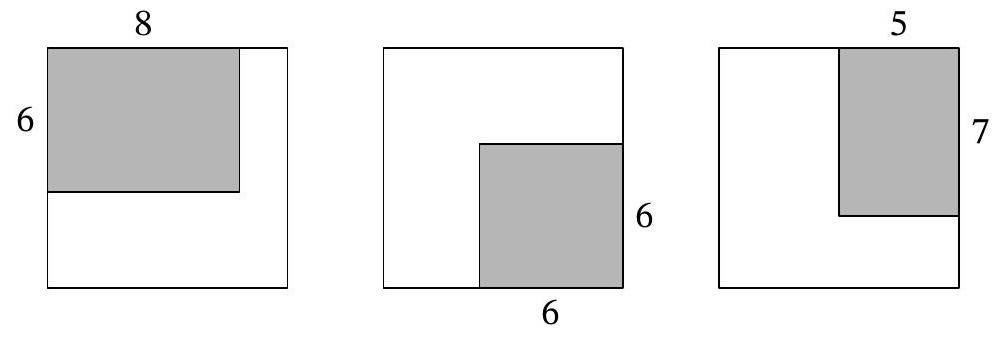
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-



|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
|
Answer: 13.
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity coefficient is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $ABC$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $AC$, point $K$ is marked, and on side $BC$, points $L$ and $M$ are marked such that $KL=KM$ (point $L$ lies on segment $BM$).
Find the length of segment $LM$, if it is known that $AK=4$, $BL=31$, and $MC=3$.
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
Fig. 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
|
Answer: -6.
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them by $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side by $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the largest integer value that $N$ can take?
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose the teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Andrey, Boris, Vasily, Gennady, and Dmitry played table tennis in pairs such that every two of them played with every other pair exactly once. There were no draws in the tennis matches. It is known that Andrey lost exactly 12 times, and Boris lost exactly 6 times. How many times did Gennady win?
Om vem: Gennady won 8 times.
|
Solution. The first pair can be formed in $5 \times 4: 2=10$ ways, the second pair can be formed in $3 \times 2: 2=3$ ways. In total, we get $10 \times 3: 2=15$ games. Andrei played in 4 pairs, and they played with 3 pairs. Therefore, Andrei played $4 \times 3=12$ times. According to the problem, he lost 12 times, which means he lost all his games. Together with him, Boris lost 3 times in a pair. Since Boris won 6 times against Andrei when playing with Vasily (2 times), with Gennady, and with Dmitry, the rest of the games he lost, that is, 3 times with Andrei and once each with Vasily (against Gennady and Dmitry), with Gennady, and with Dmitry. Therefore, Gennady lost 3 times with Andrei and once with Boris, a total of 4 times. Thus, he won 8 times.
Criteria. If the solution is incorrect - 0 points.
If the reasoning is correct but there is a computational error - 3 points. If the solution is correct - 7 points.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the maximum number of pawns that can be placed on a chessboard (no more than one pawn per square), if: 1) a pawn cannot be placed on the $e4$ square; 2) no two pawns can stand on squares that are symmetric with respect to the $e4$ square?
Answer: 39 pawns.
|
Solution. All fields of the board except for the vertical $a$, the horizontal 8, and the field e4 can be divided into pairs that are symmetrical relative to e4. Such pairs form 24. According to the condition, no more than one pawn can be placed on the fields of each pair. In addition, no more than one pawn can be placed on the fields of the vertical $a$ and the horizontal 8. There are 15 such fields. On the field $e 4$, according to the condition, no pawns can be placed. Therefore, in total, no more than

39 pawns can be placed. An example of placing 39 pawns is shown in the figure (the fields for pawns are shaded).
Criteria. If the solution is incorrect - 0 points.
If only the correct example - 3 points.
If only the correct estimate - 3 points.
If the correct solution (any correct example and justification of the estimate) - 7 points.
|
39
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Borya and Vova are playing the following game on an initially white $8 \times 8$ board. Borya moves first and on each of his turns, he colors any four white cells black. After each of his moves, Vova colors an entire row (row or column) completely white. Borya aims to color as many cells black as possible, while Vova aims to prevent him. What is the maximum number of black cells that can be on the board after Borya's move, no matter how Vova plays?
Answer: 25 cells.
|
Solution. Let Vova make white the row with the most black cells on each of his moves. Then, as soon as Borya achieves a row of no less than four black cells (we will call such a row "rich"), Vova will remove at least four cells, meaning that Borya will not be able to increase the number of black cells compared to his previous move. And further, with the presence of
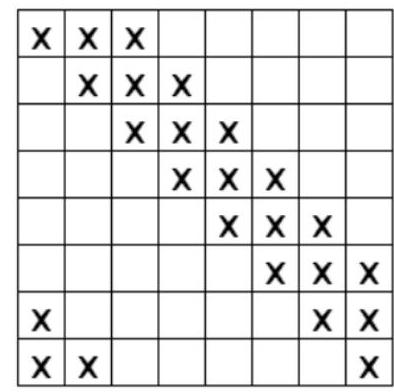
rich rows, Vova removes at least 4 black cells, and Borya adds four after that, meaning he cannot increase his maximum result. At the same time, before the first and all subsequent moments of creating a rich row when there are no rich rows on the board, there were a maximum of \(7 \cdot 3 = 21\) black cells—seven rows of 3 black cells, since Vova just made a row of this direction white. Thus, Borya always creates a structure with a maximum of 25 black cells. Now we will show that Borya can always achieve 25 black cells. Let's highlight 24 cells on the board as shown in the figure—three in each vertical and horizontal row. Suppose Borya always colors only the cells of this set, as long as there are white cells among them. Then Vova, with his next move, can remove a maximum of three black cells, meaning the number of black cells after each pair of their moves will increase by at least 1. Therefore, at some point, Borya will be able to make all these cells black (and possibly some others). Then, after Vova's move, there will be no fewer than 21 black cells left, and Borya, with his next move, will achieve at least 25 black cells. Thus, with correct play by both, the maximum number of black cells on the board that Borya can ensure is 25.
Criteria. If the solution is incorrect - 0 points.
If only the correct example is provided - 3 points.
If only the correct estimate is provided - 3 points.
If the correct solution (any correct example and justification of the estimate) - 7 points.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The password consists of four different digits, the sum of which is 27. How many password options exist
|
Answer: 72.
Solution. Among the digits of the password, there is a 9. Otherwise, since all digits of the password are different, the maximum sum of the digits will not exceed $8+7+6+5=26$. If there are 9 and 8, then the other two digits are no more than 7, and their sum is 10. There are two possible cases: 7,3 and 6,4, resulting in the sets $9,8,7,3$ and $9,8,6,4$. If there is no digit 8, then the only set is $-9,7,6,5$. Let's count the number of possible passwords. In each set, the four digits can be permuted in $4 \cdot 3 \cdot 2 \cdot 1=24$ ways. In total, there are 24 . $3=72$ password variants.
Comment. The correct answer is obtained by the method of complete enumeration - 7 points. The correct answer is obtained by the method of incomplete enumeration, and quite obvious cases are discarded without explanation - 6 points. If the correct method of counting is used but there are errors in finding the number of variants - deduct 2 points for each error. Only established that among the digits of the password there is a 9 - 1 point. For useful ideas - 1-2 points.
|
72
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Eight cards have the numbers $1,1,2,2,3,3,4,4$ written on them. Can these cards be placed in a row so that there is one card between the ones, two cards between the twos, three cards between the threes, and exactly four cards between the fours?
|
Answer: Yes.
Solution: For example, this: 41312432.
Instructions for checking:
The score can only be one of two: 0 points or 7 points.
|
41312432
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. Masha wrote a three-digit number on the board, and Vera wrote the same number next to it, but she swapped the last two digits. After that, Polina added the obtained numbers and got a four-digit sum, the first three digits of which are 195. What is the last digit of this sum? (The answer needs to be justified.)
Answer: 4.
|
Solution. Let Masha write the number $100 x+10 y+z$. Then Vera wrote the number $100 x+10 z+y$, and the sum of these numbers is $200 x+11 y+11 z$. For $x \leqslant 8$ this expression does not exceed 1798, and therefore cannot start with 195. Thus, $x=9$. Then $11(y+z)$ is a three-digit number starting with 15. Among three-digit numbers starting with 15, only 154 is divisible by 11, so the last digit of the sum is 4.
Note. Masha could have written the numbers 959, 968, 977, 986, or 995.
## Criteria
1 p. The correct answer is provided.
2 p. It is determined that Masha's number starts with the digit 9, but there is no further progress.
2 p. An example of a three-digit number that satisfies the condition of the problem is provided.
3 p. It is determined that Masha's number starts with the digit 9, and an example of a three-digit number that satisfies the condition of the problem is provided.
4 p. The correct answer and justification are provided.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The function $f(x)$ is such that for all values of $x$, the equality $f(x+1)-f(x)=x+1$ holds. It is known that $f(0)=4$. Find $f(62)$.
#
|
# Solution.
$$
f(62)-f(61)=61+1=62 \rightarrow f(62)-f(0)=31 * 63=1953
$$
Therefore, $f(62)=1957$.
|
1957
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1.1. Let $A, B, C, D, E, F, G, H$ - be different digits from 0 to 7 - satisfy the equation
$$
\overline{A B C}+\overline{D E}=\overline{F G H}
$$
Find $\overline{D E}$, if $\overline{A B C}=146$.
(The notation $\overline{A B C}$ represents a three-digit number consisting of digits $A, B, C$, similarly constructed are the numbers $\overline{F G H}$ and $\overline{D E$).
|
Answer: 57.
Solution. Substitute 146 for $\overline{A B C}$ and write the example in a column:
$$
\begin{array}{r}
146 \\
+\quad D E \\
\hline F G H
\end{array}
$$
$D, E, F, G, H$ can only be the digits $0,2,3,5,7$. Let's consider $E$.
- If $E=0$, then $H=6$ - but this contradicts the fact that $C=6$.
- If $E=2$, then $H=8$ - but we don't have such a digit.
- If $E=3$, then $H=9$ - but we don't have such a digit.
- If $E=5$, then $H=1$ - but this contradicts the fact that $A=1$.
By the method of elimination, we understand that $E=7$ :
$$
\begin{array}{r}
146 \\
+\quad D 7 \\
\hline F G 3
\end{array}
$$
Since numbers cannot start with zero, it can only correspond to one digit - this is the digit $G$ :
$$
\begin{array}{r}
146 \\
+\quad D 7 \\
\hline F 03
\end{array}
$$
Now it is not difficult to fully restore the example:
| 146 |
| ---: |
| $+\quad 57$ |
| 203 |
|
57
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2.1. In the figure, rays $O A, O B, O C, O D, O E, O F$ are such that:
- $O B$ is the bisector of angle $A O C$
- $O E$ is the bisector of angle $D O F$;
- $\angle A O F=146^{\circ}, \angle C O D=42^{\circ}$.
How many degrees does angle $B O E$ measure?
|
Answer: $94^{\circ}$.
Solution. Let's find the sum of angles $A O B$ and $E O F$:
$$
\angle A O B+\angle E O F=\frac{\angle A O C}{2}+\frac{\angle D O F}{2}=\frac{\angle A O F-\angle C O D}{2}=\frac{146^{\circ}-42^{\circ}}{2}=52^{\circ}
$$
Now it is not difficult to find the required angle:
$$
\angle B O E=\angle A O F-(\angle A O B+\angle E O F)=146^{\circ}-52^{\circ}=94^{\circ} .
$$
|
94
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4.1. Brothers Lёsha and Sasha decided to get to the skate park. They left at the same time, but Lёsha walked with the skateboard in his hands, while Sasha rode on the skateboard. It is known that Sasha rides the skateboard 3 times faster than Lёsha walks with the skateboard. After some time, they simultaneously switched their modes of transportation: Lёsha started riding the skateboard, and Sasha started walking. As a result, each of their speeds changed by a factor of 2: Lёsha's speed increased, and Sasha's speed decreased. It turned out that they arrived at the skate park at the same time. How many meters did Sasha ride on the skateboard, if the distance from home to the skate park is 3300 meters?
|
Answer: 1100.
Solution. Let $v$ be the walking speed of Lёsha, then $3v$ is the skateboarding speed of Sasha. After switching their modes of transportation, each of their speeds changed by a factor of 2, so $2v$ is Lёsha's skateboarding speed, and $1.5v$ is Sasha's walking speed. Therefore, on the second part of the journey, Lёsha's speed was $\frac{2v}{1.5v} = \frac{4}{3}$ times greater than Sasha's speed.
Let Lёsha walk $x$ meters, then Sasha skates $3x$ meters. Then Lёsha covers his remaining $(3300 - x)$ meters, and Sasha covers $(3300 - 3x)$ meters. The problem requires finding $3x$. Knowing the ratio of the speeds of the boys after changing their mode of transportation, we set up the proportion:
$$
\begin{gathered}
\frac{3300 - x}{3300 - 3x} = \frac{4}{3} \\
9900 - 3x = 13200 - 12x \\
9x = 3300 \\
3x = 1100
\end{gathered}
$$
|
1100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5.1. Points $A, B, C, D, E, F$ on the diagram satisfy the following conditions:
- points $A, C, F$ lie on the same line;
- $A B=D E=F C$
- $\angle A B C=\angle D E C=\angle F C E$
- $\angle B A C=\angle E D C=\angle C F E$
- $A F=21, C E=13$.
Find the length of segment $B D$.
|
# Answer: 5.
Solution. Note that triangles $A B C, D E C$ and $F C E$ are equal by the second criterion of triangle congruence.
Since $\angle D E C=\angle F C E$, lines $D E$ and $A F$ are parallel. Therefore, $\angle A C B=\angle C D E=$ $\angle C A B$, so all three triangles are isosceles, and their lateral sides are equal to 13.
It remains to calculate the answer:
$$
B D=B C-C D=13-A C=13-(A F-C F)=13-(21-13)=5 .
$$
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.6.1. In a row, there are 10 boxes. These boxes contain balls of two colors: red and blue. In some boxes, all the balls may be of the same color; there are no empty boxes. It is known that in each subsequent box (from left to right), there are no fewer balls than in the previous one. It is also known that there are no two boxes with the same set of red and blue balls. How many blue and how many red balls are in the rightmost box, if the total number of red balls in all the boxes is 11 and the total number of blue balls is 13?
|
Answer: 1 red ball, 3 blue balls.
Solution. Among all the boxes, there can be:
- a maximum of 2 boxes with one ball (one with a red ball, the other with a blue ball),
- a maximum of 3 boxes with two balls (one with two red balls, another with one red and one blue, and the third with two blue balls),
- a maximum of 4 boxes with three balls (one with three red balls, another with two red and one blue, the third with one red and two blue, and the fourth with three blue balls).
Thus, in the first nine boxes, there will be at least $2 \cdot 1 + 3 \cdot 2 + 4 \cdot 3 = 20$ balls. Then, in the rightmost box, there will be no more than $11 + 13 - 20 = 4$ balls. However, from the above reasoning, it follows that if a box contains 1, 2, or 3 balls, it must be one of the first nine boxes. Therefore, the rightmost box must contain exactly 4 balls, and the first nine boxes must contain exactly 20 balls.
It is not difficult to understand that the first nine boxes contain 10 red and 10 blue balls. Then, in the rightmost box, there will be $11 - 10 = 1$ red and $13 - 10 = 3$ blue balls. $\square$
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7.1. A seven-digit natural number $N$ is called interesting if:
- it consists of non-zero digits;
- it is divisible by 4;
- any number obtained from the number $N$ by permuting its digits is divisible by 4.
How many interesting numbers exist?
|
Answer: 128.
Solution. We will use the divisibility rule for 4: a number is divisible by 4 if and only if the number formed by its last two digits is divisible by 4.
In an interesting number, the digits can be rearranged in any way, and the divisibility by 4 should remain unchanged. This implies that there are no odd digits in its representation (otherwise, any of them could be placed at the end, and the resulting number would not be divisible by 4).
Let's consider which two non-zero even digits an interesting number can end with. As we remember, the two-digit number formed by these digits must be divisible by 4.
- 24 - this option does not work, because when the last two digits are swapped, the number will end in 42, and 42 is not divisible by 4;
- 28 - this option does not work, because when the last two digits are swapped, the number will end in 82, and 82 is not divisible by 4;
- 44 - this option works;
- 48 - this option works;
- 64 - this option does not work, because when the last two digits are swapped, the number will end in 46, and 46 is not divisible by 4;
- 68 - this option does not work, because when the last two digits are swapped, the number will end in 86, and 86 is not divisible by 4;
- 84 - this option works;
- 88 - this option works.
From this, it follows that an interesting number can consist only of the digits 4 and 8. It is also clear that any number whose digits are all 4 or 8 is interesting. Thus, each digit of a seven-digit interesting number can take exactly 2 values, and there are exactly $2^{7}=128$ such numbers.
|
128
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 Given a triangle $A B C$. Point $P$ is the incenter. Find the angle $B$, if it is known that $R_{A B C}=R_{A P C}$, where $R_{A B C}, R_{A P C}$ are the radii of the circumcircles of triangles $ABC$ and $APC$ respectively.
|
10.4. Given a triangle $A B C$. Point $P$ is the incenter. Find the angle $B$, if it is known that $R_{A B C}=R_{A P C}$, where $R_{A B C}, R_{A P C}$ are the radii of the circumcircles of triangles $ABC$ and $APC$ respectively.
Answer: $60^{\circ}$. Hint: Let $\alpha=\angle A B C$. Then $\angle A P C=90^{\circ}+\frac{\alpha}{2}$, since $\angle A P C=180^{\circ}-\frac{1}{2}(\angle B+\angle C)=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\alpha\right)$. Let $R=R_{A B C}=R_{A P C}$. By the known formula (for the Law of Sines) $A C=2 R \sin \alpha$ (in triangle $A B C$) and $A C=2 R \sin \left(90^{\circ}+\frac{\alpha}{2}\right)$ (in triangle $\mathrm{APC})$. From this, we get the equation $\sin \alpha=\sin \left(90^{\circ}+\frac{\alpha}{2}\right) \Leftrightarrow$ $2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}=\cos \frac{\alpha}{2} \Leftrightarrow \sin \frac{\alpha}{2}=\frac{1}{2} \Leftrightarrow \frac{\alpha}{2}=30^{\circ}$ (since $\alpha<180^{\circ}$ ).
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The distance between points A and B is 90 km. At 9:00, a bus left point A for point B at a speed of 60 km/h. Starting from 9:00, every 15 minutes, buses leave point B towards point A at a speed of 80 km/h. The bus that left point A, after traveling 45 km, reduces its speed to 20 km/h due to a breakdown and continues at this speed. A passenger in this bus is considering whether to continue the slow journey to point B or return to point A in the first passing bus. How much time does the passenger have to make a decision?
|
2. A bus leaving point A will travel 45 km in $\frac{45}{60}$ hours. During this time, a bus leaving point B at 9:00 will travel $\frac{45}{60} \cdot 80=60$ km and will be closer to point A than the bus leaving point A. A bus leaving point B at 9:15 will travel $\left(\frac{45}{60}-\frac{15}{60}\right) \cdot 80=40$ km and will be 5 km away from the bus leaving point A. Therefore, the time it will take for them to meet is $\frac{5}{20+80}=\frac{1}{20}$ hours. The passenger has 3 minutes to make a decision.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the country, there are 20 cities. An airline wants to organize two-way flights between them so that from any city, it is possible to reach any other city with no more than $\mathrm{k}$ transfers. At the same time, the number of air routes should not exceed four. What is the smallest $\mathrm{k}$ for which this is possible?
|
5. $\mathrm{k}=2$. At least two transfers will be required. From an arbitrary city A, one can reach no more than four cities without a transfer, and with one transfer - no more than $4 \times 3=12$ cities. That is, if using no more than one transfer, one can fly to no more than 16 other cities, but 19 are required.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Semyon was solving the quadratic equation $4 x^{2}+b x+c=0$ and found that its two roots are the numbers $\operatorname{tg} \alpha$ and $3 \operatorname{ctg} \alpha$ for some $\alpha$. Find $c$.
|
Answer: 12
Solution. By Vieta's theorem, $c / 4$ equals the product of the roots. Considering that $\operatorname{tg} \alpha \cdot \operatorname{ctg} \alpha=1$, we get $c / 4=3$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Given an arithmetic progression $a_{1}, a_{2}, \ldots, a_{100}$. It is known that $a_{3}=9.5$, and the common difference of the progression $d=0.6$. Find the sum $\left\{a_{1}\right\}+\left\{a_{2}\right\}+\ldots+\left\{a_{100}\right\}$. The notation $\{x\}$ represents the fractional part of the number $x$, i.e., the difference between $x$ and the greatest integer not exceeding $x$, for example: $\{4.7\}=0.7,\left\{-5 \frac{1}{3}\right\}=\frac{2}{3}$, etc.
|
Answer: 50
Solution. Let's look at the first digits after the decimal point in the decimal representation of the terms of the progression. Since $d=0.6$ and $a_{3}=9.5$, the sequence of these digits is: $3,9,5,1,7,3,9,5,1,7, \ldots$ It is periodic with a period of 5. Then the sum of the fractional parts of any five consecutive terms in the progression is $0.3+0.9+0.5+0.1+0.7=2.5$. Therefore, the desired sum of the fractional parts is $20 \cdot 2.5=50$.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. A random number sensor outputs a number $a$ - one of the natural numbers $1,2, \ldots, 100$ (with equal probability). For this value of $a$, we find the maximum possible value $M$ of the function
$$
f(x)=\frac{700}{x^{2}-2 x+2 a}
$$
The probability that $M>10$ is $n$ percent. What is $n$?
|
Answer: 35
Solution. The minimum value of the quadratic trinomial $x^{2}-2 x+2 a$ is $2 a-1$. Since for the considered values of $a$ we have $2 a-1>0$ (which is true for $a>1 / 2$), the maximum value of $f(x)$ is $M=\frac{700}{2 a-1}$. Next, the condition $M>10$ (for $2 a-1>0$) is equivalent to the following conditions: $700>10(2 a-1) \Leftrightarrow$ $71>2 a$. Among the natural numbers $a=1,2, \ldots, 100$, the last inequality is satisfied by the first 35 values.
|
35
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. In a row, the numbers are written: $100^{100}, 101^{101}, 102^{102}, \ldots, 876^{876}$ (i.e., the numbers of the form $n^{n}$ for natural numbers n from 100 to 876.) How many of the written numbers are perfect cubes? (A perfect cube is the cube of an integer.)
|
# Answer: 262
Solution. Consider a number of the form $m^{k}$, where $m$ and $k$ are natural numbers. If $k$ is divisible by 3, then $m^{k}$ is a perfect cube. Otherwise, $m^{k}$ is a perfect cube if and only if $m$ is a perfect cube. Thus, the answer to our problem is the total number of numbers that are divisible by 3 and the perfect cubes that are not divisible by 3 in the set of numbers $\{100,101,102, \ldots, 876\}$. The number of needed numbers divisible by 3 is $(876-99) / 3=259$. The number of needed perfect cubes is exactly $3: 5^{3}, 7^{3}, 8^{3}$. Therefore, the total number of required numbers is $259+3=262$.
|
262
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In a triangular pyramid $A B C D$, it is known that: $A B=C D=6, A D=B C=10, \angle A B C=120^{\circ}$. Find $R^{2}$, where $R$ is the radius of the smallest sphere that can contain such a pyramid.
|
Answer: 49
Solution. Since the segment $AC$ fits inside the sphere, $2R \geqslant AC$. On the other hand, the sphere constructed with $AC$ as its diameter covers both the triangle $ABC$, since $\angle ABC > 90^{\circ}$, and the congruent (by three sides) triangle $BAD$, and thus covers the entire tetrahedron. Therefore, the desired value of $R$ is $AC / 2$, and $R^{2} = AC^{2} / 4$.
Next, by the cosine rule we have $AC^{2} = AB^{2} + BC^{2} - 2 AB \cdot BC \cdot \cos 120^{\circ} = 6^{2} + 10^{2} + 2 \cdot 6 \cdot 10 / 2 = 4(3^{2} + 5^{2} + 3 \cdot 5) = 4 \cdot 49$
|
49
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. On the coordinate plane, a triangle $O A B$ is drawn, where the point of intersection of the medians is at $\left(\frac{19}{3}, \frac{11}{3}\right)$, and points $A$ and $B$ have natural coordinates. Find the number of such triangles. (Here, $O$ denotes the origin - the point $(0,0)$; two triangles with the same set of vertices are considered the same, i.e., $O A B$ and $O B A$ are considered the same triangle.)
|
Answer: 90.
Let $M$ be the midpoint of $AB$. Then, by the property of the median, $OM = \frac{3}{2} OG$, where $G$ is the centroid. Therefore, $M$ has coordinates $\left(\frac{19}{2}, \frac{11}{2}\right)$.
Let $\left(x_{a}, y_{a}\right)$ and $\left(x_{b}, y_{b}\right)$ be the coordinates of points $A$ and $B$. Since $M$ is the midpoint of segment $AB$, we have $x_{a} + x_{b} = 19$ and $y_{a} + y_{b} = 11$. Then, for $x_{a}$, there are 18 possible natural values: $1, 2, \ldots, 18$, each of which uniquely corresponds to a natural $x_{b} = 19 - x_{a}$. Similarly, for $y_{a}$, there are 10 possibilities. In total, there are $18 \cdot 10 = 180$ possibilities for choosing point $A$, and for each of them, a suitable point $B$ is uniquely determined. According to our agreement (triangles $OAB$ and $OBA$ are considered the same), we have $180 / 2 = 90$ variants.
Note that in all the specified variants, point $A$ (and $B$) does not lie on the line $OM$, i.e., triangle $OAB$ does not degenerate (otherwise, $y_{a} / x_{a} = 11 / 19$ would hold). Thus, all the found variants are indeed valid.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 6.4. On a computer keyboard, the key with the digit 1 is not working. For example, if you try to type the number 1231234, only the number 23234 will be printed.
Sasha tried to type an 8-digit number, but only 202020 was printed. How many 8-digit numbers meet this condition?
|
Answer: 28.
Solution. It is clear that 2 units were not printed. There are 7 positions where they can be located (they can be in the same position or in different ones):
- X202020;
- 2 X 02020;
- $20 \times 2020$
- $202 \times 020$
- $2020 \times 20$
- $20202 \mathrm{X} 0$
- $202020 \mathrm{X}$.
Case 1. If the first unit is placed in the first position, then there are 7 options left for the second unit (in any of the above positions).
Case 2. If the first unit is placed in the second position, then there are 6 options left for the second unit (in any of the above positions except the first, as this option has already been counted).
Case 3. If the first unit is placed in the third position, then there are 5 options left for the second unit (in any of the above positions except the first and second, as these options have already been counted).
$\cdots$
Case 7. If the first unit is placed in the seventh position, then there is 1 option left for the second unit (only in the seventh position; all other options have already been counted).
In total, there are exactly $1+2+3+4+5+6+7=28$ options.
|
28
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.