problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
15. How many people are in the team if the average age of all team members is 25 years, the team leader is 45 years old, and the average age of the team members without the team leader is 23 years?
|
15. Let there be $x$ people in the brigade, then we have $25 x=23(x-1)+45$, from which $2 x=22$ and $x=11$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. On one plot of 14 hectares, unsorted potatoes were planted, and on another plot of 4 hectares, sorted potatoes were planted. The average yield per hectare on these two plots is 20 centners higher than the average yield of the first plot. By how many centners is the yield of sorted potatoes higher than the yield of unsorted potatoes?
|
16. Let the average yield of non-variety potatoes be $x$ centners per hectare, and that of variety potatoes be $-y$ centners per hectare. Then the average yield of the two plots is $(x+20)$ centners per hectare. We have
$$
(x+20) \cdot 18=x \cdot 14+y \cdot 4
$$
from which $4 y-4 x=360 ; y-x=90$, which means that the yield of variety potatoes is higher than that of non-variety potatoes by 90 centners.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. Helping the collective farm with the harvest, 5th Grade A class collected 45715 kg of potatoes over 5 days. How many students were there in total, and how much did each student collect on average per day, if the average daily output of one student is a whole number of kilograms?
|
17. Let there be $x$ students, and the average daily output of a student be $y$ kg. Then $y \cdot x \cdot 5=45715$, from which $x y=9143$. Since $9143=41 \cdot 223$ and there cannot be 223 students in a class, there were 41 students, and each of them collected on average 223 kg of potatoes daily.
|
41
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. When the young fishermen were asked how many fish each of them had caught, the first one answered: "I caught half the number of fish that my friend caught, plus 10 fish." The second one said: "And I caught as many as my friend, plus 20 fish." How many fish did the fishermen catch?
|
21. Let the second one catch $x$ fish, then the first one catches $\frac{1}{2} x+10$ fish. According to the second fisherman's statement, he caught $\left(\frac{1}{2} x+10\right)+20$ fish. We have the equation $x=\left(\frac{1}{2} x+10\right)+20$, from which $x=60$, i.e., the second one caught 60 fish. Then the first one caught $\frac{1}{2} \cdot 60+10=40$ fish, and together -100 fish.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. Yura left the house for school 5 minutes later than Lena, but walked twice as fast as she did. How many minutes after leaving will Yura catch up to Lena?
|
22. If Lena walks $a$ m in 1 min, then Yura walks $2a$ m. Let him catch up with her after $x$ min from his start. Then we have $a \cdot 5 + a \cdot x = 2a \cdot x$, from which $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. Preparing his son for school, the father bought him a new uniform for 24 r. How did he pay for the purchase, if he only had 5 r bills, and the cashier only had 3 r bills?
|
24. If the buyer gave the cashier $x$ bills and received $y$ bills as change, we have the equation $5 x-3 y=24$, from which $x=\frac{24+3 y}{5}$. Since $x$ must be an integer, $24+3 y$ must be divisible by 5. This is possible with the smallest value of $y=2$. Therefore, the buyer gave 6 bills (30 p.) and received 6 p. as change (2 bills of 3 p.).
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. In a competition of fun and ingenuity, 9 points were awarded for each correctly completed task, and 5 points were deducted for each uncompleted or incorrectly completed task. It is known that the team was offered no more than 15 tasks and scored 57 points. How many tasks did the team complete correctly?
|
26. Let $x$ be the number of tasks completed correctly, and $y$ be the number of tasks completed incorrectly or not at all. Then we have $9 x-5 y=57$, from which $x=\frac{57+5 y}{9}$. Since $x$ is a natural number, $(57+5 y)$ must be divisible by 9. The smallest value of $y$ for which this condition is met is 3. In this case, $x=8$. Since $8+3=11$ and $11<15$, the found value of $x$ satisfies the condition.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. If the team had scored 97 points in the last sport, the average number of points scored by it in one sport would have been 90; if it had scored 73 points in this last sport, the average number of points per sport would have been 87. In how many sports did the team compete?
|
27. Let the team compete in $x$ sports and score $n$ points in all sports except the last one. Then we have
$$
(97+n): x=90 ;(73+n): x=87
$$
which means $97+n=90 x$ and $73+n=87 x$, so $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. In response to a question about his age, the grandfather answered: “The number expressing my age in years is a two-digit number equal to the sum of the number of its tens and the square of its units.” How old is the grandfather?
|
28. Let the grandfather be $(10 a+b)$ years old. Then $10 a+b=a+b^{2}$, hence
$$
9 a=b^{2}-b, \text{ or } a=\frac{b(b-1)}{9}
$$
Since $a$ and $b$ are single-digit numbers, the equality holds only when $b=9$. In this case, $a=8$. Therefore, the grandfather is 89 years old.
|
89
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29. In the parking lot, there were passenger cars and motorcycles. The number of motorcycles with sidecars was half the number of those without sidecars. What could be the maximum number of cars if the total number of wheels on these cars and motorcycles was $115?$
|
29. If the number of motorcycles with sidecars is $x$, then the number without sidecars is $2x$. Let the number of cars be $y$, then the total number of wheels is $3x + 2x \cdot 2 + 4y = 7x + 4y$. According to the condition, $7x + 4y = 115$, from which
$$
y=\frac{115-7x}{4}
$$
The value of $y$ is greatest when $x$ is smallest. Let $x=1$, then $y=27$. Therefore, the maximum number of cars is 27.
|
27
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Several girls were picking mushrooms. They divided the collected mushrooms among themselves as follows: one of them was given 20 mushrooms and 0.04 of the remainder, another - 21 mushrooms and 0.04 of the new remainder, the third - 22 mushrooms and 0.04 of the remainder, and so on. It turned out that everyone received an equal share. How many girls were there and how many mushrooms did they collect?
|
30. Let the girls collected $x$ mushrooms. The first one received $20+0.04(x-20)$, the second one received $21+0.04(x-21-20-0.04(x-20))$ mushrooms. According to the condition $20+0.04 x-$ $-0.8=21+0.04(x-21-20-0.04(x-20))$, from which
$$
0.0016 x=0.192 \text { and } x=120 .
$$
Thus, 120 mushrooms were collected, each girl received 24 mushrooms, and there were 5 girls.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. When shooting at a target, Misha hit the bullseye several times, scored 8 points as many times, and hit the five several times. In total, he scored 99 points. How many shots did Misha take if $6.25\%$ of his shots did not score any points?
|
32. Let's say Mishka hit the ten and the eight $x$ times each, and the five $y$ times. Then $10 x + 8 x + 5 y = 99$, or $18 x + 5 y = 99$. The term $5 y$ can end in 5 or 0, so $18 x$ must end in 4 or 9. But $18 x$ cannot end in 9, so $18 x$ must end in 4. Since $18 x < 99$, then $x = 3$. We have $18 \cdot 3 + 5 y = 99$, from which $y = 9$. Therefore, the total number of hits was $3 + 3 + 9 = 15$, which is $93.75\%$ of the total number of shots, so the number of shots made is $16\left(\frac{15 \cdot 100}{93.75} = 16\right)$.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. In a constructed school boarding house, several rooms were double-occupancy, and the rest were triple-occupancy. In total, the boarding house is designed for more than 30 but fewer than 70 places. When $\frac{1}{5}$ of the available places were occupied, the number of unoccupied places turned out to be the same as the total number of places would be if the number of double-occupancy rooms was the same as the actual number of triple-occupancy rooms, and the number of triple-occupancy rooms was the same as the actual number of double-occupancy rooms. For how many places is the boarding house built?
|
33. Let there be $x$ two-person rooms and $y$ three-person rooms in the boarding school. Then the total number of places in the boarding school is $2 x + 3 y$. If $\frac{1}{5}$ of the places were occupied, then $\frac{4}{5}$ of the places remained unoccupied, i.e., $\frac{4}{5}(2 x + 3 y)$. According to the condition, $\frac{4}{5}(2 x + 3 y) = 3 x + 2 y$, from which we get $2 y = 7 x$. Considering that $x$ and $y$ are natural numbers, we will have $x_{1} = 2 ; y_{1} = 7$; $x_{2} = 4 ; y_{2} = 14$ and so on. If $x = 2$ and $y = 7$, then the total number of places is 25; if $x = 4, y = 14$, then the number of places is 50; if $x = 6 ; y = 21$, then the number of places is 75. Since only $50(30 < 50 < 70)$ satisfies the condition, the total number of places in the boarding school was 50.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. The front tires of a car wear out after 25,000 km, while the rear tires wear out after 15,000 km. When is it advisable to swap the tires to ensure they wear out evenly? (Assume that the tires are swapped once, although drivers do this more frequently in practice.)
|
36. It is advisable to change the tires so that their wear occurs at the same mileage for all wheels. Let's say they should be changed at $x$ km of mileage, then the front wheels have $(25000-x)$ km left to wear. But if they are put in place of the rear wheels, they can only travel $\frac{15000}{25000}=\frac{3}{5}$ of the distance they would still travel if they remained in their previous position, i.e., $\frac{3}{5}(25000-x)$. The rear wheels will travel $x$ km before the change, and if they remained in their place, they would travel another $(15000-x)$ km. In the position of the front wheels, they would travel $\frac{5}{3}(15000-x)$ km. After the tire change, the wheels should travel the same distance until wear, so $\frac{3}{5}(25000-x)=\frac{5}{3}(15000-x)$, from which $x=9375$ km.
|
9375
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Two people, who have one bicycle, need to get from point $A$ to point $B$, which is 40 km away from $A$. The first person walks at a speed of 4 km/h and rides the bicycle at 30 km/h, while the second person walks at a speed of 6 km/h and rides the bicycle at 20 km/h. What is the minimum time they can take to reach point $B$? (The bicycle can be left unattended.)
|
37. Let the first person travel $x$ hours by vehicle and $y$ hours on foot, then the second person travels $y$ hours by vehicle and $x$ hours on foot. We have the equation $30 x + 4 y = 20 y + 6 x$, from which $x = \frac{2}{3} y$. Therefore, the first person walked $y$ hours and traveled $\frac{2}{3} y$ hours by vehicle, while the second person walked $\frac{2}{3} y$ hours and traveled $y$ hours by vehicle. Knowing the total distance, we can form the equation $4 y + \frac{2}{3} y \cdot 30 = 40$, from which $y = \frac{5}{3}$ hours. The first person was on the road for $\frac{5}{3} + \frac{2}{3} \cdot \frac{5}{3} = 2 \frac{7}{9}$ (hours), and the second person was on the road for the same amount of time, as he walked $1 \frac{1}{9}$ hours and traveled $1 \frac{2}{3}$ hours. Therefore, the minimum time it takes for them to reach point $B$ is 2 hours 46 minutes 40 seconds.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
38. While doing his homework, Petya was in a hurry to get to football and, as always in such cases, made mistakes. Instead of squaring the number, he doubled it and got a two-digit number, written with the same digits as the required square, only in reverse order. What is the correct answer that Petya should have obtained?
|
38. Let Pete need to square the number $x$. He should have obtained $x^{2}=10 a+b$, but in fact, he got $2 x=10 b+a$. This means $x=\frac{10 b+a}{2}$. From this, it follows that the number $x$ is a single-digit number (since $x^{2}$ is a two-digit number), and the number $10 b+a$ is an even two-digit number. The number $10 b+a$ should be sought among the numbers 12, $14,16,18$. The condition of the problem is satisfied only by the number 18. Therefore, $x=18: 2=$ $=9$ and $x^{2}=81$. Pete should have obtained 81, but he got 18.
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41. On one of the three cards, the number 18 was written, on another - the number 75, and on the third - some two-digit number. If you add up all the different six-digit numbers that can be formed by arranging these cards in a row, the result is 2606058. What number is written on the third card?
|
41. Let the number on the third card be the one with $a$ tens and $b$ units, i.e., $\overline{a b}$. Then, by arranging the cards in a row, we can obtain the following numbers:
$\overline{1875 a b}, \overline{18 a b 75}, \overline{7518 a b}, \overline{75 a b 18}, \overline{a b 7518}, \overline{a b 1875 .}$
We can represent each of these numbers as a sum, for example, like this: $\overline{1875 a b}=$ $=180000+7500+\overline{a b}$. Then, when determining the sum of these six six-digit numbers, we get
$$
181818+181818+757575+757575+\overline{a b a b a b}+\overline{a b a b a b}
$$
or $1878786+2 \overline{a b a b a b}=2606058$, from which $\overline{a b a b a b}=363636$, and thus, $\overline{a b}=36$. Therefore, the number on the third card was 36.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42. Ten identical books cost no more than 11 p., while 11 such books cost more than $12 \mathrm{p}$. How much does one book cost?
|
42. Let one book cost $x$ k. Then we have $x \cdot 10 \leqslant 1100$ and $x \cdot 11 > 1200$ or $x \leqslant 110$ and $x > 109 \frac{1}{11}$. Therefore, $x=110$ k., i.e., the book costs 1 p. 10 k.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
44. At a mathematics evening, there were students from grades V and VI. Together, they were more than 70 but less than 90. The total number of rows of chairs in which the students sat in the hall was 3 more than the number of sixth-graders in each row, and the fifth-graders sat 3 in each row. How many sixth-graders and fifth-graders were there separately?
|
44. If there were $x$ rows, then in each of them there were $(x-3)$ sixth graders. Since there were 3 fifth graders in each row, there were $x$ students in each row. Then the total number of students at the evening was $x \cdot x=x^{2}$. According to the condition $x^{2}>70$ and $x^{2}<90$. This condition is satisfied only by $x=9 ; 9^{2}=81$. Therefore, there were 9 rows, there were $54(6 \cdot 9=54)$ sixth graders, and there were $27(3 \cdot 9=$ $=27)$ fifth graders.
|
54
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46. During the holidays for eight classes of the school, each with the same number of students, a trip to the museum was organized, and for the rest of the students in the school, who turned out to be 15% more, - a cultural trip to the puppet theater. How many students are there in the school, if it is known that there are no more than 520, and a total of more than 230 students participated in the excursion?
|
46. Let in one of the eight classes that participated in the excursion, there were $x$ students, then the museum was visited by $8 x$ students. By the condition $8 x>230$, hence $x>28 \frac{3}{4}$. The puppet theater was visited by $8 x+x \cdot 0.15=9.2 x$. Therefore, the total number of students in the school is $8 x+9.2 x=17.2 x$. By the condition $17.2 x \leqslant 520$, hence $x \leqslant 30 \frac{10}{43}$. Therefore, $x=29$ or $x=30$. Considering that only $17.2 \cdot 30$ is an integer, the condition is satisfied only by $x=30$. Therefore, the total number of students in the school is $17.2 \cdot 30=516$
|
516
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the length of the side of a square whose area is numerically equal to its perimeter.
|
2. Let the side length of the square be $a$, then the area $S=a \cdot a$, and the perimeter $P=4 a$. According to the condition $a \cdot a=4 a$, from which $a=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On one of the sides of a triangle, 60 points are taken, and on another - 50. (These points are distinct from the vertices of the triangle.) Each vertex at the base is connected by straight line segments to the points taken on the opposite side. How many intersection points of these segments are formed in this case?
|
4. Each of the 60 segments drawn from one vertex intersects each of the 50 segments drawn from another vertex, so we get 3000 such points $(50 \cdot 60=$ $=3000)$.
|
3000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. A school plot of rectangular shape has a perimeter of $160 \mathrm{m}$. How will its area change if the length of each side is increased by 10 m?
|
11. Let the length of the plot be $x$ m, then its width is $(80-x)$ m (Fig. 19) (the semi-perimeter is $160: 2=80$). If $A D=x$, then $C D=80-x ; C P=10$ m and $E K=$ $=10$ m. The area of the plot will increase by an amount equal to the sum of the areas of the rectangles $A D E M$ and $C E K P$, i.e., by $x \cdot 10+(80-x+10) \cdot 10=10 x+$ $+900-10 x=900$. Thus, the area of the plot will increase by $900 \mathrm{~m}^{2}$.
|
900
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. A cube with an edge length of 0.5 m is cut into cubes, each with an edge length of 2 mm. The resulting cubes are laid out in a single continuous row. What is the length of this row
|
13. $0.5 \text{m} = 500$ mm. The volume of the given cube is $500 \cdot 500 \cdot 500 \text{m}^{3}$, the volume of each cube obtained after cutting is $2 \cdot 2 \cdot 2 \text{mm}^{3}$. As a result of cutting, the number of cubes obtained is $(500 \cdot 500 \cdot 500):(2 \cdot 2 \cdot 2)=15625000$. Therefore, the length of the row will be $2 \text{mm} \cdot 15625000=31$ km $250 \text{m}$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. Assemble a square using four $1 \times 1$ square tiles, eight $2 \times 2$ square tiles, twelve $3 \times 3$ square tiles, and sixteen $4 \times 4$ square tiles.
|
16. The area of all the tiles, and thus of the desired square, is $1 \cdot 4 + 4 \cdot 8 + 9 \cdot 12 + 16 \cdot 16 = 400$ (sq. units). Therefore, we need to form a square with a side length of 20 units. The available tiles can be arranged as shown in Fig. 24.
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. How many matches can be obtained from a wooden cube with an edge of 1 m, if each match must have a length of 5 cm, a width of 2 mm, and a height of 2 mm? (Assume that no material is lost to sawing.)
|
23. $1 \mathrm{m}^{3}=1000000 \mathrm{~cm}^{3}$; one match has a volume of $5 \cdot 0.2 \cdot 0.2=0.2\left(\mathrm{~cm}^{3}\right)$; $1000000: 0.2=5000000$. Therefore, 5 million matches.
|
5000000
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. A scout is in a house with four windows arranged in a rectangular shape. He needs to signal to the sea at night by lighting a window or several windows. How many different signals can he send?
|
25. Let's schematically represent the windows and measure them:
a) Lighting all four windows gives one signal;
b) Lighting one of the windows is perceived as one signal, as in the dark, the position of the windows relative to the house cannot be distinguished;
c) Lighting two windows can give 4 different signals: one signal by lighting windows 1,4 or 2,3; one signal by lighting windows 1,2 or 4,3; two signals by lighting windows 1,3 and 2,4, i.e., we have the following configurations:
1)
2) $\bullet \cdot 3)$
- 4)
d) Lighting three windows can give four signals: $1,2,3$; $2,3,4$; $3,4,1$ and $4,1,2$, i.e., we have the following configurations:
1)
2)
3)
4)
In total, we have different signals: $1+1+4+4=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. What is the maximum number of intersection points that a closed broken line consisting of 7 segments can have? (The common ends of the segments of the broken line are not counted.)
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
30. Take a broken line consisting of two segments. By adding a third segment, it can only intersect one of the two original segments, resulting in one point (1) (Fig. 30). Taking a fourth segment, it can intersect a maximum of two of the three existing segments, resulting in two more points $(2,3)$. A fifth segment can intersect a maximum of 3 segments, resulting in three more points $(4,5,6)$. A sixth segment can intersect a maximum of 4 segments, resulting in 4 more points $(7,8,9,10)$. A seventh segment can intersect a maximum of 4 segments, resulting in four more points $(11,12,13,14)$. Thus, the maximum possible number of self-intersection points is 14.
Fig. 29
Fig. 30
|
14
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
10. Working in a collective farm orchard harvesting fruits, schoolchildren collected 22 crates, some of which contained apples, others pears, and still others plums. Can it be asserted that there are at least 8 crates, the contents of which are one of the specified types of fruit?
|
10. Let's consider the most "unfavorable" case. Suppose there are 7 boxes of apples, pears, and plums each. This makes a total of 21 boxes. If the 22nd box is with apples, then there will be 8 boxes of apples; if this box is with pears, then there will be 8 boxes of pears; if this box is with plums, then there will be 8 boxes of plums. In other cases, there will be more than 8 boxes containing one of the three types of fruits.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. In a dark storeroom, there are boots of the same size: 12 pairs of black and as many brown. What is the smallest number of boots that need to be taken so that among them there is at least one pair (left and right boot) of the same color, if in the dark it is impossible to distinguish not only the color of the boot but also the left from the right?
|
13. Let's consider the most "unfavorable" case. If you take 24 shoes, they might all be for one foot. By taking one more shoe, it will definitely match one of the previously taken ones. It is possible that you initially took 12 shoes for different feet but of different colors, but in this case, the result will be the same. Therefore, you need to take 25 shoes.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. In the box, there are 120 colored pencils: 35 red, 23 green, 14 yellow, 26 blue, 11 brown, and 11 black. What is the smallest number of pencils that need to be taken from the box in the dark (without seeing the pencils) to ensure that there are at least 18 pencils of one color among them?
|
16. Let's consider the most "unfavorable" case: among the taken pencils, there could be 14 yellow, 11 brown, 11 black, 17 red, 17 green, and 17 blue. Thus, if we take 87 pencils $14+11+$ $+11+17+17+17=87$, it might happen that among them there will not be 18 pencils of the same color. By taking one more pencil, we will have either 18 red, 18 green, or 18 blue. Therefore, we need to take 88 pencils. In other cases, among the 88 taken pencils, there will be more than 18 pencils of one color.
|
88
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. In a photo lab, there are 130 photographs, of which 35 are from the fourth grade, 30 from the fifth, 25 from the sixth, 20 from the seventh, and the rest are from grades 1-III. The photographs are mixed and cannot be distinguished by touch. What is the smallest number of photographs that need to be taken, without seeing them, to ensure that among them there are at least 15 from one of the grades IV-VII?
|
17. Let's consider the most "unfavorable" case: we take all the photographs of classes I-III $(130-(35+30+25+20)=20)$, then it may turn out that 14 photographs were taken from each of the IV-VII classes, making a total of $14 \cdot 4+20=76$ photographs. Now, if we take one more, then one of the IV-VII classes will have 15. Therefore, we need to take 77 photographs.
|
77
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. The traffic inspector noticed that out of 20 cars that passed on the road to the airport, 14 were "Ladas," 15 were dark-colored, 17 were driven by men, and in 18 cars, there were passengers besides the driver. For what minimum number of cars could all 4 of these characteristics be true?
|
18. Out of the total number of cars, 6 did not have the first feature (not "Zhiguli"), 5 did not have the second, 3 did not have the third, and 2 did not have the fourth. Therefore, the maximum number of cars that do not have at least one feature is 16 $(6+5+3+2=16)$. The remaining $4(20-16=4)$ have all four features.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Schoolchildren helped the collective farm workers to harvest vegetables. The fourth grade collected 18 tons of cabbage and as much carrots as the sixth grade collected onions. The fifth grade worked only on cucumber harvesting and collected a whole number of tons of cucumbers, which is less than the amount of cucumbers collected by the sixth grade but more than the amount of carrots collected by the fourth grade. The sixth grade collected 7 tons of onions, and cucumbers - half as much as the cabbage collected by the fourth grade. How many tons of vegetables did the schoolchildren collect in total?
|
20. The sixth grade collected 9 centners of cucumbers $(18: 2=9)$ and 7 centners of onions, which means the fourth grade collected 7 centners of carrots. The fifth grade collected fewer cucumbers than 9 centners but more than 7 centners, so 8 centners. Thus, the students collected in total $18+7+8+9+7=49$ (centners).
|
49
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. The chain has broken into five parts,
But I hope you will
Join them as quickly as you can,
Doing the minimum work.
To cut and solder a link-
It takes two minutes...
Remember, the task is given
For a very thoughtful look.
Note. Each link has three rings.
|
22. Cut 3 rings of one link and join the remaining 4 links with the three resulting rings (by welding). This will take 6 minutes.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. In one book, the following 100 statements were written:
1) “In this book, there is exactly one false statement.”
2) “In this book, there are exactly two false statements ...”
3) “In this book, there are exactly one hundred false statements.”
Which of these statements is true?
|
25. If we assume that the first statement is true, this would mean that there is exactly one false statement in the book, and all the others are true, i.e., the second, third, and so on are true, which contradicts the first statement, since, for example, the second statement claims that there are exactly two false statements, the third claims exactly three, and so on. Conducting such reasoning up to the 98th statement inclusive, we will come to the same conclusion. If, however, the 99th statement is true, this means that there are exactly 99 false statements, i.e., all except the 99th statement. Therefore, it is false that there is exactly one, two, ..., 98, or 100 false statements. The hundredth statement cannot be true, because in this case all statements (according to the hundredth statement) are false. Thus, the true statement is the 99th.
|
99
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. A problem solved by Poisson (1781-1840) in his youth. Someone has 12 pints (a unit of volume) of honey and wants to pour out half of this amount, but he does not have a container with a capacity of 6 pints. He has 2 containers: one with a capacity of 8 pints, and the other with a capacity of 5 pints. How can he pour 6 pints of honey into the 8-pint container? What is the minimum number of transfers required to do this? (This problem determined Poisson's life path: he dedicated his entire life to mathematics.)
|
28. Let's represent it with such a diagram:
| Vessel | | |
| :---: | :---: | :---: |
| 12 pints | 8 pints | 5 pints |
| 12 | - | - |
| 4 | 8 | - |
| 4 | 3 | 5 |
| 9 | - | - |
| 1 | 8 | 3 |
| 1 | 6 | 3 |
| 6 | 6 | - |
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29. How can you use a balance scale and a 200g weight to divide 9 kg of sugar into two bags - 2 kg and 7 kg, if you are allowed to weigh no more than three times?
|
29. Place a weight on one pan and distribute the available sugar across the pans so that the scales are in balance. Then, on one pan there will be 4 kg 600 g of sugar, and on the other (where the weight is) - 4 kg 400 g of sugar. The second time, distribute 4 kg 600 g of sugar across the pans. On one of them (without the weight) there will be 2 kg 400 g of sugar, and on the other - 2 kg 200 g. The last (third) time, from 2 kg 200 g of sugar, weigh out 200 g using the available weight, and 2 kg will remain. (During the second weighing, the weight can be not used, and 2 kg 400 g can be evenly distributed on the pans.)
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. In one month, three Wednesdays fell on even dates. What date will the second Sunday of the month be?
|
31. If in one month three Wednesdays fall on even dates, this is possible under the condition that the month is not February and starts on a Tuesday. Then Wednesday will be on the 2nd, 16th, and 30th, and the second Sunday will be on the 13th.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. In which cases does a month have the maximum number of Saturdays? What is this number?
|
32. The maximum number of Saturdays in one month is 5, since $7 \cdot 4=28 ; 28<30$ and $28<31$. In February, there can be 5 Saturdays if it is a leap year and the month starts on a Saturday. April, June, September, and November will have 5 Saturdays if they start on a Saturday or a Friday. The remaining months can have 5 Saturdays if they start on a Saturday, Friday, or Thursday.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Football teams were holding a round-robin tournament. One of the fans of this game, returning from vacation, found the following situation: the total number of points scored by all teams was 44; one team, which scored the fewest points, received one point; the two teams occupying the first and second places scored the same number of points. How many teams are participating in the tournament and how many games do they still have to play?
|
37. Since $1+2+3+4+5+6+7+8+8=44$, there are 9 teams participating in the tournament. In total, they should score 72 points ( $8 \cdot 9=72$ ). Therefore, they still need to score 28 points $(72-44=28)$, which can be achieved in 14 games $(28: 2=14)$.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
38. In a tournament where each pair of teams played each other twice, 4 teams participated. For each win, two points were awarded, for a draw - one, and for a loss - 0. The team that finished in last place scored 5 points. How many points did the team that finished in first place score?
|
38. There were 12 games in total $(3 \cdot 4=12)$. In each match, -2 points were awarded, and the total points were -24. Since $5+6+7+8=26>24$, this case is impossible.
Therefore, $5+6+6+7=24$. This means the winning team scored 7 points.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. In a chess tournament, each of the 8 participants plays one game with each other. All participants scored a different number of points (an integer), and the second-place finisher scored as many points as all the chess players who finished from fifth to eighth place combined. How did the players who finished in third and fifth place play against each other?
|
39. The participant who took second place, out of a total of 28 points scored by all participants together, scored no more than six points, as otherwise, they would have taken either first place or shared the first and second places, which contradicts the condition. The only possible scenario is: $28=7+6+5+4+3+2+1+0$. On the other hand, if the participants who took fifth through eighth place inclusive scored 6 points, then these points were earned by playing against each other, losing all games to the chess players who took the top four places. Therefore, the participant who took third place won against the one who took fifth.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 22. Find the minimum value of the expression $(x+y) \cdot(x+z),$ if $x, y, z-$ are positive numbers and $x \cdot y \cdot z \cdot(x+y+z)=1$.
|
Solution. Let $a=y+z ; b=x+z ; c=x+y$. Consider a triangle with sides $a, b, c$ (it is not difficult to verify that such a triangle exists for any $x, y, z$). Then:
$$
\begin{gathered}
(x+y) \cdot(x+z)=b \cdot c \\
x y z(x+y+z)=(p-a)(p-b)(p-c) p=S^{2}=1
\end{gathered}
$$
But $b \cdot c=\frac{2 S}{\sin A}=\frac{2}{\sin A}$, and $|\sin A| \leq 1$. In this case, it is clear that the minimum value of the product $b \cdot c$ is 2. Therefore, the minimum value of the expression $(x+y) \cdot(x+z)$ under the given conditions is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
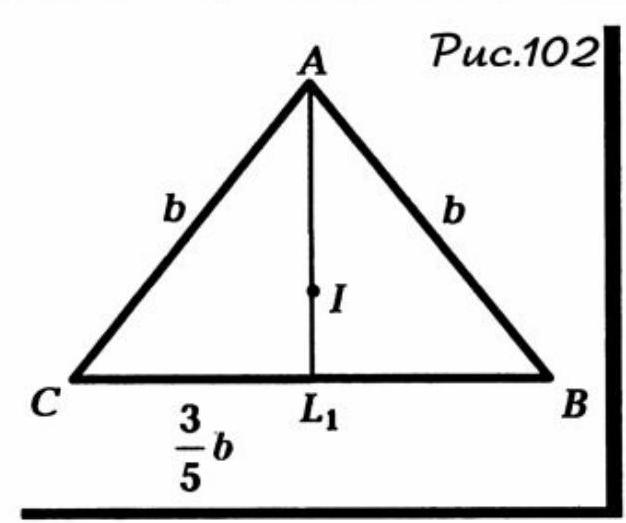
Problem 101. The center of the inscribed circle divides the height of an isosceles triangle, drawn to the base, into segments of 5 cm and 3 cm, measured from the vertex. Find the sides of the triangle.
|
Solution. Let in triangle $A B C \quad b=c$ and $\frac{A I}{I L_{1}}=\frac{5}{3}$ (Fig. 102). Then $\frac{b+c}{a}=\frac{2 b}{a}=\frac{5}{3}$, or $a=\frac{6}{5} b$. Then $\quad C L_{1}=B L_{1}=\frac{a}{2}=\frac{3}{5} b . \quad$ By the Pythagorean theorem for triangle $A L_{1} C \quad A L_{1}=\frac{4}{5} b$. Thus:
76
$$
\frac{4}{5} b=8 \text { cm, from which } b=10 \text { cm. Therefore } a=\frac{6}{5} b=12 \text { cm. }
$$
We will demonstrate how the property $\frac{A I}{I L_{1}}=\frac{b+c}{a}$ can be applied in trigonometry.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 130. Given an angle of $54^{\circ}$. Divide it into three equal parts using a compass and a straightedge.
|
Solution. We will use the fact that $\frac{1}{3} \cdot 54^{\circ}=18^{\circ}$. By supplementing the angle $54^{\circ}$ to a right angle, we obtain the angle $36^{\circ}$ (Fig. 122). The bisector of the angle $36^{\circ}$ will give us the desired angle $18^{\circ}$.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. Two natural numbers both give a remainder of 2 when divided by 3. What remainder does their product give when divided by 3?
|
19. $(3 m+2)(3 n+2)=3(m n+m+n+1)+1$.
Translating the above text into English, while preserving the original text's line breaks and format, results in:
19. $(3 m+2)(3 n+2)=3(m n+m+n+1)+1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
44. How many common multiples do the numbers 180 and 300 have? Which one is the smallest? If the smallest is determined, how can the others be obtained? How many common divisors do these numbers have and what are they?
|
44. These numbers (like any pair of numbers) have an infinite number of common multiples; the smallest of them is 900; all other common multiples are obtained by multiplying 900 by any integer; the common divisors of the given numbers are: $2,3,5 ; 4,6,10$, $15 ; 12,20,30 ; 60$. (The number of common divisors is always finite).
|
900
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. What whole number is equal to the sum of all the whole numbers preceding it? Is there only one such number?
|
65. $1+2=3$. No other number $>3$ has the required property: indeed, if we move forward in the sequence of natural numbers, then with each step taken, the sum of natural numbers increases by $3, 4, 5$, etc., while each subsequent natural number increases only by 1, and therefore the difference between the sum of natural numbers preceding a given number and this number will continue to grow. -Otherwise: the sum of integers preceding the number $n$ is $\frac{(n-1) n}{2}$. If it is to equal $n$, then $\frac{n-1}{2}=1$, from which $n-1=2, \quad n=3$
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. Write a polynomial arranged in descending powers of the number five, with coefficients being integers, non-negative, and less than 5. How can this polynomial be symbolically recorded in a manner similar to the notation of numbers in our decimal system? (See the previous question).
|
99. For example, the polynomial $3.5^{6}+1.5^{3}+2.5^{2}+4.5+1$ can be briefly written as 3001241 or, to avoid misunderstandings, as (3001241), where the 5 outside the parentheses indicates that the base of the numeral system is 5. Conversely, the symbol (432) represents the polynomial $4.5^{2}+3.5+2=117$ (in the decimal system). It can also be said that the number 117 in the decimal system is expressed in the base-5 system as 432.
|
432
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
100. Write a polynomial arranged in descending powers of 2, with coefficients equal to 1 or 0. How can this polynomial be symbolically represented? (See previous questions).
|
100. For example, $(110101101)_{2}=2^{8}+2^{7}+2^{5}+2^{3}+2^{2}+1=429$. Conversely, the number $15=2^{3}+2^{2}+2+1=(1111)_{\mathbf{2}}$.
|
429
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
102. A certain number is written in the duodecimal system; for which divisor $m$ is the following divisibility rule valid: if the sum of the digits of the number is divisible by $m$, then the number is also divisible by $m$?
|
102. $m=11$, because $12=11\cdot1+1, \quad 12^{2}=11\cdot13+1$ and so on.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
140. How to express with one equality sign that among three numbers $a, b, c$ at least one is equal to zero
|
140. $a b c=0$.
The above text has been translated into English, maintaining the original text's line breaks and format.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
152. The cooperative purchased various goods from the trust after the prices, marked in the old price list, were increased by $10 \%$. However, the cooperative receives a $10 \%$ discount from the trust. For the entire purchase, the cooperative paid $N$ rubles in cash. By what number is $N$ divisible without a remainder?
|
152. To 99.
|
99
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
287. How many solutions does the system of equations generally have
$$
\begin{gathered}
a x^{2}+b x y+c y^{2}=d \\
a_{1} x^{2}+b_{1} x y+c_{1} y^{2}=d_{1} ?
\end{gathered}
$$
In particular, how many solutions does the system of question 280 have?
|
287. Generally four. Excluding $d$ and $d_{1}$, we obtain a homogeneous equation of the second degree, which, generally, will determine two values of the ratio $\frac{x}{y}$ (see question 284) $\frac{x}{y}=k_{1}$ and $\frac{x}{y}=k_{2}$, from which $x=k_{1} y, x=k_{2} y$. Substituting each of these expressions sequentially into one of the given equations, we will obtain a quadratic equation each time, which will determine two values for $y$, and consequently for $x$. In total, generally, four solutions will be obtained.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
368. Which of the three functions
\[
\begin{aligned}
& y=100 x \\
& y=1000+100 x \\
& y=10000+99 x
\end{aligned}
\]
increases faster than the others?
|
368. $100(x+h)-100 x=100 h$
$$
[1000+100(x+h)]-(1000+100 x)=100 h \cdot .(2)
$$
$$
[10000+99(x+h)]-(10000+99 x)=99 h . .(3)
$$
The first two increase at the same rate and faster than the third. 369. $\quad[2(x+h)+3]-(2 x+3)=2 h$
$$
\begin{array}{r}
{\left[\frac{1}{2}(x+h)+18\right]-\left[\frac{1}{2} x+18\right]=\frac{1}{2} h} \\
4(x+h)-4 x=4 h \\
{[4(x+h)-4]-(4 x-4)=4 h}
\end{array}
$$
Thus: the functions (3) and (4) increase the fastest and at the same rate, while (2) increases the slowest.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
423. Can the sum of a finite number of terms of a geometric progression be zero?
|
423. If all members of the progression are real numbers, then in the trivial case only, when the progression coefficient \( q = -1 \) and the number of terms is even.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
454. Prove that the third difference of the function $n^{3}$ is constantly equal to 6. Give the general form of a function that possesses this property.
|
454. The first differences of the function $n^{3}$ are expressed by the function $3 n^{2}+3 n+1$, the second differences by $6 n+6$; consequently, the third differences are constant and equal to 6. If we add to $n^{3}$ an arbitrary function $\varphi(n)$, the third differences of which are zero, then the third differences of the resulting function $n^{3}+\varphi(n)$ will also be 6.
As is known (question 453), the most general form of $\varphi(n)$ is a quadratic trinomial.
|
6
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
456. Prove that the third difference of the function
$$
f(n)=1^{2}+2^{2}+\ldots+n^{2}
$$
is constantly equal to 2.
|
456. $f(n+1)-f(n)=(n+1)^{2}$; therefore, the first differences of $f(n)$ are $(n+1)^{2}$; the second differences are $(n+1)^{2}-n^{2}=2 n+1$, from which it is clear that the third differences are constantly equal to 2.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
489. The more sides a regular polygon has, the more convex its periphery becomes; to what limit does the internal (external) angle tend when the number of sides increases indefinitely?
|
489. The angle of a regular $n$-sided polygon $\frac{180^{\circ}(n-2)}{n}=180^{\circ}$ $\left(1-\frac{2}{n}\right)$ approaches $180^{\circ}$ as $n \rightarrow \infty$. The polygon approaches the shape of a circle, and the angle (interior) between two consecutive sides approaches the angle (at $180^{\circ}$) formed by two halves of the tangent to the circle.
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
521. Through a point lying outside a plane, how many: a) lines perpendicular to the plane can be drawn? b) lines parallel to it? c) planes perpendicular to this plane? d) planes parallel to it?
|
521. a) One, b) an infinite set - generating a plane parallel to the given one, c) an infinite set - passing through the perpendicular dropped from this point, d) one (see b).
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
551. On one of the sides of triangle $A B C$ there is a point $P$; draw a line through $\boldsymbol{P}$ that cuts off from triangle $\boldsymbol{A} \boldsymbol{B} \boldsymbol{C}$ a triangle similar to it. How many solutions?
|
551. In general, there are 4 solutions. If the triangle is isosceles or equilateral, the number of solutions decreases accordingly.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
641. Study the symmetric properties of an equilateral triangle.
|
641. 3 axes of symmetry; no center of symmetry, for if such existed, it could only be (see question 634) the point of intersection of the altitudes. But it divides the altitudes in the ratio $1: 2$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
740. Show that a rectangle is the only convex polygon in which all angles are right angles.
|
740. From the equation $\frac{180^{\circ}(n-2)}{n}=90^{\circ}$ it follows that $n=4$.
|
4
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
833. How many different values does the expression $\sin \frac{k \pi}{3}$ take when $k$ takes all integer values from 0 to $+\infty$?
|
833. Let $q$ be the integer quotient of the division of $k$ by $3$, and $r$ the remainder, which lies between -2 and 2, then $k=3 q+r$.
We have $\sin \frac{k \pi}{3}=\sin \left(q \pi+\frac{r \pi}{3}\right)=\sin \left( \pm \frac{r \pi}{3}\right)$. Everything reduces to the number of different values of the seven members of the series
$$
\sin \left(-\frac{2 \pi}{3}\right), \sin \left(-\frac{\pi}{3}\right), \sin 0^{\circ}, \sin \frac{\pi}{3}, \sin \frac{2 \pi}{3}
$$
In this series, the first two and the last two members are equal; as a result, we have 3 different values, two of which differ only in sign.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Are the equations
$$
\frac{2(x-10)}{x^{2}-13 x+30}=1 \quad \text { and } \quad x^{2}-15 x+50=0
$$
equivalent?
|
Solution. We will solve the first equation. By getting rid of the denominator, i.e., multiplying both sides of the original equation by the expression $x^{2}-13 x+30$, we obtain the equation
$$
2 x-20=x^{2}-13 x+30
$$
The set of all roots of this equation consists of two numbers: $x_{1}=10$ and $x_{2}=5$. As a result of the transformation, extraneous roots could have appeared; therefore, it is necessary to check. The check shows that the number $x_{1}=10$ is not a root of the original equation, while the number $x_{2}=5$ is its root, i.e., the first equation has a single root $x=5$.
The equation $x^{2}-15 x+50=0$ has two solutions: $x_{1}=5$ and $\boldsymbol{x}_{2}=10$. Comparing the sets of roots of the given equations, we get: the second equation is a consequence of the first.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 19. Solve the equation
$$
\sqrt{x+11}=x-1
$$
|
Solution.
The first method. The domain of definition (DOD) of equation (7) is given by the condition $x \geqslant-11$. Considering that
$$
f(x)=g(x) \Rightarrow f^{2}(x)=g^{2}(x)
$$
we have
$$
\text { (7) } \begin{aligned}
\Rightarrow x+11=x^{2}-2 x+1 \Leftrightarrow x^{2}-3 x-10=0 \Leftrightarrow \\
\Leftrightarrow(x-5)(x+2)=0 \Leftrightarrow\left[\begin{array}{l}
x=5 \\
x=-2
\end{array}\right.
\end{aligned}
$$
## 14 CH. 1. EQUIVALENT EQUATIONS AND INEQUALITIES
Thus, the solutions of the original equation are among the numbers $x_{1}=5$ and $x_{2}=-2$.
Before making the check, let us draw the reader's attention to a common mistake. Transitioning from the given equation to its consequence, roots are found. Then, it is checked whether the found roots belong to the DOD of the original equation. The roots that do not belong to the DOD are discarded, and the remaining ones (belonging to the DOD of the original equation) are listed in the answer. This is where the mistake lies. It is not enough to check whether the found roots belong to the DOD of the equation. It is necessary to check whether the roots of the consequence, which belong to the DOD of the original equation, satisfy the original equation itself. This is confirmed by the given example.
Indeed, both roots of the system satisfy the DOD, but the number 5 satisfies equation (7), while the number -2 does not satisfy it. Therefore, equation (7) has a single root $x=5$.
The second method. The equation $\sqrt{\alpha(x)}=\beta(x)$ is equivalent to the system
$$
\left\{\begin{array}{l}
\beta(x) \geqslant 0 \\
\alpha(x)=\beta^{2}(x)
\end{array}\right.
$$
since $\beta^{2}(x) \geqslant 0$, and the equality $\alpha(x)=\beta^{2}(x)$ imposes a non-negativity condition on $\alpha(x)$.
When solving equations of type (7) by equivalent transitions, it is not necessary to find the DOD of this equation, but it is mandatory to impose the non-negativity condition on the function $\beta(x)$.
Considering this, for the given example, we have
(7) $\Leftrightarrow\left\{\begin{array}{l}x-1 \geqslant 0, \\ x+11=x^{2}-2 x+1\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geqslant 1, \\ x^{2}-3 x-10=0\end{array} \Leftrightarrow\right.\right.$
$$
\Leftrightarrow\left\{\begin{array}{l}
x \geqslant 1 \\
{\left[\begin{array}{l}
x=-2, \\
x=5
\end{array}\right.}
\end{array} \Leftrightarrow x=5\right.
$$
Thus, $x=5$ is the only solution to equation (7).
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Solve the equation
$$
\left|\frac{x^{2}-6 \sqrt{x}+7}{x^{2}+6 \sqrt{x}+7}\right|=1
$$
|
Solution. The given equation is equivalent to the system of equations
$\left[\begin{array}{l}\frac{x^{2}-6 \sqrt{x}+7}{x^{2}+6 \sqrt{x}+7}=1, \\ \frac{x^{2}-6 \sqrt{x}+7}{x^{2}+6 \sqrt{x}+7}=-1\end{array} \Leftrightarrow\right.$
$$
\Leftrightarrow\left[\begin{array}{l}
\frac{-12 \sqrt{x}}{x^{2}+6 \sqrt{x}+7}=0 \\
\frac{2 x^{2}+14}{x^{2}+6 \sqrt{x}+7}=0
\end{array} \Leftrightarrow \sqrt{x}=0 \Leftrightarrow x=0\right.
$$
Thus, the only solution to the original equation is the number 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Solve the equation
$$
|x-| 4-x||-2 x=4
$$
|
Solution. The given equation is equivalent to the combination of two systems:
$$
\left\{\begin{array} { l }
{ 4 - x \geqslant 0 } \\
{ | x - ( 4 - x ) | - 2 x = 4 , }
\end{array} \quad \left\{\begin{array}{l}
4-x4 \\
-2 x=0
\end{array}\right.\right.
$$
The second system of the combination (4) has no solutions.
The first system of the combination (4) is equivalent to the combination of the following two systems:
$$
\left\{\begin{array} { l }
{ x \leqslant 4 , } \\
{ 2 x - 4 \geqslant 0 , } \\
{ ( 2 x - 4 ) - 2 x = 4 , }
\end{array} \quad \left\{\begin{array}{l}
x \leqslant 4 \\
2 x-4<0 \\
-(2 x-4)-2 x=4
\end{array}\right.\right.
$$
i.e., the combination
The only solution to the combination (5), and therefore to the original equation, is the number 0.
Consider an equation of the form
$$
\left|f_{1}(x)\right|+\left|f_{2}(x)\right|+\left|f_{3}(x)\right|+\ldots+\left|f_{n}(x)\right|=g(x)
$$
where \( f_{1}(x), \ldots, f_{n}(x), g(x) \) are some functions. If this equation is solved by sequentially opening the absolute value signs, then after opening one absolute value sign, a combination of two systems is obtained, after opening the second absolute value sign, a combination of four systems, and so on. This method is very cumbersome. Such equations are easier to solve using the interval method. For this, first find all points where at least one of the functions \( f_{1}(x), f_{2}(x), \ldots, f_{n}(x) \) changes sign. These points divide the domain of admissible values of equation (6) into intervals, on each of which all functions \( f_{1}(x), f_{2}(x), \ldots, f_{n}(x) \) retain their sign. Then, using the definition of absolute value, transition
Fig. 2.2
from equation (6) to a combination of systems without absolute value signs.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Solve the equation
$$
3 \sqrt{x+3}-\sqrt{x-2}=7
$$
|
Solution. Isolate one of the roots on the left side:
$$
3 \sqrt{x+3}=\sqrt{x-2}+7
$$
By squaring both sides of the obtained equation, we have
$$
9(x+3)=x-2+14 \sqrt{x-2}+49
$$
Combining like terms and isolating the radical on the right side, we get the equation
$$
4 x-10=7 \sqrt{x-2}
$$
By squaring both sides of the obtained equation, we have
$$
16 x^{2}-80 x+100=49(x-2)
$$
i.e., the equation
$$
16 x^{2}-129 x+198=0
$$
which is a consequence of the original equation. We find the roots of this equation: $x_{1}=6, x_{2}=2 \frac{1}{16}$.
Substitute each of these roots into the original equation.
For $x=6$, we get a true numerical equality. Therefore, $x_{1}=6$ is a root of the original equation.
For $x=2 \frac{1}{16}$, the left side of the original equation equals $6 \frac{1}{2}$, and its right side equals 7. Since $6 \frac{1}{2} \neq 7$, the number $x_{2}=2 \frac{1}{16}$ does not satisfy the original equation, i.e., it is an extraneous root for it.
Thus, $x_{1}=6$ is the only root of the original equation.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Solve the equation
$$
\sqrt{11 x+3}-\sqrt{2-x}-\sqrt{9 x+7}+\sqrt{x-2}=0
$$
|
Solution. Isolate two radicals on each side so that after squaring we get the simplest equation:
$$
\sqrt{11 x+3}-\sqrt{2-x}=\sqrt{9 x+7}-\sqrt{x-2}
$$
Perform a chain of transformations:
$$
\begin{gathered}
11 x+3-2 \sqrt{(11 x+3)(2-x)}+2-x= \\
=9 x+7-2 \sqrt{(9 x+7)(x-2)}+x-2 \\
\sqrt{6+19 x-11 x^{2}}=\sqrt{9 x^{2}-11 x-14} \\
6+19 x-11 x^{2}=9 x^{2}-11 x-14 \\
20 x^{2}-30 x-20=0 \\
2 x^{2}-3 x-2=0
\end{gathered}
$$
The last equation is a consequence of the original equation and has roots $x_{1}=2$ and $x_{2}=-0.5$.
When $x=2$, the original equation turns into a true numerical equality. Therefore, $x_{1}=2$ is its root.
When $x=-0.5$, in the left part of the original equation, we have the expression $\sqrt{-0.5-2}$, which is meaningless; therefore, the number $x_{2}=-0.5$ does not satisfy the original equation.
Thus, $x_{2}=2$ is the only root of the original equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Solve the equation
$$
\sqrt[3]{2 x-1}+\sqrt[3]{x-1}=1
$$
|
Solution. Raising both sides of the equation to the third power, we get
$$
3 x-2+3 \sqrt[3]{(2 x-1)(x-1)}(\sqrt[3]{2 x-1}+\sqrt[3]{x-1})=1
$$
By the condition, the expression $\sqrt[3]{2 x-1}+\sqrt[3]{x-1}$ equals one. Substituting this expression with one in the obtained equation, we get the equation
$$
3 x-2+3 \sqrt[3]{(2 x-1)(x-1)}=1
$$
which is a consequence of the original equation, since equation (1) may have a root that does not necessarily satisfy the relation:
$$
1=\sqrt[3]{2 x-1}+\sqrt[3]{x-1}
$$
Raising equation (1) to the third power:
$$
(2 x-1)(x-1)=(1-x)^{3}
$$
The last equation has roots $x_{1}=0$ and $x_{2}=1$.
Verification shows that $x_{1}=0$ is an extraneous root of the original equation, while $x_{2}=1$ satisfies it.
Thus, $x_{2}=1$ is the only root of the original equation.
For an equation of the form
$$
\sqrt[3]{f(x)}+\sqrt[3]{g(x)}=\varphi(x)
$$
where $f(x), g(x), \varphi(x)$ are some functions, they are usually solved as follows. Both sides of the equation are raised to the third power to obtain the equation
$$
f(x)+g(x)+3 \sqrt[3]{f(x) g(x)}(\sqrt[3]{f(x)}+\sqrt[3]{g(x)})=\varphi^{3}(x)
$$
In this equation, the expression $\sqrt[3]{f(x)}+\sqrt[3]{g(x)}$, which is the left-hand side of the original equation, is replaced by $\varphi(x)$, which is its right-hand side. As a result, we get the equation
$$
f(x)+g(x)+3 \sqrt[3]{f(x) g(x)} \varphi(x)=\varphi^{3}(x)
$$
which (since it is solved under the condition $\sqrt[3]{f(x)}+\sqrt[3]{g(x)}=$ $=\varphi(x)$) is a consequence of the original equation. After isolating the radical and raising the obtained equation to the third power, we find its roots, and then by direct substitution of each of the found numbers into the original equation, we select those that are roots of the original equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 10. Solve the equation
$$
\sqrt{x+16}-x+4=0
$$
|
Solution. The domain of the equation: $x \geqslant-16$. Isolating the radical, we get the equation $\sqrt{x+16}=x-4$. Squaring both sides of this equation and combining like terms, we obtain the equation $x^{2}-9 x=0$, the roots of which are: $x_{1}=0$ and $x_{2}=9$. Each of these roots belongs to the domain of the original equation.
For the root $x_{1}=0$, the parts of the equation $\sqrt{x+16}=x-4$ being squared have different signs; therefore, $x_{1}=0$ is an extraneous root of the original equation.
By substitution, we verify that $x=9$ is the only root of the original equation.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Solve the equation
$$
\sqrt{x^{2}+3 x-4}=\sqrt{2 x+2}
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{l}
x^{2}+3 x-4 \geqslant 0 \\
2 x+2 \geqslant 0
\end{array}\right.
$$
we find the domain of the equation: $x \geqslant 1$.
By squaring both sides of the original equation, we obtain the equation
$$
x^{2}+3 x-4=2 x+2
$$
which is a consequence of it. The roots of this equation are: $x_{1}=2$ and $x_{2}=-3$.
The root $x_{2}=-3$ does not belong to the domain of the original equation and is therefore extraneous.
Substituting the number 2 into the original equation, we get a true equality; hence, $x=2$ is its only root.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 12. Solve the equation
$$
\sqrt{2 x+5}+\sqrt{x-1}=8
$$
|
Solution. Domain of the equation: $x \geqslant 1$. Squaring both sides of the equation and performing transformations, we obtain the equation
$$
2 \sqrt{2 x^{2}+3 x-5}=60-3 x
$$
After squaring both sides of this equation, we get the equation
$$
4\left(2 x^{2}+3 x-5\right)=(60-3 x)^{2}
$$
which is a consequence of the original equation. The roots of this equation are: $x_{1}=10$ and $x_{2}=362$.
The number $x_{2}=362$ is an extraneous root of the original equation, as for it, the equation being squared $2 \sqrt{2 x^{2}+3 x-5}=60-3 x$ has parts of different signs.
The number $x_{1}=10$ belongs to the domain of the original equation and satisfies it; therefore, it is its only root.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 15. Solve the equation
$$
\sqrt{x+7} \sqrt{3 x-2}=3 \sqrt{x-1} \sqrt{x+2}
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{r}
x+7 \geqslant 0 \\
3 x-2 \geqslant 0 \\
x-1 \geqslant 0 \\
x+2 \geqslant 0
\end{array}\right.
$$
we find the domain of the equation: $x \geqslant 1$. Squaring both sides of the equation and combining like terms, we obtain the equation
$$
3 x^{2}-5 x-2=0
$$
which is a consequence of the original equation. The roots of this equation are $x_{1}=-1 / 3$ and $x_{2}=2$.
The root $x_{1}=-1 / 3$ does not belong to the domain of the original equation.
The root $x_{2}=2$ belongs to the domain of the original equation and, when substituted, turns it into a true numerical equality.
Thus, $x_{1}=2$ is the only root of the original equation.
The equation $f(x)=g(x) \alpha(x)$ is a consequence of the equation
$$
\frac{f(x)}{\alpha(x)}=g(x)
$$
If the domain of the function $\varphi(x)$ is not narrower than the domain of the equation $f(x)=g(x)$, then the equation
$$
f(x) \varphi(x)=g(x) \varphi(x)
$$
is a consequence of the equation
$$
f(x)=g(x)
$$
Therefore, if in the process of solving an equation, transformations are performed that consist of eliminating the denominator from the equation or multiplying the equation by an expression whose domain is not narrower than the domain of the given equation, the domain of the original equation may be expanded, and, consequently, extraneous roots may appear. In this case, verification is also a necessary part of solving the equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 17. Solve the equation
$$
\frac{2}{2-\sqrt{x}}+\frac{1}{2}=\frac{4}{2 \sqrt{x}-x}
$$
|
Solution. The domain of the equation is determined by the system of inequalities
$$
\left\{\begin{array}{r}
x \geqslant 0 \\
2-\sqrt{x} \neq 0 \\
2 \sqrt{-} x-x \neq 0
\end{array}\right.
$$
i.e., $x>0, x \neq 4$.
Multiplying both sides of the original equation by the expression $2(2 \sqrt{ } \bar{x}-x)$, we obtain the equation
$$
4 \sqrt{ } \bar{x}+2 \sqrt{x}-x=8
$$
which is a consequence of the original equation (equation (5) has a wider domain: $x \geqslant 0$).
Solving equation (5), we find two roots: $x_{1}=16$ and $x_{2}=4$. The number $x_{2}=4$ does not belong to the domain of equation (4) and is therefore an extraneous root. Substituting the number $x_{1}=16$ into equation (4) shows that it is the only root of the equation.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 18. Solve the equation
$$
x=(\sqrt{1+x}+1)(\sqrt{10+x}-4)
$$
|
Solution. The domain of definition (DOD) of equation (6): $x \geqslant-1$. Multiplying both sides of equation (6) by the expression $\sqrt{1+x}-1$, we obtain the equation
$$
x(\sqrt{1+x}-\sqrt{10+x}+3)=0
$$
which is a consequence of equation (6). This equation has two roots: $x_{1}=0$ and $x_{2}=-1$ (note that the DOD has not been extended). Both found roots belong to the DOD of equation (6); nevertheless, checking shows that $x_{1}=0$ is an extraneous root of equation (6), while $x_{2}=-1$ satisfies it.
Thus, equation (6) has a unique root $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 25. Solve the equation
$$
\sqrt{4-6 x-x^{2}}=x+4
$$
|
Solution. The given equation is equivalent to the system
$$
\left\{\begin{array}{l}
x+4 \geqslant 0 \\
4-6 x-x^{2}=(x+4)^{2}
\end{array}\right.
$$
i.e., the system
$$
\left\{\begin{array}{l}
x \geqslant-4 \\
x^{2}+7 x+6=0
\end{array}\right.
$$
## 68
Solving the equation \(x^{2}+7 x+6=0\), we find its two roots: \(x_{1}=-1\) and \(x_{2}=-6\). The condition \(x \geqslant-4\) is satisfied only by \(x_{1}=-1\). Therefore, the only root of the original equation is the number \((-1)\).
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 26. Solve the equation
$$
\sqrt{x+5}+\sqrt{2 x+8}=7
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{r}
x+5 \geqslant 0 \\
2 x+8 \geqslant 0
\end{array}\right.
$$
we find the domain of the equation (12): $x \geqslant-4$. We have:
$$
\text { (12) } \begin{aligned}
\Leftrightarrow & \left\{\begin{array}{l}
x \geqslant-4 \\
x+5+2 \sqrt{x+5} \sqrt{2 x+8}+2 x+8=49
\end{array} \Leftrightarrow\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
x \geqslant-4, \\
2 \sqrt{(x+5)(2 x+8)}=3(12-x)
\end{array} \Leftrightarrow\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ x \geqslant - 4 , } \\
{ x \leqslant 1 2 , } \\
{ 4 ( x + 5 ) ( 2 x + 8 ) = 9 ( 1 2 - x ) ^ { 2 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
-4 \leqslant x \leqslant 12, \\
x^{2}-288 x+1136=0
\end{array}\right.\right.
\end{aligned}
$$
Solving the equation $x^{2}-288 x+1136=0$, we find its roots: $x_{1}=284$ and $x_{2}=4$. The condition $-4 \leqslant x \leqslant 12$ is satisfied only by $x_{2}=4$. Therefore, $x=4$ is the only root of equation (12).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Solve the equation
$$
5^{2 x}-2 \cdot 5^{x}-15=0
$$
|
Solution. Let $t=5^{x}$. Then $t^{2}-2 t-15=0$. From this, we find $t_{1}=5, t_{2}=-3$. Thus, the given equation is equivalent to the system of equations
$$
5^{x}=5, \quad 5^{x}=-3
$$
## § 3. EXPONENTIAL EQUATIONS
The second equation of this system has no roots, since $-3<0$ for any $x$, while from the first equation we find that $x=1$ is the only root of the original equation.
An equation of the form
$$
a^{f(x)}=b
$$
where $a>0, a \neq 1, b>0$, can be solved by taking the logarithm of both sides (this is possible since both sides of the equation are positive). Taking the logarithm, we obtain the equation
$$
f(x)=\log _{a} b,
$$
which is equivalent to equation (3).
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 15. Solve the equation
$$
27^{x}+12^{x}=2 \cdot 8^{x}
$$
|
Solution. This equation is similar in appearance to equation (6): the exponent of the bases is the same, but the bases 27, 12, and 8 of the three consecutive terms of a geometric progression do not form one.
Consecutive (but four) terms of a geometric progression are the numbers $27, 18, 12$, and 8. Therefore, we can assume that the term containing $18^{x}$ enters the given equation with a zero coefficient.
We divide all terms of equation (11) by $8^{x}$ and obtain
$$
(3 / 2)^{3 x}+(3 / 2)^{x}=2
$$
Let $t=(3 / 2)^{x}$; then we have the equation $t^{3}+t-2=0$. Since $t^{3}+t-2=(t-1)\left(t^{2}+t+2\right)$, this equation has a unique root $t_{1}=1$. Thus, the original equation is equivalent to the equation
$$
(3 / 2)^{x}=1
$$
the only root of which is $x=0$.
An equation of the form
$$
\alpha \cdot a^{f(x)}+\beta \cdot b^{f(x)}+c=0
$$
where $\alpha, \beta, c$ are real numbers, and the bases $a$ and $b$ are positive numbers that are reciprocals of each other (i.e., $a b=1$), can be solved as follows.
Introduce the variable $t=a^{f(x)}$ and, using the equality $a b=1$, transition from equation (12) to the equation
$$
\alpha t^{2}+c t+\beta=0
$$
Then equation (12) will be equivalent to the combination of two exponential equations:
$$
a^{f(x)}=t_{1}, \quad a^{f(x)}=t_{2},
$$
where $t_{1}, t_{2}$ are the roots of equation (12'). If equation (12') has no solutions, then equation (12) also has no solutions.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 16. Solve the equation
$$
5 \cdot 2^{3 x-3}-3 \cdot 2^{5-3 x}+7=0
$$
|
Solution. Using the properties of exponents, rewrite the given equation as
$$
\frac{5}{8} \cdot 2^{3 x}-\frac{96}{2^{3 x}}+7=0
$$
This equation is of the form (12).
Let $t=2^{3 x}$; then we have $\frac{5}{8} t-\frac{96}{t}+7=0$, i.e., $5 t^{2}+56 t-768=0$. From this, we find $t_{1}=-96 / 5, t_{2}=8$.
Thus, equation (13) is equivalent to the equation
$$
2^{3 x}=8
$$
from which $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Solve the equation:
a) $\log _{x+1}\left(x^{2}-3 x+1\right)=1$
b) $\log _{x}\left(2 x^{2}-3 x-4\right)=2$.
|
Solution. a) The given equation is equivalent to the system
$$
\left\{\begin{array} { l }
{ x + 1 > 0 } \\
{ x + 1 \neq 1 , } \\
{ x ^ { 2 } - 3 x + 1 = x + 1 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>-1 \\
x \neq 0 \\
x^{2}-4 x=0
\end{array} \Leftrightarrow x=4\right.\right.
$$
Therefore, the only root of the equation is the number 4.
b) The original equation is equivalent to the system
$$
\left\{\begin{array} { l }
{ x > 0 , } \\
{ x \neq 1 , } \\
{ 2 x ^ { 2 } - 3 x - 4 = x ^ { 2 } }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ x > 0 , } \\
{ x \neq 1 , } \\
{ x ^ { 2 } - 3 x - 4 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>0, \\
x \neq 1, \\
(x+1)(x-4)=0
\end{array} \Leftrightarrow\right.\right.\right.
$$
Thus, the only root of the equation is the number 4.
An equation of the form
$$
\log _{f(x)} g(x)=\log _{f(x)} h(x)
$$
can be replaced by an equivalent system in two ways.
First method:
$$
\log _{f(x)} g(x)=\log _{f(x)} h(x) \Leftrightarrow\left\{\begin{array}{l}
g(x)>0 \\
f(x)>0 \\
f(x) \neq 1 \\
g(x)=h(x)
\end{array}\right.
$$
102
CH. 2. EQUATIONS WITH ONE UNKNOWN
Second method:
$$
\log _{f(x)} g(x)=\log _{f(x)} h(x) \Leftrightarrow\left\{\begin{array}{l}
h(x)>0 \\
f(x)>0 \\
f(x) \neq 1 \\
g(x)=h(x)
\end{array}\right.
$$
An equation of the form
$$
\log _{g(x)} f(x)=\log _{p(x)} f(x)
$$
can be replaced by an equivalent system in two ways.
First method:
$$
\log _{g(x)} f(x)=\log _{p(x)} f(x) \Leftrightarrow\left\{\begin{array}{l}
f(x)>0 \\
g(x)>0 \\
g(x) \neq 1 \\
g(x)=p(x)
\end{array}\right.
$$
Second method:
$$
\log _{g(x)} f(x)=\log _{p(x)} f(x) \Leftrightarrow\left\{\begin{array}{l}
f(x)>0 \\
p(x)>0 \\
p(x) \neq 1 \\
g(x)=p(x)
\end{array}\right.
$$
Note that the choice of a system equivalent to the given equation is determined by which of the inequalities $g(x)>0$ or $h(x)>0(p(x)>0)$ is easier to solve.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 12. Solve the equation:
a) $\log _{3}(x-2)+\log _{3} x=\log _{3} 8$;
b) $\lg (x-9)+2 \lg \sqrt{2 x-1}=2$;
B) $\frac{1}{2} \log _{5}(x+5)+\log _{5} \sqrt{x-3}=\frac{1}{2} \log _{5}(2 x+1)$.
|
Solution. a) The equation is equivalent to the system
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ x - 2 > 0 , } \\
{ x > 0 , } \\
{ \operatorname { log } _ { 3 } ( x ( x - 2 ) ) = \operatorname { log } _ { 3 } 8 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>2, \\
x>0, \\
x(x-2)=8
\end{array} \Leftrightarrow\right.\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
x>2, \\
(x-4)(x+2)=0
\end{array} \Leftrightarrow x=4\right.
\end{aligned}
$$
Thus, the only root of the original equation is the number 4.
b) The equation is equivalent to the system
$$
\begin{aligned}
\left\{\begin{array}{l}
x-9>0 \\
2 x-1>0, \\
\lg (x-9)(2 x-1)=\lg 100
\end{array}\right. & \Leftrightarrow\left\{\begin{array}{l}
x>9 \\
x>1 / 2, \\
(x-9)(2 x-1)=100
\end{array}\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
x>9 \\
2(x-13)(x+7 / 2)=0
\end{array} \Leftrightarrow x=13\right.
\end{aligned}
$$
Therefore, the only root of the original equation is the number 13.
c) The equation is equivalent to the equation
$$
\log _{5}(x+5)+2 \log _{5} \sqrt{x-3}=\log _{5}(2 x+1)
$$
which is equivalent to the system
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ x - 3 > 0 } \\
{ x + 5 > 0 , } \\
{ \operatorname { log } ( ( x + 5 ) ( x - 3 ) ) = \operatorname { log } _ { 5 } ( 2 x + 1 ) }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>3 \\
x>-5 \\
(x+5)(x-3)=2 x+1
\end{array} \Leftrightarrow\right.\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ x > 3 , } \\
{ x ^ { 2 } - 1 6 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>3 \\
(x-4)(x+4)=0
\end{array} \Leftrightarrow x=4\right.\right.
\end{aligned}
$$
Thus, the only root of the original equation is the number 4.
An equation of the form
$$
\log _{a} \alpha(x)-\log _{a} \beta(x)=\log _{a} f(x)-\log _{a} g(x), \quad a>0, \quad a \neq 1
$$
is equivalent to the equation
$$
\log _{a} \alpha(x)+\log _{a} g(x)=\log _{a} f(x)+\log _{a} \beta(x)
$$
which is equivalent to the system
$$
\left\{\begin{array}{l}
\alpha(x)>0 \\
g(x)>0 \\
f(x)>0 \\
\beta(x)>0 \\
\log _{a}(\alpha(x) g(x))=\log _{a}(f(x) \beta(x))
\end{array}\right.
$$
i.e., the system
$$
\left\{\begin{array}{l}
\alpha(x)>0 \\
g(x)>0 \\
\beta(x)>0 \\
f(x)>0 \\
\alpha(x) g(x)=f(x) \beta(x)
\end{array}\right.
$$
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 15. Solve the equation
$$
\log _{1 / 3}\left(x^{2}+3 x-4\right)=\log _{1 / 3}(2 x+2)
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{l}
x^{2}+3 x-4>0 \\
2 x+2>0
\end{array}\right.
$$
we find the domain of definition (ODZ) of equation (10): $x>1$.
Potentiating equation (10), we obtain the equation
$$
x^{2}+3 x-4=2 x+2
$$
which is a consequence of it.
Equation (11) has two roots: $x_{1}=2$ and $x_{2}=-3$. The number $x_{1}=2$ falls within the ODZ of equation (10) and is therefore its root. The number $x_{2}=-3$ does not fall within the ODZ of equation (10) and is thus an extraneous root.
Thus, the number 2 is the only root of equation (10).
Formulas of logarithms. Let $f$ and $g$ be some functions and $a>0, a \neq 1$. Then, if $f>0$ and $g>0$, we have
$1^{\circ} . \log _{a}(f g)=\log _{a} f+\log _{a} g$.
2.. $\log _{a} \frac{f}{g}=\log _{a} f-\log _{a} g$.
$3^{\circ} . \log _{a} f^{\alpha}=\alpha \log _{a} f$.
$4^{\circ} . \log _{a^{\beta}} f^{\alpha}=\frac{\alpha}{\beta} \log _{a} f$.
Applying any of these formulas formally (without considering the inequalities $f>0$ and $g>0$), one should keep in mind that the domains of definition (ODZ) of the left and right parts of each of them may be different. For example, the expression $\log _{a} f+\log _{a} g$ is defined for $f>0$ and $g>0$, while the expression $\log _{a}(f g)$ is defined both for $f>0, g>0$ and for $f<0, g<0$. Similarly, the ODZ of the left part of formulas $2^{\circ}-4^{\circ}$ may be wider than the ODZ of the right part.
Thus, transforming an equation by formally using formulas $1^{\circ}-4^{\circ}$ "from right to left" leads to an equation that is a consequence of the original equation (its ODZ may be wider). In this case, extraneous roots of the original equation may appear; therefore, at the end of the solution, one must check the membership of each root of the last equation to the ODZ of the original equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 20. Solve the equation
$$
3 x^{\log _{5} 2}+2^{\log _{5} x}=64
$$
|
Solution. The domain of the equation: $x>0$. On this set
$$
x^{\log _{5} 2}=2^{\log _{5} x}
$$
therefore, the given equation is equivalent to the equation
$$
3 \cdot 2^{\log _{5} x}+2^{\log _{5} x}=64
$$
i.e., the equation
$$
2^{\log _{5} x}=16
$$
From this, we get $\log _{5} x=4$, i.e., $x=625$. The number 625 belongs to the domain of the original equation and, therefore, is its only root.
Sometimes it is advisable to take the logarithm of both sides of the equation to reduce its solution to one of the simplest equations. As a rule, this has to be done for mixed-type equations containing both exponential and logarithmic functions.
|
625
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Solve the inequality
$$
\sqrt{6-x}\left(5^{x^{2}-7.2 x+3.9}-25 \sqrt{5}\right) \geqslant 0
$$
|
Solution. The domain of definition of inequality (1) is determined by the condition $6-x \geqslant 0$, i.e., $x \leqslant 6$. Inequality (1) is equivalent to a combination consisting of an equation and a system of two inequalities:
$$
\sqrt{6-x}=0, \quad\left\{\begin{array}{l}
5^{x^{2}-7.2 x+3.9}-25 \sqrt{5} \geqslant 0 \\
x<6
\end{array}\right.
$$
From the equation $\sqrt{6-x}=0$ we find $x=6$.
Since $25 \sqrt{5}=5^{2} \cdot 5^{1 / 2}=5^{2.5}$, the first inequality of the system is equivalent to the inequality
$$
5^{x^{2}-7.2 x+3.9} \geqslant 5^{2.5}
$$
which is equivalent to the inequality
$x^{2}-7.2 x+3.9 \geqslant 2.5 \Leftrightarrow x^{2}-7.2 x+1.4 \geqslant 0 \Leftrightarrow(x-1 / 5)(x-7) \geqslant 0$.
Therefore, the first inequality of the system is equivalent to the combination of simple inequalities
$$
x \leqslant 1 / 5, \quad x \geqslant 7
$$
Considering the condition $x<6$, we obtain the solution of the system, which is the interval $-\infty<x \leqslant 1 / 5$.
Therefore, the solutions of inequality (1) are the number $x=6$ and all numbers in the interval $-\infty<x \leqslant 1 / 5$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 22. Solve the inequality
$$
\left(\sqrt{x^{2}-4 x+3}+1\right) \log _{2} \frac{x}{5}+\frac{1}{x}\left(\sqrt{8 x-2 x^{2}-6}+1\right) \leqslant 0
$$
|
Solution. The domain of admissible values of the original inequality consists of all $x$ satisfying the system
$$
\left\{\begin{array}{l}
x>0 \\
x^{2}-4 x+3 \geqslant 0 \\
8 x-2 x^{2}-6 \geqslant 0
\end{array}\right.
$$
i.e., the system
$$
\left\{\begin{array}{l}
x>0 \\
x^{2}-4 x+3 \geqslant 0 \\
x^{2}-4 x+3 \leqslant 0
\end{array}\right.
$$
It follows that the domain of admissible values consists of all $x$ satisfying the system
$$
\left\{\begin{array}{l}
x>0 \\
x^{2}-4 x+3=0
\end{array}\right.
$$
Since the quadratic equation $x^{2}-4 x+3=0$ has positive roots $x_{1}=1$ and $x_{2}=3$, the domain of admissible values of the original inequality is $x=1$ and $x=3$. The solutions of the original inequality lie within its domain of admissible values; therefore, the solutions are among the numbers 1 and 3.
Let $x=1$. Substituting this value into the left-hand side of inequality (18), we get $\log _{5} \frac{1}{5}+1=-1+1=0$, i.e., the value $x=1$ is a solution of the inequality.
Let $x=3$. Then the left-hand side of the original inequality is
$$
\log _{5} \frac{3}{5}+\frac{1}{3}=\log _{5} 3-1+\frac{1}{3}=\log _{5} 3-\frac{2}{3}=\log _{5} \frac{3}{5^{2 / 3}}
$$
Since $27>25$, then $3>5^{2 / 3}$, i.e., $\frac{3}{5^{2 / 3}}>1$; therefore, $\log _{5} \frac{3}{5^{2 / 3}}>0$. Hence, the value $x=3$ is not a solution of the original inequality.
Thus, the set of solutions of the original inequality consists of the single number $x=1$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find an integer whose cube is equal to the sum of the cubes of the three preceding consecutive numbers.
|
12. Answer. 6. We obtain an interesting identity:
$$
3^{3}+4^{3}+5^{3}=6^{3}
$$
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. The number $n^{k}$ for $k \geqslant 2$ is the sum of $n$ consecutive odd numbers.
|
15. $(2 a+1)+(2 a+3)+\ldots+(2 a+2 n-1)=n^{k}$, $(2 a+n) n=n^{k}, a=\frac{n^{k-1}-n}{2} ;$ for example, for $3^{5}$ we have: $a=$ $=\frac{3^{4}-3}{2}=39 ; 3^{5}=79+81+83$.
|
39
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Find the remainder when the number $50^{13}$ is divided by 7.
|
52. $50^{13}=(49+1)^{13}=49 n+1$ (by the binomial theorem); therefore, the remainder of the division of $50^{13}$ by 7 (and also by 49) is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
98. For what integer values of $x$ is the number $a\left(x^{3}+a^{2} x^{2}+\right.$ $\left.+a^{2}-1\right)$ divisible by 6 for any integer $a$?
As is known, the difference $a^{n}-b^{n}$ is divisible by $a-b$ for any natural number $n$; $a^{n}-b^{n}$ is divisible by $a+b$ for even $n$; $a^{n}+b^{n}$ is divisible by $a+b$ for odd $n$.
Prove the following statements (Nos. 99 - 127):
|
98. $x=3 t$ and $x=3 t-a^{2}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
150. $N=p^{\lambda_{1}} q^{\lambda_{2}}$, where $p$ and $q$ are different prime numbers; $N^{2}$ has 15 divisors. How many divisors does the number $N^{3}$ have?
|
150. Since $N^{2}=p^{2 \lambda_{1}} q^{2 \lambda_{2}}$, then $\left(2 \lambda_{1}+1\right)\left(2 \lambda_{2}+1\right)=15$, from which $\left\{\begin{array}{l}2 \lambda_{1}+1=3 \\ 2 \lambda_{2}+1=5\end{array}, \lambda_{1}=1, \lambda_{2}=2\right.$.
Given that $N^{3}=p^{3 \lambda_{1}} q^{3 \lambda_{2}}$, the number of all divisors of the number $N^{3}$ is $\left(1+3 \lambda_{1}\right)\left(1+3 \lambda_{2}\right)=28$.
|
28
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
153*. The number $N$ has the form $p^{\alpha} q^{\beta} r^{\gamma}$, where $p, q, r$ are prime numbers, and $p q - r = 3, p r - q = 9$; furthermore, the numbers $\frac{N}{p}, \frac{N}{q}, \frac{N}{r}$ have respectively 20, 12, and 15 fewer divisors than the number $N$. Find the number $N$.
14
|
153. From the system $\left\{\begin{array}{l}p q-r=3 \\ p r-q=9\end{array}\right.$, we find $(p+1)(r-q)=6$, hence $\left\{\begin{array}{l}p+1=3 \\ r-q=2\end{array}, p=2 ;\left\{\begin{array}{l}2 q-r=3 \\ r-q=2\end{array}, q=5, r=7\right.\right.$.
The combination $p+1=6$ and $r-q=1$ does not yield the required results. Therefore, the desired number has the form $N=$ $=2^{\alpha} \cdot 5^{\beta} \cdot 7^{\gamma}$. The number of all divisors of $N$ is $(\alpha+1)(\beta+1)(\gamma+1)$.
The number of all divisors for $\frac{N}{2}$ is $\alpha(\beta+1)(\gamma+1)$, for $\frac{N}{5}$ is $\beta(\alpha+1)(\gamma+1)$, and for the number $\frac{N}{7}$ is $\gamma(\alpha+1)(\beta+1)$.
According to the problem, we get the system:
$$
\left\{\begin{array}{l}
(\beta+1)(\gamma+1)=20 \\
(\alpha+1)(\gamma+1)=12 \\
(\alpha+1)(\beta+1)=15
\end{array}\right.
$$
Multiplying, we find $(\alpha+1)(\beta+1)(\gamma+1)=60 ; \quad$ therefore, $\alpha=2, \beta=4, \gamma=3$.
Answer. 857500.
|
857500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
154. a) Find the number if the product of all its divisors is 108.
b) Find the number if the product of its divisors is 5832.
|
154. b) $5832=2^{3} \cdot 3^{6}$; therefore, the required number $A=2^{x} 3^{y}$, where $x<3 ; y<6$. Based on № 151, we find:
$$
\left(2^{x} \cdot 3^{y}\right)^{\frac{1}{2}(x+1)(y+1)}=2^{3} \cdot 3^{6}
$$
From the system $\left\{\begin{array}{l}\frac{x(x+1)(y+1)}{2}=3 \\ \frac{y(x+1)(y+1)}{2}=6\end{array}\right.$, by dividing we find $y=$ $=2 x$; substituting $y=2 x$ into the last equation of the system, we get $x(x+1)(2 x+1)=6$, hence $x=1, y=2$.
Answer. 18.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
160. Find a number of the form $2^{l} 3^{m}$, if the sum of all its divisors is 403.
|
160. $\left(2^{l+1}-1\right)\left(3^{m+1}-1\right)=2 \cdot 13 \cdot 31$. This is only possible when $\left\{\begin{array}{l}2^{l+1}-1=31 \\ 3^{m+1}-1=26\end{array}\right.$
Answer. 144.
|
144
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
162. Find a perfect number of the form $p q$, where $p$ and $q$ are prime numbers.
|
162. $\frac{\left(p^{2}-1\right)\left(q^{2}-1\right)}{(p-1)(q-1)}-p q=p q, \quad q=1+\frac{2}{p-1}, \quad$ from here $p_{1}=2, p_{2}=3, q_{1}=3, q_{2}=2$.
Answer. 6 .
42
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
164. Find a perfect number of the form $p^{2} q$.
|
164. From the equation $\left(p^{2}+p+1\right)(q+1)=2 p^{2} q$, we find $q=1+\frac{2(p+1)}{p^{2}-p-1}$, from which we obtain:
1) $p^{2}-p-1=1, p=2, q=7$
2) $p^{2}-p-1=2$, no solutions.
Moreover, the numbers $p+1$ and $p^{2}-p-1$ have no common divisors, since $\gcd \left(p+1, p^{2}-p-1\right)=\gcd[p(p+1), p^{2}-p-1]=\gcd(2 p+1, p+1)=\gcd(p, p+1)=1$.
Answer. 28.
|
28
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
166. Find a perfect number of the form $16 p$.
Note: The translation maintains the original text's line breaks and format.
|
166. From the equation $31(p+1)=32 p$ we find $p=31$.
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.