problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
171. Find $\varphi(360)$.
|
171. $\varphi(360)=\varphi\left(2^{3} \cdot 3^{2} \cdot 5\right)=360\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)=$ $=96$.
|
96
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
179. Find $N=p^{3}$, if $\varphi(N)=100$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
179. From the equation $p^{3}\left(1-\frac{1}{p}\right)=100$ we get $p^{2}(p-1)=$ $=25 \cdot 4$, from which it is clear that $p=5$.
We can also do it this way: $p^{3}-p^{2}-100=0, p^{3}-125-\left(p^{2}-25\right)=$ $=0,(p-5)\left(p^{2}+4 p+20\right)=0$, from which $p=5$.
Answer. 125.
|
125
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
180. Find $N=p q$, if $\varphi(N)=120$, and the numbers $p$ and $q$ are twin prime numbers, i.e., $p-q=2$.
|
180. From the system of equations $\left\{\begin{array}{l}p q\left(1-\frac{1}{p}\right)\left(1-\frac{1}{q}\right)=120 \\ p-q=2\end{array}\right.$ we find $p=13, q=11$.
Answer. 143.
|
143
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
262. Find a triangular number whose square is also a triangular number.
|
262. From the equation $\left[\frac{x(x+1)}{2}\right]^{2}=\frac{y(y+1)}{2}$, we find:
$$
y=\frac{-1+\sqrt{2 x^{2}(x+1)^{2}+1}}{2}
$$
Let $x(x+1)=z$, then $2 z^{2}+1=t^{2}, t^{2}-2 z^{2}=1$.
Solving this Pell's equation, we get an infinite set of values $z=2,12,70,408 \ldots$. From the equation $x(x+1)=2$, we have $x=1$, the corresponding triangular number is 1. From the equation $x(x+1)=12$, we find $x=3$, the triangular number will be 6. The values $z=70$ and $z=408$ do not lead to triangular numbers.
60
It has been proven that, apart from 1 and 6, there are no triangular numbers that satisfy the requirement of the problem.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
272. Find a three-digit number that is equal to the sum of the tens digit, the square of the hundreds digit, and the cube of the units digit.
$273 *$. Find the number $\overline{a b c d}$, which is a perfect square, if $\overline{a b}$ and $\bar{c} \bar{d}$ are consecutive numbers, with $\overline{a b}>\overline{c d}$.
|
272. $100 x+10 y+z=y+x^{2}+z^{3}$, from here $9 y=(z-$ $-1)(z+1) z+x^{2}-x-99 x, \quad(z-1) z(z+1)+x(x-1)$ must be divisible by 9; since $z(z-1)(z+1)$ is divisible by $3, x(x-1)$ is also divisible by 3, therefore, $x=1$, $3,4,6,7,9$.
When $x=3 y=\frac{z^{3}-z-291}{9}, z^{3}>z+291$, hence $z=7$, 8,9, but only when $z=7$ the number $\frac{z^{3}-z-291}{9}$ will be an integer; therefore $z=7, y=5$. The desired number is 357.
Verification. $357=5+3^{2}+7^{3}$.
Let $x=4$, then $y=\frac{z^{3}-z-384}{9},$ therefore, $z^{3}>z+384$, hence $z=8,9$, but for these values of $z$ we do not get an integer for $y$. Considering the values $x=6,7,9,1$, we will not find valid values for $y$ and $z$.
Answer. 357.
|
357
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
277. Find a two-digit number that is equal to the sum of the cube of its tens digit and the square of its units digit.
|
277. From the equality $10 x+y=x^{3}+y^{2}$ we find $x(10-$ $\left.-x^{2}\right)=y(y-1)$, hence $0<x<\sqrt{10}$; therefore, $x=1$, 2,3 ; but $y(y-1)$ is an even number, so $x$ is also even; $x=2$, then $y=4$.
Answer. 24.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
283. Find a number of the form $7 x 36 y 5$, divisible by 1375.
|
283. Answer. 713625.
|
713625
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
288. What whole number should the number 999999999 be multiplied by to get a number consisting of all ones.
|
288. We have $999999999=10^{9}-1,\left(10^{9}-1\right) x=\frac{10^{k}-1}{9}$; $x=\frac{10^{k}-1}{9\left(10^{9}-1\right)}$.
To make $x$ an integer, it is sufficient to take $k=81$; indeed, $x=\frac{10^{81}-1}{9\left(10^{9}-1\right)}=\frac{\left(10^{9}\right)^{9}-1}{9\left(10^{9}-1\right)}=\frac{\left(10^{9}\right)^{8}+\left(10^{9}\right)^{7}+\ldots+1}{9}$; since the sum of the digits of the numerator is 9, $x$ is an integer.
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
296. The difference between a number and the product of its digits is equal to the sum of the digits of this number. Find this number.
## Chapter $I X$.
## VARIOUS PROBLEMS
|
296. Let the desired number contain $n$ digits $a, b, c$, $\ldots, k, l$. According to the condition $a \cdot 10^{n-1}+b \cdot 10^{n-2}+\ldots+$ $+k \cdot 10+l-a b c d \ldots k l=a+b+c+\ldots+k+l, \quad$ from which $9 k=a\left(b c \ldots k l+1-10^{n-1}\right)+b\left(1-10^{n-2}\right)+c\left(1-10^{n-3}\right)+$ $+\ldots(1)$.
In the general case, this equality is impossible. Indeed,
$$
b c \ldots k l-\left(10^{n-1}-1\right)<10^{n-1}-\left(10^{n-1}-1\right)
$$
$b c \ldots k l-\left(10^{n-1}-1\right)<1$; since $b c \ldots k l-\left(10^{n-1}-1\right)-$ is an integer, not equal to zero, it is negative; thus, the right side of equality (1) is negative, while the left side is non-negative.
The only possible case is $n=2$ (by the problem's meaning $n \neq 1$), then $10 a+b-a b=a+b$, from which $b=9 ; a-$ is any digit (not zero). The problem is satisfied by two-digit numbers ending in 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
315. The numbers $2 \overline{a c}+1$ and $3 \overline{a c}+1$ are perfect squares. Find $\overline{a c}$.
|
315. First method. By setting $\overline{a c}=x$, we obtain the system $\left\{\begin{array}{l}2 x+1=y^{2} \\ 3 x+1=z^{2}\end{array}\right.$, i.e., $\frac{y^{2}-1}{2}$ and $\frac{z^{2}-1}{3}$ represent equal integers.
It is easy to find $x=2 t^{2}+2 t$ and $x=3 t_{1}^{2} \pm 2 t_{1}$. According to the problem's condition, we get $\left\{\begin{array}{l}2 t^{2}+2 t>9 \\ 2 t^{2}+2 t<100\end{array}\right.$ and $\left\{\begin{array}{l}3 t_{1}^{2} \pm 2 t_{1} \geq 9 \\ 3 t_{1}^{2} \pm 2 t_{1}<100\end{array}\right.$, from which we find $x=12,24,40,60,84 ; x=21,40,65$, $96,16,33,56,85$.
From this, we conclude that $\overline{a c}=40$.
Second method. Excluding $x$ from the system $\left\{\begin{array}{l}2 x+1=y^{2} \\ 3 x+1=z^{2}\end{array}\right.$, we find the equation $3 y^{2}-2 z^{2}=1$.
Solving this equation using the method indicated in № 266, we get $y=9, z=11$, hence $x=40$.
|
40
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
320. At the end of 1960, a student arrived at the school. When asked about his age, he replied: “My age is equal to the sum of the digits of the year of my birth.” How old is the student?
|
320. Given the school age, we can write the year of birth as $1900+10 x+y$. According to the problem, $1960-(1900+10 x+y)=1+9+x+y$, or $11 x + 2 y=50$ (1), from which it is clear that $x=2 x_{1}$, then $y=25-11 x_{1}$.
From the system of inequalities $\left\{\begin{array}{l}25-11 x_{1} \geqslant 0 \\ 25-11 x_{1}<10\end{array}\right.$ we find $x_{1}=2$, $x=4, y=3$.
The year of birth is 1943, age 17 years.
We can also reason as follows. According to the problem, $x$ equals 4 and 5. But from (1) it is clear that $x$ is even, therefore, $x=4, y=3$.
|
17
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
329. The number $a^{100}$ when divided by 73 gives a remainder of 2, and the number $a^{101}$ when divided by the same number gives a remainder of 69. Find the remainder of the number $a$ when divided by 73.
|
329. $a^{100}=73 m+2$, from which $a^{101}=73 n+2 a$ (1). In addition, $a^{101}=73 q+69(2)$. From (1) and (2) we find $73 k+2 a=$ $=69(3)$.
Noting that equation (3) is satisfied by the values $k=1$ and $a=-2$, we get $a=73 t-2$, which can be written as: $a=73 t+71$. The required remainder is 71.
|
71
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
331. Find the last two digits of the number $137^{42}$.
|
331. The problem reduces to finding the remainder of the division of the number $137^{42}$ by 100. Since 137 and 100 are coprime, $137^{\varphi(100)}-1$ is divisible by $100, \quad$ but $\varphi(100)=$ $=100\left(1-\frac{1}{2}\right)\left(1-\frac{1}{5}\right)=40 ; \quad$ therefore, $\quad 137^{40}-1$ is divisible by 100. Hence, $137^{42}=137^{2}\left(137^{40}-1\right)+137^{2}=$ $=137^{2} \cdot\left(137^{40}-1\right)+(100+37)^{2}=100 n+37^{2}=100 n+$ $+1369=100 n+1300+69$, from which it is immediately clear that the desired remainder is 69.
|
69
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
333. Find the remainder of the division of the number $\left(85^{70}+19^{32}\right)^{16}$ by 21.
|
333. $85^{70}=(84+1)^{70}=21 n+1$; since $\varphi(21)=12$, then $19^{12}-1$ is divisible by 21; therefore, $19^{32}=$ $=19^{8}\left(19^{24}-1\right)+19^{8}=21 m+19^{8} . \quad$ Therefore $\quad\left(85^{70}+\right.$
$.\left.+19^{32}\right)^{16}=\left(21 n+1+21 m+19^{8}\right)^{16}=[21 k+1+(21-$
$.\left.-2)^{8}\right]^{16}=\left(21 q+1+2^{8}\right)^{16}=(21 r+5)^{16}=21 t+5^{16}=$
$=21 t+5^{4}\left(5^{12}-1\right)+5^{4}=21 t+21 r+625=21 u+16$.
The required remainder is 16.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
335. Find the last two digits of the number $3^{5^{17}}$.
|
335. Answer. 43.
Hint. The last digit of the number $a^{n}(n>4)$ is the same as the last digit of the number $a^{r}$, where $r>0$ is the remainder of the division of $n$ by 4; if $r=0$, then the last digit of the number $a^{n}$ coincides with the last digit of the number $a^{4}$ (see № 89). If $(a, 10)=1$, then the last two digits of the number $a^{n}(n>40)$ are the same as the last two digits of the number $a^{r}$, where $r$ is the non-zero remainder of the division of $n$ by 40; if $r=0$, then the last two digits of the number $a^{n}$ are the same as the last two digits of the number $a^{40}$. It is recommended that readers prove the last statement.
|
43
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Bank Check. A person came to the bank to get money by check. The cashier, paying the check, made a mistake and instead of the dollars owed, gave the same number of cents and accordingly, instead of cents - dollars. The person, without counting the money, put it in their pocket, and even dropped a 5 cent coin, and upon arriving home, discovered that they had exactly twice as much money as was stated on the check. For what amount was the check issued?
|
1. The check was issued for the amount of 31 dollars and 63 cents. The person received 63 dollars and 31 cents. After losing a five-cent coin, 63 dollars and 26 cents remained, which is twice the amount specified on the check.
|
31
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Charity. A generous person distributed the same amount of money equally among those who asked him for assistance every week. One day he noticed:
- If the number of petitioners is five less next week, each will receive two dollars more.
But, alas, after a week, the number of petitioners did not decrease but increased by four.
- This means,--the benefactor noted,--that each will receive one dollar less.
How much did each petitioner receive this last time?
|
4. At first, there were 20 people and each received 6 dollars. Fifteen people (five fewer) would have received 8 dollars each. But their number increased to 24 (by four people), and each received only 5 dollars. Thus, the weekly donation amount is 120 dollars.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The "Reverse" Game. Seven friends decided to play cards by somewhat unusual rules. The one who won had to pay each of the other players as much money as they had in their pocket. The players played seven rounds and, strangely enough, they won in alphabetical order of their names, starting with $A, B, C, D, E, F$ and $G$.
After finishing the game, the friends discovered that each of them had exactly 1 dollar and 28 cents left. How much money did each player have before the game started?
|
8. Players \(A, B, C, D, E, F\) and \(G\) had, before the game began, 4 dollars 49 cents, 2 dollars 25 cents, 1 dollar 13 cents, 57 cents, 29 cents, 15 cents, and 8 cents, respectively. The answer can be obtained by working from the end of the problem to the beginning, but a simpler method is as follows: \(7+1=8 ; 2 \times 7+1=15 ; 4 \times 7+1=29\) and so on (the first multipliers represent successive powers of two, that is, the numbers \(2,4,8,16,32\) and 64\()\).
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Seven apple vendors. Seven vendors had 20, 40, 60, 80, 100, 120, and 140 apples respectively. They went to the market and sold all their apples at the same price, earning the same revenue. At what price did the vendors sell the apples?
|
12. All seven vendors sold apples at 1 cent for 7 pieces; in cases where fewer than seven apples remained, they were sold at 3 cents per piece. Thus, each vendor earned 20 cents. Without in any way disputing the ingenuity of this problem, I have always found its solution unsatisfactory due to its ambiguity, even if we assume that with such an eccentric method of trading, one can speak of a single "price" for apples. We could just as well assume that the vendors sell apples at one price but with different discounts; sell apples of different varieties at different prices; sell at one price per basket; sell by weight, while the apples are of different sizes; reduce the price for less fresh apples, etc.
In general, we can say that \(n\) vendors, who have \(n a+(n-1), n(a+b)+(n-2), n(a+2 b)+(n-3), \ldots\), \(n[a+b(n-1)]\) apples respectively, can sell them in bunches of \(n\) pieces for 1 cent, and the remaining apples for \(b\) cents each, and each of the vendors will earn \(a+b(n-1)\) cents. In the case of our problem, \(a=2, b=3, n=7\).
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Distribution of Money. Nine friends $A, B, C, D, E, F, G$, $H, K$, gathering one evening to spend time together, did the following. First, $A$ gave each of the other eight people as much money as they already had. Then $B, C$, and so on up to $K$ did the same. After this, it turned out that all nine friends had the same amount of money.
Can you find the smallest sum in cents that each of the participants could have had initially?
|
18. The smallest sum (in cents) that one of the participants could have must exceed the number of participants by one. The sums belonging to the other participants can be found by sequential doubling and subtracting 1. Thus, we get \(10,19,37,73,145,289,577,1153\) and 2305 cents. Let the one with the most money start first. Then, in the end, each participant will have \(2^{9}\) (512) cents, that is, 5 dollars and 12 cents.
|
512
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Horses and Oxen. A livestock trader bought a certain number of horses at $344 each and a certain number of oxen at $265 each. He found that the total cost of the horses was $33 more than the total cost of the oxen. What is the smallest number of horses and oxen he could have bought under these conditions?
|
20. The task reduces to solving the indeterminate equation \(344 x=265 y+33\). The methods for solving such equations are well known, so we will not dwell on them. Solving the equation, we find that \(x=252\) and \(y=327\). Thus, if the trader buys 252 horses for 344 dollars each and 327 oxen for 265 dollars each, the horses will cost him 33 dollars more than the oxen.
|
252
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. The Unfortunate Grocer. A grocer, the owner of a small shop, decided to set aside a small amount of money - all in dollar bills and coins of fifty cents and twenty-five cents. He distributed the entire amount into 8 bags, so that in each bag there was the same number of dollar bills and coins of each denomination. One evening, the grocer decided to redistribute all this money into 7 bags so that the number of dollar bills and coins of each denomination remained equal in all bags. The next evening, he similarly redistributed all the money into 6 bags.
Then the unfortunate madman tried to redistribute everything into 5 bags, but after hours of hard work, he died in complete exhaustion, bitterly mourned by his neighbors. What is the smallest amount of money that the grocer could have set aside for a rainy day?
|
22. The grocer set aside 168 paper dollars, 168 half-dollar coins, and 168 quarter-dollar coins for a rainy day, totaling 294 dollars. In each of the six bags, there should be 28 monetary units of each type; in each of the seven bags, 24; and in each of the eight bags, 21 monetary units of each type.
|
294
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. The League of Red Death. During a raid on the headquarters of a secret organization, the police found a scrap of paper, depicted in the image.

- "I've been working on this piece of paper for three days now," the detective said. "It shows the total amount of membership fees for this year: $3007.37, but the number of members (I know there are no more than 500) and the amount of one fee are obscured so that they cannot be read. How many members are there in the League of Red Death, and what is the amount of the membership fee?"
Of course, the fee cannot contain fractional cents.
|
24. The total amount of contributions, expressed in cents, is 300737. This number can be represented as the product of two prime factors: 311 and 967. Since we know that the League of Red Death has no more than 500 members, the number of members is 311, and the contribution is 967 cents, or 9 dollars and 67 cents.
There can be no other solutions.
|
311
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. Boys and Girls. Nine boys and three girls decided to share their pocket money equally. Each boy gave the same amount to each girl, and each girl also gave the same amount (but a different one) to each boy. After this, all the children had the same amount of money. What is the smallest amount of money that each of them could have had initially?
|
26. Each boy initially had 12 cents, and he gave 1 cent to each girl. Each girl had 36 cents, from which she gave 3 cents to each boy. After this, each child had 18 cents.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46. The Clocks from the Land of Dreams. In a dream, I traveled to a country where wondrous things happened. One incident was so memorable that I didn't forget it even after I woke up. In my dream, I saw a clock and spoke aloud the time it showed, but my guide corrected me. He said:
- Clearly, you don't know that our minute hands always move in the direction opposite to the hour hands. In every other way, our clocks are exactly the same as the ones you are used to.
If at the moment I was looking at the clock, both hands coincided and were between the four and five o'clock marks, and at noon they both pointed to XII, then what time was it on a regular clock?
|
46. If these were ordinary clocks, they would show 4 hours \(23 \frac{1}{13}\) minutes. But since the minute hand moved in the direction opposite to the hour hand, the true time was 4 hours \(36 \frac{12}{13}\) minutes. To get the true time, you need to subtract from 60 the number of minutes that the clock shows.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
48. Indistinguishable Clock Hands. A person had a clock on which it was impossible to distinguish the hour hand from the minute hand. If this clock was started at noon, when would it first be impossible to tell the exact time?
The reader should remember that in such clock puzzles, there is a convention that we are able to determine fractions of a second. With this assumption, an exact answer can be given.
|
48. This will first occur at 12 hours \(5 \frac{5}{143}\) minutes, which could be incorrectly interpreted (due to the identical positions of the hands) as 1 hour \(\frac{60}{143}\) minutes.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 51. Mixed-Up Hands.
- Yesterday, between two and three o'clock, - said Colonel Crackham, - I looked at my watch and, mistaking the hour hand for the minute hand, I was wrong in my estimate of the time. The erroneous time was 55 minutes less than the actual time. What was the actual time?
|
51. The true time was 2 hours \(5 \frac{5}{11}\) minutes.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Equal Distances. A few days ago, Professor Rackbrain stunned his students with the following puzzle:
- When between three and four o'clock is the minute hand at the same distance from VIII as the hour hand is from XII?
|
52. At 3 hours \(23 \frac{1}{13}\) minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. To the right and to the left. At what time between three and four o'clock is the minute hand the same distance to the left of XII as the hour hand is to the right of XII?
|
53. At 3 hours \(41 \frac{7}{13}\) minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54. At a Right Angle. Once during breakfast, Professor Rackbrain asked his young friends a simple question:
- When between five and six o'clock will the hour and minute hands be exactly at a right angle?
|
54. For the angle between the hands to be a right angle, the minute hand must be exactly 15 minutes ahead of or behind the hour hand. Each of these positions will occur 11 times in 12 hours, that is, every 1 hour \(5 \frac{5}{11}\) minutes. If eight such intervals pass after 9 o'clock, the clock will show 5 hours \(43 \frac{7}{11}\) minutes. On the other hand, if two such intervals pass after 3 o'clock, we get 5 hours \(10 \frac{10}{11}\) minutes. These are the two moments in time,
\footnotetext{
* Here M. Gardner is not entirely correct, as Dudeney considers IX as a combination of two digits: I and X.
}
that were required to find in the problem, with the second moment, of course, occurring earlier than the first.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 57. The Speed of a Car.
- I was walking down the road at a speed of $3 \frac{1}{2}$ km/h,- said Mr. Pipkins,- when suddenly a car sped past me, nearly knocking me off my feet ${ }^{2}$.
- How fast was it going? - asked his friend.
- I'll tell you. From the moment it sped past me until it disappeared around the bend, I took 27 steps and then, without stopping, I walked another 135 steps to reach the bend.[^4]- Then we can easily determine the speed of the car, assuming that our speeds were constant.
|
57. Since a person takes 27 steps in the time it takes a car to travel a distance of 162 steps, it is clear that the car is moving 6 times faster than the person. The person moves at a speed of \(3 \frac{1}{2}\) km \(/ h\); therefore, the speed of the car is 21 km \(/ h\).
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
59. A Walk. One man set out for a walk from Appleminster to Boniham at noon, and his friend left Boniham for Appleminster at two o'clock of the same day. On the way, they met. The meeting took place at five minutes to five, after which the friends arrived simultaneously at their final destinations. When did they finish their journey
|
59. It should be noted (and this is the key to the solution) that the person from B. covers 7 km in the same time that the person from E. covers 5 km. Let's assume, for example, that the distance between the cities is 24 km, then they met 14 km from E. The person from E. was moving at a speed of \(3 \frac{3}{7}\) km/h, and the person from B. - at a speed of \(4 \frac{4}{5}\) km/h. Both completed their journey at 7 p.m.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
62. Escalator. While on one of the escalators in the London Underground, I found that by walking 26 steps, I would reach the platform in $30 \mathrm{s}$. But if I walked 34 steps, the entire descent would take 18 s. How many steps are there on the escalator? Time is measured from the moment the top step begins to descend until I step off the last step onto the platform.
|
62. If I walk down 26 steps, it will take me 30 seconds to descend, and if 34, it will take -18 seconds. Multiplying 30 by 34 and 26 by 18, we get 1020 and 468, the difference between these numbers is 552. Dividing this by the difference between 30 and 18 (that is, by 12), we get 46, the number of steps on the escalator, which moves at a speed of 1 step per \(1 \frac{1}{2}\) seconds. The speed at which I move on the escalator does not matter, since the step I step off reaches the platform at the same moment regardless of what I did before.
|
46
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. Motorcycle with a sidecar. Atkins, Baldwin, and Clark decided to go on a trip. Their journey will be 52 km. Atkins has a motorcycle with a one-person sidecar. He needs to take one of his companions for some distance, drop him off to walk the rest of the way, return, pick up the other companion who started walking at the same time, and continue so that all three arrive at the destination at the same time. How can this be done?
The motorcycle's speed is 20 km/h, Baldwin can walk at a speed of 5 km/h, and Clark at 4 km/h. Of course, each one tries to move as quickly as possible and does not stop anywhere along the way.
The problem could be made more complex by introducing more passengers, but in our case, it is so simplified that even all distances are expressed in whole kilometers.
|
65. Atkins drives Clark 40 km and drops him off to walk the remaining 12 km. Then he returns and picks up Baldwin 16 km from the start and drives him to the end. The three of them spend 5 hours on the road. Another solution is for Atkins to first drive Baldwin 36 km and return for Clark, who by this time has walked 12 km. In both cases, the motorcycle has traveled 100 km, including 24 km without passengers.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
68. From Pickleminster to Quickville. Trains $A$ and $B$ depart from Pickleminster to Quickville at the same time as trains $C$ and $D$ depart from Quickville to Pickleminster. Train $A$ meets train $C$ 120 miles from Pickleminster and train $D$ 140 miles from Pickleminster. Train $B$ meets train $C$ 126 miles from Quickville, and train $D$ at the halfway point between Pickleminster and Quickville. What is the distance from Pickleminster to Quickville? All trains travel at constant speeds, not too different from the usual.
|
68. There are two distances that satisfy the condition of the problem - 210 and 144 miles. The latter case is excluded, as the problem states that the trains move at speeds "not too different from the usual." (If we had taken the distance to be 144 miles, then \(A\) would have traveled 140 miles in the same time that \(B\) and \(D\) traveled 4 miles. So if the latter were traveling at 2 miles/hour, then the former would be traveling at 70 miles/hour, a speed that certainly cannot be called "not too different from the usual"!) If the distance is 210 miles, it turns out that the speeds of \(B\) and \(D\) are half the speed of \(A\), and the speed of \(C\) is \(\frac{3}{4}\) of the speed of \(A\), which seems quite reasonable.
|
210
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69. Faulty Locomotive. We set off by railway from Angchester to Clinkerton. But an hour after the train started, a locomotive malfunction was discovered. We had to continue the journey at a speed that was $\frac{3}{5}$ of the original. As a result, we arrived in Clinkerton 2 hours late, and the driver said that if the malfunction had occurred 50 miles further, the train would have arrived 40 minutes earlier.
What is the distance from Angchester to Clinkerton?
|
69. The distance from Angchester to Clinkerton is 200 miles. The train traveled 50 miles at a speed of 50 miles/h and 150 miles at a speed of 30 miles/h. If the breakdown had occurred 50 miles further, the train would have traveled 100 miles at a speed of 50 miles/h and 100 miles at a speed of 30 miles/h.
|
200
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
72. Determine the distance. Jones set out from $A$ to $B$ and on the way, 10 km from $A$, he met his friend Kenward, who had set out from $B$ at the same time as him. Upon reaching $B$, Jones immediately turned back. Kenward did the same upon reaching $A$. The friends met again, but this time 12 km from $B$. Of course, each walked at a constant speed. What is the distance between $A$ and $B$?
There is a simple rule that anyone can use to find the required distance mentally in a few seconds. If you know how to proceed, the problem is solved with unusual ease.
|
72. The distance between two points is 18 km. The meeting points are 10 km and 12 km away from \(A\) and \(B\) respectively. Multiply 10 (the first distance) by 3 and subtract the second distance -12. What could be simpler? Try other distances to the meeting points (making sure the first distance is more than \(\frac{2}{3}\) of the second) and you will find that this rule works with unfailing success.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 73. Man and Dog.
- Walking the dog, - a mathematician friend once told me, - gives me plenty of food for thought. Once, for example, my dog, after waiting for me to go out, looked to see which way I was going to head, and when I started down the path, he raced to the end of it. Then he returned to me, ran to the end of the path again, and returned, and so on, doing this 4 times in total. All this time he moved at a constant speed, and when he ran to me for the last time, he covered the remaining distance of 81 m. Measuring the distance from my door to the end of the path later, I found it to be 625 m. At what speed did my dog run, if I was walking at a speed of 4 km/h?
|
73. The dog ran at a speed of 16 km/h. The key to solving the problem lies in the following considerations. The distance the man had left to walk alongside the dog was 81 m, or \(3^{4}\) (the dog returned 4 times), and the length of the path was \(625 \mathrm{m}\), or \(5^{4}\). Therefore, the difference in speeds (expressed in km/h) between the man and the dog (i.e., 12) and the sum of their speeds (20) should be in the ratio \(3: 5\).
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
74. Baxter's Dog. Here is an interesting puzzle, complementing the previous one. Anderson left the hotel in San Remo at 9 o'clock and was on the road for a whole hour when Baxter set out after him along the same route. Baxter's dog ran out at the same time as its owner and kept running back and forth between him and Anderson until Baxter caught up with Anderson. Anderson's speed is 2 km/h, Baxter's is 4 km/h, and the dog's is 10 km/h. How many kilometers did the dog run by the time Baxter caught up with Anderson?
The reader who sent me this problem, being a meticulous person, deemed it necessary to specify that "the length of the dog and the time spent turning can be neglected." I would add, on my part, that the dog's name and the day of the week can equally be neglected.
|
74. It is quite obvious that Baxter will catch up with Anderson in one hour, by which time they will have each traveled 4 km in the same direction. Furthermore, the dog’s speed is 10 km/h; therefore, in this hour, it will have run 10 km! When this puzzle was presented to a French mathematics professor, he exclaimed, “Mon Dieu, quelle série!”*, completely failing to notice how simple it was to solve.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
75. Исследование пустыни. Девять участников экспедиции (каждый на автомашине) встречаются на восточной окраине пустыни. Они хотят исследовать ее внутренние районы, двигаясь все время на запад. Каждому автомобилю полного бака (содержащего 1 галлон бензина) хватает на 40 миль пути. Кроме того, он может взять с собой еще 9 канистр бензина по галлону каждая (но не больше). Целые канистры можно передавать с одного автомобиля на другой. На какое максимальное расстояние исследователи могут проникнуть в пустыню, не создавая складов топлива, необходимого для возвращения назад
|
75. Девять исследователей \(A, B, C, D, E, F, G, H, J\) проезжают 40 миль, затратив на это по полному баку горючего. Затем \(A\) передает по 1 галлону остальным восьми участникам и поворачивает назад, причем у него остается 1 галлон на обратную дорогу. Остальные восемь участников едут еще 40 миль, затем \(B\) передает по 1 галлону семи другим исследователям. Двух галлонов ему как раз хватает на обратный путь. Семеро исследователей проезжают еще 40 миль, затем \(C\) передает остальным шести по 1 галлону и возвращается домой, затратив на обратный путь 3 галлона. Шестеро исследователей проезжают еще 40 миль, после чего \(D\) передает каждому по 1 галлону и возвращается назад. Пятеро оставшихся проезжают еще 40 миль, затем \(E\) дает каждому по 1 галлону и возвращается назад. Теперь уже четверо исследователей продвигаются еще на 40 миль в глубь пустыни, \(F\) раздает каждому по 1 галлону и возвращается назад. \(G, H, J\) преодолевают еще 40 миль, \(G\) дает каждому по 1 галлону и едет назад. \(H\) и \(J\) проезжают еще 40 миль, \(H\) отдает 1 галлон \(J\) и возвращается. Наконец, последний путешественник \(J\) проезжает еще 40 миль, располагая 9 галлонами на обратный путь. Таким образом, \(J\) достигает пункта, расположенного в 360 милях от начального. Это наибольшее расстояние, которое можно проехать по прямой при заданных условиях.
|
360
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
78. The Walking Passenger. The train is moving at a speed of 60 km/h. A passenger is walking from the end of the train to its beginning through the passageways between the cars at a speed of 3 km/h. What is the speed of the passenger relative to the railway track?
We are not going to engage in sophistry here, like Zeno's paradox of the flying arrow, or Einstein's theory of relativity, but are talking about movement in the ordinary sense of the word relative to the railway track.
|
78. Suppose a train travels for an hour and has an incredible length of 3 km. Then (see figure) in this time it will travel from \(B\) to \(C\) 60 km, while the passenger will move from \(A\) to \(C\), or 63 km. C
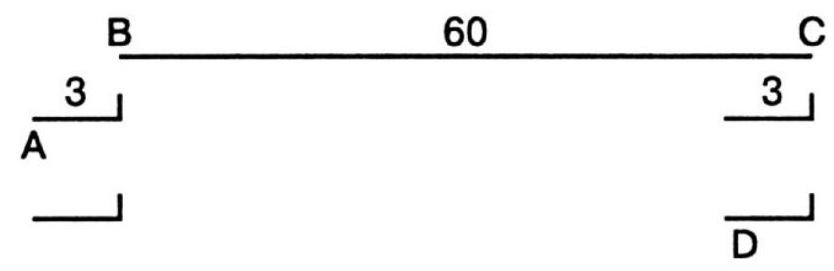
On the other hand, if the passenger walked from the locomotive to the end of the train, the train would have traveled the distance from \(B\) to \(C\) (again 60 km), while the passenger would have moved only the distance from \(B\) to \(D\), that is, 57 km. Therefore, in the first case, the passenger's speed relative to the railway track is 63, and in the second case, \(-57 \mathrm{km} /\) h \(^{*}\).
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
79. Oncoming Trains. At Wurzltown station, an old lady, looking out the window, shouted:
- Conductor! How long is it from here to Madville?
- All trains take 5 hours in either direction, ma'am, - he replied.
- And how many trains will I meet on the way?
This absurd question puzzled the conductor, but he readily answered:
- Trains from Wurzltown to Madville and from Madville to Wurzltown depart at five minutes past one, five minutes past two, and so on, with an interval of exactly one hour.
The old lady made one of her fellow passengers in the compartment find the answer to her question.
So how many trains will she meet on the way?
|
79. Since the train travels for 5 hours, we will divide the journey into 5 equal intervals. When the lady departs from Wurzeltown, 4 oncoming trains are already en route, and the fifth one is just leaving the station. She will meet each of these 5 trains. When the lady has traveled \(\frac{1}{5}\) of the distance, a new oncoming train will depart from Madville, when she has traveled \(\frac{2}{5}\) of the distance - another one, \(\frac{3}{5}\) - another one, \(\frac{4}{5}\) - another one, and finally, when she arrives in Madville, another, the fifth, train will be just departing from there. If we assume, as we should, that
\footnotetext{
* The answer follows directly from the theorem of velocity addition in mechanics, and the author's solution is merely an explanation of this theorem for the specific case under consideration.
}
she does not meet the last train "on the way" or the one that arrived in Wurzeltown when her train departed from there, then on the way from Wurzeltown to Madville, the lady will meet 9 trains.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 81. Escalator.
- Descending on the escalator, I counted 50 steps, - said Walker.
- I counted 75, - objected Trotman, - but I was going down three times faster than you.
If the escalator had stopped, how many steps could be counted on its visible part? It is assumed that both people moved at a constant speed and that the speed of the escalator was constant.
|
81. Let \(n\) be the number of steps on the escalator; the time it takes for one step to disappear at the bottom, we will take as a unit.
Trotman walks 75 steps in \(n-75\) units of time, or at a speed of 3 steps in \(\frac{n-75}{25}\) units of time. Therefore, Walker covers 1 step in \(\frac{n-75}{25}\) units of time. But he also covers 50 steps in \(n-50\) units of time, or 1 step in \(\frac{n-50}{50}\) units of time. Therefore, \(\frac{n-50}{50}=\frac{n-75}{25}\), from which \(n=100\).
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. The Fly and the Cars. The length of the road is 300 km. Car $A$ starts at one end of the road at noon and moves at a constant speed of 50 km/h. At the same time, at the other end of the road, car $B$ starts at a constant speed of 100 km/h and a fly, flying at 150 km/h. Upon meeting car $A$, the fly turns and flies towards $B$.
1) When will the fly meet $B$?
2) If, upon meeting $B$, the fly turned, flew towards $A$, met him, turned again, and continued flying back and forth between $A$ and $B$ until they collided, when would the cars crush the fly?
|
85. 1) The fly will meet \(B\) in 1 hour 48 minutes.
2) There is no need to determine the distance the fly will fly. This is too difficult a task. Instead, we can simply find the time when the cars could have collided, which is 2 hours. In reality, the fly flies (in kilometers):
\[
\frac{270}{1}+\frac{270}{10}+\frac{270}{100}+\frac{270}{1000}+\cdots \text { to infinity; }
\]
the sum of this infinite decreasing geometric progression is 300 km.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
86. Metro Stairs. Once, while exiting the "Kerli-street" metro station, we ran into a young athlete named Percy Longman. He stopped on the escalator and said:
- I always walk up the escalator. You know, extra training never hurts. This escalator is the longest on the line - almost a thousand steps. But here’s what’s interesting - and it applies to the other, smaller escalator I often have to climb: if, while climbing up, I step over two steps, the last step is one step; if I step over three steps, it’s two steps; if over four, it’s five steps; if over five, it’s four steps; if over six, it’s five steps; and finally, if I step over seven steps, the last step is six steps. I don’t know why this happens.
When Percy continued up, stepping over three steps at a time, we laughed, and my companion said:
- He probably doesn’t suspect that if he took steps of 20 steps, he would have 19 steps left on the last step!
How many steps are there on the escalator at the "Kerli-street" station, if the upper platform is counted as a step, but the lower one is not?*
|
86. The least common multiple of the numbers \(2,3,4,5,6\) and 7 is 420. Subtracting 1 from it, we get 419 - a possible number of steps. In addition, the conditions of the problem will be satisfied by numbers obtained by sequentially adding multiples of 420 to 419. Therefore, the number of steps in the escalator can be 419, \(839,1259,1679\) and so on. Since the escalator of interest contains fewer than 1000 steps and there is another escalator on the line with fewer steps, possessing the same properties as the first, the escalator at "Kerli-street" contains 839 steps.
|
839
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
87. Bus Ride. George went on a bus ride with his girlfriend, but after counting his limited resources, he realized they would have to walk back.
If the bus speed is 9 km/h, and the couple walks at 3 km/h, then how far can they ride so that the entire trip there and back takes 8 hours?
|
87. Young people travel three times faster by bus than on foot; therefore, \(\frac{3}{4}\) of the total time they need to spend on the return trip and only \(\frac{1}{4}\) of the time to travel by bus. Thus, they will travel for 2 hours, covering a distance of 18 km, and walk for 6 hours. They will return exactly 8 hours after departure.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Transportation Puzzle. Twelve soldiers need to get to a point 20 km away from their location as quickly as possible. To do this, they stopped a small car.
- I drive at a speed of 20 km/h, - the driver said, - but I can only take four of you at a time. How fast do you walk?
- Each of us walks 4 km/h, - one of the soldiers replied.
- Excellent, - the driver exclaimed, - then I will drive forward with four of you, take them part of the way, then return and pick up another four, take them as well, and return for the rest. All you need to do is walk whenever you are not in the car, I will take care of the rest.
The soldiers set off at exactly noon. When will they arrive at their destination[^5]
|
88. The driver must transport four soldiers 12 km and drop them off 8 km from the destination. Then he must return 8 km and pick up another four soldiers (out of eight) who will be there by then, transport them 12 km and drop them off 4 km from the destination. Returning 8 km to pick up the remaining soldiers, who by then will have walked 8 km from the starting point, he must transport them 12 km to the end. All soldiers will arrive at the destination simultaneously, and the car will have traveled 52 km in \(2 \frac{3}{5}\) hours. Therefore, the soldiers will arrive at the destination in 2 hours and 36 minutes.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
93. A small train puzzle. The express from Basltown to Ironchester travels at a speed of 60 km/h, and the express from Ironchester to Basltown, which departs simultaneously with it, travels at a speed of 40 km/h.
How far apart will they be one hour before meeting?
I couldn't find these cities on any map or in any reference, so I don't know the exact distance between them. Let's assume it does not exceed 250 km.
|
93. To solve the problem, no algebraic calculations are required, nor do you need to know the distance between the cities. Let's send both trains back from the meeting point, wherever it may have occurred, at the same speeds. Then in one hour, the first train will travel 60 km, and the second 40 km. Therefore, the distance between the trains one hour before the meeting is \(60+40\), or 100 km.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
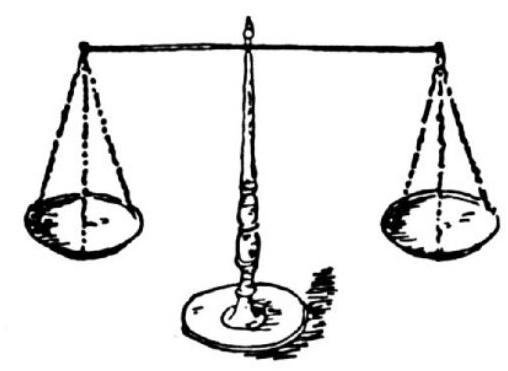
96. Incorrect scales. When the pudding was placed on one pan of the scales, they showed 4 g more than $\frac{9}{11}$ of its true weight. When it was placed on the other pan, the scales showed 48 g more than in the first case. What is the true weight of the pudding?
|
96. If the scales were incorrect due to the different weights of their pans, the true weight of the pudding would be 154 g; the first indication of the scales would give 130, and the second 178 g. Half the sum of the scale readings (the arithmetic mean) is 154. However, from the diagram in the problem, it is clear that the pans weigh the same and that the error is due to the difference in the lengths of the lever arms*. Therefore, the scale readings were 121 and 169 g, and the true weight is 143 g. Taking the square root of the product of the scale readings, we get 143 (the geometric mean). The lengths of the lever arms are in the ratio of 11 to 13.
If we denote the true weight by \(x\), then for the cases discussed, we get the following equations:
\[
\begin{gathered}
\frac{\left(\frac{9}{11} x+4\right)+\left(\frac{9}{11} x+52\right)}{2}=x, \quad \text { from which } x=154 \\
\sqrt{\left(\frac{9}{11} x+4\right)+\left(\frac{9}{11} x+52\right)}=x \quad \text { from which } x=143
\end{gathered}
\]
|
143
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 98. Weighing the Child.
- Last summer I witnessed a funny incident at a railway station, said my friend. - A small family stood in front of the automatic scales, which were calibrated for 200 pounds, trying in vain to solve the difficult problem of weighing the child. As soon as the parents left the child alone on the scales, he would start crying and jump off, and the father had to hold the dog, which also wanted to participate in this operation. Finally, the father, together with the child and Fido, climbed onto the scales, and I took a photo of them.
At this point, my friend showed me the photo, from which I copied only the scale reading, as the rest did not interest me (see the figure).
- After that, the man turned to his wife and said, "I think, dear, that together with the child I weigh 162 pounds more than the dog, and the dog weighs 70% less than the child. We should think it over at home."
I also wanted to figure it out for myself. What do you think the cute child weighed?

|
98. It is important to note that the father, child, and dog together weighed 180 pounds, as shown in the figure. Further, the difference between 180 and 162 is 18, which matches twice the weight of the dog. Therefore, the dog weighs 9 pounds, and the child 30 pounds, since if you subtract \(70\%\) of this weight from 30 pounds, you get exactly 9.
\footnotetext{
* One can agree with the author's statement only with great reservation. Indeed, the scales in the figure appear to be in balance with unequal (the right one is longer) lever arms, which precisely means that the pans have different weights! In favor of the author's interpretation is the fact that the pans look the same, and thus weigh the same. But then one must assume that the scales are not depicted in a position of equilibrium but are passing through the point of equilibrium. In a moment, the right pan will begin to descend. Perhaps, instead of appealing to the figure, the author should have simply analyzed the two cases presented.
}
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. Fruits for Jam. For making jam, it was necessary to weigh fresh fruits. It turned out that apples, pears, and plums balance each other as shown in the figure.

Could you tell how many plums would balance one pear? The relative sizes of the fruits in the figure are depicted incorrectly (this is done intentionally), but we should assume that fruits of the same type weigh the same.
Obviously, 3 apples and a pear weigh as much as 10 plums, and that an apple and 6 plums balance one pear. But how many plums would be needed to balance a pear?
|
99. On the first scales, we see that an apple and 6 plums weigh the same as a pear, so on the second scales, we can replace the pear with an apple and 6 plums without disrupting the balance. Then we can remove 6 plums from each side and find that 4 apples weigh the same as 4 plums. Therefore, one apple weighs the same as one plum. By replacing the apple with a plum on the first scales, we get that one pear weighs the same as 7 plums. As they write in old textbooks: Q.E.D.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
101. A special number. What number is formed from five consecutive digits (not necessarily in order) such that the number formed by the first two digits, multiplied by the middle digit, gives the number formed by the last two digits. (For example, if we take the number 12896, then 12, multiplied by 8, gives 96. However, unfortunately, $1,2,6,8,9$ are not consecutive digits, so this example is not a valid solution.)
|
101. The desired number is 13452. The consecutive digits are \(1,2,3,4,5 ; 13 \times 4=52\).
[For a six-digit number, V. Milli proposed the following solution: \(947658.94 \times 7=658 .-M . G\).
|
13452
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
103. Digits and Squares. What is the smallest square of an integer that ends with the longest sequence of identical digits?
If the longest sequence of identical digits were five, for example, the number 24677777 would fit (if it were the smallest square, but this is not true). Zero is not considered a valid digit.
|
103. If the square of an integer ends in repeating digits, then these digits can only be 4, as in the case of \(144=12^{2}\). However, the number of such repeating digits cannot exceed three; therefore, the answer is the number \(1444=38^{2}\).
|
1444
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
105. Repeating quartet of digits. If we multiply 64253 by 365, we get 23452345, where the first four digits repeat.
What is the largest number by which 365 must be multiplied to obtain a similar product containing eight digits, the first four of which repeat?
|
105. Multiplying 273863 by 365, we get 99959 995. Notice that any eight-digit number, where the first four digits are repeated, is divisible by 73 (and by 137). Moreover, if such a number ends in 5 or 0, it is also divisible by 365 (or by 50005). Knowing these facts, we can immediately write down the answer.
|
273863
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
108. Two Fours. I am constantly asked about the old puzzle "Four Fours." I published it in 1899, but later found out that it was first published in the first volume of the magazine Knowledge in 1881. Since then, various authors have referred to it. The puzzle is formulated as follows: "Find all possible numbers that can be obtained from four fours (no more and no less) using various arithmetic signs. For example, the number 17 can be represented as $4 \times 4 + 4 / 4$, the number 50 as $44 + 4 + \sqrt{4}$, and so on. Similarly, all numbers up to 112 inclusive can be written using only the signs of addition, subtraction, multiplication, division, square root, decimal point* and the factorial sign (for example, you can write 4!, which means just $1 \times 2 \times 3 \times 4$, or 24). The number 113 cannot already be represented as a combination of four fours.
It is necessary to determine which numbers can be written using one, two, and three fours. Major difficulties arise because some numbers are not easily represented in this way. For example, I think that very few will be able to express 64 using two fours. Will the reader be able to do this?
|
108. Here is how the number 64 can be expressed using two fours and arithmetic signs:
\[
\sqrt{(\sqrt{\sqrt{4}})^{4!}}=\sqrt{(\sqrt{2})^{24}}=\sqrt{2^{12}}=\sqrt{4096}=64
\]
[Interest in the "Four Fours" problem has periodically revived since its publication. I wrote about a relatively recent discussion of this problem in the January 1964 issue of Scientific American (see also the note in the answers section of the following issue of the same magazine). A table expressing all numbers from 1 to 100 using four fours can be found in the books: L. Harwood Clarke "Fun With Figures" (N. Y., 1954, pp. 51-53) and Angela Dunn "Mathematical Bafflers" (N. Y., 1964, pp. 5-8).
The number 64 can easily be expressed using four fours: \((4+4) \times(4+4)\), as well as using three fours: \(4 \times 4 \times 4\). M. Bicknell and V. E. Hoggatt in the journal Recreational Mathematics Magazine (14, 1964) list 64 ways to express 64 using four fours.
Knuth in the journal Mathematics Magazine (37, 1964, pp. 308-310) showed how to represent 64 using only one four and three types of symbols: the square root sign, the factorial sign, and parentheses. To express 64 in this way, 57 square root signs, 9 factorial signs, and 18 parentheses are required. With the help of a computer, it was determined that all positive integers up to 208 can be expressed in a similar manner. Knuth conjectures that this method is applicable to all positive integers.
Dudeney is partially correct in his statement regarding 113. As far as I know, no one has managed to represent this number without using highly non-standard symbols or extremely complex procedures, such as the one proposed by Knuth. -M. [\.
|
64
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
115. Division by 37. I would like to know if the number 49129308213 is divisible by 37, and if not, what the remainder is. How can I do this without performing the division? It turns out that with a skilled approach, the answer to my question can be obtained in a few seconds.
|
115. Let's write the numbers \(1,10,11\) from right to left under our number, as shown below:
\[
\begin{array}{rrrrrrrrrrr}
4 & 9 & 1 & 2 & 9 & 3 & 0 & 8 & 2 & 1 & 3 \\
10 & 1 & 11 & 10 & 1 & 11 & 10 & 1 & 11 & 10 & 1
\end{array}
\]
Now, let's multiply the numbers 1 and 10 at the bottom by the numbers above them and sum the products; then do the same with the numbers 11 and subtract the second sum from the first. The result is: \(13 + 08 + 29 + 49 = 99\); \(11 \times (2 + 3 + 1) = 66\). The difference is 33, which coincides with the remainder of our number when divided by 37.
This is the key to solving the problem. If we divide \(1,10,100,1000\) and so on by 37, we will sequentially get the remainders: \(1,10,26\) and again \(1,10,26\) and so on. It is more convenient to subtract 37 from 26 and say that the remainder is minus 11. If you apply this method to the number 49629708213, you will find that the first sum is 99, and the second sum is 165. The difference is minus 66. Add 37 and you get minus 29. Since the answer is negative, add 37 again, and you get the correct answer, which is 8. Now you can apply a similar method to other prime divisors. In the case of 7 and 13, this is easy. In the first case, you write \(1,3,2\) \((1,3,2), 1,3,2\) and so on from right to left, with the numbers in parentheses taken with a negative sign. In the second case, you need to write \(1(3,4,1), 3,4\), \(1(3,4,1)\) and so on.
\footnotetext{
" Alternatively, we can say: the probability that a randomly chosen number is divisible by 11 is \(\frac{11}{126}\).
}
|
33
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
118. Threes and sevens. What is the smallest number that is written using only the digits 3 and 7 and that both the number itself and the sum of its digits are divisible by 3 and 7? For example, 7733733 is divisible by 3 and 7 without a remainder, but the sum of its digits (33) is divisible by 3, not by 7, so it cannot serve as a solution to the problem.
|
118. The smallest possible number is 3333377733. It is divisible by 3 and 7, and the sum of its digits (42) has the same property. The number must contain at least 3 sevens and 7 threes, with the sevens being moved as far to the right as possible.
|
3333377733
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
122. Digits and Cubes. Professor Rackbrain recently asked his young friends to find all five-digit squares for which the sum of the numbers formed by the first two and the last two digits is a perfect cube. For example, if we take the square of 141, which is 19881, and add 81 to 19, we get 100 - a number that, unfortunately, is not a perfect cube.
How many solutions exist?
|
122. There are three solutions: \(56169\left(237^{2}\right)\), where \(56+69=125\) \(\left(5^{3}\right) ; 63001\left(251^{2}\right)\), where \(63+01=64\left(4^{3}\right)\) and \(23104\left(152^{2}\right)\), where \(23+04=\) \(27\left(3^{3}\right)\).
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
123. In reverse order. What nine-digit number, when multiplied by 123456 789, gives a product where the nine least significant digits are 9,8,7,6,5,4,3, 2,1 (in that exact order)?
|
123. The product of the numbers 989010989 and 123456789 is 122100120987654321, which is what we needed to find.
|
989010989
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
125. Formation of integers. Can the reader name the sum of all integers formed from the four digits $1,2,3,4$? In other words, it is required to calculate the sum of such numbers as $1234,1423,4312$, etc. Of course, one could write down all such numbers in a row and then add them up. However, it is more interesting to find a simple rule that can be used to find the sums of numbers formed from four different arbitrarily chosen (non-zero) digits.
|
125. If you multiply 6666 by the sum of four given digits, you will get the correct answer. Since \(1,2,3,4\) add up to 10,
multiplying 6666 by 10 gives us the answer 66660. If we seek the sum of all combinations of four different digits, we get 16798320, or \(6666 \times 2520\).
|
66660
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
126. Summation of numbers. Professor Rackbrain would like to know the sum of all numbers that can be formed from nine digits (0 is excluded), using each digit in each number only once.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
126. This problem can be solved in several ways. The answer, of course, is the same in all cases, equal to 201599999798400. The sum of nine digits is 45 and
\[
45 \times 8!=1814400
\]
Writing further
\[
18144
\]
18144
18144
18144 \( \qquad \)
nine times, adding them up and appending 00 at the end, we get the answer.
\(\rightleftarrows \rightleftarrows \rightleftarrows \rightleftarrows\)
|
201599999798400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
133. Digits and Prime Numbers. Using each of the nine digits once and only once, form prime numbers (numbers that do not divide evenly by any integer except 1 and themselves) whose sum is the smallest.
For example, four prime numbers
61
+283
47
59
450
contain all nine digits once and only once, and their sum is 450, but it can be significantly reduced. This is a very simple puzzle.
|
133. The digits 4, 6, and 8 must be in the second place, since no prime number can end in these digits. The digits 2 and 5 can appear in the units place only if the prime number is a single digit, meaning there are no other digits. After this, the solution can be completed without much difficulty:
\[
\begin{array}{r}
47 \\
61 \\
+\quad 89 \\
2 \\
3 \\
5 \\
\hline 207
\end{array}
\]
|
207
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
136. Twenty-four. In one book it was written: “Write the number 24 using three identical digits, different from 8. (There are two solutions to this problem.)”
The book also provided two answers: $22+2=24$ and $3^{3}-3=24$. Readers familiar with the old puzzle “Four Fours” and similar puzzles might ask why there are only the two solutions given above. Can you find more?
|
136. It is not difficult to represent the number 24 using three fours, fives, eights, or nines:
\[
\begin{gathered}
(4+4-4)! \\
\left(5-\frac{5}{5}\right)! \\
\left(\sqrt{9}+\frac{9}{9}\right)!
\end{gathered}
\]
The number 24 can also be represented using three ones, sixes, and sevens. Indeed,
\[
\begin{gathered}
\left(\frac{6}{.6}-6\right)!=24 \\
\left(7-\left[\sqrt{\frac{7}{.7}}\right]\right)!=24 \\
\left(1-\left[\sqrt{\frac{1}{.1}}\right]\right)!=24^{*}
\end{gathered}
\]
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
137. Nine Barrels. In how many ways can nine barrels be arranged in three tiers so that the numbers written on the barrels to the right of any barrel or below it are greater than the number written on the barrel itself?

The first correct arrangement that comes to mind is one where the top row is 123, the next row is 456, and the bottom row is 789. In the figure, I provide a second arrangement. In how many ways can the barrels be arranged?
|
137. The barrels can be arranged in 42 different ways. The positions of barrels 1 and 9 always remain unchanged. Let's agree to place barrel 2 so that it ends up below barrel 1. Then, if barrel 3 is placed below barrel 2, we get five variants of barrel placement. If, however, barrel 3 is placed to the right of barrel 1, then in five variants, barrel 4 ends up below barrel 2, in five - barrel 5, in four - barrel 6, and in two - barrel 7. In total, we get 21 variants. But there is no need to place barrel 2 below barrel 1. It can just as well be placed to the right of barrel 1. This way, we get another 21 variants. Upon careful examination, this set of placements turns out to be not new: all variants transform into one of the first variants when mirrored and flipped "upside down". In the center, barrels 4, 5, or 6 are always placed.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
140. An example of multiplication. One morning at breakfast, the Crackhams were discussing high matters, when suddenly George asked his sister Dora to quickly multiply
$$
1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times 0
$$
How long will it take the reader to find this product?
|
140. George's question did not catch Dora off guard. She immediately gave the correct answer: 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
141. An interesting factor. What number has the property that if it is multiplied by $1, 2, 3, 4, 5$ or 6, the result will contain only the digits present in the original number's notation
|
141. The desired number is 142857. It matches the periodically repeating sequence of digits in the fractional part of the number \(\frac{1}{7}\), written in decimal form.
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
142. Sum of Cubes. The numbers 407 and 370 match the sum of the cubes of their digits. For example, the cube of 4 is 64, the cube of 0 is 0, and the cube of 7 is 343. Adding 64, 0, and 343 gives 407. Similarly, the cube of 3 (27) added to the cube of 7 (343) results in 370.
Could you find a number, not containing zero and having the same property? Of course, we exclude the trivial case of the number being 1.
|
142. The desired number is 153. The cubes of the numbers 1, 5, and 3 are 1, 125, and 27, respectively, and their sum is 153.
[The author did not notice the fourth number: 371. If 1 is not counted, then 407, 370, 153, and 371 are the only four numbers that equal the sum of the cubes of their digits. For a more general problem of finding numbers that equal the sum of the \(n\)-th powers of their digits, see Joseph S. Madachy’s book “Mathematics on Vacation” (N. Y., 1966, pp. 163-165). - M. G.]
|
153
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
153. The Merchant's Secret. A merchant, wishing to keep his accounts secret, chose a ten-letter word (all different) like ZACHERKNUTY, where each letter corresponds to a digit in the following order: $1,2,3,4,5,6,7,8,9,0$. For example, in the case of the given keyword, ZA means 12, CHER - 345, and so on. If the sum
$$
\begin{gathered}
\begin{array}{r}
\text { DESKCH } \\
\text { INWOP }
\end{array} \\
\hline \text { PDSIWN }
\end{gathered}
$$
is written in this code, what keyword did the merchant use? It is not difficult to find the answer.
|
153. The only word (not a meaningless set of letters) that meets the given conditions is LAMP. The sum is deciphered as follows:
\[
\begin{array}{r}
36407 \\
+\quad 98521 \\
\hline 134928
\end{array}
\]
|
134928
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
154. "Bee's wax". In a certain secret code, the word BEESWAX* represents a number. The police could not find the key to this code until they discovered the following note among the papers
$$
\begin{aligned}
& E A S E B S B S X \\
& B P W W K S E T Q \\
& \hline K P E P W E K K Q
\end{aligned}
$$
The detectives suspected that this might represent a sum, but they could not decipher it. Then one of them had a brilliant idea that perhaps it was not addition but subtraction. The guess turned out to be correct: by substituting different digits for different letters, the detectives cracked the code.
What number is written in this code as $B E E S W A X$ ?[^7]
|
154. The key to the code has the form
\[
\begin{array}{cccccccccc}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 0 \\
A & T & Q & B & K & X & S & W & E & P
\end{array}
\]
from which we get
\[
\begin{array}{r}
-917947476 \\
-408857923 \\
\hline 509089553
\end{array}
\]
and BEESWAX stands for the number 4997816.
|
4997816
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 155. From "Wrong" to "Right".
- You can't make a "Right" out of two "Wrongs," someone said at breakfast.
- I'm not so sure about that,- countered Colonel Crackham - Here's an example (each letter represents a different digit, and all the encoded digits are non-zero):
$$
\begin{aligned}
& W R O N G \\
& \frac{W R O N G}{R I G H T^{*}}
\end{aligned}
$$
If you substitute the correct digits, the equation will hold true. This can be done in several ways.
|
155.
\[
\begin{array}{r}
+25938 \\
+25938 \\
\hline 51876
\end{array}
\]
|
51876
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
156. Умножение букв. В этом маленьком примере на умножение пять букв соответствуют пяти различным цифрам. Каким именно? Среди цифр нет нуля.
$$
\begin{gathered}
\times S E A M \\
T M E A T S
\end{gathered}
$$
|
156.
\[
\begin{array}{r}
4973 \\
\times \quad 8 \\
\hline 39784
\end{array}
\]
|
39784
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
157. Secret Code. Two conspirators had a secret code. Sometimes their correspondence contained simple arithmetic operations that looked completely innocent. However, in the code, each of the ten digits represented its own letter of the alphabet. Once, a sum was encountered which, after substituting the corresponding letters for the digits, took the form
$$
\begin{gathered}
F L Y \\
F O R \\
Y O U R \\
\hline L I F E^{* *}
\end{gathered}
$$
It would be interesting to restore this sum, knowing that $I$ and $O$ represent the digits 1 and 0, respectively.
|
157.
598
\[
+507
\]
\[
\begin{array}{r}
8047 \\
\hline 9152
\end{array}
\]
|
9152
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
162. Egg Sales. A woman brought eggs to the market and sold some of them. The next day, her hens worked hard, doubling the remaining eggs, and the owner sold as many as she did the previous day. On the third day, the new remainder was tripled, and the woman sold as many eggs as she did on the previous days. On the fourth day, the new remainder was quadrupled, and on the fifth day, it was quintupled, with the woman selling the same number of eggs each day. By the end of the fifth day, all the eggs were sold.
What is the smallest number of eggs the woman could have brought to the market on the first day, and how many eggs did she sell daily?
|
162. The smallest possible number of eggs is 103, and the woman sold 60 eggs daily. Any multiples of these numbers can be used as answers to the problem. For example, the woman could have brought 206 eggs and sold 120 daily, or brought 309 eggs and sold 180. Since the smallest number was required, the answer is unique.
|
103
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 163. The Cat and the Mouse.
- One of these barrels has a mouse in it,- said the dog.
- Which one? - asked the cat.
- Well, the five hundredth.
- What do you mean by that? There are only five barrels here.
- The barrel I mean will be the five hundredth if you start counting forward and backward like this.
And the dog explained how exactly one should count:
| 1 | 2 | 3 | 4 | 5 |
| ---: | ---: | ---: | ---: | ---: |
| 9 | 8 | 7 | 6 | |
| | 10 | 11 | 12 | 13 |
For example, the seventh barrel will coincide with the one that has the number 3, and the twelfth barrel with the one that has the number 4.
- This will take a lot of time,- said the cat and began to count patiently. Several times she got confused and started all over again.
- Damn it!-exclaimed the dog.-Hurry up, or it will be too late!
- Be damned yourself! You made me lose my count again, now I have to start all over.
Meanwhile, the mouse, having heard the entire conversation, gnawed a hole and slipped away just as the cat jumped into the right barrel.
- I knew it would happen, - said the dog. - Your education I would not dare to call too brilliant. A little familiarity with arithmetic would not hurt any cat, just as it does not hurt any dog. What am I saying! Even some snakes are so diligent in this science that they have to wear glasses!
Which of the barrels was the five hundredth? Could you find the answer without counting to 500?

|
163. You just need to divide the given number by 8. If it divides evenly, with no remainder, the mouse is in the second barrel. If the remainder is 1, 2, 3, 4, or 5, the barrel number will match this remainder. If the remainder is greater than 5, subtract it from 10. The resulting difference is the barrel number. The number 500, when divided by 8, gives a remainder of 4, so the number on the sought-after barrel is 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
164. Army formation. An army formation, consisting of a little more than 20 thousand people, includes 5 brigades. It is known that $\frac{1}{3}$ of the first brigade, $\frac{2}{7}$ of the second, $\frac{7}{12}$ of the third, $\frac{9}{13}$ of the fourth, and $\frac{15}{22}$ of the fifth brigade have equal numbers.
How many people are in each brigade?
|
164. Five brigades consist of 5670, 6615, 3240, 2730, and 2772 people respectively. After converting all fractions to a common denominator (12012), the numerators will be 4004, 3432, 7007, 8316, and 8190 respectively. By combining all the different divisors contained in these numbers, we get 7567560, which when divided by each of the numbers will give 1890, 2205, 1080, 910, and 924 respectively. Since the problem states that the combined force consists of "slightly more than 20,000 people," we multiply the obtained numbers by 3, which gives the correct total number of 21027 people.
|
21027
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
165. The Decisive Vote. The Congress of the United Society of Wandering Beggars (better known as the Union of Vagrants) convened to decide whether to declare a strike, demanding a shorter working day and increased alms. It was decided that during the vote, those members of the society who would vote in favor of the strike would remain standing, while those against would sit down.
- Gentlemen,-- said the chairman of the meeting after counting the votes,--I have the pleasure to inform you that the strike has been approved by a majority constituting one quarter of the opposition. (Loud cries of approval.)
- Mr. Chairman,-- someone shouted from the back,--some of us couldn't sit down.
- Why not?
- Because there are no chairs here.
- Then, perhaps, those who wanted to sit but couldn't, would not mind raising their hands... I see there are twelve of you, so the strike is canceled by a majority of one vote. (Whistles and disorder in the hall.)
How many members of the Society of Beggars participated in the vote?
|
165. A total of 207 people voted. Initially, 115 voters were in favor and 92 against, with a majority of 23 votes, which is exactly one quarter of 92. But when 12 people, for whom there were no seats, joined the opposition, it turned out that 103 votes were in favor and 104 against. Thus, the opponents of the strike won by a majority of one vote.
|
207
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
167. House Number. One person said that his friend's house is located on a long street (and on the side where the house is located, the houses are numbered in order: $1,2,3$ and so on) and that the sum of the house numbers from the beginning of the street to his friend's house is the same as the sum of the house numbers from his friend's house to the end of the street. It is also known that on the side of the street where the friend's house is located, there are more than 50 but fewer than 500 houses.
What is the house number where the friend of the storyteller lives?
|
167. The sum of the numbers of the houses located on one side of a given house will equal the sum of the numbers on the other side in the following cases: 1) if the number of the given house is 1 and there are no other houses; 2) if the number is 6 and there are a total of 8 houses; 3) if the number is 35, and there are a total of 49 houses; 4) if the number of the house is 204, and there are a total of 288 houses; 5) if the number of the house is 1189, and there are a total of 1681 houses.
ANSWER
and so on. However, we know that the number of houses is greater than 50 and less than 500; therefore, the required number is 204.
Solving the equation \(\frac{x^{2}+x}{2}=y^{2}\) in integers, we get the answers:
\begin{tabular}{rc}
Number & Number \\
of houses \(x\) & of the house \(y\) \\
1 & 1 \\
8 & 6 \\
49 & 35 \\
288 & 204 \\
1681 & 1189
\end{tabular}
and so on.
|
204
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
168. Another house number puzzle. Brown lives on a street with more than 20 but fewer than 500 houses (all houses are numbered in sequence: $1,2,3$ and so on). Brown discovered that the sum of all numbers from the first to his own, inclusive, is half the sum of all numbers from the first to the last, inclusive.
What is the number of his house
|
168. The house number of Brown is 84, and there are a total of 119 houses on the street. The sum of the numbers from 1 to 84 is 3570, and the sum of the numbers from 1 to 119 is 7140, which, as required, is exactly twice as much.
Let's write down the consecutive solutions (in integers) of the equation \(2 x-1=y^{2}\):
\[
\begin{array}{rr}
\frac{x}{1} & \frac{y}{1} \\
5 & 7 \\
29 & 41 \\
169 & 239 \\
985 & 1393
\end{array}
\]
and so on. Then the integer part \({ }^{*} \frac{x}{2}\) will give us the house number, and the integer part \(\frac{y}{2}\) will give us the total number of houses. Thus (omitting the trivial case \(0-0\)), we get \(2-3,14-20,84-119,492-696\) and so on.
|
84
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
173. Offspring of a Cow. "Suppose," said my friend the farmer Hodge, "that my cow gives birth to a heifer at the age of two. Suppose also that she will give birth to a heifer every year and that each heifer, upon reaching the age of two, will follow her mother's example and give birth to a heifer annually, and so on. Now, tell me, how many offspring will this cow have in 25 years?
From Hodge's explanation, it was clear that he was counting the time from the birth of the very first cow and that over the entire 25 years, he would not have any of his own beef or veal.[^9]
|
173. Let's write down the following sequence of numbers, first studied by Leonardo Fibonacci (born in 1175), who almost introduced the familiar Arabic numerals to Europe:
\[
0,1,1,2,3,5,8,13,21,34, \ldots, 46368
\]
Each subsequent number is the sum of the two preceding ones. The sum of all numbers from the first to the given one is 1 less than the number that follows the given one by two. If you double any member of the sequence and add the previous one, you get the member that follows the given one by two. Further, in the first year, the offspring will be 0 calves, in the second 1, in the third 1, in the fourth 2, and so on. This way, the members of this sequence will be obtained. The twenty-fifth member is 46368, and if we add all 25 members, we get the correct answer 121392. But there is no need to perform this addition. By finding the twenty-fourth and twenty-fifth members, we can simply say that 46368, multiplied by 2, plus 28657 equals 121393, and then subtract 1.
|
121392
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
177. "Common Divisor". Here is a puzzle that readers often ask me (of course, the specific numbers in it are different). A correspondent of a provincial newspaper reported that many teachers had undermined their health in vain attempts to solve it! Probably, he exaggerated a bit, because the question is actually simple, if you know which angle to approach it from.
It is as follows. Find a number that, when dividing the three numbers 480608, 508811, and 723217, would give the same remainder.
|
177. When dividing these numbers by the sought number, the remainders are the same. Therefore, if we subtract one number from the other as shown below, the difference will be divisible by the sought number without a remainder.

The prime divisors of the number 28203 are \(3, 7, 17, 79\), and \(214406 - 2, 23\), 59, 79. The only common divisor of the two differences is 79. Therefore, the sought number is 79, and the common remainder is 51. Simple, isn't it?
|
79
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
178. Strange Multiplication. I was often asked to explain the following fact, which will undoubtedly interest many readers who were not previously aware of it. If someone correctly performs addition but cannot multiply or divide by numbers greater than 2, it turns out that they can obtain the product of any two numbers using the following strange method. For example, suppose we need to multiply 97 by 23. We form two columns of numbers:
| 97 | 23 |
| ---: | :---: |
| 48 | (46) |
| 24 | (92) |
| 12 | (184) |
| 6 | (368) |
| 3 | 736 |
| 1 | 1472 |
| | 2231 |
We successively divide the numbers in the first column by 2, discarding the remainder, until we get 1, and multiply the numbers in the second column by 2 the same number of times. If we cross out the products that stand opposite even numbers in the left column (we have enclosed them in parentheses) and add the remaining ones, we get the correct answer: 2231
Why?
|
178. Let's write down in a row the remainders from dividing the numbers in the first column by 2. We get 1000011, or, if written in reverse order, 1100001. But the last number is 97 in the binary system, that is, \(1+2^{5}+2^{6}\). By adding the numbers in the second column opposite the remainders equal to 1, we get \(23 \times 1+23 \times 2^{5}+23 \times 2^{6}=2231\). Now it is clear why the correct answer is obtained: we simply act in the binary system.
|
2231
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
180. Twenty Questions. I recalled an old game that I often played in my youth. Someone thinks of something specific, for example, Big Ben, a knocker on a front door, the chime of a clock in the next room, the top button on a friend's jacket, or Mr. Baldwin's pipe. You have to determine what was thought of by asking no more than 20 questions, to each of which the answer can only be "yes" or "no."
Questions should be asked carefully, as, for example, by asking: "Is it an animal, plant, or mineral?", you might get an unsatisfactory answer of "yes" and thus waste one question. An experienced player of "Twenty Questions" rarely makes mistakes; I know of extremely difficult cases where a solution was still found under such conditions.
Recently, I was offered a new version of this game, which requires some ingenuity, and different people may approach the solution differently. The game is as follows. I think of a six-digit number. Can you guess it by asking only 20 questions, to which I will answer only "yes" or "no"? After the twentieth question, you must name the number.
|
180. There are different ways to solve this puzzle, but the simplest one, I believe, is as follows. Suppose the six-digit number is 843712.
1) Is it divisible by 2 without a remainder? Yes.
2) Is the quotient divisible by 2 without a remainder? Yes.
3) Is the new quotient divisible by 2 without a remainder? Yes.
Your twenty questions should all be the same. Write down 0 for each "yes" and 1 for each "no" from right to left. After asking the 20th question, you will get 11001101111111000000. This is nothing but our number 843712 written in binary. Since there are 6 zeros on the right, the first 1 from the right represents \(2^{6}\), the next one \(2^{7}\), and so on. By adding all the powers of two from \(2^{6}\) to \(2^{15}\) and adding \(2^{18}\) and \(2^{19}\), you will get the number 843712 in decimal notation.
If the number is not too large, for example, 100000, then 17 questions would be sufficient if you knew that the quotient is 0. The last three questions would add three extra zeros in the higher places of your binary number. To avoid confusion, it is better to assume from the beginning that 0 is divisible by 2 without a remainder, and the quotient is 0.
|
843712
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
182. Quarrelsome Children. A man married a widow, and each of them had children from their previous marriages. After 10 years, a battle broke out in which all the children (by then there were 12) participated. The mother ran to the father, shouting:
- Come quickly. Your children and my children are beating our children!
Each now had 9 children of their own.
How many children were born in these 10 years?
|
182. Each of the parents had 3 children from their first marriage, and 6 children were born from their second marriage.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
185. Squares and triangular numbers. What is the third largest number (the smallest number is considered the first) that is both a triangular number ${ }^{*}$ and a square? Of course, the first two numbers with this property are 1 and 36. What is the next number?
|
185. To find a number that is both a square and a triangular number, one must solve the Pell equation: \(8 x^{2}+1=y^{2}\). Successive values for \(x\) are \(1,6,35\), etc., and for \(y\) are \(3,17,99\), etc. The answer is the number 1225 \(\left(35^{2}\right)\), which has the required properties.
|
1225
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
188. Перестановка цифр. Если мы хотим умножить 571428 на 5 и разделить на 4 , то для этого нам нужно лишь переставить 5 из начала в конец: число 714285 дает верный ответ.[^10]
Не сумели бы вы найти число, которое можно было бы умножить на 4 и разделить затем на 5 столь же просто: переставив первую цифру в конец?
Разумеется, если бы разрешалось переставлять цифру из конца в начало, то 714285 подошло бы и на этот раз. Однако цифру следует переставлять именно из начала в конец.
|
188. Ответ имеет вид
\[
2173913043478260869565 .
\]
Данное число можно умножить на 4 и разделить затем на 5 , просто перенеся 2 из начала в конец.
|
2173913043478260869565
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
195. Разность кубов. Число 1234567 можно представить в виде разности квадратов, стоит только выписать два числа, 617284 и 617283 (половина данного числа плюс $\frac{1}{2}$ и минус $\frac{1}{2}$ соответственно), и взять разность их квадратов ${ }^{*}$. Найти же два куба, разность которых равнялась бы 1234567 , несколько труднее.
|
195. \(642^{3}=264609288 ; 641^{3}=263374721\) и разность между кубами равна 1234567.
|
1234567
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
196. Composite Squares. Can you find two three-digit squares (with no zeros) that, when written consecutively, form a six-digit number which itself is a square? For example, from 324 and $900\left(18^{2}\right.$ and $\left.30^{2}\right)$ we get $324900\left(570^{2}\right)$, but the number 900 contains two zeros, which is prohibited by the condition.
The problem has only one solution.
|
196. The answer is the number 225625 (the squares of the numbers 15 and 25, written down one after the other), which equals the square of 475.
|
225625
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
198. Square Supplement. "What number," asked Colonel Crackham, "has the property that if it is added to the numbers 100 and 164 separately, a perfect square is obtained each time?"
|
198. If we add 125 to 100 and 125 to 164, the resulting numbers are \(225=15^{2}\) and \(289=17^{2}\).
|
125
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
202. Nuts for Monkeys. One person brought a bag of nuts to the monkey enclosures. It turned out that if he divided these nuts equally among 11 monkeys in the first cage, there would be one extra nut; if he divided them among 13 monkeys in the second cage, there would be 8 nuts left; and finally, if he divided them among 17 monkeys in the last cage, there would be 3 nuts left.
It also turned out that if he divided the nuts equally among 41 monkeys in all three cages or among monkeys in any two cages, in any of these cases there would be leftover nuts.
What is the smallest number of nuts that could have been in the bag?
|
202. The smallest number of nuts is 2179. It is best to deal only with the first two cases at first and find out that 34 (or 34 plus any multiple of 143) satisfies the condition for 11 and 13 monkeys. Then, the smallest number of this kind that satisfies the condition for 17 monkeys should be found.
|
2179
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
206. Распределение орехов. Тетушка Марта купила орехов. Томми она дала один орех и четверть оставшихся, и Бесси получила один орех и четверть оставшихся, Боб тоже получил один орех и четверть оставшихся, и, наконец, Джесси получила один орех и четверть оставшихся. Оказалось, что мальчики получили на 100 орехов больше, чем девочки.
Сколько орехов тетушка Марта оставила себе
|
206. Первоначально было 1021 орех. Томми получил 256 , Бесси 192, Боб 144 и Джесси 108 орехов. Всего девочки получили 300, а мальчики 400 орехов. Тетушка Марта оставила себе 321 орех.
|
321
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
207. Young Bandits. Three young "highwaymen," returning from the cinema, met a vendor with apples. Tom grabbed half of all the apples, but threw 10 back into the basket. Ben took a third of the remaining apples, but returned 2 apples he didn't like. Jim took half of the remaining apples, but threw back one wormy one. The vendor was left with only 12 apples in the basket.
How many apples did the vendor have before the raid?
|
207. The vendor had 40 apples. Tom left her 30, Bob 22 and Jim 12 apples.
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
208. Biscuits. A trader packed his biscuits (all of the same quality) into boxes weighing $16, 17, 23, 39$, and 40 pounds respectively and was unwilling to sell them in any other way than whole boxes. A customer asked him to supply 100 pounds of biscuits.
Could you fulfill this order? If not, how close can you get to the number 100? Of course, the trader has enough boxes of each weight.
|
208. You need to give the customer four boxes at 17 pounds each and two at 16 pounds, which will make exactly 100 pounds.
|
100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
211. "Boomerang". I call "boomerang" one of the oldest types of arithmetic puzzles. Someone is asked to think of a number and after a series of calculations, to state the result. Upon hearing the result, the person who asked the question immediately announces the thought-of number. There are hundreds of different versions of this puzzle.
The oldest recorded example of this puzzle appears to be in the "Arithmetica" of Nicomachus, who died around 120 AD. He asks you to think of any whole number from 1 to 100 and then divide it successively by 3, 5, and 7, reporting the remainder each time. Having received this information, he immediately guesses the number you thought of.
Could the reader devise a simple method to perform this feat mentally? If not, perhaps he would be interested to learn how the ancient mathematician did it.
|
211. Get the remainder of the division by 3, multiply it by 70, get the remainder of the division by 5 and multiply it by 21, and get the remainder of the division by 7 and multiply it by 15. Add the results, and you will get either the number you thought of or a number that differs from the thought number by an integer multiple of 105. Thus, if the number 79 was thought of, then 1, multiplied by 70, plus 4, multiplied by 21, plus 2, multiplied by 15, will give 184. Subtract 105, and you get 79 - the number you thought of.
|
79
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
216. Blindness in Bats. One naturalist, trying to mystify Colonel Crackham, told him that he had studied the question of blindness in bats.
- I found,- he said, - that the ingrained habit of bats to sleep during the day in dark corners and fly only at night has led to the spread of blindness among them, although some individuals saw well with both or one eye. Two of the bats I examined saw with the right eye, three with the left, four did not see with the left eye, and five did not see with the right eye.
Could you calculate the smallest number of bats the naturalist had to examine to obtain such results?
|
216. The smallest number of mice is 7, with three possible cases:
1) 2 see well, 1 is blind only in the right eye, and 4 are completely blind
2) 1 sees well, 1 is blind only in the left eye, 2 are blind only in the right eye, and 3 are completely blind;
3) 2 are blind only in the left eye, 3 only in the right eye, and 2 are completely blind.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
219. Sheep Division. A certain Australian farmer, on his deathbed, left his sheep to his three sons. Alfred is to receive $20 \%$ more than John and $25 \%$ more than Charles. John's share is 3600 sheep.
How many sheep will Charles receive? Perhaps the reader will be able to solve the problem in a few seconds.
|
219. Charles's share amounts to 3456 sheep. Some readers probably first found Alfred's share and then subtracted \(25 \%\), but such a solution is, of course, incorrect.
|
3456
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
222. Marching Column. A military unit was moving in a marching column, in which the number of ranks exceeded the number of soldiers in a rank by 5. When the enemy appeared, a reformation into 5 ranks took place, as a result of which the number of soldiers in each rank increased by 845.
How many people were in the unit
|
222. There were a total of 4550 people in the unit. Initially, the soldiers marched in a column of 70 ranks with 65 people in each; then they reformed into 5 ranks with 910 soldiers in each.
|
4550
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
224. Boxes with Shells. Shells for six-inch howitzers were packed in boxes of 15, 18, and 20.
- Why do you have different boxes? - I asked the officer at the warehouse.
- You see, - he replied, - this allows us to deliver the required number of shells to the battery without opening the boxes.
Indeed, this system worked flawlessly when a large number of shells was needed, but it proved to be useless if, for example, 5, 10, 25, or 61 shells were required.
What is the largest number of shells that cannot be delivered to the battery in whole boxes, containing 15, 18, and 20 shells each? It is not too large.
|
224. An officer at the warehouse must issue the required number of shells in boxes of 18 shells until the remaining number of shells is a multiple of 5. If the number of shells is not 5, 10, or 25, the remaining shells should be issued in boxes of 15 and 20 shells. The largest number of shells for which the system fails is 72 plus 25, that is, 97. If the number of shells in the warehouse is greater, for example, 133, and 108 shells are packed in 6 boxes of 18 shells each, then the officer should issue only 1 box of 18 shells, and the remaining 115 shells should be repackaged into 1 box holding 15 shells and 5 boxes containing 20 shells each. If there are 97 shells in the warehouse, the officer will only have a remainder that is a multiple of 5, that is, 25 shells, after issuing 72 shells.
|
97
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
225. Fruit Garden. The gardener decided to create a new fruit garden. He planted young trees in rows so that a square was formed. In doing so, he had 146 extra seedlings left. But to increase the square by adding an extra row, the gardener had to buy 31 more trees.
How many trees are there in the garden at the end of the work?
|
225. Initially, there were 7890 saplings, from which a square of \(88 \times 88\) was formed, and 146 trees were left over. By purchasing an additional 31 trees, the gardener was able to increase the square to \(89 \times 89\), and the number of trees in the garden became 7921.
|
7921
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
227. Find the triangle. The sides and height of a certain triangle are expressed by four consecutive integers. What is the area of this triangle?
|
227. The sides of a triangle are 13, 14, and 15, with the base being 14, the height 12, and the area 84. There are infinitely many rational triangles whose sides are expressed as consecutive integers, such as 3, 4, and 5 or 13, 14, and 15, but only one of them satisfies our conditions for the height.
Triangles with sides expressed as three consecutive integers and an integer area are as follows:
\[
\begin{array}{lll}
3 & 4 & 5
\end{array}
\]
\(\begin{array}{lll}13 & 14 & 15\end{array}\)
\(\begin{array}{lll}51 & 52 & 53\end{array}\)
193 194 195
723 724 725 and so on.
They can be found very easily:
\[
\begin{aligned}
52 & =4 \times 14-4 \\
194 & =4 \times 52-14 \\
724 & =4 \times 194-52
\end{aligned}
\]
or in general \(U_{n}=4 U_{n-1}-U_{n-2}\). There is another way to construct these triangles. Find \(x\) such that \(3\left(x^{2}-1\right)\) is a perfect square. It will correspond to a triangle with sides \(2 x, 2 x+1, 2 x-1\).
|
84
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
228. Cow, Goat, and Goose. A certain farmer found out that his cow and goat eat the grass on the meadow in 45 days, the cow and goose in 60 days, and the goat and goose in 90 days. If he releases the cow, goat, and goose on the field at the same time, how many days will it take them to eat all the grass on the meadow?
Sir Isaac Newton once showed how to solve puzzles where the grass on the meadows does not stop growing. However, in our puzzle, for the sake of simplicity, we will assume that due to unfavorable weather conditions, the grass has stopped growing.
|
228. Since the cow and the goat eat \(\frac{1}{45}\), the cow and the goose \(\frac{1}{60}\), and the goat and the goose \(\frac{1}{90}\) of all the grass in a day, we easily find that the cow eats \(\frac{5}{360}\), the goat \(\frac{3}{360}\), and the goose \(\frac{1}{360}\) of all the grass in a day. Therefore, all together they eat \(\frac{9}{360}\) (or \(\frac{1}{40}\)) of all the grass in a day, so, since there will be no growth of grass, they will eat all the grass in 40 days.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.