problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
233. Multiplication of dates. In 1928, there were four dates with a remarkable property: when written in the usual way, the product of the day and the month gives the year of the XX century. Here are these dates: $28 / 1-28, 14 / 2-28, 7 / 4-28$ and $4 / 7-28$.
How many times in the XX century (from 1901 to 2000 inclusive) does this property occur? Perhaps you will try to find the year of our century in which the number of such dates is maximal? There is only one such year.
|
233. In the XX century, there are 215 dates with the specified property, if cases like \(\frac{25}{4}-00\) are included. The most "productive" in this regard turned out to be 1924, in which there were 7 such dates: \(24 / 1-24\), \(12 / 2-24, 2 / 12-24, 8 / 3-24, 3 / 8-24, 6 / 4-24, 4 / 6-24\). To solve the problem, one only needs to find the years containing as many divisors as possible.
|
215
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
235. Another curious example of multiplication. Here is another puzzle from Professor Rackbrain.
What number, when multiplied by $18, 27, 36, 45, 54, 63, 72$, 81 or 99, gives a product whose first and last digits match the corresponding digits of the multiplier, and when multiplied by 90, gives a product whose last two digits match the digits of the multiplier?
|
235. The desired number is 987654321, which when multiplied by 18 gives 17777777778 with 1 and 8 at the beginning and end, respectively. The same is true for other multipliers, except for 90, when we get 88888888890 with 90 at the end.
[The author did not notice numbers like 1001, 10101, and 100101, composed of 0 and 1, with 1 at the ends and not containing two consecutive 1s, each of which is also a solution to the problem. \(-M . \Gamma\).
|
987654321
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
237. Counting Losses. An English officer recounted that he was part of a detachment that initially numbered 1000 people. During one of the operations, the detachment suffered heavy losses, and those who survived were captured and sent to a prisoner-of-war camp.
On the first day of the journey, \(\frac{1}{6}\) of all the remaining members of the detachment managed to escape, on the second day, \(\frac{1}{8}\) of the remaining and one person died, on the third day, \(\frac{1}{4}\) of all the remaining escaped. The remaining prisoners were divided into 4 equal groups upon arrival at the camp.
How many people died during the operation?
|
237. During the fighting, 472 people were killed. By making calculations, the reader will find that each of the four camp groups had 72 people.
The general solution can be obtained from the indeterminate equation
\[
\frac{35 x-48}{768}=\text { an Integer, }
\]
where \(x\) is the number of survivors. Solving it in the usual way, we get \(x=528\). Therefore, the number of those killed is 472 \((1000-528)\).
|
472
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
239. Fence Order. One person ordered a fence with a total length of 297 m. The fence was to consist of 16 sections, each containing a whole number of meters. Moreover, 8 sections were to have the maximum length, while the others were to be 1, 2, or 3 meters shorter.
How should this order be carried out? Suppose that the 8 sections of maximum length contain 15 m each, then the remaining sections have lengths of 14, 13, or 12 m; naturally, it is not necessary to take sections of each of these sizes.
|
239. 8 sections of 20 m each, 1 section 18 m long, and 7 sections of 17 m each were manufactured. Thus, a total of 16 sections with a total length of \(297 \mathrm{m}\) were obtained, as required by the customer.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
241. Paving. Two square sections of pavement need to be laid with square tiles measuring $1 \mathrm{~m}^{2}$. A total of 2120 tiles are required for this, and the side of one section is 12 m longer than the side of the other.
What are the dimensions of each section?
|
241. One side of one plot measures 38 m (1444 tiles), one side of the other - 26 m (676 tiles).
|
38
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
243. Обезьяна и груз. Вот одна забавная задачка, которая представляет собой симбиоз нескольких головоломок, в том числе головоломок Льюиса Кэрролла «Обезьяна и груз» и Сэма Лойда «Сколько лет Мэри?» Хорошенько подумав, вы ее безусловно решите.
Через блок перекинута веревка, на одном конце которой висит обезьяна, а на другом груз. Длина обоих концов веревки одинакова, и система находится в равновесии. Каждый фут веревки весит
4 унции. Возраст обезьяны вместе с возрастом ее матери составляет 4 года. Обезьяна весит столько фунтов ${ }^{*}$, сколько лет ее матери. Мать обезьяны вдвое старше, чем была обезьяна, когда ее мать была вдвое моложе, и чем будет обезьяна, когда она станет в три раза старше, чем была ее мать, когда та была втрое старше обезьяны. Вес веревки с грузом в полтора раза больше разницы между весом груза и еще таким весом и весом обезьяны.
Чему равна длина веревки
|
243. Сначала мы находим возраст обезьяны ( \(1 \frac{1}{2}\) года) и возраст ее матери ( \(2 \frac{1}{2}\) года). Следовательно, обезьяна весит \(2 \frac{1}{2}\) фунта и столько же весит груз. Затем мы находим, что вес веревки составляет \(1 \frac{1}{4}\) фунта, или 20 унций, а поскольку каждый фут весит 4 унции, то длина веревки равна 5 футам.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
244. Annoying Breakdowns. On the occasion of the holiday, many residents of the town gathered to spend the day in the great outdoors. For this purpose, they hired all the available vans, with the same number of people in each van. Halfway through, 10 vans broke down, so each remaining van had to take one extra person. When everyone decided to head home, unfortunately, it turned out that another 15 vans had broken down. Therefore, each van had to take three more people than it had in the morning.
How many people participated in this mass outing?
|
244. There were 900 people in total. Initially, 100 vans, each carrying 9 people, set off. After 10 vans broke down, the remaining vans had 10 people each (one extra person). When 15 more vans broke down during the return trip, each of the 75 remaining vans had 12 people (three more people than in the morning when they set off).
|
900
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
247. Сколько весит рыба? Крэкхэмы задумали остановиться во время своего путешествия в каком-нибудь месте, где есть хорошая рыбная ловля, поскольку дядя Джейбз был заядлым рыболовом и они хотели доставить ему удовольствие. Они выбрали очаровательное местечко и, воспользовавшись случаем, устроили там пикник. Когда дядя принес великолепную форель, разгорелась дискуссия о том, сколько она может весить. Полковник представил все в виде головоломки, сказав:
- Допустим, что хвост весит 9 унций, голова весит столько же, сколько хвост вместе с половиной туловища, а туловище - столько же, сколько голова и хвост.
Скажите-ка теперь, если все это верно, сколько весит рыба?
|
247. Рыба весит 72 унции, или \(4 \frac{1}{2}\) фунта. Хвост весит 9 унций, туловище 36 и голова 27 унций.
|
72
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
248. Cats and Mice. One morning at Professor Rackbrain's table, the lively discussion was about the extermination of rodents when suddenly the professor said:
- If a certain number of cats ate a total of 999,919 mice, and all the cats ate the same number of mice, how many cats were there in total?
Someone suggested that perhaps one cat ate all the mice, but Rackbrain objected, saying he had said "cats." Then someone else ventured to suggest that each cat had eaten one mouse, to which the professor remarked that he had said "mice." He also added, to help those present, that each cat had eaten more mice than there were cats.
What, then, would be the correct answer?
|
248. It is clear that 999919 cannot be a prime number and that, since we need to find a unique solution, it must factorize into a product of two prime factors. These factors are 991 and 1009. We know that each cat caught more mice than there were cats. Therefore, there were 991 cats, and each of them caught 1009 mice.
|
991
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
249. Egg Cabinet. A person has a cabinet where he stores a collection of bird eggs. This cabinet has 12 drawers, and all of them (except the top one, where the catalog is stored) are divided into cells by wooden partitions, each of which extends the entire length or width of the corresponding drawer. In each subsequent drawer, the number of cells is greater than in the previous one. The bottom drawer (No. 12) has 12 times as many cells as partitions, drawer No. 11 has 11 times as many cells as partitions, and so on.
How are the drawers divided (how many cells and partitions are in each drawer)? In each case, specify the smallest possible number of cells and partitions.
|
249. Let the box number be \(n\). Then it will have \(2 n-1\) partitions in one direction and \(2 n-3\) in the other, which will give \(4 n^{2}-4 n\) cells and \(4 n-4\) partitions. Thus, in the twelfth box, there are 23 and 21 partitions (a total of 44) and 528 cells. This rule applies to all boxes except the second, where there can be any number of partitions in one direction and one partition in the other. So 1 and 1 will work (a single partition is not suitable, as such a "partitioning" would be absurd). Thus, in total, there are 262 partitions and 2284 cells (not 264 and 2288).
|
262
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
256. Lines and Squares. Here is one simple question. What is the smallest number of straight lines needed to construct exactly 100 squares? In the figure on the left, nine lines are used to construct 20 squares (12 with side length $A B$, 6 with side length $A C$, and 2 with side length $A D$). In the figure on the right, there is one more line, and the number of squares has increased to 17. Thus, what matters is not the total number of lines, but how they are drawn. Remember, the goal is to get exactly 100 squares (no more and no less).

|
256. If 15 lines are drawn as shown in the figure, exactly 100 squares will be formed. Forty of them have a side equal to \(A B\), twenty have a side equal to \(-A C\), eighteen have a side equal to \(-A D\), ten have a side equal to \(-A E\), and four have a side equal to \(-A F\). With 15 lines, it is even possible to form 112 squares, but we are required to form exactly 100. With 14 lines, you cannot form more than 91 squares.

In general, with \(n\) lines, \(\frac{(n-3)(n-1)(n+1)}{24}\) squares can be formed if \(n\) is odd, and \(\frac{(n-2) n(n-1)}{24}\) squares if \(n\) is even.
If we have 15 lines perpendicular to another \(n\) lines, where \(m\) is less than \(n\), the number of squares is
\[
\frac{m(m-1)(3 n-m-1)}{6}
\]
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
270. The Runner's Puzzle. $A B C D$ is a square field with an area of 19.36 hectares. $B E$ is a straight path, and $E$ is 110 meters from $D$. During the competition, Adams ran straight from $A$ to $D$, while Brown started running from $B$, reached $E$, and then continued towards $D$.
Each ran at a constant speed, and when Brown reached $E$, he saw Adams 30 meters ahead of him.
Who won the competition and by what margin?
|
270. Each side of the field is 440 m, \(B A E\) is a right-angled triangle. Therefore, \(A E=330\) m, \(B E=550\) m. If Brown runs 550 m in the same time it takes Adams to run 360 m \((330+30)\), then Brown can run the remaining 100 m in the time it takes Adams to run only \(72 \mathrm{m}\). But \(30+72=102 \mathrm{m}\), so Brown wins, beating his opponent by 8 m.
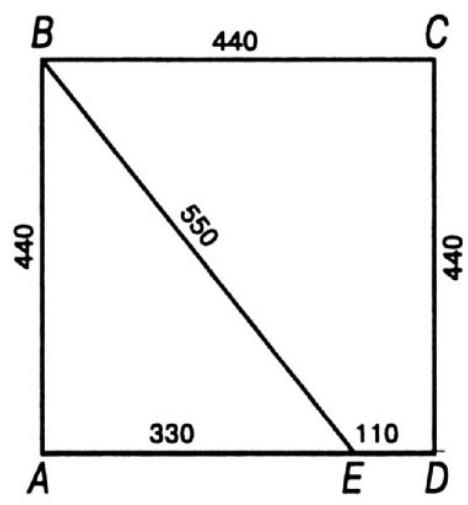
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
271. Three Tablecloths. One morning at breakfast, Mrs. Crackham announced to all present that a friend had given her three wonderful tablecloths, all square with a side of 144 cm. Mrs. Crackham asked those present to name the maximum dimensions of a square table that could be covered with all three tablecloths at the same time. The tablecloths could be placed on the table in any way, as long as the entire surface of the table was covered. The answer was required to be given to the nearest centimeter.
|
271. Three tablecloths measuring \(144 \times 144\) cm will cover a table measuring \(183 \times 183\) cm if they are placed as shown in the figure. Square \(A B C D\) is the tabletop, and squares 1, 2, and 3 are the tablecloths. Parts of the second and third tablecloths, of course, will hang off the table.
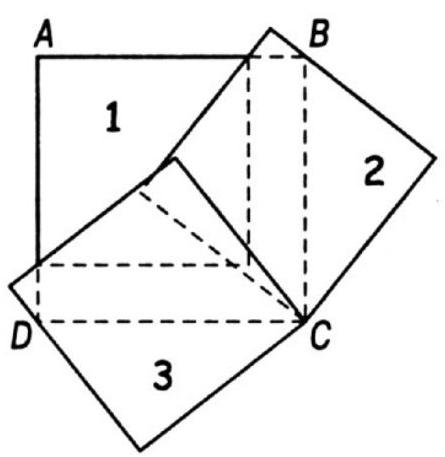
|
183
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
275. The Pen Puzzle. Answers to well-known puzzles given in old books are often completely wrong. Nevertheless, it seems that no one ever notices these errors. Here is one such example.
A farmer had a pen with a fence that was 50 rails long, in which only 100 sheep could fit. Suppose the farmer wanted to expand the pen so that it could hold twice as many sheep.
How many additional rails would the farmer need?
|
275. The old answer is that if you arrange the poles as shown in case \(A\), then by adding two poles at each end, as in case \(B\), you will get double the area. It should be noted that, firstly, the problem does not specify the shape of the enclosure. Secondly, even if it were required that the original enclosure had dimensions of \(24 \times 1\), the answer would still be incorrect, because if you arrange the poles as in case \(C\), the area will increase from 24 "square poles" to 156, and the enclosure will hold 650 sheep, with the number of poles remaining the same. Moreover, you can double the area as in case \(D\), using only 28 poles. If it is required to use all the poles and double the area exactly, you can do so as shown in case \(E\).
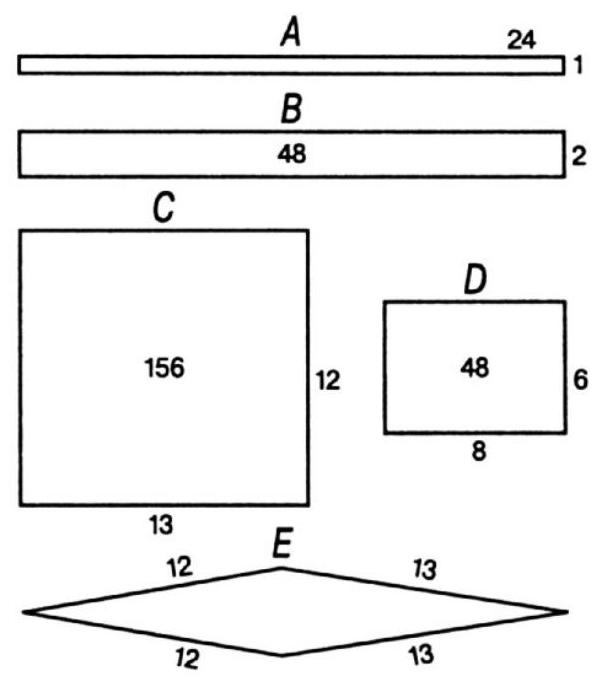
|
28
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
279. Motorcyclists again. Here is another case involving the motorcyclists mentioned in the previous puzzle. On the map segment (see figure), three roads form a right-angled triangle. When asked about the distance between $A$ and $B$, one of the motorcyclists replied that after he traveled from $A$ to $B$, then to $C$, and back to $A$, the speedometer showed 60 km. The second motorcyclist added that he happened to know that $C$ is 12 km from the road connecting $A$ with $B$, that is, from point $D$ (the dashed line in the figure). Then the person asking, after making a very simple calculation in his mind, said:
- It's clear, from $A$ to $B \ldots$
Could the reader also determine this distance so quickly?
|
279. The distances are shown in the figure. The person asking the question only needed to square the 60 km traveled by the first motorcyclist (3600), and divide the result by twice the sum of these 60 and 12 km, which is the distance from road \(A B\) to \(C\), i.e., by 144. Doing the calculations in his head, he, of course, noticed that
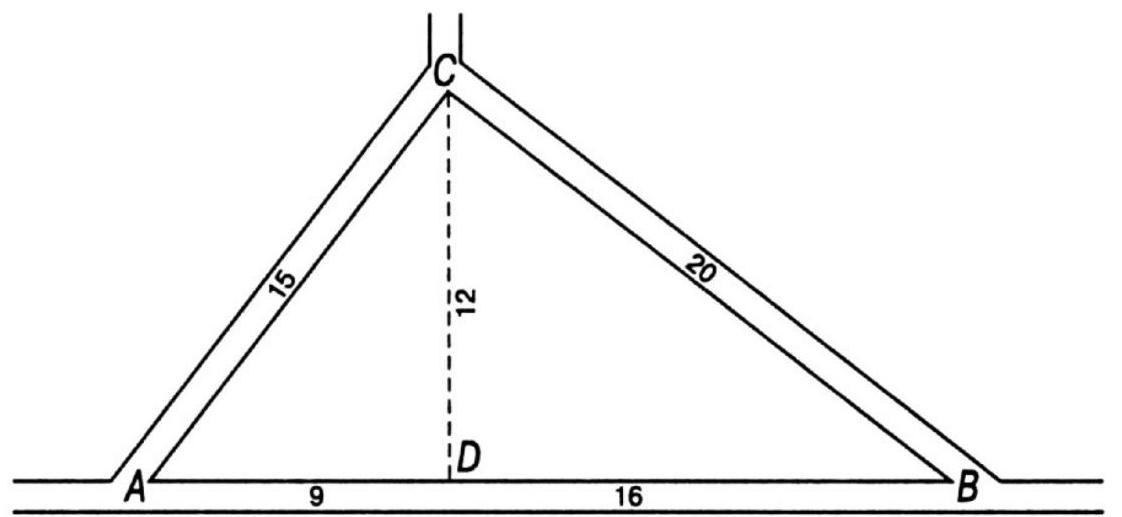
the result could be obtained by dividing 300 by 12, and therefore immediately found the correct answer - 25 km. I do not show here how to determine, if necessary, the other distances; it is quite easy to do.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
282. Cross of chips. Arrange 20 chips in the shape of a cross, as shown in the figure. How many different cases can you count where four chips form a perfect square?
For example, squares are formed by the chips at the ends of the cross, the chips located in the center, as well as the chips marked with the letters $A$ and $B$.
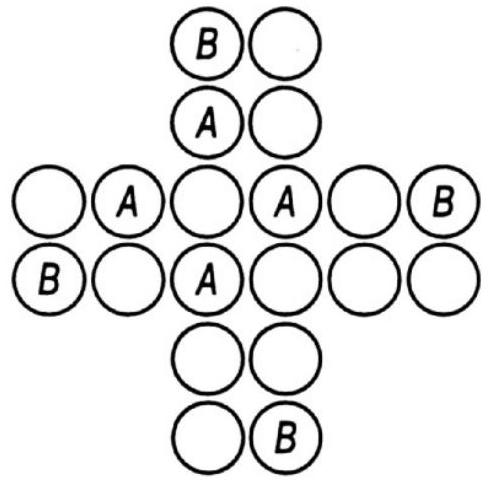
Which 6 chips should be removed so that no four of the remaining chips are located at the vertices of any square?
|
282. There are 19 such squares in total. Of these, 9 are the same size as the square marked with the letters \(a\), 4 are the same size as the square marked with the letters \(b\), 4 are the size of \(c\), and 2 are the size of \(d\). If 6 chips marked with the letter \(e\) are removed, it will be impossible to form any square from the remaining chips.
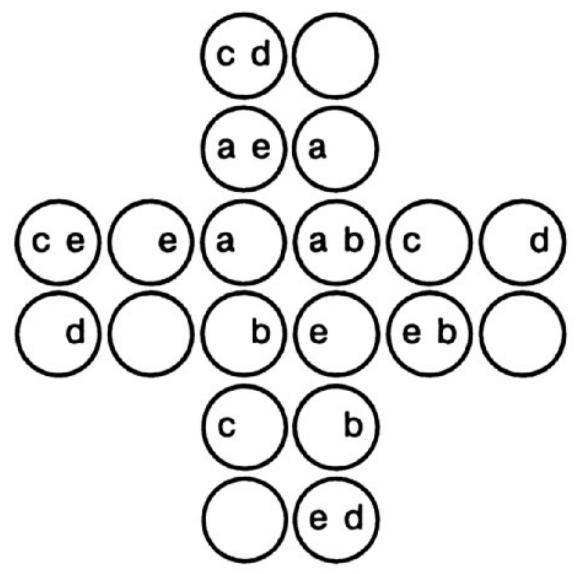
[In fact, there are 21 squares. Will the reader be able to find the two squares that Dudeney missed? The answer to the second part of the problem remains correct, nevertheless. - M. G.]
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
322. Cigarette Packaging. Cigarettes are shipped from the factory in boxes of 160. They are arranged in 8 rows of 20 each, completely filling the box.
Can more than 160 cigarettes be placed in the same box with a different packaging method? If so, how many more cigarettes can be added?
At first glance, it seems absurd to think that extra cigarettes can be added to a fully filled box, but after a moment's thought, you might find the key to this paradox.
|
322. Let the diameter of a cigarette be 2 units, and let 8 rows of 20 cigarettes each (see case \(A\)) completely fill a box. In this case, the internal length of the box is 40, and the depth is 16 units. Now, if we place 20 cigarettes in the bottom row and if instead of 20 in the next row we place 19, as shown in case \(B\), we save 0.268 (more precisely \(2-\sqrt{3}\)) in height. This second row and each additional row of 20 or 19 (alternating) cigarettes increases the height by 1.732. Therefore, we will get nine rows with a total height of \(2 + 8 \times 1.732 = 15.856\) units, which is less than our depth of 16 units. Thus, we will increase the number of cigarettes by 20 (thanks to the additional
ANSWER
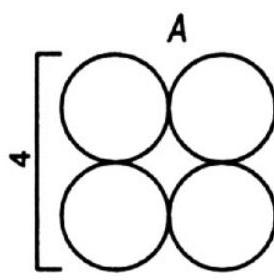
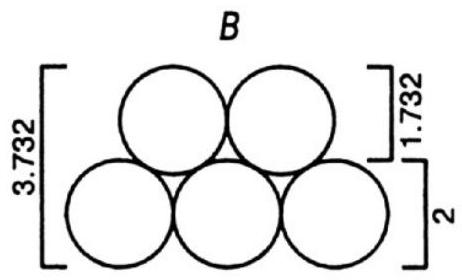
row) and decrease it by 4 (1 unit in each row of 19), resulting in a net increase of 16 cigarettes.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
339. Three Greek Crosses from One. In the figure shown here, you see an elegant solution to the problem of cutting two smaller Greek crosses of the same shape from a larger symmetrical Greek cross. Part $A$ is cut out as a whole, and it is not difficult to assemble a similar cross from the remaining 4 parts.
However, here is a more challenging question: how can you obtain three crosses of the same shape but smaller size from one large Greek cross, by cutting the large cross into the smallest possible number of pieces?
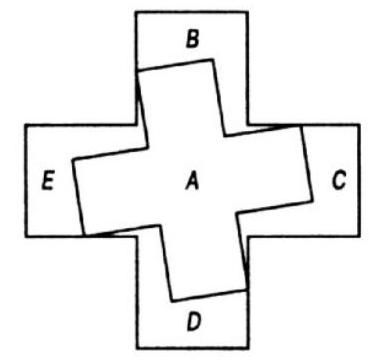
Note that this problem can be solved using only 13 pieces. I believe many readers who are adept at geometry will enjoy pondering this problem. Of course, all three crosses must be of the same size.
|
339. Cut off the top and bottom parts of the cross and place them in positions \(A\) and \(B\) (case \(I\)), and cut the remaining larger part into 3 pieces so that the 5 pieces obtained can be used to form the rectangle shown in case II. It can be said that this rectangle is composed of 15 squares - 5 squares for each new cross. The remaining cuts are not difficult to make. From parts \(2,5,8,9\) a cross is clearly formed; from parts 13,6, 10,7, and 11 - the second cross (case \(I I I\)), and from \(1,3,4,12\) the third cross (case \(I V)\). The area of each end of the small cross is \(\frac{1}{3}\) of the area of any end of the large cross.
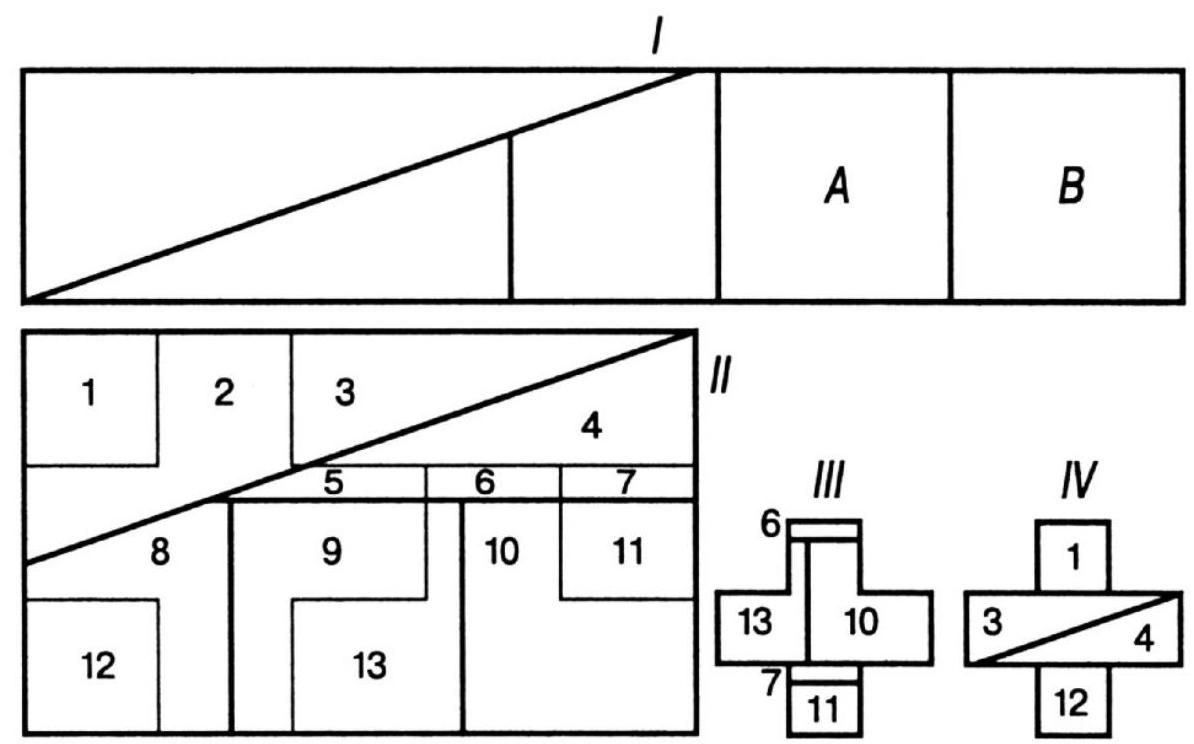
[The number of parts can be reduced to \(12 .-M \Gamma\).]
|
13
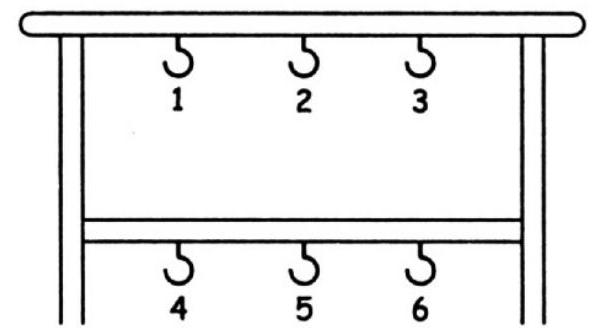
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
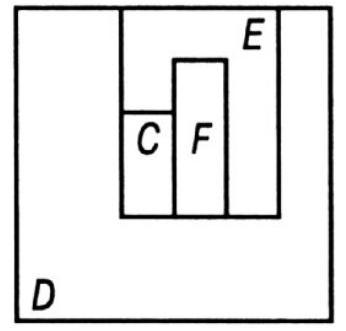
348. The Cabinetmaker's Problem. A cabinetmaker had a $7 \times 7$ chessboard piece made of excellent plywood, which he wanted to cut into 6 pieces so that they could be used to form 3 new squares (all of different sizes).
How should he proceed, without losing any material and making cuts strictly along the lines?
|
348. The figure shows how a piece of plywood can be cut. Squares \(A\) and \(B\) are cut out entirely (1), and from the four pieces \(C, D\), \(E\) and \(F\), a third square can be formed (2).
2
[There are solutions to this problem that involve only five pieces. Could the reader find a solution with five pieces where the total length of the cuts is 16 units \(3-M . \Gamma\).]
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
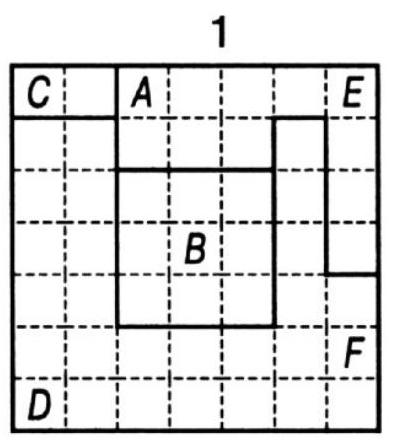
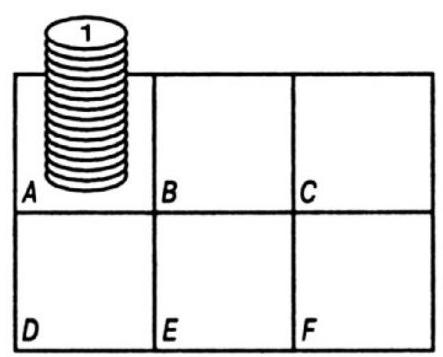
361. Moving Chips. Divide a sheet of paper into 6 squares and place a stack of 15 chips numbered $1,2,3, \ldots, 15$ in square $A$ (see figure), with the numbers going from top to bottom. The puzzle is to move the entire stack to square $F$ in the fewest possible moves. You can move one chip at a time to any square, but a chip with a higher number cannot be placed on a chip with a lower number.
For example, if you place chip 1 in square $B$ and chip 2 in square $C$, you can then place chip 1 on top of chip 2, but not chip 2 on top of chip 1.
|
361. In 9 moves, form a stack of five chips (from 1 to 5) in square \(B\). In 7 moves, build a stack of four chips (from 6 to 9) in square \(C\). Form a stack of three chips (from 10 to 12) in \(D\) in 5 moves. Place a stack of two chips (13 and 14) in \(E\) in 3 moves. Move one chip (15) to \(F\) in 1 move. Move 13 and 14 to \(F\) in 3 moves, 10 and 12 to \(F\) in 5 moves, from 6 to 9 in 7 moves, and from 1 to 5 in 9 moves. In total, this will take 49 moves.
|
49
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
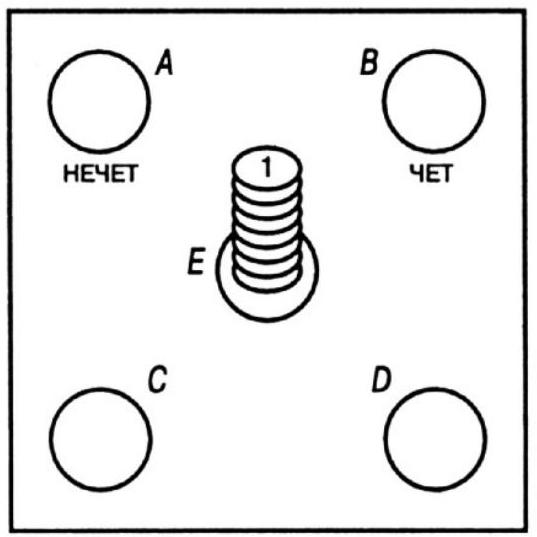
364. Even and Odd Chips. Place a stack of eight chips in the central circle, as shown in the figure,
such that the numbers from top to bottom are in order from 1 to 8. The goal is to move the chips $1,3,5,7$ to the circle labeled NEЧET, and $2,4,6,8$ to the circle labeled ЧЕТ. Only one chip can be moved at a time from one circle to another, and a chip with a larger number cannot be placed on a chip with a smaller number. It is also forbidden to place chips of different parity in the same circle simultaneously. For example, you can place chip 1 on chip 3, chip 3 on chip 7, chip 2 on chip 6, or chip 2 on chip 4, but you cannot place chip 1 on chip 2, or chip 4 on chip 7, as this would result in even and odd numbers being in the same circle.
What is the minimum number of moves?
|
364. The least number of moves is 24. You should act as follows. (It is only necessary to indicate with letters from which circle to which the chip is moved. Only one chip can be moved at a time.) So, \(E\) to \(A\), \(E\) to \(B\), \(E\) to \(C\), \(E\) to \(D\), \(B\) to \(D\), \(E\) to \(B\), \(C\) to \(B\), \(A\) to \(B\), \(E\) to \(C\), \(E\) to \(A\), \(B\) to \(A\), \(C\) to \(E\), \(B\) to \(C\), \(A\) to \(C\), \(B\) to \(A\), \(C\) to \(B\), \(C\) to \(A\), \(B\) to \(A\), \(E\) to \(C\), \(E\) to \(B\), \(C\) to \(B\), \(D\) to \(E\), \(D\) to \(B\), \(E\) to \(B\) - a total of 24 moves.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
365. Railway Switch. How can two trains pass each other using the switch depicted here and continue moving forward with their locomotives? The small side spur is only sufficient to accommodate either a locomotive or one car at a time. No tricks with ropes or flying are allowed. Each change of direction made by one locomotive counts as one move. What is the minimum number of moves?

For a more convenient solution, draw the railway tracks on a piece of paper and place a hryvnia coin and three two-kopek coins (heads up) to represent the left train, and a hryvnia coin with two two-kopek coins (tails up) to represent the right train.
|
365. Draw the path diagram as shown in the figure, take 5 chips marked \(X, L, R, A\) and \(B\). The locomotives are \(L\) and \(R\), the two cars on the right are \(-A\) and \(B\). The three cars on the left should not be separated, so we will denote them as \(X\). The dead-end is marked as \(S\). Next,
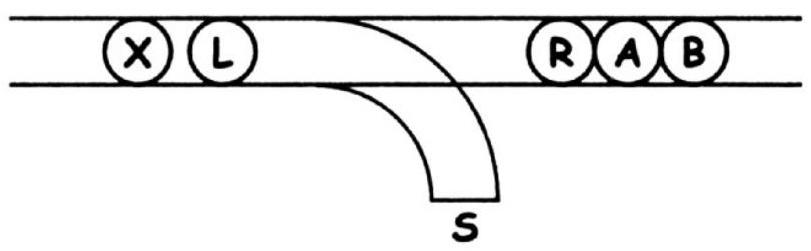
proceed as follows: \(R\) to the left, \(R\) to \(S, X L\) to the right, \(R\) to the left, \(X L A\) to the left, \(L\) pushes \(A\) to \(S, L\) to the left, \(X L\) to the right, \(R\) to \(A, R A\) to the left, \(X L B\) to the left, \(L\) directs \(B\) to \(S, L\) to the left, \(L X\) to the right, \(R A\) to \(B, R A B\) straight. In total, it took 14 moves, since in the first and third moves (\(R\) to the left and \(X L\) to the right) there is no change in direction. It is impossible to solve the problem in fewer moves.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
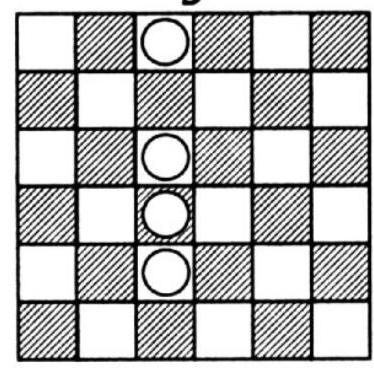
|
Yes
|
olympiads
| false
|
368. Black and White. One day over a cup of tea, Professor Rackbrain showed his friends the following old puzzle.

Arrange 4 white and 4 black chips in a row, alternating as shown in the picture. The puzzle is to move two adjacent chips to one of the ends, then move two other adjacent chips to the vacated space, and so on, until after 4 moves all the chips form a straight line without gaps, with the 4 black chips followed by the 4 white chips. Remember, you can only move adjacent chips.
- Now,- said Rackbrain,-since you have learned how to play this game, try another version. The conditions remain the same, but when moving two adjacent chips, you must swap their positions. For example, if you move chips 5,6 to the end, you must place them in the order 6,5. How many moves will it take now?
|
368. In the first case, move the pairs in the following order: place 6 and 7 before 1, then 3 and 4, 7 and 1, and 4 and 8 in the free spaces. This will result in the following arrangement of chips: 6,4, 8,2,7,1,5,3.
In the second case, move the chips 3,4 and place them in reverse order (4,3) before chip 1. Then move, simultaneously reversing the order of the chips, the pairs 6,7 (after rearrangement 7,6), 6,5 (after rearrangement 5,6), 3,1 (after rearrangement 1,3), and 6,8 (after rearrangement 8,6). The chips will be arranged in the sequence \(4,8,6,2,7,1,3,5\) in just 5 moves.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
377. Difference Squares. Can you arrange 9 digits in a square so that in any row, any column, and on each of the main diagonals, the differences between the sum of two digits and the third digit are the same? In the square provided in our diagram, all rows and columns meet the required condition - the difference in them is 3 (for example, $4+2-3,1+9-7,6+5-8$, etc.), but the diagonals "fall short," since the differences $8-(4+1)$ and $6-(1+2)$ are obtained in a prohibited manner: one digit should not be subtracted from the sum of two others, but rather the sum of two minus one.
How many solutions exist in total?
| 4 | 3 | 2 |
| :--- | :--- | :--- |
| 7 | 1 | 9 |
| 6 | 5 | 8 |
|
377. Apparently, there are only three solutions provided here. In each case, the difference is 5.
OTBETM
277

|
3
|
Logic and Puzzles
|
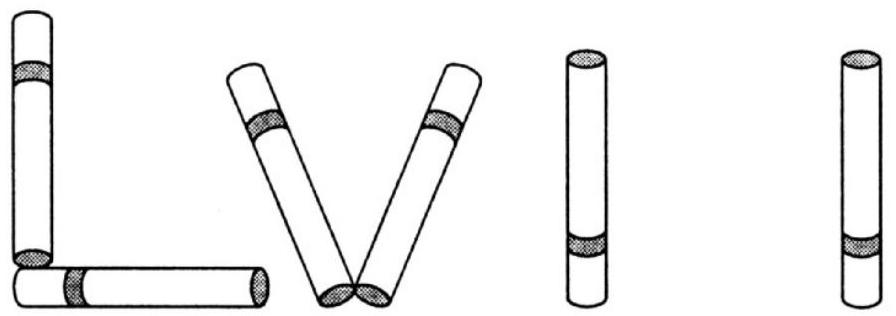
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
378. Is it that simple? Before you is a simple magic square, in which the sums of the numbers in any row, any column, and on the main diagonals are equal to 72. The puzzle con-
| 27 | 20 | 25 |
| :--- | :--- | :--- |
| 22 | 24 | 26 |
| 23 | 28 | 21 |
sists in transforming it into a multiplicative magic square, in which the products of the numbers in any row, any column, or on any of the major diagonals are the same. You are not allowed to swap the numbers, add anything to them, or use any arithmetic signs! You can only move the digits within one cell. Thus, instead of 27, you can take 72.
If you manage to find the "key" to the solution, the task will turn out to be incredibly simple. Otherwise, solving the puzzle is almost impossible.
|
378. To solve the puzzle, you just need to move the right digit up in each cell to get powers of 2. Revealing these powers, you will find that the resulting square meets the required condition with a product of 4096. Of course, anyone familiar with arithmetic knows that 20 equals 1.
|
4096
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
393. By the Stream. There is a general opinion that puzzles requiring the measurement of a certain amount of liquid can only be solved by a series of trials, but in such cases, general formulas for solutions can be found. Taking advantage of an unexpected leisure, I examined this question more closely. As a result, some very interesting things were discovered. Let's consider, for example, the simplest case, where a person comes to a stream with only two vessels and wants to measure a certain amount of water. If we are dealing with, say, a barrel of wine, we may encounter various complications related to whether the barrel is empty or full, whether we know its capacity and contents, whether the loss of wine is allowed, and whether it is possible to pour the wine back into the barrel. By the stream, all these complications disappear. Perhaps the problem has simplified to such an extent that it makes no sense to talk about it as a puzzle at all? Let's see.
A person comes to a stream with two vessels of 15 and 16 liters capacity. How can he measure exactly 8 liters of water in the fewest number of operations? Filling a vessel, emptying it, or pouring water from one vessel to another counts as one operation.
This puzzle is not difficult, but I think the reader will find it quite entertaining and instructive. It goes without saying that no tricks, such as marks on the vessels or tilting them, are allowed.
|
393.
\(A\)
\(B\)
\begin{tabular}{|c|c|c|c|c|c|c|c|}
\hline 15 l & 16 l & \(15 \pi\) & 16 l & 15 l & 16 l & 15 l & 16 l \\
\hline 0 & \(16^{*}\) & 15 & \(5^{*}\) & \(15^{*}\) & 0 & 0 & 11 \\
\hline 15 & \(1^{*}\) & 0 & 5 & 0 & 15 & 15 & 11 \\
\hline 0 & 1 & 5 & 0 & 15 & 15 & \(10^{*}\) & 16 \\
\hline 1 & 0 & 5 & 16 & \(14^{*}\) & 16 & 10 & 0 \\
\hline 1 & 16 & 15 & \(6^{*}\) & 14 & 0 & 0 & 10 \\
\hline 15 & \(2^{*}\) & 0 & 6 & 0 & 14 & 15 & 10 \\
\hline 0 & 2 & 6 & 0 & 15 & 14 & \(9^{*}\) & 16 \\
\hline 2 & 0 & 6 & 16 & \(13^{*}\) & 16 & 9 & 0 \\
\hline 2 & 16 & 15 & \(7^{*}\) & 13 & 0 & 0 & 9 \\
\hline 15 & \(3^{*}\) & 0 & 7 & 0 & 13 & 15 & 9 \\
\hline 0 & 3 & 7 & 0 & 15 & 13 & \(8^{*}\) & 16 \\
\hline 3 & 0 & 7 & 16 & \(12^{*}\) & 16 & & \\
\hline 3 & 16 & 15 & \(8^{*}\) & 12 & 0 & & \\
\hline 15 & \(4^{*}\) & 0 & 8 & 0 & 12 & & \\
\hline 0 & 4 & 8 & 0 & 15 & 12 & & \\
\hline 4 & 0 & 8 & 16 & \(11^{*}\) & 16 & & \\
\hline & 16 & & & 11 & & & \\
\hline
\end{tabular}
Each row in the column represents an operation. Thus, in the case of \(A\), we first fill the 16-liter container, then pour 15 liters into another container, leaving 1 liter; then, by emptying the 15-liter container, we pour the 1 liter from the 16-liter container into it, and so on.
The asterisks show how we can sequentially measure 1, 2, 3, 4 liters, and so on. We can also proceed differently, as shown in case \(B\): first fill the 15-liter container, and then sequentially measure 14, 13, 12, 11 liters, and so on. Continuing the "strategy" of \(A\), we get the pouring scheme \(B\) in reverse order. From this, it is clear that to measure from 1 to 7 liters, we should use method \(A\), and from 8 to 14 liters, method \(B\). Using method \(A\), we can measure 8 liters in 30 operations, and using method \(B\) in only 28, which is the correct answer.
Surprisingly, using any two coprime measures (i.e., measures that do not have common divisors, such as 15 and 16), we can measure any integer number of liters from 1 to the largest measure. Using 4-liter and 6-liter containers (each divisible by 2), we can only measure 2, 4, and 6 liters. With 3-liter and 9-liter containers, we can only measure 3, 6, and 9 liters. In our table, the measurable volumes are in the correct sequence. However, if we take 9-liter and 16-liter containers and apply method \(A\), we get 6, 14, 5, 12, 3 liters, and so on, with a cyclic difference of 7 (16 - 9 = 7). In other words, by adding 7 to 14 and subtracting 16, we get 5, and by adding 7 to 12 and subtracting 16, we get 3, and so on.
[For a good method of solving such puzzles using isometric graph paper, see my note in Scientific American, September 1963, and for further discussion of this method, see T. H. O'Beirne's book "Puzzles and Paradoxes" (Oxford University Press, 1965). - M. G.]
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
397. Measuring Water. A maid was sent to a spring with two vessels of 7 and 11 pints capacity. She needs to bring back exactly 2 pints of water.
What is the minimum number of operations in this case? By "operation" we mean either filling a vessel, emptying it, or pouring water from one vessel to another.
|
397. Two pints of water can be measured in 14 operations, if the vessels above the line are empty, and each line corresponds to one operation.
\begin{tabular}{cr}
7 l & 11 l \\
\hline 7 & 0 \\
0 & 7 \\
7 & 7 \\
3 & 11 \\
3 & 0 \\
0 & 3 \\
7 & 3 \\
0 & 10 \\
7 & 10 \\
6 & 11 \\
6 & 0 \\
0 & 6 \\
7 & 6 \\
2 & 11
\end{tabular}
The contents of the vessels, specified after each operation, do not require explanations.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
401. The Road to Tipperary. A popular bard assures us that "the road is long to Tipperary." Look at the attached map and tell us if you can find the best route there. The straight segments represent transitions from city to city. You need to get from London to Tipperary in an even number of transitions. It is not difficult to do this in 3, 5, 7, 9, or 11 transitions, but all these are odd numbers. The issue is that with an odd number of transitions, one very important sea crossing is omitted.
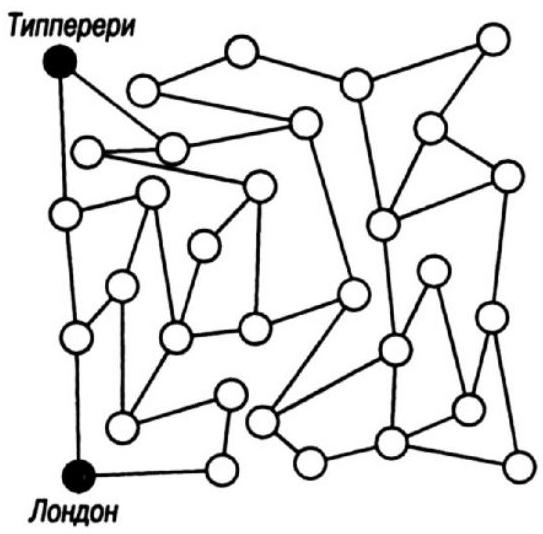
If you manage to achieve your goal and reach your destination in an even number of transitions, it will be because you have crossed the Irish Sea. Which segment of the journey crosses the Irish Sea?
|
401. The thick line on the diagram shows the route from London to Tipperary, made in 18 moves. To reach the destination in an even number of moves, it is absolutely necessary to include in the route the move marked by the words Irish Sea.
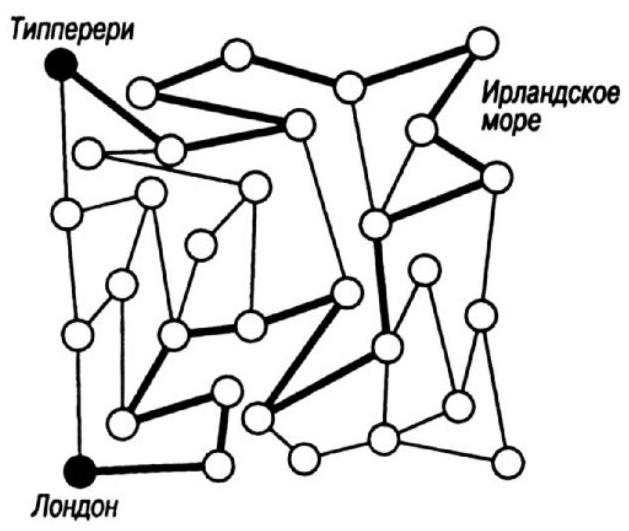
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
413. Railway Routes. The diagram shows a simplified railway network. We want to find out how many different ways there are to travel from \(A\) to \(E\), without passing through the same segment more than once on any route.
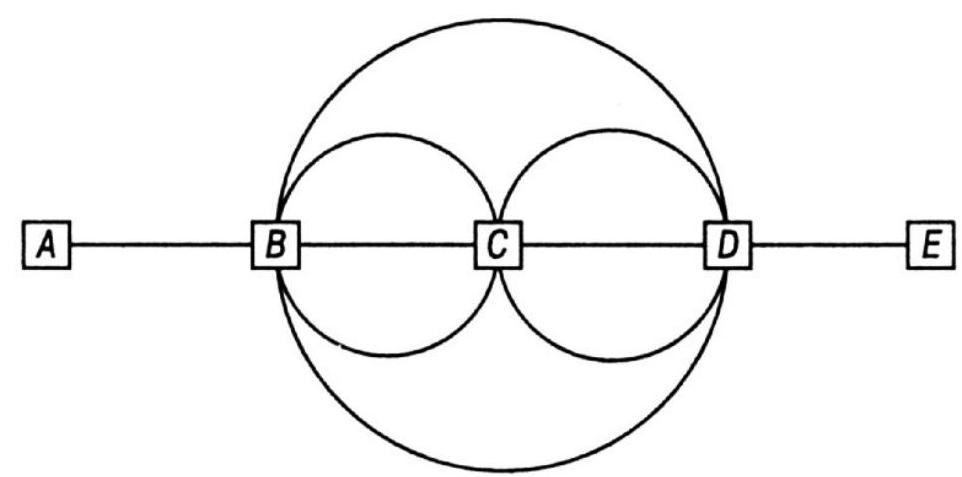
The question is very simple. However, it is practically impossible to answer it until you come up with a method to record all the routes. The issue is that there are too many routes, ranging from the short \(A B D E\), which includes one large arc, to the long \(A B C D B C D B C D E\), which includes every segment of our system and allows for various variations.
How many different routes are there in total?
|
413. There are 2501 routes from \(B\) to \(D\), specifically:
\begin{tabular}{cccr}
\begin{tabular}{c}
Number of \\
segments
\end{tabular} & \begin{tabular}{c}
Number of \\
variations
\end{tabular} & \begin{tabular}{c}
Number of \\
routes
\end{tabular} & \\
1 & 1 & 2 & 2 \\
2 & 1 & 9 & 9 \\
3 & 2 & 12 & 24 \\
4 & 5 & 18 & 90 \\
5 & 4 & 72 & 288 \\
6 & 14 & 36 & 504 \\
8 & 22 & 72 & 1584 \\
\({ } &{ } &{2501}\)
\end{tabular}
It is sufficient to consider the routes from \(B\) to \(D\). A route consisting of 1 segment leads directly to \(D\). The route with 2 segments is \(C D\). The routes with 3 segments are \(C B D\) and \(D C D\). The five routes with 4 segments are \(D B C D, D C B D, C B C D, C D C D\) and \(C D B D\). Each of these routes has variations associated with
the choice of specific segments, and the number of such variations is the same for any route containing the same number of segments. There are no routes with seven segments.
|
2501
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
433. Gifted Paintings. A wealthy collector had 10 valuable paintings. He wanted to make a gift to a museum, but the collector couldn't figure out how many gift options he had: after all, he could give any one painting, any two, any three paintings, and so on, he could even give all ten paintings.
The reader might think that answering this question would require a long and tedious calculation; however, I will provide a small rule that allows one to answer in all similar cases without any difficulties and thankless work.
|
433. Multiply 2 by itself as many times as there are pictures, and subtract 1. Thus, 2 to the tenth power is 1024. Subtracting 1, we get 1023, which is the correct answer. Suppose we have only three pictures. Then one of them can be chosen in three ways,
\footnotetext{
* It can be said that Dudeney proved a local, not a global theorem.
}
two in three ways, and three in one way, which adds up to 7 ways. But 7 is exactly \(2^{3}-1^{*}\).
|
1023
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
434. Parliamentary Elections. How many different ways are there to elect 615 members of parliament if there are only four parties: Conservatives, Liberals, Socialists, and Independents? The mandates can be distributed, for example, as follows: Conservatives - 310, Liberals - 152, Socialists - 150, Independents - 3. Other distributions are also possible: Conservatives - 0, Liberals - 0, Socialists - 0, Independents - 615 or Conservatives - 205, Liberals - 205, Socialists - 205, Independents - 0, etc. We do not distinguish between candidates from each party, as only their total number is important to us.
|
434. There are 39147416 different ways in total. Add 3 to the number of members (which gives 618) and subtract 1 from the number of parties (which gives 3). Then the answer is the number of ways to choose 3 items from 618, that is,
\[
\frac{618 \times 617 \times 616}{1 \times 2 \times 3}=39147416 \text { ways }
\]
The general solution is as follows. Let \(p\) be the number of parties, and \(m\) be the number of members of parliament. The number of ways is equal to the number of combinations of \(m+p-1\) objects taken \(\mathrm{p}-1\) at a time.
|
39147416
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
436. The Crossing. Six relatives need to cross a river in a small boat that can only hold two people at a time. Mr. Webster, who was in charge of the crossing, had a falling out with his father-in-law and son. Unfortunately, I must also note that Mrs. Webster is not speaking to her mother and her daughter-in-law. The tension between them is so high that it would be unsafe to allow feuding parties to cross together or to remain on the same bank of the river. Additionally, to prevent further disputes, no man can be left with two women or two men with three women.
How can this respectable family cross to the opposite bank in the fewest number of trips? No tricks such as using a rope or swimming to another bank are allowed.
|
436. The puzzle can be solved in 9 crossings as follows:
1) Mr. and Mrs. Webster cross together;
2) Mrs. Webster returns;
3) the mother and daughter-in-law cross
4) Mr. Webster returns;
5) the father-in-law and son cross
6) the daughter-in-law returns;
7) Mr. Webster and the daughter-in-law cross;
8) Mr. Webster returns;
9) Mr. and Mrs. Webster cross together.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
438. Escape across the river. During the flight of the Turkish troops at Treise, a small detachment found itself on the bank of a wide and deep river. Here they found a boat in which two boys were boating. The boat was so small that it could only hold two children or one adult.
How did the officer manage to cross the river with his 357 soldiers, returning the boat to the boys at the end of the crossing? How many times did the boat have to cross from bank to bank?
|
438. Two children are rowing to the other shore. One of them gets out, and the other returns. A soldier ferries across, gets out, and the boy returns. Thus, to ferry one adult across, the boat has to make 4 trips from shore to shore. Therefore, it had to make \(4 \times 358=1432\) trips to ferry the officer and 357 soldiers, and in the end, the boat was back with the children.
|
1432
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
443. Four chips in a straight line. Before you is a board of 36 squares, on which 4 chips are arranged in a straight line such that any square on the board is on the same row, column, or diagonal as at least one of the chips. In other words, if we consider our chips as chess queens, then every square on the board is under attack by at least one queen. The puzzle is to determine how many ways 4 chips can be arranged in a straight line so that every square is on the same line as one of the chips.

Two positions are considered different if the sets of 4 squares occupied by the chips are at least partially different. For example, in the given example, all chips can be moved to the adjacent column to the right or placed on any of the two central rows. Thus, we have found 4 different solutions that can be obtained from each other by rotations and reflections. Remember that the chips must always be arranged in a straight line. This puzzle is not too difficult and is quite engaging.
|
443. There are 9 main solutions presented in the figure. Solution \(A\) is the one given in the problem statement. Of these 9 solutions, \(D\), \(E\), and \(J\) each generate 8 solutions through rotations and reflections, as explained earlier, while the others yield only 4 solutions each. Therefore, there are a total of 48 different solutions to this puzzle.
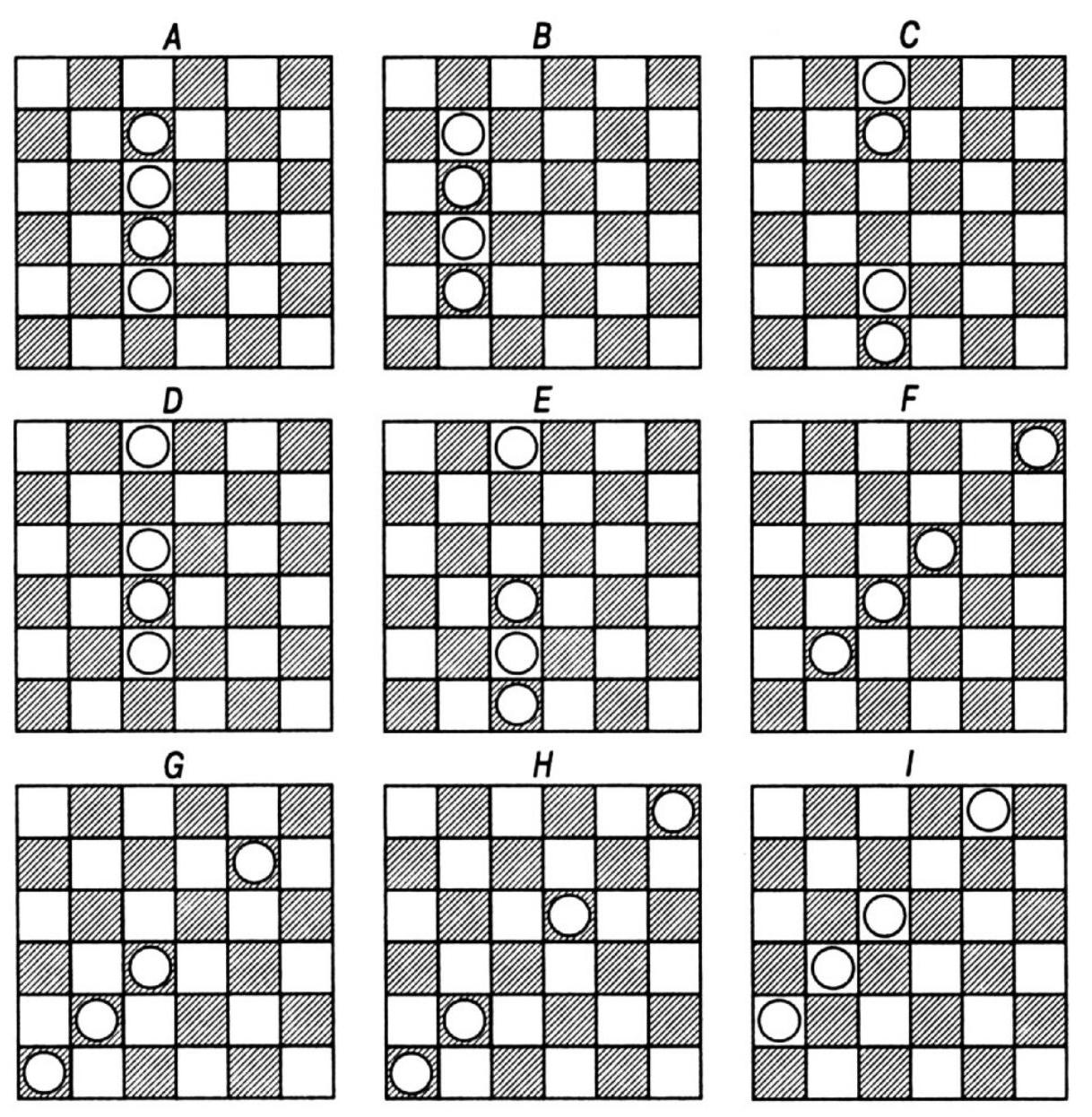
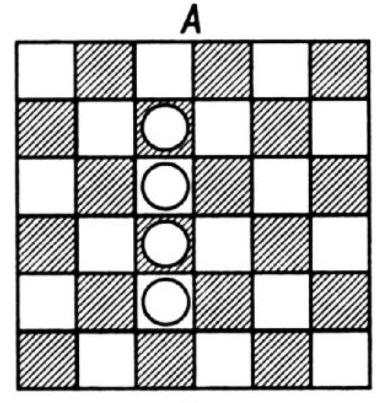
D
G
E
H
\(F\)

I
The reader may find it interesting to know that on an \(8 \times 8\) chessboard, five tokens can be arranged in a straight line under the same conditions in four main ways, generating 20 different solutions.
|
48
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
445. At Lunch. The clerks of the firm "Pilkings and Popinjay" decided that they would sit three at a time at the same table every day until any 3 people would be forced to sit at this table again. The same number of clerks of the firm "Redson, Robson and Ross" decided to do the same, but with 4 people at a time. When they started to implement their plan, it turned out that the clerks of the second firm could continue rearranging themselves exactly three times longer than their neighbors.
What is the smallest number of clerks that could have served in each of the two firms?
|
445. If Pilkins had 11 clerks and Redson 12, they could have sat at a table in 165 and 495 ways respectively, which would have been the solution to the problem. However, we know that both firms had an equal number of clerks. Therefore, the answer is 15 clerks, sitting three at a time for 455 days, and 15 clerks, sitting four at a time for 1365 days.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
449. Ten Barrels. A merchant had 10 barrels of sugar, which he arranged into a pyramid as shown in the figure. Each barrel, except one, was marked with its own number. It turned out that the merchant had accidentally placed the barrels in such a way that the sum of the numbers along each row was 16.
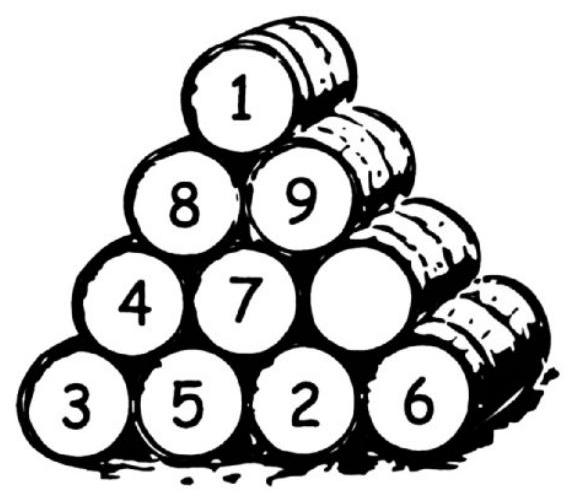
Could you rearrange the barrels so that the sum of the numbers along each row equals the smallest possible number? Of course, the central barrel (which happened to be barrel number 7 in the figure) does not count in the sum.
|
449. Arrange 10 barrels in the following two ways, so that the sum of the numbers along each side equals 13 - the smallest possible number:
By changing the position of the numbers (but not the numbers themselves) on each side, we can obtain 8 solutions in each case, if we do not distinguish solutions that are rotations or reflections of each other.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
450. Signal Lights. Two spies on opposite banks of a river came up with a way to signal at night using a frame (similar to the one shown in the picture) and three lamps. Each lamp could emit white, red, or green light. The spies developed a code in which each signal meant something.
Of course, you understand that one lamp, no matter which hook it is hung on, will have only one value. Two lamps hung on the upper hooks 1 and 2 are indistinguishable from two lamps hung on hooks 4 and 5. Two red lamps on hooks 1 and 5 can be distinguished from lamps on hooks 1 and 6, and two lamps on hooks 1 and 2 are different from two lamps on hooks 1 and 3.
Considering all this variety of lamp positions on the hooks and the color of the signals, answer how many different signals can be sent.
|
450. With three red, white, or green lamps, we can obtain 15 different combinations (45). With one red and two white lamps, we can also obtain 15 combinations, and for each of them, there are 3 more combinations of the order of colors; in total, 45 combinations. The same result will be obtained with one red and two green lamps, one white and two red lamps, one white and two green lamps, one green and two white lamps, and one green and two red lamps (270). With one red, one white, and one green lamp, we can obtain 6 times 15 combinations (90). With two red, two white, or two green lamps, we can obtain 7 combinations each (21). With one red and one white, or one red and one green, or one white and one green lamp, we can obtain 14 combinations each (42). Using only one lamp, we can send only 1 signal each (3). Now add the numbers in parentheses, and you will get the answer - 471 signals.
|
471
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
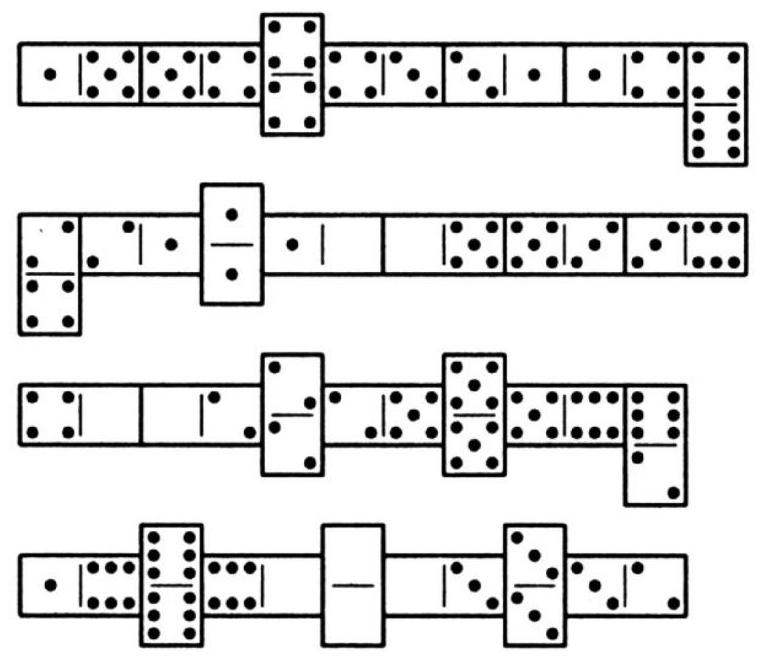
469. Groups of Dominoes. Is it known to any of my readers that if all 28 dominoes are laid out in a single line according to the usual rule (6 to 6, 2 to 2, blank to blank, etc.), the numbers at the ends will always match, so that the dominoes can actually be arranged in a circle? A very old trick involves hiding one of the dominoes (but don't take a double), and then asking someone to arrange the remaining dominoes in a line while you turn away. The audience is amazed when you, without looking at what has been done, name the numbers at the ends. These numbers match those on your hidden domino, since all the dominoes form a circle. If we arrange the dominoes as shown in the figure, and then break the chain into four pieces, each with 7 dominoes, it can be found that the sum of the points in the first group is 49, in the second 34, in the third 46, and in the fourth 39.
I would like to arrange the dominoes into 4 groups such that the sums of the points in each group are equal. Can you do this?
|
469. The figure shows one of the solutions. The chain of dominoes is broken into 4 parts, each containing 7 pieces, and the sum of the points in each part is 22.
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
478. Setting up dominoes. One day someone reminded Professor Rackbrain about his promise to say how many ways there are to arrange 28 domino tiles in a single line according to the usual rules of the game, if arrangements from left to right and from right to left are considered different. After some time, he reported that there are 7959229931520 such ways, and added that this problem is very complex.
Then the professor suggested to those present to solve a similar problem for 15 tiles (which remain after removing all tiles with five or six spots), with the condition that two domino chains, obtained by "reading" the same chain once from left to right and once from right to left, are considered different. Of course, in this case, the tiles should also be arranged according to the usual rules: 1 to 1, 6 to 6, etc.
\section*{PUZZLES WITH MATCHES}
|
478. There are 126760 different ways to arrange 15 dominoes in a line, if the two directions are distinguished.
|
126760
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
479. Matchstick Puzzle. Taking a box of matches, I found that I could form any pair of regular polygons shown in our diagram using all the matches each time. So, if I had 11 matches, I could use them to form, as shown, either a triangle and a pentagon, or a pentagon and a hexagon, or a square and a triangle (using only 3 matches for the triangle); but with 11 matches, I could not form either a triangle and a hexagon, or a square and a pentagon, or a square and a hexagon. Of course, each side of the figure must use the same number of matches.
What is the smallest number of matches that could be in my box?
|
479. The smallest possible number is 36 matches. We can form a triangle and a square from 12 and 24 matches, a triangle and a pentagon from 6 and 30 matches, a triangle and a hexagon from 6 and 30 matches, a square and a pentagon from 16 and 20 matches, a square and a hexagon from 12 and 24 matches, and a pentagon and a hexagon from 30 and 6 matches. These pairs of numbers can be varied in all cases except the fourth and the last. The total number of matches cannot be less than 36. For a triangle and a hexagon, the number of matches must be divisible by 3; for a square and a hexagon, an even number of matches is required. Therefore, the desired number must be among the numbers divisible by 6, such as \(12,18,24,30,36\), but fewer than 36 matches cannot form a pentagon and a hexagon.
|
36
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
484. Zero from fifty-seven. After the previous puzzle, this one will seem quite simple.
In our drawing, you see 6 cigarettes (matches would work just as well) arranged to form the number 57. The puzzle is to move two of the cigarettes without touching the others to get 0.
Remember, you can only move two cigarettes. There are two completely different solutions. Can you find one or even both?
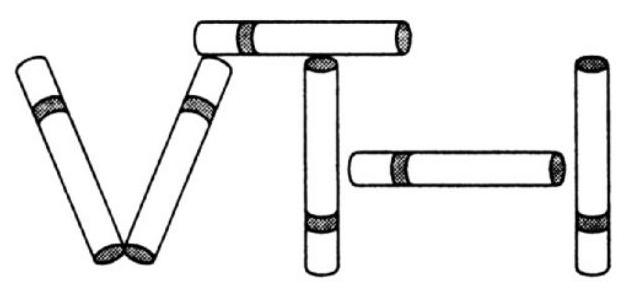
|
484. Move the two cigarettes forming the letter \(L\), and place them as shown in the figure. We have the square root of 1 minus 1 (i.e., \(1-1\)), which is obviously equal to 0. In the second case, we can move the same two cigarettes, placing one next to V and the other next to the second I, so that the word NIL (nothing) is formed.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
495. Count the Matches. A friend writes that he bought a small box of short matches, each an inch long. He found that he could arrange them in the form of a triangle, the area of which contained as many square inches as there were matches. Then he used 6 matches, and it turned out that from the remaining ones, he could form a new triangle, the area of which contained as many square inches as there were matches left. And after using another 6 matches, he managed to do the same again.
How many matches did he have in the box originally? This number is less than 40.
\section*{VARIOUS PUZZLES}
|
495. There were 36 matches in the box, from which my friend could form a triangle \((17,10,9)\) with an area of 36 square inches. After using 6 matches, the remaining 30 formed a triangle \((13,12,5)\) with an area of 30 square inches, and using another 6 matches, he was able to form a triangle \((10,8,6)\) with an area of 24 square inches from the remaining 24 matches.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
497. Shuffling Cards. An elementary method of shuffling cards consists of taking a deck face down in the left hand and transferring the cards one by one to the right hand; each successive card is placed on top of the previous one: the second on top of the first, the fourth on top of the third, and so on until all the cards have been transferred. If you repeat this procedure several times with any even number of cards, you will find that after a certain number of repeated shuffles, the cards will return to their original order. If you have \(2,4,8,16,32,64\) cards, it will take \(2,3,4,5\), 6,7 shuffles respectively for the cards to return to their original order.
\footnotetext{
* The correct order is: Ace, Two, Three, Four, Five, Six, Seven, Eight, Nine, Ten, Jack, Queen, King.
}
How many times do you need to shuffle a deck of 14 cards?
|
497. To shuffle 14 cards in the manner described above and return them to their original order, it takes 14 shuffles, although in the case of 16 cards, only 5 are required. We cannot delve into the nature of this phenomenon here, but the reader may find it interesting to conduct an independent investigation of this question.
[For the mathematical theory of such shuffling, see W. W. Rouse Ball, “Mathematical Recreations and Essays” (N. Y., 1960, pp. 310-311). This shuffling is sometimes called “Monge’s shuffle,” after the famous 18th-century French mathematician Gaspard Monge, who first invented it. M. G.]
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The Absent-Minded Secretary. The typist typed ten letters and addresses on ten envelopes, but the absent-minded secretary placed these letters into the envelopes without any regard for the correspondence between the letter and the addressee. However, she did place only one letter in each envelope. What is the probability that exactly nine letters ended up in their intended envelopes?
|
1. If nine letters have gone into their intended envelopes, then the tenth letter will certainly do the same. Therefore, the probability that exactly nine letters have gone into their envelopes is zero.
$$
[M . M ., \mathbf{3 3}, 210(\text { March 1950).] }
$$
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Zero-sum test. A certain test consists of 26 questions. For each incorrect answer, five points are deducted from the test-taker, and for each correct answer, eight points are awarded.
The test-taker answered all the questions. How many questions did he answer correctly if the total number of points he received was zero?
|
4. The ratio of the number of answers of each type is equal to the inverse ratio of the corresponding points. Therefore, the number of correct answers is $\frac{5}{5+8} \cdot 26=10$.
[M. M., 31, 237 (March 1958).]
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Mental arithmetic. Square 85 in your mind.
|
7. Since $(10 a+5)^{2}=100 a^{2}+100 a+25=a(a+1) 100+25$, we get that $(85)^{2}=8 \cdot 9 \cdot 100+25=7225 \star$.
$$
[\text { M. M., 24, } 273 \text { (May 1951).] }
$$
|
7225
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Fourth-order equation. How many negative roots does the equation
$$
x^{4}-5 x^{3}-4 x^{2}-7 x+4=0 ?
$$
have?
|
8. The equation $x^{4}-5 x^{3}-4 x^{2}-7 x+4=0$ can be rewritten as $\left(x^{2}-2\right)^{2}=5 x^{3}+7 x$. Since for any negative $x$ the left side of the equation is positive, while the right side is negative, the original equation cannot have negative roots.
[P. E. Horton, M. M., 24, 114 (November 1950).]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Flower Seller. A girl bought $x$ roses in the store, paying $y$ dollars for all ( $x$ and $y$ are integers). When she was about to leave, the seller told her: "If you bought 10 more roses, I would give you all the roses for 2 dollars, and you would save 80 cents on each dozen." Find $x$ and $y$.
|
20. Since $y$ is an integer $<2, y=1^{\star}$. Then, expressing the cost of one rose in cents, we get
$$
\frac{100}{x}-\frac{200}{x+10}=\frac{80}{12}, \text{ or } x^{2}+25 x-150=0.
$$
The only positive root of this equation is $x=5$. This is the number of roses the girl initially bought.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. The End of the World. On April 1, 1946, the newspaper "Jericho Daily Lapse" reported: "A famous astrologer and numerologist from Guyasuela, Professor Euclid Paracelsus Bombast Umbugio, predicted that the end of the world will occur in 2141. His prediction is based on deep mathematical and historical research. Professor Umbugio calculated the expression
$$
1492^{n}-1770^{n}-1863^{n}+2141^{n}
$$
for \( n=0,1,2,3 \) and so on up to 1945, and found that all the numbers he obtained after months of painstaking work are divisible by 1946. The numbers 1492, 1770, and 1863 represent historical dates: the discovery of the New World, the Boston Massacre, and the Gettysburg Address, respectively. What could happen in 2141? Obviously, the end of the world."
We should strip such a professor of his title! Obtain his result with a simple calculation.
|
23. All that is needed to solve the problem is that $x^{n}-y^{n}$ for $n=0,1,2, \ldots$ is divisible by $x-y$. Let the quantity the professor was calculating be $F(n)$. Then, since $2141-1863=$ $1770-1492=278, F(n)$ is divisible by 278 for any $n$. Similarly, $2141-1770=1863-1492=371$, a number coprime with 278. Thus, $F(n)$ is always divisible by $278 \cdot 371=53 \cdot 1946$ and, of course, by the number 1946 itself.
[E. P. Stark, A. M. M., 54, 43 (January 1947).]
|
1946
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
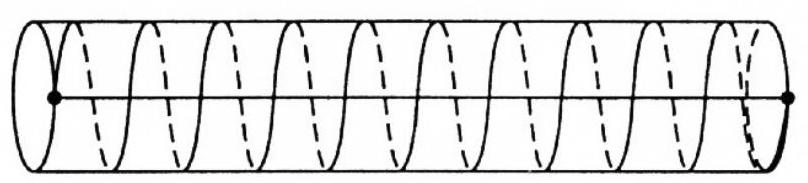
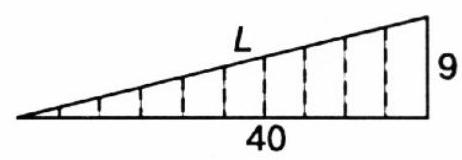
25. Length of a spiral. A piece of wire is wound in a spiral around a cylindrical tube, forming 10 turns. The length of the tube is 9 cm, and the length of its outer circumference is 4 cm. The ends of the spiral lie on the same generatrix of the cylinder. Find the length of the wire.
|
25. Let's unroll the surface of the cylinder along with the wire onto a plane. The generatrix (9 cm), the tenfold repeated circumference ($10 \cdot 4$ cm), and the wire ($L$) now form a right triangle. Therefore, $L=(81+1600)^{\frac{1}{2}}=41$ cm.
From this, it follows, among other things, that if the wire is not wound around the cylinder in such a way that it intersects the generatrices at a constant angle, it may loosen over time.
[M. M., 23, 278 (May 1950).]
|
41
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. Minimum problem. Show that for any positive numbers $p, q, r$ and $s$ the fraction
$$
\frac{\left(p^{2}+p+1\right)\left(q^{2}+q+1\right)\left(r^{2}+r+1\right)\left(s^{2}+s+1\right)}{p q r s}
$$
is not less than 81.
|
26. The given fraction can be rewritten as
$$
\left(p+1+\frac{1}{p}\right)\left(q+1+\frac{1}{q}\right)\left(r+1+\frac{1}{r}\right)\left(s+1+\frac{1}{s}\right)
$$
Further, the sum of two positive reciprocal numbers $\geqslant 2$. Therefore, each bracket $\geqslant 3$, and the entire product $\geqslant 81$.
[R. L. Moehlman, S. S. M., 54, 667 (November 1954).]
From this, it directly follows that
$$
\frac{\left(a_{1}^{2}+a_{1}+1\right)\left(a_{2}^{2}+a_{2}+1\right) \ldots\left(a_{n}^{2}+a_{n}+1\right)}{a_{1} a_{2} \ldots a_{n}} \geqslant 3^{n}
$$
for any positive $a_{i}$.
|
81
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
30. Unknown remainder. Find the remainder of the division of $f\left(x^{5}\right)$ by $f(x)$, if
$$
f(x)=x^{4}+x^{3}+x^{2}+x+1
$$
|
30. Since $f(x)=x^{4}+x^{3}+x^{2}+x+1,(x-1) f(x)=x^{5}-1$. Further, $f\left(x^{5}\right)=\left(x^{20}-1\right)+\left(x^{15}-1\right)+\left(x^{10}-1\right)+\left(x^{5}-1\right)+4+1$. But $x^{5}-1$, and therefore $f(x)$, are divisors of each of the brackets. Hence,
$$
f\left(x^{5}\right)=[\text { multiple of } f(x)]+5
$$
[N. Anning, S. S. M., 54, 576 (October 1954).]
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. Simple multiplication. Multiply 5746320819 by 125.
|
33. Since $125=1000: 8, \quad 5746320819 \cdot 125=$ $5746320819000: 8=718290102375$
$[M$. M., 25, 289 (May 1952).]
|
718290102375
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Simplifying Radicals. Simplify the expression
$$
\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}
$$
|
35. Let $\sqrt[3]{2+\sqrt{5}}=a, \quad \sqrt[3]{2-\sqrt{5}}=b, \quad a+b=x$. Then
$$
x^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}=a^{3}+b^{3}+3 a b(a+b)=4+3(\sqrt[3]{-1}) x
$$
Thus, $x^{3}+3 x-4=0$, and the only real root of this equation is 1.
$[$ [K. Adler, A. M. M., 59, 328 (May 1952).]
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41. The Dozing Schoolboy. A schoolboy, waking up at the end of an algebra lesson, heard only a fragment of the teacher's phrase: "… I will only say that all the roots are real and positive." Glancing at the board, he saw there a 20th-degree equation assigned as homework, and tried to quickly write it down. He managed to write down only the first two terms $x^{20}-20 x^{19}$, before the teacher erased the board; however, he remembered that the constant term was +1. Could you help our unfortunate hero solve this equation?
|
41. The roots are positive; their arithmetic mean is $-\frac{(-20)}{20}$, and their geometric mean is $(+1)^{\frac{1}{20}}$. Since both these values coincide, it follows that all roots are equal to 1.
[D. S. Greenstein, A. M. M., 63, 493 (September 1956).]
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
48. Book Series. A certain series of books was published at seven-year intervals. When the seventh book was released, the sum of all the years in which the books of this series were published was 13524. When was the first book of the series published?
|
48. The arithmetic mean of the years of publication is $\frac{13524}{7}=$ 1932, or the middle term of our arithmetic progression. The first term of this progression differs from the middle term by three differences. Therefore, the first book was published in 1932 $-3 \cdot 7=1911$.
$[M$. M., 34, 372 (September 1961).]
|
1911
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. An equation containing sums. Find $n$, if
$$
\frac{1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}}{2^{3}+4^{3}+6^{3}+\cdots+(2 n)^{3}}=\frac{199}{242}
$$
|
51. First, note that if \(a: b = c: d\), then obviously \((a+b): b = (c+d): d\). Applying such a transformation to the fractions in our equation, we get
\[
\frac{1^{3}+2^{3}+3^{3}+\cdots+(2 n)^{3}}{2^{3}\left(1^{3}+2^{3}+3^{3}+\cdots+n^{3}\right)}=\frac{441}{242}
\]
Then, applying the known formula for the sum of cubes of natural numbers \({ }^{*}\), we get
\[
\begin{aligned}
\frac{(2 n)^{2}(2 n+1)^{2}}{4}: \frac{8 n^{2}(n+1)^{2}}{4} & =\frac{441}{242}=\frac{(21)^{2}}{2 \cdot(11)^{2}} \\
\frac{(2 n+1)^{2}}{(n+1)^{2}} & =\frac{(21)^{2}}{(11)^{2}}
\end{aligned}
\]
From this, it is clear that \(n=10\). (The negative square root leads to a negative \(n\).)
52*. If we place a stack of \((k-1)\) rectangular parallelepipeds, each of length \(2x\), on the \(k\)-th horizontal parallelepiped of the same kind and shift our stack until its center of gravity is vertically aligned with the edge of this \(k\)-th parallelepiped, then the center of gravity of the entire configuration will be horizontally distant from the edge of the \(k\)-th parallelepiped by a distance of \(\frac{x}{k}\).
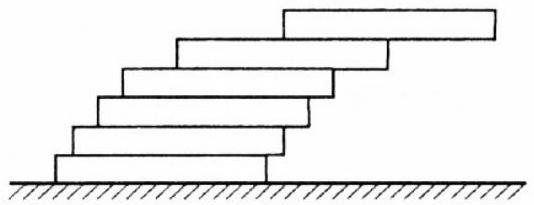
From this, it follows that \(n\) domino tiles in our stack (with \(x = 1\) inch) can be shifted between two vertical parallel planes, which are 1 inch apart, such that the total length of the "protruding" edges, moving from top to bottom, is expressed as \(1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n-1}\). In this case, the domino tiles form a semi-arch that will be in equilibrium. This sum represents a partial sum of the harmonic series; since this series diverges, we can, by choosing a sufficiently large \(n\), achieve any horizontal distance between the edge of the top tile and the edge of the bottom tile.
To have the entire top tile extend beyond the edge of the bottom tile, \(n\) must be at least 5. In this case, the total length of the "protruding" edges will be \(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}\), or approximately 2.083 inches.
If we now shift our tiles so that all the \(2 \times 0.25\) faces are parallel to the same plane, and the center of gravity of each upper part of our stack is located above the corner of the nearest lower tile, then the horizontal distance between the corners of the topmost and bottommost tiles will increase compared to the previous case by \(\left[1^{2} + \left(\frac{1}{2}\right)^{2}\right]^{\frac{1}{2}} = \frac{\sqrt{5}}{2}\) times.
\[
\text { [P. M. E. J., 1, } 411 \text { (April 1954).] }
\]
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. Dice. A die, on the faces of which the numbers $0,1,2,3,4,5$ are depicted, is rolled until the total sum of the points rolled exceeds 12. What is the most likely value of this sum?
|
53. Consider the penultimate throw. After this throw, the sum of points can be $12, 11, 10, 9$ or 8. If it is 12, then after the last throw, the final sum of points can, with equal probability, take the values $13, 14, 15, 16$ or 17. Similarly, if this sum is 11, then the final sum can, with equal probability, take the values $13, 14, 15$ or 16, and so on. From this, it is clear that the most probable value of the final sum of points is 13.
[N. J. Fine, A. M. M., 55, 98 (February 1948).]
If instead of 12, we take any $N>3$, then the most probable value of the sum is $N+1^{\star}$.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. Probability of divisibility. Find the probability that if the digits $0,1,2, \ldots, 9$ are placed in random order in the empty spaces in the sequence of digits
$$
5-383-8-2-936-5-8-203-9-3-76
$$
then the resulting number will be divisible by 396.
|
56. The number 76, formed by the last two digits, is divisible by 4. The difference between 73 (the sum of all digits in even positions) and $17+45$ (the sum of all digits in odd positions) is divisible by 11 regardless of the order in which the empty places are filled*. The sum of all digits, $90+45$, is divisible by 9. Therefore, our number is divisible by $4 \cdot 11 \cdot 9=396$. Hence, the desired probability is 1.
[P. Nagara, A. M. M., 58, 700 (December 1951).]
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. The son of a mathematics professor. The mathematics professor wrote a polynomial $f(x)$ with integer coefficients on the board and said:
- Today is my son's birthday. If his age $A$ is substituted into this polynomial instead of $x$, then the equation $f(A)=A$ holds. Note also that $f(0)=P$, where $P$ is a prime number greater than $A$.
How old is the professor's son?
|
58. Since $f(0)=P$,
$$
f(x)=x \cdot q(x)+P \quad \text { and } \quad f(A)=A \cdot q(A)+P=A .
$$
Therefore, $P$ is divisible by $A$. Since $P>A$ and $P$ is prime, $A=1$. Thus, the professor's son is 1 year old. The professor could have written down any polynomial from an infinite class of such polynomials, for example $x^{3}-3 x^{2}+3$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
60. Meteorological observations. At a weather station, it was noticed that during a certain period of time, if it rained in the morning, it was clear in the evening, and if it rained in the evening, it was clear in the morning. In total, there were 9 rainy days, with clear evenings 6 times and clear mornings 7 times. How many days did this entire period cover?
|
60. There were $\frac{1}{2}(6+7-9)=2$ completely clear days, so the period under consideration covered $9+2=11$ days.
$[$ [M. M., 34, 244 (March 1961).]
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71. Cutting a Sphere. Into what maximum number of congruent pieces can a sphere be cut so that each side of each piece represents an arc of a great circle that is less than a quarter of such a circle?
|
71. Inscribed in this sphere is a regular dodecahedron or icosahedron, and perpendiculars are dropped from the center of the sphere to each face. Construct 60 isosceles triangles whose vertices are at the bases of these perpendiculars and whose bases are the sides of the corresponding faces. Now project these triangles from the center of the sphere onto the sphere. The resulting isosceles spherical triangles will be the congruent pieces into which the sphere should be cut.
[O. R. Ransom, A. M. M., 40, 114 (February 1933).]
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
74. A curious number. Find such a positive number that $\frac{1}{5}$ of it, multiplied by its $\frac{1}{7}$, equals this number.
|
74. If $(N: 5)(N: 7)=N$, then $N(N-35)=0$, so $N=35$. In other words, if the given number is multiplied by itself, the result will be 35 times greater than if we multiply $\frac{1}{5}$ of this number by $\frac{1}{7}$ of it. Therefore, the number we are looking for is 35.
In the general case, if a number equals $\prod_{i=1}^{k}\left(\frac{1}{a_{i}}\right.$ of this number), then it equals $\left(\prod_{i=1}^{k} a_{i}\right)^{\frac{1}{(k-1)}}$
|
35
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. Sheep Buyers. A farmer died, leaving a herd of cows to his two sons. The sons sold the herd, receiving as many dollars for each head as there were heads in the herd. With the money, the brothers bought sheep at 10 dollars each and one lamb, which cost less than 10 dollars. Then they divided the sheep and the lamb between themselves so that each brother received the same number of animals. How much should the brother who received only sheep pay to his brother to ensure that each heir receives an equal share?
|
81. Let $x$ be the number of cows in the herd, $y$ the number of sheep, and $z$ the cost of a lamb. Then $x^{2}=10 y+z$, where $y$ is an odd number, and $z<10$. But the second-to-last digit of a square is odd if and only if the last digit is $6^{*}$. Thus, $z=6$, and the luckier son should pay his brother 2 dollars.
[И. Kaplansky, A. M. M., 51, 166 (March 1944).]
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. Contest. Euclid Paracelsus Bombast Umbugio tries to supplement his meager professor's salary by participating in company-sponsored soap production contests. In one such competition, it was required to determine the number of paths along which the word MATHEMATICIAN* could be read on a given diagram. Umbugio counted 1587 paths starting from one of the first five lines. When it was time to announce the results, he was quite perplexed, to say the least. Help the professor count all the paths using as few calculations as possible.
```
M
M A M
M A T A M
M A T H T A M
M A T H E H T A M
M A T H E M E H T A M
M A T H E M A M E H T A M
M A T H E M A T A M E H T A M
M A T H E M A T I T A M E H T A M
M A T H E M A T I C I T A M E H T A M
M A T H E M A T I C I C I T A M E H T T A M
M A T H E M A T I C I A I C I T A M E H T A M
M A T H E M A T I C I A N A I C I T A M E E H T A A M
```
|
85. A path can be traced by moving "backwards" from $N$. If we consider the left half of the diagram, including the central column, then at each step backward we have a choice between two possible directions, giving us $2^{12}$ paths. Doubling this number and subtracting 1 (to avoid counting the central column twice), we get $2^{13}-1=8191$ paths.
[J. F. Leech, A. M. M., 68, 296 (March 1961).]
|
8191
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Choosing a pair. Among the pairs of numbers listed below, one and only one does not satisfy the equation $187 x-104 y=41$. Which one exactly
1) $x=3, \quad y=5$
2) $x=107, \quad y=192$
3) $x=211, \quad y=379$
4) $x=314, \quad y=565$
5) $x=419, \quad y=753$.
|
88. Since the difference between the two terms on the left side of the equation is the odd number 41, one of these terms must be odd and the other even. Since $104 y$ is even, $187 x$ is odd, and therefore $x$ is odd. Thus, the pair $x=314$, $y=565$ does not satisfy our equation.
[D. Woods, S. S. M., 64, 242 (March 1964).]
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
97. The Fibonacci sequence. Consider the Fibonacci sequence $1,1,2,3,5,13, \ldots$, whose terms $F_{n}$ (Fibonacci numbers) satisfy the relation $F_{n+2}=F_{n}+F_{n+1}$, $F_{1}=F_{2}=1$. Now consider the sequence of digits in the units place of the Fibonacci numbers. Will this sequence be cyclic, that is, can it be obtained by the unlimited repetition of the same finite set of digits, as is true, for example, in the case of the sequence $055055 \ldots$.
|
97. Yes, it is possible. Each member of the desired sequence $11235831 \ldots$ can be obtained by adding the previous two members and taking the digit in the units place of this sum.
In this sequence, two odd and one even members alternate. There are $5 \cdot 5=25$ ordered pairs composed of odd digits. Therefore, after no more than $3 \cdot 25=$
75 consecutive additions, one of these odd pairs will repeat, and a new cycle will begin. Since the sum (or difference) of two digits is unique, this repeating pair must coincide with the first odd pair (with which the sequence begins) rather than with any of the "internal" odd pairs. Indeed, it turns out that only 60 additions are required, and a new cycle of 60 digits will begin: 1123583145943707 74156178538190998752796516730336954 $932572910^{*} 11 \ldots$.
Similar reasoning will be valid in any number system, as well as not only for the Fibonacci sequence but also for any sequence that satisfies the recurrence relation.
$$
A_{n+k}=A_{n}+A_{n+1}+\cdots+A_{n+k-1}
$$
|
60
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
104. Divisibility condition. For which integer $a$ does the polynomial $x^{13}+x+90$ divide by $x^{2}-x+a ?$
|
Let $f(x)=x^{2}-x+a, g(x)=x^{13}+x+90$. Then $f(0)=$ $a, f(1)=a, g(0)=90, g(1)=92$. Therefore, the greatest common divisor of 90 and 92, which is 2, must divide $a$. Further, $f(-1)=$ $a+2, g(-1)=88$; hence $a$ is neither 1 nor $-2 ; f(-2)=a+6$, $g(-2)=-8104$, so $a \neq-1$. Therefore,
$$
\begin{gathered}
a=2^{\star} \quad \text { and } \frac{x^{13}+x+90}{x^{2}-x+2}= \\
=x^{11}+x^{10}-x^{9}-3 x^{8}-x^{7}+5 x^{6}+7 x^{5}- \\
-3 x^{4}-17 x^{3}-11 x^{2}+23 x+45
\end{gathered}
$$
[L. E. Bash, A. M. M., 71, 640 (June 1964).]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
105. The Farmer's Task. A certain farmer must buy 100 heads of cattle for 100 dollars. If each calf costs 10 dollars, each lamb 3, and each piglet 0.5 dollars, then how many calves, lambs, and piglets will the farmer buy?
|
105. The average cost of one head of cattle is 1 dollar. The cost of each calf differs from the average by +9 dollars, each lamb by +2 dollars, and each piglet by $-\frac{1}{2}$ dollar. Therefore, for each calf, the farmer must buy 18 piglets, and for each lamb, 4 piglets. Consequently, since $5(1+18)+(1+4)=100$, he must buy 5 calves, 1 lamb, and 94 piglets.
[B. E. Mitchell, M. M., 26, 153 (January 1953).]
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
108. Unique Square. What square is equal to the product of four consecutive odd numbers?
|
108. If $n(n+2)(n+4)(n+6)=m^{2}$, then $\left(n^{2}+6 n+4\right)^{2}=m^{2}+16$. However, among the squares, only 0 and 9 have the form $a^{2}-16$; and since $m^{2}$ is odd, the sought square is $9=(-3)(-1)(1)(3)$.
[D. L. Silverman, M. M., 38, 60 (January 1965).]
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
110. Sum of Cosines. Calculate the sum
$$
\cos 5^{\circ}+\cos 77^{\circ}+\cos 149^{\circ}+\cos 221^{\circ}+\cos 293^{\circ}
$$
|
110. Project the sides of an arbitrary polygon onto a line lying in the plane of this polygon. Then the sum of such projections, taken with the appropriate sign, is zero. Now let's take a regular pentagon with a unit side and note that its exterior angle is $72^{\circ}$. The terms
of our sum represent the projections of the sides of this pentagon onto a line that forms an angle of $5^{\circ}$ with one of these sides. Therefore,
$$
\cos 5^{\circ}+\cos 77^{\circ}+\cos 149^{\circ}+\cos 221^{\circ}+\cos 293^{\circ}=0
$$
[M. S. Klamkin, M. M., 28, 293 (May 1955).]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
117. Two Ferries. Two ferries travel between two opposite banks of a river at constant speeds. Upon reaching a bank, each immediately starts moving in the opposite direction. The ferries departed from opposite banks simultaneously, met for the first time 700 meters from one of the banks, continued to their respective banks, then turned around and met again 400 meters from the other bank. Determine the width of the river in your mind.
|
117. Ferry $A$ departs from the shore, travels 700 m, and meets ferry $B$. By this time, they have covered a total distance equal to the width of the river. $A$ continues to the opposite shore, turns around, and after turning, travels another 400 m, meeting $B$ again. By this time, they have covered a total distance equal to three times the width of the river. Since their speeds are constant, $A$ has traveled a total distance of $3 \times 700 = 2100$ m. The width of the river is 400 m less than the distance traveled by $A$, which means it is 1700 m.
[U. K. Rufus, A. M. M., 47, 111 (February 1940).]
|
1700
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
120. Три водителя. Три водителя грузовиков зашли в придорожное кафе. Один водитель купил четыре сандвича, чашку кофе и десять пончиков на общую сумму 1 доллар 69 центов. Второй водитель купил три сандвича, чашку кофе и семь пончиков за 1 доллар 26 центов. Сколько заплатил третий водитель за сандвич, чашку кофе и пончик?
|
120. Используя данные относительно покупок первых двух водителей, можно составить два уравнения:
$$
\begin{aligned}
4 s+c+10 d & =169 \\
3 s+c+7 d & =126
\end{aligned}
$$
где $s, c$ и $d$ обозначают соответственно стоимость в центах одного сандвича, одной чашки кофе и одного пончика ${ }^{*}$. Умножим первое уравнение на 2 , а второе - на 3 , при этом получим
$$
\begin{aligned}
& 8 s+2 c+20 d=338 \\
& 9 s+3 c+21 d=378
\end{aligned}
$$[^28]
Вычтем из последнего уравнения предпоследнее:
$$
s+c+d=40
$$
Таким образом, третий водитель заплатил 40 центов.
$[$ S. S. M., 66, 561 (June 1966).]
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
123. Problem with prime numbers. The product of a certain three-digit number by a certain two-digit number has the form
| $p p p$ |
| ---: |
| $p p$ |
| $p p p p$ |
| $p p p p$ |
| $p p p p p$ |
Here the letter $p$ can represent any prime digit other than one (not necessarily the same one). Restore all the numbers and show that the solution to this problem is unique.
|
123. We need to find a three-digit and a one-digit number, the product of which is a four-digit number, and only the digits $2,3,5$ or 7 are allowed. There are only four possible solutions: $3 \cdot 775=2325, 5 \cdot 555=2775$, $5 \cdot 755=3775$ and $7 \cdot 325=2275$.
Since none of the three-digit numbers in these four products appear more than once, we conclude that the sought two-digit number consists of identical digits. Thus, the only solution is of the form
| 775 |
| ---: |
| 33 |
| 2325 |
| 2325 |
| 25575 |
[W. E. Baker, A. M. M., 43, 499 (October 1936).]
|
25575
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
125. Dear club. Ten people decided to found a club. If there were 5 more people, each would contribute 100 dollars less. How much money did each member contribute?
|
125. If the original number of participants increases by $50 \%$, then each person's share is only $\frac{2}{3}$ of the previous individual contribution. Thus, 100 dollars constitute $\frac{1}{3}$ of the original contribution, and each club member paid 300 dollars.
$[$ [ M. M., 32, 229 (March 1959).]
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
136. Joint system. For which values of $k$ is the system given below consistent?
$$
\left\{\begin{aligned}
x+y & =1 \\
k x+y & =2 \\
x+k u & =3
\end{aligned}\right.
$$
|
136. Adding the second and third equations of the given system, we get
$$
x+y+k(x+y)=5
$$
Considering the first equation, we find from here the desired value $k=4$. For this $k$ we have $x=\frac{1}{3}, y=\frac{2}{3}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
139. Moving Digits. A certain number, which is written using fewer than 30 digits, starts (if we move from left to right) with the digits 15, that is, it has the form $15 \ldots$. If we multiply it by 5, the result can be obtained simply by moving these two digits to the right end; in the end, we get a number of the form ... 15. Find the original number.
|
139. Let $f$ be a proper fraction, in the decimal periodic expansion of which one period coincides exactly with the initial number $15 \ldots$ By the conditions of this problem, $5 f=$ $0, \ldots 15 \ldots 15 \ldots$, and $100 f=15, \ldots 15 \ldots 15$, from which $95 f=15$ and $f=\frac{3}{19}$. Expanding $\frac{3}{19}$ into a decimal fraction, we find that its period consists of 18 digits: 157894736842105263. This is the number we are looking for. It is unique if we consider numbers not exceeding 30 digits. If, however, we change this restriction and consider, for example, numbers that are written using no more than 50 digits, then there will be another solution to the problem - a 36-digit number, coinciding with two periods of the fraction $f$.
[H. T. R. Aude, A. M. M., 41, 268 (April 1934).]
|
157894736842105263
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
143. Mental arithmetic. Multiply 96 by 104.
|
143. Applying the identity $(a-b)(a+b)=a^{2}-b^{2}$, we get: (96) $(104)=(100-4)(100+4)=10000-16=9984$.
|
9984
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
149. Scattered set. In a printing house, a multiplication line of the form $\overline{a b c} \cdot \overline{b c a} \cdot \overline{c a b}^{*}$ was being set; but the set scattered, and the digits of the product got mixed up. As a result, the product was printed as 2342355286. It is known that $a>b>c$ and that the units digit of the printed product is the correct digit 6. Restore the true value of the product.
|
149. Let $n=a b c$, and $N$ be the desired product. If $c=1$, then the largest possible $n$, namely 981, would yield a product $N=159080922$, which is too small. Therefore, $982 \leqslant n \leqslant$ 987. The sum of the digits of $N$ is $35 \equiv 2(\bmod 3)$; hence, $n$ and the numbers obtained by permuting the digits of $n$ give a remainder of 2 when divided by 3. Thus, $n$ is either 986 or 983. However, a 6 in the units place of the product will only occur if $n=983$. Therefore, the correctly typed line should be
$$
(983)(839)(398)=328245326
$$
[W. R. Talbot, A. M. M., 66, 726 (October 1959).]
|
328245326
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
153. The product of three prime numbers. A certain number is the product of three prime factors, the sum of the squares of which is 2331. There are 7560 numbers (including 1) less than this number and coprime with it. The sum of all divisors of this number (including 1 and the number itself) is 10560. Find this number.
|
153. Let $N=p q r$. Then $p^{2}+q^{2}+r^{2}=2331$; hence, each of these prime numbers is less than $(2331)^{\frac{1}{2}}<49$, and all prime numbers are odd.
The sum of all divisors of the number $N$ is $(1+p) \cdot(1+q) \cdot(1+r)=$ $=10560=11 \cdot 960$. The only multiple of 11 not exceeding 49 and greater than some prime number by 1 is 44, so[^30]$r=43$. Therefore, $p^{2}+q^{2}=482$ and each of these two numbers is less than $(482)^{\frac{1}{2}}<22$. Next, note that the square of an odd number can end only in 1, 5, or 9, so both $p^{2}$ and $q^{2}$ end in 1. Consequently, $p=11, q=19$ and $N=11 \cdot 19 \cdot 43=8987^{\star}$.
|
8987
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
157. Ballot Papers. A physical society needed to hold elections for three leadership positions. For each of the three positions, there were 3, 4, and 5 candidates, respectively. To ensure that the number under which each candidate is listed on the ballot does not influence the voting results, it was decided to apply a rule that in the list of candidates for each position, each candidate must appear under each number an equal number of times. What is the minimum number of different ballots required to comply with this rule?
|
157. Perhaps someone will immediately say that it is necessary to take $3 \cdot 4 \cdot 5=60$ different ballots. However, if we add two fictitious names to the group of three candidates and one fictitious name to the group of four candidates, then only 5 different ballots will be required. This technique not only reduces printing costs but also allows for the collection of statistical[^31] material, which can help determine what has a greater influence on the voting results: the number under which a candidate is listed, or their surname.
[М. S. Klamkin, M. M., 30, 110 (November 1956).]
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
162. In a nonagon. Let $A B$ and $B C$ be two adjacent sides of a regular nonagon inscribed in a circle with center $O$. Let, further, $M$ be the midpoint of $A B$, and $N$ be the midpoint of the radius perpendicular to $B C$. Show that the angle $O M N=30^{\circ}$.
|
162. Arc $A B=40^{\circ}$, and arc $A D=60^{\circ}$, so triangle $A O D$ is equilateral and $A N$ is the perpendicular dropped to $O D$. Therefore, points $A, M, N, O$ lie on a circle, the diameter of which coincides with $A O$. Thus, $\angle O M N=\angle O A N=30^{\circ}$, since they are inscribed in the same circle and subtend the same arc.
[Howard Eves, A. M. M., 63, 423 (June 1956).]
|
30
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
163. Reduced Share. A father gave his children 6 dollars for entertainment, which was to be divided equally. But two young cousins joined the company. The money was divided equally among all the children, so that each child received 25 cents less than originally intended. How many children were there in total?
|
163. The share of each child decreased by $\frac{2}{24}$ of the entire sum. Further, $24=2 \cdot 12=3 \cdot 8=4 \cdot 6$. From these representations of the number 24, we choose the pair $q_{1} c_{1}=q_{2} c_{2}$ such that $q_{1}+1=q_{2}$, and $c_{1}=c_{2}+2$. Thus, there were initially 6 children, and then there were 8.
$[$ [
$164^{\star}$. Let
$$
\begin{gathered}
S=1+2 x+3 x^{2}+4 x^{3}+\ldots \\
x S=\quad x+2 x^{2}+3 x^{3}+\ldots \\
(1-x) \cdot S=1+x+x^{2}+x^{3}+\cdots=\frac{1}{(1-x)}
\end{gathered}
$$
From this, $S=\frac{1}{(1-x)^{2}}$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
167. Inscribed Circles. Which of the two triangles has a larger inscribed circle: the triangle with sides 17, 25, and 26, or the triangle with sides 17, 25, and 28?
|
167. Answer: none. The radius of the inscribed circle of a triangle with sides $a, b, c$ is calculated by the formula
$$
r=\frac{S}{p}=\left[\frac{(p-a)(p-b)(p-c)}{p}\right]^{\frac{1}{2}}, \quad \text { where } \quad 2 p=a+b+c
$$
From this, for each of our triangles, the radius value will be 6.
A rare example of "obtuse twins" are triangles with sides equal to $97,169,122$ and 97,169, 228. Each of them has an inscribed circle radius of 30.
[B. H. Brown, M. M., 29, 275-276 (May 1956).]
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
170. Antifreeze. The radiator of a car with a capacity of 21 quarts* is filled with an 18% alcohol solution. How many quarts of this solution need to be drained from the radiator so that, by replacing them with the same amount of 90% solution, a 42% alcohol solution is obtained in the end.
|
170. The percentage of alcohol in the old solution differs from the percentage of alcohol in the new (or mixed) solution by $-24 \%$, and the percentage of alcohol in the solution added to the radiator differs from the percentage of alcohol in the new solution by $+48 \%$. Therefore, for each quart of $90 \%$ solution added to the radiator, there should be 2 quarts of the old $18 \%$ solution. Hence, $\frac{1}{3}$ of the total volume, or 7 quarts of the old solution, should be drained from the radiator.
[B. E. Mitchell, M. M., 26, 153 (January 1953).]
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
175. A divisor of its palindrome. In what base does 792 divide 297?
Note: The original problem statement is in Russian, but the provided translation is in English as requested.
|
175. In any number system with base $B \geqslant 10$ the following inequalities hold:
$$
2(297)<2(300)=600<792<800=4(200)<4(297)
$$
Therefore, $792=3(297)$, so $7 B^{2}+9 B+2=3\left(2 B^{2}+9 B+7\right)$, or $B^{2}-18 B-19=0$. Discarding the negative root of this quadratic equation, we get $B=19$.
[D. L. Silverman, M. M., 38, 124 (March 1965).]
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
179. Determinant of Pascal's Triangle. Pascal arranged the binomial coefficients in the following table (Pascal's Triangle) $)^{*}$
| 1 | 1 | 1 | 1 | 1 | 1 | $\ldots$ |
| ---: | ---: | ---: | ---: | ---: | ---: | :--- |
| 1 | 2 | 3 | 4 | 5 | 6 | $\cdots$ |
| 1 | 3 | 6 | 10 | 15 | 21 | $\cdots$ |
| 1 | 4 | 10 | 20 | 35 | 56 | $\cdots$ |
| 1 | 5 | 15 | 35 | 70 | 126 | $\cdots$ |
| 1 | 6 | 21 | 56 | 126 | 252 | $\cdots$ |
| . | . | . | . | . | . | $\cdots$ |
Prove that if we cut out any square of any size from this infinite table, the first row (or column) of which is not located on the first row (column) of this table, then the determinant of any such square will be equal to 1.
|
179. The law according to which our table is composed is that each element is equal to the sum of two other elements, one of which is directly above the given element, and the other is to the left of the given element. Applying to our determinant of the $n$-th order the operation of subtracting columns (column) $_{i} - $ (column) $_{i-1}$, where $i=n, (n-1), \ldots, 2$, and then expanding it along the first row, we will obtain a determinant of the $(n-1)$-th order, equal to the minor defined by the element in the lower left corner of the original determinant. Continuing this process, we will eventually arrive at the value 1.
For example:
$$
\begin{aligned}
& \left|\begin{array}{rrrr}
1 & 1 & 1 & 1 \\
3 & 4 & 5 & 6 \\
6 & 10 & 15 & 21 \\
10 & 20 & 35 & 56
\end{array}\right|=\left|\begin{array}{rrrr}
1 & 0 & 0 & 0 \\
3 & 1 & 1 & 1 \\
6 & 4 & 5 & 6 \\
10 & 10 & 15 & 21
\end{array}\right|=\left|\begin{array}{rrr}
1 & 1 & 1 \\
4 & 5 & 6 \\
10 & 15 & 21
\end{array}\right|= \\
& =\left|\begin{array}{rrr}
1 & 0 & 0 \\
4 & 1 & 1 \\
10 & 5 & 6
\end{array}\right|=\left|\begin{array}{ll}
1 & 0 \\
5 & 1
\end{array}\right|=1
\end{aligned}
$$
Since the original table is symmetric with respect to the main diagonal, the proof provided remains valid for determinants whose first column is located in the first column of the table. In this case, rows should be subtracted instead of columns.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
197. Test Series. Professor Tester conducts a series of tests, based on which he assigns the test subject an average score. After answering the last test, John realized that if he had scored 97 points on this last test, his average score would have been 90. On the other hand, if he had scored only 73 points on the last test, his average score would still have been 87. How many tests are in Professor Tester's series?
|
197. If the difference in points obtained in one test, equal to $97-73=24$ points, causes a change in the average score by $90-87=3$ points, then the series contains a total of $\frac{24}{3}=8$ tests.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
202. Invariant remainder. Find a number that, when dividing the numbers $1108, 1453, 1844$, and 2281, gives the same remainder.
|
202. Since the remainder does not change, the divisor must be odd. Further, $1453-1108=345,1844-1453=391,2281-1844=$ 437. Now notice that $437-391=391-345=46=2 \cdot(23)$. Since it is always true that
$$
\left(N_{1} d+r\right)-\left(N_{2} d+r\right)=d\left(N_{1}-N_{2}\right)
$$
the desired number is 23, and the corresponding remainder is 4.
$[$ [ $2 .$, 3. 35, 62 (January 1962).]
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
203. Nine digits. Find a nine-digit number, all digits of which are different and do not contain zero, and the square root of which has the form $\overline{a b a b c}$, where $\overline{a b}=c^{3}$.
|
203. The digit $c$ can only coincide with 3 or 4. However, the number $(64644)^{2}$ is ten-digit. Therefore, the only solution to our problem will be $(27273)^{2}=743816529$.
[N. Farnum, S. S. M., 63, 603 (October 1963).]
This solution will be unique even if we drop the restriction $a b=c^{3}$. Moreover, $27273=3(9091)$, and 9091 is the largest prime divisor of any square composed of nine distinct non-zero digits.
|
743816529
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
206. Characteristics of men. In a certain group of men, $70 \%$ have brown eyes; $70 \%$ have dark hair, $85 \%$ are taller than 5 feet 8 inches, and $90 \%$ weigh more than 140 pounds. What percentage of men definitely have all four of these characteristics?
|
206. Let's take 100 men and record each of the four characteristics for each man who possesses the characteristic. As a result, we will have $70+75+85+90=320$ records. Since there are 320 records for 100 men, we can observe that with the most even distribution of characteristics among the men, each man would have at least 3 characteristics. Therefore*, at least 20 men (or 20%) possess all four characteristics. In the general case, if $n$ is the number of different characteristics and $p_{i}$ is the percentage of men possessing the $i$-th characteristic, then the percentage $P$ of men possessing all $n$ characteristics is given by the formula
$$
P=\sum_{i=1}^{n} p_{i}-100(n-1)
$$
[M. M., 38, 211 (September 1965).]
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
209. "Fibonacci Tetrahedron". Find the volume of the tetrahedron whose vertices are located at the points with coordinates $\left(F_{n}, F_{n+1}, F_{n+2}\right), \quad\left(F_{n+3}, F_{n+4}, F_{n+5}\right), \quad\left(F_{n+6}, F_{n+7}, F_{n+8}\right)$ and $\left(F_{n+9}, F_{n+10}, F_{n+11}\right)$, where $F_{i}$ is the $i$-th term of the Fibonacci sequence: $1,1,2,3,5,8 \ldots$.
|
209. The Fibonacci sequence satisfies the recurrence relation $F_{n}+F_{n+1}=F_{n+2}$, so any three consecutive Fibonacci numbers satisfy the equation $x+y=z$. Consequently, all four vertices of our tetrahedron lie in the same plane, and its volume is 0.
We can observe that all the reasoning remains valid even if the coordinates of the vertices do not coincide with 12 consecutive Fibonacci numbers. It is sufficient for the coordinates of each vertex to coincide with any three consecutive Fibonacci numbers.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
227. Isosceles Triangle. In isosceles triangle \( A B C \), the angle at vertex \( C = 20^{\circ} \). Points \( M \) and \( N \) are chosen on the lateral sides \( A C \) and \( B C \) respectively, such that angle \( A B M = 60^{\circ} \) and angle \( B A N = 50^{\circ} \). Prove, without using trigonometry, that angle \( B M N = 30^{\circ} \).
|
227. Since the sum of the interior angles of a triangle is two right angles, or \(180^{\circ}\), \(\angle CBA = \angle CAB = 80^{\circ}\), \(\angle CBM = 20^{\circ}\), and \(\angle BAN = 50^{\circ} = \angle BNA\) (so \(BN = AB\)). Draw \(MR\)
parallel to \(AB\) and connect points \(A\) and \(R\) with segment \(AR\), intersecting \(BM\) at point \(D\). Draw \(ND\). Due to symmetry, triangles \(ABD\) and \(DRM\) are isosceles; thus, their angles are equal to each other. Further, \(BD = AB = BN\), so \(\angle BND = \angle BDN = 80^{\circ}\) and \(\angle NDR = 40^{\circ}\). Now notice that \(\angle MRC = 80^{\circ}\); therefore, \(\angle NRD = 40^{\circ} = \angle NDR\) and \(ND = NR\). Since \(DM = MR\), segment \(NM\) is perpendicular to segment \(DR\) and bisects it. Thus, \(\angle BMN = \frac{60^{\circ}}{2} = 30^{\circ}\).
[ [M. M., 39, 253 (September 1966).]
|
30
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
231. Henry's Walk. Henry went for a walk in the countryside sometime between 8 and 9 in the morning, when the hands of his clock were aligned. He arrived at his destination between 2 and 3 in the afternoon; at this time, the hands of his clock were pointing in exactly opposite directions. How long did Henry's walk last?
|
231. The walk lasted 6 hours. Suppose we extended the hour hand in the opposite direction. If at the beginning of the walk the hour and minute hands were coincident, then after six hours the hour hand and its extension will simply have swapped places, while the minute hand, having completed exactly six full circles, will return to its initial position and, consequently, will coincide with the extension of the hour hand.
[Ch. Salkind, M. M., 28, 241 (March 1955).]
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 236. How old is Willie?
- Is this problem your teacher gave you? - I asked Willie. - It looks quite boring.
- No, - Willie replied, - I came up with it myself. - See this polynomial? My age is its root. I mean, if you substitute the number of years I was when I last celebrated my birthday for \( x \), the polynomial will turn into zero.
- Hold on, - I noted, - this doesn't seem too hard. Our equation has integer coefficients, and we need to find an integer root... Let me try \( x = 7 \ldots \) No, it results in 77.
- Do I look that young? - Willie asked.
- Alright, let's try a larger integer... No, now it results in 85, not zero.
- You're always joking, - Willie said. - You know very well that I'm not a little kid.
How old is Willie?
|
236. Willie's friend, relying too much on the "trial and error" method, overlooked one fact that could have been very useful. The fact is that if we take a polynomial \( P(x) \) with integer coefficients and two different integers \( a \) and \( b \), then \( P(a) - P(b) \) will be divisible by \( a - b \). Let's denote Willie's age by \( A \), and the larger number that Willie's friend substituted into the equation by \( N \). Then \( 85 - 77 = 8 \) will be divisible by \( N - 7 \); 77 will be divisible by \( A - 7 \); 85 will be divisible by \( A - N \), and the inequality \( 7 < N < A \) will hold. From this, it follows that \( N \) coincides with one of the numbers 8, 9, 11, 15, and \( A \) with one of the numbers 14, 18, 84. Since 85 is divisible by \( A - N \), the number \( N \) must be 9, and \( A = 14 \). Thus, Willie is 14 years old.
[D. K. B. Marsh, A. M. M., 64, 593 (October 1957).]
The polynomial from our problem must have the form
\[
(x-7)(x-9)(x-14) Q(x) - 3 x^{2} + 52 x - 140
\]
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
249. Bonus Fund. In a certain institution, there was a bonus fund. It was planned to distribute it so that each employee of the institution would receive 50 dollars. But it turned out that the last person on the list would receive only 45 dollars. To maintain fairness, it was then decided to give each employee 45 dollars; as a result, 95 dollars remained undistributed, which were allocated to the fund for the next year. What was the initial amount of the fund?[^13]
|
249. In fact, $5 was seized from $95: 5=19$ people; therefore, the original amount of the fund was $20 \cdot 50-5=$ $=995$ dollars.
|
995
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
250. The Court Mathematician's Salary. Once, the court mathematician received his entire annual salary in silver talers, from which he formed nine piles, together constituting a magic square. The king, upon seeing this, was impressed but regretfully noted that in none of the piles was the number of coins a prime number.
- If I had nine more coins, - said the mathematician, - by adding one coin to each pile, I would get a magic square consisting only of prime numbers.
The king calculated and was convinced that this was indeed the case. He was about to give the mathematician nine more talers when the court jester, unexpectedly exclaiming, "Wait!", removed one coin from each pile, and everyone saw that a new magic square, containing only prime numbers, had been formed. Thus, the jester saved the king nine talers. What is the court mathematician's annual salary?
|
250. As established by L. S. Fryer, the elements of an arbitrary magic square of the third order can actually be represented using three parameters:
$$
\begin{array}{ccc}
(e+x), & (e-x-y) & (e+y) \\
(e-x+y), & e, & (e+x-y) \\
(e-y), & (e+x+y) & (e-x)
\end{array}
$$
It is clear that these numbers can be rearranged so that each row forms an arithmetic progression with the same difference, and each column also forms an arithmetic progression with a common difference:
$$
\begin{array}{ccc}
(e-x-y), & (e-y), & (e+x-y) \\
(e-x), & e, & (e+x), \\
(e-x+y), & (e+y), & (e+x+y)
\end{array}
$$
We need to construct a magic square of the third order from a set of prime numbers \( p_i \) that have the property that all \( p_i + 2 \) are also prime. Further, note that all \( p_i \) (not equal to 3 and 5) must end in 9, 7, or 1. Therefore, the parameter \( e \) represents the arithmetic mean of two prime numbers that end in either 9 and 9, 7 and 1, 7 and 7, or 1 and 1. Consequently, the elements of our square should be sought among the sequence of the smaller of consecutive prime twins:
$$
\begin{aligned}
& 3, \quad 5, \quad 11, \quad 17, \quad 29, \quad 41, \quad 59, \quad 71, \quad 101, \quad 107, \\
& 137, \quad 149, \quad 179, \quad 191, \quad 197, \quad 227, \quad 239, \quad 269, \quad 281, \ldots
\end{aligned}
$$
The smallest value of \( e \) ending in 9, which represents the arithmetic mean of at least four pairs of prime numbers, is determined by the equations
$$
\begin{aligned}
2(149) & =107+191=101+197=71+227=59+239= \\
& =29+269=17+281
\end{aligned}
$$
(For any prime number \( < 149 \) and ending in 1 and 7, there are no more than three members of the given sequence with the same final digit.) Substituting into the middle row of the above square, sequentially replacing \( e \) with 149, and \( (e-x) \) and \( (e+x) \) with the obtained pairs of numbers, we find that only one arrangement allows three of the remaining pairs to be placed in the correct positions, namely:
From this, we immediately find three magic squares as mentioned in the problem:
| 191 | 17 | 239 | | 192 | 18 | 240 | | 193 | 19 | 241 |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| 197 | 149 | 101 | | 198 | 150 | 102 | | 199 | 151 | 103 |
| 59 | 281 | 107 | | 60 | 282 | 108 | 61 | 283 | 109 | |
The court mathematician was paid annually
\( 9 e + 9(149 + 1) = 1350 \) thalers.
This result was also obtained by another method \( -A . M . M ., \mathbf{5 5}\), 429 (September 1948).
The next solution was found by W. Benson:
| 2088 | 1302 | 4800 |
| ---: | ---: | ---: |
| 5442 | 2730 | 18 |
| 660 | 4158 | 3372 |
In this case, the annual salary of the court mathematician is 24570 thalers.
|
1350
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
251. Packing Cylinders. Forty cylinders with a diameter of 1 cm and the same height were tightly packed in a box in 5 rows of 8 cylinders each so that they would not "rattle" during transportation. How many cylinders need to be removed from the box so that, by moving the remaining cylinders and adding the removed cylinders and one more cylinder at the end, 41 cylinders of the same size can be packed in this box? Will the cylinders "rattle" in this case?
|
251. Only two cylinders need to be removed from the box. Let's renumber the cylinders as shown in the figure. Remove cylinders 6 and 16.
Move cylinders $7-10$ to the right and up (see the figure). Move cylinders 11-15 to the left, cylinders 17-20 up and to the left, and cylinders 21-25 to the left. The remaining cylinders can be moved in different ways. For example, move cylinders 26, 28, 29, 30, 31 to the left; press cylinder 32 against cylinders 31 and 37; move cylinder 27 against cylinders 28 and 32; move cylinder 26 against cylinders 21 and 22. Move cylinder 31 to the left; press cylinder 32 against cylinders 36 and 37; move cylinder 27 up to cylinder 31; move cylinders $28, 29, 30$ up and to the left; move cylinders $33, 34, 35$ up and to the right. Insert cylinders 6, 16, and 41 into the positions indicated in the figure. If the cylinders in the new arrangement are tightly pressed against each other, the distance between the lines of centers of adjacent "columns" will be $\sqrt{\frac{3}{2}}$ cm. Therefore, the entire packaging will take up a length of $8\left(\frac{\sqrt{3}}{2}\right)+1=4 \sqrt{3}+1 \approx 7.928 < 8$ cm.
Thus, the cylinders will now "rattle" slightly during transportation.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
256. Palindromic Squares. A certain square is written in the base-6 numeral system using 5 different non-zero digits. If the digit in the units place is moved from the end of this number to the beginning, the square root of the resulting number matches the square root of the original number, written in reverse order. Find the original number.
|
256. $12345 \leqslant N^{2} \leqslant 54321$, so $113 \leqslant N \leqslant 221$. If we write the digits of the number $N$ in reverse order, the resulting number will also satisfy these inequalities. The number $N^{2}$ is divisible by 5, so $N$ is also divisible by 5. Let's list all three-digit numbers divisible by 5 and satisfying these inequalities: $113, 122, 131, 140, 145, 154, 203, 212$ and 221. Among them, there is only one pair of palindromes. By squaring it, we confirm that it provides the only solution to our problem: $(221)^{2}=53241, 15324=(122)^{2}$.
As a "free bonus," we find that $(203)^{2}=42013$ - another permutation of five consecutive digits.
|
53241
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
266. When division is exact. For which positive integer $n$ will the quantity $n^{4}+n^{2}$ be divisible by $2 n+1$?
|
266.
$$
\begin{aligned}
f(n) & =\frac{n^{4}+n^{2}}{2 n+1}=\frac{n^{2}\left(n^{2}+1\right)}{2 n+1}=\frac{n^{2}}{4}\left[\frac{4 n^{2}+4}{2 n+1}\right]= \\
& =\left(\frac{n}{2}\right)^{2} \cdot\left[2 n-1+\frac{5}{2 n+1}\right]
\end{aligned}
$$
It is obvious that the greatest common divisor of the numbers $n$ and $2n+1$ is 1. Therefore, $f(n)$ can be an integer only when $\frac{5}{2n+1}$ is an integer, which occurs when $n=2, 0, -1$, or $-3$. Consequently, the only positive integer for which $f(n)$ will be an integer is $n=2$. [In this case, $f(n)=4$.]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.