problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
26. Does there exist a three-digit number that is divisible by each of eight consecutive natural numbers?
|
26. The only such number is 840. It is divisible by $1,2,3,4,5,6,7,8$.
|
840
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. Find the smallest number that can be represented as the sum of five, six, and seven consecutive natural numbers.
|
27. The sum of five consecutive natural numbers has the form:
$$
n+(n+1)+(n+2)+(n+3)+(n+\dot{4})=5(n+2)
$$
i.e., this sum is divisible by 5. Similarly, we prove that the sum of seven consecutive natural numbers is divisible by 7, and the sum of six consecutive natural numbers has the form $3(2 n+5)$, i.e., it is an odd number divisible by 3. The smallest odd natural number that is divisible by 3, 5, and 7 is 105. Indeed, $105=19+20+$ $+21+22+23=15+16+17+18+19+20=12+13+14+15+$ $+16+17+18$
|
105
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. Find the smallest prime number that can be represented as the sum of two, three, four, five, and six different prime numbers.
|
28. It is clear that the sought prime number is not less than $2+3+5+7+11+13=41$. The number 41 is prime, but it cannot be represented as the sum of two prime numbers. Indeed, since one of these two numbers must be the even prime number, i.e., 2, the second number would need to be 39, but it is not prime.
The next prime number in sequence, 43, can be represented as the sum of two primes $(43=2+41)$, but it cannot be represented as the sum of six distinct prime numbers.
For the same reason as 41, the prime numbers 47, 53, and 59 are also ruled out. However, the next prime number, 61, satisfies all the conditions of the problem. Indeed, $61=2+59=$ $=3+5+53=2+5+7+47=3+5+7+17+29=2+3+5+7+$ $+13+31$.
|
61
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. Find all prime numbers $p$ such that $p^{2}+14$ is also a prime number.
|
31. It is easy to notice that the prime number $p=3$ satisfies the condition of the problem. If $p \neq 3$, then $p^{2}$ has the form $3 \mathrm{k}+1$ (see problem 5 a). Then $p^{2}+14=3 k+15=3(k+5)$. The obtained number is composite. Therefore, the problem has a unique solution $p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. Find the smallest number \( n > 1980 \) such that the number
\[
\frac{x_{1}+x_{2}+x_{3}+\ldots+x_{n}}{5}
\]
is an integer for any assignment of integers \( x_{1}, x_{2}, x_{3}, \ldots, x_{n} \), none of which are divisible by 5.
|
33. In problem 12, it was shown that for any integer $n$ not divisible by 5, the number $n^{4}-1$ is divisible by 5. Therefore, the fourth power of an integer not divisible by 5, when divided by 5, leaves a remainder of one. Hence, the given expression in the problem will be an integer only if the number of terms in the numerator is a multiple of 5. The smallest number divisible by 5 and greater than 1980 is 1985.
|
1985
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. Find the prime number $p$, given that the number $13 p+1$ is a perfect cube.
|
36. If $13 p+1=n^{3}$, then $13 p=(n-1)\left(n^{2}+n+1\right)$. Since on the left side of the last equation we have the product of two prime numbers, there are only three possible cases:
$$
\left\{\begin{array} { l }
{ n - 1 = 1 } \\
{ n ^ { 2 } + n + 1 = 1 3 p ; }
\end{array} \quad \left\{\begin{array} { l }
{ n - 1 = \mathrm { p } } \\
{ n ^ { 2 } + n + 1 = 1 3 ; }
\end{array} \quad \left\{\begin{array}{l}
n-1=13 \\
n^{2}+n+1=p
\end{array}\right.\right.\right.
$$
The first system has no solutions in natural numbers. From the second and third systems, we find respectively: $n=3$, $p=2$ and $n=14, p=211$. Indeed, $13 \cdot 2+1=3^{3}$ and $13 \cdot 211+$ $+1=14^{3}$
|
211
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. This square should be cut by a broken line into two parts of equal area so that each segment of the broken line is parallel to the side or diagonal of the square, and the sum of the lengths of the segments parallel to the sides equals the length of the side, while the sum of the lengths of the segments parallel to the diagonals equals the length of the diagonal. What is the minimum number of segments such a broken line can have?
$$
7-8 \text { grades }
$$
|
18. It is obvious that each segment of the broken line must be shorter than the side or diagonal of the square parallel to it, since otherwise, this segment alone would already divide the square into two parts. From this, it follows that the number of segments of the broken line cannot be less than four. We will now show,
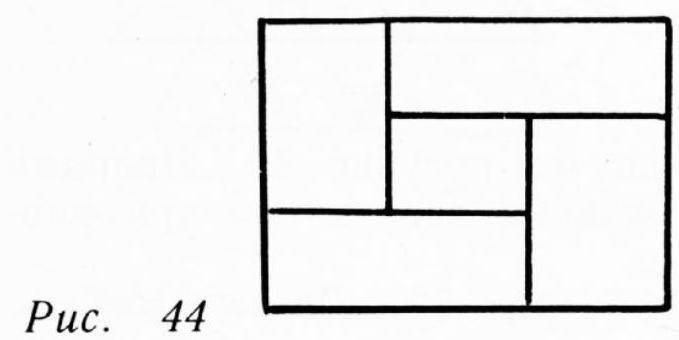
Fig. 45
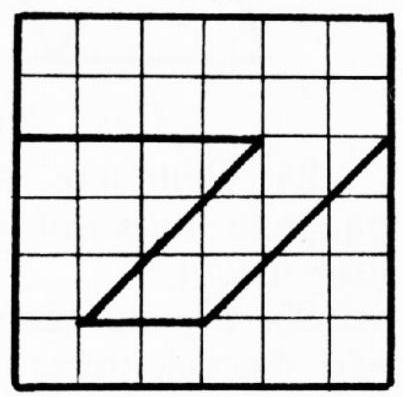
that there exists a broken line with four segments that meets all the requirements of the problem. Divide the given square into 36 equal squares. Construct the broken line shown in Figure 45. It is easy to verify that this broken line is the one we are looking for.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. List all two-element subsets of a five-element set.
|
7. Let's take the five-element set $\{A ; B ; C ; D ; E\}$. We will list its two-element subsets:
$\{A ; B\},\{A ; C\},\{A ; D\},\{A ; E\},\{B ; C\},\{B ; D\},\{B ; E\},\{C ; D\}$, $\{C ; E\},\{D ; E\}$. In total, we have 10 subsets.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
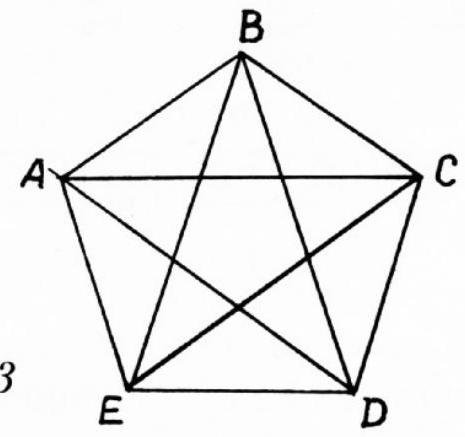
8. Given 5 points, no three of which lie on the same line. How many segments need to be drawn to connect each pair of points?
|
8. The solution to the problem is shown in Figure 93. We will obtain 10 segments. It is useful to compare this problem with problem 7.
Fig. 93
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. In how many ways can two identical pencils be distributed among five people?
|
10. If we give one pencil at a time, we will have 10 ways of distributing the pencils (equal to the number of two-element subsets of a five-element set). We will get another 5 ways if we give both pencils to one person. Ultimately, we will have 15 ways.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Write down all the letter combinations that can be obtained by rearranging the letters in the word MAMA.
|
11. We will get the following 6 letter combinations: MAMA, MMAA, MAAM, AMAM, AAMM, AMMA.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. In how many ways can four people be seated on four chairs?
|
13. To solve this problem, it is advisable to use the previous problem as a model. We will get the same number of ways, i.e., 24.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. There are 5 different books: three on mathematics and two on physics. In how many ways can two books be selected: one on mathematics and one on physics?
|
14. Let's denote the mathematics books as $M_{1}, M_{2}, M_{3}$, and the physics books as $\Phi_{1}$, and $\Phi_{2}$. We obtain the following 6 ways: $M_{1} \Phi_{1}, M_{2} \Phi_{1}, M_{3} \Phi_{1}, M_{1} \Phi_{2}, M_{2} \Phi_{2}, M_{3} \Phi_{2}$. We can also reason as follows: the selection of a mathematics book can be done in three ways, and for each of these ways, there are 2 ways to choose a physics book. In total, we will have $3 \cdot 2=6$ ways.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. In how many ways can two letters be chosen from the word УЧЕБНИК so that one of the letters is a consonant and the other is a vowel?
|
15. The number of ways can be visually represented using the graph shown in Figure 94. In total, we get \(4 \cdot 3 = 12\) ways.
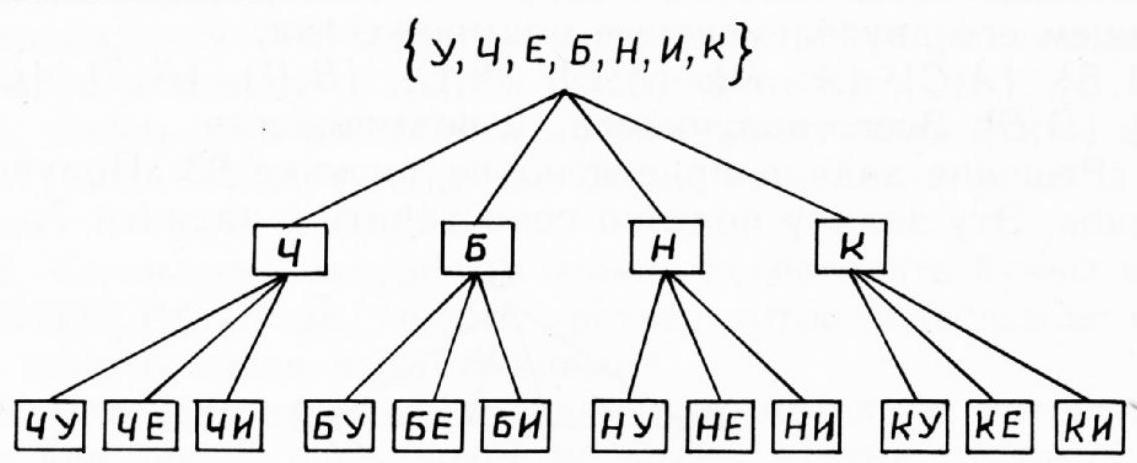
Fig. 94
After solving problems 14 and 15, it is appropriate to formulate the multiplication rule for two selections.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. From city $A$ to city $B$, one can travel by one of three types of transport, and from city $B$ to city $C$ - by one of four types of transport. In how many ways can one travel from city $A$ to city $C$, visiting city $B$ along the way?
|
16. From city $A$ to city $B$, there are three ways to travel, after which from city $B$ to city $C$, there are four ways. By the rule of product, from city $A$ to city $C$, there are $3 \cdot 4=12$ ways to travel.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. In the class, there are 16 boys and 14 girls. In how many ways can two students be assigned duty in the class: one boy and one girl?
|
17. By the rule of product, we get $16 \cdot 14=224$ ways.
|
224
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. How many different two-digit numbers can be formed from the digits: a) $1,2,3,4,5,6$; b) $0,1,2,3,4,5,6$?
|
18. a) The choice of both the first and second digit can be made in six ways. In total, we will have $6 \cdot 6=36$ two-digit numbers.
b) The choice of the first digit can be made in six ways (zero cannot be taken), and the choice of the second digit can be made in seven ways. Thus, we will have $6 \cdot 7=42$ two-digit numbers.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. In how many ways can two people be elected from ten for two different positions?
|
20. There are ten ways to choose for the first position, after which there are only nine ways to choose for the second position. In total, we get $10 \cdot 9=90$ ways.
|
90
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Ten people exchanged photographs. How many photographs were needed?
|
21. The choice of one person can be made in ten ways, after which this person can give a photograph to nine remaining people. In total, $10 \cdot 9=90$ photographs are required.
|
90
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. How many different positions can appear on a chessboard if both players, starting from the initial position, make only one move each?
|
22. In the initial position, each pawn and each knight can move in two ways, while the other pieces cannot make a move. Therefore, from the initial position, 20 different moves can be made by both the white and black pieces. Thus, after each player makes one move, $20 \cdot 20=400$ different positions can result.
|
400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. In the canteen for lunch, 4 first-course dishes, 5 second-course dishes, and 3 desserts are prepared for selection. In how many ways can one lunch be composed?
|
23. Applying the multiplication rule for the case of three choices, we get: $4 \cdot 5 \cdot 3=60$.
|
60
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. The teacher prepared three problems for the class to solve. In how many ways can he offer these problems to the students, if there are 30 students in the class?
|
24. Tasks can be proposed to students $30 \cdot 29 \cdot 28=$ $=24360$ ways.
|
24360
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. How many even four-digit numbers can be formed from the digits $0,1,2,3,4,5$?
|
25. Since zero cannot be the first digit, the first digit can be chosen in five ways. The second and third digits can each be chosen in six ways. Finally, the fourth digit, which must be even, can be chosen in three ways. Then, by the rule of product, we will have $5 \cdot 6 \cdot 6 \cdot 3=540$ four-digit even numbers.
|
540
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. How many four-digit numbers can be formed from the digits $0,1,2,3,4,5,6$, if the repetition of digits in the number is not allowed?
|
26. $6 \cdot 6 \cdot 5 \cdot 4=720$ numbers.
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. In how many ways can 6 people be seated on six chairs?
|
27. The first person can choose a chair in six ways, the second in five ways, and so on. Finally, only one chair will remain for the sixth person. In total, we get $6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=720$ ways.
Note. The product of the first $n$ natural numbers is denoted by $n$! (read: n factorial). Thus, $6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=6!$.
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. At the meeting, there are 25 people present. In how many ways can four people be elected from them to fill 4 different positions
|
28. There are $25 \cdot 24 \cdot 23 \cdot 22=303600$ different possibilities for the election to the positions.
|
303600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29. In how many ways can 5 different items be distributed among three people?
|
29. Each item can be distributed in three ways. By the rule of product, we get: $3 \cdot 3 \cdot 3 \cdot 3 \cdot 3=3^{5}=243$.
|
243
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. In how many ways can 3 different items be distributed among five people?
|
30. Each item can be distributed in five ways. In total, we will have $5 \cdot 5 \cdot 5=5^{3}=125$ ways.
|
125
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. In how many ways can 5 different items be distributed into eight boxes if no more than one item can be placed in one box?
|
31. The choice of the box for the first item can be made in eight ways, for the second in seven ways, and so on. In total, we get $8 \cdot 7 \cdot 6 \cdot 5 \cdot 4=6720$ ways.
|
6720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. How many five-digit numbers are there that read the same from left to right and right to left?
|
32. The first digit can be chosen in nine ways, and the second and third digits can be chosen in ten ways each. Since the fourth digit must match the second, and the fifth must match the first, each of the last two digits can be chosen in only one way. Thus, the number of such numbers will be $9 \cdot 10 \cdot 10 \cdot 1 \cdot 1=900$.
|
900
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. How many even five-digit numbers are there that read the same from left to right and from right to left?
|
33. Since the last digit must be even, the first digit will also be even. But the first digit cannot be zero. Therefore, there are only 4 ways to choose the first digit. In total, we get $4 \cdot 10 \cdot 10 \cdot 1 \cdot 1=400$ required even numbers.
|
400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34. How many five-digit numbers are divisible by 5?
|
34. Since the last digit can be chosen in only two ways (0 or 5), we will get a total of $9 \cdot 10 \cdot 10 \cdot 10 \cdot 2=18000$ required numbers. The same result can be obtained by dividing the total number of five-digit numbers by $5: 9 \cdot 10^{4}: 5=18000$.
|
18000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. How many five-digit numbers are there in which at least the first two digits are the same?
|
36. $9 \cdot 1 \cdot 10 \cdot 10 \cdot 10 \cdot=9000$ numbers.
|
9000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. How many five-digit numbers are there in which at least the last two digits are different?
|
37. $9 \cdot 10 \cdot 10 \cdot 10 \cdot 9=81000$ numbers.
|
81000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
38. How many six-digit numbers are there in which only the middle two digits are the same?
|
38. $9 \cdot 9 \cdot 8 \cdot 1 \cdot 7 \cdot 6=27216$ numbers.
|
27216
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. How many six-digit numbers are there with the second-to-last digit being 1, which are divisible by 4?
|
39. It is clear that the numbers divisible by 4 are those and only those numbers whose last two digits form a number divisible by 4. Then, if the second-to-last digit is 1, the last digit can only be 2 or 6. In total, we get $9 \cdot 10 \cdot 10 \cdot 10 \cdot 1 \cdot 2=18000$ required numbers.
|
18000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. How many even four-digit numbers are there that do not contain the digits 5 and 6?
|
40. The first digit can be chosen in seven ways (we cannot take 0, 5, and 6), the second and third digits can each be chosen in eight ways, and the last digit, which must be even, can be chosen in four ways (we cannot take 6). In total, we get $7 \cdot 8 \cdot 8 \cdot 4 = 1792$ numbers.
|
1792
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41. In how many ways can 5 people be seated in a row so that Kolya and Olya sit next to each other?
|
41. First, let's seat Kolya and Olya. There are 4 ways to seat them next to each other with Olya sitting to the right of Kolya, and 4 ways with Olya sitting to the left of Kolya. Thus, for 5 free seats, there are 8 ways to seat Kolya and Olya next to each other. After seating Kolya and Olya, 3 seats will remain free. These can be occupied in $3!=6$ ways. Therefore, the total number of ways to seat 5 people will be $8 \cdot 6=48$.
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42. In how many ways can all ten digits be arranged in a row so that the digits $2,5,8$ stand together?
|
42. We will consider the three digits $2,5,8$ as one number 258. Together with the other seven digits, we will have 8 numbers: $258,0,1,3,4,6,7,9$. There are $8!=40320$ ways to arrange them in a row. In this case, the digits $2,5,8$ will always be together and in the specified order.
|
40320
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. On a bookshelf, there are ten different books, three of which are on mathematics. In how many ways can all these books be arranged in a row so that the mathematics books are together?
|
43. Let's bind three mathematics books together so that they form a single book. Then we will have 8 books. They can be arranged in a row on a bookshelf in $8!=40320$ ways. Obviously, in each such arrangement, the mathematics books will continue to remain together if they are rearranged among themselves. This can be done in $3!=6$ ways. In total, we get $40320 \cdot 6=241920$ ways of the required arrangement of books on the shelf.
|
241920
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45. Five girls are sitting on five chairs in a row, and opposite them, on five chairs, are sitting five boys. It was decided that the boys would swap places with the girls. In how many ways can this be done?
|
45. Boys can be seated on the girls' chairs in $5!=$ $=120$ ways. The girls can also be seated on the boys' chairs in the same number of ways. Ultimately, we will have $120 \cdot 120=14400$ ways.
|
14400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. In the room, there are 6 light bulbs, each with its own switch. In how many ways can the room be illuminated if at least one light bulb must be turned on?
|
49. The number of ways to light a room will be equal to the number of subsets of a set of six elements, except for the case when the subset is the empty set. Thus, $2^{6}-1=63$.
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
50. How many five-digit numbers are there that are divisible by 5 and do not have any repeated digits in their representation?
|
50. The number of numbers that end in 0 and do not have identical digits in their representation is $9 \cdot 8 \cdot 7 \cdot 6 \cdot 1$. The number of numbers that end in 5 and do not have identical digits in their representation is $8 \cdot 8 \cdot 7 \cdot 6 \cdot 1$. Therefore, the total number of numbers of interest to us is $9 \cdot 8 \cdot 7 \cdot 6+8 \cdot 8 \cdot 7 \cdot 6=5712$.
|
5712
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. How many four-digit numbers contain only one even digit?
|
51. Four-digit numbers, in which only the first digit is even, amount to $4 \cdot 5 \cdot 5 \cdot 5=500$. Four-digit numbers, in which only the second (third, fourth) digit is even, amount to $5 \cdot 5 \cdot 5 \cdot 5$. Then, the total number of four-digit numbers, in which only one digit is even, will be $4 \cdot 5 \cdot 5 \cdot 5+3 \cdot 5 \cdot 5 \cdot 5 \cdot 5=2375$.
|
2375
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. How many four-digit numbers contain at least one even digit?
|
53. From four-digit numbers, we need to discard all those numbers that do not have a single even digit. We will get: $9 \cdot 10 \cdot 10 \cdot 10-5 \cdot 5 \cdot 5 \cdot 5 \cdot 5=8375$ numbers.
|
8375
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54. How many five-digit numbers are there in which
a) the digit 5 appears exactly once?
b) the digit 5 appears no more than once?
c) the digit 5 appears at least once?
|
54. a) The number of five-digit numbers where only the first digit is 5 is $1 \cdot 9 \cdot 9 \cdot 9 \cdot 9=9^{4}$. The number of five-digit numbers where only the second (third, fourth, fifth) digit is 5 is $8 \cdot 9^{3}$. Therefore, the total number of required five-digit numbers is $9^{4}+4 \cdot 8 \cdot 9^{3}=41 \cdot 9^{3}$.
b) If we add the number of five-digit numbers that do not contain the digit 5 (see problem 35) to the number of five-digit numbers that have exactly one digit 5 (see problem 54 a), we get the number of five-digit numbers in which the digit 5 appears no more than once: $8 \cdot 9^{4}+41 \cdot 9^{3}=113 \cdot 9^{3}$.
c) If we subtract the number of five-digit numbers that do not contain the digit 5 (see problem 35) from the total number of five-digit numbers, we get the number of five-digit numbers that contain at least one digit 5: $9 \cdot 10^{4}-8 \cdot 9^{4}=37512$.
|
37512
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
55. How many different letter combinations can be obtained by rearranging the letters in the word a) NONNA; b) MATHEMATICA?
|
55. a) The word NONNA contains 5 letters. If all of them were different, we could obtain $5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120$ different letter combinations from this word. In reality, in each such combination, the letter N is repeated three times. Permuting these three letters among themselves does not change the combination. Since three letters allow 6 permutations, we will get a total of $120: 6=20$ different letter combinations.
b) By analogy with the previous problem, we find that as a result of all possible permutations of the letters in the word MATEМАТИКА, we will have $10!:(2!2!3!)=151200$ different letter combinations.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. In the class, 12 subjects are studied. In how many ways can 5 different subjects be scheduled for Monday?
|
56. For the first lesson, the subject can be chosen in twelve ways, for the second - only eleven, and so on. Thus, using the multiplication rule, we get that a schedule of five different subjects, if there are 12 subjects in total, can be created $12 \cdot 11 \cdot 10 \cdot 9 \cdot 8=9504$ ways.
|
9504
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
62. Each member of a team consisting of 20 people bought three lottery tickets. It turned out that the team won three different prizes. In how many ways can these prizes be distributed?
|
62. A n s w e r. $20^{3}=8000$.
|
8000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. In how many ways can 3 identical books be distributed among twelve schoolchildren if no more than one book can be given to any one child?
|
64. If the books were different, the number of ways to distribute them among twelve schoolchildren would be 12.11 * ... * 10 = 1320. Let's choose any three schoolchildren. If, having three different books, we distribute them, giving one to each of these schoolchildren, it will be found that there are 6 ways to distribute the books. Under the same conditions, three identical books can be distributed in only one way. And this will be the case for any three schoolchildren. Therefore, the number of ways to distribute three identical books among 12 schoolchildren will be 3! times less than if the books were different. Finally, we get $12 \cdot 11 \cdot 10: 3!=220$ ways.
|
220
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
66. In how many ways can a delegation of three people be selected from twelve people?
|
66. Answer. $C_{12}^{3}=220$. It is useful to compare with problem 64.
|
220
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
68. In how many ways can 5 girls and 5 boys be seated at a round table so that no two people of the same gender sit next to each other?
|
68. Let's renumber the seats at the round table from first to tenth. We will seat the boys in the seats with odd numbers, and the girls in the seats with even numbers. This can be done in (5!) ${ }^{2}$ ways. We will get the same number of ways if we switch the boys and girls. Ultimately, we will have $2(5!)^{2}=28800$ ways.
|
28800
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69. In how many ways can two people divide 10 different items between themselves, with each person getting 5 items?
|
69. If one person selects 5 items, then the other will also have 5 items left. But 5 items out of 10 can be selected in $C_{10}^{5}=252$ ways.
|
252
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71. In how many ways can 10 athletes be divided into two teams of 5 people each, if two athletes wish to play on the same team?
|
71. Let's highlight the two athletes who wish to play together. To form two teams of 5 people each, we need to add three more athletes to them. This can be done in $C_{8}^{3}=56$ ways. Answer. 56.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
72. In how many ways can 10 athletes be divided into two teams of 5 people each, if two athletes wish to play on different teams?
|
72. If we temporarily separate two athletes who refused to play on the same team, 8 athletes will remain. Let's add four more athletes to one of the previously separated athletes. This can be done in $C_{8}^{4}=70$ ways. The remaining 4 athletes will join the team of the second athlete. A n s w e r. 70.
|
70
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
73. In the brigade, there are 10 men and 8 women. In how many ways can the brigade elect a delegation consisting of 3 men and 2 women?
|
73. Three men can be chosen in $C_{10}^{3}=120$ ways. Two women can be chosen in $C_{8}^{2}=28$ ways. By the rule of product, we get $120 \cdot 28=3360$ ways to elect a delegation of the required composition.
|
3360
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
75. Among the cards that differ only in color, there are 5 red, 3 blue, 2 green, and one yellow. In how many ways can they be laid out in a row to form a colored strip?
|
75. Answer. $11!:(5!\cdot 3!\cdot 2!\cdot 1!)=27720$.
|
27720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
77. How many four-digit numbers are there in which each subsequent digit
a) is less than the previous one?
b) is greater than the previous one?
|
77. a) We will select any 4 digits out of ten. This can be done in $C_{10}^{4}=210$ ways. For each such quartet, there is a unique way to arrange it in descending order of digits. A n s w e r. 210.
b) Since a natural number cannot start with zero, in this case, the selection of four digits is made from nine digits. A n s w e r. $C_{9}^{4}=126$.
|
210
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
79. How many four-digit numbers are there in which no two adjacent digits are the same?
|
79. The first digit can be chosen in nine ways (zero cannot be taken). Each subsequent digit can also be chosen in nine ways, as the digit used in the previous place cannot be taken. Finally, we get: $9 \cdot 9 \cdot 9 \cdot 9=6561$
|
6561
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
80. In how many ways can three identical items be distributed among ten people if there is no limit to the number of items offered to one person?
|
80. Answer. $C_{10}^{3}+2 C_{10}^{2}+C_{10}^{1}=220$ ways.
|
220
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
82. In how many ways can 6 people be seated at a round table, considering the arrangements different if at least some of the seated individuals have new neighbors?
|
82. New neighbors will not appear if the seating arrangements are obtained from one another by rotation around a circle or by symmetric reflection. In the previous problem, only rotation around a circle was considered. To account for symmetric reflection, the result of the previous problem should be divided by 2. Answer. $120: 2=60$.
|
60
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
83. At a school evening, there are 12 girls and 10 boys present. In how many ways can 4 pairs for dancing be formed from them?
|
83. Four girls can be chosen in $C_{12}^{4}=495$ ways. Now we need to choose four boys in a specific order. This can be done in $A_{10}^{4}=5040$ ways. Finally, we get $495 \cdot 5040=2494800$ ways. We can also first choose four boys, and then four girls in a specific order. Of course, we will get the same result.
|
2494800
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. Along a groove, there are 12 white balls lying. In how many ways can 8 black balls be placed among them so that no two black balls end up next to each other?
|
85. Among 12 white balls, there are 13 positions where black balls can be placed. This can be done in $C_{13}^{8}=$ $=1287$ ways.
|
1287
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
86. From a bag containing 8 white and 5 black balls, all balls are drawn one by one. How many different sequences of the balls' appearance are possible if the balls of the same color are indistinguishable?
|
86. A n s w e r. $13!:(8!\cdot 5!)=1287$.
|
1287
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
87. How many different divisors does the number have a) 800; b) 126000?
|
87. a) Since $800=2^{5} \cdot 5^{2}$, the power of two can be part of the divisor of this number in six ways $\left(2^{0}, 2^{1}, 2^{2}, 2^{3}, 2^{4}, 2^{5}\right)$, and the power of five in three ways ( $5^{0}, 5^{1}, 5^{2}$ ). Therefore, by the rule of multiplication, we get that the number 800 has $6 \cdot 3=18$ different divisors.
b) Since $126000=2^{4} \cdot 3^{2} \cdot 5^{3} \cdot 7$, the number of divisors of this number is $(4+1)(2+1)(3+1)(1+1)=120$.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Among the balls that differ only in color, there are 6 white, 4 black, and 8 red. In how many ways can two boys divide these balls (not necessarily equally) between themselves so that each of them gets at least two balls of each color?
|
88. When the boys take two balls of each color, they will have left to divide 2 white and 4 red balls. This can be done in $(2+1)(4+1)=15$ ways. (Compare with problem 87.$)$
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. Several students went to take a math exam. One student calculated that even if none of them "fail," there could still be 59049 different exam outcomes. How many students were there?
|
90. Let there be $n$ students. For each of them, there are three possible outcomes of the exam: "satisfactory", "good", and "excellent". Therefore, for $n$ students, we get $3^{n}$ outcomes. We have the equation: $3^{n}=59049$, from which $n=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
91. In how many ways can the letters in the word МАТЕМАТИКА be rearranged so that the two letters "А" are never next to each other
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
91. The word МАТЕМАТИКА, except for the three letters А, contains another 7 letters. They can be rearranged in $7!:(2!\cdot 2!)=1260$ ways. Each such permutation has 8 positions for placing the letter А. Therefore, in each such case, this can be done in $C_{8}^{3}=56$ ways. Finally, we get: $1260 \cdot 56=70560$.
|
70560
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. In how many ways can the letters in the word INTEGRAL be rearranged so that the third, fifth, and seventh positions are occupied by consonants?
|
92. The word INTEGRAL contains 5 consonant letters. Out of them, three letters can be chosen in a certain order (for the third, fifth, and seventh positions) in $A_{5}^{3}=60$ ways. The remaining 5 letters of the word can be arranged in $5!=120$ ways. In total, we get $60 \cdot 120=7200$ required arrangements of the letters in the word INTEGRAL.
|
7200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
93. How many five-digit numbers are there in which no two digits of the same parity stand next to each other?
|
93. The first digit can be chosen in nine ways. The second digit must have a parity different from that of the first digit. In any case, the second digit can be chosen in five ways. The third, fourth, and fifth digits can also be chosen in the same number of ways. Therefore, the number of required five-digit numbers will be $9 \cdot 5 \cdot 5 \cdot 5 \cdot 5=5625$.
|
5625
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
94. How many six-digit numbers are there in which three digits are even and three are odd?
|
94. The places for odd digits can be chosen in $C_{6}^{3}=20$ ways. On each of the remaining three places, there will be an even digit. Thus, after choosing places for the odd digits, each digit of the required six-digit number can be chosen in five ways (either even or odd). In total, we get $20 \cdot 5^{6}$ numbers. However, among them will be those that start with zero. There are $C_{5}^{3} \cdot 5^{5}=10 \cdot 5^{5}$ such numbers. Finally, we get $20 \cdot 5^{6}-10 \cdot 5^{6}=281250$ required six-digit numbers.
|
281250
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
96. In how many ways can 9 identical items be distributed into four boxes?
|
96. Let's add three more identical items, different from the given ones. We will then have 12 items of two types. From these, we can obtain $12!:(9!\cdot 3!)=$ $=C_{12}^{3}=220$ different permutations. In each such permutation, the items we added divide the given items into 4 parts (obviously, some of these parts may not contain any items). These 4 parts can be considered as the contents of four boxes. Answer. 220.
|
220
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Cut a plate weighing 11 g into three pieces so that, using these pieces as weights, it is possible to weigh on balance scales any whole number of grams from 1 g to 11 g.
$(4-5$ grade.)
|
4.1. The plate needs to be cut into parts weighing 1 g, 3 g, and 7 g. To weigh 2 g, you need to place 3 g on one pan of the scales, and on the other pan - a 1 g counterweight and the substance to be weighed. For the other cases, we get: $4=3+1,5=7+1-3,6=7-1,8=7+1$, $9=7+3-1,10=7+3,11=7+3+1$.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. In a school, there are 30 classes and 1000 students. Prove that there is a class with at least 34 students.
$$
\text { (4-5 grades) }
$$
|
5.1. Suppose that in each class there are no more than 33 students. Then, in the entire school, there would be no more than $33 \cdot 30=990$ students, which contradicts the condition of the problem. Therefore, there will be at least one class with more than 33 students, i.e., there will be no fewer than 34.
|
34
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.1. If Petya performs a certain task in such a way that each subsequent day he does twice as much as in all the previous days combined, then the entire task will take him 12 days. How many days will it take for Petya and Kolya to complete this task if Kolya works in the same way as Petya?
$$
\text { (4-8 grades) }
$$
|
9.1. It is clear that in 11 days, Petya will complete exactly half of the entire work, since on the twelfth day, he must complete as much work as he did in the previous 11 days combined, after which the entire work will be completed. If Kolya works together with Petya, then Kolya will also complete half of the entire work in 11 days. Thus, both boys together will complete the entire work in 11 days.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.1. Find the smallest natural number consisting of identical digits and divisible by 18.
$$
(5-6 \text { cl.) }
$$
|
12.1. It is clear that the desired number must be even and have a sum of digits divisible by 9. Among two-digit numbers consisting of identical digits, there is no such number. Among three-digit numbers, the number 666 fits this description. It will be the smallest.
保留源文本的换行和格式,翻译结果如下:
12.1. It is clear that the desired number must be even and have a sum of digits divisible by 9. Among two-digit numbers consisting of identical digits, there is no such number. Among three-digit numbers, the number 666 fits this description. It will be the smallest.
|
666
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.1. From 22 kg of fresh mushrooms, 2.5 kg of dried mushrooms are obtained, which still contain $12 \%$ water. What percentage of water is contained in fresh mushrooms?
$$
\text { (5-7 grades) }
$$
|
13.1. Let's find the mass of water contained in 2.5 kg of dry mushrooms. We get: $2.5 \cdot 12: 100=0.3$ kg. Therefore, the anhydrous mass is $2.5-0.3=2.2$ kg. This constitutes one-tenth of 22 kg, i.e., $10 \%$. Then, the remaining $90 \%$ is water.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.1. Calculate: $2^{15}-2^{14}-2^{13}-\ldots-2^{1}-1$.
$$
\text { (6-7 grades) }
$$
|
16.1. Noticing that $2^{15}-2^{14}=2 \cdot 2^{14}-2^{14}=2^{14}$, we will reduce the given expression to the following:
$$
2^{14}-2^{13}-2^{12}-\ldots-2-1
$$
Continuing to proceed in this manner further and further, we will find that the desired sum is 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18.1. What is the smallest natural number by which 720 must be multiplied so that the result is a cube of a natural number?
|
18.1. We have: $720=2^{4} \cdot 3^{2} \cdot 5$. To obtain a perfect cube from this number, it needs to be multiplied by a number such that the exponents of two, three, and five in the resulting product are divisible by three. Clearly, the smallest such multiplier will be the number $2^{2} \cdot 3 \cdot 5^{2}=300$. Indeed, in this case $720 \cdot 300=$ $=2^{6} \cdot 3^{3} \cdot 5^{3}=\left(2^{2} \cdot 3 \cdot 5\right)^{3}=60^{3}$.
|
300
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20.1. A boy wrote a certain number. In the second place, he wrote the number 7, in the third place - the difference between the second and the first number, in the fourth place - the difference between the third and the second number, and so on. What number will be in the $200-\mathrm{m}$ place?
$$
\text { (6-8 grades) }
$$
4
|
20.1. Let the first number be denoted by $x$. Then, following the condition of the problem, we get the following sequence of numbers: $x, 7, 7-x, -x, -7, x-7, x, 7, \ldots$ 18
As we can see, the seventh and eighth numbers repeat the first and second, i.e., we have a periodic repetition of numbers with a period of 6. Since 200 divided by 6 leaves a remainder of 2, we will have the same number on the two hundredth place as on the second place, i.e., 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21.1. A motorcyclist set out from city A to city B. If he travels at a speed of 50 km per hour, he will arrive in B one hour earlier than the scheduled time. If he travels at a speed of 35 km per hour, he will be two hours late. Find the distance between cities A and B.
$$
(7-8 \text { th grade })
$$
|
21.1. Let $A B=x$. Then we easily arrive at the equation: $x: 50+1=x: 35-2$, from which $x=350$. A n s w e r. $A B=350$ km.
|
350
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22.1. Calculate the expression $2 x^{4}+3 x^{2} y^{2}+y^{4}+y^{2}$, given that $x^{2}+y^{2}=1$.
$$
\text { (7-8 grades) }
$$
|
22.1. Taking into account that $x^{2}+y^{2}=1$, we get:
$$
\begin{gathered}
2 x^{4}+3 x^{2} y^{2}+y^{4}+y^{2}=2 x^{4}+2 x^{2} y^{2}+x^{2} y^{2}+y^{4}+y^{2}= \\
=2 x^{2}\left(x^{2}+y^{2}\right)+y^{2}\left(x^{2}+y^{2}\right)+y^{2}=2 x^{2}+y^{2}+y^{2}= \\
=2\left(x^{2}+y^{2}\right)=2
\end{gathered}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29.1. Find the three-digit number $\overline{a b c}$, if it is known that
$$
\begin{gathered}
8 a+5 b+c=100 \\
a+b+c=20
\end{gathered}
$$
|
29.1. Subtracting the second equation of the system from the first, we get
$$
7 a+4 b=80
$$
From this equality, it follows that $a$ is divisible by 4, i.e., $a=4$ or $a=8$. But $a$ cannot be equal to 4, because in this case, from the equation $7 a+4 b=80$, it would follow that $b=13$. However, this is impossible, since $b$ is a digit, i.e., $b \leqslant 9$. Therefore, $a=8$. Then from the equation $7 a+4 b=80$, it follows that $b=6$. Finally, from the equation $a+b+c=20$, we find that $c=6$. Answer: 866.
|
866
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32.1. Find all such prime numbers that can be represented both as the sum of two prime numbers and as their difference. $(7-10$ grades $)$
|
32.1. It is obvious that neither of the prime numbers 2 and 3 can be represented as the sum of two prime numbers. Now, let's take a prime number \( p > 3 \). It can be represented as the sum of two prime numbers only if \( p-2 \) is a prime number, since in the sum of two prime numbers, one of the addends must be equal to 2. Similarly, if a prime number \( p > 3 \) can be represented as the difference of two prime numbers, then the number \( p+2 \) must be prime, since in the difference of two prime numbers, the subtrahend must be equal to 2. Therefore, if a prime number \( p \) can be represented both as the sum and as the difference of two prime numbers, then the numbers \( p-2 \) and \( p+2 \) must be prime simultaneously. It is clear that the number 5 satisfies the condition of the problem, since \( 5 = 3 + 2 = 7 - 2 \), where all four numbers \( 2, 3, 5, 7 \) are prime. We will prove that the problem has no other solutions. For this, it is sufficient to prove that for a prime \( p > 5 \), the numbers \( p-2 \) and \( p+2 \) cannot be prime simultaneously. Indeed, a prime number \( p > 5 \) when divided by 3 gives a remainder of 1 or 2, i.e., it has one of two forms: \( p = 3k + 1 \) or \( p = 3k + 2 \), where \( k > 1 \). In the first case, the number \( p + 2 = 3k + 1 + 2 = 3(k + 1) \) will be composite, and in the second case, the number \( p - 2 = 3k + 2 - 2 = 3k \) will be composite.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33.1. A six-digit number starts with one. If this one is moved to the end of the number, the resulting number will be three times the given number. Find the given number.
$$
\text { (7-10 grades) }
$$
|
33.1. The desired six-digit number has the form $1 \overline{a b c d e}$. According to the problem, $3 \cdot 1 \overline{a b c d e}=\overline{a b c d e} 1$ or $3(100000+\overline{a b c d e})=1+10 \cdot \overline{a b c d e}$. From this, $7 \cdot \overline{a b c d e}=299999$, i.e., $\overline{a b c d e}=42857$. Therefore, the desired number is 142857.
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34.1. Prove that there exists a natural number, the square of which begins with exactly nine nines.
$$
(7-10 \text { cl.) }
$$
|
34.1. To solve the problem, it is sufficient to provide at least one example. Let's prove, for instance, that the square of the number $9999999999=$ $=10^{10}-1$ starts with exactly nine nines. Indeed,
$$
\begin{aligned}
& \left(10^{10}-1\right)^{2}=10^{20}-2 \cdot 10^{10}+1=10^{10}\left(10^{10}-2\right)+1= \\
& =9999999998 \cdot 10^{10}+1=9999999980000000001
\end{aligned}
$$
|
9999999980000000001
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
35.1. How many natural numbers $n$ exist such that
$$
100<\sqrt{n}<101 ?
$$
$$
\text { (8-9 grades) }
$$
|
35.1. If $100<\sqrt{ } \bar{n}<101$, then $10000<n<10201$. The last inequality is satisfied by 200 natural numbers: 10001, 10002, ..., 10200. These and only these numbers satisfy the given inequality. Answer. 200.
|
200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
47.1. Find the sum of all three-digit numbers divisible by 7.
$(9-10$ grade $)$
6
|
47.1. There are a total of 900 three-digit numbers. Among them, multiples of seven will be $\left[\frac{900}{7}\right]=128$ numbers. It is easy to find that the first such number is 105, and the last one is 994. Thus, we need to find the sum of 128 terms of an arithmetic progression with the first term 105 and the last term 994. We get:
$$
S_{128}=\frac{105+994}{2} \cdot 128=1099 \cdot 64=70336 .
$$
|
70336
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
48.1. Let the decimal representations of the numbers $2^{1985}$ and $2^{1986}$ contain $p$ and $q$ digits, respectively. Find the sum $p+q$.
|
48.1. Let:
$$
a=2^{1985}, \quad b=5^{1985} \text {. }
$$
## Then
$$
p-1<\lg a<p, \quad q-1<\lg b<q .
$$
By adding these two inequalities and considering that $\lg (a b)=$ $=1985$, we get:
$$
p+q-2<1985<p+q, \text { hence } \quad 1985<p+q<1987
$$
Therefore, $p+q=1986$.
|
1986
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. One sixth of the fourth-grade students received fives on their math test, one third received threes, and half received fours. How many students in this class received unsatisfactory grades?
$$
\text { (4-5 grade) }
$$
|
4.2. From Figure 12, we see that
$$
\frac{1}{6}+\frac{1}{3}+\frac{1}{2}=\frac{1}{6}+\frac{2}{6}+\frac{3}{6}=1
$$
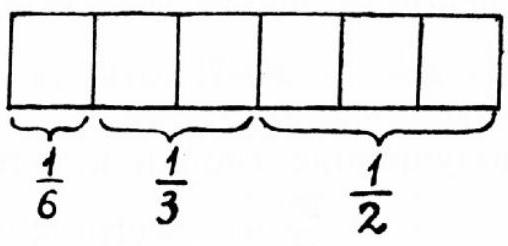
Fig. 12
i.e., the students who received grades of five, three, and four make up the entire class. Therefore, no student received an unsatisfactory grade.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. Calculate: $1+2-3-4+5+6-7-8+\ldots+1982-1983-$ $-1984+1985+1986$.
$$
(4-6 \text { grades })
$$
|
6.2. Without touching the first and last terms of the given sum, we will group the other terms into sets of four consecutive terms, namely: $1+(2-3-4+5)+(6-7-8+9)+\ldots+$ ( $1982-1983-1984+1985)+1986$. It is easy to notice that the sum in each bracket is zero. Therefore, the total sum is $1+1986=1987$.
|
1987
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. The product of three natural numbers is 60. What is the greatest possible value of their sum?
$$
\text { (4-6 grades) }
$$
|
8.2. The greatest value of the sum will be obtained in the case when we take the three natural numbers as $60,1,1$. Then the sum will be equal to $60+1+1=62$.
|
62
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. If 100 is divided by some unknown number, the remainder is 16, and if 200 is divided by the same number, the remainder is 4. Find this number.
$$
\text { (5-6 grades) }
$$
|
10.2. It is clear that the desired number is greater than 16. Moreover, the numbers $100-16=84$ and $200-4=196$ must be divisible by the desired number. Since $84=3 \cdot 4 \cdot 7$ and $196=2 \cdot 2 \cdot 7 \cdot 7$, it is easy to conclude that these numbers have only one common divisor greater than 16, namely 28. Answer: 28.
|
28
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.2. The sum of half and a third of a number is 7 units greater than its quarter. What is this number?
$$
(6-7 \text { grade })
$$
|
12.2. Let the desired number be denoted by $x$. Then
$$
\frac{1}{2} x+\frac{1}{3} x=\frac{1}{4} x+7, \text { from which } x=12
$$
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.2. A third of the sixth-grade students received threes for their math test. How many students received fives if only one student received a two, and fives were received by $\frac{5}{13}$ of the sixth-graders?
$$
(6-7 \text { grade) }
$$
|
13.2. Students who received threes and fours constitute
$$
\frac{1}{3}+\frac{5}{13}=\frac{28}{39} \text { of the entire class. }
$$
Therefore, the number of students in this class is divisible by 39. Since the class size does not exceed 50 students, there are 39 students in total in the class, with 28 of them receiving threes and fours on the test. Therefore, fives were received by $39-28-1=10$ students.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.2. For 9 identical books, more than 11 rubles were paid, and for 13 such books, less than 16 rubles were paid. How much does one book cost?
$$
(6-7 \text { grade) }
$$
|
14.2. According to the condition of the problem, the cost of one book in kopecks is within the following limits:
$$
\frac{1100}{9}<x<\frac{1600}{13} \text { or } \quad 122 \quad \frac{2}{9}<x<123 \frac{1}{13}
$$
from which we conclude that one book costs 123 kopecks = 1 r. 23 kopecks.
|
123
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.2. Find the largest natural number, the remainder of the division of which by 91 is equal to the square of the quotient.
$$
\text { (6-7 grades) }
$$
|
15.2. When dividing by 91, the largest remainder that is a perfect square is 81. Therefore, the quotient is 9. The desired number is then \(91 \cdot 9 + 81 = 900\).
|
900
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.2. Every third student in the sixth grade is a member of the math club, every fourth is a member of the history club, every sixth is a member of the chemistry club, and all the others are members of the literature club. How many people are in the chemistry club if there are three more people in the math club than in the literature club?
$$
(6-7 \text { grade) }
$$
|
16.2. Students attending the literary club constitute $1-\frac{1}{3}-\frac{1}{4}-\frac{1}{6}=\frac{1}{4}$ of the class. If $x$ is the total number of students in the sixth grade, then according to the problem, $\frac{1}{3} x-\frac{1}{4} x=3$, from which $x=36$. Therefore, the number of students attending the chemistry club is $36: 6=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18.2. A segment 20 cm long is divided into two segments, and a square is constructed on each of them as a side. Find the lengths of the sides of these squares, if the difference in the areas of the squares is $120 \mathrm{~cm}^{2}$.
$$
\text { (7-8 grades) }
$$
|
18.2. Let the side of the larger square be $x$. Then the side of the smaller square is $20-x$. According to the problem, we have:
$$
x^{2}-(20-x)^{2}=120, \text { hence } 40 x=520, \text { i.e., } x=13 .
$$
Answer: The sides of the squares are 13 cm and 7 cm.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19.2. What is the last digit of the sum
$$
3^{13}+3^{15}+3^{17}+\ldots+3^{43} ?
$$
|
19.2. There are 16 addends in total in this sum. By sequentially dividing them into 8 pairs, we get:
$$
\begin{gathered}
3^{13}(1+9)+3^{17}(1+9)+\ldots+3^{41}(1+9)= \\
=\left(3^{13}+3^{17}+\ldots+3^{41}\right) \cdot 10
\end{gathered}
$$
Thus, the considered sum ends in 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.