problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
21.2. In triangle $A B C$, the bisectors of angles $B A C$ and $A B C$ intersect at point $O$. Find angle $A C B$ if angle $A O B$ is $125^{\circ}$.
$(7-8$ grade $)$
|
21.2. In triangle $A B C$ (Fig. 15), we have: $\angle O A B + \angle O B A = 180^{\circ} - 125^{\circ} = 55^{\circ}$. Since $A O$ and $B O$ are the bisectors of angles $C A B$ and $C B A$, the sum of these angles is $2 \cdot 55^{\circ} = 110^{\circ}$. Then $\angle A C B = 180^{\circ} - (\angle C A B + \angle C B A) = 180^{\circ} - 110^{\circ} = 70^{\circ}$.
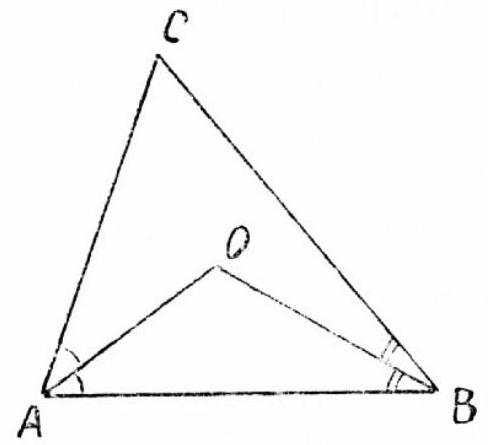
Fig. 15
|
70
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26.2. Find the smallest natural number divisible by 11, which after being increased by 1, would be divisible by 13.
$$
\text { (7-8 grades) }
$$
|
26.2. Let the desired number be denoted by $n$. According to the problem, we have: $n=11 k$ and $n+1=13 m$, where $k$ and $m$ are natural numbers. Then $11 k=13 m-1$ or $(13-2) k=13 m-1$, from which we get $13(k-m)=2 k-1$. In the obtained equation, the left side is divisible by 13. Therefore, the right side must also be divisible by 13. The smallest value of $k$ for which this is true is 7. Then $n=11 \cdot 7=77$.
|
77
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28.2. Among all triangles for which the sum of the medians is 3, find the triangle with the greatest sum of altitudes.
$$
(7-9 \text { grades })
$$
|
28.2. In any triangle, the height dropped to any side is not greater than the median drawn to the same side. Therefore, the sum of the heights of the triangle is not greater than the sum of its medians. In the conditions of this problem, the greatest sum of heights is 3, which will be the case for an equilateral triangle.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29.2. Find the smallest natural number that ends in 56, is divisible by 56, and has the sum of its digits equal to 56.
$$
(7-10 \text { cl.) }
$$
|
29.2. The desired number can be represented as $100k + 56$. Since $100k$ must be divisible by 56, the number $k$ must be divisible by 14, i.e., it is even, divisible by 7, and has a sum of digits equal to $56 - 5 - 6 = 45$. The smallest even number with a sum of digits 45 is 199998, but it is not divisible by 7. The next largest even numbers with the same sum of digits will be: 289998, 298998, etc. The first of these is also not divisible by 7, whereas the second one is. Thus, the answer to the problem is the number $298998 \cdot 100 + 56 = 29899856$.
|
29899856
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30.2. Find the largest natural number that is divisible by 37 and in which each subsequent digit is less than the previous one.
$$
\text { (7-10 grades) }
$$
|
30.2. The largest natural number with decreasing digits is the ten-digit number 9876543210. We will divide it by 37. During the division, we notice that it is not divisible by 37, whereas the eight-digit number 98765432 is divisible by 37. Therefore, the nine-digit number 987654320 is also divisible by 37. It is evident that it will be the largest among the nine-digit numbers where each subsequent digit is less than the previous one, i.e., it will be the answer to the problem.
|
987654320
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35.2. Two motorcyclists set out simultaneously from points $A$ and $B$ towards each other and met 50 km from $B$. Upon arriving at points $A$ and $B$, the motorcyclists immediately turned around and met again 25 km from $A$. How many kilometers is it from $A$ to $B$?
|
35.2. Let the motorcyclists meet for the first time at point $C$, and for the second time at point $D$ (Fig. 19). Then $B C=50$ km and $A D=25$ km.

Fig. 19
Let $A B=x$ km. Clearly, before the first meeting, the motorcyclists traveled $x$ km, and before the second meeting, they traveled $3 x$ km, i.e., three times more. Therefore, before the second meeting, each motorcyclist traveled three times the distance they traveled before the first meeting. Since the second motorcyclist traveled 50 km before the first meeting, he traveled 150 km before the second meeting. On the other hand, it is easy to see that before the second meeting, the second motorcyclist traveled $(x+25)$ km. Thus, we have the equation: $x+25=150$, from which $x=125$, i.e., $A B=125$ km.
|
125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
44.2. The sum of the first $n$ terms of an arithmetic progression is equal to $n^{2}+5 n$. Find the tenth term of the progression.
$$
\text { (9-10 grades) }
$$
|
44.2. The tenth term of the given progression can be found as the difference between the sums of its first ten and first nine terms. These sums can be found from the expression $n^{2}+5 n$, by substituting $n=10$ and $n=9$ respectively. Thus, the desired tenth term is
$$
\left(10^{2}+5 \cdot 10\right)-\left(9^{2}+5 \cdot 9\right)=150-126=24 .
$$
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45.2. Find the natural number that is 40 times less than the sum of all preceding natural numbers.
$$
(9-10 \text { th } )
$$
10
|
45.2. We have the equation:
$$
\begin{gathered}
1+2+3+\ldots+(n-1)=40 n \text {, i.e., } \frac{1}{2} n(n-1)=40 n, \\
\text { hence } n=81 .
\end{gathered}
$$
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.3. How to weigh 1 kg of cereal on balance scales using two weights of 300 g and 650 g?
$$
(4-5 \text { grade })
$$
|
1.3. This can be done in two weighings: first, weigh out 650 g, and then $650-300=350$ g.
|
350
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3. Write the number 100 using four fives and arithmetic signs.
$(4-5$ grade.)
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
3.3. The two solutions to this problem are given below:
1) $(5+5)(5+5)=100$
2) $(5 \cdot 5-5) \cdot 5=100$
|
100
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
5.3. In three piles, there are 22, 14, and 12 nuts. It is required to equalize the number of nuts in all piles by making three moves, while adhering to the following condition: from one pile to another, only as many nuts can be moved as there are in the pile to which the nuts are being moved.
$$
\text { (4-6 grades) }
$$
|
5.3. Move 14 nuts from the first pile to the second. After this, the piles will contain 8, 28, and 12 nuts, respectively. Next, move 12 nuts from the second pile to the third. Now the piles will contain 8, 16, and 24 nuts, respectively. Finally, move 8 nuts from the third pile to the first, after which each of the three piles will contain 16 nuts.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. An old problem. On a hot summer day, 6 mowers drank a barrel of kvass in 8 hours. How many mowers will drink the same barrel of kvass in 3 hours?
$$
\text { (4-7 grades) }
$$
|
6.3. If 6 mowers drank a barrel of kvass in 8 hours, then one mower would drink this barrel in 48 working hours. Therefore, 16 mowers would drink the barrel of kvass in three hours.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Add a digit to the left and right of the number 10 so that the resulting number is divisible by 72.
$$
(5-6 \text { grade) }
$$
|
9.3. The desired number must be divisible by 8 and 9, i.e., it must be even and the sum of its digits must be divisible by 9. Only 5 numbers need to be checked: $8100, 6102, 4104, 2106, 9108$. Among these numbers, only 4104 is divisible by 72. Answer: 4104.
|
4104
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Can two digits be appended to the number 277 so that the resulting number is divisible by any number from 2 to 12?
|
10.3. For a number to be divisible by 10, it must end in zero. Let's choose the second-to-last digit so that the resulting number is divisible by 9. In this case, the sum of the digits of this number should be equal to 18. Therefore, we get the number 27720. The problem has a solution only if the found number is divisible by each of the numbers 7, 8, and 11. It is easy to check that this is indeed the case. This means that the number 27720 is divisible by any number from 2 to 12 inclusive.
|
27720
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.3. A 30% hydrochloric acid solution was mixed with a 10% solution, resulting in 600 g of a 15% solution. How many grams of each solution were taken?
$$
\text { (6-7 grades) }
$$
|
14.3. Let $x$ be the number of grams of the 30% solution. Then the 10% solution was taken in the amount of ( $600-x$ ) g. We have the equation: $0.3 x + 0.1(600-x) = 0.15 \cdot 600$. From this, $x=150$. Answer: 150 g of the 30% solution and 450 g of the 10% solution were taken.
36
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.3. Boys are dividing nuts. The first one took 3 nuts and a fifth of the remainder; the second took twice 3 nuts and a fifth of the new remainder; the third took thrice 3 nuts and a fifth of the next remainder, and so on. How many boys were there if it turned out that as a result of such division, each received an equal number of nuts?
$$
\text { (6-8 grades) }
$$
|
15.3. Let the number of all boys be denoted by $n$. Then the last boy received $3 n$ nuts with nothing left over. The second-to-last boy received $3(n-1)$ nuts and one fifth of the remainder. Since the second-to-last boy received as many nuts as the last one, i.e., $3 n$ nuts, the one fifth of the remainder amounts to $3 n-3(n-1)=3$ nuts, and the entire remainder before the second-to-last boy took his one fifth consisted of 15 nuts. Therefore, the last boy received $15-3=12$ nuts. Then $3 n=12$, from which $n=4$. Answer: There were 4 boys in total.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19.3. Can the number of diagonals of a polygon be exactly twice the number of its sides?
$(6-8$ grades $)$
|
19.3. From one vertex of an $n$-sided polygon, $n-3$ diagonals emanate. Then the product $n(n-3)$ expresses twice the number of all diagonals, since in this counting each diagonal was counted twice. It remains to check whether the equation $0.5 n(n-3)=2 n$ has a solution in natural numbers. It is easy to see that such a solution is $n=7$. Thus, the number of diagonals of a convex heptagon is twice the number of its sides.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20.3. The collective farm placed a certain amount of money in the savings bank. If the number of hundreds is added to the number formed by the last two digits, then the result is the annual income from this amount, calculated at $2 \%$ per annum. What is the amount of the deposit placed in the savings bank?
$(7-8$ grades$)$
|
20.3. Let the number of hundreds in the deposited amount be denoted by $x$, and the number formed by the last two digits of this amount be denoted by $y$. We have the equation: $x+y=(100 x+y) \cdot 0.02$. From this, we find: $50 x=49 y$. The obtained equality allows us to conclude that $y$ is divisible by 50. Since $y$ is a two-digit number, then $y=50$. Then $x=49$. Answer: 4950.
|
4950
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23.3. We have 10 natural numbers whose sum is 1001. What is the greatest value that the greatest common divisor of these numbers can take?
$$
\text { (7-8 grades) }
$$
|
23.3. It is clear that the greatest common divisor of these ten numbers will also be a divisor of the number 1001. Let's consider the divisors of this number. We have: $1001=7 \cdot 11 \cdot 13$. The sought greatest common divisor cannot be equal to $11 \cdot 13=143$, since $143 \cdot 10>1001$. However, it can be equal to $7 \cdot 13=91$, if nine of the ten given numbers are taken to be 91, and the tenth is 182.
|
91
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28.3. On the sides $B C$ and $C D$ of the square $A B C D$, points $K$ and $M$ are chosen such that the perimeter of triangle $K M C$ is equal to twice the side length of the square $A B C D$. Find the angle $K A M$.
$$
(7-10 \text { grades })
$$
|
28.3. Rotate triangle $A M D$ around point $A$ by an angle of $90^{\circ}$ until segment $A D$ coincides with segment $A B$ (Fig. 25). Let
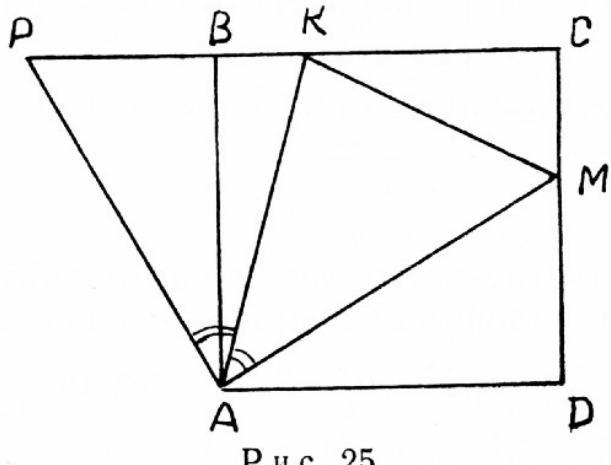
Fig. 25
point $M$ move to point $P$. We obtain triangle $A P K$, which is equal to triangle $A M K$ by the three sides: side $A K$ is common, $A P=A M, K M=P K$ (since by the condition of the problem $K M=B K+M D=$ $=B K+P B=P K$). Since angle $M A P$ is a right angle, angle $M A K$ is $45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
38.3. Find a four-digit number that is 4 times less than the number written with the same digits but in reverse order.
$$
\text { (8-10 grades) }
$$
|
38.3. It is required to find the number $\overline{a b c e}$ such that $4 \cdot \overline{a b c e}=\overline{e c b a}$. Since the product $4 \cdot \overline{a b c e}$ is even, the number $\overline{e c b a}$ is also even, i.e., the digit $a$ is even. Then it is easy to see that $a=2$ (since for $a>2$ the product $4 \cdot \overline{a b c e}$ would be a five-digit number). Moreover, since the product $4 \cdot e$ must end in $a$, i.e., in 2, then $e=8$. Thus, $4 \cdot \overline{2 b c 8}=\overline{8 c b 2}$. From this it follows that $4 \cdot \overline{b c}+3=\overline{c b}$, i.e., $40 b+4 c+3=10 c+b$ or $13 b+1=2 c$. The obtained equation for the digits $b$ and $c$ has a unique solution: $b=1, c=7$. Answer: $\overline{a b c e}=2178$.
|
2178
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Using arithmetic operation signs, write the largest natural number with two twos.
|
$\triangle$ Let's write down all natural numbers using two twos. There are not many of them:
$$
2+2=4, \quad 2 \cdot 2=4, \quad 2^{2}=4,22
$$
The largest of these is the number 22. Interestingly, for its representation, no arithmetic operation symbols were needed at all.
Answer: 22.
|
22
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. What is the smallest natural number by which the number 7 must be multiplied to obtain a number that consists only of nines?
|
$\triangle$ Let's find this number using division
$$
\text { 9999... } 7
$$
However, the quotient here is unknown, and the number of nines in the dividend is also unknown. We will perform the division by 7, appending nines to the dividend until the division is performed without a remainder for the first time. We get:
$$
\begin{array}{ll}
\frac{999999}{29} & \frac{7}{142857} \\
\frac{\frac{19}{\frac{59}{39}}}{\frac{39}{\frac{49}{0}}} & \\
&
\end{array}
$$
Answer: 142857.
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
114*. What is the maximum number of natural numbers that can be written in a row so that the sum of any three consecutive numbers is even, and the sum of any four consecutive numbers is odd?
|
Let's denote the consecutive natural numbers of the row as $a_{1}, a_{2}, a_{3}$, and so on.
By the condition, the sums
$$
a_{1}+a_{2}+a_{3}, \quad a_{2}+a_{3}+a_{4}, \quad a_{3}+a_{4}+a_{5}, \quad a_{4}+a_{5}+a_{6}
$$
and others are even. By subtracting each sum, starting from the second, from the previous one, we get that the differences
$$
a_{4}-a_{1}, \quad a_{5}-a_{2}, \quad a_{6}-a_{3}, \ldots
$$
are even, and therefore, the pairs of numbers $a_{1}$ and $a_{4}, a_{2}$ and $a_{5}, a_{3}$ and $a_{6}$, etc., have the same parity.
Let's write down the odd sums consisting of four consecutive numbers:
$$
\begin{gathered}
a_{1}+a_{2}+a_{3}+a_{4}=\left(a_{1}+a_{2}+a_{3}\right)+a_{4} \\
a_{2}+a_{3}+a_{4}+a_{5}=\left(a_{2}+a_{3}+a_{4}\right)+a_{5} \\
a_{3}+a_{4}+a_{5}+a_{6}=\left(a_{3}+a_{4}+a_{5}\right)+a_{6}, \ldots
\end{gathered}
$$
From this, it follows that the numbers $a_{4}, a_{5}, a_{6}$, etc., are odd. But then the sum $a_{4}+a_{5}+a_{6}$ is odd, which contradicts the condition.
This contradiction arises every time the number of numbers is not less than 6. Let's try to take 5 numbers.
Reasoning similarly, we establish that the numbers $a_{4}$ and $a_{5}$ are odd, and therefore, by the previous, the numbers $a_{1}$ and $a_{2}$ are also odd. Then, since the sum $a_{1}+a_{2}+a_{3}$ is even, the number $a_{3}$ is even.
Let's do one more check and verify that if we take five numbers
$$
a_{1}, a_{2}, a_{3}, a_{4}, a_{5}
$$
where the number $a_{3}$ is even, and the others are odd, then each of the sums
$$
a_{1}+a_{2}+a_{3}, \quad a_{2}+a_{3}+a_{4}, \quad a_{3}+a_{4}+a_{5}
$$
is even, and each of the sums
$$
a_{1}+a_{2}+a_{3}+a_{4}, \quad a_{2}+a_{3}+a_{4}+a_{5}
$$
is odd.
Answer: 5
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
121. Find all values of the digit $a$, if the number $\overline{875 a}$ is divisible by 6.
|
$\triangle$ Since this number is divisible by 6, it is divisible by 2 and 3, and vice versa.
Let's apply the divisibility rule for 3. For this, we will find the sum of the digits of the number:
$$
8+7+5+a=20+a
$$
From the divisibility of $(20+a): 3$ it follows that the digit $a$ is 1, 4, or 7. But according to the divisibility rule for 2, this digit must be even, so only $a=4$ fits.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
141. Find all values of the digit $a$, if the number $\overline{a 719}$ is divisible by 11.
|
$\triangle$ Divisibility of this number by 11 is equivalent to the divisibility by 11 of the sum $a-7+1-9=$ $=a-15$. The difference $a-15$ is divisible by 11 only when $a=4$.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
146. From a natural number, the sum of its digits was subtracted, and then one digit was erased from the resulting difference. The sum of the remaining digits of the difference is 131. Which digit was erased?
|
$\triangle$ The difference between a natural number and the sum of its digits is divisible by 9 (see problem 130). Let the erased digit be denoted by $x$. Then the sum $131+x$ is divisible by 9, from which $x=4$.
Answer: 4
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
152. Find the smallest natural number that is written with identical digits and is divisible by 18.
|
$\triangle$ Let the desired number be denoted as
$$
\overline{a a a \ldots a} \text { ( } n \text { digits). }
$$
Since it is divisible by 18, and therefore by 2, $a$ must be an even digit.
Applying the divisibility rule for 9:
$$
(a+a+a+\ldots+a): 9, \quad \text { na:9 }
$$
Since $a$ is an even digit, the number is even.
1) Let $a=18$.
From this, the minimum possible value of $n$ is 3, from which $a=6$.
2) Now let $na$ be 36, or 54, or 72, etc.
If we take $n=3$ here, then $a$ is respectively 12, 18, 24, etc., which is impossible. Taking values of $n$ greater than 3 makes no sense.
Therefore, the desired number is the one obtained in the first case. Answer: 666.
|
666
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
158*. Using the digits from 1 to 9 once each, form the smallest nine-digit number that is divisible by 11.
|
$\triangle$ The sum of all digits of the desired number is equal to
$$
1+2+3+\ldots+9=45
$$
Let the sum of the digits in odd positions be denoted by $S_{1}$, and the sum of the digits in even positions by $S_{2}$. Then $S_{1}+S_{2}=45$.
The difference $S_{1}-S_{2}$, according to the divisibility rule by 11, is divisible by 11. Moreover, it is odd, since the sum $S_{1}+S_{2}$ is odd, and the sum and difference of two integers have the same parity. Therefore, this difference can take the values 11, $-11, 33$, and -33. Let's consider four cases.
1) Suppose $S_{1}-S_{2}=11$.
From the system of equations
$$
\left\{\begin{array}{l}
S_{1}+S_{2}=45 \\
S_{1}-S_{2}=11
\end{array}\right.
$$
we find that $S_{1}=28, S_{2}=17$.
2) Suppose $S_{1}-S_{2}=-11$.
Then
$$
\left\{\begin{array}{l}
S_{1}+S_{2}=45 \\
S_{1}-S_{2}=-11
\end{array}\right.
$$
from which $S_{1}=17, S_{2}=28$
3) Suppose $S_{1}-S_{2}=33$.
From the system of equations
$$
\left\{\begin{array}{l}
S_{1}+S_{2}=45 \\
S_{1}-S_{2}=33
\end{array}\right.
$$
we get that $S_{1}=39, S_{2}=6$. However, the equality $S_{2}=6$ is impossible, since if this sum consists even of 4 (and not 5) addends $a, b, c$, and $d$, then
$$
S_{2}=a+b+c+d \geq 1+2+3+4>6
$$
4) Suppose $S_{1}-S_{2}=-33$.
Similarly, we establish that this case is also impossible. Thus, for $S_{1}$ and $S_{2}$, only the values 28 and 17 (in some order) remain.
Let's try to start the desired nine-digit number with: 12345; since we need the smallest number divisible by 11. The four remaining digits we will denote in sequential order by $k, l, m$, and $n$. We get the number $12345 \mathrm{klmn}$.
If the sum $1+3+5=9$ is supplemented to 28 with the digits $l$ and $n$, then $l+n=28-9=19$, which is impossible.
If the sum $2+4=6$ is supplemented to 28 with the digits $k$ and $m$, then $k+m=22$, which is also impossible.
Therefore, it is impossible to start the desired number with the five-digit number 12345, since then neither the sum $S_{1}$ nor the sum $S_{2}$ can be equal to 28.
Let's try to start the desired number with the four-digit number 1234, and denote the number itself as $\overline{1234 a b c d e}$. Since $1+3=4, 2+4=6$, then
$$
a+c+e=28-4=24, \quad b+d=17-6=11
$$
or
$$
a+c+e=17-4=13, \quad b+d=28-6=22
$$
The second option is immediately ruled out. Only the first remains:
$$
\left\{\begin{array}{l}
a+c+e=24 \\
b+d=11
\end{array}\right.
$$
In this case, $a, b, c, d$, and $e$ take different values from the set $\{5 ; 6 ; 7 ; 8 ; 9\}$.
The digit $a$ should be as small as possible. But the value $a=5$, as we have seen, is impossible; the value $a=6$ is also impossible, since then $c+e=18$, from which the digits $c$ and $e$ are equal: $c=e=9$. Let's try $a=7$. In this case:
$$
\left\{\begin{array}{l}
c+e=17 \\
b+d=11
\end{array}\right.
$$
From the first equation $c=8, e=9$ (but not $c=9, e=8$), and from the second $b=5, d=6$. Answer: 123475869.
|
123475869
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
274. How many natural numbers divisible by 3 or 7 are there among the natural numbers from 1 to 500?
|
$\triangle$ First, let's calculate how many natural numbers from 1 to 500 are divisible by 3. Let's list all such numbers:
$$
3, \quad 6=3 \cdot 2, \quad 9=3 \cdot 3, \quad 12=3 \cdot 4, \ldots, \quad 498=3 \cdot 166
$$
From this, we can see that the number of such numbers is 166.
Now let's find how many natural numbers within the same range are divisible by 7. Let's list them:
$$
7, \quad 14=7 \cdot 2, \quad 21=7 \cdot 3, \ldots, \quad 497=7 \cdot 71
$$
Thus, the number of these numbers is 71.
But this is not all: among these numbers, there are some that are divisible by both 3 and 7, which means they are also divisible by 21. Since these numbers are included in both the 166 numbers divisible by 3 and the 71 numbers divisible by 7, they are counted twice in \(166+71=237\) numbers. Let's count how many there are. Let's list the numbers from 1 to 500 that are divisible by 21:
$$
21, \quad 42=21 \cdot 2, \quad 63=21 \cdot 3, \ldots, \quad 481=21 \cdot 23
$$
Thus, there are 23 such numbers. Therefore, the total number of numbers divisible by 3 or 7 is \(237-23=214\).
Answer: 214.
When solving this problem, the principle of inclusion and exclusion for the case of two sets can be applied:
$$
n(A \cup B)=n(A)+n(B)-n(A \cap B)
$$
(see [18], § 4, formula (1)). Let's also recall the similar formula for the case of three sets:
$$
\begin{gathered}
n(A \cup B \cup C)= \\
=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C)+n(A \cap B \cap C) .
\end{gathered}
$$
|
214
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
381. The numbers $p$ and $p+15$ are prime. Find all such $p$.
|
$\triangle$ When $p=2$, we get that the number $p+15=17$ is prime.
Let $p>2$. Then $p$ is odd. Consequently, the number $p+15$ is even. Hence, this number is composite. Therefore, no prime $p>2$ works.
Answer: 2.
$382^{\circ}$. Prove that the numbers $p, p+2$, and $p+4$ are all prime only in the case when they form the triplet $3,5,7$.
$\triangle$ Consider several cases depending on $p$.
When $p=2$, the number $p+2=4$ is composite, so the value $p=2$ is ruled out.
When $p=3$, we get the triplet $3,5,7$, mentioned in the problem statement.
When $p=5$, the number $p+2=7$ is prime, but the number $p+4=9$ is composite, so $p=5$ must be discarded.
When $p=7$, the number $p+2=9$ is composite.
When $p=11$, the number $p+4=15$ is also composite.
It seems that only $p=3$ works. Let's prove it.
It is not hard to notice that the values $p=5, p=7$, and $p=11$ did not work because either $p+2$ or $p+4$ is divisible by 3. Let's confirm that this will always be the case for a prime $p>3$.
A prime number greater than 3 does not divide by 3 and, therefore, when divided by 3, can only leave a remainder of 1 or 2. Let's consider both cases.
1) Suppose $p$ when divided by 3 leaves a remainder of $1: p=3k+1(k \in \mathbb{N})$. Then the number
$$
p+2=(3k+1)+2=3k+3
$$
is divisible by 3, and the quotient of this division is greater than 1. Thus, the number $p+2$ is composite.
2) Suppose $p=3k+2(k \in \mathbb{N})$. Then the number
$$
p+4=(3k+2)+4=3k+6
$$
is composite.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
425*. A two-digit number was divided by a number written with the same digits but in reverse order, and the quotient and remainder were equal. Find all such two-digit numbers.
|
$\triangle$ Let the desired number be denoted by $\overline{x y}$. Then
$$
10 x+y=(10 y+x) r+r, \quad 10 x+y=(10 y+x+1) r
$$
where $r-$ is the remainder (and the quotient at the same time). Obviously, $1 \leqslant r < 10$. But this is impossible.
Answer: 52.
|
52
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
427. If the numbers 826 and 4373 are divided by the same natural number, the remainders will be 7 and 8, respectively. Find all values of the divisor.
|
$\triangle$ Let's write the corresponding equalities:
$$
826=b q_{1}+7, \quad 4373=b q_{2}+8
$$
where $b-$ is the unknown divisor, $q_{1}$ and $q_{2}$ are the incomplete quotients. Then
$$
b q_{1}=819, \quad b q_{2}=4365
$$
Let's factorize the numbers 819 and 4365 into prime factors:
$$
819=3^{2} \cdot 7 \cdot 13, \quad 4365=3^{2} \cdot 5 \cdot 97
$$
Therefore, the common divisors of the numbers 819 and 4365 are the numbers 1, 3, and 9. But common divisors equal to 1 and 3 are impossible, as the remainder must be less than the divisor. The only remaining number is 9.
Answer: 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
431. When dividing a natural number $a$ by 2, the remainder is 1, and when dividing by 3, the remainder is 2. What remainder will be obtained when dividing $a$ by 6?
|
$\triangle$ Let
$$
a=6 q+r
$$
where the remainder $r$ satisfies the inequality $0 \leqslant r \leqslant 5$. We will consider all possible values of $r$.
The case $r=0$ is impossible, otherwise the number $a$ would be divisible by 2 and 3.
The case $r=1$ is also impossible, because then $a$ when divided by 3 would leave a remainder of 1, not 2.
For similar reasons, the cases $r=2, r=3$, and $r=4$ are also ruled out.
The case $r=5$ is possible, for example, when $a=5$ or $a=11$.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
438*. What remainder does $46^{925}$ give when divided by $21?$
|
$\triangle$ The solution method we applied in the last problems is too cumbersome here due to the large base of the exponent and the large divisor. Let's try to modify it.
Divide 46 by 21 with a remainder and transform the exponent:
$$
46^{925}=(21 \cdot 2+4)(21 \cdot 2+4) \ldots(21 \cdot 2+4)
$$
If we multiply 925 identical sums together, then all the terms in the resulting sum are divisible by 21, except for the term $4^{925}$. Therefore, the remainder of the division of the power $46^{925}$ by 21 coincides with the remainder of the division of the power $4^{925}$ by 21.
Let's use the fact that
$$
4^{3}=64=21 \cdot 3+1
$$
We get:
$4^{925}=4 \cdot 4^{924}=4 \cdot\left(4^{3}\right)^{308}=4 \cdot 64^{308}=4 \cdot(21 \cdot 3+1)^{308}=4 \cdot(21 k+1)=4 \cdot 21 k+4$.
Therefore, the desired remainder is 4.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
447. Find the greatest common divisor of the numbers 111111 and 111111111.
|
$\triangle$ Obviously, each of the given numbers is divisible by 111, i.e., the number 111 is their common divisor. But will 111 be their greatest common divisor?
To answer this question, we will divide the given numbers by 111 and determine whether the resulting quotients are coprime numbers. We will have:
$$
111111=111 \cdot 1001, \quad 1111111111=111 \cdot 1001001
$$
Divide 1001001 by 1001 with a remainder:
$$
1001001=1001 \cdot 1000+1
$$
From this, it is clear that the numbers 1001001 and 1001 are coprime: if they had a greatest common divisor $d>1$, then from the last equation it would follow that the remainder, which is 1, is also divisible by $d$, which is impossible (a smaller natural number cannot be divisible by a larger one). Therefore, the greatest common divisor of the given numbers is 111.
Answer: 111.
|
111
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
449. Find the greatest common divisor of all nine-digit numbers, in the representation of which each of the digits $1,2,3, \ldots, 9$ appears exactly once.
|
$\triangle$ Let's denote this greatest common divisor by $d$.
From all nine-digit numbers of the specified form, we will take only two - 123456798 and 123456789.
Since these numbers are divisible by $d$, their difference, which is 9, is also divisible by $d$: $9: d$. Therefore, $d=1, d=3$ or $d=9$.
Which of these cases gives the answer? To determine the truth, we will use the divisibility rules for 3 and 9 to check if each of the nine-digit numbers is divisible by 3 or 9. For this purpose, we will find the sum of the digits of any of them:
$$
1+2+3+\ldots+9=45
$$
Since 45 is divisible by 9, each of the nine-digit numbers is divisible by 9. From the previous, it follows that 9 is their greatest divisor.
Answer: 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
459. Find all values of the greatest common divisor of the numbers $8 a+3$ and $5 a+2$, where $a$ is a natural number.
|
$\triangle$ Let's denote the greatest common divisor of these numbers by $d$. Then
$$
(8 a+3): d, \quad(5 a+2): d
$$
Multiply the sum $8 a+3$ by 5, and the sum $5 a+2$ by 8. We get:
$$
(40 a+15): d, \quad(40 a+16): d
$$
But two consecutive natural numbers $40 a+15$ and $40 a+16$ are coprime (see the statement of problem 454), therefore, $d=1$.
Answer: 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
472. For which number and for which natural $a$ are the fractions reducible:
a) $\frac{a^{4}+a^{3}-a^{2}+a+1}{a^{2}-1}$;
b) $\frac{a^{4}+6 a^{3}+15 a^{2}+18 a+8}{a^{4}+6 a^{3}+13 a^{2}+12 a+3}$?
473 $3^{\circ}$. Let $a$ and $b$ be natural numbers, where $a > b$, and the number $a$ is divided by the number $b$ with a remainder:
$$
a = bq + r \quad (0 < r < b).
$$
Prove that
$$
\text{GCD}(a, b) = \text{GCD}(b, r).
$$
|
$\triangle$ Let's introduce the notation:
$$
\text { GCD }(a, b)=d_{1}, \quad \text { GCD }(b, r)=d_{2} .
$$
Since the numbers $a$ and $b$ are divisible by $d_{1}$, from the initial equation we get that the remainder $r$ is also divisible by $d_{1}$. Therefore, $d_{1}$ is a common divisor of the numbers $b$ and $r$. But $d_{2}$ is the greatest common divisor of the same numbers; hence, $d_{2} \geqslant d_{1}$.
Since the numbers $b$ and $r$ are divisible by $d_{2}$, from the initial equation $a$ is also divisible by $d_{2}$. Therefore, $d_{2}$ is a common divisor of the numbers $a$ and $b$. But $d_{1}$ is the greatest common divisor of these numbers, so $d_{1} \geqslant d_{2}$.
From the inequalities $d_{2} \geqslant d_{1}$ and $d_{1} \geqslant d_{2}$, it follows that $d_{1}=d_{2}$.
The statement of problem 473 is the basis for the following method of finding the greatest common divisor of two natural numbers.
474 $4^{\circ}$. Let $a$ and $b$ be natural numbers, $a>b$. Divide $a$ by $b$ with a remainder; divide the number $b$ by the obtained remainder $r_{1}$ with a remainder; divide the number $r_{1}$ by the new remainder $r_{2}$ with a remainder; divide $r_{2}$ by the new remainder $r_{3}$ with a remainder, and so on. Prove that then the greatest common divisor of the numbers $a$ and $b$ is equal to the last non-zero remainder.
$\triangle$ Write down the equations corresponding to the conditions of the problem:
$$
\begin{aligned}
& a=b q_{1}+r_{1} \quad\left(r_{1}<b\right) \\
& b=r_{1} q_{2}+r_{2} \quad\left(r_{2}<r_{1}\right) \\
& r_{1}=r_{2} q_{3}+r_{3} \quad\left(r_{3}<r_{2}\right) \\
& \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\
& r_{n-2}=r_{n-1} q_{n}+r_{n} \quad\left(r_{n}<r_{n-1}\right) \\
& r_{n-1}=r_{n} q_{n+1} .
\end{aligned}
$$
Why do we eventually come to a remainder equal to zero? Because the remainders form a decreasing sequence of non-negative integers
$$
r_{1}, r_{2}, r_{3}, \ldots, r_{n}
$$
and therefore, this process must end.
Now we get, using the statement of problem 473:
$$
\text { GCD }(a, b)=\text { GCD }\left(b, r_{1}\right)=\text { GCD }\left(r_{1}, r_{2}\right)=\ldots=\text { GCD }\left(r_{n-1}, r_{n}\right)=r_{n} .
$$
(The equality GCD $\left(r_{n-1}, r_{n}\right)=r_{n}$ is explained by the fact that, as seen from the last initial equation, the number $r_{n-1}$ is divisible by the number $r_{n}$.)
The proven statement gives a method for finding the greatest common divisor of two numbers. It is called the Euclidean algorithm, which Euclid described in his work "Elements." The Euclidean algorithm is used in cases where natural numbers are quite large; if they are small, it is better to use the usual method - by factoring the numbers into prime factors.
Using the Euclidean algorithm, let's find, for example, the greatest common divisor of the numbers 9240 and 8568. We get:
$$
\begin{aligned}
& 9240=8568 \cdot 1+672 \\
& 8568=672 \cdot 12+504 \\
& 672=504 \cdot 1+168 \\
& 504=168 \cdot 3
\end{aligned}
$$
Since the last non-zero remainder here is 168, the greatest common divisor of the numbers 9240 and 8568 is 168.
|
168
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
477*. What is the greatest common divisor of all numbers $7^{n+2}+8^{2 n+1}(n \in N)$?
|
$\triangle$ Let's denote the greatest common divisor of all such numbers by $d$. Replacing $n$ with $n+1$ in the given sum, we get the sum $7^{n+3} + 8^{2n+3}$, which must also be divisible by $d$. Additionally, let's multiply the sum $7^{n+2} + 8^{2n+1}$ by 7:
$$
\left(7^{n+2} + 8^{2n+1}\right) \cdot 7 = 7^{n+3} + 7 \cdot 8^{2n+1}
$$
Now we get:
$$
\begin{aligned}
& \left(7^{n+3} + 8^{2n+3}\right) : d \\
& \frac{-\left(7^{n+3} + 7 \cdot 8^{2n+1}\right) : d}{8^{2n+1} \cdot (64 - 7) : d}
\end{aligned}
$$
Since $d$ is odd, $57 : d$, so $d$ can take the values $1, 3, 19$, and 57.
Do all the found values of $d$ work? Let's set $n = 1$ in the sum $7^{n+2} + 8^{2n+1}$:
$$
7^{3} + 8^{3} = 343 + 512 = 855
$$
and 855 is divisible by 57 (check this!). Moreover, from the solution process, it is clear that if the sum $7^{n+2} + 8^{2n+1}$ is divisible by 57 for some natural $n$, then it is also divisible by 57 when this $n$ is replaced by $n+1$. Therefore, the given sum is divisible by 57 for any natural $n$.
(Actually, the proof here was conducted using mathematical induction - see, for example, [18], § 14, point 14.7.)
Answer: 57
|
57
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
479*. For what least natural $n$ are each of the fractions
irreducible
$$
\frac{5}{n+6}, \quad \frac{6}{n+7}, \frac{7}{n+8}, \ldots, \quad \frac{24}{n+25}
$$
|
$\triangle$ Transform the given fractions as follows:
$$
\frac{5}{n+6}=\frac{5}{(n+1)+5}, \quad \frac{6}{n+7}=\frac{6}{(n+1)+6}, \ldots, \frac{24}{n+25}=\frac{24}{(n+1)+24}
$$
From this, it is clear that each of these fractions is irreducible if and only if the number $n+1$ is coprime with each of the numbers $5,6,7, \ldots, 24$. Then $n+1$ is also coprime with the numbers 25 (otherwise, the fractions with numerators $5,10,15,20$ are reducible by 5), 26, 27, and 28. Thus, none of the values of $n+1$ from 2 to 28 are suitable. However, the value $n+1=29$ is suitable, as the number 29 is coprime with each of the natural numbers from 5 to 24. Therefore, the smallest value of $n$ is 28.
Answer: 28.
|
28
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
485. A father and son were walking one behind the other on a snow-covered road. The father's step length is $-80 \mathrm{~cm}$, the son's $-60 \mathrm{~cm}$. Their steps coincided 601 times, including at the beginning and the end of the journey. What distance did they cover?
|
$\triangle$ Let's find the distance that the father and son walked from one coincidence of steps to the next. It is equal to the least common multiple of the numbers 80 and 60, i.e., $240 \mathrm{~cm}=2.4$ m. Therefore, the entire distance they walked is
$$
600 \cdot 2.4 \mathrm{M}=1440 \mathrm{~m}=1 \mathrm{Km} 440 \mathrm{M}
$$
Answer: 1 km 440 m.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
487. A customer wanted to buy all the eggs the seller had and asked how many eggs she had. She replied that she didn't remember, but she knew that if the eggs were divided into groups of $2, 3, 4, 5$ or 6, there would always be one egg left over. What is the smallest number of eggs the seller could have had?
|
$\triangle$ Let's temporarily set aside one egg. The number of remaining eggs is equal to the least common multiple of the numbers $2,3,4,5$ and 6, i.e., 60. We need to add one more egg to this number.
Answer: 61.
|
61
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
526. A six-digit number ends with the digit 7. If this digit is moved to the beginning of the number, the number increases by 5 times. What is this number?
|
The problem can be solved in two ways.
1) We will solve it as a problem of restoring the record.
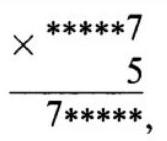
where the five-digit numbers denoted by asterisks in the first multiplier and in the product are the same. We sequentially obtain:
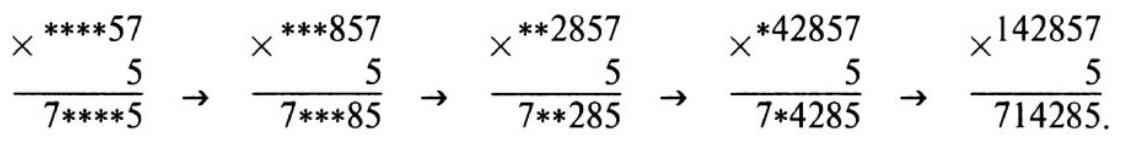
The original number turned out to be 142857.
2) Let the desired number be $10 x+7$, where $x$ is the number of tens in the number. We get the equation
$$
(10 x+7) 5=7 \cdot 10^{5}+x
$$
From this, we find $x$, and then calculate $10 x+7$:
$$
\begin{gathered}
50 x+35=700000+x, \quad 49 x=699965 \\
x=14285, \quad 10 x+7=142857
\end{gathered}
$$
Answer: 142857.
The number 142857, which resulted in the answer, often appears when solving similar problems. From it, by moving the last digit to the first place, we sequentially find five such six-digit numbers:
$$
714285, \quad 571428, \quad 857142, \quad 285714, \quad 428571.
$$
The factorization of the number 142857 into prime factors is as follows:
$$
142857=3^{3} \cdot 11 \cdot 13 \cdot 37
$$
Therefore, this number is divisible by 27. But all the above six-digit numbers are also divisible by 27, and some are divisible by 81. The number 142857 is divisible by 11, 13, and 37. But all the other six-digit numbers are also divisible by 11, 13, and 37! (Check or find the statement of problem 256 from § 8.) In addition, if the number 142857 is multiplied by the numbers 2, $3,4,5$, and 6, then the following numbers are obtained:
$$
285714, \quad 428571, \quad 571428, \quad 714285, \quad 857142
$$
(check!) - the same five numbers, only recorded in a different order. Finally,
$$
142857 \cdot 7=999999
$$
Therefore, 142857 is an unusual number, worthy of attention. It will meet us again.
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
532. A six-digit number starts with the digit 2. If this digit is moved to the last place, the number increases by 3 times. What is this number?
|
$\triangle$ Let's solve the problem in two ways.
1) Restore the record:
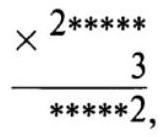
where the five-digit numbers denoted by asterisks in the first multiplier and in the product coincide. We sequentially obtain:
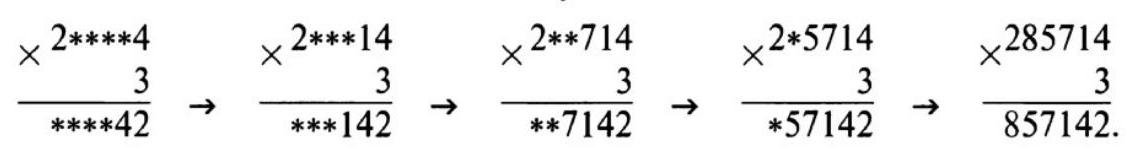
(Here, we first find the digit 4 in the first multiplier and then place it in the corresponding position in the product; we first find the digit 1 in the first multiplier and then place it in the product, and so on.)
We get the number 285714.
2) Let the desired number be $200000 + x$, where $x$ is the number formed by the last five digits. Then
$$
(200000 + x) \cdot 3 = 10x + 2
$$
From this,
$$
x = 85714, \quad 200000 + x = 285714
$$
Answer: 285714.
|
285714
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
543. Does there exist a six-digit number that increases by 6 times when the first three digits, without changing their order, are moved to the end of the number?
|
$\triangle$ Let the desired number be denoted as $\overline{a b c d e f}$. Then
$$
\overline{a b c d e f} \cdot 6=\overline{d e f a b c}
$$
Let
$$
\overline{a b c}=x, \quad \overline{d e f}=y
$$
The equation becomes
$$
(1000 x+y) \cdot 6=1000 y+x
$$
Simplify it:
$$
6000 x+6 y=1000 y+x, \quad 5999 x=994 y, \quad 857 x=142 y
$$
Since the numbers 857 and 142 are coprime, from the last equation we have $x=142, y=857$.
Therefore, the six-digit number is
$$
1000 x+y=142857
$$
Answer: It exists and is unique - 142857.
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
552. Find all four-digit numbers that are 9 times greater than their reversals.
|
$\triangle$ Let the desired number be denoted as $\overline{a b c d}$. Then
$$
\overline{a b c d}=9 \cdot \overline{d c b a}
$$
Two digits, $d$ and $a$, can be found immediately. Since the product $9 \cdot \overline{d c b a}$ is a four-digit number, the digit $d$ can only be 1. Since the product $9a$ ends with the digit $d=1$ (consider the last digit of each four-digit number), then $a=9$.
The number $\overline{a b c d}=\overline{9 b c 1}$ is divisible by 9, so the sum of its digits is divisible by 9:
$$
(10+b+c): 9
$$
Thus, $b+c=8$ or $b+c=17$.
Now, let's use the statement from problem 550, considering that the number of digits in $\overline{a b c d}$ is even: the sum
$$
\overline{a b c d}+\overline{d c b a}
$$
must be divisible by 11. Transform it:
$$
\overline{a b c d}+\overline{d c b a}=9 \cdot \overline{d c b a}+\overline{d c b a}=10 \cdot \overline{d c b a}=10 \cdot \overline{1 c b 9}
$$
Then the number $\overline{1 c b 9}$ is divisible by 11. By the divisibility rule for 11, the sum
$$
1+b-c-9=b-c-8
$$
is divisible by 11. Therefore, $b-c=8$ or $b-c=-3$.
Compare the values of $b+c$ with the values of $b-c$. Since the sum and difference of two integers have the same parity (see the statement of problem 93 in § 4), out of the four possible cases here, it is sufficient to consider two.
1) The system of equations
$$
\left\{\begin{array}{l}
b+c=8 \\
b-c=8
\end{array}\right.
$$
has the solution $b=8, c=0$.
2) The system of equations
$$
\left\{\begin{array}{l}
b+c=17 \\
b-c=-3
\end{array}\right.
$$
has the solution $b=7, c=10$, but it is not valid.
Answer: 9801.
|
9801
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
560. How many zeros are at the end of the product of all natural numbers from 1 to 60?
|
$\triangle$ Since zeros in the product of natural numbers are formed by multiplying twos by fives, it is desirable to know how many twos and fives are in the prime factorization of the given product. However, since there are more twos than fives in this factorization, it is sufficient to count the number of fives.
First of all, fives are present in the prime factorizations of the numbers
$$
5,10,15,20,25,30,35,40,45,50,55,60 .
$$
There are 12 such numbers.
In addition, there is one extra five in the numbers 25 and 50. In total, this results in 14 fives. Therefore, the given product ends with 14 zeros. Answer: 14
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
582. The number $n^{2}+2 n(n \in N)$ ends with the digit 4. Find all possible values of its second-to-last digit.
|
$\triangle$ Add 1 to both sides of the equality
$$
n^{2}+2 n=10 a+4
$$
where $a-$ is the number of tens in the number $n^{2}+2 n$, to get:
$$
n^{2}+2 n+1=10 a+5, \quad(n+1)^{2}=10 a+5
$$
From this, it is clear that the number $n+1$ ends in 5, and therefore, its square ends in 25 (see the statement of problem 563). Then the number $a$ ends in 2, i.e., the second-to-last digit of the original number $n^{2}+2 n$ is 2.
Answer: 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
585. Find the last non-zero digit of the product of all natural numbers from 1 to 40.
|
$\triangle$ First, let's find the last non-zero digit of the product $1 \cdot 2 \cdot 3 \cdot \ldots \cdot 10$. For this, we will remove the factors 10, 2, and 5 from the number. The remaining product is
$$
3 \cdot 4 \cdot 6 \cdot 7 \cdot 8 \cdot 9
$$
which, as is not difficult to calculate, ends with the digit 8.
For the same reason, each of the products
$$
11 \cdot 12 \cdot 13 \cdot \ldots \cdot 20, \quad 21 \cdot 22 \cdot 23 \cdot \ldots \cdot 30, \quad 31 \cdot 32 \cdot 33 \cdot \ldots \cdot 40
$$
has the last digit, different from zero, equal to 8. Then the last non-zero digit of the entire given product coincides with the last digit of the number
$$
8 \cdot 8 \cdot 8 \cdot 8=8^{4}=2^{12}=4096
$$
i.e., it is equal to 6.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
590. The last two digits of the decimal representation of the square of some natural number are equal and different from zero. What are these digits? Find all solutions.
|
$\triangle$ The square of a natural number can end in the digits $0,1,4,5,6$ or 9. The digit 0 is not suitable in this case. Then the square can end in
$$
11,44,55,66,99
$$
However, cases where the square ends in 11, 55, or 99 are impossible, as if the last digit of the square of a natural number is odd, then the second-to-last digit must be even (see supporting problem 566). The case where the square ends in 66 is also ruled out, as based on the divisibility rules for 2 and 4, a natural number that ends in 66 is divisible by 2 but not by 4.
The remaining option is 44. The fact that the square of a natural number can end in 44 is demonstrated by the example $12^{2}=144$.
Answer: 4 and 4.
|
44
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
595*. Does there exist a three-digit number whose cube ends in three sevens?
|
Let's denote this three-digit number as $x$. Then
$$
x^{3}=1000 a+777
$$
where $a$ is the number of thousands in $x^{3}$.
Since $x^{3}$ ends with the digit 7, the number $x$ ends with the digit 3: $x=10 k+3$, and the number $k$ is two-digit. We obtain:
$$
\begin{gathered}
(10 k+3)^{3}=1000 a+777, \quad 1000 k^{3}+900 k^{2}+270 k+27=1000 a+777 \\
100 k^{3}+90 k^{2}+27 k=100 a+75
\end{gathered}
$$
From this, it is clear that the number $k$ is divisible by 5.
Since then, in the left part of the last equation, the terms $100 k^{3}$ and $90 k^{2}$ are divisible by 25, and the right part of the equation is also divisible by 25, $k$ is divisible by 25: $k=25 b$, where $b$ is a digit not exceeding 3. We obtain:
$$
x=10 k+3=250 b+3
$$
Let's consider three possibilities.
1) Suppose $b=1$. Then:
$$
x=253, \quad x^{3}=253^{3}=16194277
$$
This case does not fit, as the number $x^{3}$ ends with two, not three sevens.
2) Suppose $b=2$. Therefore,
$$
x=503, \quad x^{3}=503^{3}=117263527
$$
This case also does not fit.
3) Suppose $b=3$. We get:
$$
x=753, \quad x^{3}=753^{3}=426957777
$$
This variant satisfies the condition of the problem: the number $x^{3}$ ends not with three, but with four sevens.
Answer: It exists and is unique - 753.
|
753
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
620. Find the smallest natural number that, when multiplied by 2, becomes a perfect square, and when multiplied by 3, becomes a perfect cube.
|
$\triangle$ The desired number $x$ is divisible by 2 or 3. Since it is the smallest of all natural numbers with the given properties, its prime factorization consists only of twos and threes:
$$
x=2^{k} \cdot 3^{l} \quad(k \in N, l \in N)
$$
After multiplying the number $x$ by 2, the result is a perfect square, and after multiplying by 3, the result is a perfect cube, so
$$
2 x=2^{k+1} \cdot 3^{\prime}=a^{2}, \quad 3 x=2^{k} \cdot 3^{\prime+1}=b^{2}
$$
where $a$ and $b$ are natural numbers. Then
$$
\begin{aligned}
& (k+1): 2, \quad l: 2 \\
& k: 3, \quad(l+1): 3
\end{aligned}
$$
We need to find the smallest $k$ and $l$ that satisfy these divisibility conditions: $k=3, l=2$. Therefore, $x=2^{3} \cdot 3^{2}=72$.
Answer: 72.
|
72
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
629. Prove that the number
$$
1998^{2}+1998^{2} \cdot 1999^{2}+1999^{2}
$$
is a perfect square.
|
$\triangle$ Let's replace 1998 with $a$ and transform the resulting expression:
$$
\begin{gathered}
a^{2}+a^{2}(a+1)^{2}+(a+1)^{2}=a^{2}+a^{4}+2 a^{3}+a^{2}+a^{2}+2 a+1= \\
=a^{4}+2 a^{3}+3 a^{2}+2 a+1=\left(a^{2}+a+1\right)^{2}
\end{gathered}
$$
Therefore, the given number is the square of the number $1998^{2}+1998+1=3994003$.
|
3994003
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
635. What exact square is equal to the product of four consecutive odd numbers?
|
Let's denote the smallest of the odd numbers by $n$. Then
$$
n(n+2)(n+4)(n+6)=a^{2}
$$
where $a$ is an integer, and also odd. We transform the left side of this equation by multiplying the first factor by the fourth, and the second by the third:
$$
\left(n^{2}+6 n\right)\left(n^{2}+6 n+8\right)=a^{2}, \quad\left(n^{2}+6 n\right)^{2}+8\left(n^{2}+6 n\right)=a^{2}
$$
We complete the left side of the last equation to a perfect square. For this, we add 16 to both sides of the equation:
$$
\begin{gathered}
\left(n^{2}+6 n\right)^{2}+8\left(n^{2}+6 n\right)+16=a^{2}+16, \quad(n+6 n+4)^{2}=a^{2}+16 \\
\left(n^{2}+6 n+4\right)^{2}-a^{2}=16
\end{gathered}
$$
When do two perfect squares differ by 16? To answer this question, we list the sequence of perfect squares, starting from 0, until the difference between even consecutive squares becomes greater than 16:
$$
0 ; 1 ; 4 ; 9 ; 16 ; 25 ; 36 ; 49 ; 64 ; 81
$$
From this, we see that the difference between two perfect squares equals 16 in only two cases:
$$
16=16-0=25-9
$$
But since $a$ is odd, only the second option fits:
$$
\left(n^{2}+6 n+4\right)^{2}=25, \quad a^{2}=9
$$
We get two equations with $n$:
$$
n^{2}+6 n+4=5, \quad n^{2}+6 n+4=-5
$$
The first of these has non-integer roots, while from the second we find that $n=-3$.
Answer: $9=(-3) \cdot(-1) \cdot 1 \cdot 3$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
650. Find all natural $k$ for which the number
$$
2^{k}+8 k+5
$$
is a perfect square.
|
$\triangle$ Checking shows that the value $k=1$ does not work, the value $k=2$ works, and the values $k=3,4,5,6$ do not work. It seems that no $k>2$ satisfies the condition of the problem. Let's prove our assumption.
Assume that there exists such a $k>2$ that the number $2^{k}+8 k+5$ is a perfect square. Since this number is odd, we have
$$
2^{k}+8 k+5=(2 a-1)^{2},
$$
where $a$ is an integer. We get:
$$
2^{k}+8 k+5=4 a^{2}-4 a+1, \quad 2^{k}+8 k+4=4 a(a-1) .
$$
In the last equation, the right-hand side is divisible not only by 4 but also by 8. However, the left-hand side is not divisible by 8, so such an equation is impossible. We have reached a contradiction. Therefore, no $k>2$ has the required property.
Answer: 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
663. Find all natural $n$ for which the number $n^{2}+3 n$ is a perfect square.
|
$\triangle$ For a natural $n$, the inequality holds:
$$
(n+1)^{2} \leqslant n^{2}+3 n<(n+2)^{2}
$$
(check it!). But since the numbers $(n+1)^{2}$ and $(n+2)^{2}$ are the two closest perfect squares to each other, the number $n^{2}+3 n$ will be a perfect square only when the left inequality turns into an equality:
$$
n^{2}+3 n=(n+1)^{2}, \quad n^{2}+3 n=n^{2}+2 n+1, \quad n=1
$$
Answer: 1.
The method of solution we used in problem 663 is called the "pinching" method.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
678. The number 43 is written in the septenary (base-7) numeral system. In which system is it written with the same digits but in reverse order?
|
$\triangle$ First, let's convert the number 43 to the decimal system:
$$
43_{7}=4 \cdot 7+3=28+3=31
$$
139
Now, let's determine the base $d$ of the system in which the equality $31=34_{d}$ holds. We will have:
$$
31=3 d+4, \quad 3 d=27, \quad d=9
$$
Answer: in base 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
700*. In what number system is the number $11111_{d}$ a perfect square?
|
$\triangle$ Let's represent this number as a sum, decomposing it by powers of $d$:
$$
11111_{d}=d^{4}+d^{3}+d^{2}+d+1
$$
We need to find a natural number $d>1$ such that the resulting sum is a square of a quadratic trinomial with argument $d$ and integer coefficients.
We will bound this sum between two squares:
$$
\left(d^{2}+\frac{d}{2}\right)^{2}<d^{4}+d^{3}+d^{2}+d+1<\left(d^{2}+\frac{d}{2}+1\right)^{2}
$$
(verify the inequality!). Multiply the last inequality by 4 to avoid fractions:
$$
\left(2 d^{2}+d\right)^{2}<4 d^{4}+4 d^{3}+4 d^{2}+4 d+4<\left(2 d^{2}+d+2\right)^{2}
$$
Since the left and right parts of this double inequality are squares of natural numbers differing by 2, and the middle part must also be a square of a natural number, the base of the latter square can only be $2 d^{2}+d+1$. Solve the corresponding equation:
$$
\begin{gathered}
\left(2 d^{2}+d+1\right)^{2}=4 d^{4}+4 d^{3}+4 d^{2}+4 d+4 \\
4 d^{4}+d^{2}+1+4 d^{3}+4 d^{2}+2 d=4 d^{4}+4 d^{3}+4 d^{2}+4 d+4 \\
d^{2}-2 d-3=0, \quad d=3
\end{gathered}
$$
Answer: in the ternary system.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
719. Find all numbers of the form $222 \ldots 2$ that can be represented as the sum of two perfect squares.
|
$\triangle$ Let
$$
222 \ldots 2=a^{2}+b^{2}
$$
where $a$ and $b$ are integers. Then the numbers $a$ and $b$ can only be odd:
$$
a=2 k+1, b=2 l+1 \quad(k \in Z, l \in Z)
$$
Therefore, the sum $a^{2}+b^{2}$ when divided by 8 gives a remainder of 2:
$$
a^{2}+b^{2}=(2 k+1)^{2}+(2 l+1)^{2}=4 k(k+1)+4 l(l+1)+2
$$
On the other hand, of the numbers of the form $222 \ldots 2$, only the number 2 gives a remainder of 2 when divided by 8, since if the number of twos in this number is greater than 1, then
$$
22 \ldots 2=22 \ldots 2 \cdot 100+22
$$
where the first term of the obtained sum is divisible by 8, and the second term gives a remainder of 6 when divided by 8.
Answer: 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
746. There are containers of two types: 130 kg and 160 kg. How many containers of the first type and how many of the second type are there if together they weigh 3 tons? List all solutions.
|
Let's denote the number of containers of the first type by $x$, and the second type by $y$. We get the equation
$$
130 x + 160 y = 3000, \quad 13 x + 16 y = 300
$$
Let's try to use divisibility by 13. For this, we represent $16 y$ as $13 y + 3 y$, and divide 300 by 13 with a remainder:
$$
13 x + 13 y + 3 y = 13 \cdot 23 + 1, \quad 3 y - 1 = 13 \cdot 23 - 13 x - 13 y .
$$
The right side of the last equation is divisible by 13, so the left side must also be divisible by 13. To find the values of $y$ for which the difference $3 y - 1$ is divisible by 13, we will use trial and error. Instead of assigning $y$ consecutive values $1, 2, 3$, etc., it is easier to set $3 y - 1$ to numbers divisible by 13: $13, 26, 39, 52, 65$, etc., and determine each time whether the root of the corresponding equation is an integer or a fraction. Integer roots are obtained in the following cases:
$$
3 y - 1 = 26, \quad y = 9 ; \quad 3 y - 1 = 65, \quad y = 22
$$
and so on. But the value $y = 22$ is already too large, since in this case
$$
16 y = 16 \cdot 22 = 352 > 300 .
$$
For $y = 9$, we can find $x$ from the equation:
$$
13 x + 16 \cdot 9 = 300, \quad 13 x = 156, \quad x = 12
$$
Answer: 12 containers of 130 kg each and 9 of 160 kg each.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
752. Find the smallest natural number that is divisible by 28, and when divided by 15, gives a remainder of 4.
|
$\triangle$ The desired number is, on the one hand, $28 x$, and on the other $-15 y+4$, where $x$ and $y$ are natural numbers. We obtain the equation
$$
28 x=15 y+4
$$
We do not need to find all solutions to this equation in natural numbers, but only one solution - the one for which the values of $x$ and $y$ are minimal. For this purpose, we transform the equation using considerations of divisibility by 15:
$$
30 x-2 x=15 y+4, \quad 30 x-15 y=4+2 x
$$
from which
$$
(2 x+4): 15, \quad(x+2): 15
$$
Since we need the smallest value of $x$ that satisfies the last divisibility, we set $x+2$ equal to 15:
$$
x+2=15, \quad x=13 \text {. }
$$
Answer: 364.
|
364
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
755. "Forty mice were walking, carrying forty groats,
Two poorer mice carried two groats each, Many mice - with no groats at all. The bigger ones carried seven each. And the rest carried four each.
How many mice walked without groats?"
|
$\triangle$ Let the number of mice that walked without groats be denoted by $x$, the number of large mice by $y$, and the number of those that carried four groats by $z$. We can set up a system of equations with the unknowns $x, y$, and $z$:
$$
\left\{\begin{array} { l }
{ 2 \cdot 2 + 7 y + 4 z = 4 0 , } \\
{ 2 + x + y + z = 4 0 , }
\end{array} \quad \left\{\begin{array}{l}
7 y+4 z=36 \\
x+y+z=38
\end{array}\right.\right.
$$
This is a system of two linear equations with three unknowns.
To solve this system, note that from the first equation, $y$ must be divisible by 4. Additionally,
$$
7 y<7 y+4 z, \quad 7 y<36
$$
from which $y \leqslant 5$. There is only one such $y$: $y=4$. Then, from the first equation, we find $z$, and subsequently from the second equation, we find $x$:
$$
7 \cdot 4+4 z=36, \quad 4 z=8, \quad z=2 ; \quad x+4+2=38, \quad x=32
$$
Answer: 32.
|
32
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
757. Find all three-digit numbers that are 11 times the sum of their digits.
|
$\triangle$ Let the desired number be $\overline{a b c}$. We get:
$$
\overline{a b c}=11(a+b+c), \quad 100 a+10 b+c=11 a+11 b+11 c, \quad 89 a=b+10 c
$$
Let's try using divisibility by 10 (but we can also use 11):
$$
90 a-a=b+10 c, \quad 90 a-10 c=a+b .
$$
Therefore, the sum $a+b$ is divisible by 10, i.e., $a+b=10$. Then the last equation becomes:
$$
90 a-10 c=10, \quad 9 a-c=1, \quad 9 a=c+1
$$
From this, $a=1, c=8$. Let's find $b$ using the fact that $a+b=10: \quad b=9$.
Answer: 198.
|
198
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
778*. Find the smallest natural number that can be represented in exactly two ways as $3 x+4 y$, where $x$ and $y$ are natural numbers.
|
$\triangle$ Let
$$
3 x+4 y=n
$$
where $n-$ is a natural number. Let's solve this equation first in integers:
$$
\begin{array}{cl}
3 x=n-4 y, & x=\frac{n-4 y}{3}=-y+\frac{n-y}{3} \\
\frac{n-y}{3}=t \in Z ; \quad n-y=3 t, \quad y=n-3 t ; \quad x=-(n-3 t)+t=4 t-n
\end{array}
$$
Next, let's find all $t$ for which $x$ and $y$ are positive:
$$
\left\{\begin{array}{l}
4 t-n>0 \\
n-3 t>0
\end{array}\right.
$$
From this, $\frac{n}{4}<t<\frac{n}{3}$.
Now, let's consider that, first, $t$ must be an integer, and second, the interval $\left(\frac{n}{4}, \frac{n}{3}\right)$ must contain exactly two integer points.
Let's think: what can be the length of this interval?
If it is greater than 3, then, obviously, the interval contains at least three integer points. If the length of the interval does not exceed 3 but is greater than 2, then the interval contains two or three such points (examples can be the intervals $(2,4 ; 4,9)$ and $(2,9; 5,3)$). If the length of the interval does not exceed 2 but is greater than 1, then it contains two or one integer point (examples are the intervals $(4,7; 6,1)$ and $(4,1; 5,9)$). If the length does not exceed 1, then the interval contains one or even no integer points.
Therefore, the length of the interval of interest must be within the limits from 1 to 3, including 3 but excluding 1.
The length of the interval $\left(\frac{n}{4}, \frac{n}{3}\right)$ is $\frac{n}{3}-\frac{n}{4}=\frac{n}{12}$. Then
$$
1<\frac{n}{12} \leqslant 3, \quad 12<n \leqslant 36
$$
Now let's perform a check of the values of $n$, starting with $n=13$.
If $n=13$, then the inequality $\frac{n}{4}<t<\frac{n}{3}$ takes the form:
$$
\frac{13}{4}<t<\frac{13}{3}, \quad 3 \frac{1}{4}<t<4 \frac{1}{3}
$$
But this interval contains only one integer.
If $n=14$, then
$$
\frac{14}{4}<t<\frac{14}{3}, \quad 3 \frac{1}{2}<t<4 \frac{2}{3} .
$$
And this case should be discarded.
The same picture is obtained for $n=15,16,17,18$ (check it!).
And only for $n=19$ does it change:
$$
\frac{19}{4}<t<\frac{19}{3}, \quad 4 \frac{3}{4}<t<6 \frac{1}{3}
$$
and this interval contains two integer points - 5 and 6.
Answer: 19.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
841*. A natural number is equal to the cube of the number of its thousands. Find all such numbers.
|
$\triangle$ Let's denote the desired number as $1000 x+y$, where $x-$ is the number of its thousands, and $y<1000$. Estimate the number $k$ from above:
$$
k=\frac{y}{x}<\frac{1000}{31}<33
$$
However, the sum $1000+k$ must be a square of a natural number. Only $k=24$ fits:
$$
1000+k=1024=32^{2}
$$
Therefore, $x=32$. Let's find $y$ as well: $y=k x=24 \cdot 32=768$.
Answer: 32768.
|
32768
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
925. What is the smallest number of members in a math club if the number of girls in it is more than $40 \%$, but less than $50 \%$?
|
Let in the club there be $a$ girls, and the total number of club members is $b$. Then the ratio of the number of girls to the total number of club members is $\frac{a}{b}$.
Since $40 \%$ is $\frac{2}{5}$, and $50 \% - \frac{1}{2}$ of the club members, then by the condition
$$
\frac{2}{5}<\frac{a}{b}<\frac{1}{2}
$$
We need to find the smallest natural number $b$, for which there exists such a natural number $a$, for which the written inequality is true.
This is a problem of the same type as problem 922. Therefore, the further solution is carried out in the same way. Complete it independently.
Answer: 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
930. How many solutions in integers $x$ and $y$ does the inequality
$$
|x|+|y|<10 ?
$$
have?
|
$\triangle$ From the condition, it is clear that
$$
|x|<10, \text { i.e. }-10<x<10
$$
Let's consider all cases.
If $x= \pm 9$, then $y=0$. We have two solutions: $(9 ; 0)$ and $(-9 ; 0)$.
If $x= \pm 8$, then $y=0, \pm 1$. This gives us six solutions: $(8 ; 0),(-8 ; 0),(8 ; 1),(-8 ; 1)$, $(8 ;-1)$ and $(-8 ;-1)$.
When $x= \pm 7$, the unknown $y$ takes values $0, \pm 1, \pm 2$. This gives us another 10 solutions.
Similarly, for $x= \pm 6, \pm 5, \pm 4, \pm 3, \pm 2, \pm 1$, we get 14, 18, 22, 26, 30, and 34 solutions, respectively.
Finally, if $x=0$, then $y$ takes values $0, \pm 1, \pm 2, \ldots, \pm 9$. This gives us another 19 solutions to the inequality.
It remains to count the total number of solutions:
$$
(2+6+10+14+18+22+26+30+34)+19=162+19=181
$$
Answer: 181.
|
181
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
998. Find a natural number that is divisible by 9 and 5 and has 14 different divisors.
|
$\triangle$ Let the desired number be denoted by
$$
a=3^{\alpha_{1}} \cdot 5^{\alpha_{2}} \cdot p_{3}^{\alpha_{3}} \ldots p_{n}^{\alpha_{n}}
$$
where $p_{3}, p_{4}, \ldots, p_{n}$ are distinct prime numbers (different from 3 and 5), $\alpha_{1}, \alpha_{2}$ are natural numbers, and $\alpha_{3}, \alpha_{4}, \ldots, \alpha_{n}$ are non-negative integers.
By the condition,
$$
\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)\left(\alpha_{3}+1\right) \ldots\left(\alpha_{n}+1\right)=14
$$
with $\alpha_{1} \geqslant 2, \alpha_{2} \geqslant 1$.
If $\alpha_{1}=2$, then $\alpha_{1}+1=3$. But since 14 is not divisible by 3, this case is impossible.
Let $\alpha_{1}>2$. Then already at $\alpha_{1}=3$ we get:
$$
\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)=4\left(\alpha_{2}+1\right) \geqslant 8
$$
Therefore, the product
$$
\left(\alpha_{3}+1\right)\left(\alpha_{4}+1\right) \ldots\left(\alpha_{n}+1\right)
$$
can only be equal to 1, otherwise
$$
\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)\left(\alpha_{3}+1\right) \ldots\left(\alpha_{n}+1\right)>14
$$
Hence,
$$
\alpha_{3}=\alpha_{4}=\ldots=\alpha_{n}=0
$$
i.e., the number $a$ has no other prime divisors except 3 and 5. We have:
$$
\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)=14
$$
Then
$$
\alpha_{1}+1=7, \quad \alpha_{2}+1=2 ; \quad \alpha_{1}=6, \quad \alpha_{2}=1 ; \quad a=3^{6} \cdot 5=729 \cdot 5=3645
$$
Answer: 3645.
|
3645
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1000. A certain natural number has only two prime divisors (in some powers), and its square has 35 different divisors. How many different divisors does the cube of this number have?
|
$\triangle$ Let the original number have the form:
$$
a=p_{1}^{\alpha_{1}} \cdot p_{2}^{\alpha_{2}}
$$
where $p_{1}$ and $p_{2}$ are distinct prime numbers, and $\alpha_{1}$ and $\alpha_{2}$ are natural numbers. Then
$$
a^{2}=p_{1}^{2 \alpha_{1}} \cdot p_{2}^{2 \alpha_{2}}, \quad a^{3}=p_{1}^{3 \alpha_{1}} \cdot p_{2}^{3 \alpha_{2}}
$$
Since $a^{2}$ has 35 distinct divisors, we have
$$
\left(2 \alpha_{1}+1\right)\left(2 \alpha_{2}+1\right)=35
$$
From this, we obtain:
$$
2 \alpha_{1}+1=5, \quad 2 \alpha_{2}+1=7 ; \quad \alpha_{1}=2, \quad \alpha_{2}=3
$$
Therefore,
$$
\tau\left(a^{3}\right)=\left(3 \alpha_{1}+1\right)\left(3 \alpha_{2}+1\right)=7 \cdot 10=70
$$
Answer: 70.
$1001^{\circ}$. Prove that a natural number has an odd number of distinct divisors if and only if it is a square of a natural number.
$\triangle$ Apply the statement of problem 995 (with the same notation). The product
$$
\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \ldots\left(\alpha_{n}+1\right)
$$
is odd if and only if all its factors are odd, i.e., when all numbers $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}$ are even, i.e., when the original number
$$
a=p_{1}^{\alpha_{1}} \cdot p_{2}^{\alpha_{2}} \cdot \ldots \cdot p_{n}^{\alpha_{n}}
$$
is a square of a natural number.
|
70
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1007. From a natural number, the sum of its digits was subtracted, and from the resulting difference, the sum of its digits was subtracted again. If this process continues, with what number will the calculations end?
|
$\triangle$ The difference between a natural number and the sum of its digits is divisible by 9 (see supporting problem 120 from § 5), and this property is preserved at each step of the computation. But such a difference is non-negative and decreases with further continuation of the computations, so its last value is zero.
Answer: 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1008. Does there exist a natural number $n$ such that
$$
n+S(n)=125
$$
where $S(n)$ is the sum of the digits of $n ?$
|
$\triangle$ The number $n$ can only be a three-digit number, and its first digit is equal to 1. Let $n=\overline{1 a b}$. We get:
$$
\overline{1 a b}+1+a+b=125, \quad 100+10 a+b+1+a+b=125, \quad 11 a+2 b=24
$$
The last equation has a unique solution in digits: $a=2, b=1$.
Answer: It exists and is unique - 121.
|
121
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1038. A piece of the book fell out. The first page of the piece has the number 163, and the number of the last page consists of the same digits but in a different order. How many sheets fell out of the book
|
$\triangle$ The last page of the piece has the number 316, as it must end with an even digit. Now we find the number of pages, and then the number of sheets in the piece:
$$
316-162=154, \quad 154: 2=77
$$
Answer: 77.
|
77
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1048. Which is greater and by how much: the sum of all even two-digit numbers or the sum of all odd two-digit numbers?
|
$\triangle$ First, let's calculate the total number of two-digit numbers. There are 99 numbers in total from 1 to 99, including both single-digit and two-digit numbers. Among them, there are 9 single-digit numbers. Therefore, the number of two-digit numbers is $99-9=90$.
Out of the 90 two-digit numbers, 45 are even and 45 are odd. Let's divide all the two-digit numbers into pairs:
$$
10 \text { and } 11, \quad 12 \text { and } 13, \quad 14 \text { and } 15, \ldots, 98 \text { and } 99 .
$$
In each pair, the odd number is 1 greater than the even number. Since there are 45 such pairs, the sum of all odd two-digit numbers is 45 greater than the sum of all even two-digit numbers.
Answer: The second sum is greater by 45.
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1053. A vendor was selling eggs. To the first customer, she sold half of all the eggs she had and another half-egg, to the second - half of the remainder and another half-egg, to the third - half of the new remainder and another half-egg, to the fourth - half of the last remainder and another half-egg. After this, she had no eggs left. How many eggs did she have initially?
|
$\triangle$ Let's solve the problem from the beginning.
After the third customer, the seller had one egg left.
After the second $-2 \cdot 1+1=3$. Let's check: she sold half of the previous remainder plus half an egg to the third customer, i.e., $3 / 2+1 / 2=2$, and she was left with $3-2=1$ egg. After the first customer, the seller had $2 \cdot 3+1=7$ eggs left. (Check it!) Finally, at the beginning, she had $2 \cdot 7+1=15$ eggs.
Answer: 15.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1061. There are candies in three boxes. In the first box, there are 8 candies less than in the other two together, and in the second box, there are 12 less than in the first and third together. How many candies are in the third box?
|
$\triangle$ Let the number of candies in the first, second, and third boxes be denoted by $a, b$, and $c$ respectively. We obtain the system of equations:
$$
\left\{\begin{array}{l}
a=b+c-8 \\
b=a+c-12
\end{array}\right.
$$
Adding these equations term by term:
$$
a+b=(a+b)+2 c-20
$$
Then
$$
2 c-20=0, \quad c=10
$$
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1067. Kolya had to square a certain natural number for his homework. Instead, he mistakenly doubled the number and got a two-digit number, written with the same digits as the square of the number, but in reverse order. What should the correct answer be?
|
$\triangle$ Let's denote the original number by $x$, its square - by $\overline{a b}$. Then
$$
\left\{\begin{array}{l}
x^{2}=10 a+b \\
2 x=10 b+a
\end{array}\right.
$$
From here, it is clear that the number $x$ is a single-digit number.
Let's add the equations of this system:
$$
x(x+2)=11(a+b)
$$
Then either $x$, or $x+2$ equals 11. But the equality $x=11$ is impossible, and when $x+2=11$ we find:
$$
x=9, \quad \overline{a b}=81
$$
We need to check the second equation of the system. For $x=9, a=8, b=1$ the equality holds.
Answer: 81.
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1082. How many terms of the sum
$$
1+2+3+\ldots+n
$$
are needed to get a three-digit number that is written with identical digits?
|
$\triangle$ Let's denote this three-digit number as $\overline{a a a}$. Applying the formula for the sum of $n$ terms of an arithmetic progression, we get:
$$
\frac{n(n+1)}{2}=\overline{a a a}=a \cdot 111, \quad n(n+1)=2 \cdot a \cdot 111=2 \cdot 3 \cdot 37 \cdot a
$$
From this, either $n$ or $n+1$ is divisible by 37, and more precisely, it equals 37, because if, for example, $n+1$ is at least $2 \cdot 37=74$, then $n=3 a \leqslant 27$, which is impossible.
Let $n+1=37$, i.e., $n=36$. Then
$$
36 \cdot 37=2 \cdot 3 \cdot 37 \cdot a, \quad 36=6 a, \quad a=6
$$
Let $n=37$. We get:
$$
37 \cdot 38=2 \cdot 3 \cdot 37 \cdot a, \quad 3 a=19
$$
But the last equation is impossible.
Answer: 36.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 4. FERRIES
Two ferries shuttle across a river at constant speeds, turning at the banks without losing time. They depart simultaneously from opposite banks and meet for the first time 700 feet from one of the banks, continue to the banks, return, and meet for the second time 400 feet from the opposite bank. As an oral exercise, determine the width of the river. (In the UK and US, a foot is denoted by a prime: 700 feet $-700^{\prime}$.)
Fig. 5
|
Solution. The total distance covered by the ferries at the time of their first meeting is exactly equal to the width of the river (Fig. 5). However, it may be surprising that by the time they meet again, the total distance they have covered is three times the width of the river. Since the speeds are constant, the second meeting will occur after a time three times longer than the first. Before the first meeting, ferry A, for example, had traveled 700 feet. In three times the duration, it would have traveled 2100 feet. But by the time of the second meeting, it reaches the riverbank and, turning back, travels an additional 400 feet. Thus, the width of the river is $2100-400=1700$ feet.
|
1700
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 13. TIC-TAC-TOE
Consider the game of "tic-tac-toe" on a three-dimensional cube $8 \times 8 \times 8$. How many straight lines can be indicated on which 8 symbols lie in a row?
|
Solution. This is not a difficult problem; it can be solved by simple counting. However, there is a brilliant solution proposed by Leo Moser. It involves considering a $10 \times 10 \times 10$ cube, obtained by covering the given $8 \times 8 \times 8$ cube with a layer of unit thickness. A winning line in the inner $8 \times 8 \times 8$ cube intersects two of the unit cubes surrounding this cube, and each unit cube in the shell is intersected by one winning line. Thus, each winning line corresponds to a unique pair of unit cubes in the outer shell, and the number of winning lines is half the number of unit cubes in the shell, which is
$$
\frac{10^{3}-8^{3}}{2}=\frac{1000-512}{2}=244
$$
This approach is entirely general. The number of winning lines for a cube with side length $k$ in $n$-dimensional space is
$$
\frac{(k+2)^{n}-k^{n}}{2}
$$
|
244
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 20. ROLLING DICE
A regular die has the numbers $1,2,3,4,5,6$ on its faces. It is rolled randomly until the sum of the points that come up exceeds the number 12.
What is the most likely total sum of points?
|
Solution. Consider the penultimate roll. After it, the total sum should be either $12,11,10,9,8$,
or 7. If it is 12, the overall result will with equal probability take the values $13,14,15$, $16,17,18$. Similarly, with a sum of 11, the final result will with equal probability take the values 13, 14, $15,16,17$, and so on. The number 13 appears as an equal candidate in each case and is the only number of this kind. Therefore, the number 13 is the most probable.
In general, the same arguments show that the most probable sum, first exceeding $n(n \geqslant 6)$, is $n+1$.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 27. MATHEMATICAL JOKE
A person bought several one-cent stamps at the post office, as many two-cent stamps so that $3 / 4$ of their quantity equals the number of one-cent stamps, as many five-cent stamps so that $3 / 4$ of their quantity equals the number of two-cent stamps, and five eight-cent stamps. He paid for them with one banknote without change. How many stamps of each denomination did he buy?
|
Solution. Suppose a person bought $y$ one-cent stamps. Then he bought $3 y / 4$ two-cent stamps and $9 y / 16$ five-cent stamps. Since $9 y / 16$ is an integer, $y$ is divisible by 16. Then for some integer $16 x=y$ and the purchase consisted of 16 one-cent, $12 x$ two-cent, $9 x$ five-cent, and 5 eight-cent stamps. Suppose he paid for the stamps with a $k$-dollar bill. Thus, the cost is
$$
16 x+2 \cdot(12 x)+5 \cdot(9 x)+8 \cdot 5=100 k
$$
i.e.
$$
\begin{aligned}
85 x+40 & =100 k \\
17 x=20 k-8 \quad \text { and } \quad x & =\frac{20 k-8}{17}=k+\frac{3 k-8}{17}
\end{aligned}
$$
Since the numbers $x$ and $k$ are integers, then
$$
\frac{3 k-8}{17} \text { is also an integer. }
$$
But $k$ must be one of the numbers $1,2,5,10,20,50,100$,
1000 or 10000. The only value of $k$ among them for which $(3 k-8) / 17$ is an integer is $k=1000$, which means the person bought 18816 one-cent, 14112 two-cent, 10584 five-cent, and 5 eight-cent stamps.
|
18816
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 33. SNOWBALLS
A boy made two snowballs, one of which has a diameter twice as large as the other. He brought them into a warm room and let them melt. Since only the surface of the snowball is exposed to the warm air, assume that the melting rate is proportional to the surface area. When half of the volume of the larger snowball has melted, how much of the smaller snowball will remain?
|
Solution. We will prove that the assumption that the melting rate of a snowball is proportional to the area of its surface leads to a surprising result, namely that the radius decreases at a constant rate regardless of the size of the snowball. Therefore, both radii will decrease by the same amount.
The volume and surface area are respectively $V=4 \pi r^{3} / 3$ and $S=4 \pi r^{2}$.
Denoting time by $t$, we get that the melting rate is
$$
\frac{d V}{d t}=\frac{4}{3} \pi \cdot 3 r^{2} \cdot \frac{d r}{d t}=4 \pi r^{2} \frac{d r}{d t}
$$
Since this rate is proportional to the surface area $S=4 \pi r^{2}$, we have
$$
4 \pi r^{2} \frac{d r}{d t}=k\left(4 \pi r^{2}\right)
$$
where $k$ is a constant. Hence,
$$
\frac{d r}{d t}=k
$$
as claimed.
58
Suppose initially the radii were $2 r$ and $r$. Then the volume of the larger snowball is
$$
V=\frac{4}{3} \pi(2 r)^{3}=\frac{32}{3} \pi r^{3}
$$
After half of it has melted, it will have a volume of
$$
V=\frac{16}{3} \pi r^{3}=\frac{4}{3} \pi(r \sqrt[3]{4})^{3}
$$
from which its radius is $r \sqrt[3]{4}$. Each radius will thus decrease by $(2-\sqrt[3]{4}) r$. Then the smaller snowball will have a radius of
$$
r-(2-\sqrt[3]{4}) r=r(\sqrt[3]{4}-1)
$$
and its volume will be
$$
V=\frac{4}{3} \pi r^{3}(\sqrt[3]{4}-1)^{3}
$$
which is very close to $1 / 5$ of the original volume $\left((\sqrt[3]{4}-1)^{3} \approx 0.2027\right)$.
## PROBLEM Z4. DIGITS OF NUMBERS FROM ONE to a BILLION
What is the sum of all the digits used in writing all the numbers, the first of which is one and the last is a billion?
Solution. Adding zero, we can form half a billion pairs of numbers:
(0; 999999999), (1; 999999998), (2; 999999997), ...
..., (499999998; 500000001), (499999999; 500000000).
The sum of the digits in each pair will be $9 \cdot 9=81$.
If we add 1 to the sum of the digits for the unaccounted number 1000000000, we get the sum quite simply:
$$
500000000 \cdot 81+1=40500000001 .
$$
|
40500000001
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 40. PERFECT NUMBERS
The ancient Greeks discovered that some natural numbers $n$ have a remarkable property: the sum of the divisors of the number $n$ equals the number $n$ itself (the number itself is not considered a divisor). For example, $n=28$ gives
$$
1+2+4+7+14=28
$$
Such numbers were called "perfect." Using the arithmetic function $\sigma(n)$, which denotes the sum of all positive divisors of the number $n$ (including the number $n$ itself), we can say that a number $n$ is perfect if $\sigma(n)=2 n$. Perfect numbers are very rare. The first five of them are $6,28,496,8128$, 33550336. In 1976, only 24 perfect numbers were known, with the largest being $2^{19936} \cdot\left(2^{19937}-1\right)$, containing about 6000 digits *).
In the eighteenth century, Euler proved that every even perfect number $m$ can be represented in the form $m=2^{n-1}\left(2^{n}-1\right)$, where $2^{n}-1$ is a prime number.
Prove the following two not-so-difficult statements independently, which we will need later:
1) $\sigma(n)$ is a multiplicative function, i.e., $\sigma(a \cdot b)=\sigma(a) \cdot \sigma(b)$ provided that $a$ and $b$ are coprime numbers.
2) If $2^{n}-1$ is a prime number, then the number $n$ is also a prime number.
*) By 1989, 52 had been found, the largest being $2^{56687} \cdot\left(2^{56667}-1\right) .-\Pi_{p}$ note by the translator.
74
In light of these premises, the task in this problem is to find all perfect numbers $n$ for which $\sigma[\sigma(n)]$ is also a perfect number.
|
Solution. First, let us assume that $n$ is an odd perfect number. Then $\sigma(n)=2n$, where 2 and $n$ are coprime, and we get
$$
\sigma[\sigma(n)]=\sigma(2n)=\sigma(2)\sigma(n)=3\sigma(n)=3 \cdot 2n=6n
$$
Clearly, $6n$ is even, and if it is also perfect, then for some prime number $p$ we must have
$$
6n=2^{p-1}(2^{p}-1)
$$
($p$ must be prime since $2^{p}-1$ is prime). However, since $n$ is odd, the number $6n$ contains the factor 2 only once (in the number 6). This means that
$$
2^{p-1}=2^{1}, \quad \text{so } p=2.
$$
Accordingly,
$$
6n=2(2^{2}-1)=6, \quad \text{so } n=1
$$
But 1 is not an odd perfect number, and we have reached a contradiction. Therefore, there are no odd perfect numbers $n$ for which $\sigma[\sigma(n)]$ is also a perfect number.
Now, let us assume that $n$ is an even perfect number. As stated, for some prime number $p$ we can write
$$
n=2^{p-1}(2^{p}-1)
$$
where $2^{p}-1$ is a prime number. In this case, 2 and $2^{p}-1$ are coprime, and we have
$$
\begin{aligned}
\sigma[\sigma(n)]=\sigma(2n)= & \sigma\left[2^{p}(2^{p}-1)\right]=\sigma\left(2^{p}\right) \cdot \sigma\left(2^{p}-1\right)= \\
& =\left(2^{p+1}-1\right)\left[(2^{p}-1)+1\right]=2^{p}(2^{p+1}-1),
\end{aligned}
$$
since $2^{p}-1$ is prime.
Clearly, this number is even, and if it is also perfect, then it is already represented in the Eulerian form for such numbers. This implies that the exponent $p+1$ must be a prime number. Thus, the numbers $p$ and $p+1$ must both be prime numbers and, since they are consecutive, they can only be 2 and 3. Therefore,
$$
n=2^{p-1}(2^{p}-1)=2 \cdot (2^{2}-1)=6
$$
and
$$
\sigma[\sigma(n)]=\sigma[\sigma(6)]=\sigma(12)=28
$$
Therefore, $n=6$ is the only solution.
|
6
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 44. COWS AND SHEEP
Two men jointly owned $x$ cows, which they sold for $x$ dollars a head. With the money they received, they bought sheep at 12 dollars a head. Since the proceeds from the sale of the cows did not divide by 12, they used the remaining money to buy a lamb. Then they divided the flock so that each of them had the same number of animals. The man with the lamb was therefore somewhat shortchanged. To make up for it, the second man gave him his harmonica. How much is the harmonica worth?
|
Solution. The revenue from sales equals $x^{2}$ dollars. If $x$ were divisible by 6, then $x^{2}$ would be divisible by 36, and consequently, by 12. Since this is not the case, $x$ is not divisible by 6. In this case, $x=12 k+r$, where $|r|=1,2,3,4$ or 5. Accordingly,
$$
\frac{x^{2}}{12}=\frac{(12 k+r)^{2}}{12}=\frac{144 k^{2}+24 k r+r^{2}}{12}=12 k^{2}+2 k r+\frac{r^{2}}{12}
$$
Now, since both people have the same number of animals, the total number of animals is even, which means there is an odd number of sheep and one lamb. Therefore, the quotient of dividing the number $x^{2}$ by 12, which equals the number of sheep bought for $x^{2}$ dollars, must be an odd number. But $12 k^{2}+2 k r$ is an even number. Therefore, the number $r^{2} / 12$ must contribute an odd value to the quotient. This implies that $r^{2}$ must exceed 12, leading to $|r|=4$ or 5. For $|r|=5$ we have
$$
\frac{r^{2}}{12}=\frac{25}{12}=2+\frac{1}{12}
$$
80
giving an even number as the contribution to the quotient. Therefore, $|r|$ must be 4 and $r^{2}=16$. Thus,
$$
\frac{r^{2}}{12}=\frac{16}{12}=1+\frac{4}{12}
$$
and the remainder is 4 (not -4). Therefore, the lamb costs 4 dollars. Consequently, one person had a 4-dollar lamb, and the other had a 12-dollar sheep, and the transfer of a 4-dollar harmonica would bring each of them to a level of 8 dollars.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 47. RED AND BLUE POINTS
Consider points arranged in a square of 20 columns and 20 rows, each of which is colored either red or blue. Whenever two points of the same color are adjacent in some row or column, they are connected by a segment of the same color. Adjacent points of different colors are connected by black segments. Among the points, 219 are red, 39 of which are on the boundary of the square, but none are in the corners. There are also 237 black segments. How many blue segments are there?
|
Solution. Each row contains 19 segments, so we get $19 \cdot 20=380$ horizontal segments. There are as many vertical segments, so their total number is 760. Since 237 of them are black, the remaining 523 are blue or red.
Let $k$ be the number of red segments and let's count how many times red points are endpoints of segments. Each black segment has one red end, and each red segment has both ends red, so in total
$237+2k$ red ends.
But 39 red points are on the boundary and are endpoints of three segments, while each of the other 180 red points is inside and is an endpoint of four segments. Thus, the number of cases where a red point is an endpoint of a segment is
$$
39 \cdot 3 + 180 \cdot 4 = 837
$$
Therefore,
$$
237 + 2k = 837 \text{ and } k = 300
$$
The number of blue segments is then $523 - 300 = 223$.
A similar problem was proposed in the journal "American Mathematical Monthly" (1971) by T. S. Brown and solved by Stefan B. Maurer.
Consider a rectangular arrangement of red and blue points with an even number of rows and an even number of columns. In each row, half the points are red and half are blue; the same is true for the columns. Whenever two points of the same color are adjacent in a row or column, they are connected by a segment of the same color. Show that the total number of red segments equals the total number of blue segments.
Solution:
Consider two adjacent rows of points, say the $i$-th and $(i+1)$-th. If two points of the same color are one above the other, then this pair is connected by a segment. Call such points "paired," and pairs of different colored points "unpaired." Now recall that in each row, half the points are red and the other half are blue. Therefore, the rows have the same number of red points. It is clear that adjacent rows have the same number of paired red points, and therefore the same number of unpaired red points. Since under each unpaired red point in the $i$-th row there is an unpaired blue point in the $(i+1)$-th row, we have that the number of unpaired blue points in the $(i+1)$-th row =
= the number of unpaired red points in the $i$-th row =
= the number of unpaired red points in the $(i+1)$-th row.
Then in the $(i+1)$-th row, we have the same number of unpaired red points and unpaired blue points. Since the $(i+1)$-th row contains the same total number of red and blue points, it follows that there will be the same number of paired red points and paired blue points. This implies that the number of blue and red segments connecting the rows is equal. The same is true for adjacent columns, from which the final conclusion follows.
|
223
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{n^{3}-(n-1)^{3}}{(n+1)^{4}-n^{4}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{n^{3}-(n-1)^{3}}{(n+1)^{4}-n^{4}}=\lim _{n \rightarrow \infty} \frac{n^{3}-n^{3}+3 n^{2}-3 n+1}{\left((n+1)^{2}-n^{2}\right) \cdot\left((n+1)^{2}+n^{2}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{3 n^{2}-3 n+1}{\left(n^{2}+2 n+1-n^{2}\right)\left(n^{2}+2 n+1+n^{2}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{3}}\left(3 n^{2}-3 n+1\right)}{\frac{1}{n^{3}}(2 n+1)\left(2 n^{2}+2 n+1\right)}=\lim _{n \rightarrow \infty} \frac{\frac{3}{n}-\frac{3}{n^{2}}+\frac{1}{n^{3}}}{\left(2+\frac{1}{n}\right)\left(2+\frac{2}{n}+\frac{1}{n^{2}}\right)}= \\
& =\frac{0-0+0}{(2+0) \cdot(2+0+0)}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 3-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}}-\sqrt{n^{2}+5}}{\sqrt[5]{n^{7}}-\sqrt{n+1}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}}-\sqrt{n^{2}+5}}{\sqrt[5]{n^{7}}-\sqrt{n+1}}=\lim _{n \rightarrow \infty} \frac{n^{-\frac{7}{5}}\left(\sqrt[3]{n^{2}}-\sqrt{n^{2}+5}\right)}{n^{-\frac{7}{5}}\left(\sqrt[5]{n^{7}}-\sqrt{n+1}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2} \cdot n^{-\frac{21}{5}}}-\sqrt{n^{2} \cdot n^{-\frac{14}{5}}+5 n^{-\frac{14}{5}}}}{\sqrt[5]{n^{7} \cdot n^{-7}}-\sqrt{n \cdot n^{-\frac{14}{5}}}+n^{-\frac{14}{5}}}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{-\frac{11}{5}}}-\sqrt{n^{-\frac{4}{5}}+5 n^{-\frac{14}{5}}}}{\sqrt[5]{1}-\sqrt{n^{-\frac{9}{5}}+n^{-\frac{14}{5}}}}= \\
& =\frac{\sqrt[3]{0}-\sqrt{0+5 \cdot 0}}{1-\sqrt{0+0}}=\frac{0}{1}=0
\end{aligned}
$$
Problem Kuznetsov Limits 4-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty}\left(\frac{n+3}{n+1}\right)^{-n^{2}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty}\left(\frac{n+3}{n+1}\right)^{-n^{2}}=\lim _{n \rightarrow \infty}\left(\frac{n+1+2}{n+1}\right)^{-n^{2}}= \\
& =\lim _{n \rightarrow \infty}\left(1+\frac{2}{n+1}\right)^{-n^{2}}=\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{n+1}{2}\right)}\right)^{-n^{2}}= \\
& =\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{n+1}{2}\right)}\right)^{\left(\frac{n+1}{2}\right)\left(\frac{2}{n+1}\right)\left(-n^{2}\right)}= \\
& =\left(\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{n+1}{2}\right)}\right)^{\left(\frac{n+1}{2}\right)}\right)^{\lim _{n \rightarrow \infty}\left(\frac{2}{n+1}\right)\left(-n^{2}\right)} \\
& =\{\text { Using the second remarkable limit }\}= \\
& =e^{\lim _{n \rightarrow \infty} \frac{-2 n^{2}}{n+1}}=e^{\lim _{n \rightarrow \infty} \frac{\frac{1}{n}\left(-2 n^{2}\right)}{\frac{1}{n}(n+1)}}=e^{\lim _{n \rightarrow \infty} \frac{-2 n}{1+\frac{1}{n}}}= \\
& =\left\{e^{\frac{-\infty}{1+0}}=e^{-\infty}=\left(\frac{1}{e}\right)^{\infty}\right\}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 7-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[7]{x}}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[7]{x}}=\lim _{x \rightarrow 0} \frac{(\sqrt{1+x}-\sqrt{1-x})(\sqrt{1+x}+\sqrt{1-x})}{\sqrt[7]{x}(\sqrt{1+x}+\sqrt{1-x})}= \\
& =\lim _{x \rightarrow 0} \frac{1+x-(1-x)}{\sqrt[7]{x}(\sqrt{1+x}+\sqrt{1-x})}=\lim _{x \rightarrow 0} \frac{2 x}{x^{\frac{1}{7}}(\sqrt{1+x}+\sqrt{1-x})}= \\
& =\lim _{x \rightarrow 0} \frac{2 x^{\frac{6}{7}}}{\sqrt{1+x}+\sqrt{1-x}}=\frac{2 \cdot 0^{\frac{6}{7}}}{\sqrt{1+0}+\sqrt{1-0}}=\frac{0}{1+1}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 11-22
This problem may have a different condition (possibly due to different editions or errors). See below for more details.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{e^{3 x}-e^{2 x}}{\sin 3 x-\tan 2 x}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{e^{3 x}-e^{2 x}}{\sin 3 x-\tan 2 x}=\lim _{x \rightarrow 0} \frac{\left(e^{3 x}-1\right)-\left(e^{2 x}-1\right)}{\sin 3 x-\tan 2 x}= \\
& =\lim _{x \rightarrow 0} \frac{\frac{1}{x}\left(\left(e^{3 x}-1\right)-\left(e^{2 x}-1\right)\right)}{\frac{1}{x}(\sin 3 x-\tan 2 x)}= \\
& =\frac{\lim _{x \rightarrow 0} \frac{1}{x}\left(\left(e^{3 x}-1\right)-\left(e^{2 x}-1\right)\right)}{\lim _{x \rightarrow 0} \frac{1}{x}(\sin 3 x-\tan 2 x)}= \\
& =\left(\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}-\lim _{x \rightarrow 0} \frac{e^{2 x}-1}{x}\right) /\left(\lim _{x \rightarrow 0} \frac{\sin 3 x}{x}-\lim _{x \rightarrow 0} \frac{\tan 2 x}{x}\right)=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$e^{3 x}-1 \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$e^{2 x}-1 \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
$\sin 3 x \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$\tan 2 x \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
We get:
$$
=\frac{\lim _{x \rightarrow 0} \frac{3 x}{x}-\lim _{x \rightarrow 0} \frac{2 x}{x}}{\lim _{x \rightarrow 0} \frac{3 x}{x}-\lim _{x \rightarrow 0} \frac{2 x}{x}}=\frac{\lim _{x \rightarrow 0} 3-\lim _{x \rightarrow 0} 2}{\lim _{x \rightarrow 0} 3-\lim _{x \rightarrow 0} 2}=\frac{3-2}{3-2}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{1-\sqrt{\cos x}}{1-\cos \sqrt{x}}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{1-\sqrt{\cos x}}{1-\cos \sqrt{x}}=\lim _{x \rightarrow 0} \frac{(1-\sqrt{\cos x})(1+\sqrt{\cos x})}{(1-\cos \sqrt{x})(1+\sqrt{\cos x})}= \\
& =\lim _{x \rightarrow 0} \frac{1-\cos x}{(1-\cos \sqrt{x})(1+\sqrt{\cos x})}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$$
\begin{aligned}
& 1-\cos x \sim \frac{x^{2}}{2}, \text { as } x \rightarrow 0 \\
& 1-\cos \sqrt{x} \sim \frac{(\sqrt{x})^{2}}{2}, \text { as } x \rightarrow 0
\end{aligned}
$$
We get:
$$
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{\frac{x^{2}}{2}}{\frac{(\sqrt{x})^{2}}{2}(1+\sqrt{\cos x})}= \\
& =\lim _{x \rightarrow 0} \frac{x^{2}}{x(1+\sqrt{\cos x})}=\lim _{x \rightarrow 0} \frac{x}{1+\sqrt{\cos x}}= \\
& =\frac{0}{1+\sqrt{\cos 0}}=\frac{0}{1+\sqrt{1}}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 16-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\cos \left(\frac{x}{\pi}\right)\right)^{1+x}$
|
## Solution
$\lim _{x \rightarrow 0}\left(\cos \left(\frac{x}{\pi}\right)\right)^{1+x}=\left(\cos \left(\frac{0}{\pi}\right)\right)^{1+0}=1^{1}=1$
## Problem Kuznetsov Limits 18-22
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 1}(\sqrt{x}+1)^{\frac{\pi}{\operatorname{arctg} x}}$
|
## Solution
$\lim _{x \rightarrow 1}(\sqrt{x}+1)^{\frac{\pi}{\operatorname{arctg} x}}=(\sqrt{1}+1)^{\frac{\pi}{\operatorname{arctg} 1}}=2^{\frac{\pi}{\left(\frac{\pi}{4}\right)}}=2^{4}=16$
## Problem Kuznetsov Limits 20-22
|
16
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(-1 ; 2 ;-3), B(3 ; 4 ;-6), C(1 ; 1 ;-1)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(3-(-1) ; 4-2 ;-6-(-3))=(4 ; 2 ;-3)$
$\overrightarrow{A C}=(1-(-1) ; 1-2 ;-1-(-3))=(2 ;-1 ; 2)$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \cos (\overrightarrow{A B, A \overrightarrow{A C}})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}= \\
& =\frac{4 \cdot 2+2 \cdot(-1)+(-3) \cdot 2}{\sqrt{4^{2}+2^{2}+(-3)^{2}} \cdot \sqrt{2^{2}+(-1)^{2}+2^{2}}}= \\
& =\frac{8-2-6}{\sqrt{16+4+9} \cdot \sqrt{4+1+4}}=\frac{0}{\sqrt{29} \cdot \sqrt{9}}=0
\end{aligned}
$$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B, A C})=0$
and consequently the angle
$\overrightarrow{A B, A C}=\frac{\pi}{2}$
## Problem Kuznetsov Analytic Geometry 4-4
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the area of the parallelogram constructed on vectors $a$ and $b$.
$a=3 p-2 q$
$b=p+5 q$
$|p|=4$
$|q|=\frac{1}{2}$
$(\widehat{p, q})=\frac{5 \pi}{6}$
|
## Solution
The area of the parallelogram constructed on vectors $a$ and $b$ is numerically equal to the modulus of their vector product:
$S=|a \times b|$
We compute $a \times b$ using the properties of the vector product:
$a \times b=(3 p-2 q) \times(p+5 q)=3 \cdot p \times p+3 \cdot 5 \cdot p \times q-2 \cdot q \times p-2 \cdot 5 \cdot q \times q=$
$=15 \cdot p \times q-2 \cdot q \times p=15 \cdot p \times q+2 \cdot p \times q=(15+2) \cdot p \times q=17 \cdot p \times q$
We compute the area:
$$
\begin{aligned}
& S=|a \times b|=|17 \cdot p \times q|=17 \cdot|p \times q|=17 \cdot|p| \cdot|q| \cdot \sin (\widehat{p, q})= \\
& =17 \cdot 4 \cdot \frac{1}{2} \cdot \sin \frac{5 \pi}{6}=34 \cdot \sin \frac{5 \pi}{6}=34 \cdot \frac{1}{2}=17
\end{aligned}
$$
Thus, the area of the parallelogram constructed on vectors $a$ and $b$ is 17.
## Problem Kuznetsov Analytic Geometry 5-4
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(2 ; 1 ;-1), B(6 ;-1 ;-4), C(4 ; 2 ; 1)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(6-2 ;-1-1 ;-4-(-1))=(4 ;-2 ;-3)$
$\overrightarrow{A C}=(4-2 ; 2-1 ; 1-(-1))=(2 ; 1 ; 2)$
We find the cosine of the angle $\phi_{\text{between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{4 \cdot 2+(-2) \cdot 1+(-3) \cdot 2}{\sqrt{4^{2}+(-2)^{2}+(-3)^{2}} \cdot \sqrt{2^{2}+1^{2}+2^{2}}}=$
$=\frac{8-2-6}{\sqrt{16+4+9} \cdot \sqrt{4+1+4}}=\frac{0}{\sqrt{29} \cdot \sqrt{9}}=0$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=0$
and consequently the angle
$\widehat{A B,} \overrightarrow{A C}=\frac{\pi}{2}$
## Problem Kuznetsov Analytic Geometry 4-11
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Calculate the area of the parallelogram constructed on vectors $a_{\text {and }} b$.
$a=3 p+2 q$
$$
\begin{aligned}
& b=p-q \\
& |p|=10 \\
& |q|=1 \\
& (\widehat{p, q})=\frac{\pi}{2}
\end{aligned}
$$
|
## Solution
The area of the parallelogram constructed on vectors $a$ and $b$ is numerically equal to the modulus of their vector product:
$S=|a \times b|$
We compute $a \times b$ using the properties of the vector product:
$a \times b=(3 p+2 q) \times(p-q)=3 \cdot p \times p-3 \cdot p \times q+2 \cdot q \times p-2 \cdot q \times q=$
$=-3 \cdot p \times q+2 \cdot q \times p=-3 \cdot p \times q-2 \cdot p \times q=(-3-2) \cdot p \times q=-5 \cdot p \times q$
We compute the area:
$S=|a \times b|=|-5 \cdot p \times q|=5 \cdot|p \times q|=5 \cdot|p| \cdot|q| \cdot \sin (\widehat{p, q})=$
$=5 \cdot 10 \cdot 1 \cdot \sin \frac{\pi}{2}=50 \cdot \sin \frac{\pi}{2}=50 \cdot 1=50$
Thus, the area of the parallelogram constructed on vectors $a$ and $b$ is 50.
## Problem Kuznetsov Analytical Geometry 5-11
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A(-2 ; 3 ;-3)$
$a: 3 x+2 y-z-2=0$
$k=\frac{3}{2}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 3 x+2 y-z-3=0$
Substitute the coordinates of point $A$ into the equation $a^{\prime}$:
$3 \cdot(-2)+2 \cdot 3-(-3)-3=0$
$-6+6+3-3=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-11
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty} \frac{(2 n+1)!+(2 n+2)!}{(2 n+3)!}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{(2 n+1)!+(2 n+2)!}{(2 n+3)!}=\lim _{n \rightarrow \infty}\left(\frac{(2 n+1)!}{(2 n+3)!}+\frac{(2 n+2)!}{(2 n+3)!}\right)= \\
& =\lim _{n \rightarrow \infty}\left(\frac{1}{(2 n+2)(2 n+3)}+\frac{1}{2 n+3}\right)=0+0=0
\end{aligned}
$$
## Problem Kuznetsov Limits 6-2
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.