problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
5. There were 5 times more strawberry bushes on the first bed than on the second. When 22 bushes were transplanted from the first bed to the second, the number of strawberry bushes on each bed became the same. How many bushes were there on each bed?
|
## 5. First method of solving.
Let's build a graphical model of the problem's condition
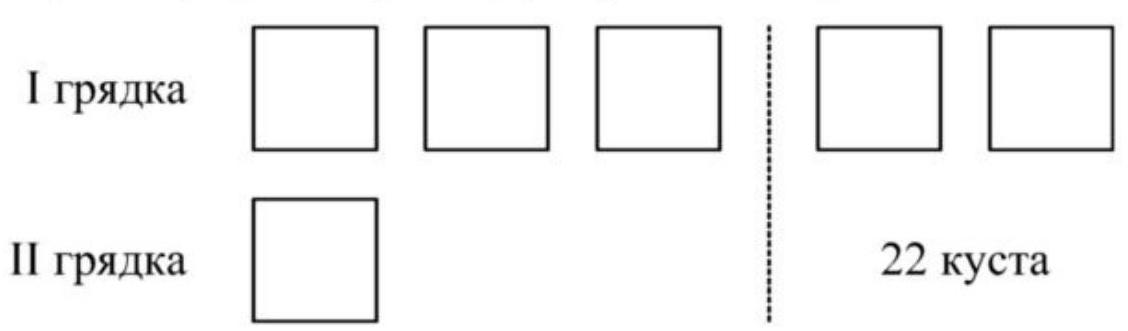
1) $22: 2=11$ (bushes) - this is $1/5$ of all the bushes (that were on the second bed);
2) $11 \times 5=55$ (bushes) - this was on the first bed.
Second method of solving (Nikolai Zherebtsov - student of School No. 46).
1) $5+1=6$ (parts) - in total;
2) $6: 2=3$ (parts) - this is how many parts each bed has;
3) $5-3=2$ (parts) - this is how many parts were transplanted from the first bed to the second;
4) $22: 2=11$ (bushes) - this is how many bushes are in one part (there were on the second bed)
5) $11 \times 5=55$ (bushes) - this was on the first bed.
Third method of solving (Vitaliy Semikin - student of School No. 48).
1) $22+22=44$ (bushes) - this is how many fewer bushes there are on the second bed compared to the first;
2) $44: 4=11$ (bushes) - this is how many bushes are in one part (there were on the second bed)
3) $11 \times 5=55$ (bushes) - this was on the first bed.
Answer: 11 bushes were on the second bed, 55 bushes were on the first.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Between the numbers $1,2,3,4,5,6,7,8,9$ insert arithmetic operation signs and parentheses so that the resulting expression has a value of 100.
|
1. a) $1+2+3+4+5+6+7+8 \times 9=100$;
b) $1 \times 2 \times 3+4+5+6+7+8 \times 9=100$;
c) $1+2 \times 3+4 \times 5-6+7+8 \times 9=100$;
d) $1 \times 2 \times 3 \times 4+(5+6-7)+8 \times 9=100$
e) $(1 \times 2+3) \times 4 \times 5+6-7-8+9=100$;
f) $(1+2+3) \times(4+5+6)-7+8+9=100$;
g) $((1+2): 3+4+5-6) \times 7+8 \times 9=100$.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let 2 cups and 2 pitchers weigh as much as 14 plates, 1 pitcher weighs as much as 1 cup and 1 plate. How many plates will balance a pitcher
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
4. First method of solution (graphical).
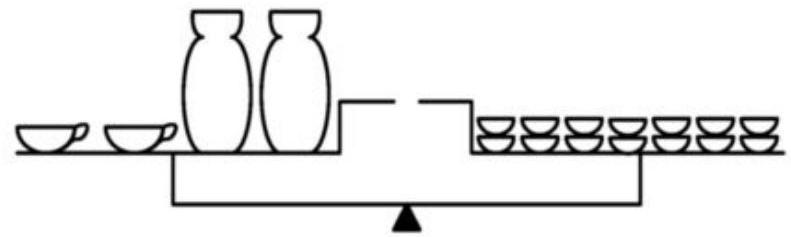
Reduce the number of items on each scale by half.

Now replace the jug on the left scale with a plate and a cup.
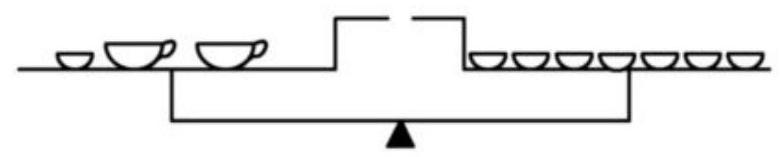
Remove a plate from each scale.
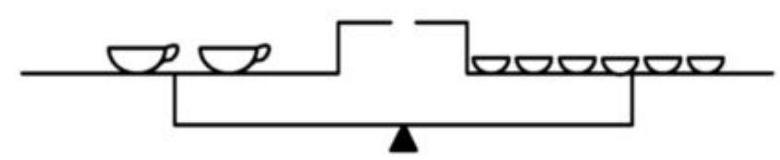
Reduce the number of items on each scale by half.

Since one jug weighs as much as one cup and one plate, we get:
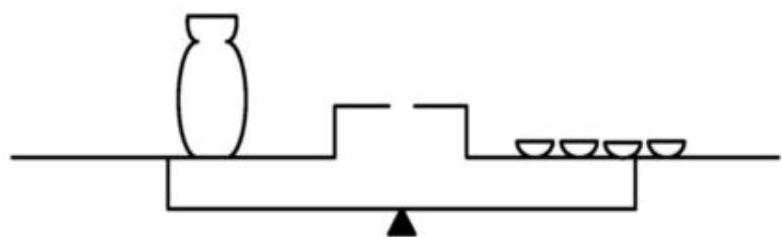
Second method of solution (analytical).
According to the problem, 2 cups + 2 jugs = 14 plates. Dividing both sides of the equation by 2, we get 1 cup + 1 jug = 7 plates. According to the second condition, 1 jug = 1 cup + 1 plate. From the subsequent two equations, we have:
$$
\begin{aligned}
& 1 \text{ cup } + 1 \text{ jug } = 7 \text{ plates; } \\
& 1 \text{ jug } = 1 \text{ cup } + 1 \text{ plate; } \\
& 1 \text{ cup } + 1 \text{ cup } + 1 \text{ plate } = 7 \text{ plates; } \\
& 2 \text{ cups } = 6 \text{ plates; } \\
& 1 \text{ cup } = 3 \text{ plates; } \\
& 1 \text{ jug } = 1 \text{ cup } + 1 \text{ plate } = 3 \text{ plates } + 1 \text{ plate } = 4 \text{ plates. }
\end{aligned}
$$
Third method of solution (arithmetic).
1) $14 \div 2 = 7$ (plates) - will balance 1 cup and 1 plate;
2) $7 - 1 = 6$ (plates) - will balance 2 cups;
3) $6 \div 2 = 3$ (plates) - will balance 1 cup;
4) $3 + 1 = 4$ (plates) - will balance 1 jug.
Answer: one jug balances 4 plates.
|
4
|
Logic and Puzzles
|
other
|
Yes
|
Yes
|
olympiads
| false
|
5. A group of third-graders decided to go on a trip to Moscow on March 19 after a math olympiad. Each student contributed the same amount of money monthly, and over 9 months, they collected 22725 rubles. How many students were in the class and how much did each student contribute monthly?
|
5. 6) $22725: 9=2525$ (rubles) — the amount the students paid for one month.
To determine how much each student paid monthly, we need to know the number of students in the class. This is unknown in the problem. However, from the problem's condition, it follows that this is a natural number that is a divisor of 2525.
$$
\begin{gathered}
2525: 5=505 \\
505: 5=101
\end{gathered}
$$
Thus, there could have been 5, 25, or 101 students in the class. Since it is impossible to have 101 students in a class, the number of students was either 5 or 25.
2) $2525: 5=505$ (rubles)
3) $2525: 25=101$ (rubles)
Answer: 5 students paid 505 rubles each or 25 students paid 101 rubles each.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Write the smallest four-digit number in which all digits are different.
|
1. According to the problem, to record a four-digit number, four different digits should be used. They can be chosen from $0,1,2,3,4,5,6,7,8,9$.
The smallest digit in the thousands place can be $1: 1^{* * *}$.
The smallest digit in the hundreds place can be $0: 10^{* *}$.
Since we have already used 1 and 0, the digit in the tens place will be $2: 102 *$.
As a result, we get the number 1023.
Answer: 1023.
|
1023
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest number that gives a remainder of 1 when divided by 2, and a remainder of 2 when divided by 3.
|
3. First, let's write down the numbers that give a remainder of 1 when divided by 2:
$$
3,5,7,9,11 \ldots
$$
Next, let's write down the numbers that give a remainder of 2 when divided by 3:
$$
5,8,11,14,17 \ldots
$$
We will choose from the obtained numbers the one that satisfies both conditions and is the smallest. This number is 5.
We could have reasoned differently. After writing down the numbers that give a remainder of 1 when divided by 2, we find which of them will give a remainder of 2 when divided by 3, and then choose the smallest one among them (5, 11, 17 ...), or we could first write down the numbers that give a remainder of 2 when divided by 3, and then choose the smallest one among them that gives a remainder of 1 when divided by 2.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A motorcyclist traveled 980 km over three days. In the first two days, he traveled 725 km, and on the second day, he traveled 123 km more than on the third day. How many kilometers did he travel each of these three days?
|
6. Let's represent the condition of the problem in a drawing
980 km
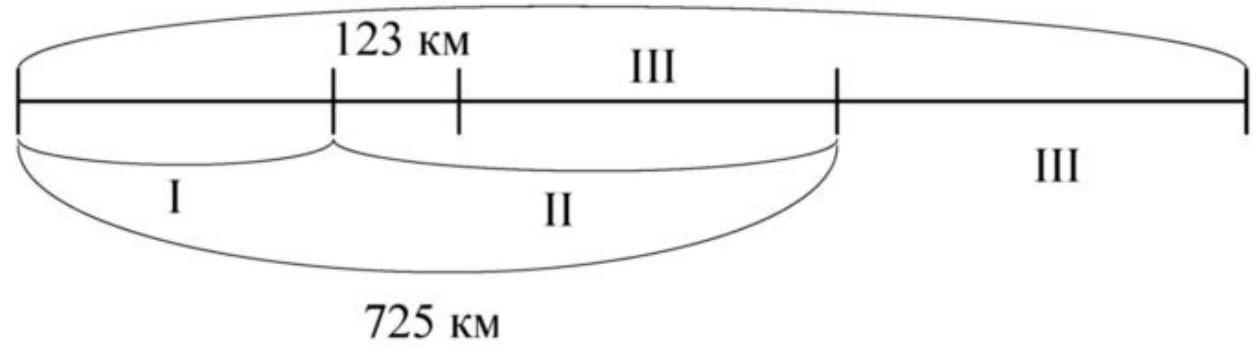
1) $980-725=255$ (km) - traveled on the third day.
2) $255+123=378$ (km) - traveled on the second day.
3) $725-378=347$ (km) - traveled on the first day.
Answer: On the first day, he traveled 347 km, on the second day - 378 km, on the third day - 255 km.
|
347
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many tiles with dimensions $15 \times 15$ cm are needed to tile a wall that is 3 m 6 dm long and 27 dm wide $?$
|
1. The first method of solving.
1) $15 \times 15=225$ (cm$^2$ - the area of one tile;
2) $360 \times 270=97200\left(\mathrm{~cm}^{2}\right)$ - the area of the walls;
3) $97200: 225=432$ (tiles).
The second method of solving (Rukhov Arseny, student of School No. 25).
1) $360: 15=24$ (tiles) - will fit in one row along the length of the wall;
2) $270: 15=18$ (tiles) - will fit in one row along the width of the wall;
3) $24 \times 18=432$ (tiles).
Answer: 432 tiles will be required.
|
432
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given the sequence of numbers $0,1,2,6,16,44,120, \ldots$ Extend it and write down the next two numbers.
|
4. All numbers, starting from the third, in the given sequence are formed according to the rule:
$$
\begin{gathered}
a_{n}=\left(a_{n-1}+a_{n-2}\right) \times 2 \\
(0+1) \times 2=2 \\
(1+2) \times 2=6 \\
(2+6) \times 2=16 \\
(16+6) \times 2=44 \\
(44+16) \times 2=120 \\
(44+120) \times 2=328
\end{gathered}
$$
Thus, we obtain the following sequence of numbers:
$$
0,1,2,6,16,44,120,328 \ldots
$$
|
328
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many days have passed from March 19, 1990 to March 23, 1996 inclusive
|
5. 6) \(365 \times 6 + 2 = 2192\) (days) - have passed from 19.03.1990 to 19.03.1996
2) \(23 - 19 = 4\) (days) - have passed from 19.03.1990 to 23.03.1996
3) \(2192 + 4 = 2196\) (days) - have passed from 19.03.1990 to 23.03.1996\).
Answer: a total of 2196 days have passed.
|
2196
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. It is known that the perimeter of one rectangle is greater than the perimeter of another rectangle. Compare the areas of these rectangles.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
6. The solution to this problem can be obtained by students as a result of conducting a computational experiment with various rectangles, for example:
a) $a=3 \text{~cm}, b=4 \text{~cm}$;
$$
\begin{aligned}
& a=4 \text{~cm}, b=2 \text{~cm} ; \\
& p_{2}=12 \text{~cm} ; \\
& S_{2}=8 \text{~cm}^{2}
\end{aligned}
$$
$$
\begin{aligned}
& p_{1}=14 \text{~cm} ; \\
& S_{1}=12 \text{~cm}^{2} ;
\end{aligned}
$$
$$
S_{1}>S_{2}
$$
b) $a=6 \text{~cm}, b=1 \text{~cm}$;
$$
\begin{aligned}
& a=4 \text{~cm}, b=2 \text{~cm} ; \\
& p_{2}=12 \text{~cm} \\
& S_{2}=8 \text{~cm}^{2}
\end{aligned}
$$
$$
\begin{aligned}
& p_{1}=14 \text{~cm} \\
& S_{1}=6 \text{~cm}^{2}
\end{aligned}
$$
$$
S_{1}<S_{2} .
$$
c) $a=10 \text{~cm}, b=2 \text{~cm}$;
$$
\begin{aligned}
& a=5 \text{~cm}, b=4 \text{~cm} \\
& p_{1}=18 \text{~cm} \\
& S_{1}=20 \text{~cm}^{2}
\end{aligned}
$$
$$
\begin{aligned}
& p_{1}=24 \text{~cm} ; \\
& S_{1}=20 \text{~cm}^{2}
\end{aligned}
$$
$$
S_{1}=S_{2} .
$$
Thus, we have three variants of the relationships between the areas of the rectangles.
Answer: the area of one rectangle can be greater than, less than, or equal to the area of another rectangle.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Which of the following time intervals is the largest? a) 1500 minutes b) 10 hours c) 1 day.
|
1. To compare time intervals, it is necessary to express them in units of the same denomination, for example, in hours:
$1500: 60=25$ (hours);
1 day $=24$ hours.
Thus, the greatest time interval is 1500 minutes.
Answer: the greatest time interval is 1500 minutes.
|
1500
|
Other
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. In the box, there are geometric shapes: triangles, squares, and circles. In total, there are 24 shapes. There are 7 times as many triangles as squares. How many of each shape could be in the box?
|
3. The first method of solving. Let's represent the condition of the problem in the form of a drawing.
squares

triangles

circles

From this, it is clear that the sum of the triangles and squares should be divisible by eight. There are only two numbers less than 24 and divisible by eight - these are 16 and 8. Let's check each of them.
1) \(16 \div 8 = 2\) (squares); \(\quad\) 1) \(8 \div 8 = 1\) (squares);
2) \(2 \times 7 = 14\) (triangles)
3) \(1 \times 7 = 7\) (triangles);
4) \(24 - 16 = 8\) (circles).
5) \(24 - 8 = 16\) (circles).
The second method of solving. Since, according to the condition, there are 7 times more triangles than squares, there could not be more than three squares, otherwise, the total number of figures would exceed 24.
Let's assume there was 1 square, then there were 7 times more triangles, that is, 7. The number of circles can be determined by calculating the difference between 24 and 8. There were 16 circles.
Let's assume there were 2 squares, then there were \(14 = 2 \times 7\) triangles, and \(8 (24 - (14 + 2)) = 8\) circles.
Let's assume there were 3 squares, then there would be 21 triangles, and their sum would be 24. In this case, there would be no circles, which contradicts the condition of the problem.
The third method of solving (by Yelena Viazmina, a student of School No. 46).
There are 7 times more triangles than squares. In total, there are 8 such parts. 24 is divisible by 8, but we still have circles. We take the nearest number that is divisible by 8. This number is 16.
1) \(16 \div 8 = 2\) (squares)
2) \(2 \times 7 = 14\) (triangles)
3) \(24 - 16 = 8\) (circles).
Answer: 2 squares, 14 triangles, 8 circles or 1 square, 7 triangles, 16 circles.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. 12 baskets of apples and 14 baskets of pears weigh 6 c 92 kg. Moreover, the weight of one basket of pears is 10 kg less than the weight of one basket of apples. How much does one basket of pears and one basket of apples weigh separately?
|
4. This problem can be solved both analytically and arithmetically.
The first method of solving. Given that the weight of one basket of pears is 10 kg less than the weight of one basket of apples, we can write the following equation:
$$
A = P + 10 .
$$
Using the first condition of the problem (12A + 14P = 692), we can derive an equation to determine the weight of one basket of pears:
$$
\begin{gathered}
12 \times (P + 10) + 14 \times P = 692 \\
26 \times P + 120 = 692 \\
26 \times P = 572 \\
P = 22(\text{kg})
\end{gathered}
$$
Then, a basket of apples weighs 32 kg (22 + 10 = 32).
The second method of solving.
1) $10 \times 14 = 140$ (kg) - this is how much less 14 baskets of pears weigh compared to 14 baskets of apples;
2) $692 + 140 = 832$ (kg) - this would be the total if all baskets were filled with apples;
3) $832 \div 26 = 32$ (kg) - the weight of one basket of apples;
4) $32 - 10 = 22$ (kg) - the weight of one basket of pears.
The third method of solving (Andrey Belokopytov, student of School No. 12).
1) $10 \times 12 = 120$ (kg) - this is how much more 12 baskets of apples weigh;
2) $692 - 120 = 572$ (kg) - the weight of apples and pears if they were equal;
3) $572 \div 26 = 22$ (kg) - the weight of one basket of pears;
4) $22 + 10 = 32$ (kg) - the weight of one basket of apples.
Answer: A basket of pears weighs 22 kg and a basket of apples weighs 32 kg.
|
22
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. By how much is the largest five-digit number greater than the smallest five-digit number
|
6. The largest five-digit number is 99999, and the smallest is 10000.
$$
99999-10000=89999
$$
Answer: greater by 89999.
|
89999
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of all three-digit numbers that can be written using the digits $1,2,3$ such that all digits in each number are different.
|
1. Let's first determine the three-digit numbers that can be formed using the digits $1,2,3$ such that all digits in each number are different.
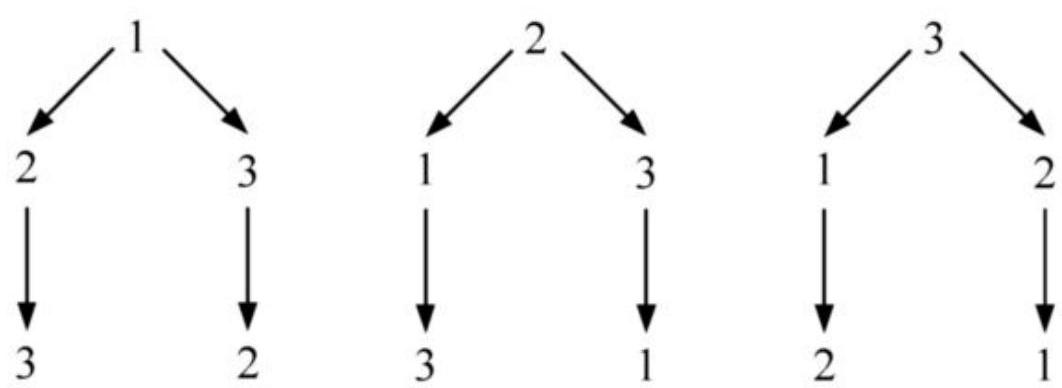
Thus, we have the following numbers that satisfy the condition of the problem: $123,132,213,231,312,321$. Let's find their sum.
$$
123+132+213+231+312+321=1332
$$
Answer: 1332.
|
1332
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Anton was given a scale, and he started weighing his toys. A car was balanced by a ball and two cubes, and a car with a cube - two balls. How many cubes balance a car? (All of Anton's balls are the same, and the cubes are the same too.)
|
4. First method of solving. Since the machine is balanced by the ball and two cubes, the machine with a cube will be balanced by the ball and three cubes. From the second condition, we have that 2 balls balance a ball and 3 cubes, meaning one ball by mass is equal to 3 cubes. Thus, the machine can be balanced by 5 cubes.
Second method of solving. This problem can be solved analytically, for which each condition of the problem can be written as an equality:
$$
\begin{aligned}
& \mathrm{M}=\mathrm{Mball}+2 \mathrm{~K} \\
& \mathrm{M}+\mathrm{K}=2 \mathrm{Mball}
\end{aligned}
$$
Substituting into the second equality the sum of Mball $+2 K$ for M, we get
$$
\text { Mball + } 2 \mathrm{~K}+\mathrm{K}=2 \text { Mball. }
$$
From which it is easy to find that
$$
\text { 3K = Mball. }
$$
From the obtained ratio and the first equality, we get:
$$
\begin{gathered}
\mathrm{M}=2 \mathrm{~K}+3 \mathrm{~K} \\
\mathrm{M}=5 \mathrm{~K}
\end{gathered}
$$
Answer: the machine can be balanced by 5 cubes.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A chocolate bar consists of $5 \times 8$ square pieces. The bar is broken along straight lines, separating the pieces until 40 individual pieces are obtained. How many times will the bar need to be broken?
|
6. To get 40 equal pieces from a chocolate bar, you first need to divide it into 8 strips along its length. For this, 7 breaks are required. Then, each of the 8 strips needs to be divided into 5 pieces. For this, 4 breaks are needed in each strip. In total, the chocolate bar will need to be broken 28 times $(7 \times 4=28)$.
Answer: 28 times.
|
28
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two numbers were first multiplied, and then the larger number was divided by the smaller one, resulting in equal outcomes. What are these numbers? How many such pairs of numbers exist?
|
2. Let $a$ and $b$ be the two numbers mentioned in the problem, with $a > b$. According to the problem,
$$
a \times b = a : b
$$
or
$$
a b^{2} - a = 0
$$
Factoring out the common factor, we get
$$
a \left(b^{2} - 1\right) = 0
$$
From this, we can conclude that $b = 1$, and $a$ can be any number.
Students might reason as follows: find a number such that when multiplied and divided by it, the result is the same. This number is one. Then the first number can be any number, because multiplying it by one and dividing it by one will yield the same number.
Answer: $b = 1$, $a$ can be any number. There are infinitely many such pairs.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Katya is 6 times younger than her great-grandfather; if a 0 is placed between the digits of her age, the age of her great-grandfather is obtained. How old is she
|
1. The first way to solve the problem. From the problem statement, it follows that Katya's age is a two-digit number, and her great-grandfather's age is a three-digit number. The number of units in Katya's age, when multiplied by 6, gives a number in which the number of units will be the same as in Katya's age. Let's find such numbers:
$1 \times 6=6-$ does not fit;
$2 \times 6=12$ - does not fit;
$3 \times 6=18-$ does not fit;
$4 \times 6=24$ - fits;
$5 \times 6=30$ - does not fit;
$6 \times 6=36$ - fits;
$7 \times 6=42$ - does not fit;
$8 \times 6=48$ - fits;
$9 \times 6=42$ - does not fit.
Thus, Katya's age ends in 4, 6, or 8. The digit in the units place of Katya's age cannot be greater than one, as in this case, a number greater than one hundred would result, which does not contain a 0 in the tens place. Therefore, we need to check the numbers $14, 16, 18$. The numbers 14 and 16 do not fit because when multiplied by 6, they result in two-digit numbers. Only one number remains - 18.
The second way to solve the problem (Lida Frolova, a student at Gymnasium No. 24).
If we place a 0 between the digits of Katya's age, we get her great-grandfather's age. This means Katya is a two-digit number of years old, and her great-grandfather is a three-digit number of years old with a 0 in the middle.
The numbers $10, 11, 12, 13, 14, 15, 16$ - do not fit, as when each of them is multiplied by 6, they result in two-digit numbers. Only $17, 18, 19$ remain to be checked:
$17 \times 6=102$ - does not fit;
$18 \times 6=108-$ fits;
$19 \times 6=114$ - does not fit.
Answer: Katya is 18 years old.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many three-digit numbers do not contain the digit 8?
|
2. First method of solving. There are a total of 900 three-digit numbers. To find out how many of them do not contain the digit 8, we need to subtract from 900 the number of three-digit numbers that contain the digit 8. Let's determine the number of these numbers. From 800 to 899, there are one hundred such numbers. Other numbers containing the digit 8 will be $152=19 \times 8$. Thus, the number of numbers that do not contain the digit 8 is $648(900-100-152=648)$.
Second method of solving (Sergey Podkovinsky, student of School No. 46).
From 100 to 199, there are a total of 100 numbers. Nineteen of them contain the digit 8.
$100-19=81$ numbers - in the hundred do not contain the digit 8. There will be eight times 81 such numbers.
Numbers from $800-899$ should be excluded as they all contain 8. As a result, we get
$$
81 \times 8=648 \text { numbers. }
$$
Answer: 648 numbers.
|
648
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Apples were divided into two unequal piles. When half of the apples from the first pile were moved to the second pile, and then half of the apples from the second pile were moved back to the first pile, there were 18 apples in the first pile and 8 in the second. How many apples were in each pile originally?
|
3. The first method of solving.
1) $8 \times 2=16$ (beans) - was in the second pile after half was moved from the first pile;
2) $18-8=10$ (beans) - was in the first pile after half was moved from it;
3) $10 \times 2=20$ (beans) - was originally in the first pile;
4) $16-10=6$ (beans) - was originally in the second pile.
The second method of solving (Sofia Bekesova, student of Gymnasium No. 24).
| I pile | II pile | |
| :---: | :---: | :--- |
| 18 | 8 | became after moving from the second pile to the first |
| 10 | 16 | became after moving half from the first pile |
| 20 | 6 | was originally |
Answer: originally, there were 20 in the first pile and 6 in the second.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a triangle with side lengths of 7 cm, 12 cm, and 9 cm respectively. Explain how to construct a segment connecting a vertex and the opposite side with a length of 9 cm so that the perimeters of the two resulting triangles are equal.
|
6. First method of solution. Since in the obtained triangles one side will be common ( $A D$ ), in order for the perimeters to be equal, it is necessary that the side of 9 cm be divided into parts, the difference in lengths of which would equal the difference of the other two sides ( $12-7=5 \text{ cm}$ ). Based on this, the number 9 should be represented as the sum of two addends, one of which is 5 more than the other. The numbers that satisfy this condition are 2 and 7. Thus, we get the following solution:
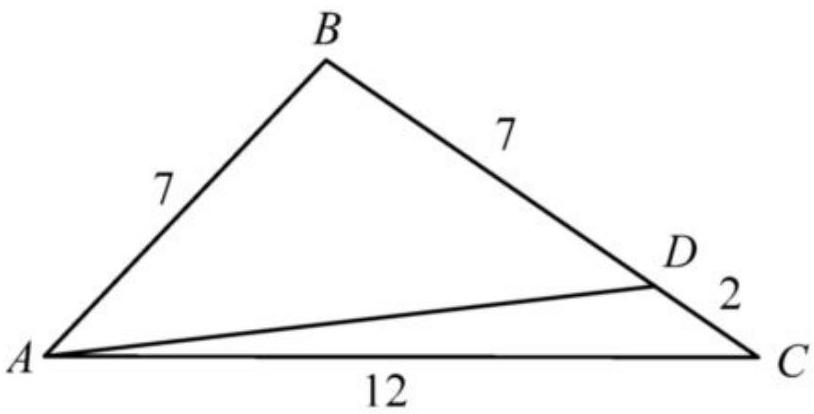
Second method of solution. The solution to this problem will be easily found if the perimeter is represented as the sum of segments:
$$
\begin{aligned}
& P_{\triangle A D C}=A C+C D+D A \\
& P_{\triangle A B D}=A B+B D+D A
\end{aligned}
$$
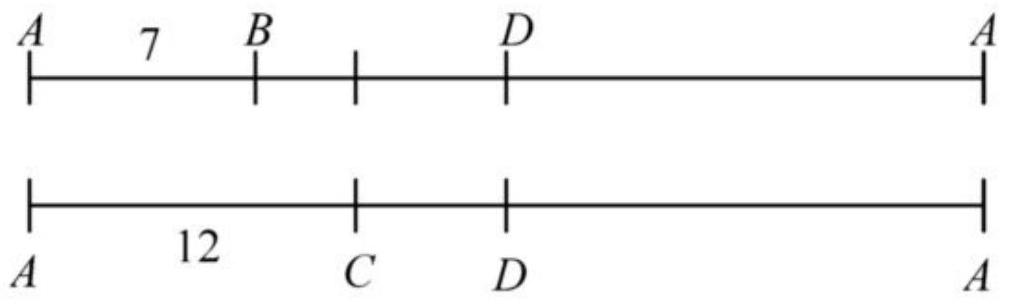
1) $12-7=5$ (cm) - by this much $B D$ should be longer than $D C$;
2) $9-5=4$ (cm) - two segments $C D$;
3) $4: 2=2$ (cm) - the length of segment $C D$;
4) $2+5=7$ (cm) - the length of segment $B D$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many times will a three-digit number increase if the same number is appended to it?
|
1. Let's write down a random three-digit number (531) and append the same number to it, resulting in -531531. Let's find their quotient:
$$
531 \times 531: 531=1001
$$
The pattern found is also valid for other three-digit numbers.
Answer: The three-digit number will increase by 1001 times.
|
1001
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
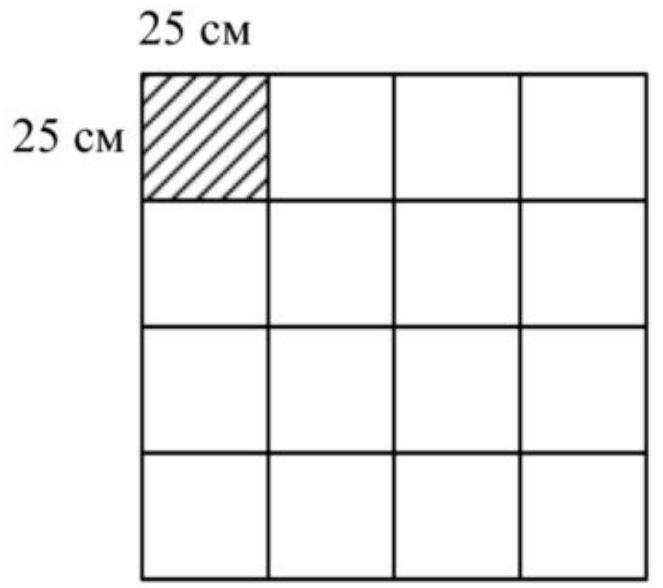
2. Carlson has a runny nose. He uses square handkerchiefs measuring 25 cm $\times 25 \mathrm{~cm}$. Over eight days, Carlson used $3 \mathrm{~m}^{2}$ of fabric. How many handkerchiefs did Carlson use per day?
|
2. First method of solving.
1) $25 \times 25=625\left(\mathrm{~cm}^{2}\right)-$ area of one handkerchief;
2) $3 \times 10000=30000\left(\mathrm{~cm}^{2}\right)$ - contained in $3 \mathrm{~m}^{2}$;
3) $30000: 625=48$ (handkerchiefs) - Carlson used over 8 days
4) $48: 8=6$ (handkerchiefs) - Carlson used per day.
Second method of solving (Setov Mikhail, student of School No. 15).
From 1 m², 16 handkerchiefs can be obtained (see diagram). Carlson used $3 \mathrm{~m}^{2}$, which means $3 \times 16=48$ handkerchiefs over 8 days. Therefore, he used 6 handkerchiefs per day $(48: 8=6)$.
Third method of solving (Babenko Dima, student of School No. 28).
1) $300 \cdot 100=30000\left(\mathrm{~cm}^{2}\right)-$ was in $3 \mathrm{~m}^{2}$;
2) $300: 25=12$ (h.) - on one side
3) $100: 25=4$ (h.) - on the other side.
4) $12 \times 4=48$ (h.) — in total.
5) $48: 8=6$ (h.) — Carlson used per day.
Fourth method of solving (Selemin Alexei, student of School No. 9)
1) $25 \times 25=625\left(\mathrm{~cm}^{2}\right)$ - area of one handkerchief;
2) $3 \times 10000=30000\left(\mathrm{~cm}^{2}\right)$ - contained in 3 square meters;
3) $30000: 8=3750\left(\mathrm{~cm}^{2}\right)$ — fabric Carlson used per day;
4) $3750: 625=6$ (h.) — Carlson used per day.
Answer: 6 handkerchiefs.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If a schoolboy bought 11 notebooks, he would have 8 rubles left, but for 15 notebooks, he would be short of 12 rubles and 24 kopecks. How much money did the schoolboy have?
|
3. Let's represent the condition of the problem in a drawing:
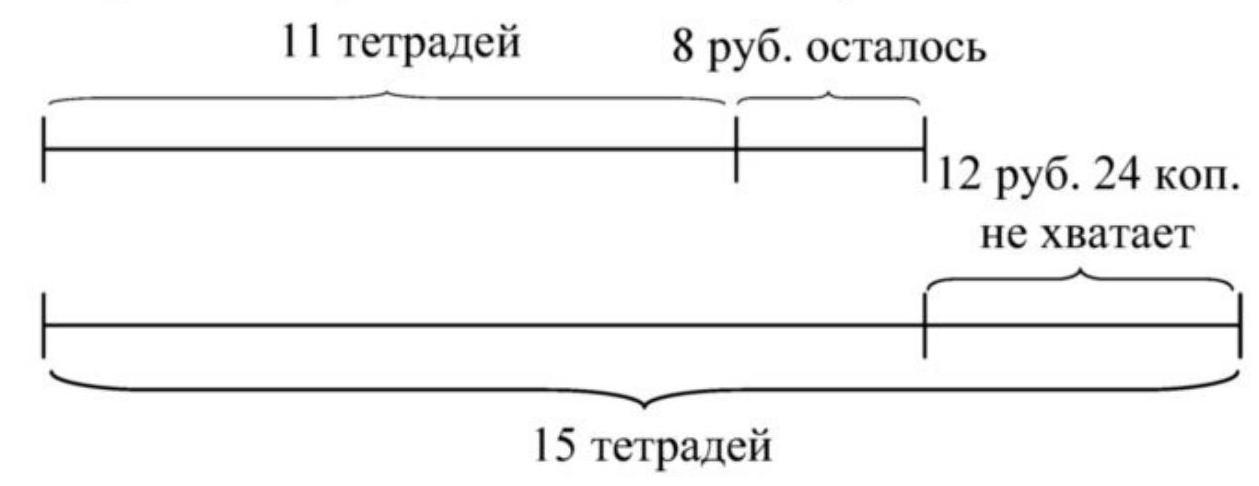
1) $15-11=4$ (notebooks) - the difference in the number of notebooks purchased;
2) $800+1224=2024$ (kop.) - the cost of 4 notebooks;
3) $2024: 4=506$ (kop.) - the cost of one notebook;
4) $506 \times 11=5566$ (kop.) - the cost of 11 notebooks;
5) $5566+800=6366$ (kop.) $=63$ rubles 66 kop. - the amount the schoolboy had.
Answer: the schoolboy had 63 rubles 66 kop.
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a box, there are 7 blue and 5 red balls. What is the minimum number of balls that need to be taken out to ensure that among them there are at least 2 blue and 1 red?
|
5. The worst-case scenario is if we draw 7 balls and they all turn out to be blue. To get another red ball, we need to draw one more ball. In this case, there will definitely be one red ball and 2 blue balls among the balls.
Answer: 8 balls.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The boy caught a fish. When asked how much the caught fish weighed, he said: “I think the tail weighs 1 kg, and the head weighs as much as the tail and half the body, and the body weighs as much as the head and the tail together.” How much does the fish weigh?
|
2. From the problem statement, it is known that the tail ( $X$ ) weighs 1 kg. The weight of the head is equal to the weight of the tail plus an additional $1 / 2$ of the body weight (T):
$$
\Gamma=\mathrm{X}+\mathrm{T} / 2 \text { or } 2 \Gamma=2 \mathrm{X}+\mathrm{T} .
$$
Since the tail weighs 1 kg, then $2 \Gamma=2+$ T .
From another condition, it is known that $\mathrm{T}=\Gamma+\mathrm{X}$ or $\mathrm{T}=\Gamma+1$.
From the obtained equations, we have:
$$
2 \Gamma=2+\Gamma+1, \Gamma=3, \mathrm{a} T=4 .
$$
Thus, the fish weighs $1+3+4=8$ (kg).
Answer: 8 kg.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. This figure consists of 6 identical squares. Its perimeter is 84 cm. Find the area of this figure.
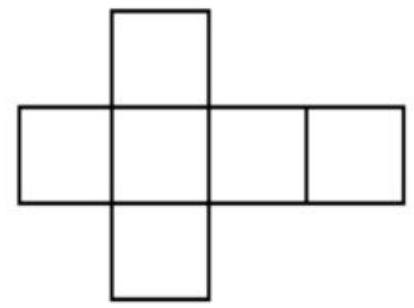
|
3. 1 ) $84: 14=6$ (cm) - the length of the side of the square.
2) $6 \times 6=36$ (cm$^2$) - the area of one square.
3) $36 \times 6=216$ (cm$^2$) - the area of the entire figure.
Answer: 216 sq. cm.
|
216
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many numbers less than 96 are divisible by 2 and 3?
|
5. We need to select numbers from 1 to 95 that are divisible by 2 and 3, which means they are divisible by 6. Such numbers are: $6,12,18$, $24,30,36,42,48,54,60,66,72,78,84,90$. There are 15 such numbers in total.
The number of such numbers could also be determined as follows:
$$
95: 6=15 \text { (remainder 5). }
$$
Answer: 15 numbers.
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. If from each of two numbers you subtract half of the smaller one, the remainder of the larger one is three times the remainder of the smaller one. How many times larger is the larger number than the smaller one?
|
1. The first way to solve the problem is to represent the condition of the problem in the form of a drawing.
From the drawing, it is clear that the first number is twice as large as the second.
The second way to solve the problem is to solve it without relying on a drawing. Since the remainder of the smaller number is half of the number itself, the larger number contains 4 halves of the smaller number and is therefore twice as large as the smaller one.
The third way to solve (Shabanov Konstantin, student of Gymnasium No. 24).
Let there be two numbers \(a\) and \(b\), where \(a > b\). Then
\[
\begin{aligned}
& a - b / 2 = x \\
& b - b / 2 = y, \quad y = b / 2
\end{aligned}
\]
By the condition
\[
x : y = 3, \quad x = 3 y
\]
that is
\[
x = 3 b / 2 \text{.}
\]
Since \(a - b / 2 = x\) and \(x = 3 b / 2\), we can find
\[
a = b / 2 + x = x = b / 2 + 3 b / 2 = 2 b \text{.}
\]
The larger number \(a\) is twice as large as the smaller \(b\).
The fourth way to solve (Lakhov Evgeny, student of School No. 12).
It became: the larger one \(-3x\), the smaller one \(-x\).
It was: the larger one \(3x + x = 4x\)
The smaller one \(x + x = 2x, \quad 4x : 2x = 2\) (times).
Answer: the larger number is 2 times larger.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Three teams scored 285 points in the Olympiad. If the team from School No. 24 had scored 8 points less, the team from School No. 46 had scored 12 points less, and the team from School No. 12 had scored 7 points less, then all of them would have scored equally. How many points did the teams from Schools No. 24 and No. 12 score together?
|
2. First method of solving. Let's make a brief record of the problem in the form of a drawing
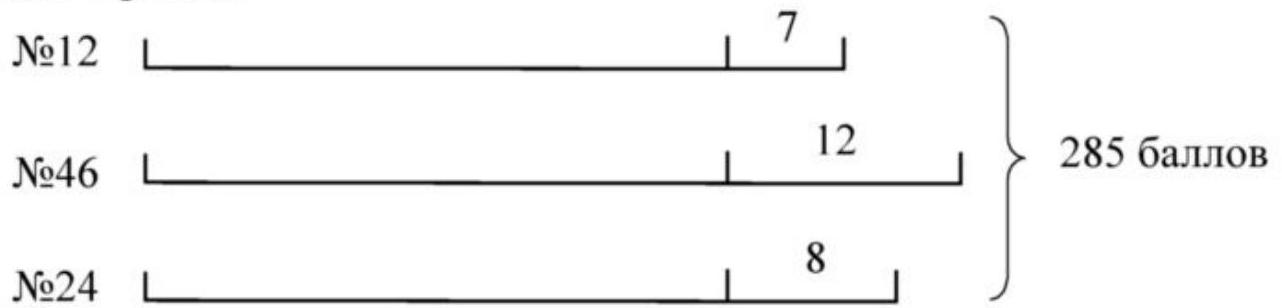
1) $7+12+8=27$ (points) - this is how many fewer points all schools scored;
2) $285-27=258$ (points) - this would be their total sum;
3) $258: 3=86$ (points) - each school would have scored;
4) $86+7=93$ (points) — School No. 12 scored;
5) $93+(86+8)=187$ (points) — Schools No. 12 and No. 24 scored together.
Second method of solving. This problem can also be solved algebraically. Let $x$ be the number of points scored by School No. 12, then we can set up the equation:
$$
\begin{aligned}
& x+(x+1)+(x+5)=285 \\
& 3 x=279 \\
& x=93 \\
& 93 \times 2+1=187
\end{aligned}
$$
Answer: 187 points.
|
187
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There were 2 minutes left before the electric train departed when the motorist was 2 km from the station. For the first minute, he drove at a speed of 30 km/h. At what speed should he drive during the second minute to catch the train?
|
5. The first method of solving.
1) $2 \times 1000=2000$ (m) - need to travel;
2) $30 \times 1000=30000(\mathrm{m} / \mathrm{h})$ - speed of the car;
3) $30000: 60=500$ (m/s) - speed in the first minute;
4) $2000-500=1500$ (m) - left to travel in 1 minute;
5) $1500 \times 60=90000(\mathrm{m} / \mathbf{h})=90(\mathrm{km} / \mathbf{h})$.
The second method of solving (Alexei Petrov, student of School No. 14).
If the speed is 30 km/h, then in 1 minute the motorist will travel $1 / 2$ km. He has 1.5 km left. 1.5 km is exactly 3 times $1 / 2$. Therefore, the speed should be three times greater $30 \times 3=90$ (km/h).
The third method of solving (Denis Skrynnikov, student of School No. 14).
To travel the entire distance in 1 minute, the motorist needs to travel at a speed of 120 km/h, and to travel in 2 minutes, he needs to travel at a speed of 60 km/h. But he traveled at a speed of 30 km/h for one minute, so he needs to travel the second minute at a speed of $120-30=90$ (km/h).
Answer: the motorist should travel at a speed of 90 km/h.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. One side of the square was increased by 5 times, and the other side was reduced by 2 times, resulting in a rectangle with an area of $160 \mathrm{~cm}^{2}$. What is the side length of the square
|
6. First method of solution.
1) $160: 5=32\left(\mathrm{~cm}^{2}\right)$ - area of half the square;
2) $32 \times 2=64\left(\mathrm{~cm}^{2}\right)$ - area of the original square;
3) $64: 8=8$ (cm) - side of the square.
Second method of solution. The algebraic solution of this problem is as follows: let $x$ be the side of the square, then $x / 2$ and $5 x$ are the sides of the rectangle. Its area is 160 sq.cm.
$$
5 x \times x / 2=160 \text { or } 5 x \times x=320, x \times x=64, x=8(\text { cm). }
$$
Answer: the side of the square is 8 cm.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate in the most rational way
$$
12 \times 171+29 \times 9+171 \times 13+29 \times 16
$$
|
$$
\begin{aligned}
& 12 \times 171 + 29 \times 9 + 171 \times 13 + 29 \times 16 = \\
& = (171 \times 12 + 171 \times 13) + 29 \times 9 + 29 \times 16 = \\
& = 171 \times (12 + 13) + 29 \times (9 + 16) = \\
& = 171 \times 25 + 29 \times 25 = (171 + 29) \times 25 = \\
& = 200 \times 25 = 5000
\end{aligned}
$$
Answer: 5000.
|
5000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. From two points $A$ and $B$, the distance between which is 300 km, two cars set off simultaneously. The speed of the car that set off from $A$ is 40 km/h. Determine the speed of the second car, given that after two hours the distance between the cars was 100 km.
|
3. Since the problem does not specify the direction they were traveling, we need to consider two cases: moving in the same direction and moving in different directions.
First case. Moving in the same direction. Let the first car travel from $A$ to $B$ at a speed of 40 km/h.

1) $40 \times 2=80$ (km) - the first car traveled in two hours $(A C)$
2) $300-80=220$ (km) - the remaining distance for the first car to reach $B(C B)$.
Since the second car was not moving towards the first, in this case, there cannot be a distance of 100 km between the first and second car after 2 hours, and the problem has no solution in this case.
Now let the first car travel from $A$ in the direction opposite to $B$.

1) $40 \times 2=80$ (km) - the first car traveled in two hours $(A C)$
2) $100-80=20$ (km) - the remaining distance for the second car to reach $A$;
3) $300-20=280$ (km) - the distance the second car traveled in 2 hours;
4) $280: 2=140(\kappa m / h)$ - the speed of the second car.
Second case. The cars are moving in different directions. In this case, they can move in opposite directions or towards each other. In the first situation, it is obvious that there is no solution. Let's consider the second situation.

1) $40 \times 2=80$ (km) - the first car traveled in two hours;
2) $300-100-80=120$ (km) — the distance the second car traveled in two hours;
3) $120: 2=60(\mathrm{km} / \mathrm{h})$ - the speed of the second car.
Answer: depending on the direction of movement, the speed of the second car is 60 km/h or 140 km/h.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In 1996, a farmer bought two sheep. This year he did not get any offspring. The first sheep gave birth to 1 sheep every three years, and the second sheep gave birth to 1 sheep every two years. All the born sheep gave birth to 1 sheep annually. How many sheep will the farmer have in the year 2000?
|
6. Let's draw a diagram according to the problem statement.

Answer: 9 sheep.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Arrange the order of operations in the expression
$$
1891-(1600: a+8040: a) \times c .
$$
and calculate its value when $a=40$ and $c=4$. Show how the expression can be modified without changing its numerical value.
|
$$
\begin{aligned}
& 1891-\left(1600: 40+8040^{5}: 40\right)^{4} \times 4= \\
& =1891-(40+201) \times 4= \\
& =1891-241 \times 4=1891-964=927 .
\end{aligned}
$$
Based on the properties of arithmetic operations, we can write:
$$
\begin{aligned}
& 1891-(1600: a+8040: a) \times c= \\
& =1891-(8040: a+1600: a) \times c= \\
& =1891-((1600+8040): a) \times c= \\
& =1891-(1600: a) \times c-(8040: a) \times c= \\
& =1891-(1600 \times c): a-(8040 \times c): a= \\
& =1891-(1600 \times c+8040 \times c): a
\end{aligned}
$$
Answer: 927.
|
927
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In this century, 200 years will be marked since the birth of the famous Russian mathematician, a native of Kaluga Governorate, Pafnuty Lvovich Chebyshev. Among the numbers that record his year of birth, the sum of the digits in the hundreds and thousands place is three times the sum of the digits in the units and tens place, and the digit in the tens place is greater than the digit in the units place. Determine the year of birth of P.L. Chebyshev, given that he was born and died in the same century and lived for 73 years.
|
3. Since in the 21st century the 200th anniversary will be marked, the first digit in the number will be -1, and the second will be 8, and the year of birth has the form $18 a c$.
The sum of the digits in the hundreds and thousands place is 9, and it is three times the sum of the digits in the units and tens place ($9: 3=3$ - this is the sum of the digits in the units and tens place). The number 3 can be represented as the sum of two addends in the following way:
$$
3=0+3=1+2 \text {. }
$$
From this, we can conclude that the digits in the tens and units can be 3 and 0, 1 and 2. Thus, the year of his birth can be $1803, 1812, 1821, 1830$. Since the digit in the tens place is greater than the digit in the units place, only two dates remain: 1821 and 1830. The latter year does not satisfy the condition that he was born and died in the same century $(1830+73=1903)$.
Answer: 1821.
|
1821
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The perimeter of quadrilateral $A B C D$ is 100 cm. The length of side $A B$ is 41 cm, side $B C$ is 18 cm shorter than side $A B$, but 6 cm longer than side $C D$. Find the length of side $A D$.
|
1. The first method of solving.
1) $41-18=23$ cm - the length of side $B C$;
2) $23-6=17$ cm - the length of side $C D$;
3) $41+23+17=61$ cm - the sum of sides $A B, B C$, and $C D$;
4) $100-61=19$ cm - the length of side $A D$.
The second method of solving. Another approach can be used to solve this problem. First, determine the tripled length of side $A B$. Then, subtract the excess length from the obtained number
$$
41 \times 3-(18 \times 2+6)=81 \text {. }
$$
On the last step, determine $A D$
$$
100-81=19
$$
To make this solution more understandable, it is necessary to make a brief record of the problem's conditions.
Answer: the length of side $A D$ is 19 cm.
|
19
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. First, three, and then four people shook hands with each other. How many handshakes were there? Find the pattern in counting the number of handshakes and determine their number for 7 people.
|
6. When solving this problem, we should use incomplete induction. Let's analyze the first situation and try to find a pattern in determining the number of handshakes based on the number of participants. In the first case, when there were three people, the following options are possible:
$$
\text { 1-2, 1-3, 2-3. }
$$
The number of handshakes is three $(1+2=3)$.
Thus, we can hypothesize that the number of handshakes is equal to the sum of the numbers less than the number of participants by 1. Let's test this hypothesis for the second case. If four people participated in the handshakes, the following options are possible:
$$
1-2,1-3,1-4,2-3,2-4,3-4
$$
The total number of handshakes will be $6(1+2+3=6)$. The hypothesis is confirmed.
Now we can determine the number of handshakes for 7 people:
$$
1+2+3+4+5+6=21
$$
Answer: 21 handshakes.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. From 16 m of fabric, 4 men's and 2 children's coats were sewn. How many meters of fabric are needed to sew one men's and one children's coat, if from 18 m of the same fabric, 2 men's and 6 children's coats can be sewn
|
7. Let's make a brief record of the problem's condition:
$$
\begin{aligned}
& 4 \text { m, } 2 \text { d }-16 \text { m; } \\
& 2 \text { m, } 6 \text { d }-18 \text { m. }
\end{aligned}
$$
To ensure that the brief record contains the same quantities, we will double the second order:
$$
\begin{aligned}
& 4 \text { m, } 2 \text { d }-16 \text { m} ; \\
& 4 \text { m, } 12 \text { d }-36 \text { m} .
\end{aligned}
$$
1) $12-2=10$ (d) - by this much more children's coats were ordered the second time;
2) $36-16=20$ (m) - by this much more fabric was used for children's coats the second time;
3) $20: 10=2$ (m) - the amount of fabric needed to sew one children's coat;
4) $16-2 \times 2=12$ (m) - the amount of fabric remaining for the first order of 4 men's coats;
5) $12: 4=3$ (m) - the amount of fabric needed to sew one men's coat.
Answer: 3 meters of fabric are needed to sew one men's coat, and 2 meters for one children's coat.
## SEVENTEENTH
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The teacher cut a square sheet of paper with a side of 5 cm into two rectangles. The perimeter of one of these rectangles is $16 \mathrm{cm}$. What is the perimeter of the other?
|
1. The first method of solving.
1) $16: 2=8$ cm - the semi-perimeter of the first rectangle;
2) $8-5=3$ cm - the width of the first rectangle;
3) $5-3=2$ cm - the width of the second rectangle;
4) $(2+5) \times 2=14 \text{cm} -$ the perimeter of the second rectangle.
The second method of solving. Before solving by the second method, it is necessary to make a drawing.
1) $16: 2=8$ cm - the semi-perimeter of the first rectangle;
2) $8-5=3$ cm - the width of the first rectangle;
3) $5 \times 4=20$ cm - the perimeter of the square;
4) $3 \times 2=6$ cm - the doubled width of the first rectangle;
5) $20-6=14$ cm - the perimeter of the second rectangle.
Answer: 14 cm.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The sum of three numbers is 1281. From the first number, 329 was subtracted, and to the second number, 401 was added. What needs to be done with the third number so that the sum does not change? Will the solution to the problem change if the word "sum" is replaced with "difference"?
|
2. First method of solving. Find out by how much the sum has increased ( $401-329=72$ ). To keep the sum the same, it is necessary to subtract 72 from the third number.
Second method of solving. Let $a, b, c$ be the first, second, and third numbers. According to the condition, their sum is 1281
$$
a+b+c=1281
$$
From the first number, 329 is subtracted $(a-329)$, and to the second number, 401 is added $(b+401)$. Their sum is
$$
a-329+b+401=a+b+72
$$
To keep the sum of the three numbers $a, b, c$ unchanged and equal to 1281, the third number must be reduced by $72(c-72)$.
If the word "sum" in the condition is replaced with "difference," the first step is to find out by how much the difference between $a$ and $b$ will decrease $(329+401=770)$. To keep the difference between $a, b$, and $c$ unchanged, 770 must be subtracted from the last number.
Answer: the third number must be reduced by 72. The solution to the problem will change.
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two trains leave from two cities at the same time. The first one travels at 40 km/h, while the second one travels at 48 km/h. How far apart will these trains be from each other after 8 hours, if they are moving in the same direction and the distance between the cities is 892 km?
|
3. The trains are moving in the same direction, so they can move in the direction of $A B$ or $B A$. Let's consider each of these cases.
The trains are moving in the direction of $A B$.
1) $40 \times 8=320$ km - the first train traveled;
2) $48 \times 8=384$ km - the second train traveled;
3) $384-320=64$ km - by this much the distance between them increased
4) $892+64=956$ km - the distance between the trains.
The trains are moving in the direction of $B A$.
1) $40 \times 8=320$ km - the first train traveled;
2) $48 \times 8=384$ km - the second train traveled;
3) $384-320=64$ km - by this much the distance between them decreased
4) $892-64=828$ km - the distance between the trains.
Instead of the first three steps, we could have performed two: $48-40=8$ km - by this much the distance between the trains increased (decreased) in one hour. Multiplying by 8, we find out by how much the distance between the trains increased (decreased) in eight hours: $8 \times 8=64$ km.
Answer: the distance between the trains is 956 km or 828 km.
|
956
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In A.S. Pushkin's fairy tale "The Priest and His Workman Balda," it is said: "Balda sat on the mare and rode a verst so that the dust rose in a column." Determine how many tens of meters are contained in the length of the path that Balda rode on the mare. $(1$ verst $=500$ sazhen, 1 sazhen $=3$ arshins, 1 arshin $=$ $71 \mathrm{~cm})$.
|
1. 2) $3 \times 500=1500$ arshins - in one verst;
2) $71 \times 1500=106500$ cm - in one verst;
3) $106500: 100=1065$ m - in one verst;
4) $1065: 10=106$ tens (remainder 5) — the number of tens of meters.
Answer: in one verst there are 106 tens of meters.
|
106
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the mathematics olympiad in two rounds, it is necessary to solve 14 problems. For each correctly solved problem, 7 points are given, and for each incorrectly solved problem, 12 points are deducted. How many problems did the student solve correctly if he scored 60 points?
|
3. Let's determine the number of problems solved by the student, given that he received 7 points for each problem: $60: 7=8$ (remainder 4). Since 12 points were deducted for each incorrectly solved problem, the number of correctly solved problems was more than 8. Further, by trial and error, we can establish that there were 12.
Answer: The student solved 12 problems correctly.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. One side of a rectangle is $5 \mathrm{~cm}$, and the other is the smallest two-digit number that is divisible by 3. For the second rectangle, one side is equal to the shorter side of the first. The area of one rectangle is $25 \mathrm{~cm}^{2}$ greater than the area of the other. Determine the unknown side of the second rectangle.
|
6. First, let's determine the unknown side of the rectangle. For this, we will find the smallest two-digit number that is divisible by 3, which is 12. According to the problem, one side of the second rectangle is $5 \mathrm{~cm}$. Let's determine the area of the first rectangle $(12 \times 5=60)$. Since the problem does not specify which rectangle's area is larger by $25 \mathrm{~cm}^{2}$, we need to consider two cases.
First case. Suppose the area of the first rectangle is $25 \mathrm{~cm}^{2}$ larger than the area of the second rectangle. In this case, the area of the second rectangle is $35 \mathrm{~cm}^{2}(60-25=35)$. Knowing that one side of the second rectangle is 5 cm and its area is 35 $\mathrm{cm}^{2}$, we can determine the second side $-7 \mathrm{~cm}(35: 5=7)$.
Second case. Suppose the area of the second rectangle is $25 \mathrm{~cm}^{2}$ larger than the area of the first rectangle. In this case, the area of the second rectangle is $85 \mathrm{~cm}^{2}(60+25=85)$. Knowing that one side of the second rectangle is 5 cm and its area is 85 $\mathrm{cm}^{2}$, we can determine the second side $-17 \mathrm{~cm}(85: 5=17)$.
Answer: 7 cm or 17 cm.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. To number the pages in a mathematics textbook, 390 digits were required. How many pages are in the mathematics textbook?
|
7. For writing the first nine pages, 9 digits are needed $(1,2,3,4,5,6,7,8,9)$.
For numbering pages from 10 to 99, 90 two-digit numbers are needed, which use $90 \times 2=180$ digits.
In the next step, we determine how many digits were used to write three-digit numbers $(390-180-9=201)$. Now we find out how many pages were written using three-digit numbers $(201: 3=67)$.
On the last step, we find the answer to the problem $(9+90+$ $+67=166)$
Answer: the mathematics textbook has 166 pages.
## EIGHTEENTH
|
166
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The pages of materials for conducting a math club session are numbered. The last page is numbered 128. How many digits were needed to number all the pages?
|
2. For numbering the first nine pages, 9 numbers are needed.
For numbering pages from 10 to 99, 90 two-digit numbers are needed, which use $90 \times 2=180$ digits.
Let's find out how many three-digit numbers were used for numbering the pages. There will be $29(128-99=29)$. Determine how many digits were used to write 29 three-digit numbers $(29 \times 3=87)$. For numbering all the pages of the book, 276 digits were needed ($9+$ $+180+87=276)$.
Answer: 276 digits.
|
276
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If the thought number is multiplied by 6, and then 382 is added to the product, the result will be the largest three-digit number written with two identical even numbers and one odd number. Find the thought number.
|
3. Let's determine the largest three-digit number written with two identical even digits and one odd digit — this is 988. Subtract 382 from the obtained number, we get 606. This is the sixfold of the thought number. Dividing 606 by 6, we determine the thought number -101.
Answer: 101.
|
101
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A sheet of cardboard measuring 48 cm in length and 36 cm in width needs to be cut into cards measuring 16 cm in length and 12 cm in width. How can this be done to obtain the maximum number of cards?
|
1. In the first step, it is necessary to determine how many cards will fit if the length of each is $16 (48: 16=3)$. Then determine how many cards will fit in the width (36:12 = 3).
Finally, find the number of cards $(3 \times 3=9)$. Then conduct similar reasoning for the case where the cards are laid out by width ( $48: 12=4,36: 16=2$ (remainder 4), $4 \times 2=8$ ). Now we can conclude that the maximum number of cards is 9.
Answer: cut the length into three equal parts of 16 cm, and then cut each of the resulting parts into 3 more parts - 12 cm each.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The sum of three numbers is 121,526. One addend is the largest five-digit number, all digits of which are even; the second is the smallest four-digit number, all digits of which are odd. What is the third number?
|
2. We will sequentially consider all the conditions of the problem. Given that the first addend is a five-digit number, it follows that five digits will be used for its notation (XXXXX). Since it must be the largest and all its numbers are even, this will be the number 88888. The second addend is a four-digit number (XXXX), and since it is the smallest, all of its numbers are odd, so this will be 1111. By determining their sum $(88888+1111=89999)$, we can find the unknown addend. To do this, we subtract the sum of the two found addends from the known sum $(121526-89999=31527)$.
Answer: 31527.
|
31527
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (Ancient Indian problem 3-4th century AD). Of the four sacrificial donors, the second gave twice as many coins as the first, the third three times as many as the second, the fourth four times as many as the third, and all together gave 132 coins. How many did the first give?
|
4. The first method of solving. By analyzing the condition of the problem, one can conclude that the number of coins given by the first person will not be more than 10. We will then refine this number through trial and error. Let's try the number 5.
$$
5+5 \times 2+5 \times 2 \times 3+5 \times 2 \times 3 \times 4=5+10+30+120=165
$$
Since the obtained number is greater than the given number, we made a mistake in our choice. Let's take the number 4. Checking shows that it satisfies the conditions of the problem.
The second method of solving. When solving this problem, it is useful to make a drawing, representing each number as a segment. This way, it will be immediately clear that 33 identical segments equal 132. From this, it is easy to determine the amount of money given by the first donor.
The third method of solving. This problem can also be solved using an equation. For this, let $x$ be the amount of money given by the first donor. Based on the condition, the following equation can be formed:
$$
\begin{gathered}
x+2 x+(2 x) \times 3+(2 x \times 3) \times 4=132 \\
x+2 x+6 x+24 x=132,33 x=132, x=4
\end{gathered}
$$
Answer: the first person gave four coins.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Nikolai was walking to a math olympiad, covering 100 meters per minute. After 36 minutes, he stepped into School No. 15. Then he remembered that he had left the pen at home, with which he had won the school olympiad, and ran back home at a speed of 3 meters per second. How much time did he spend on the return trip?
|
5. 6) $100 \times 36=3600$ m - the distance from home to school;
2) $3 \times 60=180$ m - the number of meters he ran per minute on the way back;
3) $3600: 180=20$ min - the time he spent on the return trip.
Alternatively, the second step could have determined the number of seconds spent on the return trip $(3600: 3=1200$ seconds), and then convert them to minutes ( $1200: 60=20$ minutes).
In this problem, the answer can be represented in seconds, minutes, or hours.
Answer: 1200 seconds (20 min, $1 / 3$ hour).
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two boats departed from piers $A$ and $C$. The speed of the boat traveling from $A$ is 7 km per hour, and from $C$ is 3 km per hour. Determine after how much time the boats will meet, if the distance between the piers is 20 km, and the speed of the river current from $A$ to $C$ is 2 km per hour.
|
4. Since the problem does not specify the direction in which the boats are moving, we need to consider various scenarios: they are moving towards each other; they are moving in the same direction downstream; they are moving in the same direction upstream; they are moving in opposite directions. Given that the boats must meet, we can exclude the last two cases.
Case one - the boats are moving towards each other.
1) $7+2=9$ km/h - the speed of the first boat;
2) $3-2=1 \text{ km/h} -$ the speed of the second boat;
3) $9+1=10$ km/h - the closing speed;
4) $20: 10=2$ hours.
Case two - the boats are moving downstream.
1) $7+2=9$ km/h - the speed of the first boat;
2) $3+2=5$ km/h - the speed of the second boat;
3) $9-5=4$ km/h - the closing speed;
4) $20: 4=5$ hours.
Answer: They will meet in 2 or 5 hours.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (An old entertaining problem). Divide 46 rubles into 8 parts so that each part is 50 kopecks (50 cents) more than the previous one.
|
5. First method of solution. Let the first part be $x$, then the second is $x+50$, the third is $-x+50 \times 2$, the fourth is $-x+50 \times 3$, the fifth is $x+50 \times 4$, the sixth is $-x+50 \times 5$, the seventh is $-x+50 \times 6$, and the eighth is $x+50 \times 7$. We will calculate the sum of all parts.
$$
\begin{gathered}
x+x+50+x+50 \times 2+x+50 \times 3+x+50 \times 4+ \\
x+50 \times 5+x+50 \times 6+x+50 \times 7= \\
=8 x+50 \times 28=8 x+1400 .
\end{gathered}
$$
Since 1400 kopecks is equal to 14 rubles, we get $8 x+14$. According to the problem, this sum is equal to 46 rubles.
We get the equation
$$
8 x+14=46,8 x=32, x=4
$$
The first part is 4 rubles, the second is 4 rubles 50 kopecks (4 rubles + 50 kopecks = 4 rubles 50 kopecks), the third is 5 rubles, the fourth is 5 rubles 50 kopecks, the fifth is 6 rubles, the sixth is 6 rubles 50 kopecks, the seventh is 7 rubles, and the eighth is 7 rubles 50 kopecks.
Second method of solution. The problem can be solved using a brief record of the problem's condition in the form of a diagram.
1) $50 \times 28=1400$ kopecks - was more than if all parts were like the first;
2) $4600-1400=3200$ kopecks - is the amount for eight equal parts;
3) $3200: 8=400$ kopecks $=4$ rubles - the first part.
Answer: 4 rubles, 4 rubles 50 kopecks, 5 rubles, 5 rubles 50 kopecks, 6 rubles, 6 rubles 50 kopecks, 7 rubles, 7 rubles 50 kopecks.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A wire 104 centimeters long was bent into a rectangular frame. The length and width of this frame are whole numbers of centimeters. In how many ways can the frame be obtained?
|
6. First, let's determine what the sum of the length and width is, that is, we will calculate the semi-perimeter. For this, we divide 104 by 2 and get 52. Let's represent the number 52 as the sum of two addends:
$$
52=1+51=2+50=3+49=\ldots=25+27=26+26 \text {. }
$$
We get 26 ways.
Answer: 26 ways.
|
26
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From points $A$ and $B$, which are 300 km apart, two cars set off simultaneously. The speed of the car that left from $A$ is 40 km/h. Determine the speed of the second car, given that after two hours the distance between them was 100 km.
|
2. The problem statement does not specify the direction in which the cars are moving, so all possible scenarios should be considered: moving in opposite directions, towards each other, both in the direction of $A B$, and both in the direction of $B A$.
Assume the cars are moving in opposite directions. This scenario, as well as the scenario where both cars move in the direction of $A B$, is impossible because the distance between the cars would be greater than 100 km.
Assume the cars are moving towards each other.
1) $40 \times 2=80$ km - the first car traveled in two hours;
2) $80+100=180$ km - the distance from $A$ to the second car;
3) $300-180=120$ km - the second car traveled in two hours;
4) $120: 2=60 \text{ km} / \text{h}$ - the speed of the second car.
Assume both cars are moving in the direction of $B A$.
1) $40 \times 2=80$ km - the first car traveled in two hours;
2) $300+80=380$ km - the distance from $B$ to the first car;
3) $380-100=280$ km - the second car traveled in two hours;
4) $280: 2=140$ km $/$ h - the speed of the second car.
Answer: The speed of the second car is 140 km $/$ h or 60 km $/$ h.
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The great commander, Marshal of the Soviet Union, Georgy Konstantinovich Zhukov, was born in the village of Strelkovka, Kaluga Governorate. He lived for 78 years. In the 20th century, he lived 70 years longer than in the 19th century. In what year was G.K. Zhukov born?
|
3. Let's make a brief record of the problem statement

1) $78-70=8$ years - doubled the time of life in the 19th century;
2) $8: 2=4$ years - G.K. Zhukov lived in the 19th century;
3) $1900-4=1896$ - the birth year of G.K. Zhukov
Answer: Zhukov was born in 1896.
|
1896
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. If a schoolboy bought 11 pens, he would have 8 rubles left, but for 15 pens, he would be short of 12 rubles 24 kopecks. How much money did the schoolboy have?
|
4. 5) $15-11=4$ pens - bought more the second time;
2) $8+12=20$ rubles - amount to four pens;
3) $20: 4=5$ rubles - cost of one pen;
4) $5 \times 11+8=63$ rubles - the schoolboy had.
Answer: the schoolboy had 63 rubles.
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A string 60 dm long was cut into three pieces. The length of one of them is 1 cm more than another and 1 cm less than the third. Find the length of each piece.
|
2. First method of solving. Let's make a drawing according to the problem statement.
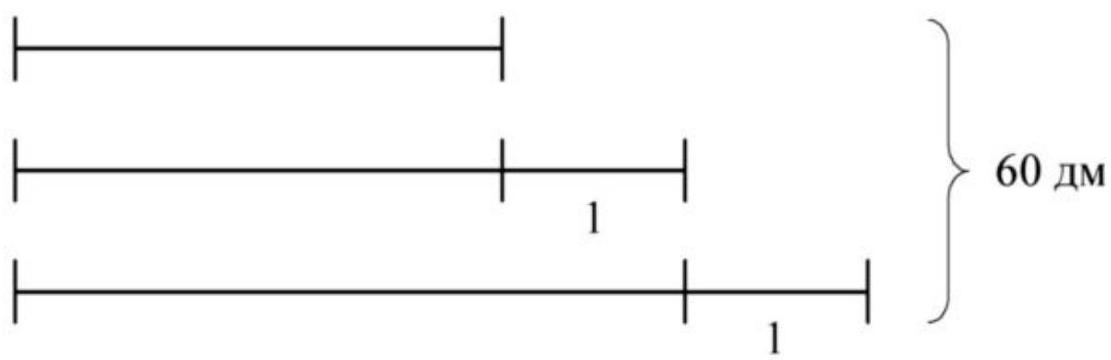
1) $600-3=597$ cm - the length of the string if all parts were as small as the smallest one
2) $597: 3=199$ cm - the length of the first part;
3) $199+1=200$ cm - the length of the second part;
4) $200+1=201$ cm - the length of the third part.
Second method of solving. Let's denote one part of the rope as $a$, then the other is $a-1$, and the third is $a+1$. Since the length of the rope is 600 cm (60 dm $=600$ cm), we can form the equation: $a + a - 1 + a + 1 = 600, 3a = 600, a = 200$ cm. Now let's find the lengths of the other two parts: $200 - 1 = 199, 200 + 1 = 201$.
Answer: the length of the first part is 199 cm, the second is $200$ cm, and the third is $201$ cm.
|
199
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. From a class of 20 people, a team of three students is formed to participate in mathematics, Russian language, and informatics olympiads. In this class, all students excel academically. How many ways are there to form the team of olympiad participants, if each member of the team participates in one olympiad?
|
6. We can select a participant for the mathematics olympiad in twenty ways, for the Russian language olympiad in nineteen ways, and for informatics in eighteen ways. In total, this results in 6840 ways $(20 \times 19 \times 18=6840)$.
Answer: 6840 ways to form the team.
|
6840
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many three-digit numbers less than 500 do not contain 1?
|
2. Let's determine which digit can represent the hundreds place of $-2.3$ or 4. Consider numbers of the form $2 x x$. There will be a total of one hundred such numbers. The digit 1 can be in the tens or units place. If 1 is in the tens place ($21 x$), we get the numbers: $210, 211, 212, 213, 214, 215, 216, 217, 218, 219$. There are ten such numbers. In each ten, 1 can be in the units place:
$$
\text { 201, 211, 221, 231, 241, 251, 261, 271, 281, } 291 .
$$
There are also ten such numbers. Since the number 211 appears twice, the total number of numbers containing the digit 1 will be $19(10+9=19)$. Therefore, the number of numbers not containing the digit 1 in three-digit numbers of the form $2 x x$ will be $81(100-19=81)$.
Similarly, considering numbers of the form $3 x x$ and $4 x x$, we can establish that the total number of three-digit numbers less than 500 that do not contain the digit 1 will be $243(81 \times 3=243)$.
Answer: 243 numbers.
|
243
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two friends collected 300 stamps. One collected 5 per week, the other - 3. The second boy collected for 20 weeks longer than the first. How many days did each boy collect stamps?
|
2. 3) $20 \times 3=60 \text{m}$ - the second boy collected in 20 weeks;
2) $300-60=240 \text{m}$ - the boys collected during the time the first boy was collecting;
3) $5+3=8$ m - they collected per day;
4) $240: 8=30$ days - the first boy collected;
5) $30+20=50$ days - the second boy collected.
Answer: the first boy collected stamps for 30 days, and the second for 50.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Every 24 hours, the clock runs ahead by 3 minutes. They were set accurately. After what shortest time will the clock hands show the exact time again?
|
4. To make the clock show the exact time, it is necessary for it to run ahead by 12 hours. Let's find out how many minutes are in 12 hours $\operatorname{cax}(12$ hours $=60$ min. $\times 12=720$ min.). Determine the number of days $-720: 3=240$.
Answer: 240 days.
|
240
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In this century, the 200th anniversary of the birth of the famous Russian mathematician, a native of the Kaluga province P.L. Chebyshev, will be celebrated. In the number that records his year of birth, the sum of the numbers in the hundreds and thousands place is three times the sum of the numbers in the tens and units place, and the digit in the tens place is greater than the digit in the units place. Determine the year of birth of P.L. Chebyshev, given that he was born and died in the same century and lived for 73 years.
|
6. Since in the 21st century the 200th anniversary of P.L. Chebyshev's birth will be celebrated, he was born in the 19th century - 18th. The sum of the numbers in the thousands and hundreds place is $9(1+8=9)$. The sum of the numbers in the tens and units place is three times less than 9. Therefore, it is $3(a+b=3)$. The number three can be represented as the sum of the following two addends: $3=0+3=1+2$. The numbers $a$ and $b$ can take the values 0 and 3 or 1 and 2. The year of birth can fall on $1803, 1830, 1812, 1821$. The numbers 1803 and 1812 should be excluded, as they do not satisfy the condition that the number of tens must be greater than the number of units. Only 1830 and 1821 remain. According to the last condition, P.L. Chebyshev lived for 73 years, was born and died in the same century. This condition is met only by the number - 1821. ( $1830+73=1903-$ this is the $\mathrm{XX}$ century).
Answer: 1821.
|
1821
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. How many numbers less than 2011 are divisible by 117 and 2?
|
7. When solving this problem, one can reason as follows. First, list the numbers less than 2011 and divisible by 117 (2), then among them, select those that are divisible by 2 (117), and determine how many there are.
Since the number is divisible by both 2 and 117, it will also be divisible by their product $2 \times 117=234$. By dividing 2011 by 234, we can determine the number of such numbers (2011:234 $=8$ (remainder 128).
Answer: eight numbers.
## TWENTY-SECOND
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A rectangular section of road with a length of 800 m and a width of 50 m was paved with asphalt. For every 100 m$^{2}$ of road, 3 tons 800 kg of asphalt were used. How many tons of asphalt were used?
|
1. 2) $800 \times 50=40000 \mathrm{~m}^{2}$ - the area of the road;
2) $40000: 100=400$ times - the road contains $100 \mathrm{m}^{2}$ segments;
3) $3800 \times 400=1520000 \mathrm{~kg}=1520 \mathrm{~T}$ - the amount of asphalt used.
Answer: 1520 tons of asphalt were used.
|
1520
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What digits stand in the natural number sequence at the thirteenth and one hundred twentieth positions?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
2. Let's write down the first fifteen numbers:
$$
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
$$
To fill the first nine positions, 9 digits are required, and then two digits are needed to write each two-digit number. Starting from the tenth position, two-digit numbers are written. For each of them, two places are allocated. To determine which digit is in the thirteenth position, we need to find out which digit of the units or tens of which two-digit number will be written. For this, we find the difference between thirteen and nine (four) and divide it by two $(4: 2=2)$. This means that the thirteenth position is occupied by the units digit of the second two-digit number, which is 1. Similarly, the 120th position is occupied by the tens digit of $55(120-9): 2=55$ (remainder 1).
Answer: 6.
|
6
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. A two-digit number was increased by 3, and it turned out that the sum is divisible by 3. When 7 was added to this same two-digit number, the resulting sum was divisible by 7. If 4 is subtracted from this two-digit number, the resulting difference is divisible by four. Find this two-digit number.
|
4. Since the sum of a two-digit number and three is divisible by three and the second addend is also divisible by three, the unknown two-digit number is divisible by three. Similarly, we can establish that the two-digit number is also divisible by seven and four. Thus, it is divisible by $84(3 \times 4 \times 7=84)$. Among the two-digit numbers divisible by eighty-four, there is only one - 84.
Answer: 84.
|
84
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. At $17-00$ the speed of the racing car was 30 km/h. Every 5 minutes thereafter, the speed increased by 6 km/h. Determine the distance traveled by the car from $17-00$ to $20-00$ of the same day.
|
5. Let's write down the sequence of numbers expressing the speed at which the car was traveling on the highway: $30,36,42,48,54 \ldots 240$. To determine the distance, we need to calculate the sum:
$$
\begin{aligned}
30: 12 & +36: 12+42: 12+\ldots .+234: 12+240: 12= \\
& =(30+36+42+. .+234+240): 12
\end{aligned}
$$
If we add the first and last terms, the second and second-to-last terms, and other similar pairs of numbers, we will always get $270(30+240=36+234=42+228$ and so on). Let's determine how many such pairs there are. The speed increased 12 times every hour ( $60: 5=12$ ). Over three hours, it increased 36 times. Therefore, there are 18 such pairs. To determine the distance, we multiply 270 by 18 and divide by 12. We get 405 km $(270 \times 18: 12=4860: 12=405)$.
Answer: 405 km.
|
405
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A cube with a side of 8 dm is cut into cubes with sides of 4 cm. How many cubes will be obtained?
|
2. Let's find out how many 4 cm cubes fit into one side of the larger cube $(80: 4=20)$. Then, in the first layer of cubes, there will be 400 $(20 \times 20=400)$. We have 20 such layers. In total, there will be 8000 cubes $(400 \times 20=8000)$.
Answer: 8000 cubes.
|
8000
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Each of the three boys was bought candies by their parents. Vitya was given 35 candies, Maria was given fewer than Vitya, and Sasha was given as many candies as Vitya and Maria together, and the number of candies he has is even. What is the maximum number of candies the boys could have been bought?
|
3. According to the condition, Maria has fewer candies than Petya. Therefore, she can have 34, 33... 1 candies. Since Sasha has an even number of candies, Maria must have an odd number $(33,31,29 \ldots 3,1)$. We need to find the greatest number of candies, so Maria will have 33 candies. Sasha will have 68 candies $(35+33=68)$, and all the children together will have $136(35+33+68=136)$.
Answer: the greatest number of candies is 136.
|
136
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Students from one of the schools are tasked with making 455 Christmas tree ornaments for kindergartens in the city. All students should make the same number of ornaments. More than 10, but fewer than 70 people participated in making the ornaments. How many students made the ornaments, and how many did each of them make?
|
4. Let's represent the number 455 as the product of several numbers. Since the number ends in 5, it is divisible by $5 (455: 5=91)$. The number 91 is also divisible by $7 (91: 7=13)$. Thus, the number 455 can be represented as the product of the following numbers: $455=5 \times 7 \times 13$.
Now let's represent the number 455 as the product of two numbers, one of which will represent the number of toys made by one student, and the other will represent the number of students making the toys:
$$
\begin{aligned}
& 455=1 \times 455=455 \times 1 ; 455=5 \times 91=91 \times 5 \\
& 455=7 \times 65=65 \times 7 ; 455=13 \times 35=35 \times 13
\end{aligned}
$$
Since the number of students is more than 10 but less than 70, the following options remain: $455=65 \times 7 ; 455=13 \times 35=35 \times 13$.
Answer: 65 students made 7 toys each, 13 students made 35 toys each, 35 students made 13 toys each.
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. How many different products that are divisible by 10 (order does not matter) can be formed from the numbers $2,3,5,7,9$? Numbers in the product do not repeat!
|
7. For a number to be divisible by 10, it must be divisible by 2 and 5.
Thus, the product must necessarily include 2 and 5. We get the first product $-2 \times 5$.
Now, let's add one more factor to this product:
$$
2 \times 5 \times 3, 2 \times 5 \times 7, 2 \times 5 \times 9
$$
Add one more factor to the obtained products:
$$
2 \times 5 \times 3 \times 7, 2 \times 5 \times 3 \times 9, 2 \times 5 \times 7 \times 9
$$
Add one more factor:
$$
2 \times 5 \times 3 \times 7 \times 9
$$
In total, we have eight products $1+3+3+1=8$.
Answer: eight products.
## TWENTY-THIRD
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From 2 kg 600 grams of copper, three items were made: a spoon, a candlestick, and a teapot. Each item is three times heavier than the previous one. What is the weight of the teapot?
|
1. Let's make a brief record of the problem statement.

1) $1+3+9=13$ (parts) - corresponds to 2 kg 600 grams;
2) $2600: 13=200$ (grams) - weight of the spoon;
3) $200 \times 3=600$ (grams) — weight of the candlestick;
4) $600 \times 3=1800$ (grams) - weight of the teapot.
Answer: the weight of the teapot is 1800 grams.
|
1800
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the fourth grades of School No. 15, 100 students are studying. 37 of them have enrolled in the football section, 40 - in the swimming section, 15 people have enrolled in both sections. How many students have not enrolled in any section?
|
4. 5) $40-15=25$ (students) - enrolled only in the swimming section;
2) $37-15=22$ (students) - enrolled only in the football section;
3) $25+22+15=62$ (students) - enrolled in the football and tennis sections;
4) $100-62=38$ (students) - did not enroll in any section.
Answer: 38 students did not enroll in any section.
|
38
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a village, two houses $A$ and $B$ stand along a straight road, 50 meters apart from each other. At what point on the road should a well be built so that the sum of the distances from the well to the houses is minimized?
|
$\triangle$ If we act fairly, we should build the well in the middle between the houses: then the distance to each house will be 25 meters, and in total 50. However, from the point of view of the problem's condition, any point $X$ on the road segment between $A$ and $B$ is equally good, since the segments $A X$ and $X B$ in total make up 50 meters. (For example, if the well is built 10 meters from $A$, the distances will be 10 and 40 meters, which is 50 in total.) $\triangleleft$
|
50
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In village $A$, there are 100 schoolchildren, and in village $B$, there are 50 schoolchildren. The distance between the villages is 3 kilometers. At what point on the road from $A$ to $B$ should a school be built to minimize the total distance traveled by all schoolchildren?
|
$\triangle$ It seems fair to build the school closer to $A$, as there are more students there. But how much closer? Sometimes it is suggested to build the school one kilometer from $A$ and two kilometers from $B$ (twice as many students, so the school is twice as close). However, from the perspective of the given problem (minimizing the total distance traveled), this option is not the best; it is better to build the school directly at $A$.
This can be verified as follows: if the distances from the school to $A$ and $B$ are $x$ and $3-x$ respectively, then the total distance traveled by all students is $100x + 50(3-x) = 100x + 150 - 50x = 50x + 150$, so it is minimized (and equals 150 km) when $x=0$. $\triangleleft$
The same can be explained without formulas: each meter the school is moved towards $A$ reduces the distance for 100 students by one meter and increases the distance for 50 students by one meter, thus reducing the total distance by 50 meters.
It can also be said this way: divide all students at $A$ arbitrarily into two groups of 50 people each. If the second group did not exist, it would not matter where to build the school (the problem of the well) - but from the perspective of the second group, it is best to build it at $A$.
## A Few More Problems
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. How many degrees does the minute hand turn in a minute? The hour hand?
|
$\Delta$ In one hour, the minute hand makes a full revolution, and in half an hour, it turns by $180^{\circ}$ (a straight angle). Half an hour is 30 minutes, so in one minute, it turns by $1 / 30$ of the angle in $180^{\circ}$, which is $180 / 30=6^{\circ}$.
The hour hand moves $1 / 12$ of a circle in one hour, meaning it moves 12 times slower than the minute hand. In one minute, it turns by $0.5^{\circ} . \triangleleft$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. Five rays emanating from a single point divide the plane into five equal angles. Find the measure of these angles.
|
$\Delta$ If the sum of these five angles is a full circle, that is, two straight angles, which is $2 \times 180^{\circ}=360^{\circ}$. Each of them is one fifth of $360^{\circ}$, that is, $360 / 5=72^{\circ}$. $\triangleleft$
This problem and its solution require some comments. The reason is that different geometry textbooks interpret the concept of an angle differently. One can consider an angle as a geometric figure composed of two rays. Or one can consider an angle as the part of the plane contained between these rays. With this understanding, two rays with a common vertex define two angles: they are obtained by making cuts along the sides. One of these angles is less than a straight angle, and the other is greater.
With the first approach, the maximum possible angle is $180^{\circ}$ (a straight angle), while with the second approach, it is $360^{\circ}$ (a full circle, which can be conditionally considered as the supplement to an angle of $0^{\circ}$).
What does this have to do with the previous problem? Here's how: if we allow angles greater than $180^{\circ}$, everything is simple - an angle of $360^{\circ}$ is divided into 5 equal parts, the sum of which is $360^{\circ}$, and so on. If, however, we do not want to talk about angles greater than $180^{\circ}$, then this reasoning does not work and we need to act a bit more complicated. Draw any line through the given point, which will divide two of the five angles into parts. In total, there will be 7 parts. The sum of these parts is the same as the sum of our five angles (each cut angle is equal to the sum of its two parts). On the other hand, these parts add up to two straight angles, so in total they give $2 \times 180^{\circ}$.
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
132. In a triangle, all sides are equal. Find its angles.
|
$\Delta$ An equilateral triangle (in which all sides are equal) is a special case of an isosceles triangle, and any side can be taken as the base. Therefore, all angles in it are equal. Since the angles sum up to $180^{\circ}$ (from the previous problem), each of them is $60^{\circ} . \triangleleft$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
141. What is the sum of the exterior angles at three vertices of a triangle?
|
$\Delta$ Together with the three interior angles (which sum up to $180^{\circ}$), this results in three straight angles, that is, $540^{\circ}$, so the sum of the exterior angles is $540-180=360^{\circ} . \triangleleft$
|
360
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
142. What is the sum of the exterior angles at the four vertices of a convex quadrilateral?
|
$\Delta$ To find the sum of these angles (they are shown on the diagram with single arcs, but this does not mean they are equal!), consider the corresponding interior angles. Together with the 4 interior angles (which sum up to $360^{\circ}$), we get 4 straight angles, that is, $720^{\circ}$, so the sum of the exterior angles is $720-360=360^{\circ} . \triangleleft$
|
360
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
143. What is the sum of the exterior angles at the five vertices of a convex pentagon?
|
$\checkmark$ Together with the 5 interior angles (which sum up to $540^{\circ}$), we get 5 straight angles, that is, $900^{\circ}$, so the sum of the exterior angles is $900-540=360^{\circ} . \triangleleft$
Similarly, one can verify that the sum of the exterior angles of a convex hexagon, heptagon, and generally any $n$-sided polygon is $360^{\circ}$. Indeed, together with the interior angles, we get $n$ straight angles, that is, $n \cdot 180^{\circ}$, and the interior angles sum up to $(n-2) \cdot 180^{\circ}$, so the difference, which is the sum of the exterior angles, is $2 \cdot 180=360^{\circ}$.
However, there is another, more intuitive (though less formal) explanation. Imagine a car that drives around the perimeter of the polygon. The angles of the polygon are the points where the car turns. At each point, it turns by an angle equal to the exterior angle of the polygon.
After completing the circuit, the car will have made a full rotation, that is, it will have turned $360^{\circ}$.
|
360
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
161. Find the angles of a right isosceles triangle.
|
$>$ The angles at the base of an isosceles triangle are equal, and together they sum up to $90^{\circ}$, so each of them is $45^{\circ} . \triangleleft$
Several of the following problems provide criteria for the congruence of right triangles.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
207. What angle does the diagonal of a square form with its side?
|
$\Delta$ This is an acute angle in a right isosceles triangle, which equals $45^{\circ} . \triangleleft$
## A few more problems
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
265. Inside the square $A B C D$, an equilateral triangle $A B M$ is constructed, and vertex $M$ is connected to points $C$ and $D$. Find the angles of triangle $C M D$.
|
$\Delta$ The angles of an equilateral triangle are $60^{\circ}$, so the angle at vertex $A$ of the isosceles triangle $A M D$ is $90-60=30^{\circ}$. Therefore, the angles at its base are $(180-30) / 2=75^{\circ}$. Thus, the angle $C D M$ is $90-75=15^{\circ}$ (as well as $\angle M C D$ ). $\triangleleft$
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
315. Two of the angles of a trapezoid are $60^{\circ}$ and $130^{\circ}$. What can be said about its other angles?
|
$\Delta$ The angles at the lateral side of the trapezoid add up to $180^{\circ}$ (as interior alternate angles). Therefore, there are also angles $180^{\circ}-60^{\circ}=120^{\circ}$ and $180^{\circ}-130^{\circ}=50^{\circ}$ in the trapezoid. Thus, all four angles have been found. $\triangleleft$
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
390. A circle is divided into five equal arcs by five points. Find the measure of each of them.
|
$\triangleright$ The total of all arcs is $360^{\circ}$, so each of them is $360^{\circ} / 5=72^{\circ} . \triangleleft$
(The Inscribed Angle Theorem) Let $A, B$ and $C$ be points on a circle with center $O$. Then the angle $B A C$ is equal to half the measure of the arc $B C$, that is, half the angle $B O C$.
The angle $B A C$ is called an inscribed angle subtending the arc $B C$. Then we can say: an inscribed angle is equal to half the arc it subtends.
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
449. Two points $A$ and $B$ are 8 units apart. How many lines exist that are 5 units away from point $A$ and 3 units away from point $B$?
|
$\triangleright$ The line $l$ is at a distance $d$ from the point $A$ when it is tangent to the circle of radius $d$ centered at $A$. Therefore, the problem can be restated as follows: given two circles with radii 3 and 5, and the distance between their centers is 8. How many common tangents exist?
We have already solved this problem; since $3+5=8$, the circles touch each other externally, and there will be three common tangents. $\triangleleft$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
500. Find the area of a rectangle with sides 3 and 5.
|
$\triangleright$ Such a rectangle can be cut into 15 unit squares, so its area is equal to the sum of the areas of these squares, that is, $15 . \triangleleft$
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
501. How many square centimeters are in a square meter
|
$\triangleright$ A square with a side length of 1 meter can be divided into $100 \times 100$ squares with a side length of 1 centimeter, so in one square meter, there are $100 \cdot 100=10000$ square centimeters. $\triangleleft$
|
10000
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
521. By what factor should the side of a square be increased to make its area four times larger?
|
$\triangleright$ The area of a rectangle with sides $a$ and $b$ is $a b$, so the area of a square with side $a$ is $a \cdot a=a^{2}$. By doubling the side of the square, we increase its area by four times: $(2 a)^{2}=2^{2} a^{2}=4 a^{2} . \triangleleft$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
577. Draw an isosceles right triangle on graph paper with the legs equal to the side of a cell, and check the Pythagorean theorem for it: the area of the square built on the hypotenuse is equal to the sum of the areas of the squares built on the legs.
|
$\triangleright$ The squares built on the legs have a unit area. The square built on the hypotenuse is divided into four triangles, each of which makes up half of a grid square, and thus has an area of 2 - as required. $\triangleleft$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
578. Check the Pythagorean theorem for a right triangle with legs 1 and 2.
|
$\triangleright$ The squares constructed on the legs have areas of 1 and 4. It remains to find the area of the square constructed on the hypotenuse. This can be done in two ways. First, it can be cut into 4 triangles and a central square. The triangles are equal to the original (legs 1 and 2) and have an area of 1. The area of four such triangles is 4, plus the unit square in the center, totaling 5, as required.
Another way to calculate the area of the square constructed on the hypotenuse is to surround it with triangles on all four sides, completing it to a larger square. By adding four triangles equal to the original, we get a square $3 \times 3=9$, thus the desired area is $9-4=5 . \triangleleft$
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
662. Point $A$ was moved 13 units to the right and resulted in a point with a coordinate of 8. What was the coordinate of point $A$?
|
$\triangleright$ Let $A$ have the coordinate $a$. Then $a+13=8$, and $a=8-13=(-5) . \triangleleft$
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
663. The grasshopper jumped from the point with coordinate 8 to the point with coordinate 17.5. Then it made another jump of the same length (in the same direction). At the point with what coordinate did it end up?
|
$\triangleright$ The length of the jump is $17.5-8=9.5$; another jump will give $17.5+9.5=27 . \triangleleft$
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
664. Given two points $A(-3)$ and $B(7)$ (the coordinates are given in parentheses). Find the coordinate of the midpoint of segment $A B$.
|
$\triangle$ The distance $A B$ is $7-(-3)=10$, half of the distance is 5. Shifting $A$ 5 units to the right (or $B$ 5 units to the left), we get the point with coordinate 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.