problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
13.064. The hay reserve is such that 96 kg can be issued daily for all the horses. In fact, the daily portion for each horse could be increased by 4 kg because two horses were sold. How many horses were there originally?
|
Solution.
Let there initially be $x$ horses. The daily portion for each horse was $\frac{96}{x}$ kg. Since two horses were sold to another collective farm, the number of horses became $x-2$, and the daily portion for each horse became $\frac{96}{x}+4$ kg. According to the condition, $\left(\frac{96}{x}+4\right)(x-2)=96$, from which $x=8$.
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.066. At a machine-building plant, a new type of parts for generators has been developed. From 875 kg of metal, they now produce three more new-type parts than old-type parts were produced from 900 kg. What is the mass of the new and old type parts, if two new-type parts are 0.1 tons lighter than one old-type part?
|
## Solution.
Let $x$ kg be the mass of the new type of part, and $y$ kg be the mass of the old type. According to the problem, $y-2 x=100$. From 875 kg, $\frac{875}{x}$ new type parts are made, and from 900 kg, $\frac{900}{y}$ old type parts were made. According to the problem, $\frac{875}{x}-\frac{900}{y}=3$. Solving the system $\left\{\begin{array}{l}\frac{875}{x}-\frac{900}{y}=3, \\ y-2 x=100,\end{array}\right.$ we find $x=175$ kg, $y=450$ kg.
Answer: 175 and 450 kg.
|
175
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.067. On the first day of the sports competitions, $1 / 6$ of the boys' team and $1 / 7$ of the girls' team did not meet the qualifying standards and were eliminated from further competition. Over the rest of the competition period, an equal number of athletes dropped out from both teams due to failing to meet the standards. By the end of the competition, a total of 48 boys and 50 girls did not meet the qualifying standards, but among those who did meet the standards, the number of girls was twice that of the boys. What was the initial number of athletes in each team?
|
## Solution:
Let $x$ be the number of boys who met the credit standards and $2x$ be the number of girls. Then the initial number of team members is $x+48$ boys and $2x+50$ girls. By the end of the first day of the competition, $\frac{1}{6}(x+48)$ boys and $\frac{1}{7}(2x+50)$ girls dropped out. Later, an equal number of athletes dropped out from both teams, so $48-\frac{1}{6}(x+48)=50-\frac{1}{7}(2x+50)$, from which $x=24$. Therefore, the initial number of team members is 72 boys and 98 girls.
Answer: 72 boys and 98 girls.
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.068. The working hour of masters $A$ and $B$ is paid differently, but both masters worked the same number of hours. If $A$ had worked one hour less, and $B$ had worked five hours less, then $A$ would have earned 720 rubles, and $B$ 800 rubles. If, on the contrary, $A$ had worked five hours less, and $B$ had worked one hour less, then $B$ would have earned 360 rubles more than $A$. How much did each master actually earn?
|
## Solution:
Let the masters have worked $x$ hours. If $A$ had worked 1 hour less, he would have earned $\frac{720}{x-1}$ rubles per hour; if $B$ had worked 5 hours less, he would have earned $\frac{800}{x-5}$ rubles per hour. According to the condition, $\frac{800}{x-5}(x-1)-\frac{720}{x-1}(x-5)=360$, from which $x=25$. In reality, $A$ earned $\frac{720}{25-1} \cdot 25=750$ rubles, and $B$ earned $\frac{800}{20} \cdot 25=1000$ rubles.
Answer: 750 and 1000 rubles.
|
750
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.069. In one pool there are 200 m $^{3}$ of water, and in another - 112 m $^{3}$. Taps are opened, through which the pools are filled. After how many hours will the amount of water in the pools be the same, if 22 m $^{3}$ more water is poured into the second pool per hour than into the first?
|
Solution.
Let the amount of water in the pools become equal after $x$ hours. Let $y$ m$^{3}$ of water be added to the first pool per hour, and $y+22$ m$^{3}$ - to the second. According to the condition, $200+x y=112+x(y+22)$, from which $x=4$.
Answer: in 4 hours.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.072. The city $C$, located between points $A$ and $B$, is supplied with gas from these points, the distance between which is 500 km. From reservoir $A$, 10000 $\mathrm{M}^{3}$ of gas is pumped out every minute, and from reservoir $B$ - 12% more. In this case, the gas leakage in each pipeline is 4 m $^{3}$ per kilometer of pipe. Knowing that gas arrives in city $C$ from reservoirs $A$ and $B$ equally, find the distance between city $C$ and point $A$.
|
## Solution.
Let $x$ km be the distance between $A$ and $C$, and $500-x$ km be the distance between $C$ and $B$. Considering the gas leakage, $10000-4 x$ m$^3$ of gas is delivered from $A$ to $C$, and $10000 \cdot 1.12 - 4(500-x)$ m$^3$ of gas is delivered from $B$ to $C$. According to the condition, $10000-4 x = 1.12 \cdot 10000 - 4(500-x)$, from which $x=100$.
Answer: 100 km.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.075. Two workers together produced 72 parts per shift. After the first worker increased their productivity by $15 \%$, and the second by $25 \%$, together they started producing 86 parts per shift. How many parts does each worker produce per shift after the increase in productivity?
|
## Solution.
Initially, the workers produced $x$ and $72-x$ parts per shift, and then $1.15x$ and $1.25(72-x)$ parts. According to the condition, $1.15x + 90 - 1.25x = 86$; $0.1x = 4; x = 40; 1.15 \cdot 40 = 46$.
Answer: 46 and 40 parts.
|
46
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.076. The collection of corn from the fields of a livestock farm was 4340 centners. The following year, it is planned to obtain 5520 centners of corn by increasing the area by 14 hectares and increasing the yield by 5 centners per hectare. Determine the area occupied by corn and the yield in centners per hectare (the yield was less than 40 centners per hectare).
|
Solution.
Let $x$ ha be the area occupied by corn, $\frac{4340}{x}$ centners/ha the yield. The next year, the area is $x+14$ ha, and the yield is $\frac{4340}{x}+5$ centners/ha. According to the condition, $\left(\frac{4340}{x}+5\right)(x+14)=5520$, from which $x=98$ ha or $x=124$ ha. The yield is $\frac{4340}{98} \approx 44.3$ centners/ha or $\frac{4340}{124}=35$ centners/ha.
Answer: 124 ha; 35 centners per ha.
|
124
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.077. The older brother on a motorcycle and the younger brother on a bicycle made a two-hour non-stop trip to the forest and back. During this time, the motorcyclist traveled each kilometer 4 minutes faster than the cyclist. How many kilometers did each of the brothers travel in 2 hours, if it is known that the distance covered by the older brother in this time is 40 km more?
|
## Solution.
Let $x$ km be the distance the younger brother traveled, and $x+40$ km be the distance the older brother traveled. The younger brother took $\frac{120}{x}$ minutes to travel 1 km, and the older brother took $\frac{120}{40+x}$ minutes. According to the condition, $\frac{120}{x}-4=\frac{120}{40+x}$, from which we get $x=20$.
Answer: 20 and 60 km.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.078. A tourist traveled $5 / 8$ of the total distance by car and the remaining part by boat. The boat's speed is 20 km/h less than the car's speed. The tourist traveled by car for 15 minutes longer than by boat. What are the speeds of the car and the boat if the total distance of the tourist's journey is 160 km?
|
## Solution.
The tourist drove 160 * 5/8 = 100 km by car, and 160 - 100 = 60 km by boat. Let \( x \) km/h be the speed of the boat, and \( 20 + x \) km/h the speed of the car. The tourist traveled by car for \( \frac{100}{20+x} \) hours, and by boat for \( \frac{60}{x} \) hours. According to the problem, \( \frac{100}{20+x} - \frac{60}{x} = 0.25 \), from which \( x = 60 \) or \( x = 80 \).
Answer: the speed of the car is 100 or 80 km/h; the speed of the boat is 80 or 60 km/h.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.079. The first tourist, after riding a bicycle for 1.5 hours at a speed of $16 \mathrm{~km} / \mathrm{h}$, makes a stop for 1.5 hours, and then continues the journey at the initial speed. After 4 hours from the departure of the first tourist, the second tourist sets off in pursuit on a motorcycle at a speed of $56 \mathrm{km} / \mathrm{h}$. What distance will they cover before the second tourist catches up with the first?
|
## Solution.
The motion graph is shown in Fig. 13.3. Let $t$ be the time (in hours) it takes for the second tourist to catch up with the first. Since $v_{\text {bike }}=16 \mathrm{km} / \mathbf{h}$, $\mathrm{v}_{\text {motor }}=56 \mathrm{km} /$ h, then $S_{\text {bike }}=(2.5+t) 16, S_{\text {motor }}=56 t$. Therefore, $56 t=16 t+40$, i.e., $t=1$ (h). Thus, $S=56$ km.
Answer: 56 km.
|
56
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.081. A motorcyclist set off from point $A$ to point $B$, which is 120 km away from $A$. On the way back, he set off at the same speed, but had to stop for 10 minutes after an hour of travel. After this stop, he continued his journey to $A$, increasing his speed by 6 km/h. What was the initial speed of the motorcyclist, given that he spent as much time on the return trip as he did on the trip from $A$ to $B$?
|
## Solution.
By the condition $A C=C D$ (Fig. 13.4). We have $A C=\frac{120}{x}$, where $x-$ is the initial speed; $C D=1+\frac{1}{6}+\frac{120-x}{x+6} \Rightarrow \frac{120}{x}=\frac{7}{6}+\frac{120-x}{x+6}$, from which $x=48($ km $/ h)$.
Answer: 48 km $/$ h
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.082. Two groups of tourists must walk towards each other from tourist bases $A$ and $B$, the distance between which is 30 km. If the first group leaves 2 hours earlier than the second, they will meet 2.5 hours after the second group leaves. If the second group leaves 2 hours earlier than the first, the meeting will occur 3 hours after the first group leaves. At what average speed does each group walk?
|
Solution.
Let $x$ km/h be the speed of the first group, $y$ km/h be the speed of the second. If the first group starts earlier than the second, then $2.5 y + (2.5 + 2) x = 30$. If the second group starts earlier than the first, then $3 x + (3 + 2) y = 30$. Solving the system $\left\{\begin{array}{l}2.5 y + 4.5 x = 30, \\ 3 x + 5 y = 30,\end{array}\right.$ we find $x = 5$ km/h, $y = 3$ km/h.
Answer: 5 and 3 km/h.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.083. A freight train was delayed on the way for 12 minutes, and then at a distance of 60 km, it made up for the lost time by increasing its speed by 15 km/h. Find the original speed of the train.
|
## Solution.
Let the speed of the train before the delay be $x$ km/h, and after the delay $(x+15)$ km/h. Then (Fig. 13.5) $A B=\frac{x}{5}, C E=60, C D=60-\frac{x}{5}$, $B D=\frac{60-\frac{x}{5}}{x}, A E=\frac{60}{x+15}$. Since $B D=A E$, then $\frac{60-\frac{x}{5}}{x}=\frac{60}{x+15}$, from which $x=60($ km $/ \mathbf{4})$.
Answer: $60 \mathrm{km} / \mathrm{h}$.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.085. Two brothers took their bicycles and set off simultaneously with the intention of riding $42 \mathrm{km}$. The older brother maintained the same speed throughout the journey; while the younger brother fell behind by 4 km every hour. However, since the older brother rested for a whole hour during the trip, and the younger brother only rested for 20 minutes, they arrived at the finish line simultaneously. How long did the trip last?
|
## Solution.
Let $x$ km/h be the speed of the older brother, then $(x-4)$ km/h is the speed of the younger brother. The older brother was on the road for $t_{\text {old }}=\frac{42}{x}+1$, and the younger brother for $t_{\text {young }}=\frac{42}{x-4}+\frac{1}{3}$. According to the problem, $t_{\text {old }}=t_{\text {young }}$, that is, $\frac{42}{x}+1=\frac{42}{x-4}+\frac{1}{3}$, from which $x=18$ and $t=1+\frac{42}{18}=3 \frac{1}{3}$.
Answer: 3 hours 20 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.086. A positive integer is thought of. To its notation, the digit 7 is appended on the right, and from the resulting new number, the square of the thought number is subtracted. The remainder is reduced by $75\%$ of this remainder, and the thought number is subtracted again. In the final result, zero is obtained. What number was thought of?
|
Solution.
Let the number be $x$. Consider the numbers $10 x+7, 10 x+7-x^{2}$, and the remainder $\frac{25}{100}\left(10 x+7-x^{2}\right)$. Then $\frac{1}{4}\left(10 x+7-x^{2}\right)-x=0, x^{2}-6 x-7=0 \Rightarrow$ $\Rightarrow x=7$
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.087. A positive integer is thought of. The digit 5 is appended to its right, and from the resulting new number, the square of the thought number is subtracted. The difference is divided by the thought number, and then the thought number is subtracted, and the result is one. What number is thought of?
|
## Solution.
Let $x$ be the number thought of. Then the new number can be represented as $10 x + 5$. According to the condition, $\frac{10 x + 5 - x^2}{x} - x = 1$, from which $x = 5$.
Answer: 5.
Fig. 13.6
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.089. A train traveled a certain distance at a speed of 120 km/h. After that, it traveled a distance 75 km longer at a speed of 150 km/h, and the remaining distance, 135 km shorter than the distance traveled, at a speed of 96 km/h. How long is the entire journey if the average speed of the train turned out to be 120 km/h?
|
Solution.
| Section | Distance | Speed | Time |
| :---: | :---: | :---: | :---: |
| First | $x \mathrm{km}$ | $120 \mathrm{km} / \mathrm{h}$ | $\frac{x}{120} \mathrm{h}$ |
| Second | $75+x \mathrm{km}$ | $150 \mathrm{km} / \mathrm{h}$ | $\frac{75+x}{150} \mathrm{h}$ |
| Third | | | |
The entire distance is $x+75+x+2x-60=4x+15$, the total time is $\frac{x}{120}+\frac{75+x}{150}+\frac{2x-60}{96}=\frac{43x-150}{1200}$. The average speed of the train: $\frac{4x+15}{\frac{43x-150}{1200}}=120$.
From this, $x=100$ km. The entire distance will be: $4 \cdot 100+15=415$ km.
Answer: 415 km.
|
415
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.091. The 300 kg of goods in stock were sold in unequal quantities to two organizations at a price of 37.5 rubles per kg. The first organization transports the purchased goods a distance of 20 km, while the second organization transports them 30 km. Transporting 10 kg of goods costs 1.5 rubles per km. Knowing that the second organization paid 2700 rubles more than the first for the purchase and transportation of the goods, determine how many kilograms each organization bought and how much they paid for the goods and their transportation.
|
Solution.
Using the condition of the problem, we will form a table
| Organization | Product (tons) | Cost (rubles) | Transportation (rubles) | Total cost (rubles) |
| :---: | :---: | :---: | :---: | :---: |
| № 1 | $x$ | $37.5 x$ | $3 x$ | $40.5 x$ |
| № 2 | $300-x$ | $37.5(300-x)$ | $4.5(300-x)$ | $42(300-x)$ |
According to the condition of the problem, we have $42(300-x)-40.5 x=2700$, from which $x=120$ (kg), $300-x=180$ (kg); $40.5 x=4860$ (rubles), $42(300 - x) = 7560$ (rubles).
Answer: 120 kg and 4860 rubles; 180 kg and 7560 rubles.
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.092. A monetary prize was distributed among three inventors: the first received half of the entire prize minus $3 / 22$ of what the other two received together. The second received $1 / 4$ of the entire prize and $1 / 56$ of the money received by the other two together. The third received 30000 rubles. How large was the prize and how much money did each inventor receive?
|
## Solution.
Let $x$ rubles be the prize for the first inventor, and $y$ rubles be the prize for the second. According to the condition, the total prize is $x+y+30000$ rubles. Then
$$
\left\{\begin{array}{l}
x=\frac{1}{2}(x+y+30000)-\frac{3}{22}(y+30000) \\
y=\frac{1}{4}(x+y+30000)+\frac{1}{56}(x+30000)
\end{array} \text {, from which } x=40000, y=25000 .\right. \text { The total }
$$
prize is $40000+25000+30000=95000$ rubles.
Answer: 95000 rubles; 40000, 25000, and 30000 rubles.
|
95000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.097. The distance from $A$ to $B$ by railway is 88 km, while by river it is 108 km. The train from $A$ departs 1 hour later than the riverboat and arrives in $B$ 15 minutes earlier. Find the average speed of the train, given that it is 40 km/h greater than the average speed of the riverboat.
|
## Solution.
Let $x$ km/h be the speed of the train, and $x-40$ km/h be the speed of the steamer. The train was on the way for $\frac{88}{x}$ hours, and the steamer for $\frac{108}{x-40}$ hours. According to the condition, $\frac{108}{x-40}-\frac{88}{x}=1+\frac{1}{4}$, from which $x=88$.
Answer: 88 km/h.
|
88
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.098. A pedestrian and a cyclist set off simultaneously towards each other from cities $A$ and $B$, the distance between which is 40 km, and meet 2 hours after departure. Then they continue their journey, with the cyclist arriving in $A$ 7 hours and 30 minutes earlier than the pedestrian in $B$. Find the speeds of the pedestrian and the cyclist, assuming that they remained constant throughout.
|
Solution.
We will fill in the table of speed, distance, and time values in the order indicated by the numbers (1), (2), ..., (12):
| Tourist | Before Meeting | | | After Meeting | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | speed, km $/ \mathbf{4}$ | time, h | distance, | speed, km $/ \mathbf{4}$ | time, | distance, km |
| Pedestrian | (1) $x$ | (3) 2 | (5) $2 x$ | (7) $x$ | (11) $40-2 x$ | (9) $40-2 x$ |
| Cyclist | (2) $20-x$ | (4) 2 | (6) $40-2 x$ | (8) $20-x$ | (12) $\frac{2 x}{20-x}$ | (10) $2 x$ |
According to the condition $\frac{40-2 x}{x}-\frac{2 x}{20-x}=\frac{15}{2}$, from which $x=4$ (km/h).
Answer: 4 and 16 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.100. Determine the positive integer based on the following data: if it is written in digits and the digit 4 is appended to the right, the resulting number is divisible without a remainder by a number that is 4 greater than the sought number, and the quotient is a number that is 27 less than the divisor.
|
Solution.
Let $x$ be the required number. According to the condition $\frac{10 x+4}{x+4}=x+4-27$, from which $x=32$.
Answer: 32.
|
32
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.103. From the railway station to the tourist base, one can walk along the highway or a path, with the path being 5 km shorter. Two friends agreed that one would walk along the highway at a constant speed of $\mathrm{v}$ km/h, while the other would take the path at a speed of 3 km/h. The second one arrived at the tourist base 1 hour earlier than the first. Find the distance from the station to the tourist base along the highway and the speed $v$ of the first friend, given that $v$ is an integer.
|
Solution.
Let $x$ km be the distance from the station to the tourist base by road, and $x-5$ km by trail. According to the problem, $\frac{x}{v}-\frac{x-5}{3}=1$, from which $x=\frac{2 v}{v-3}$. The expression makes sense for $v>3$. By trial, we find: at $v=4$ km/h, $x=8$ km. Other solutions to this equation do not satisfy the condition $x-5>0$.
Answer: 8 km, 4 km/h.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.104. The length of the bus route is 16 km. During peak hours, the bus switches to express mode, i.e., it significantly reduces the number of stops, as a result of which the travel time from the beginning to the end of the route is reduced by 4 minutes, and the average speed of the bus increases by 8 km/h. At what speed does the bus travel in express mode?
|
Solution.
Let $x$ km/h be the speed of the bus in express mode. Then the travel time in this mode will be $\left(\frac{16}{x-8}-\frac{1}{15}\right)$ hours. According to the condition, $\left(\frac{16}{x-8}-\frac{1}{15}\right) x=16$, from which $x=48$ km/h.
Answer: 48 km/h.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.105. On one of the tram lines, trams of a new design have started to operate. A trip of 20 km now takes 12 minutes less, as the average speed of the new design tram is 5 km/h higher than the average speed of the outdated design tram. How much time does the new design tram take for the trip and what is its average speed?
|
## Solution.
Let $x$ km/h be the average speed of the new tram model.
Then the time it takes for the trip is $-\frac{20}{x}$ hours. According to the problem, $\frac{20}{x}=\frac{20}{x-5}-\frac{1}{5}$, from which $x=25$ km/h, and the time $-\frac{20}{25}=\frac{4}{5}$ hours $=48$ minutes.
Answer: 48 min, 25 km/h.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.106. The plane must fly 2900 km. Having flown 1700 km, it made an emergency landing for 1 hour 30 minutes, after which it flew at a speed 50 km/h less than before. Find the original speed of the plane, given that it arrived at its destination 5 hours after takeoff.
|
## Solution.
Let $x$ km/h be the original speed of the airplane. Before landing, it was in the air for $\frac{1700}{x}$ hours, and after landing, it was in the air for $\frac{1200}{x-50}$ hours. According to the condition, $\frac{1700}{x} + 1.5 + \frac{1200}{x-50} = 5$, from which we find $x = 850$ km/h.
Answer: 850 km/h.
|
850
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.107. Two brigades, working together, were supposed to repair a given section of a highway in 18 days. In reality, however, only the first brigade worked at first, and the second brigade, which has a higher labor productivity than the first, finished the repair of the road section. As a result, the repair of the given road section took 40 days, with the first brigade completing $2 / 3$ of the work during its working time. How many days would it take for each brigade to repair the given road section separately?
|
Solution.
Let $x$ be the work rate of the first team, and $y$ be the work rate of the second team. Working together, the teams will repair the section in $\frac{1}{x+y}$ days. According to the problem, $\frac{1}{x+y}=18$. The productivity of the first team is $\frac{1}{x}$, and the second team's productivity is $\frac{1}{y}$. According to the problem, $\frac{2}{3} \cdot \frac{1}{x}+\frac{1}{3} \cdot \frac{1}{y}=40$. Solving the system $\left\{\begin{array}{l}\frac{1}{x+y}=18, \\ \frac{2}{3} \cdot \frac{1}{x}+\frac{1}{3} \cdot \frac{1}{y}=40,\end{array}\right.$ we find: $\frac{1}{x}=45$ days; $\frac{1}{y}=30$ days or $\frac{1}{x}=24$ days, $\frac{1}{y}=72$ days. Considering the conditions of the problem, finally: $\frac{1}{x}=45$ days, $\frac{1}{y}=30$ days. Therefore, the first team will repair the entire section in 45 days, and the second team in 30 days.
Answer: 45 and 30 days.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.109. Two cyclists set off simultaneously towards each other from two places, the distance between which is 270 km. The second cyclist travels 1.5 km less per hour than the first, and meets him after as many hours as the first cyclist travels in kilometers per hour. Determine the speed of each cyclist.
|
## Solution.
Let $x$ km/h be the speed of the first cyclist, and $x-1.5$ km/h be the speed of the second cyclist. Before they meet, the first cyclist traveled $x \cdot x$ km, and the second cyclist traveled $x(x-1.5)$ km. According to the problem, $x^{2}+x(x-1.5)=270$, from which $x=12$ km/h; $12-1.5=10.5$ km/h.
Answer: 12 and 10.5 km/h.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.112. Two bodies move towards each other from two places, the distance between which is 390 km. The first body traveled 6 m in the first second, and in each subsequent second, it traveled 6 m more than in the previous one. The second body moved uniformly at a speed of $12 \mathrm{~m} / \mathrm{c}$ and started moving 5 seconds after the first. After how many seconds from the start of the first body will they meet?
|
## Solution.
Let $t$ s be the time of movement of the first body until the meeting; $t-5$ s of the second. The first traveled until the meeting $\frac{a t^{2}}{2}=\frac{6 t^{2}}{2}=3 t^{2}$ km; the second $12(t-5)$ km. According to the condition $3 t^{2}+12(t-5)=360$, from which $t=10$ s.
Answer: in $10 \mathrm{s}$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.113. A material particle entered the pipe through an opening, and 6.8 minutes later, a second particle entered the same opening. Upon entering the pipe, each particle immediately began linear motion along the pipe: the first particle moved uniformly at a speed of 5 m/min, while the second particle covered 3 m in the first minute and 0.5 m more in each subsequent minute than in the previous one. How many minutes will it take for the second particle to catch up with the first?
|
## Solution.
Let $t$ be the time (in minutes) it takes for the second particle to catch up with the first. The distance traveled by the second particle is equal to the sum of $t$ terms of an arithmetic progression with $a_{1}=3, d=0.5$; therefore, $s=\frac{2 a_{1}+d(t-1)}{2} t=\frac{6+0.5(t-1)}{2} t$. The same distance traveled by the first particle is $5(6.8+t)=34+5 t$. Thus, $\frac{6+0.5(t-1)}{2} t=34+5 t$, from which $t=17$ (min).
Answer: 17 min.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.115. Tourist $A$ set off from city $M$ to city $N$ at a constant speed of 12 km/h. Tourist $B$, who was in city $N$, upon receiving a signal that $A$ had already traveled 7 km, immediately set off towards him and traveled 0.05 of the total distance between $M$ and $N$ each hour. From the moment $B$ set off until his meeting with $A$, the number of hours that passed is equal to the number of kilometers $B$ traveled per hour. Find the distance between the cities $M$ and $N$, given that it is not less than 100 km.
|
## Solution.
Let $x$ km be the distance between $M$ and $N$. Then the speed of tourist $B$ is $B-0.05 x$ km/h. Before the meeting, $A$ traveled $7+0.05 x \cdot 12$ km; $B$ traveled $(0.05 x)^{2}$ km. According to the condition, $7+0.05 x \cdot 12+(0.05 x)^{2}=x$, from which $x_{1}=20$ km; $x_{2}=140$ km. Considering that $x \geq 100$ km, we find $x=140$ km.
Answer: $140 \text{ km}$.
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.117. A cyclist traveled 60 km from point $A$ to point $B$. On the return trip, he rode the first hour at the same speed, then stopped for 20 minutes. Resuming his journey, he increased his speed by 4 km/h and therefore spent as much time traveling from $B$ to $A$ as he did traveling from $A$ to $B$. Determine the cyclist's speed on the trip from $A$ to $B$.
|
## Solution.
Let $x$ km/h be the speed of the cyclist on the way from $A$ to $B$. The time spent on the way from $A$ to $B$ is $\frac{60}{x}$ hours; the time spent on the return trip is $-1+\frac{1}{3}+\frac{60-x}{x+4}$. According to the condition, $\frac{60}{x}=1+\frac{1}{3}+\frac{60-x}{x+4}$, from which $x=20$ km/h.
Answer: 20 km/h.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.118. Two buses left the factory simultaneously and headed to the recreation area, to the lake. The distance between the factory and the lake is 48 km. The first bus arrived at the lake 10 minutes earlier than the second, and the average speed of the second bus is 4 km/h less than the average speed of the first. Calculate the speeds of the buses.
|
## Solution.
Let $x$ km/h be the speed of the first bus, and $x-4$ km/h be the speed of the second bus. The first bus arrived at the lake in $\frac{48}{x}$ hours, and the second bus in $\frac{48}{x-4}$ hours. According to the condition, $\frac{48}{x-4}-\frac{48}{x}=\frac{1}{6}$, from which $x=36$ km/h, $36-4=32$ km/h.
Answer: 32 and 36 km/h.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.123. The motorcyclist was delayed at the barrier for 24 minutes. After increasing his speed by $10 \mathrm{km} / \mathrm{h}$, he made up for the delay on an 80 km stretch. Determine the motorcyclist's speed before the delay.
|
Solution.
Let $x$ km/h be the motorcyclist's speed before the delay, and $x+10$ km/h on the segment. Without the delay, the motorcyclist would have traveled 80 km in $t$ hours,
but he traveled 80 km at a speed of $x+10$ km/h in $t-0.4$ hours. Then $\left\{\begin{array}{l}(x+10)(t-0.4)=80, \\ x \cdot t=80,\end{array}\right.$
Answer: 40 km/h.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.124. Two steamers left the port simultaneously, with one heading south and the other heading east. After 2 hours, the distance between them was 174 km. Find the average speed of each steamer, given that one of them traveled 3 km more on average per hour,

Fig. 13.8 than the other.
|
## Solution.
Let $x$ km/h be the speed of the second steamboat, and $x+3$ km/h be the speed of the first. In 2 hours, the first steamboat traveled $2(x+3)$ km, and the second $2x$ km. From the right triangle (Fig. 13.8), by the Pythagorean theorem, $(2x)^2 + (2(x+3))^2 = 174^2$, from which $x = 60$ km/h.
Answer: 60 and 63 km/h.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.129. At 9 AM, a self-propelled barge left $A$ upstream and arrived at point $B$; 2 hours after arriving at $B$, the barge set off on the return journey and arrived back at $A$ at 7:20 PM on the same day. Assuming the average speed of the river current is 3 km/h and the barge's own speed is constant throughout, determine when the barge arrived at point $B$. The distance between $A$ and $B$ is 60 km.
|
Solution.
Let $v$ km/h be the own speed of the barge. From $A$ to $B$, the barge sailed $\frac{60}{v-3}$ hours, and on the way back $-\frac{60}{v+3}$ hours. According to the condition, $\frac{60}{v-3}+2+\frac{60}{v+3}=10 \frac{1}{3}$, from which $v=15$ km/h. The barge arrived in $B$ at $9+\frac{60}{15-3}=14$ hours.
Answer: at 14 hours.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.135. A team of mechanics can complete a certain task of processing parts 15 hours faster than a team of apprentices. If the team of apprentices works for 18 hours on this task, and then the team of mechanics continues working on the task for 6 hours, only 0.6 of the entire task will be completed. How much time does the team of apprentices need to complete this task independently?
|
## Solution.
Let $x$ hours be necessary for the students to complete the task; $x-15$ hours for the team of mechanics. In 18 hours, the students will complete $\frac{1}{x} \cdot 18$ of the entire task, and in 6 hours, the mechanics will complete $\frac{6}{x-15}$ of the entire task. According to the condition, $\frac{18}{x}+\frac{6}{x-15}=0.6$, from which $x=45$ hours.
Answer: 45 hours.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.138. Two workers, the second of whom started working 1.5 days later than the first, independently wallpapered several rooms in 7 days, counting from the moment the first worker started. If this work had been assigned to each separately, the first would have needed 3 days more than the second to complete it. How many days would each of them take to complete the same work individually?
|
Solution.
Let the first worker complete the entire job in $x$ days, the second in $x-3$ days. In 7 days, the first worker completed $\frac{7}{x}$ of the entire job, and in $7-1.5=5.5$ days, the second worker completed $\frac{5.5}{x-3}$ of the job. Therefore, $\frac{7}{x}+\frac{5.5}{x-3}=1$, from which $x=14$ days.
Answer: in 14 and 11 days.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.139. Find a two-digit number, the quotient of which when divided by the product of its digits is $8 / 3$, and the difference between the number and the number written with the same digits but in reverse order is 18.
|
## Solution.
Let's represent the desired number as $10 x + y$. Then, according to the condition,
$$
\left\{\begin{array}{l}
\frac{10 x + y}{x y} = \frac{8}{3}, \\
10 x + y = 10 y + x + 18,
\end{array} \text { from which } x = 6, y = 4. \text { The desired number is } 64. \right.
$$
Answer: 64.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.140. On one of two machines, a batch of parts is processed 3 days longer than on the other. How many days would it take for each machine to process this batch of parts separately, if it is known that when working together, these machines processed a batch of parts three times larger in 20 days?
|
Solution.
Time $(t)$, the amount of work done per unit of time, i.e., productivity ( $W$ ), and the total volume of work ( $V$ ) are related by $V=W t$. Let $V=1$ and fill in the following table:
| Machine | Time, days | Volume of work | Productivity |
| :---: | :---: | :---: | :---: |
| First | $x$ | 1 | $\frac{1}{x}$ |
| Second | $x-3$ | 1 | $\frac{1}{x-3}$ |
| Both together | 20 | 3 | $\frac{3}{20}$ |
Since the productivity of the machines adds up when they work together, $\frac{1}{x}+\frac{1}{x-3}=\frac{3}{20}$, from which $x=15$.
Answer: 15 and 12 days.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.141. An integer was given. It was required to increase it by 200000 and then triple the resulting number. Instead, the digit 2 was appended to the right of the digital representation of the given number, and the correct result was obtained: What number was given?
|
## Solution.
Let $x$ be the desired number. By appending the digit 2 to this number, we get the number $10 x+2$. According to the condition, $10 x+2=3(x+200000)$, from which $x=85714$.
Answer: 85714.
|
85714
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.144. The sum of all even two-digit numbers is divisible by one of them without a remainder. The quotient obtained differs from the divisor only in the order of the digits, and the sum of its digits is 9. What two-digit number was the divisor?
|
Solution.
Let's represent the divisor in the form $10a + b$. Then, according to the condition, we have $\left\{\begin{array}{l}\frac{2430}{10a + b} = 10b + a, \\ a + b = 9,\end{array}\right.$ from which $a = 4, b = 5$. The required number is 54.
Answer: 54.
|
54
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.145. First, the motorboat traveled 10 km downstream, and then twice that distance - across the lake into which the river flows. The entire trip lasted 1 hour. Find the boat's own speed, if the river current speed is 7 km/h.
|
## Solution.
Let $v$ km/h be the own speed of the boat. Downstream, the boat traveled $\frac{10}{v+7}$ hours, and on the lake $-\frac{20}{v}$ hours. According to the condition, $\frac{10}{v+7}+\frac{20}{v}=1$, from which $v^{2}-23 v-140=0$, i.e., $v=28$ (km/h).
Answer: 28 km/h.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.148. A photograph measuring $12 \times 18$ cm is inserted into a frame of constant width. Determine the width of the frame if its area is equal to the area of the photograph itself.
|
## Solution.
Let $x$ cm be the width of the frame (Fig. 13.9). Then its area is $2 \cdot 12 x + 2(18 + 2 x) x$ cm. According to the condition, $2 \cdot 12 x + 2(18 + 2 x) x = 12 \cdot 18$, from
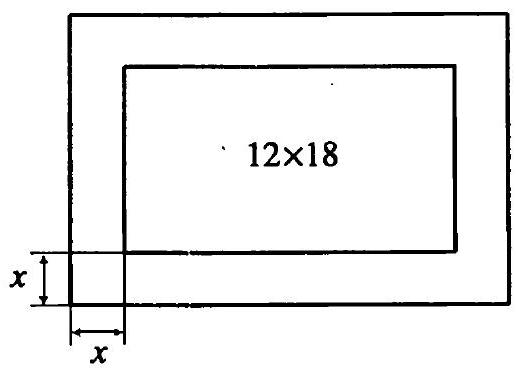
Fig. 13.9 where $x=3$ cm.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.153. A plot in the shape of a rectangle with a diagonal of 185 m was allocated for a sports field. During construction, the length of each side was reduced by 4 m. The rectangular shape was maintained, but the area was reduced by \(1012 \mathrm{~m}^{2}\). What are the actual dimensions of the sports field?
Fig. 13.10
|
Solution.
Let $x$ be the length and $y$ be the width of the plot. By the Pythagorean theorem, $x^{2}+y^{2}=185^{2}$. Additionally, $(x-4)(y-4)=x y-1012$, from which $x y-4(x+y)=$ $=x y-1028 ; x+y=257 ; y=257-x$. Solving the quadratic equation $x^{2}+(257-x)^{2}-185^{2}=0$, we find $x_{1}=104, x_{2}=153$.
Answer: $100 \times 149$ m.
13.154.3a 1 kg of one product and 10 kg of another cost 20 rubles. If, due to seasonal price changes, the first product increases in price by $15 \%$, and the second decreases in price by $25 \%$, then the same amount of these products will cost 18 rubles 20 kopecks. What is the cost of 1 kg of each product?
Solution.
Let $x$ rubles be the price of one product, and $y$ rubles be the price of the other. According to the problem, $x+10 y=20$. With the seasonal price changes, 1 kg of the first product will cost $1.15 x$ rubles, and 1 kg of the second product will cost $0.75 y$ rubles. Then $1.15 x+10 \cdot 0.75 y=18.2$. Solving the system $\left\{\begin{array}{l}1.15 x+0.75 \cdot 10 y=18.2, \\ x+10 y=20,\end{array}\right.$ we find $x=8$ rubles, $y=1.2$ rubles.
Answer: 8 rubles and 1 ruble 20 kopecks.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.155. In the first week of their vacation trip, the friends spent 60 rubles less than $2 / 5$ of the amount of money they brought with them; in the second week, $1 / 3$ of the remainder and another 12 rubles on theater tickets; in the third week, $3 / 5$ of the new remainder and another 31 rubles 20 kopecks on boat rides, after which they had 420 rubles left. How much money was spent over the three weeks of the trip?
|
Solution.
Let the initial amount be $x$ rubles.
| Week | Spent | Balance |
| :--- | :---: | :---: |
| First | $\frac{2}{5} x-60$ (rubles) | $\frac{3}{5} x+60$ (rubles) |
| Second | $\frac{1}{3}\left(\frac{3}{5} x+60\right)+12=\frac{1}{5} x+32$ (rubles) | $\frac{2}{5} x+28$ (rubles) |
| Third | $\frac{3}{5}\left(\frac{2}{5} x+28\right)+31 \frac{1}{5} x=$ | $\frac{2}{5} x+28-\frac{6}{25} x-48=$ |
| | $=\frac{6}{25} x+48$ (rubles) | $=\frac{4}{25} x-20$ (rubles) |
According to the condition $\frac{4}{25} x-20=420$, from which $x=2750$ rubles. Over three weeks, $2750-420=2330$ (rubles) were spent.
Answer: 2330 rubles.
|
2330
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.156. A motorboat with a speed of 20 km/h traveled the distance between two points along the river and back without stopping in 6 hours and 15 minutes. The distance between the points is 60 km. Determine the speed of the river current.
|
Solution.
Let $v_{\text {r }}$ km/h be the speed of the river current; the boat traveled 60 km downstream in $\frac{60}{20+v_{\mathrm{r}}}$ hours, and upstream in $\frac{60}{20-v_{\mathrm{r}}}$ hours. According to the problem, $\frac{60}{20+v_{\mathrm{r}}}+\frac{60}{20-v_{\mathrm{r}}}=6.25$, from which $v_{\mathrm{r}}=4$ km/h.
Answer: 4 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.157. Find a two-digit number such that if it is divided by the product of the digits it is composed of, the quotient is $16 / 3$, and if 9 is subtracted from it, the difference will also be a two-digit number that differs from the desired number only in the order of the digits.
|
## Solution.
Let $10 x+y$ be the desired two-digit number. Then
$$
\left\{\begin{array}{l}
\frac{10 x+y}{x y}=\frac{16}{3}, \\
10 x+y-9=10 y+x,
\end{array} \text { from which } x=3, y=2 . \text { The desired number is } 32 .\right.
$$
Answer: 32.
|
32
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.158. Apples of the 1st grade for a total of 228 rubles and apples of the 2nd grade for a total of 180 rubles were delivered to the store. During unloading, the delivered apples were accidentally mixed. It was found that if all the apples are now sold at one price - 90 kopecks lower than the price per kilogram of 1st grade apples, the previously planned amount will be earned. How many kilograms of apples were delivered, if it is known that there were 5 kg more of 2nd grade apples than 1st grade apples?
|
## Solution.
Let $x$ kg of apples of the first grade and $x+5$ kg of apples of the second grade be delivered to the store. In total, $2x+5$ kg of apples were delivered. A kilogram of apples of the 1st grade costs $\frac{228}{x}$ rubles. The new price of apples $-\left(\frac{228}{x}-0.9\right)$ rubles. The amount received from the sale of all apples $-\left(\frac{228}{x}-0.9\right)(2 x+5)$. According to the condition $\left(\frac{228}{x}-0.9\right)(2 x+5)=228+180$, from which $x=40$ kg. In total, $2 \cdot 40+5=85$ kg of apples were delivered.
Answer: 85 kg.
|
85
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.159. Three departments of the institute have submitted applications for the purchase of additional equipment for laboratories. The cost of the equipment in the application of the first department is $45\%$ of the application of the second department, and the cost of the equipment in the application of the second department is $80\%$ of the application of the third department. The cost of the equipment in the application of the third department exceeds the application of the first by 640 thousand rubles. What is the total cost of the equipment in the applications of all three departments?
|
## Solution.
Let $x, y, z$ thousand rubles be the cost of equipment in the applications of the first,
second, and third departments, respectively. According to the conditions $\left\{\begin{array}{l}x=0.45 y, \\ y=0.8 z, \\ z=x+640,\end{array}\right.$ from
which $x=360$ thousand rubles, $y=800$ thousand rubles, $z=1000$ thousand rubles. The total cost of the equipment in the applications of all three departments is $360+800+$ $+1000=2160$ (thousand rubles)
Answer: 2 million 160 thousand rubles.
|
2160
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.160. If a two-digit number is divided by the sum of its digits, the quotient is 4 and the remainder is 3. If this number is divided by the product of its digits, the quotient is 3 and the remainder is 5. Find this number.
|
Solution.
Let the desired number be $10 x+y$. Then, according to the condition, we have the system $\left\{\begin{array}{l}10 x+y-3=4(x+y), \\ 10 x+y-5=3 x y\end{array} \Rightarrow x=2, y=3\right.$.
Answer: 23.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.162. A certain product was purchased in the fall for 825 rubles. A kilogram of this product in the fall was 1 ruble cheaper than in the spring, and therefore, for the same amount in the spring, 220 kg less was purchased. How much does 1 kg of the product cost in the spring and how much of it was purchased in the fall?
|
## Solution.
Let $x$ kg of the product be purchased in the fall. In the spring, $x-220$ kg of the product was purchased for the same amount of money. The cost of 1 kg in the fall is $\frac{825}{x}$ rubles, and in the spring it is $\frac{825}{x-220}$ rubles. According to the condition, $\frac{825}{x-220}-\frac{825}{x}=1$, from which $x=550$ kg. The cost of 1 kg of the product in the spring is $\frac{825}{550-220}=2$ rubles 50 kopecks.
Answer: 2 rubles 50 kopecks; 550 kg.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.163. When harvesting, 210 centners of wheat were collected from each of two plots. The area of the first plot is 0.5 hectares less than the area of the second plot. How many centners of wheat were collected per hectare on each plot if the wheat yield on the first plot was 1 centner per hectare more than on the second?
|
Solution.
Let $x$ ha be the area of the first plot, $(x+0.5)$ ha be the area of the second. From 1 ha on the first plot, $\frac{210}{x}$ centners of wheat were collected, and from the second plot, $\frac{210}{x+0.5}$ centners. According to the condition, $\frac{210}{x}-\frac{210}{x+0.5}=1$, from which $x=10$ ha. From 1 ha on the first plot, $\frac{210}{10}=21$ centners of wheat were collected, and from the second - 20 centners.
Answer: 21 and 20 centners.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.164. The cost of 60 copies of the first volume and 75 copies of the second volume is 2700 rubles. In reality, only 2370 rubles were paid for all these books, as a discount was applied: 15% on the first volume and 10% on the second. Find the original price of these books.
|
Solution.
Let $x$ and $y$ rub. - the original price of the first and second volumes, respectively. According to the condition, $60 x + 75 y = 2700$. After the discount, the price of the first volume became $0.85 x$ rub., the second - $0.9 y$ rub. According to the condition, $60 \cdot 0.85 x + 75 \cdot 0.9 y = 2370$. Solving the system
$$
\left\{\begin{array}{l}
60 x + 75 y = 2700, \\
60 \cdot 0.85 x + 75 \cdot 0.9 y = 2370,
\end{array} \text { we find } x = 20 \text { rub., } y = 20\right. \text { rub. }
$$
Answer: 20 rub.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.167. A motorboat and a sailboat, being 30 km apart on a lake, move towards each other and meet after 1 hour. If the motorboat were 20 km behind the sailboat and was catching up to it, it would take 3 hours and 20 minutes. Determine the speeds of the boat and the sailboat, assuming they are constant and unchanged in both cases.
|
## Solution.
Let $x$ km/h be the speed of the boat, and $y$ km/h be the speed of the sailboat. According to the problem, $x \cdot 1 + y \cdot 1 = 30$. In the second case, in 3 hours and 20 minutes, the boat would have traveled
$3 \frac{1}{3} y + 20$ km. Then $\frac{3 \frac{1}{3} y + 20}{x} = 3 \frac{1}{3}$. Solving the system $\left\{\begin{array}{l}x + y = 30, \\ \frac{3 \frac{1}{3} y + 20}{x} = 3 \frac{1}{3},\end{array}\right.$
we find $x = 18 \text{ km/h}, y = 12 \text{ km/h}$.
Answer: 18 and 12 km/h.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.168. A one-digit number was increased by 10 units. If the resulting number is increased by the same percentage as the first time, the result is 72. Find the original number.
|
Solution.
Let $x$ be the number we are looking for, which was increased by $y \cdot 100\%$. Then $x+10=y x$, from which $y=\frac{x+10}{x}$. According to the condition $(x+10) \cdot \frac{x+10}{x}=72$, from which $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.170. One tractor brigade plowed 240 ha, and the other plowed $35 \%$ more than the first. The first brigade processed 3 ha less daily than the second, but finished the work 2 days earlier than the second. How many hectares did each brigade process per working day, given that the planned daily norm of 20 ha was exceeded by both brigades?
|
Solution.
The second brigade plowed $240 \cdot 1.35=324$ hectares. Let $x$ hectares be the amount the first brigade processed daily, and $(x+3)$ hectares - the second brigade; $y$ days the first brigade worked, and $(y+2)$ days - the second brigade. According to the problem,
$$
\left\{\begin{array}{l}
x \cdot y=240, \\
(x+3)(y+2)=324,
\end{array}\right.
$$
Answer: 24 and 27 hectares.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.173. If an unknown two-digit number is divided by the number represented by the same digits but in reverse order, the quotient is 4 and the remainder is 3. If the sought number is divided by the sum of its digits, the quotient is 8 and the remainder is 7. Find this number.
|
Solution.
Let $10 x+y$ be the desired number. Then $\left\{\begin{array}{l}10 x+y=(10 y+x) \cdot 4+3, \\ 10 x+y=(y+x) \cdot 8+7,\end{array}\right.$ from which $x=7, y=1$. The desired number is 71.
Answer: 71.
|
71
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.178. Two parks with a total area of 110 hectares are divided into an equal number of plots. The plots of each park are equal in area to each other, but differ from the plots of the other park. If the first park were divided into plots of the same area as the second, it would have 75 plots, and if the second park were divided into plots of the same area as the first, it would contain 108 plots. Determine the area of each park.
|
Solution.
Let $S$ be the area of the park, $n$ be the number of equal-sized plots, and $Q$ be the area of a plot. Then $S: n=Q$. We will fill in the table with the given and required values in the sequence indicated by the numbers (1), (2),
| Park | Initially | | | With new division | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | $\bar{S}$ | $\bar{n}$ | $Q$ | $\bar{S}$ | $\bar{n}$ | $Q$ |
| First | (7) $x$ | (11) $\frac{108 x}{110-x}$ | $(9)$ $\frac{110 x}{108}$ | (1) $x$ | (3) 75 | $(5)$ $\frac{x}{75}$ |
| Second | $(8)$ $110^{-x}$ | $\frac{75(110-x)}{x}$ | $(10)$ $\frac{x}{75}$ | $(2)$ $110-x$ | $(4)$ 108 | $(6)$ $\frac{110-x}{108}$ |
$$
\text { According to the condition } \frac{108 x}{110-x}=\frac{75(110-x)}{x} \text {, from which } x=50 \text {. }
$$
Answer: 50 and 60 hectares.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.181. A team of workers was supposed to manufacture 7200 parts per shift, with each worker making the same number of parts. However, three workers fell ill, and therefore, to meet the entire quota, each of the remaining workers had to make 400 more parts. How many workers were in the team?
|
Solution.
Let there be $x$ workers in the team. Each worker made $\frac{7200}{x}$ parts. After the team size was reduced to $x-3$ workers, each worker started making $\frac{7200}{x}+400$ parts. According to the condition, $\left(\frac{7200}{x}+400\right)(x-3)=7200$, from which $x=9$.
## Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.185. When testing two engines, it was found that the first one consumed 300 g, and the second one 192 g of gasoline, with the second engine working 2 hours less than the first. The first engine consumes 6 g more gasoline per hour than the second. How much gasoline does each engine consume per hour?
|
## Solution.
Let $x$ g of gasoline be consumed per hour by the second engine, and $(6+x)$ g per hour - by the first. The first engine worked for $\frac{300}{x+6}$ hours, the second - for $\frac{192}{x}$ hours. According to the condition, $\frac{300}{x+6}-\frac{192}{x}=2$, from which $x=24$ g per hour is consumed by the second engine, $24+6=30$ g per hour - by the first.
Answer: 30 and 24 g.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.186. A brigade of masons took on the task of laying $432 \mathrm{~m}^{3}$ of masonry, but in reality, 4 fewer people showed up for work. How many masons are there in the brigade if it is known that each working mason had to lay $9 \mathrm{~m}^{3}$ more than initially planned?
|
## Solution.
Let there be $x$ masons in the team. Each mason lays $\frac{432}{x}$ m $^{3}$ of masonry. Since $x-4$ masons were working, each had to lay $\frac{432}{x}+9$ m $^{3}$ of masonry. Therefore, $\left(\frac{432}{x}+9\right)(x-4)=432$, from which $x=16$.
## Answer: 16.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.191. Two forces are applied to a material point, the angle between which is $30^{\circ}$. The magnitude of one of the applied forces is $7 \sqrt{3}$ times the magnitude of the other, and the magnitude of the resultant force is $24 \mathrm{N}$ greater than the magnitude of the smaller force. Determine the magnitude of the smaller force and the resultant force.
|
## Solution.
Let $x \mathrm{H}$ be the modulus of the smaller force (Fig. 13.11). By the cosine rule: $\quad(24+x)^{2}=x^{2}+(7 \sqrt{3} x)^{2}-2 x \cdot 7 \sqrt{3} x \cdot \cos \left(180^{\circ}-30^{\circ}\right)$, from which $x=2 \mathrm{H}$ is the modulus of the smaller force; $24+2=26 \mathrm{H}$ is the modulus of the resultant force.
Answer: 2 and $26 \mathrm{H}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.193. During exercises, a reconnaissance boat approached the lead ship of the squadron and received an order to conduct reconnaissance ahead of the squadron in the direction of its movement at a distance of 70 km. Determine how long it will take for the boat to return to the lead ship of the squadron, which continues to move forward, if it is known that the speed of the boat is 28 km/h, and the squadron must move at a speed of 14 km/h.
|
Solution.
Let the boat return to the lead ship after $x$ hours. In this time, the squadron will travel $14 x$ km. Therefore, the boat must travel $70+70-14 x$ km. According to the condition, $140-14 x=28 x$, from which $x=3 \frac{1}{3}$ hours.
Answer: in 3 hours 20 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.194. The front wheel of a moving model makes 6 more revolutions than the rear wheel over a distance of 120 m. If the circumference of the front wheel is increased by $1 / 4$ of its length, and the circumference of the rear wheel is increased by $1 / 5$ of its length, then over the same distance, the front wheel will make 4 more revolutions than the rear wheel. Find the lengths of the circumferences of the front and rear wheels.
|
Solution.
The circumference of the wheel $C$, the number of revolutions $n$, and the distance $s$ are related by the formula $\mathrm{Cn}=s$. We will fill in the table of values for these quantities in the order indicated by the numbers (1), (2), ..., (12):
| Wheel | Before change | | | After change | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | $C$ | $s$ | $n$ | $C$ | $s$ | $n$ |
| Front | (1) $x$ | (3) 120 | (5) $\frac{120}{x}$ | (7) $\frac{5 x}{4}$ | (9) 120 | (11) $\frac{120 \cdot 4}{5 x}$ |
| Rear | (2) $y$ | (4) 120 | (6) $\frac{120}{y}$ | (8) $\frac{6 y}{5}$ | (10) 120 | (12) $\frac{120 \cdot 5}{6 y}$ |
According to the problem, we have the system $\left\{\begin{array}{l}\frac{120}{x}-\frac{120}{y}=6, \\ \frac{96}{x}-\frac{100}{y}=4,\end{array}\right.$ from which $x=4$ (m), $y=5$ (m).
Answer: 4 and $5 \mathrm{m}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.196. Two hours after leaving the factory, the driver looked at the speedometer and noticed that he had only traveled 112 km. He mentally calculated that if he continued at the same speed, he would be 30 minutes late in delivering the cargo to the station. Therefore, the driver increased his speed and arrived at the station even 30 minutes early. Determine the initial and subsequent speeds of the car, if the distance from the factory to the station according to the speedometer is 280 km.
|
Solution.
The initial speed of the car is $\frac{112}{2}=56$ km/h. The driver was on the road for a total of $\frac{280}{56}-1=4$ hours. Let the driver increase the speed by $x$ km/h. With this speed, he drove for 2 hours and covered $280-112=168$ km. Therefore, $2(56+x)=168$, from which the new speed of the car is $84 \mathrm{km} / \mathrm{h}$.
Answer: 56 and 84 km/h.
|
56
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.197. A cinema hall has two doors, a wide one and a narrow one. After a screening, the audience exits the hall through both doors in 3 minutes and 45 seconds. If the audience is let out through only the wide door, it takes 4 minutes less than if they are let out through only the narrow door. How much time is required for the audience to exit the cinema hall through each door separately?
|
## Solution.
Let $x$ min be necessary to release the audience only through the wide door, $(x+4)$ min - only through the narrow door. In one minute, $\frac{1}{x}$ people exit through the wide door, and $\frac{1}{x+4}$ people exit through the narrow door. According to the condition: $\frac{1}{x}+\frac{1}{x+4}=\frac{1}{3 \frac{3}{4}}$, from which $x=6$ min.
Answer: 6 and 10 min.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.199. On the way from the village to the field, the truck's wheel makes 100 fewer revolutions than the bicycle's wheel and 150 more revolutions than the tractor's track. Find the distance between the village and the field, given that the circumference of the truck's wheel is $4 / 3$ of the circumference of the bicycle's wheel and 2 m shorter than the tractor's track.
|
## Solution.
Let $x$ m be the distance between the village and the field, $y$ m be the circumference of the bicycle wheel; $\frac{4}{3} y$ m be that of the truck, $\left(\frac{4}{3} y+2\right)$ m be that of the tractor.
The truck wheel makes $\frac{x}{\frac{4}{3} y}$ revolutions; the bicycle wheel makes $-\frac{x}{y}$ revolutions; the tractor wheel makes $-\frac{x}{\frac{4}{3} y+2}$ revolutions. According to the conditions, $\left\{\begin{array}{l}\frac{x}{\frac{4}{3} y}=\frac{x}{y}-100, \\ \frac{x}{\frac{4}{3} y}=\frac{x}{\frac{4}{3} y+2}+150,\end{array}\right.$ from which $x=600$ m.
Answer: 600 m.
|
600
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.200. Two skins with a total cost of 22500 rubles were sold at an auction with a profit of $40 \%$. What is the cost of each skin if a profit of $25 \%$ was made on the first one, and $50 \%$ on the second one?
|
Solution.
Let $x$ rubles be the cost of the first pelt, and 22500 - $x$ rubles be the cost of the second. The first pelt was sold for $1.25 x$ rubles, and the second for $1.5(22500-x)$ rubles. According to the condition, $1.25 x + 1.5(22500-x) = 1.4 \cdot 22500$, from which $x = 9000$ rubles.
Answer: 9000 and 13500 rubles.
|
9000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.205. If a two-digit number is divided by the sum of its digits, the quotient is 3 and the remainder is 7. If then the sum of the squares of the digits of this number is taken and the product of the same digits is subtracted from it, the original number is obtained. Find this number.
|
Solution.
Let $10 x+y$ be the desired number. According to the condition $\left\{\begin{array}{l}10 x+y=3(x+y)+7, \\ x^{2}+y^{2}-x y=10 x+y,\end{array}\right.$ from which $x=3, y=7$. The desired number is 37.
Answer: 37.
|
37
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.206. A three-digit number ends with the digit 2. If it is moved to the beginning of the number, the resulting number will be 18 more than the original. Find this number.
|
## Solution.
Let the desired three-digit number be of the form $100x + 10y + 2$; then after moving the digit 2, it will take the form $200 + 10x + y$ (1). According to the problem, $200 + 10x + y - (100x + 10y + 2) = 18$, from which we get $10x + y = 20$. Substituting this expression into (1), we get $200 + 20 = 220$. Therefore, the original three-digit number is 202.
Answer: 202.
|
202
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.207. The express train travels the distance from Moscow to St. Petersburg 3 hours and 30 minutes faster than the passenger train, as it covers 35 km more in 1 hour. How many kilometers per hour does each of them travel, if the distance between Moscow and St. Petersburg is rounded to 650 km?
|
## Solution.
Let $x$ km/h be the speed of the passenger train, and $x+35$ km/h be the speed of the express train. According to the condition, $\frac{650}{x}-\frac{650}{x+35}=3.5$, from which $x=65$ km/h.
Answer: 65 and 100 km/h.
|
65
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.322 A=\sqrt{y^{2}-6 y+9}-|y-9|+2$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.322 A=\sqrt{y^{2}-6 y+9}-|y-9|+2$.
|
Solution. $A=\sqrt{(y-3)^{2}}-|y-9|+2=|y-3|-|y-9|+2$.
Consider 3 cases.
1) $\left\{\begin{array}{l}y9, \\ A=y-3-(y-9)+2\end{array} \Leftrightarrow\left\{\begin{array}{l}y>9, \\ A=8 .\end{array}\right.\right.$
Answer: if $y>9$, then $A=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.275 $\frac{2+x}{2-x}+\sqrt{x}=1+x$
|
Solution. $\frac{2+x}{2-x}-1=x-\sqrt{x} \Leftrightarrow \frac{2 x}{2-x}=\sqrt{x}(\sqrt{x}-1)$. Let $y=\sqrt{x}$, then $\frac{2 y^{2}}{2-y^{2}}=y(y-1) \Leftrightarrow\left[\begin{array}{l}y=0, \\ y \neq \sqrt{2}, \\ y^{3}-y^{2}+2=0\end{array} \Leftrightarrow\right.$ $\Leftrightarrow\left[\begin{array}{l}y=0 . \\ (y+1)\left(y^{2}-2 y+2\right)=0\end{array} \Leftrightarrow \sqrt{x}=0\right.$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.277 \sqrt{x-1}+\sqrt{x+3}+2 \sqrt{(x-1)(x+3)}=4-2 x
$$
6.277 \sqrt{x-1}+\sqrt{x+3}+2 \sqrt{(x-1)(x+3)}=4-2 x
$$
|
Solution. Let $u=\sqrt{x-1}, v=\sqrt{x+3}$, then $u+v+2uv=-(u^2+v^2)+6 \Leftrightarrow$ $(u+v)^2+(u+v)-6=0 \Leftrightarrow\left[\begin{array}{l}u+v=-3, \\ u+v=2\end{array} \Leftrightarrow\left[\begin{array}{l}\varnothing, \\ \sqrt{x-1}+\sqrt{x+3}=2 .\end{array}\right.\right.$
Since $x \geq 1$, then $\sqrt{x+3} \geq 2 \Rightarrow x=1$ is the only solution to the last equation.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.278 \sqrt{2 x+3}+\sqrt{x+1}=3 x+2 \sqrt{2 x^{2}+5 x+3}-16$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$6.278 \sqrt{2 x+3}+\sqrt{x+1}=3 x+2 \sqrt{2 x^{2}+5 x+3}-16$.
|
Solution. $\sqrt{2 x+3}+\sqrt{x+1}=3 x-16+2 \sqrt{(2 x+3)(x+1)}$.
Let $u=\sqrt{2 x+3}, v=\sqrt{x+1}$, then $u+\dot{v}=u^{2}+v^{2}-20+2 u v \Leftrightarrow$
$$
\Leftrightarrow(u+v)^{2}-(u+v)-20=0 . \Leftrightarrow\left[\begin{array}{l}
u+v=5, \\
u+v=-4
\end{array} \Leftrightarrow \sqrt{2 x+3}+\sqrt{x+1}=5 \Leftrightarrow\right.
$$
$$
\begin{aligned}
& \Leftrightarrow\left\{\begin{array} { l }
{ x \geq - 1 , } \\
{ 3 x + 4 + 2 \sqrt { ( 2 x + 3 ) ( x + 1 ) } = 2 5 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq-1, \\
x \leq 7, \\
4(2 x+3)(x+1)=9(7-x)^{2}
\end{array} \Leftrightarrow\right.\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
-1 \leq x \leq 7, \\
x^{2}-146 x+429=0
\end{array} \Leftrightarrow x=3 .\right.
\end{aligned}
$$
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.279 \sqrt[4]{x+8}-\sqrt[4]{x-8}=2$
|
Solution. Let $u=\sqrt[4]{x+8}, v=\sqrt[4]{x-8}$, then $\left\{\begin{array}{l}u-v=2, \\ u^{4}-v^{4}=16\end{array} \Rightarrow\right.$ $\Rightarrow(v+2)^{4}-v^{4}=16 \Leftrightarrow\left((v+2)^{2}-v^{2}\right)\left((v+2)^{2}+v^{2}\right)=16 \Leftrightarrow(v+1)(v+2 v+2)=2$.
Since $v \geq 0$, then $v+1 \geq 1, v^{2}+2 v+2 \geq 2 \Rightarrow v=0$ is the only solution to the last equation.
Answer: $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.280 \sqrt{x}-\sqrt{x+1}-\sqrt{x+4}+\sqrt{x+9}=0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$6.280 \sqrt{x}-\sqrt{x+1}-\sqrt{x+4}+\sqrt{x+9}=0$.
|
Solution. $\sqrt{x}+\sqrt{x+9}=\sqrt{x+1}+\sqrt{x+4} \Leftrightarrow$
$\Leftrightarrow\left\{\begin{array}{l}x \geq 0, \\ x+x+9+2 \sqrt{x(x+9)}=x+1+x+4+2 \sqrt{(x+1)(x+4)}\end{array} \Leftrightarrow\right.$
$\Leftrightarrow\left\{\begin{array}{l}x \geq 0, \\ 2+\sqrt{x(x+9)}=\sqrt{(x+1)(x+4)}\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geq 0 \\ 4+x^{2}+9 x+4 \sqrt{x(x+9)}=x^{2}+5 x+4\end{array} \Leftrightarrow\right.\right.$ $\Leftrightarrow\left\{\begin{array}{l}x \geq 0, \\ x+\sqrt{x(x+9)}=0\end{array} \Leftrightarrow x=0\right.$.
Answer: $x=0$.
## $6.281 \sqrt[3]{x+5}+\sqrt[3]{x+6}=\sqrt[3]{2 x+11}$
Solution. Raise both sides to the third power:
$2 x+11+3 \sqrt[3]{(x+5)(x+6)} \cdot(\sqrt[3]{x+5}+\sqrt[3]{x+6})=2 x+11 \Leftrightarrow$
$\sqrt[3]{(x+5)(x+6)} \cdot(\sqrt[3]{x+5}+\sqrt[3]{x+6})=0 \Leftrightarrow \sqrt[3]{(x+5)(x+6)(2 x+11)}=0 \Rightarrow\left[\begin{array}{l}x=-5, \\ x=-6, \\ x=-\frac{11}{2} .\end{array}\right.$
By checking, we confirm that all these values are roots of the original equation.
Answer: $x_{1}=-6 ; x_{2}=-5.5 ; x_{3}=-5$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.282 \sqrt{x^{2}-x-1}+\sqrt{x^{2}+x+3}=\sqrt{2 x^{2}+8}, x>0$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$6.282 \sqrt{x^{2}-x-1}+\sqrt{x^{2}+x+3}=\sqrt{2 x^{2}+8}, x>0$.
|
Solution. Raise both sides to the square:
$\left\{\begin{array}{l}x^{2}-x-1 \geq 0, ; \\ 2 x^{2}+2+2 \sqrt{\left(x^{2}-x-1\right)\left(x^{2}+x+3\right)}=2 x^{2}+8, \\ x>0\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}x^{2}-x-1 \geq 0, \\ \sqrt{\left(x^{2}-x-1\right)\left(x^{2}+x+3\right)} \\ x>0\end{array}, \Leftrightarrow\left\{\begin{array}{l}x>0, \\ \left(x^{2}-x-1\right)\left(x^{2}+x+3\right)=9\end{array} \Leftrightarrow\right.\right.$
$\Leftrightarrow\left\{\begin{array}{l}x>0, \\ x^{4}+x^{2}-4 x-12=0\end{array} \Leftrightarrow\left\{\begin{array}{l}x>0, \\ (x-2)\left(x^{3}+2 x^{2}+5 x+6\right)=0\end{array} \Leftrightarrow x=2\right.\right.$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.283 \frac{x \sqrt[5]{x}-1}{\sqrt[5]{x^{3}}-1}+\frac{\sqrt[5]{x^{3}}-1}{\sqrt[5]{x}-1}=16$
|
## Solution.
Let $y=\sqrt[5]{x}$, then $\frac{y^{6}-1}{y^{3}-1}+\frac{y^{3}-1}{y-1}=16 \Leftrightarrow y^{3}+y^{2}+y-14=0 \Leftrightarrow$ $\Leftrightarrow(y-2)\left(y^{2}+3 y+7\right)=0 \Leftrightarrow \sqrt[5]{x}=2 \Leftrightarrow x=32$.
Answer: $x=32$.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.287 \frac{1}{\sqrt{x}+\sqrt[3]{x}}+\frac{1}{\sqrt{x}-\sqrt[3]{x}}=\frac{1}{3}$.
|
Solution. $\frac{\sqrt{x}-\sqrt[3]{x}+\sqrt{x}+\sqrt[3]{x}}{(\sqrt{x}+\sqrt[3]{x})(\sqrt{x}-\sqrt[3]{x})}=\frac{1}{3} \Leftrightarrow\left\{\begin{array}{l}6 \sqrt{x}=x-\sqrt[3]{x^{2}} \\ \sqrt{x} \neq \sqrt[3]{x} .\end{array}\right.$
Let $\sqrt[6]{x}=y$, then $\left\{\begin{array}{l}6 y^{3}=y^{6}-y^{4}, \\ y^{3}-y^{2} \neq 0\end{array} \Leftrightarrow y^{3}-y-6=0 \Leftrightarrow\right.$ $\Leftrightarrow(y-2)\left(y^{2}+2 y+3\right)=0 \Leftrightarrow y=2$.
Answer: $x=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.288 \frac{x^{2}}{\sqrt{2 x+15}}+\sqrt{2 x+15}=2 x$.
|
Solution.
$$
\begin{aligned}
& \frac{x^{2}}{\sqrt{2 x+15}}+\sqrt{2 x+15}-2 x=0 \Leftrightarrow\left(\frac{x}{\sqrt[4]{2 x+15}}-\sqrt[4]{2 x+15}\right)^{2}=0 \Leftrightarrow \\
& \Leftrightarrow \frac{x}{\sqrt[4]{2 x+15}}=\sqrt[4]{2 x+15} \Leftrightarrow x=\sqrt{2 x+15} \Leftrightarrow\left\{\begin{array}{l}
x \geq 0, \\
x^{2}=2 x+15
\end{array} \Leftrightarrow x=5 .\right.
\end{aligned}
$$
Answer: $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.290 \sqrt{x+2 \sqrt{x-1}}+\sqrt{x-2 \sqrt{x-1}}=x-1$.
|
Solution. $\sqrt{(x-1)+2 \sqrt{x-1}+1}+\sqrt{(x-1)-2 \sqrt{x-1}+1}=x-1 \Leftrightarrow$ $\Leftrightarrow \sqrt{(\sqrt{x-1}+1)^{2}}+\sqrt{(\sqrt{x-1}-1)^{2}}=x-1 \Leftrightarrow \sqrt{x-1}+1+|\sqrt{x-1}-1|=x-1 \Leftrightarrow$ $\Leftrightarrow \sqrt{x-1}+|\sqrt{x-1}-1|=x-2$.
Since $x \geq 2$, then $\sqrt{x-1} \geq 1$. Therefore, the last equation is equivalent to the system:
$\left\{\begin{array}{l}2 \sqrt{x-1}-1=x-2, \\ x \geq 2\end{array} \Leftrightarrow\left\{\begin{array}{l}2 \sqrt{x-1}=x-1, \\ x \geq 2\end{array} \Leftrightarrow\left\{\begin{array}{l}2=\sqrt{x-1}, \\ x \geq 2\end{array} \Leftrightarrow x=5\right.\right.\right.$.
Answer: $x=5$.
$6.2918,4 \sqrt[12]{x^{-7}}-0.2 \sqrt[4]{x^{-1} \cdot \sqrt[3]{x^{2}}}=\sqrt[12]{x^{11}}$
Solution. Note that $\sqrt[4]{x^{-1} \cdot \sqrt[3]{x^{2}}}=\sqrt[12]{x^{-1}}$. Multiply both sides of the equation by $\sqrt[12]{x}: \frac{8.4}{\sqrt{x}}-0.2=x$. Let $y=\sqrt{x}$, then $5 y^{3}+y-42=0 \Leftrightarrow$ $\Leftrightarrow(y-2)\left(5 y^{2}+10 y+21\right)=0 \Leftrightarrow y=2 \Leftrightarrow x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.293
$$
\frac{\sqrt[7]{x-\sqrt{2}}}{2}-\frac{\sqrt[7]{x-\sqrt{2}}}{x^{2}}=\frac{x}{2} \cdot \sqrt[7]{\frac{x^{2}}{x+\sqrt{2}}}
$$
|
Solution. $\frac{\sqrt[7]{x^{2}-2}}{2}-\frac{\sqrt[7]{x^{2}-2}}{x^{2}}=\frac{x}{2} \cdot \sqrt[7]{x^{2}} \Leftrightarrow \sqrt[7]{x^{2}-2} \cdot\left(x^{2}-2\right)=x^{3} \cdot \sqrt[7]{x^{2}} \Leftrightarrow$ $\Leftrightarrow\left(x^{2}-2\right)^{8}=x^{23} \Leftrightarrow\left|x^{2}-2\right|=x^{\frac{23}{8}}$.
Consider two cases:
1) $\left\{\begin{array}{l}x^{2}-2=x^{\frac{23}{8}} \\ x \geq \sqrt{2}\end{array}, \Leftrightarrow \varnothing\right.$, since $x^{\frac{23}{8}} \geq x^{2}$ for $\dot{x}>1$.
2) $\left\{\begin{array}{l}2-x^{2}=x^{\frac{23}{8}} \\ 00$. Therefore, the equation $f(x)=2$ has a unique root $x=1$ for $0 \leqslant x<\sqrt{2}$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.299 \frac{2}{19}\left(\sqrt{x^{2}+37 x+336}-\sqrt{x^{2}+18 x+32}\right)=\sqrt{\frac{21+x}{16+x}}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$6.299 \frac{2}{19}\left(\sqrt{x^{2}+37 x+336}-\sqrt{x^{2}+18 x+32}\right)=\sqrt{\frac{21+x}{16+x}}$.
|
Solution. Note that $x^{2}+37 x+336 \geq x^{2}+18 x+32$, i.e., $x \geq-16$.
Therefore, the original equation is equivalent to
$$
\begin{aligned}
& \left\{\begin{array}{l}
\frac{2}{19} \sqrt{x+16}(\sqrt{x+21}-\sqrt{x+2})=\frac{\sqrt{x+21}}{\sqrt{x+16}}, \Leftrightarrow \\
x>-16
\end{array}\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
\frac{2(x+16)(\sqrt{x+21}-\sqrt{x+2})}{(x+21)-(x+2)}=\sqrt{x+21}, \Leftrightarrow \frac{2(x+16)}{\sqrt{x+21}+\sqrt{x+2}}=\sqrt{x+21} \Leftrightarrow \\
x>-16
\end{array}\right. \\
& \Leftrightarrow 2(x+16)=x+21+\sqrt{x+21} \cdot \sqrt{x+2} \Leftrightarrow\left\{\begin{array}{l}
(x+11)^{2}=(x+21)(x+2), \\
x \geq-2
\end{array} \Leftrightarrow x=79\right.
\end{aligned}
$$
Answer: $x=79$.
$$
|
79
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.300 \sqrt{x-2}+\sqrt{4-x}=x^{2}-6 x+11
|
Solution. $\sqrt{(x-3)+1}+\sqrt{1-(x-3)}=\left(x^{2}-6 x+9\right)+2$.
Let $y=x-3$, then $\sqrt{y+1}+\sqrt{1-y}=y^{2}+2 \Leftrightarrow$ $y^{4}+4 y^{2}+2\left(1-\sqrt{1-y^{2}}\right)=0$.
Since $1 \geq \sqrt{1-y^{2}}$, the last equation is equivalent to the system:
$$
\left\{\begin{array}{l}
y^{4}+4 y^{2}=0 \\
1=\sqrt{1-y^{2}}
\end{array} \Leftrightarrow y=0 .\right.
$$
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.355 Prove that for any natural $n$
$\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots+\frac{1}{(n+1)(n+2)}=\frac{n+1}{n+2}$
and using this equality, solve the equation
$$
(1+3+5+\ldots+(2 n+1)):\left(\frac{1}{2}+\frac{1}{6}+\ldots+\frac{1}{342}\right)=342
$$
|
## Solution.
$\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots+\frac{1}{(n+1)(n+2)}=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\ldots+\left(\frac{1}{n}-\frac{1}{n+1}\right)+$ $+\left(\frac{1}{n+1}-\frac{1}{n+2}\right)=1-\frac{1}{n+2}=\frac{n+1}{n+2}$.
$1+3+5+\ldots+(2 n+1)=\frac{1+(2 n+1)}{2}(n+1)=(n+1)^{2}$.
$\frac{1}{2}+\frac{1}{6}+\ldots+\frac{1}{342}=\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots+\frac{1}{18 \cdot 19}=\frac{18}{19}$. Then the original equation becomes: $\frac{19(n+1)^{2}}{18}=342 \Leftrightarrow(n+1)^{2}=18^{2} \Leftrightarrow n=17$.
Answer: $n=17$.
|
17
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6.365 Solve the equation $\left(x^{3}+x^{-3}\right)+\left(x^{2}+x^{-2}\right)+\left(x+x^{-1}\right)=6$.
|
Solution. $\left(x^{3}-2+\frac{1}{x^{3}}\right)+\left(x^{2}-2+\frac{1}{x^{2}}\right)+\left(x-2+\frac{1}{x}\right)=0 \Leftrightarrow \frac{\left(x^{3}-1\right)^{2}}{x^{3}}+\frac{\left(x^{2}-1\right)^{2}}{x^{2}}+\frac{(x-1)^{2}}{x}=0$ $(x-1)^{2}\left(\left(x^{2}+x+1\right)^{2}+x(x+1)^{2}+x^{2}\right)=0 \Leftrightarrow$ $\Leftrightarrow(x-1)^{2}\left(\left(x^{2}+x+1\right)^{2}+x\left(x^{2}+2 x+1\right)+x^{2}\right)=0 \Leftrightarrow x=1$ or $\left(x^{2}+x+1\right)^{2}+x\left(x^{2}+x+1\right)+2 x^{2}=0$. Let $v=x, u=x^{2}+x+1$, then $\left[\begin{array}{l}x=1 \\ u^{2}+u v+2 v^{2}=0\end{array} \Leftrightarrow\left[\begin{array}{l}x=1 \\ x \in \varnothing\end{array} \Rightarrow x=1\right.\right.$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.370 Solve the equation $\sqrt[4]{x^{4}+x-2}+\sqrt{x^{4}+x-2}=6$ given that $\boldsymbol{x}>\mathbf{0}$.
|
Solution. Let $y=\sqrt[4]{x^{4}+x-2}$, then $y^{2}+y-6=0 \Leftrightarrow \sqrt[4]{x^{4}+x-2}=2 \Leftrightarrow$ $\Leftrightarrow x^{4}+x-18=0 \Leftrightarrow(x-2)\left(x^{3}+2 x^{2}+4 x+9\right)=0$.
Since $x>0$, then $x^{3}+2 x^{2}+4 x+9>0 \Rightarrow x=2$.
Answer: $x=2$.
## pRoGReSSiOnS
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.069 Find a three-digit number whose digits form a geometric progression. If 792 is subtracted from this number, the result is a number written with the same digits but in reverse order. If 4 is subtracted from the digit representing the hundreds, and the other digits of the desired number are left unchanged, the resulting number will have digits that form an arithmetic progression.
|
Solution. Let the desired number have the form:
$100 x+10 y+z \Rightarrow 100 x+10 y+z=792+100 z+10 y+x \Rightarrow x=8+z \Rightarrow\left[\begin{array}{l}z=0, x=8, \\ z=1, x=9 .\end{array}\right.$
Since the digits $x, y, z$ form a geometric progression, then $z \neq 0 \Rightarrow z=1$. The possible cases are:
1) $x z=y^{2} \Rightarrow y=3$
2) $x y=z^{2} \Rightarrow \varnothing$;
3) $y z=x^{2} \Rightarrow \varnothing$.
By verification, we find that the number 931 satisfies the other conditions of the problem.
Answer: 931.
|
931
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.070 It is known that for any $n$ the sum of the first $n$ terms of a certain numerical sequence is expressed by the formula $S_{n}=2 n^{2}+3 n$. Find the tenth term of this sequence and prove that this sequence is an arithmetic progression.
|
Solution. Let $a_{1}, a_{2}, \ldots a_{n}$ be the given sequence. Then
$a_{n}=S_{n}-S_{n-1}=2 n^{3}+3 n-\left(2(n-1)^{2}+3(n-1)\right)=4 n+1$ for $n \geq 2$. Further, $a_{n+1}-a_{n}=(4(n+1)+1)-(4 n+1)=4$ for $n \geq 2$. It remains to check the difference $a_{2}-a_{1}: a_{2}=4 \cdot 2+1=9, a_{1}=S_{1}=2 \cdot 1^{2}+3 \cdot 1=5 \Rightarrow a_{2}-a_{1}=4$.
Therefore, $a_{1}, a_{2}, \ldots, a_{n}$ is an arithmetic progression and $a_{10}=41$.
Answer: 41.
|
41
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.075 The sequence of numbers $1,8,22,43, \ldots$ has the property that the differences between two consecutive terms (the subsequent and the previous) form an arithmetic progression: $7,14,21, \ldots$. Find the index of the term in the sequence that equals 35351.
|
Solution. Let the numbers of the given sequence $1, 8, 22, \ldots$ be denoted as $a_{1}, a_{2}, a_{3}, \ldots$.
By the condition, $a_{2}-a_{1}=7 \cdot 1, a_{3}-a_{2}=7 \cdot 2, \ldots, a_{n}-a_{n-1}=7(n-1)$.
Adding these equations term by term, we have: $\left(a_{2}-a_{1}\right)+\left(a_{3}-a_{2}\right)+\ldots+$
$+\left(a_{n-1}-a_{n-2}\right)+\left(a_{n}-a_{n-1}\right)=7(1+2+\ldots+(n-1)) \Leftrightarrow a_{n}-a_{1}=7 \cdot \frac{n(n-1)}{2} \Rightarrow$
$\Rightarrow a_{n}=a_{1}+\frac{7(n-1) n}{2}$. Since $a_{n}=35351$, then $n(n-1)=10100 \Rightarrow n=101$.
Answer: 101.
|
101
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.084 In a volleyball competition, $n$ teams participated. Each team played with all the others once. For each game, the winning team was awarded one point, and no points were awarded for a loss, as there are no draws in volleyball. At the end of the competition, it turned out that the points scored by the teams formed an arithmetic progression. How many points did the team that finished in last place score?
|
Solution. Let the points scored by the teams form a non-decreasing arithmetic progression $a_{1}, a_{2}, \ldots, a_{n}$ with a common difference $d$. A total of $\frac{n(n-1)}{2}$ games were played. Therefore, the total number of points scored by all teams is $\frac{n(n-1)}{2}$, from which we have $a_{1}+a_{2}+\ldots+a_{n}=\frac{n(n-1)}{2} \Rightarrow \frac{n}{2}\left(2 a_{1}+(n-1) d\right)=\frac{n(n-1)}{2} \Rightarrow 2 a_{1}=(n-1)(1-d)$.
Since $d$ and $a_{1}$ are integers, we have $\left[\begin{array}{l}d=1, \\ d=0 .\end{array}\right.$ However, according to the problem, there is a team that finished in the last place, so $d=1 \Rightarrow a_{1}=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.085 In an angle containing $60^{\circ}$, five circles are inscribed such that each subsequent circle, starting from the second, touches the previous one; How many times greater is the sum of the areas of all five corresponding circles compared to the area of the smallest circle?
|
## Solution.

$\angle O_{1} A B_{1}=30^{\circ} \Rightarrow A O_{1}=2 a, A O_{2}=2 b$. But $A O_{2}=b+a+A O_{1}=3 a+b \Rightarrow \frac{b}{a}=3$.
Therefore, if $r_{i}$ is the radius of the $i$-th inscribed circle, then $\frac{r_{i}}{r_{i-1}}=3$, i.e., $r_{1}, r_{2}, r_{3}, r_{4}, r_{5}$ form a geometric progression with a common ratio of 3. If $S_{i}$ is the area of the $i$-th circle, then $S_{1}+S_{2}+S_{3}+S_{4}+S_{5}=\pi r_{1}^{2}\left(1+3^{2}+3^{4}+3^{6}+3^{8}\right)=S_{1} \cdot 7381$.
## Answer: 7381 times.
LOGARITHMS. EXPONENTIAL AND LOGARITHMIC EQUATIONS
Simplify the expressions (7.295 - 7.299):
|
7381
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.296
$2 \log _{a}^{\frac{1}{2}} b \cdot\left(\left(\log _{a} \sqrt[4]{a b}+\log _{b} \sqrt[4]{a b}\right)^{\frac{1}{2}}-\left(\log _{a} \sqrt[4]{\frac{b}{a}}+\log _{b} \sqrt[4]{\frac{a}{b}}\right)^{\frac{1}{2}}\right), a, b>1$.
|
Solution.
1) $\left(\log _{a} \sqrt[4]{a b}+\log _{b} \sqrt[4]{a b}\right)^{\frac{1}{2}}=\left(\frac{1}{4}\left(\log _{a} b+1+\log _{b} a+1\right)\right)^{\frac{1}{2}}=$
$=\left(\frac{1}{4}\left(2+\log _{a} b+\frac{1}{\log _{a} b}\right)\right)^{\frac{1}{2}}=\frac{1}{2}\left(\frac{\left(\log _{a} b+1\right)^{2}}{\log _{a} b}\right)^{\frac{1}{2}}=\frac{\log _{a} b+1}{2 \sqrt{\log _{a} b}}$.
2) $\left(\log _{a} \sqrt[4]{\frac{b}{a}}+\log _{b} \sqrt[4]{\frac{a}{b}}\right)^{\frac{1}{2}}=\left(\frac{1}{4} \log _{a} b-\frac{1}{4}+\frac{1}{4} \log _{b} a-\frac{1}{4}\right)^{\frac{1}{2}}=\frac{1}{2}\left(\frac{\left(\log _{a} b-1\right)^{2}}{\log _{a} b}\right)^{\frac{1}{2}}=$
$$
=\frac{\left|\log _{a} b-1\right|}{2 \sqrt{\log _{a} b}} .
$$
3) $2 \log _{a}^{\frac{1}{2}} b \cdot\left(\frac{\log _{a} b+1}{2 \sqrt{\log _{a} b}}-\frac{\left|\log _{a} b-1\right|}{2 \sqrt{\log _{a} b}}\right)=\log _{a} b+1-\left|\log _{a} b-1\right|$.
Answer: 2, if $1<a \leq b ; 2 \log _{a} b$, if $1<b<a$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.308 \quad(\sqrt[3]{0.5}+\sqrt[3]{4})^{x}=13.5$.
|
## Solution.
$$
\left(\frac{1}{\sqrt[3]{2}}+\sqrt[3]{4}\right)^{x}=\frac{27}{2} \Leftrightarrow\left(\frac{3}{\sqrt[3]{2}}\right)^{x}=\frac{27}{2} \Leftrightarrow\left(\frac{27}{2}\right)^{\frac{x}{3}}=\left(\frac{27}{2}\right)^{1} \Leftrightarrow x=3
$$
Answer: $x=3$.
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3092 \log _{9}^{2} x=\log _{3} x \cdot \log _{3}(\sqrt{2 x+1}-1)
|
Solution. $\frac{\log _{3}^{2} x}{2}=\log _{3} x \cdot \log _{3}(\sqrt{2 x+1}-1) \Leftrightarrow \log _{3} x \cdot\left(\log _{3} x-2 \log _{3}(\sqrt{2 x+1}-1)\right)=0$
Answer: $x_{1}=1, x_{2}=4$.
$7.310\left(1+\log _{x} \frac{4-x}{10}\right) \lg x=\lg \lg 10^{3}-1$.
Solution. $\log _{x} \frac{(4-x) x}{10} \cdot \lg x=\lg 3-1 \Leftrightarrow \log _{x} \frac{(4-x) x}{10}=\frac{\lg \frac{3}{10}}{\lg x} \Leftrightarrow$ $\Leftrightarrow \log _{x} \frac{(4-x) x}{10}=\log _{x} \frac{3}{10} \Leftrightarrow\left\{\begin{array}{l}x>0, \\ x \neq 1, \\ (4-x) x=3\end{array} \Leftrightarrow x=3\right.$.
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.313 \log _{x+1}\left(x^{3}-9 x+8\right) \cdot \log _{x-1}(x+1)=3$.
|
## Solution.
$\log _{x+1}\left((x-1)\left(x^{2}+x-8\right)\right) \cdot \log _{x-1}(x+1)=3 \Leftrightarrow$
$\Leftrightarrow\left\{\begin{array}{l}\log _{x+1}\left((x-1)\left(x^{2}+x-8\right)\right)=3 \log _{x+1}(x-1), \\ x \neq 2\end{array} \Leftrightarrow\left\{\begin{array}{l}x-1>0, \\ x \neq 2, \\ (x-1)\left(x^{2}+x-8\right)=(x-1)^{3}\end{array} \Leftrightarrow\right.\right.$
$\Leftrightarrow\left\{\begin{array}{l}x-1>0, \\ x \neq 2, \\ x^{2}+x-8=(x-1)^{2}\end{array} \Leftrightarrow x=3\right.$
Answer: $x=3$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.317 \log _{4} x+\log _{x} 2-\log _{4} \sqrt{x}=1$
|
Solution. $\frac{1}{2} \log _{2} x+\frac{1}{\log _{2} x}-\frac{1}{4} \log _{2} x=1 \Leftrightarrow \log _{2}^{2} x-4 \log _{2} x+4=0 \Leftrightarrow$ $\left(\log _{2} x-2\right)^{2}=0 \Leftrightarrow x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.