problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
7.029. $0.25^{\log _{2} \sqrt{x+3}-0.5 \log _{2}\left(x^{2}-9\right)}=\sqrt{2(7-x)}$.
|
## Solution.
Domain of definition: $\quad\left\{\begin{array}{l}x+3>0, \\ x^{2}-9>0.33 . \Rightarrow x_{1}=5, x_{2}=-1 ; x_{2}=-1 \text{ does not fit the domain of definition.}\end{array}\right.$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.031. $\log _{5}(x-2)+\log _{\sqrt{5}}\left(x^{3}-2\right)+\log _{0.2}(x-2)=4$.
|
## Solution.
Domain of definition: $\quad x-2>0, x>2$.
From the condition we have
$$
\log _{5}(x-2)+2 \log _{5}\left(x^{3}-2\right)-\log _{5}(x-2)=4, \log _{5}\left(x^{3}-2\right)=2
$$
from which $x^{3}-2=25, x^{3}=27$. Then $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.034. $\lg \left(3^{x}-2^{4-x}\right)=2+0.25 \lg 16-0.5 x \lg 4$.
|
Solution.
Domain of definition: $3^{x}-2^{4-x}>0$.
From the condition
$$
\begin{aligned}
& \lg \left(3^{x}-2^{4-x}\right)=\lg 100+\lg 2-\lg 2^{x} \Rightarrow \lg \left(3^{x}-2^{4-x}\right)=\lg \frac{100 \cdot 2}{2^{x}} \\
& 3^{x}-2^{4-x}=\frac{200}{2^{x}}
\end{aligned}
$$
From here $6^{x}=216$, hence $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.035. $\log _{3}\left(81^{x}+3^{2 x}\right)=3 \log _{27} 90$.
|
## Solution.
From the condition $\log _{3}\left(81^{x}+3^{2 x}\right)=\log _{3} 90, 9^{2 x}+9^{x}-90=0$, from which we find $9^{x}=-10$, which is not suitable, or $9^{x}=9$, from which we have $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.039. $\lg \left(10^{\lg \left(x^{2}-21\right)}\right)-2=\lg x-\lg 25$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{2}-21>0, \\ x>0,\end{array} x>\sqrt{21}\right.$.
From the condition we have
$$
\lg \left(x^{2}-21\right)-\lg 100=\lg x-\lg 25, \lg \frac{x^{2}-21}{100}=\lg \frac{x}{25}, \quad \frac{x^{2}-21}{100}=\frac{x}{25}
$$
We obtain the quadratic equation $x^{2}-4 x-21=0$, the roots of which are $x_{1}=7, x_{2}=-3 ; x_{2}=-3$ does not satisfy the domain of definition.
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.042. $x(\lg 5-1)=\lg \left(2^{x}+1\right)-\lg 6$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
7.042. $x(\lg 5-1)=\lg \left(2^{x}+1\right)-\lg 6$.
|
Solution.
$$
\begin{aligned}
& x(\lg 5-\lg 10)=\lg \left(2^{x}+1\right)-\lg 6, \quad x \lg \frac{5}{10}=\lg \frac{2^{x}+1}{6} \\
& \lg 2^{-x}=\lg \frac{2^{x}+1}{6}, 2^{-x}=\frac{2^{x}+1}{6}, 2^{2 x}+2^{x}-6=0
\end{aligned}
$$
Solving this equation as a quadratic in terms of $2^{x}$, we find $2^{x}=-3$ (not valid), $2^{x}=2$, from which we have $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.045. $\log _{5}(3 x-11)+\log _{5}(x-27)=3+\log _{5} 8$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}3 x-11>0, \\ x-27>0,\end{array} \quad x>27\right.$.
## We have
$$
\begin{aligned}
& \log _{5}(3 x-11)+\log _{5}(x-27)=\log _{5} 125+\log _{5} 8 \\
& \log _{5}(3 x-11) \cdot(x-27)=\log _{5}(125 \cdot 8) \quad(3 x-11)(x-27)=125 \cdot 8 \\
& 3 x^{2}-92 x-703=0
\end{aligned}
$$
from which we find $x_{1}=37, x_{2}=-\frac{19}{3} ; x_{2}=-\frac{19}{3}$ does not satisfy the domain of definition.
Answer: 37.
|
37
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.047. Find the natural number $n$ from the equation
$$
3^{2} \cdot 3^{5} \cdot 3^{8} \cdots 3^{3 n-1}=27^{5}
$$
|
## Solution.
$3^{2+5+8+\ldots+3 n-1}=3^{15}, 2+5+8+\ldots+3 n-1=15$.
On the left side of the equation, we have the sum of the terms of an arithmetic progression $S_{k}$, where $a_{1}=2, d=3, a_{k}=3 n-1, k=\frac{a_{k}-a_{1}}{d}+1=\frac{3 n-1-2}{3}+1=n$.
Then $S_{k}=\frac{a_{1}+a_{k}}{2} \cdot k=\frac{2+3 n-1}{2} \cdot n=\frac{3 n^{2}+n}{2}$, and the equation becomes $\frac{3 n^{2}+n}{2}=15,3 n^{2}+n-30=0$, from which $n=3$.
Answer: 3.
Solve the equations (7.048 - 7.127):
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.048. $0.5\left(\lg \left(x^{2}-55 x+90\right)-\lg (x-36)\right)=\lg \sqrt{2}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{2}-55 x+90>0 \\ x-36>0\end{array}\right.$
From the condition
$$
\begin{aligned}
& 0.5\left(\lg \left(x^{2}-55 x+90\right)-\lg (x-36)\right)=0.5 \lg 2, \lg \frac{x^{2}-55 x+90}{x-36}=\lg 2 \\
& \frac{x^{2}-55 x+90}{x-36}=2
\end{aligned}
$$
We have $x^{2}-57 x+162=0$ for $x \neq 36$. Hence, $x_{1}=54, x_{2}=3$; $x_{2}=3$ does not satisfy the domain of definition.
Answer: 54.
|
54
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.050. $\log _{2} \frac{x-5}{x+5}+\log _{2}\left(x^{2}-25\right)=0$.
|
## Solution.
Domain of definition: $\frac{x-5}{x+5}>0$ or $x \in(-\infty ;-5) \cup(5 ; \infty)$.
We have $\log _{2} \frac{(x-5)\left(x^{2}-25\right)}{x+5}=0,(x-5)^{2}=1$, from which $x-5=-1$ or $x-5=1$. Then $x_{1}=4, x_{2}=6 ; x_{1}=4$ does not fit the domain of definition.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.051. $\frac{\lg 8-\lg (x-5)}{\lg \sqrt{x+7}-\lg 2}=-1$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x-5>0, \\ x+7>0, \quad x>5 . \\ \sqrt{x+7} \neq 2,\end{array}\right.$
## From the condition
$$
\begin{aligned}
& \lg 8-\lg (x-5)=\lg 2-\lg \sqrt{x+7}, \quad \lg \frac{8}{x-5}=\lg \frac{2}{\sqrt{x+7}} \\
& \frac{8}{x-5}=\frac{2}{\sqrt{x+7}}, \quad 4 \sqrt{x+7}=x-5, \quad 16 x+112=x^{2}-10 x+25, x>5
\end{aligned}
$$
We have $x^{2}-26 x-87=0$, from which $x_{1}=29, x_{2}=-3 ; x_{2}=-3$ does not satisfy the domain of definition.
Answer: 29.
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.053. $\lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.053. $\lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}\lg x>0, \\ \lg x^{3}-2>0,\end{array} \quad x>\sqrt[3]{100}\right.$.
From the condition we have
$\lg \left(\lg x \cdot\left(\lg x^{3}-2\right)\right)=0, \quad \lg x(3 \lg x-2)=1$,
$3 \lg ^{2} x-2 \lg x-1=0$.
Solving this equation as a quadratic equation in terms of $\lg x$, we find $(\lg x)_{1}=-\frac{1}{3}$, hence $x_{1}=\frac{1}{\sqrt[3]{10}}$, or $(\lg x)_{2}=1$, hence $x_{2}=10 ; x_{1}=\frac{1}{\sqrt[3]{10}}$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.054. $\log _{2} x+\log _{4} x+\log _{8} x=11$.
|
## Solution.
Domain: $x>0$.
We have $\log _{2} x+\frac{1}{2} \log _{2} x+\frac{1}{3} \log _{2} x=11, \log _{2} x=6$, from which $x=2^{6}=64$.
Answer: 64.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.055. $\log _{3}\left(3^{x}-8\right)=2-x$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
7.055. $\log _{3}\left(3^{x}-8\right)=2-x$.
|
Solution.
Domain of definition: $3^{x}-8>0$.
By the definition of logarithm, we have $3^{x}-8=3^{2-x}, 3^{x}-8=\frac{9}{3^{x}}$, $3^{2 x}-8 \cdot 3^{x}-9=0$, from which, solving this equation as a quadratic equation in terms of $3^{x}$, we find $3^{x}=-1, \varnothing$; or $3^{x}=9$, from which $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.056. $7^{\lg x}-5^{\lg x+1}=3 \cdot 5^{\lg x-1}-13 \cdot 7^{\lg x-1}$.
|
## Solution.
Domain: $x>0$.
From the condition
$$
7^{\lg x}-5 \cdot 5^{\lg x}=\frac{3}{5} \cdot 5^{\lg x}-\frac{13}{7} \cdot 7^{\lg x}, \quad 35 \cdot 7^{\lg x}+65 \cdot 7^{\lg x}=21 \cdot 5^{\lg x}+175 \cdot 5^{\lg x},
$$
$100 \cdot 7^{\lg x}=196 \cdot 5^{\lg x},\left(\frac{7}{5}\right)^{\lg x}=\left(\frac{7}{5}\right)^{2}$,
from which $\lg x=2$ and $x=100$.
Answer: 100.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.057. $5^{x+6}-3^{x+7}=43 \cdot 5^{x+4}-19 \cdot 3^{x+5}$.
|
Solution.
We have $5^{6} \cdot 5^{x}-43 \cdot 5^{4} \cdot 5^{x}=3^{7} \cdot 3^{x}-19 \cdot 3^{5} \cdot 3^{x},\left(\frac{5}{3}\right)^{x}=\left(\frac{5}{3}\right)^{-3}$, from which $x=-3$.
Answer: -3.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.061. $\sqrt{2} \cdot 0.5^{\frac{5}{5^{x}+10}}-16^{\left.\frac{1}{2(\sqrt{x}+1}\right)}=0$.
|
## Solution.
Domain of definition: $x \geq 0$.
From the condition
$$
2^{\frac{1}{2}} \cdot 2^{-\frac{5}{4 \sqrt{x}+10}}=2^{\frac{2}{\sqrt{x}+1}}, 2^{\frac{1}{2}-\frac{5}{4 \sqrt{x}+10}}=2^{\frac{2}{\sqrt{x}+1}}
$$
it follows that
$$
\frac{1}{2}-\frac{5}{4 \sqrt{x}+10}=\frac{2}{\sqrt{x}+1} \Rightarrow(\sqrt{x})^{2}-3 \sqrt{x}-10=0
$$
Solving this equation as a quadratic equation in $\sqrt{x}$, we find $\sqrt{x}=-2, \varnothing$; or $\sqrt{x}=5$, from which $x=25$.
Answer: 25.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.066. $2^{\frac{1}{\sqrt{x}-1}} \cdot 0.5^{\frac{1}{\sqrt{x}+1}}=4^{\frac{\sqrt{x}}{x+\sqrt{x}}}$
|
Solution.
Domain of definition: $0<x \neq 1$.
We have: $2^{\frac{1}{\sqrt{x}-1}} \cdot 2^{-\frac{1}{\sqrt{x}+1}}=2^{\frac{2 \sqrt{x}}{x+\sqrt{x}}}, 2^{\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}}=2^{\frac{2 \sqrt{x}}{x+\sqrt{x}}}$.
Then $\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}=\frac{2 \sqrt{x}}{x+\sqrt{x}}, x-\sqrt{x}-2=0$. Solving this equation as a quadratic equation in terms of $\sqrt{x}$, we find $\sqrt{x}=-1, \varnothing$; or $\sqrt{x}=2$, from which we have $x=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.069. $\log _{\sqrt{5}}\left(4^{x}-6\right)-\log _{\sqrt{5}}\left(2^{x}-2\right)=2$.
|
Solution.
Domain of Definition (DOD): $\left\{\begin{array}{l}4^{x}-6>0 \\ 2^{x}-2>0 .\end{array}\right.$
We have $\log _{\sqrt{5}} \frac{4^{x}-6}{2^{x}-2}=2, \frac{2^{2 x}-6}{2^{2}-2}=5,2^{2 x}-5 \cdot 2^{x}+4=0$. Solving this equation as a quadratic in terms of $2^{x}$, we find $\left(2^{x}\right)=1$, from which we get $x_{1}=0$, or $\left(2^{x}\right)_{2}=4$, from which we get $x_{2}=2 ; x_{1}=0$ does not satisfy the DOD.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.071. $3 \cdot 5^{2 x-1}-2 \cdot 5^{x-1}=0.2$.
|
## Solution.
From the condition $3 \cdot 5^{2 x}-2 \cdot 5^{x}=1,3 \cdot 5^{2 x}-2 \cdot 5^{x}-1=0$. Solving this equation as a quadratic in terms of $5^{x}$, we get $5^{x}=-\frac{1}{3}, \varnothing$; or $5^{x}=1$, from which $x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.076. $9^{\sqrt{x-5}}-27=6 \cdot 3^{\sqrt{x-5}}$.
7.076. $9^{\sqrt{x-5}}-27=6 \cdot 3^{\sqrt{x-5}}$.
|
Solution.
Domain of definition: $x-5 \geq 0, x \geq 5$.
$$
3^{2 \sqrt{x-5}}-6 \cdot 3^{\sqrt{x-5}}-27=0
$$
We solve the equation as a quadratic equation in terms of $3^{\sqrt{x-5}}$. We have $3^{\sqrt{x-5}}=-3$. (not suitable) or $3^{\sqrt{x-5}}=9$, from which $\sqrt{x-5}=2$, or $x-5=4$. Then $x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.080. $\lg (\sqrt{6+x}+6)=\frac{2}{\log _{\sqrt{x}} 10}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}6+x \geq 0, \\ x>0, \\ x \neq 1,\end{array} \quad 0<x \neq 1\right.$.
We will switch to base 10. We have
$\lg (\sqrt{6+x}+6)=2 \lg \sqrt{x}, \quad \lg (\sqrt{6+x}+6)=\lg x$.
Then $\sqrt{6+x}+6=x, \sqrt{6+x}=x-6 \Rightarrow\left\{\begin{array}{l}x^{2}-13 x+30=0, \\ x \geq 6,\end{array}\right.$
from which $x=10$.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.084. $\frac{2^{x}+10}{4}=\frac{9}{2^{x-2}}$.
7.084. $\frac{2^{x}+10}{4}=\frac{9}{2^{x-2}}$.
|
## Solution.
From the condition
$$
\frac{2^{x}+10}{4}=\frac{9}{2^{x} \cdot 2^{-2}}, \frac{2^{x}+10}{4}=\frac{36}{2^{x}}, 2^{2 x}+10 \cdot 2^{x}-144=0 .
$$
Solving this equation as a quadratic in terms of $2^{x}$, we find $2^{x}=-18, \varnothing$, or $2^{x}=8$, from which $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.091. $\log _{2}\left(4 \cdot 3^{x}-6\right)-\log _{2}\left(9^{x}-6\right)=1$.
|
## Solution.
oDZ: $\left\{\begin{array}{l}4 \cdot 3^{x}-6>0 \\ 9^{x}-6>0\end{array}\right.$
We have $\log _{2} \frac{4 \cdot 3^{x}-6}{3^{2 x}-6}=1, \frac{4 \cdot 3^{x}-6}{3^{2 x}-6}=2 \Rightarrow 3^{2 x}-2 \cdot 3^{x}-3=0$. Solving it as a quadratic equation in terms of $3^{x}$, we find $3^{x}=-1, \varnothing$; or $3^{x}=3$, from which $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.098. $\lg \sqrt{x-3}+\lg \sqrt{x+3}=2-0.5 \lg 625$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x-3>0, \\ x+3>0\end{array} x>3\right.$.
## We have
$\lg \sqrt{x-3}+\lg \sqrt{x+3}=\lg 100-\lg 25, \lg \sqrt{x^{2}-9}=\lg 4, \sqrt{x^{2}-9}=4$, from which $x^{2}=25, x_{1}=-5, x_{2}=5, x_{1}=-5$ does not satisfy the domain of definition.
Answer: 5 .
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.099. $\lg (3-x)-\frac{1}{3} \lg \left(27-x^{3}\right)=0$.
|
## Solution.
Domain of definition: $3-x>0, x<3$.
## Rewrite the equation as
$$
3 \lg (3-x)=\lg \left(27-x^{3}\right), \lg (3-x)^{3}=\lg \left(27-x^{3}\right)
$$
Then $(3-x)^{3}=27-x^{3} \Rightarrow x^{2}-9 x=0$, from which $x_{1}=0, x_{2}=9 ; x_{2}=9$ does not satisfy the domain of definition.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.101. $\lg 8-\lg \sqrt{x+6}=\lg 16-\lg (x-2)$
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+6>0, \\ x-2>0,\end{array} \quad x>2\right.$.
We have
$$
\lg \frac{8}{\sqrt{x+6}}=\lg \frac{16}{x-2}, \quad \frac{8}{\sqrt{x+6}}=\frac{16}{x-2}, \quad 2 \sqrt{x+6}=x-2, x^{2}-8 x-20=0
$$
from which $x_{1}=10, x_{2}=-2 ; x_{2}=-2$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.103. $\frac{\lg (2 x-19)-\lg (3 x-20)}{\lg x}=-1$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}2 x-19>0, \\ 3 x-20>0,\end{array} \quad x>\frac{19}{2}\right.$.
## From the condition
$$
\begin{aligned}
& \lg (2 x-19)-\lg (3 x-20)=-\lg x, \lg (2 x-19)+\lg x=\lg (3 x-20) \\
& x(2 x-19)=3 x-20, x^{2}-11 x+10=0 .
\end{aligned}
$$
From here $x_{1}=10, x_{2}=1 ; x_{2}=1$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.104. $\frac{\lg x^{2}}{\lg (6 x-5)}=1$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq 0, \\ 6 x-5>0,\end{array}, \frac{5}{6}<x \neq 1\right.$.
We have $\lg x^{2}=\lg (6 x-5)$, from which $x^{2}=6 x-5, x^{2}-6 x+5=0$, hence $x_{1}=5$ and $x_{2}=1 ; x_{2}=1$ does not satisfy the domain of definition.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.109. $5^{2 x-1}+2^{2 x}-5^{2 x}+2^{2 x+2}=0$.
|
Solution.
Write the equation as
$$
\begin{aligned}
& \frac{5^{2 x}}{5}-5^{2 x}=-2^{2 x}-4 \cdot 2^{2 x},-\frac{4}{5} \cdot 5^{2 x}=-5 \cdot 2^{2 x} \\
& \left(\frac{5}{2}\right)^{2 x}=\left(\frac{5}{2}\right)^{2}, x=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.110. $\log _{2}\left(9-2^{x}\right)=10^{\lg (3-x)}$.
7.110. $\log _{2}\left(9-2^{x}\right)=10^{\lg (3-x)}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}9-2^{x}>0, \\ 3-x>0,\end{array} \quad x<3\right.$.
We have $\log _{2}\left(9-2^{x}\right)=3-x, 9-2^{x}=2^{3-x}, 2^{2 x}-9 \cdot 2^{x}+8=0$. Solving this equation as a quadratic in terms of $2^{x}$, we get $\left(2^{x}\right)=1$ or $\left(2^{x}\right)_{2}=8$, hence $x_{1}=0, x_{2}=3 ; x_{2}=3$ does not satisfy the domain of definition.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.111. $\frac{1}{3} \lg \left(271+3^{2 \sqrt{x}}\right)+\lg 10=2$.
|
## Solution.
Domain: $x \geq 0$.
From the condition $\frac{1}{3} \lg \left(271+3^{2 \sqrt{x}}\right)+1=2, \lg \left(271+3^{2 \sqrt{x}}\right)=3$. Then $271+3^{2 \sqrt{x}}=$ $=1000,3^{2 \sqrt{x}}=3^{6}$, from which $\sqrt{x}=3, x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.112. $\left.(\sqrt[5]{27})^{\frac{x}{4}-\sqrt{\frac{x}{3}}}\right)^{\frac{x}{4}+\sqrt{\frac{x}{3}}}=\sqrt[4]{3^{7}}$.
|
## Solution.
Domain of definition: $x \geq 0$.
Rewrite the equation as $3^{\frac{3}{5}\left(\frac{x}{4}-\sqrt{\frac{x}{3}}\right)\left(\frac{x}{4}+\sqrt{\frac{x}{3}}\right)}=3^{\frac{7}{4}}$. Then
$$
\frac{3}{5}\left(\frac{x}{4}-\sqrt{\frac{x}{3}}\right)\left(\frac{x}{4}+\sqrt{\frac{x}{3}}\right)=\frac{7}{4}, 3 x^{2}-16 x-140=0
$$
from which $x_{1}=10, x_{2}=-\frac{14}{3} ; x_{2}=-\frac{14}{3}$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.114. $\lg (x(x+9))+\lg \frac{x+9}{x}=0$.
|
## Solution.
Domain of definition: $x(x+9)>0, x \in(-\infty ;-9) \cup(0 ; \infty)$.
We have $\lg \frac{x(x+9)(x+9)}{x}=0$, from which $(x+9)^{2}=1$. Then $(x+9)_{1}=-1$, $x_{1}=-10$ or $(x+9)_{2}=1, x_{2}=-8 ; x_{2}=-8$ does not fit the domain of definition.
Answer: -10.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.117. $2^{\log _{3} x^{2}} \cdot 5^{\log _{3} x}=400$.
|
Solution.
Domain: $x>0$.
From the condition $4^{\log _{3} x} \cdot 5^{\log _{3} x}=400, 20^{\log _{3} x}=20^{2}$, hence $\log _{3} x=2$, $x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.121. $\log _{2}\left(4^{x}+4\right)=x+\log _{2}\left(2^{x+1}-3\right)$
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.121. $\log _{2}\left(4^{x}+4\right)=x+\log _{2}\left(2^{x+1}-3\right)$
|
## Solution.
Domain of definition: $2^{x+1}-3>0$.
Rewrite the equation as
$$
\begin{aligned}
& \log _{2}\left(2^{2 x}+4\right)-\log _{2}\left(2 \cdot 2^{x}-3\right)=x, \quad \log _{2} \frac{2^{2 x}+4}{2 \cdot 2^{x}-3}=x \\
& \frac{2^{2 x}+4}{2 \cdot 2^{x}-3}=2^{x}, 2^{2 x}-3 \cdot 2^{x}-4=0 .
\end{aligned}
$$
Solving this equation as a quadratic in terms of $2^{x}$, we get $2^{x}=-1, \varnothing$; or $2^{x}=4$, hence $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.127. $\log _{2}\left(25^{x+3}-1\right)=2+\log _{2}\left(5^{x+3}+1\right)$
|
Solution.
Domain of definition: $25^{x+3}-1>0, 25^{x+3}>25^{0}, x>-3$.
From the condition
$\log _{2}\left(25^{3} \cdot 25^{x}-1\right)=\log _{2} 4\left(5^{3} \cdot 5^{x}+1\right) 25^{3} \cdot 5^{2 x}-1=4 \cdot 5^{3} \cdot 5^{x}+4$, $3125 \cdot 5^{2 x}-100 \cdot 5^{x}-1=0$,
from which, solving this equation as a quadratic in terms of $5^{x}$, we have $5^{x}=-\frac{1}{125}, \varnothing ;$ or $5^{x}=5^{-2}$, from which $x=-2$.
Answer: -2.
Solve the systems of equations (7.128-7.149):
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.010. Find the positive integer values of $x$ that satisfy the inequality $\frac{5 x+1}{x-1}>2 x+2$.
|
Solution.
We have
$$
\begin{aligned}
& \frac{5 x+1}{x-1}-2 x-2>0 \Leftrightarrow \frac{5 x+1-2(x+1)(x-1)}{x-1}>0 \Leftrightarrow \frac{-2 x^{2}+5 x+3}{x-1}>0 \Leftrightarrow \\
& \Leftrightarrow\left(2 x^{2}-5 x-3\right)(x-1)<0 \Leftrightarrow 2\left(x+\frac{1}{2}\right)(x-3)(x-1)<0
\end{aligned}
$$
Using the number line, we find that $x=2$.
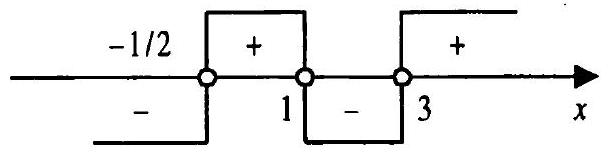
Answer: $\quad x=2$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.012. Find the natural values of $x$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
\log _{\sqrt{2}}(x-1)<4 \\
\frac{x}{x-3}+\frac{x-5}{x}<\frac{2 x}{3-x}
\end{array}\right.
$$
|
Solution.
From the condition
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ 0 0 \text { for } x \in R, \\
x(x-3)<0 .
\end{array}\right.
\end{aligned}
$$
Using the number line, we find the solution to the system $x=2$.
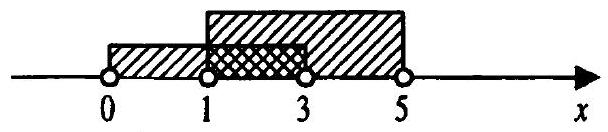
Answer: $x=2$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.007. An isosceles trapezoid with a side length of 17 cm is circumscribed around a circle with a diameter of 15 cm. Find the bases of the trapezoid.
|
Solution.
According to the condition, $K Q=15 \mathrm{~cm}, A B=C D=17 \mathrm{~cm}, B C+A D=A B+C D=34$. In $\triangle C E D \angle C E D=90^{\circ}, C E=K Q$ (Fig. 10.7) We have $D E=\sqrt{289-225}=8 \mathrm{~cm}$, $A D=2 E D+B C=16+B C, B C+16+B C=34, B C=9 \mathrm{~cm}, A D=25 \mathrm{~cm}$.
Answer: 9 cm $; 25$ cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.013. Given a triangle with sides 12, 15, and \(18 \, \text{cm}\). A circle is drawn that touches both smaller sides and has its center on the larger side. Find the segments into which the center of the circle divides the larger side of the triangle.
|
## Solution.
Using the cosine theorem, from Fig. 10.13 we have:
$$
\begin{aligned}
& A B^{2}=B C^{2}+A C^{2}-2 \cdot B C \cdot A C \cdot \cos \alpha \Rightarrow \\
& \Rightarrow 12^{2}=15^{2}+18^{2}-2 \cdot 15 \cdot 18 \cos \alpha, \cos \alpha=\frac{3}{4}, \sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\frac{\sqrt{7}}{4} \\
& B C^{2}=A B^{2}+A C^{2}-2 \cdot A B \cdot A C \cdot \cos \beta \Rightarrow \\
& \Rightarrow 15^{2}=12^{2}+18^{2}-2 \cdot 12 \cdot 18 \cdot \cos \beta, \cos \beta=\frac{9}{16}, \sin \beta=\sqrt{1-\cos ^{2} \beta}=\frac{5 \sqrt{7}}{16}
\end{aligned}
$$
$$
\begin{aligned}
& \sin \alpha=\frac{O M}{O C}=\frac{R}{18-x}, \sin \beta=\frac{O K}{A O}=\frac{R}{x} \text { and } \frac{\sin \alpha}{\sin \beta}=\frac{x}{18-x}=\frac{4}{5} \\
& 5 x=72-4 x, 9 x=72, x=8, y=10 . A O=8 \text{ cm}, O C=10 \text{ cm}
\end{aligned}
$$
Answer: 8 and 10 cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.017. Given a point $P$, which is 7 cm away from the center of a circle with a radius of $11 \mathrm{~cm}$. A chord of length 18 cm is drawn through this point. What are the lengths of the segments into which the chord is divided by point $P$?
|
## Solution.
Draw the diameter $C D$ through point $P$ (Fig. 10.17), which will divide it into segments $P D$ and $C P$ of lengths $11-7=4$ and $11+7=18$ (cm). Let $A P=x$; then $P B=18-x$. Since $A P \cdot P B=C P \cdot P D=4 \cdot 18$, we have $x(18-x)=72$ or $x^{2}-18 x+72=0$, from which $x_{1}=12, x_{2}=6$, i.e., the chord $A B$ is divided by point $P$ into segments of lengths 12 and 6 cm.
Answer: 12 and 6 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.024. The lengths of the parallel sides of the trapezoid are 25 and 4 cm, and the lengths of the non-parallel sides are 20 and 13 cm. Find the height of the trapezoid.
|
## Solution.
Given $B C=4 \text{ cm}, A D=25 \text{ cm}, A B=20 \text{ cm}, C D=13 \text{ cm}$ (Fig. 10.24). Draw $B E \perp A D$ and $C F \perp A D$. Let $B E=C F=h, A E=x$, $F D=y$. Then from $\triangle A B E$ and $\triangle C F D$ we find $h^{2}=20^{2}-x^{2}=13^{2}-y^{2}$. Considering that $y=25-4-x=21-x$, we have $20^{2}-x^{2}=13^{2}-(21-x)^{2}$ or $42 x=672$, from which $x=16$ (cm). Therefore, $h=\sqrt{20^{2}-16^{2}}=12$ (cm).
Answer: 12 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.033. A tangent, parallel to the base, is drawn to the circle inscribed in an isosceles triangle with a base of 12 cm and a height of 8 cm. Find the length of the segment of this tangent, enclosed between the sides of the triangle.
|
## Solution.
Let's find the length of the side $B C$ (Fig. 10.33): $B C=\sqrt{B M^{2}+M C^{2}}=$ $=\sqrt{6^{2}+8^{2}}=10$ (cm). Considering that $A O$ is the bisector of $\triangle A B M$, we have $M O / O B=A M / A B$ or $r /(8-r)=6 / 10$, from which $r=3$ (cm). Since $D E \| A C$, then $\triangle D B E \sim \triangle A B C$, i.e., $D E / A C=B N / B M$ or $D E / 12=(8-2 r) / 8$, from which $D E=3$ cm.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.038. The perimeter of a parallelogram is 90 cm and the acute angle is $60^{\circ}$ (Fig. 10.38). A diagonal of the parallelogram divides its obtuse angle in the ratio $1: 3$. Find the sides of the parallelogram.
|
Solution.
According to the condition $2 B C+2 C D=90 \text{ cm}, \angle B C D=60^{\circ}, \frac{\angle A B D}{\angle D B C}=\frac{3}{1}$. We have $B C+C D=45, \angle A B C+\angle B C D=180^{\circ}$. Let $\angle C B D=x, \angle A B D=3 x$, therefore, $3 x+x+60^{\circ}=180^{\circ}$ and $x=30^{\circ}, \angle A B D=90^{\circ}$. In $\triangle A B D$ $A B=A D \cdot \cos 60^{\circ}, A B=\frac{A D}{2}=\frac{B C}{2}, A B=C D ; B C+\frac{B C}{2}=45,3 B C=90$; $B C=30$ cm. $A D=D C=15 \text{ cm}$.
Answer: 15 and 30 cm.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.039. The lines containing the non-parallel sides of an isosceles trapezoid intersect at a right angle (Fig. 10.39). Find the lengths of the sides of the trapezoid if its area is \(12 \mathrm{~cm}^{2}\) and the height is \(2 \mathrm{~cm}\).
Fig. 10.39
Fig. 10.40
|
## Solution.
Given $S_{\triangle A B C D}=12 \mathrm{~cm}^{2}, B E=2 \mathrm{~cm} ; \angle O A D=\angle O D A=\frac{90^{\circ}}{2}=45^{\circ}$, $\frac{B E}{\sin 45^{\circ}}=A B, A B=\frac{2}{\sqrt{2}} \cdot 2=2 \sqrt{2}=C D, A E=B E=2, \frac{B C+A D}{2} \cdot B E=12$, $\frac{B C+A D}{2} \cdot 2=12, B C+A D=12$, then $2 B C+2 A E=12, B C+A E=6$, $B C+2=6, B C=4 \mathrm{~cm}, A D=4+4=8 \mathrm{~cm}$.
Answer: 4 and 8 cm; $2 \sqrt{2}$ and $2 \sqrt{2}$ cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.042. One of the angles of the trapezoid is $30^{\circ}$, and the lines containing the lateral sides of the trapezoid intersect at a right angle (Fig. 10.42). Find the length of the shorter lateral side of the trapezoid if its midline is 10 cm, and one of the bases is $8 \mathrm{~cm}$.
|
## Solution.
Given $\angle B C A=30^{\circ}, \angle A B C=90^{\circ}, K M=10$ cm, $D E=8$ cm, $\frac{8+A C}{2}=10, A C=12$ cm (since $K M$ is the midline). Since $\triangle D B E \sim \triangle A B C$, then $\frac{A B}{D B}=\frac{A C}{D E} ; \frac{x+D B}{D B}=\frac{12}{8}$ (where $A D=x$ ), $x=D B \cdot \frac{1}{2}$. In $\triangle D B E, \angle D B E=90^{\circ}, \angle B E D=\angle B C A=30^{\circ}, D B=D E \cdot \sin 30^{\circ}=8 / 2=4$, so, $x=4 \cdot \frac{1}{2}=2$ cm.
Answer: 2 cm.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.045. The common chord of two intersecting circles is seen from the centers at angles of $90^{\circ}$ and $60^{\circ}$. Find the radii of the circles if the distance between their centers is $\sqrt{3}+1$.
|
Solution.
Let $r$ be the radius of one circle, and $R$ be the radius of the other circle. According to the problem, $\angle A O_{1} B=90^{\circ}, \angle A O_{2} B=60^{\circ}, O_{1} O_{2}=\sqrt{3}+1 ; A B=r \sqrt{2} ;$ $O_{1} E=A B / 2 ; O_{1} E=r \frac{\sqrt{2}}{2}, A B=2 R \cdot \sin 30^{\circ}=R\left(\angle A O_{2} E=\frac{\angle A O_{2} B}{2}\right)$, therefore, $R=r \sqrt{2}, E O_{2}=R \frac{\sqrt{3}}{2}=r \frac{\sqrt{6}}{2}, O_{1} O_{2}=O_{1} E+O_{2} E=\frac{r \sqrt{6}}{2}+\frac{r \sqrt{2}}{2}=$ $=\sqrt{3}+1, r(\sqrt{6}+\sqrt{2})=(\sqrt{3}+1) \cdot 2, r=\sqrt{2} ; R=\sqrt{2} \cdot \sqrt{2}=2$ (Fig. 10.45).
Answer: 2 and $\sqrt{2}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.047. The perimeter of a right-angled triangle $ABC$ ( $\angle C=90^{\circ}$ ) is 72 cm, and the difference between the lengths of the median $CK$ and the altitude $CM$ is 7 cm (Fig. 10.47). Find the length of the hypotenuse.
|
Solution.
According to the condition $C K - C M = 7 \text{ cm}, P_{A B C} = 72 \text{ cm}, p = \frac{P_{A B C}}{2} = 36$. If the radius of the inscribed circle, then $r = p - A B, S = p \cdot r = p \cdot (p - A B)$. Let $A B = x, K$ be the center of the circumscribed circle, $C K = A K = K B = \frac{A B}{2} = \frac{x}{2}; S = 36 \cdot (36 - x); \frac{x}{2} - C M = 7$ (by condition) $C M = \frac{x}{2} - 7$; $S = \frac{x}{2} \left( \frac{x}{2} - 7 \right) \cdot \frac{x^2}{4} - \frac{7x}{2} = 36^2 - 36x, x^2 + 130x - 5184 = 0, x = 32$ cm.
Answer: $32 \text{ cm}$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.049. A point on the hypotenuse, equidistant from both legs, divides the hypotenuse into segments of length 30 and $40 \mathrm{~cm}$. Find the legs of the triangle.
|
Solution.
Given $\angle C=90^{\circ}, A D=30 \text{ cm}, B D=40$ cm (Fig. 10.49). Let $A C=x, B C=y$. Since the point equidistant from the sides of an angle lies on its bisector, $\frac{x}{y}=\frac{30}{40}$, i.e., $y=\frac{4 x}{3}$. But $x^{2}+y^{2}=A B^{2}$ or $x^{2}+\frac{16 x^{2}}{9}=70^{2}$, from which $x^{2}=1764$. Therefore, $x=42$ (cm), $y=56$ (cm).
Answer: 42 and 56 cm.
|
42
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.051. Three circles of different radii touch each other pairwise. The segments connecting their centers form a right triangle. Find the radius of the smallest circle, if the radii of the largest and medium circles are 6 and 4 cm.
|
Solution.
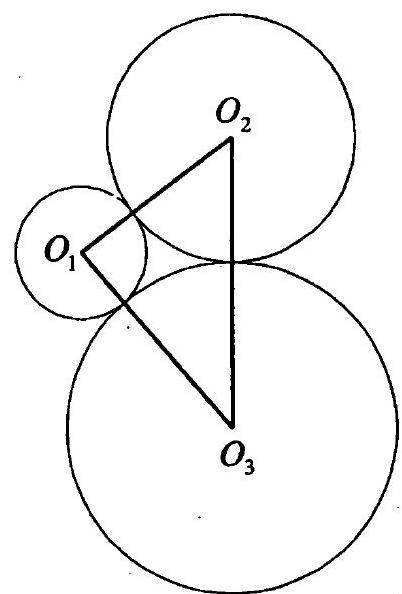
Fig. 10.51
Fig. 10.52
Let $r$ be the radius of the smaller circle. Then $O_{1} O_{2}=r+4$, $O_{1} O_{3}=r+6$ (Fig. 10.51). Since $O_{2} O_{3}^{2}=O_{1} O_{2}^{2}+O_{1} O_{3}^{2}$, we have $10^{2}=(r+4)^{2}+(r+6)^{2}, r^{2}+10 r-24=0$, from which $r=2$ cm (the root $r=-12$ does not satisfy the condition).
Answer: $2 \text{ cm}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.064. The lateral side of an isosceles triangle is $10 \mathrm{~cm}$, and the base is $12 \mathrm{~cm}$. Tangents are drawn to the inscribed circle of the triangle, parallel to the height of the triangle, and cutting off two right triangles from the given triangle. Find the lengths of the sides of these triangles.
|
## Solution.
The area of the triangle is found using the formula (Fig. 10.63):
$$
S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{16(16-10)(16-10)(16-12)}=48
$$
The radius of the inscribed circle $r=\frac{S}{p}=\frac{48}{16}=3$ (cm); $r=D H . H C=D C-$ $-D H=6-3=3 \text{ cm} ; \triangle B C D$ and $\triangle F C H$ are similar, so $\frac{D C}{H C}=\frac{B C}{F C}$. Therefore, $F C=\frac{B C \cdot H C}{D C}=\frac{10 \cdot 3}{6}=5$ cm. From $\triangle F C H$ it follows that $F C^{2}=$ $=F H^{2}+H C^{2} ; F H=\sqrt{F C^{2}-H C^{2}}=\sqrt{5^{2}-3^{2}}=4$ (cm).
## Answer: 3 cm, 4 cm, 5 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.067. Inside a circle with a radius of 15 cm, a point $M$ is taken at a distance of 13 cm from the center. Through point $M$, a chord of length 18 cm is drawn. Find the lengths of the segments into which point $M$ divides the chord.
|
Solution.
Draw $O C \perp A B$ (Fig. 10.66). Then $C B=\frac{1}{2} A B=9$ cm. From $\triangle O B C$
Fig. 10.67
Fig. 10.68
we find $O C=\sqrt{O B^{2}-B C^{2}}=12$ (cm), and from $\triangle O M C$ we get $M C=$ $=\sqrt{O M^{2}-O C^{2}}=5$ (cm). Therefore, $A M=9+5=14$ (cm), $M B=$ $=9-5=4$ (cm).
Answer: $\quad 14$ and 4 cm.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.096. The area of an isosceles trapezoid circumscribed around a circle is $32 \sqrt{3} \mathrm{~cm}^{2}$ (Fig. 10.92). Determine the lateral side of the trapezoid, given that the acute angle at the base is $\pi / 3$.
|
Solution.
$\triangle C E D-$ is a right triangle and $\sin 60^{\circ}=\frac{2 R}{C D}$. Therefore, $2 R=\frac{\sqrt{3}}{2} C D$, $C D=x \Rightarrow 2 R=\frac{\sqrt{3}}{2} x$. The area of the trapezoid $S=\frac{a+b}{2} h=2 R x=\frac{\sqrt{3}}{2} x^{2}$. According to the condition $\frac{\sqrt{3}}{2} x^{2}=32 \sqrt{3} \Rightarrow x^{2}=64, x=8$ (cm).
Answer: 8 cm.
Fig. 10.93
Fig. 10.94
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.100. A regular hexagon $A B C D E F$ consists of two trapezoids sharing a common base $C F$ (Fig. 10.96). It is known that $A C=13$ cm, $A E=10$ cm. Find the area of the hexagon.
|
Solution.
$\triangle C K A$ is a right triangle, $A K=\frac{1}{2} A E=5$ (cm), $C K=\sqrt{A C^{2}-A K^{2}}=$ $=\sqrt{13^{2}-5^{2}}=12(\text{cm}), \cos \varphi=\frac{12}{13} ; \sin \varphi=\frac{5}{13}$. Consider $\triangle C O B(\angle C O B=$ $\left.=90^{\circ}\right): \sin 2 \varphi=\frac{5}{x}$ and $\sin 2 \varphi=2 \sin \varphi \cos \varphi=2 \cdot \frac{5}{13} \cdot \frac{12}{13}=\frac{120}{169}$. Therefore, $x=$ $=\frac{169 \cdot 5}{120}=\frac{169}{24}(\text{cm}), \quad \cos 2 \varphi=\frac{C O}{x} ; \cos 2 \varphi=\cos ^{2} \varphi-\sin ^{2} \varphi=\frac{144}{169}-$

Fig. 10.97

Fig. 10.98
$-\frac{25}{169}=\frac{119}{169} \cdot$. Therefore, $C O=\frac{169}{24} \cdot \frac{119}{169}=\frac{119}{24}$ (cm), $C O=K F, C F=C O+O F=$ $=C K+K F=12+\frac{119}{24}=\frac{407}{24}$ (cm). The area of the desired hexagon: $S_{A B C D E F}=2 S_{C D E F}=2 \cdot \frac{1}{2}(C F+E D) \cdot E K=\left(\frac{407}{24}+\frac{169}{24}\right) \cdot 5=120\left(\text{cm}^{2}\right)$.
Answer: $120 \text{ cm}^{2}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.122. The larger base of the trapezoid has a length of 24 cm (Fig. 10.113). Find the length of its smaller base, given that the distance between the midpoints of the diagonals of the trapezoid is 4 cm.
|
Solution.
$A E=E C ; D F=F B, K E=D C / 2 ; F T=D C / 2 ; D C=x, K T=2 K E+E F=$ $=x+4$. On the other hand, $K T=\frac{x+24}{2}$. Solving the equation $x+4=\frac{x+24}{2}$, we get $x=16$ (cm).
Answer: $16 \mathrm{~cm}$.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.142. A circle is inscribed in an equilateral triangle, and a regular hexagon is inscribed in the circle. Find the ratio of the areas of the triangle and the hexagon.
|
## Solution.
Let the side of the equilateral triangle be $a$. Then its area $S_{1}=\frac{a^{2} \sqrt{3}}{4} \cdot$ The radius of the circle inscribed in the triangle, $r=\frac{a \sqrt{3}}{6}$.
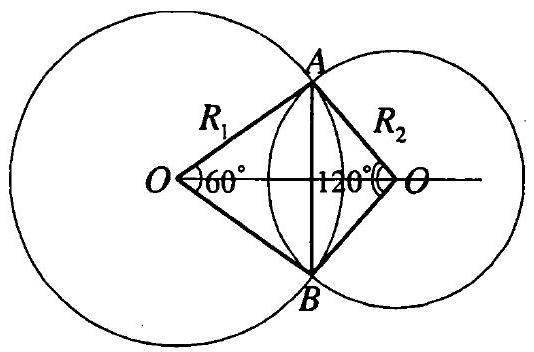
Fig. 10.128
Fig. 10.129
It will be equal to the side of the hexagon inscribed in this circle: $a_{6}=\frac{a \sqrt{3}}{6} \cdot$ And the radius of the circle inscribed in this hexagon:
$$
r=\frac{a_{6}}{2 \operatorname{tg} \frac{180^{\circ}}{6}}=\frac{a_{6} \sqrt{3}}{2}=\frac{a}{4}
$$
The area of the hexagon
$$
S_{2}=\frac{6 a_{5} r}{2}=\frac{a^{2} \sqrt{3}}{8} ; \frac{S_{1}}{S_{2}}=\frac{a^{2} \sqrt{3} \cdot 8}{4 a^{2} \sqrt{3}}=2
$$
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.147. In a parallelogram with a perimeter of 32 cm, the diagonals are drawn. The difference between the perimeters of two adjacent triangles is 8 cm. Find the lengths of the sides of the parallelogram.
|
Solution.
Let the sides of the parallelogram be denoted by $a$ and $b$. Then its perimeter is $p=2(a+b)=32$. The perimeter of one triangle is $p_{1}=b+\frac{d_{1}}{2}+\frac{d_{2}}{2}$, and the second is $p_{2}=a+\frac{d_{1}}{2}+\frac{d_{2}}{2}$, where $d_{1}, d_{2}$ are the diagonals of the parallelogram. The difference $p_{1}-p_{2}=b-a=8$. We obtain the system: $\left\{\begin{array}{l}a+b=16, \\ b-a=8 .\end{array}\right.$ Solving it, we find $a=4, b=12$.
Answer: 12 cm, 4 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.157. Through points $R$ and $E$, belonging to sides $A B$ and $A D$ of parallelogram $A B C D$, and such that $A R=(2 / 3) A B, A E=(1 / 3) A D$, a line is drawn. Find the ratio of the area of the parallelogram to the area of the resulting triangle.
|
## Solution.
Let $h$ be the height of parallelogram $ABCD$, and $h_{1}$ be the height of triangle $ARE$ (Fig. 10.134). Then $S_{ABCD} = AD \cdot h$, and $S_{\triangle ARE} = \frac{1}{2} AE \cdot h_{1}$. But $\frac{h}{h_{1}} = \frac{AB}{AR} = \frac{3}{2}$. Therefore, $\frac{S_{ABCD}}{S_{\triangle ARE}} = \frac{AD \cdot h}{\frac{1}{2} AE \cdot h_{1}} = \frac{AD \cdot h}{\frac{1}{2} \cdot \frac{1}{3} AD \cdot \frac{2}{3} h} = 9$.
Answer: 9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.160. In a trapezoid with an area of $594 \mathrm{~m}^{2}$, the height is 22 m, and the difference between the parallel sides is $6 \mathrm{~m}$. Find the length of each of the parallel sides.
|
## Solution.
Since $S=\frac{1}{2}(a+b) h$, then $\frac{1}{2}(a+b) \cdot 22=594$, from which $a+b=54$. From the system of equations $\left\{\begin{array}{l}a+b=54, \\ a-b=6\end{array}\right.$ we find $a=30$ (m), $b=24$ (m).
Answer: $\quad 30$ m and 24 m.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.185. In an isosceles trapezoid, the length of the midline is 5, and the diagonals are perpendicular to each other. Find the area of the trapezoid.
|
Solution.
Let the bases of the trapezoid be $a$ and $b$, and the height be $h$. Then the area
Fig. 10.153
Fig. 10.154
is $S=\frac{a+b}{2} h$. On the other hand, $S=h^{2}$. Therefore, $h=\frac{a+b}{2}=5$, from which $S=25$.
Answer: 25.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.186. The lengths of the bases of an isosceles trapezoid are in the ratio 5:12, and the length of its height is 17 cm. Calculate the radius of the circle circumscribed around the trapezoid, given that its midline is equal to the height.
|
Solution.
Let $B C=5 k, A D=12 k$ (Fig. 10.153). Then $\frac{B C+A D}{2}=h=17$, $\frac{12 k+5 k}{2}=17$, from which $k=2$. Therefore, $B C=10, A D=24$. Let $C L \perp A D$, $B K \perp A D, A K=L D=\frac{A D-B C}{2}=7$ (cm); $C D=\sqrt{C L^{2}+L D^{2}}=\sqrt{17^{2}+7^{2}}=$ $=13 \sqrt{2}, \sin \alpha=\frac{C L}{C D}=\frac{17}{13 \sqrt{2}}$. From $\triangle A L C$ we find $A C=\sqrt{C L^{2}+A L^{2}}=$ $=\sqrt{17^{2}+17^{2}}=17 \sqrt{2}$. By the Law of Sines $\frac{A C}{\sin \alpha}=2 R$, therefore, $\frac{17 \sqrt{2} \cdot 13 \sqrt{2}}{17 \cdot 2}=R, R=13(\text{cm})$.
Answer: 13 cm.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.189. A square is inscribed in a segment whose arc is $60^{\circ}$. Calculate the area of the square if the radius of the circle is $2 \sqrt{3}+\sqrt{17}$.
|
Solution.
Let $B C=C D=D A=A B=x$ (Fig. 10.156). Consider $\triangle O N C$,

Fig. 10.156
Fig. 10.157
$\angle O N C=90^{\circ}$. We have $O N^{2}+N C^{2}=O C^{2}$, where $O C=R=2 \sqrt{3}+\sqrt{17}$. $O N \doteq$ $=O M+M N=O M+x, N C=\frac{x}{2}$. In $\triangle O M F \quad \angle O M F=90^{\circ}, \angle M O F=$ $=\frac{\angle E O F}{2}=30^{\circ}$, then $O M=O F \cdot \frac{\sqrt{3}}{2}=R \cdot \frac{\sqrt{3}}{2}$, therefore, $O N=$ $=\frac{R \sqrt{3}}{2}+x$. Thus, we have $\left(\frac{R \sqrt{3}}{2}+x\right)^{2}+\frac{x^{2}}{4}=R^{2}$. Solving the quadratic equation, we get $x=\frac{2 R}{10}(\sqrt{17}-2 \sqrt{3}) ; S_{A B C D}=x^{2}$; $x=\frac{(2 \sqrt{3}+\sqrt{17})(\sqrt{17}-2 \sqrt{3})}{5}=1, S_{A B C D}=1$.
Answer: 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.007. Find the ratio of the volume of a cube to the volume of a regular tetrahedron, the edge of which is equal to the diagonal of the face of the cube.
|
## Solution.
For a tetrahedron where all edges are equal, denote the edges as $a$. The radius of the circumscribed circle around the base of the tetrahedron is $R=\frac{a \sqrt{3}}{3}$. The foot of the height $H$ is the center of the circumscribed circle around $\triangle A B C$ (see Fig. 11.5). Therefore, $H=\sqrt{a^{2}-R^{2}}=\frac{\sqrt{2} a}{\sqrt{3}}$ and the volume $V_{1}=\frac{1}{3} S_{\text {base }} \cdot H$. Since $\triangle A B C$ is equilateral, $S_{\text {base }}=\frac{a^{2} \sqrt{3}}{4}$. Thus, $V_{1}=\frac{a^{3} \sqrt{2}}{12}$. Let the edge of the cube be $b$. The diagonal of the cube is $b \sqrt{2}$. It is equal to the edge of the tetrahedron $b \sqrt{2}=a$, hence $b=\frac{a}{\sqrt{2}}$. The volume of the cube $V_{2}=b^{3}=\frac{a^{3}}{2 \sqrt{2}}$. The ratio $\frac{V_{2}}{V_{1}}=\frac{a^{3} \cdot 12}{2 \sqrt{2} \cdot a^{3} \sqrt{2}}=3$.
Answer: 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.073. The measurements of a rectangular parallelepiped are 2, 3, and 6 cm. Find the length of the edge of a cube such that the volumes of these bodies are in the same ratio as their surface areas.
|
Solution.
The volume of a rectangular parallelepiped is $V_{\text {par }}=2 \cdot 3 \cdot 6=36 \mathrm{~cm}^{3}$. The volume of a cube is $V_{\mathrm{x}}=a^{3}$. The area of the complete surface of a rectangular parallelepiped is calculated as follows: $S_{\text {par }}=S_{\text {side }}+2 S_{\text {base }}=P H+2 S_{\text {base }}=2(2+3) \cdot 6+$ $+2 \cdot 3 \cdot 2=72 \mathrm{~cm}^{2}$. The area of the complete surface of a cube is $S_{\mathrm{K}}=6 a^{2}$. From the condition $\frac{V_{\text {par }}}{V_{\mathrm{K}}}=\frac{S_{\text {par }}}{S_{\mathrm{K}}}$. Hence, $\frac{36}{a^{3}}=\frac{72}{6 a^{2}}$. We get $a=3$ cm.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.022. Find the angle of a triangle if it is known that the sides enclosing this angle are 1 and 3, and the bisector of the angle is \(0.75 \sqrt{3}\).
|
## Solution.
In $\triangle A B C$ we have: $A C=1, B C=3, \angle A C C_{1}=\angle B C C_{1}, C C_{1}=0.75 \sqrt{3}$; we need to find $\angle A C B$ (Fig. 12.25).
We use the formula $l_{c}=\frac{2 a b \cos (C / 2)}{a+b}$ (see "Some relations between elements of figures", p. 713). Expressing $\cos \frac{C}{2}$ from this, we get
$$
\cos \frac{C}{2}=\frac{l_{c}(a+b)}{2 a b}
$$
or, after substituting the values $a=1, b=3, l_{c}=0.75 \sqrt{3}$, we find
$$
\cos \frac{C}{2}=\frac{3 \sqrt{3} \cdot 4}{4 \cdot 2 \cdot 1 \cdot 3}=\frac{\sqrt{3}}{2}
$$
Therefore, $\frac{C}{2}=30^{\circ}$, from which $C=60^{\circ}$.
Answer: $60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.040. The height of an isosceles trapezoid is $h$. The upper base of the trapezoid is seen from the midpoint of the lower base at an angle of $2 \alpha$, and the lower base is seen from the midpoint of the upper base at an angle of $2 \beta$. Find the area of the trapezoid in this general case and calculate it without tables if $h=2, \alpha=15^{\circ}, \beta=75^{\circ}$.
|
## Solution.
In trapezoid $ABCD$, we have: $AB=CD, BC \| AD, M \in AD, AM=MD$, $N \in BC, BN=NC, BE \perp AD, BE=h, \angle BMC=2\alpha, \angle AND=2\beta$ (Fig. 12.42). Since $\triangle ABM = \triangle CMD$ and $\triangle ABN = \triangle NCD$ (by two sides and the included angle), we have $BM=MC$ and $AN=ND$. From $\triangle AMN$ and $\triangle BMN$, we find $AM = h \tan \beta$ and $BN = h \tan \alpha$. Therefore, $S_{ABCD} = (AM + BN)h = h^2 (\tan \alpha + \tan \beta) = \frac{h^2 \sin (\alpha + \beta)}{\cos \alpha \cos \beta}$. For $h=2, \alpha=15^\circ$ and $\beta=75^\circ$, we have
Fig. 12.43
Fig. 12.44
$$
S_{ABCD} = \frac{4 \sin 90^\circ}{\cos 15^\circ \cos 75^\circ} = \frac{4}{\cos 15^\circ \sin 15^\circ} = \frac{8}{\sin 30^\circ} = 16
$$
Answer: $\frac{h^2 \sin (\alpha + \beta)}{\cos \alpha \cos \beta} ; 16$.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.003. In two barrels, there are 70 liters of milk. If 12.5% of the milk from the first barrel is poured into the second barrel, then both barrels will have the same amount. How many liters of milk are in each barrel?
|
## Solution.
Let the initial amount of milk in the first bucket be $x$, and in the second bucket $70-x$ liters. After transferring, the first bucket has $x-0.125x=0.875x$ liters left, and the second bucket has $70-x+0.125x$ liters. According to the condition, $70-x+0.125x=0.875x$, from which $x=40$. There were 40 liters in the first bucket and 30 liters in the second bucket of milk.
Answer: 40 and 30 liters.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.005. The sum of the digits of a two-digit number is 12. If 36 is added to the desired number, the result is a number written with the same digits but in reverse order. Find the number.
|
## Solution.
Let the desired number be of the form $10x + y$. Then, according to the condition, $x + y = 12$ (1) and $10x + y + 36 = 10y + x$, i.e., $x - y + 4 = 0$ (2). Adding (1) and (2), we get $2x = 8$, from which $x = 4$, and $y = 8$.
Answer: 48.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.006. A tractor driver plowed three plots of land. The area of the first is $2 / 5$ of the area of all three plots, and the area of the second is to the area of the third as $3 / 2: 4 / 3$. How many hectares were there in all three plots if the third plot was 16 hectares less than the first?
|
Solution.
Let the areas of the plots be $x, y, x-16$ (ha). According to the condition, $x=\frac{2}{5}(x+y-16+x)$ and $y:(x-16)=3 / 2: 4 / 3$, from which $y=\frac{9}{8}(x-16)$. We have
$x=\frac{2}{5}\left(2 x-16+\frac{9}{8} x-18\right) \Leftrightarrow x=\frac{2}{5}\left(\frac{25 x}{8}-34\right), x=\frac{272}{5}$. Next, we find $y=\frac{9}{8}\left(\frac{272}{5}-16\right)=\frac{216}{5}$. The total area is $\frac{544}{5}+\frac{216}{5}-16=136$ (ha).
Answer: 136 ha.
|
136
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.008. Seawater contains $5 \%$ salt by mass. How much fresh water needs to be added to 30 kg of seawater to make the salt concentration $1.5 \%$?
|
## Solution.
Let $x$ kg of salt in 30 kg of seawater. $x$ kg is $5 \%$. Hence, $x=1.5$ kg, $30 \text{kg}-100 \%$. In the diluted seawater: 1.5 kg of salt is $1.5 \%$, $a$ kg is $100 \%$, from which $a=100$ kg of diluted seawater. Therefore, we need to add $100-30=70$ kg of fresh water.
Answer: $70 \text{kg}$.
|
70
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.009. In the library, there are books in English, French, and German. English books make up $36 \%$ of all foreign language books, French books make up $75 \%$ of the English books, and the remaining 185 books are German. How many foreign language books are there in the library?
|
## Solution.
Let $x$ be the total number of books in foreign languages. The number of English books is $0.36x$; the number of French books is $0.75 \cdot 0.36x$. According to the problem, $0.36x + 0.75 \cdot 0.36x + 185 = x$, from which we find $x = 500$.
Answer: 500
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.010. A pump can extract $2 / 3$ of the water from a pool in 7.5 min. After working for 0.15 h, the pump stopped. Find the capacity of the pool, if after the pump stopped, there was still 25 m $^{3}$ of water left in the pool.
|
Solution.
Let $x$ m $^{3}$ be the capacity of the pool. In 7.5 minutes, the pump can extract $\frac{2}{3} x$ water. In $0.15 \text{ h} = 9$ minutes, the pump extracted $\frac{9 \cdot \frac{2}{3} x}{7.5}=0.8 x$ water. In the pool, $0.2 x$ water remained. According to the problem, $0.2 x=25$, from which $x=125$.
Answer: $125 \text{ m}^{3}$.
|
125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.011. Due to the reconstruction of equipment, the labor productivity of a worker increased twice during the year by the same percentage. By what percentage did the labor productivity increase each time, if during the same time a worker used to produce goods worth 2500 rubles, and now produces goods worth 2809 rubles?
|
Solution.
Let a worker produce a parts in 8 hours of work. Then the rate is $\frac{2500}{a}$ rubles per part, and the labor productivity is $\frac{a}{8}$ parts per hour. After the first increase in productivity by $x \%$, the worker started producing $\frac{a}{8}+\frac{x \cdot a}{100 \cdot 8}$ parts per hour; after the second increase in productivity by $x \% - \frac{a}{8}\left(1+\frac{x}{100}\right)\left(1+\frac{x}{100}\right)$ parts per hour. In 8 hours, he started producing $a\left(1+\frac{x}{100}\right)^{2}$ parts and earned $a\left(1+\frac{x}{100}\right)^{2} \cdot \frac{2500}{a}$ rubles. According to the condition, $a\left(1+\frac{x}{100}\right)^{2} \cdot \frac{2500}{a}=2809$, from which $x=6 \%$.
Answer: $6 \%$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.012. The working day has been reduced from 8 to 7 hours. By what percentage does labor productivity need to increase to ensure that, with the same rates, the wage increases by $5 \%$?
|
Solution.
Let the master produce $a$ parts and earn $b$ rubles for 8 hours of work. Then the rate is $b / a$ rubles per part, and the labor productivity is $a / 8$ parts per hour. After increasing productivity by $x \%$, the master started producing $\frac{a}{8}+\frac{x a}{8 \cdot 100}$ parts per hour. Therefore, in 7 hours, he produced $\frac{7 a}{8}\left(1+\frac{x}{100}\right)$ parts and earned $\frac{7 a}{8}\left(1+\frac{x}{100}\right) \frac{b}{a}=\frac{7 b}{8}\left(1+\frac{x}{100}\right)$ rubles. According to the condition, $\frac{7 a}{8}\left(1+\frac{x}{100}\right)=1.05 b$, from which $x=20 \%$.
Answer: $20 \%$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.015. A tourist traveled the distance between two cities in 3 days. On the first day, he traveled $1 / 5$ of the total distance and an additional 60 km, on the second day $1 / 4$ of the total distance and an additional 20 km, and on the third day $23 / 80$ of the total distance and the remaining 25 km. Find the distance between the cities.
|
Solution.
Let $x$ km be the distance between the cities. We can form the following table:
| Day | Distance traveled in a day |
| :---: | :---: |
| First | $\frac{1}{5} x+60$ (km) |
| Second | $\frac{1}{4} x+20$ (km) |
| Third | $\frac{23}{80} x+25$ (km) |
According to the condition, $\frac{1}{5} x+60+\frac{1}{4} x+20+\frac{23}{80} x+25=x$, from which $x=400$.
Answer: 400 km.
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.017. Find the sum of three numbers, knowing that the third is related to the first as $18.48: 15.4$ and constitutes $40 \%$ of the second, and the sum of the first and second is 400.
|
Solution.
Let $x, y, z$ be the given numbers. According to the condition, we have: $\frac{z}{x}=\frac{1848}{1540}=\frac{6}{5}$, $z=0.4 y, x+y=400$. Since $y=\frac{5}{2} z$ and $z=\frac{6}{5} x$, then $y=3 x$ and $x+3 x=400 \Rightarrow$ $\Rightarrow x=100, z=\frac{6}{5} x=120$. Then
$S=x+y+z=400+120=520$.
Answer: 520.
|
520
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.018. The depositor withdrew from his savings account at the savings bank first $1 / 4$ of his money, then $4 / 9$ of the remaining money and another 640 rubles. After this, he had $3 / 20$ of all his money left on the savings book. How large was the deposit?
|
Solution.
Let the deposit be $x$ rubles. Then the first remainder is $\frac{3 x}{4}$; the second remainder $-\frac{3 x}{4}-\frac{4}{9} \cdot \frac{3 x}{4}-640=\frac{3 x}{20}$. We have $\frac{3 x}{4}-\frac{x}{3}-\frac{3 x}{20}=640$, from which $x=2400$ (rubles).
Answer: 2400 rubles.
|
2400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.019. Two snow-clearing machines are working on snow removal. The first can clear the entire street in 1 hour, while the second can do it in $75\%$ of this time. Starting the cleaning simultaneously, both machines worked together for 20 minutes, after which the first machine stopped. How much more time is needed for the second machine to finish the work?
|
## Solution.
Let's consider the entire volume of work as 1. The productivity of the first machine is 1 (per hour), and the second machine's productivity is $1: \frac{3}{4}=\frac{4}{3}$ (per hour). Working together for $\frac{1}{3}$ of an hour, they will complete $\frac{1}{3} \cdot 1 + \frac{1}{3} \cdot \frac{4}{3} = \frac{7}{9}$ of the entire work. Then, the remaining work for the second machine will be $\frac{2}{9}$, which will require $\frac{2}{9} : \frac{4}{3} = \frac{1}{6}$ (hours).
Answer: 10 min.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.020. The sum of the first three terms of the proportion is 58. The third term is $2 / 3$, and the second term is $3 / 4$ of the first term. Find the fourth term of the proportion and write it down.
|
Solution.
Let the proportion be $\frac{a}{b}=\frac{c}{d}$. Given that $a+b+c=58$; $c=\frac{2}{3} a$; $b=\frac{3}{4} a$. Therefore, $a+\frac{3}{4} a+\frac{2}{3} a=58$, from which $a=24$; $c=16$; $b=18$. Thus, $d=\frac{b c}{a}=12$.
Answer: $12 ; \frac{24}{18}=\frac{16}{12}$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.021. One brigade can harvest the entire field in 12 days. The second brigade needs $75\%$ of this time to complete the same work. After the first brigade worked alone for 5 days, the second brigade joined, and together they finished the work. How many days did the brigades work together?
|
## Solution.
Let the teams work together for $x$ days. The productivity of the first team is $-\frac{1}{12}$; the productivity of the second team is $-\frac{1}{12 \cdot 0.75}=\frac{1}{9}$. According to the condition, $\frac{1}{12} \cdot 5+\left(\frac{1}{12}+\frac{1}{9}\right) \cdot x=1$, from which $x=3$ days.
Answer: 3 days.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.022. On the mathematics entrance exam, $15 \%$ of the applicants did not solve a single problem, 144 people solved problems with errors, and the number of those who solved all problems correctly is to the number of those who did not solve any at all as 5:3. How many people took the mathematics exam that day
|
Solution.
Let $x$ be the total number of people who took the exam. $0.15x$ people did not solve any problems; $0.25x$ people solved all the problems, which is $\frac{0.15x \cdot 5}{3}=0.25x$ people. According to the problem, $0.15x + 144 + 0.25x = x$, from which we get $x = 240$.
Answer: 240.
|
240
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.023. Identical parts are processed on two machines. The productivity of the first machine is $40 \%$ higher than that of the second. How many parts were processed during the shift on each machine, if the first machine worked for 6 hours during this shift, and the second - 8 hours, and both machines together processed 820 parts?
|
Solution.
Let the productivity of the second machine be $x$; then the productivity of the first machine is $1.4x$ parts per hour. The first machine processed $1.4x \cdot 6$ parts in the shift; the second machine processed $x \cdot 8$ parts. According to the condition, $1.4x \cdot 6 + x \cdot 8 = 820$, from which $x = 50$. Therefore, the first machine processed $1.4 \cdot 50 \cdot 6 = 420$ parts in the shift; the second machine processed $50 \cdot 8 = 400$ parts.
Answer: 420 and 400 parts.
|
420
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.024. A tractor team can plow 5/6 of a plot of land in 4 hours and 15 minutes. Before the lunch break, the team worked for 4.5 hours, after which 8 hectares remained unplowed. How large was the plot?
|
## Solution.
Let $x$ ha be the entire plot. Before lunch, the team plowed $\frac{4.5 \cdot \frac{5}{6} x}{4.25}=\frac{15}{17} x$ ha. According to the condition, $\frac{15}{17} x + 8 = x$, from which $x = 68$ ha.
Answer: 68 ha.
|
68
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.026. A tourist traveled 90 km by boat along the river and walked 10 km on foot. For the walking route, 4 hours less were spent compared to the river journey. If the tourist had walked for as long as he had rowed, and rowed for as long as he had walked, these distances would have been equal. How long did he walk and how long did he row?
|
## Solution.
Let $x$ be the number of hours the tourist walked. Then he spent $(x+4)$ hours on the boat. The tourist's walking speed is $\frac{10}{x}$ km/h; the speed on the boat is $-\frac{90}{x+4}$ km/h. According to the problem, $\frac{10}{x}(x+4)=\frac{90}{x+4} \cdot x$, from which $x=2$ hours.
Answer: 2 and 6 hours.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.031. A group of students went on a hike through the Moscow region during their vacation. The first 30 km they walked, $20 \%$ of the remaining part of the route they traveled by raft along the river, and then they walked again, covering a distance 1.5 times greater than the distance they traveled by raft. The remaining part of the journey was covered in 1 hour 30 minutes by hitching a ride on a passing truck, which was traveling at a speed of 40 km/h. What is the total length of the route?
|
## Solution.
Let $x$ km be the total length of the route. Then the students floated on a raft for $(x-30) \cdot 0.2$ km, and then walked another $1.5(x-30) \cdot 0.2$ km. According to the problem, $30+(x-30) \cdot 0.2+1.5(x-30) \cdot 0.2+40 \cdot 1.5=x$, from which $x=150$ km.
Answer: 150 km.
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.032. In 3.5 hours of operation, one stamping press can produce $42\%$ of all ordered parts. The second press can produce $60\%$ of all parts in 9 hours, and the work speeds of the third and second presses are in the ratio of $6:5$. How long will it take to complete the entire order if all three presses work simultaneously?
|
Solution.
Let $x$ parts be the entire order. Then the working speed of the first press is $-\frac{0.42 x}{3.5}$ parts/hour; the second press is $\frac{0.6 x}{9}$ parts/hour; the third press is $\frac{6}{5} \cdot \frac{0.6 x}{9}$ parts/hour. Therefore, all three presses working simultaneously will complete the entire order in $\frac{x}{\frac{0.6 x}{9}+\frac{0.42 x}{3.5}+\frac{6}{5} \cdot \frac{0.6 x}{9}}=3.75$ (hours) $=3$ hours 45 minutes.
Answer: $i n ~ 3$ hours 45 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.033. Each of the two typists retyped a manuscript of 72 pages. The first typist retyped 6 pages in the same time it took the second to retype 5 pages. How many pages did each typist retype per hour, if the first finished the work 1.5 hours faster than the second?
|
Solution.
Let $x$ pages per hour be the typing speed of the first typist, then the second typist's speed is $\frac{5}{6} x$. The first typist worked $\frac{72}{x}$ hours; the second - $\frac{72}{5}$ hours. According to the problem, $\frac{72}{x}=\frac{72}{\frac{5}{6} x}-1.5$, from which $x=9.6($ pages/hour); the second typist typed $\frac{5}{6} \cdot 9.6=8$ pages/hour.
Answer: 8 and 9.6 pages/hour.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.035. A shoe factory completed $20 \%$ of the monthly plan in the first week, produced $120 \%$ of the amount of products made in the first week in the second week, and produced $60 \%$ of the products made in the first two weeks combined in the third week. What is the monthly production plan for shoes, if it is known that to complete it, it is necessary to manufacture 1480 pairs of shoes in the last week of the month?
|
## Solution.
Let $x$ be the monthly production plan for shoes. In the first week, the factory produced $0,2 x$ pairs of shoes, in the second week - $1,2 \cdot 0,2 x$; in the third week - $0,6(0,2 x+1,2 \cdot 0,2 x)$ pairs. According to the condition,
$0,2 x+1,2 \cdot 0,2 x+0,6(0,2 x+1,2 \cdot 0,2 x)+1480=x$, from which $x=5000$ pairs.
Answer: 5000.
|
5000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.041. A 30% hydrochloric acid solution was mixed with a 10% solution to obtain 600 g of a 15% solution. How many grams of each solution were taken?
|
## Solution.
Let $x$ g of a $30\%$ hydrochloric acid solution and $(600-x)$ g of a $10\%$ solution be taken. The mass of hydrochloric acid in the $30\%$ solution is $0.3x$ g; in the $10\%$ solution, it is $0.1(600-x)$ g. In the resulting $15\%$ solution, the mass of hydrochloric acid is $0.15 \cdot 600 = 90$ g. According to the condition, $0.3x + 0.1(600-x) = 90$, from which $x = 150$ g of the $30\%$ solution; $600 - 150 = 450$ g of the $10\%$ solution.
Answer: 150 and 450 g.
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.047. A musical theater announced a competition for admission to the orchestra. Initially, it was planned that the number of places for violinists, cellists, and trumpeters would be distributed in the ratio $1.6: 1: 0.4$. However, it was then decided to increase the intake, and as a result, 25% more violinists and 20% fewer cellists were admitted than originally planned. How many musicians of each genre were admitted to the orchestra if a total of 32 people were admitted?
|
## Solution.
Let it be planned to recruit $1.6 x$ violinists, $x$ - cellists, $0.4 x$ trumpeters. Then, they recruited $1.25 \cdot 1.6 x$ violinists, $(1-0.2) x$ cellists, $0.4 x$ trumpeters. According to the condition, $1.25 \cdot 1.6 x + (1-0.2) x + 0.4 x = 32$, from which $x=10$. Therefore, they recruited $1.25 \cdot 1.6 \cdot 10=20$ violinists; $0.8 \cdot 10=8$ cellists; $0.4 \cdot 10=4$ trumpeters.
Answer: 20 violinists, 8 cellists, 4 trumpeters.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.050. The worker's wages for October and November were in the ratio of $3 / 2: 4 / 3$, and for November and December, they were in the ratio of $2: 8 / 3$. In December, he received 450 rubles more than in October, and for exceeding the quarterly plan, the worker was awarded a bonus of $20 \%$ of his three-month earnings. Find the size of the bonus.
|
Solution.
Let $x$ rubles be the worker's salary for November. Then for October, it is $\left(\frac{3}{2} : \frac{4}{3}\right) x = \frac{9}{8} x$ rubles; for December, it is $\left(\frac{8}{3} : 2\right) x = \frac{4}{3} x$ rubles. According to the condition, $\frac{4}{3} x = \frac{9}{8} x + 450$, from which $x = 2160$ rubles - the salary for November; $\frac{9}{8} \cdot 2160 = 2430$ rubles - for October; $\frac{4}{3} \cdot 2160 = 2880$ rubles - for December. Then the bonus amount is $-(2160 + 2430 + 2880) \cdot 0.2 = 1494$ rubles.
Answer: 1494 rubles.
|
1494
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.051. Two cylinders roll down an inclined board 6 m long, one of which has a circumference of 3 dm, and the other 2 dm. Can the circumferences of both cylinders be increased by the same amount so that on the same path one of them makes 3 more revolutions than the other?
|
Solution.
Assume that the lengths of the circumferences can be increased by $x$ dm. Then the first cylinder will make $\frac{60}{3+x}$ revolutions, and the second will make $-\frac{60}{2+x}$. According to the condition, $\frac{60}{3+x}+3=\frac{60}{2+x}$, from which we get $x^{2}+5 x-14=0$. Solving this equation, we find that the lengths of the circumferences can be increased by $x=2$ dm.
Answer: can be increased by 2 dm.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.053. A crystal, while in the formation stage, uniformly increases its mass. Observing the formation of two crystals, it was noted that over a year, the first crystal increased its initial mass by $4 \%$, while the second increased by $5 \%$, at the same time the mass increase of the first crystal over 3 months was equal to the mass increase of the second crystal over 4 months. What were the initial masses of these crystals, if it is known that after each of them increased by 20 g, the ratio of the mass of the first crystal to the mass of the second crystal reached the number 1.5?
|
Solution.
Let $a$ be the initial mass of the first crystal; $b$ be the second; and let $x$ be the mass increase of the first crystal over 3 months. Over a year, the mass increase of the first crystal is $4x$; of the second crystal - $3x$. According to the problem, $a+4x=1.04a, b+3x=1.05b$. According to the problem, $\frac{a+20}{b+20}=1.5$. Solving the system $\left\{\begin{array}{l}a+4x=1.04a \\ b+3x=1.05b \\ a+20=1.5(b+20),\end{array}\right.$ we find that $a=100 \text{ g}; b=60 \text{ g}$.
Answer: 100 and 60 g.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.054. One farmer obtained an average buckwheat yield of 21 tons per hectare, while another, who had 12 hectares less under buckwheat, achieved an average yield of 25 tons per hectare. As a result, the second farmer collected 300 tons more buckwheat than the first. How many tons of buckwheat were collected by each farmer?
|
Solution.
Let's compile the following table:
| Farmer | Area, ha | Yield, c/ha | Mass, c |
| :---: | :---: | :---: | :---: |
| First | $x$ | 21 | $21 x$ |
| Second | $x-12$ | 25 | $25(x-12)$ |
According to the condition $25(x-12)-21 x=300$, from which $x=150$. Then $21 x=3150$ (c); $25(x-12)=3450$ c.
Answer: 3150 and 3450 c.
|
3150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.059. On both sides of a 1200 m long street, there are rectangular strips of land allocated for plots, one being 50 m wide, and the other 60 m wide. How many plots is the entire village divided into, if the narrower strip contains 5 more plots than the wider one, given that each plot on the narrower strip is 1200 m$^{2}$ smaller than each plot on the wider strip?
|
## Solution.
Let $x$ be the number of plots on the wide strip, $x+5$ plots - on the narrow strip, $y$ m - the width of a plot on the narrow strip, and $y+1200$ m - on the wide strip. According to the problem, $\left\{\begin{array}{l}(x+5) y=1200 \cdot 50, \\ x(y+1200)=1200 \cdot 60 .\end{array}\right.$ Solving the system, we find $x=20$ plots on the wide strip. Therefore, on the narrow strip, there are 25 plots. In total, $20+25=$ $=45$ plots.
Answer: 45.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.060. A load with a mass of 60 kg presses on a support. If the mass of the load is reduced by 10 kg, and the area of the support is reduced by 5 dm², then the mass per square decimeter of the support will increase by 1 kg. Determine the area of the support.
|
Solution.
Let $x$ dm $^{2}$ be the area of the support. Then $\frac{60}{x}$ kg/dm² is the mass per 1 dm ${ }^{2}$ of the support. After reducing the mass of the load and the area of the support, this mass is $\frac{50}{x-5}$ kg/dm². According to the condition, $\frac{50}{x-5}-1=\frac{60}{x}$, from which $x=15$.
Answer: 15 dm $^{2}$.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.061. To pay for the delivery of four parcels, 4 different postage stamps were needed for a total of 84 kopecks. Determine the cost of the stamps purchased by the sender, if these costs form an arithmetic progression, and the most expensive stamp is 2.5 times more expensive than the cheapest one.
|
Solution.
Let $x$ kop. - the cost of the cheapest stamp, $x+d, x+2 d$, $x+3 d$ - the costs of the other stamps. By condition
$$
\left\{\begin{array}{l}
x+x+d+x+2 d+x+3 d=84, \\
x+3 d=2.5 x,
\end{array} \text { from which } x=12 ; d=6\right. \text {. Costs of the }
$$
stamps: 12 kop., 18 kop., 24 kop, 30 kop.
Answer: 12 kop., 18 kop., 24 kop, 30 kop.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.062. An apprentice turner is machining pawns for a certain number of chess sets. He wants to learn to produce 2 more pawns per day than he does now; then he would complete the same task 10 days faster. If he could learn to produce 4 more pawns per day than he does now, the time required to complete the same task would be reduced by 16 days. How many chess sets does this apprentice supply with pawns, if 16 pawns are needed for each set?
|
## Solution:
Let the turner provide $x$ sets of chess pieces. He completes the task in $y$ days. According to the problem,
$$
\left\{\begin{array}{l}
\left(\frac{16 x}{y}+2\right)(y-10)=16 x \\
\left(\frac{16 x}{y}+4\right)(y-16)=16 x
\end{array}, \text { from which } x=15\right.
$$
Answer: 15.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.063. In the club's auditorium, there were 320 seats arranged in identical rows. After the number of seats in each row was increased by 4 and one more row was added, the auditorium had 420 seats. How many rows are there in the auditorium now?
|
Solution:
Let there be $x$ rows in the auditorium; $\frac{320}{x}$ - the number of seats in one row. After the number of seats in a row was increased by 4 and one row was added, the total number of seats in the hall became $\left(\frac{320}{x}+4\right)(x+1)=420$, from which $x=20$. Therefore, there are now 21 rows in the auditorium.
Answer: 21.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.