problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1.009.
$$
\frac{0.4+8\left(5-0.8 \cdot \frac{5}{8}\right)-5: 2 \frac{1}{2}}{\left(1 \frac{7}{8} \cdot 8-\left(8.9-2.6: \frac{2}{3}\right)\right) \cdot 34 \frac{2}{5}} \cdot 90
$$
|
Solution.
$$
\begin{aligned}
& \frac{0.4+8\left(5-0.8 \cdot \frac{5}{8}\right)-5: 2 \frac{1}{2}}{\left(1 \frac{7}{8} \cdot 8-\left(8.9-2.6: \frac{2}{3}\right)\right) \cdot 34 \frac{2}{5}} \cdot 90=\frac{\left(0.4+40-4-5 \cdot \frac{2}{5}\right) \cdot 90}{\left(\frac{15}{8} \cdot 8-\frac{89}{10}+\frac{13}{5} \cdot \frac{3}{2}\right) \cdot \frac{172}{5}}= \\
& =\frac{34.4 \cdot 90}{\left(\frac{150}{10}-\frac{89}{10}+\frac{39}{10}\right) \cdot \frac{172}{5}}=\frac{344 \cdot 9}{2 \cdot 172}=9 .
\end{aligned}
$$
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.010. $\frac{\left(5 \frac{4}{45}-4 \frac{1}{6}\right): 5 \frac{8}{15}}{\left(4 \frac{2}{3}+0.75\right) \cdot 3 \frac{9}{13}} \cdot 34 \frac{2}{7}+\frac{0.3: 0.01}{70}+\frac{2}{7}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(5 \frac{4}{45}-4 \frac{1}{6}\right): 5 \frac{8}{15}}{\left(4 \frac{2}{3}+0.75\right) \cdot 3 \frac{9}{13}} \cdot 34 \frac{2}{7}+\frac{0.3: 0.01}{70}+\frac{2}{7}=\frac{\left(\frac{229}{45}-\frac{25}{6}\right): \frac{83}{15}}{\left(\frac{14}{3}+\frac{3}{4}\right) \cdot \frac{48}{13}} \cdot \frac{240}{7}+\frac{30}{70}+\frac{2}{7}= \\
& =\frac{\frac{93}{90} \cdot \frac{15}{83}}{\frac{65}{12} \cdot \frac{48}{13}} \cdot \frac{240}{7}+\frac{5}{7}=\frac{1}{6 \cdot 20} \cdot \frac{240}{7}+\frac{5}{7}=\frac{2}{7}+\frac{5}{7}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.011. $\frac{\left(\frac{3}{5}+0.425-0.005\right): 0.1}{30.5+\frac{1}{6}+3 \frac{1}{3}}+\frac{6 \frac{3}{4}+5 \frac{1}{2}}{26: 3 \frac{5}{7}}-0.05$.
|
## Solution.
$$
\frac{\left(\frac{3}{5}+0.425-0.005\right): 0.1}{30.5+\frac{1}{6}+3 \frac{1}{3}}+\frac{6 \frac{3}{4}+5 \frac{1}{2}}{26: 3 \frac{5}{7}}-0.05=
$$
$=\frac{(0.6+0.42) \cdot 10}{\frac{61}{2}+\frac{1}{6}+\frac{10}{3}}+\frac{12 \frac{1}{4} \cdot 26}{26 \cdot 7}-0.05=$
$=\frac{10.2}{34}+\frac{7}{4}-\frac{1}{20}=\frac{3}{10}+\frac{7}{4}-\frac{1}{20}=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.012. $\frac{3 \frac{1}{3} \cdot 1.9+19.5: 4 \frac{1}{2}}{\frac{62}{75}-0.16}: \frac{3.5+4 \frac{2}{3}+2 \frac{2}{15}}{0.5\left(1 \frac{1}{20}+4.1\right)}$.
|
## Solution.
$\frac{3 \frac{1}{3} \cdot 1.9 + 19.5 : 4 \frac{1}{2}}{\frac{62}{75} - 0.16} : \frac{3.5 + 4 \frac{2}{3} + 2 \frac{2}{15}}{0.5 \left(1 \frac{1}{20} + 4.1\right)} = \frac{\frac{10}{3} \cdot \frac{19}{10} + \frac{39}{2} \cdot \frac{2}{9}}{\frac{62}{75} - \frac{4}{25}} \cdot \frac{\frac{1}{2} \left(\frac{21}{20} + \frac{41}{10}\right)}{\frac{7}{2} + \frac{14}{3} + \frac{32}{15}}=$
$= \frac{\frac{19}{3} + \frac{13}{3}}{\frac{2}{3}} \cdot \frac{\frac{103}{40}}{\frac{103}{10}} = \frac{16}{4} = 4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.014. $\frac{\left(4.5 \cdot 1 \frac{2}{3}-6.75\right) \cdot \frac{2}{3}}{\left(3 \frac{1}{3} \cdot 0.3+5 \frac{1}{3} \cdot \frac{1}{8}\right): 2 \frac{2}{3}}+\frac{1 \frac{4}{11} \cdot 0.22: 0.3-0.96}{\left(0.2-\frac{3}{40}\right) \cdot 1.6}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(4.5 \cdot 1 \frac{2}{3}-6.75\right) \cdot \frac{2}{3}}{\left(3 \frac{1}{3} \cdot 0.3+5 \frac{1}{3} \cdot \frac{1}{8}\right): 2 \frac{2}{3}}+\frac{1 \frac{4}{11} \cdot 0.22: 0.3-0.96}{\left(0.2-\frac{3}{40}\right) \cdot 1.6}=\frac{\left(\frac{9}{2} \cdot \frac{5}{3}-\frac{27}{4}\right) \cdot \frac{2}{3}}{\left(\frac{10}{3} \cdot \frac{3}{10}+\frac{16}{3} \cdot \frac{1}{8}\right) \cdot \frac{3}{8}}+ \\
& +\frac{\frac{15}{11} \cdot \frac{11}{50} \cdot \frac{10}{3}-\frac{24}{25}}{\left(\frac{1}{5}-\frac{3}{40}\right) \cdot \frac{8}{5}}=\frac{\left(\frac{30}{4}-\frac{27}{4}\right) \cdot \frac{2}{3}}{\left(1+\frac{2}{3}\right) \cdot \frac{3}{8}}+\frac{1-\frac{24}{25}}{\frac{1}{8} \cdot \frac{8}{5}}=\frac{1}{2} \cdot \frac{8}{5}+\frac{1}{5}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.016. $\left(16 \frac{1}{2}-13 \frac{7}{9}\right) \cdot \frac{18}{33}+2.2\left(\frac{8}{33}-\frac{1}{11}\right)+\frac{2}{11}$.
|
## Solution.
$$
\begin{aligned}
& \left(16 \frac{1}{2}-13 \frac{7}{9}\right) \cdot \frac{18}{33}+2.2\left(\frac{8}{33}-\frac{1}{11}\right)+\frac{2}{11}=\left(\frac{33}{2}-\frac{124}{9}\right) \cdot \frac{6}{11}+ \\
& +\frac{22}{10}\left(\frac{8}{33}-\frac{3}{33}\right)+\frac{2}{11}=\frac{49}{18} \cdot \frac{6}{11}+\frac{1}{3}+\frac{2}{11}=\frac{49}{33}+\frac{17}{33}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.017. $\frac{0.128: 3.2+0.86}{\frac{5}{6} \cdot 1.2+0.8} \cdot \frac{\left(1 \frac{32}{63}-\frac{13}{21}\right) \cdot 3.6}{0.505 \cdot \frac{2}{5}-0.002}$.
|
## Solution.
$$
\begin{aligned}
& \frac{0.128: 3.2+0.86}{\frac{5}{6} \cdot 1.2+0.8} \cdot \frac{\left(1 \frac{32}{63}-\frac{13}{21}\right) \cdot 3.6}{0.505 \cdot \frac{2}{5}-0.002}=\frac{0.04+0.86}{1+0.8} \cdot \frac{\left(\frac{95}{63}-\frac{39}{63}\right) \cdot \frac{18}{5}}{0.202-0.002}= \\
& =\frac{9}{18} \cdot \frac{8}{9} \cdot \frac{18}{0.2 \cdot 5}=8
\end{aligned}
$$
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.018. $\frac{3 \frac{1}{3}: 10+0.175: 0.35}{1.75-1 \frac{11}{17} \cdot \frac{51}{56}}-\frac{\left(\frac{11}{18}-\frac{1}{15}\right): 1.4}{\left(0.5-\frac{1}{9}\right) \cdot 3}$.
|
Solution.
$$
\begin{aligned}
& \frac{3 \frac{1}{3}: 10+0.175: 0.35}{1.75-1 \frac{11}{17} \cdot \frac{51}{56}}-\frac{\left(\frac{11}{18}-\frac{1}{15}\right): 1.4}{\left(0.5-\frac{1}{9}\right) \cdot 3}=\frac{\frac{1}{3}+\frac{1}{2}}{\frac{7}{4}-\frac{28}{17} \cdot \frac{51}{56}}-\frac{\frac{49}{90} \cdot \frac{5}{7}}{\frac{7}{18} \cdot 3}= \\
& =\frac{5}{6\left(\frac{7}{4}-\frac{3}{2}\right)}-\frac{7 \cdot 18}{18 \cdot 7 \cdot 3}=\frac{10}{3}-\frac{1}{3}=3 .
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.019. $\frac{0.125: 0.25+1 \frac{9}{16}: 2.5}{(10-22: 2.3) \cdot 0.46+1.6}+\left(\frac{17}{20}+1.9\right) \cdot 0.5$.
|
## Solution.
$$
\begin{aligned}
& \frac{0.125: 0.25+1 \frac{9}{16}: 2.5}{(10-22: 2.3): 0.46+1.6}+\left(\frac{17}{20}+1.9\right) \cdot 0.5=\frac{\frac{1}{2}+\frac{5}{8}}{\left(10-\frac{220}{23}\right) \cdot \frac{23}{50}+\frac{8}{5}}+\frac{17}{40}+\frac{19}{20}= \\
& =\frac{\frac{9}{8}}{\frac{1}{5}+\frac{8}{5}}+\frac{17}{40}+\frac{38}{40}=\frac{5}{8}+\frac{11}{8}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.020. $\left(\left(1 \frac{1}{7}-\frac{23}{49}\right): \frac{22}{147}-\left(0.6: 3 \frac{3}{4}\right) \cdot 2 \frac{1}{2}+3.75: 1 \frac{1}{2}\right): 2.2$.
|
## Solution.
$$
\begin{aligned}
& \left(\left(1 \frac{1}{7}-\frac{23}{49}\right): \frac{22}{147}-\left(0.6: 3 \frac{3}{4}\right) \cdot 2 \frac{1}{2}+3.75: 1 \frac{1}{2}\right): 2.2= \\
& =\left(\left(\frac{8}{7}-\frac{23}{49}\right) \frac{147}{22}-0.16 \cdot 2.5+2.5\right): 2.2=\left(\frac{33}{49} \cdot \frac{147}{22}-0.4+2.5\right): 2.2= \\
& =(4.5-0.4+2.5) \cdot \frac{10}{22}=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.022. $\frac{0.5+\frac{1}{4}+\frac{1}{6}+0.125}{\frac{1}{3}+0.4+\frac{14}{15}}+\frac{(3.75-0.625) \frac{48}{125}}{12.8 \cdot 0.25}$.
|
Solution.
$\frac{0.5+\frac{1}{4}+\frac{1}{6}+0.125}{\frac{1}{3}+0.4+\frac{14}{15}}+\frac{(3.75-0.625) \frac{48}{125}}{12.8 \cdot 0.25}=\frac{\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}}{\frac{1}{3}+\frac{2}{5}+\frac{14}{15}}+\frac{3.125 \cdot 48}{3.2 \cdot 125}=$
$=\frac{25}{24} \cdot \frac{3}{5}+\frac{1.2}{3.2}=0.625+0.375=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.024. $\frac{0.725+0.6+\frac{7}{40}+\frac{11}{20}}{0.128 \cdot 6 \frac{1}{4}-0.0345: \frac{3}{25}} \cdot 0.25$.
|
## Solution.
$$
\begin{aligned}
& \frac{0.725+0.6+\frac{7}{40}+\frac{11}{20}}{0.128 \cdot 6 \frac{1}{4}-0.0345: \frac{3}{25}} \cdot 0.25=\frac{1.325+\frac{29}{40}}{0.128 \cdot 6.25-0.0345: 0.12} \cdot 0.25= \\
& =\frac{1.325+0.725}{0.8-0.2875} \cdot 0.25=\frac{2.05}{0.5125} \cdot 0.25=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.025. $\left((520 \cdot 0.43): 0.26-217 \cdot 2 \frac{3}{7}\right)-\left(31.5: 12 \frac{3}{5}+114 \cdot 2 \frac{1}{3}+61 \frac{1}{2}\right)$.
|
Solution.
$$
\begin{aligned}
& \left((520 \cdot 0.43): 0.26-217 \cdot 2 \frac{3}{7}\right)-\left(31.5: 12 \frac{3}{5}+114 \cdot 2 \frac{1}{3}+61 \frac{1}{2}\right)= \\
& =\left(223.6: 0.26-217 \cdot \frac{17}{7}\right)-\left(\frac{63}{2} \cdot \frac{5}{63}+114 \cdot \frac{7}{3}+\frac{123}{2}\right)= \\
& =(860-527)-\left(\frac{5}{2}+266+\frac{123}{2}\right)=333-330=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.026. $\frac{(3.4-1.275) \cdot \frac{16}{17}}{\frac{5}{18} \cdot\left(1 \frac{7}{85}+6 \frac{2}{17}\right)}+0.5\left(2+\frac{12.5}{5.75+\frac{1}{2}}\right)$.
|
Solution.
$$
\begin{aligned}
& \frac{(3.4-1.275) \cdot \frac{16}{17}}{\frac{5}{18} \cdot\left(1 \frac{7}{85}+6 \frac{2}{17}\right)}+0.5\left(2+\frac{12.5}{5.75+\frac{1}{2}}\right)=\frac{2.125 \cdot \frac{16}{17}}{\frac{5}{18}\left(\frac{92}{85}+\frac{104}{17}\right)}+\frac{1}{2}\left(2+\frac{12.5}{6.25}\right)= \\
& =\frac{\frac{17}{8} \cdot \frac{16}{17}}{\frac{5}{18} \cdot \frac{612}{85}}+1+1=1+2=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.027. $\left(\frac{3.75+2 \frac{1}{2}}{2 \frac{1}{2}-1.875}-\frac{2 \frac{3}{4}+1.5}{2.75-1 \frac{1}{2}}\right) \cdot \frac{10}{11}$.
|
Solution.
$\left(\frac{3.75+2 \frac{1}{2}}{2 \frac{1}{2}-1.875}-\frac{2 \frac{3}{4}+1.5}{2.75-1 \frac{1}{2}}\right) \cdot \frac{10}{11}=\left(\frac{3.75+2.5}{2.5-1.875}-\frac{2.75+1.5}{2.75-1.5}\right) \cdot \frac{10}{11}=$
$=\left(\frac{6.25}{0.625}-\frac{4.25}{1.25}\right) \cdot \frac{10}{11}=\left(10-\frac{17}{5}\right) \cdot \frac{10}{11}=\frac{33}{5} \cdot \frac{10}{11}=6$.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.028. $((21.85: 43.7+8.5: 3.4): 4.5): 1 \frac{2}{5}+1 \frac{11}{21}$.
|
## Solution.
$$
\begin{aligned}
& ((21.85: 43.7+8.5: 3.4): 4.5): 1 \frac{2}{5}+1 \frac{11}{21}=\left((0.5+2.5): 4 \frac{1}{2}\right): \frac{7}{5}+\frac{32}{21}= \\
& =\left(3 \cdot \frac{2}{9}\right) \cdot \frac{5}{7}+\frac{32}{21}=\frac{10}{21}+\frac{32}{21}=\frac{42}{21}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.029. $\left(1 \frac{2}{5}+3.5: 1 \frac{1}{4}\right): 2 \frac{2}{5}+3.4: 2 \frac{1}{8}-0.35$.
|
## Solution.
$$
\begin{aligned}
& \left(1 \frac{2}{5}+3.5: 1 \frac{1}{4}\right): 2 \frac{2}{5}+3.4: 2 \frac{1}{8}-0.35= \\
& =(1.4+3.5: 1.25): 2.4+3.4: 2.125-0.35=(1.4+2.8): 2.4+ \\
& +1.6-0.35=4.2: 2.4+1.25=1.75+1.25=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.032. $\frac{\left(3^{-1}-\sqrt{1 \frac{7}{9}}\right)^{-2}: 0.25}{\frac{37}{300}: 0.0925}+12.5 \cdot 0.64$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(3^{-1}-\sqrt{1 \frac{7}{9}}\right)^{-2}: 0.25}{\frac{37}{300}: 0.0925}+12.5 \cdot 0.64=\frac{\left(\frac{1}{3}-\sqrt{\frac{16}{9}}\right)^{-2} \cdot 4}{\frac{37}{300} \cdot \frac{400}{37}}+8= \\
& =\frac{\left(\frac{1}{3}-\frac{4}{3}\right)^{-2} \cdot 4}{\frac{4}{3}}+8=3(-1)^{-2}+8=3+8=11
\end{aligned}
$$
Answer: 11.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.033. $\frac{\left(\frac{5}{8}+2 \frac{17}{24}\right): 2.5}{\left(1.3+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}} \cdot 0.5$.
|
## Solution.
$\frac{\left(\frac{5}{8}+2 \frac{17}{24}\right): 2.5}{\left(1.3+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}} \cdot 0.5=\frac{\left(\frac{5}{8}+\frac{65}{24}\right) \cdot \frac{2}{5} \cdot \frac{1}{2}}{\left(\frac{13}{10}+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}}=\frac{\frac{10}{3} \cdot \frac{1}{5}}{\frac{401}{165} \cdot \frac{110}{401}}=\frac{2}{3}: \frac{2}{3}=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.039. $\left(\frac{(3.2-1.7): 0.003}{\left(\frac{29}{35}-\frac{3}{7}\right) \cdot 4: 0.2}-\frac{\left(1 \frac{13}{20}-1.5\right) \cdot 1.5}{\left(2.44+1 \frac{14}{25}\right) \cdot \frac{1}{8}}\right): 62 \frac{1}{20}+1.364: 0.124$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{(3.2-1.7): 0.003}{\left(\frac{29}{35}-\frac{3}{7}\right) \cdot 4: 0.2}-\frac{\left(1 \frac{13}{20}-1.5\right) \cdot 1.5}{\left(2.44+1 \frac{14}{25}\right) \cdot \frac{1}{8}}\right): 62 \frac{1}{20}+1.364: 0.124= \\
& =\left(\frac{1.5: 0.003}{\frac{14}{35} \cdot 4 \cdot 5}-\frac{\frac{3}{20} \cdot \frac{3}{2}}{4 \cdot \frac{1}{8}}\right): \frac{1241}{20}+11=\left(\frac{500}{8}-\frac{9}{40} \cdot 2\right) \cdot \frac{20}{1241}+11= \\
& =\left(\frac{125}{2}-\frac{9}{20}\right) \cdot \frac{20}{1241}+11=\frac{1241}{20} \cdot \frac{20}{1241}+11=12
\end{aligned}
$$
Answer: 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.041. $\frac{\left(4-3.5 \cdot\left(2 \frac{1}{7}-1 \frac{1}{5}\right)\right): 0.16}{X}=\frac{3 \frac{2}{7}-\frac{3}{14}: \frac{1}{6}}{41 \frac{23}{84}-40 \frac{49}{60}}$.
|
## Solution.
$$
\begin{aligned}
& X=\frac{\left(4-3.5 \cdot\left(2 \frac{1}{7}-1 \frac{1}{5}\right)\right): 0.16 \cdot\left(41 \frac{23}{84}-40 \frac{49}{60}\right)}{3 \frac{2}{7}-\frac{3}{14}: \frac{1}{6}}= \\
& =\frac{\left(4-3.5 \cdot\left(\frac{15}{7}-\frac{6}{5}\right)\right): 0.16 \cdot \frac{16}{35}}{\frac{23}{7} \cdot \frac{9}{7}}=\frac{\left(4-\frac{7}{2} \cdot \frac{33}{35}\right): \frac{4}{25} \cdot \frac{16}{35}}{2} \\
& =\frac{\left(4-\frac{33}{10}\right): \frac{4}{25} \cdot \frac{16}{35}}{2}=\frac{\frac{7}{10} \cdot \frac{25}{4} \cdot \frac{16}{35}}{2}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.043. $\frac{0.125 X}{\left(\frac{19}{24}-\frac{21}{40}\right) \cdot 8 \frac{7}{16}}=\frac{\left(1 \frac{28}{63}-\frac{17}{21}\right) \cdot 0.7}{0.675 \cdot 2.4-0.02}$.
|
Solution.
$X=\frac{\left(1 \frac{28}{63}-\frac{17}{21}\right) \cdot 0.7 \cdot\left(\frac{19}{24}-\frac{21}{40}\right) \cdot 8 \frac{7}{16}}{(0.675 \cdot 2.4-0.02) \cdot 0.125}=\frac{\left(\frac{91}{63}-\frac{17}{21}\right) \cdot \frac{7}{10} \cdot \frac{4}{15} \cdot \frac{135}{16}}{(1.62-0.02) \cdot 0.125}=$ $=\frac{\frac{40}{63} \cdot \frac{63}{40}}{1.6 \cdot 0.125}=\frac{1}{0.2} 5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.046.
$$
\frac{\sqrt{6.3 \cdot 1.7} \cdot\left(\sqrt{\frac{6.3}{1.7}}-\sqrt{\frac{1.7}{6.3}}\right)}{\sqrt{(6.3+1.7)^{2}-4 \cdot 6.3 \cdot 1.7}}
$$
|
Solution.
$$
\begin{aligned}
& \frac{\sqrt{6.3 \cdot 1.7} \cdot\left(\sqrt{\frac{6.3}{1.7}}-\sqrt{\frac{1.7}{6.3}}\right)}{\sqrt{(6.3+1.7)^{2}-4 \cdot 6.3 \cdot 1.7}}=\frac{\sqrt{6.3 \cdot 1.7} \cdot\left(\sqrt{\frac{6.3}{1.7}}-\sqrt{\frac{1.7}{6.3}}\right)}{\sqrt{6.3^{2}+2 \cdot 6.3 \cdot 1.7+1.7^{2}-4 \cdot 6.3 \cdot 1.7}}= \\
& =\frac{\sqrt{6.3 \cdot 1.7} \cdot \frac{\sqrt{6.3^{2}}-\sqrt{1.7^{2}}}{\sqrt{6.3 \cdot 1.7}}}{\sqrt{6.3^{2}-2 \cdot 6.3 \cdot 1.7+1.7^{2}}}=\frac{6.3-1.7}{\sqrt{(6.3-1.7)^{2}}}=\frac{6.3-1.7}{6.3-1.7}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.047. $\left(\frac{\sqrt{561^{2}-459^{2}}}{4 \frac{2}{7} \cdot 0.15+4 \frac{2}{7}: \frac{20}{3}}+4 \sqrt{10}\right): \frac{1}{3} \sqrt{40}$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{\sqrt{561^{2}-459^{2}}}{4 \frac{2}{7} \cdot 0.15+4 \frac{2}{7} : \frac{20}{3}}+4 \sqrt{10}\right): \frac{1}{3} \sqrt{40}=\left(\frac{\sqrt{(561+459)(561-459)}}{\frac{30}{7} \cdot \frac{3}{20}+\frac{30}{7} \cdot \frac{3}{20}}+4 \sqrt{10}\right) \times \\
& \times \frac{3}{2 \sqrt{10}}=\left(\frac{\sqrt{1020 \cdot 102}}{\frac{9}{7}}+4 \sqrt{10}\right) \cdot \frac{3}{2 \sqrt{10}}=\frac{7 \sqrt{102^{2} \cdot 10}+36 \sqrt{10}}{9} \cdot \frac{3}{2 \sqrt{10}}= \\
& =\frac{714 \sqrt{10}+36 \sqrt{10}}{9} \cdot \frac{3}{2 \sqrt{10}}=\frac{750 \sqrt{10}}{9} \cdot \frac{3}{2 \sqrt{10}}=\frac{375}{3}=125 .
\end{aligned}
$$
Answer: 125.
|
125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.049. $\frac{2^{-2}+5^{0}}{(0.5)^{-2}-5(-2)^{-2}+\left(\frac{2}{3}\right)^{-2}}+4.75$.
|
Solution.
$$
\begin{aligned}
& \frac{2^{-2}+5^{0}}{(0.5)^{-2}-5(-2)^{-2}+\left(\frac{2}{3}\right)^{-2}}+4.75=\frac{\frac{1}{2^{2}}+1}{-\frac{1}{(0.5)^{2}}-\frac{5}{(-2)^{-2}}+\left(\frac{3}{2}\right)^{2}}+4.75= \\
& =\frac{\frac{1}{4}+1}{\frac{1}{0.25}-\frac{5}{4}+\frac{9}{4}}+4.75=\frac{-\frac{4}{4}}{4+1}+4.75=\frac{1}{4}+4 \frac{3}{4}=5 .
\end{aligned}
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.019. $\frac{\left(x^{2}-y^{2}\right)(\sqrt[3]{x}+\sqrt[3]{y})}{\sqrt[3]{x^{5}}+\sqrt[3]{x^{2} y^{3}}-\sqrt[3]{x^{3} y^{2}}-\sqrt[3]{y^{5}}}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right) x=64$.
|
Solution.
$$
\begin{aligned}
& \text { Domain: } z=\sqrt[3]{x^{5}}+\sqrt[3]{x^{2} y^{3}}-\sqrt[3]{x^{3} y^{2}}-\sqrt[3]{y^{5}} \neq 0 \\
& \frac{\left(x^{2}-y^{2}\right)(\sqrt[3]{x}+\sqrt[3]{y})}{\sqrt[3]{x^{5}}+\sqrt[3]{x^{2} y^{3}}-\sqrt[3]{x^{3} y^{2}}-\sqrt[3]{y^{5}}}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)= \\
& =\frac{(x-y)(x+y)(\sqrt[3]{x}+\sqrt[3]{y})}{\sqrt[3]{x^{2}}\left(\sqrt[3]{x^{3}}+\sqrt[3]{y^{3}}\right)-\sqrt[3]{y^{2}}\left(\sqrt[3]{x^{3}}+\sqrt[3]{y^{3}}\right)}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)= \\
& =\frac{(x-y)(x+y)(\sqrt[3]{x}+\sqrt[3]{y})}{\sqrt[3]{x^{2}}(x+y)-\sqrt[3]{y^{2}}(x+y)}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)= \\
& =\frac{(x-y)(x+y)(\sqrt[3]{x}+\sqrt[3]{y})}{(x+y)\left(\sqrt[3]{x^{2}}-\sqrt[3]{y^{2}}\right)}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)= \\
& =\frac{(x-y)(\sqrt[3]{x}+\sqrt[3]{y})}{(\sqrt[3]{x}-\sqrt[3]{y})(\sqrt[3]{x}+\sqrt[3]{y})}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)= \\
& =\frac{x-y}{\sqrt[3]{x}-\sqrt[3]{y}}-\left(\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)=\frac{(\sqrt[3]{x})^{3}-(\sqrt[3]{y})^{3}}{\sqrt[3]{x}-\sqrt[3]{y}}-\sqrt[3]{x y}-\sqrt[3]{y^{2}}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{(\sqrt[3]{x}-\sqrt[3]{y})\left(\sqrt[3]{x^{2}}+\sqrt[3]{x y}+\sqrt[3]{y^{2}}\right)}{\sqrt[3]{x}-\sqrt[3]{y}}-\sqrt[3]{x y}-\sqrt[3]{y^{2}}= \\
& =\sqrt[3]{x^{2}}+\sqrt[3]{x y}+\sqrt[3]{y^{2}}-\sqrt[3]{x y}-\sqrt[3]{y^{2}}=\sqrt[3]{x^{2}}=\sqrt[3]{64^{2}}= \\
& =\sqrt[3]{4^{3 \cdot 2}}=4^{2}=16
\end{aligned}
$$
Answer: 16.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.025. $\frac{a^{3}-a-2 b-b^{2} / a}{\left(1-\sqrt{\frac{1}{a}+\frac{b}{a^{2}}}\right) \cdot(a+\sqrt{a+b})}:\left(\frac{a^{3}+a^{2}+a b+a^{2} b}{a^{2}-b^{2}}+\frac{b}{a-b}\right) ;$
$a=23 ; b=22$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{3}-a-2 b-b^{2} / a}{\left(1-\sqrt{\frac{1}{a}+\frac{b}{a^{2}}}\right) \cdot(a+\sqrt{a+b})}:\left(\frac{a^{3}+a^{2}+a b+a^{2} b}{a^{2}-b^{2}}+\frac{b}{a-b}\right)= \\
& =\frac{\frac{a^{4}-a^{2}-2 a b-b^{2}}{a}}{\left(1-\sqrt{\frac{a+b}{a^{2}}}\right) \cdot(a+\sqrt{a+b})}:\left(\frac{a^{2}(a+1)+a b(a+1)}{(a-b)(a+b)}+\frac{b}{a-b}\right)= \\
& =\frac{a^{4}-\left(a^{2}+2 a b+b^{2}\right)}{(a-\sqrt{a+b})(a+\sqrt{a+b})}:\left(\frac{a(a+1)(a+b)}{(a-b)(a+b)}+\frac{b}{a-b}\right)= \\
& =\frac{a^{4}-(a+b)^{2}}{a^{2}-a-b}:\left(\frac{a(a+1)}{a-b}+\frac{b}{a-b}\right)= \\
& =\frac{\left(a^{2}-a-b\right)\left(a^{2}+a+b\right)}{a^{2}-a-b}: \frac{a^{2}+a+b}{a-b}= \\
& =\frac{\left(a^{2}+a+b\right)(a-b)}{a^{2}+a+b}=a-b=23-22=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.030. $\sqrt{\frac{\sqrt{2}}{a}+\frac{a}{\sqrt{2}}+2}-\frac{a \sqrt[4]{2}-2 \sqrt{a}}{a \sqrt{2 a}-\sqrt[4]{8 a^{4}}}$.
2.030. $\sqrt{\frac{\sqrt{2}}{a}+\frac{a}{\sqrt{2}}+2}-\frac{a \sqrt[4]{2}-2 \sqrt{a}}{a \sqrt{2 a}-\sqrt[4]{8 a^{4}}}$.
(Note: The original text and the translation are identical as the expression is already in a mathematical form that does not require translation.)
|
Solution.
Domain of definition: $\left\{\begin{array}{l}a>0, \\ a \neq \sqrt{2} .\end{array}\right.$
$$
\sqrt{\frac{\sqrt{2}}{a}+\frac{a}{\sqrt{2}}+2}-\frac{a^{2} \sqrt[4]{2}-2 \sqrt{a}}{a \sqrt{2 a}-\sqrt[4]{8 a^{4}}}=\sqrt{\frac{a^{2}+2 a \sqrt{2}+(\sqrt{2})^{2}}{a \sqrt{2}}}-
$$
$$
\begin{aligned}
& -\frac{a^{2} \cdot 2^{1 / 4}-2 \cdot a^{1 / 2}}{a^{3 / 2} \cdot 2^{1 / 2}-2^{3 / 4} \cdot a}=\frac{\sqrt{(a+\sqrt{2})^{2}}}{\sqrt{a \sqrt{2}}}-\frac{2^{1 / 4} \cdot a^{1 / 2} \cdot\left(a^{3 / 2}-2^{3 / 4}\right)}{2^{1 / 2} \cdot a \cdot\left(a^{1 / 2}-2^{1 / 4}\right)}= \\
& =\frac{a+\sqrt{2}}{a^{1 / 2} \cdot 2^{1 / 4}}-\frac{2^{1 / 4} \cdot a^{1 / 2} \cdot\left(\left(a^{1 / 2}\right)^{3}-\left(2^{1 / 4}\right)^{3}\right)}{2^{1 / 2} \cdot a \cdot\left(a^{1 / 2}-2^{1 / 4}\right)}=\frac{a+2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}- \\
& -\frac{\left(a^{1 / 2}-2^{1 / 4}\right)\left(a+2^{1 / 4} \cdot a^{1 / 2}+2^{1 / 2}\right)}{a^{1 / 2} \cdot 2^{1 / 4} \cdot\left(a^{1 / 2}-2^{1 / 4}\right)}=\frac{a+2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}-\frac{a+2^{1 / 4} \cdot a^{1 / 2}+2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}= \\
& =\frac{a+2^{1 / 2}-a-2^{1 / 4} \cdot a^{1 / 2}-2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}=\frac{-2^{1 / 4} \cdot a^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}=-1
\end{aligned}
$$
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.039. $\frac{9 b^{4 / 3}-\frac{a^{3 / 2}}{b^{2}}}{\sqrt{a^{3 / 2} b^{-2}+6 a^{3 / 4} b^{-1 / 3}+9 b^{4 / 3}}} \cdot \frac{b^{2}}{a^{3 / 4}-3 b^{5 / 3}} ; \quad b=4$.
|
Solution.
$$
\begin{aligned}
& \frac{9 b^{4 / 3}-\frac{a^{3 / 2}}{b^{2}}}{\sqrt{a^{3 / 2} b^{-2}+6 a^{3 / 4} b^{-1 / 3}+9 b^{4 / 3}}} \cdot \frac{b^{2}}{a^{3 / 4}-3 b^{5 / 3}}=\frac{\frac{9 b^{4 / 3} \cdot b^{2}-a^{3 / 2}}{b^{2}}}{\sqrt{\frac{a^{3 / 2}}{b^{2}}+\frac{6 a^{3 / 4}}{b^{+1 / 3}}+9 b^{4 / 3}}} \times \\
& \times \frac{b^{2}}{a^{3 / 4}-3 b^{5 / 3}}=\frac{9 b^{10 / 3}-a^{3 / 2}}{\sqrt{\frac{a^{3 / 2}+6 a^{3 / 4} b^{5 / 3}+9 b^{10 / 3}}{b^{2}}} \cdot\left(a^{3 / 4}-3 b^{5 / 3}\right)}= \\
& =\frac{-\left(\left(a^{3 / 4}\right)^{2}-\left(3 b^{5 / 3}\right)^{2}\right)}{\sqrt{\frac{\left(a^{3 / 4}\right)^{2}+6 a^{3 / 4} b^{5 / 3}+\left(3 b^{5 / 3}\right)^{2}}{b^{2}}} \cdot\left(a^{3 / 4}-3 b^{5 / 3}\right)}= \\
& =\frac{-\left(a^{3 / 4}-3 b^{5 / 3}\right)\left(a^{3 / 4}+3 b^{5 / 3}\right)}{\frac{\sqrt{\left(a^{3 / 4}+3 b^{5 / 3}\right)^{2}}}{b} \cdot\left(a^{3 / 4}-3 b^{5 / 3}\right)}=\frac{-\left(a^{3 / 4}+3 b^{5 / 3}\right) b}{a^{3 / 4}+3 b^{5 / 3}}=-b=-4 .
\end{aligned}
$$
Answer: -4.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.044. $\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1} ; x>a>0$.
2.044. $\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1} ; x>a>0$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1}= \\
& =\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{(\sqrt{x-a})^{2}}{\sqrt{x-a}(\sqrt{x+a}-\sqrt{x-a})}\right): \sqrt{\frac{x^{2}-a^{2}}{a^{2}}}= \\
& =\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{\sqrt{x-a}}{\sqrt{x+a}-\sqrt{x-a}}\right) \cdot \frac{a}{\sqrt{x^{2}-a^{2}}}= \\
& =\frac{\sqrt{x-a}(\sqrt{x+a}-\sqrt{x-a})+\sqrt{x-a}(\sqrt{x+a}+\sqrt{x-a})}{(\sqrt{x+a}+\sqrt{x-a})(\sqrt{x+a}-\sqrt{x-a})} \cdot \frac{a}{\sqrt{x^{2}-a^{2}}}= \\
& =\frac{\sqrt{x^{2}-a^{2}}-x+a+\sqrt{x^{2}-a^{2}}+x-a}{x+a-x+a} \cdot \frac{a}{\sqrt{x^{2}-a^{2}}}=\frac{2 \sqrt{x^{2}-a^{2}} \cdot a}{2 a \sqrt{x^{2}-a^{2}}}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.046. $\frac{\sqrt{1-x^{2}}-1}{x} \cdot\left(\frac{1-x}{\sqrt{1-x^{2}}+x-1}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)$
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq 0, \\ -1 \leq x<1 .\end{array}\right.$
$$
\begin{aligned}
& \frac{\sqrt{1-x^{2}}-1}{x} \cdot\left(\frac{1-x}{\sqrt{1-x^{2}}+x-1}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)=\frac{\sqrt{1-x^{2}}-1}{x} \times \\
& \times\left(\frac{(\sqrt{1-x})^{2}}{\sqrt{1-x}(\sqrt{1+x}-\sqrt{1-x})}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)=\frac{\sqrt{1-x^{2}}-1}{x} \times
\end{aligned}
$$
$$
\begin{aligned}
& \times\left(\frac{\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)=\frac{\sqrt{1-x^{2}}-1}{x} \cdot \frac{\sqrt{1-x}+\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}=
\end{aligned}
$$
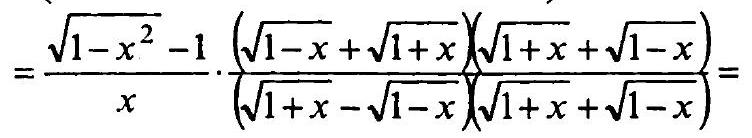
$$
\begin{aligned}
& =\frac{\sqrt{1-x^{2}}-1}{x} \cdot \frac{1-x+2 \sqrt{1-x^{2}}+1+x}{1+x-1+x}=\frac{\sqrt{1-x^{2}}-1}{x} \cdot \frac{2\left(\sqrt{1-x^{2}}+1\right)}{2 x}= \\
& =\frac{\left(\sqrt{1-x^{2}}-1\right)\left(\sqrt{1-x^{2}}+1\right)}{x^{2}}=\frac{1-x^{2}-1}{x^{2}}=\frac{-x^{2}}{x^{2}}=-1
\end{aligned}
$$
Answer: -1 .
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.051. $\frac{\left(a^{2}-b^{2}\right)\left(a^{2}+\sqrt[3]{b^{2}}+a \sqrt[3]{b}\right)}{a \sqrt[3]{b}+a \sqrt{a}-b \sqrt[3]{b}-\sqrt{a b^{2}}}: \frac{a^{3}-b}{a \sqrt[3]{b}-\sqrt[6]{a^{3} b^{2}}-\sqrt[3]{b^{2}}+a \sqrt{a}} ;$
$$
a=4.91 ; b=0.09
$$
|
Solution.
$$
\begin{aligned}
& \frac{\left(a^{2}-b^{2}\right)\left(a^{2}+\sqrt[3]{b^{2}}+a \sqrt[3]{b}\right)}{a \sqrt[3]{b}+a \sqrt{a}-b \sqrt[3]{b}-\sqrt{a b^{2}}}: \frac{a^{3}-b}{a \sqrt[3]{b}-\sqrt[6]{a^{3} b^{2}}-\sqrt[3]{b^{2}}+a \sqrt{a}}= \\
& =\frac{(a-b)(a+b)\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}{a(\sqrt{a}+\sqrt[3]{b})-b(\sqrt{a}+\sqrt[3]{b})}: \frac{a^{3}-b}{a(\sqrt{a}+\sqrt[3]{b})-\sqrt[3]{b}(\sqrt{a}+\sqrt[3]{b})}= \\
& =\frac{(a-b)(a+b)\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}{(\sqrt{a}+\sqrt[3]{b})(a-b)}: \frac{a^{3}-(\sqrt[3]{b})^{3}}{(\sqrt{a}+\sqrt[3]{b})(a-\sqrt[3]{b})}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{(a+b)\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}{\sqrt{a}+\sqrt[3]{b}} \cdot \frac{(\sqrt{a}+\sqrt[3]{b})(a-\sqrt[3]{b})}{(a-\sqrt[3]{b})\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}= \\
& =a+b=4.91+0.09=5
\end{aligned}
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.054. $\frac{3 a^{2}+2 a x-x^{2}}{(3 x+a)(a+x)}-2+10 \cdot \frac{a x-3 x^{2}}{a^{2}-9 x^{2}}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq \pm \frac{a}{3}, \\ x \neq-a .\end{array}\right.$
$$
\begin{aligned}
& \frac{3 a^{2}+2 a x-x^{2}}{(3 x+a)(a+x)}-2+10 \cdot \frac{a x-3 x^{2}}{a^{2}-9 x^{2}}=\frac{-(x+a)(x-3 a)}{(3 x+a)(a+x)}-2+ \\
& +10 \cdot \frac{x(a-3 x)}{(a-3 x)(a+3 x)}=\frac{-x+3 a}{3 x+a}-2+\frac{10 x}{3 x+a}= \\
& =\frac{-x+3 a-6 x-2 a+10 x}{3 x+a}=\frac{3 x+a}{3 x+a}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.058. $\left(\left(\frac{1}{a}+\frac{1}{b+c}\right):\left(\frac{1}{a}-\frac{1}{b+c}\right)\right):\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)$;
$$
a=1 \frac{33}{40} ; b=0.625 ; c=3.2
$$
|
Solution.
$$
\begin{aligned}
& \left(\left(\frac{1}{a}+\frac{1}{b+c}\right):\left(\frac{1}{a}-\frac{1}{b+c}\right):\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)=\right. \\
& =\left(\frac{a+b+c}{a(b+c)}: \frac{-a+b+c}{a(b+c)}\right): \frac{2 b c+b^{2}+c^{2}-a^{2}}{2 b c}= \\
& =\left(\frac{a+b+c}{a(b+c)} \cdot \frac{a(b+c)}{-a+b+c}\right): \frac{\left(b^{2}+2 b c+c^{2}\right)-a^{2}}{2 b c}= \\
& =\frac{a+b+c}{-a+b+c} \cdot \frac{2 b c}{(b+c)^{2}-a^{2}}=\frac{2(a+b+c) b c}{(-a+b+c)(b+c-a)(b+c+a)}= \\
& =\frac{2 b c}{(-a+b+c)^{2}}=\frac{2 \cdot 0.625 \cdot 3.2}{\left(-1 \frac{33}{40}+0.625+3.2\right)^{2}}=\frac{4}{(-1.825+3.825)^{2}}=\frac{4}{4}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.068. $\frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}\right)(a+b+2 c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}} ; \quad a=7.4 ; b=\frac{5}{37}$.
|
Solution.
$$
\begin{aligned}
& \frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}\right)(a+b+2 c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}}=\frac{\frac{a+b-2 c}{a b} \cdot(a+b+2 c)}{\frac{a^{2}+2 a b+b^{2}-4 c^{2}}{a^{2} b^{2}}}= \\
& =\frac{\frac{(a+b-2 c)(a+b+2 c)}{a b}}{\frac{(a+b)^{2}-(2 c)^{2}}{a^{2} b^{2}}}=\frac{(a+b-2 c)(a+b+2 c) a^{2} b^{2}}{\left((a+b)^{2}-(2 c)^{2}\right) a b}= \\
& =\frac{(a+b-2 c)(a+b+2 c) a b}{(a+b-2 c)(a+b+2 c)}=a b=7.4 \cdot \frac{5}{37}=\frac{37}{5} \cdot \frac{5}{37}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.073. $\frac{\sqrt{5-2 \sqrt{6}}}{(\sqrt[4]{3}+\sqrt[4]{2})(\sqrt[4]{3}-\sqrt[4]{2})}$.
|
Solution.
$$
\begin{aligned}
& \frac{\sqrt{5-2 \sqrt{6}}}{(\sqrt[4]{3}+\sqrt[4]{2})(\sqrt[4]{3}-\sqrt[4]{2})}=\frac{\sqrt{3-2 \sqrt{3 \cdot 2}+2}}{(\sqrt[4]{3})^{2}-(\sqrt[4]{2})^{2}}= \\
& =\frac{\sqrt{(\sqrt{3})^{2}-2 \sqrt{3} \cdot \sqrt{2}+(\sqrt{2})^{2}}}{\sqrt{3}-\sqrt{2}}= \\
& =\frac{\sqrt{(\sqrt{3}-\sqrt{2})^{2}}}{\sqrt{3}-\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.078. $\left(\frac{1}{t^{2}+3 t+2}+\frac{2 t}{t^{2}+4 t+3}+\frac{1}{t^{2}+5 t+6}\right)^{2} \cdot \frac{(t-3)^{2}+12 t}{2}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}t \neq-3, \\ t \neq-2, \\ t \neq-1 .\end{array}\right.$
$$
\begin{aligned}
& \left(\frac{1}{t^{2}+3 t+2}+\frac{2 t}{t^{2}+4 t+3}+\frac{1}{t^{2}+5 t+6}\right)^{2} \cdot \frac{(t-3)^{2}+12 t}{2}= \\
& =\left(\frac{1}{(t+2)(t+1)}+\frac{2 t}{(t+3)(t+1)}+\frac{1}{(t+3)(t+2)}\right)^{2} \cdot \frac{t^{2}-6 t+9+12 t}{2}= \\
& =\left(\frac{t+3+2 t(t+2)+t+1}{(t+1)(t+2)(t+3)}\right)^{2} \cdot \frac{t^{2}+6 t+9}{2}=\left(\frac{2(t+2)+2 t(t+2)}{(t+1)(t+2)(t+3)}\right)^{2} \cdot \frac{(t+3)^{2}}{2}= \\
& =\frac{(2(t+2)(t+1))^{2}(t+3)^{2}}{2((t+1)(t+2)(t+3))^{2}}=\frac{4(t+2)^{2}(t+1)^{2}(t+3)^{2}}{2(t+2)^{2}(t+1)^{2}(t+3)^{2}}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.084. $\left(\frac{2-b}{b-1}+2 \cdot \frac{a-1}{a-2}\right):\left(b \cdot \frac{a-1}{b-1}+a \cdot \frac{2-b}{a-2}\right)$;
$a=\sqrt{2}+0.8 ; b=\sqrt{2}-0.2$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{2-b}{b-1}+2 \cdot \frac{a-1}{a-2}\right):\left(b \cdot \frac{a-1}{b-1}+a \cdot \frac{2-b}{a-2}\right)=\frac{(2-b)(a-2)+2(a-1)(b-1)}{(b-1)(a-2)} \\
& \frac{b(a-1)(a-2)+a(2-b)(b-1)}{(b-1)(a-2)}=\frac{a b-2}{(b-1)(a-2)} \cdot \frac{(b-1)(a-2)}{a^{2} b-a b^{2}-2 a+2 b}= \\
& =\frac{a b-2}{a b(a-b)-2(a-b)}=\frac{a b-2}{(a-b)(a b-2)}=\frac{1}{a-b}=\frac{1}{\sqrt{2}+0.8-\sqrt{2}+0.2}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.105. $\left(\frac{1+\sqrt{1-x}}{1-x+\sqrt{1-x}}+\frac{1-\sqrt{1+x}}{1+x-\sqrt{1+x}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}-1<x<1, \\ x \neq 0 .\end{array}\right.$
$$
\begin{aligned}
& \left(\frac{1+\sqrt{1-x}}{1-x+\sqrt{1-x}}+\frac{1-\sqrt{1+x}}{1+x-\sqrt{1+x}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& \left.\left.=\left(\frac{1+\sqrt{1-x}}{\sqrt{1-x}(\sqrt{1-x}+1}\right)+\frac{1-\sqrt{1+x}}{\sqrt{1+x}(\sqrt{1+x}-1}\right)\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\left(\frac{1}{\sqrt{1-x}}-\frac{1}{\sqrt{1+x}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1-x^{2}}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\frac{1+x-2 \sqrt{1-x^{2}}+1-x}{1-x^{2}} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\frac{2\left(1-\sqrt{1-x^{2}}\right)}{1-x^{2}} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =-1+\sqrt{1-x^{2}}-\sqrt{1-x^{2}}=-1
\end{aligned}
$$
Answer: -1 .
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.109. $\left(-4 a^{3} \sqrt{\frac{\sqrt{a x}}{a^{2}}}\right)^{3}+\left(-10 a \sqrt{x} \cdot \sqrt{(a x)^{-1}}\right)^{2}+\left(-2\left(\sqrt[3]{a^{4} \sqrt{\frac{x}{a}}}\right)^{2}\right)^{3} ;$
$$
a=3 \frac{4}{7} ; x=0.28
$$
|
## Solution.
$$
\begin{aligned}
& \left(-4 a^{3} \sqrt{\frac{\sqrt{a x}}{a^{2}}}\right)^{3}+\left(-10 a \sqrt{x} \cdot \sqrt{(a x)^{-1}}\right)^{2}+\left(-2\left(\sqrt[3]{a \sqrt{\frac{x}{a}}}\right)^{2}\right)^{3}= \\
& =\frac{-64 a^{3} \sqrt{a x}}{a^{2}}+\frac{100 a^{2} x}{a x}-\frac{8 a^{2} \sqrt{x}}{\sqrt{a}}=-64 a \sqrt{a x}+100 a-8 a \sqrt{a x}= \\
& =100 a-72 a \sqrt{a x}=100 \cdot 3 \frac{4}{7}-72 \cdot 3 \frac{4}{7} \cdot \sqrt{3 \frac{4}{7} \cdot 0.28}= \\
& =100 \cdot \frac{25}{7}-72 \cdot \frac{25}{7} \cdot \sqrt{\frac{25}{7} \cdot \frac{7}{25}}=\frac{2500}{7}-\frac{1800}{7}=\frac{700}{7}=100
\end{aligned}
$$
Answer: 100.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.123. $2 \sqrt{40 \sqrt{12}}+3 \sqrt{5 \sqrt{48}}-2 \sqrt[4]{75}-4 \sqrt{15 \sqrt{27}}$.
|
Solution.
$$
\begin{aligned}
& 2 \sqrt{40 \sqrt{12}}+3 \sqrt{5 \sqrt{48}}-2 \sqrt[4]{75}-4 \sqrt{15 \sqrt{27}}= \\
& =2 \sqrt{40 \sqrt{4 \cdot 3}}+3 \sqrt{5 \sqrt{16 \cdot 3}}-2 \sqrt[4]{25 \cdot 3}-4 \sqrt{15 \sqrt{9 \cdot 3}}= \\
& =2 \sqrt{40 \cdot 2 \sqrt{3}}+3 \sqrt{5 \cdot 4 \sqrt{3}}-2 \sqrt{\sqrt{25 \cdot 3}}-4 \sqrt{15 \cdot 3 \sqrt{3}}= \\
& =2 \sqrt{80 \sqrt{3}}+3 \cdot 2 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-4 \sqrt{45 \sqrt{3}}= \\
& =2 \sqrt{16 \cdot 5 \sqrt{3}}+6 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-4 \sqrt{9 \cdot 5 \sqrt{3}}= \\
& =2 \cdot 4 \sqrt{5 \sqrt{3}}+6 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-4 \cdot 3 \sqrt{5 \sqrt{3}}= \\
& =8 \sqrt{5 \sqrt{3}}+6 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-12 \sqrt{5 \sqrt{3}}=14 \sqrt{5 \sqrt{3}}-14 \sqrt{5 \sqrt{3}}=0 .
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.126. $(4+\sqrt{15})(\sqrt{10}-\sqrt{6}) \cdot \sqrt{4-\sqrt{15}}=2$.
|
## Решение.
Возведем обе части равенства в квадрат. Тогда
$$
\begin{aligned}
& (4+\sqrt{15})^{2}(\sqrt{10}-\sqrt{6})^{2}(4-\sqrt{15})=4 \\
& (4+\sqrt{15})(4-\sqrt{15})(4+\sqrt{15})(10-2 \sqrt{60}+6)=4 \\
& \left(4^{2}-(\sqrt{15})^{2}\right)(4+\sqrt{15})(16-2 \sqrt{60})=4 \\
& (16-15)(4+\sqrt{15}) \cdot 2 \cdot(8-\sqrt{60})=4, \quad(4+\sqrt{15})(8-\sqrt{4 \cdot 15})=2, \\
& (4+\sqrt{15})(8-2 \sqrt{15})=2, \quad(4+\sqrt{15}) \cdot 2 \cdot(4-\sqrt{15})=2, \\
& (4+\sqrt{15})(4-\sqrt{15})=1, \quad 4^{2}-(\sqrt{15})^{2}=1, \quad 16-15=1, \quad 1=1
\end{aligned}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.127. $\sqrt{3-\sqrt{5}} \cdot(3+\sqrt{5}) \cdot(\sqrt{10}-\sqrt{2})=8$.
|
## Solution.
Let's square both sides of the equation. Then
$$
(\sqrt{3-\sqrt{5}})^{2}(3+\sqrt{5})^{2}(\sqrt{2}(\sqrt{5}-1))^{2}=64
$$
$(3-\sqrt{5})(3+\sqrt{5})^{2} \cdot 2(\sqrt{5}-1)^{2}=64$,
$(3-\sqrt{5})(3+\sqrt{5})(3+\sqrt{5})(5-2 \sqrt{5}+1)=32$,
$\left(3^{2}-(\sqrt{5})^{2}\right)(3+\sqrt{5})(6-2 \sqrt{5})=32$,
$(9-5)(3+\sqrt{5}) \cdot 2 \cdot(3-\sqrt{5})=32,8(3+\sqrt{5})(3-\sqrt{5})=32$,
$8\left(3^{2}-(\sqrt{5})^{2}\right)=32, \quad 8(9-5)=32, \quad 8 \cdot 4=32, \quad 32=32$.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.129. $\frac{25 \cdot \sqrt[4]{2}+2 \sqrt{5}}{\sqrt{250}+5 \sqrt[4]{8}}-\sqrt{\frac{\sqrt{2}}{5}+\frac{5}{\sqrt{2}}+2}=-1$.
|
## Solution.
Let's set
$$
X=\frac{25 \cdot \sqrt[4]{2}+2 \sqrt{5}}{\sqrt{250}+5 \sqrt[4]{8}}=\frac{\sqrt[4]{5^{8} \cdot 2}+\sqrt[4]{5^{2} \cdot 2^{4}}}{\sqrt[4]{5^{6} \cdot 2^{2}}+\sqrt[4]{5^{4} \cdot 2^{3}}}=\frac{\sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{6}}+\sqrt[4]{2^{3}}\right)}{\sqrt[4]{5^{2} \cdot 2} \cdot \sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)}=
$$
$$
\begin{aligned}
& =\frac{\left(\sqrt[4]{5^{2}}\right)^{3}+(\sqrt[4]{2})^{3}}{\sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)}=\frac{\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)\left(\left(\sqrt[4]{5^{2}}\right)^{2}-\sqrt[4]{5^{2} \cdot 2}+(\sqrt[4]{2})^{2}\right)}{\sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)}= \\
& =\frac{\sqrt[4]{5^{4}}-\sqrt[4]{5^{2} \cdot 2}+\sqrt[4]{2^{2}}}{\sqrt[4]{5^{2} \cdot 2}}
\end{aligned}
$$
$Y=\sqrt{\frac{\sqrt{2}}{5}+\frac{5}{\sqrt{2}}+2}=\sqrt{\frac{2+2 \cdot 5 \sqrt{2}+25}{5 \sqrt{2}}}=\sqrt{\frac{(5+\sqrt{2})^{2}}{\sqrt{5^{2} \cdot 2}}}=\frac{5+\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}$.
## Conclusion
$$
\begin{aligned}
& X-Y=\frac{5-\sqrt[4]{5^{2} \cdot 2}+\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}-\frac{5+\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}=\frac{5-\sqrt[4]{5^{2} \cdot 2}+\sqrt{2}-5-\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}= \\
& =\frac{-\sqrt[4]{5^{2} \cdot 2}}{\sqrt[4]{5^{2} \cdot 2}}=-1
\end{aligned}
$$
We obtained $-1=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.130. $\frac{\sqrt{\sqrt[4]{27}+\sqrt{\sqrt{3}-1}}-\sqrt{\sqrt[4]{27}-\sqrt{\sqrt{3}-1}}}{\sqrt{\sqrt[4]{27}-\sqrt{2 \sqrt{3}}+1}}=\sqrt{2}$.
|
## Решение.
Возведем обе части равенства в квадрат. Тогда
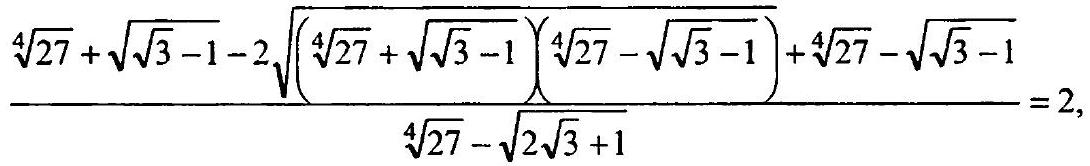
$$
\begin{aligned}
& \frac{2 \sqrt[4]{27}-2 \sqrt{(\sqrt[4]{27})^{2}-(\sqrt{\sqrt{3}-1})^{2}}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=2, \frac{\sqrt[4]{27}-\sqrt{\sqrt{27}-\sqrt{3}+1}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=1
\end{aligned}
$$
$\frac{\sqrt[4]{27}-\sqrt{3 \sqrt{3}-\sqrt{3}+1}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=1, \quad \frac{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=1, \quad 1=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.135. $\frac{x^{3}-a^{-2 / 3} \cdot b^{-1}\left(a^{2}+b^{2}\right) x+b^{1 / 2}}{b^{3 / 2} \cdot x^{2}} ; x=a^{2 / 3} b^{-1 / 2}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}a \neq 0, \\ b \neq 0 .\end{array}\right.$
$$
\begin{aligned}
& \frac{\left(a^{2 / 3} b^{-1 / 2}\right)^{3}-a^{2 / 3} \cdot b^{-1}\left(a^{2}+b^{2}\right)^{2 / 3} b^{-1 / 2}+b^{1 / 2}}{b^{3 / 2} \cdot\left(a^{2 / 3} b^{-1 / 2}\right)^{2}}= \\
& =\frac{a^{2} b^{-3 / 2}-a^{0} b^{-3 / 2}\left(a^{2}+b^{2}\right)+b^{1 / 2}}{b^{3 / 2} a^{4 / 3} b^{-1}}= \\
& =\frac{\frac{a^{2}}{b^{3 / 2}}-\frac{a^{2}+b^{2}}{b^{3 / 2}}+b^{1 / 2}}{b^{1 / 2} a^{4 / 3}}=\frac{\frac{a^{2}-a^{2}-b^{2}+b^{2}}{b^{3 / 2}}}{b^{1 / 2} a^{4 / 3}}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.136. $\frac{1-b}{\sqrt{b}} \cdot x^{2}-2 x+\sqrt{b} ; \quad x=\frac{\sqrt{b}}{1-\sqrt{b}}$.
2.136. $\frac{1-b}{\sqrt{b}} \cdot x^{2}-2 x+\sqrt{b} ; \quad x=\frac{\sqrt{b}}{1-\sqrt{b}}$.
|
## Solution.
Domain of definition: $0<b \neq 1$.
$$
\begin{aligned}
& \frac{1-b}{\sqrt{b}} \cdot\left(\frac{\sqrt{b}}{1-\sqrt{b}}\right)^{2}-2 \cdot \frac{\sqrt{b}}{1-\sqrt{b}}+\sqrt{b}=\frac{(1-\sqrt{b})(1+\sqrt{b})}{\sqrt{b}} \cdot \frac{b}{(1-\sqrt{b})^{2}}-\frac{2 \sqrt{b}}{1-\sqrt{b}}+ \\
& +\sqrt{b}=\frac{(1+\sqrt{b}) \sqrt{b}}{1-\sqrt{b}}-\frac{2 \sqrt{b}}{1-\sqrt{b}}+\sqrt{b}=\frac{\sqrt{b}+b}{1-\sqrt{b}}-\frac{2 \sqrt{b}}{1-\sqrt{b}}+\sqrt{b}= \\
& =\frac{\sqrt{b}+b-2 \sqrt{b}+\sqrt{b}-b}{1-\sqrt{b}}=0 .
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.141. $\frac{(1-y)(y+2)}{y^{2}(y+1)^{2}} ; \quad y=\frac{\sqrt{3}-1}{2}$.
|
Solution.
$$
\begin{aligned}
& \frac{\left(1-\frac{\sqrt{3}-1}{2}\right) \cdot\left(\frac{\sqrt{3}-1}{2}+2\right)}{\left(\frac{\sqrt{3}-1}{2}\right)^{2} \cdot\left(\frac{\sqrt{3}-1}{2}+1\right)^{2}}=\frac{-\left(\frac{\sqrt{3}-1}{2}-1\right) \cdot\left(\frac{\sqrt{3}-1}{2}+2\right)}{\left(\frac{\sqrt{3}-1}{2} \cdot\left(\frac{\sqrt{3}-1}{2}+1\right)\right)^{2}}= \\
& =-\frac{\left(\frac{\sqrt{3}-1}{2}\right)^{2}+\frac{\sqrt{3}-1}{2}-2}{\left(\left(\frac{\sqrt{3}-1}{2}\right)^{2}+\frac{\sqrt{3}-1}{2}\right)^{2}}=-\frac{\frac{4-2 \sqrt{3}}{4}+\frac{\sqrt{3}-1}{2}-2}{\left(\frac{4-2 \sqrt{3}}{4}+\frac{\sqrt{3}-1}{2}\right)^{2}}= \\
& =-\frac{\frac{2-\sqrt{3}}{2}+\frac{\sqrt{3}-1}{2}-2}{\left(\frac{2-\sqrt{3}}{2}+\frac{\sqrt{3}-1}{2}\right)^{2}}=-\frac{\frac{2-\sqrt{3}+\sqrt{3}-1}{2}-2}{\left(\frac{2-\sqrt{3}+\sqrt{3}-1}{2}\right)^{2}}=6 .
\end{aligned}
$$
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.145. $\frac{1-a x}{1+a x} \cdot \sqrt{\frac{1+b x}{1-b x}} ; \quad x=\frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}} ; \quad 0<\frac{b}{2}<a<b$.
|
Solution.
$\frac{1-a \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}}{1+a \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}} \cdot \sqrt{\frac{1+b \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}}{1-b \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}}}=\frac{1-\sqrt{\frac{2 a-b}{b}}}{1+\sqrt{\frac{2 a-b}{b}}} \times$
$$
\begin{aligned}
& \times \sqrt{\frac{1+\frac{1}{a} \cdot \sqrt{\frac{b^{2}(2 a-b)}{b}}}{1-\frac{1}{a} \cdot \sqrt{\frac{b^{2}(2 a-b)}{b}}}}=\frac{1-\frac{\sqrt{2 a-b}}{\sqrt{b}}}{1+\frac{\sqrt{2 a-b}}{\sqrt{b}}} \cdot \sqrt{\frac{\frac{a+\sqrt{b(2 a-b)}}{a}}{\frac{a-\sqrt{b(2 a-b)}}{a}}}=\frac{\sqrt{b}-\sqrt{2 a-b}}{\sqrt{b}+\sqrt{2 a-b}} \times \\
& \times \sqrt{\frac{a+\sqrt{b(2 a-b)}}{a-\sqrt{b(2 a-b)}}}=\frac{(\sqrt{b}-\sqrt{2 a-b})(\sqrt{b}-\sqrt{2 a-b})}{(\sqrt{b}+\sqrt{2 a-b})(\sqrt{b}-\sqrt{2 a-b})} \times \\
& \times \sqrt{\frac{(a+\sqrt{b(2 a-b)})(a+\sqrt{b(2 a-b)})}{(a-\sqrt{b(2 a-b)})(a+\sqrt{b(2 a-b)})}}=\frac{b-2 \sqrt{b(2 a-b)}+2 a-b}{b-2 a+b} \times \\
& \times \sqrt{\frac{(a+\sqrt{b(2 a-b)})^{2}}{a^{2}-b(2 a-b)}}=\frac{2 a-2 \sqrt{b(2 a-b)}}{2 b-2 a} \cdot \sqrt{\frac{(a+\sqrt{b(2 a-b)})^{2}}{a^{2}-2 a b+b^{2}}}= \\
& =\frac{a-\sqrt{b(2 a-b)}}{b-a} \cdot \sqrt{\left(\frac{a+\sqrt{b(2 a-b)}}{a-b}\right)^{2}}=\frac{a-\sqrt{b(2 a-b)}}{b-a} \cdot \frac{a+\sqrt{b(2 a-b)}}{b-a}= \\
& =\frac{a^{2}-b(2 a-b)}{(b-a)^{2}}=\frac{a^{2}-2 a b+b^{2}}{(b-a)^{2}}=\frac{(b-a)^{2}}{(b-a)^{2}}=1 \text {. }
\end{aligned}
$$
Answer: 1.
Rationalize the denominator of the fraction (2.146-2.151):
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.154. What is the value of $\sqrt{25-x^{2}}+\sqrt{15-x^{2}}$, given that the difference $\sqrt{25-x^{2}}-\sqrt{15-x^{2}}=2$ (the value of $x$ does not need to be found)?
|
Solution.
Domain of definition: $\left\{\begin{array}{l}25-x^{2} \geq 0, \\ 15-x^{2} \geq 0\end{array} \Leftrightarrow-\sqrt{15} \leq x \leq \sqrt{15}\right.$.
Multiplying both sides of the equation by $\sqrt{25-x^{2}}+\sqrt{15-x^{2}}$, we have
$$
\begin{aligned}
& \left(\sqrt{25-x^{2}}-\sqrt{15-x^{2}}\right)\left(\sqrt{25-x^{2}}+\sqrt{15-x^{2}}\right)= \\
& =2\left(\sqrt{25-x^{2}}+\sqrt{15-x^{2}}\right) \Leftrightarrow \\
& \Leftrightarrow 25-x^{2}-15+x^{2}=2\left(\sqrt{25-x^{2}}+\sqrt{15-x^{2}}\right)
\end{aligned}
$$
from which $\sqrt{25-x^{2}}+\sqrt{15-x^{2}}=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.156. Calculate the sum of the cubes of two numbers if their sum and product are 11 and 21, respectively.
|
Solution.
Let $a+b=11$ and $a b=21$. Then
$$
\begin{aligned}
& a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)=(a+b)\left((a+b)^{2}-3 a b\right)=11\left(11^{2}-3 \cdot 21\right)= \\
& =11(121-63)=638
\end{aligned}
$$
Answer: 638.
|
638
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.040. $\frac{1-\cos 4 \alpha}{\cos ^{-2} 2 \alpha-1}+\frac{1+\cos 4 \alpha}{\sin ^{-2} 2 \alpha-1}=2$.
|
Solution.
$$
\begin{aligned}
& \frac{1-\cos 4 \alpha}{\cos ^{-2} 2 \alpha-1}+\frac{1+\cos 4 \alpha}{\sin ^{-2} 2 \alpha-1}=\frac{1-\cos 4 \alpha}{\frac{1}{\cos ^{2} 2 \alpha}-1}+\frac{1+\cos 4 \alpha}{\frac{1}{\sin ^{2} 2 \alpha}-1}= \\
& =\frac{(1-\cos 4 \alpha) \cos ^{2} 2 \alpha}{1-\cos ^{2} 2 \alpha}+\frac{(1+\cos 4 \alpha) \sin ^{2} 2 \alpha}{1-\sin ^{2} 2 \alpha}=\frac{(1-\cos 4 \alpha) \cos ^{2} 2 \alpha}{\sin ^{2} 2 \alpha}+ \\
& +\frac{(1+\cos 4 \alpha) \sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}=\frac{\left(1-\left(1-\sin ^{2} 2 \alpha\right) \cos ^{2} 2 \alpha\right.}{\sin ^{2} 2 \alpha}+\frac{\left(1+2 \cos ^{2} 2 \alpha-1\right) \sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}= \\
& =\frac{2 \sin ^{2} 2 \alpha \cos ^{2} 2 \alpha}{\sin ^{2} 2 \alpha}+\frac{2 \cos ^{2} 2 \alpha \sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}=2 \cos ^{2} 2 \alpha+2 \sin ^{2} 2 \alpha= \\
& =2\left(\cos ^{2} 2 \alpha+\sin ^{2} 2 \alpha\right)=2 .
\end{aligned}
$$
The identity is proven.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.081. $\sin ^{2}\left(\alpha-\frac{3 \pi}{2}\right)\left(1-\operatorname{tg}^{2} \alpha\right) \operatorname{tg}\left(\frac{\pi}{4}+\alpha\right) \cos ^{-2}\left(\frac{\pi}{4}-\alpha\right)$.
|
Solution.
$$
\begin{aligned}
& \sin ^{2}\left(\alpha-\frac{3 \pi}{2}\right)\left(1-\operatorname{tg}^{2} \alpha\right) \operatorname{tg}\left(\frac{\pi}{4}+\alpha\right) \cos ^{-2}\left(\frac{\pi}{4}-\alpha\right)= \\
& =\left(\sin \left(\frac{3}{2} \pi-\alpha\right)\right)^{2}\left(1-\operatorname{tg}^{2} \alpha\right) \operatorname{tg}\left(\frac{\pi}{4}+\alpha\right) \cdot \frac{1}{\cos ^{2}\left(\frac{\pi}{4}-\alpha\right)}= \\
& =\cos ^{2} \alpha\left(1-\frac{1-\cos 2 \alpha}{1+\cos 2 \alpha}\right) \cdot \frac{1-\cos \left(\frac{\pi}{2}+2 \alpha\right)}{\sin \left(\frac{\pi}{2}+2 \alpha\right)} \cdot \frac{1}{\frac{1+\cos \left(\frac{\pi}{2}-2 \alpha\right)}{2}}= \\
& =\frac{1+\cos 2 \alpha}{2} \cdot \frac{1+\cos 2 \alpha-1+\cos 2 \alpha}{1+\cos 2 \alpha} \cdot \frac{1+\sin 2 \alpha}{\cos 2 \alpha} \cdot \frac{2}{1+\sin 2 \alpha}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.088. $\frac{\operatorname{ctg}\left(270^{\circ}-\alpha\right)}{1-\operatorname{tg}^{2}\left(\alpha-180^{\circ}\right)} \cdot \frac{\operatorname{ctg}^{2}\left(360^{\circ}-\alpha\right)-1}{\operatorname{ctg}\left(180^{\circ}+\alpha\right)}$.
|
## Solution.
$\frac{\operatorname{ctg}\left(270^{\circ}-\alpha\right)}{1-\operatorname{tg}^{2}\left(\alpha-180^{\circ}\right)} \cdot \frac{\operatorname{ctg}^{2}\left(360^{\circ}-\alpha\right)-1}{\operatorname{ctg}\left(180^{\circ}+\alpha\right)}=\frac{\operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha} \cdot \frac{\operatorname{ctg}^{2} \alpha-1}{\operatorname{ctg} \alpha}=\frac{2 \operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha} \times$ $\times \frac{\operatorname{ctg}^{2} \alpha-1}{2 \operatorname{ctg} \alpha}=\operatorname{tg} 2 \alpha \operatorname{ctg} 2 \alpha=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.098. $\sin \left(2 \alpha-\frac{3}{2} \pi\right)+\cos \left(2 \alpha-\frac{8}{3} \pi\right)+\cos \left(\frac{2}{3} \pi+2 \alpha\right)$.
|
## Solution.
Let
$$
\begin{aligned}
& X=\sin \left(2 \alpha-\frac{3}{2} \pi\right)+\cos \left(2 \alpha-\frac{8}{3} \pi\right)+\cos \left(\frac{2}{3} \pi+2 \alpha\right)= \\
& =-\sin \left(\frac{3}{2} \pi-2 \alpha\right)+\cos \left(\frac{8}{3} \pi-2 \alpha\right)+\cos \left(\frac{2}{3} \pi+2 \alpha\right) \\
& -\sin \left(\frac{3}{2} \pi-2 \alpha\right)=\cos 2 \alpha \\
& \cos \left(\frac{8}{3} \pi-2 \alpha\right)=\cos \left(\frac{9 \pi-\pi}{3}-2 \alpha\right)=\cos \left(3 \pi-\left(\frac{\pi}{3}+2 \alpha\right)\right)= \\
& =-\cos \left(\frac{\pi}{3}+2 \alpha\right)=-\cos \frac{\pi}{3} \cos 2 \alpha+\sin \frac{\pi}{3} \sin 2 \alpha=-\frac{1}{2} \cos 2 \alpha+\frac{\sqrt{3}}{2} \sin 2 \alpha
\end{aligned}
$$
$$
\cos \left(\frac{2}{3} \pi+2 \alpha\right)=\cos \frac{2}{3} \pi \cos 2 \alpha-\sin \frac{2}{3} \pi \sin 2 \alpha=-\frac{1}{2} \cos 2 \alpha-\frac{\sqrt{3}}{2} \sin 2 \alpha
$$
$$
X=\cos 2 \alpha-\frac{1}{2} \cos 2 \alpha+\frac{\sqrt{3}}{2} \sin 2 \alpha-\frac{1}{2} \cos 2 \alpha-\frac{\sqrt{3}}{2} \sin 2 \alpha=0
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.105. $\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos (6 \alpha-\pi)}{\cos 2 \alpha}$.
|
## Solution.
$\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos (6 \alpha-\pi)}{\cos 2 \alpha}=\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos (\pi-6 \alpha)}{\cos 2 \alpha}=\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos 6 \alpha}{\cos 2 \alpha}=$
$=\frac{\sin 6 \alpha \cos 2 \alpha-\cos 6 \alpha \sin 2 \alpha}{\sin 2 \alpha \cos 2 \alpha}=\frac{\sin 4 \alpha}{\sin 2 \alpha \cos 2 \alpha}=\frac{2 \sin 4 \alpha}{2 \sin 2 \alpha \cos 2 \alpha}=$
$=\frac{2 \sin 4 \alpha}{\sin 4 \alpha}=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.148. $\left(\sin 160^{\circ}+\sin 40^{\circ}\right)\left(\sin 140^{\circ}+\sin 20^{\circ}\right)+\left(\sin 50^{\circ}-\sin 70^{\circ}\right) \times$
$$
\times\left(\sin 130^{\circ}-\sin 110^{\circ}\right)=1
$$
|
Solution.
$\left(\sin 160^{\circ}+\sin 40^{\circ}\right)\left(\sin 140^{\circ}+\sin 20^{\circ}\right)+\left(\sin 50^{\circ}-\sin 70^{\circ}\right)\left(\sin 130^{\circ}-\sin 110^{\circ}\right)=$
$$
\begin{aligned}
& =\left(\sin \left(180^{\circ}-20^{\circ}\right)+\sin 40^{\circ}\right)\left(\sin \left(180^{\circ}-40^{\circ}\right)+\sin 20^{\circ}\right)+ \\
& +\left(\sin 50^{\circ}-\sin 70^{\circ}\right)\left(\sin \left(180^{\circ}-50^{\circ}\right)-\sin \left(180^{\circ}-70^{\circ}\right)\right)= \\
& =\left(\sin 20^{\circ}+\sin 40^{\circ}\right)\left(\sin 40^{\circ}+\sin 20^{\circ}\right)+\left(\sin 50^{\circ}-\sin 70^{\circ}\right)\left(\sin 50^{\circ}-\sin 70^{\circ}\right)= \\
& =\left(\sin 20^{\circ}+\sin 40^{\circ}\right)^{2}+\left(\sin 50^{\circ}-\sin 70^{\circ}\right)^{2}=\left(2 \sin 30^{\circ} \cos 10^{\circ}\right)^{2}+ \\
& +\left(2 \cos 60^{\circ} \sin 10^{\circ}\right)^{2}=\left(2 \cdot \frac{1}{2} \cos 10^{\circ}\right)^{2}+\left(2 \cdot \frac{1}{2} \sin 10^{\circ}\right)^{2}=\cos ^{2} 10^{\circ}+\sin ^{2} 10^{\circ}=1
\end{aligned}
$$
The equality holds.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.153. $\sin ^{2} \frac{\pi}{8}+\cos ^{2} \frac{3 \pi}{8}+\sin ^{2} \frac{5 \pi}{8}+\cos ^{2} \frac{7 \pi}{8}$.
|
Solution.
$$
\begin{aligned}
& \sin ^{2} \frac{\pi}{8}+\cos ^{2} \frac{3 \pi}{8}+\sin ^{2} \frac{5 \pi}{8}+\cos ^{2} \frac{7 \pi}{8}= \\
& =\frac{1-\cos \frac{\pi}{4}}{2}+\frac{1+\cos \frac{3 \pi}{4}}{2}+\frac{1-\cos \frac{5 \pi}{4}}{2}+\frac{1+\cos \frac{7 \pi}{4}}{2}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{4-\cos \frac{\pi}{4}+\cos \frac{4 \pi-\pi}{4}-\cos \frac{4 \pi+\pi}{4}+\cos \frac{8 \pi-\pi}{4}}{2}= \\
& =\frac{4-\cos \frac{\pi}{4}+\cos \left(\pi-\frac{\pi}{4}\right)-\cos \left(\pi+\frac{\pi}{4}\right)+\cos \left(2 \pi-\frac{\pi}{4}\right)}{2}= \\
& =\frac{4-\cos \frac{\pi}{4}-\cos \frac{\pi}{4}+\cos \frac{\pi}{4}+\cos \frac{\pi}{4}}{2}=\frac{4}{2}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.154. $\operatorname{tg} 435^{\circ}+\operatorname{tg} 375^{\circ}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
3.154. $\operatorname{tan} 435^{\circ}+\operatorname{tan} 375^{\circ}$.
|
## Solution.
$$
\begin{aligned}
& \tan 435^{\circ}+\tan 375^{\circ}=\tan\left(450^{\circ}-15^{\circ}\right)+\tan\left(360^{\circ}+15^{\circ}\right)= \\
& =\cot 15^{\circ}+\tan 15^{\circ}=\frac{\cos 15^{\circ}}{\sin 15^{\circ}}+\frac{\sin 15^{\circ}}{\cos 15^{\circ}}=\frac{\cos ^{2} 15^{\circ}+\sin ^{2} 15^{\circ}}{\sin 15^{\circ} \cos 15^{\circ}}= \\
& =\frac{1}{\sin 15^{\circ} \cos 15^{\circ}}=\frac{2}{2 \sin 15^{\circ} \cos 15^{\circ}}=\frac{2}{\sin 30^{\circ}}=\frac{2}{\frac{1}{2}}=4
\end{aligned}
$$
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.177. Calculate $(1+\operatorname{ctg} \alpha)(1+\operatorname{ctg} \beta)$, if $\alpha+\beta=\frac{3 \pi}{4}$.
|
Solution.
$$
\begin{aligned}
& (1+\operatorname{ctg} \alpha)(1+\operatorname{ctg} \beta)=\left(1+\frac{\cos \alpha}{\sin \alpha}\right)\left(1+\frac{\cos \beta}{\sin \beta}\right)=\frac{\sin \alpha+\cos \alpha}{\sin \alpha} \times \\
& \times \frac{\sin \beta+\cos \beta}{\sin \beta}=\frac{\cos \alpha \cos \beta+\sin \alpha \sin \beta+\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\sin \alpha \sin \beta}= \\
& =\frac{\cos (\alpha-\beta)+\sin (\alpha+\beta)}{\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))}=\frac{2\left(\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}\right)}{\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.178. Calculate $(1+\operatorname{tg} \alpha)(1+\operatorname{tg} \beta)$, if $\alpha+\beta=\frac{\pi}{4}$.
|
Solution.
$$
(1+\operatorname{tg} \alpha)(1+\operatorname{tg} \beta)=\left(1+\frac{\sin \alpha}{\cos \alpha}\right)\left(1+\frac{\sin \beta}{\cos \beta}\right)=\frac{\cos \alpha+\sin \alpha}{\cos \alpha} \times
$$
$$
\begin{aligned}
& \times \frac{\cos \beta+\sin \beta}{\cos \beta}=\frac{\cos \alpha \cos \beta+\sin \alpha \sin \beta+\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta}= \\
& =\frac{\cos (\alpha-\beta)+\sin (\alpha+\beta)}{\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta))}=\frac{2\left(\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}\right)}{\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.003. In a shooting competition, for each miss in a series of 25 shots, the shooter received penalty points: for the first miss - one penalty point, and for each subsequent miss - half a point more than for the previous one. How many times did the shooter hit the target, having received 7 penalty points?
|
Solution.
Let $a_{1}=1$ be the first term of the arithmetic progression, $d=\frac{1}{2}$ be its common difference, and $S_{n}=7$ be the sum of the first $n$ terms of this progression, where $n$ is the number of terms. Using formula (4.5), we have
$$
\frac{2+(n-1) \cdot \frac{1}{2}}{2} \cdot n=7, n^{2}+3 n-28=0
$$
from which $n_{1}=-7$ (not suitable); $n_{2}=4$. Therefore: the shooter hit the target 21 times.
Answer: 21 times.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.012. The sum of the third and ninth terms of an arithmetic progression is 8. Find the sum of the first 11 terms of this progression.
|
Solution.
From the condition, we have $a_{3}+a_{9}=8$. Using formula (4.1), we get $a_{1}+2 d+a_{1}+8 d=8, 2 a_{1}+10 d=8$, and using formula (4.5), we find $S_{11}=\frac{2 a_{1}+10 d}{2} \cdot 11=44$.
Answer: 44.
|
44
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.013. The sum of the first three terms of an increasing arithmetic progression is 15. If 1 is subtracted from the first two terms of this progression, and 1 is added to the third term, the resulting three numbers will form a geometric progression. Find the sum of the first 10 terms of the arithmetic progression.
|
## Solution.
From the condition, we have: $a_{1}-1, a_{1}+d-1, a_{1}+2 d+1 \cdots$ - three consecutive terms of a geometric progression. Using formula (4.5), we find $S_{3}=\frac{2 a_{1}+2 d}{2} \cdot 3=15$ or $a_{1}+d=5$. Using formula (4.7), we get $\left(a_{1}+d-1\right)^{2}=\left(a_{1}-1\right)\left(a_{1}+2 d+1\right)$. Substituting the value $a_{1}=5-d$ into this equation, we obtain $16=(4-d)(6+d), d^{2}+2 d-8=0$. From this, $d_{1}=-4$, $d_{2}=2$. Then $a_{1}^{\prime}=9, a_{2}^{\prime}=5, a_{3}^{\prime}=1 ; a_{1}^{\prime \prime}=3, a_{2}^{\prime \prime}=5, a_{3}^{\prime \prime}=7$. Considering that by the condition $a_{1}<a_{2}<a_{3}$, we get $a_{1}=3, d=2$. Then
$$
S_{10}=\frac{2 \cdot 3+2 \cdot 9}{2} \cdot 10=120
$$
Answer: 120.
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.015. Calculate
$$
\left(1+3^{2}+5^{2}+\ldots+(2 n-1)^{2}+\ldots+199^{2}\right)-\left(2^{2}+4^{2}+6^{2}+(2 n)^{2}+\ldots+200^{2}\right)
$$
|
## Solution.
From the condition we have
$$
\begin{aligned}
& 1+3^{2}+5^{2}+\ldots+(2 n-1)^{2}+\ldots+199^{2}-2^{2}-4^{2}-6^{2}-(2 n)^{2}-\ldots-200^{2}= \\
& =(1-2)^{2}+\left(3^{2}-4^{2}\right)+\left(5^{2}-6^{2}\right)+\ldots+\left((2 n-1)^{2}-(2 n)^{2}\right)+\ldots+\left(199^{2}-200^{2}\right)= \\
& =(1-2)(1+2)+(3-4)(3+4)+(5-6)(5+6)+\ldots+(2 n-1-2 n)(2 n-1+2 n)+ \\
& +\ldots+(199-200)(199+200)=-3-7-11-\ldots-(4 n-1)-\ldots-399
\end{aligned}
$$
From here, \(a_{1}=-3, d=-4, a_{n}=-399\). Using the formulas (4.4) and \(n=\frac{a_{n}-a_{1}}{d}+1\), we get
$$
S_{n}=\frac{-3-399}{2}\left(\frac{-399+3}{-4}+1\right)=-20100
$$
Answer: -20100.
|
-20100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.018. The denominator of the geometric progression is $1 / 3$, the fourth term of this progression is $1 / 54$, and the sum of all its terms is 121/162. Find the number of terms in the progression.
|
Solution.
From the condition we have $\left\{\begin{array}{l}b_{4}=\frac{1}{54}, \\ S_{n}=\frac{121}{162}\end{array}\right.$.
Using formulas (4.6) and (4.11), we get
$$
\begin{aligned}
& b_{4}=b_{1} q^{3}=b_{1}\left(\frac{1}{3}\right)^{3} ; \frac{b_{1}}{27}=\frac{1}{54}, b_{1}=\frac{1}{2} ; \\
& S_{n}=\frac{b_{1}\left(1-q^{n}\right)}{1-q} ; \frac{\frac{1}{2}\left(1-\left(\frac{1}{3}\right)^{n}\right)}{1-\frac{1}{3}}=\frac{121}{162} \Rightarrow 243\left(3^{n}-1\right)=242 \cdot 3^{n} \Rightarrow \\
& \Rightarrow 3^{n}=243, n=5
\end{aligned}
$$
Answer: $n=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.028. Find the number of terms in a finite geometric progression, where the first, second, and last terms are 3, 12, and 3072, respectively.
|
Solution.
From the condition we have $b_{1}=3, b_{2}=12, \ldots, b_{n}=3072$.
By formula (4.6) we get
$$
\left\{\begin{array} { l }
{ b _ { 1 } = 3 , } \\
{ b _ { 1 } q = 1 2 , } \\
{ b _ { 1 } q ^ { n - 1 } = 3 0 7 2 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
b_{1}=3, \\
q=4, \\
4^{n-1}=1024
\end{array} \Rightarrow 4^{n-1}=4^{5} \Leftrightarrow n-1=5 \Rightarrow n=6\right.\right.
$$
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.029. Find the sum of all positive even two-digit numbers that are divisible by 3.
|
## Solution.
From the condition, we have $a_{1}=12, a_{n}=96, d=12$.
Using formulas (4.4) and (4.5), we get
$$
n=\frac{a_{n}-a_{1}}{d}+1 ; n=\frac{96-12}{6}+1=15, S_{n}=\frac{12+96}{2} \cdot 15=810 \text {. }
$$
Answer: 810.
|
810
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.031. It is known that the interior angles of a certain convex polygon, the smallest of which is $120^{\circ}$, form an arithmetic progression with a difference of $5^{\circ}$. Determine the number of sides of the polygon.
|
Solution.
From the condition, we have $a_{1}=120^{\circ}, d=5^{\circ}$. Using the formulas for the sum of terms of an arithmetic progression (4.5) and the sum of the interior angles of an $n$-sided polygon $S_{n}=180^{\circ}(n-2)$, we get
$$
\frac{240^{\circ}+(n-1) 5^{\circ}}{2} \cdot n=180^{\circ}(n-2), n^{2}-25 n+144=0 \Rightarrow
$$
$\Rightarrow n_{1}=9, n_{2}=16$ (the latter does not fit, as in this case
$\Rightarrow a_{16}=120^{\circ}+5^{\circ} \cdot 15=195^{\circ}$, while the interior angle of a convex $n$-sided polygon is always less than $\left.180^{\circ}\right)$.
Answer: 9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.012. $(x-1)\left(x^{2}-3\right)+(2 x-1)\left(x^{2}+2\right)=3$.
|
Solution.
Domain of definition: $x \in R$.
## We have
$$
\begin{aligned}
& x^{3}-x^{2}-3 x+3+2 x^{3}-x^{2}+4 x-2=3 \Leftrightarrow \\
& \Leftrightarrow 3 x^{3}-2 x^{2}+x-2=0 \Leftrightarrow 3 x^{3}-3 x^{2}+x^{2}-x+2 x-2=0 \Leftrightarrow \\
& \Leftrightarrow 3 x^{2}(x-1)+x(x-1)+2(x-1)=0 \Leftrightarrow(x-1)\left(3 x^{2}+x+2\right)=0 \\
& x-1=0, x_{1}=1 \text { or } 3 x^{2}+x+2=0, x_{2,3} \in \varnothing(D<0)
\end{aligned}
$$
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.014. $\frac{4}{x^{2}+4}+\frac{5}{x^{2}+5}=2$.
|
## Solution.
Domain: $x \in R$.
$\frac{2 x^{4}+9 x^{2}}{\left(x^{2}+4\right)\left(x^{2}+5\right)}=0 \Leftrightarrow 2 x^{4}+9 x^{2}=0 \Leftrightarrow x^{2}\left(2 x^{2}+9\right)=0$,
$x^{2}=0, x_{1}=0$ or $2 x^{2}+9=0, x_{2,3} \in \varnothing$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.031. $\sqrt{3 x+4}+\sqrt{x-4}=2 \sqrt{x}$.
|
## Solution.
Domain of definition: $3 x+4 \geq 0, x-4 \geq 0, x \geq 0 \Rightarrow x \geq 4$.
Squaring both sides of the equation, we get
$$
\begin{aligned}
& 3 x+4+2 \sqrt{(3 x+4)(x-4)}+x-4=4 x \Leftrightarrow \\
& \Leftrightarrow 2 \sqrt{(3 x+4)(x-4)}=0
\end{aligned}
$$
Squaring again, we get: $(3 x+4)(x-4)=0$. From this, we have $3 x+4=0$ or $x-4=0, x_{1}=-\frac{4}{3}, x_{2}=4 ; x_{1}=-\frac{4}{3}$ does not satisfy the domain of definition. Checking $x=4$ by direct substitution into the original equation, we get:
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.032. $\sqrt{x+\sqrt{x+11}}+\sqrt{x-\sqrt{x+11}}=4$.
6.032. $\sqrt{x+\sqrt{x+11}}+\sqrt{x-\sqrt{x+11}}=4$.
|
Solution.
Let $\sqrt{x+11}=y \geq 0$ or $x+11=y^{2}$, i.e., $x=y^{2}-11$. Then
$$
\sqrt{y^{2}+y-11}+\sqrt{y^{2}-y-11}=4 \text { or } \sqrt{y^{2}+y-11}=4-\sqrt{y^{2}-y-11}
$$
Squaring both sides of the equation, we get
$$
y^{2}+y-11=16-8 \sqrt{y^{2}-y-11}+y^{2}-y-11, 8 \sqrt{y^{2}-y-11}=16-2 y
$$
or $4 \sqrt{y^{2}-y-11}=8-y$. Squaring both sides of the equation again, we find
$$
\begin{aligned}
& 16 y^{2}-16 y-176=64-16 y+y^{2}, 0<y \leq 8 \Rightarrow \\
& \Rightarrow\left\{\begin{array}{l}
15 y^{2}=240, \\
0<y \leq 8
\end{array} \text { or } y=4 .\right.
\end{aligned}
$$
From this, we get $\sqrt{x+11}=4$ or $x+11=16, x=5$. Checking, we confirm that this is a root of the original equation.
Answer: $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.034. $1+\sqrt{1+x \sqrt{x^{2}-24}}=x$.
6.034. $1+\sqrt{1+x \sqrt{x^{2}-24}}=x$.
|
Solution.
Write the equation as $\sqrt{1+x \sqrt{x^{2}-24}}=x-1$. Squaring both sides of the equation, we get
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ 1 + x \sqrt { x ^ { 2 } - 2 4 } = x ^ { 2 } - 2 x + 1 , } \\
{ x - 1 \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \sqrt{x^{2}-24}=x^{2}-2 x, \\
x \geq 1
\end{array}\right.\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
\sqrt{x^{2}-24}=x-2, \\
x \geq 1
\end{array}\right. \\
& \Rightarrow x^{2}-24=x^{2}-4 x+4 \text { or } 4 x=28 ; x=7 .
\end{aligned}
$$
Checking $x=7$ by direct substitution into the original equation, we have:
Answer: $x=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.037. $\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}}=2$.
|
Solution.
Domain of definition: $x \geq 0$.
Raising both sides of the equation to the third power, we get
$$
\begin{aligned}
& 1+\sqrt{x}+3 \sqrt[3]{(1+\sqrt{x})^{2}(1-\sqrt{x})}+3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})^{2}}+1-\sqrt{x}=8 \Leftrightarrow \\
& \Leftrightarrow 3 \sqrt[3]{(1+\sqrt{x})^{2}(1-\sqrt{x})}+3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})^{2}}=6 \Leftrightarrow \\
& \Leftrightarrow 3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})}(\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}})=6
\end{aligned}
$$
Since $\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}}=2$, the equation becomes:
$3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})} \cdot 2=6 \Leftrightarrow \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})}=1 \Leftrightarrow \sqrt[3]{1-x}=1 \Leftrightarrow$ $\Leftrightarrow 1-x=1, x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.040. $\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}}=1$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
6.040. $\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}}=1$.
|
## Solution.
Domain of definition: $x \geq 0$.
Raising both sides of the equation to the third power, we get
$$
\begin{aligned}
& 24+\sqrt{x}-3 \sqrt[3]{(24+\sqrt{x})^{2}(5+\sqrt{x})}+3 \sqrt[3]{(24+\sqrt{x})(5+\sqrt{x})^{2}}-5-\sqrt{x}=1 \Leftrightarrow \\
& \Leftrightarrow-3 \sqrt[3]{(24+\sqrt{x})}(5+\sqrt{x})(\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}})=-18
\end{aligned}
$$
Since $\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}}=1$ by the condition, we obtain
$\sqrt[3]{(24+\sqrt{x})}(5+\sqrt{x})=6 \Leftrightarrow(24+\sqrt{x})(5+\sqrt{x})=216$,
$(\sqrt{x})^{2}+29 \sqrt{x}-96=0$.
From which $\sqrt{x}=3, \sqrt{x}=-3$ (not suitable). Therefore, $x=9$.
Answer: $x=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.049. $\sqrt{x^{3}+8}+\sqrt[4]{x^{3}+8}=6$.
6.049. $\sqrt{x^{3}+8}+\sqrt[4]{x^{3}+8}=6$.
|
## Solution.
Domain of definition: $x^{3}+8 \geq 0 \Leftrightarrow x^{3} \geq-8 \Leftrightarrow x \geq-2$.
Let $\sqrt[4]{x^{3}+8}=y, y>0$, and the equation becomes $y^{2}+y=6 \Leftrightarrow$ $\Leftrightarrow y^{2}+y-6=0$, from which $y_{1}=-3, y_{2}=2 ; y_{1}=-3$ is not suitable. Then $\sqrt[4]{x^{3}+8}=2, x^{3}+8=16, x^{3}=8, x=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.052.
$$
\frac{1}{x-\sqrt{x^{2}-x}}-\frac{1}{x+\sqrt{x^{2}-x}}=\sqrt{3}
$$
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{2}-x \geq 0, \\ x \neq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}x(x-1) \geq 0, \\ x \neq 0\end{array} \Leftrightarrow x \in(-\infty ; 0) \cup[1 ;+\infty)\right.\right.$.
From the condition we get
$$
\begin{aligned}
& \frac{x+\sqrt{x^{2}-x}-x+\sqrt{x^{2}-x}}{x^{2}-x^{2}+x}=\sqrt{3} \Leftrightarrow \frac{2 \sqrt{x^{2}-x}}{x}=\sqrt{3} \Leftrightarrow \\
& \Leftrightarrow \frac{2 \sqrt{x} \sqrt{x-1}}{x}=\sqrt{3} \Leftrightarrow \frac{2 \sqrt{x-1}}{\sqrt{x}}=\sqrt{3}(x \neq 0)
\end{aligned}
$$
Squaring both sides of the equation, we get $\frac{4 x-4}{x}=3$ or $x=4$. By verification, we confirm that $x=4$ is a root of the last equation with radicals.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.053. $\frac{\sqrt[3]{x^{4}}-1}{\sqrt[3]{x^{2}}-1}-\frac{\sqrt[3]{x^{2}}-1}{\sqrt[3]{x}+1}=4$
|
## Solution.
Domain of definition: $x \neq \pm 1$.
Let $\sqrt[3]{x}=y, y \neq \pm 1$. The equation in terms of $y$ becomes
$$
\begin{aligned}
& \frac{y^{4}-1}{y^{2}-1}-\frac{y^{2}-1}{y+1}=4 \Leftrightarrow \frac{\left(y^{2}-1\right)\left(y^{2}+1\right)}{y^{2}-1}-\frac{(y-1)(y+1)}{y+1}=4 \Leftrightarrow \\
& \Leftrightarrow y^{2}+1-y+1=4 \Leftrightarrow y^{2}-y-2=0
\end{aligned}
$$
from which we find $y_{1}=-1, y_{2}=2$. Then $\sqrt[3]{x}=-1, x_{1}=-1$, or $\sqrt[3]{x}=2$, $x_{2}=8 ; x_{1}=-1$ does not satisfy the domain of definition.
Answer: $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.054. $\sqrt{5+\sqrt[3]{x}}+\sqrt{5-\sqrt[3]{x}}=\sqrt[3]{x}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}5+\sqrt[3]{x} \geq 0 \\ 5-\sqrt[3]{x} \geq 0\end{array} \Leftrightarrow -125 \leq x \leq 125\right.$.
By squaring both sides of the equation, we get the equation
$$
\begin{aligned}
& 5+\sqrt[3]{x}+2 \sqrt{(5+\sqrt[3]{x})(5-\sqrt[3]{x})}+5-\sqrt[3]{x}=\sqrt[3]{x^{2}} \Leftrightarrow \\
& \Leftrightarrow 2 \sqrt{25-\sqrt[3]{x^{2}}}=\sqrt[3]{x^{2}}-10 \Rightarrow 100-4 \sqrt[3]{x^{2}}=\sqrt[3]{x^{4}}-20 \sqrt[3]{x^{2}}+100 \Leftrightarrow \\
& \Leftrightarrow \sqrt[3]{x^{4}}-16 \sqrt[3]{x^{2}}=0 \Leftrightarrow \sqrt[3]{x^{2}}\left(\sqrt[3]{x^{2}}-16\right)=0
\end{aligned}
$$
from which $\sqrt[3]{x^{2}}=0, x_{1}=0$, or $\sqrt[3]{x^{2}}-16=0, \sqrt[3]{x^{2}}=16, x_{2}=64$. Upon verification, $x_{1}=0$ does not satisfy the original equation.
Answer: $x=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.055. $\sqrt{x \sqrt[5]{x}}+\sqrt[5]{x \sqrt{x}}=56$.
6.055. $\sqrt{x \sqrt[5]{x}}+\sqrt[5]{x \sqrt{x}}=56$.
|
## Solution.
Domain of definition: $x \geq 0$.
From the condition we have
$$
x^{\frac{6}{10}}-x^{\frac{3}{10}}=56 \Leftrightarrow\left(x^{\frac{3}{10}}\right)^{2}-x^{\frac{3}{10}}-56=0
$$
Let $x^{\frac{3}{10}}=y \geq 0$. The equation in terms of $y$ becomes $y^{2}-y-56=0$, from which $y_{1}=-7$ or $y_{2}=8 ; y_{1}=-7<0$ is not valid. Therefore, $x^{\frac{3}{10}}=8$. Hence, $x=8^{\frac{10}{3}}, x=\left(2^{3}\right)^{\frac{10}{3}}, x=2^{10}=1024$.
Answer: $x=1024$.
|
1024
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.058. $\sqrt[3]{\frac{5-x}{x+3}}+\sqrt[7]{\frac{x+3}{5-x}}=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq-3, \\ x \neq 5\end{array}\right.$
Let $\sqrt[7]{\frac{5-x}{x+3}}=z, z \neq 0$. The equation in terms of $z$ becomes $z+\frac{1}{z}=2 \Leftrightarrow z^{2}-2 z+1=0 \Leftrightarrow(z-1)^{2}=0 \Leftrightarrow z-1=0, z=1$.
Then $\sqrt[7]{\frac{5-x}{x+3}}=1 \Leftrightarrow \frac{5-x}{x+3}=1 ; x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.061. $2 \sqrt[3]{x}+5 \sqrt[6]{x}-18=0$.
|
## Solution.
Domain of definition: $x \geq 0$.
Let $\sqrt[6]{x}=y \geq 0$. The equation in terms of $y$ becomes $2 y^{2}+5 y-18=0$, from which we find $y_{1}=-\frac{9}{2}, y_{2}=2 ; y_{1}=-\frac{9}{2}<0$ is not valid.
Then $\sqrt[6]{x}=2, x=2^{6}=64$.
Answer: $x=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.063. $\frac{\sqrt{x}+\sqrt[3]{x}}{\sqrt{x}-\sqrt[3]{x}}=3$.
|
## Solution.
Domain of definition: $0<x \neq 1$.
Rewrite the equation as
$$
\frac{\sqrt[6]{x^{3}}+\sqrt[6]{x^{2}}}{\sqrt[6]{x^{3}}-\sqrt[6]{x^{2}}}=3 \Leftrightarrow \frac{\sqrt[6]{x^{3}}(\sqrt[6]{x}+1)}{\sqrt[6]{x^{3}}(\sqrt[6]{x}-1)}=3 \Leftrightarrow \frac{\sqrt[6]{x}+1}{\sqrt[6]{x}-1}=3 \Leftrightarrow
$$
$$
\begin{aligned}
& \Leftrightarrow \frac{\sqrt[6]{x}+1}{\sqrt[6]{x}-1}-3=0, x \neq 1 \Leftrightarrow \frac{\sqrt[6]{x}+1-3 \sqrt[6]{x}+3}{\sqrt[6]{x}-1}=0 \Leftrightarrow \\
& \Leftrightarrow-2 \sqrt[6]{x}+4=0 \Leftrightarrow \sqrt[6]{x}=2, x=2^{6}=64
\end{aligned}
$$
Answer: $x=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.064. $\sqrt{x+2}+\sqrt{3 x+8}=\sqrt{2 x+6}$.
6.064. $\sqrt{x+2}+\sqrt{3 x+8}=\sqrt{2 x+6}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+2 \geq 0, \\ 3 x+8 \geq 0, \\ 2 x+6 \geq 0\end{array} \Leftrightarrow x \geq-2\right.$.
Write the equation in the form $\sqrt{x+2}-\sqrt{2 x+6}=-\sqrt{3 x+8}$ and square both sides:
$$
\begin{aligned}
& x+2-2 \sqrt{(x+2)(2 x+6)}+2 x+6=3 x+8 \Leftrightarrow \\
& \Leftrightarrow \sqrt{(x+2)(2 x+6)}=0
\end{aligned}
$$
from which $x+2=0, x_{1}=-2$, or $2 x+6=0, x_{2}=-3$ - does not satisfy the domain of definition. By checking, we confirm that $x=-2$ is a root of the given equation.
Answer: $x=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.065. $\sqrt{2 x+5}+\sqrt{5 x+6}=\sqrt{12 x+25}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}2 x+5 \geq 0, \\ 5 x+6 \geq 0, \\ 12 x+25 \geq 0\end{array} \Leftrightarrow x \geq-\frac{6}{5}\right.$.
By squaring both sides of the equation, we have
$$
\begin{aligned}
& 2 x+5+2 \sqrt{(2 x+5)(5 x+6)}+5 x+6=12 x+25 \Leftrightarrow \\
& \Leftrightarrow 2 \sqrt{(2 x+5)(5 x+6)}=5 x+14 \Rightarrow \\
& \Rightarrow 4(2 x+5)(5 x+6)=25 x^{2}+140 x+196 \Leftrightarrow 15 x^{2}+8 x-76=0
\end{aligned}
$$
from which $x_{1}=-\frac{38}{15}, x_{2}=2 ; x_{1}=-\frac{38}{15}$ does not satisfy the domain of definition. By checking, we confirm that $x=2$ is a root of the equation.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.126. For what integer value of $k$ is one of the roots of the equation $4 x^{2}-(3 k+2) x+\left(k^{2}-1\right)=0$ three times smaller than the other?
|
Solution.
From the condition, by Vieta's theorem, we have
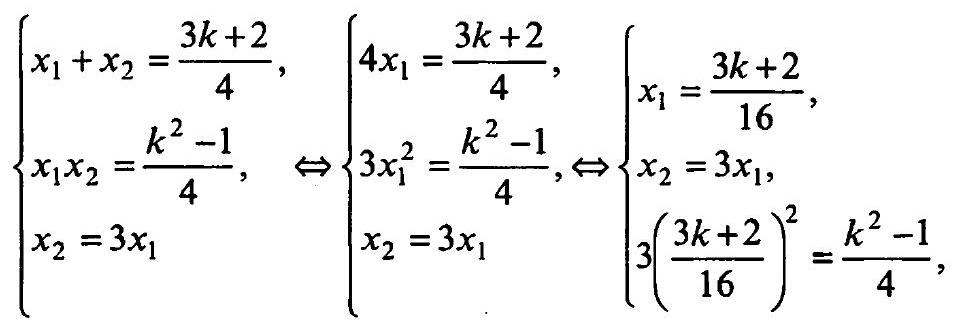
where $k \in \mathbb{Z}$. From this, $37 k^{2}-36 k-76=0, k_{1}=2, k_{2}=-\frac{38}{37} \notin \mathbb{Z}$ (does not fit).
Answer: $k=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.129. For what value of $a$ do the equations $x^{2}+a x+8=0$ and $x^{2}+x+a=0$ have a common root?
|
## Solution.
Let $x_{1}$ be the common root, then
$$
\left\{\begin{array}{l}
x_{1}^{2}+a x_{1}+8=0, \\
x_{1}^{2}+x_{1}+a=0
\end{array} \Rightarrow a x_{1}-x_{1}+8-a=0, x_{1}=\frac{a-8}{a-1}\right.
$$
From the second equation of the system, we have
$$
\begin{aligned}
& \left(\frac{a-8}{a-1}\right)^{2}+\left(\frac{a-8}{a-1}\right)+a=0, \frac{a^{3}-24 a+72}{(a-1)^{2}}=0 \Leftrightarrow\left\{\begin{array}{l}
a^{3}-24 a+72=0, \\
a \neq 1,
\end{array}\right. \\
& a^{3}+216-216-24 a+72=0,\left(a^{3}+216\right)-24 a-144=0, \\
& \left(a^{3}+6^{3}\right)-24(a+6)=0 \\
& (a+6)\left(a^{2}-6 a+36\right)-24(a+6)=0 \\
& (a+6)\left(a^{2}-6 a+12\right)=0
\end{aligned}
$$
from which $a=-6$. For the quadratic equation, $D<0, \varnothing$.
Answer: $a=-6$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.130. In the equation $x^{2}-2 x+c=0$, determine the value of $c$ for which its roots $x_{1}$ and $x_{2}$ satisfy the condition $7 x_{2}-4 x_{1}=47$.
|
Solution.
From the condition by Vieta's theorem we have $\left\{\begin{array}{l}x_{1}+x_{2}=2, \\ x_{1} \cdot x_{2}=c, \\ 7 x_{2}-4 x_{1}=47 .\end{array}\right.$ From here, $x_{2}=2-x_{1}$ and we obtain
$$
\left\{\begin{array} { l }
{ x _ { 1 } ( 2 - x _ { 1 } ) = c } \\
{ 7 ( 2 - x _ { 1 } ) - 4 x _ { 1 } = 4 7 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x_{1}\left(2-x_{1}\right)=c \\
x_{1}=-3
\end{array}\right.\right.
$$
Thus, $c=-15$.
Answer: $c=-15$.
|
-15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.131. Without solving the equation $x^{2}-(2 a+1) x+a^{2}+2=0$, find the value of $a$ for which one of the roots is twice the other.
|
Solution.
From the condition, by Vieta's theorem, we have
$$
\left\{\begin{array} { l }
{ x _ { 1 } + x _ { 2 } = 2 a + 1 , } \\
{ x _ { 1 } \cdot x _ { 2 } = a ^ { 2 } + 2 , } \\
{ x _ { 2 } = 2 x _ { 1 } }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ 3 x _ { 1 } = 2 a + 1 , } \\
{ 2 x _ { 1 } ^ { 2 } = a ^ { 2 } + 2 } \\
{ x _ { 2 } = 2 x _ { 1 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x_{1}=\frac{2 a+1}{3} \\
x_{1}^{2}=\frac{a^{2}+2}{2} \\
x_{2}=2 x_{1}
\end{array}\right.\right.\right.
$$
From here,
$$
\begin{aligned}
& \left(\frac{2 a+1}{3}\right)^{2}=\frac{a^{2}+2}{2} \Leftrightarrow \frac{4 a^{2}+4 a+1}{9}=\frac{a^{2}+2}{2} \Leftrightarrow \\
& \Leftrightarrow a^{2}-8 a+16=0 \Leftrightarrow(a-4)^{2}=0
\end{aligned}
$$
Thus, $a=4$.
Answer: $a=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.134. For what integer value of $b$ do the equations $2 x^{2}+(3 b-1) x-3=0$ and $6 x^{2}-(2 b-3) x-1=0$ have a common root?
|
Solution.
Let $x_{1}$ be the common root. Then
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ 2 x _ { 1 } ^ { 2 } + ( 3 b - 1 ) x _ { 1 } - 3 = 0 , } \\
{ 6 x _ { 1 } ^ { 2 } - ( 2 b - 3 ) x _ { 1 } - 1 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
6 x^{2}+(9 b-3) x-9=0, \\
6 x^{2}-(2 b-3) x_{1}-1=0
\end{array}\right.\right. \\
& \Leftrightarrow(9 b-3) x+(2 b-3) x-9+1=0, \quad x=\frac{8}{11 b-6} .
\end{aligned}
$$
From the first equation we have
$2\left(\frac{8}{11 b-6}\right)^{2}+(3 b-1)\left(\frac{8}{11 b-6}\right)-3=0,99 b^{2}-164 b-68=0$,
$b_{1}=-\frac{34}{99}, b_{2}=2$
$b_{1}=-\frac{34}{99}$ is not an integer value.
Answer: $b=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.001. $\sqrt{25^{\frac{1}{\log _{6} 5}}+49^{\frac{1}{\log _{8} 7}}}$
|
## Solution.
$$
\begin{aligned}
& \sqrt{\frac{1}{25^{\log _{6} 5}}+49^{\frac{1}{\log _{8} 7}}}=\sqrt{5^{2 \log _{5} 6}+7^{2 \log _{7} 8}}=\sqrt{5^{\log _{5} 6^{2}}+7^{\log _{7} 8^{2}}}= \\
& =\sqrt{6^{2}+8^{2}}=10
\end{aligned}
$$
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.002. $81^{\frac{1}{\log _{5} 3}}+27^{\log _{9} 36}+3^{\frac{4}{\log _{7} 9}}$.
|
Solution.
$81^{\frac{1}{\log _{5} 3}}+27^{\log _{9} 36}+3^{\frac{4}{\log _{7} 9}}=3^{4 \log _{3} 5}+3^{\frac{3}{2^{2} \log _{3} 36}}+3^{\frac{4}{2} \log _{3} 7}=5^{4}+36^{\frac{3}{2}}+49=$ $=625+216+49=890$.
Answer: 890.
|
890
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.003. $-\log _{2} \log _{2} \sqrt{\sqrt[4]{2}}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.003. $-\log _{2} \log _{2} \sqrt{\sqrt[4]{2}}$.
|
Solution.
$$
-\log _{2} \log _{2} \sqrt{\sqrt[4]{2}}=-\log _{2} \log _{2} 2^{\frac{1}{8}}=-\log _{2} \frac{1}{8} \log _{2} 2=-\log _{2} 2^{-3}=3
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.004. $-\log _{3} \log _{3} \sqrt[3]{\sqrt[3]{3}}$.
7.004. $-\log _{3} \log _{3} \sqrt[3]{\sqrt[3]{3}}$.
|
## Solution.
$-\log _{3} \log _{3} \sqrt[3]{\sqrt[3]{3}}=-\log _{3} \log _{3} 3^{\frac{1}{9}}=-\log _{3} \frac{1}{9} \log _{3} 3=-\log _{3} 3^{-2}=2$.
Answer: 2.
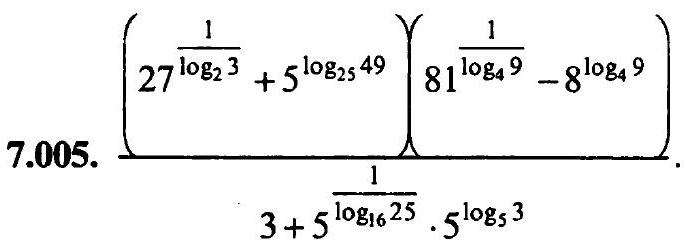
## Solution.
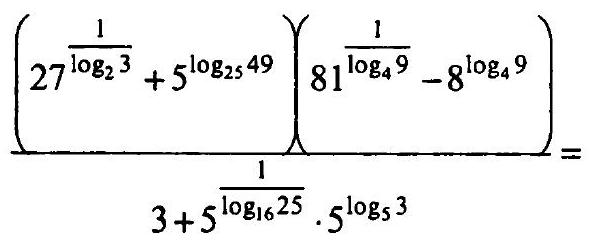
$=\frac{\left(\left(3^{3}\right)^{\log _{3} 2}+5^{\log _{5} 27^{2}}\right)\left(\left(9^{2}\right)^{\log _{9} 4}-\left(2^{3}\right)^{\log _{2} 23^{2}}\right)}{3+5^{\log _{5} 24^{2}} \cdot 3}=$
$=\frac{\left(3^{\log _{3} 2^{3}}+5^{\log _{5} 7}\right)\left(9^{\log _{9} 4^{2}}-2^{\log _{2} 3^{3}}\right)}{3+5^{\log _{5} 4} \cdot 3}=\frac{\left(2^{3}+7\right)\left(4^{2}-3^{3}\right)}{3+4 \cdot 3}=$
$=\frac{15 \cdot(-11)}{15}=-11$.
Answer: -11.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.007. $\left(81^{\frac{1}{4}-\frac{1}{\log _{9} 4}}+25^{\log _{125} 8}\right) \cdot 49^{\log _{7} 2}$.
|
Solution.
$$
\begin{aligned}
& \left(81^{\frac{1}{4}-\frac{1}{2} \log _{9} 4}+25^{\log _{125} 8}\right) \cdot 49^{\log _{7} 2}=\left(\frac{81^{\frac{1}{4}}}{\left(9^{2}\right)^{\frac{1}{2} \log _{9} 4}}+5^{2 \log _{5} 32^{3}}\right) \cdot 7^{2 \log _{7} 2}= \\
& =\left(\frac{3}{4}+4\right) \cdot 4=19
\end{aligned}
$$
Answer: 19.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.008. $\frac{81^{\frac{1}{\log _{5} 9}}+3^{\frac{3}{\log _{\sqrt{6}} 3}}}{409} \cdot\left((\sqrt{7})^{\frac{2}{\log _{25} 7}}-125^{\log _{25} 6}\right)$
|
## Решение.
$$
\frac{81^{\frac{1}{\log _{5} 9}}+3^{\frac{3}{\log _{\sqrt{6}}}}}{409} \cdot\left((\sqrt{7})^{\frac{2}{\log _{25} 7}}-125^{\log _{25} 6}\right)=
$$
$=\frac{9^{2 \log _{9} 5}+3^{3 \log _{3} \sqrt{6}}}{409} \cdot\left(\left(7^{\frac{1}{2}}\right)^{2 \log _{7} 25}-5^{3 \log _{5} 26}\right)=\frac{9^{\log _{9} 5^{2}}+3^{\log _{3}(\sqrt{6})}}{409} \times$
$\times\left(7^{\log _{7} 25}-5^{\log _{5} 6^{\frac{3}{2}}}\right)=\frac{\left(25+6^{\frac{3}{2}}\right)\left(25-6^{\frac{3}{2}}\right)}{409}=\frac{625-216}{409}=1$.
Omвem: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.009. $\left(N^{\frac{1}{\log _{2} N}} \cdot N^{\frac{1}{\log _{4} N}} \cdot N^{\frac{1}{\log _{8} N}} \cdots N^{\frac{1}{\log _{64} N}}\right)^{\frac{1}{15}}$ (the bases of the logarithms are consecutive natural powers of the number 2).
|
## Solution.
$$
\begin{aligned}
& \left(N^{\frac{1}{\log _{2} N}} \cdot N^{\frac{1}{\log _{4} N}} \cdot N^{\frac{1}{\log _{8} N}} \cdots N^{\frac{1}{\log _{512} N}}\right)^{\frac{1}{15}}= \\
& =\left(N^{\log _{N} 2} \cdot N^{\log _{N} 4} \cdot N^{\log _{N} 8} \cdots N^{\log _{N} 512}\right)^{\frac{1}{15}}= \\
& =(2 \cdot 4 \cdot 8 \cdots 512)^{\frac{1}{15}}=\left(2^{1} \cdot 2^{2} \cdot 2^{3} \cdots 2^{9}\right)^{\frac{1}{15}}=\left(2^{1+2+3+\ldots+9}\right)^{\frac{1}{15}}
\end{aligned}
$$
The expression $S_{n}=1+2+3+\ldots+9$ is the sum of the terms of an arithmetic progression, where $a_{1}=1, d=1, a_{n}=9, n=9$. Then $S_{n}=\frac{a_{1}+a_{n}}{2} n=$ $=\frac{1+9}{2} \cdot 9=45$. Therefore, $\left(2^{45}\right)^{\frac{1}{15}}=2^{3}=8$.
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.021. $3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
7.021. $3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
|
Solution.
Domain of definition: $3^{x}-5^{2-x}>0$.
$\log _{5} 8+2 \log _{5} 5-\log _{5}\left(3^{x}-25 \cdot 5^{-x}\right)=x \Leftrightarrow \log _{5} \frac{8 \cdot 25}{3^{x}-25 \cdot 5^{-x}}=x$,
from which $\frac{200}{3^{x}-25 \cdot 5^{-x}}=5^{x} \Leftrightarrow 15^{x}=15^{2}$. Therefore, $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.028. $5^{2\left(\log _{5} 2+x\right)}-2=5^{x+\log _{5} 2}$.
|
## Solution.
$\left(5^{x+\log _{5} 2}\right)^{2}-5^{x+\log _{5} 2}-2=0$; solving this equation as a quadratic equation in terms of $5^{x+\log _{5} 2}$, we find $5^{x+\log _{5} 2}=-1$ and $5^{x+\log _{5} 2}=2 ; 5^{x+\log _{5} 2}=-1$ has no solutions.
Thus,
$$
5^{x+\log _{5} 2}=2 \Rightarrow \log _{5} 5^{x+\log _{5} 2}=\log _{5} 2, x+\log _{5} 2=\log _{5} 2
$$
from which $x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.