problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
8.5. Snow White entered a room where 30 chairs were arranged around a round table. Some of the chairs were occupied by dwarfs. It turned out that Snow White could not sit down without having someone next to her. What is the minimum number of dwarfs that could have been at the table? Explain how the dwarfs should have been seated.
|
Answer: 10.
Solution: If there were three consecutive empty chairs at the table in some place, Snow White could sit down in such a way that no one would sit next to her. Therefore, in any set of three consecutive chairs, at least one must be occupied by a dwarf. Since there are 30 chairs in total, there cannot be fewer than 10 dwarfs. We will show that it is possible to seat 10 dwarfs in such a way that the condition of the problem is satisfied: we will seat the dwarfs every three chairs: on the first chair, on the fourth chair, on the seventh chair, and so on. Then the condition of the problem will be met.
Internet resources: http://www.problems.ru, https://olimpiada.ru.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On Eeyore's Birthday, Winnie-the-Pooh, Piglet, and Owl came to visit. When Owl left, the average age in this company decreased by 2 years, and when Piglet left, the average age decreased by another 1 year. How many years older is Owl than Piglet?
Answer: Owl is 6 years older than Piglet.
|
Solution. Let the average age of those who remained after Piglet be x, and Piglet's age be y. Then $2x + y = 3(x + 1)$, which means $y = x + 3$. Let Owl's age be K. Then $3(x + 1) + K = 4(x + 3)$, which means $K = x + 9$. Therefore, Owl is older than Piglet by $(x + 9) - (x + 3) = 6$ years.
Criteria. If the solution is incorrect - 0 points.
If the reasoning is correct but there is a computational error - 3 points. If the solution is correct - 7 points.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. In the park, all bicycle paths run from north to south or from west to east. Petya and Kolya simultaneously started from point $A$ and rode their bicycles at constant speeds: Petya - along the route $A-B-C$, Kolya - along the route $A-D-E-F-C$ (see fig.), and both spent 12 minutes on the road. It is known that Kolya rides 1.2 times faster than Petya. How much time did he spend on the segment $D E$? The scale in the figure is not preserved.
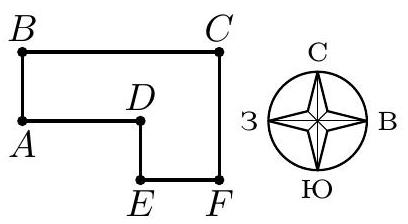
|
Answer: 1 minute.
Solution. Draw the segment $D H$, as shown in Fig. 2. Kolya travels 1.2 times faster than Petya, so it would take him $12 / 1.2=10$ minutes to travel the route $A-B-C$. The difference in time

Fig. 2 $12-10=2$ minutes - this is the time spent moving down the segment $D E$ and moving up the segment $F H$. From the equality $D E=F H$, it follows that Petya will take 1 minute to cover the distance $D E$.
Comment. A correct answer without justification - 2 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. Around a round table, 12 people sat down, some of them are knights, and the rest are liars (knights always tell the truth, while liars always lie). Then each of them said: "Among my neighbors, there is a liar." What is the maximum number of people sitting at the table who can say: "Among my neighbors, there is a knight"?
|
# Answer: 8.
Solution. Note that two liars cannot sit next to each other (otherwise, each of them would be telling the truth). Therefore, no liar can say the second phrase.
On the other hand, 3 knights also cannot sit next to each other (otherwise, the middle one would have lied by saying that he has a neighbor who is a liar). Therefore, among any three sitting next to each other, there is a liar, meaning that no more than two of them can say the second phrase. By dividing the people sitting into four groups of three sitting next to each other, we get that no more than \(4 \cdot 2 = 8\) people could have said the second phrase.
Exactly 8 (knights) of those sitting at the table could have said the required phrase if the people at the table are seated in the following order: LRR LRR LRR LRR.
Remark. For a knight to say the second phrase, he must sit next to another knight. From this, it is not difficult to see that the optimal example is unique (up to rotation of the table).
Comment. Noted that 3 knights cannot sit next to each other - 1 point.
Noted that 2 liars cannot sit next to each other - 1 point.
Shown that the number of people who said the required phrase is no more than \(8 - 3\) points.
Provided an example showing that exactly 8 of those sitting at the table could have said the required phrase - 2 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Sixteen boys gathered for fishing. It is known that every boy who put on boots also put on a cap. Without boots, there were 10 boys, and without a cap - two. Which boys are more and by how many: those who wore a cap but no boots, or those who put on boots? Be sure to explain your answer.
|
Answer. Those who were in caps but without boots were 2 more than those who were in boots.
Solution. Out of 16 boys, 10 were without boots, which means 6 were in boots. Two were without caps, so 14 were in caps. Since everyone who wore boots also wore a cap, out of the 14 who wore caps, 6 also wore boots, and the remaining 8 did not wear boots. Therefore, those who were in caps and without boots (8 people) are 2 more than those who were in boots (6 people).
This reasoning can be conducted based on the diagram:
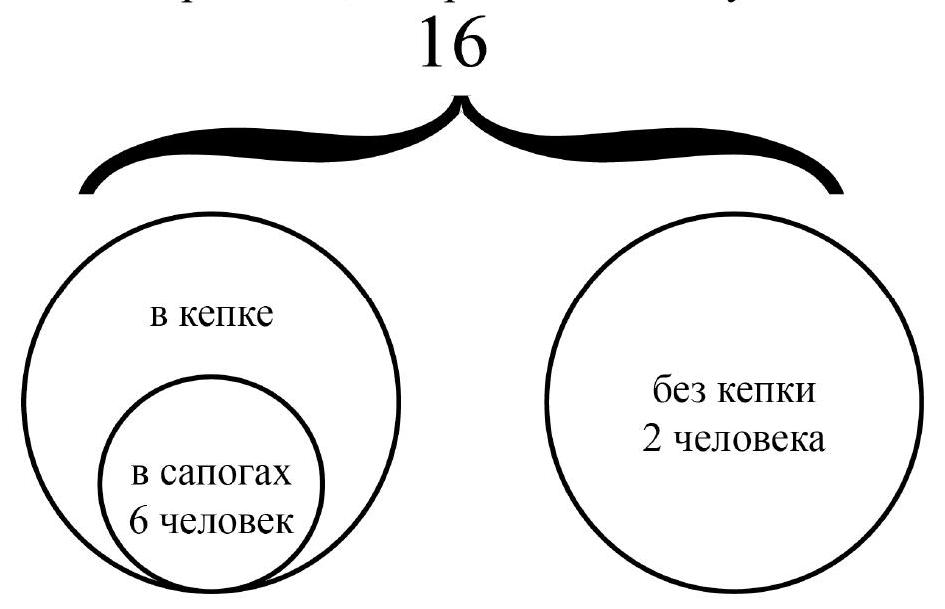
## Grading Criteria.
- Complete and justified solution - 7 points.
- Correct reasoning was conducted, but the final step was not taken (the number of those in caps and without boots and those in boots were given separately), 6 points.
- A correct diagram was drawn or correct reasoning was started, but the solution was not completed - 2 points.
- Correct answer without explanation (but with verification that everything matches) 2 points.
- Only the correct answer - 1 point.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Rectangle $A B C D$ was divided into four
smaller rectangles with equal perimeters (see figure). It is known that $A B=18$ cm, and $B C=16$ cm. Find the lengths of the sides of the other rectangles. Be sure to explain your answer.
|
Answer. 2 cm and 18 cm are the lengths of the sides of rectangle $A B L E$, 6 cm and 14 cm are the lengths of the sides of the other rectangles.
Solution. Since the perimeters of the three vertical rectangles are equal and the segments $E D, F G, K H$ and $L C$ are also equal, the segments $E F$, $F K$ and $K L$ are also equal. Therefore, each of
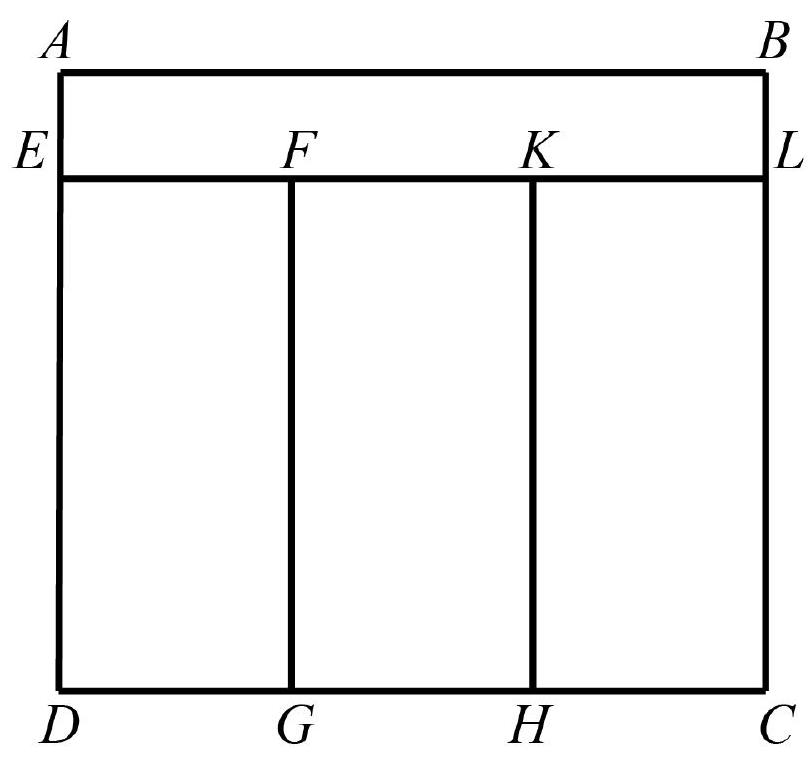
the segments $E F, F K$ and $K L$ is
$$
18 \text { cm : } 3=6 \text { cm. }
$$
The perimeter of rectangle $A B L E$ is equal to the perimeter of rectangle $D E F G$. We can solve this by setting up an equation or by trying to solve it without one.
Method 1. Let $A E=x$ cm, then $18+18+x+x=6+6+16-x+16-x$. From this, we find $x=2$. Therefore, $A E=2$ cm, and $E D=14$ cm.
Method 2. From the condition, it follows that $D E+E F=A E+A B$, that is, $D E+6=A E+18$. Then the difference in the lengths of segments $D E$ and $A E$ is 12 cm, and their sum is 16 cm according to the condition. Therefore, $A E=2$ cm, and $D E=14$ cm.
## Grading Criteria.
- Correct answer and complete explanation - 7 points.
- Correct answer with incomplete explanation - 5-6 points.
- Correct reasoning but with an arithmetic error - 3 points.
- Something is written on the picture, and the correct answer is obtained - 1-2 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A point in a triangle is connected to the vertices by three segments. What is the maximum number of these segments that can equal the opposite side?
#
|
# Answer: One.
## Solution:
Let $B M = A C$ and $A B = M C$ (see fig.). Triangles $A B M$ and $M C A$ are equal by three sides. Therefore, angle $B A M$ is equal to angle $A M C$, which means $A B \parallel M C$.
Similarly, $A C \parallel M B$.
Thus, $A B M C$ is a parallelogram, but this is not the case, because angle $B M C$, lying in this parallelogram, is greater than a straight angle.
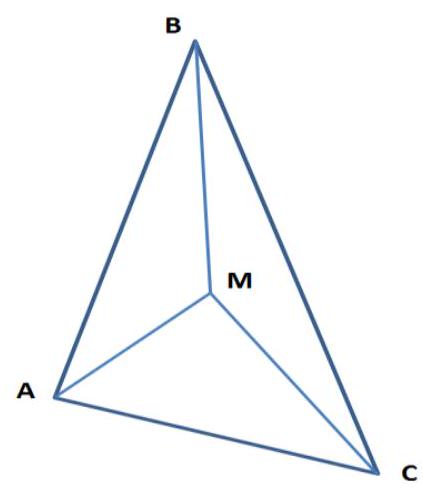
## Comment on the interpretation of the condition:
The words "Point in the triangle" imply "inside the triangle." Indeed, the solution remains valid even if point $M$ is on the boundary of the triangle. If point $M$ is chosen at a vertex, we consider this to not meet the condition of the problem ("A point in the triangle is connected to the vertices by three segments" - if the point coincides with a vertex, the segment becomes degenerate).
In other words, by default, it is assumed that the point is chosen strictly inside the triangle.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Buratino buried two ingots on the Field of Wonders: a gold one and a silver one. On the days when the weather was good, the gold ingot increased by $30 \%$, and the silver one by $20 \%$. On the days when the weather was bad, the gold ingot decreased by $30 \%$, and the silver one by $20 \%$. After a week, it turned out that one of the ingots had increased, while the other had decreased. How many days was the weather good?
|
Solution. Increasing a number by $20 \%$ is equivalent to multiplying it by 1.2, and decreasing a number by $20 \%$ is equivalent to multiplying it by 0.8 (for $30 \%$ - by 1.3 and 0.7, respectively). Therefore, the result does not depend on the sequence of good and bad weather days, but only on the number of good and bad days.
After one good and one bad day, both ingots decrease: $1.2 \cdot 0.81$, while $1.3^{4} \cdot 0.7^{3}<1$. On the other hand, after two good and one bad day, the gold ingot increases. Therefore, it also increases after four good and two bad days, and even more so after five good and two bad days. Thus, if there are five or more good days, the gold ingot grows. Therefore, only when there are four good days does one ingot grow while the other decreases. Answer: four.
Comment. If the fact that the answer does not depend on the sequence of good and bad days is used without justification, no more than 4 points are awarded.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all positive roots of the equation $x^{x}+x^{1-x}=x+1$.
#
|
# Solution
Since $x>0$, then
$0=x^{2 x}+x-x^{x+1}-x^{x}=x^{x}\left(x^{x}-1\right)-x\left(x^{x}-1\right)=x\left(x^{x}-1\right)\left(x^{x-1}-1\right)$.
Thus, $x=1$.
## Answer $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Several numbers are written on the board. It is known that the square of any written number is greater than the product of any two other written numbers. What is the maximum number of numbers that can be on the board
#
|
# Answer. 3 numbers.
Solution. Suppose there are at least four numbers, and $a-$ is the number with the smallest absolute value. Among the remaining numbers, at least two have the same sign (both non-negative or both non-positive). Let these numbers be $b$ and $c$; then $bc = |bc| \geqslant |a|^2 = a^2$, which contradicts the condition.
It remains to provide an example of three numbers that satisfy the condition. For example, the numbers $1, 2, -3$ work.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. At one meal, Karlson can eat no more than 5 kg of jam. If he opens a new jar of jam, he must eat it completely during this meal. (Karlson will not open a new jar if he has to eat more than 5 kg of jam together with what he has just eaten.)
Little Boy has several jars of raspberry jam weighing a total of 50 kg, each weighing no more than 1 kg. In the least number of meals, how many meals will Karlson definitely be able to eat all the jam?
|
Answer: 12.
Solution. We will prove that in 12 meals, Karlson will always be able to eat all the jam.
We will distribute the jars into piles according to the following algorithm. In each pile (starting with the first, then the second, and so on), we will place jars one by one until the pile contains more than 5 kg of jam. The last jar we place in the pile will be called the extra jar. Since Little has 50 kg of jam, there will be no more than 10 such piles.
Obviously, if we remove the extra jar from a pile, Karlson will be able to eat all the remaining jam in one meal. That is, Karlson will eat all the jam except the extra jars in 10 meals. And he will spend no more than 2 meals on the extra jars, as there are no more than 10 of them, and each weighs no more than 1 kg.
Now we will show that Karlson will not always be able to eat all the jam in 11 meals. Suppose there are a total of $5 \cdot 11 + 1 = 56$ jars, and each contains $\frac{25}{28}$ kg of jam. If Karlson managed to eat all of this in 11 meals, then by the pigeonhole principle, there would be a meal during which he ate at least 6 jars of jam. But $6 \cdot \frac{25}{28} = \frac{150}{28} > 5$, a contradiction.
Another construction example. We will demonstrate that Karlson will be able to eat at least $\frac{25}{6}$ kg of jam in one meal if there is at least that much jam left.
First, we will select jars one by one until we accumulate more than $\frac{25}{6}$ kg of jam. Then we will start returning the selected jars one by one so that the total remains at least $\frac{25}{6}$ kg of jam.
Suppose we can no longer return any of the selected jars, but the total amount of jam in them is still more than 5 kg. Clearly, then we have at least 6 jars, and the smallest of them contains no more than $\frac{1}{6}$ of the total mass of jam. We will select and return it; then there will be at least $\frac{5}{6} \cdot 5 = \frac{25}{6}$ kg of jam left. Contradiction. Therefore, Karlson can open and eat the remaining selected jars in one meal.
Thus, Karlson will be able to eat at least $\frac{25}{6}$ kg of jam in one meal, except for the last time when he finishes the remaining. Then, obviously, in $\frac{50}{\frac{25}{6}} = 12$ meals, he will manage.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The graph of the function $y=x^{2}+a x+b$ is shown in the figure. It is known that the line $A B$ is perpendicular to the line $y=x$. Find the length of the segment $O C$.
---
The text has been translated while preserving the original formatting and line breaks.
|
Answer: 1.
Solution. Since $y(0)=b$, then $B(0 ; b)$. Now let's find the length of the segment $O A$.
First method. Since the line $A B$ is perpendicular to the line $y=x$, it is parallel to the line $y=-x$. Moreover, this line passes through the point $B(0 ; b)$. Therefore,
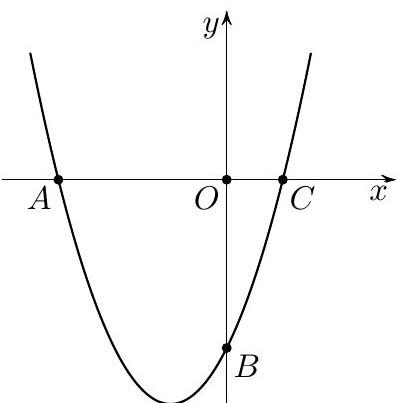
it is described by the equation $y=-x+b$. Since $y=0$ when $x=b$, then $O A=-b$.
Second method. From the problem statement, it follows that the bisector of triangle $A O B$, drawn to the side $A B$, lies on the line $y=x$, and therefore coincides with the height of this triangle. Consequently, $O A=O B=-b$.
Thus, the number $b$ and the desired length $c$ of the segment $O C$ are the roots of the quadratic equation $x^{2}+a x+b=0$. By Vieta's theorem: $b c=b$. Since $b \neq 0$, then $c=1$.
## Grading criteria: + correct answer and complete justified solution $\pm$ correct answer and solution with minor gaps in justification 干 only proved that $O A=O B$, with no further progress Ғ used the equality $O A=$ OB without proof, and then obtained the correct answer in a justified manner 干 the correct answer was obtained based on specific numerical values of a and b - only the answer is provided
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. The heights $A D$ and $B E$ of an acute-angled triangle $A B C$ intersect at point $H$. The circumcircle of triangle $A B H$ intersects sides $A C$ and $B C$ at points $F$ and $G$ respectively. Find $F G$, if $D E=$ $=5$ cm.
|
Answer: 10 cm.
Solution. Let $\angle H B F=\alpha$ (see Fig. 9.5). Then $\angle F A H=\angle H B F=\alpha$ (inscribed angles subtending the same arc). From the right triangle $A D C: \angle C=90^{\circ}-\alpha$, and from the right triangle $E C B: \angle E B C=90^{\circ}-\angle C=\alpha$.
Thus, $B E$ is the height and the angle bisector of triangle $F B C$, which means this triangle is isosceles and $B E$ is its median, i.e., $F E = E C$. Similarly, it can be shown that $C D = D G$. Therefore, $E D$ is the midline of triangle $F C G$. Hence, $F G = 2 D E = 10$ (cm).
## Grading Criteria:
+ - a complete and well-reasoned solution
- only the answer provided
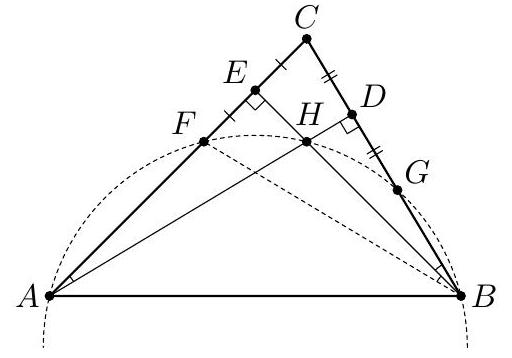
Fig. 9.5
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A natural number $n$ is called good if each of its natural divisors, increased by 1, is a divisor of the number $n+1$. Find all good natural numbers.
(S. Berlov)
|
Answer. One and all odd prime numbers.
Solution. It is clear that $n=1$ satisfies the condition. Also, all odd primes satisfy it: if $n=p$, then its divisors increased by 1 are 2 and $p+1$; both of them divide $p+1$. On the other hand, any number $n$ that satisfies the condition has a divisor 1; hence, $n+1$ is divisible by $1+1$, which means $n$ is odd.
Now suppose that some composite $n$ satisfies the condition. We have $n=a b$, where $a \geqslant b \geqslant 2$. Then the number $n+1$ is divisible by $a+1$; moreover, the number $n+b=(a+1) b$ is also divisible by $a+1$. Therefore, the number $b-1=(n+b)-(n+1)$ is also divisible by $a+1$. Since $b-1>0$, we get that $b-1 \geqslant a+1$. But this contradicts the inequality $b \leqslant a$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the sum $\sin x + \sin y + \sin z$, given that $\sin x = \tan y$, $\sin y = \tan z$, $\sin z = \tan x$
|
Answer: 0.
First solution. From $\sin x = \operatorname{tg} y$, we get $\sin x \cos y = \sin y$. Therefore, $|\sin x| \cdot |\cos y| = |\sin y|$. This means $|\sin x| \geq |\sin y|$, and the inequality becomes an equality only if either $\sin y = \sin x = 0$ or $|\cos y| = 1$ (which again implies $\sin y = \sin x = 0$). Similarly, from the remaining equations, we obtain the inequalities $|\sin y| \geq |\sin z|$ and $|\sin z| \geq |\sin x|$. Thus, $|\sin x| \geq |\sin y| \geq |\sin z| \geq |\sin x|$. Therefore, $|\sin x| = |\sin y| = |\sin z|$. Since all inequalities have become equalities, we have $\sin x = \sin y = \sin z = 0$, and $\sin x + \sin y + \sin z = 0$.
Second solution. If one of the sines is zero, then the tangent equal to it is also zero, which means the sine in the numerator of the tangent is zero. Consequently, the other sines and tangents are also zero. In this case, $\sin x + \sin y + \sin z = 0$.
Suppose none of the sines are zero. Multiplying all three equations, we get $\sin x \sin y \sin z = \operatorname{tg} y \operatorname{tg} z \operatorname{tg} x = \frac{\sin x \sin y \sin z}{\cos x \cos y \cos z}$. Since $\sin x \sin y \sin z \neq 0$, we have $\cos x \cos y \cos z = 1$. This is only possible if $|\cos x| = |\cos y| = |\cos z| = 1$, which means the sines are zero, and the considered case is impossible.
Comment. A correct answer without justification - 0 points.
An answer obtained by considering an example - 1 point.
At least one case is incorrectly considered (or omitted) - no more than 3 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. In the castle, there are 16 identical square rooms forming a $4 \times 4$ square. Sixteen people, who are either liars or knights (liars always lie, knights always tell the truth), have settled in these rooms, one person per room. Each of these 16 people said: "At least one of the rooms adjacent to mine is occupied by a liar." What is the maximum number of knights that could be among these 16 people? Rooms are considered adjacent if they share a wall.
|
Answer: 12 knights.
Solution: Note that for each knight, at least one of their neighbors must be a liar. We will show that there must be no fewer than 4 liars (thus showing that there are no more than 12 knights). Suppose there are no more than 3 liars, then there will be a "vertical row" of rooms where only knights live. However, each of these knights must have a neighbor who is a liar (and these neighbors are different). Therefore, there must be at least 4 liars.
The diagram below shows how 12 knights and 4 liars could be accommodated.
| $\mathrm{P}$ | L | $\mathrm{P}$ | $\mathrm{P}$ |
| :--- | :--- | :--- | :--- |
| $\mathrm{P}$ | $\mathrm{P}$ | $\mathrm{P}$ | L |
| L | $\mathrm{P}$ | $\mathrm{P}$ | $\mathrm{P}$ |
| $\mathrm{P}$ | $\mathrm{P}$ | L | $\mathrm{P}$ |
Comment: A correct answer without justification - 0 points.
Example of accommodating 4 liars and 12 knights - 2 points.
Proved that there are no more than 12 knights - 5 points.
Note 1: In the example, liars should not be neighbors.
Note 2: The estimate can be obtained by noting that in three rooms - a corner room and the two adjacent to it - at least one liar must reside.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a square grid of cells, some cells are painted black. It turned out that no black cell shares a side with more than one other black cell? What is the maximum number of cells that could be painted black?
In a square of cells, some cells are painted black. It turned out that no black cell shares a side with more than one other black cell? What is the maximum number of cells that could be painted black?
|
Solution. An example of properly coloring 8 squares is shown in Fig. 1a. Suppose more than 8 were colored, then at least one of the four $2 \times 2$ squares would have at least three cells colored (Fig. 1b). But then at least one of them would share adjacent sides with two other black cells. This contradiction completes the proof.

a)
b)
Fig. 1
Answer: 8.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the tournament, 15 volleyball teams are playing, and each team plays against all other teams only once. Since there are no draws in volleyball, there is a winner in each match. A team is considered to have performed well if it loses no more than two matches. Find the maximum possible number of teams that performed well.
|
Answer: 5.
Solution.
Evaluation. If the number of teams that played well is not less than 6, then consider six of them. They could have lost no more than $6 \times 2=12$ matches. But the games between them amounted to $6 \times 5 / 2=15$. Thus, they lost no fewer than 15 matches in total. Contradiction.
Example. Place the captains of 5 teams in a circle facing the center. Let each team lose to the two teams whose captains are to the right of their captain in the circle, and win against the two teams whose captains are to the left, and also win against the remaining 10 teams. The games between the 10 teams can end in any way. The five teams whose captains stand in the circle performed well. The rest lost no fewer than five matches.
Criteria. Any correct solution: 7 points.
The evaluation that 6 or more teams cannot be good: 4 points.
An example for 5 good teams is provided: 2 points.
Only the answer: 0 points.
## Grading Criteria:
| Points | Correctness (incorrectness) of the solution |
| :---: | :---: |
| 7 | Complete correct solution. |
| 6-7 | Correct solution. There are minor flaws that do not significantly affect the solution. |
| 5-6 | The solution is generally correct. However, it contains several errors or the omission of individual cases, but can become correct with minor corrections or additions. |
| 4 | One of the two (more complex) significant cases is correctly considered, or in a problem of the type "evaluation + example," the evaluation is correctly obtained. |
| 2-3 | Auxiliary statements that help in solving the problem are proven, or in a problem of the type "evaluation + example," a correct example is constructed. |
| 1 | Individual important cases are considered in the absence of a solution (or in the case of an incorrect solution). |
| 0 | The solution is incorrect, and there is no progress. |
| 0 | The solution is absent. |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let there be $x$ seventh-graders participating in the tournament, who together scored $n$ points. Then the number of eighth-graders participating in the tournament is $10 * x$ people, and the total points they scored is $4.5 * n$ points. Therefore, a total of $11 * x$ students participated in the tournament, and they collectively scored $5.5 * n$ points. The total number of points scored by all participants is equal to the number of games played. We get the equation:
$$
\begin{gathered}
5.5 * n = \frac{11 * x * (11 x - 1)}{2} \\
n = x * (11 x - 1)
\end{gathered}
$$
Each seventh-grader played $11 x - 1$ games (since there are a total of $11 x$ participants). Therefore, $x$ seventh-graders could collectively score $n$ points, i.e., $x * (11 x - 1)$ points, only if each of them won all their games. This is only possible when $x = 1$ (two seventh-graders cannot simultaneously win against each other).
|
Answer: 1 student from 7th grade participated in the tournament and scored 10 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) In Sun City, they exchange a honey cake for 6 pretzels, and for 9 pretzels, they give 4 doughnuts. How many doughnuts will they give for 3 honey cakes? Explain your answer.
|
Answer: 8.
Solution.
If for one cookie you get 6 pretzels, then for 3 cookies you will get $3 \times 6=18$ pretzels. 18 pretzels is 2 times 9 pretzels. Therefore, for them, you will get 2 times 4 gingerbread cookies, i.e., 8 gingerbread cookies.
## Grading Criteria.
- Any correct and justified solution - 7 points.
- Correct initial reasoning is provided, but incorrect conclusions are drawn or no conclusions are made - 2 points.
- The solution is complete, but one arithmetic error is made - 2 points.
- Only the correct answer - 1 point.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. For a natural number $a$, the product $1 \cdot 2 \cdot 3 \cdot \ldots \cdot a$ is denoted as $a$ !.
(a) (2 points) Find the smallest natural number $m$ such that $m$ ! is divisible by $23 m$.
(b) (2 points) Find the smallest natural number $n$ such that $n$ ! is divisible by $33n$.
|
# Answer:
(a) (2 points) 24.
(b) (2 points) 12.
Solution. (a) The condition is equivalent to $(m-1)!$ being divisible by 23. Since 23 is a prime number, at least one of the numbers $1, 2, \ldots, m-1$ must be divisible by 23, so $m-1 \geqslant 23$ and $m \geqslant 24$. Clearly, $m=24$ works, since in this case $\frac{24!}{23 \cdot 24}=22!$.
(b) The condition is equivalent to $(n-1)!$ being divisible by $33=3 \cdot 11$. Since 3 and 11 are prime numbers, at least one of the numbers $1, 2, \ldots, n-1$ must be divisible by 11, so $n-1 \geqslant 11$ and $n \geqslant 12$. Clearly, $n=12$ works, since in this case $\frac{12!}{33 \cdot 12}=\frac{10!}{3}=8! \cdot 3 \cdot 10$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. In the morning, 5 foreign cars were parked along the road. By noon, 2 domestic cars were parked between each pair of foreign cars. And by evening, a motorcycle was parked between each pair of adjacent cars. How many motorcycles were parked in total $?$
Answer: 12 .
|
Solution. Between 5 foreign cars there are 4 gaps, so there were $4 \cdot 2=8$ domestic cars parked there; that is, a total of $5+8=13$ cars were parked. Between them, 12 motorcycles were parked.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the table, there were cards with digits from 1 to 9 (a total of 9 cards). Katya chose four cards such that the product of the digits on two of them equals the product of the digits on the other two. Then Anton took one more card from the table. In the end, the cards with the digits $1,4,5,8$ remained on the table. Which card did Anton take?
|
# Answer: 7.
Solution. One of the cards that is not currently on the table has the number 7. Note that Katya could not have taken the 7, because then one of her products would be divisible by 7, while the other would not. Therefore, Anton took the 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Yulia thought of a number. Dasha added 1 to Yulia's number, and Anya added 13 to Yulia's number. It turned out that the number obtained by Anya is 4 times the number obtained by Dasha. What number did Yulia think of?
|
Answer: 3.
Solution. Note that since Anya's number is 4 times greater than Dasha's number, the difference between these numbers is 3 times greater than Dasha's number. Thus, Dasha's number is $(13-1): 3=4$. Therefore, Yulia's number is 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. Aся, Borya, Vasilina, and Grisha bought tickets to the cinema for one row. It is known that:
- There are a total of 9 seats in the row, numbered from 1 to 9.
- Borya did not sit in seat 4 or 6.
- Aся sat next to Vasilina and Grisha, and no one sat next to Borya.
- There were no more than two seats between Aся and Borya.
In which seat, with what number, was someone definitely sitting?
Answer: 5.
|
Solution. Note that Asey, Vasilina, and Grisha occupy three seats in a row, and Borya sits one seat away from them. Let's seat another child, Dima, in the free seat. Then, 5 children sit in a row. Thus, someone is sitting in the central seat of the row (that is, seat number 5). For any other seat, we can come up with an arrangement such that it is not occupied.
What if Dima is sitting in the 5th seat? Then Borya (since they are sitting next to each other) must sit either in seat 4 or 6, but this contradicts the condition. Therefore, in seat 5, either Asey, Borya, Vasilina, or Grisha is sitting.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. Masha braided her dolls: half of the dolls got one braid each, a quarter of the dolls got two braids each, and the remaining quarter of the dolls got four braids each. She tied a ribbon in each braid. How many dolls does Masha have if she needed 24 ribbons in total?
|
Answer: 12.
Solution. Note that since a quarter of the dolls have four braids, the total number of ribbons used on them is the same as the total number of dolls. Half of the dolls have one braid, so the number of ribbons used on them is half the total number of dolls. And a quarter of the dolls have two braids, so the number of ribbons used on them is also half the total number of dolls.
This means that the number of ribbons is twice the number of dolls. Therefore, Masha has a total of 12 dolls.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. Variant 1.
A square piece of paper is folded as follows: the four corners are folded to the center so that they meet at one point (see figure),
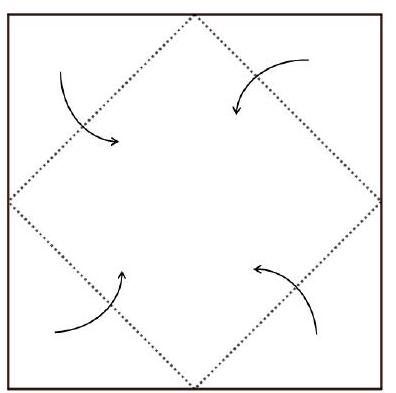
resulting in a square again. After performing this operation several times, a square with a side length of 3 cm and a thickness of 16 sheets of paper is obtained. Find the side length of the original square in centimeters.
|
Answer: 12.
Solution: After each operation, the thickness of the square doubles, and the area is halved. Since the thickness has become 16 sheets, the operation was applied 4 times. In this process, the area decreased by a factor of 16 and became equal to 9 square centimeters. Therefore, the area of the original square was $16 \times 9 = 12 \times 12 = 144$ square centimeters. Thus, the side length of the original square is 12 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the sequence of numbers $a_{1}, a_{2}, \ldots$, is an arithmetic progression, and the sequence of numbers $a_{1} a_{2}, a_{2} a_{3}, a_{3} a_{4} \ldots$, is a geometric progression. It is known that $a_{1}=1$. Find $a_{2017}$.
|
Answer: $a_{2017}=1$;
Trunov K.V.
## Solution:
Since the sequence of numbers $a_{1} a_{2}, a_{2} a_{3}, a_{3} a_{4} \ldots$, is a geometric progression, then $\left(a_{n} a_{n+1}\right)^{2}=\left(a_{n-1} a_{n}\right)\left(a_{n+1} a_{n+2}\right)$ for $n \geq 2$. From this, we obtain that $a_{n} a_{n+1}=a_{n-1} a_{n+2}$ (since $a_{n} \neq 0$ for any $n$, otherwise the geometric progression would contain an infinite number of zeros, which would mean that the arithmetic progression $a_{1}, a_{2}, \ldots$, contains an infinite number of zeros, which is impossible). Since $a_{1}, a_{2}, \ldots$, is an arithmetic progression, we can write $a_{n} a_{n+1}=a_{n-1} a_{n+2}$ as $a_{n}\left(a_{n}+d\right)=\left(a_{n}-d\right)\left(a_{n}+2 d\right) \Leftrightarrow$
$\Leftrightarrow a_{n}^{2}+a_{n} d=a_{n}^{2}+a_{n} d-2 d^{2} \Leftrightarrow-2 d^{2}=0 \Leftrightarrow d=0 \Rightarrow a_{2017}=1$.
## Recommendations for checking.
Only the answer is given without justification - 0 points.
#
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let's call a four-digit number accompanying the year $\overline{20 a b}$ if it also ends in $\overline{a b}$ and, in addition, is divisible by $\overline{a b}$ (a two-digit number), for example, the number 4623 accompanies the year 2023. How many numbers accompany the year $2022?$
|
Solution. $\overline{m n 22}=\overline{m n} \cdot 100+22 \Rightarrow \overline{m n} \cdot 100: 22 \Rightarrow \overline{m n}: 11: 11,22,33,44,55,66,77$, 88,99 - 9 numbers.
Answer 9.
## Grading Criteria.
Correct answer with valid reasoning - 7 points.
Valid reasoning for divisibility by 11 and description of the set of numbers, but incorrect answer - 5 points.
Valid reasoning for divisibility by 11 - 3 points.
Valid reasoning for divisibility by 22, leading to answers $22,44,66,88$ - 4 numbers - 1 point.
Incorrect solution or only the answer - 0 points.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many solutions does the rebus $\frac{B+O+C+b+M+O+\breve{U}}{K+J+A+C+C}=\frac{22}{29}$ have, where different letters represent different digits, and the same letters represent the same digits? It is known that the digit 0 is not used.
|
Solution. In the rebus, 9 different letters are used, i.e., all non-zero digits are used. $1+2+3+0+0 \leq K+Л+A+C+C \leq 6+7+8+9+9$, i.e.
$$
6 \leq K+Л+A+C+C \leq 39 . \quad \text { Since the fraction } \frac{22}{29} \text { is irreducible, the number }
$$
$K+Л+A+C+C$ must be divisible by 29, the only case that satisfies all conditions is $K+Л+A+C+C=29$. Therefore, $B+O+C+b+M+O+\breve{И}=22$, in the word, 6 different letters are used (O is repeated twice). Note that $1+2+3+4+5+6=21$, doubling 1 gives 22, so $\mathrm{O}=1$. The unused digits form the word КЛА, so $7+8+9+\mathrm{C}+\mathrm{C}=29,2 \mathrm{C}=5$, but C cannot be non-integer. There are no solutions.
## Answer 0
## Grading Criteria.
Correct answer obtained with justification - 7 points.
Correctly shown that the numerator is 22 and the denominator is 29 without further progress - $\underline{2}$ points.
Shown that O must be equal to 1 - $\underline{\mathbf{1} \text { point. }}$
Underlined points are summed.
Incorrect solution or only the answer - 0 points.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Different positive numbers $x, y, z$ satisfy the equations
$$
x y z=1 \quad \text{and} \quad x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}
$$
Find the median of them. Justify your answer.
|
# Solution:
Method 1. Consider the polynomial $P(t)=(t-x)(t-y)(t-z)$. The numbers $x, y, z$ are its roots. Expanding the brackets or using Vieta's theorem for cubic polynomials, we get $P(t)=t^{3}+a t^{2}+b t+c$, where $a=-(x+y+z)$, $b=xy+xz+yz$, and $c=-xyz$. The condition of the problem shows that $a=-b$ and $c=-1$. Then we have $P(t)=t^{3}-b t^{2}+b t-1=(t-1)(t^{2}-b t+1)$. This means that one of the roots of the polynomial $P(t)$ is 1, and the other two are the roots of the quadratic trinomial $t^{2}-b t+1$. By Vieta's theorem, their product is 1. Since both are positive numbers, one of them is greater than 1, and the other is less than 1.
Method 2. Express $z$ from the first equation and substitute it into the second: $z=\frac{1}{xy}$, and then
\[
\begin{gathered}
x+y+\frac{1}{xy}=\frac{1}{x}+\frac{1}{y}+xy \\
x^{2}y+xy^{2}+1=y+x+x^{2}y^{2} \\
x^{2}(y-y^{2})+x(y^{2}-1)+1-y=0 \\
(1-y)(x^{2}y-xy-x+1)=0 \\
(1-y)(x-1)(xy-1)=0
\end{gathered}
\]
Thus, either $x=1$, or $y=1$, or $xy=1 \Leftrightarrow z=1$. In any of these cases, the product of the other two numbers is 1, as follows from the first condition. Since the numbers are distinct and positive, one of them is less than 1, the second is equal to 1, and the third is greater than 1.
Answer: 1.
Note: Reference to Vieta's theorem is accepted without proof.
| in progress | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| The problem is reduced to finding the roots of a cubic equation | 2 points |
| The problem is reduced to an equation with two variables | 1 point |
| An example of numbers satisfying the conditions of the problem is provided | 0 points |
| Incorrect solution or its absence | 0 points |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. From a $7 \times 7$ square grid, an equal number of $2 \times 2$ squares and $1 \times 4$ rectangles were cut out along the grid lines. What is the maximum number of these figures that could have been cut out?
|
Answer: 12.
Solution: Both the square and the rectangle consist of 4 cells. Therefore, the number of cut-out figures is no more than 49/4, that is, no more than 12. There are an equal number of figures of both types, so there are no more than 6 squares $2 \times 2$ and rectangles $1 \times 4$. The diagram shows how to cut out 6 squares $2 \times 2$ and 6 rectangles $1 \times 4$ from the square.
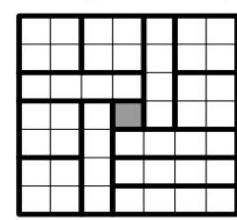
Comment: Only proved that there are no more than twelve figures - 3 points. Only provided an example of placing 12 figures - 6 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The beetle is 3 times heavier than the cat, the mouse is 10 times lighter than the cat, the turnip is 60 times heavier than the mouse. How many times heavier is the turnip than the beetle? Justify your answer.
|
# Answer. 2 times.
Solution. Cat $=10$ mice, turnip $=60$ mice. Therefore, the turnip is 6 times heavier than the cat. That is, the turnip $=6$ cats. According to the condition, Zhuchka $=3$ cats. Therefore, the turnip is 2 times heavier than Zhuchka.
## Grading Criteria.
- Correct solution - 7 points.
- Correct answer, partial explanations (some of the relationships are found), but no full justification - 3 points.
- Correct answer without explanations, how it was obtained - 2 points.
- Partial progress, for example, found that the turnip is 6 times heavier than the cat - up to 2 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.7. Initially, a natural number $N$ is written on the board. At any moment, Misha can choose a number $a>1$ on the board, erase it, and write down all natural divisors of $a$, except for $a$ itself (the same numbers can appear on the board). After some time, it turned out that there are $N^{2}$ numbers on the board. For which $N$ could this have happened?
(M. Fadin, K. Kovalenko)
|
Answer. Only for $N=1$.
Solution. Lemma. For any natural $n>1$, the inequality holds
$$
\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{n^{2}}<1
$$
Proof. Consider the function $f(t) = \frac{1}{t^{2}}$ for $t > 1$. The function $f(t)$ is decreasing for $t > 1$. Let $1 = d_{1} < d_{2} < \ldots < d_{k} < d_{k+1} = N$ be the divisors of the number $N$. Then the numbers $N / d_{1} > N / d_{2} > \ldots > N / d_{k} > N / d_{k+1}$ are also divisors of the number $N$. Therefore, they are equal to the numbers $d_{k+1}, d_{k}, \ldots, d_{2}, d_{1}$ respectively. Taking the lemma into account, we get that the total number of numbers on the board will not exceed the number
$$
\begin{aligned}
d_{1}^{2}+d_{2}^{2} & +\ldots+d_{k}^{2}=\frac{N^{2}}{d_{k+1}^{2}}+\frac{N^{2}}{d_{k}^{2}}+\ldots+\frac{N^{2}}{d_{2}^{2}}= \\
& =N^{2}\left(\frac{1}{d_{2}^{2}}+\frac{1}{d_{3}^{2}}+\ldots+\frac{1}{d_{k+1}^{2}}\right) \leqslant \\
& \leqslant N^{2}\left(\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{N^{2}}\right)<N^{2} \cdot 1=N^{2}
\end{aligned}
$$
which is what we needed to prove.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. In the castle, there are 16 identical square rooms forming a $4 \times 4$ square. Sixteen people, who are either liars or knights (liars always lie, knights always tell the truth), moved into these rooms, one person per room. Each of these 16 people said: "At least one of the rooms adjacent to mine is occupied by a liar." What is the maximum number of liars that could be among these 16 people? Rooms are considered adjacent if they share a wall.
|
Answer: 8 liars.
Solution: Note that liars cannot live in adjacent rooms (otherwise, they would be telling the truth). Let's divide the rooms into 8 pairs of adjacent rooms. Then, in each pair, there can be no more than one liar. Therefore, there can be no more than 8 liars in total. Consider a chessboard coloring of the rooms in black and white. If we place 8 liars in the "black" rooms and 8 knights in the "white" rooms, the condition of the problem will be satisfied (all liars will be lying, and all knights will be telling the truth).
Comment: A correct answer without justification - 0 points.
Example of placing 8 liars and 8 knights - 2 points.
Proven that there are no more than 8 liars - 5 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Initially, there were 10 piles of candies on the table, containing $1, 2, \ldots, 10$ candies respectively. The Child decided to redistribute the candies. On each odd minute, he chooses one pile and divides it into two piles, each containing at least one candy. On each even minute, he chooses two piles and merges them into one (thus, his first action is to divide a pile into two). Can it happen at some point that all piles on the table contain the same number of candies?
(N. Agakhanov, jury)
|
Answer: Yes.
Solution. We will provide an example of how Little One can achieve such a distribution. On the first minute, he divides the pile of 10 candies into two piles of 5 candies each. Then, on the 2nd, 4th, 6th, and 8th minutes, he combines the piles of 1+9, 2+8, 3+7, 4+6 respectively, and on the 3rd, 5th, 7th, and 9th minutes, he divides the pile of 10 candies he just received into two equal parts. By the 9th minute, he has 11 piles of 5 candies each.
Remark. There are other ways to get 11 piles of 5 candies. On the other hand, the number of piles on the table is always 10 or 11; from this, it is not hard to see that if the required result occurs, then there are exactly 11 piles of 5 candies each on the table.
Comment. Answer only - 0 points.
Any correct algorithm leading to the goal - 7 points.
|
11
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) Anya multiplied 20 twos, and Vanya multiplied 17 fives. Now they are going to multiply their huge numbers. What will be the sum of the digits of the product?
|
Answer: 8.
Solution. In total, 20 twos and 17 fives are multiplied. Let's rearrange the factors, alternating twos and fives. This results in 17 pairs of $2 \cdot 5$ and three additional twos, which multiply to 8. Thus, the number 8 needs to be multiplied by 10, 17 times. This results in a number consisting of the digit 8 followed by 17 zeros. The sum of the digits is 8. Another way to write the same reasoning using the properties of exponents is:
$$
2^{20} \cdot 5^{17}=2^{3} \cdot 2^{17} \cdot 5^{17}=8 \cdot(2 \cdot 5)^{17}=8 \cdot 10^{17}=800000000000000000 .
$$
## Grading Criteria.
- Any complete and correct solution - 7 points.
- Correct solution approach, correct product obtained, but the sum of digits not indicated - 5 points.
- Grouping of twos and fives into pairs that give tens, but the answer is not obtained or is incorrect - 2 points.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
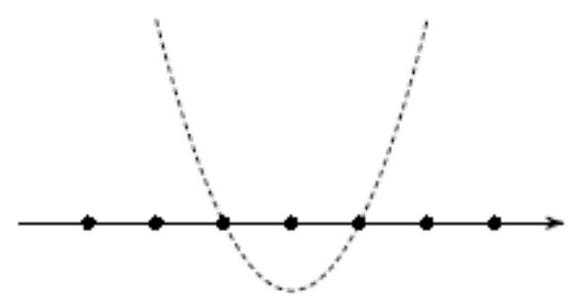
3. (7 points) The graph of a reduced quadratic trinomial is shown in the figure (the y-axis is erased, the distance between adjacent marked points is 1). What is the discriminant of this trinomial?
|
Solution. Let $x_{1}$ and $x_{2}$ be the roots of the given quadratic ( $x_{1}<x_{2}$ ). From the condition, it follows that $x_{2}-x_{1}=2$. Since $x_{2}=\frac{-b+\sqrt{D}}{2}, x_{1}=\frac{-b-\sqrt{D}}{2}$, we get that $x_{2}-x_{1}=\sqrt{D}$, hence $D=4$.
## Answer. 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) The graphs of the functions $y=k x+b$ and $y=b x+k$ intersect. Find the x-coordinate of the point of intersection.
#
|
# Solution.
Method 1. The desired abscissa is the solution to the equation $k x + b = b x + k$. This equation can be reduced to $(k - b) x = k - b$. Since the given graphs intersect (do not coincide), $k \neq b$, so $x = 1$.
Method 2. Notice that $x = 1$ is a solution to the problem, because when $x = 1$, both given linear functions take the same value $y = k + b$. Since their graphs intersect, meaning these lines have exactly one common point, there are no other solutions.
Answer. $x = 1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $\mathrm{ABC}$ with sides $\mathrm{AB}=5, \mathrm{BC}=\sqrt{17}$, and $\mathrm{AC}=4$, a point $\mathrm{M}$ is taken on side $\mathrm{AC}$ such that $\mathrm{CM}=1$. Find the distance between the centers of the circumcircles of triangles $\mathrm{ABM}$ and $\mathrm{BCM}$.
|
Answer: 2.
Solution: Draw the height BH to side AC. Let $\mathrm{CH}=x$, then $\mathrm{BH}=$ 4 - $x$. By the Pythagorean theorem from two triangles, we have $B H^{2}=B C^{2}-C H^{2}=17-x^{2}$ and $B H^{2}=A B^{2}-A H^{2}=25-(4-x)^{2}$. Equating the right sides of both equations, we get $x=1$, which means points M and H coincide. Then triangles ABM and BCM are right triangles, the centers of the circumscribed circles lie on the midpoints of the hypotenuses AB and BC. The distance between the centers is equal to the length of the midline parallel to side AC, i.e., it is equal to 2.
## MATHEMATICS
10th GRADE
Grading criteria: Correct and justified solution - 7 points, incorrect solution or only answer $-\mathbf{0}$ points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
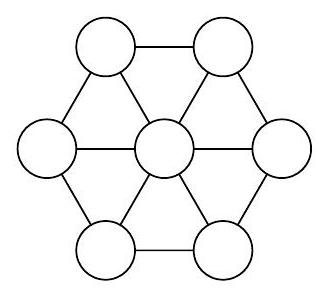
Problem 8.1. Gleb placed the numbers $1,2,7,8,9,13,14$ at the vertices and the center of a regular hexagon such that in any of the 6 equilateral triangles, the sum of the numbers at the vertices is divisible by 3. What number could Gleb have written in the center? It is sufficient to provide one suitable example.
|
Answer: 9.
Solution. Let's add the sums of the numbers in all six triangles; denote this value by $X$. On the one hand, $X$ is divisible by 3, since each term was divisible by 3 according to the condition. On the other hand, each number at the vertex of the hexagon entered $X$ twice (from two triangles), and the central number entered it 6 times. Subtracting from $X$ twice the sum of all numbers, which is $2 \cdot 54$, we get the quadrupled central number.
Divisibility by 3 is preserved in this process. This means that the number in the center is a multiple of 3. We have only one such number, which is 9.
The other numbers can be arranged around the perimeter of the hexagon so that their remainders when divided by 3 alternate; for example, in the order $1,2,7,8,13,14$.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. A field was partially planted with corn, oats, and millet. If the remaining part is completely planted with millet, then millet will occupy half of the entire field. If the remaining part is equally divided between oats and corn, then oats will occupy half of the entire field. By what factor will the amount of corn increase if the remaining part is completely planted with corn?
|
Answer: 3.
Solution. Let the area of the entire field be 1, and the empty part be $x$. Then, from the first condition, millet occupies $\frac{1}{2}-x$, and from the second condition, oats occupy $\frac{1}{2}-\frac{1}{2} x$.
Corn is left with $1-x-\left(\frac{1}{2}-x\right)-\left(\frac{1}{2}-\frac{1}{2} x\right)=\frac{1}{2} x$. If we add $x$ to this, we get $\frac{3}{2} x$, which means the area planted with corn will triple.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Semyon has 20 numbers: $1,2,3, \ldots, 19,20$. He formed 10 fractions by writing ten of these numbers in some order as numerators, and the remaining ten in some order as denominators. What is the maximum number of integers Semyon could obtain after simplifying all the written fractions?
|
Answer: 8 numbers.
## Solution:
For the fractions to have an integer value, the prime numbers $11, 13, 17, 19$ can only be numerators with a denominator of 1. Therefore, to form fractions equal to an integer, no more than 17 numbers can be used, meaning no more than 8 fractions can be formed. Example: 20/10, 19/1, $18 / 9, 16 / 8, 15 / 5, 14 / 7, 12 / 6, 4 / 2$.
## Criteria:
Correct answer without a correct example of fractions - 1 point.
Correct answer with an example of 8 fractions - 3 points.
The idea that each of the numbers 11, 13, 17, and 19 can only be present in one reducible fraction - 2 points.
(If all the above is present, only a correct conclusion remains to be drawn - and to get a full 7 points.)
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. What is the total number of emeralds in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
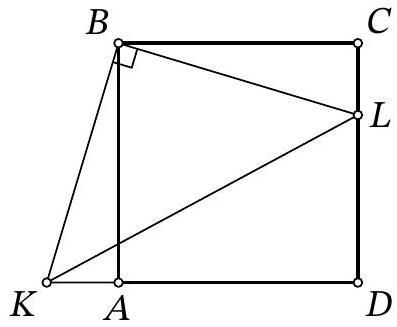
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $ABCD$ is a square, then $AB=BC=CD=AD$.
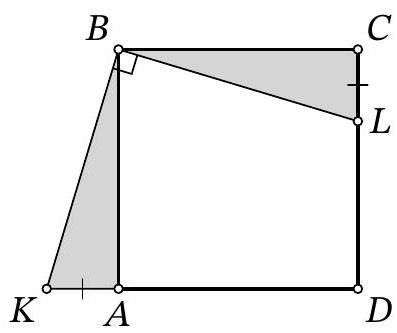
Fig. 1: to the solution of problem 8.4
Notice that $\angle ABK = \angle CBL$, since they both complement $\angle ABL$ to $90^{\circ}$. Therefore, right triangles $ABK$ and $CBL$ are congruent by the acute angle and the leg $AB = BC$ (Fig. 1). Consequently, $AK = CL = 6$. Then
$$
LD = CD - CL = AD - CL = (KD - AK) - CL = KD - 2 \cdot CL = 19 - 2 \cdot 6 = 7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
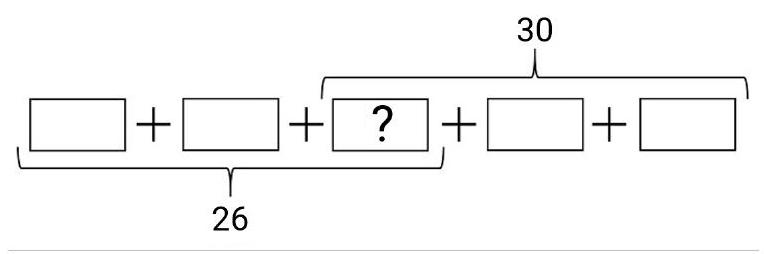
2.1. The numbers 7, 8, 9, 10, 11 are arranged in a row in some order. It turned out that the sum of the first three of them is 26, and the sum of the last three is 30. Determine the number standing in the middle.
|
Answer: 11
Solution. If we add the sum of the first three and the sum of the last three, we get the sum of all four numbers once and the middle number twice. Since the sum of all five numbers is $7+8+9+10+11=45$, and the sum of 26 and 30 is 56, then the number counted twice is 11.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Alina travels to school by bus. The bus runs on a schedule every 15 minutes. It always takes the girl the same number of minutes to get to the bus stop. If she leaves home at 8:20, she will be at school at 8:57, but if she leaves home at 8:21, she will be late for school. Classes start at 9:00. How many minutes will Alina be late for school if she leaves home at 8:23?
|
Answer: 12
Solution. Since Alina is late for school if she leaves home one minute after 8:20, leaving 1, 2, ... 15 minutes after 8:20, she will catch the next bus, which means she will arrive at school 15 minutes later than 8:57, i.e., she will arrive at school at 9:12.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Each of the 37 hexagonal cells has 3, 4, or 6 neighbors. Some of the cells were filled with chips. After that, in each free cell that is adjacent to at least two cells containing chips, the number of these neighboring chips was written. Then the chips were removed, and only the numbers remained on the diagram. How many chips were there?
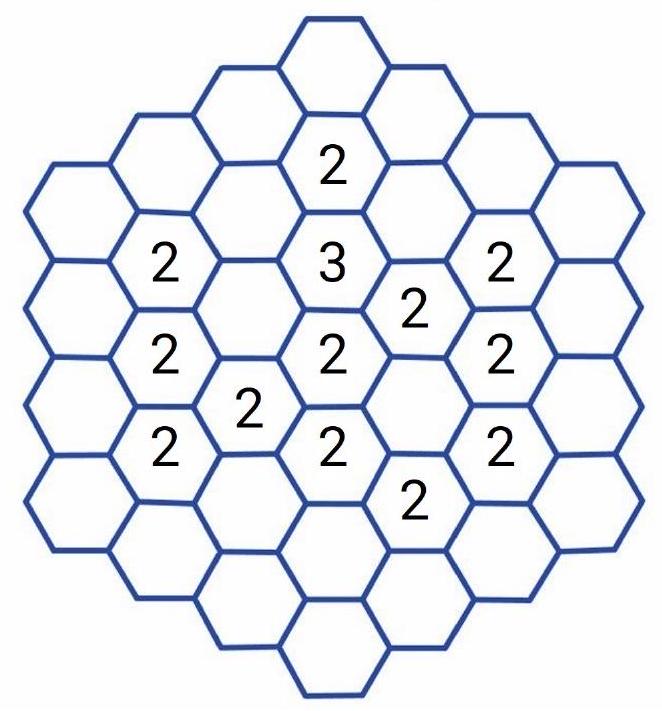
#
|
# Answer: 8
Solution. Let's look at the picture on the left. Consider the triplet and the central pair. We understand that the chips must be placed at the positions of the yellow crosses. Next, we understand the red minuses - the absence of chips. Then we place the chips at the positions of the green crosses. And the blue minuses - the absence of chips. The purple question mark - can a chip be placed here? We understand that no, because otherwise, at the position of the adjacent blue minus, there should be a 2, but there isn't one. Therefore, we place the chips at the positions of the purple crosses (also considering that no empty cells should be adjacent to two chips, otherwise, there would be numbers in them).
In the end, the chips are placed as shown in the picture on the right.
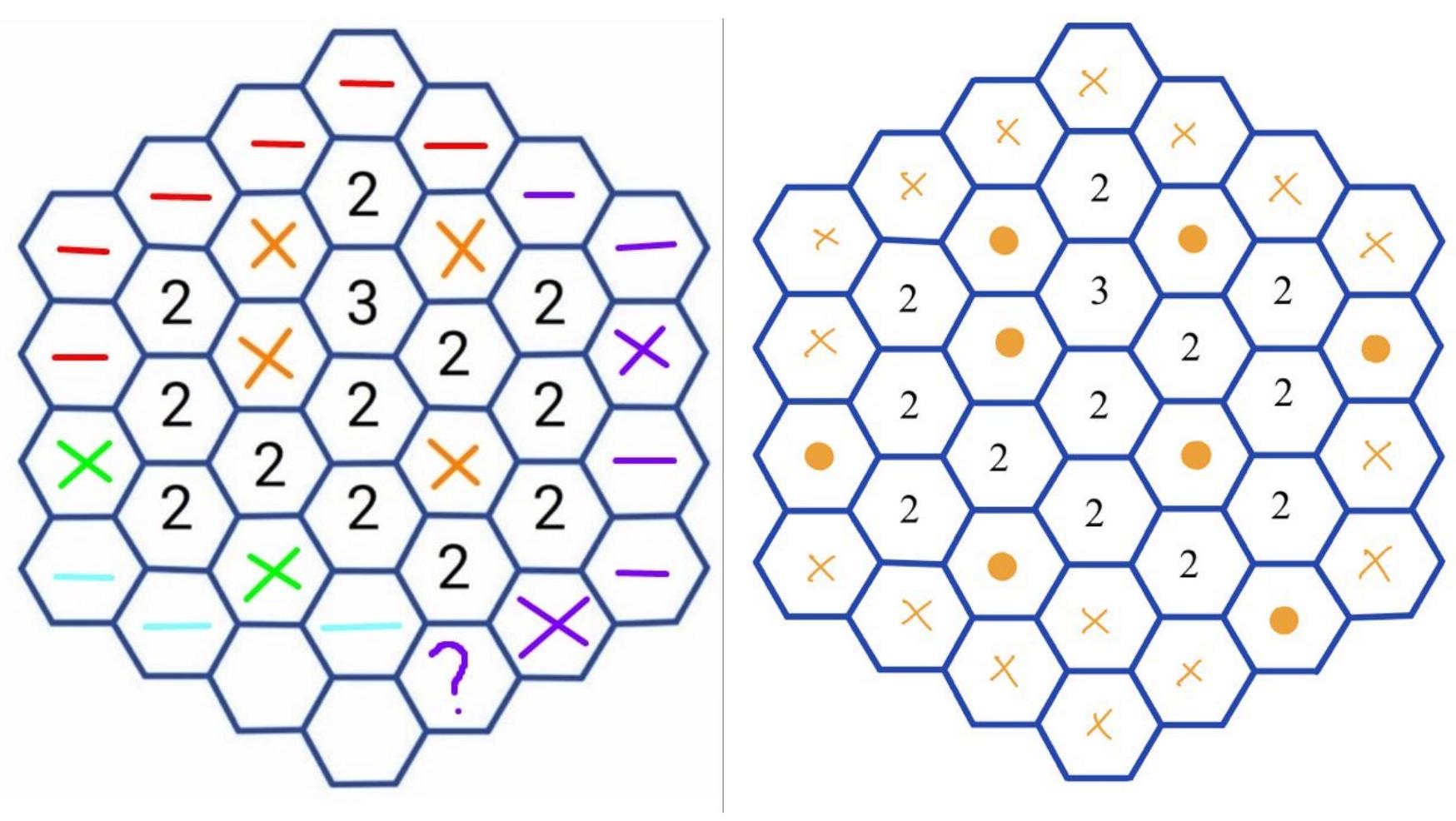
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a football tournament where each team played against each other once, teams A, B, C, D, E, and F participated. Teams received 3 points for a win, 1 point for a draw, and 0 points for a loss. In the end, it turned out that teams A, B, C, D, and E each had 7 points. What is the maximum number of points that team $\mathrm{E}$ could have?
|
4. In a match where one of the teams won, the teams together score 3 points; in a match that ended in a draw, - 2 points. Since 7 is not divisible by 3, a team that scored 7 points must have at least one draw. Since there are five such teams, there were at least three draws in the tournament. In total, as is easy to check, 15 matches were played. Therefore, all teams together scored no more than $2 \cdot 3 + 3 \cdot 12 = 42$ points. Of these, 35 points were scored by teams A, B, V, G, and D. Therefore, team $\mathrm{E}$ scored no more than $42 - 35 = 7$ points. How it could have scored exactly 7 points is shown in the table.
| | A | B | V | G | D | E |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| A | X | 3 | 3 | 1 | 0 | 0 |
| B | 0 | X | 3 | 3 | 1 | 0 |
| V | 0 | 0 | X | 3 | 3 | 1 |
| G | 1 | 0 | 0 | X | 3 | 3 |
| D | 3 | 1 | 0 | 0 | X | 3 |
| E | 3 | 3 | 1 | 0 | 0 | X |
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Sasha invited Dima to visit, saying that he lives in entrance 10, apartment No. 333, but forgot to mention the floor. Approaching the building, Dima noticed that the building is nine-story. Which floor should he go to?
|
3. $333=9 \cdot 37=10 \cdot 33+3$. Therefore, the number of apartments in the entrance is less than 37 but more than 33. In this range, only 36 is divisible by 9. So, there are 36 apartments in the entrance, and 4 on each floor. Since $333=9 \cdot 36+2 \cdot 4+1$, apartment 333 is on the third floor.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The graphs of the functions $y=a x^{2}+b x+1$ and $y=x^{2}+c x+d$ intersect at the point with coordinates ( $2 ; 4$ ). What is the value of the expression $4 a+d$, if $b+c=1$ ?
|
Answer: 1.
Solution: Since the graphs pass through the point with coordinates (2; 4), then $4=4a+2b+1$ and $4=4+2c+d$. Therefore, $4a+2b=3$, and $2c+d=0$, or $4a=3-2b, d=-2c$. Summing up the obtained expressions: $4a+d=3-2b-2c=3-2(b+c)=3-2=1$. Note: The condition is satisfied by the functions $y=ax^2+bx+1$ and $y=x^2+cx+d$ when $a=1, b=-1/2, c=3/2, d=-3$.
Criteria: Only the answer - 0 points. If the solution is found by selecting suitable values of $a, b, c$ and $d-3$ points. Correctly found values of the expressions $4a+2b=3$ and $2c+d=0$, but no further progress in the solution (or incorrect further solution) - 4 points. 7 points for a complete and correct solution.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two candles of different thickness, each 24 cm long, are lit simultaneously. The thin candle burns out in 4 hours, the thick one in 6 hours. After what time will one candle be half the length of the other? It is assumed that each candle burns uniformly, meaning it decreases by the same height over equal time intervals. The comparison is made between the unburned portions of the candles.
|
Solution. Let $x$ hours $(x<4)$ have passed since the candles were lit. Since the thin candle decreases by $24: 4=6$ cm every hour, it will decrease by a length of $6 x$ in this time, leaving an unburned stub of length $24-6 x$. Similarly, the stub of the second candle will have a length of $24-4 x$. For one candle to become half the length of the other, the condition $2(24-6 x)=24-4 x$ must be satisfied, from which $x=3$. Answer: in 3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. On a sheet of paper, three intersecting circles are drawn, forming 7 regions. We will call two regions adjacent if they share a common boundary. Regions that border at exactly one point are not considered adjacent.
Two regions already have numbers written in them. Write integers in the remaining 5 regions so that the number in each region equals the sum of all numbers in adjacent regions. What number should be in place of the question mark?
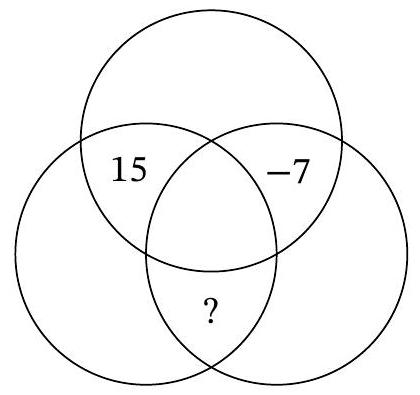
|
Answer: -8.
Solution. Let the unknown number be $x$. Then we can place the numbers in the other regions as follows:
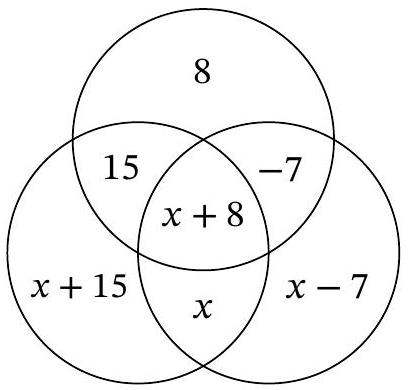
The sum of the numbers in the regions surrounding $x$ should be equal to $x$. We can write this as:
$$
(x+15)+(x+8)+(x-7)=x
$$
Solving the equation, we get $x=-8$. It is easy to verify that the condition of the problem is also satisfied for the other regions.
|
-8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. Petya and Daniil are playing the following game. Petya has 36 candies. He lays out these candies in the cells of a $3 \times 3$ square (some cells may remain empty). After this, Daniil chooses four cells forming a $2 \times 2$ square and takes all the candies from there. What is the maximum number of candies that Daniil can guarantee to take?
|
# Answer: 9.
Solution. If Petya places 9 candies in each corner cell (and does not place any candies in the other cells), then in any $2 \times 2$ square there will be exactly 9 candies. After this, Daniil will be able to take only 9 candies.
Let's prove that Daniil can get at least 9 candies. Suppose the opposite: let him be able to take no more than 8 candies for any choice of a $2 \times 2$ square. Let him then sequentially take candies from all $x$ four $2 \times 2$ squares: first from one (no more than 8 candies), then the remaining candies from the next square (also no more than 8), then from the third square, and then from the fourth. At each step, he could take no more than 8 candies, so in total he will take no more than 32. But there should be 36. Contradiction.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.2. During a physical education class, 25 students from 5B class lined up. Each of the students is either an excellent student who always tells the truth, or a troublemaker who always lies.
Excellent student Vlad stood in the 13th place. Everyone except Vlad stated: "There are exactly 6 troublemakers between me and Vlad." How many troublemakers are there in the line?
|
Answer: 12.
Solution. Note that students in places $7-12$ are troublemakers, since there are fewer than 6 people between each of them and Vlad. Therefore, the student with number 6 is an excellent student. The same can be said about the student in the 5th place, then about the 4th, the 3rd, the 2nd, and the 1st.
Thus, the first six places are occupied by excellent students, the next six places are occupied by troublemakers, and Vlad is already at place 13. Similar reasoning can be applied to students in places $14-25$. Therefore, there are exactly $6+6=12$ troublemakers in the line.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5.4. Masha drew two little people in her notebook. The area of each cell is 1.
Which of the little people has a larger area?
What is the difference? If the areas are the same, write "0" in the answer.
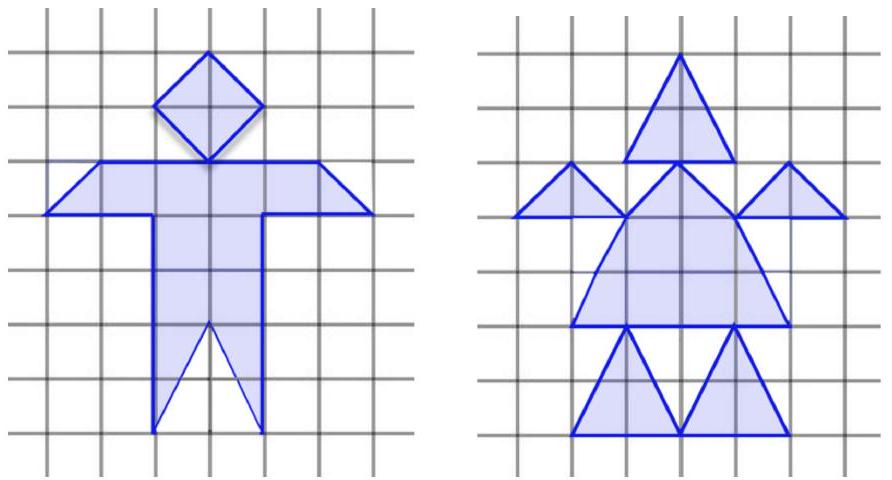
|
Answer: The area of the right human figure is 2 more than the area of the left one.
Solution. Let's calculate the areas of the human figures.
As can be seen from the figure on the right, the first human figure consists of
- 8 whole cells,
- 6 small triangles (each of which is equal to half a cell),
- 2 large triangles (each of which is equal to half a rectangle $1 \times 2$).
Every two small triangles "add up to one whole cell" in total, so their total area is 1. Every two large triangles "add up to one rectangle $1 \times 2$" in total, so their total area is 2.
Then the area of the first human figure is
$$
8 \cdot 1 + 3 \cdot 1 + 1 \cdot 2 = 13
$$
As can be seen from the figure on the right, the second human figure consists of
- 4 whole cells,
- 6 small triangles (each of which is equal to half a cell),
- 8 large triangles (each of which is equal to half a rectangle $1 \times 2$).
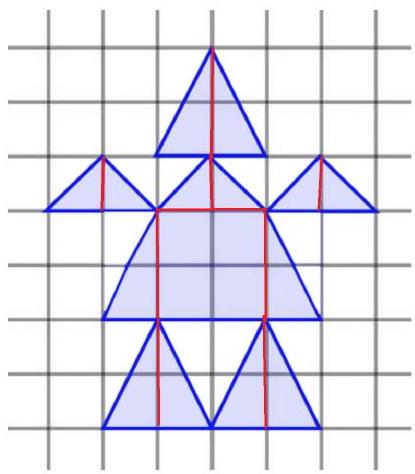
Then the area of the second human figure is
$$
4 \cdot 1 + 3 \cdot 1 + 4 \cdot 2 = 15
$$
Thus, the area of the second (right) human figure is 2 more than the area of the first (left) one.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. 20 schoolchildren came to the mathematics Olympiad. Everyone who brought a pencil also brought a pen. 12 people forgot their pencils at home, and 2 schoolchildren forgot their pen. By how many fewer schoolchildren brought a pencil than those who brought a pen but forgot a pencil?
|
Answer: 2.
Solution: 8 students brought a pencil, which means they also brought a pen. 18 students brought a pen. Therefore, 10 students brought a pen without a pencil. Then 10-8=2.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. 5.1. An isosceles trapezoid \(ABCD\) is inscribed in a circle with diameter \(AD\) and center at point \(O\). A circle is inscribed in triangle \(BOC\) with center at point \(I\). Find the ratio of the areas of triangles \(AID\) and \(BIC\), given that \(AD=15, BC=5\).
|
Answer: 9.
## Solution.
From the fact that $A D$ is the diameter of the circle circumscribed around the trapezoid, it follows that $A O = B O = C O = D O$ as radii. Therefore, triangle $B O D$ is isosceles. Hence, $\angle O B D = \angle O D B = \angle D B C$ (the last equality is due to $A D \parallel B C$). Thus, $B D$ is the bisector of angle $O B C$. Similarly, $A C$ is the bisector of angle $O C B$. Since the center of the inscribed circle in triangle $B O C$ coincides with the intersection of the angle bisectors, we have: $I = A C \cap B D$. Further, due to the similarity of triangles $A I D$ and $B I C$, the areas are proportional to the square of the similarity coefficient: $\left(\frac{A D}{B C}\right)^{2} = \left(\frac{15}{5}\right)^{2} = 9$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Petya writes on the board such different three-digit natural numbers that each of them is divisible by 3, and the first two digits differ by 2. What is the maximum number of such numbers he can write if they end in 6 or 7?
|
Answer: 9
Solution. A number is divisible by 3 if the sum of its digits is a multiple of 3. If the number ends in 6, then the sum of the other two digits leaves a remainder of 0 when divided by 3. Such numbers are: 2,4 and 4,2; 5,7 and 7,5. If the number ends in 7, then the sum of the other two digits leaves a remainder of 2 when divided by 3. Such numbers are: 2,0; 3,5 and 5,3; 6,8 and 8,6. In total, there are 9 numbers: 246, 426, 576, 756, 207, 357, 537, 687, 867.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Every hour, between two adjacent nettle bushes in a row, two more of the same grow. How many bushes do you need to plant initially so that after three hours, the total number of bushes together is 190?
|
Answer: 8
Solution. If at the moment there are $\mathrm{n}$ bushes, then on the next move their number increases by $2(n-1)$. Thus, if after 3 hours the total number of bushes should be 190, then one hour before that, there should be $\frac{190-1}{3}+1=64$. One more hour back, $\frac{64-1}{3}+1=22$. And on the next move $\frac{22-1}{3}+1=8$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. 40 people came into a room where there were 40 chairs, black and white, and sat on them. All of them said they were sitting on black chairs. Then they somehow resat, and exactly 16 claimed they were sitting on white chairs. Each of those sitting either lied both times or told the truth both times. How many of them lied the second time and were sitting on black chairs?
|
Answer: 8
Solution. Initially, everyone who told the truth sat on black chairs, and everyone who lied sat on white ones. After some of them switched chairs, 16 claimed they were sitting on white chairs. Obviously, this group includes those who told the truth and were sitting on white chairs, and those who switched with them - they lied and were sitting on black chairs. Since their numbers are equal, exactly half of them - 8 - lied and were sitting on black chairs.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. On Fyodor's bookshelf, there are volumes of works by various authors. When a friend borrowed two volumes of Pushkin, Fyodor noticed that among the remaining books, he had read at least half of them in full. After the friend returned the two volumes of Pushkin and borrowed two volumes of Lermontov, Fyodor realized that among the remaining books, he had read less than one third of them in full. What is the greatest number of volumes that could have been on the shelf at Fyodor's?
|
Answer: 12
Solution. Let's number all of Fyodor's books from 1 to $\mathrm{n}$.
Let the first two volumes be Pushkin's, $s_{1}$ - the number of them read by Fyodor; the last two - Lermontov's, $s_{2}$ - the number of them read by Fyodor. $S$ - the number of read volumes among the books from 3 to $n-2$.
According to the condition,
$S+s_{2} \geqslant \frac{n-2}{2}, S+s_{1}<\frac{n-2}{3}$,
$3 S+3 s_{1}<n-2 \leqslant 2 S+2 s_{2}$,
$3 S+3 s_{1}<2 S+2 s_{2}$
$S<2 s_{2}-3 s_{1} \leqslant 4$
Thus, $S$ does not exceed 3. Then the maximum possible $S=3$. From this, $n \leqslant 12$. Example for 12 (1 read, 0 - not read): 001110000011.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. There are nuts in three boxes. In the first box, there are six fewer nuts than in the other two boxes combined, and in the second box, there are ten fewer nuts than in the other two boxes combined. How many nuts are in the third box? Justify your answer.
|
Solution: Let there be $x$ nuts in the first box, $y$ and $z$ in the second and third boxes, respectively. Then the condition of the problem is given by the equations $x+6=y+z$ and $x+z=y+10$. From the first equation, $x-y=z-6$, and from the second, $x-y=10-z$. Therefore, $z-6=10-z$, from which $z=8$.
Answer: 8 nuts.
| in progress | points |
| :--- | :--- |
| correct and fully justified answer | 7 points |
| an incorrect answer due solely to arithmetic errors | 6 points |
| the system of equations describing the problem condition is correctly set up but not solved | 3 points |
| a specific example (examples) of the distribution of nuts in the boxes (and, therefore, the correct answer) is provided | 1 point |
| only the correct answer is given without justification (or with incorrect justification) | 0 points |
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
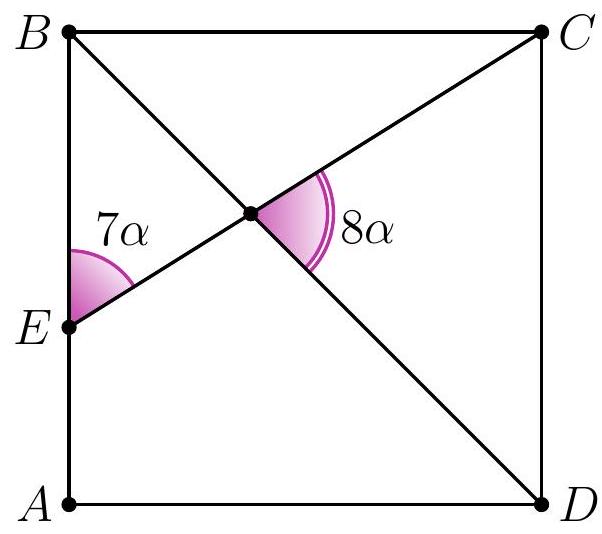
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
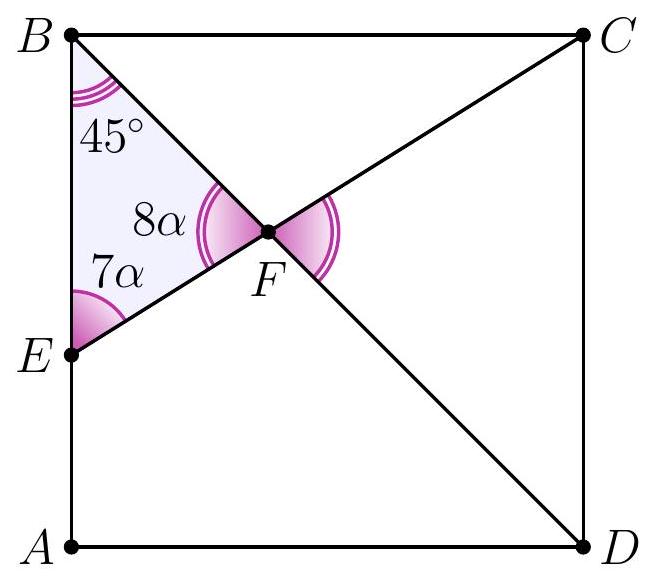
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
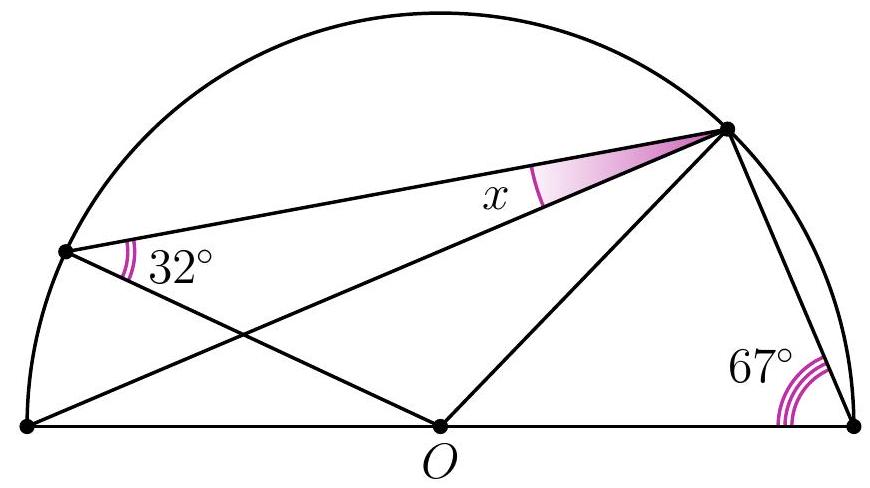
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. All values of the quadratic trinomial $f(x)=a x^{2}+b x+c$ on the interval $[0 ; 2]$ do not exceed 1 in absolute value. What is the greatest value that the quantity $|a|+|b|+|c|$ can have under these conditions? For which function $f(x)$ is this value achieved?
|
Answer: the maximum value is 7; for example, it is achieved for $f(x)=2 x^{2}-4 x+1$.
Solution. By the condition, the values of $f(x)=a x^{2}+b x+c$ on the interval $[0 ; 2]$ do not exceed one in absolute value. In particular, $|f(0)| \leqslant 1,|f(1)| \leqslant 1,|f(2)| \leqslant 1$, which is equivalent to the system
$$
\left\{\begin{array}{r}
|c| \leqslant 1 \\
|a+b+c| \leqslant 1 \\
|4 a+2 b+c| \leqslant 1
\end{array}\right.
$$
Since the absolute value of the sum of numbers does not exceed the sum of their absolute values, we obtain the inequalities
$$
\begin{aligned}
& |2 a|=|(4 a+2 b+c)-2(a+b+c)+c| \leqslant|4 a+2 b+c|+2|(a+b+c)|+|c| \leqslant 4 \\
& |2 b|=|4(a+b+c)-(4 a+2 b+c)-3 c| \leqslant 4|a+b+c|+|4 a+2 b+c|+3|c| \leqslant 8
\end{aligned}
$$
from which $|a| \leqslant 2,|b| \leqslant 4$, and thus, $|a|+|b|+|c| \leqslant 7$.
For the function $f(x)=2 x^{2}-4 x+1$, the quantity $|a|+|b|+|c|$ is exactly 7. Moreover, the quadratic trinomial $f(x)=2 x^{2}-4 x+1=2(x-1)^{2}-1$ satisfies the condition of the problem, since for $x \in[0 ; 2]$
$$
-1=f(1) \leqslant f(x) \leqslant f(0)=f(2)=1
$$
Thus, the maximum value of the quantity $|a|+|b|+|c|$ under the given conditions is 7.
Criteria. Correct answer -0 points. The inequality $|c| \leqslant 1$ is proven -1 point. Only one of the inequalities $|a| \leqslant 2$ or $|b| \leqslant 4$ is proven - another 2 points. It is proven that the sum of the absolute values does not exceed $7,-5$ points (not cumulative with previous points). Example of a function without justification of the estimate 2 points. Full solution -7 points.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. It is known that the quadratic equations in $x$, $2017 x^{2} + p x + q = 0$ and $u p x^{2} + q x + 2017 = 0$ (where $p$ and $q$ are given real numbers) have one common root. Find all possible values of this common root and prove that there are no others.
|
Solution: Let $x_{0}$ be the common root of these equations, that is, the equalities $2017 x_{0}^{2} + p x_{0} + q = 0$ and $p x_{0}^{2} + q x_{0} + 2017 = 0$ are satisfied. Multiply both sides of the first equation by the number $x_{0}$ and subtract the second equation. We get the consequential equation: $2017 x_{0}^{3} - 2017 = 0$, from which $x_{0} = 1$. Substituting this root into any of the original equations, we get the equality $p + q + 2017 = 0$. This means that when $p + q = -2017$, both equations indeed have a common root equal to 1, and if this sum equals another number, there are simply no common roots.
Answer: 1.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Correctly written roots of both quadratic equations and at least one case of coinciding roots is correctly investigated | 4 points |
| Noted that if $1$ is a root, then this root is common, but not proven that there can be no other common roots | 1 point |
| Correct answer without justification and/or calculations from which the solution process is not visible | 0 points |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. On a plane, a semicircle with diameter $A B=36$ cm was constructed; inside it, a semicircle with diameter $O B=18$ cm was constructed ($O-$ the center of the larger semicircle). Then, a circle was constructed that touches both semicircles and the segment АО. Find the radius of this circle. Justify your answer.
|
Solution: Let the desired radius be $x$. Let points $C$ and $Q$ be the centers of the smaller semicircle and the inscribed circle, respectively, and $D$ be the point of tangency of the inscribed circle with the diameter $AB$. Due to the tangency of the circle and the larger semicircle, the ray $OQ$ passes through the point of tangency, so $OQ = 18 - x$. Due to the tangency of the circle and the smaller semicircle, the segment $CQ$ passes through the point of tangency, so $CQ = 9 + x$. Due to the tangency of the circle and the segment $AB$, the segment $QD$ equals $x$ and is the height of triangle $QOC$. In triangle $QOC$, all three sides and the height are expressed through $x$. We will find the area of the triangle in two ways. The semiperimeter of the triangle is $\frac{9 + (18 - x) + (9 + x)}{2} = 18$ and by Heron's formula, its area is $\sqrt{18 \cdot (18 - 9) \cdot (18 - (18 - x)) \cdot (18 - (9 + x))} = \sqrt{18 \cdot 9 \cdot x \cdot (9 - x)}$. This area is also equal to half the product of the height and the side to which the height is drawn, that is, it is equal to $\frac{9 \cdot x}{2}$. From the equation $\sqrt{18 \cdot 9 \cdot x \cdot (9 - x)} = \frac{9 \cdot x}{2}$, we find $x = 8$.
Answer: 8 cm
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The correct approach to the solution resulted in an incorrect answer due to errors in calculations (algebraic or arithmetic) | 6 points |
| The elements of triangle $QOC$ are correctly written (in terms of the unknown), fully defining the triangle, but the solution is not completed to the answer | 5 points |
| Triangle $QOC$ is considered, but not all elements defining it are found (expressed) | 3 points |
| The correct application of the coordinate method, which is not completed to the answer (depending on the degree of progress) | 1 - 3 points |
| Correct answer without justification and/or any calculations from which the solution process is not clear | 0 points |
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. We will call a natural number semi-prime if it is greater than 25 and is the sum of two distinct prime numbers. What is the maximum number of consecutive natural numbers that can be semi-prime? Justify your answer.
|
Solution: There are many sets of five consecutive semiprime numbers, for example $30(=13+17), 31(=2+29), 32(=3+29), 33(=2+31), 34$ $(=5+29)$ or $102(=5+97), 103(=2+101), 104(=31+73), 105(=2+103)$, $106(=47+59)$. We will show that there are no six consecutive semiprime numbers.
Indeed, among any six consecutive numbers, exactly three are odd, and these odd numbers increase by a step of 2. If an odd number is represented as the sum of two natural numbers, then one of the addends is even, and the other is odd. If both addends are prime, then the even one must be 2. Therefore, these odd semiprime numbers have the form $2+p_{1}, 2+p_{2}$, and $2+p_{3}$. In this case, the numbers $p_{1}, p_{2}$, $p_{3}$ are consecutive odd numbers. Among any three consecutive odd numbers, one is divisible by 3. Since it is prime, it must be 3. Then one of the numbers is 5, and it is not semiprime because it is less than 25. Contradiction.
Answer: 5 numbers.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| If the proof that there are no more than 5 numbers is correct, but the example of 5 consecutive semiprime numbers is missing | 4 points |
| Only an example (or examples) of 5 consecutive semiprime numbers is provided | 2 points |
| Correct answer without justification and/or examples of consecutive semiprime numbers in a quantity less than 5, and/or a more crude estimate of their quantity. | 0 points |
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Inside a convex pentagon, a point is marked and connected to all vertices. What is the maximum number of the ten segments drawn (five sides and five segments connecting the marked point to the vertices of the pentagon) that can have a length of 1? (A. Kuznetsov)
|
Answer: 9 segments.
Solution. First, we prove that all 10 segments cannot have a length of 1. Assume the opposite. Let $A B C D E$ be a pentagon, $O$ be a point inside it, and all 10 drawn segments have a length of 1 (see Fig. 6). Then triangles $O A B, O B C$, $O C D, O D E$, and $O E A$ are equilateral, so $\angle A O B = \angle B O C = \angle C O D = \angle D O E = \angle A O E = 60^{\circ}$. The sum of these angles should be $360^{\circ}$, but $5 \cdot 60^{\circ} = 300^{\circ}$, which is a contradiction.
Fig. 6
Fig. 7
It remains to provide an example where 9 segments have a length of 1 (see Fig. 7). Mark points $A$ and $O$ on the plane at a distance of 1. Choose points $B, C, D$, and $E$ sequentially so that triangles $A O B, B O C, C O D$, and $D O E$ are equilateral. Then point $O$ lies inside the pentagon $A B C D E$, and out of the 10 drawn segments, all except $A E$ have a length of 1.
Remark. In the given example, points $A, B, C, D$, and $E$ are five vertices of a regular hexagon with side length 1.
Comment. Only the proof that there are no more than 9 segments of unit length - 3 points.
Only the example showing that 9 segments of unit length can be found - 3 points.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. Masha lives in apartment No. 290, which is located in the 4th entrance of a 17-story building. On which floor does Masha live? (The number of apartments is the same in all entrances of the building on all 17 floors; apartment numbers start from 1.$)$
|
# Answer: 7.
Solution. Let $x$ be the number of apartments per floor, then there are $17 x$ apartments in each entrance. Thus, in the first three entrances, there are $51 x$ apartments, and in the first four $68 x$.
If $x \geqslant 6$, then in the first three entrances there are at least 306 apartments, so apartment No. 290 cannot be located in the fourth entrance. And if $x \leqslant 4$, then in the first four entrances there will be no more than 272 apartments, which again means that apartment No. 290 cannot be located in the fourth entrance. The only remaining option is when $x=5$.
Then in the first three entrances, there are 255 apartments, and apartment No. 290 is the 35th in the fourth entrance, i.e., it is located on the 7th floor.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. The product of positive numbers $a$ and $b$ is 1. It is known that
$$
(3 a+2 b)(3 b+2 a)=295
$$
Find $a+b$.
|
Answer: 7.
Solution. Expanding the brackets, we get
$$
295=6 a^{2}+6 b^{2}+13 a b=6\left(a^{2}+b^{2}\right)+13
$$
from which $a^{2}+b^{2}=47$. Then
$$
(a+b)^{2}=a^{2}+b^{2}+2 a b=47+2=49=7^{2}
$$
which gives $a+b=7$ (note that $a+b>0$, since $a>0$ and $b>0$).
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Real numbers $a$ and $b$ are such that $a^{5}+b^{5}=3, a^{15}+b^{15}=9$. Find the value of the expression $a^{10}+b^{10}$.
|
Answer: 5.
Solution. Let $x=a^{5}, y=b^{5}$. Then $x+y=3, x^{3}+y^{3}=9 ;(x+y)\left(x^{2}-x y+y^{2}\right)=9$; $3\left(x^{2}-x y+y^{2}\right)=9 ; x^{2}-x y+y^{2}=3 ; x^{2}+2 x y+y^{2}=9 ; 3 x y=6 ; x y=2 ; x^{2}+y^{2}=9-2 x y=9-$ $2 \cdot 2=5 ; a^{10}+b^{10}=x^{2}+y^{2}=5$
Criteria. Simplification using substitution was done, but the solution is not complete: 1 point.
The value $x y=2$ was found, but the solution is not complete: 3 points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. In each cell of a $6 \times 6$ table, numbers are written. All the numbers in the top row and all the numbers in the left column are the same. Each of the other numbers in the table is equal to the sum of the numbers written in the two adjacent cells - the cell to the left and the cell above. What number can be written in the top-left corner cell if the number in the bottom-right corner cell is 2016?
|
Answer: 8. Let $a$ be the number written in the corner cell at the top left. Then the table is filled in sequentially. For the bottom right corner, we get the relation $252 a = 2016$, from which it follows that $a = 8$.
Comment. An answer with a chain of calculations - 7 points. An answer obtained using combinatorial considerations - Pascal's triangle - 7 points.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A $5 \times 5$ square is to be cut into two types of rectangles: $1 \times 4$ and $1 \times 3$. How many rectangles can result from the cutting? Justify your answer.
|
5. Answer: 7.
Solution. Example:
If there are no more than 6 rectangles, then they occupy no more than $6 \cdot 4 = 24$ cells, while there are 25 cells. Therefore, there must be at least 7 rectangles.
A rectangle that is completely located in a column will be called vertical, and one that is completely located in a row will be called horizontal. Suppose we managed to cut the square into such rectangles. Consider the rectangle that contains the central cell of the $5 \times 5$ square. If necessary, rotate the $5 \times 5$ square so that this rectangle is horizontal. The cells of this rectangle are located in at least three columns, and there are no vertical rectangles in these columns. There are a total of 10 possible rectangles: 5 vertical and 5 horizontal. But 3 vertical rectangles are impossible, so there can be no more than $10 - 3 = 7$ rectangles.
The number of rectangles can only be 7.
## Grading Criteria.
Only the example: 2 points.
Proved that there are at least 7 rectangles: 1 point.
Shown that there are no more than 9 rectangles, as 9 would occupy at least 27 cells: 1 point.
Attempted to enumerate to prove that there cannot be 8 rectangles: 1 point.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For what value of the parameter m is the sum of the squares of the roots of the equation
$$
x^{2}-(m+1) x+m-1=0
$$
the smallest?
|
3. $\mathrm{m}=3$.
Note that the discriminant $\mathrm{D}$ of the equation is equal to
$$
\mathrm{D}=(\mathrm{m}+1)^{2}-4(\mathrm{~m}-1)=(\mathrm{m}-1)^{2}+4>0
$$
therefore, the equation has two roots for any $\mathrm{m}$. Let's represent the sum of the squares of the roots $\mathrm{x}_{1}$ and $\mathrm{x}_{2}$ as
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}
$$
From Vieta's theorem, we get
$$
x_{1}^{2}+x_{2}^{2}=\frac{(m+1)^{2}}{4}-2(m-1)
$$
The minimum value of $x_{1}^{2}+x_{2}^{2}$ is achieved at the minimum point of the function $\mathrm{f}(\mathrm{m})=(\mathrm{m}+1)^{2}-8(\mathrm{~m}-1)$, which is $\mathrm{m}_{\min }=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. Arina wrote down a number and the number of the month of her birthday, multiplied them and got 248. In which month was Arina born? Write the number of the month in your answer.

|
Answer: 8
Solution. $248=2 * 2 * 2 * 31$. Obviously, 31 is the number, then 8 is the month number.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. It is known that in the past chess tournament, in each round all players were paired, the loser was eliminated (there were no draws). It is known that the winner played 6 games. How many participants in the tournament won at least 2 games more than they lost?
|
Answer: 8
Solution. Since the winner played 6 games, there were a total of $2^{6}=64$ players. The win-loss ratio for those eliminated in the 1st round is -1; for those who lost in the 2nd round, it is 0; for those who lost in the 3rd round, it is +1; for those who lost in the 4th round and beyond, it is at least +2. 8 participants reached the $4th$ round.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. In a basketball team, there is a certain number of players. The coach added up all their heights and divided by the number of players (let's call this the average height), getting 190 cm. After the first game, the coach removed Nikolai, who is 197 cm tall, and replaced him with Petr, who is 181 cm tall, after which the average height of the players in the team was 188 cm. How many people are in the team?
|
Answer: 8
Solution. The change in the total height of the players by $197-181=16$ cm leads to a change in the average height of the team by $190-188=2$ cm, so the team has $\frac{16}{2}=8$ people.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all natural $\boldsymbol{n}$ such that the value of the expression $\frac{2 n^{2}-2}{n^{3}-n}$ is a natural number.
|
Solution. $\frac{2 n^{2}-2}{n^{3}-n}=\frac{2(n-1)(n+1)}{n(n-1)(n+1)}$. For $n \neq \pm 1$, this expression is identically equal to $\frac{2}{n}$. Since $n \neq 1$, the value of the last expression is a natural number only when $n=2$.
Answer: $n=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $A B C D$ is a square, then $A B=B C=C D=A D$.
Fig. 1: to the solution of problem 8.4
Notice that $\angle A B K=\angle C B L$, since they both complement $\angle A B L$ to $90^{\circ}$. Then the right triangles $A B K$ and $C B L$ are equal by the acute angle and the leg $A B=B C$ (Fig. 1). Therefore, $A K=C L=6$. Then
$$
L D=C D-C L=A D-C L=(K D-A K)-C L=K D-2 \cdot C L=19-2 \cdot 6=7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. While tidying up the children's room before the guests arrived, mom found 9 socks. Among any four socks, at least two belong to the same owner. And among any five socks, no more than three belong to the same owner. How many children scattered the socks, and how many socks does each child own?
Answer. There are three children, and each owns three socks.
|
Solution. No child owned more than three socks, as otherwise the condition "among any five socks, no more than three belonged to one owner" would not be met. There are a total of 9 socks, so there are no fewer than three children. On the other hand, among any four socks, there are two socks belonging to one child, so there are fewer than four children. Therefore, there are three children in the family, and each scattered no more than three socks, with a total of 9 socks. This means that each child owns 3 of the socks found by the mother.
Grading Criteria.
- Complete answer with correct explanation - 7 points.
- Justified that there are three children - 5 points.
- Correct reasoning, but the solution is not fully completed - 1-2 points.
- Answer without justification - 0 points.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many natural numbers $n$ exist for which $4^{n}-15$ is a square of an integer?
|
Answer. Two.
Solution. Let $4^{n}-15=x^{2}$, where $x$ is an integer. It is obvious that $x \neq 0$. If $x$ is negative, then $(-x)^{2}$ is also equal to $4^{n}-15$; therefore, we will assume that $4^{n}-15=x^{2}$, where $x$ is a natural number. From the equation $2^{2 n}-15=x^{2}$, we get: $2^{2 n}-x^{2}=15$, and using the formula for factoring the difference of squares: $\left(2^{n}-x\right)\left(2^{n}+x\right)=15$. Since $x$ is a natural number, the second factor on the left in the last equation is positive, and therefore the first factor must also be positive. The number 15 can be factored into natural numbers in two ways: $15=3 \cdot 5=1 \cdot 15$. Since $x>0$, we have $2^{n}+x>2^{n}-x$. Thus, there are only two possible cases:
$\left\{\begin{array}{l}2^{n}-x=1, \\ 2^{n}+x=15\end{array}\right.$ or $\left\{\begin{array}{l}2^{n}-x=3, \\ 2^{n}+x=5 .\end{array}\right.$
Solving the first system of equations (it is most convenient to simply add the equations), we get that $2 \cdot 2^{n}=16$, i.e., $n=3$. Similarly, from the second system, we get that $n=2$.
We could solve without limiting ourselves to natural values of $x$, but then the number of systems to be considered would increase, as the cases $15=(-1) \cdot(-15)=(-3) \cdot(-5)$ would also be possible.
Grading criteria.
- Correct answer with full justification - 7 points.
- Cases of factoring 15 into negative factors not considered without justification, why negative factors can be ignored - 6 points.
- Systems for determining $n$ correctly set up, but not checked for natural solutions - 5 points.
- Only one of the two possible factorizations of the number 15 considered - 5 points.
- Reasonable arguments that did not lead to a solution - 1-2 points.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.1
## Condition:
Grandma is embroidering her grandchildren's names on their towels. She embroidered the name "ANNA" in 20 minutes, and the name "LINA" in 16 minutes. She spends the same amount of time on the same letters, and possibly different times on different letters. How long will it take her to embroider the name "LILI"?
|
Express the answer in minutes.
Answer: 12
Exact match of the answer - 1 point
Solution.
Since the grandmother spends the same amount of time on identical letters, she will spend $20: 2=10$ minutes on the syllable "NA". Then she will spend
$16-10=6$ minutes on the syllable "LI". Therefore, she will spend $6+6=12$ minutes on the name "LILI".
## Condition:
Mashenka is signing gifts beautifully for New Year. She wrote "MAMA" in 12 minutes, and the name "MILA" in 8 minutes. She spends the same amount of time on identical letters, and possibly different amounts of time on different letters. How long will it take her to write the name "LILI"?
Express the answer in minutes.
Answer: 4
Exact match of the answer - 1 point
Solution by analogy with task № 3.1.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 4.1
## Condition:
On an island of knights, who always tell the truth, and liars, who always lie, a five-story building was built. One resident lived on each floor. One day, each of them made the same statement:
"There are more liars above me than knights below me!"
How many liars can live in this building?
|
# Answer: 3
## Exact match of the answer -1 point
## Solution.
Notice that the person living on the 5th floor is definitely lying, as there is no one living above them, including liars. Therefore, there are 0 liars above them, and 0 or more knights below. Now consider the resident on the 1st floor. They definitely told the truth, as there are 0 knights below them, and at least 1 liar living above, specifically the one on the 5th floor.
Now let's focus on the resident on the 4th floor. Above them lives exactly 1 liar, and below - at least 1 knight on the 1st floor. Therefore, their statement is false in any case. This means they are a liar. Then, the resident on the 2nd floor, similar to the reasoning about the one on the 1st floor, is a knight. The only one left to determine is the resident on the 3rd floor. Above them live 2 liars, and below - 2 knights. Therefore, their statement is false. Hence, they are a liar.
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 4.3
## Condition:
On an island of knights, who always tell the truth, and liars, who always lie, a six-story building was built. One resident lived on each floor. One day, each of them made the same statement:
"There are more liars above me than knights below me!" How many liars can live in this building?
|
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with task No. 4.1.
## Condition:
On an island of knights, who always tell the truth, and liars, who always lie, a five-story building was built. One resident lived on each floor. One day, each of them made the same statement:
"There are more liars below me than knights above me!" How many knights can live in this building?
## Answer: 2
Exact match of the answer - 1 point
Solution by analogy with task No. 4.1.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 5.1
## Condition:
In a correct equation, identical digits were replaced with the same letters, and different digits with different letters. The result is
$$
P+\mathrm{P}+\mathrm{A}+3+Д+\mathrm{H}+\mathrm{U}+\mathrm{K}=\mathrm{U} \mathrm{U}
$$
What can U be equal to?
|
# Answer:
$\circ 1$
$\circ 2$
$\checkmark 3$
$\circ 4$
० 5
० 6
○ 7
○ 8
$\circ 9$
$\circ 0$
Exact match of the answer - 1 point
## Solution.
Notice that the expression involves 9 different letters, meaning all digits except one are used. On the left, we have the sum of eight different single-digit numbers. The sum of all single-digit numbers is $0+1+2+3+4+5+6+7+8+9=45$. Let's see which two-digit numbers with identical digits can be obtained by summing eight numbers.
$44=45-1, 33=45-12, 22=45-23, 11=45-34$. The last two are not possible because the maximum sum of two single-digit numbers is $17=8+9$. Also, 44 is not suitable because to get it, we would need to use all numbers except 0 and 1, but then U cannot be 4 because 4 is already used on the left. The variant 33 is quite suitable. $12=3+9$, and we get the equality:
$$
0+1+2+4+5+6+7+8=33
$$
## Condition:
In a correct equality, identical digits were replaced by identical letters, and different digits by different letters. The result is
$$
П+\mathrm{O}+\mathrm{Б}+\mathrm{E}+Д+\mathrm{И}+Ш+\mathrm{b}=\mathrm{AA} .
$$
What can $A$ be equal to?
## Answer:
$\circ 1$
$\circ 2$
$\checkmark 3$
$\circ 4$
$\circ 5$
○ 6
○ 7
○ 8
० 9
$\circ 0$
Exact match of the answer - 1 point
Solution by analogy with problem № 5.1.
## Condition:
In a correct equality, identical digits were replaced by identical letters, and different digits by different letters. The result is
$$
\mathrm{C}+\mathrm{y}+П+\mathrm{E}+\mathrm{P}+\mathrm{K}+Л+\mathrm{A}+Д=\mathrm{AA}
$$
What can $A$ be equal to?
## Answer:
$\circ 1$
$\circ 2$
$\circ 3$
$\checkmark 4$
$\circ 5$
० 6
○ 7
○ 8
० 9
$\circ 0$
Exact match of the answer - 1 point
Solution by analogy with problem № 5.1.
## Condition:
In a correct equality, identical digits were replaced by identical letters, and different digits by different letters. The result is
$$
Г+\mathrm{P}+\mathrm{A}+Д+\mathrm{y}+\mathrm{C}+\mathrm{H}+\mathrm{И}+\mathrm{K}=\text { ИИ. }
$$
What can И be equal to?
## Answer:
$\circ 1$
$\circ 2$
$\circ 3$
$\checkmark 4$
$\circ 5$
० 6
○ 7
○ 8
० 9
○ 0
Exact match of the answer - 1 point
Solution by analogy with problem № 5.1.
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 6.1
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
|
Answer: 9
Exact match of the answer - 1 point
## Solution.
Unfold the paper and mark the lines of the cuts.
Now it is easy to count the resulting pieces. For convenience, they are highlighted in color.
## Problem:
A sheet of paper was folded like an accordion as shown in the picture, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
Answer: 8
Exact match of the answer - 1 point
Solution by analogy with problem № 6.1.
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.1
## Condition:
On the Misty Planet, santiks, kubriks, and tugriks are in circulation. One santik can be exchanged for 1 kubrik or 1 tugrik, 1 kubrik can be exchanged for 3 santiks, and 1 tugrik can be exchanged for 4 santiks. No other exchanges are allowed. Jolly U, initially having 1 santik, made 20 exchanges, and now he has 25 santiks (and no other money). How many times did he exchange kubriks for santiks?
|
# Answer: 6
## Exact match of the answer -1 point
## Solution.
To increase the number of santiks, we need to exchange them for kubriks or tugriks. In essence, we need to perform a double exchange, that is, first convert a santik into a tugrik or kubrik at a 1:1 ratio, and then increase the number of coins. Since the total number of exchanges is 20, 10 "double exchanges" were conducted. When exchanging a kubrik, the number of coins increases by 2, and when exchanging a tugrik, it increases by 3. Starting with 1 coin, it became 25 - the number of coins increased by 24. If all exchanges were made using kubriks, the number of coins would have increased by 20. In our case, it increased by 24, so 4 exchanges were made with tugriks, and 6 with kubriks.
#
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.2
Condition:
In the city of Abracodabra, funtics, tubrics, and santics are in circulation. One funtic can be exchanged for 1 tubric or 1 santic, 1 tubric for 5 funtics, and 1 santic for 2 funtics. No other exchanges are allowed. Lunatic, initially having 1 funtic, made 24 exchanges and now has 40 funtics (and no other money). How many times did he exchange tubrics for funtics?
|
Answer: 9
Exact match of the answer -1 point
Solution by analogy with task No. 7.1.
## Condition:
On the planet Mon Calamari, dataries, flans, and pegats are in circulation. One datary can be exchanged for 1 flan or 1 pegat, 1 flan - for 2 dataries, and 1 pegat - for 4 dataries. No other exchanges are allowed. Meray, initially having 1 datary, made 20 exchanges, and now he has 25 dataries (and no other money). How many times did he exchange flans for dataries?
Answer: 3
Exact match of the answer -1 point
Solution by analogy with task No. 7.1.
## Condition:
In the machine, there are tokens, wrappers, and stamps. The machine can exchange 1 token for 1 wrapper or 1 stamp, 1 stamp for 2 tokens, or 1 wrapper for 3 tokens. No other exchanges can be made by the machine. Nезнайка, initially having 1 token, made 30 exchanges, and now he has 20 tokens (and no more wrappers or stamps). How many times did he exchange wrappers for tokens?
Answer: 4
Exact match of the answer -1 point
Solution by analogy with task No. 7.1.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. $\left(7\right.$ points) Calculate $\frac{(2009 \cdot 2029+100) \cdot(1999 \cdot 2039+400)}{2019^{4}}$.
|
# Solution.
$2009 \cdot 2029+100=(2019-10) \cdot(2019+10)+100=2019^{2}-10^{2}+100=2019^{2}$.
$1999 \cdot 2039+400=(2019-20) \cdot(2019+20)+400=2019^{2}-20^{2}+400=2019^{2}$.
Then $\frac{2019^{2} \cdot 2019^{2}}{2019^{4}}=1$
Answer. 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) Find all natural solutions to the equation $2 n-\frac{1}{n^{5}}=3-\frac{2}{n}$.
#
|
# Solution.
1 method. $2 n-\frac{1}{n^{5}}=3-\frac{2}{n}, 2 n-3=\frac{1}{n^{5}}-\frac{2}{n}, 2 n-3=\frac{1-2 n^{4}}{n^{5}}$.
For $n=1$ the equality is true, for $n>1 \quad 2 n-3>0, \frac{1-2 n^{4}}{n^{5}}<0$.
Answer. $n=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 In Pokémon hunting, 11 adults and $n$ children participated. Together, they caught $n^{2}+3 n-2$ Pokémon, with all adults catching the same number, and all children catching the same number, but each child catching 6 fewer than an adult. How many children participated in the game?
|
Solution: Let each child catch $m$ pokemons. Then $n m+11(m+6)=n^{2}+3 n-2$. From this, $(n+11) m=n^{2}+3 n-68$. Therefore, the right side is divisible by $n+11$. We have $n^{2}+3 n-68=$ $n(n+11)-8(n+11)+20$, so 20 is divisible by $n+11$. The only divisor of 20 greater than 10 is 20 itself, so $n+11=20, n=9$.
## Criteria:
- No points are deducted for the lack of an example for $n=9$.
- It is shown that $n=9$ works, but it is not proven that there are no other options -1 point.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. One side of a rectangle was increased by 3 times, and the other was reduced by 2 times, resulting in a square. What is the side of the square if the area of the rectangle is $54 \mathrm{m}^{2} ?$
|
Answer: 9 m.
Let's reduce the side of the given rectangle by half (see Fig. 5.3a). Then the area of the resulting rectangle will be 27 m $^{2}$ (see Fig. 5.3b). Next, we will increase the other side by three times, that is, "add" two more rectangles (see Fig. 5.3c). The area of the resulting figure will become $27 \cdot 3=81$ (m ${ }^{2}$ ). Since, by the condition, a square has formed, its area is $81 \mathrm{~m}^{2}$. Therefore, the side of the resulting square is 9 meters.
Fig. 5.3a

Fig. 5.3b
Fig. 5.3c
+ complete justified solution
$\pm$ the area of the square is correctly obtained, but the side is not found or is found incorrectly
Ғ only the correct answer is provided or the correct answer is obtained by considering a specific case (a rectangle with specific sides)
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №3
The base and the lateral side of an isosceles triangle are 34 and 49, respectively.
a) Prove that the midline of the triangle, parallel to the base, intersects the inscribed circle of the triangle.
b) Find the length of the segment of this midline that is contained within the circle.
|
# Answer: 8.
## Solution
a) Let $\mathrm{O}$ be the center of the inscribed circle in triangle $ABC$ with sides $AB = AC = 49$, $BC = 34$, and $AH$ be the height of the triangle. Points $M$ and $N$ are the midpoints of sides $AB$ and $AC$, respectively, and $K$ is the intersection point of $AH$ and $MN$. Since $MN$ is the midline of the isosceles triangle, point $K$ is the common midpoint of $MN$ and $AH$.
From the right triangle $ABH$, we find that
$$
A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{49 - 17^{2}} = 8 \sqrt{33},
$$
so, $K H = 4 \sqrt{33}$.
Let $r$ be the radius of the inscribed circle of triangle $ABC$. Then
$$
r = \frac{S_{ABC}}{p} = \frac{\frac{1}{2} BC \cdot AH}{AB + BH} = \frac{17 \cdot 8 \sqrt{33}}{49 + 17} = \frac{68 \sqrt{33}}{33}
$$
and the diameter of the inscribed circle is $2r = \frac{136 \sqrt{33}}{33}$. Clearly, $\frac{136}{33} > 4$, so $2r = \frac{136 \sqrt{33}}{33} > 4 \sqrt{33} = KH$.
Therefore, the inscribed circle intersects the midline $MN$ of the triangle.
b) To calculate the length of the segment of the midline, we introduce a coordinate system on the plane as follows: the $OX$ axis is directed along the base of the triangle, and the $OY$ axis is directed along the height.
Then the inscribed circle in the triangle is given by the equation
$$
x^{2} + \left(y - \frac{68 \sqrt{33}}{33}\right)^{2} = \left(\frac{68 \sqrt{33}}{33}\right)^{2}
$$
and the midline of the triangle is given by the equation
$$
y = 4 \sqrt{33}.
$$
Substituting this value into the equation of the circle, we get the values
$$
x_{1} = -4 \quad \text{and} \quad x_{2} = 4.
$$
Thus, the length of the segment of the midline inside the circle is 8.
|
8
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Dima wrote a sequence of 0s and 1s in his notebook. Then he noticed that a 1 follows a 0 sixteen times, a 0 follows a 1 fifteen times, and a 0 follows 01 eight times. How many times does a 0 follow 11?
|
# Answer. 7.
Solution. The combination 01 appears 16 times in the tetrad, while the combination 10 appears 15 times. Therefore, the string starts with 0, meaning that before each combination 10 there is either 0 or 1. According to the condition, eight times it is 0, so the combination 110 appears $15-8=7$ times.
Criteria. Full solution - 7 points. Noted that the string starts with 0 without further progress - 2 points. Considered specific cases of concrete sequences and obtained the correct answer - 1 point. Only answer - 0.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. How much greater is one of two positive numbers than the other if their arithmetic mean is $2 \sqrt{3}$ and the geometric mean is $\sqrt{3}$?
(Hint: the geometric mean of two numbers $m$ and $n$ is the number $p=\sqrt{\mathrm{mn}}$).
|
# Solution.
Let the unknown numbers be denoted by $x$ and $y$. Then, from the problem statement, we get:
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ \frac { x + y } { 2 } = 2 \sqrt { 3 } , } \\
{ \sqrt { x y } = \sqrt { 3 } , }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x+y=4 \sqrt{3}, \\
x y=3 .
\end{array}\right.\right. \\
& \text { Then }|x-y|=\sqrt{(x-y)^{2}}=\sqrt{(x+y)^{2}-4 x y}=\sqrt{4^{2} \cdot 3-4 \cdot 3}=6 .
\end{aligned}
$$
Other methods of solution are possible.
Answer: 6 .
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the largest natural number $\mathrm{n}$, for which the system of inequalities
$1<x<2, 2<x^{2}<3, \ldots, n<x^{n}<n+1$
has a solution. (6 points)
|
Solution. From the condition $: n=4$.
Rewrite the inequalities as:
$\left\{\begin{aligned} & 16^{3} \text{, then for } n=5 \text{ the given system is already inconsistent: the intervals } [\sqrt[3]{3}, \sqrt[4]{4}] \text{ and } [\sqrt[5]{2}, \sqrt[5]{6}] \text{ do not intersect.} \\ & \text{For } n=4 \text{, it is not difficult to find a value of } x \text{ that satisfies all four inequalities (for example, } x=1.45 \text{).} \end{aligned}\right.$
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There is a bag with 16 letters: А, А, А, А, В, В, Д, И, И, М, М, Н, Н, Н, Я, Я. Anna, Vanya, Danya, and Dima each took 4 letters from it, after which the bag was empty. How many of them could have successfully spelled out their names? Explain your answer.
|
2. Answer: 3.
Solution. All of them could not have formed their names, as there were not enough letters D. Anna, Vanya, and Dima could have drawn cards from which they could form their names, while Danya would have been left with the cards: V, I, M, Ya.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.