problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4. In city $\mathrm{N}$, only blondes and brunettes live. Blondes always lie, while brunettes always tell the truth. Every day, the residents dye their hair the opposite color. On one Monday in October, everyone born in the fall was asked: "Were you born this month?" - and 200 residents answered "yes," while no one answered "no." On Friday of the same week, everyone born in the fall was asked again: "Were you born this month?" - and this time only 50 of them gave an affirmative answer. How many "yes" answers were given to the same question on the last Monday of September, if there were exactly four Mondays in October of that year and no one in the city $\mathrm{N}$ was born in November?
|
4. Answer. 0.
Solution. Note that on Monday and Friday of the same week, the residents have the same hair color: Monday - Tuesday - Wednesday - Thursday - Friday. Then, if the same people answer differently on Monday and Friday, it means that the month has changed, and the brunettes will answer "no" to the same question.
If the month has changed, then it is the last Monday of October. Since there were 4 Mondays in October, the residents will have the same hair color again on the last Monday of September: M (September) - M1 - M2 - M3 - M4 (October) (since the hair color changes each subsequent Monday). The first time all brunettes answered "yes," it means that all residents who were brunettes on that day were born in October. On the following Friday and the last Monday of September, they will also be brunettes, but since the month will change, all of them will answer "no."
Let's pay attention to the blondes. The first time all of them answered "yes," it means that none of them were born in October. We also know that no one was born in November. Therefore, all blondes were born in September and will also answer "no" on the last Monday of September.
Thus, on the last Monday of September, 0 residents will answer "yes."
## Grading Criteria:
Correct and justified solution - 7 points. In all other cases - $\mathbf{0}$ points.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A tournament of dodgeball was held at school. In each game, two teams competed. 15 points were awarded for a win, 11 for a draw, and no points for a loss. Each team played against each other once. By the end of the tournament, the total number of points scored was 1151. How many teams were there?
|
5. Answer: 12 teams.
Solution. Let there be $\mathrm{N}$ teams. Then the number of games was $\mathrm{N}(\mathrm{N}-1) / 2$. For each game, a total of 15 or 22 points are scored. Therefore, the number of games was no less than 53 $(1151 / 22)$ and no more than $76(1151 / 15)$.
Note that if there were no more than 10 teams, then the number of games would not exceed 45. And if there were no fewer than 13 teams, then the number of games would be no less than 78.
Thus, the number of teams was 11 (55 games) or 12 (66 games). In each game, teams score exactly 15 points in total! And 7 additional points if there was a draw. Therefore, the total number of draws is (1151-55*15)/7 (a non-integer - this could not have been the case) or (1151-66*15)/7=23. Therefore, the only option is that there were 12 teams.
## Grading Criteria.
Correct and justified solution - 7 points.
Justified that the number of teams is 11 or 12 without further progress - 3 points. Justified that the number of games was no less than 53 and no more than 76 without further progress - $\mathbf{2}$ points. Correct answer with a constructed example - $\mathbf{2}$ points. Just the correct answer - $\mathbf{0}$ points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. A polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-8$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -24. (b) 6.
Solution. (a) Since the graph of $G(x)$ is symmetric with respect to the line $x=-8$, the points at which it takes the same value must be divided into pairs of symmetric points, except possibly one point that lies on the axis of symmetry. Therefore, the middle of the five given points should lie on the axis of symmetry, i.e., $x_{3}=-8$. The first and fifth points should be symmetric with respect to the line $x=-8$, so $x_{1}+x_{5}=2 \cdot(-8)=-16$. Therefore, $x_{1}+x_{3}+x_{5}=-24$.
(b) Consider the auxiliary polynomial $F(x)=G(x-8)-2022$. Clearly, the degree of $F(x)$ coincides with the degree of $G(x)$. The graph of $F(x)$ is obtained by a parallel shift of the graph of $G(x)$ 8 units to the right and 2022 units down. Then this graph is symmetric with respect to the line $x=0$, and at five points $F(x)$ takes the value 0. It is clear that $F(x)$ has exactly 5 distinct roots, so its degree is at least 5. On the other hand, since the graph of $F(x)$ is symmetric with respect to the line $x=0$, the function $F(x)$ is even, so the degree of $F(x)$ is also even. Therefore, the degree of $F(x)$, and hence the degree of $G(x)$, is at least 6.
As an example of a polynomial of degree 6, we can take $F(x)=(x+2)(x+1)x^{2}(x-1)(x-2)$. It corresponds to $G(x)=(x+10)(x+9)(x+8)^{2}(x+7)(x+6)+2022$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.3.1. The polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-8$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -24 . (b) 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.3.4. The polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-6$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -18 . (b) 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.7.4. Let $N$ be the least common multiple of ten different natural numbers $a_{1}<a_{2}<a_{3}<\ldots<a_{10}$.
(a) (2 points) What is the smallest value that $N / a_{6}$ can take?
(b) (2 points) Identify all possible values of $a_{6}$ in the interval $[1 ; 2000]$, for which the value of $N / a_{1}$ can take its smallest value.
|
Answer: (a) 5. (b) $504,1008,1512$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the $3000-$th year, the World Hockey Championship will be held under new rules: 12 points will be awarded for a win, 5 points will be deducted for a loss, and no points will be awarded for a draw. If the Brazilian national team plays 38 matches in this championship, scores 60 points, and loses at least once, how many victories can they achieve? Provide all possible options and explain why there cannot be any others.
|
Solution. Let Brazil win in x matches and lose in y matches. We form the equation $12 x-5 y=60$. We see that $12 \mathrm{x} \vdots 12$ and $60 \vdots 12$. GCD(5, 12)=1, i.e., $y \vdots 12$. Possible: a) $y=12$. Then we get the equation $12 x-60=60$. Thus, $x=10$. This is possible. b) $y=24$. We get the equation: $12 x-120=60$. Hence, $x=15$. This is impossible, as the number of matches already exceeds 38. c) $y=36$. We get $12 x-180=60$. Hence, $x=20$, which is also impossible. Larger values of x do not fit, as the number of matches played will already exceed 38.
Answer. 10 wins.
Recommendations for checking. Only the correct answer - 0 points. Only the correct answer with verification - 1 point. The equation is correctly set up, but there is no further progress (even with the correct answer and verification) - 2 points. The equation is set up, there is an idea of divisibility, but there is no further progress - 3 points. After setting up the equation, there is an idea of divisibility, only the first case is considered, and the correct answer is obtained - 4 points. After setting up the equation, there is an idea of divisibility, only the first and second cases are considered, and the correct answer is obtained - 5 points. After considering the second case without explanation, it is written that the number of matches increases further - do not deduct points. Full enumeration with one computational error and the correct answer - 5 points. One case is missed in the full enumeration - no more than 4 points. More than one case is missed in the full enumeration with the correct answer - 1 point, with the wrong answer - 0 points.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Find all natural $k$ such that the product of the first $k$ prime numbers, decreased by 1, is a perfect power of a natural number (greater than the first).
(V. Senderov)
|
Answer. $k=1$.
Solution. Let $n \geqslant 2$, and $2=p_{1}<p_{2}<\ldots<p_{k}$; then $k>1$. The number $a$ is odd, so it has an odd prime divisor $q$. Then $q>p_{k}$, otherwise the left side of the equation $(*)$ would be divisible by $q$, which is impossible. Therefore, $a>p_{k}$.
Without loss of generality, we can assume that $n$ is a prime number (if $n=s t$, then we can replace $n$ with $t$, and $a$ with $a^{s}$). Note that $n>2$, since $a^{2}+1$ cannot be divisible by $3=p_{2}$.
We will now show that $n>p_{k}$. Otherwise, we have $n=p_{i}$ for some $1<p_{i} \leqslant p_{k}$. Since $a>p_{k}$ and $n>p_{k}$, it follows that $a^{n}+1>p_{k}^{p_{k}}>p_{1} p_{2} \ldots p_{k}$, which contradicts the equation $(*)$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On the board, a certain natural number $N$ was written nine times (one under the other). Petya appended a non-zero digit to the left or right of each of the 9 numbers; all the appended digits are different. What is the maximum number of prime numbers that could result among the 9 obtained numbers?
(I. Efremov)
|
Answer: 6.
Solution. Let $S$ be the sum of the digits of the number $N$. Then the sums of the digits of the obtained numbers will be $S+1, S+2, \ldots, S+9$. Three of these sums will be divisible by 3. By the divisibility rule for 3, the corresponding three numbers on the board will also be divisible by 3. Since these numbers will be greater than 3, they will be composite. Therefore, more than 6 prime numbers cannot appear on the board.
Six prime numbers can appear even when $N=1$ - for example, if Petya gets, among others, the numbers 11, 13, 41, 61, 17, and 19.
Remark. Petya can get six prime numbers even if he only appends digits to one side, for example, from the number $N=3$ he can get the numbers 13, 23, 43, 53, 73, and 83.
Comment. Only an example is provided where 6 prime numbers appeared on the board - 2 points.
Only proven that more than six prime numbers could not appear - 5 points.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. All cells of a $100 \times 100$ square table are numbered in some order with numbers from 1 to 10000. Petya colors the cells according to the following rules. Initially, he colors $k$ cells at his discretion. Then, on each move, Petya can color one more uncolored cell with number $a$ if at least one of the two conditions is met: either there is an already colored cell with a number less than $a$ in the same row; or there is an already colored cell with a number greater than $a$ in the same column. What is the smallest $k$ such that, regardless of the initial numbering, Petya can color all the cells of the table in several moves?
(S. Berlov)
|
Answer. $k=1$.
Solution. First, let's prove the following statement.
Lemma. For any two cells $A$ and $B$, there exists a cell $C$ such that by coloring it, one can then color both $A$ and $B$ (possibly $C$ coincides with $A$ or $B$).
Proof. We can assume that the number $a$ of cell $A$ is less than the number $b$ of cell $B$. Let $D$ be the cell in the same column as $A$ and in the same row as $B$, and let $d$ be its number (possibly $D=A$ or $D=B$). Then, if $d < a$, after coloring $A$, one can sequentially color $D$ and $B$. If $d > b$, after coloring $B$, one can sequentially color $D$ and $A$. Therefore, in any case, one can choose $C$ as one of the cells $A$, $B$, or $D$. The lemma is proved.
Now, let's proceed to the solution of the problem. It is clear that $k \geqslant 1$; hence, it is sufficient to prove that when $k=1$, the coloring is always possible.
Fix an arbitrary numbering of the cells. Consider all ways of coloring the cells according to the condition (for $k=1$) and choose the one in which the number of colored cells is maximal. Let $A$ be the first colored cell in this way. Suppose that in this way, some cell $B$ remains uncolored. Then, by choosing the corresponding cell $C$ according to the Lemma and starting the coloring from it, we can then color $B$, $A$, and, consequently, all the cells that were colored in the chosen way. Thus, we will color at least one more cell. The contradiction with the choice of the way shows that in fact, all cells will be colored in our way. This means that $k=1$ works.
## 10th grade
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 About numbers a and b, it is known that the system of equations
$$
\left\{\begin{array}{l}
y^{2}=x^{2}+a x+b \\
x^{2}=y^{2}+a y+b
\end{array}\right.
$$
has no solutions. Find a.
|
Solution: Since the system has no solutions, in particular, there are no solutions with $x=y$. When $x=y$, both equations of the system are equivalent to the equation $a x+b=0$. This linear equation has no roots only when its slope coefficient $a$ is zero.
## Criteria:
- Points are not deducted for the absence of an example of a system with $a=0$ that has no solutions.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 Another participant in the competition for meaningless activity marked the centers of 13 cells in a grid rectangle of size $(N-1) \times(N+1)$ such that the distance between any two marked points is greater than 2. What is the smallest value that $N$ can take?
|
Solution: We will show that it is impossible to mark cells in a $6 \times 8$ rectangle (and thus in any smaller size) in such a way. Indeed, let's divide the rectangle into $2 \times 2$ squares. In each of them, the pairwise distances between the centers of the cells do not exceed $\sqrt{2}$, so no more than one cell is marked in each. Therefore, the total number of marked cells does not exceed 12.
Example for a $7 \times 9$ rectangle:
| | | | $\mathrm{X}$ | | | | | $\mathrm{X}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | $\mathrm{X}$ | | | | | $\mathrm{X}$ | | |
| | | | | $\mathrm{X}$ | | | | |
| $\mathrm{X}$ | | $\mathrm{X}$ | | | | | $\mathrm{X}$ | |
| | | | | | $\mathrm{X}$ | | | |
| | $\mathrm{X}$ | | $\mathrm{X}$ | | | | | $\mathrm{X}$ |
Criteria:
- Only proved that $N>7-3$ points;
- Only provided an example for $N=8-3$ points;
- No points are deducted for the lack of justification in the example.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Consider natural numbers $a, b$, and $c$ such that the fraction
$$
k=\frac{a b+c^{2}}{a+b}
$$
is a natural number less than $a$ and $b$. What is the smallest number of natural divisors that the number $a+b$ can have?
(P. Kozlov)
|
Answer. Three divisors.
First solution. Since the number $a+b$ is greater than one, it has at least two distinct divisors. We will prove that there cannot be exactly two, i.e., that the number $a+b$ cannot be prime. Multiplying the equality from the condition by the denominator, we get $a b+c^{2}=k a+k b$ or, equivalently, $a b-k a-k b+k^{2}=k^{2}-c^{2}$. Factoring both sides, we arrive at the relation
$$
(a-k)(b-k)=(k-c)(k+c)
$$
Since $k<a$ and $k<b$, both parentheses on the left side are positive, and thus, $c<k$. Then there exist natural numbers $x, y, z$ and $t$ such that
$$
a-k=x y, \quad b-k=z t, \quad k-c=x z \quad \text { and } \quad k+c=y t .
$$
For example, we can set $x=\text{GCD}(a-k, k-c), t=\text{GCD}(b-k, k+c), y=(a-k) / x$ and $z=(b-k) / t$. Then the first two equalities are satisfied by definition; on the other hand, $k-c$ divides $x z$, and $k+c$ divides $y t$, so the written equalities follow from the equality of the products.
Therefore,
$$
\begin{aligned}
& a+b=(a-k)+(b-k)+(k-c)+(k+c)= \\
& =x y+z t+x z+y t=(x+t)(y+z)
\end{aligned}
$$
Thus, the number $a+b$ can be represented as the product of two natural numbers greater than 1, and therefore, it is not prime.
Finally, it is not difficult to see that $a+b$ can have exactly three distinct divisors. For example, if $a=10, b=15, c=5$, then $k=\frac{10 \cdot 15+5^{2}}{10+15}=7$, and $a+b=25=5^{2}$ has three divisors.
Remark. For no $a$ and $b$ can the sum $a+b$ equal $2^{2}$ or $3^{2}$. But for any prime number $p \geqslant 5$, there exist numbers $a, b$ and $c$ satisfying the condition of the problem such that $a+b=p^{2}$. For the case $a \leqslant b$, all suitable $a, b, c$ and $k$ have the form $a=n p$, $b=(p-n) p, c=m p$ and $k=n p-n^{2}+m^{2}$, where $2 \leqslant n \leqslant \frac{p-1}{2}$, $1 \leqslant m \leqslant n-1$. In particular, for $p=5$ the example is unique up to the permutation of the numbers $a$ and $b$.
Second solution. We will provide another proof that the number $p=a+b$ cannot be prime. Assume the contrary.
Assume $a \leqslant b$. Then the number $k p=a b+c^{2}=a(p-a)+c^{2}=a p+c^{2}-a^{2}$ is divisible by $p$ and less than $a p$. Therefore, the number $a^{2}-c^{2}=(a-c)(a+c)$ is positive and divisible by $p$. Then the first parenthesis is positive and $a-c<a+b=p$, so it does not divide $p$. The second parenthesis is also positive and $a+c<2 a \leqslant a+b=p$, so it also does not divide $p$. We have reached a contradiction, so the assumption is false. Thus, $a+b$ is a composite number and, therefore, it has at least three divisors.
Comment. Only the answer - 0 points.
Only the answer and an example where $a+b$ is the square of a prime number (i.e., it has three divisors) - 2 points.
Only the proof that the number $a+b$ cannot be prime (i.e., it has more than two divisors) - 4 points.
It is well known that the number of divisors of a natural number $n$, having a prime factorization of the form $n=p_{1}^{\alpha_{1}} \ldots p_{k}^{\alpha_{k}}$, is $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \ldots\left(\alpha_{k}+1\right)$. If this formula is used without proof - points are not deducted.
In the first solution, the representation (*) is known. If it is used without proof - points are not deducted. If it is used with an incorrect proof - 1 point is deducted.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Natural numbers starting from 1 are written in a row. This results in a sequence of digits: 1234567891011121314... What digit is in the 2021st position?
|
Answer. 1.
Solution. Note that the sum of the digits of all single-digit and two-digit numbers is $1892021$. Therefore, the digit in the 2021st position belongs to the recording of some three-digit number.
Let $x$ be some three-digit number, then the sum of the digits in the sequence from 1 to $x$ is $n=189+3(x-99)$. We have $189+3(x-99)<2021, 3x<2129, x<709 \frac{2}{3}$. The sequence of numbers from 1 to 709 contains $189+3 \cdot(709-99)=2019$ digits. Therefore, the digit in the 2021st position is the second digit of the number 710, which is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The bathtub fills with cold water in 6 minutes 40 seconds, with hot water - in 8 minutes. In addition, if the plug is removed from a full bathtub, the water will drain in 13 minutes 20 seconds. How long will it take to fill the bathtub completely, provided that both taps are open, but the bathtub is not plugged?
|
Solution: First, we will convert the time in seconds to minutes: 6 minutes 40 seconds will be replaced by $6+2 / 3$, or $20 / 3$, and 13 minutes 20 seconds will be replaced by $13+1 / 3$, or $40 / 3$. Then, in one minute, the cold water will fill $3 / 20$ of the bathtub, the hot water will fill $1 / 8$ of the bathtub, and $3 / 40$ of the bathtub will drain. Therefore, in one minute, the bathtub will fill $3 / 20+1 / 8-3 / 40$, i.e., $1 / 5$ of the bathtub. Thus, the entire bathtub will be filled in 5 minutes.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Six people are standing in a circle, each of whom is either a knight - who always tells the truth, or a liar - who always lies. Each of them said one of two phrases: "There is a liar next to me" or "There is a liar opposite me." What is the minimum number of liars among them? Provide an example and prove that there cannot be fewer liars.
|
Answer: 2.
Solution. Let's number all the people standing clockwise (this way, people with numbers 1 and 4, 2 and 5, 3 and 6 will stand opposite each other).
Zero liars is obviously impossible (then there would be only knights and no one could say any of the phrases).
If there is one liar, let's say his number is 1, then the knight with number 3 has two knight neighbors and a knight standing opposite him. This means he cannot say either of these two phrases.
Example with two liars. Liars have numbers 1 and 2 and say "There is a liar opposite me," which is also said by knights 4 and 5. The remaining knights (3 and 6) say "There is a liar next to me."
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. In Solar City, 6 dwarfs eat donuts daily, 8 dwarfs eat donuts every other day, and the rest do not eat donuts at all. Yesterday, 11 dwarfs ate donuts. How many dwarfs will eat donuts today?
|
Answer: 9.
Solution: Of the 11 dwarfs who ate donuts yesterday, 6 dwarfs eat them daily, so the remaining $11-6=5$ eat them every other day. Therefore, these five will not eat donuts today, while the other $8-5=3$ from those who eat every other day will. So today, these three will eat donuts, as well as the six who always eat donuts. We get the answer $3+6=9$.
Comment: Correct answer without justification -2 points.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. A round table was sat by 10 people - liars and knights. Liars always lie, while knights always tell the truth. Each of them was given a coin. Then each of those sitting passed their coin to one of their two neighbors. After that, 5 people said: “I have one coin,” while the other 5 said: “I have no coins.” What is the maximum number of knights that could have been sitting at the table?
|
# Answer: 7.
Solution. After passing the coins, each person sitting at the table can have 0, 1, or 2 coins. The total number of coins will be 10. Note that if a person lies, they will state a number of coins that differs from the actual number by 1 or 2. Since the total number of coins based on the answers differs from the actual total by $10-5=5$, at least 3 people must have lied. Therefore, there are no more than 7 knights at the table. Suppose the knights sitting at the table pass the coins as follows (arrows indicate the direction of the coin transfer; the number of coins after the transfer is in parentheses): $\leftarrow \mathrm{P}(0)-\mathrm{P}(0) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{L}(1) \rightarrow$ $\mathrm{L}(2) \leftrightarrow \mathrm{L}(2) \leftarrow$. In this case, all knights tell the truth, while the liars lie, saying they have 0 coins.
Comment. It is proven that there are no more than 7 knights at the table - 5 points. It is proven that there can be 7 knights at the table - 2 points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3 In triangle $A B C$, the median $A M$ is drawn (point $M$ lies on side $\mathrm{BC}$). It is known that angle $C A M$ is $30^{\circ}$, and side $A C$ is 2. Find the distance from point $B$ to the line $A C$.
Omвem: 1.
|
Solution: See fig.
Triangle СKM is equal to triangle ВHM (these are right triangles, the hypotenuses СM and ВM of which are equal, and the angles are the same).
Therefore, $\mathrm{BH}=$ СK. But in triangle СKA, the leg СK lies opposite the angle $30^{\circ}$ and is equal to half the hypotenuse АC: СK=1.
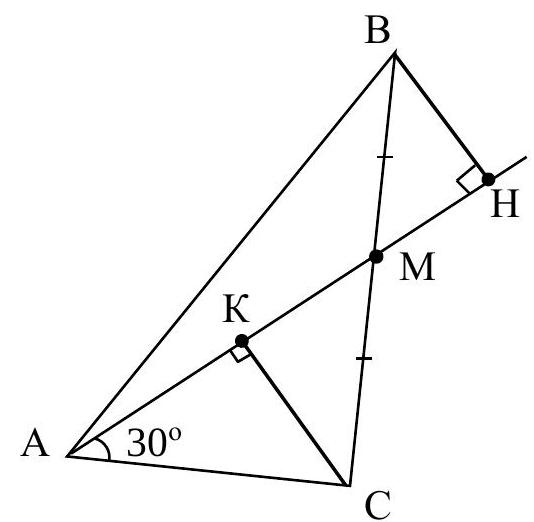
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Given natural numbers $M$ and $N$, both greater than ten, consisting of the same number of digits, and such that $M = 3N$. To obtain the number $M$, one of the digits of $N$ must be increased by 2, and each of the other digits must be increased by an odd digit. What digit could the number $N$ end with? Find all possible answers.
(n. Agakhanov)
|
Answer. The digit 6.
Solution. By the condition, $M=3 N$, so the number $A=M-$ $-N=2 N$ is even. However, by the condition, the number $A$ is composed of odd digits and the digit 2. Therefore, $A$ ends in 2. Thus, the number $N$, which is half of $A$, ends in either 1 or 6.
We will show that $N$ cannot end in 1. If $N$ ends in 1, then when it is doubled, there is no carry from the last digit to the second-to-last digit. This means that the second-to-last digit of the number $A=2 N$ will be even, but it must be odd. This is a contradiction.
Remark. Pairs of numbers $N$ and $M$ that satisfy the condition do exist, for example, $N=16, M=48$. Moreover, there are infinitely many such pairs. All suitable numbers $N$ can be described as follows: the first digit is 1 or 2, followed by several (possibly zero) digits, each of which is 5 or 6, and the last digit is 6.
Comment. The correct answer and an example of a number $N$ ending in the digit 6 - 1 point.
It is established that the last digit of the number $M$ is 2 more than the last digit of the number $N$ - 1 point.
It is shown that the last digit of the number $N$ can only be 1 or 6 - 2 points.
Points for different advancements are cumulative.
Note that the problem does not require providing an example of such a number. It is sufficient to prove that no digit other than 6 can be the last digit.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.

|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
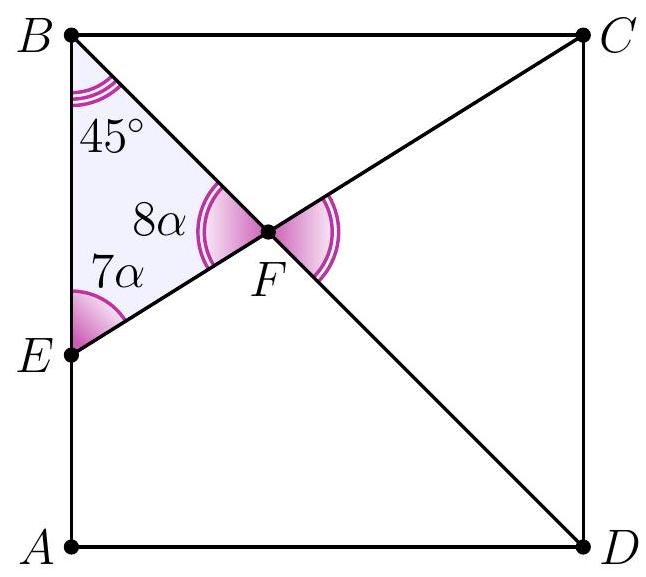
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-5. In a tournament, 6 teams $P, Q, R, S, T$ and $U$ participate, and each team must play against every other team exactly once. Each day, they are divided into 3 pairs, and all three matches are played simultaneously. The "Sports" channel has chosen which match it will broadcast each day:
$$
\begin{array}{c|c|c|c|c}
1 \text { day } & 2 \text { day } & 3 \text { day } & 4 \text { day } & 5 \text { day } \\
\hline P-Q & R-S & P-T & T-U & P-R
\end{array}
$$
On which day can teams $S$ and $U$ play against each other? Mark all possible options.
|
Answer. Only in the 1st.
Solution. Let's look at team $P$: on the 1st, 3rd, and 5th days, it will play against teams $Q, T$, and $R$. Therefore, in the remaining two days, it must play against teams $S$ and $U$. Since on the 2nd day $S$ plays against $R$, $P$ has no choice but to play against $U$ on the 2nd day, and against $S$ on the 4th day.
$$
\begin{array}{l|l|l|l|l}
1 \text { day } & 2 \text { day } & 3 \text { day } & 4 \text { day } & 5 \text { day } \\
\hline P-Q & R-S & P-T & T-U & P-R \\
& P-U & & P-S &
\end{array}
$$
| 1 day | 2 day | 3 day | 4 day | 5 day |
| :---: | :---: | :---: | :---: | :---: |
| $P-Q$ | $R-S$ $P-U$ | $P-T$ | $T-U$ $P-S$ | $P-R$ |
| | $T-Q$ | | $Q-R$ | |
Similarly, let's look at team $T$. On the 5th day, it must play either against $R$ or $S$; $R$ is already playing against $P$, so $T$ will play against $S$. Therefore, the match $T-R$ must take place on the 1st day:
| 1 day | 2 day | 3 day | 4 day | 5 day |
| :---: | :---: | :---: | :---: | :---: |
| $P-Q$ | $R-S$ | $P-T$ | $T-U$ | $P-R$ |
| $T-R$ | $P-U$ | | $P-S$ | $T-S$ |
| | $T-Q$ | | $Q-R$ | |
Thus, the remaining match on the 1st day is the match $S-U$, which is what we were looking for.
Comment. The situation described in the problem is indeed possible:
| 1 day | 2 day | 3 day | 4 day | 5 day |
| :---: | :---: | :---: | :---: | :---: |
| $P-Q$ | $R-S$ | $P-T$ | $T-U$ | $P-R$ |
| $T-R$ | $P-U$ | $Q-S$ | $P-S$ | $T-S$ |
| $S-U$ | $T-Q$ | $R-U$ | $Q-R$ | $Q-U$ |
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
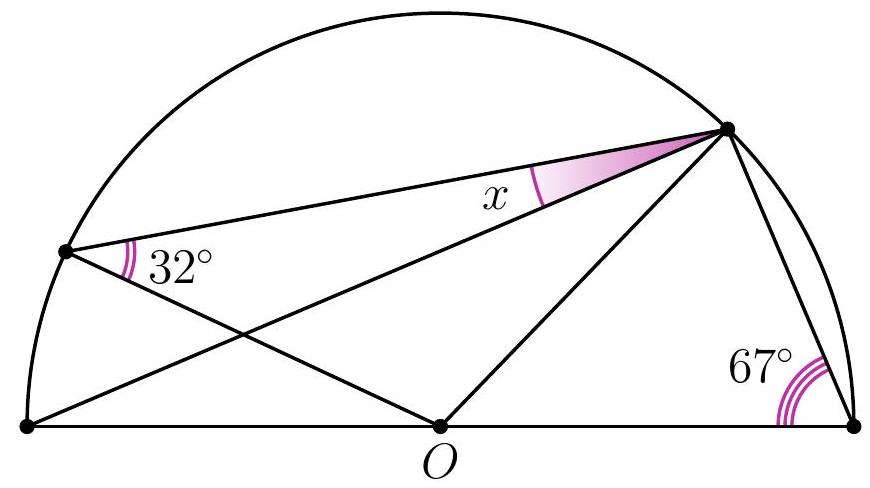
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
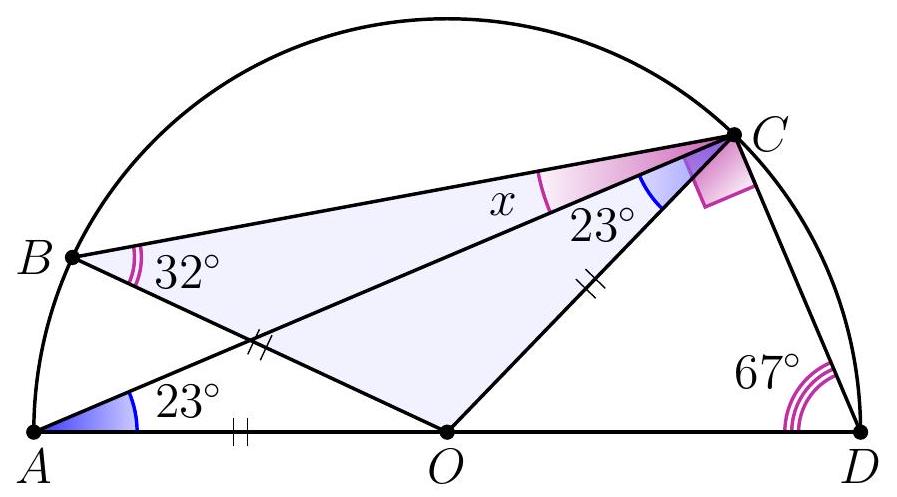
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-1. Twins Paolo and Sevilla are celebrating their birthday at a cafe with friends. If the final bill amount is divided equally among everyone, then each person should pay 12 euros. But if the bill is divided equally among everyone except Paolo and Sevilla, then each person should pay 16 euros. How many friends came to Paolo and Sevilla's birthday?
|
Answer: 6.
Solution. Let $n$ be the number of friends who arrived. Then we get the equation $12(n+2)=16n$, from which $n=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Variant 1.
It is known that
$$
\left(x^{2}-x+3\right)\left(y^{2}-6 y+41\right)\left(2 z^{2}-z+1\right)=77
$$
Find $\frac{x y}{z}$.
|
# Answer: 6.
Solution.
$$
\begin{aligned}
& x^{2}-x+3=(x-0.5)^{2}+2.75 \geq 2.75 \\
& y^{2}-6 y+41=(y-3)^{2}+32 \geq 32 \\
& 2 z^{2}-z+1=2(z-0.25)^{2}+0.875 \geq 0.875
\end{aligned}
$$
Therefore, $\left(x^{2}-x+3\right)\left(y^{2}-6 y+41\right)\left(2 z^{2}-z+1\right) \geq 77$ and if at least one of the three inequalities is strict, then the left side is greater than 77. Thus, all three inequalities must be equalities. This occurs when $x=0.5, y=3, z=0.25$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Variant 1.
Given a parallelogram $A B C D$. Let $B P$ and $C Q$ be the perpendiculars dropped from vertices $B$ and $C$ to diagonals $A C$ and $B D$ respectively (point $P$ lies on segment $A C$, and point $Q$ lies on segment $B D$). Find the ratio $\frac{10 B D}{A C}$, if $\frac{A P}{A C}=\frac{4}{9}$ and $\frac{D Q}{D B}=\frac{28}{81}$.
|
Answer: 6.
Solution: Let $O$ be the point of intersection of the diagonals. Note that points $B, C, Q, P$ lie on the same circle (segment $B C$ is seen from points $P$ and $Q$ at a right angle). Therefore, triangles $B O P$ and $C O Q$ are similar. Let $A C=2 a, B D=2 b$. Then $P O=a-\frac{8 a}{9}=\frac{a}{9}, Q O=$ $b-\frac{56 b}{81}=\frac{25 b}{81}$. From the similarity of triangles $B O P$ and $C O Q$, we have $\frac{P O}{Q O}=\frac{B O}{C O} \cdot \frac{a}{9}: \frac{25 b}{81}=\frac{b}{a} \cdot \frac{81 a}{9 \cdot 25 b}=\frac{b}{a}$, from which $\frac{b}{a}=\frac{3}{5}$.
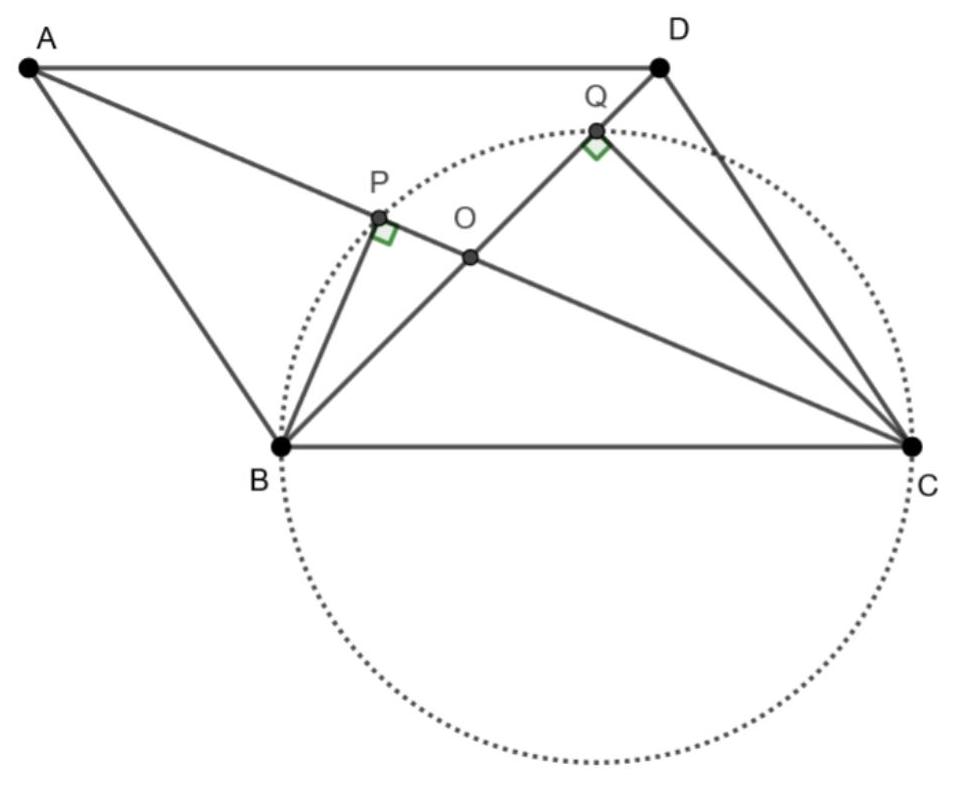
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Draw a row of 11 circles, each of which is either red, blue, or green. Moreover, among any three consecutive circles, there should be at least one red, among any four consecutive circles, there should be at least one blue, and there should be more than half green. How many red circles did you get?
|
Answer: 3 red circles
Hint. The circles are arranged only as follows: ZZKSKZKSKZZ.
Solution. (1) Three non-overlapping triplets of circles can be identified, each containing at least one red circle. Therefore, there are no fewer than three red circles. (2) Two non-overlapping quartets of circles can be identified, each containing at least one blue circle. Therefore, there are no fewer than two blue circles. (3) According to the condition, there are no fewer than six green circles. (4) Since $3+2+6=11$, all the constraints must turn into equalities. In particular, there are 3 red circles.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Represent the number 32 as the product of three integer factors, the sum of which is 3. What is the smallest of the factors?
|
Answer: -4.
Example: $32=(-4) \cdot(-1) \cdot 8$.
Solution. The given factorization is unique. This can be proven.
If all three factors are positive, then the largest of them is not less than 4, and the sum is greater than 3, which contradicts the condition. Therefore, two of the factors are negative, and the third is positive.
The number 32 has only one odd factor, and the sum of the three factors is odd. Therefore, one of them is +1 or -1. From the previous remark, it follows that this factor is -1. It is not difficult to enumerate: $32=(-1) \cdot(-2) \cdot 16=(-1) \cdot(-4) \cdot$ $8=(-1) \cdot(-16) \cdot 2=(-1) \cdot(-8) \cdot 4$. Only the second option fits.
|
-4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.7. Petya told Misha that in his class exactly two thirds of all the girls are blondes, exactly one seventh of the boys are blonds, and in total, a third of the class has light hair. Misha said: "You once told me that there are no more than 40 people in your class. 0 ! I know how many girls are in your class!" How many?
|
Answer: 12 girls
Solution. Let there be $x$ girls and $y$ boys in the class. From the problem statement, we have the following relationship:
$\frac{2}{3} x+\frac{1}{7} y=\frac{1}{3}(x+y)$,
which, after transformation, becomes $7 x=4 y$.
From the condition and the derived relationship, it follows that the number $x$ is divisible by 3 and 4, so it is divisible by 12. Let $x=12 n$, where $n$ is a natural number. From the derived equation, it follows that $y=21 n$.
Therefore, there are $x+y=12 n+21 n=33 n$ students in the class. According to the condition, this number is no more than 40, so $n=1$. In the class, there are $x=12 n=12$ girls.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Represent the number 36 as the product of three integer factors, the sum of which is 4. What is the smallest of the factors?
|
Answer: -4.
Example: $36=(-4) \cdot(-1) \cdot 9$.
Solution. The given factorization is unique. This can be proven.
If all three factors are positive, then the largest of them is not less than 4 (since $3^{3}<36$), and the sum is greater than 4, which contradicts the condition. Therefore, two of the factors are negative, and the third is positive.
Then the positive factor is 9. Indeed, if it is not more than 6, then the sum of the absolute values of the other two is greater than 2; if it is not less than 12, then the sum of the absolute values of the other two is less than 8. Then the two negative factors are either -4 and -1, or -2 and -2. Only the first variant satisfies the condition.
|
-4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Given a parallelogram $A B C D, \angle D=100^{\circ}, B C=12$. On side $A D$ there is a point $L$ such that $\angle A B L=50^{\circ}, L D=4$. Find the length of $C D$.
|
Answer: 8.
Solution. By the property of a parallelogram, $\angle A B C=\angle D=100^{\circ}, A D=B C=12$ and $C D=A B$. Therefore, $\angle C B L=\angle A B C-\angle A B L=100^{\circ}-50^{\circ}=50^{\circ}$ and $A L=A D-L D=12-4=8$. Since $\angle A L B=\angle C B L$ (as alternate interior angles when $A D$ and $B C$ are parallel and $B L$ is the transversal) and $\angle C B L=\angle A B L=50^{\circ}$, we get that $\angle A L B=\angle A B L$, so triangle $A B L$ is isosceles and $A B=A L=8$. Therefore, $C D=A B=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Four boys and three girls went to the forest to pick mushrooms. Each found several mushrooms, in total they collected 70. No two girls collected the same amount, and any three boys together brought no fewer than 43 mushrooms. The number of mushrooms collected by any two children differed by no more than 5 times. Masha collected the most among the girls. How many mushrooms did she bring?
|
Answer: 5 mushrooms.
Solution. Any three boys collected at least 43 mushrooms together, so there is a boy who collected no less than 15 mushrooms (since $14 \cdot 3 < 43$). Therefore, this boy and the other three collected no less than $15 + 43 = 58$ pieces.
If there is a boy who collected no less than 15 pieces, then any girl collected no less than $15 \div 5 = 3$ mushrooms. Therefore, the girls collected different numbers of mushrooms, meaning they collected at least $3 + 4 + 5 = 12$ pieces together.
Since $58 + 12 = 70$ is the total number of mushrooms collected, the girls must have collected 3, 4, and 5 mushrooms, so Masha brought 5 pieces.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7.5 (7 points)
On a plane, 6 lines are drawn and several points are marked. It turned out that on each line exactly 3 points are marked. What is the minimum number of points that could have been marked?
|
# Solution:
The vertices of the triangle, the midpoints of its sides, and the point of intersection of the medians - 7 points lying in threes on 6 lines (3 sides and 3 medians).
P.S. It doesn't have to be medians specifically.
Proof of the estimate: If we have a point through which at least 4 lines pass, then we will have no fewer than $1+4 \cdot 2=9$ marked points (on these 4 lines, there are 2 other marked points each). If we have
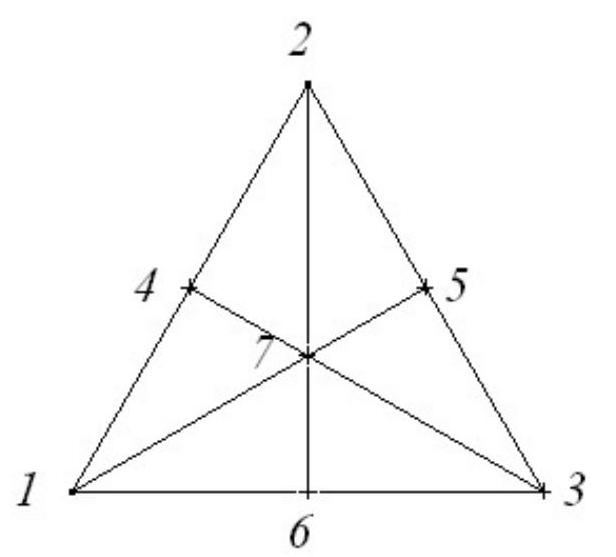
a point through which exactly 3 lines pass, then we will have no fewer than $1+3 \cdot 2=7$ marked points. If, however, through each marked point, no more than two lines pass, then the number of marked points will be no less than $6 \cdot 3 / 2=9$ (6 lines with 3 points each, each point is counted no more than twice). Therefore, we will have no fewer than 7 marked points.
| Criteria | Points |
| :--- | :---: |
| Complete solution | 7 |
| Proof of the estimate without an example | 4 |
| Example without the estimate | 3 |
| Incorrect answer | 0 |
## Answer: 7 points
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Misha has a $7 \times 7$ square of paper, all cells of which are white. Misha wants to color $N$ cells black. What is the smallest $N$ for which Misha can color the cells so that after coloring, no completely white rectangle with at least ten cells can be cut out from the square?
|
Answer: 4.
Solution. Divide the $7 \times 7$ square into 5 rectangles: four $3 \times 4$ rectangles (each corner of such a rectangle coincides with one of the corners of the $7 \times 7$ square) and a $1 \times 1$ square. If only three cells are colored, there will be a white rectangle consisting of 12 cells. Example for 4 cells: color $b 4, d 2, d 6, f 4$ in chess notation.
Criteria. Only the answer - 0 points. Correct example for 4 cells - 3 points. Proof that 3 black cells are not enough - 4 points. Points for parts of this problem are summed.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the side $A D$ of the square $A B C D$, point $K$ is marked, and on the extension of ray $A B$ beyond point $B$ - point $L$. It is known that $\angle L K C=45^{\circ}, A K=1, K D=2$. Find $L B$.
|
Answer: $L B=2$.
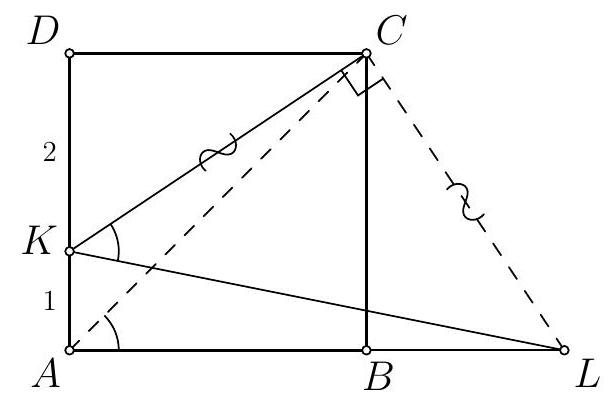
Fig. 1: to the solution of problem 5
Solution. Note that $\angle L A C=45^{\circ}=\angle L K C$, which implies that quadrilateral $L A K C$ is cyclic. Then $\angle K C L=90^{\circ}$ (Fig. 1). Therefore, triangle $L C K$ is an isosceles right triangle, i.e., $L C=K C$. Right triangles $B L C$ and $D K C$ are congruent by hypotenuse and leg, so $B L=K D=2$.
Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used
3 6. The cyclic nature of quadrilateral $L A K C$ is proven, but there is no further progress.
1 6. The correct answer is provided, but there is no justification.
06. The problem is not solved or is solved incorrectly.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. An excursion group of 6 tourists is visiting attractions. At each attraction, three people take photos, while the others photograph them. After what minimum number of attractions will each tourist have photos of all other participants in the excursion?
Answer: after 4 attractions.
|
Solution. Evaluation. A total of $6 \cdot 5=30$ photographs need to be taken (considering only photographs between two people $A$ and $B$, that is, if person $A$ photographs 3 other participants $B, C, D$ in one photograph - this counts as 3 photographings $A \rightarrow B, A \rightarrow C, A \rightarrow D$).
At one landmark, no more than $3 \cdot 3=9$ new photographings can occur. Thus, three landmarks are insufficient.
We can provide an example of how to organize the photographings around four landmarks. Let's number the people from 1 to 6. Then we can organize everything as follows:
- $(123) \rightarrow(456)$
- $(145) \rightarrow(236)$
- $(256) \rightarrow(134)$
- $(346) \rightarrow(125)$.
It is not difficult to verify that each person will photograph every other person at least once.
## Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used:
2 6. It is proven that the tourists need to visit at least 4 landmarks, but the method of photographing is not specified
2 6. A method of photographing at four landmarks is specified to meet the conditions of the problem, but the evaluation is not proven
0 6. The correct answer is provided, but there is no justification
0 6. The problem is not solved or is solved incorrectly.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of the numbers $1-2+3-4+5-6+\ldots+2013-2014$ and $1+2-3+4-5+6-\ldots-2013+2014$.
|
1. Answer: 2.
Notice that for each term of the first sum, except for 1, there is an opposite term in the second sum. The sum of opposite numbers is 0. Therefore, the total sum is $1+1=2$.
Grading criteria:
Correct answer with proper justification: 7 points.
Incorrect answer with the right idea in the justification: 2 points. Correct answer only: 1 point.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Misha painted all integers in several colors such that numbers whose difference is a prime number are painted in different colors. What is the smallest number of colors that Misha could have used? Justify your answer.
|
5. Answer: 4 colors
Evaluation. Consider the numbers $1,3,6,8$. The difference between any two of them is a prime number, which means that all of them must be of different colors, and at least four colors are needed.
Example. Paint numbers of the form $4 \mathrm{k}$ in the first color, numbers of the form $4 \mathrm{k}+1$ in the second color, numbers of the form $4 \mathrm{k}+2$ in the third color, and numbers of the form $4 \mathrm{k}+3$ in the fourth color ( $\mathrm{k}$ - an integer). The difference between any two numbers of the same color is a multiple of 4 and cannot be a prime number.
Grading criteria:
Correct example provided: 3 points. Correct evaluation provided: 3 points.
Only the correct answer provided: 0 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How to measure 8 liters of water when you are near a river and have two buckets with a capacity of 10 liters and 6 liters? (8 liters of water should end up in one bucket).
|
Solution. Let's write the sequence of filling the buckets in the form of a table:
| | Bucket with a capacity of 10 liters | Bucket with a capacity of 6 liters | Comment |
| :--- | :--- | :--- | :--- |
| Initially | 0 liters | 0 liters | |
| Step 1 | 10 liters | 0 liters | Filled the first bucket from the river |
| Step 2 | 4 liters | 6 liters | Poured from the first bucket into the second until it was full |
| Step 3 | 4 liters | 0 liters | Poured the second bucket back into the river |
| Step 4 | 0 liters | 4 liters | Poured from the first bucket into the second bucket |
| Step 5 | 10 liters | 4 liters | Filled the first bucket from the river again |
| Step 6 | 8 liters | 6 liters | Poured from the first bucket into the second until it was full |
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Snow White entered a room where there were 30 chairs around a round table. Some of the chairs were occupied by dwarfs. It turned out that Snow White could not sit down without having someone next to her. What is the minimum number of dwarfs that could have been at the table? (Explain how the dwarfs should have been seated and why, if there were fewer dwarfs, there would be a chair with no one sitting next to it).
|
Answer: 10.
Solution: If there were three consecutive empty chairs at the table in some place, Snow White could sit down in such a way that no one would sit next to her. Therefore, in any set of three consecutive chairs, at least one must be occupied by a dwarf. Since there are 30 chairs in total, there cannot be fewer than 10 dwarfs. We will show that it is possible to seat 10 dwarfs in such a way that the condition of the problem is satisfied: we will seat the dwarfs every three chairs: on the first chair, on the fourth chair, on the seventh chair, and so on. Then the condition of the problem will be met.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How to measure 2 liters of water when you are near a river and have two buckets with a capacity of 10 liters and 6 liters? (2 liters of water should end up in one bucket).
|
Solution. Let's write the sequence of filling the buckets in the form of a table:
| | Bucket with a capacity of 10 liters | Bucket with a capacity of 6 liters | Comment |
| :---: | :---: | :---: | :---: |
| Initially | 0 liters | 0 liters | |
| Step 1 | 10 liters | 0 liters | The first bucket is filled from the river |
| Step 2 | 4 liters | 6 liters | Poured from the first bucket into the second until it is full |
| Step 3 | 4 liters | 0 liters | Poured the second bucket back into the river |
| Step 4 | 0 liters | 4 liters | Poured from the first bucket into the second |
| Step 5 | 10 liters | 4 liters | The first bucket is filled from the river |
| Step 6 | 8 liters | 6 liters | Poured from the first bucket into the second until it is full |
| Step 7 | 8 liters | 0 liters | Poured the second bucket back into the river |
| Step 8 | 2 liters | 6 liters | Poured from the first bucket into the second until it is full |
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Each of the 10 dwarfs either always tells the truth or always lies. It is known that each of them loves exactly one type of ice cream: butter, chocolate, or fruit. First, Snow White asked those who love butter ice cream to raise their hands, and everyone raised their hands, then those who love chocolate ice cream - and half of the dwarfs raised their hands, then those who love fruit ice cream - and only one dwarf raised his hand. How many of the dwarfs are truthful?
#
|
# Answer. 4.
Solution. The gnomes who always tell the truth raised their hands once, while the gnomes who always lie raised their hands twice. In total, 16 hands were raised (10+5+1). If all the gnomes had told the truth, 10 hands would have been raised. If one truthful gnome is replaced by one liar, the number of raised hands increases by 1. Since there were 6 "extra" hands raised, 6 gnomes lied, and 4 told the truth.
## 8th Grade. Grading Recommendations.
Each problem is scored out of 7 points. Each score is an integer from 0 to 7. Some guidelines for grading are provided below. Naturally, the creators cannot foresee all cases. When evaluating a solution, it should be determined whether the provided solution is generally correct (although it may have flaws) - in which case the solution should be scored at least 4 points. Or if it is incorrect (although it may have significant progress) - in which case the score should not exceed 3 points.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Each of the 10 dwarfs either always tells the truth or always lies. It is known that each of them loves exactly one type of ice cream: butter, chocolate, or fruit. First, Snow White asked those who love butter ice cream to raise their hands, and everyone raised their hands, then those who love chocolate ice cream - and half of the dwarfs raised their hands, then those who love fruit ice cream - and only one dwarf raised their hand. How many of the dwarfs are truthful?
|
# Answer. 4.
Solution. The gnomes who always tell the truth raised their hands once, while the gnomes who always lie raised their hands twice. In total, 16 hands were raised (10+5+1). If all the gnomes had told the truth, 10 hands would have been raised. If one truthful gnome is replaced by one liar, the number of raised hands increases by 1. Since 6 "extra" hands were raised, 6 gnomes lied, and 4 told the truth.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Given natural numbers $M$ and $N$, both greater than ten, consisting of the same number of digits, and such that $M = 3N$. To obtain the number $M$, one of the digits of $N$ must be increased by 2, and each of the other digits must be increased by an odd digit. What digit could the number $N$ end with? Find all possible answers.
(N. Agakhanov)
|
Answer. The digit 6.
Solution. By the condition, $M=3 N$, so the number $A=M-N=2 N$ is even. However, by the condition, the number $A$ is composed of odd digits and the digit 2. Therefore, $A$ ends in 2. Thus, the number $N$, which is half of $A$, ends in either 1 or 6.
We will show that $N$ cannot end in 1. If $N$ ends in 1, then when it is doubled, there is no carry from the last digit to the second-to-last digit. This means that the second-to-last digit of the number $A=2 N$ would be even, but it must be odd. This is a contradiction.
Remark. Pairs of numbers $N$ and $M$ as described in the condition do exist, for example, $N=16, M=48$. Moreover, there are infinitely many such pairs. All suitable numbers $N$ can be described as follows: the first digit is 1 or 2, followed by several (possibly zero) digits, each of which is 5 or 6, and the last digit is 6.
Comment. A correct answer and an example of a number $N$ ending in the digit 6 - 1 point.
It is established that the last digit of the number $M$ is 2 more than the last digit of the number $N$ - 1 point.
It is shown that the last digit of the number $N$ can only be 1 or 6 - 2 points.
Points for various advancements are cumulative.
Note that the problem does not require providing an example of such a number. It is sufficient to prove that no digit other than 6 can be the last digit.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the edge $A A^{\prime}$ of the cube $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with edge length 2, a point $K$ is marked. In space, a point $T$ is marked such that $T B=\sqrt{11}$ and $T C=\sqrt{15}$. Find the length of the height of the tetrahedron $T B C K$, dropped from vertex $C$.
|
Answer: 2.
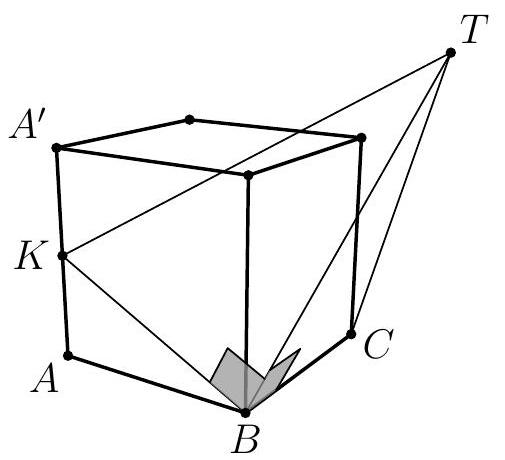
Fig. 5: to problem 5
Solution. Notice that
$$
T B^{2}+B C^{2}=11+4=15=T C^{2}
$$
From this, by the converse of the Pythagorean theorem, it follows that angle $T B C$ is a right angle. Therefore, $T B \perp B C$, which means $T$ lies in the plane of the face $A A^{\prime} B^{\prime} B$. Thus, $B C$ is the height dropped from vertex $C$, and its length is 2.
Remark. There are two possible positions of point $T$, symmetric with respect to the plane $K B C$.
## Criteria
## 4 p. Correct solution.
0 p. Only the correct answer.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) Percival's castle had a square shape. One day, Percival decided to expand his domain and added a square extension to the castle. As a result, the perimeter of the castle increased by $10 \%$. By what percentage did the area of the castle increase?
|
Answer: $4 \%$.
Solution. Let the width of the castle be $a$, and the width of the extension be $b$. Then the original perimeter is $4 a$, and the final perimeter is $4 a+2 b$. Therefore:
$$
1.1 \cdot 4 a=4 a+2 b \Leftrightarrow b=0.2 a
$$
From this, the area of the castle becomes $a^{2}+(0.2 a)^{2}=1.04 a^{2}$, which means the area has increased by $4 \%$.
Criteria. Any correct solution: 7 points.
The side of the extension is correctly found, but the further solution is missing or incorrect: 4 points.
Only the correct answer is provided: 0 points.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) It is known that $a^{2}+b=b^{2}+c=c^{2}+a$. What values can the expression $a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right)$ take?
## Answer: 0.
|
Solution. Note that the equality $a^{2}+b=b^{2}+c$ can be written as: $a^{2}-b^{2}=c-b$. Similarly, we have $b^{2}-c^{2}=a-c, c^{2}-a^{2}=b-a$. Substituting these equalities into the desired expressions, we get that
$$
a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right)=a(c-b)+b(a-c)+c(b-a)=0
$$
Criteria. Any correct solution: 7 points.
Only the correct answer is provided: 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a football tournament where each team played against each other once, teams A, B, C, D, and E participated. For a win, a team received 3 points, for a draw 1 point, and for a loss 0 points. In the end, it turned out that teams A, B, C, D, and E each had 7 points. What is the maximum number of points that team $\mathrm{E}$ could have?
|
Answer: 7 points.
Solution: In a match where one of the teams won, the teams together score 3 points, in a match that ended in a draw - 2 points. Since 7 is not divisible by 3, the team that scored 7 points must have at least one draw. Since there are five such teams, there were at least three draws in the tournament. There were a total of 15 matches, as is easily verified. Therefore, all teams together scored no more than $2 \cdot 3 + 3 \cdot 12 = 42$ points. Of these, teams A, B, C, D, and E scored 35 points. Therefore, team F scored no more than $42 - 35 = 7$ points. How it could have scored exactly 7 points is shown in the table on the right.
Comment: A realization is proposed - 3 points, an estimate is made - 4 points, points are summed. In the absence of a solution, 2-3 points for potentially useful ideas and approaches. Answer without justification - 0 points.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Solve the equation
$$
\sqrt{3 x-2-x^{2}}+\sqrt{x^{2}-4 x+3}=\sqrt{2}(1-\sqrt{x})
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{c}
3 x-2-x^{2} \geq 0 \\
x^{2}-4 x+3 \geq 0
\end{array}\right.
$$
we obtain that the domain of the function on the left side of the equation is $\{1\}$. The domain of the function on the right side of the equation is the numerical ray $[0 ;+\infty)$. Therefore, the domain of the equation is $\{1\}$. By verification, we find that $x=1$ is a root of the equation.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Each of the thirteen dwarfs is either a knight, who always tells the truth, or a liar, who always lies. One day, all the dwarfs in turn made the statement: “Among the statements made previously, there are exactly two more false ones than true ones.” How many knights could there have been among the dwarfs?
|
Answer: 6
Solution. The first two statements are obviously false, as there were fewer than two statements made before each of them. The third statement is true, as there were 2 false statements and zero true statements made before it. The fourth statement is false, as it adds one true statement to the two false ones, while the fifth statement is true again.
Reasoning similarly, we find that all gnomes making an even-numbered statement were lying, while those making an odd-numbered statement were telling the truth. Thus, the knights are the gnomes who spoke under the numbers: $3,5,7,9,11$ and 13.
Evaluation criteria.
"+" A complete and well-reasoned solution with the correct answer is provided
“士” A generally correct reasoning with minor gaps or inaccuracies and the correct answer is provided
"干" Only the numbers of the gnomes who told the truth are correctly indicated, but any explanations are missing
“-" Only the answer is provided
“-" An incorrect solution is provided or it is missing
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
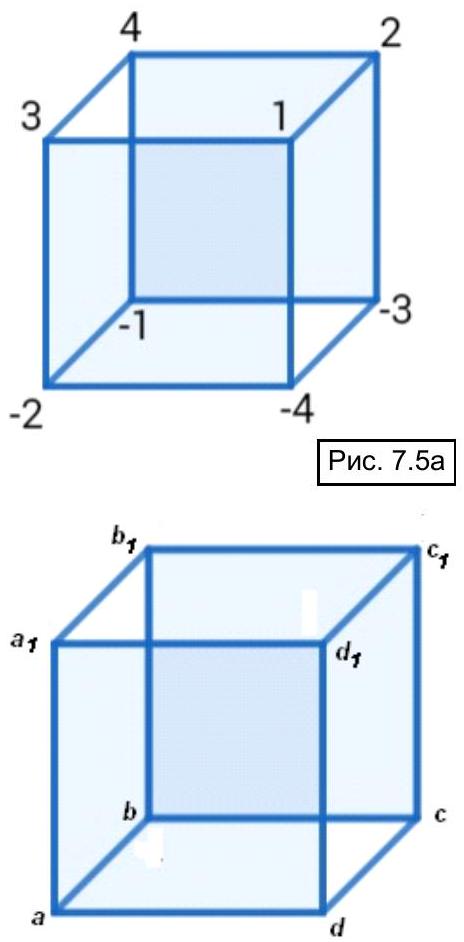
7.5. At each vertex of a cube lives a number, not necessarily positive. All eight numbers are distinct. If a number is equal to the sum of the three numbers living in the adjacent vertices, then it is happy. What is the maximum number of happy numbers that can live at the vertices of the cube?
|
Answer: 8.
Solution. See, for example, Fig. 7.5a. It is easy to verify that each vertex of the cube contains a lucky number.
There are other examples as well. Let's understand how they are structured (this was not required of the olympiad participants). Let's denote the numbers at the vertices of the cube (see Fig. 7.5b). First, write down two equations for the opposite vertices of the lower square: $a=a_{1}+b+d$ (1); $c=c_{1}+b+d$ (2). Subtracting equation (2) from equation (1), we get: $a-c=a_{1}-c_{1}$ (3).
Now, write down similar equations for two vertices of the vertical edge: $b=b_{1}+a+c$ (4); $b_{1}=b+a_{1}+c_{1}$ (5). Substituting $b_{1}$ from equation (5) into equation (4), we get: $a+c=-a_{1}-c_{1}$ (6). Combining equations (3) and (6) into a system, we get that $a=-c_{1}$; $c = -a_{1}$. Thus, the numbers in opposite vertices of the cube must be opposite (similar equations for the other two pairs of numbers follow from the symmetry of the cube).
Therefore, to construct any example, it is sufficient to choose one vertex of the cube and denote the numbers in the adjacent vertices, for example, as $x$, $y$, and $z$. To make the chosen vertex lucky, place the number $x+y+z$ in it. It is only required that the absolute values of the numbers $x$, $y$, $z$, and $x+y+z$ be pairwise distinct. Then, place the numbers $-x$, $-y$, $-z$, and $-x-y-z$ in the opposite vertices, respectively. It is easy to verify that all eight numbers are lucky.
Grading criteria.
“+" Correct answer and correct example provided
“-" Only the answer is provided
“-” Incorrect example or no example provided
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. In the numerical example АБВ $+9=$ ГДЕ, the letters А, Б, В, Г, Д, and Е represent six different digits. What digit is represented by the letter Д?
|
Answer: 0.
Solution: In the addition, the second digit of the first addend АБВ has changed (Д instead of Б). This could only happen if 1 was carried over from the units place to the tens place during the addition. However, the first digit also changed (Г instead of А). This means that 1 was also carried over from the tens place to the hundreds place during the addition. This is only possible if Б $+1=10$. Therefore, $Б=9$, and then $Д=0$.
Note: The puzzle has solutions, for example, $194+9=203$.
Comment: The score is not reduced if the correct answer is given, it is stated that $Б=9$, $Д=0$, but detailed explanations are not provided.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. In the room, there are 10 people - liars and knights (liars always lie, and knights always tell the truth). The first said: "In this room, there is at least 1 liar." The second said: "In this room, there are at least 2 liars." The third said: "In this room, there are at least 3 liars." And so on,
up to the tenth, who said: "In this room, everyone is a liar." How many liars could there be among these 10 people?
|
Answer: 5.
Solution: Let there be $k$ liars in the room. Then the first $k$ people told the truth (and thus were knights), while the remaining $(10-k)$ lied (and were liars). Therefore, $k=10-k$, from which $k=5$.
Comment: The answer is obtained by considering an example -3 points.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the island, there live knights who always tell the truth and liars who always lie. In the island's football team, there are 11 people. Player number 1 said: "In our team, there are as many knights as there are liars." Player number 2 said: "In our team, the number of knights and the number of liars differ by one," and so on. Player number 11 said: "In our team, the number of knights and the number of liars differ by ten." How many knights are in the team, and if there are any, what are their numbers? Find all possible answers to this question.
|
4. Answer: There are either no knights at all, or there is only one and he plays under number 10. The two answers cannot both be true, as they contradict each other. This means there can be no more than one true answer. If there is no true answer, then the team consists entirely of liars, in which case indeed none of the answers are true. If there is 1 knight and 10 liars in the team, then the answer of the player under number 10 is true, and the rest of the answers are false.
Criteria: correct solution - 7 points. Stated but not explained why there cannot be two correct answers, no other errors - 5 points. The case of no knights in the team is lost - 2 points. Only noted that there may be no knights - 1 point. Only the answer - 0 points.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2 Out of 24 matches, a figure in the form of a $3 \times 3$ square is laid out (see figure), the side length of each small square is equal to the length of a match. What is the smallest number of matches that can be removed so that there are no whole $1 \times 1$ squares left, formed from matches.

|
Answer: 5 matches.
Solution: Estimation: It is impossible to manage with four matches, as by removing a match, we "ruin" no more than two squares (each match is a side of one or two adjacent squares), but initially, we have 9 small squares. Example for 5 matches:
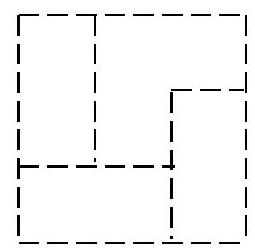
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Two given quadratic trinomials $f(x)$ and $g(x)$ each have two roots, and the equalities $f(1)=g(2)$ and $g(1)=f(2)$ hold. Find the sum of all four roots of these trinomials.
|
Answer: 6.
First solution. Let $f(x)=x^{2}+a x+b, g(x)=x^{2}+$ $+c x+d$. Then the conditions of the problem can be written as
$$
1+a+b=4+2 c+d \quad \text { and } \quad 4+2 a+b=1+c+d
$$
Subtracting the second equation from the first, we get $-3-a=3+c$, which means $a+c=-6$. By Vieta's theorem, $-a$ is the sum of the roots of the first quadratic, and $-c$ is the sum of the roots of the second quadratic, from which the required result follows.
Second solution. Consider the auxiliary quadratic polynomial $h(x)=g(3-x)$ (it is also a monic polynomial!). Then $h(x)-f(x)$ is a linear polynomial with roots 1 and 2; hence, it is identically zero, i.e., $f(x)=g(3-x)$. Therefore, if $x_{0}$ is a root of $f(x)$, then $3-x_{0}$ is a root of $g(x)$, and the sum of these two roots is 3. Similarly, the sum of the other roots of these polynomials is also 3.
Comment. Only the correct answer - 0 points.
Only the correct answer with an example of two polynomials satisfying the conditions of the problem - 1 point.
Proved that $a+c=-6$ (in the notation of the first solution) - 3 points.
Proved that $f(x)=g(3-x)$ - 3 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Each of the 10 people is either a knight, who always tells the truth, or a liar, who always lies. Each of them thought of some integer. Then the first said: “My number is greater than 1”, the second said: “My number is greater than 2”, \ldots, the tenth said: “My number is greater than 10”. After that, all ten, speaking in some order, said: “My number is less than 1”, “My number is less than 2”, \ldots, “My number is less than 10” (each said exactly one of these ten phrases). What is the maximum number of knights that could have been among these 10 people?
(O. Podlipsky)
|
Answer: 8 knights.
Solution. We will prove that none of the knights could have said either of the phrases "My number is greater than 9" or "My number is greater than 10." Indeed, if this were possible, the integer thought of by the knight would be at least 10. But then he could not have said any of the phrases "My number is less than 1," "My number is less than 2," ..., "My number is less than 10." Therefore, there could not have been more than eight knights.
We will show that there could have been 8 knights. Suppose the first knight thought of the number 2, the second -3, ..., the eighth -9, and the liars thought of the numbers 5 and 6. Then the $k$-th knight could have said the phrases "My number is greater than $k$" and "My number is less than $k+2$," while the liars could have said the phrases: one - "My number is greater than 9" and "My number is less than 1," and the other - "My number is greater than 10" and "My number is less than 2."
Note. The example given above ceases to be valid if the liars think of numbers outside the interval $[1; 10]$, as then some of their statements become true.
Comment. Proved that there are no more than $9-$ 0 points.
Proved that there are no more than 8 knights (or, equivalently, at least two liars -3 points.
Provided an example showing that there could have been 8 knights, with a correct indication of which person said which phrase - 4 points.
If the example provided does not fully describe the situation (for example, it is not specified what numbers the liars thought of, or it is not clearly indicated who said which phrase) - out of 4 points for the example, no more than 2 points are given.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. For what least natural $n$ do there exist integers $a_{1}, a_{2}, \ldots, a_{n}$ such that the quadratic trinomial
$$
x^{2}-2\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2} x+\left(a_{1}^{4}+a_{2}^{4}+\ldots+a_{n}^{4}+1\right)
$$
has at least one integer root?
(P. Kozlov)
|
Answer. For $n=6$.
Solution. For $n=6$, we can set $a_{1}=a_{2}=a_{3}=a_{4}=1$ and $a_{5}=a_{6}=-1$; then the quadratic trinomial from the condition becomes $x^{2}-8 x+7$ and has two integer roots: 1 and 7. It remains to show that this is the smallest possible value of $n$.
Suppose the numbers $a_{1}, a_{2}, \ldots, a_{n}$ satisfy the condition of the problem; then the discriminant of the quadratic trinomial from the condition, divided by 4, must be a perfect square. It is equal to
$$
d=\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{4}-\left(a_{1}^{4}+a_{2}^{4}+\ldots+a_{n}^{4}+1\right)
$$
Then the number $d$ is odd and is a square, so it gives a remainder of 1 when divided by 8.
Rewrite the above equality as
$$
d+1+a_{1}^{4}+a_{2}^{4}+\ldots+a_{n}^{4}=\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{4}
$$
and consider it modulo 8. It is not hard to check that the fourth powers of integers give only remainders 0 and 1 when divided by 8, so the right-hand side of the equality gives a remainder of 0 or 1. The left-hand side, however, is comparable to $1+1+k$, where $k$ is the number of odd numbers among $a_{i}$. Therefore, $n \geqslant k \geqslant 6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. In a notebook, a triangular grid is drawn (see figure). Tanya placed integers at the nodes of the grid. We will call two numbers close if they are in adjacent nodes of the grid. It is known that
- the sum of all ten numbers is 43;
- the sum of any three numbers such that any two of them are close is 11.
What is the central number?

|
Answer: 10.
Solution. Let's denote the numbers by variables as shown in the figure.
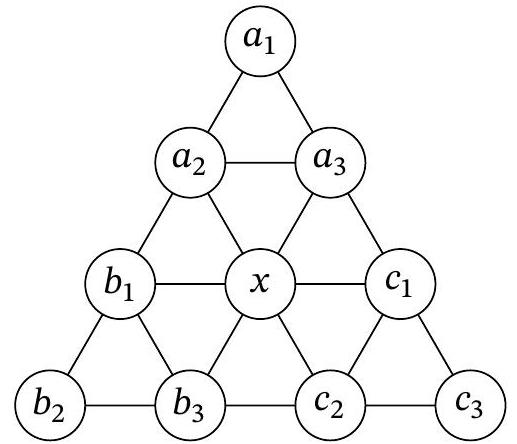
Then
\[
\begin{gathered}
a_{1}+a_{2}+a_{3}=b_{1}+b_{2}+b_{3}=c_{1}+c_{2}+c_{3}=11 \\
\left(a_{1}+a_{2}+a_{3}\right)+\left(b_{1}+b_{2}+b_{3}\right)+\left(c_{1}+c_{2}+c_{3}\right)+x=43
\end{gathered}
\]
From this, we get that \( x=10 \).
An example of a suitable arrangement of numbers is shown below.
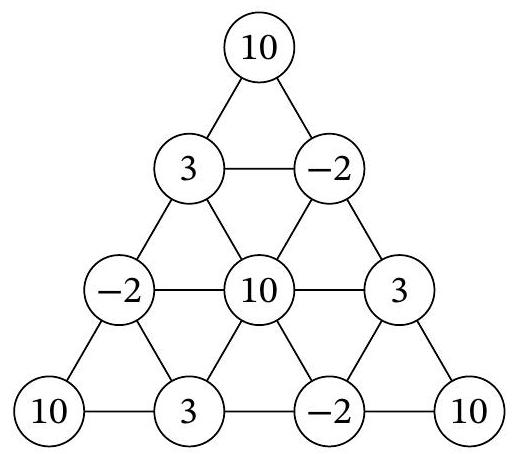
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.3. The teacher wrote a fraction on the board, where the numerator and the denominator are natural numbers. Misha added 30 to the numerator of the given fraction and wrote the resulting fraction in his notebook, while Lesha subtracted 6 from the denominator of the fraction written on the board and also wrote the resulting fraction in his notebook. The fractions recorded by the boys turned out to be equal to the same number. What is this number?
|
Answer: 5.
Solution. Let $\frac{a}{b}$ be the original fraction. Then Misha wrote down the fraction $\frac{a+30}{b}$ in his notebook, and Lёsha wrote down $-\frac{a}{b-6}$.
Let's write the equation
$$
\frac{a+30}{b}=\frac{a}{b-6}
$$
Transforming it, we get
$$
\begin{gathered}
(a+30)(b-6)=a b \\
a b+30 b-6 a-180=a b ; \\
30 b=6 a+180 \\
\frac{a+30}{b}=5
\end{gathered}
$$
This is the value of the fraction obtained by Misha. It should also have been obtained by Lёsha.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Pantelej and Gerasim received 20 grades each in November, and Pantelej received as many fives as Gerasim received fours, as many fours as Gerasim received threes, as many threes as Gerasim received twos, and as many twos as Gerasim received fives. At the same time, their average grade for November is the same. How many twos did Pantelej receive in November?
|
Solution. Let's add one to each of Gerasim's grades. His total score will increase by 20. On the other hand, it will become greater than Pantelej's total score by four times the number of Pantelej's twos.
Answer: 5 twos.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In triangle $\mathrm{ABC}$, $\mathrm{AC}=1$, $\mathrm{AB}=2$, $\mathrm{O}$ is the point of intersection of the angle bisectors. A segment passing through point O and parallel to side $\mathrm{BC}$ intersects sides $\mathrm{AC}$ and $\mathrm{AB}$ at points K and M, respectively. Find the perimeter of triangle $\mathrm{AKM}$.
|
8.3. $\angle \mathrm{KCO}=\angle \mathrm{BCO}=\angle \mathrm{KOC}$ (alternate interior angles). Therefore, OK = KC, and similarly BM = OM. Then
$$
A K+A M+K M=A K+K C+A M+B M=3 .
$$
Answer: 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. We will call a natural number interesting if the sum of its digits is a prime number. What is the maximum number of interesting numbers that can be among five consecutive natural numbers?
(
#
|
# Answer: 4.
Solution. Among five consecutive natural numbers, there can be 4 interesting numbers. For example, the numbers 199, 200, 201, 202, 203 (with digit sums 19, 2, 3, 4, and 5) will work.
Now, let's prove that all 5 numbers cannot be interesting. Among our five numbers, there are three that lie within the same decade. Then their digit sums are consecutive numbers; hence, they cannot all be prime simultaneously.
Remark 1. There are other examples of five consecutive numbers, four of which are interesting. Moreover, the number divisible by 10 can also be in a different position, as in the set 197, 198, 199, 200, 201. However, in any such example, the digit sums of two of the numbers in the set must be 2 and 3.
Remark 2. One can also prove that five consecutive numbers cannot all be interesting in a different way. Among our numbers, at least two have even digit sums (even if there is a transition "across a decade"). But both of these sums cannot equal 2, since the digit sum 2 is only found in numbers of the form $10 \ldots 010 \ldots 0$ and $20 \ldots 0$, and two such numbers cannot appear among 5 consecutive natural numbers.
Comment. Only the answer - 0 points.
Providing an example of five consecutive numbers, four of which are interesting - 3 points.
Providing only an example of five consecutive numbers, among which fewer than 4 are interesting - 0 points.
Proving that there do not exist five consecutive interesting numbers - 3 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. At the New Year's celebration, schoolchildren organized an exchange game: if they were given five tangerines, they would exchange them for three crackers and a candy, and if they were given two crackers, they would exchange them for three tangerines and a candy. Father Frost played this game with them several times and received a total of 50 candies. Initially, he only had a bag of tangerines, and after all the exchanges, he had no crackers left. How many tangerines did Father Frost give to the children?
|
Solution. Ded Moroz conducted 50 exchanges, as he was given 50 candies. At the end of the game, he had no crackers left, meaning he exchanged all of them back. For every two exchanges of tangerines for crackers (ten given - six received), he conducted three exchanges of crackers for tangerines (six given - nine received). Therefore, every five exchanges, Ded Moroz irreversibly gave away one tangerine. All exchanges can be divided into ten such groups. Therefore, Ded Moroz gave away 10 tangerines in total.
Answer. Ded Moroz gave away 10 tangerines.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-1. Piglet has balloons of five colors. He managed to arrange them in a row in such a way that for any two different colors in the row, there will always be two adjacent balloons of these colors. What is the minimum number of balloons Piglet could have?
|
Answer: 11 balls.
Solution. Consider the balls of color $a$. Their neighbors must be balls of all 4 other colors. But one ball can have no more than two neighbors, so there must be at least 2 balls of color $a$. This is true for each of the 5 colors, so there must be at least 10 balls in total.
Notice that some ball of color $b$ is at the end of the row. It has only one neighbor, so two balls of this color have no more than 3 neighbors. Therefore, to meet the conditions, we need to add at least one more ball of color $b$. Thus, we need at least 11 balls in total.
We will show that 11 balls are sufficient. Let $a, b, c, d, e$ be the colors of the balls. They can be arranged, for example, as follows: $a b c d e c a d b e a$.
Criteria. Only the answer - 0 points. Estimation (that there are no fewer than 11 balls) - 4 points. Example of the required arrangement - 3 points.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-5. From 80 identical Lego parts, several figures were assembled, with the number of parts used in all figures being different. For the manufacture of the three smallest figures, 14 parts were used, and in the three largest, 43 were used in total. How many figures were assembled? How many parts are in the largest figure?
|
Answer: 8 figurines, 16 parts.
Solution. Let the number of parts in the figurines be denoted by $a_{1}43$, so $a_{n-2} \leq 13$.
Remove the three largest and three smallest figurines. In the remaining figurines, there will be $80-14$ - 43 $=23$ parts, and each will have between 7 and 12 parts. One figurine is clearly insufficient, and three would be too many (7 $+8+9=24$). Therefore, 23 parts form 2 figurines. This is possible, and in only one way: $23=11+12$.
We have $43=13+14+16$ - the only decomposition with $a_{6} \geq 13$.
Criteria. Only the answer - 0 points. Only correct estimates for $a_{3}$ and $a_{n-3}-3$ points. Only a justified answer for the number of figurines - 5 points. Complete solution - 7 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1 Two ants are running along a circle towards each other at constant speeds. While one of them runs 9 laps, the other runs 6. At the point where the ants meet, a red dot appears. How many red dots will there be on the circle?
#
|
# Answer: 5
Solution. The ratio of the speeds of the ants is $\frac{9}{6}=\frac{3}{2}$. Without loss of generality, assume the circumference of the circle is 5, and let the ants meet at some moment at point 0. Place points $1, 2, 3,$ and 4 clockwise so that they, together with point 0, divide the circle into 5 equal parts. If the slower ant runs counterclockwise, they will meet again at point 2. Now we can consider this point as the starting point, and thus they will meet next at point 4, and then at point 1 (since $4+2=6$, but the circumference is 5). The next meeting will be at point 3, then 0, after which the process will repeat, and there will be a total of 5 points.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. 16 travelers, each of whom is either a liar or a knight (liars always lie, knights always tell the truth), settled into 3 rooms of a hotel. When everyone gathered in their rooms, Basil, who was staying in the first room, said: "There are more liars than knights in this room right now. Although no - there are more knights than liars in this room right now." After that, Basil went to the second room and said the same two statements there. And then he went to the third room and said the same two statements there as well. How many knights could there have been among these 16 travelers?
|
Answer: 9 knights.
Solution: Since Vasily's statements contradict each other, Vasily is a liar. Therefore, both of Vasily's statements (about each room) are false, and in each room (when he was there) the number of liars and knights was equal. This means that in each room, without Vasily, there was one more knight than liar. Therefore, among the 15 remaining travelers, there are 3 more knights than liars, which means there are 9 knights and 6 liars among them.
Comment: Correct answer without justification - 0 points.
Showing that Vasily is a liar - 1 point.
Proving that in each room, without Vasily, there is one more knight than liar - 4 points.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. It is known that the numbers EGGPLANT and FROG are divisible by 3. What is the remainder when the number CLAN is divided by 3? (Letters represent digits, the same letters represent the same digits, different letters represent different digits).
Answer: 0
|
Solution. By the divisibility rule for 3, the sums B+A+K+L+A+Z+A+N and Z+A+B+A are divisible by 3, and therefore the difference of these sums $K+N+A+H$ is also divisible by 3, which by the rule means that the number KLAN is divisible by 3, hence the remainder is 0.
Criteria. Only the answer - 0 points
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Find the value of the expression $\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}$, if $a+b+c=0$.
|
Answer: 3.
Solution. $(a+b+c)^{3}=a^{3}+b^{3}+c^{3}+(a+b+c)(3 a b+3 b c+3 c a)-3 a b c$. Using the condition $a+b+c=0$, we get: $a^{3}+b^{3}+c^{3}=3 a b c$. Then $\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}=\frac{a^{3}+b^{3}+c^{3}}{a b c}=\frac{3 a b c}{a b c}=3$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At present, the exchange rates of the US dollar and the euro are as follows: $D=6$ yuan and $E=7$ yuan. The People's Bank of China determines the yuan exchange rate independently of market conditions and adheres to a policy of approximate equality of currencies. One bank employee proposed the following scheme for changing the exchange rate to the management. Over one year, the exchange rates $D$ and $E$ are allowed to change according to the following four rules. Either change $D$ and $E$ to the pair $(D+E, 2D \pm 1)$, or to the pair $(D+E, 2E \pm 1)$. Moreover, it is forbidden for the exchange rates of the dollar and euro to be equal at any time.
For example: From the pair $(6,7)$, after one year, the following pairs can be made: $(13,11)$, $(11,13)$, $(13,15)$, or $(15,13)$. What is the smallest value that the difference between the larger and smaller of the resulting exchange rates can take after 101 years?
|
# Solution.
Note that if $D$ and $E$ have different parity, their sum is odd, and if they have the same parity, their sum is even. The second number in the pair is always odd. Initially, we have a pair $О Н$ (Odd, Odd).
After one year
After two years $\quad \mathrm{H}+\mathrm{H}=$ О, Н. And so on.
That is, after an odd number of years, there will be a pair of odd numbers.
Since they do not coincide, the smallest difference can only be 2.
We will also prove that after an even number of years, a difference of 1 can be achieved. We will prove this fact by mathematical induction.
For $n=1$, i.e., after one year $(13,11)$, the difference is 2. For $n=2(24,13 \cdot 2$ - $1=25)$. The difference is 1. Suppose for $n=2 k$ the difference is 1, i.e., $(2 m ; 2 m-1) \Rightarrow(4 m-$ $1 ; 4 m-3)$, the difference is 2. If $n=2 k-1$, the difference, by the induction hypothesis, is 2, then for $n=2 k$ from two courses $(2 m ; 2 m+2) \Rightarrow(4 m+2 ; 4 m+3)$. The difference is 1. Therefore, after 101 years, the smallest difference can be 2.
Answer: 2.
## Recommendations for checking.
Proved only the fact of the alternation of the parity of the difference of the courses - 2 points
Answer without justification - 0 points
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. It is known that $a^{2}+b=b^{2}+c=c^{2}+a$. What values can the expression
$$
a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right) ?
$$
take?
|
Answer: 0.
Solution. From the condition, it follows that $a^{2}-b^{2}=c-b$, $b^{2}-c^{2}=a-c$, and $c^{2}-a^{2}=b-a$. Therefore, $a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right)=a(c-b)+b(a-c)+c(b-a)=0$.
## Grading Criteria:
+ a complete and justified solution is provided
the correct answer is obtained by considering specific examples
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. Waiting for customers, a watermelon seller sequentially weighed 20 watermelons (weighing 1 kg, 2 kg, 3 kg, ..., 20 kg), balancing the watermelon on one scale pan with one or two weights on the other pan (possibly identical). In the process, the seller wrote down on a piece of paper the weights he used. What is the smallest number of different numbers that could have appeared in his notes, if the weight of each weight is an integer number of kilograms?
|
Answer: 6 numbers.
Solution. Let's check that with weights of 1 kg, 3 kg, 5 kg, 7 kg, 9 kg, and 10 kg, one can weigh any of the given watermelons. Indeed, $2=1+1 ; 4=3+1 ; 6=5+1 ; 8=7+1 ; 11=10+1$; $12=9+3 ; 13=10+3 ; 14=9+5 ; 15=10+5 ; 16=9+7 ; 17=10+7 ; 18=9+9 ; 19=10+9 ;$ $20=10+10$. Thus, 6 different numbers could have been recorded.
We will show that five types of weights are insufficient for the required weighings. If there are five weights, then, generally speaking, twenty watermelons can be weighed. Specifically: five watermelons can be balanced with single weights, five with double weights, and the remaining $\frac{5 \cdot 4}{2}=10$ watermelons with pairs of different weights. However, each combination of weights must be used exactly once.
Notice that half of the watermelons have an odd mass. Let $k$ be the number of weights with an odd mass, and $(5-k)$ be the number of weights with an even mass. Then the number of ways to weigh a watermelon with an odd mass is exactly $k+k(5-k)=6k-k^2$. However, for no $k=0 ; 1 ; 2 ; 3 ; 4 ; 5$ does this expression equal 10 (this can be verified either by substitution or by solving the quadratic equation $6k-k^2=10$).
Therefore, the seller could not have recorded fewer than 6 numbers.
## Grading criteria:
+ a complete and well-reasoned solution is provided
$\pm$ a generally correct solution is provided, containing minor gaps or inaccuracies
$\pm$ it is proven that fewer than six numbers could not have been recorded, a correct set of six weights is indicated, but it is not shown how exactly to weigh the watermelons
dry it is only proven that five weights are insufficient
Ғ it is not proven that five weights are insufficient, but a correct set of six weights is provided (regardless of whether it is shown how exactly to weigh the watermelons)
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The working day at the enterprise lasted 8 hours. During this time, the labor productivity was as planned for the first six hours, and then it decreased by $25 \%$. The director (in agreement with the labor collective) extended the shift by one hour. As a result, it turned out that again the first six hours were worked with planned productivity, and then it decreased by $30 \%$. By what percentage did the overall labor productivity for the shift increase as a result of extending the working day?
|
2. Answer: by 8 percent. Solution. Let's take 1 as the planned labor productivity (the volume of work performed per hour). Then before the shift extension, workers completed $6+1.5=7.5$ units of work per shift. And after the extension, $8+2.1=8.1$ units. Thus, the overall productivity per shift became $8.1: 7.5 \times 100 \% = 108 \%$ of the initial, meaning it increased by $8 \%$. Grading criteria. Correct solution - 7 points. Initial and final productivity per shift correctly expressed in conditional units, but the percentage ratio is expressed incorrectly - 4 points. In all other cases - 0 points.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In pentagon $A B C D E \quad A B=A E=C D=1, \quad B C+D E=1$, $\angle A B C=\angle A E D=90^{\circ}$. Find the area of the pentagon.
|
6. Answer: 1. Solution. Extend the segment $C B$ beyond point $B$ to segment $B F=D E$, and then draw segments $C A, C E$ and $A F$. It is easy to see that triangles $C D E$ and $A B F$ are equal. Therefore, $C E=A F$ and the areas of the pentagon and quadrilateral $A E C F$ coincide. But triangles $A E C$ and $A F C$ are equal by three sides, and the area of triangle $A F C$ is $1 / 2$. Therefore, the area of quadrilateral $A E C F$ is 1. Grading criteria. Correct solution - 7 points. In all other cases - 0 points.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) In a building, on all floors in all entrances there is an equal number of apartments (more than one). Also, in all entrances there are an equal number of floors. The number of floors is greater than the number of apartments per floor, but less than the number of entrances. How many floors are there in the building if there are a total of $715$ apartments?
|
Answer: 11.
Solution. Let the number of apartments per floor be K, the number of floors be F, and the number of entrances be E. According to the condition, $1<K<F<E$. The number 715 can be factored into numbers greater than one in only one way: $715=5 \cdot 11 \cdot 13$. Therefore, $K=5, F=11, E=13$.
Criterion. Correct solution: 7 points.
Answer without explanation: 3 points.
Incorrect answer: 0 points.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Anya left the house, and after some time Vanya left from the same place and soon caught up with Anya. If Vanya had walked twice as fast, he would have caught up with Anya three times faster. How many times faster would Vanya have caught up with Anya (compared to the actual time) if, in addition, Anya walked twice as slow
|
Answer: 7.
Solution: Let Ane's speed be $v$, and Vanya's speed be $V$. The distance Ane has walked is proportional to $v$, while Vanya catches up with her at a speed of $u=V-v$. When Vanya doubles his speed, this difference triples, i.e., $u+V=2V-v=3u$. From this, we get $V=2u=2v$. If Vanya's speed doubles and Ane's speed is halved, the new difference in speeds will be $3.5v$, which is 7 times the new speed of Masha. Therefore, Vanya will catch up to her 7 times faster.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Solve the equation $\sqrt{2 x-1}+\sqrt[3]{x}=\sqrt[4]{17-x}$.
|
Answer: 1.
Solution. It is easy to verify that $x=1$ is a root of the equation.
Since the left side of the equation is an increasing function (as the sum of two increasing functions), and the right side is a decreasing function, there are no other roots.
Comment. The correct answer without proof of its uniqueness - 2 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In a chess tournament, each of the 10 players played one game against each other, and Petya came in last place (scored fewer points than any other participant). Then two players were disqualified, and all points earned in matches against them were annulled, and these two players were removed from the table. It turned out that as a result, Petya became the winner of the tournament (scored more points than any other participant). How many points did Petya end up with (after the disqualification of the players)? 1 point is awarded for a win, 0.5 points for a draw, and 0 points for a loss.
|
Answer: 4 points.
Solution. In a tournament with 10 players, played in a single round, $\frac{10 \cdot 9}{2}=45$ points are distributed. Therefore, there will be a player who scores no more than $45: 10=4.5$ points. This means that the player who finished in absolute last place scored no more than 4 points. Similarly, in a tournament with $10-2=8$ players, played in a single round, $\frac{8 \cdot 7}{2}=28$ points are distributed. In such a tournament, there will be a player who scores no less than $28: 8=3.5$ points. This means that the player who finished in absolute first place (after the disqualification) scored no less than 4 points. Therefore, Petya could have scored only 4 points.
Comment. A correct answer without justification - 0 points.
A correct answer obtained by considering an example - 1 point.
One of the two estimates for the number of points Petya scored (before or after disqualification) is correctly proven - 3 points.
Note. The tournament described in the problem is possible. Providing an example of such a tournament is not required, as it follows from the problem statement that such a tournament exists. Points are not deducted for the lack of such an example.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In the notebook, all irreducible fractions with the numerator 15 are written, which are greater than $\frac{1}{16}$ and less than $\frac{1}{15} \cdot$ How many such fractions are written in the notebook?
|
Answer: 8 fractions.
Solution. We look for all suitable irreducible fractions of the form $\frac{n}{15}$. Since $\frac{1}{16} < \frac{15}{n}$, then $\frac{15}{225} > \frac{15}{n}$, and $n > 225$. Therefore, $225 < n < 240$. The fraction $\frac{n}{15}$ is irreducible, meaning $n$ is not divisible by 3 or 5. It is not difficult to verify that out of the range from 226 to 239 (14 numbers), we need to exclude 6 numbers (228, 230, 231, 234, 235, 237). This leaves 8 possible values for $n$.
## Criteria.
1 point. Correct answer without correct justification.
2 points. Correctly obtained range for $n$.
0 points. Not all cases considered when listing fractions.
Comment. It is quite possible that participants will try to list all such fractions and then justify why the denominator cannot be greater or less, carefully monitoring the accuracy of such justifications.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In an isosceles triangle \(ABC\), the angle \(A\) at the base is \(75^\circ\). The bisector of angle \(A\) intersects side \(BC\) at point \(K\). Find the distance from point \(K\) to the base \(AC\), if \(BK=10\).
|
Answer: 5.
Solution. In triangle $ABC$, $\angle B = (180^0 - 75^0 - 75^0) = 30^0$. Drop perpendiculars from point $K$: $KH$ to side $AB$, and $KN$ to side $AC$. In the right triangle $HBK$, the hypotenuse $BK$ is 10. Angle $B$ is 30 degrees, and the side opposite to it is half the hypotenuse, so $HK = 5$. Triangles $AHK$ and $ANK$ are equal by hypotenuse and acute angle, so $KN = KH = 5$.
## Criteria.
1 point. A perpendicular is dropped from point $K$ to side $AB$.
2 points. The length of the perpendicular dropped from point $K$ to side $AB$ is found. Comment. Points for criteria are summed.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Given a triangle $A B C$. A line parallel to $A C$ intersects sides $A B$ and $B C$ at points $P$ and $T$ respectively, and the median $A M$ at point $Q$. It is known that $P Q=3$, and $Q T=5$. Find the length of $A C$.
|
Answer: $AC=11$.
Solution. First method. Draw a line through point $Q$ parallel to $BC$ (where $N$ and $L$ are the points of intersection of this line with sides $AB$ and $AC$ respectively, see Fig. 9.3a). Since $AM$ is the median of triangle $ABC$, then $LQ=NQ$. Moreover, $PT \| AC$, so $PQ$ is the midline of triangle $ANL$. Therefore, $AL=2PQ=6$. Additionally, $QL \| TC$ and $QT \| LC$, hence $LQTC$ is a parallelogram, from which $LC=QT=5$. Thus, $AC=AL+LC=6+5=11$.
Fig. 9.3a
Fig. 9.3b

Fig. 9.3c
Second method. Draw the midline $XM$ in triangle $ABC$ (see Fig. 9.3b). Then $XM \| PT \| AC$, hence $\triangle APQ \sim \triangle AXM$ and $\triangle QMT \sim \triangle AMC$, from which it follows that $\frac{PQ}{XM}=\frac{AQ}{AM}$ and $\frac{QT}{AC}=\frac{QM}{AM}$, that is, $\frac{PQ}{XM}+\frac{QT}{AC}=1$. Substituting the values from the problem and considering that $AC=2MX$, we get $\frac{6}{AC}+\frac{5}{AC}=1$, from which $AC=11$.
Third method. Draw the midline $MN$ in triangle $ABC$ (see Fig. 9.3c). Since $QT \| AC$, then $QT$ is bisected by segment $MN$. From the similarity of triangles $APQ$ and $MXQ$, we get $\frac{AQ}{QM}=\frac{3}{2.5}=\frac{6}{5}$. Then $\frac{MQ}{AM}=\frac{5}{11}$, from which $\frac{QT}{AC}=\frac{5}{11}$, that is, $AC=11$.
Fourth method. Write the Menelaus theorem for triangle $BPT$ and line $AM: \frac{PQ}{QT} \cdot \frac{TM}{MB} \cdot \frac{BA}{AP}=1$. Let $BP=x, AP=y$. Then $\frac{BT}{TC}=\frac{x}{y}$ and $\frac{TM}{MB}=\left(\frac{x+y}{2}-y\right): \frac{x+y}{2}=\frac{x-y}{x+y}$. Thus, $\frac{3}{5} \cdot \frac{x-y}{x+y} \cdot \frac{x+y}{y}=1$, from which $\frac{x-y}{y}=\frac{5}{3}$, that is, $\frac{x}{y}=\frac{8}{3}$. Since $\frac{PT}{AC}=\frac{x}{x+y}$, then $AC=11$.
Grading criteria:
+ fully justified solution
± a correct, overall, solution with an arithmetic error
干 the problem is not solved, but there is a correct idea for an additional construction
- only the correct answer is provided
- the problem is not solved or solved incorrectly
- a special case is considered (e.g., the problem is solved for an isosceles triangle)
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. There are nuts in three boxes. In the first box, there are six nuts fewer than in the other two boxes combined, and in the second box, there are ten fewer nuts than in the other two boxes combined. How many nuts are in the third box? Justify your answer.
|
Solution: Let there be $x$ nuts in the first box, $y$ and $z$ in the second and third boxes, respectively. Then the condition of the problem is defined by the equations $x+6=y+z$ and $x+z=y+10$. From the first equation, $x-y=z-6$, and from the second, $x-y=10-z$. Therefore, $z-6=10-z$, from which $z=8$.
Answer: 8 nuts.
| in progress | points |
| :--- | :--- |
| correct and fully justified answer | points |
| an incorrect answer due solely to arithmetic errors | 6 points |
| the system of equations describing the problem condition is correctly set up but not solved | 3 points |
| a specific example (examples) of the distribution of nuts in the boxes (and, therefore, the correct answer) is provided | 1 point |
| only the correct answer is given without justification (or with incorrect justification) | 0 points |
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. For what least natural $\mathrm{k}$ does the quadratic trinomial
$$
y=k x^{2}-p x+q \text { with natural coefficients } p \text{ and } q \text{ have two }
$$
distinct positive roots less than 1?
|
Solution. First, let's estimate the coefficient $\mathrm{k}_{\text{from below. Let }} 0k^{2} x_{1}\left(1-x_{1}\right) x_{2}\left(1-x_{2}\right) \geq 1 \Rightarrow k>4 \text{. Thus, we have obtained the }$
$$
$$
lower bound. To show the accuracy of the estimate, it is sufficient to construct an example with $k=5: y=5 x^{2}-5 x+1$.
Recommendations for checking: Constructing only an example, without an estimate - 3 points;
Obtaining only the estimate (without an example) - 4 points.
## Recommendations for checking
Constructing only an example, without an estimate - 3 points;
Obtaining only the estimate (without an example) - 4 points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Among the numbers from 1 to $10^{23}$, which are more numerous - those with a two-digit sum of digits or those with a three-digit sum? Answer: those with a three-digit sum.
|
Solution. The number $10^{23}$ has a digit sum of 1, so we will not consider it. We will write numbers as 23-digit numbers, adding leading zeros. We will call digits "complementary" if their sum is 9. To each number with a two-digit digit sum, we will correspond a number by replacing each digit with its "complementary" counterpart. Each number will be paired with a unique number. If the digit sum of a number is x, then the digit sum of its paired number will be $9 * 23 - x = 207 - x \geq 207 - 99 = 108$, and it will not exceed $9 * 23$, that is, it will be a three-digit number. Therefore, the number of numbers with a three-digit digit sum is no less than those with a two-digit digit sum. However, there is also, for example, the number $99...99$ (23 nines), which is not paired with any number.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.2. Petya has 25 coins, each with a denomination of $1, 2, 5$, or 10 rubles. Among these coins, 19 are not two-ruble coins, 20 are not ten-ruble coins, and 16 are not one-ruble coins. How many five-ruble coins does Petya have?
|
Answer: 5.
Solution. Since among Petya's coins, 19 are not two-ruble coins, Petya has a total of 6 two-ruble coins. Similarly, it follows that Petya has 5 ten-ruble coins and 9 one-ruble coins.
Thus, Petya has $25-6-5-9=5$ five-ruble coins.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. By September 1st, Vlad bought himself several ballpoint and gel pens. He noticed that if all the pens he bought were gel pens, he would have paid 4 times more than he actually did. And if all the pens were ballpoint pens, the purchase would have cost him 2 times less than the actual price. How many times more expensive is a gel pen compared to a ballpoint pen?
|
Answer: 8.
Solution. If all the pens were gel pens, their price would be 4 times the actual price, which in turn is 2 times more than if all the pens were ballpoint pens. Therefore, gel pens cost $4 \cdot 2=8$ times more than ballpoint pens. Consequently, one gel pen is 8 times more expensive than one ballpoint pen.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.7. Jerry the mouse decided to give Tom the cat a square cake $8 \times 8$ for his birthday. In three pieces marked with the letter "P," he put fish, in two pieces marked with the letter "K," he put sausage, and in one piece, he added both, but did not mark it (all other pieces are without filling). Jerry also told Tom that in any $6 \times 6$ square, there are at least 2 pieces with fish, and in any $3 \times 3$ square, there is no more than one piece with sausage.
What is the minimum number of pieces of cake Tom needs to eat to ensure that he gets a piece with both fish and sausage?
| | | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | P | | | | | | |
| | K | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | P | K | | |
| | | | | | | | |
| | P | | | | | | |
|
# Answer: 5.
Solution. Let's call a piece with fish and sausage a coveted piece.
According to the problem, in any $6 \times 6$ square, there are at least 2 pieces with fish. In any such square, at least one known piece with fish is already included; consider the squares that contain only 1 known piece of fish (all of them are adjacent to the right edge of the pie). It can be seen that they have a common rectangle of $4 \times 6$ (gray in Figure 1). Therefore, the coveted piece must be in this rectangle.
Figure 1: Solution to problem 5.7
Next, according to the problem, in any $3 \times 3$ square, there is no more than 1 piece with sausage. Therefore, in any such square that already contains a known piece of sausage, the coveted piece will not be there. Such squares cover areas of $5 \times 5$ centered on each piece of sausage (shaded in the figure).
There remain exactly 5 cells (gray but not shaded). It is not difficult to verify that each of these 5 cases satisfies the conditions of the problem. If Tom eats no more than 4 pieces of the pie, one of the above-mentioned five cells will definitely remain untouched, and the coveted piece may be in it. If Tom eats 5 pieces in these cells, then among them, there will definitely be the coveted one.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. A natural number $n$ is called good if 2020 gives a remainder of 22 when divided by $n$. How many good numbers exist?
|
Answer: 10.
Solution. In the subsequent solution, the expression of the form $a^{k}$ - the number $a$ raised to the power of $k$ - is the number $a$ multiplied by itself $k$ times. We will also consider $a^{0}=1$. For example, $3^{2}=3 \cdot 3=9$, and $2^{0}=1$.
Since 2020 gives a remainder of 22 when divided by $n$, then $2020-22=1998$ is divisible by $n$, and also $n>22$ (since the remainder of the division is less than the divisor). Therefore, we need to find the number of divisors of 1998 that are greater than 22. Clearly, any such number is a good number.
Let's factorize 1998 into prime factors: $1998=2 \cdot 3^{3} \cdot 37$. Any of its divisors that are divisible by 37 are greater than 22, so they are good numbers. Such divisors are represented in the form $2^{a} \cdot 3^{b} \cdot 37$, where $a$ can take one of the values 0,1 (2 options), and $b$ can take one of the values $0,1,2,3$ (4 options). Therefore, there are $2 \cdot 4=8$ such divisors.
Now let's count the number of divisors that are not divisible by 37. Such divisors are represented in the form $2^{c} \cdot 3^{d}$, where $c$ can take one of the values 0,1, and $d$ can take one of the values $0,1,2,3$. If $d>22$, so it is a good number. There are only two such divisors: $3^{3}$ and $2 \cdot 3^{3}$.
In total, there are $8+2=10$ good numbers.
Remark. Knowing that $1998=2 \cdot 3 \cdot 3 \cdot 3 \cdot 37$, we can simply list all 16 divisors of this number and verify that exactly 10 of them exceed 22:
$$
1,2,3,6,9,18,27,37,54,74,111,222,333,666,999,1998
$$
## 7th grade
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. Four children were walking along an alley and decided to count the number of firs planted along it.
- Anya said: "There are a total of 15 firs along the alley."
- Borya said: "The number of firs is divisible by 11."
- Vера said: "There are definitely fewer than 25 firs."
- Gena said: "I am sure that their number is divisible by 22."
One boy and one girl were right, while the other two were wrong. How many firs grow along the alley?
|
Answer: 11.
Solution. Let $N-$ be the number of elms along the alley.
Suppose Genya told the truth, and $N$ is divisible by 22. But then $N$ is also divisible by 11, i.e., Borya also told the truth. But according to the problem, one of the boys was wrong. Therefore, Genya must have been wrong, but Borya was right. So, $N$ is divisible by 11 but not by 22.
Since 15 is not divisible by 11, Anya must have been wrong. Then Vera told the truth, and $N<25$. But there is exactly one number less than 25 that is divisible by 11 and not by 22, which is 11. It is easy to verify that $N=11$ satisfies all the conditions of the problem.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. In a class, there are 20 students. Thinking about which girls to send a Valentine's card to on February 14, each boy made a list of all the girls in the class he finds attractive (possibly an empty list). It is known that there do not exist three boys whose lists have the same number of girls. What is the minimum number of girls that can be in the class?
|
Answer: 6.
Solution. Let the number of girls in the class be $d$. According to the condition, there are no three boys whose lists match in the number of girls, so there can be a maximum of 2 empty lists, 2 lists with one girl, 2 lists with two girls, ..., 2 lists with $d$ girls. This means that the number of lists, and thus boys, does not exceed $2(d+1)$.
The total number of children in the class is 20 and does not exceed $2(d+1)+d=3d+2$, from which we get that $d \leqslant 6$.
It is not difficult to understand that this could happen if there were 6 girls and 14 boys in total. Two boys should have empty lists, two others should have 1 girl in their lists, another two should have 2 girls, ..., and the last two should have 6 girls (it does not matter which specific girls are in the lists, what matters is their number). In total, this results in exactly 14 lists.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.

|
Answer: 3.
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the problem's condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. How many pairs of natural numbers $a$ and $b$ exist such that $a \geqslant b$ and
$$
\frac{1}{a}+\frac{1}{b}=\frac{1}{6} ?
$$
|
Answer: 5.
Solution. From the condition, it follows that $\frac{1}{6}=\frac{1}{a}+\frac{1}{b} \leqslant \frac{2}{b}$, from which $b \leqslant 12$. Also, $\frac{1}{6}=\frac{1}{a}+\frac{1}{b}>\frac{1}{b}$, so $b>6$. Therefore, $b$ can take values from 7 to 12 inclusive.
Using $\frac{1}{a}=\frac{1}{6}-\frac{1}{b}=\frac{b-6}{6 b}$, we get
$$
a=\frac{6 b}{b-6}=6+\frac{36}{b-6}
$$
Substitute the possible values of $b$ and check if the number $a$ is natural.
If $b=7$, then $a=6+\frac{36}{7-6}=42$ - fits.
If $b=8$, then $a=6+\frac{36}{8-6}=24$ - fits.
If $b=9$, then $a=6+\frac{36}{9-6}=18$ - fits.
If $b=10$, then $a=6+\frac{36}{10-6}=15$ - fits.
If $b=11$, then $a=6+\frac{36}{11-6}=6+\frac{36}{5}$ - not an integer, does not fit.
If $b=12$, then $a=6+\frac{36}{12-6}=12$ - fits.
It is easy to see that all 5 pairs $(42,7),(24,8),(18,9),(15,10),(12,12)$ are solutions to the original equation.
Another solution. Multiplying the equation by the denominators (since $a$ and $b$ are natural, they can be multiplied and divided), we get
$$
6 a+6 b=a b
$$
This equation can be easily transformed into the following:
$$
(a-6)(b-6)=36
$$
From this, it is clear that the numbers $a-6$ and $b-6$ must be divisors of 36, and natural, because if they were negative integers, the smaller of them would be no more than -6, which is impossible.
The first factor is no less than the second by condition. By considering the possible factorizations
$$
(a-6)(b-6)=36 \cdot 1=18 \cdot 2=12 \cdot 3=9 \cdot 4=6 \cdot 6
$$
we get the same 5 solutions.
## 10th grade
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. Yura has $n$ cards, on which numbers from 1 to $n$ are written. After losing one of them, the sum of the numbers on the remaining cards turned out to be 101. What number is written on the lost card?
|
Answer: 4.
Solution. Suppose that $n \leqslant 13$. Then $1+2+\ldots+n=\frac{n(n+1)}{2} \leqslant 91101$, a contradiction.
Therefore, $n=14$, and the missing number is $1+2+\ldots+14-101=105-101=4$.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Around a round table, $2 n(n>5)$ people are sitting - knights and liars. Liars give a false answer to any question, while knights give a true answer. Each of them knows who is a knight and who is a liar. Each of them answered two questions: "Who is your left neighbor?", "Who is your right neighbor?". A wise man, who knows that there are liars at the table but there are fewer of them than knights, was informed of the number of answers "Knight" and the number of answers "Liar", and he accurately named the number of knights. How many answers "Knight" did the wise man receive? Explain your answer.
|
5. Two adjacent knights (R), like two adjacent liars (L), give answers "R" and "R", while adjacent R and L give answers "L" and "L". If the number of L is less than \( n-1 \), then in a group of consecutive R, the outermost R can be replaced by L, and we get the same set of answers with a different number of R. Also, L can be replaced by R if there are at least two L next to each other. Therefore, L is exactly \( n-1 \) and no two of them sit next to each other. Then the arrangement around the table looks either like -R-LR-...-L-RRR-L-, or -R-L-R-...-L-RR-L-...-R-L-RR-L-...-L-. In both cases, we get 4 answers "R".
Answer: 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5.1. In the cells of a $12 \times 12$ table, natural numbers are arranged such that the following condition is met: for any number in a non-corner cell, there is an adjacent cell (by side) that contains a smaller number. What is the smallest number of different numbers that can be in the table?
(Non-corner cells are those that are not in the corner of the table. There are exactly 140 of them.)
|
Answer: 11.
Solution. First, let's provide an example with the arrangement of 11 different numbers.
| 1 | 2 | 3 | 4 | 5 | 6 | 6 | 5 | 4 | 3 | 2 | 1 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2 | 3 | 4 | 5 | 6 | 7 | 7 | 6 | 5 | 4 | 3 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 8 | 7 | 6 | 5 | 4 | 3 |
| 4 | 5 | 6 | 7 | 8 | 9 | 9 | 8 | 7 | 6 | 5 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 | 10 | 9 | 8 | 7 | 6 | 5 |
| 6 | 7 | 8 | 9 | 10 | 11 | 11 | 10 | 9 | 8 | 7 | 6 |
| 6 | 7 | 8 | 9 | 10 | 11 | 11 | 10 | 9 | 8 | 7 | 6 |
| 5 | 6 | 7 | 8 | 9 | 10 | 10 | 9 | 8 | 7 | 6 | 5 |
| 4 | 5 | 6 | 7 | 8 | 9 | 9 | 8 | 7 | 6 | 5 | 4 |
| 3 | 4 | 5 | 6 | 7 | 8 | 8 | 7 | 6 | 5 | 4 | 3 |
| 2 | 3 | 4 | 5 | 6 | 7 | 7 | 6 | 5 | 4 | 3 | 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 6 | 5 | 4 | 3 | 2 | 1 |
Now, let's prove that in any arrangement satisfying the condition, there are at least 11 different numbers. We will draw arrows between cells: if two adjacent cells contain different numbers, we will draw an arrow from the larger number to the smaller one. By the condition, at least one arrow comes out of each non-corner cell.
Consider the cell in the 6th row and 6th column (one of the four "central" cells). We will construct a directed path starting from it: we will sequentially move from a cell along any of the arrows coming out of it. Since the number of cells in the table is finite, we will either eventually arrive at a cell we have already visited (obviously, this is impossible, as the numbers in the cells of our path are constantly decreasing), or we will arrive at a corner cell. To reach a corner cell, it is necessary to change rows at least 5 times and columns at least 5 times, which means making at least \(5 + 5 = 10\) moves. Therefore, our directed path passes through at least 11 cells, and all the numbers in them are clearly different.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Option 1.
It is known that the equations $x^{2}+(2 a-5) x+a^{2}+1=0$ and $x^{3}+(2 a-5) x^{2}+\left(a^{2}+1\right) x+a^{2}-4=0$ have common roots. Find the sum of these roots.
|
Answer: 9.
Solution. The left side of the second equation is obtained from the left side of the first equation by multiplying by $x$ and adding the expression $a^{2}-4$. Therefore, $a^{2}-4=0$, from which $a=2$ or $a=-2$. If $a=2$, then the first equation has no roots. Therefore, $a=-2$, and then we get that the first equation is of the form: $x^{2}-9 x+5=0$. By Vieta's theorem, we find that the desired sum is 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.7. On the board, 99 numbers were written, none of which are equal. In a notebook, $\frac{99 \cdot 98}{2}$ numbers were written—all differences between two numbers from the board (each time subtracting the smaller number from the larger one). It turned out that the number 1 was written exactly 85 times in the notebook. Let $d$ be the largest number written in the notebook. Find the smallest possible value of $d$.
(L. Samoilov)
|
Answer. $d=7$.
Solution. We will prove that $d \geqslant 7$. All numbers on the board can be divided into chains of numbers of the form $a, a+1, a+2, \ldots, a+t$ such that numbers from different chains do not differ by exactly 1. Such a partition is not difficult to construct by connecting any two numbers that differ by 1 with a segment and considering the resulting broken lines.
Let there be $k$ chains, in which there are $n_{1}, n_{2}, \ldots, n_{k}$ numbers respectively (some chains may consist of a single number). In a chain of $n_{i}$ numbers, there are exactly $n_{i}-1$ pairs of numbers that differ by 1. Therefore, the total number of ones in the notebook is
\[
\left(n_{1}-1\right)+\left(n_{2}-1\right)+\ldots+\left(n_{k}-1\right)=\left(n_{1}+n_{2}+\ldots+n_{k}\right)-k=99-k,
\]
from which $k=99-85=14$. Thus, in one of the chains, there are at least 99/14 numbers, that is, at least 8 numbers. The difference between the largest and smallest numbers in such a chain is at least $8-1=7$.
It remains to provide an example where $d=7$. Such an example is given, for example, by the numbers
\[
0=\frac{0}{14}, \frac{1}{14}, \frac{2}{14}, \ldots, \frac{98}{14}=7
\]
Indeed, in this example, $d=7$, and exactly the first 85 of these numbers in the set have a number that is one greater.
Remark. The provided example is not the only one. All possible optimal examples are structured such that there is exactly one chain of 8 numbers (from $a$ to $a+7$), and 13 chains, each of 7 numbers; all numbers of these other chains must be located between $a$ and $a+7$.
Comment. Only the answer - 0 points.
Providing only an example with $d=7$ that satisfies the conditions of the problem - 2 points.
Providing only the estimate showing that $d \geqslant 7$ - 5 points.
The statement that all numbers can be divided into chains, in each of which the numbers differ by 1 (and the differences between numbers from different chains are not equal to 1) is accepted without proof. The statement that in a chain of $n_{i}$ numbers there are no more than $n_{i}-1$ unit differences is also accepted without proof.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.9. Find the largest number $m$ such that for any positive numbers $a, b$, and $c$, the sum of which is 1, the inequality
$$
\sqrt{\frac{a b}{c+a b}}+\sqrt{\frac{b c}{a+b c}}+\sqrt{\frac{c a}{b+c a}} \geqslant m
$$
holds.
(l. Emelyanov)
|
Answer. $m=1$.
First solution. First, we prove that $m=1$ satisfies the requirements of the problem. Notice that $ab + c = ab + c(a + b + c) = (c + a)(c + b)$. Therefore,
\[
\begin{aligned}
& \sqrt{\frac{ab}{c + ab}} + \sqrt{\frac{bc}{a + bc}} + \sqrt{\frac{ca}{b + ca}} = \\
& = \sqrt{\frac{ab}{(c + a)(c + b)}} + \sqrt{\frac{bc}{(a + b)(a + c)}} + \sqrt{\frac{ca}{(b + c)(b + a)}} = \\
& = \frac{\sqrt{ab} \sqrt{a + b} + \sqrt{bc} \sqrt{b + c} + \sqrt{ca} \sqrt{c + a}}{\sqrt{(a + b)(b + c)(c + a)}}.
\end{aligned}
\]
Thus, it remains to prove the inequality
\[
\sqrt{ab} \sqrt{a + b} + \sqrt{bc} \sqrt{b + c} + \sqrt{ca} \sqrt{c + a} \geq \sqrt{(a + b)(b + c)(c + a)}
\]
Square this inequality; it will take the form
\[
\begin{gathered}
ab(a + b) + bc(b + c) + ca(c + a) + 2 \sqrt{ab^2 c(a + b)(b + c)} + \\
+ 2 \sqrt{bc^2 a(b + c)(c + a)} + 2 \sqrt{ca^2 b(c + a)(a + b)} \geq \\
\geq a^2 b + ab^2 + a^2 c + ac^2 + b^2 c + bc^2 + 2abc
\end{gathered}
\]
After simplification, the left side will remain the sum of the square roots, and the right side will be $2abc$. But any of the square roots is not less than $abc$; indeed, for example, $\sqrt{ab^2 c(a + b)(b + c)} \geq \sqrt{ab^2 c \cdot ac} = abc$. This is where the required inequality follows.
It remains to prove that for any $m > 1$, the inequality is not always satisfied; it is sufficient to show this for $1a \geq \frac{1}{3}$, so the inequality is not always satisfied - 2 points.
Proving only that $m=1$ satisfies the requirements of the problem - 5 points.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.