problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
11. (3b,9-11) In the conditions of a chess match, the winner is declared as the one who outperforms the opponent by two wins. Draws do not count. The probabilities of winning for the opponents are equal. The number of decisive games in such a match is a random variable. Find its mathematical expectation.
|
# Solution.
Let $\mathrm{X}$ be the number of successful games. At the beginning of the match, the difference in the number of wins between the two participants is zero. Let's list the possible cases of two successful games, denoting a win by the first participant as 1 and a win by the second participant as 2: $11, 12, 21, 22$. Two out of the four cases mean a win in the match, specifically, 11 and 22. The other two cases bring us back to the initial state with a zero difference in the number of wins. Thus, with a probability of $\frac{2}{4}=\frac{1}{2}$, the number of wins $X=2$ and with the same probability $X=2+\tilde{X}$ where $\tilde{X}$ is distributed the same as $X$. From this, we derive the equation for the expectation
$$
\begin{gathered}
\mathrm{M} X=2 \cdot \frac{1}{2}+(2+\mathrm{M} \tilde{X}) \cdot \frac{1}{2}=2 \cdot \frac{1}{2}+(2+\mathrm{M} X) \cdot \frac{1}{2} \\
\frac{1}{2} \mathrm{M} X=2 ; \mathrm{M} X=4
\end{gathered}
$$
Answer: 4.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. (4b, 8-11) In Anchuria, a checkers championship is being held in several rounds. The days and cities for the rounds are determined by a draw. According to the championship rules, no two rounds can take place in the same city, and no two rounds can take place on the same day. Among the fans, a lottery is organized: the main prize goes to the person who correctly guesses before the championship begins in which cities and on which days all the rounds will take place. If no one guesses correctly, the main prize will go to the championship organizing committee. There are eight cities in Anchuria, and the championship is allocated a total of eight days. How many rounds should the organizing committee schedule to have the highest probability of winning the main prize themselves?
|
# Solution.
In an $8 \times 8$ tour table, you need to select $k$ cells such that no more than one cell is chosen in any row or column. The value of $k$ should be chosen to maximize the number of combinations.
The number of combinations is given by $C_{8}^{k} A_{8}^{k}=\frac{8!\cdot 8!}{(8-k)!\cdot(8-k)!\cdot k!}$, where $C_{8}^{k}$ is the number of ways to choose $k$ cities from eight without regard to order, and $A_{8}^{k}$ is the number of ways to choose $k$ days from eight with regard to order, since each day must correspond to one of the cities. From the table
| $k$ | Number of Combinations |
| :---: | :---: |
| 0 | 1 |
| 1 | 64 |
| 2 | 1568 |
| 3 | 18816 |
| 4 | 117600 |
| 5 | 376320 |
| $\mathbf{6}$ | $\mathbf{5 6 4 4 8 0}$ |
| 7 | 322560 |
| 8 | 40320 |
it is clear that the maximum number of combinations occurs when $k=6$.
Answer: 6.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Buratino the Statistician (from 7th grade, 2 points). Every month, Buratino plays in the "6 out of 45" lottery organized by Karabas-Barabas. In the lottery, there are 45 numbered balls, and in each draw, 6 random winning balls are drawn.
Buratino noticed that in each subsequent draw, there are no balls that appeared in the previous draw: in the second draw, there were no balls from the first, in the third draw, there were no balls from the second, and so on.
Buratino does not believe in events with a probability of less than 0.01. If such an event occurs, Buratino begins to suspect something is amiss. After which draw will Buratino start to suspect that Karabas-Barabas is cheating?
|
Solution. The probability that no numbers from the first draw will be repeated in the second draw is $a=\frac{39 \cdot 38 \cdot 37 \cdot \ldots \cdot 34}{45 \cdot 44 \cdot 43 \cdot \ldots 40}=0.40056 \ldots$, which is slightly more than 0.4. The probability that there will be no repetitions from the previous draw in both the second and third draws is the square of this number, that is, $a^{2}$. The probability of no repetitions in the draws from the second to the fourth is $a^{3}$, and so on. The fifth power of the number $a$ is greater than 0.01: $a^{5}>0.4^{5}=10^{-5} \cdot 2^{10}=0.01024$, while the sixth is already less: $a^{6}=0.0041 \ldots$. Therefore, Pinocchio can accuse Karabas-Barabas after this phenomenon repeats 6 times, that is, after the seventh draw.
## Answer: after the seventh.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Winter Camp. In the winter camp, Vanya and Grisha live in a room. Every evening they draw lots to decide who will turn off the light before going to bed: the switch is near the door, and the loser has to go to bed in complete darkness, bumping into chairs.
Usually, Vanya and Grisha draw lots without any complications, but this time Grisha came up with a special way to draw lots:
- Let's toss a coin. If an eagle (heads) comes up on any even throw, we stop tossing: I win. If a tail (tails) comes up on any odd throw, you win.
a) (from 8th grade, 2 points). What is the probability of Grisha winning?
b) (from 8th grade, 2 points). Find the expected number of coin tosses until the end of the draw.
|
Solution. a) Let's assume that heads in a coin toss give a one, and tails give a zero in the fractional part of a binary fraction. This results in some number $x$ represented by a binary fraction. For example, if the sequence of tosses starts with HTH, then the binary fraction is 0.101.
Obviously, $0 \leq x \leq 1$, and the probability of the event $0 \leq x \leq a$ is $a$ for any non-negative $a \leq 1$ (try to prove this rigorously).
It is easy to see that Grisha will win only if the sequence of tosses gives a number $x$ that is greater than
$$
0.10101010101 \ldots = 0 + \frac{1}{2} + \frac{0}{4} + \frac{1}{8} + \frac{0}{16} + \frac{1}{32} + \ldots = \frac{1}{2} \cdot \frac{1}{1 - 1/4} = \frac{2}{3}
$$
The probability of this is $\frac{1}{3}$. If the obtained fraction is less than $\frac{2}{3}$, Vanya wins. The event "exactly $\frac{2}{3}$" has a zero probability.
Another solution can be obtained by considering the first two tosses. Grisha wins only in the case of HH, and in the case of HT, no one wins, and the game starts again. Therefore, the probability of Grisha's win $p$ can be found from the equation
$$
p = \frac{1}{4} + \frac{1}{4} p, \text{ hence } p = \frac{1}{3}
$$
b) Let's call a successful toss one where the outcome is decided, i.e., heads on an even toss or tails on an odd toss. The probability of success on each individual toss is 0.5. Due to the independence of the tosses, the expected number of tosses is 2.
Answer: a) $1 / 3 ;$ b) 2.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
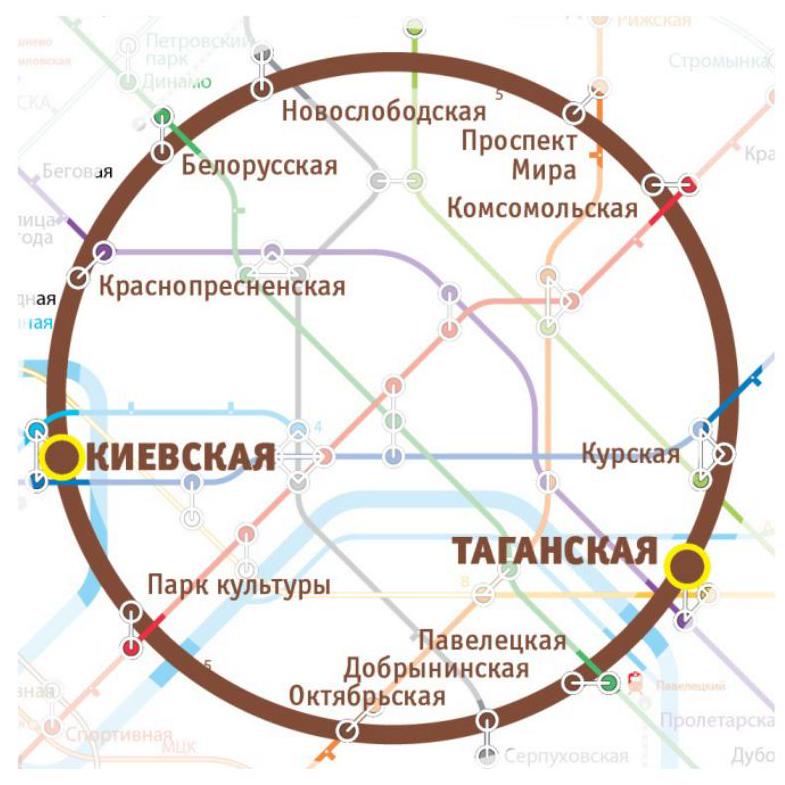
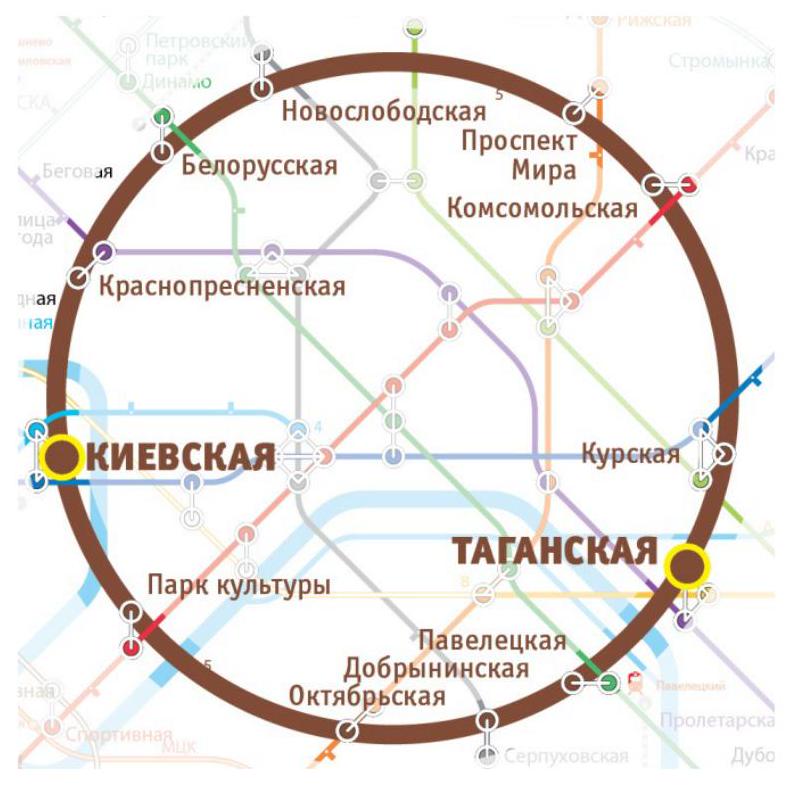
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.
|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Magic Pen (recommended for 8th grade, 1 point). Katya correctly solves a problem with a probability of $4 / 5$, while the magic pen correctly solves a problem without Katya's help with a probability of $1 / 2$. In the test, there are 20 problems, and to get a B, one needs to solve at least 13 of them correctly. How many problems should Katya solve on her own, and how many should she entrust to the magic pen, so that the expected number of correct answers is at least 13?
|
Solution. Let $x$ be the number of examples Katya solves herself, and $20-x$ be the number of examples solved by the pen. Then the expected number of correctly solved problems is
$$
\frac{4}{5} x+\frac{1}{2}(20-x)=0.3 x+10
$$
From the inequality $0.3 x+10 \geq 13$ we get that $x \geq 10$. Therefore, Katya needs to try to solve at least 10 examples on her own.
Answer: at least 10 examples.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. New Year's Problem (recommended for 8th grade, 4 points). On the New Year's table, there are 4 glasses in a row: the first and third are filled with orange juice, while the second and fourth are empty. While waiting for guests, Vanya absent-mindedly and randomly pours the juice from one glass to another. In one move, she can take a full glass and pour all its contents into one of the two empty glasses.
Find the expected number of pourings after which, for the first time, everything will be the opposite: the first and third glasses will be empty, and the second and fourth will be full.
|
Solution. We will encode full glasses with the digit 1 and empty ones with the digit 0. We will construct a graph of possible pourings (Fig. 4). This graph turns out to be the graph of an octahedron. From each state to any adjacent one, one can move with a probability of $1 / 4$, and each edge is "traversable" in both directions.
From the initial state (1010) to the final state (0101), one can transition through any of the remaining four states. Let's identify these four intermediate states. We get a simpler graph with three vertices (Fig. 5).
For brevity, let's denote the initial and final states by $A$ and $C$, and all intermediate states by a single vertex $B$, without distinguishing between them. We will make the edges directed, showing all possible movements in the graph, except for the edge $C \rightarrow B$, which we do not need, since we are interested in the moment of the first arrival of the random process at vertex $C$. We will write the probabilities of the corresponding steps next to the edges. For example, the probability of the step $A \rightarrow B$ is 1, and the probability of the reverse step $B \rightarrow A$ is $1 / 4$. The probability of the step $B \rightarrow B$ is $1 / 2$.
Let $X$ be the random variable "the number of steps leading from A to C for the first time," and $Y$ "the number of steps leading from B to C for the first time."
It is clear that from $A$ one can only go to $B$, and after that, to reach vertex $C$, it will take $Y$ steps. Therefore,
$$
X=1+Y
$$
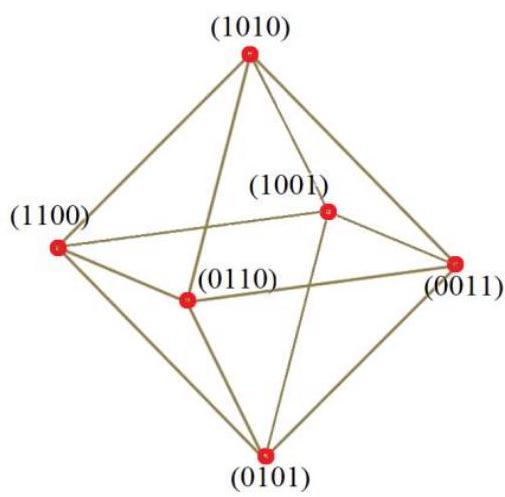
Fig. 4
Exiting from $B$, the process can go three ways, each of which we will invent an indicator for: let $I_{A}, I_{B}$, and $I_{C}$ be three random variables, each of which is 1 if the process transitions from point $B$ to $A, B$, or $C$ respectively, and 0 otherwise.
If the process from $B$ reaches the initial point $A$, then one step is spent and it will take another $X_{1}$ steps to reach $C$, and the quantities $X$ and $X_{1}$ are identically distributed. If the process from $B$ reaches $B$ again, then one step is spent, but nothing changes and it will take $Y_{1}$ steps to reach $C$, and the quantities $Y$ and $Y_{1}$ are identically distributed. Only in the case of transitioning to $C$ does the process end. We get the equation
$$
Y=I_{A}\left(1+X_{1}\right)+I_{B}\left(1+Y_{1}\right)+I_{C} \cdot 1
$$
The indicators $I_{A}, I_{B}$, and $I_{C}$ relate to the step taken from point $B$, while the quantities $X_{1}$ and $Y_{1}$ relate to subsequent steps. Therefore, the quantities $I_{A}$ and $X_{1}$ are independent, and $I_{B}$ and $Y_{1}$ are independent. Transitioning to mathematical expectations in equations (1) and (2), we get the system
$$
\left\{\begin{array}{l}
\mathrm{E} X=1+\mathrm{E} Y, \\
\mathrm{E} Y=\mathrm{E} I_{A} \cdot\left(1+\mathrm{E} X_{1}\right)+\mathrm{E} I_{B} \cdot\left(1+\mathrm{E} Y_{1}\right)+\mathrm{E} I_{C}
\end{array}\right.
$$
Let's find the mathematical expectations of the indicators:
$$
\mathrm{E} I_{A}=\mathrm{P}\left(I_{A}=1\right)=\mathrm{P}(B \rightarrow A)=\frac{1}{4}, \mathrm{E} I_{B}=\frac{1}{2} \text { and } \mathrm{E} I_{C}=\frac{1}{4} .
$$
Let $\mathrm{E} X=\mathrm{E} X_{1}=x$ and $\mathrm{E} Y=\mathrm{E} Y_{1}=y$. The system takes the form
$$
\left\{\begin{array}{l}
x=1+y \\
y=1+\frac{1}{4} x+\frac{1}{2} y,
\end{array}\right.
$$
Answer: 6.
Comment. The solution can be made more concise if we use the properties of conditional mathematical expectations.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. Messengers (recommended for 9th grade, 3 points). Once, the beautiful Queen Guinevere, while staying at her parental castle, asked King Arthur to send her 20 pearls. The roads are not safe, and Arthur, just in case, decided to send 40 pearls, with different messengers, ordering them to ride on different roads. Bandits may lie in wait for the messengers. The probability that each individual messenger will be robbed is $p$, independently of the chosen road and the fate of other messengers $(0<p<1)$.
The king is in a dilemma: should he send two messengers, giving each 20 pearls, send three messengers, giving one 20 and the other two 10 pearls each, or send four messengers, giving each 10 pearls? Which option should the king choose so that the queen has the highest probability of receiving at least 20 pearls?
|
Solution. The probability of not saving at least 20 pearls if there are two messengers:
$$
\mathrm{P}_{2}=p^{2}
$$
The probability of not saving at least 20 pearls if there are three messengers:
$$
\mathrm{P}_{3}=p^{3}+2 p^{2}(1-p)=p^{2}(2-p) .
$$
The probability of not saving at least 20 pearls if there are four messengers:
$$
\mathrm{P}_{4}=p^{4}+4 p^{3}(1-p)=p^{3}(4-3 p)
$$
Dividing all probabilities by \( p^{2} \), we get three functions:
$$
f_{2}=1, f_{3}=2-p, f_{4}=4 p-3 p^{2}
$$
Clearly, \( f_{2}<f_{3} \) for all \( p \in(0 ; 1) \) (Fig. 6), so the option with three messengers is inferior under any conditions. Let's compare \( f_{2} \) and \( f_{4} \):
$$
1<4 p-3 p^{2} ; 3 p^{2}-4 p+1<0, \text { hence } \frac{1}{3}<p<1
$$
Thus, when \( 0<p<\frac{1}{3} \), it is more advantageous to send four messengers, and when \( \frac{1}{3} \leq p<1 \) - two. In fact, when \( p=\frac{1}{3} \), two or four messengers will perform equally well, but why send four messengers if two are sufficient?
Answer: when \( 0<p<\frac{1}{3} \), it is more advantageous to send four messengers, and when \( \frac{1}{3} \leq p<1 \) - two.
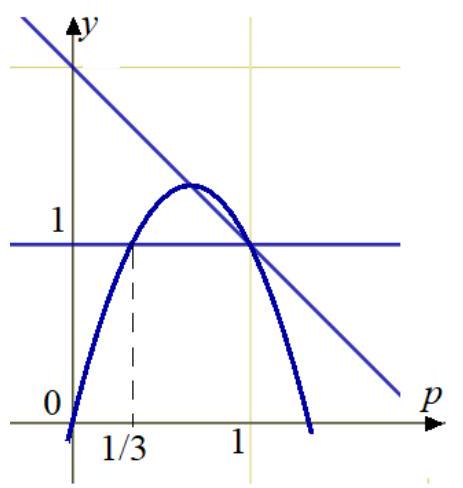
Fig. 6.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Lonely Cars. (From 9th grade, 4 points.) On a very long narrow highway, where overtaking is impossible, $n$ cars are driving in a random order, each with its own preferred speed. If a fast car catches up to a slower one, the fast car has to slow down and drive at the same speed as the slower one. Thus, the cars form groups. Find the expected number of "lonely" cars, that is, groups consisting of a single car.
|
Solution. Let $I_{k}$ be the indicator of the event "the $k$-th car in line is alone." For $k \leq n$, this event consists of the slowest car among the first $k+1$ cars being the last, and the second slowest being the second to last. The probability of this is $\frac{1}{(k+1) k}$. If $k=n$, then this event consists of the slowest car being the last (probability $\frac{1}{n}$).
The random variable $X$ "number of lonely cars" is equal to the sum of all indicators, therefore
$$
\begin{gathered}
\mathrm{E} X=\mathrm{E} I_{1}+\mathrm{E} I_{2}+\ldots+\mathrm{E} I_{n}=\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots .+\frac{1}{(n-1) n}+\frac{1}{n}= \\
=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\ldots+\frac{1}{n-1}-\frac{1}{n}+\frac{1}{n}=1
\end{gathered}
$$
Answer: 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The smallest set. (From 6th grade, 2 points) In a numerical set, the median is 3, the arithmetic mean is 5, and the only mode of the set is 6. What is the smallest number of numbers that can be in a set with the given properties?
|
Solution. It is clear that the number 6 appears at least twice in the set, and in addition, there are at least two more numbers.
If the set contains exactly four numbers $a, b, 6, 6$, then we can assume that $a \leq b \leq 3$ and, moreover, the sum of all numbers is 20, so $a+b=20-6-6=8$. Contradiction. The set cannot contain exactly four numbers.
If the set contains exactly five numbers, then the set has the form $a, b, 3, 6, 6$, where $a \leq b \leq 3$ and $a+b=25-6-6-3=10$. Contradiction. The set cannot consist of exactly five numbers.
A set of six numbers with the specified properties exists. For example, $-2, -1, 0, 6, 6, 21$.
## Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Patrick and Slippers. Every day, the dog Patrick gnaws one slipper from the existing supply in the house. With a probability of 0.5, Patrick wants to gnaw a left slipper, and with a probability of 0.5 - a right slipper. If the desired slipper is not available, Patrick gets upset. How many pairs of identical slippers need to be bought so that with a probability of at least 0.8, Patrick does not get upset for a whole week (7 days)?
|
Solution. It is clear that if 7 pairs are bought, Patrick will definitely have enough of the desired, even if he chooses only left slippers every day. The question is about the smallest number of slippers that need to be bought so that with a probability of 0.8 or higher, Patrick will not be disappointed. Probability theory often helps to solve a problem not with absolute certainty, but practically with certainty ${ }^{1}$, which is more important in real life.
Assume for definiteness that during the week Patrick will want to eat $S$ left and $7-S$ right slippers. We need to find such a $k$ that the inequality
$$
\mathrm{P}(S \leq k \cap 7-S \leq k) \geq 0.8
$$
holds. $k$ will be the required number of pairs. Rewrite the event in parentheses as:
$$
\mathrm{P}(7-k \leq S \leq k) \geq 0.8
$$
The probability on the left side of the inequality is equal to the sum
$$
C_{7}^{7-k} \frac{1}{2^{7}}+C_{7}^{8-k} \frac{1}{2^{7}}+\ldots+C_{7}^{k} \frac{1}{2^{7}}=\frac{1}{128} \cdot\left(C_{7}^{7-k}+C_{7}^{8-k}+\ldots+C_{7}^{k}\right)=\frac{1}{64} \cdot\left(C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k}\right)
$$
Then
$$
C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k} \geq 64 \cdot 0.8=51.2
$$
Considering that the left side is an integer, we need to find the smallest $k$ for which the inequality
$$
C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k} \geq 52
$$
holds.
Write out the 7th row of Pascal's triangle, starting from $C_{7}^{4}$:
| $C_{7}^{4}$ | $C_{7}^{5}$ | $C_{7}^{6}$ | $C_{7}^{7}$ |
| :---: | :---: | :---: | :---: |
| 35 | 21 | 7 | 1 |
The sum $C_{7}^{4}+C_{7}^{5}=35+21>52$, so the smallest $k$ is 5.
Answer: 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
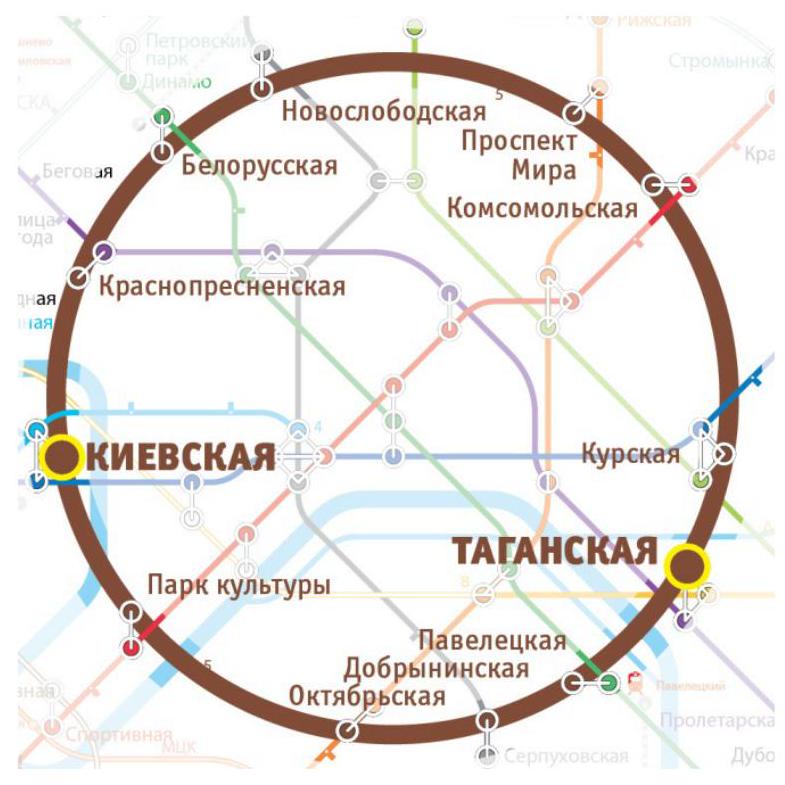
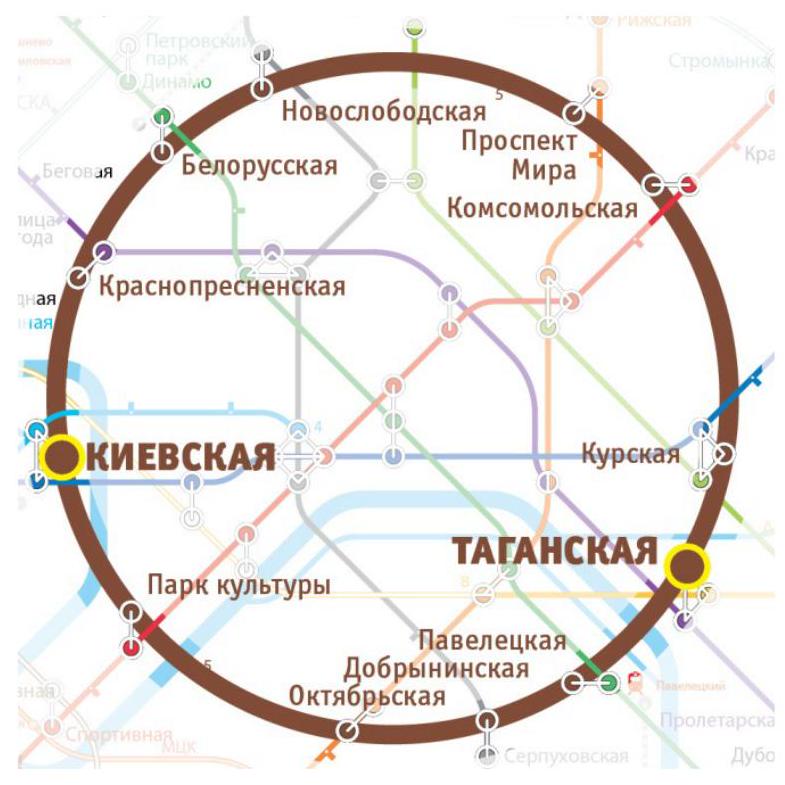
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.
|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. There are fewer than 30 people in the class. The probability that a randomly chosen girl is an excellent student is $\frac{3}{13}$, and the probability that a randomly chosen boy is an excellent student is $\frac{4}{11} \cdot$ How many excellent students are there in the class?
|
# Solution.
According to classical probability theory, the probability that a randomly chosen girl is an excellent student is equal to the ratio of the number of excellent girl students to the total number of girls in the class. Accordingly,
$$
\frac{3}{13}=\frac{\text { number of girls-excellent students }}{\text { number of girls }}
$$
Considering that the number of girls is a natural number, and that there are fewer than 30 people (and thus fewer than 30 girls) in the class, we find that there are either 13 girls (3 excellent students) or 26 (6 excellent students).
Applying the same reasoning to boys, we find that:
$$
\frac{4}{11}=\frac{\text { number of boys-excellent students }}{\text { number of boys }}
$$
In the class, there are either 11 boys (4 excellent students) or 22 (8 excellent students). Further, considering that there are fewer than 30 people in the class, we find that there are 13 girls (3 excellent students) and 11 boys (4 excellent students). Therefore, the number of excellent students is $3+4=7$.
Answer: 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Disks (from 9th grade. 3 points). At a familiar factory, metal disks with a diameter of 1 m are cut out. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, there is a measurement error, and therefore the standard deviation of the radius is 10 mm. Engineer Sidorov believes that a stack of 100 disks will on average weigh 10000 kg. By how much is Engineer Sidorov mistaken?
|
Solution. Given $\mathrm{E} R=0.5 \mathrm{m}, \mathrm{D} R=10^{-4}$ (sq.m). Let's find the expected value of the area of one disk:
$$
\mathrm{ES}=\mathrm{E}\left(\pi R^{2}\right)=\pi \mathrm{E} R^{2}=\pi\left(D R+\mathrm{E}^{2} R\right)=\pi\left(10^{-4}+0.25\right)=0.2501 \pi
$$
Thus, the expected value of the mass of the disk is $\frac{0.2501 \pi}{0.25 \pi} \cdot 100=100.04$ kg. Therefore, a stack of 100 disks on average will weigh 10004 kg.
Answer: 4 kg.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.

|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.
|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Ring Line (from 8th grade. 3 points). On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow metro from the station "Taganskaya" to the station "Kievskaya", and back in the evening (see the diagram).
Upon entering the station, the Scientist boards the first train that arrives. It is known that trains run at approximately equal intervals in both directions, and that the train traveling on the northern route (through "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while the train on the southern route (through "Paveletskaya") takes 11 minutes.
Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives at the same station. The same is true for "Taganskaya";
- the average travel time from home to work is 1 minute less than the travel time from work to home.
Find the expected interval between trains traveling in the same direction.
|
Solution. If the Scientist boarded trains of different directions with equal probabilities, the average travel time in one direction and the average travel time in the other would be the same. Therefore, the probabilities are not equal.
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is
$$
11 p + 17(1-p) = 17 - 6p
$$
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is
$$
17 p + 11(1-p) = 11 + 6p
$$
According to the condition, $11 + 6p - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the favorite stations. Then
$$
\mathrm{E} T = \frac{\mathrm{E} Y}{1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3
$$
Answer: 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
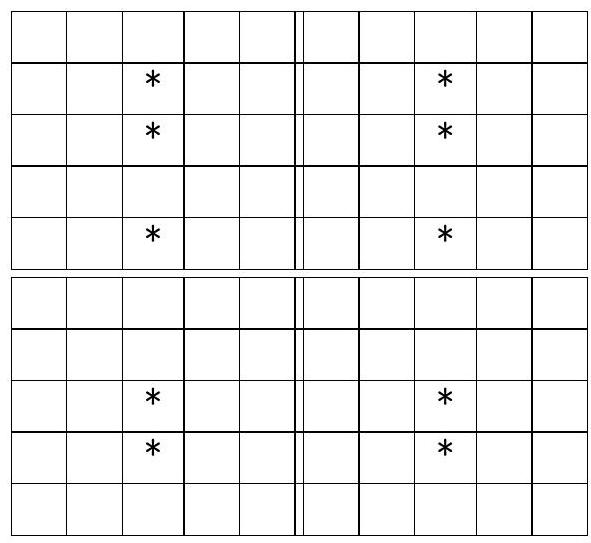
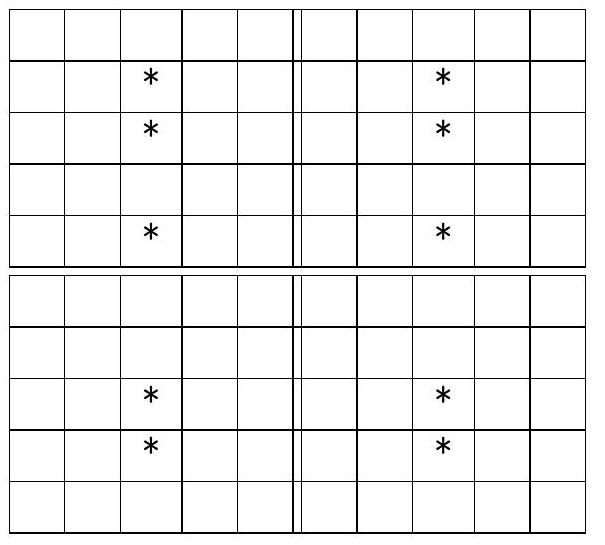
4. Stem-and-leaf plot. (From 6th grade, 2 points). To represent whole numbers or decimal fractions, a special type of diagram called a "stem-and-leaf plot" is often used. Such diagrams are convenient for representing people's ages. Suppose that in the studied group, there are 5 people aged 19, 34, 37, 42, and 48. For this group, the diagram will look as shown in Fig. 2. The left column is the "stem," and to the right of it are the "leaves."
When studying a certain group of patients, on December 1, the doctor created a diagram of their ages (Fig. 3a). On Fig. 3b, a new diagram of their ages is shown, which was also created on December 1, several years later. Over these years, the composition of the group remained the same - all those who were there remained, and no one new joined the group. However, the numbers on the new diagram are not visible - they are replaced by asterisks. Determine how many years have passed and restore the diagram.
$$
\begin{array}{l|llllll}
0 & & & & & & \\
1 & 0 & 0 & 1 & 2 & 2 & 3 \\
2 & 1 & 5 & 6 & & & \\
3 & 0 & 2 & 4 & 6 & & \\
4 & 1 & 6 & & & &
\end{array}
$$
Fig. 3 a)

Fig. 3 b)
|
Solution. The digits from 0 to 5, representing decades of years, can be placed immediately (Fig. 4a). It is clear that less than 10 years have passed, otherwise there would be no digits in line "1".
If 7 or more years had passed, then the person who is 13 years old would have moved to line "2", and there would be fewer than six values left in line "1". But this did not happen, so less than 7 years have passed.
No one from line "1" moved to line "2", but two people, aged 25 and 26, moved from line "2" to line "3". However, the number of values in line "3" did not change, which means that those who were 34 and 36 years old moved to line "4". Therefore, at least 6 years have passed.
Thus, exactly 6 years have passed, and the diagram shown in Fig. 4b) was obtained. [^0]

Fig. 4 a)

Fig. 4 b)
Answer: 6 years, see Fig. 4 b).
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Solution. Suppose for clarity of reasoning that when a bite occurs, the Absent-Minded Scholar immediately pulls out and re-casts the fishing rod, and does so instantly. After this, he waits again. Consider a 6-minute time interval. During this time, on average, there are 3 bites on the first fishing rod and 2 bites on the second fishing rod. Therefore, in total, there are on average 5 bites on both fishing rods in these 6 minutes. Consequently, the average waiting time for the first bite is $6: 5=1.2$ minutes.
|
Answer: 1 minute 12 seconds.
Evaluation Criteria
| Correct and justified solution | 3 points |
| :--- | :---: |
| It is shown that on average there are 5 bites in 6 minutes, or an equivalent statement is proven | 1 point |
| The solution is incorrect or missing (in particular, only the answer is given) | 0 points |
|
1
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Solution.
a) Suppose there are 9 numbers in the set. Then five of them do not exceed the median, which is the number 2. Another four numbers do not exceed the number 13. Therefore, the sum of all numbers in the set does not exceed
$$
5 \cdot 2 + 4 \cdot 13 = 62
$$
Since the arithmetic mean is 7, the sum of the numbers in the set is $7 \cdot 9 = 63$. This is a contradiction. The set cannot consist of 9 numbers.
b) Let the number of numbers in the set be $2n + 1$ ($n$ is a natural number). In the set, there will be exactly $n + 1$ numbers, each of which does not exceed the median, which is the number 2. The remaining $n$ numbers do not exceed the number 13. Therefore, the sum of all numbers in the set does not exceed
$$
13n + 2(n + 1) = 15n + 2
$$
On the other hand, this sum is equal to $7(2n + 1) = 14n + 7$. From the inequality $14n + 7 \leq 15n + 2$, we get that $n \geq 5$. Therefore, the set contains no fewer than $2 \cdot 5 + 1 = 11$ numbers. To show that this is possible, consider the following example. The set
$$
2; 2; 2; 2; 2; 2; 13; 13; 13; 13; 13
$$
consists of 11 numbers and satisfies conditions 1-4.
|
Answer: a) no; b) 11.
Scoring criteria
| Both parts solved correctly or only part (b) | 3 points |
| :--- | :---: |
| The correct estimate of the number of numbers in part (b) is found, but no example is given | 2 points |
| Part (a) is solved correctly | 1 point |
| The solution is incorrect or missing (in particular, only the answer is given) | 0 points |
|
11
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Solution.
a) Suppose the set contains 7 numbers. Then four of them are not less than the median, which is the number 10. Another three numbers are not less than one. Then the sum of all numbers in the set is not less than
$$
3+4 \cdot 10=43
$$
Since the arithmetic mean is 6, the sum of the numbers in the set is $6 \cdot 7=42$. Contradiction. The set cannot consist of 7 numbers.
b) Let the number of numbers in the set be $2 n+1$ (where $n$ is a natural number). In the set, there will be exactly $n+1$ numbers, each of which is not less than the median, which is the number 10. The remaining $n$ numbers are not less than the number 1. Then the sum of all numbers in the set is not less than
$$
n+10(n+1)=11 n+10
$$
On the other hand, this sum is equal to $6(2 n+1)=12 n+6$. From the inequality $12 n+6 \geq 11 n+10$ we get that $n \geq 4$. Therefore, the set contains no fewer than $2 \cdot 4+1=9$ numbers. Let's provide an example to show that this is possible. The set
$$
\text { 1; 1; 1; 1; 10; 10; 10; 10; } 10
$$
consists of 9 numbers and satisfies conditions 1-4.
|
Answer: a) no; b) 9.
## Grading Criteria
| Both parts solved correctly or only part (b) | 3 points |
| :--- | :---: |
| Correct estimate of the number of numbers in part (b), but no example | 2 points |
| Part (a) solved correctly | 1 point |
| Solution is incorrect or missing (including only the answer) | 0 points |
|
9
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. All students in the class scored different numbers of points (positive integers) on the test, with no duplicate scores. In total, they scored 119 points. The sum of the three lowest scores is 23 points, and the sum of the three highest scores is 49 points. How many students took the test? How many points did the winner score?
|
Solution. Let's denote all the results in ascending order $a_{1}, a_{2}, \ldots, a_{n}$, where $n$ is the number of students. Since $a_{1}+a_{2}+a_{3}=23$ and $a_{n-2}+a_{n-1}+a_{n}=49$, the sum of the numbers between $a_{3}$ and $a_{n-2}$ is $119-23-49=47$.
Since $a_{1}+a_{2}+a_{3}=23$, then $a_{3} \geq 9$ (otherwise, $a_{1}+a_{2}+a_{3} \leq 6+7+8=21$).
Therefore, between $a_{3}$ and $a_{n-2}$, there can only be the numbers $10,11,12,13,14$. Their sum is 60, but it should be 47. Therefore, all these numbers are present except for the number 13.
This results in the sequence $a_{1}, a_{2}, 9,10,11,12,14,15, a_{n-1}, a_{n}$, where $a_{1}+a_{2}=14$ and $a_{n-1}+a_{n}=34$. Thus, $n=10$, $a_{1}=6$, $a_{2}=8$, $a_{n-1}=16$, and $a_{n}=18$.
Note that it is not enough to simply specify the required set. A proof of uniqueness is needed.
Answer: A) 10 students; B) 18 points.
Answer to variant 212: A) 10 participants; B) 18 points.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. One mole of an ideal gas undergoes a closed cycle, in which:
$1-2$ - isobaric process, during which the volume increases by 4 times;
$2-3$ - isothermal process, during which the pressure increases;
$3-1$ - a process in which the gas is compressed according to the law $T=\gamma V^{2}$.
Find how many times the volume in state 3 exceeds the initial volume in state 1.
|
Solution. Let the initial volume and pressure be denoted as $\left(V_{0} ; P_{0}\right)$. Then $V_{2}=4 V_{0}$.
From the Mendeleev-Clapeyron law, we have three relationships:
$$
P_{0} V_{0}=R T_{1}, P_{0} V_{2}=R T, P_{3} V_{3}=R T
$$
Dividing the third relationship by the second, we get: $\frac{P_{3}}{P_{0}}=\frac{V_{2}}{V_{3}}$.
From the dependence of temperature on volume in the process $3-1$, there is a linear relationship between pressure and volume: $P=\gamma V$. Then we can write the relationship between the parameters corresponding to states 1 and $3: \frac{P_{3}}{P_{0}}=\frac{V_{3}}{V_{0}}$.
From the two obtained relationships, it follows that:
$$
\frac{V_{2}}{V_{3}}=\frac{V_{3}}{V_{0}} \Rightarrow V_{3}^{2}=V_{2} V_{0} \Rightarrow V_{3}=2 V_{0}
$$
Answer: 2.
Answer to variant 212: 2.
|
2
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. All students in the class scored a different number of points (positive integers) on the test, with no duplicate scores. In total, they scored 119 points. The sum of the three lowest scores is 23 points, and the sum of the three highest scores is 49 points. How many students took the test? How many points did the winner score?
|
Solution. Let's denote all the results in ascending order $a_{1}, a_{2}, \ldots, a_{n}$, where $n$ is the number of students. Since $a_{1}+a_{2}+a_{3}=23$ and $a_{n-2}+a_{n-1}+a_{n}=49$, the sum of the numbers between $a_{3}$ and $a_{n-2}$ is $119-23-49=47$.
Since $a_{1}+a_{2}+a_{3}=23$, then $a_{3} \geq 9$ (otherwise, $a_{1}+a_{2}+a_{3} \leq 6+7+8=21$).
Therefore, between $a_{3}$ and $a_{n-2}$, there can only be the numbers $10,11,12,13,14$. Their sum is 60, but it should be 47. Therefore, all these numbers are present except for the number 13.
This results in the sequence $a_{1}, a_{2}, 9,10,11,12,14,15, a_{n-1}, a_{n}$, where $a_{1}+a_{2}=14$ and $a_{n-1}+a_{n}=34$. Thus, $n=10$, $a_{1}=6$, $a_{2}=8$, $a_{n-1}=16$, and $a_{n}=18$.
Note that it is not enough to simply specify the required set. A proof of uniqueness is needed.
Answer: A) 10 students; B) 18 points.
Answer to variant 212: A) 10 participants; B) 18 points.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A ten-liter bucket was filled to the brim with currants. Gavrila immediately said that there were 10 kg of currants in the bucket. Glafira thought about it and estimated the weight of the berries in the bucket more accurately. How can this be done if the density of the currant can be approximately considered equal to the density of water?
|
Solution. In approximate calculations, the sizes of the berries can be considered the same and much smaller than the size of the bucket. If the berries are laid out in one layer, then in the densest packing, each berry will have 6 neighbors: the centers of the berries will be at the vertices of equilateral triangles with sides equal to the diameter of the berries. When pouring the next layer, the berries will be located in the depressions between the berries of the previous layer. In such a packing, each berry will have 12 neighbors, and the centers of the berries will be at the vertices of regular tetrahedrons.
To calculate the fraction of the volume occupied by the berries, one can mentally "cut out" a parallelepiped from the lattice formed by the centers of the berries with edges of length $2 N R$, where $R$ is the radius of the berries, and $N$ is the number of berries that fit along one side, and in two opposite vertices of the edge, they meet at an angle of $60^{\circ}$. The volume of such a parallelepiped is $4 \sqrt{2} N^{3} R^{3}$, and it contains approximately $N^{3}$ berries, each with a volume of $\frac{4}{3} \pi R^{3}$ (berries near the walls are not fully placed, but their number is of the order of $N^{2}$, so this can be neglected for large $N$). Therefore, the ratio of the volume of the berries to the volume of the bucket is approximately $\frac{\pi \sqrt{2}}{6} \approx 0.74$, so in a 10-liter bucket, with the densest packing, there are about 7.4 kg of berries. In reality, there are somewhat fewer due to the lack of density.
The ratio of the volume of the berries to the volume of the container can also be calculated differently. For example, consider a rectangular parallelepiped in which the berries are laid out in layers, the distance between which is equal to the height of the tetrahedron mentioned above $\frac{2 \sqrt{2} R}{\sqrt{3}}$. In each layer, the distance between rows is equal to the height of the equilateral triangle $R \sqrt{3}$. Thus, $N^{3}$ berries will occupy a parallelepiped with a length of $2 R N$, a width of $\sqrt{3} R N$, and a height of $\frac{2 \sqrt{2} R N}{\sqrt{3}}$. The ratio of volumes is $\frac{N^{3} \cdot \frac{4}{3} \pi R^{3}}{2 R N \cdot \sqrt{3} R N \cdot \frac{2 \sqrt{2} R N}{\sqrt{3}}}=\frac{\pi}{3 \sqrt{2}}=\frac{\pi \sqrt{2}}{6}$.
Answer: about 7 kg.
Criteria: 20 points - correct (not necessarily the same as above) solution and the correct answer (from 7 to 7.4 kg); 15 points - generally ideologically correct solution, with errors that did not affect the answer; 10 points - ideologically correct solution with significant errors; also evaluated are solutions in which the packing density coefficient $\frac{\pi \sqrt{2}}{6}$ (or 74%) is used without proof; 5 points - the packing in the layer is taken into account, but the packing between layers is not; **0** points - everything else.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Hot oil at a temperature of $100^{\circ} \mathrm{C}$ in a volume of two liters is mixed with one liter of cold oil at a temperature of $20^{\circ} \mathrm{C}$. What volume will the mixture have when thermal equilibrium is established in the mixture? Heat losses to the external environment can be neglected. The coefficient of volumetric expansion of the oil is $2 \cdot 10^{-3} 1 /{ }^{\circ} \mathrm{C}$.
|
Answer: 3
Let $V_{1}=2$ L be the volume of hot oil, and $V_{2}=1$ L be the volume of cold oil. Then we can write $V_{1}=U_{1}\left(1+\beta t_{1}\right), V_{2}=U_{2}\left(1+\beta t_{2}\right)$, where $U_{1}, U_{2}$ are the volumes of the respective portions of oil at zero temperature; $t_{1}=100^{\circ} \mathrm{C}, t_{2}=20^{\circ} \mathrm{C} ; \beta=2 \cdot 10^{-3} 1 /{ }^{\circ} \mathrm{C}$ is the coefficient of volumetric expansion.
From the heat balance equation: $c m_{1}\left(t-t_{1}\right)+c m_{2}\left(t-t_{2}\right)=0 \Leftrightarrow t=\frac{m_{1} t_{1}+m_{2} t_{2}}{m_{1}+m_{2}}$, where $m_{1}, m_{2}$ are the masses of the hot and cold portions of oil, respectively; $t$ is the temperature of the mixture. Note that $m_{1}=U_{1} \rho, m_{2}=U_{2} \rho$, where $\rho$ is the density of the oil at zero temperature.
Then $W_{1}=U_{1}(1+\beta t), W_{2}=U_{2}(1+\beta t)$. Here $W_{1}, W_{2}$ are the volumes of the initial portions of oil at temperature $t$.
The new total volume of the oil will be equal to
$$
\begin{aligned}
& W_{1}+W_{2}=\left(U_{1}+U_{2}\right)(1+\beta t)=\left(\frac{m_{1}}{\rho}+\frac{m_{2}}{\rho}\right)(1+\beta t)=\frac{1}{\rho}\left(m_{1}+m_{2}+\left(m_{1}+m_{2}\right) \beta t\right)= \\
& \frac{1}{\rho}\left(m_{1}+m_{2}+m_{1} \beta t_{1}+m_{2} \beta t_{2}\right)=\frac{1}{\rho}\left(m_{1}+m_{1} \beta t_{1}\right)+\frac{1}{\rho}\left(m_{2}+m_{2} \beta t_{2}\right)=\frac{m_{1}}{\rho}\left(1+\beta t_{1}\right)+\frac{m_{2}}{\rho}(1+
\end{aligned}
$$
$\left.\beta t_{2}\right)$
That is, $W_{1}+W_{2}=U_{1}\left(1+\beta t_{1}\right)+U_{2}\left(1+\beta t_{2}\right)=V_{1}+V_{2}$
Thus, the volume will not change.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Grandma baked 19 pancakes. The grandchildren came from school and started eating them. While the younger grandson eats 1 pancake, the older grandson eats 3 pancakes, and during this time, grandma manages to cook 2 more pancakes. When they finished, there were 11 pancakes left on the plate. How many pancakes did the older grandson eat?
|
Solution. In one "cycle", the grandsons eat $1+3=4$ pancakes, and the grandmother bakes 2 pancakes, which means the number of pancakes decreases by 2. There will be ( $19-11$ ) $/ 2=4$ such cycles. This means, in these 4 cycles, the younger grandson ate 4 pancakes, the older grandson ate 12 pancakes, and the grandmother baked 8 pancakes during this time. Indeed, $19+8-4-12=11$.
Answer: 12.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. All students in the class scored different numbers of points (positive integers) on the test, with no duplicate scores. In total, they scored 119 points. The sum of the three lowest scores is 23 points, and the sum of the three highest scores is 49 points. How many students took the test? How many points did the winner score?
|
Solution. Let's denote all the results in ascending order $a_{1}, a_{2}, \ldots, a_{n}$, where $n$ is the number of students. Since $a_{1}+a_{2}+a_{3}=23$ and $a_{n-2}+a_{n-1}+a_{n}=49$, the sum of the numbers between $a_{3}$ and $a_{n-2}$ is $119-23-49=47$.
Since $a_{1}+a_{2}+a_{3}=23$, then $a_{3} \geq 9$ (otherwise, $a_{1}+a_{2}+a_{3} \leq 6+7+8=21$).
Therefore, between $a_{3}$ and $a_{n-2}$, there can only be the numbers $10,11,12,13,14$. Their sum is 60, but it should be 47. Therefore, all these numbers are present except for the number 13.
Thus, we get the sequence $a_{1}, a_{2}, 9,10,11,12,14,15, a_{n-1}, a_{n}$, where $a_{1}+a_{2}=14$ and $a_{n-1}+a_{n}=34$. Therefore, $n=10$, $a_{1}=6$, $a_{2}=8$, $a_{n-1}=16$, and $a_{n}=18$.
Answer: A) 10 students; B) 18 points.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. The friends who came to visit Gavrila occupied all the three-legged stools and four-legged chairs in the room, but there was no place left for Gavrila himself. Gavrila counted that there were 45 legs in the room, including the "legs" of the stools and chairs, the legs of the visiting guests (two for each!), and Gavrila's own two legs. How many people were in the room?
|
Answer: 9. Solution. If there were $n$ stools and $m$ chairs, then the number of legs in the room is $3 n+4 m+2 \cdot(n+m)+2$, from which we get $5 n+6 m=43$. This equation in integers has the solution $n=5-6 p, m=3+5 p$. The values of $n$ and $m$ are positive only when $p=0$. Therefore, there were 5 stools and 3 chairs. Thus, the number of people in the room is: $5+3+$ Gavril.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. A grenade lying on the ground explodes into a multitude of small identical fragments, which scatter in a radius of $L=90$ m. Determine the time interval (in seconds) between the moments of impact on the ground of the first and the last fragment, if such a grenade explodes in the air at a height of $H=10 \mathrm{m}$. The acceleration due to gravity is considered to be $g=10$ m/s ${ }^{2}$. Air resistance is negligible.
|
Answer: 6. Solution. From the motion law for a body thrown from ground level at an angle $\alpha$ to the horizontal, the range of flight is determined by the relation $L=\frac{V_{0}^{2}}{g} \sin 2 \alpha$. Therefore, the maximum range of flight is achieved at $\alpha=45^{\circ}$ and is equal to $L=\frac{V_{0}^{2}}{g}$. This means $V_{0}=\sqrt{g L}$.
The fragment that falls to the ground first is the one that flies vertically downward, and the last one is the one that flies vertically upward. After time $\tau=\frac{2 V_{0}}{g}$, the last fragment will return to the explosion site, which means it will be in the same situation as the first fragment. Therefore, the required time interval is $\tau=\frac{2 V_{0}}{g}$ (independent of height $H$). Thus, $\tau=\frac{2 \sqrt{g L}}{g}=2 \sqrt{\frac{L}{g}}=6$ seconds.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Gavriil and Glafira took a glass filled to the brim with water and poured a little water into three ice cube trays, then placed them in the freezer. When the ice froze, they put the three resulting ice cubes back into the glass. Gavriil predicted that some water would spill out of the glass because ice expands in volume when it freezes. Glafira, however, claimed that the water level would be below the rim of the glass because part of the floating ice would protrude above the water surface. Who is right and why?
|
Solution. Let $V$ be the volume of water in the molds. Then the volume $W$ of ice in the molds can be determined from the law of conservation of mass $V \cdot \rho_{\text {water }}=W \cdot \rho_{\text {ice }}$. When ice of volume $W$ is floating, the submerged part of this volume $U$ can be determined from the condition of floating bodies $U \cdot \rho_{\text {water }}=W \cdot \rho_{\text {ice }}$. It is therefore obvious that $V=U$.
Answer: No one is right. The water will fill the glass exactly to its edges.
Grading criteria: 20 points - correct (not necessarily the same as above) solution and correct answer; 10 points - correct answer, but insufficiently clear justification.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the greatest whole number of liters of water that can be heated to boiling temperature using the amount of heat obtained from the combustion of solid fuel, if in the first 5 minutes of combustion, 480 kJ is obtained from the fuel, and for each subsequent five-minute period, 25% less than the previous one. The initial temperature of the water is $20^{\circ} \mathrm{C}$, the boiling temperature is $100^{\circ} \mathrm{C}$, and the specific heat capacity of water is 4.2 kJ.
|
Answer: 5 liters
Solution: The amount of heat required to heat a mass $m$ of water under the conditions of the problem is determined by the relation $Q=4200(100-20) m=336 m$ kJ. On the other hand, if the amount of heat received in the first 5 minutes is $Q_{0}=480$ kJ. Then the total (indeed over an infinite time) amount of heat received will be $Q=4 Q_{0}$. Then the mass $m$ will be determined from the relation $m=\frac{4 Q_{0}}{336} \approx 5.7$
That is, the whole number of liters of water heated to 100 degrees is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A new model car travels $4 \frac{1}{6}$ kilometers more on one liter of gasoline compared to an old model car. At the same time, its fuel consumption per 100 km is 2 liters less. How many liters of gasoline does the new car consume per 100 km?
|
Answer: 6 liters.
Instructions. The fuel consumption of the new car is $x$ liters, and the consumption of the old car is $x+2$
liters. Equation: $\frac{100}{x}-\frac{100}{x+2}=\frac{25}{6} \Leftrightarrow \frac{4(x+2-x)}{x(x+2)}=\frac{1}{6} \Leftrightarrow x^{2}+2 x-48=0 \Leftrightarrow x=-8 ; x=6$. Therefore, $x=6$ liters.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Solve the equation $\sqrt{15 x^{2}-52 x+45} \cdot(3-\sqrt{5 x-9}-\sqrt{3 x-5})=1$.
|
Solution. Rewrite our equation in the form
$$
\sqrt{3 x-5} \cdot \sqrt{5 x-9} \cdot(3-\sqrt{5 x-9}-\sqrt{3 x-5})=1
$$
Such a transformation is possible because the solution to the original equation exists only for $x>\frac{9}{5}$. Let $\sqrt{3 x-5}=a>0, \sqrt{5 x-9}=b>0$. We have
$$
a+b+\frac{1}{a b}=3
$$
Apply the Cauchy inequality to the left side
$$
a+b+\frac{1}{a b} \geq 3 \sqrt[3]{a \cdot b \cdot \frac{1}{a b}}=3
$$
Thus, for the solution of our equation, it is necessary that the Cauchy inequality holds as an equality and $a=b=\frac{1}{a b}$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Solve the equation $\log _{5}(3 x-4) \cdot \log _{5}(7 x-16) \cdot\left(3-\log _{5}\left(21 x^{2}-76 x+64\right)\right)=1$.
|
Solution. Rewrite our equation in the form
$$
\log _{5}(3 x-4) \cdot \log _{5}(7 x-16) \cdot\left(3-\log _{5}(3 x-4)-\log _{5}(7 x-16)\right)=1
$$
Such a transformation is possible because the solution to the original equation exists only for $x>\frac{16}{7}$. Let $\log _{5}(3 x-4)=a>0, \log _{5}(7 x-16)=b>0$. Note that both logarithms must be positive. Indeed, the positivity of the first logarithm follows from the domain of existence. Suppose that $\log _{5}(7 x-16)<0 \Leftrightarrow \frac{16}{7}<x<\frac{17}{7}$. In this case, two factors in the left-hand side are positive, and one is negative, which is impossible. Thus, we have
$$
a+b+\frac{1}{a b}=3
$$
Apply the Cauchy inequality to the left-hand side
$$
a+b+\frac{1}{a b} \geq 3 \sqrt[3]{a \cdot b \cdot \frac{1}{a b}}=3
$$
Thus, for the solution of our equation, it is necessary that the Cauchy inequality holds as an equality and $a=b=\frac{1}{a b}$.
## Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (4 points)
The price of a new 3D printer is 625000 rubles. Under normal operating conditions, its resale value decreases by $20 \%$ in the first year, and then by $8 \%$ each subsequent year. After how many years will the resale value of the printer be less than 400000 rubles?
|
Solution:
Let's calculate the cost of the printer year by year:
1 year $=625000 * 0.8=500000$ rubles
2 year $=500000 * 0.92=460000$ rubles (1 point)
3 year $=460000 * 0.92=423200$ rubles (1 point)
4 year $=423200 * 0.92=397694$ rubles. (1 point)
Answer: in 4 years. ( $\mathbf{1}$ point)
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What was NOT used as money?
1) gold
2) stones
3) horses
4) dried fish
5) mollusk scales
6) all of the above were used
|
Answer: 6. All of the above were used as money.
|
6
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
7. What is a sign of a financial pyramid?
1) an offer of income significantly above average
2) incomplete information about the company
3) aggressive advertising
4) all of the above
|
Answer: 4. All of the above are signs of a financial pyramid.
|
4
|
Other
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10. (4 points)
To buy new headphones costing 275 rubles, Katya decided to save money on sports activities. Until now, she has been buying a single-visit ticket to the swimming pool, including a visit to the sauna for 250 rubles, to warm up. However, summer has arrived, and the need to visit the sauna has disappeared. Visiting only the swimming pool costs 200 rubles more than visiting the sauna. How many times does Katya need to visit the swimming pool without the sauna to save enough to buy the headphones? (Provide the answer as a whole number, without spaces or units of measurement.)
Answer: 11.
## Comment:
|
Solution: one visit to the sauna costs 25 rubles, the price of one visit to the swimming pool is 225 rubles. Katya needs to visit the swimming pool 11 times without going to the sauna in order to save up for buying headphones.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Leshа has 10 million rubles. Into what minimum number of banks should he deposit them to receive the full amount through ACB insurance payouts in case the banks cease operations?
|
Answer: 8. The maximum insurance payout is 1,400,000, which means no more than this amount should be deposited in each bank.
|
8
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How much did the euro exchange rate change over the 2012 year (from January 1, 2012 to December 31, 2012)? Provide the answer in rubles, rounded to the nearest whole number.
|
Answer: 1 or -1. On January 1, 2012, the euro was worth 41.6714, and on December 31, it was 40.2286. $40.2286-41.6714=-1.4428 \approx-1$.
Note: This problem could have been solved using the internet. For example, the website https://news.yandex.ru/quotes/region/23.html
|
-1
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The Petrovs family has decided to renovate their apartment. They can hire a company for a "turnkey renovation" for 50,000 or buy materials for 20,000 and do the renovation themselves, but for that, they will have to take unpaid leave. The husband earns 2000 per day, and the wife earns 1500. How many working days can they spend on the renovation so that it turns out to be more cost-effective than hiring workers?
|
Answer: 8. The combined daily salary of the husband and wife is $2000+1500=3500$ rubles. The difference between the cost of a turnkey repair and buying materials is $50000-20000=30000$.
$30000: 3500 \approx 8.57$, so the family can spend no more than 8 days on the repair.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (15 points) Purchase a meat grinder at "Technomarket" first, as it is more expensive, which means the largest bonuses can be earned on it, and then purchase a blender using the accumulated bonuses. In this case, she will spend
$$
\text { 4800+1500-4800*0.2=5340 rubles. }
$$
This is the most cost-effective way to make the purchases.
## Maximum 30 points
## Problem 5
Student Alexei informed his parents that he is already an adult and can manage his finances independently. His mother suggested he use a duplicate of the bank card linked to her account. To participate in a charitable New Year's program, Alexei wants to buy 40 "Joy" chocolate bars and donate them to a children's home. However, the bank, whose clients are Alexei's parents, has implemented a new system to protect against unauthorized card payments. The protection system analyzes the root mean square (RMS) value of the last 3 purchases (S) using the formula $S=\sqrt{\frac{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}{3}}$, where $\mathrm{x}_{1}, \mathrm{x}_{2}$, and $\mathrm{x}_{3}$ are the amounts of the last 3 purchases, and compares the value of $S$ with the amount of the current purchase. If the current payment exceeds the value of $S$ by three times, the bank blocks the transaction and requires additional verification (e.g., a call from his mother to the call center). Over the past month, only payments for mobile phone service have been made, each for 300 rubles. How many minimum receipts should Alexei split the purchase into to buy all 40 "Joy" chocolate bars at a cost of 50 rubles each?
|
# Solution:
The root mean square value of the last purchases is $\sqrt{(300 * 300+300 * 300+300 * 300) / 3}=300$ rubles. Therefore, the permissible first purchase is no more than $300 * 3=900$ rubles, with which 18 chocolates can be bought. It remains to buy 22 chocolates for a total of $22 * 50=1100$ rubles.
For the second purchase, the average value considering the first purchase will be $\sqrt{(300 * 300+300 * 300+900 * 900) / 3}=\sqrt{330000}$, which is more than 500 rubles. Therefore, the second purchase can be for more than $500 * 3=1500$ rubles, which is sufficient to buy the remaining chocolates. The minimum number of receipts is 2.
## Maximum 15 points
15 points - a fully detailed correct solution and the correct answer.
10 points - correct calculation of the permissible amount of the first purchase, the correct number of chocolates in the first purchase, and the correct calculation of the amount for the second purchase.
5 points - correct calculation of the permissible amount of the first purchase.
## Appendix to Problem No. 1
Insurance is a system of relationships between insurers (insurance company) and insured individuals (for example, any citizen), which allows reducing property risks by insuring, for example, property against possible adverse events...
Property insurance is one of the types of insurance according to the Civil Code of the Russian Federation. Real estate is one of the types of property. Houses, apartments, and land plots are considered real estate.
## To insure a risk:
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The park is a $10 \times 10$ grid of cells. A lamp can be placed in any cell (but no more than one lamp per cell).
a) The park is called illuminated if, no matter which cell a visitor is in, there is a $3 \times 3$ square of 9 cells that contains both the visitor and at least one lamp. What is the minimum number of lamps in an illuminated park?
b) The park is called reliably illuminated if it remains illuminated even after the failure of any one lamp. What is the minimum number of lamps in a reliably illuminated park?
|
Solution. a) 4. Divide the park into 4 quarters (squares $5 \times 5$), then there must be at least one lamp in each quarter (to illuminate, for example, the corner cells). By placing one lamp in the center of each quarter, we get an example.
b) 10.
Estimate. In each corner square $3 \times 3$ there must be at least two lamps (to illuminate the corner cell). Temporarily leave only these 8 lamps. Each of them illuminates only within its own quarter, and if the lamp in the center of the quarter breaks (or if it is absent), then a five-cell strip inside this quarter, adjacent to another quarter, will definitely not be illuminated. Note that the union of two such strips for opposite quarters cannot be illuminated by one lamp in any case, so at least two more lamps are needed.
Example:
Criteria. In part a) 1 point is given for the estimate and 1 point for the example. In part b) 3 points are given for the estimate (1 point if it is proven that 8 lamps are insufficient), and 2 points for the example.

International Mathematical Olympiad
«Formula of Unity» / «The Third Millennium»
Year 2022/2023. Qualifying round
## Problems for grade R9
Each task is assessed at 7 points. Some problems have their own criteria (printed in gray).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Once Valera left home, walked to the cottage, painted 11 fence boards there, and returned home 2 hours after leaving. Another time, Valera and Olga went to the cottage together, painted 9 fence boards (without helping or hindering each other), and returned home together 3 hours after leaving. How many boards will Olga be able to paint alone if she needs to return home 1 hour after leaving? The physical abilities, diligence, and working conditions of Valera and Olga remain unchanged.
(V. P. Fedorov)
|
Solution. The strange result (working together for a longer time, the characters managed to do less work) is explained by the different times spent walking, since the speed of "joint" walking is equal to the lower of the two walkers' speeds. The second time, Valery's working time decreased, which means the travel time increased by more than an hour; hence, Olga spends more than an hour on the trip to the cottage and back. Therefore, in an hour, she wouldn't even have time to get there and return.
Answer: 0 boards
Criteria. Only the answer - 0 points. Understanding that two people walk at the speed of the slower walker (i.e., Olga) - 2 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A natural number $n>5$ is called new if there exists a number that is not divisible by $n$, but is divisible by all natural numbers less than $n$. What is the maximum number of consecutive numbers that can be new?
|
Solution. Answer: 3.
Example: the number 7 is new (60 is divisible by the numbers from 1 to 6, but not by 7);
the number 8 is new (420 is divisible by the numbers from 1 to 7, but not by 8);
the number 9 is new (840 is divisible by the numbers from 1 to 8, but not by 9).
Evaluation: every fourth number has the form $n=4k+2=2(2k+1)$; if some number is divisible by 2 and $2k+1$, then it is also divisible by $2(2k+1)$, therefore such an $n$ cannot be new.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The pond has a square shape. On the first frosty day, the part of the pond within 10 meters of the nearest shore froze. On the second day, the part within 20 meters froze, on the third day, the part within 30 meters, and so on. On the first day, the area of open water decreased by $19 \%$. How long will it take for the pond to freeze completely?
|
Solution. It is not hard to understand that a pond of $200 \times 200$ fits, for which the answer is - in 10 days (since each day the side decreases by 20 meters). There are no other options, as the larger the side of the pond, the smaller the percentage that will freeze on the first day.
More rigorously: let the side of the pond be $x$ meters, then the initial area is $x^{2}$ m $^{2}$; then after the first day, $0.81 x^{2}=(0.9 x)^{2}$ remains, that is, the side of the pond after the first day is $0.9 x$. Therefore, the side decreased by $0.1 x$ on the first day. At the same time, it decreased by 20 m, hence $0.1 x=20, x=200$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In several packages, there are 20 candies, and there are no two packages with the same number of candies and no empty packages. Some packages may be inside other packages (then it is considered that a candy lying in the inner package also lies in the outer package). However, it is forbidden to place a package inside another package that already contains a package. What is the maximum possible number of packages?
|
Solution. 8. Example: ((6)(2)) ((3)(4)) ((1)4) (there are other examples).
There cannot be more than 8 packages. Indeed, then the sum of the number of candies in the packages (or rather, the number of incidences of candies to packages) is not less than $1+2+\ldots+9=45$. But there are 20 candies, so at least one of them lies in at least three packages, which is not allowed.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The pond has a rectangular shape. On the first frosty day, the part of the pond within 10 meters of the nearest shore froze. On the second day, the part within 20 meters froze, on the third day, the part within 30 meters, and so on. On the first day, the area of open water decreased by 20.2%, and on the second day, it decreased by 18.6% of the original area. On which day will the pond be completely frozen?
|
Solution. First method. Let the sides of the pond be $a$ and $b$ meters, then
$(a-20)(b-20)=(1-0.202) a b, (a-40)(b-40)=(1-0.388) a b$,
from which $20(a+b)-400=0.202 a b, 40(a+b)-1600=0.388 a b$, that is, $800=0.016 a b, a b=5000$ and further $a+b=525$. It turns out that the sides are 400 and 125 meters.
Answer: on the seventh day

Second method. Notice that each day 800 m $^{2}$ less freezes than the previous day. This is evident from the diagram, which shows that the "outer frame" consists of pieces equal to the corresponding pieces of the "inner frame," plus eight 10 x 10 m squares. Therefore, the percentage of the frozen part also decreases by the same amount each day. That is, on the first day, 20.2% of the area freezes, on the second day 18.6%, on the third day 17.0%, and so on. Note that the sum of the first six terms of this progression is less than 100%, while the sum of the first seven terms is already more than 100%. Therefore, the pond will freeze on the seventh day.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The park is a $10 \times 10$ grid of cells. A lamp can be placed in any cell (but no more than one lamp per cell).
a) The park is called illuminated if, no matter which cell a visitor is in, there is a $3 \times 3$ square of 9 cells that contains both the visitor and at least one lamp. What is the minimum number of lamps in an illuminated park?
b) The park is called reliably illuminated if it remains illuminated even after the failure of any one lamp. What is the minimum number of lamps in a reliably illuminated park?
|
Solution. a) 4. Divide the park into 4 quarters (squares $5 \times 5$), then there must be at least one lamp in each quarter (to illuminate, for example, the corner cells). By placing one lamp in the center of each quarter, we get an example.
b) 10.
Estimate. In each corner square $3 \times 3$ there must be at least two lamps (to illuminate the corner cell). Temporarily leave only these 8 lamps. Each of them illuminates only within its own quarter, and if the lamp in the center of the quarter breaks (or if it is absent), then a five-cell strip inside this quarter, adjacent to another quarter, will definitely not be illuminated. Note that the union of two such strips for opposite quarters cannot be illuminated by one lamp in any case, so at least two more lamps are needed.
Example:
Criteria. In part a) 1 point is given for the estimate and 1 point for the example. In part b) 3 points are given for the estimate (1 point if it is proven that 8 lamps are insufficient), and 2 points for the example.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Once Valera left home, walked to the cottage, painted 11 fence boards there, and returned home 2 hours after leaving. Another time, Valera and Olga went to the cottage together, painted 8 fence boards (without helping or hindering each other), and returned home together 3 hours after leaving. How many boards will Olga manage to paint alone if she needs to return home 1.5 hours after leaving? The physical abilities, diligence, and working conditions of Valera and Olga remain constant. (V. P. Fedorov)
|
Solution. This is a more complex version of problem 5 for 5th grade.
The strange result (that the characters accomplished less work in more time when working together) is explained by the different times spent walking, since the speed of "joint" walking is equal to the lower of the two walkers' speeds. The second time, Valera worked no more than $2 \cdot \frac{8}{11}$ hours, so they must have spent at least $3-\frac{16}{11}=\frac{17}{11}>1.5$ hours on the journey. This means that in one and a half hours, Olga would not have enough time to even walk to the cottage and back.
Answer: 0 boards.
Scoring. Only the answer - 0 points.
Evaluated progressions:
1) Understanding that two people walk at the speed of the slower one (this is stated explicitly or used in the solution) - 1 point.
2) With this in mind, it is indicated that Olga spends more than an hour on the journey (or at least an hour more than Valera, or something similar) - another +2 points.
3) It is calculated that in the second case, Valera would have completed the work alone in 16/11 hours (or that he would have completed it in less than 1.5 hours) - 2 points (added to progressions 1 and 2).
For example, the solution "In the second case, they spent an hour longer walking, so Olga spends an hour more on the journey than Valera, so in the third case, she will have a maximum of half an hour to work, and it's unclear what to do next" earns 3 points (progressions 1 and 2).
A solution like "In the second case, Valera would have worked alone for no more than $2 \cdot 8 / 11$ hours, and since it took them longer, Olga must have been in the way; so, alone, Olga would paint nothing (or a negative number of boards)" earns 2 points (only progression 3).
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Several plants and zombies (no more than 20 creatures in total) attended the "Plants VS Zombies" gathering, and it turned out that all creatures were of different heights. Plants always tell the truth to those who are shorter than them and lie to those who are taller. Zombies, on the contrary, lie to shorter creatures and tell the truth to taller ones. Upon meeting, each participant approached every other and said either "I am taller than you" or "I am shorter." The phrase "I am shorter" was heard 20 times. When saying goodbye, each had to approach every other and say "I am taller and I am a plant." If a creature could not say this, it clapped. There were 18 claps. Determine how many creatures attended the gathering, and arrange them by height.
(P. D. Mulyenko)
|
Solution. Let the total number of beings be $n$, and exactly $z$ of them are zombies. When plants greet, they say to everyone “I am taller than you”, and zombies say to everyone “I am shorter”. Each zombie said this phrase to everyone except themselves, so we get $z(n-1)=20$. Given that $n-1<20$, the possible cases are: $z=2, n-1=10 ; \quad z=4, n-1=5 ; \quad z=5, n-1=4$ (larger $z$ are impossible since $z \leqslant n$).
Now let's examine the farewells. When a plant addresses someone who is shorter, it must tell the truth, and the phrase “I am taller and I am a plant” is true. When addressing someone who is taller, it must lie, and this phrase is a lie (the first part is false). For zombies, this phrase is always a lie, so they can say it to everyone who is shorter, but not to those who are taller. Therefore, all the slaps are performed by zombies to those who are taller. It is not hard to see that of the three cases, only $z=2, n=11$ fits (otherwise, there would be fewer than 18 slaps). Out of 11 beings, the zombies must be the shortest and the third from the bottom in height - only then do we get $10+8=18$ slaps (in other cases, it is either $10+9$ or no more than 17).
Answer: 11 beings; when ordered by increasing height - ZPZPPPPPPP.
Criteria. 3 points if the participant could determine that the number of zombies can be 2, 4, or 5.
Deduct 1 point if the arrangement of beings by height is not explicitly indicated in the solution, but everything else is explained.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The magical clock, in addition to the usual pair of hands, has a second pair that is symmetrical to the first at every moment relative to the vertical axis. It is impossible to determine which hands are real from a photograph of the clock. Furthermore, just like with ordinary clocks, it is impossible to distinguish morning from evening using the magical clock. Therefore, the same photograph of the clock can correspond to several different times (for example, 1:15, $10:45$, and $22:45$ look the same as shown on the right).
A robot takes several photographs of the clock over the course of a day (from 0:00 to 24:00). It remembers the order in which the photographs were taken but not the time they were taken. Sometimes, from such a series of photographs, it is possible to determine the exact time some of them were taken; such photographs will be called definite. If, however, there are several moments when a photograph could have been taken (even considering the other photographs in the series), it is called indefinite. For example, in the series of photographs shown on the right, photograph №2 is definite (it was taken at 9:00), while photograph №4 is indefinite (it could have been taken at either $16:00$ or 20:00).
Suppose there is a series of 100 photographs taken over the course of a day, none of which look the same, and none of which were taken at 0:00, $6:00$, $12:00$, $18:00$, or 24:00. What is the minimum number of indefinite photographs that can be among them?
(A. A. Tsel)
|
Solution. See the solution to problem 6 for 10th grade.
Instead of the last paragraph of the solution to problem 6 for 10th grade, it is sufficient to provide an example with exactly three undefined photographs and prove that there are exactly three. For example, let the first three photos be taken at 5:50, 11:40, 17:30, and the rest in the interval from 20:00 to 23:00. Then, from the appearance of the photographs, it can be determined that the first one was taken no earlier than 5:50, which means the second one was taken no earlier than 11:40, and the third one no earlier than 17:30, and finally, the rest after 18:00, where only one option remains for them, meaning they are defined.
## Answer: 3.
Criteria. 1 point for providing an example with exactly 3 undefined photographs, +1 additional point if it is proven that the example is correct.
1 point for stating the proposition "each photograph corresponds to four possible times: $t, 12-t, 12+t, 24-t$."
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all real solutions of the system of equations
$$
\left\{\begin{array}{l}
\frac{1}{x}=\frac{32}{y^{5}}+\frac{48}{y^{3}}+\frac{17}{y}-15 \\
\frac{1}{y}=\frac{32}{z^{5}}+\frac{48}{z^{3}}+\frac{17}{z}-15 \\
\frac{1}{z}=\frac{32}{x^{5}}+\frac{48}{x^{3}}+\frac{17}{x}-15
\end{array}\right.
$$
(A. B. Vladimirov)
|
Solution. Let $F(t)=32 t^{5}+48 t^{3}+17 t-15$. Then the system has the form $F\left(\frac{1}{y}\right)=\frac{1}{x}, F\left(\frac{1}{z}\right)=\frac{1}{y}$, $F\left(\frac{1}{x}\right)=\frac{1}{z}$. From this, it follows that $F\left(F\left(F\left(\frac{1}{x}\right)\right)\right)=\frac{1}{x}$. Note that $F(0.5)=0.5$ and the function $F(t)-t$ is strictly increasing. Therefore, if $t>0.5$, then $t < F(F(F(t)))$. But this means that $\frac{1}{x}=0.5$, and the original system has a unique solution $x=y=z=2$.
Criteria. 1 point is given for finding the solution. 3 points for the solution under the assumption $x=y=z$. If the uniqueness of the solution to $F(t)=t$ is not proven, 2 points are deducted.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Three people want to travel from city A to city B, which is 45 kilometers away from A. They have two bicycles. The speed of a cyclist is 15 km/h, and the speed of a pedestrian is 5 km/h. What is the minimum time they can reach B, if the bicycle can be left unattended on the road?
|
Solution. Two people ride a bicycle for 10 kilometers, then one of them leaves the bicycle by the road and walks the next 10 kilometers, while the other continues for the next 10 kilometers and also leaves the bicycle (which the first one should pick up later), the third one walks the first 10 kilometers and then rides the bicycle picked up by the first one for the remaining distance.
In any case, they will collectively ride 60 km and walk 30 km. Therefore, there will be at least one of them who will walk no less than 10 kilometers and ride the rest. If he walks exactly 10 kilometers and rides 20 kilometers, it will take 3 hours and 20 minutes, and any increase in the 10 kilometers will only worsen the result.
Criteria. A complete solution consists of two parts: a description of how the cyclists should ride, and a proof that this result cannot be improved. If only one of these parts is present, the problem is not solved, and we give 2 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the Olympionov family, it is a tradition to especially celebrate the day when a person turns as many years old as the sum of the digits of their birth year. Kolya Olympionov had such a celebration in 2013, and Tolya Olympionov had one in 2014. Who is older and by how many years?
|
Solution. Let's determine in which year a person could be born if adding the sum of the digits of their birth year results in 2013 or 2014. It is clear that the year of such a birth cannot be later than 2014. Since the sum of the digits of each number from 1 to 2014 does not exceed \(1+9+9+9=28\), the birth year cannot be earlier than 2013-28=1985. By checking all years from 1985 to 2013, we find that Kolya could have been born in 1992 or 2010, and Tolya in 1988 or 2006.
Therefore, the possible scenarios are: Tolya is 4 years older; Tolya is 22 years older; Kolya is 14 years older.
## Criteria.
Complete solution. The solution should include a check or at least indicate the range of the check. Justifications such as "It is sufficient to check only from 1985 to 2014 because the sum of the digits is no more than 28" are not required - it is enough for the range to include the years from 1988 to 2010.
Errors. If nothing is written about the check, and it is immediately stated, "Kolya could have been born in 1992 or 2010, and Tolya in 1988 or 2006, therefore... " and the correct answer follows, this is considered a solution with an error and is scored 5 points.
Progress. If one of the possible birth years for Kolya and one for Tolya is indicated - 1 point is given. If one variant is found for one brother and both for the other, 2 points are given.
If there are "extra" birth years given, the solution is scored no more than 2 points. A correct (complete) answer without indicating the years they could have been born - 2 points.
Note. Strictly speaking, we found the difference in birth years, but the difference in ages can lie in the range from 3 to 5 years or from 21 to 23 years or from -15 to -13 years. Mentioning this is not required but is not penalized.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A fly is sitting at vertex $A$ of a triangular room $A B C$ ( $\angle B=60^{\circ}, \angle C=45^{\circ}, A C=5$ m). At some point, it flies out in a random direction, and each time it reaches a wall, it turns $60^{\circ}$ and continues flying in a straight line (see figure). Can it happen that after some time, the fly has flown more than 9.9 meters?
|
Solution. Let the fly take off at an angle of 60 degrees to the line $A C$. Consider the equilateral triangle $A K C$ with side $A C$. Note that its sides $A K$ and $K C$ can be divided into parts (into infinitely many parts) such that each part equals the next segment of the fly's trajectory. The sum of these parts is $A K + K C = 10$ m, so at some point, the fly will have flown more than 10 meters.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Pasha and Igor are flipping a coin. If it lands on heads, Pasha wins; if tails, Igor wins. The first time the loser pays the winner 1 ruble, the second time - 2 rubles, then - 4, and so on (each time the loser pays twice as much as the previous time). After 12 games, Pasha is 2023 rubles richer than he was initially. How many of these games did he win?
(L. S. Korechkova, A. A. Tessler)
|
Answer: 9 (all except 4, 8, and 1024).
Solution. We need to place the signs in the equation $\pm 1 \pm 2 \pm 2^{2} \pm 2^{3} \pm \ldots \pm 2^{9} \pm 2^{10} \pm 2^{11}=2023$. If we choose all plus signs, the sum will be $2^{0}+\ldots+2^{11}=2^{12}-1=4095$, so we need to replace plus signs with minus signs before the numbers whose sum is $\frac{4095-2023}{2}=1036$. There is only one such set of numbers (due to the uniqueness of the binary representation of a number): $1036=1024+8+4$.
Criteria. 1 point - it is stated that the total sum of money is 4095;
another 1 point - it is found that Pasha won 3059;
2 points - the correct answer with an example;
-2 points for the lack of proof of the uniqueness of the representation of 1036.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Pasha and Igor are flipping a coin. If it lands on heads, Pasha wins; if tails, Igor wins. The first time the loser pays the winner 1 ruble, the second time - 2 rubles, then - 4, and so on (each time the loser pays twice as much as the previous time). At the beginning of the game, Pasha had a single-digit amount of money, and Igor had a four-digit amount. By the end, Igor had a two-digit amount, and Pasha had a three-digit amount. What is the minimum number of games Pasha could have won? The players cannot go into debt.
(L. S. Korechkova, A. A. Tessler)
|
Solution. Let $n$ be the amount of money Pasha has become richer (and Igor poorer). Note that Pasha won the last game (otherwise, he would have lost more money than he gained in all previous stages). Therefore, the sequence of games can be divided into series, in each of which Pasha won the last game and lost all the others (a series can consist of just one game). If a series started with game number $k$ and ended with game number $m$, then Pasha won $-2^{k}-2^{k+1}-\ldots-2^{m-2}+2^{m-1}=2^{k}$ rubles for it. Thus, the binary representation of the number $n$ uniquely describes the set of games Pasha won (except for the number of the last game): the term $2^{k}$ means that the next series started with game number $k+1$, i.e., Pasha won game number $k$.
According to the problem, $901 \leqslant n \leqslant 998$. But all numbers from 901 to 998 contain $2^{7}+2^{8}+2^{9}$ in their binary representation, so Pasha won the seventh, eighth, and ninth games, as well as the last one (its number is greater than 9, otherwise there would be no term $2^{9}$) - already a minimum of 4 games.
In addition, Pasha must have won at least 3 times in the first 6 games:
1) at least one out of the first four games, since $9-1-2-4-8<0$;
2) at least one out of the next two, since $9 \pm 1 \pm 2 \pm 4 \pm 8-16-32<0$;
3) if only one out of the first four was won, then after them the sum is no more than 10, and the fifth and sixth must definitely be won.
Thus, Pasha won at least 7 games. Here is an example for 7 games: initially, Pasha had 9 rubles, and Igor had 1000 rubles, a total of 10 games were played. Then $n=985=2^{0}+2^{3}+$ $2^{4}+2^{6}+2^{7}+2^{8}+2^{9}=\left(-2^{0}-2^{1}+2^{2}\right)+\left(2^{3}\right)+\left(2^{4}\right)+\left(-2^{5}+2^{6}\right)+\left(2^{7}\right)+\left(2^{8}\right)+\left(2^{9}\right)$, i.e., Pasha won games with numbers $3,4,6,7,8,9,10$, and Igor - games $1,2,5$. In the end, Pasha will have 994 rubles, and Igor - 15 rubles.
Answer: 7 games.
Criteria. 5 points are given for the estimate (1 point for estimating that there were at least 10 games in total), 2 points for the example.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Calculate the area of the set of points on the coordinate plane that satisfy the inequality $(y+\sqrt{x})\left(y-x^{2}\right) \sqrt{1-x} \leqslant 0$.
|
Solution. The left side makes sense only for $0 \leqslant x \leqslant 1$. In this case, it is required that $y+\sqrt{x}$ and $y-x^{2}$ have different signs (or one of them equals zero), or that $x$ equals 1. If we exclude the case $x=1$ (which gives a zero area), we are left with a part of the plane bounded by the segment of the line $x=1$ and parts of the parabolas $y=-\sqrt{x}$ and $y=x^{2}$. By cutting this figure into two parts along the x-axis and placing the upper part below the lower one, we get a square of area 1.
Answer: the area is 1.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Flint has five sailors and 60 gold coins. He wants to distribute them into wallets, and then give the wallets to the sailors so that each gets an equal number of coins. But he doesn't know how many sailors will be alive by the time of the distribution. Therefore, he wants to distribute the coins in such a way that they can be evenly divided among two, three, four, or five sailors. What is the minimum number of wallets he will need? Don't forget to prove that the number you found is the smallest.
|
Solution. Answer: 9 wallets. Example: $12,12,8,7,6,5,4,3,3$.
We will prove that 8 wallets are insufficient.
1) Note that each wallet should contain no more than 12 coins. Therefore, 15 coins must be made up of at least two wallets. This means that when we divide 8 wallets among four pirates, each should receive two wallets. Thus, they form four pairs with a sum of 15.
2) When dividing among five pirates, at least two pirates will receive one wallet each. Therefore, there are two wallets with 12 coins.
3) From point 1, it follows that these two wallets must be paired with two wallets containing 3 coins.
4) If there are only two wallets with 12 coins, the rest must form pairs with a sum of 12. Then, in addition to each wallet with 3 coins, there must be a wallet with 9 coins. And then each of them needs a pair with 6 coins (to make a sum of 15). Thus, the set of wallets is: $12,12,3,3,9,9,6,6$. Clearly, 20 coins cannot be obtained with these (20 is not divisible by 3).
5) If there are more than two wallets with 12 coins, i.e., at least three, then there must be at least three wallets with 3 coins (which complement them to 15 coins, see point 1). However, from such a set of wallets, it is impossible to form even one portion of 20 coins; to be able to get three such portions, at least three more wallets need to be added, then there will be no fewer than nine.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all natural numbers $n$ for which $2^{n}+n^{2016}$ is a prime number.
|
Solution. Let's consider three cases.
- If $n$ is even, then the given number is also even (and greater than two for $n>0$).
- If $n$ is odd and not divisible by 3, then $2^{n}$ gives a remainder of 2 when divided by 3, and $n^{2016}=\left(n^{504}\right)^{4}$ gives a remainder of 1 when divided by 3, so the sum is divisible by 3 (and greater than three for $n>1$). For $n=1$, the result is 3, which is a prime number.
- Finally, let $n$ be divisible by 3 (and odd, which is not used). Then the number in question is the sum of cubes: if $n=3k$, then
$2^{n}+n^{2016}=\left(2^{k}\right)^{3}+\left(n^{672}\right)^{3}=\left(2^{k}+n^{672}\right) \cdot\left(2^{2k}-2^{k} \cdot n^{672}+n^{2 \cdot 672}\right)-$ a composite number (it is obvious that $1<2^{k}+n^{672}<2^{n}+n^{2016}$ for $n \geqslant 3$).
Answer: $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In the game "set," all possible four-digit numbers consisting of the digits $1,2,3$ (each digit appearing exactly once) are used. It is said that a triplet of numbers forms a set if, in each digit place, either all three numbers contain the same digit or all three numbers contain different digits.
The complexity of a set is defined as the number of digit places where all three digits are different.
For example, the numbers 1232, 2213, 3221 form a set of complexity 3 (in the first place, all three digits are different, in the second place, only the digit 2 appears, in the third place, all three digits are different, and in the fourth place, all three digits are different); the numbers $1231,1232,1233$ form a set of complexity 1 (in the first three places, the digits are the same, and only in the fourth place are all digits different). The numbers 1123, 2231, 3311 do not form a set at all (in the last place, two ones and a three appear).
Which sets have the highest complexity in the game, and why?
|
Solution. Note that for any two numbers, there exists exactly one set in which they occur. Indeed, the third number of this set is constructed as follows: in the positions where the first two numbers coincide, the third number has the same digit; in the position where the first two numbers differ, the third number gets the remaining digit. For example, for the numbers 1231 and 1223, the third in the set will be 1212.
Let's call an "ordered set" a set of three four-digit numbers with their order taken into account. Note that each unordered set $\{a, b, c\}$ corresponds to six ordered sets: $(a, b, c)$, $(a, c, b)$, $(b, a, c)$, $(b, c, a)$, $(c, a, b)$, $(c, b, a)$. Therefore, instead of the number of unordered sets, we can compare the number of ordered sets (which is six times more). Each ordered set $(a, b, c)$ is uniquely determined by an ordered pair of numbers $(a, b)$.
Let's count the number of ordered sets of complexity $k>0$. Each such set can start with any number $a$ (81 options). In this number, we need to choose $k$ positions ($C_{4}^{k}$ ways to choose) and replace the digit in each of them with one of the two different ones ($2^{k}$ ways). As a result, we get a number $b$, which uniquely determines the set. In total, we get $81 \cdot C_{4}^{k} \cdot 2^{k}$ ordered sets of complexity $k$.
Comparing the numbers $f(k)=C_{4}^{k} \cdot 2^{k}$ for different $k$, we get: $f(1)=8$, $f(2)=24$, $f(3)=32$, $f(4)=16$. As we can see, the largest number of sets has complexity $k=3$.
Answer: the most sets have complexity 3.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Petya prints five digits on the computer screen, none of which are zeros. Every second, the computer removes the initial digit and appends to the end the last digit of the sum of the remaining four digits. (For example, if Petya enters 12345, after one second it will become 23454, then 34546, and so on. However, he can enter any five digits, not necessarily 12345.) At some point, Petya stops the process. What is the minimum possible sum of the five digits that could be on the screen at that moment?
(A. A. Tesler)
|
Answer: 2.
Solution. The record 00000 cannot appear on the screen, as it can only result from 00000. A record with four zeros and one also cannot appear, since in that case, the last digit would not equal the remainder of the division of the sum of the first four by 10.
However, a sum of digits equal to 2 is possible. For example, by working backwards, we can find an example of obtaining the record 00011 (or 10001):
$00011 \leftarrow 10001 \leftarrow 91000 \leftarrow 09100 \leftarrow 00910 \leftarrow 20091 \leftarrow 72009 \leftarrow 17200 \leftarrow 01720 \leftarrow 40172 \leftarrow$ $24017 \leftarrow 52401 \leftarrow 95240 \leftarrow 89524$.
Criteria. 5 points for the example, 2 points for the proof of the impossibility of smaller sums.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The pond has a square shape. On the first frosty day, the part of the pond that is no more than 10 meters away from the nearest point on the shore froze. On the second day, the part no more than 20 meters away froze, on the third day, the part no more than 30 meters away, and so on. On the first day, the area of open water decreased by $35 \%$. On which day will the pond be completely frozen?
|
Solution. Note that the larger the side of the pond, the smaller the percentage that will freeze on the first day. If the side of the pond is 100 m, then 36% will freeze on the first day, and if the side is 120 m, then on the first day, $1-\frac{100^{2}}{120^{2}}=11 / 36<1 / 3$ of the pond's area will freeze. Therefore, the side of the pond is between 100 and 120 meters. Therefore, it will freeze completely on the sixth day.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all such numbers $k$ for which
$$
(k / 2)!(k / 4)=2016+k^{2}
$$
The symbol $n!$ denotes the factorial of the number $n$, which is the product of all integers from 1 to $n$ inclusive (defined only for non-negative integers; $0!=1$).
|
Solution. Note that the left side makes sense only for even values of $k$. We directly verify that $k=2,4,6,8,10$ do not work, while $k=12$ gives a correct equality.
With each further increase of $k$ by 2, the expression $(k / 2)!$ increases by at least 7 times, i.e., the left side grows by more than 7 times. At the same time, the right side increases by less than double: $(k+1)^{2}-k^{2}<12$. Therefore, for $k>12$, the left side is greater than the right side.
Answer: $k=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let's call a rectangular parallelepiped typical if all its dimensions (length, width, and height) are different. What is the smallest number of typical parallelepipeds into which a cube can be cut? Don't forget to prove that this is indeed the smallest number.
|
Solution. A cube can be cut into four typical parallelepipeds. For example, a cube $5 \times 5 \times 5$ can be cut into parallelepipeds $5 \times 3 \times 1, 5 \times 3 \times 4, 5 \times 2 \times 1, 5 \times 2 \times 4$.
It is impossible to cut the cube into a smaller number of typical parallelepipeds. Indeed, a cube has 8 vertices; if it is cut into three or fewer parallelepipeds, then at least one of them contains at least three vertices of the cube.
If all three vertices are located on the same face of the cube (for example, on the top face), then the parallelepiped contains the entire top face of the cube; thus, it has two identical dimensions. If two vertices are located on the top face of the cube and one on the bottom, then the parallelepiped contains at least one edge of the top face, and its height is equal to the height of the cube. Again, we have two identical dimensions.
Answer: into 4 typical parallelepipeds.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Petya's favorite TV game is called "Sofa Lottery." During the game, viewers can send SMS messages with three-digit numbers containing only the digits $1, 2, 3$, and 4. At the end of the game, the host announces a three-digit number, also consisting only of these digits. An SMS is considered a winning one if the number in it differs from the host's number by no more than one digit (for example, if the host announced the number 423, then the messages 443 and 123 are winning, but 243 and 224 are not).
Petya wants to send as few messages as possible to ensure that at least one is definitely a winner. How many SMS messages will he have to send? (L. S. Korechkova)
|
Answer: 8.
Solution. An example of eight suitable SMS messages: 111, 122, 212, 221, 333, 344, 434, 443. Indeed, no matter what number the host names, it contains either at least two digits from the set $\{1,2\}$, or at least two from the set $\{3,4\}$. If the third digit is from the other set, we replace it with a digit from the same set as the other two, so that the sum of the digits is odd - this will definitely result in one of the specified options.
Now suppose there are fewer than 8 messages. Then some digit (for example, the digit 1) begins at most one message. Without loss of generality, let this message be 111 (if it exists at all). Consider the cases when the host names the numbers 122, 123, $124,132,133,134,142,143,144$. There are 9 of them, and for each of them, a separate message is needed (since the first digit is not 1, the second and third must be guessed).
Remark. The problem can be reformulated as: "What is the minimum number of rooks needed to cover a $4 \times 4 \times 4$ chessboard?". The general solution (for a board $n \times n \times n$) is provided, for example, in the comment at http://math.hashcode.ru/questions/52123.
Criteria. 4 points are given for the estimate, 3 points for the example. 1 point is given for the assertion that at least 7 SMS messages are necessary.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the maximum number of numbers that can be chosen from the set $\{1,2, \ldots, 12\}$ so that the product of no three chosen numbers is a perfect cube?
|
Solution. 9: all except $4,9,12$. Note that to remove the cubes, we need to remove at least one element from each of the sets $\{1,2,4\},\{3,6,12\},\{2,4,8\},\{1,3,9\},\{2,9,12\}$, $\{3,8,9\},\{4,6,9\}$. Note that all numbers, except 9, are in no more than three of these seven triples. Therefore, if we remove two numbers different from 9, at least one triple will remain. If, however, we remove the number 9, then among the remaining triples there will be two non-intersecting $(\{1,2,4\},\{3,6,12\})$, so no matter which second number we remove, one of the triples will remain.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest possible value of the expression
$$
\left(\frac{x y}{z}+\frac{z x}{y}+\frac{y z}{x}\right)\left(\frac{x}{y z}+\frac{y}{z x}+\frac{z}{x y}\right)
$$
where $x, y, z$ are non-zero real numbers.
|
Solution. Note that the signs of all six numbers $\frac{x y}{z}, \frac{z x}{y}$, etc., are the same. If all of them are negative, then replace the numbers $x, y, z$ with their absolute values. As a result, each term ($\frac{x y}{z}$, etc.) will change its sign. The modulus of each bracket will remain the same, but the sign will change, so the product of the two brackets will remain the same. Therefore, any value taken by the expression is also taken when $x, y, z$ are positive.
For positive values of $x, y, z$, we use the inequality of the arithmetic mean and the geometric mean. We get:
$\left(\frac{x y}{z}+\frac{z x}{y}+\frac{y z}{x}\right)\left(\frac{x}{y z}+\frac{y}{z x}+\frac{z}{x y}\right) \geqslant 3 \sqrt{\frac{x y}{z} \cdot \frac{z x}{y} \cdot \frac{y z}{x}} \cdot 3 \sqrt{\frac{x}{y z} \cdot \frac{y}{z x} \cdot \frac{z}{x y}}=9 \sqrt{\frac{(x y z)^{2}}{x y z} \cdot \frac{x y z}{(x y z)^{2}}}=9$.
Obviously, the value 9 is achieved, for example, when $x=y=z=1$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The edge of a regular tetrahedron $A B C D$ is 1. Through a point $M$, lying on the face $A B C$ (but not on the edge), planes parallel to the other three faces are drawn. These planes divide the tetrahedron into parts. Find the sum of the lengths of the edges of the part that contains point $D$.
|
5. See the figure at the end of the file.
Note that the part of the tetrahedron we are interested in is bounded by three of its faces containing point $D$, and by three planes parallel to the faces. Therefore, this is a parallelepiped.
Consider the faces $A B C$ and $A D C$. Align these faces so that vertex $B$ coincides with $D$, and edge $A C$ remains in place. Note that the lines of intersection of these faces with the plane passing through $M$ parallel to $(B C D)$ will coincide, since they are at the same distance from $C D$ (from $B C$). The same is true for the plane parallel to $(A B D)$. As a result, one of the faces of our parallelepiped transforms into a parallelogram with diagonal $BM$.
Reasoning similarly for the other two faces, we see that three faces of our parallelepiped are equal to three parallelograms with vertex $M$ lying in the face $A B C$. If we denote the edges of the parallelepiped as $a, b$, and $c$, then the result shown in Figure 2 is obtained. Since all triangles in this figure are equilateral, $a+b+c=1$. Therefore, the sum of the lengths of the edges of the parallelepiped is $4 a+4 b+4 c=4$.
Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Prove that $\sqrt[3]{\sqrt{5}+2}-\sqrt[3]{\sqrt{5}-2}$ is a rational number.
|
Solution: Let $x=\sqrt[3]{\sqrt{5}+2}-\sqrt[3]{\sqrt{5}-2}$. Then $x^{3}=(\sqrt{5}+2)-(\sqrt{5}-2)-$ $3 \sqrt[3]{(\sqrt{5}+2)(\sqrt{5}-2)} \times(\sqrt[3]{\sqrt{5}+2}-\sqrt[3]{\sqrt{5}-2})=4-3 x ; x^{3}+3 x-4=0.0=x^{3}+$ $3 x-4=(x-1)\left(x^{2}+x+4\right), x-1=0$ or $x^{2}+x+4=0$. The second equation has no roots because its discriminant is negative. Therefore, $x=1$ is a rational number.
Criteria: It is written that the value of the given sum is equal to 1 - 1 point. The root of the obtained equation is found and it is not proven that there are no other roots - 5 points.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation
$$
x^{2018}+\frac{1}{x^{2018}}=1+x^{2019}
$$
|
Answer: $x=1$.
Solution: $x^{2018}+\frac{1}{x^{2018}} \geq 2$ for $x \neq 0$, because $x^{4036}-2 x^{2018}+1=\left(x^{2018}-1\right)^{2} \geq 0 . x^{2019}=x^{2018}+\frac{1}{x^{2018}}-1 \geq 2-1=1 . x \geq 1$. If $\quad x>1, \quad x^{2019}+1>$ $x^{2018}+\frac{1}{x^{2018}}$, because $x^{2019}=x * x^{2018}>x^{2018}$ and $1>\frac{1}{x^{2018}}$. Contradiction, so $x=1, x<=1$, so $x=1$. $x=1$ is indeed a solution to the equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A black and white chocolate bar consists of individual pieces forming $n$ horizontal and $m$ vertical rows, arranged in a checkerboard pattern. Yan ate all the black pieces, and Maxim ate all the white pieces. What is $m+n$, if it is known that Yan ate $8 \frac{1}{3} \%$ more pieces than Maxim.
|
Solution. The number of black and white segments can only differ by 1. Therefore, Yan ate 1 segment more than Maksim. If 1 segment is 8 $\frac{1}{3} \%$, then Maksim ate 12 segments, Yan ate 13 segments, and together they ate 25 segments. This means the chocolate bar was $5 \times 5$.
Answer: 10.
Criteria: 14 points for a justified correct solution. 12 points for a correct solution with an arithmetic error. 6 points for stating that Yan ate 1 segment more than Maksim. 2 points for the correct answer only. (Do not deduct points for the answer $26-25+1$.)
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. There are books of three colors: white, blue, and green. To make the shelf look beautiful, the boy first arranged the white books, and then placed blue books in each gap between them. Finally, he placed green books in each gap between the standing books. In the end, there were 41 books on the shelf. How many white books did the boy place on the shelf?
|
Answer: 11
9. The sum of two natural numbers is 2017. If you append 9 to the end of the first number and remove the digit 8 from the end of the second number, the numbers will be equal. Find the largest of these numbers.
Answer: 1998
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. In a row, $n$ integers are written such that the sum of any three consecutive numbers is positive, while the sum of any five consecutive numbers is negative. For what largest $n$ is this possible
|
Answer: 6.
Solution: Let's provide an example for $n=6: 3,-5,3,3,-5,3$. We will prove that for $n \geq 7$ it will not be possible to write down a sequence of numbers that satisfy the condition of the problem. We will construct a table for the first 7 numbers in this sequence
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ |
| :--- | :--- | :--- | :--- | :--- |
| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ |
| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ |
By the condition: the sum of the numbers in each row must be negative, and in each column positive. Therefore, the sum of all the numbers in the table should be positive on one side and negative on the other. Contradiction.
Criteria: Only for the correct answer - 1 point. Correct answer with an example - 2 points.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Find the value of the expression $\sqrt[3]{7+5 \sqrt{2}}-\sqrt[3]{5 \sqrt{2}-7}$
|
Answer: 2
Task 2.B The bases $AD$ and $BC$ of an isosceles trapezoid $ABCD$ are $16 \sqrt{3}$ and $8 \sqrt{3}$, respectively, and the acute angle at the base is $30^{\circ}$. What is the length of the lateral side of the trapezoid?
Answer: 8
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the table, there are 10 stacks of playing cards (the number of cards in the stacks can be different, there should be no empty stacks). The total number of cards on the table is 2015. If a stack has an even number of cards, remove half of the cards. If the number of remaining cards in the stack is still even, remove half again, and so on, until the number of cards in the stack becomes odd. Do this for each stack. Explain:
a) What is the maximum possible number of cards remaining on the table?
b) What is the minimum possible number of cards remaining on the table?
In each case, provide an example of how the playing cards can be distributed among the stacks.
|
# Solution
a) Since 2014 is an odd number, in any distribution of cards into 10 piles, there will be at least one pile with an even number of cards. Therefore, the number of cards in this pile, and thus the total number of cards, will definitely decrease by at least one card (if there are 2 cards in this pile). This means the final number of cards on the table will always be less than 2015. With the distribution $\underbrace{1,1, \ldots, 1}_{8}, 2,2005$, it is easy to verify that the final number of cards remaining on the table is 2014.
b) The smallest number of cards remaining in a pile is 1. Therefore, the final number of cards remaining on the table cannot be less than 10. In the following example, the final number of cards remaining on the table is 10:
1024, 512, 256, 128, 64, 16, 8, 4, 2, 1.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation in integers $x^{2}+y^{2}=3 x y$.
---
Note: The translation maintains the original format and line breaks as requested.
|
Answer: $x=y=0$.
Solution: If both numbers are not equal to 0, divide the numbers $x$ and $y$ by their greatest common divisor, resulting in coprime numbers $a$ and $b$. The right side of the equation is divisible by 3, so the left side must also be. The square of an integer can give a remainder of 0 or 1 when divided by 3, so $a^{2}$ and $b^{2}$ are divisible by 3, which means $a$ and $b$ are divisible by 3. This is a contradiction because $a$ and $b$ are coprime and have a common divisor 3, which is greater than 1.
Criteria: Only for the correct answer - 1 point. Noted that $x$ and $y$ must be divisible by $3-3$ points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 6. Find the value of the expression $\left(\sqrt[3]{x^{2}} \cdot x^{-0.5}\right):\left(\left(\sqrt[6]{x^{2}}\right)^{2} \cdot \sqrt{x}\right)$ at $x=\frac{1}{2}$
|
Answer: 2
Problem 7. The diagonals of trapezoid $ABCD (BC \| AD)$ are perpendicular to each other, and $CD = \sqrt{129}$. Find the length of the midline of the trapezoid, given that $BO = \sqrt{13}, CO = 2\sqrt{3}$, where $O$ is the point of intersection of the diagonals of the trapezoid.
Answer: 10
Problem 8. Four numbers are given, the first three of which form a geometric progression, and the last three form an arithmetic progression with a difference of 999. It is known that the first and last numbers are the same. Find these numbers and give their sum in the answer.
Answer: 2331
Problem 9. The function $f(x)$ is defined for all $x$ except 1 and satisfies the equation: $(x+2) f\left(\frac{x+1}{x-1}\right) = x - f(x)$. Find $f(-1)$.
Answer: 1
Problem 10. Find the number of integer solutions to the inequality $\frac{\left(6 x-5-x^{2}\right)\left(2-x-x^{2}\right)(1+x)}{\left(x^{2}-3 x-10\right)(1-x)} \geq 0$
Answer: 2.
Problem 11. A tourist left the camp and walked along a country road to a mountain, climbed to the top of the mountain, and then returned to the camp along the same route, spending a total of 5 hours on the entire journey. What distance did the tourist travel if his speed along the country road was 4 km/h, he climbed the mountain at a speed of 3 km/h, and descended from the mountain at a speed of 6 km/h?
Answer: 20 km
Problem 12. Find the sum of all solutions to the equation
$$
(x-2)^{2}-\frac{24}{4 x-x^{2}}=18
$$
Answer: 8
Problem 13. In trapezoid $ABCD$, the bases $BC$ and $AD$ are in the ratio $1:3$, $AC = 12 \sqrt[4]{5}$, $AD = 18 \sqrt[4]{5}$, $\cos \angle CAD = \frac{1}{9}$. Find the area of the trapezoid.
Answer: 320
Problem 14. Solve the equation in integers for all natural $n$:
$$
x^{4} + n = y(2-y) + 1
$$
In the answer, write the number of solutions.
Answer: 5
Problem 15. Two cars are participating in a race. The first car moves at a speed of 120 km/h, the second at 180 km/h. There are gas stations along the route. The first car spends $a$ minutes at each gas station, and the second car spends twice as long. They started and finished at the same time. The length of the route is 300 km. How many gas stations could there be on the route if $a$ is an integer greater than 5? In the answer, indicate the number of solutions.
Answer: 3
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Ten consecutive natural numbers are written on the board. What is the maximum number of them that can have a digit sum equal to a perfect square?
|
Answer: 4.
Solution: Note that the sums of the digits of consecutive natural numbers within the same decade are consecutive natural numbers. Since there are 10 numbers, they span two decades. Also note that among ten consecutive natural numbers, there can be no more than 3 perfect squares, and three perfect squares can only occur if there are 9 numbers. Therefore, among the 10 consecutive natural numbers written on the board, there cannot be more than 4 numbers with a sum of digits equal to the square of a natural number. We can provide an example where there are exactly 4 such numbers: $\{1,2,3,4,5,6,7,8,9,10\}$.
Grading criteria. Full solution - 20 points. Only the estimate - 12 points. Answer + example - 9 points. Only the answer - 3 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all real roots of the equation
$(x+1)^{5}+(x+1)^{4}(x-1)+(x+1)^{3}(x-1)^{2}+(x+1)^{2}(x-1)^{3}+(x+1)(x-1)^{4}+(x-1)^{5}=0$
|
Solution. Multiply both sides of the equation by $(x+1)-(x-1)$ (this factor equals 2). Use the formula $a^{6}-b^{6}=(a-b)\left(a^{5}+a^{4} b+a^{3} b^{2}+a^{2} b^{3}+a b^{4}+b^{5}\right)$.
$$
\begin{gathered}
(x+1)^{6}-(x-1)^{6}=0 \\
(x+1)^{6}=(x-1)^{6}
\end{gathered}
$$
The equation
$$
x+1=x-1
$$
has no solutions. The equation
$$
x+1=-(x-1)
$$
has the solution $x=0$. Since we multiplied the equation by the number 2, we did not obtain any extraneous roots.
Answer. 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Four points $A, B, C, D$ are on a plane. It is known that $A B=1, B C=$ $2, C D=\sqrt{3}, \angle A B C=60^{\circ}, \angle B C D=90^{\circ}$. Find $A D$.
|
Solution. Let's construct the diagram. Let the line $CD$ intersect the line $AB$ at point $O$

(according to the condition, these lines are not parallel). There are two possible positions for point $D$ on the line $CD$ - on the segment $CO$ and outside this segment. Triangle $BOC$ is a right triangle, with the angle at vertex $O$ equal to $30^{\circ}$. We find $AB=4$, $OA=3$, $OC=2\sqrt{3}$. For $OD$, considering $CD=\sqrt{3}$, we get two possible values, $OD=\sqrt{3}$ or $OD=3\sqrt{3}$. In triangle $AOD$, two sides and the angle at vertex $O$ are known. Using the cosine rule, we find $AD$. We get two values: $AD=3$ or $AD=\sqrt{3}$. Answer. 3 and $\sqrt{3}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. In a seven-story building, domovoi (Russian house spirits) live. The elevator travels between the first and the last floors, stopping at every floor. On each floor, starting from the first, one domovoi entered the elevator, but no one exited. When the thousandth domovoi entered the elevator, it stopped. On which floor did this happen? Explain your answer.
|
Answer: on the fourth floor.
Solution. First, let's find out how many housekeepers ended up in the elevator after the first trip from the first to the seventh floor and back, until the elevator returned to the first floor. One housekeeper entered on the first and seventh floors, and on all other floors, two housekeepers entered. Thus, in one such trip, 12 housekeepers ended up in the elevator.
Now, let's find out how many such complete trips the elevator managed to make. When dividing 1000 by 12, the quotient is 83 and the remainder is 4. This means that after 83 ascents and descents, 4 more housekeepers can still enter the elevator: on the first, second, third, and fourth floors.
## Grading criteria:
+ correct answer and a fully justified solution
$\pm$ correct answer and a generally correct solution, but there are gaps and deficiencies in the justification
干 correct answer only
干 correct answer is missing, but the correct idea of dividing the elevator trips into "cycles" of 12 housekeepers is indicated
- the problem is not solved or solved incorrectly
(Note: The "干" characters in the grading criteria should be replaced with appropriate English terms, such as "partially correct" or "incomplete.")
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the maximum possible area of a quadrilateral in which the product of any two adjacent sides is 1.
|
1. Find the maximum possible area of a quadrilateral for which the product of any two adjacent sides is 1.
OTBET: 1.
SOLUTION.
Let the quadrilateral have sides $a, b, c, d$. Then $a b=b c=c d=d a=1$. From the equality $a b=b c$, it follows that $a=c$, and from the equality $b c=c d$, we get that $b=d$. Therefore, the given quadrilateral is a parallelogram. Let $\alpha$ be the angle between sides $a$ and $b$. Then $S=a \cdot b \sin \alpha$, and the area is maximized if $\sin \alpha=1$. Thus, $S=a \cdot b=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The graph of the linear function $y=k x+k+1(k>0)$ intersects the $O x$ axis at point $A$, and the $O y$ axis at point $B$ (see the figure). Find the smallest possible value of the area of triangle $A B O$.
|
Answer: 2.
Solution. The abscissa of point $A$ of intersection with the $O x$ axis: $0=k x+k+1 ; x=$
$-\left(1+\frac{1}{k}\right)$. The ordinate of point $B$ of intersection with the $O y$ axis: $y=k \cdot 0+k+1 ; y=k+1$. Therefore, $S_{A B O}=\frac{1}{2} \cdot O A \cdot O B=\frac{1}{2}(k+1)\left(1+\frac{1}{k}\right)=\frac{1}{2}\left(2+k+\frac{1}{k}\right)$. By the inequality between the arithmetic mean and the geometric mean, $k+\frac{1}{k} \geq 2$, and equality is achieved when $k=1$, so the minimum value of $S_{A B O}$ is also achieved when $k=1$. Thus, the smallest possible area of triangle $A B O$ is 2.
Comment. The correct answer is found based on the consideration of an example, and the minimality is not proven - 1 point. The expression for the area of the triangle in terms of $k$ is found - 5 points. If the logic is correct but errors in transformations prevent obtaining the correct answer - 4 points. The statement that the minimum value of the expression $k+\frac{1}{k}$ is achieved when $k=1$ can be used without proof.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.7. In a magic shop, for 20 silver coins you can buy an invisibility cloak and get 4 gold coins as change. For 15 silver coins you can buy an invisibility cloak and get 1 gold coin as change. How many silver coins will you get as change if you buy an invisibility cloak for 14 gold coins?
|
Answer: 10.
Solution. In the first case, compared to the second, by paying 5 extra silver coins, one can receive 3 extra gold coins in change. Therefore, 5 silver coins are equivalent to 3 gold coins.
In the second case, by paying 15 silver coins (which is equivalent to $3 \cdot 3=9$ gold coins), one can get the cloak and 1 gold coin in change. Therefore, the cloak costs 8 gold coins.
In the third case, by paying 14 gold coins for a cloak worth 8 coins, one would receive 6 gold coins in change, which is equivalent to $5 \cdot 2=10$ silver coins.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Each of the 33 bogatyrs (Russian epic heroes) either always lies or always tells the truth. It is known that each bogatyr has exactly one favorite weapon: a sword, spear, axe, or bow.
One day, Ded Chernomor asked each bogatyr four questions:
- Is your favorite weapon a sword?
- Is your favorite weapon a spear?
- Is your favorite weapon an axe?
- Is your favorite weapon a bow?
To the first question, 13 bogatyrs answered affirmatively, to the second question - 15 bogatyrs, to the third - 20 bogatyrs, and to the fourth - 27 bogatyrs.
How many bogatyrs always tell the truth?
|
Answer: 12.
Solution. Note that each of the truth-telling heroes answers affirmatively to only one question, while each of the lying heroes answers affirmatively to exactly three questions. Let the number of truth-telling heroes be $x$, and the number of lying heroes be $-(33-x)$. Then the total number of affirmative answers was $13+15+20+27=x+3 \cdot(33-x)$, from which we get $75=99-2 x$ and $x=12$. Note also that the number of truth-telling heroes can be exactly 12. Suppose 8 lying heroes love the sword the most, another 6 lying heroes love the spear, another 1 lying hero loves the axe, another 6 lying heroes love the bow, and another 12 truthful heroes love the bow. It is not difficult to verify that all conditions of the problem are satisfied in this case.
## 6th grade
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.3. In a new math textbook, there are a total of 91 problems. Yura started solving them in the mornings, beginning on September 6.
Every morning, starting from September 7, he solves one fewer problem than the previous morning (until the problems run out).
By the evening of September 8, Yura realized that there were still 46 problems left to solve in the textbook. On which day of September will he finish solving the textbook?
|
Answer: 12.
Solution. In the first 3 days, Yura solved $91-46=45$ problems. Let's say on September 7th, he solved $z$ problems, then on September 6th, he solved $(z+1)$ problems, and on September 8th, he solved $(z-1)$ problems. We get that $45=(z+1)+z+(z-1)=3 z$, from which $z=15$.
Since $91=16+15+14+13+12+11+10$, Yura will solve problems for exactly 7 days, from September 6th to September 12th.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2. Petya bought himself shorts for football at the store.
- If he had bought shorts with a T-shirt, the cost of the purchase would have been twice as much.
- If he had bought shorts with cleats, the cost of the purchase would have been five times as much.
- If he had bought shorts with shin guards, the cost of the purchase would have been three times as much.
How many times greater would the cost of the purchase have been if Petya had bought shorts, a T-shirt, cleats, and shin guards?
|
Answer: 8.
Solution. Let the shorts cost $x$. Since the shorts with a T-shirt cost $2x$, the T-shirt also costs $x$. Since the shorts with boots cost $5x$, the boots cost $4x$. Since the shorts with shin guards cost $3x$, the shin guards cost $2x$. Then, if Petya bought shorts, a T-shirt, boots, and shin guards, his purchase would amount to $x+x+4x+2x=8x$, which is 8 times more than $x$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $A B C D$ is a square, then $A B=B C=C D=A D$.
Fig. 1: to the solution of problem 8.4
Notice that $\angle A B K=\angle C B L$, since they both complement $\angle A B L$ to $90^{\circ}$. Then the right triangles $A B K$ and $C B L$ are equal by the acute angle and the leg $A B=B C$ (Fig. 1). Therefore, $A K=C L=6$. Then
$$
L D=C D-C L=A D-C L=(K D-A K)-C L=K D-2 \cdot C L=19-2 \cdot 6=7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. Vanya runs from home to school at a constant speed. If he had initially increased his speed by 2 m/s, he would have arrived at school 2.5 times faster. How many times faster would he have arrived at school if he had initially increased his speed by 4 m/s?
#
|
# Answer: 4.
Solution. Let Vasya's initial speed be $v$ m/s. If he ran at a speed of $(v+2)$ m/s, he would cover the same distance to school 2.5 times faster. This means that $\frac{v+2}{v}=2.5$, from which we find $v=\frac{4}{3}$. If he had initially run at a speed of $(v+4)$ m/s, he would have arrived at school $\frac{v+4}{v}$ times faster. Substituting $v=\frac{4}{3}$ into this expression, we get the answer 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. The entire surface of a cube $13 \times 13 \times 13$ was painted red, and then this cube was sawn into smaller cubes $1 \times 1 \times 1$. All the faces of the smaller cubes $1 \times 1 \times 1$ that were not painted red were painted blue. By what factor is the total area of the blue faces greater than the total area of the red faces?
|
Answer: 12.
Solution. Each face of the original cube consists of exactly $13^{2}$ $1 \times 1$ squares, so a total of $6 \cdot 13^{2}$ $1 \times 1$ squares were painted red. Since there are exactly $13^{3}$ $1 \times 1 \times 1$ cubes, and each has 6 faces, the number of $1 \times 1$ squares painted blue is $6 \cdot 13^{3}-6 \cdot 13^{2}$. Therefore, the answer to the problem is
$$
\frac{6 \cdot 13^{3}-6 \cdot 13^{2}}{6 \cdot 13^{2}}=13-1=12
$$
Remark. The same answer could have been obtained in a different way, by understanding that each $1 \times 1$ red square on the surface of the original cube corresponds to exactly 12 blue $1 \times 1$ squares inside the cube. These 12 blue squares are obtained from the red one by applying a parallel translation of length 1 "into the cube," perpendicular to the face of the red square.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. Petya wrote down ten natural numbers in a row as follows: the first two numbers he wrote down arbitrarily, and each subsequent number, starting from the third, was equal to the sum of the two preceding ones. Find the fourth number if the seventh is 42 and the ninth is 110.
|
Answer: 10.
Solution. From the condition, it follows that the eighth number is equal to the difference between the ninth and the seventh, i.e., $110-42=68$. Then the sixth is $68-42=26$, the fifth is $42-26=16$, and the fourth is $26-16=10$.
Remark. In fact, the numbers on the board are the doubled Fibonacci numbers.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Oleg wrote down several composite natural numbers less than 1500 on the board. It turned out that the greatest common divisor of any two of them is 1. What is the maximum number of numbers that Oleg could have written down?
|
Answer: 12.
Solution. Prime numbers less than $\sqrt{1500}$ will be called small. There are exactly 12 such numbers: $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37$.
Note that each of Oleg's numbers has a small divisor (otherwise it would be not less than $43^{2} > 1500$), and different numbers have different small divisors (otherwise the GCD of these numbers would be greater than 1). Therefore, the number of Oleg's numbers is no less than the total number of small numbers, i.e., no less than 12.
An example with 12 numbers is easy to construct: these are the numbers $2^{2}, 3^{2}, 5^{2}, 7^{2}, 11^{2}, 13^{2}, 17^{2}, 19^{2}, 23^{2}, 29^{2}, 31^{2}, 37^{2}$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. There are 22 batteries, 15 of which are charged and 7 are discharged. The camera works with three charged batteries. You can insert any three batteries into it and check if it works. How can you guarantee to turn on the camera in 10 such attempts?
|
Solution. Let's number the batteries: $1,2, \ldots, 22$. The first six tests will involve inserting batteries into the camera as follows: $1,2,3 ; 4,5,6 ; \ldots, 16,17,18$. If at least one of these groups turns on the camera, everything is fine. If not, then among the first 18 batteries, there are at least 6 discharged ones, which means that among the last four batteries, there is at most one discharged one. The next four tests will involve trying all combinations of the remaining batteries: $19,20,21 ; 19,20,22 ; 19,21,22 ; 20,21,22$ - and we will definitely find a group of three charged batteries.
- See also problem 1 for 10th grade.
- For an answer without justification - 0 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Inside triangle ABC, two points are given. The distances from one of them to the lines AB, BC, and AC are 1, 3, and 15 cm, respectively, and from the other - 4, 5, and 11 cm. Find the radius of the circle inscribed in triangle ABC.
|
Answer: 7 cm. First solution. Let $M_{1}$ and $M_{2}$ be the first and second given points, and let point $O$ be such that point $M_{2}$ is the midpoint of segment $O M_{1}$. Drop perpendiculars $M_{1} N_{1}, M_{2} N_{2}$, and $O N_{3}$ to line $A B$. Then segment $M_{2} N_{2}$ will be the midline of trapezoid $O N_{3} N_{1} M_{1}$. Therefore, $M_{2} N_{2}=\left(O N_{3}+M_{1} N_{1}\right) / 2 \Rightarrow 4=\left(O N_{3}+1\right) / 2$, from which $O N_{3}=7$. Similarly, we find that the perpendiculars $O M_{3}$ and $O K_{3}$ from point $O$ to lines $B C$ and $A C$ respectively are also equal to 7. Thus, point $O$ is the center of the inscribed circle of triangle $A B C$, which has a radius of 7. Second solution. Let $A B=c, B C=a$, $A C=b$. Then $3 a+15 b+c=5 a+11 b+4 c=r(a+b+c)=2 S_{A B C}$. From the first equality, we get $a=(4 b-3 c) / 2$. Substituting the found $a$ into the second equality $5 a+11 b+4 c=r(a+b+c)$, we find $r=7$.
- For an answer without justification - 0 points.
Problem 6. On the board, there are five "equations" of the form $x^{2}+\ldots x+\ldots=0$. Two players take turns writing natural numbers from 1 to 10 in place of the ellipses, with each number being used only once. The game ends when all numbers are written. The player who makes the first move wants to have as few equations with two distinct roots as possible at the end, while his opponent wants to have as many as possible. What is the best result the first player can achieve regardless of the second player's moves?
Answer. The first player can ensure that there are no more than three equations with two distinct roots on the board. This result cannot be improved. Solution. To create two equations without roots, the first player needs to use the first two moves to write the smallest of the numbers not yet written in the coefficient of $x$ in an "equation" where no numbers have been written yet. This is possible because if no more than two pairs of moves have been made, then at least one coefficient has been written in no more than four "equations". Let $x^{2}+p x+q=0$ be one of the equations obtained at the end of the game, where the coefficient $p$ was written by the first player on one of the first two moves. Then, obviously, $p \leq 3$ and $q \geq p+1$, from which $p^{2}-4 q \geq p^{2}-4(p+1)=p(p-4)-40$.
- For an answer without justification - 0 points. If there is a strategy for only one of the players, the solution is scored out of 4 points: 2 points for describing the strategy and 2 points for justifying it.
## SOURCES AND AUTHORS OF THE PROBLEMS
XII Tournament of Mathematical Flash Battles "League of Discoveries", Kazan, 2022: 6-4, 7-4.
Based on problems from Kostroma olympiads: 7-2, 9-2.
District-city round of the Chelyabinsk Region Olympiad 1999/2000: 9-1.
District-city round of the Chelyabinsk Region Olympiad 1998/1999: 11-5.
Third Kostroma City Tournament of Mathematical Battles, 1998 (numerical data changed): $9-3$.
Tatarstan, Olympiad for 6th grade, final round, 2014: 10-1.
Udmurtia, district round, 1979: 11-1
Folklore: $5-4=6.3,11-4$.
All other problems were composed by I.S. Rubanov specifically for this olympiad.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A teacher fills in the cells of a class journal of size $7 \times 8$ (7 rows, 8 columns). In each cell, she puts one of three grades: 3, 4, or 5. After filling in the entire journal, it turns out that in each row, the number of threes is not less than the number of fours and not less than the number of fives, and in each column, the number of fours is not less than the number of fives and not less than the number of threes. How many fives could the teacher have put?
|
Answer: 8 fives.
## Solution.
First step.
In each row, there are no fewer threes than fours, so in the entire journal, there are no fewer threes than fours. In each column, there are no fewer fours than threes, so in the entire journal, there are no fewer fours than threes. Therefore, the number of threes and fours in the journal is the same.
Second step.
Suppose in some column, there are more fours than threes. Since in the other columns, there are no fewer fours than threes, we would get that in the entire journal, there are more fours than threes. This is a contradiction. Therefore, in each column, the number of fours and threes is the same.
Third step.
Consider all possible distributions of threes, fours, and fives in a column: 1) $0,0,7 ; 2) 1,1,5 ; 3) 2,2,3$ - these do not work, as then there would be more fives. The only remaining case is $3,3,1$. Then, in the entire journal, there can be 8 fives.
Fourth step.
Such a distribution is possible (we need to consider that in the rows, the number of fours and threes is also the same),
| $\mathbf{5}$ | $\mathbf{5}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{5}$ | $\mathbf{5}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ |
| $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{5}$ | $\mathbf{4}$ | $\mathbf{3}$ |
| $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{5}$ | $\mathbf{5}$ |
| $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ |
| $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ |
| $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ |
see the example in the figure.
Criteria. If the solution is incorrect - 0 points.
If only the correct example is given - 3 points.
If only the correct estimate is given - 4 points.
If the solution is correct (any correct example and justification of the estimate) - 7 points.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A car left point A for point B, which are 10 km apart, at 7:00. After traveling $2 / 3$ of the way, the car passed point C, from which a cyclist immediately set off for point A. As soon as the car arrived in B, a bus immediately set off from there in the opposite direction and arrived in point A at 9:00. At what distance from B did the bus catch up with the cyclist, if the cyclist arrived in point A at 10:00 and the speed of each participant in the movement was constant?
|
Solution. Let $v_{a}$ be the speed of the car, $v_{\varepsilon}$ be the speed of the cyclist, and $v_{a \varepsilon}$ be the speed of the bus. From the problem statement, we derive the following system of equations:
$$
\left\{\begin{array}{l}
\frac{20 / 3}{v_{a}}+\frac{20 / 3}{v_{s}}=3 \\
\frac{10}{v_{a}}+\frac{10}{v_{a \varepsilon}}=2
\end{array}\right.
$$
We need to find $\frac{\frac{10}{3}+\frac{10}{3 v_{a}} v_{g}}{v_{a \varepsilon}-v_{s}} v_{a \varepsilon}=\frac{\frac{10}{3 v_{s}}+\frac{10}{3 v_{a}}}{1 / v_{b}-1 / v_{a \varepsilon}}$.
From the system of equations, we get
$$
\left\{\begin{array} { l }
{ \frac { 1 0 } { 3 v _ { a } } + \frac { 1 0 } { 3 v _ { s } } = \frac { 3 } { 2 } , } \\
{ \frac { 1 0 } { 3 v _ { a } } + \frac { 1 0 } { 3 v _ { a \varepsilon } } = \frac { 2 } { 3 } , \quad \frac { 1 0 } { 3 v _ { a } } + \frac { 1 0 } { 3 v _ { s } } = \frac { 3 } { 2 } , \quad \frac { 1 0 } { 3 v _ { s } } - \frac { 1 0 } { 3 v _ { a \varepsilon } } = \frac { 5 } { 6 } }
\end{array} \left\{\begin{array}{l}
\frac{10}{3 v_{a}}+\frac{10}{3 v_{s}}=\frac{3}{2} \\
\frac{1}{v_{s}}+\frac{1}{v_{a \varepsilon}}=\frac{1}{4}
\end{array}\right.\right.
$$
Substituting the obtained values into expression (*), we get $\frac{3 / 2}{1 / 4}=\frac{3}{2} \cdot 4=6$.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.