problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
8.2. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved three seats to the right, Galia had moved one seat to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she stood up?
|
Answer: 3
Solution. Let's see how the seat number changed for everyone except Anya. Varya's seat number increased by 3, Galia's decreased by 1, and the sum of Diana's and Eli's seat numbers did not change. At the same time, the total sum of the seat numbers did not change, so Anya's seat number must have decreased by 2. But then the seat left for her cannot be seat 5 (since there is no seat 6), so the seat left for her must be seat 1, and initially, she had seat 3.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved one seat to the right, Galia had moved three seats to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she got up?
|
# Answer: 3
Solution. Let's see how the seat number of everyone except Anya has changed. Varya's seat number increased by 1, Galia's decreased by 3, and the sum of Diana's and El's seat numbers did not change. At the same time, the total sum of the seats did not change, so Anya's seat number must have increased by 2. However, the seat left for her cannot be seat 1 (since there is no seat 0 or -1), so the seat left for her must be seat 5, and initially, she had seat 3.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved one seat to the right, Galia had moved two seats to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she got up?
|
# Answer: 4
Solution. Let's see how the seat number of everyone except Anya has changed. Varya's seat number increased by 1, Galia's decreased by 2, and the sum of Diana's and Eli's seat numbers did not change. At the same time, the total sum of the seat numbers did not change, so Anya's seat number must have increased by 1. However, the seat left for her cannot be seat 1 (since there is no seat 0), so the seat left for her must be seat 5, and initially, she had seat 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the pantry, Winnie-the-Pooh keeps 11 pots, seven of which contain jam, and four contain honey. All the pots are lined up, and Winnie remembers that the pots with honey are standing together. What is the minimum number of pots Winnie-the-Pooh needs to check to find a pot with honey?
|
Answer: one.
Solution. Let's number the pots from 1 to 11 in the order of their arrangement in a row. Exactly one of the pots numbered 4 and 8 contains honey. Therefore, it is sufficient to check one of them. It is impossible to identify the pot with honey without checking, as any pot may contain either honey or jam.
Criteria. Any correct solution: 7 points.
It is stated that the 4th (8th) pot should be checked, but it is not specified what to do if it contains jam: 3 points.
Only the correct answer is provided: 0 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. To the number $A$, consisting of eight non-zero digits, a seven-digit number, consisting of identical digits, was added, and the eight-digit number $B$ was obtained. It turned out that the number $B$ can be obtained from the number $A$ by rearranging some of the digits. What digit can the number $A$ start with if the last digit of the number $B$ is 5?
|
Answer: 5.
Solution: Since the numbers $A$ and $B$ have the same sum of digits, their difference is divisible by 9. Therefore, the added seven-digit number with identical digits is divisible by 9. This means it consists of nines. That is, we can consider that $10^7$ was added to the number $A$ and 1 was subtracted. This means that the number $B$ is obtained from the number $A$ by increasing the first digit by 1 and decreasing the last digit by 1 (since there are no zeros in $A$ and $B$ is eight-digit), while the other digits remain unchanged. Since the number $B$ can be obtained from the number $A$ by permuting some digits, the last digit of the number $B$ coincides with the first digit of the number $A$ (and vice versa). Therefore, the number $A$ can only start with the digit 5.
Comment: It is proven that the added number consists of nines - 2 points.
Answer obtained by considering an example - 1 point.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. On a checkerboard of size $8 \times 8$, 8 checkerboard ships of size $1 \times 3$ are placed such that no two cells occupied by different ships share any points. One shot is allowed to pierce all 8 cells of one row or one column. What is the minimum number of shots needed to guarantee hitting at least one ship?
|
Answer: 2 shots.
Solution. We will make 2 shots as shown in Fig. 5. Suppose we did not hit any ship. Then there are no ships in area 1. In each of areas 2 and 3, there is no more than 1 ship. Therefore, there are at least 6 ships in area 4.
Area 4 is a $5 \times 5$ square. Then in this area, horizontally placed ships cannot lie in adjacent rows, and vertically placed ships cannot lie in adjacent columns. Therefore, in this area, there are 3 "vertical" and 3 "horizontal" ships, and one of them lies
Fig. 5 in the central row, and another in the central column of the area. But then both of these ships contain the central cell of the area. Contradiction. Therefore, at least one ship is hit.
We will show that if only one shot is made, it is possible not to hit any ship. Suppose the shot was made in some row. Note that in one row, two ships can be placed. Then if the shot was made in a row with an odd number, two ships could stand in rows with numbers $2, 4, 6$, and 8. If the shot was made in a row with an even number, two ships could stand in rows with numbers $1, 3, 5$, and 7.
Remark. It can be shown that even 5 ships cannot be placed in area 4.
Comment. Only shown how to wound a ship with 2 shots - 4 points.
Only proven that 1 shot may not be enough - 2 points.
A correct example of two shots is given, but it is not explained why at least one ship will be hit - 1 point (instead of 4 points for the first criterion).
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From Central Square to the station, there is a straight street divided by 11 intersections into 12 equal blocks. At each intersection, there is a traffic light. All traffic lights simultaneously turn green for 3 minutes, then red for 1 minute. It takes the bus two minutes to travel one block (from intersection to intersection), while a car takes one minute to travel one block. The bus and the car start from the square at the same time, at which moment all traffic lights turn green. Which vehicle will arrive at the station first, and how many minutes earlier?
|
Solution. A car will travel three blocks without obstacles in the first three minutes. Upon approaching the intersection separating the third and fourth blocks, the car will stop at the traffic light for 1 minute. Thus, to travel three blocks and start moving on the fourth block, the car will need four minutes. The car's movement will then repeat, and it will leave the ninth block along with the intersection after 12 minutes. The next three blocks will be traveled in 3 minutes, and since there is no traffic light after the twelfth block, it will arrive at the station 15 minutes after leaving the square.
The bus will travel the first block, the first intersection, and the second block without stopping and will approach the second intersection at the moment when the red light changes to green. Therefore, at the beginning of the third block, the same situation will occur as at the beginning of the first block - the bus starts moving on the third block when the traffic light turns green. It will then pass all intersections without stopping at traffic lights again. The bus's travel time is 24 minutes.
Thus, the car will arrive 9 minutes earlier.
Answer. The car will arrive first, overtaking the bus by 9 minutes.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The head of the fish weighs as much as the tail and half of the body, the body weighs as much as the head and the tail together. The tail weighs 1 kg. How much does the fish weigh?
|
Answer: 8 kg.
Solution 1. The body weighs as much as the head and tail, i.e., two tails and half the body. This means that half the body weighs as much as two tails, i.e., the body weighs 4 kg. Then the head weighs $1+2=3$ kg, and the whole fish weighs $4+3+1=8$ kg.
Solution 2. Let $\Gamma, T, X$ be the weight of the head, body, and tail, respectively. Then, according to the condition, $\Gamma=T / 2+X, T=\Gamma+X$. From this, $\Gamma=(\Gamma+X) / 2+X$, i.e., $\Gamma=3 X$. Therefore, the fish weighs $\Gamma+T+X=3 X+(3 X+X)+X=8 X=8$ kg.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Real numbers $x, y, z$ (non-zero) satisfy the equation: $x+y=z$. Find all possible values that the expression $\frac{z}{x}+\frac{y}{z}-\frac{x}{y}+\frac{x}{z}+\frac{z}{y}-\frac{y}{x}$ can take.
|
1. Answer: 3.
Solution. Transform the expression $\frac{z}{x}+\frac{y}{z}-\frac{x}{y}+\frac{x}{z}+\frac{z}{y}-\frac{y}{x}=$
$=\frac{z}{x}-\frac{y}{x}+\frac{z}{y}-\frac{x}{y}+\frac{y}{z}+\frac{x}{z}=\frac{z-y}{x}+\frac{z-x}{y}+\frac{y+x}{z}$.
Using the condition $x+y=z$ and the derived formulas $y=z-x$ and $x=$ $z-y$, we get:
$\frac{z-y}{x}+\frac{z-x}{y}+\frac{y+x}{z}=\frac{x}{x}+\frac{y}{y}+\frac{z}{z}=3$.
Grading criteria:
Correct answer with justification provided: 7 points.
Only the correct answer provided without justification: 0 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. For different numbers $a$ and $b$, it is known that $\frac{a}{b}+a=\frac{b}{a}+b$. Find $\frac{1}{a}+\frac{1}{b}$.
|
Answer: -1.
Solution. The given equality can be written as $\frac{a}{b}-\frac{b}{a}=b-a$, from which $\frac{a^{2}-b^{2}}{a b}=b-a$ or $\frac{(a-b)(a+b)}{a b}=b-a$. Since the numbers $a$ and $b$ are different, we can divide both sides of the equation by $a-b$, after which we get: $\frac{a+b}{a b}=-1$. This is the required value, since $\frac{a+b}{a b}=\frac{1}{a}+\frac{1}{b}$.
## Grading Criteria:
+ correct answer and complete solution provided
$\pm$ correct answer and generally correct calculations provided, but no justification for the possibility of dividing by $(a-b)$
干 correct reasoning provided, but a computational error was made
- only the answer provided
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. During a math test, Oleg was supposed to divide a given number by 2, and then add 6 to the result. But he hurried and instead multiplied the given number by 2, and then subtracted 6 from the result. Nevertheless, he got the correct answer. What number was given to Oleg
|
Answer: 8.
Solution. Since Oleg multiplied the number by 2 instead of dividing it, he got a result that is four times greater than the required one. This means that the difference between these two results is three times greater than the required result. However, according to the condition, this difference is equal to $6+6=12$. Therefore, the required result is $12: 3=4$. Then the guessed number is $4 \cdot 2=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. In the kingdom, there live counts, dukes, and marquises. One day, each count dueled with three dukes and several marquises. Each duke dueled with two counts and six marquises. Each marquise dueled with three dukes and two counts. It is known that all counts dueled with an equal number of marquises. How many marquises did each count duel with?
|
Answer: With 6 marquises.
Solution. Let there be $x$ counts, $y$ dukes, and $z$ marquises in the kingdom. Each count fought with three dukes, so there were $3 x$ duels between counts and dukes. But each duke fought with two counts, meaning there were $2 y$ such duels. Therefore, $3 x=2 y$.
Each duke fought with six marquises. Thus, there were $6 y$ duels between dukes and marquises. Each marquis fought with three dukes, so there were $3 z$ such duels. Therefore, $6 y=3 z$, from which $z=2 y=3 x$.
Each marquis fought with two counts, so there were $2 z=6 x$ duels between counts and marquises. Therefore, each count fought with six marquises.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. On an island, there live knights who always tell the truth, and liars who always lie. One day, 15 natives, among whom were both knights and liars, stood in a circle, and each said: "Of the two people standing opposite me, one is a knight, and the other is a liar." How many of them are knights?
|
Answer: 10 knights.
Solution. Consider any knight. He tells the truth, which means that opposite him stand a knight and a liar. One of the people opposite the found liar is the initial knight, so next to him stands another knight. Opposite this new knight stands the previously found liar and another person, who must be a knight. Repeating these considerations, we see that in the circle, there are two knights, then one liar, then again two knights, then another liar, and so on. This means that the liars make up a third of the total number of participants. Therefore, the number of liars is $15 \div 3 = 5$, and the number of knights is $15 - 5 = 10$.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 6.1
## Condition:
Given a triangle $\mathrm{ABC}$, in which $\mathrm{AB}=5$. The median $\mathrm{BM}$ is perpendicular to the bisector $\mathrm{AL}$. Find $\mathrm{AC}$.
|
Answer: 10
Exact match of the answer -1 point
Solution.
Consider triangle ABM: since the bisector drawn from vertex A is perpendicular to side $\mathrm{BM}$, triangle ABM is isosceles.
Therefore, $\mathrm{AB}=\mathrm{AM}=\mathrm{MC}$. Hence, $\mathrm{AC}=10$.
#
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.1
## Condition:
Artist Ivan Konstantinovich decided to sell several of his paintings at the Broken Auction. The rules of the Broken Auction are as follows: first, Ivan Konstantinovich names a certain starting price for his painting, after which the participants who want to buy this painting begin to bid on it - increasing the price, but only by a factor of two, - that is, the new price can only be twice the last one offered; the participant after whom no one dares to raise the price by another factor of two gets the painting; if no one bids on the painting, that is, no one offers a price higher than the initial one, the painting remains unsold. For each of his paintings, Ivan Konstantinovich decided to set the starting price at 1000 rubles. How many paintings did he sell at the Broken Auction if all his paintings were bought for different prices, and his total revenue from all the sold paintings amounted to 250000 rubles?
|
Answer: 6
Exact match of the answer -1 point
## Solution.
It is claimed that each painting by Ivan Konstantinovich was sold for $1000 \times 2^{\text {x }}$ rubles, where $\mathrm{x}$ is some natural number. Indeed, initially, the painting's price is 1000 rubles, and each participant doubles its price, meaning the price is multiplied by 2. Therefore, when the painting reaches the last participant and is sold, its price is multiplied by 2 several times (possibly once) and becomes $1000 \times 2 \times \ldots \times 2$, or $1000 \times 2^{x}$ rubles. Here, $\mathrm{x}$ cannot be 0 because the painting cannot be sold for 1000 rubles if no one doubles the price; the painting would remain unsold, and the problem only concerns sold paintings.
Thus, Ivan Konstantinovich's total revenue is the sum of several such numbers of the form $1000 \times 2^{\mathrm{a}}$, where the exponent of 2 is some natural number. This means it is 1000 multiplied by some sum of powers of 2. Since all prices, according to the problem, were different, no power of 2 in this sum is repeated. We need to represent the number $250000 / 1000=250$ as a sum of different powers of 2, and the number of terms in such a decomposition will show us the number of paintings sold. Let's do this: $250=128+64+32+16+8+2 \Rightarrow 6$ terms $\Rightarrow$ 6 paintings were sold.
The uniqueness of such a decomposition can be explained using simple reasoning about what can and cannot be in the decomposition: there are no powers of 2 greater than 128 in the sum, as otherwise the sum would be at least 256, but it should be 250. Moreover, 128 must be included, otherwise the maximum sum would be $64+32+16+8+4+2=126$, since all numbers in the sum are different (as the prices are different by condition). It remains to make up the difference of 250$128=122$. Similarly, it can be shown that 64, 32, 16, and 8 must be included in the sum. After that, only 2 remains to be added, which is exactly the number 2.
#
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.2
## Condition:
Artist Ivan Konstantinovich decided to sell several of his paintings at the Broken Auction. The rules of the Broken Auction are as follows: first, Ivan Konstantinovich names a certain starting price for his painting, after which the participants who want to buy this painting begin to bid on it - increasing the price, but only by a factor of two, - that is, the new price can only be twice the last one offered; the participant after whom no one dares to raise the price by another factor of two gets the painting; if no one bids on the painting, that is, no one offers a price higher than the initial one, the painting remains unsold. For each of his paintings, Ivan Konstantinovich decided to set the starting price at 1000 rubles. How many paintings did he sell at the Broken Auction if all his paintings were bought for different prices, and his total revenue from all the sold paintings amounted to 300000 rubles?
|
Answer: 4
Exact match of the answer - 1 point
Solution by analogy with task №7.1
#
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 7.3
## Condition:
Artist Ivan Konstantinovich decided to sell several of his paintings at the Broken Auction. The rules of the Broken Auction are as follows: first, Ivan Konstantinovich names a certain starting price for his painting, after which the participants who want to buy this painting begin to bid on it - increasing the price, but only by two times, - that is, the new price can only be twice the last one offered; the participant after whom no one dares to raise the price by another two times gets the painting; if no one bids on the painting, that is, no one offers a price higher than the initial one, the painting remains unsold. For each of his paintings, Ivan Konstantinovich decided to set the starting price at 1000 rubles. How many paintings did he sell at the Broken Auction if all his paintings were bought for different prices, and his total revenue from all the sold paintings amounted to 350000 rubles?
|
Answer: 6
Exact match of the answer - 1 point
Solution by analogy with task №7.1
#
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In triangle $ABC$, the median $BM$ was drawn. It turned out that $\angle ABM=40^{\circ}$, $\angle MBC=70^{\circ}$. Find the ratio $AB: BM$. Justify your answer.
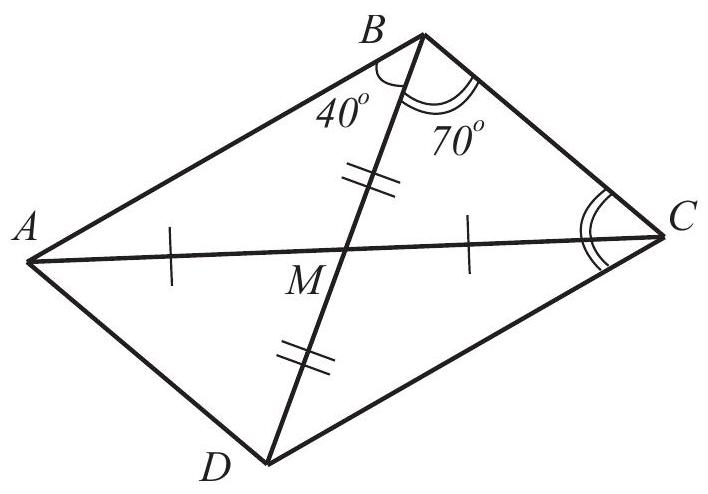
To solve problem 9.2 Solution: Extend the median $BM$ beyond point $M$ and lay off a segment $MD = BM$ (see the figure). In quadrilateral $ABCD$, the diagonals bisect each other, so this quadrilateral is a parallelogram. Then $\angle ABC + \angle BCD = 180^{\circ}$, from which $\angle BCD = 70^{\circ} = \angle MBC = \angle DBC$. This means that triangle $BCD$ is isosceles, as is the congruent triangle $BAD$. Therefore,
$$
AB: BM = AB: \frac{BD}{2} = AB: \frac{AB}{2} = 2
$$
|
Answer: $A B: B M=2$.
| in progress | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| An example of a triangle satisfying the conditions of the problem is provided | 0 points |
| Incorrect solution or its absence | 0 points |
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. After the bankruptcy of the company "Horns and Hooves," 17 horns, 2 hooves, and one weight remained. All this wealth was divided equally by weight between Pankovskiy and Balaganov, with the weight entirely going to Balaganov. The horns and hooves were not cut into pieces. Each horn is heavier than each hoof and lighter than the weight by the same amount. How many horns and hooves did Pankovskiy get? Provide all possible options and prove that there are no others.
|
Solution: Let one hoof weigh $k$, and one horn weigh $k+\delta$ (all weights in the same units of measurement, for example, in puds). Then, according to the condition, the weight of the weight (the iron piece) is $k+2\delta$, and the total weight of the divided property is $20k+19\delta$. Each person received $10k+9.5\delta$. Balaganov took the weight, and with horns and hooves, he gathered $9k+7.5\delta$. This weight is less than the weight of 9 horns but more than the weight of 7 horns and 2 hooves. Therefore, Balaganov took fewer than 9 but more than 7 horns, which means 8.8 horns weigh $8k+8\delta$, and for hooves, Balaganov has $k-0.5\delta$ left, which is less than the weight of one hoof. This means all hooves and all other horns went to Panikovsky. Incidentally, we established that $k-0.5\delta=0$, meaning the horn is 3 times heavier than the hoof, and the weight is 5 times heavier than the hoof.
Answer: 9 horns and 2 hooves.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer with the derived relationship between the weights of the horn, hoof, and weight | 7 points |
| Proven that all hooves went to Panikovsky | 2 points |
| Proven that Balaganov could only have 9 horns | 2 points |
| The problem is solved for specifically chosen weights of horns, hooves, and the weight | 0 points |
| Correct answer without justification | 0 points |
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1.
Masha is distributing tennis balls into identical boxes. If she uses 4 boxes, there is still room for 8 more balls in the last box, and if she uses 3 boxes, 4 balls will not fit into the boxes. How many balls is one box designed to hold?
|
Answer: 12
Solution.
Method 1
Notice that if the balls are in 3 boxes, there are 4 tennis balls left. Take these 4 balls and put them in the fourth box. According to the condition, there will still be room for 8 more balls in this box. This means that the box can hold a total of 12 balls.
Method 2.
Let the box hold $x$ balls. Then $3 x+4=4 x-8$. From this, $x=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 2.
Café "Buratino" operates 6 days a week with a day off on Mondays. Kolya made two statements: "from April 1 to April 20, the café was open for 18 days" and "from April 10 to April 30, the café was also open for 18 days." It is known that he was wrong once. How many days was the café open from April 1 to April 13?
|
Answer: 11
Option 3.
The cafe "Buratino" operates 6 days a week with a day off on Mondays. Kolya made two statements: "the cafe was open for 18 days from April 1 to April 20" and "the cafe was also open for 18 days from April 10 to April 30." It is known that he was wrong once. How many days was the cafe open from April 8 to April 20?
Answer: 11
#
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1.
Petya wrote 9 consecutive natural numbers on the board. Kolya calculated their sum and got the answer 43040102. It turned out that he made a mistake only in the first digit of the sum. What should the first digit be
|
Answer: 8.
Solution: Let the consecutive natural numbers be $a-4, a-3, \cdots, a+3, a+4$. The sum of nine consecutive numbers is divisible by 9, indeed, this sum is equal to $(a-4)+(a-3)+\cdots+(a+3)+(a+4)=9a$. Therefore, the desired sum must be divisible by 9. This means that the sum of the digits of the obtained answer must also be divisible by 9. The sum of all digits except the first one is 10. Therefore, the first digit must be 8. A suitable number would be 83040102.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. On a line, there are blue and red points, with no fewer than 5 red points. It is known that on any segment with endpoints at red points, containing a red point inside, there are at least 3 blue points. And on any segment with endpoints at blue points, containing 2 blue points inside, there are at least 2 red points. What is the maximum number of blue points that can be on a segment with endpoints at red points, not containing other red points?
|
# Answer. 3.
Solution. Note that on a segment with endpoints at red points, not containing other red points, there cannot be 4 blue points. Indeed, in this case, between the outermost blue points there will be 2 blue points, which means there will be at least 2 more red points. Therefore, there are no more than 3 blue points on such a segment.
We will show that 3 blue points can lie on a segment with endpoints at red points, not containing other red points. Suppose the points are arranged on a line in the following order: 2 red - 3 blue - 2 red - 3 blue - 2 red. Then all conditions are satisfied, and there is a segment with 3 blue points.
Comment. It is proven that there are no more than 3 blue points between neighboring red points - 4 points.
A correct example with 3 blue points is provided - 3 points.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. Petya runs down from the fourth floor to the first floor 2 seconds faster than his mother rides the elevator. Mother rides the elevator from the fourth floor to the first floor 2 seconds faster than Petya runs down from the fifth floor to the first floor. How many seconds does it take Petya to run down from the fourth floor to the first floor? (The lengths of the stair flights between all floors are the same).
|
Answer: 12 seconds.
Solution. Between the first and fourth floors, there are 3 flights, and between the fifth and first floors, there are 4. According to the problem, Petya runs 4 flights in 2 seconds longer than it takes his mother to ride the elevator, and 3 flights in 2 seconds less than his mother. Therefore, Petya runs one flight in 4 seconds. Then from the fourth floor to the first (i.e., 3 flights), Petya runs down in $4 \times 3 = 12$ seconds.
## Grading Criteria.
7 points. Correct answer with a complete solution.
5 points. Explained that one flight takes 4 seconds, and the answer is 4 seconds.
3 points. Correct reasoning under the assumption that the distance from the fifth floor to the first is 1.25 times the distance from the fourth floor to the first, and the answer is 16 seconds. Only the answer $-\mathbf{0}$ points.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Three people are playing table tennis, with the player who loses a game giving way to the player who did not participate in it. In the end, it turned out that the first player played 10 games, the second - 21. How many games did the third player play?
|
Answer: 11 games.
Solution: According to the condition, the second player played 21 games, so there were at least 21 games in total. Out of any two consecutive games, the first player must participate in at least one, which means there were no more than \(2 \cdot 10 + 1 = 21\) games. Therefore, a total of 21 games were played, and the second player participated in each of them. In 10 games, he met the first player, and in the remaining 11 games, he met the third player.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Let x be some natural number. Among the statements:
$2 \times$ greater than 70
x less than 100
$3 x$ greater than 25
x not less than 10
x greater than 5
three are true and two are false. What is x
|
Answer: 9.
Solution
The first statement is equivalent to x > 35, and the third statement is equivalent to $\mathrm{x}>8$, since x is a natural number. The first statement is false, because if it were true, then the third, fourth, and fifth statements would also be true, i.e., there would be at least 4 true statements. Therefore, x does not exceed 35. From this, it follows that the second statement is true. But then the fourth statement is false (otherwise, the third and fifth statements would also be true, and again we would have at least 4 true statements). Therefore, statements 3 and 5 are true. And from the falsity of the fourth statement and the truth of the third statement, it immediately follows that $x=9$.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Twelve chairs are arranged in a row. Sometimes a person sits on one of the free chairs. In this case, exactly one of his neighbors (if they were there) stands up and leaves. What is the maximum number of people that can be sitting simultaneously, if initially all the chairs were empty?
|
Answer: 11.
Solution. Evaluation. Note that it is impossible to occupy all chairs simultaneously, as at the moment when a person sits on the last unoccupied chair, one of his neighbors will stand up. Therefore, the number of people sitting simultaneously cannot exceed 11.
Example. We will show how to seat 11 people. Number the chairs from 1 to 12. The first chair is easy to occupy. The second chair can be occupied in two stages. In the first stage, a person sits on the third chair, and in the second stage, we seat a person on the second chair, and the person on the third chair stands up. We proceed similarly: if chairs numbered from 1 to \( k \) are occupied, we first seat a person on the chair numbered \( k+2 \), and then seat a person on the chair numbered \( k+1 \), thereby freeing the chair numbered \( k+2 \). After this operation is performed for all \( k \) from 1 to 10, the chairs numbered from 1 to 11 will be occupied, and the twelfth chair will be free.
## Evaluation Criteria:
+ A complete and justified solution is provided
± The correct answer is provided and it is explained how to seat 11 (a correct example is given), but it is not explained why there cannot be 12 sitting (no evaluation)
干 The correct answer is provided and it is explained why there cannot be 12 sitting, but the seating example for 11 is not provided or is incorrect
- Only the answer is provided
- The problem is not solved or is solved incorrectly
8.5. Inside an equilateral triangle \( ABC \), a point \( M \) is marked. Prove that it is possible to choose a point \( C_{1} \) on side \( AB \), a point \( A_{1} \) on side \( BC \), and a point \( B_{1} \) on side \( AC \) such that the lengths of the sides of triangle \( A_{1} B_{1} C_{1} \) are equal to the segments \( MA, MB \), and \( MC \).
Solution. Mark points \( C_{1} \) on side \( AB \), \( A_{1} \) on side \( BC \), and \( B_{1} \) on side \( AC \) such that \( M C_{1} \parallel BC, M A_{1} \parallel AC, M B_{1} \parallel AB \) (see Fig. 8.5). Then the segments \( M A_{1}, M B_{1} \), and \( M C_{1} \) will divide the given triangle into three trapezoids. From the parallelism, it follows that each angle at the larger base of these trapezoids is \( 60^{\circ} \), so these trapezoids are isosceles. Consequently, in each trapezoid, the diagonals are equal: \( B_{1} C_{1} = MA \), \( A_{1} C_{1} = MB \), \( A_{1} B_{1} = MC \), which is what we needed to prove.
Evaluation Criteria:
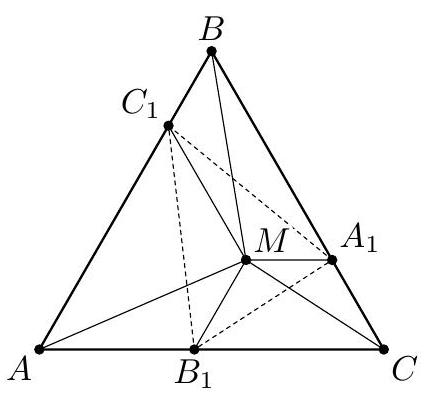
Fig. 8.5
+ A complete and justified solution is provided
± A correct construction is provided, but it is not explained (or explained incorrectly) why the sides of the resulting triangle are the desired ones
- The problem is not solved or is solved incorrectly
The presence of any reasoning about the number of ways to mark the desired points in the solution does not affect the evaluation result.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) Consider the equation $\sin ^{3}(x)+\cos ^{3}(x)=-1$. How many solutions does it have on the interval $[0 ; 6 \pi]$?
Answer: 6.
|
Solution. From the main trigonometric identity, we have $\sin ^{2}(x)+$ $\cos ^{2}(x)=1$. Adding this to the given equality, we get
$$
0=\sin ^{2}(x) \cdot(1+\sin (x))+\cos ^{2}(x) \cdot(1+\cos (x))
$$
In this expression, all factors are non-negative, so both terms $\sin ^{2}(x)(1+\sin (x))$ and $\cos ^{2}(x)(1+\cos (x))$ are equal to 0.
Case 1. Let $\sin (x)=0$. Then $\cos (x) \neq 0$, so $\cos (x)=-1$. Therefore, $x=\pi+2 \pi k$.
Case 2. Let $\sin (x) \neq 0$. Then $\sin x=-1$, which implies $\cos (x)=0$. Therefore, $x=\frac{3 \pi}{2}+2 \pi n$.
It is easy to see that all numbers of the form $\pi+2 \pi k$ and $\frac{3 \pi}{2}+2 \pi n$ are roots of the original equation. In the required interval, three roots of the first form fall, where $k=0,1,2$ and three roots of the second form, where $n=0,1,2$. In total, we have $3+3=6$ roots.
Criteria. Any correct solution: 7 points.
General formulas for the roots are obtained, but the number of roots on the interval $[0 ; 6 \pi]$ is calculated incorrectly: 5 points.
Only the answer, even with the full set of roots presented: 1 point.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. At a ball, princesses and knights gathered - a total of 22 people. The first princess danced with seven knights, the second with eight knights, the third with nine knights, ..., the last danced with all the knights present. How many princesses were at the ball?
|
Answer: 8.
Solution. Note that the number of knights the princess danced with is 6 more than her number. Let there be $x$ princesses in total, then the last one has the number $x$ and danced with all the knights, and there are $x+6$ of them in total. We get that there were $x+$ $(x+6)=2x+6=22$ people at the ball, which means there were 8 princesses.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.3. Dima, Misha, and Yura decided to find out who among them is the most athletic. For this, they held 10 competitions. The winner received 3 points, the second place 1 point, and the third place received nothing (in each competition, there was a first, second, and third place). In total, Dima scored 22 points, and Misha scored 8 points. How many points did Yura score?
|
Answer: 10.
Solution. In each competition, the boys in total received $3+1+0=4$ points. For all competitions, they scored $4 \cdot 10=40$ points. Dima and Misha in total scored $22+8=30$ points, so the remaining $40-30=10$ points were scored by Yura.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.4. On her birthday, Katya treated her classmates with candies. After giving out some candies, she noticed that she had 10 more candies left than Artem received. After that, she gave everyone one more candy, and it turned out that all the children in the class (including Katya) had the same number of candies. How many classmates does Katya have?
|
Answer: 9.
Solution. Initially, the number of candies Kati and Artyom had differed by 10. When Kati gave everyone one more candy, the number of candies Artyom had increased by 1, and the number of candies Kati had decreased by the number of her classmates, and they ended up with the same amount. This means that 10 is the number of her classmates plus 1. Therefore, Kati has 9 classmates.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. Cat Matroskin, Uncle Fyodor, Postman Pechkin, and Sharik sat down at a round table. In front of each of them was a plate with 15 sandwiches. Every minute, three of them ate a sandwich from their own plate, while the fourth ate a sandwich from their neighbor's plate. After 5 minutes of the meal, there were 8 sandwiches left in Uncle Fyodor's plate. What is the minimum number of sandwiches that could have remained on Cat Matroskin's plate?
|
# Answer: 7
Solution. We will call the sandwiches eaten from a neighbor's plate stolen. Note that in 5 minutes, exactly 5 sandwiches were stolen.
At the same time, 7 sandwiches disappeared from Uncle Fyodor's plate, of which he himself ate no more than 5, meaning that at least 2 were stolen. From this, it is clear that no more than 3 sandwiches were stolen from Matroskin's plate, that is, no more than 8 sandwiches in total disappeared from there. Therefore, at least 7 sandwiches remained.
Note that exactly 7 sandwiches could remain if Uncle Fyodor and Matroskin always ate sandwiches from their own plates, while Sharik sat between them and ate 2 sandwiches from Uncle Fyodor's plate and 3 sandwiches from Matroskin's plate.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There are 9 cards with numbers $1,2,3,4,5,6,7,8$ and 9. What is the maximum number of these cards that can be laid out in some order in a row so that on any two adjacent cards, one of the numbers is divisible by the other?
|
2. Answer: 8.
Note that it is impossible to arrange all 9 cards in a row as required. This follows from the fact that each of the cards with numbers 5 and 7 can only have one neighbor, the card with the number 1. Therefore, both cards 5 and 7 must be at the ends, and the card with the number 1 must be adjacent to each of them, which is impossible. It is possible to select 8 cards and arrange them in a row according to the requirements of the problem, for example: $9,3,6,2,4,8,1,5$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Petya bought one cupcake, two muffins, and three bagels, Anya bought three cupcakes and a bagel, and Kolya bought six muffins. They all paid the same amount of money for their purchases. Lena bought two cupcakes and two bagels. How many muffins could she have bought for the same amount she spent?
|
3. Answer. 5 cupcakes.
The total cost of Petya and Anya's purchases is equal to the cost of two of Kolya's purchases. If we denote $x, y$, and $z$ as the costs of a cake, a cupcake, and a bagel respectively, we get the equation: $(x+2 y+3 z)+(3 x+z)=12 y, \quad$ from which it follows that $\quad 4 x+4 z=10 y$, \quad that is, \quad $2 x+2 z=5 y$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the minimum number of L-shaped corners consisting of 3 cells that need to be painted in a $6 \times 6$ square of cells so that no more L-shaped corners can be painted? (Painted L-shaped corners should not overlap.)
|
5. Answer. 6.
Let the cells of a $6 \times 6$ square be painted in such a way that no more corners can be painted.
Then, in each $2 \times 2$ square, at least 2 cells are painted, otherwise, a corner in this square can still be painted. By dividing the $6 \times 6$ square into 9 $2 \times 2$ squares, we get that at least $9 \cdot 2 = 18$ cells are painted. Therefore, at least 6 corners are painted. The figure below shows how to paint 6 corners so that no more corners can be painted.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Three pirates divided the diamonds they had obtained during the day in the evening: twelve each for Bill and Sam, and the rest went to John, who couldn't count. At night, Bill stole one diamond from Sam, Sam stole one from John, and John stole one from Bill. As a result, the average weight of Bill's diamonds decreased by one carat, Sam's decreased by two carats, and John's increased by four carats. How many diamonds did John get?
|
Answer: 9 diamonds.
Solution. The first method (arithmetic). Note that the number of diamonds each pirate has did not change overnight. Since Bill has 12 diamonds, and their average weight decreased by 1 carat, the total weight of his diamonds decreased by 12 carats. Similarly, Sam also has 12 diamonds, and their average weight decreased by 2 carats, so the total weight of his diamonds decreased by 24 carats. Since the total weight of the diamonds of Bill and Sam decreased by 36 carats, the total weight of John's diamonds increased by the same 36 carats. Since the average weight of John's diamonds increased by 4 carats, he had $36: 4=9$ diamonds.
The second method (algebraic). Let John have $x$ diamonds. Let the average weight of the diamonds that Bill received be denoted by $b$, Sam's by $s$, and John's by $d$. Then the total weight of the diamonds that Bill had was $12 b$, Sam's was $-12 s$, and John's was $-x d$.
In the morning, the number of diamonds each had did not change, but the average weight of the diamonds became: for Bill - $(b-1)$, for Sam - $(s-2)$, for John - $(d+4)$. The total weight of the diamonds became: for Bill $12(b-1)$, for Sam $-12(s-2)$, for John $-x(d+4)$. Since the total weight of the diamonds of the three pirates did not change, we have $12 b+12 s+x d=12(b-1)+12(s-2)+x(d+4)$. Expanding the brackets and combining like terms, we get: $4 x-36=0$, so $x=9$.
## Grading criteria:
+ a complete and well-reasoned solution is provided
$\pm$ a generally correct solution is provided, but an arithmetic error is made
干 the equation is correctly set up, but not solved or solved incorrectly
干 the correct answer is obtained from a specific example
- only the answer is provided
- the problem is not solved or solved incorrectly
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. The numbers $x, y, z$ are such that $x \in[-3,7], y \in[-2,5], z \in[-5,3]$.
(a) (1 point) Find the smallest possible value of the quantity $x^{2}+y^{2}$.
(b) (3 points) Find the smallest possible value of the quantity $x y z - z^{2}$.
|
# Answer:
(a) (1 point) 0.
(b) (3 points) -200.
Solution. (a) Note that $x^{2} \geqslant 0$ and $y^{2} \geqslant 0$, so $x^{2}+y^{2} \geqslant 0$. The value $x^{2}+y^{2}=0$ is possible when $x=0, y=0$.
(b) Note that $|x y z|=|x||y||z| \leqslant 7 \cdot 5 \cdot 5$ and $z^{2} \leqslant 5^{2}$, so $x y z-z^{2} \geqslant-7 \cdot 5 \cdot 5-5^{2}=-200$. The value $x y z-z^{2}=200$ is possible when $x=7, y=5, z=-5$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The graph of the quadratic function $y=a x^{2}+c$ intersects the coordinate axes at the vertices of an equilateral triangle. What is the value of ac?
|
Answer: -3.
Solution. Since the graph intersects the OX axis at two points, the numbers a and c have different signs. The points of intersection are: $A\left(\sqrt{-\frac{c}{a}} ; 0\right) ; B\left(-\sqrt{-\frac{c}{a}} ; 0\right)$. The graph intersects the OY axis at point $C(0 ; c)$. Then the side $AB$ of the equilateral triangle is $2 \sqrt{-\frac{c}{a}}$, and its height is $|c|$. Since the side $a$ and the height $h$ of an equilateral triangle are related by $h=\frac{a \sqrt{3}}{2}$, we have $|c|=\frac{\sqrt{3}}{2} \cdot 2 \sqrt{-\frac{c}{a}}$, from which $c^{2}=-3 \cdot \frac{c}{a}$, so $a c=-3$.
There are other ways to obtain the equation relating a and c, for example, by using that $A B=A C$.
Grading criteria.
“+” A complete and well-reasoned solution is provided
“士” A generally correct reasoning is provided, containing minor gaps or inaccuracies (e.g., only considering $s > 0$)
“Ғ” Correct reasoning, but a computational error is made
“ๆ” Only the correct answer is provided
“-” The problem is not solved or is solved incorrectly
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given $n>2$ natural numbers, among which there are no three equal, and the sum of any two of them is a prime number. What is the largest possible value of $n$?
|
1. Answer: 3. Note that the triplet $1,1,2$ satisfies the condition. Suppose there are more than 3 numbers. Consider any 4 of them a, b, c, d. Among these four numbers, there cannot be two even numbers, otherwise their sum would be an even prime greater than two. Therefore, at least 3 of them must be odd. Their pairwise sums are even primes. Then all three considered numbers must be 1, which violates the condition.
Grading recommendations:
only answer - 0 points
example for three numbers provided - 2 points.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) The kids were given the task to convert the turtle's speed from centimeters per second to meters per minute. Masha got an answer of 25 m/min, but she thought there were 60 cm in a meter and 100 seconds in a minute. Help Masha find the correct answer.
|
Answer: 9 m/min.
Solution. The turtle covers a distance of 25 Machine "meters" in one Machine "minute," meaning it crawls $25 \cdot 60$ centimeters in 100 seconds. Therefore, the speed of the turtle is $\frac{25 \cdot 60}{100}=15$ cm/sec. Thus, in 60 seconds, the turtle will crawl $15 \cdot 60$ centimeters, which is $\frac{15 \cdot 60}{100}=9$ meters.
Criteria. Any correct solution: 7 points.
Correctly found the speed in centimeters per second, but the subsequent part is not done or done with an error: 3 points.
Only the answer without a solution: 1 point.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) Two pedestrians set out at dawn. Each walked at a constant speed. One walked from $A$ to $B$, the other from $B$ to $A$. They met at noon (i.e., exactly at 12 o'clock) and, without stopping, arrived: one at $B$ at 4 PM, and the other at $A$ at 9 PM. At what time was dawn that day?
|
Answer: at 6 AM.
Solution. Let's denote the meeting point as $C$. Let $x$ be the number of hours from dawn to noon.
The speed of the first pedestrian on segment $A C$ is $A C / x$, and on segment $B C$ it is $B C / 4$. Since his speed is constant, we have $\frac{A C}{x}=\frac{B C}{4}$, which can be rewritten as $\frac{A C}{B C}=\frac{x}{4}$.
Similarly for the second pedestrian: the equality of speeds on segments $B C$ and $A C$ results in the ratio $\frac{B C}{x}=\frac{A C}{9}$, which we can rewrite as $\frac{A C}{B C}=\frac{9}{x}$.
We get $\frac{x}{4}=\frac{9}{x}$, and by the property of proportions, $x^{2}=36, x=6$. Dawn was 6 hours before noon, i.e., at 6 AM.
Criteria. Any correct solution: 7 points.
The time interval from dawn to the meeting is correctly found, but the time of dawn is not found or is found with an error: 5 points.
Only the answer without a solution: 1 point.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. There are three acrobat brothers. Their average height is 1 meter 74 centimeters. The average height of two of these brothers: the tallest and the shortest - 1 meter 75 centimeters. What is the height of the middle brother? Justify your answer.
|
Answer: 1 meter 72 centimeters.
Solution. Since the average height of all three is 1 meter 74 centimeters, the total height of all three is 5 meters 22 centimeters. The average height of the two brothers is 1 meter 75 centimeters, so their combined height is 3 meters 50 centimeters. Therefore, the height of the middle brother is 1 meter 72 centimeters.
## Criteria
2 p. Correct solution approach, but an arithmetic error was made.
4 p. The correct answer and justification are provided.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the island, there live knights who always tell the truth and liars who always lie. In the island's football team, there are 11 people. Player number 1 said: "In our team, the number of knights and the number of liars differ by one." Player number 2 said: "In our team, the number of knights and the number of liars differ by two," and so on. Player number 11 said: "In our team, the number of knights and the number of liars differ by eleven." How many knights are in the team, and if there are any, what are their numbers?
|
3. Answer: the only knight plays under number 9. The solution is that the number of knights cannot be equal to the number of liars, so one of the answers must be correct. Two answers cannot be true, as they contradict each other. Therefore, there is exactly 1 knight and 10 liars in the team, which is stated by the player under number 9.
Criteria: correct solution - 7 points. Failure to indicate that the number of knights in the team cannot be equal to the number of liars - 2 points deducted. Correct answer with an explanation of its validity - 2 points. Only answer - 0 points.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A student passed 31 exams over 5 years of study. Each subsequent year, he passed more exams than the previous year, and in the fifth year, he passed three times as many exams as in the first year. How many exams did he pass in the fourth year?
|
# Answer: 8.
Solution: Let $a, b, c, d, e$ be the number of exams taken in each year of study. According to the problem, $a+b+c+d+e=31, a<b<c<d<e$.
Replace the numbers $b, c, d, e$ in the equation with definitely not larger values:
$a+(a+1)+(a+2)+(a+3)+3a \leq 31$. We get $7a \leq 25$. Replacing these numbers with definitely not smaller values, we get $a+(3a-3)+(3a-2)+(3a-1)+3a \geq 31$. We get $13a \geq 37$. Therefore, $a=3$. In this case, $e=9, b+c+d=19$.
If $d<8$, then this sum is no more than $5+6+7=18$. The numbers 5, 6, 8 fit. Evaluation criteria. The answer alone is not scored. An answer with an example of all five numbers - 2 points.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
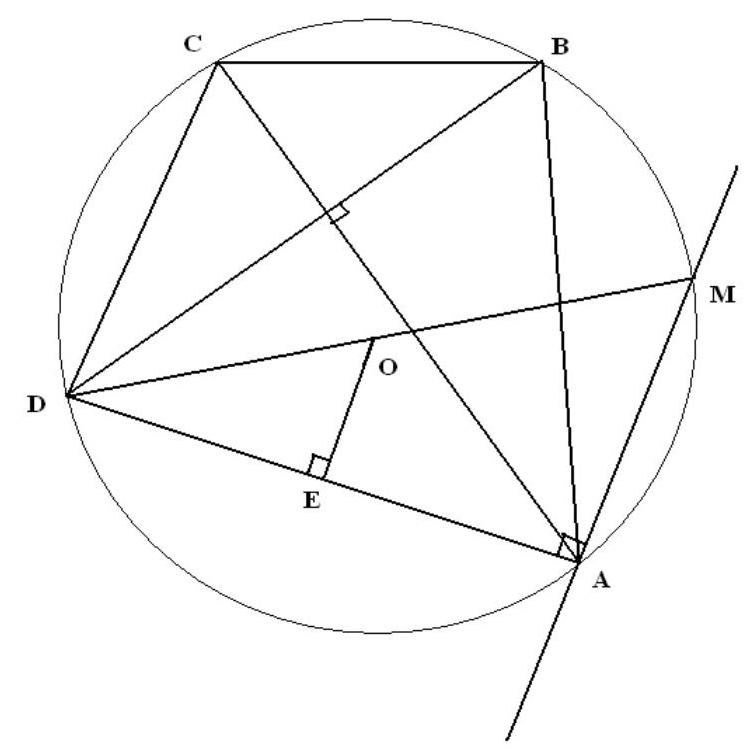
4. A circle with center at point $O$ is circumscribed around quadrilateral $A B C D$. The diagonals of the quadrilateral are perpendicular. Find the length of side $B C$, if the distance from point $O$ to side $A D$ is 1.
|
Answer: $B C=2$
Solution. Let $O E \perp A D$, then $O E=1$. Draw a line through point $A$ perpendicular to $A D$, which intersects the circle at point $M$. Then $D M$ is a diameter and $D O=O M$. Since $\angle D B A=\angle D M A$ (as inscribed angles subtending the same arc), $\angle M D A=90^{\circ}-\angle D M A$ and $\angle C A B=90^{\circ}-\angle D B A$, then $\angle C A B=\angle M D A$. Therefore, arc $A M$ is equal to arc $B C$ and $B C=A M$. $\triangle M D A$ is similar to $\triangle O D E$ (by two equal angles) with a similarity ratio of $\frac{1}{2}$, so $2 O E=A M=B C=2$.
## Grading Criteria.
Similarity of $\triangle O E D$ and $\triangle C B A$ is proven - 2 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. There are 9 cards with numbers $1,2,3,4,5,6,7,8$ and 9. What is the maximum number of these cards that can be laid out in some order in a row so that on any two adjacent cards, one of the numbers is divisible by the other?
|
Answer: 8.
Solution: Note that it is impossible to arrange all 9 cards in a row as required. This follows from the fact that each of the cards with numbers 5 and 7 can only have one neighbor, the card with the number 1. Therefore, both cards 5 and 7 must be at the ends, and the card with the number 1 must be adjacent to each of them, which is impossible.
It is possible to select 8 cards and arrange them in a row according to the requirements of the problem, for example: $9,3,6,2,4,8,1,5$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Rational numbers $a, b$ and $с$ are such that $(a+b+c)(a+b-c)=2 c^{2}$. Prove that $c=0$.
---
Translation:
4. Rational numbers $a, b$ and $c$ are such that $(a+b+c)(a+b-c)=2 c^{2}$. Prove that $c=0$.
|
Solution. The initial equality is equivalent to the following $(a+b)^{2}-c^{2}=2 c^{2}$, or $(a+b)^{2}=3 c^{2}$. If $c \neq 0$, we get $((a+b) / c)^{2}=3 .|(a+b) / c|={ }^{-}$. On the left, we have a rational number, since the sum, quotient, and absolute value of rational numbers are rational, while on the right, we have an irrational number, and the equality is impossible. Therefore, $c=0$.
Criteria. The equality $(a+b)^{2}=3 c^{2}$ is obtained, but there is no further progress: 1 point.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Given three quadratic trinomials $f(x)=a x^{2}+b x+c, g(x)=b x^{2}+c x+a, h(x)=c x^{2}+$ $a x+b$, where $a, b, c$ are distinct non-zero real numbers. From them, three equations were formed: $f(x)=g(x), f(x)=h(x), g(x)=h(x)$. Find the product of all roots of these three equations, given that each of them has two distinct roots.
|
Answer. 1.
Solution. Since it is known that all equations have roots, we can use Vieta's theorem. Then the product of all roots will be equal to $\frac{c-a}{a-b} \cdot \frac{a-b}{b-c} \cdot \frac{b-c}{c-a}=1$.
Comment. Correct answer without justification - 0 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. In a $4 \times 4$ square, each of the 16 cells was painted either black or white. Then, in each of the nine $2 \times 2$ squares that can be identified within this square, the number of black cells was counted. The resulting numbers were 0, 2, 2, 3, 3, 4, 4, 4, 4. How many black cells can there be in the large square? List all possible options.
|
Answer: 11
Solution. Note that squares with 0 white cells and 4 white cells cannot intersect. If a square with 0 white cells is not in a corner, then it does not intersect with more than three other squares (the square can be in the center or adjacent to the middle of a side). Let the white square be in the bottom-left corner, then we have 5 squares suspected of containing 4 black cells, of which 4 are entirely black, and one has 2 or 3 black cells. Note that the squares marked in Figure 1 contain no more than 2 black cells, so exactly 2. Then the three corner squares either all contain 4 cells, but then 5 squares contain 4 black cells; or two corners contain 4, and one contains 3. In total, this results in 11 cells. Figures 2 and 3 show examples of such arrangements.
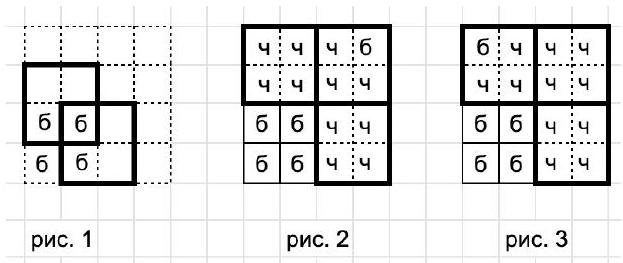
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. What is the largest number of different natural numbers that can be chosen so that the sum of any three of them is a prime number?
|
Answer: 4 numbers. Example: $1,3,7,9$. Indeed, the numbers $1+3+7=11, 1+3+9=13$, $1+7+9=17, 3+7+9=19$ are prime. Evaluation. Note that among five natural numbers, it is always possible to choose three whose sum is a composite number. Consider the remainders of these five numbers when divided by 3. If there are three identical remainders, then the sum of the corresponding numbers is divisible by 3. If there are no three identical remainders, then each of the three possible remainders $0,1,2$ must be present. Then the sum of three numbers with different remainders when divided by 3 is divisible by 3. This sum is not equal to 3, since all numbers are different and natural. Therefore, this sum is a composite number.
Remarks. An example of four numbers without evaluation - no more than 3 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Solve the inequality: $\sqrt{(x-2)^{2}\left(x-x^{2}\right)}<\sqrt{4 x-1-\left(x^{2}-3 x\right)^{2}}$.
|
11.1. Answer: $x=2$.
The left side of the original inequality is defined at $x=2$ and. At the point $x=2$, the inequality is true. We will prove that there are no solutions on the interval $[0 ; 1]$. For this, we will square both sides and bring the inequality to the form $x^{2}(1-x)<-1$. The last inequality is not satisfied for $x \in [0 ; 1]$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. All horizontal and vertical distances between adjacent points are equal to 1. What is the area of the triangle with vertices at the black points?
|
Answer. 1.
Solution. The area of the triangle can be found, for example, by subtracting from half the area of the square the area of the square and the areas of two right triangles. We get $S=10-4-2-3=1$. The figure can be divided in other ways.
Comment. An answer without justification - 0 points. A partition that allows finding the area but lacks calculations - 2 points. With the correct method of solution, there are calculation errors - deduct 2 points for each error.
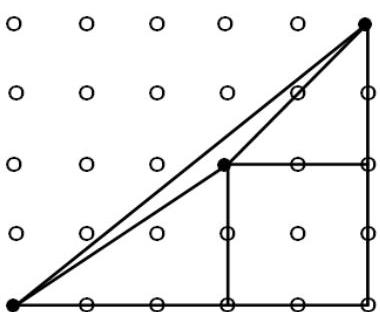
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. In the picture, nine small squares are drawn, with arrows on eight of them. The numbers 1 and 9 are already placed. Replace the letters in the remaining squares with numbers from 2 to 8 so that the arrows from the square with the number 1 point in the direction of the square with the number 2 (the number 2 can be in square $A$ or $B$), the arrows from the square with the number 2 point in the direction of the square with the number 3, and so on, the arrows from the square with the number 8 point in the direction of the square with the number 9.
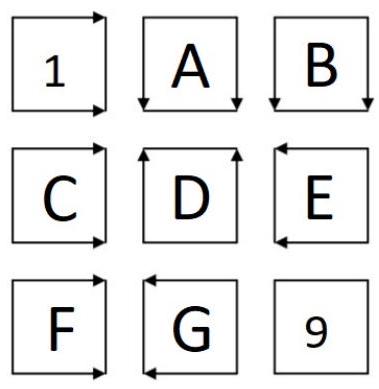
Construct the correspondence.
- In square $A$
- In square $B$
- In square $C$
- In square $D$
- In square $E$
- In square $F$
- In square $G$
- stands the number 2.
- stands the number 3.
- stands the number 4.
- stands the number 5.
- stands the number 6.
- stands the number 7.
- stands the number 8.
|
Answer: In square $A$ there is the number 6, in $B-2$, in $C-4$, in $D-5$, in $E-3$, in $F-8$, in $G-7$.
Solution. Let's order all the squares by the numbers in them. This "increasing chain" contains all nine squares.
Notice that in this chain, immediately before $C$ can only be $E$ (only the arrows from $E$ point to $C$). Similarly, immediately before $E$ can only be $B$ (not $C$, because $C$ is after $E$). Immediately before $B$ can only be 1. Therefore, the numbers in squares $B, E, C$ are $2,3,4$ respectively. Then 5 is definitely in $D$, 6 is definitely in $A$, 7 is definitely in $G$, and 8 is definitely in $F$.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.

|
Answer: 7.
Solution. Since $ABCD$ is a square, then $AB = BC = CD = AD$.
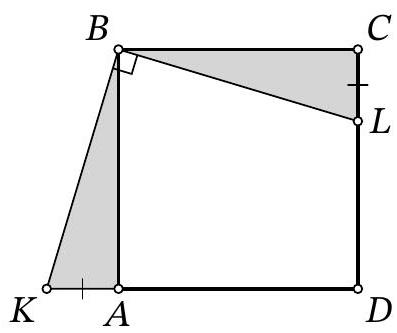
Fig. 1: to the solution of problem 8.4
Notice that $\angle ABK = \angle CBL$, since they both complement $\angle ABL$ to $90^{\circ}$. Therefore, right triangles $ABK$ and $CBL$ are congruent by the acute angle and the leg $AB = BC$ (Fig. 1). Consequently, $AK = CL = 6$. Then
$$
LD = CD - CL = AD - CL = (KD - AK) - CL = KD - 2 \cdot CL = 19 - 2 \cdot 6 = 7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Each of the 10 people is either a knight, who always tells the truth, or a liar, who always lies. Each of them thought of some number (not necessarily an integer). Then the first said: “My number is greater than 1”, the second said: “My number is greater than $2”, \ldots$, the tenth said: “My number is greater than $10”. After that, all ten, speaking in some order, said: “My number is less than 1”, “My number is less than $2”, \ldots$, “My number is less than 10” (each said exactly one of these ten phrases). What is the maximum number of knights that could have been among these 10 people?
(O. Podlipsky)
|
Answer: 9 knights.
Solution. Estimation. Note that none of the knights could have said the phrase "My number is greater than 10," otherwise the number they thought of would indeed be greater than 10. But then he could not have said any of the phrases "My number is less than 1," "My number is less than 2," ..., "My number is less than 10." Therefore, there is at least one liar, and there are no more than 9 knights.
Example. Let's show that there could have been 9 knights. Suppose the first person thought of the number 1.5, the second -2.5, ..., the ninth -9.5, and the tenth person thought of the number 5. Then for $k=1,2, \ldots, 9$, the $k$-th person could have said the true phrases "My number is greater than $k$" and "My number is less than $k+1$" (i.e., he is a knight), while the tenth person is a liar, saying the phrases "My number is greater than 10" and "My number is less than 1."
Remark. The example given above ceases to be valid if the tenth person thinks of a number outside the interval $(0 ; 10)$, as then exactly one of his answers is true.
Comment. It is proven that there are no more than 9 knights (or, equivalently, there is at least one liar) - 3 points.
The example showing that there could have been 9 knights, with the indication of which person said which phrases - 4 points.
If the example provided is not fully described (for example, it is not specified what number the liar thought of, or it is not clearly indicated who said which phrase) - out of 4 points for the example, no more than 2 points are given.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. One day Uncle Fyodor weighed Sharik and Matroskin. It turned out that Sharik is 6 kg heavier than Matroskin, and Matroskin is three times lighter than Sharik. How much did Matroskin weigh?
|
Answer: 3 kg.
Solution: Since Matroskin is three times lighter than Sharik, Matroskin is lighter than Sharik by two of his own weights. According to the condition, this is equal to 6 kg, i.e., Matroskin weighs $6: 2=3$ kg.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Mom bought a box of lump sugar (sugar in cubes). The children first ate the top layer - 77 cubes, then the side layer - 55 cubes, and finally, the front layer. How many sugar cubes are left in the box?
|
Answer: 300 or 0.
Solution. A box has three dimensions: height, width, and depth. To find out how many cubes are in the top layer, you need to multiply the width by the depth, and for the side layer, multiply the height by the depth. After the top layer is eaten, the height decreases by 1, while the depth remains the same. Therefore, 77 and 55 must be divisible by the original depth of the box. Since the common factors of 77 and 55 are only 1 and 11. If the depth is 1, then nothing is left after the front layer is eaten. If we assume that some sugar is still left, then the depth of the box is 11. Then the width is 77:11=7 cubes, and the height after the top layer is eaten is 55:11=5 cubes. After the side layer is eaten, the width decreases by 1 (becoming 7-1=6 cubes), and after the front layer is eaten, the depth decreases by 1 and becomes 11-1=10. Therefore, the remaining height of the sugar in the box is 5, the width is 6, and the depth is 10 cubes. That is, there are $5 * 6 * 10=300$ cubes of sugar left in the box.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 10.5. (7 points)
At a joint conference of the party of liars and the party of truth-tellers, 32 people were elected to the presidium and seated in four rows of eight. During the break, each member of the presidium claimed that among their neighbors there are representatives of both parties. It is known that liars always lie, and truth-tellers always tell the truth. What is the minimum number of liars in the presidium for the described situation to be possible? (Two members of the presidium are neighbors if one of them sits to the left, right, in front of, or behind the other).
|
Answer: with eight liars.
Solution: Divide all the seats in the presidium into eight groups as shown in the figure. If there are fewer than eight liars, then in one of these groups, only truth-tellers will be sitting, which is impossible. The contradiction obtained shows that there are no fewer than eight liars. The figure shows how eight liars can be seated in the presidium so that the condition of the problem is satisfied.
Comments. Without an example of seating the liars - 5 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-2-1. Petya writes down a sequence of numbers: if the current number is equal to $x$, then the next one is $\frac{1}{1-x}$. The first number in the sequence is 2. What is the five hundredth number?
|
Answer: -1.
Solution variant 1. Let's list the first few terms of the obtained sequence:
$$
2,-1,1 / 2,2, \ldots
$$
We see that the sequence has entered a cycle with a period of 3. Since the number 500 when divided by 3 gives a remainder of 2, the 500th term will be the same as the 2nd. That is, the five hundredth number will be equal to -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a coordinate plane with the origin at point $O$, a parabola $y=x^{2}$ is drawn. Points $A, B$ are marked on the parabola such that $\angle A O B$ is a right angle. Find the smallest possible value of the area of triangle $A O B$.
|
5. Answer: 1. Solution. Let $A\left(a, a^{2}\right), B\left(b, b^{2}\right)$ be arbitrary points on the parabola. Then, by the Pythagorean theorem, $a^{2}+a^{4}+b^{2}+b^{4}=(a-b)^{2}+\left(a^{2}-b^{2}\right)^{2} \Leftrightarrow a b=-1$. From this, we find the expression for the area of the triangle: $2 S=\sqrt{a^{2}+a^{4}} \cdot \sqrt{\frac{1}{a^{2}}+\frac{1}{a^{4}}}=\sqrt{2+\left(a^{2}+\frac{1}{a^{2}}\right)} \geq 2$ (the last inequality follows from the inequality between the arithmetic mean and the geometric mean). It is clear that the value 1 is achieved for an isosceles triangle with vertices $O$, $A(1,1), B(-1,1)$.
Grading criteria. Correct solution - 7 points. The necessary inequality is proven, but it is not indicated that there exists a triangle with such an area - 5 points. The relationship between the coordinates of the points on the parabola is obtained, but there is no further progress - 1 point. The relationship between the coordinates is obtained and the formula for the area is written, but the estimate for the area is not made - 2 points. In all other cases - 0 points.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In the notebook, all irreducible fractions with the numerator 15 are written down, which are greater than $\frac{1}{16}$ and less than $\frac{1}{15}$. How many such fractions are written down in the notebook?
|
Answer: 8 fractions.
Solution. We look for all suitable irreducible fractions of the form $\frac{n}{15}$. Since $\frac{1}{16}<\frac{15}{n}$, then $\frac{15}{225}>\frac{15}{n}$, and $n>225$. Therefore, $225<n<240$. The fraction $\frac{n}{15}$ is irreducible, meaning $n$ is not divisible by 3 or 5. It is not difficult to verify that out of the range from 226 to 239 (14 numbers), we need to exclude 6 numbers (228, 230, 231, 234, 235, 237). This leaves 8 possible values for $n$.
## Criteria.
1 point. Correct answer without correct justification.
3 points. Correctly obtained range for $n$.
$\mathbf{0}$ points. Not all cases considered when listing fractions.
Comment. It is quite possible that participants will try to list all such fractions and then justify why the denominator cannot be greater or less, carefully watch the accuracy of such justifications.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 2001 coins on the table. Two players play the following game: they take turns, on each turn the first player can take any odd number of coins from 1 to 99, the second player can take any even number of coins from 2 to 100, and so on. The player who cannot make a move loses. Who wins with correct play?
|
5. The first one wins. Winning strategy: the first player should take 81 coins from the table on the first move. On each subsequent move, if the second player takes x coins, then the first player should take (101 - x) coins. He can always do this because if x is an even number from 2 to 100, then (101 - x) is an odd number from 1 to 99. Since 2001 = 101 * 19 + 81 + 1, after 19 such "responses" the first player will leave 1 coin on the table after his move, and the second player will not be able to make a move, i.e., will lose.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In a class, there are 18 children. The parents decided to gift the children from this class a cake. To do this, they first asked each child the area of the piece they wanted to receive. After that, they ordered a square cake, the area of which is exactly equal to the sum of the 18 named numbers. However, upon seeing the cake, the children wanted their pieces to be square as well. The parents can cut the cake with cuts parallel to the sides of the cake (cuts are not required to start or end on the side of the cake). For what largest $k$ can the parents guarantee to cut out $k$ square pieces from the ordered cake, which can be given to $k$ children, so that each of them gets what they want?
(A. Ibragimov, I. Bogdanov)
|
Answer. $k=12$.
Solution. We always assume that the area of the cake is 1. We will show that for some children's requests, the parents will not be able to cut out more than 12 required pieces. Choose a number $1 / 15 > x > 1 / 16$. Suppose that 15 main children ordered a piece of cake with an area of $x$ each (and the other three made arbitrary orders so that the total area of the ordered pieces is equal to 1). Mentally divide the cake into 16 equal squares and mark all 9 vertices of these squares that do not lie on the boundary of the cake (see Fig. 3). Then strictly inside any square piece of area $x$ will lie one of the marked points, that is, no more than nine such pieces can be cut out. Therefore, at least six children will not get their desired pieces.
It remains to prove that 12 children will always be able to get what they want. Let $a_{1} \geqslant a_{2} \geqslant \ldots \geqslant a_{18}$ be the side lengths of the pieces that the children want to get, that is,
$$
a_{1}^{2}+a_{2}^{2}+\ldots+a_{18}^{2}=1
$$
We will show that from a square, pieces with sides $a_{7}, a_{8}, \ldots, a_{18}$ can be cut out.
For this, we need the inequalities
$$
a_{7}+a_{10}+a_{13}+a_{16} \leqslant 1 \quad \text { and } \quad a_{7}+a_{8}+a_{9} \leqslant 1
$$
To prove the first inequality, note that
$$
\begin{aligned}
1 \geqslant & a_{1}^{2}+a_{2}^{2}+\ldots+a_{16}^{2} \geqslant 4 a_{4}^{2}+4 a_{8}^{2}+4 a_{12}^{2}+4 a_{16}^{2} \geqslant \\
& \geqslant 4\left(a_{7}^{2}+a_{10}^{2}+a_{13}^{2}+a_{16}^{2}\right) \geqslant\left(a_{7}+a_{10}+a_{13}+a_{16}\right)^{2}
\end{aligned}
$$
In the last transition, we used the inequality between the quadratic mean and the arithmetic mean. The second inequality is proved similarly:
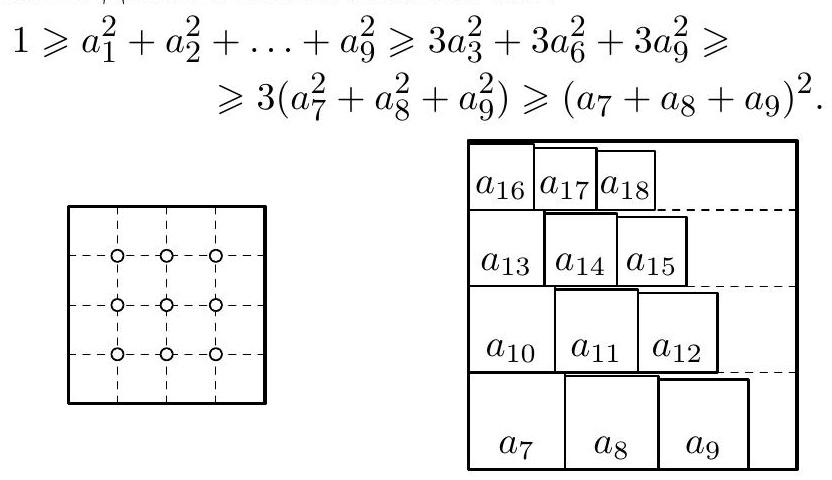
| $a_{16}$ | $a_{17} \mid a$ | |
| :---: | :---: | :---: |
| $a_{13}$ | $a_{14}$ | $a_{15}$ |
| $a_{10}$ | $a_{11}$ | $a_{12}$ |
| $a_{7}$ | $a_{\S}$ | $a$ |
$1 \geqslant a_{1}^{2}+a_{2}^{2}+\ldots+a_{9}^{2} \geqslant 3 a_{3}^{2}+3 a_{6}^{2}+3 a_{9}^{2} \geqslant$
$\geqslant 3\left(a_{7}^{2}+a_{8}^{2}+a_{9}^{2}\right) \geqslant\left(a_{7}+a_{8}+a_{9}\right)^{2}$.
Fig. 3
Fig. 4
From inequalities $(*)$ it follows that the cake can be cut into horizontal
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
|
Answer: -6.
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Grandfather is 31 times older than his grandson. In how many years will he be 7 times older than his grandson, given that the grandfather is more than 50 but less than 90 years old?
|
Answer: In 8 years.
Solution: Grandfather's age is divisible by 31. But the only such number greater than 50 and less than 90 is 62. Therefore, the grandfather is 62 years old, and the grandson is 2 years old. In x years, the grandfather will be x+62 years old, and the grandson will be x+2 years old. If at that time he will be 7 times older than the grandson, then x+62=7(x+2), from which x=8.
Comment: It is written that the grandfather's age is 62 years - 3 points.
Internet resources: http://www.problems.ru, https://olimpiada.ru.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation $\left(x^{2}-|x|-2\right)^{2}+\sqrt{|2 x+1|-3}=0$.
|
# Solution
Since each term of the original equation is non-negative, the equation can have solutions if and only if both terms are equal to zero. We obtain the equivalent system of equations
$$
\left\{\begin{array}{l}
x^{2}-|x|-2=0 \\
|2 x+1|-3=0
\end{array}\right.
$$
The solution to this system is $x=-2$.
## Criteria
The equivalent system is formulated and justified, but solved incorrectly - 4 points. The equivalent system is formulated and solved, but not justified - 5 points.
The equivalent system is formulated, but not justified and solved with an error - 3 points.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A $3 \times 3$ table was filled with prime numbers. It turned out that the sum of the numbers in any two adjacent cells is a prime number. What is the maximum number of different numbers that can be in the table? Provide an example and prove that there cannot be more different numbers.
Fill the $3 \times 3$ table with prime numbers such that the sum of the numbers in any two adjacent cells is a prime number. Determine the maximum number of different prime numbers that can be used and provide an example. Prove that it is not possible to use more different prime numbers.
|
3. Answer: 6.
Example:
| 5 | 2 | 29 | |
| :---: | :---: | :---: | :---: |
| 2 | 3 | 2 | |
| 11 | 2 | 17 | |
| | -2 | | 0 |

We will prove that it cannot be more. Divide the cells of the table into 4 pairs of adjacent cells and one central cell. In each pair of adjacent cells, the sum of the numbers is a prime number. But the sum of two odd primes is an even number greater than two and, therefore, composite. Thus, in each pair, there must be a number 2. Therefore, there must be at least four 2s. The different numbers can be the five remaining and the 2, meaning there are no more than 6 different numbers.
## Grading Criteria.
Only the correct example is provided: 3 points.
Proved that there are at least four 2s, 6 different numbers, but no example: 4 points.
It can also be proved by coloring the board in a checkerboard pattern and explaining that on each color, the numbers have the same parity.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the greatest length of an arithmetic progression of natural numbers
$a_{1}, a_{2}, \ldots, a_{n}$ with a difference of 2, in which for all $k=1,2 \ldots, n$ all numbers $a_{k}^{2}+1$ are prime
|
Solution.
All members of the progression must be even numbers. Consider the remainders when divided by 5. Since the common difference of the arithmetic progression is 2, the remainders in the progression will appear in the order
$\ldots 2,4,1,3,0,2,4,1,3,0, \ldots$ This means that among the terms of the progression, there will be numbers of the form $a_{k}=5 t+2$ and $a_{k}=5 t+3\left(t-\right.$ natural). For these numbers, we calculate $a_{k}^{2}+1=$ $25 t^{2}+20 t+5$ and $a_{k}^{2}+1=25 t^{2}+30 t+10$. We have found that the specified terms of the progression $a_{k}=5 t+2$ and $a_{k}=5 t+3$ yield expressions $a_{k}^{2}+1$ that are divisible by 5 and are not prime. The longest set of terms in the arithmetic progression that does not contain numbers of the form $a_{k}=5 t+2$ and $a_{k}=5 t+3$ consists of two numbers. Therefore, the number of consecutive terms of the progression that meet our criteria cannot exceed two. The only case where a sequence of three numbers can be obtained is by including the number 5 in $a_{k}^{2}+1$. Indeed, the numbers $2,4,6$ form an arithmetic progression and yield the corresponding sequence of prime numbers 5, 17, 37. Answer. $n=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A $10 \times 10$ square was cut into 17 rectangles, each with both side lengths greater than 1. What is the smallest number of squares that could be among these rectangles? Provide an example of such a cutting.
|
Answer: one square.
Solution. Suppose that among the rectangles, there is not a single square. Let $a$ and $b$ be the sides of an arbitrary rectangle, with $a > b$. Since the integer $b$ is greater than 1, then $b \geqslant 2$, and thus $a \geqslant 3$. Therefore, the area of each such rectangle $a \times b$ is at least $2 \cdot 3 = 6$ cells. However, then 17 rectangles should occupy at least $17 \cdot 6 = 102$ cells, while the original square $10 \times 10$ has only 100 cells.
In Figure 1, an example of cutting the $10 \times 10$ square into 17 rectangles, among which there is exactly one square, is provided.
Criteria. Only the answer - 0 points. Proved that the area of each non-square rectangle is at least 6 cells - 1 point. Proved,
Fig. 1 that among the rectangles there is a square - another 3 points. Correct example of cutting - another 3 points. Full solution - 7 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The diagonals of quadrilateral $A B C D$ intersect at point $O$. It is known that $A B=B C=$ $=C D, A O=8$ and $\angle B O C=120^{\circ}$. What is $D O ?$
|
Answer: $D O=8$.
Solution. Mark a point $E$ on the line $A C$ such that triangle $B O E$ is equilateral (Fig. 2). We will prove the equality of triangles $B A E$ and $B C O$. Indeed, since $A B=B C$, triangle $A B C$ is isosceles, and thus $\angle B A C=\angle B C A$. Additionally, note another pair of equal angles $\angle A E B=\angle B O C=120^{\circ}$. Therefore, triangles $B A E$ and $B C O$ are equal by one side and two angles, hence $A E=C O$ and $A O=A E+E O=C O+B O$.
If we mark a point $F$ on the line $B D$ such that triangle $C O F$ is equilateral, then by similar reasoning we get $D O=B O+C O$. Therefore, it follows that $D O=A O=8$.
Fig. 2
Criteria. Only the answer - 0 points. Correct additional construction related to the equilateral triangle - 2 points. The equality $A O=C O+B O$ or its equivalent $D O=B O+C O$ is established - 4 points. Complete solution - 7 points.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A seagull is being fed from a moving boat. A piece of bread is thrown down, the seagull takes 3 seconds to pick up the piece from the sea surface, and then it takes 12 seconds to catch up with the boat. Upon entering the bay, the boat reduces its speed by half. How much time will it now take the seagull to catch up with the boat after picking up the piece of bread?
Om vem: 2 seconds.
|
Solution. Let the speed of the seagull relative to the boat be $x$ (m/s). Then in 12 seconds, it flies $12 x$ (m). The boat covers this distance in 3 seconds, so its speed is $4 x$ (m/s), and the speed of the seagull is $5 x$ (m/s). In the bay, the boat's speed becomes $2 x$ (m/s). In 3 seconds, it travels $6 x$ (m). The speed of the seagull relative to the boat is now $5 x - 2 x = 3 x$ (m/s). Therefore, it will take her 2 seconds to catch up with the boat.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer - 0 points.
If the reasoning is correct and there is a computational error - 3 points. If the solution is correct - 7 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
|
Answer: 3.
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the problem's condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. The lateral faces of the pentagonal pyramid $S A B C D E$ are acute-angled triangles. We will call a lateral edge of the pyramid good if it is equal to the height of the opposite lateral face, drawn from the vertex of the pyramid (for example, the edge $S A$ is good if it is equal to the height of the triangle $S C D$, drawn from the vertex $S$). What is the maximum number of good edges that the pyramid can have?
|
# Answer. 2.
Solution. We will show that two non-adjacent lateral edges of the pyramid cannot both be good. Suppose this is not the case, and, for example, edges $S A$ and $S C$ are good, meaning $S A = S P$ is the height of face $S C D$, and $S C = S Q$ is the height of face $S A E$. However, by the property of the height in an acute triangle, $S P < S C$, and $S Q < S A$. Therefore, $S A = S P < S C = S Q < S A$ - a contradiction.
Now, note that among the three lateral edges of a pentagonal pyramid, there will always be two non-adjacent edges. Thus, the pyramid can have no more than two good edges. We will show that there exists a pentagonal pyramid with two good lateral edges. Consider a square $A M N E$ with center $O$. Let the line passing through vertex $M$ and perpendicular to $E M$, and the line passing through vertex $N$ and perpendicular to $A N$, intersect at point $C$. Choose points $B$ and $D$ such that points $M$ and $N$ are the midpoints of segments $B C$ and $D C$, respectively. Choose an arbitrary point $S$ on the perpendicular to the plane $A B C$ passing through point $O$. Then, by the theorem of three perpendiculars, $S M$ and $S N$ are the heights of triangles $S B C$ and $S D C$. And, as follows from the isosceles nature of triangles $E S M$ and $A S N$, edges $S E$ and $S A$ are good.
Comment. Correct answer without justification - 0 points.
Proved that the pyramid cannot have more than 2 good edges - 4 points.
Provided an example of a pyramid with 2 good edges - 3 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1 Two couples want to sit on a bench. In how many ways can they sit so that each boy sits next to his girlfriend, if the left and right sides of the bench are distinguishable?
|
# Answer: 8
Solution. Let's number the seats from 1 to 4. If one of the couple sits in seat number 1, then the second must sit in seat 2. Thus, each couple either sits on the left (seats 1 and 2) or on the right (seats 3 and 4). Each couple can sit in two ways (boy on the left or right), and the couples themselves can switch places. In total, $2 \cdot 2 \cdot 2=8$ ways.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.1.2. A sports team consists of two boys and two girls. In the relay, the stages run by girls must alternate with the stages run by boys. In how many ways can the stages be distributed
#
|
# Answer: 8
Solution. Boys can run stages 1 and 3, or stages 2 and 4. If they run stages 1 and 3, they can be distributed in two ways, and girls can be distributed in two ways, making a total of 4 ways. In the second case, there are another 4 ways, making a total of 8 ways.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.1.3 Two mothers with their children want to sit on a bench with 4 seats. In how many ways can they sit so that each mother sits next to her child? Each mother is walking with one child.
#
|
# Answer: 8
Solution. Let's number the seats from 1 to 4. If someone from a family sits in seat number 1, then the second person must sit in seat 2. Thus, each family either sits on the left (seats 1 and 2) or on the right (seats 3 and 4). Each family can sit in two ways (child on the left or right), and the families can switch places. In total, $2 \cdot 2 \cdot 2=8$ ways.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1 For Eeyore's Birthday, Winnie-the-Pooh, Owl, and Piglet decided to give balloons. Winnie-the-Pooh prepared twice as many balloons as Piglet, and Owl prepared three times as many balloons as Piglet. When Piglet was carrying his balloons, he was in a hurry, stumbled, and some of the balloons burst. Eeyore received a total of 31 balloons for his party. How many balloons did Piglet end up giving?
|
# Answer: 1
Solution. If Piglet hadn't burst his balloons, then Eeyore would have received exactly 6 times more balloons than Piglet prepared. The next number after 31 that is a multiple of 6 is $36, 36: 6=6$, which means Piglet prepared no less than 6 balloons.
If all of Piglet's balloons had burst, then Eeyore would have received exactly 5 times more than Piglet prepared. If Piglet initially had 7 or more balloons, then even now Eeyore would have received at least 35 balloons, which is not the case. Therefore, Piglet prepared exactly 6 balloons. If everything had been fine, Eeyore would have received 36 balloons, but since 5 burst, Piglet gave 1 balloon.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2 For Eeyore's Birthday, Winnie-the-Pooh, Owl, and Piglet decided to give balloons. Winnie-the-Pooh prepared three times as many balloons as Piglet, and Owl prepared four times as many balloons as Piglet. When Piglet was carrying his balloons, he was in a great hurry, stumbled, and some of the balloons burst. Eeyore received a total of 60 balloons for his party. How many balloons did Piglet end up giving?
|
# Answer: 4
Solution. If Piglet hadn't burst his balloons, then Eeyore would have received exactly 8 times more balloons than Piglet prepared. The next number after 60 that is a multiple of 8 is $64, 64: 8=8$, which means Piglet prepared no less than 8 balloons.
If all of Piglet's balloons had burst, then Eeyore would have received exactly 7 times more than Piglet prepared. If Piglet initially had 9 or more balloons, then even now Eeyore would have received at least 63 balloons, which is not the case. Therefore, Piglet prepared exactly 8 balloons. If everything had been fine, Eeyore would have received 64 balloons, but since 4 burst, it means Piglet gave 4 balloons.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.3 For Eeyore's Birthday, Winnie-the-Pooh, Owl, and Piglet decided to give balloons. Winnie-the-Pooh prepared twice as many balloons as Piglet, and Owl prepared four times as many balloons as Piglet. When Piglet was carrying his balloons, he was in a great hurry, stumbled, and some of the balloons burst. Eeyore received a total of 44 balloons for his party. How many balloons did Piglet end up giving?
|
# Answer: 2
Solution. If Piglet hadn't burst his balloons, then Eeyore would have received exactly 7 times more balloons than Piglet prepared. The next number after 44 that is a multiple of 7 is 49, $49: 7=7$, which means Piglet prepared no less than 6 balloons.
If all of Piglet's balloons had burst, then Eeyore would have received exactly 6 times more than Piglet prepared. If Piglet initially had 8 or more balloons, then even now Eeyore would have received at least 48 balloons, which is not the case. Therefore, Piglet prepared exactly 7 balloons. If everything had been fine, Eeyore would have received 36 balloons, but it turned out that 5 burst, so Piglet gave 2 balloons.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1 Six children stood in a circle and whispered their favorite number to the neighbors on their right and left. Each child added the two numbers they heard and said them out loud. The picture shows what three of the children said. What number did the girl think of, next to whom there is a question mark?

#
|
# Answer: 6.
Solution. Let's add the numbers we know: $16+12+8=36$. We get that 36 is the sum of the numbers marked on the diagram as A, B, and the question mark, but taken twice. Therefore, $36: 2=18$, and the sum of numbers A and B is 12. This means the girl guessed the number 6, which can be found by subtracting 12 from 18.

|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2 Six children stood in a circle and whispered their favorite number to the neighbors on their right and left. Each child added the two numbers they heard and said them out loud. The picture shows what three of the children said. What number did the girl think of, next to whom there is a question mark?

|
Answer: 5.
Solution. Let's add the numbers we know: $8+14+12=34$. We get that 34 is the numbers marked on the diagram as A, B, and under the question mark, but taken twice. Therefore, 34:2 = 17, and the sum of the numbers A and B is 12. Thus, the girl guessed the number 5, which can be found by subtracting 12 from 17.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. A rectangle with a perimeter of 100 cm was divided into 88 smaller identical rectangles by seven vertical and ten horizontal cuts. What is the perimeter of each of them, if the total length of all the cuts is 434 cm?
## Answer: 11
|
Solution. Note that the sum of seven vertical and seven horizontal cuts is 7.50 $=350$ cm, so the three extra horizontal cuts have a total length of 84 cm, each of which is 28 cm. This is the length of the horizontal side of the original rectangle. The vertical side of it is $50-28=22$ cm. After the cuts, the resulting rectangle has a horizontal side of $28 / 8=3.5$ cm and a vertical side of $22 / 11=2$ cm, so its perimeter is 11 cm.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.6.3 A rectangle with a perimeter of 96 cm was divided into 108 smaller identical rectangles by eight vertical and eleven horizontal cuts. What is the perimeter of each of them, if the total length of all the cuts is 438 cm?
|
# Answer: 9
Solution. Note that the sum of eight vertical and eight horizontal cuts is $8 \square 48=384$ cm, so the three extra horizontal cuts have a total length of 54 cm, each of which is 18. This is the length of the horizontal side of the original rectangle. The vertical side of it is $48-18=30 \text{~cm}$. After the cuts, the resulting rectangle has a horizontal side of $18 / 9=2$ cm, and a vertical side of $30 / 12=2.5$ cm, so its perimeter is 9 cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2 On the Island of Truth and Lies, there are knights who always tell the truth, and liars who always lie. One day, 15 residents of the island lined up by height (from tallest to shortest, the tallest being the first) for a game. Each had to say one of the following phrases: "There is a liar below me" or "There is a knight above me." In the end, those standing from the fourth to the eighth position said the first phrase, while the rest said the second. How many knights were among these 15 people, given that all residents have different heights?
|
# Answer: 11
Solution. The formation cannot consist of only liars (in such a case, 4-8 would be telling the truth). Consider the tallest knight, let's call him R. He could only say the first phrase, so the positions 1, 2, and 3 must be occupied by liars, and R stands from 4 to 8. In addition, there is a liar who is shorter than R, let's call him L. This liar cannot say the second phrase, so he must say the first phrase and stand no later than the 8th position but no earlier than the 5th position. Therefore, from the 9th to the 15th position, only knights stand. A liar cannot stand at the 4th position, as L is shorter than him. Therefore, R stands at the 4th position. If there are other liars between R and L, they must also say the first phrase, but L is shorter than them, which is a contradiction.
We conclude that liars stand at positions $1, 2, 3,$ and 8, while the remaining positions are occupied by knights.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. How many seven-digit natural numbers exist, for which the product of the first three digits is 30, the product of the three digits in the center is 7, and the product of the last three digits is 15?
|
Answer: 4.
Solution: Let the number be $\overline{\operatorname{abcdefg}}$. According to the condition, $c d e=7$, which means one of these digits is 7, and the other two are 1. Since 30 and 15 are not divisible by $7, d=7, c=e=1$. The number $30=5 \cdot 6 \cdot 1$, so we get two three-digit numbers $\overline{a b c}$: 561 and 651. The number $15=1 \cdot 3 \cdot 5$, from which we get two three-digit numbers $\overline{e f g}$: 135 and 153. Finally, we get $2 \cdot 2=4$ numbers.
Comment: Full solution of the problem - 7 points. Only the values of the three middle digits found - 2 points. Correct answer given without explanation - 0 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. At a round table, 10 people are sitting, each of whom is either a knight, who always tells the truth, or a liar, who always lies. Each of them was given a token. Then each of them passed their token to one of their two neighbors. After that, 5 people said: "I have one token," while the other 5 said: "I have no tokens." What is the maximum number of knights that could have been among these 10 people?
|
# Answer. 7.
Solution. Evaluation. After passing the chips, each person sitting at the table can have 0, 1, or 2 chips. The total number of chips will be 10. Note that if a person lies, they will state a number of chips that differs from the actual number by 1 or 2. Since the total number of chips according to the answers differs from the actual number by \(10-5=5\), at least 3 people must have lied. Therefore, there are no more than 7 knights at the table.
Example. Suppose the knights sitting at the table pass the chips as follows (arrows indicate the direction of the chip transfer; the number of chips after the transfer is in parentheses):
$$
\leftarrow \mathrm{P}(0)-\mathrm{P}(0) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{L}(1) \rightarrow \mathrm{L}(2) \leftrightarrow \mathrm{L}(2) \leftarrow
$$
In this case, all knights tell the truth, while the liars lie, saying they have 0 chips.
Comment. A fully justified solution - 7 points. Correct evaluation - 5 points, a correct example constructed - 2 points, points are cumulative. The problem is not solved or solved incorrectly - 0 points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Having walked $4 / 9$ of the length of the bridge, the traveler noticed that a car was catching up to him, but it had not yet entered the bridge. Then he turned back and met the car at the beginning of the bridge. If he had continued his movement, the car would have caught up with him at the end of the bridge. Find the ratio of the car's speed to the traveler's speed.
#
|
# Solution
From the condition, it follows that the time it takes for the car to approach the bridge is equal to the time it takes for the traveler to walk $4 / 9$ of the bridge. Therefore, if the traveler continues moving, by the time the car reaches the bridge, he will have walked ${ }^{8} / 9$ of the bridge. This means that during the time it takes for the car to cross the bridge, the traveler manages to walk one-ninth of the bridge, so the speed of the car is 9 times greater than the speed of the traveler.
## Answer 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given various real numbers $p$ and $q$. It is known that there exists a number $x$ such that the equations $x^{2} + p x + q = 0$ and $x^{2} + q x + p = 0$ are satisfied. What values can the sum $p + q$ take?
|
Solution. Let $x$ be such that both equalities from the problem statement are satisfied. Then $x^{2}+p x+q=x^{2}+q x+p$, from which $(p-q) x=p-q$. Since $p \neq q$, it follows that $x=1$. Substituting this value into any of the equations, we find that $p+q+1=0$, that is, $p+q=-1$. Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a football tournament, seven teams played: each team played once with each other. Teams that scored thirteen or more points advance to the next round. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round?
|
Solution. Evaluation. Note that the total number of games will be $\frac{7 \cdot 6}{2}=21$. Then the total number of points does not exceed $21 \cdot 3=63$. This means that no more than $\left[\frac{63}{13}\right]=4$ teams can advance to the next round.
Example. We will show that 4 teams can advance to the next round. For this, we will provide an example of a suitable tournament table (the symbol "x" denotes insignificant results):
| $№$ | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | $\mathbf{7}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathbf{1}$ | - | 1 | 3 | 3 | 3 | 3 | 0 |
| $\mathbf{2}$ | 1 | - | 0 | 3 | 3 | 3 | 3 |
| $\mathbf{3}$ | 0 | 3 | - | 3 | 3 | 3 | 1 |
| $\mathbf{4}$ | 0 | 0 | 0 | - | $\mathrm{x}$ | $\mathrm{x}$ | 0 |
| $\mathbf{5}$ | 0 | 0 | 0 | $\mathrm{x}$ | - | $\mathrm{x}$ | 0 |
| $\mathbf{6}$ | 0 | 0 | 0 | $\mathrm{x}$ | $\mathrm{x}$ | - | 0 |
| $\mathbf{7}$ | 3 | 0 | 1 | 3 | 3 | 3 | - |
Answer: 4.
Comment. The correct evaluation is obtained - no more than 3 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. For real numbers $x$ and $y$, define the operation $\star$ as follows: $x \star y=x y+4 y-3 x$.
Calculate the value of the expression
$$
((\ldots)(((2022 \star 2021) \star 2020) \star 2019) \star \ldots) \star 2) \star 1
$$
|
Answer: 12.
Solution. Let $t=(\ldots(((2022 \star 2021) \star 2020) \star 2019) \star \ldots) \star 4$. Then the value of the expression from the problem condition is
$$
\begin{aligned}
((t \star 3) \star 2) \star 1 & =((3 t+12-3 t) \star 2) \star 1=12 \star 2 \star 1= \\
& =(24+8-36) \star 1=(-4) \star 1=-4+4+12=12
\end{aligned}
$$
## 9th grade
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. The numbers $a$ and $b$ are such that each of the two quadratic trinomials $x^{2} + a x + b$ and $x^{2} + b x + a$ has two distinct roots, and the product of these trinomials has exactly three distinct roots. Find all possible values of the sum of these three roots.
(S. Berlov)
|
Answer: 0.
Solution: From the condition, it follows that the quadratic polynomials $x^{2}+a x+b$ and $x^{2}+b x+a$ have a common root $x_{0}$, as well as roots $x_{1}$ and $x_{2}$ different from it; in particular, $a \neq b$. Then $0=\left(x_{0}^{2}+a x_{0}+b\right)-\left(x_{0}^{2}+b x_{0}+a\right)=(a-b)\left(x_{0}-1\right)$, that is, $x_{0}=1$. Substituting this root into any quadratic polynomial, we get $0=1+a+b$, that is, $b=-a-1$. Thus, our quadratic polynomials have the form $x^{2}+a x-(a+1)=(x-1)(x+a+1)$ and $x^{2}-(a+1) x+a=(x-1)(x-a)$. Their roots are the numbers $1, a$, and $-(a+1)$ (for $a \neq 1,-2,-1 / 2$ they are distinct), the sum of which is zero.
Remark. After obtaining the equality $0=1+a+b$, the solution can be completed differently. By Vieta's theorem, we have $x_{0}+x_{1}=-a, x_{0}+x_{2}=-b$, from which $x_{0}+x_{1}+x_{2}=-a-b-x_{0}=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Natural numbers $a, x$ and $y$, greater than 100, are such that $y^{2}-1=$ $=a^{2}\left(x^{2}-1\right)$. What is the smallest value that the fraction $a / x$ can take?
|
# Answer. 2.
First solution. Rewrite the condition of the problem as $y^{2}=a^{2} x^{2}-a^{2}+1$. Notice that $y100$, if we set $a=2 x, y=a x-1=2 x^{2}-1$.
Second solution. We provide another proof of the estimate $a / x \geqslant 2$. Rewrite the equality from the condition as
$$
(a x-y)(a x+y)=a^{2} x^{2}-y^{2}=a^{2}-1
$$
The numbers $a^{2}-1$ and $a x+y$ are positive, so the number $k=a x-y$ is also positive (and natural). Then $a x+y=\frac{a^{2}-1}{k}$. Adding the two equations, we get
$$
2 a x=\frac{a^{2}-1}{k}+k=a^{2}+\frac{(k-1)\left(k-a^{2}+1\right)}{k} \leqslant a^{2}
$$
since $1 \leqslant k \leqslant a^{2}-1$. Thus, $2 a x \leqslant a^{2}$, which means $a / x \geqslant 2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. $B$ of trapezoid $A B C D: \angle A=\angle B=90^{\circ}, A D=2 \sqrt{7}, A B=\sqrt{21}, B C=2$. What is the minimum value that the sum of the lengths $X A+X B+X C+X D$ can take, where $X-$ is an arbitrary point in the plane?
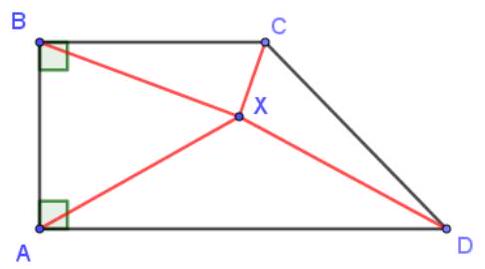
|
# Answer: 12
Solution. By the triangle inequality $X A+X C \geqslant A C$, and equality is achieved when $X$ lies on the segment $A C$. Similarly, $X B+X D \geqslant B D$, and equality is achieved when $X$ lies on the segment
$B D$. Thus, $X A+X B+X C+X D \geqslant A C+B D$, and equality is achieved when $X$ is the intersection point of the diagonals. By the Pythagorean theorem $A C=\sqrt{A B^{2}+B C^{2}}=5, B D=\sqrt{A B^{2}+A D^{2}}=7$, hence $A C+B D=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. On the parabola $y=x^{2}-4 x-1$, three different points $A\left(x_{a}, y_{a}\right), B\left(x_{b}, y_{b}\right), C\left(x_{c}, y_{c}\right)$ are taken. It is known that $x_{c}=5$ and $y_{a}=y_{b}$. Find the abscissa of the point of intersection of the medians of triangle $A B C$.
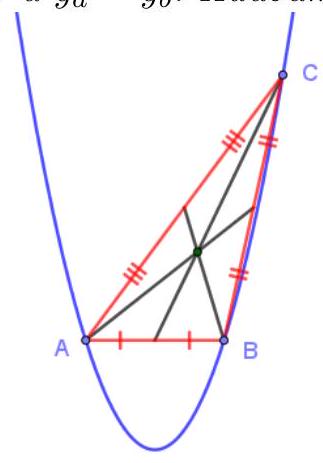
|
# Answer: 3
Solution. Since $y_{a}=y_{b}$, points $A$ and $B$ are symmetric with respect to the axis of the parabola, which means the midpoint $K$ of segment $A B$ has an abscissa equal to the abscissa of the vertex of the parabola $x_{k}=2$. Next, by the property of the median, the point of intersection of the medians $M$ divides the median $C K$ in the ratio $2: 1$, counting from the vertex, so the abscissa $x_{m}$ of point $M$ is found from the equality $x_{c}-x_{k}=3\left(x_{m}-x_{k}\right)$. Finally: $x_{m}=\frac{x_{c}+2 x_{k}}{3}=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Little One gave Karlson 111 candies. They immediately ate some of them together, $45\%$ of the remaining candies went to Karlson for lunch, and a third of the candies left after lunch were found by Fräulein Bok during cleaning. How many candies did she find?
|
Answer: 11.
First method. Let Carlson have had $n$ candies before lunch. Then, after lunch, there were $\frac{55}{100} n$ left, and Fräulein Bock found $\frac{1}{3} \cdot \frac{55}{100} n=\frac{11 n}{60}$ candies. Since the number of candies must be an integer, $11 n$ is divisible by 60. Since the numbers 11 and 60 are coprime, $n$ must be a multiple of 60. There is only one number that is divisible by 60 and less than 111, which is 60. Therefore, $n=60$, meaning Fräulein Bock found 11 candies.
Similar reasoning: if Carlson had $n$ candies before lunch, then he ate $0.45 n=\frac{9 n}{20}$ candies, and since the numbers 9 and 20 are coprime, $n$ is divisible by 20. After lunch, there were $0.55 n=\frac{11 n}{20}$ candies left, and this number must be divisible by 3. But 11 is not divisible by 3, so $n$ must be divisible by 3. Thus, $n$ is divisible by 3 and on
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.