problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. (7 points) A seller bought a batch of pens and sold them. Some customers bought one pen for 10 rubles, while others bought 3 pens for 20 rubles. It turned out that the seller made the same profit from each sale. Find the price at which the seller bought the pens.
|
Answer: 5 rubles.
Solution. Let the purchase price of a pen be $x$. Then the profit from one pen is $10-x$, and from 3 pens is $20-3x$. Solving the equation $10-x=20-3x$, we get $x=5$.
Criteria. Correct solution by any method: 7 points.
If it is not justified that the purchase price of the pen should be 5 rubles, but it is verified that the condition is met in this case: 4 points.
Only the correct answer without any explanation: 2 points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-5. Santa Claus is preparing gifts. He has distributed 115 candies into bags, with each bag containing a different number of candies. In the three smallest gifts, there are 20 candies, and in the three largest - 50. How many bags are the candies distributed into? How many candies are in the smallest gift?
|
Answer: 10 packages, 5 candies.
Solution. Let's number the gifts from the smallest to the largest, from 1 to n. If the third gift has 7 or fewer candies, then the three smallest gifts have no more than $7+6+5=18$ candies. This contradicts the condition. Therefore, the third gift has at least 8 candies. Similarly, the third from the last gift has no more than 15 candies $(16+17+18=51>50)$.
Remove the three largest and the three smallest gifts. In the remaining gifts, there will be 115 - 20 $50=45$ candies, and each will have between 9 and 14 candies. Three packages are clearly not enough ( $14+13+12=39$ ), and five would be too many ( $9+10+11+12+13=55$ ). Therefore, 45 candies are distributed in 4 packages. This is possible: $47=9+11+12+13$. Note that the fourth package cannot have more than 9 candies: $10+11+12+13=46>45$.
If the fourth package has 9 candies, then the third has no more than 8, the second no more than 7, so the first package has at least $20-8-7=5$ candies. But no more, since $6+7+8=21$.
Criteria. Only the answer - 0 points. Only correct estimates for $a_{3}$ and $a_{n-3}-3$ points. Only a justified answer for the number of packages - 5 points. Full solution - 7 points.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. The numbers from 1 to 10 were written in some order and resulted in the numbers \(a_{1}, a_{2}, a_{3}, \ldots, a_{10}\), and then the sums \(S_{1}=a_{1}\), \(S_{2}=a_{1}+a_{2}\), \(S_{3}=a_{1}+a_{2}+a_{3}\), \ldots, \(S_{10}=a_{1}+a_{2}+a_{3}+\ldots+a_{10}\) were calculated. What is the maximum number of prime numbers that could be among the numbers \(S_{1}, S_{2}\), \(S_{3}, \ldots, S_{10}\)?
|
Answer: 7.
Among the numbers from 1 to 10, there are five odd numbers. Adding an odd number changes the parity of the sum. Let $y_{1}^{\prime}, y_{2}, y_{3}, y_{4}, y_{5}$ be the odd numbers, in the order they appear on the board. After adding $y_{2}$, the sum will become even and greater than 2, as it will after adding $y_{4}$. These sums are composite numbers, as is $S_{10}=55$. Therefore, among the sums, there are no more than 7 prime numbers.
Example of writing the numbers: $2,1,4,3,7,6,8,10,5,9$. The resulting sums: $2,3,7,10,17,23,31,41,46,55$.
Comment. An answer without justification - 0 points. A correct answer with an example - 3 points (the example provided in the solution is not unique). An estimate of the number of prime sums (without an example) - 3 points.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
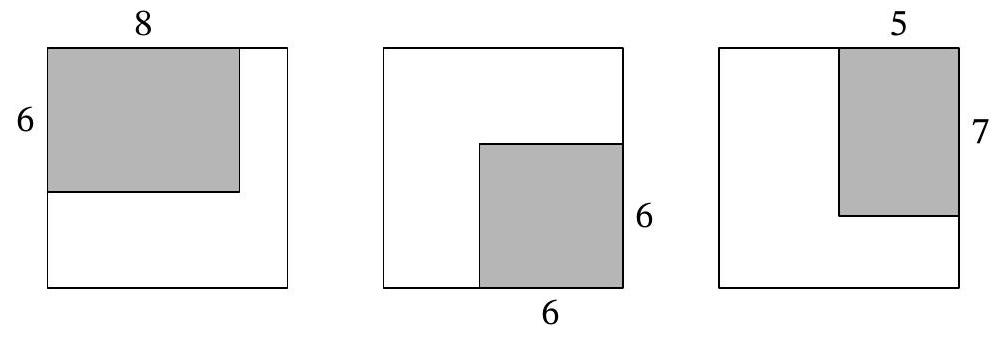
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
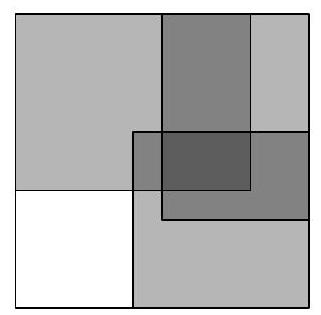
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. In the figure, two equal triangles are depicted: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
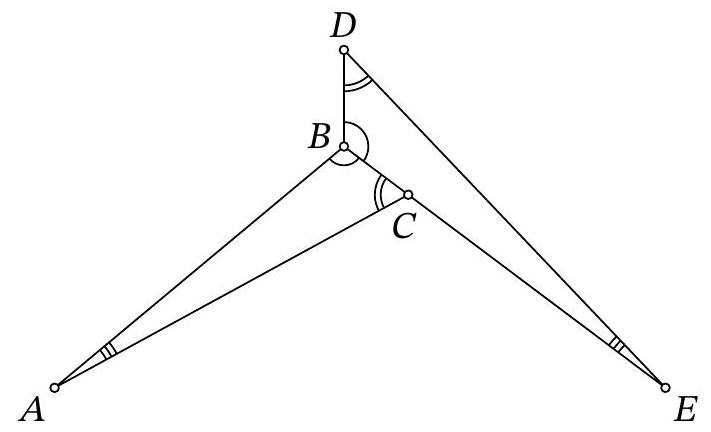
|
Answer: 7.
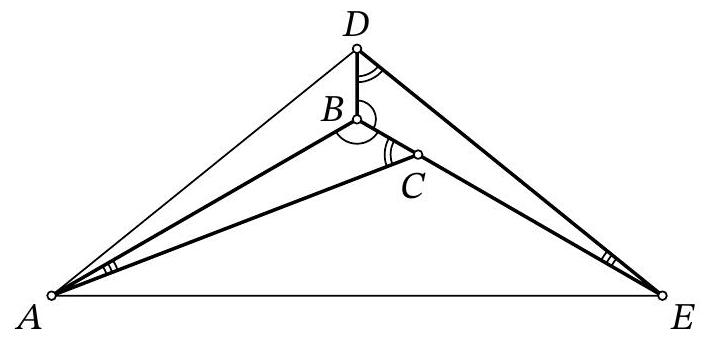
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
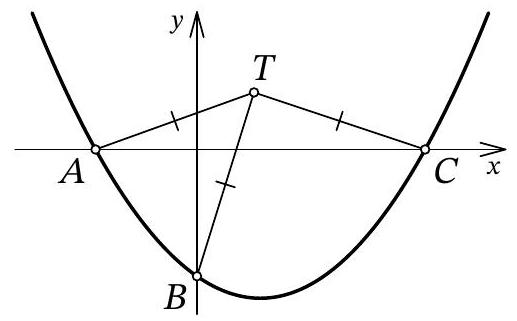
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
|
Answer: -6.
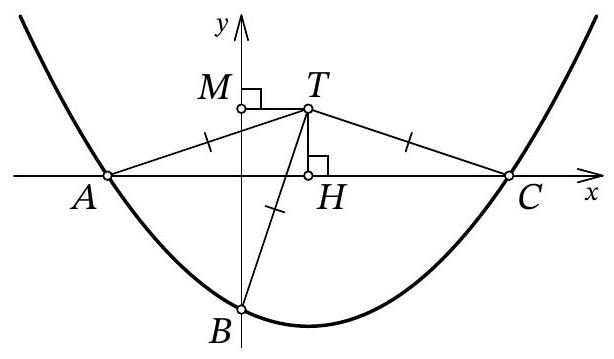
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
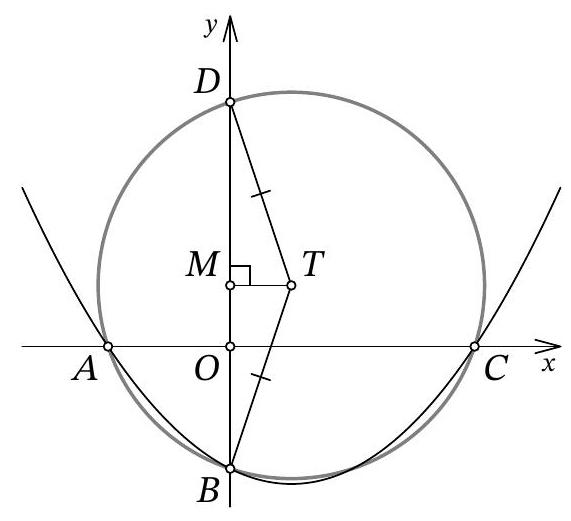
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. CONDITION
The sequence of numbers $\mathrm{a}_{1}, \mathrm{a}_{2}, \mathrm{a}_{3}, \ldots, \mathrm{a}_{\mathrm{n}}, \ldots$ satisfies the relations $\mathrm{a}_{\mathrm{n}}=\mathrm{a}_{\mathrm{n}-1} \cdot \mathrm{a}_{\mathrm{n}-3}$ for $\mathrm{n}=4,5,6, \ldots$ Find $\mathrm{a}_{2019}$, given that $\mathrm{a}_{1}=1, \mathrm{a}_{2}=1, \mathrm{a}_{3}=-1$.
|
Solution. It is clear that all members of this sequence are equal to $\pm 1$. We find:
$$
\begin{aligned}
& a_{n}=\left(a_{n-1}\right) \cdot a_{n-3}=\left(a_{n-2} \cdot a_{n-4}\right) \cdot a_{n-3}=\left(a_{n-2}\right) \cdot a_{n-4} \cdot a_{n-3}= \\
& =\left(a_{n-3} \cdot a_{n-4}\right) \cdot a_{n-4} \cdot a_{n-3}=a_{n-3}^{2} \cdot a_{n-4} \cdot a_{n-5}=a_{n-4} \cdot a_{n-5}= \\
& =\left(a_{n-4}\right) \cdot a_{n-5}=\left(a_{n-5} \cdot a_{n-7}\right) \cdot a_{n-5}=a_{n-5}^{2} \cdot a_{n-7}=a_{n-7}
\end{aligned}
$$
That is, the sequence is periodic with a period of 7. Therefore,
$$
\mathrm{a}_{2019}=\mathrm{a}_{288 \cdot 7+3}=\mathrm{a}_{3}=-1
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A 2019-digit number written on the board is such that any number formed by any two adjacent digits (in the order they follow) is divisible by 13. Find the last digit of this number, given that the first digit is 6.
|
1. Answer: 2.
Two-digit numbers divisible by 13: $13,26,39,52,65,78,91$. If the first digit of the number is 6, then the second digit must be 5 (forming the number 65, which is divisible by 13), the third digit is 2 (forming 52), and the fourth digit is again 6 (forming 26). Thus, the digits will be arranged in triplets: $652652 \ldots$ Since 2019 is divisible by 3, the last digit is 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
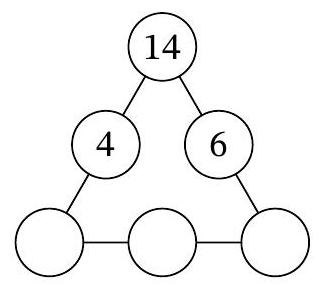
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
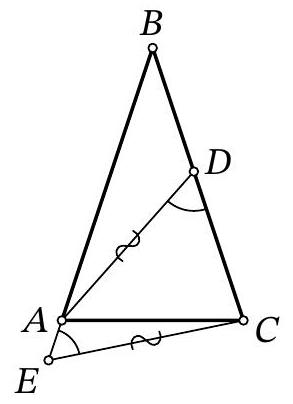
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
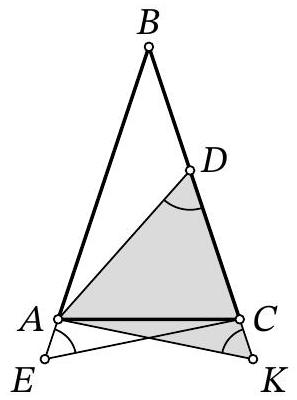
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are both $60^{\circ}$, so it is an equilateral triangle, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. If $x=5 m+4$, then $(5 m+4)^{2}+1=25 m^{2}+40 m+17$ is not divisible by 5.
|
Answer: $\left\{\begin{array}{c}x=5 m+2, \\ y=5 m^{2}+4 m+1 .\end{array}\right.$ or $\left\{\begin{array}{c}x=5 m+3, \\ y=5 m^{2}+6 m+2 .\end{array}\right.$ where $m \in \mathbb{Z}$.
5 points - the solution is correct, complete, and contains no errors.
4 points - if the answer is incorrect, the solution method is correct, but a computational error or typo has been made, and the solution is completed with this error.
3 points - the problem is solved to the correct answer by trial and error, but not all possible cases are considered or the sequence of trials is not completed.
1 point - the solution is incorrect, but contains reasonable considerations, has some progress in solving the problem.
0 points - the solution is incorrect or missing.
## №3. (6 points)
In an isosceles triangle $ABC$, a circle is inscribed. A tangent to the circle, parallel to the base $AC$, intersects the lateral sides at points $D$ and $E$. Find the radius of the circle if $DE=8$ and $AC=18$.
Solution: Drop perpendiculars from points $D$ and $E$ to side $AC$ - we get a rectangle $DEMK$, in which $KM=DE=8$.
The diameter of the circle is equal to the perpendicular $DK$, to calculate the length of which we first need to find the length of segment $AD$.
Consider the right triangles $ADK$ and $CEM$. They are equal by the leg ($DK=EM$) and the acute angle ($\angle A = \angle C$ since $\triangle ABC$ is isosceles). From the equality of the triangles, it follows that the segments $AK=MC=5$.
Since in a quadrilateral circumscribed around a circle, the sums of the lengths of opposite sides are equal,
$AD + EC = DE + AC = 8 + 18 = 26 \Rightarrow AD = EC = \frac{26}{2} = 13$. The diameter of the circle is $DK = \sqrt{AD^2 - AK^2} = \sqrt{13^2 - 5^2} = 12$. Therefore, the radius is $\frac{12}{2} = 6$.
Answer: 6.
6 points - the solution is correct, complete, and contains no errors.
5 points - the solution is correct, but insufficiently justified or contains inaccuracies.
2 points - the solution is incorrect, but contains reasonable considerations, has some progress in solving the problem.
1 point - only the answer is recorded.
0 points - the solution is incorrect or missing.
## №4. (7 points)
Solve the equation: $x \sqrt{1-y^{2}} + y \sqrt{2-z^{2}} + z \sqrt{3-x^{2}} = 3$.
Solution: Applying the inequality between the arithmetic mean and the geometric mean to the numbers $x^2$ and $1-y^2$, we get: $|x| \sqrt{1-y^2} \leq \frac{x^2 + 1 - y^2}{2}$.
Similarly, $|y| \sqrt{2-z^2} \leq \frac{y^2 + 2 - z^2}{2}$ and $|z| \sqrt{3-x^2} \leq \frac{z^2 + 3 - x^2}{2}$. Adding these inequalities and considering that $U \leq |l|$, we have
$$
x \sqrt{1-y^2} + y \sqrt{2-z^2} + z \sqrt{3-x^2} \leq 3
$$
Therefore, equality is achieved in all the above inequalities. This is possible only if $x^2 = 1 - y^2$, $y^2 = 2 - z^2$, and $z^2 = 3 - x^2$. Solving the system, we get:
$x = \pm 1, y = 0, z = \pm \sqrt{2}$. Note that for negative values of $x$ and $z$, the inequality $(*)$ is strict. Therefore, the equation has a unique solution when: $x = 1, y = 0, z = \sqrt{2}$.
Answer: $x = 1, y = 0, z = \sqrt{2}$
7 points - the solution is correct, complete, and contains no errors.
6 points - the solution is correct, but insufficiently justified or contains inaccuracies.
4 points - the solution is found, but the uniqueness of the solution is not proven.
3 points - the solution is constructed without justification, assuming each term equals one.
2 points - the solution is incorrect, but contains reasonable considerations, has some progress in solving the problem.
1 point - only the answer is recorded.
0 points - the solution is incorrect or missing.
## №5. (7 points)
How many different pairs can be formed from 28 domino tiles so that the tiles in the pair can be placed next to each other? (Tiles can be placed next to each other if some number of dots appears on both tiles).
## Solution
Choosing a pair of tiles is simpler to consider as choosing two cards, but it is clear that there are half as many unordered pairs as ordered ones. It is easier to find the number of ordered pairs, as in this case, the rule of product can be applied.
Choose the first tile - this can be done in 28 ways, of which in 7 cases the tile will be a double, i.e., a tile of the form

In 21 cases, it will be a tile of the form $a < b$. In the first case, the second tile can be chosen in 6 ways, and the number of ways to choose a pair of tiles by the rule of product is $7 \cdot 6 = 42$.
In the second case, the second tile can be chosen in 12 ways - 6
pairs, so the number of ways is $21 \cdot 12 = 252$.
Therefore, by the rule of sum, the total number of ways to choose an ordered pair is $42 + 252 = 294$.
Answer: 147 pairs.
7 points - the task is completed correctly.
5 points - the solution contains minor errors, gaps in justification, but is generally correct and can become fully correct after minor corrections or additions.
2 points - important cases are considered in the absence of a solution (or an incorrect solution).
1 point - only the answer is recorded.
0 points - the solution is incorrect or missing.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a school chess tournament, boys and girls competed, with the number of boys being five times the number of girls. According to the tournament rules, each chess player played against every other player twice. How many players in total participated if it is known that the boys scored exactly twice as many points in total as the girls? (1 point is awarded for a win, -0.5 points for a draw, and 0 points for a loss.)
|
Answer: 6 players.
Solution. Let $d$ girls and $5d$ boys participate in the tournament. Then the total number of players was $d + 5d = 6d$; playing two matches each with every other, they played a total of $2 \cdot \frac{1}{2} \cdot 6d(6d-1) = 6d(6d-1)$ matches. Since each match awards one point, the total number of points scored by all participants is also $6d(6d-1)$. Of these, two-thirds of the points belong to the boys, and one-third to the girls, meaning the girls scored $\frac{1}{3} \cdot 6d(6d-1) = 2d(6d-1)$ points.
Note that if each girl won against all the boys, the girls together could have scored a maximum of $2 \cdot d \cdot 5d = 10d^2$ points, and playing against each other, the girls distributed $2 \cdot \frac{1}{2} \cdot d(d-1)$ points. Therefore, the maximum number of points the girls could have scored is $10d^2 + d(d-1) = 11d^2 - d$. Thus,
$$
2d(6d-1) \leq 11d^2 - d \quad \Longleftrightarrow \quad d^2 \leq d
$$
Therefore, there could not have been more than one girl. If there was one girl, then there were five boys, making a total of 6 players. Six players played a total of $6 \cdot 5 = 30$ matches and awarded 30 points. The girl scored 10 points, winning two matches against each of the five boys. Playing against each other, the boys distributed the remaining 20 points.
Criteria. Only the answer - 0 points. Correct example - 2 points. Calculation of the total number of points scored by all girls - 2 points. Estimation of the number of points scored by the girls - 4 points. Criteria are not cumulative. Full solution - 7 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.7. For natural numbers $a>b>1$, define the sequence $x_{1}, x_{2}, \ldots$ by the formula $x_{n}=\frac{a^{n}-1}{b^{n}-1}$. Find the smallest $d$ such that this sequence does not contain $d$ consecutive terms that are prime numbers, for any $a$ and $b$.
(V. Senderov)
|
10.7. Answer. 2.
For $a=4, b=2$ we have $\frac{a^{1}-1}{b^{1}-1}=3, \frac{a^{2}-1}{b^{2}-1}=5$. It remains to show that more than two consecutive prime numbers will not occur.
We will prove a stronger statement than required: for $n \geqslant 2$ at least one of the numbers $\frac{a^{n}-1}{b^{n}-1}, \frac{a^{n+1}-1}{b^{n+1}-1}$ is not prime. Suppose the opposite; then
\[
\begin{aligned}
& (a-1)\left(a^{n-1}+\ldots+a+1\right)=p(b-1)\left(b^{n-1}+\ldots+b+1\right) \\
& (a-1)\left(a^{n}+\ldots+a+1\right)=q(b-1)\left(b^{n}+\ldots+b+1\right)
\end{aligned}
\]
where $p$ and $q$ are prime numbers.
Suppose that $a-1$ does not divide $b-1$. Then some prime number $r$ appears in the factorization of the number $b-1$ with a power greater than in $a-1$. From (1) and (2) we get that $r$ is a common divisor of the numbers $a^{n-1}+\ldots+a+1$ and $a^{n}+\ldots+a+1$, but
\[
\begin{aligned}
& \text{GCD}\left(a^{n-1}+\ldots+a+1, a^{n}+\ldots+a+1\right)= \\
&= \text{GCD}\left(a^{n-1}+\ldots+a+1, a^{n}\right)=1
\end{aligned}
\]
Contradiction.
Thus, the number $k=\frac{a-1}{b-1}$ is an integer. From (1) we have
\[
k\left(a^{n-1}+\ldots+a+1\right)=p\left(b^{n-1}+\ldots+b+1\right)
\]
where $1<k<p$, since $b^{n-1}+\ldots+b+1<a^{n-1}+\ldots+a+1$. Therefore, $\text{GCD}(k, p)=1$, so $b^{n-1}+\ldots+b+1 \vdots k$. Similarly, from (2) it follows that $k<q$ and $b^{n}+\ldots+b+1 \vdots k$. But this contradicts the fact that $\text{GCD}\left(b^{n-1}+\ldots+b+1, b^{n}+\ldots+b+1\right)=1$.
Remark. Two consecutive prime numbers in such a sequence can be any two prime numbers of the form $p=b+1, q=b^{2}+1$. Indeed, setting $a=b^{2}$, we have $p=\frac{a-1}{b-1}, q=\frac{a^{2}-1}{b^{2}-1}$. Such pairs include, for example, $(7,37),(11,101)$ and $\left(2^{2^{3}}+1,2^{2^{4}}+1\right)$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There are 25 coins, 12 of which are counterfeit and differ in weight by exactly 1 g from the genuine ones. All coins weigh an integer number of grams. Some may be lighter than the genuine ones, while others may be heavier. There are balance scales without weights, with a needle that shows the difference in weight. What is the minimum number of weighings needed to determine whether a given coin is counterfeit or not?
|
Solution. We will prove that one weighing is sufficient. Set aside the coin under investigation, and place the rest on the scales, 12 coins on each side. If the scales show a difference in an even number of grams, then the coin is genuine; if in an odd number, then it is counterfeit. Indeed, if an odd number of counterfeit coins lie on the pan, then its mass differs from the mass of 12 genuine coins by an odd number of grams (the sum of an odd number of odd numbers), otherwise - by an even number. Depending on the coin under investigation, there are 11 or 12 counterfeit coins on the pans, which can be divided into two groups with different or the same parity of the number of coins, respectively. Answer: one weighing.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the hypotenuse of a right triangle if the height drawn to it is 1 cm, and one of the angles of the triangle is $15^{\circ}$. If the answer is not an integer, round it to the tenths.
|
Solution. Let's call the original triangle $ABC$. Let $CH$ be the height drawn to the hypotenuse; $\angle C=90^{\circ}$, and $\angle A=15^{\circ}$. Draw the median $CM$. It is clear that $CM=MA=MB$, so triangle $CMA$ is isosceles $\left(CM=MA \text{ and } \angle MCA=\angle MAC=15^{\circ}\right)$. Note that $\angle BMC=30^{\circ}$ (the exterior angle of the triangle), but then $CM=2 \cdot CH=2$. Since $CM=MA=MB=2$, the hypotenuse $AB=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 In the fishing, 11 experienced fishermen and $n$ children participated. Together they caught $n^{2}+$ $5 n+22$ fish, with all experienced fishermen catching the same amount, and all children catching the same amount, but each 10 less than an experienced fisherman. Who was there more of at the fishing - experienced fishermen or children?
|
Solution: Let each child catch $m$ fish. Then $n m+11(m+10)=n^{2}+5 n+22$. From this, $(n+11) m=n^{2}+3 n-88$. Therefore, the right side is divisible by $n+11$. We have $n^{2}+5 n-88=$ $(n+11)(n-6)-22$, so 22 is divisible by $n+11$. The only divisor of 22 greater than 11 is 22 itself, so $n+11=22, n=11$. Therefore, the experienced fishermen and children were equal in number.
## Criteria:
- No points are deducted for the absence of an example for $n=11$.
- It is shown that $n=11$ works, but it is not proven that there are no other options - 1 point.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4 Is there a rectangular box, all three dimensions of which (height, width, and depth) are expressed as irrational numbers, while the surface area and volume are integers?
|
Solution 1: Consider a box with sides $\sqrt{2}-1, \sqrt{2}-1,3+2 \sqrt{2}$. Its volume is $(\sqrt{2}-1)^{2}(3+2 \sqrt{2})=(3-2 \sqrt{2})(3+2 \sqrt{2})=1$, and the surface area is $2(\sqrt{2}-1)^{2}+4(\sqrt{2}-1)(3+2 \sqrt{2})=2(3-2 \sqrt{2})+4(\sqrt{2}+1)=10$.
Solution 2: Consider the polynomial $f(x)=x^{3}-30 x^{2}+31 x-1$. Since $f(0) < 0, f(2) > 0$, the equation $f(x)=0$ has three positive roots. The numbers $\pm 1$ are not roots, so all roots of the equation are irrational. Take them as the dimensions of the box. By Vieta's theorem, their sum of pairwise products is 31 (from which the surface area is 62), and their product is 1.
## Criteria:
- If the irrationality of the box's sides, their positivity, and/or the integrity of the volume and surface area are not obvious - up to 3 points are deducted;
- If the measurements are given as roots of a polynomial, but it is not verified that this polynomial has three irrational positive roots - no more than 3 points are awarded;
- The statement "the root of an integer to an integer power is either an integer or an irrational number" and its consequences are accepted without proof.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5 What is the largest number of non-overlapping groups into which all integers from 1 to 20 can be divided so that the sum of the numbers in each group is a perfect square?
|
Solution: A group consisting of a single number can only be formed by 4 squares. The remaining 16 numbers must be divided into groups of at least two. Therefore, there will be no more than 12 groups in total. Let's check that exactly 12 groups are not possible. Indeed, in such a case, the numbers 1, 4, 9, 16 would form separate groups, and the remaining numbers would be divided into pairs. Then, the number 8 can only be paired with 17, and the number 19 can only be paired with 6, so the number 10 can only be paired with 15. The number 12 can only be paired with 13, the number 18 only with 7, the number 20 only with 5, and then the number 11 can only be paired with 14. Thus, for all non-squares except 2 and 3, we have uniquely restored the pairs, but 2 and 3 cannot form a group because their sum is not a square. Contradiction.
An example of a partition into 11 groups is the specified partition of non-squares into pairs, and the numbers 2 and 3 are combined into a group with 4.
## Criteria:
- Only proved that there are no more than 11 groups, no example provided - 4 points;
- Provided an example, but did not prove that 12 groups are not possible - 2 points.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the numerical value of the expression
$$
\frac{1}{a^{2}+1}+\frac{1}{b^{2}+1}+\frac{2}{a b+1}
$$
if it is known that $a$ is not equal to $b$ and the sum of the first two terms is equal to the third.
|
Answer: 2.
Solution. Let's bring the condition to a common denominator
$$
\frac{1}{a^{2}+1}+\frac{1}{b^{2}+1}=\frac{2}{a b+1}
$$
we get
$$
\frac{\left(a^{2}+b^{2}+2\right)(a b+1)-2\left(a^{2}+1\right)\left(b^{2}+1\right)}{\left(a^{2}+1\right)\left(b^{2}+1\right)(a b+1)}=0
$$
expand all brackets in the numerator, combine like terms, we get the equality $(a-b)^{2}(a b-1)=0$. Since $a \neq b$, then $a b=1$. From this, the third term equals 1, and then the entire sum equals 2.
Criteria. Full solution - 7 points. Correctly brought to a common denominator, like terms correctly combined, but without further progress - 1 point. Reasoning of the type "if $a$ is taken this way, and $b$ another way, then something will result" is rated 0 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of integer points $(x, y)$ satisfying the equation $\frac{1}{|x|}+\frac{1}{|y|}=\frac{1}{2017}$.
|
Solution. Transform the original equation $\frac{1}{|x|}+\frac{1}{|y|}=\frac{1}{2017} \Rightarrow$
$2017(|x|+|y|)-|x||y|=0 \Rightarrow 2017 \cdot|x|+2017 \cdot|y|-|x||y|-2017^{2}=-2017^{2}$, from which it follows that $(|x|-2017)(|y|-2017)=2017^{2}$. Since 2017 is a prime number and $|x|$ and $|y|$ are natural numbers, the last equation is equivalent to the union of systems of equations $\left\{\begin{array}{c}|x|-2017=1 \\ |y|-2017=2017^{2}\end{array},\left\{\begin{array}{c}|x|-2017=2017 \\ |y|-2017=2017\end{array},\left\{\begin{array}{c}|x|-2017=2017^{2} \\ |y|-2017=1\end{array}\right.\right.\right.$. Each system of equations has four distinct solutions that do not coincide with the solutions of the other systems. Therefore, the number of points sought is 12.
Answer. 12.
Recommendations for checking. The factorization of the form $(|x|-2017)(|y|-2017)=2017^{2}$ or an equivalent form within another solution method - 3 points.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The brother left the house 6 minutes after his sister, following her, and caught up with her after 12 minutes. How many minutes would it have taken him to catch up if he had walked twice as fast? Both the brother and the sister walk at a constant speed.
|
# Answer: 3 minutes.
Solution. Since the brother walked for 12 minutes before meeting his sister, and the sister walked for 18 minutes, the brother's speed was $3 / 2$ times the sister's speed. If the brother's speed is 3 times the sister's speed, which is 2 times faster than before, then the difference of 6 minutes will be covered 4 times faster than before, that is, in 3 minutes.
## Grading Criteria:
- The correct answer with a complete justification is given - 7 points;
- The correct answer and a generally correct justification, with gaps or inaccuracies, is given - 5 points;
- The correct answer with verification is given, but the uniqueness is not proven - no more than 3 points;
- The correct answer is given without justification - 1 point;
- The incorrect answer is given - 0 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the neighboring houses on Happy Street in Sunny Village, two families of 10 people each lived, with the average weight of the members of one family being 1 kg more than the average weight of the members of the other family. After the eldest sons from both families left to study in the city, it turned out that the average weight of the remaining members of one of these families was 1 kg more than the average weight of the remaining members of the other family. By how many kilograms is the weight of one of the departed sons greater than the weight of the other? List all possible options and prove that there are no others.
|
Answer: by 1 kg or by 19 kg.
Solution. The total weight of the members of one of the families before the departure of the elder sons was 10 kg more than the total weight of the members of the other family. If the heavier family remained heavier, then its total weight became 9 kg more than the total weight of the other family, meaning the weight of its departed son was 1 kg more than the other departed son. In the opposite case, its total weight became 9 kg less, meaning the weight of its departed son was 19 kg less than the other departed son.
## Grading Criteria:
- Both answers are provided with full justification - 7 points;
- The correct answer and a generally correct justification are provided, but with gaps or inaccuracies - 5 points;
- One answer is provided with justification - 4 points;
- The correct answer is provided without justification - 2 points;
- An incorrect answer is provided - 0 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5 The numbers $x$, $y$, and $z$ satisfy the equations
$$
x y + y z + z x = x y z, \quad x + y + z = 1
$$
What values can the sum $x^{3} + y^{3} + z^{3}$ take?
|
Solution 1: Let $x y z=p$. Then, from the condition $x y+y z+z x$ is also equal to $p$. Therefore, by Vieta's theorem, the numbers $x, y$, and $z$ are the roots of the polynomial $t^{3}-t^{2}+p t-p$. However, the number 1 is a root of such a polynomial, so one of the numbers is equal to 1. Then the other two numbers are opposite, and the sum of the cubes of all three is 1.
Solution 2: From the condition $x y z=x y+y z+z x$. Then $x^{3}+y^{3}+z^{3}=3 x y z+(x+y+z)\left(x^{2}+y^{2}+\right.$ $\left.z^{2}-x y-y z-z x\right)=3(x y+y z+z x)+\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)=(x+y+z)^{2}=1$.
Solution 3: From the condition
$$
0=(x y z-x y-y z-z x)+(x+y+z-1)=(x-1)(y-1)(z-1) .
$$
Therefore, one of the numbers is equal to 1. Then the other two numbers are opposite, and the sum of the cubes of all three is 1.
## Criteria:
- If it is stated without proof that one of the numbers is equal to 1, and the answer to the problem is derived from this -1 point;
- If it is proven that one of the numbers is equal to 1, but the problem is not solved to the answer -6 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5 On an island, there live 25 people: knights, liars, and tricksters. Knights always tell the truth, liars always lie, and tricksters answer the questions posed to them in turn, alternating between truth and lies. All the islanders were asked three questions: "Are you a knight?", "Are you a trickster?", "Are you a liar?" (the questions were asked in the exact order specified). To the first question, 21 people answered affirmatively, to the second - 17 people, to the third - 6 people. How many knights live on this island?
|
Solution. Each knight will answer "yes" to the first question and "no" to the other two. Each liar will answer "yes" to the first two questions and "no" to the last one. The tricksters can be divided into those who answered the first question truthfully (tricksters of the first type) and those who answered the first question falsely (tricksters of the second type). Tricksters of the first type will answer "no" to all questions, while tricksters of the second type will answer "yes" to all questions. The results can be recorded in a table:
| Type of inhabitant | Are you a knight? | Are you a trickster? | Are you a liar? |
| :---: | :---: | :---: | :---: |
| Knight | yes | no | no |
| Liar | yes | yes | no |
| Trickster 1 type | no | no | no |
| Trickster 2 type | yes | yes | yes |
| Number of "yes" answers | 21 | 17 | 6 |
Note that only tricksters of the second type will answer affirmatively to the last question. Therefore, there are 6 tricksters of the second type. Only tricksters of the first type will not answer affirmatively to the first question, and there are $25-21=4$ of them. The second question will be answered affirmatively by liars and tricksters of the second type (and only them), so there are $17-6=11$ liars. Therefore, the number of knights on the island is $25-6-4-11=4$.
Answer: 4 knights.
| IS IN THE SOLUTION | SCORE |
| :--- | :---: |
| Correct and justified answer | 7 points |
| Correct approach with arithmetic errors, possibly leading to an incorrect answer | deduct 1 point for each error |
| Correctly and justifiedly found only the number of liars or only the number of tricksters | 3 points |
| Considering two types of tricksters (not leading to a solution) | 2 points |
| Correct answer without justification | 1 point |
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. What is the maximum number of L-shaped pieces
| |
| :--- |
consisting of three $1 x 1$ squares, that can be placed in a 5x7 rectangle? (The L-shaped pieces can be rotated and flipped, but they cannot overlap).
|
Solution: The area of the corner is 3, and the area of the rectangle is 35, so 12 corners cannot fit into the rectangle. The image below shows one way to place 11 corners in the rectangle.

Answer: 11
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In triangle $A B C$, the lengths of the sides are known: $A B=4, B C=5, C A=6$. Point $M$ is the midpoint of segment $B C$, and point $H$ is the foot of the perpendicular dropped from $B$ to the angle bisector of angle $A$. Find the length of segment $H M$. If necessary, round your answer to the hundredths.
#
|
# Answer. 1.
Solution. Let $D$ be the intersection point of line $B H$ with line $A C$. Triangle $A B D$ is isosceles because in it the bisector and the altitude from vertex $A$ coincide. Therefore, $H$ is the midpoint of segment $B D$. Then $H M$ is the midline of triangle $B C D$. Note that $C D = A C - A D = A C - A B = 6 - 4 = 2$, from which $H M = C D / 2 = 1$.
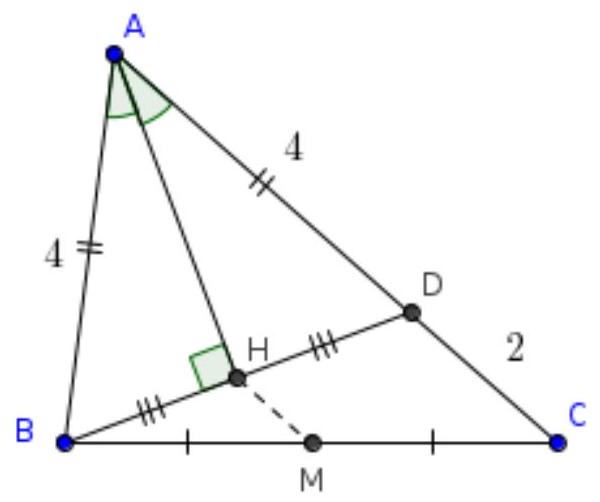
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The school stage of the Magic and Wizardry Olympiad consists of 5 spells. Out of 100 young wizards who participated in the competition,
- 95 correctly performed the 1st spell
- 75 correctly performed the 2nd spell
- 97 correctly performed the 3rd spell
- 95 correctly performed the 4th spell
- 96 correctly performed the 5th spell.
What is the minimum number of students who could have correctly performed exactly 4 out of 5 spells under the described conditions?
|
# Answer: 8.
Solution. The number of students who correctly performed all spells is no more than 75, since only 75 students correctly performed the second spell. The number of students who made mistakes in the 1st, 3rd, 4th, or 5th spells is no more than $(100-95)+(100-97)+(100-95)+(100-96)=$ $5+3+5+4=17$. If a student made a mistake in at least two spells, then they definitely made a mistake in a spell other than the second. Therefore, the number of students who made a mistake in at least two spells does not exceed 17. Then the desired number of students is no less than $100-75-17=8$.
It remains to show that such a number of students is possible. Indeed, let the first 25 students make a mistake in the second spell. Among them, five made a mistake in the first, three in the third, five in the fourth, and four in the fifth. Since $5+3+5+4=17$ is less than 25, these 17 students can be different.
## Information about other clones
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Rational numbers a, b, and c are such that $(a+b+c)(a+b-c)=4 c^{2}$. Prove that $\mathrm{a}+\mathrm{b}=0$.
---
The translation maintains the original text's line breaks and formatting.
|
Solution. The initial equality is equivalent to the following $(a+b)^{2}-c^{2}=4 c^{2}$, or $(a+b)^{2}=5 c^{2}$. If $c \neq 0$, we get $((a+b) / c)^{2}=5 .|(a+b) / c|={ }^{-}$. On the left, we have a rational number, since the sum, quotient, and absolute value of rational numbers are rational, while on the right, we have an irrational number, and the equality is impossible. Therefore, $c=0$ and, consequently, $(a+b)^{2}=0$, and $a+b=0$.
Criteria. The equality $(a+b)^{2}=5 c^{2}$ is obtained, but there is no further progress: 1 point.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. The bisectors $\mathrm{AD}$ and $\mathrm{BE}$ of triangle $\mathrm{ABC}$ intersect at point I. It turns out that the area of triangle ABI is equal to the area of quadrilateral CDIE. Find $AB$, if $CA=9, CB=4$.
|
Answer: 6.
Solution. Let $\mathrm{S}(\mathrm{CDIE})=\mathrm{S}_{1}, \mathrm{~S}(\mathrm{ABI})=\mathrm{S}_{2}$, $S(B D I)=S_{3}, S(A I E)=S_{4}$ (see figure). Since the ratio of the areas of triangles with a common height is equal to the ratio of the bases, and the angle bisector divides the opposite side in the ratio of the adjacent sides, we have $\left(\mathrm{S}_{1}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{2}+\mathrm{S}_{3}\right)=\mathrm{CD} / \mathrm{BD}$ $=\mathrm{AC} / \mathrm{AB} . \quad$ Similarly, $\left(\mathrm{S}_{2}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{1}+\mathrm{S}_{3}\right)$ $=A E / E C=A B / B C$. Since $S_{1}=S_{2}$, then $\left(\mathrm{S}_{1}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{2}+\mathrm{S}_{3}\right)=\quad\left(\mathrm{S}_{2}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{1}+\mathrm{S}_{3}\right) \quad$ from which $A B / B C=A C / A B . \quad A B / 4=9 / A B . \quad A B^{2}=36$,

$\mathrm{AB}=6$ (since the length of a segment is a positive number). It is not difficult to verify that such a triangle exists $(4+6>9)$.
Criteria. The length of the side is found correctly, but there is no check for the existence of the triangle: 6 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A road 28 kilometers long was divided into three unequal parts. The distance between the midpoints of the extreme parts is 16 km. Find the length of the middle part.
|
Answer: 4 km.
Solution. The distance between the midpoints of the outermost sections consists of half of the outer sections and the entire middle section, i.e., twice this number equals the length of the road plus the length of the middle section. Thus, the length of the middle section $=16 * 2-28=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. The older brother took identical uncolored cubes from Misha and used them to build a large cube. After that, he completely painted some (not all) faces of the large cube red. When the paint dried, Misha disassembled the large cube and found that exactly 343 small cubes had no red faces. How many faces of the large cube did Misha's brother paint? Justify your answer.
|
Solution: We will call a small cube that has a red face painted. The size of the large cube is greater than 7 (since only the unpainted cubes amount to $343=7^{3}$, and there are also painted ones), but less than 9 (since all "internal" cubes are unpainted - no more than $7^{3}$). Therefore, it is equal to 8. Out of $8^{3}=512$ cubes that make it up, $6^{3}=216$ are "internal." There remain $343-216=127$ unpainted cubes, which lie on the boundary of the large cube. Each unpainted face will give 36 such cubes (the inner square $6 \times 6$), so there are fewer than four unpainted faces. We will prove that there are at least three. Indeed, if there are fewer, then all corner cubes are painted, and the number of unpainted boundary cubes is even. Therefore, three faces, which have a common vertex, are not painted. Let's check that an $8 \times 8 \times 8$ cube with three unpainted adjacent faces fits. In it, there are $3 \cdot 6^{2}=108$ unpainted cubes (inner cubes of the faces) plus $3 \cdot 6=18$ - cubes on the common edge of two unpainted faces plus one corner - exactly 127 cubes.
Answer: 3 faces.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Proven that there can only be 3 faces, but not shown that the described situation is possible | 6 points |
| Justified that the cube has a size of $8 \times 8 \times 8$, but not proven that the number of painted faces cannot differ from 3 | 4 points |
| Correct answer and an example of a cube and coloring, but the uniqueness is not justified | 2 points |
| Answer without justification and/or incorrect answer | 0 points |
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. A cube lies on a plane. Each face is marked with 1 to 6 points such that the sum of points on opposite faces is always 7. The cube is rolled over the plane as shown in the picture. How many points will be on the top face of the cube when it lands on the last cell?
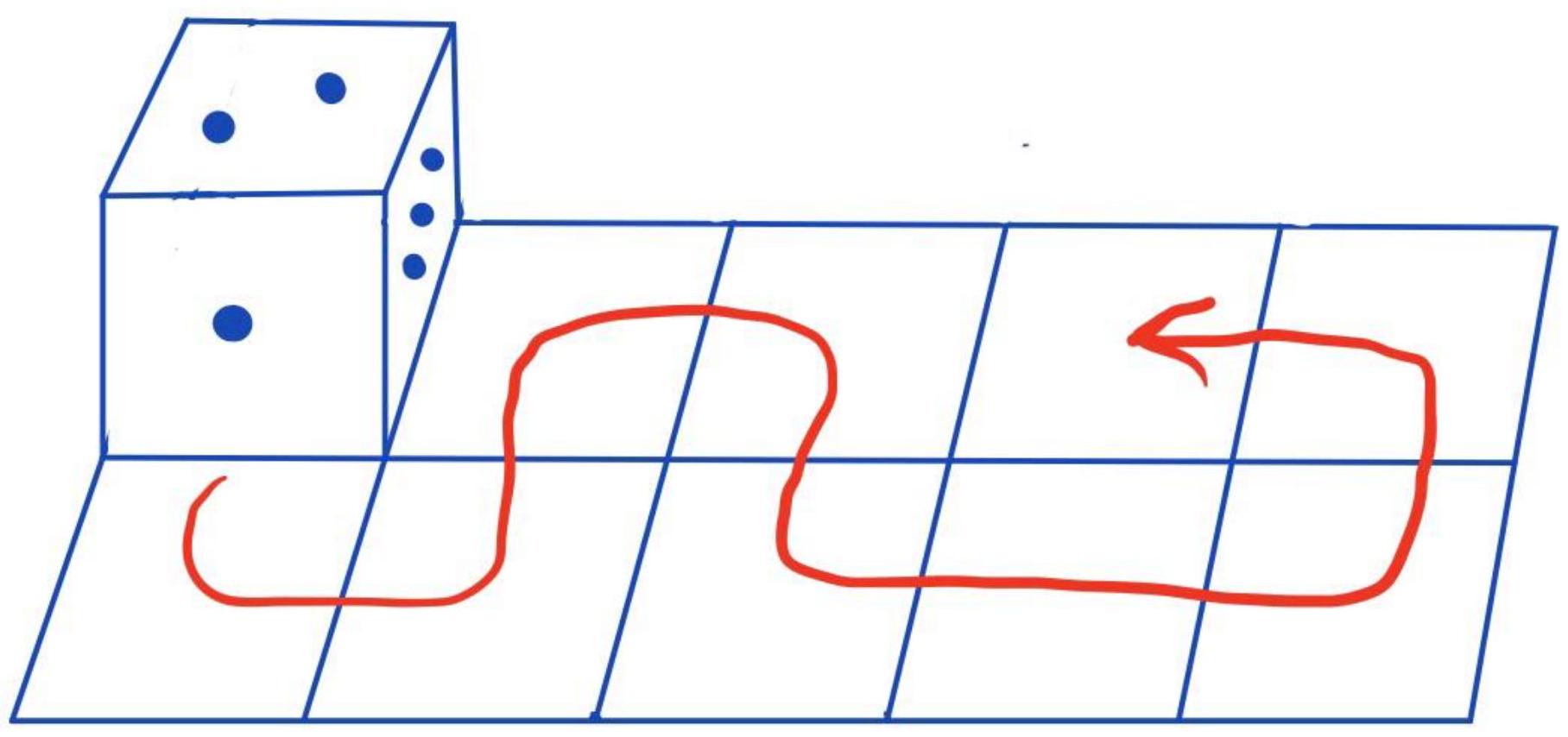
|
Answer: 5
Solution. To find out the answer, you need to imagine rolling the die in the opposite direction and each time keep track of where the face that will end up on top will be. It turns out that this face will be at the bottom in the initial position of the die. Since the top face has 2 dots, the bottom face now has 5 dots.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. On the board, there are five "equations" of the form $x^{2}+\ldots x+\ldots=0$. Two players take turns filling in the dots with natural numbers from 1 to 10, with each number being used only once. The game ends when all numbers are filled in. The player who makes the first move wants to have as many equations as possible with two distinct roots at the end of the game, while his opponent wants to have as few as possible. What is the best result the first player can achieve regardless of the second player's moves?
|
Answer. 3. Solution. To obtain three equations, each having two distinct roots, the first player needs to use the three initial moves to write the largest of the numbers not yet written in the place of the coefficient of $x$ in the "equation" where no number has yet been written. This is possible because if no more than two pairs of moves have been made, the coefficients could have appeared in a maximum of four "equations."
Let $x^{2}+p x+q=0$ be one of the equations obtained at the end of the game, where the coefficient $p$ was written by the first player on one of the first three moves. Then, obviously, $q \leq p-1$, from which $p^{2}-4 q \geq p^{2}-4(p-1)=(p-2)^{2}>0$, because even on the third move of the first player, $p \geq 6$, as only four numbers were used in the first two pairs of moves. Thus, the first player can ensure three equations with two roots each.
To prevent the first player from obtaining more than three equations with two roots, the second player needs to use the first two moves to write the smallest of the numbers not yet written in the place of the coefficient of $x$ in the "equation" where no number has yet been written. Let $x^{2}+p x+q=0$ be one of the equations obtained at the end of the game, where the coefficient $p$ was written by the second player on one of the first two moves. Then, obviously, $p \leq 4$ and $q \geq p+1$, from which $p^{2}-4 q \geq p^{2}-4(p+1)=p(p-4)-4<0$, meaning the equation has no roots.
- Answer without justification - 0 points. If there is a strategy for only one of the players, the solution is evaluated out of 4 points: 2 points for describing the strategy and 2 points for its justification.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 10.5
The altitudes AD and $\mathrm{BE}$ of an acute-angled triangle $\mathrm{ABC}$ intersect at point $\mathrm{H}$.
The circumcircle of triangle $\mathrm{ABH}$ intersects sides $\mathrm{AC}$ and $\mathrm{BC}$ at points $\mathrm{F}$ and $\mathrm{G}$, respectively. Find FG, if $\mathrm{DE}=5$ cm.
## Number of points 7
#
|
# Answer:
$\mathrm{FG}=10 \mathrm{~cm}$
## Solution
We have only one numerical given.
So, the length of FG will either be equal to ED or a multiple of it. It doesn't seem to be equal. It should be larger (judging by the diagram), by some factor. What do we know about such relationships? There is the midline of a triangle, which is half the length of the base. Let's try to show that ED is the midline in triangle FCG. We need E to be the midpoint of FC. Let's look at triangle FCB. It has a height BE. Let's try to show that it is also a bisector (since we also have a circumscribed circle, and a circle involves angles). On FH, there are two angles: FAH and HBF. They are equal. Let's denote them as $\alpha$. Then from the right triangles, we get $\angle \mathrm{C}=90^{0}-\alpha$ and $\angle \mathrm{CBE}=90^{0}-\left(90^{0}-\alpha\right)=\alpha$. We have confirmed that BE is both a height and a bisector, and therefore a median. Similarly, $\mathrm{AD}$ is a median for triangle CAG. Thus, ED is the midline in triangle FCG, and therefore $\mathrm{FG}=10 \mathrm{~cm}$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Cut a $3 \times 9$ rectangle into 8 squares.
7 points are awarded for a complete solution to each problem
The maximum total score is 35
|
5. First, cut the rectangle into three squares of size $3 \times 3$. Leave two of them, and from the third, cut out a square of size $2 \times 2$. Cut the remaining part into 5 squares of size $1 \times 1$. In total, you will have 8 squares.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. The cells of the pyramid are filled according to the following rule: above every two adjacent numbers, their arithmetic mean is written. Some numbers were erased, and the structure shown in the figure was obtained. What number was in the bottom right cell? (The arithmetic mean of two numbers is their sum divided by 2.)
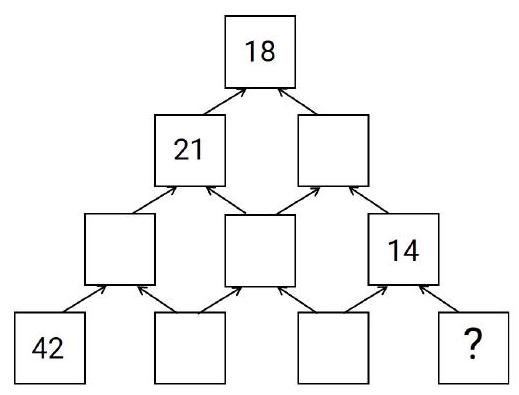
|
Answer: 6.
Solution. Let's restore the numbers in the table by going through it from top to bottom. For example, if the numbers 21 and $x$ are in the second row, then from $18=\frac{1}{2}(21+x)$ we get $x=15$. Similarly, in the third row, we get that next to the number 14 is 16, and next to it is -26; in the last row, the numbers are $42,10,22$ and 6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find $x^{2}+y^{2}+z^{2}$, if $x+y+z=2, \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$.
|
# 9.1. Answer: 4.
## 9th grade
By getting rid of the denominators in the second equation, we get $x y + y z + z x = 0$. Squaring the first equation, we get $x^{2} + y^{2} + z^{2} + 2(x y + y z + z x) = 4$. From this, we obtain the answer.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. For four consecutive natural numbers, it is known that the largest of them is a divisor of the product of the other three. Find all values that the largest of these numbers can take.
|
Answer: 6.
First solution. Let our numbers be $n-3, n-2, n-1, n$, where $n-3 \geqslant 1, n \geqslant 4$. Since the numbers $n-1$ and $n$ are coprime, $(n-3)(n-2)$ is divisible by $n$. Note that $(n-3)(n-2) = n^2 - 5n + 6 = n(n-5) + 6$, and since both numbers $(n-3)(n-2)$ and $n(n-5)$ are divisible by $n$, 6 is also divisible by $n$. Therefore, $n \leqslant 6$, and since the largest number is not greater than 6, we need to check the cases $n=4, n=5$, and $n=6$. Clearly, only $n=6$ works.
Second solution. Let our numbers be $n, n+1, n+2, n+3$. Note that if the largest of these numbers is divisible by a prime $p$, then one of the remaining numbers must also be divisible by $p$, but then their difference, which is no more than 3, must also be divisible by $p$, so $p \leqslant 3$. Therefore, $n+3 = 2^m 3^k$.
If $n+3$ is divisible by 9, then the numbers $n+1$ and $n+2$ are not divisible by 3, so $n$ must be divisible by 9. But then $3 = n+3 - n$ would be divisible by 9. This contradiction shows that $k \leqslant 1$. If $n+3$ is divisible by 4, then the numbers $n$ and $n+2$ are not divisible by 2, so $n+1$ must be divisible by 4. But then $2 = n+3 - (n+1)$ would be divisible by 4. This contradiction shows that $m \leqslant 1$. Therefore, the possible values for the largest number are $1, 2, 3, 6$. Clearly, only the last option works.
Comment. Only the answer - 1 point.
Proved that the largest number has the form $2^m 3^k - 2$ points.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 The Oddball marked the centers of 17 cells in an $N \times N$ grid such that the distance between any two marked points is greater than 2. What is the smallest value that $N$ can take?
|
Solution: We will show that in an $8 \times 8$ square (and then in any smaller size), it is impossible to mark the cells in this way. Indeed, let's divide the square into $2 \times 2$ squares. In each of them, the pairwise distances between the centers of the cells do not exceed $\sqrt{2}$, so no more than one cell is marked in each of the four cells. Therefore, the total number of marked cells does not exceed 16.
Example for a $9 \times 9$ square:
| | | $\mathrm{X}$ | | | | | $\mathrm{X}$ | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathrm{X}$ | | | | | $\mathrm{X}$ | | | |
| | | | X | | | | | $\mathrm{X}$ |
| | $\mathrm{X}$ | | | | | $\mathrm{X}$ | | |
| | | | | $\mathrm{X}$ | | | | |
| | | $\bar{X}$ | | | | | $\mathrm{X}$ | |
| $\mathrm{X}$ | | | | | X | | | |
| | | | X | | | | | $\mathrm{X}$ |
| | $\mathrm{X}$ | | | | | X | | |
## Criteria:
- Only proved that $N>8-3$ points;
- Only provided an example for $N=9-3$ points;
- No points are deducted for the lack of justification in the example.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Dima wrote a sequence of zeros and ones in his notebook. Then he noticed that a one follows a zero 16 times, a one follows 01 seven times, and a zero follows 01 eight times. What could be the last two digits on the board? (In your answer, indicate all options and prove that there are no others).
|
Answer. 01.
Solution. The combination 01 occurs 16 times in the tetrad. After it, $7+8=15$ times there is a 0 or 1, and one time there is not. Therefore, one of the combinations 01 stands at the end of the line.
Criteria. Full solution - 7 points. Partial examples of sequences with the correct answer - 1. Only answer - 0 -
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. CONDITION
A tourist goes on a hike from $A$ to $B$ and back, and completes the entire journey in 3 hours and 41 minutes. The route from $A$ to $B$ first goes uphill, then on flat ground, and finally downhill. Over what distance does the road pass on flat ground, if the tourist's speed is 4 km/h when climbing uphill, 5 km/h on flat ground, and 6 km/h when descending, and the distance $AB$ is 9 km?
|
Solution. Let $x$ km of the path be on flat ground, then $9-x$ km of the path (uphill and downhill) the tourist travels twice, once (each of the ascent or descent) at a speed of 4 km/h, the other at a speed of 6 km/h, and spends $(9-x) / 4+(9-x) / 6$ hours on this part. Since the tourist walks $2 x / 5$ hours on flat ground, and the round trip takes 3 hours and 41 minutes, then $2 x / 5+(9-x) / 4+(9-x) / 6=221 / 60$, from which $x=4$ km.
Answer: 4 km.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Three circles with radii 1, 2, 3 touch each other externally at three points. Find the radius of the circle passing through these three points.
|
Answer: 1.
Solution: Let $\mathrm{O}_{1}, \mathrm{O}_{2}$ and $\mathrm{O}_{3}$ be the centers of the given circles, K, M, N the points of tangency, such that $\mathrm{O}_{1} \mathrm{~K}=\mathrm{O}_{1} \mathrm{~N}=1, \mathrm{O}_{2} \mathrm{~K}=\mathrm{O}_{2} \mathrm{M}=2$ and $\mathrm{O}_{3} \mathrm{~N}=$ $\mathrm{O}_{3} \mathrm{M}=3$. It is known that when two circles touch, the point of tangency lies on the segment connecting their centers. Therefore, K, M, N are points on the sides of the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$. Note that the desired circle coincides with the circle inscribed in the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$. Indeed, since the equalities $\mathrm{O}_{1} \mathrm{~K}=\mathrm{O}_{1} \mathrm{~N}, \mathrm{O}_{2} \mathrm{~K}=\mathrm{O}_{2} \mathrm{M}$ and $\mathrm{O}_{3} \mathrm{~N}=\mathrm{O}_{3} \mathrm{M}$ hold, the points $\mathrm{K}, \mathrm{M}, \mathrm{N}$ are the points of tangency of the inscribed circle with the sides of the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$.
Let $r$ be the desired radius, write the area of the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ in terms of the perimeter and $r$, and using Heron's formula. We get the equation:
$$
\frac{1}{2}(3+4+5) r=\sqrt{6(6-3)(6-4)(6-5)} \Rightarrow 6 r=6 \Rightarrow r=1
$$
## ALL-RUSSIAN SCHOOL OLYMPIAD 2022/23
## MATHEMATICS 11th GRADE
Grading criteria: Correct and justified solution - 7 points, incorrect solution or only answer - $\mathbf{0}$ points.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. What is the minimum number of cells that need to be marked on a 5 by 5 board so that among the marked cells there are no adjacent ones (having a common side or a common vertex), and adding any one cell to these would violate the first condition?
|
Answer: 4 cells.
Solution: Estimation. Divide the board into four parts (see fig.). In each of them, a cell must be marked, otherwise the black cell contained in it can be added.
Example. The four black cells in the figure satisfy both conditions.
Criteria: Answer only - 0 points. Estimation only - 5 points. Example only - 2 points. 7 points are given if both estimation and example are present.
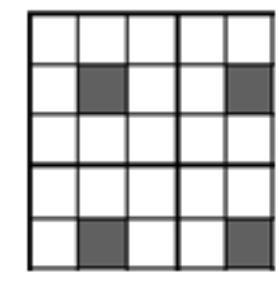
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a white $10 \times 10$ square, on the first move, a $1 \times 1$ cell rectangle is painted, on the second move - a $1 \times 2$ cell rectangle, on the third - $1 \times 3$ and so on, as long as it is possible to do so. After what minimum number of moves could this process end? (Cells cannot be painted over again.)
#
|
# Answer: after 6 moves.
Solution. Evaluation. On the board, 16 rectangles of size $1 \times 6$ can be highlighted, of which a maximum of $1+2+3+4+5=15$ will contain colored cells, meaning that a sixth move is always possible. Example. The process is illustrated in the diagram, showing a scenario where a seventh move is no longer possible.
Criteria. If the solution is incorrect - 0 points.
If only a correct example is provided - 3 points.
If only the correct evaluation is provided - 3 points.
If the solution is correct (any correct example and justification of the evaluation) - 7 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
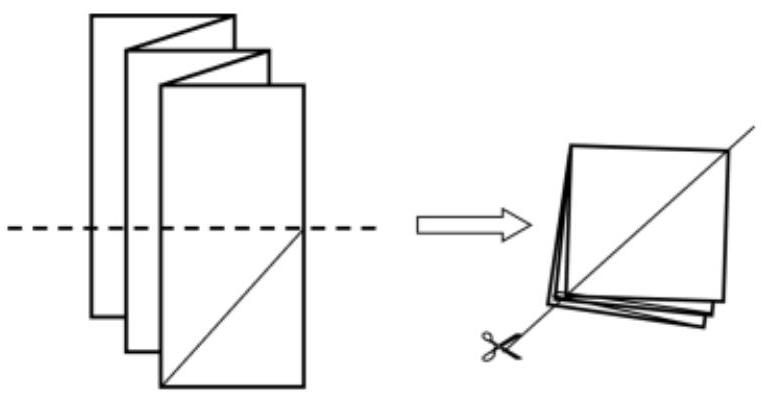
# Task No. 6.1
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
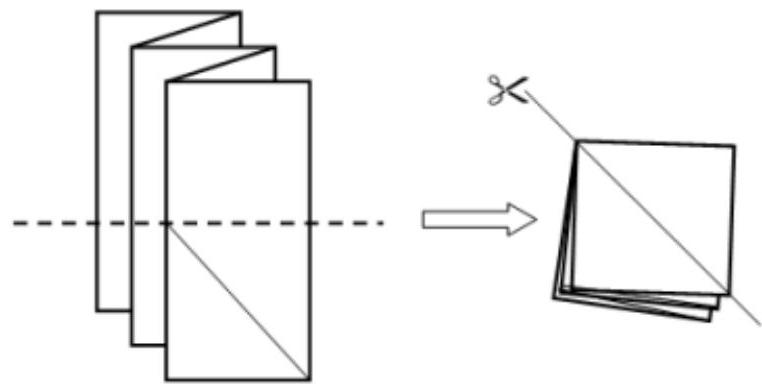
How many pieces of paper were obtained after this?
|
Answer: 9
Exact match of the answer - 1 point
## Solution.
Unfold the paper and mark the lines of the cuts.
Now it is easy to count the resulting pieces. For convenience, they are highlighted in color.
## Problem:
A sheet of paper was folded like an accordion as shown in the picture, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
Answer: 8
Exact match of the answer - 1 point
Solution by analogy with problem № 6.1.
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
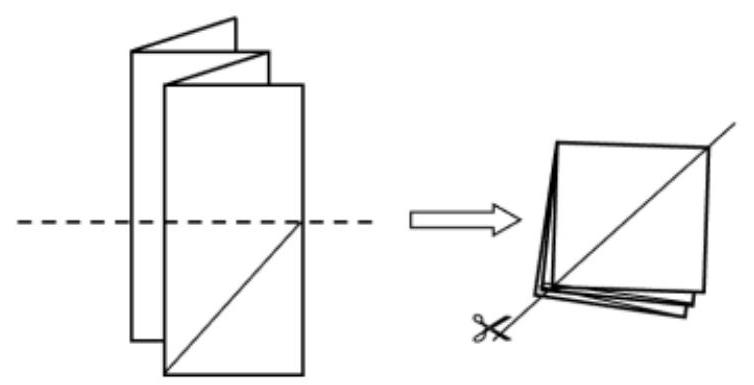
# Task No. 6.3
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
|
Answer: 9
Exact match of the answer -1 point
Solution by analogy with task No. 6.1.
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
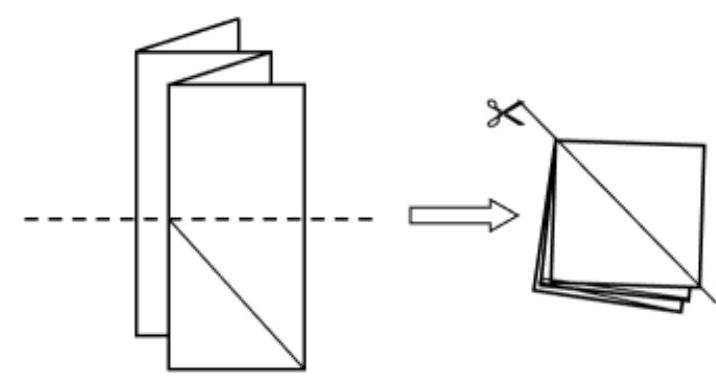
How many pieces of paper were obtained after this
## Answer: 7
Exact match of the answer -1 point
Solution by analogy with task No. 6.1.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In a box, there are several (more than three) balls. Each is painted in some color. If you take out any three balls from the box, there will definitely be at least one red and at least one blue among them. How many balls can be in the box
|
Answer: 4. Solution. In the box, there are no more than two red and blue balls (otherwise, it would be possible to draw three red or three blue balls) and no more than one ball of other colors (otherwise, it would be possible to draw one blue or red ball and two balls of other colors). Therefore, there are no more than five balls in the box, and if there are five, then among them are two blue and two red balls and one of some third color. But then we could draw a ball of the third color and two blue balls. This means that there cannot be five balls in the box. Therefore, there are four: two blue and two red.
Comment. Answer - 0 points, example - 2 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Option 1.
In a box, there are chips. Tolya and Kolya were asked how many chips are in the box. Tolya answered: “Less than 7”, and Kolya answered: “Less than 5”. How many chips can be in the box if it is known that one of the answers is correct? Find all the options. In the answer, write their sum.
|
Answer: 11.
Solution: If there are 7 or more chips in the box, then both boys are lying. If there are 4 or fewer chips in the box, then both boys are telling the truth. If there are 5 or 6 chips in the box, then Tolya is telling the truth, and Kolya is lying.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Variant 1. In the kindergarten, 5 children eat porridge every day, 7 children eat porridge every other day, and the rest never eat porridge. Yesterday, 9 children ate porridge. How many children will eat porridge today?
|
Answer: 8.
Solution. Of the 9 boys who ate porridge yesterday, 5 boys eat it every day, so the remaining $9-5=4$ eat it every other day. Therefore, these four will not eat porridge today, while the other $7-4=3$ of those who eat every other day will. So today, these three, as well as the five who always eat porridge, will eat it. We get the answer $3+5=8$.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1. On a rectangular plot measuring $5 \times 6$ meters, there is a triangular flower bed (see figure). Find the area of this flower bed (in square meters).
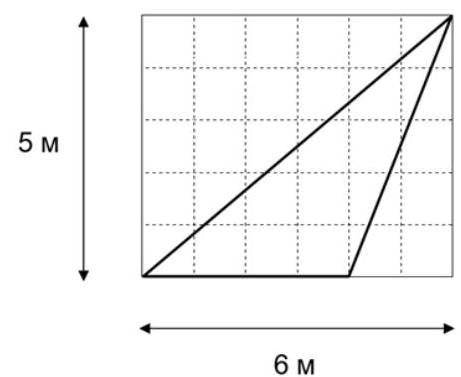
|
Answer: 10.
Solution. The area of the flower bed can be calculated as the difference between the area of the plot and the sum of the areas of the two triangular parts not occupied by the flower bed:
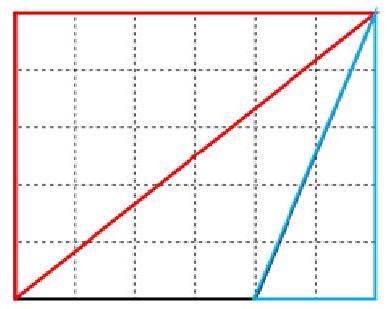
1) $(6 \cdot 5): 2=15\left(\mathrm{m}^{2}\right)-$ area of the red part
2) $(5 \cdot 2): 2=5\left(\mathrm{m}^{2}\right)-$ area of the blue part
3) $5 \cdot 6=30\left(\mathrm{~m}^{2}\right)-$ area of the plot
4) $30-15-5=10\left(\mathrm{~m}^{2}\right)-$ area of the flower bed
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is a paper square $7 \times 7$, all cells of which are white. What is the minimum number of cells that need to be painted black so that it is impossible to cut out a rectangle from it with at least 10 cells, all of which are white?
|
# Answer: 4.
Solution. Divide the $7 \times 7$ square into 5 rectangles (see figure): four $3 \times 4$ and a $1 \times 1$ square. If only three cells are shaded, there will be a white rectangle of 12 cells. How to shade 4 cells is shown in the following figure:
Grading criteria.
Example of four black cells: 3 points.
Estimation that three are not enough: 4 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. A group of schoolchildren decided to buy pizza. Each pizza is cut into 12 pieces. They calculated that if each boy eats 7 pieces and each girl eats 2 pieces, then three pizzas would not be enough. If they buy four pizzas, then each boy can have 8 pieces and each girl can have 4 pieces, and there will still be some left over. How many boys and how many girls are in this group?
|
Answer: 1 girl and 5 boys.
Solution: Let the number of boys be $m$, and the number of girls be $d$. Notice that $7 m+2 d > 36, 8 m+4 d \geq 14$, from which we get $m \geq 5$. But then from the inequality $4 m+2 d \leq 22$ we get that $d \leq 1$, so either $d=0$ or $d=1$. If $d=0$, then $7 m > 36, m > 5$, and $8 m \leq 44, m \leq 5$, a contradiction. If $d=1$, then $7 m > 34, m \geq 5$, and $8 m \leq 40, m \leq 5$, from which $m=5$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the minimum number of 3-cell corners that need to be painted in a $5 \times 5$ square so that no more corners can be painted? (Painted corners should not overlap.)
|
# 3. Answer. 4.
Let the cells of a $5 \times 5$ square be painted in such a way that no more corners can be painted. Consider the 4 corners marked on the diagram. Since none of these corners can be painted, at least one cell in each of them must be painted. Note that one corner cannot paint cells of two marked corners. Therefore, at least 4 corners must be painted.

The following diagram shows how to paint 4 corners so that no more corners can be painted.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. We will call a number greater than 25 semi-prime if it is the sum of some two distinct prime numbers. What is the maximum number of consecutive natural numbers that can be semi-prime?
|
4. Answer. 5.
Note that an odd semiprime number can only be the sum of two and an odd prime number.
Let's show that three consecutive odd numbers \(2n+1, 2n+3\), and \(2n+5\), greater than 25, cannot all be semiprimes simultaneously. Assuming the contrary, we get that the numbers \(2n-1, 2n+1\), and \(2n+3\) are prime, and all of them are greater than 3. But one of these three numbers is divisible by 3, which is a contradiction. Note that among any six consecutive numbers, there are three consecutive odd numbers; therefore, there cannot be more than five consecutive semiprime numbers. Five consecutive numbers can be semiprimes; for example, \(30 = 17 + 13\),
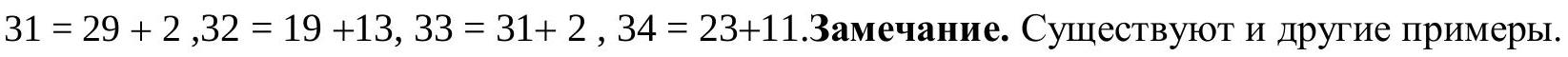
The segment \(C_1M\) is the median of the right triangle \(CC_1A\), so \(CM = \underline{AC} = MA\) (see the figure). Then \(\angle CMA = \pi - 2\angle BAC\). Similarly, \(\angle AMC = \pi - 2\angle BCA\).
From this, \(\angle C_1MA + \angle A_1MC = 2(\pi - \angle BAC - \angle BCA) = 2\angle ABC\),
\(\angle A_1MC_1 = \pi - (\angle AMC_1 + \angle CMA_1) = \pi - 2\angle ABC\).
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
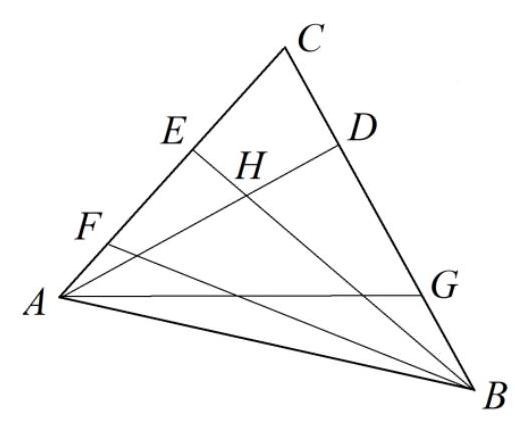
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
|
Answer: 3.
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the problem's condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) The function $f$ is such that for any $x>0, y>0$ the equality $f(x y)=f(x)+f(y)$ holds. Find $f(2019)$, if $f\left(\frac{1}{2019}\right)=1$.
|
Solution. When $y=1 \quad f(x)=f(x)+f(1), f(1)=0$.
When $x=2019 \quad y=\frac{1}{2019} f(1)=f(2019)+f\left(\frac{1}{2019}\right)$,
$f(2019)=f(1)-f\left(\frac{1}{2019}\right)$
$f(2019)=-f\left(\frac{1}{2019}\right)=-1$.
Answer. $f(2019)=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the GCD of all numbers obtained by all possible permutations of the digits of the number 202120222023
Solution. By the divisibility rule, all these numbers are divisible by 9 (the sum of the digits is 18). A sufficient condition to prove that there are no other numbers is that the difference between any two such numbers is also divisible by the GCD. For example, 222222100032 - 222222100023 = 9 is divisible by 9 and cannot be greater than 9.
|
Answer: 9.
## Criteria
7 points - complete solution;
3 points - GCD found, but not proven that there can be no other divisors.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
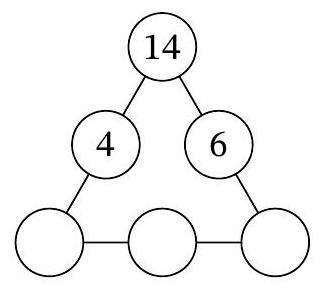
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
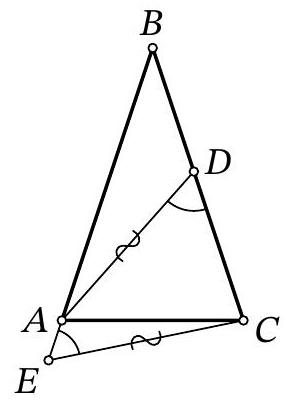
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
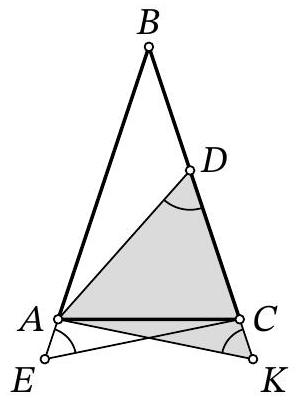
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are $60^{\circ}$, so it is equilateral, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Among fifty consecutive natural numbers, exactly 8 are divisible by 7 without a remainder. What is the remainder when the eleventh number in the sequence is divided by 7?
#
|
# Answer: 3
Solution. The closest numbers that give the same remainder when divided by 7 differ by 7. Therefore, among fifty consecutive numbers, 6 groups of numbers with the same remainder are formed, each containing 7 numbers, and only one group containing 8 numbers, with the first and last numbers among them. Thus, the first number is exactly divisible by 7. Then the eleventh number gives the same remainder when divided by 7 as the fourth, and this remainder is 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. We will build a sequence of numbers in the following way. We will place the number 7 in the first position, and after each number, we will place the sum of the digits of its square, increased by one. For example, the second position will hold the number 14, since $7^{2}=49$, and $4+9+1=14$. The third position will hold the number 17, since $14^{2}=196$, and $1+9+6+1=17$, and so on. What number stands in the 2016th position?
|
Solution Let's continue finding the first few terms of the sequence: $7 ; 14 ; 17 ; 20 ; 5 ; 8 ; 11 ; 5 ; \ldots$ - the number 5 is repeated. This means the sequence has a period of length 3: the numbers 5; 8; 11 will repeat subsequently. The number 8 is in the sixth position, so for any $\mathrm{k}>0$, the number 8 will also be in the $3 \mathrm{k}$-th position. Since $2016=3 \times 672$, the number 8 is in the 2016-th position.
Answer: 8.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
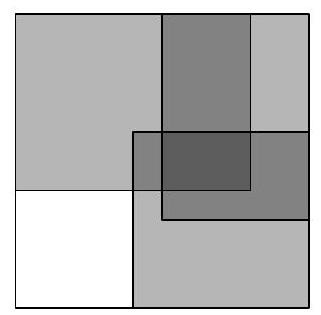
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
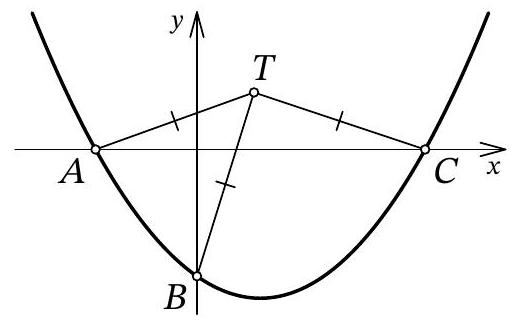
|
Answer: -6.
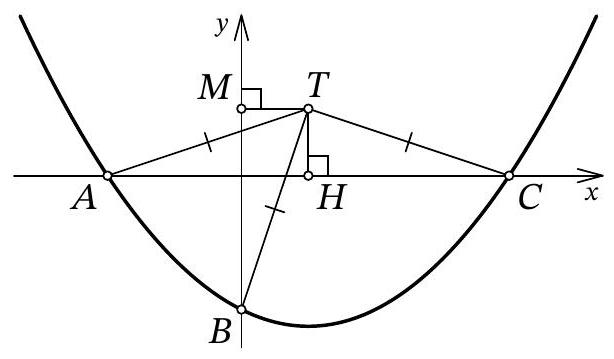
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
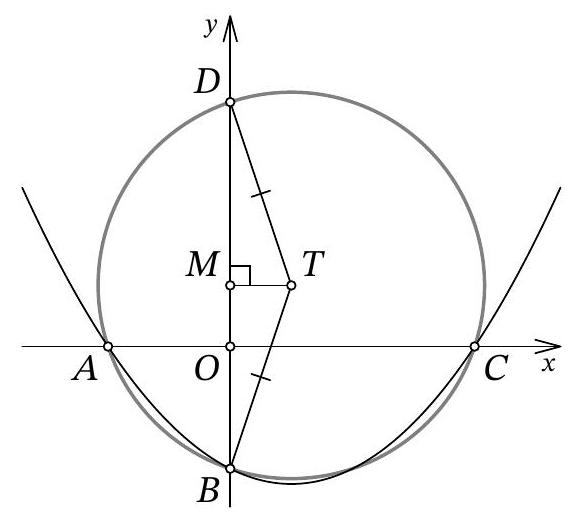
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 Points A, B, C, D are consecutive vertices of a regular n-gon. What is n if $\angle \mathrm{ACD}=120^{\circ}$?
|
Solution. We consider the given n-gon as inscribed.
Each small arc between adjacent vertices is $\frac{1}{\mathrm{n}} \cdot 360^{\circ}$. The angle $\mathrm{ACD}$ is an inscribed angle and subtends an arc consisting of $\mathrm{n}-3$ small arcs, i.e., an arc of $(\mathrm{n}-3) \cdot \frac{1}{\mathrm{n}} \cdot 360^{\circ}$. Therefore, $\angle \mathrm{ACD}=\frac{1}{2} \cdot \frac{\mathrm{n}-3}{\mathrm{n}} \cdot 360^{\circ}=\frac{\mathrm{n}-3}{\mathrm{n}} \cdot 180^{\circ}$. According to the problem, $\frac{\mathrm{n}-3}{\mathrm{n}} \cdot 180^{\circ}=240^{\circ}$. Solving for $\mathrm{n}$, we get $\mathrm{n}=9$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3 Let a, b, c be non-negative integers such that $28a + 30b + 31c = 365$. Prove that $a + b + c = 12$.
|
Solution. If it were $\mathrm{a}+\mathrm{b}+\mathrm{c} \leq 11$, then we would have $28 \mathrm{a}+30 \mathrm{~b}+31 \mathrm{c} \leq 31(\mathrm{a}+\mathrm{b}+\mathrm{c}) \leq 31 \cdot 11 < 365$. Therefore, $\mathrm{a}+\mathrm{b}+\mathrm{c} \geq 12$. We will show that the inequality $\mathrm{a}+\mathrm{b}+\mathrm{c} \geq 13$ is also excluded. For this, note that due to the equality $28 \mathrm{a}+30 \mathrm{~b}+31 \mathrm{c}=365$, the number $\mathrm{c}$ is odd (otherwise, the left side of the equality would represent an even number, while 365 is an odd number). Therefore, $c \geq 1$. Further, if $\mathrm{a}+\mathrm{b}+\mathrm{c} \geq 13$, then we get
$28 \mathrm{a}+30 \mathrm{~b}+31 \mathrm{c}=28(\mathrm{a}+\mathrm{b}+\mathrm{c})+2 \mathrm{~b}+3 \mathrm{c} \geq 28 \cdot 13+2 \cdot 0+3 \cdot 1=267-$ too much! Therefore, $\mathrm{a}+\mathrm{b}+\mathrm{c} \leq 12$. Finally, $\mathrm{a}+\mathrm{b}+\mathrm{c}=12$.
|
12
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. In a chess tournament, 30 chess players participated, each playing against each other exactly once. A win was awarded 1 point, a draw - $1 / 2$, and a loss - 0. What is the maximum number of chess players who could have ended up with exactly 5 points by the end of the tournament?
|
Answer: 11.
Solution. Let $N-$ be the number of chess players with 5 points.
Assume $N \geqslant 12$. In each game between two playing chess players, 1 point is played, so the sum of points of all chess players who scored 5 points at the end of the tournament is no less than $\frac{N \cdot(N-1)}{2}$. Then, by the pigeonhole principle, there will be one among them with points no less than $\frac{\stackrel{2}{N-1}}{2} \geqslant 5.5$, a contradiction. Therefore, $N \leqslant 11$.
We will show that the value $N=11$ is possible. Divide the 30 chess players into two groups: the first with 11 people, and the second with 19. Let each person in each group play to a draw with each other, and also let each person in the first group lose to each person in the second group. It is easy to see that exactly 5 points were scored by all chess players in the first group, and there are 11 of them.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. The frame for three square photographs has the same width everywhere (see figure). The perimeter of one opening is 60 cm, the perimeter of the entire frame is 180 cm. What is the width of the frame?
|
Answer: 5 cm.
Solution. From the condition of the problem, it follows that the length of one hole's side is 15 cm. Let $d$ cm be the width of the frame, then the perimeter of the rectangle is $8 \cdot 15 + 12 d = 120 + 12 d$ (cm). According to the condition, $120 + 12 d = 180$, which means $d = 5$.
Similar reasoning can be conducted without setting up an equation.
## Evaluation Criteria:
+ fully justified solution
$\pm$ the equation is correctly set up (correct line of reasoning), but an arithmetic error is made in solving the equation (in performing a certain operation)
干 the correct answer is guessed and verified that it satisfies the condition
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. The arithmetic mean of four numbers is 10. If one of these numbers is erased, the arithmetic mean of the remaining three increases by 1; if instead another number is erased, the arithmetic mean of the remaining numbers increases by 2; and if only the third number is erased, the arithmetic mean of the remaining increases by 3. By how much will the arithmetic mean of the remaining three numbers change if the fourth number is erased?
|
Answer: will decrease by 6.
Solution. From the fact that the arithmetic mean of four numbers is 10, it follows that the sum of these numbers is 40. Similarly, the sum of three numbers (excluding the first) is 33, the sum of three numbers (excluding the second) is 36, and the sum of three numbers (excluding the third) is 39. From these conditions, we get: the first number is 7, the second is 4, the third is 1. Thus, the arithmetic mean of the first three numbers is 4, which is 6 less than 10.
Similar reasoning can be conducted algebraically. Denoting the four numbers by $a, b, c$, and $d$ respectively, we get four equations: $(a+b+c+d): 4=10, (b+c+d): 3=11, (a+c+d): 3=12$, $(a+b+d): 3=13$. The solution to this system is the set of numbers: $(7,4,1,28)$.
## Evaluation Criteria:
+ fully justified solution
$\pm$ correct line of reasoning (the system of equations is correctly set up), but an arithmetic error is made
the answer is not obtained, but it is proven that the arithmetic mean of the first three numbers is less than 10
$\mp$ the correct answer is obtained by selecting a set of four numbers and verifying that it satisfies the condition (but it is not proven that the found set of four numbers is the only possible one)
- a set of four numbers is given, but it is not even verified
- an error is made in the definition of the arithmetic mean
- the problem is not solved or is solved incorrectly
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.8. On the board, there are $N \geqslant 9$ different non-negative numbers, each less than one. It turns out that for any eight different numbers on the board, there is a ninth, different from them, such that the sum of these nine numbers is an integer. For which $N$ is this possible?
(F. Nilov)
|
Answer. Only for $N=9$.
Solution. It is clear that for $N=9$ the required is possible - it is sufficient to write 9 different positive numbers on the board with a unit sum. We will show that for $N>9$ the required is impossible. Suppose the opposite; let $S$ be the sum of all numbers on the board.
Choose arbitrary numbers $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{7}$ with sum $T$; let $A$ be the set of all other numbers on the board. By the condition, for any number $\beta \in A$ there exists a number $\gamma \in A$ different from it such that the number $T+\beta+\gamma$ is an integer. We say that the number $\gamma$ corresponds to the number $\beta$. Note that such a number $\gamma$ is unique. Indeed, if there were another number $\gamma^{\prime} \in A$ for which the sum $T+\beta+\gamma^{\prime}$ is an integer, then the number $\gamma-\gamma^{\prime}=(T+\beta+\gamma)-\left(T+\beta+\gamma^{\prime}\right)$ would also be an integer; this is impossible, since $0<|\gamma-\gamma^{\prime}|<1$, as $N=7+2 \ell>9$.
Now consider the sum
$$
\Sigma=\left(T+\beta_{1}+\gamma_{1}\right)+\left(T+\beta_{2}+\gamma_{2}\right)+\ldots+\left(T+\beta_{\ell}+\gamma_{\ell}\right)
$$
Then $\Sigma$ is an integer. On the other hand, each number from $A$ appears in $\Sigma$ exactly once; hence, $\Sigma=\ell T+(S-T)=S+(\ell-1) T$, from which $T=\frac{\Sigma-S}{\ell-1}$.
Now, choosing the numbers $\alpha_{2}, \alpha_{3}, \alpha_{4}, \ldots, \alpha_{8}$ on the board and denoting their sum by $T^{\prime}$, we similarly obtain that $T^{\prime}=\frac{\Sigma^{\prime}-S}{\ell-1}$ for an integer $\Sigma^{\prime}$. Therefore,
$$
\alpha_{1}-\alpha_{8}=\frac{\Sigma-S}{\ell-1}-\frac{\Sigma^{\prime}-S}{\ell-1}=\frac{\Sigma-\Sigma^{\prime}}{\ell-1}
$$
Since $\alpha_{1}$ and $\alpha_{8}$ could be any two numbers on the board, we get that the difference of any two numbers on the board has the form $\frac{k}{\ell-1}$ for an integer $k$.
Let $\mu$ be the smallest number on the board. Then the board can only contain the numbers $\mu, \mu+\frac{1}{\ell-1}, \ldots, \mu+\frac{\ell-2}{\ell-1}$ (all larger numbers will already be at least 1) - a total of $\ell$ numbers. However, the total number of numbers on the board is $N=7+2 \ell>\ell$; hence, they cannot all be different. Contradiction.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. There is a balance scale without weights and 11 visually identical coins, among which one may be counterfeit, and it is unknown whether it is lighter or heavier than the genuine coins (genuine coins have the same weight). How can you find at least 8 genuine coins in two weighings?
|
Solution. Let's divide the coins into three piles of three coins each. Compare pile 1 and pile 2, and then compare pile 2 and pile 3. If all three piles weigh the same, then all the coins in them are genuine, and we have found 9 genuine coins. Otherwise, one of the piles differs in weight from the others, and the counterfeit coin can only be in it. Then the genuine coins are in the other two piles plus the two remaining coins that we did not weigh.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Find all numbers of the form $22 \ldots 2$ that can be represented as the sum of two perfect squares.
|
Answer: 2.
Solution. Let $22 \ldots 2=a^{2}+b^{2}$ for some integers $a$ and $b$.
If the numbers $a$ and $b$ are even, then the sum of their squares is divisible by 4, but the number $22 \ldots 2$ is not.
Thus, the numbers $a$ and $b$ can only be odd:
$$
a=2 k+1, b=2 l+1(k, l \in Z)
$$
Therefore, the sum
$$
a^{2}+b^{2}=(2 k+1)^{2}+(2 l+1)^{2}=4 k(k+1)+4 l(l+1)+2
$$
when divided by 8 leaves a remainder of 2.
On the other hand, among the numbers of the form 222... 2, only the number 2 leaves a remainder of 2 when divided by 8, since if the number of twos in this number is greater than 1, then
$22 \ldots 2=22 \ldots 2200+22$, in which the first term of the obtained sum is divisible by 8, and the second term leaves a remainder of 6 when divided by 8.
Comments on evaluation. It is shown that the numbers $a$ and $b$ can only be odd - 2 points.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.1. Find any natural $x$ such that the value of the expression $2^{x}+2^{8}+2^{11}$ is a square of a natural number.
|
Answer: 12.
Solution. Note that $x=12$ works: $2^{12}+2^{8}+2^{11}=\left(2^{6}\right)^{2}+\left(2^{4}\right)^{2}+2 \cdot 2^{6} \cdot 2^{4}=\left(2^{6}+2^{4}\right)^{2}$. Remark. The number $x=12$ is the only one that fits the condition of the problem.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. There are 36 balls lying in a circle, each of which is either red or blue (balls of each of these colors are present). It is known that:
- for any red ball, there is exactly one red ball such that there is exactly one ball between them;
- for any red ball, there is exactly one red ball such that there are exactly three balls between them.
(a) (2 points) Suppose there are no two adjacent red balls. How many red balls can lie in a circle? Indicate all possible options.
(b) (2 points) Suppose there are two adjacent red balls. How many red balls can lie in a circle? Indicate all possible options.
|
Answer:
(a) (2 points) 12.
(b) (2 points) 24.
Solution. By the condition, there will be two red balls, between which lies exactly one ball. Number the balls clockwise with numbers \(1, 2, \ldots, 36\) such that the 1st and 3rd balls are red. From the condition, it follows that the 35th ball is blue (otherwise, the first condition is false for the 1st ball), the 5th ball is blue (otherwise, the first condition is false for the 3rd ball), the 7th ball is red (otherwise, the second condition is false for the 3rd ball), and the 9th ball is red (otherwise, the first condition is false for the 7th ball). Thus, assuming that the 1st and 3rd balls are red, we have that the 5th ball is blue, and the 7th and 9th balls are red. Continuing this reasoning, we get that the 11th ball is blue, the 13th and 15th balls are red, and so on.
Two-thirds of the balls are red, and one-third are blue.
(a) Suppose there are no two adjacent red balls. It is easy to see that then there are no red balls among the balls with even numbers. Therefore, the total number of red balls is \(\frac{36}{2} \cdot \frac{2}{3} = 12\). An example with 12 red balls is shown below.
(b) Suppose there are two adjacent red balls. It is easy to see that then among the balls with even numbers, red balls also constitute two-thirds. Therefore, the total number of red balls is \(36 \cdot \frac{2}{3} = 24\). An example with 24 red balls is shown below.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
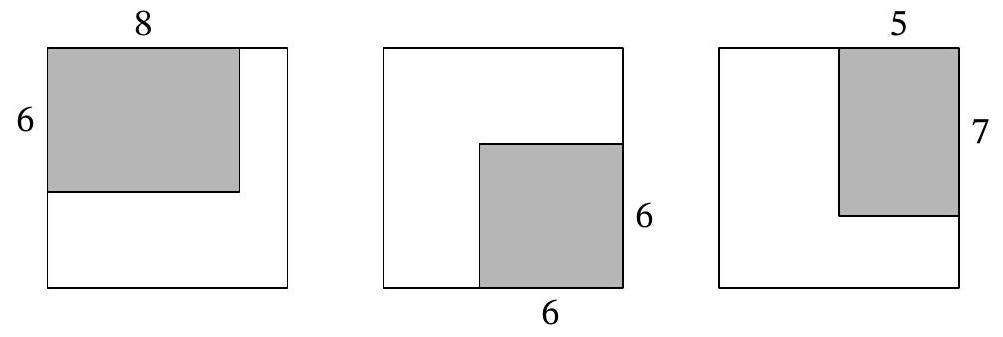
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
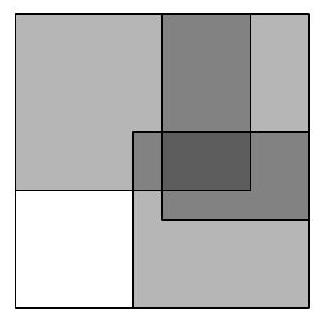
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.

|
Answer: -6.
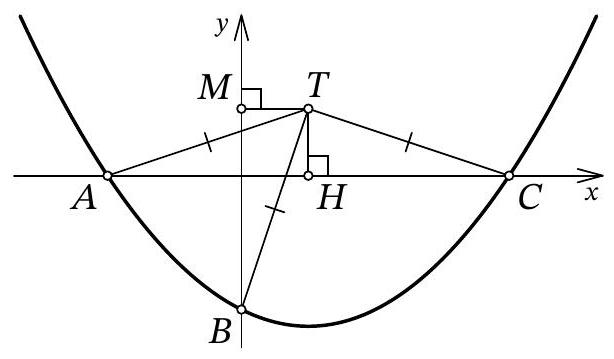
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
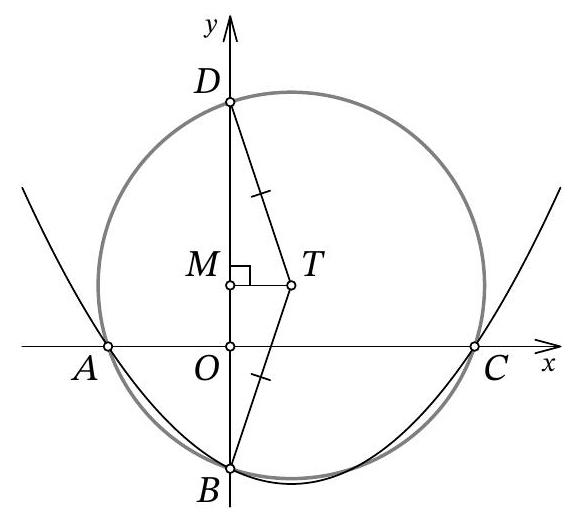
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a room, 15 chairs are arranged in a circle. Three jewelers, when no one is watching, sit on three adjacent chairs, and the one sitting in the middle chair hides a diamond in the chair he is sitting on. The inspector has several detectors that show whether someone has sat on a chair or not. What is the minimum number of detectors he should place on the chairs before the jewelers arrive, so that he can determine from their readings where the diamond is?
|
Answer: 9 detectors.
Instructions. Evaluation. Consider five chairs such that between any two nearest ones there are two other chairs. If there is no detector in two nearest ones, then by adding to the two chairs between them any of them, we get two possible seating arrangements of jewelers, in which the detector readings are the same. To have a detector in any two nearest ones, it is necessary to place at least three detectors in them. Such different quintets can be formed three times. This means that at least $3 \cdot 3=9$ detectors are needed. Example. They need to be placed in groups of three on adjacent chairs in intervals, between which there are two chairs without detectors. The number of activated detectors easily determines which three chairs were occupied.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. What is the total number of emeralds in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $ABCD$ is a square, then $AB=BC=CD=AD$.
Fig. 1: to the solution of problem 8.4
Notice that $\angle ABK = \angle CBL$, since they both complement $\angle ABL$ to $90^{\circ}$. Therefore, right triangles $ABK$ and $CBL$ are congruent by the acute angle and the leg $AB = BC$ (Fig. 1). Consequently, $AK = CL = 6$. Then
$$
LD = CD - CL = AD - CL = (KD - AK) - CL = KD - 2 \cdot CL = 19 - 2 \cdot 6 = 7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Petya runs down from the fourth floor to the first floor 2 seconds faster than his mother rides the elevator. Mother rides the elevator from the fourth floor to the first floor 2 seconds faster than Petya runs down from the fifth floor to the first floor. How many seconds does it take for Petya to run down from the fourth floor to the first floor? (The lengths of the stair flights between all floors are the same).
|
Answer: 12 seconds.
Solution. Between the first and fourth floors, there are 3 flights, and between the fifth and first floors, there are 4. According to the problem, Petya runs 4 flights 2 seconds longer than it takes his mother to ride the elevator, and 3 flights 2 seconds faster than his mother. Therefore, it takes Petya 4 seconds to run one flight. Then from the fourth floor to the first (i.e., 3 flights), Petya runs down in $4 \cdot 3=12$ seconds.
Grading criteria.
- Correct answer with a complete solution - 7 points.
- Explained that it takes 4 seconds for one flight, and the answer is 4 seconds - 5 points.
- Correct reasoning assuming the distance from the fifth floor to the first is 1.25 times the distance from the fourth floor to the first, and the answer is 16 seconds - 3 points.
- Only the answer - 0 points.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the number line, points with integer coordinates are painted red and blue according to the following rules: a) points whose coordinate difference is 7 must be painted the same color; b) points with coordinates 20 and 14 should be painted red, and points with coordinates 71 and 143 - blue. In how many ways can all points with integer coordinates be painted, while adhering to these rules?
|
Answer. In eight ways.
Solution. From part a), it follows that the coloring of all points with integer coordinates is uniquely determined by the coloring of the points corresponding to the numbers $0,1,2,3,4,5$, and 6. The point $0=14-2 \cdot 7$ must be colored the same as 14, i.e., red. Similarly, the point $1=71-10 \cdot 7$ must be colored blue, the point $3=143-20 \cdot 7$ - blue, and $6=20-2 \cdot 7$ - red. Therefore, it remains to count the number of different ways to color the points corresponding to the numbers 2, 4, and 5. Since each point can be colored in two ways - red or blue - the total number of ways is $2 \cdot 2 \cdot 2=8$.
Note. When counting the number of ways to color the points 2, 4, and 5, one can simply list all the ways, for example, in a table:
| 2 | 4 | 5 |
| :--- | :--- | :--- |
| $\kappa p$ | $\kappa p$ | $\kappa p$ |
| $\kappa p$ | $\kappa p$ | $c i n$ |
| $\kappa p$ | $c u n$ | $\kappa p$ |
| $\kappa p$ | $c u n$ | $c i n$ |
| $c u n$ | $\kappa p$ | $\kappa p$ |
| $c i n$ | $\kappa p$ | $c i n$ |
| $c i n$ | $c i n$ | $\kappa p$ |
| $c i n$ | $c i n$ | $c i n$ |
Grading criteria.
- Correct answer with proper justification - 7 points.
- The problem is reduced to counting the number of ways to color 3 points, but the answer is 6 or 7 - 4 points.
- The problem is reduced to counting the number of ways to color 3 points, but the calculation of the number of ways is missing or the answer is different from the ones mentioned earlier - 3 points.
- Answer (including the correct one) without justification - 0 points.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a rectangle $A B C D$. Point $M$ is the midpoint of side $A B$, point $K$ is the midpoint of side $B C$. Segments $A K$ and $C M$ intersect at point $E$. How many times smaller is the area of quadrilateral $M B K E$ compared to the area of quadrilateral $A E C D$?
|
Answer: 4 times.
Solution. Draw segments $MK$ and $AC$. Quadrilateral $MBKE$ consists of triangles $MBK$ and $MKE$, while quadrilateral $AEC D$ consists of triangles $AEC$ and $ACD$. We can reason in different ways.
1st method. Triangles $MBK$ and $ACD$ are right-angled, and the legs of the first are half the length of the legs of the second, so they are similar, and the area of triangle $ACD$ is 4 times the area of triangle $MBK$.
Since $M$ and $K$ are the midpoints of $AB$ and $BC$ respectively, $MK$ is the midline of triangle $ABC$, so $MK \parallel AC$ and $MK = 0.5 AC$. From the parallelism of lines $MK$ and $AC$, it follows that triangles $MKE$ and $AEC$ are similar, and since the similarity coefficient is 0.5, the area of triangle $AEC$ is 4 times the area of triangle $MKE$.
Now: $S_{AEC D} = S_{AEC} + S_{ACD} = 4 S_{MKE} + 4 S_{MBK} = 4 (S_{MKE} + S_{MBK}) = 4 S_{MBKE}$.
2nd method. Let the area of rectangle $ABCD$ be $S$. Then the area of triangle $ACD$ is $\frac{1}{2} S$ (the diagonal of the rectangle divides it into two equal triangles), and the area of triangle $MBK$ is $\frac{1}{2} MB \cdot BK = \frac{1}{2} \cdot \frac{1}{2} AB \cdot \frac{1}{2} BC = \frac{1}{8} AB \cdot BC = \frac{1}{8} S$.
Since $M$ and $K$ are the midpoints of segments $AB$ and $BC$, $AK$ and $CM$ are medians of triangle $ABC$, so $E$ is the centroid of triangle $ABC$, i.e., the distance from $E$ to $AC$ is $\frac{1}{3} h$, where $h$ is the height of triangle $ABC$ from vertex $B$. Then the area of triangle $AEC$ is $\frac{1}{2} AC \left(\frac{1}{3} h\right) = \frac{1}{3} \left(\frac{1}{2} AC h\right) = \frac{1}{3} S_{ABC} = \frac{1}{3} \left(\frac{1}{2} S\right) = \frac{1}{6} S$. Therefore, for the area of quadrilateral $AEC D$, which is the sum of the areas of triangles $AEC$ and $ACD$, we get: $\frac{1}{2} S + \frac{1}{6} S = \frac{2}{3} S$.
Furthermore, since $MK$ is the midline of triangle $ABC$, the area of triangle $MKE$ is $\frac{1}{2} MK \cdot \left(\frac{1}{2} h - \frac{1}{3} h\right) = \frac{1}{2} \left(\frac{1}{2} AC\right) \left(\frac{1}{6} h\right) = \frac{1}{12} \left(\frac{1}{2} AC h\right) = \frac{1}{12} S_{ACD} = \frac{1}{24} S$. Therefore, for the area of quadrilateral $MBKE$, which is the sum of the areas of triangles $MBK$ and $MKE$, we get: $\frac{1}{8} S + \frac{1}{24} S = \frac{1}{6} S$.
Thus, the ratio of the areas of quadrilaterals $AEC D$ and $MBKE$ is $\frac{2}{3} S : \left(\frac{1}{6} S\right) = 4$.
Grading criteria.
- Correct solution and correct answer - 7 points.
- Correct solution, but incorrect answer due to an arithmetic error - 5 points.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. There are 40 pencils of four colors - 10 pencils of each color. They were distributed among 10 children so that each received 4 pencils. What is the smallest number of children that can always be selected to ensure that pencils of all colors are found among them, regardless of the distribution of pencils?
(I. Bogdanov, O. Podlipsky)
|
10.1. Answer. 3 boys.
We will show that it is always possible to choose three boys such that they have pencils of all colors. Since there are 10 pencils of each color and each boy received 4 pencils, at least one boy must have received pencils of at least two different colors. It remains to add to him two boys who have pencils of the remaining two colors.
Now, let's show how to distribute the pencils to the boys so that any two of them together have pencils of no more than three colors. Distribute 4 pencils of the second color to two boys, 4 pencils of the third color to two boys, 4 pencils of the fourth color to two boys, 4 pencils of the first color to one boy, 2 pencils of the first and second colors to one boy, 2 pencils of the first and third colors to one boy, and 2 pencils of the first and fourth colors to one boy.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Plot the graph of the function $\mathrm{y}=\sqrt{4 \sin ^{4} x-2 \cos 2 x+3}+\sqrt{4 \cos ^{4} x+2 \cos 2 x+3}$.
|
Answer. The graph of the function will be the line $y = 4$.
## Solution.
$\mathrm{y}=\sqrt{4 \sin ^{4} x-2 \cos 2 x+3}+\sqrt{4 \cos ^{4} x+2 \cos 2 x+3}$
$\mathrm{y}=\sqrt{4 \sin ^{4} x-2+4 \sin ^{2} x+3}+\sqrt{4 \cos ^{4} x+4 \cos ^{2} x-2+3}$
$\mathrm{y}=\sqrt{4 \sin ^{4} x+4 \sin ^{2} x+1}+\sqrt{4 \cos ^{4} x+4 \cos ^{2} x+1}$
$\mathrm{y}=2 \sin ^{2} x+1+2 \cos ^{2} x+1, \mathrm{y}=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
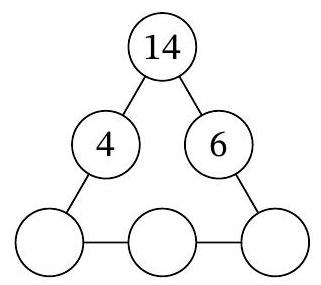
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.

|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
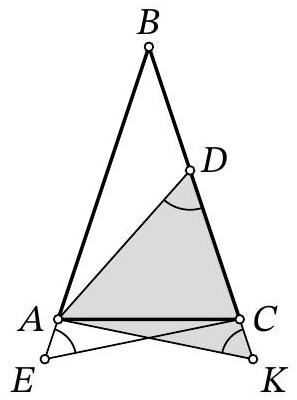
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are $60^{\circ}$, so it is equilateral, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. What is the maximum number of digits that a natural number can have, where all digits are different, and it is divisible by each of its digits?
|
Answer: 7 digits.
Evaluation. There are 10 digits in total. The number cannot contain the digit 0, so there are no more than 9. If all 9, then the digit 5 must be at the end of the number (divisibility rule for 5), but in this case, the number must also be divisible by 2. Therefore, the digit 5 is not in this number. If the number lacks only 0 and 5, then it contains 9, and the sum of the digits of this number will be 40, which contradicts divisibility by 9. Thus, there are no more than seven digits.
An example of such a number is 9176328. Verification. The three-digit number formed by the last three digits is 328, which is divisible by 8, meaning the given number is divisible by its digits 2 and 8. The sum of the digits of this number is 36, so it is divisible by 3 and 9, and also by 6. It is easy to see that it is divisible by 7: $9176328: 7=1310904$.
Remarks. An example of a seven-digit number with verification is provided - 3 points. It is proven that there are no more than seven digits, but an example of such a number is not provided - 3 points. If both are present, 7 points.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Dima was supposed to arrive at the station at 18:00. By this time, his father was supposed to pick him up in a car. However, Dima managed to catch an earlier train and arrived at the station at 17:05. He didn't wait for his father and started walking towards him. On the way, they met, Dima got into the car, and they arrived home 10 minutes earlier than the planned time. At what speed was Dima walking before the meeting with his father, if the car's speed was $60 \mathrm{km} / \mathrm{h}$?
|
Answer: 6 km/h
Solution. Dima arrived home 10 minutes earlier, during which time the car would have traveled the distance Dima walked twice. Therefore, on the way to the station, the father saved 5 minutes and met Dima at 17:55. This means Dima walked the distance from the station to the meeting point in 50 minutes, so he walked 10 times slower than the car, and his speed was 6 km/h.
## Grading Criteria.
- Complete correct solution - 7 points.
- Generally correct solution with insufficient justifications (in particular, a diagram of the movement is drawn with incomplete justifications) - 5 points.
- Correct approach but incorrect answer due to arithmetic error - 4 points.
- It is found that the meeting time is 17:55, but there is no further progress - 2 points.
- It is found that the father saved 5 minutes on the way to the station, but it is incorrectly assumed that Dima walked for 55 minutes before the meeting - 2 points.
- Only the correct answer is provided - 1 point.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $ABC$, the median from vertex $A$ is perpendicular to the bisector of angle $B$, and the median from vertex $B$ is perpendicular to the bisector of angle $A$. It is known that side $AB=1$. Find the perimeter of triangle $ABC$.
|
Answer: 5.
Solution. Let $A M$ be the median drawn from vertex $A$. Then, in triangle $A B M$, the bisector of angle $B$ is perpendicular to side $A M$, i.e., the bisector is also an altitude. Therefore, this triangle is isosceles, $A B = B M = 1$. Hence, $B C = 2 B M = 2$. Similarly, from the second condition, we get that side $A C$ is twice the length of $A B$, so the perimeter of triangle $A B C$ is $1 + 2 + 2 = 5$.

## Grading Criteria.
- Correct solution - 7 points.
- It is determined that the triangle cut off by one of the medians is isosceles, but there is no further progress - 3 points.
- Only the correct answer is provided - 1 point.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There are three vessels with volumes of 3 liters, 4 liters, and 5 liters, without any markings, a water tap, a sink, and 3 liters of syrup in the smallest vessel. Can you, using pourings, obtain 6 liters of a water-syrup mixture such that the amount of water is equal to the amount of syrup in each vessel?
|
Solution.
For example, as follows (see the table below, c - syrup, w - water, f - final mixture).
| |  | 4-liter container | 5-liter container |
| :---: | :---: | :---: | :---: |
| Pour the syrup into the 5-liter container, and using the 3- and 4-liter containers, get 2 liters of water in the 4-liter container. | $3 \mathrm{c}$ | 0 | 0 |
| | 0 | 0 | $3 \mathrm{c}$ |
| | Zw | 0 | $3 \mathrm{c}$ |
| | 0 | Zw | $3 \mathrm{c}$ |
| | Zw | Zw | $3 \mathrm{c}$ |
| | 2B | 4B | $3 \mathrm{c}$ |
| | 2B | 0 | $3 \mathrm{c}$ |
| | 0 | 2B | $3 \mathrm{c}$ |
| Then fill the 4-liter container with syrup to get 4 liters of the required mixture. | 0 | $2 \mathrm{~B}+2 \mathrm{c}=4$ f | $1 \mathrm{c}$ |
|  | Zi | 1f | $1 \mathrm{c}$ |
| | Zi | $1 f+1 c$ | 0 |
| | 0 | $1 f+1 c$ | Zi |
| | $1 f+1 c$ | 0 | Zi |
| | 1 f $+1 c+1$ w $=3$ f | 0 | Zi |
## Grading Criteria.
- Correct algorithm - 7 points.
- Less than 6 liters of the required mixture obtained (i.e., the required mixture is obtained in one container, but the ratio is not maintained in the other) — no more than 1 point.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
|
Answer: 3.
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 2.3
## Condition:
Dmitry has socks in his wardrobe: 14 pairs of blue socks, 24 pairs of black socks, and 10 pairs of white socks. Dmitry bought some more pairs of black socks and found that now the black socks make up 3/5 of the total number of socks. How many pairs of black socks did Dmitry buy?
|
Answer: 12
Exact match of the answer -1 point
Solution by analogy with task №2.1.
#
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 6.4
## Condition:
On the faces of a cube, 6 letters are drawn: A, B, V, G, D, E. The picture shows three images of the cube from different angles. Which letter is drawn on the face opposite the face with the letter $\mathrm{A}$?

## Answer Options:
○ A
$\circ$ B
$\circ$ V
$\circ$ G
$\circ$ D
○ E
## Correct Answer:
○ B
Exact match of the answer - 1 point
|
Solution by analogy with problem №6.1.
## Condition:
Anya, Borya, and Vasya took the same test consisting of 6 questions, each of which can be answered with "yes" or "no." The answers are presented in the table:
| Question No. | 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Anya | no | no | yes | yes | yes | yes |
| Borya | yes | no | no | yes | yes | yes |
| Vasya | no | yes | no | no | no | no |
It turned out that Anya has two incorrect answers, and Borya has only two correct answers. How many correct answers does Vasya have?
Answer: 3
Exact match of the answer - 1 point
## Solution.
Anya has 4 correct answers, and Borya has 2. Therefore, there are at least two questions on which Anya answered correctly, and Borya answered incorrectly. However, Anya and Borya gave different answers to exactly two questions: the first and third. Therefore, it is precisely on these questions that Anya answered correctly, and Borya answered incorrectly. Vasya's answer to the first question matches Anya's, and on the third question, it does not. Therefore, among these two of Vasya's answers, exactly one is correct. Anya's and Borya's answers to the four remaining questions coincide. Therefore, among them, two are correct and two are incorrect. Vasya's answers to all these questions are opposite to Anya's and Borya's. Therefore, among them, two are correct (where Anya and Borya's answers are incorrect) and two are incorrect (where Anya and Borya's answers are correct). Adding 1 and 2, we get the answer.
## Condition:
Anya, Borya, and Vasya took the same test consisting of 6 questions, each of which can be answered with "yes" or "no." The answers are presented in the table:
| Question No. | 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Anya | yes | no | no | yes | no | yes |
| Borya | no | no | yes | yes | no | yes |
| Vasya | no | yes | no | no | yes | no |
It turned out that Anya has two incorrect answers, and Borya has only two correct answers. How many incorrect answers does Vasya have?
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with problem №7.1.
## Condition:
Anya, Borya, and Vasya took the same test consisting of 6 questions, each of which can be answered with "yes" or "no." The answers are presented in the table:
| Question No. | 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Anya | no | no | yes | yes | yes | yes |
| Borya | yes | no | yes | yes | yes | no |
| Vasya | no | yes | no | no | no | no |
It turned out that Anya has two incorrect answers, and Borya has only two correct answers. How many correct answers does Vasya have?
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with problem №7.1.
|
3
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
10.6. On the board, the expression $\cos x$ is written. It is allowed to add or multiply several expressions written on the board (an expression can be used multiple times) and write the new obtained expression on the board. Is it possible to get an expression that takes the value 0 when $x=\pi$ after several actions?
(N. Agakhanov)
|
Answer. Yes, it is possible.
Solution. The first action is to append $\cos ^{2} x$, the second is to append $\cos ^{2} x+\cos x$. Since $\cos \pi=-1$, the value of the last expression at $x=\pi$ is 0.
Comment. An answer without presenting the required expression - 0 points.
Only presenting any correct required expression without indicating the sequence of steps leading to it - 6 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Three lines intersect to form 12 angles, and $n$ of them turn out to be equal. What is the maximum possible value of $n$?
|
Answer: 6.
Solution: Three lines limit a certain triangle. If this triangle is equilateral, then out of twelve angles, six are $60^{\circ}$, and the other six are $120^{\circ}$.
Can any external angle of the triangle be equal to its internal angle? It is equal to the sum of the non-adjacent internal angles, so it is greater than each of the non-adjacent ones. Therefore, it can only be equal to the adjacent one. Then each of them is $90^{\circ}$, and there are 4 such angles (they share a common vertex). There are no other right angles in this construction. But then the other external angles are not equal to the internal ones. Equal can only be the internal ones (and the vertical ones to them) or only the external ones (and the vertical ones to them). Then there will be no more than 4 equal angles of each type.
Criteria: 3 points for an example with six equal angles, 3 points for comparing external and internal angles. 1 point for an answer without justification.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1
In trapezoid $A B C D(A D \| B C)$, the bisectors of angles $D A B$ and $A B C$ intersect on side $C D$. Find $A B$, if $A D=5, B C=2$.
|
Answer: 7.
Solution.
Mark point $L$ on side $AB$ such that $LB = BC$. Let $K$ be the intersection point of the angle bisectors of $\angle DAB$ and $\angle ABC$. Then triangles $LBK$ and $BCK$ are congruent by angle and two adjacent sides $\Rightarrow \angle BLK = \angle BCK$. Therefore, $\angle ALK = 180^\circ - \angle BLK = 180^\circ - \angle BCK = \angle ADC$ (the last equality holds because $AD \parallel BC$). Finally, $\triangle ALK = \triangle ADC$ by angles and a common side. Thus, $AB = AD + BC$.
## Variant 2
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 5$, $BC = 3$.
Answer: 8.
## Variant 3
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 7$, $BC = 2$.
Answer: 9.
## Variant 4
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 11$, $BC = 5$.
Answer: 16.
## Variant 5
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 10$, $BC = 3$.
Answer: 13.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.5. The hedgehogs collected 65 mushrooms and divided them so that each hedgehog got at least one mushroom, but no two hedgehogs had the same number of mushrooms. What is the maximum number of hedgehogs that could be
|
Answer: 10
Solution: If there were 11 hedgehogs, then together they would have collected no less than $1+2+3+\ldots+10+11=66$ mushrooms, which exceeds the total number of mushrooms collected. Therefore, there were fewer than 11 hedgehogs. We will show that there could have been 10 hedgehogs. Suppose the first found 1 mushroom, the second found 2 mushrooms, the third found 3, and so on, the ninth found 9 mushrooms. Then the nine hedgehogs collected $1+2+\ldots+8+9=45$ mushrooms. If the tenth found 20, then all together they collected 65 mushrooms.
Comment. Only the correct answer - 0 points. If an example for 10 hedgehogs is shown without proving the impossibility for 11, then - 4 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.