problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
10.5. Given an odd number $n>10$. Find the number of ways to arrange the natural numbers $1,2,3, \ldots, n$ in a circle in some order so that each number is a divisor of the sum of the two adjacent numbers. (Ways that differ by rotation or reflection are considered the same.) (D. Khramov)
|
Answer. Two ways
Solution. Consider an arbitrary arrangement of numbers from 1 to $n$ that satisfies the conditions. Suppose that two even numbers $x$ and $y$ are adjacent, and the next number is $z$. Since $x+z$ is divisible by $y$, the number $z$ is also even. Continuing this movement around the circle, we get that all numbers in the arrangement are even, which is impossible. Therefore, no two even numbers are adjacent; hence, some two odd numbers are adjacent, and the even and odd numbers alternate.
Note that both neighbors of the number $n$ cannot be even; indeed, otherwise their sum would be divisible by $2n$, i.e., it would be at least $2n$. Therefore, for any odd number less than $n$, either both neighbors are even, or one of the neighbors is the number $n$.
Suppose that the numbers $n$ and $n-2$ are neighbors, and the other neighbor of the number $n-2$ is the number $t$. The number $t+n=(n-2)+(t+2)$ must be divisible by $n-2$, which is only possible if $t=n-4$. But then three odd numbers $n, n-2, n-4$ are adjacent, which, as we have shown, is impossible.
Thus, both neighbors of the odd number $n-2$ are even, and therefore their sum is divisible by $2(n-2)$, i.e., this sum is at least $2(n-2)$; this is only possible if these neighbors are $n-1$ and $n-3$. In particular, the numbers $n-1$ and $n-2$ are neighbors. If the pair $n-1, n-2$ continues with numbers in descending order up to the number 1, we arrive at the circular arrangement $n-1, n-2, n-3, n-4, \ldots, 3, 2, 1, n$, which obviously satisfies the condition.
Now suppose that the pair $n-1, n-2$ continues with numbers in descending order up to the number $d>1$, and after it follows the number $x \neq d-1$. Thus, we have the numbers $n-1, n-2, \ldots, d+1, d, x, y, \ldots$ in a row around the circle. Since $x+(d+1)=(x+1)+d$ is divisible by $d$, then $x+1$ is divisible by $d$, in particular, $x \geq d-1$. But $x$ is different from the numbers $d-1, d, \ldots, n-2, n-1$; hence, the only remaining option is $x=n$.
Let $n=2k+1$. We have obtained that the number $n+1=2k+2$ is divisible by $d$; since $d<10$, the only possible values for $d$ are 1, 2, or 4. If $d=1$, the arrangement is $n, n-1, n-2, n-3, \ldots, 3, 2, 1$, which satisfies the condition. If $d=2$, the arrangement is $2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, k-1, k-2, \ldots, 1$, which also satisfies the condition. If $d=4$, the arrangement is $2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, k-1, k-2, \ldots, 1$, which also satisfies the condition.
For $n>10$, the arrangement $n, n-1, n-2, n-3, \ldots, 3, 2, 1$ is the only one that satisfies the condition.
Comment. Only the correct answer or the correct answer with the presentation of one of the two required arrangements - 0 points.
Points for the following advancements from different parts a), b), c) are summed.
a) Two examples of arrangements that satisfy the condition are found - 1 point.
b) It is proven that the numbers $n-1$ and $n-2$ are adjacent - 2 points.
If it is only proven that two even numbers do not stand next to each other - 1 point out of these 2.
c) Assuming that $n-1$ and $n-2$ are adjacent, it is proven that the chain uniquely continues to one of the examples $(n-1, n-2, n-3, \ldots, 2, 1, n)$ or $(2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, k-1, k-2, \ldots) - 4$ points.
If it is only proven that the continuation has the form $(n-1, n-2, \ldots, d+1, d, n, \ldots)$ for some $d$ - 1 point out of these 4.
If it is proven that the continuation has the form $(n-1, n-2, n-3, \ldots, 2, 1, n)$ or $(2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, \ldots) - 3$ points out of these 4.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Given quadratic trinomials $f_{1}(x), f_{2}(x), \ldots, f_{100}(x)$ with the same coefficients for $x^{2}$, the same coefficients for $x$, but different constant terms; each of them has two roots. For each trinomial $f_{i}(x)$, one root was chosen and denoted by $x_{i}$. What values can the sum $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{100}\left(x_{99}\right)+f_{1}\left(x_{100}\right)$ take?
(N. Agakhanov)
|
Answer: Only 0.
Solution: Let the $i$-th quadratic polynomial have the form $f_{i}(x)=a x^{2}+b x+c_{i}$. Then
$f_{2}\left(x_{1}\right)=a x_{1}^{2}+b x_{1}+c_{2}=\left(a x_{1}^{2}+b x_{1}+c_{1}\right)+\left(c_{2}-c_{1}\right)=c_{2}-c_{1}$, since $f_{1}\left(x_{1}\right)=0$. Similarly, we obtain the equalities $f_{3}\left(x_{2}\right)=$ $=c_{3}-c_{2}, \ldots, f_{100}\left(x_{99}\right)=c_{100}-c_{99}$ and $f_{1}\left(x_{100}\right)=c_{1}-c_{100}$.
By adding the obtained equalities, we get $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{1}\left(x_{100}\right)=\left(c_{2}-c_{1}\right)+\ldots+\left(c_{1}-c_{100}\right)=0$. Therefore, the only possible value of the sum is zero.
Comment: A correct answer without justification - 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. King Hiero has 11 metal ingots that are indistinguishable in appearance; the king knows that their weights (in some order) are 1, $2, \ldots, 11$ kg. He also has a bag that will tear if more than 11 kg is placed in it. Archimedes has learned the weights of all the ingots and wants to prove to Hiero that the first ingot weighs 1 kg. In one step, he can load several ingots into the bag and demonstrate to Hiero that the bag does not tear (the bag cannot be torn!). What is the minimum number of bag loadings Archimedes needs to achieve the required result?
(I. Bogdanov, K. Knop)
|
Answer. In 2 loads.
Solution. We will show that Archimedes can use the bag only twice. Let him first put in the bag ingots weighing 1, 2, 3, and 5 kg, and then ingots weighing 1, 4, and 6 kg. In both cases, the bag will not tear.
We will prove that this could only happen if the 1 kg ingot was used twice. Indeed, if Archimedes used ingots weighing $w_{1}, \ldots, w_{6}$ kg instead of ingots weighing 1, ..., 6 kg, these weights would satisfy the system of inequalities $w_{1}+w_{2}+w_{3}+w_{5} \leqslant 11, w_{1}+w_{4}+w_{6} \leqslant 11$. Adding these inequalities, we get $w_{1}+(w_{1}+w_{2}+\ldots+w_{6}) \leqslant 22$. The sum in parentheses is the sum of six different natural numbers, so it is at least $1+2+\ldots+6=21$. Therefore, $w_{1} \leqslant 22-21=1$. Hence, $w_{1}=1$, which means the 1 kg ingot is uniquely determined.
It remains to show that one load is insufficient. If Archimedes loads only one ingot, the bag will not tear in any case, so no ingot can be identified. Suppose Archimedes loads more than one ingot, and the bag does not tear. If the 1 kg ingot is not loaded into the bag, then replacing it with any ingot in the bag will not change the result; in this case, Hiero will not be able to determine whether this ingot is in the bag. If the required ingot is in the bag, then Hiero will not be able to determine which of the (at least two) loaded ingots is the required one.
Remark. After the specified two loads, the group of weights 2, 3, and 5 kg, as well as the group of weights 4 and 6 kg, are also uniquely determined.
Comment. Only proved that one load is insufficient - 1 point.
Only provided a correct example of two loads, but did not prove that it works - 3 points (these points can be combined with the previous one).
Provided a correct example of two loads, proved that it works, but did not prove that one load is insufficient - 6 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Given quadratic trinomials $f_{1}(x), f_{2}(x), \ldots, f_{100}(x)$ with the same coefficients for $x^{2}$, the same coefficients for $x$, but different constant terms; each of them has two roots. For each trinomial $f_{i}(x)$, one root was chosen and denoted by $x_{i}$. What values can the sum $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{100}\left(x_{99}\right)+f_{1}\left(x_{100}\right)$ take?
|
Answer: Only 0.
Solution. Let the $i$-th quadratic polynomial have the form $f_{i}(x)=a x^{2}+b x+c_{i}$. Then
$$
f_{2}\left(x_{1}\right)=a x_{1}^{2}+b x_{1}+c_{2}=\left(a x_{1}^{2}+b x_{1}+c_{1}\right)+\left(c_{2}-c_{1}\right)=c_{2}-c_{1},
$$
since $f_{1}\left(x_{1}\right)=0$. Similarly, we obtain the equalities $f_{3}\left(x_{2}\right)=$ $=c_{3}-c_{2}, \ldots, f_{100}\left(x_{99}\right)=c_{100}-c_{99}$ and $f_{1}\left(x_{100}\right)=c_{1}-c_{100}$.
Adding the obtained equalities, we get $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{1}\left(x_{100}\right)=\left(c_{2}-c_{1}\right)+\ldots+\left(c_{1}-c_{100}\right)=0$. Therefore, the only possible value of the sum is zero.
Comment. A correct answer without justification - 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. What different values can the digit U take in the puzzle U$\cdot$LAN + U$\cdot$DE = 2020? Justify your answer. (Identical digits are replaced by the same letters, different digits by different letters.)
|
Answer: two. $\mathrm{V}=2, \mathrm{y}=5$.
Solution: Factor out the common factor: У$\cdot$(ЛАН + ДЭ) $=2020$. Note that У, Л, and Э are not equal to 0.
Factorize the right-hand side: $2020=1 \cdot 2 \cdot 2 \cdot 5 \cdot 101$. Since У is a digit, consider all possible values: $\mathrm{V}=1,2,4,5$.
1) $У=1$. Then ЛАН + ДЭ $=2020$, but ЛАН + ДЭ $<999+99=1098<2020$. No solutions.
2) $\mathbf{y}=2$, ЛАН + ДЭ $=1010$.
There are 8 different solutions, for example, $2 \cdot 974+2 \cdot 36=2020$
3) $У=4$, ЛАН + ДЭ $=505$. Clearly, Л $\leq 5$.
Л $\neq 5$, because otherwise ЛАН $\geq 501$, but then ДЭ cannot be a two-digit number.
$Л \neq 4$, because $У=4$.
For Л $=3$, АН + ДЭ $=205$. But АН + ДЭ $\leq 99+99=198$ < 205. No solutions.
4) $\mathbf{y}=\mathbf{5}$, ЛАН + ДЭ $=404$.
There are 14 different solutions, for example, $5 \cdot 306+5 \cdot 98=2020$
# Criteria:
7 points - correct answer and complete correct solution;
only one answer found and justified - 4 points;
only answer - 0 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. Each cell of a $7 \times 8$ table (7 rows and 8 columns) is painted in one of three colors: red, yellow, or green. In each row, the number of red cells is not less than the number of yellow cells and not less than the number of green cells, and in each column, the number of yellow cells is not less than the number of red cells and not less than the number of green cells. How many green cells can there be in such a table?
|
Answer: 8.
Solution. 1) In each row of the table, there are no fewer red cells than yellow ones, so in the entire table, there are no fewer red cells than yellow ones.
In each column of the table, there are no fewer yellow cells than red ones, so in the entire table, there are no fewer yellow cells than red ones.
Thus, in the table, there is an equal number of red
| 3 | 3 | ॠ | $\mathbf{K}$ | Ж世 | К | WK | $\mathbf{K}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| К | Ж | 3 | 3 | К | Ж | $\mathbf{K}$ | Ж |
| З | $\boldsymbol{\kappa}$ | $\mathbf{K}$ | Ж | 3 | 6 | ऊ | |
| К | Ж | ЖК | $\mathbf{K}$ | ЗК | К | 3 | 3 |
| ЗК | $\mathbf{K}$ | $\mathbf{K}$ | Ж | K | Ж | $\mathbf{K}$ | |
| K | ऊ币 | $\overline{\mathbf{K}}$ | Ж | $\mathbf{K}$ | ऊ | $\mathbf{K}$ | ज्ञ |
| Ж | $\mathbf{K}$ | З | $\mathbf{K}$ | ЗK | K | Ж | |
and yellow cells.
2) Suppose that in some column, there are more yellow cells than red ones. Since in each of the other columns, there are no fewer yellow cells than red ones, then in the entire table, there would be more yellow cells than red ones, but this is not the case (see 1). Therefore, in each of the eight columns, there are an equal number of red and yellow cells.
3) Since in each column, there are no fewer yellow cells than green ones, the cases where in each column: a) 1 yellow, 1 red, 5 green cells and b) 2 yellow, 2 red, 3 green cells are excluded.
The only remaining case is when in each column there are 3 red, 3 yellow, and 1 green cell. Then, in total, there are 8 green cells in the table.
This case is possible. For example, see the table.
## Evaluation Criteria
+ A complete and well-reasoned solution is provided
$\pm$ A generally correct solution is provided, containing minor gaps or inaccuracies
干 It is proven that there can only be 8 green cells, but an example is not provided
Ғ Only the correct answer and an example are provided
- Only the answer is provided
- The problem is not solved or is solved incorrectly
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Alyosha and Vitya set off from point $N$ to point $M$, the distance between which is 20 km. Unfortunately, they have only one bicycle between them. From $N$, Alyosha sets off on the bicycle, while Vitya starts walking. Alyosha can leave the bicycle at any point along the road and continue on foot. When Vitya reaches this point, he switches to the bicycle. Alyosha's walking speed is 4 km/h, and his cycling speed is 15 km/h. Vitya's walking speed is 5 km/h, and his cycling speed is 20 km/h. At what point should Alyosha leave the bicycle so that they both arrive in $M$ at the same time?
|
Answer. 12 km from point $N$.
Solution. Let $x$ (km) be the distance from $N$ to the point where Alyosha leaves the bicycle. Then Alyosha will spend $\frac{x}{15}+\frac{20-x}{4}$ hours on the entire journey, and Vitya will spend $\frac{x}{5}+\frac{20-x}{20}$ hours. By setting up and solving the equation, we find $x=12$ (km).
Comment. Only the answer - 1 point. The equation for finding the distance is correctly set up, but not solved - 3 points. An arithmetic error is made in solving the equation, but the rest is correct - 5 points.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
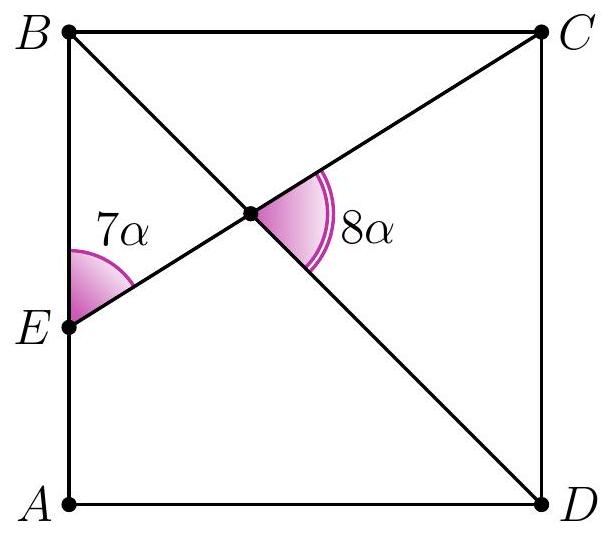
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
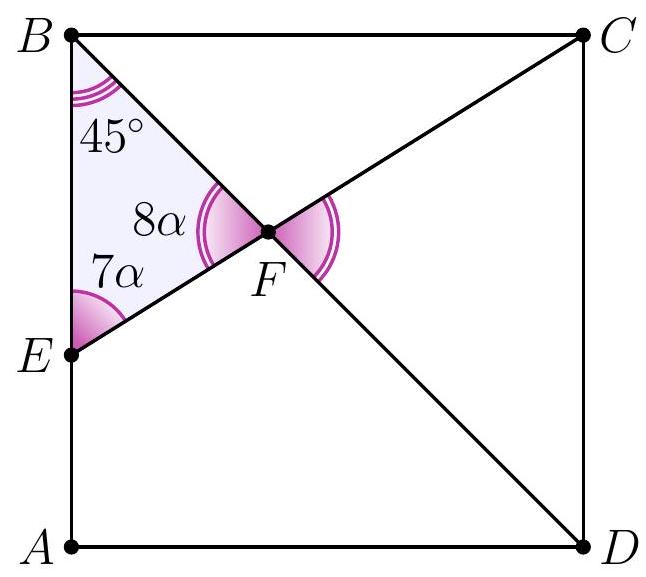
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
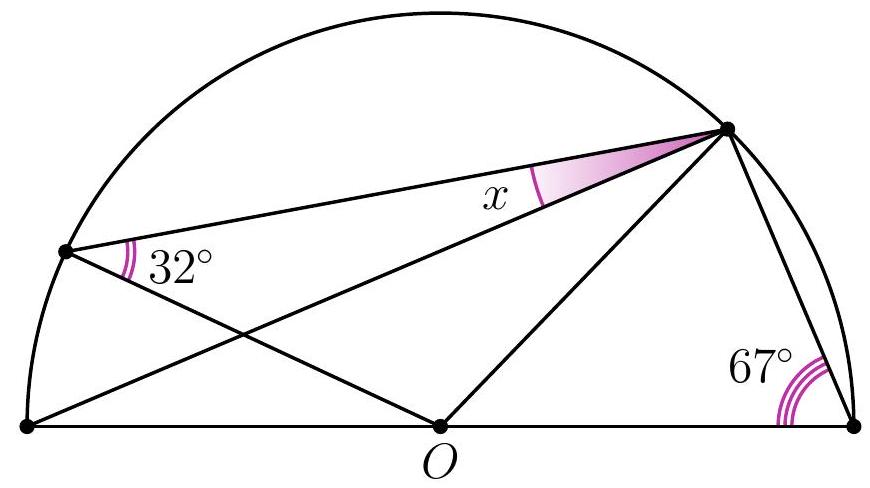
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
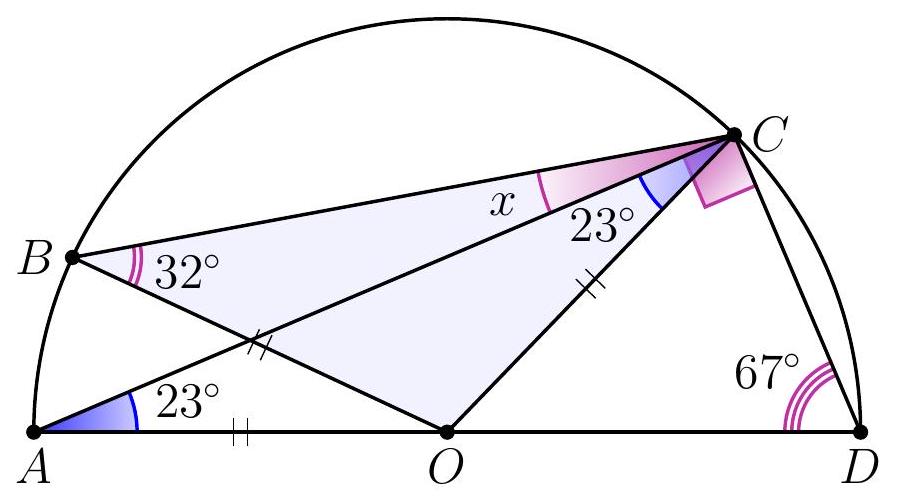
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. In a bag, there were cards with numbers from 1 to 20. Vlad drew 6 cards and said that all these cards can be divided into pairs so that the sums of the numbers in each pair are the same. Lena managed to peek at 5 of Vlad's cards: the numbers on them were $2, 4, 9, 17, 19$. What number was on the card that Lena didn't manage to peek at? (It is sufficient to provide one suitable answer.)
|
Answer: 12.
Solution. To calculate the answer, one needs to select four numbers out of the given five such that the sum of two of them equals the sum of the other two. By enumeration, it is not difficult to verify that these numbers are $2,4,17,19(2+19=4+17)$.
Thus, the number on the remaining card is $12(2+19=4+17=9+12)$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A row of 11 numbers is written such that the sum of any three consecutive numbers is 18. Additionally, the sum of all the numbers is 64. Find the central number.
|
Answer: 8.
Solution. Number the numbers from left to right from 1 to 11.
Notice that the sum of the five central numbers (from the fourth to the eighth) is 64 (the sum of all numbers) $-2 \cdot 18$ (the sum of the numbers in the first and last triplets) $=28$.
Then the sixth (central) number is 18 (the sum of the fourth, fifth, and sixth numbers) +18 (the sum of the sixth, seventh, and eighth numbers) -28 (the sum of the central five numbers) $=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the numerical value of the expression
$$
\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{2}{x y+1}
$$
if it is known that $x$ is not equal to $y$ and the sum of the first two terms is equal to the third.
|
Answer: 2.
Solution. Let's bring the condition to a common denominator
$$
\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}=\frac{2}{x y+1}
$$
we get
$$
\frac{\left(x^{2}+y^{2}+2\right)(x y+1)-2\left(x^{2}+1\right)\left(y^{2}+1\right)}{\left(x^{2}+1\right)\left(y^{2}+1\right)(x y+1)}=0
$$
expand all brackets in the numerator, combine like terms, we get the equality $(x-y)^{2}(x y-1)=0$. Since $x \neq y$, then $x y=1$. From this, the third term equals 1, and then the entire sum equals 2.
Criteria. Full solution - 7 points. Correctly brought to a common denominator, like terms correctly combined, but without further progress - 1 point. Reasoning of the type "if $x$ is taken this way, and $y$ another way, then something will result" is rated 0 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. A football team coach loves to experiment with the lineup. During training sessions, he divides 20 available field players into two teams of 10 players each, adds goalkeepers, and arranges a game between the teams. He wants any two field players to end up on different teams at some training session. What is the minimum number of training sessions that must take place for this to happen?
|
# 9.5. 5 Training Sessions.
Note that four training sessions are insufficient. Let's take 10 football players who played on the same team during the first training session. During the second training session, at least five of them will be on the same team again. During the third training session, at least three of these five will be on the same team again. Finally, two of these three will be on the same team during the fourth training session.
However, five training sessions are sufficient. Here is an example of team distribution.
| | Team 1 | Team 2 |
| :--- | :---: | :---: |
| Training 1 | $1-10$ | $11-20$ |
| Training 2 | $1-5,11-15$ | $6-10,16-20$ |
| Training 3 | $1-3,6-7,11-13,16-17$ | $4-5,8-10,14-15,18-20$ |
| Training 4 | $1-2,4,6,8,11-12,14,16,18$ | $3,5,7,9-10,13,15,17,19-20$ |
| Training 5 | $2,4,6,8,10,12,14,16,18,20$ | $1,3,5,7,9,11,13,15,17,19$, |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Fishermen caught several carp and pike. Each caught as many carp as all the others caught pike. How many fishermen were there if the total number of carp caught was 10 times the number of pike? Justify your answer.
|
# Solution:
Method 1. Each fisherman caught as many carp and pike together as the total number of pike caught. Summing the catches of all fishermen, we get that the total catch of all fishermen (in terms of the number of fish) is equal to the total number of pike caught, multiplied by the number of fishermen. On the other hand, there are 10 times more carp than pike, so the total catch in terms of the number of fish is 11 times the number of pike. Therefore, there are 11 fishermen in total.
Method 2. Let the total number of fishermen be $n$, and the $i$-th fisherman caught $a_{i}$ pike and $b_{i}$ carp $(i=\overline{1, n})$. Then $b_{k}=\left(\sum_{i=1}^{n} a_{i}\right)-a_{k}$ for all $k$. Summing these equalities over $k$, we get
$\sum_{i=1}^{n} b_{i}=n \cdot \sum_{i=1}^{n} a_{i}-\sum_{i=1}^{n} a_{i}=(n-1) \cdot \sum_{i=1}^{n} a_{i}$. But $\sum_{i=1}^{n} b_{i}=10 \cdot \sum_{i=1}^{n} a_{i}$, from which $n-1=10$ and $n=11$.
Answer: 11 fishermen.
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| A correct approach but an incorrect answer due to arithmetic or algebraic errors | 5 points |
| Correctly formulated but unsolved system of equations, fully describing the problem's conditions | 3 points |
| Only specific cases are considered, for example, when all fishermen caught the same number of pike | 1 point |
| Correct answer without justification or illustrated by a finite number of examples | 0 points |
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. We consider all possible pairs of quadratic equations $x^{2} + p x + q = 0$ and $x^{2} + q x + p = 0$ such that each equation has two distinct roots. Is it true that the expression $\frac{1}{x_{1} x_{3}} + \frac{1}{x_{1} x_{4}} + \frac{1}{x_{2} x_{3}} + \frac{1}{x_{2} x_{4}}$, where the numbers $x_{1}, x_{2}$ are the roots of the first equation, and the numbers $x_{3}, x_{4}$ are the roots of the second, is the same for all such pairs (i.e., does not depend on the numbers $p$ and $q$)? Justify your answer.
|
Solution: According to Vieta's theorem
$$
x_{1} x_{2}=-\left(x_{3}+x_{4}\right)=q \text { and } x_{3} x_{4}=-\left(x_{1}+x_{2}\right)=p
$$
Then
$$
\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}=\frac{x_{3}+x_{4}}{x_{1} x_{3} x_{4}}=-\frac{q}{p x_{1}}
$$
Similarly
$$
\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}=-\frac{q}{p x_{2}}
$$
Then
$$
\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}+\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}=-\frac{q}{p}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}\right)=-\frac{q}{p} \cdot \frac{x_{2}+x_{1}}{x_{1} x_{2}}=-\frac{q}{p} \cdot\left(-\frac{p}{q}\right)=1
$$
that is, the same for all pairs of equations.
Note 1: Such pairs of equations exist. The task does not require providing examples of such pairs.
Note 2: The problem can also be solved "head-on," by writing the roots of the equations using the root formula (via discriminants), substituting them into the expression, and performing the necessary transformations. The solution will be somewhat longer, but that's all.
Answer: Correct.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The solution does not include examples of pairs of such equations | points not reduced |
| Roots of the equations are correctly found and substituted into the expression Or Vieta's theorem is correctly written for both equations, but further transformations are incorrect or incomplete | 2 points |
| :--- | :--- |
| The correct answer is illustrated with several examples | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.3. In the distant times of stagnation in the Soviet Union, 15 and 20 kopeck coins were in circulation. Schoolboy Valera had a certain amount of money only in such coins. Moreover, the number of 20 kopeck coins was greater than the number of 15 kopeck coins. Valera spent one-fifth of all his money, paying two coins for a movie ticket. He then spent half of the remaining money on lunch, paying with three coins. How many coins of each denomination did Valera have initially? Justify your answer.
|
Solution: One fifth of Valera's capital could be either 30, 35, or 40 kopecks. Then, after buying the ticket, he should have had 120, 140, or 160 kopecks left, and the cost of the lunch was either 60, 70, or 80 kopecks. The maximum value of three coins is 60 kopecks, so the last two scenarios are impossible. Therefore, Valera had lunch for 60 kopecks, paying with three "twenty-kopeck" coins, paid 30 kopecks for the movie ticket (using 2 "fifteen-kopeck" coins), and had 60 kopecks left. This amount could be made up either with 4 coins of 15 kopecks each, or 3 coins of 20 kopecks each. In the first case, it turns out that Valera had 6 "fifteen-kopeck" coins and 3 "twenty-kopeck" coins, which contradicts the condition. The second case leads to the correct answer: 2 coins of 15 kopecks and 6 coins of 20 kopecks.
Answer: 2 coins of 15 kopecks and 6 coins of 20 kopecks.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| In the correct solution, there are computational errors (possibly leading to an incorrect answer) | deduct 1 point for each error |
| In the exhaustive solution, exactly one case was not considered | 4 points |
| :--- | :--- |
| In the exhaustive solution, more than one case was not considered | 2 points |
| Correct answer supported by calculations, but without proof of its uniqueness | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The city center is a rectangle measuring $5 \times 8$ km, consisting of 40 blocks, each $1 \times 1$ km, with boundaries formed by streets that create 54 intersections. What is the minimum number of police officers needed to be placed at the intersections so that any intersection can be reached by at least one police officer driving no more than 2 km along the city streets?
Answer: 6 police officers.
|
Solution. Evaluation. Consider the intersections on the boundary. There are 26 in total. Each police officer can control no more than 5 intersections (if he is on the boundary, then exactly 5, if he is inside the city, then no more than 3 on each side and no more than 5 in the corner). Therefore, at least 6 police officers are needed.
Example (see fig).
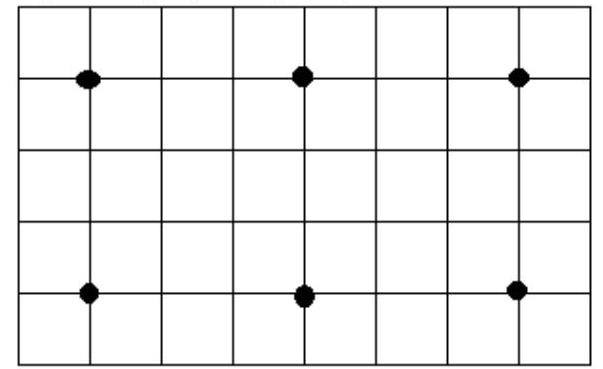
Criteria. If the solution is incorrect - 0 points.
If only an example is constructed - 2 points.
If only the evaluation is proven - 4 points.
If the correct solution (both example and evaluation) - 7 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. The hunter told a friend that he saw a wolf with a one-meter tail in the forest. That friend told another friend that a wolf with a two-meter tail had been seen in the forest. Passing on the news further, ordinary people doubled the length of the tail, while cowards tripled it. As a result, the 10th channel reported about a wolf with a tail 864 meters long. How many ordinary and how many cowardly people "grew" the wolf's tail? Provide all possible answers and prove that there are no others.
|
Solution: Note that when information is transmitted by ordinary people, the length of the tail is multiplied by 2, and when transmitted by cowardly people, it is multiplied by 3. Therefore, the number of twos in the product equals the number of ordinary people (and the number of threes equals the number of cowardly people) through whom the information has passed. This number does not depend on the order in which the information reached these people. Let's factorize the number 864 into prime factors. We get $864=2^{5} \cdot 3^{3}$. Therefore, the number of ordinary and cowardly people who grew the wolf's tail was 5 and 3, respectively.
Answer: 5 ordinary people and 3 cowardly people.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| Answer is incorrect only due to arithmetic errors | 6 points |
| Correct answer is confirmed by an example showing how the wolf's tail length could have "changed" | 4 points |
| It is justified that the length of the "grown" tail does not depend on the order in which the information was transmitted by ordinary and cowardly people, but there is no solution. | 2 points |
| Correct answer without justification | 1 point |
| Principally incorrect reasoning | 0 points |
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Lisa wrote a quadratic equation. Artem erased its free term, so the equation now looks like $\operatorname{\operatorname {mak}} 2 x^{2}+20 x+\ldots=0$. Lisa doesn't remember what number Artem erased, but she remembers that the equation has exactly one real root. What is this root?
|
# Answer: -5
Solution. A quadratic equation has one root if and only if its discriminant is 0. And if the discriminant is 0, then the root is calculated using the formula $x_{1}=-b /(2 a)=-20 / 4=-5$.
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. A paper rectangle $4 \times 8$ was folded along the diagonal as shown in the figure. What is the area of the triangle that is covered twice?
|
Answer: 10.
Solution. By the Pythagorean theorem, $A C=\sqrt{A B^{2}+B C^{2}}=4 \sqrt{5}$. Triangle $A E C$ is isosceles, and if we drop the height $E H$ in it, then triangle $A E H$ will be similar to triangle $A C D$. Therefore, $A H / E H=A D / D C=2 . A H=2 \sqrt{5}$, since the height in an isosceles triangle is also a median. Thus, $E H=\sqrt{5}, S(A E C)=\sqrt{5} \cdot 4 \sqrt{5} / 2=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Real $x, y, z$ are such that $x y + x z + y z + x + y + z = -3, x^{2} + y^{2} + z^{2} = 5$. What is $x + y + z$?
|
Answer: -1
Solution. Add twice the first equation to the second, we get $(x+y+z)^{2}+2(x+y+z)=-1$. Therefore, $(x+y+z+1)^{2}=0, x+y+z=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A $7 \times 7$ checkered board was assembled using three types of figures (see the image), not necessarily all. How many figures, composed of four cells, could have been used?
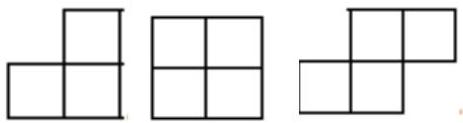
|
Answer: only one.
Solution. We will prove that only one figure consisting of four cells can be used. We will color the cells of the board as shown in Fig. 11.5a: Each of the given figures can cover no more than one shaded cell, therefore, the number of figures must be no less than 16.
Since 16 three-cell figures cover 48 cells, one such figure consisting of four cells must be used. More than one cannot be used.

Indeed, if at least two figures consisting of four cells are used, and the remaining 14 figures are three-cell ones, together they will occupy \(2 \cdot 4 + 14 \cdot 3 = 50\) cells, which exceeds the size of the board.
An example of a board composed of one four-cell figure and fifteen three-cell figures is shown in Fig. 11.56.
There are other examples as well. They can be obtained by highlighting 7 rectangles of size \(3 \times 2\) on the board, each of which can be divided into two three-cell corners, and placing one three-cell and one four-cell figure in the remaining part of the board.
Evaluation criteria.
«+» A complete and justified solution is provided
Fig. 11.56 «士» It is proven that there are no fewer than 16 figures and the correct answer is given, but the example is missing
«Ғ» Only the correct answer and the correct example are provided
«-» Only the answer is provided
«-» The problem is not solved or is solved incorrectly
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the basket, there are fruits (no less than five). If you randomly pick three fruits, there will definitely be an apple among them. If you randomly pick four fruits, there will definitely be a pear among them. What fruits can be picked and in what quantities if you randomly pick five fruits?
|
Solution. From the condition of the problem, it follows that the "non-apples" in the box are no more than two fruits (otherwise, you could pull out 3 fruits, none of which would be apples). Similarly, "non-pears" are no more than three fruits (otherwise, you could pull out 4 fruits, none of which would be pears). Thus, there are exactly 5 fruits in the box: three apples and two pears. These are the ones that will be pulled out. Answer: three apples and two pears.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation: $\cos ^{4}\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)+\sin ^{4}\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)=\sin ^{-2}\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)$.
|
# Solution.
Let's make the substitution $t=\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)$. Clearly, $0<t \leq \frac{\pi}{2}$.
$\cos ^{4} t+\sin ^{4} t=\sin ^{-2} t$.
$\cos ^{4} t+\sin ^{4} t=\left(\cos ^{2} t+\sin ^{2} t\right)^{2}-2 \sin ^{2} t \cdot \cos ^{2} t=1-2 \sin ^{2} t \cdot \cos ^{2} t \leq 1 . \frac{1}{\sin ^{2} t} \geq 1$.
Equality is possible only if $\cos ^{4} t+\sin ^{4} t=1$ and $\sin ^{-2} t=1$ simultaneously. This is possible only when $\sin ^{2} t=1$.
Considering that $0<t \leq \frac{\pi}{2}, t=\frac{\pi}{2}$. Then $x=0$.
## Answer: 0
## Recommendations for checking.
The answer $x=0$ is given, but it is not proven that there are no other roots - 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the height of the pyramid if, by cutting it only along the lateral edges and unfolding the lateral faces onto the plane of the base, outside of it, you get a square with a side of 18. If it is impossible to get such a square, explain why.
#
|
# Solution:
The figure shows such a net. If we flip the pyramid and place it on the face $A B C$, it is easy to calculate the volume of the pyramid $V=\frac{1}{3} \cdot \frac{1}{2} \cdot 9 \cdot 9 \cdot 18=3^{5}$. We determine the area of the base $B D C$ as the difference between the area of the square and the areas of three triangles. $18^{2}-\frac{1}{2}(9 \cdot 9+9 \cdot 18+9 \cdot 18)=\frac{3^{5}}{2}$
We determine the volume of the pyramid in two ways. $V=\frac{1}{3} H \cdot \frac{3^{5}}{2}=3^{5}$, where H is the height of the pyramid we are looking for. From the equality, we find that $H=6$.
## Answer: 6
## Recommendations for checking.
The net of the pyramid is correctly drawn - 4 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. On the board, nine quadratic trinomials are written: $x^{2}+a_{1} x+b_{1}, x^{2}+a_{2} x+b_{2}, \ldots, x^{2}+a_{9} x+b_{9}$. It is known that the sequences $a_{1}, a_{2}, \ldots, a_{9}$ and $b_{1}, b_{2}, \ldots, b_{9}$ are arithmetic progressions. It turned out that the sum of all nine trinomials has at least one root. What is the maximum number of the original trinomials that can have no roots?
(I. Bogdanov)
|
10.2. Answer. 4.
Let $P_{i}(x)=x^{2}+a_{i} x+b_{i}, P(x)=P_{1}(x)+\ldots+P_{9}(x)$. Notice that $P_{i}(x)+P_{10-i}(x)=2 x^{2}+\left(a_{i}+a_{10-i}\right) x+\left(b_{i}+b_{10-i}\right)=$ $=2 P_{5}(x)$. Therefore, $P(x)=9 P_{5}(x)$, and the condition is equivalent to $P_{5}(x)$ having at least one root.
Let $x_{0}$ be any of its roots. Then $P_{i}\left(x_{0}\right)+P_{10-i}\left(x_{0}\right)=2 P_{5}\left(x_{0}\right)=0$, which means that either $P_{i}\left(x_{0}\right) \leqslant 0$ or $P_{10-i}\left(x_{0}\right) \leqslant 0$. Since the leading coefficients of the quadratic polynomials are positive, this implies that in each of the pairs $(P_{1}, P_{9})$, $\left(P_{2}, P_{8}\right),\left(P_{3}, P_{7}\right),\left(P_{4}, P_{6}\right)$, at least one of the polynomials has a root. Therefore, there are at least five polynomials that have at least one root. Hence, there are no more than four polynomials without roots.
It remains to provide an example where exactly five polynomials (one of them being $-P_{5}$) have at least one root. For example, the polynomials $x^{2}-4, x^{2}-3, x^{2}-2, \ldots, x^{2}+4$ will do.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Anya has a chocolate bar of size 5 x 6 squares. It contains 6 squares, forming a $2 \times 3$ rectangle, in which there are nuts (the rectangle can be positioned either vertically or horizontally). Anya does not know exactly where the nuts are. She wants to eat the smallest number of squares, but in such a way that at least one of them contains nuts. How many squares does she need to eat? Show which squares she should eat and prove that a smaller number is not sufficient.
|
2. Answer: 5.
Solution. An example of which slices to eat.
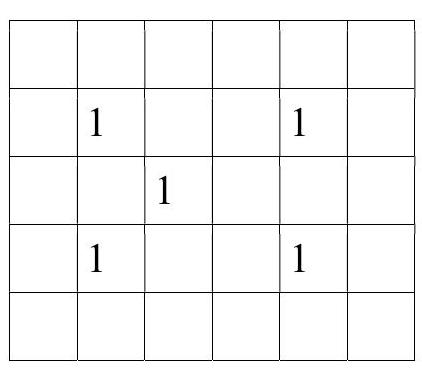
Evaluation. Let's number the slices as shown in the figure.
| 1 | 1 | 2 | 2 | 3 | 3 |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 2 | 2 | 3 | 3 |
| 1 | 1 | 2 | 2 | 3 | 3 |
| 4 | 4 | 4 | 5 | 5 | 5 |
| 4 | 4 | 4 | 5 | 5 | 5 |
Note that we need to eat at least one slice with each number, otherwise the nuts could be in all the slices marked with the number we did not touch.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.

|
Answer: 7.
Solution. Since $A B C D$ is a square, then $A B=B C=C D=A D$.

Fig. 1: to the solution of problem 8.4
Notice that $\angle A B K=\angle C B L$, since they both complement $\angle A B L$ to $90^{\circ}$. Then the right triangles $A B K$ and $C B L$ are equal by the acute angle and the leg $A B=B C$ (Fig. 1). Therefore, $A K=C L=6$. Then
$$
L D=C D-C L=A D-C L=(K D-A K)-C L=K D-2 \cdot C L=19-2 \cdot 6=7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) Mom is walking around a lake with a stroller and completes a full lap around the lake in 12 minutes. Vanya rides a scooter on the same path in the same direction and meets (overtakes) mom every 12 minutes. At what intervals will Vanya meet mom if he rides at the same speed but in the opposite direction?
|
Answer: Every 4 minutes.
Solution. Since Mom completes a full lap around the lake in 12 minutes and meets Vanya every 12 minutes, in 12 minutes Vanya rides around the lake exactly 2 times, while Mom completes one lap. Therefore, Vanya's speed is twice that of Mom's. From this, it follows that when Vanya was riding in the same direction as Mom, their closing speed was equal to Mom's speed. If Vanya rides in the opposite direction, their closing speed will be three times Mom's speed, i.e., three times faster. Therefore, he will meet Mom three times more frequently, i.e., every 4 minutes.
This reasoning can be conducted by introducing a notation for the length of the path.
Let \( l \) be the length of the path around the lake (in meters), then Mom's speed is \( \frac{l}{12} \) (m/min), and Vanya's speed is \( -\frac{l}{6} \) (m/min). The closing speed when Mom and Vanya are riding towards each other is \( \frac{3l}{12} = \frac{l}{4} \) (m/min). Therefore, with this speed, they will cover \( l \) meters together in 4 minutes, i.e., they will meet every 4 minutes.
## Grading Criteria.
- Any complete and correct solution - 7 points.
- Correctly found that Vanya's speed is twice that of Mom's, correctly found the sum of speeds, but the final conclusion is incorrect - 2 points.
- Correctly and justifiedly found that Vanya's speed is twice that of Mom's, but further reasoning is either unjustified or not completed - 1 point.
- A solution that provides specific distances and speeds and arrives at the correct answer - 1 point.
- Only the correct answer - 0 points.
Maximum score for all completed tasks - 35.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.2. Condition:
On an island, there are two tribes: knights, who always tell the truth, and liars, who always lie. Four islanders lined up, each 1 meter apart from each other.
- The leftmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
- The rightmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
It is known that there are two knights and two liars in the row. What distances could the second and third islanders from the left have mentioned? List all possible options.
## Options for matching:
Second islander 1 m
Third islander $\quad 2 \mathrm{~m}$
3 m
$4 \mathrm{M}$
#
|
# Answer:
The second islander is 1 m
The third islander is 1 m.
## Solution.
Let's number the islanders from left to right. Suppose the first one is a knight. Then from his statement, it follows that the third one is also a knight; by the principle of exclusion, the second and fourth must be liars. The fourth said that his fellow islander stands two meters away. This is true, but the fourth is a liar, which leads to a contradiction. Therefore, the first one must be a liar.
Notice that a similar situation is created for the fourth and the first: if we look at the row from right to left, the fourth will be the first in it, and the same reasoning will apply to him. That is, the fourth must also be a liar. It follows that the second and third are knights, as the liars are the first and fourth.
From the above, it follows that the second and third are knights, who will say "one meter."
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. There is a set of 2021 numbers. Moreover, it is known that if each number in the set is replaced by the sum of the others, the same set will be obtained. Prove that the set contains a zero.
|
Solution. Let the sum of the numbers in the set be $M$, then the number $a$ in the set is replaced by the number $b=M-a$. Summing these equations for all $a$:
$$
b_{1}+\ldots+b_{2021}=2021 M-\left(a_{1}+\ldots+a_{2021}\right)
$$
from which $M=0$, since $b_{1}+\ldots+b_{2021}=a_{1}+\ldots+a_{2021}=M$. Therefore, for any $a$ the number $b=-a$ is also in the set, and all numbers can be paired as $(a,-a)$. From the odd number of elements, it follows that the set includes a number $a=-a$, that is, $a=0$.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Variant 1
It is known that $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{1}{5}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{4}{5}}$. Find $\cos (\alpha-\beta)+\cos (\beta-$ $\gamma)+\cos (\gamma-\alpha)$
|
Answer: -1.
Solution. Consider the expression $(\cos \alpha+\cos \beta+\cos \gamma)^{2}+(\sin \alpha+\sin \beta+\sin \gamma)^{2}$ and expand the brackets: $\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma+2(\cos \alpha \cdot \cos \beta+\cos \alpha \cdot \cos \gamma+\cos \beta \cdot \cos \gamma)+\sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma+2(\sin \alpha \cdot \sin \beta+\sin \alpha \cdot \sin \gamma+\sin \beta \cdot \sin \gamma)$. We transform, then apply the fundamental trigonometric identity and the cosine difference formula: $\left(\cos ^{2} \alpha+\sin ^{2} \alpha\right)+\left(\cos ^{2} \beta+\sin ^{2} \beta\right)+\left(\cos ^{2} \gamma+\sin ^{2} \gamma\right)+2(\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta)+2(\cos \alpha \cdot \cos \gamma+\sin \alpha \cdot \sin \gamma)+2(\cos \beta \cdot \cos \gamma+\sin \beta \cdot \sin \gamma)=3+2(\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha))$. Substituting the initial expression $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{1}{5}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{4}{5}}$ we get the equation: $\left(\sqrt{\frac{1}{5}}\right)^{2}+\left(\sqrt{\frac{4}{5}}\right)^{2}=3+2(\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha))$, from which we find the answer.
## Variant 2
It is known that $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{10}{7}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{11}{7}}$. Find $\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha)$
## Answer: 0.
## Variant 3
It is known that $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{10}{3}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{17}{3}}$. Find $\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha)$
Answer: 3.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Option 1
Initially, there were 20 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{25}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{16}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
|
Answer: 4.
Solution: Let there be $a$ white balls, $b$ blue balls, and $c$ red balls in the box. We can set up the following equations:
$$
\begin{gathered}
a+b+c=20 \\
\frac{a}{20}=\frac{a}{20+b}+\frac{1}{25} \\
\frac{b}{20}+\frac{1}{16}=\frac{b}{20-a}
\end{gathered}
$$
Transform the second equation: $\frac{a b}{20(20+b)}=\frac{1}{25}$ and the third equation: $\frac{1}{16}=\frac{a b}{20(20-a)}$. Finally, $\frac{20+b}{25}=\frac{20-a}{16}$ and, substituting into the second equation, after simplification, we get a quadratic equation for $a$ (for $a \neq 20$): $\frac{a}{20}=\frac{16 a}{25(20-a)}+\frac{1}{25} \Leftrightarrow$ $100 a-5 a^{2}=64 a+80-4 a \Leftrightarrow a^{2}-8 a+16=0 \Leftrightarrow a=4$. Then, from the first and second equations, we have: $b=5, c=11$.
## Variant 2
Initially, there were 30 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{36}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{25}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 5.
## Variant 3
Initially, there were 42 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{49}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{36}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 6.
## Variant 4
Initially, there were 56 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{64}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{49}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 7.
## Variant 5
Initially, there were 72 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{81}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{64}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 8.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1
At the base of the quadrilateral pyramid $S A B C D$ lies a square $A B C D, S A$ - the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $S C$ and $A D$. What is the maximum value that the area of triangle $B S A$ can have if $M N=3 ?$
|
Answer: 9.
Solution: Let $O$ be the center of the square $ABCD$. Then $MO$ is the midline of the triangle $SAC$, so $SA = 2MO$. Similarly, $ON$ is the midline of the triangle $BDA$, so $AB = 2ON$. Therefore, $SA^2 + AB^2 = 4(MO^2 + ON^2) = MN^2 = 36$. Let $SA = x, AB = y$. From the formula $S = 0.5 \cdot SA \cdot AB = 0.5xy$, the equality $x^2 + y^2 = SB^2 = 36$, and the inequality $x^2 + y^2 \geq 2xy$, it follows that the area of the triangle is maximized when $2xy = x^2 + y^2$, and it is equal to 9.
## Variant 2
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 4$?
Answer: 16.
## Variant 3
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 5$?
Answer: 25.
## Variant 4
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 6$?
Answer: 36.
## Variant 5
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 2$?
Answer: 4.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In the village, seven people live. Some of them are liars (always lie), and the rest are knights (always tell the truth). Each of them said about each of the others whether they are a knight or a liar. Out of the 42 answers received, 24 were “He is a liar.” What is the smallest number of knights that can live in the village?
|
Answer: 3.
Solution: The phrase "He is a knight" would be said by a knight about a knight and by a liar about a liar, while the phrase "He is a liar" would be said by a knight about a liar and by a liar about a knight. Therefore, in each pair of knight-liar, the phrase "He is a liar" will be said twice. Since this phrase was said 24 times in total, there are 12 pairs of knight-liar, from which we find that there are 3 knights and 4 liars, or vice versa.
Comment: A correct answer without justification - 0 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. In a row, there are 27 matchboxes, each containing a certain number of matches. It is known that in any four consecutive boxes, the total is 25 matches, and in all of them, the total is 165. How many matches are in the eighth box?
|
Answer: 10
Solution. In the first 24 boxes, there are a total of $6 \cdot 25=150$ matches. In the last three boxes, there are 15 matches. Therefore, the 4th from the end (or 24th from the start) has 10 matches. Then, in boxes $24, 23, 22, 21$, there are 25 matches in total, meaning in boxes $21, 22, 23$, there are 15 matches. But in boxes $23, 22, 21$, and 20, there are also 25 matches, so box 20 has 10 matches, the same as box 24. Thus, in every 4th box with a number divisible by 4, there will be 10 matches, including the box with number 8.
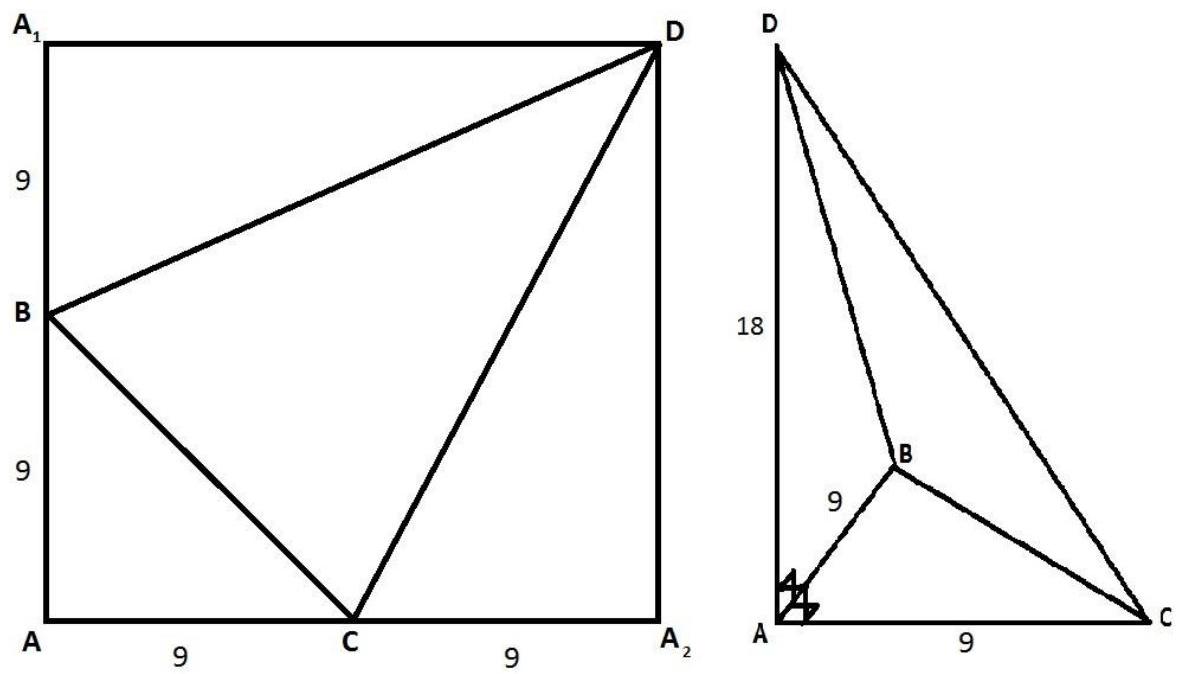
On the same road, Emilia and Eduard set out at the same speed. It is known that Arkady met Emilia at 13:00, and Eduard at 16:00. Arina met Emilia at 15:00. At what time will Arina meet Eduard?
Answer: 18
Solution. Arkady and Arina met Emilia with a 2-hour interval. The speeds of Arina and Arkady are equal, as are the speeds of Emilia and Eduard. Therefore, the distance between Arkady and Arina is constant, as is the distance between Emilia and Eduard. This means the speed of approach between Arkady and Emilia is equal to the speed of approach between Arkady and Eduard, and the same speed of approach will be between Arina and Emilia, and Arina and Eduard. Since the speeds of approach of Emilia and Eduard to the pair Arkady-Arina are equal, they will each pass the pair Arkady-Arina in the same amount of time, i.e., 2 hours. If Arkady met Eduard at 16:00, then Arina will meet him 2 hours later, i.e., at 18:00.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A $7 \times 7$ board has a chessboard coloring. In one move, you can choose any $m \times n$ rectangle of cells and repaint all its cells to the opposite color (black cells become white, white cells become black). What is the minimum number of moves required to make the board monochromatic?
Answer: in 6 moves.
|
Solution. Consider segments of length equal to the side of a cell, separating pairs of cells adjacent to the side of the board. Along each side of the board, there are 6 such segments, totaling $6 \cdot 4=24$. Each of these segments separates cells that initially have different colors, so each segment must end up on the side of at least one of the chosen rectangles. It is easy to see that no more than four of the considered segments can lie on the sides of one rectangle. Thus, to make the board monochromatic, at least $24: 4=6$ moves are required. It remains to show that six moves are sufficient. We choose 6 rectangles of size $1 \times 6$, covering the cells of the second, fourth, and sixth rows and the second, fourth, and sixth diagonals.
Criteria for evaluation.
Only the answer - 0 points.
An example of repainting in 6 moves without proving minimality - 2 points.
Proof of minimality without an example - 5 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is a ruler 10 cm long without divisions. What is the smallest number of intermediate divisions that need to be made on the ruler so that segments of length 1 cm, 2 cm, 3 cm, ..., 10 cm can be laid off, applying the ruler in each case only once.
|
Answer: 4
Solution: First, let's prove that three divisions are not enough. There are a total of 10 segments with endpoints at five points. Therefore, if three divisions are made, each length from 1 to 10 should be obtained exactly once. If any division is made at a non-integer distance from the left end, there will be segments of non-integer length, meaning not all lengths from 1 to 10 can be obtained. Therefore, for each division, only nine options are possible. Thus, a segment of length 9 can only be obtained in one way: by making a division at a distance of 1 from one of the ends of the ruler. Without loss of generality, we can assume that this division is made at a distance of 1 from the left end, and denote this division as T. How can a segment of length 8 be obtained? Again, consider the fact that segments of non-integer length should not be formed. This means that a segment of length 8 can be obtained either by making a division at a distance of 2 from one of the ends, or from two divisions, each made at a distance of 1 from the left and right ends of the ruler. The second case is impossible, as it results in two identical segments (length 1). If the division is made at a distance of 2 from the left end, two segments of length 1 are again formed. Therefore, the only option left is to make the division at a distance of 2 from the right end. Denote this division as S. A segment of length 3 cannot be obtained using the ends of the ruler: it results in extra segments of length 1 or 2. Therefore, the third point N is such that either NT=3 or NS=4 (in each case, uniqueness follows from the fact that N lies on the ruler). Denote the left end of the ruler as A, and the right end as B. If NT=3, then AN=NS=4, leading to a contradiction. If SN=3, then AN=NB=5, again contradicting the fact that all segment lengths are different. Thus, we have proven that three divisions are not enough to complete the task.
Four points are sufficient, as they can be arranged as follows: AC=1, AD=4, AE=5, AF=8, where A is the left end of the segment.
Criteria:
Only the answer without construction --- 0 points.
Proving that all segments from 1 to 10 must be obtained exactly once --- 2 points.
Proving that three points are not enough --- 6 points.
Proving that four points are sufficient --- 1 point.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
|
Answer: -6.
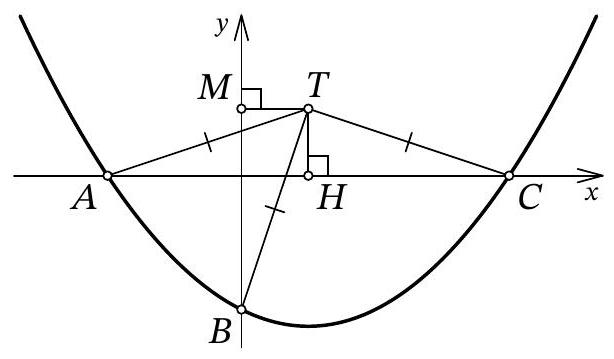
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.

Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 A group of friends went for a morning run around a lake. During the run, one by one they realized they had miscalculated their strength, and switched from running to walking. One of the friends calculated that he had run one-eighth of the total distance that the entire group had run, and walked one-tenth of the total distance that they had walked. How many people were on the outing?
|
Solution 1: Let the person who ran cover $x$ part of the road, then $0<x<1$, and he walked $(1-x)$ part of the way. If there were $n$ people in total, then according to the condition, the total distance covered by the group (expressed in terms of parts) is on one side $n$, and on the other side $8 x + 10(1-x) = 10 - 2 x$. Therefore, $2 x$ is an integer, so the only option is $x=0.5$, and $n=9$.
Solution 2: If this friend ran $a$ km and walked $b$ km, then the total distance covered by the group on one side is $8 a + 10 b$, and on the other side $n(a + b)$. Thus, $n = \frac{8 a + 10 b}{a + b} = 9 + \frac{b - a}{a + b}$. Since $a$ and $b$ are non-zero numbers, the last fraction can only be an integer if $a = b$, otherwise the absolute value of the non-zero numerator will be less than the absolute value of the denominator, and the fraction will not be an integer.
Criteria: The correct equation for the total distance was set up, but no conclusions were drawn, -2 points.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The midpoints of adjacent sides of a rectangle with a perimeter of 32 were connected by segments. The same operation was performed on the resulting quadrilateral: the midpoints of adjacent sides were connected by segments (see figure). How many times in total does one need to perform such an operation so that the perimeter of the resulting quadrilateral first becomes less than 1?
|
Answer: 11.
Solution: After two operations, a quadrilateral is obtained, the sides of which are the midlines of triangles with bases parallel to the sides of the original rectangle. Therefore, this quadrilateral is a rectangle, and each of its sides is half the length of the corresponding side of the original rectangle. Thus, after 2 operations, the perimeter is halved. After 5 pairs of operations, the perimeter will decrease by a factor of $2^{5}=32$ and will become equal to 1. From the triangle inequality, it is clear that the perimeter decreases with each operation. Therefore, after 11 operations, the perimeter will be less than 1.
Comment: A specific case is considered (for example, calculations are performed for a rectangle with sides given by specific numbers), but the method of calculations can be applied to any rectangle - 4 points; the method is applicable only to rectangles of a certain type - 1-2 points. If the first two operations were not taken into account when counting the number of operations, deduct 1 point. If it is not proven that the perimeter decreases with each operation, deduct 1 point.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. All 25 students in class 7A participated in a quiz consisting of three rounds. In each round, each participant scored a certain number of points. It is known that in each round, as well as in the total of all three rounds, all participants scored a different number of points.
Student Kolya from 7A was third in the first round of the quiz, fourth in the second, and fifth in the third. What is the lowest place Kolya could have taken among all classmates in the total points for all three rounds of the quiz?
|
Answer: 10.
Solution. In the first round, 2 classmates overtook Kolya, in the second - 3, in the third - 4. Then, in the sum of all three rounds, he could be overtaken by no more than $2+3+4=9$ classmates, i.e., in the sum of the three rounds, he could not end up lower than 10th place.
Now let's provide an example of how Kolya could end up exactly in 10th place. Suppose
- in each of the rounds, Kolya scored 100 points;
- in the first round, Andrey and Boris scored 1000 and 2000 points respectively and took the first two places
- in the second round, Vlad, Gennady, and Denis scored 10000, 20000, 30000 points respectively and took the first three places
- in the third round, Masha, Svetlana, Tanya, and Katya scored 100000, 200000, 300000, 400000 points respectively and took the first four places;
- in each of the rounds, all other participants after Kolya were ordered alphabetically and scored a number of points equal to their position in the ranking from the end.
It is easy to see that all the conditions of the problem are satisfied.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. What is the minimum number of unit-radius circles required to completely cover a triangle with sides $2 ; 3 ; 4$?
|
Answer: three circles. Solution. Let $A C=4, A B=2, B C=3$ and let $C_{1}, A_{1}$ and $B_{1}$ be the midpoints of sides $A B, B C$ and $A C$ respectively. Note that angle $B$ is obtuse, since $A C^{2}>A B^{2}+B C^{2}$. Therefore, points $B$ and $B_{1}$ lie inside the circle of radius 1 with center at point $O$ - the midpoint of segment $C_{1} A_{1}$ (here we take into account that $\angle C_{1} B_{1} A_{1}=\angle B$ and that the length of the midline is half of $A C$). Thus, the parallelogram $B A_{1} B_{1} C_{1}$ is covered by a unit circle with center $O$. Two other unit circles with centers $M$ and $N$ at the midpoints of $A B_{1}$ and $B_{1} C$ will cover triangles $A C_{1} B_{1}$ and $B_{1} A_{1} C$ (here again we use the fact that angles $A C_{1} B_{1}$ and $B_{1} A_{1} C$ are equal to angle $B$, and thus are obtuse). We will now show that two unit circles are insufficient. Otherwise, their centers must coincide with points $M$ and $N$ (otherwise, segment $A C$ of length 4 could not be covered by two circles of diameter 2). But then point $B$ lies outside both of these circles, since otherwise
the triangle inequality would be violated for triangle $A B M \quad(A B<A M+M B)$ or for triangle $N B C(B C<N B+N C)^{\circ}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
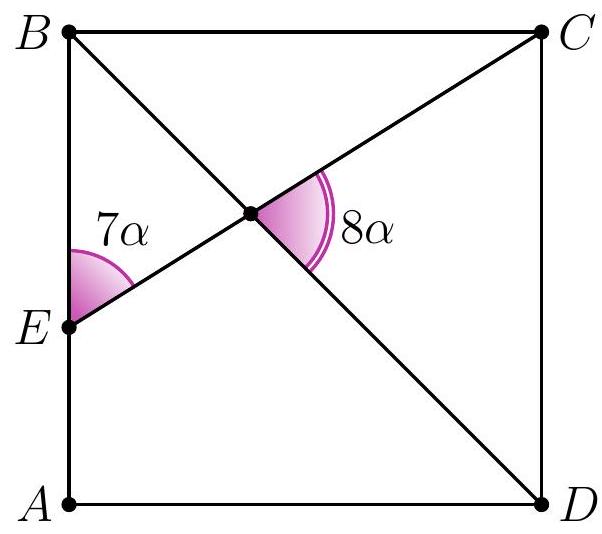
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
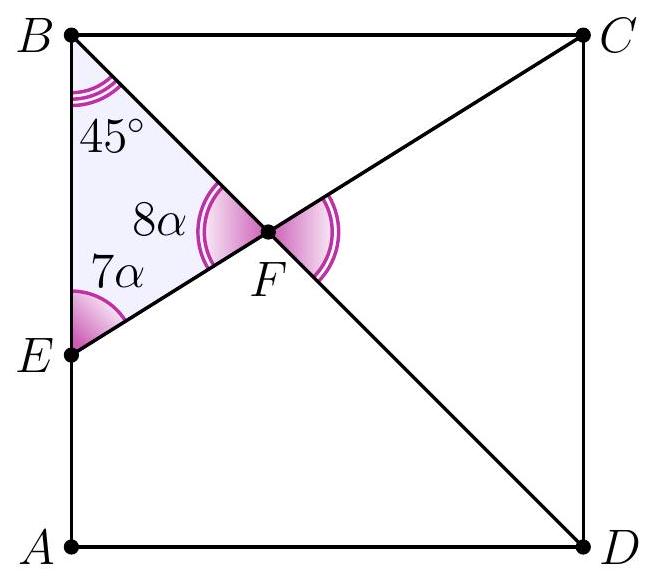
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
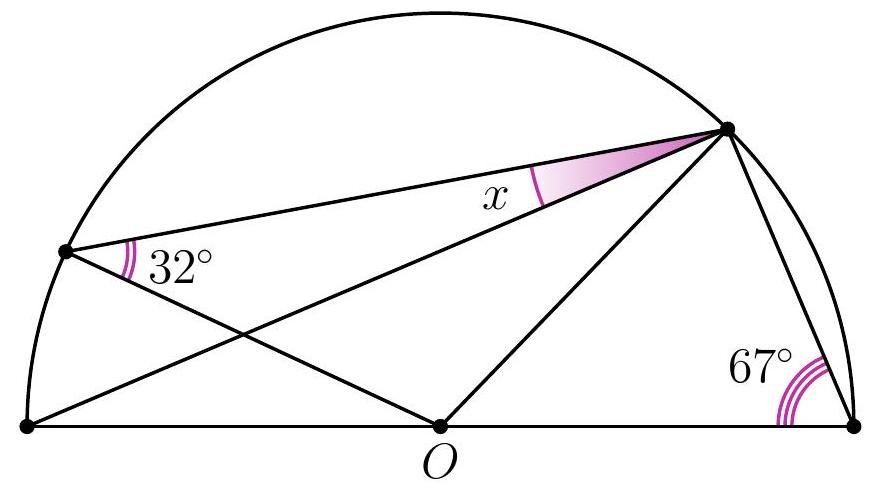
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
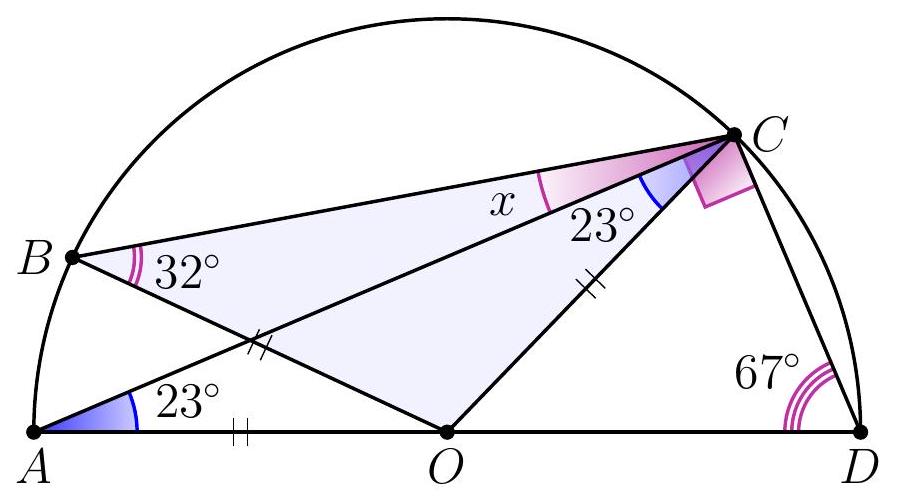
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. After teacher Mary Ivanovna moved Vovochka from the first row to the second, Vanechka from the second row to the third, and Mashenka from the third row to the first, the average age of students sitting in the first row increased by one week, those sitting in the second row increased by two weeks, and those sitting in the third row decreased by four weeks. It is known that there are 12 people sitting in the first and second rows. How many people are sitting in the third row?
|
3. Let there be x people in the third row. Since the average age is the sum of the ages divided by the number of people, after the rearrangement, the total age of the children in the first row increased by 12 weeks, in the second row by 24 weeks, and in the third row by -4x weeks. Since the total sum of the ages of all students could not have changed, $4x = 12 + 24$, i.e., $x = 9$.
Answer: 9 people.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. While waiting for customers, the watermelon seller sequentially weighed 20 watermelons (weighing 1 kg, 2 kg, 3 kg, ..., 20 kg), balancing the watermelon on one scale pan with one or two weights on the other pan (possibly identical). The seller recorded on a piece of paper the weights of the weights he used. What is the smallest number of different numbers that could have appeared in his records, if the weight of each weight is an integer number of kilograms?
|
Answer: 6.
Solution. With one or two weights of 1 kg, 3 kg, 5 kg, 7 kg, 9 kg, and 10 kg, any of the given watermelons can be weighed. Indeed, $2=1+1, 4=3+1$, $6=5+1, 8=7+1, 11=10+1, 12=9+3, 13=10+3, 14=9+5, 15=10+5, 16=9+7, 17$ $=10+7, 18=9+9, 19=10+9, 20=10+10$. Thus, six different numbers could have been recorded.
We will show that five types of weights are insufficient for the required weighings. If there are five weights, then, generally speaking, twenty watermelons can be weighed. Specifically: five watermelons can be balanced with single weights, five with double weights, and the remaining $5 \cdot 4: 2=10$ watermelons with pairs of different weights. However, each combination of weights must be used exactly once.
Notice that half of the watermelons have an odd mass. Let $k$ of the five weights have an odd mass, and $5-k$ have an even mass. Then the number of ways to weigh a watermelon with an odd mass is exactly $k+k(5-k)=6k-k^2$. However, for no $k=0,1,2,3,4,5$ does this expression equal 10 (this can be verified either by substitution or by solving the quadratic equation $6k-k^2=10$).
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the notebook, all irreducible fractions with the numerator 15 are written down, but which are greater than $\frac{1}{16}$ and less than $\frac{1}{15}$. How many such fractions are written in the notebook?
|
Answer: 9 fractions.
## Solution:
We are looking for all suitable irreducible fractions of the form $\frac{15}{n}$. Since $\frac{1}{16}<\frac{15}{n}<\frac{1}{15}$, then $15 \cdot 15<n<15 \cdot 16$ or $225<n<240$ (with the fraction $\frac{15}{n}$ being irreducible, meaning $n$ is not divisible by 3 or 5). It is not difficult to verify that from this range (of 14 numbers), we need to exclude the numbers 228, 230, 231, 234, 235, 237 - 6 numbers. This leaves 9 possible values for $n$.
## Criteria:
Correct answer without a correct justification - 1 point.
Participants might try to list all such fractions and then justify why the denominator cannot be larger or smaller - carefully monitor the accuracy of such justifications.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In each cell of a $2 \times 2$ table, a number was written, and all the numbers are different. It turned out that the sum of the numbers in the first row is equal to the sum of the numbers in the second row, and the product of the numbers in the first column is equal to the product of the numbers in the second column. What can the sum of all four numbers in the table be? Find all possible options and explain why there are no others.
|
# Answer: 0.
## Solution:
| $a$ | $b$ |
| :--- | :--- |
| $c$ | $d$ |
Let's denote the numbers in the table as shown on the left. According to the condition, $a+b=c+d$, $ac=bd$. Then $a=c+d-b$, substitute this into the product equality: $(c+d-b)c=bd$. Expand the brackets and move everything to the left: $c^2 + cd - bc - bd = 0$. Factorize: $(c+d)(c-b)=0$. Since $c-b \neq 0$ (all numbers are different), then $c+d=0$. Therefore, the sum in the first row is also 0, and accordingly, the sum in the entire table is also 0.
## Criteria:
Correct answer without correct justification - 1 point.
If it is not justified why $c$ can be canceled out - deduct 2 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The organizers of a mathematics olympiad decided to photograph 60 participants. It is known that no more than 30 participants can fit in a single photograph, however, any two students must appear together in at least one photograph. What is the minimum number of photographs needed to achieve this?
|
# Answer: 6.
## Solution:
Example with 6 photos: divide 60 participants into 4 groups of 15 people (groups $A, B, B$, Г). Take 6 photos of all possible pairs of groups: $A+D, A+B, A+\Gamma, B+B, B+\Gamma, B+\Gamma$ - in each photo, there will be 30 people, and it is easy to see that in this way any two people will be photographed together.
We will prove that fewer photos are not sufficient. Suppose no more than 5 photos were taken. After each photo, give each photographed person a candy. Then, in total, the participants received no more than $30 \cdot 5 = 150$ candies (since no more than 30 people are in each photo, and there are no more than 5 photos). Since there are 60 participants, there will be a participant who received no more than 2 candies (otherwise, a total of at least $60 \cdot 3 = 180$ candies would have been given). Then he was photographed with no more than 29 other participants in one photo and with no more than 29 other participants in another photo (if there is such a photo) - that is, with no more than $29 \cdot 2 = 58$ other participants of the olympiad, while he should have been photographed with all 59 participants (i.e., with everyone except himself). This is a contradiction, so five or fewer photos are insufficient to meet the condition of the problem.
## Criteria:
A correct answer without a correct example is not scored.
Example for 6 photos - 2 points.
Correct estimation (justification why 5 or fewer photos are insufficient) - another 5 points.
Examples or estimates for 7 or more photos are not scored.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.2. (7 points)
Twelve people are carrying 12 loaves of bread. Each man carries 2 loaves, each woman carries half a loaf, and each child carries a quarter of a loaf. How many men, women, and children were there?
|
Answer: 5 men, one woman, and 6 children.
Solution: Let $x$ be the number of men, $y$ be the number of women, and $z$ be the number of children; $x, y, z$ are natural numbers.
Then $x+y+z=12$ and $2 x+\frac{y}{2}+\frac{z}{4}=12$. From the last equation, it follows that $8 x+2 y+z=48$.
Transform the last equation: $7 x+y+(x+y+z)=48$. Considering the first equality, we get: $7 x+y=36, x=\frac{36-y}{7}$.
Since $x, y$ are natural numbers, $y$ can take the values 1, 8, 15, 22, 29. The values of $y$, equal to 15, 22, and 29, do not meet the condition of the problem $(y<12)$.
When $y=8: x=4, z=0$ - this contradicts the condition of the problem.
Let $y=1$, then $x=5, z=6$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Solve the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+2}\left(1+\frac{1}{x+1}\right)\right)=x$.
Answer: 2
|
Solution.
$1+\frac{1}{x+1}=\frac{x+2}{x+1}$, therefore the given equation is equivalent to the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+1}\right)=x$ under the condition that $\mathrm{x} \neq-2$. Acting similarly, we get that $1+\frac{3}{x+3}=x$, where $\mathrm{x} \neq-2$ and $\mathrm{x} \neq-3$. The roots of this equation are the numbers 2 and -2, so the only root of the original equation is the number 2.
## Grading Criteria
- Only the correct answer is provided - 1 point.
- The correct solution process, but the extraneous root is not discarded - 3 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The math teacher agreed with the eleven students who came to the elective that he would leave the classroom, and the students would agree among themselves who would be a liar (always lie) and who would be a knight (always tell the truth). When the teacher returned to the class, he asked each student to say about each of the others whether they were a knight or a liar. Out of 110 answers, 56 were "He is a liar." What is the maximum number of knights that could have been among the students?
|
Answer: 7.
Solution: The phrase "He is a knight" would be said by a knight about a knight and by a liar about a liar, while the phrase "He is a liar" would be said by a knight about a liar and by a liar about a knight. Therefore, in each pair of "knight-liar," the phrase "He is a liar" will be said twice. Since this phrase was said 56 times in total, there are 28 pairs of "knight-liar," from which we find that there are 7 knights and 4 liars, or vice versa.
Comment: A correct answer without justification - 0 points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. At competitions, an athlete's performance is evaluated by 7 judges, each of whom gives a score (an integer from 0 to 10). To obtain the final score, the best and worst scores from the judges are discarded, and the arithmetic mean is calculated. If the average score were calculated based on all seven scores, the athletes would be ranked in the exact reverse order. What is the maximum number of athletes that could have participated in the competition?
|
# Answer. 5.
Solution. Suppose there are no fewer than six dancers. Let $A, a, S_{A}$ be the best score, the worst score, and the sum of all non-discarded scores of the winner, respectively, and $B, b, S_{B}$ be the same for the last athlete. Instead of averages, we can arrange the dancers by the sum of all scores or the sum of all except the extreme ones. From the condition, it follows that such sums are different for all and go in the opposite order. Since the sums are integers and there are at least six dancers, the inequalities must hold:
$$
S_{A}-S_{B} \geq 5 \text { and }\left(B+b+S_{B}\right)-\left(A+a+S_{A}\right) \geq 5 \text {. }
$$
Adding these inequalities, we get $B+b-A-a \geq 10$.
From this, $b \geq A+a+(10-B) \geq A$, i.e., the worst score of the last athlete is not less than the best score of the winner. But then each score of the last athlete is not less than that of the winner, i.e., $S_{B} \geq S_{A}$. We have reached a contradiction.
Example of score distribution among athletes: $0-0-0-0-0-0-10,0-0-0-0-0-1-8$, $0-0-0-0-1-1-6,0-0-0-1-1-1-4,0-0-1-1-1-1-2$.
Comment. Example - 3 points, evaluation - 4 points.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. In a regular pentagon $A B C D E$, a point $F$ is marked on side $A B$, and a point $G$ is marked on side $B C$ such that $F G=G D$. Find the angle $C D G$, if the angle $F D E$ is $60^{\circ}$.
|
Answer: $6^{\circ}$.
Solution. The angles of a regular pentagon are each $108^{\circ}, \angle E D A = 36^{\circ}, \angle F D E = 60^{\circ}$. Therefore, $\angle A D F = 24^{\circ}$.
Additional construction: Take point $O$ such that $B O = C O = B C$. Then $\triangle B O C$ is equilateral, $\angle A B O = O C D = 108^{\circ} - 60^{\circ} = 48^{\circ}$. We get that $\triangle A B O = \triangle O C D$, where $\angle B A O = \angle B O A = \angle C O D = \angle C D O = 66^{\circ}, A O = O D$.
Thus, there exists a circle with center at point $O$ and radius $r = O A = O D$. Let this circle intersect side $A B$ at point $K$. Then
$\angle A K O = \angle K A O = 66^{\circ}, \angle K O A = 48^{\circ}$. We obtain that $\angle A D K = A D F = 24^{\circ}$. Therefore, $K = F$. Then $\angle K A D = \angle B A D = \angle B A E - \angle D A E = 72^{\circ}$, and $\angle A F D = 84^{\circ}$, $\angle O F D = 18^{\circ}$.
Let $H$ be the midpoint of $F D$, then $O H$ and $G H$ are medians, altitudes, and angle bisectors of $\triangle F O D$ and $\triangle F G D$ respectively (thus, $G O \perp F D$). We get $\angle F O H = \angle D O H = \angle D O G = 90^{\circ} - 18^{\circ} = 72^{\circ}$.
$\angle G O D + G C D = 180^{\circ} \Rightarrow O G C D$ is inscribed in a circle $\Rightarrow O C D = \angle O G D = 48^{\circ} = \angle H G D$. Then $\angle G D H = 90^{\circ} - 48^{\circ} = 42^{\circ}$. We obtain that $\angle C D G = 108^{\circ} - 60^{\circ} - 42^{\circ} = 6^{\circ}$.
Comment. It is proven that point $O$, the vertex of the equilateral triangle constructed on segment $B C$, is equidistant from vertices $A, F, D$ - 3 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. During a physical education class, all students in the class lined up in a row. It turned out that boys and girls alternated in the row. It is known that exactly $52 \%$ of the students are girls. Find the number of boys in the class. Justify your answer.
|
Solution: Since there are more than half girls, the first and last student in the row are girls. Let's remove the last girl from the row - there will be an equal number of boys and girls left. In this row, all the boys in the class make up $48 \%$. There are as many girls, another $48 \%$. The remaining $100-2 \cdot 48=4 \%$ corresponds to the removed girl. Thus, one person constitutes $4 \%$, and the number of students in the class is $100: 4=25, 48$ percent of this number is 12 people.
Answer: 12 boys.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| In the correct solution, there is an arithmetic error, possibly leading to an incorrect answer | 6 points |
| Noted that there is one more girl than boys | 1 point |
| Correct answer without any justification | 0 points |
To the condition of problem 7.2
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that the equations $x^{2}+a x+b=0$ and $x^{3}+b x+a=0$ have a common root and $a>b>0$. Find it.
|
Answer: -1.
Solution. Multiply the first equation by $x$ and subtract the second from it. The common root of the original equations will also be a root of the resulting equation
$$
\left(x^{3}+a x^{2}+b x\right)-\left(x^{3}+b x+a\right)=0 \quad \Longleftrightarrow \quad a\left(x^{2}-1\right)=0
$$
The last equation has two roots, which are 1 and -1. If the common root is $x=1$, then substituting it into each equation yields the equality $1+a+b=0$, which cannot hold given the condition $a>b>0$, leading to a contradiction.
If the common root is $x=-1$, then substituting it into the equations yields $1-a+b=0$, which does not contradict the condition.
Remark. Other methods of solution are possible.
Criteria. Only the answer - 0 points. Excess roots not eliminated - 2 points deducted. No verification of the root $x=-1$ for compliance with the condition - another 2 points deducted. One of the possible roots is missed - no more than 3 points. Complete solution - 7 points.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Pasha is playing a computer game. The game takes place on an infinite grid. Each cell contains either a treasure or a natural number. The number indicates the distance to the nearest treasure in cells (if it takes $A$ steps vertically and $B$ steps horizontally to reach the treasure, the cell contains the number $A+B$). In one move, Pasha can reveal the contents of one cell. The goal of the game is to find at least one treasure.
a) Pasha revealed three cells in a row horizontally. Each of them contained the number 5. What is the minimum number of additional moves Pasha needs to make to definitely find a treasure?
(2 points)
b) Pasha revealed some three cells, and they contained numbers. Could it be that from this information, Pasha can definitely find a treasure with the next move?
(3 points)
c) Pasha knows that each number on the field does not exceed some fixed $K \geqslant 3$. Can Pasha definitely find a treasure by making no more than $K+3$ moves?
2) Pasha knows that each number on the field does not exceed 2023. Will 20 moves be enough for Pasha to definitely find a treasure?
|
Solution. a) Note that if Pasha finds a certain number $K$ in a cell, then at least one treasure must be located in the cells along the perimeter of a square rotated by $45^{\circ}$ relative to the grid lines, where the side of the square is exactly $K+1$ cells. At the same time, there cannot be any treasures inside such a square. Let's construct such squares around the fives found by Pasha. The treasure related to the central five can only be located above or below it at a distance of 5 cells, as the other cells on the perimeter will be covered by other squares. But one of these cells may not contain a treasure, so Pasha will need more than one move to guarantee finding it. For other fives or cells outside the squares, it is also impossible to determine the exact location of the treasure. Therefore, Pasha needs at least two moves (these moves are marked with a star in the figure).
To the solution of problem $7.5 \mathrm{a}$
To the solution of problem $7.5 \mathrm{b}$
b) The figure shows one of the possible situations where the position of the treasure can be determined unambiguously. The treasure is located in the cell marked with a star, as the other cells of the square around the one are covered by the inner cells of the squares around the twos.
c) Suppose Pasha checks two adjacent cells horizontally with his first two moves. The numbers in these cells are either equal or differ by 1 (if, of course, a treasure is found, then Pasha has completed the task). In both cases, the squares around these two numbers will overlap such that the treasure related to the smaller number (or any of the equal numbers) will be located in cells forming only two sides of the square. Let the smaller number be $N \leqslant K$, and, without loss of generality, the specified sides will be to the left of it. The situation is shown in the figure (the sizes of the square are shown schematically).
With the next moves, Pasha will check the cells from left to right, from 1 to a maximum of $N-1$—until the number in the cell matches the number of this cell. If 1 matches, then the treasure should be searched in the three cells around it, and if it does not match, then there is definitely no treasure in these three cells. If 2 matches, the treasure should be searched two cells above or below, and if it does not match, then there is definitely no treasure in these two cells, and so on. If, as a result of such actions, no number matches in any cell, including the number $N-1$, then the treasure should be searched in the last two cells—above or below the number $N$.
Thus, to find the treasure, Pasha will spend: 2 initial moves, no more than $K-1$ moves horizontally, 2 moves to find the treasure above or below the number (3 moves if he gets lucky on the first cell). In total, $2+(K-1)+2=K+3$ moves. Or $2+1+3=6$ moves, but $6 \leqslant K+3$ by the condition.
d) The first two moves will be made in the same way as in part c). For the remaining corner of two sides of the square around the number $N$, we will make three more moves—to its ends and the central cell. If the treasure is still not found, then the suspicious cells will remain in two diagonal segments, containing $N-1 \leqslant 2022$ cells.
Now let's describe the next operation. If in such a segment we select $M+1$ consecutive cells, then there exists a square for which the selected cells form a side. At the same time, all other cells of the square lie strictly inside the square with side $N$ obtained by the first two moves, and therefore definitely do not contain the treasure. Then Pasha can check the central cell of the square—if it turns out to be the number $M$, then among the selected $M+1$ cells there is a treasure, and if not $M$—then there is no treasure. For convenience, this operation will be performed for any $M \geqslant 0$, and for $M=0$ the square together with the boundary is just one cell.
Using the described operation, Pasha will first leave one of the two segments. Then we will divide the segment in half—selecting half of the cells from one of the edges (if the number of cells is odd—half of all, not counting the central one). Then even in the worst case, he will need no more than 12 moves, since $2^{11}>2022$. Indeed, the number of unverified options in 11 moves will not exceed 1011, 506, 253, 127, 64, 32, 16, 8, 4, 2, 1 cells, respectively. In total, Pasha will spend no more than $2+3+1+12=18$ moves, which is even less than the proposed twenty.
Answer. a) 2 moves b) It could.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. Ivan on a tractor and Petr in a "Mercedes" left point A for point B. Petr arrived at point B, waited for 10 minutes, and called Ivan to find out that Ivan had only covered a third of the distance and was currently passing by a cafe. Petr drove to meet him. Not noticing Ivan, he reached the cafe and spent half an hour on a snack, then drove to point B. In the end, Petr arrived at point B at the same time as Ivan. How much time did Ivan spend on the entire journey, if both he and Petr traveled at constant speeds?
|
Solution. From the fact that Ivan had traveled a third of the distance by the time Peter had traveled the whole distance and waited for 10 minutes, we can conclude that by the time Ivan reaches point B, Peter could have traveled the route three times and waited for half an hour. Instead, he traveled the route $1+2 / 3+2 / 3=7 / 3$ times and waited for 40 minutes. This means that for Peter, $2 / 3$ of the journey in the first ratio is equivalent to 10 minutes of waiting in the second. From this, we can conclude that Peter takes 15 minutes to travel the entire route, and a third of Ivan's journey is 25 minutes. Therefore, Ivan's entire journey is 75 minutes.
Answer. 1 hour and 15 minutes.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 11.1. Solve the equation
$$
x^{4}+2 x \sqrt{x-1}+3 x^{2}-8 x+4=0
$$
|
Solution. Let's check that $x=1$ is a root. Indeed,
$$
1^{4}+2 \sqrt{1-1}+3 \cdot 1^{2}-8+4=1+3-8+4=0
$$
We will show that there are no other roots. Since the left side of the equation is defined only for $x \geqslant 1$, it is sufficient to consider the case $x>1$. Using the valid inequalities in this case $x^{4}>x^{2}, x \sqrt{x-1}>0$ and $(x-1)^{2}>0$, we obtain for the left side the inequality
$$
x^{4}+2 x \sqrt{x-1}+3 x^{2}-8 x+4>4 x^{2}-8 x+4=4(x-1)^{2}>0
$$
which holds for all $x>1$. Thus, there are no roots for $x>1$.
Answer. $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In how many ways can all natural numbers from 1 to $2 n$ be arranged in a circle so that each number is a divisor of the sum of its two neighboring numbers? (Ways that differ only by rotation or symmetry are considered the same)
|
Solution. Note that if the numbers in the circle do not alternate in parity, then some two even numbers are adjacent. An even number is a divisor of the sum of the even number adjacent to it and the second adjacent number, which means the latter is also even. Continuing this reasoning around the circle, we get that all numbers in the circle are even, which is incorrect. Consider the number $2n-1$. By the proven fact, both of its neighbors are even, and their sum is divisible by $2n-1$, so the sum is at least $4n-2$. The maximum sum of the two remaining numbers is $2n + (2n-2) = 4n-2$. Therefore, the numbers adjacent to $2n-1$ are $2n$ and $2n-2$. Without loss of generality, let them be in descending order clockwise. Now and further, the situation will be as follows: around the circle, the numbers from $2n$ to $k$ are already placed in descending order clockwise, where $k>1$. One of the neighbors of the number $k$ is $k+1$, and the other neighbor is no more than $k-1$, so the sum of the adjacent numbers is greater than $k$ and no more than $2k$, which means it is equal to $2k$. It turns out that the next number after $k$ is $k-1$. We again get the situation described above. Therefore, the numbers are arranged in a circle from $2n$ to 1 in descending order clockwise or counterclockwise (these are the same options) and no other way.
Answer. 1 option.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. A pair of natural numbers $a>b$ is called good if the least common multiple (LCM) of these numbers is divisible by their difference. Among all natural divisors of the number $n$, exactly one good pair was found. What can $n$ be?
|
36. Answer: $n=2$. Two odd numbers cannot form a good pair. Therefore, the number $n$ has an even divisor, and thus it is even. But then it has two good pairs of divisors: $(2,1)$ and $(n, n / 2)$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all integers $x, y$ for which $x+y, 2x+3y$ and $3x+y$ are perfect squares.
|
Answer: $x=y=0$. Let $x+y=a^{2}, 2 x+3 y=b^{2}$ and $3 x+y=c^{2}$. Note that $2 b^{2}+c^{2}=7 a^{2}$. We will prove that this equation has a unique solution: $a=b=c=0$. Indeed, let $(a, b, c)$ be a solution with the minimal sum $a^{2}+b^{2}+c^{2}$, in which not all numbers $a, b, c$ are equal to 0. Then $2 b^{2}+c^{2}: 7$. It is easy to see that this is possible only if $b \vdots 7$ and $c \vdots 7$. But then $7 a^{2} \vdots 49$, from which $a \vdots 7$. Reducing $a, b, c$ by 7, we get a new non-zero solution with a smaller sum $a^{2}+b^{2}+c^{2}$. Contradiction. Thus, $a=b=c=0$. Then $x=\frac{c^{2}-a^{2}}{2}=0$ and $y=a^{2}-x=0$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. When preparing a district olympiad, each jury member participated in no more than 10 discussions. Discussions can be large or small. In a small discussion, 7 jury members participate, each sending exactly one email to each of the other 6. In a large discussion, 15 jury members participate, each sending exactly one email to each of the other 14. A total of 1994 emails were sent, not counting the emails sent by the jury secretary. In how many discussions did the secretary participate?
|
28. Answer: The secretary participated in 6 small discussions and 2 large ones.
In a small discussion, 7 jury members participate, each sending exactly one email to each of the 6 others, so in the end, 42 emails are sent in a small discussion. Similarly, participants in a large discussion send 210 emails.
Let a total of $M$ small and $B$ large discussions take place, and the secretary participated in $m \leqslant M$ small and $b \leqslant B$ large discussions, with $m+b \leqslant 10$ by condition. A participant in a small discussion sends 6 emails, and a participant in a large discussion sends 14 emails. Thus, the secretary sent $6 m+14 b$ emails. Adding to this the 1994 emails sent by the other jury members, we get all the emails written as a result of all discussions, i.e., $42 M+210 B$ emails. Therefore,
$$
1994+6 m+14 b=42 M+210 B
$$
The right-hand side of this equation is divisible by 42. Thus,
$$
6 m+14 b \equiv-1994 \equiv 22 \quad(\bmod 42)
$$
Thus, theoretically, the sum $6 m+14 b$ can take values $22, 22+42=64, 22+42 \cdot 2=106$, $22+42 \cdot 3=148$, etc. But since $m+b \leqslant 10$, the sum $6 m+14 b$ cannot be too large:
$$
6 m+14 b \leqslant 14 m+14 b=14(m+b) \leqslant 14 \cdot 10=140 .
$$
Thus, we only need to check whether the equations
$$
6 m+14 b=22, \quad 6 m+14 b=64, \quad 6 m+14 b=106
$$
have solutions in non-negative integers $m$ and $b$, where $m+b \leqslant 10$. This check is performed by a simple enumeration. As a result, we find that the first and third equations do not have such solutions. The second equation has a solution $m=6, b=2$, which seems to suit us.
Now we need to ensure that for the found values of $m$ and $b$, we can choose numbers $M \geqslant m$, $B \geqslant b$ such that the equation $(*)$ is satisfied, i.e.,
$$
42 M+210 B=2058
$$
For example, we can take $B=b=2$, then we find that $M=39$.
Thus, we have found that the situation described in the condition is possible only in the case where the secretary participated in 8 discussions.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. There are $2 n$ cards, each with a number from 1 to $n$ (each number appears on exactly two cards). The cards are lying on the table face down. A set of $n$ cards is called good if each number appears exactly once. Baron Munchausen claims that he can point out 80 sets of $n$ cards, at least one of which is guaranteed to be good. For what largest $n$ can Baron's words be true?
|
Answer: $n=7$. We will present an algorithm for how to indicate $2^{n-1}$ sets on $2n$ cards, one of which is suitable. (In our case, this is $2^{6}=64<80$ sets.) Imagine that identical cards are connected by (invisible to us for now) red edges. We will arbitrarily pair the cards with blue edges. The red-blue graph is a collection of cycles, and any set of the form "cards every other in each cycle" will suit us. Any such set has the obvious property: on each blue edge, exactly one vertex is selected. Therefore, by checking all $2^{n}$ sets with this property, we will certainly find the suitable one. Moreover, all such sets are divided into pairs of opposites (and in each pair, either both sets are suitable or both are not), so it is enough to check $2^{n-1}$ sets.
Now suppose that for 16 cards, 80 sets of 8 cards each are indicated. We will prove that it is possible to write numbers on the cards so that none of these sets are suitable.
For each set, mark all $8^{2}$ pairs of cards where one card is in the set and the other is not; in total, $80 \cdot 8^{2}$ pairs will be marked. There are $16 \cdot 15 / 2$ pairs in total, so some pair will be marked no more than $80 \cdot 8^{2} /(16 \cdot 15 / 2)=(8 / 15) \cdot 80$ times. Therefore, this pair is "split" by no more than 42 sets. We will write the number 1 on this pair of cards. All sets that contain both of these cards or neither of them are already rejected. We will now consider only the remaining $a \leqslant 42$ sets that potentially could be suitable.
Each of them contains exactly 7 of the remaining 14 cards. Similarly to the previous step, some pair of them will be "split" by no more than $[(7 / 13) \cdot a] \leqslant[7 / 13] \cdot 42]=22$ sets. We will write the number 2 on this pair and thereby reject all sets except no more than 22.
We continue in the same manner, eventually leaving 4 free cards and one set of two cards. We will write the number 7 on the cards of this set, and the number 8 on the two remaining cards; this set will also be rejected.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. A polynomial of degree 10 has three distinct roots. What is the maximum number of zero coefficients it can have?
(A. Khryabrov)
|
24. Answer: Answer: 9 zero coefficients. For example, the polynomial $x^{10}-x^{8}$ has roots $0,1,-1$. If a polynomial has only one non-zero coefficient, it is of the form $a x^{10}$, and therefore has exactly one root.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the bank of the river stand 10 sheikhs, each with a harem of 100 wives. Also at the bank stands an $n$-person yacht. By law, a woman should not be on the same bank, on the yacht, or even at a transfer point with a man if her husband is not present. What is the smallest $n$ for which all the sheikhs and their wives can cross to the other bank without breaking the law?
|
Answer: 10. Example: first, all 1000 wives move quietly, then one returns and 10 sheikhs leave. Finally, another returns and picks up the first. Evaluation: let the number of places not exceed 9. Consider the moment when the first sheikh appears on the other shore - or several at once, but not all, for they could not have crossed all at once. Then, together with them, their harems are also there, and with the remaining sheikhs, their harems are there. But then for the return trip, there is only one option: all the sheikhs present on the second shore return immediately, and they accumulate again on the first shore. Thus, all the sheikhs will never leave from there.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a prime number $p$. All natural numbers from 1 to $p$ are written in a row in ascending order. Find all $p$ for which this row can be divided into several blocks of consecutive numbers so that the sums of the numbers in all blocks are equal.
|
Answer: $p=3$. Let $k-$ be the number of blocks, $S-$ be the sum in each block. Since $p(p+1) / 2=k S$, either $k$ or $S$ is divisible by $p$. Clearly, $k<p$, so $S$ is a multiple of $p$. Let the leftmost group consist of numbers from 1 to $m$. Then $m(m+1) / 2$ is a multiple of $p$, from which $m \geqslant p-1$, i.e., $m=p-1$. But this means that the sum of the numbers from 1 to $p-1$ is equal to $p$, which is only possible when $p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Given $n$ distinct natural numbers, any two of which can be obtained from each other by permuting the digits (zero cannot be placed in the first position). For what largest $n$ can all these numbers be divisible by the smallest of them?
|
Answer: 9. It is clear that there cannot be more than nine numbers.
We will use a known property of the period of a purely periodic rational fraction $\alpha=$ $a / b<1$ with coprime $(a, b)$: the length of the period is the smallest natural $t$ for which $\left(10^{t}-1\right) \vdots b$, and the period $T$ itself is the number $\left(10^{t}-1\right) \alpha$.
From this, it follows that if $a_{1} / b$ and $a_{2} / b$ are two proper irreducible fractions, and $a_{1}=k a_{2}$, then the period of the first fraction is exactly $k$ times the period of the second.
Consider the fractions 2/19, 4/19, 6/19, 8/19, 10/19, 12/19, 14/19, 16/19, 18/19. They have periods of the same length, and all of them are divisible by the period of 2/19, which is 105263157894736842. On the other hand, it can be verified that 10 is a primitive root modulo 19. Therefore, the numbers $2 \cdot 10^{s} / 19$ for $0 \leqslant s \leqslant 17$
It can be verified that 10 is a primitive root modulo 19. Therefore, the numbers $10^{s} / 19$ for $0 \leqslant s \leqslant 17$ after removing the integer part are all 18 proper irreducible fractions with the denominator 19. Their periods have the same length and are obtained from the period of the fraction $2 / 19$ by cyclic shifts of $s$ digits to the right. In particular, they all consist of the same set of digits. (And all, except $1 / 19$, do not start with zero, i.e., they represent natural numbers of the same length). From the previous paragraph, it follows that the periods of the fractions $4 / 19,6 / 19,8 / 19,10 / 19,12 / 19,14 / 19,16 / 19,18 / 19$ are divisible by the period of the fraction $2 / 19$ and together they form an example of 9 numbers.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Olya wrote fractions of the form $1 / n$ on cards, where $n-$ are all possible divisors of the number $6^{100}$ (including one and the number itself). She arranged these cards in some order. After that, she wrote the number on the first card on the board, then the sum of the numbers on the first and second cards, then the sum of the numbers on the first three cards, and so on, finally, the sum of the numbers on all the cards. Each sum Olya wrote on the board as an irreducible fraction. What is the smallest number of different denominators that could appear on the board?
(O. Ivanova)
|
52. Answer: two denominators. Let's represent all fractions in the form $a_{n} / 6^{100}$, then $a_{1}, a_{2}, \ldots$ are again all divisors of the number $6^{100}$, each appearing once. Let the partial sums be denoted by $S_{n} / 6^{100}$. Then the denominator of the irreducible representation of the partial sum depends on the powers of the prime factors 2 and 3 in the numerator $S_{n}$.
It is not difficult to understand that among $S_{n}$ there are both even and odd numbers, so in some $S_{n}$, the factor 2 enters with a zero power, and in others, with a non-zero power. Therefore, the answer in the problem is at least 2.
Let's provide an example of an arrangement with two different denominators. First, write down the divisor $a_{1}=1$. Then write down in any order all divisors that are multiples of 2 and 3. Up to this point, all partial sums $S_{n}$ are neither divisible by 2 nor by 3, i.e., they contain 2 and 3 in the same (zero) power, and the last of them gives a remainder of 1 when divided by both 2 and 3. It remains to write down all divisors of the form $2^{k}$ and $3^{k}$ ( $k$ from 1 to 100). First, write down the powers of two, alternating $2^{k} \equiv 1(\bmod 3)$ and $2^{k} \equiv 2(\bmod 3)$ (i.e., powers with even and odd exponents). All the resulting partial sums will still be odd and not divisible by three. Finally, write down the powers of three, alternating their remainders modulo 4 so that all remaining partial sums are not divisible by 4. In this case, they will remain not divisible by three, and the factor 2 will enter them no more than in the first power! Thus, in this example, the factor 3 enters all $S_{n}$ in the zero power, and the factor 2 in the zero or first power.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. A grasshopper starts moving in the top-left cell of a $10 \times 10$ square. It can jump one cell down or to the right. Additionally, the grasshopper can fly from the bottom cell of any column to the top cell of the same column, and from the rightmost cell of any row to the leftmost cell of the same row. Prove that the grasshopper will need at least 9 flights to visit each cell of the square at least once.
(N. Vlasova)
|
13. Consider the diagonal running from the bottom-left corner to the top-right corner. We will paint all 10 cells on this diagonal red. Note that from any red cell, without making any jumps, you can only move to cells that are to the right of it, below it, or to the right and below it. Therefore, it is impossible to move from one red cell to another red cell without jumping. The grasshopper must visit all 10 red cells in some order, so it must make at least 9 jumps between these visits.
|
9
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
66. An isosceles triangle \(ABC\) with a perimeter of 12 is inscribed in a circle \(\omega\). Points \(P\) and \(Q\) are the midpoints of the arcs \(ABC\) and \(ACB\) respectively. The tangent to the circle \(\omega\) at point \(A\) intersects the ray \(PQ\) at point \(R\). It turns out that the midpoint of segment \(AR\) lies on the line \(BC\). Find the length of segment \(BC\).
\[
\text{(A. Kuznetsov)}
\]
|
66. Answer: 4. Let $I_{A}, I_{B}, I_{C}$ be the centers of the excircles of triangle $ABC$, touching sides $BC, CA$, and $AB$ respectively. Then the lines $A I_{A}, B I_{B}, C I_{C}$ will be the angle bisectors of triangle $ABC$, and the lines $I_{B} I_{C}, I_{C} I_{A}, I_{A} I_{B}$ will be its external angle bisectors. Therefore, points $A, B, C$ will be the feet of the altitudes of triangle $I_{A} I_{B} I_{C}$, and circle $\omega$ will be its nine-point circle. Then point $P$ is the point of intersection of $I_{A} I_{C}$ with $\omega$ other than $B$. Therefore, $P$ is the midpoint of $I_{A} I_{C}$. Similarly, $Q$ is the midpoint of $I_{A} I_{B}$. Thus, $PQ$ is the midline of triangle $I_{A} I_{B} I_{C}$.
Let $K$ and $L$ be the feet of the external and internal angle bisectors of angle $A$ of triangle $ABC$, and let $M$ be the point of intersection of lines $AR$ and $BC$. By the problem's condition, we know that $AM = MR$. We will prove that $AM = ML = MK$. Indeed, $\angle MAL = \angle MAC + \angle CAL = \angle ABC + \angle LAB = \angle ALM$ (point $M$ lies on ray $BC$ since $R$ lies on $PQ$). Therefore, $AM = ML$, and since triangle $AKL$ is right-angled, $AM = MK$.
Thus, $AM = ML = MK = MR$. Therefore, $ALRK$ is a rectangle and $LR \parallel I_{B} I_{C}$. We obtain that lines $PQ$ and $LR$ are parallel to $I_{B} I_{C}$ and have a common point $R$. Then these lines coincide. This means that point $L$ lies on the midline of triangle $I_{A} I_{B} I_{C}$ and, therefore, divides segment $A I_{A}$ in half. Further, applying the property of the external angle bisector to triangles $ABL$ and $ACL$, we get $AB / BL = AC / CL = AI_{A} / I_{A} L = 2$. Then $AB + AC = 2BC$ and, therefore, $BC = 4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. What is the maximum number of solutions that the equation $\max \left\{a_{1} x+b_{1}, \ldots, a_{10} x+b_{10}\right\}=0$ can have, if $a_{1}, \ldots, a_{10}, b_{1}, \ldots, b_{10}$ are real numbers, and all $a_{i}$ are not equal to 0?
|
49. Answer: 2 solutions. For example, 5 functions $-x-1$ and 5 functions $x-1$.
Suppose this equation has three roots: $u<v<w$. At point $v$, one of the linear functions $a_{i} x+b_{i}$ is zero. On the other hand, its values at points $u$ and $w$ do not exceed zero. However, such a linear function can only be a constant, which is prohibited by the condition.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. In the table, there are 25 columns and 300 rows, and Kostya painted all its cells in three colors. Then Lesha, looking at the table, names one of the three colors for each row and marks all the cells of this color in that row. (If there are no cells of the specified color in the row, he marks nothing in it.) After that, all columns that contain at least one marked cell are erased from the table. Kostya wants as few columns as possible to remain in the table, while Lesha wants as many as possible. What is the maximum number of columns that Lesha can guarantee to leave?
|
52. Answer: Two columns. To leave at least two columns, Lesha must for each row name a color that does not appear in the first two cells of that row. With this strategy, the first two columns will not be crossed out.
Note now that $300=C_{25^{2}}$. Using this observation, we can associate each row with its own pair of columns. Let Kostya paint in each row the cells in the corresponding two columns in the 1st and 2nd colors, and the rest of the cells in the third color. If Lesha chooses the 3rd color in some row, this will immediately cross out everything except two columns. If, however, Lesha always chooses the 1st or 2nd color, then at most one column will remain! Indeed, suppose some two columns remain. Since there is a row in which the cells of these columns are painted in the 1st and 2nd colors, one of these columns must be destroyed by Lesha's choice for that row!
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. What is the minimum number of colors needed to color the cells of a $5 \times 5$ square so that among any three consecutive cells in a row, column, or diagonal, there are no cells of the same color?
(M. Antipov)
|
30. Answer: in five colors.
Consider a cross of five cells, the central cell of which coincides with the central cell of the square. By the condition, three cells in its column have different colors. Similarly, the colors of the three cells in its row are also different. Finally, any two cells at the "ends" of the cross are also of different colors. For example, cells $A$ and $B$ in the figure have different colors, since by the condition
among the cells $A, B, C$ there are no cells of the same color. Thus, the colors of all five cells in the cross are different, so there are at least five colors.
An example of coloring in five colors is shown on the right. In this example, each subsequent row is obtained from the previous one by a cyclic shift of two cells to the left.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. Many city residents engage in dancing, many in mathematics, and at least one in both. Those who engage only in dancing are exactly $p+1$ times more than those who engage only in mathematics, where $p-$ is some prime number. If you square the number of all mathematicians, you get the number of all dancers. How many residents are interested in both mathematics and dancing at the same time?
|
36. Answer: 1 person is engaged in both dancing and mathematics.
Let $a$ people be engaged only in mathematics, and $b \geqslant 1$ people be engaged in both dancing and mathematics. Then, according to the condition, $(a+b)^{2}=(p+1) a+b$. Subtract $a+b$ from both sides: $(a+b)^{2}-(a+b)=p a$. Factor out the common term on the left side: $(a+b)(a+b-1)=p a$. Since $p$ is prime, one of the brackets on the left side must be divisible by $p$. Then $a$ must be divisible by the other bracket! But it is clear that the first bracket is greater than $a$, and the second is not less than $a$. Therefore, $a$ can only be divisible by the second bracket, and only in the case where the second bracket equals $a$. This is possible only when $b=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
66. The sum
$$
\begin{gathered}
2 \\
3 \cdot 6
\end{gathered}+\begin{gathered}
2 \cdot 5 \\
3 \cdot 6 \cdot 9
\end{gathered}+\ldots+\begin{gathered}
2 \cdot 5 \cdot \ldots \cdot 2015 \\
3 \cdot 6 \cdot \ldots \cdot 2019
\end{gathered}
$$
was written as a decimal fraction. Find the first digit after the decimal point.
|
66. Answer: the first digit after the decimal point is 5.
To start, let's simplify the given sum. Each term can be written as a difference
$$
\begin{aligned}
\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}=\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1) \cdot(3 k+3)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}- & \frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1) \cdot(3 k+2)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}= \\
& =\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot 3 k}-\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1) \cdot(3 k+2)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}
\end{aligned}
$$
Then the entire sum will telescope to the difference of the extreme terms $\frac{2}{3}-\frac{2 \cdot 5 \cdot \ldots \cdot 2018}{3 \cdot 6 \cdot \ldots \cdot 2019}$.
Now let's estimate the subtrahend. Introduce the variables
$$
\begin{gathered}
A=\frac{1 \cdot 3 \cdot 6 \cdot \ldots \cdot 2016}{1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2017}, \quad B=\frac{1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2017}{2 \cdot 5 \cdot 8 \cdot \ldots \cdot 2018}, \quad C=\frac{2 \cdot 5 \cdot 8 \cdot \ldots \cdot 2018}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot 2019}, \quad D=\frac{3 \cdot 6 \cdot 9 \cdot \ldots \cdot 2019}{4 \cdot 7 \cdot 10 \cdot \ldots \cdot 2020} \\
E=\frac{4 \cdot 7 \cdot 10 \cdot \ldots \cdot 2020}{5 \cdot 8 \cdot 11 \cdot \ldots \cdot 2022}
\end{gathered}
$$
We want to estimate the value of the number $C$.
Since $\frac{a-1}{a}<\frac{a}{a+1}$ for natural $a$, the inequalities $A<B<C<D<E$ hold, from which $A B C<C^{3}<C D E$. Substituting these inequalities into the formulas for our numbers and simplifying the fractions, we get
$$
\frac{1}{2019}<C^{3}<\frac{2}{2022}, \quad \frac{1}{15}<\sqrt[3]{\frac{1}{2019}}<C<\sqrt[3]{\frac{2}{2022}}<\frac{1}{6}, \text { and thus, } \quad \frac{1}{2}<\frac{2}{3}-\frac{2 \cdot 5 \cdot \ldots \cdot 2018}{3 \cdot 6 \cdot \ldots \cdot 2019}<\frac{3}{5}
$$
Thus, the first digit after the decimal point of the original number is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. From the edge of a large square sheet, a small square was cut off, as shown in the figure, and as a result, the perimeter of the sheet increased by $10 \%$. By what percent did the area of the sheet decrease?
|
5. Answer: by $4 \%$.
Let the side of the larger square be denoted by $a$, and the side of the smaller square by $b$. As a result of cutting out the smaller square from the perimeter of the sheet, one segment of length $b$ disappears, and three such segments appear instead, meaning the perimeter increases by $2 b$. Therefore, $2 b$ constitutes $10 \%$ of the old perimeter: $2 b=0.1 \cdot 4 a$. From this, $b=0.2 a$. Thus, the area of the sheet has decreased by $b^{2}=0.04 a^{2}$, i.e., by $4 \%$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Sasha went to bed at 10 PM and set the alarm clock (with hands and a 12-hour dial) for 7 AM. During the night, at some point, the alarm clock, which had been working properly, broke, and its hands started moving in the opposite direction (at the same speed). Nevertheless, the alarm rang exactly at the scheduled time in the morning. At what time did the alarm clock break? Justify your answer.
(A. Kuznetsov, D. Shiryayev)
|
1. Answer: the alarm clock broke at 1 o'clock at night.
Let's imagine that the minute hand on the alarm clock is missing, and the hour hand, at the moment when the alarm clock broke, split into two halves, one of which (as stated in the condition) started moving in the opposite direction, while the other continued its normal movement. Then at 7 o'clock in the morning, both hands will meet! This means that both hands have traveled half the clock face and the split occurred directly "opposite" the 7 mark, i.e., at 1 o'clock at night.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the inequality $2021 \cdot \sqrt[202]{x^{2020}}-1 \geq 2020 x$ for $x \geq 0$. (10 points)
|
Solution. Transform the inequality into the form:
$$
\begin{aligned}
& \frac{2020 x+1}{2021} \leq \sqrt[202]{x^{2020}}, \text { from which } \\
& x+x+\ldots+x+1
\end{aligned}
$$
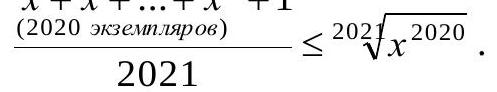
But by the relation for the arithmetic mean and the geometric mean, $x+x+\ldots+x+1$
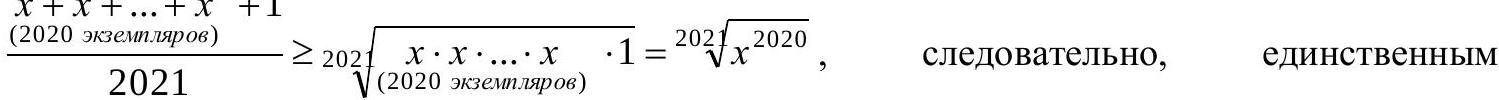
the solution to the inequality is $x=1$.
Answer. $x=1$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $2021 x=2022 \cdot \sqrt[2022]{x^{2021}}-1 .(10$ points $)$
|
Solution. $x \geq 0$. Transform the equation to the form:
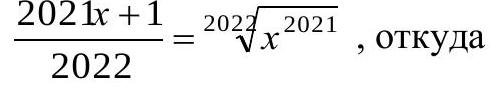
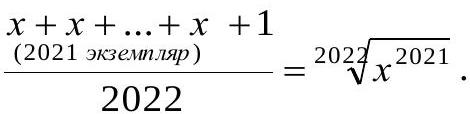
But by the relation for the arithmetic mean and the geometric mean
$x+x+\ldots+x+1$
the inequality holds for $x=1$.
Answer. $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $2021 \cdot \sqrt[202]{x^{2020}}-1=2020 x$ for $x \geq 0 \cdot$ (10 points)
|
Solution. Transform the equation to the form:
$$
\begin{aligned}
& \frac{2020 x+1}{2021}=\sqrt[202]{x^{2020}}, \text { from which } \\
& x+x+\ldots+x+1 \\
& \frac{(2020 \text { instances) }}{2021}=\sqrt[202]{x^{2020}}
\end{aligned}
$$
But by the relation for the arithmetic mean and the geometric mean
the solution to the equation is $x=1$.
Answer. $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two adjacent faces of a tetrahedron, which are isosceles right triangles with a hypotenuse of 2, form a dihedral angle of 60 degrees. The tetrahedron is rotated around the common edge of these faces. Find the maximum area of the projection of the rotating tetrahedron onto the plane containing
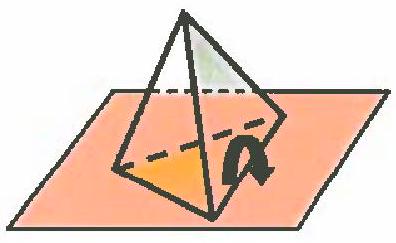
the given edge. (12 points)
Solution. Let the area of each of the given faces be \( S \). If the face lies in the plane of projection, then the projection of the tetrahedron is equal to the area of this face \( \Pi = S \).
When rotated by an angle \( 0 < \varphi < 30^\circ \), the area of the projection is \( \Pi = S \cos \varphi < S \).
When rotated by an angle \( 30^\circ < \varphi < 90^\circ \), the area of the projection is
\[
\Pi = S \cos \varphi + S \cos \psi = S \cos \varphi + S \cos \left(\pi - \frac{\pi}{3} - \varphi\right) = S \cos \varphi + S \cos \left(\frac{2\pi}{3} - \varphi\right).
\]
\[
\Pi' = S \left(-\sin \varphi + \sin \left(\frac{2\pi}{3} - \varphi\right)\right), \quad \Pi' = 0 \text{ when } \varphi = \frac{\pi}{3}.
\]
The maximum of the function in the considered interval is achieved at
\[
\varphi = \frac{\pi}{3}, \quad \Pi = 2 S \cos \left(\frac{\pi}{3}\right) = 2 S \cdot \frac{1}{2} = S.
\]
When rotated by an angle \( 90^\circ < \varphi < 120^\circ \), the area of the projection is \( \Pi = S \cos \left(\frac{\pi}{2} - \varphi\right) = S \sin \varphi < S \).
When \( \varphi = \frac{2\pi}{3} \), the area \( \Pi = S \).
|
Answer. $\Pi=S=\frac{1}{2} \cdot \sqrt{2}^{2}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $2021 \cdot \sqrt[202]{x^{2020}}-1=2020 x$ for $x \geq 0$. (10 points)
|
Solution. Transform the equation to the form:
$$
\begin{aligned}
& \frac{2020 x+1}{2021}=\sqrt[202]{x^{2020}}, \text { from which } \\
& \frac{\begin{array}{l}
x+x+\ldots+x+1 \\
(2020 \text { terms) }
\end{array}}{2021}=\sqrt[202]{x^{2020}} .
\end{aligned}
$$
But by the inequality between the arithmetic mean and the geometric mean
the solution to the equation is $x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. An athlete with a mass of 78.75 kg is testing a net used by firefighters to save people. The net sags by 100 cm when the athlete jumps from a height of 15 m. Assuming the net behaves elastically like a spring, calculate how much it will sag when a person with a mass of 45 kg jumps from a height of 29 m.
Given:
$m_{1}=78.75$ kg;
$x_{1}=1 \mathrm{~m} ;$
$h_{1}=15 \mathrm{~m} ;$
$m_{2}=45 \mathbf{~ kg ; ~}$
$h_{2}=29 \mathrm{~m}:$
|
Solution. The mechanical system "Earth-athlete-net" $x_{2}-?$ can be considered closed. According to the law of conservation of energy, when the athlete jumps, his potential energy should completely transform into the energy of the elastic deformation of the net: $m_{2} g\left(h_{2}+x_{2}\right)=\frac{k x_{2}^{2}}{2} ;$
$m_{1} g\left(h_{1}+x_{1}\right)=\frac{k x_{1}^{2}}{2} ;$
$\frac{m_{2}}{m_{1}} \cdot \frac{\left(h_{2}+x_{2}\right)}{\left(h_{1}+x_{1}\right)}=\frac{x_{2}^{2}}{x_{1}^{2}} ;$
$\frac{45}{78.75} \cdot \frac{\left(29+x_{2}\right)}{(15+1)}=x_{2}^{2}$;
$\frac{\left(29+x_{2}\right)}{16}=\frac{x_{2}^{2} \cdot 78.75}{45} ;$
$29+x_{2}=x_{2}^{2} \cdot 1.75 \cdot 16$
$28 x_{2}^{2}-x_{2}-29=0$
$D=1+4 \cdot 28 \cdot 29=3249=57^{2}$
$x_{2}=\frac{1+57}{56} \approx 1.04 \mathrm{M}$.
3. Mass spectrometry is one of the most precise methods of substance identification, used in almost all areas of human activity: pharmaceuticals, medicine, ecology,
oil and gas industry, nuclear energy. It is a kind of "weighing" of molecules: components are ionized, and then the mass-to-charge ratio of the ions is determined. It turned out that when separating ions with comparable mass, for example, two isotopes of argon ( ${ }^{36} \mathrm{Ar}$ and ${ }^{38} \mathrm{Ar}$ ), difficulties arise. Calculate the radius of curvature required for these particles to be 1.2 mm apart.
Ions, after passing through crossed electric and magnetic fields, and after the velocity selector, enter only the magnetic field and move along the arc of a circle.
$\left\{\begin{array}{c}v=\frac{E}{B} \\ q v B^{\prime}=\frac{m v^{2}}{R}\end{array} \rightarrow m=\frac{q B B^{\prime} R}{E}\right.$.
$x=D_{2}-D_{1}=2\left(R_{2}-R_{1}\right)$
All quantities except $R$ in formula (1) are determined by the parameters of the setup, therefore, for particles with the same charge, it is valid
$\frac{R_{2}}{R_{1}}=\frac{m_{2}}{m_{1}}=38 / 36=1.056$
$R_{2}-R_{1}=\frac{x}{2}=0.6(\mathrm{MM})$
$0.6+R_{1}=1.056 R_{1}$
$R_{1}=10.7$ mm
$R_{2}=11.3 \mathrm{Mm}$
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $9^{x}+4 \cdot 3^{x+1}=13$.
|
Solution: $3^{2 x}+4 \cdot 3^{x+1}=13, 3^{2 x}+12 \cdot 3^{x}-13=0$,
$\left(3^{x}\right)_{1,2}=\frac{-12 \pm \sqrt{144+52}}{2}=\frac{-12 \pm 14}{2}=\left[\begin{array}{l}1, \\ -13 .- \text { n.s. }\end{array} 3^{x}=1 \Rightarrow x=0\right.$. Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=3 \sin x+4 \cos x$.
|
Solution: $f(x)=3 \sin x+4 \cos x=\sqrt{3^{2}+4^{2}} \sin \left(x+\operatorname{arctg} \frac{4}{3}\right)=5 \sin \left(x+\operatorname{arctg} \frac{4}{3}\right)$.
Answer: The maximum value is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $9^{x-1}+3^{x+2}=90$.
|
Solution: $9^{x-1}+3^{x+2}=90,\left(3^{x-1}\right)^{2}+27 \cdot 3^{x-1}=90$, $3^{x-1}=\frac{-27 \pm \sqrt{3^{6}+4 \cdot 3^{2} \cdot 10}}{2}=\frac{-27 \pm 3 \sqrt{121}}{2}=\frac{-27 \pm 33}{2}=\left[\begin{array}{l}3, \\ -30 .\end{array} \quad x-1=1, x=2\right.$ Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{x-3}{2 x+1}}+2=3 \sqrt{\frac{2 x+1}{x-3}}$.
|
Solution: $t=\frac{x-3}{2 x+1}>0 ; \sqrt{t}+2=\frac{3}{\sqrt{t}}, \sqrt{t}+2 \sqrt{t}-3=0, \sqrt{t}=\left[\begin{array}{l}1 \\ -3 \text {, but this is not valid }\end{array}\right.$
$\frac{x-3}{2 x+1}=1 ; x-3=2 x+1, x=-4, \sqrt{\frac{-7}{-7}}+2=3 \sqrt{\frac{-7}{-7}}$. Answer: $x=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{2 x+2}{x+2}}-\sqrt{\frac{x+2}{2 x+2}}=\frac{7}{12}$.
|
Solution: $\sqrt{\frac{2 x+2}{x+2}}-\sqrt{\frac{x+2}{2 x+2}}=\frac{7}{12} ; t=\frac{2 x+2}{x+2}>0, \sqrt{t}-\sqrt{\frac{1}{t}}=\frac{7}{12}$,
$\sqrt{t}=\frac{7 \pm \sqrt{49+4 \cdot 144}}{24}=\frac{7 \pm 25}{24}=\left[\begin{array}{l}\frac{32}{24}=\frac{4}{3} \\ -\frac{18}{24}=-\frac{3}{4}\end{array}, \frac{2 x+2}{x+2}=\frac{16}{9}, 16 x+18=16 x+32\right.$,
$2 x=14, x=7$. Verification: $\sqrt{\frac{16}{9}}-\sqrt{\frac{9}{16}}=\frac{7}{12}$. Answer: $x=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=6 \sin x+8 \cos x$.
|
Solution: $f(x)=6 \sin x+8 \cos x=\sqrt{6^{2}+8^{2}} \sin \left(x+\operatorname{arctg} \frac{8}{6}\right)$.
Answer: The maximum value is 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the greatest and least values of the function $y=x^{3}-3 x^{2}+5$ on the interval $[1 ; 3]$.
|
Solution: $y=x^{3}-3 x^{2}+5,[1 ; 3] ; y^{\prime}=3 x^{2}-6 x=3 x(x-2) \Rightarrow x=0 ; 2$
$y(1)=3 ; y(3)=5 ; y(2)=1$.
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Calculate $\sqrt{4+\sqrt{12}}-\sqrt{4-\sqrt{12}}$.
|
Solution: $\sqrt{4+\sqrt{12}}-\sqrt{4-\sqrt{12}}=A ; A^{2}=8-2 \sqrt{16-12}=4 ; \quad A= \pm 2$ Answer: $A=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Calculate $\sqrt{3+\sqrt{8}}-\sqrt{3-\sqrt{8}}$.
|
Solution: $\sqrt{3+\sqrt{8}}-\sqrt{3-\sqrt{8}}=A ; A^{2}=6-2 \sqrt{9-8}=4, \quad A= \pm 2, \quad A=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $3 \cdot 9^{x}+2 \cdot 3^{x}=1$.
|
Solution: $3 \cdot 9^{x}+2 \cdot 3^{x}=1,3 \cdot\left(3^{x}\right)^{2}+2 \cdot 3^{x}-1=0,3^{x}=\frac{-2 \pm \sqrt{4+12}}{6}=\left[\begin{array}{l}\frac{1}{3}, \\ -1-\text { not valid }\end{array} \quad x=-1\right.$.
Answer: $x=-1$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Two vertices of a square with an area of $256 \mathrm{~cm}^{2}$ lie on a circle, while the other two vertices lie on a tangent to this circle. Find the radius of the circle.
|
Solution: $S_{A B C D}=256 \, \text{cm}^{2} \Rightarrow a=16 \, \text{cm}=x$,
$E F=2 R-x, F O=R-E F=R-(2 R-x)=x-R$,
$\triangle F C O: F O^{2}=R^{2}-F C^{2} \Rightarrow(x-R)^{2}=R^{2}-8^{2}$,
$x^{2}-2 R x+R^{2}=R^{2}-8^{2}, 2 R x=16^{2}+8^{2} \Rightarrow R=\frac{16^{2}+8^{2}}{2 \cdot 16}=10$. Answer:
$R=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{x+3}{3 x-5}}+1=2 \sqrt{\frac{3 x-5}{x+3}}$.
|
Solution:
$$
\sqrt{\frac{x+3}{3 x-5}}+1=2 \sqrt{\frac{3 x-5}{x+3}}
$$
$\frac{x+3}{3 x-5}>0$
$t=\frac{x+3}{3 x-5}, \sqrt{t}+1=\frac{2}{\sqrt{t}}, \frac{t+\sqrt{t}-2}{\sqrt{t}}=0, \sqrt{t}=\frac{-1 \pm \sqrt{1+8}}{2}=\frac{-1 \pm 3}{2}=\left[\begin{array}{l}-2 \\ 1\end{array}\right.$
$t=1, \frac{x+3}{3 x-5}=1,3 x-5=x+3,2 x=8, x=4$. Verification: $\sqrt{\frac{7}{7}}+1=2 \sqrt{\frac{7}{7}}$. Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.