problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
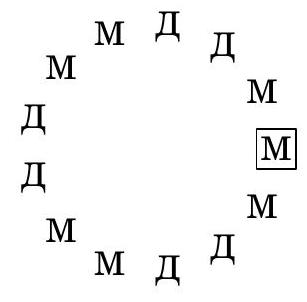
Problem 4. 13 children sat at a round table and agreed that boys would lie to girls, but tell the truth to each other, and girls, on the contrary, would lie to boys, but tell the truth to each other. One of the children said to their right neighbor: "The majority of us are boys." The latter said to their right neighbor: "The majority of us are girls," and he to his right neighbor: "The majority of us are boys," and so on, until the last child said to the first: "The majority of us are boys." How many boys were at the table?
[6 points] (A. V. Khachatryan)
|
# Answer: 7.
Solution. It is clear that there were both boys and girls at the table. Let's see how the children were seated. After a group of boys sitting next to each other comes a group of girls, then boys again, then girls, and so on (a group can consist of just one person). Groups of boys and girls alternate, so their number is even. The incorrect statements were made at the transitions from one group to another, so their number is also even. Since seven statements of "most of us are boys" were made, six of the statements "most of us are girls" must be incorrect, and there were also six groups.
The alternation of correct and incorrect statements means that there were two children in each group. Only the first and last child sitting next to each other said the same thing, so there were three people in their group. These are boys, as they are in the majority. In total, there were $2+2+2=6$ girls and $2+2+3=7$ boys sitting at the table.
The diagram shows exactly how the children were seated at the table. The first speaker is outlined in a frame.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Small Island and Big Island have a rectangular shape and are divided into rectangular counties. In each county, a road is laid along one of the diagonals. On each island, these roads form a closed path that does not pass through any point more than once. Here is how Small Island is organized, with a total of 6 counties (see Fig. 1). Draw how Big Island might be organized if it has an odd number of counties. How many counties did you get?
[7 points] (A. V. Shapovalov)
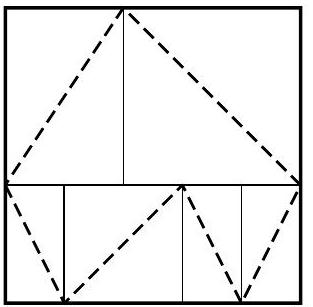
Fig. 1
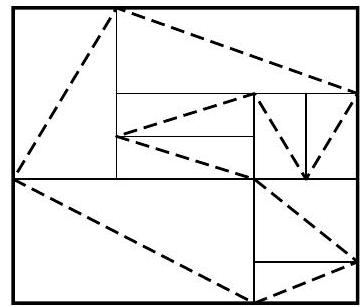
Fig. 2
|
Answer. Figure 2 provides an example for 9 counties.
Comment. We will show that examples do not exist for 7 counties (or fewer), while at the same time pointing out a property characteristic of all such examples.
All roads can be divided into two types: some roads connect the top-left corner of a county with the bottom-right, while others connect the bottom-left with the top-right. If the roads of different types always alternated when traversing a closed path, their total number would be even (just like the groups of boys and girls in the previous problem). On the Large Island, where the number of counties is odd, there must, therefore, be two roads of the same type in a row.
For example, suppose two roads $A B$ and $B C$ of the same type are in a row (see the figure). In addition to the counties in which they are constructed, two more counties, shaded in gray, adjoin vertex $B$. By the condition, the roads in these counties do not pass through point $B$. Let's draw them.
Now there are four roads on the figure. To have a total of seven, three segments are needed to connect them into a single chain. To do this, it would be necessary to connect some two ends of the roads in the "gray counties" with a segment, which is impossible.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In the square, some cells are shaded as shown in the figure. It is allowed to fold the square along any grid line and then unfold it back. Cells that coincide with shaded cells when folded are also shaded. Can the entire square be shaded:
a) in 5 or fewer;
b) in 4 or fewer;

c) in 3 or fewer such foldings?
(If yes, write the number of the fold after which each cell will be shaded for the first time, draw the fold line and mark it with the same number. If no, prove it.) [4 points] (T. I. Goleneva-Kutuzova, M. A. Raskin, I. V. Yashchenko)
|
Answer. It is possible (even with 3 bends).
Solution. For example, it is possible to paint the entire lower half of the board with two vertical bends, after which the upper half can be painted with one horizontal bend - see the figure. (There are other solutions as well.)
Comment. It is impossible to paint all cells in 2 bends. Indeed, with each bend, the number of cells increases by no more than 2 times. Initially, there are 6 painted cells; therefore, after two bends, no more than $6 \cdot 2 \cdot 2=24$ cells out of 36 will be painted.
| 3 | 3 | 3 | 3 | 3 | 3 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 |
| | 1 | | 1 | 2 | 2 |
| 2 | | 1 | 2 | 2 | |
| 1 | 2 | 2 | | | 2 |
| | | 1 | 2 | | |
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. A bag of sunflower seeds was passed around a table. The first person took 1 seed, the second took 2, the third took 3, and so on: each subsequent person took one more seed than the previous one. It is known that in the second round, the total number of seeds taken was 100 more than in the first round. How many people were sitting at the table?
$[4$ points
(A. V. Shapovalov)
|
Answer: 10 people.
Solution: Let there be $n$ people sitting at the table. Then on the second round, the first person took the $n+1$-th sunflower seed, the second person took the $n+2$-th - and generally, each person took $n$ more seeds than on the first round. Altogether, on the second round, they took $n \cdot n=n^{2}$ more seeds than on the first. Since $n^{2}=100$, then $n=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Three square paths with a common center are 1 m apart from each other (see figure). Three ants start simultaneously from the lower left corners of the paths and run at the same speed: Mu and Ra counterclockwise, and Wei clockwise. When Mu reaches the lower right corner of the largest path, the other two, who have not yet completed a full circle, are on the right sides of their paths, and all three are on the same straight line. Find the sides of the squares.
[6 points] (A. V. Shapovalov)
|
Answer: 4 m, 6 m, 8 m.
Solution: The lengths of the sides of two adjacent paths differ by 2 m (Fig. 3). Therefore, at the moment when Mu reached the corner, Ra had run 2 m along the right side of the path and was at a distance of $2+1=3$ m from the "lower" side of the outer path. Since $\mathrm{Pa}$ is halfway between Mu and Vee, Vee is at twice the distance from this side, 6 m (since the two highlighted right triangles in Fig. 4 are equal in hypotenuse and angles). That is, Vee still has to run $6-1-1=4$ m along the side.
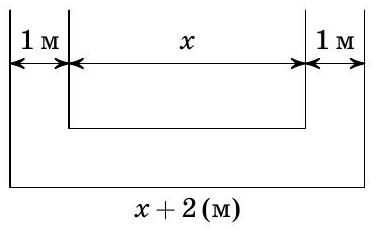
Fig. 3
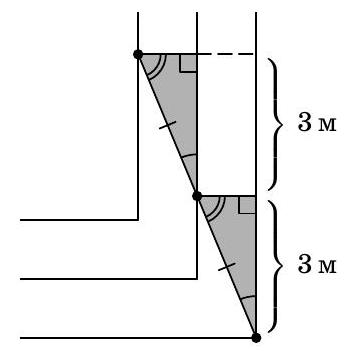
Fig. 4
But if Vee had run counterclockwise, he would have run the entire lower side and another 4 m along the right side (since this side is 4 m shorter than the side of the outer square), i.e., he would have ended up at the same point. Since Vee ends up at the same point whether he runs clockwise or counterclockwise, this point is the upper right corner of the square. Therefore, the side of this square is 4 m. Accordingly, the sides of the other two squares are $4+2=6$ m and $6+2=8$ m.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Fox Alice and Cat Basil have grown 20 fake banknotes on a tree and are now filling in seven-digit numbers on them. Each banknote has 7 empty cells for digits. Basil calls out one digit at a time, either "1" or "2" (he doesn't know any others), and Alice writes the called digit in any free cell of any banknote and shows the result to Basil.
When all cells are filled, Basil takes as many banknotes with different numbers as possible (if there are several with the same number, he takes only one), and the rest go to Alice. What is the maximum number of banknotes Basil can get, no matter how Alice acts? [8 points] (A. V. Shapovalov)
|
Answer: 2.
Solution: Basil can always get two banknotes: he knows the place where the last digit should be written and names it so that it differs from the digit in the same place on some other banknote. Then the numbers on these two banknotes will be different, and the cat can take them.
We will show how Alice can ensure that there are no more than two different numbers. She arranges the banknotes one above the other so that the cells for the digits form a table.
When the cat names a one, Alice writes it in the leftmost column where there is a free cell (in any of the cells), and when the cat names a two - in the rightmost column.
If both ones and twos start to appear in some column, then all other columns are already filled: ones on the left, twos on the right. This means there will be at most one column where both ones and twos appear. Therefore, if the numbers do differ, they will differ only by the digit in this column. Since there are only two digits, there will be no more than two different numbers.
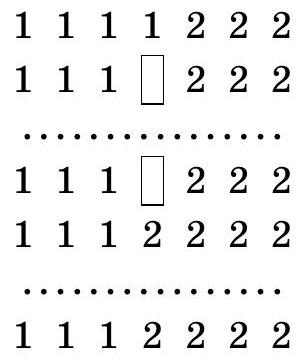
$\begin{array}{lllllllllllll}1 & 1 & 1 & 1 & 2 & 2 & 2\end{array}$


$\begin{array}{lllllll}1 & 1 & 1 & 2 & 2 & 2 & 2\end{array}$
$\begin{array}{lllllll}1 & 1 & 1 & 2 & 2 & 2 & 2\end{array}$
The 11th Oral City Mathematical Olympiad for 6-7 grades will take place on March 17, 2013.
Students who have received a diploma or certificate as a prize winner or honorable mention in at least one of the following mathematical competitions are invited to participate:
- Mathematical Festival (19.02.12 or 17.02.13),
- 10th City Oral Olympiad (09.03.12),
- Winter Archimedes Tournament (22.01.12 or 20.01.13),
- Spring Archimedes Tournament for 5th grade (individual competition, 01.04.12).
To participate in the Olympiad, you need to register in advance by March 5, 2013. Details on the website olympiads.mccme.ru/ustn/
## Information on Enrollment in 5-8 Grades with Advanced Mathematics in 2013
| School | Phone, URL | Address | Grades | Periods |
| :---: | :---: | :---: | :---: | :---: |
| 2 | (499) $137-17-69$ (499) $137-69-31$ www.sch2.ru | Fotieva St., 18 (m. "Oktyabrskaya") | 7,8 | March-May |
| 25 | sch25.ru nabor@mathbaby.ru | University Ave., 7 (m. "University") | $7 ;$ additional in 8 | from February |
| 54 | (499) 245-99-72 (499) 245-54-25 moscowschool54.ru | Dovator St., 5/9 (m. "Sportivnaya") | 8 | February-May |
| 57 | (495) $691-85-72$ (495) $691-54-58$ sch57.msk.ru | Mal. Znamensky Lane, 7/10, bld. 5 (m. "Borovitskaya") | 8 | from March 13 Wednesdays |
| 179 | (495) $692-48-51$ www.179.ru | Bol. Dmitrovka St., 5/6, bld. 7 (m. "Okhotny Ryad") | 7,8 | from March 22 |
| 192 | (499) $137-33-55$ (499) $137-72-85$ www.sch192.ru | Leninsky Prospekt 34-A (m. "Leninsky Prospekt") | 5,$7 ;$ additional in 8 | April-May Fridays at $16^{00}$ |
| 218 | (499) 976-19-85 school218.ru | Dmitrovskoye Shosse, 5a (m. "Dmitrovskaya") | 8 (IUP) | from March 25 to May 18 |
| 444 | (495) 465-23-52 $(495) 465-60-52$ schv444.mskobar.ru | Nizh. Pervomayskaya St., 14 (m. "Pervomayskaya") | 8 | March-May |
| 1329 | co1329.mskzapad.ru nabor@mathbaby.ru | Nikulin St., 10 (m. "Yugo-Zapadnaya") | 5,8 | from February |
| 1543 | (495) $433-16-44$ $(495) 434-26-44$ www. $1543 . r u$ | 26 Baku Commissars St., 3, bld. 5 (m. "Yugo-Zapadnaya") | 8 | April |
| 2007 | (495) 716-29-35 fmsh2007.ru | Gorchakova St., 9, bld. 1 (m. "Gorchakova St.") | $5-7 ;$ additional in 8 | April |
| Intel- lectual | (499) 445-52-10 sch-int.ru | Kremenchugskaya St., 13 (m. "Slavyanskiy Bulvar") | $5 ;$ additional in 6,7 | March-June |
The information is provided by the schools to the MCCME. It is published free of charge.
Detailed information on enrollment in these and other classes is available on the website www.mccme.ru
Current information on olympiads is available on the website www.olimpiada.ru
The page of the Mathematical Festival (problems, solutions, lists of winners) www.mccme.ru/matprazdnik /
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
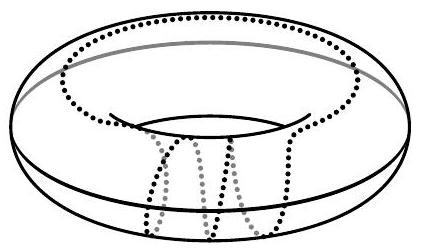
Problem 1. On the surface of a planet shaped like a donut, two snails crawled, leaving trails behind: one along the outer equator, and the other along a spiral line (see figure). Into how many parts did the snails' trails divide the surface of the planet? (It is sufficient to write the answer.)
## [4 points] (S.K. Smirnov, I.V. Yashchenko)
|
Answer: 3.
Comment. Let's imagine the surface of a donut made of paper. Cut it along the path of the first snail and unfold it. We will get the lateral surface of a cylinder. The path of the second snail will be cut in three places. That is, on the resulting surface, the trail of the second snail represents three lines connecting the bottom base of the cylinder with the top. It is not difficult to realize that they divide the lateral surface of the cylinder into 3 parts.
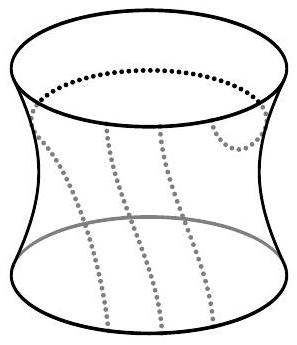
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
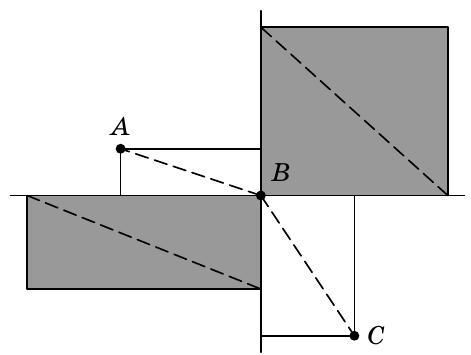
Problem 6. On the sides \(AB\) and \(BC\) of square \(ABCD\) with side length 10, points \(K\) and \(L\) are marked such that \(AK = CL = 3\). On segment \(KL\), a point \(P\) is chosen, and on the extension of segment \(AB\) beyond point \(B\), a point \(Q\) is chosen such that \(AP = PQ = QL\) (see figure).
a) Prove that \(\angle PAB = \angle BLQ\).
b) Find the length of segment \(BQ\).
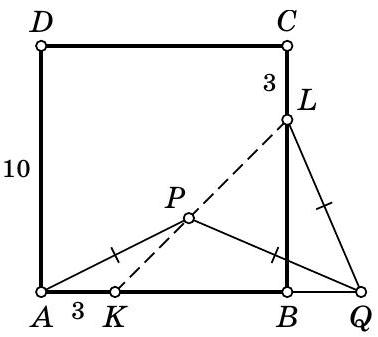
[4 points]
[4 points] * In solving part b), you can use the statement from part a).
(F. A. Ivlev, A. A. Mardanov)
a) Solution. Note that \(KB = AB - AK = 10 - 3 = BC - CL = BL\). Therefore, triangle \(KBL\) is isosceles and right-angled, so \(\angle KLB = 45^\circ\).
Let \(\angle BLQ = \alpha\). Since triangle \(PQL\) is isosceles, we have \(\angle LPQ = \angle PLQ = 45^\circ + \alpha\). From the sum of the angles in triangle \(PQL\), we find \(\angle PQL = 180^\circ - 2 \cdot (45^\circ + \alpha) = 90^\circ - 2\alpha\).
From the sum of the angles in triangle \(BLQ\), we find that \(\angle LQB = 90^\circ - \alpha\). Now we find \(\angle PQA = \angle LQA - \angle LQP = 90^\circ - \alpha - (90^\circ - 2\alpha) = \alpha\). Finally, since triangle \(APQ\) is isosceles, \(\angle PQA = \angle PAQ = \alpha = \angle BLQ\), which is what we needed to prove.
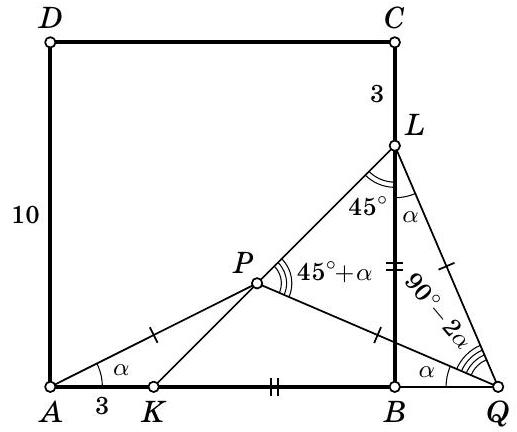
b) Answer. \(BQ = 4\).
|
Solution. Drop a perpendicular $PH$ from point $P$ to side $AB$. Since triangle $KBL$ is isosceles and right-angled, $\angle PKH = 45^\circ$. Therefore, triangle $KPH$ is also isosceles and $KH = HP$.
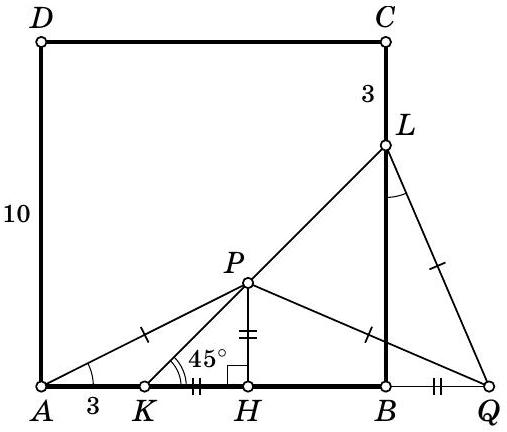
Notice that right triangles $APH$ and $LQB$ are equal by hypotenuse ($AP = LQ$) and acute angle ($\angle PAH = \angle BLQ$). Therefore, $KH = PH = BQ$.
Since $PH$ is the height in the isosceles triangle $APQ$ drawn to its base, it is also the median. Then $AH = HQ$ and we can write the following relationship:
\[
\begin{gathered}
AB + BQ = AQ = 2AH = 2(AK + KH) = 2(AK + BQ) \\
10 + BQ = 2(3 + BQ) = 6 + 2BQ
\end{gathered}
\]
from which $BQ = 4$.
|
4
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Small Island and Big Island have a rectangular shape and are divided into rectangular counties. In each county, a road is laid along one of the diagonals. On each island, these roads form a closed path that does not pass through any point more than once. Here is how Small Island is organized, with a total of 6 counties (see Fig. 1). Draw how Big Island might be organized if it has an odd number of counties. How many counties did you get?
[7 points] (A. V. Shapovalov)

Fig. 1

Fig. 2
|
Answer. Figure 2 provides an example for 9 counties.
Comment. We will show that examples do not exist for 7 counties (or fewer), while at the same time pointing out a property characteristic of all such examples.
All roads can be divided into two types: some roads connect the top-left corner of a county with the bottom-right, while others connect the bottom-left with the top-right. If the roads of different types always alternated when traversing a closed path, their total number would be even (just like the groups of boys and girls in the previous problem). On the Large Island, where the number of counties is odd, there must, therefore, be two roads of the same type in a row.
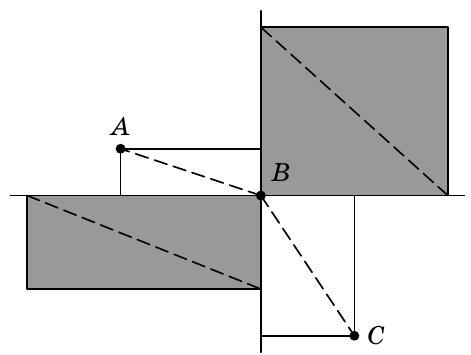
For example, suppose two roads $A B$ and $B C$ of the same type are in a row (see the figure). In addition to the counties in which they are constructed, two more counties, shaded in gray, adjoin vertex $B$. By the condition, the roads in these counties do not pass through point $B$. Let's draw them.
Now there are four roads on the figure. To have a total of seven, three segments are needed to connect them into a single chain. To do this, it would be necessary to connect some two ends of the roads in the "gray counties" with a segment, which is impossible.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In the square, some cells are shaded as shown in the figure. It is allowed to fold the square along any grid line and then unfold it back. Cells that coincide with shaded cells when folded are also shaded. Can the entire square be shaded:
a) in 5 or fewer;
b) in 4 or fewer;

c) in 3 or fewer such foldings?
(If yes, write the number of the fold after which each cell will be shaded for the first time, draw the fold line and mark it with the same number. If no, prove it.) [4 points] (T. I. Golenishcheva-Kutuzova, M. A. Raskin, I. V. Yashchenko)
|
Answer. It is possible (even with 3 bends).
Solution. For example, it is possible to paint the entire lower half of the board with two vertical bends, after which the upper half can be painted with one horizontal bend - see the figure. (There are other solutions as well.)
Comment. It is impossible to paint all cells in 2 bends. Indeed, with each bend, the number of cells increases by no more than 2 times. Initially, there are 6 painted cells; therefore, after two bends, no more than $6 \cdot 2 \cdot 2=24$ cells out of 36 will be painted.
| 3 | 3 | 3 | 3 | 3 | 3 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 |
| | 1 | | 1 | 2 | 2 |
| 2 | | 1 | 2 | 2 | |
| 1 | 2 | 2 | | | 2 |
| | | 1 | 2 | | |
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. The numbers $2,3,4, \ldots, 29,30$ are written on the board. For one ruble, you can mark any number. If a number is already marked, you can freely mark its divisors and numbers that are multiples of it. What is the minimum number of rubles needed to mark all the numbers on the board? [6 points]
(I.V. Yashchenko)
|
Answer. For 5 rubles.
Solution. Let's mark the numbers $17, 19, 23$, and 29, spending four rubles. Then mark the number 2, spending another ruble. After this, we can freely mark all even numbers (since they are divisible by 2), and then all odd numbers not exceeding 15 - for any of them (let's say for the number $n$), the even number $2n$ is marked, and we can mark $n$ as its divisor. It remains to mark 21, 25, and 27, and this is also done for free: 25 is divisible by the marked number 5, and 21 and 27 are divisible by the marked number 3. In any way of solving the problem, the prime numbers 17, 19, 23, and 29, which exceed 15, will have to be marked for money, as they are not divisors or multiples of any numbers on the board. So, 4 rubles will be spent only on them. To mark anything else, we will have to spend a fifth ruble. Therefore, it is impossible to fulfill the conditions of the problem for less than five rubles.
Comment. In fact, after marking the "large" prime numbers, we could have marked any of the remaining numbers on the board instead of two. Indeed, then we will freely mark its smallest prime divisor $p$. If $p=2$, we act according to the algorithm described above. If not, we mark $2p$ (this is possible since $p<15$), then mark two, and then everything else in the known way.
A similar solution is applicable for an arbitrarily long set $2, 3, 4, \ldots, N$ - we are forced to mark all "large" prime numbers (exceeding $N / 2$) for money, and then mark any of the remaining numbers for a ruble. Then we freely mark two in the way described above, then all even numbers, then all "small" prime numbers (not exceeding $N / 2$), because any "small" $p$ will be a divisor of $2p$. Now we can mark all other unmarked numbers: each of them will be divisible by its minimal prime divisor - a "small" prime number.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A rectangular sheet of paper was folded, aligning a vertex with the midpoint of the opposite shorter side (Fig. 12). It turned out that triangles I and II are equal. Find the longer side of the rectangle if the shorter side is 8.
[6 points] (A. V. Khachatryan)
|
Answer: 12.
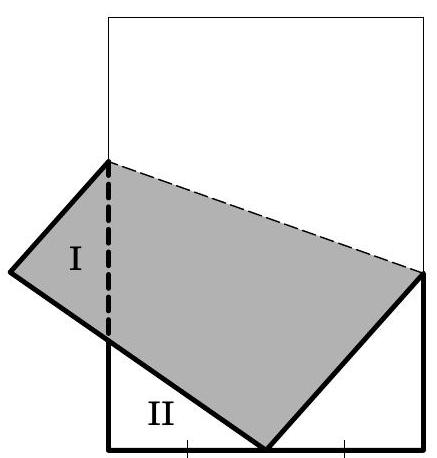
Fig. 12
Solution. Let's mark the equal segments (Fig. 13 - here we used the fact that in congruent triangles, sides opposite equal angles are equal). We see that the length of the larger side is $a+b+4$, and the length of the smaller side is $a+b$. Therefore, $a+b=8$ and the larger side has a length of $a+b+4=8+4=12$.
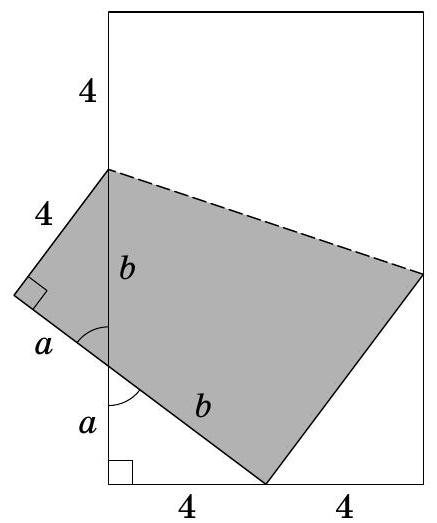
Fig. 13
Comment. By applying the Pythagorean theorem, we can find the lengths of the sides of triangles I and II. It turns out that these are Egyptian triangles - triangles with sides 3, 4, and 5.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Pete liked the puzzle, he decided to glue it together and hang it on the wall. In one minute, he glued together two pieces (initial or previously glued). As a result, the entire puzzle was joined into one complete picture in 2 hours. How long would it have taken to assemble the picture if Pete had glued together three pieces per minute instead of two?
[5 points] (A. V. Shapovalov)
|
Answer: In one hour.
Solution 1. Each gluing reduces the number of pieces on the table by 1. Since after 120 gluings one piece (the complete puzzle) was obtained, there were 121 pieces at the beginning. Now, if three pieces are glued together per minute (i.e., the number of pieces is reduced by 2), one piece will remain after 60 minutes.
Solution 2. In one minute, Petya made one gluing and spent 2 hours assembling the puzzle. If he glued three pieces together, he would make two gluings per minute, i.e., work twice as fast and thus spend 1 hour.
Comment. The time spent gluing the entire puzzle does not depend on the order in which Petya took the pieces. For example, he could add one piece at a time to the already glued part. Or he could glue the pieces in pairs or triplets and then glue them together. In the first case, it would take him 2 hours, and in the second case, 1 hour. In the first solution, this fact is proven by counting the total number of pieces. In the second solution, it is taken as obvious. Therefore, strictly speaking, the second solution is incomplete: it provides the correct answer, but does not prove its uniqueness.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5. Replace in the equation
$$
\text { PIE = SLICE + SLICE + SLICE + ... + SLICE }
$$
identical letters with identical digits, and different letters with different digits, so that the equation is true, and the number of "slices of pie" is the largest possible.
|
Answer. The maximum number of "pieces" is seven, for example: ПИРОГ $=95207$, КУСОК $=13601$.
Solution. An example for seven "pieces" is given above. We will show that there cannot be more than seven "pieces". For this, it is convenient to rewrite the condition as a multiplication example: ПИРОГ $=$ КУСОК $\cdot n$, where $n$ is the number of "pieces".
It is clear that if there are 10 or more "pieces", the right side will exceed 100000, so there will be no solutions.
A solution is also impossible for nine "pieces". For ПИРОГ $=$ КУСОК $\cdot 9$ to be a five-digit number, $К$ must be 1. But then ПИРОГ starts and ends with a nine, which should not be the case.
Now we will prove that there cannot be eight "pieces". Let КУСОК $\cdot 8=$ ПИРОГ. Since all the digits in ПИРОГ are different, ПИРОГ $\leqslant 98765$, and then КУСОК $\leqslant 98765 / 8=12345.675$, so КУСОК $\leqslant 12345$. Then it is clear that $К=1$ and $\Gamma=8$. The letter О represents a digit, the product of which by 8 ends in the same digit. It is easy to see that this can only be zero. Since the digits 0 and 1 are already used, and $\mathrm{V} \leqslant 2$ and $\mathrm{C} \leqslant 3$, then $\mathrm{V}=2$ and $\mathrm{C}=3$. Thus, there is only one possibility: КУСОК $=12301$. But this number does not work, as $12301 \cdot 8=98408$, and in 98408 the digits are repeated, which should not be the case.
The example given for seven "pieces" is not the only one; there are three more: $14051 \cdot 7=98357, 12351 \cdot 7=86457, 12051 \cdot 7=84357$. Of course, it was sufficient to provide one example.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Let param1. What is the largest possible value of param2?
It is given that param1. Find the largest possible value of param2.
| param 1 | param 2 | Answer |
| :---: | :---: | :---: |
| $\frac{9 \cos ^{2} x-7+12 \sin x}{16-9 \sin ^{2} x+6 \sqrt{5} \cos x}=3$ | $6 \sin x$ | 4 |
| $\frac{25 \sin ^{2} x-37+40 \cos x}{35-25 \cos ^{2} x-30 \sin x}=4$ | $10 \cos x$ | 8 |
| $\frac{33-16 \cos ^{2} x-24 \sin x}{16 \sin ^{2} x-19-8 \sqrt{7} \cos x}=2$ | $12 \sin x$ | 9 |
| :---: | :---: | :---: |
| $\frac{15-9 \cos ^{2} x+6 \sin x}{9 \sin ^{2} x-7+12 \sqrt{2} \cos x}=\frac{1}{2}$ | | |
## Condition
Let $\frac{9 \cos ^{2} x-7+12 \sin x}{16-9 \sin ^{2} x+6 \sqrt{5} \cos x}=3$. What is the largest possible value of $6 \sin x$?
Answer.
4
#
|
# Solution
Notice that $\frac{9 \cos ^{2} x-7+12 \sin x}{16-9 \sin ^{2} x+6 \sqrt{5} \cos x}=\frac{6-(3 \sin x-2)^{2}}{2+(3 \cos x+\sqrt{5})^{2}}$. The obtained expression can equal 3 only if $3 \sin x-2=0$ and $3 \cos x+\sqrt{5}=0$. Therefore, the expression $6 \sin x$ can only take the value 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the smallest number of different integers that need to be taken so that among them one can choose both a geometric and an arithmetic progression of length $5$?
(M.A. Evdokimov)
|
Solution. Let's provide an example of six integers that satisfy the condition: $-8, -2, 1, 4, 10, 16$. The numbers $1, -2, 4, -8, 16$ form a geometric progression, while the numbers $-8, -2, 4, 10, 16$ form an arithmetic progression.
We will show that no five distinct integers satisfy the condition of the problem. Suppose the contrary: let there be five integers that simultaneously form a geometric progression and, possibly in a different order, an arithmetic progression. Then they have the form $b$, $b q, b q^{2}, b q^{3}, b q^{4}$ where $b \in \mathbb{Z}$. Note that $b \neq 0$ and $q \neq 0$ by the definition of a geometric progression. The numbers $b, b q^{2}, b q^{4}$ are always of the same sign and in an arithmetic progression, they either appear consecutively for $q > 0$ or $q < 0$. In any case, the equality $2 b q^{2} = b + b q^{4}$ must hold, i.e., $b\left(q^{2}-1\right)^{2}=0$, from which $q = \pm 1$, but then there are equal numbers among them. Contradiction. Therefore, five numbers are insufficient.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On an island, there live chameleons of five colors. When one chameleon bites another, the color of the bitten chameleon changes according to some rule, and the new color depends only on the color of the biter and the color of the bitten. It is known that 2023 red chameleons can agree on a sequence of bites, after which all of them will turn blue. For what smallest $k$ can it be guaranteed that $k$ red chameleons can agree to turn blue?
For example, the rules might be: if a red chameleon bites a green one, the bitten one changes color to blue; if a green chameleon bites a red one, the bitten one remains red, i.e., "changes color to red"; if a red chameleon bites a red one, the bitten one changes color to yellow, and so on. (The specific rules for color changes may be different.)
(2022-60, M. Raskin)
|
# Answer. For $k=5$. Solution.
First, let's provide an example of rules under which the described recoloring would require at least 5 red chameleons. Let's number the colors so that red is the first color and blue is the last. Then, let the rules be as follows: if a chameleon of color $k1$ can reduce the number of its color by means of a bite from a chameleon of color $l<k$. In other words, chameleons of colors $1, \ldots, k$ can become colors $1, \ldots, k-1$. By applying this reasoning several times, we will get that our chameleons can all change their color to blue.
Comment. It is not hard to notice that for $n$ colors, $n$ chameleons will be needed. In fact, this problem is one of many questions around (in general) Petri nets. With slight modifications to the problem, the minimum size of the initial population can increase significantly.
For example, suppose that upon biting, both chameleons can change their color differently, and the goal is to reach a state with one green chameleon and many blue ones. In this case, the minimum number can grow faster than any polynomial in $n$, and even faster than
known as the Ackermann function.
Fortunately, if all chameleons must be of the same color both at the beginning and at the end, the situation simplifies significantly. The requirement that only one of the chameleons changes color upon biting even further simplifies the situation. It corresponds to "immediate observation" or "one-way communication" in Petri nets (immediate observation, one-way communication).
In this variant, for example, it is shown—using combinatorial methods accessible to school students—that if two sets of chameleon colors, and after adding the same number of blue chameleons to the first, it becomes possible to obtain the second, then it is sufficient to add $n^{3}$ chameleons.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (B. Novikov) On each cell of an $8 \times 8$ board, a guard is placed. Each guard can look in one of four directions (along the lines of the board) and watch all the guards on the line of his sight. For what largest $k$ can the guards' gazes be directed so that each guard is watched by at least $k$ other guards?
|
Solution: Answer: 5. We will prove that $k \leq 5$. For this, assume that $k \geqslant 6$. Consider the guards standing at the corners of the board. Each of them is watched by at least 6 guards, and these guards must stand at the edge of the board. Moreover, if a guard sees one of the corner guards, they do not see the other corner guards. Thus, at least 24 guards standing at the edge of the board are looking along the sides of the board. Then, inside the board, not at the corner guards, there are no more than four guards standing at the boundaries.
Now consider the guards standing in the central $6 \times 6$ square. Let's count the maximum possible number of "incoming gazes" for them. (We will not count gazes directed at guards on the boundary of the board). This number does not exceed $184=24+100+48+12$. (24 - from four guards on the boundary, 100 - 5 gazes from each of the 20 guards on the boundary of the $6 \times 6$ square, 48 - 4 gazes from each of the 12 guards on the boundary of the $4 \times 4$ square, 12 - 3 gazes from each of the 4 guards in the central $2 \times 2$ square.) Thus, for 36 guards, there are $184=36 \cdot 5+4<36 \cdot 6$ gazes. Therefore, among the guards, there are those who received fewer than 6 gazes.
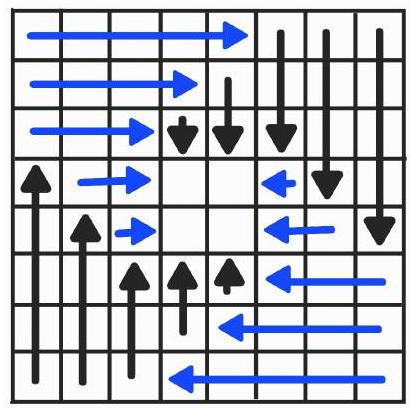
Examples for $k=5$ can be arranged differently. One of the variants is shown in the figure (long arrows mean that several guards in a row are looking in the same direction, guards in the center can look in any direction).
## Criteria.
Arithmetic errors (or errors in counting the number of certain cells) do not affect the evaluation if they did not affect the solution process. “+” - a correct and justified solution is provided;
“土” - a correct example and evaluation with minor (easily fixable) flaws that do not simplify the evaluation;
“干” - a correct example or a correct evaluation is provided;
“-.“ - an evaluation with minor flaws is provided;
“-” - all other cases, including if an evaluation with any significant flaws is provided, the evaluation is greater than 5, or the example is less than 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the largest natural number $n$ with the following property: for any odd prime $p$ less than $n$, the difference $n-p$ is also a prime number.
(I. Akulich)
|
Answer: 10
Solution: Suppose that $n>10$. Notice that the numbers $n-3, n-5, n-7$ are all greater than three, and one of them is divisible by three, and consequently composite. Contradiction.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Among any five nodes of a regular grid paper, there will definitely be two nodes, the midpoint of the segment between which is also a node of the grid paper. What is the minimum number of nodes of a grid made of regular hexagons that need to be taken so that among them, there will definitely be two nodes, the midpoint of the segment between which is also a node of this grid?
(A. Kulygin)
#
|
# Answer. 9
Lemma. Among any five nodes of a grid of equilateral triangles, there will be two such that the midpoint of the segment between them is also a grid node.
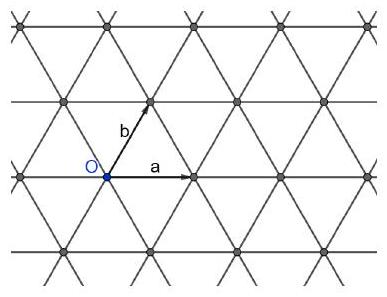
Proof. Introduce the origin at one of the grid nodes and denote by $\vec{a}$ and $\vec{b}$ the radius vectors to the two nearest nodes (see picture). Then the nodes of the grid are points of the form $m \vec{a}+n \vec{b}$ for integers $m$ and $n$. By the pigeonhole principle, among five points, there will be two points $m_{1} \vec{a}+n_{1} \vec{b}$ and $m_{2} \vec{a}+n_{2} \vec{b}$, for which the parity of $m_{1}$ and $m_{2}$ and the parity of $n_{1}$ and $n_{2}$ coincide simultaneously. The midpoint of the segment connecting these two points is the point $\frac{m_{1}+m_{2}}{2} \vec{a}+\frac{n_{1}+n_{2}}{2} \vec{b}$. It is a grid node due to the identical parity of $m_{1}$ and $m_{2}, n_{1}$ and $n_{2}$.
Solution. In the first picture, you can see an example of the placement of 8 grid nodes, among which there are no two such that the midpoint of the segment between them is a grid node. We will prove that nine nodes are sufficient. Note that the hexagonal grid is divided into the union of two triangular grids (see the second picture). By the pigeonhole principle, among any nine nodes, at least five will be in one of these two triangular grids. By the lemma, among these five nodes, there will be two of the required ones.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A polyhedron with vertices at the midpoints of the edges of a certain cube is called a cuboctahedron. When the cuboctahedron is intersected by a plane, a regular polygon is obtained. What is the maximum number of sides this polygon can have?
(M. A. Evdokimov)
|
Solution.
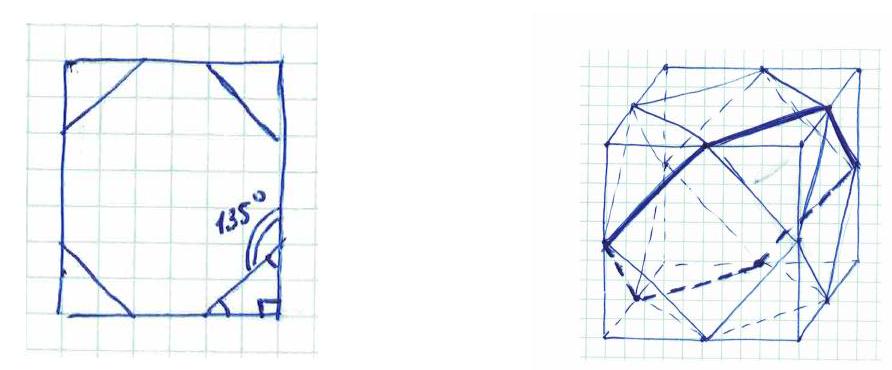
Let the edge of the original cube, from which the cuboctahedron is obtained, be 1. Consider the sections of the cuboctahedron by a plane parallel to the base of the cube at a distance of $08$. Then the vertices of this $n$-gon must lie on the edges of the cuboctahedron, and no more than two vertices of the $n$-gon can belong to one edge. Consider the section of the original cube, which is a regular hexagon (see fig.), as well as sections that are obtained from this by rotating by $90^{\circ}, 180^{\circ}$, and $270^{\circ}$ about the vertical axis of the cube. Note that the union of the sides of these four regular hexagons is the union of all the edges of the cuboctahedron. We will show that on the sides of one of the four chosen regular hexagons, there lie at least 3 vertices of the $n$-gon. Indeed, if on the sides of each such hexagon there are no more than two vertices, then the total number of vertices will not exceed eight. Therefore, the plane of the section of the $n$-gon coincides with the plane of this hexagon, and a hexagon is obtained in the section of the cuboctahedron. This leads to a contradiction.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (I. Akulich) Find the largest natural $n$ with the following property: for any odd prime $p$ less than $n$, the difference $n-p$ is also a prime number.
|
Solution: Answer: 10. Indeed, $10=3+7=5+5$. We will prove that numbers greater than 10 do not work. Let $n$ be a number greater than 10. Note that the numbers $3, 5, 7$ give different remainders when divided by 3. Then the numbers $n-3, n-5, n-7$ give different remainders when divided by 3, meaning one of them is divisible by 3. It remains to note that this number is greater than 3, so it is composite. Contradiction.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
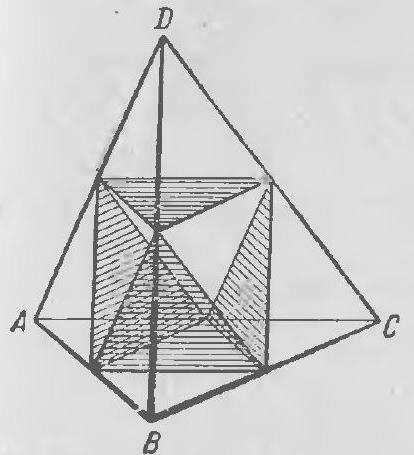
14. What is the smallest number of triangular pyramids (tetrahedrons) into which a cube can be divided?
|
14. It is easy to see that the cube $A B C D A_{1} B_{1} C_{1} D_{1}$ can be divided into five tetrahedra: if we cut off the tetrahedra $B A C B_{1}$ and $D A C D_{1}$, as well as the tetrahedra $A_{1} B_{1} D_{1} A$ and $C_{1} B_{1} D_{1} C$, we will have one more (fifth) tetrahedron $A C B_{1} D_{1}$ left (Fig. 51; the tetrahedron $A C B_{1} D_{1}$ is even a regular one). It is more difficult to establish that the cube cannot be divided into fewer than five tetrahedra.
Indeed, suppose that the cube $A B C D A_{1} B_{1} C_{1} D_{1}$ is divided into some number of tetrahedra. In this case, the face $A B C D$ of the cube is divided into parts that are faces of at least two tetrahedra (the square $A B C D$ can be divided into two or more triangles), and the sum of the areas
Fig. 51. of the bases of these tetrahedra is equal to $a^{2}$, and the height of each of them does not exceed $a$; therefore, the sum of the volumes of the tetrahedra adjacent to the face $A B C D$ of the division does not exceed $\frac{1}{3} a^{2} \cdot a = \frac{a^{3}}{3}$. Similarly, the face $A_{1} B_{1} C_{1} D_{1}$ of the cube is adjacent to at least two tetrahedra, and the total volume of these tetrahedra also does not exceed $\frac{a^{3}}{3}$. Since no tetrahedron can simultaneously have faces that are part of the square $A B C D$ and part of the square $A_{1} B_{1} C_{1} D_{1}$ (since no tetrahedron has parallel faces!), we already have at least four tetrahedra, and the total number of tetrahedra in the division is not yet exhausted, since the total volume of the specified tetrahedra does not exceed $\frac{a^{3}}{3} + \frac{a^{3}}{3} = \frac{2}{3} a^{3}$, which is less than the volume $a^{3}$ of the cube. Hence, the number of tetrahedra in the division cannot be less than five.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. Let $h_{a}=\beta_{b}=m_{c}$, where $h_{a}=A P, \beta_{b}=B L$ and $m_{c}=C F-$ are the altitude, bisector, and median drawn from three different vertices of some triangle $A B C$. What value can the ratio of the greatest side of triangle $A B C$ to its smallest side have?
|
49. First of all, note that if for triangle \(ABC\) the inequality \(m_{a}b = CA\) holds. This immediately follows from the known formula \(^{2}\) \(m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}\), but it can also be proven without calculations. Translate triangle \(ABC\) parallel to vector \(\overline{ED}\) to position \(A' B' C'\) (Fig. 128). Since \(B' D = B E\), by the condition \(B' D = B E > A D\); therefore,
Fig. 128. thus \(B' P > A P\), where \(P\) is the projection of point \(D\) on \(AB\). Since \(A A' = B B'\), then \(B P > A' P\), and consequently,
\[
\frac{a}{2} = B D > A' D = \frac{b}{2}, \quad \text{or} \quad a > b.
\]
Now suppose triangle \(ABC\) is such that \(h_{a} = \beta_{b} = m_{c}\). Since, by the result of problem 48, \(h_{u} = \beta_{b} \geqslant h_{b}\) and \(h_{a} = m_{c} \geqslant h_{c}\), the height \(h_{a}\)
1) This also follows from the fact that in any other arrangement of points \(P, K\), and \(D\), the problem of constructing triangle \(ABC\) from three segments \(h_{a}, \beta_{a}\), and \(m_{n}\) would be unsolvable, as mentioned later (compare with problem 112 from book [17]).
\(^{2}\) See, for example, Adamar [13], p. 124.
is the largest; therefore, from the equality \(h_{a} = m_{c}\) it follows that \(\angle C < 60^{\circ}\) (see problem 50 below). On the other hand, the median \(m_{c}\) is the smallest in triangle \(ABC\), because \(m_{c} = h_{\alpha} \leqslant m_{\alpha}\) and \(m_{c} = \beta_{b} \leqslant m_{b}\) (see problem 48); therefore, by what has just been proven, \(c\) is the largest side of triangle \(ABC\), and \(C\) is its largest angle. Since the sum of the three angles of a triangle is \(180^{\circ} = 3 \cdot 60^{\circ}\), and since \(\angle C \leqslant 60^{\circ}\), all angles of the triangle are \(60^{\circ}\), triangle \(ABC\) is equilateral, and the ratio of its largest side to its smallest side is 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In space, there are 4 points not lying in the same plane. How many planes can be drawn equidistant from these points?
|
1. Since the four points do not lie in the same plane, the plane equidistant from these points cannot be located on the same side of all of them. Therefore, there are only two possible cases: 1) three points lie on one side of the considered plane, and the fourth point lies on the other side, and 2) two points lie on each side of the plane.
Fig. 27.
Consider the first case. Let points \(A, B\), and \(C\) lie on one side of the plane \(\Pi\), equidistant from points \(A, B, C\), and \(D\), while point \(D\) lies on the other side (Fig. 27). Points \(A, B\), and \(C\) cannot lie on the same line—otherwise, all four points would lie in the same plane. Since the plane \(\Pi\) is equidistant from points \(A, B\), and \(C\), which are located on the same side of it, this plane must be parallel to the plane \(ABC\). For the distance from point \(D\) to this plane to be equal to the distance from it to the three points \(A, B\), and \(C\), the plane \(\Pi\) must pass through the midpoint of the perpendicular \(DP\) dropped from point \(D\) to the plane \(ABC\) (see Fig. 27). Thus, the plane \(\Pi\), equidistant from points \(A, B, C\), and \(D\), with points \(A, B\), and \(C\) on one side and point \(D\) on the other, is uniquely determined.
Similarly, the plane equidistant from the given four points, with only point \(C\) (or point \(B\), or point \(A\)) on one side and the other three points on the other side, can be found. In total, there are four planes equidistant from the given four points such that only one point is on one side of them, and the other three are on the other side.
Consider the second case. Let points \(A\) and \(B\) lie on one side of the plane \(\Pi\), equidistant from points \(A, B, C\), and \(D\), while points \(C\) and \(D\) lie on the other side (Fig. 28). Since the plane \(\Pi\) is equidistant from points \(A\) and \(B\), which lie on the same side of \(\Pi\), it must be parallel to the line \(AB\). Similarly, it can be proven that this plane must be parallel to the line \(CD\). Since points \(A, B, C\), and \(D\) do not lie in the same plane, the lines \(AB\) and \(CD\) must be skew. Draw two parallel planes through the skew lines \(AB\) and \(CD\); it is clear that the plane \(\Pi\) must be parallel to these planes and equidistant from them, i.e., it must pass exactly midway between these planes (see Fig. 28). Thus, there is a unique plane equidistant from points \(A, B, C\), and \(D\) such that points \(A\) and \(B\) lie on one side of it, and points \(C\) and \(D\) lie on the other.
Similarly, there is a unique plane equidistant from our four points such that the point \(A\) and only the point \(C\) (or point \(D\)) lie on the same side, while the other two points (\(B\) and \(D\) or \(B\) and \(C\)) lie on the other side. Therefore, there are three planes equidistant from the given four points such that two of the four points lie on one side of each of them, and the other two lie on the other side.
Thus, the total number of planes equidistant from the given four points in space is \(4 + 3 = 7\). If we consider a triangular pyramid (tetrahedron) with vertices \(A, B, C\), and \(D\),
a)
b)
Fig. 29.
then four of these seven planes will pass parallel to the faces of the pyramid through the midpoints of the corresponding heights (Fig. 29, a), and the remaining three will pass parallel to pairs of opposite edges at equal distances from them (Fig. 29, b).
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many spheres exist that touch all the faces of the given triangular pyramid $T$?
|
3. The task is to determine how many points (centers of the sought spheres) are equidistant from the four faces of the pyramid.
The geometric locus of points equidistant from the faces of a given dihedral angle is a plane passing through the edge of the dihedral angle and bisecting this angle — the bisector plane of the dihedral angle.
Since two intersecting planes form two pairs of vertical dihedral angles, the geometric locus of points equidistant from two intersecting planes consists of two planes passing through the line of intersection of the first two planes.
The geometric locus of points equidistant from the faces of a trihedral angle is the line of intersection of the bisector planes of the three dihedral angles of the trihedral angle — the bisector line of the trihedral angle.
Since three intersecting planes form four pairs of vertical trihedral angles, the geometric locus of points equidistant from three intersecting planes consists of four lines passing through the point of intersection of the three planes.
Let $\mathrm{II}_{1}, \mathrm{II}_{2}, \mathrm{II}_{3}$, and $\mathrm{II}_{4}$ be the planes of the faces of the pyramid. Consider the trihedral angle of the pyramid formed by the planes $\mathrm{II}_{1}, \mathrm{II}_{2}$, and $\mathrm{II}_{3}$. The geometric locus of points equidistant from the three faces of this angle consists of four lines $\beta_{1}, \beta_{2}, \beta_{3}$, and $\beta_{4}$. Further, the geometric locus of points equidistant from the planes $\mathrm{II}_{1}$ and $\mathrm{II}_{4}$ consists of two planes $B_{1}$ and $B_{2}$. It is clear that each of the points of intersection of one of the lines $\beta_{1}, \beta_{2}, \beta_{3}$, and $\beta_{4}$ with one of the planes $B_{1}$ and $B_{2}$ (and only these points) will be equidistant from the planes $\mathrm{II}_{1}, \mathrm{II}_{2}, \mathrm{II}_{3}$, and $\mathrm{II}_{4}$. Thus, in general, we obtain eight points equidistant from the planes of the faces of the pyramid, and consequently, eight spheres tangent to these faces. It is not difficult to see that out of these eight spheres, one is enclosed inside the pyramid (the inscribed sphere; Fig. 35, a), four are located outside the pyramid, one inside each of its trihedral angles (the "exscribed" spheres; Fig. 35, b), and three are located inside the dihedral angles of the pyramid and inside the angles vertical to the opposite dihedral angles (Fig. 35, c).
a)
b)
c:
Fig. 35.
Note that in special cases, a tetrahedral pyramid may have fewer than eight spheres tangent to the planes of all its faces. For example, a regular tetrahedron has only five such spheres (spheres of only the types shown in Fig. 35, a and b). This is because in some cases, some of the lines $\beta_{1}, \beta_{2}, \beta_{3}$, and $\beta_{4}$ may be parallel to some of the planes $B_{1}$ and $B_{2}$.
Remark. It can be shown that if the sum of the areas of two faces of a triangular pyramid is equal to the sum of the areas of the other two faces, then there are only 7 spheres tangent to the planes of all the faces; if the areas of the faces are pairwise equal, then there are 6 such spheres; finally, if all the faces of the pyramid are equal in area (and therefore equal; see, for example, problem 29 in the book by D. O. Shklyarsky, N. N. Chentsov, and I. M. Yaglom, Selected Problems and Theorems of Elementary Mathematics, part 3, "Mathematical Circle Library," issue 3), then there are only 5 such spheres. See "Elementary Geometry" by J. Hadamard, part 2 (Moscow, Uchpedgiz, 1951), solution to problem 701.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69. What is more likely: to win 3 games out of 4 or 5 games out of 8 against an equally matched opponent?
|
69. The total number of possible outcomes of a sequence of four matches we get by combining a win or loss in the first match with a win or loss in the second, third, and fourth matches. This number is equal to $2^{4}=16$. All these outcomes are equally probable, as the opponents are of equal strength, and for each separate match, the probability of winning is the same for each of the two opponents. Favorable outcomes here are those in which the first of the opponents wins in three out of four cases; the number of such outcomes is obviously 4 (these four cases correspond to losing the first, second, third, or fourth match and winning the rest). Thus, the desired probability is $\frac{4}{16}=\frac{1}{4}$. Similarly, in the case of eight matches, the total number of outcomes is $2^{8}=256$. The number of favorable outcomes here is the number of ways in which five matches can be won out of eight, i.e., it is equal to $C_{8}^{5}=$ $=\frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3}=56$. Therefore, the probability of winning five matches out of eight is $\frac{56}{256}=\frac{7}{32}<\frac{1}{4}$.
Answer: winning three matches out of four against an equally strong opponent is more likely than winning five matches out of eight ${ }^{1}$).
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
103*. The bus network of the city, consisting of several (more than two) routes, is organized in such a way that:
$1^{\circ}$ each route has at least three stops,
$2^{\circ}$ from any stop to any other stop, one can travel without transferring, and
$3^{\circ}$ for each pair of routes, there is one (and only one) stop where one can transfer from one of these routes to the other.
a) Prove that each bus route has the same number of stops and that each stop is served by the same number of routes (equal to the number of stops on each route).
b) Find the number of stops on each bus route if the total number of routes in the city is 57.
|
103. a) Let \( n \) be the number of stops on one of the bus routes in the city. We need to prove that in this case, each route will have exactly \( n \) stops and that exactly 2 routes will pass through each stop.
Let's denote the route with \( n \) stops by \( a \), and the stops on this route by \( A_{1}, A_{2}, \ldots, A_{n} \). Consider an arbitrary bus stop \( B \) located outside the route \( a \) (Fig. 92). According to condition \( 2^{\circ} \), from stop \( B \) one can reach each of the \( n \) stops \( A_{1}, A_{2}, \ldots, A_{n} \) by one of the routes. By condition \( 3^{\circ} \), each of the routes passing through \( B \) must pass through one of the stops \( A_{1}, A_{2}, \ldots, A_{n} \) (otherwise, it would be impossible to transfer to route \( a \) from this route), and only through one of them (otherwise, it would be possible to transfer to route \( a \) from this route at two stops), and no two routes passing through \( B \) pass through the same stop on route \( a \) (otherwise, it would be possible to transfer from one of these routes to another at two stops: at stop \( B \) and at the stop where they meet route \( a \)). Therefore, the number of routes passing through stop \( B \) is the same as the number of stops on route \( a \), i.e., exactly \( n \) routes.
Now consider an arbitrary route \( c \) different from \( a \) (Fig. 93). According to condition \( 1^{\circ} \), route \( c \) has at least three stops, and by condition \( 3^{\circ} \), one of these stops is also a stop on route \( a \). Outside route \( c \), there are obviously \( n-1 \) stops of route \( a \); let's show that there is at least one more stop outside \( c \) that does not lie on \( a \). Indeed, let \( A_{1} \) be one of the \( n-1 \) stops of route \( a \) located outside \( c \), and let \( C_{1} \) be one of the stops of route \( c \) located outside \( a \) (there are at least 2 such stops). By condition \( 2^{\circ} \), there is a bus route \( b \) passing through stops \( A_{1} \) and \( C_{1} \), and by condition \( 3^{\circ} \), this route has at least one more stop \( B \) outside \( c \) and outside \( a \).
We know that exactly \( n \) routes pass through each bus stop located outside \( a \); this applies, in particular, to stop \( B \). Each of the \( n \) routes passing through \( B \) intersects route \( c \) at exactly one stop by condition \( 3^{\circ} \); furthermore, by condition \( 2^{\circ} \), at least one route passing through \( B \) also passes through each stop of route \( c \). Therefore, the number of stops on route \( c \) is equal to the number of routes passing through \( B \), i.e., \( n \). Thus, we have proved that each bus route in the city has the same number \( n \) of stops.
It remains to prove that exactly \( n \) routes pass through each of the stops \( A_{1}, A_{2}, \ldots, A_{n} \) on route \( a \). To do this, it is sufficient to show that for any of these stops, there is a route that does not pass through this stop: indeed, this route, like any other, will have \( n \) stops, and we already know that exactly \( n \) routes pass through any stop located outside a route with \( n \) stops (see the proof at the beginning of the solution that \( n \) routes pass through \( B \)). Since the total number of routes is at least two, there is another route \( b \) besides \( a \) that, by condition \( 3^{\circ} \), intersects route \( a \) at exactly one stop. Let this stop be \( A_{1} \); then the stops \( A_{2}, A_{3}, \ldots, A_{n} \) will be located outside \( b \) and, therefore, exactly \( n \) routes will pass through them. Furthermore, on \( b \) there are other stops besides \( A_{1} \) (at least two); let \( B \) be one of these stops. In this case, the route passing through \( B \) and \( A_{2} \) (such a route exists by \( 2^{\circ} \)) will not pass through \( A_{1} \); therefore, there is at least one route outside \( A_{1} \) and exactly \( n \) routes pass through \( A_{1} \). Thus, the problem is solved.
b) By the result of part a), in this case, each route has the same number \( n \) of stops, and exactly \( n \) routes pass through each stop. Let \( a \) be one of the routes; through each of the \( n \) stops of this route, besides \( a \), \( n-1 \) other routes pass. From condition \( 3^{\circ} \), it easily follows that no two of the \( n(n-1) \) routes obtained in this way coincide with each other and that each of the routes different from \( a \) is among these \( n(n-1) \) routes (see the solution of part a)). Thus, the total number of bus routes in the city (including \( a \)) is \( n(n-1)+1 \). From this, we obtain the quadratic equation for determining \( n \):
\[
\begin{aligned}
n(n-1)+1 & =57 \\
n^{2}-n-56 & =0 ; \\
n & =8
\end{aligned}
\]
(the second root of the equation \( n=-7 \) is, of course, not suitable).
|
8
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4.11. The centers of three spheres, with radii of 3, 4, and 6, are located at the vertices of an equilateral triangle with a side length of 11. How many planes exist that are tangent to all three spheres simultaneously?
## § 3. Two intersecting circles lie on the same sphere
|
4.11. Consider a plane tangent to all three given spheres, and draw a plane through the center of the sphere of radius 3 parallel to it. The resulting plane is tangent to the spheres of radii $4 \pm 3$ and $6 \pm 3$, concentric with the spheres of radii 4 and 6. When the signs of the number 3 are the same, the tangency is external, and when they are different, the tangency is internal. It is also clear that for each plane tangent to all spheres, the plane symmetric to it with respect to the plane passing through the centers of the spheres is also tangent to all spheres.
To determine whether there exists a plane passing through a given point and tangent to two given spheres, we can use the result of problem 12.11. In all cases except for the internal tangency with spheres of radii 1 and 9, the tangent planes exist (see Fig. 36). We will prove that there is no plane tangent internally to the spheres of radii 1 and 9 with centers $B$ and $C$ and passing through the point $A$. Let $\alpha$ be the angle between the line $A B$ and the tangent from $A$ to the sphere with center $B$, and $\beta$ be the angle between the line $A C$ and the tangent from $A$ to the sphere with center $C$. It is sufficient to check that $\alpha + \beta > 60^{\circ}$, i.e., $\cos (\alpha + \beta) < 1 / 2$. Since $\sin \alpha = 1 / 11$ and $\sin \beta = 9 / 11$, we have $\cos \alpha = \sqrt{120} / 11$, $\cos \beta = \sqrt{40} / 11$. Then $\cos (\alpha + \beta) = (40 \sqrt{3} - 9) / 121$. Thus, the inequality $\cos (\alpha + \beta) < 1 / 2$ is equivalent to the inequality $80 \sqrt{3} < 139$; the latter inequality is verified by squaring.
In the end, we find that there are 3 pairs of tangent planes.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.19. Chord $A B$ of a sphere with radius 1 has a length of 1 and is positioned at an angle of $60^{\circ}$ to the diameter $C D$ of this sphere. It is known that $A C=\sqrt{2}$ and $A C<B C$. Find the length of the segment $B D$.
|
4.19. Let $O$ be the center of the sphere. Take a point $E$ such that $\overrightarrow{C E}=\overrightarrow{A B}$. Since $\angle O C E=60^{\circ}$ and $C E=1=O C$, then $O E=1$. Point $O$ is equidistant from all vertices of the parallelogram $A B E C$, so $A B E C$ is a rectangle and the projection $O_{1}$ of point $O$ onto the plane of this rectangle coincides with its center, i.e., with the midpoint of segment $B C$. Segment $O O_{1}$ is the midline of triangle $C B D$, therefore $B D=20 O_{1}=2 \sqrt{O C^{2}-B C^{2} / 4} \Rightarrow$ $=2 \sqrt{1-\left(A B^{2}+A C^{2}\right) / 4}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.35. a) Prove that the sum of the cosines of the dihedral angles of a regular tetrahedron is 2.
b) The sum of the plane angles of a trihedral angle is \(180^{\circ}\). Find the sum of the cosines of its dihedral angles.
## § 5. Orthocentric Tetrahedron
Definition. A tetrahedron is called orthocentric if all its altitudes (or their extensions) intersect at one point.
|
6.35. a) Let $\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{3}$ and $\mathbf{e}_{4}$ be unit vectors, non-perpendicular to the faces and directed outward. Since the areas of all faces are equal, then $\mathbf{e}_{1}+\mathbf{e}_{2}+\mathbf{e}_{3}+\mathbf{e}_{4}=0$ (see problem 7.19). Therefore, $0=\left|e_{1}+\mathbf{e}_{2}+\mathbf{e}_{3}+\mathbf{e}_{4}\right|^{2}=$ $=4+2 \sum\left(\mathrm{e}_{i}, \mathbf{e}_{j}\right)$. It remains to note that the scalar product $\left(\mathrm{e}_{i}, \mathrm{e}_{j}\right)$ is equal to $-\cos \varphi_{i j}$, where $\varphi_{i j}$ is the dihedral angle between the faces numbered $i$ and $j$.
b) Take an arbitrary point $A$ on one edge of the given trihedral angle with vertex $S$ and draw segments $A B$ and $A C$ to intersect the other edges such that $\angle S A B=$ $=\angle A S C$ and $\angle S A C=\angle A S B$. Then $\triangle S C A=\triangle A B S$. Since the sum of the angles of triangle $A C S$ is equal to the sum of the planar angles at vertex $S$, then $\angle S C A=\angle C S B$. Therefore, $\triangle S C A=$ $=\triangle C S B$, which means the tetrahedron $A B C S$ is equifacial. According to problem a), the sum of the cosines of the dihedral angles at the edges of this tetrahedron is 2, and this sum is twice the sum of the cosines of the dihedral angles of the given trihedral angle.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7.37. What is the maximum number of planes of symmetry that a spatial figure consisting of three pairwise non-parallel lines can have?
Symmetry with respect to a line $l$ is a transformation of space that maps a point $X$ to a point $X^{\prime}$ such that the line $l$ passes through the midpoint of the segment $X X^{\prime}$ and is perpendicular to it. This transformation is also called axial symmetry, and $l$ is called the axis of symmetry:
|
7.37. Let $P$ be a plane of symmetry of a figure consisting of three pairwise non-parallel lines. There are only two possible cases: 1) each given line is symmetric relative to $P$; 2) one line is symmetric relative to $P$, and the other two lines are symmetric to each other.
In the first case, either one line is perpendicular to $P$, and the other two belong to $P$, or all three lines belong to $P$. Thus, the plane $P$ is defined by some pair of the given lines. Therefore, the number of planes of symmetry of this type is no more than 3.
In the second case, the plane $P$ passes through the bisector of the angle between two given lines and is perpendicular to the plane containing these lines. For each pair of lines, there are exactly 2 such planes, so the number of planes of symmetry of this type is no more than 6.
Thus, the total number of planes of symmetry is no more than 9. Moreover, a figure consisting of three pairwise perpendicular lines passing through one point has exactly 9 planes of symmetry.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.26. a) How many pairwise non-equal spatial quadrilaterals exist with one and the same set of side vectors?
b) Prove that the volumes of all tetrahedra defined by these spatial quadrilaterals are equal.
|
8.26. a) We fix one of the vectors of the sides. It can be followed by any of the three remaining vectors, and then by any of the two remaining ones. Therefore, there are exactly 6 different quadrilaterals.
b) Let $\mathbf{a}, \mathbf{b}, \mathbf{c}$, and $\mathbf{d}$ be the given vectors of the sides. Consider the parallelepiped defined by the vectors $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ (Fig. 61); its diagonal is the vector $\mathbf{d}$. A simple enumeration shows that all 6 different quadrilaterals are among the quadrilaterals whose sides are the edges of this parallelepiped and its diagonal $\mathbf{d}$ (it is convenient to fix the vector $\mathbf{d}$ during enumeration). The volume of each corresponding tetrahedron is $1/6$ of the volume of the parallelepiped.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.9. a) Prove that it is possible to choose 8 vertices of a dodecahedron such that they are the vertices of a cube. How many ways can this be done?
b) Prove that it is possible to choose 4 vertices of a dodecahedron such that they are the vertices of a regular tetrahedron.
|
9.9. a) From the solution to problem 9.2, it is clear that there exists a cube whose vertices are located at the vertices of the dodecahedron. Moreover, one edge of the cube is located on each face of the dodecahedron. It is also clear that choosing any of the five diagonals of a certain face of the dodecahedron as an edge of the cube uniquely determines the entire cube. Therefore, there are 5 different cubes with vertices at the vertices of the dodecahedron.
b) By placing the cube such that its vertices are located at the vertices of the dodecahedron, it is then possible to place a regular tetrahedron such that its vertices are located at the vertices of that cube.
|
5
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
15.22. What is the smallest number of tetrahedra into which a cube can be cut?
|
15.22. If a tetrahedron \(A^{\prime} B C^{\prime} D\) is cut out from the cube \(A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}\), the remaining part of the cube splits into 4 tetrahedra, i.e., the cube can be cut into 5 tetrahedra.
We will prove that the cube cannot be cut into fewer than 5 tetrahedra. The face \(A B C D\) cannot be a face of the tetrahedra into which the cube is divided, so at least two tetrahedra adjoin it. Consider all tetrahedra adjacent to the face \(A B C D\). Their heights dropped onto this face do not exceed \(a\), where \(a\) is the edge of the cube, and the sum of the areas of their faces lying on \(A B C D\) is equal to \(a^{2}\). Therefore, the sum of their volumes does not exceed \(a^{3} / 3\). Since the faces of one tetrahedron cannot lie on opposite faces of the cube, at least 4 tetrahedra adjoin the faces \(A B C D\) and \(A^{\prime} B^{\prime} C^{\prime} D^{\prime}\), and the sum of their volumes does not exceed \(2 a^{3} / 3 < a^{3}\). Therefore, there is still one more tetrahedron in the partition.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.32. A plane intersects the lower base of a cylinder along its diameter and has only one common point with the upper base. Prove that the area of the cut-off part of the lateral surface of the cylinder is equal to the area of its axial section.
|
15.32. Let 0 be the center of the lower base of the cylinder; $AB$ - the diameter along which the plane intersects the base; $\alpha$ - the angle between the base and the intersecting plane; $r$ - the radius of the cylinder. Consider an arbitrary generatrix $XY$ of the cylinder, having a common point $Z$ with the intersecting plane (point $X$ lies on the lower base). If $\angle AOX = \varphi$, then the distance from point $X$ to the line $AB$ is $r \sin \varphi$. Therefore, $XZ = r \sin \varphi \operatorname{tg} \alpha$. It is also clear that $r \operatorname{tg} \alpha = h$, where $h$ is the height of the cylinder.
268
Unfold the surface of the cylinder onto a plane tangent to it at point $A$. Introduce a coordinate system on this plane, choosing point $A$ as the origin, and directing the $Oy$ axis upwards, parallel to the axis of the cylinder. Point $X$ transitions to point $(r \varphi, 0)$ upon unfolding, and point $Z$ transitions to point $(r \varphi, h \sin \varphi)$. Thus, the unfolded surface of the section is bounded by the $Ox$ axis and the graph of the function $y = h \sin (x / r)$ (Fig. 112). Its area is
$$
\int_{0}^{\pi r} h \sin (x / r) d x = \left.(-h r \cos (x / r))\right|_{0} ^{\pi r} = 2 h r
$$
It remains to note that the area of the axial section of the cylinder is also equal to $2 h r$.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
16.16. Given three pairwise tangent spheres $\Sigma_{1}$, $\Sigma_{2}$, $\Sigma_{3}$ and a set of spheres $S_{1}, S_{2}, \ldots, S_{n}$, such that each sphere $S_{i}$ is tangent to all three spheres $\Sigma_{1}$, $\Sigma_{2}$, $\Sigma_{3}$, as well as to the spheres $S_{i-1}$ and $S_{i+1}$ (it is meant that $S_{0}=S_{n}$ and $S_{n+1}=$ $=S_{1}$). Prove that if all points of tangency of the spheres are pairwise distinct and $n>2$, then $n=6$.
|
16.16. Consider the inversion with the center at the point of tangency of spheres $\Sigma_{1}$ and $\Sigma_{2}$. In this case, they transform into a pair of parallel planes, and the images of all other spheres touch these planes, and therefore their radii are equal. Thus, in a section by a plane equidistant from these parallel planes, we obtain what is shown in Fig. 117.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
61. Determine the remainder of the division by 7 of the number
$$
3^{100}
$$
The 10-arithmetic and 7-arithmetic we have discussed are special cases of residue arithmetic modulo $m$, or $m$-arithmetic. Let $m$ be any positive integer. The elements of $m$-arithmetic are the numbers $0,1,2, \ldots, m-1$. Addition and multiplication in $m$-arithmetic are defined as follows: to add (or multiply) two numbers, one must take the remainder of the division by $m$ of their ordinary sum (respectively product).
|
61. Let's compute $3^{100}$ in 7-arithmetic:
$$
3^{2}=2,3^{8}=6,3^{4}=4,3^{5}=5,3^{6}=1
$$
Therefore,
$$
3^{100}=3^{6 \cdot 16+4}=\left(3^{6}\right)^{16} \cdot 3^{4}=3^{4} \Rightarrow 4
$$
$14^{*}$
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
117. Let three elements $x, y, z$ of the circular sequence $\breve{\Phi}_{m}$ be arranged such that the distance between $x$ and $y$ is equal to the distance between $y$ and $z$ (Fig. 54). Prove that if $x=y=0$, then $z=0$.
|
117. The number $y=0$ is at an equal distance from $x$ and $z$. Therefore, based on problem 116, either $x+z=0$ or $x-z=0$. Since $x=0$, in both cases $z=0$,
|
0
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
120. Prove that if a circular sequence without repetitions $\Phi_{m}$ contains zero and consists of an odd number of elements, then the number of its elements is three.
|
120. If the circular sequence $\breve{\Phi}_{m}$ contains zero and consists of an odd number of terms, then there will be a pair of adjacent elements $x, y$ located at the same distance from zero (Fig. 143). According to problem 116, either
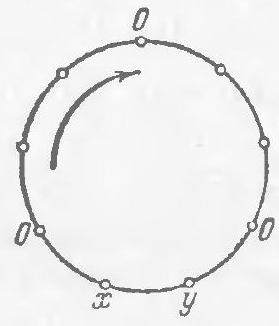
Fig. 143.
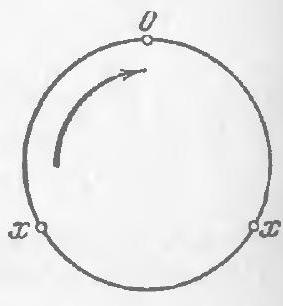
Fig. 144.
$x+y=0$, or $x-y=0$ and, therefore, one of the elements of the sequence adjacent to the pair $x, y$ is equal to zero. By problem 117, the second element adjacent to this pair is also equal to zero. From this, it follows that $x=y$, and since the sequence in question is a sequence without repetitions, it has the form shown in Fig. 144.
|
3
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
191. The following experiment is conducted. Two urns that look identical are placed in a room. The left one contains $a$ balls, and the right one contains $b$ balls. People enter the room one by one, and each person moves a ball from the left urn to the right or from the right urn to the left. It is assumed that the probability of a ball being moved from the left urn to the right is the same as the probability of a ball being moved from the right urn to the left, which is $\frac{1}{2}$. The experiment continues until one of the urns is empty. What is the probability that the left urn will be empty? What is the probability that the right urn will be empty? What is the probability that the experiment will never end?
Fig. 63.
|
191. We will represent the number of balls in the left urn using a chip placed on a number line. At the initial
1) A. P. Kiselev, Algebra, Part 2, 23rd edition, Uchpedgiz, M., 1946, p. 78.
18 Law. Zzya. E. Dynkin and V. Uspenskii
moment, the chip is located at point $a$ (Fig. 156). After each unit of time, it moves to the right with a probability of $\frac{1}{2}$ (a ball is moved from the right urn to the left, increasing the number of balls in the left urn by one) and to the left with a probability of $\frac{1}{2}$ (a ball is moved from the left urn to the right, decreasing the number of balls in the left urn by one), until it first reaches one of the points 0 or $a+b$. The arrival of the chip at point 0 means that the left urn is empty, and its arrival at point $a+b$ means that the right urn is empty. Let the probability of the chip reaching 0, given that it started from point $k$, be denoted by $p_{k}$ (we need to find $p_{a}$). Clearly, $p_{0}=1, p_{a+b}=0$.
Suppose the chip is at point $k$.
Consider two events:
$A$: "the chip moves to $k+1$ in one step,"

Fig. 156.
By the condition, $\mathbf{P}(A)=\mathbb{P}(B)=1 / 2$. If event $A$ occurs, the probability of the chip reaching 0 is $p_{k+1}$, and if event $B$ occurs, the probability of the chip reaching 0 is $p_{k-1}$. By the formula for total probability, we have
$$
p_{k}=\frac{1}{2} p_{k+1}+\frac{1}{2} p_{k-1}
$$
or after transformation
$$
2 p_{k}=p_{k+1}+p_{k-1}, \quad p_{k+1}-p_{k}=p_{k}-p_{k-1}
$$
Denoting the constant difference $p_{k+1}-p_{k}$ by $d$, we write
$$
\begin{array}{r}
p_{k}-p_{k-1}=d_{2} \\
p_{k-1}-p_{k-2}=d \\
\cdots \cdot \cdot \cdot \\
p_{2}-p_{1}=d \\
p_{1}-p_{0}=d
\end{array}
$$
Adding these equations, we get
$$
\begin{aligned}
& p_{k}-p_{0}=k d, \\
& p_{k}-1=k d, \\
& p_{k}=1+k d
\end{aligned}
$$
or, setting $k=a+b$,
$$
\begin{gathered}
0=p_{a+b}=1+(a+b) d, \quad d=-\frac{1}{a+b} \\
p_{k}=1-\frac{k}{a+b}=\frac{a+b-k}{a+b}
\end{gathered}
$$
The probability we are interested in is
$$
p_{a}=\frac{b}{a+b}
$$
it is clear,
The probability that the right urn will be empty is
$$
p_{b}=\frac{a}{a+b}
$$
The probability that the experiment will end, i.e., that one of the urns will be empty, is, by property 2
$$
\frac{b}{a+b}+\frac{a}{a+b}=1
$$
The probability that the experiment will never end is $1-1=0$ (property 3).
Remark. This problem is known in the history of mathematics as the "ruin problem." The classical formulation of this problem is as follows:
Two players are playing. The probability of winning each game for each of them is $\frac{1}{2}$. The first player has $a$ rubles, and the second player has $b$ rubles. The game continues until one of the players is left with no money. What is the probability of ruin for each player?
In problem 191, the players are replaced by urns, and the money by balls.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Three circles with radii 1, 2, and 3 touch each other externally. Find the radius of the circle passing through the points of tangency of these circles.
|
2. Note that the circle passing through the points of tangency is inscribed in a triangle with vertices at the centers of the circles. By equating the expressions for the area of the triangle obtained using Heron's formula and as the product of the semiperimeter and the radius of the inscribed circle, we find \( r=1 \).
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a trapezoid, the diagonals are equal to 3 and 5, and the segment connecting the midpoints of the bases is equal to 2. Find the area of the trapezoid.
|
7. Let (Fig. 2) $ABCD$ be the given trapezoid ($BCAD$). Draw a line through $C$ parallel to $BD$, and denote by $K$ the point of intersection of this line with the line $AD$. The area of $\triangle ACK$ is equal to the area of the trapezoid, the sides $AC$ and $CK$ are equal to the diagonals of the trapezoid, and the median $CL$ is equal to the distance between the midpoints of $AD$ and $BC$. Extend $CL$ and take a point $M$ on the extension such that $|LLM| = |CL|$. We obtain $\triangle CKM$, which is equal in area to trapezoid $ABCD$, with sides equal to its diagonals and twice the distance between the midpoints of the bases. In our case, the sides of $\triangle CKM$ are 3.5 and 4.
Answer: $S=6$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A circle of radius 1 is inscribed in triangle $A B C$, where $\cos \widehat{A B C}=0.8$. This circle touches the midline of triangle $A B C$, parallel to side $A C$. Find the length of side $A C$.
|
9. It follows from the condition that the height to side $AC$ is equal to two diameters of the inscribed circle, i.e., 4. If $M, N$ and $K$ are the points of tangency with $AB, BC$ and $CA$, then
$$
|BM|=|BN|=r \operatorname{ctg} \frac{\widehat{ABC}}{2}=1 \cdot \sqrt{\frac{1+0.8}{1-0.8}}=\sqrt{9}=3
$$
If $|MA|=|AK|=x,|KC|=|NC|=y$, then, expressing the area through the semiperimeter and the radius of the inscribed circle and through the base and height, we get
$$
(3+x+y)=(x+y) 2, \quad x+y=3
$$
Answer: $|AC|=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35*. What is the greatest number of rays in space that form pairwise obtuse angles?
|
35. It is easy to see that it is possible to draw four rays, each pair of which forms obtuse angles: for example, it is sufficient to connect the center $O$ of a regular tetrahedron $ABCD$ with all its vertices (it is clear, for example, that $\angle AOB > \angle AO_1B = 90^\circ$, where $O_1$ is the center of the face $BCD$ of the tetrahedron). Now let's prove that it is impossible to specify more than four rays in space, each pair of which forms obtuse angles.
Let $l_1, l_2, l_3$, and $l_4$ be four rays emanating from a point $O$ and forming obtuse angles with each other, and let $\pi_1, \pi_2, \pi_3$, and $\pi_4$ be planes passing through the point $O$ and perpendicular to the rays $l_1, l_2, l_3$, and $l_4$, respectively. All rays forming obtuse angles with the ray $l_1$ must lie on the other side of the plane $\pi_1$ from the ray $l_1$. All rays forming obtuse angles with both rays $l_1$ and $l_2$ must lie within the dihedral angle formed by the half-planes $\pi_1$ and $\pi_2$; this dihedral angle (Fig. 83a) is acute, since the angle between the rays perpendicular to its faces is obtuse. All rays forming obtuse angles with each of the three rays $l_1, l_2, l_3$ must lie within the intersection of the dihedral angles $\pi_1\pi_2$ and $\pi_1\pi_3$. This intersection is a trihedral angle $\pi_1\pi_2\pi_3$, or $OABC$ (Fig. 83b), which, as proven above, has all dihedral angles acute. The ray $l_4$ must lie within it; we will show that it forms acute angles with all other rays lying inside this angle.
Let the plane passing through $OA$ and the ray $l_4$ intersect the face $BOC$ along the ray $OA'$. One of the dihedral angles with edge $OA'$ is acute; let this be the angle $AOA'C$. Then all dihedral angles of the trihedral angle $OAA'C$ are acute; hence, all plane angles of this trihedral angle are also acute (see, for example, the solution to problem 28 in the book by D. O. Sharygin et al., cited in the footnote on page 151). But $\angle AOL_4$ is only a part of the angle $AOA'$; therefore, the angle between the rays $OA$ and $l_4$ is acute. Similarly, the ray $l_4$ forms acute angles with $OB$ and $OC$. Therefore, all
1) Consider how this reasoning changes if we are talking about points in space (although the case where all points lie in the same plane does not contradict the condition of problem b).
three rays $OA, OB, OC$ lie on the same side of the plane $\pi_4$ as the ray $l_4$, and thus all internal points of the trihedral angle $OABC$ lie on the same side of $\pi_4$ as the ray $l_4$. Therefore, any ray $l_5$ located inside the trihedral angle $\pi_1\pi_2\pi_3$,
a)
b)
Fig. 83.
lies on the same side of the plane $\pi_4$, and thus no such ray $l_5$ can form an obtuse angle with $l_4$. This proves the required statement.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Given a triangle $T$.
a) Place a centrally symmetric polygon $m$ of the largest possible area inside $T$.
What is the area of $m$ if the area of $T$ is 1?
b) Enclose $T$ in a convex centrally symmetric polygon $M$ of the smallest possible area.
What is the area of $M$ if the area of $T$ is 1?
|
52. a) If $O$ is the center of the sought centrally symmetric polygon $m$, then by symmetrically reflecting the given $\triangle ABC \equiv T$ together with $m$ (which will transform into itself), we can see that $m$ is also inscribed in $\triangle A_{1} B_{1} C_{1} \equiv T_{1}$, which is symmetric to $\triangle ABC$ with respect to $O$. Since the intersection ${ }^{1}$ ) $n=T \cap T_{1}$ of triangles $T$ and $T_{1}$ is clearly a centrally symmetric polygon with center $O$, the smallest centrally symmetric polygon inscribed in $T$ with center $O$ has an area of $\frac{1}{2} S_{ABC}$, because if the height $OP$ of triangle $AOB$ were less than half the height $CH$ of triangle $ABC$, then point $C'$ would lie outside $\triangle ABC$ (beyond side $AB$) and the intersection of $\triangle ABC$ and $\triangle A'B'C'$ would not be a parallelogram.
In the second case, the convex hull of the considered points is a centrally symmetric hexagon $A C' B A' C B'$ (Fig. $109, \sigma$), the area of which is exactly twice the area of $\triangle ABC$. Indeed,
\[
\begin{aligned}
& S_{A C' B A' C B'} = S_{O A B'} + S_{O A' B} + S_{O C A'} + S_{O C' A} + S_{O B C'} + S_{O B' C} = \\
&= 2 S_{O A B'} + 2 S_{O C A'} + 2 S_{O B C'}
\end{aligned}
\]
but
\[
S_{O A B'} = S_{O A B}
\]
since $AO$ is the median of triangle $AB'B$, and similarly
\[
S_{O C A'} = S_{O C A}, \quad S_{O B C'} = S_{O B C}
\]
thus,
\[
S_{A C' B A' C B'} = 2 S_{O A B} + 2 S_{O C A} + 2 S_{O B C} = 2 S_{ABC}
\]
The simplest example of a centrally symmetric polygon (of the smallest possible area) with an area of $2 S_{ABC}$ (i.e., an area of 2 if $S_{ABC} = 1$), containing $\triangle ABC$ inside, is the parallelogram $A B A' C$ (Fig. $109, b$).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. On a plane, there are 4 points $A_{1}, A_{2}, A_{3}, A_{4}$, the distance between any two of which is not less than 1. What is the maximum possible number of line segments $A_{i} A_{j}$ of length 1 connecting these points pairwise?
|
90. The number $v_{2}(4)<6$, otherwise the number of diameters of a system of four points on a plane could equal the "complete" number of six segments connecting our points, and by the result of problem 87 a) this is not the case. However, the number of segments equal to 1, connecting the points of our system of four points on a plane, can equal 5:
$$
v_{2}(4)=5
$$
(Fig. 159).
Note. It is also obvious that $v_{2}(3)=3$ and generally
$v_{k}(n)=C_{n}^{2}\left(=\frac{n(n-1)}{2}\right) \quad$ for $\quad n \leqslant k+1$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. a) Points $A$ and $B$ move uniformly and with equal angular velocities along circles centered at $O_{1}$ and $O_{2}$, respectively (clockwise). Prove that vertex $C$ of the equilateral triangle $A B C$ also moves uniformly along some circle.
b) The distances from a fixed point $P$ on the plane to two vertices $A, B$ of an equilateral triangle $A B C$ are $A P=2$ and $B P=3$. Determine the maximum value that the distance $C P$ can have.
|
6. a) Let $\overrightarrow{\mathrm{O}_{1} \mathrm{O}_{3}}$ be the vector obtained by rotating $\overrightarrow{O_{1} O_{2}}$ by $60^{\circ}$ (in the same direction as the rotation that transforms $\overrightarrow{A B}$ into $\overrightarrow{A C}$). Points $A^{\prime}$ and $B^{\prime}$ are the images of $A$ and $B$ under the same rotation around $O_{1}$. When vectors $\overrightarrow{O_{1} A}$ and $\overrightarrow{O_{2} B}$ rotate uniformly with the same angular velocity, $\triangle O_{1} A^{\prime} A$ will rotate around $O_{1}$, vectors $\overrightarrow{O_{3} B^{\prime}}$ and $\overrightarrow{B^{\prime} C}=\overrightarrow{A^{\prime} A}$, and thus their sum $\overrightarrow{O_{3} C}$ will rotate around $O_{8}$ (Fig. 23).
Fig. 23
Fig. 24
b) Answer: 5. Fix point $B$ at a distance of 3 from $P$ (Fig. 24). As point $A$ moves along a circle of radius 2 centered at $P$, vertex $C$ will move along a circle of radius 2, with its center $O$ located at a distance $O P=3$ from $P$ ( $\triangle O P B$ is equilateral). The farthest point on this circle from $P$ is at a distance $C O + O P = 5$.
$\nabla$ In the inequality to be proven, $P C \leqslant A P + B P$ (for any equilateral triangle $A B C$ and any point $P$), equality is achieved for all points $P$ on the arc $A B$ of the circumscribed circle of $\triangle A B C$, not containing point $C$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Kolya and Petya are dividing $2 n+1$ nuts, $n \geqslant 2$, with each wanting to get as many as possible. There are three ways of dividing (each goes through three stages).
1st stage: Petya divides all the nuts into two parts, each containing no fewer than two nuts.
2nd stage: Kolya divides each part again into two, each containing no fewer than one nut.
(1st and 2nd stages are common for all three ways.)
3rd stage: in the first way, Kolya takes the larger and the smaller parts; in the second way, Kolya takes both middle parts; in the third way, Kolya takes either the larger and the smaller parts or both middle parts, but in exchange for the right to choose, he gives Petya one nut.
Determine which way is the most advantageous for Kolya and which is the least advantageous for him.
|
10. Answer: the most profitable way for Kolya is the first one; with the second and third, he will get one nut less with correct play. (In general, as we will see, the dispute in this division is over one nut.)
No matter what piles (of $a$ and $b$ nuts, $a<b$) form after Petya's first move, Kolya can split the larger one into two parts of 1 and $b-1$ nuts, which will be the largest and the smallest, i.e., with the first division method, he can take $b \geqslant n+1$ nuts. (By taking $a=n, b=n+1$, Petya can prevent him from achieving more.) With the second division method, after the first move, $a=2, b=2n+1$, and with the best response $2=1+1$, $2n-1=n-1+n$, Kolya will get only $n$ nuts. (But with any other first move, he can get no less than $n+1$.) With the third method, Petya's move $a=n, b=n+1$ does not allow Kolya to achieve more than taking $n+1$ nuts (the sums of the two middle piles and the two outer ones will always be $n$ and $n+1$), so the extra nut that needs to be given away becomes decisive.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Let's take any 1962-digit number divisible by 9. The sum of its digits will be denoted by $a$, the sum of the digits of $a$ by $b$, and the sum of the digits of $b$ by $c$. What is $c$?[^0]
|
21. Answer. $c=9$. The sum of the digits of any number gives the same remainder when divided by 9 as the number itself (PZ). On the other
Fig. 30 hand, $a \leqslant 1962.9<19999$, so $b \leqslant 1+4 \cdot 9=37$ and $c \leqslant 9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. What is the maximum area that a triangle with sides \(a, b, c\) can have, given the following constraints:
\[
0 \leqslant a \leqslant 1 \leqslant b \leqslant 2 \leqslant c \leqslant 3 \text { ? }
\]
|
23. Answer: 1. Among triangles with two sides $a, b$ that satisfy the conditions $0<a \leqslant 1,1 \leqslant b \leqslant 2$, the one with the largest area is the right triangle with legs $a=1, b=2$ (indeed, $s \leqslant a b / 2 \leqslant 1$, since the height dropped to side $b$ is no more than $a$). The third side of this triangle $c=\sqrt{5}$ satisfies the condition $2 \leqslant c \leqslant 3$, therefore, among all the considered triangles, it has the largest area.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. For each of the numbers from 1 to 1000000000, the sum of its digits is calculated, and for each of the resulting billion numbers, the sum of its digits is calculated again, and so on, until a billion single-digit numbers are obtained. Which number will there be more of: 1 or 2?
|
43. Answer: the number of ones will be one more than the number of twos.
Any number gives the same remainder when divided by 9 as the sum of its digits (DS). Therefore, in our problem, ones come from numbers that give a remainder of 1 when divided by 9, i.e., from the numbers 1, 10, 19, 28, ..., 999999991, 1000000000, and twos come from numbers that give a remainder of 2, i.e., from the numbers $2,11,20,29, \ldots$ ... 999999992.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46. Solve the equation in integers
$$
\sqrt{\sqrt{x+\sqrt{x+\sqrt{x+\ldots+\sqrt{x}}}}}=y
$$
|
46. Answer: the only solution is $x=y=0$.
Let $\boldsymbol{x}$ and $\boldsymbol{y}$ be integers satisfying the condition. After a series of squaring, we are convinced that $\sqrt{x+\sqrt{x}}=\boldsymbol{m}$ and $\sqrt{x}=k$ are integers, and
$$
m^{2}=k(k+1)
$$
If $k>0$, then it must be that $k^{2}<m^{2}<(k+1)^{2}$, so $k<m<k+1$ and therefore $m$ is not an integer. Thus, $k=0$, i.e., $x=0$.
$\nabla$ Note that the contradiction of equation (*) also follows from problem 42.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. What is the smallest number of non-overlapping tetrahedra into which a cube can be divided?
|
53. It is easy to see that a cube can be divided into 5 tetrahedra. In Fig. 40, these are the tetrahedra $A A^{\prime} B^{\prime} D^{\prime}, A B^{\prime} B C, A C D D^{\prime}, B^{\prime} C^{\prime} D^{\prime} C$, and $A C D^{\prime} B^{\prime}$.
Let us now prove that it is impossible to divide the cube into fewer tetrahedra. Suppose the cube is divided into several tetrahedra. There are at least two of them whose bases lie on the face $A B C D$ of the cube. Similarly, there are at least 2 tetrahedra with bases on the face $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$.
These tetrahedra are certainly different from the first two, since a tetrahedron cannot have two parallel faces. Thus, we already have 4 tetrahedra. Their total volume is no more than $2 a^{3} / 3$, i.e., less than the volume of the cube. Therefore, it is impossible to divide the cube into 4 tetrahedra.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. Three consecutive vertices of a rhombus lie on the sides $A B, B C, C D$ of a given square with side 1. Find the area of the figure filled by the fourth vertices of such rhombi.
|
92. Answer: $S=1$.
Let $K, L, N$ be the vertices of the rhombus on the sides $A B, B C$, and $A D$ of the square (Fig. $52, a$). Note that the length $K B$ is equal to the distance from point $M$ to the line $A D$. Therefore, if we fix point $K$, the possible positions of point $M$ fill a certain segment $M_{1} M_{2}$ parallel to side $A D$.
The lower position $M_{1}$ of point $M$ corresponds to the case $N_{1}=A$, and the upper position $M_{2}$ corresponds to the case $L_{2}=C$.
To determine the positions of points $M_{1}$ and $M_{2}$ depending on the location of point $K$, we introduce a coordinate system as shown in Fig. 52.
Simple calculations show that if the abscissa of point $K$ is $x>0$, then $M_{1}=(-x, \sqrt{2 x})$, and $M_{2}=(-x, \sqrt{1-2 x}+1)$. Using the symmetry of the set of points $M$ with respect to the $O y$ axis, we find that this set forms a figure marked with hatching. There is no need to take integrals to calculate the area: in Fig. 51, the figures marked with the numbers 1 and 2 are equal.
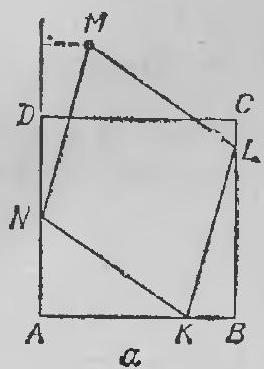

Fig. 52

6
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. In a regular $n$-gon ( $n>5$ ), the difference between the largest and smallest diagonals is equal to the side. Find $n$.
|
99. Answer: $n=9$.
Let $a_{n}$ be the side length, and $D_{n}$ and $d_{n}$ be the lengths of the largest and smallest diagonals of a regular $n$-gon. For $n=4$ and $n=5$, all diagonals are equal. For $n=6$ and $n=7$, $D_{n}-a_{n}=2 A K=D_{8}-d_{8}$. For $n=9$ (Fig. 55,6), similarly, we get $\angle A B K=30^{\circ}$, so $A B=a_{9}=2 A K=D_{9}-d_{9}$.
We will further consider the $n$-gon inscribed in a circle of radius 1. For $n>9$, obviously, $D_{n} \geqslant D_{9}, d_{n}D_{9}-d_{9}=a_{9}>a_{n}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
123. In a certain state, the airline system is arranged in such a way that any city is connected by air routes to no more than three other cities, and from any city to any other, one can travel with no more than one layover.
What is the maximum number of cities that can be in this state?
|
123. Answer: 10 cities.
From any city $A$, one can reach no more than three cities, and from each of them no more than two (excluding $A$). Thus, the total number of cities is no more than $1+3+3 \cdot 2=$ $=10$.
The example in Fig. 60 shows that the required system of air routes in a state with ten cities exists.
$\nabla$ The graph in Fig. 60 is often used as an example and even has a special name, the "Petersen graph".
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
131. How many sides in a convex polygon can be equal in length to the longest diagonal?
|
131. Answer: no more than two. An example of a polygon with two sides equal to the largest diagonal is shown in Fig. 61.
Suppose there are more than two such sides. We select two of them, $A B$ and $C D$, which do not share any vertices (this is possible, [^3] since a polygon with diagonals is not a triangle). Then at least one of the diagonals $A C$ or $B D$ is longer than side $A B$: if these diagonals intersect at some point $K$, then
$$
\begin{aligned}
& A C+B D=A K+K C+B K+ \\
& \quad+K D>A B+C D=2 A B
\end{aligned}
$$
Fig. 61
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
190. Among the numbers of the form $36^{k}-5^{l}$, where $k$ and $l$ are natural numbers, find the smallest in absolute value. Prove that the found number is indeed the smallest.
|
190. Answer: $11=36-5^{2}$.
The last digit of the number $36^{h}=6^{2 k}$ is 6, the last digit of the number $5^{t}$ is 5. Therefore, the number $\left|6^{2 k}-5^{t}\right|$ ends in either 1 (if $6^{2 k}>5^{t}$) or 9 (if $6^{2 k}<5^{t}$).
The equation $6^{2 k}-5^{t}=1$ is impossible, because then it would be $5^{l}=\left(6^{k}-1\right)\left(6^{k}+1\right)$, and the number $6^{k}+1$ is not divisible by 5. For $k=1$ and $l=2$, we get $36^{k}-5^{t}=11$.
The equation $5^{t}-6^{2 k}=9$ is also impossible, because $5^{t}$ for a natural $l$ is not divisible by 3.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
238. Several black and white chips are arranged in a circle. Two players take turns performing the following operation: the first player removes all black chips that have a white neighbor (at least on one side), and the second player then removes all white chips that have a black neighbor. They continue doing this until only chips of one color remain.
a) Suppose there were 40 chips initially. Is it possible that after each player makes two moves, only one chip remains on the circle?
b)* Initially, there were 1000 chips on the circle. What is the minimum number of moves after which only one chip can remain on the circle?
|
238. Answers: a) yes, b) 8 moves (each player - per move).
Fig. 102 shows an example of arranging 41 chips; next to each chip is its rank-number, indicating how many moves before the end it will be removed. The construction of such an arrangement is convenient "from the end"; to the remaining last black chip of rank 0, add two white chips of rank 1, next to each of them add two black chips of rank 2 (on both sides), next to each black chip add two white chips of rank 3, and so on. It is clear that this method gives the maximum possible number of chips of the corresponding rank at each step. Thus, for each $t$, an arrangement is obtained with the maximum possible number $a_{t}=b_{t}+w_{t}$ of chips - $b_{t}$ black and $w_{t}$ white, which can be transformed into one black chip in $t$ moves ($b_{0}=1$, $w_{0}=0$); the rule for sequential calculation of ($b_{t}, w_{t}$) is very simple: when transitioning from $\boldsymbol{t}$ to $\boldsymbol{t}+1$, the larger of the numbers $\boldsymbol{b}_{t}$, $w_{t}$ does not change, and to the smaller, the doubled larger is added.
| $\boldsymbol{t}$ | 0 | 1 | 2 | 3 | 4 | 5 | | 7 | |
| :---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| $b_{t}$ | 1 | 1 | 5 | 5 | 29 | 29 | 169 | 169 | 985 |
| $w_{t}$ | 0 | 2 | 2 | 12 | 12 | 70 | 70 | 408 | 408 |
| $a_{t}$ | 1 | 3 | 7 | 17 | 41 | 99 | 239 | 577 | 1393 |
To solve problem a), it is sufficient to remove one chip of rank 4 from the 41 points in Fig. 102, which does not affect the situation after the first move (i.e., standing next to another chip "4"), for example, to maintain symmetry, the one marked with a star.
The transition from 1000 chips to one cannot occur in fewer than 8 moves, as can be seen from the table, $a_{7}=577<1000$. An example with exactly 1000 chips can be obtained from the maximum arrangement for 8 moves with $a_{8}=1393$ chips, by removing 393 chips of rank 8, which do not affect the situation after the first move - this can be done since $2 \cdot 408=816$ chips of rank 8, placed among 577 chips of rank no more than 7, form no fewer than $816-577=239$ pairs of adjacent chips.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
306. We will say that a number has the property $\mathrm{P}(k)$ if it can be factored into the product of $k$ consecutive natural numbers, all greater than 1.
a) Find $k$ such that some number $N$ simultaneously has the properties $\mathrm{P}(k)$ and $\mathrm{P}(k+2)$.
b) Prove that there are no numbers that simultaneously have the properties $P(2)$ and $\mathbf{P}(4)$.
|
306. a) $k=3 ; 720=2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=8 \cdot 9 \cdot 10$.
b) If $m(m+1)=n(n+1)(n+2)(n+3)$, then $m^{2}+m+1=\left(n^{2}+3 n+1\right)^{2}$, which is impossible.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
325. a) Find the smallest possible value of the polynomial
$$
P(x, y)=4+x^{2} y^{4}+x^{4} y^{2}-3 x^{2} y^{2}
$$
b) ${ }^{*}$ Prove that this polynomial cannot be represented as a sum of squares of polynomials in the variables $x, y$.
|
325. a) Answer: 3 at $x=y=1$.
From the inequality of the arithmetic mean, it follows that $1+x^{2} y^{4}+x^{4} y^{2} \geqslant 3 x^{2} y^{2}$.
b) Let $P(x, y)=g_{1}^{2}(x, y)+g_{2}^{2}(x, y)+\ldots+g_{n}^{2}(x, y)$, where $g_{i}(x, y), i=1,2, \ldots, n-$ are polynomials. Since $P(x, 0)=$ $=P(0, y)=4$, the polynomials $g_{i}$ cannot contain monomials of the form $a x^{k}$ and $b y^{2}$. Therefore, the coefficient of $x^{2} y^{2}$ must be positive.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
389. The sequence $x_{n}$ is defined recursively: $\quad x_{1}=1 ; x_{2}=1 ; x_{n+2}=x_{n+1}^{2}-\frac{1}{2} x_{n}, \quad$ if $n \geqslant 1$. Prove that the sequence $x_{n}$ has a limit, and find it.
390 *. In the white cells of a chessboard of size $1983 \times 1984$, numbers 1 or -1 are written such that for any black cell, the product of the numbers in the adjacent white cells is 1. Prove that this is possible only if all the written numbers are 1.
|
389. Answer: $\lim _{n \rightarrow \infty} x_{n}=0\left(\left|x_{n+7}\right| \leqslant \frac{1}{4}\left(\frac{5}{6}\right)^{n}\right.$ for $\left.n \geqslant 1\right)$.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
432. Milk is poured into 30 glasses. A boy is trying to make the amount of milk equal in all glasses. For this, he takes any two glasses and pours milk from one to the other until the amount of milk in them is equal. Is it possible to pour milk into the glasses in such a way that the boy cannot achieve his goal, no matter how long he spends pouring?
|
432. Answer: it is possible. You need to pour 100 g of milk into all the glasses except one, and into the remaining one - 200 g
256
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
456. Every evening, Uncle Chernomor appoints 9 or 10 out of 33 bogatyrs for duty, at his discretion. What is the smallest number of days after which it can happen that each of the bogatyrs has been on duty the same number of times?
|
456. Answer: 7 days. Let $k$ be the number of days when 9 bogatyrs were on duty, and $l$ be the number of days when 10 bogatyrs were on duty, with each of them being on duty $m$ times. Then $9 k + 10 l = 33 m$. For $m=1$ there are no solutions, but for $m=2$ we have $k=4$ and $l=3$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.3. Replace the ellipsis with such a natural number $p$ so that the answer to the following question is unique: how many lines are drawn on the plane, if it is known that they intersect at ... different points?
|
1.3. Answer. $p=2$.
We will prove that if there are two intersection points, there can only be three lines. Suppose there are only two intersection points $A$ and $B$, and let $l_{1}$ and $l_{2}$ be the lines intersecting at point $A$, and $l_{3}$ be a line not passing through $A$ (such a line exists, otherwise all lines would intersect at $A$). Line $l_{3}$ intersects only one of the lines $l_{1}, l_{2}$, say $l_{1}$, at point $B$, and is parallel to the other line $l_{2}$ (figure a). Verify that no more lines can be drawn without increasing the number of intersection points.
a)
Fig. 1.3.
Note that the proof uses Euclid's "fifth postulate" - the axiom stating that through a point, no more than one line can be drawn parallel to a given line.
We will prove that the number of intersection points cannot be different from 2. If there is only one intersection point, the number of lines can be any number starting from 2, provided that all lines pass through this point. If the number of intersection points $n>2$, the number of lines is not uniquely determined. This is illustrated by the example of the arrangement of lines shown in figure b: a line $l_{n+1}$ can be drawn parallel to $l_{n}$, or it can be not drawn, without affecting the number of intersection points.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. Six pennies lie on the table, forming a closed chain (i.e., the first penny touches the second, the second touches the third, and so on, the sixth touches the first). A seventh penny, also lying on the table, rolls without slipping along the outer side of the chain, touching each of the six pennies in the chain in turn. How many revolutions will this penny make before returning to its original position?
## QUADRILATERAL AND FOUR CIRCLES
|
6.3. Answer. 4 turns.
From figure $a$, it can be seen that during the time the moving coin, depicted with a dashed line, rolls along the arc $\alpha$ of the stationary coin with center $O$, it rotates by an angle of $2 \alpha$: in this figure, $M^{\prime} A^{\prime}$ is the new position of the radius $M A$, the radii $M A$ and $M^{\prime} A^{\prime \prime}$ are parallel, $\angle A^{\prime \prime} M^{\prime} B = \angle A O B = \alpha$, and since the arcs $A^{\prime} B$ and $A B$ are equal, $\angle B M^{\prime} A^{\prime} = \alpha$, therefore, the entire angle $\angle A^{\prime \prime} M^{\prime} A^{\prime}$, by which the moving coin rotates, is $2 \alpha$.
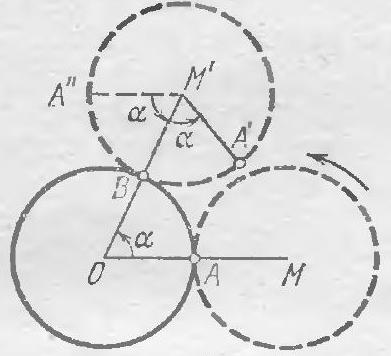
a)
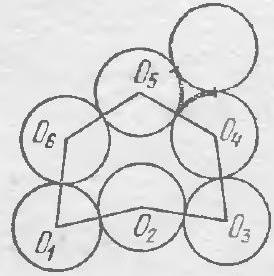
b)
Fig. 6.3.
Now let's find the sum of the arcs (in degrees) consisting of points of the stationary coins that the moving coin touched while rolling along the chain. Let $O_{1}, O_{2}, \ldots, O_{6}$ be the centers of the stationary coins (see figure b). The sum of the arcs lying inside the hexagon $O_{1} O_{2} \ldots O_{6}$ is equal to the sum of its interior angles, i.e., $180^{\circ} \cdot 6 - 360^{\circ} = 720^{\circ}$. Indeed, the sum of the interior angles of any $n$-sided polygon, not necessarily convex, is $180^{\circ} n - 360^{\circ}$ (prove this yourself or read the proof, for example, in the book by D. O. Shklyarsky et al., "Selected Problems and Theorems in Planimetry," "Nauka," 1967, problem 108). The sum of the arcs lying outside this hexagon is $360^{\circ} \cdot 6 - 720^{\circ} = 1440^{\circ}$. From this, we need to subtract the sum of the arcs lying in the indentations between two adjacent coins, where the moving coin will not reach; in each of the six indentations, the sum of the two such arcs is $120^{\circ}$ (on figure 6, these arcs are shown with a bold line). Thus, the total sum of the arcs along which the coin will roll is $1440^{\circ} - 120^{\circ} \cdot 6 = 720^{\circ}$, and the desired number of turns is obtained by multiplying this value by 2 and dividing by $360^{\circ}$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the board in the laboratory, two numbers are written. Every day, senior researcher Petya erases both numbers from the board and writes down their arithmetic mean and harmonic mean instead. On the morning of the first day, the numbers 1 and 2 were written on the board. Find the product of the numbers written on the board in the evening of the 1999th day. (The arithmetic mean of two numbers $a$ and $b$ is the number $\frac{a+b}{2}$, and the harmonic mean is the number $\frac{2}{1 / a+1 / b}$.)
|
1. The product of the numbers on the board does not change. Indeed,
$$
\frac{a+b}{2} \cdot \frac{2}{1 / a+1 / b}=\frac{a+b}{2} \cdot \frac{2 a b}{a+b}=a b
$$
Therefore, on the 1999th day, the product will be the same as it was on the first day. See also fact 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 *. Find all pairs of natural numbers $x, y$ such that $x^{3}+y$ and $y^{3}+x$ are divisible by $x^{2}+y^{2}$.
|
3. Let's first prove that $x$ and $y$ are coprime. Assume the opposite. Then $x$ and $y$ are divisible by some prime number $p$. Let $p$ enter the prime factorizations of $x$ and $y$ with powers $a \geqslant 1$ and $b \geqslant 1$ respectively (see fact 10). Without loss of generality, we can assume that $a \geqslant b$. Then the maximum power of $p$ that divides $x^{3}+y$ is $b$ (since $x^{3}$ is divisible by $p^{3 a}$ and therefore by $p^{b+1}$, but $y$ is divisible by $p^{b}$ and not by $p^{b+1}$). On the other hand, $x^{2}+y^{2}$ is divisible by $p^{2 b}$, so $x^{3}+y$ cannot be divisible by $x^{2}+y^{2}$. This contradiction shows that $x$ and $y$ are coprime (see fact 5).
Next, by the condition, $x\left(x^{2}+y^{2}\right)-\left(x^{3}+y\right)=y(x y-1)$ must be divisible by $x^{2}+y^{2}$. Note that $y$ and $x^{2}+y^{2}$ cannot have a common divisor greater than 1 (since $x$ and $y$ are coprime), so $x y-1$ must be divisible by $x^{2}+y^{2}$ (see fact 9). But if we assume that $x y-1>0$, this is impossible, since $x^{2}+y^{2} \geqslant 2 x y>x y-1$. Therefore, $x y=1$, which means $x=y=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4*. Find all such positive integers $k$ for which the number
$$
\underbrace{1 \ldots 1 \overbrace{2 \ldots 2}^{k}}_{2000}-\underbrace{2 \ldots 2}_{1001}
$$
is a perfect square.
|
4. Let $n=1000$. Consider two cases.
$1^{\circ} . k>n$. Then
$$
\underbrace{1 \ldots 12 \ldots 2}_{2 n}-\underbrace{2 \ldots 2}_{n+1}=\underbrace{1 \ldots 1}_{2 n-k} \overbrace{2 \ldots 2}^{k-(n+1)} \underbrace{0 \ldots 0}_{n+1} .
$$
This number ends with $n+1=1001$ zeros. But if a number is a square of a natural number, it must end with an even number of zeros! Therefore, this number cannot be a square of a natural number.
$2^{\circ} . k \leqslant n$. Then
$$
\begin{aligned}
\underbrace{1 \ldots 1 \overbrace{2 \ldots 2}^{k}}_{2 n}-\underbrace{2 \ldots 2}_{n+1}=\underbrace{1 \ldots 10 \ldots 0}_{2 n-k}-\underbrace{2 \ldots 20 \ldots 0}_{k} & = \\
& =10^{k}(\underbrace{1 \ldots 1}_{2 n-k}-\underbrace{2 \ldots 2}_{n+1-k})
\end{aligned}
$$
This number ends with $k$ zeros. As explained above, for it to be a square of a natural number (henceforth, we will call squares of natural numbers perfect squares), $k$ must be even. Let $l=\frac{k}{2}$.
It is clear that the number (1) is a perfect square if and only if the number
$$
A=\underbrace{1 \ldots 1}_{2 n-2 l}-\underbrace{2 \ldots 2}_{n+1-2 l}
$$
is a perfect square.
Notice that
$$
A=\frac{1}{9} \cdot \underbrace{9 \ldots 9}_{2 n-2 l}-\frac{2}{9} \cdot \underbrace{9 \ldots 9}_{n+1-2 l}=\frac{1}{9}\left(10^{2 n-2 l}-1-2\left(10^{n+1-2 l}-1\right)\right)
$$
(see fact 11). Let $B=9 A$. The number $A$ is a perfect square if and only if $B=9 A$ is a perfect square. Write the expression for $B$ in the following form:
$$
B=10^{2 n-2 l}-2 \cdot 10^{n+1-2 l}+1=\left(10^{n-l}\right)^{2}-2 \cdot 10^{n-l} \cdot 10^{1-l}+1
$$
For $l=1$, the right-hand side of (2) becomes the formula for the square of a difference:
$$
B=\left(10^{n-1}\right)^{2}-2 \cdot 10^{n-1}+1=\left(10^{n-1}-1\right)^{2}
$$
Let $l>1$.
Now notice that if $X=Y^{2}$ is a square of a natural number, then the nearest perfect square (less than $X$) is $(Y-1)^{2}=Y^{2}-2 Y+1$. That is, if a number $Z$ is such that
$$
Y^{2}-2 Y+1\left(10^{n-l}\right)^{2}-2 \cdot 10^{n-l}+1
$$
Then, by the previous observation, this number cannot be a perfect square, so only $l=1$ (and, therefore, only $k=2$) satisfies the condition.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a convex quadrilateral $A B C D$, points $E$ and $F$ are the midpoints of sides $B C$ and $C D$ respectively. Segments $A E, A F$, and $E F$ divide the quadrilateral into 4 triangles, the areas of which are consecutive natural numbers. What is the maximum possible value of the area of triangle $A B D$?
|
3. Let the areas of the triangles be $n, n+1, n+2$, $n+3$. Then the area of the quadrilateral $A B C D$ is $4 n+6$. It is easy to see that the area of triangle $B C D$ is four times the area of triangle $E C F$, so this area is at least $4 n$. Therefore,
$$
S_{A B D}=S_{A B C D}-S_{B C D} \leqslant(4 n+6)-4 n=6 .
$$
Equality is achieved if triangle $E C F$ has the smallest area
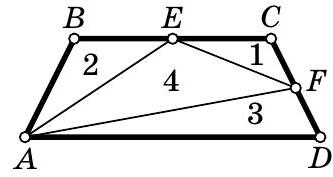
Fig. 151 of the four triangles mentioned.
It remains to prove that the value 6 is possible. An example is an isosceles trapezoid with bases $A D=6, B C=4$ and height 2 (the numbers in Fig. 151 denote the areas of the triangles).
Comment. It is easy to see that the area of triangle $A B D$ is always either 2 or 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. For a convex polyhedron, the internal dihedral angle at each edge is acute. How many faces can the polyhedron have?
|
5. For each of the faces, consider the vector of the external normal, i.e., a vector perpendicular to this face and directed outward from the polyhedron.
$1^{\circ}$. Let's prove that the angle between any two external normals is obtuse or straight. Suppose this is not the case, and there exist two faces $\Gamma_{1}$ and $\Gamma_{2}$, the external normals of which form an angle not greater than $\pi / 2$. Then the faces $\Gamma_{1}$ and $\Gamma_{2}$ belong to half-planes $\Pi_{1}$ and $\Pi_{2}$, which form a dihedral angle of at least $\pi / 2$.
Take a point $P$ on the face $\Gamma_{2}$. Let $P^{\prime}$ be the projection of the point $P$ onto the plane of the face $\Gamma_{1}$. Since the angle between
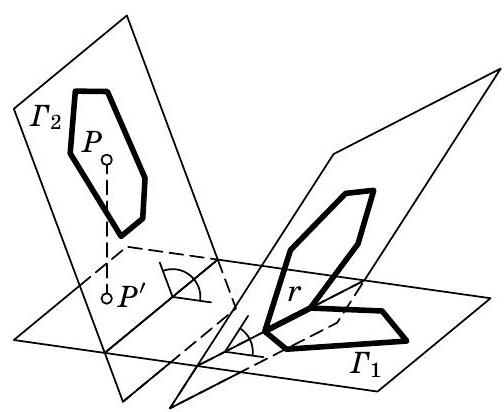
Fig. 167 the external normals to the faces $\Gamma_{1}$ and $\Gamma_{2}$ is not greater than $\pi / 2$, and our polyhedron is convex, the point $P^{\prime}$ lies outside the polygon $\Gamma_{1}$. Therefore, there exists a line containing some edge $r$ of the face $\Gamma_{1}$ and separating $P^{\prime}$ from $\Gamma_{1}$. The polyhedron lies inside the acute dihedral angle corresponding to the edge $r$, but $P$ lies outside this dihedral angle (Fig. 167). Contradiction.
$2^{\circ}$. It remains to show that in space, there do not exist more than four vectors, the pairwise angles between which are obtuse or straight.
Suppose this is not the case, and $\vec{u}_{0}, \vec{u}_{1}, \vec{u}_{2}, \vec{u}_{3}, \vec{u}_{4}$ are five vectors, the pairwise angles between which are obtuse or straight. Introduce a rectangular coordinate system such that the $O z$ axis is directed along $\vec{u}_{0}$.
Denote by $\vec{v}_{i}$ the projection of the vector $\vec{u}_{i}$ onto the plane $O x y$. Let $\vec{u}_{i}=\left(x_{i}, y_{i}, z_{i}\right)$, then $x_{0}=y_{0}=0, z_{0}>0$ and $v_{0}=0$.
The condition that all angles are obtuse or straight is equivalent to all scalar products being negative. In particular,
$$
z_{0} z_{i}=\left(\vec{u}_{0}, \vec{u}_{i}\right) < 0 \quad \text{for} \quad 1 \leqslant i \leqslant 4.
$$
Since $z_{0} > 0$, it follows that $z_{i} < 0$ for $1 \leqslant i \leqslant 4$. Now consider the scalar products between the projections:
$$
\left(\vec{v}_{i}, \vec{v}_{j}\right)=\left(\vec{u}_{i}, \vec{u}_{j}\right)-z_{i} z_{j} < 0 \quad \text{for} \quad 1 \leqslant i, j \leqslant 4.
$$
Thus, $\vec{v}_{1}, \vec{v}_{2}, \vec{v}_{3}, \vec{v}_{4}$ are four vectors on the plane, the angles between which are obtuse or straight. But this is impossible.
Therefore, a polyhedron has four faces. Note that a polyhedron with four faces can only be a tetrahedron.
Idea of another solution. First, prove that at each vertex of the polyhedron, three faces meet. For this, it is sufficient to prove that the sum of the dihedral angles of any $n$-hedral angle is greater than $\pi(n-2)$. Since an $n$-hedral angle can be cut into $n-2$ trihedral angles, it is sufficient to prove this statement for a trihedral angle. Now, it can be shown that all planar angles at each vertex are acute. From this, it is not difficult to deduce that all faces are triangles. Now, it is not difficult to verify that the polyhedron is a tetrahedron.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A square sheet of checkered paper $8 \times 8$ was folded several times along the grid lines so that a $1 \times 1$ square was obtained. It was then cut along a segment connecting the midpoints of two opposite sides of the square. Into how many pieces could the square have split as a result?
|
2. Let the cut be vertical (the case of a horizontal cut is analogous). Draw vertical segments in all $1 \times 1$ squares, connecting the midpoints of opposite sides. Notice that when folding along the grid lines, these
Fig. 180 segments overlap each other. Therefore, when cutting, only these segments are cut. By counting the number of resulting parts, we see that the square has split into 9 parts.
Comment. It was important to solve the problem for any folding, not just a specific example. In particular, the problem does not specify that each fold was made in half.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Given a line $l$, two points $A$ and $B$ on the same side of it, and a segment $a$. Find a segment $X Y$ on the line $l$ of length $a$ such that the length of the broken line $A X Y B$ is the smallest (Fig. 42).
|
35. Since the length of the segment $X Y$ is equal to $a$, it is necessary that the sum $A X + B Y$ be minimal. Suppose that the segment $X Y$ is laid out. The sliding symmetry with the axis $l$ "of the parallel translation magnitude $a$ translates point $B$ to $B'$, and point $Y$ to $X$ (Fig. 144); therefore, $B Y = B' X$ and, consequently, $A X + B Y = A X + B' X$. Thus, it is required that the length of the broken line $A X B'$ be the smallest. From this, it follows that $X$ is the point of intersection of the line $l$ with the segment $A B'$.
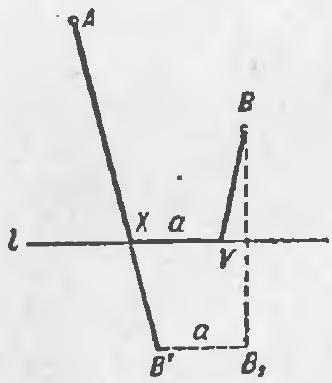
Fig. 144.
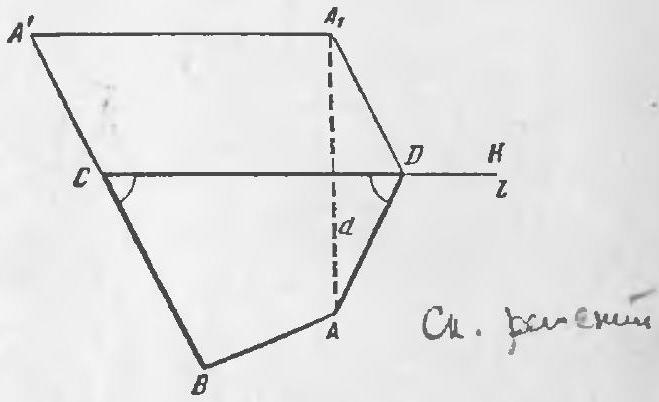
Fig. 145.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. How many real solutions does the system of two equations with three unknowns have:
$$
\left\{\begin{aligned}
x+y & =2 \\
x y-z^{2} & =1 ?
\end{aligned}\right.
$$
|
Sol 1. From the second equation, it follows that $x y \geqslant 1$. The numbers $x$ and $y$ cannot both be negative, since their sum is 2. Therefore, the numbers $x$ and $y$ are positive and $x+y \geqslant 2 \sqrt{x y} \geqslant 2$, and the equality $x+y=2$ is possible only when $x=y=1$. In this case, $z=0$.
Part 2. Solve the system of equations:
$$
\left\{\begin{aligned}
x^{3}-y^{3} & =26 \\
x^{2} y-x y^{2} & =6
\end{aligned}\right.
$$
Sol 2. Let $y=k x$. Immediately note that $k \neq 1$. From the equations
$$
\begin{aligned}
x^{3}-k^{3} x^{3} & =26 \\
k x^{3} y-k^{2} x^{3} & =6
\end{aligned}
$$
we get $x^{3}=\frac{26}{1-k^{3}}$ and $x^{3}=\frac{6}{k-k^{2}}$. Therefore,
$$
\frac{26}{1-k^{3}}=\frac{6}{k-k^{2}}
$$
This equation can be multiplied by $1-k$. As a result, we get
$$
\frac{26}{1+k+k^{2}}=\frac{6}{k}
$$
from which $k=3$ or $\frac{1}{3}$. Therefore, $x^{3}=-1$ or $x^{3}=27$. In the end, we get the following solutions: $(-1,-3)$, $\left(\frac{1 \pm i \sqrt{3}}{2}, \frac{3}{2}(1 \pm i \sqrt{3})\right),(3,1),\left(\frac{-3 \pm 3 i \sqrt{3}}{2}, \frac{1}{2}(-1 \pm i \sqrt{3})\right)$.
Part 3. Find the sum
$$
1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}
$$
Sol 3. By induction on $m$, it is easy to prove that $1^{3}+2^{3}+3^{3}+\cdots+m^{3}=\left(\frac{m(m+1)}{2}\right)^{2}$. Indeed, the base of induction is obvious, so we only need to check the equality
$$
\frac{m^{2}(m+1)^{2}}{2}+(m+1)^{3}=\frac{(m+1)^{2}(m+2)^{2}}{.}
$$
After canceling by $m+1$ and multiplying by 4, we get the obvious equality $m^{2}+4(m+1)=(m+2)^{2 *}$
Thus, $1^{3}+2^{3}+3^{3}+\cdots+(2 n-1)^{3}+(2 n)^{3}=\left(\frac{2 n(2 n+1)}{2}\right)$, i.e., $1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}+2^{3}\left(1^{3}+2^{3}+\cdots+n^{3}\right)=\left(\frac{2 n(2 n+1)}{2}\right)^{2}$. Transform the last equality, using the fact that $1^{3}+2^{3}+\cdots+n^{3}=\left(\frac{n(n+1)}{2}\right)^{2}$. As a result, we get $1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}=n^{2}\left(2 n^{2}-1\right)$.
## Series C
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. The city's bus network is organized as follows: 1) from any stop to any other stop, you can get without transferring;
2) for any pair of routes, there is, and only one, stop where you can transfer from one of these routes to the other;
3) on each route, there are exactly three stops.
How many bus routes are there in the city?
|
Solve 5. Answer: 7. We will prove that if the given conditions are satisfied, then the number of stops $n$ and the number of routes $N$ are related by the formula $N=n(n-1)+1$. Let $a$ be one of the routes, and $B$ be a stop that route $a$ does not pass through. Each route passing through $B$ intersects route $a$. Therefore, exactly $n$ routes pass through $B$. Similarly, it can be proven that through each stop of route $a$, $n-1$ routes different from $a$ pass. In total, we get $n(n-1)$ different routes and the route $a$ itself.
## 9 - 10 grades
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. In a chess tournament, students from grades IX and X participated. There were 10 times more students from grade X than from grade IX, and they scored 4.5 times more points in total than all the students from grade IX. How many points did the students from grade IX score? Find all solutions.
|
Solution 1. Let $x$ be the number of ninth graders in the tournament. Then there were a total of $11x$ participants, and they scored $\frac{11x(11x-1)}{2}$ points. According to the problem, the ratio of the number of points scored by the ninth graders to the number of points scored by the tenth graders is $1:4.5$. Therefore, the ninth graders scored $x(11x-1)$ points, which means each ninth grader won all $11x-1$ games they played. However, if there were two ninth graders among the participants, they would have had to both win their game against each other, which is impossible. Therefore, only one ninth grader participated in the tournament; he scored 10 points.
Part 2. Given the sequence of numbers: $0,1,1,2,3,5,8,13,21,34,55,89, \ldots$, where each number, starting from the third, is the sum of the two preceding numbers. Will there be a number among the first hundred million ($10^8 + 1$) terms of this sequence that ends with four zeros?
Solution 2. Answer: Yes, there will be. Replace each of the given numbers with its remainder when divided by 1000. Let $a_{1}=0, a_{2}, \ldots$ be the resulting numbers. If we know the numbers $a_{k}$ and $a_{k+1}$, then we also know $a_{k-1}$, since in the original sequence the $(k-1)$-th term is the difference between the $(k+1)$-th and $k$-th terms. Therefore, if for some $k$ and $n$ the equalities $a_{k}=a_{k+n}$ and $a_{k+1}=a_{k+n+1}$ hold, then $a_{k-1}=a_{k+n-1}, a_{k-2}=a_{k+n-2}, \ldots, a_{1}=a_{n+1}$. But $a_{1}=0$, so $a_{n+1}=0$, i.e., in the original sequence, the number at the $(n+1)$-th position ends with four zeros.
It remains to prove that among the pairs $\left(a_{1}, a_{2}\right),\left(a_{2}, a_{3}\right), \ldots,\left(a_{10^{8}}, a_{10^{8}+1}\right),\left(a_{10^{8}+1}, a_{10^{8}+2}\right)$, there will be two identical pairs. But from the numbers $0,1,2, \ldots, 9999$, it is impossible to form more than $10^8$ different pairs, while we are considering $10^8 + 1$ pairs.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. In the city, there are 57 bus routes. It is known that:
1) from any stop to any other stop, one can travel without transferring;
2) for any pair of routes, there is one, and only one, stop where one can transfer from one of these routes to the other;
3) each route has no fewer than three stops.
How many stops does each of the 57 routes have?
|
Solution 4. Answer: 8. We will prove that if the given conditions are satisfied, then the number of stops $n$ and the number of routes $N$ are related by the formula $N=n(n-1)+1$. First, we will show that if a route has $n$ stops, then any other route also has $n$ stops, and furthermore, each stop is served by $n$ routes. Let's take a stop $B$ that is not on the considered route $a$. From $B$, there is a route to each of the $n$ stops on route $a$, and such a route is unique, since two different routes cannot have two common stops. Each route passing through $B$ intersects route $a$. Therefore, exactly $n$ routes pass through $B$. Now it is clear that a route $b$ that does not pass through stop $B$ also has exactly $n$ stops. Indeed, exactly $n$ routes pass through $B$, each intersecting $b$ at one point, two routes cannot intersect $b$ at the same point, and each stop on route $b$ is served by one of these routes. Now it is clear that each stop is served by $n$ routes. In particular, each stop on route $a$ is served by $n-1$ routes other than $a$ itself. In total, we get $n(n-1)$ different routes and the route $a$ itself.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. There is a piece of chain consisting of 60 links, each weighing 1 g. What is the smallest number of links that need to be unbuckled so that from the resulting parts, all weights of 1 g, 2 g, 3 g, \(\ldots, 60\) g can be formed (an unbuckled link also weighs 1 g)
|
Solution 5. Answer: 3 links. Let's determine the greatest \(n\) for which it is sufficient to break \(k\) links of an \(n\)-link chain so that all weights from 1 to \(n\) can be formed from the resulting parts. If \(k\) links are broken, then any number of links from 1 to \(k\) can be formed from them. But \(k+1\) links cannot be formed if there is no part with \(k+1\) or fewer links (we do not consider the broken links here). The most advantageous situation is to have a part with exactly \(k+1\) links. Then we can get any number of links from 1 to \(2k+1\). (Otherwise, we can only get a number of links from 1 to \(l_1 + k\), where \(l_1 \leq k\).) Next, the most advantageous situation is to have a part with \(2(k+1)\) links, then with \(4(k+1)\) links, and so on. Thus, if we break \(k\) links, the most advantageous situation is when the \(k+1\) parts obtained consist of \(k+1, 2(k+1), 4(k+1), 8(k+1)\), \(\ldots, 2^k(k+1)\) links (we do not consider the broken links here). In this case, any number of links from 1 to \(n = 2^{k+1}(k+1) - 1\) can be formed. Therefore, if \(2^k k \leq n \leq 2^{k+1}(k+1) - 1\), then \(k\) breaks are sufficient and \(k-1\) breaks are insufficient. In particular, if \(24 \leq n \leq 63\), then the minimum number of broken links is 3. The four parts of the chain obtained by breaking should consist of \(4, 8, 16, 29\) links.
\footnotetext{
\({ }^{6}\) It is allowed for the vertices of the quadrilateral to lie not only on the sides of the trapezoid but also on their extensions. (Editor's note)
}
\section*{9 - 10 grades}
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. There is a piece of chain consisting of 150 links, each weighing 1 g. What is the smallest number of links that need to be unbuckled so that from the resulting parts, all weights of 1 g, 2 g, 3 g, \(\ldots, 150\) g can be formed (an unbuckled link also weighs 1 g)?
|
Solution 4. Answer: 4 links. According to the solution of problem 5 for grades \(7-8\) for a chain consisting of \(n\) links, where \(64 \leqslant n \leqslant 159\), it is sufficient to unfasten 4 links.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-rd 5. When dividing the polynomial \(x^{1951}-1\) by \(x^{4}+x^{3}+2 x^{2}+x+1\), a quotient and a remainder are obtained. Find the coefficient of \(x^{14}\) in the quotient.
|
Solve 5. Answer: -1. The equalities \(x^{4}+x^{3}+2 x^{2}+x+1=\left(x^{2}+1\right)\left(x^{2}+x+1\right)\) and \(x^{12}-1=(x-1)\left(x^{2}+x+\right.\)
1) \(\left(x^{3}+1\right)\left(x^{2}+1\right)\left(x^{4}-x^{2}+1\right)\) show that
\[
\begin{aligned}
x^{4}+x^{3}+2 x^{2}+x+1 & =\frac{x^{12}-1}{(x-1)\left(x^{3}+1\right)\left(x^{4}-x^{2}+1\right)}= \\
& =\frac{x^{12}-1}{x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1}
\end{aligned}
\]
Therefore, dividing the polynomial \(x^{1951}-1\) by \(x^{4}+x^{3}+2 x^{2}+x+1\) is the same as first dividing it by \(x^{12}-1\) and then multiplying by \(x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1\). But
\[
\frac{x^{1951}-1}{x^{12}-1}=x^{1939}+x^{1927}+x^{1915}+\cdots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}
\]
so the desired coefficient is the coefficient of \(x^{14}\) in the product
\[
\left(x^{1939}+\cdots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}\right)\left(x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1\right)
\]
\section*{9th - 10th Grades}
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. Five people play several games of dominoes (two on two) so that each player has each other as a partner once and as an opponent twice. Find the number of games played and all possible ways of distributing the players.
|
Solution 5. Answer: 5 games; the distribution of players is unique (up to their numbering). First, let's see who the 1st player played with. We can assume that the 1st and 2nd played against the 3rd and 4th, and the 1st and 5th played against the 2nd and 3rd (this can be achieved by swapping the 3rd and 4th). The 3rd player has already been an opponent of the 1st twice, so the 2nd and 5th play against the 1st and 4th. After this, the 2nd cannot play against the 1st, so the 4th and 5th play against the 1st and 3rd. The last game remains: the 2nd and 4th play against the 3rd and 5th.
\section*{10th Grade}
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-2. Points \(A_{1}, A_{2}, A_{3}, A_{4}, A_{5}, A_{6}\) divide a circle of radius 1 into six equal parts. From \(A_{1}\), a ray \(l_{1}\) is drawn in the direction of \(A_{2}\), from \(A_{2}\) - a ray \(l_{2}\) in the direction of \(A_{3}, \ldots\), from \(A_{6}\) - a ray \(l_{6}\) in the direction of \(A_{1}\). From point \(B_{1}\), taken on ray \(l_{1}\), a perpendicular is dropped onto ray \(l_{6}\), from the foot of this perpendicular a perpendicular is dropped onto \(l_{5}\), and so on. The foot of the sixth perpendicular coincides with \(B_{1}\). Find the segment \(B_{1} A_{1}\).
|
Solve 2. Answer: \(B_{1} A_{1}=2\).
Let \(B_{2}, B_{3}, \ldots, B_{7}\) be the feet of the perpendiculars dropped from \(l_{6}, l_{5}, \ldots, l_{1} ; x_{1}=A_{2} B_{1}, x_{2}=\) \(A_{1} B_{2}, x_{3}=A_{6} B_{3}, \ldots, x_{7}=A_{2} B_{7}\). Then \(x_{k+1}=\frac{1}{2}\left(1+x_{k}\right)\). By the condition \(x_{1}=x_{7}\). But
\[
x_{7}=\frac{1}{2}\left(1+x_{6}\right)=\frac{1}{2}\left(1+\frac{1}{2}\left(1+x_{5}\right)\right)=\frac{1}{2}\left(1+\frac{1}{2}\left(1+\frac{1}{2}\left(1+x_{5}\right)\right)\right)=\ldots
\]
therefore
\[
x_{7}=\frac{1}{2}+\frac{x_{6}}{2}=\frac{3}{4}+\frac{x_{5}}{4}=\frac{7}{8}+\frac{x_{4}}{8}=\cdots=\frac{63}{64}+\frac{x_{1}}{64}
\]
Thus, we get the equation \(\frac{63}{64}+\frac{x_{1}}{64}=x_{1}\), from which \(x_{1}=1\). It is also clear that \(B_{1} A_{1}=1+x\).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-3. We took three numbers \(x, y, z\). We calculated the absolute values of the pairwise differences \(x_{1}=|x-y|\), \(y_{1}=|y-z|, z_{1}=|z-x|\). In the same way, from the numbers \(x_{1}, y_{1}, z_{1}\) we constructed the numbers \(x_{2}, y_{2}, z_{2}\) and so on. It turned out that for some \(n\), \(x_{n}=x\), \(y_{n}=y\), \(z_{n}=z\). Knowing that \(x=1\), find \(y\) and \(z\).
|
Solve 3. Answer: \(y=z=0\).
The numbers \(x_{n}, y_{n}, z_{n}\) are non-negative, so the numbers \(x, y, z\) are also non-negative. If all the numbers \(x\), \(y, z\) were positive, then the largest of the numbers \(x_{1}, y_{1}, z_{1}\) would be strictly less than the largest of the numbers \(x, y, z\), and then the largest of the numbers \(x_{n}, y_{n}, z_{n}\) would be strictly less than the largest of the numbers \(x, y, z\). Therefore, among the numbers \(x, y, z\) there is a 0. Similarly, it is proved that among the numbers \(x_{1}, y_{1}, z_{1}\) there is a 0 (for \(n=1\) there is nothing to prove, because then \(x_{1}=x, y_{1}=y, z_{1}=z\)). This means that two of the numbers \(x, y, z\) are equal. In the end, we get that the unordered set of numbers \(x, y, z\) can be either 0,0, 1, or \(0,1,1\). Obviously, the second set does not have the required property.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. In a rectangular table composed of positive numbers, the product of the sum of the numbers in any column and the sum of the numbers in any row equals the number at their intersection. Prove that the sum of all numbers in the table is one.
|
Solution 4. First solution. Let \(x_{1}, \ldots, x_{n}\) be the sums of the numbers in the rows, and \(y_{1}, \ldots, y_{m}\) be the sums of the numbers in the columns. At the intersection of the \(i\)-th row and the \(j\)-th column, the number \(x_{i} y_{j}\) is placed. Therefore, the sum of the numbers in the \(i\)-th row is \(x_{i} y_{1} + x_{i} y_{2} + \cdots + x_{i} y_{m}\). On the other hand, this sum is equal to \(x_{i}\). Thus, \(x_{i} = x_{i} (y_{1} + y_{2} + \cdots + y_{m})\). The number \(x_{i}\) is positive; in particular, it is not zero, so \(y_{1} + y_{2} + \cdots + y_{m} = 1\). But the sum \(y_{1} + y_{2} + \cdots + y_{m}\) is precisely the sum of all the numbers in the table.
\(s s l\) Let \(a_{j i}\) be the number at the intersection of the \(i\)-th column and the \(j\)-th row. By the condition, \(a_{j i} = \left(\sum_{p=1}^{m} a_{p i}\right) \left(\sum_{q=1}^{n} a_{j q}\right)\).
Therefore, \(\sum_{i, j} a_{j i} = \sum_{i, j} \left(\sum_{p=1}^{m} a_{p i}\right) \left(\sum_{q=1}^{n} a_{j q}\right) = \left(\sum_{i, j} a_{j i}\right)^{2}\). For the number \(S = \sum_{i, j} a_{j i}\), we have obtained the equation \(S^{2} = S\). But \(S > 0\), so \(S = 1\).
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3-6. All values of the quadratic trinomial \(a x^{2}+b x+c\) on the interval \([0,1]\) do not exceed 1 in absolute value. What is the maximum value that the quantity \(|a|+|b|+|c|\) can have in this case?
|
Solve 6.
\section*{9th Grade}
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.90. What is the maximum number of acute angles a convex polygon can have
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
6.90. Let a convex $n$-gon have $k$ acute angles. Then the sum of its angles is less than $k \cdot 90^{\circ} + (n-k) \cdot 180^{\circ}$. On the other hand, the sum of the angles of an $n$-gon is $(n-2) \cdot 180^{\circ}$. Therefore, $(n-2) \cdot 180^{\circ} < k \cdot 90^{\circ} + (n-k) \cdot 180^{\circ}$, i.e., $k < 4$. Since $k$ is an integer, $k \leqslant 3$.
For any $n \geqslant 3$, there exists a convex $n$-gon with three acute angles (Fig. 6.17).
Fig. 6.17
Fig. 6.18
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.68. Using a compass and a ruler, divide an angle of $19^{\circ}$ into 19 equal parts.
|
8.68. If there is an angle of magnitude $\alpha$, then angles of magnitude $2 \alpha, 3 \alpha$, etc., can be constructed. Since $19 \cdot 19^{\circ}=361$, an angle of $361^{\circ}$, which coincides with an angle of $1^{\circ}$, can be constructed.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.18*. How many sides can a convex polygon have if all its diagonals have the same length?
|
9.18. We will prove that the number of sides of such a polygon does not exceed 5. Suppose that all diagonals of the polygon $A_{1} \ldots A_{n}$ have the same length and $n \geqslant 6$. Then the segments $A_{1} A_{4}, A_{1} A_{5}, A_{2} A_{4}$, and $A_{2} A_{5}$ have the same length, as they are diagonals of this polygon. However, in the convex quadrilateral $A_{1} A_{2} A_{4} A_{5}$, the segments $A_{1} A_{5}$ and $A_{2} A_{4}$ are opposite sides, while $A_{1} A_{4}$ and $A_{2} A_{5}$ are diagonals. Therefore, $A_{1} A_{5} + A_{2} A_{4} < A_{1} A_{4} + A_{2} A_{5}$. This leads to a contradiction.
It is also clear that a regular pentagon and a square satisfy the required condition.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.22. In a triangle, the lengths of two sides are 3.14 and 0.67. Find the length of the third side, given that it is an integer.
|
9.22. Let the length of the third side be $n$. By the triangle inequality, $3.14-0.67<n<3.14+$ $+0.67$. Since $n$ is an integer, then $n=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.32. The perimeter of a convex quadrilateral is 4. Prove that its area does not exceed 1.
|
9.32. According to problem $9.31 S_{A B C D} \leqslant(A B+C D)(B C+A D) / 4$. Since $a b \leqslant(a+$ $+b)^{2} / 4$, then $S_{A B C D} \leqslant(A B+C D+A D+B C)^{2} / 16=1$.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
25.25*. A regular octagon with side 1 is cut into parallelograms. Prove that among them there are at least two rectangles, and the sum of the areas of all rectangles is 2.
## §5. Plane, cut by lines
Let $n$ pairwise non-parallel lines be drawn on the plane, with no three intersecting at the same point. Problems 25.26-25.30 consider the properties of the figures into which these lines divide the plane. A figure is called $n$-linked if it is bounded by $n$ links (i.e., segments or rays).
|
25.25. Let us consider two mutually perpendicular pairs of opposite sides in a regular octagon and, as in problem 25.1, chains of parallelograms connecting opposite sides. At the intersections of these chains, there are rectangles. By considering two other pairs of opposite sides, we will obtain at least one more rectangle.
The parallelograms in each chain can be further cut so that the chain splits into several "paths," where in each path, adjacent parallelograms touch each other with entire sides, not parts of sides. The union of the rectangles in the new partition coincides with the union of the rectangles in the original partition, so the proof is sufficient to conduct for the new partition. Each path has a constant width; therefore, the length of one side of each rectangle in the path is equal to the width of the path, and the sum of the lengths of all other sides is equal to the sum of the widths of the paths corresponding to the second pair of sides. Consequently, the area of all rectangles in one path is equal to the product of the width of the path by the length of the side of the polygon, i.e., numerically equal to the width of the path. Therefore, the area of all rectangles corresponding to two perpendicular pairs of opposite sides is 1, and the area of all rectangles in general is 2.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
43. It is obvious that any figure with a diameter of 1 can be enclosed within a square with a side of 2: for this, it is sufficient for the center of the square to coincide with any point of the figure. What is the side of the smallest square that can enclose any figure with a diameter of 1?
Note. One can also pose a problem analogous to problems 42 and 43, replacing the square (problem 43) or circle (problem 42) with any other figure. For example, it can be shown that the smallest equilateral triangle that can enclose any figure with a diameter of 1 is a triangle with a side of \(\sqrt{3}\), and the smallest regular hexagon with the same property is a hexagon with a side of \(\frac{\sqrt{3}}{3}\) (see problem 31 in the book by I. M. Yaglom and V. G. Boltyansky, cited on page 10).
|
43. It is obvious that a circle with a diameter of 1 cannot be enclosed in any square whose side is less than 1. On the other hand, it is almost equally clear that any figure with a diameter of 1 can be enclosed in a square with a side of 1. Indeed, any square that encloses some figure $\Phi$ can always be reduced so that at least one pair of opposite sides of the square "touch" the figure (Fig. 123). But if $A$ and $B$ are points of the figure $\Phi$ with a diameter of 1, lying on opposite sides of the square containing $\Phi$ inside itself, then the distance between these sides of the square (or, equivalently, the side of the square) does not exceed $AB$, and $AB \leqslant 1$.
Thus, the smallest square in which any figure with a diameter of 1 can be enclosed has a side equal to 1.

Fig. 123.
Fig. 124.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. How many circles of radius 1 can be applied ${ }^{1}$ ) to a given unit circle $\mathcal{S}$ so that no two of these circles intersect? So that no one of these circles contains the center of another circle inside itself?
|
49. Since a unit circle tangent to $S$ is seen from the center $O$ of circle $S$ at an angle of $60^{\circ}$ (Fig. $132, a$), no more than $6\left(=\frac{360}{60^{\circ}}\right)$ non-overlapping unit circles can be applied to $S$. Six circles can obviously be applied (Fig. 132, b).
Further, if $O_{1}$ and $O_{2}$ are the centers of two unit circles $C_{1}$ and $C_{2}$ applied to $S$ such that $O_{1}$ does not lie inside $C_{2}$ and $O_{2}$ does not lie inside $C_{1}$ (Fig. $133, a$), then $O_{1} O_{2} \geqslant 1, O O_{1}=$ $=O O_{2}=2$ and $\angle O_{1} O O_{2} \geqslant 2 \arcsin \frac{1}{4} \approx 29.0^{\circ}$. It follows that no more than 12 (12 is the integer part of the fraction $\frac{360^{\circ}}{29.0^{\circ}}$) unit circles can be applied to $S$ such that no circle contains the center of another circle; 12 circles can obviously be applied (Fig. 133, b).
a)
Fig. 132.
Fig. 133.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. What is the greatest number of squares with side 1 that can be placed ${ }^{1}$ ) next to a given unit square $K$ so that no two of them intersect?
$^{1}$) The superscript "1" is kept as is, since it might refer to a footnote or additional information in the original text.
|
51. First solution. Let $O$ be the center of the main square $K$, and $O_{1}$ and $O_{2}$ be the centers of the non-overlapping squares $K_{1}$ and $K_{2}$ attached to it (Fig. $135, a$). Since the smallest distance from the center of a unit square to its boundary is $\frac{1}{2}$, the segments $O O_{1}$, $O O_{2}$, and $O_{1} O_{2}$ are not less than 1. Furthermore, since the squares $K$ and $K_{1}$ touch at some point $A$, we have $O O_{1} \leqslant O A + O_{1} A \leqslant \sqrt{2}$ (since the greatest distance from the center of a unit square to its boundary is $\frac{\sqrt{2}}{2}$). Therefore, the points $O_{1}$ and $O_{2}$ lie within the annulus centered at $O$ and bounded by circles of radii 1 and $\sqrt{2}$; and since $O_{1} O_{2} \geqslant 1$, the angle $O_{1} O O_{2}$, by the result of problem 46, is not less than $2 \arcsin \frac{1}{2 \sqrt{2}} \approx 41.4^{\circ}$. From this,
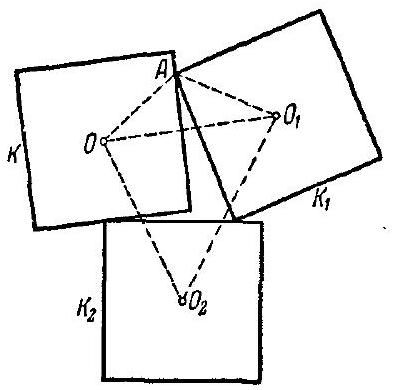
a)

b)
Fig. 135.
it follows that more than eight non-overlapping unit squares cannot be attached to the square $K$, since $9 \times 41.4^{\circ} > 360^{\circ}$. That eight squares can be attached is evident from Fig. 135, b.
Note. This problem can also be solved without using trigonometric tables. $2 \arcsin \frac{1}{2 \sqrt{2}}$ is the angle at the vertex of an isosceles triangle with legs $\sqrt{2}$ and base 1. If we attach nine such triangles to each other as shown in Fig. 136, the sum of the lengths of the bases of all these triangles will exceed the length of the circumference of radius $\sqrt{2}$; indeed, $2 \pi \sqrt{2} < 360^{\circ}$, which is what we needed to show.
Second solution. Let $A B C D$ be the original square $K$; we will take the length of its side as the unit. Consider the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with side 2, having the same center as the square $K$ and the same orientation of sides (Fig. $137, a$); the perimeter of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is obviously 8. We will show that the length $l$ of the part of the perimeter of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ cut by the side of one attached square cannot be less than 1; from this it will follow that no more than eight non-overlapping squares can be attached to $K$. Consider all possible positions of the attached square.
a)
b)
Fig. 137.
$1^{\circ}$ Suppose no vertex of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ falls inside the attached square (cases of squares $E F G H$ and $E_{1} F_{1} G_{1} H_{1}$ in Fig. 137, a). If in this case only one vertex of the attached square falls inside the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ (as in the case of square $E F G H$), then, denoting the angle between the sides $B C$ and $E F$ by $\alpha$, we have
$$
\begin{aligned}
& l = M K + K N = E K \operatorname{tg} \alpha + E K \operatorname{ctg} \alpha = \frac{1}{2} \left( \operatorname{tg} \alpha + \frac{1}{\operatorname{tg} \alpha} \right) = \\
& = 1 + \frac{1}{2} \left( \sqrt{\operatorname{tg} \alpha} - \frac{1}{\sqrt{\operatorname{tg} \alpha}} \right)^2 \geqslant 1
\end{aligned}
$$
If two vertices of the attached square fall inside the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ (as in the case of square $E_{1} F_{1} G_{1} H_{1}$), then obviously $l = M_{1} N_{1} \geqslant N_{1} L_{1} = 1$.
$2^{\circ}$ Suppose one vertex of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ falls inside the attached square (squares $A F_{2} C_{2} H_{2}$, $E_{3} F_{3} C_{3} H_{3}$, and $E_{4} F_{4} G_{4} H_{4}$ in Fig. 137, b). If the attached square touches the square $A B C D$ at a point on the boundary other than a vertex (case of square $E_{3} F_{3} G_{3} H_{3}$), then
$$
\begin{aligned}
l = M B^{\prime} + B^{\prime} N & = \left( P B^{\prime} + B^{\prime} Q \right) + (Q N - P M) = \\
& = 1 + (Q N - P M).
\end{aligned}
$$
But (Fig. $137, \sigma$)
$P M = E_{3} P \operatorname{tg} \alpha, \quad Q N = R Q \operatorname{tg} \alpha, \quad R Q - E_{3} P = R B - E_{3} B \geqslant 0$, since $\alpha \leqslant 45^{\circ}$. Therefore, $Q N > P M$ and $l > 1$. These same arguments apply in the case where the attached square touches the square $A B C D$ at a vertex (case of square $A F_{2} G_{2} H_{2}$); in this case only $P^{\prime} M^{\prime} = Q^{\prime} N^{\prime}$ and, therefore, $l = M^{\prime} A^{\prime} + A^{\prime} N^{\prime} = 1$. Finally, if the attached square touches the vertex of the square $A B C D$ with a side (case of square $E_{4} F_{4} G_{4} H_{4}$), then
$$
l = M_{1} D^{\prime} + D^{\prime} N_{1} > M_{1} N_{1} \geqslant G_{4} F_{4} = 1
$$
Thus, in all cases, the length of the part $M N$ of the perimeter of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ indeed cannot be less than 1.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54. What is the smallest number of circles with which a circle of twice the radius can be completely covered?
|
54. Since the diameter of the smaller circles is equal to the radius $R$ of the larger circle, each such circle intersects the circumference of the larger circle at points no more than $R$ apart, and thus covers an arc of this circumference no greater than $60^{\circ}$. It follows that at least six smaller circles are required to cover the entire circumference of the larger circle; in this case, six circles are sufficient only when these circles have diameters equal to the six sides of a regular hexagon inscribed in the larger circle, and in all other cases, at least seven circles are required. However, if the circumference of the larger circle is covered by six circles, then at least one more small circle is required to cover the remaining part of the larger circle (since the first six circles do not cover, for example, the center of the larger circle). In this case, one circle is sufficient to cover the remaining part of the larger circle (Fig. 143; from the fact that $O_{1} M=\frac{1}{2} R$, it follows that $O_{1} M$ is the median of the right triangle $O O_{1} A$ with an angle of $30^{\circ}$ and, therefore, $\left.O M=\frac{1}{2} R\right)$. Thus, we see that the smallest number of circles with radius $\frac{1}{2} R$ required to cover a circle with radius $R$ is 7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
102. Given a triangle $ABC$. A point $M$, located inside the triangle, moves parallel to side $BC$ until it intersects side $CA$, then moves parallel to $AB$ until it intersects side $BC$, then - parallel to $AC$ until it intersects $AB$, and so on. Prove that after a certain number of such steps, the point will return to its initial position, and find this number of steps.
Fig. 25.
|
102. If point $M$ lies on any of the medians of triangle $ABC$, for example, on $M_{3} M_{1}$, then it is obvious that after four steps it will return to its initial position (Fig. $227, a$). Now suppose that $M$ does not lie on any of the three medians of triangle $ABC$.
Let $M_{1}, M_{2}, M_{3}, M_{4}, M_{5}, M_{6}, M_{7}$ be the points on the sides of triangle $ABC$ that point $M$ sequentially reaches during its movement (Fig. 227, b). We need to prove that $M_{7}$ coincides with $M_{1}$. Let $M^{\prime}$ be the point of intersection of $M M_{1}$ with $AB$. It is sufficient to show that $M_{6}$ coincides with $M^{\prime}$. Draw a line through point $M^{\prime}$ parallel to $AC$. Let $M_{0}$ be the point of intersection of this line with $BC$.
a)
b)
Fig. 227.
Triangle $M^{\prime} B M_{0}$ is equal to triangle $M_{1} M_{2} C$, triangle $M_{1} M_{2} C$ is equal to triangle $A M_{3} M_{4}$, and triangle $A M_{3} M_{4}$ is equal to triangle $B M_{5} M_{6}$. Therefore, triangle $M^{\prime} B M_{0}$ is equal to triangle $B M_{5} M_{6}$, and thus $M_{6} M_{5} = M^{\prime} M_{0}$. From this, it follows that $M_{6}$ coincides with $M^{\prime}$, and $M_{5}$ with $M$; hence, $M_{7}$ coincides with $M_{1}$. This will happen in seven steps.
|
7
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
31. a) The third term of an arithmetic progression is equal to 0. Find the sum of the first 5 terms.
b) The third term of a geometric progression is equal to 4. Find the product of the first 5 terms.
|
31. a) We know that for an arithmetic progression $u_{1}=u_{3}-2 d ; u_{2}=u_{3}-d$; $u_{4}=u_{3}+d ; \quad u_{5}=u_{3}+2 d$. Therefore, the sum of the first five terms is
$$
\begin{aligned}
& \delta_{5}=u_{1}+u_{2}+u_{3}+u_{4}+u_{5}=\left(u_{3}-2 d\right)+ \\
& +\left(u_{3}-d\right)+u_{3}+\left(u_{3}+d\right)+ \\
& +\left(u_{3}+2 d\right)=5 u_{3}=0
\end{aligned}
$$
b) We need to find
$$
P_{5}=u_{1} \cdot u_{2} \cdot u_{3} \cdot u_{4} \cdot u_{5}
$$
We know that for a geometric progression
$\boldsymbol{u}_{1}=\frac{u_{3}}{q^{2}} ; \quad u_{2}=\frac{u_{3}}{q} ; \quad u_{4}=u_{3} q ; \quad u_{5}=u_{3} q^{2}$.
Therefore,
$$
P_{5}=\frac{u_{3}}{q^{2}} \cdot \frac{u_{3}}{q} \cdot u_{3} \cdot u_{3} q \cdot u_{3} q^{2}=u_{3}^{5}=4^{5}=1024
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. Mom has two apples and three pears. Every day for five consecutive days, she gives out one fruit. In how many ways can this be done?
|
56. Here is one way to distribute apples and pears: 000 'on the 1st and 3rd day - apples, on the 2nd, 4th, and 5th days - pears),
## 000
(on the first three days - pears, on the last two days - apples). Thus, we need to count all the tables with two light and three dark circles; but we have already done this when solving problem 44. The answer is $C_{5}^{2}=10$
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. Determine the sum of the coefficients of the polynomial that results from expanding and combining like terms in the expression $\left(1+x-3 x^{2}\right)^{1965}$.
|
81. If we expand the expression $\left(1+x-3 x^{2}\right)^{1965}$ and combine like terms, we get a polynomial $a_{0}+a_{1} \cdot x+$ $+a_{2} \cdot x^{2}+a_{3} \cdot x^{3}+\ldots$. Note that the sum of its coefficients is equal to the value of the polynomial at $x=1$
$$
\begin{aligned}
& a_{0}+a_{1} \cdot 1+a_{2} \cdot 1^{2}+a_{3} \cdot 1^{3}+\ldots= \\
&=a_{0}+a_{1}+a_{2}+a_{3}+\ldots
\end{aligned}
$$
Of course, there is no need to actually expand the brackets and combine like terms. It is sufficient to substitute $x=1$ into the original expression
$$
\left(1+1-3 \cdot 1^{2}\right)^{1965}=(-1)^{1965}=-1
$$
Thus, $a_{0}+a_{1}+a_{2}+a_{3}+\ldots=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.