problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. The AC-2016 calculator can perform two operations: taking the cube root and calculating the tangent. Initially, the number $2^{-243}$ was entered into the calculator. What is the minimum number of operations required to obtain a number greater than 1?
|
Answer: 7
## Examples of answer notation:
## 10
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Dima took the fractional-linear function $\frac{a x+2 b}{c x+2 d}$, where $a, b, c, d-$ are positive numbers, and added it to all the remaining 23 functions that result from it by permuting the numbers $a, b, c, d$. Find the root of the sum of all these functions, independent of the numbers $a, b, c, d$.
|
Answer: -1
## Examples of answer notation:
14
$1 / 4$
$-1.4$
#
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the last digit of the integer part of the number $(\sqrt{37}+\sqrt{35})^{2016}$.
|
Answer: 1
## Examples of answer recording:
## 0
#
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
Circles $O_{1}, O_{2}$, and $O_{3}$ are located inside circle $O_{4}$ with radius 6, touching it internally, and touching each other externally. Moreover, circles $O_{1}$ and $O_{2}$ pass through the center of circle $O_{4}$. Find the radius of circle $O_{3}$.
#
|
# Answer: 2
## Solution:
We will solve the problem in general for all cases, specifically proving that if the radius of circle $O_{4}$ is $R$, then the radius of circle $O_{3}$ is $\frac{R}{3}$.
Since circles $O_{1}$ and $O_{2}$ pass through the center of circle $O_{4}$ and are internally tangent to it, for each of them, the center of circle $O_{4}$ is diametrically opposite to the point of tangency. This means that the radius of each of them is $\frac{R}{2}$. Additionally, they touch each other at the center of circle $O_{4}$, which means that the centers of all three circles lie on the same straight line.
Now consider the triangle formed by the centers of circles $O_{1}$ and $O_{2}$ (let's call them $A$ and $B$) and the point of tangency of circles $O_{2}$ and $O_{3}$ (let's call it $C$). By symmetry, it is clear that $A C = B C$. Moreover, point $O$ (the center of circle $O_{4}$) is the midpoint of side $A B$. Therefore, triangle $O A C$ is a right triangle, with $O A = \frac{R}{2}$ and $O C = R$.
Now consider point $X$ (the center of circle $O_{3}$). It lies on segment $O C$, so triangle $O A X$ is also a right triangle. Its legs are $O A = \frac{R}{2}$ and $O X = R - r$, and the hypotenuse is $A X = \frac{R}{2} + r$, where $r$ is the desired radius of circle $O_{3}$. By the Pythagorean theorem, $\frac{R^{2}}{4} + R^{2} - 2 R r + r^{2} = \frac{R^{2}}{4} + R r + r^{2} = R^{2}$, from which $3 R r = R^{2}$ and $r = \frac{R}{3}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given triangle $\mathrm{ABC}: \mathrm{BK}, \mathrm{CL}$ - angle bisectors, M - the point of their intersection. It turns out that triangle $\mathrm{AMC}$ is isosceles, one of whose angles is 150 degrees. Find what the perimeter of triangle $\mathrm{ABC}$ can be, if it is known that $\mathrm{BK}=4-2 \sqrt{3}$.
|
Answer: 4
## Examples of how to write answers:
14
$1 / 4$
0.25
#
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of solutions in natural numbers for the equation $(x-4)^{2}-35=(y-3)^{2}$.
|
Answer: 3
## Examples of answer notation:
14
#
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the hitmen convention, 1000 participants gathered, each receiving a registration number from 1 to 1000. By the end of the convention, it turned out that all hitmen, except number 1, were killed. It is known that each hitman could only kill hitmen with higher numbers, and the number of his victims could not exceed his number. What is the minimum number of hitmen who could have participated in the killings at the convention?
|
Answer: 10
## Examples of answer notation:
5
#
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (3 points)
Natural numbers $a$ and $b$ are such that $2a + 3b = \operatorname{LCM}(a, b)$. What values can the number $\frac{\operatorname{LCM}(a, b)}{a}$ take? List all possible options in ascending or descending order, separated by commas. If there are no solutions, write the number 0.
|
Answer: 0 (no solutions)
## Solution:
Let $d=\operatorname{GCD}(a, b)$. Then $a=x d, b=y d, \operatorname{LCM}(a, b)=x y d$, where $x$ and $y$ are coprime. We get $2 x d+3 y d=x y d$. Dividing by $d$ yields $2 x+3 y=x y$.
The right side of this equation is divisible by $x$, so $2 x+3 y$ is divisible by $x$, which means $3 y$ is divisible by $x$. Since $x$ and $y$ are coprime, 3 must be divisible by $x$. Therefore, $x=3$ or $x=1$. Similarly, 2 must be divisible by $y$.
If $x=3$, the equation becomes $6+3 y=3 y$, which is false. If $x=1$, we get $2+3 y=y$, from which $y$ is negative, which is also impossible.
Therefore, there are no solutions.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Find the minimum value of the expression $x^{2}+4 x \sin y-4 \cos ^{2} y$.
|
Answer: -4.
Solution: Add and subtract $4 \sin ^{2} y$. We get the expression $x^{2}+4 x \sin y+4 \sin ^{2} y-4=(x+2 \sin y)^{2}-4$. It is clear that this expression has a minimum value of -4.
Idea of Solution 2: To find the minimum value, we can take the derivatives of this expression with respect to $x$ and $y$ and find the point where both these derivatives are zero. The derivative with respect to $x$ is zero when $x=-2 \sin y$.
The derivative with respect to $y$ is $4 x \cos y+8 \sin y \cos y$. It is zero in two cases: when $x=-2 \sin y$ and when $\cos y=0$. After this, it is necessary to determine which of these points are indeed local minima and why a global minimum exists.
A rigorous proof of this in terms of derivatives unfortunately goes beyond the school curriculum, so for school students, this solution can serve more as a hint to the answer and to the solution presented above.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Find the minimum value of the expression $x^{2}-6 x \sin y-9 \cos ^{2} y$.
|
Answer: -9.
Solution: Add and subtract $9 \sin ^{2} y$. We get the expression $x^{2}-6 x \sin y+9 \sin ^{2} y-9=(x-3 \sin y)^{2}-9$. It is clear that this expression has a minimum value of -9.
Idea of Solution 2: To find the minimum value, we can take the derivatives of this expression with respect to $x$ and $y$ and find the point where both these derivatives are zero. The derivative with respect to $x$ is zero when $x=3 \sin y$.
The derivative with respect to $y$ is $-6 x \cos y+18 \sin y \cos y$. It is zero in two cases: when $x=3 \sin y$ and when $\cos y=0$. After this, it is necessary to determine which of these points are indeed local minima and why a global minimum exists.
A rigorous proof of this in terms of derivatives unfortunately goes beyond the school curriculum, so for school students, this solution can serve more as a hint to the answer and to the solution presented above.
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Find the minimum value of the expression $4 x^{2}+4 x \sin y-\cos ^{2} y$.
|
Answer: -1.
Solution: Add and subtract $\sin ^{2} y$. We get the expression $4 x^{2}+4 x \sin y+\sin ^{2} y-1=(x+2 \sin y)^{2}-1$. It is clear that this expression has a minimum value of -1.
Idea of Solution 2: To find the minimum value, we can take the derivatives of this expression with respect to $x$ and $y$ and find the point where both these derivatives are zero. The derivative with respect to $x$ is zero when $2 x=-\sin y$.
The derivative with respect to $y$ is $4 x \cos y-2 \sin y \cos y$. It is zero in two cases: when $x=-2 \sin y$ and when $\cos y=0$. After this, it is necessary to determine which of these points are indeed local minima and why a global minimum exists.
A rigorous proof of this in terms of derivatives unfortunately goes beyond the school curriculum, so for school students, this solution can serve more as a hint to the answer and to the solution presented above.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Among six different quadratic trinomials that differ by the permutation of coefficients, what is the maximum number that can have no roots?
|
Answer: 6
Solution:
Consider, for example, the coefficients 1000, 1001, 1002. The square of any of them is obviously less than the quadruple product of the other two, so all discriminants will be negative.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Among six different quadratic trinomials that differ by the permutation of coefficients, what is the maximum number that can have two distinct roots
|
Answer: 6
Solution: Let's take, for example, the coefficients, $-5,1,2$.
If the number -5 is the leading coefficient or the constant term, the equation obviously has two roots of different signs.
For the case when -5 is the second coefficient, let's calculate the discriminant: $5^{2}-1 \cdot 2=23>0$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the greatest value that the sum $\sin ^{2} a+\sin ^{2}\left(a+60^{\circ}\right)+\sin ^{2}\left(a+120^{\circ}\right)+\ldots+\sin ^{2}\left(a+300^{\circ}\right)$ can take?
|
Answer: 3
## Examples of how to write the answer:
1,7
$1 / 7$
17
#
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What integer can be written in the form $\sqrt{12-\sqrt{12-\sqrt{12-\ldots}}}$ (the number of roots is infinite).
|
Answer: 3
## Examples of how to write the answer:
1,7
#
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The fox builds "pyramids" from 5 cubes in the following way: each "pyramid" consists of one or several levels; on each level, the number of cubes is strictly less than on the previous one; each new level consists of one or several consecutive cubes. You can see an example of a "pyramid" made of ten cubes in the picture:
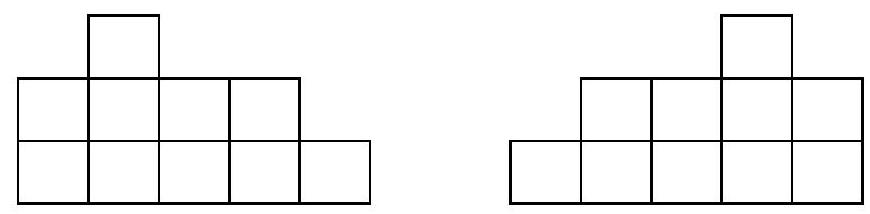
How many different "pyramids" can the fox build?
(It is important where the right edge and the left edge of the "pyramid" are — the "pyramids" in the picture are different).
|
Answer: 7
## Examples of answer notation:
12
#
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $A B D E, B C E F, C D F A$ - cyclic quadrilaterals with the intersection points of the diagonals $K, L$ and $M$ respectively. It is known that point $K$ lies on segments $B L$ and $A M$, point $M$ - on segment $C L$. Moreover, $E L=F L=K L=5, D M=4, A K=M K=6$. Find the length of segment $M C$. If there are multiple possible answers, list them in any order separated by a semicolon.
|
Answer: 4
## Examples of how to write answers:
$1 / 4$
0.25
$4 ; 10$
#
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (2 points)
What is the maximum number of different reduced quadratic equations that can be written on the board, given that any two of them have a common root, but no four have a root common to all.
|
Answer: 3
Solution:
Consider three such equations. There are two cases:
1) These equations have a common root $a$. Then they can be represented in the form $(x-a)(x-b)=0, (x-a)(x-c)=0$ and $(x-a)(x-d)=0$, where $b, c$ and $d$ are their remaining roots (they are not equal to each other, otherwise the equations coincide; one of these numbers can coincide with $a$, which is not important).
The fourth equation cannot have the root $a$; then it must have the roots $b, c$ and $d$ simultaneously, which means it is not quadratic.
We get a contradiction.
2) The equations do not have a common root. Then they can be represented as $(x-a)(x-b)=0$, $(x-a)(x-c)=0$ and $(x-b)(x-c)=0$. In this case, the fourth equation can only have one of the roots $a, b$ and $c$, otherwise it coincides with one of the previously described.
If it has a root, for example, $a$, then it cannot have a common root with $(x-$ $b)(x-c)=0$. Again, we get a contradiction.
Therefore, there cannot be more than three different equations.
An example can easily be constructed for the first case by taking arbitrary numbers $a, b, c, d$.
#
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (2 points)
What is the maximum number of different reduced quadratic equations that can be written on the board, given that any two of them have a common root, but no five have a root common to all.
|
Answer: 4
## Solution:
Consider 4 such equations. There are two cases:
1) These equations have a common root $a$. Then they can be represented in the form $(x-a)(x-b)=0,(x-a)(x-c)=0,(x-a)(x-d)=0$ and $(x-a)(x-e)=0$, where $b, c, d$ and $e$ are their remaining roots (they are not equal to each other, otherwise the equations coincide; one of these numbers can coincide with $a$, which is not important).
The fifth equation cannot have the root $a$; then it must have the roots $b, c, d$ and $e$ simultaneously, which means it is not quadratic. This leads to a contradiction.
2) The equations do not have a common root. Then three of them can be represented as $(x-$ $a)(x-b)=0,(x-a)(x-c)=0$ and $(x-b)(x-c)=0$. In this case, the fourth equation can only have one of the roots $a, b$ and $c$, otherwise it coincides with one of the previously described equations.
If it has a root, for example, $a$, then it cannot have a common root with $(x-$ b) $(x-c)=0$. Again, we get a contradiction. Therefore, in this case, there cannot be more than three different equations.
An example can easily be constructed for the first case by taking arbitrary numbers $a, b, c, d$ and $e$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many pairs of natural numbers exist for which the number 189 is the LCM? (The numbers in the pair can be the same, the order of the numbers in the pair does not matter)
|
Answer: 11
Only digits are allowed as input
#
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
$A B C$ is an equilateral triangle with a side length of 10. On side $A B$, a point $D$ is taken; on side $A C$, a point $E$ is taken; on side $B C$, points $F$ and $G$ are taken such that triangles $A D E$, $B D G$, and $C E F$ are also equilateral. $A D=3$. Find $F G$.
|
# Answer: 4
## Solution:
$B D=A B-A D=10-3=7$, so all sides of triangle $B D G$ are equal to 7.
$C E=A C-A E=A C-A D=10-3=7$, so all sides of triangle $C E F$ are also equal to 7.
Thus, $B G+C F=14$. This is greater than the length of segment $B C=10$, so $G F=14-10=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. (3 points)
Alice the Fox thought of a two-digit number and told Pinocchio that this number is divisible by $2, 3, 4, 5$, and $6$. However, Pinocchio found out that exactly two of these five statements are actually false. What numbers could Alice the Fox have thought of? In your answer, indicate the number of possible variants.
|
# Answer: 8
## Solution:
If a number is not divisible by 2, then it is not divisible by 4 or 6 either, and we already have three false statements. Therefore, the number must be divisible by 2. If an even number is divisible by 3, it is also divisible by 6, which means the statements about divisibility by 4 and 5 are false. If the number is not divisible by 3, it is not divisible by 6, and the statements about divisibility by 4 and 5 should be true instead.
In the first case, we get numbers that are divisible by 6 but not by 4 or 5. There are exactly five such two-digit numbers: 18, 42, 54, 66, and 78. In the second case, we get numbers that are divisible by 20 but not by 3. There are three such numbers: 20, 40, and 80. In total, we have 8 numbers.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The gnomes dug a system of tunnels that formed a rectangular grid 7 by 2. The main entrance is located at the bottom-left vertex $(0,0)$, and the main exit is at the top-right vertex $(7,2)$. The tunnels are numbered as follows: the tunnel connecting vertices $(x, k)$ and $(x+1, k)$ has a number equal to $7 k + x + 1$, and the tunnel connecting vertices $(m, y)$ and $(m, y+1)$ has a number equal to $21 + 8 y + m + 1$. A collapse occurred, as a result of which all tunnels with numbers that are prime numbers became non-functional. In how many ways can one now travel from the main entrance to the main exit, passing through each tunnel no more than once?
|
Answer: 8
Only digits are allowed as input
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
On the side $B C$ of triangle $A B C$, points $A_{1}$ and $A_{2}$ are marked such that $B A_{1}=6, A_{1} A_{2}=8$, $C A_{2}=4$. On the side $A C$, points $B_{1}$ and $B_{2}$ are marked such that $A B_{1}=9, C B_{2}=6$. Segments $A A_{1}$ and $B B_{1}$ intersect at point $K$, and $A A_{2}$ and $B B_{2}$ intersect at point $L$. Points $K, L$ and $C$ lie on the same line. Find $B_{1} B_{2}$.
|
# Answer: 12
## Solution:
Let $M$ be the point of intersection of line $KL$ and side $AB$. We write two Ceva's theorems, for point $K$ and for point $L$:
$$
\frac{AM}{MB} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A}=1 ; \quad \frac{AM}{MB} \cdot \frac{BA_2}{A_2C} \cdot \frac{CB_2}{B_2A}=1
$$
From this, we get $\frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A}=\frac{BA_2}{A_2C} \cdot \frac{CB_2}{B_2A}$. Four segments in this equality are known to us. $A_1C = A_2C \pm A_1A_2 = A_2C + A_1A_2$, since $A_1A_2 > A_2C$. Similarly, $BA_2 = BA_1 + A_1A_2$. For the other two segments, $AB_2 = AB_1 \pm B_1B_2$ and $CB_1 = CB_2 \pm B_1B_2$ (the signs $\pm$ are the same). Substituting, we get
$$
\begin{gathered}
\frac{BA_1}{A_2C + A_1A_2} \cdot \frac{CB_2 \pm B_1B_2}{B_1A} = \frac{BA_1 + A_1A_2}{A_2C} \cdot \frac{CB_2}{AB_1 \pm B_1B_2} \\
(CB_2 \pm B_1B_2)(AB_1 \pm B_1B_2) = \frac{(BA_1 + A_1A_2)CB_2(A_2C + A_1A_2)B_1A}{A_2C \cdot BA_1} \\
(6 \pm B_1B_2)(9 \pm B_1B_2) = \frac{14 \cdot 6 \cdot 12 \cdot 9}{4 \cdot 6} = 378
\end{gathered}
$$
Since $378 > 6 \cdot 9$, the signs $\pm$ are resolved as +, and we get the quadratic equation $B_1B_2^2 + 15B_1B_2 - 324 = 0$. This equation has roots 12 and -27, of which we are interested in the positive one.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (3 points)
$4^{27000}-82$ is divisible by $3^n$. What is the greatest natural value that $n$ can take?
|
Answer: 5
Solution:
$4^{27000}=(1+3)^{27000}=1+27000 \cdot 3+\frac{27000 \cdot 26999 \cdot 3^{2}}{2}+\frac{27000 \cdot \ldots \cdot 26998 \cdot 3^{3}}{6}+$
$+\frac{27000 \cdot \ldots \cdot 26997 \cdot 3^{4}}{24}+\frac{27000 \cdot \ldots \cdot 26996 \cdot 3^{5}}{120} \ldots$
The last two terms listed are divisible by $3^{6}$, as are all other terms included in the ellipsis.
$$
1+27000 \cdot 3+\frac{27000 \cdot 26999 \cdot 3^{2}}{2}+\frac{27000 \cdot 26999 \cdot 26998 \cdot 3^{3}}{6}=1+81000+
$$
$$
+\frac{27000 \cdot 26999 \cdot 3^{2}+27000 \cdot 26999 \cdot 26998 \cdot 3^{2}}{2}
$$
$1+81000=1+81(1+999)=1+81+81 \cdot 999=1+82+81 \cdot 999$, which gives a remainder of 82 when divided by $3^{6}$, since the last term is divisible by $3^{6}$.
$\frac{27000 \cdot 26999 \cdot 3^{2}+27000 \cdot 26999 \cdot 26998 \cdot 3^{2}}{2}=\frac{27000 \cdot 26999 \cdot 3^{2} \cdot(1+26998)}{2}$, and this number is clearly divisible by $3^{5}$, but not by $3^{6}$. Therefore, $4^{27000}-82$ is also divisible by $3^{5}$, but not by $3^{6}$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
Positive numbers $x, y$, and $z$ are such that $x+y+z=5$. What is the smallest value that the quantity $x^{2}+y^{2}+2 z^{2}-x^{2} y^{2} z$ can take?
|
# Answer: -6
## Solution:
Rewrite the condition as $\frac{x}{2}+\frac{x}{2}+\frac{y}{2}+\frac{y}{2}+z=5$ and write the inequality for the arithmetic mean and the quadratic mean of these five numbers:
$$
1=\frac{\frac{x}{2}+\frac{x}{2}+\frac{y}{2}+\frac{y}{2}+z}{5} \leqslant \sqrt{\frac{\frac{x^{2}}{4}+\frac{x^{2}}{4}+\frac{y^{2}}{4}+\frac{y^{2}}{4}+z^{2}}{5}}=\sqrt{\frac{x^{2}+y^{2}+2 z^{2}}{10}}
$$
from which $x^{2}+y^{2}+2 z^{2} \geqslant 10$. Now write the inequality for the arithmetic mean and the geometric mean of these same numbers:
$$
1=\frac{\frac{x}{2}+\frac{x}{2}+\frac{y}{2}+\frac{y}{2}+z}{5} \geqslant \sqrt[5]{\frac{x}{2} \cdot \frac{x}{2} \cdot \frac{y}{2} \cdot \frac{y}{2} \cdot z}
$$
from which $x^{2} y^{2} z \leqslant 16$. Therefore, $x^{2}+y^{2}+2 z^{2}-x^{2} y^{2} z \geqslant 10-16=-6$. The minimum is achieved when all numbers for which the inequalities of means are applied are equal, that is, $x=y=2$, $z=1$.
#
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) On a $3 \times 3$ chessboard, there are knights, who always tell the truth, and liars, who always lie. Each of them said: "Among my neighbors, there are exactly three liars." How many liars are on the board?
Neighbors are considered to be people on cells that share a common side.
|
Answer: 5.
Solution: The people in the corner cells are obviously liars: they simply do not have three neighbors.
If the person in the center is a knight, then all the people in the side cells are also liars. But in this case, the knight has 4 liar neighbors, not three. This leads to a contradiction.
If the person in the center is a liar, then the people in the side cells each have three liar neighbors, so they are knights. Now we check that the person in the center is indeed a liar: they do not have three liar neighbors.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) On a $2 \times 4$ chessboard, there are knights, who always tell the truth, and liars, who always lie. Each of them said: "Among my neighbors, there are exactly three liars." How many liars are on the board?
Neighbors are considered to be people on cells that share a common side.
|
Answer: 6.
Solution: On the corner cells, liars are obviously standing: they simply do not have three neighbors.
A situation where all people on the board are liars is impossible, as it would mean that four of these liars are telling the truth.
Therefore, there is at least one knight. Then all his neighbors are liars, and we get the following situation (accurate up to symmetry):
| $L$ | $\mathrm{P}$ | $L$ | $L$ |
| :---: | :---: | :---: | :---: |
| $L$ | $L$ | $?$ | $L$ |
The cell marked with a question mark can only be a knight, since all his neighbors are liars. Don't forget to check that the left and upper neighbors of this knight have only two liar neighbors, meaning they are indeed lying.
Thus, we end up with 6 liars.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given the function $f(x)=\frac{\sqrt{3} x-1}{x+\sqrt{3}}$. Find $\underbrace{f(f(\ldots(1) \ldots))}_{2013 \text { times }}$.
|
Answer: -1
## Examples of how to write answers:
$1 / 4$
0.25
10
#
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Four spheres of radius $r$ touch each other externally. A sphere of radius $\sqrt{6}+2$ touches all of them internally. Find $r$.
|
Answer: 2
## Examples of how to write answers:
$1 / 4$
0.25
10
#
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is a trapezoid with bases $A D=15$ and $\mathrm{BC}=10$. $O$ is one of the intersection points of the circles constructed on the lateral sides of the trapezoid as diameters, and this point lies inside the trapezoid. Triangle $B C M$ is constructed on side $B C$ on the external side relative to the trapezoid and is similar to triangle $A D O$ (the vertices of the triangles are listed in the order in which they correspond to each other). Line $O M$ intersects the bases $B C$ and $A D$ at points $K$ and $L$ respectively. It is known that $O K=4, O L=9$. Find the smallest possible value of the length of segment $B K$.
|
Answer: 4
## Examples of answer notations:
$1 / 4$
0.25
10
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In a row without spaces, all natural numbers are written in ascending order: $1234567891011 . .$. What digit stands at the 2017th place in the resulting long number?
|
Answer: 7.
Solution: The first 9 digits are contained in single-digit numbers, the next 180 - in two-digit numbers. $2017-180-9=1828$. Next, $1828: 3=609 \frac{1}{3}$. This means that the 2017-th digit is the first
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Given the cryptarithm: ЖАЛО + ЛОЖА = ОСЕНЬ. Identical letters represent identical digits, different letters represent different digits. Find the value of the letter А.
|
Answer: 8
Solution: The rebus can be rewritten as ОСЕНЬ $=($ ЖА + ЛО $) \cdot 101$. First, this means that the last digit of ЖА + ЛО is Ь. Second, if ЖА + ЛО $<100$, the result will be a four-digit number. Let $Ж А+Л О=1 Х Ь$, where $X$ is some digit.
Then ОСЕНЬ $=1 Х Ь 00+1 Х Ь$. If $\mathrm{b}<9$, then the second and fourth digits of this number should match, but they do not. Therefore, $\mathrm{b}=9$. Consequently, $\mathrm{A}+\mathrm{O}=9$. But О is 1, so А is 8.
There are many examples, for instance, $7861+6178=14039$.
7. (4 points) Alice and Bob each have three equal segments. First, Alice breaks one of the segments into two unequal parts. Then, Bob breaks another of the original segments into any two parts. As a result, there are five segments, from which ten sets of three segments can be chosen. Alice wins if at least 4 of these ten sets form a triangle. Otherwise, Bob wins. Who will win if both players play optimally?
Answer: Bob wins.
Solution: Let the original segments have a length of 1, and Alice breaks one of the segments into parts $x$ and $1-x$, with $x<1-x$ for definiteness. Then Bob needs to break another segment into parts $1-y$ and $y$ such that $y$ is very small, specifically, the inequalities $y<x$, $y<(1-x)-x$, and $y<(1-y)-(1-x)$, or $2 y<x$, are satisfied. Clearly, he can choose such a $y$.
Using the triangle inequality: to form a triangle, it is necessary and sufficient that the largest side of the triangle is less than the sum of the other two. With such a choice of $y$, it is not greater than the difference between any two other segments, and therefore cannot form a triangle with any of them. There are exactly 6 sets of three segments that include the segment $y$. Additionally, the remaining segment of length 1 and the segments Alice obtained also do not form a triangle. This is the seventh set of segments that does not form a triangle. Thus, Alice is left with only 3 sets of segments that can form a triangle, and she loses.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In a row without spaces, all natural numbers from 999 to 1 are written in descending order: 999998 ...321. What digit is in the 2710th position of the resulting long number?
|
Answer: 9.
Solution: The first $3 \cdot 900=2700$ digits are contained in three-digit numbers. Therefore, we need to count another 10 digits in two-digit numbers. That is, we need the first digit of the fourth largest two-digit number. This number is 96, so we need the digit 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Given the cryptarithm: RIVER + SQUARE = ABVAD. Identical letters represent identical digits, different letters represent different digits. Find the value of the letter B.
|
Answer: 2
Solution: The rebus can be rewritten as ABVAD $=(\mathrm{KA}+\mathrm{PE}) \cdot 101$. First, this means that the last digit of $\mathrm{KA}+\mathrm{PE}$ is D. Second, if $\mathrm{KA}+\mathrm{PE}<100$, the result will be a four-digit number. Let $\mathrm{KA}+\mathrm{PE}=1X$D, where $X$ is some digit.
Then ABVAD $=1X$D$00+1X$D. If D $<9$, then the second and fourth digits of this number should match, but they do not. Therefore, D $=9$ and the second digit of the number ABVAD is one more than the fourth. But A is 1, so B is 2.
There are many examples, for instance, $5861+6158=12019$.
7. (4 points) Alice and Bob have three equal segments. First, Alice breaks one of the segments into two parts. Then, Bob breaks another of the original segments into two arbitrary parts. As a result, five segments are obtained, from which ten ways to choose three segments are possible. Alice wins if at least 4 of these ten ways give triples of segments that form a triangle. Otherwise, Bob wins. Who will win with correct play by both opponents?
Answer: Alice wins.
Solution: We use the triangle inequality: to form a triangle, it is necessary and sufficient that the largest side of the triangle is less than the sum of the other two.
Let the original segments have a length of 1. Alice breaks one of the segments into two equal parts. Let Bob break his segment into parts of length $x$ and $1-x$, and for definiteness, let $x<1-x$. $1-x<\frac{1}{2}+\frac{1}{2}$, so this triple forms a triangle. Also, the triple formed by Alice's segments and Bob's smaller segment forms a triangle. Two more suitable triples are obtained when we take the segments $1,1-x$ and $\frac{1}{2}$.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (3 points)
Natural numbers $x, y, z$ are such that $\operatorname{GCD}(\operatorname{LCM}(x, y), z) \cdot \operatorname{LCM}(\operatorname{GCD}(x, y), z)=1400$.
What is the greatest value that $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$ can take?
#
|
# Answer: 10
## Solution:
Notice that $\operatorname{LCM}(\operatorname{GCD}(x, y), z)$ is divisible by $z$, and $z$ is divisible by $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$, so $\operatorname{LCM}(\operatorname{GCD}(x, y), z)$ is divisible by $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$.
$1400=2^{3} \cdot 5^{2} \cdot 7$ and in the second factor, each prime number appears with an exponent no less than in the first. Therefore, the maximum possible value of $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$ is $2 \cdot 5=10$. This value is achieved when $x=y=10, z=140$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. (3 points)
Let $f(x)$ be a quadratic trinomial with integer coefficients. Given that $f(\sqrt{3}) - f(\sqrt{2}) = 4$. Find $f(\sqrt{10}) - f(\sqrt{7})$.
|
# Answer: 12
## Solution:
Let $f(x)=c x^{2}+d x+e$. Then $f(\sqrt{3})-f(\sqrt{2})=3 c+\sqrt{3} d+e-(2 c+\sqrt{2} d+e)=c+d(\sqrt{3}-\sqrt{2})$. This number can only be an integer if $d=0$. Therefore, $f(x)=c x^{2}+e$ and $f(\sqrt{3})-f(\sqrt{2})=c$.
Then $f(\sqrt{10})-f(\sqrt{7})=10 c+e-(7 c+e)=3 c=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (3 points)
Positive numbers $x, y, z$ are such that $x y + y z + x z = 12$.
Find the smallest possible value of $x + y + z$.
#
|
# Answer: 6
## Solution:
By adding the inequalities $x^{2}+y^{2} \geqslant 2 x y, x^{2}+z^{2} \geqslant 2 x z$ and $y^{2}+z^{2} \geqslant 2 y z$ and dividing by 2, we get $x^{2}+y^{2}+z^{2} \geqslant x y+y z+x z$.
$(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z) \geqslant 3(x y+y z+x z)=36$, from which $x+y+z \geqslant 6$. Equality is achieved when $x=y=z=2$.
#
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (3 points)
From point $K$ on side $A C$ of triangle $A B C$, perpendiculars $K L_{1}$ and $K M_{1}$ were dropped to sides $A B$ and $B C$ respectively. From point $L_{1}$, a perpendicular $L_{1} L_{2}$ was dropped to $B C$, and from point $M_{1}$, a perpendicular $M_{1} M_{2}$ was dropped to $A B$.
It turned out that triangles $B L_{1} M_{1}$ and $B L_{2} M_{2}$ are similar (point $L_{1}$ in the first triangle corresponds to point $M_{2}$ in the second). In addition, $B L_{2}=6$ and $L_{2} M_{1}=4$. Find $L_{1} L_{2}$.
|
# Answer: 8
## Solution:
Notice that the quadrilateral $L_{1} M_{2} L_{2} M_{1}$ is cyclic, since $\angle L_{1} M_{2} M_{1}=\angle L_{1} L_{2} M_{1}=$ $90^{\circ}$. Therefore, $\angle B M_{2} L_{2}=180^{\circ}-\angle L_{1} M_{2} L_{2}=\angle L_{2} M_{1} L_{1}=\angle B M_{1} L_{1}$. Similarly, $\angle B L_{2} M_{2}=\angle B L_{1} M_{1}$, so triangles $B L_{1} M_{1}$ and $B L_{2} M_{2}$ are similar, with point $L_{1}$ in the first triangle corresponding to point $L_{2}$ in the second. However, the problem states that they are similar in another way, which means these two triangles are isosceles. From this, we get $B L_{1}=B M_{1}=B L_{2}+L_{2} M_{1}$ and, by the Pythagorean theorem, we find $L_{1} L_{2}=\sqrt{B L_{1}^{2}-B L_{2}^{2}}=\sqrt{\left(B L_{2}+L_{2} M_{1}\right)^{2}-B L_{2}^{2}}$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
The graphs of the quadratic trinomials $f(x)$ and $g(x)$ intersect at the point $(3 ; 8)$. The trinomial $f(x)+g(x)$ has a single root at 5. Find the leading coefficient of the trinomial $f(x)+g(x)$.
#
|
# Answer: 4
## Solution:
Since the quadratic polynomial $f(x)+g(x)$ has a unique root 5, it can be represented as $a(x-5)^{2}$, where $a$ is precisely the leading coefficient we are looking for. Additionally, the value of this quadratic polynomial at the point 3 is equal to the sum of the values of the polynomials $f(x)$ and $g(x)$, which is 16.
Thus, $a \cdot(-2)^{2}=16$, from which we get $a=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (3 points)
It is known that $a^{2} b+a^{2} c+b^{2} a+b^{2} c+c^{2} a+c^{2} b+3 a b c=30$ and $a^{2}+b^{2}+c^{2}=13$.
Find $a+b+c$.
|
Answer: 5
## Solution:
$(a+b+c)^{3}-(a+b+c)\left(a^{2}+b^{2}+c^{2}\right)=2\left(a^{2} b+a^{2} c+b^{2} a+b^{2} c+c^{2} a+c^{2} b+3 a b c\right)$. Let $a+b+c$ be $x$, substitute the known values of the expressions from the condition, and we get the equation $x^{3}-13 x-60=0$.
It is not hard to notice that the number 5 is a root of this equation. Dividing $x^{3}-13 x-60$ by $x-5$, we get $x^{2}+5 x+12$. This quadratic has no roots, so 5 is the only possible answer.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
Circles $O_{1}$ and $O_{2}$ touch circle $O_{3}$ with radius 13 at points $A$ and $B$ respectively and pass through its center $O$. These circles intersect again at point $C$. It is known that $O C=12$. Find $A B$.
|
# Answer: 10
## Solution:
Since circles $O_{1}$ and $O_{2}$ touch circle $O_{3}$ at points $A$ and $B$ respectively and pass through its center $O$, $AO$ and $BO$ are their diameters. Therefore, angles $\angle OCA$ and $\angle OCB$ are right angles. These cannot be the same angle, as this would mean that circles $O_{1}$ and $O_{2}$ coincide, so they are adjacent angles. Right triangles $OCA$ and $OCB$ are equal by the leg $OC$ and hypotenuses. Therefore, $AB = 2AC = 2\sqrt{OA^2 - OC^2} = 2\sqrt{13^2 - 12^2} = 10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
32 volleyball teams participate in a tournament according to the following scheme. In each round, all remaining teams are randomly paired; if the number of teams is odd, one team skips this round. In each pair, one team wins and the other loses, as there are no draws in volleyball. After three losses, a team is eliminated from the tournament. When all teams except one are eliminated, this team is declared the winner and the tournament ends.
What is the minimum number of rounds the tournament can last?
|
# Solution:
For all teams to be eliminated except one, they must suffer at least 93 losses, meaning at least 93 matches must be played.
We also note that after each round, the number of teams decreases by at most half, because no more than half of the teams lose. In particular, in the final round, only 2 teams could have participated, and they played one match. In the penultimate round, a maximum of 4 teams participated and played a maximum of 2 matches. One round before that, a maximum of 4 matches were played, and another round before that, a maximum of 8. In total, in the last 4 rounds, no more than 15 matches were played.
This means that at least 78 matches were played before that. In each of the remaining rounds, no more than 16 matches were played, so there were at least 5 such rounds. In total, we get at least $4+5=9$ rounds.
The teams could manage in 9 rounds. Indeed, in the first 4 rounds, the teams could pair up, and in each pair, they could inflict 2 losses on each other. After this, each team has one loss left, and we get a standard Olympic system of 5 rounds, in each of which half of the teams are eliminated.
Answer: 9
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (2 points)
In a class, each student has either 5 or 6 friends (friendship is mutual), and any two friends have a different number of friends in the class. What is the smallest number of students, greater than 0, that can be in the class?
|
Answer: 11
## Solution:
Let's look at some person. Suppose he has five friends. Then each of these five people has six friends. Similarly, there are at least another 6 people with five friends each. In total, there are 11 people.
It is quite easy to construct an example: two groups of 5 and 6 people, people from different groups are friends with each other, but not within the same group.
#
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (2 points)
In a positive non-constant geometric progression, the arithmetic mean of the second, seventh, and ninth terms is equal to some term of this progression. What is the minimum possible number of this term?
|
Answer: 3
Solution:
The second element is either the larger or the smaller of the three specified, so it cannot be equal to the arithmetic mean of all three. The first element is even less suitable.
To prove that the answer "3" is possible, let's introduce the notation: let $b_{n}=$ $b q^{n-1}$. Then we need to solve the equation $3 b q^{2}=b q+b q^{6}+b q^{8}$. Simplifying it, we get $q^{7}+q^{5}-$ $3 q+1=0$.
This equation has a root $q=1$, but it does not suit us because the progression is not constant. $q^{7}+q^{5}-3 q+1=(q-1)\left(q^{6}+q^{5}+2 q^{4}+2 q^{3}+q^{2}+2 q-1\right)$. The second factor is negative at $q=0$ and positive at $q=1$, so this expression has a root between zero and one. Thus, we can choose the common ratio of the progression and take any positive number as the first term for the answer 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
In a class, each student has either 5 or 7 friends (friendship is mutual), and any two friends have a different number of friends in the class. What is the smallest number of students, greater than 0, that can be in the class?
Answer: 12
|
Solution:
Let's look at some person. Suppose he has five friends. Then each of these five people has seven friends. Similarly, there are at least seven more people with five friends each. In total, there are 12 people.
It is quite easy to construct an example: two groups of 5 and 7 people, people from different groups are friends with each other, but not within the same group.
#
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (2 points)
In a positive non-constant geometric progression, the arithmetic mean of the third, fourth, and eighth terms is equal to some term of this progression. What is the minimum possible number of this term?
|
Answer: 4
Solution:
The third element is either the larger or the smaller of the three specified, so it cannot be equal to the arithmetic mean of all three. The first and second elements are even less suitable.
To prove that the answer "4" is possible, let's introduce the notation: let $b_{n}=$ $b q^{n-1}$. Then we need to solve the equation $3 b q^{3}=b q^{2}+b q^{3}+b q^{7}$. Simplifying it, we get $q^{5}-$ $2 q+1=0$.
This equation has a root $q=1$, but it does not suit us because the progression is not constant. $q^{5}-2 q+1=(q-1)\left(q^{4}+q^{3}+q^{2}+q-1\right)$. The second factor is negative at $q=0$ and positive at $q=1$, so this expression has a root between zero and one. Thus, we can choose the common ratio of the progression and take any positive number as the first term for the answer 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is a trapezoid with bases $\mathrm{AD}=6$ and $\mathrm{BC}=10$. It turns out that the midpoints of all four sides of the trapezoid lie on the same circle. Find its radius.
If there are multiple correct answers, list them in any order separated by a semicolon.
|
Answer: 4.
## Examples of answer notation:
45
$4 ; 5$
#
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Three consecutive terms of a geometric progression with a common ratio $q$ were used as coefficients of a quadratic trinomial, with the middle term being the leading coefficient. For what largest integer $q$ will the resulting trinomial have two distinct roots regardless of how the other two coefficients are arranged?
|
Answer: -1
## Examples of answer notation:
2
5;9
#
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) On the Island of Misfortune, there live knights, who always tell the truth, and liars, who always lie. One day, $n$ islanders gathered in a room. $\quad 30$
The first one said: "Exactly every first person present in this room is a liar."
The second one said: "Exactly every second person present in this room is a liar." and so on
The person with number $n$ said: "Exactly every $n$-th person present in this room is a liar." How many people could have been in the room?
|
# Answer: 2
## Solution:
Let's note that among these people, there is definitely one knight, otherwise it would mean that the first islander is a liar telling the truth, which is impossible. Moreover, the first person is definitely a liar.
Furthermore, there is exactly one knight, since all the speakers contradict each other. This means there are no more than half knights. On the other hand, all the islanders claim that there are no fewer than half knights. Therefore, there are exactly half, i.e., there are two people in the room.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) On the Island of Misfortune, there live knights who always tell the truth, and liars who always lie. One day, $n$ islanders gathered in a room.
The first one said: "Exactly every second person in this room is a liar."
The second one said: "Exactly every third person in this room is a liar."
and so on
The person with number $n$ said: "Exactly every ( $n_{33} 1$ )-th person in this room is a liar."
How many people could have been in the room, given that not all of them are liars?
|
# Answer: 2
Solution:
According to the condition, there is at least one knight among these people. Therefore, there must be at least two people, otherwise the first person would be a knight who is lying.
Moreover, there is exactly one knight, as all the speakers contradict each other. Thus, there cannot be more than half knights. On the other hand, all the islanders, including the knight who tells the truth, claim that there are at least half knights. Therefore, there must be exactly half, i.e., there are two people in the room.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) At a knight's tournament, each knight gave each of his acquainted ladies as many flowers as she had acquainted knights, except for him. After this, every two knights arranged as many duels as they had common acquainted ladies. What was more: the given flowers or the arranged duels, and by how many times?
Answer: Flowers were more by two times.
|
Solution: For each trio consisting of a lady and two of her acquainted knights, one duel will take place. Regarding the flowers, the first knight will give the lady one flower for introducing him to the second, and the second will give one for being introduced to the first, making a total of two flowers.
## Grade 9 2nd variant
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) With the number written on the board, one of the following operations is allowed:
1) If there is a digit in the original number that is not 9 and has two neighboring digits greater than 0, you can increase this digit by 1, and decrease the neighboring digits by 1.
2) Subtract 1 from any non-zero digit except the last one, and add 3 to the next digit.
3) Decrease any sufficiently large digit by 7.
If, as a result of any of these operations, there are zeros in the leading positions of the number, they are automatically discarded.
Initially, the number on the board was a hundred eights. In the end, a single-digit number remained. Which one exactly?
|
Answer: 3
Solution:
The first operation corresponds to subtracting a number of the form $910 \cdot 0$, the second and third - subtracting $70 \cdot 0$. Both these operations do not change the remainder of the original number when divided by 7, since 91 is divisible by 7.
$1001=c d o t 91$, and $888888=888 \cdot 1001$. Therefore, to find the remainder of the original number when divided by 7, the number of eights that are multiples of 6 can be discarded. The remaining number is $8888=8008+875+5=8 \cdot 1001+7 \cdot 125+5$ which gives a remainder of 5.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) With the number written on the board, one of the following operations is allowed:
1) If there is a digit in the original number that is not equal to 9 and has two neighboring digits greater than 0, you can increase this digit by 1, and decrease the neighboring digits by 1.
2) Subtract 1 from any non-zero digit except the last one, and add 3 to the next digit.
3) Decrease any sufficiently large digit by 7.
If, as a result of any of these operations, there are zeros in the number on one or more of the leading positions, they are automatically discarded.
Initially, the number consisting of one hundred nines was written on the board. In the end, a single-digit number remained. Which one exactly?
|
# Answer: 3
Solution:
The first operation corresponds to subtracting a number of the form $910 \cdot 0$, the second and third - subtracting $70 \cdot 0$. Both these operations do not change the remainder of the original number when divided by 7, since 91 is divisible by 7.
$1001 = 91 \cdot 11$, and $999999 = 999 \cdot 1001$. Therefore, to find the remainder of the original number when divided by 7, the number of nines that are multiples of 6 can be discarded. The remaining number is $9999 = 9009 + 987 + 3 = 9 \cdot 1001 + 7 \cdot 141 + 3$, which gives a remainder of 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) Find what $x+y$ can be equal to, given that $x^{3}-6 x^{2}+15 x=12$ and $y^{3}-6 y^{2}+15 y=16$.
|
Answer: 4.
Solution:
Let $u=x-2$ and $v=y-2$. Then the original equations transform into $u^{3}+3 u=-2$ and $v^{3}+3 v=2$. Adding these equations, we get $(u+v)\left(u^{2}-u v+v^{2}+3\right)=0$. The second bracket is always positive, so the first one must be zero, from which we have $x+y=u+v+4=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) Find what $x+y$ can be equal to, given that $x^{3}+6 x^{2}+16 x=-15$ and $y^{3}+6 y^{2}+16 y=-17$.
|
Answer: -4
Solution: Let $u=x+2$ and $v=y+2$. Then the original equations transform into $u^{3}+4 u=1$ and $v^{3}+4 v=-1$. Adding these equations, we get $(u+v)\left(u^{2}-u v+v^{2}+4\right)=0$. The second bracket is always positive, so the first one must be zero, from which we have $x+y=u+v-4=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $O$ is the center of a certain circle, $A$ is a point outside the circle, $B$ is a point on the circle such that $AB$ is a tangent. $AO=6$. Find the greatest possible value of the area of triangle $AOB$.
|
Answer: 9.
## Examples of answer notations:
17
$1 / 7$
1.7
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Circle $S_{1}$ intersects circle $S_{2}$ at points $A$ and $B$ and is tangent to circle $S_{3}$ at point $Z$. The common tangent of circles $S_{1}$ and $S_{3}$ intersects line $A B$ at point $C$. Also, through $C$ passes line $X Y$, which is tangent to circle $S_{2}$ at point $X$ and to circle $S_{3}$ at point $Y$.
It is known that $A B=7, B C=5, X Z=4 \sqrt{6}$. Find $Y Z$.
It is assumed that points denoted by different letters do not coincide. If there are multiple possible answers, write them in any order separated by a semicolon.
|
Answer: 12
Allowed for input are digits, a period or comma, a division sign, a semicolon
#
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a rectangle $\mathrm{ABCD}$. The length of side $\mathrm{BC}$ is one and a half times less than the length of side $\mathrm{AB}$. Point $\mathrm{K}$ is the midpoint of side AD. Point $\mathrm{L}$ on side $\mathrm{CD}$ is such that $\mathrm{CL}=\mathrm{AK}$. Point $\mathrm{M}$ is the intersection of line BL and the perpendicular bisector of segment DL. It is known that $\mathrm{KL}=4$. Find the length of segment BM.
(A rectangle is a figure such that its opposite sides are equal, and the angles are each $90^{\circ}$. )
|
Answer: 8
## Examples of answer recording:
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The function $f(x)$ is such that $f(x+1)+f(x-1)=5.2 f(x)$. It is known that $f(0)=-98$, and $\mathrm{f}(3)=249.2$. Find $f(1)$.
|
Answer: -10
## Examples of how to write answers:
17
$-1.7$
$1 / 7$
#
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Prove that for $n=6002$ the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}-$ the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in all other cases.
|
# Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are discarded).
Let's denote this sum as $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 1998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{1999} S_{2}=4^{999} \cdot 2 C_{2}^{1}=4^{1000}$, which gives a remainder of 1 when divided by 3.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Prove that for $n=9002$ the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}-$ the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in all other cases.
|
Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are discarded).
Let's denote this sum as $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 2998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{2999} S_{2}=4^{1499} \cdot 2 C_{2}^{1}=4^{1500}$, which gives a remainder of 1 when divided by 3.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Prove that for $n=12002$ the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}-$ the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in all other cases.
|
# Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are discarded).
Let's denote this sum as $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 3998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{3999} S_{2}=4^{1999} \cdot 2 C_{2}^{1}=4^{2000}$, which gives a remainder of 1 when divided by 3.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. A grid rectangle $4 \times 11$ is divided into $2 \times 2$ squares and strips of three cells. What is the maximum number of strips that can participate in this division?
|
Answer: 12
## Examples of answer notation:
100
90
#
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $O$ is the center of a certain circle, $A$ is a point outside the circle, $B$ is a point on the circle such that $AB$ is a tangent. $AO=6$. Find the greatest possible value of the area of triangle $AOB$.
|
Answer: 9.
## Examples of answer notations:
17
$1 / 7$
1.7
#
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the number $\sqrt{3}+\sqrt{5}$ is a root of a polynomial of the fourth degree with integer coefficients, the leading coefficient of which is 1. What is the sum of the coefficients of this polynomial?
|
Answer: -11
2. It is known that the number $\sqrt{3}+\sqrt{7}$ is a root of a polynomial of the fourth degree with integer coefficients, the leading coefficient of which is 1. What is the sum of the coefficients of this polynomial?
Answer: -3
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that the function $f(x)$ satisfies the equality for any $x$:
$3 \sin x+f(x)=f(x+2)$
Find the value of $\mathrm{f}(2017) \sin 1$, given that $f(1)=\frac{3 \cos ^{2} 1008}{\sin 1}$.
|
Answer: 3
## Examples of answer notations:
17
$1 / 7$
1.7
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) In space, there is a cube $1000 \times 1000 \times 1000$ with a vertex at the origin and faces parallel to the coordinate planes. Vectors are drawn from the origin to all integer points inside and on the boundary of this cube. Find the remainder when the sum of the squares of the lengths of these vectors is divided by 13.
#
|
# Answer: 0
Solution:
The sum of the squares of the lengths of these vectors is the sum of the squares of all their coordinates, that is, $3 \cdot 1001^{2} \cdot\left(0^{2}+1^{2}+\right.$ $2^{2}+\ldots+1000^{2}$ ), which is divisible by 13, since 1001 is divisible by 13.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) In space, there is a cube $1000 \times 1000 \times 1000$ with a vertex at the origin and faces parallel to the coordinate planes. Vectors are drawn from the origin to all integer points inside and on the boundary of this cube. Find the remainder when the sum of the squares of the lengths of these vectors is divided by 11.
#
|
# Answer: 0
## Solution:
The sum of the squares of the lengths of these vectors is the sum of the squares of all their coordinates, that is, $3 \cdot 1001^{2} \cdot\left(0^{2}+1^{2}+\right.$ $\left.2^{2}+\ldots+1000^{2}\right)$, which is divisible by 11, since 1001 is divisible by 11.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Let $x, y, z$ and $t$ be non-negative numbers such that $x+y+z+t=5$. Prove the inequality
$$
\sqrt{x^{2}+y^{2}}+\sqrt{x^{2}+1}+\sqrt{z^{2}+y^{2}}+\sqrt{z^{2}+t^{2}}+\sqrt{t^{2}+9} \geqslant 10
$$
|
# Solution:
Consider the following points on the plane: $A(0,0) ; B(x, 1) ; C(x+y, 1+x) ; D(x+y+z, 1+$ $x+y) ; E(x+y+z+t, 1+x+y+z) ; F(x+y+z+t+3,1+x+y+z+t)$. Then the length of the broken line $A B C D E F$ coincides with the expression that needs to be evaluated. By the triangle inequality, the length of the broken line $A B C D E F$ is not less than the length of the segment $A F$. Given that $x+y+z+t=5$, the coordinates of point $F$ are $(8,6)$ and the length of segment $A F=10$.
|
10
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Let $x, y, z$ and $t$ be non-negative numbers such that $x+y+z+t=2$. Prove the inequality
$$
\sqrt{x^{2}+z^{2}}+\sqrt{x^{2}+1}+\sqrt{z^{2}+y^{2}}+\sqrt{y^{2}+t^{2}}+\sqrt{t^{2}+4} \geqslant 5
$$
|
Solution:
Consider the following points on the plane: $A(0,0) ; B(x, z) ; C(x+1, z+x) ; D(x+1+z, z+x+y) ; E(x+1+z+y, z+x+y+t) ; F(x+1+z+y+t, z+x+y+t+2)$. Then the length of the broken line $A B C D E F$ coincides with the expression that needs to be evaluated. By the triangle inequality, the length of the broken line $A B C D E F$ is not less than the length of the segment $A F$. Given that $x+y+z+t=2$, the coordinates of point $F$ are $(3,4)$ and the length of segment $A F=5$.
|
5
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Boys were collecting apples. Each collected either 10 apples or $10\%$ of the total number of apples collected, and there were both types. What is the smallest number of boys there could have been?
|
# Answer: 6
Solution: Example: one boy collected 10 apples, the rest collected 2 each, totaling 20.
Evaluation: Let's prove that there could not have been fewer boys. We know that $10\%$ of the total number of apples is an integer, let's denote it as $k$. Suppose $n$ people collected ten apples each, and $m$ people collected $10\%$ each, then $10n = (10-m)k$, which means $10n$ is divisible by $10-m$. When $m=1$ or $m=3$, we get that $10n$ is divisible by 9 or 7, respectively, meaning $n$ is divisible by 9 or 7, which is too large. When $m=2$ or $m=4$, we get that $10n$ is divisible by 8 or 6, respectively, meaning $n$ is divisible by 4 or 3, and $m+n \geqslant 6$. When $m \geqslant 5$, the total number of boys is at least 1 more, meaning, again, at least 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Solve the system of equations: $\left\{\begin{array}{l}x y=6(x+y) \\ x z=4(x+z) \\ y z=2(y+z)\end{array}\right.$
|
Answer: $x=y=z=0$ or $x=-24, y=\frac{24}{5}, y=\frac{24}{7}$
Solution: It is easy to verify that if one of the variables is 0, then the others are also 0. Otherwise, the system can be transformed into
$\left\{\begin{array}{l}\frac{1}{6}=\frac{1}{x}+\frac{1}{y} \\ \frac{1}{4}=\frac{1}{x}+\frac{1}{z} \\ \frac{1}{2}=\frac{1}{z}+\frac{1}{y}\end{array}\right.$
By adding the first two equations and subtracting the last one, we get $\frac{1}{6}+\frac{1}{4}-\frac{1}{2}=\frac{2}{x}$, from which $-\frac{1}{12}=\frac{2}{x}$, that is, $x=-24$. Similarly, we find the other unknowns.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two quadratic trinomials have a common root -3, and for one of them, it is the larger root, while for the other, it is the smaller root. The length of the segment cut off by the graphs of these trinomials on the y-axis is 12. Find the length of the segment cut off by the graphs of the trinomials on the x-axis.
|
Answer: 4
Allowed for input are digits, the division sign, and a period or comma as a decimal separator
#
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two racers with speeds of $100 \mathrm{~m} / \mathrm{c}$ and $70 \mathrm{~m} / \mathrm{c}$ started simultaneously in the same direction from the same place on a circular track of length $800 \mathrm{m}$. How many times did the racers meet after the start if both drove for 320 seconds?
|
Answer: 12
## Examples of writing answers:
45
## Problem 4 (2 points).
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Seven dwarfs lined up by height, starting with the tallest. The first (i.e., the tallest) said: "My height is 60 cm." The second said: "My height is 61 cm." In order next: "My height is 62 cm," "My height is 63 cm," "My height is 64 cm," "My height is 65 cm," and finally the shortest said: "My height is 66 cm." What is the maximum number of dwarfs who could have told the truth?
|
1. Answer: 1.
No two dwarfs could tell the truth, because in this case the taller one would name the shorter height. However, one dwarf (any one) could tell the truth.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. Find the largest natural number that cannot be represented as the sum of two composite numbers. (Recall that a natural number is called composite if it is divisible by some natural number other than itself and one.)
|
17. Answer: 11.
All large numbers can be represented in the required way: odd numbers as "9 + an even number greater than two", and even numbers as "8 + an even number greater than two".
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. Grandfather Frost has many identical dials in the form of regular 12-sided polygons, on which numbers from 1 to 12 are printed. He places these dials in a stack on top of each other (one by one, face up). In doing so, the vertices of the dials coincide, but the numbers in the coinciding vertices do not necessarily match. The Christmas tree will light up as soon as the sums of the numbers in all 12 columns have the same remainder when divided by 12. How many dials can be in the stack at this moment?
|
19. Answer: 12.
Let there be $k$ clock faces in the stack. Consider any two adjacent columns. The sum of the numbers in them differs by either $k$ or $k-12s$ (where $s$ is the number of clock faces for which one column has 12 and the next has 1). For $k=1,2, \ldots, 11$, all these differences are not divisible by 12, but for $k=12$ they become divisible by 12.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40.
$$
\frac{x^{2}}{x^{2}+2 y z}+\frac{y^{2}}{y^{2}+2 z x}+\frac{z^{2}}{z^{2}+2 x y} \geqslant 1
$$
|
40. Since $2 x y \leqslant x^{2}+y^{2}$, we get
$$
\begin{aligned}
\frac{x^{2}}{x^{2}+2 y z}+\frac{y^{2}}{y^{2}+2 z x} & +\frac{z^{2}}{z^{2}+2 x y} \geqslant \\
& \geqslant \frac{x^{2}}{x^{2}+y^{2}+z^{2}}+\frac{y^{2}}{x^{2}+y^{2}+z^{2}}+\frac{z^{2}}{x^{2}+y^{2}+z^{2}}=1
\end{aligned}
$$
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
41.
$$
\frac{x^{2}+2 y^{2}+2 z^{2}}{x^{2}+y z}+\frac{y^{2}+2 z^{2}+2 x^{2}}{y^{2}+z x}+\frac{z^{2}+2 x^{2}+2 y^{2}}{z^{2}+x y}>6
$$
|
41. Transform the left side using $2 x y \leqslant x^{2}+y^{2}$, multiplying the numerator and denominator by 2:
$$
\begin{aligned}
& \frac{x^{2}+2 y^{2}+2 z^{2}}{x^{2}+y z}+\frac{y^{2}+2 z^{2}+2 x^{2}}{y^{2}+z x}+\frac{z^{2}+2 x^{2}+2 y^{2}}{z^{2}+x y} \geqslant \\
& \geqslant 2\left(\frac{x^{2}+2 y^{2}+2 z^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{y^{2}+2 z^{2}+2 x^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{z^{2}+2 x^{2}+2 y^{2}}{2 z^{2}+x^{2}+y^{2}}\right) \geqslant \\
& \quad \geqslant 2\left(\frac{x^{2}+y^{2}+2 z^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{y^{2}+z^{2}+2 x^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{z^{2}+x^{2}+2 y^{2}}{2 z^{2}+x^{2}+y^{2}}\right)
\end{aligned}
$$
Now apply the transinequality (for the numerators and the reciprocals of the denominators) to the expression in parentheses:
$$
\begin{aligned}
& 2\left(\frac{x^{2}+y^{2}+2 z^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{y^{2}+z^{2}+2 x^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{z^{2}+x^{2}+2 y^{2}}{2 z^{2}+x^{2}+y^{2}}\right) \geqslant \\
& \quad \geqslant 2\left(\frac{y^{2}+z^{2}+2 x^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{z^{2}+x^{2}+2 y^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{x^{2}+y^{2}+2 z^{2}}{2 z^{2}+x^{2}+y^{2}}\right)=6
\end{aligned}
$$
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
65. What is the smallest degree that a polynomial $P$ can have if it is known that there exists an integer $b$ such that $A_{P}$ contains elements both greater and less than $b$, but does not contain $b$?
|
65. Answer: 4.
For example, consider the polynomial $P(x)=(x-3)(x-1)(x+1)(x+3)$. It is even. Therefore, if $c \neq P(0)$, then $l_{P}(c)$ is even. Therefore, in $A$ there can only be one odd number, namely, $l_{P}(P(0))$. Thus, $b=1$ or $b=3$ is the desired number, since $0,4 \in A_{P}$. Why can't the degree be less? Consider, for example, a cubic polynomial $P$. Since its derivative is a quadratic polynomial, it has no more than two roots, and thus $P$ has no more than three intervals of monotonicity, specifically 1 or 3. Let's consider the most complex case immediately - when $P$ has three intervals of monotonicity. Suppose it has a local minimum $m$ and a local maximum $M$. Then for $x \in(-\infty, m) \cup(M,+\infty)$, $l_{P}(x)=1$, $l_{P}(m)=l_{P}(M)=2$, and for $x \in(m, M)$, $l_{P}(x)=3$. The other cases are even simpler to analyze.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. What is the smallest degree that a polynomial $P$ can have if it is known that there exists an integer $b$ such that $A_{P}$ contains elements both greater and smaller than $b$, but does not contain $b$?
|
65. Answer: 4.
For example, consider the polynomial $P(x)=(x-3)(x-1)(x+1)(x+3)$. It is even. Therefore, if $c \neq P(0)$, then $l_{P}(c)$ is even. Therefore, in $A$ there can only be one odd number, namely, $l_{P}(P(0))$. Thus, $b=1$ or $b=3$ is the desired number, since $0,4 \in A_{P}$. Why can't the degree be less? Consider, for example, a cubic polynomial $P$. Since its derivative is a quadratic polynomial, it has no more than two roots, and thus $P$ has no more than three intervals of monotonicity, specifically 1 or 3. Let's consider the most complex case immediately - when $P$ has three intervals of monotonicity. Suppose it has a local minimum $m$ and a local maximum $M$. Then for $x \in(-\infty, m) \cup(M,+\infty)$, $l_{P}(x)=1$, $l_{P}(m)=l_{P}(M)=2$, and for $x \in(m, M)$, $l_{P}(x)=3$. The other cases are even simpler to analyze.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The number 2015 was divided into 12 addends, after which all numbers that can be obtained by adding some of these addends (from one to nine) were written down. What is the minimum number of numbers that could have been written down?
|
5.
Answer: 10
Example: Let's break down 2015 into 11 numbers of 155 and one number of 310. In this case, the sum of the addends can range from $155 \times 1$ to $155 \times 10$.
We will prove that it is impossible to get fewer than 10 different numbers: first, note that 2015 is not divisible by 12, so we will have at least 2 different numbers. Arrange all the numbers in ascending order. First, select only the first number, then the first and second, and so on—finally, select the first 9 numbers—this gives us 9 different sums. Now, take the last 9 numbers—the new sum exceeds all previous sums, so there are at least 10 different numbers on the board.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Seven natives from several tribes are sitting in a circle by the fire. Each one says to the neighbor on their left: “Among the other five, there are no members of my tribe.” It is known that the natives lie to foreigners and tell the truth to their own. How many tribes are represented around the fire?
|
Solution. If there are at least 4 natives from one tribe, then two of them sit next to each other, and one of them will lie to the other, although they should tell the truth. If there is only one native from a certain tribe, then he tells the truth to his left neighbor, although he should lie. Therefore, each tribe has two or three representatives.
Then, with two tribes, there are no more than $3+3=6$, so there are exactly three tribes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 20 chocolate candies on the table. Masha and Bear are playing a game according to the following rules. Players take turns. In one move, a player can take one or several candies from the table and eat them. Masha goes first, but on this move, she cannot take all the candies. In all other moves, players cannot take more candies than anyone has already taken in one move. The player who takes the last candy wins. For this, he will get a whole cake! Who among the players can ensure their victory?
|
Solution. Masha will win if she eats 4 candies on her first move.
Let's arrange the candies in a row, number them, and assume that the players take candies in a row from left to right.
Suppose Masha eats one candy on her first move. In this case, she will lose, as until the end of the game, the players will take one candy each, and all even-numbered candies, including the last 20th candy, will go to the Bear.
Suppose Masha eats two candies on her first move. Then the Bear will take two candies until Masha takes one candy. If Masha never takes one candy, the Bear will take candies 3, 4, 7, 8, 11, 12, 15, 16, 19, 20 and win. If Masha takes one candy, its number will be odd. Then the players will take one candy each in turn, and the Bear will get candies with even numbers. Masha will lose again.
Suppose Masha eats three candies on her first move. Then the Bear will take one candy on his first move, and with the remaining moves, he will again eat all the remaining even-numbered candies, and Masha will lose.
Suppose Masha eats 4 candies on her first move. Then Masha will act as follows: if the Bear eats 4 candies, Masha will also eat 4; if the Bear eats 3 candies, Masha will eat one; if the Bear eats 2 candies, Masha will also eat 2; if the Bear eats one candy, Masha will also eat one. If the Bear always takes 4 candies, Masha will eat candies 1, 2, 3, 4, 9, 10, 11, 12, 17, 18, 19, 20 and win. After the Bear eats three or one candy, an odd number of candies will remain on the table, and all the remaining candies with even numbers will go to Masha. Masha will win again. After the Bear eats two candies, 20 - 4 - 2 = 14 or 20 - 4 - 4 - 4 - 2 = 6 candies will remain on the table. Then the players will eat two candies each (the case with one candy we have already discussed), and Masha will get the 19th and 20th candies. Therefore, in this game, Masha will win if she eats 4 candies on her first move.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Petya thought of a 9-digit number obtained by rearranging the digits of the number 123456789. Vitya is trying to guess it. For this, he chooses any 9-digit number (possibly with repeated digits and zeros) and tells it to Petya, who then responds with how many digits of this number match the ones in his thought number. Can Vitya find out the first digit of Petya's number in no more than 4 moves? (A match is a digit standing in the same place.)
|
Solution. Vitya's first move is to name the number 122222 222. Then Petya can only respond with 0, 1, or 2.
If Petya answers 0, then neither the one nor the two hit their places. This means the two must be in the first position. There's no need to ask further.
If Petya answers 2, then both the one and the two hit their places. This means the one is in the first position. There's no need to ask further.
If Petya answers 1, then neither the one nor the two can be in the first position. In this case, Vitya will name the next number 344444444. After Petya's response, Vitya will either learn the first digit of Petya's number or understand that it is neither a three nor a four. Next, Vitya will name the numbers 566666666 and 788888888 until he learns the first digit. If Petya also answers 1 to the number 788888888, then the first digit of his number will be the only remaining unchecked digit - 9.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a string of 2021 letters A and B. Consider the longest palindromic substring. What is its minimum possible length? A palindrome is a string that reads the same from right to left and from left to right.
|
Solution. The minimum possible length of the maximum palindrome is 4.
We will prove that it cannot be less than 4. Consider the 5 letters in the center of the string. If these are alternating letters, then it is a palindrome of length 5. Suppose among these five letters there are two identical letters standing next to each other. Take the maximal contiguous block of identical letters. It is at least 2 in length, and adding one opposite letter on each side, we get 4 (if there are no other letters on the sides, then we have reached the end of the string and there are many identical letters in a row, since we started from the center of the string).
Let's provide an example of a string where the maximum palindrome has a length of 4. This is a string where the sequence ABABAB repeats periodically: ABABABABABABABABABAB.... By checking all possible positions of the centers of palindromes, one can verify that there are no palindromes longer than 4 in this string. Due to the periodicity of the string, only a small number of cases need to be checked.
Comments. The specified example is unique up to shift and reflection.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the bus route, there are only four stops - "Initial", "First", "Final", and "Last". At the first two stops, passengers only got on, and at the remaining stops, they only got off. It turned out that 30 passengers got on at the "Initial" stop, and 14 passengers got off at the "Last" stop. At the "First" stop, three times fewer passengers got on than got off at the "Final" stop. Which passengers are more - those traveling from "Initial" to "Last", or those traveling from "First" to "Final", and by how many?
Solution:
|
Answer: Those traveling from "First" to "Final" are six more.
Let $x$ be the number of people who got on at "First". Then, $3x$ people got off at "Final". Since the number of people getting on equals the number of people getting off, we have $30 + x = 3x + 14$, from which $x = 8$. Let $y$ be the number of people traveling from "Initial" to "Final". Then, the number of people traveling from "Initial" to "Final" is $8 - y$. Together with those traveling from "First" to "Final", they make up 14 people. Therefore, the number of people traveling from "First" to "Final" is $14 - 8 + y = 6 + y$. That is, six more people are traveling from "First" to "Final" than from "Initial" to "Final".
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Baron Munchausen placed a horse in some cells of an $N \times N$ board. He claims that no one will find two different $4 \times 4$ squares on this board (with sides along the grid lines) with the same number of horses. For what largest $N$ can his words be true?
#
|
# Solution:
Answer: $N=7$.
The number of knights in a $4 \times 4$ square can range from 0 to 16, i.e., there are 17 possible variants. The number of $4 \times 4$ squares on an $N \times N$ board is $(N-3)^{2}$ (since the top-left cell of the square can occupy positions from the far left to the fourth from the right horizontally, and the same vertically). To avoid repetitions, the number of squares must be no more than 17, i.e., $(N-3)^{2} \leqslant 17$. Therefore, $N$ cannot be greater than seven, since then $(N-3)^{2} \geqslant(8-3)^{2}=25>17$.
For $N=7$, an example can be constructed as shown on the right (knights are placed in the shaded cells, and the number of knights in each square is indicated in the top-left cell of each $4 \times 4$ square).
| 16 | 15 | 14 | 13 | | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 12 | 11 | 10 | 9 | | | |
| 8 | 7 | 6 | 5 | | | |
| 4 | 3 | 2 | 1 | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In a $4 \times 4$ square, cells are colored in several colors such that in any $1 \times 3$ rectangle, there are two cells of the same color. What is the maximum number of colors that can be used?
|
Solution. Maximum 9 colors. See example in the picture. We will prove that more is not possible. Any row (row or column) gives a maximum of three colors, so the first row + first column will give a maximum of $3+3-1=5$ colors.
We will prove that the remaining $3 \times 3$ square will give a maximum of 4 colors. Indeed, suppose we used 5 colors in it. Since in one row there are no more than two different colors, there will be two rows in which 4 different colors are used, 2 colors in each row. Then in the remaining row, there will be at least one cell of the fifth color. In the column containing this cell, all cells will be of different colors. Contradiction.
Thus, on the entire board, there are no more than $4+5=9$ different colors.
Criteria. Full solution (there is an estimate and there is an example) - 7 points.
Of these:
There is an example for 9 colors - 2 points.
Full proof of the estimate - 5 points, of which: 2 points for one row + one column and 3 points for the proof that the $3 \times 3$ square will give a maximum of 4 colors.

|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In the company, there are elves, fairies, and gnomes. Each elf is friends with all fairies except for three, and each fairy is friends with twice as many elves. Each elf is friends with exactly three gnomes, and each fairy is friends with all gnomes. Each gnome is friends with exactly half of the elves and fairies combined. How many gnomes are there in the company?
|
Solution. Answer: 12.
Let $n$ be the number of elves, $m$ be the number of fairies, and $k$ be the number of gnomes. Then the number of friendly pairs "elf-fairy" is $n(m-3)$, and "fairy-elf" is $-m \cdot 2(m-3)$. But these are the same pairs, therefore,
$$
n(m-3)=2 m(m-3)
$$
From which, $n=2 m$. Counting the friendly pairs with gnomes, we arrive at the equation
$$
k \cdot \frac{n+m}{2}=3 n+m k
$$
Substituting $n=2 m$, we get
$$
k \cdot \frac{3}{2} m=6 m+m k
$$
Dividing by $m$, we get $k=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Today's date is written as: 22.11.2015. How many other days in this year can be written with the same set of digits?
|
Solution. The month number cannot start with a two, so it is either 11 or 12. In the first case, it is 22.11, in the second case 12.12 and 21.12. Answer: two.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.4. Let initially each island is inhabited by one colony, and let one of the islands have $d$ neighboring islands. What can the maximum possible number of colonies that can settle on this island be equal to?
|
Solution. Answer: $d+1$.
Example. We will prove that in a vertex of degree $d$, $d+1$ colonies can gather. Suspend the tree from this vertex as the root and prove that in each vertex from which $e$ edges go down, $e+1$ colonies can gather, conducting only migrations within its subtree. We will prove this by "induction from the lower vertices to the upper ones." For leaves, the statement is obvious (they already have one colony), and for any other vertex, it is sufficient to gather the required number of colonies in its immediate children, after which perform one migration for each of them.
Estimate. We will show that any available distribution of numbers on the tree can be obtained by organizing migrations so that each colony does not move further than to a neighboring island. From this, it will follow that the answer is no more than $d+1$.
We prove this by induction on the number of migrations. Base case - zero migrations, is obvious.
Inductive step. Suppose a migration is about to occur from island $v$. By the inductive hypothesis, all colonies on it are from it and neighboring islands. Since a migration is possible, by the inductive hypothesis, there are colonies on the island from at least $\operatorname{deg} v-1$ neighboring islands; we will send them back to their islands. If there is a colony from the remaining neighboring island, we will also send it back, and if there is a colony from the island itself, we will send it to any of the neighboring islands.
## Plot 2.
Two circles inscribed in an angle with vertex $R$ intersect at points $A$ and $B$. A line through $A$ intersects the smaller circle at point $C$ and the larger circle at point $D$. It turns out that $A B=A C=A D$.
|
+1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The gnomes went to work, and Snow White is feeling lonely. She laid out a pile of 36 stones on the table. Every minute, Snow White splits one of the existing piles into two, and then adds a new stone to one of them. After some time, she had seven piles, each with an equal number of stones. How many stones ended up in each pile?
|
Solution. There will be seven piles after six moves. After six moves, there will be $36+6=42$ stones - meaning, 6 stones in each pile.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Seven people stood in a circle, each of whom is either a knight, who always tells the truth, or a liar, who always lies, or a traveler, who alternates between truth and lies.
The first and second said in unison: "Among us there is exactly 1 liar," the second and third: "Among us there are exactly 2 knights," the third and fourth: "Among us there are exactly 3 liars," $\vdots$
the sixth and seventh: "Among us there are exactly 6 knights," the seventh and first: "Among us there are exactly 7 liars."
Who is who among them?
|
Solution. If all 7 statements are lies, then everyone lied, meaning everyone is a liar, and then 7 and 1 told the truth. This means that at least one statement is true. On the other hand, there are no more than 2 true statements (one about the liars, the other about the knights). That is, there are either 0 or 1 knights, but the latter is impossible, since everyone said there are more than 1 knight. Therefore, there are no knights, but someone told the truth. This means the statement about the liars was true, and it was told by two visitors. Hence, 5 and 6 are visitors, and all others are liars.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. When the child was born, their parents were not yet 40 years old, but they were already adults. When the child turned 2 years old, the age of exactly one of the parents was divisible by 2; when the child turned 3 years old, the age of exactly one of the parents was divisible by 3, and so on. How long could such a pattern have continued?
|
Solution. The condition means that at the moment of the child's birth, the age of exactly one of the parents was divisible by 2, the age of exactly one of the parents - by 3, and so on (as long as this pattern continued).
Let one of the parents be 24 years old, and the other 35 years old. Then this pattern could continue until the child turned 8. Beyond that, the pattern must break. Indeed, suppose the child turned 9, and the pattern continues. Then at the moment of the child's birth, exactly one of the parents had an even number of years, exactly one - a multiple of 3, exactly one - a multiple of 6, exactly one - a multiple of 8, and exactly one - a multiple of 9. So it is the same parent, and they must be at least 72 years old, i.e., they are too old.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In triangle $A B C$, angle $A$ is equal to $50^{\circ}, B H$ is the altitude. Point $M$ on $B C$ is such that $B M=B H$. The perpendicular bisector of segment $M C$ intersects $A C$ at point $K$. It turns out that $A C=2 \cdot H K$. Find the angles of triangle $A B C$.
|
Solution. Draw a perpendicular to $BC$ from point $M$. Let $K^{\prime}$ be the point of its intersection with $AC$. Then the segment $MK$ is the midline in $\triangle K^{\prime}MC$, that is, $K^{\prime}K = KC$. From the fact that $HK = KC + AH$, we get $AH = HK^{\prime}$. Right triangles $BHA$ and $BHK^{\prime}$ are equal by two legs, $BHK^{\prime}$ and $BMK^{\prime}$ are equal by a leg and hypotenuse. Then
$$
\angle B = 3 \angle AHB = 3 \cdot (90^{\circ} - 50^{\circ}) = 120^{\circ} \text{.}
$$
The remaining angle $C$ is
$$
180^{\circ} - 50^{\circ} - 120^{\circ} = 10^{\circ}
$$
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Konstantin pronounced the names of all natural numbers from 180 to 220 inclusive, while Mikhail - from 191 to 231 inclusive. Who pronounced more words and by how many?
|
Solution. Let's remove the numbers that both have: 191-220. Then each will have 11 numbers left: Konstantin has 180-190, and Mikhail has 221-231. Note that in the names of the numbers 181-189, 221-229, and 231, there are three words each, while in 180, 190, and 230, there are two words each. This means that Mikhail said one more word.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. At the festival "Hobbits - for cultural diversity!", more than 20 participants arrived. A correspondent found out that among any 15 participants of the festival, there are at least 4 humans and at least 5 elves. How many hobbits participated in the festival? Provide all possible answers and prove that there are no others.
|
Solution. Suppose there is at least one hobbit. If there are 10 people among the participants, then in their company with the hobbit and 4 other participants, there will not be 5 elves, which contradicts the condition. Therefore, there are no more than 9 people. Since the total number of participants is more than 20, there will be 12 participants who are not people. But then, by adding 3 participants to them, we will get a company that contradicts the condition. This means that there were no hobbits at all.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Yesterday at the market, with one hundred tugriks you could buy 9 gingerbreads and 7 pastries (and even get some change), but today this amount is no longer enough. However, with the same one hundred tugriks today, you can buy two gingerbreads and 11 pastries (also with some change), but yesterday this amount would not have been enough. A gingerbread and a pastry cost a whole number of tugriks, and the price of each sweet changed by no more than one tugrik overnight. $A$ How much does one gingerbread cost today?
|
Solution. Note that something has become more expensive (otherwise, the situation where we could buy a set yesterday but not today could not have arisen), and another sweet has become cheaper for similar reasons. Nine cookies and seven cakes together have become more expensive, so the cookie has become more expensive, and the cake has become cheaper. This set has become 2 tugriks more expensive overnight, i.e., it cost 99 tugriks yesterday and 101 tugriks today. Thus, today 9 cookies = 101 tugriks - 7 cakes, i.e., by subtracting a multiple of 7 from 101, we should get a number that is a multiple of 9. This is only possible in one case: 101 - 56 = 45. Then a cookie today costs 5 tugriks, and a cake costs 8 tugriks.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.