problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. During the physical education lesson, all students of grade 8 lined up. It turned out that boys and girls alternated in the line. It is known that exactly $52\%$ of the students in grade 8 are boys. Find the number of girls in grade 8. Don't forget to justify your answer.
|
Answer: 12. Solution. If there were an even number of students in the row, the number of boys and girls would be equal. But according to the condition, there are more boys. Therefore, the number of students in the row is odd, and boys stand in odd positions. Let there be $n$ girls in the class. Then there are $n+1$ boys, and from the condition, we get that $n+1=0.52(2n+1)$, from which $n=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For what largest natural $\mathrm{k}$ can the cells of a $5 \times 5$ table be filled with zeros and ones (each cell must contain exactly one number) so that there are $k$ rows, in each of which the sum of the numbers is at least 3, and $k$ columns, in each of which the sum of the numbers is at most 2? (O. Nechaeva, I. Rubanov)
|
Answer. For $k=4$. Solution. For $k=5$, it is impossible to fill the table in the required manner, since when calculating the sum of the numbers in the table by adding the sums of the rows, it turns out that it is not less than $3 \cdot 5=15$, while when calculating the same sum by the columns, it turns out that it is not
| 1 | 1 | 0 | 0 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 |
more than $2 \cdot 5=10$. An example of filling the table that satisfies the condition of the problem for $k=4$ is shown on the right.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find all natural numbers $n$ for which the number $n^{7}+n^{6}+n^{5}+1$ has exactly three natural divisors. (O. Nechaeva, I. Rubanov)
|
Answer. 1. Solution. For $n=1, n^{7}+n^{6}+n^{5}+1=4$. The number 4 has exactly three divisors: 1, 2, 4. Notice further that $n^{7}+n^{6}+n^{5}+1=\left(n^{7}+n^{5}\right)+\left(n^{6}+1\right)=n^{5}\left(n^{2}+1\right)+\left(n^{2}+1\right)\left(n^{4}-n^{2}+1\right)=\left(n^{2}+1\right)\left(n^{5}+n^{4}-n^{2}+1\right)=\left(n^{2}+1\right)(n+1)\left(n^{4}-n+1\right) . \quad$ For $n>1$, the inequalities $n^{2}+1>n+1>1$ are satisfied, and the number $\left(n^{2}+1\right)(n+1)\left(n^{4}-n+1\right)$ has at least four distinct divisors: $1, n+1, n^{2}+1$ and $\left(n^{2}+1\right)(n+1)$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In parallelogram $A B C D$ with side $A B=1$, point $M$ is the midpoint of side $B C$, and angle $A M D$ is 90 degrees. Find the side $B C$.
|
Answer: 2. First solution. Draw the median $M N$ in triangle $A M D$. $A B M N$ is a parallelogram since $B M$ and $A N$ are equal and parallel, thus $M N = B C = 1$. But the median $M N$ is half the hypotenuse $A D$ in the right triangle $A M D$, from which it follows that $B C = A D = 2$. Second solution. Extend the segment $A M$ and side $C D$ until they intersect at point $K$. Consider triangle $A D K$. Segment $M C$ is parallel to the base $A D$ and equal to half of it. Therefore, $M C$ is the midline, $A M = M K$, and $K D = 2 C D = 2$. But in the considered triangle, the median $D M$ coincides with the altitude, so it is isosceles and $A D = 2 A B = 2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of two-digit numbers that can be written in a row so that any two adjacent numbers are not coprime, while any two non-adjacent numbers are coprime?
|
Answer: 10. Solution: Ten numbers can be written: 11, 77, 91, 65, 85, 51, 57, 38, 46, 23. Suppose we managed to write 11 such numbers. Let's list the common divisor, different from 1, for each pair of adjacent numbers. This will result in 10 numbers, any two of which are coprime. All these numbers are either single-digit or double-digit. But it is impossible to choose more than four single-digit numbers, different from 1, any two of which are coprime. Therefore, in the constructed sequence of 10 numbers, there will be no fewer than six double-digit numbers. This means that some two of them will be adjacent, and some number in the original sequence will be divisible by each of them. Since they are coprime, it is also divisible by their product. But a double-digit number cannot be divisible by the product of two double-digit numbers.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the side $A C$ of triangle $A B C$, a point $E$ is chosen. The bisector $A L$ intersects the segment $B E$ at point $X$. It turns out that $A X=X E$ and $A L=B X$. What is the ratio of the angles $A$ and $B$ of the triangle? (S. Berlov)
|
Answer. 2. Solution. Let the line passing through point $E$ parallel to $A L$ intersect lines $B C$ and $B A$ at points $P$ and $Q$ respectively. From the similarity of triangles $A B L$ and $Q B P$, we have $P Q / A L = B E / B X = B E / A L$, from which it follows that $P Q = B E$. Due to the parallelism of lines $A L$ and $P Q$, we have $\angle A Q E = \angle B A X = \angle X A E = \angle A E Q$, from which it follows that $A E = A Q$. Moreover, from the equality $A X = X E$, it follows that $\angle A E B = \angle A E X = \angle X A E$, from which it follows that $\angle A E B = \angle A Q E$. Thus, triangles $A Q P$ and $A E B$ are equal by two sides and the angle between them. Therefore, $A P = A B$ and $\angle B A E = \angle P A Q = 2 \angle C B A$, from which we obtain the answer.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given two non-zero numbers. If you add one to each of them, as well as subtract one from each of them, then the sum of the reciprocals of the four resulting numbers will be equal to 0. What number can result if you subtract the sum of their reciprocals from the sum of the original numbers? Find all possibilities. (S. Berlov)
|
Answer: 0. Solution: Let the given numbers be a and b. We transform the sum of the four numbers given in the condition: $0=\frac{1}{a+1}+\frac{1}{a-1}+\frac{1}{b+1}+\frac{1}{b-1}=\frac{2 a}{a^{2}-1}+\frac{2 b}{b^{2}-1}$. Let $x=\frac{a}{a^{2}-1}=-\frac{b}{b^{2}-1}$. Then
$$
a-\frac{1}{a}+b-\frac{1}{b}=\frac{a^{2}-1}{a}+\frac{b^{2}-1}{b}=\frac{1}{x}-\frac{1}{x}=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Tom Sawyer took on the task of painting a very long fence, adhering to the condition: any two boards, between which there are exactly two, exactly three, or exactly five boards, must be painted in different colors. What is the smallest number of different colors he can manage with.
|
Answer: Three. Solution. Note that between the first and fourth, and the fourth and seventh boards, there are two boards each, and between the first and seventh boards, there are five boards. Therefore, the first, fourth, and seventh boards of the fence must be painted in different colors, so Tom will need at least three different paints. On the other hand, three colors will be enough for him, for example, if he paints like this: AAABBBCCCAAABBBCCC...: here, between any two same-colored boards, there are at least 6 boards.
Grading Guidelines. Only the answer - 0 points. Proven that two colors are not enough, but no example for three colors - 3 points. Only a correct example for three colors without explanation of why it works - no more than 3 points (3 points if the explanation is obvious, as in our example, and from 0 to 2 points otherwise, depending on the complexity of the justification). Proven that two colors are not enough and provided a correct example, but without explanation of why it works - from 5 to 7 points, depending on the complexity of the justification.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a coffee shop, 55 Indians and Turks met, each drinking tea or coffee. All Indians tell the truth when drinking tea and lie when drinking coffee, while all Turks do the opposite. When asked "Are you drinking coffee?" 44 people answered "yes," when asked "Are you a Turk?" 33 people answered "yes," and 22 people agreed with the statement "It is raining outside." How many Indians in the coffee shop are drinking tea?
|
Answer: 0. Solution. Let $h_{\psi}, h_{\kappa}$ be the number of Indians drinking tea and coffee, respectively. Similarly, define the quantities $T_{4}$ and $T_{k}$. Then from the first question, it follows that $T_{4}+T_{\kappa}=44$, and from the second question, it follows that $h_{\kappa}+T_{\kappa}=33$. Suppose that "It is raining outside" is a false statement. Then $h_{k}+T_{4}=22$. Adding the first two equations and subtracting the third, we get $2 T_{\kappa}=55$, a contradiction. Therefore, it is raining, from which $h_{4}+T_{\kappa}=22$. Adding all three equations and subtracting the obvious equation $h_{4}+h_{k}+T_{4}+T_{\kappa}=55$, we get $2 T_{\kappa}=44$, from which $T_{\kappa}=22$ and $h_{4}=0$.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the vertices of a regular 300-gon, numbers from 1 to 300 are placed once each in some order. It turns out that for each number a, among the 15 nearest numbers to it in the clockwise direction, there are as many numbers less than a as there are among the 15 nearest numbers to it in the counterclockwise direction. A number that is greater than all 30 nearest numbers to it is called huge. What is the smallest possible number of huge numbers? (S. Berlov)
|
Answer: 10. Solution: Estimation. To prove that there are no fewer than 10 huge numbers, it is sufficient to prove that among any 30 consecutive numbers, there will be a huge one. Indeed, suppose this is not the case. Then consider the largest of these 30 numbers. On one side of it, all 15 nearest numbers will be part of this set of thirty, and therefore will be less than it. But then, according to the condition, the 15 nearest numbers on the other side of it will also be less than it, meaning it will be huge. Contradiction. Example. All numbers ending in 0 can be arranged in the following order: 300, 280, 260, 240, ..., 20, 290, 270, 250, ..., 10. After them, in a similar order, we can arrange the numbers ending in 1: 291, 271, ..., 11, 281, ..., 1, and then similarly arrange the numbers ending in 2, and so on until the cycle is complete. It is not difficult to verify that all conditions will be met, and the huge numbers will be only those from 291 to 300.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In each cell of a $2 \times 2$ table, one number is written. All numbers are distinct, the sum of the numbers in the first row is equal to the sum of the numbers in the second row, and the product of the numbers in the first column is equal to the product of the numbers in the second column. Find the sum of all four numbers.
|
Answer: 0. Solution: Let the numbers in the top row of the table be (from left to right) $a$ and $b$, and the numbers in the bottom row (from left to right) be $c$ and $d$. By the condition, $a+b=c+d$ and $a c=b d$. Expressing $c$ from the first equation and substituting into the second, we get $a(a+b-d)=b d \Leftrightarrow(a+b)(a-d)=0$, from which, since $a-d \neq 0$, we obtain $a=-b$. Similarly, $d=-c$, from which we get the answer.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Each of the 10 people is either a knight, who always tells the truth, or a liar, who always lies. Each of them thought of some natural number. Then the first said: “My number is greater than 1”, the second said: “My number is greater than 2”, ..., the tenth said: “My number is greater than 10”. After that, they, in a different order, said (each one phrase): “My number is less than 1”, “My number is less than 2”, ..., “My number is less than 10”. What is the maximum number of knights that could have been among these 10 people? (O. Podlipsky)
|
Answer: 8. Solution: Those who in the first series of answers said that their numbers are greater than 9 and 10 are definitely liars, because these answers are incompatible with any of the answers in the second series. Therefore, there are no more than eight knights. An example when there are exactly 8 knights: the first eight in the first series of answers thought of the numbers $2, \ldots, 9$ respectively, and they give the answers "My number is less than 3", ..., "My number is less than 10" in the second series of answers. Each of the two liars thought of the number 5, and they give the last two answers of the first series and the first two answers of the second series.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numbers 1, 2, 3, 4, 5, 6, 7 were written in a circle in some order. We will call a written number good if it is equal to the sum of the two numbers written next to it. What is the maximum possible number of good numbers among the written ones? (E. Bakayev)
|
Answer: 3. Solution: If the numbers are written, for example, in the order 2, 7, 5, 6, 1, 4, 3, then the numbers 7, 6, and 4 will be good. It remains to show that there cannot be more than three good numbers.
Note that a good number is greater than both of its neighbors, so two good numbers cannot stand next to each other. Therefore, the number following a good number clockwise should not be good, and the numbers following different good numbers should be different and not good. Consequently, among all the written numbers, the good ones do not exceed half, and thus, there are no more than three.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From the natural numbers from 1 to 25, Dasha chose six such that the difference between any two chosen numbers is divisible by 4. What is the maximum number of prime numbers that Dasha could have chosen?
|
Answer: Five. First solution. The difference of two numbers is divisible by 4 if and only if these numbers have the same remainder when divided by 4. Let's list all prime numbers less than 25 and their remainders when divided by 4: 2-2, 3-3, 5-1, 7-3, 11-3, 13-1, 17-1, 19-3, 23-3. The most common remainder is 3, which appears five times, giving us the answer. Second solution. Since $5-2=3,13-11=19-17=2$, from the groups of prime numbers $\{2,3,5\},\{11,13\},\{17,19\}$ Dasha could choose no more than one number from each. Among the primes less than 25, the only numbers not in these groups are 7 and 23, so the number of prime numbers Dasha could choose is no more than five. An example where there are exactly five is given in the first solution.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle ABC, the median BM is drawn. It is known that $\angle A B M=40^{\circ}$, and $\angle C B M=70^{\circ}$. Find the ratio $A B: B M$.
|
Answer: 2. First solution. Complete the triangle $A B C$ to a parallelogram $A B C D$. Since the diagonals of a parallelogram bisect each other, point $M$ is the point of their intersection and $B D=2 B M$. On the other hand, $\angle B D A=\angle C B D=70^{\circ}$, and $\angle B A D=180^{\circ}-\angle B D A-\angle A B D=70^{\circ}=\angle B D A$, from which $A B=B D=2 B M$ and $A B: B M=2 B M: B M=2$. Second solution. Note that $B C$ is the bisector of the external angle at vertex $B$ of triangle $A B M$. Therefore, $A B: B M=A C: C M=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The cells of an $n \times n$ square are colored black and white with the condition that no four cells, located at the intersection of two rows and two columns, can all be the same color. What is the largest possible value of $n$?
|
Solution. An example for $n=4$ is shown in the figure on the right. We will prove by contradiction that it is impossible to color a $5 \times 5$ square in this way. Let's call a row predominantly black if it has more black squares than white, and predominantly white otherwise. Among the five rows, there will be either three predominantly black rows or three predominantly white rows; without loss of generality, let's assume we have found three predominantly black rows. In these rows, there are at least nine black cells.
| B | W | B | W |
| :---: | :---: | :---: | :---: |
| B | B | W | W |
| W | B | B | W |
| W | W | W | B |
Now we consider only these three rows. If in some column (let's call it A) there are three black cells, then the remaining four columns have at least six black cells. Therefore, there will be a column (let's call it B) where there are two black cells. Then, taking columns A and B and the two rows where the two black cells of column B are located, we get a contradiction.
Thus, in each column, there are no more than two black cells. But this is only possible if there are at least two black cells in at least four columns. Since there are only three ways to color two out of three cells black, in some two columns the coloring is the same, and we again get a contradiction.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A numerical sequence is given:
$x_{0}=\frac{1}{n} ; x_{k}=\frac{1}{n-k}\left(x_{0}+x_{1}+\ldots+x_{k-1}\right) ; k=1,2, \ldots, n-1$.
Find $S_{n}=x_{0}+x_{1}+\ldots+x_{n-1}$, if $n=2021$.
|
# Solution.
We will prove by mathematical induction that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$. For $k=0$, this equality holds. For $k=1$, $x_{0}+x_{1}=\frac{1}{n}+\frac{1}{n-1} \cdot \frac{1}{n}=\frac{1}{n-1}$. Suppose this equality holds for all $m \leq k$, then it should also hold for $k+1$. Let's check this:
$$
\begin{aligned}
& \left(x_{0}+x_{1}+\ldots+x_{k}\right)+x_{k+1}=\frac{1}{n-k}+x_{k+1}=\frac{1}{n-k}+\frac{1}{n-(k+1)}\left(x_{0}+x_{1}+\ldots+x_{k}\right)= \\
& =\frac{1}{n-k}+\frac{1}{(n-k-1)(n-k)}=\frac{1}{n-(k+1)} .
\end{aligned}
$$
Thus, this equality also holds for $k+1$. Therefore, our assumption that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$ is correct.
Then, for $n=2021$ and $k=n-1=2020: S_{2021}=x_{0}+x_{1}+\ldots+x_{2020}=\frac{1}{2021-2020}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A numerical sequence is given:
$$
x_{0}=\frac{1}{n} ; x_{k}=\frac{1}{n-k}\left(x_{0}+x_{1}+\ldots+x_{k-1}\right) ; k=1,2, \ldots, n-1
$$
Find $S_{n}=x_{0}+x_{1}+\ldots+x_{n-1}$, if $n=2022$.
|
# Solution.
We will prove by mathematical induction that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$. For $k=0$, this equality holds. For $k=1$, $x_{0}+x_{1}=\frac{1}{n}+\frac{1}{n-1} \cdot \frac{1}{n}=\frac{1}{n-1}$. Suppose this equality holds for all $m \leq k$, then it should also hold for $k+1$. Let's check this:
$$
\begin{aligned}
& \left(x_{0}+x_{1}+\ldots+x_{k}\right)+x_{k+1}=\frac{1}{n-k}+x_{k+1}=\frac{1}{n-k}+\frac{1}{n-(k+1)}\left(x_{0}+x_{1}+\ldots+x_{k}\right)= \\
& =\frac{1}{n-k}+\frac{1}{(n-k-1)(n-k)}=\frac{1}{n-(k+1)} .
\end{aligned}
$$
Thus, this equality also holds for $k+1$. Therefore, our assumption that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$ is correct.
Then, for $n=2022$ and $k=n-1=2021: S_{2022}=x_{0}+x_{1}+\ldots+x_{2021}=\frac{1}{2022-2021}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1} \mathrm{c}$ is inscribed in a sphere with base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. Segment $C D$ is the diameter of this sphere, point $K$ and $L$ are the midpoints of edge $A A_{1}$ and $A B$ respectively. Find the volume of the prism if $D L=\sqrt{2}, D K=\sqrt{3}$.
|
# Solution.
The planes of the bases $ABC$ and $A_1B_1C_1$ of the prism intersect the sphere along the circumcircles of the equilateral triangles $ABC$ and $A_1B_1C_1$, with their centers at points $O$ and $O_1$ respectively.
It is easy to show that the midpoint $M$ of the segment $OO_1$ is the center of the sphere (Fig. 5).
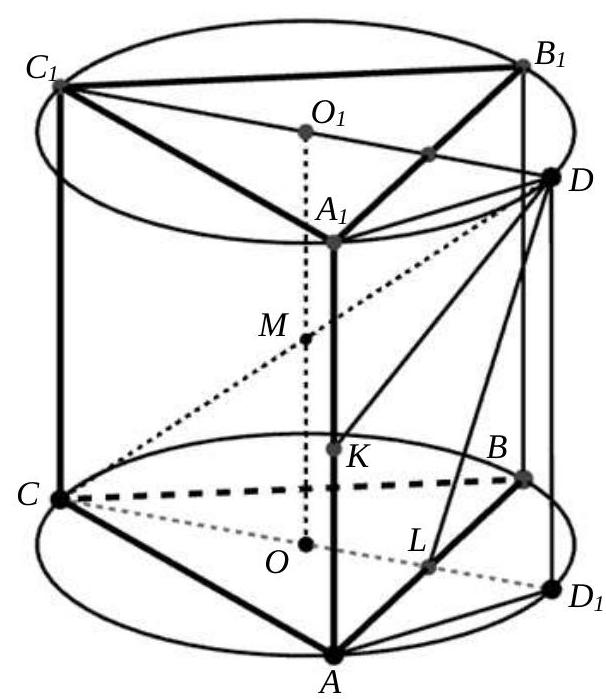
Fig. 5.
Draw a diameter $C_1D$ of the circle centered at point $O_1$ through point $C_1$. We will show that $CD$ is a diameter of the sphere. Indeed, the plane $CC_1D$ is perpendicular to the planes of the bases and, therefore, contains the segment $OO_1$ along with point $O_1$. Since $C_1D = 2DO_1$, the line $CD$ intersects the segment $OO_1$ at its midpoint, i.e., at the center $M$ of the given sphere.
Let $D_1$ be the projection of point $D$ onto the plane of the base $ABC$, the height of the prism is $h$, and the radii of the circles centered at $O$ and $O_1$ are $r$. Consider triangles $KA_1D$ and $LDD_1$. Given that $A_1D = AD_1 = r$ (triangle $A_1O_1D$ is equilateral), $LD_1 = \frac{r}{2}$, $DD_1 = h$, $KA_1 = \frac{h}{2}$, by the Pythagorean theorem, we obtain the system of equations
$$
\left\{\begin{array}{l}
\frac{h^2}{4} + r^2 = (\sqrt{3})^2 \\
h^2 + \frac{r^2}{4} = (\sqrt{2})^2
\end{array}\right.
$$
Solving the system, we find that $r = \frac{2\sqrt{6}}{3}$, $h = \frac{2\sqrt{3}}{3}$. Then the side of the base is $2\sqrt{2}$, its area $S = 2\sqrt{3}$, and consequently, the volume of the prism $V = S \cdot h = 4$.
Answer. 4.
## Mathematics. Variant-32 $10-11$ grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ is inscribed in a sphere with the base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. The segment $C_{1} D$ is the diameter of this sphere, and point $K$ is the midpoint of edge $C C_{1}$. Find the volume of the prism if $D K=2, D A=\sqrt{6}$.
|
# Solution.
The planes of the bases $ABC$ and $A_1B_1C_1$ of the prism intersect the sphere along the circumcircles of the equilateral triangles $ABC$ and $A_1B_1C_1$, with their centers at points $O$ and $O_1$ respectively.
It is easy to show that the midpoint $M$ of the segment $OO_1$ is the center of the sphere (Fig. 5).
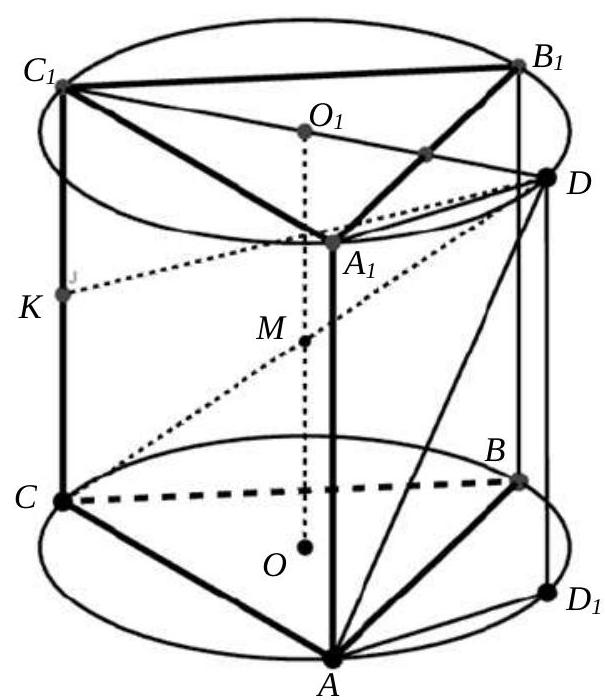
Fig. 5
Draw a diameter $C_1D$ of the circle centered at point $O_1$ through point $C_1$. We will show that $CD$ is a diameter of the sphere. Indeed, the plane $CC_1D$ is perpendicular to the planes of the bases and, therefore, contains the segment $OO_1$ along with point $O_1$. Since $C_1D = 2DO_1$, the line $CD$ intersects the segment $OO_1$ at its midpoint, i.e., at the center $M$ of the given sphere.
Let $D_1$ be the projection of point $D$ onto the plane of the base $ABC$, the height of the prism is $h$, and the radii of the circles centered at $O$ and $O_1$ are $r$. Consider the triangles $KC_1D$ and $ADD_1$. Given that $C_1D = 2r$, $AD_1 = r$ (triangle $A_1O_1D$ is equilateral), $DD_1 = h$, $KC_1 = \frac{h}{2}$, by the Pythagorean theorem, we obtain the system of equations
$$
\left\{\begin{array}{l}
\frac{h^2}{4} + 4r^2 = 2^2 \\
h^2 + r^2 = (\sqrt{6})^2
\end{array}\right.
$$
Solving the system, we find that $r = \frac{\sqrt{6}}{3}$, $h = \frac{4\sqrt{3}}{3}$. Then the side of the base is $\sqrt{2}$, its area $S = \frac{\sqrt{3}}{2}$, and consequently, the volume of the prism $V = S \cdot h = 2$.
Answer. 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. If we now take into account that after reflections in the mirrors, the ray EC' has entered the eyepiece, that is, the direction of the ray after two deflections coincides with the direction of DA, it follows that the total deflection of the ray EC' is equal to the angle between the rays EC' and DA
$$
\mathrm{psi}_{\text {total }}=2 \mathrm{phi}=\text { alpha }
$$
from which
$$
\text { phi }=0.5 \mathrm{alpha}=15^{\circ}
$$
Thus, we have shown that if the ray $\mathrm{EC}$' after deflections overlaps with the ray $\mathrm{DA}$, then the angle between the mirrors must be equal to half the angle alpha, and this equality will not change after the platform is rotated: the angle alpha will remain the same, and therefore, the angle between the mirrors, which is 15 degrees, must be maintained.
|
Answer: There is no need to rotate mirror C relative to point C. The angle of rotation of mirror C relative to the platform is $0^{\circ}$.
## Solution Method 2.
|
0
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
8. Finally, let's calculate the change in resistance when the switch is closed:
$$
\Delta R=R_{p}-R_{3}=33[\text { Ohms] }-30[\text { Ohms] }=3[\text { Ohms] }
$$
|
Answer: 3.0 Ohms
Criteria (maximum 10 points)
|
3
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle touches the extensions of two sides $A B$ and $A D$ of square $A B C D$ with side $2 \sqrt{3} \mathrm{~cm}$. Two tangents are drawn from point $C$ to this circle. Find the radius of the circle if the angle between the tangents is $30^{\circ}$, and it is known that $\sin 15^{\circ}=\frac{\sqrt{3}-1}{2 \sqrt{2}}$.
#
|
# Solution.
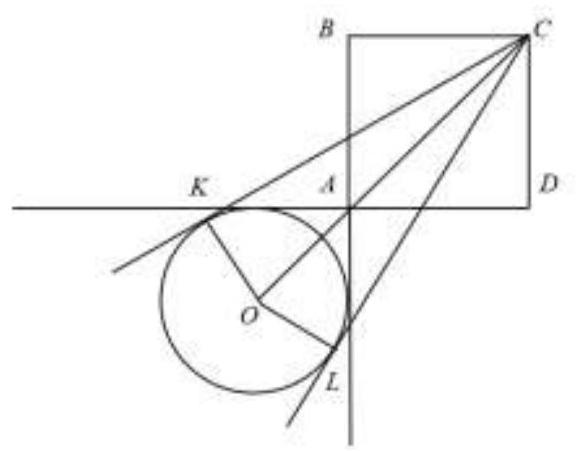
Fig. 1
The segment cut off from vertex $A$ by the point of tangency of the circle is equal to the radius of this circle. The diagonal of the square $A B C D A C=2 \sqrt{6}$. If radii of the circle are drawn to the points of tangency, a square with side $R$ is formed. Then $O A=R \sqrt{2}$, $O C=\frac{O K}{\sin 15^{\circ}}=\frac{2 \sqrt{2} R}{\sqrt{3}-1}$. As a result, we get the equation $\frac{2 \sqrt{2} R}{\sqrt{3}-1}=R \sqrt{2}+2 \sqrt{6}$, from which $R=\frac{2 \sqrt{6}}{\sqrt{6}+\sqrt{2}-\sqrt{2}}=2$.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Determine the amount of substance of sodium carbonate
According to the chemical reaction equation:
$$
\mathrm{n}\left(\mathrm{CO}_{2}\right)=\mathrm{n}\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)=0.125 \text { mol }
$$
Determination of the amount of substance - 2 points
19. Calculate the mass of sodium carbonate
$$
m\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)=n \cdot M=0.125 \cdot 106=13.25 \text { g }
$$
Determination of the mass of the substance - 2 points
20. Determine the mass fraction of sodium carbonate in the initial solution:
$$
\omega\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)=\frac{m\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right) \cdot 100 \%}{m_{\mathrm{p}-\mathrm{pa}}\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)}=\frac{13.25 \cdot 100 \%}{132.5}=10 \%
$$
Determination of the mass fraction of the substance in the solution - 2 points
|
Answer: $10 \%$
## TOTAL 10 points
## TASK № 2
Aluminum oxide was melted with potash. The resulting product was dissolved in hydrochloric acid and treated with excess ammonia water. The precipitate that formed was dissolved in excess sodium hydroxide solution. Write the equations for the four reactions described.
## Solution:
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. Let's determine the amount of sulfur substance
According to the chemical reaction equation:
$$
\mathrm{n}(\mathrm{S})=\mathrm{n}\left(\mathrm{SO}_{2}\right)=1 \text { mole }
$$
29. Let's calculate the mass of pure sulfur:
$$
m(S)=n \cdot M=1 \cdot 32=32 \text { g }
$$
Determination of the mass of the substance - 2 points
30. Thus, in a sample of natural sulfur weighing 38 g, there are 32 g of pure substance.
Let's calculate the mass of the impurity:
$m($ impurity $)=38-32=6$ g
Determination of the mass of the impurity - 2 points
|
Answer: 6 g.
## TOTAL 10 points
## TASK № 2
Potassium phosphate was calcined with coke in the presence of river sand. The simple substance formed reacted with excess chlorine. The resulting product was added to an excess of potassium hydroxide solution. The formed solution was treated with lime water. Write the equations for the four described reactions.
## Solution:
|
6
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. Let's calculate the volume of carbon dioxide.
According to Avogadro's law, the following rule applies: in equal volumes of different gases taken at the same temperatures and pressures, the same number of molecules is contained.
From the chemical reaction equation, it follows that the ratio of the amount of substance (in moles) is $2: 1$, which means the volume of carbon dioxide is half the volume of oxygen.
$V\left(\mathrm{CO}_{2}\right)=\frac{1}{2} V\left(\mathrm{O}_{2}\right)=\frac{1}{2} \cdot 14=7$ liters
Determining the volume of carbon dioxide - 4 points
|
Answer: 7 l.
## TOTAL 10 points
## TASK № 2
Chromium (III) oxide was melted with potassium sulfite. The resulting product was added to water. To the precipitate formed, a mixture of bromine and sodium hydroxide was added, resulting in a yellow solution. Upon adding hydrogen sulfide water to the obtained solution, a precipitate formed. Write the equations for the four described reactions.
## Solution:
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) Find the smallest natural solution of the inequality $\left(\frac{2023}{2022}\right)^{27+18+12+8+\ldots+27 \cdot\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{72}$.
|
Solution.
$\left(\frac{2023}{2022}\right)^{27+18+12+8+\ldots+27 \cdot\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{72}$
We transition to an equivalent inequality
$27+18+12+8+\ldots+27 \cdot\left(\frac{2}{3}\right)^{n}>72$
$27\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\left(\frac{2}{3}\right)^{3}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>72$
$\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\left(\frac{2}{3}\right)^{3}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>\frac{8}{3}$
The left side of the inequality represents the sum of a geometric progression
$\frac{1-\left(\frac{2}{3}\right)^{n+1}}{1-\frac{2}{3}}>\frac{8}{3}, 1-\left(\frac{2}{3}\right)^{n+1}>\frac{8}{9}, \frac{1}{9}>\left(\frac{2}{3}\right)^{n+1},\left(\frac{2}{3}\right)^{n}\frac{1}{6},\left(\frac{2}{3}\right)^{5}=\frac{32}{243}=\frac{64}{486}=\frac{1}{6} \cdot \frac{64}{81}<\frac{1}{6}$.
Thus, the smallest natural value of $n=5$.
Answer. 5.
|
5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) Find the smallest natural solution of the inequality $\left(\frac{2023}{2022}\right)^{36+24+16+\ldots+36\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{96}$.
|
Solution.
$\left(\frac{2023}{2022}\right)^{36+24+16+\ldots+36\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{96}$.
$36+24+16+. .+36 \cdot\left(\frac{2}{3}\right)^{n}>96$
$36\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>96$
$\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>\frac{8}{3}$
The left side of the inequality represents the sum of a geometric progression
$\frac{1-\left(\frac{2}{3}\right)^{n+1}}{1-\frac{2}{3}}>\frac{8}{3}, 1-\left(\frac{2}{3}\right)^{n+1}>\frac{8}{9}, \frac{1}{9}>\left(\frac{2}{3}\right)^{n+1},\left(\frac{2}{3}\right)^{n}\frac{1}{6},\left(\frac{2}{3}\right)^{5}=\frac{32}{243}=\frac{64}{486}=\frac{1}{6} \cdot \frac{64}{81}<\frac{1}{6}$.
Thus, the smallest natural value of $n=5$.
Answer. 5.
|
5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle with a radius of 15 touches two adjacent sides $AB$ and $AD$ of the square $ABCD$. On the other two sides, the circle intersects at points, cutting off segments of 6 cm and 3 cm from the vertices, respectively. Find the length of the segment that the circle cuts off from vertex $B$ at the point of tangency.
|
# Solution.

Fig. 1
Let $X$ be the desired segment, then $X+15$ is the side of the square. The segment $K L=15+X-6-3=X+6$. Consider $\triangle O N L$. By the Pythagorean theorem, the following equality holds:
$$
15^{2}=X^{2}+\left(\frac{X+6}{2}\right)^{2}
$$
This is a quadratic equation in terms of $X$, which has only one positive root 12.
Answer. 12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle with a radius of 10 touches two adjacent sides $AB$ and $AD$ of the square $ABCD$. On the other two sides, the circle intersects at points, cutting off segments of 4 cm and 2 cm from the vertices, respectively. Find the length of the segment that the circle cuts off from vertex $B$ at the point of tangency.
|
Solution.
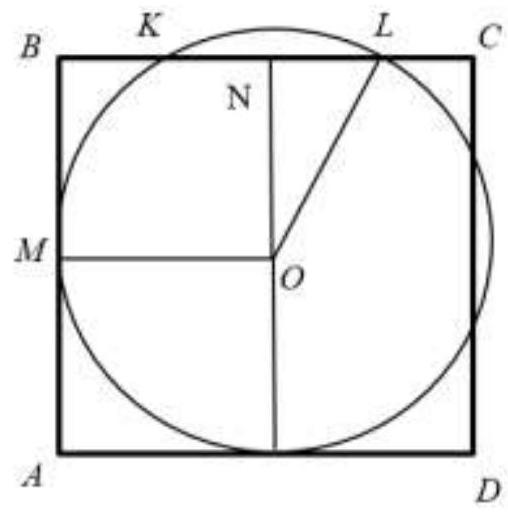
Fig. 1
Let $X$ be the desired segment, then $X+10$ is the side of the square. The segment $K L=10+X-4-2=X+4$. Consider $\triangle O N L$. By the Pythagorean theorem, the following equality holds:
$$
10^{2}=X^{2}+\left(\frac{X+4}{2}\right)^{2}
$$
This is a quadratic equation in terms of $X$, which has only one positive root 8.
Answer. 8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle touches two adjacent sides $AB$ and $AD$ of square $ABCD$ and cuts off segments of length 4 cm from vertices $B$ and $D$ at the points of tangency. On the other two sides, the circle intersects and cuts off segments of 2 cm and 1 cm from the vertices, respectively. Find the radius of the circle.
|
# Solution.
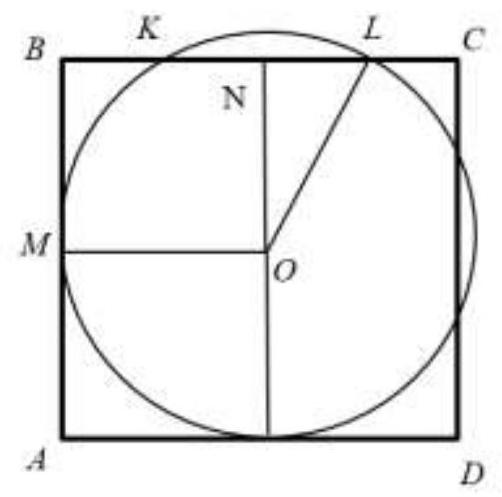
Fig. 1
Let $R$ be the radius of the circle, then $R+4$ is the side of the square. The segment $K L=4+R-2-1=R+1$. Consider the triangle $O N L$. By the Pythagorean theorem, the following equality holds:
$$
R^{2}=4^{2}+\left(\frac{1+R}{2}\right)^{2}
$$
This is a quadratic equation in terms of $R$, which has only one positive root 5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle touches two adjacent sides $AB$ and $AD$ of square $ABCD$ and cuts off segments of length 8 cm from vertices $B$ and $D$ at the points of tangency. On the other two sides, the circle intersects and cuts off segments of 4 cm and 2 cm from the vertices, respectively. Find the radius of the circle.
|
# Solution.
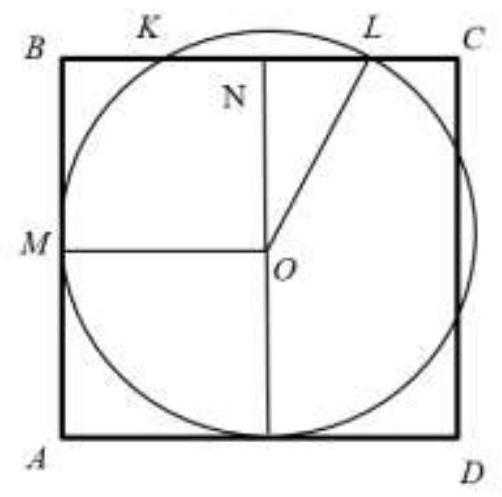
Fig. 1
Let $R$ be the radius of the circle, then $R+8$ is the side of the square. The segment $K L=8+R-4-2=R+2$. Consider $\triangle O N L$. By the Pythagorean theorem, the following equality holds:
$$
R^{2}=8^{2}+\left(\frac{2+R}{2}\right)^{2}
$$
This is a quadratic equation in terms of $R$, which has only one positive root 10.
Answer. 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Development of a Method for Optimizing a Mathematical Problem
Problem Statement. At Unit 3 of an oil and gas company, the task is to optimize the operation of the navigation system elements. The task of this unit is to receive encrypted signals from Unit 1 and Unit 2, synthesize the incoming data packets, and further transmit them to the Data Processing Center. Write a program that receives one natural number from each unit as input, and returns a third number calculated by raising the value received from the first unit to the power of the number received from the second unit. Only the last digit of the resulting value will be sent to the Center. Use the following test values:
- From the first unit: 954950230952380948328708
- From the second unit: 470128749397540235934750230
|
Solution to the problem. Solving the problem "head-on" by raising one number to the power of another is bound to exceed the computational power not only of a single computer but even a data center would require a certain amount of time to perform the calculations. Since we only need to send the last digit, let's focus on calculating just that. Note that when raising numbers to a certain power, the last digit always has a certain cycle from a limited set of elements. For example: $2^{2}=4,2^{3}=8,2^{4}=16,2^{5}=32,2^{4}=64$.
Thus, we only need to take the last digit of the first number and the remainder of the second number divided by 4, and only then raise the first number to the power of the second.
Example of program implementation in Python
```
number = input()
degree = input()
number = int(str(number)[-1])
degree = int(str(degree)[-2] + str(degree)[-1]) % 4
if degree == 0:
degree = 4
print((number ** degree))
```
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Development of a Method for Optimizing a Mathematical Problem
Problem Statement. At Unit 3 of an oil and gas company, the task is to optimize the operation of the navigation system elements. The task of this unit is to receive encrypted signals from Unit 1 and Unit 2, synthesize the incoming data packets, and further transmit them to the Data Processing Center. Write a program that takes one natural number from each unit as input and returns a third number, calculated by raising the value received from the first unit to the power of the number received from the second unit. Only the last digit of the resulting value will be sent to the Center. Use the following test values:
- From the first unit: 954950230952380948328708
- From the second unit: 470128749397540235934750230
|
Solution to the problem. Solving the problem "head-on" by raising one number to the power of another is bound to exceed the computational power not only of a single computer but even a data center would require a certain amount of time to perform the calculations. Since we only need to send the last digit, let's focus on calculating just that. Note that when raising numbers to a certain power, the last digit always has a certain cycle from a limited set of elements. For example: $2^{2}=4,2^{3}=8,2^{4}=16,2^{5}=32,2^{4}=64$.
Thus, we only need to take the last digit of the first number and the remainder of the second number divided by 4, and only then raise the first number to the power of the second.
Example of program implementation in Python
```
number = input()
degree = input()
number = int(str(number)[-1])
degree = int(str(degree)[-2] + str(degree)[-1]) % 4
if degree == 0:
degree = 4
print((number ** degree))
```
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Does there exist a natural number that, when divided by the sum of its digits, gives both a quotient and a remainder of 2014? If there is more than one such number, write their sum as the answer. If no such numbers exist, write 0. (12 points)
#
|
# Solution:
Suppose there exists a natural number $\boldsymbol{n}$ with the sum of its digits $\boldsymbol{s}$, such that $n=2014 s+2014$, from which we get $n-s=2013 s+2014$. By the divisibility rule, $n-s$ is divisible by 3. However, the number $2013 s+2014$ is not divisible by 3, since the number $2013s$ is a multiple of 3, while the number 2014 is not. This is a contradiction.
Answer: 0.
| Points | Criteria for evaluating the performance of task № $\mathbf{5}$ |
| :---: | :--- |
| $\mathbf{1 2}$ | A correct and justified sequence of all steps of the solution is provided. All transformations and calculations are performed correctly. The correct answer is obtained. |
| $\mathbf{1 0}$ | A correct sequence of all steps of the solution is provided. There are gaps in the justification of divisibility by 3 or a computational error or typo that does not affect the further course of the solution. As a result of this error or typo, an incorrect answer may be obtained. |
| $\mathbf{5}$ | The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, the equation for the desired number is correctly written); - the other part is either not performed or performed incorrectly, possibly even with logical errors (for example, the desired number is found or its absence is incorrectly justified). The solution may be incomplete. |
| $\mathbf{0}$ | All cases of the solution that do not correspond to the above criteria for scoring 5, 10, and 12 points. |
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. Maximum 20 points
Svetlana is convinced that any feline can be interesting to her for two purposes - catching mice and conducting cat therapy. Based on these considerations, Svetlana has decided to acquire 2 kittens, each of which has an equal probability of being either a male or a female. The weekly production possibility curve for males is $\mathrm{M}=80-4 \mathrm{~K}$, and for females $\mathrm{M}=16-0.25 \mathrm{~K}$, where $\mathrm{M}$ is the number of mice caught per week, and $\mathrm{K}$ is the number of hours devoted to cat therapy.
(a) Determine the maximum number of mice that 2 kittens can catch in a week with the optimal combination of males and females for this purpose.
(b) Determine the number of different variants of the combined production possibility curve Svetlana has when acquiring 2 kittens.
(c) Determine the analytical and graphical form of the combined production possibility curve for 2 kittens for each of the possible combinations of males and females.
(d) In the end, the kitten seller delivered the order, consisting of a male and a female, but also noted that the male has a twin brother, whom Svetlana can receive for free in her caring hands. Determine the analytical and graphical form of the combined production possibility curve if Svetlana agrees to the offer to take the third kitten.
|
# Solution:
(a) Males catch mice better than females. Two males can catch $40 \cdot 2=80$ mice in a week.
Answer: 160 (2 points).
(b) There are 3 options: one male and one female, two males, two females.
Answer: 3 (2 points).
(c) Two males with individual PPFs: $M=80-4K$. The opportunity costs for males are constant and equal (they can produce cat therapy in any order). The first produces $K_1$ units of cat therapy, and the second produces $K_2$ units of cat therapy. $K_{1}+K_{2}=K$. Joint PPF: $M=80-4 K_{1}+80-4 K_{2}$.
$$
M=80-4\left(K-K_{2}\right)+80-4 K_{2}=160-4 K
$$
Answer: two males $M=160-4 K, K \leq 40+$ graph (2 points).
Two females with individual PPFs: $M=16-0.25 K$. The solution is similar to the previous part: $M=32-0.25 K, K \leq 128$.
Answer: two females $M=32-0.25 K, K \leq 128+$ graph (2 points).
One male $M_{1}=80-4 K_{1}$ and one female $M_{2}=16-0.25 K_{2}$. The opportunity costs for the female are lower, so she produces cat therapy first.
$$
\begin{gathered}
K_{1}=0, K_{2}=K, K \leq 64 \\
K_{1}=K-64, K_{2}=64,64<K \leq 84
\end{gathered}
$$
The joint PPF can be obtained by substituting these values into the function $M=M_1 + M_2 = 80-4 K_{1} + 16-0.25 K_{2}$:
PPF:
$$
\begin{aligned}
& M=96-0.25 K, 0<K \leq 64 \\
& M=336-4 K, 64<K \leq 84
\end{aligned}
$$
Answer:
$$
M=96-0.25 K, 0<K \leq 64
$$
$M=336-4 K, 64<K \leq 84+$ graph (4 points)
(d) The problem reduces to finding the joint PPF for three individual functions:
$M=80-2 K, M=80-2 K, M=16-0.25 K$. Clearly, the problem can be simplified by combining the joint PPF of two males from the previous part $M=160-4 K$ with the PPF of one female $M=16-0.25 K$.
Similarly to the reasoning in the previous part, we get:
$$
\begin{gathered}
K_{1}=0, K_{2}=K, K \leq 64 \\
K_{1}=K-64, K_{2}=64,64<K \leq 104
\end{gathered}
$$
Substituting these values of $K_{1}$ and $K_{2}$ into $M=M_{1}+M_{2}=160-4 K_{1}+16-0.25 K_{2}$.
Joint PPF of two males and one female:
$$
\begin{gathered}
M=176-0.25 K, 0<K \leq 64 \\
M=416-4 K, 64<K \leq 104
\end{gathered}
$$
Answer:
$$
\begin{gathered}
M=176-0.25 K, 0<K \leq 64 \text { (4 points) } \\
M=416-4 K, 64<K \leq 104+\text { graph (4 points) }
\end{gathered}
$$
Arithmetic errors that did not lead to a distortion of the meaning of the problem - penalty 2 points.
Answers without solutions are not credited.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. Maximum 15 points
Find the values of the variable $x$ such that the four expressions: $2 x-6, x^{2}-4 x+5, 4 x-8, 3 x^{2}-12 x+11$ differ from each other by the same number. Find all possible integer values of the variable $x$ for any order of the expressions.
|
# Solution:
From the properties of numbers that differ from the following in a numerical sequence by the same number, we form two equations:
$$
\begin{gathered}
x^{2}-4 x+5-(2 x-6)=4 x-8-\left(x^{2}-4 x+5\right) \\
4 x-8-\left(x^{2}-4 x+5\right)=3 x^{2}-12 x+11-(4 x-8)
\end{gathered}
$$
Only \( x=4 \) satisfies both equations.
## Criteria.
- A correct solution to the problem and the correct answer are provided - 15 points (maximum),
- A correct solution to the problem is provided, but the wrong answer or no answer is given - 8 points (rounded to the nearest whole number, half the maximum),
- An error in the solution, but the correct answer is obtained - 7 points (rounded to the nearest whole number, half the maximum minus one),
- The solution is incorrect or missing, but the correct answer is obtained - 1 point (under any circumstances),
- The solution is incorrect or missing, and the wrong answer or no answer is given - 0 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. Maximum 20 points
Let's say in country A there are only two firms engaged in research and development in a certain field. Currently, each of them independently decides whether to participate in the development of a new technology. It is known that if a firm develops a new technology, it will bring it $V$ monetary units of income in the future, provided the second firm is either unsuccessful or does not participate in the development. If both firms develop the new technology, each will receive $0.5 \mathrm{~V}$ monetary units. The investment costs for research and development for each firm will be IC monetary units regardless of the success of the development. Let the probability of success for each firm be $\alpha, 0<\alpha<1$. Then we can write the expected income of each firm as $\alpha(1-\alpha) V+0.5 \alpha^{2} V$, if both firms participate in the development, or $\alpha V$, if only the given firm participates in the development.
(a) Under what conditions will both firms participate in the development?
(b) How many firms will participate in the development if $V=16, \alpha=0.5$, and $I C=5$?
(c) Let's assume that social welfare can be assessed as the total profit of the firms. Will the number of firms found in part (b) be socially optimal? Comment on the result obtained.
|
# Solution and Grading Scheme:
(a) For each firm to decide to participate in the development, it is necessary that the expected profit from participation for each firm is greater than 0 (we use the formula for expected income in the case where both firms are involved in development):
$\alpha(1-\alpha) V+0.5 \alpha^{2} V-I C \geq 0$ (4 points)
(b) Substitute the known variables into the inequality from part (a) and check its validity:
$$
\begin{gathered}
0.5^{2} \cdot 16+0.5 \cdot 0.5^{2} \cdot 16-5 \geq 0 \\
4+2-5>0 \text { (4 points) }
\end{gathered}
$$
It makes no sense to check the equilibrium where only one firm is involved in development, as two inequalities must be satisfied simultaneously:
$$
\alpha V-\text { IC } \geq 0 \text { and } \alpha(1-\alpha) V+0.5 \alpha^{2} V-\text { IC }<0
$$
We know that the second one is not satisfied. (2 points)
(c) Calculate in which case the total profit will be greater:
1) both firms participate in development:
$\pi_{1}+\pi_{2}=2\left((1-\alpha) V+0.5 \alpha^{2} V-I C\right)=2(6-5)=2$ (3 points)
2) one firm participates in development.
$\pi_{\text {one }}=\alpha V-\mathrm{IC}=0.5 \cdot 16-5=8-5=3$. (3 points)
We see that it is more efficient for one firm to be involved in development. This is due to the fact that in the case of two firms participating, the duplication of research costs leads to a greater increase in costs than the increase in potential revenue for the firms due to the increased probability of discovery. (4 points)
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 5. Maximum 15 points
In the treasury of the Magic Kingdom, they would like to replace all old banknotes with new ones. There are a total of 3,628,800 old banknotes in the treasury. Unfortunately, the machine that prints new banknotes requires major repairs and each day it can produce fewer banknotes: on the first day, it can only produce half of the banknotes that need to be replaced; on the second day, only a third of the remaining old banknotes in the treasury; on the third day, only a quarter, and so on. Each run of the machine in any state costs the treasury 90,000 monetary units (m.u.), and major repairs will cost 800,000 m.u. After major repairs, the machine can produce no more than one million banknotes per day. The kingdom has allocated no more than 1 million m.u. for the renewal of banknotes in the treasury.
(a) After how many days will 80% of the old banknotes be replaced?
(b) Will the kingdom be able to replace all the old banknotes in the treasury?
|
# Solution:
(a) If a major repair is to be carried out, it is most effective to do so on the second day, as this will allow the production of new banknotes to increase from 604,800 to 1 million on that day, and the production will also be 1 million in subsequent days, which is more than the possibilities without major repairs. It is not efficient to carry out the major repair on the first day, as the production without it is 1,814,400 banknotes. (9 points).
With the major repair, the budget will cover the repair itself and 2 launches of the machine, thus the maximum number of banknotes that can be replaced is 1,814,400 + 1,000,000 = 2,814,400 banknotes, which is less than 80% of the number of old banknotes (2 points).
Let's consider the option of not repairing the machine. We have enough funds for only 11 launches. In percentage terms, the remaining amount is:
After the first day: 50%.
After the second day: 200/3.
After the third day: 25%.
After the fourth day: 20%.
Thus, it will take 4 days (2,903,040 banknotes will be replaced), which is 80% of the banknotes. (2 points)
(b) After 11 launches, we will only be able to replace 3,326,400 banknotes, i.e., in any case, we will not be able to recast all the banknotes without repairing the machine.
It can also be noted that with any launch, there will always be a part of the banknotes that remain unreplaced. (2 points)
# Federal State Budget Educational Institution of Higher Education Russian Presidential Academy of National Economy and Public Administration
Olympiad of Schoolchildren of RANEPA in Economics 2022 - 2023 academic year 10-11 grade Final stage Variant 2.
#
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. Maximum 20 points
Let's say in country A there are only two firms engaged in research and development in a certain field. Currently, each of them independently decides whether to participate in the development of a new technology. It is known that if a firm develops a new technology, it will bring it $V$ monetary units of income in the future, provided the second firm is either unsuccessful or does not participate in the development. If both firms develop the new technology, each will receive $0.5 \mathrm{~V}$ monetary units. The investment costs for research and development for each firm will be IC monetary units regardless of the success of the development. Let the probability of success for each firm be $\alpha, 0<\alpha<1$. Then we can write the expected income of each firm as $\alpha(1-\alpha) V+0.5 \alpha^{2} V$, if both firms participate in the development, or $\alpha V$, if only the given firm participates in the development.
(a) Under what conditions will both firms participate in the development?
(b) How many firms will participate in the development if $V=24, \alpha=0.5$, and $I C=7$?
(c) Let's assume that social welfare can be assessed as the total profit of the firms. Will the number of firms found in part (b) be socially optimal? Comment on the result obtained.
|
# Solution and Grading Scheme:
(a) For each firm to decide to participate in the development, it is necessary that the expected profit from participation for each firm is greater than 0 (we use the formula for expected income in the case where both firms are involved in development):
$\alpha(1-\alpha) V+0.5 \alpha^{2} V-I C \geq 0$ (4 points)
(b) Substitute the known variables into the inequality from part (a) and check its validity:
$$
0.5^{2} \cdot 24+0.5 \cdot 0.5^{2} \cdot 24-7 \geq 0
$$
$6+3-7>0$ (4 points)
It makes no sense to check the equilibrium where only one firm is involved in development, as two inequalities must be satisfied simultaneously:
$\alpha V - IC \geq 0$ and $\alpha(1-\alpha) V+0.5 \alpha^{2} V - IC < 0$.
We know that the second one is not satisfied. (2 points)
(c) Calculate in which case the total profit will be greater:
1) both firms participate in development:
$\pi_{1}+\pi_{2}=2\left((1-\alpha) V+0.5 \alpha^{2} V-I C\right)=2(9-7)=4$ (3 points)
2) one firm participates in development.
$\pi_{\text {one }}=\alpha V-I C=0.5 \cdot 24-7=12-7=5$. (3 points)
We see that it is more efficient for one firm to be involved in development. This is due to the fact that in the case of two firms participating, the duplication of research costs leads to a greater increase in costs than the increase in potential income for the firms due to the increased probability of discovery. (4 points)
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 3. Maximum 20 points
Consider a consumer who plans to use a coffee machine. Let's assume the consumer lives for two periods and values the benefit of using the coffee machine at 10 monetary units in each period. Coffee machines can be produced in two types: durable, working for two periods, and low-quality, completely breaking down at the end of each period. It is known that the technology for producing durable machines allows them to be produced with constant average costs of 6 monetary units. Low-quality coffee machines can be produced with constant average costs of C monetary units.
(a) Suppose coffee machines are produced only by a monopoly. For what average costs C will the monopoly produce only durable coffee machines?
(b) How would your answer to part (a) change if coffee machines of both types are produced in a perfectly competitive market?
(c) What conditions for choosing the lifespan of a coffee machine have we not considered? Come up with at least one and explain how its inclusion in the model would affect the choice in the conditions of part (a) and part (b).
|
# Solution and Grading Scheme:
(a) When coffee machines are produced by a monopoly, it sets a selling price that will extract all consumer surplus:
1) when producing a durable machine, the price equals the consumer's benefit from using the coffee machine for 2 periods $\mathrm{p}_{\mathrm{L}}=2 \cdot 10=20$ (1 point)
2) when producing a low-quality coffee machine, the price will be equal to the benefit from using it for one period $\mathrm{p}_{\mathrm{s}}=10 .(\mathbf{1}$ point)
Calculate the profit from producing a durable machine: $\pi_{\mathrm{L}}=20-6=14$. ( $\mathbf{1}$ point)
Profit from producing a low-quality coffee machine: $\pi_{\mathrm{S}}=10$ - c. ( $\mathbf{1}$ point)
For the monopolist to find it profitable to produce a durable machine, the profit from its production must be greater than the profit from producing two low-quality machines (since the service life of the durable one is twice as long):
$$
14>2(10 \text { - c) (2 points) }
$$
From this, it follows that c $>3$. ( $\mathbf{1}$ point)
(b) In this case, coffee machines will be sold at prices equal to the costs of their production: $\mathrm{q}_{\mathrm{L}}=6$ and $\mathrm{q}_{\mathrm{s}}=\mathrm{c}$. (2 points) For only durable machines to be produced, it is necessary that consumers prefer to buy only them.
The net consumer surplus from buying a durable machine will be $2 \cdot 10-\mathrm{q}_{\mathrm{L}}=20-$ $6=14$. ( 2 points)
The net consumer surplus from buying two low-quality coffee machines will be $2\left(10-\mathrm{q}_{\mathrm{s}}\right)=2(10-\mathrm{c}) .(\mathbf{2}$ points)
Thus, the decision to buy only durable machines will be made if the inequality $14>2(10-$ c) and c $>3$ is satisfied, i.e., the answer does not change. ( $\mathbf{1}$ point)
(c) costs of purchasing (going to the store, searching online - can vary over two periods), costs of disposing of a broken coffee machine (need to recycle it), etc. You need to demonstrate how the inequalities change with the addition of this new condition. (6 points)
|
3
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 5. Maximum 20 points
In Moscow, a tennis tournament is being held. Each team consists of 3 players. Each team plays against every other team, with each participant of one team playing against each participant of the other exactly one match. Due to time constraints, a maximum of 150 matches can be played in the tournament. How many teams can participate in the tournament so that everyone gets to play?
|
# Solution:
Assume there are two teams - then each of the three members of one team plays against each of the other - i.e., $3 * 3 = 9$ games. The number of team pairs can be $150: 9 = 16.6 \ldots$ a maximum of 16. Two teams form only one pair; three teams form three pairs. If there is a fourth team, add 3 more pairs, so in total 6. With each subsequent team, the number of pairs increases by one more: (2 teams - 1 pair, 3 teams $-1+2$ pairs, 4 teams $-1+2+3$ pairs, etc.) Thus, if there are 6 teams, $1+2+3+4+5=15$ pairs. On the seventh day, it is already $15+6=21$, which exceeds the maximum of 16. Therefore, the answer is: 6 teams.
## Criteria:
Correct answer obtained with sound reasoning - 20 points Correct chain of reasoning, but an arithmetic error leads to an incorrect answer - 5 points.
## Federal State Budget Educational Institution of Higher Education Russian Presidential Academy of National Economy and Public Administration
## RANEPA School Olympiad in Economics 2022 - 2023 Academic Year 8-9 grade Final Stage Variant 2.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 3. Maximum 20 points
Consider a consumer who plans to use a coffee machine. Let's assume the consumer lives for two periods and evaluates the benefit from using the coffee machine at 20 monetary units in each period. Coffee machines can be produced in two types: durable, working for two periods, and low-quality, completely breaking down at the end of each period. It is known that the technology for producing durable machines allows them to be produced with constant average costs of 12 monetary units. Low-quality coffee machines can be produced with constant average costs of C monetary units.
(a) Suppose coffee machines are produced only by a monopoly. For what average costs C will the monopoly produce only durable coffee machines?
(b) How would your answer to part (a) change if coffee machines of both types are produced in a perfectly competitive market?
(c) What conditions for choosing the lifespan of a coffee machine have we not considered? Come up with at least one and explain how its inclusion in the model would affect the choice in the conditions of part (a) and part (b).
|
# Solution and Grading Scheme:
(a) When coffee machines are produced by a monopoly, it sets a selling price that will extract all consumer surplus:
1) when producing a durable machine, the price equals the consumer's benefit from using the coffee machine for 2 periods $\mathrm{p}_{\mathrm{L}}=2 \cdot 20=40$ (1 point)
2) when producing a low-quality coffee machine, the price will be equal to the benefit from using it for one period $\mathrm{p}_{\mathrm{s}}=20$. (1 point)
Let's calculate the profit from producing a durable machine: $\pi_{\mathrm{L}}=40-12=28$. (1 point)
Profit from producing a low-quality coffee machine: $\pi_{\mathrm{s}}=20$ - c. (1 point)
For the monopolist to find it profitable to produce a durable machine, the profit from its production must be greater than the profit from producing two low-quality machines (since the service life of the durable one is twice as long):
$$
28>2(20-c) (2 \text{ points) }
$$
From this, it follows that c $>6$. (1 point)
(b) In this case, coffee machines will be sold at prices equal to the costs of their production: $\mathrm{q}_{\mathrm{L}}=12$ and $\mathrm{q}_{\mathrm{S}}=\mathrm{c}$. (2 points) For only durable machines to be produced, it is necessary that consumers prefer to buy only them.
The net consumer surplus from buying a durable machine will be $2 \cdot 20-\mathrm{q}_{\mathrm{L}}=40-$ $12=28. (2$ points)
The net consumer surplus from buying two low-quality coffee machines will be $2\left(20-\mathrm{q}_{s}\right)=2(20-\mathrm{c}). (2$ points)
Thus, the decision to buy only durable machines will be made if the inequality $28>2(20-$ c) and c $>6$ is satisfied, i.e., the answer does not change. (1 point)
(c) costs of purchasing (going to the store, searching online - can vary over two periods), costs of disposing of a broken coffee machine (need to recycle it), etc. It is necessary to demonstrate how the inequalities change with the addition of this new condition. (6 points)
|
6
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 5. Maximum 20 points
In Moscow, a tennis tournament is being held. Each team consists of 3 players. Each team plays against every other team, with each participant of one team playing against each participant of the other exactly one match. Due to time constraints, a maximum of 200 matches can be played in the tournament. How many teams can participate in the tournament so that everyone gets to play?
#
|
# Solution:
Assume there are two teams - then each of the three members of one team plays against each of the other - i.e., $3 * 3=9$ games. The number of team pairs can be $200: 9=22.2 \ldots$ a maximum of 22. Two teams form only one pair; three teams form three pairs. If there is a fourth team, add 3 more pairs, so in total 6. With each subsequent team, one more is added to the number of pairs from the previous number: (2 teams - 1 pair, 3 teams $-1+2$ pairs, 4 teams $-1+2+3$ pairs, etc.). Thus, on the seventh day, it is possible to form $1+2+3+4+5+6=21$ pairs. On the eighth day, it is already $21+7=28$, which exceeds the maximum of 22. Therefore, the answer is: 7 teams.
## Criteria:
Correctly derived the correct answer - 20 points The chain of reasoning is correct, but due to an arithmetic error, an incorrect answer is obtained - 5 points.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a certain kingdom, the workforce consists only of the clan of dwarves and the clan of elves. Historically, in this kingdom, dwarves and elves have always worked separately, and no enterprise has ever hired both at the same time. The aggregate supply of labor resources of the dwarves is represented by the function $w_{\text {dwarves }}^{S}=1+L / 3$, and the aggregate supply of labor resources of the elves is $w_{\text {elves }}^{S}=3+L$. The inverse function of the aggregate demand for dwarf labor is $w_{\text {dwarves }}^{D}=10-2 L / 3$, and the inverse function of the aggregate demand for elf labor is $w_{\text {elves }}^{D}=18-2 L$. The king, who recently ascended to the throne, is very concerned that the wage rates of his subjects are different, so he issued a law stipulating that the wages of elves and dwarves must be the same and that workers in the kingdom should not be discriminated against based on clan affiliation. At the same time, the king believes that regulatory wage rate control will have a negative impact on the economy of his kingdom and requires all his subjects to behave in a perfectly competitive manner. By what factor will the wage of the group of workers whose wage was lower before the king's intervention increase, if firms in the kingdom are indifferent to hiring elves or dwarves?
|
# Solution:
Before the law was introduced, the wages of elves and gnomes were determined by the condition of equality of supply and demand in each market:
$w_{\text {gnome }}^{S}=w_{\text {gnome }}^{D}$, from which $1+\frac{L}{3}=10-2 L / 3$ and $L_{\text {gnome }}=9$ and $w_{\text {gnome }}=4$
$w_{\text {elf }}^{S}=w_{\text {elf }}^{D}$, from which $3+L=18-2 L$ and $L_{\text {elf }}=5 w_{\text {elf }}=8$
After the law was introduced, all market participants must behave in a perfectly competitive manner, and the total demand for labor resources must equal the total supply of labor resources. Therefore,
$L_{\text {gnome }}^{S}+L_{\text {elf }}^{S}=L_{\text {elf }}^{D}+L_{\text {gnome }}^{D}$, where
$L_{\text {gnome }}^{S}+L_{\text {elf }}^{S}=\left\{\begin{array}{l}3 w-3, \text { if } w \leq 3 \\ 4 w-6, \text { if } w>3\end{array}\right.$
$L_{\text {elf }}^{D}+L_{\text {gnome }}^{D}=\left\{\begin{array}{l}9-w / 2, \text { if } w \geq 10 \\ 24-2 w, \text { if } w solutions. All transformations and calculations are correct. The correct answer is obtained. | $\mathbf{1 0}$ |
| The correct sequence of all steps in the solution is provided. There are gaps in the justification of the choice of number combinations (for example, one extra solution (0+4) is not considered, pairs of digits are not divided by 2, etc.) or a computational error or typo that does not affect the further course of the solution. As a result of this error or typo, an incorrect answer may be obtained. | |
| The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, part of the combinations is considered and calculated correctly); | |
| - the other part is either not performed or performed incorrectly, possibly | |
| even with logical errors (for example, most combinations are not considered | |
| or extra combinations are considered, combinations are calculated incorrectly, cases of erasing the same digit (2+2, | |
| 5+5, 8+8) are not considered, etc.); | |
| In this case, the solution may be incomplete. | |
All cases of the solution that do not meet the above criteria for scoring 3 and 6 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a 2015-digit number divisible by 9. Let the sum of its digits be $\boldsymbol{a}$, the sum of the digits of $\boldsymbol{a}$ be $\boldsymbol{b}$, and the sum of the digits of $\boldsymbol{b}$ be $\boldsymbol{c}$. Find the number $\boldsymbol{c}$. (14 points).
|
Solution:
The sum of the digits of any number gives the same remainder when divided by 9 as the number itself.
The largest 2015-digit number consists of 2015 nines. The sum of its digits is $2015 * 9 = 18135$, i.e., it has 5 digits.
The sum of the digits of the largest 5-digit number is 45 (b).
Numbers less than 45 and divisible by 9 are 9, 18, 27, 36, and 45. The sum of their digits is 9.
## Answer: 9.
| Points | Criteria for evaluating the performance of task № 3 |
| :---: | :--- |
| $\mathbf{1 4}$ | A correct and justified sequence of all steps of the solution is provided. All transformations and calculations are performed correctly. The correct answer is obtained. |
| $\mathbf{1 0}$ | A correct sequence of all steps of the solution is provided. There are gaps in the justification of upper estimates or possible values of the numbers $\boldsymbol{a}$ and (or) $\boldsymbol{b}$, or a computational error or typo that does not affect the further course of the solution. As a result of this error or typo, an incorrect answer may be obtained. |
| $\mathbf{5}$ | The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, a correct upper estimate is obtained only for the number $\boldsymbol{a}$ or only for the number $\boldsymbol{b}$); - the other part is either not performed or performed incorrectly, possibly even with logical errors (for example, finding another upper estimate). In this case, the solution may be incomplete. |
| $\mathbf{0}$ | All cases of the solution that do not correspond to the above criteria for scoring 5 and 10 points. |
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the extensions of sides $\boldsymbol{A B}, \boldsymbol{B C}, \boldsymbol{C D}$ and $\boldsymbol{A}$ of the convex quadrilateral $\boldsymbol{A} \boldsymbol{B C D}$, points $\boldsymbol{B}_{1}, \boldsymbol{C}_{1}, \boldsymbol{D}_{1}$ and $\boldsymbol{A}_{1}$ are taken such that $\boldsymbol{B} \boldsymbol{B}_{1}=\boldsymbol{A B}, \boldsymbol{C} \boldsymbol{C}_{1}=\boldsymbol{B C}, \boldsymbol{D} \boldsymbol{D}_{1}=\boldsymbol{C D}$ and $\boldsymbol{A} \boldsymbol{A}_{1}=\boldsymbol{D} \boldsymbol{A}$. How many times larger is the area of quadrilateral $\boldsymbol{A}_{1} \boldsymbol{B}_{1} \boldsymbol{C}_{1} \boldsymbol{D}_{1}$ compared to the area of quadrilateral $A B C D .(10$ points)
|
# Solution:
Let the area of quadrilateral $\boldsymbol{A} \boldsymbol{B C D}$ be $\boldsymbol{S}$. The median divides the area of a triangle in half. Therefore, $S_{A B C}=S_{C B B 1}=S_{C B 1 C 1}$. Consequently, $S_{B B 1 C 1}=2 S_{A B C}$. Similarly, we have $S_{C C 1 D 1}=2 S_{B C D}$, $S_{D D 1 A 1}=2 S_{C D A}$, and $S_{A A 1 B 1}=2 S_{D A B}$. Adding these four equations, we get: $S_{B B 1 C 1}+S_{C C 1 D 1}+S_{D D 1 A 1}+S_{A A 1 B 1}=2\left(S_{A B C}+S_{B C D}+S_{C D A}+S_{D A B}\right)=4 S$. Therefore, $S_{A I B I C I D 1}=4 S+S=5 S$.
Answer: 5.
| Points | Criteria for evaluating the performance of task № 3 |
| :---: | :--- |
| $\mathbf{1 0}$ | A correct and justified sequence of all steps of the solution is provided. All transformations and calculations are performed correctly. The correct answer is obtained. |
| $\mathbf{8}$ | A correct sequence of all steps of the solution is provided. There are gaps in the justification of the area relationships of triangles or a computational error or typo that does not affect the further course of the solution. As a result of this error or typo, an incorrect answer may be obtained. |
| $\mathbf{5}$ | The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, the property of the median of a triangle is given or the areas of right triangles are correctly calculated); - another part is either not performed or performed incorrectly, possibly even with logical errors (for example, the area relationships of triangles are obtained incorrectly or only a special case of a quadrilateral is considered). The solution may be incomplete. |
| $\mathbf{0}$ | All cases of the solution that do not meet the criteria for scoring 5, 8, and 10 points. |
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The power in the kingdom of gnomes was seized by giants. The giants decided to get rid of the gnomes and told them the following: "Tomorrow we will line you up so that each of you will see those who stand after and not see those who stand before (i.e., the 1st sees everyone, the last sees no one). We will put either a black or a white hat on each of you (equally likely, each will have either a black or a white hat) and ask what color it is. Those who answer correctly will be released, and those who answer incorrectly will be executed." How many gnomes can be risked at a minimum with certain agreements before the execution, if there are p gnomes in the kingdom and p $<\infty$. Justify your answer. (12 points)
#
|
# Solution:
The gnomes agree as follows: they risk the first gnome, telling him the following: "Denote a white hat as 1 and a black hat as 0, and count the sum of the remaining n-1 gnomes. If the sum is even, say 'white'; if it is odd, say 'black'. Under this condition, the first gnome dies with a probability of $1 / 2$. The second gnome counts the sum of the (n-2) gnomes. If the sum has changed, it means he has a white hat. The others hear him and adjust the parity of the remaining gnomes, and so on. Answer: 1 gnome.
Answer: 1.
| Points | Criteria for evaluating the completion of task № 5 |
| :---: | :---: |
| 12 | A correct and justified sequence of all steps of the solution is provided. The correct answer is obtained. |
| 10 | A correct sequence of all steps of the solution is provided. There are gaps in the justification of the parity of the sum, but they do not affect the further course of the solution. |
| 8 | The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, it is proposed to denote a white hat as 1 and a black hat as 0); - another part is either not performed or performed incorrectly, possibly even with logical errors (for example, the necessity of adjusting the parity of the sum is not proven). The solution may be incomplete. |
| 5 | The problem is not solved, but there is some progress in its solution, i.e.: - the initial part of the solution is performed correctly (for example, the assumption about the probable death of the first gnome is correctly stated or the cases of even and odd numbers of gnomes are considered); - the main part is either not performed or performed incorrectly, possibly even with logical errors (for example, the correspondence between the color of the hat and the numbers is not shown, or the probability of the first gnome's death is insufficiently justified, or an incorrect conclusion is drawn from the parity and non-parity of the number of gnomes, or the assumption is made that the gnomes can exchange additional information or that execution occurs immediately upon an incorrect answer and the others see it). The solution may be incomplete. |
| $\mathbf{0}$ | All cases of the solution that do not meet the criteria for scoring 5, 8, 10, and 12 points. |
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the extensions of sides $\boldsymbol{A B}, \boldsymbol{B C}, \boldsymbol{C D}$ and $\boldsymbol{A}$ of the convex quadrilateral $\boldsymbol{A} \boldsymbol{B C D}$, points $\boldsymbol{B}_{1}, \boldsymbol{C}_{1}, \boldsymbol{D}_{1}$ and $\boldsymbol{A}_{1}$ are taken such that $\boldsymbol{B} \boldsymbol{B}_{1}=\boldsymbol{A B}, \boldsymbol{C} \boldsymbol{C}_{1}=\boldsymbol{B C}, \boldsymbol{D D}_{1}=\boldsymbol{C D}$ and $\boldsymbol{B} \boldsymbol{B}_{1}=\boldsymbol{A B}$ and $\boldsymbol{A} \boldsymbol{A}_{1}=\boldsymbol{A}$. How many times smaller is the area of quadrilateral $\boldsymbol{A} \boldsymbol{B} \boldsymbol{C D}$ compared to the area of quadrilateral $\boldsymbol{A}_{1} \boldsymbol{B}_{1} C_{1} \boldsymbol{D}_{1}$. (10 points)
|
# Solution:
Let the area of quadrilateral $\boldsymbol{A} \boldsymbol{B C D}$ be $\boldsymbol{S}$. A median divides the area of a triangle in half. Therefore, $S_{A B C}=S_{C B B 1}=S_{C B 1 C 1}$. Consequently, $S_{B B 1 C 1}=2 S_{A B C}$. Similarly, we have $S_{C C 1 D 1}=2 S_{B C D}$, $S_{D D 1 A 1}=2 S_{C D A}$, and $S_{A A 1 B 1}=2 S_{D A B}$. Adding these four equalities, we get: $S_{B B 1 C 1}+S_{C C 1 D 1}+S_{D D 1 A 1}+S_{A A 1 B 1}=2\left(S_{A B C}+S_{B C D}+S_{C D A}+S_{D A B}\right)=4 S$. Therefore, $S_{A I B I C I D 1}=4 S+S=5 S$.
## Answer: 5.
| Points | Criteria for evaluating the performance of task No. 3 |
| :---: | :--- |
| $\mathbf{9}$ | A correct and justified sequence of all steps of the solution is provided. All transformations and calculations are performed correctly. The correct answer is obtained. |
| $\mathbf{6}$ | A correct sequence of all steps of the solution is provided. There are gaps in the justification of the area relationships of the triangles or a computational error or typo that does not affect the further course of the solution. As a result of this error or typo, an incorrect answer may be obtained. |
| $\mathbf{3}$ | The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, the property of the median of a triangle is given); - another part is either not performed or performed incorrectly, possibly even with logical errors (for example, the area relationships of the triangles are obtained incorrectly). The solution may be incomplete. |
| $\mathbf{0}$ | All cases of the solution that do not correspond to the above criteria for scoring 9, 6, and 3 points. |
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In all other cases, $-\mathbf{0}$ points.
## Task 4
Maxim Andreevich, a former university lecturer, gives math lessons to groups of schoolchildren. The cost of one hour (60 minutes) of Maxim Andreevich's lesson with a group of schoolchildren is 3 thousand rubles (after all taxes). In addition to income from tutoring, he has a steady income from investment activities, which amounts to 14 thousand rubles per month. Maxim Andreevich dedicates his weekends entirely to his family and does not work. Maxim Andreevich is very disciplined and strictly monitors the distribution of his time and income. On working days, of which there are exactly 21 in each month, he sleeps for eight hours a day, works for some time, devotes some time to his hobby - creating metal engravings, and spends the rest of the time on rest and household chores. He considers his hobby an important part of his life, so if he works L hours in a day, he will definitely spend 2L hours on creating engravings. He does not sell the engravings but gives them to friends and acquaintances. In addition, Maxim Andreevich is an active philanthropist and donates money to a fund for helping sick children. Every working day, he sets aside exactly $\mathrm{k} / 3$ thousand rubles for charity if he spends a total of $\mathrm{k}$ hours on rest and household chores that day. He spends 70 thousand rubles per month on all household expenses, hobbies, and household management (excluding charitable donations), and he has no other expenses. Of course, Maxim Andreevich loves to rest and do household chores, but he has to work, and every working day he decides for himself how many lessons with students he will conduct that day.
(a) What is the maximum amount of money Maxim Andreevich can donate to charity each month?
(b) Since Maxim Andreevich is a very good math teacher, the parents of the students he teaches are willing to offer him a higher rate for additional lessons (beyond those he already conducts daily). Maxim Andreevich has long taken care of the days when he will no longer be able to work, so he confidently spends all the money he receives each month. Will Maxim Andreevich agree to their offer? If yes, what should the pay for the extra lessons be for him to agree to conduct additional lessons? If no, explain why he would refuse such an offer.
|
# Solution and Grading Scheme:
(a) Maxim Andreevich works $\left(24-8-2 L_{i}-k_{i}\right)=16-2 L_{i}-k_{i}$ hours a day, where $L_{i}$ is the number of hours he works as a tutor on the $i$-th working day, and $k_{i}$ is the number of hours he spends on rest and household chores on the $i$-th working day. The number of working hours in one working day can differ from the number of working hours in another working day.
Then $16-2 L_{i}-k_{i}=L_{i}$, or $L_{i}=\left(16-k_{i}\right) / 3$
His daily earnings from tutoring are $3 L_{i}=3\left(16-k_{i}\right) / 3=16-k_{i}$.
In a month, Maxim Andreevich earns from tutoring
$$
\begin{gathered}
3 L_{1}+3 L_{2}+\cdots+3 L_{20}=\left(16-k_{1}\right)+\left(16-k_{2}\right)+\cdots+\left(16-k_{20}\right) \\
3\left(L_{1}+L_{2}+\cdots+L_{20}\right)=21 * 16-\left(k_{1}+k_{2}+\cdots+k_{20}\right)
\end{gathered}
$$
Or $3 L^{*}=336-K^{*}$,
where $L^{*}$ is the total number of working hours in a month, and $K^{*}$ is the total number of hours in a month that Maxim Andreevich spends on rest and household chores.
His monthly expenses amount to $70+\left(k_{1}+k_{2}+\cdots+k_{20}\right) / 3=70+K^{*} / 3$. Since he spends all his earnings, including income from investment activities, then
$14+336-K^{*}=70+K^{*} / 3$, from which we find the maximum number of hours in a month that Maxim Andreevich spends on rest and household chores: $K^{*}=210$.
Then in a month, Maxim Andreevich will spend a maximum of $\frac{K^{*}}{3}=\frac{210}{3}=$ 70 thousand rubles on charity.
Full solution - 10 points.
For a partial solution assuming that the number of working hours, leisure, etc., are the same every day of the month - 6 points.
If only the equations for the number of hours are written - 2 points.
(b) If Maxim Andreevich declines the offer to work more, then in a month he will work $L^{*}=(336-70) / 3=42$ hours.
Suppose Maria Ivanovna would agree to work extra for a higher hourly wage A>3. Then her monthly earnings from tutoring would be
$3 * 42+A(\tilde{L}-42)=126-42 \mathrm{~A}+\mathrm{A} \tilde{L}$
Since $L_{i}=\left(16-k_{i}\right) / 3$, then with the new distribution of working time, as before
$\tilde{L}=L_{1}+L_{2}+\cdots+L_{20}=\left(16-k_{1}\right) / 3+\left(16-k_{2}\right) / 3+\cdots+\left(16-k_{20}\right) / 3=16 * 21 / 3-$ $\widetilde{K} / 3$
Then in a month, including investments, Maxim Andreevich will earn
$126-42 A+A(112-\widetilde{K} / 3)+14$ thousand rubles.
Since the maximum expenses will equal the income with the proportions in the distribution of time between work and rest, then
$$
\begin{gathered}
126-42 A+A(112-\widetilde{K} / 3)+14=70+\widetilde{K} / 3 \\
70(A+1)=\frac{\widetilde{K}}{3}(A+1)
\end{gathered}
$$
And, as in part (a), we get: $K^{*}=210$. That is, Maria Ivanovna will not agree to work more than the hours she works at a rate of 2 thousand rubles/hour, regardless of the increased wage rate.
Full justification - 10 points,
Partial justification - 5 points
## Task 5
Company "Zolotnik" is engaged in gold and precious stone mining. "Zolotnik" has signed a contract to process a square plot of land with an area of 10 km². The workers of "Zolotnik" suffer from chronic fatigue due to the very labor-intensive work, which leads to a 2-fold decrease in their productivity each day. The amount of land that any worker can process on the first day of work is $1 / 2$ km². The salary of one worker for the entire period of work is 3 monetary units (mon. units), and the daily rental cost of equipment for processing the entire plot of land is 7 mon. units. The contract with a team of workers, which can consist of any number of workers, can only be signed on the first day the contract for processing the plot of land comes into effect.
(a) Find the minimum number of workers required to process the specified plot of land.
(b) Find the number of workers who can process the plot of land in one day.
(c) If "Zolotnik" minimizes its costs for processing the plot of land, how many workers will the company hire and how long will the processing take? What will be the total costs of the company for renting equipment and paying workers?
(a) Answer: 11.
We will prove by contradiction that no smaller number of workers can complete the task. Suppose $n$ workers processed the entire plot of land in $k$ days, where $n \leq 10$. Then each of them processed no more than
$\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^{k}}=1-\frac{1}{2^{k}}$
square kilometers of land, which is strictly less than 1.
Thus, in total, all workers processed no more than
$$
n\left(1-\frac{1}{2^{k}}\right)=n-\frac{n}{2^{k}} \leq 10-\frac{10}{2^{k}}10
$$
Thus, 11 is the minimum number of workers required to process the given plot of land.
## Full justification - 5 points
(b) Answer: 20.
Indeed, on the first day, each worker processes $\frac{1}{2}$ square kilometers of land, so to process the entire plot, $10: \frac{1}{2}=20$ workers are required.
## Full justification - 5 points
(c) Answer: the company will hire 14 workers for 2 days;
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
## Maximum 15 points
Find the value of the expression under the condition that the summation is performed infinitely
$$
\sqrt{20+\sqrt{20+\sqrt{20+\cdots}}}
$$
#
|
# Solution:
Let $x=\sqrt{20+\sqrt{20+\sqrt{20+\cdots}}}, x>0$.
Square both sides of the obtained equation. We get:
$x^{2}=20+x$
$x^{2}-x-20=0 ;$
$D=1+80=81 ; x_{1}=\frac{1-9}{2}=-4-$ does not satisfy the condition $x>0$;
$x_{1}=\frac{1+9}{2}=5-$ fits.
Answer: 5.
## Criteria
0 points - If calculated approximately, then $0 \%$.
8 points - If both roots of the equation are given: -4 and 5, then $50 \%$.
15 points - If the answer is correct, and a valid and justified solution is provided without using a calculator, then $100 \%$.
#
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Consider the vectors $\vec{a}=(3, x), \vec{b}=(\sqrt{x-2}, 4)$, then $\vec{a} \cdot \vec{b} \leq|\vec{a}||\vec{b}|$, which is equivalent to
$$
3 \sqrt{x-2}+4 x \leq \sqrt{\left(9+x^{2}\right)(x+14)}
$$
Equality is possible if and only if the vectors are collinear
$$
\frac{\sqrt{x-2}}{3}=\frac{4}{x}>0 \Leftrightarrow x \sqrt{x-2}=12
$$
The left side of the considered equation is a monotonically increasing function on the domain of definition, so the equation has no more than one root. By trial, we find $x=6$.
|
Answer: 1. 6. 2.6 3.74. 7.
## Checking Criteria:
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Maximum 15 points. A school economics teacher believes it is extremely important to know the basics of both microeconomics and macroeconomics. Therefore, for his subject, he has introduced the following final grading system. First, the student's study of the basics of microeconomics ( $O_{\text {micro }}$ ) is assessed out of 5 points, and then the basics of macroeconomics ( $O_{\text {macro }}$ ) are assessed out of 5 points. The final grade in economics is formed as the minimum value of two quantities: $0.25 * O_{\text {micro }}+0.75 * O_{\text {macro }}$ and $0.75 * O_{\text {micro }}+0.25 * O_{\text {macro }}$ (the final value is rounded to the nearest integer according to the rules of mathematical rounding). Student Ivanov seriously approached the planning of time for studying each school subject and decided that he would spend no more than 4.6 time units on studying economics. However, studying the basics of one area of economics is more difficult for Ivanov than the other. Thus, each unit of time spent on studying macroeconomics increases his final score (in points) in this area by exactly 1.5 points, while the same unit of time invested in preparing for microeconomics increases the final score in this area by 2.5 points.
(a) What is the maximum grade that student Ivanov can get in economics?
(b) Explain why the final grade in economics reflects the teacher's opinion that it is extremely important to know both microeconomics and macroeconomics. Will this always be the case with such a grading system?
|
# Solution:
(a) If the minimum value of the two is determined by the expression $0.75 * O_{\text {мИкро }} + 0.25 * O_{\text {мАкро }}$, i.e., $O_{\text {мИкро }}O_{\text {мАкро }}$, then it is more advantageous for Ivanov to spend an additional unit of time studying macroeconomics.
Thus, to achieve the highest grade, Ivanov should not spend time studying only one area of economics. How should he correctly allocate his time? As long as the expressions $0.25 * O_{\text {мИкро }} + 0.75 * O_{\text {мАкро }}$ and $0.75 * O_{\text {мИкро }} + 0.25 * O_{\text {мАкро }}$ are not equal, as shown above, it will always be more advantageous to switch to studying one of the areas, increasing the resulting grade. Therefore, the maximum final grade can only be achieved if the time is allocated such that $0.25 * O_{\text {мИкро }} + 0.75 * O_{\text {мАкро }} = 0.75 * O_{\text {мИкро }} + 0.25 * O_{\text {мАкро }}$. From this, $O_{\text {мИкро }} = O_{\text {мАкро }}$. To achieve this, with the full use of the time resource, it is necessary to spend $5 / 8$ of the total time on studying macroeconomics, and the rest on studying microeconomics. Then the calculated final grade in economics will be $O_{\text {мИкро }} = O_{\text {мАкро }} = 3 * 2.5 * 4.6 / 8 = 4.3125$, and after mathematical rounding, it will be 4 points.
It should be noted that since the grade was rounded down, Ivanov can achieve a grade of 4 without using the entire planned time resource of 4.6 time units, and can spend the remaining time on another activity.
(b) Using this formula, it turns out that the student will know both microeconomics and macroeconomics. However, if the coefficients for the grades for knowledge of microeconomics and/or macroeconomics, and the coefficients of the labor intensity of studying both areas of economics were different, it could result in a boundary solution where the student would spend time preparing only for one area of economics (for example, if the labor intensity ratio was $1: 5$ with the given formula for the final grade).
## Grading Scheme:
(a) Total 10 points:
- 5 points for a complete justification that the solution will be internal (that $O_{\text {мИкро }} = O_{\text {мАкро }}$);
- 5 points for finding the maximum grade.
(b) Total 5 points:
- 2 points for explaining the internal solution;
- 3 points for explaining the possibility of a boundary solution.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the segment $A B$ of length 10, a circle $\omega$ is constructed with $A B$ as its diameter. A tangent to $\omega$ is drawn through point $A$, and a point $K$ is chosen on this tangent. A line through point $K$, different from $A K$, is tangent to the circle $\omega$ at point $C$. The height $C H$ of triangle $A B C$ intersects segment $B K$ at point $L$. Find the area of triangle $C K L$, given that $B H: A H=1: 4$.
|
Answer: 8.

Solution. Let $O$ be the center of $\omega$. Note that
$$
B H=\frac{1}{5} A B=2, \quad A H=8, \quad O H=\frac{1}{2} A B-B H=3, \quad C H=\sqrt{O C^{2}-O H^{2}}=4
$$
Right triangles $B H C$ and $O A K$ are similar because
$$
\angle A B C=\frac{1}{2} \angle A O C=\frac{1}{2}\left(180^{\circ}-\angle A K C\right)=90^{\circ}-\angle A K O=\angle A O K
$$
Then
$$
\frac{A B}{A K}=2 \cdot \frac{A O}{O K}=2 \cdot \frac{B H}{C H}=1
$$
from which $\angle A B K=45^{\circ}$ and $L H=B H=2$. Therefore,
$$
S_{C K L}=\frac{1}{2} \cdot C L \cdot A H=\frac{1}{2} \cdot(C H-L H) \cdot A H=\frac{1}{2} \cdot 2 \cdot 8=8
$$
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A knight is placed in each cell of a chessboard. What is the smallest number of knights that can be removed from the board so that no knight remains that attacks exactly three other knights? (A knight attacks the squares that are one square away horizontally and two squares away vertically, or vice versa.)
|
Answer: 8 knights.
Solution 1. We will say that a knight controls a square on the board if it attacks this square or stands on it. First, we will prove that it is impossible to remove fewer than 8 knights. It is sufficient to check that at least 4 knights must be removed from each half of the board. Consider, for definiteness, the upper half and mark six knights on it as shown in the figure:
(for convenience, they are highlighted in different colors). We will call the squares marked with a circle on the figure multiple, and the other squares simple. We will divide the figure into two $4 \times 4$ squares and fix one of them. The black knights standing in the square attack exactly three squares. Therefore, one of the following actions must be performed.
1) Remove two knights standing on simple squares controlled by black knights (they can be the black knights themselves).
2) Remove a knight standing on a multiple square. As a result, the white knight from this square will attack exactly three other knights. Therefore, it will be necessary to remove another knight from a simple square controlled by the white knight (possibly the white knight itself).
The same actions must be performed for the other square. Thus, each square determines a pair of squares in the upper half of the board from which knights need to be removed. These pairs do not intersect, since no two marked knights from different squares control the same squares. In other words, the actions with the squares are performed independently of each other. Therefore, at least four knights will have to be removed from the upper half of the board.
We will provide an example showing that 8 knights are sufficient. The knights that need to be removed from the board are marked on the figure.
Solution 2. We will first show that it is necessary to remove at least 8 knights. Mark 12 knights on the board as shown in the left figure:

(for convenience, they are highlighted in different colors). We will call a square useful if it is occupied or attacked by at least one black knight, and useless otherwise. If a square is attacked by two black knights, it is called key (on the left figure, key squares are marked with circles). We will divide the board into four $4 \times 4$ squares. Since black knights attack exactly three squares on the board, the following two facts are true.
1) In each square, at least one useful square must be cleared.
2) If in some square exactly one useful square is cleared, then it must be a key square. Suppose that no more than 7 knights can be removed from the board. Then in some square, exactly one knight will be removed. Let this be, for definiteness, the top-left square. By 2), the knight must be removed from a key square, after which the white knights from this square will attack exactly three knights. Therefore, for each white knight, it will be necessary to clear another square. By assumption, these squares do not lie in the top-left square (and, therefore, they are different). Thus, one of the squares will lie in the bottom-left square, and the other in the top-right square. Obviously, both of them are useless.
By 1), there is at least one cleared square in the top-left and bottom-right squares. Therefore, in the top-right and bottom-left squares, a total of no more than five squares will be cleared. Then in some square (for example, the top-right square), no more than two squares will be cleared. One of them, as shown above, is useless. Therefore, by 1) and 2), another square will be cleared, and it will be a key square. After this, for the white knights standing in the top-right square, it will be necessary to clear two more useless squares - one in the top-left square, and the other in the bottom-right square. In the end, we will clear 4 useless squares (they are different since they lie in different squares), and at least 4 useful squares by 1). Thus, at least 8 knights will be removed, which is impossible.
We will now provide an example showing that 8 knights are sufficient. The knights that need to be removed from the board are marked on the right figure.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A knight is placed in each cell of a chessboard. What is the minimum number of knights that can be removed from the board so that no knight remains that attacks exactly four other knights? (A knight attacks the squares that are one square away horizontally and two squares away vertically, or vice versa.)
|
Answer: 8 knights.
Solution. First, we will show that no fewer than 8 knights need to be removed. On the left diagram, all knights that attack exactly 4 squares of the board are marked (for convenience, they are highlighted in different colors). Let's call such knights bad. To stop a knight from attacking four others, one must remove either this knight or one of those it attacks. We will show that even to get rid of the bad black knights, one must free no fewer than 8 squares. On the middle diagram, the circles mark the squares under attack by the bad black knights. Three bad black knights in the upper left corner attack four squares marked with the symbol $\odot$. If only one of these squares is freed, one of the black knights will remain bad. Therefore, for this trio of knights, at least two squares need to be cleared. Thus, for all four trios, at least $4 \cdot 2 = 8$ squares need to be freed.
Now, let's provide an example showing that 8 knights are sufficient. On the right diagram, the knights that need to be removed from the board are marked.

|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For a natural number ending not in zero, one of its digits was replaced by zero (if it is the leading digit, it was simply erased). As a result, the number decreased by 9 times. How many numbers exist for which this is possible?
|
Answer: 7.
Solution. Let's represent the original number in the form $m+10^{k} a+10^{k+1} n$, where $a$ is a decimal digit, and $k, m, n$ are non-negative integers, with $m>0$, otherwise $m=a=0$. Then the number $8 m$ is a multiple of 10 and therefore ends in 0. By the condition, the number $m$ does not end in 0. Thus, the last digit of $m$ is 5 and the number $m$ is odd. Therefore, $8 m$ is not divisible by 16, which implies $k \leqslant 3$. Let's consider three cases.
1) Suppose $k=3$. Then $m=125 a$. Since the number $m$ is odd and less than 1000, the digit $a$ can take the values $1,3,5,7$, which gives us 4 options.
2) Suppose $k=2$. Then $m=\frac{25 a}{2}$. Since the number $m$ is odd and less than 100, the digit $a$ is 2 or 6. These values give us another 2 options.
3) Suppose $k=1$. Then $m=\frac{5 a}{4}$. Since the number $m$ is odd and less than 10, we get $a=4$.
Note that in 1) we get four-digit numbers, in 2) - three-digit numbers, in 3) - two-digit numbers. Therefore, each number satisfying the condition of the problem falls into exactly one of the sets 1) - 3). Thus, the total number of options is $4+2+1=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the table, there are three cones standing on their bases, touching each other. The radii of their bases are 6, 24, and 24. A truncated cone is placed on the table with its smaller base down, and it shares a generatrix with each of the other cones. Find the radius of the smaller base of the truncated cone.
|
Answer: 2.
Solution. Let $C$ be the center of the smaller base of the truncated cone, and $r$ be the radius of this base. Let $O_{1}, O_{2}, O_{3}$ be the centers of the bases of the other cones. Denote by $\mathcal{K}_{0}$ the cone that completes the truncated cone to a regular cone, and by $\mathcal{K}_{1}$ the cone with the base center at $O_{1}$. On the left diagram, the section of $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$ by the plane $\Pi$ passing through points $O_{1}$ and $C$ and perpendicular to the table is shown. By the problem's condition, $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$ have a common generatrix, which lies in $\Pi$ since it passes through the vertices of the cones. Let $B$ be the point of intersection of this generatrix with the table. Then $B$ lies on the boundaries of the bases of $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$, as well as on the segment $C O_{1}$ connecting the centers of the bases. Hence, the bases of $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$ touch each other at point $B$, i.e., $B C = r$. Similarly, it can be verified that the distance from $C$ to the bases of the other two cones is also $r$. Therefore, the following equalities hold:
$$
r = C O_{1} - 6 = C O_{2} - 24 = C O_{3} - 24
$$
Then $C O_{2} = C O_{3}$, which means that point $C$ lies on the common tangent $A O_{1}$ to the bases of the larger cones (see the right diagram). Note that
$$
A O_{1} = \sqrt{O_{1} O_{2}^{2} - A O_{2}^{2}} = \sqrt{30^{2} - 24^{2}} = 18
$$
Therefore,
$$
(24 + r)^{2} = C O_{2}^{2} = 24^{2} + A C^{2} = 24^{2} + (A O_{1} - r - 6)^{2} = 24^{2} + (12 - r)^{2}, \quad \text{from which } r = 2
$$
## Variant 6
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the table, there are three cones standing on their bases, touching each other. The radii of their bases are 23, 46, and 69. A truncated cone is placed on the table with its smaller base down, and it shares a generatrix with each of the other cones. Find the radius of the smaller base of the truncated cone.
#
|
# Answer: 6.
Solution. Let $C$ be the center of the smaller base of the truncated cone, $R$ be the radius of this base, and $O_{1}, O_{2}, O_{3}$ be the centers of the bases of the other cones. Denote by $\mathcal{K}_{0}$ the cone that completes the truncated cone to a regular cone, and by $\mathcal{K}_{1}$ the cone with the base center at $O_{1}$. On the left diagram, the section of $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$ by the plane $\Pi$ passing through points $O_{1}$ and $C$ and perpendicular to the table is shown. By the problem's condition, $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$ have a common generatrix, which lies in $\Pi$ since it passes through the vertices of the cones. Let $B$ be the point of intersection of this generatrix with the table. Then $B$ lies on the boundaries of the bases of $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$, as well as on the segment $C O_{1}$ connecting the centers of the bases. Hence, the bases of $\mathcal{K}_{0}$ and $\mathcal{K}_{1}$ touch each other at point $B$, i.e., $B C=R$. Similarly, it can be verified that the distance from $C$ to the bases of the other two cones is also $R$. Let $r=23$ and note that
$$
O_{1} O_{2}=3 r, \quad O_{1} O_{3}=4 r, \quad O_{2} O_{3}=5 r
$$
which means that triangle $O_{1} O_{2} O_{3}$ is a right triangle. Direct the coordinate axes along the rays $O_{1} O_{3}$ and $O_{1} O_{2}$ (see the right diagram). Let the coordinates of point $C$ be $(x, y)$. Since
$$
C O_{1}=B O_{1}+B C=r+R, \quad C O_{2}=2 r+R, \quad C O_{3}=3 r+R
$$
the following equalities hold:
$$
(r+R)^{2}-x^{2}=y^{2}=(3 r+R)^{2}-(4 r-x)^{2} \Longleftrightarrow r^{2}+2 r R=6 r R+8 r x-7 r^{2} \Longleftrightarrow 2 x=2 r-R
$$
and also
$$
(r+R)^{2}-y^{2}=x^{2}=(2 r+R)^{2}-(3 r-y)^{2} \Longleftrightarrow r^{2}+2 r R=4 r R+6 r y-5 r^{2} \Longleftrightarrow 3 y=3 r-R
$$
Since $x^{2}+y^{2}=C O_{1}^{2}=(r+R)^{2}$, we get
$$
36(r+R)^{2}=(6 r-3 R)^{2}+(6 r-2 R)^{2} \Longleftrightarrow 23 R^{2}+132 r R-36 r^{2}=0
$$
This equation in terms of $R$ has a unique positive solution $R=\frac{6}{23} r=6$.
## Variant 8
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the table, there are three cones standing on their bases, touching each other. The heights of the cones are the same, and the radii of their bases are 1, 2, and 3. A sphere is placed on the table, touching all the cones. It turns out that the center of the sphere is equidistant from all points of contact with the cones. Find the radius of the sphere.
|
Answer: 1.
Solution: Let $O_{1}, O_{2}, O_{3}$ be the centers of the bases of the cones, $O$ be the center of the sphere, $R$ be the radius of the sphere, $C$ be the point of contact of the sphere with the table, $2 \alpha$ and $2 \beta$ be the angles at the vertices of the first and second cones, $A$ and $B$ be the points of intersection of the segments $C O_{1}$ and $C O_{2}$ with the bases of the cones. The left diagram shows the section of the first cone by the plane $C O O_{1}$. The contact of the sphere with the first cone means that the perpendicular $O E$, dropped from point $O$ to the generatrix $P A$, is equal to $R$. Indeed, in this case, the sphere and the cone touch the plane passing through the generatrix $P A$ perpendicular to the section, and lie on opposite sides of it. Then the sphere touches the lines $A C$ and $A E$ at points $C$ and $E$, from which
$$
O C=O E=R, \quad A C=A E \quad \text { and } \quad \angle A O C=\frac{1}{2} \angle E O C=\frac{\pi}{4}-\frac{\alpha}{2} .
$$
Therefore, $A C=R \cdot \operatorname{tg}\left(\frac{\pi}{4}-\frac{\alpha}{2}\right)$ and, similarly, $B C=R \cdot \operatorname{tg}\left(\frac{\pi}{4}-\frac{\beta}{2}\right)$. Let
$$
\lambda=\operatorname{tg}\left(\frac{\pi}{4}-\frac{\alpha}{2}\right), \quad \mu=\operatorname{tg}\left(\frac{\pi}{4}-\frac{\beta}{2}\right)
$$
Since $O_{1} O_{2}=3, O_{1} O_{3}=4, O_{2} O_{3}=5$, the triangle $O_{1} O_{2} O_{3}$ is a right triangle. By the condition, point $C$ is equidistant from the points of contact of the bases of the cones. Then $C$ lies at the intersection of the angle bisectors of triangle $O_{1} O_{2} O_{3}$ and, therefore, is the center of its inscribed circle, the radius of which is 1. By calculating $C O_{1}^{2}$ and $C O_{2}^{2}$ in two ways, we get
$$
\left\{\begin{array} { l }
{ ( 1 + \lambda R ) ^ { 2 } = 2 , } \\
{ ( 2 + \mu R ) ^ { 2 } = 5 }
\end{array} \Longleftrightarrow \left\{\begin{array} { l }
{ \lambda ^ { 2 } R ^ { 2 } + 2 \lambda R = 1 , } \\
{ \mu ^ { 2 } R ^ { 2 } + 4 \mu R = 1 }
\end{array} \Longleftrightarrow \left\{\begin{array}{l}
\lambda^{2} R^{2}+2 \lambda R-1=0, \\
\left(\lambda^{2}-\mu^{2}\right) R^{2}=2 R(2 \mu-\lambda)
\end{array}\right.\right.\right.
$$
(we subtracted the second equation from the first). Note that
$$
\frac{1}{\lambda}-\lambda=\frac{1+\operatorname{tg} \frac{\alpha}{2}}{1-\operatorname{tg} \frac{\alpha}{2}}-\frac{1-\operatorname{tg} \frac{\alpha}{2}}{1+\operatorname{tg} \frac{\alpha}{2}}=\frac{4 \operatorname{tg} \frac{\alpha}{2}}{1-\operatorname{tg}^{2} \frac{\alpha}{2}}=2 \operatorname{tg} \alpha \quad \text { and, similarly, } \quad \frac{1}{\mu}-\mu=2 \operatorname{tg} \beta
$$
By the equality of the heights of the cones, the relation $\operatorname{tg} \beta=2 \operatorname{tg} \alpha$ holds. Therefore,
$$
1-\mu^{2}=\frac{2 \mu}{\lambda}\left(1-\lambda^{2}\right) \quad \text { and } \quad \lambda^{2}-\mu^{2}=\lambda^{2}-1+1-\mu^{2}=\frac{\left(1-\lambda^{2}\right)(2 \mu-\lambda)}{\lambda}
$$
The second equation of $(*)$ gives
$$
R=\frac{2(2 \mu-\lambda)}{\left(\lambda^{2}-\mu^{2}\right)}=\frac{2 \lambda}{\left(1-\lambda^{2}\right)} \Longleftrightarrow R-\lambda^{2} R=2 \lambda
$$
From the first equation of the system $(*)$, it follows that $\lambda R=\sqrt{2}-1$. Excluding $\lambda$, we get
$$
R-\frac{(\sqrt{2}-1)^{2}}{R}=\frac{2(\sqrt{2}-1)}{R} \Longleftrightarrow R^{2}=(\sqrt{2}-1)(\sqrt{2}+1)=1 \Longleftrightarrow R=1
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Inside an angle of $30^{\circ}$ with vertex $A$, a point $K$ is chosen, the distances from which to the sides of the angle are 1 and 2. Through point $K$, all possible lines are drawn, intersecting the sides of the angle. Find the minimum area of the triangle cut off by the line from the angle.
|
Answer: 8.
Solution 1. Choose points $P$ and $Q$ on the sides of the angle such that point $K$ is the midpoint of segment $P Q$. We will show that line $P Q$ cuts off a triangle of the smallest area. Take another line passing through point $K$. Let it intersect the sides of the angle at points $X$ and $Y$. By swapping $P$ with $Q$ and $X$ with $Y$ if necessary, we can assume that $X$ lies on segment $A P$. It is sufficient to prove that $K X < K Y$. Suppose $K X \geqslant K Y$. Mark a point $Z$ on segment $K X$ such that $K Z = K Y$ (see the left figure). Triangles $K Q Y$ and $K P Z$ are equal by two sides and the angle, hence
$$
\angle K Q Y = \angle K P Z \quad \text{and} \quad \angle Z P Q + \angle A Q P = 180^{\circ}.
$$
But this is impossible, since point $Z$ lies inside triangle $A P Q$ and
$$
\angle Z P Q + \angle A Q P \leqslant \angle A P Q + \angle A Q P = 150^{\circ}.
$$
2. The area of triangle $A X Y$ is expressed by the function
$$
S(x) = \frac{x^2}{x-2}, \quad \text{hence} \quad S'(x) = \frac{x(x-4)}{(x-2)^2}
$$
Thus, the derivative $S$ is negative for $x \in (2,4)$ and positive for $x > 4$. Therefore, the minimum value of $S$ is achieved at $x = 4$ and is equal to 8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the table, there are three cones standing on their bases, touching each other. The heights of the cones are the same, and the radii of their bases are $2r$, $3r$, and $10r$. A sphere with a radius of 2 is placed on the table, touching all the cones. It turns out that the center of the sphere is equidistant from all points of contact with the cones. Find $r$.
|
Answer: 1.
Solution: Let $O_{1}, O_{2}, O_{3}$ be the centers of the bases of the cones, $O$ be the center of the sphere, $R$ be the radius of the sphere, $C$ be the point of contact of the sphere with the table, $2 \alpha$ and $2 \beta$ be the angles at the vertices of the first and second cones, $A$ and $B$ be the points of intersection of the segments $C O_{1}$ and $C O_{2}$ with the bases of the cones. The left diagram shows the section of the first cone by the plane $C O O_{1}$. The contact of the sphere with the first cone means that the perpendicular $O E$, dropped from point $O$ to the generatrix $P A$, is equal to $R$. Indeed, in this case, the sphere and the cone touch the plane passing through the generatrix $P A$ perpendicular to the section, and lie on opposite sides of it. Then the sphere touches the lines $A C$ and $A E$ at points $C$ and $E$, from which
$$
O C=O E=2, \quad A C=A E \quad \text { and } \quad \angle A O C=\frac{1}{2} \angle E O C=\frac{\pi}{4}-\frac{\alpha}{2} .
$$
Therefore, $A C=2 \operatorname{tg}\left(\frac{\pi}{4}-\frac{\alpha}{2}\right)$ and, similarly, $B C=2 \operatorname{tg}\left(\frac{\pi}{4}-\frac{\beta}{2}\right)$. Let
$$
\lambda=\operatorname{tg}\left(\frac{\pi}{4}-\frac{\alpha}{2}\right), \quad \mu=\operatorname{tg}\left(\frac{\pi}{4}-\frac{\beta}{2}\right)
$$
Since $O_{1} O_{2}=5 r, O_{1} O_{3}=12 r, O_{2} O_{3}=13 r$, the triangle $O_{1} O_{2} O_{3}$ is a right triangle. By the condition, point $C$ is equidistant from the points of contact of the bases of the cones. Then $C$ lies at the intersection of the angle bisectors of triangle $O_{1} O_{2} O_{3}$ and, therefore, is the center of its inscribed circle, the radius of which is $2 r$. Calculating $C O_{1}^{2}$ and $C O_{2}^{2}$ in two ways, we get
$$
\left\{\begin{array} { l }
{ ( 2 r + 2 \lambda ) ^ { 2 } = 8 r ^ { 2 } , } \\
{ ( 3 r + 2 \mu ) ^ { 2 } = 1 3 r ^ { 2 } }
\end{array} \Longleftrightarrow \left\{\begin{array} { l }
{ 4 \lambda ^ { 2 } + 8 \lambda r = 4 r ^ { 2 } , } \\
{ 4 \mu ^ { 2 } + 1 2 \mu r = 4 r ^ { 2 } }
\end{array} \Longleftrightarrow \left\{\begin{array}{l}
\lambda^{2}+2 \lambda r-r^{2}=0 \\
\lambda^{2}-\mu^{2}=r(3 \mu-2 \lambda)
\end{array}\right.\right.\right.
$$
(we subtracted the second equation from the first). Note that
$$
\frac{1}{\lambda}-\lambda=\frac{1+\operatorname{tg} \frac{\alpha}{2}}{1-\operatorname{tg} \frac{\alpha}{2}}-\frac{1-\operatorname{tg} \frac{\alpha}{2}}{1+\operatorname{tg} \frac{\alpha}{2}}=\frac{4 \operatorname{tg} \frac{\alpha}{2}}{1-\operatorname{tg}^{2} \frac{\alpha}{2}}=2 \operatorname{tg} \alpha \quad \text { and, similarly, } \quad \frac{1}{\mu}-\mu=2 \operatorname{tg} \beta
$$
By the equality of the heights of the cones, the relation $\operatorname{tg} \beta=\frac{3}{2} \operatorname{tg} \alpha$ holds. Therefore,
$$
1-\mu^{2}=\frac{3 \mu}{2 \lambda}\left(1-\lambda^{2}\right) \quad \text { and } \quad \lambda^{2}-\mu^{2}=\lambda^{2}-1+1-\mu^{2}=\frac{\left(1-\lambda^{2}\right)(3 \mu-2 \lambda)}{2 \lambda}
$$
The second equation of $(*)$ gives
$$
r=\frac{\lambda^{2}-\mu^{2}}{3 \mu-2 \lambda}=\frac{1-\lambda^{2}}{2 \lambda}=\frac{1}{2}\left(\frac{1}{\lambda}-\lambda\right)
$$
From the first equation of the system $(*)$, it follows that $\lambda=r(\sqrt{2}-1)$. Excluding $\lambda$, we get
$$
2 r=\frac{\sqrt{2}+1}{r}-(\sqrt{2}-1) r \Longleftrightarrow \sqrt{2}+1=(\sqrt{2}+1) r^{2} \Longleftrightarrow r=1
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Cells of an infinite grid paper are painted in $k$ colors (each cell is painted entirely in one color). What is the largest $k$ such that in every grid rectangle with sides 3 and 4, cells of all these colors will be found?
|
Answer: 10.
Solution. Divide the infinite grid paper into ten-cell figures as shown in the figure.

The required coloring with 10 colors can be achieved by coloring one such figure in 10 colors and coloring the rest in exactly the same way.
It is obvious that the sheet cannot be painted in more than 12 colors in the required manner. Suppose there is a coloring in 11 or 12 colors. Assume that there is a coloring in 11 colors such that in each $3 \times 3$ square all colors are different. Consider one such square. In the containing $3 \times 4$ rectangle, there are only 11 different colors. Therefore, in the additional $3 \times 1$ strip, some two colors coincide. Then, in the $3 \times 3$ square containing this strip, some two colors coincide.
Suppose we have a coloring in $n$ colors, where $n$ is 11 or 12. Choose a $3 \times 3$ square in which there are no more than $n-3$ different colors. Extend it to rectangles $3 \times 4$ and $4 \times 4$ as shown in the figure. Then, in the strips $3 \times 1$ and $1 \times 3$, the same triplets of colors are represented. Cover the cell marked with a cross with a horizontal rectangle $3 \times 4$. Then this rectangle will contain 5 cells from the strips, meaning it has at least two pairs of cells of the same color, so the total number of colors does not exceed 10. Contradiction.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Positive numbers $a, b, c$ are such that $a^{2} b+b^{2} c+c^{2} a=3$. Find the minimum value of the expression
$$
A=a^{7} b+b^{7} c+c^{7} a+a b^{3}+b c^{3}+c a^{3}
$$
|
Answer: 6.
Solution. By the Cauchy-Schwarz inequality
$$
A=\left(a^{7} b+a b^{3}\right)+\left(b^{7} c+b c^{3}\right)+\left(c^{7} a+c a^{3}\right) \geqslant 2\left(a^{4} b^{2}+b^{4} c^{2}+c^{4} a^{2}\right) \geqslant \frac{2}{3}\left(a^{2} b+b^{2} c+c^{2} a\right)^{2}=6
$$
Equality is achieved when $a=b=c=1$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $a, b, c > 0$, find the maximum value of the expression
$$
A=\frac{a^{3}+b^{3}+c^{3}}{(a+b+c)^{3}-26 a b c}
$$
|
Answer: 3.
Solution. Note that $(a+b+c)^{3}=a^{3}+b^{3}+c^{3}+6 a b c+B$, where
$$
B=3\left(a^{2} b+a b^{2}+b^{2} c+b c^{2}+c^{2} a+c a^{2}\right) \geqslant 18 \sqrt[6]{a^{6} b^{6} c^{6}}=18 a b c
$$
(we used the Cauchy inequality). Then
$$
a^{3}+b^{3}+c^{3} \leqslant(a+b+c)^{3}-24 a b c
$$
Let $t=\frac{(a+b+c)^{3}}{a b c}$. By the Cauchy inequality, $t \geqslant 27$, hence
$$
A \leqslant \frac{(a+b+c)^{3}-24 a b c}{(a+b+c)^{3}-26 a b c}=\frac{t-24}{t-26}=1+\frac{2}{t-26} \leqslant 3
$$
Equality is achieved when $a=b=c$.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $a, b, c > 0$, find the maximum value of the expression
$$
A=\frac{a^{4}+b^{4}+c^{4}}{(a+b+c)^{4}-80(a b c)^{4 / 3}}
$$
|
Answer: 3.
Solution. Note that $(a+b+c)^{4}=a^{4}+b^{4}+c^{4}+B$, where
\[
\begin{aligned}
& B=4\left(a^{3} b+a b^{3}+b^{3} c+b c^{3}+c^{3} a+c a^{3}\right)+6\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)+12\left(a b c^{2}+b c a^{2}+c a b^{2}\right) \geqslant \\
& \geqslant 24 \sqrt[6]{(a b c)^{8}}+18 \sqrt[3]{(a b c)^{4}}+36 \sqrt[3]{(a b c)^{4}}=78(a b c)^{4 / 3}
\end{aligned}
\]
(we used the Cauchy inequality). Then
\[
a^{4}+b^{4}+c^{4} \leqslant(a+b+c)^{4}-78(a b c)^{4 / 3}
\]
Let $t=\frac{(a+b+c)^{4}}{(a b c)^{4 / 3}}$. By the Cauchy inequality, $t \geqslant 81$, hence
\[
A \leqslant \frac{(a+b+c)^{4}-78(a b c)^{4 / 3}}{(a+b+c)^{4}-80(a b c)^{4 / 3}}=\frac{t-78}{t-80}=1+\frac{2}{t-80} \leqslant 3
\]
Equality is achieved when $a=b=c$.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $a, b, c > 0$, find the maximum value of the expression
$$
A=\frac{a^{2}(b+c)+b^{2}(c+a)+c^{2}(a+b)}{a^{3}+b^{3}+c^{3}-2 a b c}
$$
|
Answer: 6.
Solution. By the Cauchy-Schwarz inequality,
$$
a^{2}(b+c)+b^{2}(c+a)+c^{2}(a+b)=\frac{1}{3}\left((a+b+c)^{3}-\left(a^{3}+b^{3}+c^{3}+6 a b c\right)\right) \leqslant \frac{1}{3}\left((a+b+c)^{3}-9 a b c\right)
$$
Note that
$$
a^{3}+b^{3}+c^{3}-2 a b c \geqslant \frac{1}{9}(a+b+c)^{3}-2 a b c=\frac{1}{9}\left((a+b+c)^{3}-18 a b c\right)
$$
Let $t=\frac{(a+b+c)^{3}}{a b c}$. By the Cauchy-Schwarz inequality, $t \geqslant 27$, hence
$$
A \leqslant \frac{3\left((a+b+c)^{3}-9 a b c\right)}{(a+b+c)^{3}-18 a b c}=\frac{3(t-9)}{t-18}=3\left(1+\frac{9}{t-18}\right) \leqslant 6
$$
Equality is achieved when $a=b=c$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $a, b, c > 0$, find the maximum value of the expression
$$
A=\frac{a^{3}(b+c)+b^{3}(c+a)+c^{3}(a+b)}{(a+b+c)^{4}-79(a b c)^{4 / 3}}
$$
|
Answer: 3.
Solution. By the Cauchy-Schwarz inequality,
$a^{3}(b+c)+b^{3}(c+a)+c^{3}(a+b)=(a+b+c)\left(a^{3}+b^{3}+c^{3}\right)-\left(a^{4}+b^{4}+c^{4}\right) \leqslant(a+b+c)\left(a^{3}+b^{3}+c^{3}\right)-3(a b c)^{4 / 3}$.
Note that $(a+b+c)^{3}=a^{3}+b^{3}+c^{3}+6 a b c+B$, where
$$
B=3\left(a^{2} b+a b^{2}+b^{2} c+b c^{2}+c^{2} a+c a^{2}\right) \geqslant 18 \sqrt[6]{a^{6} b^{6} c^{6}}=18 a b c
$$
(we used the Cauchy-Schwarz inequality). Then $a^{3}+b^{3}+c^{3} \leqslant(a+b+c)^{3}-24 a b c$ and
$(a+b+c)\left(a^{3}+b^{3}+c^{3}\right)-3(a b c)^{4 / 3} \leqslant(a+b+c)^{4}-24 a b c(a+b+c)-3(a b c)^{4 / 3} \leqslant(a+b+c)^{4}-75(a b c)^{4 / 3}$.
Let $t=\frac{(a+b+c)^{4}}{(a b c)^{4 / 3}}$. By the Cauchy-Schwarz inequality, $t \geqslant 81$, hence
$$
A \leqslant \frac{(a+b+c)^{4}-75(a b c)^{4 / 3}}{(a+b+c)^{4}-79(a b c)^{4 / 3}}=\frac{t-75}{t-79}=1+\frac{4}{t-79} \leqslant 3
$$
Equality is achieved when $a=b=c$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (10 points) Minister K. issued an order that citizens will only be received if the number of ways to choose a group of four people from those who have come is less than the number of ways to choose a group of two people from them. Determine the maximum number of citizens that the minister can receive?
|
Answer: 5.
Solution: The number of ways to choose a group of four people from $n$ people is $C_{n}^{4}$; a group of two people is $C_{n}^{2}$. We are interested in the maximum natural number $n$ such that $C_{n}^{4}<C_{n}^{2}$. Transforming:
$$
\frac{n(n-1)(n-2)(n-3)}{1 \cdot 2 \cdot 3 \cdot 4}<\frac{n(n-1)}{2} \Leftrightarrow \frac{(n-2)(n-3)}{3 \cdot 4}<1
$$
Solving the inequality using the interval method, we get that $-1<n<6$. Therefore, the maximum $n$ is 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) From village $A$ to village $B$, the Indians take three times as long to travel by canoe as from village $B$ to village $A$. How many times longer than usual can the Indians take to travel from $B$ to $A$ by canoe without paddles?
|
Answer: 3 times.
Solution: It is not hard to see that village V is upstream from village A. Let's denote the speed of the river current as $v_{r}$, and the average speed of the canoe in still water as $v$. If $S$ is the distance along the river from A to V, then from the condition we have
$$
3 \frac{S}{v+v_{r}}=\frac{S}{v-v_{r}}
$$
From this, we get that
$$
v=2 v_{r}
$$
Let the time it takes for the Indians to travel from V to A without paddles (i.e., only by the river current) be $k$ times longer than with paddles. This gives us the equation
$$
k \frac{S}{v+v_{r}}=\frac{S}{v_{r}}
$$
Then, taking into account $(*)$, we find that $k=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (40 points) To enter Ali Baba's cave, it is necessary to zero out 28 counters, each set to a natural number in the range from 1 to 2017. Treasure hunters are allowed, in one move, to decrease the values of some of the counters by the same number, which they can change from move to move. Indicate the minimum number of moves in which the treasure hunters can, with certainty, zero out the counters (regardless of the initial values) and enter the cave.
|
Answer: In 11 moves.
## Solution:
Estimation. Suppose the counters are set to all powers of two from 1 to 1024 and some 17 other numbers. Since the order of moves does not matter, we can arrange them in descending order of the numbers being subtracted. We will show by induction that after the $k$-th move, there is a number on the board that is not less than $2^{10-k}$. The base case - 0 moves - is obvious. Suppose after $k$ moves, there is a number on the board that is not less than $2^{10-k}$. If we subtract a number greater than $2^{10-k-1}$ on the $k$-th move, then this and the previous moves have not affected the number $2^{10-k-1}$, and the proof is complete. Otherwise, after the subtraction, there will be a number not less than $2^{10-k-1}$, which is not less than $2^{10-k}$. From the proven statement, it follows that after 10 moves, there will still be a number on the board that is not less than $2^{0}=1$, meaning that at least 11 moves are required.
Example. By subtracting $2^{10}$ from all numbers not less than $2^{10}$, we will make all numbers less than $2^{10}$. The next step will similarly make all numbers less than $2^{9}$, and so on. After the tenth step, all numbers will be less than $2^{0}=1$, that is, they will all be zeros.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In each cell of a $2017 \times 2017$ board, there is a chip. In one operation, you can remove a chip that has a non-zero even number of neighbors (neighbors are chips located in cells that share a side or a corner). What is the minimum number of chips that can be left on the board using such operations?
#
|
# Answer: 2
Solution. If there are only two chips on the board, then each of them has no more than one neighbor, and according to the rules, they cannot be removed. Therefore, at least two chips will remain. We will show how to leave exactly two chips on the board. For this, we will provide an algorithm that allows clearing two adjacent rows (or two adjacent columns) on an $m \times n$ board. Let's assume we want to clear the top two rows. We will number the cells from 1 to $n$. First, we will remove the chip from the 2nd cell of the second row (this can be done because it has 8 neighbors), then we will remove the corner chip (it now has 2 neighbors), then the 3rd chip from the first row (it has 4 neighbors), then the 2nd chip from the first row (it has 2 neighbors), and the 1st chip from the second row (it also has 2 neighbors). Next, moving from left to right, we will sequentially remove all the chips from the first row (each of them will have 4 neighbors at the moment of removal, except for the last one, which will have 2 neighbors), and then similarly remove the chips from the second row. This way, we will clear the two top rows. We will apply these actions sequentially, alternating between rows and columns, until only the chips in a $3 \times 3$ square remain. Dealing with them is quite simple: we remove the central one, then the four corner ones in any order, then the remaining top one, and finally, the remaining bottom one.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an island, there live knights who always tell the truth, and liars who always lie. In a room, 15 islanders gathered. Each of those in the room said two phrases: "Among my acquaintances in this room, there are exactly six liars" and "among my acquaintances in this room, there are no more than seven knights." How many knights can there be in this room?
|
Answer: 9 knights
Solution. If there is a liar in the room, then his statement "among my acquaintances in this room, there are no more than seven knights" is a lie, and there are no fewer than 8 knights in the room. If there is a knight in the room, then his statement "among my acquaintances in this room, there are exactly six liars" is true, and there are no fewer than 6 liars in the room. Therefore, there are both knights and liars in the room, with no fewer than 8 knights and no fewer than 6 liars. This means there are no more than $15-6=9$ knights. Suppose there are exactly 8 knights. Then there are 7 liars in the room, and each of them has more than 7 acquaintances who are knights. Therefore, each of them is acquainted with all the knights in the room. This means that each knight is also acquainted with all the liars in the room, i.e., each knight has 7 acquaintances who are liars. But then he would be lying. Therefore, there cannot be 8 knights. Thus, there are 9 knights in the room. Such a situation is possible if each knight knows each liar, and no one else is acquainted with anyone else.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (40 points) Let $P(n)$ denote the product of the digits of a natural number $n$. For what largest natural number $k$ does there exist a natural number $n>10$ such that
$$
P(n)<P(2 n)<\ldots<P(k n) ?
$$
|
# Answer: 9.
Solution: First, let's show that $k<10$. Indeed, for $k \geqslant 10$, the set of numbers includes $P(10 n)$. It equals zero because the number $10 n$ ends in 0. Then $P(n)<0$, which is impossible.
Now let's provide an implementation for $k=9$. We can take $n$ as a number of the form $\underbrace{\overline{11 \ldots 1}}_{j}$ for any $j \geqslant 2$. In this case, $P(s n)=s^{j}, s=1, \ldots, k$, and the numbers $s^{j}$ clearly increase.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) During the draw before the math marathon, team captains were asked to name the smallest possible sum of the digits in the decimal representation of the number $n+1$, given that the sum of the digits of the number $n$ is 2017. What was the answer given by the captain of the team that won the draw?
|
Answer: 2.
Solution: First, we show that the answer is not less than 2. If the sum of the digits of the number $n+1$ is 1, then $n+1=10 \ldots 0$, and the decimal representation of $n$ consists entirely of nines. Then the number $n$ is divisible by 9, and the sum of its digits, therefore, is also. But this is impossible since 2017 is not divisible by 9.
It remains to provide an example of a number $n+1$ whose sum of digits is 2. Since $2017=224 \cdot 9+1$, we can set $n=19 \ldots 9$, where the digit 9 is repeated 224 times. Indeed, in this case, $n+1=20 \ldots 0$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Inside the circle $\omega$ are located intersecting at points $K$ and $L$ circles $\omega_{1}$ and $\omega_{2}$, touching the circle $\omega$ at points $M$ and $N$. It turned out that points $K, M$, and $N$ lie on the same line. Find the radius of the circle $\omega$, if the radii of the circles $\omega_{1}$ and $\omega_{2}$ are 3 and 5, respectively.
|
Answer: 8.
Solution. Let $O, O_{1}, O_{2}$ be the centers of the circles $\omega, \omega_{1}, \omega_{2}$, respectively. The radii $O M$ and $O_{1} M$ of the circles $\omega$ and $\omega_{1}$ are perpendicular to their common tangent at point $M$. Therefore, they are parallel, which means that point $O_{1}$ lies on the segment $O M$. Similarly, it follows that point $O_{2}$ lies on the segment $O N$ (see the figure). Since triangles $O M N, O_{1} M K$, and $O_{2} K N$ are isosceles,
$$
\angle M K O_{1} = \angle K M O_{1} = \angle K N O_{2} = \angle N K O_{2}
$$
Therefore, $K O_{1} \| N O$ and $K O_{2} \| M O$, which means that $O O_{1} K O_{2}$ is a parallelogram. Then
$$
M O = M O_{1} + O_{1} O = M O_{1} + K O_{2} = 3 + 5 = 8
$$
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Inside the circle $\omega$ is a circle $\omega_{1}$ that is tangent to it at point $K$. The circle $\omega_{2}$ is tangent to the circle $\omega_{1}$ at point $L$ and intersects the circle $\omega$ at points $M$ and $N$. It turns out that points $K, L$, and $M$ lie on the same line. Find the radius of the circle $\omega$, if the radii of the circles $\omega_{1}$ and $\omega_{2}$ are 4 and 7, respectively.
|
Answer: 11.
Solution. Let $O, O_{1}, O_{2}$ be the centers of the circles $\omega, \omega_{1}, \omega_{2}$, respectively. The radii $O K$ and $O_{1} K$ of the circles $\omega$ and $\omega_{1}$ are perpendicular to their common tangent at point $K$. Therefore, they are parallel, which means that point $O_{1}$ lies on the segment $O K$ (see the figure). Since triangles $O K M$, $O_{1} K L$, and $O_{2} L M$ are isosceles,
$$
\angle K M O = \angle L K O_{1} = \angle K L O_{1} = \angle M L O_{2} = \angle L M O_{2}
$$
Therefore, $K O \parallel M O_{2}$ and $O_{1} O_{2} \parallel M O$, which means that $O O_{1} O_{2} M$ is a parallelogram. Then
$$
O M = O_{1} O_{2} = O_{1} L + L O_{2} = 4 + 7 = 11
$$
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In an arm wrestling tournament, 510 athletes are participating. 1 point is awarded for a win, and 0 points for a loss. If the winner initially had fewer points than the opponent, the winner additionally receives one point from the loser. In each round, participants with a difference of no more than 1 point in their scores compete. The tournament ends as soon as a sole leader is determined. What is the minimum number of rounds that need to be played?
|
# Answer: 9.
Solution. Let there be $N=2 m+k$ athletes in the leading group before the next round, with $2 m$ of them meeting each other, and $k$ meeting participants who have one point less. Note that if athletes with $n$ and $n+1$ points meet, they will end up with $n$ and $n+2$ points regardless of the outcome. Therefore, after the round, there will be $m+k$ participants in the leading group. The minimum value of this sum is $\frac{N}{2}$ for even $N$ and $\frac{N+1}{2}$ for odd $N$. According to the problem, after the first round, there will be no fewer than 255 leaders, after the second round - no fewer than 128, and after each subsequent round, the number of leaders will decrease by no more than half. Therefore, it will take no fewer than $2+\log _{2} 128=9$ rounds.
We will show that the tournament can be completed in 9 rounds. We will prove two statements.
1) In a tournament with $2^{n}$ participants, the winner can be determined in $n$ rounds. We will use induction on $n$. For $n=1$, this is obvious. Suppose the statement is true for some $n$. Then, in a tournament with $2^{n+1}$ participants, after the first round, $2^{n}$ athletes will have 0 points and $2^{n}$ will have 1 point. We will conduct two independent tournaments in these groups. By the induction hypothesis, both can be completed in $n$ rounds. The winner of the second tournament will become the overall winner, and he will be determined in $n+1$ rounds.
2) For $n \geqslant 3$, in a tournament with $2^{n}-2$ participants, the winner can be determined in $n$ rounds. After the first round, $2^{n-1}-1$ athletes will have 0 points and $2^{n-1}-1$ will have 1 point. If in the second round, only one pair of opponents has a different number of points, then after the round, $2^{n-2}$ participants will have 0 points and 2 points, and $2^{n-1}-2$ participants will have 1 point. We will now use induction on $n$. For $n=3$, we will pair athletes with the same number of points, after which the tournament will end. Suppose $n>3$ and the statement is true for $n-1$. By statement 1) and the induction hypothesis, independent tournaments can be organized in the groups with 0, 1, and 2 points, and the first and third groups will end in $n-2$ rounds, while the second group will end in $n-1$ rounds (but the last round will not be needed). The winner of the third group will win the entire tournament, as he will have $n+1$ points, while participants from other groups will have no more than $n$ points. In total, the tournament will last $n$ rounds.
It remains to apply statement 2) for $n=9$.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression for $a, b \geqslant 0$
$$
\frac{|a-3 b-2|+|3 a-b|}{\sqrt{a^{2}+(b+1)^{2}}}
$$
|
Answer: 2.
Solution 1. The minimized expression is $d_{1}+d_{2}$, where $d_{1}, d_{2}$ are the distances from points $A(1,3)$ and $B(3,1)$ to the line $\ell$ defined by the equation $a x-(b+1) y+1=0$. It can be rewritten as
$y=\frac{a}{b+1} x+\frac{1}{b+1}$ or $y=p x+q$, where $p \geqslant 0, q \in(0,1]$. We can assume that the line $\ell$ intersects the segment $A B$, otherwise we can rotate it around the point $C(0, q)$ towards $A B$, reducing $d_{1}$ and $d_{2}$. Then $d_{1}+d_{2}=A B \cdot \sin \alpha$, where $\alpha$ is the angle between the lines $\ell$ and $A B$. The right side reaches its minimum when the angle $\alpha$ is the smallest, which is realized when $\alpha=\angle C A B$ or $\alpha=\angle C B A$. Both of these angles are not less than $\frac{\pi}{4}$, and $\angle C B A=\frac{\pi}{4}$ when $a=b=0$. Therefore, the minimum of $d_{1}+d_{2}$ is $A B \cdot \frac{\sqrt{2}}{2}=2$.
Solution 2. Let $A$ be the maximized expression, $c=b+1 \geqslant 1$. Then
$$
A=\frac{|a-3 c+1|+|3 a-c+1|}{\sqrt{a^{2}+c^{2}}}
$$
Consider three cases.
1) Suppose $c \geqslant 3 a+1$. Then
$$
A=\frac{3 c-a-1+c-3 a-1}{\sqrt{a^{2}+c^{2}}}=\frac{4 c-4 a-2}{\sqrt{a^{2}+c^{2}}} \geqslant \frac{8 a+2}{\sqrt{a^{2}+(3 a+1)^{2}}}=\frac{8 a+2}{\sqrt{10 a^{2}+6 a+1}}
$$
and the inequality becomes an equality when $c=3 a+1$. Moreover,
$$
\frac{(8 a+2)^{2}}{10 a^{2}+6 a+1}=\frac{64 a^{2}+32 a+4}{10 a^{2}+6 a+1} \geqslant \frac{40 a^{2}+24 a+4}{10 a^{2}+6 a+1}=4
$$
and equality is achieved when $a=0$. Thus, the minimum of $A$ is realized when $a=0, c=1$ and is equal to 2.
2) Suppose $\frac{a+1}{3} \leqslant c \leqslant 3 a+1$. Then
$$
A=\frac{3 c-a-1+3 a-c+1}{\sqrt{a^{2}+c^{2}}}=\frac{2 c+2 a}{\sqrt{a^{2}+c^{2}}} \geqslant \frac{2 \left(\frac{a+1}{3}\right)+2 a}{\sqrt{a^{2}+\left(\frac{a+1}{3}\right)^{2}}}=\frac{\frac{8}{3} a+\frac{2}{3}}{\sqrt{a^{2}+\left(\frac{a+1}{3}\right)^{2}}}=\frac{8 a+2}{\sqrt{10 a^{2}+2 a+1}} \geqslant \frac{8 a+2}{\sqrt{10 a^{2}+6 a+1}} \geqslant 2
$$
Thus, in this case, the minimum of $A$ is not realized.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Points $K, L$ and $M$ are the midpoints of sides $AB, BC$ and $CD$ of parallelogram $ABCD$. It turned out that quadrilaterals $KBLM$ and $BCDK$ are cyclic. Find the ratio $AC: AD$.
---
The translation is provided as requested, maintaining the original formatting and structure.
|
Answer: 2.
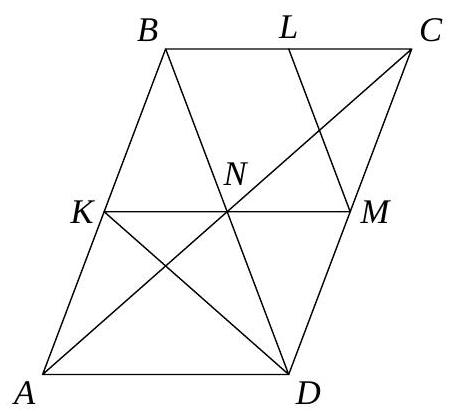
Solution. Let $N$ be the point of intersection of the diagonals of the parallelogram. Quadrilateral $K B L M$ is an inscribed trapezoid, so $K B = L M$. Multiplying this equality by 2, we get $A B = B D$. Then $A K = D N$ and
$$
\angle A K N = 180^{\circ} - \angle K A D = 180^{\circ} - \angle A D N = \angle D N K
$$
Thus, triangles $A K N$ and $D N K$ are equal, from which $D K = A N$. On the other hand, $B C D K$ is also an inscribed trapezoid, so $D K = B C = A D$. Then
$$
\frac{A C}{A D} = \frac{2 A N}{A D} = \frac{2 A N}{D K} = 2
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a qualification arm wrestling tournament, 896 athletes participate. A victory earns 1 point, a defeat earns 0 points. Before each round, pairs are formed by drawing lots among participants with an equal number of points (those who do not find a pair are awarded a point without playing). After the second defeat, an athlete is eliminated from the tournament. As soon as a sole leader is determined, the tournament ends, and all remaining athletes on the tournament are considered to have passed the qualification. Find the number of such athletes.
|
Answer: 10.
Solution. Note that $896=1024-128$. First, let's prove an auxiliary statement.
In a tournament with $2^{n}$ participants, for any $m \in\{1, \ldots, n\}$, after the $m$-th round, there will be $2^{n-m}$ athletes without any losses and $m \cdot 2^{n-m}$ athletes with one loss. We will use induction on $m$. For $m=1$, everything is obvious. Suppose for some $m<n$ the statement is true. Then before the $(m+1)$-th round, all participants will be paired. After the round, the number of athletes without any losses will be halved, i.e., it will become $2^{n-m-1}$. One loss will be incurred by those who lost in the group of leaders (there are $2^{n-m-1}$ such people), and by those who already had one loss and won (by the induction hypothesis, there are $m \cdot 2^{n-m-1}$ such people). In total, we will have $(m+1) \cdot 2^{n-m-1}$. The remaining participants will leave the tournament. Thus, the inductive step is completed.
Suppose that parallel to ours, a second qualifying tournament with 128 participants is held under the same rules. We can treat these two tournaments as parts of one (with 1024 participants) up to the seventh round. We will pair only athletes from their own tournament in each round. This is possible because, by the above, the number of leaders and participants with one loss in the second and overall tournament will be even, and thus in the first one as well. We will record the remaining participants as pairs $(a, b)$, where $b$ is the number of leaders, and $a$ is the number of athletes with one loss. By the auxiliary statement, after the seventh round, in the overall tournament, there will be $(56,8)$ participants, and in the second one - $(7,1)$. Therefore, in our tournament, there will be $(49,7)$ athletes, and their number will change as follows:
$$
(49,7) \rightarrow(28,4) \rightarrow(16,2) \rightarrow(9,1)
$$
Thus, the tournament will end after the tenth round, and 10 athletes will qualify.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression for $a, b>0$
$$
\frac{(2 a+2 a b-b(b+1))^{2}+\left(b-4 a^{2}+2 a(b+1)\right)^{2}}{4 a^{2}+b^{2}}
$$
|
Answer: 1.
Solution 1. The minimized expression is the sum of the squares of the distances from point $A(1,2 a)$ to the lines $\ell_{1}$ and $\ell_{2}$, given by the equations
$$
\ell_{1}: 2 a x+b y-b(b+1)=0 \quad \text { and } \quad \ell_{2}: b x-2 a y+2 a(b+1)=0
$$
These lines are perpendicular and intersect at point $B(0, b+1)$. Then, by the Pythagorean theorem, we need to find the minimum of $A B^{2}=1+(b+1-2 a)^{2}$, which is 1 and is achieved, for example, when $a=b=1$.
Solution 2. Transform the numerator of the fraction:
$$
\begin{aligned}
& (2 a+2 a b-b(b+1))^{2}+\left(b-4 a^{2}+2 a(b+1)\right)^{2}= \\
& =4 a^{2}+4 a^{2} b^{2}+b^{2}(b+1)^{2}+8 a^{2} b-4 a b(b+1)-4 a b^{2}(b+1)+ \\
& +b^{2}+16 a^{4}+4 a^{2}(b+1)^{2}-8 a^{2} b+4 a b(b+1)-16 a^{3}(b+1)= \\
& \quad=\left(4 a^{2}+b^{2}\right)\left(1+4 a^{2}+(b+1)^{2}-4 a(b+1)\right)=\left(4 a^{2}+b^{2}\right)\left(1+(b+1-2 a)^{2}\right)
\end{aligned}
$$
Thus, we need to find the minimum of the function $(b+1-2 a)^{2}+1$ for positive $a$ and $b$. It is 1 and is achieved, for example, when $a=b=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In an arm wrestling tournament, $2^{n}$ athletes participate, where $n$ is a natural number greater than 7. One point is awarded for a win, and zero points for a loss. Before each round, pairs are formed by drawing lots among participants with the same number of points (those who do not find a pair are simply given a point). After the seventh round, it turned out that exactly 42 participants had 5 points. What is $n$?
|
Answer: 8.
Solution. Let $f(m, k)$ be the number of participants who have scored $k$ points after $m$ rounds. We will prove by induction on $m$ that
$$
f(m, k)=2^{n-m} \cdot C_{m}^{k}, \quad \text { where } 0 \leqslant k \leqslant m \leqslant 2^{n}
$$
If $m=0$, then $k=0$, and $f(0,0)=2^{n}$. We will now perform the inductive step. Suppose that for some $m<n$ the required equality holds. Then each group with the same number of points contains an even number of participants, so all participants can be paired. After the $(m+1)$-th round, the groups of athletes with no wins and no losses will be halved. Therefore,
$$
f(m+1,0)=\frac{1}{2} f(m, 0)=\frac{1}{2} \cdot 2^{n-m}=2^{n-(m+1)} \cdot C_{m+1}^{0} \quad \text { and } \quad f(m+1, m+1)=\frac{1}{2} f(m, m)=2^{n-(m+1)} \cdot C_{m+1}^{m+1}
$$
Now let $k \in\{1, \ldots, m\}$. After the $(m+1)$-th round, $k$ points will be scored by those who had $k$ points and lost, as well as by those who had $k-1$ point and won. Therefore,
$$
f(m+1, k)=\frac{1}{2} \cdot f(m, k)+\frac{1}{2} \cdot f(m, k-1)=2^{n-m-1}\left(C_{m}^{k}+C_{m}^{k-1}\right)=2^{n-(m+1)} \cdot C_{m+1}^{k}
$$
(in the last transition, we used the main identity of Pascal's triangle). Thus, the inductive step is completed. It remains to note that
$$
42=f(7,5)=2^{n-7} \cdot C_{7}^{5}=2^{n-7} \cdot \frac{7 \cdot 6}{2}=42 \cdot 2^{n-8}, \quad \text { that is } n=8 .
$$
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression for $a, b>0$
$$
\frac{(3 a b-6 b+a(1-a))^{2}+\left(9 b^{2}+2 a+3 b(1-a)\right)^{2}}{a^{2}+9 b^{2}}
$$
|
# Answer: 4.
Solution 1. The minimized expression is the sum of the squares of the distances from point $A(3 b,-2)$ to the lines $\ell_{1}$ and $\ell_{2}$, given by the equations
$$
\ell_{1}: a x+3 b y+a(1-a)=0 \quad \text { and } \quad \ell_{2}: 3 b x-a y+3 b(1-a)=0
$$
These lines are perpendicular and intersect at point $B(a-1,0)$. Then, by the Pythagorean theorem, we need to find the minimum of $A B^{2}=(a-1-3 b)^{2}+4$, which is 4 and is achieved, for example, when $a=4$ and $b=1$.
Solution 2. Transform the numerator of the fraction:
$$
\begin{aligned}
& (3 a b-6 b+a(1-a))^{2}+\left(9 b^{2}+2 a+3 b(1-a)\right)^{2}= \\
& =36 b^{2}+9 a^{2} b^{2}+a^{2}(1-a)^{2}-36 a b^{2}-12 a b(1-a)+6 a^{2} b(1-a)+ \\
& +4 a^{2}+81 b^{4}+9 b^{2}(1-a)^{2}+36 a b^{2}+12 a b(1-a)+54 b^{3}(1-a)= \\
& \quad=\left(a^{2}+9 b^{2}\right)\left(4+9 b^{2}+(1-a)^{2}+6 b(1-a)\right)=\left(a^{2}+9 b^{2}\right)\left(4+(1-a+3 b)^{2}\right)
\end{aligned}
$$
Thus, we need to find the minimum of the function $(1-a+3 b)^{2}+1$ for positive $a$ and $b$. It is 4 and is achieved, for example, when $a=4$ and $b=1$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y, z \in (0,2]$, find the maximum value of the expression
$$
A=\frac{\left(x^{3}-6\right) \sqrt[3]{x+6}+\left(y^{3}-6\right) \sqrt[3]{y+6}+\left(z^{3}-6\right) \sqrt[3]{z+6}}{x^{2}+y^{2}+z^{2}}
$$
|
Answer: 1.
Solution. For $x \in(0,2]$, the inequalities $\sqrt[3]{x+6} \leqslant 2$ and $x^{3} \leqslant 2 x^{2}$ hold, from which
$$
\left(x^{3}-6\right) \sqrt[3]{x+6} \leqslant 2\left(2 x^{2}-6\right)
$$
Similarly, the other two terms in the numerator of $A$ are estimated. Therefore,
$$
A \leqslant 2 \cdot \frac{2 x^{2}-6+2 y^{2}-6+2 z^{2}-6}{x^{2}+y^{2}+z^{2}}=4-\frac{36}{x^{2}+y^{2}+z^{2}} \leqslant 4-\frac{36}{12}=1
$$
Equality is achieved when $x=y=z=2$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The diagonals of the inscribed quadrilateral $ABCD$ intersect at point $O$. Inside triangle $AOB$, a point $K$ is chosen such that line $KO$ is the bisector of angle $CK$. Ray $DK$ intersects the circumcircle of triangle $COK$ again at point $L$, and ray $CK$ intersects the circumcircle of triangle $DOK$ again at point $M$. Find the ratio of the areas of triangles $ALO$ and $BMO$.
|
Answer: 1.
Solution. Let $r_{1}$ and $r_{2}$ be the radii of the circumcircles of triangles $C O K$ and $D O K$, respectively. Note that
$$
\angle L K O=180^{\circ}-\angle D K O=180^{\circ}-\angle C K O=\angle M K O
$$
from which $\frac{L O}{M O}=\frac{r_{1}}{r_{2}}$. Moreover, the inscribed quadrilateral $A B C D$ implies that triangles $A O D$ and $B O C$ are similar by two angles. Then
$$
\frac{A O}{B O}=\frac{O D}{O C}=\frac{r_{2}}{r_{1}}
$$
since the chords $O D$ and $O C$ correspond to equal inscribed angles. Therefore,
$$
\frac{L O}{M O} \cdot \frac{A O}{B O}=1 \Longleftrightarrow L O \cdot A O=M O \cdot B O
$$
Since $\angle K M O=\angle K D O$ and $\angle K L O=\angle K C O$, triangles $M C O$ and $D L O$ are similar, from which
$$
\begin{gathered}
\angle A O L=\angle A O M+\angle L O M=180^{\circ}-\angle C O M+\angle L O M= \\
\quad=180^{\circ}-\angle D O L+\angle L O M=\angle B O L+\angle L O M=\angle B O M
\end{gathered}
$$
Thus,
$$
S_{A O L}=\frac{1}{2} \cdot L O \cdot A O \cdot \sin \angle A O L=\frac{1}{2} \cdot M O \cdot B O \cdot \sin \angle B O M=S_{B O M}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $x, y, z \geqslant 3$ find the minimum value of the expression
$$
A=\frac{\left(x^{3}-24\right) \sqrt[3]{x+24}+\left(y^{3}-24\right) \sqrt[3]{y+24}+\left(z^{3}-24\right) \sqrt[3]{z+24}}{x y+y z+z x}
$$
|
Answer: 1.
Solution. For $x \geqslant 3$, the inequalities $\sqrt[3]{x+24} \geqslant 3$ and $x^{3} \geqslant 3 x^{2}$ hold, from which
$$
\left(x^{3}-24\right) \sqrt[3]{x+24} \geqslant 3\left(3 x^{2}-24\right)
$$
Similarly, the other two terms in the numerator of $A$ are estimated. Therefore,
$$
A \geqslant 3 \cdot \frac{3 x^{2}-24+3 y^{2}-24+3 z^{2}-24}{x y+y z+z x}=9\left(\frac{x^{2}+y^{2}+z^{2}}{x y+y z+z x}-\frac{24}{x y+y z+z x}\right) \geqslant 9\left(1-\frac{24}{27}\right)=1
$$
Equality is achieved when $x=y=z=3$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides $AB$ and $AC$ of an acute-angled triangle $ABC$, points $K$ and $L$ are marked such that the quadrilateral $B K L C$ is cyclic. Inside this quadrilateral, a point $M$ is chosen so that the line $AM$ is the bisector of angle $BMC$. The ray $BM$ intersects the circumcircle of triangle $AMC$ again at point $P$, and the ray $CM$ intersects the circumcircle of triangle $AMB$ again at point $Q$. Find the ratio of the areas of triangles $ALP$ and $AKQ$.
|
Answer: 1.

Solution. Let $r_{1}$ and $r_{2}$ be the radii of the circumcircles of triangles $A M B$ and $A M C$, respectively. Since $A M$ is the bisector of angle $B M C$, the following equalities hold:
$$
\angle A M B = \angle A M C \quad \text{and} \quad \angle A M P = \angle A M Q
$$
from which $\frac{A B}{A C} = \frac{r_{1}}{r_{2}} = \frac{A Q}{A P}$. Moreover, from the inscribed quadrilateral $B K L C$, it follows that
$$
\angle A L K = 180^{\circ} - \angle K L C = \angle A B C
$$
Thus, triangles $A L K$ and $A B C$ are similar by two angles. Therefore,
$$
\frac{A L}{A K} = \frac{A B}{A C} = \frac{A Q}{A P} \Longrightarrow A L \cdot A P = A K \cdot A Q
$$
From the equalities $\angle A B M = \angle A Q M$ and $\angle A P M = \angle A C M$, it follows that $\angle B A P = \angle C A Q$, from which
$$
\angle L A P = \angle C A P = \angle B A P - \angle B A C = \angle C A Q - \angle B A C = \angle B A Q = \angle K A Q
$$
Thus,
$$
S_{A L P} = \frac{1}{2} \cdot A L \cdot A P \cdot \sin \angle L A P = \frac{1}{2} \cdot A K \cdot A Q \cdot \sin \angle K A Q = S_{A K Q}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given $x, y, z \geqslant 1$, find the minimum value of the expression
$$
A=\frac{\sqrt{3 x^{4}+y}+\sqrt{3 y^{4}+z}+\sqrt{3 z^{4}+x}-3}{x y+y z+z x}
$$
|
Answer: 1.
Solution. Note that for $x, y \geqslant 1$
$$
\sqrt{3 x^{4}+y}-1=\sqrt{x^{4}+2 x^{4}+y}-1 \geqslant \sqrt{x^{4}+2 x^{2}+1}-1=x^{2}
$$
Similarly, it can be shown that
$$
\sqrt{3 y^{4}+z}-1 \geqslant y^{2}, \quad \sqrt{3 z^{4}+x}-1 \geqslant z^{2}
$$
Therefore,
$$
A \geqslant \frac{x^{2}+y^{2}+z^{2}}{x y+y z+z x} \geqslant 1
$$
Equality is achieved when $x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a cyclic quadrilateral $A B C D$ with perpendicular diagonals. On the circle circumscribed around it, a point $E$ is marked, diametrically opposite to $D$, and the segments $A B$ and $D E$ do not intersect. Find the ratio of the areas of triangle $B C D$ and quadrilateral $A B E D$.
|
Answer: 1.
Solution. Let $N$ be the intersection point of $A C$ and $B D$, and $H$ be the foot of the perpendicular dropped from point $E$ to line $A C$. By the problem's condition, $D E$ is the diameter of the circle. Therefore, $\angle D B E=90^{\circ}$, which implies $B E \| A C$. Additionally, $\angle D C E=90^{\circ}$ and
$$
\angle C D E=90^{\circ}-\angle D E C=90^{\circ}-\angle D A C=\angle A D B
$$
from which it follows that $C E=A B$. Thus, $A B E C$ is an isosceles trapezoid, and
$$
C N=A C-A N=A C-C H=A H
$$
It remains to note that
$$
2 \cdot S_{A B E D}=B D \cdot A N+B D \cdot B E=B D \cdot A H=B D \cdot C N=2 \cdot S_{B C D}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y, z \in(0,1]$ find the maximum value of the expression
$$
A=\frac{\sqrt{8 x^{4}+y}+\sqrt{8 y^{4}+z}+\sqrt{8 z^{4}+x}-3}{x+y+z}
$$
|
Answer: 2.
Solution. Note that for $x, y \in(0,1]$
$$
\sqrt{8 x^{4}+y}-1=\sqrt{4 x^{4}+4 x^{4}+y}-1 \leqslant \sqrt{4 x^{2}+4 x+1}-1=2 x .
$$
Similarly, it can be shown that
$$
\sqrt{3 y^{4}+z}-1 \leqslant 2 y, \quad \sqrt{3 z^{4}+x}-1 \leqslant 2 z
$$
Therefore,
$$
A \leqslant \frac{2 x+2 y+2 z}{x+y+z}=2
$$
Equality is achieved when $x=y=z=1$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The diagonal $AC$ of the inscribed quadrilateral $ABCD$ is the diameter of the circumscribed circle $\omega$ around it. A line perpendicular to the segment $BC$ was drawn from point $D$, intersecting the circle $\omega$ again at point $E$. Find the ratio of the areas of triangle $BCD$ and quadrilateral $ABEC$.
|
Answer: 1.

Solution. Let $N$ be the intersection point of $B C$ and $D E$, and $H$ be the foot of the perpendicular dropped from point $A$ to line $D E$. By the problem's condition, $A C$ is the diameter of the circle. Therefore, $\angle A B C=90^{\circ}$, which implies $A B \| D E$. Additionally, $\angle A D C=90^{\circ}$ and
$$
\angle A C D=90^{\circ}-\angle D A C=90^{\circ}-\angle D E C=90^{\circ}-\angle N E C=\angle E C B
$$
from which it follows that $A D=B E$. Thus, $D A B E$ is an isosceles trapezoid, and
$$
D N=D E-E N=D E-D H=E H
$$
It remains to note that
$$
2 \cdot S_{A B E C}=B C \cdot E N+B C \cdot A B=B C \cdot E H=B C \cdot D N=2 \cdot S_{B C D}
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y \in(0,1]$, find the maximum value of the expression
$$
A=\frac{\left(x^{2}-y\right) \sqrt{y+x^{3}-x y}+\left(y^{2}-x\right) \sqrt{x+y^{3}-x y}+1}{(x-y)^{2}+1}
$$
|
Answer: 1.
Solution. Note that
$$
y+x^{3}-x y-x^{2}=\left(y-x^{2}\right)(1-x)
$$
If $y \geqslant x^{2}$, then
$$
\sqrt{y+x^{3}-x y} \geqslant x \quad \text { and } \quad\left(x^{2}-y\right)\left(\sqrt{y+x^{3}-x y}-x\right) \leqslant 0
$$
and when $y<x^{2}$
$$
\sqrt{y+x^{3}-x y} \leqslant x \quad \text { and } \quad\left(x^{2}-y\right)\left(\sqrt{y+x^{3}-x y}-x\right) \leqslant 0
$$
In both cases, the inequality $\left(x^{2}-y\right) \sqrt{y+x^{3}-x y} \leqslant x^{3}-x y$ holds. Estimating the second term in the numerator of $A$ similarly, we get
$$
A \leqslant \frac{x^{3}+y^{3}-2 x y+1}{(x-y)^{2}+1} \leqslant \frac{x^{2}+y^{2}-2 x y+1}{(x-y)^{2}+1}=1
$$
Equality is achieved when $x=y=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the side $AB$ of an acute-angled triangle $ABC$, a point $M$ is marked. A point $D$ is chosen inside the triangle. Circles $\omega_{A}$ and $\omega_{B}$ are circumscribed around triangles $AMD$ and $BMD$ respectively. The side $AC$ intersects the circle $\omega_{A}$ again at point $P$, and the side $BC$ intersects the circle $\omega_{B}$ again at point $Q$. The ray $PD$ intersects the circle $\omega_{B}$ again at point $R$, and the ray $QD$ intersects the circle $\omega_{A}$ again at point $S$. Find the ratio of the areas of triangles $ACR$ and $BCS$.
|
# Answer: 1.
Solution. Notice that
$$
\angle P A M=180^{\circ}-\angle P D M=\angle R D M=\angle R B M
$$
from which it follows that $B R \| A C$. Therefore, the distances from points $B$ and $R$ to the line $A C$ are the same. Thus, triangles $A B C$ and $A C R$ have the same base $A C$ and the same heights dropped to $A C$. Therefore, the areas of these triangles are equal. Additionally,
$$
\angle Q B M=180^{\circ}-\angle Q D M=\angle M D S=180^{\circ}-\angle M A S
$$
from which it follows that $A S \| B C$. Therefore, the distances from points $A$ and $S$ to the line $B C$ are the same. Thus, triangles $A B C$ and $B C S$ have the same base $B C$ and the same heights dropped to $B C$. Therefore, the areas of these triangles are also equal. As a result, we get $S_{A C R}=S_{A B C}=S_{B C S}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y \in[1,3]$ find the minimum value of the expression
$$
A=\frac{\left(3 x y+x^{2}\right) \sqrt{3 x y+x-3 y}+\left(3 x y+y^{2}\right) \sqrt{3 x y+y-3 x}}{x^{2} y+y^{2} x}
$$
|
Answer: 4.
Solution. Note that
$$
3 x y+x-3 y-x^{2}=(3 y-x)(x-1) \geqslant 0
$$
since $x \geqslant 1$ and $x \leqslant 3 \leqslant 3 y$. Then
$$
\left(3 x y+x^{2}\right) \sqrt{3 x y+x-3 y} \geqslant 3 x^{2} y+x^{3} \quad \text { and, similarly, } \quad\left(3 x y+y^{2}\right) \sqrt{3 x y+y-3 x} \geqslant 3 y^{2} x+y^{3} .
$$
Moreover, by the Cauchy inequality
$$
x^{2} y+y^{2} x=x y(x+y) \leqslant \frac{1}{4}(x+y)^{3}
$$
Therefore,
$$
A \geqslant \frac{3 x y(x+y)+x^{3}+y^{3}}{\frac{1}{4}(x+y)^{3}}=4 \cdot \frac{(x+y)^{3}}{(x+y)^{3}}=4
$$
Equality is achieved when $x=y=1$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the side $B C$ of triangle $A B C$ with obtuse angle $C$, a point $M$ is marked. Point $D$ is chosen such that triangle $B C D$ is acute, and points $A$ and $D$ lie on opposite sides of line $B C$. Circles $\omega_{B}$ and $\omega_{C}$ are circumscribed around triangles $B M D$ and $C M D$ respectively. Side $A B$ intersects circle $\omega_{B}$ again at point $P$, and ray $A C$ intersects circle $\omega_{C}$ again at point $Q$. Segment $P D$ intersects circle $\omega_{C}$ again at point $R$, and ray $Q D$ intersects circle $\omega_{B}$ again at point $S$. Find the ratio of the areas of triangles $A B R$ and $A C S$.
|
# Answer: 1.

Solution. Notice that
$$
\angle S B M=180^{\circ}-\angle S D M=\angle M D Q=180^{\circ}-\angle M C Q
$$
from which $S B \| A C$. Therefore, the distances from points $B$ and $S$ to line $A C$ are the same. Thus, triangles $A B C$ and $A S C$ have the same base $A C$ and equal heights dropped to $A C$. Therefore, the areas of these triangles are equal. Additionally,
$$
\angle P B M=\angle P D M=\angle R D M=\angle R C M
$$
from which $B P \| R C$. Therefore, the distances from points $R$ and $C$ to line $A B$ are the same. Thus, triangles $A B C$ and $A B R$ have the same base $A B$ and equal heights dropped to $A B$. Therefore, the areas of these triangles are also equal. As a result, we get $S_{A S C}=S_{A B C}=S_{A B R}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For $x, y, z \in(0,1]$ find the minimum value of the expression
$$
A=\frac{(x+2 y) \sqrt{x+y-x y}+(y+2 z) \sqrt{y+z-y z}+(z+2 x) \sqrt{z+x-z x}}{x y+y z+z x}
$$
|
Answer: 3.
Solution. Note that for $x, y \in(0,1]$
$$
\sqrt{x+y-x y}=\sqrt{x+y(1-x)} \geqslant \sqrt{x} \geqslant x
$$
Then $(x+2 y) \sqrt{x+y-x y} \geqslant x^{2}+2 x y$ and similarly,
$$
(y+2 z) \sqrt{y+z-y z} \geqslant y^{2}+2 y z, \quad(z+2 x) \sqrt{z+x-z x} \geqslant z^{2}+2 z x
$$
Therefore,
$$
A \geqslant \frac{x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x}{x y+y z+z x}=\frac{(x+y+z)^{2}}{x y+y z+z x} \geqslant 3
$$
Equality is achieved when $x=y=z=1$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a quadratic trinomial $f(x)$ such that the equation $(f(x))^{3}-f(x)=0$ has exactly three solutions. Find the ordinate of the vertex of the trinomial $f(x)$.
|
# Answer: 0.
Solution. Suppose the leading coefficient of the trinomial is positive. Note that $(f(x))^{3}-f(x)=f(x) \cdot(f(x)-1) \cdot(f(x)+1)$. The equation $f(x)=0$ has more roots than the equation $f(x)=-1$, and fewer roots than the equation $f(x)=1$. It is also clear that no two equations have common roots. Therefore, the equation $f(x)=0$ has exactly one root. Consequently, the ordinate of the vertex of the trinomial $f(x)$ is zero. Similarly, the case where the leading coefficient of the trinomial is negative is also considered.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given a board $2016 \times 2016$. For what smallest $k$ can the cells of the board be colored in $k$ colors such that
1) one of the diagonals is painted in the first color;
2) cells symmetric with respect to this diagonal are painted in the same color;
3) any two cells located in the same row on opposite sides of the cell of the first color are painted in different colors (the cells do not necessarily have to be adjacent to the cell of the first color).
|
Answer: 11.
Solution. Let the cells of the diagonal running from the top left corner to the bottom right corner be painted in the first color. Denote by $C_{i}$ the set of colors in which the cells of the $i$-th row, located to the left of the diagonal of a single color, are painted. We will prove that $C_{i} \neq C_{j}$ for $i<j$. Indeed, the cell located in the $i$-th row and $j$-th column has a color not included in $C_{i}$. But the cell located in the $j$-th row and $i$-th column is painted in the same color, and its color is included in $C_{j}$. Thus, the sets $C_{1}, C_{2}, \ldots, C_{2016}$ are different subsets of the set $\{1,2, \ldots, k\}$. Then there are no more than $2^{k}$ of them. Therefore, $k \geqslant 11$.
By induction, we will show how to paint the board $2^{k} \times 2^{k}$ in $k$ colors as required. This will be sufficient, since by leaving only the rows from 1 to 2016 and the columns from 1 to 2016, we will obtain a $2016 \times 2016$ board with the required coloring.
Base case $k=1$ is obvious, since a $2 \times 2$ board can be painted in one color. Inductive step from $k$ to $k+1$. If we already know how to paint a $2^{k} \times 2^{k}$ board as required, then we will paint a $2^{k+1} \times 2^{k+1}$ board as follows: place two copies of the $2^{k} \times 2^{k}$ board, one in the top left corner and the other in the bottom right corner, and paint the remaining cells in the $(k+1)$-th color.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a quadratic trinomial $f(x)$ such that the equation $(f(x))^{3}-4 f(x)=0$ has exactly three solutions. How many solutions does the equation $(f(x))^{2}=1$ have?
|
Answer: 2.
Solution. Suppose the leading coefficient of the polynomial is positive. Note that $(f(x))^{3}-4 f(x)=f(x) \cdot(f(x)-2) \cdot(f(x)+2)$. The equation $f(x)=0$ has more roots than the equation $f(x)=-2$, and fewer roots than the equation $f(x)=2$. It is also clear that no two equations have common roots. Then the equation $f(x)=0$ has exactly one root. Therefore, the equation $f(x)=1$ has exactly two roots, and the equation $f(x)=-1$ has no roots. Thus, the equation $(f(x))^{2}-1=(f(x)+1)(f(x)-1)=0$ has two roots. Similarly, the case when the leading coefficient of the polynomial is negative is considered.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.