problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
6. Find all natural numbers $n$ such that the number $2^{n}+n^{2}+25$ is a cube of a prime number.
|
Answer: $n=6$
Solution. Let $2^{n}+n^{2}+25=p^{3}$ for some prime number $p$. Since $p>3$, $p$ is an odd prime number. Then $n$ is an even number, and $2^{n}$ gives a remainder of 1 when divided by three. If $n$ is not divisible by three, then $n^{2}$ gives a remainder of 1 when divided by three, and then $2^{n}+n^{2}+25$ is divisible by three, which is impossible. Therefore, $n$ is divisible by six and can be written as $n=6 k$. Consequently, $2^{n}+n^{2}+25=64^{k}+36 k^{2}+25>\left(4^{k}\right)^{3}$. Therefore,
$$
64^{k}+36 k^{2}+25 \geqslant\left(4^{k}+1\right)^{3}=64^{k}+3 \cdot 16^{k}+3 \cdot 4^{k}+1 .
$$
If $k \geqslant 2$, then $3 \cdot 4^{k}>25$ and $3 \cdot 16^{k} \geqslant 36 k^{2}$ (the latter follows, for example, from the easily verifiable by induction inequality $4^{k} \geqslant 6 k$). Thus, $k=1$ and $n=6$. It remains to verify that such $n$ works: $2^{6}+6^{2}+25=125=5^{3}$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all values of $a$ for which the quadratic trinomials $x^{2}+2 x+a$ and $x^{2}+a x+2=0$ have two roots each, and the sum of the squares of the roots of the first trinomial is equal to the sum of the squares of the roots of the second trinomial.
|
Answer: $a=-4$
Solution. If $x_{1}$ and $x_{2}$ are the roots of the quadratic polynomial $x^{2}+p x+q$, then by Vieta's theorem
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=p^{2}-2 q
$$
Therefore, we need to find such numbers $a$ for which $2^{2}-2 a=a^{2}-2 \cdot 2$. Thus, we need to solve the equation $a^{2}+2 a-8=0$. Its roots are $a=-4$ and $a=2$. The first solution is valid, while the second solution is not valid, since the quadratic polynomial $x^{2}+2 x+2$ does not have roots.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all values of $a$ for which the quadratic trinomials $x^{2}-6 x+4 a$ and $x^{2}+a x+6=0$ have two roots each, and the sum of the squares of the roots of the first trinomial is equal to the sum of the squares of the roots of the second trinomial.
|
Answer: $a=-12$
If $x_{1}$ and $x_{2}$ are the roots of the quadratic polynomial $x^{2}+p x+q$, then by Vieta's theorem
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=p^{2}-2 q
$$
Therefore, we need to find such numbers $a$ for which $6^{2}-8 a=a^{2}-2 \cdot 6$. Thus, we need to solve the equation $a^{2}+8 a-48=0$. Its roots are $a=-12$ and $a=4$. The first solution is valid, while the second solution is not valid, since the quadratic polynomial $x^{2}-6 x+16$ does not have roots.
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points) We will call a date diverse if in its representation in the form DD/MM/YY (day-month-year) all digits from 0 to 5 are present. How many diverse dates are there in the year 2013?
|
Answer: 2.
Solution. Note that in any date of 2013 in the specified format, the digits 1 and 3 are used, so for the day and month of a diverse date, the digits left are 0, 2, 4, and 5.
Let $Д_{1}$ and $Д_{2}$ be the first and second digits in the day's notation, and $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$ be the first and second digits in the month's notation. Since there are 12 months in a year, $\mathrm{M}_{1} \leqslant 1$, hence $\mathrm{M}_{1}=0$. Moreover, no month has more than 31 days, and of the remaining digits, only 2 is suitable for $Д_{1}$. The digits 4 and 5 can be placed in positions $Д_{2}$ and $\mathrm{M}_{2}$ in any order, giving a valid date.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (10 points) We will call a word any finite sequence of letters of the Russian alphabet. How many different six-letter words can be formed from the letters of the word СКАЛКА? And how many seven-letter words from the letters of the word ТЕФТЕЛЬ? In your answer, indicate the quotient of dividing the larger of the found numbers by the smaller.
#
|
# Answer: 7.
Solution. The word СКАЛКА has six letters, but the letter А and the letter K each appear twice. Therefore, the number of different words will be $\frac{6!}{2!\cdot 2!}$. In
the word ТЕФТЕЛЬ, there are seven letters, and the letters $\mathrm{T}$ and $\mathrm{E}$ each appear twice, so the number of different words that can be formed from the letters of this word will be greater and will be equal to $\frac{7!}{2!2!}$. It is easy to see that the quotient of dividing the larger by the smaller will be equal to 7.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (20 points) Let a sequence of non-negative integers be given
$$
k, k+1, k+2, \ldots, k+n
$$
Find the smallest $k$, for which the sum of all numbers in the sequence is equal to 100.
#
|
# Answer: 9.
Solution. The given sequence of numbers is an arithmetic progression with $n+1$ terms. Its sum is $\frac{(n+1)(2 k+n)}{2}$. Therefore, the condition can be rewritten as $(n+1)(2 k+n)=200$, where $n$ is a non-negative integer. It is clear that $k$ decreases as $n$ increases. Thus, we need to find the largest $n$ for which $k$ is an integer. Note that
$$
200=(n+1)(2 k+n)>n^{2} \Longrightarrow n<\sqrt{200} \Longrightarrow n \leqslant 14
$$
Moreover, $200=2^{3} \cdot 5^{2}$. Let's consider two cases.
1) $n$ is even. The largest $n \leqslant 14$ for which 200 is divisible by $n+1$ is 4, from which $k=\frac{40-4}{2}=18$.
2) $n$ is odd. Then $n$ can only be $1, 3, 7$ (otherwise 200 is not divisible by $n+1$). For $n=7$, we get $k=9$. This will be the smallest.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (50 points) A $5 \times 5$ square of cells was cut into several pieces of different areas, each consisting of an integer number of cells. What is the maximum number of pieces that could result from such a cutting?
|
Answer: 6.
Solution. We will show that there cannot be more than 6 parts. Indeed, the total area of 7 parts cannot be less than $1+2+3+4+5+6+7=28$, which exceeds the area of the square.
Now we will show how a $5 \times 5$ square can be cut into 6 parts of different sizes:

Thus, the areas of the pieces will be $2, 8, 3, 7, 1,$ and 4.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (50 points) Each of the 12 knights sitting around a round table has thought of a number, and all the numbers are different. Each knight claims that the number they thought of is greater than the numbers thought of by their neighbors to the right and left. What is the maximum number of these claims that can be true?
|
Answer: 6.
Solution. Let's renumber the knights in order with numbers from 1 to 12. In the pairs $(1,2),(3,4)$, $\ldots,(11,12)$, at least one of the knights is lying (specifically, the one who guessed the smaller number). Therefore, there can be no more than 6 true statements. Now let's provide an example where exactly 6 statements are true. Suppose the knights with odd numbers guessed the numbers from 1 to 6, and those with even numbers guessed the numbers from 7 to 12 (in any order). Then all the knights with even numbers are telling the truth.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Quadrilateral $A B C D$ is inscribed in a circle. A tangent line $\ell$ is drawn to this circle at point $C$. Circle $\omega$ passes through points $A$ and $B$ and is tangent to line $\ell$ at point $P$. Line $P B$ intersects segment $C D$ at point $Q$. Find the ratio $\frac{B C}{C Q}$, given that $B$ is the point of tangency of circle $\omega$.
|
Answer: 1.
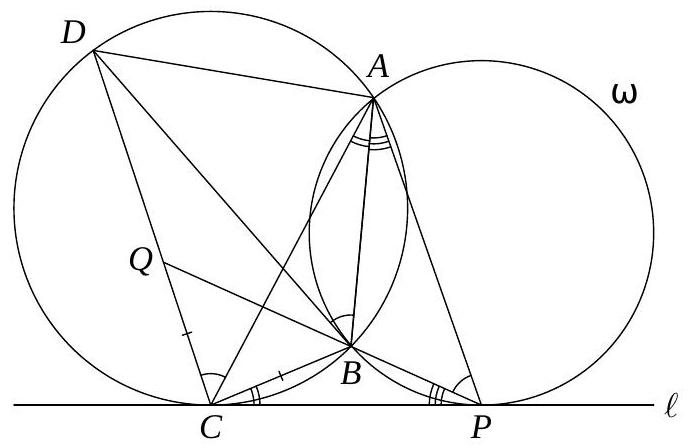
Solution. The angle between the tangent $BD$ and the chord $AB$ of the circle $\omega$ is equal to the inscribed angle that subtends $AB$, so $\angle APB = \angle ABD = \angle ACD$. Therefore, the quadrilateral $APCQ$ is cyclic, from which $\angle CQB = \angle CAP$. Applying the tangent-secant theorem twice more, we also get the equalities $\angle BCP = \angle BAC$ and $\angle BPC = \angle BAP$. Then,
$$
\angle CBQ = 180^{\circ} - \angle CBP = \angle BCP + \angle BPC = \angle BAC + \angle BAP = \angle CAP = \angle CQB
$$
Thus, triangle $BCQ$ is isosceles, from which $BC = CQ$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Each cell of a $5 \times 6$ table is colored in one of three colors: blue, red, or yellow. In each row of the table, the number of red cells is not less than the number of blue cells and not less than the number of yellow cells, and in each column of the table, the number of blue cells is not less than the number of red cells and not less than the number of yellow cells. How many yellow cells can there be in such a table? Provide an example of a corresponding coloring.
|
Answer: 6.
| $\mathrm{C}$ | $\mathrm{C}$ | $\mathrm{C}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{C}$ | $\mathrm{C}$ | $\mathrm{C}$ |
| $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{C}$ | $\mathrm{C}$ |
| $\mathrm{C}$ | $\mathrm{C}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ |
| $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{C}$ | $\mathrm{C}$ | $\mathrm{K}$ | $\mathrm{K}$ |
Solution. Since in each row there are no fewer red cells than blue ones, there are no fewer of them in the entire table. Then the number of red and blue cells is the same in each column. Indeed, if in one of the columns there are fewer red cells than blue ones, then there will be fewer of them in the entire table, since in the other columns there are no more blue ones. In addition, the number of blue cells in each column is no less than $\frac{5}{3}$, that is, it is at least 2. Therefore, the table contains at least 12 blue cells and as many red ones. Therefore, there are no more than 6 yellow cells in the table. On the other hand, in each column the total number of red and blue cells is even, so there is at least one yellow cell in it. Therefore, the table contains no fewer than 6 yellow cells. An example of coloring with six yellow cells is shown in the figure.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Each cell of a $5 \times 5$ table is colored in one of three colors: blue, red, or yellow. In each row of the table, the number of yellow cells is not less than the number of red cells and not less than the number of blue cells, and in each column of the table, the number of red cells is not less than the number of yellow cells and not less than the number of blue cells. How many blue cells can there be in such a table? Provide an example of a corresponding coloring.
|
Answer: 5.
| $\mathrm{C}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ |
| :---: | :---: | :---: | :---: | :---: |
| $\mathrm{K}$ | $\mathrm{C}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ |
| $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{C}$ | $\mathrm{K}$ | $\mathrm{K}$ |
| $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{C}$ | $\mathrm{K}$ |
| $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{K}$ | $\mathrm{C}$ |
Solution. Since in each row the number of yellow cells is not less than the number of red cells, the same is true for the entire table. Therefore, the number of yellow and red cells is the same in each column. Indeed, if in one of the columns the number of yellow cells is less than the number of red cells, then there will be fewer of them in the entire table, since in the other columns their number is not greater than the number of red cells. Moreover, the number of red cells in each column is not less than $\frac{5}{3}$, that is, it is at least 2. Thus, the table contains at least 10 red cells and the same number of yellow cells. Therefore, there are no more than 5 blue cells in the table. On the other hand, in each column the total number of yellow and red cells is even, so there is at least one blue cell in each column. Thus, the table contains no fewer than 5 blue cells. An example of coloring with five blue cells is shown in the figure.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the minimum number of cells that need to be marked in a $7 \times 7$ table so that every vertical or horizontal strip $1 \times 4$ contains at least one marked cell?
|
Answer: 12.
Solution. Consider a more general problem when the table has size $(2 n-1) \times(2 n-1)$, and the strip is $-1 \times n$. Let's call the $n$-th row and the $n$-th column central, and the marked cells on them, except for the center of the board, - axial. Suppose there are $k$ axial cells in the central row and $m$ axial cells in the central column. In rows and columns that do not contain axial cells, there should be at least two marked cells. In total, in such rows, there will be at least $2 \cdot(2 n-2-m)=4(n-1)-2 m$ marked cells, and in columns - at least $4(n-1)-2 k$ cells. At the same time, each cell will be counted no more than twice. Taking into account the axial cells, we get that there are at least
$$
\frac{1}{2}(4(n-1)-2 m+4(n-1)-2 k)+k+m=4(n-1) \text { cells. }
$$
The value $4(n-1)$ is achieved if all cells of the central row and column, except for the center of the board, are marked. Assuming $n=4$, we get the answer.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given numbers $x, y, z \in\left[0, \frac{\pi}{2}\right]$. Find the minimum value of the expression
$$
A=\cos (x-y)+\cos (y-z)+\cos (z-x)
$$
|
Answer: 1.
Solution. We can assume that $x \leqslant y \leqslant z$, since the expression $A$ does not change under pairwise permutations of the variables. Notice that
$$
\cos (x-y)+\cos (z-x)=2 \cos \left(\frac{z-y}{2}\right) \cos \left(\frac{z+y}{2}-x\right)
$$
The first cosine in the right-hand side is positive and does not depend on $x$, while the argument of the second cosine lies in $\left[0, \frac{\pi}{2}\right]$, since $\frac{\pi}{2} \geqslant \frac{z+y}{2} \geqslant x$. Therefore, the right-hand side will be the smallest when $x=0$. In this case,
$$
A=\cos y+\cos z+\cos (y-z)=\cos z+2 \cos \frac{z}{2} \cdot \cos \left(y-\frac{z}{2}\right)
$$
Notice that $-\frac{z}{2} \leqslant y-\frac{z}{2} \leqslant \frac{z}{2}$, hence $\cos \left(y-\frac{z}{2}\right) \geqslant \cos \frac{z}{2}$. Therefore,
$$
A \geqslant \cos z+2 \cos ^{2} \frac{z}{2}=2 \cos z+1 \geqslant 1
$$
Equality is achieved when $x=0, y=z=\frac{\pi}{2}$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given numbers $x, y, z \in [0, \pi]$. Find the minimum value of the expression
$$
A=\cos (x-y)+\cos (y-z)+\cos (z-x)
$$
|
Answer: -1.
Solution. We can assume that $x \leqslant y \leqslant z$, since the expression $A$ does not change under pairwise permutations of the variables. Notice that
$$
\cos (x-y)+\cos (z-x)=2 \cos \left(\frac{z-y}{2}\right) \cos \left(\frac{z+y}{2}-x\right)
$$
The first cosine in the right-hand side is non-negative and does not depend on $x$, while the argument of the second cosine lies in the interval $[0, \pi]$, since $\pi \geqslant \frac{z+y}{2} \geqslant x$. Therefore, the right-hand side will be the smallest when $x=0$. In this case,
$$
A=\cos y+\cos z+\cos (y-z)=\cos z+2 \cos \frac{z}{2} \cdot \cos \left(y-\frac{z}{2}\right)
$$
Notice that $-\frac{\pi}{2} \leqslant-\frac{z}{2} \leqslant y-\frac{z}{2} \leqslant \frac{z}{2} \leqslant \frac{\pi}{2}$, hence
$$
A=\cos z+2 \cos \frac{z}{2} \cdot \cos \left(y-\frac{z}{2}\right) \geqslant \cos z \geqslant-1
$$
Equality is achieved when $x=0, y=z=\pi$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $3 \times 3$ table, 9 numbers are arranged such that the six products of these numbers in the rows and columns of the table are all different. What is the maximum number of these numbers that can equal one?
|
Answer: 5.
Solution. Let's call the index of the table the total number of its rows and columns consisting of ones. According to the condition, the index does not exceed 1. Let $n$ be an element of the table different from 1. Then in one row or one column with $n$ there is another number not equal to 1 (otherwise the products in the row and column containing $n$ would be equal to $n$). Therefore, non-unit elements occur in pairs. There are at least two such pairs, otherwise the index of the table would be no less than 3. If there are exactly two pairs, then they do not intersect, otherwise the index of the table is 2. Thus, the table contains at least 4 numbers different from 1, and the number of ones does not exceed 5. An example of a table with 5 ones is given below.
| 1 | 1 | 1 |
| :--- | :--- | :--- |
| 1 | 2 | 3 |
| 5 | 7 | 1 |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $3 \times 4$ table, 12 numbers are arranged such that all seven sums of these numbers in the rows and columns of the table are distinct. What is the maximum number of numbers in this table that can be zero?
|
Answer: 8.
Solution. Let's call the index of the table the total number of its zero rows and columns. According to the condition, the index does not exceed 1. Let $n$ be a non-zero element of the table. Then in the same row or in the same column with $n$ there is another non-zero number (otherwise the sums in the row and column containing $n$ are equal to $n$). Therefore, non-zero elements occur in pairs. There are at least two such pairs, otherwise the index of the table is not less than 4. If there are exactly two pairs, then they do not intersect, otherwise the index of the table is 3. Thus, the table contains at least 4 non-zero numbers, and the number of zeros does not exceed 8. An example of a table with 8 zeros is given below.
| 0 | 0 | 0 | 0 |
| :--- | :--- | :--- | :--- |
| 1 | 2 | 0 | 0 |
| 0 | 0 | 4 | 5 |
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given numbers $x, y, z \in [0, \pi]$. Find the maximum value of the expression
$$
A=\sin (x-y)+\sin (y-z)+\sin (z-x)
$$
|
Answer: 2.
Solution 1. We can assume that $x \leqslant y$ and $x \leqslant z$, since the expression $A$ does not change under cyclic permutation of the variables. Notice that
$$
\sin (x-y)+\sin (z-x)=2 \sin \left(\frac{z-y}{2}\right) \cos \left(\frac{z+y}{2}-x\right)
$$
The argument of the sine on the right-hand side lies in $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, and the cosine in $[0, \pi]$, since $\pi \geqslant \frac{z+y}{2} \geqslant x$. Consider two cases.
1) $z>y$. The right-hand side will be maximized at the maximum possible $x$, i.e., when $x=y$, and the value of $A$ will be zero.
2) $z \leqslant y$. For fixed $y$ and $z$, the right-hand side will reach its maximum when $x=0$. In this case,
$$
A=\sin z-\sin y+\sin (y-z)=-\sin y+2 \sin \frac{y}{2} \cdot \cos \left(\frac{y}{2}-z\right) \leqslant 2 \sin \frac{y}{2}-\sin y \leqslant 2
$$
Thus, $A \leqslant 2$. Equality is achieved when $x=0, y=\pi, z=\frac{\pi}{2}$.
Solution 2. Let $a=x-y, b=y-z, c=z-x$. The sum of the numbers $a, b, c$ is zero, so at least one of them is non-positive. Suppose, for example, $c \leqslant 0$. Then $c \in[-\pi, 0]$, hence $\sin c \leqslant 0$. Therefore,
$$
A=\sin a+\sin b+\sin c \leqslant \sin a+\sin b \leqslant 2
$$
Equality is achieved when $x=0, y=\pi, z=\frac{\pi}{2}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (40 points) For the quadratic function $p(x)=a x^{2}+b x+c$, for some integers $n$, the equality $p(n)=p\left(n^{2}\right)$ holds. Provide an example of the function $p(x)$ for which the number of such numbers $n$ is the largest. What is this largest number of numbers $n$?
|
Answer: The maximum number of numbers $n$ is 4. An example of a function: $p(x)=x^{2}-6 x+1$.
Solution: Since $0=0^{2}$ and $1=1^{2}$, for any function $p(x)$ there are at least two such numbers $n$.
Write the equality $p(n)=p\left(n^{2}\right)$ and transform it:
$$
a n^{2}+b n+c=a n^{4}+b n^{2}+c \Leftrightarrow a n^{2}\left(n^{2}-1\right)=b n(1-n)
$$
Further, assuming that $n \neq 0$ and $n \neq 1$, we get that $b=-a n(n+1)$.
For each function $p(x)$, the value $-\frac{b}{a}$ is known and fixed. Therefore, the values of $n$ of interest can be obtained as solutions to the quadratic equation $n^{2}+n+\frac{b}{a}=0$. Its roots are $n_{1,2}=\frac{-1 \pm \sqrt{D}}{2}$, where $D=1-4 \frac{b}{a}$. It is not difficult to see that the roots of the equation will be integers only if the numerator of the fraction is even, which means the discriminant must be a perfect square of some odd number; and in this case, we will have two integer solutions to the equation; in all other cases, there will be no integer roots.
The relationship between $n_{1}$ and $n_{2}$ follows from Vieta's theorem: $n_{1}+n_{2}=-1$, i.e., $n_{2}=-1-n_{1}$.
Thus, the set of numbers for which the condition of the problem is satisfied is the set $\left\{0,1, n_{1},-1-n_{1}\right\}$. Now let's determine whether there are such $n_{1}$ that this set consists of four numbers. It is easy to see that the conditions
$$
\left\{\begin{array} { l }
{ n _ { 1 } \neq 0 , } \\
{ n _ { 1 } \neq 1 , } \\
{ - 1 - n _ { 1 } \neq 0 , } \\
{ - 1 - n _ { 1 } \neq 1 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
n_{1} \neq 0 \\
n_{1} \neq 1 \\
n_{1} \neq-1 \\
n_{1} \neq-2
\end{array}\right.\right.
$$
Obviously, such $n_{1}$ exist, and therefore, the maximum number of numbers $n$ for which the condition of the problem is satisfied is 4. To construct an example, let $n_{1}=2, a=1$. We get that $n_{2}=-1-n_{1}=-3$ and $b=-a n_{1}\left(n_{1}+1\right)=-1 \cdot 2 \cdot 3=-6$. Let $c=1$. Then we get that $p(x)=x^{2}-6 x+1$. Let's check: $p(0)=p\left(0^{2}\right)=1$, $p(1)=p\left(1^{2}\right)=-4, p(2)=p\left(2^{2}\right)=-7, p(-3)=p\left((-3)^{2}\right)=28$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (20 points) Find the number of different four-digit numbers that can be obtained by rearranging the digits of the number 2021 (including this number itself).
|
Answer: 9.
Solution: The number of options can be found by enumerating the permutations of the digits: 2021, 2012, 2201, 2210, 2102, 2120, 1022, 1202, 1220.
The number of options can also be calculated using combinatorial methods. The position of zero can be chosen in three ways, as it should not be the first. Then, in three ways, we choose the position of 1, and on the two remaining places, we put the twos. In the end, we get $3 \cdot 3=9$ possible numbers.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. All three-digit numbers from 100 to 999 are written in a row without spaces. Kostya underlined \( k \) consecutive digits in this sequence, and Andrey underlined other \( k \) consecutive digits in this sequence. It turned out that the \( k \)-digit numbers underlined by the boys are equal. For what largest \( k \) could this have happened?
|
Answer: $k=5$.
Solution. An example of a five-digit number that satisfies the condition of the problem is 22923. Indeed, Kostya could underline the fragment «22923» at the junction of the numbers 229 and 230, and Andrey - at the junction of the numbers 922 and 923.
Now we will show that it is not possible to choose a six-digit fragment. First, let's note two obvious facts.
1) If the middle digits of two consecutive three-digit numbers are different, then the smaller number ends in 9, and the larger one - in 0.
2) If the leading digits of two consecutive three-digit numbers are different, then the smaller number ends in 99, and the larger one - in 00.
Suppose the boys underlined a six-digit fragment «abcdef». It can be highlighted in the string in one of three ways, as shown in the diagram:
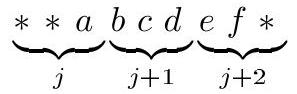
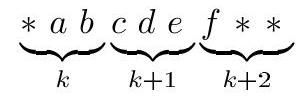
(here $i, j, k$ are three-digit numbers, and asterisks denote some digits). Note that Kostya and Andrey used different methods, otherwise they would have underlined the same block. Suppose Kostya chose his block using the third method. Then $b$ and $e$ are the last digits of the consecutive numbers $k$ and $k+1$, so they are different. If Andrey used the second configuration, then the numbers $j+1$ and $j+2$ have different leading digits. By 2), the number $j+2$ ends in 00, and in particular, $f=0$. If Andrey used the first configuration, then the numbers $i$ and $i+1$ have different middle digits, and $f=0$ by 1). But $f \neq 0$, since the number $k+2$ is a three-digit number. The case where the boys used the first two configurations is handled similarly.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. All four-digit numbers from 1000 to 9999 are written in a row without spaces. Kostya underlined \( k \) consecutive digits in this sequence, and Andrey underlined other \( k \) consecutive digits in this sequence. It turned out that the \( k \)-digit numbers underlined by the boys are equal. For what largest \( k \) could this have happened?
|
Answer: $k=7$.
Solution. An example of a seven-digit number that satisfies the condition of the problem is 2229223. Indeed, Kostya could underline the fragment «2229223» at the junction of the numbers 2229 and 2230, and Andrey - at the junction of the numbers 9222 and 9223.
Now we will show that it is impossible to choose an eight-digit fragment. First, note the obvious fact: if the second-to-last digits of two consecutive four-digit numbers are different, then the smaller number ends in 9, and the larger one ends in 0. Suppose the boys underlined an eight-digit fragment «abcdefgh». It can be highlighted in the string in one of four ways, as shown in the diagram:
$$
\underbrace{a b c d}_{i} \underbrace{e f g h}_{i+1} \underbrace{* a b c}_{j} \underbrace{d e f g}_{j+1} \underbrace{h * * *}_{j+2} \underbrace{* * a b}_{k} \underbrace{c d e f}_{k+1} \underbrace{g h * *}_{k+2} \underbrace{* * * a}_{m} \underbrace{b c d e}_{m+1} \underbrace{f g h *}_{m+2}
$$
(here $i, j, k, m$ are four-digit numbers, and asterisks denote some digits). Note that Kostya and Andrey used different methods, otherwise they would have underlined the same block. Suppose Kostya chose his block in the first way, and Andrey in the second. Then $c$ and $g$ are the last digits of adjacent numbers $j$ and $j+1$, so they are different. Therefore, the numbers $i$ and $i+1$ have different second-to-last digits. According to the above remark, the number $i+1$ ends in 0, that is, $h=0$. But this is impossible, since the number $j+2$ is a four-digit number. Other configurations are analyzed similarly.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the maze diagram in Fig. 1, each segment (link) is a corridor, and each circle is a small room. In some rooms, there are beacons that hum - each with its own voice. When in any room, the robot hears the signal from each beacon and determines the distance to it by the attenuation, i.e., the number of links on the shortest path to the beacon. For example, if a beacon is located in room $A$ (in chess notation, this is room a4), and the robot is in room $B$ (this is room g4), the distance between them is 7 links. The robot has the maze diagram and the beacons are marked on it. For what minimum number of beacons can the robot, when in any room, uniquely determine its location by sound?
a) Indicate how such a number of beacons can be placed. Why will the robot be able to determine its room by them?
b) Prove that it is impossible to manage with a smaller number of beacons.
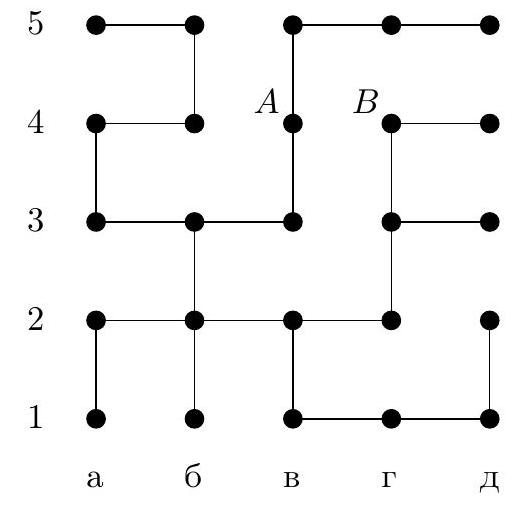
Fig. 1: Maze
|
Answer: the minimum number of beacons is 3, for example, they can be placed in rooms a1, d3, a5.
## Solution.
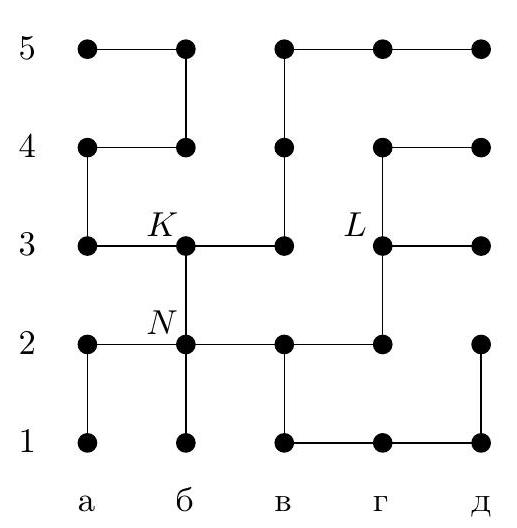
Fig. 2: Parts of the maze
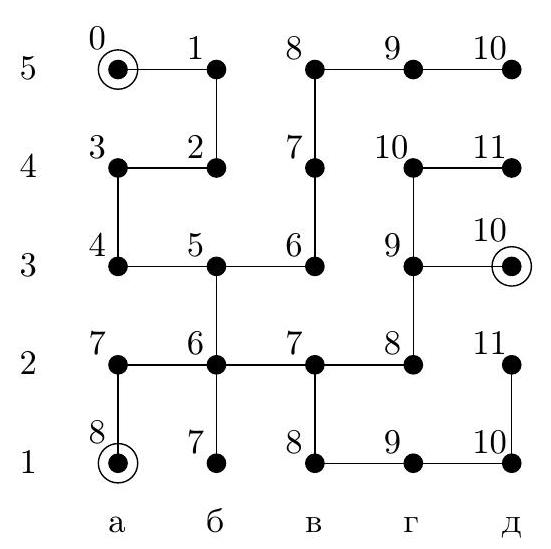
Fig. 3: Distances to beacon a5
b) Estimation. We will prove that two beacons are not enough. Consider three parts of our maze (Fig. 2): part $\mathcal{K}$ is room $K$ and two long dead-end corridors that lead from it to the left and right, part $\mathcal{L}$ is room $L$ and two dead-end corridors that lead from it upwards and to the right, part $\mathcal{N}$ is room $N$ and two dead-end corridors that lead from it to the left and downwards. If there are no more than 2 beacons, then one of these parts will not have a beacon. For example, let this be part $\mathcal{K}$, signals from beacons will reach this part via the edge entering room $K$ from below. Then a robot in room a3 will hear the same signals as in room b3, and therefore will not be able to distinguish which of these two rooms it is in. Similarly, indistinguishable rooms can be found in other parts if they do not contain a beacon.
a) Example. Let's check that beacons in rooms a1, d3, a5 will allow the robot to orient itself in this maze. Here, it is easier to perform a case-by-case check than to come up with general considerations. In Fig. 3, we marked the distances from all rooms to beacon a5. As we can see, rooms with distances from 0 to 5 are uniquely defined. Rooms with a distance of 6 are at different distances from beacon d3. Similarly, rooms with distances of $8, 9, 10, 11$. As for the four rooms with a distance of 7, two of them, v2 and v4, are at distances of 3 and 7 from beacon d3 and are thus uniquely defined by the distances to a5 and to d3. The other two rooms, a2 and b1, are at a distance of 5 from d3, but they are at different distances from a1.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the maze diagram in Fig. 7, each segment (link) is a corridor, and each circle is a small room. In some rooms, there are beacons that hum - each with its own voice. When in any room, the robot hears the signal from each beacon and determines the distance to it by the attenuation, i.e., the number of links on the shortest path to the beacon. For example, if a beacon is in room $A$ (in chess notation, this is room a4), and the robot is in room $B$ (this is room g4), the distance between them is 5 links. The robot has the maze diagram and the beacons are marked on it. For what minimum number of beacons can the robot, when in any room, uniquely determine its location by sound?
a) Indicate how such a number of beacons can be placed. Why will the robot be able to determine its room by them?
b) Prove that it is impossible to manage with fewer beacons.
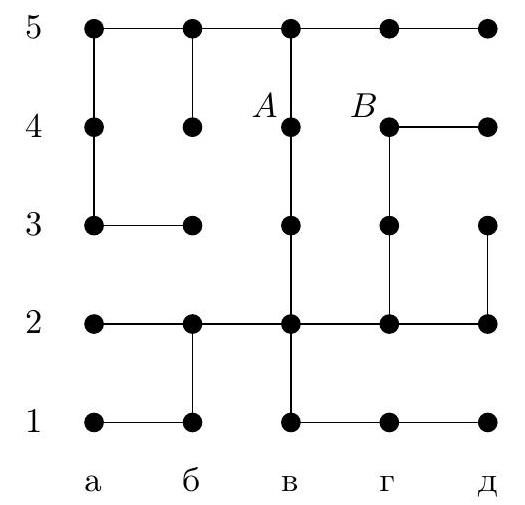
Fig. 7: Maze
|
Answer: the minimum number of beacons is 3, for example, they can be placed in rooms a1, b3, d4.
Solution.
b) Estimation. We will prove that two beacons are not enough. Consider three parts of our maze (Fig. 8): part $\mathcal{K}$ is room $K$, the long dead-end corridor that exits from it to the left, and the dead-end corridor below, part $\mathcal{L}$ is room $L$ and the two dead-end corridors that exit from it upwards and to the right, part $\mathcal{N}$ is room $N$ and the two dead-end corridors that exit from it to the left and below. If there are no more than 2 beacons, then one of these parts will not have a beacon. For example, let this be part $\mathcal{K}$, signals from the beacons will reach this part via the link entering room $K$ from the right. Then a robot, being in room a5, will hear the same signals as in room b4, and therefore will not be able to distinguish,
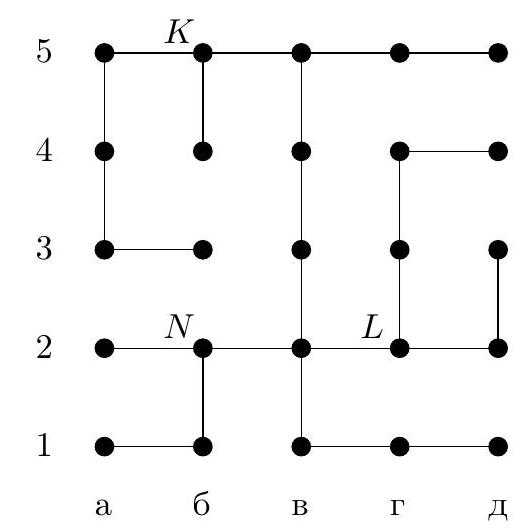
Fig. 8: Parts of the maze
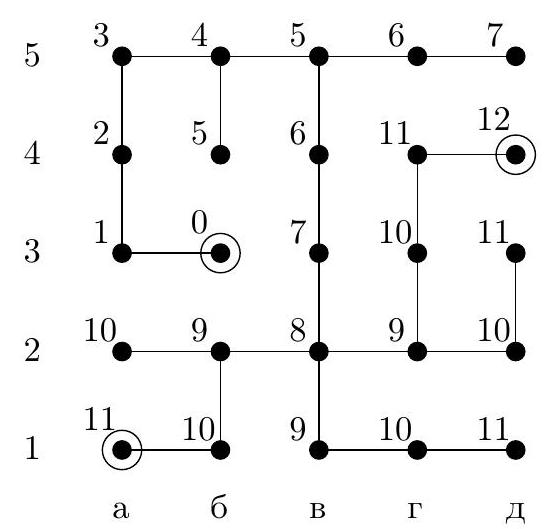
Fig. 9: Distances to beacon b3
which of these two rooms it is in. Similarly, indistinguishable rooms can be found in other parts if they do not contain a beacon.
a) Example. Let's check that beacons in rooms a1, b3, d4 will allow the robot to orient itself in this maze. Here, it is easier to perform a case-by-case analysis rather than come up with general considerations. In Fig. 9, we marked the distances from all rooms to beacon b3. As we can see, rooms with distances $0,1,2,3,4,8$ and 12 are uniquely defined. Rooms with a distance of 5 are at different distances from beacon a1. Similarly, rooms with a distance of 6 and 7. There are three rooms with a distance of 9: one of them - b2 is at a distance of 2 from beacon a1, and the other two are at a distance of 4 from a1, but they have different distances to d4. Two rooms with a distance of 10 - d2 and g3 - are at distances of 4 and 2 from beacon d4, and the other three - b1, a2, and g1 - are at a distance of 6 from d4, but at different distances from a1. Finally, two rooms with a distance of 11 - d3 and g4 - are at distances of 5 and 1 from beacon d4, and the other two - a1 and d1 - are at a distance of 7 from d4, but at different distances from a1.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the maze diagram in Fig. 13, each segment (link) is a corridor, and each circle is a small room. Some rooms have beacons that hum, each with its own voice. When in any room, the robot hears the signal from each beacon and determines the distance to it by the attenuation, i.e., the number of links on the shortest path to the beacon. For example, if a beacon is in room $A$ (in chess notation, this is room a4), and the robot is in room $B$ (this is room g4), the distance between them is 5 links. The robot has the maze diagram and the beacons are marked on it. For what minimum number of beacons can the robot, when in any room, uniquely determine its location by sound?
a) Indicate how such a number of beacons can be placed. Why will the robot be able to determine its room by them?
b) Prove that it is impossible to manage with fewer beacons.
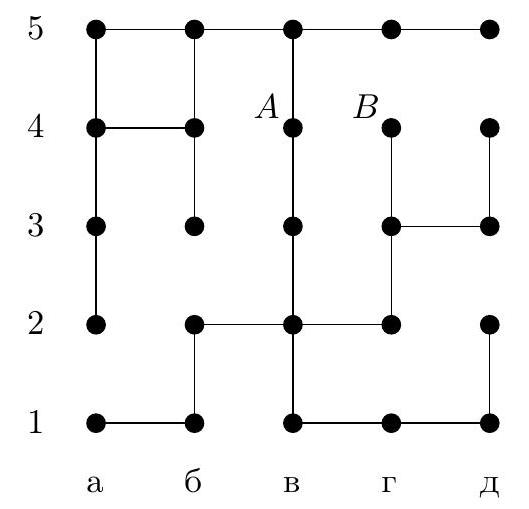
Fig. 13: Maze
|
Answer: the minimum number of beacons is 3, for example, they can be placed in rooms a1, b3, d4.
## Solution.
b) Estimation. We will prove that two beacons are not enough. Consider three parts of our maze (Fig. 14): part $\mathcal{K}$ is room $K$ and the dead-end corridors that lead from it to the right and down, part $\mathcal{L}$ is room $L$ and the two dead-end corridors that lead from it up and to the right, part $\mathcal{N}$ is room $N$ and the two dead-end corridors that lead from it to the left and down. If there are no more than 2 beacons, then one of these parts will not have a beacon. For example, let this be part $\mathcal{K}$, signals from beacons will reach this part via the link entering room $K$ from the right. Then the robot, being in room a3, will hear the same signals as in room b4, and therefore will not be able to distinguish which of these two rooms it is in. Similarly, indistinguishable rooms can be found in other parts if they do not contain a beacon.
a) Example. Let's check that beacons in rooms a1, b3, d4 will allow the robot to orient itself in this maze. Here, it is easier to perform a case-by-case analysis than to come up with some general considerations. In Figure 15, we marked the distances from all rooms to beacon b3. As we can see, rooms with distances $0,1,2,5$ and 8 are uniquely defined. Rooms with a distance of 3 are at different distances from beacon a1. Similarly, rooms with distances of 4, 6, and 7. There are three rooms with a distance of 9: one of them -62- is at a distance of 2 from beacon a1, while the other two are at a distance of 4 from a1, but they have different
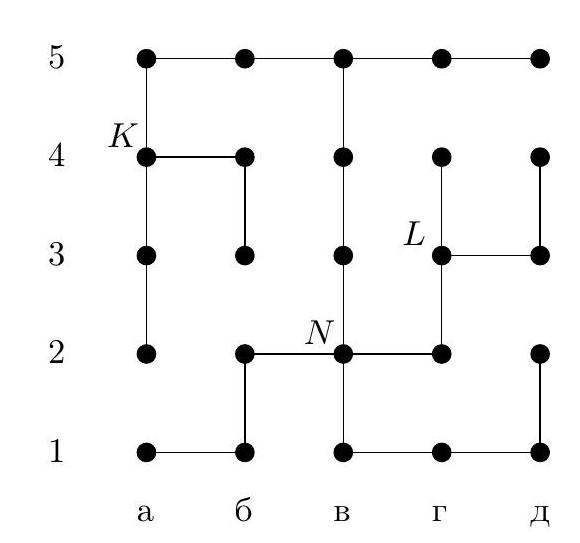
Fig. 14: Parts of the maze
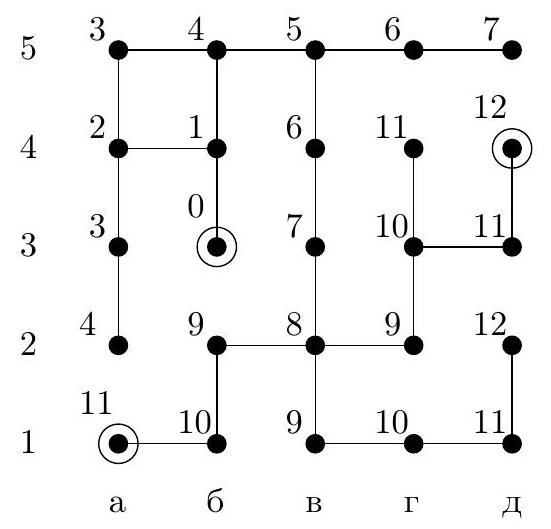
Fig. 15: Distances to beacon b3
distances to d4. Two rooms with a distance of 10 - g1 and g3 - are at a distance of 5 from beacon a1, but they differ in their distance to d4, while another one - b1 - is at a distance of 1 from a1 and thus differs from the previous two. Two rooms with a distance of 11 - d3 and g4 - are at distances of 1 and 3 from beacon d4, while the other two - a1 and d1 - are at a distance of 7 from d4, but at different distances from a1. Finally, rooms with a distance of 12 differ in their distance to d4.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all primes $p$ for which the numbers $p+1$ and $p^{2}+1$ are double the squares of natural numbers.
#
|
# Answer: $p=7$
First solution. Let $p+1=2 x^{2}$ and $p^{2}+1=2 y^{2}$, then $2\left(y^{2}-x^{2}\right)=p(p-1)$. Therefore, either $y-x$ or $y+x$ is divisible by $p$. From the inequality $xy-x \geqslant p$ and, thus, $2(y-x)(y+x) \geqslant 2 p^{2}>p(p-1)$, which is impossible. Therefore, $y+x$ is divisible by $p$. Note that $\frac{y^{2}}{x^{2}}=\frac{p^{2}+1}{p+1}>\frac{p^{2}-1}{p+1}=p-1$. Then if $p \geqslant 11$, $y^{2}>12 x^{2}$, hence $y>3 x$ and, thus, $2(y-x)>y+x \geqslant p$. Therefore, $2(y-x)(y+x)>p^{2}>p(p+1)$, which is also impossible. Thus, it remains to consider the cases $p=3, p=5$, and $p=7$. In the first two cases, $p+1$ is not a doubled square, while $p=7$ fits.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all primes $p$ for which the numbers $p+7$ and $p^{2}+7$ are double the squares of natural numbers.
|
Answer: $p=11$
First solution. Let $p+7=2 x^{2}$ and $p^{2}+7=2 y^{2}$, then $2\left(y^{2}-x^{2}\right)=p(p-1)$. Since $p-$ is odd, $p \geqslant 3$ and $2 p^{2}>p^{2}+7$. Therefore, $xy-x \geqslant p$ and, thus, $2(y-x)(y+x) \geqslant 2 p^{2}>p(p-1)$, which is impossible. Therefore, $y+x$ is divisible by $p$. Note that $\frac{y^{2}}{x^{2}}=\frac{p^{2}+7}{p+7}>\frac{p^{2}-49}{p+7}=p-7$. Then if $p \geqslant 17$, $y^{2}>10 x^{2}$, from which $y>3 x$ and, thus, $2(y-x)>y+x \geqslant p$. Therefore, $2(y-x)(y+x)>p^{2}>p(p+1)$, which is also impossible. Thus, it remains to consider the cases $p=3, p=5, p=7, p=11$ and $p=13$. In the last, as well as in the first three of them, $p+7$ is not a doubled square, while $p=11$ fits.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The sum of positive numbers $a, b, c$ and $d$ is not less than 8. Find the minimum value of the expression
$\frac{a^{4}}{(a+b)(a+c)(a+d)}+\frac{b^{4}}{(b+c)(b+d)(b+a)}+\frac{c^{4}}{(c+d)(c+a)(c+b)}+\frac{d^{4}}{(d+a)(d+b)(d+c)}$.
|
Answer: 1
First solution. By the inequality of means for four numbers, we have
$$
\begin{aligned}
\frac{a^{4}}{(a+b)(a+c)(a+d)}+\frac{a+b}{16}+\frac{a+c}{16} & +\frac{a+d}{16} \geqslant \\
& \geqslant 4 \sqrt[4]{\frac{a^{4}}{(a+b)(a+c)(a+d)} \cdot \frac{a+b}{16} \cdot \frac{a+c}{16} \cdot \frac{a+d}{16}}=\frac{a}{2}
\end{aligned}
$$
Therefore,
$$
\frac{a^{4}}{(a+b)(a+c)(a+d)} \geqslant \frac{a}{2}-\left(\frac{a+b}{16}+\frac{a+c}{16}+\frac{a+d}{16}\right)=\frac{5 a}{16}-\frac{b+c+d}{16}
$$
Summing this inequality with three similar ones, we get
$$
\begin{aligned}
& \frac{a^{4}}{(a+b)(a+c)(a+d)}+\frac{b^{4}}{(b+c)(b+d)(b+a)}+\frac{c^{4}}{(c+d)(c+a)(c+b)}+\frac{d^{4}}{(d+a)(d+b)(d+c)} \geqslant \\
& \geqslant\left(\frac{5 a}{16}-\frac{b+c+d}{16}\right)+\left(\frac{5 b}{16}-\frac{c+d+a}{16}\right)+\left(\frac{5 c}{16}-\frac{d+a+b}{16}\right)+\left(\frac{5 d}{16}-\frac{a+b+c}{16}\right)= \\
& =\frac{2(a+b+c+d)}{16} \geqslant 1 .
\end{aligned}
$$
If $a=b=c=d=2$, then the sum of the fractions in the problem condition is 1, so the minimum value of the expression is 1.
Second solution. For brevity, let
$$
K=\frac{a^{4}}{(a+b)(a+c)(a+d)}+\frac{b^{4}}{(b+c)(b+d)(b+a)}+\frac{c^{4}}{(c+d)(c+a)(c+b)}+\frac{d^{4}}{(d+a)(d+b)(d+c)}
$$
By the Cauchy-Bunyakovsky inequality for the sets of numbers
$$
\frac{a^{4}}{(a+b)(a+c)(a+d)}, \frac{b^{4}}{(b+c)(b+d)(b+a)}, \frac{c^{4}}{(c+d)(c+a)(c+b)}, \frac{d^{4}}{(d+a)(d+b)(d+c)} \text { and }
$$
we have
$$
\begin{aligned}
& (2(a+b+c+d)) K=((a+d)+(b+a)+(c+b)+(d+c)) K \geqslant \\
& \quad \geqslant\left(\frac{a^{2}}{\sqrt{(a+b)(a+c)}}+\frac{b^{2}}{\sqrt{(b+c)(b+d)}}+\frac{c^{2}}{\sqrt{(c+d)(c+a)}}+\frac{d^{2}}{\sqrt{(d+a)(d+b)}}\right)^{2}
\end{aligned}
$$
Let the last expression in parentheses be denoted by $L$ and estimate it by the Cauchy-Bunyakovsky inequality for the sets
$$
\begin{aligned}
& \frac{a^{2}}{\sqrt{(a+b)(a+c)}}, \quad \frac{b^{2}}{\sqrt{(b+c)(b+d)}}, \quad \frac{c^{2}}{\sqrt{(c+d)(c+a)}}, \quad \frac{d^{2}}{\sqrt{(d+a)(d+b)}} \text { and } \\
& \sqrt{(a+b)(a+c)}, \quad \sqrt{(b+c)(b+d)}, \quad \sqrt{(c+d)(c+a)}, \quad \sqrt{(d+a)(d+b)} .
\end{aligned}
$$
Then $L M \geqslant(a+b+c+d)^{2}$, where
$$
M=\sqrt{(a+b)(a+c)}+\sqrt{(b+c)(b+d)}+\sqrt{(c+d)(c+a)}+\sqrt{(d+a)(d+b)}
$$
Thus,
$$
K \geqslant \frac{L^{2}}{2(a+b+c+d)} \geqslant \frac{(a+b+c+d)^{4}}{2(a+b+c+d) M^{2}}=\frac{(a+b+c+d)^{3}}{2 M^{2}}
$$
Finally, by the inequality of means for two numbers $\sqrt{(x+y)(x+z)} \leqslant \frac{(x+y)+(x+z)}{2}$, therefore
$$
M \leqslant \frac{2 a+b+c}{2}+\frac{2 b+c+d}{2}+\frac{2 c+d+a}{2}+\frac{2 d+a+b}{2}=2(a+b+c+d)
$$
Thus,
$$
K \geqslant \frac{1}{2} \cdot \frac{(a+b+c+d)^{3}}{(2(a+b+c+d))^{2}}=\frac{a+b+c+d}{8} \geqslant 1
$$
If $a=b=c=d=2$, then $K=1$, so the minimum value of $K$ is 1.
Third solution. For brevity, let
$$
K=\frac{a^{4}}{(a+b)(a+c)(a+d)}+\frac{b^{4}}{(b+c)(b+d)(b+a)}+\frac{c^{4}}{(c+d)(c+a)(c+b)}+\frac{d^{4}}{(d+a)(d+b)(d+c)}
$$
By the Cauchy-Bunyakovsky inequality for the sets of numbers
$$
\begin{aligned}
& \frac{a^{4}}{(a+b)(a+c)(a+d)}, \frac{b^{4}}{(b+c)(b+d)(b+a)}, \frac{c^{4}}{(c+d)(c+a)(c+b)}, \frac{d^{4}}{(d+a)(d+b)(d+c)} \text { and } \\
& (a+c)(a+d), \quad(b+d)(b+a), \quad(c+a)(c+b), \quad(d+b)(d+c)
\end{aligned}
$$
we have
$$
\begin{aligned}
(a+b+c+d)^{2} K & =((a+c)(a+d)+(b+d)(b+a)+(c+a)(c+b)+(d+b)(d+c)) K \geqslant \\
& \geqslant\left(\frac{a^{2}}{\sqrt{a+b}}+\frac{b^{2}}{\sqrt{b+c}}+\frac{c^{2}}{\sqrt{c+d}}+\frac{d^{2}}{\sqrt{d+a}}\right)^{2}
\end{aligned}
$$
Let the last expression in parentheses be denoted by $L$ and estimate it by the Cauchy-Bunyakovsky inequality for the sets
$$
\frac{a^{2}}{\sqrt{a+b}}, \quad \frac{b^{2}}{\sqrt{b+c}}, \quad \frac{c^{2}}{\sqrt{c+d}}, \quad \frac{d^{2}}{\sqrt{d+a}} \text { and } \sqrt{a+b}, \sqrt{b+c}, \sqrt{c+d}, \sqrt{d+a}
$$
Then $L M \geqslant(a+b+c+d)^{2}$, where $M=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+d}+\sqrt{d+a}$. Thus,
$$
K \geqslant \frac{L^{2}}{(a+b+c+d)^{2}} \geqslant \frac{1}{(a+b+c+d)^{2}} \cdot \frac{(a+b+c+d)^{4}}{M^{2}}=\left(\frac{a+b+c+d}{M}\right)^{2}
$$
By the inequality of means for two numbers $2 \sqrt{x+y} \leqslant \frac{x+y+4}{2}$, therefore
$$
M \leqslant \frac{a+b+4}{4}+\frac{b+c+4}{4}+\frac{c+d+4}{4}+\frac{d+a+4}{4}=\frac{2 s+16}{4}
$$
where $s=a+b+c+d \geqslant 8$. Thus, we have proved that
$$
K \geqslant\left(\frac{s}{M}\right)^{2} \geqslant\left(\frac{4 s}{2 s+16}\right)^{2}
$$
It remains to note that $4 s=2 s+2 s \geqslant 2 s+16$, so the last expression is not less than 1. If $a=b=c=d=2$, then $K=1$, so the minimum value of $K$ is 1.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) At the Journalism Faculty of the University of Enchanted Commonwealth, 4 chickens are applying. The faculty has 2 places in the daytime program and 3 places in the evening program. Assuming all 4 chickens will be admitted to the faculty, determine the number of outcomes in which exactly two chickens will be admitted to the evening program.
|
Answer: 6.
Solution. The faculty has a total of 5 places, to which 4 applicants are applying. Since exactly two chickens will be admitted to the evening department, the other two will be admitted to the daytime department. The number of ways to choose 2 out of 4 applicants to be admitted to the daytime department is $C_{4}^{2}=6$.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. (40 points) For real numbers $a, b$ and $c$ it is known that $a b + b c + c a = 3$. What values can the expression $\frac{a\left(b^{2}+3\right)}{a+b}+\frac{b\left(c^{2}+3\right)}{b+c}+\frac{c\left(a^{2}+3\right)}{c+a}$ take?
|
Answer: 6.
Solution. Consider the first term of the desired expression. Using the condition that $a b+b c+c a=3$. Then
$$
b^{2}+3=b^{2}+a b+b c+c a=(b+a)(b+c)
$$
Therefore,
$$
\frac{a\left(b^{2}+3\right)}{a+b}=\frac{a(b+a)(b+c)}{a+b}=a(b+c) \text {. }
$$
Similarly for the second and third terms, we get
$$
\frac{b\left(c^{2}+3\right)}{b+c}=b(c+a), \quad \frac{c\left(a^{2}+3\right)}{c+a}=c(a+b)
$$
Thus,
$$
\begin{gathered}
\frac{a\left(b^{2}+3\right)}{a+b}+\frac{b\left(c^{2}+3\right)}{b+c}+\frac{c\left(a^{2}+3\right)}{c+a}=a(b+c)+b(c+a)+c(a+b)= \\
\quad=a b+a c+b c+b a+c a+c b=2(a b+b c+c a)=2 \times 3=6
\end{gathered}
$$
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The quadratic trinomial $f(x)=a x^{2}+b x+c$ has exactly one root, the quadratic trinomial $2 f(2 x-3)-f(3 x+1)$ also has exactly one root. Find the root of the trinomial $f(x)$.
|
Answer: -11.
Solution. Since dividing all the coefficients of the quadratic polynomial $f(x)$ by $a$ does not change its roots or the roots of the polynomial $g(x)=2 f(2 x-3)-f(3 x+1)$, we can assume that $a=1$. A quadratic polynomial has exactly one root if and only if its discriminant is zero. Therefore, $b^{2}=4 c$ and, hence, $f(x)=x^{2}+b x+\frac{b^{2}}{4}$. Then,
\[
\begin{aligned}
g(x) & =2 f(2 x-3)-f(3 x+1)=2(2 x-3)^{2}+2 b(2 x-3)+\frac{b^{2}}{2}-\left((3 x+1)^{2}+b(3 x+1)+\frac{b^{2}}{4}\right)= \\
& =-x^{2}+(b-30) x+\left(17-7 b+\frac{b^{2}}{4}\right)
\end{aligned}
\]
Therefore,
\[
0=(b-30)^{2}+4\left(17-7 b+\frac{b^{2}}{4}\right)=2 b^{2}-88 b+968=2(b-22)^{2}
\]
Thus, the discriminant of the polynomial $g(x)$ is 0 only when $b=22$, which means $f(x)=$ $x^{2}+22 x+121$ and its only root is -11.
|
-11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The quadratic trinomial $f(x)=a x^{2}+b x+c$ has exactly one root, the quadratic trinomial $f(3 x+2)-2 f(2 x-1)$ also has exactly one root. Find the root of the trinomial $f(x)$.
|
Answer: -7.
Solution. Since dividing all the coefficients of the quadratic polynomial $f(x)$ by $a$ does not change its roots or the roots of the polynomial $g(x)=f(3 x+2)-2 f(2 x-1)$, we can assume that $a=1$. A quadratic polynomial has exactly one root if and only if its discriminant is zero. Therefore, $b^{2}=4 c$ and, hence, $f(x)=x^{2}+b x+\frac{b^{2}}{4}$. Then
\[
\begin{aligned}
g(x) & =f(3 x+2)-2 f(2 x-1)=(3 x+3)^{2}+b(3 x+2)+\frac{b^{2}}{2}-\left((2 x-1)^{2}+b(2 x-1)+\frac{b^{2}}{4}\right)= \\
& =x^{2}+(20-b) x+\left(2+4 b-\frac{b^{2}}{4}\right)
\end{aligned}
\]
Therefore,
\[
0=(20-b)^{2}-4\left(2+4 b-\frac{b^{2}}{4}\right)=2 b^{2}-56 b+392=2(b-14)^{2}
\]
Thus, the discriminant of the polynomial $g(x)$ is 0 only when $b=14$, which means $f(x)=$ $x^{2}+14 x+49$ and its only root is -7.
|
-7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given the quadratic trinomial $f(x)=a x^{2}-a x+1$. It is known that $|f(x)| \leqslant 1$ for all $x \in[0,1]$. What is the greatest value that $a$ can take?
|
Answer: 8
Solution. It is not difficult to check that $a=8$ works. Indeed, $|2 x-1| \leqslant 1$ for $x \in[0,1]$, so $f(x)=8 x^{2}-8 x+1=2(2 x-1)^{2}-1 \leqslant 1$, and the inequality $f(x) \geqslant-1$ holds for all $x$.
Suppose that $a>8$. Then
$$
f\left(\frac{1}{2}\right)=\frac{a}{4}-\frac{a}{2}+1=1-\frac{a}{4}=\frac{4-a}{4}<-1
$$
which is impossible by the condition.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given trapezoid $A B C D$ with bases $A B$ and $C D$, angles $\angle C=30^{\circ}$ and $\angle D=80^{\circ}$. Find $\angle A C B$, if it is known that $D B$ is the bisector of angle $\angle D$.
|
Answer: $10^{\circ}$
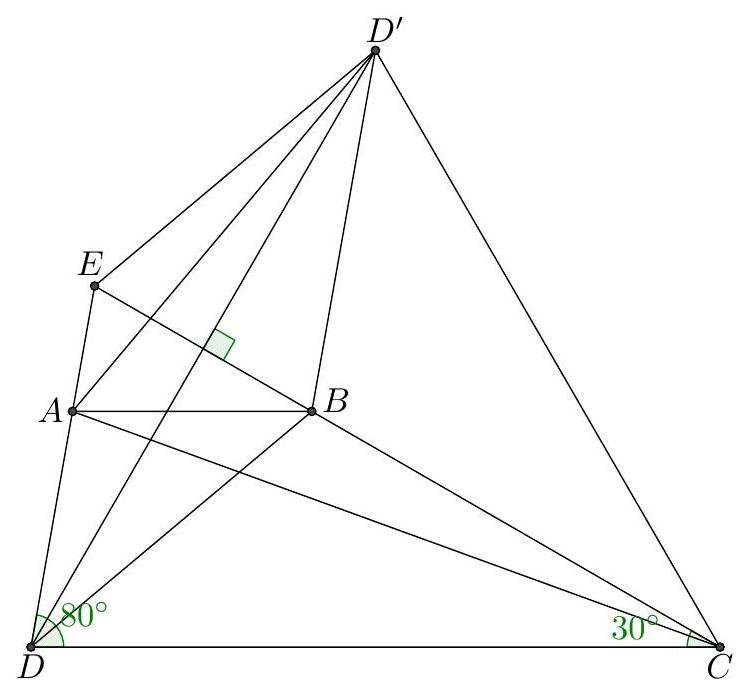
Let $E$ be the intersection point of lines $A D$ and $B C$, and $D^{\prime}$ be the point symmetric to point $D$ with respect to line $B C$. Then $C D = C D^{\prime}$ and $\angle D C D^{\prime} = 2 \angle B C D = 60^{\circ}$. Therefore, triangle $D C D^{\prime}$ is equilateral and $D D^{\prime} = C D$. By symmetry, $D E = D^{\prime} E$ and triangle $D E D^{\prime}$ is isosceles. Thus, $\angle E D^{\prime} D = \angle E D D^{\prime} = \angle A D C - \angle C D D^{\prime} = 80^{\circ} - 60^{\circ} = 20^{\circ}$.
By Thales' theorem, $\frac{E A}{A D} = \frac{E B}{B C}$, and by the property of the angle bisector, $\frac{E B}{B C} = \frac{E D}{D C} = \frac{E D^{\prime}}{D D^{\prime}}$. Therefore, $\frac{E A}{A D} = \frac{E D^{\prime}}{D D^{\prime}}$ and $D^{\prime} A$ is the angle bisector of $\angle E D^{\prime} D$, so $\angle A D^{\prime} D = \angle A D^{\prime} E = 10^{\circ}$. Therefore, $\angle A D^{\prime} C = \angle A D^{\prime} D + \angle D D^{\prime} C = 10^{\circ} + 60^{\circ} = 70^{\circ} = \angle A E C$. Thus, quadrilateral $A E D^{\prime} C$ is cyclic and $\angle A C B = \angle A C E = \angle A D^{\prime} E = 10^{\circ}$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points) Chess clubs from Moscow, Saint Petersburg, and Kazan agreed to hold a tournament. Each Muscovite played exactly 9 Saint Petersburg residents and $n$ Kazan residents. Each Saint Petersburg resident played exactly 6 Muscovites and 2 Kazan residents. Each Kazan resident played exactly 8 Muscovites and 6 Saint Petersburg residents. What is $n$?
|
# Answer: 4.
Solution. Let the team from Moscow consist of $m$ participants, the team from Saint Petersburg - of $p$ participants, and the team from Kazan - of $k$ participants.
According to the problem, each Muscovite, i.e., each of the $m$ people, played exactly 9 games with the Saint Petersburg residents; and each Saint Petersburg resident, i.e., each of the $p$ people, played exactly 6 games with the Muscovites. Clearly, the games played by Muscovites with Saint Petersburg residents are the same games played by Saint Petersburg residents with Muscovites, i.e., $m \cdot 9 = p \cdot 6$.
Similarly, $m \cdot n = k \cdot 8$ and $p \cdot 2 = k \cdot 6$. We have
$$
\left\{\begin{array} { l }
{ 9 m = 6 p , } \\
{ n m = 8 k , } \\
{ 2 p = 6 k ; }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ 3 m = 2 p , } \\
{ n m = 8 k , } \\
{ p = 3 k ; }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ 3 m = 2 \cdot 3 k , } \\
{ n m = 8 k , } \\
{ p = 3 k ; }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ m = 2 k , } \\
{ n m = 8 k , } \\
{ p = 3 k ; }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
m=2 k \\
n \cdot 2 k=8 k \\
p=3 k
\end{array}\right.\right.\right.\right.\right.
$$
From this, $n=4$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) At a market in Egypt, a tourist is bargaining with a seller over a souvenir worth 10000 Egyptian pounds. The tourist first reduces the price by x percent $(0<x<100)$, then the seller increases the price by $x$ percent, and so on. The number $x$ remains constant throughout the bargaining, and the seller increases the price at least once. The bargaining continues until one of the participants receives a non-integer value for the price of the souvenir. Find the maximum possible number of price changes during such a bargaining session (including the final non-integer price).
|
Answer: 5.
Solution. The final cost of the souvenir can be found using one of two formulas (depending on who had the last word): $10000 \cdot\left(1-\frac{x}{100}\right)^{n} \cdot\left(1+\frac{x}{100}\right)^{n}$ or $10000 \cdot\left(1-\frac{x}{100}\right)^{n+1} \cdot\left(1+\frac{x}{100}\right)^{n}$.
After some transformations, we get $\frac{(100-x)^{n}(100+x)^{n}}{100^{2 n-2}}$ and $\frac{(100-x)^{n+1}(100+x)^{n}}{100^{2 n-2}}$.
An expression of the form $(100-x)^{a}(100+x)^{b}$ is divisible by $100^{t}$ for $a>0, b>0, x>0$ and $t>0$ at least once for $x=10 i, i=1, \ldots, 9$ (an even number, a multiple of 5).
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (30 points) The bases $AB$ and $CD$ of trapezoid $ABCD$ are 15 and 19, respectively. $AH$ and $BG$ are heights to the line $DC$, and $CF$ is a height to the line $AB$. Points $K, L, M$, and $N$ are the midpoints of segments $AB, CF, CD$, and $AH$ respectively. Find the ratio of the area of trapezoid $ABCD$ to the area of quadrilateral $KLMN$, if $DG=17$.
|
Answer: 2 or $\frac{2}{3}$.

Solution. Let the trapezoid $ABCD$ be labeled in a clockwise direction, with the bases assumed to be horizontal. Since the problem does not specify where point $G$ lies on line $DC$, we need to consider all possible cases. There are two scenarios: point $G$ lies to the left of point $D$ (see the left diagram) and point $G$ lies to the right of point $D$ (see the right diagram). In the second case, since
$$
DG = 17 < 19 = DC
$$
point $G$ lies on segment $DC$.
Let $h$ be the height of the trapezoid. By the problem's condition, points $N$ and $L$ are the midpoints of the heights of the trapezoid. Note that the area of quadrilateral $KLMN$ is the sum of the areas of triangles $KNL$ and $MNL$, which share a base and have heights equal to half the height of the trapezoid, i.e.,
$$
S_{KLMN} = S_{KNL} + S_{MNL} = 2 \cdot S_{KNL} = 2 \cdot \frac{1}{2} \cdot NL \cdot \frac{h}{2} = NL \cdot \frac{h}{2}
$$
Thus, the desired ratio of areas is
$$
\frac{S_{ABCD}}{S_{KLMN}} = \frac{\frac{AB + DC}{2} \cdot h}{NL \cdot \frac{h}{2}} = \frac{AB + CD}{NL}
$$
$NL$ is the distance between lines $AH$ and $CF$. In the case where point $G$ lies to the left of point $D$, i.e., does not fall on base $CD$, the value of $NL = AB + BG + DC = 15 + 17 + 19 = 51$. In the second case, $NL = HG + GC = AB + (DC - DG) = 15 + (19 - 17) = 17$. Therefore, we get two answers: $\frac{AB + CD}{NL} = \frac{34}{51} = \frac{2}{3}$ and $\frac{AB + CD}{NL} = \frac{34}{17} = 2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the maze diagram in Fig. 1, each segment (link) is a corridor, and each circle is a small room. In some rooms, there are beacons that hum - each with its own voice. When in any room, the robot hears the signal from each beacon and determines the distance to it by the attenuation, i.e., the number of links on the shortest path to the beacon. For example, if a beacon is located in room $A$ (in chess notation, this is room a4), and the robot is in room $B$ (this is room g4), the distance between them is 7 links. The robot has the maze diagram and the beacons are marked on it. For what minimum number of beacons can the robot, when in any room, uniquely determine its location by sound?
a) Indicate how such a number of beacons can be placed. Why will the robot be able to determine its room by them?
b) Prove that it is impossible to manage with a smaller number of beacons.
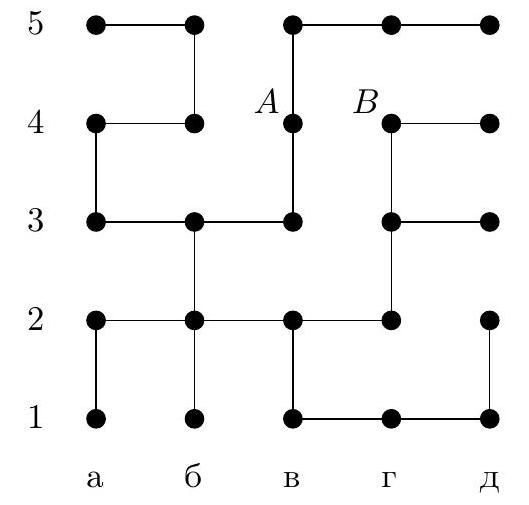
Fig. 1: Maze
|
Answer: the minimum number of beacons is 3, for example, they can be placed in rooms a1, d3, a5.
## Solution.
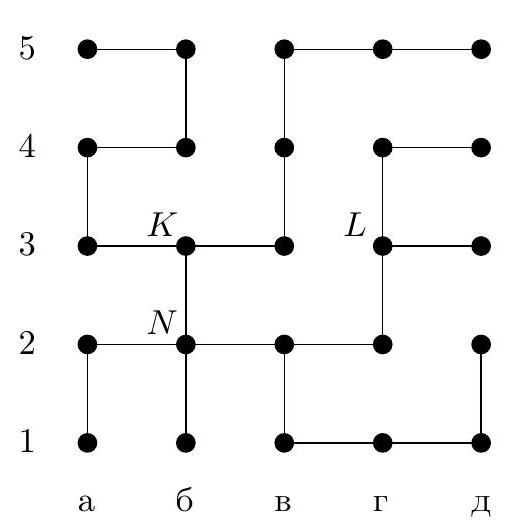
Fig. 2: Parts of the maze
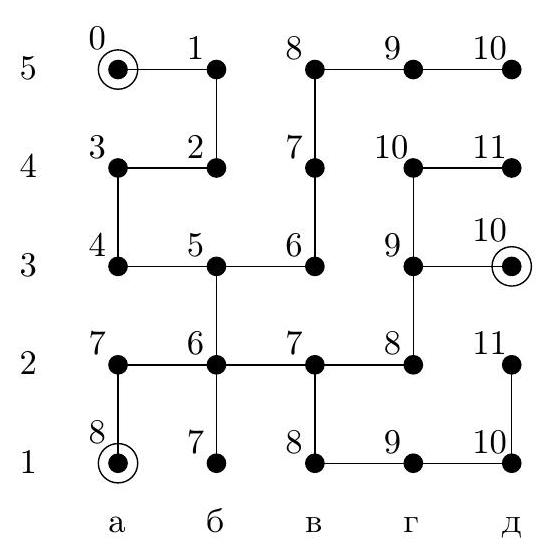
Fig. 3: Distances to beacon a5
b) Estimation. We will prove that two beacons are not enough. Consider three parts of our maze (Fig. 2): part $\mathcal{K}$ is room $K$ and two long dead-end corridors that lead from it to the left and right, part $\mathcal{L}$ is room $L$ and two dead-end corridors that lead from it upwards and to the right, part $\mathcal{N}$ is room $N$ and two dead-end corridors that lead from it to the left and downwards. If there are no more than 2 beacons, then one of these parts will not have a beacon. For example, let this be part $\mathcal{K}$, signals from beacons will reach this part via the edge entering room $K$ from below. Then a robot in room a3 will hear the same signals as in room b3, and therefore will not be able to distinguish which of these two rooms it is in. Similarly, indistinguishable rooms can be found in other parts if they do not contain a beacon.
a) Example. Let's check that beacons in rooms a1, d3, a5 will allow the robot to orient itself in this maze. Here, it is easier to perform a case-by-case check than to come up with general considerations. In Fig. 3, we have marked the distances from all rooms to beacon a5. As we can see, rooms with distances from 0 to 5 are uniquely defined. Rooms with a distance of 6 are at different distances from beacon d3. Similarly, rooms with distances of $8, 9, 10, 11$. As for the four rooms with a distance of 7, two of them, v2 and v4, are at distances of 3 and 7 from beacon d3 and are thus uniquely defined by the distances to a5 and to d3. The other two rooms, a2 and b1, are at a distance of 5 from d3, but they are at different distances from a1.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the maze diagram in Fig. 7, each segment (link) is a corridor, and each circle is a small room. In some rooms, there are beacons that hum - each with its own voice. When in any room, the robot hears the signal from each beacon and determines the distance to it by the attenuation, i.e., the number of links on the shortest path to the beacon. For example, if a beacon is in room $A$ (in chess notation, this is room a4), and the robot is in room $B$ (this is room g4), the distance between them is 5 links. The robot has the maze diagram and the beacons are marked on it. For what minimum number of beacons can the robot, when in any room, uniquely determine its location by sound?
a) Indicate how such a number of beacons can be placed. Why will the robot be able to determine its room by them?
b) Prove that it is impossible to manage with fewer beacons.
Fig. 7: Maze
|
Answer: the minimum number of beacons is 3, for example, they can be placed in rooms a1, b3, d4.
Solution.
b) Estimation. We will prove that two beacons are not enough. Consider three parts of our maze (Fig. 8): part $\mathcal{K}$ is room $K$, the long dead-end corridor that exits from it to the left, and the dead-end corridor below, part $\mathcal{L}$ is room $L$ and the two dead-end corridors that exit from it upwards and to the right, part $\mathcal{N}$ is room $N$ and the two dead-end corridors that exit from it to the left and below. If there are no more than 2 beacons, then one of these parts will not have a beacon. For example, let this be part $\mathcal{K}$, signals from the beacons will reach this part via the link entering room $K$ from the right. Then a robot, being in room a5, will hear the same signals as in room b4, and therefore will not be able to distinguish,

Fig. 8: Parts of the maze

Fig. 9: Distances to beacon b3
which of these two rooms it is in. Similarly, indistinguishable rooms can be found in other parts if they do not contain a beacon.
a) Example. Let's check that beacons in rooms a1, b3, d4 will allow the robot to orient itself in this maze. Here, it is easier to perform a case-by-case check than to come up with some general considerations. In Figure 9, we marked the distances from all rooms to beacon b3. As we can see, rooms with distances $0,1,2,3,4,8$ and 12 are uniquely defined. Rooms with a distance of 5 are at different distances from beacon a1. Similarly, rooms with a distance of 6 and 7. There are three rooms with a distance of 9: one of them - b2 is at a distance of 2 from beacon a1, and the other two are at a distance of 4 from a1, but they have different distances to d4. Two rooms with a distance of 10 - d2 and g3 - are at distances of 4 and 2 from beacon d4, and the other three - b1, a2, and g1 - are at a distance of 6 from d4, but at different distances from a1. Finally, two rooms with a distance of 11 - d3 and g4 - are at distances of 5 and 1 from beacon d4, and the other two - a1 and d1 - are at a distance of 7 from d4, but at different distances from a1.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the maze diagram in Fig. 13, each segment (link) is a corridor, and each circle is a small room. Some rooms have beacons that hum, each with its own voice. When in any room, the robot hears the signal from each beacon and determines the distance to it by the attenuation, i.e., the number of links on the shortest path to the beacon. For example, if a beacon is in room $A$ (in chess notation, this is room a4), and the robot is in room $B$ (this is room g4), the distance between them is 5 links. The robot has the maze diagram and the beacons are marked on it. For what minimum number of beacons can the robot, when in any room, uniquely determine its location by sound?
a) Indicate how such a number of beacons can be placed. Why will the robot be able to determine its room by them?
b) Prove that it is impossible to manage with fewer beacons.
Fig. 13: Maze
|
Answer: the minimum number of beacons is 3, for example, they can be placed in rooms a1, b3, d4.
## Solution.
b) Estimation. We will prove that two beacons are insufficient. Consider three parts of our maze (Fig. 14): part $\mathcal{K}$ is room $K$ and the dead-end corridors that lead from it to the right and down, part $\mathcal{L}$ is room $L$ and the two dead-end corridors that lead from it up and to the right, part $\mathcal{N}$ is room $N$ and the two dead-end corridors that lead from it to the left and down. If there are no more than 2 beacons, then one of these parts will not have a beacon. For example, let this be part $\mathcal{K}$, signals from beacons will reach this part via the link entering room $K$ from the right. Then a robot in room a3 will hear the same signals as in room b4, and therefore will not be able to distinguish which of these two rooms it is in. Similarly, indistinguishable rooms can be found in other parts if they do not contain a beacon.
a) Example. Let's check that beacons in rooms a1, b3, d4 will allow the robot to orient itself in this maze. Here, it is easier to perform a case-by-case analysis than to come up with general considerations. In Fig. 15, we marked the distances from all rooms to beacon b3. As we can see, rooms with distances $0,1,2,5$ and 8 are uniquely defined. Rooms with a distance of 3 are at different distances from beacon a1. Similarly, rooms with distances of 4, 6, and 7. There are three rooms with a distance of 9: one of them -62- is at a distance of 2 from beacon a1, while the other two are at a distance of 4 from a1, but they have different
Fig. 14: Parts of the maze
Fig. 15: Distances to beacon b3
distances to d4. Two rooms with a distance of 10 - g1 and g3 - are at a distance of 5 from beacon a1, but differ in their distance to d4, while another one - b1 - is at a distance of 1 from a1 and thus differs from the previous two. Two rooms with a distance of 11 - d3 and g4 - are at distances of 1 and 3 from beacon d4, while the other two - a1 and d1 - are at a distance of 7 from d4, but at different distances from a1. Finally, rooms with a distance of 12 differ in their distance to d4.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. From the town "U $" to the town "A x" at $10^{00}$ AM, Ivan set off on his bicycle. After traveling two-thirds of the way, he passed the town "Ox," from which at that moment Peter set off on foot towards the town "U x". At the moment Ivan arrived in the town "A x", Nikolai set off from there in the opposite direction on his bicycle and arrived in the town "U x" by the morning of the same day. At what distance from the town "A x" did Nikolai catch up with Peter, if Peter arrived in the town "U x" at $12^{00}$ AM of the same day, and the speed of each participant was constant, with the distance between the towns "U x" and "A x" being 10 km in total. (7 points)
|
Answer: 6 km.
## Solution:
We will solve the problem using a graphical-geometric method. Let's represent Ivan's movement as segment $K L$, Nikolai's movement as segment $L M$, and Petr's movement as segment $N P$ in a coordinate system $(t ; s)$, where $t$ is time in hours and $s$ is distance in kilometers from point A (Fig.1). Let $Q$ be the intersection point of $L M$ and $N P$. According to the problem, $M K=2$ and $P M=1$. Draw $M G \| N Q, G \in K L$, then by Thales' theorem we have
$$
N G: G K=P M: M K=1: 2 .
$$
Thus, if $N G=2 x$, then $G K=4 x$, and $L N=3 x$. Therefore, by Thales' theorem again, we have
$$
L Q: Q M=L N: N G=3 x: 2 x=3: 2
$$
Thus, the required distance is $\frac{3}{5} \cdot 10=6$ (km.)
Note that when finding the ratio $L Q: Q M$, we can use Menelaus' theorem. Points $N, Q$, and $P$ lie on the same line, so $\frac{K N}{N L} \cdot \frac{L Q}{Q M} \cdot \frac{M P}{P K}=1$ or $\frac{2}{1} \cdot \frac{L Q}{Q M} \cdot \frac{1}{3}=1$. Therefore, $\frac{L Q}{Q M}=$ $\frac{3}{2}$.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. From the town "U ${ }^{\prime}$ " to the town " $A x$ ", Ivan set off on his bicycle at $11^{00}$ AM, having traveled two fifths of the distance, he passed the town " $O x$ ", from which at that moment Peter set off on foot towards the town "Ux". At the moment when Ivan arrived in the town " $A x$ ", from there in the opposite direction Nikolai set off on his bicycle and arrived in the town "Ux" at $12^{00}$ of the same day. How many kilometers from the town " $A x$ " did Nikolai catch up with Peter, if Peter arrived in the town "U $\$ " at $13^{30}$ of the same day, while the speed of each participant was constant, and the distance between the towns "U" and " $A x$ " is
7 km.
( 7 points)
|
Answer: 5 km.
Solution: a similar solution to this problem is present in option 1 under the same number.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the value of the expression
$$
\frac{1}{1+m+m n}+\frac{1}{1+n+n k}+\frac{1}{1+k+k m} \text { given that } m=\frac{1}{n k} \text {. }
$$
|
Answer: 1.
## Solution.
$$
\begin{gathered}
\frac{1}{1+m+m n}+\frac{1}{1+n+n k}+\frac{1}{1+k+k m}=\frac{k}{k+k m+k m n}+\frac{k m}{k m+k m n+k m n k}+\frac{1}{1+k+k m}= \\
=\frac{k}{k+k m+1}+\frac{k m}{k m+1+k}+\frac{1}{1+k+k m}=\frac{k+k m+1}{1+k+k m}=1
\end{gathered}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For the quadratic trinomials $f_{1}(x)=a x^{2}+b x+c_{1}, f_{2}(x)=a x^{2}+b x+c_{2}$, $\ldots, f_{2020}(x)=a x^{2}+b x+c_{2020}$, it is known that each of them has two roots.
Denote by $x_{i}$ one of the roots of $f_{i}(x)$, where $i=1,2, \ldots, 2020$. Find the value
$$
f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\cdots+f_{2020}\left(x_{2019}\right)+f_{1}\left(x_{2020}\right)
$$
|
Answer: 0.
## Solution:
Since $f_{1}\left(x_{1}\right)=0$, then $f_{2}\left(x_{1}\right)=f_{1}\left(x_{1}\right)+\left(c_{2}-c_{1}\right)=c_{2}-c_{1}$.
Similarly, we can obtain the following equalities:
$$
f_{3}\left(x_{2}\right)=c_{3}-c_{2}, \ldots, f_{2020}\left(x_{2019}\right)=c_{2020}-c_{2019}, f_{1}\left(x_{2020}\right)=c_{1}-c_{2020}
$$
Adding these equalities, we get
$$
f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\cdots+f_{2020}\left(x_{2019}\right)+f_{1}\left(x_{2020}\right)=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a sports store, over two days, thirteen pairs of sneakers, two sports suits, and one T-shirt were sold, with the same amount of money earned on the first day as on the second day (from the sale of the aforementioned items). One pair of sneakers is cheaper than a sports suit and more expensive than a T-shirt by the same amount. How many pairs of sneakers and suits were sold in one day with a T-shirt?
|
Answer: 8 pairs of sneakers and no sports suits.
Solution. Let in one day $x$ suits and $y$ pairs of sneakers were sold with a T-shirt. Then in the other day, $(2-x)$ suits and $(13-y)$ pairs of sneakers were sold.
Let $c$ be the price of one pair of sneakers, and $s$ be the price difference.
Then, from the condition of the problem, it follows that
$$
\begin{aligned}
& x(c+s)+y c+(c-s)=(2-x)(c+s)+(13-y) c \\
&(14-2 x-2 y) c=(2 x-3) s .
\end{aligned}
$$
The number $x$ can take the values 0, 1, or 2. Let's consider each of them in turn
1) $x=0 \Rightarrow(2 y-14) c=3 s$. Since $0<s<c$, then $0<(2 y-14) c<3 c \Rightarrow$
$$
0<(2 y-14)<3 \Rightarrow y=8-\text { unit integer }
$$
2) $x=1 \Rightarrow(2 y-12) c=s$. Since $0<s<c$, then $0<(2 y-12) c<$ c $\Rightarrow$
$$
0<(2 y-12)<1 \Rightarrow y-\text { no integers. }
$$
3) $x=2 \Rightarrow(10-2 y) c=s$. Since $0<s<c$, then $0<(10-2 y) c<$ c $\Rightarrow$
$$
0<(10-2 y)<1 \Rightarrow y \text { - no integers. }
$$
Thus, the situation described in the problem can only occur when $x=0, y=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Misha invited eighteen friends from his sports club and two of his brothers to celebrate his birthday, a total of twenty guests. All the guests and Misha himself, seated at two tables, ate all the hot dogs served equally on both tables, and everyone ate only from their own table. Each friend from the sports club ate more hot dogs than each of Misha's brothers, but less than Misha by the same number of pieces. How many friends from the sports club and how many brothers sat at the same table with Misha?
|
# Answer: 9 friends from the sports club and no brothers.
Solution. Let $x$ be the number of brothers and $y$ be the number of friends from the sports club sitting at the same table with Misha. Then, at the other table, there were $2-x$ brothers and $18-y$ friends from the sports club.
Let $c$ be the number of hot dogs each friend from the sports club ate, and $s$ be the constant difference in hot dogs mentioned in the problem.
Then, according to the problem's condition, we can write
$$
\begin{gathered}
x(c-s)+y c+(c+s)=(2-x)(c-s)+(18-y) c \\
(2 x+2 y-19) c=(2 x-3) s .
\end{gathered}
$$
The number $x$ can take the values 0, 1, or 2. Let's consider each of them in turn.
1) $x=0 \Rightarrow(19-2 y) c=3 s$. Since $0<s<c$, then $0<(19-2 y) c<3 c \Rightarrow$
$$
0<(19-2 y)<3 \Rightarrow y=19-\text { a single integer }
$$
2) $x=1 \Rightarrow(17-2 y) c=s$. Since $0<s<c$, then $0<(17-2 y) c<$ c $\Rightarrow$ $0<(17-2 y)<1 \Rightarrow y-$ no integers.
3) $x=2 \Rightarrow(2 y-15) c=s$. Since $0<s<c$, then $0<(2 y-15) c<$ c $\Rightarrow$
$$
0<(2 y-15)<1 \Rightarrow y-\text { no integers. }
$$
Thus, the situation described in the problem can only occur when $x=0, y=9$.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of roots of the equation: $2^{\lg \left(x^{2}-2023\right)}-\lg 2^{x^{2}-2022}=0$.
|
# Answer: 4 roots.
Solution: Using the properties of logarithms, rewrite the equations in the following form
$$
\left(x^{2}-2023\right)^{\lg 2}-\lg 2^{x^{2}-2022}=0
$$
Introduce the notations $z=x^{2}-2023, a=1 \mathrm{~g} 2$, in this case $z>0, a \in(0,1)$. Then $z^{a}=(z+1) a$
Let $y_{1}(z)=z^{a}, y_{2}(z)=(z+1) a$.
Since $y_{1}(1)=1, y_{2}(1)=2 a$, and $y_{1}(1)=1=\lg 10>\lg 4=2 \lg 2=2 a$ and considering the monotonicity and convexity of the functions $y_{1}(z), y_{2}(z)$ for $a \in(0,1)$, we get that the equation $z^{a}=(z+1) a$ has two roots $z_{1}$ and $z_{2}$, one of which, for example $z_{1}$ is less than one but greater than zero, and the other root $z_{2}$ will be greater than one. Then, recalling the substitution $z=x^{2}-2023$ and returning to the original variable $x$, we conclude that the original equation will have 4 roots: $\pm \sqrt{z_{1}+2023}, \pm \sqrt{z_{2}+2023}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The cosine of the angle between the lateral sides $A D$ and $B C$ of trapezoid $A B C D$ is 0.8. A circle is inscribed in the trapezoid, and the side $A D$ is divided by the point of tangency into segments of lengths 1 and 4. Determine the length of the lateral side $B C$ of the trapezoid.
|
Answer: 4 or $\frac{100}{7}$.
Solution: Let $S$ be the intersection point of lines $A D$ and $B C$; $K, L, M$ be the points of tangency of the inscribed circle with sides $A B, A D$, and $C D$ respectively, and $O$ be its center. Then $O K \perp A B, O M \perp C D$, as radii, and since $A B \| C D$, points $K, O, M$ lie on the same line, meaning $KM$ is a diameter. The problem's conditions correspond to two possible cases for the position of point $L$ on side $A D$.
1) In this case, $A L=1, D L=4$ (Fig.2). Then $A K=A L=1, D M=D L=4$. Drop $A N \perp C D$. Considering that $A N \| K M$, we get $N M=1, D N=3$. In the right triangle $A D N$, the hypotenuse is $A D=5$, and the leg $D N=3$, so $A N=4$. Therefore, $\cos \angle D A N = \frac{4}{5}$, and given the problem's conditions, we conclude that $\angle D A N = \angle D S C$, and line $S C \parallel A N$. Thus, $\angle C$ of the trapezoid is a right angle, and the length $B C = A N = 4$.
2) In this case, $A L=4, D L=1$ (Fig.3). As before, the length of the perpendicular $A N=4, D N=3$, $\cos \angle A D N=\frac{3}{5}, \sin \angle A D N=\frac{4}{5}$. The acute angle $A D N$ is an external angle for the trapezoid and triangle $D S C$, so $\angle A D N = \angle C + \angle S$. Given that $\cos \angle S=\frac{4}{5}$, we find $\sin \angle S=\frac{3}{5}$, $\sin \angle C=\sin (\angle A D N - \angle S)=\frac{7}{25}$. Since $A N = B C \cdot \sin \angle C$, then $B C = \frac{100}{7}$.
## MINISTRY OF SCIENCE AND HIGHER EDUCATION OF THE RF COUNCIL OF RECTORS OF UNIVERSITIES OF TOMSK REGION OPEN REGIONAL INTERUNIVERSITY OLYMPIAD 2018-2019 MATHEMATICS (9th GRADE) FINAL STAGE 2nd VARIANT (ANSWERS)
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For the quadratic trinomial $f(x)=a x^{2}+b x+c$, it is known that
$$
f\left(\frac{a-b-c}{2 a}\right)=f\left(\frac{c-a-b}{2 a}\right)=0
$$
Find the value of the product $f(-1) \cdot f(1)$.
|
Answer: 0.
## Solution:
$$
f\left(\frac{a-b-c}{2 a}\right)=\frac{a(a-b-c)^{2}}{4 a^{2}}+\frac{b(a-b-c)}{2 a}+c=\frac{(a-b+c)(a+b+c)}{4 a}=\frac{f(-1) \cdot f(1)}{4 a}=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Compute $2022!\cdot\left(S_{2021}-1\right)$, if $S_{n}=\frac{1}{2!}+\frac{2}{3!}+\cdots+\frac{n}{(n+1)!}$.
|
Answer: -1.
Solution.
Given that $\frac{n}{(n+1)!}=\frac{n+1}{(n+1)!}-\frac{1}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!}$, we get
$S_{2021}=\frac{1}{2!}+\frac{2}{3!}+\cdots+\frac{2021}{2022!}=\left(\frac{1}{1!}-\frac{1}{2!}\right)+\left(\frac{1}{2!}-\frac{1}{3!}\right)+\cdots+\left(\frac{1}{2021!}-\frac{1}{2022!}\right)=1-\frac{1}{2022!}$.
Then $\quad 2022!\cdot\left(S_{2021}-1\right)=2022!\cdot\left(1-\frac{1}{2022!}-1\right)=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the value of the expression $\frac{1}{a b}+\frac{1}{b c}+\frac{1}{a c}$, if it is known that $a, b, c$ are three different real numbers satisfying the conditions $a^{3}-2022 a^{2}+1011=0, b^{3}-2022 b^{2}+1011=0, c^{3}-2022 c^{2}+1011=0$.
|
Answer: -2.
## Solution.
The cubic equation $t^{3}-2022 t^{2}+1011=0$ has three distinct roots (since for $\left.f(t)=t^{3}-2022 t^{2}+1011: f(-3000)0, f(10)0\right)$.
Let these roots be $a, b, c$. Then, by Vieta's formulas:
$$
\left\{\begin{array}{l}
a+b+c=2022 \\
a b+b c+a c=0 \\
a b c=-1011
\end{array}\right.
$$
We find the value of the expression: $\quad \frac{1}{a b}+\frac{1}{b c}+\frac{1}{a c}=\frac{c+a+b}{a b c}=\frac{2022}{-1011}=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Compute $2023!\cdot\left(S_{2022}-1\right)$, if $S_{n}=\frac{1}{2!}+\frac{2}{3!}+\cdots+\frac{n}{(n+1)!}$.
|
Answer: -1.
Solution.
Given that $\frac{n}{(n+1)!}=\frac{n+1}{(n+1)!}-\frac{1}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!}$, we get
$S_{2022}=\frac{1}{2!}+\frac{2}{3!}+\cdots+\frac{2022}{2023!}=\left(\frac{1}{1!}-\frac{1}{2!}\right)+\left(\frac{1}{2!}-\frac{1}{3!}\right)+\cdots+\left(\frac{1}{2022!}-\frac{1}{2023!}\right)=1-\frac{1}{2023!}$.
Then $\quad 2023!\cdot\left(S_{2022}-1\right)=2023!\cdot\left(1-\frac{1}{2023!}-1\right)=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the value of the expression $\frac{1}{a b}+\frac{1}{b c}+\frac{1}{a c}$, if it is known that $a, b, c$ are three different real numbers satisfying the conditions $a^{3}-2020 a^{2}+1010=0, b^{3}-2020 b^{2}+1010=0, \quad c^{3}-2020 c^{2}+1020=0$.
|
Answer: -2.
## Solution.
The cubic equation $t^{3}-2020 t^{2}+1010=0$ has three distinct roots (since for $\left.f(t)=t^{3}-2020 t^{2}+1010: f(-3000)0, f(10)0\right)$.
Let these roots be $a, b, c$. Then, by Vieta's formulas:
$$
\left\{\begin{array}{l}
a+b+c=2020 \\
a b+b c+a c=0 \\
a b c=-1010
\end{array}\right.
$$
We find the value of the expression: $\quad \frac{1}{a b}+\frac{1}{b c}+\frac{1}{a c}=\frac{c+a+b}{a b c}=\frac{2020}{-1010}=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the value of the expression $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$, if it is known that $a, b, c$ are three different real numbers satisfying the conditions:
$a^{3}-2022 a+1011=0, \quad b^{3}-2022 b+1011=0, \quad c^{3}-2022 c+1011=0$.
|
Answer: 2.
## Solution.
The cubic equation $t^{3}-2022 t+1011=0$ has three distinct roots (since for $\left.f(t)=t^{3}-2022 t+1011: f(-100)0, f(10)0\right)$.
Let these roots be $a, b, c$. Then, by Vieta's theorem:
$$
\left\{\begin{array}{l}
a+b+c=0 \\
a b+b c+a c=-2022 \\
a b c=-1011
\end{array}\right.
$$
We find the value of the expression: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{a b+b c+a c}{a b c}=\frac{-2022}{-1011}=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the value of the expression $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$, if it is known that $a, b, c$ are three distinct real numbers satisfying the conditions:
$a^{3}-2020 a+1010=0, \quad b^{3}-2020 b+1010=0, c^{3}-2020 c+1010=0$.
|
Answer: 2.
Solution.
The cubic equation $t^{3}-2020 t+1010=0$ has three distinct roots (since for $\left.f(t)=t^{3}-2020 t+1010: f(-100)0, f(10)0\right)$.
Let these roots be $a, b, c$. Then, by Vieta's theorem:
$$
\left\{\begin{array}{l}
a+b+c=0 \\
a b+b c+a c=-2020 \\
a b c=-1010
\end{array}\right.
$$
We find the value of the expression: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{a b+b c+a c}{a b c}=\frac{-2020}{-1010}=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. To walk 2 km, ride 3 km on a bicycle, and drive 20 km by car, Uncle Vanya needs 1 hour 6 minutes. If he needs to walk 5 km, ride 8 km on a bicycle, and drive 30 km by car, it will take him 2 hours 24 minutes. How much time will Uncle Vanya need to walk 4 km, ride 5 km on a bicycle, and drive 80 km by car?
|
# Answer: 2 hours 54 minutes. (2.9 hours.)
## Solution:
Let $\frac{1}{x}, \frac{1}{y}, \frac{1}{z}$ be the walking speed, cycling speed, and driving speed, respectively. Then, according to the problem, we can set up the system:
$$
\left\{\begin{array} { c }
{ 2 x + 3 y + 2 0 z = 6 6 } \\
{ 5 x + 8 y + 3 0 z = 1 4 4 . }
\end{array} \Rightarrow \left\{\begin{array} { c }
{ 2 x + 3 y = 6 6 - 2 0 z } \\
{ 5 x + 8 y = 1 4 4 - 3 0 z }
\end{array} \Rightarrow \left\{\begin{array}{l}
x=96-70 z \\
y=40 z-42
\end{array}\right.\right.\right.
$$
Therefore, $4 x+5 y+80 z=4(96-70 z)+5(40 z-42)+80 z=174$ minutes. 174 minutes $=2$ hours 54 minutes.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The base of the pyramid $S A B C D$ is a rectangle $A B C D$, with the height being the edge $S A=25$. Point $P$ lies on the median $D M$ of the face $S C D$, point $Q$ lies on the diagonal $B D$, and the lines $A P$ and $S Q$ intersect. Find the length of $P Q$, if $B Q: Q D=3: 2$.
|
# Answer: 10.
## Solution:
Since lines $A P$ and $S Q$ intersect, points $A, P, S, Q$ lie in the same plane. Let $R$ be the intersection point of $S P$ and $A Q$. Then
$$
\frac{R Q}{A Q}=\frac{D Q}{B Q}=\frac{2}{3} \Rightarrow \frac{R Q}{R A}=\frac{2}{5}
$$
We will prove that $\frac{R M}{R S}=\frac{2}{5}$. Note that $\frac{D Q}{B A}=\frac{2}{3} \Rightarrow \frac{D Q}{C D}=\frac{2}{3} \Rightarrow \frac{C D}{D Q}=\frac{1}{2}$.
Let $H$ be a point on edge $S C$ such that $R H \| D M$. Then
$$
\frac{C H}{H M}=\frac{C R}{R D}=\frac{1}{2} \Rightarrow \frac{M S}{M H}=\frac{3}{2} \Rightarrow \frac{M H}{S H}=\frac{2}{5} \Rightarrow \frac{R M}{R S}=\frac{2}{5}
$$
From the similarity of triangles $R P Q$ and $R S A$, we get that
$$
\frac{P Q}{S A}=\frac{2}{5} \Rightarrow \frac{P Q}{25}=\frac{2}{5} \Rightarrow P Q=10
$$
## Evaluation criteria are provided in the table:
| Points | Evaluation Criteria |
| :---: | :--- |
| $\mathbf{7}$ | Complete and justified solution. |
| $\mathbf{6}$ | Justified solution with minor flaws. |
| $\mathbf{5 - 6}$ | The solution contains minor errors, gaps in justification, but is generally correct and can become fully correct with minor corrections or additions. |
| $\mathbf{4}$ | The problem is more solved than not, for example, one of the two (more complex) significant cases is correctly considered. |
| $\mathbf{2 - 3}$ | The problem is not solved, but formulas, diagrams, considerations, or auxiliary statements relevant to the solution of the problem are provided. |
| $\mathbf{1}$ | The problem is not solved, but an attempt at a solution has been made, for example, individual (partial) cases have been considered in the absence of a solution or in the case of an incorrect solution. |
| $\mathbf{0}$ | The solution is absent or does not meet any of the criteria listed above. |
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Real
numbers
$x, y, z$
satisfy
$$
4 x^{2}-2 x-30 y z=25 y^{2}+5 y+12 x z=9 z^{2}-3 z-20 x y .
$$
relations:
Find the maximum of the sum $a+b+c$, where $a=2 x+5 y, b=3 z+5 y, c=3 z-2 x$.
|
Solution. Note that
$$
a-b+c=0
$$
Let $A=4 x^{2}-2 x-30 y z, B=25 y^{2}+5 y+12 x z$ and $C=9 z^{2}-3 z-20 x y$. Subtracting these equations from each other, we get
$$
\begin{aligned}
& A-B=a \cdot(2 x-6 z-5 y-1)=0 \\
& B-C=b \cdot(5 y+4 x-3 z+1)=0 \\
& A-C=c \cdot(1-2 x-10 y-3 z)=0
\end{aligned}
$$
Assume that all three numbers $a, b, c$ are non-zero. Then $2 x-6 z-5 y-1=0, 5 y+4 x-3 z+1=0$ and $1-2 x-10 y-3 z=0$, which is impossible, as adding the second equation to the third and subtracting the first, we get $3=0$. Therefore, at least one of the numbers $a, b, c$ is zero. Consider the possible cases:
1) All three numbers $a, b, c$ are zero. The triplet $a=b=c=0$ clearly satisfies the conditions of the problem (it is sufficient to take $x=y=z=0$).
2) Only two of the numbers $a, b, c$ are zero. This is impossible: if two numbers are zero, then, according to (1), the third is also zero.
3) Only one of the numbers $a, b, c$ is zero:
- $a=0$. Then $x=-\frac{5 y}{2}$. From system (2) we find $b=c=1$;
- $b=0$. Then $a=-c=1$;
- $c=0$. Then $a=b=-1$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a triangle with sides $a, b, c$ and angles $\alpha, \beta, \gamma$, the equality $3 \alpha + 2 \beta = 180^{0}$ is satisfied. The sides $a, b, c$ lie opposite the angles $\alpha, \beta, \gamma$ respectively. Find the length of side $c$ when $a=2, b=3$.
|
Solution: From the condition, it follows that $c > b$. Let's find a point $D$ on the segment $AB$ such that $AC = AD$. Then the triangle $ACD$ is isosceles and $\angle ACD = \angle ADC = 90^\circ - \alpha / 2$. The angle $\angle ADC$ is the external angle of the triangle $CBD$. Therefore, $\angle BCD + \beta = \angle ADC = 90^\circ - \frac{\alpha}{2} = \alpha + \beta$. Hence, $\angle BCD = \alpha$, and the triangles $CDB$ and $ABC$ are similar. We have $\frac{BD}{BC} = \frac{BC}{AB}$ or $\frac{c - b}{a} = \frac{a}{c'}$, from which it follows that $a^2 + bc - c^2 = 0$. The quadratic equation $c^2 - 3c - 4 = 0$ has a unique positive root $c = 4$.
## Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides $B C$ and $C D$ of the square $A B C D$, points $E$ and $F$ are chosen such that the angle $E A F$ is $45^{\circ}$. The length of the side of the square is 1. Find the perimeter of triangle $C E F$.
|
Solution: If point $D$ is reflected relative to line $A F$, and then relative to line $A E$, it will transition to point $B$. Indeed, the composition of two axial symmetries relative to intersecting lines is a rotation by twice the angle between the lines. In our case, these two symmetries are equivalent to a $90^{\circ}$ rotation around point $A$. This means that the image of point $D$ under symmetry relative to $A F$ and the image of point $B$ under symmetry relative to $A E$ are
## Interregional School Olympiad in Mathematics for Students of Departmental Educational Organizations
the same point; on the diagram, it is denoted by $K$. From point $K$, segments $A E$ and $A F$ are seen at an angle of $90^{0}$ (angles are preserved under symmetry, so, for example, angles $A B E$ and $A K E$ are equal). Therefore, point $K$ is the foot of the perpendicular dropped from point $A$ to line $E F$. Finally, since $B E = E K$ and $D F = F K$ (lengths of segments are preserved under symmetry), we see that the perimeter of triangle $C E F$ is equal to the sum of the lengths of sides $B C$ and $C D$ of the square.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Eight numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $b_{1}, b_{2}, b_{3}, b_{4}$ satisfy the relations
$$
\left\{\begin{array}{c}
a_{1} b_{1}+a_{2} b_{3}=1 \\
a_{1} b_{2}+a_{2} b_{4}=0 \\
a_{3} b_{1}+a_{4} b_{3}=0 \\
a_{3} b_{2}+a_{4} b_{4}=1
\end{array}\right.
$$
It is known that $a_{2} b_{3}=7$. Find $a_{4} b_{4}$.
|
Solution. We will prove that ${ }^{1}$
$$
a_{2} b_{3}=a_{3} b_{2}
$$
Multiply equation (a) of the original system by $b_{2}$ and subtract from it equation (b) multiplied by $b_{1}$. The result is
$$
a_{2} \cdot \Delta=b_{2}
$$
Here $\Delta=b_{2} b_{3}-b_{1} b_{4}$. Similarly, from (c) and (d) we find that
$$
a_{3} \cdot \Delta=b_{3}
$$
Note that $\Delta \neq 0$, otherwise from (3) it would follow that $b_{3}=0$, and thus $a_{2} b_{3}=0$, which contradicts the problem's condition. It remains to express $a_{2}$ and $a_{3}$ from (2) and (3) and substitute the obtained expressions into (1). The validity of relation (1) will thereby be proven.
Further, from equation (d) and equality (1), it follows that $a_{4} b_{4}=1-a_{3} b_{2}=1-a_{2} b_{3}=-6$.
Answer: $a_{4} b_{4}=-6$.
Comment. ${ }^{1}$ The system of equations in the problem is the component-wise recording of the matrix equality
$$
\mathbf{A} \cdot \mathbf{B}=\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right) \text {, where } \mathbf{A}=\left(\begin{array}{ll}
a_{1} & a_{2} \\
a_{3} & a_{4}
\end{array}\right) \text { and } \mathbf{B}=\left(\begin{array}{ll}
b_{1} & b_{2} \\
b_{3} & b_{4}
\end{array}\right)
$$
It is well known that if the product of two matrices is the identity matrix, then these matrices commute, which means the system of equations in the problem will remain valid if all $a_{i}$ are replaced by $b_{i}$ and vice versa. From this observation, equality (1) follows immediately.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The function $y=f(x)$ is defined on the set $(0,+\infty)$ and takes positive values on it. It is known that for any points $A$ and $B$ on the graph of the function, the areas of the triangle $A O B$ and the trapezoid $A B H_{B} H_{A}$ are equal to each other $\left(H_{A}, H_{B}\right.$ - the bases of the perpendiculars dropped from points $A$ and $B$ to the x-axis; $O$ - the origin). Find all such functions. Given $f(1)=4$, write the number $f(4)$ in the answer.
|
# Solution:
Let $M$ be the intersection point of segments $O B$ and $A H_{A}$. Since the areas of triangle $A O B$ and trapezoid $A B H_{B} H_{A}$ are equal, then
the areas of triangles $A M O$ and trapezoid $M B H_{B} H_{A}$ are also equal. From this, it follows that the areas of triangles $A O H_{A}$ and trapezoid $B O H_{B}$ are also equal. Let the abscissas of points $H_{A}$ and $H_{B}$ be $x$ and $t$ respectively. Then we have the equality $x \cdot f(x) = t \cdot f(t)$. For a fixed $t$, we get the conclusion: $f(x) = \frac{c}{x}, c > 0$.
Answer: 1
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $x_{1}$ and $x_{2}$ be the largest roots of the polynomials
$$
\begin{gathered}
f(x)=1-x-4 x^{2}+x^{4} \\
\text { and } \\
g(x)=16-8 x-16 x^{2}+x^{4}
\end{gathered}
$$
respectively. Find $\frac{x_{2}}{x_{1}}$.
|
Solution:
Notice that $f(-2)>0, f(-1)<0, f(0)>0, f(1)<0$. Therefore, the polynomial $f(x)$ has 4 real roots. Similarly, from the inequalities $g(-4)>0, g(-2)<0, g(0)>0, g(2)<0$ it follows that the polynomial $g(x)$ has 4 real roots.
Comparison of the coefficients of the polynomials
$$
f(x)=1-x-4 x^{2}+x^{4} \text { and } g(x)=16-8 x-16 x^{2}+x^{4}
$$
shows that according to Vieta's formulas, the roots of the polynomial $g(x)$ are double the roots of the polynomial $f(x)$. Hence, it follows that $\frac{x_{2}}{x_{1}}=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Points $F$ and $G$ are chosen on the sides $AB$ and $BC$ of rectangle $ABCD$, respectively. A perpendicular $FK$ is dropped from point $F$ to side $CD$. A perpendicular $GH$ is dropped from point $G$ to side $AD$. The intersection point of $FK$ and $GH$ is denoted as $E$. Find the area of triangle $DFG$, given that the areas of rectangles $ABCD$ and $HEK$ are 20 and 8, respectively.
|
# Solution:
Let $A D=a, D C=b, H D=x$, and $D K=y$.
$$
\begin{aligned}
S_{D F G}=S_{A B C D} & -S_{A F D}-S_{F G B}-S_{D G C}=a b-\frac{1}{2} a y-\frac{1}{2}(b-y)(a-x)-\frac{1}{2} b x \\
& =a b-\frac{1}{2} a y-\frac{1}{2} a y(a b-b x-a y+x y)-\frac{1}{2} b x \\
& =a b-\frac{1}{2} a y-\frac{1}{2} a b+\frac{1}{2} b x+\frac{1}{2} a y-\frac{1}{2} x y-\frac{1}{2} b x=\frac{a b-x y}{2}=\frac{S_{A B C D}-S_{H E K D}}{2}=6
\end{aligned}
$$
Answer: 6
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Eight numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $b_{1}, b_{2}, b_{3}, b_{4}$ satisfy the relations
$$
\left\{\begin{array}{l}
a_{1} b_{1}+a_{2} b_{3}=1 \\
a_{1} b_{2}+a_{2} b_{4}=0 \\
a_{3} b_{1}+a_{4} b_{3}=0 \\
a_{3} b_{2}+a_{4} b_{4}=1
\end{array}\right.
$$
It is known that $a_{2} b_{3}=7$. Find $a_{4} b_{4}$.
|
Solution. We will prove that ${ }^{1}$
$$
a_{2} b_{3}=a_{3} b_{2}
$$
Interregional Olympiad for Schoolchildren Based on Departmental Educational Organizations in Mathematics
$$
\begin{cases}a_{1} b_{1}+a_{2} b_{3}=1 & \text { (a) } \\ a_{1} b_{2}+a_{2} b_{4}=0 & \text { (b) } \\ a_{3} b_{1}+a_{4} b_{3}=0 & \text { (c) } \\ a_{3} b_{2}+a_{4} b_{4}=1 & \text { (d) }\end{cases}
$$
Multiply equation (a) by $b_{2}$ and subtract from it equation (b) multiplied by $b_{1}$. The result is
$$
a_{2} \cdot \Delta=b_{2}
$$
Here $\boldsymbol{\Delta}=\mathbf{b}_{\mathbf{2}} \boldsymbol{b}_{\mathbf{3}}-\boldsymbol{b}_{\mathbf{1}} \boldsymbol{b}_{\mathbf{4}}$. Similarly, from (c) and (d) we find that
$$
a_{3} \cdot \Delta=b_{3} \text {. }
$$
Note that $\Delta \neq 0$, because otherwise from (3) it would follow that $b_{3}=0$, and thus $a_{2} b_{3}=0$, which contradicts the problem's condition. It remains to express $a_{2}$ and $a_{3}$ from (2) and (3) and substitute the obtained expressions into (1). The validity of relation (1) will thereby be proven.
Further, from equation (d) and equality (1), it follows that $a_{4} b_{4}=1-a_{3} b_{2}=1-a_{2} b_{3}=-6$.
Answer: $a_{4} b_{4}=-6$.
Comment. ${ }^{1}$ The system of equations in the problem is the component-wise recording of the matrix equality $\mathbf{A} \cdot \mathbf{B}=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$, where $\mathbf{A}=\left(\begin{array}{ll}a_{1} & a_{2} \\ a_{3} & a_{4}\end{array}\right)$ and $\mathbf{B}=\left(\begin{array}{ll}b_{1} & b_{2} \\ b_{3} & b_{4}\end{array}\right)$. It is well known that if the product of two matrices is the identity matrix, then these matrices commute, which means the system of equations in the problem remains valid if all $a_{i}$ are replaced by $b_{i}$ and vice versa. From this observation, equality (1) follows immediately.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (4 points) Oleg usually arrives on a business trip by the 11 o'clock train. A car arrives at the station for this train. This time, the train arrived an hour earlier, and Oleg started walking towards the car. Meeting the car on the way, he got in, and as a result, arrived 10 minutes earlier than planned. Determine the time Oleg met the car.
|
4. 10 hours 55 minutes.
$+(4$ points) - solution is correct (by any method)
+- (3 points) - solution is correct, but there are arithmetic errors
-+ (2 points) - there are reasonable ideas in solving the problem, but the problem is not solved in general
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (4 points) Let two sequences of numbers $\left(x_{0}, x_{1}, \ldots, x_{2009}\right)$, $\left(y_{0}, y_{1}, \ldots, y_{2009}\right)$ be constructed according to the following rules:
a) $x_{0}=12, x_{1}=\frac{1}{3}, y_{0}=4, y_{1}=\frac{1}{18}$,
b) $x_{i+1}=x_{i-1}+4 x_{i}$ and $y_{i+1}=y_{i-1}-4 y_{i}$ for $i=1, \ldots, 2008$.
Calculate the value of $x_{2009} y_{2008}+x_{2008} y_{2009}$.
|
5. 2 .
$+(4$ points) - solution is correct
+- (3 points) - the idea of the recurrence relation is proven, but there are arithmetic errors in the solution
-+ (2 points) - the idea of the recurrence relation is formulated, but the problem is not completed
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Non-zero numbers $a$ and $b$ are roots of the quadratic equation $x^{2}-5 p x+2 p^{3}=0$. The equation $x^{2}-a x+b=0$ has a unique root. Find $p$. Justify your solution.
|
Solution. Since the equation $x^{2}-a x+b=0$ has a unique root, then $b=\frac{a^{2}}{4}$. By Vieta's theorem, we have the equalities: $a+b=5 p ; a b=2 p^{3}$. Substituting $b=\frac{a^{2}}{4}$ into the last equality, we get: $a=2 p$. Considering that $a$ and $b$ are non-zero, we find $p=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the sides $B C$ and $C D$ of the square $A B C D$, points $E$ and $F$ are chosen such that the angle $E A F$ is $45^{\circ}$. The length of the side of the square is 1. Find the perimeter of triangle $C E F$. Justify your solution.
|
Solution. If point $D$ is reflected across line $A F$, and then across line $A E$, it will transition to point $B$. Indeed, the composition of two axial symmetries relative to intersecting lines is a rotation by twice the angle between the lines. In our case, these two symmetries are equivalent to a $90^{\circ}$ rotation around point $A$.
This means that the image of point $D$ under the symmetry relative to $A F$ and the image of point $B$ under the symmetry relative to $A E$ are the same point; on the diagram, it is denoted by $K$. From point $K$, segments $A E$ and $A F$ are seen at a $90^{\circ}$ angle (since angles are preserved under symmetry, for example, angles $A B E$ and $A K E$ are equal). Therefore, point $K$ is the foot of the perpendicular dropped from point $A$ to line $E F$.
Finally, since $B E = E K$ and $D F = F K$ (lengths of segments are preserved under symmetry), we see that the perimeter of triangle $C E F$ is equal to the sum of the lengths of sides $B C$ and $C D$ of the square.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Eight numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $b_{1}, b_{2}, b_{3}, b_{4}$ satisfy the relations
$$
\left\{\begin{aligned}
a_{1} b_{1}+a_{2} b_{3} & =1 \\
a_{1} b_{2}+a_{2} b_{4} & =0 \\
a_{3} b_{1}+a_{4} b_{3} & =0 \\
a_{3} b_{2}+a_{4} b_{4} & =1
\end{aligned}\right.
$$
It is known that $a_{2} b_{3}=7$. Find $a_{4} b_{4}$.
|
Solution. We will prove that ${ }^{1}$
$$
a_{2} b_{3}=a_{3} b_{2}
$$
Multiply equation (a) of the original system
$$
\begin{cases}a_{1} b_{1}+a_{2} b_{3}=1 & \text { (a) } \\ a_{1} b_{2}+a_{2} b_{4}=0 & \text { (b) } \\ a_{3} b_{1}+a_{4} b_{3}=0 & \text { (c) } \\ a_{3} b_{2}+a_{4} b_{4}=1\end{cases}
$$
by $b_{2}$ and subtract from it equation (b) multiplied by $b_{1}$. The result is
$$
a_{2} \cdot \Delta=b_{2}
$$
Here $\Delta=b_{2} b_{3}-b_{1} b_{4}$. Similarly, from (c) and (d) we find that
$$
a_{3} \cdot \Delta=b_{3}
$$
Note that $\Delta \neq 0$, otherwise from (3) it would follow that $b_{3}=0$, and thus $a_{2} b_{3}=0$, which contradicts the problem's condition. It remains to express $a_{2}$ and $a_{3}$ from (2) and (3) and substitute the obtained expressions into (1). The validity of relation (1) will thereby be proven.
Further, from equation (d) and equality (1), it follows that $a_{4} b_{4}=1-a_{3} b_{2}=1-a_{2} b_{3}=-6$.
Answer: $a_{4} b_{4}=-6$.
Comment. ${ }^{1}$ The system of equations in the problem is the component-wise recording of the matrix equality $\mathbf{A} \cdot \mathbf{B}=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$, where $\mathbf{A}=\left(\begin{array}{ll}a_{1} & a_{2} \\ a_{3} & a_{4}\end{array}\right)$ and $\mathbf{B}=\left(\begin{array}{ll}b_{1} & b_{2} \\ b_{3} & b_{4}\end{array}\right)$. It is well known that if the product of two matrices is the identity matrix, then these matrices commute, which means the system of equations in the problem remains valid if all $a_{i}$ are replaced by $b_{i}$ and vice versa. From this observation, equality (1) follows immediately.
Interregional Olympiad for Schoolchildren Based on Departmental Educational Organizations in Mathematics
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides $B C$ and $C D$ of the square $A B C D$, points $E$ and $F$ are chosen such that the angle $E A F$ is $45^{\circ}$. The length of the side of the square is 1. Find the perimeter of triangle $C E F$. Justify your solution.
|
# Solution:
If point $D$ is reflected relative to line $A F$, and then relative to line $A E$, it will transition to point $B$. Indeed, the composition of two axial symmetries relative to intersecting lines is a rotation by twice the angle between the lines. In our case, these two symmetries are equivalent to a $90^{\circ}$ rotation around point $A$.
## Interregional School Olympiad in Mathematics for Students of Departmental Educational Organizations
This means that the image of point $D$ under symmetry relative to $A F$ and the image of point $B$ under symmetry relative to $A E$ are the same point; on the diagram, it is denoted as $K$. From point $K$, segments $A E$ and $A F$ are seen at a $90^{\circ}$ angle (angles are preserved under symmetry, so, for example, angles $A B E$ and $A K E$ are equal). Therefore, point $K$ is the foot of the perpendicular dropped from point $A$ to line $E F$.
Finally, since $B E = E K$ and $D F = F K$ (lengths of segments are preserved under symmetry), we see that the perimeter of triangle $C E F$ is equal to the sum of the lengths of sides $B C$ and $C D$ of the square.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Points $F$ and $G$ are chosen on the sides $AB$ and $BC$ of rectangle $ABCD$, respectively. A perpendicular $FK$ is dropped from point $F$ to side $CD$. A perpendicular $GH$ is dropped from point $G$ to side $AD$. The intersection point of $FK$ and $GH$ is denoted as $E$. Find the area of triangle $DFG$, given that the areas of rectangles $ABCD$ and $HEKD$ are 20 and 8, respectively.
|
# Solution:
Let $A D=a, D C=b, H D=x$, and $D K=y$.
$$
\begin{aligned}
S_{D F G}=S_{A B C D} & -S_{A F D}-S_{F G B}-S_{D G C}=a b-\frac{1}{2} a y-\frac{1}{2}(b-y)(a-x)-\frac{1}{2} b x \\
& =a b-\frac{1}{2} a y-\frac{1}{2} a y(a b-b x-a y+x y)-\frac{1}{2} b x \\
& =a b-\frac{1}{2} a y-\frac{1}{2} a b+\frac{1}{2} b x+\frac{1}{2} a y-\frac{1}{2} x y-\frac{1}{2} b x=\frac{a b-x y}{2}=\frac{S_{A B C D}-S_{H E K D}}{2}=6
\end{aligned}
$$
Answer: 6
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (3 points) Let two sequences of numbers $\left(x_{0}, x_{1}, \ldots, x_{2009}\right)$, $\left(y_{0}, y_{1}, \ldots, y_{2009}\right)$ be constructed according to the following rules:
a) $x_{0}=12, x_{1}=\frac{1}{3}, y_{0}=4, y_{1}=\frac{1}{18}$
b) $x_{i+1}=x_{i-1}+4 x_{i}$ and $y_{i+1}=y_{i-1}-4 y_{i}$ for $i=1, \ldots, 2008$.
Calculate the value of $x_{2009} y_{2008}+x_{2008} y_{2009}$.
|
2. 2 .
$+(3$ points) - the solution is correct
+- (2 points) - the idea of the recurrence relation is proven, but there are arithmetic errors in the solution
-+ (1 point) - the idea of the recurrence relation is formulated, but the problem is not completed
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Real numbers $x, y, z$ satisfy the relations:
$$
4 x^{2}-2 x-30 y z=25 y^{2}+5 y+12 x z=9 z^{2}-3 z-20 x y .
$$
Find the maximum of the sum $a+b+c$, where $a=2 x+5 y, b=3 z+5 y, c=3 z-2 x$.
|
Solution. Note that
$$
a-b+c=0
$$
Let $A=4 x^{2}-2 x-30 y z, B=25 y^{2}+5 y+12 x z$ and $C=9 z^{2}-3 z-20 x y$. Subtracting these equations from each other, we get
$$
\begin{aligned}
& A-B=a \cdot(2 x-6 z-5 y-1)=0 \\
& B-C=b \cdot(5 y+4 x-3 z+1)=0 \\
& A-C=c \cdot(1-2 x-10 y-3 z)=0
\end{aligned}
$$
Assume that all three numbers $a, b, c$ are non-zero. Then $2 x-6 z-5 y-1=0, 5 y+4 x-3 z+1=0$ and $1-2 x-10 y-3 z=0$, which is impossible, as adding the second equation to the third and subtracting the first, we get $3=0$. Therefore, at least one of the numbers $a, b, c$ is zero. Consider the possible cases:
1) All three numbers $a, b, c$ are zero. The triplet $a=b=c=0$ clearly satisfies the conditions of the problem (it is sufficient to take $x=y=z=0$).
2) Only two of the numbers $a, b, c$ are zero. This is impossible: if two numbers are zero, then, according to (1), the third is also zero.
3) Only one of the numbers $a, b, c$ is zero:
- $a=0$. Then $x=-\frac{5 y}{2}$. From system (2) we find $b=c=1$;
## Interregional Olympiad for Schoolchildren Based on Departmental Educational Organizations
in mathematics- $b=0$. Then $a=-c=1$;
- $c=0$. Then $a=b=-1$.
Thus, there are 4 possible options: $(0,0,0),(0,1,1),(1,0,-1),(-1,-1,0)$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In quadrilateral $A B C D$, the diagonals intersect at point $O$. It is known that $S_{A B O}=S_{C D O}=\frac{3}{2}$, $B C=3 \sqrt{2}$, $\cos \angle A D C=\frac{3}{\sqrt{10}}$. Find the smallest area that such a quadrilateral can have.
|
Solution. We will prove that quadrilateral $ABCD$ is a parallelogram. Let $x_{1}, x_{2}, y_{1}, y_{2}$ be the segments into which the diagonals are divided by their point of intersection. Denote the angle between the diagonals as $\alpha$. By the condition, the areas of triangles $ABO$ and $CDO$ are equal, that is, $\frac{1}{2} x_{1} y_{2} \sin \alpha = \frac{1}{2} x_{2} y_{1} \sin \alpha$. Hence, $\frac{x_{1}}{x_{2}} = \frac{y_{1}}{y_{2}}$, and,

consequently, triangles $BOC$ and $AOD$ are similar by the first similarity criterion: two sides ($x_{1}$ and $y_{1}$) of triangle $BOC$ are proportional to two sides ($x_{2}$ and $y_{2}$) of triangle $AOD$, and the angles formed by these sides ($\angle BOC$ and $\angle AOD$) are equal. Let $k = \frac{x_{1}}{x_{2}} = \frac{y_{1}}{y_{2}}$ be the similarity coefficient of triangles $BOC$ and $AOD$. Denote by $S$ the areas of triangles $ABO$ and $CDO$ (by the condition $S = \frac{3}{2}$). Then $S_{BOC} = k \cdot S$ and $S_{AOD} = S / k$. In the end, the area of quadrilateral $ABCD$ can be represented as:
$$
S_{ABCD} = S_{AOD} + S_{CDO} + S_{BOC} + S_{ABO} = 2S + S\left(k + \frac{1}{k}\right)
$$
It is known that for $k > 0$ the minimum value of the expression $k + \frac{1}{k}$ is achieved at $k = 1$. Therefore, $x_{1} = x_{2}$ and $y_{1} = y_{2}$, which means that the diagonals of the quadrilateral are bisected by their point of intersection, so $ABCD$ is a parallelogram. Its area $S_{ABCD} = 4S = 6$.
Answer: 6.
## Interregional School Olympiad in Mathematics for Students of Vedomstvennye Educational Organizations
5. Find the sum of all prime numbers whose decimal representation has the form 101010...01.
Solution. Let $2n+1$ be the number of digits in the number $A = 101010 \ldots 101$. Let $q = 10$ be the base of the number system. Then $A = q^{0} + q^{2} + \cdots + q^{2n} = \frac{q^{2n+2} - 1}{q^{2} - 1}$. Consider the cases of even and odd $n$.
- $n = 2k \Rightarrow A = \frac{q^{2n+2} - 1}{q^{2} - 1} = \frac{q^{2k+1} - 1}{q - 1} \cdot \frac{q^{2k+1} + 1}{q + 1}$. Thus, the number $A$ is represented as the product of two integers (by the theorem of Bezout, the polynomial $q^{2k+1} \pm 1$ is divisible without remainder by the polynomial $q \pm 1$), each of which is different from 1. Therefore, for even $n$, the number $A$ is not prime.
- $n = 2k-1 \Rightarrow A = \frac{q^{2n+2} - 1}{q^{2} - 1} = \frac{q^{2k} - 1}{q^{2} - 1} \cdot (q^{2k} + 1)$. For $k > 1$, both factors are integers and different from 1; therefore, the number $A$ is composite. It remains to verify that for $k = 1$, we get the prime number $A = q^{0} + q^{2} = 101$.
## Answer: 101.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let $x_{1}$ and $x_{2}$ be the largest roots of the polynomials $f(x)=1-x-4 x^{2}+x^{4}$ and $g(x)=16-8 x-$ $16 x^{2}+x^{4}$ respectively. Find $\frac{x_{2}}{x_{1}}$.
|
# Solution:
Notice that $f(-2)>0, f(-1)<0, f(0)>0, f(1)<0$. Therefore, the polynomial $f(x)$ has 4 real roots. Similarly, from the inequalities $g(-4)>0, g(-2)<0, g(0)>0, g(2)<0$, it follows that the polynomial $g(x)$ has 4 real roots.
Comparison of the coefficients of the polynomials
$$
f(x)=1-x-4 x^{2}+x^{4} \text { and } g(x)=16-8 x-16 x^{2}+x^{4}
$$
shows that, according to Vieta's formulas, the roots of the polynomial $g(x)$ are twice the roots of the polynomial $f(x)$. Hence, it follows that $\frac{x_{2}}{x_{1}}=2$.
## Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (3 points) Oleg usually arrives on a business trip by the 11 AM train. A car arrives at the station for this train. This time, the train arrived an hour earlier, and Oleg started walking towards the car. Meeting the car on the way, he got in, and as a result, arrived 10 minutes earlier than planned. Determine the time Oleg met the car.
|
1. 10 hours 55 minutes.
+ (3 points) - the solution is correct (by any method)
$+-(2$ points) - the solution is correct, but there are arithmetic errors
-+ (1 point) - there are reasonable ideas in solving the problem, but the problem is not solved overall
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $\mathrm{ABC}$, the sides $A B=4, B C=6$. Point $M$ lies on the perpendicular bisector of segment $A B$, and lines $A M$ and $A C$ are perpendicular. Find $M A$, if the radius of the circumscribed circle around triangle $A B C$ is 9.
|
Solution. Introduce a coordinate system with the origin at point A such that point C lies on the x-axis. From the problem statement, point M lies on the y-axis. Let's introduce notations for the unknown coordinates: $\mathrm{A}(0,0), \mathrm{B}\left(\mathrm{x}_{\mathrm{B}}, \mathrm{y}_{\mathrm{B}}\right), \mathrm{C}\left(\mathrm{x}_{\mathrm{C}}, 0\right), \mathrm{M}\left(0, \mathrm{y}_{\mathrm{M}}\right)$. Let $\mathrm{N}$ be the midpoint of $\mathrm{AB}$ and 0 be the center of the circumscribed circle, then $N\left(\frac{x_{B}}{2}, \frac{y_{B}}{2}\right)$ and $O\left(\frac{x_{C}}{2}, y_{0}\right)$. From the perpendicularity of vectors $\overrightarrow{\mathrm{AB}}$ and $\overrightarrow{\mathrm{MN}}$, it follows that $\mathrm{x}_{\mathrm{B}} \frac{\mathrm{x}_{\mathrm{B}}}{2}+\mathrm{y}_{\mathrm{B}}\left(\mathrm{y}_{\mathrm{M}}-\frac{\mathrm{y}_{\mathrm{B}}}{2}\right)=0$. From this, considering $\mathrm{AB}^{2}=\mathrm{x}_{\mathrm{B}}^{2}+\mathrm{y}_{\mathrm{B}}^{2}=16$, we get $\mathrm{y}_{\mathrm{M}}=\frac{8}{\mathrm{y}_{\mathrm{b}}}$. From the perpendicularity of vectors $\overrightarrow{\mathrm{AB}}$ and $\overrightarrow{\mathrm{MO}}$, it follows that $\mathrm{x}_{\mathrm{B}} \frac{\mathrm{x}_{C}}{2}+\mathrm{y}_{\mathrm{B}}\left(\mathrm{y}_{\mathrm{M}}-\mathrm{y}_{0}\right)=0$. Additionally, $\mathrm{BC}^{2}=\left(\mathrm{x}_{\mathrm{B}}-\mathrm{x}_{C}\right)^{2}+\mathrm{y}_{\mathrm{B}}^{2}=36$ and $\mathrm{AO}^{2}=\left(\frac{\mathrm{x}_{\mathrm{C}}}{2}\right)^{2}+\mathrm{y}_{0}^{2}=81$. These equations are sufficient to obtain $\mathrm{MA}=\left|\mathrm{y}_{\mathrm{M}}\right|=6$.
Answer: 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many solutions of the equation $x^{2}-2 x \cdot \sin (x \cdot y)+1=0$ fall within the circle $x^{2}+y^{2} \leq 100$?
|
Solution. We will interpret the left side of the equation as a quadratic trinomial in terms of $x$. For the roots to exist, the discriminant must be non-negative, i.e., $D=4 \sin ^{2}(x \cdot y)-4 \geq 0 \Leftrightarrow \sin ^{2}(x \cdot y)=1 \Leftrightarrow \cos 2 x y=-1 \Leftrightarrow x y=\frac{\pi}{2}+\pi n, n \in \mathbb{Z}$. For even $n$, we get the equation $x^{2}-2 x+1=0 \Leftrightarrow x=1$, and for odd $n$, we find $x=-1$. The left side of the equation is an even function of $x$, so for $x=1$ and $x=-1$, the corresponding values of $y$ will be the same. The solution has the form $(x, y)=\left( \pm 1, \frac{\pi}{2}+2 \pi k\right), k \in \mathbb{Z}$. Only 6 solutions fall within the circle $x^{2}+y^{2} \leq 100$.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (5 points) From point $A$, lying on a circle of radius 3, chords $A B, A C$ and tangent $A D$ are drawn. The angle between the chords is $\frac{\pi}{4}$, and the angle between chord $A C$ and tangent $A D$, which does not contain chord $A B$, is $\frac{5 \pi}{12}$. Calculate the integer area of triangle $A B C$.
#
|
# Solution:
Let $\angle D A C=\alpha, \angle B A C=\beta$, and the radius of the circle be $R$. It is known that $\angle A C B=\angle D A C=\alpha$.
By the Law of Sines, $\quad \frac{|A B|}{\sin \alpha}=\frac{|B C|}{\sin \beta}=2 R$. Therefore, $\quad|A B|=2 R \sin \alpha$, and $|B C|=2 R \sin \beta$.
$S_{\triangle A B C}=\frac{1}{2}|A B| \cdot|B C| \cdot \sin (\angle A B C)$.
Thus,
$S_{\triangle A B C}=2 R^{2} \sin \alpha \sin \beta \sin (\alpha+\beta)$
To calculate the area, we need to know the values of $\sin \alpha$ and $\sin (\alpha+\beta)$. We will compute these values under the conditions of the problem.
For this, we will calculate $\sin \alpha$ and $\cos \alpha$.
$$
\begin{aligned}
& \sin \alpha=\sin \frac{5 \pi}{12}=\sin \left(\frac{\pi}{2}-\frac{\pi}{12}\right)=\cos \frac{\pi}{12}=\sqrt{\frac{1}{2}\left(1+\cos \frac{\pi}{6}\right)}=\frac{1}{2} \sqrt{2+\sqrt{3}}=\frac{1+\sqrt{3}}{2 \sqrt{2}} \\
& \cos \alpha=\cos \frac{5 \pi}{12}=\cos \left(\frac{\pi}{2}-\frac{\pi}{12}\right)=\sin \frac{\pi}{12}=\sqrt{\frac{1}{2}\left(1-\cos \frac{\pi}{6}\right)}=\frac{1}{2} \sqrt{2-\sqrt{3}}=\frac{-1+\sqrt{3}}{2 \sqrt{2}} \\
& \sin (\alpha+\beta)=\sin \left(\frac{\pi}{4}+\frac{5 \pi}{12}\right)=\sin \frac{2 \pi}{3}=\frac{\sqrt{3}}{2}
\end{aligned}
$$
Substituting the obtained values into (2), it is not difficult to get that $S_{\triangle A B C}=\frac{9}{4}(3+\sqrt{3})$.
It remains to compute the answer.
Answer: 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (5 points) From point $A$, lying on a circle, chords $A B$, $A C$, and tangent $A D$ are drawn. The angle between the chords is $\frac{\pi}{6}$, and the angle between chord $A C$ and tangent $A D$, which does not contain chord $A B$, is $\frac{5 \pi}{12}$. Calculate the integer part of the radius of the circle if the area of triangle $A B C$ is 32.
|
# Solution:
Let $\angle D A C=\alpha, \angle B A C=\beta$, and the radius of the circle be $R$. It is known that $\angle A C B=\angle D A C=\alpha$.

By the Law of Sines, $\quad \frac{|A B|}{\sin \alpha}=\frac{|B C|}{\sin \beta}=2 R$. Therefore, $\quad|A B|=2 R \sin \alpha$, and $|B C|=2 R \sin \beta$. $S_{\square A B C}=\frac{1}{2}|A B| \cdot|B C| \cdot \sin (\angle A B C)$.
Thus, $S_{\triangle A B C}=2 R^{2} \sin \alpha \sin \beta \sin (\alpha+\beta)$.
$$
R=\sqrt{\frac{S_{\triangle A B C}}{2 \sin \alpha \sin \beta \sin (\alpha+\beta)}}
$$
To calculate the radius, we need to know the values of $\sin \alpha$ and $\sin (\alpha+\beta)$. We will compute these values under the conditions of the problem. First, we will calculate $\sin \alpha$ and $\cos \alpha$.
$$
\begin{aligned}
& \sin \alpha=\sin \frac{5 \pi}{12}=\sin \left(\frac{\pi}{2}-\frac{\pi}{12}\right)=\cos \frac{\pi}{12}=\sqrt{\frac{1}{2}\left(1+\cos \frac{\pi}{6}\right)}=\frac{1}{2} \sqrt{2+\sqrt{3}}=\frac{1+\sqrt{3}}{2 \sqrt{2}} \\
& \cos \alpha=\cos \frac{5 \pi}{12}=\cos \left(\frac{\pi}{2}-\frac{\pi}{12}\right)=\sin \frac{\pi}{12}=\sqrt{\frac{1}{2}\left(1-\cos \frac{\pi}{6}\right)}=\frac{1}{2} \sqrt{2-\sqrt{3}}=\frac{-1+\sqrt{3}}{2 \sqrt{2}} \\
& \sin (\alpha+\beta)=\sin \left(\frac{\pi}{6}+\frac{5 \pi}{12}\right)=\sin \left(\frac{7 \pi}{12}\right)=\sin \left(\frac{\pi}{2}+\frac{\pi}{12}\right)=\cos \frac{\pi}{12}=\frac{1+\sqrt{3}}{2 \sqrt{2}}
\end{aligned}
$$
Substituting the obtained values into (2), it is not difficult to get that $R=\frac{16}{1+\sqrt{3}}$. It remains to compute the answer.
Answer: 5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. In a triangle with sides $a, b, c$ and angles $\alpha, \beta, \gamma$, the equality $3 \alpha + 2 \beta = 180^{0}$ is satisfied. The sides $a, b, c$ lie opposite the angles $\alpha, \beta, \gamma$ respectively. Find the length of side $c$ when $a=2, b=3$.
|
Solution: From the condition, it follows that $c > b$. Let's find a point $D$ on the segment $AB$ such that $AC = AD$. Then the triangle $ACD$ is isosceles and $\angle ACD = \angle ADC = 90^\circ - \alpha / 2$. The angle $\angle ADC$ is the external angle of the triangle $CBD$. Therefore, $\angle BCD + \beta = \angle ADC = 90^\circ - \frac{\alpha}{2} = \alpha + \beta$. Hence, $\angle BCD = \alpha$, and the triangles $CDB$ and $ABC$ are similar. We have $\frac{BD}{BC} = \frac{BC}{AB}$ or $\frac{c - b}{a} = \frac{a}{c'}$, from which it follows that $a^2 + bc - c^2 = 0$. The quadratic equation $c^2 - 3c - 4 = 0$ has a unique positive root $c = 4$.
Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A circle touches the sides of an angle at points $A$ and $B$. A point $M$ is chosen on the circle. The distances from $M$ to the sides of the angle are 24 and 6. Find the distance from $M$ to the line $A B$.
|
Solution: $\angle \mathrm{XBM}=\angle \mathrm{ZAM}=\frac{1}{2} \overline{\mathrm{BM}}$, therefore, triangles ВМХ and ZAM are similar, so $\frac{\mathrm{XM}}{\mathrm{ZM}}=\frac{\mathrm{BM}}{\mathrm{AM}} \cdot \angle \mathrm{ABM}=\angle \mathrm{YAM}=\frac{1}{2} \overline{\mathrm{AM}}$, therefore, triangles $\mathrm{AMY}$ and $\mathrm{BMZ}$ are similar, so $\frac{\mathrm{YM}}{\mathrm{ZM}}=$ $\frac{\mathrm{AM}}{\mathrm{BM}} \cdot$ Therefore,
$$
\mathrm{ZM}^{2}=\mathrm{XM} \cdot \mathrm{YM}=24 \cdot 6=144, \quad \mathrm{ZM}=12
$$
Answer: 12
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Non-zero numbers $a$ and $b$ are roots of the quadratic equation $x^{2}-5 p x+2 p^{3}=0$. The equation $x^{2}-a x+b=0$ has a unique root. Find $p$.
|
Solution. Since the equation $x^{2}-a x+b=0$ has a unique root, then $b=\frac{a^{2}}{4}$. By Vieta's theorem, we have the equalities: $a+b=5 p ; a b=2 p^{3}$. Substituting $b=\frac{a^{2}}{4}$ into the last equality, we get: $a=2 p$. Considering that $a$ and $b$ are non-zero, we find $p=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the sides $B C$ and $C D$ of the square $A B C D$, points $E$ and $F$ are chosen such that the angle $E A F$ is $45^{\circ}$. The length of the side of the square is 1. Find the perimeter of triangle $C E F$.
|
Solution. If point $D$ is reflected across line $A F$, and then across line $A E$, it will transition to point $B$. Indeed, the composition of two axial symmetries relative to intersecting lines is a rotation by twice the angle between the lines. In our case, these two symmetries are equivalent to a $90^{\circ}$ rotation around point $A$.
This means that the image of point $D$ under the symmetry relative to $A F$ and the image of point $B$ under the symmetry relative to $A E$ are the same
point; on the diagram, it is denoted by $K$. From point $K$, segments $A E$ and $A F$ are seen at a $90^{\circ}$ angle (since angles are preserved under symmetry, for example, angles $A B E$ and $A K E$ are equal). Therefore, point $K$ is the foot of the perpendicular dropped from point $A$ to line $E F$.
Finally, since $B E = E K$ and $D F = F K$ (lengths of segments are preserved under symmetry), we see that the perimeter of triangle $C E F$ is equal to the sum of the lengths of sides $B C$ and $C D$ of the square.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (5 points) The sides of a parallelogram are 5 and 13, and the angle between them is $\arccos \frac{6}{13}$. Two mutually perpendicular lines divide this parallelogram into four equal-area quadrilaterals. Find the lengths of the segments into which these lines divide the sides of the parallelogram.
#
|
# Solution:
Let in parallelogram $ABCD$, $|AB| = |CD| = a$, $|AD| = |BC| = b$, $\angle BAC = \alpha = \arccos c$. Clearly, $\cos \alpha = c$, and $\cos (\pi - \alpha) = -c$.
Denote $|DN| = x$, $|LC| = y$.
By contradiction, it can be shown that the mutually perpendicular lines $MN$ and $KL$, specified in the problem, must pass through the intersection point of the diagonals of parallelogram $ABCD$. It is evident that $\square KON = \square LON$.
From this and the equality of areas, $S_{\text{KOND}} = S_{\text{LONC}}$, it follows that the areas coincide, $S_{\square KND} = S_{\square LNC}$. This fact implies the validity of the equality
$$
\frac{1}{2}(a-x) y \cdot \sin \alpha = \frac{1}{2}(b-y) x \cdot \sin (\pi - \alpha),
$$
from which the relation follows
$$
y = \frac{b}{a} x
$$
Based on the equality $|KN| = |LN|$ and the cosine theorem, we can write the equation
$$
(a-x)^2 + y^2 - 2(a-x) y \cdot \cos \alpha = (b-y)^2 + x^2 - 2(b-y) x \cdot \cos (\pi - \alpha)
$$
from which and from (1), in turn, follows the equation
$$
\frac{4 b c}{a} x^2 - \left(2a - \frac{2b^2}{a} + 4bc\right) x + a^2 - b^2 = 0
$$
For $a = 5$, $b = 13$, and $c = \frac{6}{13}$, the solutions to (2) are $x = -10$ and $x = 3$. The first is discarded for geometric reasons. The corresponding value of $y = \frac{39}{5}$.
Answer: 3 and $2, \frac{39}{5}$ and $\frac{26}{5}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) For a natural number $x$, five statements are made:
$$
3 x>91
$$
$$
\begin{aligned}
& x37 \\
& 2 x \geq 21 \\
& x>7
\end{aligned}
$$
It is known that only three of them are true, and two are false. Find $x$.
|
Solution. Let's transform the original system of inequalities
$$
\begin{aligned}
& x>\frac{91}{3} \\
& x \geq \frac{21}{2} \\
& x>\frac{37}{4} \\
& x>7 \\
& x<120
\end{aligned}
$$
The first inequality does not hold, since otherwise, four inequalities would be satisfied immediately. Therefore, $x \leq \frac{91}{3}$, and the fifth inequality is satisfied.
The second inequality also does not hold, since otherwise, four inequalities would be satisfied: the second, third, fourth, and fifth. Therefore, $x<\frac{21}{2}$.
Now it is immediately clear that the desired number $x=10$.
Answer: $x=10$
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A square table consists of 2014 rows and 2014 columns. In each cell at the intersection of the row with number $i$ and the column with number $j$, the number $a_{i, j}=(-1)^{i}(2015-i-j)^{2}$ is written. Find the sum of all the numbers in the table
|
Problem 3. Answer: $\mathbf{0 .}$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Eight numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $b_{1}, b_{2}, b_{3}, b_{4}$ satisfy the relations
$$
\left\{\begin{array}{l}
a_{1} b_{1}+a_{2} b_{3}=1 \\
a_{1} b_{2}+a_{2} b_{4}=0 \\
a_{3} b_{1}+a_{4} b_{3}=0 \\
a_{3} b_{2}+a_{4} b_{4}=1
\end{array}\right.
$$
It is known that $a_{2} b_{3}=7$. Find $a_{4} b_{4}$.
Interregional Olympiad for Schoolchildren based on Departmental Educational Organizations
|
Solution. We will prove that ${ }^{1}$
Multiply the equation (a) of the original system
$$
a_{2} b_{3}=a_{3} b_{2}
$$
$$
\begin{cases}a_{1} b_{1}+a_{2} b_{3}=1 & (\mathrm{a}) \\ a_{1} b_{2}+a_{2} b_{4}=0 & \text { (b) } \\ a_{3} b_{1}+a_{4} b_{3}=0 & \text { (c) } \\ a_{3} b_{2}+a_{4} b_{4}=1 & \text { (d) }\end{cases}
$$
by $b_{2}$ and subtract from it the equation (b), multiplied by $b_{1}$. As a result, we get
$$
a_{2} \cdot \Delta=b_{2}
$$
Here $\boldsymbol{\Delta}=\mathbf{b}_{\mathbf{2}} \boldsymbol{b}_{\mathbf{3}}-\boldsymbol{b}_{\mathbf{1}} \boldsymbol{b}_{\mathbf{4}}$. Similarly, from (c) and (d) we find that
$$
a_{3} \cdot \Delta=b_{3}
$$
Note that $\Delta \neq 0$, otherwise from (3) it would follow that $b_{3}=0$, and thus $a_{2} b_{3}=0$, which contradicts the condition of the problem. It remains to express $a_{2}$ and $a_{3}$ from (2) and (3) and substitute the obtained expressions into (1). The validity of the relation (1) will thereby be proven.
Further, from equation (d) and equality (1), it follows that $a_{4} b_{4}=1-a_{3} b_{2}=1-a_{2} b_{3}=-6$.
Answer: $a_{4} b_{4}=-6$.
Comment. ${ }^{1}$ The system of equations in the problem is the component-wise recording of the matrix equality $\mathbf{A} \cdot \mathbf{B}=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$, where $\mathbf{A}=\left(\begin{array}{ll}a_{1} & a_{2} \\ a_{3} & a_{4}\end{array}\right)$ and $\mathbf{B}=\left(\begin{array}{ll}b_{1} & b_{2} \\ b_{3} & b_{4}\end{array}\right)$. It is well known that if the product of two matrices is equal to the identity matrix, then such matrices commute, which means that the system of equations in the problem will remain valid if all $a_{i}$ are replaced by $b_{i}$ and vice versa. From this observation, equality (1) follows immediately.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (4 points) Find the area of a triangle if two of its medians are equal to $\frac{15}{7}$ and $\sqrt{21}$, and the cosine of the angle between them is $\frac{2}{5}$.
#
|
# Solution:
Let $|A D|=a$ and $|B E|=b$ be the medians of the triangle, and $\cos (\angle A O F)=c$.
It is known that the area
$$
\begin{aligned}
& S_{A O E}=\frac{1}{6} \cdot S_{A B C} \\
& S_{A O E}=\frac{1}{2} \cdot\left(\frac{2}{3} \cdot a\right) \cdot\left(\frac{1}{3} \cdot b\right) \cdot \sin (\angle A O F)
\end{aligned}
$$
or, equivalently,
$S_{A O E}=\frac{a b}{9} \sqrt{1-c^{2}}$.
Therefore, $S_{A B C}=\frac{2 a b}{3} \sqrt{1-c^{2}}$.
Substituting the specific values of the parameters, we get the answer.
Answer: 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (4 points) Find the area of a triangle if two of its medians are equal to 3 and $2 \sqrt{7}$, and the cosine of the angle between them is $-\frac{3}{4}$.
#
|
# Solution:
Let $|A D|=a$ and $|B E|=b$ be the medians of the triangle, and $\cos (\angle A O F)=c$.
It is known that the area
$$
\begin{aligned}
& S_{A O E}=\frac{1}{6} \cdot S_{A B C} \cdot \\
& S_{A O E}=\frac{1}{2} \cdot\left(\frac{2}{3} \cdot a\right) \cdot\left(\frac{1}{3} \cdot b\right) \cdot \sin (\angle A O F)
\end{aligned}
$$
or, equivalently,
$S_{A O E}=\frac{a b}{9} \sqrt{1-c^{2}}$.
Therefore, $S_{A B C}=\frac{2 a b}{3} \sqrt{1-c^{2}}$.
Substituting the specific values of the parameters, we get the answer.
Answer: 7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Eight numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $b_{1}, b_{2}, b_{3}, b_{4}$ satisfy the relations
$$
\left\{\begin{array}{l}
a_{1} b_{1}+a_{2} b_{3}=1 \\
a_{1} b_{2}+a_{2} b_{4}=0 \\
a_{3} b_{1}+a_{4} b_{3}=0 \\
a_{3} b_{2}+a_{4} b_{4}=1
\end{array}\right.
$$
It is known that $a_{2} b_{3}=7$. Find $a_{4} b_{4}$.
|
Solution. We will prove that ${ }^{1}$
$$
a_{2} b_{3}=a_{3} b_{2}
$$
Multiply equation (a) of the original system
$$
\begin{cases}a_{1} b_{1}+a_{2} b_{3}=1 & (\mathrm{a}) \\ a_{1} b_{2}+a_{2} b_{4}=0 & \text { (b) } \\ a_{3} b_{1}+a_{4} b_{3}=0 & \text { (c) } \\ a_{3} b_{2}+a_{4} b_{4}=1 & \text { (d) }\end{cases}
$$
by $b_{2}$ and subtract from it equation (b), multiplied by $b_{1}$. The result is
$$
a_{2} \cdot \Delta=b_{2}
$$
Here $\Delta=b_{2} b_{3}-b_{1} b_{4}$. Similarly, from (c) and (d) we find that
$$
a_{3} \cdot \Delta=b_{3}
$$
Note that $\Delta \neq 0$, otherwise from (3) it would follow that $b_{3}=0$, and thus $a_{2} b_{3}=0$, which contradicts the problem's condition. It remains to express $a_{2}$ and $a_{3}$ from (2) and (3) and substitute the obtained expressions into (1). The validity of relation (1) will thereby be proven.
Further, from equation (d) and equality (1), it follows that $a_{4} b_{4}=1-a_{3} b_{2}=1-a_{2} b_{3}=-6$.
Answer: $a_{4} b_{4}=-6$.
Comment. ${ }^{1}$ The system of equations in the problem is the component-wise recording of the matrix equality $\mathbf{A} \cdot \mathbf{B}=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)$, where $\mathbf{A}=\left(\begin{array}{ll}a_{1} & a_{2} \\ a_{3} & a_{4}\end{array}\right)$ and $\mathbf{B}=\left(\begin{array}{ll}b_{1} & b_{2} \\ b_{3} & b_{4}\end{array}\right)$. It is well known that if the product of two matrices is the identity matrix, then these matrices commute, which means the system of equations in the problem will remain valid if all $a_{i}$ are replaced by $b_{i}$ and vice versa. From this observation, equality (1) follows immediately.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the first day, $2^{n}$ schoolchildren played ping-pong in a "knockout" format: first, two played, then the winner played with the third, the winner of this pair played with the fourth, and so on until the last schoolchild (there are no draws in ping-pong). On the second day, the same schoolchildren played for the cup: first, they arbitrarily split into pairs and played, the losers were eliminated, and the winners again arbitrarily split into pairs and played, and so on. It turned out that the sets of pairs that played on the first and second days were the same (possibly with different winners). Find the largest possible value of $n$.
B. Frenkin
|
Answer: 3.
Solution. Let's construct the following graph: vertices are players, edges are played matches. According to the condition, for both tournaments, this graph is the same. Consider the first tournament and select the matches where the winners had not won before (for example, the first match). Then the corresponding edges form a path, and the other edges are connected to this path by one end. In particular, if we remove all pendant vertices, only our path without the end vertices will remain.
Now consider the same graph as the graph of the cup tournament. If we remove the pendant vertices from it, a graph of the tournament on $2^{n-1}$ winners of the first stage will remain. It is obviously a path only for $n \leq 3$, otherwise, the tournament winner will have a degree of at least 3. Therefore, $n \leq 3$.
It remains to provide an example for $n=3$. Let the participants be numbered from 1 to 8 and the pairs in the cup be as follows (the loser is indicated first, the winner second): $1-2,3-4,5-6,7-8,2-4,6-8$, 4-8. Then in the knockout stage, the pairs could have been as follows (the winner is again indicated second): $1-2$, $2-4,3-4,4-8,7-8,8-6,6-5$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [8] The three medians of a triangle divide its angle into six angles, of which exactly $k$ are greater than $30^{\circ}$. What is the greatest possible value of $k$?
(N. Sedrakyan)
|
Answer. $k=3$.
Evaluation. First method. Let $h_{1} \leq h_{2} \leq h_{3}$ be the heights of the triangle, and $m_{1}, m_{2}, m_{3}$ be the medians from the corresponding vertices (in fact, $m_{1} \leq m_{2} \leq m_{3}$, but this will not be used). Then we have $m_{3} \geq h_{i}$ for $i=1,2$, 3. Dropping perpendiculars from the end of $m_{3}$ to the adjacent sides, each of them equals half of the corresponding height and, therefore, is not greater than $m_{3} / 2$. Thus, the angles adjacent to $m_{3}$ are not greater than $30^{\circ}$. Similarly, one of the angles at $m_{2}$ is not greater than $30^{\circ}$.
Second method. Let there be a triangle $A B C$ with medians $A X, B Y, C Z$. Both angles $B A X$ and $B C Z$ cannot be greater than $30^{\circ}$: otherwise, points $A$ and $C$ lie inside a circle with chord $Z X$ and a diameter twice as large as $Z X$, but then $A C=2 Z X$, meaning a segment equal to the diameter lies strictly inside the circle - a contradiction. Similarly, in each of the other two pairs, at most one angle is greater than $30^{\circ}$.
Example 1. Consider first a triangle $A B C$ where $\angle C=90^{\circ}, \angle A=30^{\circ}$. Let $B K$ and $C L$ be its medians. Then $\angle A C L=30^{\circ}, \angle B C L=60^{\circ}, \angle C B K>30^{\circ}$ (since the angle bisector of angle $B$ lies between the leg and the median). Now slightly decrease the leg $A C$. In this case, the angle $A C L$ will slightly increase (i.e., become greater than $30^{\circ}$), while the angles $B C L$ and $C B K$ will slightly decrease but remain greater than $30^{\circ}$.
Example 2. Consider a right triangle with legs 4 and 6 (see figure). We have $\operatorname{tg} 30^{\circ}<\operatorname{tg} \alpha<\operatorname{tg} \beta<\operatorname{tg} \gamma$, since $\frac{1}{\sqrt{3}}<\frac{2}{3}<\frac{3}{4}<\frac{3}{2}$.

|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2.
In a table consisting of $n$ rows and $m$ columns, numbers (not necessarily integers) were written such that the sum of the elements in each row is 408, and the sum of the elements in each column is 340. After that, $k$ columns were added to the table, the sum of the elements in each of which is 476, and a column, the sum of the elements in which is 272. The resulting table has a sum of elements in each row equal to 544. Find the numbers $n, m$, and $k$ for which the expression $2n - 3m + 6k$ takes the smallest possible natural value. For the found parameters $n, m$, and $k$, provide an example of the specified table.
|
Answer: 4 when $n=65, m=78, k=18$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. The director of an aluminum plant wants the advertisement of his plant, which lasts 1 min. 30 sec., to be shown exactly every 18 min. 30 sec. after the end of the previous advertising break. How much time will the advertisement of the aluminum plant be shown in a week?
a) 12 h.
b) 12 h. 12 min.
c) 12 h. 24 min.
d) 12 h. 36 min.
e) 12 h. 48 min.
|
12. answer: g. In a week, there are $7 \cdot 24=168$ hours. For every hour, advertisements are shown for $1.5 \cdot 3=4.5$ minutes. Therefore, in a week, advertisements make up $4.5 \cdot 168=756=12$ hours and 36 minutes of airtime. In a week, there are $7 \cdot 24=168$ hours. For every hour, advertisements are shown for $1.5 \cdot 3=4.5$ minutes. Therefore, in a week, advertisements make up $4.5 \cdot 168=756=12$ hours and 36 minutes of airtime.
|
12
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
16. At the quiz in the Museum of Entertaining Sciences of SFU, 10 schoolchildren are participating. In each round, the students are divided into pairs. Each participant meets every other participant exactly once. A win in a match earns 1 point, a draw earns 0.5 points, and a loss earns 0 points. What is the minimum number of rounds after which an early winner can appear?
## Answers and solutions:
## Translation of the question and answers into English:
16. At the quiz in the Museum of Entertaining Sciences of SFU, 10 schoolchildren are participating. In each round, the students are divided into pairs. Each participant meets every other participant exactly once. A win in a match earns 1 point, a draw earns 0.5 points, and a loss earns 0 points. What is the minimum number of rounds after which an early winner can appear?
## Answers and solutions:
|
16. 7. Evaluation. After the sixth round, 30 points have been played, and the leader has no more than 6 points, while the other nine participants have collectively scored no less than 24 points. Therefore, among them, there is at least one participant with more than three points. Since there are still 3 rounds ahead, the winner is still unknown.
Example. Suppose in the first 7 rounds, the leader won all their matches, and all other matches ended in draws. Then two students who have not yet faced the leader have 3.5 points each, while the others have 3 points each. Since only 2 rounds remain until the end of the tournament, the winner is already determined.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Young researcher Petya noticed that the iron at home heats up by $9^{\circ} \mathrm{C}$ every 20 seconds, and after being turned off, it cools down by $15^{\circ} \mathrm{C}$ every 30 seconds. Last evening, after turning off the iron, it cooled down for exactly 3 minutes. How long was the iron turned on?
a) 3 min 20 sec
b) 3 min 40 sec
c) 3 min
d) 4 min
e) 5 min
|
8. answer: a. 3 minutes $=180$ seconds. In 180 seconds, the iron cools down by $180 / 30 \cdot 15=90$ degrees. To heat up by 90 degrees, the iron takes $90 / 9 \cdot 20=200$ seconds. 200 seconds $=3$ minutes 20 seconds.
|
3
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
12. The security guard of the aluminum plant works on Tuesdays, Fridays, and on odd-numbered days. What is the maximum number of consecutive days the security guard can work?
a) 3
b) 4
c) 5
d) 6
e) 7
|
12. answer: g. 6 days. An example of such a situation: 29th (odd), 30th (Tuesday), 31st (odd), 1st (odd), 2nd (Friday), 3rd (odd).
|
6
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
16. A worker at an aluminum plant can produce 16 blanks or 10 parts from blanks in one shift. It is known that exactly one part is made from each blank. What is the maximum number of blanks the worker can produce in one shift to make parts from them in the same shift?
|
16. 6. Let's denote by $x$ the duration of the worker's working day in hours. Then the worker makes one part from a blank in $\frac{x}{10}$ hours, one blank in $\frac{x}{16}$ hours, and a blank and a part from it in $\frac{x}{10}+\frac{x}{16}=\frac{13 x}{80}$ hours. Since $x: \frac{13 x}{80}=6 \frac{2}{13}$, the maximum number of blanks that the worker can make in a day so that parts can be made from all of them on the same day is 6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. What is greater: 1 or $\frac{21}{64}+\frac{51}{154}+\frac{71}{214} ?$
|
Answer: One is greater.
## First solution.
$$
\frac{21}{64}+\frac{51}{154}+\frac{71}{214}<\frac{21}{63}+\frac{51}{153}+\frac{71}{213}=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1
$$
## Second solution.
$$
\begin{aligned}
\frac{21}{64}+\frac{51}{154}+\frac{71}{214} & =\frac{21 \cdot 154 \cdot 214+64 \cdot 51 \cdot 214+64 \cdot 154 \cdot 71}{64 \cdot 154 \cdot 214}= \\
& =\frac{692076+698496+699776}{2109184}=\frac{2090348}{2109184}\left[=\frac{522587}{527296}\right]<1 .
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.