problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 2. In a football tournament, seven teams played: each team played once with each other. In the next round, teams that scored thirteen or more points qualify. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round?
|
Answer: 4.
Solution. In total, the teams played $\frac{7 \cdot 6}{2}=21$ games, each of which awarded 2 or 3 points. Therefore, the maximum total number of points that all teams can have is $21 \cdot 3=63$. Hence, the number of teams $n$ advancing to the next stage satisfies the inequality $n \cdot 13 \leqslant 63$, from which $n \leqslant 4$.
On the other hand, an example of a tournament table can be provided where 4 teams advance to the next round:
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | $\mathrm{X}$ | 0 | 1 | 3 | 3 | 3 | 3 | 13 |
| 2 | 3 | $\mathrm{X}$ | 0 | 1 | 3 | 3 | 3 | 13 |
| 3 | 1 | 3 | $\mathrm{X}$ | 0 | 3 | 3 | 3 | 13 |
| 4 | 0 | 1 | 3 | $\mathrm{X}$ | 3 | 3 | 3 | 13 |
| 5 | 0 | 0 | 0 | 0 | $\mathrm{X}$ | 1 | 1 | 2 |
| 6 | 0 | 0 | 0 | 0 | 1 | $\mathrm{X}$ | 1 | 2 |
| 7 | 0 | 0 | 0 | 0 | 1 | 1 | $\mathrm{X}$ | 2 |
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. For what least natural $k$ is the expression $2017 \cdot 2018 \cdot 2019 \cdot 2020+k$ a square of a natural number?
|
Answer: 1.
Solution. We will prove that $k=1$ already works. Let $n=2018$, then for $k=1$ the expression from the condition equals
$$
\begin{aligned}
(n-1) n(n+1)(n+2)+1 & =(n-1)(n+2) \cdot n(n+1)+1=\left(n^{2}+n-2\right)\left(n^{2}+n\right)+1= \\
& =\left(\left(n^{2}+n-1\right)-1\right)\left(\left(n^{2}+n-1\right)+1\right)+1=\left(n^{2}+n-1\right)^{2}
\end{aligned}
$$
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a football tournament, seven teams played: each team played once with each other. In the next round, teams that scored twelve or more points qualify. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round?
|
Answer: 5.
Solution. In total, the teams played $\frac{7 \cdot 6}{2}=21$ games, each of which awarded 2 or 3 points. Therefore, the maximum total number of points that all teams can have is $21 \cdot 3=63$. Hence, the number of teams $n$ advancing to the next stage satisfies the inequality $n \cdot 12 \leqslant 63$, from which $n \leqslant 5$.
On the other hand, an example of a tournament table can be provided where 5 teams advance to the next round:
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | $\mathrm{X}$ | 0 | 0 | 3 | 3 | 3 | 3 | 12 |
| 2 | 3 | $\mathrm{X}$ | 0 | 0 | 3 | 3 | 3 | 12 |
| 3 | 3 | 3 | $\mathrm{X}$ | 0 | 0 | 3 | 3 | 12 |
| 4 | 0 | 3 | 3 | $\mathrm{X}$ | 0 | 3 | 3 | 12 |
| 5 | 0 | 0 | 3 | 3 | $\mathrm{X}$ | 3 | 3 | 12 |
| 6 | 0 | 0 | 0 | 0 | 0 | $\mathrm{X}$ | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | $\mathrm{X}$ | 1 |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. For what least natural $k$ is the expression $2019 \cdot 2020 \cdot 2021 \cdot 2022 + k$ a square of a natural number?
|
Answer: 1.
Solution. We will prove that $k=1$ already works. Let $n=2020$, then for $k=1$ the expression from the condition equals
$$
\begin{aligned}
(n-1) n(n+1)(n+2)+1 & =(n-1)(n+2) \cdot n(n+1)+1=\left(n^{2}+n-2\right)\left(n^{2}+n\right)+1= \\
& =\left(\left(n^{2}+n-1\right)-1\right)\left(\left(n^{2}+n-1\right)+1\right)+1=\left(n^{2}+n-1\right)^{2}
\end{aligned}
$$
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. What is greater: 1 or $\frac{23}{93}+\frac{41}{165}+\frac{71}{143}$?
|
Answer: One is greater.
## First solution.
$$
\frac{23}{93}+\frac{41}{165}+\frac{71}{143}<\frac{23}{92}+\frac{41}{164}+\frac{71}{142}=\frac{1}{4}+\frac{1}{4}+\frac{1}{2}=1 .
$$
## Second solution.
$$
\begin{aligned}
\frac{23}{93}+\frac{41}{165}+\frac{71}{143} & =\frac{23 \cdot 165 \cdot 143+93 \cdot 41 \cdot 143+93 \cdot 165 \cdot 71}{93 \cdot 165 \cdot 143}= \\
& =\frac{542685+545259+1089495}{2194335}=\frac{2177439}{2194335}\left[=\frac{65983}{66495}\right]<1
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a football tournament, eight teams played: each team played once with each other. In the next round, teams that scored fifteen or more points qualify. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round?
|
Answer: 5.
Solution. In total, the teams played $\frac{8 \cdot 7}{2}=28$ games, in each of which 2 or 3 points were at stake. Therefore, the maximum total number of points that all teams can have is $28 \cdot 3=84$. Hence, the number of teams $n$ that advance to the next stage satisfies the inequality $n \cdot 15 \leqslant 84$, from which $n \leqslant 5$.
On the other hand, an example of a tournament table can be provided in which 5 teams qualify for the next round:
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Sum |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | $\mathrm{X}$ | 0 | 0 | 3 | 3 | 3 | 3 | 3 | 15 |
| 2 | 3 | $\mathrm{X}$ | 0 | 0 | 3 | 3 | 3 | 3 | 15 |
| 3 | 3 | 3 | $\mathrm{X}$ | 0 | 0 | 3 | 3 | 3 | 15 |
| 4 | 0 | 3 | 3 | $\mathrm{X}$ | 0 | 3 | 3 | 3 | 15 |
| 5 | 0 | 0 | 3 | 3 | $\mathrm{X}$ | 3 | 3 | 3 | 15 |
| 6 | 0 | 0 | 0 | 0 | 0 | $\mathrm{X}$ | 1 | 1 | 2 |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | $\mathrm{X}$ | 1 | 2 |
| 8 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | $\mathrm{X}$ | 2 |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. For what least natural $k$ is the expression $2018 \cdot 2019 \cdot 2020 \cdot 2021+k$ a square of a natural number
|
Answer: 1.
Solution. We will prove that $k=1$ already works. Let $n=2019$, then for $k=1$ the expression from the condition equals
$$
\begin{aligned}
(n-1) n(n+1)(n+2)+1 & =(n-1)(n+2) \cdot n(n+1)+1=\left(n^{2}+n-2\right)\left(n^{2}+n\right)+1= \\
& =\left(\left(n^{2}+n-1\right)-1\right)\left(\left(n^{2}+n-1\right)+1\right)+1=\left(n^{2}+n-1\right)^{2}
\end{aligned}
$$
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a football tournament, six teams played: each team played once with each other. In the next round, teams that scored twelve or more points qualify. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round?
|
Answer: 3
Solution. In total, the teams played $\frac{6 \cdot 5}{2}=15$ games, each of which awarded 2 or 3 points. Therefore, the maximum total number of points that all teams can have is $15 \cdot 3=45$. Hence, the number of teams $n$ that advance to the next stage satisfies the inequality $n \cdot 12 \leqslant 45$, from which $n \leqslant 3$.
On the other hand, an example of a tournament table can be provided where 3 teams advance to the next round:
| | 1 | 2 | 3 | 4 | 5 | 6 | Sum |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | $\mathrm{X}$ | 0 | 3 | 3 | 3 | 3 | 12 |
| 2 | 3 | $\mathrm{X}$ | 0 | 3 | 3 | 3 | 12 |
| 3 | 0 | 3 | $\mathrm{X}$ | 3 | 3 | 3 | 12 |
| 4 | 0 | 0 | 0 | $\mathrm{X}$ | 1 | 1 | 2 |
| 5 | 0 | 0 | 0 | 1 | $\mathrm{X}$ | 1 | 2 |
| 6 | 0 | 0 | 0 | 1 | 1 | $\mathrm{X}$ | 2 |
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. For what least natural $k$ is the expression $2016 \cdot 2017 \cdot 2018 \cdot 2019 + k$ a square of a natural number?
|
Answer: 1.
Solution. We will prove that $k=1$ already works. Let $n=2017$, then for $k=1$ the expression from the condition equals
$$
\begin{aligned}
(n-1) n(n+1)(n+2)+1 & =(n-1)(n+2) \cdot n(n+1)+1=\left(n^{2}+n-2\right)\left(n^{2}+n\right)+1= \\
& =\left(\left(n^{2}+n-1\right)-1\right)\left(\left(n^{2}+n-1\right)+1\right)+1=\left(n^{2}+n-1\right)^{2}
\end{aligned}
$$
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. In the surgical department, there are 4 operating rooms: I, II, III, and IV. In the morning, they were all empty. At some point, an operation began in operating room I, then after some time in operating room II, then after some more time in operating room III, and finally in operating room IV.
All four operations ended simultaneously, and the total duration of all operations was 2 hours and 32 minutes. Thirty minutes before the completion of all operations, the total duration of the ongoing operations was 52 minutes, and ten minutes before that, it was 30 minutes. Which operating rooms' operation durations can be determined from these data, and which cannot?
|
Answer: Only the duration of the operation in Operating Room IV can be determined.
Solution. First, let's prove that the durations of the operations in Operating Rooms I, II, and III cannot be determined uniquely. Indeed, it is not difficult to verify that if the durations of the operations are 70, 39, 33, 10 or 56, 54, 32, 10 minutes, then all conditions of the problem are satisfied. However, in these two variants, the durations of the operations in Operating Rooms I, II, and III are different.
Now let's prove that the duration of the operation in Operating Room IV can be uniquely restored. For this, let's note that the total duration of the operations 40 and 30 minutes before the end of the operations increased by 22 minutes. This means that 30 minutes before the end of the operations, the operations in Operating Rooms I, II, and III were already in progress, otherwise, the total duration would have increased by no more than 20 minutes. Then, by the end of all operations, their total duration is $52 + 30 \cdot 3 = 142$ minutes. Therefore, the operation in Operating Room IV lasted $152 - 142 = 10$ minutes.
Comment. The durations of the operations can be (in minutes) $(70; 36+s; 36-s; 10)$, where $s \in [0; 4]$ or $(55+t; 55-t; 32; 10)$, where $t \in [0; 15]$.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what greatest value of the parameter $a$ will the coefficient of $x^{4}$ in the expansion of the polynomial $\left(1-2 x+a x^{2}\right)^{8}$ be equal to -1540?
|
Answer: -5.
Solution. Applying the polynomial formula, we get
$$
\left(1-2 x+a x^{2}\right)^{8}=\sum_{n_{1}+n_{2}+n_{3}=8} \frac{8!}{n_{1}!\cdot n_{2}!\cdot n_{3}!} \cdot 1^{n_{1}} \cdot(-2 x)^{n_{2}} \cdot\left(a x^{2}\right)^{n_{3}}=\sum_{n_{1}+n_{2}+n_{3}=8} \frac{8!}{n_{1}!\cdot n_{2}!\cdot n_{3}!} \cdot(-2)^{n_{2}} \cdot a^{n_{3}} \cdot x^{n_{2}+2 n_{3}}
$$
To determine which terms in the sum contain $x^{4}$, we need to solve the system of equations in non-negative integers:
$$
\left\{\begin{array}{l}
n_{1}+n_{2}+n_{3}=8 \\
n_{2}+2 n_{3}=4
\end{array}\right.
$$
From the second equation, it follows that $n_{2}$ is even. Due to the non-negativity of the variables, $n_{2}$ can take the values 0, 2, and 4. Solving the system for each of these $n_{2}$, we will have three cases:
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what greatest value of the parameter $a$ will the coefficient of $x^{4}$ in the expansion of the polynomial $\left(1-3 x+a x^{2}\right)^{8}$ be equal to $70$?
|
Answer: -4.
Solution. Applying the polynomial formula, we get
$$
\left(1-3 x+a x^{2}\right)^{8}=\sum_{n_{1}+n_{2}+n_{3}=8} \frac{8!}{n_{1}!\cdot n_{2}!\cdot n_{3}!} \cdot 1^{n_{1}} \cdot(-3 x)^{n_{2}} \cdot\left(a x^{2}\right)^{n_{3}}=\sum_{n_{1}+n_{2}+n_{3}=8} \frac{8!}{n_{1}!\cdot n_{2}!\cdot n_{3}!} \cdot(-3)^{n_{2}} \cdot a^{n_{3}} \cdot x^{n_{2}+2 n_{3}}
$$
To determine which terms in the sum contain $x^{4}$, we need to solve the system of equations in non-negative integers:
$$
\left\{\begin{array}{l}
n_{1}+n_{2}+n_{3}=8 \\
n_{2}+2 n_{3}=4
\end{array}\right.
$$
From the second equation, it follows that $n_{2}$ is even. Due to the non-negativity of the variables, $n_{2}$ can take the values 0, 2, and 4. Solving the system for each of these $n_{2}$, we will have three cases:
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (Option 1) The decimal representation of the natural number $n$ contains sixty-three digits. Among these digits, there are twos, threes, and fours. No other digits are present. The number of twos is 22 more than the number of fours. Find the remainder when $n$ is divided by 9.
|
# Answer. 5.
(Option 2) The decimal representation of a natural number $n$ contains sixty-one digits. Among these digits, there are threes, fours, and fives. No other digits are present. The number of threes is 11 more than the number of fives. Find the remainder when $n$ is divided by 9.
Answer. 8.
Criteria. "干" The correct answer is obtained by considering a specific case.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. For what values of the parameter $a$ does the equation
$$
3^{x^{2}-2 a x+a^{2}}=a x^{2}-2 a^{2} x+a^{3}+a^{2}-4 a+4
$$
have exactly one solution?
|
Answer: Only when $a=1$.
Solution. Let's denote $x-a$ by $t$. Note that the number of solutions of the equation does not change with such a substitution. Then the original equation will take the form
$$
3^{t^{2}}=a t^{2}+a^{2}-4 a+4.
$$
Notice that the expressions on both sides do not change when $t$ is replaced by $-t$, so the equation can have an odd number of solutions (in particular, exactly one solution) only if $t=0$ is its root:
$$
3^{0}=a \cdot 0+a^{2}-4 a+4
$$
i.e., $a^{2}-4 a+3=0$, from which $a=3$ or $a=1$. Thus, besides these two numbers, no other values of the parameter $a$ can satisfy the condition.
Let $a=1$. Then the equation will take the form $3^{t^{2}}=t^{2}+1$. Note that $3^{x}>x \ln 3+1$ for $x>0$ (which can be proven, for example, by taking the derivatives of both sides). Then for $t \neq 0$ we get $3^{t^{2}}>t^{2} \ln 3+1>t^{2}+1$. Therefore, when $a=1$, the equation has a unique solution.
Let $a=3$. Then the equation will take the form $3^{t^{2}}=3 t^{2}+1$. Note that $3^{1}=3,3 \cdot 1+1=4$, but $3^{2^{2}}=81$, $3 \cdot 2^{2}+1=13$, i.e., at $t=1$ the left side is less than the right, and at $t=2$ the opposite is true. Therefore, by the intermediate value theorem, the equation has at least one more root in the interval $(1,2)$. Therefore, $a=3$ does not satisfy the condition.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10. Points $M, N$, and $K$ are located on the lateral edges $A A_{1}, B B_{1}$, and $C C_{1}$ of the triangular prism $A B C A_{1} B_{1} C_{1}$ such that $A M: A A_{1}=1: 2, B N: B B_{1}=1: 3, C K: C C_{1}=1: 4$. Point $P$ belongs to the prism. Find the maximum possible value of the volume of the pyramid $M N K P$, if the volume of the prism is 16.
|
Answer: 4.
Solution. Suppose we have found the position of point $P$ such that the volume of pyramid $M N K P$ is maximized. Draw a plane $\alpha$ through it, parallel to the plane $M N K$, and call $M_{1}, N_{1}$, and $K_{1}$ the points of intersection of this plane with the edges $A A_{1}, B B_{1}$, and $C C_{1}$, respectively. Note that
$V_{M N K P}=\frac{1}{3} V_{M N K M_{1} N_{1} K_{1}}$. Draw planes $\beta$ and $\beta_{1}$ through points $M$ and $M_{1}$, parallel to the plane $A B C$, and call $R$ and $R_{1}$ the points of intersection with edge $B B_{1}$, and $S$ and $S_{1}$ with edge $C C_{1}$. Note that the figures $M N K R S$ and $M_{1} N_{1} K_{1} R_{1} S_{1}$ are obtained from each other by a parallel translation, and thus are equal, and their volumes are also equal. Therefore, the volumes of prisms $M N K M_{1} N_{1} K_{1}$ and $M R S M_{1} R_{1} S_{1}$ are also equal. But $V_{M R S M_{1} R_{1} S_{1}}=\frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$, from which we get that $V_{M N K P}=\frac{1}{3} \frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$.
We need to find the position of plane $\alpha$ such that $M M_{1}$ is maximized. Note that at least one of the points $M_{1}, N_{1}, K_{1}$ lies within the original prism, from which $M M_{1}=N N_{1}=K K_{1} \leq \max \left\{A M, A_{1} M, B N, B_{1} N, C K, C_{1} K\right\}$. Substituting the given ratios in the problem, we finally get that $M M_{1}=N N_{1}=K K_{1}=C_{1} K=\frac{3}{4} C C_{1}$, from which $V_{M N K P}=\frac{1}{3} \frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}=\frac{1}{3} \frac{3}{4} 16=4$.
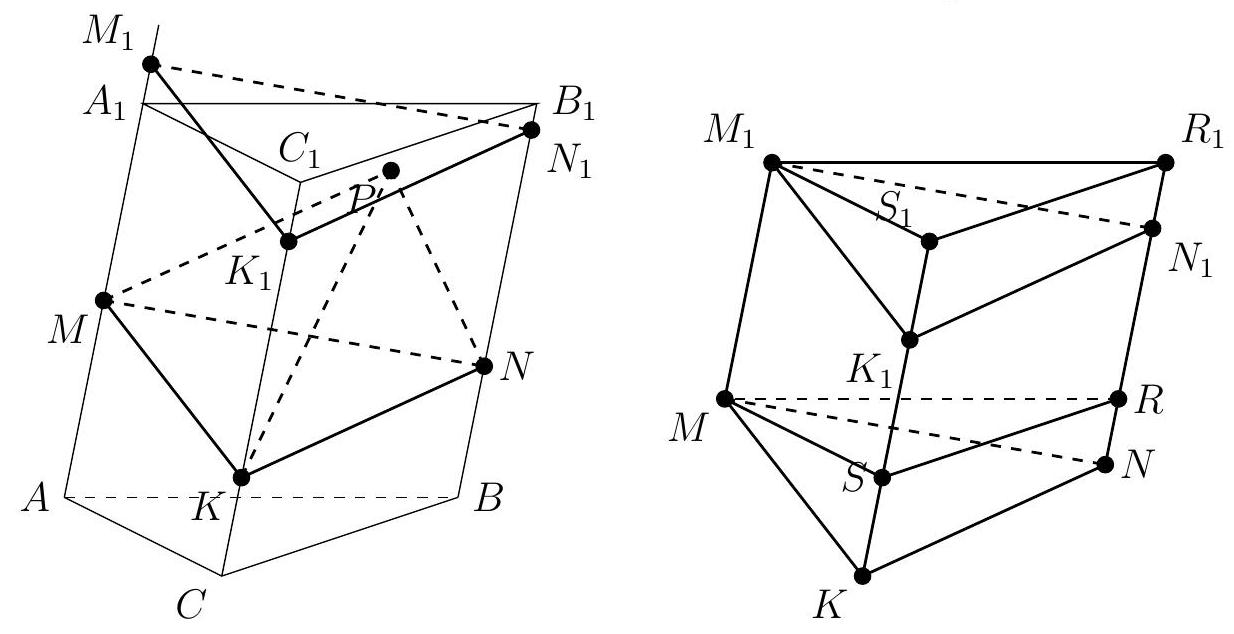
## Variant II
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. For what values of the parameter $a$ does the equation
$$
3^{x^{2}+6 a x+9 a^{2}}=a x^{2}+6 a^{2} x+9 a^{3}+a^{2}-4 a+4
$$
have exactly one solution?
|
Answer: Only when $a=1$.
Solution. Let's denote $x+3a$ by $t$. Note that the number of solutions to the equation does not change with this substitution. Then the original equation will take the form
$$
3^{t^{2}}=a t^{2}+a^{2}-4 a+4
$$
Notice that the expressions on both sides do not change when $t$ is replaced by $-t$, so the equation can have an odd number of solutions (in particular, exactly one solution) only if $t=0$ is a root:
$$
3^{0}=a \cdot 0+a^{2}-4 a+4
$$
i.e., $a^{2}-4 a+3=0$, from which $a=3$ or $a=1$. Thus, besides these two numbers, no other values of the parameter $a$ can satisfy the condition.
Let $a=1$. Then the equation will take the form $3^{t^{2}}=t^{2}+1$. Note that $3^{x}>x \ln 3+1$ for $x>0$ (which can be proven, for example, by taking the derivatives of both sides). Then for $t \neq 0$ we get $3^{t^{2}}>t^{2} \ln 3+1>t^{2}+1$. Therefore, when $a=1$, the equation has a unique solution.
Let $a=3$. Then the equation will take the form $3^{t^{2}}=3 t^{2}+1$. Note that $3^{1}=3, 3 \cdot 1+1=4$, but $3^{2^{2}}=81$, $3 \cdot 2^{2}+1=13$, i.e., at $t=1$ the left side is less than the right, and at $t=2$ the opposite is true. Therefore, by the intermediate value theorem, the equation has at least one more root in the interval $(1,2)$. Therefore, $a=3$ does not satisfy the condition.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10. Points $M, N$, and $K$ are located on the lateral edges $A A_{1}, B B_{1}$, and $C C_{1}$ of the triangular prism $A B C A_{1} B_{1} C_{1}$ such that $A M: A A_{1}=2: 3, B N: B B_{1}=3: 5, C K: C C_{1}=4: 7$. Point $P$ belongs to the prism. Find the maximum possible value of the volume of the pyramid $M N K P$, if the volume of the prism is 27.
|
# Answer: 6.
Solution. Suppose we have found the position of point $P$ such that the volume of pyramid $M N K P$ is maximized. Draw a plane $\alpha$ through it, parallel to the plane $M N K$, and call $M_{1}, N_{1}$, and $K_{1}$ the points of intersection of this plane with the edges $A A_{1}, B B_{1}$, and $C C_{1}$, respectively. Note that $V_{M N K P}=\frac{1}{3} V_{M N K M_{1} N_{1} K_{1}}$. Draw planes $\beta$ and $\beta_{1}$ through points $M$ and $M_{1}$, parallel to the plane $A B C$, and call $R$ and $R_{1}$ the points of intersection with edge $B B_{1}$, and $S$ and $S_{1}$ with edge $C C_{1}$. Note that the figures $M N K R S$ and $M_{1} N_{1} K_{1} R_{1} S_{1}$ are obtained from each other by a parallel translation, and thus are equal, and their volumes are also equal. Therefore, the volumes of prisms $M N K M_{1} N_{1} K_{1}$ and $M R S M_{1} R_{1} S_{1}$ are also equal. But $V_{M R S M_{1} R_{1} S_{1}}=\frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$, from which we get that $V_{M N K P}=\frac{1}{3} \frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$.
We need to find the position of plane $\alpha$ such that $M M_{1}$ is maximized. Note that at least one of the points $M_{1}, N_{1}, K_{1}$ lies within the original prism, from which $M M_{1}=N N_{1}=K K_{1} \leq \max \left\{A M, A_{1} M, B N, B_{1} N, C K, C_{1} K\right\}$. Substituting the given ratios in the problem, we finally get that $M M_{1}=N N_{1}=K K_{1}=A M=\frac{2}{3} A A_{1}$, from which $V_{M N K P}=\frac{1}{3} \frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}=\frac{12}{3} \frac{2}{3} 27=6$.
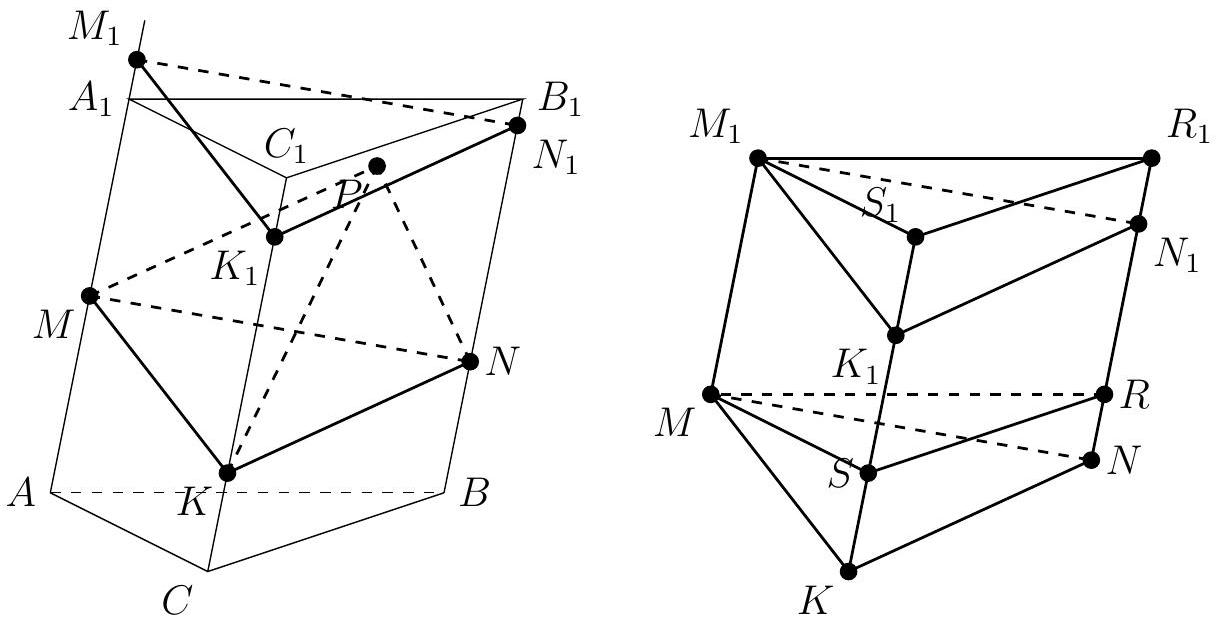
## Variant III
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 8. For what values of the parameter $a$ does the equation
$$
5^{x^{2}-6 a x+9 a^{2}}=a x^{2}-6 a^{2} x+9 a^{3}+a^{2}-6 a+6
$$
have exactly one solution?
|
Answer: Only when $a=1$.
Solution. Let's denote $x-3a$ by $t$. Note that the number of solutions to the equation does not change with this substitution. Then the original equation will take the form
$$
5^{t^{2}}=a t^{2}+a^{2}-6a+6
$$
Notice that the expressions on both sides do not change when $t$ is replaced by $-t$, so the equation can have an odd number of solutions (in particular, exactly one solution) only if $t=0$ is a root:
$$
5^{0}=a \cdot 0+a^{2}-6a+6
$$
i.e., $a^{2}-6a+5=0$, from which $a=5$ or $a=1$. Thus, besides these two numbers, no other values of the parameter $a$ can satisfy the condition.
Let $a=1$. Then the equation will take the form $5^{t^{2}}=t^{2}+1$. Note that $5^{x}>x \ln 5+1$ for $x>0$ (which can be proven, for example, by taking the derivatives of both sides). Then for $t \neq 0$ we get $5^{t^{2}}>t^{2} \ln 5+1>t^{2}+1$. Therefore, when $a=1$, the equation has a unique solution.
Let $a=5$. Then the equation will take the form $5^{t^{2}}=5t^{2}+1$. Note that $5^{1}=5, 5 \cdot 1+1=6$, but $5^{2^{2}}=625$, $5 \cdot 2^{2}+1=21$, i.e., at $t=1$ the left side is less than the right, and at $t=2$ the opposite is true. Therefore, by the Intermediate Value Theorem, the equation has at least one more root in the interval $(1,2)$. Therefore, $a=5$ does not satisfy the condition.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10. Points $M, N$, and $K$ are located on the lateral edges $A A_{1}, B B_{1}$, and $C C_{1}$ of the triangular prism $A B C A_{1} B_{1} C_{1}$ such that $A M: A A_{1}=3: 7, B N: B B_{1}=2: 5, C K: C C_{1}=4: 9$. Point $P$ belongs to the prism. Find the maximum possible value of the volume of the pyramid $M N K P$, if the volume of the prism is 40.
|
Answer: 8.
Solution. Suppose we have found the position of point $P$ such that the volume of pyramid $M N K P$ is maximized. Draw a plane $\alpha$ through it, parallel to the plane $M N K$, and call $M_{1}, N_{1}$, and $K_{1}$ the points of intersection of this plane with the edges $A A_{1}, B B_{1}$, and $C C_{1}$, respectively. Note that
$V_{M N K P}=\frac{1}{3} V_{M N K M_{1} N_{1} K_{1}}$. Draw planes $\beta$ and $\beta_{1}$ through points $M$ and $M_{1}$, parallel to the plane $A B C$, and call $R$ and $R_{1}$ the points of intersection with edge $B B_{1}$, and $S$ and $S_{1}$ with edge $C C_{1}$. Note that the figures $M N K R S$ and $M_{1} N_{1} K_{1} R_{1} S_{1}$ are obtained from each other by a parallel translation, and thus are equal, and their volumes are also equal. Therefore, the volumes of prisms $M N K M_{1} N_{1} K_{1}$ and $M R S M_{1} R_{1} S_{1}$ are also equal. But $V_{M R S M_{1} R_{1} S_{1}}=\frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$, from which we get that $V_{M N K P}=\frac{1}{3} \frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$.
We need to find the position of plane $\alpha$ such that $M M_{1}$ is maximized. Note that at least one of the points $M_{1}, N_{1}, K_{1}$ lies within the original prism, from which $M M_{1}=N N_{1}=K K_{1} \leq \max \left\{A M, A_{1} M, B N, B_{1} N, C K, C_{1} K\right\}$. Substituting the given ratios in the problem, we finally get that $M M_{1}=N N_{1}=K K_{1}=B_{1} N=\frac{3}{5} B B_{1}$, from which $V_{M N K P}=\frac{1}{3} \frac{N N_{1}}{B B_{1}} V_{A B C A_{1} B_{1} C_{1}}=\frac{1}{3} \frac{3}{5} 40=8$.
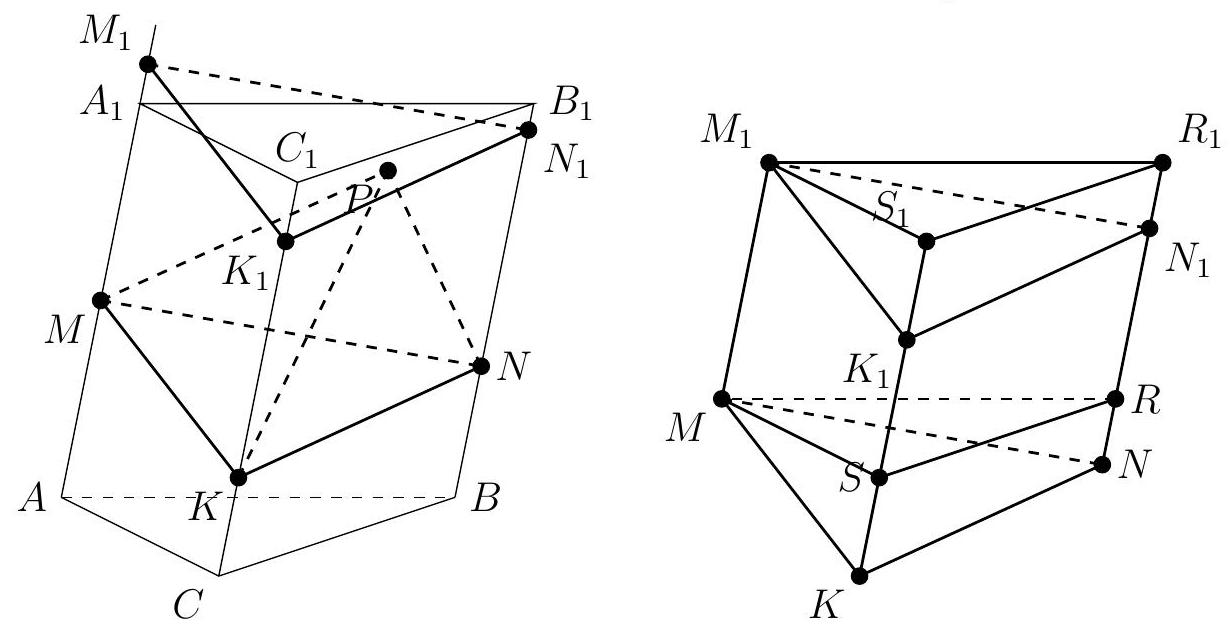
## Variant IV
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. For what values of the parameter $a$ does the equation
$$
5^{x^{2}+2 a x+a^{2}}=a x^{2}+2 a^{2} x+a^{3}+a^{2}-6 a+6
$$
have exactly one solution?
|
Answer: Only when $a=1$.
Solution. Let's denote $x+a$ by $t$. Note that the number of solutions of the equation does not change with such a substitution. Then the original equation will take the form
$$
5^{t^{2}}=a t^{2}+a^{2}-6 a+6
$$
Notice that the expressions on both sides do not change when $t$ is replaced by $-t$, so the equation can have an odd number of solutions (in particular, exactly one solution) only if $t=0$ is its root:
$$
5^{0}=a \cdot 0+a^{2}-6 a+6
$$
i.e., $a^{2}-6 a+5=0$, from which $a=5$ or $a=1$. Thus, apart from these two numbers, no other values of the parameter $a$ can satisfy the condition.
Let $a=1$. Then the equation will take the form $5^{t^{2}}=t^{2}+1$. Note that $5^{x}>x \ln 5+1$ for $x>0$ (which can be proven, for example, by taking the derivatives of both sides). Then for $t \neq 0$ we get $5^{t^{2}}>$ $t^{2} \ln 5+1>t^{2}+1$. Therefore, when $a=1$, the equation has a unique solution.
Let $a=5$. Then the equation will take the form $5^{t^{2}}=5 t^{2}+1$. Note that $5^{1}=5,5 \cdot 1+1=6$, but $5^{2^{2}}=625$, $5 \cdot 2^{2}+1=21$, i.e., at $t=1$ the left side is less than the right, and at $t=2$ the opposite is true. Therefore, by the intermediate value theorem, the equation has at least one more root in the interval $(1,2)$. Therefore, $a=5$ does not satisfy the condition.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
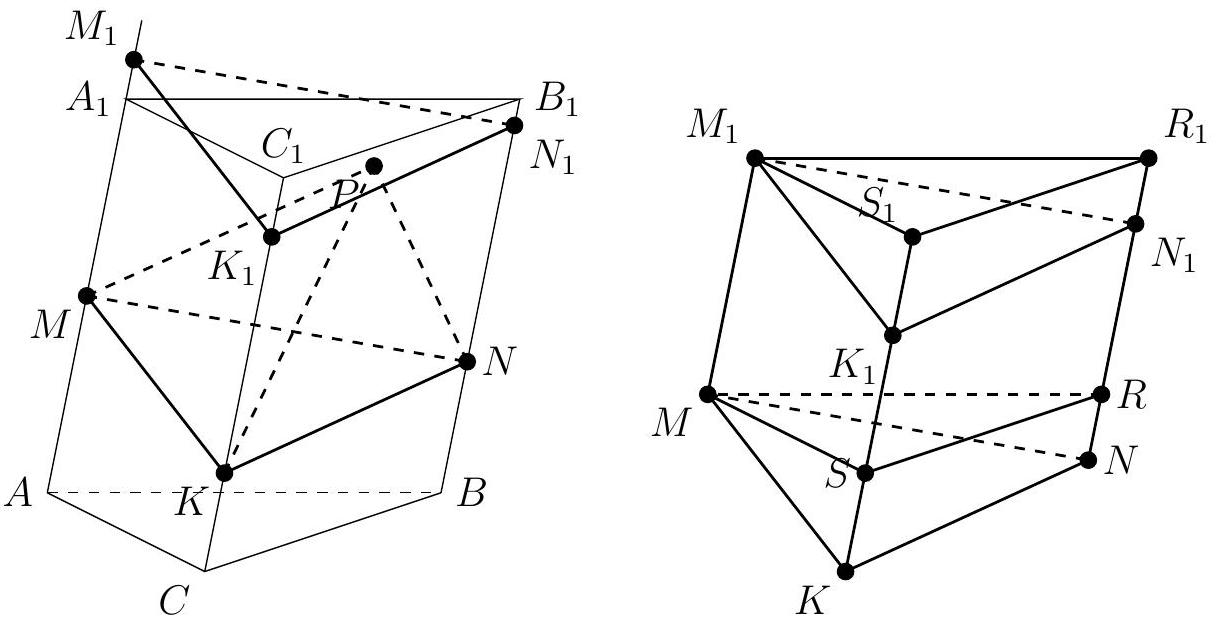
Problem 10. Points $M, N$, and $K$ are located on the lateral edges $A A_{1}, B B_{1}$, and $C C_{1}$ of the triangular prism $A B C A_{1} B_{1} C_{1}$ such that $A M: A A_{1}=5: 6, B N: B B_{1}=6: 7, C K: C C_{1}=2: 3$. Point $P$ belongs to the prism. Find the maximum possible value of the volume of the pyramid $M N K P$, if the volume of the prism is 35.
|
Answer: 10.
Solution. Suppose we have found the position of point $P$ at which the volume of pyramid $M N K P$ is maximized. Draw a plane $\alpha$ through it, parallel to the plane $M N K$, and call $M_{1}, N_{1}$, and $K_{1}$ the points of intersection of this plane with the edges $A A_{1}, B B_{1}$, and $C C_{1}$, respectively. Note that $V_{M N K P}=\frac{1}{3} V_{M N K M_{1} N_{1} K_{1}}$. Draw planes $\beta$ and $\beta_{1}$ through points $M$ and $M_{1}$, parallel to the plane $A B C$, and call $R$ and $R_{1}$ the points of intersection with edge $B B_{1}$, and $S$ and $S_{1}$ with edge $C C_{1}$. Note that the figures $M N K R S$ and $M_{1} N_{1} K_{1} R_{1} S_{1}$ are obtained from each other by a parallel translation, and therefore are equal, and their volumes are also equal. Then the volumes of prisms $M N K M_{1} N_{1} K_{1}$ and $M R S M_{1} R_{1} S_{1}$ are also equal. But $V_{M R S M_{1} R_{1} S_{1}}=\frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$, from which we get that $V_{M N K P}=\frac{1}{3} \frac{M M_{1}}{A A_{1}} V_{A B C A_{1} B_{1} C_{1}}$.
We need to find the position of plane $\alpha$ such that $M M_{1}$ is maximized. Note that at least one of the points $M_{1}, N_{1}, K_{1}$ lies within the original prism, from which $M M_{1}=N N_{1}=K K_{1} \leq \max \left\{A M, A_{1} M, B N, B_{1} N, C K, C_{1} K\right\}$. Substituting the given ratios in the problem, we finally get that $M M_{1}=N N_{1}=K K_{1}=B N=\frac{6}{7} B B_{1}$, from which $V_{M N K P}=\frac{1}{3} \frac{N N_{1}}{B B_{1}} V_{A B C A_{1} B_{1} C_{1}}=\frac{16}{3} \frac{6}{7} 35=10$.
[^0]: ${ }^{1}$ see https://ru.wikipedia.org/wiki/Малая_теорема_Ферма\#Альтернативная_формулировка
[^1]: ${ }^{2}$ see https://ru.wikipedia.org/wiki/Малая_теорема_Ферма\#Альтернативная_формулировка
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In a right triangle $ABC$, a circle is constructed on the leg $AC$ as its diameter, which intersects the hypotenuse $AB$ at point $E$. A tangent to the circle is drawn through point $E$, which intersects the leg $CB$ at point $D$. Find the length of $DB$, if $AE=6$, and $BE=2$.
|
Answer: 2.
Solution. The solution is based on two simple observations. First, $\angle A E C=90^{\circ}$, since it subtends the diameter. Second, $D E$ and $D C$ are tangents to the circle from the condition, so $D E=D C$. Therefore, in the right triangle $C E B$, a point $D$ is marked on the hypotenuse $B C$ such that $D E=D C$; it is well known that then $D$ is the midpoint of this hypotenuse, $B D=B C / 2$.
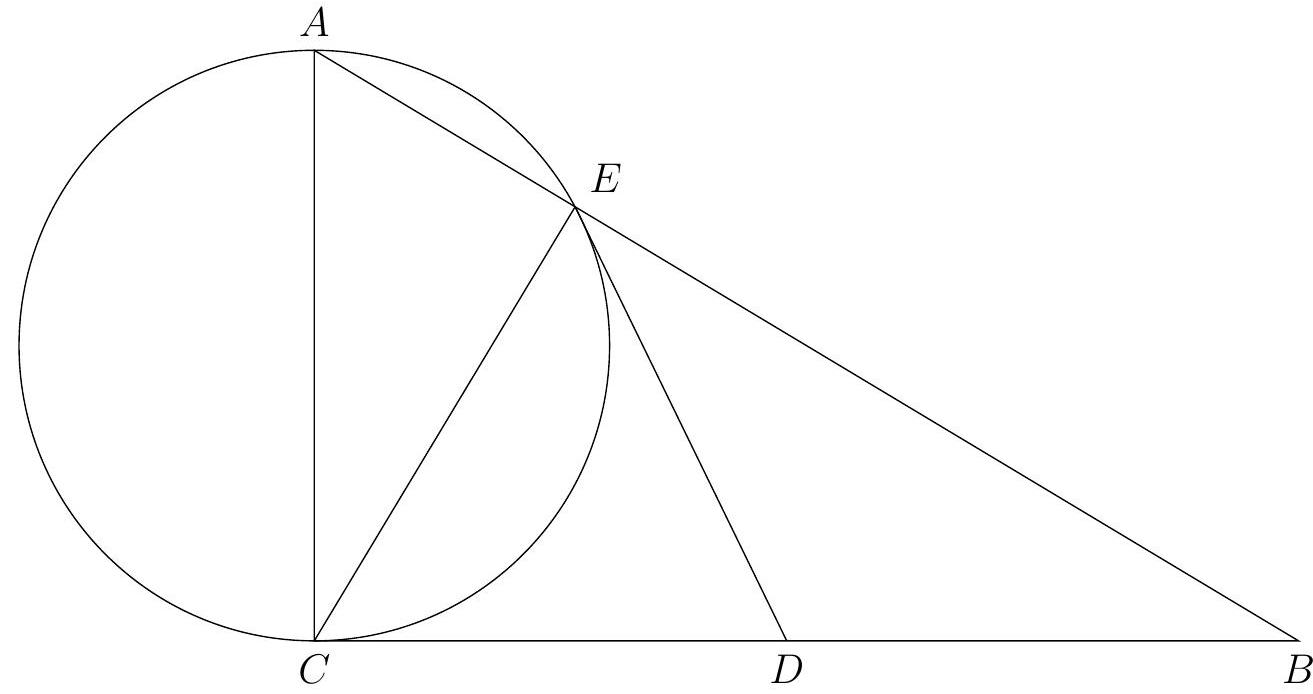
The solution can be completed in several ways; we will present two of them.
First method, height of a right triangle and the Pythagorean theorem. In the right triangle $A B C$, the height $C E$ divides the hypotenuse $A B$ into segments $A E=6$ and $B E=2$. We get that $C E^{2}=A E \cdot B E=6 \cdot 2$; by the Pythagorean theorem $B C^{2}=B E^{2}+C E^{2}=2^{2}+2 \cdot 6=16, B D=B C / 2=2$.
Second method, the tangent-secant theorem. According to the tangent-secant theorem for the tangent $B C$ and the secant $B A$, we have: $B C^{2}=B E \cdot B A=2 \cdot(2+6)=16, B D=B C / 2=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In a right triangle $P Q R$, a circle is constructed on the leg $P R$ as its diameter, which intersects the hypotenuse $P Q$ at point $T$. A tangent to the circle is drawn through point $T$, which intersects the leg $R Q$ at point $S$. Find the length of $S Q$, if $P T=15$, and $Q T=5$.
|
Answer: 5.
Solution. The solution is based on two simple observations. First, $\angle P T R=90^{\circ}$, since it subtends the diameter. Second, $S T$ and $S R$ are tangents to the circle from the given conditions, so $S T=S R$. Therefore, in the right triangle $R T Q$, a point $S$ is marked on the hypotenuse $Q R$ such that $S T=S R$; it is well known that then $S$ is the midpoint of this hypotenuse, $Q S=Q R / 2$.
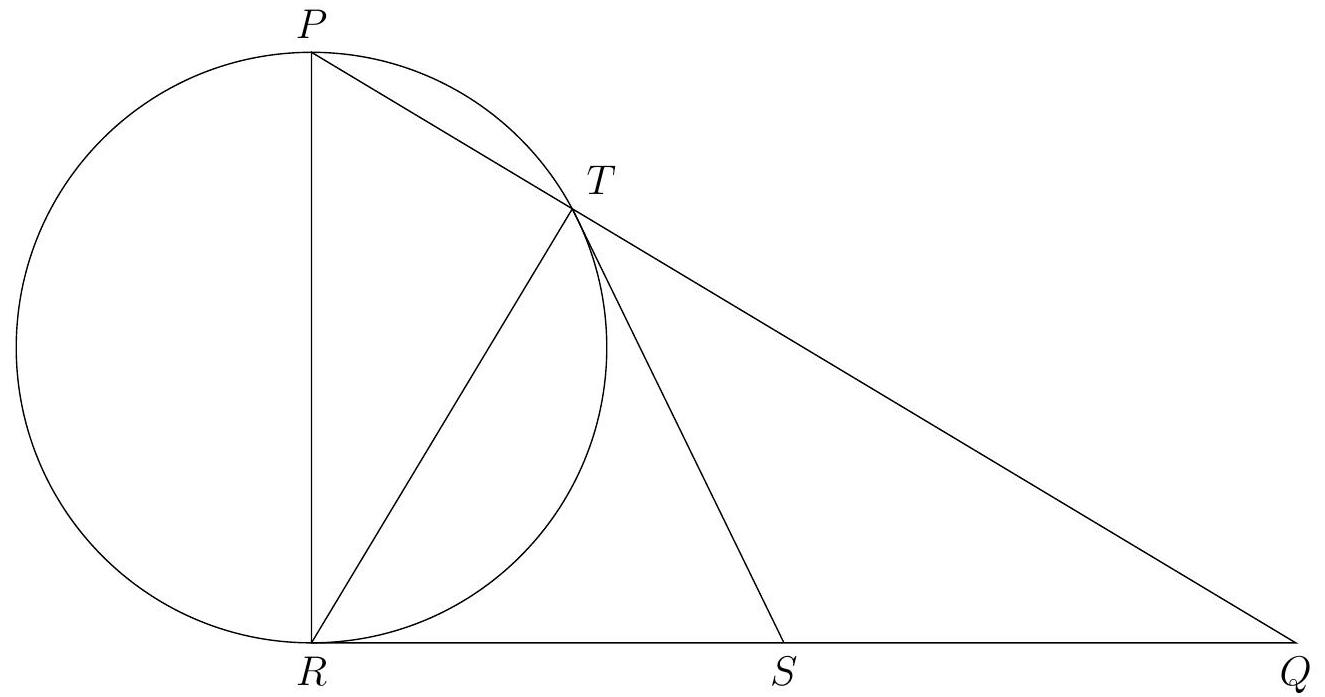
The solution can be completed in several ways; we will present two of them.
First method, height of a right triangle and the Pythagorean theorem. In the right triangle $P Q R$, the height $R T$ divides the hypotenuse $P Q$ into segments $P T=15$ and $Q T=5$. We get that $R T^{2}=P T \cdot Q T=15 \cdot 5$; by the Pythagorean theorem $Q R^{2}=Q T^{2}+R T^{2}=5^{2}+15 \cdot 5=100, Q S=Q R / 2=5$.
Second method, the tangent-secant theorem. According to the tangent-secant theorem for the tangent $Q R$ and the secant $Q P$, we have: $Q R^{2}=Q T \cdot Q P=5 \cdot(5+15)=100, Q S=Q R / 2=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In a right triangle $X Y Z$, a circle is constructed on the leg $X Z$ as its diameter, which intersects the hypotenuse $X Y$ at point $W$. A tangent to the circle is drawn through point $W$, which intersects the leg $Z Y$ at point $V$. Find the length of $V Y$, if $X W=12$, and $Y W=4$.
|
Answer: 4.
Solution. The solution is based on two simple observations. First, $\angle X W Z=90^{\circ}$, since it subtends the diameter. Second, $V W$ and $V Z$ are tangents to the circle from the condition, so $V W=V Z$. Therefore, in the right triangle $Z W Y$, a point $V$ is marked on the hypotenuse $Y Z$ such that $V W=V Z$; it is well known that then $V$ is the midpoint of this hypotenuse, $Y V=Y Z / 2$.
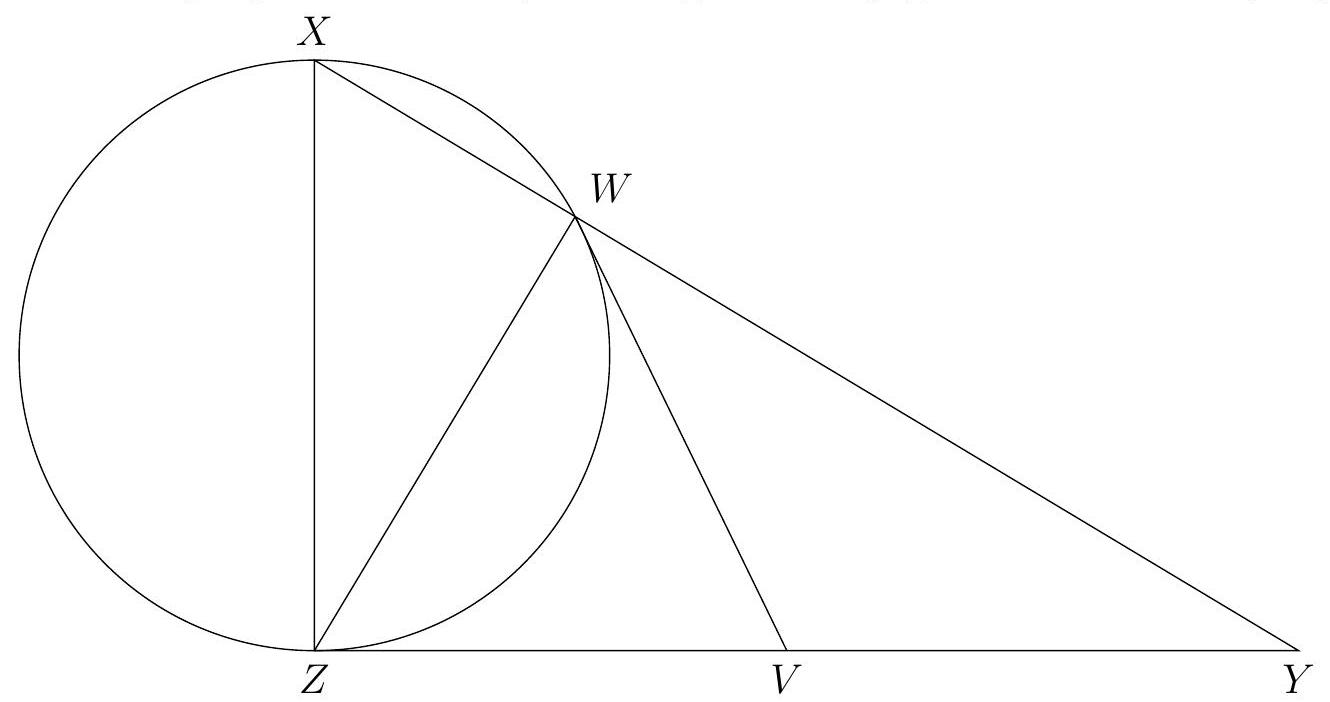
The solution can be completed in several ways; we will present two of them.
First method, height of a right triangle and the Pythagorean theorem. In the right triangle $X Y Z$, the height $Z W$ divides the hypotenuse $X Y$ into segments $X W=12$ and $Y W=4$. We get that $Z W^{2}=X W \cdot Y W=12 \cdot 4$; by the Pythagorean theorem, $Y Z^{2}=Y W^{2}+Z W^{2}=4^{2}+12 \cdot 4=64, Y V=Y Z / 2=4$.
Second method, the tangent-secant theorem. According to the tangent-secant theorem for the tangent $Y Z$ and the secant $Y X$, we have: $Y Z^{2}=Y W \cdot Y X=4 \cdot(4+12)=64, Y V=Y Z / 2=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In a right triangle $KLM$, a circle is constructed on the leg $KM$ as its diameter, which intersects the hypotenuse $KL$ at point $G$. A tangent to the circle is drawn through point $G$, intersecting the leg $ML$ at point $F$. Find the length of $FL$, if $KG=5$ and $LG=4$.
|
Answer: 3.
Solution. The solution is based on two simple observations. First, $\angle K G M=90^{\circ}$, since it subtends the diameter. Second, $F G$ and $F M$ are tangents to the circle from the condition, so $F G=F M$. Therefore, in the right triangle $M G L$, a point $F$ is marked on the hypotenuse $L M$ such that $F G=F M$; it is well known that then $F$ is the midpoint of this hypotenuse, $L F=L M / 2$.
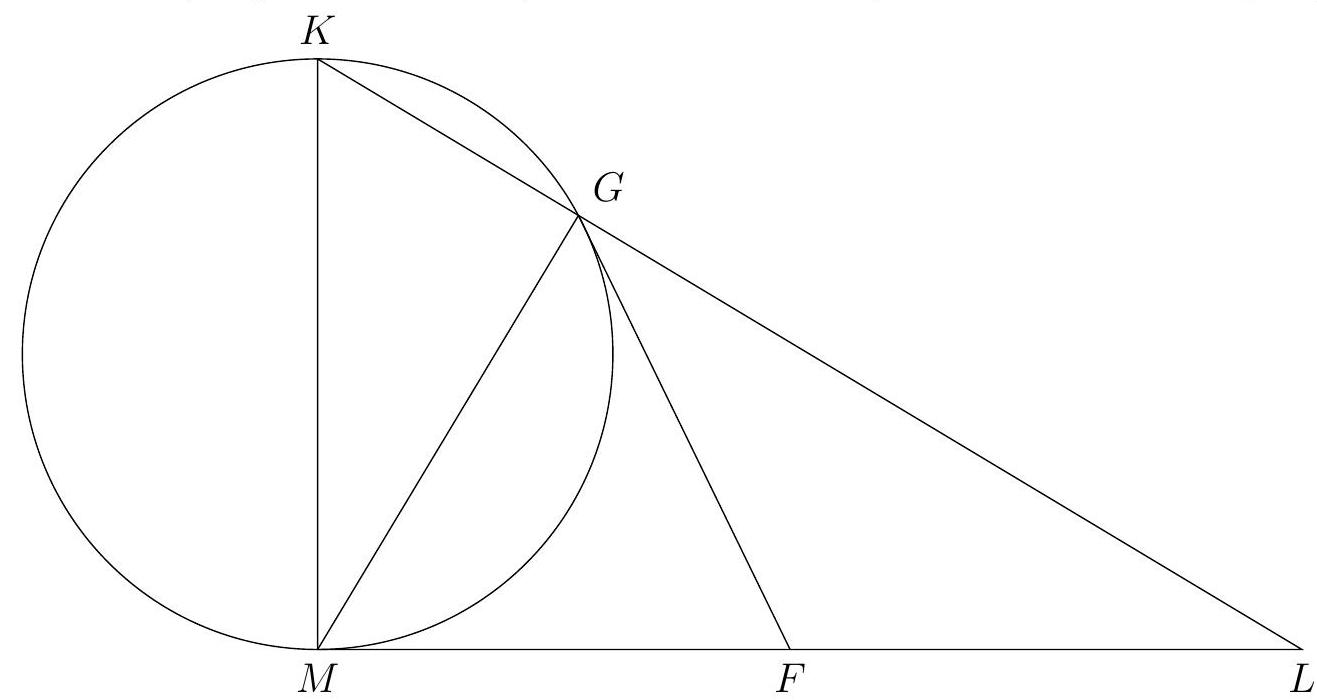
The solution can be completed in several ways; we will present two of them.
First method, height of a right triangle and the Pythagorean theorem. In the right triangle $K L M$, the height $M G$ divides the hypotenuse $K L$ into segments $K G=5$ and $L G=4$. We get that $M G^{2}=K G \cdot L G=5 \cdot 4$; by the Pythagorean theorem $L M^{2}=L G^{2}+M G^{2}=4^{2}+5 \cdot 4=36, L F=L M / 2=3$.
Second method, the tangent-secant theorem. According to the tangent-secant theorem for the tangent $L M$ and the secant $L K$, we have: $L M^{2}=L G \cdot L K=4 \cdot(4+5)=36, L F=L M / 2=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. Each knight gives one affirmative answer to four questions, while a liar gives three. In total, there were $105+45+85+65=300$ affirmative answers. If all the residents of the city were knights, the total number of affirmative answers would be 200. The 100 extra "yes" answers come from the lies of the liars. Thus, the number of liars is $\frac{100}{2}=50$. Let $k$ be the number of knights living in district B, then $45-k$ is the number of affirmative answers to the second question given by the liars. Therefore, the number of liars living in district B is $50-(45-k)=k+5$. In the other districts, the number of liars is less than the number of knights.
|
Answer: in Block B, on 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Each of the two workers was assigned to process the same number of parts. The first completed the work in 8 hours. The second spent more than 2 hours on setting up the equipment and with its help finished the work 3 hours earlier than the first. It is known that the second worker processed as many parts in 1 hour after the equipment started as the first did by that time. By what factor does the equipment increase labor productivity?
|
Answer: 4 times.
Solution: Let $x$ be the time spent on equipment setup. Then the second worker worked (on the equipment) $8-3-x=5-x$ hours, producing as much per hour as the first worker in $x+1$ hours. Therefore, $\frac{8}{5-x}=\frac{x+1}{1}$. We get $x^{2}-4 x+3=0$. But by the condition $x>2$, so $x=3$, and the required ratio is $\frac{x+1}{1}=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. The function $f$ is such that $f(2 x-3 y)-f(x+y)=-2 x+8 y$ for all $x, y$. Find all possible values of the expression $\frac{f(5 t)-f(t)}{f(4 t)-f(3 t)}$.
|
Answer: 4.
Solution. By substituting $y=-x$, we get that $f(5 x)=-10 x+f(0)$, i.e., $f(t)=-2 t+c$ (where $c$ is some constant). Therefore, the desired expression is always (when it is defined) equal to 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. The function $f$ is such that $f(2 x-3 y)-f(x+y)=-2 x+8 y$ for all $x, y$. Find all possible values of the expression $\frac{f(4 t)-f(t)}{f(3 t)-f(2 t)}$.
|
Answer: 3.
Solution. By substituting $y=-x$, we get that $f(5 x)=-10 x+f(0)$, i.e., $f(t)=-2 t+c$ (where $c$ is some constant). Therefore, the desired expression is always (when it is defined) equal to 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. The function $f$ is such that $f(x+2 y)-f(3 x-2 y)=2 y-x$ for all $x, y$. Find all possible values of the expression $\frac{f(5 t)-f(t)}{f(4 t)-f(3 t)}$.
|
Answer: 4.
Solution. Substituting $x=-2 y$, we get that $f(0)-f(-8 y)=-4 y$, i.e., $f(t)=\frac{1}{2} t+c$ (where $c$ is some constant). Therefore, the desired expression is always (when it is defined) equal to 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. The function $f$ is such that $f(x+2 y)-f(3 x-2 y)=2 y-x$ for all $x, y$. Find all possible values of the expression $\frac{f(4 t)-f(t)}{f(3 t)-f(2 t)}$.
|
Answer: 3.
Solution. Substituting $x=-2 y$, we get that $f(0)-f(-8 y)=-4 y$, i.e., $f(t)=\frac{1}{2} t+c$ (where $c$ is some constant). Therefore, the desired expression is always (when it is defined) equal to 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. A team of workers was working on pouring the rink on the large and small fields, with the area of the large field being twice the area of the small field. In the part of the team that worked on the large field, there were 4 more workers than in the part that worked on the small field. When the pouring of the large rink was completed, the part of the team that was on the small field was still working. What is the maximum number of workers that could have been in the team
|
Answer: 10.
Solution. Let the number of workers on the smaller field be $n$, then the number of workers on the larger field is $n+4$, and the total number of people in the team is $2n+4$. The problem "implicitly assumes" that the productivity of each worker is the same, denoted as $a$. Therefore, the productivities of each part of the team are $an$ and $a(n+4)$. If the area of the smaller field is $S$, then the area of the larger field is $2S$. The time spent on completing the entire work by each team is $\frac{S}{an}$ and $\frac{2S}{a(n+4)}$, respectively. According to the problem, $\frac{S}{an} > \frac{2S}{a(n+4)}$. Due to the positivity of all variables, this inequality is equivalent to the inequality $n+4 > 2n$, or $n < 4$. Therefore, $n \leqslant 3$, and $2n+4 \leqslant 10$. The equality situation is clearly possible: just take any positive $S$ and $a$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Point $O$ is the center of the circumcircle of triangle $ABC$ with sides $BC=8$ and $AC=4$. Find the length of side $AB$ if the length of the vector $4 \overrightarrow{OA} - \overrightarrow{OB} - 3 \overrightarrow{OC}$ is 10.
|
Answer: 5.
Answer: Let the radius of the circumscribed circle be denoted by $R$. Then for any numbers $x, y, z$, the following equality holds:
$$
\begin{aligned}
& (x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C})^{2}= \\
& =x^{2} O A^{2}+y^{2} O B^{2}+z^{2} O C^{2}+2 x y(\overrightarrow{O A} \cdot \overrightarrow{O B})+2 y z(\overrightarrow{O B} \cdot \overrightarrow{O C})+2 x z(\overrightarrow{O A} \cdot \overrightarrow{O C})= \\
& =\left(x^{2}+y^{2}+z^{2}\right) R^{2}+x y\left(O A^{2}+O B^{2}-A B^{2}\right)+y z\left(O B^{2}+O C^{2}-B C^{2}\right)+x z\left(O A^{2}+O C^{2}-A C^{2}\right)= \\
& =\left(x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 x z\right) R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}= \\
& =(x+y+z)^{2} R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}
\end{aligned}
$$
Then, for $x=4, y=-1, z=-3$, we obtain the equality $10^{2}=0 \cdot R^{2}+4 A B^{2}-3 B C^{2}+12 A C^{2}$, from which $A B^{2}=\frac{1}{4}\left(100-12 A C^{2}+3 B C^{2}\right)=25$, i.e., $A B=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what values of the parameter $a$ does the equation
$$
\log _{2}^{2} x+(a-6) \log _{2} x+9-3 a=0
$$
have exactly two roots, one of which is four times the other?
|
Answer: $-2.2$
Solution. Let $t=\log _{2} x$, then the equation becomes $t^{2}+(a-6) t+(9-3 a)=0$. Notice that $3 \cdot(3-a)=9-3 a, 3+(3-a)=6-a$, from which, by the theorem converse to Vieta's theorem, the roots of this equation are -3 and $3-a$. We make the reverse substitution: $\log _{2} x=3$ or $\log _{2} x=3-a$, i.e., either $x=8$, or $x=2^{3-a}$. We get two cases: $8=4 \cdot 2^{3-a}$ or $2^{3-a}=4 \cdot 8$. In the first case $a=2$, in the second $a=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Point $O$ is the center of the circumcircle of triangle $ABC$ with sides $AB=8$ and $AC=5$. Find the length of side $BC$ if the length of the vector $\overrightarrow{OA}+3 \overrightarrow{OB}-4 \overrightarrow{OC}$ is 10.
|
Answer: 4.
Answer: Let the radius of the circumscribed circle be denoted by $R$. Then for any numbers $x, y, z$, the following equality holds:
$$
\begin{aligned}
& (x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C})^{2}= \\
& =x^{2} O A^{2}+y^{2} O B^{2}+z^{2} O C^{2}+2 x y(\overrightarrow{O A} \cdot \overrightarrow{O B})+2 y z(\overrightarrow{O B} \cdot \overrightarrow{O C})+2 x z(\overrightarrow{O A} \cdot \overrightarrow{O C})= \\
& =\left(x^{2}+y^{2}+z^{2}\right) R^{2}+x y\left(O A^{2}+O B^{2}-A B^{2}\right)+y z\left(O B^{2}+O C^{2}-B C^{2}\right)+x z\left(O A^{2}+O C^{2}-A C^{2}\right)= \\
& =\left(x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 x z\right) R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}= \\
& =(x+y+z)^{2} R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}
\end{aligned}
$$
Then, for $x=1, y=3, z=-4$, we obtain the equality $10^{2}=0 \cdot R^{2}-3 A B^{2}+12 B C^{2}+4 A C^{2}$, from which $B C^{2}=\frac{1}{12}\left(100+3 A B^{2}-4 A C^{2}\right)=16$, i.e., $B C=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. A team of workers was laying linoleum in a store's warehouse and in the cash hall, with the warehouse area being 3 times larger than the cash hall area. In the part of the team working in the warehouse, there were 5 more workers than in the part working in the cash hall. When the work in the warehouse was completed, the part of the team working in the cash hall was still working. What is the maximum number of workers that could have been in the team?
|
Answer: 9.
Solution. Let the number of workers in the cash hall be denoted as $n$, then the number of workers in the warehouse is $n+5$, and the total number of people in the team is $2n+5$. The problem "implicitly assumes" that the productivity of each worker is the same, denoted as $a$. Therefore, the productivity of each part of the team is $an$ and $a(n+5)$. If the area of the cash hall is $S$, then the area of the warehouse is $3S$. The time spent on completing the entire work by each part of the team is $\frac{S}{an}$ and $\frac{3S}{a(n+5)}$, respectively. According to the problem, $\frac{S}{an} > \frac{3S}{a(n+5)}$. Due to the positivity of all variables, this inequality is equivalent to $n+5 > 3n$, or $2n < 5$. Therefore, $n \leqslant 2$, and $2n+5 \leqslant 9$. The equality situation is clearly possible: just take any positive $S$ and $a$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Point $O$ is the center of the circumcircle of triangle $ABC$ with sides $BC=5$ and $AB=4$. Find the length of side $AC$ if the length of the vector $3 \overrightarrow{OA}-4 \overrightarrow{OB}+\overrightarrow{OC}$ is 10.
|
Answer: 8.
Answer: Let the radius of the circumscribed circle be denoted by $R$. Then for any numbers $x, y, z$, the following equality holds:
$$
\begin{aligned}
& (x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C})^{2}= \\
& =x^{2} O A^{2}+y^{2} O B^{2}+z^{2} O C^{2}+2 x y(\overrightarrow{O A} \cdot \overrightarrow{O B})+2 y z(\overrightarrow{O B} \cdot \overrightarrow{O C})+2 x z(\overrightarrow{O A} \cdot \overrightarrow{O C})= \\
& =\left(x^{2}+y^{2}+z^{2}\right) R^{2}+x y\left(O A^{2}+O B^{2}-A B^{2}\right)+y z\left(O B^{2}+O C^{2}-B C^{2}\right)+x z\left(O A^{2}+O C^{2}-A C^{2}\right)= \\
& =\left(x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 x z\right) R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}= \\
& =(x+y+z)^{2} R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}
\end{aligned}
$$
Then, for $x=3, y=-4, z=1$, we obtain the equality $10^{2}=0 \cdot R^{2}+12 A B^{2}+4 B C^{2}-3 A C^{2}$, from which $A C^{2}=\frac{1}{3}\left(12 A C^{2}+4 B C^{2}-100\right)=64$, i.e., $A C=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Point $O$ is the center of the circumcircle of triangle $ABC$ with sides $AB=5, AC=8$, and $BC=4$. Find the length of the vector $\overrightarrow{O A}-4 \overrightarrow{O B}+3 \overrightarrow{O C}$.
|
Answer: 10.
Answer: Let the radius of the circumscribed circle be denoted by $R$. Then for any numbers $x, y, z$, the following equality holds:
$$
\begin{aligned}
& (x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C})^{2}= \\
& =x^{2} O A^{2}+y^{2} O B^{2}+z^{2} O C^{2}+2 x y(\overrightarrow{O A} \cdot \overrightarrow{O B})+2 y z(\overrightarrow{O B} \cdot \overrightarrow{O C})+2 x z(\overrightarrow{O A} \cdot \overrightarrow{O C})= \\
& =\left(x^{2}+y^{2}+z^{2}\right) R^{2}+x y\left(O A^{2}+O B^{2}-A B^{2}\right)+y z\left(O B^{2}+O C^{2}-B C^{2}\right)+x z\left(O A^{2}+O C^{2}-A C^{2}\right)= \\
& =\left(x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 x z\right) R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}= \\
& =(x+y+z)^{2} R^{2}-x y A B^{2}-y z B C^{2}-x z A C^{2}
\end{aligned}
$$
Then, for $x=1, y=-4, z=3$, we obtain the equality $(\overrightarrow{O A}-4 \overrightarrow{O B}+3 \overrightarrow{O C})^{2}=0 \cdot R^{2}+4 A B^{2}+12 B C^{2}-$ $3 A C^{2}=100$, i.e., the answer is 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. How many natural numbers $n>1$ exist, for which there are $n$ consecutive natural numbers, the sum of which is equal to 2016?
|
Answer: 5.
Solution. Suppose that for some $n$ there exist $n$ consecutive natural numbers $a$, $a+1, \ldots, a+(n-1)$, the sum of which is 2016. Then $n a+(n-1) n / 2=2016$, or, after algebraic transformations, $n(2 a+n-1)=4032=2^{6} \cdot 3^{2} \cdot 7$.
Note that $n$ and $2 a+n-1$ have different parity. Therefore, if $n$ is even, then $n$ must be divisible by $2^{6}=64$, from which $n \geqslant 64, 2 a+n-1 \leqslant 4032 / 64=63$, which contradicts $2 a+n-1>n$.
Thus, $n$ is an odd divisor of the number 4032, i.e., a divisor of the number 63. Let's check that each of them fits. If $n=3: 2 a+3-1=1344, a=671$; if $n=7: 2 a+7-1=576, a=285$; if $n=9$ : $2 a+9-1=448, a=220$; if $n=21: 2 a+21-1=192, a=86$; if $n=63: 2 a+63-1=64, a=1$. In total, there are five suitable $n$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
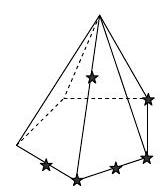
7.4. On the surface of a pentagonal pyramid (see fig.), several gnomes live in pairwise distinct points, and they can live both inside the faces and on the edges or at the vertices. It turned out that on each face (including the vertices and edges that bound it) a different number of gnomes live. What is the minimum number of gnomes living on the pyramid?
|
Answer: 6
Solution: There are 6 faces in total, so at least 5 gnomes live on the most "populated" one. If there are exactly 5 gnomes in total, then all of them live on one face (let's call it face $A$), so the faces where 4 and 3 gnomes live (let's call them $B$ and $C$ respectively) are adjacent to it. Then, on the edge $A-B$ there should be 4, and on the edge $A-C$ there should be 3 gnomes. This means there are already at least 7 gnomes, and we could have counted only one of them twice - the one sitting at the vertex connecting faces $A$, $B$, and $C$. Therefore, there are at least 6 gnomes - a contradiction. An example with 6 gnomes is shown in the figure.
## Criteria:
Only the answer - 0 points.
Only a correct example - 2 points.
Only proof that there cannot be fewer than 5 - 1 point.
Only proof that there cannot be fewer than 6 - 3 points.
These points DO NOT add up.
Justification of the example is not required.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Ten chess players over nine days played a full round-robin tournament, during which each of them played exactly one game with each other. Each day, exactly five games were played, with each chess player involved in exactly one of them. For what maximum $n \leq 9$ can it be claimed that, regardless of the schedule, at the end of some game day with number $k \leq 8$, there will definitely be $n$ chess players who have already played all their scheduled games with each other?
|
Answer. $n=5$.
Solution. By the end of the eighth day, each chess player has played 8 games, meaning they have not played one. The unplayed games divide the chess players into 5 non-intersecting pairs. By the Pigeonhole Principle, among any six chess players, there will always be two belonging to the same pair, that is, who have not played against each other even by the end of the penultimate day of the tournament. Therefore, $n \leq 5$.
We will show that by the end of the seventh day of the tournament, regardless of the schedule, there will always be five chess players who have already played all their scheduled games with each other, from which it follows that $n=5$. We will construct a chain of chess players: the first is any player, the second is the one who played the first on the eighth day, the third is the one who played the second on the ninth day, the fourth is the one who played the third on the eighth day, and so on. Since the number of chess players is finite, at some point in the chain, a repetition will occur for the first time. This cannot happen at any player except the first, otherwise, the repeated player would have played at least three games in two days. Therefore, the chain will form a cycle of even length, as the days of the games considered alternate when moving along it. If the constructed cycle includes all 10 chess players, we stop; if not, we choose any player not included in it and repeat the procedure for constructing the cycle. The new cycle will not intersect with the already constructed one. After several steps, we will construct several cycles of even length, not less than 4, including all 10 chess players (there are few options - either 10 or $6+4$). We select half of the participants from each cycle, every other one, totaling 5 chess players. No two of them are adjacent in the cycles, so they did not play against each other on the eighth and ninth days.
Therefore, all games between them were played in the first 7 days. Thus, $n \geq 5$, and hence $n=5$. In this case, $k=7$.
Grading criteria. ($\cdot$) Proof that $n \leq 5: 3$ points. ($\cdot$) Proof that $n \geq 5: 4$ points.
10.5.. Find the maximum value of the sum $x_{1}\left(1-x_{2}\right)+x_{2}\left(1-x_{3}\right)+\ldots+x_{6}\left(1-x_{7}\right)+x_{7}\left(1-x_{1}\right)$ for arbitrary numbers $x_{1}, x_{2}, \ldots, x_{7}$ from the interval $[0,1]$.
Answer. 3.
Solution. We isolate in the left-hand side of the inequality all terms containing the variable $x_{1}$, obtaining $x_{1}\left(1-x_{2}-x_{7}\right)$. For fixed other variables, this expression, and hence the entire left-hand side, reaches its maximum when $x_{1}=1$ if $x_{2}+x_{7}<1$ and when $x_{1}=0$ if $x_{2}+x_{7} \geq 1$. Therefore, if we replace each variable, starting from $x_{1}$ to $x_{7}$, with 1 or 0 according to the condition whether the sum of the neighboring variables is less than 1 or not less than 1, we will not decrease the value of the sum on the right-hand side of the inequality. Thus, the maximum of the right-hand side is achieved for a set of $x_{1}, x_{2}, \ldots, x_{7}$ where each variable is either 1 or 0. Moreover, in such a set, two adjacent variables cannot both be 1, as in this case, the second one could not have appeared according to the replacement rules. Therefore, the set contains no more than 3 ones, and the rest are zeros, meaning that no more than three terms in the right-hand side of the inequality are non-zero, each obviously not exceeding 1, and the entire sum is no more than 3. An example where the value 3 is achieved: $x_{1}=x_{3}=x_{5}=1$, the rest are 0.
Grading criteria. Proven that the maximum of the sum does not exceed 3: 5 points. Example where the value 3 is achieved: 2 points.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. At a round table, 410 deputies sat down, each of whom was either a knight, who always tells the truth, or a liar, who always lies. Each of the deputies said: "Among my twenty neighbors to the left and twenty neighbors to the right, there are exactly 20 liars in total." It is known that at least half of the people at the table are liars. How many knights are there at the table?
|
Answer: None.
Solution: Let's divide all the people sitting at the table into ten groups of 41 people each. Then, at least one group will have at least 21 liars. Otherwise, in each group, there would be a maximum of 20, i.e., no more than \(20 \times 10 = 200\) in total, which is less than half of the total number. Consider this group.
If a knight is sitting in the center, he tells the truth, and there are exactly 20 liars in this group. But we have already established that there are at least 21. Contradiction. Therefore, a liar is sitting in the center, and there are at least 22 liars in the group (there cannot be exactly 21, as otherwise, the central person would be telling the truth). Now consider the left neighbor of the central liar. Among his 40 neighbors, there are at least 21 liars, since we lost one extreme neighbor (who might be a liar) by shifting to the left, but gained a liar neighbor who was previously central. Repeating the reasoning for him, we get that he is also a liar. Shift left again and continue this process. Eventually, we will get that everyone sitting at the table is a liar.
## Criteria:
Only the answer, answer with verification - 0 points.
Proved that there will be a group with 21 liars - 2 points.
Proved that in this group, a liar is sitting in the center - another 1 point.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. On a circular route, 12 trams run in one direction at the same speed and at equal intervals. How many trams need to be added so that at the same speed, the intervals between trams decrease by one fifth?
#
|
# Answer: 3.
Solution: Let's take the entire distance as 60 arbitrary units, which means the trams are currently 5 arbitrary units apart. We want this distance to be reduced by $1 / 5$, making it equal to 4 arbitrary units. For this, we need $60: 4=15$ trams, which is 3 more than the current number.
Criteria: only the answer - 0 points, answer with verification - 2 points, deduct no less than 2 points for arithmetic errors.
|
3
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Each digit of the natural number $N$ is strictly greater than the one to its left. What is the sum of the digits of the number $9 N$?
|
Answer: 9.
Solution: Note that $9 N=10 N-N$. Let's perform this subtraction in a column. In the units place, there will be the difference between 10 and the last digit of the number $N$, in the tens place - the last and the second-to-last digit, decreased by 1. In all subsequent places, there will be the difference between two adjacent digits, as the smaller digit will always be subtracted from the larger one. Each digit will appear once as the minuend and once as the subtrahend. When finding the sum of the digits, all these minuends and subtrahends will cancel each other out. Only the aforementioned $10-1=9$ will remain.
Criteria: only the answer, the answer with verification on specific cases - 0 points, the scheme of proof by example -2 points, the transition $9 N=10 N-N-1$ point. These points $\mathrm{NE}$ are not summed.
## Solutions to the tasks of the first stage of the All-Siberian Open Olympiad for schoolchildren in mathematics 2014-15
## 9th grade
## Each task is worth 7 points
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In the morning, a dandelion blooms, it flowers yellow for three days, on the fourth morning it turns white, and by the evening of the fifth day, it withers. On Monday afternoon, there were 20 yellow and 14 white dandelions on the meadow, and on Wednesday - 15 yellow and 11 white. How many white dandelions will there be on the meadow on Saturday?
|
Answer. Six dandelions.
Solution. A blooming dandelion is white on the fourth and fifth day. This means that on Saturday, the dandelions that bloomed on Tuesday or Wednesday will be white. Let's determine how many there are. The dandelions that were white on Monday had already flown away by Wednesday, and 20 yellow ones definitely survived until Wednesday (possibly turning white).
On Wednesday, there were $15+11=26$ dandelions on the meadow. We know that 20 of them were on the meadow since Monday, and the remaining $26-20=6$ bloomed on Tuesday and Wednesday.
Criteria. The correct answer is guessed with verification: 2 points.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Inside a semicircle of radius 12, there are a circle of radius 6 and a small semicircle, each touching the others pairwise, as shown in the figure. Find the radius of the small semicircle.
|
Answer: 4.
Solution. Let the radius of the small semicircle be $x$, the center of the large semicircle be $A$, the center of the circle be $B$, and the center of the small semicircle be $C$. The centers of the tangent circles and semicircle, and the corresponding points of tangency, lie on the same straight line, so $A B C$ is a right triangle with legs $A B=6, A C=12-x, B C=6+x$. By the Pythagorean theorem, we have $(x+6)^{2}=6^{2}+(12-x)^{2}$, from which $x=4$.
Criteria. It should be clearly explained why $A B=6, A C=12-x, B C=6+x$, otherwise 2 points will be deducted.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. In a semicircle with a radius of 18 cm, a semicircle with a radius of 9 cm is constructed on one of the halves of the diameter, and a circle is inscribed, touching the larger semicircle from the inside, the smaller semicircle from the outside, and the second half of the diameter. Find the radius of this circle.
#
|
# Answer: 8 cm.
Solution. Let O, O_1, O_2 be the centers of the large semicircle, the small semicircle, and the inscribed circle, respectively, and let P, Q, R be the points of tangency of the inscribed circle with the diameter of the large semicircle, the small semicircle, and the large semicircle, respectively. Then the points O_1, Q, O_2 lie on the same line, and the points O, O_2, R lie on the same line. Let the radius of the inscribed circle be x. From the Pythagorean theorem for triangle OO_2P, we have OP = \sqrt{(18-x)^2 - x^2} = \sqrt{324 - 36x}. From the Pythagorean theorem for triangle O_1O_2P, we have O_1P = \sqrt{(9 + x)^2 - x^2} = \sqrt{81 + 18x}. Therefore, O_1P = OP + 9 = \sqrt{324 - 36x} + 9 = \sqrt{81 + 18x}. Dividing by 3, we get \sqrt{36 - 4x} + 3 = \sqrt{9 + 2x}. From the last equation, x = 8.
Criteria. There is no clear justification for the calculation of OP and O_1P: deduct 2 points. The equation for x is correctly set up, but not solved: 3 points.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. The road from point A to point B first goes uphill and then downhill. A cat takes 2 hours and 12 minutes to travel from A to B, and the return trip takes 6 minutes longer. The cat's speed going uphill is 4 km/h, and downhill is 5 km/h. How many kilometers is the distance from A to B? (Provide a complete solution, not just the answer.)
|
Solution: When a cat goes uphill, it takes 15 minutes for 1 km, and when it goes downhill, it takes 12 minutes. That is, when the direction changes, the time spent on 1 km changes by 3 minutes. Since the cat spent 6 minutes more on the return trip, the uphill section on the return trip is 2 km longer.
Let the length of the uphill section on the way from A to B be $x$. Then we can set up the equation $15 x + 12(x + 2) = 132$, from which $x = 4$. Therefore, the total distance is $x + (x + 2) = 4 + 6 = 10$ km.
Comment: Other solutions are possible. For example, a system of equations could have been set up and solved immediately. Or it could have been proven that the difference between the two sections of the path is 2 km, then the answer could be guessed, and then its uniqueness could be proven.
Criteria: Only the answer - 0 points.
Answer with verification - 1 point.
Correct system of equations - 2 points.
Proven that the difference between the two sections of the path is 2 km - 1 point.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. On a certain island, there live 100 people, each of whom is either a knight, who always tells the truth, or a liar, who always lies. One day, all the inhabitants of this island lined up, and the first one said: "The number of knights on this island is a divisor of the number 1." Then the second said: "The number of knights on this island is a divisor of the number 2," and so on until the hundredth, who said: "The number of knights on this island is a divisor of the number 100." Determine how many knights can live on this island. (Find all answers and prove that there are no others.)
|
Solution: If there are no knights, then all the speakers are lying, since 0 is not a divisor of any natural number.
If there are knights, let there be $a$ of them. Then only the people with numbers $a k$ for $k=1,2, \ldots$ are telling the truth. On the other hand, since exactly $a$ people are telling the truth, $k$ changes precisely from 1 to $a$.
Thus, $a$ is such a number that the person with number $a \cdot a$ is still in the row $\left(a^{2} \leqslant 100\right)$, while the person with number $a \cdot(a+1)$ is not $(a(a+1)>100)$. Clearly, only $a=10$ fits, as for $a10$ - the first.
In total, there are either 0 or 10 knights.
Criteria: Only the answer - 0 points.
The case where there are no knights - 1 point.
Noted that the people with numbers $a, 2 a, \ldots, k a$ should be telling the truth - 2 points.
Proven that $k=a$ - another 2 points.
Proven that then $a=10$ - another 2 points.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. The perimeter of triangle $ABC$ is 24 cm, and the segment connecting the point of intersection of its medians with the point of intersection of its angle bisectors is parallel to side $AC$. Find the length of $AC$.
|
Answer: 8 cm.
Solution. Let AK be the median from vertex A, M - the point of intersection of the medians ABC, and I - the point of intersection of its angle bisectors AA1, BB1, CC1. Draw a line through K parallel to AC, intersecting the angle bisector BB1 at point P - its midpoint. By Thales' theorem, $PI: IB1 = KM: MA = 2$, so $BI: IB1 = 1$. By the property of angle bisectors AI and CI in triangles $ABB1$ and $CBB1$, we have
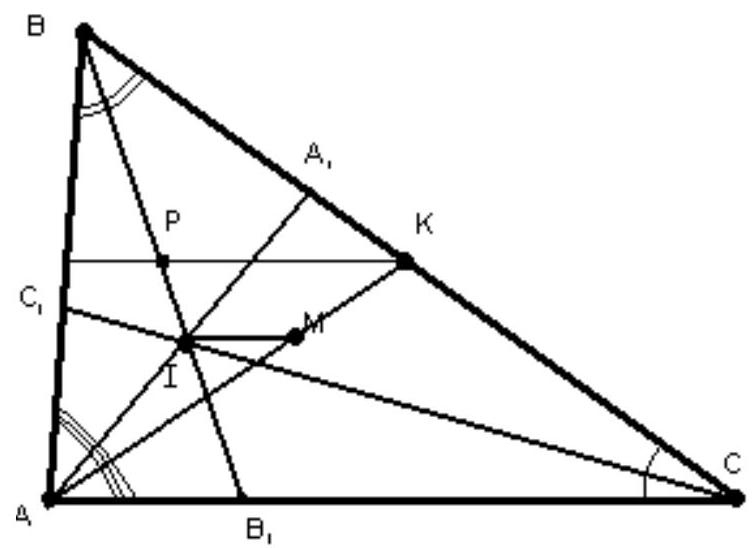
$AB: AB1 = BI: IB1 = CB: CB1 = 1$. Therefore, $AC = \frac{1}{2}(AB + BC) = \frac{1}{3}(AB + BC + AC) = 8$.
Evaluation. Just the answer: 0 points. Finding the ratio $BI: IB1 = 1: 3$: 1 point. Finding the ratios $AB: AB1 = BI: IB1 = CB: CB1 = 1: 2$: 2 points.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
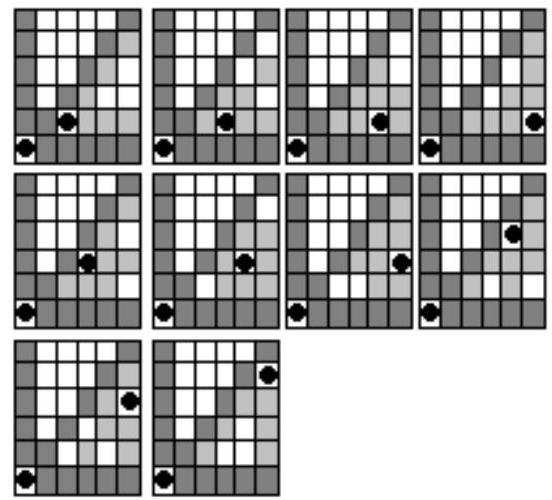
9.5. What is the smallest number of colors needed to color all the cells of a 6 by 6 square so that in each row, column, and diagonal of the square, all cells have different colors? Explanation: a diagonal of the square is understood to mean all rows of at least two cells running diagonally from one edge of the square to the other at an angle of $45^{\circ}$ or $135^{\circ}$ to the horizontal.
|
Answer: In 7 colors.
Solution. Let's provide an example of coloring in 7 colors that satisfies the condition of the problem. Consider a 7 by 7 square, and color it in the required way using 7 colors with a known technique: the coloring of each subsequent row is obtained from the coloring of the previous row by a cyclic shift of 2 cells. Then, we select the left lower corner 6 by 6 square from it, which will be the required example.
Let's prove the minimality of 7 colors. Each row of the square contains 6 cells, so at least 6 colors are required for a correct coloring. Suppose we managed to color the square in 6 colors in the required way, then there will be exactly 6 cells of each color, and they will all be in different verticals and horizontals of the square. Let's call the color of the left lower corner cell A of the square black, and show that the remaining 5 black cells cannot be located in the upper right 5 by 5 square in different verticals and horizontals and at the same time not lie on its main diagonal, already controlled by cell A. Otherwise, we can assume that at least three of them would be located below the main diagonal in a "staircase" figure consisting of 10 cells, made up of 4 strips of 4, 3, 2, and 1 cells respectively. However, it is directly verified that for any cell of the "staircase," cells not in the same row, column, or diagonal can correctly contain no more than one black cell. The possible positions of this second black cell are shown in the figure. Cells controlled by it are colored light gray.
Therefore, it is impossible to color the 6 by 6 square in the required way in 6 colors.
Grading criteria. Any explicit and correct example with 7 colors: 3 points. Its correctness does not need to be proven.
Noted that there should be no fewer than 6 colors: 1 point. Proven that there should be no fewer than 7 colors: 4 points.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. In the city, there are 9 bus stops and several buses. Any two buses have no more than one common stop. Each bus has exactly three stops. What is the maximum number of buses that can be in the city
|
Answer: 12.
Solution: if some stop is common for 5 routes, then no two of them have any more common stops, which means there are at least $1+5*2=11$ stops, which contradicts the condition. Therefore, each stop is the intersection of no more than 4 routes, then the total number of stops made by buses is no more than 94, and since there are 3 buses on each route, the total number of buses is no more than $94 / 3=12$.
Buses in the city can run, for example, as follows (stops are marked with numbers): $(1,2,3),(4,5,6),(7,8,9)$ $(1,4,7),(2,5,8),(3,6,9)$ $(1,5,9),(2,6,7),(3,4,8)$ $(3,5,7),(2,4,9),(1,6,8)$.
Criteria: only the example - 3 points; only the estimation that it cannot be more than 12 - 3 points; only the remark that one stop cannot be in more than 4 routes - 1 point; only the answer - 0 points.
## 8th grade
## Each problem is worth 7 points
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In the city, there are 9 bus stops and several buses. Any two buses have no more than one common stop. Each bus has exactly three stops. What is the maximum number of buses that can be in the city?
|
Answer: 12.
Solution: if some stop is common for 5 routes, then no two of them have any more common stops, which means there are at least $1+5*2=11$ stops, which contradicts the condition. Therefore, each stop is the intersection of no more than 4 routes, then the total number of stops made by buses is no more than 94, and since there are 3 buses on each route, the total number of buses is no more than $94 / 3=12$.
Buses in the city can operate, for example, as follows (stops are denoted by numbers):
$(1,2,3),(4,5,6),(7,8,9)$
$(1,4,7),(2,5,8),(3,6,9)$
$(1,5,9),(2,6,7),(3,4,8)$
$(3,5,7),(2,4,9),(1,6,8)$.
Criteria: only the example - 3 points; only the estimation that it cannot be more than 12 - 3 points; only the remark that one stop cannot be in more than 4 routes - 1 point; only the answer - 0 points.
## 9th grade
Each problem is worth 7 points
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. The electronic clock on the building of the station shows the current hours and minutes in the format HH:MM from 00:00 to 23:59. How much time in one day will the clock display four different digits?
|
Answer: 10 hours 44 minutes.
Solution. Each possible combination of four digits burns on the clock for one minute. Consider separately the time of day from 00:00 to 19:59 and from 20:00 to 23:59. In the first case, the number of valid combinations according to the problem's conditions will be: 2 (the tens digit of the hour in the first position), multiplied by 5 (the tens digit of the minute in the third position, except for the one already burning in the first position), multiplied by 8 (the units digit of the hour, not equal to the digits in the 1st and 3rd positions) and multiplied by 7 (the units digit of the minute in the fourth position, not equal to the digits in the 1st, 2nd, and 3rd positions). This results in 560 combinations, burning for 560 minutes, which is 9 hours and 20 minutes per day.
In the second case, the number of valid combinations according to the problem's conditions will be: 1 (the tens digit of the hour in the first position, equal to 2), multiplied by 3 (the units digit of the hour in the second position, not equal to 2), multiplied by 4 (the tens digit of the minute in the third position, except for those already burning in the 1st and 2nd positions) and multiplied by 7 (the units digit of the minute in the fourth position, not equal to the digits in the 1st, 2nd, and 3rd positions). This results in 84 combinations, burning for 84 minutes, which is 1 hour and 24 minutes per day. Together, we get 10 hours and 44 minutes.
## Grading Criteria.
The idea of dividing the consideration into cases for the time of day from 00:00 to 19:59 and from 20:00 to 23:59: 2 points.
The idea of counting the number of options by digits in a convenient order of position: 3 points.
The correct calculation after this: 2 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In a fairy-tale country, every piglet either always lies or always tells the truth, and each piglet reliably knows whether every other piglet is a liar. One day, Nif-Nif, Naf-Naf, and Nuf-Nuf met for a cup of tea, and two of them made statements, but it is unknown who exactly said what. One of the three piglets said: “Nif-Nif and Naf-Naf both always lie.” Another said: “Nif-Nif and Nuf-Nuf both always lie.” Determine how many liars are among the three piglets.
|
# Answer: Two
Solution: If at least one of the statements is true, then the piglets mentioned in it are liars, which means there are at least two liars. At the same time, the one making this true statement must be telling the truth. Therefore, there are no more than two liars. In total, if at least one of the spoken phrases is true, then there are two liars. Note that this is possible, for example, if the first phrase is said by Nuf-Nuf.
If both statements are false, then those who say them are liars. This means there are at least two liars. At the same time, for each phrase to be false, at least one honest piglet must be mentioned. This means there is one, so there are no more than two liars. Thus, in this case, there are exactly two liars. Note that this situation is possible if the only honest piglet is Nif-Nif and he is silent.
Criteria: Only the answer - 0 points.
Example that there can be 2 liars, no other progress - 1 point.
Enumerative solution, missing cases - no more than 4 points.
For the absence of verification that there can indeed be two liars, do not deduct points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. On a certain island, only knights, who always tell the truth, and liars, who always lie, live. One day, 99 inhabitants of this island stood in a circle, and each of them said: "All ten people following me in a clockwise direction are liars." How many knights could there be among those standing in the circle?
|
Answer: 9 knights.
Solution. Note that all people cannot be liars, because then it would mean that each of them is telling the truth. Therefore, among these people, there is at least one knight. Let's number all the people so that the knight is 99th in the sequence. Then, the 10 people with numbers from 1 to 10 are liars (this follows from the knight's statement). Moreover, the 10 people with numbers 89-98 are also liars, since they made an incorrect statement (there is a knight among the ten people standing after them). Therefore, since these 10 people stand in a row along our circle after person number 88, he told the truth and, consequently, is also a knight. Repeating the reasoning for him, we get that people with numbers 78-87 are liars, and so on. In the end, we get that the knights are people with numbers 99, 88, 77, ..., 11, that is, there are 9 of them in total.
For completeness, note that we have proven that if the arrangement is possible, it must look exactly like this. It is not difficult to check that there are no contradictions, and that the people could indeed stand this way.
Criteria. Only the answer - 0 points.
Only the answer with an example of the arrangement - 2 points.
The case where there are no knights is not considered - no points deducted.
The obtained arrangement is not verified - no points deducted.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. We consider all possible tilings of an 8 by 8 chessboard with dominoes, each consisting of two adjacent squares. Determine the maximum natural number \( n \) such that for any tiling of the 8 by 8 board with dominoes, one can find some rectangle composed of \( n \) squares of the board that does not contain any domino in its entirety. The lengths of the sides of the rectangle in squares can be any natural numbers, starting from one.
|
Answer. $n=4$.
Solution. 1) We will prove that $n \leq 4$. Consider the following tiling of an 8 by 8 chessboard with dominoes. Divide the board into 2 by 2 squares, color each of them in red and blue in a checkerboard (relative to the 4 by 4 board) pattern, and divide the red squares into pairs of horizontal dominoes, and the blue squares into pairs of vertical dominoes. Any rectangle with an area greater than 4 either contains a 1 by 5 rectangle or a 2 by 3 rectangle. It is easy to verify that for the considered tiling, a 1 by 5 rectangle or a 2 by 3 rectangle in any position on the board contains at least one entire domino.
2) We will prove that for any tiling of an 8 by 8 board with dominoes, one can find some rectangle of area 4, composed of cells, that does not contain any entire domino. Consider the domino in the tiling that contains cell d4; we can, by rotating the board if necessary, assume it is horizontal. We will consider in detail the case where it consists of cells c4, d4; the case where it consists of cells d4, e4 is analogous. Consider the cells c3, d3 and c5, d5. If at least one of these cells, say c3 (other cases are analogous), lies in a horizontal domino of the tiling, then the vertical rectangle c2, c3, c4, c5 does not contain any entire domino of the tiling. If all these cells lie in vertical dominoes of the tiling, then the dominoes containing c3 and d3 are vertical, so the rectangle b3, c3, d3, e3 does not contain any entire domino of the tiling. Note that by choosing cell d4 to start the reasoning, we ensure that the selected 1 by 4 strip cannot extend beyond the board.
Grading criteria. ($\cdot$) If the point 1) that $n \leq 4$ is proven: 2 points. ($\cdot$) If the point 2) that one can always find some suitable rectangle of area 4: 5 points. ($\cdot$) If an example of a tiling is provided where any rectangle with more than 4 cells always contains an entire domino, and it is correct, the score is not reduced for lack of meticulous verification. ($\cdot$) In a generally correct reasoning about selecting a 1 by 4 strip of cells that does not contain any entire domino, the possibility of extending beyond the edge of the board is not considered: minus 2 points. ($\cdot$) In the reasoning, the possibility of the sought rectangle extending beyond the edge of the board is allowed: the solution is given 0 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. What is the minimum sum of digits in the decimal representation of the number $f(n)=17 n^{2}-11 n+1$, where $n$ runs through all natural numbers?
# Answer. 2.
|
Solution. When $n=8$, the number $f(n)$ is 1001, so the sum of its digits is 2. If $f(n)$ for some $n$ had a sum of digits equal to 1, it would have the form $100, \ldots 00$ and would either be equal to 1 or divisible by 10. The function of a real variable $f(x)$ reaches its minimum at $x=\frac{11}{34}1$, and $f(n)$ cannot take the value 1. Furthermore, it is easy to notice that $f(n)$ is always an odd number, so it cannot be divisible by 10. Therefore, the minimum sum of the digits of the number $f(n)=17 n^{2}-11 n+1$ is 2, and it is achieved when $n=8$.
Grading Criteria. Correct answer with verification for $n=8$: 2 points. Proven that $f(n)>1$ and that $f(n)$ cannot take the value 1: 2 points. Proven that $f(n)$ is always an odd number, so it cannot be divisible by 10: 3 points.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. It is known that $70 \%$ of mathematicians who have moved to IT regret their change of activity. At the same time, only $7 \%$ of all people who have moved to IT regret the change. What percentage of those who have moved to IT are mathematicians, if only they regret the change of activity?
|
Solution. Let a total of $x$ people went into IT, and $y$ of them are mathematicians. According to the condition of the change in activity, on the one hand, $0.07 x$ people regret, and on the other - $0.7 y$. From this, we get that $0.07 x=0.7 y$, from which $y / x=0.1$, that is, $10 \%$.
Criteria. Only the answer - 1 point.
Solution in a particular case (let there be 100 people in total...) without reference to the general - no more than 5 points.
|
10
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. What is the maximum number of rooks that can be placed on an 8x8 chessboard so that each rook attacks no more than one other? A rook attacks all squares on the same row and column it occupies.
|
Answer: 10.
Solution: It is clear that in each column and row there are no more than two rooks. Let $k$ rooks be placed while satisfying the condition. On each square where a rook is placed, write the number 0. In each of the 8 columns, perform the following operation: if there are two numbers in the column, add 1 to both; if there is one number, add 2 to it (do nothing in an empty column). Then perform the same operation for each row. Clearly, on the square of each of the $k$ rooks, the result will be either 3 or 4 (if 2 is written, then this rook is under attack by two others), so the sum $S$ of all the written numbers is at least $3k$. On the other hand, since we added no more than 2 in each of the 8 columns and then in each of the 8 rows, $S \leq 32$. Therefore, $3k \leq S \leq 32$, from which $k \leq 10$. An example is easily constructed.
Criterion: Only the answer - 0 points. An example is worth 2 points, the estimation of the number of rooks is worth 5 points (points are cumulative).
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Find all natural $n$, for which on a square grid of size $n$ by $n$ cells, it is possible to mark $n$ cells, each in different rows and different columns, that can be sequentially visited by a knight's move in chess, starting from some cell, without landing on the same cell twice, and returning to the starting cell. The knight can only land on the marked cells.
|
Answer. $n=4$.
Solution. An example for $n=4$ is not difficult:
We will prove that for $n \neq 4$, the required set of cells does not exist.
Suppose that for a given $n$, it is possible to mark $n$ cells in different rows and different columns of an $n \times n$ board, which can be sequentially traversed by a knight's move and return to the initial marked cell. Consider the horizontal displacements of the knight during its sequential moves to the marked cells in the columns of the board. The knight either moves to a cell in column a (the first from the left) from a cell in column b (the second from the left), and then moves to a cell in column c (the third from the left), or vice versa. In the first case (the second case is symmetric to the first), to avoid repeating columns, the knight can only move to column b from column d, and can only move from column c to column e. All preceding moves to column d and subsequent moves from column e are made with a horizontal displacement of 2, except for one with a displacement of 1, which will close the chain of the knight's movements and can only occur at the right edge of the board. In total, the knight will move horizontally 2 times by one cell and $n-2$ times by two cells. The same can be said about its vertical movements along the rows of the board. Each move of the knight involves a displacement of one cell in one direction and two cells in the other, so in the total set of all $2n$ displacements in both directions, the number of displacements by one cell must equal the number of displacements by two cells, from which $2n-4=4$ and $n=4$.
Grading criteria. The idea of considering moves along the three outermost columns (rows) of the board: 2 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Two athletes with constant speeds run on an oval track of a sports ground, the first of them runs the track completely 5 seconds faster than the second. If they run on the track from the same starting point in the same direction, they will meet again for the first time after 30 seconds. How many seconds will it take for them to meet again for the first time if they run on the track from the same starting point in opposite directions
|
Answer. In 6 seconds.
Solution. Let the length of the track be $S$ meters, and the speeds of the first and second runners be $x$ and $y$ meters per second, respectively. From the first condition: $\frac{S}{x} + 5 = \frac{S}{y}$, and from the second condition $\frac{S}{x-y} = 30$, since in this case the first runner catches up with the second runner who is initially $S$ meters behind. From the second equation, we express $S = 30(x - y)$, substitute it into the first equation, make the substitution $t = \frac{x}{y} > 1$, and obtain the equation $t^2 - \frac{13}{6} t + 1 = 0$, from which $t = \frac{3}{2} = \frac{x}{y}$. Express $y = \frac{2}{3} x$, substitute it into the second equation, we have $\frac{S}{x} = 10$, that is, $S = 10 x$.
If the runners run in opposite directions, their speeds will add up, and they will meet after covering the track in $\frac{S}{x+y} = \frac{S}{\frac{5}{3} x} = \frac{3}{5} \frac{S}{x} = 6$ seconds.
Grading criteria. Correct formulation of the system of equations: 3 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. In a row from left to right, all natural numbers from 1 to 37 are written in such an order that each number, starting from the second to the 37th, divides the sum of all numbers to its left: the second divides the first, the third divides the sum of the first and second, and so on, the last divides the sum of the first thirty-six. The number 37 is on the first place from the left, what number is on the third place?
|
Answer: 2.
Solution. If the first number is the prime number 37, then the second must be 1, and the third must be a divisor of the number $37+1=38$, that is, 2 or 19. However, 19 must be in the last position, since the number 37 minus an even number must divide the sum of all the other numbers and itself, that is, divide the sum of all the numbers, which is $\frac{(1+37) \cdot 37}{2}=19 \cdot 37$, and must equal 19, as 37 is already occupied. Therefore, the number 2 is in the third position.
Grading Criteria. The solution does not require providing an example of the arrangement of numbers that satisfies the condition. If a complete correct example with the number 2 in the third position is provided without proving its uniqueness: 3 points. For constructing an example of the arrangement, if everything else is correctly proven, no additional points are added.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Each cell of a $5 \times 5$ table is painted in one of several colors. Lada shuffled the rows of this table so that no row remained in its original position. Then Lera shuffled the columns so that no column remained in its original position. To their surprise, the girls noticed that the resulting table was the same as the original one. What is the maximum number of different colors this table can be painted with?
|
# Answer: 7.
Solution: Let's renumber the colors and reason about numbers instead. Both columns and rows could have been cyclically permuted or divided into a pair and a triplet. If a cyclic permutation of columns was used, then all columns consist of the same set of numbers, i.e., no more than five different numbers. The same situation applies to a cyclic permutation of rows.
If, however, both columns and rows were divided into a pair and a triplet, the table can be conditionally divided into squares $2 \times 2$ and $3 \times 3$, as well as rectangles $2 \times 3$ and $3 \times 2$, in each of which both columns and rows are cyclically permuted. In the squares, there can be no more than two and three different numbers, respectively (because the set of numbers in each column is the same), and in the rectangles, no more than one (since both in columns and rows, the set of numbers must be the same).
Example for seven numbers see in the figure.
Criteria: Only the estimate - 3 points
Only the example - 3 points.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. For what minimum natural $n$ can $n$ distinct natural numbers $s_{1}, s_{2}, \ldots, s_{n}$ be found such that $\left(1-\frac{1}{s_{1}}\right)\left(1-\frac{1}{s_{2}}\right) \ldots\left(1-\frac{1}{s_{n}}\right)=\frac{7}{66} ?$
|
Answer. $n=9$.
Solution. We can assume that $1<s_{1}<s_{2}<\ldots<s_{n}$, then for any $k=1, \ldots, n$ the inequality $s_{k} \geq k+1$ holds. Therefore, $\frac{7}{66}=\left(1-\frac{1}{s_{1}}\right)\left(1-\frac{1}{s_{2}}\right) \ldots\left(1-\frac{1}{s_{n}}\right) \geq\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) \ldots\left(1-\frac{1}{n+1}\right)=\frac{1}{2} \cdot \frac{2}{3} \cdot \ldots \cdot \frac{n}{n+1}=\frac{1}{n+1}$, from which $n \geq 9$.
Example of nine numbers satisfying the condition: $2,3,4,5,6,8,9,10,11$.
Grading criteria. Estimation $n \geq 9: 5$ points. Example of nine numbers satisfying the condition: 2 points.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. A finite set of distinct real numbers $X$ is called good if each number in $X$ can be represented as the sum of two other distinct numbers in $X$. What is the minimum number of elements that a good set $X$ can contain?
#
|
# Answer: 6.
Solution. From the condition, it follows that $X$ contains no less than three numbers, which means there are non-zero numbers in it. By multiplying all numbers by minus one if necessary, we can assume that $X$ contains positive numbers. Let's choose the largest number $M$ from them. According to the condition, it is equal to the sum of two other distinct numbers from $X$, each of which is smaller than it. From the maximality of $M$, it follows that both of these numbers are positive. Therefore, $X$ contains no less than three distinct positive numbers. Consider the smallest positive number $\boldsymbol{m}$, it is equal to the sum of two other distinct numbers from $X$, one of which must be negative due to the minimality of $\boldsymbol{m}$. Now let's choose the smallest negative number $\mathrm{N}$ from $X$, it is also equal to the sum of two other distinct numbers from $X$, each of which is greater than it. From the minimality of $\mathrm{N}$, it follows that both of these numbers are negative. Therefore, $X$ contains no less than three distinct negative numbers. Thus, a good set $X$ must contain no fewer than six numbers.
An example of a good set with six elements is the set $X=\{-3,-2,-1,1,2,3\}$.
Grading Criteria. ($\cdot$) An example of a good set with six numbers is provided: 2 points. ($\cdot$) It is proven that $X$ contains no less than 3 positive or negative numbers: 3 points. ($\cdot$) It is proven that $X$ must contain numbers of different signs: 2 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. What is the maximum number of colors in which all cells of a 4 by 4 square can be painted so that any 2 by 2 square of cells necessarily contains at least two cells of the same color?
|
Answer: In 11 colors.
Solution. We will prove that the maximum number of colors under the conditions of the problem does not exceed 11. Consider in a 4x4 square five 2x2 squares: four corner ones and the central one. The corner 2x2 squares do not intersect, and the central one shares one common cell with each of the corner ones. According to the condition, each corner 2x2 square contains cells of no more than three different colors, totaling no more than 12. But if there are no repeating colors among these four sets of three colors in the corner 2x2 squares, then the central 2x2 square must contain cells of four different colors - one from each set of three, which contradicts the condition. Therefore, the total number of different colors in which the cells of the 4x4 square are painted does not exceed 12-1=11. If, however, in at least one of the corner 2x2 squares no more than two different colors are used, then the total number of different colors is immediately no more than 11.
An example of coloring a 4x4 square in 11 colors, satisfying the condition of the problem, looks like this: the bottom horizontal row of the square is painted in different colors $1,2,3$ and 4, the second horizontal row - entirely in color 5, the third horizontal row in different colors $6,7,8$ and 9, and the fourth horizontal row - in colors $10,7,11,9$.
Grading criteria. ($\cdot$) Proof of the maximum of 11 colors: 4 points, ($\cdot$) If the case where in one of the corner 2x2 squares no more than two different colors are used is not considered at all in the proof of the maximum of 11 colors: minus 1 point. ($\cdot$) Example of a correct coloring in 11 colors: 3 points.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In a kindergarten, each child was given three cards, each of which had either "MA" or "NYA" written on it. It turned out that 20 children could form the word "MAMA" from their cards, 30 children could form the word "NYANYA," and 40 children could form the word "MANYA." How many children had all three cards the same?
|
Answer: 10 children.
Solution. Let's denote the number of children who received three "MA" cards as $x$, two "MA" cards and one "NA" card as $y$, two "NA" cards and one "MA" card as $z$, and three "NA" cards as $t$. Then, the word "MAMA" can be formed by all children from the first and second groups and only them, the word "NANA" - by all children from the third and fourth groups and only them, and the word "MANA" - by all children from the second and third groups and only them. Therefore, $x+y=20, z+t=30, y+z=40$, so the desired number is $x+t=(x+y)+(z+t)-(y+z)=20+30-40=10$ children.
Grading criteria. A guessed answer with some examples is not to be evaluated. Formulating but not solving the system of equations: 3 points. Misinterpreting the problem: 0 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. For seven natural numbers $a, b, c, a+b-c, a+c-b, b+c-a, a+b+c$ it is known that all of them are different prime numbers. Find all values that the smallest of these seven numbers can take.
|
Answer: 3.
Solution. From the condition, it follows that $a, b, c$ are also primes. If the smallest of the seven numbers were equal to two, the last four numbers would be different even numbers, which means they could not all be prime. If all seven numbers are greater than three, due to their primality, they are not divisible by 3, and their remainders when divided by 3 are 1 or -1. Consider the remainders of the numbers $a, b, c$ when divided by 3. If all their remainders are equal, then the number $a+b+c$ is divisible by 3. If two of them are equal and the third has the opposite sign, then one of the numbers $a+b-c, a+c-b, b+c-a$ is divisible by 3. In both cases, one of the seven numbers is divisible by 3 and, by assumption, is greater than 3, which contradicts its primality. Therefore, the smallest of the seven numbers in the condition can only be equal to 3. An example of such numbers: $a=7, b=13, c=17, a+b-c=3, a+c-b=11, b+c-a=23, a+b+c=37$.
Grading criteria. Correct answer with an example: 2 points. Proof of the minimality of the number 3: 5 points. If the case with two is not considered - deduct 2 points.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Daniil has 6 cards with letters, from which he managed to form the word WNMWNM shown in the picture. Note that this word has a remarkable property: if you rotate it 180 degrees, you get the same word. How many words with such a property can Daniil form using all 6 cards at once?

|
Answer: 12 words.
## Solution:
(1) According to the problem, Danil has 2 cards with the letter $\mathrm{N}$, which remains the same when flipped, and 4 cards with the letter M, which turns into the letter W when flipped. Clearly, to get a word with the desired properties, we need to arrange 2 letters M and one $\mathrm{N}$ in the first half, and the second half of the word will be uniquely determined.
(2) The letter $\mathrm{N}$ can be placed in three ways, after which the letter M can be placed on the first of the remaining positions in two ways (flip or not), and on the last position also in two ways. In total, there are $3 * 2 * 2=12$ options.
## Criteria:
Only the answer - 1 point.
Only the idea that the first three letters uniquely determine the word (part (1) of the solution) - 2 points (can be combined with the previous one).
After noting (1), listing all options with at least one missed case - no more than three points.
All 12 options are listed, but it is not explained why there are no other options - 1 point.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 The banker leaves home, and at that exact moment, a car from the bank arrives to take him to the bank. The banker and the car always leave at the same time, and the car always travels at a constant speed. One day, the banker left home 55 minutes earlier than usual and, for fun, started walking in the direction opposite to the bank. The car caught up with him and took him to the bank 10 minutes later than usual. Find the ratio of the car's speed to the banker's speed.
|
Answer. The speed of the car is 12 times greater than the speed of the banker.
Solution. Indeed, the car delivered the banker to the bank 10 minutes later than usual, which means it caught up with him 5 minutes later than usual, i.e., from the moment he usually leaves his house. Therefore, the car traveled from the banker's house to the meeting point (or capture point) for 5 minutes. The banker, having left 55 minutes earlier than usual and being caught (captured) by the car, had walked from his house for $55+5=60$ minutes by the time of the meeting. Thus, the car travels 12 times faster than the banker walks.
Grading criteria. ($\cdot$) Proven that the car traveled from the banker's house to the meeting point for 5 minutes: 3 points. ($\cdot$) Proven that the banker had walked for 60 minutes by the time of the meeting: 2 points. ($\cdot$) Proven that the car travels 12 times faster than the banker walks: 2 points.
9.3.. Let $\sqrt{x}-\sqrt{y}=10$. Prove that $x-2 y \leq 200$.
Proof. Rewrite the condition as $\sqrt{x}=\sqrt{y}+10$. Both sides of the equation are non-negative, so we square both sides: $x=100+20 \sqrt{y}+y$. Then $x-2 y=100+20 \sqrt{y}-y=200-(10-\sqrt{y})^{2} \leq 200$, which is what we needed to prove.
Grading criteria. Not mentioning the non-negativity of both sides of the equation before squaring: minus 1 point.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Find the value of the expression $\frac{1}{1+x^{2}}+\frac{1}{1+y^{2}}+\frac{2}{1+x y}$, given that $x \neq y$ and the sum of the first two terms of the expression is equal to the third.
|
Answer: 2.
Solution. Let's write the condition of the equality of the sum of the first two terms to the third one as: $\frac{1}{1+x^{2}}-\frac{1}{1+x y}=\frac{1}{1+x y}-\frac{1}{1+y^{2}} \quad$ and bring it to a common denominator:
$\frac{x(y-x)}{(1+x^{2})(1+x y)}=\frac{y(y-x)}{(1+y^{2})(1+x y)}$. Given $x \neq y$, we cancel $x-y$ and $1+x y$: $x(1+y^{2})=y(1+x^{2})$. The latter is equivalent to $(x-y)(x y-1)=0$, and again we cancel $x-y$, obtaining $x y=1$ and the desired expression equals $\frac{2}{1+x y} \cdot 2=2$.
Grading criteria. Any suitable $x \neq y$ guessed and the answer: 1 point.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. A set for playing lotto contains 90 barrels numbered with natural numbers from 1 to 90. The barrels are somehow distributed among several bags (each bag contains more than one barrel). We will call a bag good if the number of one of the barrels in it equals the product of the numbers of the other barrels in the same bag (for example, the bag "2, 3, 6" is good, while "4, 5, 10" is not). What is the maximum possible number of good bags?
|
Answer: 8.
Solution: In each good bag, there are no fewer than three barrels. The smallest number in each good bag must be unique; otherwise, the largest number in this bag would not be less than $10 \times 11=110$, which is impossible. For the same reason, if a good bag contains a barrel with the number 1, it must also contain another barrel with a single-digit number. Therefore, the number of good bags does not exceed 8.
On the other hand, an example can be provided where there are exactly 8 good bags. We can gather 8 good bags $(2,17,34),(3,16,48),(4,15,60),(5,14,70),(6,13,78),(7,12,84),(8$, $11,88)$, and $(9,10,90)$. All other numbers can be placed in a separate bag that is not good.
Criteria: Example only - 3 points.
Estimate only - 3 points.
Noting that each bag must contain a single-digit number - 1 point, can be combined with the example.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Experienced sawyer Garik knows how to make cuts. In one day of continuous work, he can saw 600 nine-meter logs into identical three-meter logs (they differ from the original only in length). How much time will the experienced sawyer Garik need to saw 400 twelve-meter logs (they differ from the nine-meter logs only in length) into the same three-meter logs?
|
Answer: one day
Solution: to turn a 9-meter log into 3 three-meter pieces, 2 cuts are needed. Therefore, Garik makes $2 * 600=1200$ cuts per day. To turn a 12-meter log into three-meter pieces, 3 cuts are needed, and for 400 logs, $400 * 3=1200$ cuts are needed, which means it will take the same amount of time.
Criteria: only answer -1 point.
|
1
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. The ore contains $21 \%$ copper, enriched - $45 \%$ copper. It is known that during the enrichment process, $60 \%$ of the mined ore goes to waste. Determine the percentage content of ore in the waste.
|
Answer: $5 \%$.
Solution. In the extracted 100 kg of ore, there are 21 kg of copper. From these 100 kg of enriched ore, 40 kg will be obtained, containing 18 kg of copper. Therefore, the 60 kg of waste that went to the dump contain 3 kg of copper, that is, $5 \%$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. A square box 3 by 3 is divided into 9 cells. It is allowed to place balls in some cells (possibly a different number in different cells). What is the minimum number of balls that need to be placed in the box so that each row and each column of the box contains a different number of balls?
|
Answer: 8.
Solution: Add up the number of balls in all rows and columns. Since these are 6 different non-negative numbers, this sum is at least $0+1+\ldots+5=15$.
Now notice that the sum of the numbers in the rows is equal to the sum of the numbers in the columns, since these sums are equal to the total number of balls in the box. Therefore, the sum of the six numbers is twice the sum of the numbers in the rows, which means it is even. Thus, twice the number of balls in the box is greater than 15, so the number of balls is greater than 7. An example with 8 is shown alongside.
Criteria: only the answer - 0 points, only the example - 2 points, only noted that the sum of 6 numbers is not less than $15-1$ point. Only the correct estimate - 3 points.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find all natural numbers $n$ such that $\frac{1}{n}=\frac{1}{p}+\frac{1}{q}+\frac{1}{p q}$ for some primes $p$ and $q$
|
Answer. $n=1$.
Solution. Bringing the expression in the condition to a common denominator, we get: $n(p+q+1)=pq$. From the simplicity of $p$ and $q$, it follows that the divisors of the right-hand side can only be the numbers $1, p, q$, and $pq$, one of which must equal $p+q+1$. Since $1, p$, and $q$ are less than $p+q+1$, we obtain $pq=p+q+1$ and $n=1$. Rewriting the last equation as $(p-1)(q-1)=2$, we get $p=2, q=3$ or $p=3, q=2$.
Grading Criteria. Guessed $n=1$ and $p=2, q=3$ or $p=3, q=2$: 1 point. Proved that $n=1$ is the only number that can satisfy the condition: 5 points. Shown that it satisfies the condition for $p=2, q=3$ or $p=3, q=2$: 2 points. (It is sufficient to simply provide the example $p=2, q=3$ or $p=3, q=2$)
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. What is the maximum number of different rectangles that an 8 by 8 chessboard can be cut into? All cuts must follow the grid lines. Rectangles are considered different if they are not equal as geometric figures.
|
Answer: 12.
Solution. Let's list the possible sizes of different integer rectangles of minimal areas that can fit along the grid lines on an 8 by 8 board in ascending order of these areas: 1 by 1, 1 by 2, 1 by 3, 1 by 4, 2 by 2, 1 by 5, 1 by 6, 2 by 3, 1 by 7, 1 by 8, 2 by 4, 3 by 3, 2 by 5. There are already 13 rectangles, and the sum of their areas is 73, which is greater than the area of the board. Therefore, it is impossible to cut the board into more than 12 rectangles in the required manner.
On the other hand, the sum of the areas of all of them except the 3 by 3 is exactly 64, and it is possible to provide an example of such a partition into all 12 rectangles except the 3 by 3: the first four verticals of the board can be cut into strips of width 1 and lengths 1 and 7, 2 and 6, 3 and 5, and 8, respectively. The remaining 4 verticals can be divided into two vertical rectangles 2 by 7, composed of rectangles 2 by 5 and 2 by 2, and 2 by 4 and 2 by 3. Above them, add a horizontal strip 1 by 4.
Other examples of such a partition are also possible.
Grading criteria. It is proven that the number of rectangles in the partition does not exceed 12: 4 points. A correct example for 12 rectangles is provided: 3 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. It is known that the values of the quadratic trinomial $a x^{2}+b x+c$ on the interval $[-1,1]$ do not exceed 1 in absolute value. Find the maximum possible value of the sum $|a|+|b|+|c|$. Answer. 3.
|
Solution. Substituting the values $x=0,1,-1$ from the interval $[-1,1]$ into the polynomial $a x^{2}+b x+c$, we obtain three inequalities: $-1 \leq c \leq 1$, $-1 \leq a+b+c \leq 1$, and $-1 \leq a-b+c \leq 1$. Adding the second and third inequalities, we also get $-1 \leq a+c \leq 1$. Subtracting the second from the third (they are double and symmetric!), we have $-1 \leq b \leq 1$. Subtracting $-1 \leq c \leq 1$ from $-1 \leq a+c \leq 1$, we get $-2 \leq a \leq 2$. Due to the symmetry of the problem's conditions with respect to multiplication by -1, we can assume the coefficient $a$ is positive. If $b, c \geq 0$, then $|a|+|b|+|c|=$ $a+b+c \leq 1$ as proven. If $b<0, c \geq 0$, then $|a|+|b|+|c|=a-b+c \leq 1$, as proven. If $b \geq 0, c<0$, then $|a|+|b|+|c|=a+b-c=(a+b+c)-2 c \leq 1+2=3$. If $b, c<0$, then $|a|+|b|+|c|=a-b-c=(a-b+c)-2 c \leq 1+2=3$. Thus, the sum $|a|+|b|+|c|$ under the conditions of the problem does not exceed 3.
The value 3 is achieved, for example, on the polynomial $f(x)=2 x^{2}-1$: its minimum value is reached inside the interval at the vertex of the parabola when $x=0$, and its maximum values are reached at the ends of the interval when $x=1,-1$.
Grading criteria. Only the boundaries of the coefficients of the equation and their sums from statements 1-3 are found: 2-3 points. The estimate $|a|+|b|+|c| \leq 3$ is proven: 5 points. An example is provided and justified where this boundary is achieved: 2 points. If the example is provided without justification: minus 1 point. Any incorrect boundary: 0 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. What is the maximum number of integers that can be written in a row so that the sum of any five consecutive ones is greater than zero, and the sum of any seven consecutive ones is less than zero?
|
Answer. Ten.
Solution. The sum of any seven written numbers is negative, while the sum of the five outermost numbers from this seven is positive, which means the sum of the two leftmost and the sum of the two rightmost numbers from this seven are negative. Therefore, the sum of any two adjacent numbers, with at least five more numbers to the right or left, is negative.
This means that if we assume more than ten numbers are written, the sum of any two adjacent numbers is negative.
In every sequence of five consecutive numbers, the sum of all is positive, while the sum of two pairs of adjacent numbers is negative, so the outermost and middle numbers of each five are positive. If there are at least nine (or eleven) numbers, each of them will be the outermost in some five, meaning all written numbers will be positive, which contradicts the condition of the negativity of the sums of sevens. Therefore, the number of written numbers is no more than ten.
Let's construct an example for ten numbers. From the previous reasoning, it follows that the numbers with indices $1,3,5,6,8,10$ should be positive, while the others should be negative. Suppose all positive numbers are equal to ${ }^{x}$, and all negative numbers are equal to ${ }^{-y}$. The sum of any five consecutive numbers will be $3 x-2 y>0$, and the sum of any seven consecutive numbers will be $4 x-3 y<0$, from which $\frac{4}{3} x<y<\frac{3}{2} x$. We can take, for example, $x=5, y=7$, then the desired example will be: 5,-7,5,-7,5,5,-7,5,-7,5.
Grading criteria. Noted that the sum of the two leftmost and the sum of the two rightmost numbers from this seven are negative: 1 point. Noted that if there are more than ten numbers, the sum of any two adjacent numbers is negative: 2 points. Noted that the outermost and middle numbers of each five are positive: 1 point. Noted that if there are at least eleven numbers, all numbers will be positive: 1 point. Any correct example for ten numbers: 2 points.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Petya wrote 10 integers on the board (not necessarily distinct).
Then he calculated the pairwise products (that is, he multiplied each of the written numbers by each other). Among them, there were exactly 15 negative products. How many zeros were written on the board?
|
Answer: 2.
Solution. Let there be $A$ positive numbers and $B$ negative numbers on the board. Then $A+B \leq 10$ and $A \cdot B=15$. Since a negative product is obtained when we multiply a negative and a positive number. From this, it is easy to understand that the numbers $A$ and $B$ are 3 and 5 (1). Therefore, $A+B=8$ and there are exactly two zeros on the board.
Criteria. Correct answer without justification - 1 point. Correctly found intermediate relationship (1) - 4 points. Correct answer with justification - 7 points.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. Find all natural numbers $x$ such that the product of all digits in the decimal representation of $x$ equals $x^{2}-10 x-22$
|
Answer: $x=12$.
Solution: First, the product of all digits of a natural number is non-negative, so $x^{2}-10 x-22$, from which $x \geq \frac{10+\sqrt{188}}{2}$, that is, $x \geq 12$. Second, if in the product of all digits of a natural number, all digits except the first are replaced by tens, the product will not decrease, but will not exceed the number itself, so the product of all digits of the number does not exceed the number itself, hence $x^{2}-11 x-22 \leq 0$, from which $x \leq \frac{11+\sqrt{209}}{2}$, that is, $x \leq 12$. For $x=12$, the condition is obviously satisfied, therefore, this is the only answer.
Grading criteria. Only the answer with verification: 1 point. Proof that the product of all digits of the number does not exceed the number itself: 3 points.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. Find all natural numbers $n$ that can be represented as $n=\frac{x+\frac{1}{x}}{y+\frac{1}{y}}$, for some natural numbers $x$ and $y$.
|
Answer. $n=1$
Solution. Transform the equality in the condition to the form $n=\frac{\left(x^{2}+1\right) y}{\left(y^{2}+1\right) x}$. Note that the numbers $x^{2}+1$ and $x$, as well as the numbers $y^{2}+1$ and $y$ are coprime, so $x$ in the denominator can only cancel out with $y$ in the numerator, meaning $y$ is divisible by $x$ and, in particular, $y$ is not less than $x$. Similarly, $y^{2}+1$ in the denominator can only cancel out with $x^{2}+1$ in the numerator, so $y^{2}+1$ divides $x^{2}+1$, in particular, does not exceed it, from which it follows that $y$ does not exceed $x$. Therefore, $y$ equals $x$ and $n=1$. The number $n=1$ is obtained for any pair of equal $x$ and $y$, for example, when they are both equal to 1.
Grading criteria. A statement in the solution like “the numbers $x^{2}+1$ and $x$, as well as the numbers $x^{2}+1$ and $y$ are coprime” can be considered correct without detailed explanations. If there are no references to coprimality: the score will not exceed 2 points. If it is not explicitly stated that the number $n=1$ is still obtained for any pair of equal $x$ and $y$, for example, when they are equal to something specific: 1 point will be deducted.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2 Sergey arranged several (more than two) pairwise distinct real numbers in a circle so that each number turned out to be equal to the product of its neighbors. How many numbers could Sergey have arranged?
|
Answer: 6.
Solution: Let's denote the two adjacent numbers as $a$ and $b$. Then, next to them stands $b / a$, followed by $1 / a, 1 / b, a / b$, and again $a$. Thus, it is impossible to arrange more than 6 numbers.
If 3 numbers can be arranged, then $a=1 / a$, which means $a$ is 1 or -1. In the first case, $b$ and $b / a$ coincide. In the second case, we get the triplet: $-1, b, -b$, where $-1=b * (-b)$, meaning this triplet is $-1, 1, -1$.
If 4 numbers can be arranged, then $a=1 / b$, resulting in the quartet of numbers $a, 1 / a, 1 / a^2, 1 / a$. There are repeating numbers.
If 5 numbers can be arranged, then $a=a / b$, which means $b=1$. This results in the quintet of numbers $a, 1, 1 / a, 1 / a, 1$. There are repeating numbers.
Finally, 6 numbers can be arranged: $2, 3, 3 / 2, 1 / 2, 1 / 3, 2 / 3$.
Criteria: Proving that there are no more than 6 numbers - 3 points.
For considering each case - 1 point each.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Given a triangle $A B C$, side $A B$ is divided into 4 equal segments $A B_{1}=B_{1} B_{2}=B_{2} B_{3}=B_{3} B$, and side $A C$ into 5 equal segments $A C_{1}=C_{1} C_{2}=C_{2} C_{3}=C_{3} C_{4}=C_{4} C$. How many times larger is the area of triangle $A B C$ compared to the sum of the areas of triangles $C_{1} B_{1} C_{2}, C_{2} B_{2} C_{3}, C_{3} B_{3} C_{4}, C_{4} B C$?
|
Answer: 2 times.
Solution: Let the area of $A B_{1} C_{1}$ be $S$. Then the area of $B_{1} C_{1} C_{2}$ is also $S$, since $B_{1} C_{1}$ is the median in $A B_{1} C_{2}$. Similarly, the area of $B_{1} B_{2} C_{2}$ is $2S$, as $C_{2} B_{1}$ is the median in $A B_{2} C_{2}$. The area of $B_{2} C_{2} C_{3}$ is half the area of $A B_{2} C_{2}$, because these triangles share the same height, and the base $C_{2} C_{3}$ is half the length of the base $A C_{2}$. Therefore, the area of $B_{2} C_{2} C_{3}$ is $2S$. From similar reasoning, the area of $B_{2} C_{3} B_{3}$ is half the area of $A B_{2} C_{3}$, which is $3S$. Since $C_{3} C_{4}$ is one-third of $A C_{3}$, the area of $B_{3} C_{3} C_{4}$ is one-third of $A B_{3} C_{3}$ and equals $3S$. Similarly, the areas of $B_{3} C_{4} B$ and $C_{4} B C$ are each $4S$. Therefore, the total area of the shaded part is $S + 2S + 3S + 4S = 10S$, and the unshaded part is $S + 2S + 3S + 4S = 10S$, meaning the shaded area is half of the entire triangle.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Masha and Misha set out to meet each other simultaneously, each from their own house, and met one kilometer from Masha's house. Another time, they again set out to meet each other simultaneously, each from their own house, but Masha walked twice as fast, and Misha walked twice as slow as the previous time. This time, they met one kilometer from Misha's house. What is the distance between Masha's and Misha's houses?
|
# Answer: 3 km.
Solution: We will prove that they spent the same amount of time on the first and second occasions. Suppose this is not the case, and they spent less time on the second occasion. Then, on the first occasion, Masha walked 1 km, and on the second occasion, less than 2 km (her speed was twice as high, but the time was less). Misha walked 1 km on the second occasion, so on the first occasion, he walked more than 2 km (for similar reasons). Therefore, the total distance is more than 3 km (1 km from Masha and more than 2 km from Misha on the first occasion), but at the same time, it is less than 3 km (1 km from Misha and less than 2 km from Masha on the second occasion). This is impossible. If they walked longer on the second occasion, similar reasoning will lead to a contradiction (due to the symmetry of the situations).
Thus, they moved for the same amount of time both times. Therefore, on the second occasion, Masha walked 2 km, and Misha walked 1 km. Consequently, their houses are 3 kilometers apart.
Criteria: answer, answer with verification - 0 points, not proven that the time was the same in the first and second cases, when using this - no more than 2 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Find all positive integer solutions of the equation $(n+2)!-(n+1)!-(n)!=n^{2}+n^{4}$. Answer. $n=3$.
|
Solution. Rewrite the equation as $n!=\left(n^{*}\left(n^{2}+1\right)\right) /(n+2)$. Transforming the right side, we get $n!=n^{2}-2 n+5-10:(n+2)$. The last fraction will be an integer for $n=3$ and $n=8$, but the latter number is not a solution (substitute and check!)
Grading criteria. Acquiring extraneous solutions: minus 3 points. Guessed and verified answer: 1 point.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2 To buy an apartment, you need to take either exactly 9 small, 6 medium, and one large loan, or exactly 3 small, 2 medium, and 3 large loans. How many only large loans would be required to buy an apartment?
|
Answer: 4 large loans.
Solution: Let's denote small, medium, and large loans by the letters m, c, and b, respectively. Rewrite the condition using these notations:
$$
9 \mathrm{M}+6 \mathrm{c}+\sigma=3 \mathrm{~m}+2 \mathrm{c}+3 b
$$
Simplifying, we get $6 \mathrm{~m}+4 \mathrm{c}=2$ b or $3 \mathrm{~m}+2 \mathrm{c}=$ b, which means $3 \mathrm{~m}+2 \mathrm{c}+3 b=4 b$.
Criteria: Only the answer - 0 points.
Correctly formulated equation - 1 point.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. It is known that the sum of the digits of number A is 59, and the sum of the digits of number B is 77. What is the minimum sum of the digits that the number A+B can have?
|
Answer. 1.
Solution. It is sufficient to consider A=9999995, B=999999990000005, then $\mathrm{A}+\mathrm{B}=1000000000000000$, the sum of the digits is 1 - the minimum possible.
Grading Criteria. Correct answer and example: 7 points. Presence of arithmetic errors: minus 1-2 points. Any other answer: 0 points.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On an island, 20 people live, some of whom are knights who always tell the truth, and the rest are liars who always lie. Each islander knows for sure who among the others is a knight and who is a liar. When asked by a visitor how many knights live on the island, the first islander answered: "None," the second: "No more than one," the third: "No more than two," the fourth: "No more than three," and so on, the twentieth stated: "No more than nineteen." So how many knights live on the island?
|
Answer: 10.
Solution: If the first islander were a knight, he would have lied in his answer, which cannot be the case. Therefore, the first is a liar, and there are no more than 19 knights on the island. This means the twentieth islander told the truth, so he is a knight, and there is at least one knight on the island. Then, if the second islander were a knight, there would already be two knights including the twentieth, and he would have lied, so the second is a liar, and there are no more than 18 knights. Therefore, the nineteenth told the truth and is a knight. Continuing this way, it is easy to see that the first to tenth islanders are all liars, and the eleventh to twentieth are all knights.
Grading Criteria: Established that the first is a liar: 1 point. Established that the first is a liar and the second is a knight: 2 points. Given the correct answer and constructed an example with verification: 3 points. Any incorrect answer: 0 points.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Find the value of the expression $\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}$, given that $\frac{1}{y+z}+\frac{1}{x+z}+\frac{1}{x+y}=5$ and $x+y+z=2$.
|
Answer: 7.
Solution. Transform: $\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=\frac{x+y+z}{y+z}+\frac{y+x+z}{x+z}+\frac{z+x+y}{x+y}-3=$ $=(x+y+z)\left(\frac{1}{y+z}+\frac{1}{x+z}+\frac{1}{x+y}\right)-3=2 \cdot 5-3=7$.
Grading Criteria. Presence of arithmetic errors: minus 1-2 points. Correct answer calculated on some example: 1 point.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The bathtub fills up in 23 minutes from the hot water tap, and in 17 minutes from the cold water tap. Pete first opened the hot water tap. After how many minutes should he open the cold water tap so that by the time the bathtub is full, one and a half times more hot water has been added than cold water?
|
# 9.2. Answer. In 7 minutes.
In one minute, the hot water tap fills $\frac{1}{23}$ of the bathtub, and the cold water tap fills $\frac{1}{17}$ of the bathtub. After filling the bathtub, the hot water should make up $\frac{3}{5}$ of the bathtub, and the cold water should make up $\frac{2}{5}$ of the bathtub. Therefore, the hot water tap should be open for $\frac{3}{5} / \frac{1}{23} = \frac{69}{5}$ minutes, and the cold water tap should be open for $\frac{2}{5} / \frac{1}{17} = \frac{34}{5}$ minutes. Thus, the cold water tap should be opened $\frac{69}{5} - \frac{34}{5} = 7$ minutes after the hot water tap is opened.
Grading Remarks. If the answer is only guessed, give 0 points. If the answer is guessed and its correctness is neatly verified, give 3 points. If the equation or system is correctly set up but solved with errors, give 4 to 6 points depending on the type of error.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. What is the maximum number of 4-element subsets that can be selected from a set of 8 elements such that the intersection of any three of the selected subsets contains no more than one element?
|
Answer. Eight.
Solution. We will provide two different examples of choosing eight 4-element subsets in a set $\mathrm{X}$ of eight elements, satisfying the condition of the problem. Both examples are constructed as geometric objects.
Example 1. We will consider the elements of $\mathrm{X}$ as the vertices of a unit cube, six of the chosen subsets will be the faces of this cube, and the remaining two will be the vertices of two inscribed regular tetrahedra with edge length $\sqrt{2}$. No two vertices of these tetrahedra lie on the same edge of the cube.
If among any three of the chosen subsets, both tetrahedra are included, or two parallel faces, the intersection is empty. If it is two adjacent faces and a tetrahedron, the intersection of the faces gives an edge, which intersects the tetrahedron at exactly one vertex. If it is three pairwise adjacent faces, their intersection contains the unique vertex of the trihedral angle formed by these faces.
Example 2. We will consider the elements of $\mathrm{X}$ as the vertices of a regular octagon. Number the vertices clockwise from 1 to 8, and mark the quadrilateral $\mathrm{M}$ with vertices numbered $1,2,3,5$. The chosen subsets will be $\mathrm{M}$ and seven other quadrilaterals obtained from $\mathrm{M}$ by rotations of angles $\frac{2 \pi k}{8}, k=1,2, \ldots, 6,7$. If the intersection of any three of them contained at least two vertices, i.e., some side or diagonal of the octagon other than the main ones, then by rotating all three quadrilaterals back to coincide with $\mathrm{M}$, we would obtain three different segments of the same length connecting the vertices of $\mathrm{M}$. The latter is impossible because the lengths of the sides and diagonals of $\mathrm{M}$, measured in sides, are $1,1,2,2,3,4$, and there are no more than two equal lengths among them. If the main diagonal of length 4 is mentioned, it is clear that it is contained in only two of the eight considered quadrilaterals.
We will prove that if in an 8-element set $\mathrm{X}$, nine 4-element subsets are arbitrarily chosen, then the intersection of some three of them contains more than one element. The sum of the cardinalities of the chosen subsets is 36, so one of the elements of $\mathrm{X}$, denoted by $\boldsymbol{x}$, is contained in at least $k \geq 5$ of them. Remove $\boldsymbol{x}$ from these $k$ subsets and consider the $k \geq 5$ resulting 3-element subsets in the 7-element set Y, which is equal to X without $\boldsymbol{x}$. The sum of the cardinalities of the resulting sets is at least 15, so one of the elements of Y, denoted by $\boldsymbol{y}$, is contained in at least three of the $k$ resulting 3-element subsets. Therefore, the pair of elements $\boldsymbol{x}$ and $\boldsymbol{y}$ is contained in at least three of the nine chosen 4-element subsets from $\mathrm{X}$.
Grading Criteria. ($\cdot$) Example for eight subsets: 3 points. ($\cdot$) Proof of the estimate: 4 points. ($\cdot$) Lack of justification for the example: minus 1 point.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. At the Olympiad, students from gymnasiums, lyceums, and regular schools met. Some of them stood in a circle. Gymnasium students always lie to regular school students, lyceum students lie to gymnasium students, and regular school students lie to lyceum students. In all other cases, the students tell the truth. Each one said to their right neighbor: “I am a gymnasium student.” How many students from regular schools were in this circle?
|
Answer: There were no ordinary school students in the circle.
Solution: Let's assume there was an ordinary school student in the circle. Consider his left neighbor. This neighbor could not be another ordinary school student or a lyceum student, because they would tell the truth. But he also cannot be a gymnasium student, because then he would have lied, and he said the truth. Therefore, the neighbor of the ordinary school student cannot be anyone. Consequently, ordinary school students did not join the circle. Criteria: only the answer - 0 points, answer with verification - 1 point. For the claim that to the right of a gymnasium student there must be a gymnasium student or a lyceum student (in reality, it can be either a lyceum student or a gymnasium student) - deduct 3 points.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Given a convex quadrilateral $A B C D$ with side $A D$ equal to 3. Diagonals $A C$ and $B D$ intersect at point $E$, and it is known that the areas of triangles $A B E$ and $D C E$ are both 1. Find the side $B C$, given that the area of $A B C D$ does not exceed 4.
|
# Answer: 3.
Solution: Triangles $A B D$ and $A C D$ have the same area, as they are composed of the common $A E D$ and equal-area $A B E$ and $D C E$. Since $A B D$ and $A C D$ have the same base $A D$, their heights to this base are equal. Therefore, $B C$ is parallel to $A D$, meaning our quadrilateral is a trapezoid.
Let $B C$ be $x$. Triangles $B E C$ and $A E D$ are similar, so $B E / E D = B C / A D = x / 3$. Additionally, the area of $B E C$ is $B E / E D$ of the area of $B C D$, since these triangles have the same base, and their heights are in the ratio of $B E$ to $E D$. Therefore, the area of $B E C$ is $x / 3$. Similarly, the area of $A E D$ is $3 / x$.
Since the area of the entire quadrilateral does not exceed 4, $x / 3 + 3 / x \leq 2$.
However, the sum of the reciprocals of positive quantities is always at least 2, and equality is achieved only when the terms are equal, i.e., in our case, $x / 3 = 3 / x$, from which $x$ equals 3.
Criteria: Only the answer - 0 points. Proved that $A B C D$ is a trapezoid - plus 2 points. Obtained the equation - plus 1 point. Not explained why the inequality is possible only when the terms are equal - deduct 1 point.
## Criteria for Determining Winners and Prize Winners of the All-Siberian Open Mathematics Olympiad for Schoolchildren (2015-2016 academic year)
According to the Regulations, the winners and prize winners of the Olympiad were determined based on the results of the Final Stage of the Olympiad. The total number of winners and prize winners was 380 out of 1578 participants, which is 24.08%. The number of winners was 85, which is 5.38%.
Based on the overall ranking of participants and considering the noticeable gaps in the scores of the top-ranked groups, the Olympiad jury developed the following criteria for determining winners and prize winners: The maximum possible score is 35 points.
## 11th Grade:
Winners:
Participants who scored more than 77% of the maximum possible points, i.e., from 27 to 35 points; Prize winners:
2nd degree - more than 62% of the maximum possible points, i.e., from 22 to 26 points 3rd degree - more than 51% of the maximum possible points, i.e., from 18 to 21 points
10th Grade:
Winners:
Participants who scored more than 85% of the maximum possible points, i.e., from 30 to 35 points;
Prize winners:
2nd degree - more than 62% of the maximum possible points, i.e., from 22 to 29 points
3rd degree - more than 51% of the maximum possible points, i.e., from 18 to 21 points
9th Grade:
Winners:
Participants who scored more than 85% of the maximum possible points, i.e., from 30 to 35 points;
Prize winners:
2nd degree - more than 65% of the maximum possible points, i.e., from 24 to 29 points
3rd degree - more than 51% of the maximum possible points, i.e., from 18 to 23 points
8th Grade:
Winners:
Participants who scored more than 82% of the maximum possible points, i.e., from 29 to 35 points;
Prize winners:
2nd degree - more than 62% of the maximum possible points, i.e., from 22 to 28 points 3rd degree - more than 48% of the maximum possible points, i.e., from 17 to 21 points
7th Grade:
Winners:
Participants who scored more than 85% of the maximum possible points, i.e., from 30 to 35 points;
Prize winners:
2nd degree - more than 71% of the maximum possible points, i.e., from 24 to 29 points
3rd degree - more than 42% of the maximum possible points, i.e., from 15 to 21 points
Co-Chair of the Mathematics Jury

A.Yu. Avdyushenko
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Find all triples of distinct natural numbers, the least common multiple of which is equal to their sum. The least common multiple of several numbers is the smallest natural number that is divisible by each of these numbers.
|
Answer. All triples of the form $\{n, 2 n, 3 n\}$ for any natural number $n$.
Solution. Let the required numbers be $a<b<c$. By the condition, their least common multiple, which is equal to $a+b+c$, is divisible by $c$, so $c$ divides the sum $a+b<2 c$. Therefore, $a+b=c$. Next, $a+b+c=2 a+2 b$ is divisible by $b$, so $b$ divides $2 a<2 b$. Therefore, $2 a=b$ and $c=a+b=3 a$, and the natural number $a$ can be any.
On the other hand, for any triple of natural numbers of the form $a=n, b=2 n, c=3 n$, their least common multiple is $6 n$. Indeed, it must divide $3 n$, but it is not equal to $3 n$, because $3 n$ does not divide $2 n$, so it is not less than $3 n \cdot 2=6 n$. It remains to note that $6 n$ divides each of the numbers $a=n, b=2 n, c=3 n$.
Evaluation criteria. Only the example of triples of the form $\{n, 2 n, 3 n\}$ for any natural number $n: 2$ points. Example for specific $n: 1$ point. Proved that $a+b=c: 2$ points.
Proved that $2 a=b: 2$ points.
9.4.. In triangle $\mathrm{ABC}$, point $M$ is the midpoint of side $\mathrm{BC}$, and $\mathrm{H}$ is the foot of the altitude dropped from vertex $\mathrm{B}$. It is known that angle $\mathrm{MCA}$ is twice the angle $\mathrm{MAC}$, and the length of $\mathrm{BC}$ is 10 cm. Find the length of segment $\mathrm{AH}$.
Answer. $\mathrm{AH}=5$ cm.
Solution. In the right triangle $\mathrm{BHC}$, segment $\mathrm{HM}$ is the median to the hypotenuse, so the length of $\mathrm{HM}$ is half the length of $\mathrm{BC}$, which is 5 cm.
Triangle $\mathrm{CHM}$ is isosceles with $\mathrm{HM}=\mathrm{MC}$, so angle $\mathrm{MHC}$ equals angle $\mathrm{MCH}=\mathrm{MCA}$ and is twice the angle $\mathrm{MAC}$.
Angle $\mathrm{MHC}$ is the exterior angle for triangle $\mathrm{AMH}$, its measure is equal to the sum of angles $\mathrm{MAH}$ and $\mathrm{AMH}$ and it is twice $\mathrm{MAH}=\mathrm{MAC}$. Therefore, angles $\mathrm{MAH}$ and $\mathrm{AMH}$ are equal, triangle $\mathrm{AMH}$ is isosceles, so $\mathrm{AH}=\mathrm{HM}=5$ cm.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. For non-negative numbers $a, b, c, d$, the following equalities are satisfied:
$\sqrt{a+b}+\sqrt{c+d}=\sqrt{a+c}+\sqrt{b+d}=\sqrt{a+d}+\sqrt{b+c}$. What is the maximum number of distinct values that can be among the numbers $a, b, c, d$?
|
Answer. Two.
Solution. Square the first equality, combine like terms, cancel by 2, square again, combine like terms once more, ultimately obtaining the equality $a c+b d=a b+c d$, equivalent to $(a-d)(c-b)=0$, from which either $a=d$ or $b=c$. Performing similar manipulations with the second equality, we get $a=b$ or $d=c$. Any equality from the first pair shares a common letter with any equality from the second pair, so three out of the four numbers must be equal to each other, and among the numbers $a, b, c, d$ there cannot be more than two distinct numbers. On the other hand, any set of four non-negative numbers, where three are the same and the fourth is arbitrary, clearly satisfies the condition of the problem, so among the numbers $a, b, c, d$ there can be exactly two distinct numbers.
Grading criteria. Proof that among the numbers $a, b, c, d$ there cannot be more than two distinct numbers: 5 points. Example where there are exactly two distinct numbers: 2 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. What is the maximum number of colors needed to color all cells of a 4 by 4 square so that for every pair of different colors, there are two cells of these colors that are either in the same row or in the same column of the square?
|
Answer: In 8 colors.
Solution. If the cells were painted in 9 or more colors, there would be a color in which only one cell is painted. There are only 6 cells located in the same row or column with it, so there are no more than 6 other colors forming a pair with it, as required by the condition - a contradiction. Therefore, the cells can be painted in no more than 8 colors.
Let's provide two essentially different examples of the required coloring in 8 colors, with each color being used for exactly two cells of the square.
| 5 | 6 | 3 | 8 |
| :--- | :--- | :--- | :--- |
| 3 | 4 | 2 | 7 |
| 2 | 1 | 6 | 5 |
| 1 | 7 | 8 | 4 |
| 6 | 7 | 8 | 3 |
| :--- | :--- | :--- | :--- |
| 4 | 5 | 2 | 6 |
| 2 | 3 | 4 | 5 |
| 1 | 1 | 7 | 8 |
Grading criteria. It is proven that the cells cannot be painted in more than 8 colors (i.e., an upper bound on the number of colors is established): 3 points.
A correct example of the required coloring in 8 colors is explicitly provided: 3 points. Justification of it and description of the construction idea are not required.
Both the example and the estimate are present: 7 points.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. A set for playing lotto contains 90 barrels numbered with natural numbers from 1 to 90. The barrels are somehow distributed into several bags (each bag contains more than one barrel). We will call a bag good if the number of one of the barrels in it equals the product of the numbers of the other barrels in the same bag (for example, the bag "2, 3, 6" is good, while "4, 5, 10" is not). What is the maximum possible number of good bags?
|
# Answer: 8.
Solution: In each good bag, there are no fewer than three barrels. The smallest number in each good bag must be unique, otherwise the largest number in this bag would be no less than $10 \times 11=110$, which is impossible. For the same reason, if a good bag contains a barrel with the number 1, it must also contain another barrel with a single-digit number. Therefore, the number of good bags does not exceed 8.
On the other hand, an example can be provided where there are exactly 8 good bags. We can gather 8 good bags $(2,17,34),(3,16,48),(4,15,60),(5,14,70),(6,13,78),(7,12,84),(8,11,88)$, and $(9,10,90)$. All other numbers can be placed in a separate bag that is not good.
Criteria: Example only - 3 points.
Estimate only - 3 points.
Noting that each bag must contain a single-digit number - 1 point, can be combined with the example.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In the math test, each of the 25 students could receive one of four grades: $2, 3, 4$ or 5. It turned out that the number of students who received fours was 4 more than those who received threes. How many people received twos, if it is known that the sum of all grades for this test is 121?
|
# 7.3. Answer: 0.
Let's assume that the 4 students who received fours skipped school, then 21 students should have scored 105 points on the test, which is only possible if all of them received fives. Therefore, in the real situation, no one received a two.
## Comments on Evaluation.
Answer only: 1 point. Answer with verification: 2 points.
#
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.