problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let \( a, b, c \) be strictly positive real numbers. Show that
$$
\frac{a}{b c}+\frac{b}{a c}+\frac{c}{a b} \geqslant \frac{2}{a}+\frac{2}{b}-\frac{2}{c}.
$$
Note, there is indeed a "minus" in the right-hand side!
|
By multiplying both sides by abc, the inequality to be shown can be rewritten as
$$
\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2} \geqslant 2 \mathrm{bc}+2 \mathrm{ac}-2 \mathrm{ab}
$$
By moving 2ab to the other side, we can factorize. The inequality to be shown becomes
$$
(a+b)^{2}+c^{2} \geqslant 2(a+b) c
$$
By moving everything to the left, the inequality is finally equivalent to
$$
(a+b-c)^{2} \geqslant 0
$$
which is always true. Moreover, we have equality if and only if $\mathrm{c}=\mathrm{a}+\mathrm{b}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient a, b, c des réels strictement positifs. Montrer que
$$
\frac{a}{b c}+\frac{b}{a c}+\frac{c}{a b} \geqslant \frac{2}{a}+\frac{2}{b}-\frac{2}{c} .
$$
Attention, il y a bien un "moins" dans le membre de droite!
|
En multipliant les deux membres par abc, l'inégalité à montrer se réécrit
$$
\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2} \geqslant 2 \mathrm{bc}+2 \mathrm{ac}-2 \mathrm{ab}
$$
En passant 2 ab de l'autre côté, on peut factoriser. L'inégalité à montrer devient
$$
(a+b)^{2}+c^{2} \geqslant 2(a+b) c
$$
En passant tout à gauche, l'inégalité est finalement équivalente à
$$
(a+b-c)^{2} \geqslant 0
$$
qui est bien toujours vraie. De plus, on a égalité si et seulement si $\mathrm{c}=\mathrm{a}+\mathrm{b}$.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi3-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
63b5ea29-ef36-5e47-8efc-e3f1f5571289
| 607,707
|
1. Let $a, b$ and $c$ be three real numbers such that
$$
|a| \geqslant|a+b|,|b| \geqslant|b+c| \text { and }|c| \geqslant|c+a| \text {. }
$$
Show that $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$.
2. Let $a, b, c$ and $d$ be four real numbers such that
$$
|a| \geqslant|a+b|,|b| \geqslant|b+c|,|c| \geqslant|c+d| \text { and }|d| \geqslant|d+a|
$$
Do we necessarily have $\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{d}=0$?
|
1. Among the three numbers, there are at least two of the same sign. We can assume that these are $a$ and $b$ and that they are positive, the other cases being treated similarly. We then have
$$
a=|a| \geqslant|a+b|=a+b \geqslant a
$$
thus we have equality everywhere, so $b=0$. Since $|b| \geqslant|b+c|$, we have $0 \geqslant|c|$, so $c=0$. Finally, since $|c| \geqslant|c+a|$, we have $0 \geqslant|a|$, so $a=0$. Therefore, the three numbers are all zero.
2. No. For example, we can take $a=c=1$ and $b=d=-1$. We then have
$$
a+b=b+c=c+d=d+a=0
$$
so the condition is satisfied, even though the chosen numbers are non-zero.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
1. Soient $a, b$ et $c$ trois nombres réels tels que
$$
|a| \geqslant|a+b|,|b| \geqslant|b+c| \text { et }|c| \geqslant|c+a| \text {. }
$$
Montrer que $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$.
2. Soient $a, b, c$ et d quatre nombres réels tels que
$$
|a| \geqslant|a+b|,|b| \geqslant|b+c|,|c| \geqslant|c+d| \text { et }|d| \geqslant|d+a|
$$
A-t-on forcément $\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{d}=0$ ?
|
1. Parmi les trois nombres, il y en a au moins deux de même signe. On peut supposer que ce sont $a$ et $b$ et qu'ils sont positifs, les autres cas se traitant de la même manière. On a alors
$$
a=|a| \geqslant|a+b|=a+b \geqslant a
$$
donc on a égalité partout, donc $b=0$. Comme $|b| \geqslant|b+c|$, on a donc $0 \geqslant|c|$, donc $c=0$. Finalement, comme $|c| \geqslant|c+a|$, on a $0 \geqslant|a|$ donc $a=0$ donc les trois nombres sont nuls.
2. Non. Par exemple, on peut prendre $a=c=1$ et $b=d=-1$. On a alors
$$
a+b=b+c=c+d=d+a=0
$$
donc la condition est vérifiée, bien que les nombres choisis soient non nuls.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi3-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
814b989f-ab33-5b24-81ee-bee95aa3692e
| 607,708
|
Let $\left(a_{n}\right)_{n \geqslant 1}$ be an increasing sequence of strictly positive integers and $k$ a strictly positive integer. Suppose that for some $r \geqslant 1$, we have $a \frac{r}{a_{r}}=k+1$. Show that there exists an integer $s \geqslant 1$ such that $\frac{s}{a_{s}}=k$.
|
Let $v_{n}=\mathrm{n}-\mathrm{ka}_{\mathrm{n}}$ for all $\mathrm{n} \geqslant 1$. The problem reduces to showing that there exists $s$ such that $v_{s}=0$.
We observe that $\nu_{1}=1-k a_{1} \leqslant 0$, that $\nu_{r}=r-k a_{r}=a_{r}>0$ and finally $\nu_{n+1}=$ $(n+1)-k a_{n+1}=n-k a_{n+1}+1 \leqslant n-k a_{n}+1=v_{n}+1$, since the sequence $\left(a_{n}\right)_{n}$ is increasing.
Intuitively, we have a sequence of integers starting from a negative number, reaching a strictly positive number, and can only increase by at most 1 at each step: it must reach 0. Let's prove it: let $s$ be the largest integer less than $r$ such that $v_{s} \leqslant 0$ (it exists because $\nu_{1} \leqslant 0$). Then, since $v_{r}>0$, we have $s<\mathrm{r}$, so $v_{s+1}>0$. Therefore, $v_{s+1} \geqslant 1$, so $0 \geqslant v_{s} \geqslant v_{s+1}-1 \geqslant 0$, hence $v_{s}=0$, so $\frac{s}{a_{s}}=k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $\left(a_{n}\right)_{n \geqslant 1}$ une suite croissante d'entiers strictement positifs et $k$ un entier strictement positif. Supposons que pour un certain $r \geqslant 1$, on $a \frac{r}{a_{r}}=k+1$. Montrer qu'il existe un entier $s \geqslant 1$ tel que $\frac{s}{a_{s}}=k$.
|
Soit $v_{n}=\mathrm{n}-\mathrm{ka}_{\mathrm{n}}$ pour tout $\mathrm{n} \geqslant 1$. Le problème revient à montrer qu'il existe $s$ tel que $v_{s}=0$.
On observe que $\nu_{1}=1-k a_{1} \leqslant 0$, que $\nu_{r}=r-k a_{r}=a_{r}>0$ et qu'enfin $\nu_{n+1}=$ $(n+1)-k a_{n+1}=n-k a_{n+1}+1 \leqslant n-k a_{n}+1=v_{n}+1$, car la suite $\left(a_{n}\right)_{n}$ est croissante.
Intuitivement, on a donc une suite d'entiers qui part d'un nombre négatif, atteint un nombre strictement positif, et ne peut augmenter que d'au plus 1 à chaque fois : elle doit atteindre 0 . Prouvons-le : soit $s$ le plus grand entier inférieur à $r$ tel que $v_{s} \leqslant 0$ (il existe car $\nu_{1} \leqslant 0$ ). Alors, comme $v_{r}>0$, on a $s<\mathrm{r}$, donc $v_{s+1}>0$. On a donc $v_{s+1} \geqslant 1$, donc $0 \geqslant v_{s} \geqslant v_{s+1}-1 \geqslant 0$, donc $v_{s}=0$, de sorte que $\frac{s}{a_{s}}=k$.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi3-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
3487b01e-08da-5114-a811-21acc6d3d2de
| 607,710
|
Let $a, b, c > 0$ such that $a^{2} + b^{2} + c^{2} + (a + b + c)^{2} \leqslant 4$. Show that
$$
\frac{a b + 1}{(a + b)^{2}} + \frac{b c + 1}{(b + c)^{2}} + \frac{c a + 1}{(c + a)^{2}} \geqslant 3
$$
|
By developing $(\mathrm{a}+\mathrm{b}+\mathrm{c})^{2}$ and dividing everything by 2, the hypothesis can be rewritten as
$$
a^{2}+b^{2}+c^{2}+a b+b c+c a \leqslant 2 .
$$
We now seek to homogenize the left-hand side of the inequality to be proven, that is, to ensure that all terms have the same degree. For this, we introduce a 2 in place of the 1 and use our hypothesis:
$$
\begin{aligned}
\frac{a b+1}{(a+b)^{2}} & =\frac{1}{2} \frac{2 a b+2}{(a+b)^{2}} \\
& \geqslant \frac{1}{2} \frac{2 a b+a^{2}+b^{2}+c^{2}+a b+b c+c a}{(a+b)^{2}} \\
& =\frac{1}{2}\left(1+\frac{c^{2}+a b+b c+c a}{(a+b)^{2}}\right) \\
& =\frac{1}{2}+\frac{1}{2} \frac{(c+a)(c+b)}{(a+b)^{2}}
\end{aligned}
$$
Similarly, we obtain $\frac{b c+1}{(b+c)^{2}} \geqslant \frac{1}{2}+\frac{1}{2} \frac{(a+b)(a+c)}{(b+c)^{2}}$ and $\frac{c a+1}{(c+a)^{2}} \geqslant \frac{1}{2}+\frac{1}{2} \frac{(b+c)(b+a)}{(c+a)^{2}}$. By summing, the left-hand side is at least
$$
\frac{3}{2}+\frac{1}{2}\left(\frac{(c+a)(c+b)}{(a+b)^{2}}+\frac{(a+b)(a+c)}{(b+c)^{2}}+\frac{(b+c)(b+a)}{(c+a)^{2}}\right) .
$$
However, according to the arithmetic-geometric mean inequality, we have
$$
\begin{aligned}
& \frac{(c+a)(c+b)}{(a+b)^{2}}+\frac{(a+b)(a+c)}{(b+c)^{2}}+\frac{(b+c)(b+a)}{(c+a)^{2}} \\
\geqslant & 3 \sqrt[3]{\frac{(c+a)(c+b)}{(a+b)^{2}} \times \frac{(a+b)(a+c)}{(b+c)^{2}} \times \frac{(b+c)(b+a)}{(c+a)^{2}}}=3
\end{aligned}
$$
thus the left-hand side is at least $\frac{3}{2}+\frac{3}{2}=3$, hence the result.
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b, c>0$ tels que $a^{2}+b^{2}+c^{2}+(a+b+c)^{2} \leqslant 4$. Montrer que
$$
\frac{a b+1}{(a+b)^{2}}+\frac{b c+1}{(b+c)^{2}}+\frac{c a+1}{(c+a)^{2}} \geqslant 3
$$
|
En développant $(\mathrm{a}+\mathrm{b}+\mathrm{c})^{2}$ et en divisant tout par 2, l'hypothèse se réécrit
$$
a^{2}+b^{2}+c^{2}+a b+b c+c a \leqslant 2 .
$$
On cherche maintenant à homogénéiser le membre de gauche de l'inégalité à montrer, c'est-à-dire à faire en sorte que tous les termes aient le même degré. Pour cela, on fait apparaître un 2 à la place du 1 et on utilise notre hypothèse :
$$
\begin{aligned}
\frac{a b+1}{(a+b)^{2}} & =\frac{1}{2} \frac{2 a b+2}{(a+b)^{2}} \\
& \geqslant \frac{1}{2} \frac{2 a b+a^{2}+b^{2}+c^{2}+a b+b c+c a}{(a+b)^{2}} \\
& =\frac{1}{2}\left(1+\frac{c^{2}+a b+b c+c a}{(a+b)^{2}}\right) \\
& =\frac{1}{2}+\frac{1}{2} \frac{(c+a)(c+b)}{(a+b)^{2}}
\end{aligned}
$$
De même, on obtient $\frac{b c+1}{(b+c)^{2}} \geqslant \frac{1}{2}+\frac{1}{2} \frac{(a+b)(a+c)}{(b+c)^{2}}$ et $\frac{c a+1}{(c+a)^{2}} \geqslant \frac{1}{2}+\frac{1}{2} \frac{(b+c)(b+a)}{(c+a)^{2}}$. En sommant, le membre de gauche vaut au moins
$$
\frac{3}{2}+\frac{1}{2}\left(\frac{(c+a)(c+b)}{(a+b)^{2}}+\frac{(a+b)(a+c)}{(b+c)^{2}}+\frac{(b+c)(b+a)}{(c+a)^{2}}\right) .
$$
Or, d'après l'inégalité de la moyenne arithmético-géométrique, on a
$$
\begin{aligned}
& \frac{(c+a)(c+b)}{(a+b)^{2}}+\frac{(a+b)(a+c)}{(b+c)^{2}}+\frac{(b+c)(b+a)}{(c+a)^{2}} \\
\geqslant & 3 \sqrt[3]{\frac{(c+a)(c+b)}{(a+b)^{2}} \times \frac{(a+b)(a+c)}{(b+c)^{2}} \times \frac{(b+c)(b+a)}{(c+a)^{2}}}=3
\end{aligned}
$$
donc le membre de gauche vaut au moins $\frac{3}{2}+\frac{3}{2}=3$, d'où le résultat.
## Exercices du groupe A
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi3-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
000aaea2-86f4-5706-b577-c7cada31de27
| 607,712
|
Let $x_{1}, \ldots, x_{n}$ be any real numbers. Show that
$$
\sum_{i=1}^{n} \sum_{j=1}^{n}\left|x_{i}+x_{j}\right| \geqslant n \sum_{i=1}^{n}\left|x_{i}\right| .
$$
|
Among the $n$ numbers, we assume that $r$ are positive (or zero), and $s=n-r$ are strictly negative. We denote $\left(a_{i}\right)_{1 \leqslant i \leqslant r}$ as the list of positive (or zero) numbers, and $\left(-b_{j}\right)_{1 \leqslant j \leqslant s}$ as the list of strictly negative numbers, such that all the $a_{i}$ and the $b_{j}$ are positive.
We define
$$
A=\sum_{i=1}^{r} a_{i}, B=\sum_{j=1}^{s} b_{j}
$$
We denote $M_{1}$ and $M_{2}$ as the left-hand side and the right-hand side of the statement, respectively. By changing all the signs if necessary, we can assume $A \geqslant B$.
We then have
$$
M_{1}=2 r A+2 s B+2 \sum_{1 \leqslant i \leqslant r} \sum_{1 \leqslant j \leqslant s}\left|a_{i}-b_{j}\right|,
$$
where $2 r A$ is the sum of the terms $\left|x_{i}+x_{j}\right|$ with $x_{i}, x_{j} \geqslant 0$ and similarly $2 s B$ is the sum of the terms $\left|x_{i}+x_{j}\right|$ with $x_{i}, x_{j}<0$ and $\sum \sum\left|a_{i}-b_{j}\right|$ is the sum of the terms $\left|x_{i}+x_{j}\right|$ where $x_{i}$ and $x_{j}$ have different signs. Furthermore, we have $M_{2}=(r+s)(A+B)$. Showing that $M_{1} \geqslant M_{2}$ is therefore equivalent to showing
$$
2 \sum_{i=1}^{r} \sum_{j=1}^{s}\left|a_{i}-b_{j}\right| \geqslant(s-r)(A-B)
$$
If $s \leqslant r$, the result is obvious because the left-hand side is positive and the right-hand side is negative. We therefore assume $s>r$. We then have
$$
\begin{aligned}
2 \sum_{i=1}^{r} \sum_{j=1}^{s}\left|a_{i}-b_{j}\right| & \geqslant \sum_{i=1}^{r} \sum_{j=1}^{s}\left|a_{i}-b_{j}\right| \\
& \geqslant \sum_{i=1}^{r} \sum_{j=1}^{s} a_{i}-b_{j} \\
& =s A-r B \\
& =(s-r) A+r A-r B \\
& \geqslant(s-r) A \\
& \geqslant(s-r)(A-B)
\end{aligned}
$$
since $s>r$ and $A \geqslant B$. We have thus shown what we wanted.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x_{1}, \ldots, x_{n}$ des réels quelconques. Montrer que
$$
\sum_{i=1}^{n} \sum_{j=1}^{n}\left|x_{i}+x_{j}\right| \geqslant n \sum_{i=1}^{n}\left|x_{i}\right| .
$$
|
Parmi les $n$ nombres, on suppose que $r$ sont positifs (ou nuls), et $s=n-r$ sont strictement négatifs. On note $\left(a_{i}\right)_{1 \leqslant i \leqslant r}$ la liste des nombres positifs (ou
nuls), et $\left(-b_{j}\right)_{1 \leqslant j \leqslant s}$ la liste des nombres strictement négatifs, de sorte que tous les $a_{i}$ et les $b_{j}$ sont positifs.
On pose
$$
A=\sum_{i=1}^{r} a_{i}, B=\sum_{j=1}^{s} b_{j}
$$
On note $M_{1}$ et $M_{2}$ le membre de gauche et le membre de droite dans l'énoncé respectivement. Quitte à changer tous les signes, on peut supposer $A \geqslant B$.
On a alors
$$
M_{1}=2 r A+2 s B+2 \sum_{1 \leqslant i \leqslant r} \sum_{1 \leqslant j \leqslant s}\left|a_{i}-b_{j}\right|,
$$
où $2 r A$ est la somme des termes $\left|x_{i}+x_{j}\right|$ avec $x_{i}, x_{j} \geqslant 0$ et de même $2 s B$ est la somme des termes $\left|x_{i}+x_{j}\right|$ avec $x_{i}, x_{j}<0$ et $\sum \sum\left|a_{i}-b_{j}\right|$ est la somme des termes $\left|x_{i}+x_{j}\right|$ où $x_{i}$ et $x_{j}$ sont de signes différents. De plus, on a $M_{2}=(r+s)(A+B)$. Montrer que $M_{1} \geqslant M_{2}$ est donc équivalent à montrer
$$
2 \sum_{i=1}^{r} \sum_{j=1}^{s}\left|a_{i}-b_{j}\right| \geqslant(s-r)(A-B)
$$
Si $s \leqslant r$, le résultat est évident car le membre de gauche est positif et celui de droite est négatif. On suppose donc $s>r$. On a alors
$$
\begin{aligned}
2 \sum_{i=1}^{r} \sum_{j=1}^{s}\left|a_{i}-b_{j}\right| & \geqslant \sum_{i=1}^{r} \sum_{j=1}^{s}\left|a_{i}-b_{j}\right| \\
& \geqslant \sum_{i=1}^{r} \sum_{j=1}^{s} a_{i}-b_{j} \\
& =s A-r B \\
& =(s-r) A+r A-r B \\
& \geqslant(s-r) A \\
& \geqslant(s-r)(A-B)
\end{aligned}
$$
car $s>r$ et $A \geqslant B$. On a donc montré ce qu'on voulait.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi3-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
25e363e0-2091-510c-af7d-891fec94b442
| 607,714
|
It is said that two permutations $a_{1}, \ldots, a_{4035}$ and $b_{1}, \ldots, b_{4035}$ of the integers $1, \ldots, 4035$ intersect if there exists an integer $k \leqslant 4035$ such that $a_{k}=b_{k}$. An ensemble $E$ of permutations is said to be unavoidable if every permutation of the integers $1, \ldots, 4035$ intersects a permutation belonging to $E$.
a) Show that there exists an unavoidable ensemble containing 2018 permutations.
b) Does there exist an unavoidable ensemble containing 2017 permutations?
|
a) For all $i \in \{1, \ldots, 2018\}$, we denote $\sigma^{(i)}$ as the permutation
$$
\mathfrak{i}+1, \mathfrak{i}+2, \ldots, 2018,1,2, \ldots, \mathfrak{i}, 2019,2020, \ldots, 4035
$$
In other words, $\sigma^{(i)}$ is the permutation such that:
$\triangleright$ for all $\mathfrak{j} \leqslant 2018, \sigma_{\mathfrak{j}}^{(i)}$ is the unique element of $\{1, \ldots, 2018\}$ such that $\sigma_{\mathfrak{j}}^{(\mathfrak{i})} \equiv \mathfrak{i}+\mathfrak{j}(\bmod 2018)$;
$\triangleright$ for all $j \geqslant 2019, \sigma_{j}^{(i)}=j$.
Then the set $E=\left\{\sigma^{(1)}, \ldots, \sigma^{(2018)}\right\}$ is unavoidable. Indeed, let $b_{1}, \ldots, b_{4035}$ be a permutation. Among the integers $\mathrm{b}_{1}, \ldots, \mathrm{~b}_{2018}$, there is at least one that is less than or equal to 2018, since the set $\{2019, \ldots, 4035\}$ contains only 2017 elements. Let $i$ be an integer such that $i \leqslant 2018$ and $b_{i} \leqslant 2018$, and let $j$ be the unique element of $\{1, \ldots, 2018\}$ such that $j \equiv b_{i}-i(\bmod 2018)$. Then $b_{i} \equiv \mathfrak{i}+\mathfrak{j} \equiv \sigma_{i}^{(\mathfrak{j})}(\bmod 2018)$, and since $1 \leqslant b_{i}, \sigma_{i}^{(j)} \leqslant 2018$, this shows that $b_{i}=\sigma_{i}^{(j)}$, hence that $b$ intersects the permutation $\sigma^{(j)}$.
b) Let $E$ be a set containing 2017 permutations. For any permutation $b_{1}, \ldots, b_{4035}$, we call a collision of $b$ an integer $i$ such that there exists a permutation $a$ in $E$ for which $a_{i} = b_{i}$, and we call the weight of $b$ the number of collisions of $b$. We then consider a permutation $b$ of minimum weight: we will show that this weight is zero.
Indeed, suppose this weight is non-zero. Let $i$ be a collision of $b$. The set $\bar{X}=\{x \in \{1, \ldots, 4035\} \mid \exists a \in E$ such that $\left.a_{x}=b_{i}\right\}$ has cardinality at most $|E|=2017$, so the set $X=\left\{x \in \{1, \ldots, 4035\} \mid \forall a \in E, a_{x} \neq b_{i}\right\}$ has cardinality at least $4035-2017=2018$.
We then consider the set $Y=\left\{b_{x} \mid x \in X\right\}$, which also has cardinality at least 2018. According to the pigeonhole principle, there exists an integer $y \in Y$ such that $a_{i} \neq y$ for every permutation $a$ in $E$. Let $x \in X$ such that $y=b_{x}$.
We then consider the permutation $b^{\prime}$ obtained from $b$ by swapping the values of $b_{i}$ and $b_{x}$. By construction, neither $i$ nor $x$ are collisions of $b^{\prime}$. The other collisions of $b^{\prime}$ are all collisions of $b$. Consequently, $b^{\prime}$ has a strictly lower weight than $b$. This contradicts the definition of $b$, which invalidates our assumption and shows that no set containing 2017 permutations is unavoidable.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On dit que deux permutations $a_{1}, \ldots, a_{4035}$ et $b_{1}, \ldots, b_{4035}$ des entiers $1, \ldots, 4035$ s'intersectent s'il existe un entier $k \leqslant 4035$ tel que $a_{k}=b_{k}$. On dit qu'un ensemble $E$ de permutations est inévitable si chaque permutation des entiers $1, \ldots, 4035$ intersecte une permutation appartenant à E .
a) Montrer qu'il existe un ensemble inévitable contenant 2018 permutations.
b) Existe-t-il un ensemble inévitable contenant 2017 permutations?
|
a) Pour tout $i \in\{1, \ldots, 2018\}$, on note $\sigma^{(i)}$ la permutation
$$
\mathfrak{i}+1, \mathfrak{i}+2, \ldots, 2018,1,2, \ldots, \mathfrak{i}, 2019,2020, \ldots, 4035
$$
En d'autres termes, $\sigma^{(i)}$ est la permutation telle que:
$\triangleright$ pour tout $\mathfrak{j} \leqslant 2018, \sigma_{\mathfrak{j}}^{(i)}$ est le seul élément de $\{1, \ldots, 2018\}$ tel que $\sigma_{\mathfrak{j}}^{(\mathfrak{i})} \equiv \mathfrak{i}+\mathfrak{j}(\bmod 2018)$;
$\triangleright$ pour tout $j \geqslant 2019, \sigma_{j}^{(i)}=j$.
Alors l'ensemble $E=\left\{\sigma^{(1)}, \ldots, \sigma^{(2018)}\right\}$ est inévitable. En effet, soit $b_{1}, \ldots, b_{4035}$ une permutation. Parmi les entiers $\mathrm{b}_{1}, \ldots, \mathrm{~b}_{2018}$, il y en a au moins un qui est inférieur ou égal à 2018, puisque l'ensemble $\{2019, \ldots, 4035\}$ ne compte que 2017 éléments. Soit i un entier tel que $i \leqslant 2018$ et $b_{i} \leqslant 2018$, et soit $j$ l'unique élément de $\{1, \ldots, 2018\}$ tel que $j \equiv b_{i}-i(\bmod 2018)$. Alors $b_{i} \equiv \mathfrak{i}+\mathfrak{j} \equiv \sigma_{i}^{(\mathfrak{j})}(\bmod 2018)$, et puisque $1 \leqslant b_{i}, \sigma_{i}^{(j)} \leqslant 2018$, cela montre que $b_{i}=\sigma_{i}^{(j)}$, donc que $b$ intersecte la permutation $\sigma^{(j)}$.
b) Soit E un ensemble contenant 2017 permutations. Pour toute permutation $b_{1}, \ldots, b_{4035}$, on appelle collision de $b$ un entier $i$ tel qu'il existe une permutation a dans E pour laquelle $a_{i}=$ $b_{i}$, et on appelle poids de $b$ le nombre de collisions de $b$. On considère alors une permutation $b$ de poids minimum : on va montrer que ce poids est nul.
En effet, supposons ce poids non nul. Soit alors $i$ une collision de $b$. L'ensemble $\bar{X}=\{x \in$ $\{1, \ldots, 4035\} \mid \exists a \in E$ tel que $\left.a_{x}=b_{i}\right\}$ est de cardinal au plus $|E|=2017$, donc l'ensemble $X=\left\{x \in\{1, \ldots, 4035\} \mid \forall a \in E, a_{x} \neq b_{i}\right\}$ est de cardinal au moins $4035-2017=2018$.
On considère alors l'ensemble $Y=\left\{b_{x} \mid x \in X\right\}$, de cardinal au moins 2018 lui aussi. Toujours d'après le principe des tiroirs, il existe un entier $y \in Y$ tel que $a_{i} \neq y$ pour toute permutation $a$ dans $E$. Soit $x \in X$ tel que $y=b_{x}$.
On considère alors la permutation $b^{\prime}$ obtenue à partir de $b$ en échangeant les valeurs de $b_{i}$ et de $b_{x}$. Par construction, ni $i$ ni $x$ ne sont des collisions de $b^{\prime}$. Les autres collisions de $b^{\prime}$ sont toutes des collisions de b. Par conséquent, $b^{\prime}$ est de poids strictement inférieur au poids de b. Ceci contredit la définition de b, ce qui invalide notre supposition et montre donc que nul ensemble contenant 2017 permutations n'est inévitable.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
9570c43f-e5e3-586e-be13-d23fa0399612
| 607,719
|
Consider a $2018 \times 2018$ table where each cell contains a non-zero natural number. Noémie modifies these numbers at her discretion, applying the following operations:
$\triangleright$ choose a row and then multiply by 2 all the integers in this row;
$\triangleright$ choose a column and then subtract 1 from all the integers in this column.
Show that, by applying these operations, Noémie can manage to obtain a table where each cell contains the integer 0.
|
Let's say a column is positive if it contains only non-zero natural numbers, and is null if it contains only 0s. Note that, every time Noémie doubles the integers in a row, the positive columns remain positive and the null columns remain null. We will say that an integer $n$ is a pivotal value if columns 1 to $n$ are null and columns $n+1$ to 2018 are positive. Note that a grid does not necessarily have a pivotal value; however, all the grids we will consider will have one.
Initially, 0 is a pivotal value. We will show that, starting from a grid with a pivotal value $n$, Noémie can apply the operations described to obtain a grid with $n+1$ as the pivotal value. To do this, we call the weight of the $(n+1)^{\text{th}}$ column the largest integer it contains. If this weight is strictly greater than 1, Noémie reduces it as follows:
$\triangleright$ first, she doubles the integers in each row whose $(n+1)$-th integer is 1 (and will therefore be 2 after doubling);
$\triangleright$ then she subtracts 1 from all the integers in the $(n+1)^{\text{th}}$ column.
By doing so, the $(n+1)^{\text{th}}$ column has indeed seen its weight decrease by 1, and $n$ remains the pivotal value of the grid. Finally, if the $(n+1)^{\text{th}}$ column has a weight of 1, then Noémie subtracts 1 from all the integers in this column, making it a null column.
She thus obtains a grid where $n+1$ is the pivotal value. By repeating this process, she eventually arrives at a grid where 2018 is the pivotal value, which means the grid contains only the integer 0.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On considère un tableau de taille $2018 \times 2018$ dont chaque case contient un entier naturel non nul. Noémie modifie ces entiers à sa guise, en appliquant les opérations suivantes :
$\triangleright$ choisir une ligne puis multiplier par 2 tous les entiers contenus dans cette ligne;
$\triangleright$ choisir une colonne puis soustraire 1 à tous les entiers contenus dans cette colonne.
Montrer que, en appliquant ces opérations, Noémie peut se débrouiller pour obtenir un tableau dont chaque case contient l'entier 0.
|
On va dire qu'une colonne est positive si elle ne contient que des entiers naturels non nuls, et est nulle si elle ne contient que des 0 . Remarquons que, chaque fois que Noémie double les entiers contenus sur une ligne, les colonnes positives restent positives et les colonnes nulles restent nulles. On dit enfin qu'un entier $n$ est une valeur charnière si les colonnes 1 à $n$ sont nulles et les colonnes $n+1$ à 2018 sont positives. Notons qu'une grille n'a pas nécessairement de valeur charnière; ce sera néanmoins le cas de toutes les grilles que nous considérerons.
Initialement, 0 est une valeur charnière. On va montrer que, partant d'une grille ayant une valeur charnière $n$, Noémie peut appliquer les opérations de l'énoncé pour obtenir une grille ayant $n+1$ pour valeur charnière. Pour ce faire, on appelle poids de la $(n+1)^{\text {ème }}$ colonne le plus grand entier qu'elle contient. Si ce poids est strictement supérieur à 1, Noémie le fait baisser comme suit :
$\triangleright$ tout d'abord, elle double les entiers de chacune des lignes dont le ( $n+1$ )ème entier vaut 1 (et vaudra donc 2 après doublement);
$\triangleright$ puis elle retranche 1 à tous les entiers de la $(n+1)^{\text {ème }}$ colonne.
Ce faisant, la $(n+1)^{\text {ème }}$ colonne a bien vu son poids diminuer de 1 , et $n$ est toujours la valeur charnière de la grille. Enfin, si la $(n+1)^{\text {ème }}$ colonne a un poids de 1, alors Noémie retranche 1 à tous les entiers de cette colonne, et en fait une colonne nulle.
Elle obtient ainsi une grille dont $\mathrm{n}+1$ est la valeur charnière. En réitérant ce processus, elle finit par aboutir à une grille dont 2018 est la valeur charnière, ce qui signifie que la grille ne contient que l'entier 0.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
e178930d-fabc-5963-a91c-cc1c51b631f9
| 607,720
|
Show that, among 2048 integers, one can always find 1024 whose sum is divisible by 1024.
|
We will prove by induction on $n \geqslant 0$ the property $P(n)$ which states that among $2^{n+1}$ integers, one can always find $2^{n}$ whose sum is divisible by $2^{n}$. First, for $n=0$, the result is obvious, since every integer is divisible by $2^{0}=1$. Therefore, the property $P(0)$ is true.
Now consider an integer $n \geqslant 0$ such that $P(n)$ is true, and we will show $P(n+1)$. Consider a set of $2^{n+2}$ arbitrary integers, which we arbitrarily divide into two piles of $2^{n+1}$ integers each. Thanks to the property $P(n)$, we extract from the first pile a set $E_{1}$ of $2^{n}$ integers whose sum is divisible by $2^{n}$. Similarly, we extract from the second pile a set $E_{2}$ of $2^{n}$ integers whose sum is divisible by $2^{n}$. Finally, among the $2^{n+1}$ integers that do not belong to $E_{1}$ or $E_{2}$, we extract again a set $E_{3}$ of $2^{n}$ integers whose sum is divisible by $2^{n}$.
The three sets $E_{1}, E_{2}$, and $E_{3}$ are disjoint, and their sums are congruent to 0 or $2^{n}$ modulo $2^{n+1}$. Therefore, two of these sums are equal modulo $2^{n+1}$. The union of the associated sets is thus a set of $2^{n+1}$ integers whose sum is divisible by $2^{n+1}$, which shows $P(n+1)$ and concludes the exercise.
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Montrer que, parmi 2048 entiers, on peut toujours en trouver 1024 dont la somme est divisible par 1024.
|
On va montrer par récurrence sur $n \geqslant 0$ la propriété $P(n)$ selon laquelle, parmi $2^{n+1}$ entiers, on peut toujours en trouver $2^{n}$ dont la somme est divisible par $2^{n}$. Tout d'abord, pour $n=0$, le résultat est évident, puisque tout entier est divisible par $2^{0}=1$. La propriété $\mathrm{P}(0)$ est donc vraie.
On considère maintenant un entier $n \geqslant 0$ tel que $P(n)$ est vraie, et on va montrer $P(n+1)$. Considérons un ensemble de $2^{n+2}$ entiers quelconques, que l'on coupe arbitrairement en deux tas de $2^{\mathrm{n}+1}$ entiers chacun. Grâce à la propriété $P(n)$, on extrait du premier tas un ensemble $E_{1}$ de $2^{n}$ entiers dont la somme est divisible par $2^{n}$. De même, on extrait du second tas un ensemble $\mathrm{E}_{2}$ de $2^{n}$ entiers dont la somme est divisible par $2^{n}$. Enfin, parmi les $2^{n+1}$ entiers n'appartenant ni à $E_{1}$ ni à $E_{2}$, on extrait de nouveau un ensemble $E_{3}$ de $2^{n}$ entiers dont la somme est divisible par $2^{n}$.
Les trois ensembles $E_{1}, E_{2}$ et $E_{3}$ sont disjoints, et ont des sommes congrues à 0 ou à $2^{n}$ modulo $2^{\mathrm{n+1}}$. Deux de ces sommes sont donc égales modulo $2^{\mathrm{n+1}}$. L'union des ensembles associés est donc un ensemble de $2^{n+1}$ entiers dont la somme est divisible par $2^{n+1}$, ce qui montre $P(n+1)$ et conclut l'exercice.
## Exercices du groupe A
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
313fce9e-bbbd-5d26-8aba-0a36a1d993be
| 607,721
|
It is said that a set $B$ of integers is an interval of integers if there exist integers $i \leqslant j$ such that $B=\{i, i+1, \ldots, j\}$, and we denote by $\mathcal{J}$ the set of intervals of integers. Furthermore, if $A=\left\{a_{1}, \ldots, a_{k}\right\}$ is a set of integers, with $a_{1}<\ldots<a_{k}$, we define
$$
f(A)=\max _{1 \leqslant i<k}\left(a_{i+1}-a_{i}\right) \text { and } g(A)=\max _{B \subseteq A, B \in \mathcal{J}}|B| \text {. }
$$
We recall that the notation $|B|$ denotes the number of elements in the set $B$. If $A$ is empty or a singleton, we also set $f(A)=0$. Finally, for any integer $n \geqslant 1$, we define
$$
F(n)=\sum_{A \subseteq\{1, \ldots, n\}} f(A) \text { and } G(n)=\sum_{A \subseteq\{1, \ldots, n\}} g(A) .
$$
Show that there exists a natural number $m$ such that $F(n)>G(n)$ for all integers $n \geqslant m$.
|
In this solution, we will denote by $E_{n}$ the set of subsets of $\{1, \ldots, n\}$ and $S_{n}$ the set of subsets $A$ of $\{1, \ldots, n\}$ such that $\{1, n\} \subseteq A$. If $A$ is a set and $k$ is an integer, we will also denote by $A+k$ the set $\{x+k \mid x \in A\}$.
For a given set $A \in E_{n}$, $f(A)$ is the largest difference between successive elements of $A$, while $g(A)+1$ is the largest difference between successive elements of $\{0, \ldots, n+1\} \backslash A$, or equivalently of $\{1, \ldots, n+2\} \backslash(A+1)$.
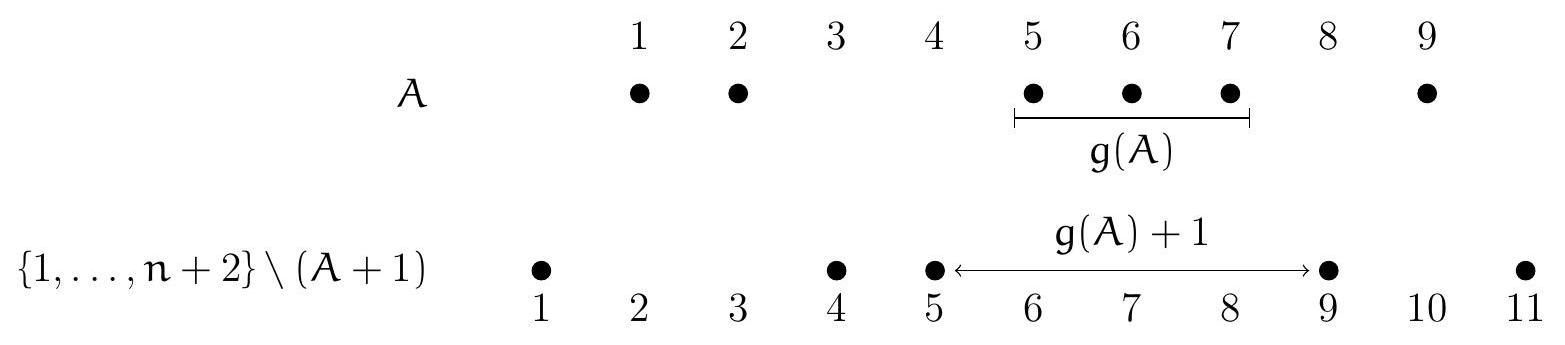
We therefore have $g(A)+1=f(\{1, \ldots, n+2\} \backslash(A+1))$. When $A$ runs through the set $E_{n},\{1, \ldots, n+2\} \backslash(A+1)$ runs through $S_{n+2}$. We thus have
$$
\mathrm{G}(\mathrm{n})=\sum_{A \in \boldsymbol{S}_{n+2}}(\mathrm{f}(\mathrm{~A})-1)
$$
We then wish to compare $F(n)$ to the sum $\sum_{A \in S_{n+2}} f(A)$. To do this, we introduce the bijection $\varphi: E_{n} \mapsto S_{n+2}$ defined as follows: $\varphi(\emptyset)=\{1, \ldots, n+2\}$ and, if $A$ is a non-empty subset of $\{1, \ldots, n\}$, with minimum $a$ and maximum $b$, then $\varphi(A)=\{1, \ldots, a\} \cup\{x+1 \mid x \in A$ and $a<x<b\} \cup\{b+2, \ldots, n+2\}$.
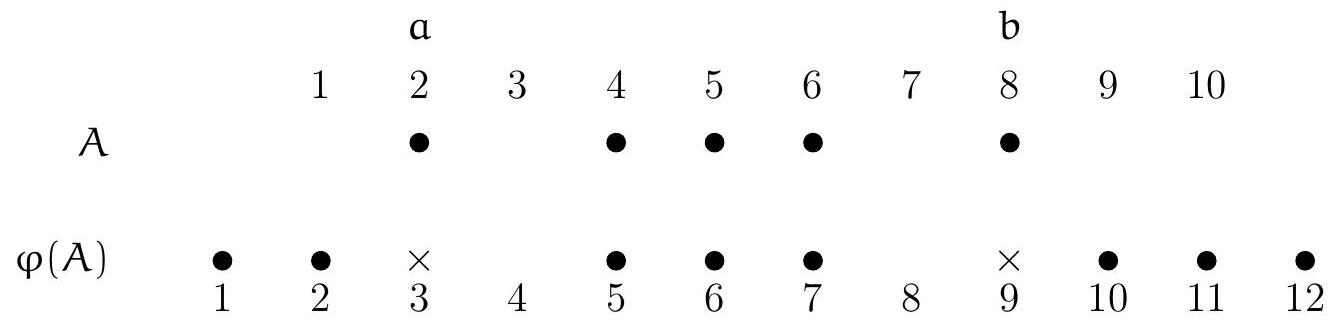
Note that, from $\varphi(A)$, we can compute $a$ and $b$, and thus recover $A$ itself, so $\varphi$ is injective. Since $E_{n}$ and $S_{n+2}$ both have cardinality $2^{n}$, $\varphi$ is indeed a bijection.
Furthermore, observe that for any $A \in E_{n}$ such that $|A| \geqslant 2$, with minimum $a$ and maximum $b$, we have $f(\varphi(A)) \leqslant f(A)+1$, with equality if and only if $a+f(A)$ is the second smallest element of $A$, or $b-f(A)$ is the second largest element of $A$. On the other hand, if $|A| \leqslant 1$, then $f(A)=0$ and $f(\varphi(A)) \leqslant 2$.
We then say that a set $A \in E_{n}$ is good if $|A| \geqslant 2$ and if $f(\varphi(A)) \leqslant f(A)$, and denote by $e_{n}$ the number of good sets in $E_{n}$. Then
$$
\begin{aligned}
\sum_{A \in S_{n}+2} f(A) & =\sum_{A \in E_{n}} f(\varphi(A)) \leqslant \sum_{A \in E_{n},|A| \geqslant 2, A \text { good }} f(A)+\sum_{A \in E_{n},|A| \geqslant 2, A \text { not good }}(f(A)+1)+\sum_{A \in E_{n},|A| \leqslant 1} 2 \\
& \leqslant \sum_{A \in E_{n},|A| \geqslant 2}(f(A)+1)-e_{n}+2(n+1)=\sum_{A \in E_{n}}(f(A)+1)-e_{n}+n+1
\end{aligned}
$$
Now, if $n \geqslant 5$, any set $A$ of the form $\{1,2, n-1, n\} \cup(X+3)$, where $X$ is an element of $E_{n-5}$, is necessarily good, since $f(A) \geqslant 2$. Therefore, there are at least $2^{n-5}$ good sets in $E_{n}$, which shows that $e_{n} \geqslant 2^{n-5}$. In particular, we have $e_{10} \geqslant 2^{5}=32>10+1$, and an immediate induction shows that $e_{n}>n+1$ for all $n \geqslant 10$. It follows that, if $n \geqslant 10$, then
$$
\begin{aligned}
G(n) & =\sum_{A \in S_{n+2}} f(A)-\left|S_{n+2}\right| \leqslant \sum_{A \in E_{n}}(f(A)+1)-e_{n}+n+1-\left|S_{n+2}\right| \\
& \leqslant F(n)+\left|E_{n}\right|-e_{n}+n+1-\left|S_{n+2}\right|=F(n)-e_{n}+n+1<F(n)
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On dit qu'un ensemble B d'entiers est un intervalle d'entiers s'il existe des entiers $i \leqslant j$ tels que $B=\{i, \mathfrak{i}+1, \ldots, j\}$, et on note $\mathcal{J}$ l'ensemble des intervalles d'entiers. Par ailleurs, si $A=\left\{a_{1}, \ldots, a_{k}\right\}$ est un ensemble d'entiers, avec $a_{1}<\ldots<a_{k}$, on pose
$$
f(A)=\max _{1 \leqslant i<k}\left(a_{i+1}-a_{i}\right) \text { et } g(A)=\max _{B \subseteq \mathcal{A}, B \in \mathcal{J}}|B| \text {. }
$$
On rappelle que la notation $|B|$ désigne le nombre d'éléments de l'ensemble B. Si A est vide ou est un singleton, on pose également $f(A)=0$. Enfin, pour tout entier $n \geqslant 1$, on définit
$$
F(n)=\sum_{A \subseteq\{1, \ldots, n\}} f(A) \text { et } G(n)=\sum_{A \subseteq\{1, \ldots, n\}} g(A) .
$$
Montrer qu'il existe un entier naturel $m$ tel que $F(n)>G(n)$ pour tout entier $n \geqslant m$.
|
Dans toute cette soluion, on notera $E_{n}$ l'ensemble des parties de $\{1, \ldots, n\}$ et $S_{n} l^{\prime}$ ensemble des parties $A$ de $\{1, \ldots, n\}$ telles que $\{1, n\} \subseteq A$. Si $A$ est un ensemble et $k$ un entier, on notera également $A+k$ l'ensemble $\{x+k \mid x \in A\}$.
Pour un ensemble $A \in E_{n}$ donné, $f(A)$ est la plus grande différence entre des éléments successifs de $A$, tandis que $g(A)+1$ est la plus grande différence entre des éléments successifs de $\{0, \ldots, n+1\} \backslash A$, ou encore de $\{1, \ldots, n+2\} \backslash(A+1)$.

On a donc $g(A)+1=f(\{1, \ldots, n+2\} \backslash(A+1))$. Or, quand $A$ parcourt l'ensemble $E_{n},\{1, \ldots, n+$ $2\} \backslash(A+1)$ parcourt $S_{n+2}$. On a donc
$$
\mathrm{G}(\mathrm{n})=\sum_{A \in \boldsymbol{S}_{n+2}}(\mathrm{f}(\mathrm{~A})-1)
$$
On souhaite alors comparer $F(n)$ à la somme $\sum_{A \in S_{n+2}} f(A)$. Pour ce faire, on introduit la bijection $\varphi: E_{n} \mapsto S_{n+2}$ définie comme suit : $\varphi(\emptyset)=\{1, \ldots, n+2\}$ et, si A est une partie non vide de $\{1, \ldots, n\}$, de minimum $a$ et de maximum $b$, alors $\varphi(A)=\{1, \ldots, a\} \cup\{x+1 \mid x \in A$ et $a<x<$ b $\} \cup\{\boldsymbol{b}+2, \ldots, \boldsymbol{n}+2\}$.

Notons que, à partir de $\varphi(A)$, on peut calculer a et b, donc retrouver A lui-même, de sorte que $\varphi$ est injective. Puisque $E_{n}$ et $S_{n+2}$ sont tous deux de cardinal $2^{n}, \varphi$ est donc bien une bijection.
En outre, remarquons que, pour tout $A \in E_{n}$ tel que $|A| \geqslant 2$, de minimum a et de maximum $b$, on a $f(\varphi(A)) \leqslant f(A)+1$, avec égalité si et seulement si $a+f(A)$ est le deuxième plus petit élément de $A$, ou $b-f(A)$ est le deuxième plus grand élément de $A$. D'autre part, si $|A| \leqslant 1$, alors $f(A)=0$ et $f(\varphi(A)) \leqslant 2$.
On dit alors qu'un ensemble $A \in E_{n}$ est bon si $|A| \geqslant 2$ et si $f(\varphi(A)) \leqslant f(A)$, et note $e_{n}$ le nombre de bons ensembles de $E_{n}$. Alors
$$
\begin{aligned}
\sum_{A \in S_{n}+2} f(A) & =\sum_{A \in E_{n}} f(\varphi(A)) \leqslant \sum_{A \in E_{n},|A| \geqslant 2, A \text { bon }} f(A)+\sum_{A \in E_{n},|A| \geqslant 2, A \text { pas bon }}(f(A)+1)+\sum_{A \in E_{n},|A| \leqslant 1} 2 \\
& \leqslant \sum_{A \in E_{n},|\mathcal{A}| \geqslant 2}(f(A)+1)-e_{n}+2(n+1)=\sum_{A \in E_{n}}(f(A)+1)-e_{n}+n+1
\end{aligned}
$$
Or, si $n \geqslant 5$, tout ensemble $A$ de la forme $\{1,2, n-1, n\} \cup(X+3)$, où $X$ est un élément de $E_{n-5}$, est nécessairement bon, puisque $f(A) \geqslant 2$. Il existe donc au moins $2^{n-5}$ bons ensembles dans $E_{n}$, ce qui montre que $e_{n} \geqslant 2^{n-5}$. En particulier, on a $e_{10} \geqslant 2^{5}=32>10+1$, et une récurrence immédiate montre que $e_{n}>n+1$ pour tout $n \geqslant 10$. Il s'ensuit que, si $n \geqslant 10$, alors
$$
\begin{aligned}
G(n) & =\sum_{A \in S_{n+2}} f(A)-\left|S_{n+2}\right| \leqslant \sum_{A \in E_{n}}(f(A)+1)-e_{n}+n+1-\left|S_{n+2}\right| \\
& \leqslant F(n)+\left|E_{n}\right|-e_{n}+n+1-\left|S_{n+2}\right|=F(n)-e_{n}+n+1<F(n)
\end{aligned}
$$
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
98646805-ed21-57c1-81c7-4a9a43539b79
| 607,724
|
Adalbert and Babette are playing dominoes on a rectangular grid that is 2 cells high and 2018 cells wide. Adalbert starts by placing a domino of size $1 \times 2$ horizontally, covering exactly two cells of the grid. Then Babette plays a domino of size $1 \times 2$ vertically, and so on. The first player who cannot place a domino without overlapping an already placed domino loses. Show that Adalbert has a winning strategy.
|
Divide the grid into 1009 consecutive blocks of size $2 \times 2$. Adalbert starts by placing a domino in one of these blocks. He is then assured of being able to complete it later with another domino. Babette must then play in another block (and she cannot play across two blocks, as her dominos are vertical). Adalbert plays in a third block, etc. When he plays for the 505th time, he starts a 505th block, which guarantees him the possibility of playing 505 more times. He can therefore place a total of 1010 dominos. Since a maximum of 2018 dominos can be placed in total, Babette can place at most 1008, so she will be blocked before Adalbert, who wins.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Adalbert et Babette jouent aux dominos sur une grille rectangulaire de 2 cases de hauteur et 2018 cases de largeur. Adalbert commence en posant un domino de taille $1 \times 2$ en position horizontale, de façon à ce qu'il recouvre exactement deux cases de la grille. Puis Babette joue de même un domino $1 \times 2$ en position verticale, et ainsi de suite. Le premier qui ne peut plus jouer sans chevaucher un domino déjà posé a perdu. Montrer qu'Adalbert a une stratégie gagnante.
|
Divisons la grille en 1009 blocs consécutifs de taille $2 \times 2$. Adalbert commence par poser un domino dans un de ces blocs. Il est alors assurer de pouvoir le compléter plus tard par un autre domino. Babette doit alors jouer dans un autre bloc (et elle ne peut pas jouer à cheval entre deux blocs, car ses dominos sont verticaux). Adalbert joue dans un troisième bloc, etc. Lorsqu'il joue pour la 505-ème fois, il entame un 505-ème bloc, ce qui lui garantit la possibilité de jouer encore 505 fois. Il pourra donc poser 1010 dominos au total. Comme on peut poser au plus 2018 dominos au total, Babette pourra en poser au plus 1008, elle sera donc bloquée avant Adalbert, qui l'emporte.
|
{
"resource_path": "French/segmented/envois/fr-pofm_2017-2018-envoi5-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
030a837b-f9d2-52e5-8f9b-c9db2567ed82
| 607,726
|
Let $ABC$ be an equilateral triangle and $P$ a point on its circumcircle, distinct from $A, B$, and $C$. The lines passing through $P$ and parallel to $(BC), (CA)$, and $(AB)$ intersect $(AC)$ at $M$, $(AB)$ at $N$, and $(BC)$ at $Q$, respectively. Prove that $M, N$, and $Q$ are collinear.
|
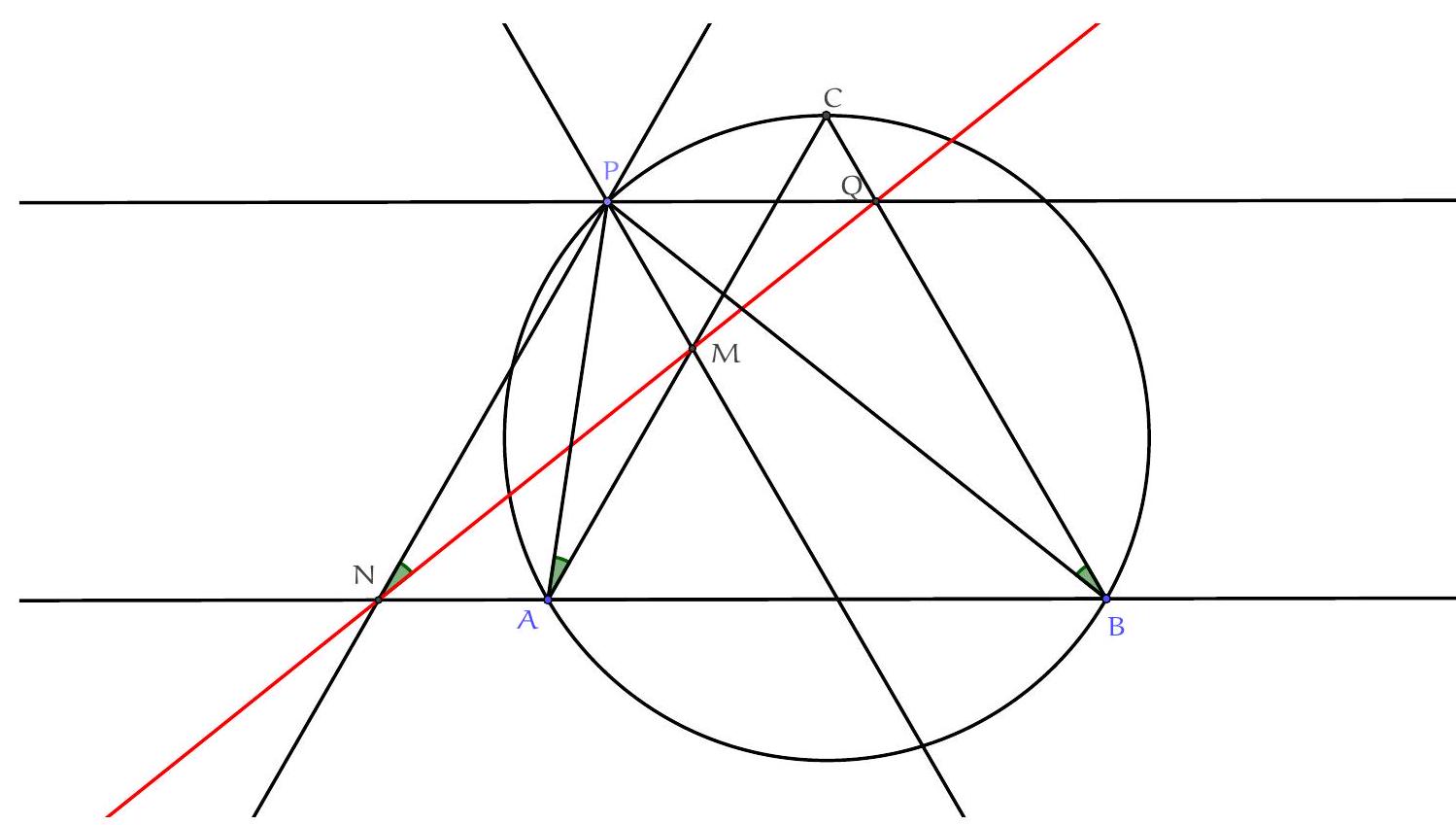
Without loss of generality, we can assume that $P$ is on the arc $(AC)$, as shown in the figure. There are many parallel lines, so angle equalities, and thus likely more cyclic points giving even more angle equalities... Indeed, $(NP) \parallel (AC)$ and $(PM) \parallel (CB)$, so $\widehat{NPM} = \widehat{ACB} = 60^\circ$. And $\widehat{NAM} = 180^\circ - \widehat{CAB} = 120^\circ$. Therefore, $\widehat{NPM} + \widehat{NAM} = 180^\circ$, so $P, M, A, N$ are cyclic. Thus,
$$
\widehat{PNM} = \widehat{PAM} = \widehat{PAC}.
$$
Note that $\widehat{PNM}$ is of interest to us: if we prove that $\widehat{PNM} = \widehat{PNQ}$, then we will have shown that $M, N$, and $Q$ are collinear.
Now let's work on $\widehat{PNQ}$: we observe as before that $P, Q, B, N$ are cyclic, so
$$
\widehat{PNQ} = \widehat{PBQ} = \widehat{PBC}
$$
But $\widehat{PBC} = \widehat{PAC}$ because $P, B, A, C$ are cyclic. Therefore, $\widehat{PNQ} = \widehat{PNM}$ and $M, N, Q$ are collinear.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle équilatéral et $P$ un point de son cercle circonscrit, distinct de $A, B$ et $C$. Les droites passant par $P$ et parallèles à $(B C),(C A)$ et $(A B)$ intersectent respectivement $(A C)$ en $M$, $(A B)$ en $N$ et (BC) en $Q$. Prouver que $M, N$ et $Q$ sont alignés.
|

Sans perte de généralité, on peut supposer que $P$ est sur l'arc ( $A C$ ), comme sur la figure. Il y a de nombreuses droites parallèles, donc égalités d'angles, donc sans doute des points cocycliques donnant encore plus d'égalité d'angles... En effet, (NP)//(AC) et $(\mathrm{PM}) / /(\mathrm{CB})$ donc $\widehat{\mathrm{NPM}}=\widehat{\mathrm{ACB}}=60^{\circ}$. Et $\widehat{N A M}=180^{\circ}-\widehat{C A B}=120^{\circ}$. Donc $\widehat{N P M}+\widehat{N A M}=180^{\circ}$, donc $P, M, A, N$ sont cocycliques. Ainsi,
$$
\widehat{P N M}=\widehat{P A M}=\widehat{P A C} .
$$
Notons que $\widehat{P N M}$ a un certain intérêt pour nous : si on prouve que $\widehat{P N M}=\widehat{\mathrm{PNQ}}$, alors on aura montré que $M, N$ et Q sont alignés.
Cherchons désormais à travailler sur $\widehat{\mathrm{PNQ}}$ : on constate comme précédemment que $\mathrm{P}, \mathrm{Q}, \mathrm{B}, \mathrm{N}$ sont cocycliques, donc
$$
\widehat{\mathrm{PNQ}}=\widehat{\mathrm{PBQ}}=\widehat{\mathrm{PBC}}
$$
Or $\widehat{\mathrm{PBC}}=\widehat{\mathrm{PAC}}$ car $\mathrm{P}, \mathrm{B}, \mathrm{A}, \mathrm{C}$ sont cocycliques. Donc $\widehat{\mathrm{PNQ}}=\widehat{\mathrm{PNM}}$ et $M, N, Q$ sont alignés.
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-pofm_2017-2018-envoi5-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
153a7141-c069-5d48-b31b-83b552447368
| 607,727
|
Let $\mathcal{C}$ be a circle, $P$ a point outside it, $A$ and $B$ the points of tangency of the two tangents to $\mathcal{C}$ passing through $P$. Let $K$ be any point on $(AB)$, distinct from $A$ and $B$. We call $T$ the second intersection of $\mathcal{C}$ and the circumcircle of triangle $PBK$. Furthermore, we call $P'$ the symmetric point of $P$ with respect to $A$.
Show that $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}'\mathrm{KA}}$.
|
Let's prove that triangles PBT and KAT are similar (in this order of vertices): according to the theorem of the angle inscribed in a tangent, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{TAB}}=\widehat{\mathrm{TAK}}$. Since $\mathrm{P}, \mathrm{T}, \mathrm{B}, \mathrm{K}$ are concyclic, $\widehat{\mathrm{TPB}}=180^{\circ}-\widehat{\mathrm{TKB}}=\widehat{\mathrm{TKA}}$. We deduce that PBT and KAT are similar, and that
$$
\frac{\mathrm{PT}}{\mathrm{KT}}=\frac{\mathrm{PB}}{\mathrm{KA}}.
$$
Since $\mathrm{PB}=\mathrm{PA}=\mathrm{P}^{\prime} \mathrm{A}$, we have
$$
\frac{\mathrm{PT}}{\mathrm{KT}}=\frac{\mathrm{P}^{\prime} \mathrm{A}}{\mathrm{KA}}
$$
and $\mathrm{P}^{\prime} A K$ and PTK are similar. Therefore, $\widehat{\mathrm{P}^{\prime} \mathrm{KA}}=\widehat{\mathrm{PKT}}$. Since $\widehat{\mathrm{PKT}}=\widehat{\mathrm{PBT}}$ by the inscribed angle theorem, this concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\mathcal{C}$ un cercle, P un point extérieur à celui-ci, $A$ et $B$ les points de contact des deux tangentes à $\mathcal{C}$ passant par $P$. Soit $K$ un point quelconque sur $(A B)$, distinct de $A$ et de $B$. On appelle $T$ la seconde intersection de $\mathcal{C}$ et du cercle circonscrit au triangle PBK . En outre, on appelle $\mathrm{P}^{\prime}$ le symétrique de $P$ par rapport à $A$.
Montrer que $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
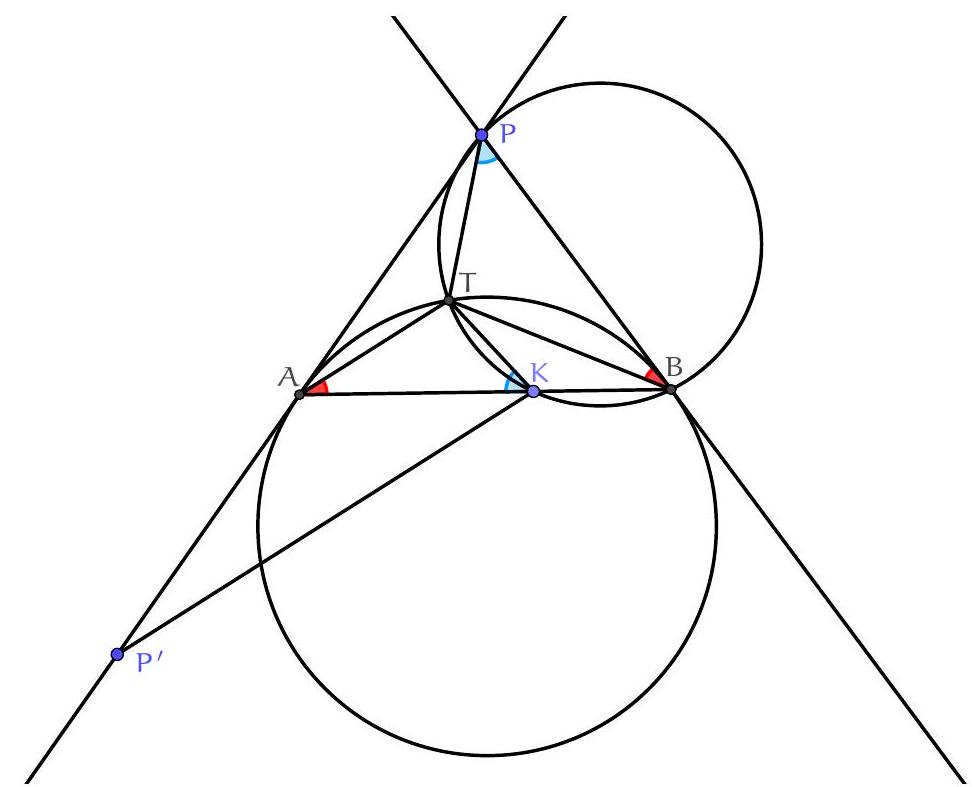
Prouvons que les triangles PBT et KAT sont semblables (dans cet ordre des sommets) : d'après le théorème de l'angle inscrit à la tangente, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{TAB}}=\widehat{\mathrm{TAK}}$. Comme $\mathrm{P}, \mathrm{T}, \mathrm{B}, \mathrm{K}$ sont cocycliques,
$\widehat{\mathrm{TPB}}=180^{\circ}-\widehat{\mathrm{TKB}}=\widehat{\mathrm{TKA}}$. On en déduit que PBT et KAT sont semblables, et que
$$
\frac{\mathrm{PT}}{\mathrm{KT}}=\frac{\mathrm{PB}}{\mathrm{KA}} .
$$
Or $\mathrm{PB}=\mathrm{PA}=\mathrm{P}^{\prime} \mathrm{A}$. Donc
$$
\frac{\mathrm{PT}}{\mathrm{KT}}=\frac{\mathrm{P}^{\prime} \mathrm{A}}{\mathrm{KA}}
$$
et $\mathrm{P}^{\prime} A K$ et PTK sont semblables. Donc $\widehat{\mathrm{P}^{\prime} \mathrm{KA}}=\widehat{\mathrm{PKT}}$. Or $\widehat{\mathrm{PKT}}=\widehat{\mathrm{PBT}}$ par théorème de l'angle inscrit, ce qui conclut.
|
{
"resource_path": "French/segmented/envois/fr-pofm_2017-2018-envoi5-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
898648dc-91f2-5a11-87e3-8ab190eab586
| 607,729
|
We define a sequence $\left(a_{n}\right)_{n \geqslant 0}$ as follows: we choose $a_{0}, a_{1} \in \mathbb{N}^{*}$, and for all integers $n \geqslant 0$, we set
$$
a_{n+2}=\left\lfloor\frac{2 a_{n}}{a_{n+1}}\right\rfloor+\left\lfloor\frac{2 a_{n+1}}{a_{n}}\right\rfloor,
$$
where $\lfloor x\rfloor$ denotes the greatest integer that does not exceed $x$. Prove that there exists $m \in \mathbb{N}$ such that $a_{m}=4$ and $\boldsymbol{a}_{\mathfrak{m}+1} \in\{3,4\}$.
|
For all $\mathrm{a}, \mathrm{b} \in \mathbb{N}^{*}$, we denote $\mathrm{g}(\mathrm{a}, \mathrm{b}):=\left\lfloor\frac{2 \mathrm{a}}{\mathrm{b}}\right\rfloor+\left\lfloor\frac{2 \mathrm{~b}}{\mathrm{a}}\right\rfloor$. It is well known that $\left(\frac{\sqrt{a}}{\sqrt{b}}-\frac{\sqrt{b}}{\sqrt{a}}\right)^{2}=\frac{a}{b}+\frac{b}{a}-2$, and since a square is always positive, $\frac{a}{b}+\frac{b}{a} \geqslant 2$, with equality if and only if $\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{b}}{\sqrt{a}}$, i.e., $a=b$. For any real number $x$, we have $\lfloor x\rfloor > x - 1$. Therefore, $g(a, b) > 2\left(\frac{a}{b}+\frac{b}{a}\right)-2 \geqslant 2$. Since $g(a, b)$ is an integer, $g(a, b) \geqslant 3$. Thus, $a_{n} \geqslant 3$ for all $n \geqslant 2$ (which also justifies the well-definition of the sequence $(a_{n})$: it never becomes zero, so the terms in the denominator in the statement do not pose a problem).
For $n \geqslant 2$, let $u_{n}=\max \left(a_{n}, a_{n+1}\right)$. We observe that for $a \geqslant b \geqslant 3, g(a, b) \leqslant \frac{2 \max (a, b)}{3}+2$, so if $\max (a, b)>6$, we have $g(a, b)<a$. Therefore, if $u_{n}>6, a_{n+2}<u_{n}$. If in addition $a_{n+1}<u_{n}$, then $u_{n+1}<u_{n}$. Otherwise, $u_{n+1}=u_{n}$, and $a_{n+3}<u_{n+1}$ as before, so $u_{n+2}<u_{n+1}$. Thus, if $u_{n}>6, u_{n+1}<u_{n}$ or $u_{n+2}<u_{n}$. Since $(u_{n})$ is a sequence of integer values, $\min \left(u_{n+1}, u_{n+2}\right) \leqslant u_{n}-1$. Continuing in this way, we necessarily arrive after a finite number of steps at an integer $\boldsymbol{l}$ such that $\mathfrak{u}_{\boldsymbol{l}} \leqslant 6$. Therefore, $\mathfrak{a}_{l}, \boldsymbol{a}_{l+1} \in\{3,4,5,6\}$. We easily prove by induction on $\mathfrak{n} \geqslant \mathrm{l}$ that $3 \leqslant a_{n} \leqslant 6$, using the fact that $g(a, b) \leqslant \frac{2 \max (a, b)}{3}+2$. Thus, the sequence $(a_{n})$ will always take its values in $\{3,4,5,6\}$. And, we easily observe that if $a \in\{3,4,5,6\}, g(a, 4)=g(4, a) \in\{3,4\}$. It thus suffices to show that $a_{m}=4$ for some $m \geqslant l$. It remains to study the case where $a_{l}, a_{l+1} \in\{3,5,6\}$. We verify by a small case study that $g(a, b) \leqslant 5$ for all $a, b \in\{3,4,5,6\}$, so $a_{l+2}, a_{l+3} \in\{3,4,5\}$. If $a_{l+2}=4$ or $a_{l+3}=4$, we are done. Otherwise, we verify that for $a, b \in\{3,5\}, g(a, b)=4$, which allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On définit une suite $\left(a_{n}\right)_{n \geqslant 0}$ ainsi : on choisit $a_{0}, a_{1} \in \mathbb{N}^{*}$, et pour tout entier $n \geqslant 0$, on pose
$$
a_{n+2}=\left\lfloor\frac{2 a_{n}}{a_{n+1}}\right\rfloor+\left\lfloor\frac{2 a_{n+1}}{a_{n}}\right\rfloor,
$$
où $\lfloor x\rfloor$ désigne le plus grand entier qui ne dépasse pas $x$. Prouver qu'il existe $m \in \mathbb{N}$ tel que $a_{m}=4$ et $\boldsymbol{a}_{\mathfrak{m}+1} \in\{3,4\}$.
|
Pour tous $\mathrm{a}, \mathrm{b} \in \mathbb{N}^{*}$, on note $\mathrm{g}(\mathrm{a}, \mathrm{b}):=\left\lfloor\frac{2 \mathrm{a}}{\mathrm{b}}\right\rfloor+\left\lfloor\frac{2 \mathrm{~b}}{\mathrm{a}}\right\rfloor$. Il est bien connu que $\left(\frac{\sqrt{a}}{\sqrt{b}}-\frac{\sqrt{b}}{\sqrt{a}}\right)^{2}=\frac{a}{b}+\frac{b}{a}-2$, or un carré est toujours positif, donc $\frac{a}{b}+\frac{b}{a} \geqslant 2$, avec égalité si et seulement si $\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{b}}{\sqrt{a}}$, soit $a=b$. Et pour tout réel $x$, on $a\lfloor x\rfloor>x-1$. Donc $g(a, b)>2\left(\frac{a}{b}+\frac{b}{a}\right)-2 \geqslant 2$. Or $g(a, b)$ est entier, donc $g(a, b) \geqslant 3$. Ainsi, $a_{n} \geqslant 3$ pour tout $n \geqslant 2$ (ce qui permet au passage de justifier la bonne définition de la suite ( $a_{n}$ ) : elle ne s'annule jamais, donc les termes au dénominateur
dans l'énoncé ne posent pas de problème).
Pour $n \geqslant 2$, posons $u_{n}=\max \left(a_{n}, a_{n+1}\right)$. On remarque que pour $a \geqslant b \geqslant 3, g(a, b) \leqslant \frac{2 \max (a, b)}{3}+2$, donc si $\max (a, b)>6$, on a $g(a, b)<a$. Donc, si $u_{n}>6, a_{n+2}<u_{n}$. Si de plus $a_{n+1}<u_{n}$, alors $u_{n+1}<u_{n}$. Sinon, $u_{n+1}=u_{n}$, et $a_{n+3}<u_{n+1}$ comme précédemment, donc $u_{n+2}<u_{n+1}$. Ainsi, si $u_{n}>6, u_{n+1}<u_{n}$ ou $u_{n+2}<u_{n}$. Or $\left(u_{n}\right)$ est une suite à valeurs entières, donc $\min \left(u_{n+1}, u_{n+2}\right) \leqslant$ $u_{n}-1$. En continuant de cette façon, on arrive nécessairement après un nombre fini d'étapes sur un entier $\boldsymbol{l}$ tel que $\mathfrak{u}_{\boldsymbol{l}} \leqslant 6$. On a donc $\mathfrak{a}_{l}, \boldsymbol{a}_{l+1} \in\{3,4,5,6\}$. On prouve aisément par récurrence sur $\mathfrak{n} \geqslant \mathrm{l}$ que $3 \leqslant$ $a_{n} \leqslant 6$, en utilisant le fait que $g(a, b) \leqslant \frac{2 \max (a, b)}{3}+2$. Ainsi, la suite $\left(a_{n}\right)$ prendra toujours ses valeurs dans $\{3,4,5,6\}$. Et, on constate facilement que si $a \in\{3,4,5,6\}, g(a, 4)=g(4, a) \in\{3,4\}$. Il suffit ainsi de montrer que $a_{m}=4$, pour un certain $m \geqslant l$. Il reste donc à étudier le cas où $a_{l}, a_{l+1} \in\{3,5,6\}$. On vérifie par une petite étude de cas que $g(a, b) \leqslant 5$ pour tout $a, b \in\{3,4,5,6\}$, donc $a_{l+2}, a_{l+3} \in\{3,4,5\}$. Si $a_{l+2}=4$ ou $a_{l+3}=4$, c'est gagné. Sinon, on vérifie que pour $a, b \in\{3,5\}, g(a, b)=4$, ce qui nous permet de conclure.
|
{
"resource_path": "French/segmented/envois/fr-pofm_2017-2018-envoi5-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
92d5bf49-5d6c-5cab-b508-425ef8e490c3
| 607,731
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles intersecting at $M$ and $N$. Let $A$ and $B$ be the points of tangency of these two circles with their nearest common external tangent to $M$. Let $C$ and $D$ be the symmetrics of $A$ and $B$ with respect to $M$, and $E$ and $F$ the points of intersection (other than $M$) of the circumcircle of $MCD$ with $\Gamma_{1}$ and $\Gamma_{2}$ respectively. Show that the circumcircles of $MEF$ and $NEF$ have the same radius.
|
The statement as formulated may seem curious, but we notice that it suffices to prove that $\widehat{\mathrm{EMF}} + \widehat{\mathrm{ENF}} = 180^{\circ}$ to obtain the desired result.
Let $L$ be the intersection of $(MN)$ and $(AB)$. $L$ is on the radical axis of $\Gamma_{1}$ and $\Gamma_{2}$, so its power with respect to these two circles is the same, i.e., $LA^2 = LB^2$, hence $L$ is the midpoint of $[AB]$.
By the construction of $C$ and $D$, $ABCD$ is a parallelogram with center $M$, so $(AD) \parallel (BC) \parallel (MN)$.
Let's prove that $B, C, F$ are collinear: by the inscribed angle theorem, $\widehat{CFM} = \widehat{CDM}$. But $\widehat{CDM} = \widehat{DBA} = \widehat{MBA}$ and $\widehat{MBA} = \widehat{BFM}$ by the inscribed angle theorem at the tangent. Therefore, $B, C, F$ are collinear, and the same applies to $A, D, E$ by symmetry.
Thus, $AMNF$ and $BMNE$ are trapezoids whose four vertices are concyclic, and the inscribed angle theorem shows that they are isosceles. Therefore, $\widehat{MNE} = \widehat{AMN}$ and $\widehat{MNP} = \widehat{NMB}$, which implies that $\widehat{\mathrm{ENF}} = \widehat{\mathrm{AMB}} = 180^{\circ} - \widehat{\mathrm{BMC}}$. It remains to establish that $\widehat{\mathrm{BMC}} = \widehat{\mathrm{EMF}}$.
We even prove that $\triangle CMB$ and $\triangle EMF$ are similar (which allows us to conclude): since $C, D, E, F, M$ are concyclic, $\widehat{MCB} = 180^{\circ} - \widehat{MCF} = \widehat{MEF}$ and $\widehat{MBC} = \widehat{MDA} = 180^{\circ} - \widehat{MDE} = \widehat{MFE}$, so $\triangle CMB$ and $\triangle EMF$ are indeed similar.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma_{1}$ et $\Gamma_{2}$ deux cercles s'intersectant en $M$ et $N$. Soit $A$ et $B$ les points de contact de ces deux cercles avec leur tangente extérieure commune la plus proche de $M$. Soient C et D les symétriques respectifs de $A$ et $B$ par rapport à $M$, et $E$ et $F$ les points d'intersection (autres que $M$ ) du cercle circonscrit à MCD avec $\Gamma_{1}$ et $\Gamma_{2}$ respectivement. Montrer que les cercles circonscrits à MEF et NEF ont le même rayon.
|
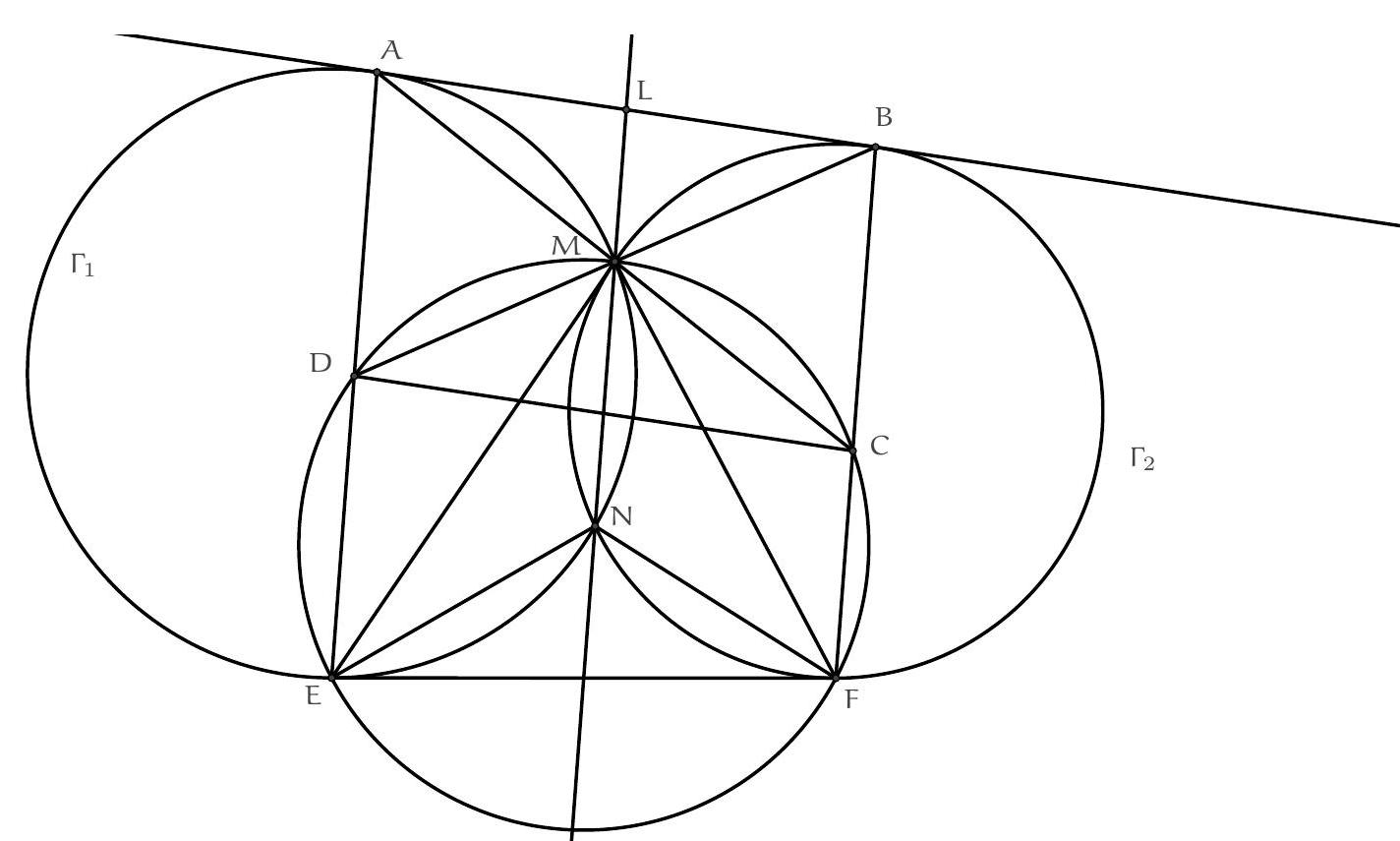
L'énoncé ainsi formulé peut sembler curieux, mais on remarque qu'il suffit de prouver que $\widehat{\mathrm{EMF}}+\widehat{\mathrm{ENF}}=$ $180^{\circ}$ pour obtenir le résultat voulu.
Soit L l'intersection de ( MN ) et ( AB ). L est sur l'axe radical de $\Gamma_{1}$ et $\Gamma_{2}$, donc sa puissance par rapport à ces deux cercles est la même, soit $L A^{2}=L B^{2}$, donc $L$ est le milieu de $[A B]$.
Par construction de $C$ et $D, A B C D$ est un parallèlogramme de centre $M$, donc (AD)//(BC)//(MN).
Prouvons que $B, C, F$ sont alignés : par théorème de l'angle inscrit, $\widehat{C F M}=\widehat{C D M}$. Or $\widehat{C D M}=\widehat{D B A}=$ $\widehat{M B A}$ et $\widehat{M B A}=\widehat{B F M}$ par théorème de l'angle inscrit à la tangente. Donc $B, C, F$ sont alignés, et il en va de même pour $A, D, E$ par symétrie.
Ainsi, $A M N F$ et $B M N E$ sont des trapèzes dont les quatre sommets sont cocycliques, le théorme de l'angle inscrit montre qu'ils sont isocèles. Donc $\widehat{M N E}=\widehat{A M N}$ et $\widehat{M N P}=\widehat{N M B}$, ce qui implique que $\widehat{\mathrm{ENF}}=\widehat{\mathrm{AMB}}=180^{\circ}-\widehat{\mathrm{BMC}}$. Il reste donc à établir que $\widehat{\mathrm{BMC}}=\widehat{\mathrm{EMF}}$.
On prouve même que CMB et EMF sont semblables (ce qui permet de conclure) : comme C, D, E, F, M sont cocycliques, $\widehat{M C B}=180^{\circ}-\widehat{M C F}=\widehat{M E F}$ et $\widehat{M B C}=\widehat{M D A}=180^{\circ}-\widehat{M D E}=\widehat{M F E}$, donc CMB et EMF sont bien semblables.
|
{
"resource_path": "French/segmented/envois/fr-pofm_2017-2018-envoi5-corrige.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution de l'exercice 9"
}
|
1187ddc5-7c5b-5905-b1f7-f27104b43d0c
| 607,733
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. We denote $\Delta_{1}$ and $\Delta_{2}$ as the images of the line $(A B)$ under the symmetries whose axes are respectively the internal bisectors of $\widehat{C A D}$ and $\widehat{C B D}$. Let $P$ be the intersection of $\Delta_{1}$ and $\Delta_{2}$.
Prove that $(O P)$ and $(C D)$ are perpendicular.
|
We only treat the case where $O$ is inside $ABCD$ (the other cases being similar). According to the properties of the inscribed angle, the two considered bisectors intersect at a point on the circle, denoted by $S$, which is the midpoint of the arc $CD$. In particular, $(OS)$ and $(CD)$ are perpendicular. It is therefore sufficient to show that $P, O, S$ are collinear.
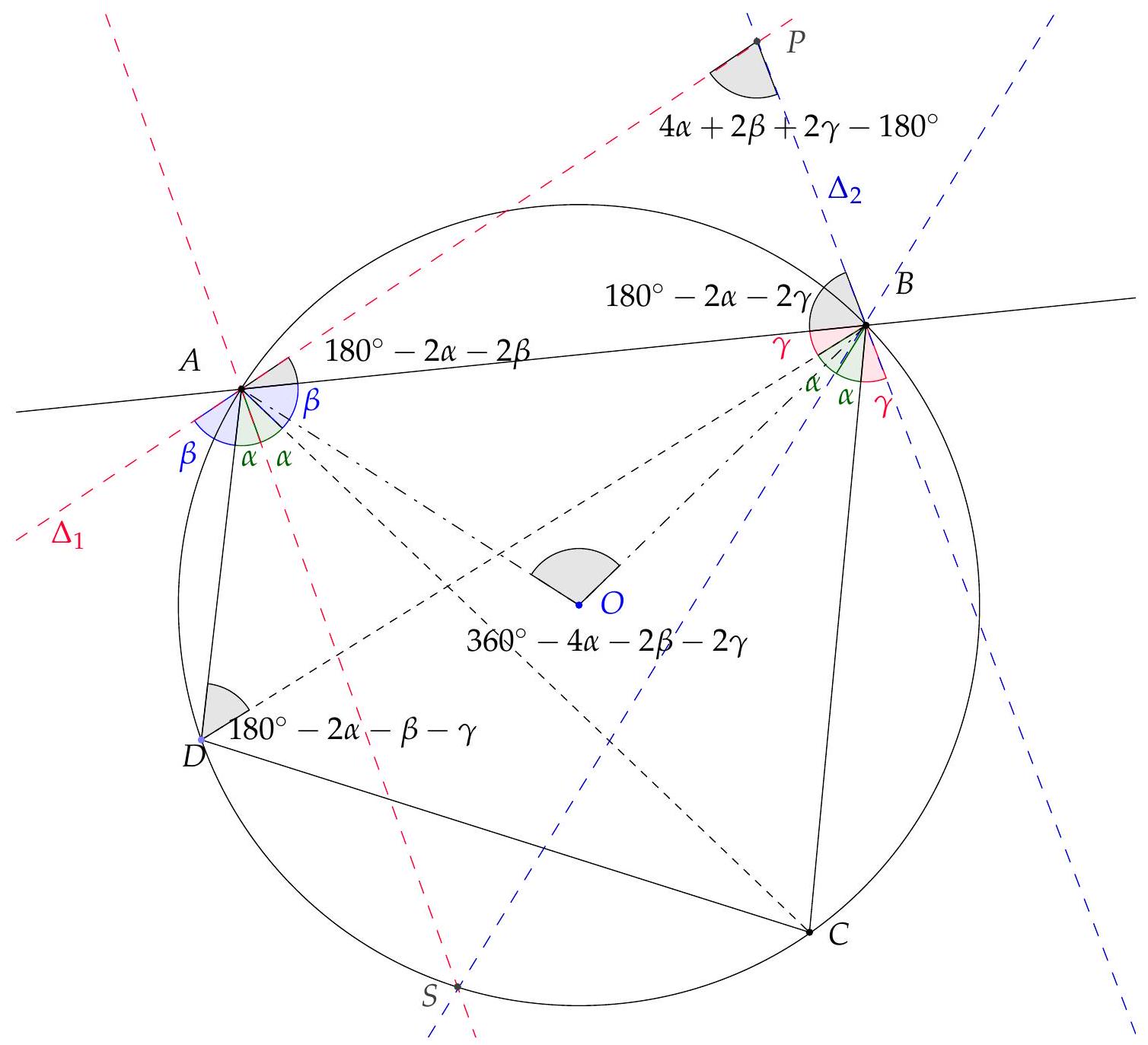
An angle chase (see figure) yields $\widehat{APB} + \widehat{AOB} = 180^\circ$. Thus, $A, P, B, O$ are concyclic. Then $\widehat{POB} = \widehat{PAB} = 180^\circ - 2\alpha - 2\beta$. Since $A, B, C, D$ are concyclic, we have $\widehat{BOC} = 2\widehat{BAC} = 2\beta$ and $\widehat{COS} = 2\widehat{SBC} = 2\alpha$. Therefore, $\widehat{POB} + \widehat{BOC} + \widehat{COS} = 180^\circ$. The points $P, O, S$ are thus collinear, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère inscrit dans un cercle de centre $O$. On note $\Delta_{1}$ et $\Delta_{2}$ les images de la droite $(A B)$ par les symétries dont les axes sont respectivement les bissectrices intérieures de $\widehat{C A D}$ et $\widehat{C B D}$. Soit $P$ l'intersection de $\Delta_{1}$ et $\Delta_{2}$.
Prouver que $(O P)$ et $(C D)$ sont perpendiculaires.
|
On traite uniquement le cas où $O$ est à l'intérieur de $A B C D$ (les autres cas étant similaires). D'après les propriétés de l'angle inscrit, les deux bissectrices considérées s'intersectent en un point du cercle noté $S$, qui est le milieu de l'arc $C D$. En particulier, (OS) et $(C D)$ sont perpendiculaires. Il suffit donc de montrer que $P, O, S$ sont alignés.

Une chasse aux angles (voir figure) fournit $\widehat{A P B}+\widehat{A O B}=180^{\circ}$. Ainsi, $A, P, B, O$ sont cocycliques. Alors $\widehat{P O B}=\widehat{P A B}=180^{\circ}-2 \alpha-2 \beta$. Comme $A, B, C, D$ sont cocyliques, on a $\widehat{B O C}=2 \widehat{B A C}=2 \beta$ et $\widehat{C O S}=2 \widehat{S B C}=2 \alpha$. Ainsi, $\widehat{P O B}+\widehat{B O C}+\widehat{C O S}=180^{\circ}$. Les points $P, O, S$ sont donc alignés, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2011-2012-ofm-2011-2012-test-janvier-corrige.jsonl",
"problem_match": "## Exercice 3\n",
"solution_match": "\nSolution."
}
|
b29b63e2-8740-5fd7-9c8c-5a4bbde28ae2
| 604,159
|
Let $a, b, c, d$ be natural numbers such that $0<|a d-b c|<\min (c, d)$.
Prove that for all integers $x, y>1$ that are coprime, the number $x^{a}+y^{b}$ is not divisible by $x^{c}+y^{d}$.
|
By contradiction: suppose that the integers $x, y>1$ are coprime and that $s=x^{c}+y^{d}$ divides $x^{a}+y^{b}$. We then have:
$$
x^{c}=-y^{d} \quad \bmod s \quad \text { and } \quad x^{a}=-y^{b} \quad \bmod s .
$$
Thus,
$$
x^{a d}=(-1)^{d} y^{b d} \bmod s \quad \text { and } \quad x^{b c}=(-1)^{c} y^{b d} \bmod s .
$$
So $x^{a d}=(-1)^{b-d} x^{b c} \bmod s$.
Since $c>0$ and $x$ and $y$ are coprime, it is clear that $x$ and $s$ are coprime. We can therefore divide by $x^{\min (a d, b c)}$ in the above congruence, and we get $x^{|a d-b c|}=(-1)^{b-d} \bmod s$. Similarly, we have $y^{|a d-b c|}=(-1)^{a-c} \bmod s$.
We deduce that:
$$
x^{|a d-b c|}+y^{|a d-b c|} \text { or } x^{|a d-b c|}-y^{|a d-b c|} \text { is divisible by } s .
$$
But we have $x^{|a d-b c|}-y^{|a d-b c|} \neq 0$ because $x$ and $y$ are coprime, greater than 1, and $|a d-b c|>0$. Furthermore, $|a d-b c|<\min (c, d)$, so we have the inequalities
$$
0<\left|x^{|a d-b c|}-y^{|a d-b c|}\right|<x^{|a d-b c|}+y^{|a d-b c|}<x^{c}+y^{d}=s,
$$
which contradicts (1).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a, b, c, d$ des entiers naturels tels que $0<|a d-b c|<\min (c, d)$.
Prouver que pour tous entiers $x, y>1$ premiers entre eux, le nombre $x^{a}+y^{b}$ n'est pas divisible par $x^{c}+y^{d}$.
|
Par l'absurde : on suppose que les entiers $x, y>1$ sont premiers entre eux et que $s=x^{c}+y^{d}$ divise $x^{a}+y^{b}$. On a alors:
$$
x^{c}=-y^{d} \quad \bmod s \quad \text { et } \quad x^{a}=-y^{b} \quad \bmod s .
$$
D'où
$$
x^{a d}=(-1)^{d} y^{b d} \bmod s \quad \text { et } \quad x^{b c}=(-1)^{c} y^{b d} \bmod s .
$$
Ainsi $x^{a d}=(-1)^{b-d} x^{b c} \bmod s$.
Or, puisque $c>0$ et que $x$ et $y$ sont premiers entre eux, on a clairement $x$ et $s$ premiers entre eux. On peut donc diviser par $x^{\min (a d, b c)}$ dans la congruence ci-dessus, et il vient $x^{|a d-b c|}=(-1)^{b-d} \bmod s$. De même, on a $y^{|a d-b c|}=(-1)^{a-c} \bmod s$.
On en déduit que :
$$
x^{|a d-b c|}+y^{|a d-b c|} \text { ou } x^{|a d-b c|}-y^{|a d-b c|} \text { est divisible par } s .
$$
Mais on a $x^{|a d-b c|}-y^{|a d-b c|} \neq 0$ car $x$ et $y$ sont premiers entre eux, supérieurs à 1 , et $|a d-b c|>0$. De plus $|a d-b c|<\min (c, d)$ donc on a les inégalités
$$
0<\left|x^{|a d-b c|}-y^{|a d-b c|}\right|<x^{|a d-b c|}+y^{|a d-b c|}<x^{c}+y^{d}=s,
$$
ce qui contredit (1).
|
{
"resource_path": "French/segmented/tests/fr-2011-2012-ofm-2011-2012-test-janvier-corrige.jsonl",
"problem_match": "## Exercice 4\n",
"solution_match": "\nSolution."
}
|
e7434207-e21d-510d-a917-b3abb96f641f
| 604,180
|
Let $n$ and $k$ be two strictly positive integers. Consider an assembly of $k$ people such that, for any group of $n$ people, there is a $(n+1)$-th person who knows them all (if $A$ knows $B$ then $B$ knows $A$).
1) If $k=2n+1$, prove that there exists a person who knows everyone else.
2) If $k=2n+2$, give an example of such an assembly in which no one knows everyone else.
|
1) We start by constructing, by induction, a group of $n+1$ people who all know each other: it is clear that we can find two people who know each other. Suppose that for a fixed $p \in\{2, \ldots, n\}$, we have managed to find a group of $p$ people who all know each other. By adding $n-p$ arbitrary people to this group, we form a group of $n$ people, and we know that there is an $(n+1)^{st}$ person who knows them all. By adding this person to our group of $p$ people, we thus form a group of $p+1$ people who all know each other.
We therefore consider a group $G$ of $n+1$ people who all know each other. Since $k=2 n+1$, there are therefore $n$ people left who form a disjoint group $G^{\prime}$. For this group $G^{\prime}$, we know that there is a person who necessarily belongs to $G$ and who knows all its members. This person then knows everyone.
2) We divide the people into $n+1$ disjoint pairs, and assume that each person knows everyone else except the one who is in the same pair as them. Thus, no one knows everyone.
Let $G$ be a group of $n$ people from this assembly. Since there are $n+1$ pairs, there must be a pair, say $\{A, B\}$, of which neither member is in $G$. Therefore, $A$ knows all the members of $G$, and the conditions of the statement are satisfied.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient $n$ et $k$ deux entiers strictement positifs. On considère une assemblée de $k$ personnes telle que, pour tout groupe de $n$ personnes, il y en ait une $(n+1)$-ième qui les connaisse toutes (si $A$ connaît $B$ alors $B$ connaît $A$ ).
1) Si $k=2 n+1$, prouver qu'il existe une personne qui connaît toutes les autres.
2) Si $k=2 n+2$, donner un exemple d'une telle assemblée dans laquelle personne ne connaît tous les autres.
|
1) On commence par construire, par récurrence, un groupe de $n+1$ personnes qui se connaissent deux à deux : il est clair que l'on peut trouver deux personnes qui se connaissent. Supposons que pour $p \in\{2, \ldots, n\}$ fixé, on ait réussi à trouver un groupe de $p$ personnes qui se connaîssent deux à deux. En complétant ce groupe par $n-p$ personnes quelconques, on forme un groupe de $n$ personnes dont on sait qu'il en existe une $(n+1)^{i e ̀ m e}$ qui les connaît toutes. En ajoutant cette personne à notre groupe de $p$ personnes, on forme ainsi un groupe de $p+1$ personnes qui se connaissent deux à deux.
On considère donc un groupe $G$ de $n+1$ personnes qui se connaissent deux à deux. Puisque $k=2 n+1$, il reste donc $n$ personnes qui forment un groupe $G^{\prime}$ disjoint du précédent. Pour ce groupe $G^{\prime}$, on sait qu'il existe une personne appartenant nécessairement à $G$ qui en connaît tous les membres. Cette personne connaît alors tout le monde.
2) On divise les personnes en $n+1$ paires disjointes, et on suppose que chaque personne connaît toutes les autres sauf celle qui est dans la même paire qu'elle. Ainsi, personne ne connaît tout le monde.
Soit $G$ un groupe de $n$ personnes de cette assemblée. Puisqu'il y a $n+1$ paires, c'est donc qu'il existe une paire, disons $\{A, B\}$, dont aucun des deux membres n'est dans $G$. Par suite, $A$ connaît tous les membres de $G$, et les conditions de l'énoncé sont satisfaites.
|
{
"resource_path": "French/segmented/tests/fr-2011-2012-ofm-2011-2012-test-mars-corrige.jsonl",
"problem_match": "## Exercice 1\n",
"solution_match": "## Solution."
}
|
59fb4cac-ea1d-50c4-838e-e343a5163494
| 604,195
|
Let $ABC$ be an acute triangle with $AB \neq AC$. We denote $\Gamma$ as its circumcircle, $H$ as its orthocenter, and $O$ as the center of $\Gamma$. Let $M$ be the midpoint of $[BC]$. The line $(AM)$ intersects $\Gamma$ again at $N$, and the circle with diameter $[AM]$ intersects $\Gamma$ again at $P$.
Prove that the lines $(AP)$, $(BC)$, and $(OH)$ are concurrent if and only if $AH = HN$.
|
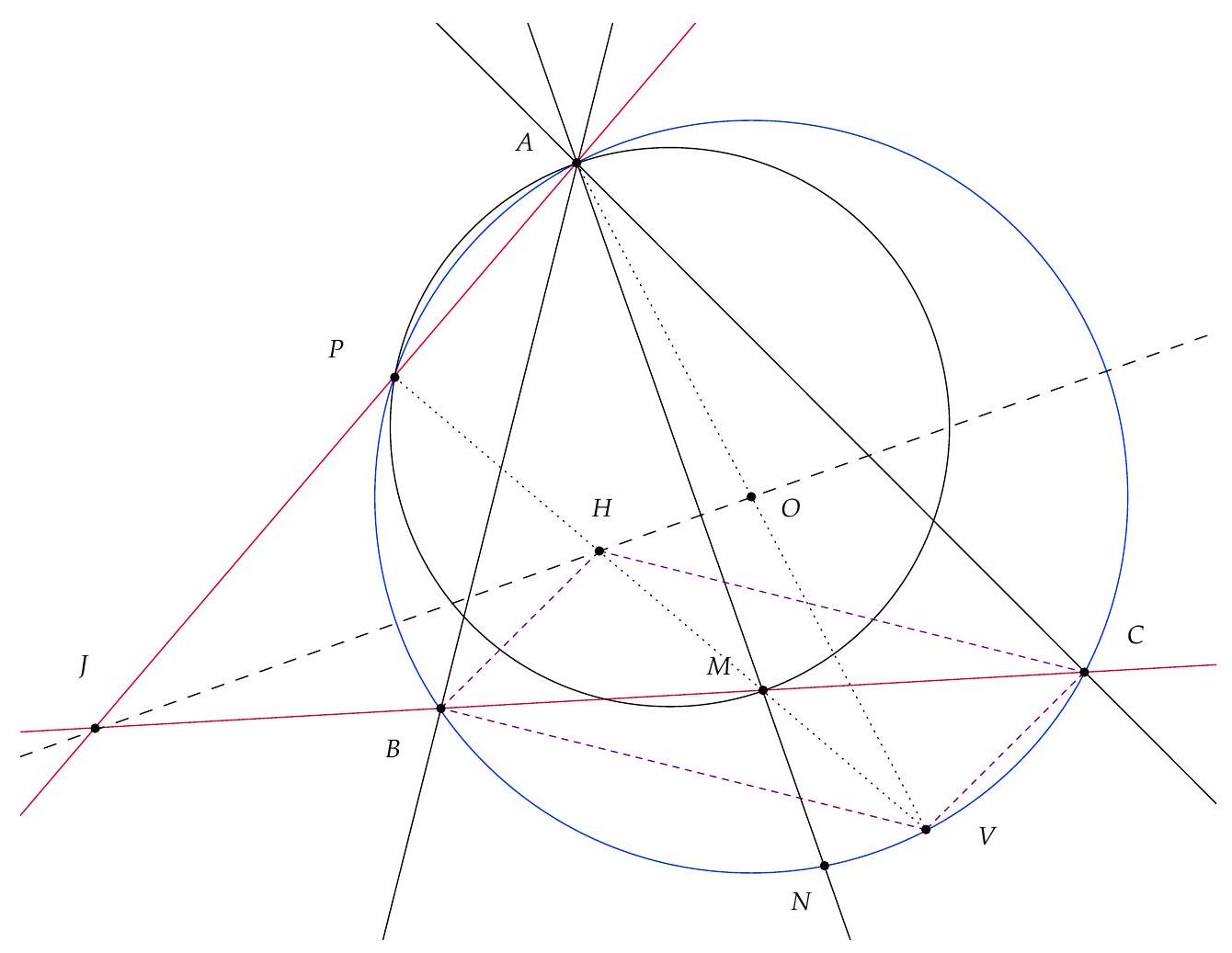
First, let's show that $P, H, M$ are collinear. To this end, introduce $V$, the point diametrically opposite to $A$ on $\Gamma$. Then $(V C) \perp (A C)$ and therefore $(B H) \parallel (V C)$. Similarly, we see that $(C H) \parallel (V B)$. It follows that $B H C V$ is a parallelogram with center $M$. The points $H, M, V$ are therefore collinear. If we denote $U$ as the second intersection of $(H V)$ with $\Gamma$, by cocyclicity we obtain $\widehat{A U V} = \widehat{A B V} = 90^{\circ}$. Since $\widehat{A P V} = \widehat{A P M} = 90^{\circ}$, we conclude that $U = P$ and therefore that $P, H, M$ are collinear.
Let $J$ be the intersection of $(A P)$ and $(BC)$. Since $(A H)$ and $(M P)$ are altitudes of triangle $A J M$, $H$ is also the orthocenter of $A J M$. Thus, $(O H)$ passes through $J$ if and only if $(O H) \perp (A N)$. Since $O A = O N$, this implies that $(O H) \perp (A N)$ if and only if $(O H)$ is the perpendicular bisector of $[A N]$, which is to say if and only if $H A = H N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle avec $A B \neq A C$. On note $\Gamma$ son cercle circonscrit, $H$ son orthocentre et $O$ le centre de $\Gamma$. Soit $M$ le milieu de $[B C]$. La droite $(A M)$ recoupe $\Gamma$ en $N$ et le cercle de diamètre $[A M]$ recoupe $\Gamma$ en $P$.
Prouver que les droites $(A P),(B C),(O H)$ sont concourantes si, et seulement si, $A H=H N$.
|
Montrons d'abord que $P, H, M$ sont alignés. À cet effet, introduisons $V$, le point diamétralement opposé à $A$ sur $\Gamma$. Alors $(V C) \perp(A C)$ et donc $(B H) / /(V C)$. De même on voit que $(C H) / /(V B)$. Il s'ensuit que $B H C V$ est un parallélogramme de centre $M$. Les points $H, M, V$ sont donc alignés. Si on note $U$ la deuxième intersection de $(H V)$ avec $\Gamma$, par cocyclicité on obtient $\widehat{A U V}=\widehat{A B V}=90^{\circ}$. Comme $\widehat{A P V}=\widehat{A P M}=90^{\circ}$, on conclut que $U=P$ et donc que $P, H, M$ sont alignés.
Soit J l'intersection de $(A P)$ et de (BC). Comme $(A H)$ et $(M P)$ sont des hauteurs du triangle $A J M, H$ est aussi l'orthocentre de $A J M$. Ainsi, $(O H)$ passe par $J$ si, et seulement si, $(O H) \perp(A N)$. Or $O A=O N$, ce qui implique que $(O H) \perp(A N)$ si, et seulement si $(O H)$ est la médiatrice de de $[A N]$, c'est-à-dire si, et seulement si, $H A=H N$.
|
{
"resource_path": "French/segmented/tests/fr-2011-2012-ofm-2011-2012-test-mars-corrige.jsonl",
"problem_match": "## Exercice 2\n",
"solution_match": "## Solution."
}
|
b2d4fe4c-887a-5a48-a627-dce86a42e2a5
| 604,211
|
Let $ABCD$ be a convex quadrilateral such that the lines $(AD)$ and $(BC)$ are not parallel. Suppose that the circles with diameters $[AB]$ and $[CD]$ intersect at two points $E$ and $F$ located inside $ABCD$. Let $\Gamma_{E}$ be the circle passing through the orthogonal projections of $E$ onto $(AB)$, $(BC)$, and $(CD)$, and $\Gamma_{F}$ be the circle passing through the orthogonal projections of $F$ onto $(CD)$, $(DA)$, and $(AB)$.
Prove that the midpoint of $[EF]$ lies on the line passing through the two points of intersection of $\Gamma_{E}$ and $\Gamma_{F}$.
|
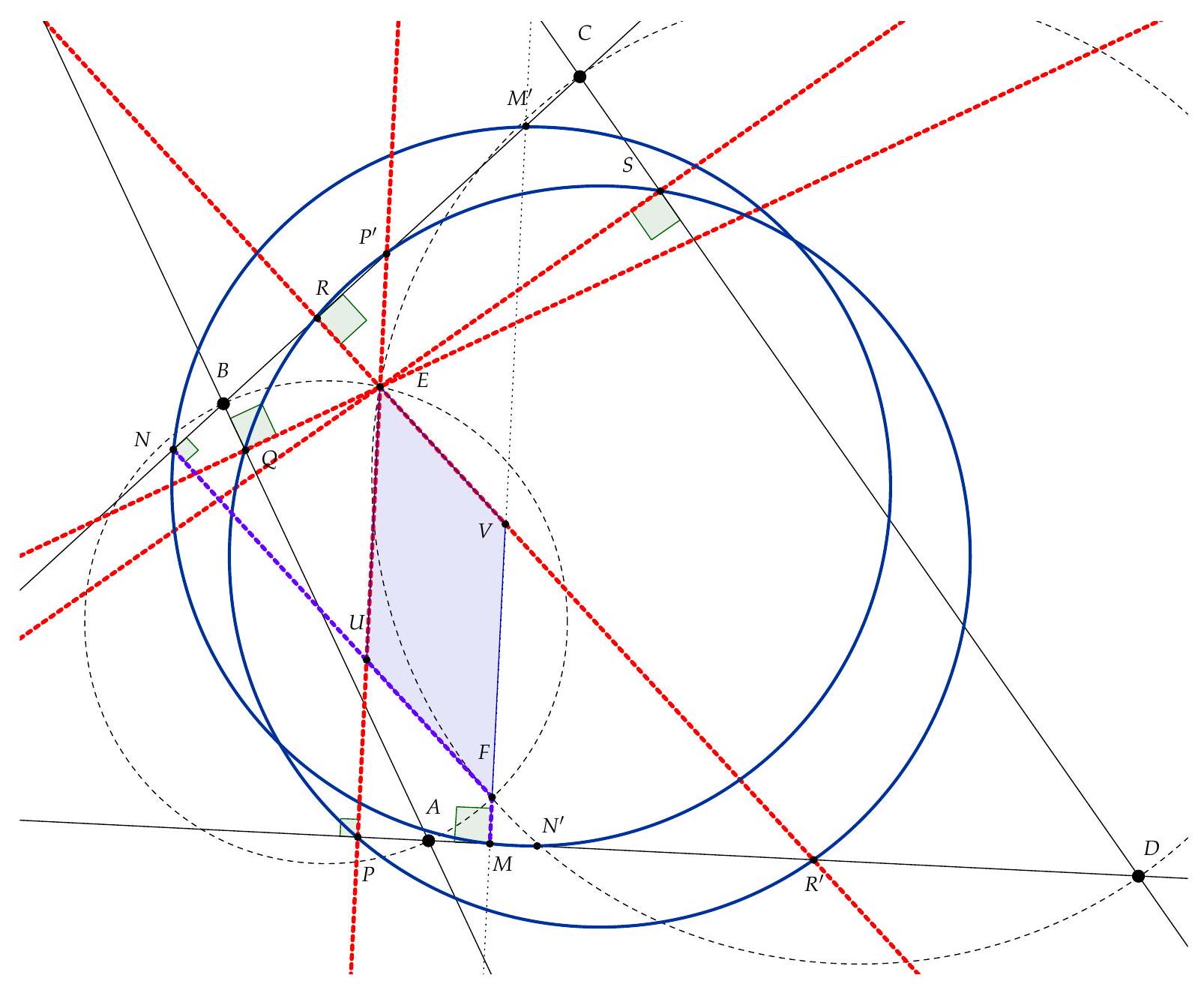
Let $P, Q, R, S$ be the projections of $E$ onto the lines $(D A), (A B), (B C), (C D)$. The points $P$ and $Q$ belong to the circle with diameter $[A E]$, so that $\widehat{Q P E} = \widehat{Q A E}$. Similarly, $\widehat{Q R E} = \widehat{Q B E}$. Thus:
$$
\widehat{Q P E} + \widehat{Q R E} = \widehat{Q A E} + \widehat{Q B E} = 90^{\circ}
$$
Similarly, we show that $\widehat{Q P S} + \widehat{Q R S} = 90^{\circ} + 90^{\circ} = 180^{\circ}$. Therefore, the points $P, Q, R, S$ lie on $\Gamma_{E}$. Similarly, the orthogonal projections of $F$ onto the sides of $A B C D$ lie on $\Gamma_{F}$.
Let $K$ be the intersection of $(A D)$ and $(B C)$. Without loss of generality, assume that $A \in [D K]$. It is easy to see that $\widehat{C K D} < 90^{\circ}$ (otherwise, the circle with diameter $[C D]$ would cover the entire $A B C D$). Therefore, the lines $(E P)$ and $(B C)$ intersect at a point $P^{\prime}$, and the lines $(E R)$ and $(A D)$ intersect at a point $R^{\prime}$. We will show that $P^{\prime}$ and $R^{\prime}$ are on $\Gamma_{E}$. By the cocyclicity of the points $R, E, Q, B$:
$$
\widehat{Q R K} = \widehat{Q E B} = 90^{\circ} - \widehat{Q B E} = \widehat{Q A E} = \widehat{Q P E}.
$$
Thus, $\widehat{Q R K} = \widehat{Q P P^{\prime}}$, which implies that $P^{\prime} \in \Gamma_{E}$. Similarly, $R^{\prime} \in \Gamma_{E}$.
Similarly, let $M$ and $N$ be the projections of $F$ onto $(A D)$ and $(B C)$, and let $M^{\prime}$ be the intersection of $(F M)$ and $(B C)$, and $N^{\prime}$ be the intersection of $(F N)$ and $(A D)$. Using the same arguments as before, we see that $M^{\prime}$ and $N^{\prime}$ are on $\Gamma_{F}$.
Finally, let $U$ be the intersection of $(N N^{\prime})$ with $(P P^{\prime})$ and $V$ be the intersection of $(M M^{\prime})$ with $(R R^{\prime})$. Since the angles at $N$ and $P$ are right angles, $N, N^{\prime}, P, P^{\prime}$ are cocyclic. The power of $U$ with respect to the circle passing through these points is therefore:
$$
U N \cdot U N^{\prime} = U P \cdot U P^{\prime}
$$
Thus, $U$ lies on the radical axis of $\Gamma_{E}$ and $\Gamma_{F}$. Similarly, $V$ lies on this radical axis. Since $E U F V$ is a parallelogram, this implies that $(U V)$ intersects $[E F]$ at its midpoint.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe tel que les droites $(A D)$ et $(B C)$ ne sont pas parallèles. On suppose que les cercles de diamètre $[A B]$ et $[C D]$ se coupent en deux points $E$ et $F$ situés à l'intérieur de $A B C D$. Soit $\Gamma_{E}$ le cercle qui passe par les projetés orthogonaux de $E$ sur $(A B),(B C)$ et $(C D)$, et $\Gamma_{F}$ le cercle qui passe par les projetés orthogonaux de $F$ sur $(C D),(D A)$ et $(A B)$.
Prouver que le milieu de $[E F]$ appartient à la droite passant par les deux points d'intersection de $\Gamma_{E}$ et $\Gamma_{F}$.
|
Soient $P, Q, R, S$ les projections de $E$ sur les droites $(D A),(A B),(B C),(C D)$. Les points $P$ et $Q$ appartiennent au cercle de diamètre $[A E]$ de sorte que $\widehat{Q P E}=\widehat{Q A E}$. De même, $\widehat{Q R E}=\widehat{Q B E}$. Ainsi :
$$
\widehat{Q P E}+\widehat{Q R E}=\widehat{Q A E}+\widehat{Q B E}=90^{\circ}
$$
De même, on montre que $\widehat{Q P S}+\widehat{Q R S}=90^{\circ}+90^{\circ}=180^{\circ}$. Ainsi, les points $P, Q, R, S$ appartiennent à $\Gamma_{E}$. De même, les projetés orthogonaux de $F$ sur les côtés de $A B C D$ sont sur $\Gamma_{F}$.
Soit $K$ le point d'intersection de $(A D)$ et $(B C)$. Sans perte de généralité, on suppose que $A \in[D K]$. On voit facilement que $\widehat{C K D}<90^{\circ}$ (sinon le cercle de diamètre $[C D]$ couvre entièrement $A B C D$ ). Les droites $(E P)$ et $(B C)$ s'intersectent donc en un point $P^{\prime}$ et les droites $(E R)$ et $(A D)$ en un point $R^{\prime}$. Montrons que $P^{\prime}$ et $R^{\prime}$ sont sur $\Gamma_{E}$. Par cocyclicité des points $R, E, Q, B$ :
$$
\widehat{Q R K}=\widehat{Q E B}=90^{\circ}-\widehat{Q B E}=\widehat{Q A E}=\widehat{Q P E} .
$$
Donc $\widehat{Q R K}=\widehat{Q P P^{\prime}}$, ce qui implique que $P^{\prime} \in \Gamma_{E}$. De même, $R^{\prime} \in \Gamma_{E}$.
De même, soient $M$ et $N$ les projections respectives de $F$ sur $(A D)$ et (BC), et soient $M^{\prime}$ le point d'intersection de $(F M)$ et $(B C)$ et $N^{\prime}$ le point d'intersection de $(F N)$ et $(A D)$. En utilisant les mêmes arguments que précédemment on voit que $M^{\prime}$ et $N^{\prime}$ sont sur $\Gamma_{F}$.
Soient finalement $U$ l'intersection de $\left(N N^{\prime}\right)$ avec $\left(P P^{\prime}\right)$ et $V$ l'intersection de ( $\left.M M^{\prime}\right)$ avec $\left(R R^{\prime}\right)$. Comme les angles en $N$ et $P$ sont droits, $N, N^{\prime}, P, P^{\prime}$ sont cocycliques. La puissance de $U$ par rapport au cercle passant par ces points vaut donc:
$$
U N \cdot U N^{\prime}=U P \cdot U P^{\prime}
$$
Ainsi, $U$ appartient à l'axe radical de $\Gamma_{E}$ et $\Gamma_{F}$. De même $V$ appartient à cet axe radical. Or $E U F V$ est un parallelogramme, ce qui implique que $(U V)$ coupe $[E F]$ en son milieu.
|
{
"resource_path": "French/segmented/tests/fr-2011-2012-ofm-2011-2012-test-mars-corrige.jsonl",
"problem_match": "## Exercice 6\n",
"solution_match": "\nSolution."
}
|
72d82937-8683-5f80-80a8-7a0945f23c32
| 604,291
|
On the circle $\Gamma$, points $A, B, C$ are chosen such that $A C = B C$. Let $P$ be a point on the arc $A B$ of $\Gamma$ that does not contain $C$. The line passing through $C$ and perpendicular to the line (PB) meets (PB) at D.
Prove that $\mathrm{PA} + \mathrm{PB} = 2 \mathrm{PD}$.
|
Extend the ray $[\mathrm{PB})$ and introduce the point Q such that $B Q=P A$.
We thus have $A P=B Q$ and $A C=B C$ as well as $\widehat{\mathrm{QBC}}=\pi-\widehat{\mathrm{CBP}}=\widehat{\mathrm{PAC}}$. This ensures that the triangles $C B Q$ and $C A P$ are congruent, and therefore that $C P=C Q$. Consequently, the triangle $C P Q$ is isosceles and the point $D$, the foot of the altitude from $C$, is then the midpoint of $[\mathrm{PQ}]$.
We thus have $P A+P B=B Q+P B=P Q=2 P D$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Sur le cercle $\Gamma$, on choisit les points $A, B, C$ de sorte que $A C=B C$. Soit $P$ un point de l'arc $A B$ de $\Gamma$ qui ne contient pas $C$. La droite passant par $C$ et perpendiculaire à la droite ( PB ) rencontre (PB) en D.
Prouver que $\mathrm{PA}+\mathrm{PB}=2 \mathrm{PD}$.
|
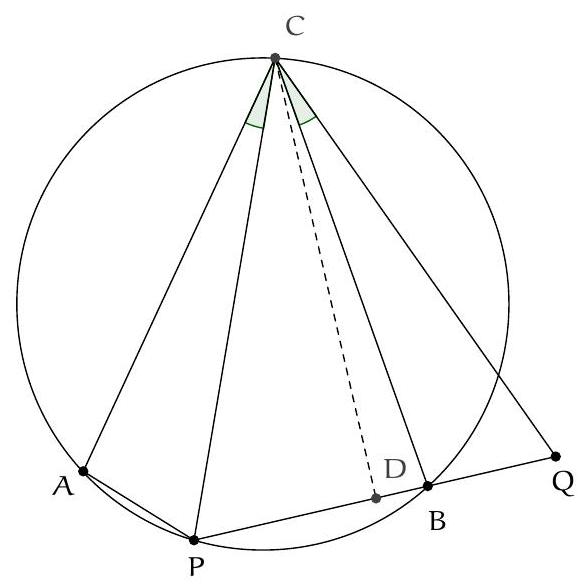
Prolongeons la demi-droite $[\mathrm{PB})$ et introduisons le point Q tel que $B Q=P A$.
On a donc $A P=B Q$ et $A C=B C$ ainsi que $\widehat{\mathrm{QBC}}=\pi-\widehat{\mathrm{CBP}}=\widehat{\mathrm{PAC}}$. Cela assure que les triangles $C B Q$ et $C A P$ sont égaux, et donc que $C P=C Q$. Par suite, le triangle $C P Q$ est isocèle et le point $D$, pied de la hauteur issue de $C$, est alors le milieu de $[\mathrm{PQ}]$.
On a donc $P A+P B=B Q+P B=P Q=2 P D$.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution."
}
|
6d7b9a56-e10e-54bc-b400-0331d384cb49
| 604,322
|
On a $2013 \times 2013$ grid, chairs are placed at the vertices of the grid. Each chair is occupied by a person. Some people decide to change places: some move one step to the right, others move two steps forward, others move three steps to the left, and others move six steps backward. In the end, each chair is still occupied by one person.
Prove that at least one person did not change their place.
|
Let \( a \) (resp. \( b \), \( c \), \( d \)) be the number of people who move to the right (resp. left, forward, backward). We can assume that there exists a coordinate system such that all people have integer coordinates \(\left(x_{i}, y_{i}\right)\). Since \(\sum_{i} x_{i}\) does not change, but moving one step to the right (resp. three steps to the left) increases (resp. decreases) \(\sum_{i} x_{i}\) by the amount \( a \) (resp. \( 3c \)), we deduce that \( a = 3c \), and thus \( a \) and \( c \) have the same parity. Similarly, \( 2b = 6d \) so \( b \) and \( d \) have the same parity. Finally, \( a + b + c + d = (a + b) + (c + d) \) is even, and therefore cannot be equal to 2013, which implies that at least one person did not move.

## Olympic Subject
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Sur un terrain, $2013 \times 2013$ chaises sont placées sur les sommets d'un quadrillage. Chaque chaise est occupée par une personne. Certaines personnes décident alors de changer de place : certaines se décalent d'un cran vers la droite, d'autres de 2 crans vers l'avant, d'autres de 3 crans vers la gauche, et d'autres de 6 crans vers l'arrière. A la fin, chaque chaise est toujours occupée par une seule personne.
Prouver qu'au moins une personne n'a pas changé de place.
|
Soit a (resp. b, c, d) le nombre de personnes qui se décalent vers la droite (resp. la gauche, l'avant, l'arrière). On peut supposer qu'il existe un repère tel que les personnes ont toutes des coordonnées entières $\left(x_{i}, y_{i}\right)$. Comme $\sum_{i} x_{i}$ ne change pas, mais que le déplacement d'un cran vers la droite (resp. 3 crans vers la gauche) a pour effet de faire augmenter (resp. diminuer) $\sum_{i} x_{i}$ de la quantité $a$ (resp. 3c), on en déduit que $a=3 c$, et donc $a$ et $c$ ont la même parité. De même, $2 \mathrm{~b}=6 \mathrm{~d}$ donc b et $d$ ont la même parité. Finalement, $a+b+c+d=(a+b)+(c+d)$ est pair, donc ne peut pas être égal à 2013, ce qui implique qu'au moins une personne ne s'est pas déplacée.

## Sujet Olympique
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
151c2e6f-e349-5db9-9719-608f07ab0bcc
| 604,339
|
Let $0 \leqslant x_{1} \leqslant x_{2} \leqslant \cdots \leqslant x_{n} \leqslant 1$ and $0 \leqslant y_{1} \leqslant y_{2} \leqslant \cdots \leqslant y_{n} \leqslant 1$ be real numbers. We set $x_{n+1}=1$.
Prove that
$$
\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)+n \sum_{i=1}^{n}\left(x_{i+1}-x_{i}\right) y_{i} \geqslant 0
$$
|
We will reason by induction on $\mathrm{n} \geqslant 1$.
- For $n=1$, consider two real numbers $x_{1}, y_{1} \in [0,1]$ and set $x_{2}=1$. We need to prove that $\left(x_{1}-y_{1}\right)+\left(x_{2}-x_{1}\right) y_{1} \geqslant 0$.
Indeed, we have $\left(x_{1}-y_{1}\right)+\left(x_{2}-x_{1}\right) y_{1}=\left(x_{1}-y_{1}\right)+\left(1-x_{1}\right) y_{1}=x_{1}\left(1-y_{1}\right) \geqslant 0$, which concludes the proof.
- Suppose that for some $n \geqslant 1$ and for all real numbers $0 \leqslant a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant 1$ and $0 \leqslant b_{1} \leqslant b_{2} \leqslant \cdots \leqslant b_{n} \leqslant 1$ with $a_{n+1}=1$, we have
$$
\sum_{i=1}^{n}\left(a_{i}-b_{i}\right)+n \sum_{i=1}^{n}\left(a_{i+1}-a_{i}\right) b_{i} \geqslant 0
$$
Consider then real numbers $0 \leqslant x_{1} \leqslant x_{2} \leqslant \cdots \leqslant x_{n+1} \leqslant 1$ and $0 \leqslant y_{1} \leqslant y_{2} \leqslant \cdots \leqslant y_{n+1} \leqslant 1$ and set $x_{n+2}=1$.
By isolating the contributions of $x_{1}$ and $y_{1}$, we have
$$
\begin{aligned}
& \sum_{i=1}^{n+1}\left(x_{i}-y_{i}\right)+(n+1) \sum_{i=1}^{n+1}\left(x_{i+1}-x_{i}\right) y_{i} \\
&= \sum_{i=2}^{n+1}\left(x_{i}-y_{i}\right)+n \sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right) y_{i}+x_{1}-y_{1}+\sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right) y_{i} \\
& \quad+(n+1)\left(x_{2}-x_{1}\right) y_{1}
\end{aligned}
$$
applied to the real numbers $a_{i}=x_{i+1}$ and $b_{i}=y_{i+1}$
$$
\geqslant x_{1}-y_{1}+\sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right) y_{1}+(n+1)\left(x_{2}-x_{1}\right) y_{1} \text{ since } y_{1} \leqslant y_{i} \text{ and } x_{i+1} \geqslant x_{i} \text{ for }
$$
all $i$
$$
\begin{aligned}
& =x_{1}+y_{1}\left[-1+(n+1)\left(x_{2}-x_{1}\right)+\sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right)\right] \\
& =x_{1}+y_{1}\left[n x_{2}-(n+1) x_{1}\right] \\
& =x_{1}\left(1-y_{1}\right)+n y_{1}\left(x_{2}-x_{1}\right) \\
& \geqslant 0
\end{aligned}
$$
which proves the desired result for the value $n+1$ and completes the proof.

|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $0 \leqslant x_{1} \leqslant x_{2} \leqslant \cdots \leqslant x_{n} \leqslant 1$ et $0 \leqslant y_{1} \leqslant y_{2} \leqslant \cdots \leqslant y_{n} \leqslant 1$ des réels. On pose $x_{n+1}=1$.
Prouver que
$$
\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)+n \sum_{i=1}^{n}\left(x_{i+1}-x_{i}\right) y_{i} \geqslant 0
$$
|
On va raisonner par récurrence sur $\mathrm{n} \geqslant 1$.
- Pour $n=1$, on considère deux réels $x_{1}, y_{1} \in[0,1]$ et on pose $x_{2}=1$. Il s'agit de prouver que $\left(x_{1}-y_{1}\right)+\left(x_{2}-x_{1}\right) y_{1} \geqslant 0$.
Or, on a $\left(x_{1}-y_{1}\right)+\left(x_{2}-x_{1}\right) y_{1}=\left(x_{1}-y_{1}\right)+\left(1-x_{1}\right) y_{1}=x_{1}\left(1-y_{1}\right) \geqslant 0$, ce qui conclut.
- Supposons que pour un certain $n \geqslant 1$ et pour tous réels $0 \leqslant a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant 1$ et $0 \leqslant b_{1} \leqslant b_{2} \leqslant \cdots \leqslant b_{n} \leqslant 1$ et avec $a_{n+1}=1$, on ait
$$
\sum_{i=1}^{n}\left(a_{i}-b_{i}\right)+n \sum_{i=1}^{n}\left(a_{i+1}-a_{i}\right) b_{i} \geqslant 0
$$
On considère alors des réels $0 \leqslant x_{1} \leqslant x_{2} \leqslant \cdots \leqslant x_{n+1} \leqslant 1$ et $0 \leqslant y_{1} \leqslant y_{2} \leqslant \cdots \leqslant y_{n+1} \leqslant 1$ et on pose $x_{n+2}=1$.
En isolant les contributions de $x_{1}$ et $y_{1}$, on a
$$
\begin{aligned}
& \sum_{i=1}^{n+1}\left(x_{i}-y_{i}\right)+(n+1) \sum_{i=1}^{n+1}\left(x_{i+1}-x_{i}\right) y_{i} \\
&= \sum_{i=2}^{n+1}\left(x_{i}-y_{i}\right)+n \sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right) y_{i}+x_{1}-y_{1}+\sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right) y_{i} \\
& \quad+(n+1)\left(x_{2}-x_{1}\right) y_{1}
\end{aligned}
$$
appliquée aux réels $a_{i}=x_{i+1}$ et $b_{i}=y_{i+1}$
$$
\geqslant x_{1}-y_{1}+\sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right) y_{1}+(n+1)\left(x_{2}-x_{1}\right) y_{1} \text { puisque } y_{1} \leqslant y_{i} \text { et } x_{i+1} \geqslant x_{i} \text { pour }
$$
tout $i$
$$
\begin{aligned}
& =x_{1}+y_{1}\left[-1+(n+1)\left(x_{2}-x_{1}\right)+\sum_{i=2}^{n+1}\left(x_{i+1}-x_{i}\right)\right] \\
& =x_{1}+y_{1}\left[n x_{2}-(n+1) x_{1}\right] \\
& =x_{1}\left(1-y_{1}\right)+n y_{1}\left(x_{2}-x_{1}\right) \\
& \geqslant 0
\end{aligned}
$$
ce qui prouve le résultat cherché pour la valeur $n+1$ et achève la démonstration.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution."
}
|
a97643c1-ff8d-5482-ae3b-72b4903de365
| 604,350
|
A, B, C, D, E are five points on the same circle, such that $A B C D E$ is convex and $A B=B C$ and $C D=D E$. We assume that the lines $(A D)$ and $(B E)$ intersect at $P$, and that the line (BD) meets the line (CA) at $Q$ and the line (CE) at $T$.
Prove that the triangle PQT is isosceles.
|
Let $\alpha$ and $\beta$ be the angles $(\overrightarrow{A B}, \overrightarrow{A C})$ and $(\overrightarrow{A C}, \overrightarrow{A D})$ respectively. According to the inscribed angle theorem and the hypotheses of the problem, we have
$$
\begin{aligned}
& \alpha=(\overrightarrow{\mathrm{DB}}, \overrightarrow{\mathrm{DC}})=(\overrightarrow{\mathrm{EB}}, \overrightarrow{\mathrm{EC}})=(\overrightarrow{\mathrm{CA}}, \overrightarrow{\mathrm{CB}})=(\overrightarrow{\mathrm{DA}}, \overrightarrow{\mathrm{DB}}) \\
& \beta=(\overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BD}})=(\overrightarrow{\mathrm{EC}}, \overrightarrow{\mathrm{ED}})=(\overrightarrow{\mathrm{BD}}, \overrightarrow{\mathrm{BE}})=(\overrightarrow{\mathrm{CD}}, \overrightarrow{\mathrm{CE}})
\end{aligned}
$$
We deduce that
$$
\begin{aligned}
(\overrightarrow{\mathrm{BD}}, \overrightarrow{\mathrm{BP}}) & =\beta=(\overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BQ}}) \\
(\overrightarrow{\mathrm{DP}}, \overrightarrow{\mathrm{DB}}) & =\alpha=(\overrightarrow{\mathrm{CA}}, \overrightarrow{\mathrm{CB}})
\end{aligned}
$$
Therefore, triangles $BPD$ and $BQC$ are similar. It follows that $\frac{B Q}{B P}=\frac{B C}{B D}$.
Since $(\overrightarrow{B Q}, \overrightarrow{B P})=\beta=(\overrightarrow{B C}, \overrightarrow{B D})$, triangles $BQP$ and $BCD$ are similar, which implies that $\frac{B P}{P Q}=\frac{B D}{C D}$.
By swapping the roles of $(A, B)$ and $(E, D)$, we obtain that $\frac{D P}{P T}=\frac{B D}{B C}$. Dividing the two previous equalities, we deduce that
$$
\frac{B P}{D P} \times \frac{P T}{P Q}=\frac{B C}{C D}
$$
Since $BDP$ and $BDC$ are (indirectly) similar, as $(\overrightarrow{B D}, \overrightarrow{B P})=\beta=(\overrightarrow{B C}, \overrightarrow{B D})$ and $(\overrightarrow{D P}, \overrightarrow{D B})=\alpha=(\overrightarrow{D B}, \overrightarrow{D C})$, we have $\frac{B P}{D P}=\frac{B C}{C D}$, and finally $P T=P Q$.
$\underline{\text { Analytical solution. }}$
We can assume that the affixes $a, b, c, d, e$ of points $A, B, C, D, E$ are complex numbers of modulus 1. The fact that $ABC$ is isosceles at $B$ translates to the equality $b^{2}=a c$ since $\frac{b}{a}=e^{i \theta}=\frac{c}{b}$ where $\theta$ is the angle $(\overrightarrow{O A}, \overrightarrow{O B})=(\overrightarrow{O B}, \overrightarrow{O C})$. Similarly, we have $d^{2}=c e$.
To calculate the affix $p$ of point $P$, we express that $B, P, E$ are collinear, which translates to the fact that $\frac{p-b}{p-e}$ is real, or equivalently
$$
\frac{p-b}{p-e}=\frac{\bar{p}-\bar{b}}{\bar{p}-\bar{e}}
$$
We eliminate the denominators and simplify:
$$
(\bar{b}-\bar{e}) p-(b-e) \bar{p}+b \bar{e}-\bar{b} e=0
$$
Since $\overline{b}-\overline{e}=\frac{1}{b}-\frac{1}{e}=-\frac{b-e}{be}$ and $b \overline{e}-\overline{b} e=\frac{b}{e}-\frac{e}{b}=\frac{b^{2}-e^{2}}{be}=\frac{(b-e)(b+e)}{be}$, we deduce
$$
-\frac{(b-e)}{be} p-(b-e) \bar{p}+(b-e) \frac{b+e}{be}=0
$$
which simplifies to
$$
p+b e \bar{p}=b+e
$$
Similarly, the fact that $A, P, D$ are collinear translates to $p+a d \bar{p}=a+d$. Subtracting the two previous equalities and dividing by $be - ad$, we get
$$
\bar{p}=\frac{b+e-a-d}{b e-a d} .
$$
Similarly, $\bar{q}=\frac{b+d-a-c}{b d-a c}$. Subtracting the two previous equalities:
$$
\overline{p}-\overline{q}=\frac{(bd-ac)(b+e-a-d)-(be-ad)(b+d-a-c)}{(be-ad)(bd-ac)}
$$
We expand the numerator and replace all $b^{2}$ with $ac$ and all $d^{2}$ with $ce$, which gives
$$
\begin{aligned}
\bar{p}-\bar{q} & =\frac{a(-b c+a c+c d-a d+b e-c e)}{(b e-a d)(b d-a c)} \\
& =\frac{a(-b c+a c+c d-a d+b e-c e)}{b(b e-a d)(d-b)}
\end{aligned}
$$
considering $ac=b^2$. By swapping the roles of $(a, b)$ and $(e, d)$, we get
$$
\bar{p}-\bar{t}=\frac{e(-c d+c e+b c-b e+a d-a c)}{d(a d-b e)(b-d)}
$$
We see that $\bar{p}-\overline{t}=-\frac{be}{ad}(\overline{p}-\overline{q})$. Taking the modulus of both sides, we conclude that $PQ=PT$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A, B, C, D, E sont cinq points d'un même cercle, de sorte que $A B C D E$ soit convexe et que l'on ait $A B=B C$ et $C D=D E$. On suppose que les droites $(A D)$ et $(B E)$ se coupent en $P$, et que la droite (BD) rencontre la droite (CA) en $Q$ et la droite (CE) en $T$.
Prouver que le triangle PQT est isocèle.
|
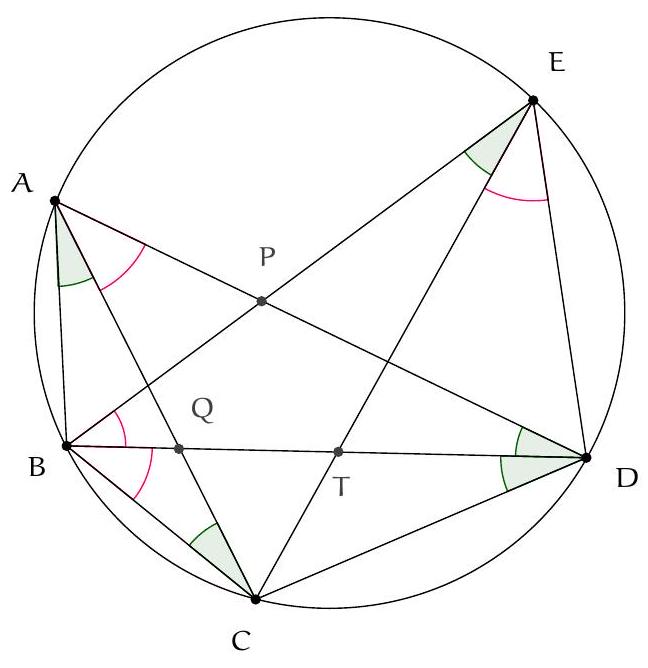
Notons $\alpha$ et $\beta$ les angles $(\overrightarrow{A B}, \overrightarrow{A C})$ et $(\overrightarrow{A C}, \overrightarrow{A D})$ respectivement. D'après le théorème de l'angle inscrit et les hypothèses de l'énoncé, on a
$$
\begin{aligned}
& \alpha=(\overrightarrow{\mathrm{DB}}, \overrightarrow{\mathrm{DC}})=(\overrightarrow{\mathrm{EB}}, \overrightarrow{\mathrm{EC}})=(\overrightarrow{\mathrm{CA}}, \overrightarrow{\mathrm{CB}})=(\overrightarrow{\mathrm{DA}}, \overrightarrow{\mathrm{DB}}) \\
& \beta=(\overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BD}})=(\overrightarrow{\mathrm{EC}}, \overrightarrow{\mathrm{ED}})=(\overrightarrow{\mathrm{BD}}, \overrightarrow{\mathrm{BE}})=(\overrightarrow{\mathrm{CD}}, \overrightarrow{\mathrm{CE}})
\end{aligned}
$$
On en déduit que
$$
\begin{aligned}
(\overrightarrow{\mathrm{BD}}, \overrightarrow{\mathrm{BP}}) & =\beta=(\overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BQ}}) \\
(\overrightarrow{\mathrm{DP}}, \overrightarrow{\mathrm{DB}}) & =\alpha=(\overrightarrow{\mathrm{CA}}, \overrightarrow{\mathrm{CB}})
\end{aligned}
$$
donc BPD et $B Q C$ sont semblables. Il s'ensuit $\frac{B Q}{B P}=\frac{B C}{B D}$.
Or, $(\overrightarrow{B Q}, \overrightarrow{B P})=\beta=(\overrightarrow{B C}, \overrightarrow{B D})$, donc $B Q P$ et $B C D$ sont semblables, ce qui entrainne que $\frac{B P}{P Q}=\frac{B D}{C D}$.
En échangeant les rôles de $(A, B)$ et de $(E, D)$, on obtient que $\frac{D P}{P T}=\frac{B D}{B C}$. En divisant les deux égalités précédentes, on en déduit que
$$
\frac{B P}{D P} \times \frac{P T}{P Q}=\frac{B C}{C D}
$$
Or, $B D P$ et $B D C$ sont (indirectement) semblables, puisque $(\overrightarrow{B D}, \overrightarrow{B P})=\beta=(\overrightarrow{B C}, \overrightarrow{B D})$ et $(\overrightarrow{D P}, \overrightarrow{D B})=$ $\alpha=(\overrightarrow{D B}, \overrightarrow{D C})$, donc $\frac{B P}{D P}=\frac{B C}{C D}$, et finalement $P T=P Q$.
$\underline{\text { Solution analytique. }}$
On peut supposer que les affixes $a, b, c, d, e$ des points $A, B, C, D, E$ sont des nombres complexes de module 1. Le fait que $A B C$ est isocèle en $B$ se traduit par l'égalité $b^{2}=a c$ puisque $\frac{b}{a}=e^{i \theta}=\frac{c}{b}$ où $\theta$ est l'angle $(\overrightarrow{O A}, \overrightarrow{O B})=(\overrightarrow{O B}, \overrightarrow{O C})$. De même, on a $d^{2}=c e$.
Pour calculer l'affixe $p$ du point $P$, on exprime que $B, P, E$ sont alignés, ce qui se traduit par le fait que $\frac{p-b}{p-e}$ est réel, ou encore
$$
\frac{p-b}{p-e}=\frac{\bar{p}-\bar{b}}{\bar{p}-\bar{e}}
$$
On chasse les dénominateurs et on simplifie :
$$
(\bar{b}-\bar{e}) p-(b-e) \bar{p}+b \bar{e}-\bar{b} e=0
$$
Comme $\overline{\mathrm{b}}-\overline{\mathrm{e}}=\frac{1}{\mathrm{~b}}-\frac{1}{\mathrm{e}}=-\frac{\mathrm{b}-\mathrm{e}}{\mathrm{be}}$ et $\mathrm{b} \overline{\mathrm{e}}-\overline{\mathrm{b}} e=\frac{\mathrm{b}}{\mathrm{e}}-\frac{\mathrm{e}}{\mathrm{b}}=\frac{\mathrm{b}^{2}-\mathrm{e}^{2}}{\mathrm{be}}=\frac{(\mathrm{b}-\mathrm{e})(\mathrm{b}+\mathrm{e})}{\mathrm{be}}$, on en déduit
$$
-\frac{(b-e)}{b e} p-(b-e) \bar{p}+(b-e) \frac{b+e}{b e}=0
$$
ce qui se simplifie en
$$
p+b e \bar{p}=b+e
$$
De même, le fait que $A, P, D$ sont alignés se traduit par $p+a d \bar{p}=a+d$. En soustrayant les deux égalités précédentes et en divisant par be - ad, on obtient
$$
\bar{p}=\frac{b+e-a-d}{b e-a d} .
$$
De même, $\bar{q}=\frac{b+d-a-c}{b d-a c}$. On soustrait les deux égalités précédentes :
$$
\overline{\mathrm{p}}-\overline{\mathrm{q}}=\frac{(\mathrm{bd}-\mathrm{ac})(\mathrm{b}+\mathrm{e}-\mathrm{a}-\mathrm{d})-(\mathrm{be}-\mathrm{ad})(\mathrm{b}+\mathrm{d}-\mathrm{a}-\mathrm{c})}{(\mathrm{be}-\mathrm{ac})(\mathrm{bd}-\mathrm{ac})}
$$
On développe le numérateur et on remplace tous les $b^{2}$ par $a c$ et tous les $\mathrm{d}^{2}$ par ce , ce qui donne
$$
\begin{aligned}
\bar{p}-\bar{q} & =\frac{a(-b c+a c+c d-a d+b e-c e)}{(b e-a d)(b d-a c)} \\
& =\frac{a(-b c+a c+c d-a d+b e-c e)}{b(b e-a d)(d-b)}
\end{aligned}
$$
compte tenu de $\mathrm{ac}=\mathrm{b}^{2}$. En échangeant les rôles de $(\boldsymbol{a}, \mathrm{b})$ et $(e, d)$, on obtient
$$
\bar{p}-\bar{t}=\frac{e(-c d+c e+b c-b e+a d-a c)}{d(a d-b e)(b-d)}
$$
On voit que $\bar{p}-\overline{\mathrm{t}}=-\frac{\mathrm{be}}{\mathrm{ad}}(\overline{\mathrm{p}}-\overline{\mathrm{q}})$. En prenant le module des deux membres, on en conclut que $\mathrm{PQ}=\mathrm{PT}$.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution."
}
|
46303509-c43d-5062-ae19-217238b2a83a
| 604,374
|
Let $ABC$ be an isosceles triangle at $A$. We denote $O$ as the center of its circumcircle. Let $D$ be a point on $[BC]$. The line parallel to $(AB)$ passing through $D$ intersects $(AC)$ at $E$. The line parallel to $(AC)$ passing through $D$ intersects $(AB)$ at $F$. Show that $A, E, O, F$ are concyclic.
|
Let $R$ be the rotation centered at $O$ with angle $(\overrightarrow{O B}, \overrightarrow{O A})$. We have $R(B)=A$ and $R(A)=C$.
Since ( DF$) / /(\mathrm{AC})$, we have $\widehat{\mathrm{FDB}}=\widehat{\mathrm{ACB}}=\widehat{\mathrm{CBA}}=\widehat{\mathrm{DBF}}$, so FBD is isosceles at F. Therefore, $\mathrm{BF}=\mathrm{FD}$. Since $A E D F$ is a parallelogram, $\mathrm{FD}=A E$, hence $B F=A E$. We deduce that $R(F)$ and $E$ are two points on $[A, C]$ that are the same distance from $A$, so $R(F)=E$.
We deduce the equality of the vector angles $(\overrightarrow{O F}, \overrightarrow{O E})=(\overrightarrow{O B}, \overrightarrow{O A})$. Consequently, $2(\overrightarrow{O F}, \overrightarrow{O E})=$ $(\overrightarrow{O B}, \overrightarrow{O A})+(\overrightarrow{O A}, \overrightarrow{O C})=(\overrightarrow{O B}, \overrightarrow{O C})=2(\overrightarrow{A B}, \overrightarrow{A C})=2(\overrightarrow{A F}, \overrightarrow{A E})$, so the angles of the lines $(A F, A E)$ and $(\mathrm{OF}, \mathrm{OE})$ are equal, which concludes.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$. On note $O$ le centre de son cercle circonscrit. Soit $D$ un point de $[B C]$. La droite parallèle à $(A B)$ passant par $D$ coupe $(A C)$ en $E$. La droite parallèle à $(A C)$ passant par $D$ coupe $(A B)$ en $F$. Montrer que $A, E, O, F$ sont cocycliques.
|
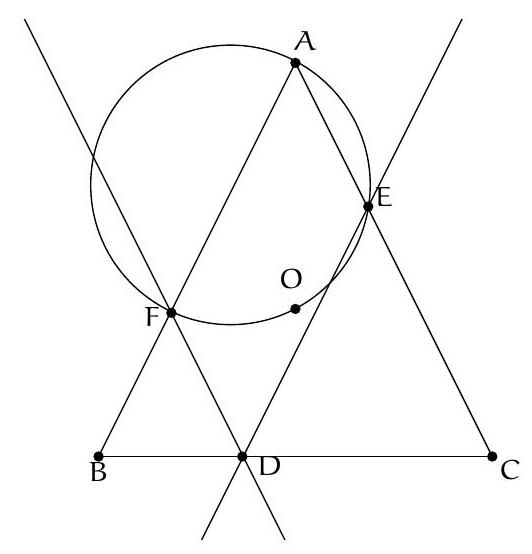
Soit $R$ la rotation de centre $O$ et d'angle $(\overrightarrow{O B}, \overrightarrow{O A})$. On a $R(B)=A$ et $R(A)=C$.
Comme ( DF$) / /(\mathrm{AC})$, on a $\widehat{\mathrm{FDB}}=\widehat{\mathrm{ACB}}=\widehat{\mathrm{CBA}}=\widehat{\mathrm{DBF}}$, donc FBD est isocèle en F. Par conséquent, $\mathrm{BF}=\mathrm{FD}$. Or, $A E D F$ est un parallélogramme, donc $\mathrm{FD}=A E$, d'où $B F=A E$. On en déduit que $R(F)$ et $E$ sont deux points de $[A, C]$ qui sont à même distance de $A$, donc $R(F)=E$.
On en déduit l'égalité entre les angles de vecteurs $(\overrightarrow{O F}, \overrightarrow{O E})=(\overrightarrow{O B}, \overrightarrow{O A})$. Par conséquent, $2(\overrightarrow{O F}, \overrightarrow{O E})=$ $(\overrightarrow{O B}, \overrightarrow{O A})+(\overrightarrow{O A}, \overrightarrow{O C})=(\overrightarrow{O B}, \overrightarrow{O C})=2(\overrightarrow{A B}, \overrightarrow{A C})=2(\overrightarrow{A F}, \overrightarrow{A E})$, donc les angles de droites $(A F, A E)$ et $(\mathrm{OF}, \mathrm{OE})$ sont égaux, ce qui conclut.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution."
}
|
e83f1eff-5db9-5c21-b0e8-88e6f5a04bfa
| 604,397
|
Let $\left(a_{n}\right)_{n \in \mathbb{N}}$ be a non-constant, increasing sequence of strictly positive integers such that $a_{n}$ divides $n^{2}$ for all $n \geqslant 1$. Prove that one of the following statements is true:
a) There exists an integer $n_{1}>0$ such that $a_{n}=n$ for all $n \geqslant n_{1}$.
b) There exists an integer $n_{2}>0$ such that $a_{n}=n^{2}$ for all $n \geqslant n_{2}$.
|
First, since for all integers $n$, we have $a_{n} \in \mathbb{N}^{*}$, and the sequence $(a_{n})$ is increasing and not constant, there exists an integer $n_{0}$ such that $a_{n} \geqslant 2$ for all $n \geqslant n_{0}$. Consequently, for any prime number $p > n_{0}$, we have $a_{p}=p$ or $a_{p}=p^{2}$.
- Suppose that for all integers $n \geqslant 1$, we have $a_{n} \leqslant n$. Let $p > n_{0}$ be a prime number. We will prove by induction that $a_{n}=n$ for all $n \geqslant p$. Indeed, from the above, we have $a_{p}=p$. Furthermore, if $a_{n}=n$ for some $n \geqslant p \geqslant 2$, then $n=a_{n} \leqslant a_{n+1} \leqslant n+1$, hence $a_{n+1}=n$ or $a_{n+1}=n+1$. However, $a_{n+1}$ divides $(n+1)^{2}$, while $n$ does not divide $(n+1)^{2}$. Thus, we have $a_{n+1}=n+1$, which completes the induction.
It is then sufficient to choose $n_{1}=p$ to conclude in this case.
- Suppose there exists an integer $m \geqslant 1$ such that $a_{m}>m$. Since these are integers, it follows that $a_{m} \geqslant m+1$. But, $m+1 \geqslant 2$ and $m+1$ is coprime with $m^{2}$, so $m+1$ cannot divide $m^{2}$, and we have $a_{m} \geqslant m+2$. We deduce that $a_{m+1} \geqslant a_{m}>m+1$. An immediate induction ensures that $a_{n}>n$ for all $n \geqslant m$.
In particular, given our initial remark, if $p \geqslant m$ is a prime number, we have $a_{p}=p^{2}$. Let $p > m$ be an odd prime number. We will prove by induction that $a_{n}=n^{2}$ for all $n \geqslant p$. We have just seen that this is true for $n=p$. Suppose that $a_{n}=n^{2}$ for some integer $n \geqslant p$. Then $n \geqslant 3$, hence $a_{n+1} \geqslant a_{n}=n^{2}>\frac{1}{2}(n+1)^{2}$. Since $a_{n+1}$ divides $(n+1)^{2}$, we have $a_{n+1}=(n+1)^{2}$. This completes the induction.
It is therefore sufficient to choose $n_{2}=p$ to conclude in this case.

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\left(a_{n}\right)_{n \in \mathbb{N}}$ une suite croissante et non constante d'entiers strictement positifs tels que $a_{n}$ divise $n^{2}$ pour tout $n \geqslant 1$. Prouver que l'une des affirmations suivantes est vraie:
a) Il existe un entier $n_{1}>0$ tel que $a_{n}=n$ pour tout $n \geqslant n_{1}$.
b) Il existe un entier $n_{2}>0$ tel que $a_{n}=n^{2}$ pour tout $n \geqslant n_{2}$.
|
Tout d'abord, puisque pour tout entier $n$, on a $a_{n} \in \mathbb{N}^{*}$, et que la suite ( $a_{n}$ ) est croissante et non constante, il existe un entier $n_{0}$ tel que $a_{n} \geqslant 2$ pour tout $n \geqslant n_{0}$. Par conséquent, pour tout nombre premier $p>n_{0}$, on a $a_{p}=p$ ou $a_{p}=p^{2}$.
- Supposons que, pour tout entier $n \geqslant 1$, on ait $a_{n} \leqslant n$. Soit $p>n_{0}$ un nombre premier. Prouvons par récurrence que $a_{n}=n$ pour tout $n \geqslant p$. En effet, d'après ci-dessus, on a $a_{p}=p$. De plus, si $a_{n}=n$ pour un certain $n \geqslant p \geqslant 2$, alors $n=a_{n} \leqslant a_{n+1} \leqslant n+1$, d'où $a_{n+1}=n$ ou $a_{n+1}=n+1$. Mais, $a_{n+1}$ divise $(n+1)^{2}$, tandis que $n$ ne divise pas $(n+1)^{2}$. Ainsi, on a $a_{n+1}=n+1$, ce qui achève la récurrence.
Il suffit alors de choisir $\mathrm{n}_{1}=\mathrm{p}$ pour conclure dans ce cas.
- Supposons qu'il existe un entier $m \geqslant 1$ tel que $a_{m}>m$. S'agissant d'entiers, c'est donc que $a_{m} \geqslant m+1$. Mais, $m+1 \geqslant 2$ et $m+1$ est premier avec $m^{2}$, donc $m+1$ ne peut diviser $m^{2}$, et on a alors $a_{m} \geqslant m+2$. On en déduit que $a_{m+1} \geqslant a_{m}>m+1$. Une récurrence immédiate assure donc que $a_{n}>n$ pour tout $n \geqslant m$.
En particulier, compte-tenu de notre remarque initiale, si $p \geqslant m$ est un nombre premier, on a $a_{p}=p^{2}$. Soit donc $p>m$ un nombre premier impair. Nous allons prouver par récurrence que $a_{n}=n^{2}$ pour tout $n \geqslant p$. Nous venons de voir que c'est vrai pour $n=p$. Supposons que $a_{n}=n^{2}$ pour un certain entier $n \geqslant p$. Alors $n \geqslant 3$, d'où $a_{n+1} \geqslant a_{n}=n^{2}>\frac{1}{2}(n+1)^{2}$. Or, $a_{n+1}$ divise $(n+1)^{2}$, donc $\mathrm{a}_{\mathrm{n}+1}=(\mathrm{n}+1)^{2}$. Cela achève la récurrence.
Il suffit donc de choisir $\mathrm{n}_{2}=\mathrm{p}$ pour conclure dans ce cas.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution."
}
|
37161fd4-f7ca-56d8-a051-a85ec155c9d7
| 604,407
|
Prove that for all strictly positive real numbers $a, b, c$ such that $a b c=1$, we have
$$
\frac{1}{1+a^{2}+(b+1)^{2}}+\frac{1}{1+b^{2}+(c+1)^{2}}+\frac{1}{1+c^{2}+(a+1)^{2}} \leqslant \frac{1}{2}
$$
|
Let $a, b, c$ be strictly positive real numbers.
Given the well-known inequality $x^{2}+y^{2} \geqslant 2 x y$ valid for all real numbers $x, y$, we have
$$
\frac{1}{1+a^{2}+(b+1)^{2}}=\frac{1}{2+a^{2}+b^{2}+2 b} \leqslant \frac{1}{2(1+a b+b)}
$$
Similarly, and since $a b c=1$, we have
$$
\frac{1}{1+b^{2}+(c+1)^{2}} \leqslant \frac{1}{2(1+b c+c)}=\frac{a b}{2\left(a b+a b^{2} c+a b c\right)}=\frac{a b}{2(1+a b+b)}
$$
and
$$
\frac{1}{1+c^{2}+(a+1)^{2}} \leqslant \frac{1}{2(1+a c+a)}=\frac{b}{2(b+a b c+a b)}=\frac{b}{2(1+a b+b)}
$$
By summing member by member, we get
$$
\begin{aligned}
& \frac{1}{1+\mathrm{a}^{2}+(\mathrm{b}+1)^{2}}+\frac{1}{1+\mathrm{b}^{2}+(\mathrm{c}+1)^{2}}+\frac{1}{1+\mathrm{c}^{2}+(\mathrm{a}+1)^{2}} \\
& \leqslant \frac{1}{2}\left(\frac{1}{1+\mathrm{ab}+\mathrm{b}}+\frac{\mathrm{ab}}{1+\mathrm{ab}+\mathrm{b}}+\frac{\mathrm{b}}{1+\mathrm{ab}+\mathrm{b}}\right)=\frac{1}{2}
\end{aligned}
$$

|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que pour tous réels strictement positifs $a, b, c$ tels que $a b c=1$, on a
$$
\frac{1}{1+a^{2}+(b+1)^{2}}+\frac{1}{1+b^{2}+(c+1)^{2}}+\frac{1}{1+c^{2}+(a+1)^{2}} \leqslant \frac{1}{2}
$$
|
Soit $a, b, c$ des réels strictement positifs.
Compte tenu de l'inégalité bien connue $x^{2}+y^{2} \geqslant 2 x y$ valable pour tous réels $x, y$, on a
$$
\frac{1}{1+a^{2}+(b+1)^{2}}=\frac{1}{2+a^{2}+b^{2}+2 b} \leqslant \frac{1}{2(1+a b+b)}
$$
De même, et puisque $a b c=1$, on a
$$
\frac{1}{1+b^{2}+(c+1)^{2}} \leqslant \frac{1}{2(1+b c+c)}=\frac{a b}{2\left(a b+a b^{2} c+a b c\right)}=\frac{a b}{2(1+a b+b)}
$$
et
$$
\frac{1}{1+c^{2}+(a+1)^{2}} \leqslant \frac{1}{2(1+a c+a)}=\frac{b}{2(b+a b c+a b)}=\frac{b}{2(1+a b+b)}
$$
en sommant membre à membre, il vient
$$
\begin{aligned}
& \frac{1}{1+\mathrm{a}^{2}+(\mathrm{b}+1)^{2}}+\frac{1}{1+\mathrm{b}^{2}+(\mathrm{c}+1)^{2}}+\frac{1}{1+\mathrm{c}^{2}+(\mathrm{a}+1)^{2}} \\
& \leqslant \frac{1}{2}\left(\frac{1}{1+\mathrm{ab}+\mathrm{b}}+\frac{\mathrm{ab}}{1+\mathrm{ab}+\mathrm{b}}+\frac{\mathrm{b}}{1+\mathrm{ab}+\mathrm{b}}\right)=\frac{1}{2}
\end{aligned}
$$

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution."
}
|
65477acb-bc9e-5354-a2e4-028a587baa92
| 604,420
|
1) Let $a$ and $b$ be real numbers such that $a^{n}+b^{n}$ is an integer for $n=1,2,3,4$. Show that $a^{n}+b^{n}$ is an integer for all $n \in \mathbb{N}^{*}$.
2) Is it true that if $a$ and $b$ are real numbers such that $a^{n}+b^{n}$ is an integer for $\boldsymbol{n}=1,2,3$ then $a^{n}+b^{n}$ is an integer for all $n \in \mathbb{N}^{*}$?
|
1) Let $s=a+b$ and $p=ab$. Let $S_{n}=a^{n}+b^{n}$. By hypothesis, $S_{n}$ is an integer for $1 \leqslant n \leqslant 4$. Since for all $n \geqslant 1$ we have
$$
S_{n+1}=a^{n+1}+b^{n+1}=(a+b)\left(a^{n}+b^{n}\right)-ab\left(a^{n-1}+b^{n-1}\right)=S_{1} S_{n}-p S_{n-1},
$$
if we show that $p$ is an integer, then by immediate induction it will follow that $S_{n}$ is an integer for all $n$.
We have
$$
S_{2}=(a+b)^{2}-2ab=s^{2}-2p
$$
so $2p=S_{1}^{2}-S_{2}$ is an integer. We have
$$
S_{4}=\left(a^{2}+b^{2}\right)^{2}-2(ab)^{2}=S_{2}^{2}-2p^{2}
$$
so $2p^{2}=S_{2}^{2}-S_{4}$ is an integer. We deduce that $(2p)^{2}=2(2p^{2})$ is an even integer. Since $2p$ is an integer, it is even, so $p$ is indeed an integer.
2) We have
$$
S_{3}=(a+b)\left(a^{2}+b^{2}\right)-ab^{2}-a^{2}b=S_{1} S_{2}-ps
$$
so if $p$ is a half-integer (i.e., $p-\frac{1}{2}$ is an integer) and if $s$ is an even integer, then $S_{1}, S_{2}, S_{3}$ are integers while $S_{4}$ is a half-integer. For example, if $a=1+\frac{1}{\sqrt{2}}$ and $b=1-\frac{1}{\sqrt{2}}$ then $s=2$, $p=\frac{1}{2}$, $S_{1}=2$, $S_{2}=3$, $S_{3}=5$, $S_{4}=17 / 2$.

|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
1) Soient $a$ et $b$ deux nombres réels tels que $a^{n}+b^{n}$ est un entier pour $n=1,2,3,4$. Montrer que $a^{n}+b^{n}$ est un entier pour tout $n \in \mathbb{N}^{*}$.
2) Est-il vrai que si $a$ et $b$ sont deux nombres réels tels que $a^{n}+b^{n}$ est un entier pour $\boldsymbol{n}=1,2,3$ alors $a^{n}+b^{n}$ est un entier pour tout $n \in \mathbb{N}^{*}$ ?
|
1) Notons $s=a+b$ et $p=a b$. Soit $S_{n}=a^{n}+b^{n}$. Par hypothèse, $S_{n}$ est un entier pour $1 \leqslant n \leqslant 4$. Comme pour tout $\mathrm{n} \geqslant 1$ on a
$$
S_{n+1}=a^{n+1}+b^{n+1}=(a+b)\left(a^{n}+b^{n}\right)-a b\left(a^{n-1}+b^{n-1}\right)=S_{1} S_{n}-p S_{n-1},
$$
si on montre que $p$ est un entier alors par récurrence immédiate il s'ensuivra que $S_{n}$ est un entier pour tout $n$.
On a
$$
S_{2}=(a+b)^{2}-2 a b=s^{2}-2 p
$$
donc $2 p=S_{1}^{2}-S_{2}$ est un entier. On a
$$
S_{4}=\left(a^{2}+b^{2}\right)^{2}-2(a b)^{2}=S_{2}^{2}-2 p^{2}
$$
donc $2 p^{2}=S_{2}^{2}-S_{4}$ est un entier. On en déduit que $(2 p)^{2}=2\left(2 p^{2}\right)$ est un entier pair. Comme $2 p$ est entier, il est pair donc $p$ est bien entier.
2) On a
$$
S_{3}=(a+b)\left(a^{2}+b^{2}\right)-a b^{2}-a^{2} b=S_{1} S_{2}-p s
$$
donc si $p$ est un demi-entier (c'est-à-dire que $p-\frac{1}{2}$ est un entier) et si $s$ est un entier pair, alors $S_{1}, S_{2}, S_{3}$ sont des entiers alors que $S_{4}$ est un demi-entier. Par exemple, si $a=1+\frac{1}{\sqrt{2}}$ et $b=1-\frac{1}{\sqrt{2}}$ alors $s=2$, $p=\frac{1}{2}, S_{1}=2, S_{2}=3, S_{3}=5, S_{4}=17 / 2$.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution."
}
|
ff85a3b0-15e8-53fa-a2a2-661b463fd8b5
| 604,459
|
Starting from a triplet of integers $(x, y, z)$, an operation consists of adding to one of these three integers a multiple of one of the other two (this multiple can be positive or negative). Prove that if $a, b, c$ are integers that are coprime as a set, one can go from the triplet $(a, b, c)$ to the triplet $(1,0,0)$ in at most five operations.
|
If $b$ and $c$ are zero, then since $\operatorname{pgcd}(a, b, c)=1$, we must have $a=1$ or $a=-1$. In the first case, there is nothing to do. In the second case, by three successive operations, we can go from $(-1,0,0)$ to $(-1,1,0)$, then to $(1,1,0)$, and finally to $(1,0,0)$.
We can therefore assume that $b$ or $c$ is non-zero.
The goal is to reach a triplet of the form $(1, \mathrm{~s}, \mathrm{t})$ in at most three steps, since with two additional steps, it is then immediate to obtain $(1,0,0)$.
We assume that $\mathrm{c} \neq 0$, the case $\mathrm{b} \neq 0$ being treated similarly.
To achieve the above goal, it suffices to find an integer $n$ such that $c$ and $\mathrm{b}+\mathrm{na}$ are coprime: indeed, suppose for the moment that such an integer $n$ has been determined and see how the conclusion will follow.
We set $b^{\prime}=b+n a$ and, with a first operation, we can go from $(a, b, c)$ to $\left(a, b^{\prime}, c\right)$. Then, by Bézout's theorem, we know that there exist two integers $u$ and $v$ such that $u b^{\prime}+v c=1$. After multiplying by $a-1$, there therefore exist two integers $x$ and $y$ such that $x b^{\prime}+y c=a-1$. We then use a second operation to go from $\left(a, b^{\prime}, c\right)$ to $\left(a-x b^{\prime}, b^{\prime}, c\right)$, and a third to go from $\left(a-x b^{\prime}, b^{\prime}, c\right)$ to $\left(a-x b^{\prime}-y c, b^{\prime}, c\right)=\left(1, b^{\prime}, c\right)$.
To conclude, it only remains to prove that such an integer $n$ exists.
Let $E$ be the set of prime divisors of $c$ that also divide at least one number of the form $b+k a$, where $k \in \mathbb{Z}$.
If $E=\emptyset$ then any integer $n$ is such that $\operatorname{pgcd}(\mathrm{c}, \mathrm{b}+\mathrm{na})=1$.
Otherwise, we note that $E$ is finite because it only contains prime divisors of $c$, with $c \neq 0$. Next, for each $p \in E$, there exists an integer $k_{p}$ such that $b+k_{p} a=0 \bmod [p]$. We note that such a number $p$ does not divide $a$ because otherwise $p$ would also divide $b$, in contradiction with $\operatorname{pgcd}(a, b, c)=1$.
By the Chinese remainder theorem, there exists an integer $n$ such that $n=k_{p}+1 \bmod [p]$ for all $p \in E$. Let's prove that this integer $n$ works:
- If $p$ divides $c$ and $p \notin E$ then $p$ does not divide any number of the form $b+k a$ and therefore, in particular, does not divide $b + na$.
- If $p \in E$ then $b+n a=b+k_{p} a+a=a \neq 0 \bmod [p]$.
Thus, no prime divisor of $c$ divides $\mathrm{b}+\mathrm{na}$, which ensures that $c$ and $\mathrm{b}+\mathrm{na}$ are indeed coprime.

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Partant d'un triplet d'entiers relatifs $(x, y, z)$, une opération consiste à ajouter à l'un de ces trois entiers un multiple de l'un des deux autres (ce multiple peut être positif ou négatif). Prouver que si $a, b, c$ sont des entiers premiers entre eux dans leur ensemble, on peut passer du triplet ( $a, b, c$ ) au triplet $(1,0,0)$ en au plus cinq opérations.
|
Si $b$ et $c$ sont nuls alors, puisque $\operatorname{pgcd}(a, b, c)=1$, on doit avoir $a=1$ ou $a=-1$. Dans le premier cas, il n'y a rien à faire. Dans le second, par trois opérations successives, on peut passer de $(-1,0,0)$ à $(-1,1,0)$, puis à $(1,1,0)$ et enfin à $(1,0,0)$.
On peut donc supposer que b ou c est non nul.
L'objectif est d'atteindre un triplet de la forme $(1, \mathrm{~s}, \mathrm{t})$ en au plus trois étapes, puisqu'avec deux étapes supplémentaires, il est alors immédiat d'obtenir $(1,0,0)$.
On suppose que $\mathrm{c} \neq 0$, le cas $\mathrm{b} \neq 0$ se traitant de façon analogue.
Afin d'atteindre l'objectif ci-dessus, il suffit de trouver un entier n tel que c et $\mathrm{b}+\mathrm{na}$ soient premiers entre eux : en effet, supposons pour le moment qu'un tel entier n ait été déterminé et voyons comment la conclusion va en découler.
On pose $b^{\prime}=b+n a$ et, avec une première opération, on peut passer de $(a, b, c) a ̀\left(a, b^{\prime}, c\right)$. Ensuite, d'après le théorème de Bézout, on sait qu'il existe deux entiers $u$ et $v$ tels que $u b^{\prime}+v c=1$. Après multiplication par $a-1$, il existe donc deux entiers $x$ et $y$ tels que $x b^{\prime}+y c=a-1$. On utilise alors une seconde opération pour passer de $\left(a, b^{\prime}, c\right)$ à $\left(a-x b^{\prime}, b^{\prime}, c\right)$, puis une troisième pour passer de $\left(a-x b^{\prime}, b^{\prime}, c\right) a ̀\left(a-x b^{\prime}-y c, b^{\prime} c\right)=\left(1, b^{\prime}, c\right)$.
Pour conclure, il ne reste donc plus qu'à prouver qu'un tel entier n existe.
Soit E l'ensemble des diviseurs premiers de c qui divisent également au moins un nombre de la forme $b+k a$, où $k \in \mathbb{Z}$.
$\operatorname{Si} E=\emptyset$ alors tout entier n est tel que $\operatorname{pgcd}(\mathrm{c}, \mathrm{b}+\mathrm{na})=1$.
Sinon, on note tout d'abord que E est fini car il ne contient que des diviseurs premiers de c , avec $c \neq 0$. Ensuite, pour chaque $p \in E$, il existe un entier $k_{p}$ tel que $b+k_{p} a=0 \bmod [p]$. On remarque qu'un tel nombre $p$ ne divise pas a car sinon $p$ diviserait aussi $b$, en contradiction avec $\operatorname{pgcd}(a, b, c)=1$.
D'après le théorème chinois, il existe un entier $n$ tel que $n=k_{p}+1 \bmod [p]$ pour tout $p \in E$. Prouvons que cet entier n convient :
- Si $p$ divise $c$ et $p \notin E$ alors $p$ ne divise aucun nombre de la forme $b+k a$ et donc, en particulier, ne divise pas b + na.
- Si $p \in E$ alors $b+n a=b+k_{p} a+a=a \neq 0 \bmod [p]$.
Ainsi, aucun diviseur premier de c ne divise $\mathrm{b}+\mathrm{na}$, ce qui assure que c et $\mathrm{b}+\mathrm{na}$ sont bien premiers entre eux.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution."
}
|
f852b237-515a-5aad-9c54-3c9758a5fab4
| 604,471
|
Let $ABC$ be a triangle. Let $D \in [AC]$ and $E \in [AB]$ such that $BE = CD$. Let $P$ be the intersection point of $(BD)$ and $(CE)$. The circumcircles of $BEP$ and $CDP$ intersect at $Q$. Let $K$ and $L$ be the midpoints of $[BE]$ and $[CD]$, respectively. Let $R$ be the intersection of the perpendicular to $(QK)$ passing through $K$ and the perpendicular to $(QL)$ passing through $L$. Show that
1) $R$ lies on the circumcircle of $ABC$;
2) $Q$ lies on the bisector of the angle $\widehat{BAC}$.
|
Let's first recall the method for constructing the center of a direct similarity that maps two distinct points $A$ and $B$ to two distinct points $A'$ and $B'$, respectively.
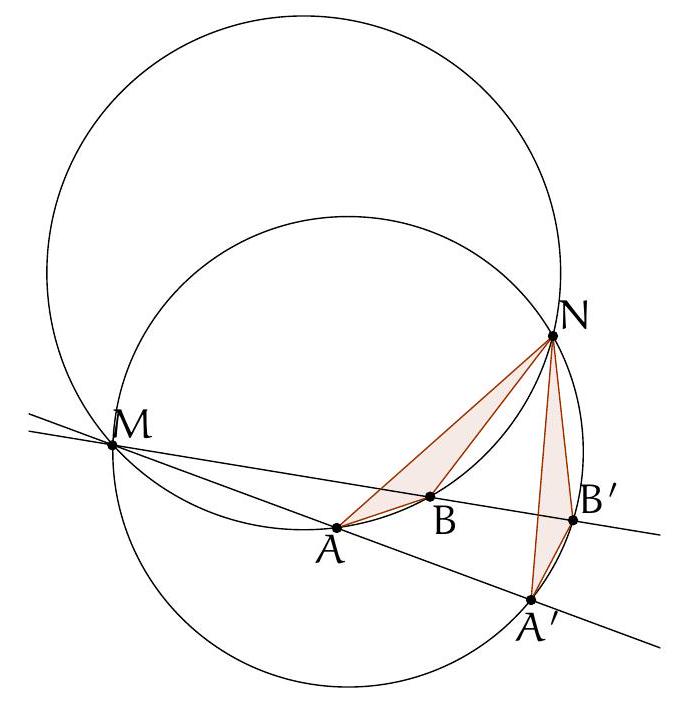
Suppose that $A \neq A'$, $B \neq B'$, and that the lines $(A A')$ and $(B B')$ are not parallel. Let $M$ be the intersection point of $(A A')$ and $(B B')$. Then the circles $MAB$ and $MA'B'$ intersect at a point $N$. Since $(NA, NB) = (MA, MB) = (MA', MB') = (NA', NB')$ and $(AB, AN) = (MB, MN) = (MB', MN) = (A'B', A'N)$, the triangles $NAB$ and $NA'B'$ are directly similar. Therefore, the similarity with center $N$ and ratio $NA' / NA$ maps $A$ to $A'$ and $B$ to $B'$. We verify that the result remains true if $A = A'$ or $B = B'$.
If $(A A')$ and $(B B')$ are parallel, then $N$ is the intersection point of $(AB)$ and $(A'B')$.
Let's return to the exercise. First, let's prove the second assertion.
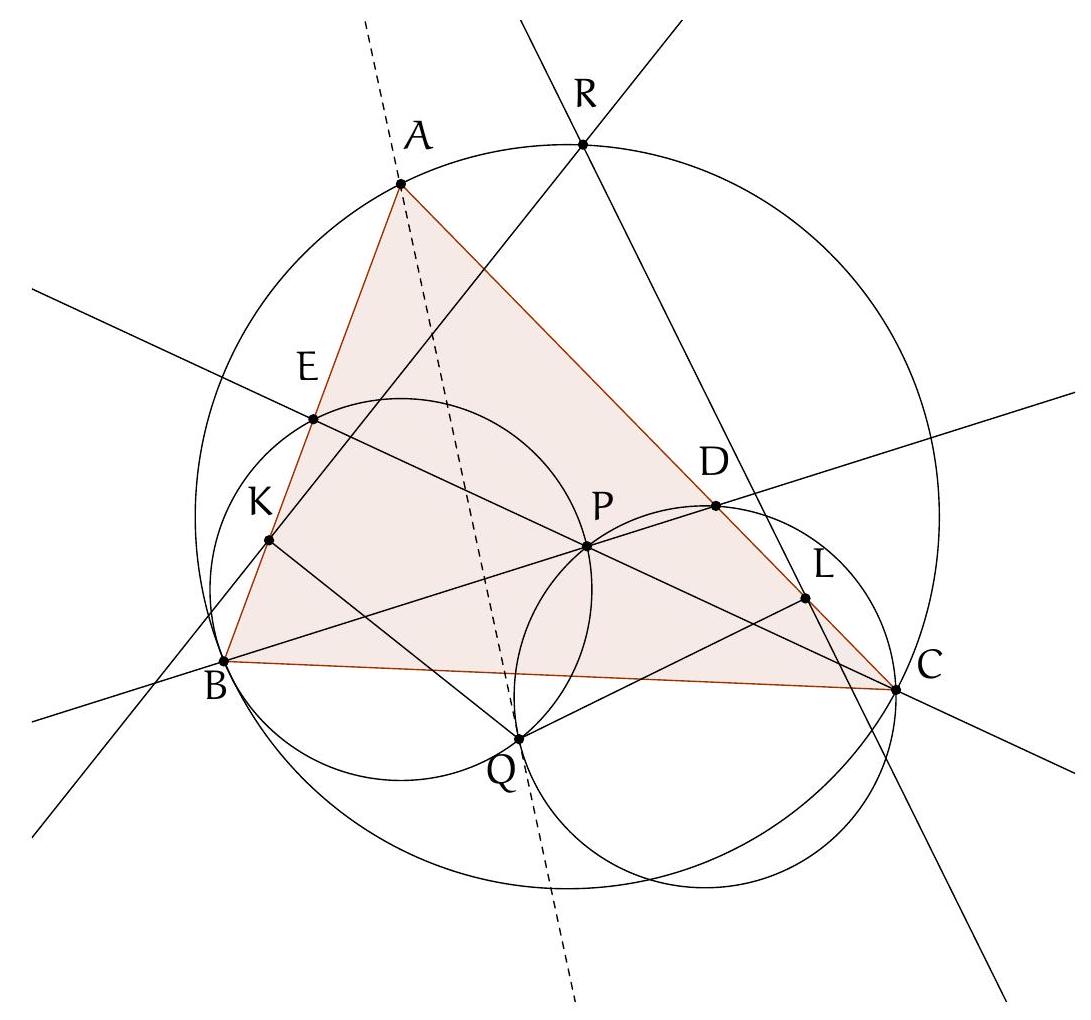
According to the preliminary, $Q$ is the center of the direct similarity that maps $B$ to $D$ and $E$ to $C$. Since $BE = CD$, this similarity is a rotation, which we will denote by $r$. Since $r$ maps $(AB)$ to $(AC)$, $Q$ is equidistant from $(AB)$ and $(AC)$, so $Q$ lies on a bisector of the angle $\widehat{BAC}$. Let's verify that it is the internal bisector.
By a continuity argument, it suffices to restrict ourselves to the case where $E$ and $D$ are strictly inside the segments $[AB]$ and $[AC]$. In this case, $A, B$, and $E$ being collinear and not cocyclic, $Q \neq A$.
Furthermore, when $ABC$ is isosceles at $A$ and $D$ and $E$ tend towards $A$, the circumcircles of $BPE$ and $CPD$ tend towards the circles $\Gamma_1$ passing through $B$ and tangent to $(AC)$ at $A$ and $\Gamma_2$ passing through $C$ and tangent to $(AB)$ at $A$. The circle $\Gamma_1$ and the triangle are on the same side of the line $(AC)$, and the circle $\Gamma_2$ and the triangle are on the same side of $(AB)$, so $Q$ tends towards a point inside the angle $\widehat{BAC}$ or the opposite angle by the vertex. This will therefore be a point on the internal bisector (different from $A$ since $(AB) \neq (AC)$).
By varying the points $A, D$, and $E$, the point $Q$ remains on the union of the two bisectors and does not pass through $A$, so it must, by continuity, remain on the internal bisector.
Now let's prove the first assertion. Since $r$ maps $(QK)$ to $(QL)$ and $(AK)$ to $(AL)$, the angles between the lines $(QK, QL)$ and $(AK, AL)$ are equal, so $A, K, Q, L$ are concyclic.
Since the triangles $KQR$ and $LQR$ are right-angled at $K$ and $L$, the circle with diameter $[QR]$ passes through $K$ and $L$, so the circumcircle of $QKL$ meets $R$, which shows that $A, K, Q, L, R$ are concyclic.
Let $r'$ be the direct similarity that maps $K$ to $B$ and $L$ to $C$. According to the preliminary, the center of $r'$ is the second intersection point of the circumcircle of $ABC$ with the circumcircle of $AKL$, which is $R$. Since $r'$ maps the lines $(RK)$ and $(RL)$ to $(RB)$ and $(RC)$ respectively, we deduce that $(RB, RC) = (RK, RL) = (AK, AL) = (AB, AC)$, where the second equality comes from the concyclicity of $A, K, L, R$. This proves that $A, B, C, R$ are concyclic.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. Soient $D \in[A C]$ et $E \in[A B]$ tels que $B E=C D$. Soit $P$ le point d'intersection de (BD) et ( $C E$ ). Les cercles circonscrits à BEP et CDP se recoupent en Q. Soient $K$ et $L$ les milieux respectifs de [BE] et [CD]. Soit R l'intersection entre la perpendiculaire à (QK) passant par K et la perpendiculaire à ( QL ) passant par L . Montrer que
1) $R$ se trouve sur le cercle circonscrit à $A B C$;
2) $Q$ se trouve sur la bissectrice de l'angle $\widehat{B A C}$.
|
Rappelons d'abord la méthode de construction du centre d'une similitude directe qui envoie deux points distincts $A$ et $B$ sur deux points distincts $A^{\prime}$ et $B^{\prime}$ respectivement.

Supposons que $A \neq A^{\prime}, B \neq B^{\prime}$, et que les droites $\left(A A^{\prime}\right)$ et $\left(B B^{\prime}\right)$ ne sont pas parallèles. Soit $M$ le point d'intersection de $\left(A A^{\prime}\right)$ et de ( $\left.B B^{\prime}\right)$. Alors les cercles $M A B$ et $M A^{\prime} B^{\prime}$ se recoupent en un point $N$. Comme $(N A, N B)=(M A, M B)=\left(M A^{\prime}, M B^{\prime}\right)=\left(N A^{\prime}, N B^{\prime}\right)$ et $(A B, A N)=(M B, M N)=$ $\left(M B^{\prime}, M N\right)=\left(A^{\prime} B^{\prime}, A^{\prime} N\right)$, les triangles $N A B$ et $N A^{\prime} B^{\prime}$ sont directement semblables, donc la similitude de centre $N$ et de rapport $N A^{\prime} / N A$ envoie $A$ sur $A^{\prime}$ et $B$ sur $B^{\prime}$. On vérifie que le résultat reste vrai si $A=A^{\prime}$ ou $B=B^{\prime}$.
$\mathrm{Si}\left(A A^{\prime}\right)$ et $\left(B B^{\prime}\right)$ sont parallèles, alors $N$ est le point d'intersection de $(A B)$ et de $\left(A^{\prime} B^{\prime}\right)$.
Revenons à l'exercice. Montrons d'abord la deuxième assertion.

D'après le préliminaire, $Q$ est le centre de la similitude directe qui envoie $B$ sur $D$ et $E$ sur $C$. Comme $B E=C D$, cette similitude est une rotation sur l'on notera $r$. Comme $r$ envoie ( $A B$ ) sur ( $A C$ ), $Q$ est équidistant de $(A B)$ et de $(A C)$ donc $Q$ est sur une bissectrice de l'angle $\widehat{B A C}$. Vérifions que c'est la bissectrice intérieure.
Par un argument de continuité, il suffit de se restreindre au cas où $E$ et $D$ sont strictement à l'intérieur des segments $[A B]$ et $[A C]$. Dans ce cas, $A, B$ et $E$ étant alignés donc non-cocycliques, $Q \neq A$.
De plus, lorsque $A B C$ est isocèle en $A$ et que $D$ et $E$ tendent vers $A$, les cercles circonscrits à $B P E$ et CPD tendent vers les cercles $\Gamma_{1}$ passant par B et tangent à (AC) en $A$ et $\Gamma_{2}$ passant par $C$ et tangent à $(A B)$ en $A$. Or, le cercle $\Gamma_{1}$ et le triangle sont du même côté de la droite $(A C)$, le cercle $\Gamma_{2}$ et le triangle sont du même côté de $(A B)$, donc $Q$ tend vers un point à l'intérieur de l'angle $\widehat{B A C}$ ou de celui opposé par le sommet. Ce sera donc un point de la bissectrice intérieure (différent de $A$ puisque $(A B) \neq(A C)$ ).
En faisant varier les points $A, D$ et $E$, le point $Q$ reste sur la réunion des deux bissectrices et ne passe pas par $A$, donc il doit par continuité rester sur la bissectrice intérieure.
Montrons maintenant la première assertion. Comme $r$ envoie ( $Q K$ ) sur ( $Q L$ ) et ( $A K$ ) sur ( $A L$ ), les angles de droites $(Q K, Q L$ ) et ( $A K, A L$ ) sont égaux donc $A, K, Q, L$ sont cocycliques.
Comme les triangles $K Q R$ et $L Q R$ sont rectangles en $K$ et $L$, le cercle de diamètre $[Q R]$ passe par $K$ et $L$, donc le cercle circonscrit à $Q K L$ rencontre $R$, ce qui montre que $A, K, Q, L, R$ sont cocycliques.
Soit $r^{\prime}$ la similitude directe qui envoie $K$ sur $B$ et $L$ sur $C$. D'après le préliminaire, le centre de $r^{\prime}$ est le second point d'intersection du cercle ABC avec le cercle AKL, c'est-à-dire R. Comme $r^{\prime}$ envoie les droites $(R K)$ et $(R L)$ sur $(R B)$ et $(R C)$ respectivement, on en déduit que $(R B, R C)=(R K, R L)=$ $(A K, A L)=(A B, A C)$ où la deuxème égalité provient de la cocyclicité de $A, K, L, R$. Ceci prouve que $A, B, C, R$ sont cocycliques.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution."
}
|
d2e87794-194e-5893-a312-30b565635a6e
| 604,482
|
Let $k \geqslant 2$ be an integer.
1) Let $n>k$ be an integer.
Does there exist $n$ strictly positive integers such that any $k$ of them are never coprime in their set, but any $k+1$ of them are always coprime in their set?
2) Does there exist an infinite sequence of strictly positive integers satisfying the two conditions above?
|
1) Let $A$ be the set of subsets of $\{1, \ldots, n\}$ of cardinality $k$. Since the set of prime numbers is infinite, there exists a family $\left(p_{I}\right)_{I \in A}$ of distinct prime numbers indexed by $A$. For all $i$, let $A(i)$ be the set of subsets $I$ of $\{1, \ldots, n\}$ of cardinality $k$ such that $i \in I$. We define
$$
a_{i}=\prod_{I \in A(i)} p_{I}
$$
If $J$ is a subset of $\{1, \ldots, n\}$, then the $a_{j}(j \in J)$ are not pairwise coprime
$\Longleftrightarrow$ they have a common prime factor
$\Longleftrightarrow$ there exists $I \in A$ such that $p_{I} \mid a_{j}$ for all $j \in J$
$\Longleftrightarrow$ there exists $I \in A$ such that $j \in I$ for all $j \in J$
$\Longleftrightarrow$ there exists $I \in A$ such that $J \subset I$
$\Longleftrightarrow \operatorname{Card}(J) \leqslant k$.
This shows that the family $\left(a_{i}\right)_{1 \leqslant i \leqslant n}$ works.
2) Suppose, for the sake of contradiction, that there is a family $\left(a_{n}\right)_{n \in \mathbb{N}}$ of strictly positive integers such that any $k$ of them are never pairwise coprime.
Let $p_{1}, \ldots, p_{m}$ be the prime divisors of $a_{0}$. Since $k \geqslant 2$, for all $n \in \mathbb{N}$, $a_{n}$ has a divisor among $p_{1}, \ldots, p_{m}$. Let $p_{i(n)}$ be one of them. Since the sequence $\left(p_{i(n)}\right)_{n \in \mathbb{N}}$ takes only a finite number of values, at least one of these values (which we will denote by $p_{\ell}$) is attained infinitely often. Therefore, there exist $i_{1}<\cdots<i_{k+1}$ such that $p_{\ell}$ divides $a_{i_{1}}, \ldots, a_{i_{k+1}}$, which shows that $a_{i_{1}}, \ldots, a_{i_{k+1}}$ are not pairwise coprime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $k \geqslant 2$ un entier.
1) Soit $n>k$ un entier.
Existe-t-il $n$ entiers strictement positifs tels que $k$ quelconques ne sont jamais premiers entre eux dans leur ensemble, mais $k+1$ quelconques sont toujours premiers entre eux dans leur ensemble?
2) Existe-t-il une suite infinie d'entiers strictement positifs vérifiant les deux conditions ci-dessus?
|
1) Soit $A$ l'ensemble des parties de $\{1, \ldots, n\}$ de cardinal $k$. Comme l'ensemble des nombres premiers est infini, il existe une famille $\left(p_{I}\right)_{I \in A}$ de nombres premiers deux à deux distincts indexée par $A$. Pour tout $i$, notons $A(i)$ l'ensemble des parties $I$ de $\{1, \ldots, n\}$ de cardinal $k$ telles que $i \in I$. On définit
$$
a_{i}=\prod_{I \in A(i)} p_{I}
$$
Si $J$ est une partie de $\{1, \ldots, n\}$, alors les $a_{j}(j \in J)$ ne sont pas premiers entre eux dans leur ensemble
$\Longleftrightarrow$ ils ont un facteur premier commun
$\Longleftrightarrow$ il existe $I \in A$ tel que $p_{I} \mid a_{j}$ pour tout $j \in J$
$\Longleftrightarrow$ il existe $I \in A$ tel que $j \in I$ pour tout $j \in J$
$\Longleftrightarrow$ il existe $I \in A$ tel que $J \subset I$
$\Longleftrightarrow \operatorname{Card}(J) \leqslant k$.
Ceci montre que la famille $\left(a_{i}\right)_{1 \leqslant i \leqslant n}$ convient.
2) Supposons par l'absurde qu'il y a une famille $\left(a_{n}\right)_{n \in \mathbb{N}}$ d'entiers strictement positifs telle que $k$ quelconques ne sont jamais premiers entre eux dans leur ensemble.
Notons $p_{1}, \ldots, p_{m}$ les diviseurs premiers de $a_{0}$. Comme $k \geqslant 2$, pour tout $n \in \mathbb{N}$, $a_{n}$ possède un diviseur parmi $p_{1}, \ldots, p_{m}$. Notons $p_{i(n)}$ l'un d'eux. Comme la suite $\left(p_{i(n)}\right)_{n \in \mathbb{N}}$ ne prend qu'un nombre fini de valeurs, au moins une de ses valeurs (que nous noterons $p_{\ell}$ ) est atteinte une infinité de fois. Il existe donc $i_{1}<\cdots<i_{k+1}$ tels que $p_{\ell}$ divise $a_{i_{1}}, \ldots, a_{i_{k+1}}$, ce qui montre que $a_{i_{1}}, \ldots, a_{i_{k+1}}$ ne sont pas premiers entre eux dans leur ensemble.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl",
"problem_match": "## Exercice 1.",
"solution_match": "\nSolution."
}
|
59961ee2-4ece-546a-a98a-8f83000def3f
| 604,497
|
Let $ABC$ be a triangle and $\omega$ a circle passing through $A$ and $B$ and intersecting the sides $[BC]$ and $[AC]$ at $D$ and $E$ respectively. The points $K$ and $L$ are the centers of the incircles of $DAC$ and $BEC$ respectively. Let $N$ be the intersection of the lines $(EL)$ and $(DK)$.
Prove that the triangle $KNL$ is isosceles.
|
We will show the equality between the angles of lines $(K L, K N)$ and $(L N, K L)$. First, note that $C, K, L$ are collinear (on the interior bisector at $C$ of triangle $A B C$).
\[
\begin{aligned}
(K L, K N) & =(C K, C D)+(D C, D N)=\frac{1}{2}((\overrightarrow{C A}, \overrightarrow{C B})+(\overrightarrow{D C}, \overrightarrow{D A})) \\
& =\frac{1}{2}[(\overrightarrow{C A}, \overrightarrow{C B})+\Pi+(\overrightarrow{D B}, \overrightarrow{D A})]
\end{aligned}
\]
where $\Pi$ is the straight angle, and
\[
\begin{aligned}
(L N, K L) & =(E L, E C)+(E C, C K)=\frac{1}{2}((\overrightarrow{E B}, \overrightarrow{E C})+(\overrightarrow{C E}, \overrightarrow{C B})) \\
& =\frac{1}{2}[(\overrightarrow{E B}, \overrightarrow{E A})+\Pi+(\overrightarrow{C A}, \overrightarrow{C B})]
\end{aligned}
\]
The angles of vectors $(\overrightarrow{D B}, \overrightarrow{D A})$ and $(\overrightarrow{E B}, \overrightarrow{E A})$ are equal since $E$ and $D$ are on the same arc delimited by $A$ and $B$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\omega$ un cercle qui passe par $A$ et $B$ et recoupe les côtés $[B C]$ et $[A C]$ respectivement en $D$ et $E$. Les points $K$ et $L$ sont respectivement les centres du cercle inscrit dans $D A C$ et du cercle inscrit dans $B E C$. Soit $N$ l'intersection des droites $(E L)$ et $(D K)$.
Prouver que le triangle $K N L$ est isocèle.
|
On va montrer l'égalité entre les angles de droites ( $K L, K N$ ) et $(L N, K L)$. Notons d'abord que $C, K, L$ sont alignés (sur la bissectrice intérieure en $C$ du triangle $A B C$ ).
$$
\begin{aligned}
(K L, K N) & =(C K, C D)+(D C, D N)=\frac{1}{2}((\overrightarrow{C A}, \overrightarrow{C B})+(\overrightarrow{D C}, \overrightarrow{D A})) \\
& =\frac{1}{2}[(\overrightarrow{C A}, \overrightarrow{C B})+\Pi+(\overrightarrow{D B}, \overrightarrow{D A})]
\end{aligned}
$$
où $\Pi$ est l'angle plat, et
$$
\begin{aligned}
(L N, K L) & =(E L, E C)+(E C, C K)=\frac{1}{2}((\overrightarrow{E B}, \overrightarrow{E C})+(\overrightarrow{C E}, \overrightarrow{C B})) \\
& =\frac{1}{2}[(\overrightarrow{E B}, \overrightarrow{E A})+\Pi+(\overrightarrow{C A}, \overrightarrow{C B})]
\end{aligned}
$$
Or, les angles de vecteurs $(\overrightarrow{D B}, \overrightarrow{D A})$ et $(\overrightarrow{E B}, \overrightarrow{E A})$ sont égaux puisque $E$ et $D$ sont sur le même arc délimité par $A$ et $B$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl",
"problem_match": "## Exercice 2.",
"solution_match": "\nSolution 1."
}
|
8e72f4dd-2564-5dea-984a-453c9457899d
| 604,511
|
Let $ABC$ be a triangle and $\omega$ a circle passing through $A$ and $B$ and intersecting the sides $[BC]$ and $[AC]$ at $D$ and $E$ respectively. The points $K$ and $L$ are the centers of the incircles of $DAC$ and $BEC$ respectively. Let $N$ be the intersection of the lines $(EL)$ and $(DK)$.
Prove that the triangle $KNL$ is isosceles.
|
Since $A, B, D, E$ are concyclic, we have the equalities of directed angles of lines
$$
\begin{aligned}
& (D A, D C)=(D A, D B)=(E A, E B)=(E C, E B) \\
& (A D, A C)=(A D, A E)=(B D, B E)=(B C, B E)
\end{aligned}
$$
thus the directed angles of $C A D$ and $C B E$ are pairwise opposite, hence the triangles $C A D$ and $C B E$ are indirectly similar. Let $f$ be the indirect similarity that maps $C, A, D$ to $C, B, E$ respectively. Then $f$ maps the incenter of $C A D$ to that of $C B E$: in other words, $f(K)=L$.
We have $(L K, L N)=(L K, E L)=(C L, E L)$ because $C, K, L$ are collinear (on the internal angle bisector at $C$ of triangle $A B C$). Furthermore, $f$ maps $C, D, K$ to $C, E, L$ respectively, so $(C L, E L)=-(C K, D K)=(K D, K C)=$ $(K N, K L)$. Finally, $(L K, L N)=(K N, K L)$, hence $L K N$ is isosceles at $N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\omega$ un cercle qui passe par $A$ et $B$ et recoupe les côtés $[B C]$ et $[A C]$ respectivement en $D$ et $E$. Les points $K$ et $L$ sont respectivement les centres du cercle inscrit dans $D A C$ et du cercle inscrit dans $B E C$. Soit $N$ l'intersection des droites $(E L)$ et $(D K)$.
Prouver que le triangle $K N L$ est isocèle.
|
Comme $A, B, D, E$ sont cocycliques, on a les égalités d'angles orientés de droites
$$
\begin{aligned}
& (D A, D C)=(D A, D B)=(E A, E B)=(E C, E B) \\
& (A D, A C)=(A D, A E)=(B D, B E)=(B C, B E)
\end{aligned}
$$
donc les angles orientés de $C A D$ et $C B E$ sont deux à deux opposés, par conséquent les triangles $C A D$ et $C B E$ sont indirectement semblables. Soit $f$ la similitude indirecte qui envoie $C, A, D$ sur $C, B, E$ respectivement. Alors $f$ envoie le centre du cercle inscrit de $C A D$ sur celui de $C B E$ : autrement dit, $f(K)=L$.
On a $(L K, L N)=(L K, E L)=(C L, E L)$ car $C, K, L$ sont alignés (sur la bissectrice intérieure en $C$ du triangle $A B C$ ). De plus, $f$ envoie $C, D, K$ sur $C, E, L$ respectivement, donc $(C L, E L)=-(C K, D K)=(K D, K C)=$ $(K N, K L)$. Finalement, $(L K, L N)=(K N, K L)$ donc $L K N$ est isocèle en $N$.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl",
"problem_match": "## Exercice 2.",
"solution_match": "\nSolution 2."
}
|
8e72f4dd-2564-5dea-984a-453c9457899d
| 604,511
|
Prove that, for all real numbers $a, b, c > 0$ and any real number $t \geqslant 0$, we have
$$
\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b} \geqslant \frac{3}{1+t} .
$$
|
Let $x=b+t c, y=c+t a, z=a+t b$. We verify that
$$
\begin{aligned}
\left(1+t^{3}\right) a & =z-t x+t^{2} y \\
\left(1+t^{3}\right) b & =x-t y+t^{2} z \\
\left(1+t^{3}\right) c & =y-t z+t^{2} x
\end{aligned}
$$
thus, according to the arithmetic-geometric mean inequality,
$$
\begin{aligned}
\left(1+t^{3}\right)\left(\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b}\right) & =\frac{z-t x+t^{2} y}{x}+\frac{x-t y+t^{2} z}{y}+\frac{y-t z+t^{2} x}{z} \\
& =\left(\frac{z}{x}+\frac{x}{y}+\frac{y}{z}\right)+t^{2}\left(\frac{y}{x}+\frac{z}{y}+\frac{x}{z}\right)-3 t \\
& \geqslant 3 \sqrt[3]{\frac{z}{x} \frac{x}{y} \frac{y}{z}}+3 t^{2} \sqrt[3]{\frac{y}{x} \frac{z}{y} \frac{x}{z}}-3 t \\
& =3\left(1-t+t^{2}\right)=3 \frac{1+t^{3}}{1+t}
\end{aligned}
$$
from which the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tous réels $a, b, c>0$ et tout réel $t \geqslant 0$, on a
$$
\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b} \geqslant \frac{3}{1+t} .
$$
|
Posons $x=b+t c, y=c+t a, z=a+t b$. On vérifie que
$$
\begin{aligned}
\left(1+t^{3}\right) a & =z-t x+t^{2} y \\
\left(1+t^{3}\right) b & =x-t y+t^{2} z \\
\left(1+t^{3}\right) c & =y-t z+t^{2} x
\end{aligned}
$$
donc, d'après l'inégalité arithmético-géométrique,
$$
\begin{aligned}
\left(1+t^{3}\right)\left(\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b}\right) & =\frac{z-t x+t^{2} y}{x}+\frac{x-t y+t^{2} z}{y}+\frac{y-t z+t^{2} x}{z} \\
& =\left(\frac{z}{x}+\frac{x}{y}+\frac{y}{z}\right)+t^{2}\left(\frac{y}{x}+\frac{z}{y}+\frac{x}{z}\right)-3 t \\
& \geqslant 3 \sqrt[3]{\frac{z}{x} \frac{x}{y} \frac{y}{z}}+3 t^{2} \sqrt[3]{\frac{y}{x} \frac{z}{y} \frac{x}{z}}-3 t \\
& =3\left(1-t+t^{2}\right)=3 \frac{1+t^{3}}{1+t}
\end{aligned}
$$
d'où la conclusion.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl",
"problem_match": "## Exercice 3.",
"solution_match": "\nSolution 1."
}
|
78f0551b-7969-5380-845e-6314f8a722cc
| 604,545
|
Prove that, for all real numbers $a, b, c > 0$ and any real number $t \geqslant 0$, we have
$$
\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b} \geqslant \frac{3}{1+t} .
$$
|
Since the inequality is homogeneous in $a, b, c$, we can assume that $a+b+c=1$. The left-hand side is equal to $a f(x)+b f(y)+c f(z)$ where $x=b+t c, y=c+t a, z=a+t b$ and $f(x)$ is the convex function $x \mapsto \frac{1}{x}$. By Jensen's inequality, the left-hand side is greater than or equal to
$$
f(a x+b y+t z)=\frac{1}{a b+t a c+b c+t b a+c a+t a b}=\frac{1}{(1+t)(a b+b c+c a)},
$$
so it suffices to prove that $a b+b c+c a \leqslant \frac{1}{3}$.
Now, $1=(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(a b+b c+c a)$, so it suffices to show that $a^{2}+b^{2}+c^{2} \geqslant \frac{1}{3}$, which follows from the inequality between the arithmetic mean and the quadratic mean of $a, b, c$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tous réels $a, b, c>0$ et tout réel $t \geqslant 0$, on a
$$
\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b} \geqslant \frac{3}{1+t} .
$$
|
Puisque l'inégalité est homogène en $a, b, c$, on peut supposer que $a+b+c=1$. Comme le membre de gauche est égal à $a f(x)+b f(y)+c f(z)$ où $x=b+t c, y=c+t a, z=a+t b$ et $f(x)$ est la fonction convexe $x \mapsto \frac{1}{x}$, d'après l'inégalité de Jensen le membre de gauche est supérieur ou égal à
$$
f(a x+b y+t z)=\frac{1}{a b+t a c+b c+t b a+c a+t a b}=\frac{1}{(1+t)(a b+b c+c a)},
$$
donc il suffit de prouver que $a b+b c+c a \leqslant \frac{1}{3}$.
Or, $1=(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(a b+b c+c a)$ donc il suffit de montrer que $a^{2}+b^{2}+c^{2} \geqslant \frac{1}{3}$, ce qui découle de l'inégalité entre la moyenne arithmétique et la moyenne quadratique de $a, b, c$.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl",
"problem_match": "## Exercice 3.",
"solution_match": "\nSolution 2."
}
|
78f0551b-7969-5380-845e-6314f8a722cc
| 604,545
|
Prove that, for all real numbers $a, b, c > 0$ and any real number $t \geqslant 0$, we have
$$
\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b} \geqslant \frac{3}{1+t} .
$$
|
According to the Cauchy-Schwarz inequality,
\[
\left(\frac{a^{2}}{a b+t c a}+\frac{b^{2}}{b c+t a b}+\frac{c^{2}}{c a+t b c}\right) \cdot((a b+t c a)+(b c+t a b)+(c a+t b c)) \geqslant(a+b+c)^{2}
\]
which can be written as
\[
\left(\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b}\right) \cdot(1+t)(a b+b c+c a) \geqslant a^{2}+b^{2}+c^{2}+2(a b+b c+c a).
\]
We have \(a^{2}+b^{2}+c^{2} \geqslant a b+b c+c a\) according to the rearrangement inequality (or the Cauchy-Schwarz inequality), so
\[
\left(\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b}\right) \cdot(1+t)(a b+b c+c a) \geqslant 3(a b+b c+c a).
\]
The required inequality follows after dividing by \((1+t)(a b+b c+c a)\).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tous réels $a, b, c>0$ et tout réel $t \geqslant 0$, on a
$$
\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b} \geqslant \frac{3}{1+t} .
$$
|
D'après l'inégalité de Cauchy-Schwarz,
$\left(\frac{a^{2}}{a b+t c a}+\frac{b^{2}}{b c+t a b}+\frac{c^{2}}{c a+t b c}\right) \cdot((a b+t c a)+(b c+t a b)+(c a+t b c)) \geqslant(a+b+c)^{2}$ ce qui s'écrit
$$
\left(\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b}\right) \cdot(1+t)(a b+b c+c a) \geqslant a^{2}+b^{2}+c^{2}+2(a b+b c+c a) .
$$
Or, on a $a^{2}+b^{2}+c^{2} \geqslant a b+b c+c a$ d'après l'inégalité de réordonnement (ou d'après celle de Cauchy-Schwarz), donc
$$
\left(\frac{a}{b+t c}+\frac{b}{c+t a}+\frac{c}{a+t b}\right) \cdot(1+t)(a b+b c+c a) \geqslant 3(a b+b c+c a)
$$
L'inégalité demandée en découle après division par $(1+t)(a b+b c+c a)$.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-stage-corrige.jsonl",
"problem_match": "## Exercice 3.",
"solution_match": "\nSolution 3."
}
|
78f0551b-7969-5380-845e-6314f8a722cc
| 604,545
|
On a line, there are 400 blue points and 200 green points. Show that one can find a segment that contains exactly 200 blue points and 100 green points.
|
Let $A_{1}, \ldots, A_{600}$ be points on a line, aligned in this order. We need to show that there exists an integer $k \in\{0, \ldots, 300\}$ such that among the points $A_{k+1}, \ldots, A_{k+300}$, there are exactly 100 green points (and therefore 200 blue points).
Introduce the function $\mathrm{f}:\{0, \ldots, 300\} \longrightarrow \mathbb{N}$ which associates to an integer $k$ the number of green points among $A_{k+1}, \ldots, A_{k+300}$. We want to show that $f$ takes the value 100. For this, note two things:
1. First, the sum $f(0)+f(300)$ counts the total number of green points, and it is therefore 200. Thus, one of the two terms in the sum is at least 100 while the other does not exceed 100. Without loss of generality, we can assume that $f(0) \leqslant 100 \leqslant f(300)$.
2. Now, consider the difference $f(k)-f(k-1)$, where $k \geqslant 1$:
- if $A_{k+300}$ and $A_{k}$ are of the same color, it is 0;
- if $A_{k+300}$ is green and $A_{k}$ is blue, it is 1;
- if $A_{k+300}$ is blue and $A_{k}$ is green, it is -1.
In particular, we have $f(k)-f(k-1) \leqslant 1$ for all $k \in\{1, \ldots, 300\}$.
Consider now the smallest integer $p$ such that $f(p) \geqslant 100$: this integer exists, since $f(300) \geqslant 100$. If $p=0$, there is nothing more to do: indeed, in this case, we have $f(0) \geqslant 100$ and $f(0) \leqslant 100$,
hence $f(0)=100$. If $p>0$, the minimality of $p$ ensures that $f(p-1) \leqslant 99$ and thus, from the above, we have $100 \leqslant f(p) \leqslant f(p-1)+1 \leqslant 100$, and thus $f(p)=100$.
Finally, in all cases, the value 100 is indeed reached by the function $f$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Sur une droite se trouvent 400 points bleus et 200 points verts. Montrer que l'on peut trouver un segment qui contient exactement 200 points bleus et 100 points verts.
|
Notons $A_{1}, \ldots, A_{600}$ les points de la droite, alignés dans cet ordre. Il s'agit de montrer qu'il existe un entier $k \in\{0, \ldots, 300\}$ tel que, parmi les points $A_{k+1}, \ldots, A_{k+300}$, il y en a exactement 100 verts (il y en aura alors forcément 200 bleus).
Introduisons la fonction $\mathrm{f}:\{0, \ldots, 300\} \longrightarrow \mathbb{N}$ qui à un entier $k$ associe le nombre de points verts parmi $A_{k+1}, \ldots, A_{k+300}$. On veut montrer que f prend la valeur 100 . Pour cela, remarquons deux choses:
1. Tout d'abord, la somme $f(0)+f(300)$ compte le nombre total de points verts, et elle vaut donc 200. Ainsi, l'un des deux termes de la somme est supérieur ou égal à 100 tandis que l'autre ne dépasse pas 100. Quitte à changer le sens de parcours des points sur la droite, on peut supposer que $f(0) \leqslant 100 \leqslant f(300)$.
2. Intéressons-nous maintenant à la différence $f(k)-f(k-1)$, où $k \geqslant 1$ :
- si $A_{k+300}$ et $A_{k}$ sont de même couleur, elle vaut 0 ;
- si $A_{k+300}$ est vert et $A_{k}$ est bleu, elle vaut 1;
- si $A_{k+300}$ est bleu et $A_{k}$ est vert, elle vaut -1 .
En particulier, on a $f(k)-f(k-1) \leqslant 1$ pour tout $k \in\{1, \ldots, 300\}$.
Considérons maintenant le plus petit entier $p$ tel que $f(p) \geqslant 100$ : cet entier existe bien, puisque $f(300) \geqslant 100$. Si $p=0$, il n'y a plus rien à faire : en effet, dans ce cas, on a $f(0) \geqslant 100$ et $f(0) \leqslant 100$,
d'où $f(0)=100$. Si $p>0$, la minimalité de $p$ assure que $f(p-1) \leqslant 99$ et donc, d'après ci-dessus, on a alors $100 \leqslant f(p) \leqslant f(p-1)+1 \leqslant 100$, et ainsi $f(p)=100$.
Finalement, dans tous les cas, la valeur 100 est bien atteinte par la fonction $f$, ce qui conclut.
## Exercices communs
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
2147bf77-172b-54ca-9a8b-5a2639fbb465
| 604,595
|
Let $a, b, c, d > 0$ be real numbers such that $a b c d = 1$.
Prove that
$$
\frac{1}{a+b+2}+\frac{1}{b+c+2}+\frac{1}{c+d+2}+\frac{1}{d+a+2} \leqslant 1 .
$$
|
It is well known that if $x, y > 0$ are real numbers, then $x + y \geqslant 2 \sqrt{xy}$.
Therefore, $\frac{1}{a+b+2} \leqslant \frac{1}{2(\sqrt{ab}+1)}$ and $\frac{1}{c+d+2} \leqslant \frac{1}{2(\sqrt{cd}+1)}$, hence
$$
\begin{aligned}
\frac{1}{a+b+2}+\frac{1}{c+d+2} & \leqslant \frac{1}{2(\sqrt{ab}+1)}+\frac{1}{2(\sqrt{cd}+1)}=\frac{1}{2(\sqrt{ab}+1)}+\frac{1}{2\left(\frac{1}{\sqrt{ab}}+1\right)} \\
& =\frac{1}{2(\sqrt{ab}+1)}+\frac{\sqrt{ab}}{2(\sqrt{ab}+1)}=\frac{1}{2}
\end{aligned}
$$
Similarly, we can prove that $\frac{1}{b+c+2}+\frac{1}{d+a+2} \leqslant \frac{1}{2}$.
By summing the two inequalities above, we immediately deduce the desired conclusion.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c, d>0$ des réels tels que $a b c d=1$.
Prouver que
$$
\frac{1}{a+b+2}+\frac{1}{b+c+2}+\frac{1}{c+d+2}+\frac{1}{d+a+2} \leqslant 1 .
$$
|
Il est bien connu que, si $x, y>0$ sont des réels, on a $x+y \geqslant 2 \sqrt{x y}$.
Par suite, $\frac{1}{a+b+2} \leqslant \frac{1}{2(\sqrt{a b}+1)}$ et $\frac{1}{c+d+2} \leqslant \frac{1}{2(\sqrt{c d}+1)}$, d'où
$$
\begin{aligned}
\frac{1}{a+b+2}+\frac{1}{c+d+2} & \leqslant \frac{1}{2(\sqrt{a b}+1)}+\frac{1}{2(\sqrt{c d}+1)}=\frac{1}{2(\sqrt{a b}+1)}+\frac{1}{2\left(\frac{1}{\sqrt{a b}}+1\right)} \\
& =\frac{1}{2(\sqrt{a b}+1)}+\frac{\sqrt{a b}}{2(\sqrt{a b}+1)}=\frac{1}{2}
\end{aligned}
$$
On prouve de même que $\frac{1}{\mathrm{~b}+\mathrm{c}+2}+\frac{1}{\mathrm{~d}+\mathrm{a}+2} \leqslant \frac{1}{2}$.
En sommant les deux inégalités précédentes, on déduit immédiatement la conclusion désirée.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl",
"problem_match": "## Exercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
87a2e7b5-4f6c-5904-aed7-834e91394e23
| 604,610
|
Let $\mathcal{C}$ and $\mathcal{C}^{\prime}$ be two external circles with centers $O$ and $O^{\prime}$. We draw two parallel radii of the same direction $[O M]$ and $\left[O^{\prime} M^{\prime}\right]$, and two other parallel radii of the same direction $[OP]$ and $\left[O^{\prime} P^{\prime}\right]$. The line $\left(M M^{\prime}\right)$ intersects $\mathcal{C}^{\prime}$ at $N$ and the line $(PP^{\prime})$ intersects $\mathcal{C}^{\prime}$ at $Q$. Show that $M, N, P, Q$ are concyclic.
|
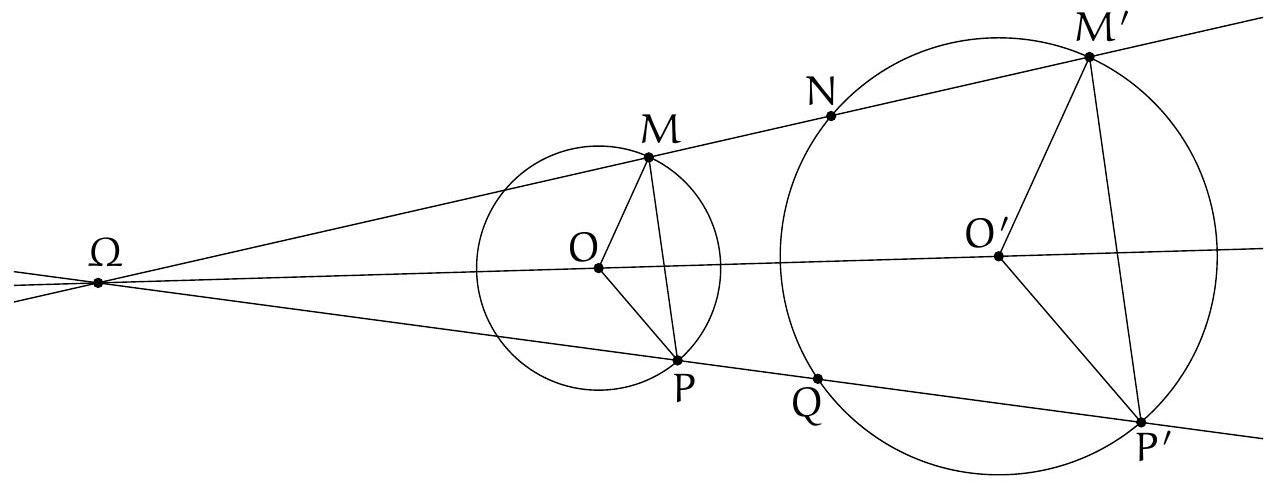
The triangles OMP and \( \mathrm{O}^{\prime} \mathrm{M}^{\prime} \mathrm{P}^{\prime} \) are isosceles at O and \( \mathrm{O}^{\prime} \) respectively. Moreover, the angles \( (\overrightarrow{\mathrm{OM}}, \overrightarrow{\mathrm{OP}}) \) and \( \left(\overrightarrow{\mathrm{O}^{\prime} \mathrm{M}^{\prime}}, \overrightarrow{\mathrm{O}^{\prime} \mathrm{P}^{\prime}}\right) \) are equal, so these two triangles are directly similar. Since (OM) and \( \left(O^{\prime} M^{\prime}\right) \) are parallel, (MP) and \( \left(M^{\prime} \mathrm{P}^{\prime}\right) \) are also parallel.
We deduce that \( (M P, M N) = \left(M^{\prime} P^{\prime}, M^{\prime} N\right) = \left(Q^{\prime}, Q N\right) = (Q P, Q N) \), so MNPQ is cyclic.
Another solution. Suppose the circles have different radii. Let \( \Omega \) be the center of the homothety \( h \) with ratio \( \lambda > 0 \) that transforms the first circle into the second. The point \( h(M) \) satisfies the same condition in the statement as the point \( M^{\prime} \), so \( h(M) = M^{\prime} \). Similarly, \( h(P) = P^{\prime} \). We have \( \Omega N \cdot \Omega M^{\prime} = \Omega Q \cdot \Omega P^{\prime} \) (power of a point with respect to a circle), so \( \lambda \Omega N \cdot \Omega M = \lambda Q \cdot \Omega P \). Simplifying by \( \lambda \) and using the power of a point with respect to a circle again, we deduce that \( M, N, P, Q \) are concyclic.
If the circles have the same radius, then there exists a translation that sends \( M \) and \( P \) to \( M^{\prime} \) and \( P^{\prime} \) respectively, so as above we have \( (M P, M N) = \left(M^{\prime} P^{\prime}, M^{\prime} N\right) = \left(Q^{\prime}, Q N\right) = (Q P, Q N) \).
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient deux cercles extérieurs $\mathcal{C}$ et $\mathcal{C}^{\prime}$ de centres $O$ et $\mathrm{O}^{\prime}$. On mène deux rayons parallèles de même sens $[O M]$ et $\left[O^{\prime} M^{\prime}\right]$, et deux autres rayons parallèles de même sens [OP] et $\left[\mathrm{O}^{\prime} \mathrm{P}^{\prime}\right]$. La droite $\left(M M^{\prime}\right.$ ) recoupe $\mathcal{C}^{\prime}$ en $N$ et la droite ( $\mathrm{PP}^{\prime}$ ) recoupe $\mathcal{C}^{\prime}$ en Q . Montrer que $M, N, P, Q$ sont cocycliques.
|

Les triangles OMP et $\mathrm{O}^{\prime} \mathrm{M}^{\prime} \mathrm{P}^{\prime}$ sont isocèles en O et $\mathrm{O}^{\prime}$ respectivement. De plus, les angles $(\overrightarrow{\mathrm{OM}}, \overrightarrow{\mathrm{OP}})$ et $\left(\overrightarrow{\mathrm{O}^{\prime} \mathrm{M}^{\prime}}, \overrightarrow{\mathrm{O}^{\prime} \mathrm{P}^{\prime}}\right)$ sont égaux, donc ces deux triangles sont directement semblables. Comme de plus (OM) et $\left(O^{\prime} M^{\prime}\right)$ sont parallèles, (MP) et $\left(M^{\prime} \mathrm{P}^{\prime}\right)$ le sont.
On en déduit $(M P, M N)=\left(M^{\prime} P^{\prime}, M^{\prime} N\right)=\left(Q^{\prime}, Q N\right)=(Q P, Q N)$, donc MNPQ est inscriptible.
Autre solution. Supposons que les cercles sont de rayons différents. Soit $\Omega$ le centre de l'homothétie $h$ de rapport $\lambda>0$ qui transforme le premier cercle en le deuxième. Le point $h(M)$ vérifie la même condition de l'énoncé que le point $M^{\prime}$, donc $h(M)=M^{\prime}$. De même, $h(P)=P^{\prime}$. On a $\Omega N \cdot \Omega M^{\prime}=\Omega Q \cdot \Omega P^{\prime}$ (puissance d'un point par rapport à un cercle), donc $\lambda \Omega N \cdot \Omega M=$ $\lambda Q \cdot \Omega P$. En simplifiant par $\lambda$ et en utilisant encore la puissance d'un point par rapport à un cercle, on en déduit que $M, N, P, Q$ sont cocycliques.
Si les cercles sont de même rayon, alors il existe une translation qui envoie $M$ et $P$ sur $M^{\prime}$ et $P^{\prime}$ respectivement, donc comme ci-dessus on a $(M P, M N)=\left(M^{\prime} P^{\prime}, M^{\prime} N\right)=\left(Q^{\prime}, Q N\right)=$ (QP, QN).
## Exercices du groupe A
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
a81648e2-f94b-539b-85da-762670a95cb2
| 604,622
|
Let $n>0$ be an integer, and $a, b, c$ be strictly positive integers such that
$$
(a+b c)(b+a c)=19^{n}
$$
Prove that $n$ is even.
|
Let us proceed by contradiction and assume that there exists a triplet $(a, b, c)$ such that $(a+bc)(b+ac)=19^n$, where $n$ is an odd integer. Without loss of generality, we can assume that $a \geqslant b$ and that the sum $a+b+c$ is minimal.
Since 19 is prime, we know that $b+ac \geqslant 2$ is a power of 19, so $b+ac \equiv 0 \pmod{19}$. If 19 divides $a$, then 19 also divides $b$: then the triplet $(\alpha, \beta, c)=\left(\frac{a}{19}, \frac{b}{19}, c\right)$ is such that $(\alpha+\beta c)(\beta+\alpha c)=19^{n-2}$, so the sum $a+b+c$ is not minimal. We therefore know that $\operatorname{GCD}(a, 19)=1$.
Furthermore, if $c=1$, then $(a+bc)(b+ac)=(a+b)^2$ is a square, so $n$ must be even. Similarly, if $a=b$, then $(a+bc)(b+ac)=(a+ac)^2$ is a square, and $n$ is even. We therefore know that $c>1$ and that $a>b$.
Then $b+ac=(a+bc)+(a-b)(c-1)>a+bc$, so there exist two natural numbers $u$ and $v$ such that $a+bc=19^u$ and $b+ac=19^{u+v}$. In particular, $a(c-1)(c+1)=ac^2-a=(b+ac)c-(a+bc)=19^u(19^vc-1)$. We therefore know that $19^u$ divides $(c-1)(c+1)$ and, since $\operatorname{GCD}(19^u, c-1, c+1)=\operatorname{GCD}(19^u, c-1, 2)=1$, we deduce that $19^u$ divides either $c-1$ or $c+1$.
However, we know that $19^u=a+bc>b+bc \geqslant c+1>c-1>0$. It is therefore impossible for $19^u$ to divide $c-1$ or $c+1$, so our initial assumption was false, and thus $n$ must be even.
Remark. The reasoning used above actually shows that, if $p$ is an odd prime, the triplets $(a, b, c)$ of strictly positive integers such that $(a+bc)(b+ac)$ is a power of $p$ are the triplets of the form $(a, p^k-a, 1)$ or $(p^k, p^k, p^\ell-1)$.
The fact that $p$ is odd is very important, as the problem is false if we take $p=2$, as evidenced by the equality $(3+1 \times 5)(1+3 \times 5)=2^7$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n>0$ un entier, et $a, b, c$ des entiers strictement positifs tels que
$$
(a+b c)(b+a c)=19^{n}
$$
Prouver que n est pair.
|
Procédons par l'absurde, et supposons qu'il existe un triplet ( $a, b, c$ ) tel que $(\mathrm{a}+\mathrm{bc})(\mathrm{b}+\mathrm{ac})=19^{\mathrm{n}}$, où $n$ est un entier impair. Sans perte de généralité, on peut supposer que $a \geqslant b$ et que la somme $a+b+c$ est minimale.
Puisque 19 est premier, on sait que $b+a c \geqslant 2$ est une puissance de 19 , donc que $b+a c \equiv 0$ $(\bmod 19)$. Si 19 divise $a$, alors 19 divise bégalement : alors le triplet $(\alpha, \beta, c)=\left(\frac{a}{19}, \frac{b}{19}, c\right)$ est tel que $(\alpha+\beta c)(\beta+\alpha c)=19^{n-2}$, de sorte que la somme $a+b+c$ n'est pas minimale. On sait donc que $\operatorname{PGCD}(\mathbf{a}, 19)=1$.
En outre, si $\mathrm{c}=1$, alors $(a+b c)(b+a c)=(a+b)^{2}$ est un carré, donc $n$ est nécessairement pair. De même, si $a=b$, alors $(a+b c)(b+a c)=(a+a c)^{2}$ est un carré, et $n$ est pair. On sait donc que $c>1$ et que $a>b$.
Alors $b+a c=(a+b c)+(a-b)(c-1)>a+b c$, de sorte qu'il existe deux entiers naturels $u$ et $v$ tels que $a+b c=19^{u}$ et $b+a c=19^{u+v}$. En particulier, $a(c-1)(c+1)=a c^{2}-a=$ $(b+a c) c-(a+b c)=19^{u}\left(19^{v} c-1\right)$. On sait donc que $19^{u}$ divise $(c-1)(c+1)$ et, puisque $\operatorname{PGCD}\left(19^{\mathbf{u}}, \mathfrak{c}-1, \mathrm{c}+1\right)=\operatorname{PGCD}\left(19^{\mathbf{u}}, \boldsymbol{c}-1,2\right)=1$, on en déduit que $19^{\mathbf{u}}$ divise soit $\mathbf{c}-1$ soit $\mathrm{c}+1$.
Or, on sait que $19^{\mathrm{u}}=\mathrm{a}+\mathrm{bc}>\mathrm{b}+\mathrm{bc} \geqslant \mathrm{c}+1>\mathrm{c}-1>0$. Il est donc impossible que $19^{\mathrm{u}}$ divise $\mathrm{c}-1$ ou $\mathrm{c}+1$, de sorte que notre supposition initiale était fausse, et donc que $n$ est nécessairement pair.
Remarque. Le raisonnement utilisé ci-dessus permet en fait de montrer que, si $p$ est un nombre premier impair, les triplets ( $a, b, c$ ) d'entiers strictement positifs tels que $(a+b c)(b+a c)$ soit une puissance de $p$ sont les triplets de la forme ( $\mathfrak{a}, \mathfrak{p}^{\mathrm{k}}-\mathfrak{a}, 1$ ) ou bien ( $\mathfrak{p}^{k}, \mathfrak{p}^{\mathrm{k}}, \mathfrak{p}^{\ell}-1$ ).
Le fait que $p$ soit impair est très important, car l'exercice est faux si on prend $p=2$, comme en témoigne l'égalité $(3+1 \times 5)(1+3 \times 5)=2^{7}$.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
737f112a-bb1a-58a8-8138-25f1ec62a705
| 604,634
|
Let $n$ and $p$ be integers $\geqslant 1$. In an assembly of $n$ people, any two people have at most $p$ common acquaintances; of course, if A knows B, then B knows A. Show that the number of unordered pairs $\{A, B\}$ of people who know each other is less than or equal to $\sqrt{\mathrm{pn}^{3}}$.
|
Let $A_{1}, \cdots, A_{n}$ be the people, and consider the simple undirected graph whose vertices are the $A_{i}$, and where two people $A_{i}$ and $A_{j}$ are connected by an edge if and only if they know each other.
For all $i$, let $d_{i}$ be the degree of $A_{i}$ (i.e., the number of people $A_{i}$ knows). We need to prove that the number of edges $a$ in this graph satisfies $a \leqslant \sqrt{pn^3}$.
It is well known that $2a = \sum_{i=1}^{n} d_{i}$.
Let $M$ be the number of pairs of edges $\{XY, YZ\}$ that share a common vertex.
For all $i$, the vertex $A_{i}$ plays the role of $Y$ as many times as we can choose two vertices adjacent to $A_{i}$. Thus,
$$
M = \sum_{i=1}^{n} \binom{d_{i}}{2}
$$
On the other hand, according to the problem statement, any two vertices have at most $p$ common adjacent vertices. Thus,
$$
M \leqslant p \binom{n}{2}.
$$
From (1) and (2), we deduce that
$$
\sum_{i=1}^{n} \binom{d_{i}}{2} \leqslant p \binom{n}{2}
$$
The function $x \longmapsto \frac{1}{2} x(x-1)$ is convex on $\mathbb{R}$, so by Jensen's inequality, we have
$$
\sum_{i=1}^{n} \binom{d_{i}}{2} \geqslant \frac{n}{2} \left( \frac{2a}{n} \right) \left( \frac{2a}{n} - 1 \right)
$$
From (3) and (4), we get $2a(2a - n) \leqslant p^2 (n-1) \leqslant n^3$, or equivalently, $4a^2 - 2na - pn^3 \leqslant 0$. If $a > \sqrt{pn^3}$, then $0 > 4a^2 - 2na - a^2 = (3a - 2n)a \geqslant (3\sqrt{pn} - 2)na \geqslant na \geqslant 0$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient $n$ et $p$ des entiers $\geqslant 1$. Dans une assemblée de $n$ personnes, deux personnes quelconques ont au plus $p$ connaissances communes ; bien sûr, si A connaît B, alors B connaît $A$. Montrer que le nombre de paires non ordonnées $\{A, B\}$ de personnes qui se connaissent est inférieur ou égal à $\sqrt{\mathrm{pn}^{3}}$.
|
Notons $A_{1}, \cdots, A_{n}$ les personnes et, considérons le graphe simple et non orienté dont les sommets sont les $A_{i}$, et où deux personnes $A_{i}$ et $A_{j}$ sont reliées par une arête si et seulement si elles se connaissent.
Pour tout $i$, notons $d_{i}$ le degré de $A_{i}$ (c'est-à-dire le nombre de personnes que connaît $A_{i}$ ). Il s'agit de prouver que le nombre d'arêtes a de ce graphe vérifie $a \leqslant \sqrt{\mathrm{pn}^{3}}$.
Il est bien connu que $2 a=\sum_{i=1}^{n} d_{i}$.
Soit $M$ le nombre de paires d'arêtes $\{X Y, Y Z\}$ ayant un sommet commun.
Pour tout $i$, le sommet $A_{i}$ joue le rôle de $Y$ autant de fois que l'on peut choisir deux sommets adjacents à $A_{i}$. Ainsi,
$$
M=\sum_{i=1}^{n}\binom{d_{i}}{2}
$$
D'autre part, d'après l'énoncé, deux sommets quelconques ont toujours au plus p sommets adjacents communs. Ainsi,
$$
M \leqslant p\binom{n}{2} .
$$
De (1) et (2), on déduit que
$$
\sum_{i=1}^{n}\binom{d_{i}}{2} \leqslant p\binom{n}{2}
$$
Or, la fonction $x \longmapsto \frac{1}{2} \chi(x-1)$ est convexe sur $\mathbb{R}$ donc, d'après l'inégalité de Jensen, on a
$$
\sum_{i=1}^{n}\binom{d_{i}}{2} \geqslant \frac{n}{2}\left(\frac{2 a}{n}\right)\left(\frac{2 a}{n}-1\right)
$$
De (3) et (4), on obtient que $2 a(2 a-n) \leqslant p^{2}(n-1) \leqslant n^{3}$, ou encore $4 a^{2}-2 n a-p n^{3} \leqslant 0$. Si $a>\sqrt{p n^{3}}$, alors $0>4 a^{2}-2 n a-a^{2}=(3 a-2 n) a \geqslant(3 \sqrt{p n}-2) n a \geqslant n a \geqslant 0$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
f2be30dd-ab0a-573d-afab-9d020dd13519
| 604,651
|
Let $C$ and $C'$ be two circles with centers $O$ and $O'$, respectively, and assume they are external to each other. A common external tangent intersects the two common internal tangents at points $M$ and $N$.
Show that $(OM)$ is perpendicular to $(O'M)$ and that $(ON)$ is perpendicular to $(O'N)$.
|
Let (T) be the external common tangent as stated. Let ( $\mathrm{T}^{\prime}$ ) be the internal common tangent passing through $M$. The lines $(T)$ and $\left(T^{\prime}\right)$ are therefore the two tangents to $C$ from $M$.
Since these two tangents are symmetric with respect to (OM), the line (OM) is a bisector of ( $T$ ) and $\left(T^{\prime}\right)$. Similarly, $\left(O^{\prime} M\right)$ is a bisector of $(T)$ and $\left(T^{\prime}\right)$.
Since the bisectors of two lines are perpendicular, $(O M)$ and $\left(O^{\prime} M\right)$ are perpendicular or coincident.
If they were coincident, $\mathrm{O}, \mathrm{O}^{\prime}, \mathrm{M}$ would be collinear, and the two tangents to ( C ) passing through $M$ would be external, which is not the case.
Therefore, $(O M) \perp\left(O^{\prime} M\right)$. Similarly, we can show that $(O N) \perp\left(O^{\prime} N\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $C$ et $\mathrm{C}^{\prime}$ deux cercles de centres $O$ et $\mathrm{O}^{\prime}$, extérieurs l'un à l'autre. Une tangente commune extérieure coupe les deux tangentes communes intérieures aux points M et N .
Montrer que (OM) est perpendiculaire à ( $O^{\prime} M$ ) et que ( $O N$ ) est perpendiculaire à ( $O^{\prime} N$ ).
|
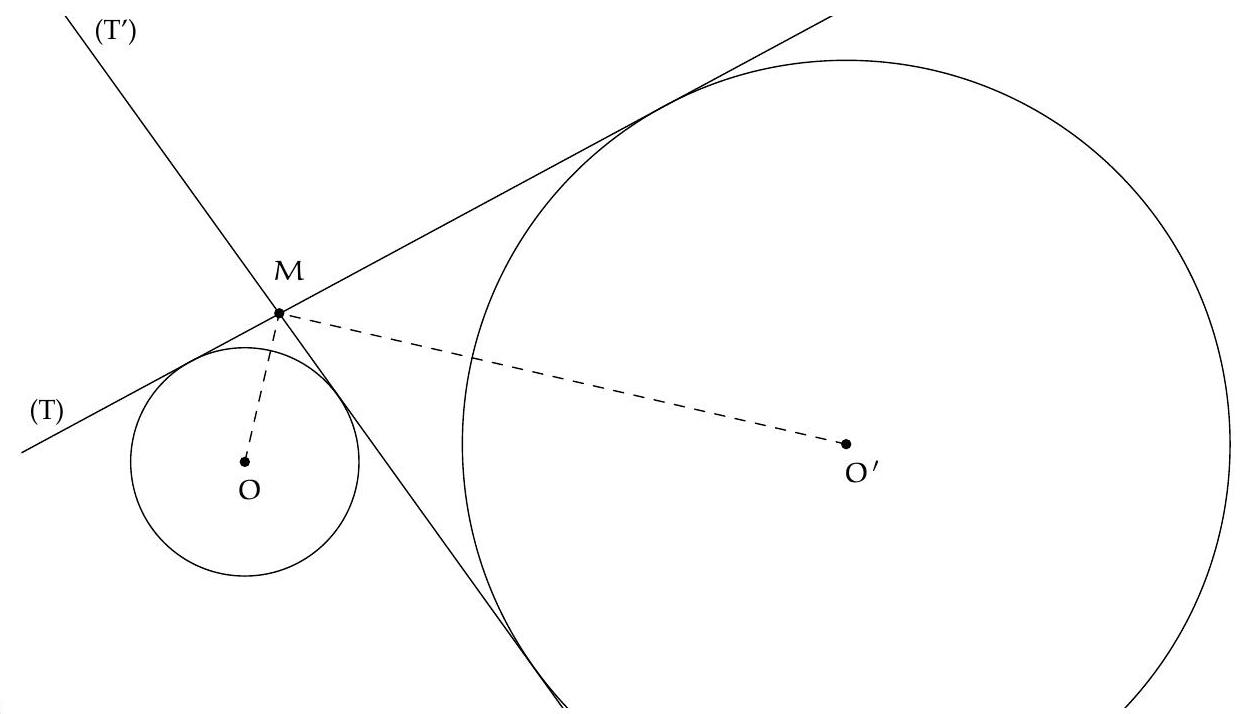
Soit (T) la tangente commune extérieure de l'énoncé. Soit ( $\mathrm{T}^{\prime}$ ) la tangente commune intérieure passant par $M$. Les droites $(T)$ et $\left(T^{\prime}\right)$ sont donc les deux tangentes à $C$ issues de $M$.
Comme ces deux tangentes sont symétriques par rapport à (OM), la droite (OM) est une bissectrice de ( $T$ ) et $\left(T^{\prime}\right)$. De même, $\left(O^{\prime} M\right.$ ) est une bissectrice de $(T)$ et $\left(T^{\prime}\right)$.
Comme les bissectrices de deux droites sont perpendiculaires, $(O M)$ et $\left(O^{\prime} M\right.$ ) sont perpendiculaires ou confondues.
Si elles étaient confondues, $\mathrm{O}, \mathrm{O}^{\prime}, \mathrm{M}$ seraient alignés, et les deux tangentes à ( C ) passant par $M$ seraient extérieures, ce qui n'est pas le cas.
Par conséquent, $(O M) \perp\left(O^{\prime} M\right)$. On montre de même que $(O N) \perp\left(O^{\prime} N\right)$.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
91720757-dbfd-5936-bfb8-503788395556
| 604,663
|
Let $k \geqslant 1$ be an integer. A telephone operator offers each customer $k$ free call numbers (if person $A$ chooses the number of $B$, then calls from $A$ to $B$ and from $B$ to $A$ are free). Consider a group of $n$ people.
1) If $n \geqslant 2 k+2$, show that there exist two people who will not be able to communicate for free.
2) If $n=2 k+1$, show that the $n$ people can arrange it so that any person can communicate for free with any other.
|
To simplify, we say that a person $A$ chooses a person $B$ if the number of $B$ is among the numbers chosen by $A$ for free communication.
3) Since each person can choose at most $k$ other people, there are at most $kn$ pairs of people who can communicate for free. However, the total number of pairs of people is $n(n-1) / 2$, and we have
$$
\frac{n(n-1)}{2} \geqslant \frac{n(2 k+1)}{2} > k n
$$
Thus, the total number of pairs of people is strictly greater than the number of pairs of people who can communicate for free. Therefore, there must be at least two people who cannot communicate for free.
2) Place the $2k+1$ people on a circle. Each person then chooses to communicate for free with the $k$ people who are immediately after them. It is easy to verify that this configuration allows any person to communicate for free with any other: by construction, each person can communicate with the $k$ people immediately after them as well as the $k$ people immediately before them, in other words, everyone can.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $k \geqslant 1$ un entier. À chaque client, un opérateur téléphonique propose $k$ numéros pour lesquels la communication est gratuite (si une personne $A$ choisit le numéro de $B$, alors les appels de $A$ vers $B$ et de $B$ vers $A$ sont gratuits). On considère un groupe de $n$ personnes.
1) Si $n \geqslant 2 k+2$, montrer qu'il existe deux personnes qui ne pourront pas communiquer gratuitement.
2) $\operatorname{Si} n=2 k+1$, montrer que les $n$ personnes peuvent faire en sorte que toute personne peut communiquer gratuitement avec n'importe quelle autre.
|
On dira pour simplifier qu'une personne $A$ choisit une personne B si le numéro de $B$ fait parti des numéros choisis par $A$ vers lesquels la communication est gratuite.
3) Comme chaque personne peut choisir au plus k autre personnes, il y a au plus kn paires de personnes qui peuvent communiquer gratuitement. Or le nombre total de paires de personnes est $n(n-1) / 2$, et on a
$$
\frac{n(n-1)}{2} \geqslant \frac{n(2 k+1)}{2}>k n
$$
Ainsi, le nombre total de paires de personnes est strictement supérieur au nombre de paires de personnes qui peuvent communiquer gratuitement. Il existe donc forcément deux personnes qui ne pourront pas communiquer gratuitement.
2) Plaçons les $2 k+1$ personnes sur un cercle. Chaque personne choisit alors de communiquer gratuitement avec les $k$ personnes qui sont situées juste après elle. On vérifie aisément que cette configuration permet à toute personne de communiquer gratuitement avec n'importe quelle autre : par construction, chaque personne peut communiquer avec les $k$ personnes situées juste après elle ainsi qu'avec les $k$ personnes situées juste avant elles, autrement dit tout le monde.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
62c9da4d-bea6-5949-92c1-75198aee11bc
| 604,673
|
Let $ABC$ be a triangle with acute angles, and such that $AB \neq AC$. We denote $D$ as the foot of the angle bisector of $\widehat{BAC}$. The point $E$ (resp. $F$) is the foot of the altitude from $B$ (resp. from $C$). The circumcircle of triangle $DBF$ intersects the circumcircle of triangle $DCE$ at a point $M$ other than $D$.
Prove that $ME = MF$.
|
Lemme 1. The circles AEF, BDF, and CDE intersect at $M$.
This immediately follows from Miquel's theorem, but let's recall the proof:
$(M F, M E) = (M F, M D) + (M D, M E) = (B F, B D) + (C D, C E) = (A B, C D) + (C D, A C) = (A B, A C)$, so $A, E, F, M$ are concyclic.
Lemme 2. The triangles $A E F$ and $A B C$ are (indirectly) similar.
The triangles $A F C$ and $A E B$ are right-angled at $F$ and $E$, and their angles at $A$ are equal, so they are similar. We deduce that $\frac{A E}{A F} = \frac{A B}{A C}$. This can be written as $\frac{A E}{A B} = \frac{A F}{A C}$. Since $\widehat{E A F} = \widehat{B A C}$, the triangles EAF and $B A C$ are similar. It is clear that the similarity is indirect since the oriented angles $(\overrightarrow{A B}, \overrightarrow{A C})$ and $(\overrightarrow{A E}, \overrightarrow{A F})$ are opposite.
Let's return to the exercise. Let $M^{\prime}$ be the other intersection point of the angle bisector of $\widehat{B A C}$ with the circle $A E F$. Similarly, define $M^{\prime \prime}$ as the other intersection point of the angle bisector of $\widehat{B A C}$ with the circle $A B C$. We will show that $M^{\prime} = M$.
$$
\begin{aligned}
\left(M^{\prime} F, M^{\prime} D\right) & = \left(M^{\prime} F, M^{\prime} A\right) \quad \text{since } A, M, D \text{ are collinear} \\
& = (E F, E A) \quad \text{since } A, E, F, M \text{ are concyclic} \\
& = (B A, B C) \quad \text{since } A E F \text{ and } A B C \text{ are indirectly similar} \\
& = (B F, B F).
\end{aligned}
$$
We deduce that $M^{\prime}$ lies on the circle BDF. Similarly, it lies on the circle CDE. Consequently, it is the intersection of the three circles BDF, CDE, and $A E F$: this proves that $M^{\prime} = M$.
Finally, since the arcs MF and ME are equal (since (AM) is the angle bisector of $\widehat{F A E}$), we have $M F = M E$.
## Another Solution.
Lemme 1. Two chords $\left[\mathrm{BB}^{\prime}\right]$ and $\left[\mathrm{CC}^{\prime}\right]$ of a circle intersect at an external point $A$. Then the triangles $A B C$ and $A C^{\prime} B^{\prime}$ are indirectly similar.
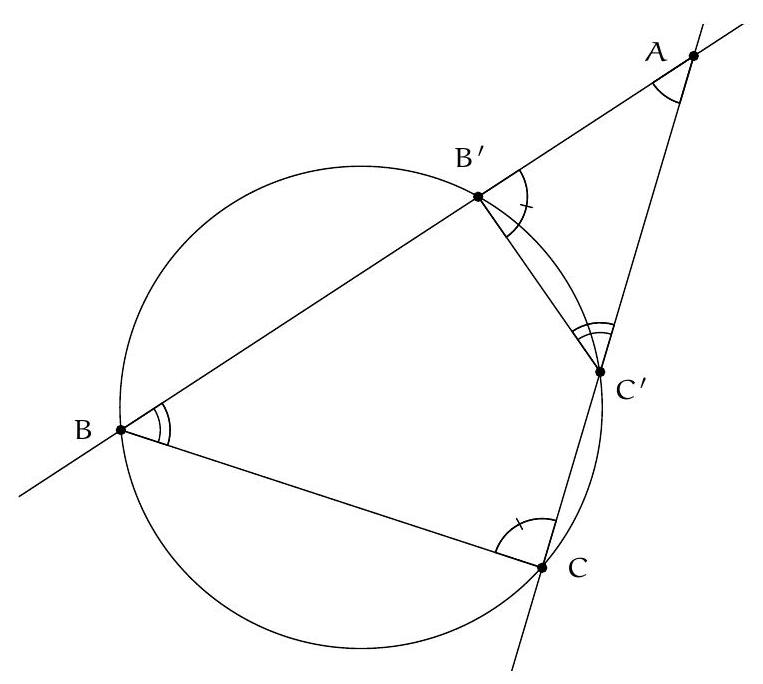
We have $\left(B^{\prime} C^{\prime}, B^{\prime} A\right) = \left(B^{\prime} C^{\prime}, B^{\prime} B\right) = \left(C C^{\prime}, C B\right) = (C A, C B)$ and similarly $\left(C^{\prime} A, C^{\prime} B^{\prime}\right) = (B C, B A)$.
Lemme 2. $\frac{D B}{D C} = \frac{A B}{A C}$.
By the law of sines, we have $\frac{A B}{D B} = \frac{\sin \widehat{A D B}}{\sin \frac{\widehat{B A C}}{2}} = \frac{\sin \widehat{C D A}}{\sin \frac{\widehat{B A C}}{2}} = \frac{A C}{D C}$.
Let's return to the exercise. Since AFC and AEB are right-angled at $F$ and $E$ and have the same angle at $A$, they are similar. We deduce that $\frac{A F}{A E} = \frac{A C}{A B}$, which can be written as $A F \cdot A B = A E \cdot A C$. In other words, $A$ has the same power with respect to the two circles BFD and CED. Consequently, $A$ lies on the radical axis (MD).
Furthermore, the lemma 1 implies that $A F M$ and $A D B$ are similar, so $\frac{B D}{B A} = \frac{M F}{M A}$. Similarly, $\frac{C D}{C A} = \frac{M E}{M A}$. According to lemma 2, we have $\frac{B D}{B A} = \frac{C D}{C A}$, so $M F = M E$.
## Exercises for Group A
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus, et tel que $A B \neq A C$. On note $D$ le pied de la bissectrice de $\widehat{B A C}$. Le point $E$ (resp. $F$ ) désigne le pied de la hauteur issue de $B$ (resp. de C). Le cercle circonscrit au triangle DBF rencontre le cercle circonscrit au triangle DCE en un point $M$ autre que $D$.
Prouver que ME $=M F$.
|
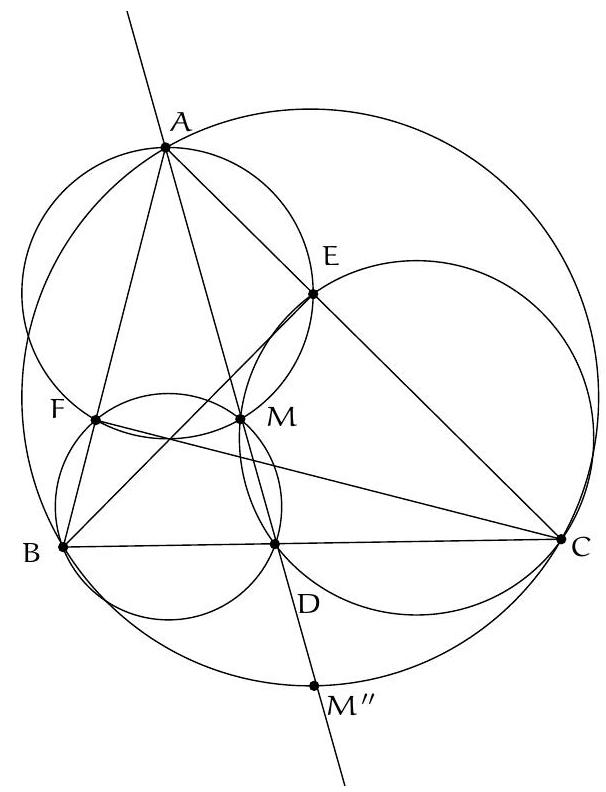
Lemme 1. Les cercles AEF, BDF et CDE sont concourants en $M$.
Cela découle immédiatement du théorème de Miquel mais rappelons tout de même la démonstration:
$(M F, M E)=(M F, M D)+(M D, M E)=(B F, B D)+(C D, C E)=(A B, C D)+(C D, A C)=$ ( $A B, A C$ ) donc $A, E, F, M$ sont cocycliques.
Lemme 2. Les triangles $A E F$ et $A B C$ sont (indirectement) semblables.
Les triangles $A F C$ et $A E B$ sont rectangles en $F$ et en $E$, et leurs angles en $A$ sont égaux, donc ils sont semblables. On en déduit que $\frac{A E}{A F}=\frac{A B}{A C}$. Ceci s'écrit encore $\frac{A E}{A B}=\frac{A F}{A C}$. Comme $\widehat{E A F}=\widehat{B A C}$, les triangles EAF et $B A C$ sont semblables. Il est clair que la similitude est indirecte puisque les angles orientés $(\overrightarrow{A B}, \overrightarrow{A C})$ et $(\overrightarrow{A E}, \overrightarrow{A F})$ sont opposés.
Revenons à l'exercice. Soit $M^{\prime}$ le point d'intersection autre que $A$ entre la bissectrice de $\widehat{B A C}$ et le cercle $A E F$. De même, on définit $M^{\prime \prime}$ comme le point d'intersection autre que $A$ entre la bissectrice de $\widehat{B A C}$ et le cercle $A B C$. Montrons que $M^{\prime}=M$.
$$
\begin{aligned}
\left(M^{\prime} F, M^{\prime} D\right) & =\left(M^{\prime} F, M^{\prime} A\right) \quad \text { car } A, M, D \text { alignés } \\
& =(E F, E A) \quad \text { car } A, E, F, M \text { cocycliques } \\
& =(B A, B C) \quad \text { car } A E F \text { et } A B C \text { indirectement semblables } \\
& =(B F, B F) .
\end{aligned}
$$
On en déduit que $M^{\prime}$ appartient au cercle BDF. De même, il appartient au cercle CDE. Par conséquent, il est l'intersection des trois cercles BDF, CDE et $A E F$ : ceci prouve que $M^{\prime}=M$.
Enfin, comme les arcs MF et ME sont égaux (puisque (AM) est la bissectrice de $\widehat{F A E}$ ), on a $M F=M E$.
## Autre solution.
Lemme 1. Deux cordes $\left[\mathrm{BB}^{\prime}\right]$ et $\left[\mathrm{CC}^{\prime}\right]$ d'un cercle se coupent en un point extérieur $A$. Alors les triangles $A B C$ et $A C^{\prime} B^{\prime}$ sont indirectement semblables.

On a $\left(B^{\prime} C^{\prime}, B^{\prime} A\right)=\left(B^{\prime} C^{\prime}, B^{\prime} B\right)=\left(C C^{\prime}, C B\right)=(C A, C B)$ et de même $\left(C^{\prime} A, C^{\prime} B^{\prime}\right)=(B C, B A)$.
Lemme 2. $\frac{D B}{D C}=\frac{A B}{A C}$.
D'après la loi des sinus, on a $\frac{A B}{D B}=\frac{\sin \widehat{A D B}}{\sin \frac{\widehat{B A C}}{2}}=\frac{\sin \widehat{C D A}}{\sin \frac{\widehat{B A C}}{2}}=\frac{A C}{D C}$.
Revenons à l'exercice. Comme AFC et AEB sont rectangles en $F$ et $E$ et ont le même angle en $A$, ils sont semblables. On en déduit $\frac{A F}{A E}=\frac{A C}{A B}$, ce qui s'écrit encore $A F \cdot A B=A E \cdot A C$. Autrement dit, $A$ a la même puissance par rapport aux deux cercles BFD et CED. Par conséquent, $A$ se trouve sur l'axe radical (MD).
$D^{\prime}$ 'autre part, le lemme 1 entraîne que $A F M$ et $A D B$ sont semblables, donc $\frac{B D}{B A}=\frac{M F}{M A}$. De même, $\frac{C D}{C A}=\frac{M E}{M A}$. D'après le lemme 2 , on a $\frac{B D}{B A}=\frac{C D}{C A}$ donc $M F=M E$.
## Exercices du groupe A
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
47c8fa32-7d4e-5613-9ae3-19a13aac97d1
| 604,697
|
It is said that a sequence $\left(u_{n}\right)_{n \geqslant 1}$ is Sicilian if $u_{1}$ is a strictly positive integer, and if for all $n$,
$$
u_{n+1}= \begin{cases}u_{n} / 2 & \text { if } u_{n} \text { is even, and } \\ u_{n}+\left[\sqrt{u_{n}}\right] & \text { if } u_{n} \text { is odd. }\end{cases}
$$
Does there exist a Sicilian sequence $\left(u_{n}\right)_{n \geqslant 1}$ such that $u_{n}>1$ for all $n$?
(N.B. $[x]$ denotes the integer part of $x$. For example, $[2.71828]=2$.)
|
Let's start with a simple observation. Let $\mathrm{f}: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ be the function that, for any non-zero natural number $n$, associates the integer $n / 2$ if $n$ is even, and $n+[\sqrt{n}]$ if $n$ is odd. It is clear that the image $f(n)$ is indeed a non-zero natural number.
We will now show that the answer to the question in the statement is negative: every Sicilian sequence $\left(u_{n}\right)_{n \geqslant 1}$ contains a term $u_{n}=1$.
Let $\left(u_{n}\right)_{n \geqslant 1}$ be a Sicilian sequence: we note that $u_{n+1}=f\left(u_{n}\right)$ for all integers $n \geqslant 1$. Let $E=\left\{u_{n} \mid n \geqslant 1\right\}$ be the set of values taken by the terms of this sequence. $E$ is a non-empty set of integers, so it has a minimum $M$, such that $M \geqslant 1$: there then exists an integer $n \geqslant 1$ such that $M=u_{n}$. Our goal is to show that $M=1$. We will therefore proceed by contradiction, and assume that $M \geqslant 2$.
If $M$ is even, then $u_{n+1}=f\left(u_{n}\right)=f(M)=M / 2<M$ and, since $u_{n+1} \in E$, this contradicts the minimality of $M$.
If $M$ is odd, let $k$ be the non-zero natural number such that $k^{2} \leqslant M<(k+1)^{2}$. If $k$ is odd, then $u_{n+1}=f(M)=M+k$, so $M+k$ is even, and $u_{n+2}=f\left(u_{n+1}\right)=f(M+k)=\frac{M+k}{2}$. Since $M>1$, we have $M-k \geqslant M-\sqrt{M}=\sqrt{M}(\sqrt{M}-1)>0$, so $u_{n+2}<M$ : since $u_{n+2} \in E$, this contradicts the minimality of $M$.
Thus, we know that $M$ is odd and that $k$ is even, so $k^{2}+1 \leqslant M<(k+1)^{2}$.
- If $k^{2}+1 \leqslant M \leqslant k^{2}+k$, then $k^{2} \leqslant f(M)=M+k<(k+1)^{2}$, and $(k+1)^{2} \leqslant f^{2}(M)=$ $M+2 k<(k+2)^{2}$, so $f^{3}(M)=M+3 k+1$ is even, and finally $f^{4}(M)=\frac{M+3 k+1}{2}$.
- If $k^{2}+k+1 \leqslant M<(k+1)^{2}$, then $(k+1)^{2} \leqslant f(M)=M+k<(k+2)^{2}$, so $f^{2}(M)=$ $M+2 k+1$ is even, and finally $f^{3}(M)=\frac{M+2 k+1}{2}$.
It follows that $M=\min E \leqslant \min \left\{f^{3}(M), f^{4}(M)\right\} \leqslant \frac{M+3 k+1}{2}$, so $M \leqslant 3 k+1$.
In particular, $k^{2} \leqslant 3 k+1$, which means that $k^{2}-3 k-1=\left(k-\frac{3}{2}\right)^{2}-\frac{13}{4} \leqslant 0$, so $k \leqslant \frac{3}{2}+\sqrt{\frac{13}{4}}<2+\sqrt{4}=4$. Since $k$ is even and $M$ is odd, we deduce that $k=2$ and that $M \in\{5,7\}$. We conclude the exercise by showing that $\mathbf{f}^{5}(5)=3<5$ and that $\mathrm{f}^{4}(7)=3<7$, which indeed establishes that no value $M \geqslant 2$ is possible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'une suite $\left(u_{n}\right)_{n \geqslant 1}$ est Sicilienne si $u_{1}$ est un entier strictement positif, et si pour tout $n$,
$$
u_{n+1}= \begin{cases}u_{n} / 2 & \text { si } u_{n} \text { est pair, et } \\ u_{n}+\left[\sqrt{u_{n}}\right] & \text { si } u_{n} \text { est impair. }\end{cases}
$$
Existe-t-il une suite Sicilienne $\left(u_{n}\right)_{n \geqslant 1}$ telle que $u_{n}>1$ pour tout $n$ ?
(N.B. $[x]$ désigne la partie entière de $x$. Par exemple, $[2,71828]=2$.)
|
Commençons par une simple remarque. Soit $\mathrm{f}: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ la fonction qui, à tout entier naturel non nul $n$, associe l'entier $n / 2$ si $n$ est pair, et $n+[\sqrt{n}]$ si $n$ est impair. Il est clair que l'image $f(n)$ est bien un entier naturel non nul.
Nous allons maintenant montrer que la réponse à la question de l'énoncé est négative : toute suite Sicilienne $\left(u_{n}\right)_{n \geqslant 1}$ contient un terme $u_{n}=1$.
Soit $\left(u_{n}\right)_{n \geqslant 1}$ une suite Sicilienne : on note que $u_{n+1}=f\left(u_{n}\right)$ pour tout entier $n \geqslant 1$. Soit alors $E=\left\{u_{n} \mid n \geqslant 1\right\}$ l'ensemble des valeurs prises par les termes de cette suite. $E$ est un ensemble d'entiers non vide, de sorte qu'il admet un minimum $M$, tel que $M \geqslant 1$ : il existe alors un entier $n \geqslant 1$ tel que $M=u_{n}$. Notre but est de montrer que $M=1$. Nous allons donc procéder par l'absurde, et supposer que $M \geqslant 2$.
Si $M$ est pair, alors $u_{n+1}=f\left(u_{n}\right)=f(M)=M / 2<M$ et, puisque $u_{n+1} \in E$, cela contredit la minimalité de $M$.
Si $M$ est impair, soit $k$ l'entier naturel non nul tel que $k^{2} \leqslant M<(k+1)^{2}$. Si $k$ est impair, alors $u_{n+1}=f(M)=M+k$, donc $M+k$ est pair, et $u_{n+2}=f\left(u_{n+1}\right)=f(M+k)=\frac{M+k}{2}$. Or, $M>1$, donc $M-k \geqslant M-\sqrt{M}=\sqrt{M}(\sqrt{M}-1)>0$, de sorte que $u_{n+2}<M$ : puisque $u_{n+2} \in E$, cela contredit la minimalité de $M$.
Ainsi, on sait que $M$ est impair et que $k$ est pair, donc que $k^{2}+1 \leqslant M<(k+1)^{2}$.
- Si $k^{2}+1 \leqslant M \leqslant k^{2}+k$, alors $k^{2} \leqslant f(M)=M+k<(k+1)^{2}$, puis $(k+1)^{2} \leqslant f^{2}(M)=$ $M+2 k<(k+2)^{2}$, donc $f^{3}(M)=M+3 k+1$ est pair, et enfin $f^{4}(M)=\frac{M+3 k+1}{2}$.
- Si $k^{2}+k+1 \leqslant M<(k+1)^{2}$, alors $(k+1)^{2} \leqslant f(M)=M+k<(k+2)^{2}$, donc $f^{2}(M)=$ $M+2 k+1$ est pair, et enfin $f^{3}(M)=\frac{M+2 k+1}{2}$.
Il s'ensuit que $M=\min E \leqslant \min \left\{f^{3}(M), f^{4}(M)\right\} \leqslant \frac{M+3 k+1}{2}$, donc que $M \leqslant 3 k+1$.
En particulier, $k^{2} \leqslant 3 k+1$, ce qui signifie que $k^{2}-3 k-1=\left(k-\frac{3}{2}\right)^{2}-\frac{13}{4} \leqslant 0$, donc que $k \leqslant \frac{3}{2}+\sqrt{\frac{13}{4}}<2+\sqrt{4}=4$. Puisque $k$ est pair et $M$ impair, en déduit que $k=2$ et que $M \in\{5,7\}$. On conclut donc l'exercice en montrant que $\mathbf{f}^{5}(5)=3<5$ et que $\mathrm{f}^{4}(7)=3<7$, ce qui permet bien d'établir que nulle valeur $M \geqslant 2$ n'est possible.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
c32a32a2-a008-5ca1-9c54-78015e421be8
| 604,708
|
We distribute weights of $1 \mathrm{~g}, 2 \mathrm{~g}, \ldots, 200 \mathrm{~g}$ on the two pans of a balance so that each pan contains 100 weights.
Prove that it is possible to exchange 50 weights from one pan with 50 weights from the other pan so that the balance becomes balanced.
|
In this solution, we will say that two weights are complementary if they weigh 201 grams together.
Consider then the 100 weights on the left plate. We can classify them into three categories:
1. the weights $a_{1}, \ldots, a_{n}$ of 100 grams or less, whose complementary is also on the left plate;
2. their complements, which are the weights $A_{1}, \ldots, A_{n}$ of 101 grams or more, whose complementary is also on the left plate (with $A_{k}=201-a_{k}$);
3. finally, the weights $b_{1}, \ldots, b_{\ell}$ whose complementary is on the right plate.
Similarly, we can classify the 100 weights on the right plate into three categories:
1. the weights $c_{1}, \ldots, c_{m}$ of 100 grams or less, whose complementary is also on the right plate;
2. their complements, which are the weights $C_{1}, \ldots, C_{m}$ of 101 grams or more, whose complementary is also on the left plate (with $C_{k}=201-c_{k}$);
3. finally, the weights $B_{1}, \ldots, B_{\ell}$ which are the complements of the weights $b_{1}, \ldots, b_{\ell}$ (with $B_{k}=201-b_{k}$); these are the weights on the right plate whose complementary is on the left plate.
Note that $100=2n+\ell=2m+\ell$, so $m=n$. Two possibilities are then open to us:
4. if $m=n \geqslant 25$, we keep on the left plate the 50 weights $a_{1}, \ldots, a_{25}$ and $A_{1}, \ldots, A_{25}$, and transfer the 50 weights $c_{1}, \ldots, c_{25}$ and $C_{1}, \ldots, C_{25}$ to it; all other weights are placed on the right plate;
5. if $m=n<25$, this means that $\ell>50$; in this case, we keep on the left plate the 50 weights $b_{1}, \ldots, b_{50}$ and transfer the 50 weights $B_{1}, \ldots, B_{50}$ to it; all other weights are placed on the right plate.
In both cases, we have transferred 50 weights from the left plate to the right plate, and vice versa. Moreover, each of the two plates is now made up of 50 pairs of complementary weights, so each weighs $50 \times 201$ grams, and thus they have the same weight.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On répartit des poids de respectivement $1 \mathrm{~g}, 2 \mathrm{~g}, \ldots, 200 \mathrm{~g}$ sur les deux plateaux d'une balance de sorte que chaque plateau contienne 100 poids.
Prouver que l'on peut échanger 50 poids d'un plateau avec 50 poids de l'autre plateau pour que la balance devienne équilibrée.
|
Dans cette solution, on dira que deux poids sont complémentaires s'ils pèsent 201 grammes à eux deux.
Considérons alors les 100 poids situés sur le plateau de gauche. On peut les classer en trois catégories:
1. les poids $a_{1}, \ldots, a_{n}$ de 100 grammes ou moins, dont le complémentaire est également sur le plateau de gauche;
2. leurs complémentaires, qui sont les poids $A_{1}, \ldots, A_{n}$ de 101 grammes ou plus, dont le complémentaire est également sur le plateau de gauche (avec $A_{k}=201-a_{k}$ );
3. enfin, les poids $b_{1}, \ldots, b_{\ell}$ dont le complémentaire est sur le plateau de droite.
De même, on peut classer les 100 poids du plateau de droite en trois catégories :
1. les poids $c_{1}, \ldots, c_{m}$ de 100 grammes ou moins, dont le complémentaire est également sur le plateau de droite;
2. leurs complémentaires, qui sont les poids $C_{1}, \ldots, C_{m}$ de 101 grammes ou plus, dont le complémentaire est également sur le plateau de gauche ; (avec $\mathrm{C}_{\mathrm{k}}=201-\mathrm{c}_{\mathrm{k}}$ );
3. enfin, les poids $B_{1}, \ldots, B_{\ell}$ qui sont les complémentaires des poids $b_{1}, \ldots, b_{\ell}$ (avec $B_{k}=$ $201-b_{k}$ ) ; ce sont les poids du plateau de droite dont le complémentaire est sur le plateau de gauche.
Notons que $100=2 \mathrm{n}+\ell=2 \mathrm{~m}+\ell$, de sorte que $\mathrm{m}=\mathrm{n}$. Deux possibilités s'offrent alors à nous:
4. si $m=n \geqslant 25$, on conserve sur le plateau de gauche les 50 poids $a_{1}, \ldots, a_{25}$ et $A_{1}, \ldots, A_{25}$, et on $y$ transfère les 50 poids $c_{1}, \ldots, c_{25}$ et $C_{1}, \ldots, C_{25}$; tous les autres poids sont mis sur le plateau de droite;
5. si $\mathrm{m}=\mathrm{n}<25$, cela signifie que $\ell>50$; dans ce cas, on conserve sur le plateau de gauche les 50 poids $b_{1}, \ldots, b_{50}$ et on y transfère les 50 poids $B_{1}, \ldots, B_{50}$; tous les autres poids sont mis sur le plateau de droite.
Dans les deux cas, on a transféré 50 poids du plateau de gauche vers le plateau de droite, et réciproquement. En outre, chacun des deux plateaux est maintenant formé de 50 paires de poids complémentaires, de sorte que chacune pèse $50 \times 201$ grammes, et donc qu'elles ont bien le même poids.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
b7c20696-9ec8-544a-a794-c3cda0a7f5e7
| 604,734
|
Two circles $O_{1}$ and $O_{2}$ intersect at $M$ and $N$. The common tangent to the two circles closest to $M$ touches $O_{1}$ and $O_{2}$ at $A$ and $B$ respectively. Let $C$ and $D$ be the reflections of $A$ and $B$ with respect to $M$ respectively. The circumcircle of triangle $D C M$ intersects the circles $O_{1}$ and $O_{2}$ at points $E$ and $F$ distinct from $M$. Show that the circumcircles of triangles $M E F$ and $N E F$ have the same radius.
|
First, let's show that $(EF)$ is the other common tangent to the two circles.
Let $E'$ and $F'$ be the points of contact of the other common tangent. Let $X$ be the intersection point of $(AB)$ and $(MN)$. We have $AX = BX$ because $X$ lies on the radical axis of the two circles. Since $ABCD$ is a parallelogram with center $M$, we have $(MX) \parallel (AD)$, which implies $(AD) \perp (O_1 O_2)$.
Furthermore, since $A$ and $E$ are symmetric with respect to $(O_1 O_2)$, we get that $A, D, E$ are collinear, and similarly, $B, C, F$ are collinear.
According to the limiting case of the inscribed angle theorem in circle $O_1$, we have $(EM, EA) = (AM, AB)$, so $(CM, CD) = (CA, CD) = (AM, AB) = (EM, EA) = (EM, ED)$. Therefore, $E'$ lies on the circle $MCD$. We conclude that $E = E'$, and similarly, $F = F'$.
By applying the symmetry with respect to the axis $(O_1 O_2)$ and then the symmetry with center $M$ to the circle $(NEF)$, we successively obtain the circle $MAB$, and then the circle $MCD$, which is the circle $MEF$. Since a symmetry preserves lengths, the circles $MEF$ and $NEF$ have the same radius.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Deux cercles $O_{1}$ et $O_{2}$ se coupent en $M$ et $N$. La tangente commune aux deux cercles la plus proche de $M$ touche $O_{1}$ et $O_{2}$ en $A$ et $B$ respectivement. Soient $C$ et $D$ les symétriques de $A$ et $B$ par rapport à $M$ respectivement. Le cercle circonscrit au triangle $D C M$ intersecte les cercles $O_{1}$ et $O_{2}$ respectivement en des points $E$ et $F$ distincts de $M$. Montrer que les cercles circonscrits aux triangles $M E F$ et $N E F$ sont de même rayon.
|
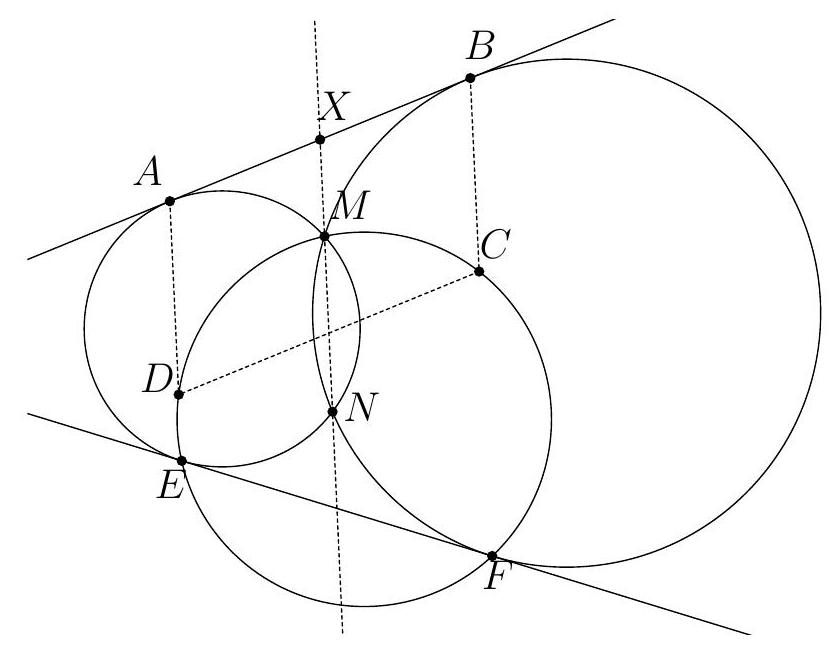
Montrons d'abord que $(E F)$ l'autre tangente commune aux deux cercles.
Soient $E^{\prime}$ et $F^{\prime}$ les points de contact de l'autre tangente commune. Soit $X$ le point d'intersection de $(A B)$ et de $(M N)$. On a $A X=B X$ car $X$ se situe sur l'axe radical des deux cercles. Comme $A B C D$ est un parallélogramme de centre $M$, on a $(M X) / /(A D)$, ce qui entraîne $(A D) \perp\left(O_{1} O_{2}\right)$.
De plus, $A$ et $E$ étant symétriques par rapport à $\left(O_{1} O_{2}\right)$ on obtient que $A, D, E$ sont alignés, et de même $B, C, F$ sont alignés.
D'après le cas limite du théorème de l'angle inscrit dans le cercle $O_{1}$, on a $(E M, E A)=(A M, A B)$, donc $(C M, C D)=(C A, C D)=(A M, A B)=(E M, E A)=(E M, E D)$, par conséquent $E^{\prime}$ appartient au cercle $M C D$. On en conclut que $E=E^{\prime}$, et de même $F=F^{\prime}$.
En appliquant la symétrie d'axe $\left(O_{1} O_{2}\right)$ puis la symétrie de centre $M$ au cercle $(N E F)$, on obtient successivement le cercle $M A B$, puis le cercle $M C D$, c'est-à-dire le cercle $M E F$. Comme une symétrie conserve les longueurs, les cercles $M E F$ et $N E F$ ont même rayon.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-mai-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
b2001151-0ce3-5051-9060-801bc1be36bd
| 604,760
|
Show that there are infinitely many positive integers $n$ such that the largest prime factor of $n^{4}+n^{2}+1$ is equal to the largest prime factor of $(n+1)^{4}+(n+1)^{2}+1$.
|
For all $n \geq 1$, we denote $p_{n}$ as the largest prime divisor of $n^{4}+n^{2}+1$, and $q_{n}$ as the largest prime divisor of $n^{2}+n+1$.
We thus have $p_{n}=q_{n^{2}}$.
Furthermore, from the identity
$$
n^{4}+n^{2}+1=\left(n^{2}+n+1\right)\left(n^{2}-n+1\right)=\left(n^{2}+n+1\right)\left((n-1)^{2}+(n-1)+1\right)
$$
it follows that $p_{n}=\max \left(q_{n}, q_{n-1}\right)$ for all $n \geq 2$.
Moreover, the number $n^{2}-n+1=n(n-1)+1$ is odd, so
$$
\operatorname{gcd}\left(n^{2}+n+1, n^{2}-n+1\right)=\operatorname{gcd}\left(2 n, n^{2}-n+1\right)=\operatorname{gcd}\left(n, n^{2}-n+1\right)=1
$$
Thus, we have $q_{n} \neq q_{n-1}$.
To conclude, it suffices to prove that the set
$$
S=\left\{n \geq 2 \mid q_{n}>q_{n-1} \text { and } q_{n}>q_{n+1}\right\}
$$
is infinite, since for all $n \in S$, we have
$$
p_{n}=\max \left(q_{n}, q_{n-1}\right)=q_{n}=\max \left(q_{n}, q_{n+1}\right)=p_{n+1} .
$$
By contradiction: suppose that $S$ is finite.
Since $q_{2}=q_{4}=7<13=q_{3}$, we can assert that $S$ is not empty. Since it is finite, it has a largest element, say $m$.
The sequence $\left(q_{n}\right)_{n \geq m}$ cannot be strictly decreasing since it consists of positive integers. Therefore, there exists $k \geq m$ such that $q_{k}<q_{k+1}$ (we recall that $q_{k} \neq q_{k+1}$). However, it is also impossible for $\left(q_{n}\right)_{n \geq k}$ to be strictly increasing because $q_{(k+1)^{2}}=p_{k+1}=\max \left(q_{k}, q_{k+1}\right)=q_{k+1}$. Let $t$ be the smallest integer greater than or equal to $k+1$ such that $q_{t}>q_{t+1}$. The minimality of $t$ ensures that $q_{t-1}<q_{t}$, and thus $t \in S$.
However, we have $t \geq k+1>k \geq m$, which contradicts the maximality of $m$.
Therefore, $S$ is infinite, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer qu'il existe une infinité d'entiers positifs $n$ tels que le plus grand facteur premier de $n^{4}+n^{2}+1$ soit égal au plus grand facteur premier de $(n+1)^{4}+(n+1)^{2}+1$.
|
Pour tout $n \geq 1$, on note $p_{n}$ le plus grand diviseur premier de $n^{4}+n^{2}+1$, et $q_{n}$ le plus grand diviseur premier de $n^{2}+n+1$.
On donc $p_{n}=q_{n^{2}}$.
De plus, de l'identité
$$
n^{4}+n^{2}+1=\left(n^{2}+n+1\right)\left(n^{2}-n+1\right)=\left(n^{2}+n+1\right)\left((n-1)^{2}+(n-1)+1\right)
$$
il découle que $p_{n}=\max \left(q_{n}, q_{n-1}\right)$ pour tout $n \geq 2$.
D'autre part, le nombre $n^{2}-n+1=n(n-1)+1$ est impair, donc
$$
\operatorname{pgcd}\left(n^{2}+n+1, n^{2}-n+1\right)=\operatorname{pgcd}\left(2 n, n^{2}-n+1\right)=\operatorname{pgcd}\left(n, n^{2}-n+1\right)=1
$$
Ainsi, on a $q_{n} \neq q_{n-1}$.
Pour conclure, il suffit alors de prouver que l'ensemble
$$
S=\left\{n \geq 2 \mid q_{n}>q_{n-1} \text { et } q_{n}>q_{n+1}\right\}
$$
est infini, puisque pour tout $n \in S$, on a
$$
p_{n}=\max \left(q_{n}, q_{n-1}\right)=q_{n}=\max \left(q_{n}, q_{n+1}\right)=p_{n+1} .
$$
Par l'absurde: supposons que $S$ soit fini.
Puisque $q_{2}=q_{4}=7<13=q_{3}$, on peut affirmer que $S$ n'est pas vide. Puisqu'il est fini, il possède alors un plus grand élément, disons $m$.
La suite $\left(q_{n}\right)_{n \geq m}$ ne peut être strictement décroissante puisqu'elle est formée d'entiers positifs. Il existe donc $k \geq m$ tel que $q_{k}<q_{k+1}$ (on rappelle que $q_{k} \neq q_{k+1}$ ). Mais, il est également impossible d'avoir $\left(q_{n}\right)_{n \geq k}$ strictement croissante car $q_{(k+1)^{2}}=p_{k+1}=\max \left(q_{k}, q_{k+1}\right)=q_{k+1}$. Notons alors $t$ le plus petit entier supérieur ou égal à $k+1$ tel que $q_{t}>q_{t+1}$. La minimalité de $t$ assure que l'on a $q_{t-1}<q_{t}$, et donc que $t \in S$.
Pourtant, on a $t \geq k+1>k \geq m$, ce qui contredit la maximalité de $m$.
Par suite, on a $S$ infini, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-mai-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
dbda2564-cde2-5feb-b55e-ef81e81a0a85
| 604,771
|
Let $n$ be a strictly positive integer and $x_{1}, \ldots, x_{n}$ be strictly positive real numbers. Show that there exist numbers $a_{1}, \ldots, a_{n} \in\{-1,1\}$ such that:
$$
a_{1} x_{1}^{2}+a_{2} x_{2}^{2}+\cdots+a_{n} x_{n}^{2} \geqslant\left(a_{1} x_{1}+a_{2} x_{2}+\cdots+a_{n} x_{n}\right)^{2} .
$$
|
Let's order the reals $x_{k}$ so that $x_{1} \geq x_{2} \geq \ldots \geq x_{n}>0$.
We will show by strong induction that a solution is provided by the sequence of coefficients defined by $a_{k}=1$ if $k$ is odd and $a_{k}=-1$ if $k$ is even.
$\triangleright$ If $n=1, a_{1} x_{1}^{2}=\left(a_{1} x_{1}\right)^{2}$, so the inequality is satisfied.
$\triangleright$ If $n=2, a_{1} x_{1}^{2}+a_{2} x_{2}^{2}=x_{1}^{2}-x_{2}^{2} \geq x_{1}^{2}-2 x_{1} x_{2}+x_{2}^{2}=\left(x_{1}-x_{2}\right)^{2}$ since $x_{1} \geq x_{2}$; the inequality is still satisfied.
$\triangleright$ Let $n \geq 3$. Suppose the result is established up to rank $n-1$ and show the inequality at rank $n$.
The difference between the two members is then
$$
a_{1} x_{1}^{2}+\ldots+a_{n} x_{n}^{2}-\left(a_{1} x_{1}+\ldots+a_{n} x_{n}\right)^{2}=\alpha x_{1}+\beta
$$
with
$$
\alpha=-2\left(a_{2} x_{2}+\ldots+a_{n} x_{n}\right)=2\left(\left(x_{2}-x_{3}\right)+\left(x_{4}-x_{5}\right)+\ldots\right) \leq 0
$$
since $x_{2} \geq x_{3}, x_{4} \geq x_{5}, \ldots$ Therefore, using the increasing function $x \mapsto \alpha x+\beta$ and $x_{1} \geq x_{2}$,
$$
\begin{aligned}
a_{1} x_{1}^{2}+\ldots+a_{n} x_{n}^{2}-\left(a_{1} x_{1}+\ldots+a_{n} x_{n}\right)^{2} & \geq \alpha x_{2}+\beta \\
& \geq a_{1} x_{2}^{2}+a_{2} x_{2}^{2} \ldots+a_{n} x_{n}^{2}-\left(a_{1} x_{2}+a_{2} x_{2}+\ldots+a_{n} x_{n}\right)^{2} \\
& \geq a_{3} x_{1}^{3}+\ldots+a_{n} x_{n}^{2}-\left(a_{3} x_{3}+\ldots+a_{n} x_{n}\right)^{2}
\end{aligned}
$$
since $a_{1}=-a_{2}$ and thus $a_{1} x_{1}^{2}+a_{2} x_{2}^{2}=a_{1} x_{1}+a_{2} x_{2}=0$. The last term is positive according to the induction hypothesis with the reals $x_{3}, \ldots, x_{n}$, which completes the proof of the inequality at rank $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n$ un entier strictement positif et $x_{1}, \ldots, x_{n}$ des réels strictement positifs. Montrer qu'il existe des nombres $a_{1}, \ldots, a_{n} \in\{-1,1\}$ tels que :
$$
a_{1} x_{1}^{2}+a_{2} x_{2}^{2}+\cdots+a_{n} x_{n}^{2} \geqslant\left(a_{1} x_{1}+a_{2} x_{2}+\cdots+a_{n} x_{n}\right)^{2} .
$$
|
Commençons par ordonner les réels $x_{k}$ de sorte à ce que $x_{1} \geq x_{2} \geq \ldots \geq x_{n}>0$.
Montrons par récurrence forte qu'une solution est fournie par la suite de coefficients définie par $a_{k}=1$ si $k$ est impair et $a_{k}=-1$ si $k$ est pair.
$\triangleright \operatorname{Si} n=1, a_{1} x_{1}^{2}=\left(a_{1} x_{1}\right)^{2}$ donc l'inégalité est vérifiée.
$\triangleright$ Si $n=2, a_{1} x_{1}^{2}+a_{2} x_{2}^{2}=x_{1}^{2}-x_{2}^{2} \geq x_{1}^{2}-2 x_{1} x_{2}+x_{2}^{2}=\left(x_{1}-x_{2}\right)^{2}$ car $x_{1} \geq x_{2}$; l'inégalité est encore vérifiée.
$\triangleright$ Soit $n \geq 3$. Supposons que le résultat est établi jusqu'au rang $n-1$ et montrons l'inégalité au rang $n$.
La différence des deux membres est alors
$$
a_{1} x_{1}^{2}+\ldots+a_{n} x_{n}^{2}-\left(a_{1} x_{1}+\ldots+a_{n} x_{n}\right)^{2}=\alpha x_{1}+\beta
$$
avec
$$
\alpha=-2\left(a_{2} x_{2}+\ldots+a_{n} x_{n}\right)=2\left(\left(x_{2}-x_{3}\right)+\left(x_{4}-x_{5}\right)+\ldots\right) \leq 0
$$
car $x_{2} \geq x_{3}, x_{4} \geq x_{5}, \ldots$ Par conséquent, en utilisant la croissance de la fonction $x \mapsto \alpha x+\beta$ et $x_{1} \geq x_{2}$,
$$
\begin{aligned}
a_{1} x_{1}^{2}+\ldots+a_{n} x_{n}^{2}-\left(a_{1} x_{1}+\ldots+a_{n} x_{n}\right)^{2} & \geq \alpha x_{2}+\beta \\
& \geq a_{1} x_{2}^{2}+a_{2} x_{2}^{2} \ldots+a_{n} x_{n}^{2}-\left(a_{1} x_{2}+a_{2} x_{2}+\ldots+a_{n} x_{n}\right)^{2} \\
& \geq a_{3} x_{1}^{3}+\ldots+a_{n} x_{n}^{2}-\left(a_{3} x_{3}+\ldots+a_{n} x_{n}\right)^{2}
\end{aligned}
$$
car $a_{1}=-a_{2}$ et donc $a_{1} x_{1}^{2}+a_{2} x_{2}^{2}=a_{1} x_{1}+a_{2} x_{2}=0$. Le dernier terme est positif d'après l'hypothèse de récurrence avec les réels $x_{3}, \ldots, x_{n}$ ce qui termine la preuve de l'inégalité au rang $n$.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-mai-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
9c5c9010-d74c-5e5e-960c-4a09a4a2ac3f
| 604,798
|
In a country, there are 100 cities. Each of these cities is connected to exactly three other cities by direct two-way roads. Prove that there exists a city $A$ from which one can travel from city to city and return to $A$, without ever using the same road twice, and using a total number of roads that is not divisible by 3 (it is not required that all cities in the country be visited during this journey).
|
Since there is only a finite number of cities, we can consider a path C of maximum length. Let $v_{0}$ be one of the cities at the ends of C and traverse C starting from $v_{0}$, numbering the cities as we go. The maximality of C ensures that the three cities connected to $v_{0}$ by a road are in C. These are $v_{1}, \nu_{i}$, and $v_{j}$ with $1<i<j$. We have thus identified three cycles:
$$
\begin{gathered}
v_{0}, v_{1}, \cdots, v_{i}, v_{0} \text {, of length } \mathfrak{i}+1, \\
v_{0}, v 1, \cdots, v_{j}, v_{0} \text {, of length } \mathfrak{j}+1 \\
v_{0}, v_{i}, v_{i+1}, \cdots, v_{j}, v_{0}, \text { of length } \mathfrak{j}-\mathfrak{i}+2
\end{gathered}
$$
If $i+1$ or $j+1$ is not divisible by 3, one of the first two cycles will do. Otherwise, it means $\boldsymbol{i}=\mathbf{j}=-1 \bmod 3, d^{\prime}$ where $\boldsymbol{j}-\mathfrak{i}+2=2 \bmod 3$ and the third cycle allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans un pays, se trouvent 100 villes. Chacune de ces villes est reliée à exactement trois autres villes par des routes directes dans les deux sens. Prouver qu'il existe une ville $A$ à partir de laquelle on peut aller de ville en ville et revenir en $A$, sans jamais passer deux fois par une même route, et en utilisant un nombre total de routes qui n'est pas divisible par 3 (il n'est pas demandé que toutes les villes du pays soient visitées au cours de ce voyage).
|
Puisqu'il n'y a qu'un nombre fini de villes, on peut considérer un chemin C de longueur maximale. Soit $v_{0}$ une des villes extrémités de C et parcourons C en partant de $v_{0}$ en numérotant les villes au fur et à mesure. La maximalité de C assure que les trois villes reliées à $v_{0}$ par une route sont dans C. Il s'agit de $v_{1}, \nu_{i}$ et $v_{j}$ avec $1<i<j$. On a ainsi identifié trois cycles :
$$
\begin{gathered}
v_{0}, v_{1}, \cdots, v_{i}, v_{0} \text {, de longueur } \mathfrak{i}+1, \\
v_{0}, v 1, \cdots, v_{j}, v_{0} \text {, de longueur } \mathfrak{j}+1 \\
v_{0}, v_{i}, v_{i+1}, \cdots, v_{j}, v_{0}, \text { de longueur } \mathfrak{j}-\mathfrak{i}+2
\end{gathered}
$$
Si $i+1$ ou $j+1$ n'est pas divisible par 3, l'un des deux premiers cycles convient. Sinon, c'est que $\boldsymbol{i}=\mathbf{j}=-1 \bmod 3, d^{\prime}$ où $\boldsymbol{j}-\mathfrak{i}+2=2 \bmod 3$ et le troisième cycle permet de conclure.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
5da42e2a-46c8-5866-9725-f876bbc3a671
| 604,825
|
Let $ABC$ be a non-isosceles triangle at $A$ and $\Gamma$ its circumcircle. Let $N$ be the midpoint of the arc of $\Gamma$ between $B$ and $C$ that contains $A$. Let $I$ be the center of the incircle of $ABC$, $J$ the center of the $A$-excircle of $ABC$, and $K$ the intersection point of $(BC)$ with the external bisector of $\angle BAC$.
Show that $(JN) \perp (IK)$.
|
Let $\mathrm{J}_{\mathrm{b}}$ and $\mathrm{J}_{\mathrm{c}}$ be the centers of the excircles opposite to angles $\widehat{\mathrm{B}}$ and $\widehat{\mathrm{C}}$. Then I is the orthocenter of $J_{b} J_{c}$. Using the fact that $B$ and $C$ lie on the circle with diameter $J_{b} J_{c}$, and that $A, B, C, N$ are concyclic, we have $\overline{\mathrm{KJ}_{\mathrm{b}}} \cdot \overline{\mathrm{KJ}} \mathrm{c}=\overline{\mathrm{KB}} \cdot \overline{\mathrm{KC}}=\overline{\mathrm{KA}} \cdot \overline{\mathrm{KN}}$, thus
$$
\begin{aligned}
\left(\overline{\mathrm{KA}}+\overline{A J_{b}}\right)\left(\overline{\mathrm{KA}}+\overline{A J_{c}}\right) & =\overline{\mathrm{KA}} \cdot(\overline{\mathrm{KA}}+\overline{\mathrm{AN}}) \\
\overline{\mathrm{KA}}\left(\overline{A J_{b}}+\overline{A J_{c}}+\overline{N A}\right) & =-\overline{A J_{b}} \cdot \overline{A J_{c}}
\end{aligned}
$$
Since $\overline{A J_{b}}+\overline{A J_{c}}+\overline{N A}=\overline{N J_{b}}+\overline{A J_{c}}=\overline{J_{c} N}+\overline{A J_{c}}=\overline{A N}$, we have $\overline{K A}=-\frac{\overline{A J_{b}} \cdot \overline{A J_{c}}}{\overline{A N}}$.
Since I is the orthocenter of $J_{b} J_{c}$, we have $\frac{I A}{A J_{b}}=\frac{A J_{c}}{A J}$. Therefore, $\frac{I A}{K A}=\frac{A N}{A J}$, so the right triangles KAI and JAN are similar. Since $(\mathrm{KA}) \perp(\mathrm{JA})$, it follows that $(\mathrm{KI}) \perp(\mathrm{JN})$.
Another solution. It suffices to show that I is the orthocenter of KJN. Since $(\mathrm{AJ}) \perp(\mathrm{KN})$, it suffices to show that (NI) $\perp(\mathrm{KJ})$.
Let $\omega$ be the circle with diameter $[\mathrm{IJ}]$. It contains the points B and C. Let L be the second intersection point of (KJ) with $\omega$. We have $\overline{\mathrm{KL}} \cdot \overline{\mathrm{KJ}}=\overline{\mathrm{KB}} \cdot \overline{\mathrm{KC}}=\overline{\mathrm{KA}} \cdot \overline{\mathrm{KN}}$, so A, N, L, J are concyclic.
Since $(J A) \perp($ AN $)$, we have $(J L) \perp(L N)$.
Moreover, since $\omega$ has diameter [IJ], we have (JL) $\perp$ (IL), so N, I, L are collinear. It follows that $(\mathrm{NI}) \perp(\mathrm{JL})$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non isocèle en $A$ et $\Gamma$ son cercle circonscrit. Soit $N$ le milieu de l'arc de $\Gamma$ entre $B$ et $C$ qui contient $A$. Soient $I$ le centre du cercle inscrit à $A B C, J$ le centre du cercle $A$-exinscrit à $A B C$ et $K$ le point d'intersection de ( $B C)$ avec la bissectrice extérieure de $\angle B A C$.
Montrer que $(\mathrm{JN}) \perp(\mathrm{IK})$.
|
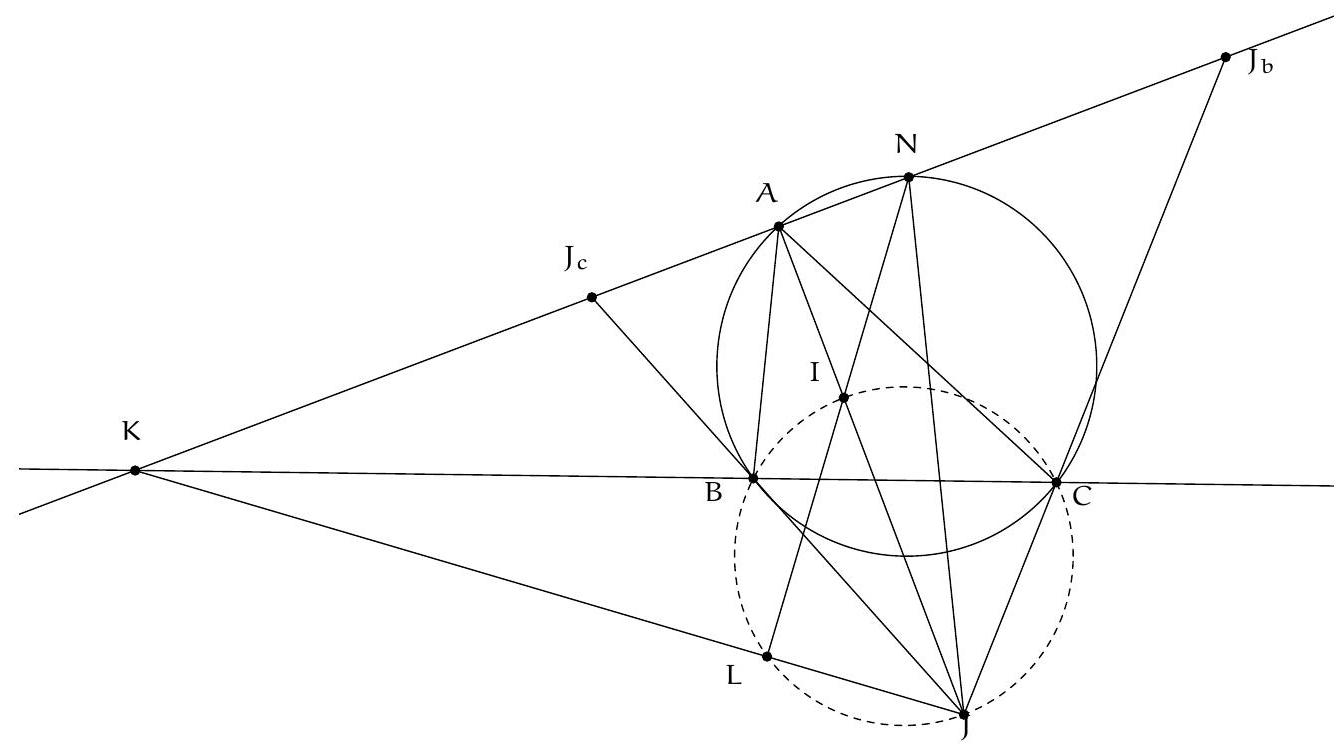
Notons $\mathrm{J}_{\mathrm{b}}$ et $\mathrm{J}_{\mathrm{c}}$ les centres des cercles exinscrits dans les angles $\widehat{\mathrm{B}}$ et $\widehat{\mathrm{C}}$. Alors I est l'orthocentre de $J_{b} J_{c}$. En utilisant le fait que $B$ et $C$ sont sur le cercle de diamètre $J_{b} J_{c}$, et que $A, B, C, N$ sont cocycliques, on a $\overline{\mathrm{KJ}_{\mathrm{b}}} \cdot \overline{\mathrm{KJ}} \mathrm{c}=\overline{\mathrm{KB}} \cdot \overline{\mathrm{KC}}=\overline{\mathrm{KA}} \cdot \overline{\mathrm{KN}}$, donc
$$
\begin{aligned}
\left(\overline{\mathrm{KA}}+\overline{A J_{b}}\right)\left(\overline{\mathrm{KA}}+\overline{A J_{c}}\right) & =\overline{\mathrm{KA}} \cdot(\overline{\mathrm{KA}}+\overline{\mathrm{AN}}) \\
\overline{\mathrm{KA}}\left(\overline{A J_{b}}+\overline{A J_{c}}+\overline{N A}\right) & =-\overline{A J_{b}} \cdot \overline{A J_{c}}
\end{aligned}
$$
Or, $\overline{A J_{b}}+\overline{A J_{c}}+\overline{N A}=\overline{N J_{b}}+\overline{A J_{c}}=\overline{J_{c} N}+\overline{A J_{c}}=\overline{A N}$, donc $\overline{K A}=-\frac{\overline{A J_{b}} \cdot \overline{A J_{c}}}{\overline{A N}}$.
Or, I étant l'orthocentre de $J_{b} J_{c}$, on a $\frac{I A}{A J_{b}}=\frac{A J_{c}}{A J}$. Il vient $\frac{I A}{K A}=\frac{A N}{A J}$, donc les triangles rectangles KAI et JAN sont semblables. Comme $(\mathrm{KA}) \perp(\mathrm{JA})$, il vient $(\mathrm{KI}) \perp(\mathrm{JN})$.
Autre solution. Il suffit de montrer que I est l'orthocentre de KJN . Comme $(\mathrm{AJ}) \perp(\mathrm{KN})$, il suffit de voir que (NI) $\perp(\mathrm{KJ})$.
Soit $\omega$ le cercle de diamètre $[\mathrm{IJ}]$. Il contient les points B et C . Soit L le second point d'intersection de (KJ) avec $\omega$. On a $\overline{\mathrm{KL}} \cdot \overline{\mathrm{KJ}}=\overline{\mathrm{KB}} \cdot \overline{\mathrm{KC}}=\overline{\mathrm{KA}} \cdot \overline{\mathrm{KN}}$ donc $A, N, L$, J sont cocycliques.
Or, $(J A) \perp($ AN $)$, donc $(J L) \perp(L N)$.
De plus, comme $\omega$ a pour diamètre [IJ], on a (JL) $\perp$ (IL), donc N, I, L sont alignés. Il vient $(\mathrm{NI}) \perp(\mathrm{JL})$.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
b35c732a-2a63-50c7-aaa3-e96e3d3b8b27
| 604,851
|
Let $n$ and $k$ be strictly positive integers. There are $n k$ objects (of the same size) and $k$ boxes that can each hold $n$ objects. Each object is colored in one of $k$ possible colors. Show that it is possible to arrange the objects in the boxes so that each box contains objects of at most 2 different colors.
|
We show this by induction on $k$. If $k=1$, the statement is obvious. Suppose the property holds for all integers $<k$.
If one of the colors $c$ is taken exactly $n$ times, we place all objects of color $c$ in the last box. The induction hypothesis allows us to place the remaining $n(k-1)$ objects in the first $k-1$ boxes such that each box contains objects of at most 2 different colors.
Suppose, therefore, that no color is taken exactly $n$ times. If all colors are taken $\leqslant n-1$ times, then there are at most $(n-1) k$ objects in total, which contradicts the hypothesis. Therefore, one of the colors $c_{1}$ is taken $\geqslant n+1$ times. Similarly, one of the colors $c_{2}$ is taken $\leqslant n-1$ times.
We then place all objects of color $c_{2}$ in the last box. We complete this box with objects of color $c_{1}$. The induction hypothesis allows us to place the remaining $n(k-1)$ objects in the first $k-1$ boxes such that each box contains objects of at most 2 different colors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient $n$ et $k$ des entiers strictement positifs. Il y a $n k$ objets (de même taille) et $k$ boîtes qui peuvent contenir chacune $n$ objets. Chaque objet est colorié en une couleur parmi $k$ couleurs possibles. Montrer qu'il est possible de ranger les objets dans les boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.
|
On le montre par récurrence sur $k$. Si $k=1 c^{\prime}$ est évident. Supposons la propriété vraie pour tous les entiers $<k$.
Si l'une des couleurs $c$ est prise exactement $n$ fois, on range tous les objets dont la couleur est $c$ dans la dernière boîte. L'hypothèse de récurrence permet de ranger les $n(k-1)$ objets restants dans les $k-1$ premières boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.
Supposons donc qu'aucune couleur ne soit prise exactement $n$ fois. Si toutes les couleurs sont prises $\leqslant n-1$ fois, alors il y a au plus $(n-1) k$ objets au total, ce qui contredit l'hypothèse. Donc l'une des couleurs $c_{1}$ est prise $\geqslant n+1$ fois. De même, l'une des couleurs $c_{2}$ est prise $\leqslant n-1$ fois.
On place alors tous les objets de couleur $c_{2}$ dans la dernière boîte. On complète cette boîte avec des objets de couleur $c_{1}$. L'hypothèse de récurrence permet de ranger les $n(k-1)$ objets restants dans les $k-1$ premières boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
e29a49dc-de10-5d51-bb5c-12db9cf94d9e
| 604,884
|
Let $ABC$ be a non-isosceles triangle. Let $\omega$ be the incircle and $I$ its center. We denote $M, N, P$ as the points of tangency of $\omega$ with the sides $[BC], [CA], [AB]$. Let $J$ be the intersection point between $(MN)$ and $(IC)$. The line $(PJ)$ intersects $\omega$ again at $K$. Show that
a) $CKIP$ is cyclic;
b) $(CI)$ is the bisector of $\widehat{PC K}$.
|
a) Since $(I N) \perp(N C)$ and $(I M) \perp(M C)$, the points $M$ and $N$ are located on the circle with diameter [IC], so $I, M, C, N$ are concyclic.
From the power of a point with respect to this circle, we have $J I \cdot J C = J M \cdot J N$. On the other hand, using the power with respect to the inscribed circle, we have $J M \cdot J N = J K \cdot J P$, so finally $J I \cdot J C = J K \cdot J P$, which implies that $P, I, K, C$ are concyclic.
b) From part a), we have $\widehat{I C P} = \widehat{I K P}$ and $\widehat{K C I} = \widehat{K P I}$. Since $I P K$ is isosceles at $I$, we have $\widehat{I K P} = \widehat{K P I}$, which implies that $\widehat{I C P} = \widehat{K C I}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non isocèle. Soit $\omega$ le cercle inscrit et $I$ son centre. On note $M, N, P$ les points de contact de $\omega$ avec les côtés $[B C],[C A],[A B]$. Soit $J$ le point d'intersection entre $(M N)$ et $(I C)$. La droite $(P J)$ recoupe $\omega$ en $K$. Montrer que
a) $C K I P$ est cyclique;
b) $(C I)$ est la bissectrice de $\widehat{P C K}$.
|
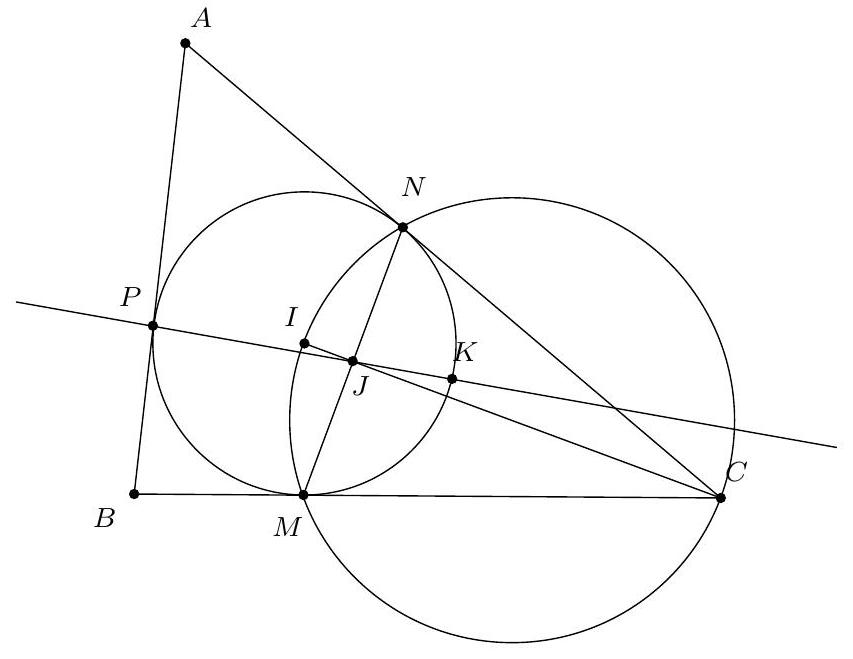
a) Comme $(I N) \perp(N C)$ et $(I M) \perp(M C)$, les points $M$ et $N$ sont situés sur le cercle de diamètre [IC], donc $I, M, C, N$ sont cocycliques.
D'après la puissance d'un point par rapport à ce cercle, on a $J I \cdot J C=J M \cdot J N$. D'autre part, en utilisant la puissance par rapport au cercle inscrit, on a $J M \cdot J N=J K \cdot J P$, donc finalement $J I \cdot J C=J K \cdot J P$, ce qui entraîne que $P, I, K, C$ sont cocycliques.
b) D'après la question a), on a $\widehat{I C P}=\widehat{I K P}$ et $\widehat{K C I}=\widehat{K P I}$. Or, $I P K$ est isocèle en $I$, donc $\widehat{I K P}=\widehat{K P I}$, ce qui entraîne que $\widehat{I C P}=\widehat{K C I}$.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
a6cacf62-0fa5-5f89-b9c4-36c53f486f8f
| 604,909
|
Let $ABCD$ be a trapezoid such that $(AB) / /(CD)$. Two circles $\omega_{1}$ and $\omega_{2}$ are located inside the trapezoid such that $\omega_{1}$ is tangent to $(DA)$, $(AB)$, $(BC)$ and $\omega_{2}$ is tangent to $(BC)$, $(CD)$, $(DA)$. Let $d_{1}$ be a line passing through $A$, other than $(AD)$, tangent to $\omega_{2}$. Let $d_{2}$ be a line passing through $C$, other than $(CB)$, tangent to $\omega_{1}$. Show that $d_{1} / / d_{2}$.
|
By continuity, we can assume that $A B \neq C D$. Furthermore, by swapping $A$ and $B$ with $C$ and $D$, as well as $\omega_{1}$ and $\omega_{2}$, we can assume $A B > C D$.
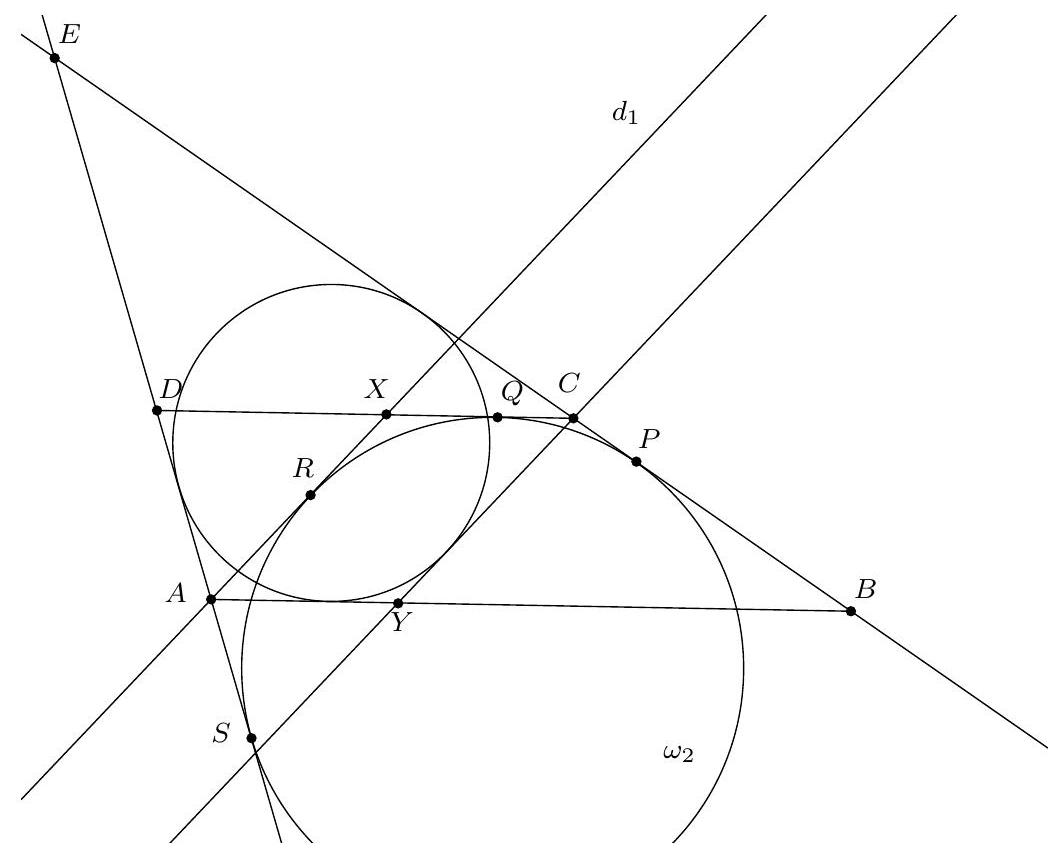
Let $E$ be the intersection of $(A D)$ and $(B C)$. Suppose that $(C D)$ intersects $\omega_{1}$.
We denote $P, Q, R, S$ as the points of tangency of $\omega_{2}$ with $(B C), (C D), d_{1}, (D A)$. Let $X$ be the intersection of $(C D)$ with $d_{1}$. Let $d_{2}^{\prime}$ be the line parallel to $d_{1}$ passing through $C$ and $Y = (A B) \cap d_{2}^{\prime}$. We orient the lines such that the algebraic measures $\overline{E A}, \overrightarrow{A B}, \overline{B C}, \overline{D C}, \overline{A X}, \overline{Y C}$ are positive.
\[
\begin{aligned}
(E A + Y C) - (C E + A Y) & = (\overline{E A} + \overline{Y C}) - (\overline{C E} + \overline{A Y}) \\
& = \overline{E S} + \overline{S A} + \overline{A X} - \overline{C P} - \overline{P E} - \overline{X C} \\
& = \overline{S A} + \overline{A X} - \overline{C P} - \overline{X C} \text{ since } \overline{E S} = \overline{P E} \\
& = \overline{R A} + \overline{A X} - \overline{X Q} = \overline{R X} - \overline{X Q} = 0
\end{aligned}
\]
Thus, $E A Y C$ is circumscribed. It follows that $d_{2}^{\prime} = (C Y) = d_{2}$, so $d_{1} \parallel d_{2}$.
If now $(C D)$ does not intersect $\omega_{1}$, we define this time $d_{1}^{\prime}$ as the line parallel to $d_{2}$ passing through $A$, $X = (C D) \cap d_{1}^{\prime}$, and $Y = (A B) \cap d_{2}$. We show as above that $E A X C$ is circumscribed (the proof is left to the reader).
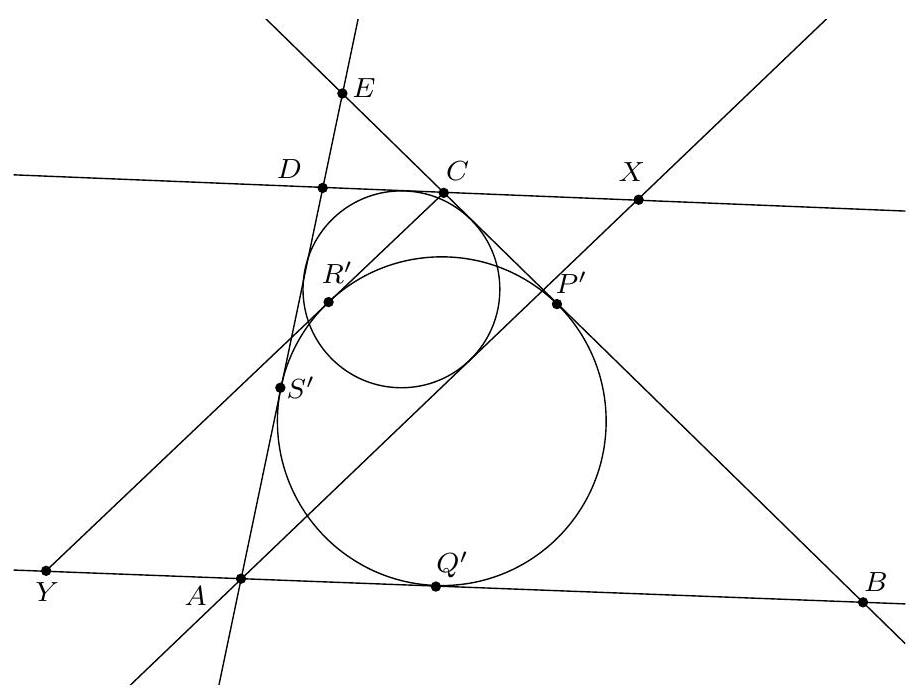
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze tel que $(A B) / /(C D)$. Deux cercles $\omega_{1}$ et $\omega_{2}$ sont situés à l'intérieur du trapèze de sorte que $\omega_{1}$ est tangent à $(D A),(A B),(B C)$ et $\omega_{2}$ est tangent à $(B C),(C D),(D A)$. Soit $d_{1}$ une droite passant par $A$, autre que $(A D)$, tangente à $\omega_{2}$. Soit $d_{2}$ une droite passant par $C$, autre que $(C B)$, tangente à $\omega_{1}$. Montrer que $d_{1} / / d_{2}$.
|
Par continuité, on peut supposer que $A B \neq C D$. De plus, quitte à échanger $A$ et $B$ avec $C$ et $D$, ainsi que $\omega_{1}$ et $\omega_{2}$, on peut supposer $A B>C D$.

Soit $E$ l'intersection de $(A D)$ et $(B C)$. Supposons que $(C D)$ coupe $\omega_{1}$.
On note $P, Q, R, S$ les points de contact de $\omega_{2}$ avec $(B C),(C D), d_{1},(D A)$. Soit $X$ l'intersection de $(C D)$ avec $d_{1}$. Soit $d_{2}^{\prime}$ la parallèle à $d_{1}$ passant par $C$ et $Y=(A B) \cap d_{2}^{\prime}$. On oriente les droites de sorte que les mesures algébriques $\overline{E A}, \overrightarrow{A B}, \overline{B C}, \overline{D C}, \overline{A X}, \overline{Y C}$ soient positives.
$$
\begin{aligned}
(E A+Y C)-(C E+A Y) & =(\overline{E A}+\overline{Y C})-(\overline{C E}+\overline{A Y}) \\
& =\overline{E S}+\overline{S A}+\overline{A X}-\overline{C P}-\overline{P E}-\overline{X C} \\
& =\overline{S A}+\overline{A X}-\overline{C P}-\overline{X C} \operatorname{car} \overline{E S}=\overline{P E} \\
& =\overline{R A}+\overline{A X}-\overline{X Q}=\overline{R X}-\overline{X Q}=0
\end{aligned}
$$
donc $E A Y C$ est circonscriptible. Il vient $d_{2}^{\prime}=(C Y)=d_{2}$, donc $d_{1} / / d_{2}$.
Si maintenant $(C D)$ ne coupe pas $\omega_{1}$, on définit cette fois $d_{1}^{\prime}$ la parallèle à $d_{2}$ passant par $A$, $X=(C D) \cap d_{1}^{\prime}$ et $Y=(A B) \cap d_{2}$. On montre comme ci-dessus que EAXC est circonscriptible (la preuve est laissée au lecteur).

|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
1d64e0a9-941a-516f-8c0d-929f893f086e
| 604,964
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be strictly positive integers. For all $k=1,2, \ldots, n$, we denote
$$
m_{k}=\max _{1 \leq \ell \leq k} \frac{a_{k-\ell+1}+a_{k-\ell+2}+\cdots+a_{k}}{\ell} .
$$
Show that for any $\alpha>0$, the number of integers $k$ such that $m_{k}>\alpha$ is strictly less than $\frac{a_{1}+a_{2}+\cdots+a_{n}}{\alpha}$.
|
Let $k_{1}$ be the largest integer $k$ such that $m_{k}>\alpha$. There exists $\ell_{1}$ such that $a_{k_{1}-\ell_{1}+1}+\cdots+a_{k_{1}}>\ell_{1} \alpha$.
Let $k_{2}$ be the largest integer $\leqslant k_{1}-\ell_{1}$ such that $m_{k}>\alpha$. There exists $\ell_{2}$ such that $a_{k_{2}-\ell_{2}+1}+\cdots+a_{k_{2}}>\ell_{2} \alpha$. ...
We thus construct a finite sequence $k_{1}>k_{2}>\cdots>k_{r}$ such that any integer $k$ satisfying $m_{k}>\alpha$ is found in one of the intervals $I_{j}=\llbracket k_{j}-\ell_{j}+1, k_{j} \rrbracket$. Moreover, these intervals are pairwise disjoint.
Consequently, the number of integers $k$ such that $m_{k}>\alpha$ is less than or equal to the sum of the lengths of the intervals, namely $\ell_{1}+\cdots+\ell_{r}$.
Now, $\sum_{j=1}^{r} \ell_{j}<\frac{1}{\alpha} \sum_{j}\left(a_{k_{j}-\ell_{j}+1}+\cdots+a_{k_{j}}\right) \leqslant \frac{1}{\alpha}\left(a_{1}+\cdots+a_{n}\right)$. QED.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a_{1}, a_{2}, \ldots, a_{n}$ des entiers strictement positifs. Pour tout $k=1,2, \ldots, n$, on note
$$
m_{k}=\max _{1 \leq \ell \leq k} \frac{a_{k-\ell+1}+a_{k-\ell+2}+\cdots+a_{k}}{\ell} .
$$
Montrer que pour tout $\alpha>0$, le nombre d'entiers $k$ tel que $m_{k}>\alpha$ est strictement plus petit que $\frac{a_{1}+a_{2}+\cdots+a_{n}}{\alpha}$.
|
Soit $k_{1}$ le plus grand entier $k$ tel que $m_{k}>\alpha$. Il existe $\ell_{1}$ tel que $a_{k_{1}-\ell_{1}+1}+\cdots+a_{k_{1}}>\ell_{1} \alpha$.
Soit $k_{2}$ le plus grand entier $\leqslant k_{1}-\ell_{1}$ tel que $m_{k}>\alpha$. Il existe $\ell_{2}$ tel que $a_{k_{2}-\ell_{2}+1}+\cdots+a_{k_{2}}>\ell_{2} \alpha$. ...
On construit ainsi une suite finie $k_{1}>k_{2}>\cdots>k_{r}$ telle que tout entier $k$ vérifiant $m_{k}>\alpha$ se trouve dans l'un des intervalles $I_{j}=\llbracket k_{j}-\ell_{j}+1, k_{j} \rrbracket$. De plus, ces intervalles sont deux à deux disjoints.
Par conséquent, le nombre d'entiers $k$ tels que $m_{k}>\alpha$ est inférieur ou égal à la somme des longueurs des intervalles, à savoir $\ell_{1}+\cdots+\ell_{r}$.
Or, $\sum_{j=1}^{r} \ell_{j}<\frac{1}{\alpha} \sum_{j}\left(a_{k_{j}-\ell_{j}+1}+\cdots+a_{k_{j}}\right) \leqslant \frac{1}{\alpha}\left(a_{1}+\cdots+a_{n}\right)$. CQFD.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution de l'exercice 6"
}
|
063f4c29-a172-5fac-9182-4c00cff1ce40
| 604,973
|
Let $a, b, c, n$ be integers, with $n \geq 2$. Let $p$ be a prime number that divides $a^{2}+a b+b^{2}$ and $a^{n}+b^{n}+c^{n}$, but does not divide $a+b+c$.
Prove that $n$ and $p-1$ are not coprime.
|
If $p$ divides $a$ and $b$, then $p$ divides $c^{n}$, hence $p$ divides $c$, which contradicts the last assertion. Therefore, by possibly swapping $a$ and $b$, we assume that $p$ does not divide $b$. By possibly multiplying $a, b, c$ by an inverse of $b$ modulo $p$, we can assume that $b=1$ and thus
$$
p \mid a^{2}+a+1, \quad p \mid a^{n}+1+c^{n}, \quad p \nmid a+1+c.
$$
Since $a^{2}+a+1$ is odd, $p$ is also odd.
Since $p$ divides $\left(a^{2}+a+1\right)(a-1)=a^{3}-1$, the order of $a$ modulo $p$ is 1 or 3.
First case: $a \equiv 1 \pmod{p}$. Then $p=3$, so $c^{n} \equiv -1 - a^{n} \equiv 1 \pmod{3}$.
In particular, $c$ is invertible modulo 3, so $c \equiv \pm 1 \pmod{3}$. Since $p \nmid a+1+c$, we must have $c \equiv -1 \pmod{3}$. Finally, since $c^{n} \equiv 1 \pmod{3}$, the integer $n$ is even, hence not coprime with $p-1$.
Second case: the order of $a$ modulo $p$ is 3. Since the order of $a$ modulo $p$ also divides $p-1$ by Fermat's little theorem, we have $3 \mid p-1$.
Suppose that $n$ is coprime with $p-1$. Then $x \mapsto x^{n}$ is a bijection from $\mathbb{Z} / p \mathbb{Z}$ to itself:
- if $n \equiv 1 \pmod{3}$ then $c^{n} \equiv -a^{n} - 1 \equiv -a - 1 \equiv a^{2} \equiv (a^{2})^{n} \pmod{p}$, so by the bijectivity of $x \mapsto x^{n}$ in $\mathbb{Z} / p \mathbb{Z}$ we have $c \equiv a^{2} \equiv -a - 1 \pmod{p}$: contradiction!
- if $n \equiv 2 \pmod{3}$ then $c^{n} \equiv -a^{n} - 1 \equiv -a^{2} - 1 \equiv a \equiv (a^{2})^{n} \pmod{p}$, so by the bijectivity of $x \mapsto x^{n}$ in $\mathbb{Z} / p \mathbb{Z}$ we have $c \equiv a^{2} \equiv -a - 1 \pmod{p}$: contradiction!
We conclude that $n \equiv 0 \pmod{3}$, so 3 is a common divisor of $n$ and $p-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a, b, c, n$ des entiers, avec $n \geq 2$. Soit $p$ un nombre premier qui divise $a^{2}+a b+b^{2}$ et $a^{n}+b^{n}+c^{n}$, mais qui ne divise pas $a+b+c$.
Prouver que $n$ et $p-1$ ne sont pas premiers entre eux.
|
Si $p$ divise $a$ et $b$, alors $p$ divise $c^{n}$ donc $p$ divise $c$, ce qui contredit la dernière assertion. Donc, quitte à échanger $a$ et $b$, on suppose que $p$ ne divise pas $b$. Quitte à multiplier $a, b, c$ par un inverse de $b$ modulo $p$, on peut supposer que $b=1$ et donc
$$
p\left|a^{2}+a+1, \quad p\right| a^{n}+1+c^{n}, \quad p \nmid a+1+c .
$$
Comme $a^{2}+a+1$ est impair, $p$ l'est aussi.
Comme $p$ divise $\left(a^{2}+a+1\right)(a-1)=a^{3}-1$, l'ordre de $a$ modulo $p$ est 1 ou 3 .
Premier cas: $a \equiv 1(\bmod p)$. Alors $p=3$, donc $c^{n} \equiv-1-a^{n} \equiv 1(\bmod 3)$.
En particulier, $c$ est inversible modulo 3 , donc $c \equiv \pm 1(\bmod 3)$. Comme $p \nmid a+1+c$, on a nécessairement $c \equiv-1(\bmod 3)$. Enfin, comme $c^{n} \equiv 1(\bmod 3)$, l'entier $n$ est pair donc n'est pas premier avec $p-1$.
Deuxième cas: l'ordre de $a$ modulo $p$ est 3 . Comme par ailleurs l'ordre de $a$ modulo $p$ divise $p-1$ en vertu du petit théorème de Fermat, on a $3 \mid p-1$.
Supposons que $n$ est premier avec $p-1$. Alors $x \mapsto x^{n}$ est une bijection de $\mathbb{Z} / p \mathbb{Z}$ sur lui-même :
- si $n \equiv 1(\bmod 3)$ alors $c^{n} \equiv-a^{n}-1 \equiv-a-1 \equiv a^{2} \equiv\left(a^{2}\right)^{n}(\bmod p)$ donc par bijectivité de $x \mapsto x^{n}$ dans $\mathbb{Z} / p \mathbb{Z}$ on a $c \equiv a^{2} \equiv-a-1(\bmod p):$ contradiction!
- si $n \equiv 2(\bmod 3)$ alors $c^{n} \equiv-a^{n}-1 \equiv-a^{2}-1 \equiv a \equiv\left(a^{2}\right)^{n}(\bmod p)$ donc par bijectivité de $x \mapsto x^{n}$ dans $\mathbb{Z} / p \mathbb{Z}$ on a $c \equiv a^{2} \equiv-a-1(\bmod p):$ contradiction!
On en déduit que $n \equiv 0(\bmod 3)$, donc 3 est un diviseur commun de $n$ et de $p-1$.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution de l'exercice 7"
}
|
68375505-6144-56d5-a747-c774520840b7
| 604,987
|
Let $a_{1}, a_{2}, \ldots, a_{2 n}$ be real numbers such that $a_{1}+a_{2}+\cdots+a_{2 n}=0$.
Prove that there exist at least $2 n-1$ pairs $\left(a_{i}, a_{j}\right)$ with $i<j$ such that $a_{i}+a_{j} \geqslant 0$.
|
Without loss of generality, we can assume that $a_{1} \leq a_{2} \leq \cdots \leq a_{2 n}$. We distinguish two cases:
- If $a_{n}+a_{2 n-1} \geq 0$ then we have $a_{i}+a_{2 n-1} \geq 0$ for $i=n, \cdots, 2 n-2$, and $a_{i}+a_{2 n} \geq 0$ for $i=n \cdots, 2 n-1$. This provides at least $2 n-1$ non-negative sums.
- If $a_{n}+a_{2 n-1}<0$ then
$$
a_{1}+\cdots+a_{n-1}+a_{n+1}+\cdots a_{2 n-2}+a_{2 n}>0
$$
On the other hand, we have $0>a_{n}+a_{2 n-1} \geq a_{n-1}+a_{2 n-2} \geq \cdots \geq a_{2}+a_{n+1}$, so
$$
a_{2}+a_{3}+\cdots+a_{n-1}+a_{n+1}+\cdots+a_{2 n-2}<0
$$
From (1) and (2), we deduce that $a_{1}+a_{2 n} \geq 0$, which ensures that $a_{i}+a_{2 n} \geq 0$ for $i=1, \cdots 2 n-1$.
Another solution. Let $b_{1} \leqslant b_{2} \leqslant \cdots \leqslant b_{\ell}$ be the non-negative integers among $a_{1}, \ldots, a_{2 n}$. First case: $\ell>n$. Then there are at least $\frac{\ell(\ell-1)}{2} \geq \frac{n(n+1)}{2}$ pairs $\left(a_{i}, a_{j}\right)$ with $i<j, a_{i} \geqslant 0$ and $a_{j} \geqslant 0$. Now, $\frac{n(n+1)}{2}-(2 n-1)=\frac{n^{2}-3 n+2}{2}=\frac{(n-1)(n-2)}{2} \geqslant 0$, so there are at least $2 n-1$ pairs $\left(a_{i}, a_{j}\right)$ with $i<j$ such that $a_{i}+a_{j} \geqslant 0$.
Second case: $\ell \leqslant n$. Let $c_{1} \leqslant \cdots \leqslant c_{\ell}$ be the smallest integers among $a_{1}, \ldots, a_{2 n}$. Since $\ell \leqslant n$, we have $c_{\ell}<0$. Moreover, $\sum_{i=1}^{2 n} a_{i}$ is equal to the sum of $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right)$ and negative terms, so $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right) \geqslant 0$. Now, $b_{\ell}+c_{\ell} \geqslant b_{i}+c_{i}$ for all $i$, so $b_{\ell}+c_{\ell} \geqslant 0$.
We thus form $2 n-\ell$ pairs $\left(a_{i}, a_{j}\right)$ by taking $a_{j}=b_{\ell}$ and $a_{i}$ other than $c_{1}, \ldots, c_{\ell-1}, b_{\ell}$.
Furthermore, for all $k=1, \ldots, \ell-1$, we have $\sum_{i=1}^{\ell}\left(b_{i}+c_{i+k}\right) \geqslant 0$ (where by convention $c_{\ell+1}=c_{1}$, $c_{\ell+2}=c_{2}$, etc.), so for all $k$ there exists $i$ such that $b_{i}+c_{i+k} \geqslant 0$. This provides $\ell-1$ additional pairs.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a_{1}, a_{2}, \ldots, a_{2 n}$ des réels tels que $a_{1}+a_{2}+\cdots+a_{2 n}=0$.
Prouver qu'il existe au moins $2 n-1$ couples $\left(a_{i}, a_{j}\right)$ avec $i<j$ tels que $a_{i}+a_{j} \geqslant 0$.
|
Sans perte de généralité, on peut supposer que $a_{1} \leq a_{2} \leq \cdots \leq a_{2 n}$. On distingue deux cas :
- Si $a_{n}+a_{2 n-1} \geq 0$ alors on a $a_{i}+a_{2 n-1} \geq 0$ pour $i=n, \cdots, 2 n-2$, et $a_{i}+a_{2 n} \geq 0$ pour $i=n \cdots, 2 n-1$. Cela fournit bien $2 n-1$ sommes positives ou nulles.
- Si $a_{n}+a_{2 n-1}<0$ alors
$$
a_{1}+\cdots+a_{n-1}+a_{n+1}+\cdots a_{2 n-2}+a_{2 n}>0
$$
D'autre part, on a $0>a_{n}+a_{2 n-1} \geq a_{n-1}+a_{2 n-2} \geq \cdots \geq a_{2}+a_{n+1}$, donc
$$
a_{2}+a_{3}+\cdots+a_{n-1}+a_{n+1}+\cdots+a_{2 n-2}<0
$$
De (1) et (2), on déduit que $a_{1}+a_{2 n} \geq 0$, ce qui assure que $a_{i}+a_{2 n} \geq 0$ pour $i=1, \cdots 2 n-1$.
Autre solution. Notons $b_{1} \leqslant b_{2} \leqslant \cdots \leqslant b_{\ell}$ les entiers positifs ou nuls parmi $a_{1}, \ldots, a_{2 n}$. Premier cas: $\ell>n$. Alors il y a au moins $\frac{\ell(\ell-1)}{2} \geq \frac{n(n+1)}{2}$ couples $\left(a_{i}, a_{j}\right)$ avec $i<j, a_{i} \geqslant 0$ et $a_{j} \geqslant 0$. Or, $\frac{n(n+1)}{2}-(2 n-1)=\frac{n^{2}-3 n+2}{2}=\frac{(n-1)(n-2)}{2} \geqslant 0$, donc il y a au moins $2 n-1$ couples $\left(a_{i}, a_{j}\right)$ avec $i<j$ tels que $a_{i}+a_{j} \geqslant 0$.
Deuxième cas : $\ell \leqslant n$. Notons $c_{1} \leqslant \cdots \leqslant c_{\ell}$ les plus petits entiers parmi $a_{1}, \ldots, a_{2 n}$. Comme $\ell \leqslant n$, on a $c_{\ell}<0$. De plus, $\sum_{i=1}^{2 n} a_{i}$ est égal à la somme de $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right)$ et de termes négatifs, donc $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right) \geqslant 0$. Or, $b_{\ell}+c_{\ell} \geqslant b_{i}+c_{i}$ pour tout $i$, donc $b_{\ell}+c_{\ell} \geqslant 0$.
On forme ainsi déjà $2 n-\ell$ couples $\left(a_{i}, a_{j}\right)$ en prenant $a_{j}=b_{\ell}$ et $a_{i}$ autre que $c_{1}, \ldots, c_{\ell-1}, b_{\ell}$.
De plus, pour tout $k=1, \ldots, \ell-1$, on a $\sum_{i=1}^{\ell}\left(b_{i}+c_{i+k}\right) \geqslant 0$ (où par convention $c_{\ell+1}=c_{1}$, $c_{\ell+2}=c_{2}$, etc.), donc pour tout $k$ il existe $i$ tel que $b_{i}+c_{i+k} \geqslant 0$. Ceci fournit encore $\ell-1$ couples supplémentaires.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
12e89f5f-191f-5c17-b74b-bb788b20c8fb
| 605,000
|
Let $ABC$ be a triangle with all angles acute, and $H$ its orthocenter. The bisectors of $\widehat{ABH}$ and $\widehat{ACH}$ intersect at a point $I$. Show that $I$ is collinear with the midpoints of $[BC]$ and $[AH]$.
|
Let $D, E, F$ be the feet of the altitudes, $O$ the center of the circumcircle, $M$ the midpoint of $[B C]$, and $N$ the midpoint of $[A H]$. We have $2 \overrightarrow{M N}=2 \overrightarrow{O N}-2 \overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O H}-\overrightarrow{O B}-\overrightarrow{O C}$.
Since $\overrightarrow{O H}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$, it follows that $\overrightarrow{M N}=\overrightarrow{O A}$. Therefore, it suffices to show that $(M I)$ is parallel to $(O A)$.
Since $B C F$ is a right triangle at $F$, the point $F$ lies on the circle centered at $M$ passing through $B$ and $C$. The same applies to point $E$. The angle bisector of $\widehat{A B H}$ passes through the midpoint of the arc $E F$, and similarly for the angle bisector of $\widehat{A C H}$, so $I$ is the midpoint of the arc $E F$. Denoting $C^{\prime}$ as the midpoint of $[A B]$, we deduce the angle equalities $(M I, M B)=2(C I, C B)=$ $(C E, C B)+(C F, C B)=(C A, C B)+(C F, A B)+(A B, C B)$.
On the other hand, $(O A, M B)=\left(O A, O C^{\prime}\right)+\left(O C^{\prime}, A B\right)+(A B, M B)=(C A, C B)+(C F, A B)+$ $(A B, C B)$ because $\left(O C^{\prime}\right)$ and $(C F)$ are parallel.
Therefore, $(O A, M B)=(M I, M B)$, which proves that $(O A)$ and $(M I)$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus, et $H$ son orthocentre. Les bissectrices de $\widehat{A B H}$ et $\widehat{A C H}$ se coupent en un point $I$. Montrer que $I$ est aligné avec les milieux de $[B C]$ et de $[A H]$.
|
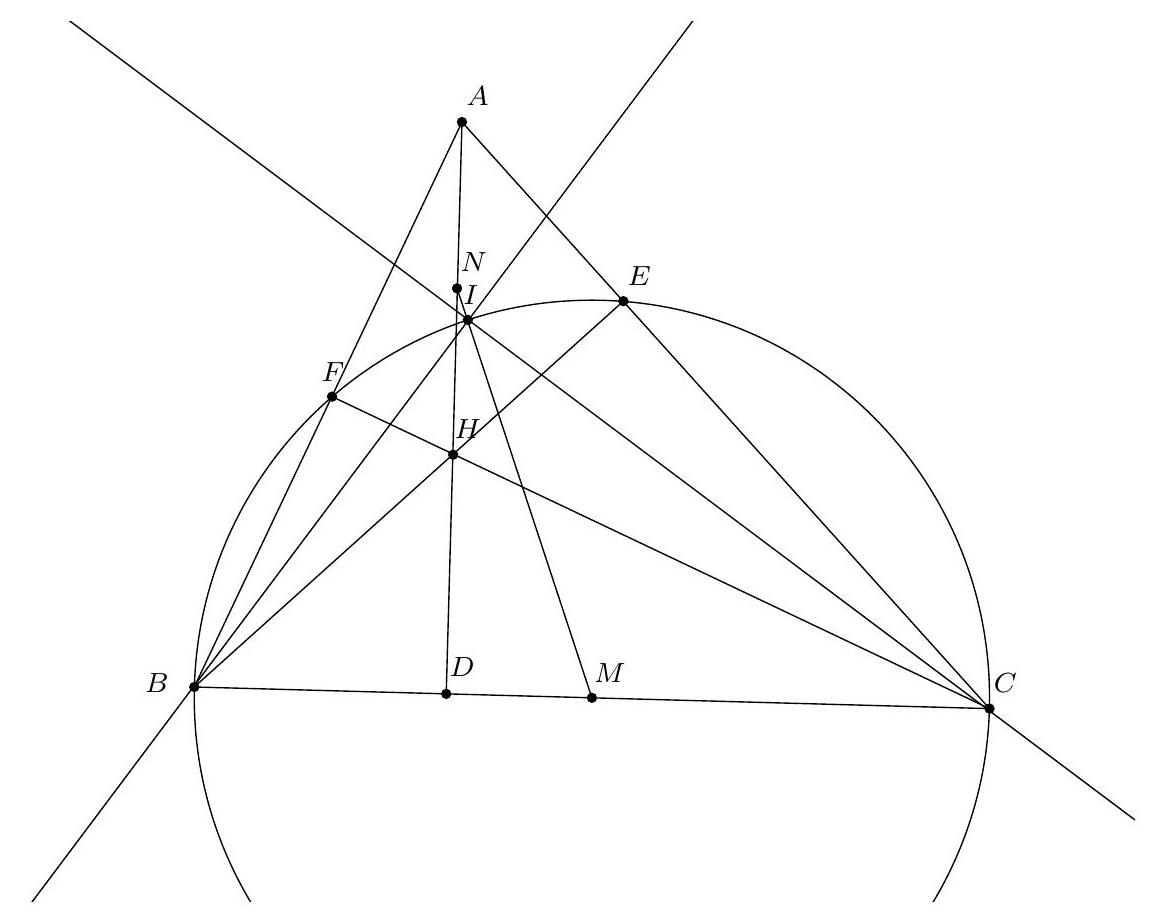
Notons $D, E, F$ les pieds des hauteurs, $O$ le centre du cercle circonscrit, $M$ le milieu de $[B C]$ et $N$ le milieu de $[A H]$. On a $2 \overrightarrow{M N}=2 \overrightarrow{O N}-2 \overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O H}-\overrightarrow{O B}-\overrightarrow{O C}$.
Or, $\overrightarrow{O H}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$ donc $\overrightarrow{M N}=\overrightarrow{O A}$. Par conséquent, il suffit de montrer que ( $M I$ ) est parallèle à $(O A)$.
Comme $B C F$ est un triangle rectangle en $F$, le point $F$ est situé sur le cercle de centre $M$ passant par $B$ et $C$. Il en va de même pour le point $E$. La bissectrice de $\widehat{A B H}$ passe par le milieu de l'arc $E F$, et de même pour la bissectrice de $\widehat{A C H}$, donc $I$ est le milieu de l'arc $E F$. En notant $C^{\prime}$ le milieu de $[A B]$, on en déduit les égalités d'angles de droites $(M I, M B)=2(C I, C B)=$ $(C E, C B)+(C F, C B)=(C A, C B)+(C F, A B)+(A B, C B)$.
D'autre part, $(O A, M B)=\left(O A, O C^{\prime}\right)+\left(O C^{\prime}, A B\right)+(A B, M B)=(C A, C B)+(C F, A B)+$ $(A B, C B)$ car $\left(O C^{\prime}\right)$ et $(C F)$ sont parallèles.
Par conséquent, $(O A, M B)=(M I, M B)$, ce qui prouve que $(O A)$ et $(M I)$ sont parallèles.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
b719225f-7780-52d8-a7fb-5586519ec306
| 605,014
|
For any integer $n \in \mathbb{N}^{*}$, we denote $v_{3}(n)$ as the 3-adic valuation of $n$, which is the greatest integer $k$ such that $n$ is divisible by $3^{k}$. We set $u_{1}=2$ and $u_{n}=4 v_{3}(n)+2-\frac{2}{u_{n-1}}$ for all $n \geqslant 2$ (provided that $u_{n-1}$ is defined and non-zero).
Show that, for any positive rational number $q$, there exists a unique integer $n \geqslant 1$ such that $u_{n}=q$.
|
First, note that $u_{1}=2, u_{2}=1, u_{3}=3, u_{4}=\frac{3}{2}, u_{5}=\frac{2}{3}$ and $u_{6}=3$. We prove by induction that, for all integers $n \geq 2$, we have $0<u_{n}$ and
$$
0<u_{3 n-1}<1<u_{3 n-2}<2<u_{3 n}=2+u_{n}:
$$
this is already true for $n=2$.
Since $u_{3 n}=u_{n}+2$, we show successively that $u_{3 n+1}, u_{3 n+2}$ and $u_{3 n+3}$ are well defined, with
$$
\begin{aligned}
& u_{3 n+1}=2-\frac{2}{u_{3 n}}=1+\frac{u_{n}}{2+u_{n}}, \text { so } 1<u_{3 n+1}<2 ; \\
& u_{3 n+2}=2-\frac{2}{u_{3 n+1}}=1+\frac{u_{n}}{1+u_{n}}, \text { so } 0<u_{3 n+2}<1 ; \\
& u_{3 n+3}=4 v_{3}(3(n+1))+2-\frac{2}{u_{3 n+2}}=4 v_{3}(n)+4-\frac{2}{u_{n}}=2+u_{n+1} .
\end{aligned}
$$
This concludes the induction.
Now, consider the function $\varphi:\{x \in \mathbb{Q}: 0<x$ and $x \notin\{1,2\}\} \mapsto\{x \in \mathbb{Q}: 0<x\}$ such that
$$
\begin{aligned}
\varphi: & x \mapsto \frac{x}{1-x} \text { if } 0<x<1 ; \\
& x \mapsto 2 \frac{x-1}{2-x} \text { if } 1<x<2 ; \\
& x \mapsto x-2 \text { if } 2<x
\end{aligned}
$$
Furthermore, for any irreducible fraction $\frac{p}{q}$, with $p \geq 0$ and $q>0$, we set $\left\|\frac{p}{q}\right\|=p+q$. Then:
- $\left\|\varphi\left(\frac{p}{q}\right)\right\|=\left\|\frac{p}{q-p}\right\|=p<p+q=\left\|\frac{p}{q}\right\|$ if $0<p<q$;
- $\left\|\varphi\left(1+\frac{p}{q}\right)\right\|=\left\|2 \frac{p}{q-p}\right\| \leq 2 q<(p+q)+q=\left\|1+\frac{p}{q}\right\|$ if $0<p<q$;
- $\left\|\varphi\left(2+\frac{p}{q}\right)\right\|=\left\|\frac{p}{q}\right\|=p+q<(p+2 q)+q=\left\|2+\frac{p}{q}\right\|$ if $0<p$ and $0<q$.
In all cases, if $x$ is a positive rational number such that $x \notin\{1,2\}$, we have $\|\varphi(x)\|<\|x\|$. Now, for any positive rational number $x$ and for all integers $n \geq 1$:
- if $0<x<1$, then $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+2}=x$;
- if $1<x<2$, then $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+1}=x$;
- if $2<x$, then $u_{n}=\varphi(x) \Leftrightarrow u_{3 n}=x$.
An induction on $\|x\|$ immediately shows that, for any positive rational number $x$, there exists a unique integer $n \geq 1$ such that $u_{n}=x$, which concludes the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier $n \in \mathbb{N}^{*}$, on note $v_{3}(n)$ la valuation 3 -adique de $n$, c'est-à-dire le plus grand entier $k$ tel que $n$ est divisible par $3^{k}$. On pose $u_{1}=2$ et $u_{n}=4 v_{3}(n)+2-\frac{2}{u_{n-1}}$ pour tout $n \geqslant 2$ (si tant est que $u_{n-1}$ soit défini et non nul).
Montrer que, pour tout nombre rationnel strictement positif $q$, il existe un et un seul entier $n \geqslant 1$ tel que $u_{n}=q$.
|
Tout d'abord, notons que $u_{1}=2, u_{2}=1, u_{3}=3, u_{4}=\frac{3}{2}, u_{5}=\frac{2}{3}$ et $u_{6}=3$. On prouve par récurrence que, pour tout entier $n \geq 2$, on a $0<u_{n}$ et
$$
0<u_{3 n-1}<1<u_{3 n-2}<2<u_{3 n}=2+u_{n}:
$$
c'est déjà vrai pour $n=2$.
Puisque $u_{3 n}=u_{n}+2$, on montre successivement que $u_{3 n+1}, u_{3 n+2}$ et $u_{3 n+3}$ sont bien définis, avec
$$
\begin{aligned}
& u_{3 n+1}=2-\frac{2}{u_{3 n}}=1+\frac{u_{n}}{2+u_{n}}, \text { donc } 1<u_{3 n+1}<2 ; \\
& u_{3 n+2}=2-\frac{2}{u_{3 n+1}}=1+\frac{u_{n}}{1+u_{n}}, \text { donc } 0<u_{3 n+2}<1 ; \\
& u_{3 n+3}=4 v_{3}(3(n+1))+2-\frac{2}{u_{3 n+2}}=4 v_{3}(n)+4-\frac{2}{u_{n}}=2+u_{n+1} .
\end{aligned}
$$
Ceci conclut la récurrence.
Maintenant, considérons la fonction $\varphi:\{x \in \mathbb{Q}: 0<x$ et $x \notin\{1,2\}\} \mapsto\{x \in \mathbb{Q}: 0<x\}$ telle que
$$
\begin{aligned}
\varphi: & x \mapsto \frac{x}{1-x} \text { si } 0<x<1 ; \\
& x \mapsto 2 \frac{x-1}{2-x} \text { si } 1<x<2 ; \\
& x \mapsto x-2 \text { si } 2<x
\end{aligned}
$$
En outre, pour toute fraction irréductible $\frac{p}{q}$, avec $p \geq 0$ et $q>0$, on pose $\left\|\frac{p}{q}\right\|=p+q$. Alors :
- $\left\|\varphi\left(\frac{p}{q}\right)\right\|=\left\|\frac{p}{q-p}\right\|=p<p+q=\left\|\frac{p}{q}\right\|$ si $0<p<q$ ;
- $\left\|\varphi\left(1+\frac{p}{q}\right)\right\|=\left\|2 \frac{p}{q-p}\right\| \leq 2 q<(p+q)+q=\left\|1+\frac{p}{q}\right\|$ si $0<p<q$ ;
- $\left\|\varphi\left(2+\frac{p}{q}\right)\right\|=\left\|\frac{p}{q}\right\|=p+q<(p+2 q)+q=\left\|2+\frac{p}{q}\right\|$ si $0<p$ et $0<q$.
Dans tous les cas, si $x$ est un rationnel strictement positif tel que $x \notin\{1,2\}$, on a $\|\varphi(x)\|<\|x\|$. Or, pour tout rationnel strictement positif $x$ et pour tout entier $n \geq 1$ :
- si $0<x<1$, alors $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+2}=x ;$
- si $1<x<2$, alors $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+1}=x$;
- si $2<x$, alors $u_{n}=\varphi(x) \Leftrightarrow u_{3 n}=x$.
Une récurrence sur $\|x\|$ montre donc immédiatement que, pour tout rationnel strictement positif $x$, il existe un entier unique entier $n \geq 1$ tel que $u_{n}=x$, ce qui conclut l'exercice.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
0be23be4-5717-5059-b3e0-23d6a3a477d5
| 605,027
|
Prove that for all integers $n \geq 2$, we have: $\sum_{k=2}^{n} \frac{1}{\sqrt[k]{(2 k)!}} \geq \frac{n-1}{2 n+2}$.
N.B. If $a>0$, we denote $\sqrt[k]{a}$ the unique positive real number $b$ such that $b^{k}=a$.
|
We reason by induction on $n \geq 2$.
For $n=2$, we have $\frac{1}{\sqrt{24}} > \frac{1}{6}$.
Suppose the desired inequality holds for the value $n-1 \geq 2$. For the value $n$, the right-hand side increases by $\frac{n-1}{2 n+2} - \frac{n-2}{2 n} = \frac{1}{n(n+1)}$.
According to the induction hypothesis, it suffices to prove that $\frac{1}{\sqrt[n]{(2 n)!}} \geq \frac{1}{n(n+1)}$.
For $k=1,2, \cdots, n$, we have $(n-k)(n-k+1) \geq 0$, so $0 \leq k(2 n-k+1) \leq n(n+1)$.
By multiplying these inequalities term by term, we get $(2 n)! \leq (n(n+1))^{n}$, from which the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tout entier $n \geq 2$, on a : $\sum_{k=2}^{n} \frac{1}{\sqrt[k]{(2 k)!}} \geq \frac{n-1}{2 n+2}$.
N.B. Si $a>0$, on note $\sqrt[k]{a}$ l'unique nombre réel $b>0$ tel que $b^{k}=a$.
|
On raisonne par récurrence sur $n \geq 2$.
Pour $n=2$, on a bien $\frac{1}{\sqrt{24}}>\frac{1}{6}$.
Supposons que l'inégalité désirée soit vraie pour la valeur $n-1 \geq 2$. Pour la valeur $n$, le membre de droite augmente de $\frac{n-1}{2 n+2}-\frac{n-2}{2 n}=\frac{1}{n(n+1)}$.
D'après l'hypothèse de récurrence, il suffit donc de prouver que $\frac{1}{\sqrt[n]{(2 n)!}} \geq \frac{1}{n(n+1)}$.
Or, pour $k=1,2, \cdots, n$, on a $(n-k)(n-k+1) \geq 0$, donc $0 \leq k(2 n-k+1) \leq n(n+1)$.
En multipliant ces inégalités membre à membre, il vient $(2 n)!\leq(n(n+1))^{n}$, $\mathrm{d}^{\prime}$ où la conclusion.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
fa2c39f5-4434-507e-9bc4-7ed4e3bdf8b2
| 605,034
|
Let $ABC$ be a non-right triangle such that $AB < AC$. We denote $H$ as the projection of $A$ onto $(BC)$, and $E, F$ as the projections of $H$ onto $(AB)$ and $(AC)$, respectively. The line $(EF)$ intersects $(BC)$ at point $D$. Consider the semicircle with diameter $[CD]$ located in the same half-plane delimited by $(CD)$ as $A$. Let $K$ be the point on this semicircle that projects onto $B$. Show that $(DK)$ is tangent to the circle $KEF$.
|
As $A E H F$ are concyclic (on the circle with diameter $[A H]$), we have $(E F, E A)=(H F, H A)=$ $(H F, C A)+(C A, C B)+(C B, H A)=(C A, C B)=(C F, C B)$, so $(E F, E B)=(C F, C B)$. Therefore, $B, E, F, C$ are concyclic. From the power of a point with respect to a circle, we have $D E \cdot D F=D B \cdot D C$. On the other hand, since $D K C$ is a right triangle at $K$, the triangles $D K B$ and $D C K$ are similar, which implies $\frac{D K}{D B}=\frac{D C}{D K}$, or equivalently $D K^{2}=D B \cdot D C$.
Thus, $D K^{2}=D E \cdot D F$, and therefore, from the power of $D$ with respect to the circle $K E F$, we conclude that $(D K)$ is tangent to the circle $K E F$ at $K$.
Remark: The choice of the semicircle is not important.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non rectangle tel que $A B<A C$. On note $H$ le projeté de $A$ sur $(B C)$, et $E, F$ les projetés respectifs de $H$ sur $(A B)$ et $(A C)$. La droite $(E F)$ coupe $(B C)$ au point $D$. On considère le demi-cercle de diamètre $[C D]$ situé dans le même demi-plan délimité par $(C D)$ que $A$. Soit $K$ le point de ce demi-cercle qui se projette sur $B$. Montrer que $(D K)$ est tangente au cercle $K E F$.
|
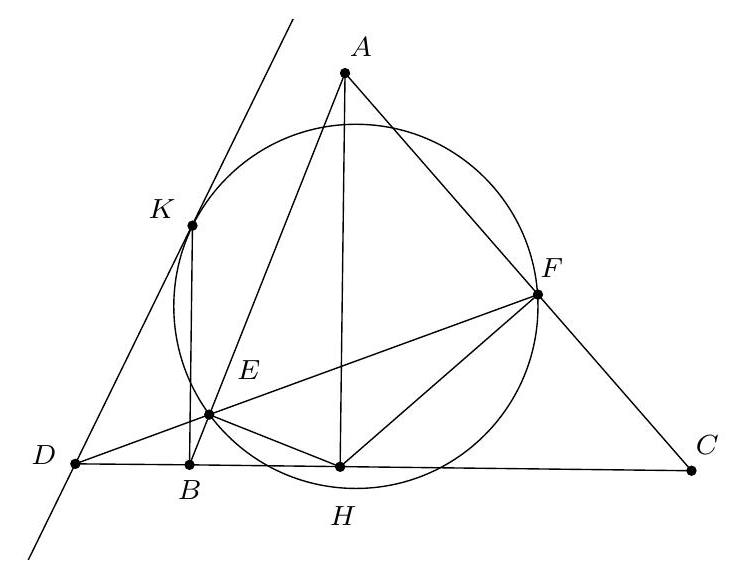
Comme $A E H F$ sont cocycliques (sur le cercle de diamètre $[A H]$ ), on a $(E F, E A)=(H F, H A)=$ $(H F, C A)+(C A, C B)+(C B, H A)=(C A, C B)=(C F, C B)$, donc $(E F, E B)=(C F, C B)$. Par conséquent, $B, E, F, C$ sont cocycliques. D'après la puissance d'un point par rapport à un cercle, on a $D E \cdot D F=D B \cdot D C$. D'autre part, comme $D K C$ est rectangle en $K$, les triangles $D K B$ et $D C K$ sont semblables, ce qui implique $\frac{D K}{D B}=\frac{D C}{D K}$, ou encore $D K^{2}=D B \cdot D C$.
Il vient $D K^{2}=D E \cdot D F$, et donc d'après la puissance de $D$ par rapport au cercle $K E F$, on en déduit que $(D K)$ est tangente en $K$ au cercle $K E F$.
Remarque : le choix du demi-cercle n'a pas d'importance.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
3a0dd58c-b34b-5fef-851f-aa5fa621c60a
| 605,050
|
Let $n \geq 1$ be an integer. A group of $2 n$ people meet. Each of these people has at least $n$ friends in this group (in particular, if $A$ is a friend of $B$ then $B$ is a friend of $A$, and one is not a friend with oneself). Prove that it is possible to arrange these $2 n$ people around a round table so that each person is between two of their friends.
|
Consider an arbitrary arrangement of guests:
AB.... $A$.
where $A, B$ denote different people, but the two $A$s represent the same person (we are around a round table).
In what follows, we will consider the arrangement as a sequence of people, ordered from left to right.
If two neighbors are not friends, we will say that it is a tension.
If there is no tension, it is over.
If there is a tension, by circular symmetry, we can always assume that $A$ and $B$ are not friends.
Since $B$ has at least $n$ friends, plus himself, we deduce that $B$ has at most $n-1$ "enemies".
Suppose that in the arrangement above and after $B$, we never find two neighbors $A'$ and $B'$ (in this order) who are friends respectively of $A$ and $B$.
Then, since such an arrangement does not occur before $B$ either, we deduce that it never appears, and therefore to the right of each friend of $A$ must be an enemy of $B$. Thus, the number of enemies of $B$ is at least equal to the number of friends of $A$, which implies $n-1 \geq n$. Contradiction.
Therefore, we can find two neighbors $A'$ and $B'$ (in this order) who are friends respectively of $A$ and $B$.
The arrangement is then of the form:
$$
A B \ldots A' B' \ldots A
$$
Under these conditions, we can eliminate the tension between $A$ and $B$ by reversing the order of the people between $B$ and $A'$:
$$
A\left(B \ldots A'\right) B' \ldots A \rightarrow A\left(A' \ldots B\right) B' \ldots A
$$
This provides a new arrangement but with at least one less tension than in the previous one, since clearly the modification does not create any new tension (however, it can eliminate a potential tension between $A'$ and $B'$).
By repeating this procedure as many times as necessary (a finite number of times in any case, since the initial number of tensions is finite), we eliminate all tensions, and the goal is achieved.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geq 1$ un entier. Un groupe de $2 n$ personnes se réunit. Chacune de ces personnes possède au moins $n$ amies dans ce groupe (en particulier, si $A$ est amie avec $B$ alors $B$ est amie avec $A$, et on n'est pas ami avec soi-même). Prouver que l'on peut disposer ces $2 n$ personnes autour d'une table ronde de sorte que chacune soit entre deux de ses amies.
|
Considérons une disposition arbitraire des invités :
AB.... $A$.
où $A, B$ désignent des personnes différentes, mais les deux $A$ représentent la même personne (on est autour d'une table ronde).
Dans ce qui suit, on considérera la disposition comme une suite de personnes, ordonnée de gauche à droite.
Si deux voisins ne sont pas amis, on dira que c'est une tension.
S'il n'y a aucune tension, c'est fini.
S'il existe une tension, par symétrie circulaire, on peut toujours supposer que $A$ et $B$ ne sont pas amis.
Comme $B$ a au moins $n$ amis, plus lui-même, on en déduit que $B$ a au plus $n-1$ "ennemis".
Supposons que dans la disposition ci-dessus et après $B$, on ne trouve jamais deux voisins $A^{\prime}$ et $B^{\prime}$ (dans cet ordre) qui sont amies respectivement de $A$ et de $B$.
Alors, comme une telle disposition n'arrive pas non plus avant $B$, on en déduit qu'elle n'apparaît jamais, et donc qu'à droite de chaque ami de $A$ doit se trouver un ennemi de $B$. Donc, le nombre d'ennemis de $B$ est au moins égal au nombre d'amis de $A$, ce qui implique $n-1 \geq n$. Contradiction.
Par suite, on peut trouver deux voisins $A^{\prime}$ et $B^{\prime}$ (dans cet ordre) qui sont amies respectivement de $A$ et de $B$.
La disposition est alors de la forme :
$$
A B \ldots A^{\prime} B^{\prime} \ldots A
$$
Dans ces conditions, on peut éliminer la tension entre $A$ et $B$ en renversant l'ordre des personnes entre $B$ et $A^{\prime}$ :
$$
A\left(B \ldots A^{\prime}\right) B^{\prime} \ldots A \rightarrow A\left(A^{\prime} \ldots B\right) B^{\prime} \ldots A
$$
Cela fournit une nouvelle disposition mais avec au moins une tension de moins que dans la précédente, puisque clairement la modification ne crée pas de nouvelle tension (par contre, elle peut éliminer une tension éventuelle entre $A^{\prime}$ et $B^{\prime}$ ).
En répétant cette procédure autant que nécessaire (un nombre fini de fois en tout cas, puisque le nombre initial de tensions est fini), on fait disparaître toutes les tensions, et l'objectif est atteint.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
4e7762bb-d4ce-5743-aede-2681082fab51
| 605,062
|
Let $ABC$ be a triangle, and $M$ the midpoint of $[BC]$. We denote $I_{b}$ and $I_{c}$ as the centers of the incircles of $AMB$ and $AMC$. Show that the second point of intersection of the circumcircles of triangles $ABI_{b}$ and $ACI_{c}$ lies on the line $(AM)$.
|
Let $T$ be the intersection between the circle with diameter $[B C]$ and the ray $\left[M A\right)$. It suffices to show that $T$ lies on the circle $A B I_{b}$ (by symmetry of the roles of $B$ and $C$, this will show that it also lies on the circle $A C I_{c}$).
Since $\widehat{B T C}$ is a right angle, we have $\widehat{A T B}=90^{\circ}+\frac{1}{2} \widehat{A M B}=\widehat{A I_{b} B}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et $M$ le milieu de $[B C]$. On note $I_{b}$ et $I_{c}$ les centres des cercles inscrits à $A M B$ et $A M C$. Montrer que le second point d'intersection des cercles circonscrits aux triangles $A B I_{b}$ et $A C I_{c}$ se situe sur la droite $(A M)$.
|
Soit $T$ l'intersection entre le cercle de diamètre $[B C]$ et la demi-droite $\left[M A\right.$ ). Il suffit de montrer que $T$ appartient au cercle $A B I_{b}$ (par symétrie des rôles de $B$ et $C$, ceci montrera qu'il appartient également au cercle $A C I_{c}$ ).
Comme $\widehat{B T C}$ est droit, on a $\widehat{A T B}=90^{\circ}+\frac{1}{2} \widehat{A M B}=\widehat{A I_{b} B}$.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
b1bd668e-0f1f-5574-8879-3575e4dca836
| 605,099
|
Let $n \geqslant 1$ be an integer. Suppose there exist exactly 2005 pairs $(x, y)$ of natural numbers such that $\frac{1}{x}+\frac{1}{y}=\frac{1}{n}$. Show that $n$ is the square of an integer.
N.B. If $x \neq y$ then $(x, y) \neq(y, x)$.
|
We notice that $x>n$ and $y>n$.
The equation can be written as $xy=n(x+y)$, or equivalently $n^2=(x-n)(y-n)$. From this, we deduce that there are exactly 2005 pairs of natural numbers $(u, v)$ such that $n^2=uv$.
If $n^2=uv$ then $u$ is a divisor of $n^2$. Conversely, if $u$ is a divisor of $n^2$ then the equation $n^2=uv$ uniquely determines $v$. We deduce that $n^2$ has exactly 2005 divisors.
Let's write $n=p_1^{\alpha_1} \cdots p_r^{\alpha_r}$ with $p_i$ distinct primes and $\alpha_i$ integers. Therefore, $n^2=p_1^{2\alpha_1} \cdots p_r^{2\alpha_r}$. We know that the number of divisors of $n^2$ is equal to $(2\alpha_1+1) \cdots (2\alpha_r+1)$. The prime factorization of 2005 is $5 \times 401$, so either $r=1$ and $2\alpha_1+1=2005$, or $r=2$ and $2\alpha_1+1=5$, $2\alpha_2+1=401$. In all cases, the $\alpha_i$ are even, so $n$ is a perfect square.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 1$ un entier. On suppose qu'il existe exactement 2005 couples $(x, y)$ d'entiers naturels tels que $\frac{1}{x}+\frac{1}{y}=\frac{1}{n}$. Montrer que $n$ est le carré d'un entier.
N.B. Si $x \neq y$ alors $(x, y) \neq(y, x)$.
|
On remarque que $x>n$ et $y>n$.
L'équation s'écrit $x y=n(x+y)$, ou encore $n^{2}=(x-n)(y-n)$. On en déduit qu'il y a exactement 2005 couples d'entiers naturels $(u, v)$ tels que $n^{2}=u v$.
Si $n^{2}=u v$ alors $u$ est un diviseur de $n^{2}$. Réciproquement, si $u$ est un diviseur de $n^{2}$ alors l'équation $n^{2}=u v$ détermine uniquement $v$. On en déduit que $n^{2}$ admet exactement 2005 diviseurs.
Ecrivons $n=p_{1}^{\alpha_{1}} \cdots p_{r}^{\alpha_{r}}$ avec $p_{i}$ premiers distincts et $\alpha_{i}$ entiers. On a donc $n^{2}=p_{1}^{2 \alpha_{1}} \cdots p_{r}^{2 \alpha_{r}}$. On sait que le nombre de diviseurs de $n^{2}$ est égal à $\left(2 \alpha_{1}+1\right) \cdots\left(2 \alpha_{r}+1\right)$. Or, la décomposition en facteurs premiers de 2005 est $5 \times 401$, donc soit $r=1$ et $2 \alpha_{1}+1=2005$, soit $r=2$ et $2 \alpha_{1}+1=5$, $2 \alpha_{2}+1=401$. Dans tous les cas, les $\alpha_{i}$ sont pairs donc $n$ est un carré parfait.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
84bf3b74-0099-58c0-8128-638557b9025c
| 605,109
|
Let $ABC$ be an isosceles triangle at $A$, where the angle at $A$ is not a right angle. Let $D$ be the point on $(BC)$ such that $(AD) \perp (AB)$. Let $E$ be the orthogonal projection of $D$ onto $(AC)$. Finally, let $H$ be the midpoint of $[BC]$. Show that $AH = HE$.
|
First, since the angles $\widehat{A H D}$ and $\widehat{A E D}$ are right angles, the points $A, H, E, D$ lie on the circle with diameter $[A D]$.
Let $\theta=\widehat{C B A}=\widehat{A C B}$. Since $A H C$ is a right triangle at $H$, $\widehat{H A C}=90^{\circ}-\theta$. Since $B A D$ is a right triangle at $A$, $\widehat{A D B}=90^{\circ}-\theta$, and thus $\widehat{A D H}=\widehat{H A E}$.
By the cocyclicity of $A, H, E, D$, the angles $\widehat{A D H}$ and $\widehat{A E H}$ are equal or supplementary, so $\widehat{H A E}=\widehat{A E H}$ or $\widehat{H A E}+\widehat{A E H}=180^{\circ}$.
The second case cannot occur because the sum of the angles in triangle $A E H$ is $180^{\circ}$, so we have $\widehat{H A E}=\widehat{A E H}$. This implies that $H A E$ is isosceles at $H$, hence $H A=H E$.
Another approach using angles between lines. We know that if $T$ is a tangent at a point $A$ to a circle $(C)$ and if $B$ and $M$ are two other points on $(C)$, then $(T, A B)=(M A, M B)$.
In the problem, since $(A B)$ is perpendicular to the diameter $(A D)$, it is tangent to the circle. Therefore, from the above, we have $(A B, A H)=(E A, E H)$. Since $A B C$ is isosceles, we have $(A B, A H)=(A H, A C)$, so $(A H, A E)=(A H, A C)=(A B, A H)=(E A, E H)$. We conclude that $H A E$ is isosceles at $H$, hence $H A=H E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, dont l'angle en $A$ n'est pas droit. Soit $D$ le point de $(B C)$ tel que $(A D) \perp(A B)$. Soit $E$ le projeté orthogonal de $D$ sur $(A C)$. Soit enfin $H$ le milieu de $[B C]$. Montrer que $A H=H E$.
|
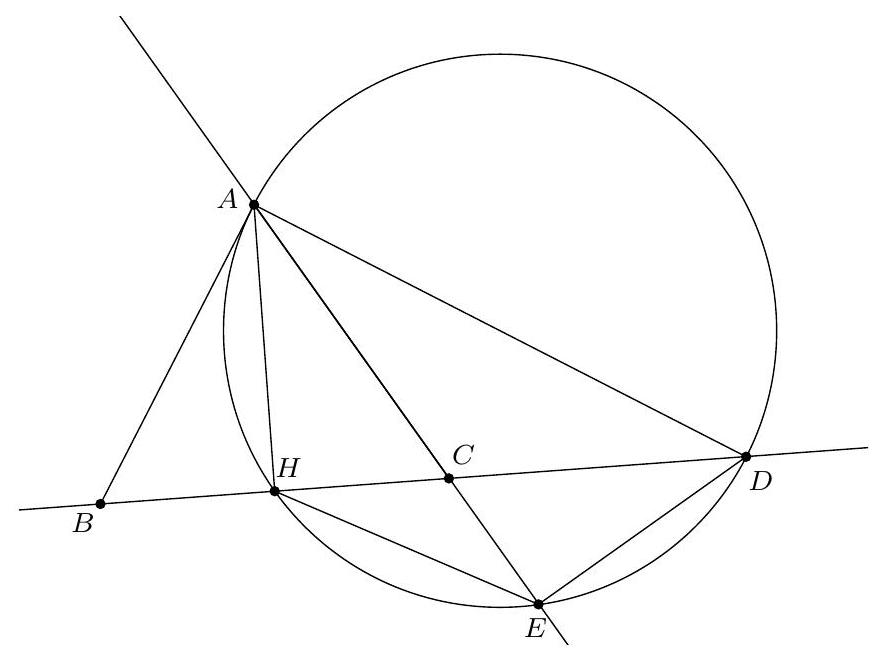
Tout d'abord, comme les angles $\widehat{A H D}$ et $\widehat{A E D}$ sont droits, les points $A, H, E, D$ sont sur le cercle de diamètre $[A D]$.
Notons $\theta=\widehat{C B A}=\widehat{A C B}$. Comme $A H C$ est rectangle en $H, \widehat{H A C}=90^{\circ}-\theta$. Comme $B A D$ est rectangle en $A, \widehat{A D B}=90^{\circ}-\theta$, et donc $\widehat{A D H}=\widehat{H A E}$.
Par cocyclicité de $A, H, E, D$, les angles $\widehat{A D H}$ et $\widehat{A E H}$ sont égaux ou supplémentaires, donc $\widehat{H A E}=\widehat{A E H}$ ou $\widehat{H A E}+\widehat{A E H}=180^{\circ}$.
Le deuxième cas ne peut pas se produire car la somme des angles du triangle $A E H$ vaut $180^{\circ}$, donc on a $\widehat{H A E}=\widehat{A E H}$. On en déduit que $H A E$ est isocèle en $H$, d'où $H A=H E$.
Autre approche avec les angles de droites. On sait que si $T$ est une tangente en un point $A$ à un cercle $(C)$ et si $B$ et $M$ sont deux autres points de $(C)$, alors $(T, A B)=(M A, M B)$.
Dans l'exercice, comme $(A B)$ est perpendiculaire au diamètre $(A D)$, elle est tangente au cercle donc d'après ce qui précède on a $(A B, A H)=(E A, E H)$. Or, comme $A B C$ est isocèle on a $(A B, A H)=(A H, A C)$ donc $(A H, A E)=(A H, A C)=(A B, A H)=(E A, E H)$. On en conclut que $H A E$ est isocèle en $H$, d'où $H A=H E$.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
482608e1-946a-5f95-adf0-359854551e57
| 605,123
|
Let $I$ be the center of the incircle of a triangle $ABC$. Let $D$ be the point diametrically opposite to $A$ on the circumcircle. Suppose that the point $E$ on the ray $[BA)$ and the point $F$ on the ray $[CA)$ satisfy the condition
$$
BE=CF=\frac{AB+BC+CA}{2}.
$$
Show that $(EF) \perp (DI)$.
|
Let $a, b, c$ be the lengths of the sides, $r$ the radius of the inscribed circle, and $p = (a + b + c) / 2$. Since $[AD]$ is a diameter, the angles $\widehat{ABD}$ and $\widehat{ACD}$ are right angles, so
\[
\begin{aligned}
DE^2 - DF^2 & = (DB^2 + BE^2) - (DC^2 + CF^2) = DB^2 - DC^2 \\
& = (AD^2 - DC^2) - (AD^2 - DB^2) = AC^2 - AB^2 \\
& = b^2 - c^2.
\end{aligned}
\]
On the other hand, if $C'$ is the point of tangency of the inscribed circle with $[AB]$, we know that $BC' = p - b$, so $C'E = BE - BC' = b$. It follows that $IE^2 = (IC')^2 + (C'E)^2 = r^2 + b^2$, and similarly $IF^2 = r^2 - c^2$, so
\[
DE^2 - DF^2 = IE^2 - IF^2.
\]
This means that the points $D$ and $I$ have the same difference in powers with respect to $E$ and $F$ (considered as circles of zero radius), so $(DI) \perp (EF)$.
Clarification: Let's explain why if $C$ and $C'$ are two circles with centers $O$ and $O'$, and if $P_C(A) - P_{C'}(A) = P_C(B) - P_{C'}(B)$, then $(AB) \perp (OO')$. Let $R$ and $R'$ be the radii of the circles, and $C, D$ the projections of $A$ and $B$ on $(OO')$.
We have $P_C(A) - P_{C'}(A) = OA^2 - O'A^2 - (R^2 - (R')^2) = OC^2 - O'C^2 - (R^2 - (R')^2)$, so $OC^2 - O'C^2 = OD^2 - O'D^2$. This can be written as $(\overline{OC} - \overline{O'C})(\overline{OC} + \overline{O'C}) = (\overline{OD} - \overline{O'D})(\overline{OD} + \overline{O'D})$, or $2 \overline{O'O} \cdot \overline{MC} = 2 \overline{O'O} \cdot \overline{MD}$ where $M$ is the midpoint of $[O'O]$. Consequently, $C = D$, and thus $(AB) = (AC) \perp (OO')$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $I$ le centre du cercle inscrit à un triangle $A B C$. Soit $D$ le point diamétralement opposé à $A$ sur le cercle circonscrit. On suppose que le point $E$ de la demi-droite $[B A)$ et le point $F$ de la demi-droite $[C A)$ satisfont la condition
$$
B E=C F=\frac{A B+B C+C A}{2} .
$$
Montrer que $(E F) \perp(D I)$.
|
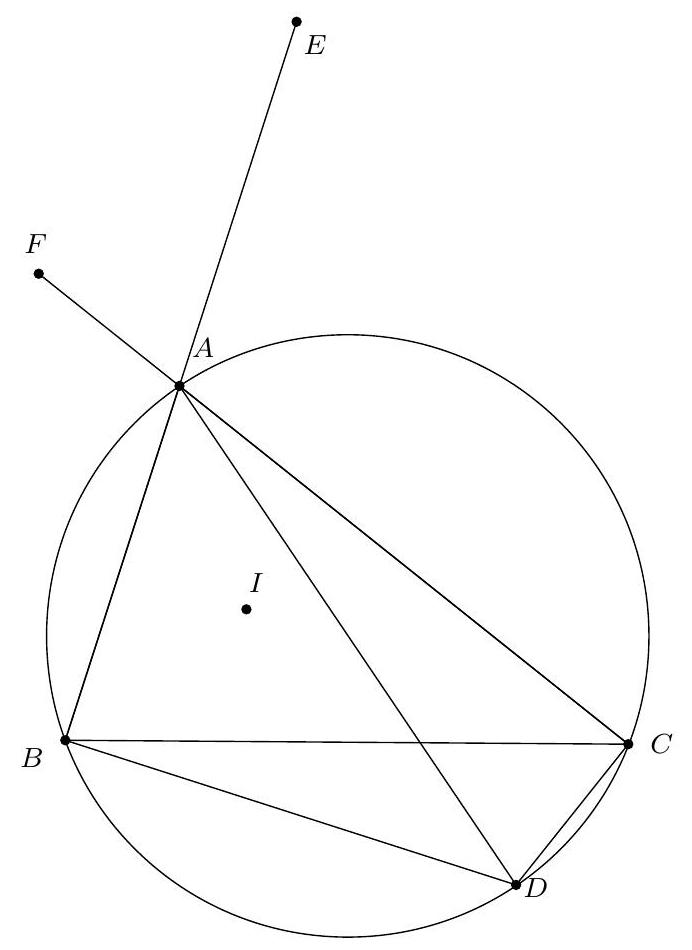
Notons $a, b, c$ les longueurs des côtés, $r$ le rayon du cercle inscrit et $p=(a+b+c) / 2$. Comme $[A D]$ est un diamètre, les angles $\widehat{A B D}$ et $\widehat{A C D}$ sont droits donc
$$
\begin{aligned}
D E^{2}-D F^{2} & =\left(D B^{2}+B E^{2}\right)-\left(D C^{2}+C F^{2}\right)=D B^{2}-D C^{2} \\
& =\left(A D^{2}-D C^{2}\right)-\left(A D^{2}-D B^{2}\right)=A C^{2}-A B^{2} \\
& =b^{2}-c^{2} .
\end{aligned}
$$
D'autre part, si $C^{\prime}$ est le point de contact du cercle inscrit avec $[A B]$, on sait que $B C^{\prime}=p-b$, donc $C^{\prime} E=B E-B C^{\prime}=b$. Il vient $I E^{2}=\left(I C^{\prime}\right)^{2}+\left(C^{\prime} E\right)^{2}=r^{2}+b^{2}$, et de même $I F^{2}=r^{2}-c^{2}$, donc
$$
D E^{2}-D F^{2}=I E^{2}-I F^{2}
$$
Ceci signifie que les points $D$ et $I$ ont la même différence de puissances par rapport à $E$ et $F$ (considérés comme des cercles de rayon nul), donc $(D I) \perp(E F)$.
Précision : expliquons pourquoi si $C$ et $C^{\prime}$ sont deux cercles de centres $O$ et $O^{\prime}$, et si $P_{C}(A)$ -$P_{C^{\prime}}(A)=P_{C}(B)-P_{C^{\prime}}(B)$ alors $(A B) \perp\left(O O^{\prime}\right)$. Notons $R$ et $R^{\prime}$ les rayons des cercles et $C, D$ les projetés respectifs de $A$ et $B$ sur $\left(O O^{\prime}\right)$.
On a $P_{C}(A)-P_{C^{\prime}}(A)=O A^{2}-O^{\prime} A^{2}-\left(R^{2}-\left(R^{\prime}\right)^{2}\right)=O C^{2}-O^{\prime} C^{2}-\left(R^{2}-\left(R^{\prime}\right)^{2}\right)$, donc $O C^{2}-$ $O^{\prime} C^{2}=O D^{2}-O^{\prime} D^{2}$. Ceci s'écrit encore $\left(\overline{O C}-\overline{O^{\prime} C}\right)\left(\overline{O C}+\overline{O^{\prime} C}\right)=\left(\overline{O D}-\overline{O^{\prime} D}\right)\left(\overline{O D}+\overline{O^{\prime} D}\right)$, ou encore $2 \overline{O^{\prime} O} \cdot \overline{M C}=2 \overline{O^{\prime} O} \cdot \overline{M D}$ où $M$ est le milieu de $\left[O^{\prime} O\right]$. Par conséquent, $C=D$, et donc $(A B)=(A C) \perp\left(O O^{\prime}\right)$.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution de l'exercice 6"
}
|
18e3c95e-e27d-5b00-a127-e36faf885fe7
| 605,176
|
Let $ABC$ be a triangle with all angles acute.
The altitudes $\left[A A_{1}\right],\left[B B_{1}\right]$, and $\left[C C_{1}\right]$ intersect at point $H$. Let $A_{2}$ be the symmetric point of $A$ with respect to $\left(B_{1} C_{1}\right)$, and let $O$ be the center of the circumcircle of $ABC$.
a) Prove that the points $O, A_{2}, B_{1}, C$ are concyclic.
b) Prove that $O, H, A_{1}, A_{2}$ are concyclic.
|
a) $A, H, B_{1}, C_{1}$ are concyclic on the circle with diameter $[A H]$, so $\widehat{A B_{1} C_{1}}=\widehat{A H C_{1}}=90^{\circ}-$ $\widehat{C_{1} A H}$. Since, $\left(A A_{2}\right) \perp\left(B_{1} C_{1}\right)$, we have $\widehat{A_{2} A B_{1}}=\widehat{C_{1} A H}$, i.e., the rays $[A H)$ and $\left[A A_{2}\right)$ are symmetric with respect to the bisector of $\widehat{B A C}$. We deduce that $A_{2} \in[A O)$. Since $A O = C O$, we have $\widehat{A C O}=\widehat{O A C}=\widehat{A A_{2} B_{1}}$, so $O, A_{2}, B_{1}, C$ are concyclic.
b) Using the power of $A$ with respect to the circles $O, A_{2}, B_{1}, C$ and $H, A_{1}, C, B_{1}$, we have $A B_{1} \cdot A C = A O \cdot A A_{2}$ and $A B_{1} \cdot A C = A H \cdot A A_{1}$. Consequently, $A O \cdot A A_{2} = A H \cdot A A_{1}$. According to the power of a point with respect to a circle, we deduce that $O A_{2}, H, A_{1}$ are concyclic.
Remark. The assumption that $A B C$ is acute is superfluous.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus.
Les hauteurs $\left[A A_{1}\right],\left[B B_{1}\right]$ et $\left[C C_{1}\right]$ se coupent au point $H$. Soit $A_{2}$ le symétrique de $A$ par rapport à $\left(B_{1} C_{1}\right)$, et soit $O$ le centre du cercle circonscrit à $A B C$.
a) Prouver que les points $O, A_{2}, B_{1}, C$ sont cocycliques.
b) Prouver que $O, H, A_{1}, A_{2}$ sont cocycliques.
|
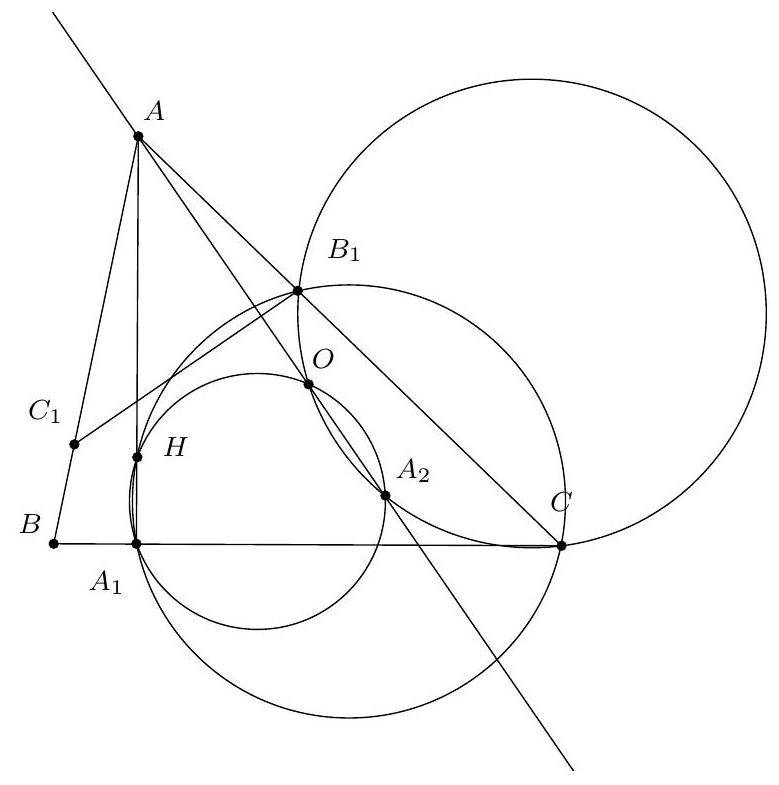
a) $A, H, B_{1}, C_{1}$ sont cocycliques sur le cercle de diamètre $[A H]$, donc $\widehat{A B_{1} C_{1}}=\widehat{A H C_{1}}=90^{\circ}-$ $\widehat{C_{1} A H}$. Or, $\left(A A_{2}\right) \perp\left(B_{1} C_{1}\right)$ donc $\widehat{A_{2} A B_{1}}=\widehat{C_{1} A H}$, i.e. les demi-droites $[A H)$ et $\left[A A_{2}\right)$ sont symétriques par rapport à la bissectrice de $\widehat{B A C}$. On en déduit que $A_{2} \in[A O)$. Comme $A O=$ $C O$, on a $\widehat{A C O}=\widehat{O A C}=\widehat{A A_{2} B_{1}}$, donc $O, A_{2}, B_{1}, C$ sont cocycliques.
b) En utilisant la puissance de $A$ par rapport aux cercles $O, A_{2}, B_{1}, C$ et $H, A_{1}, C, B_{1}$, on a $A B_{1}$. $A C=A O \cdot A A_{2}$ et $A B_{1} \cdot A C=A H \cdot A A_{1}$. Par conséquent, $A O \cdot A A_{2}=A H \cdot A A_{1}$. D'après la puissance d'un point par rapport à un cercle, on en déduit que $O A_{2}, H, A_{1}$ sont cocycliques.
Remarque. L'hypothèse que $A B C$ est acutangle est superflue.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
4177e59d-c266-55e8-a122-7d0bd2f4fdb8
| 605,226
|
Let $a_{0}, a_{1}, \ldots, a_{99}, b_{0}, b_{1}, \ldots, b_{99}$ be strictly positive real numbers.
For $k=0,1, \ldots, 198$, we set $S_{k}=\sum_{i=0}^{198} a_{i} b_{k-i}$, with $a_{j}=0$ and $b_{j}=0$ if $j<0$ or $j>99$.
Is it possible that the numbers $S_{0}, S_{1}, \ldots, S_{198}$ are all equal?
|
No. Let's reason by contradiction. Indeed, since $a_{0} b_{0}=a_{0} b_{99}+\cdots+a_{99} b_{0}$ where the $\cdots$ represent strictly positive terms, we have $a_{0} b_{0}>a_{0} b_{99}$, hence $b_{0}>b_{99}$, and similarly $a_{0}>a_{99}$. Consequently, $S_{0}=a_{0} b_{0}>a_{99} b_{99}=S_{198}$, which is contradictory.
Another proof that does not require the positivity assumption (but only the fact that $a_{99} \neq 0$ and $b_{99} \neq 0$):
Suppose that $S_{0}=S_{1}=\ldots=S_{198}=\alpha$.
Note that $\alpha \neq 0$.
Let $P(x)=a_{0}+a_{1} x+\ldots+a_{99} x^{99}$ and $Q(x)=b_{0}+b_{1} x+\ldots+b_{99} x^{99}$. Since $P(x) Q(x)=S_{0}+S_{1} x+\ldots+S_{198} x^{198}=\alpha\left(1+x+\ldots+x^{198}\right)$
$=\alpha \frac{1-x^{199}}{1-x}$ for $x \neq 1$, we observe that $P(x) Q(x) \neq 0$ for all $x \neq 1$. On the other hand, since $\alpha \neq 0$ because $P$ and $Q$ are non-zero polynomials, we have $P(1) Q(1)=199 \alpha \neq 0$.
Therefore, $P(x) Q(x) \neq 0$ for all real $x$, and thus $P$ does not have any real roots. This contradicts the fact that $P$ is of odd degree.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a_{0}, a_{1}, . ., a_{99}, b_{0}, b_{1}, \ldots, b_{99}$ des réels strictement positifs.
Pour $k=0,1, \ldots, 198$, on pose $S_{k}=\sum_{i=0}^{198} a_{i} b_{k-i}$, avec $a_{j}=0$ et $b_{j}=0$ si $j<0$ ou $j>99$.
Est-il possible que les nombres $S_{0}, S_{1}, \ldots, S_{198}$ soient tous égaux?
|
Non. Raisonnons par l'absurde. En effet, comme $a_{0} b_{0}=a_{0} b_{99}+\cdots+a_{99} b_{0}$ où les $\cdots$ représentent des termes strictement positifs, on a $a_{0} b_{0}>a_{0} b_{99}$ donc $b_{0}>b_{99}$, et de même $a_{0}>a_{99}$. Par conséquent, $S_{0}=a_{0} b_{0}>a_{99} b_{99}=S_{198}$, ce qui est contradictoire.
Autre démonstration qui ne nécessite pas l'hypothèse de positivité (mais seulement le fait que $a_{99} \neq 0$ et $b_{99} \neq 0$ :
supposons que $S_{0}=S_{1}=\ldots=S_{198}=\alpha$.
Notons que $\alpha \neq 0$.
On pose $P(x)=a_{0}+a_{1} x+\ldots+a_{99} x^{99}$ et $Q(x)=b_{0}+b_{1} x+\ldots+b_{99} x^{99}$. Comme $P(x) Q(x)=S_{0}+S_{1} x+\ldots+S_{198} x^{198}=\alpha\left(1+x+\ldots+x^{198}\right)$
$=\alpha \frac{1-x^{199}}{1-x}$ pour $x \neq 1$, on constate que $P(x) Q(x) \neq 0$ pour tout $x \neq 1$. D'autre
part, on a $\alpha \neq 0$ puisque $P$ et $Q$ sont des polynômes non nuls, donc $P(1) Q(1)=199 \alpha \neq 0$.
Par conséquent, $P(x) Q(x) \neq 0$ pour tout réel $x$, et donc $P$ n'admet pas de racine réelle. Ceci contredit le fait que $P$ est de degré impair.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
d60a40a0-aa57-5bdd-9f11-1c51b579645f
| 605,236
|
1) Pierre distributes the integers $1,2, \ldots, 2012$ into two disjoint groups such that the sums of the elements in each group are equal.
Without even looking at the distribution chosen by Pierre, Clara claims that it is possible to eliminate two numbers from each group so that, in each group, the sums of the remaining elements are still equal.
Prove that Clara is right.
2) Pierre distributes the integers $1,2, \ldots, 20$ into two disjoint groups such that the sums of the elements in each group are equal.
Without even looking at the distribution chosen by Pierre, Clara claims that it is possible to eliminate two numbers from each group so that, in each group, the sums of the remaining elements are still equal.
Prove that, this time, Clara might have been better off looking before speaking.
|
We color the elements of group $G_{1}$ in red, and those of $G_{2}$ in blue. Without loss of generality, we can assume that 1 is red. When two consecutive integers are not in the same group, we say that we have an alternation.
- If we have at least four alternations, we can find the configuration ...rb...br...rb...br..., where the dots indicate that we remain on the same color, except possibly for the last segment. In the described situation, the conclusion is assured by eliminating the integers responsible for the first and fourth alternations (we cannot use the first two alternations because $c^{\prime}$ might be the same blue number involved).
- If we have exactly three alternations ...rb...br...rb... with at least two consecutive blues in the first blue segment, we can erase the numbers involved in the first two alternations. Similarly, if there are at least two consecutive reds in the second red segment, we can erase the numbers involved in the second and third alternations.
If we are not in one of these two cases, it means we have ...rbrb...., where the first group of dots represents only reds, and the second group of dots represents only blues. Let $k$ be the number of reds in this first segment. The sum of the red numbers is then $\frac{k(k+1)}{2}+(k+2)$, while the sum of all integers from 1 to 2012 is $2012 \times 2013 / 2$. Since the sum of the numbers in each group is the same, we must have $\frac{k(k+1)}{2}+(k+2) = 2012 \times 2012 / 4$, or equivalently, $k(k+3)+4 = 2012 \times 2013 / 2$. However, this equation has no solution modulo 3, which ensures that this configuration is ultimately not possible.
- If we have exactly two alternations, we must be in the configuration ....rb...br...., where the dots indicate that there are no color changes. If there are at least two blues, we can erase the numbers involved in the two alternations. Otherwise, there is only one blue, but then it must be equal to 1012539, which is impossible.
- If there is only one alternation, we are in the configuration ....rb... If, as above, we denote $k$ as the number of reds, we must have $\frac{k(k+1)}{2} = 1012539$, or $k(k+1) = 2025078$, which also has no integer solution (we can see this modulo 10).
Finally, in all cases, we can eliminate two numbers from each group so that, in each group, the respective sums of the remaining elements are equal.
2) For example, for $n=20$, we color the integers from 1 to 14 in red, and the others in blue. The sums of the two groups are equal, but if we eliminate two reds, the sum of the reds will decrease by at most $14+13=27$, while if we eliminate two blues, the sum of the blues will decrease by at least $15+16=31$. It is then impossible that after elimination, the two groups still have equal sums.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
1) Pierre répartit les entiers $1,2, \ldots, 2012$ en deux groupes disjoints dont les sommes respectives des éléments sont égales.
Sans même regarder la répartion choisie par Pierre, Clara affirme alors que l'on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.
Prouver que Clara a raison.
2) Pierre répartit les entiers $1,2, \ldots, 20$ en deux groupes disjoints dont les sommes respectives des éléments sont égales.
Sans même regarder la répartion choisie par Pierre, Clara affirme alors que l'on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.
Prouver que, cette fois, Clara aurait peut-être mieux fait de regarder avant de parler.
|
On colorie les éléments du groupe $G_{1}$ en rouge, et ceux de $G_{2}$ en bleu. Sans perte de généralité, on peut supposer que 1 est rouge. Lorsque deux entiers consécutifs ne sont pas dans le même groupe, on dit que l'on a une alternance.
- Si l'on a au moins quatre alternances, on peut trouver la configuration ...rb...br...rb...br..., où les pointillés indiquent toujours que l'on reste sur la même couleur, sauf peut-être pour le dernier paquet. Dans la situation décrite, la conclusion est assurée en éliminant les entiers responsables des première et quatrième alternances (on ne peut utiliser les deux premières alternances car $c^{\prime}$ est peut-être le même nombre bleu qui est concerné).
- Si l'on a exactement trois alternances ...rb...br...rb... avec au moins deux bleus successifs dans le premier paquet de bleus, on peut effacer les nombres impliqués dans les deux premières alternances. De même, s'il y a au moins deux rouges successifs dans le second paquet de rouges, on peut effacer les nombres impliqués dans les seconde et troisième alternances.
Si l'on n'est pas dans un de ces deux cas, c'est que l'on a ...rbrb...., où le premier groupe de pointillés ne désigne que des rouges, et le second groupe de pointillés ne désigne que des bleus. On appelle $k$ le nombre de rouges dans ce premier paquet. La somme des nombres rouges est alors $\frac{k(k+1)}{2}+(k+2)$, alors que la somme de tous les entiers de 1 à 2012 vaut $2012 \times 2013 / 2$. Puisque la somme des nombres dans chaque groupe est la même, on doit avoir $\frac{k(k+1)}{2}+(k+2)=$ $2012 \times 2012 / 4$, autrement dit, $k(k+3)+4=2012 \times 2013 / 2$. Or, cette équation n'a pas de solution modulo 3, ce qui assure que cette configuration n'est finalement pas possible.
- Si l'on a exactement deux alternances, on est forcément dans la configuration ....rb...br...., où les pointillés indiquent qu'il n'y a pas de changements de couleurs. S'il y a au moins deux bleus, on peut effacer les nombres impliqués dans les deux alternances. Sinon, c'est qu'il n'y a qu'un bleu, mais alors il doit être égal à 1012539, ce qui est impossible.
- S'il n'y a qu'une alternance, c'est que l'on est dans la configuration ....rb... Si, comme ci-dessus, on note $k$ le nombre de rouges, on doit avoir $\frac{k(k+1)}{2}=1012539$, soit $k(k+1)=2025078$ qui n'a pas non plus de solution entière (on peut le voir modulo 10).
Finalement, dans tous les cas, on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.
2) Par exemple, pour $n=20$, on colorie en rouge les entiers de 1 à 14 , et les autres en bleu. Les sommes des deux groupes sont égales, mais si l'on élimine deux rouges, la somme des rouges diminuera d'au plus $14+13=27$, alors que si on élimine deux bleus, la somme des bleus diminuera d'au moins $15+16=31$. Il est alors impossible qu'après élimination, les deux groupes aient encore des sommes égales.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
20bffca3-cec1-575e-82c6-7a9c5f55fdf9
| 605,249
|
Let $P(x)=x^{4}-x^{3}-3 x^{2}-x+1$. Show that there are infinitely many integers $n$ such that $P\left(3^{n}\right)$ is not prime.
|
We observe that $3^{2} \equiv-1(\bmod 5)$ and $3^{4} \equiv 1(\bmod 5)$. Let $n \geqslant 1$. Let $x=3^{4 n+1}$, then $x=\left(3^{4}\right)^{n} \times 3 \equiv 3(\bmod 5)$, so $P(x) \equiv 3^{4}-3^{3}-3^{3}-3+1 \equiv 1+3+3-3+1 \equiv 0$ $(\bmod 5)$.
On the other hand, $P(x)>x^{4}-x^{3}-3 x^{3}-x^{3}=x^{3}(x-5)>x-5>3^{4 n}-5>5$, so $P\left(3^{4 n+1}\right)$ is not prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $P(x)=x^{4}-x^{3}-3 x^{2}-x+1$. Montrer qu'il existe une infinité d'entiers $n$ tels que $P\left(3^{n}\right)$ ne soit pas premier.
|
On observe que $3^{2} \equiv-1(\bmod 5)$ et $3^{4} \equiv 1(\bmod 5)$. Soit $n \geqslant 1$. Soit $x=3^{4 n+1}$, alors $x=\left(3^{4}\right)^{n} \times 3 \equiv 3(\bmod 5)$, donc $P(x) \equiv 3^{4}-3^{3}-3^{3}-3+1 \equiv 1+3+3-3+1 \equiv 0$ $(\bmod 5)$.
D'autre part, $P(x)>x^{4}-x^{3}-3 x^{3}-x^{3}=x^{3}(x-5)>x-5>3^{4 n}-5>5$, donc $P\left(3^{4 n+1}\right)$ n'est $^{\prime}$ pas premier.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
bfa47a62-5d4d-560e-8b5a-af90d54065df
| 605,280
|
Let $ABC$ be a right triangle at $C$. Let $D$ be the foot of the altitude from $C$, and $Z$ the point on $[AB]$ such that $AC = AZ$. The bisector of $\widehat{BAC}$ intersects $(CB)$ and $(CZ)$ at $X$ and $Y$ respectively. Show that the four points $B, X, Y, D$ lie on the same circle.
|
$C A Z$ is isosceles at $A$ so $(A Y)$, which is the bisector of $\widehat{C A Z}$, is perpendicular to $(C Z)$. Therefore, $A D Y C$ is cyclic.
We then have $\widehat{D Y X}=180^{\circ}-\widehat{A Y D}=180^{\circ}-\widehat{A C D}=180^{\circ}-\widehat{X B D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $C$. Soient $D$ le pied de la hauteur issue de $C$, et $Z$ le point de $[A B]$ tel que $A C=A Z$. La bissectrice de $\widehat{B A C}$ coupe $(C B)$ et $(C Z)$ en $X$ et $Y$ respectivement. Montrer que les quatre points $B, X, Y, D$ sont sur un même cercle.
|
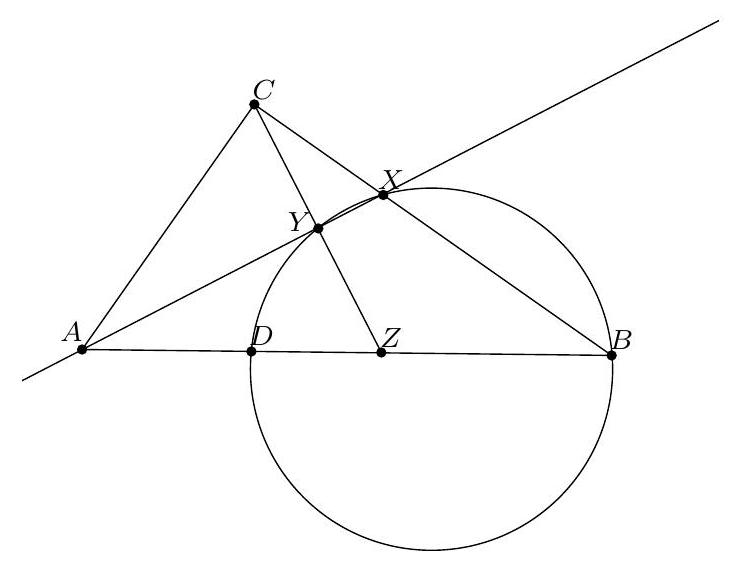
$C A Z$ est isocèle en $A$ donc $(A Y)$, qui est la bissectrice de $\widehat{C A Z}$, est perpendiculaire à $(C Z)$. Donc $A D Y C$ est cyclique.
On a alors $\widehat{D Y X}=180^{\circ}-\widehat{A Y D}=180^{\circ}-\widehat{A C D}=180^{\circ}-\widehat{X B D}$.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
0df08156-08ee-57a5-8c34-521637d730b8
| 605,290
|
Let $a \in [0 ; 1]$. We define the sequence $\left(x_{n}\right)$ by
$x_{0}=a$ and $x_{n+1}=1-\left|1-2 x_{n}\right|$, for all $n \geq 0$.
Prove that the sequence $\left(x_{n}\right)$ is periodic from a certain rank if and only if $a$ is a rational number.
(Note: we say that $\left(x_{n}\right)$ is periodic from a certain rank if there exist integers $T>0$ and $n \geqslant 0$ such that $x_{k+T}=x_{k}$ for all $k \geqslant n$.)
|
First, note that if $x_{n} \in [0 ; 1]$, then $-1 \leq 1 - 2x_{n} \leq 1$, hence $0 \leq x_{n+1} \leq 1$. Since $x_{0} \in [0 ; 1]$, we deduce by induction that $x_{n} \in [0 ; 1]$ for all $n \geq 0$.
- Suppose that $a$ is a rational number. An immediate induction ensures that, for all $n \geq 0$, $x_{n}$ is a rational number.
For all $n \geq 0$, let $x_{n} = \frac{p_{n}}{q_{n}}$, where $p_{n}$ and $q_{n}$ are positive integers and coprime. Then $x_{n+1} = \frac{q_{n} - |q_{n} - 2p_{n}|}{q_{n}}$, hence $q_{n+1} \leq q_{n}$.
The sequence $(q_{n})$, a decreasing sequence of natural numbers, is then stationary from a certain rank. Therefore, there exist integers $q > 0$ and $N \geq 0$ such that $q_{n} = q$ for all $n \geq N$.
For all $n \geq N$, the number $x_{n}$ is thus a rational number in $[0 ; 1]$ with denominator $q$. However, there are only finitely many such rationals, and there exist $n_{0} \geq N$ and $k > 0$ such that $x_{n_{0}+k} = x_{n_{0}}$. The recursive definition of $(x_{n})$ then ensures that $(x_{n})_{n \geq n_{0}}$ is periodic with period $k$.
- Now suppose that there exist integers $k > 0$ and $N \geq 0$ such that $x_{n+k} = x_{n}$ for all $n \geq N$.
For $n \geq 0$, we have $x_{n+1} = 2x_{n}$ or $x_{n+1} = 2 - 2x_{n}$ depending on whether $1 - 2x_{n}$ is positive or negative. We can thus write $x_{n+1} = a + 2b x_{n}$, where $a$ is an integer and $b = \pm 1$. It is then easy to prove by induction that, for all $i \geq 0$, there exists an integer $a_{i}$ such that $x_{N+i} = a_{i} + 2^{i} b_{i} x_{N}$ with $b_{i} = \pm 1$.
In particular, we have $x_{N} = x_{N+k} = a_{k} + 2^{k} b_{k} x_{N}$. Since $2^{k} b_{k} = \pm 2^{k} \neq 1$, this linear equation in $x_{N}$ has a unique solution $x_{N} = \frac{a_{k}}{1 - 2^{k} b_{k}}$. Thus, $x_{N}$ is a rational number. It is easy to verify that, for $m \geq 0$, if $x_{m+1}$ is rational, then $x_{m}$ is rational. Therefore, by downward induction, we deduce that $a = x_{0}$ is rational.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a \in[0 ; 1]$. On définit la suite $\left(x_{n}\right)$ par
$x_{0}=a$ et $x_{n+1}=1-\left|1-2 x_{n}\right|$, pour tout $n \geq 0$.
Prouver que la suite $\left(x_{n}\right)$ est périodique à partir d'un certain rang si et seulement si $a$ est un nombre rationnel.
(Note: on dit que $\left(x_{n}\right)$ est périodique à partir d'un certain rang s'il existe des entiers $T>0$ et $n \geqslant 0$ tels que $x_{k+T}=x_{k}$ pour tout $k \geqslant n$.)
|
On note tout d'abord que si $x_{n} \in[0 ; 1]$ alors $-1 \leq 1-2 x_{n} \leq 1$, d'où $0 \leq x_{n+1} \leq 1$. Puisque $x_{0} \in[0 ; 1]$, on déduit ainsi par récurrence que $x_{n} \in[0 ; 1]$ pour tout $n \geq 0$.
- Supposons que $a$ soit un nombre rationnel. Une récurrence immédiate assure alors que, pour tout $\mathrm{n} \geq 0, x_{n}$ est un nombre rationnel.
Pour tout $n \geq 0$, on pose $x_{n}=\frac{p_{n}}{q_{n}}$, avec $p_{n}$ et $q_{n}$ entiers positifs et premiers entre eux. Alors $x_{n+1}=\frac{q_{n}-\left|q_{n}-2 p_{n}\right|}{q_{n}}$, d'où $q_{n+1} \leq q_{n}$.
La suite $\left(q_{n}\right)$, suite décroissante d'entiers naturels, est alors stationnaire à partir d'un certain rang. Il existe donc des entiers $q>0$ et $N \geq 0$ tels que $q_{n}=q$ pour tout $n \geq N$.
Pour tout $n \geq N$, le nombre $x_{n}$ est donc un nombre rationnel de $[0 ; 1]$ dont le dénominateur vaut $q$. Or, il n'y a qu'un nombre fini de tels rationnels et il existe donc $n_{0} \geq N$ et $k>0$ tels que $x_{n_{0}+k}=x_{n_{0}}$. La définition par récurrence de $\left(x_{n}\right)$ assure alors que $\left(x_{n}\right)_{n \geq n_{0}}$ est périodique de période $k$.
- Supposons maintenant qu'il existe des entiers $k>0$ et $N \geq 0$ tels que $x_{n+k}=x_{n}$ pour tout $n \geq N$.
Pour $n \geq 0$, on a $x_{n+1}=2 x_{n}$ ou $x_{n+1}=2-2 x_{n}$ selon que $1-2 x_{n}$ est positif ou négatif. On peut donc poser $x_{n+1}=a+2 b x_{n}$, où $a$ est un entier et $b= \pm 1$. On prouve alors facilement par récurrence que, pour tout $i \geq 0$, il existe un entier $a_{i}$ tel que $x_{N+i}=a_{i}+2^{i} b_{i} x_{N}$ avec $b_{i}= \pm 1$.
En particulier, on a $x_{N}=x_{N+k}=a_{k}+2^{k} b_{k} x_{N}$. Puisque $2^{k} b_{k}= \pm 2^{k} \neq 1$, cette équation du premier degré en $x_{N}$ admet une unique solution $x_{N}=\frac{a_{k}}{1-2^{k} b_{k}}$. Ainsi, $x_{N}$ est un nombre rationnel. Or, il est facile de vérifier que, pour $m \geq 0$, si $x_{m+1}$ et rationnel alors $x_{m}$ est rationnel donc, par récurrence descendante, on déduit que $a=x_{0}$ est rationnel.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
1ede0432-ef44-5c7f-9203-644074487410
| 605,302
|
Prove that there exists an integer $n>0$ such that among the 2016 rightmost digits in the decimal representation of $2^{n}$, there are at least 1008 digits 9.
|
One can legitimately wonder when to find 9s to the right of the decimal representation of $2^{n}$. One might think it's when the power of 2 is slightly less than a power of 10. We will therefore look for numbers of the form $2^{n}+1$ that are divisible by 5 to a high power. For such a number, by multiplying by the appropriate power of 2, we will obtain a number of the form $2^{k}\left(2^{n}+1\right)=2^{n+k}+2^{k}$ divisible by a large power of 10, and it will suffice to subtract the $2^{k}$ in question to obtain the desired power of 2.
Lemma. For any integer $k \geq 1$, the number $a_{k}=2^{2 \cdot 5^{k-1}}+1$ is divisible by $5^{k}$.
Proof of the lemma. We proceed by induction on $k$:
- For $k=1$, we have $a_{1}=5$ which is indeed divisible by 5.
- Suppose the result is established for some $k \geq 1$.
Let $a=4^{5^{k-1}}=a_{k}-1$. We note that then $a=-1 \bmod 5$.
We have $a_{k+1}=4^{5^{k}}+1=a^{5}+1=(a+1)\left(a^{4}-a^{3}+a^{2}-a+1\right)$.
By the induction hypothesis, we have $a+1=0 \bmod 5^{k-1}$.
On the other hand, since $a=-1 \bmod 5$, we have $a^{4}-a^{3}+a^{2}-a+1=0 \bmod 5$.
Thus, $a_{k+1}$ is divisible by $5^{k}$, which completes the induction.
As expected, we deduce that, for all $k \geq 1$, the number $2^{2 k}\left(2^{2 \cdot 5^{2 k-1}}+1\right)=2^{2 k+2 \cdot 5^{2 k-1}}+2^{2 k}$ is divisible by $10^{2 k}$. Its decimal representation therefore ends with at least $2 k$ zeros.
Now, for $k \geq 1$, we have $2^{2 k}<10^{k}$. Thus, the decimal representation of $2^{2 k} n^{\prime}$ uses no more than $k$ digits. Consequently, among the $2 k$ rightmost digits of the decimal representation of $2^{2 k+2 \cdot 5^{2 k-1}}$, there are at least $k$ digits 9.
The desired result corresponds to $k=1008$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prouver qu'il existe un entier $n>0$ tel que parmi les 2016 chiffres de droite dans $l^{\prime}$ écriture décimale de $2^{n}$, il y a au moins 1008 chiffres 9.
|
On peut légitimement se demander quand trouver des 9 à la droite de l'écriture décimale de $2^{n}$. On peut penser que c'est quand la puissance de 2 est légèrement inférieure à une puissance de 10 . On va donc chercher des nombres de la forme $2^{n}+1$ qui sont divisibles par 5 selon une puissance élevée. Pour un tel nombre, en multipliant par la puissance de 2 adéquate, on obtiendra un nombre de la forme $2^{k}\left(2^{n}+1\right)=2^{n+k}+2^{k}$ divisible par une grande puissance de 10 , et il suffira de retrancher le $2^{k}$ en question pour obtenir le type de puissance de 2 cherché.
Lemme. Pour tout entier $k \geq 1$, le nombre $a_{k}=2^{2 \cdot 5^{k-1}}+1$ est divisible par $5^{k}$.
Preuve du lemme. On raisonne par récurrence sur $k$ :
- Pour $k=1$, on a $a_{1}=5$ qui est bien divisible par 5.
- Supposons le résultat établi pour un certain $k \geq 1$.
Posons $a=4^{5^{k-1}}=a_{k}-1$. On note qu'alors $a=-1 \bmod 5$.
On a alors $a_{k+1}=4^{5^{k}}+1=a^{5}+1=(a+1)\left(a^{4}-a^{3}+a^{2}-a+1\right)$.
D'après l'hypothèse de récurrence, on a $a+1=0 \bmod 5^{k-1}$.
D'autre part, puisque $a=-1 \bmod 5$, on a $a^{4}-a^{3}+a^{2}-a+1=0 \bmod 5$.
Ainsi, $a_{k+1}$ est divisible par $5^{k}$, ce qui achève la récurrence.
Comme prévu, on en déduit que, pour tout $k \geq 1$, le nombre $2^{2 k}\left(2^{2 \cdot 5^{2 k-1}}+1\right)=2^{2 k+2 \cdot 5^{2 k-1}}+2^{2 k}$ est divisible par $10^{2 k}$. Son écriture décimale se termine donc par au moins $2 k$ chiffres 0 .
Or, pour $k \geq 1$, on a $2^{2 k}<10^{k}$. Ainsi, l'écriture décimale de $2^{2 k} n^{\prime}$ utilise pas plus de $k$ chiffres. Par suite, parmi les $2 k$ chiffres de droite de l'écriture décimale de $2^{2 k+2 \cdot 5^{2 k-1}}$, il y a au moins $k$ chiffres 9.
Le résultat demandé correspond à $k=1008$.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
437bd1e6-cdf2-5ef4-bdef-42c4c4fd03b3
| 605,310
|
Let $n \geq 5$ be an integer, and $E_{1}, E_{2}, \ldots, E_{2 n-1}$ be distinct two-element subsets of $\{1,2, \ldots, n\}$.
Prove that among the $2 n-1$ subsets $E_{i}$, one can choose $n$ such that the union of these $n$ subsets contains no more than $\frac{2}{3} n+1$ elements.
|
We will prove by induction on $k \leq \frac{2 n-1}{3}$ that we can always eliminate $3 k$ of the $2 n-1$ parts so that the union of the remaining $2 n-1-3 k$ does not contain more than $n-k$ elements.
The case $k=0$ is immediate.
Now let $1 \leq k \leq \frac{2 n-1}{3}$. Suppose we have eliminated $3(k-1)$ of the $E_{i}$ so that the union $U_{k-1}$ of the remaining $2 n-1-3(k-1)$ does not contain more than $n-k+1$ elements.
Each of the $E_{i}$ contains two elements. From $2(2 n-1-3(k-1)) < 4(n-k+1)$, we deduce that there exists an element $x$ in $U_{k-1}$ that belongs to at most three of the $E_{i}$ that form $U_{k-1}$. Thus, by eliminating three more of the $E_{i}$ not already eliminated, including all those that contain $x$, this ensures that the union of the remaining $n-3 k$ does not contain more than $n-k$ elements.
This completes the induction.
For $k=\left\lfloor\frac{n-1}{3}\right\rfloor$, we have $n-\left\lfloor\frac{n-1}{3}\right\rfloor \leq n-\frac{n-1}{3}=\frac{2}{3} n+1$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geq 5$ un entier, et $E_{1}, E_{2}, \ldots, E_{2 n-1}$ des parties distinctes à deux éléments de $\{1,2, \ldots, n\}$.
Prouver que, parmi les $2 n-1$ parties $E_{i}$, on peut en choisir $n$ de sorte que la réunion de ces $n$ parties ne contienne pas plus de $\frac{2}{3} n+1$ éléments.
|
On va prouver par récurrence sur $k \leq \frac{2 n-1}{3}$ que l'on peut toujours éliminer $3 k$ des $2 n-1$ parties de sorte que la réunion des $2 n-1-3 k$ restantes ne contienne pas plus de $n-k$ éléments.
Le cas $k=0$ est immédiat.
Soit maintenant $1 \leq k \leq \frac{2 n-1}{3}$. On suppose que l'on a éliminé $3(k-1)$ des $E_{i}$ de sorte que la réunion $U_{k-1}$ des $2 n-1-3(k-1)$ autres ne contienne pas plus de $n-k+1$ éléments.
Chacun des $E_{i}$ contient deux éléments. De $2(2 n-1-3(k-1))<4(n-k+1)$, on déduit alors qu'il existe un élément $x$ de $U_{k-1}$ qui n'appartient qu'à au plus trois de $E_{i}$ qui forment $U_{k-1}$. Ainsi, en éliminant encore trois des $E_{i}$ non déà éliminés, dont tous ceux qui contiennent $x$, cela assure que la réunion des $n-3 k$ restants ne contient pas plus de $n-k$ éléments.
Cela achève la récurrence.
Pour $k=\left\lfloor\frac{n-1}{3}\right\rfloor$, on a $n-\left\lfloor\frac{n-1}{3}\right\rfloor \leq n-\frac{n-1}{3}=\frac{2}{3} n+1$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
11a30336-511f-537a-a3bd-f48269785af0
| 605,321
|
Let $ABC$ be a triangle. We denote $P$ as the symmetric point of $B$ with respect to $(AC)$ and $Q$ as the symmetric point of $C$ with respect to $(AB)$.
Let $T$ be the intersection between $(PQ)$ and the tangent at $A$ to the circumcircle of $(APQ)$.
Show that the symmetric point of $T$ with respect to $A$ lies on $(BC)$.
|
Let $B'$ and $C'$ be the symmetrical points of $B$ and $C$ with respect to $A$. Since triangle $A B' P$ is isosceles at $A$, we have $\widehat{A B' P} = \frac{1}{2} \left(180^{\circ} - \widehat{B' A P}\right) = \frac{1}{2} \widehat{P A B} = \widehat{B A C}$, so $\left(B' P\right) \parallel (A C)$.
Similarly, $\left(C' Q\right) \parallel (A B)$, so the lines $\left(B' P\right)$ and $\left(C' Q\right)$ intersect. Let $A'$ be their point of intersection.
Triangles $A' B' C'$ and $A C B$ are similar because their sides are pairwise parallel.
Moreover, $A B' P$ and $A C' Q$ are similar because $\widehat{A B' P} = \widehat{A C' Q}$ and because these two triangles are isosceles at $A$.
Now let's prove the required assertion. By symmetry with respect to $A$, it is equivalent to showing that $T, B', C'$ are collinear. Applying Menelaus' theorem in $A' P Q$, this is equivalent to
$$
\frac{B' P}{B' A'} \times \frac{C' A'}{C' Q} \times \frac{T Q}{T P} = 1 \quad (E)
$$
Since $T A Q$ and $T P A$ are similar, we have $\frac{T A}{T P} = \frac{T Q}{T A} = \frac{A Q}{A P}$, so $\frac{T Q}{T P} = \frac{A Q^2}{A P^2} = \frac{A C^2}{A B^2}$.
Since $A' B' C'$ and $A C B$ are similar, we have $\frac{C' A'}{B' A'} = \frac{A B}{A C}$.
Since $A B' P$ and $A C' Q$ are similar, we have $\frac{B' P}{C' Q} = \frac{A P}{A Q} = \frac{A B}{A C}$.
We deduce that $(E)$ is true.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $P$ le symétrique de $B$ par rapport à $(A C)$ et $Q$ le symétrique de $C$ par rapport à $(A B)$.
Soit $T$ l'intersection entre $(P Q)$ et la tangente en $A$ au cercle circonscrit à $(A P Q)$.
Montrer que le symétrique de $T$ par rapport à $A$ appartient à $(B C)$.
|
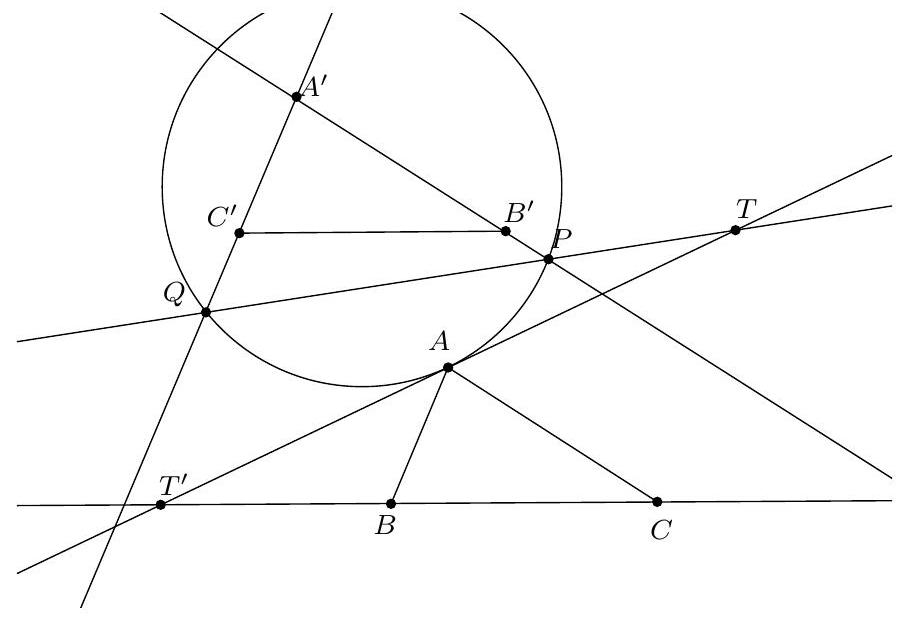
Soient $B^{\prime}$ et $C^{\prime}$ les symétriques de $B$ et $C$ par rapport à $A$. Comme le triangle $A B^{\prime} P$ est isocèle en $A$, on a $\widehat{A B^{\prime} P}=\frac{1}{2}\left(180^{\circ}-\widehat{B^{\prime} A P}\right)=\frac{1}{2} \widehat{P A B}=\widehat{B A C}$, donc $\left(B^{\prime} P\right) \|(A C)$.
De même, $\left(C^{\prime} Q\right) \|(A B)$, donc les droites $\left(B^{\prime} P\right)$ et $\left(C^{\prime} Q\right)$ sont sécantes. Notons $A^{\prime}$ leur point d'intersection.
Les triangles $A^{\prime} B^{\prime} C^{\prime}$ et $A C B$ sont semblables car leurs côtés sont deux à deux parallèles.
De plus, $A B^{\prime} P$ et $A C^{\prime} Q$ sont semblables car $\widehat{A B^{\prime} P}=\widehat{A C^{\prime} Q}$ et car ces deux triangles sont isocèles en $A$.
Montrons maintenant l'assertion demandée. Par symétrie par rapport à $A$, il revient au même de montrer que $T, B^{\prime}, C^{\prime}$ sont alignés. En appliquant le théorème de Ménélaüs dans $A^{\prime} P Q$, cela équivaut à
$$
\frac{B^{\prime} P}{B^{\prime} A^{\prime}} \times \frac{C^{\prime} A^{\prime}}{C^{\prime} Q} \times \frac{T Q}{T P}=1 \quad(E)
$$
Comme $T A Q$ et $T P A$ sont semblables, on a $\frac{T A}{T P}=\frac{T Q}{T A}=\frac{A Q}{A P}$, donc $\frac{T Q}{T P}=\frac{A Q^{2}}{A P^{2}}=\frac{A C^{2}}{A B^{2}}$.
Comme $A^{\prime} B^{\prime} C^{\prime}$ et $A C B$ sont semblables, on a $\frac{C^{\prime} A^{\prime}}{B^{\prime} A^{\prime}}=\frac{A B}{A C}$.
Comme $A B^{\prime} P$ et $A C^{\prime} Q$ sont semblables, on a $\frac{B^{\prime} P}{C^{\prime} Q}=\frac{A P}{A Q}=\frac{A B}{A C}$.
On en déduit que $(E)$ est vraie.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
0e5b7fc3-9751-57fc-b76b-381a840d1ab0
| 605,329
|
Let $a, b, c, d$ be real numbers such that $0 \leqslant a \leqslant b \leqslant c \leqslant d$. Show that
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geqslant a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
A first idea is to consider the "symmetric sums $\gg$ each other $S_{1}=a b^{3}+b^{3}+c d^{3}+d a^{3}$ and $S_{2}=a^{3} b+b^{3} c+c^{3} d+d^{3} a$. We then observe that
$S_{1}-S_{2}=\left(d^{3}-b^{3}\right)(c-a)+\left(c^{3}-a^{3}\right)(b-d)=(d-b)(c-a)\left(d^{2}+bd+d^{2}-c^{2}-ac-a^{2}\right) \geqslant 0$.
The Cauchy-Schwarz inequality then indicates that $S_{1}^{2} \geqslant S_{1} S_{2} \geqslant\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}$, which concludes.
## Exercises of Group A - Statements and Solutions
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c, d$ des réels tels que $0 \leqslant a \leqslant b \leqslant c \leqslant d$. Montrer que
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geqslant a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
Une première idée est de considérer les sommes «symétriques $\gg$ l'une de l'autre $S_{1}=a b^{3}+b^{3}+c d^{3}+d a^{3}$ et $S_{2}=a^{3} b+b^{3} c+c^{3} d+d^{3} a$. On constate alors que
$S_{1}-S_{2}=\left(d^{3}-b^{3}\right)(c-a)+\left(c^{3}-a^{3}\right)(b-d)=(d-b)(c-a)\left(d^{2}+b d+d^{2}-c^{2}-a c-a^{2}\right) \geqslant 0$.
L'inégalité de Cauchy-Schwarz indique alors que $S_{1}^{2} \geqslant S_{1} S_{2} \geqslant\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}$, ce qui conclut.
## Exercices du groupe A - Énoncés et solutions
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
e7243e7b-5fbc-5390-9011-f542b22816fe
| 605,376
|
Let $n$ be an odd natural number, and let $a_{1}, \ldots, a_{n}$ be non-zero natural numbers. We denote $A$ as the product of the integers $a_{i}$, and $d$ as their greatest common divisor.
Show that
$$
\operatorname{GCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right) \leqslant 2 d^{n}
$$
|
For all $i$, we set $b_{i}=a_{i} / d$, so that $\operatorname{PGCD}\left(b_{1}, \ldots, b_{n}\right)=1$, and we also set $B=b_{1} \times \ldots \times b_{n}$ and $\Delta=\operatorname{PGCD}\left(b_{1}^{n}+B, b_{2}^{n}+B, \ldots, b_{n}^{n}+B\right)$. Then $\operatorname{PGCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right)=d^{n} \times \Delta$, and it remains to prove that $\Delta \leqslant 2$.
We then consider a potential prime factor $p$ of $\Delta$. If $p$ divides one of the integers $b_{i}$, then it also divides $B$, so it divides each integer $b_{j}$, which is absurd. Therefore, $p$ does not divide any of the integers $b_{i}$, and does not divide $B$ either. This shows that $\Delta$ is coprime with $B$. Since $b_{1}^{n} \equiv b_{2}^{n} \equiv \ldots \equiv b_{n}^{n}=-B(\bmod \Delta)$, then $B^{n} \equiv b_{1}^{n} \times \ldots \times b_{n}^{n} \equiv(-1)^{n} B^{n} \equiv-B^{n}$ $(\bmod \Delta)$. Therefore, $\Delta$ divides $2 B^{n}$. We conclude that $\Delta$ divides 2, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier naturel impair, et soit $a_{1}, \ldots, a_{n}$ des entiers naturels non nuls. On note $A$ le produit des entiers $a_{i}$, et $d$ leur plus grand diviseur commun.
Montrer que
$$
\operatorname{PGCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right) \leqslant 2 d^{n}
$$
|
Pour tout $i$, on pose $b_{i}=a_{i} / d$, de sorte que $\operatorname{PGCD}\left(b_{1}, \ldots, b_{n}\right)=1$, et on pose également $B=b_{1} \times \ldots \times b_{n}$ et $\Delta=\operatorname{PGCD}\left(b_{1}^{n}+B, b_{2}^{n}+B, \ldots, b_{n}^{n}+B\right)$. Alors $\operatorname{PGCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right)=d^{n} \times \Delta$, et il reste à démontrer que $\Delta \leqslant 2$.
On considère alors un éventuel facteur premier $p$ de $\Delta$. Si $p$ divise un des entiers $b_{i}$, alors il divise $B$ également, donc il divise chaque entier $b_{j}$, ce qui est absurde. Par conséquent, $p$ ne divise aucun des entiers $b_{i}$, et ne divise pas $B$ non plus. Cela montre que $\Delta$ est premier avec $B$. Or, puisque $b_{1}^{n} \equiv b_{2}^{n} \equiv \ldots \equiv b_{n}^{n}=-B(\bmod \Delta)$, alors $B^{n} \equiv b_{1}^{n} \times \ldots \times b_{n}^{n} \equiv(-1)^{n} B^{n} \equiv-B^{n}$ $(\bmod \Delta)$. Par conséquent, $\Delta$ divise $2 \mathrm{~B}^{n}$. On en déduit que $\Delta$ divise 2 , ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
98aeecc1-fe8e-5bc0-9287-a16449240a7a
| 605,387
|
Let $ABC$ be a non-isosceles acute triangle. Let $O$ be the center of the circumcircle of $ABC$ and $H$ the orthocenter of $ABC$. Let $P$ and $Q$ be the points of intersection of $(AO)$ with $(BH)$ and $(CH)$, respectively.
Show that the center of the circumcircle of $P Q H$ lies on a median of the triangle $A B C$.
|
Let $\Omega$ be the circumcircle of $ABC$, $\omega$ the circumcircle of $PQH$, and $X$ the center of $\omega$. Since $B$ and $C$ play symmetric roles, we will show that $X$ lies on the median from $A$. Let $M$ be the intersection of the lines $(AX)$ and $(BC)$: we will show that $M$ is the midpoint of $[BC]$, that is, $\widehat{CMO}=90^{\circ}$.
First, a simple angle chasing shows that $\widehat{QHP}=\widehat{CAB}$, $\widehat{HPQ}=\widehat{ABC}$, and $\widehat{PQH}=\widehat{PHA}=\widehat{BCA}$. The triangles $ABC$ and $HPQ$ are therefore similar, and there exists a similarity $s$ such that $s(A)=H$, $s(B)=P$, $s(C)=Q$, and $s(O)=X$.
Furthermore, since $\widehat{PQH}=\widehat{PHA}$, we know that $(AH)$ is tangent to $\omega$ at $H$. Consequently, if we set $S=s^{-1}(\mathcal{A})$, then we know that $S$ is the intersection of $(BC)$ and the tangent to $\Omega$ at $A$. Since $s$ maps $BSO$ to $PAX$, we deduce that $\widehat{MSO}=\widehat{BSO}=\widehat{XAP}=\widehat{MAO}$, so the points $M, S, O$, and $A$ are concyclic. Now, $\widehat{SAO}=90^{\circ}$. It follows that $\widehat{SMO}=90^{\circ}$ as well, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle non isocèle. Soit O le centre du cercle circonscrit à $A B C$ et $H$ l'orthocentre de $A B C$. Soit $P$ et $Q$ les points d'intersection respectifs de ( $A O)$ avec (BH) et (CH).
Montrer que le centre du cercle circonscrit à $P Q H$ se situe sur une médiane du triangle $A B C$.
|
Soit $\Omega$ le cercle circonscrit à $A B C, \omega$ le cercle circonscrit à PQH , et $X$ le centre de $\omega$. Puisque $B$ et $C$ jouent des rôles symétriques, on va montrer que $X$ se trouve sur la médiane issue de $A$. Soit alors $M$ le point d'intersection des droites $(A X)$ et (BC) : montrons que $M$ est le milieu de $[B C]$, c'est-à-dire que $\widehat{C M O}=90^{\circ}$.
Tout d'abord, une simple chasse aux angles montre que $\widehat{\mathrm{QHP}}=\widehat{\mathrm{CAB}}, \widehat{\mathrm{HPQ}}=\widehat{\mathrm{ABC}}$ et $\widehat{\mathrm{PQH}}=$ $\widehat{P H A}=\widehat{B C A}$. Les triangles $A B C$ et $H P Q$ sont donc semblables, et il existe une similitude $s$ telle que $s(A)=H, s(B)=P, s(C)=Q$ et $s(O)=X$.
$D^{\prime}$ autre part, puisque $\widehat{P Q H}=\widehat{P H A}$ on sait que $(A H)$ est tangente à $\omega$ en $H$. Par conséquent, si on pose $S=s^{-1}(\mathcal{A})$, alors on sait que $S$ est le point d'intersection de (BC) et de la tangente à $\Omega$ en $A$. Puisque s envoie $B S O$ sur $P A X$, on en déduit que $\widehat{M S O}=\widehat{B S O}=\widehat{\mathrm{XAP}}=\widehat{\mathrm{MAO}}$, donc que les points $M, S, O$ et $A$ sont cocycliques. Or, $\widehat{S A O}=90^{\circ}$. Il s'ensuit que $\widehat{S M O}=90^{\circ}$ également, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
f7b0aac1-6abc-5134-a351-3c275c6f16b8
| 605,407
|
Let $ABC$ be a triangle. We denote $L, M, N$ as the midpoints of $[BC], [CA]$, and $[AB]$. Let $(d)$ be the tangent at $A$ to the circumcircle of $ABC$. The line $(LM)$ intersects $(d)$ at $P$, and the line $(LN)$ intersects $(d)$ at $Q$. Show that $(CP)$ and $(BQ)$ are parallel.
|
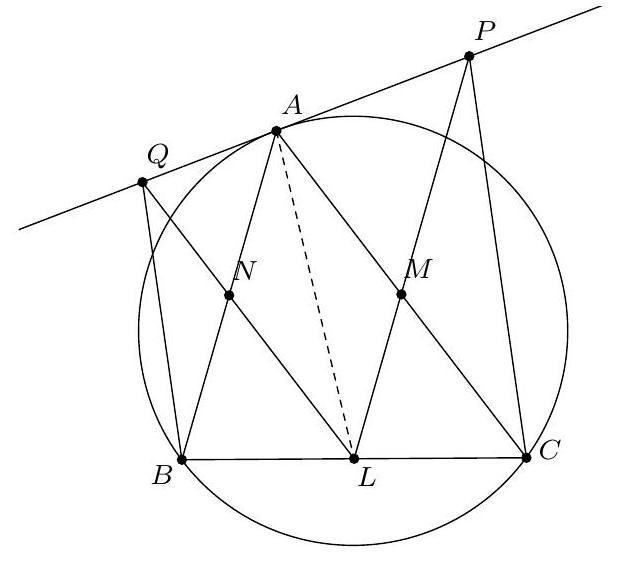
Since $(A Q, A B) = (C A, C B) = (L Q, L B)$, points $A, Q, B, L$ are concyclic, and similarly, points $A, P, C, M$ are concyclic. Therefore, $(C P, B C) = (C P, C L) = (A P, A L) = (A Q, A L) = (B Q, B L) = (B Q, B C)$, so lines $(C P)$ and $(B Q)$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $L, M, N$ les milieux de $[B C],[C A]$ et $[A B]$. Notons $(d)$ la tangente en $A$ au cercle circonscrit à $A B C$. La droite $(L M)$ coupe $(d)$ en $P$, et la droite $(L N)$ coupe $(d)$ en $Q$. Montrer que $(C P)$ et $(B Q)$ sont parallèles.
|

On a $(A Q, A B)=(C A, C B)=(L Q, L B)$ donc $A, Q, B, L$ sont cocycliques, et de même $A, P, C, M$ sont cocycliques. On a donc $(C P, B C)=(C P, C L)=(A P, A L)=(A Q, A L)=(B Q, B L)=$ $(B Q, B C)$, donc $(C P)$ et $(B Q)$ sont parallèles.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
c62af5d0-2751-54ce-be39-1357fda3b4e9
| 605,425
|
Let $p$ and $n$ be strictly positive integers, with $p$ prime, and $n \geqslant p$. Suppose that $1+n p$ is a perfect square. Show that $n+1$ is a sum of $p$ non-zero perfect squares (not necessarily distinct).
|
Let $k$ be such that $1+n p=k^{2}$, then $n p=(k-1)(k+1)$.
First case: $p$ divides $k-1$. Then we can write $k-1=p \ell$, so $k=p \ell+1$. By substituting into the equation, we get that $n+1=p \ell^{2}+2 \ell+1=(p-1) \ell^{2}+(\ell+1)^{2}$.
Second case: $p$ divides $k+1$. Using the same method, we get $n+1=p \ell^{2}-2 \ell+1=(p-1) \ell^{2}+(\ell-1)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $p$ et $n$ des entiers strictement positifs, avec $p$ premier, et $n \geqslant p$. On suppose que $1+n p$ est un carré parfait. Montrer que $n+1$ est une somme de $p$ carrés parfaits non nuls (non nécessairement distincts).
|
Soit $k$ tel que $1+n p=k^{2}$, alors $n p=(k-1)(k+1)$.
Premier cas : $p$ divise $k-1$. Alors on peut écrire $k-1=p \ell$, donc $k=p \ell+1$. En reportant dans l'égalité, on obtient que $n+1=p \ell^{2}+2 \ell+1=(p-1) \ell^{2}+(\ell+1)^{2}$.
Deuxième cas : $p$ divise $k+1$. On obtient avec la même méthode $n+1=p \ell^{2}-2 \ell+1=$ $(p-1) \ell^{2}+(\ell-1)^{2}$.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
a97d7d19-0bee-5777-80a0-1f625ec5efad
| 605,435
|
Let $ABC$ be an acute triangle, and let $P$ be a point located inside the triangle $ABC$. Let $D$ be the midpoint of the segment $[PC]$, $E$ the intersection point of the lines $(AP)$ and $(BC)$, and $Q$ the intersection point of the lines $(BP)$ and $(DE)$. Show that, if the angles $\widehat{PAC}$ and $\widehat{PCB}$ are equal, then $\sin (\widehat{BCQ})=\sin (\widehat{BAP})$.
|
Let $R$ be the intersection point of the lines $(C Q)$ and $(A P)$. It suffices to prove the equality of the angles $(C B, C Q)=(A B, A R)$. To do this, it suffices to prove that the points $B, C, A, R$ are concyclic, that is, $(B R, B C)=(A R, R C)$. Since $(A R, A C) = (C P, C B)$, it suffices to prove that $(B R, B C)=(C P, C B)$, hence that the lines $(B R)$ and $(P C)$ are parallel.
For this last point, one can use that if $X=(C P) \cap(B R)$ then $(X, D, P, C)$ is a harmonic division. One can also do without projective geometry as follows:
We use Ceva's theorem in the triangle $P C E$, since the lines $(P B)$, $(D E)$, and $(R C)$ are concurrent at $Q$, with $R \in(P E)$ and $B \in(C E)$. We deduce that
$$
1=\frac{C B}{E B} \cdot \frac{P D}{C D} \cdot \frac{R E}{R P}=\frac{C B}{E B} \cdot \frac{R E}{R P}
$$
that is,
$$
\frac{R E}{E B}=\frac{R P}{C B}
$$
By applying the converse of Thales' theorem to the triangles $B R E$ and $C P E$, we deduce from this last equality that the lines $(B R)$ and $(P C)$ are indeed parallel, which concludes.
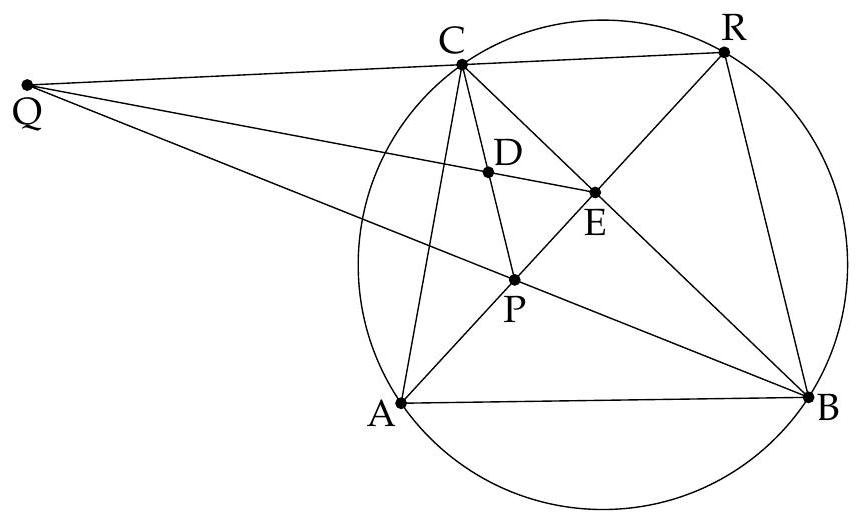
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle, et soit $P$ un point situé à l'intérieur du triangle $A B C$. Soit $D$ le milieu du segment $[P C], E$ le point d'intersection des droites $(A P)$ et $(B C)$, et $Q$ le point d'intersection des droites $(B P)$ et $(D E)$. Montrer que, si les angles $\widehat{P A C}$ et $\widehat{P C B}$ sont égaux, alors $\sin (\widehat{B C Q})=\sin (\widehat{B A P})$.
|
Soit $R$ le point d'intersection des droites $(C Q)$ et $(A P)$. Il suffit de prouver l'égalité des angles de droites $(C B, C Q)=(A B, A R)$. Pour ce faire, il suffit de prouver que les points $B, C, A, R$ sont cocycliques, c'est-à-dire que $(B R, B C)=(A R, R C)$. Comme $(A R, A C)=$ $(C P, C B)$, il suffit de prouver que $(B R, B C)=(C P, C B)$, donc que les droites $(B R)$ et $(P C)$ sont parallèles.
Pour ce dernier point, on peut utiliser que si $X=(C P) \cap(B R)$ alors $(X, D, P, C)$ est une division harmonique. On peut également se passer de géométrie projective comme suit :
On utilise le théorème de Ceva dans le triangle $P C E$, puisque les droites $(P B),(D E)$ et $(R C)$ sont concourantes en $Q$, avec $R \in(P E)$ et $B \in(C E)$. On en déduit que
$$
1=\frac{C B}{E B} \cdot \frac{P D}{C D} \cdot \frac{R E}{R P}=\frac{C B}{E B} \cdot \frac{R E}{R P}
$$
c'est-à-dire
$$
\frac{R E}{E B}=\frac{R P}{C B}
$$
En appliquant la réciproque du théorème de Thalès aux triangles $B R E$ et $C P E$, on déduit de cette dernière égalité que les droites $(B R)$ et $(P C)$ sont bien parallèles, ce qui conclut.

|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
195a7a94-00aa-5d7b-8389-152792d87599
| 605,457
|
Let $n \geqslant 2$ be a natural number. We are given $2n$ balls. On each of these balls, a number is written. We assume that whenever the balls are grouped into $n$ pairs, two of these pairs have the same sum.
(a) Show that four of these balls bear the same number.
(b) Show that the number of distinct values written on the balls is $\leqslant n-1$.
|
(a) We denote $a_{1} \geqslant a_{2} \geqslant \cdots \geqslant a_{2 n}$ the values taken by the $2 n$ balls in descending order. We pair them as follows: $\left(a_{1}, a_{2}\right),\left(a_{3}, a_{4}\right), \ldots$ Since there exist $i<j$ odd such that $a_{i}+a_{i+1}=a_{j}+a_{j+1}$, and since $a_{i} \geqslant a_{i+1} \geqslant a_{j} \geqslant a_{j+1}$, we have $a_{i}=a_{i+1}=a_{j}=a_{j+1}$.
(b) Suppose there are at least $n$ distinct values, which we order in descending order $b_{1}>b_{2}>\cdots>b_{n}$. We order the other balls in descending order $c_{1} \geqslant \cdots \geqslant c_{n}$. We form the $n$ pairs $\left(b_{i}, c_{i}\right)$, and we observe that if $i<j$ then $b_{i}+c_{i}>b_{j}+c_{j}$, which contradicts the fact that two of these sums must be equal.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geqslant 2$ un entier naturel. On se donne $2 n$ boules. Sur chacune de ces boules est écrit un nombre. On suppose que, à chaque fois que l'on regroupe les boules en $n$ paires, deux de ces paires ont la même somme.
(a) Montrer que quatre de ces boules comportent le même nombre.
(b) Montrer que le nombre de valeurs distinctes inscrites sur les boules est $\leqslant n-1$.
|
(a) On note $a_{1} \geqslant a_{2} \geqslant \cdots \geqslant a_{2 n}$ les valeurs prises par les $2 n$ boules dans l'ordre décroissant. On les apparie ainsi : $\left(a_{1}, a_{2}\right),\left(a_{3}, a_{4}\right), \ldots$ Comme il existe $i<j$ impairs tels que $a_{i}+a_{i+1}=a_{j}+a_{j+1}$, et comme $a_{i} \geqslant a_{i+1} \geqslant a_{j} \geqslant a_{j+1}$, on a $a_{i}=a_{i+1}=a_{j}=a_{j+1}$.
(b) Supposons qu'il y ait au moins $n$ valeurs distinctes, que l'on ordonne par ordre décroissant $b_{1}>b_{2}>\cdots>b_{n}$. On ordonne les autres boules dans l'ordre décroissant $c_{1} \geqslant \cdots \geqslant c_{n}$. On forme les $n$ paires $\left(b_{i}, c_{i}\right)$, et on constate que si $i<j$ alors $b_{i}+c_{i}>b_{j}+c_{j}$, ce qui contredit le fait que deux de ces sommes doivent être égales.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
377c3619-49d2-5920-9e6f-fbb280282280
| 605,494
|
Let $A B C D$ be a convex quadrilateral with area $S$. We denote $a=A B, b=B C, c=C D$ and $d=D A$. For any permutation $x, y, z, t$ of $a, b, c, d$, show that
$$
S \leqslant \frac{1}{2}(x y+z t)
$$
|
If $x$ and $y$ are adjacent, without loss of generality, we need to show that $S \leqslant \frac{1}{2}(a b+c d)$. This follows from $S_{A B C}=\frac{1}{2} A B \cdot B C \cdot \sin \widehat{A B C} \leqslant \frac{1}{2} a b$, and similarly $S_{C D A} \leqslant \frac{1}{2} c d$. If $x$ and $y$ are opposite sides, we need to show that $S \leqslant \frac{1}{2}(a c+b d)$. Let $A^{\prime}$ be the symmetric point of $A$ with respect to the perpendicular bisector of $[B D]$. Then $B A^{\prime} D$ is isometric to $D A B$. We apply the above to $A^{\prime} B C D$, which gives $S=S_{B A D}+S_{B C D}=S_{B A^{\prime} D}+S_{B C D}=S_{A^{\prime} B C D} \leqslant \frac{1}{2}\left(A^{\prime} B \cdot B C+\right.$ $\left.C D \cdot D A^{\prime}\right)=\frac{1}{2}(a c+b d)$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $A B C D$ un quadrilatère convexe d'aire $S$. On note $a=A B, b=B C, c=C D$ et $d=D A$. Pour toute permutation $x, y, z, t$ de $a, b, c, d$, montrer que
$$
S \leqslant \frac{1}{2}(x y+z t)
$$
|
Si $x$ et $y$ sont adjacents, sans perte de généralité on se ramène à montrer que $S \leqslant \frac{1}{2}(a b+c d)$. Cela découle de $S_{A B C}=\frac{1}{2} A B \cdot B C \cdot \sin \widehat{A B C} \leqslant \frac{1}{2} a b$, et de même $S_{C D A} \leqslant \frac{1}{2} c d$. Si $x$ et $y$ sont des côtés opposés, on doit montrer que $S \leqslant \frac{1}{2}(a c+b d)$. Soit $A^{\prime}$ le symétrique de $A$ par rapport à la médiatrice de $[B D]$. Alors $B A^{\prime} D$ est isométrique à $D A B$. On applique ce qui précède à $A^{\prime} B C D$, ce qui donne $S=S_{B A D}+S_{B C D}=S_{B A^{\prime} D}+S_{B C D}=S_{A^{\prime} B C D} \leqslant \frac{1}{2}\left(A^{\prime} B \cdot B C+\right.$ $\left.C D \cdot D A^{\prime}\right)=\frac{1}{2}(a c+b d)$.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
5bc5156e-ff58-5698-83ac-66d8d8b3db14
| 605,507
|
In a country, there are 64 cities. There are roads connecting certain pairs of cities, but Bob does not know which ones (the roads do not cross each other but can potentially pass over each other; furthermore, the roads can be traveled in both directions). Alice, on the other hand, knows the network perfectly. Bob can choose any pair of cities and ask Alice if they are directly connected by a road. Bob's goal is to determine whether it is possible to travel from any city to any other (by potentially taking several successive roads). Show that there is no algorithm (i.e., no strategy based on Alice's successive answers) that allows him to be sure in fewer than 2016 questions.
|
We notice that $2016=64 \times 63 / 2=\binom{64}{2}$, so there are exactly 2016 pairs of cities. The road network is an undirected graph with 64 vertices. Each pair of cities corresponds to a question, and we want to know if Bob can determine whether the graph is connected in fewer than 2016 questions. Suppose, for the sake of contradiction, that Bob has an algorithm that requires fewer than 2016 questions: consequently, for any graph with 64 vertices, if Bob follows his algorithm by asking a sequence of questions $Q_{1}, Q_{2}, \ldots$ and stops at a question $Q_{n}$ as soon as he can conclude with certainty whether the graph is connected or not, then $n \leqslant 2015$ (the integer $n$ depends on the graph). Note that the answer to $Q_{n}$ must be "yes" if the graph is connected and "no" if the graph is not connected, otherwise Bob could have already concluded at question $Q_{n-1}$.
We start with the graph $G_{0}$ having no edges. Bob, using his algorithm, asks a sequence of questions $Q_{1}, Q_{2}, \ldots, Q_{n_{0}}$ to Alice.
The question $Q_{n_{0}}$ corresponds to a pair of cities. Let $G_{1}$ be the graph obtained by adding an edge between these two cities. Following his algorithm, Bob asks the questions $Q_{1}, \ldots, Q_{n_{0}}$ again, and additional questions $Q_{n_{0}+1}, \ldots, Q_{n_{1}}$. We have $n_{1}>n_{0}$ because, for the graph $G_{1}$, the answer to $Q_{n_{0}}$ is "yes", and the answer to $Q_{n_{1}}$ is "no" since the graph $G_{1}$ is not connected.
We continue this procedure and construct a sequence of graphs $G_{0}, G_{1}, G_{2}, \ldots$, each graph being constructed from the previous one by adding an edge, until we obtain a connected graph $G_{k}$. Since $n_{k-1}>n_{k-1}>\cdots>n_{0} \geqslant 1$, we have $n_{k-1} \geqslant k$ and thus $k \leqslant 2015$.
However, $G_{k}$ has $k$ edges, so there exists a pair of cities $X$ and $Y$ that are not directly connected. On the other hand, since $G_{k}$ is connected, we can go from $X$ to $Y$ by following a path consisting of edges in $G_{k}$. Let $j$ be the largest index such that one of the edges $A$ of this path belongs to $G_{j}$ but not to $G_{j-1}$. Let $G^{\prime}$ be the graph obtained by removing the edge $A$ from $G_{k}$ and adding the edge $X Y$, then the answers to the questions $Q_{1}, \ldots, Q_{n_{j-1}}$ are the same for $G^{\prime}$ as for $G_{j-1}$. However, Bob was able to conclude with certainty that $G_{j-1}$ is not connected, so $G^{\prime}$ is not connected either.
But this is contradictory because, since $G_{k}$ is connected, $G^{\prime}$ is also connected.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans un pays se trouvent 64 villes. Il existe des routes qui relient certaines paires de villes, mais Bob ne sait pas lesquelles (les routes ne se croisent pas mais peuvent éventuellement passer les unes au-dessus des autres ; de plus, les routes peuvent être parcourues dans les deux sens). Alice, elle, connaît parfaitement le réseau. Bob peut choisir n'importe quelle paire de villes et demander à Alice si elles sont reliées directement par une route. Le but de Bob est de déterminer s'il est possible de voyager de n'importe quelle ville à n'importe quelle autre (en empruntant éventuellement plusieurs routes successives). Montrer qu'il n'existe aucun algorithme (c'est-à-dire aucune stratégie en fonction des réponses successives d'Alice) lui permettant de le savoir à coup sûr en moins de 2016 questions.
|
On remarque que $2016=64 \times 63 / 2=\binom{64}{2}$, donc il y a exactement 2016 paires de villes. Le réseau routier est un graphe non orienté ayant 64 sommets. Chaque paire de villes correspond à une
question, et on veut savoir si en moins de 2016 questions Bob peut déterminer si le graphe est connexe. Supposons par l'absurde que Bob possède un algorithme en moins de 2016 questions : par conséquent, pour tout graphe ayant 64 sommets, si Bob suit son algorithme en posant une suite de questions $Q_{1}, Q_{2}, \ldots$ et s'arrête à une question $Q_{n}$ dès qu'il peut conclure à coup sûr si le graphe est connexe ou non, alors $n \leqslant 2015$ (l'entier $n$ dépend du graphe). Remarquons que la réponse à $Q_{n}$ est nécessairement "oui" si le graphe est connexe et "non" si le graphe est non connexe, sinon Bob aurait déjà pu conclure à la question $Q_{n-1}$.
On part du graphe $G_{0}$ ne possédant aucune arête. Bob, en utilisant son algorithme, pose une suite de questions $Q_{1}, Q_{2}, \ldots, Q_{n_{0}}$ à Alice.
La question $Q_{n_{0}}$ correspond à une paire de villes. Soit $G_{1}$ le graphe consistant à rajouter une arête entre ces deux villes. En suivant son algorithme, Bob pose à nouveau les questions $Q_{1}, \ldots, Q_{n_{0}}$, et d'autres questions $Q_{n_{0}+1}, \ldots, Q_{n_{1}}$. On a bien $n_{1}>n_{0}$ car, pour le graphe $G_{1}$, la réponse à $Q_{n_{0}}$ est "oui", et la réponse à $Q_{n_{1}}$ est "non" puisque le graphe $G_{1}$ n'est pas connexe.
On continue la procédure, et on construit ainsi une suite de graphes $G_{0}, G_{1}, G_{2}, \ldots$, chaque graphe étant construit à partir du précédent en rajoutant une arête, jusqu'à obtenir un graphe connexe $G_{k}$. Comme $n_{k-1}>n_{k-1}>\cdots>n_{0} \geqslant 1$, on a $n_{k-1} \geqslant k$ donc $k \leqslant 2015$.
Or, $G_{k}$ possède $k$ arêtes, donc il existe une paire de villes $X$ et $Y$ qui ne sont pas reliées directement. En revanche, comme $G_{k}$ est connexe on peut aller de $X$ vers $Y$ en suivant un chemin consistant en des arêtes de $G_{k}$. Soit $j$ le plus grand indice tel que l'une des arêtes $A$ de ce chemin appartient à $G_{j}$ mais pas à $G_{j-1}$. Soit $G^{\prime}$ le graphe obtenu en enlevant l'arête $A$ au graphe $G_{k}$ et en ajoutant l'arête $X Y$, alors la réponse aux questions $Q_{1}, \ldots, Q_{n_{j-1}}$ est la même pour $G^{\prime}$ que pour $G_{j-1}$. Or, Bob a pu conclure à coup sûr que $G_{j-1}{\text { n'est pas connexe, donc } G^{\prime}}^{\prime}$ ne l'est pas non plus.
Mais ceci est contradictoire car, $G_{k}$ étant connexe, $G^{\prime}$ l'est aussi.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution de l'exercice 6"
}
|
3e33d5c4-86d8-5a3f-97e9-ccef14b44f71
| 605,531
|
Let $ABCD$ be a trapezoid such that $(AB)$ and $(CD)$ are parallel. Suppose that $AD < CD$ and that $ABCD$ is inscribed in a circle $\Gamma$. Let $P$ be a point on $\Gamma$ such that $(DP)$ is parallel to $(AC)$. The tangent to $\Gamma$ at $D$ intersects $(AB)$ at $E$, and the chords $[BP]$ and $[CD]$ intersect at $Q$. Show that $EQ = AC$.
|
We know that $(CQ)$ is parallel to $(\mathrm{AE})$, so the statement reduces to showing that $A C Q E$ is a parallelogram, hence it suffices to show that (EQ) and (AC) are parallel. The quadrilateral BQDE is a trapezoid, with $(B E)$ and (DQ) parallel. We will first show that it is an isosceles trapezoid. Indeed, we have
$$
\widehat{\mathrm{EDQ}}=\widehat{\mathrm{EDC}}=180^{\circ}-\widehat{\mathrm{DAC}}
$$
according to the limiting case of the inscribed angle theorem. On the other hand, we have
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{BDC}}-\widehat{\mathrm{DBP}}=180^{\circ}-\widehat{\mathrm{BAC}}-\widehat{\mathrm{DAP}}
$$
Now, the quadrilaterals $A B C D$ and $A C P D$ are inscribed trapezoids, hence isosceles, so $P C=$ $A D=B C$, thus $C$ is the midpoint of the arc between $B$ and $P$. Therefore, $\widehat{B A C}=\widehat{C A P}$, so
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{CAP}}-\widehat{\mathrm{DAP}}=180^{\circ}-\widehat{\mathrm{DAC}}=\widehat{\mathrm{EDQ}}
$$
thus the trapezoid EBQD is indeed isosceles and has an axis of symmetry. We deduce
$$
\widehat{\mathrm{DQE}}=\widehat{\mathrm{QDB}}=\widehat{\mathrm{CDB}}=\widehat{\mathrm{DCA}},
$$
using at the end the fact that $A B C D$ has an axis of symmetry. This shows that (QE) and (AC) are parallel, which concludes the proof.
## Exercise common to groups A and B - Statement and solution
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze tel que $(A B)$ et $(C D)$ sont parallèles. On suppose que $A D<$ $C D$ et que $A B C D$ est inscrit dans un cercle $\Gamma$. Soit $P$ sur $\Gamma$ tel que (DP) est parallèle à ( $A C$ ). La tangente à $\Gamma$ en $D$ recoupe $(A B)$ en $E$, et les cordes $[B P]$ et $[C D]$ s'intersectent en $Q$. Montrer que $E Q=A C$.
|
On sait que (CQ) est parallèle à $(\mathrm{AE})$, donc l'énoncé revient à montrer que $A C Q E$ est un parallélogramme, donc il suffit de montrer que (EQ) et (AC) sont parallèles. Le quadrilatère BQDE est un trapèze, avec $(B E)$ et (DQ) parallèles. On va d'abord montrer que c'est un trapèze isocèle. En effet, on a
$$
\widehat{\mathrm{EDQ}}=\widehat{\mathrm{EDC}}=180^{\circ}-\widehat{\mathrm{DAC}}
$$
d'après le cas limite du théorème de l'angle inscrit. D'autre part, on a
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{BDC}}-\widehat{\mathrm{DBP}}=180^{\circ}-\widehat{\mathrm{BAC}}-\widehat{\mathrm{DAP}}
$$
Or, les quadrilatères $A B C D$ et $A C P D$ sont des trapèzes inscriptibles, donc isocèles, donc $P C=$ $A D=B C$, donc $C$ est le milieu de l'arc entre $B$ et $P$. On a donc $\widehat{B A C}=\widehat{C A P}$, donc
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{CAP}}-\widehat{\mathrm{DAP}}=180^{\circ}-\widehat{\mathrm{DAC}}=\widehat{\mathrm{EDQ}}
$$
donc le trapèze EBQD est bien isocèle, et a un axe de symétrie. On en déduit
$$
\widehat{\mathrm{DQE}}=\widehat{\mathrm{QDB}}=\widehat{\mathrm{CDB}}=\widehat{\mathrm{DCA}},
$$
en utilisant à la fin le fait que $A B C D$ a un axe de symétrie. Cela montre que ( QE ) et ( $A C$ ) sont parallèles, ce qui conclut.
## Exercice commun aux groupes A et B - Énoncé et solution
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
1077266a-0331-570d-9960-278c8dbdd634
| 605,561
|
Determine all integers $n \geqslant 2$ satisfying the following property: for all integers $a_{1}, a_{2}, \ldots, a_{n}$ whose sum is not divisible by $n$, there exists an index $i$ such that none of the numbers
$$
a_{i}, a_{i}+a_{i+1}, \ldots, a_{i}+\cdots+a_{i+n-1}
$$
is divisible by $n$ (for $i>n$, we set $a_{i}=a_{i-n}$ ).
|
These are exactly the prime numbers!
Indeed, if $n=ab$, we can take $a_{1}=0$ and $a_{2}=\cdots=a_{n}=a$. The sum of the $a_{i}$ is $a(n-1)$, which is not divisible by $n$. However, for any $1 \leqslant i \leqslant n$, if $i+b-1 \leqslant n$, then the number $a_{i}+\cdots+a_{i+b-1}=ab=n$ is divisible by $n$. If $i+b-1>n$, then the number $a_{i}+\cdots+a_{i+b}=ab=n$ is divisible by $n$.
Conversely, suppose $n$ is prime, and let $a_{1}, \ldots, a_{n}$ be integers whose sum is not divisible by $n$. If $n$ does not satisfy the property, then for any index $i$, there exists $j(i)$ with $i+1 \leqslant j(i) \leqslant i+n$ such that
$$
a_{i}+a_{i+1}+\cdots+a_{j(i)-1}
$$
is divisible by $n$. Furthermore, since the sum of the $a_{i}$ is not divisible by $n$, we cannot have $j(i)=i+n$, so $i+1 \leqslant j(i) \leqslant i+n-1$. We then define by induction a sequence of indices $\left(i_{n}\right)$ by $i_{1}=1$ and $i_{n+1}=j\left(i_{n}\right)$. We know that for all $k$, the integer
$$
a_{i_{k}}+\cdots+a_{i_{k+1}-1}
$$
is divisible by $n$; therefore, by summing, for all indices $k<\ell$, the integer
$$
a_{i_{k}}+\cdots+a_{i_{\ell}-1}
$$
is divisible by $n$. By the pigeonhole principle, there exist $1 \leqslant k<\ell \leqslant n+1$ such that $i_{k} \equiv i_{\ell}(\bmod n)$. The number of terms in the sum (1) is then $i_{\ell}-i_{k}$, which is divisible by $n$, so each of the $a_{i}$ appears exactly $\frac{i_{\ell}-i_{k}}{n}$ times. Moreover, we know that $i_{j+1}-i_{j} \leqslant n-1$ for all $j$ and that $\ell-k \leqslant n$, so $i_{\ell}-i_{k} \leqslant n(n-1)$. The sum (1) is therefore
$$
\frac{i_{\ell}-i_{k}}{n} \times \sum_{i=1}^{n} a_{i} .
$$
But $\frac{i_{\ell}-i_{k}}{n} \leqslant n-1$ and cannot be divisible by $n$, and the sum of the $a_{i}$ is not divisible by $n$ either. Since $n$ is prime, the sum (1) is not divisible by $n$, leading to a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Déterminer tous les entiers $n \geqslant 2$ vérifiant la propriété suivante : pour tous entiers $a_{1}, a_{2}, \ldots, a_{n}$ dont la somme n'est pas divisible par $n$, $i l$ existe un indice $i$ tel qu'aucun des nombres
$$
a_{i}, a_{i}+a_{i+1}, \ldots, a_{i}+\cdots+a_{i+n-1}
$$
n'est divisible par $n$ (pour $i>n$, on pose $a_{i}=a_{i-n}$ ).
|
Ce sont exactement les nombres premiers!
En effet, si $n=a b$, on peut prendre $a_{1}=0$ et $a_{2}=\cdots=a_{n}=a$. La somme des $a_{i}$ vaut $a(n-1)$ donc n'est pas divisible par $n$. Cependant, soit $1 \leqslant i \leqslant n$. Si $i+b-1 \leqslant n$, alors le nombre $a_{i}+\cdots+a_{i+b-1}=a b=n$ est divisible par $n$. Si $i+b-1>n$, alors le nombre $a_{i}+\cdots+a_{i+b}=a b=n$ est divisible par $n$.
Réciproquement, supposons $n$ premier, et soient $a_{1}, \ldots, a_{n}$ des entiers dont la somme n'est pas divisible par $n$. Si $n$ ne vérifie pas la propriété, alors pour tout indice $i$, il existe $j(i)$ avec $\mathfrak{i}+1 \leqslant \mathfrak{j}(\mathfrak{i}) \leqslant \mathfrak{i}+\boldsymbol{n}$ tel que
$$
a_{i}+a_{i+1}+\cdots+a_{j(i)-1}
$$
est divisible par $n$. De plus, comme la somme des $a_{i} n^{\prime}$ est pas divisible par $n$, on ne peut pas avoir $\mathfrak{j}(\mathfrak{i})=\mathfrak{i}+\mathfrak{n}$, donc $\mathfrak{i}+1 \leqslant \mathfrak{j}(\mathfrak{i}) \leqslant \mathfrak{i}+\mathfrak{n}-1$. On définit alors par récurrence une suite $d^{\prime}$ 'indices $\left(i_{n}\right)$ par $i_{1}=1$ et $i_{n+1}=j\left(i_{n}\right)$. On sait que pour tout $k$, l'entier
$$
a_{i_{k}}+\cdots+a_{i_{k+1}-1}
$$
est divisible par n donc, en sommant, pour tous indices $k<\ell$, l'entier
$$
a_{i_{k}}+\cdots+a_{i_{\ell}-1}
$$
est divisible par $n$. Par le principe des tiroirs, il existe $1 \leqslant k<\ell \leqslant n+1$ tels que $\mathfrak{i}_{k} \equiv \mathfrak{i}_{\ell}(\bmod n)$. Le nombre de termes de la somme (1) vaut alors $\mathfrak{i}_{\ell}-\mathfrak{i}_{k}$ donc est divisible par $n$, donc chacun des $a_{i} y$ apparaît exactement $\frac{\boldsymbol{i}_{\ell}-\mathfrak{i}_{k}}{n}$ fois. De plus, on sait que $\mathfrak{i}_{j+1}-\mathfrak{i}_{j} \leqslant n-1$ pour tout $j$ et que $\ell-k \leqslant n$, donc $\mathfrak{i}_{\ell}-\mathfrak{i}_{k} \leqslant n(n-1)$. La somme (1) vaut donc
$$
\frac{\mathfrak{i}_{\ell}-\mathfrak{i}_{k}}{n} \times \sum_{i=1}^{n} a_{i} .
$$
Mais $\frac{i_{\ell}-i_{k}}{n} \leqslant n-1$ donc ne peut pas être divisible par $n$, et la somme des $a_{i}$ ne l'est pas non plus. Comme n est premier, la somme (1) n'est pas divisible par n , d'où la contradiction.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
4f872c5f-428c-51ae-b0ab-a06e471562e4
| 605,584
|
Let $ABC$ be a triangle with $AB \neq AC$, and let $\omega$ be the $A$-excircle of $ABC$. We denote by $D, E$ and $F$ the points of tangency of $\omega$ with $[BC]$, $[AC)$, and $[AB)$. The circumcircle of $AEF$ intersects $(BC)$ at $P$ and $Q$. We denote by $M$ the midpoint of $[AD]$. Show that the circumcircle of $MPQ$ is tangent to $\omega$.
Note. We recall that the $A$-excircle of $ABC$ is the unique circle tangent to the segment $[BC]$, to the ray $[AB)$ beyond $B$, and to the ray $[AC)$ beyond $C$.
|
Let $\Gamma$ be the circle passing through $A, E, F, P$ and $Q$. Let $T$ be the second intersection point of (AD) with $\omega$. We will show that $\omega$ and the circumcircle of MPQ are tangent at $T$. To do this, we first show that $M, P, Q$ and $T$ are concyclic.
Let $J$ be the center of $\omega$, and $N$ the midpoint of [DT]. Then the angles $\widehat{A E J}$ and $\widehat{A F J}$ are right angles, so $E$ and $F$ lie on the circle with diameter $[A J]$, hence $\Gamma$ is the circle with diameter $[A J]$. Moreover, the line (JN) is the perpendicular bisector of [DT], so the angle $\widehat{A N J}$ is also a right angle and $N \in \Gamma$. The power of $D$ with respect to $\Gamma$ then gives
$$
\mathrm{DP} \times \mathrm{DQ}=\mathrm{DA} \times \mathrm{DN}=\mathrm{DA} \times \frac{1}{2} \mathrm{DT}=\frac{1}{2} \mathrm{DA} \times \mathrm{DT}=\mathrm{DM} \times \mathrm{DT}
$$
so $M, T, P$ and $Q$ are indeed concyclic.
We now draw the tangent at $T$ to $\omega$, which intersects ( $B C$ ) at $X$. We have $X D=X T$, so the points $X$, J and $N$ are collinear on the perpendicular bisector of [DT]. The triangles XND and XDJ are then
right-angled at $N$ and $D$ and share the angle $\widehat{D R J}$, so they are similar, so $\frac{X N}{X D}=\frac{X D}{X J}$, so $\mathrm{XD}^{2}=\mathrm{XN} \times \mathrm{XJ}$. We also know that $\mathrm{XT}=\mathrm{XD}$, and the power of $X$ with respect to $\Gamma$ gives $\mathrm{XN} \times X \mathrm{~J}=\mathrm{XP} \times \mathrm{XQ}$. We then obtain
$$
X T^{2}=X P \times X Q
$$
so $(X T)$ is tangent to the circumcircle of PQT, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $A B \neq A C$, et soit $\omega$ le cercle $A$-exinscrit à $A B C$. On note $D, E$ et $F$ les points de tangence de $\omega$ avec $[B C],[A C)$ et $[A B)$. Le cercle circonscrit à $A E F$ recoupe ( $B C$ ) en $P$ et $Q$. On note $M$ le milieu de $[A D]$. Montrer que le cercle circonscrit à MPQ est tangent à $\omega$.
Remarque. On rappelle que le cercle $A$-exinscrit à $A B C$ est l'unique cercle tangent au segment $[B C]$, à la demi-droite $[A B)$ au-delà de $B$ et à la demi-droite $[A C)$ au-delà de $C$.
|
On note $\Gamma$ le cercle passant par $A, E, F, P$ et $Q$. Soit $T$ le second point d'intersection de (AD) avec $\omega$. On va montrer que $\omega$ et le cercle circonscrit à MPQ sont tangents en $T$. On commence pour cela par montrer que $M, P, Q$ et $T$ sont cocycliques.
Soient $J$ le centre de $\omega$, et $N$ le milieu de [DT]. Alors les angles $\widehat{A E J}$ et $\widehat{A F J}$ sont droits, donc $E$ et $F$ sont sur le cercle de diamètre $[A J]$, donc $\Gamma$ est le cercle de diamètre $[A J]$. De plus, la droite (JN) est la médiatrice de [DT], donc l'angle $\widehat{A N J}$ est aussi droit et $N \in \Gamma$. La puissance de $D$ par rapport à $\Gamma$ donne alors
$$
\mathrm{DP} \times \mathrm{DQ}=\mathrm{DA} \times \mathrm{DN}=\mathrm{DA} \times \frac{1}{2} \mathrm{DT}=\frac{1}{2} \mathrm{DA} \times \mathrm{DT}=\mathrm{DM} \times \mathrm{DT}
$$
donc $M, T, P$ et Q sont bien cocycliques.
On trace maintenant la tangente en $T$ à $\omega$, qui recoupe ( $B C$ ) en $X$. On a $X D=X T$, donc les points $X$, J et $N$ sont alignés sur la médiatrice de [DT]. Les triangles XND et XDJ sont alors
rectangles en $N$ et $D$ et partagent l'angle $\widehat{D R J}$, donc ils sont semblables, donc $\frac{X N}{X D}=\frac{X D}{X J}$, donc $\mathrm{XD}^{2}=\mathrm{XN} \times \mathrm{XJ}$. On sait aussi que $\mathrm{XT}=\mathrm{XD}$, et la puissance de $X$ par rapport à $\Gamma$ donne $\mathrm{XN} \times X \mathrm{~J}=\mathrm{XP} \times \mathrm{XQ}$. On obtient donc
$$
X T^{2}=X P \times X Q
$$
donc $(X T)$ est tangente au cercle circonscrit à PQT, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
e707447f-4416-5c0b-af3c-178c3d567746
| 605,598
|
Let $\omega_{1}, \omega_{2}$ be two circles tangent to each other at a point $T$, such that $\omega_{1}$ is inside $\omega_{2}$. Let $M$ and $N$ be two distinct points on $\omega_{1}$, different from $T$. Let [AB] and [CD] be two chords of the circle $\omega_{2}$ passing through $M$ and $N$ respectively. Suppose that the segments [BD], $[A C]$, and $[M N]$ intersect at a point $K$.
Show that (TK) is the bisector of the angle $\widehat{M T N}$.
|
Let $E$ and $F$ be the points of intersection of $(TM)$ and $(TN)$ with $\omega_{2}$, other than $T$. Since $\omega_{1}$ and $\omega_{2}$ are tangent at $T$, the homothety centered at $T$ that maps $\omega_{1}$ to $\omega_{2}$ also maps $M$ to $E$ and $N$ to $F$. This implies that
$$
\frac{\mathrm{TM}}{\mathrm{TN}}=\frac{\mathrm{ME}}{\mathrm{NF}}
$$
Furthermore, the power of points $M$ and $N$ with respect to $\omega_{2}$ is respectively $A M \cdot M B=T M \cdot M E$ and $C N \cdot N D=T N \cdot N F$. This shows that
$$
\frac{\mathrm{TM}^{2}}{\mathrm{TN}^{2}}=\frac{\mathrm{TM} \cdot \mathrm{ME}}{\mathrm{TN} \cdot \mathrm{NF}}=\frac{\mathrm{AM} \cdot \mathrm{MB}}{\mathrm{CN} \cdot \mathrm{ND}}
$$
On the other hand, in triangles $A M K$ and $D N K$, the law of sines indicates that
$$
A M \cdot \sin (\widehat{M A K})=M K \cdot \sin (\widehat{A K M}) \text { and that DN } \cdot \sin (\widehat{N D K})=N K \cdot \sin (\widehat{D K N}) .
$$
Since $A, B, C$ and $D$ are concyclic, we also have $\sin (\widehat{B A C})=\sin (\widehat{B D C})$, so that
$$
\sin (\widehat{M A K})=\sin (\widehat{B A C})=\sin (\widehat{B D C})=\sin (\widehat{K D N})
$$
It follows that $\frac{A M}{D N}=\frac{M K \cdot \sin (\widehat{A K M})}{N K \cdot \sin (\widehat{D K N})}$ and, similarly, that $\frac{B M}{C N}=\frac{M K \cdot \sin (\widehat{B K M})}{N K \cdot \sin (\widehat{C K N})}$. Since the angles $\widehat{B K M}$ and $\widehat{D K N}$ on one hand, and $\widehat{A K M}$ and $\widehat{C K M}$ on the other, are vertically opposite, hence equal, we deduce that
$$
\frac{A M \cdot M B}{D N \cdot N C}=\frac{M K^{2}}{N K^{2}}
$$
We conclude that TM $\cdot N K=T N \cdot M K$.
The law of sines in triangles TKM and TKN also indicates that
$$
\mathrm{TM} \cdot \sin (\widehat{\mathrm{KTM}})=\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \text { and that } \mathrm{TN} \cdot \sin (\widehat{\mathrm{KTN}})=\mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})
$$
Since $\widehat{M K T}$ and $\widehat{N K T}$ are supplementary, they have the same sine, so that
$$
\frac{\sin (\widehat{K T M})}{\sin (\widehat{\mathrm{KTN}})}=\frac{\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \cdot \mathrm{TN}}{\mathrm{TM} \cdot \mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})}=1
$$
which proves that (TK) is the angle bisector of $\widehat{M T N}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient deux cercles $\omega_{1}, \omega_{2}$ tangents l'un à l'autre en un point $T$, tels que $\omega_{1}$ soit à l'intérieur de $\omega_{2}$. Soient $M$ et $N$ deux points distincts sur $\omega_{1}$, différents de $T$. Soient [AB] et [CD] deux cordes du cercle $\omega_{2}$ passant respectivement par $M$ et $N$. On suppose que les segments [BD], $[A C]$, et $[M N]$ s'intersectent en un point $K$.
Montrer que (TK) est la bissectrice de l'angle $\widehat{M T N}$.
|
Soit $E$ et $F$ les points d'intersection respectifs de (TM) et (TN) avec $\omega_{2}$, autres que $T$. Puisque $\omega_{1}$ et $\omega_{2}$ sont tangents en $T$, l'homothétie de centre T et qui envoie $\omega_{1}$ sur $\omega_{2}$ envoie également $M$ sur $E$ et $N$ sur $F$. On en déduit que
$$
\frac{\mathrm{TM}}{\mathrm{TN}}=\frac{\mathrm{ME}}{\mathrm{NF}}
$$
En outre, la puissance des points $M$ et $N$ par rapport à $\omega_{2}$ vaut respectivement $A M \cdot M B=T M \cdot M E$ et $C N \cdot N D=T N \cdot N F$. Cela montre que
$$
\frac{\mathrm{TM}^{2}}{\mathrm{TN}^{2}}=\frac{\mathrm{TM} \cdot \mathrm{ME}}{\mathrm{TN} \cdot \mathrm{NF}}=\frac{\mathrm{AM} \cdot \mathrm{MB}}{\mathrm{CN} \cdot \mathrm{ND}}
$$
D'autre part, dans les triangles $A M K$ et $D N K$, la loi des sinus indique que
$$
A M \cdot \sin (\widehat{M A K})=M K \cdot \sin (\widehat{A K M}) \text { et que DN } \cdot \sin (\widehat{N D K})=N K \cdot \sin (\widehat{D K N}) .
$$
Puisque $A, B, C$ et $D$ sont cocycliques, on a également $\sin (\widehat{B A C})=\sin (\widehat{B D C})$, de sorte que
$$
\sin (\widehat{M A K})=\sin (\widehat{B A C})=\sin (\widehat{B D C})=\sin (\widehat{K D N})
$$
Il s'ensuit que $\frac{A M}{D N}=\frac{M K \cdot \sin (\widehat{A K M})}{N K \cdot \sin (\widehat{D K N})}$ et, de même, que $\frac{B M}{C N}=\frac{M K \cdot \sin (\widehat{B K M})}{N K \cdot \sin (\widehat{C K N})}$. Puisque les angles $\widehat{B K M}$ et $\widehat{D K N}$ d'une part, et $\widehat{A K M}$ et $\widehat{C K M}$ d'autre part, sont opposés par le sommet, donc sont égaux deux à deux, on en déduit que
$$
\frac{A M \cdot M B}{D N \cdot N C}=\frac{M K^{2}}{N K^{2}}
$$
On en conclut que TM $\cdot N K=T N \cdot M K$.
La loi des sinus dans les triangles TKM et TKN indique en outre que
$$
\mathrm{TM} \cdot \sin (\widehat{\mathrm{KTM}})=\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \text { et que } \mathrm{TN} \cdot \sin (\widehat{\mathrm{KTN}})=\mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})
$$
Puisque $\widehat{M K T}$ et $\widehat{N K T}$ sont supplémentaires, ils ont même sinus, de sorte que
$$
\frac{\sin (\widehat{K T M})}{\sin (\widehat{\mathrm{KTN}})}=\frac{\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \cdot \mathrm{TN}}{\mathrm{TM} \cdot \mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})}=1
$$
ce qui prouve que (TK) est la bissectrice de $\widehat{M T N}$.
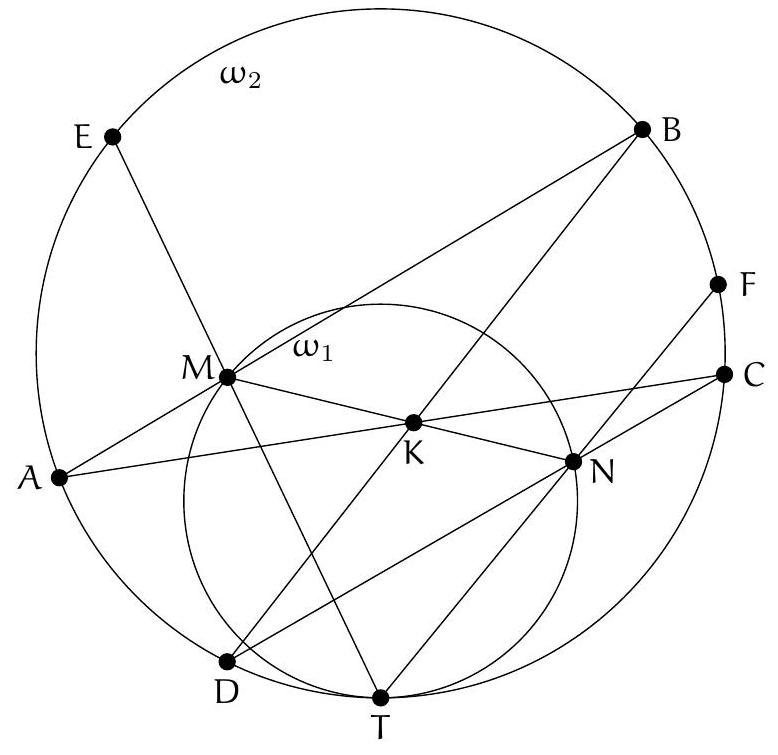
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
15bbba33-74fd-518a-8e4e-170af74e3522
| 605,617
|
In the cells of a rectangular table with $n$ rows and $m$ columns, real numbers are written. We assume that for any row or column, the sum of the numbers written in that row or column is an integer. Show that it is possible to replace each real number $x$ by the integer $\lfloor x\rfloor$ or $\lceil x\rceil$ so that the sums of each column and each row remain unchanged.
Note: We recall that if $x$ is a real number, $\lfloor x\rfloor$ is the unique integer such that $\lfloor x\rfloor \leqslant x<\lfloor x\rfloor+1$, and $\lceil x\rceil$ is the unique integer such that $\lceil x\rceil-1<x \leqslant\lceil x\rceil$.
|
By subtracting the integer part from each entry in the array, we can assume that each number is between 0 and 1. We say that a cell is "fractional" if its number is not an integer. Note that, if C is a fractional cell, then there must necessarily be another fractional cell on the same row as C, and there must also be another fractional cell on the same column as C.
Let's choose a fractional cell $C_{0}$, and for all $n \in \mathbb{N}$:
- if $n$ is even, we choose a fractional cell $C_{n+1}$ on the same row as $C_{n}$;
- if $n$ is odd, we choose a fractional cell $C_{n+1}$ on the same column as $C_{n}$.
By the pigeonhole principle, there exist two integers $k<\ell$ such that $C_{k}=C_{\ell}$. Without loss of generality, we assume that $\ell$ is as small as possible, among all choices of cells $C_{0}, C_{1}, \ldots$ and integers $k<\ell$ that we might make.
Thus, we have $k=0$, and we have a "cycle" $C_{0}, \ldots, C_{\ell-1}, C_{\ell}$ of distinct fractional cells (except $C_{0}$ and $C_{\ell}$) such that the segments $\left[C_{i}, C_{i+1}\right]$ are alternately horizontal and vertical. Since this cycle is of minimal length $\ell$, we know that each row and each column contains either 0 or 2 cells of the cycle, and these cells are consecutive in the cycle.
For all $i<\ell-1$, we denote by $x_{i}$ the number written on the cell $C_{i}$, and we set $y_{i}=x_{i}$ if $i$ is even, and $y_{i}=1-x_{i}$ if $i$ is odd. Then we replace $x_{i}$ with the real number
$$
x_{i}^{\prime}=x_{i}+(-1)^{i} \varepsilon
$$
where $\varepsilon=\min \left\{y_{i} \mid i<\ell\right\}$. By construction of $\varepsilon$, we have $0 \leqslant x_{i}^{\prime} \leqslant 1$ for all $i<\ell$, with $x_{i}^{\prime}=0$ or $x_{i}^{\prime}=1$ for at least one integer $i$.
This process has not modified the sum of any row or column, and has reduced the number of fractional cells, while assigning to each modified cell a value $x_{i}^{\prime}$ such that
$$
\left\{\left\lfloor x_{i}^{\prime}\right\rfloor,\left\lceil x_{i}^{\prime}\right\rceil\right\} \subseteq\{0,1\}=\left\{\left\lfloor x_{i}\right\rfloor,\left\lceil x_{i}\right\rceil\right\}.
$$
We can therefore repeat this process until all fractional cells are eliminated, which concludes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Dans les cases d'un tableau rectangulaire à $n$ lignes et $m$ colonnes sont écrits des nombres réels. On suppose que pour toute ligne ou colonne, la somme des nombres écrits sur cette ligne ou colonne est un entier. Montrer qu'il est possible de remplacer chaque réel $x$ par l'entier $\lfloor x\rfloor$ ou $\lceil x\rceil$ de sorte que les sommes de chaque colonne et de chaque ligne demeurent inchangées.
Remarque : On rappelle que si $x$ est un nombre réel, $\lfloor x\rfloor$ est l'unique entier tel que $\lfloor x\rfloor \leqslant x<\lfloor x\rfloor+1$, et $\lceil x\rceil$ est l'unique entier tel que $\lceil x\rceil-1<x \leqslant\lceil x\rceil$.
|
Quitte à soustraire sa partie entière à chaque entrée du tableau, on peut supposer que chaque nombre est compris entre 0 et 1 . On dit qu'une case est « fractionnaire $\gg$ si son nombre n'est pas entier. Remarquons que, si C est une case fractionnaire, alors il existe nécessairement une autre case fractionnaire sur la même ligne que C , et il existe aussi une autre case fractionnaire sur la même colonne que C .
Choisissons donc une case $C_{0}$ fractionnaire, puis, pour tout $n \in \mathbb{N}$ :
- si $n$ est pair, on choisit une case $C_{n+1}$ fractionnaire sur la même ligne que $C_{n}$;
- si $n$ est impair, on choisit une case $C_{n+1}$ fractionnaire sur la même colonne que $C_{n}$.
Par principe des tiroirs, il existe deux entiers $k<\ell$ tels que $C_{k}=C_{\ell}$. Sans perte de généralité, on suppose que $\ell$ est aussi petit que possible, parmi tous les choix de cases $C_{0}, C_{1}, \ldots$ et d'entiers $k<\ell$ que l'on aura pu faire.
On a donc $k=0$, et l'on dispose ainsi d'un $«$ cycle $\gg C_{0}, \ldots, C_{\ell-1}, C_{\ell}$ de cases fractionnaires deux à deux distinctes (sauf $C_{0}$ et $C_{\ell}$ ) et telles que les segments $\left[C_{i}, C_{i+1}\right]$ sont alternativement horizontaux et verticaux. Ce cycle étant de longueur $\ell$ minimale, on sait que chaque ligne et chaque colonne contient soit 0 , soit 2 cases du cycle, et que ces cases sont consécutives dans le cycle.
Pour tout $i<\ell-1$, on note $x_{i}$ le nombre écrit sur la case $C_{i}$, et l'on pose $y_{i}=x_{i}$ si $i$ est pair, et $y_{i}=1-x_{i}$ si $i$ est impair. Puis l'on remplace $x_{i}$ par le réel
$$
x_{i}^{\prime}=x_{i}+(-1)^{i} \varepsilon
$$
où $\varepsilon=\min \left\{y_{i} \mid i<\ell\right\}$. Par construction de $\varepsilon$, on a donc $0 \leqslant x_{i}^{\prime} \leqslant 1$ pour tout $i<\ell$, avec $x_{i}^{\prime}=0$ ou $x_{i}^{\prime}=1$ pour au moins un entier $i$.
Ce procédé n'a modifié la somme d'aucune ligne ni colonne, et a permis de réduire le nombre de cases fractionnaires, tout en affectant à chaque case modifiée une valeur $x_{i}^{\prime}$ telle que
$$
\left\{\left\lfloor x_{i}^{\prime}\right\rfloor,\left\lceil x_{i}^{\prime}\right\rceil\right\} \subseteq\{0,1\}=\left\{\left\lfloor x_{i}\right\rfloor,\left\lceil x_{i}\right\rceil\right\} .
$$
On peut donc réitérer ce procédé jusqu'à éliminer toutes les cases fractionnaires, ce qui conclut le problème.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
9c3759db-b7eb-5562-ace9-0d9813c793ee
| 605,626
|
Let $x$ and $y$ be two integers such that $5x + 6y$ and $6x + 5y$ are perfect squares. Show that $x$ and $y$ are both divisible by 11.
Note: an integer $n$ is a perfect square if it is the square of an integer.
|
Let $a$ and $b$ be integers such that $5 x + 6 y = a^2$ and $6 x + 5 y = b^2$. We note that $a^2 + b^2 = 11(x + y)$ is divisible by 11. Now, modulo 11, the squares are $0, 1, 3, 4, 5$, and 9: thus, the sum of two squares is zero (mod. 11) if and only if the two squares in question are zero (mod. 11) as well.
In our case, this means that $a$ and $b$ are divisible by 11. Therefore, there exist integers $A$ and $B$ such that $a = 11 A$ and $b = 11 B$. But then
$$
11 x = (6 \times 6 - 5 \times 5) x = 6(b^2 - 5 y) - 5(a^2 - 6 y) = 6 b^2 - 5 a^2 = 11^2 (6 B^2 - 5 A^2)
$$
so that $x = 11(6 B^2 - 5 A^2)$ is indeed divisible by 11. Similarly, we show that $y = 11(6 A^2 - 5 B^2)$ is also divisible by 11.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $x$ et $y$ deux entiers tels que $5 x+6 y$ et $6 x+5 y$ soient des carrés parfaits. Montrer que $x$ et $y$ sont tous deux divisibles par 11.
Note : on dit qu'un entier $n$ est un carré parfait si c'est le carré d'un entier.
|
Soit $a$ et $b$ deux entiers tels que $5 x+6 y=a^{2}$ et $6 x+5 y=b^{2}$. On note que $a^{2}+b^{2}=11(x+y)$ est divisible par 11 . Or, modulo 11 , les carrés sont $0,1,3,4,5$ et 9 : ainsi, la somme de deux carrés est nulle (mod. 11) si et seulement si les deux carrés en question sont nuls (mod. 11) eux aussi.
Dans notre cas, cela signifie que $a$ et $b$ sont divisibles par 11. Il existe donc des entiers $A$ et $B$ tels que $a=11 A$ et $b=11 \mathrm{~B}$. Mais alors
$$
11 x=(6 \times 6-5 \times 5) x=6\left(b^{2}-5 y^{2}\right)-5\left(a^{2}-6 y\right)=6 b^{2}-5 a^{2}=11^{2}\left(6 B^{2}-5 A^{2}\right)
$$
de sorte que $x=11\left(6 B^{2}-5 A^{2}\right)$ est bien divisible par 11. De même, on montre que $y=$ $11\left(6 A^{2}-5 B^{2}\right)$ est lui aussi divisible par 11.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
91c30962-c0bc-5ed0-90d2-0bf1c8745afd
| 605,636
|
Let $\Gamma$ be a circle with center $O$ and radius $r$, and $\ell$ be a line that does not intersect $\Gamma$. We denote $E$ as the point of intersection between $\ell$ and the line perpendicular to $\ell$ passing through $O$.
Let $M$ be a point on $\ell$ different from $E$. The tangents to the circle $\Gamma$ passing through $M$ touch $\Gamma$ at $A$ and $B$. Finally, let $H$ be the point of intersection of the lines $(AB)$ and $(OE)$.
Show that $\mathrm{OH}=\mathrm{r}^{2} / \mathrm{OE}$.
|
First, the triangles OAM, OBM, and OEM are respectively right-angled at $A, B$, and $E$, so the points $A, O, B, E, M$ all belong to the same circle with diameter [OM].
According to the law of sines in triangles OBH and OEA, we know that
$$
\frac{\mathrm{OH} \times \mathrm{OE}}{\mathrm{r}^{2}}=\frac{\mathrm{OH}}{\mathrm{OB}} \times \frac{\mathrm{OE}}{\mathrm{OA}}=\frac{\sin (\widehat{\mathrm{OBA}})}{\sin (\widehat{\mathrm{OHB}})} \times \frac{\sin (\widehat{\mathrm{OAE}})}{\sin (\widehat{\mathrm{OEA}})}
$$
Since the points $O, B, E$, and $A$ are concyclic, we know that $\widehat{O B A}=\widehat{O E A}$. On the other hand, since the lines $(\mathrm{AH})$ and $(\mathrm{HO})$ are respectively perpendicular to $(\mathrm{OM})$ and $(\mathrm{ME})$, we also know that
$$
\widehat{\mathrm{OHB}}=180^{\circ}-\widehat{\mathrm{AHO}}=180^{\circ}-\widehat{\mathrm{OME}}=180^{\circ}-\widehat{\mathrm{OAE}}
$$
This shows that $\sin (\widehat{O B A})=\sin (\widehat{O E A})$ and that $\sin (\widehat{O H B})=\sin (\widehat{O A E})$, which concludes the proof.
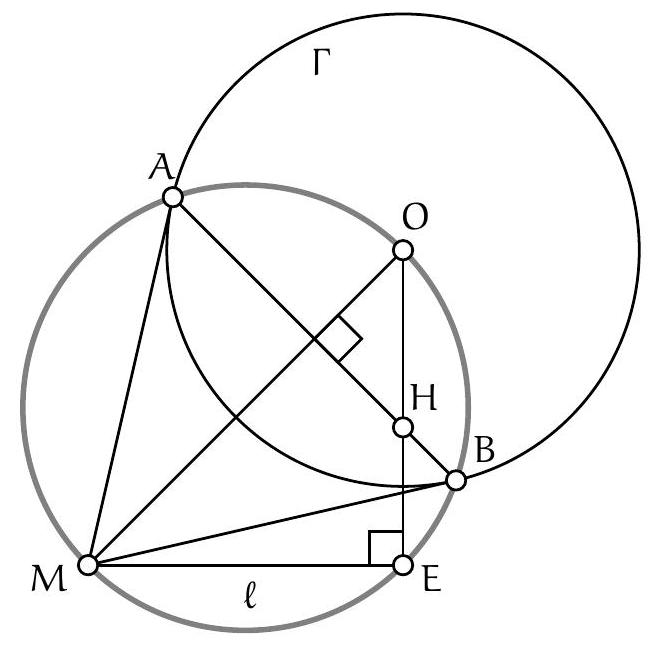
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma$ un cercle de centre $O$ et de rayon $r$ et $\ell$ une droite qui ne coupe pas $\Gamma$. On note $E$ le point d'intersection entre $\ell$ et la droite perpendiculaire à $\ell$ passant par $O$.
Soit $M$ un point de $\ell$ différent de $E$. Les tangentes au cercle $\Gamma$ et passant par $M$ touchent $\Gamma$ en $A$ et $B$. Enfin, soit $H$ le point d'intersection des droites ( $A B$ ) et ( $O E$ ).
Montrer que $\mathrm{OH}=\mathrm{r}^{2} / \mathrm{OE}$.
|
Tout d'abord, les triangles OAM, OBM et OEM sont respectivement rectangles en $A, B$ et $E$, de sorte que les points $A, O, B, E, M$ appartiennent tous à un même cercle de diamètre [OM].
Or, d'après la loi des sinus dans les triangles OBH et OEA, on sait que
$$
\frac{\mathrm{OH} \times \mathrm{OE}}{\mathrm{r}^{2}}=\frac{\mathrm{OH}}{\mathrm{OB}} \times \frac{\mathrm{OE}}{\mathrm{OA}}=\frac{\sin (\widehat{\mathrm{OBA}})}{\sin (\widehat{\mathrm{OHB}})} \times \frac{\sin (\widehat{\mathrm{OAE}})}{\sin (\widehat{\mathrm{OEA}})}
$$
Les points $O, B, E$ et $A$ étant cocycliques, on sait que $\widehat{O B A}=\widehat{O E A}$. D'autre part, puisque les droites $(\mathrm{AH})$ et $(\mathrm{HO})$ sont respectivement perpendiculaires à $(\mathrm{OM})$ et $(\mathrm{ME})$, on sait également que
$$
\widehat{\mathrm{OHB}}=180^{\circ}-\widehat{\mathrm{AHO}}=180^{\circ}-\widehat{\mathrm{OME}}=180^{\circ}-\widehat{\mathrm{OAE}}
$$
Cela montre que $\sin (\widehat{O B A})=\sin (\widehat{O E A})$ et que $\sin (\widehat{O H B})=\sin (\widehat{O A E})$, ce qui conclut.

|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
a105e586-f473-5f56-8854-213ef259f9ff
| 605,643
|
Let $n$ be an odd integer, and let $S$ be a set of $n$ points in the plane with integer coordinates. Consider a permutation $\mathrm{f}: \mathrm{S} \rightarrow \mathrm{S}$ that satisfies the following property:
For any pair of points $A$ and $B$ belonging to $S$, the distance between $f(A)$ and $f(B)$ is greater than or equal to the distance between $A$ and $B$.
Show that there exists a point $X$, belonging to $S$, such that $f(X)=X$.
|
Since $S$ has odd cardinality, $f$ admits an orbit of odd cardinality. Without loss of generality, we can therefore assume that $S$ is equal to this orbit, and even that $S=\left\{P_{1}, \ldots, P_{n}\right\}$ with $f\left(P_{i}\right)=P_{i+1}$ for all $i \leqslant n$, setting $P_{1}=n+1$.
If $f$ has no fixed point, it follows that $n \geqslant 3$. Let's show that this case is actually impossible.
Indeed, under these conditions, the statement shows that $P_{1} P_{2} \leqslant P_{2} P_{3} \leqslant \ldots \leqslant P_{n} P_{1}$, so that all these inequalities are in fact equalities. Furthermore, without loss of generality, by considering a point $P_{i}$ rather than $P_{1}$ and by performing integer translations and dividing all our coordinates by 2, we can assume that the coordinates of the vector $\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}}$ are not both even. Now, we will denote $x_{i}$ and $y_{i}$ the coordinates of the point $P_{i}$.
Since the squares modulo 4 are 0 and 1, we deduce that $P_{i} P_{i+1}^{2}=P_{1} P_{2}^{2}=\left(x_{i}-x_{i+1}\right)^{2}+$ $\left(y_{i}-y_{i+1}\right)^{2}$ is congruent to 1 or 2 modulo 4.
In the first case, it follows that the sum $\Delta_{i}=x_{i}+y_{i}+x_{i+1}+y_{i+1} \equiv 1(\bmod 2)$. We deduce that
$$
n \equiv \sum_{i=1}^{n} \Delta_{i} \equiv 2 \sum_{i=1}^{n}\left(x_{i}+y_{i}\right) \equiv 0 \quad(\bmod 2)
$$
In the second case, we have directly $\Delta_{i}^{x}=x_{i}+x_{i+1} \equiv 1(\bmod 2)$ and $\Delta_{i}^{y}=y_{i}+y_{i+1} \equiv 1$ $(\bmod 2)$, so that
$$
n \equiv \sum_{i=1}^{n} \Delta_{i}^{x} \equiv 2 \sum_{i=1}^{n} x_{i} \equiv 0 \quad(\bmod 2)
$$
Since $n$ is odd, neither of these two cases is possible, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n$ un entier impair, et soit $S$ un ensemble de $n$ points du plan à coordonnées entières. On considère une permutation $\mathrm{f}: \mathrm{S} \rightarrow \mathrm{S}$ qui satisfait la propriété suivante :
Pour toute paire de points $A$ et $B$ appartenant à $S$, la distance entre $f(A)$ et $f(B)$ est supérieure ou égale à la distance entre $A$ et $B$.
Montrer qu'il existe un point $X$, appartenant à $S$, tel que $f(X)=X$.
|
Puisque $S$ est de cardinal impair, f admet une orbite de cardinal impair. Sans perte de généralité, on peut donc supposer que $S$ est égal à cette orbite, et même que $S=\left\{P_{1}, \ldots, P_{n}\right\}$ avec $f\left(P_{i}\right)=P_{i+1}$ pour tout $i \leqslant n$, en posant $P_{1}=n+1$.
Si f n'a aucun point fixe, $\mathrm{c}^{\prime}$ est donc que $n \geqslant 3$. Montrons que ce cas est en fait impossible.
En effet, dans ces conditions, l'énoncé montre que $P_{1} P_{2} \leqslant P_{2} P_{3} \leqslant \ldots \leqslant P_{n} P_{1}$, de sorte que toutes ces inégalités sont en fait des égalités. En outre, toujours sans perte de généralité, quitte à considérer un point $P_{i}$ plutôt que $P_{1}$ et quitte à effectuer des translations à coordonnées entières et à diviser toutes nos coordonnées par 2, on peut supposer que les coordonnées du vecteur $\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}}$ ne sont pas toutes les deux paires. Maintenant, on va noter $x_{i}$ et $y_{i}$ les coordonnées du point $P_{i}$.
Puisque les carrés modulo 4 sont 0 et 1 , on en déduit que $P_{i} P_{i+1}^{2}=P_{1} P_{2}^{2}=\left(x_{i}-x_{i+1}\right)^{2}+$ $\left(y_{i}-y_{i+1}\right)^{2}$ est congru à 1 ou 2 modulo 4 .
Dans le premier cas, $c^{\prime}$ est donc que la somme $\Delta_{i}=x_{i}+y_{i}+x_{i+1}+y_{i+1} \equiv 1(\bmod 2)$. On en déduit que
$$
n \equiv \sum_{i=1}^{n} \Delta_{i} \equiv 2 \sum_{i=1}^{n}\left(x_{i}+y_{i}\right) \equiv 0 \quad(\bmod 2)
$$
Dans le deuxième cas, on a directement $\Delta_{i}^{x}=x_{i}+x_{i+1} \equiv 1(\bmod 2)$ et $\Delta_{i}^{y}=y_{i}+y_{i+1} \equiv 1$ $(\bmod 2)$, de sorte que
$$
n \equiv \sum_{i=1}^{n} \Delta_{i}^{x} \equiv 2 \sum_{i=1}^{n} x_{i} \equiv 0 \quad(\bmod 2)
$$
Puisque n est impair, aucun de ces deux cas n'est possible, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
fb5ad1a6-828d-597e-aa1a-c59fbf72ebc1
| 605,673
|
Let $ABC$ be a triangle, and let $E$ and $F$ be two points lying on the lines $(AB)$ and $(AC)$ respectively, distinct from $A, B$, and $C$. Let $\Omega$ be the circumcircle of $ABC$, $O$ the center of $\Omega$, and $\Gamma$ the circumcircle of $AEF$. Let $P$ be the intersection point of $\Gamma$ and $\Omega$ other than $A$, and let $Q$ be the reflection of $P$ over the line $(EF)$.
Show that $Q$ lies on the line $(BC)$ if and only if $O$ lies on the circle $\Gamma$.
|
Since (BC) and (EF) are two lines of notable interest, we denote 7 as their point of intersection, possibly at infinity. Then Q belongs to the line (BC) if and only if, in terms of angles between lines, we have (BT, ET) = (ET, PT).
Moreover, always in terms of angles between lines, we already know that
\[
\begin{aligned}
(\mathrm{PB}, \mathrm{PE}) & =(\mathrm{PB}, \mathrm{PA})+(\mathrm{PA}, \mathrm{PE})=(\mathrm{CB}, \mathrm{CA})+(\mathrm{FA}, \mathrm{FE}) \\
& =(\mathrm{CT}, \mathrm{CF})+(\mathrm{CF}, \mathrm{FT})=(\mathrm{CT}, \mathrm{FT})=(\mathrm{TB}, \mathrm{TE}),
\end{aligned}
\]
which means that the points \(\mathrm{P}, \mathrm{E}, \mathrm{B}\) and T are concyclic. Consequently, we know that \((B T, E T)=(B P, E P)\) and \((E T, P T)=(E B, P B)=(A B, P B)\).
We also know that \(2(B A, B P)=(O A, O P)\) and that \((E A, E P)=(B A, B P)+(B P, E P)\). Thus,
\[
\begin{aligned}
\text{Q belongs to the line }(\mathrm{BC}) & \Leftrightarrow(\mathrm{BP}, \mathrm{EP})=(\mathrm{AB}, \mathrm{~PB}) \\
& \Leftrightarrow(\mathrm{EA}, \mathrm{EP})=2(\mathrm{BA}, \mathrm{BP})=(\mathrm{OA}, \mathrm{OP}) \\
& \Leftrightarrow \mathrm{O} \text{ belongs to the circle } \Gamma.
\end{aligned}
\]
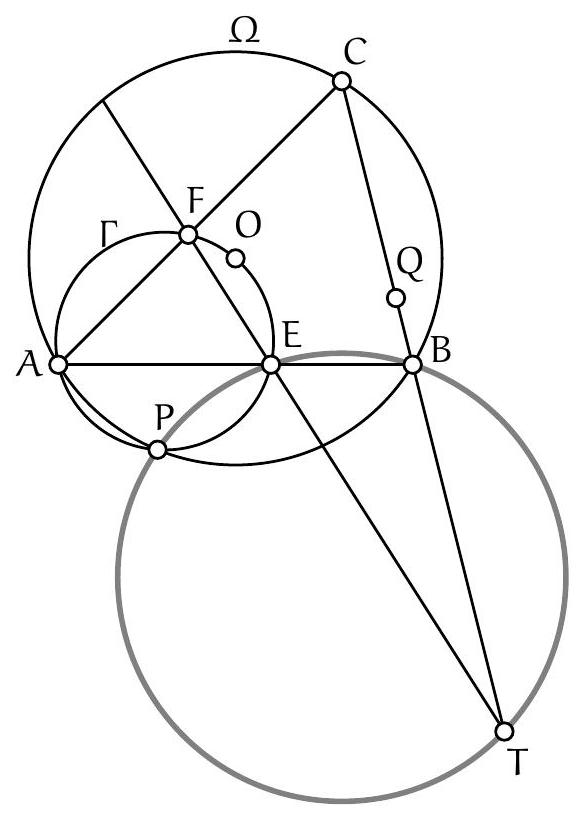
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et soit $E$ et $F$ deux points appartenant respectivement aux droites $(A B)$ et $(A C)$, distincts de $A, B$ et $C$. Soit également $\Omega$ le cercle circoncscrit à $A B C$, soit $O$ le centre de $\Omega$, et soit $\Gamma$ le cercle circonscrit à $A E F$. Enfin, soit $P$ le point d'intersection $\operatorname{de} \Gamma$ et $\Omega$ autre que $A$, et soit $Q$ le symétrique de $P$ par rapport à la droite (EF).
Montrer que Q appartient à la droite ( BC ) si et seulement si O appartient au cercle $\Gamma$.
|
Puisque (BC) et (EF) sont deux droites d'intérêt notoire, on note 7 leur point d'intersection, éventuellement rejeté à l'infini. Alors Q appartient à la droite ( BC ) si et seulement si, en angles de droites, on a (BT, ET) $=(\mathrm{ET}, \mathrm{PT})$.
Or, toujours en angles de droites, on sait déjà que
$$
\begin{aligned}
(\mathrm{PB}, \mathrm{PE}) & =(\mathrm{PB}, \mathrm{PA})+(\mathrm{PA}, \mathrm{PE})=(\mathrm{CB}, \mathrm{CA})+(\mathrm{FA}, \mathrm{FE}) \\
& =(\mathrm{CT}, \mathrm{CF})+(\mathrm{CF}, \mathrm{FT})=(\mathrm{CT}, \mathrm{FT})=(\mathrm{TB}, \mathrm{TE}),
\end{aligned}
$$
ce qui signifie que les points $\mathrm{P}, \mathrm{E}, \mathrm{B}$ et T sont cocycliques. Par conséquent, on sait que $(B T, E T)=(B P, E P)$ et $(E T, P T)=(E B, P B)=(A B, P B)$.
On sait aussi que $2(B A, B P)=(O A, O P)$ et que $(E A, E P)=(B A, B P)+(B P, E P)$. Ainsi,
$$
\begin{aligned}
\text { Q appartient à la droite }(\mathrm{BC}) & \Leftrightarrow(\mathrm{BP}, \mathrm{EP})=(\mathrm{AB}, \mathrm{~PB}) \\
& \Leftrightarrow(\mathrm{EA}, \mathrm{EP})=2(\mathrm{BA}, \mathrm{BP})=(\mathrm{OA}, \mathrm{OP}) \\
& \Leftrightarrow \mathrm{O} \text { appartient au cercle } \Gamma .
\end{aligned}
$$

|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
9cc04771-c616-5c29-b50e-5af46a0e6cb6
| 605,684
|
Let $m$ and $n$ be two natural numbers. Prove that $n!\neq m^{2}+2019$.
|
Let's proceed by contradiction and assume that we have two natural integers $m$ and $n$ such that $n!=m^{2}+2019$. First, we know that $n!\geqslant 2019>6!=720$, so $n \geqslant 7$. Consequently, $n!$ is divisible by $7!=2^{4} \times 3^{2} \times 5 \times 7$, and we have $0 \equiv m^{2}+2019$ $(\bmod 7!)$.
By virtue of the prime factorization stated above and the Chinese Remainder Theorem, this means that -2019 is a square modulo $k$ for any integer $k$, among $2^{4}$, $3^{2}$, 5, and 7.
We could show that this does not constitute a contradiction for $k=5$ and $k=7$. However, -2019 is not a square modulo 9 (nor modulo 16). Indeed, if $m^{2} \equiv -2019 \equiv -3$ $(\bmod 9)$, then 3 divides $m$, so 9 divides $m^{2}$, which should therefore be congruent to both 0 and -3 modulo 9.
Thus, as soon as $n \geqslant 7$, we actually have $n!\equiv 0 \not \equiv m^{2}-3 \equiv m^{2}+2019(\bmod 9)$, which shows that no pair of natural integers $(m, n)$ can satisfy the equation $n!=m^{2}+2019$.
Note: We also have $-2019 \equiv 5(\bmod 8)$, while $n^{2} \equiv 1(\bmod 8)$ for any odd integer $n$. Thus, as expected, -2019 is not a square modulo 8, and therefore not modulo $2^{4}$ either.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $m$ et $n$ deux entiers naturels. Démontrer que $n!\neq m^{2}+2019$.
|
Procédons par l'absurde, et supposons que l'on dispose de deux entiers naturels $m$ et $n$ tels que $n!=m^{2}+2019$. Tout d'abord, on sait que $n!\geqslant 2019>6!=720$, donc que $n \geqslant 7$. Par conséquent, $n!$ est divisible par $7!=2^{4} \times 3^{2} \times 5 \times 7$, et l'on a $0 \equiv m^{2}+2019$ $(\bmod 7!)$.
En vertu de la décomposition en produit de facteurs premiers énoncée ci-dessus et du théorème Chinois, cela signifie que -2019 est un carré modulo $k$ pour tout entier $k$, parmi $2^{4}, 3^{2}$, 5 et 7 .
On pourrait démontrer que cela ne constitue pas une contradiction pour $k=5$ et $k=7$. En revanche, -2019 n'est pas un carré modulo 9 (ni modulo 16). En effet, si m² $\equiv-2019 \equiv-3$ $(\bmod 9)$, alors 3 divise $m$, donc 9 divise $m^{2}$, qui devrait donc être congru à la fois à 0 et à -3 modulo 9.
Ainsi, dès lors que $n \geqslant 7$, on a en fait $n!\equiv 0 \not \equiv m^{2}-3 \equiv m^{2}+2019(\bmod 9)$, ce qui montre bien que nulle paire d'entiers naturels ( $m, n$ ) ne peut satisfaire l'équation $n!=m^{2}+2019$.
Note : On a également $-2019 \equiv 5(\bmod 8)$, alors que $n^{2} \equiv 1(\bmod 8)$ pour tout entier $n$ impair. Ainsi, comme prévu, -2019 n'est pas un carré modulo 8 , donc modulo $2^{4}$ non plus.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
39f147cc-4dc8-5e00-b35d-767c2b9e7946
| 605,706
|
Let $ABC$ be a triangle, and let $M$ be the foot of the median from $A$. Let $\ell_{\mathrm{b}}$ be the bisector of $\widehat{A M B}$ and $\ell_{c}$ be the bisector of $\widehat{A M C}$. Furthermore, let $B^{\prime}$ be the orthogonal projection of $B$ onto $\ell_{b}$, let $C^{\prime}$ be the orthogonal projection of $C$ onto $\ell_{c}$, and let $A^{\prime}$ be the point of intersection of the lines $(A M)$ and $(B^{\prime} C^{\prime})$.
Prove that $A^{\prime} B^{\prime}=A^{\prime} C^{\prime}$.
|
Let $\beta$ be the angle $\widehat{A M B^{\prime}}$ and $\gamma$ be the angle $\widehat{A M C^{\prime}}$. By construction, we know that $2(\beta+\gamma)=180^{\circ}$, so $\widehat{\mathrm{B}^{\prime} \mathrm{MC}^{\prime}}=\beta+\gamma=90^{\circ}$. Thus, the line $\ell_{\mathrm{b}}=\left(\mathrm{MB}^{\prime}\right)$ is perpendicular to the lines $\left(\mathrm{BB}^{\prime}\right)$ and $\ell_{c}=\left(M C^{\prime}\right)$, and the line $\ell_{c}=\left(M C^{\prime}\right)$ is perpendicular to the lines $\left(C C^{\prime}\right)$ and $\ell_{b}=\left(M B^{\prime}\right)$.
Furthermore, we notice that $\widehat{\mathrm{B}^{\prime} \mathrm{BM}}=180^{\circ}-\widehat{\mathrm{BB}^{\prime} M}-\widehat{\mathrm{BMB}^{\prime}}=180^{\circ}-90^{\circ}-\beta=\gamma$ and that, similarly, $\widehat{C^{\prime} C M}=\beta$. Thus, the two triangles $B B^{\prime} M$ and $M C^{\prime} C$ are similar. Moreover, since $M$ is the foot of the median of $A B C$ from $A$, $c^{\prime}$ is actually the midpoint of [BC], so $B M=M C$. The two triangles $B B^{\prime} M$ and $M C C^{\prime}$ are therefore isometric.
In particular, we deduce that $B B^{\prime}=M C^{\prime}$ and that $C C^{\prime}=M B^{\prime}$. But then, since the triangle $M B^{\prime} C^{\prime}$ is right-angled at $M$, it has an angle and two sides of the same measures as the triangle $B^{\prime} M B$, and it is therefore isometric with $B^{\prime} M B$ and with $C^{\prime} C M$.
We thus deduce in particular that
$$
\widehat{A^{\prime} C^{\prime} M}=\widehat{B^{\prime} C^{\prime} M}=\widehat{M B B^{\prime}}=\gamma=\widehat{A M C^{\prime}}=\widehat{A^{\prime} M C^{\prime}}
$$
so that the triangle $A^{\prime} C^{\prime} M$ is isosceles at $A^{\prime}$. Similarly, the triangle $A^{\prime} B^{\prime} M$ is isosceles at $A^{\prime}$, and we conclude as expected that $A^{\prime} B^{\prime}=A^{\prime} M=A^{\prime} C^{\prime}$.
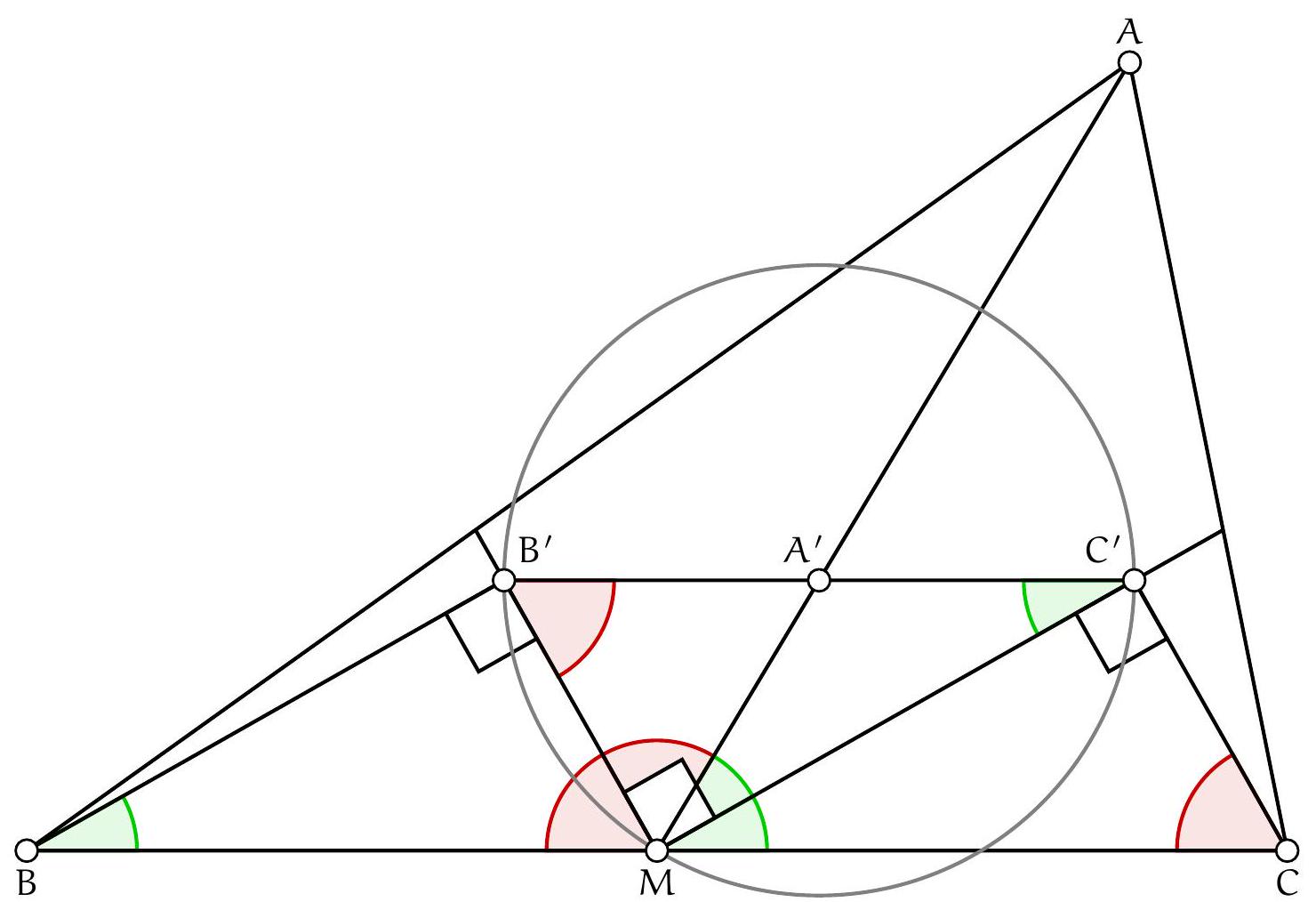
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et soit $M$ le pied de la médiane issue de $A$. Soit également $\ell_{\mathrm{b}}$ la bissectrice de $\widehat{A M B}$ et $\ell_{c}$ la bissectrice de $\widehat{A M C}$. Enfin, soit $B^{\prime}$ le projeté orthogonal de $B$ sur $\ell_{b}$, soit $C^{\prime}$ le projeté orthogonal de $C$ sur $\ell_{c}$, et soit $A^{\prime}$ le point $d^{\prime}$ intersection des droites $(A M)$ et ( $B^{\prime} C^{\prime}$ ).
Démontrer que $A^{\prime} B^{\prime}=A^{\prime} C^{\prime}$.
|
Soit $\beta$ l'angle $\widehat{A M B^{\prime}}$ et $\gamma$ l'angle $\widehat{A M C^{\prime}}$. Par construction, on sait que $2(\beta+\gamma)=180^{\circ}$, donc que $\widehat{\mathrm{B}^{\prime} \mathrm{MC}^{\prime}}=\beta+\gamma=90^{\circ}$. Ainsi, la droite $\ell_{\mathrm{b}}=\left(\mathrm{MB}^{\prime}\right)$ est perpendiculaire aux droites $\left(\mathrm{BB}^{\prime}\right)$ et $\ell_{c}=\left(M C^{\prime}\right)$, et la droite $\ell_{c}=\left(M C^{\prime}\right)$ est perpendiculaire aux droites $\left(C C^{\prime}\right)$ et $\ell_{b}=\left(M B^{\prime}\right)$.
$D^{\prime}$ autre part, on remarque que $\widehat{\mathrm{B}^{\prime} \mathrm{BM}}=180^{\circ}-\widehat{\mathrm{BB}^{\prime} M}-\widehat{\mathrm{BMB}^{\prime}}=180^{\circ}-90^{\circ}-\beta=\gamma$ et que, de même, $\widehat{C^{\prime} C M}=\beta$. Ainsi, les deux triangles $B B^{\prime} M$ et $M C^{\prime} C$ sont semblables. En outre, puisque $M$ est le pied de la médiane de $A B C$ issue de $A$, $c^{\prime}$ est en fait le milieu de [BC], donc $B M=M C$. Les deux triangles $B B^{\prime} M$ et $M C C^{\prime}$ sont donc isométriques.
En particulier, on en déduit que $B B^{\prime}=M C^{\prime}$ et que $C C^{\prime}=M B^{\prime}$. Mais alors, puisque le triangle $M B^{\prime} C^{\prime}$ est rectangle en $M$, il a un angle et deux côtés de mêmes mesures que le triangle $B^{\prime} M B$, et il est donc isométrique avec $B^{\prime} M B$ et avec $C^{\prime} C M$.
On en déduit notamment que
$$
\widehat{A^{\prime} C^{\prime} M}=\widehat{B^{\prime} C^{\prime} M}=\widehat{M B B^{\prime}}=\gamma=\widehat{A M C^{\prime}}=\widehat{A^{\prime} M C^{\prime}}
$$
donc que le triangle $A^{\prime} C^{\prime} M$ est isocèle en $A^{\prime}$. De même, le triangle $A^{\prime} B^{\prime} M$ est isocèle en $A^{\prime}$, et on en conclut comme prévu que $A^{\prime} B^{\prime}=A^{\prime} M=A^{\prime} C^{\prime}$.

|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
dc02208a-56a4-5efd-8503-92da847a6a18
| 605,714
|
Let $\mathrm{f}: \mathbb{Z} \mapsto \mathbb{R}$ be a function such that
$$
\mathbf{f}(\mathrm{n}+2)=(f(n+1)+\mathbf{f}(\mathrm{n})) / 2
$$
for all integers $n$. Suppose that $f$ is bounded, that is, there exists a real number $\mathbf{F}$ such that $-F \leqslant f(n) \leqslant F$ for all $n$.
Prove that $f$ is a constant function.
|
Suppose that $f$ is not constant. There exists an integer $n$ and a real number $\varepsilon \neq 0$ such that $f(n+1) - f(n) = \varepsilon$.
For any integer $k$, let $\Delta_k = f(k+1) - f(k)$. Then
$$
\Delta_{k+1} = f(k+2) - f(k+1) = (f(k+1) + f(k)) / 2 - f(k+1) = -\Delta_k / 2
$$
and, conversely, $\Delta_{k-1} = -2 \Delta_k$. An immediate induction then shows that $\Delta_{n-k} = (-2)^k \varepsilon$ for all $k \geq 0$.
However, for any integer $k$, we know that $|\Delta_k| \leq |f(k+1)| + |f(k)| \leq 2F$. But this is incompatible with the fact that $|\Delta_{n-k}| = 2^k |\varepsilon|$ for all $k \geq 0$. Our initial assumption was therefore absurd, and $f$ is indeed constant.
## Exercises for the Senior Group
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\mathrm{f}: \mathbb{Z} \mapsto \mathbb{R}$ une fonction telle que
$$
\mathbf{f}(\mathrm{n}+2)=(f(n+1)+\mathbf{f}(\mathrm{n})) / 2
$$
pour tout entier $n$. On suppose que f est bornée, c'est-à-dire qu'il existe un réel $\mathbf{F}$ tel que $-F \leqslant f(n) \leqslant F$ pour tout $n$.
Démontrer que $f$ est une fonction constante.
|
Supposons que f n'est pas constante. Il existe donc un entier n et un réel $\varepsilon \neq 0$ tels que $f(n+1)-f(n)=\varepsilon$.
Pour tout entier $k$, posons $\Delta_{k}=f(k+1)-f(k)$. Alors
$$
\Delta_{k+1}=f(k+2)-f(k+1)=(f(k+1)+f(k)) / 2-f(k+1)=-\Delta_{k} / 2
$$
et, réciproquement, $\Delta_{\mathrm{k}-1}=-2 \Delta_{\mathrm{k}}$. Une récurrence immédiate indique alors que $\Delta_{\mathrm{n}-\mathrm{k}}=$ $(-2)^{k} \varepsilon$ pour tout $k \geqslant 0$.
Or, pour tout entier $k$, on sait que $\left|\Delta_{k}\right| \leqslant|\mathbf{f}(k+1)|+|f(k)| \leqslant 2 \mathbf{F}$. Mais ceci est incompatible avec le fait que $\left|\Delta_{n-k}\right|=2^{k}|\varepsilon|$ pout tout $k \geqslant 0$. Notre supposition initiale était donc absurde, et $f$ est bien constante.
## Exercices du groupe Senior
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
7348577f-13a0-571e-b9ab-89722cbf7bfd
| 605,722
|
Let $A, B, C$ and $P$ be four points in the plane such that $ABC$ is an equilateral triangle and $AP < BP < CP$. We assume that the only given lengths $AP, BP$, and $CP$ allow us to uniquely determine the length $AB$.
Prove that $P$ lies on the circumcircle of $ABC$.
|
Let $\Gamma_{\mathrm{a}}, \Gamma_{\mathrm{b}}$ and $\Gamma_{\mathrm{c}}$ be the circles centered at $P$ and passing through $A$, $B$, and $C$ respectively. Let $C^{\bullet}$ be the symmetric point of $C$ with respect to $(AP)$. Note that $C^{\bullet}$ is the only point on $\Gamma_{\mathrm{c}}$, other than $C$ itself, such that $A C = A C^{\bullet}$.
Now, let $r$ be the rotation centered at $\mathcal{A}$ with an angle of $60^{\circ}$ in the clockwise direction. Without loss of generality, we assume that $C = r(B)$.
Then, for any point $B^{\prime}$ on $\Gamma_{b}$, we associate the point $C^{\prime} = r(B^{\prime})$. The triangle $A B^{\prime} C^{\prime}$ is equilateral, and the hypothesis of the problem states that for any $B^{\prime}$, the point $C^{\prime}$ can only belong to $\Gamma_{c}$ if it is equal to $C$ or $C^{\bullet}$.
As $B^{\prime}$ describes $\Gamma_{b}$, the point $C^{\prime}$ describes the circle $r(\Gamma_{b})$, centered at $r(P)$ and with radius $PB$. This circle cannot contain both points $C$ and $C^{\bullet}$, since then its center would lie on the perpendicular bisector $(AP)$ of $[C^{\bullet}]$, which is not the case for $r(P)$.
Since $r(\Gamma_{b})$ already contains $C$, it cannot contain any other point of $\Gamma_{c}$. Given that $r(P)A = PA < PB$, we know that $A$ is located inside $r(\Gamma_{b})$, which is therefore internally tangent to $\Gamma_{c}$ at the point $C$.
Since $PB = r(P)C < PC$, it follows that the points $C, r(P)$, and $P$ are collinear in that order. This implies that $PC = r(P)C + r(P)P = PB + PA$, or equivalently, $CP \cdot AB = BP \cdot AC + AP \cdot BC$. The Ptolemy's theorem then indicates that the points $A, B, C$, and $P$ are concyclic, which concludes the proof.
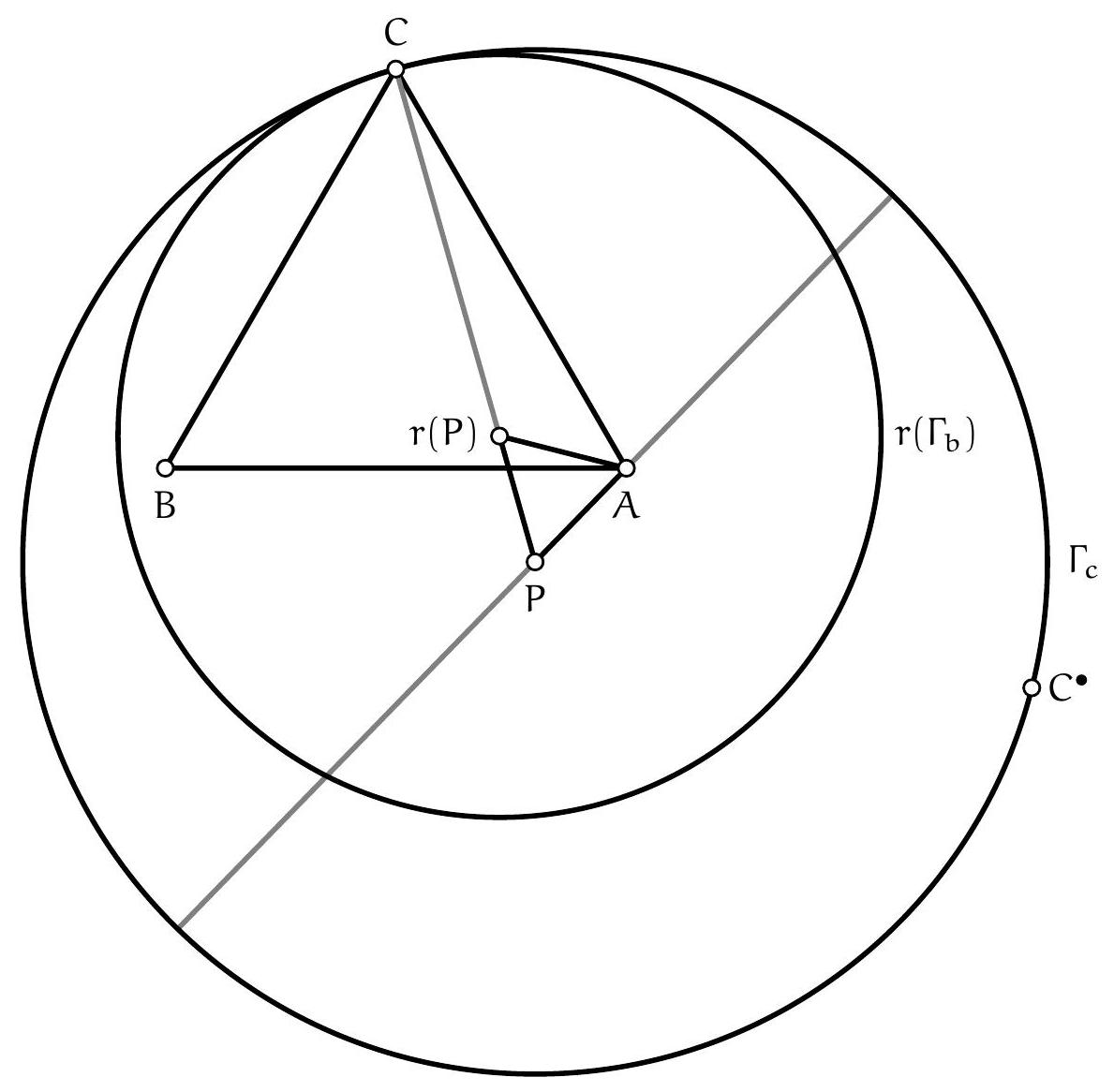
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C$ et $P$ quatre points du plan tels que $A B C$ soit un triangle équilatéral et que $A P<B P<C P$. On suppose que la seule donnée des longueurs $A P, B P$ et $C P$ nous permet de déterminer, de manière unique, la longueur $A B$.
Démontrer que P appartient au cercle circonscrit à $A B C$.
|
Soit $\Gamma_{\mathrm{a}}, \Gamma_{\mathrm{b}}$ et $\Gamma_{\mathrm{c}}$ les cercles de centre P et passant respectivement par $A$, $B$ et $C$. Soit également $C^{\bullet}$ le symétrique de $C$ par rapport à ( $A P$ ). Notons que $C^{\bullet}$ est le seul point de $\Gamma_{\mathrm{c}}$, autre que C lui-même, tel que $A C=A C^{\bullet}$.
On note maintenant r la rotation de centre $\mathcal{A}$ et d'angle $60^{\circ}$ dans le sens horaire. Quitte à faire subir une symétrie à la figure de répart, on suppose que $C=r(B)$.
Puis, à tout point $B^{\prime}$ de $\Gamma_{b}$, on associe le point $C^{\prime}=r\left(B^{\prime}\right)$. Le triangle $A B^{\prime} C^{\prime}$ est équilatéral, et l'hypothèse de l'énoncé stipule donc que, pour tout $B^{\prime}$, le point $C^{\prime}$ ne peut appartenir à $\Gamma_{c}$ que s'il est égal à $C$ ou à $C^{\bullet}$.
Or, quand $B^{\prime}$ décrit $\Gamma_{b}$, le point $C^{\prime}$ décrit le cercle $r\left(\Gamma_{b}\right)$, de centre $r(P)$ et de rayon $P B$. Ce cercle ne peut contenir à la fois les points $C$ et $C^{\bullet}$, puisque alors son centre se trouverait sur la médiatrice (AP) de $\left[C^{\bullet}\right]$, ce qui n'est pas le cas de $r(P)$.
Comme $\mathrm{r}\left(\Gamma_{\mathrm{b}}\right)$ contient déjà C , il ne peut donc pas contenir d'autre point de $\Gamma_{\mathrm{c}}$, et puisque $\mathrm{r}(\mathrm{P}) A=\mathrm{PA}<\mathrm{PB}$, on sait que $A$ est situé à l'intérieur $\operatorname{de} \mathrm{r}\left(\Gamma_{\mathrm{b}}\right)$, qui est donc tangent intérieurement, en le point $C$, à $\Gamma_{\mathrm{c}}$.
Comme $P B=r(P) C<P C, c^{\prime}$ est en fait que les points $C, r(P)$ et $P$ sont alignés dans cet ordre. On en déduit que $P C=r(P) C+r(P) P=P B+P A$, ou encore que $C P \cdot A B=B P \cdot A C+A P$. $B C$. L'égalité de Ptolémée indique donc que les points $A, B, C$ et $P$ sont cocycliques, ce qui conclut.

|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
f74011f6-10bf-5a50-a66e-410c6ee0e0a3
| 605,728
|
Let $a_{0}, a_{1}, \ldots, a_{d}$ be integers such that $\operatorname{GCD}\left(a_{0}, a_{1}\right)=1$. For any integer $n \geqslant 1$, we define
$$
u_{n}=\sum_{k=0}^{d} a_{k} \varphi(n+k)
$$
Prove that 1 is the only natural number that divides all integers $u_{n}$.
We recall that $\varphi(n+k)$ is the number of natural numbers $\ell<n+k$ such that $\operatorname{GCD}(\ell, n+k)=1$.
|
Let us proceed by contradiction and assume that there exists a prime number $p$ that divides all integers $u_{n}$.
First, since $\varphi(1)=\varphi(2)=1$ and $\varphi(\mathfrak{n})$ is even for all $\mathfrak{n} \geqslant 2$, we note that $u_{1} \equiv a_{0}+a_{1}(\bmod 2)$ and that $u_{2} \equiv a_{0}(\bmod 2)$. Since $a_{0}$ and $a_{1}$ are coprime, the integers $\mathfrak{u}_{1}$ and $\mathfrak{u}_{2}$ cannot both be even, so $p \geqslant 3$.
Let $\delta$ then be the largest integer such that $p$ does not divide $a_{\delta}$. For any integer $n \geqslant 1$, we denote by $T_{n}$ the $\delta$-tuple $(\varphi(n), \varphi(n+1), \ldots, \varphi(n+\delta-1))$, considered modulo $p$. Since $u_{n} \equiv 0(\bmod p)$, it follows that
$$
\varphi(n+\delta) \equiv-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} \varphi(n+k) \quad(\bmod p)
$$
Thus, if we denote by $\lambda:(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta} \mapsto(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta}$ the function defined by
$$
\lambda:\left(x_{0}, x_{1}, \ldots, x_{\delta-1}\right) \mapsto\left(x_{1}, x_{2}, \ldots, x_{\delta-1},-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} x_{k}\right)
$$
we have $\mathbf{T}_{\mathfrak{n}+1}=\lambda\left(\mathbf{T}_{\mathfrak{n}}\right)$. By the pigeonhole principle, there exist two integers $k, \ell \geqslant 1$ such that $\mathbf{T}_{\mathrm{k}}=\mathbf{T}_{\mathrm{k}+\ell}$. We then have $\mathbf{T}_{\mathbf{n}}=\mathbf{T}_{\mathrm{n}+\ell}$ and $\varphi(\mathrm{n}) \equiv \varphi(\mathrm{n}+\ell)(\bmod p)$ for all $n \geqslant k$.
We then prove the following lemma: for all integers $a \geqslant 1$ and $b \geqslant 3$, there exists a prime number $q>a$ such that $q \not \equiv 1(\bmod b)$. Indeed, the integer $m=\max \{a, b\}!-1$ is congruent to -1 $(\bmod b)$, so it must have a prime factor $q \not \equiv 1(\bmod b)$, and $q$ cannot divide $\mathrm{m}+1=\max \{\mathrm{a}, \mathrm{b}\}!$, so $\mathrm{q}>\mathrm{a}$.
By applying this lemma twice, we deduce that there exist two prime numbers $q$ and $r$ such that $q, r \not \equiv 1(\bmod p)$ and $q>r>k+\ell$. But then $q$ is coprime with $\ell$, so $q^{\varphi(\ell)} \equiv 1(\bmod \ell)$, and $\varphi\left(q^{\varphi(\ell)} n\right) \equiv \varphi(n)(\bmod p)$ for all $n \geqslant k$.
Since $q>r \geqslant k$, we deduce that
$$
\begin{array}{rlr}
(q-1) q^{\varphi(\ell)} & \equiv \varphi\left(q^{\varphi(\ell)+1}\right) \equiv \varphi(q) & \equiv q-1 \quad(\bmod p) \\
(r-1)(q-1) q^{\varphi(\ell)-1} & \equiv \varphi\left(r q^{\varphi(\ell)}\right) & \equiv \varphi(r)
\end{array}
$$
Since $q, r \not \equiv 1(\bmod p)$, it follows that $q^{\varphi(\ell)} \equiv(q-1) q^{\varphi(\ell)-1} \equiv 1(\bmod p)$, so $q^{\varphi(\ell)-1} \equiv 0$ $(\bmod p)$, which is impossible. We have thus obtained the desired contradiction, which concludes the proof.
Note: We can also appeal to Dirichlet's theorem, which states that for all integers $a$ and $b$ that are coprime, there are infinitely many prime numbers $q \equiv a(\bmod b)$. There then exist prime numbers $q_{0}>q_{1}>\ldots>q_{d}>p+d$ congruent to $1(\bmod p)$. Then, if we choose $k \in\{0,1\}$ such that $p$ does not divide $a_{k}$, there also exists a prime number $r$ such that $r \equiv 2(\bmod p)$ and $r \equiv k-i\left(\bmod q_{i}\right)$ for all $i \neq k$. Then $p$ does not divide $u_{r-k}$.
Exercise 7. Let $n \geqslant 2$ be an integer. Clara has a board of size $3 n \times 3 n$, similar to a chessboard. She has just invented a new piece, the leopard, which she can move as follows: by moving it one square up, one square to the right, or one square diagonally, down and to the left. Clara placed her leopard on one of the squares of the board, then moved it so that it never passes through the same square twice, until it returns to its starting square.
What is the maximum number of moves Clara could have made in this way?
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, \ldots, a_{d}$ des entiers tels que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=1$. Pour tout entier $n \geqslant 1$, on pose
$$
u_{n}=\sum_{k=0}^{d} a_{k} \varphi(n+k)
$$
Démontrer que 1 est le seul entier naturel divisant tous les entiers $u_{n}$.
On rappelle que $\varphi(n+k)$ est le nombre d'entiers naturels $\ell<n+k$ tels que $\operatorname{PGCD}(\ell, n+k)=1$.
|
Procédons par l'absurde, et supposons qu'il existe un nombre premier $p$ qui divise tous les entiers $u_{n}$.
Tout d'abord, puisque $\varphi(1)=\varphi(2)=1$ et que $\varphi(\mathfrak{n})$ est pair pour tout $\mathfrak{n} \geqslant 2$, on remarque que $u_{1} \equiv a_{0}+a_{1}(\bmod 2)$ et que $u_{2} \equiv a_{0}(\bmod 2)$. Comme $a_{0}$ et $a_{1}$ sont premiers entre eux, les entiers $\mathfrak{u}_{1}$ et $\mathfrak{u}_{2}$ ne peuvent donc pas être pairs tous les deux, de sorte que $p \geqslant 3$.
Soit alors $\delta$ le plus grand entier tel que $p$ ne divise pas $a_{\delta}$. Pour tout entier $n \geqslant 1$, on note $T_{n}$ le $\delta$-uplet $(\varphi(n), \varphi(n+1), \ldots, \varphi(n+\delta-1))$, considéré modulo $p$. Puisque $u_{n} \equiv 0(\bmod p)$, $c^{\prime}$ est que
$$
\varphi(n+\delta) \equiv-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} \varphi(n+k) \quad(\bmod p)
$$
Ainsi, si l'on note $\lambda:(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta} \mapsto(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta}$ la fonction définie par
$$
\lambda:\left(x_{0}, x_{1}, \ldots, x_{\delta-1}\right) \mapsto\left(x_{1}, x_{2}, \ldots, x_{\delta-1},-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} x_{k}\right)
$$
on a $\mathbf{T}_{\mathfrak{n}+1}=\lambda\left(\mathbf{T}_{\mathfrak{n}}\right)$. Or, d'après le principe des tiroirs, il existe deux entiers $k, \ell \geqslant 1$ tels que $\mathbf{T}_{\mathrm{k}}=\mathbf{T}_{\mathrm{k}+\ell}$. On a alors $\mathbf{T}_{\mathbf{n}}=\mathbf{T}_{\mathrm{n}+\ell}$ et $\varphi(\mathrm{n}) \equiv \varphi(\mathrm{n}+\ell)(\bmod p)$ pour tout $n \geqslant k$.
On montre alors le lemme suivant : pour tous les entiers $a \geqslant 1$ et $b \geqslant 3$, il existe un nombre premier $q>a$ tel que $q \not \equiv 1(\bmod b)$. En effet, l'entier $m=\max \{a, b\}!-1$ est congru à -1 $(\bmod b)$, donc il admet nécessairement un facteur premier $q \not \equiv 1(\bmod b)$, et $q$ ne peut pas diviser $\mathrm{m}+1=\max \{\mathrm{a}, \mathrm{b}\}!$, donc $\mathrm{q}>\mathrm{a}$.
En appliquant ce lemme deux fois de suite, on en déduit qu'il existe deux nombres premiers $q$ et $r$ tels que $q, r \not \equiv 1(\bmod p)$ et $q>r>k+\ell$. Mais alors $q$ est premier avec $\ell$, donc $q^{\varphi(\ell)} \equiv 1(\bmod \ell)$, et $\varphi\left(q^{\varphi(\ell)} n\right) \equiv \varphi(n)(\bmod p)$ pour tout $n \geqslant k$.
Puisque $q>r \geqslant k$, on en déduit que
$$
\begin{array}{rlr}
(q-1) q^{\varphi(\ell)} & \equiv \varphi\left(q^{\varphi(\ell)+1}\right) \equiv \varphi(q) & \equiv q-1 \quad(\bmod p) \\
(r-1)(q-1) q^{\varphi(\ell)-1} & \equiv \varphi\left(r q^{\varphi(\ell)}\right) & \equiv \varphi(r)
\end{array}
$$
Comme $q, r \not \equiv 1(\bmod p), c^{\prime}$ est que $q^{\varphi(\ell)} \equiv(q-1) q^{\varphi(\ell)-1} \equiv 1(\bmod p)$, donc que $q^{\varphi(\ell)-1} \equiv 0$ $(\bmod p)$, ce qui est impossible. On a ainsi obtenu la contradiction souhaitée, ce qui conclut.
Note : On peut aussi faire appel au théorème de Dirichlet, qui affirme que, pour tous les entiers $a$ et $b$ premiers entre eux, il existe une infinité de nombres premiers $q \equiv a(\bmod b)$. Il existe alors des nombres premiers $q_{0}>q_{1}>\ldots>q_{d}>p+d$ congrus à $1(\bmod p)$. Puis, si on choisit $k \in\{0,1\}$ tel que $p$ ne divise pas $a_{k}$, il existe aussi un nombre premier $r$ tel que $r \equiv 2(\bmod p)$ et $r \equiv k-i\left(\bmod q_{i}\right)$ pour tout $i \neq k$. Alors $p$ ne divise pas $u_{r-k}$.
Exercice 7 . Soit $n \geqslant 2$ un entier. Clara dispose d'un plateau de taille $3 n \times 3 n$, semblable à un échiquier. Elle vient d'inventer une nouvelle pièce, le léopard, qu'elle peut mouvoir comme suit : en le déplaçant d'une case vers le haut, d'une case vers la droite, ou bien d'une case en diagonale, vers le bas et la gauche. Clara a posé son léopard sur une des cases du plateau, puis elle l'a déplacé, de sorte qu'il ne passe jamais deux fois par la même case, jusqu'à ce qu'il revienne à sa case de départ.
Quelle est le plus grand nombre possible de déplacements que Clara a pu effectuer en procédant de la sorte?
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
a140de3f-8c00-59d6-9cc9-738145c30650
| 605,735
|
Let $A B C D$ be a trapezoid such that $(A B)$ is parallel to $(C D)$. Let $P$ be a point on $[A C]$ and $Q$ be a point on $[B D]$ such that $\widehat{A P D}=\widehat{\mathrm{BQC}}$.
Prove that $\widehat{A Q D}=\widehat{\mathrm{BPC}}$.
|
The statement gives us several angle equalities: let's exploit them! First, we notice that
$$
\widehat{\mathrm{DPC}}=180^{\circ}-\widehat{\mathrm{APD}}=180^{\circ}-\widehat{\mathrm{CQB}}=\widehat{\mathrm{DQC}},
$$
which means that the points $C, D, P$ and $Q$ are concyclic.
From this, we deduce that
$$
\widehat{\mathrm{BQP}}=180^{\circ}-\widehat{\mathrm{PQD}}=180^{\circ}-\widehat{\mathrm{PCD}}=180^{\circ}-\widehat{\mathrm{PAB}}
$$
which again means that the points $A, B, P$ and $Q$ are concyclic.
We conclude that
$$
\begin{aligned}
\widehat{\mathrm{AQD}} & =\widehat{\mathrm{AQP}}+\widehat{\mathrm{PQD}}=\widehat{\mathrm{ABP}}+\widehat{\mathrm{PCD}}=(\widehat{\mathrm{ABC}}-\widehat{\mathrm{PBC}})+(\widehat{\mathrm{BCD}}-\widehat{\mathrm{BCP}}) \\
& =(\widehat{\mathrm{ABC}}+\widehat{\mathrm{BCD}})-(\widehat{\mathrm{PBC}}+\widehat{\mathrm{BCP}})=180^{\circ}-\left(180^{\circ}-\widehat{\mathrm{CPB}}\right)=\widehat{\mathrm{CPB}}
\end{aligned}
$$
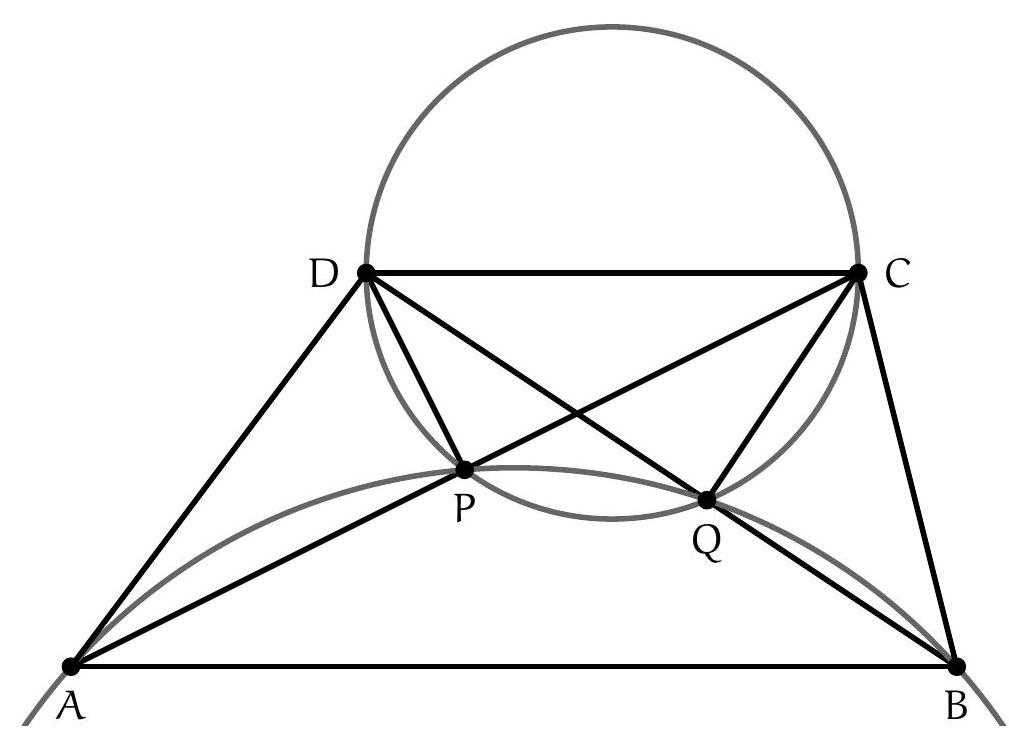
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze tel que $(A B)$ soit parallèle à $(C D)$. Soit $P$ un point de $[A C]$ et $Q$ un point de $[B D]$ tels que $\widehat{A P D}=\widehat{\mathrm{BQC}}$.
Démontrer que $\widehat{A Q D}=\widehat{\mathrm{BPC}}$.
|
L'énoncé nous donne plein d'égalités d'angles : exploitons-les! Tout d'abord, on remarque que
$$
\widehat{\mathrm{DPC}}=180^{\circ}-\widehat{\mathrm{APD}}=180^{\circ}-\widehat{\mathrm{CQB}}=\widehat{\mathrm{DQC}},
$$
ce qui signifie que les points $C, D, P$ et $Q$ sont cocycliques.
On en déduit que
$$
\widehat{\mathrm{BQP}}=180^{\circ}-\widehat{\mathrm{PQD}}=180^{\circ}-\widehat{\mathrm{PCD}}=180^{\circ}-\widehat{\mathrm{PAB}}
$$
ce qui signifie là encore que les points $A, B, P$ et $Q$ sont cocycliques.
On en conclut que
$$
\begin{aligned}
\widehat{\mathrm{AQD}} & =\widehat{\mathrm{AQP}}+\widehat{\mathrm{PQD}}=\widehat{\mathrm{ABP}}+\widehat{\mathrm{PCD}}=(\widehat{\mathrm{ABC}}-\widehat{\mathrm{PBC}})+(\widehat{\mathrm{BCD}}-\widehat{\mathrm{BCP}}) \\
& =(\widehat{\mathrm{ABC}}+\widehat{\mathrm{BCD}})-(\widehat{\mathrm{PBC}}+\widehat{\mathrm{BCP}})=180^{\circ}-\left(180^{\circ}-\widehat{\mathrm{CPB}}\right)=\widehat{\mathrm{CPB}}
\end{aligned}
$$

|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
8ecd4c63-551a-5afe-8e73-5819edd82f90
| 605,753
|
It is said that a pair of integers ( $\mathbf{a}, \mathrm{b}$ ) is Cypriot if $\mathrm{a} \geqslant \mathrm{b} \geqslant 2$, if a and b are coprime, and if $a+b$ divides $a^{b}+b^{a}$.
Prove that there are infinitely many distinct Cypriot pairs.
|
Let $k=a-b$. Since $a$ and $b$ are coprime, we know that $a \neq b$, so $k \geqslant 1$. Thus,
$$
a^{b}+b^{a} \equiv a^{b}+(-a)^{a} \equiv a^{b}\left(1+(-1)^{a} a^{k}\right) \quad(\bmod a+b)
$$
Since $a$ is coprime with $b$, it is also coprime with $a+b$.
According to Gauss's theorem, we want $a+b=2a-k$ to divide $1+(-1)^{a} a^{k}$, or equivalently $a^{\mathrm{k}}+(-1)^{\mathrm{a}}$.
For lack of a better approach, let's examine the small values of $k$. Choosing $k=1$ would mean that $a+b$ divides $a \pm 1$, which is impossible since $a+b > a+1 > a-1$. So we look at $k=2$.
In this case, we want $2a-2=2(a-1)$ to divide $a^{2}+(-1)^{a}$. Note that $a^{2}+(-1)^{a} \equiv 1+(-1)^{\mathrm{a}} \pmod{a-1}$. Consequently, and since $a \geqslant 2$, we must necessarily choose $a$ to be odd. In this case, it remains to ensure that $2(a-1)$ divides $a^{2}-1=(a-1)(a+1)$, which means that 2 must divide $a-1$. But this is indeed the case, since $a$ is odd.
In conclusion, we have shown that all pairs $(2k+1, 2k-1)$, where $k \geqslant 2$, are Cypriot.
Note: There are other Cypriot pairs. We leave it to the reader to verify that the integers $\mathrm{a}=(2\ell)^{4\ell}+2\ell-1$ and $\mathrm{b}=(2\ell)^{4\ell}-2\ell-1$ form a Cypriot pair for any integer $\ell \geqslant 1$.
## Exercise for both Junior and Senior groups
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'une paire d'entiers ( $\mathbf{a}, \mathrm{b}$ ) est chypriote si $\mathrm{a} \geqslant \mathrm{b} \geqslant 2$, si a et b sont premiers entre eux, et si $a+b$ divise $a^{b}+b^{a}$.
Démontrer qu'il existe une infinité de paires chypriotes distinctes.
|
Posons $k=a-b$. Puisque $a$ et $b$ sont premiers entre eux, on sait que $a \neq b$, donc que $k \geqslant 1$. Ainsi,
$$
a^{b}+b^{a} \equiv a^{b}+(-a)^{a} \equiv a^{b}\left(1+(-1)^{a} a^{k}\right) \quad(\bmod a+b)
$$
Or, $a$ est premier avec $b$ donc avec $a+b$ aussi.
D'après le théorème de Gauss, on souhaite donc que $a+b=2 a-k$ divise $1+(-1)^{a} a^{k}$, ou encore $a^{\mathrm{k}}+(-1)^{\mathrm{a}}$.
Faute de mieux, étudions maintenant les petites valeurs de k. Choisir $k=1$ reviendrait à souhaiter que $a+b$ divise $a \pm 1$, ce qui est impossible puisque $a+b>a+1>a-1$. On regarde donc $k=2$.
Dans ce cas, on souhaite que $2 a-2=2(a-1)$ divise $a^{2}+(-1)^{a}$. Or, notons que $a^{2}+(-1)^{a} \equiv$ $1+(-1)^{\mathrm{a}}(\bmod a-1)$. Par conséquent, et puisque $a \geqslant 2$, il nous faut nécessairement choisir $a$ impair. Dans ce cas, il reste à faire en sorte que $2(a-1)$ divise $a^{2}-1=(a-1)(a+1)$, c'est-à-dire que 2 divise $a-1$. Mais c'est justement le cas, puisque a est impair.
En conclusion, on a bien montré que toutes les paires $(2 k+1,2 k-1)$, où $k \geqslant 2$, étaient chypriotes.
Note : Il existe d'autres paires chypriotes. On laisse ainsi au lecteur le plaisir de vérifier que les entiers $\mathrm{a}=(2 \ell)^{4 \ell}+2 \ell-1$ et $\mathrm{b}=(2 \ell)^{4 \ell}-2 \ell-1$ forment également une paire chypriote pour tout entier $\ell \geqslant 1$.
## Exercice commun aux groupes Junior et Senior
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
17a52b0e-61a5-5189-81ea-9500e37c3e03
| 605,771
|
Let \( u \) be a non-zero natural number.
Prove that there are only a finite number of triplets of natural numbers \( (a, b, n) \) such that \( n! = u^a - u^b \).
Note: recall that \( 0! = 1! = 1 \).
|
Let $p$ be an odd prime that does not divide $u$, and let $k$ be an integer such that $p^{k}>u^{p-1}-1$. Set $q=p^{k-1}$. We first show that $u$ is not a $q^{\text{th}}$ power $\left(\bmod p^{k}\right)$. Indeed, if $u$ were a $q^{\text{th}}$ power $\left(\bmod p^{k}\right)$, then there would exist an integer $v$ such that $u \equiv v^{q}\left(\bmod p^{k}\right)$, and then we would have $1 \equiv v^{\varphi\left(p^{k}\right)} \equiv v^{q(p-1)} \equiv u^{p-1} \left(\bmod p^{k}\right)$, which is not the case.
Consequently, we also know, for any integer $\ell \geqslant k$, that $u$ is not a $q^{\text{th}}$ power $\left(\bmod p^{\ell}\right)$. We deduce that $p^{\ell-k}$ divides $\omega_{p^{\ell}}(u)$, where $\omega_{p^{\ell}}(u)$ denotes the order of $u\left(\bmod p^{\ell}\right)$. Indeed, let $g$ be a primitive root $\left(\bmod p^{\ell}\right)$, and let $x$ be an integer such that $u \equiv g^{x} \left(\bmod p^{\ell}\right)$. Then $1 \equiv u^{\omega_{p^{\ell}}(u)} \equiv g^{x \omega_{p^{\ell}}(u)} \left(\bmod p^{\ell}\right)$, which means that $\varphi\left(p^{\ell}\right)=(p-1)p^{\ell-1}$ divides $x \omega_{p^{\ell}}(u)$. Since $q=p^{k-1}$ does not divide $x$, it follows that $p^{\ell-k}$ divides $\omega_{p^{\ell}}(u)$.
Suppose finally that there exists a triplet $(a, b, n)$ of integers such that $u^{a}-u^{b}=n!$ and $n \geqslant kp$. Set also $d=a-b$ and $\ell=\lfloor n / p\rfloor$. Then $p^{\ell}$ divides $n!=u^{b}(u^{d}-1)$ and, since $p$ does not divide $u$, it follows that $u^{d} \equiv 1 \left(\bmod p^{\ell}\right)$. We deduce that $\omega_{p^{\ell}}(u)$ divides $d$, and therefore that $p^{\ell-k}$ divides $d$ as well. This means in particular that $d \geqslant p^{\ell-k}$, and thus
$$
2^{n(n+1)} \geqslant n^{n+1} \geqslant n!+1 \geqslant u^{d} \geqslant u^{p^{\ell-k}} \geqslant u^{p^{p / p-k}},
$$
or equivalently that $p^{k} n(n+1) \geqslant p^{n / p} \log _{2}(u)$.
Once the integers $u, p$ and $k$ are fixed, the right-hand side grows much faster than the left-hand side. Therefore, there exists an integer $\mathbf{N}$, which depends only on $u$, $p$ and $k$, such that $n \leqslant N$.
Thus, only a finite number of integers $n$ belong to a triplet $(a, b, n)$ such that $n!=u^{a}-u^{b}$. Once such an integer $n$ is fixed, we know that $u^{a}>u^{b}$, so $a \geqslant b+1$, and thus $n! \geqslant u^{a}-u^{a-1}=(u-1)u^{a-1}$, which shows that $a$ and $b$ are themselves bounded. This concludes our solution.
Note: It was not necessary to directly invoke the existence of a primitive root $\left(\bmod p^{\ell}\right)$, for example by proceeding as follows. Let $s$ be the order of $u \left(\bmod p\right)$, and let $k$ be the $p$-adic valuation of $u^{s}-1$. Then, for all $\ell \geqslant k$, one can in fact show that $u$ has order $\omega=p^{\ell-k}s \left(\bmod p^{\ell}\right)$.
To do this, we will first show by induction, for all $m \geqslant 1$, that the $p^{\text{th}}$ roots of unity $\left(\bmod p^{m}\right)$ are the integers congruent to $1 \left(\bmod p^{m-1}\right)$. Indeed, the result is immediate for $m=1$. Then, if $m \geqslant 2$ and if $x^{p} \equiv 1 \left(\bmod p^{m}\right)$, then $x^{p} \equiv 1 \left(\bmod p^{m-1}\right)$, so we can write $x=1+y^{m-2}$, and by expanding a binomial of Newton we deduce that $1 \equiv x^{p} \equiv 1+y^{m-1} \left(\bmod p^{m}\right)$, which concludes the induction.
Using the above induction, we note that $u^{s}$ has order $\varpi=p^{\ell-k} \left(\bmod p^{\ell}\right)$. Since $s$ divides $\omega$, we know in addition that $\omega=s \varpi$, which concludes.
In general, this reasoning plays a crucial role in the proof of the existence of a primitive root $\left(\bmod p^{\ell}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit u un entier naturel non nul.
Démontrer qu'il n'existe qu'un nombre fini de triplets d'entiers naturels ( $a, b, n$ ) tels que $\mathrm{n}!=\mathrm{u}^{\mathrm{a}}-\mathrm{u}^{\mathrm{b}}$.
Note : on rappelle que $0!=1!=1$.
|
Soit $p$ un nombre premier impair qui ne divise pas $u$, et soit $k$ un entier tel que $p^{k}>u^{p-1}-1$. Posons $q=p^{k-1}$. On montre tout d'abord que $u$ n'est $^{\text {pres }}$ une puissance $q^{\text {ème }}\left(\bmod p^{k}\right)$. En effet, si $u$ était une puissance $q^{\text {ème }}\left(\bmod p^{k}\right)$, alors il existerait un entier $v$ tel que $u \equiv v^{q}\left(\bmod p^{k}\right)$, et alors on aurait $1 \equiv v^{\varphi\left(p^{k}\right)} \equiv v^{q(p-1)} \equiv \mathfrak{u}^{p-1}$ $\left(\bmod p^{k}\right)$, ce qui $n^{\prime}$ est pas le cas.
Par conséquent, on sait également, pour tout entier $\ell \geqslant k$, que $u$ n'est pas non plus une puissance $q^{\text {ème }}\left(\bmod p^{\ell}\right)$. On en déduit que $p^{\ell-k}$ divise $\omega_{p^{\ell}}(u)$, où $\omega_{p^{\ell}}(u)$ désigne l'ordre de $u\left(\bmod p^{\ell}\right)$. En effet, soit $g$ une racine primitive $\left(\bmod p^{\ell}\right)$, et soit $x$ un entier tel que $u \equiv g^{x}$ $\left(\bmod \mathfrak{p}^{\ell}\right)$. Alors $1 \equiv u^{\omega_{p^{\ell}}(\mathfrak{u})} \equiv \mathrm{g}^{x \omega_{p^{\ell}}(\mathfrak{u})}\left(\bmod \mathrm{p}^{\ell}\right)$, ce qui signifie que $\varphi\left(\mathrm{p}^{\ell}\right)=(p-1) \mathrm{p}^{\ell-1}$ divise $x \omega_{p^{\ell}}(u)$. Puisque $q=p^{k-1}$ ne divise pas $x$, $c^{\prime}$ est donc que $p^{\ell-k}$ divise $\omega_{p^{\ell}}(u)$.
Supposons enfin qu'il existe un triplet ( $a, b, n$ ) d'entiers tels que $u^{a}-u^{b}=n$ ! et $n \geqslant k p$. Posons également $d=a-b$ et $\ell=\lfloor n / p\rfloor$. Alors $p^{\ell}$ divise $n!=u^{b}\left(u^{d}-1\right)$ et, puisque $p$ ne divise pas $u$, $c^{\prime}$ est donc que $a^{d} \equiv 1\left(\bmod p^{\ell}\right)$. On en déduit que $\omega_{p^{\ell}}(u)$ divise $d$, donc que $p^{\ell-k}$ divise $d$ également. Cela signifie en particulier que $d \geqslant p^{\ell-k}$, donc que
$$
2^{\mathfrak{n}(\mathfrak{n}+1)} \geqslant \mathfrak{n}^{n+1} \geqslant n!+1 \geqslant \mathfrak{u}^{d} \geqslant \mathfrak{u}^{p^{\ell-k}} \geqslant \mathfrak{u}^{p^{p / p-k}},
$$
ou encore que $p^{k} n(n+1) \geqslant p^{n / p} \log _{2}(u)$.
Une fois les entiers $u, p$ et $k$ fixés, le membre de droite croît beaucoup plus vite que le membre de gauche. Il existe donc un entier $\mathbf{N}$, qui ne dépend que de $u$, $p$ et $k$, et tel que $n \leqslant N$.
Ainsi, seul un nombre fini d'entiers $n$ appartient à un triplet ( $a, b, n$ ) tel que $n!=u^{a}-u^{b}$. Or, une fois un tel entier $n$ fixé, on sait que $u^{a}>u^{b}$, donc que $a \geqslant b+1$, et donc que $n!\geqslant \mathfrak{u}^{\mathrm{a}}-\mathfrak{u}^{\mathrm{a}-1}=(\mathfrak{u}-1) \mathfrak{u}^{\mathrm{a}-1}$, ce qui montre que $a$ et $b$ sont eux-mêmes bornés. Ceci conlut notre solution.
Note : Il n'était pas nécessaire de recourir directement à l'existence d'une racine primitive $\left(\bmod p^{\ell}\right)$, par exemple en procédant comme suit. Soit $s$ l'ordre de $_{u}(\bmod p)$, et soit $k$ la valuation $p$-adique de $u^{s}-1$. Alors, pour tout $\ell \geqslant k$, on peut en fait montrer que $u$ est $d^{\prime}$ ordre $\omega=p^{\ell-\mathrm{k}} s\left(\bmod p^{\ell}\right)$.
Pour ce faire, on va d'abord montrer par récurrence, pour tout $m \geqslant 1$, les racines $p^{\text {èmes }}$ de l'unité $^{\left(\bmod p^{\mathrm{m}}\right)}$ sont les entiers congrus à $1\left(\bmod p^{\mathrm{m}-1}\right)$. En effet, le résultat est immédiat pour $m=1$. Puis, si $m \geqslant 2$ et si $x^{p} \equiv 1\left(\bmod p^{\mathfrak{m}}\right)$, alors $x^{p} \equiv 1\left(\bmod p^{m-1}\right)$, donc on peut écrire $x=1+y^{\mathrm{m}-2}$, et en développant un binôme de Newton on en déduit que $1 \equiv x^{\mathfrak{p}} \equiv 1+y^{\mathfrak{m}-1}\left(\bmod \mathfrak{p}^{\mathfrak{m}}\right)$, ce qui conclut la récurrence.
À l'aide de la récurrence ci-dessus, on remarque donc que $u^{s}$ est d'ordre $\varpi=p^{\ell-k}$ $\left(\bmod p^{\ell}\right)$. Puisque $s$ divise $\omega$, on sait en outre que $\omega=s \varpi$, ce qui conclut.
De manière générale, ce raisonnement joue en fait un rôle crucial dans la preuve de l'existence $d^{\prime}$ une racine primitive $\left(\bmod p^{\ell}\right)$.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
88fe1a39-79db-5beb-ba72-afbdbd5faeb4
| 605,793
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.