problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus)
|
In this solution we will use the Prime Number Theorem which states that $$ \pi(m)=\frac{m}{\log m} \cdot(1+o(1)) $$ as $m$ tends to infinity. Here and below $\pi(m)$ denotes the number of primes not exceeding $m$, and $\log$ the natural logarithm. Let $m>5$ be a large positive integer and let $n:=p_{1} p_{2} \cdot \ldots \cdot p_{\pi(m)}$ be the product of all primes not exceeding $m$. Then $\varphi(d(n))=\varphi\left(2^{\pi(m)}\right)=2^{\pi(m)-1}$. Consider the number $$ \varphi(n)=\prod_{k=1}^{\pi(m)}\left(p_{k}-1\right)=\prod_{s=1}^{\pi(m / 2)} q_{s}^{\alpha_{s}} $$ where $q_{1}, \ldots, q_{\pi(m / 2)}$ are primes not exceeding $m / 2$. Note that every term $p_{k}-1$ contributes at most one prime $q_{s}>\sqrt{m}$ into the product $\prod_{s} q_{s}^{\alpha_{s}}$, so we have $$ \sum_{s: q_{s}>\sqrt{m}} \alpha_{s} \leqslant \pi(m) \Longrightarrow \sum_{s: q_{s}>\sqrt{m}}\left(1+\alpha_{s}\right) \leqslant \pi(m)+\pi(m / 2) . $$ Hence, applying the AM-GM inequality and the inequality $(A / x)^{x} \leqslant e^{A / e}$, we obtain $$ \prod_{s: q_{s}>\sqrt{m}}\left(\alpha_{s}+1\right) \leqslant\left(\frac{\pi(m)+\pi(m / 2)}{\ell}\right)^{\ell} \leqslant \exp \left(\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ where $\ell$ is the number of primes in the interval $(\sqrt{m}, m]$. We then use a trivial bound $\alpha_{i} \leqslant \log _{2}(\varphi(n)) \leqslant \log _{2} n<\log _{2}\left(m^{m}\right)<m^{2}$ for each $i$ with $q_{i}<\sqrt{m}$ to obtain $$ \prod_{s=1}^{\pi(\sqrt{m})}\left(\alpha_{s}+1\right) \leqslant\left(m^{2}\right)^{\sqrt{m}}=m^{2 \sqrt{m}} $$ Putting this together we obtain $$ d(\varphi(n))=\prod_{s=1}^{\pi(m / 2)}\left(\alpha_{s}+1\right) \leqslant \exp \left(2 \sqrt{m} \cdot \log m+\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ The prime number theorem then implies that $$ \limsup _{m \rightarrow \infty} \frac{\log (d(\varphi(n)))}{m / \log m} \leqslant \limsup _{m \rightarrow \infty} \frac{2 \sqrt{m} \cdot \log m}{m / \log m}+\limsup _{m \rightarrow \infty} \frac{\pi(m)+\pi(m / 2)}{e \cdot m / \log m}=\frac{3}{2 e} . $$ Whereas, again by prime number theorem, we have $$ \liminf _{m \rightarrow \infty} \frac{\log (\varphi(d(n)))}{m / \log m}=\liminf _{m \rightarrow \infty} \frac{\log \left(2^{\pi(m)-1}\right)}{m / \log m}=\log 2 $$ Since $\frac{3}{2 e}<\frac{3}{5}<\log 2$, this implies that $\varphi(d(n)) / d(\varphi(n))$ can be arbitrarily large. Comment 2. The original formulation of the problem was asking whether $d(\varphi(n)) \geqslant \varphi(d(n))$ for all but finitely many values of $n$. The Problem Selection Committee decided that the presented version is better suited for the Shortlist. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus)
|
In this solution we will use the Prime Number Theorem which states that $$ \pi(m)=\frac{m}{\log m} \cdot(1+o(1)) $$ as $m$ tends to infinity. Here and below $\pi(m)$ denotes the number of primes not exceeding $m$, and $\log$ the natural logarithm. Let $m>5$ be a large positive integer and let $n:=p_{1} p_{2} \cdot \ldots \cdot p_{\pi(m)}$ be the product of all primes not exceeding $m$. Then $\varphi(d(n))=\varphi\left(2^{\pi(m)}\right)=2^{\pi(m)-1}$. Consider the number $$ \varphi(n)=\prod_{k=1}^{\pi(m)}\left(p_{k}-1\right)=\prod_{s=1}^{\pi(m / 2)} q_{s}^{\alpha_{s}} $$ where $q_{1}, \ldots, q_{\pi(m / 2)}$ are primes not exceeding $m / 2$. Note that every term $p_{k}-1$ contributes at most one prime $q_{s}>\sqrt{m}$ into the product $\prod_{s} q_{s}^{\alpha_{s}}$, so we have $$ \sum_{s: q_{s}>\sqrt{m}} \alpha_{s} \leqslant \pi(m) \Longrightarrow \sum_{s: q_{s}>\sqrt{m}}\left(1+\alpha_{s}\right) \leqslant \pi(m)+\pi(m / 2) . $$ Hence, applying the AM-GM inequality and the inequality $(A / x)^{x} \leqslant e^{A / e}$, we obtain $$ \prod_{s: q_{s}>\sqrt{m}}\left(\alpha_{s}+1\right) \leqslant\left(\frac{\pi(m)+\pi(m / 2)}{\ell}\right)^{\ell} \leqslant \exp \left(\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ where $\ell$ is the number of primes in the interval $(\sqrt{m}, m]$. We then use a trivial bound $\alpha_{i} \leqslant \log _{2}(\varphi(n)) \leqslant \log _{2} n<\log _{2}\left(m^{m}\right)<m^{2}$ for each $i$ with $q_{i}<\sqrt{m}$ to obtain $$ \prod_{s=1}^{\pi(\sqrt{m})}\left(\alpha_{s}+1\right) \leqslant\left(m^{2}\right)^{\sqrt{m}}=m^{2 \sqrt{m}} $$ Putting this together we obtain $$ d(\varphi(n))=\prod_{s=1}^{\pi(m / 2)}\left(\alpha_{s}+1\right) \leqslant \exp \left(2 \sqrt{m} \cdot \log m+\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ The prime number theorem then implies that $$ \limsup _{m \rightarrow \infty} \frac{\log (d(\varphi(n)))}{m / \log m} \leqslant \limsup _{m \rightarrow \infty} \frac{2 \sqrt{m} \cdot \log m}{m / \log m}+\limsup _{m \rightarrow \infty} \frac{\pi(m)+\pi(m / 2)}{e \cdot m / \log m}=\frac{3}{2 e} . $$ Whereas, again by prime number theorem, we have $$ \liminf _{m \rightarrow \infty} \frac{\log (\varphi(d(n)))}{m / \log m}=\liminf _{m \rightarrow \infty} \frac{\log \left(2^{\pi(m)-1}\right)}{m / \log m}=\log 2 $$ Since $\frac{3}{2 e}<\frac{3}{5}<\log 2$, this implies that $\varphi(d(n)) / d(\varphi(n))$ can be arbitrarily large. Comment 2. The original formulation of the problem was asking whether $d(\varphi(n)) \geqslant \varphi(d(n))$ for all but finitely many values of $n$. The Problem Selection Committee decided that the presented version is better suited for the Shortlist. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
60fa4bf2-d7a9-5d52-9959-6d718646dc0b
| 24,033
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine)
|
We prove the following stronger statement. Claim. Let $\mathcal{S}$ be a good set consisting of $n \geqslant 2$ positive integers. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i} \nmid a_{i-1}+a_{i+1}$ and $a_{i} \nmid a_{i-1}-a_{i+1}$, for all $i=2,3, \ldots, n-1$. Proof. Say that the ordering $a_{1}, \ldots, a_{n}$ of $\mathcal{S}$ is nice if it satisfies the required property. We proceed by induction on $n$. The base case $n=2$ is trivial, as there are no restrictions on the ordering. To perform the step of induction, suppose that $n \geqslant 3$. Let $a=\max \mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{a\}$. Use the inductive hypothesis to find a nice ordering $b_{1}, \ldots, b_{n-1}$ of $\mathcal{T}$. We will show that $a$ may be inserted into this sequence so as to reach a nice ordering of $\mathcal{S}$. In other words, we will show that there exists a $j \in\{1,2, \ldots, n\}$ such that the ordering $$ N_{j}=\left(b_{1}, \ldots, b_{j-1}, a, b_{j}, b_{j+1}, \ldots, b_{n-1}\right) $$ is nice. Assume that, for some $j$, the ordering $N_{j}$ is not nice, so that some element $x$ in it divides either the sum or the difference of two adjacent ones. This did not happen in the ordering of $\mathcal{T}$, hence $x \in\left\{b_{j-1}, a, b_{j}\right\}$ (if, say, $b_{j-1}$ does not exist, then $x \in\left\{a, b_{j}\right\}$; a similar agreement is applied hereafter). But the case $x=a$ is impossible: $a$ cannot divide $b_{j-1}-b_{j}$, since $0<\left|b_{j-1}-b_{j}\right|<a$, while $a \nmid b_{j-1}+b_{j}$ by Observation A. Therefore $x \in\left\{b_{j-1}, b_{j}\right\}$. In this case, assign the number $x$ to the index $j$. Suppose now that none of the $N_{j}$ is nice. Since there are $n$ possible indices $j$, and only $n-1$ elements in $\mathcal{T}$, one of those elements (say, $b_{k}$ ) is assigned to two different indices, which then should equal $k$ and $k+1$. This means that $b_{k}$ divides the numbers $b_{k-1}+\varepsilon_{1} a$ and $a+\varepsilon_{2} b_{k+1}$, for some signs $\varepsilon_{1}, \varepsilon_{2} \in\{-1,1\}$. But then $$ b_{k-1} \equiv-\varepsilon_{1} a \equiv \varepsilon_{1} \varepsilon_{2} b_{k+1} \quad\left(\bmod b_{k}\right), $$ and therefore $b_{k} \mid b_{k-1}-\varepsilon_{1} \varepsilon_{2} b_{k+1}$, which means that the ordering of $\mathcal{T}$ was not nice. This contradiction proves the step of induction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine)
|
We prove the following stronger statement. Claim. Let $\mathcal{S}$ be a good set consisting of $n \geqslant 2$ positive integers. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i} \nmid a_{i-1}+a_{i+1}$ and $a_{i} \nmid a_{i-1}-a_{i+1}$, for all $i=2,3, \ldots, n-1$. Proof. Say that the ordering $a_{1}, \ldots, a_{n}$ of $\mathcal{S}$ is nice if it satisfies the required property. We proceed by induction on $n$. The base case $n=2$ is trivial, as there are no restrictions on the ordering. To perform the step of induction, suppose that $n \geqslant 3$. Let $a=\max \mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{a\}$. Use the inductive hypothesis to find a nice ordering $b_{1}, \ldots, b_{n-1}$ of $\mathcal{T}$. We will show that $a$ may be inserted into this sequence so as to reach a nice ordering of $\mathcal{S}$. In other words, we will show that there exists a $j \in\{1,2, \ldots, n\}$ such that the ordering $$ N_{j}=\left(b_{1}, \ldots, b_{j-1}, a, b_{j}, b_{j+1}, \ldots, b_{n-1}\right) $$ is nice. Assume that, for some $j$, the ordering $N_{j}$ is not nice, so that some element $x$ in it divides either the sum or the difference of two adjacent ones. This did not happen in the ordering of $\mathcal{T}$, hence $x \in\left\{b_{j-1}, a, b_{j}\right\}$ (if, say, $b_{j-1}$ does not exist, then $x \in\left\{a, b_{j}\right\}$; a similar agreement is applied hereafter). But the case $x=a$ is impossible: $a$ cannot divide $b_{j-1}-b_{j}$, since $0<\left|b_{j-1}-b_{j}\right|<a$, while $a \nmid b_{j-1}+b_{j}$ by Observation A. Therefore $x \in\left\{b_{j-1}, b_{j}\right\}$. In this case, assign the number $x$ to the index $j$. Suppose now that none of the $N_{j}$ is nice. Since there are $n$ possible indices $j$, and only $n-1$ elements in $\mathcal{T}$, one of those elements (say, $b_{k}$ ) is assigned to two different indices, which then should equal $k$ and $k+1$. This means that $b_{k}$ divides the numbers $b_{k-1}+\varepsilon_{1} a$ and $a+\varepsilon_{2} b_{k+1}$, for some signs $\varepsilon_{1}, \varepsilon_{2} \in\{-1,1\}$. But then $$ b_{k-1} \equiv-\varepsilon_{1} a \equiv \varepsilon_{1} \varepsilon_{2} b_{k+1} \quad\left(\bmod b_{k}\right), $$ and therefore $b_{k} \mid b_{k-1}-\varepsilon_{1} \varepsilon_{2} b_{k+1}$, which means that the ordering of $\mathcal{T}$ was not nice. This contradiction proves the step of induction.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
19ab9d25-a95b-592c-a6a0-d08ea0bb2cc3
| 24,037
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine)
|
We again prove a stronger statement. Claim. Let $\mathcal{S}$ be an arbitrary set of $n \geqslant 3$ positive integers. Then its elements can be ordered as $a_{1}, \ldots, a_{n}$ so that, if $a_{i} \mid a_{i-1}+a_{i+1}$, then $a_{i}=\max \mathcal{S}$. The claim easily implies what we need to prove, due to Observation A. To prove the Claim, introduce the function $f$ which assigns to any two elements $a, b \in \mathcal{S}$ with $a<b$ the unique integer $f(a, b) \in\{1,2, \ldots, a\}$ such that $a \mid b+f(a, b)$. Hence, if $b \mid a+c$ for some $a, b, c \in \mathcal{S}$ with $a<b<c$, then $a=f(b, c)$. Therefore, the Claim is a consequence of the following combinatorial lemma. Lemma. Let $\mathcal{S}$ be a set of $n \geqslant 3$ positive integers, and let $f$ be a function which assigns to any $a, b \in \mathcal{S}$ with $a<b$ some integer from the range $\{1, \ldots, a\}$. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so as to satisfy the following two conditions simultaneously: (i) Unimodality: There exists a $j \in\{1,2, \ldots, n\}$ such that $a_{1}<a_{2}<\ldots<a_{j}>a_{j+1}>\ldots>$ $a_{n}$; and (ii) $f$-avoidance: If $a<b$ are two elements of $\mathcal{S}$, which are adjacent in the ordering, then $f(a, b)$ is not adjacent to $a$. Proof. We call an ordering of $\mathcal{S}$ satisfying (i) and (ii) $f$-nice. We agree that $f(x, y)=x$ for $x \geqslant y$; this agreement puts no extra restriction. We proceed by induction; for the base case $n=3$, it suffices to put the maximal element in $\mathcal{S}$ onto the middle position. To perform the step of induction, let $p<q$ be the two minimal elements of $\mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{p\}$. Define a function $g$ by assigning to any elements $a<b$ of $\mathcal{T}$ the value $$ g(a, b)= \begin{cases}q, & \text { if } f(a, b)=p \\ f(a, b), & \text { otherwise }\end{cases} $$ Notice that $g(a, b) \leqslant a$ for all $a, b \in \mathcal{T}$. Use the inductive hypothesis to get a $g$-nice ordering $b_{1}, b_{2}, \ldots, b_{n-1}$ of $\mathcal{T}$. By unimodality, either $b_{1}$ or $b_{n-1}$ equals $q$; these cases differ only by reverting the order, so we assume $b_{1}=q$. Notice that, according to (1), the number $f\left(b_{2}, b_{3}\right)$ differs from both $p$ and $q$. On the other hand, the number $f\left(b_{n-1}, b_{n-2}\right)$ differs from at least one of them - say, from $r$; set $s=p+q-r$, so that $\{r, s\}=\{p, q\}$. Now, order $\mathcal{S}$ as $$ s, b_{2}, b_{3}, \ldots, b_{n-1}, r $$ By the induction hypothesis and the above choice, this ordering is nice. Comment. In the original proposal, the numbers in the set were assumed to be odd (which implies that none is a sum of two others); moreover, the proposal requested to arrange in a row all numbers but one. On the other hand, Solution 2 shows that the condition of $\mathcal{S}$ being good may be relaxed to the condition that the maximal element of $\mathcal{S}$ is not a sum of two other elements in $\mathcal{S}$. On the other hand, the set $\{1,2,3\}$ shows that the condition cannot be merely omitted. The Problem Selection Committee considered several versions of the problem and chose the best version in their opinion for the Shortlist. 61st International Mathematical Olympiad Saint Petersburg Russia
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine)
|
We again prove a stronger statement. Claim. Let $\mathcal{S}$ be an arbitrary set of $n \geqslant 3$ positive integers. Then its elements can be ordered as $a_{1}, \ldots, a_{n}$ so that, if $a_{i} \mid a_{i-1}+a_{i+1}$, then $a_{i}=\max \mathcal{S}$. The claim easily implies what we need to prove, due to Observation A. To prove the Claim, introduce the function $f$ which assigns to any two elements $a, b \in \mathcal{S}$ with $a<b$ the unique integer $f(a, b) \in\{1,2, \ldots, a\}$ such that $a \mid b+f(a, b)$. Hence, if $b \mid a+c$ for some $a, b, c \in \mathcal{S}$ with $a<b<c$, then $a=f(b, c)$. Therefore, the Claim is a consequence of the following combinatorial lemma. Lemma. Let $\mathcal{S}$ be a set of $n \geqslant 3$ positive integers, and let $f$ be a function which assigns to any $a, b \in \mathcal{S}$ with $a<b$ some integer from the range $\{1, \ldots, a\}$. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so as to satisfy the following two conditions simultaneously: (i) Unimodality: There exists a $j \in\{1,2, \ldots, n\}$ such that $a_{1}<a_{2}<\ldots<a_{j}>a_{j+1}>\ldots>$ $a_{n}$; and (ii) $f$-avoidance: If $a<b$ are two elements of $\mathcal{S}$, which are adjacent in the ordering, then $f(a, b)$ is not adjacent to $a$. Proof. We call an ordering of $\mathcal{S}$ satisfying (i) and (ii) $f$-nice. We agree that $f(x, y)=x$ for $x \geqslant y$; this agreement puts no extra restriction. We proceed by induction; for the base case $n=3$, it suffices to put the maximal element in $\mathcal{S}$ onto the middle position. To perform the step of induction, let $p<q$ be the two minimal elements of $\mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{p\}$. Define a function $g$ by assigning to any elements $a<b$ of $\mathcal{T}$ the value $$ g(a, b)= \begin{cases}q, & \text { if } f(a, b)=p \\ f(a, b), & \text { otherwise }\end{cases} $$ Notice that $g(a, b) \leqslant a$ for all $a, b \in \mathcal{T}$. Use the inductive hypothesis to get a $g$-nice ordering $b_{1}, b_{2}, \ldots, b_{n-1}$ of $\mathcal{T}$. By unimodality, either $b_{1}$ or $b_{n-1}$ equals $q$; these cases differ only by reverting the order, so we assume $b_{1}=q$. Notice that, according to (1), the number $f\left(b_{2}, b_{3}\right)$ differs from both $p$ and $q$. On the other hand, the number $f\left(b_{n-1}, b_{n-2}\right)$ differs from at least one of them - say, from $r$; set $s=p+q-r$, so that $\{r, s\}=\{p, q\}$. Now, order $\mathcal{S}$ as $$ s, b_{2}, b_{3}, \ldots, b_{n-1}, r $$ By the induction hypothesis and the above choice, this ordering is nice. Comment. In the original proposal, the numbers in the set were assumed to be odd (which implies that none is a sum of two others); moreover, the proposal requested to arrange in a row all numbers but one. On the other hand, Solution 2 shows that the condition of $\mathcal{S}$ being good may be relaxed to the condition that the maximal element of $\mathcal{S}$ is not a sum of two other elements in $\mathcal{S}$. On the other hand, the set $\{1,2,3\}$ shows that the condition cannot be merely omitted. The Problem Selection Committee considered several versions of the problem and chose the best version in their opinion for the Shortlist. 61st International Mathematical Olympiad Saint Petersburg Russia
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
19ab9d25-a95b-592c-a6a0-d08ea0bb2cc3
| 24,037
|
A magician intends to perform the following trick. She announces a positive integer $n$, along with $2 n$ real numbers $x_{1}<\ldots<x_{2 n}$, to the audience. A member of the audience then secretly chooses a polynomial $P(x)$ of degree $n$ with real coefficients, computes the $2 n$ values $P\left(x_{1}\right), \ldots, P\left(x_{2 n}\right)$, and writes down these $2 n$ values on the blackboard in non-decreasing order. After that the magician announces the secret polynomial to the audience. Can the magician find a strategy to perform such a trick? (Luxembourg) Answer: No, she cannot.
|
Let $x_{1}<x_{2}<\ldots<x_{2 n}$ be real numbers chosen by the magician. We will construct two distinct polynomials $P(x)$ and $Q(x)$, each of degree $n$, such that the member of audience will write down the same sequence for both polynomials. This will mean that the magician cannot distinguish $P$ from $Q$. Claim. There exists a polynomial $P(x)$ of degree $n$ such that $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for $i=$ $1,2, \ldots, n$. Proof. We want to find a polynomial $a_{n} x^{n}+\ldots+a_{1} x+a_{0}$ satisfying the following system of equations: $$ \left\{\begin{array}{l} \left(x_{1}^{n}+x_{2}^{n}\right) a_{n}+\left(x_{1}^{n-1}+x_{2}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \left(x_{3}^{n}+x_{4}^{n}\right) a_{n}+\left(x_{3}^{n-1}+x_{4}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \cdots \\ \left(x_{2 n-1}^{n}+x_{2 n}^{n}\right) a_{n}+\left(x_{2 n-1}^{n-1}+x_{2 n}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \end{array}\right. $$ We use the well known fact that a homogeneous system of $n$ linear equations in $n+1$ variables has a nonzero solution. (This fact can be proved using induction on $n$, via elimination of variables.) Applying this fact to the above system, we find a nonzero polynomial $P(x)$ of degree not exceeding $n$ such that its coefficients $a_{0}, \ldots, a_{n}$ satisfy this system. Therefore $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for all $i=1,2, \ldots, n$. Notice that $P$ has a root on each segment $\left[x_{2 i-1}, x_{2 i}\right]$ by the Intermediate Value theorem, so $n$ roots in total. Since $P$ is nonzero, we get $\operatorname{deg} P=n$. Now consider a polynomial $P(x)$ provided by the Claim, and take $Q(x)=-P(x)$. The properties of $P(x)$ yield that $P\left(x_{2 i-1}\right)=Q\left(x_{2 i}\right)$ and $Q\left(x_{2 i-1}\right)=P\left(x_{2 i}\right)$ for all $i=1,2, \ldots, n$. It is also clear that $P \neq-P=Q$ and $\operatorname{deg} Q=\operatorname{deg} P=n$. Comment. It can be shown that for any positive integer $n$ the magician can choose $2 n+1$ distinct real numbers so as to perform such a trick. Moreover, she can perform such a trick with almost all (in a proper sense) $(2 n+1)$-tuples of numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A magician intends to perform the following trick. She announces a positive integer $n$, along with $2 n$ real numbers $x_{1}<\ldots<x_{2 n}$, to the audience. A member of the audience then secretly chooses a polynomial $P(x)$ of degree $n$ with real coefficients, computes the $2 n$ values $P\left(x_{1}\right), \ldots, P\left(x_{2 n}\right)$, and writes down these $2 n$ values on the blackboard in non-decreasing order. After that the magician announces the secret polynomial to the audience. Can the magician find a strategy to perform such a trick? (Luxembourg) Answer: No, she cannot.
|
Let $x_{1}<x_{2}<\ldots<x_{2 n}$ be real numbers chosen by the magician. We will construct two distinct polynomials $P(x)$ and $Q(x)$, each of degree $n$, such that the member of audience will write down the same sequence for both polynomials. This will mean that the magician cannot distinguish $P$ from $Q$. Claim. There exists a polynomial $P(x)$ of degree $n$ such that $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for $i=$ $1,2, \ldots, n$. Proof. We want to find a polynomial $a_{n} x^{n}+\ldots+a_{1} x+a_{0}$ satisfying the following system of equations: $$ \left\{\begin{array}{l} \left(x_{1}^{n}+x_{2}^{n}\right) a_{n}+\left(x_{1}^{n-1}+x_{2}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \left(x_{3}^{n}+x_{4}^{n}\right) a_{n}+\left(x_{3}^{n-1}+x_{4}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \cdots \\ \left(x_{2 n-1}^{n}+x_{2 n}^{n}\right) a_{n}+\left(x_{2 n-1}^{n-1}+x_{2 n}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \end{array}\right. $$ We use the well known fact that a homogeneous system of $n$ linear equations in $n+1$ variables has a nonzero solution. (This fact can be proved using induction on $n$, via elimination of variables.) Applying this fact to the above system, we find a nonzero polynomial $P(x)$ of degree not exceeding $n$ such that its coefficients $a_{0}, \ldots, a_{n}$ satisfy this system. Therefore $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for all $i=1,2, \ldots, n$. Notice that $P$ has a root on each segment $\left[x_{2 i-1}, x_{2 i}\right]$ by the Intermediate Value theorem, so $n$ roots in total. Since $P$ is nonzero, we get $\operatorname{deg} P=n$. Now consider a polynomial $P(x)$ provided by the Claim, and take $Q(x)=-P(x)$. The properties of $P(x)$ yield that $P\left(x_{2 i-1}\right)=Q\left(x_{2 i}\right)$ and $Q\left(x_{2 i-1}\right)=P\left(x_{2 i}\right)$ for all $i=1,2, \ldots, n$. It is also clear that $P \neq-P=Q$ and $\operatorname{deg} Q=\operatorname{deg} P=n$. Comment. It can be shown that for any positive integer $n$ the magician can choose $2 n+1$ distinct real numbers so as to perform such a trick. Moreover, she can perform such a trick with almost all (in a proper sense) $(2 n+1)$-tuples of numbers.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a5243020-a376-5bcd-b0bf-a5cdd4e84f90
| 24,053
|
Let $n$ and $k$ be positive integers. Prove that for $a_{1}, \ldots, a_{n} \in\left[1,2^{k}\right]$ one has $$ \sum_{i=1}^{n} \frac{a_{i}}{\sqrt{a_{1}^{2}+\ldots+a_{i}^{2}}} \leqslant 4 \sqrt{k n} $$ (Iran)
|
Apply induction on $n$. The base $n \leqslant 16$ is clear: our sum does not exceed $n \leqslant 4 \sqrt{n k}$. For the inductive step from $1, \ldots, n-1$ to $n \geqslant 17$ consider two similar cases. Case 1: $n=2 t$. Let $x_{\ell}=\frac{a_{\ell}}{\sqrt{a_{1}^{2}+\ldots+a_{\ell}^{2}}}$. We have $$ \exp \left(-x_{t+1}^{2}-\ldots-x_{2 t}^{2}\right) \geqslant\left(1-x_{t+1}^{2}\right) \ldots\left(1-x_{2 t}^{2}\right)=\frac{a_{1}^{2}+\ldots+a_{t}^{2}}{a_{1}^{2}+\ldots+a_{2 t}^{2}} \geqslant \frac{1}{1+4^{k}} $$ where we used that the product is telescopic and then an estimate $a_{t+i} \leqslant 2^{k} a_{i}$ for $i=1, \ldots, t$. Therefore, $x_{t+1}^{2}+\ldots+x_{2 t}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$, where log denotes the natural logarithm. This implies $x_{t+1}+\ldots+x_{2 t} \leqslant \sqrt{2 k t}$. Hence, using the inductive hypothesis for $n=t$ we get $$ \sum_{\ell=1}^{2 t} x_{\ell} \leqslant 4 \sqrt{k t}+\sqrt{2 k t} \leqslant 4 \sqrt{2 k t} $$ Case 2: $n=2 t+1$. Analogously, we get $x_{t+2}^{2}+\ldots+x_{2 t+1}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$ and $$ \sum_{\ell=1}^{2 t+1} x_{\ell} \leqslant 4 \sqrt{k(t+1)}+\sqrt{2 k t} \leqslant 4 \sqrt{k(2 t+1)} $$ The last inequality is true for all $t \geqslant 8$ since $$ 4 \sqrt{2 t+1}-\sqrt{2 t} \geqslant 3 \sqrt{2 t}=\sqrt{18 t} \geqslant \sqrt{16 t+16}=4 \sqrt{t+1} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ and $k$ be positive integers. Prove that for $a_{1}, \ldots, a_{n} \in\left[1,2^{k}\right]$ one has $$ \sum_{i=1}^{n} \frac{a_{i}}{\sqrt{a_{1}^{2}+\ldots+a_{i}^{2}}} \leqslant 4 \sqrt{k n} $$ (Iran)
|
Apply induction on $n$. The base $n \leqslant 16$ is clear: our sum does not exceed $n \leqslant 4 \sqrt{n k}$. For the inductive step from $1, \ldots, n-1$ to $n \geqslant 17$ consider two similar cases. Case 1: $n=2 t$. Let $x_{\ell}=\frac{a_{\ell}}{\sqrt{a_{1}^{2}+\ldots+a_{\ell}^{2}}}$. We have $$ \exp \left(-x_{t+1}^{2}-\ldots-x_{2 t}^{2}\right) \geqslant\left(1-x_{t+1}^{2}\right) \ldots\left(1-x_{2 t}^{2}\right)=\frac{a_{1}^{2}+\ldots+a_{t}^{2}}{a_{1}^{2}+\ldots+a_{2 t}^{2}} \geqslant \frac{1}{1+4^{k}} $$ where we used that the product is telescopic and then an estimate $a_{t+i} \leqslant 2^{k} a_{i}$ for $i=1, \ldots, t$. Therefore, $x_{t+1}^{2}+\ldots+x_{2 t}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$, where log denotes the natural logarithm. This implies $x_{t+1}+\ldots+x_{2 t} \leqslant \sqrt{2 k t}$. Hence, using the inductive hypothesis for $n=t$ we get $$ \sum_{\ell=1}^{2 t} x_{\ell} \leqslant 4 \sqrt{k t}+\sqrt{2 k t} \leqslant 4 \sqrt{2 k t} $$ Case 2: $n=2 t+1$. Analogously, we get $x_{t+2}^{2}+\ldots+x_{2 t+1}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$ and $$ \sum_{\ell=1}^{2 t+1} x_{\ell} \leqslant 4 \sqrt{k(t+1)}+\sqrt{2 k t} \leqslant 4 \sqrt{k(2 t+1)} $$ The last inequality is true for all $t \geqslant 8$ since $$ 4 \sqrt{2 t+1}-\sqrt{2 t} \geqslant 3 \sqrt{2 t}=\sqrt{18 t} \geqslant \sqrt{16 t+16}=4 \sqrt{t+1} $$
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
56b51cb9-f72c-5433-ae87-ae9893563c94
| 24,058
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Denote by $A^{\prime}$ the reflection of $A$ in $B D$. We will show that that the quadrilaterals $A^{\prime} B K E$ and $A^{\prime} D L F$ are cyclic, and their circumcircles are tangent to each other at point $A^{\prime}$. From the symmetry about line $B C$ we have $\angle B E K=\angle B A K$, while from the symmetry in $B D$ we have $\angle B A K=\angle B A^{\prime} K$. Hence $\angle B E K=\angle B A^{\prime} K$, which implies that the quadrilateral $A^{\prime} B K E$ is cyclic. Similarly, the quadrilateral $A^{\prime} D L F$ is also cyclic. 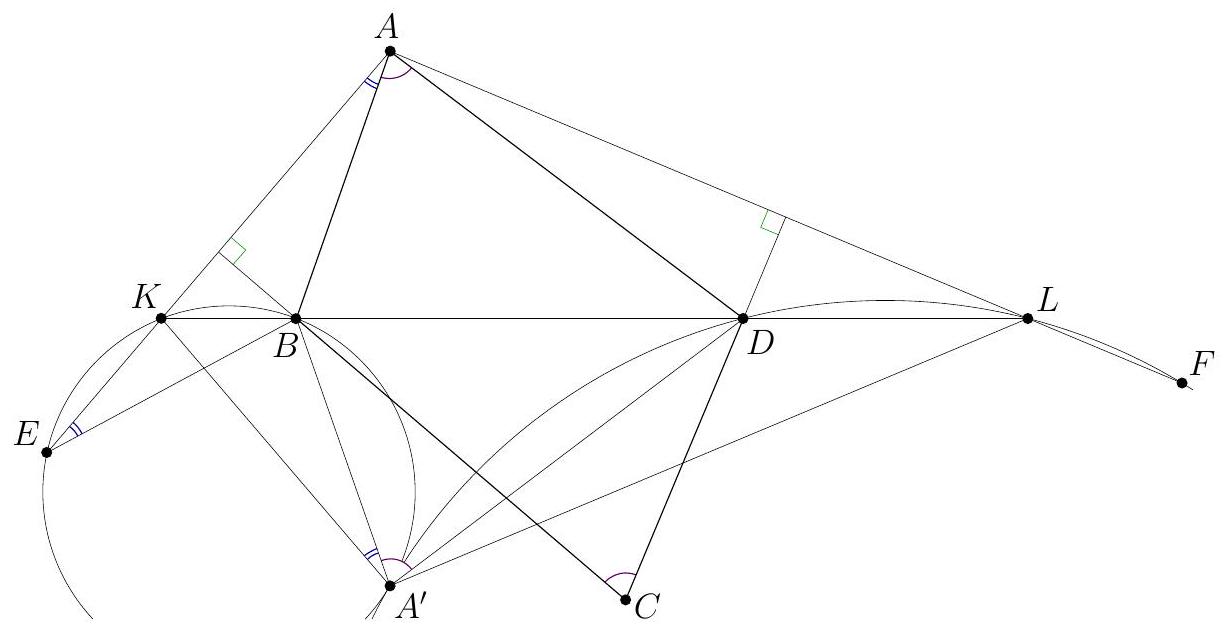 For showing that circles $A^{\prime} B K E$ and $A^{\prime} D L F$ are tangent it suffices to prove that $$ \angle A^{\prime} K B+\angle A^{\prime} L D=\angle B A^{\prime} D . $$ Indeed, by $A K \perp B C$, $A L \perp C D$, and again the symmetry in $B D$ we have $$ \angle A^{\prime} K B+\angle A^{\prime} L D=180^{\circ}-\angle K A^{\prime} L=180^{\circ}-\angle K A L=\angle B C D=\angle B A D=\angle B A^{\prime} D, $$ as required. Comment 1. The key to the solution above is introducing the point $A^{\prime}$; then the angle calculations can be done in many different ways.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Denote by $A^{\prime}$ the reflection of $A$ in $B D$. We will show that that the quadrilaterals $A^{\prime} B K E$ and $A^{\prime} D L F$ are cyclic, and their circumcircles are tangent to each other at point $A^{\prime}$. From the symmetry about line $B C$ we have $\angle B E K=\angle B A K$, while from the symmetry in $B D$ we have $\angle B A K=\angle B A^{\prime} K$. Hence $\angle B E K=\angle B A^{\prime} K$, which implies that the quadrilateral $A^{\prime} B K E$ is cyclic. Similarly, the quadrilateral $A^{\prime} D L F$ is also cyclic.  For showing that circles $A^{\prime} B K E$ and $A^{\prime} D L F$ are tangent it suffices to prove that $$ \angle A^{\prime} K B+\angle A^{\prime} L D=\angle B A^{\prime} D . $$ Indeed, by $A K \perp B C$, $A L \perp C D$, and again the symmetry in $B D$ we have $$ \angle A^{\prime} K B+\angle A^{\prime} L D=180^{\circ}-\angle K A^{\prime} L=180^{\circ}-\angle K A L=\angle B C D=\angle B A D=\angle B A^{\prime} D, $$ as required. Comment 1. The key to the solution above is introducing the point $A^{\prime}$; then the angle calculations can be done in many different ways.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6e287f18-780b-5216-a258-c9c7e4b030e8
| 24,077
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Note that $\angle K A L=180^{\circ}-\angle B C D$, since $A K$ and $A L$ are perpendicular to $B C$ and $C D$, respectively. Reflect both circles $(B E K)$ and $(D F L)$ in $B D$. Since $\angle K E B=\angle K A B$ and $\angle D F L=\angle D A L$, the images are the circles $(K A B)$ and $(L A D)$, respectively; so they meet at $A$. We need to prove that those two reflections are tangent at $A$. For this purpose, we observe that $$ \angle A K B+\angle A L D=180^{\circ}-\angle K A L=\angle B C D=\angle B A D . $$ Thus, there exists a ray $A P$ inside angle $\angle B A D$ such that $\angle B A P=\angle A K B$ and $\angle D A P=$ $\angle D L A$. Hence the line $A P$ is a common tangent to the circles $(K A B)$ and $(L A D)$, as desired. Comment 2. The statement of the problem remains true for a more general configuration, e.g., if line $B D$ intersect the extension of segment $A E$ instead of the segment itself, etc. The corresponding restrictions in the statement are given to reduce case sensitivity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Note that $\angle K A L=180^{\circ}-\angle B C D$, since $A K$ and $A L$ are perpendicular to $B C$ and $C D$, respectively. Reflect both circles $(B E K)$ and $(D F L)$ in $B D$. Since $\angle K E B=\angle K A B$ and $\angle D F L=\angle D A L$, the images are the circles $(K A B)$ and $(L A D)$, respectively; so they meet at $A$. We need to prove that those two reflections are tangent at $A$. For this purpose, we observe that $$ \angle A K B+\angle A L D=180^{\circ}-\angle K A L=\angle B C D=\angle B A D . $$ Thus, there exists a ray $A P$ inside angle $\angle B A D$ such that $\angle B A P=\angle A K B$ and $\angle D A P=$ $\angle D L A$. Hence the line $A P$ is a common tangent to the circles $(K A B)$ and $(L A D)$, as desired. Comment 2. The statement of the problem remains true for a more general configuration, e.g., if line $B D$ intersect the extension of segment $A E$ instead of the segment itself, etc. The corresponding restrictions in the statement are given to reduce case sensitivity.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6e287f18-780b-5216-a258-c9c7e4b030e8
| 24,077
|
Let $A B C D$ be a cyclic quadrilateral with no two sides parallel. Let $K, L, M$, and $N$ be points lying on sides $A B, B C, C D$, and $D A$, respectively, such that $K L M N$ is a rhombus with $K L \| A C$ and $L M \| B D$. Let $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$ be the incircles of triangles $A N K$, $B K L, C L M$, and $D M N$, respectively. Prove that the internal common tangents to $\omega_{1}$ and $\omega_{3}$ and the internal common tangents to $\omega_{2}$ and $\omega_{4}$ are concurrent. (Poland)
|
This solution is based on the following general Lemma. Lemma 2. Let $E$ and $F$ be distinct points, and let $\omega_{i}, i=1,2,3,4$, be circles lying in the same halfplane with respect to $E F$. For distinct indices $i, j \in\{1,2,3,4\}$, denote by $O_{i j}^{+}$ (respectively, $O_{i j}^{-}$) the center of homothety with positive (respectively, negative) ratio taking $\omega_{i}$ to $\omega_{j}$. Suppose that $E=O_{12}^{+}=O_{34}^{+}$and $F=O_{23}^{+}=O_{41}^{+}$. Then $O_{13}^{-}=O_{24}^{-}$. Proof. Applying Monge's theorem to triples of circles $\omega_{1}, \omega_{2}, \omega_{4}$ and $\omega_{1}, \omega_{3}, \omega_{4}$, we get that both points $O_{24}^{-}$and $O_{13}^{-}$lie on line $E O_{14}^{-}$. Notice that this line is distinct from $E F$. Similarly we obtain that both points $O_{24}^{-}$and $O_{13}^{-}$lie on $F O_{34}^{-}$. Since the lines $E O_{14}^{-}$and $F O_{34}^{-}$are distinct, both points coincide with the meeting point of those lines.  Turning back to the problem, let $A B$ intersect $C D$ at $E$ and let $B C$ intersect $D A$ at $F$. Assume, without loss of generality, that $B$ lies on segments $A E$ and $C F$. We will show that the points $E$ and $F$, and the circles $\omega_{i}$ satisfy the conditions of Lemma 2 , so the problem statement follows. In the sequel, we use the notation of $O_{i j}^{ \pm}$from the statement of Lemma 2, applied to circles $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$. Using the relations $\triangle E C A \sim \triangle E B D, K N \| B D$, and $M N \| A C$. we get $$ \frac{A N}{N D}=\frac{A N}{A D} \cdot \frac{A D}{N D}=\frac{K N}{B D} \cdot \frac{A C}{N M}=\frac{A C}{B D}=\frac{A E}{E D} $$ Therefore, by the angle bisector theorem, point $N$ lies on the internal angle bisector of $\angle A E D$. We prove similarly that $L$ also lies on that bisector, and that the points $K$ and $M$ lie on the internal angle bisector of $\angle A F B$. Since $K L M N$ is a rhombus, points $K$ and $M$ are symmetric in line $E L N$. Hence, the convex quadrilateral determined by the lines $E K, E M, K L$, and $M L$ is a kite, and therefore it has an incircle $\omega_{0}$. Applying Monge's theorem to $\omega_{0}, \omega_{2}$, and $\omega_{3}$, we get that $O_{23}^{+}$lies on $K M$. On the other hand, $O_{23}^{+}$lies on $B C$, as $B C$ is an external common tangent to $\omega_{2}$ and $\omega_{3}$. It follows that $F=O_{23}^{+}$. Similarly, $E=O_{12}^{+}=O_{34}^{+}$, and $F=O_{41}^{+}$. Comment 3. The reduction to Lemma 2 and the proof of Lemma 2 can be performed with the use of different tools, e.g., by means of Menelaus theorem, by projecting harmonic quadruples, by applying Monge's theorem in some other ways, etc. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with no two sides parallel. Let $K, L, M$, and $N$ be points lying on sides $A B, B C, C D$, and $D A$, respectively, such that $K L M N$ is a rhombus with $K L \| A C$ and $L M \| B D$. Let $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$ be the incircles of triangles $A N K$, $B K L, C L M$, and $D M N$, respectively. Prove that the internal common tangents to $\omega_{1}$ and $\omega_{3}$ and the internal common tangents to $\omega_{2}$ and $\omega_{4}$ are concurrent. (Poland)
|
This solution is based on the following general Lemma. Lemma 2. Let $E$ and $F$ be distinct points, and let $\omega_{i}, i=1,2,3,4$, be circles lying in the same halfplane with respect to $E F$. For distinct indices $i, j \in\{1,2,3,4\}$, denote by $O_{i j}^{+}$ (respectively, $O_{i j}^{-}$) the center of homothety with positive (respectively, negative) ratio taking $\omega_{i}$ to $\omega_{j}$. Suppose that $E=O_{12}^{+}=O_{34}^{+}$and $F=O_{23}^{+}=O_{41}^{+}$. Then $O_{13}^{-}=O_{24}^{-}$. Proof. Applying Monge's theorem to triples of circles $\omega_{1}, \omega_{2}, \omega_{4}$ and $\omega_{1}, \omega_{3}, \omega_{4}$, we get that both points $O_{24}^{-}$and $O_{13}^{-}$lie on line $E O_{14}^{-}$. Notice that this line is distinct from $E F$. Similarly we obtain that both points $O_{24}^{-}$and $O_{13}^{-}$lie on $F O_{34}^{-}$. Since the lines $E O_{14}^{-}$and $F O_{34}^{-}$are distinct, both points coincide with the meeting point of those lines.  Turning back to the problem, let $A B$ intersect $C D$ at $E$ and let $B C$ intersect $D A$ at $F$. Assume, without loss of generality, that $B$ lies on segments $A E$ and $C F$. We will show that the points $E$ and $F$, and the circles $\omega_{i}$ satisfy the conditions of Lemma 2 , so the problem statement follows. In the sequel, we use the notation of $O_{i j}^{ \pm}$from the statement of Lemma 2, applied to circles $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$. Using the relations $\triangle E C A \sim \triangle E B D, K N \| B D$, and $M N \| A C$. we get $$ \frac{A N}{N D}=\frac{A N}{A D} \cdot \frac{A D}{N D}=\frac{K N}{B D} \cdot \frac{A C}{N M}=\frac{A C}{B D}=\frac{A E}{E D} $$ Therefore, by the angle bisector theorem, point $N$ lies on the internal angle bisector of $\angle A E D$. We prove similarly that $L$ also lies on that bisector, and that the points $K$ and $M$ lie on the internal angle bisector of $\angle A F B$. Since $K L M N$ is a rhombus, points $K$ and $M$ are symmetric in line $E L N$. Hence, the convex quadrilateral determined by the lines $E K, E M, K L$, and $M L$ is a kite, and therefore it has an incircle $\omega_{0}$. Applying Monge's theorem to $\omega_{0}, \omega_{2}$, and $\omega_{3}$, we get that $O_{23}^{+}$lies on $K M$. On the other hand, $O_{23}^{+}$lies on $B C$, as $B C$ is an external common tangent to $\omega_{2}$ and $\omega_{3}$. It follows that $F=O_{23}^{+}$. Similarly, $E=O_{12}^{+}=O_{34}^{+}$, and $F=O_{41}^{+}$. Comment 3. The reduction to Lemma 2 and the proof of Lemma 2 can be performed with the use of different tools, e.g., by means of Menelaus theorem, by projecting harmonic quadruples, by applying Monge's theorem in some other ways, etc. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
da642403-3904-56dc-9c13-7160c2315e80
| 24,080
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other. (Slovakia)
|
Let $\Varangle(p, q)$ denote the directed angle between lines $p$ and $q$. The points $B, C, I$, and $I_{A}$ lie on the circle $\Gamma$ with diameter $I I_{A}$. Let $\omega$ and $\Omega$ denote the circles $\left(I_{A} E F\right)$ and $(A I D)$, respectively. Let $T$ be the second intersection point of $\omega$ and $\Gamma$. Then $T$ is the Miquel point of the complete quadrilateral formed by the lines $B C, B I_{A}, C I_{A}$, and $D E F$, so $T$ also lies on circle $(B D E)$ (as well as on circle $(C D F)$ ). We claim that $T$ is a desired tangency point of $\omega$ and $\Omega$. In order to show that $T$ lies on $\Omega$, use cyclic quadrilaterals $B D E T$ and $B I I_{A} T$ to write $$ \Varangle(D T, D A)=\Varangle(D T, D E)=\Varangle(B T, B E)=\Varangle\left(B T, B I_{A}\right)=\Varangle\left(I T, I I_{A}\right)=\Varangle(I T, I A) . $$ 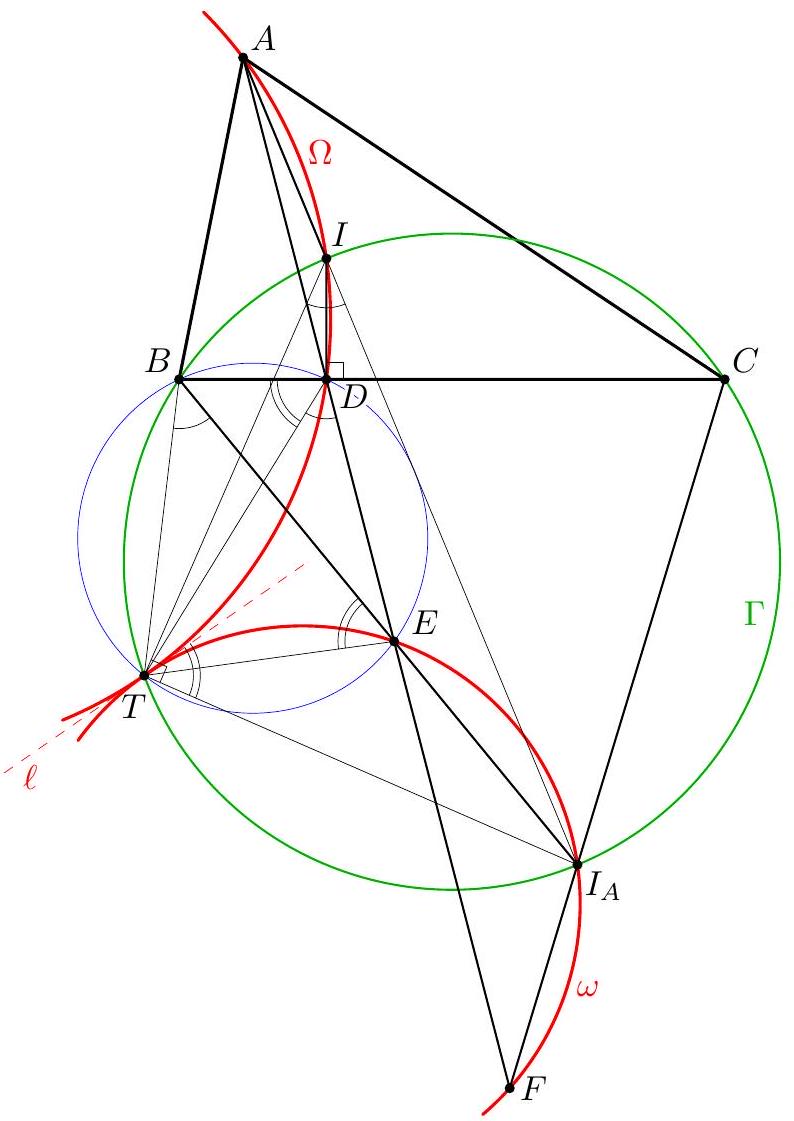 To show that $\omega$ and $\Omega$ are tangent at $T$, let $\ell$ be the tangent to $\omega$ at $T$, so that $\Varangle\left(T I_{A}, \ell\right)=$ $\Varangle\left(E I_{A}, E T\right)$. Using circles $(B D E T)$ and $\left(B I C I_{A}\right)$, we get $$ \Varangle\left(E I_{A}, E T\right)=\Varangle(E B, E T)=\Varangle(D B, D T) . $$ Therefore, $$ \Varangle(T I, \ell)=90^{\circ}+\Varangle\left(T I_{A}, \ell\right)=90^{\circ}+\Varangle(D B, D T)=\Varangle(D I, D T), $$ which shows that $\ell$ is tangent to $\Omega$ at $T$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other. (Slovakia)
|
Let $\Varangle(p, q)$ denote the directed angle between lines $p$ and $q$. The points $B, C, I$, and $I_{A}$ lie on the circle $\Gamma$ with diameter $I I_{A}$. Let $\omega$ and $\Omega$ denote the circles $\left(I_{A} E F\right)$ and $(A I D)$, respectively. Let $T$ be the second intersection point of $\omega$ and $\Gamma$. Then $T$ is the Miquel point of the complete quadrilateral formed by the lines $B C, B I_{A}, C I_{A}$, and $D E F$, so $T$ also lies on circle $(B D E)$ (as well as on circle $(C D F)$ ). We claim that $T$ is a desired tangency point of $\omega$ and $\Omega$. In order to show that $T$ lies on $\Omega$, use cyclic quadrilaterals $B D E T$ and $B I I_{A} T$ to write $$ \Varangle(D T, D A)=\Varangle(D T, D E)=\Varangle(B T, B E)=\Varangle\left(B T, B I_{A}\right)=\Varangle\left(I T, I I_{A}\right)=\Varangle(I T, I A) . $$  To show that $\omega$ and $\Omega$ are tangent at $T$, let $\ell$ be the tangent to $\omega$ at $T$, so that $\Varangle\left(T I_{A}, \ell\right)=$ $\Varangle\left(E I_{A}, E T\right)$. Using circles $(B D E T)$ and $\left(B I C I_{A}\right)$, we get $$ \Varangle\left(E I_{A}, E T\right)=\Varangle(E B, E T)=\Varangle(D B, D T) . $$ Therefore, $$ \Varangle(T I, \ell)=90^{\circ}+\Varangle\left(T I_{A}, \ell\right)=90^{\circ}+\Varangle(D B, D T)=\Varangle(D I, D T), $$ which shows that $\ell$ is tangent to $\Omega$ at $T$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1e34241f-1fe9-507f-96c0-ab66a6357293
| 24,085
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other. (Slovakia)
|
We use the notation of circles $\Gamma, \omega$, and $\Omega$ as in the previous solution. Let $L$ be the point opposite to $I$ in circle $\Omega$. Then $\angle I A L=\angle I D L=90^{\circ}$, which means that $L$ is the foot of the external bisector of $\angle A$ in triangle $A B C$. Let $L I$ cross $\Gamma$ again at $M$. Let $T$ be the foot of the perpendicular from $I$ onto $I_{A} L$. Then $T$ is the second intersection point of $\Gamma$ and $\Gamma$. We will show that $T$ is the desired tangency point. First, we show that $T$ lies on circle $\omega$. Notice that $$ \Varangle(L T, L M)=\Varangle(A T, A I) \quad \text { and } \quad \Varangle(M T, M L)=\Varangle(M T, M I)=\Varangle\left(I_{A} T, I_{A} I\right), $$ which shows that triangles $T M L$ and $T I_{A} A$ are similar and equioriented. So there exists a rotational homothety $\tau$ mapping $T M L$ to $T I_{A} A$. Since $\Varangle(M L, L D)=\Varangle(A I, A D)$, we get $\tau(B C)=A D$. Next, since $$ \Varangle(M B, M L)=\Varangle(M B, M I)=\Varangle\left(I_{A} B, I_{A} I\right)=\Varangle\left(I_{A} E, I_{A} A\right), $$ we get $\tau(B)=E$. Similarly, $\tau(C)=F$. Since the points $M, B, C$, and $T$ are concyclic, so are their $\tau$-images, which means that $T$ lies on $\omega=\tau(\Gamma)$. 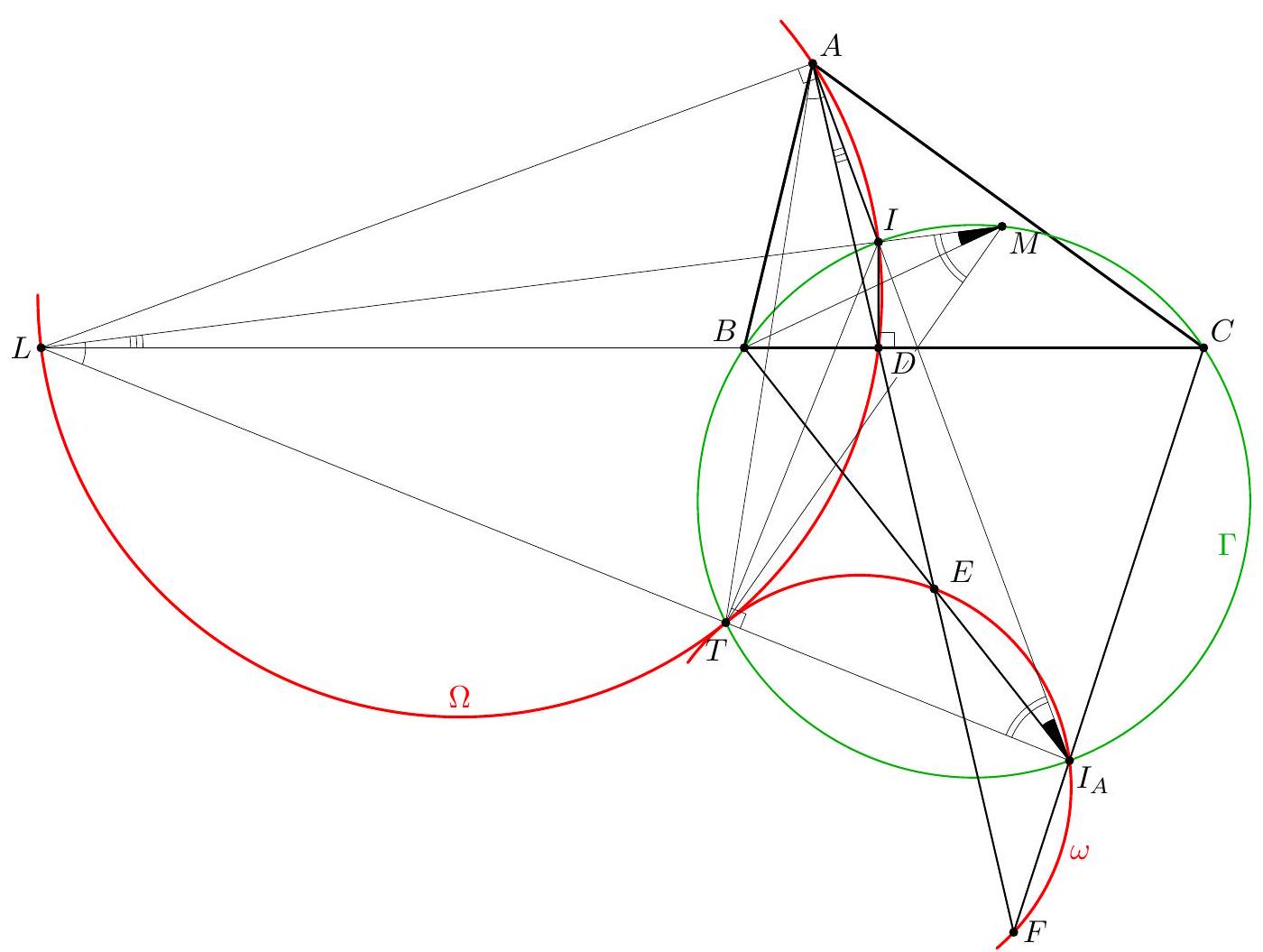 Finally, since $\tau(L)=A$ and $\tau(B)=E$, triangles $A T L$ and $E T B$ are similar so that $$ \Varangle(A T, A L)=\Varangle(E T, E B)=\Varangle\left(E I_{A}, E T\right) . $$ This means that the tangents to $\Omega$ and $\omega$ at $T$ make the same angle with the line $I_{A} T L$, so the circles are indeed tangent at $T$. Comment. In both solutions above, a crucial step is a guess that the desired tangency point lies on $\Gamma$. There are several ways to recognize this helpful property. E.g. one may perform some angle chasing to see that the tangents to $\Omega$ at $L$ and to $\omega$ at $I_{A}$ are parallel (and the circles lie on different sides of the tangents). This yields that, under the assumption that the circles are tangent externally, the tangency point must lie on $I_{A} L$. Since $I L$ is a diameter in $\Omega$, this, in turn, implies that $T$ is the projection of $I$ onto $I_{A} L$. Another way to see the same fact is to perform a homothety centered at $A$ and mapping $I$ to $I_{A}$ (and $D$ to some point $D^{\prime}$ ). The image $\Omega^{\prime}$ of $\Omega$ is tangent to $\omega$ at $I_{A}$, because $\angle B I_{A} A+\angle C I_{A} D^{\prime}=180^{\circ}$. This yields that the tangents to $\Omega$ at $I$ and to $\omega$ at $I_{A}$ are parallel. There are other ways to describe the tangency point. The next solution presents one of them.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other. (Slovakia)
|
We use the notation of circles $\Gamma, \omega$, and $\Omega$ as in the previous solution. Let $L$ be the point opposite to $I$ in circle $\Omega$. Then $\angle I A L=\angle I D L=90^{\circ}$, which means that $L$ is the foot of the external bisector of $\angle A$ in triangle $A B C$. Let $L I$ cross $\Gamma$ again at $M$. Let $T$ be the foot of the perpendicular from $I$ onto $I_{A} L$. Then $T$ is the second intersection point of $\Gamma$ and $\Gamma$. We will show that $T$ is the desired tangency point. First, we show that $T$ lies on circle $\omega$. Notice that $$ \Varangle(L T, L M)=\Varangle(A T, A I) \quad \text { and } \quad \Varangle(M T, M L)=\Varangle(M T, M I)=\Varangle\left(I_{A} T, I_{A} I\right), $$ which shows that triangles $T M L$ and $T I_{A} A$ are similar and equioriented. So there exists a rotational homothety $\tau$ mapping $T M L$ to $T I_{A} A$. Since $\Varangle(M L, L D)=\Varangle(A I, A D)$, we get $\tau(B C)=A D$. Next, since $$ \Varangle(M B, M L)=\Varangle(M B, M I)=\Varangle\left(I_{A} B, I_{A} I\right)=\Varangle\left(I_{A} E, I_{A} A\right), $$ we get $\tau(B)=E$. Similarly, $\tau(C)=F$. Since the points $M, B, C$, and $T$ are concyclic, so are their $\tau$-images, which means that $T$ lies on $\omega=\tau(\Gamma)$.  Finally, since $\tau(L)=A$ and $\tau(B)=E$, triangles $A T L$ and $E T B$ are similar so that $$ \Varangle(A T, A L)=\Varangle(E T, E B)=\Varangle\left(E I_{A}, E T\right) . $$ This means that the tangents to $\Omega$ and $\omega$ at $T$ make the same angle with the line $I_{A} T L$, so the circles are indeed tangent at $T$. Comment. In both solutions above, a crucial step is a guess that the desired tangency point lies on $\Gamma$. There are several ways to recognize this helpful property. E.g. one may perform some angle chasing to see that the tangents to $\Omega$ at $L$ and to $\omega$ at $I_{A}$ are parallel (and the circles lie on different sides of the tangents). This yields that, under the assumption that the circles are tangent externally, the tangency point must lie on $I_{A} L$. Since $I L$ is a diameter in $\Omega$, this, in turn, implies that $T$ is the projection of $I$ onto $I_{A} L$. Another way to see the same fact is to perform a homothety centered at $A$ and mapping $I$ to $I_{A}$ (and $D$ to some point $D^{\prime}$ ). The image $\Omega^{\prime}$ of $\Omega$ is tangent to $\omega$ at $I_{A}$, because $\angle B I_{A} A+\angle C I_{A} D^{\prime}=180^{\circ}$. This yields that the tangents to $\Omega$ at $I$ and to $\omega$ at $I_{A}$ are parallel. There are other ways to describe the tangency point. The next solution presents one of them.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1e34241f-1fe9-507f-96c0-ab66a6357293
| 24,085
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Let $A I, B I$, and $C I$ meet $\Gamma$ again at $D, E$, and $F$, respectively. Let $\ell$ be the common tangent to $\omega_{B}$ and $\omega_{C}$ at $I$. We always denote by $\Varangle(p, q)$ the directed angle from a line $p$ to a line $q$, taken modulo $180^{\circ}$. Step 1: We show that $Y$ lies on $\Gamma$. Recall that any chord of a circle makes complementary directed angles with the tangents to the circle at its endpoints. Hence, $$ \Varangle(B Y, B I)+\Varangle(C I, C Y)=\Varangle(I B, \ell)+\Varangle(\ell, I C)=\Varangle(I B, I C) . $$ Therefore, $$ \begin{aligned} \Varangle(B Y, B A)+\Varangle(C A, C Y)=\Varangle(B I, B A)+ & \Varangle(B Y, B I)+\Varangle(C I, C Y)+\Varangle(C A, C I) \\ & =\Varangle(B C, B I)+\Varangle(I B, I C)+\Varangle(C I, C B)=0, \end{aligned} $$ which yields $Y \in \Gamma$. 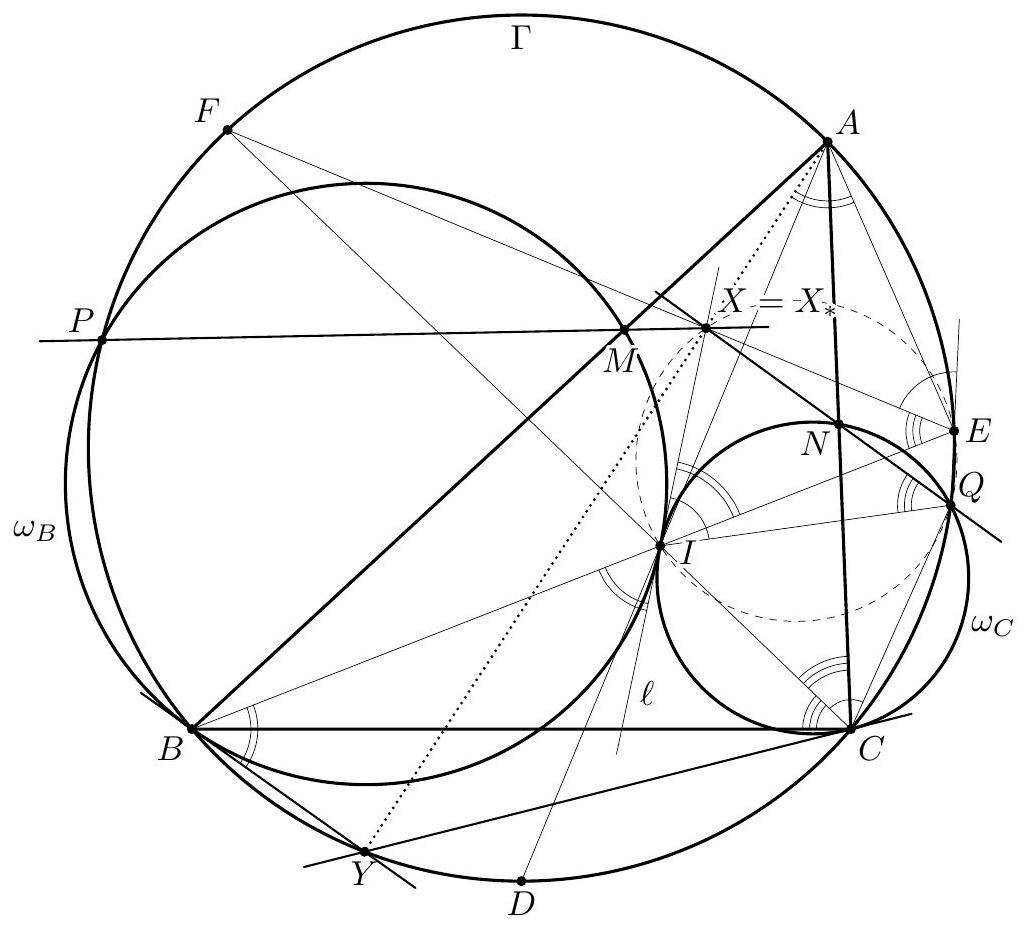 Step 2: We show that $X=\ell \cap E F$. Let $X_{*}=\ell \cap E F$. To prove our claim, it suffices to show that $X_{*}$ lies on both $P M$ and $Q N$; this will yield $X_{*}=X$. Due to symmetry, it suffices to show $X_{*} \in Q N$. Notice that $$ \Varangle\left(I X_{*}, I Q\right)=\Varangle(C I, C Q)=\Varangle(C F, C Q)=\Varangle(E F, E Q)=\Varangle\left(E X_{*}, E Q\right) ; $$ therefore, the points $X_{*}, I, Q$, and $E$ are concyclic (if $Q=E$, then the direction of $E Q$ is supposed to be the direction of a tangent to $\Gamma$ at $Q$; in this case, the equality means that the circle $\left(X_{*} I Q\right)$ is tangent to $\Gamma$ at $\left.Q\right)$. Then we have $$ \Varangle\left(Q X_{*}, Q I\right)=\Varangle\left(E X_{*}, E I\right)=\Varangle(E F, E B)=\Varangle(C A, C F)=\Varangle(C N, C I)=\Varangle(Q N, Q I), $$ which shows that $X_{*} \in Q N$. Step 3: We finally show that $A, X$, and $Y$ are collinear. Recall that $I$ is the orthocenter of triangle $D E F$, and $A$ is symmetric to $I$ with respect to $E F$. Therefore, $$ \Varangle(A X, A E)=\Varangle(I E, I X)=\Varangle(B I, \ell)=\Varangle(B Y, B I)=\Varangle(B Y, B E)=\Varangle(A Y, A E), $$ which yields the desired collinearity. Comment 1. Step 2 in the above solution seems to be crucial. After it has been performed (even without Step 1), there are different ways of finishing the solution. E.g., one may involve the notion of isogonal conjugacy. Let $X_{1}$ and $Y_{1}$ be isogonal conjugates of $X$ and $Y$, respectively, with respect to triangle $A B C$. Since $X A=X I$, triangle $A I X$ is isosceles, and hence the lines $A X$ and $X I$ form equal angles with the internal bisector $A I$ of $\angle B A C$. This means that $A X_{1} \| X I$, or $A X_{1} \| \ell$. On the other hand, the lines $B Y$ and $\ell$ form equal angles with $B I$, so that $B Y_{1} \| \ell$. Similarly, $C Y_{1} \| \ell$. This means that $Y_{1}$ is an ideal point, and $A Y_{1} \| \ell$ as well. Therefore, points $A, X_{1}$, and $Y_{1}$ are collinear, and hence $A, X$, and $Y$ are such.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Let $A I, B I$, and $C I$ meet $\Gamma$ again at $D, E$, and $F$, respectively. Let $\ell$ be the common tangent to $\omega_{B}$ and $\omega_{C}$ at $I$. We always denote by $\Varangle(p, q)$ the directed angle from a line $p$ to a line $q$, taken modulo $180^{\circ}$. Step 1: We show that $Y$ lies on $\Gamma$. Recall that any chord of a circle makes complementary directed angles with the tangents to the circle at its endpoints. Hence, $$ \Varangle(B Y, B I)+\Varangle(C I, C Y)=\Varangle(I B, \ell)+\Varangle(\ell, I C)=\Varangle(I B, I C) . $$ Therefore, $$ \begin{aligned} \Varangle(B Y, B A)+\Varangle(C A, C Y)=\Varangle(B I, B A)+ & \Varangle(B Y, B I)+\Varangle(C I, C Y)+\Varangle(C A, C I) \\ & =\Varangle(B C, B I)+\Varangle(I B, I C)+\Varangle(C I, C B)=0, \end{aligned} $$ which yields $Y \in \Gamma$.  Step 2: We show that $X=\ell \cap E F$. Let $X_{*}=\ell \cap E F$. To prove our claim, it suffices to show that $X_{*}$ lies on both $P M$ and $Q N$; this will yield $X_{*}=X$. Due to symmetry, it suffices to show $X_{*} \in Q N$. Notice that $$ \Varangle\left(I X_{*}, I Q\right)=\Varangle(C I, C Q)=\Varangle(C F, C Q)=\Varangle(E F, E Q)=\Varangle\left(E X_{*}, E Q\right) ; $$ therefore, the points $X_{*}, I, Q$, and $E$ are concyclic (if $Q=E$, then the direction of $E Q$ is supposed to be the direction of a tangent to $\Gamma$ at $Q$; in this case, the equality means that the circle $\left(X_{*} I Q\right)$ is tangent to $\Gamma$ at $\left.Q\right)$. Then we have $$ \Varangle\left(Q X_{*}, Q I\right)=\Varangle\left(E X_{*}, E I\right)=\Varangle(E F, E B)=\Varangle(C A, C F)=\Varangle(C N, C I)=\Varangle(Q N, Q I), $$ which shows that $X_{*} \in Q N$. Step 3: We finally show that $A, X$, and $Y$ are collinear. Recall that $I$ is the orthocenter of triangle $D E F$, and $A$ is symmetric to $I$ with respect to $E F$. Therefore, $$ \Varangle(A X, A E)=\Varangle(I E, I X)=\Varangle(B I, \ell)=\Varangle(B Y, B I)=\Varangle(B Y, B E)=\Varangle(A Y, A E), $$ which yields the desired collinearity. Comment 1. Step 2 in the above solution seems to be crucial. After it has been performed (even without Step 1), there are different ways of finishing the solution. E.g., one may involve the notion of isogonal conjugacy. Let $X_{1}$ and $Y_{1}$ be isogonal conjugates of $X$ and $Y$, respectively, with respect to triangle $A B C$. Since $X A=X I$, triangle $A I X$ is isosceles, and hence the lines $A X$ and $X I$ form equal angles with the internal bisector $A I$ of $\angle B A C$. This means that $A X_{1} \| X I$, or $A X_{1} \| \ell$. On the other hand, the lines $B Y$ and $\ell$ form equal angles with $B I$, so that $B Y_{1} \| \ell$. Similarly, $C Y_{1} \| \ell$. This means that $Y_{1}$ is an ideal point, and $A Y_{1} \| \ell$ as well. Therefore, points $A, X_{1}$, and $Y_{1}$ are collinear, and hence $A, X$, and $Y$ are such.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a64aad5-47da-5c02-876d-6faf56be5988
| 24,093
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Perform an inversion centered at $I$; the images of the points are denoted by primes, e.g., $A^{\prime}$ is the image of $A$. On the inverted figure, $I$ and $\Gamma^{\prime}$ are the orthocenter and the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$, respectively. The points $P^{\prime}$ and $Q^{\prime}$ lie on $\Gamma^{\prime}$ such that $B^{\prime} P^{\prime} \| C^{\prime} Q^{\prime}$ (since $B^{\prime} P^{\prime}=\omega_{B}^{\prime}$ and $C^{\prime} Q^{\prime}=\omega_{C}^{\prime}$ ). The points $M^{\prime}$ and $N^{\prime}$ are the second intersections of lines $B^{\prime} P^{\prime}$ and $C^{\prime} Q^{\prime}$ with the circumcircles $\gamma_{B}$ and $\gamma_{C}$ of triangles $A^{\prime} I B^{\prime}$ and $A^{\prime} I C^{\prime}$, respectively. Notice here that $\gamma_{C}$ is obtained from $\gamma_{B}$ by the translation at $\overrightarrow{B^{\prime} C^{\prime}}$; the same translation maps line $B^{\prime} P^{\prime}$ to $C^{\prime} Q^{\prime}$, and hence $M^{\prime}$ to $N^{\prime}$. In other words, $B^{\prime} M^{\prime} N^{\prime} C^{\prime}$ is a parallelogram, and $P^{\prime} Q^{\prime}$ partitions it into two isosceles trapezoids. Point $X^{\prime}$ is the second intersection point of circles $\left(I P^{\prime} M^{\prime}\right)$ and $\left(I Q^{\prime} N^{\prime}\right)$ that is - the reflection of $I$ in their line of centers. But the centers lie on the common perpendicular bisector $p$ of $P^{\prime} M^{\prime}$ and $Q^{\prime} N^{\prime}$, so $p$ is that line of centers. Hence, $I X^{\prime} \| B^{\prime} P^{\prime}$, as both lines are perpendicular to $p$. Finally, the point $Y$ satisfies $\Varangle(B Y, B I)=\Varangle(P B, P I)$ and $\Varangle(C Y, C I)=\Varangle(Q C, Q I)$, which yields $\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} I\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)$ and $\Varangle\left(Y^{\prime} C^{\prime}, Y^{\prime} I\right)=\Varangle\left(C^{\prime} Q^{\prime}, C^{\prime} I\right)$. Therefore, $$ \Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} C^{\prime}\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)+\Varangle\left(C^{\prime} I, C^{\prime} Q^{\prime}\right)=\Varangle\left(C^{\prime} I, B^{\prime} I\right)=\Varangle\left(A^{\prime} B^{\prime}, A^{\prime} C^{\prime}\right), $$ which shows that $Y^{\prime} \in \Gamma^{\prime}$. In congruent circles $\Gamma^{\prime}$ and $\gamma_{B}$, the chords $A^{\prime} P^{\prime}$ and $A^{\prime} M^{\prime}$ subtend the same angle $\angle A^{\prime} B^{\prime} P^{\prime}$; therefore, $A^{\prime} P^{\prime}=A^{\prime} M^{\prime}$, and hence $A^{\prime} \in p$. This yields $A^{\prime} X^{\prime}=A^{\prime} I$, and hence $\Varangle\left(I A^{\prime}, I X^{\prime}\right)=$ $\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right)$ 。 Finally, we have $$ \begin{aligned} \Varangle\left(Y^{\prime} I, Y^{\prime} A^{\prime}\right) & =\Varangle\left(Y^{\prime} I, Y^{\prime} B^{\prime}\right)+\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} A^{\prime}\right) \\ & =\Varangle\left(B^{\prime} I, B^{\prime} P^{\prime}\right)+\Varangle\left(I A^{\prime}, I B^{\prime}\right)=\Varangle\left(I A^{\prime}, B^{\prime} P^{\prime}\right)=\Varangle\left(I A^{\prime}, I X^{\prime}\right)=\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right), \end{aligned} $$ which yields that the points $A^{\prime}, X^{\prime}, Y^{\prime}$, and $I$ are concyclic. This means exactly that $A, X$, and $Y$ are collinear.  Comment 2. An inversion at $I$ may also help in establishing Step 2 in Solution 1. Indeed, relation $A^{\prime} X^{\prime}=A^{\prime} I$ yields $X A=X I$, so that $X \in E F$. On the other hand, $I X^{\prime} \| B^{\prime} P^{\prime}$ yields $I X \| \ell$, i.e., $X \in \ell$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Perform an inversion centered at $I$; the images of the points are denoted by primes, e.g., $A^{\prime}$ is the image of $A$. On the inverted figure, $I$ and $\Gamma^{\prime}$ are the orthocenter and the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$, respectively. The points $P^{\prime}$ and $Q^{\prime}$ lie on $\Gamma^{\prime}$ such that $B^{\prime} P^{\prime} \| C^{\prime} Q^{\prime}$ (since $B^{\prime} P^{\prime}=\omega_{B}^{\prime}$ and $C^{\prime} Q^{\prime}=\omega_{C}^{\prime}$ ). The points $M^{\prime}$ and $N^{\prime}$ are the second intersections of lines $B^{\prime} P^{\prime}$ and $C^{\prime} Q^{\prime}$ with the circumcircles $\gamma_{B}$ and $\gamma_{C}$ of triangles $A^{\prime} I B^{\prime}$ and $A^{\prime} I C^{\prime}$, respectively. Notice here that $\gamma_{C}$ is obtained from $\gamma_{B}$ by the translation at $\overrightarrow{B^{\prime} C^{\prime}}$; the same translation maps line $B^{\prime} P^{\prime}$ to $C^{\prime} Q^{\prime}$, and hence $M^{\prime}$ to $N^{\prime}$. In other words, $B^{\prime} M^{\prime} N^{\prime} C^{\prime}$ is a parallelogram, and $P^{\prime} Q^{\prime}$ partitions it into two isosceles trapezoids. Point $X^{\prime}$ is the second intersection point of circles $\left(I P^{\prime} M^{\prime}\right)$ and $\left(I Q^{\prime} N^{\prime}\right)$ that is - the reflection of $I$ in their line of centers. But the centers lie on the common perpendicular bisector $p$ of $P^{\prime} M^{\prime}$ and $Q^{\prime} N^{\prime}$, so $p$ is that line of centers. Hence, $I X^{\prime} \| B^{\prime} P^{\prime}$, as both lines are perpendicular to $p$. Finally, the point $Y$ satisfies $\Varangle(B Y, B I)=\Varangle(P B, P I)$ and $\Varangle(C Y, C I)=\Varangle(Q C, Q I)$, which yields $\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} I\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)$ and $\Varangle\left(Y^{\prime} C^{\prime}, Y^{\prime} I\right)=\Varangle\left(C^{\prime} Q^{\prime}, C^{\prime} I\right)$. Therefore, $$ \Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} C^{\prime}\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)+\Varangle\left(C^{\prime} I, C^{\prime} Q^{\prime}\right)=\Varangle\left(C^{\prime} I, B^{\prime} I\right)=\Varangle\left(A^{\prime} B^{\prime}, A^{\prime} C^{\prime}\right), $$ which shows that $Y^{\prime} \in \Gamma^{\prime}$. In congruent circles $\Gamma^{\prime}$ and $\gamma_{B}$, the chords $A^{\prime} P^{\prime}$ and $A^{\prime} M^{\prime}$ subtend the same angle $\angle A^{\prime} B^{\prime} P^{\prime}$; therefore, $A^{\prime} P^{\prime}=A^{\prime} M^{\prime}$, and hence $A^{\prime} \in p$. This yields $A^{\prime} X^{\prime}=A^{\prime} I$, and hence $\Varangle\left(I A^{\prime}, I X^{\prime}\right)=$ $\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right)$ 。 Finally, we have $$ \begin{aligned} \Varangle\left(Y^{\prime} I, Y^{\prime} A^{\prime}\right) & =\Varangle\left(Y^{\prime} I, Y^{\prime} B^{\prime}\right)+\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} A^{\prime}\right) \\ & =\Varangle\left(B^{\prime} I, B^{\prime} P^{\prime}\right)+\Varangle\left(I A^{\prime}, I B^{\prime}\right)=\Varangle\left(I A^{\prime}, B^{\prime} P^{\prime}\right)=\Varangle\left(I A^{\prime}, I X^{\prime}\right)=\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right), \end{aligned} $$ which yields that the points $A^{\prime}, X^{\prime}, Y^{\prime}$, and $I$ are concyclic. This means exactly that $A, X$, and $Y$ are collinear.  Comment 2. An inversion at $I$ may also help in establishing Step 2 in Solution 1. Indeed, relation $A^{\prime} X^{\prime}=A^{\prime} I$ yields $X A=X I$, so that $X \in E F$. On the other hand, $I X^{\prime} \| B^{\prime} P^{\prime}$ yields $I X \| \ell$, i.e., $X \in \ell$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a64aad5-47da-5c02-876d-6faf56be5988
| 24,093
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia) Answer: No such sequence exists.
|
Suppose that $a_{1}, \ldots, a_{n}$ satisfy the required properties. Let $d=\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)$. If $d>1$ then replace the numbers $a_{1}, \ldots, a_{n}$ by $\frac{a_{1}}{d}, \ldots, \frac{a_{n}}{d}$; all arithmetic and all geometric means will be divided by $d$, so we obtain another sequence satisfying the condition. Hence, without loss of generality, we can assume that $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$. We show two numbers, $a_{m}$ and $a_{k}$ such that their arithmetic mean, $\frac{a_{m}+a_{k}}{2}$ is different from the geometric mean of any (nonempty) subsequence of $a_{1} \ldots, a_{n}$. That proves that there cannot exist such a sequence. Choose the index $m \in\{1, \ldots, n\}$ such that $a_{m}=\max \left(a_{1}, \ldots, a_{n}\right)$. Note that $a_{m} \geqslant 2$, because $a_{1}, \ldots, a_{n}$ are not all equal. Let $p$ be a prime divisor of $a_{m}$. Let $k \in\{1, \ldots, n\}$ be an index such that $a_{k}=\max \left\{a_{i}: p \nmid a_{i}\right\}$. Due to $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$, not all $a_{i}$ are divisible by $p$, so such a $k$ exists. Note that $a_{m}>a_{k}$ because $a_{m} \geqslant a_{k}, p \mid a_{m}$ and $p \nmid a_{k}$. Let $b=\frac{a_{m}+a_{k}}{2}$; we will show that $b$ cannot be the geometric mean of any subsequence of $a_{1}, \ldots, a_{n}$. Consider the geometric mean, $g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ of an arbitrary subsequence of $a_{1}, \ldots, a_{n}$. If none of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then they are not greater than $a_{k}$, so $$ g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}} \leqslant a_{k}<\frac{a_{m}+a_{k}}{2}=b $$ and therefore $g \neq b$. Otherwise, if at least one of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then $2 g=2 \sqrt{t} \sqrt{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ is either not an integer or is divisible by $p$, while $2 b=a_{m}+a_{k}$ is an integer not divisible by $p$, so $g \neq b$ again.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia) Answer: No such sequence exists.
|
Suppose that $a_{1}, \ldots, a_{n}$ satisfy the required properties. Let $d=\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)$. If $d>1$ then replace the numbers $a_{1}, \ldots, a_{n}$ by $\frac{a_{1}}{d}, \ldots, \frac{a_{n}}{d}$; all arithmetic and all geometric means will be divided by $d$, so we obtain another sequence satisfying the condition. Hence, without loss of generality, we can assume that $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$. We show two numbers, $a_{m}$ and $a_{k}$ such that their arithmetic mean, $\frac{a_{m}+a_{k}}{2}$ is different from the geometric mean of any (nonempty) subsequence of $a_{1} \ldots, a_{n}$. That proves that there cannot exist such a sequence. Choose the index $m \in\{1, \ldots, n\}$ such that $a_{m}=\max \left(a_{1}, \ldots, a_{n}\right)$. Note that $a_{m} \geqslant 2$, because $a_{1}, \ldots, a_{n}$ are not all equal. Let $p$ be a prime divisor of $a_{m}$. Let $k \in\{1, \ldots, n\}$ be an index such that $a_{k}=\max \left\{a_{i}: p \nmid a_{i}\right\}$. Due to $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$, not all $a_{i}$ are divisible by $p$, so such a $k$ exists. Note that $a_{m}>a_{k}$ because $a_{m} \geqslant a_{k}, p \mid a_{m}$ and $p \nmid a_{k}$. Let $b=\frac{a_{m}+a_{k}}{2}$; we will show that $b$ cannot be the geometric mean of any subsequence of $a_{1}, \ldots, a_{n}$. Consider the geometric mean, $g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ of an arbitrary subsequence of $a_{1}, \ldots, a_{n}$. If none of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then they are not greater than $a_{k}$, so $$ g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}} \leqslant a_{k}<\frac{a_{m}+a_{k}}{2}=b $$ and therefore $g \neq b$. Otherwise, if at least one of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then $2 g=2 \sqrt{t} \sqrt{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ is either not an integer or is divisible by $p$, while $2 b=a_{m}+a_{k}$ is an integer not divisible by $p$, so $g \neq b$ again.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8694a387-0601-5d2e-8224-58bc5721824a
| 24,100
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia) Answer: No such sequence exists.
|
Like in the previous solution, we assume that the numbers $a_{1}, \ldots, a_{n}$ have no common divisor greater than 1 . The arithmetic mean of any two numbers in the sequence is half of an integer; on the other hand, it is a (some integer order) root of an integer. This means each pair's mean is an integer, so all terms in the sequence must be of the same parity; hence they all are odd. Let $d=\min \left\{\operatorname{gcd}\left(a_{i}, a_{j}\right): a_{i} \neq a_{j}\right\}$. By reordering the sequence we can assume that $\operatorname{gcd}\left(a_{1}, a_{2}\right)=d$, the sum $a_{1}+a_{2}$ is maximal among such pairs, and $a_{1}>a_{2}$. We will show that $\frac{a_{1}+a_{2}}{2}$ cannot be the geometric mean of any subsequence of $a_{1} \ldots, a_{n}$. Let $a_{1}=x d$ and $a_{2}=y d$ where $x, y$ are coprime, and suppose that there exist some $b_{1}, \ldots, b_{t} \in\left\{a_{1}, \ldots, a_{n}\right\}$ whose geometric mean is $\frac{a_{1}+a_{2}}{2}$. Let $d_{i}=\operatorname{gcd}\left(a_{1}, b_{i}\right)$ for $i=1,2, \ldots, t$ and let $D=d_{1} d_{2} \cdot \ldots \cdot d_{t}$. Then $$ D=d_{1} d_{2} \cdot \ldots \cdot d_{t} \left\lvert\, b_{1} b_{2} \cdot \ldots \cdot b_{t}=\left(\frac{a_{1}+a_{2}}{2}\right)^{t}=\left(\frac{x+y}{2}\right)^{t} d^{t}\right. $$ We claim that $D \mid d^{t}$. Consider an arbitrary prime divisor $p$ of $D$. Let $\nu_{p}(x)$ denote the exponent of $p$ in the prime factorization of $x$. If $p \left\lvert\, \frac{x+y}{2}\right.$, then $p \nmid x, y$, so $p$ is coprime with $x$; hence, $\nu_{p}\left(d_{i}\right) \leqslant \nu_{p}\left(a_{1}\right)=\nu_{p}(x d)=\nu_{p}(d)$ for every $1 \leqslant i \leqslant t$, therefore $\nu_{p}(D)=\sum_{i} \nu_{p}\left(d_{i}\right) \leqslant$ $t \nu_{p}(d)=\nu_{p}\left(d^{t}\right)$. Otherwise, if $p$ is coprime to $\frac{x+y}{2}$, we have $\nu_{p}(D) \leqslant \nu_{p}\left(d^{t}\right)$ trivially. The claim has been proved. Notice that $d_{i}=\operatorname{gcd}\left(b_{i}, a_{1}\right) \geqslant d$ for $1 \leqslant i \leqslant t$ : if $b_{i} \neq a_{1}$ then this follows from the definition of $d$; otherwise we have $b_{i}=a_{1}$, so $d_{i}=a_{1} \geqslant d$. Hence, $D=d_{1} \cdot \ldots \cdot d_{t} \geqslant d^{t}$, and the claim forces $d_{1}=\ldots=d_{t}=d$. Finally, by $\frac{a_{1}+a_{2}}{2}>a_{2}$ there must be some $b_{k}$ which is greater than $a_{2}$. From $a_{1}>a_{2} \geqslant$ $d=\operatorname{gcd}\left(a_{1}, b_{k}\right)$ it follows that $a_{1} \neq b_{k}$. Now the have a pair $a_{1}, b_{k}$ such that $\operatorname{gcd}\left(a_{1}, b_{k}\right)=d$ but $a_{1}+b_{k}>a_{1}+a_{2}$; that contradicts the choice of $a_{1}$ and $a_{2}$. Comment. The original problem proposal contained a second question asking if there exists a nonconstant sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers such that the geometric mean of every two terms is equal the arithmetic mean of some terms. For $n \geqslant 3$ such a sequence is $(4,1,1, \ldots, 1)$. The case $n=2$ can be done by the trivial estimates $$ \min \left(a_{1}, a_{2}\right)<\sqrt{a_{1} a_{2}}<\frac{a_{1}+a_{2}}{2}<\max \left(a_{1}, a_{2}\right) $$ The Problem Selection Committee found this variant less interesting and suggests using only the first question.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia) Answer: No such sequence exists.
|
Like in the previous solution, we assume that the numbers $a_{1}, \ldots, a_{n}$ have no common divisor greater than 1 . The arithmetic mean of any two numbers in the sequence is half of an integer; on the other hand, it is a (some integer order) root of an integer. This means each pair's mean is an integer, so all terms in the sequence must be of the same parity; hence they all are odd. Let $d=\min \left\{\operatorname{gcd}\left(a_{i}, a_{j}\right): a_{i} \neq a_{j}\right\}$. By reordering the sequence we can assume that $\operatorname{gcd}\left(a_{1}, a_{2}\right)=d$, the sum $a_{1}+a_{2}$ is maximal among such pairs, and $a_{1}>a_{2}$. We will show that $\frac{a_{1}+a_{2}}{2}$ cannot be the geometric mean of any subsequence of $a_{1} \ldots, a_{n}$. Let $a_{1}=x d$ and $a_{2}=y d$ where $x, y$ are coprime, and suppose that there exist some $b_{1}, \ldots, b_{t} \in\left\{a_{1}, \ldots, a_{n}\right\}$ whose geometric mean is $\frac{a_{1}+a_{2}}{2}$. Let $d_{i}=\operatorname{gcd}\left(a_{1}, b_{i}\right)$ for $i=1,2, \ldots, t$ and let $D=d_{1} d_{2} \cdot \ldots \cdot d_{t}$. Then $$ D=d_{1} d_{2} \cdot \ldots \cdot d_{t} \left\lvert\, b_{1} b_{2} \cdot \ldots \cdot b_{t}=\left(\frac{a_{1}+a_{2}}{2}\right)^{t}=\left(\frac{x+y}{2}\right)^{t} d^{t}\right. $$ We claim that $D \mid d^{t}$. Consider an arbitrary prime divisor $p$ of $D$. Let $\nu_{p}(x)$ denote the exponent of $p$ in the prime factorization of $x$. If $p \left\lvert\, \frac{x+y}{2}\right.$, then $p \nmid x, y$, so $p$ is coprime with $x$; hence, $\nu_{p}\left(d_{i}\right) \leqslant \nu_{p}\left(a_{1}\right)=\nu_{p}(x d)=\nu_{p}(d)$ for every $1 \leqslant i \leqslant t$, therefore $\nu_{p}(D)=\sum_{i} \nu_{p}\left(d_{i}\right) \leqslant$ $t \nu_{p}(d)=\nu_{p}\left(d^{t}\right)$. Otherwise, if $p$ is coprime to $\frac{x+y}{2}$, we have $\nu_{p}(D) \leqslant \nu_{p}\left(d^{t}\right)$ trivially. The claim has been proved. Notice that $d_{i}=\operatorname{gcd}\left(b_{i}, a_{1}\right) \geqslant d$ for $1 \leqslant i \leqslant t$ : if $b_{i} \neq a_{1}$ then this follows from the definition of $d$; otherwise we have $b_{i}=a_{1}$, so $d_{i}=a_{1} \geqslant d$. Hence, $D=d_{1} \cdot \ldots \cdot d_{t} \geqslant d^{t}$, and the claim forces $d_{1}=\ldots=d_{t}=d$. Finally, by $\frac{a_{1}+a_{2}}{2}>a_{2}$ there must be some $b_{k}$ which is greater than $a_{2}$. From $a_{1}>a_{2} \geqslant$ $d=\operatorname{gcd}\left(a_{1}, b_{k}\right)$ it follows that $a_{1} \neq b_{k}$. Now the have a pair $a_{1}, b_{k}$ such that $\operatorname{gcd}\left(a_{1}, b_{k}\right)=d$ but $a_{1}+b_{k}>a_{1}+a_{2}$; that contradicts the choice of $a_{1}$ and $a_{2}$. Comment. The original problem proposal contained a second question asking if there exists a nonconstant sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers such that the geometric mean of every two terms is equal the arithmetic mean of some terms. For $n \geqslant 3$ such a sequence is $(4,1,1, \ldots, 1)$. The case $n=2$ can be done by the trivial estimates $$ \min \left(a_{1}, a_{2}\right)<\sqrt{a_{1} a_{2}}<\frac{a_{1}+a_{2}}{2}<\max \left(a_{1}, a_{2}\right) $$ The Problem Selection Committee found this variant less interesting and suggests using only the first question.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8694a387-0601-5d2e-8224-58bc5721824a
| 24,100
|
For any odd prime $p$ and any integer $n$, let $d_{p}(n) \in\{0,1, \ldots, p-1\}$ denote the remainder when $n$ is divided by $p$. We say that $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ is a $p$-sequence, if $a_{0}$ is a positive integer coprime to $p$, and $a_{n+1}=a_{n}+d_{p}\left(a_{n}\right)$ for $n \geqslant 0$. (a) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{n}>b_{n}$ for infinitely many $n$, and $b_{n}>a_{n}$ for infinitely many $n$ ? (b) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{0}<b_{0}$, but $a_{n}>b_{n}$ for all $n \geqslant 1$ ? (United Kingdom) Answer: Yes, for both parts.
|
Fix some odd prime $p$, and let $T$ be the smallest positive integer such that $p \mid 2^{T}-1$; in other words, $T$ is the multiplicative order of 2 modulo $p$. Consider any $p$-sequence $\left(x_{n}\right)=\left(x_{0}, x_{1}, x_{2}, \ldots\right)$. Obviously, $x_{n+1} \equiv 2 x_{n}(\bmod p)$ and therefore $x_{n} \equiv 2^{n} x_{0}(\bmod p)$. This yields $x_{n+T} \equiv x_{n}(\bmod p)$ and therefore $d\left(x_{n+T}\right)=d\left(x_{n}\right)$ for all $n \geqslant 0$. It follows that the sum $d\left(x_{n}\right)+d\left(x_{n+1}\right)+\ldots+d\left(x_{n+T-1}\right)$ does not depend on $n$ and is thus a function of $x_{0}$ (and $p$ ) only; we shall denote this sum by $S_{p}\left(x_{0}\right)$, and extend the function $S_{p}(\cdot)$ to all (not necessarily positive) integers. Therefore, we have $x_{n+k T}=x_{n}+k S_{p}\left(x_{0}\right)$ for all positive integers $n$ and $k$. Clearly, $S_{p}\left(x_{0}\right)=S_{p}\left(2^{t} x_{0}\right)$ for every integer $t \geqslant 0$. In both parts, we use the notation $$ S_{p}^{+}=S_{p}(1)=\sum_{i=0}^{T-1} d_{p}\left(2^{i}\right) \quad \text { and } \quad S_{p}^{-}=S_{p}(-1)=\sum_{i=0}^{T-1} d_{p}\left(p-2^{i}\right) $$ (a) Let $q>3$ be a prime and $p$ a prime divisor of $2^{q}+1$ that is greater than 3 . We will show that $p$ is suitable for part (a). Notice that $9 \nmid 2^{q}+1$, so that such a $p$ exists. Moreover, for any two odd primes $q<r$ we have $\operatorname{gcd}\left(2^{q}+1,2^{r}+1\right)=2^{\operatorname{gcd}(q, r)}+1=3$, thus there exist infinitely many such primes $p$. For the chosen $p$, we have $T=2 q$. Since $2^{q} \equiv-1(\bmod p)$, we have $S_{p}^{+}=S_{p}^{-}$. Now consider the $p$-sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ with $a_{0}=p+1$ and $b_{0}=p-1$; we claim that these sequences satisfy the required conditions. We have $a_{0}>b_{0}$ and $a_{1}=p+2<b_{1}=2 p-2$. It follows then that $$ a_{k \cdot 2 q}=a_{0}+k S_{p}^{+}>b_{0}+k S_{p}^{+}=b_{k \cdot 2 q} \quad \text { and } \quad a_{k \cdot 2 q+1}=a_{1}+k S_{p}^{+}<b_{1}+k S_{p}^{+}=b_{k \cdot 2 q+1} $$ for all $k=0,1, \ldots$, as desired. (b) Let $q$ be an odd prime and $p$ a prime divisor of $2^{q}-1$; thus we have $T=q$. We will show that $p$ is suitable for part (b). Notice that the numbers of the form $2^{q}-1$ are pairwise coprime (since $\operatorname{gcd}\left(2^{q}-1,2^{r}-1\right)=2^{\operatorname{gcd}(q, r)}-1=1$ for any two distinct primes $q$ and $r$ ), thus there exist infinitely many such primes $p$. Notice that $d_{p}(x)+d_{p}(p-x)=p$ for all $x$ with $p \nmid x$, so that the sum $S_{p}^{+}+S_{p}^{-}=p q$ is odd, which yields $S_{p}^{+}=S_{p}(1) \neq S_{p}(-1)=S_{p}^{-}$. Assume that $\left(x_{n}\right)$ and $\left(y_{n}\right)$ are two $p$-sequences with $S_{p}\left(x_{0}\right)>S_{p}\left(y_{0}\right)$ but $x_{0}<y_{0}$. The first condition yields that $$ x_{M q+r}-y_{M q+r}=\left(x_{r}-y_{r}\right)+M\left(S_{p}\left(x_{0}\right)-S_{p}\left(y_{0}\right)\right) \geqslant\left(x_{r}-y_{r}\right)+M $$ for all nonnegative integers $M$ and every $r=0,1, \ldots, q-1$. Thus, we have $x_{n}>y_{n}$ for every $n \geqslant q+q \cdot \max \left\{y_{r}-x_{r}: r=0,1, \ldots, q-1\right\}$. Now, since $x_{0}<y_{0}$, there exists the largest $n_{0}$ with $x_{n_{0}}<y_{n_{0}}$. In this case the $p$-sequences $a_{n}=x_{n-n_{0}}$ and $b_{n}=y_{n-n_{0}}$ possess the desired property (notice here that $x_{n} \neq y_{n}$ for all $n \geqslant 0$, as otherwise we would have $\left.S_{p}\left(x_{0}\right)=S_{p}\left(x_{n}\right)=S_{p}\left(y_{n}\right)=S_{p}\left(y_{0}\right)\right)$. It remains to find $p$-sequences $\left(x_{n}\right)$ and $\left(y_{n}\right)$ satisfying the two conditions. Recall that $S_{p}^{+} \neq S_{p}^{-}$. Now, if $S_{p}^{+}>S_{p}^{-}$, then we can put $x_{0}=1$ and $y_{0}=p-1$. Otherwise, if $S_{p}^{+}<S_{p}^{-}$, then we put $x_{0}=p-1$ and $y_{0}=p+1$. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any odd prime $p$ and any integer $n$, let $d_{p}(n) \in\{0,1, \ldots, p-1\}$ denote the remainder when $n$ is divided by $p$. We say that $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ is a $p$-sequence, if $a_{0}$ is a positive integer coprime to $p$, and $a_{n+1}=a_{n}+d_{p}\left(a_{n}\right)$ for $n \geqslant 0$. (a) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{n}>b_{n}$ for infinitely many $n$, and $b_{n}>a_{n}$ for infinitely many $n$ ? (b) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{0}<b_{0}$, but $a_{n}>b_{n}$ for all $n \geqslant 1$ ? (United Kingdom) Answer: Yes, for both parts.
|
Fix some odd prime $p$, and let $T$ be the smallest positive integer such that $p \mid 2^{T}-1$; in other words, $T$ is the multiplicative order of 2 modulo $p$. Consider any $p$-sequence $\left(x_{n}\right)=\left(x_{0}, x_{1}, x_{2}, \ldots\right)$. Obviously, $x_{n+1} \equiv 2 x_{n}(\bmod p)$ and therefore $x_{n} \equiv 2^{n} x_{0}(\bmod p)$. This yields $x_{n+T} \equiv x_{n}(\bmod p)$ and therefore $d\left(x_{n+T}\right)=d\left(x_{n}\right)$ for all $n \geqslant 0$. It follows that the sum $d\left(x_{n}\right)+d\left(x_{n+1}\right)+\ldots+d\left(x_{n+T-1}\right)$ does not depend on $n$ and is thus a function of $x_{0}$ (and $p$ ) only; we shall denote this sum by $S_{p}\left(x_{0}\right)$, and extend the function $S_{p}(\cdot)$ to all (not necessarily positive) integers. Therefore, we have $x_{n+k T}=x_{n}+k S_{p}\left(x_{0}\right)$ for all positive integers $n$ and $k$. Clearly, $S_{p}\left(x_{0}\right)=S_{p}\left(2^{t} x_{0}\right)$ for every integer $t \geqslant 0$. In both parts, we use the notation $$ S_{p}^{+}=S_{p}(1)=\sum_{i=0}^{T-1} d_{p}\left(2^{i}\right) \quad \text { and } \quad S_{p}^{-}=S_{p}(-1)=\sum_{i=0}^{T-1} d_{p}\left(p-2^{i}\right) $$ (a) Let $q>3$ be a prime and $p$ a prime divisor of $2^{q}+1$ that is greater than 3 . We will show that $p$ is suitable for part (a). Notice that $9 \nmid 2^{q}+1$, so that such a $p$ exists. Moreover, for any two odd primes $q<r$ we have $\operatorname{gcd}\left(2^{q}+1,2^{r}+1\right)=2^{\operatorname{gcd}(q, r)}+1=3$, thus there exist infinitely many such primes $p$. For the chosen $p$, we have $T=2 q$. Since $2^{q} \equiv-1(\bmod p)$, we have $S_{p}^{+}=S_{p}^{-}$. Now consider the $p$-sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ with $a_{0}=p+1$ and $b_{0}=p-1$; we claim that these sequences satisfy the required conditions. We have $a_{0}>b_{0}$ and $a_{1}=p+2<b_{1}=2 p-2$. It follows then that $$ a_{k \cdot 2 q}=a_{0}+k S_{p}^{+}>b_{0}+k S_{p}^{+}=b_{k \cdot 2 q} \quad \text { and } \quad a_{k \cdot 2 q+1}=a_{1}+k S_{p}^{+}<b_{1}+k S_{p}^{+}=b_{k \cdot 2 q+1} $$ for all $k=0,1, \ldots$, as desired. (b) Let $q$ be an odd prime and $p$ a prime divisor of $2^{q}-1$; thus we have $T=q$. We will show that $p$ is suitable for part (b). Notice that the numbers of the form $2^{q}-1$ are pairwise coprime (since $\operatorname{gcd}\left(2^{q}-1,2^{r}-1\right)=2^{\operatorname{gcd}(q, r)}-1=1$ for any two distinct primes $q$ and $r$ ), thus there exist infinitely many such primes $p$. Notice that $d_{p}(x)+d_{p}(p-x)=p$ for all $x$ with $p \nmid x$, so that the sum $S_{p}^{+}+S_{p}^{-}=p q$ is odd, which yields $S_{p}^{+}=S_{p}(1) \neq S_{p}(-1)=S_{p}^{-}$. Assume that $\left(x_{n}\right)$ and $\left(y_{n}\right)$ are two $p$-sequences with $S_{p}\left(x_{0}\right)>S_{p}\left(y_{0}\right)$ but $x_{0}<y_{0}$. The first condition yields that $$ x_{M q+r}-y_{M q+r}=\left(x_{r}-y_{r}\right)+M\left(S_{p}\left(x_{0}\right)-S_{p}\left(y_{0}\right)\right) \geqslant\left(x_{r}-y_{r}\right)+M $$ for all nonnegative integers $M$ and every $r=0,1, \ldots, q-1$. Thus, we have $x_{n}>y_{n}$ for every $n \geqslant q+q \cdot \max \left\{y_{r}-x_{r}: r=0,1, \ldots, q-1\right\}$. Now, since $x_{0}<y_{0}$, there exists the largest $n_{0}$ with $x_{n_{0}}<y_{n_{0}}$. In this case the $p$-sequences $a_{n}=x_{n-n_{0}}$ and $b_{n}=y_{n-n_{0}}$ possess the desired property (notice here that $x_{n} \neq y_{n}$ for all $n \geqslant 0$, as otherwise we would have $\left.S_{p}\left(x_{0}\right)=S_{p}\left(x_{n}\right)=S_{p}\left(y_{n}\right)=S_{p}\left(y_{0}\right)\right)$. It remains to find $p$-sequences $\left(x_{n}\right)$ and $\left(y_{n}\right)$ satisfying the two conditions. Recall that $S_{p}^{+} \neq S_{p}^{-}$. Now, if $S_{p}^{+}>S_{p}^{-}$, then we can put $x_{0}=1$ and $y_{0}=p-1$. Otherwise, if $S_{p}^{+}<S_{p}^{-}$, then we put $x_{0}=p-1$ and $y_{0}=p+1$. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cf7f7f2a-e6ab-5a52-9e82-dca0984d0faa
| 24,105
|
Determine all functions $f$ defined on the set of all positive integers and taking non-negative integer values, satisfying the three conditions: (i) $f(n) \neq 0$ for at least one $n$; (ii) $f(x y)=f(x)+f(y)$ for every positive integers $x$ and $y$; (iii) there are infinitely many positive integers $n$ such that $f(k)=f(n-k)$ for all $k<n$. (Croatia) Answer: The sought functions are those of the form $f(n)=c \cdot \nu_{p}(n)$, where $p$ is some prime, $c$ is a nonnegative integer, and $\nu_{p}(n)$ denotes the exponent of $p$ in the prime decomposition of $n$.
|
We use the notion of a good number from the previous solution. As above, we also denote by $\nu_{p}(n)$ the exponent of a prime $p$ in the prime decomposition of $n$. Say that a positive integer $k$ is big if $f(k)>0$. Let $\mathcal{B}$ be the set of big primes, and let $p_{1}<p_{2}<\ldots$ list the elements of $\mathcal{B}$ (this set might be either finite or infinite). By the problem conditions, we have $$ f(n)=\sum_{i} \nu_{p_{i}}(n) f\left(p_{i}\right) $$ thus, the big numbers are those divisible by at least one big prime. For a positive integer $k$, define its essence $e(k)$ to be the largest product $e$ of (not necessarily different) big primes such that $e \mid k$. In other words, $$ e(n)=\prod_{p_{i} \in \mathcal{B}} p_{i}^{\nu_{p_{i}}(n)} $$ This yields that $k / e(k)$ is not big, so $f(k)=f(e(k))+f(k / e(k))=f(e(k))$. Lemma. Assume that $n$ is a good number. Then $e(k)=e(n-k)$ for all $k<n$. Proof. Arguing indirectly, choose a minimal $k$ for which the claim of the lemma is violated. Clearly, $k$ is big, as otherwise $f(k)=f(n-k)=0$ and hence $e(k)=e(n-k)=1$. There are $t=k / e(k)$ multiples of $e(k)$ in each of the segments $[1, k]$ and $[n-k, n-1]$. On the other hand, there are $t-1$ such multiples on $[1, k-1]$ - and, by minimality of $k$, on $[n-k+1, n-1]$ as well. This yields that $n-k$ is a multiple of $e(k)$. Therefore, $$ f(e(k))=f(k)=f(n-k)=f(e(k))+f\left(\frac{n-k}{e(k)}\right), $$ so the last summand vanishes, hence $\frac{n-k}{e(k)}$ has no big prime divisors, that is, $e(n-k)=e(k)$. This contradicts our choice. Back to the problem, assume that $|\mathcal{B}| \geqslant 2$. Take any good number $n>p_{1} p_{2}$, and let $p_{1}^{\alpha}$ be the largest power of $p_{1}$ smaller than $n$, so that $n \leqslant p_{1}^{\alpha+1}<p_{1}^{\alpha} p_{2}$. By the lemma, $e\left(n-p_{1}^{\alpha}\right)=e\left(p_{1}^{\alpha}\right)=p_{1}^{\alpha}$, which yields $p_{1}^{\alpha} \mid n$. Similarly, $p_{2} \mid n$, so that $n \geqslant p_{1}^{\alpha} p_{2}$. This contradiction shows that $|\mathcal{B}| \leqslant 1$, which by (1) yields that $f$ is listed in the answer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine all functions $f$ defined on the set of all positive integers and taking non-negative integer values, satisfying the three conditions: (i) $f(n) \neq 0$ for at least one $n$; (ii) $f(x y)=f(x)+f(y)$ for every positive integers $x$ and $y$; (iii) there are infinitely many positive integers $n$ such that $f(k)=f(n-k)$ for all $k<n$. (Croatia) Answer: The sought functions are those of the form $f(n)=c \cdot \nu_{p}(n)$, where $p$ is some prime, $c$ is a nonnegative integer, and $\nu_{p}(n)$ denotes the exponent of $p$ in the prime decomposition of $n$.
|
We use the notion of a good number from the previous solution. As above, we also denote by $\nu_{p}(n)$ the exponent of a prime $p$ in the prime decomposition of $n$. Say that a positive integer $k$ is big if $f(k)>0$. Let $\mathcal{B}$ be the set of big primes, and let $p_{1}<p_{2}<\ldots$ list the elements of $\mathcal{B}$ (this set might be either finite or infinite). By the problem conditions, we have $$ f(n)=\sum_{i} \nu_{p_{i}}(n) f\left(p_{i}\right) $$ thus, the big numbers are those divisible by at least one big prime. For a positive integer $k$, define its essence $e(k)$ to be the largest product $e$ of (not necessarily different) big primes such that $e \mid k$. In other words, $$ e(n)=\prod_{p_{i} \in \mathcal{B}} p_{i}^{\nu_{p_{i}}(n)} $$ This yields that $k / e(k)$ is not big, so $f(k)=f(e(k))+f(k / e(k))=f(e(k))$. Lemma. Assume that $n$ is a good number. Then $e(k)=e(n-k)$ for all $k<n$. Proof. Arguing indirectly, choose a minimal $k$ for which the claim of the lemma is violated. Clearly, $k$ is big, as otherwise $f(k)=f(n-k)=0$ and hence $e(k)=e(n-k)=1$. There are $t=k / e(k)$ multiples of $e(k)$ in each of the segments $[1, k]$ and $[n-k, n-1]$. On the other hand, there are $t-1$ such multiples on $[1, k-1]$ - and, by minimality of $k$, on $[n-k+1, n-1]$ as well. This yields that $n-k$ is a multiple of $e(k)$. Therefore, $$ f(e(k))=f(k)=f(n-k)=f(e(k))+f\left(\frac{n-k}{e(k)}\right), $$ so the last summand vanishes, hence $\frac{n-k}{e(k)}$ has no big prime divisors, that is, $e(n-k)=e(k)$. This contradicts our choice. Back to the problem, assume that $|\mathcal{B}| \geqslant 2$. Take any good number $n>p_{1} p_{2}$, and let $p_{1}^{\alpha}$ be the largest power of $p_{1}$ smaller than $n$, so that $n \leqslant p_{1}^{\alpha+1}<p_{1}^{\alpha} p_{2}$. By the lemma, $e\left(n-p_{1}^{\alpha}\right)=e\left(p_{1}^{\alpha}\right)=p_{1}^{\alpha}$, which yields $p_{1}^{\alpha} \mid n$. Similarly, $p_{2} \mid n$, so that $n \geqslant p_{1}^{\alpha} p_{2}$. This contradiction shows that $|\mathcal{B}| \leqslant 1$, which by (1) yields that $f$ is listed in the answer.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
74cb761b-190a-5a54-aa2a-ee735fb31571
| 24,108
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus) Answer: No, such constant does not exist.
|
Fix $N>1$, let $p_{1}, \ldots, p_{k}$ be all primes between 1 and $N$ and $p_{k+1}, \ldots, p_{k+s}$ be all primes between $N+1$ and $2 N$. Since for $j \leqslant k+s$ all prime divisors of $p_{j}-1$ do not exceed $N$, we have $$ \prod_{j=1}^{k+s}\left(p_{j}-1\right)=\prod_{i=1}^{k} p_{i}^{c_{i}} $$ with some fixed exponents $c_{1}, \ldots, c_{k}$. Choose a huge prime number $q$ and consider a number $$ n=\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-1} \cdot\left(p_{k+1} \cdot \ldots \cdot p_{k+s}\right) $$ Then $$ \varphi(d(n))=\varphi\left(q^{k} \cdot 2^{s}\right)=q^{k-1}(q-1) 2^{s-1} $$ and $$ d(\varphi(n))=d\left(\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-2} \prod_{i=1}^{k+s}\left(p_{i}-1\right)\right)=d\left(\prod_{i=1}^{k} p_{i}^{q-2+c_{i}}\right)=\prod_{i=1}^{k}\left(q-1+c_{i}\right) $$ so $$ \frac{\varphi(d(n))}{d(\varphi(n))}=\frac{q^{k-1}(q-1) 2^{s-1}}{\prod_{i=1}^{k}\left(q-1+c_{i}\right)}=2^{s-1} \cdot \frac{q-1}{q} \cdot \prod_{i=1}^{k} \frac{q}{q-1+c_{i}} $$ which can be made arbitrarily close to $2^{s-1}$ by choosing $q$ large enough. It remains to show that $s$ can be arbitrarily large, i.e. that there can be arbitrarily many primes between $N$ and $2 N$. This follows, for instance, from the well-known fact that $\sum \frac{1}{p}=\infty$, where the sum is taken over the set $\mathbb{P}$ of prime numbers. Indeed, if, for some constant $\stackrel{p}{C}$, there were always at most $C$ primes between $2^{\ell}$ and $2^{\ell+1}$, we would have $$ \sum_{p \in \mathbb{P}} \frac{1}{p}=\sum_{\ell=0}^{\infty} \sum_{\substack{p \in \mathbb{P} \\ p \in\left[2^{\ell}, 2^{\ell+1}\right)}} \frac{1}{p} \leqslant \sum_{\ell=0}^{\infty} \frac{C}{2^{\ell}}<\infty, $$ which is a contradiction. Comment 1. Here we sketch several alternative elementary self-contained ways to perform the last step of the solution above. In particular, they avoid using divergence of $\sum \frac{1}{p}$. Suppose that for some constant $C$ and for every $k=1,2, \ldots$ there exist at most $C$ prime numbers between $2^{k}$ and $2^{k+1}$. Consider the prime factorization of the factorial $\left(2^{n}\right)!=\prod p^{\alpha_{p}}$. We have $\alpha_{p}=\left\lfloor 2^{n} / p\right\rfloor+\left\lfloor 2^{n} / p^{2}\right\rfloor+\ldots$. Thus, for $p \in\left[2^{k}, 2^{k+1}\right)$, we get $\alpha_{p} \leqslant 2^{n} / 2^{k}+2^{n} / 2^{k+1}+\ldots=2^{n-k+1}$, therefore $p^{\alpha_{p}} \leqslant 2^{(k+1) 2^{n-k+1}}$. Combining this with the bound $(2 m)!\geqslant m(m+1) \cdot \ldots \cdot(2 m-1) \geqslant m^{m}$ for $m=2^{n-1}$ we get $$ 2^{(n-1) \cdot 2^{n-1}} \leqslant\left(2^{n}\right)!\leqslant \prod_{k=1}^{n-1} 2^{C(k+1) 2^{n-k+1}} $$ or $$ \sum_{k=1}^{n-1} C(k+1) 2^{1-k} \geqslant \frac{n-1}{2} $$ that fails for large $n$ since $C(k+1) 2^{1-k}<1 / 3$ for all but finitely many $k$. In fact, a much stronger inequality can be obtained in an elementary way: Note that the formula for $\nu_{p}(n!)$ implies that if $p^{\alpha}$ is the largest power of $p$ dividing $\binom{n}{n / 2}$, then $p^{\alpha} \leqslant n$. By looking at prime factorization of $\binom{n}{n / 2}$ we instantaneously infer that $$ \pi(n) \geqslant \log _{n}\binom{n}{n / 2} \geqslant \frac{\log \left(2^{n} / n\right)}{\log n} \geqslant \frac{n}{2 \log n} . $$ This, in particular, implies that for infinitely many $n$ there are at least $\frac{n}{3 \log n}$ primes between $n$ and $2 n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus) Answer: No, such constant does not exist.
|
Fix $N>1$, let $p_{1}, \ldots, p_{k}$ be all primes between 1 and $N$ and $p_{k+1}, \ldots, p_{k+s}$ be all primes between $N+1$ and $2 N$. Since for $j \leqslant k+s$ all prime divisors of $p_{j}-1$ do not exceed $N$, we have $$ \prod_{j=1}^{k+s}\left(p_{j}-1\right)=\prod_{i=1}^{k} p_{i}^{c_{i}} $$ with some fixed exponents $c_{1}, \ldots, c_{k}$. Choose a huge prime number $q$ and consider a number $$ n=\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-1} \cdot\left(p_{k+1} \cdot \ldots \cdot p_{k+s}\right) $$ Then $$ \varphi(d(n))=\varphi\left(q^{k} \cdot 2^{s}\right)=q^{k-1}(q-1) 2^{s-1} $$ and $$ d(\varphi(n))=d\left(\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-2} \prod_{i=1}^{k+s}\left(p_{i}-1\right)\right)=d\left(\prod_{i=1}^{k} p_{i}^{q-2+c_{i}}\right)=\prod_{i=1}^{k}\left(q-1+c_{i}\right) $$ so $$ \frac{\varphi(d(n))}{d(\varphi(n))}=\frac{q^{k-1}(q-1) 2^{s-1}}{\prod_{i=1}^{k}\left(q-1+c_{i}\right)}=2^{s-1} \cdot \frac{q-1}{q} \cdot \prod_{i=1}^{k} \frac{q}{q-1+c_{i}} $$ which can be made arbitrarily close to $2^{s-1}$ by choosing $q$ large enough. It remains to show that $s$ can be arbitrarily large, i.e. that there can be arbitrarily many primes between $N$ and $2 N$. This follows, for instance, from the well-known fact that $\sum \frac{1}{p}=\infty$, where the sum is taken over the set $\mathbb{P}$ of prime numbers. Indeed, if, for some constant $\stackrel{p}{C}$, there were always at most $C$ primes between $2^{\ell}$ and $2^{\ell+1}$, we would have $$ \sum_{p \in \mathbb{P}} \frac{1}{p}=\sum_{\ell=0}^{\infty} \sum_{\substack{p \in \mathbb{P} \\ p \in\left[2^{\ell}, 2^{\ell+1}\right)}} \frac{1}{p} \leqslant \sum_{\ell=0}^{\infty} \frac{C}{2^{\ell}}<\infty, $$ which is a contradiction. Comment 1. Here we sketch several alternative elementary self-contained ways to perform the last step of the solution above. In particular, they avoid using divergence of $\sum \frac{1}{p}$. Suppose that for some constant $C$ and for every $k=1,2, \ldots$ there exist at most $C$ prime numbers between $2^{k}$ and $2^{k+1}$. Consider the prime factorization of the factorial $\left(2^{n}\right)!=\prod p^{\alpha_{p}}$. We have $\alpha_{p}=\left\lfloor 2^{n} / p\right\rfloor+\left\lfloor 2^{n} / p^{2}\right\rfloor+\ldots$. Thus, for $p \in\left[2^{k}, 2^{k+1}\right)$, we get $\alpha_{p} \leqslant 2^{n} / 2^{k}+2^{n} / 2^{k+1}+\ldots=2^{n-k+1}$, therefore $p^{\alpha_{p}} \leqslant 2^{(k+1) 2^{n-k+1}}$. Combining this with the bound $(2 m)!\geqslant m(m+1) \cdot \ldots \cdot(2 m-1) \geqslant m^{m}$ for $m=2^{n-1}$ we get $$ 2^{(n-1) \cdot 2^{n-1}} \leqslant\left(2^{n}\right)!\leqslant \prod_{k=1}^{n-1} 2^{C(k+1) 2^{n-k+1}} $$ or $$ \sum_{k=1}^{n-1} C(k+1) 2^{1-k} \geqslant \frac{n-1}{2} $$ that fails for large $n$ since $C(k+1) 2^{1-k}<1 / 3$ for all but finitely many $k$. In fact, a much stronger inequality can be obtained in an elementary way: Note that the formula for $\nu_{p}(n!)$ implies that if $p^{\alpha}$ is the largest power of $p$ dividing $\binom{n}{n / 2}$, then $p^{\alpha} \leqslant n$. By looking at prime factorization of $\binom{n}{n / 2}$ we instantaneously infer that $$ \pi(n) \geqslant \log _{n}\binom{n}{n / 2} \geqslant \frac{\log \left(2^{n} / n\right)}{\log n} \geqslant \frac{n}{2 \log n} . $$ This, in particular, implies that for infinitely many $n$ there are at least $\frac{n}{3 \log n}$ primes between $n$ and $2 n$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f5672458-e54a-5cda-9432-08e4cd3a6957
| 24,114
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus) Answer: No, such constant does not exist.
|
In this solution we will use the Prime Number Theorem which states that $$ \pi(m)=\frac{m}{\log m} \cdot(1+o(1)) $$ as $m$ tends to infinity. Here and below $\pi(m)$ denotes the number of primes not exceeding $m$, and $\log$ the natural logarithm. Let $m>5$ be a large positive integer and let $n:=p_{1} p_{2} \cdot \ldots \cdot p_{\pi(m)}$ be the product of all primes not exceeding $m$. Then $\varphi(d(n))=\varphi\left(2^{\pi(m)}\right)=2^{\pi(m)-1}$. Consider the number $$ \varphi(n)=\prod_{k=1}^{\pi(m)}\left(p_{k}-1\right)=\prod_{s=1}^{\pi(m / 2)} q_{s}^{\alpha_{s}} $$ where $q_{1}, \ldots, q_{\pi(m / 2)}$ are primes not exceeding $m / 2$. Note that every term $p_{k}-1$ contributes at most one prime $q_{s}>\sqrt{m}$ into the product $\prod_{s} q_{s}^{\alpha_{s}}$, so we have $$ \sum_{s: q_{s}>\sqrt{m}} \alpha_{s} \leqslant \pi(m) \Longrightarrow \sum_{s: q_{s}>\sqrt{m}}\left(1+\alpha_{s}\right) \leqslant \pi(m)+\pi(m / 2) . $$ Hence, applying the AM-GM inequality and the inequality $(A / x)^{x} \leqslant e^{A / e}$, we obtain $$ \prod_{s: q_{s}>\sqrt{m}}\left(\alpha_{s}+1\right) \leqslant\left(\frac{\pi(m)+\pi(m / 2)}{\ell}\right)^{\ell} \leqslant \exp \left(\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ where $\ell$ is the number of primes in the interval $(\sqrt{m}, m]$. We then use a trivial bound $\alpha_{i} \leqslant \log _{2}(\varphi(n)) \leqslant \log _{2} n<\log _{2}\left(m^{m}\right)<m^{2}$ for each $i$ with $q_{i}<\sqrt{m}$ to obtain $$ \prod_{s=1}^{\pi(\sqrt{m})}\left(\alpha_{s}+1\right) \leqslant\left(m^{2}\right)^{\sqrt{m}}=m^{2 \sqrt{m}} $$ Putting this together we obtain $$ d(\varphi(n))=\prod_{s=1}^{\pi(m / 2)}\left(\alpha_{s}+1\right) \leqslant \exp \left(2 \sqrt{m} \cdot \log m+\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ The prime number theorem then implies that $$ \limsup _{m \rightarrow \infty} \frac{\log (d(\varphi(n)))}{m / \log m} \leqslant \limsup _{m \rightarrow \infty} \frac{2 \sqrt{m} \cdot \log m}{m / \log m}+\limsup _{m \rightarrow \infty} \frac{\pi(m)+\pi(m / 2)}{e \cdot m / \log m}=\frac{3}{2 e} . $$ Whereas, again by prime number theorem, we have $$ \liminf _{m \rightarrow \infty} \frac{\log (\varphi(d(n)))}{m / \log m}=\liminf _{m \rightarrow \infty} \frac{\log \left(2^{\pi(m)-1}\right)}{m / \log m}=\log 2 $$ Since $\frac{3}{2 e}<\frac{3}{5}<\log 2$, this implies that $\varphi(d(n)) / d(\varphi(n))$ can be arbitrarily large. Comment 2. The original formulation of the problem was asking whether $d(\varphi(n)) \geqslant \varphi(d(n))$ for all but finitely many values of $n$. The Problem Selection Committee decided that the presented version is better suited for the Shortlist. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus) Answer: No, such constant does not exist.
|
In this solution we will use the Prime Number Theorem which states that $$ \pi(m)=\frac{m}{\log m} \cdot(1+o(1)) $$ as $m$ tends to infinity. Here and below $\pi(m)$ denotes the number of primes not exceeding $m$, and $\log$ the natural logarithm. Let $m>5$ be a large positive integer and let $n:=p_{1} p_{2} \cdot \ldots \cdot p_{\pi(m)}$ be the product of all primes not exceeding $m$. Then $\varphi(d(n))=\varphi\left(2^{\pi(m)}\right)=2^{\pi(m)-1}$. Consider the number $$ \varphi(n)=\prod_{k=1}^{\pi(m)}\left(p_{k}-1\right)=\prod_{s=1}^{\pi(m / 2)} q_{s}^{\alpha_{s}} $$ where $q_{1}, \ldots, q_{\pi(m / 2)}$ are primes not exceeding $m / 2$. Note that every term $p_{k}-1$ contributes at most one prime $q_{s}>\sqrt{m}$ into the product $\prod_{s} q_{s}^{\alpha_{s}}$, so we have $$ \sum_{s: q_{s}>\sqrt{m}} \alpha_{s} \leqslant \pi(m) \Longrightarrow \sum_{s: q_{s}>\sqrt{m}}\left(1+\alpha_{s}\right) \leqslant \pi(m)+\pi(m / 2) . $$ Hence, applying the AM-GM inequality and the inequality $(A / x)^{x} \leqslant e^{A / e}$, we obtain $$ \prod_{s: q_{s}>\sqrt{m}}\left(\alpha_{s}+1\right) \leqslant\left(\frac{\pi(m)+\pi(m / 2)}{\ell}\right)^{\ell} \leqslant \exp \left(\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ where $\ell$ is the number of primes in the interval $(\sqrt{m}, m]$. We then use a trivial bound $\alpha_{i} \leqslant \log _{2}(\varphi(n)) \leqslant \log _{2} n<\log _{2}\left(m^{m}\right)<m^{2}$ for each $i$ with $q_{i}<\sqrt{m}$ to obtain $$ \prod_{s=1}^{\pi(\sqrt{m})}\left(\alpha_{s}+1\right) \leqslant\left(m^{2}\right)^{\sqrt{m}}=m^{2 \sqrt{m}} $$ Putting this together we obtain $$ d(\varphi(n))=\prod_{s=1}^{\pi(m / 2)}\left(\alpha_{s}+1\right) \leqslant \exp \left(2 \sqrt{m} \cdot \log m+\frac{\pi(m)+\pi(m / 2)}{e}\right) $$ The prime number theorem then implies that $$ \limsup _{m \rightarrow \infty} \frac{\log (d(\varphi(n)))}{m / \log m} \leqslant \limsup _{m \rightarrow \infty} \frac{2 \sqrt{m} \cdot \log m}{m / \log m}+\limsup _{m \rightarrow \infty} \frac{\pi(m)+\pi(m / 2)}{e \cdot m / \log m}=\frac{3}{2 e} . $$ Whereas, again by prime number theorem, we have $$ \liminf _{m \rightarrow \infty} \frac{\log (\varphi(d(n)))}{m / \log m}=\liminf _{m \rightarrow \infty} \frac{\log \left(2^{\pi(m)-1}\right)}{m / \log m}=\log 2 $$ Since $\frac{3}{2 e}<\frac{3}{5}<\log 2$, this implies that $\varphi(d(n)) / d(\varphi(n))$ can be arbitrarily large. Comment 2. The original formulation of the problem was asking whether $d(\varphi(n)) \geqslant \varphi(d(n))$ for all but finitely many values of $n$. The Problem Selection Committee decided that the presented version is better suited for the Shortlist. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f5672458-e54a-5cda-9432-08e4cd3a6957
| 24,114
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine) Common remarks. In all solutions, we call a set $\mathcal{S}$ of positive integers good if no its element is a sum of two other distinct members of $\mathcal{S}$. We will use the following simple observation. Observation A. If $a, b$, and $c$ are three distinct elements of a good set $\mathcal{S}$ with $b>a, c$, then $b \nmid a+c$. Otherwise, since $b \neq a+c$, we would have $b \leqslant(a+c) / 2<\max \{a, c\}$.
|
We prove the following stronger statement. Claim. Let $\mathcal{S}$ be a good set consisting of $n \geqslant 2$ positive integers. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i} \nmid a_{i-1}+a_{i+1}$ and $a_{i} \nmid a_{i-1}-a_{i+1}$, for all $i=2,3, \ldots, n-1$. Proof. Say that the ordering $a_{1}, \ldots, a_{n}$ of $\mathcal{S}$ is nice if it satisfies the required property. We proceed by induction on $n$. The base case $n=2$ is trivial, as there are no restrictions on the ordering. To perform the step of induction, suppose that $n \geqslant 3$. Let $a=\max \mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{a\}$. Use the inductive hypothesis to find a nice ordering $b_{1}, \ldots, b_{n-1}$ of $\mathcal{T}$. We will show that $a$ may be inserted into this sequence so as to reach a nice ordering of $\mathcal{S}$. In other words, we will show that there exists a $j \in\{1,2, \ldots, n\}$ such that the ordering $$ N_{j}=\left(b_{1}, \ldots, b_{j-1}, a, b_{j}, b_{j+1}, \ldots, b_{n-1}\right) $$ is nice. Assume that, for some $j$, the ordering $N_{j}$ is not nice, so that some element $x$ in it divides either the sum or the difference of two adjacent ones. This did not happen in the ordering of $\mathcal{T}$, hence $x \in\left\{b_{j-1}, a, b_{j}\right\}$ (if, say, $b_{j-1}$ does not exist, then $x \in\left\{a, b_{j}\right\}$; a similar agreement is applied hereafter). But the case $x=a$ is impossible: $a$ cannot divide $b_{j-1}-b_{j}$, since $0<\left|b_{j-1}-b_{j}\right|<a$, while $a \nmid b_{j-1}+b_{j}$ by Observation A. Therefore $x \in\left\{b_{j-1}, b_{j}\right\}$. In this case, assign the number $x$ to the index $j$. Suppose now that none of the $N_{j}$ is nice. Since there are $n$ possible indices $j$, and only $n-1$ elements in $\mathcal{T}$, one of those elements (say, $b_{k}$ ) is assigned to two different indices, which then should equal $k$ and $k+1$. This means that $b_{k}$ divides the numbers $b_{k-1}+\varepsilon_{1} a$ and $a+\varepsilon_{2} b_{k+1}$, for some signs $\varepsilon_{1}, \varepsilon_{2} \in\{-1,1\}$. But then $$ b_{k-1} \equiv-\varepsilon_{1} a \equiv \varepsilon_{1} \varepsilon_{2} b_{k+1} \quad\left(\bmod b_{k}\right), $$ and therefore $b_{k} \mid b_{k-1}-\varepsilon_{1} \varepsilon_{2} b_{k+1}$, which means that the ordering of $\mathcal{T}$ was not nice. This contradiction proves the step of induction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine) Common remarks. In all solutions, we call a set $\mathcal{S}$ of positive integers good if no its element is a sum of two other distinct members of $\mathcal{S}$. We will use the following simple observation. Observation A. If $a, b$, and $c$ are three distinct elements of a good set $\mathcal{S}$ with $b>a, c$, then $b \nmid a+c$. Otherwise, since $b \neq a+c$, we would have $b \leqslant(a+c) / 2<\max \{a, c\}$.
|
We prove the following stronger statement. Claim. Let $\mathcal{S}$ be a good set consisting of $n \geqslant 2$ positive integers. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i} \nmid a_{i-1}+a_{i+1}$ and $a_{i} \nmid a_{i-1}-a_{i+1}$, for all $i=2,3, \ldots, n-1$. Proof. Say that the ordering $a_{1}, \ldots, a_{n}$ of $\mathcal{S}$ is nice if it satisfies the required property. We proceed by induction on $n$. The base case $n=2$ is trivial, as there are no restrictions on the ordering. To perform the step of induction, suppose that $n \geqslant 3$. Let $a=\max \mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{a\}$. Use the inductive hypothesis to find a nice ordering $b_{1}, \ldots, b_{n-1}$ of $\mathcal{T}$. We will show that $a$ may be inserted into this sequence so as to reach a nice ordering of $\mathcal{S}$. In other words, we will show that there exists a $j \in\{1,2, \ldots, n\}$ such that the ordering $$ N_{j}=\left(b_{1}, \ldots, b_{j-1}, a, b_{j}, b_{j+1}, \ldots, b_{n-1}\right) $$ is nice. Assume that, for some $j$, the ordering $N_{j}$ is not nice, so that some element $x$ in it divides either the sum or the difference of two adjacent ones. This did not happen in the ordering of $\mathcal{T}$, hence $x \in\left\{b_{j-1}, a, b_{j}\right\}$ (if, say, $b_{j-1}$ does not exist, then $x \in\left\{a, b_{j}\right\}$; a similar agreement is applied hereafter). But the case $x=a$ is impossible: $a$ cannot divide $b_{j-1}-b_{j}$, since $0<\left|b_{j-1}-b_{j}\right|<a$, while $a \nmid b_{j-1}+b_{j}$ by Observation A. Therefore $x \in\left\{b_{j-1}, b_{j}\right\}$. In this case, assign the number $x$ to the index $j$. Suppose now that none of the $N_{j}$ is nice. Since there are $n$ possible indices $j$, and only $n-1$ elements in $\mathcal{T}$, one of those elements (say, $b_{k}$ ) is assigned to two different indices, which then should equal $k$ and $k+1$. This means that $b_{k}$ divides the numbers $b_{k-1}+\varepsilon_{1} a$ and $a+\varepsilon_{2} b_{k+1}$, for some signs $\varepsilon_{1}, \varepsilon_{2} \in\{-1,1\}$. But then $$ b_{k-1} \equiv-\varepsilon_{1} a \equiv \varepsilon_{1} \varepsilon_{2} b_{k+1} \quad\left(\bmod b_{k}\right), $$ and therefore $b_{k} \mid b_{k-1}-\varepsilon_{1} \varepsilon_{2} b_{k+1}$, which means that the ordering of $\mathcal{T}$ was not nice. This contradiction proves the step of induction.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
acd04ecf-53a5-53f5-a56d-8e904d058430
| 24,117
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine) Common remarks. In all solutions, we call a set $\mathcal{S}$ of positive integers good if no its element is a sum of two other distinct members of $\mathcal{S}$. We will use the following simple observation. Observation A. If $a, b$, and $c$ are three distinct elements of a good set $\mathcal{S}$ with $b>a, c$, then $b \nmid a+c$. Otherwise, since $b \neq a+c$, we would have $b \leqslant(a+c) / 2<\max \{a, c\}$.
|
We again prove a stronger statement. Claim. Let $\mathcal{S}$ be an arbitrary set of $n \geqslant 3$ positive integers. Then its elements can be ordered as $a_{1}, \ldots, a_{n}$ so that, if $a_{i} \mid a_{i-1}+a_{i+1}$, then $a_{i}=\max \mathcal{S}$. The claim easily implies what we need to prove, due to Observation A. To prove the Claim, introduce the function $f$ which assigns to any two elements $a, b \in \mathcal{S}$ with $a<b$ the unique integer $f(a, b) \in\{1,2, \ldots, a\}$ such that $a \mid b+f(a, b)$. Hence, if $b \mid a+c$ for some $a, b, c \in \mathcal{S}$ with $a<b<c$, then $a=f(b, c)$. Therefore, the Claim is a consequence of the following combinatorial lemma. Lemma. Let $\mathcal{S}$ be a set of $n \geqslant 3$ positive integers, and let $f$ be a function which assigns to any $a, b \in \mathcal{S}$ with $a<b$ some integer from the range $\{1, \ldots, a\}$. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so as to satisfy the following two conditions simultaneously: (i) Unimodality: There exists a $j \in\{1,2, \ldots, n\}$ such that $a_{1}<a_{2}<\ldots<a_{j}>a_{j+1}>\ldots>$ $a_{n}$; and (ii) $f$-avoidance: If $a<b$ are two elements of $\mathcal{S}$, which are adjacent in the ordering, then $f(a, b)$ is not adjacent to $a$. Proof. We call an ordering of $\mathcal{S}$ satisfying (i) and (ii) $f$-nice. We agree that $f(x, y)=x$ for $x \geqslant y$; this agreement puts no extra restriction. We proceed by induction; for the base case $n=3$, it suffices to put the maximal element in $\mathcal{S}$ onto the middle position. To perform the step of induction, let $p<q$ be the two minimal elements of $\mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{p\}$. Define a function $g$ by assigning to any elements $a<b$ of $\mathcal{T}$ the value $$ g(a, b)= \begin{cases}q, & \text { if } f(a, b)=p \\ f(a, b), & \text { otherwise }\end{cases} $$ Notice that $g(a, b) \leqslant a$ for all $a, b \in \mathcal{T}$. Use the inductive hypothesis to get a $g$-nice ordering $b_{1}, b_{2}, \ldots, b_{n-1}$ of $\mathcal{T}$. By unimodality, either $b_{1}$ or $b_{n-1}$ equals $q$; these cases differ only by reverting the order, so we assume $b_{1}=q$. Notice that, according to (1), the number $f\left(b_{2}, b_{3}\right)$ differs from both $p$ and $q$. On the other hand, the number $f\left(b_{n-1}, b_{n-2}\right)$ differs from at least one of them - say, from $r$; set $s=p+q-r$, so that $\{r, s\}=\{p, q\}$. Now, order $\mathcal{S}$ as $$ s, b_{2}, b_{3}, \ldots, b_{n-1}, r $$ By the induction hypothesis and the above choice, this ordering is nice. Comment. In the original proposal, the numbers in the set were assumed to be odd (which implies that none is a sum of two others); moreover, the proposal requested to arrange in a row all numbers but one. On the other hand, Solution 2 shows that the condition of $\mathcal{S}$ being good may be relaxed to the condition that the maximal element of $\mathcal{S}$ is not a sum of two other elements in $\mathcal{S}$. On the other hand, the set $\{1,2,3\}$ shows that the condition cannot be merely omitted. The Problem Selection Committee considered several versions of the problem and chose the best version in their opinion for the Shortlist. 61st International Mathematical Olympiad Saint Petersburg Russia
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathcal{S}$ be a set consisting of $n \geqslant 3$ positive integers, none of which is a sum of two other distinct members of $\mathcal{S}$. Prove that the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so that $a_{i}$ does not divide $a_{i-1}+a_{i+1}$ for all $i=2,3, \ldots, n-1$. (Ukraine) Common remarks. In all solutions, we call a set $\mathcal{S}$ of positive integers good if no its element is a sum of two other distinct members of $\mathcal{S}$. We will use the following simple observation. Observation A. If $a, b$, and $c$ are three distinct elements of a good set $\mathcal{S}$ with $b>a, c$, then $b \nmid a+c$. Otherwise, since $b \neq a+c$, we would have $b \leqslant(a+c) / 2<\max \{a, c\}$.
|
We again prove a stronger statement. Claim. Let $\mathcal{S}$ be an arbitrary set of $n \geqslant 3$ positive integers. Then its elements can be ordered as $a_{1}, \ldots, a_{n}$ so that, if $a_{i} \mid a_{i-1}+a_{i+1}$, then $a_{i}=\max \mathcal{S}$. The claim easily implies what we need to prove, due to Observation A. To prove the Claim, introduce the function $f$ which assigns to any two elements $a, b \in \mathcal{S}$ with $a<b$ the unique integer $f(a, b) \in\{1,2, \ldots, a\}$ such that $a \mid b+f(a, b)$. Hence, if $b \mid a+c$ for some $a, b, c \in \mathcal{S}$ with $a<b<c$, then $a=f(b, c)$. Therefore, the Claim is a consequence of the following combinatorial lemma. Lemma. Let $\mathcal{S}$ be a set of $n \geqslant 3$ positive integers, and let $f$ be a function which assigns to any $a, b \in \mathcal{S}$ with $a<b$ some integer from the range $\{1, \ldots, a\}$. Then the elements of $\mathcal{S}$ may be ordered as $a_{1}, a_{2}, \ldots, a_{n}$ so as to satisfy the following two conditions simultaneously: (i) Unimodality: There exists a $j \in\{1,2, \ldots, n\}$ such that $a_{1}<a_{2}<\ldots<a_{j}>a_{j+1}>\ldots>$ $a_{n}$; and (ii) $f$-avoidance: If $a<b$ are two elements of $\mathcal{S}$, which are adjacent in the ordering, then $f(a, b)$ is not adjacent to $a$. Proof. We call an ordering of $\mathcal{S}$ satisfying (i) and (ii) $f$-nice. We agree that $f(x, y)=x$ for $x \geqslant y$; this agreement puts no extra restriction. We proceed by induction; for the base case $n=3$, it suffices to put the maximal element in $\mathcal{S}$ onto the middle position. To perform the step of induction, let $p<q$ be the two minimal elements of $\mathcal{S}$, and set $\mathcal{T}=\mathcal{S} \backslash\{p\}$. Define a function $g$ by assigning to any elements $a<b$ of $\mathcal{T}$ the value $$ g(a, b)= \begin{cases}q, & \text { if } f(a, b)=p \\ f(a, b), & \text { otherwise }\end{cases} $$ Notice that $g(a, b) \leqslant a$ for all $a, b \in \mathcal{T}$. Use the inductive hypothesis to get a $g$-nice ordering $b_{1}, b_{2}, \ldots, b_{n-1}$ of $\mathcal{T}$. By unimodality, either $b_{1}$ or $b_{n-1}$ equals $q$; these cases differ only by reverting the order, so we assume $b_{1}=q$. Notice that, according to (1), the number $f\left(b_{2}, b_{3}\right)$ differs from both $p$ and $q$. On the other hand, the number $f\left(b_{n-1}, b_{n-2}\right)$ differs from at least one of them - say, from $r$; set $s=p+q-r$, so that $\{r, s\}=\{p, q\}$. Now, order $\mathcal{S}$ as $$ s, b_{2}, b_{3}, \ldots, b_{n-1}, r $$ By the induction hypothesis and the above choice, this ordering is nice. Comment. In the original proposal, the numbers in the set were assumed to be odd (which implies that none is a sum of two others); moreover, the proposal requested to arrange in a row all numbers but one. On the other hand, Solution 2 shows that the condition of $\mathcal{S}$ being good may be relaxed to the condition that the maximal element of $\mathcal{S}$ is not a sum of two other elements in $\mathcal{S}$. On the other hand, the set $\{1,2,3\}$ shows that the condition cannot be merely omitted. The Problem Selection Committee considered several versions of the problem and chose the best version in their opinion for the Shortlist. 61st International Mathematical Olympiad Saint Petersburg Russia
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
acd04ecf-53a5-53f5-a56d-8e904d058430
| 24,117
|
Let $n$ be an integer, and let $A$ be a subset of $\left\{0,1,2,3, \ldots, 5^{n}\right\}$ consisting of $4 n+2$ numbers. Prove that there exist $a, b, c \in A$ such that $a<b<c$ and $c+2 a>3 b$.
|
(By contradiction) Suppose that there exist $4 n+2$ non-negative integers $x_{0}<$ $x_{1}<\cdots<x_{4 n+1}$ that violate the problem statement. Then in particular $x_{4 n+1}+2 x_{i} \leqslant 3 x_{i+1}$ for all $i=0, \ldots, 4 n-1$, which gives $$ x_{4 n+1}-x_{i} \geqslant \frac{3}{2}\left(x_{4 n+1}-x_{i+1}\right) . $$ By a trivial induction we then get $$ x_{4 n+1}-x_{i} \geqslant\left(\frac{3}{2}\right)^{4 n-i}\left(x_{4 n+1}-x_{4 n}\right) \text {, } $$ which for $i=0$ yields the contradiction $$ x_{4 n+1}-x_{0} \geqslant\left(\frac{3}{2}\right)^{4 n}\left(x_{4 n+1}-x_{4 n}\right)=\left(\frac{81}{16}\right)^{n}\left(x_{4 n+1}-x_{4 n}\right)>5^{n} \cdot 1 $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be an integer, and let $A$ be a subset of $\left\{0,1,2,3, \ldots, 5^{n}\right\}$ consisting of $4 n+2$ numbers. Prove that there exist $a, b, c \in A$ such that $a<b<c$ and $c+2 a>3 b$.
|
(By contradiction) Suppose that there exist $4 n+2$ non-negative integers $x_{0}<$ $x_{1}<\cdots<x_{4 n+1}$ that violate the problem statement. Then in particular $x_{4 n+1}+2 x_{i} \leqslant 3 x_{i+1}$ for all $i=0, \ldots, 4 n-1$, which gives $$ x_{4 n+1}-x_{i} \geqslant \frac{3}{2}\left(x_{4 n+1}-x_{i+1}\right) . $$ By a trivial induction we then get $$ x_{4 n+1}-x_{i} \geqslant\left(\frac{3}{2}\right)^{4 n-i}\left(x_{4 n+1}-x_{4 n}\right) \text {, } $$ which for $i=0$ yields the contradiction $$ x_{4 n+1}-x_{0} \geqslant\left(\frac{3}{2}\right)^{4 n}\left(x_{4 n+1}-x_{4 n}\right)=\left(\frac{81}{16}\right)^{n}\left(x_{4 n+1}-x_{4 n}\right)>5^{n} \cdot 1 $$
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9902f219-469c-5eb1-8f38-d6659be5da41
| 24,121
|
Let $n$ be an integer, and let $A$ be a subset of $\left\{0,1,2,3, \ldots, 5^{n}\right\}$ consisting of $4 n+2$ numbers. Prove that there exist $a, b, c \in A$ such that $a<b<c$ and $c+2 a>3 b$.
|
Denote the maximum element of $A$ by $c$. For $k=0, \ldots, 4 n-1$ let $$ A_{k}=\left\{x \in A:\left(1-(2 / 3)^{k}\right) c \leqslant x<\left(1-(2 / 3)^{k+1}\right) c\right\} $$ Note that $$ \left(1-(2 / 3)^{4 n}\right) c=c-(16 / 81)^{n} c>c-(1 / 5)^{n} c \geqslant c-1 $$ which shows that the sets $A_{0}, A_{1}, \ldots, A_{4 n-1}$ form a partition of $A \backslash\{c\}$. Since $A \backslash\{c\}$ has $4 n+1$ elements, by the pigeonhole principle some set $A_{k}$ does contain at least two elements of $A \backslash\{c\}$. Denote these two elements $a$ and $b$ and assume $a<b$, so that $a<b<c$. Then $$ c+2 a \geqslant c+2\left(1-(2 / 3)^{k}\right) c=\left(3-2(2 / 3)^{k}\right) c=3\left(1-(2 / 3)^{k+1}\right) c>3 b $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be an integer, and let $A$ be a subset of $\left\{0,1,2,3, \ldots, 5^{n}\right\}$ consisting of $4 n+2$ numbers. Prove that there exist $a, b, c \in A$ such that $a<b<c$ and $c+2 a>3 b$.
|
Denote the maximum element of $A$ by $c$. For $k=0, \ldots, 4 n-1$ let $$ A_{k}=\left\{x \in A:\left(1-(2 / 3)^{k}\right) c \leqslant x<\left(1-(2 / 3)^{k+1}\right) c\right\} $$ Note that $$ \left(1-(2 / 3)^{4 n}\right) c=c-(16 / 81)^{n} c>c-(1 / 5)^{n} c \geqslant c-1 $$ which shows that the sets $A_{0}, A_{1}, \ldots, A_{4 n-1}$ form a partition of $A \backslash\{c\}$. Since $A \backslash\{c\}$ has $4 n+1$ elements, by the pigeonhole principle some set $A_{k}$ does contain at least two elements of $A \backslash\{c\}$. Denote these two elements $a$ and $b$ and assume $a<b$, so that $a<b<c$. Then $$ c+2 a \geqslant c+2\left(1-(2 / 3)^{k}\right) c=\left(3-2(2 / 3)^{k}\right) c=3\left(1-(2 / 3)^{k+1}\right) c>3 b $$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9902f219-469c-5eb1-8f38-d6659be5da41
| 24,121
|
Show that for all real numbers $x_{1}, \ldots, x_{n}$ the following inequality holds: $$ \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}-x_{j}\right|} \leqslant \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}\right|} $$
|
If we add $t$ to all the variables then the left-hand side remains constant and the right-hand side becomes $$ H(t):=\sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}+2 t\right|} $$ Let $T$ be large enough such that both $H(-T)$ and $H(T)$ are larger than the value $L$ of the lefthand side of the inequality we want to prove. Not necessarily distinct points $p_{i, j}:=-\left(x_{i}+x_{j}\right) / 2$ together with $T$ and $-T$ split the real line into segments and two rays such that on each of these segments and rays the function $H(t)$ is concave since $f(t):=\sqrt{|\ell+2 t|}$ is concave on both intervals $(-\infty,-\ell / 2]$ and $[-\ell / 2,+\infty)$. Let $[a, b]$ be the segment containing zero. Then concavity implies $H(0) \geqslant \min \{H(a), H(b)\}$ and, since $H( \pm T)>L$, it suffices to prove the inequalities $H\left(-\left(x_{i}+x_{j}\right) / 2\right) \geqslant L$, that is to prove the original inequality in the case when all numbers are shifted in such a way that two variables $x_{i}$ and $x_{j}$ add up to zero. In the following we denote the shifted variables still by $x_{i}$. If $i=j$, i.e. $x_{i}=0$ for some index $i$, then we can remove $x_{i}$ which will decrease both sides by $2 \sum_{k} \sqrt{\left|x_{k}\right|}$. Similarly, if $x_{i}+x_{j}=0$ for distinct $i$ and $j$ we can remove both $x_{i}$ and $x_{j}$ which decreases both sides by $$ 2 \sqrt{2\left|x_{i}\right|}+2 \cdot \sum_{k \neq i, j}\left(\sqrt{\left|x_{k}+x_{i}\right|}+\sqrt{\left|x_{k}+x_{j}\right|}\right) $$ In either case we reduced our inequality to the case of smaller $n$. It remains to note that for $n=0$ and $n=1$ the inequality is trivial.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that for all real numbers $x_{1}, \ldots, x_{n}$ the following inequality holds: $$ \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}-x_{j}\right|} \leqslant \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}\right|} $$
|
If we add $t$ to all the variables then the left-hand side remains constant and the right-hand side becomes $$ H(t):=\sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}+2 t\right|} $$ Let $T$ be large enough such that both $H(-T)$ and $H(T)$ are larger than the value $L$ of the lefthand side of the inequality we want to prove. Not necessarily distinct points $p_{i, j}:=-\left(x_{i}+x_{j}\right) / 2$ together with $T$ and $-T$ split the real line into segments and two rays such that on each of these segments and rays the function $H(t)$ is concave since $f(t):=\sqrt{|\ell+2 t|}$ is concave on both intervals $(-\infty,-\ell / 2]$ and $[-\ell / 2,+\infty)$. Let $[a, b]$ be the segment containing zero. Then concavity implies $H(0) \geqslant \min \{H(a), H(b)\}$ and, since $H( \pm T)>L$, it suffices to prove the inequalities $H\left(-\left(x_{i}+x_{j}\right) / 2\right) \geqslant L$, that is to prove the original inequality in the case when all numbers are shifted in such a way that two variables $x_{i}$ and $x_{j}$ add up to zero. In the following we denote the shifted variables still by $x_{i}$. If $i=j$, i.e. $x_{i}=0$ for some index $i$, then we can remove $x_{i}$ which will decrease both sides by $2 \sum_{k} \sqrt{\left|x_{k}\right|}$. Similarly, if $x_{i}+x_{j}=0$ for distinct $i$ and $j$ we can remove both $x_{i}$ and $x_{j}$ which decreases both sides by $$ 2 \sqrt{2\left|x_{i}\right|}+2 \cdot \sum_{k \neq i, j}\left(\sqrt{\left|x_{k}+x_{i}\right|}+\sqrt{\left|x_{k}+x_{j}\right|}\right) $$ In either case we reduced our inequality to the case of smaller $n$. It remains to note that for $n=0$ and $n=1$ the inequality is trivial.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a15fe8d7-320b-586e-97e9-7338f5c62db9
| 24,133
|
Show that for all real numbers $x_{1}, \ldots, x_{n}$ the following inequality holds: $$ \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}-x_{j}\right|} \leqslant \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}\right|} $$
|
For real $p$ consider the integral $$ I(p)=\int_{0}^{\infty} \frac{1-\cos (p x)}{x \sqrt{x}} d x $$ which clearly converges to a strictly positive number. By changing the variable $y=|p| x$ one notices that $I(p)=\sqrt{|p|} I(1)$. Hence, by using the trigonometric formula $\cos (\alpha-\beta)-\cos (\alpha+$ $\beta)=2 \sin \alpha \sin \beta$ we obtain $\sqrt{|a+b|}-\sqrt{|a-b|}=\frac{1}{I(1)} \int_{0}^{\infty} \frac{\cos ((a-b) x)-\cos ((a+b) x)}{x \sqrt{x}} d x=\frac{1}{I(1)} \int_{0}^{\infty} \frac{2 \sin (a x) \sin (b x)}{x \sqrt{x}} d x$, from which our inequality immediately follows: $$ \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}\right|}-\sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}-x_{j}\right|}=\frac{2}{I(1)} \int_{0}^{\infty} \frac{\left(\sum_{i=1}^{n} \sin \left(x_{i} x\right)\right)^{2}}{x \sqrt{x}} d x \geqslant 0 $$ Comment 1. A more general inequality $$ \sum_{i=1}^{n} \sum_{j=1}^{n}\left|x_{i}-x_{j}\right|^{r} \leqslant \sum_{i=1}^{n} \sum_{j=1}^{n}\left|x_{i}+x_{j}\right|^{r} $$ holds for any $r \in[0,2]$. The first solution can be repeated verbatim for any $r \in[0,1]$ but not for $r>1$. In the second solution, by putting $x^{r+1}$ in the denominator in place of $x \sqrt{x}$ we can prove the inequality for any $r \in(0,2)$ and the cases $r=0,2$ are easy to check by hand. Comment 2. In fact, the integral from Solution 2 can be computed explicitly, we have $I(1)=\sqrt{2 \pi}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that for all real numbers $x_{1}, \ldots, x_{n}$ the following inequality holds: $$ \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}-x_{j}\right|} \leqslant \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}\right|} $$
|
For real $p$ consider the integral $$ I(p)=\int_{0}^{\infty} \frac{1-\cos (p x)}{x \sqrt{x}} d x $$ which clearly converges to a strictly positive number. By changing the variable $y=|p| x$ one notices that $I(p)=\sqrt{|p|} I(1)$. Hence, by using the trigonometric formula $\cos (\alpha-\beta)-\cos (\alpha+$ $\beta)=2 \sin \alpha \sin \beta$ we obtain $\sqrt{|a+b|}-\sqrt{|a-b|}=\frac{1}{I(1)} \int_{0}^{\infty} \frac{\cos ((a-b) x)-\cos ((a+b) x)}{x \sqrt{x}} d x=\frac{1}{I(1)} \int_{0}^{\infty} \frac{2 \sin (a x) \sin (b x)}{x \sqrt{x}} d x$, from which our inequality immediately follows: $$ \sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}+x_{j}\right|}-\sum_{i=1}^{n} \sum_{j=1}^{n} \sqrt{\left|x_{i}-x_{j}\right|}=\frac{2}{I(1)} \int_{0}^{\infty} \frac{\left(\sum_{i=1}^{n} \sin \left(x_{i} x\right)\right)^{2}}{x \sqrt{x}} d x \geqslant 0 $$ Comment 1. A more general inequality $$ \sum_{i=1}^{n} \sum_{j=1}^{n}\left|x_{i}-x_{j}\right|^{r} \leqslant \sum_{i=1}^{n} \sum_{j=1}^{n}\left|x_{i}+x_{j}\right|^{r} $$ holds for any $r \in[0,2]$. The first solution can be repeated verbatim for any $r \in[0,1]$ but not for $r>1$. In the second solution, by putting $x^{r+1}$ in the denominator in place of $x \sqrt{x}$ we can prove the inequality for any $r \in(0,2)$ and the cases $r=0,2$ are easy to check by hand. Comment 2. In fact, the integral from Solution 2 can be computed explicitly, we have $I(1)=\sqrt{2 \pi}$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a15fe8d7-320b-586e-97e9-7338f5c62db9
| 24,133
|
Let $n \geqslant 2$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots+a_{n}=1$. Prove that $$ \sum_{k=1}^{n} \frac{a_{k}}{1-a_{k}}\left(a_{1}+a_{2}+\cdots+a_{k-1}\right)^{2}<\frac{1}{3} $$
|
For all $k \leqslant n$, let $$ s_{k}=a_{1}+a_{2}+\cdots+a_{k} \quad \text { and } \quad b_{k}=\frac{a_{k} s_{k-1}^{2}}{1-a_{k}} $$ with the convention that $s_{0}=0$. Note that $b_{k}$ is exactly a summand in the sum we need to estimate. We shall prove the inequality $$ b_{k}<\frac{s_{k}^{3}-s_{k-1}^{3}}{3} $$ Indeed, it suffices to check that $$ \begin{aligned} (1) & \Longleftrightarrow 0<\left(1-a_{k}\right)\left(\left(s_{k-1}+a_{k}\right)^{3}-s_{k-1}^{3}\right)-3 a_{k} s_{k-1}^{2} \\ & \Longleftrightarrow 0<\left(1-a_{k}\right)\left(3 s_{k-1}^{2}+3 s_{k-1} a_{k}+a_{k}^{2}\right)-3 s_{k-1}^{2} \\ & \Longleftrightarrow 0<-3 a_{k} s_{k-1}^{2}+3\left(1-a_{k}\right) s_{k-1} a_{k}+\left(1-a_{k}\right) a_{k}^{2} \\ & \Longleftrightarrow 0<3\left(1-a_{k}-s_{k-1}\right) s_{k-1} a_{k}+\left(1-a_{k}\right) a_{k}^{2} \end{aligned} $$ which holds since $a_{k}+s_{k-1}=s_{k} \leqslant 1$ and $a_{k} \in(0,1)$. Thus, adding inequalities (1) for $k=1, \ldots, n$, we conclude that $$ b_{1}+b_{2}+\cdots+b_{n}<\frac{s_{n}^{3}-s_{0}^{3}}{3}=\frac{1}{3} $$ as desired. Comment 1. There are many ways of proving (1) which can be written as $$ \frac{a s^{2}}{1-a}-\frac{(a+s)^{3}-s^{3}}{3}<0 $$ for non-negative $a$ and $s$ satisfying $a+s \leqslant 1$ and $a>0$. E.g., note that for any fixed $a$ the expression in (2) is quadratic in $s$ with the leading coefficient $a /(1-a)-a>0$. Hence, it is convex as a function in $s$, so it suffices to check the inequality at $s=0$ and $s=1-a$. The former case is trivial and in the latter case the inequality can be rewritten as $$ a s-\frac{3 a s(a+s)+a^{3}}{3}<0, $$ which is trivial since $a+s=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 2$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots+a_{n}=1$. Prove that $$ \sum_{k=1}^{n} \frac{a_{k}}{1-a_{k}}\left(a_{1}+a_{2}+\cdots+a_{k-1}\right)^{2}<\frac{1}{3} $$
|
For all $k \leqslant n$, let $$ s_{k}=a_{1}+a_{2}+\cdots+a_{k} \quad \text { and } \quad b_{k}=\frac{a_{k} s_{k-1}^{2}}{1-a_{k}} $$ with the convention that $s_{0}=0$. Note that $b_{k}$ is exactly a summand in the sum we need to estimate. We shall prove the inequality $$ b_{k}<\frac{s_{k}^{3}-s_{k-1}^{3}}{3} $$ Indeed, it suffices to check that $$ \begin{aligned} (1) & \Longleftrightarrow 0<\left(1-a_{k}\right)\left(\left(s_{k-1}+a_{k}\right)^{3}-s_{k-1}^{3}\right)-3 a_{k} s_{k-1}^{2} \\ & \Longleftrightarrow 0<\left(1-a_{k}\right)\left(3 s_{k-1}^{2}+3 s_{k-1} a_{k}+a_{k}^{2}\right)-3 s_{k-1}^{2} \\ & \Longleftrightarrow 0<-3 a_{k} s_{k-1}^{2}+3\left(1-a_{k}\right) s_{k-1} a_{k}+\left(1-a_{k}\right) a_{k}^{2} \\ & \Longleftrightarrow 0<3\left(1-a_{k}-s_{k-1}\right) s_{k-1} a_{k}+\left(1-a_{k}\right) a_{k}^{2} \end{aligned} $$ which holds since $a_{k}+s_{k-1}=s_{k} \leqslant 1$ and $a_{k} \in(0,1)$. Thus, adding inequalities (1) for $k=1, \ldots, n$, we conclude that $$ b_{1}+b_{2}+\cdots+b_{n}<\frac{s_{n}^{3}-s_{0}^{3}}{3}=\frac{1}{3} $$ as desired. Comment 1. There are many ways of proving (1) which can be written as $$ \frac{a s^{2}}{1-a}-\frac{(a+s)^{3}-s^{3}}{3}<0 $$ for non-negative $a$ and $s$ satisfying $a+s \leqslant 1$ and $a>0$. E.g., note that for any fixed $a$ the expression in (2) is quadratic in $s$ with the leading coefficient $a /(1-a)-a>0$. Hence, it is convex as a function in $s$, so it suffices to check the inequality at $s=0$ and $s=1-a$. The former case is trivial and in the latter case the inequality can be rewritten as $$ a s-\frac{3 a s(a+s)+a^{3}}{3}<0, $$ which is trivial since $a+s=1$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a92fac4-6f0f-57e7-8795-b835975f1e29
| 24,137
|
Let $n \geqslant 2$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots+a_{n}=1$. Prove that $$ \sum_{k=1}^{n} \frac{a_{k}}{1-a_{k}}\left(a_{1}+a_{2}+\cdots+a_{k-1}\right)^{2}<\frac{1}{3} $$
|
We sketch a probabilistic version of the first solution. Let $x_{1}, x_{2}, x_{3}$ be drawn uniformly and independently at random from the segment [0,1]. Let $I_{1} \cup I_{2} \cup \cdots \cup I_{n}$ be a partition of $[0,1]$ into segments of length $a_{1}, a_{2}, \ldots, a_{n}$ in this order. Let $J_{k}:=I_{1} \cup \cdots \cup I_{k-1}$ for $k \geqslant 2$ and $J_{1}:=\varnothing$. Then $$ \begin{aligned} \frac{1}{3}= & \sum_{k=1}^{n} \mathbb{P}\left\{x_{1} \geqslant x_{2}, x_{3} ; x_{1} \in I_{k}\right\} \\ = & \sum_{k=1}^{n}\left(\mathbb{P}\left\{x_{1} \in I_{k} ; x_{2}, x_{3} \in J_{k}\right\}\right. \\ + & 2 \cdot \mathbb{P}\left\{x_{1} \geqslant x_{2} ; x_{1}, x_{2} \in I_{k} ; x_{3} \in J_{k}\right\} \\ & \left.+\mathbb{P}\left\{x_{1} \geqslant x_{2}, x_{3} ; x_{1}, x_{2}, x_{3} \in I_{k}\right\}\right) \\ = & \sum_{k=1}^{n}\left(a_{k}\left(a_{1}+\cdots+a_{k-1}\right)^{2}+2 \cdot \frac{a_{k}^{2}}{2} \cdot\left(a_{1}+\cdots+a_{k-1}\right)+\frac{a_{k}^{3}}{3}\right) \\ > & \sum_{k=1}^{n}\left(a_{k}\left(a_{1}+\cdots+a_{k-1}\right)^{2}+a_{k}^{2}\left(a_{1}+\cdots+a_{k-1}\right) \cdot \frac{a_{1}+\cdots+a_{k-1}}{1-a_{k}}\right) \end{aligned} $$ where for the last inequality we used that $1-a_{k} \geqslant a_{1}+\cdots+a_{k-1}$. This completes the proof since $$ a_{k}+\frac{a_{k}^{2}}{1-a_{k}}=\frac{a_{k}}{1-a_{k}} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 2$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots+a_{n}=1$. Prove that $$ \sum_{k=1}^{n} \frac{a_{k}}{1-a_{k}}\left(a_{1}+a_{2}+\cdots+a_{k-1}\right)^{2}<\frac{1}{3} $$
|
We sketch a probabilistic version of the first solution. Let $x_{1}, x_{2}, x_{3}$ be drawn uniformly and independently at random from the segment [0,1]. Let $I_{1} \cup I_{2} \cup \cdots \cup I_{n}$ be a partition of $[0,1]$ into segments of length $a_{1}, a_{2}, \ldots, a_{n}$ in this order. Let $J_{k}:=I_{1} \cup \cdots \cup I_{k-1}$ for $k \geqslant 2$ and $J_{1}:=\varnothing$. Then $$ \begin{aligned} \frac{1}{3}= & \sum_{k=1}^{n} \mathbb{P}\left\{x_{1} \geqslant x_{2}, x_{3} ; x_{1} \in I_{k}\right\} \\ = & \sum_{k=1}^{n}\left(\mathbb{P}\left\{x_{1} \in I_{k} ; x_{2}, x_{3} \in J_{k}\right\}\right. \\ + & 2 \cdot \mathbb{P}\left\{x_{1} \geqslant x_{2} ; x_{1}, x_{2} \in I_{k} ; x_{3} \in J_{k}\right\} \\ & \left.+\mathbb{P}\left\{x_{1} \geqslant x_{2}, x_{3} ; x_{1}, x_{2}, x_{3} \in I_{k}\right\}\right) \\ = & \sum_{k=1}^{n}\left(a_{k}\left(a_{1}+\cdots+a_{k-1}\right)^{2}+2 \cdot \frac{a_{k}^{2}}{2} \cdot\left(a_{1}+\cdots+a_{k-1}\right)+\frac{a_{k}^{3}}{3}\right) \\ > & \sum_{k=1}^{n}\left(a_{k}\left(a_{1}+\cdots+a_{k-1}\right)^{2}+a_{k}^{2}\left(a_{1}+\cdots+a_{k-1}\right) \cdot \frac{a_{1}+\cdots+a_{k-1}}{1-a_{k}}\right) \end{aligned} $$ where for the last inequality we used that $1-a_{k} \geqslant a_{1}+\cdots+a_{k-1}$. This completes the proof since $$ a_{k}+\frac{a_{k}^{2}}{1-a_{k}}=\frac{a_{k}}{1-a_{k}} $$
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a92fac4-6f0f-57e7-8795-b835975f1e29
| 24,137
|
Let $A$ be a finite set of (not necessarily positive) integers, and let $m \geqslant 2$ be an integer. Assume that there exist non-empty subsets $B_{1}, B_{2}, B_{3}, \ldots, B_{m}$ of $A$ whose elements add up to the sums $m^{1}, m^{2}, m^{3}, \ldots, m^{m}$, respectively. Prove that $A$ contains at least $m / 2$ elements.
|
Let $A=\left\{a_{1}, \ldots, a_{k}\right\}$. Assume that, on the contrary, $k=|A|<m / 2$. Let $$ s_{i}:=\sum_{j: a_{j} \in B_{i}} a_{j} $$ be the sum of elements of $B_{i}$. We are given that $s_{i}=m^{i}$ for $i=1, \ldots, m$. Now consider all $m^{m}$ expressions of the form $$ f\left(c_{1}, \ldots, c_{m}\right):=c_{1} s_{1}+c_{2} s_{2}+\ldots+c_{m} s_{m}, c_{i} \in\{0,1, \ldots, m-1\} \text { for all } i=1,2, \ldots, m $$ Note that every number $f\left(c_{1}, \ldots, c_{m}\right)$ has the form $$ \alpha_{1} a_{1}+\ldots+\alpha_{k} a_{k}, \alpha_{i} \in\{0,1, \ldots, m(m-1)\} $$ Hence, there are at most $(m(m-1)+1)^{k}<m^{2 k}<m^{m}$ distinct values of our expressions; therefore, at least two of them coincide. Since $s_{i}=m^{i}$, this contradicts the uniqueness of representation of positive integers in the base- $m$ system. Comment 1. For other rapidly increasing sequences of sums of $B_{i}$ 's the similar argument also provides lower estimates on $k=|A|$. For example, if the sums of $B_{i}$ are equal to 1!, 2!, 3!, $\ldots, m$ !, then for any fixed $\varepsilon>0$ and large enough $m$ we get $k \geqslant(1 / 2-\varepsilon) m$. The proof uses the fact that the combinations $\sum c_{i}$ ! with $c_{i} \in\{0,1, \ldots, i\}$ are all distinct. Comment 2. The problem statement holds also if $A$ is a set of real numbers (not necessarily integers), the above proofs work in the real case.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A$ be a finite set of (not necessarily positive) integers, and let $m \geqslant 2$ be an integer. Assume that there exist non-empty subsets $B_{1}, B_{2}, B_{3}, \ldots, B_{m}$ of $A$ whose elements add up to the sums $m^{1}, m^{2}, m^{3}, \ldots, m^{m}$, respectively. Prove that $A$ contains at least $m / 2$ elements.
|
Let $A=\left\{a_{1}, \ldots, a_{k}\right\}$. Assume that, on the contrary, $k=|A|<m / 2$. Let $$ s_{i}:=\sum_{j: a_{j} \in B_{i}} a_{j} $$ be the sum of elements of $B_{i}$. We are given that $s_{i}=m^{i}$ for $i=1, \ldots, m$. Now consider all $m^{m}$ expressions of the form $$ f\left(c_{1}, \ldots, c_{m}\right):=c_{1} s_{1}+c_{2} s_{2}+\ldots+c_{m} s_{m}, c_{i} \in\{0,1, \ldots, m-1\} \text { for all } i=1,2, \ldots, m $$ Note that every number $f\left(c_{1}, \ldots, c_{m}\right)$ has the form $$ \alpha_{1} a_{1}+\ldots+\alpha_{k} a_{k}, \alpha_{i} \in\{0,1, \ldots, m(m-1)\} $$ Hence, there are at most $(m(m-1)+1)^{k}<m^{2 k}<m^{m}$ distinct values of our expressions; therefore, at least two of them coincide. Since $s_{i}=m^{i}$, this contradicts the uniqueness of representation of positive integers in the base- $m$ system. Comment 1. For other rapidly increasing sequences of sums of $B_{i}$ 's the similar argument also provides lower estimates on $k=|A|$. For example, if the sums of $B_{i}$ are equal to 1!, 2!, 3!, $\ldots, m$ !, then for any fixed $\varepsilon>0$ and large enough $m$ we get $k \geqslant(1 / 2-\varepsilon) m$. The proof uses the fact that the combinations $\sum c_{i}$ ! with $c_{i} \in\{0,1, \ldots, i\}$ are all distinct. Comment 2. The problem statement holds also if $A$ is a set of real numbers (not necessarily integers), the above proofs work in the real case.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
30ebebec-626a-506d-8f89-212b5aa9c419
| 24,142
|
Let $n \geqslant 1$ be an integer, and let $x_{0}, x_{1}, \ldots, x_{n+1}$ be $n+2$ non-negative real numbers that satisfy $x_{i} x_{i+1}-x_{i-1}^{2} \geqslant 1$ for all $i=1,2, \ldots, n$. Show that $$ x_{0}+x_{1}+\cdots+x_{n}+x_{n+1}>\left(\frac{2 n}{3}\right)^{3 / 2} $$
|
Lemma 1.1. If $a, b, c$ are non-negative numbers such that $a b-c^{2} \geqslant 1$, then $$ (a+2 b)^{2} \geqslant(b+2 c)^{2}+6 $$ Proof. $(a+2 b)^{2}-(b+2 c)^{2}=(a-b)^{2}+2(b-c)^{2}+6\left(a b-c^{2}\right) \geqslant 6$. Lemma 1.2. $\sqrt{1}+\cdots+\sqrt{n}>\frac{2}{3} n^{3 / 2}$. Proof. Bernoulli's inequality $(1+t)^{3 / 2}>1+\frac{3}{2} t$ for $0>t \geqslant-1$ (or, alternatively, a straightforward check) gives $$ (k-1)^{3 / 2}=k^{3 / 2}\left(1-\frac{1}{k}\right)^{3 / 2}>k^{3 / 2}\left(1-\frac{3}{2 k}\right)=k^{3 / 2}-\frac{3}{2} \sqrt{k} . $$ Summing up (*) over $k=1,2, \ldots, n$ yields $$ 0>n^{3 / 2}-\frac{3}{2}(\sqrt{1}+\cdots+\sqrt{n}) . $$ Now put $y_{i}:=2 x_{i}+x_{i+1}$ for $i=0,1, \ldots, n$. We get $y_{0} \geqslant 0$ and $y_{i}^{2} \geqslant y_{i-1}^{2}+6$ for $i=1,2, \ldots, n$ by Lemma 1.1. Thus, an easy induction on $i$ gives $y_{i} \geqslant \sqrt{6 i}$. Using this estimate and Lemma 1.2 we get $$ 3\left(x_{0}+\ldots+x_{n+1}\right) \geqslant y_{1}+\ldots+y_{n} \geqslant \sqrt{6}(\sqrt{1}+\sqrt{2}+\ldots+\sqrt{n})>\sqrt{6} \cdot \frac{2}{3} n^{3 / 2}=3\left(\frac{2 n}{3}\right)^{3 / 2} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 1$ be an integer, and let $x_{0}, x_{1}, \ldots, x_{n+1}$ be $n+2$ non-negative real numbers that satisfy $x_{i} x_{i+1}-x_{i-1}^{2} \geqslant 1$ for all $i=1,2, \ldots, n$. Show that $$ x_{0}+x_{1}+\cdots+x_{n}+x_{n+1}>\left(\frac{2 n}{3}\right)^{3 / 2} $$
|
Lemma 1.1. If $a, b, c$ are non-negative numbers such that $a b-c^{2} \geqslant 1$, then $$ (a+2 b)^{2} \geqslant(b+2 c)^{2}+6 $$ Proof. $(a+2 b)^{2}-(b+2 c)^{2}=(a-b)^{2}+2(b-c)^{2}+6\left(a b-c^{2}\right) \geqslant 6$. Lemma 1.2. $\sqrt{1}+\cdots+\sqrt{n}>\frac{2}{3} n^{3 / 2}$. Proof. Bernoulli's inequality $(1+t)^{3 / 2}>1+\frac{3}{2} t$ for $0>t \geqslant-1$ (or, alternatively, a straightforward check) gives $$ (k-1)^{3 / 2}=k^{3 / 2}\left(1-\frac{1}{k}\right)^{3 / 2}>k^{3 / 2}\left(1-\frac{3}{2 k}\right)=k^{3 / 2}-\frac{3}{2} \sqrt{k} . $$ Summing up (*) over $k=1,2, \ldots, n$ yields $$ 0>n^{3 / 2}-\frac{3}{2}(\sqrt{1}+\cdots+\sqrt{n}) . $$ Now put $y_{i}:=2 x_{i}+x_{i+1}$ for $i=0,1, \ldots, n$. We get $y_{0} \geqslant 0$ and $y_{i}^{2} \geqslant y_{i-1}^{2}+6$ for $i=1,2, \ldots, n$ by Lemma 1.1. Thus, an easy induction on $i$ gives $y_{i} \geqslant \sqrt{6 i}$. Using this estimate and Lemma 1.2 we get $$ 3\left(x_{0}+\ldots+x_{n+1}\right) \geqslant y_{1}+\ldots+y_{n} \geqslant \sqrt{6}(\sqrt{1}+\sqrt{2}+\ldots+\sqrt{n})>\sqrt{6} \cdot \frac{2}{3} n^{3 / 2}=3\left(\frac{2 n}{3}\right)^{3 / 2} $$
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cd3699f7-0caf-5e23-9e4a-1653d35c28b4
| 24,145
|
Let $n \geqslant 1$ be an integer, and let $x_{0}, x_{1}, \ldots, x_{n+1}$ be $n+2$ non-negative real numbers that satisfy $x_{i} x_{i+1}-x_{i-1}^{2} \geqslant 1$ for all $i=1,2, \ldots, n$. Show that $$ x_{0}+x_{1}+\cdots+x_{n}+x_{n+1}>\left(\frac{2 n}{3}\right)^{3 / 2} $$
|
Say that an index $i \in\{0,1, \ldots, n+1\}$ is good, if $x_{i} \geqslant \sqrt{\frac{2}{3}} i$, otherwise call the index $i$ bad. Lemma 2.1. There are no two consecutive bad indices. Proof. Assume the contrary and consider two bad indices $j, j+1$ with minimal possible $j$. Since 0 is good, we get $j>0$, thus by minimality $j-1$ is a good index and we have $$ \frac{2}{3} \sqrt{j(j+1)}>x_{j} x_{j+1} \geqslant x_{j-1}^{2}+1 \geqslant \frac{2}{3}(j-1)+1=\frac{2}{3} \cdot \frac{j+(j+1)}{2} $$ that contradicts the AM-GM inequality for numbers $j$ and $j+1$. Lemma 2.2. If an index $j \leqslant n-1$ is good, then $$ x_{j+1}+x_{j+2} \geqslant \sqrt{\frac{2}{3}}(\sqrt{j+1}+\sqrt{j+2}) . $$ Proof. We have $$ x_{j+1}+x_{j+2} \geqslant 2 \sqrt{x_{j+1} x_{j+2}} \geqslant 2 \sqrt{x_{j}^{2}+1} \geqslant 2 \sqrt{\frac{2}{3} j+1} \geqslant \sqrt{\frac{2}{3} j+\frac{2}{3}}+\sqrt{\frac{2}{3} j+\frac{4}{3}}, $$ the last inequality follows from concavity of the square root function, or, alternatively, from the AM-QM inequality for the numbers $\sqrt{\frac{2}{3} j+\frac{2}{3}}$ and $\sqrt{\frac{2}{3} j+\frac{4}{3}}$. Let $S_{i}=x_{1}+\ldots+x_{i}$ and $T_{i}=\sqrt{\frac{2}{3}}(\sqrt{1}+\ldots+\sqrt{i})$. Lemma 2.3. If an index $i$ is good, then $S_{i} \geqslant T_{i}$. Proof. Induction on $i$. The base case $i=0$ is clear. Assume that the claim holds for good indices less than $i$ and prove it for a good index $i>0$. If $i-1$ is good, then by the inductive hypothesis we get $S_{i}=S_{i-1}+x_{i} \geqslant T_{i-1}+\sqrt{\frac{2}{3} i}=T_{i}$. If $i-1$ is bad, then $i>1$, and $i-2$ is good by Lemma 2.1. Then using Lemma 2.2 and the inductive hypothesis we get $$ S_{i}=S_{i-2}+x_{i-1}+x_{i} \geqslant T_{i-2}+\sqrt{\frac{2}{3}}(\sqrt{i-1}+\sqrt{i})=T_{i} $$ Since either $n$ or $n+1$ is good by Lemma 2.1, Lemma 2.3 yields in both cases $S_{n+1} \geqslant T_{n}$, and it remains to apply Lemma 1.2 from Solution 1. Comment 1. Another way to get (*) is the integral bound $$ k^{3 / 2}-(k-1)^{3 / 2}=\int_{k-1}^{k} \frac{3}{2} \sqrt{x} d x<\frac{3}{2} \sqrt{k} . $$ Comment 2. If $x_{i}=\sqrt{2 / 3} \cdot(\sqrt{i}+1)$, the conditions of the problem hold. Indeed, the inequality to check is $$ (\sqrt{i}+1)(\sqrt{i+1}+1)-(\sqrt{i-1}+1)^{2} \geqslant 3 / 2 $$ that rewrites as $$ \sqrt{i}+\sqrt{i+1}-2 \sqrt{i-1} \geqslant(i+1 / 2)-\sqrt{i(i+1)}=\frac{1 / 4}{i+1 / 2+\sqrt{i(i+1)}}, $$ which follows from $$ \sqrt{i}-\sqrt{i-1}=\frac{1}{\sqrt{i}+\sqrt{i-1}}>\frac{1}{2 i} $$ For these numbers we have $x_{0}+\ldots+x_{n+1}=\left(\frac{2 n}{3}\right)^{3 / 2}+O(n)$, thus the multiplicative constant $(2 / 3)^{3 / 2}$ in the problem statement is sharp.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 1$ be an integer, and let $x_{0}, x_{1}, \ldots, x_{n+1}$ be $n+2$ non-negative real numbers that satisfy $x_{i} x_{i+1}-x_{i-1}^{2} \geqslant 1$ for all $i=1,2, \ldots, n$. Show that $$ x_{0}+x_{1}+\cdots+x_{n}+x_{n+1}>\left(\frac{2 n}{3}\right)^{3 / 2} $$
|
Say that an index $i \in\{0,1, \ldots, n+1\}$ is good, if $x_{i} \geqslant \sqrt{\frac{2}{3}} i$, otherwise call the index $i$ bad. Lemma 2.1. There are no two consecutive bad indices. Proof. Assume the contrary and consider two bad indices $j, j+1$ with minimal possible $j$. Since 0 is good, we get $j>0$, thus by minimality $j-1$ is a good index and we have $$ \frac{2}{3} \sqrt{j(j+1)}>x_{j} x_{j+1} \geqslant x_{j-1}^{2}+1 \geqslant \frac{2}{3}(j-1)+1=\frac{2}{3} \cdot \frac{j+(j+1)}{2} $$ that contradicts the AM-GM inequality for numbers $j$ and $j+1$. Lemma 2.2. If an index $j \leqslant n-1$ is good, then $$ x_{j+1}+x_{j+2} \geqslant \sqrt{\frac{2}{3}}(\sqrt{j+1}+\sqrt{j+2}) . $$ Proof. We have $$ x_{j+1}+x_{j+2} \geqslant 2 \sqrt{x_{j+1} x_{j+2}} \geqslant 2 \sqrt{x_{j}^{2}+1} \geqslant 2 \sqrt{\frac{2}{3} j+1} \geqslant \sqrt{\frac{2}{3} j+\frac{2}{3}}+\sqrt{\frac{2}{3} j+\frac{4}{3}}, $$ the last inequality follows from concavity of the square root function, or, alternatively, from the AM-QM inequality for the numbers $\sqrt{\frac{2}{3} j+\frac{2}{3}}$ and $\sqrt{\frac{2}{3} j+\frac{4}{3}}$. Let $S_{i}=x_{1}+\ldots+x_{i}$ and $T_{i}=\sqrt{\frac{2}{3}}(\sqrt{1}+\ldots+\sqrt{i})$. Lemma 2.3. If an index $i$ is good, then $S_{i} \geqslant T_{i}$. Proof. Induction on $i$. The base case $i=0$ is clear. Assume that the claim holds for good indices less than $i$ and prove it for a good index $i>0$. If $i-1$ is good, then by the inductive hypothesis we get $S_{i}=S_{i-1}+x_{i} \geqslant T_{i-1}+\sqrt{\frac{2}{3} i}=T_{i}$. If $i-1$ is bad, then $i>1$, and $i-2$ is good by Lemma 2.1. Then using Lemma 2.2 and the inductive hypothesis we get $$ S_{i}=S_{i-2}+x_{i-1}+x_{i} \geqslant T_{i-2}+\sqrt{\frac{2}{3}}(\sqrt{i-1}+\sqrt{i})=T_{i} $$ Since either $n$ or $n+1$ is good by Lemma 2.1, Lemma 2.3 yields in both cases $S_{n+1} \geqslant T_{n}$, and it remains to apply Lemma 1.2 from Solution 1. Comment 1. Another way to get (*) is the integral bound $$ k^{3 / 2}-(k-1)^{3 / 2}=\int_{k-1}^{k} \frac{3}{2} \sqrt{x} d x<\frac{3}{2} \sqrt{k} . $$ Comment 2. If $x_{i}=\sqrt{2 / 3} \cdot(\sqrt{i}+1)$, the conditions of the problem hold. Indeed, the inequality to check is $$ (\sqrt{i}+1)(\sqrt{i+1}+1)-(\sqrt{i-1}+1)^{2} \geqslant 3 / 2 $$ that rewrites as $$ \sqrt{i}+\sqrt{i+1}-2 \sqrt{i-1} \geqslant(i+1 / 2)-\sqrt{i(i+1)}=\frac{1 / 4}{i+1 / 2+\sqrt{i(i+1)}}, $$ which follows from $$ \sqrt{i}-\sqrt{i-1}=\frac{1}{\sqrt{i}+\sqrt{i-1}}>\frac{1}{2 i} $$ For these numbers we have $x_{0}+\ldots+x_{n+1}=\left(\frac{2 n}{3}\right)^{3 / 2}+O(n)$, thus the multiplicative constant $(2 / 3)^{3 / 2}$ in the problem statement is sharp.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cd3699f7-0caf-5e23-9e4a-1653d35c28b4
| 24,145
|
Let $S$ be an infinite set of positive integers, such that there exist four pairwise distinct $a, b, c, d \in S$ with $\operatorname{gcd}(a, b) \neq \operatorname{gcd}(c, d)$. Prove that there exist three pairwise distinct $x, y, z \in S$ such that $\operatorname{gcd}(x, y)=\operatorname{gcd}(y, z) \neq \operatorname{gcd}(z, x)$.
|
There exists $\alpha \in S$ so that $\{\operatorname{gcd}(\alpha, s) \mid s \in S, s \neq \alpha\}$ contains at least two elements. Since $\alpha$ has only finitely many divisors, there is a $d \mid \alpha$ such that the set $B=\{\beta \in$ $S \mid \operatorname{gcd}(\alpha, \beta)=d\}$ is infinite. Pick $\gamma \in S$ so that $\operatorname{gcd}(\alpha, \gamma) \neq d$. Pick $\beta_{1}, \beta_{2} \in B$ so that $\operatorname{gcd}\left(\beta_{1}, \gamma\right)=\operatorname{gcd}\left(\beta_{2}, \gamma\right)=: d^{\prime}$. If $d=d^{\prime}$, then $\operatorname{gcd}\left(\alpha, \beta_{1}\right)=\operatorname{gcd}\left(\gamma, \beta_{1}\right) \neq \operatorname{gcd}(\alpha, \gamma)$. If $d \neq d^{\prime}$, then either $\operatorname{gcd}\left(\alpha, \beta_{1}\right)=\operatorname{gcd}\left(\alpha, \beta_{2}\right)=d$ and $\operatorname{gcd}\left(\beta_{1}, \beta_{2}\right) \neq d$ or $\operatorname{gcd}\left(\gamma, \beta_{1}\right)=\operatorname{gcd}\left(\gamma, \beta_{2}\right)=d^{\prime}$ and $\operatorname{gcd}\left(\beta_{1}, \beta_{2}\right) \neq d^{\prime}$. Comment. The situation can be modelled as a complete graph on the infinite vertex set $S$, where every edge $\{s, t\}$ is colored by $c(s, t):=\operatorname{gcd}(s, t)$. For every vertex the incident edges carry only finitely many different colors, and by the problem statement at least two different colors show up on the edge set. The goal is to show that there exists a bi-colored triangle (a triangle, whose edges carry exactly two different colors). For the proof, consider a vertex $v$ whose incident edges carry at least two different colors. Let $X \subset S$ be an infinite subset so that $c(v, x) \equiv c_{1}$ for all $x \in X$. Let $y \in S$ be a vertex so that $c(v, y) \neq c_{1}$. Let $x_{1}, x_{2} \in X$ be two vertices with $c\left(y, x_{1}\right)=c\left(y, x_{2}\right)=c_{2}$. If $c_{1}=c_{2}$, then the triangle $v, y, x_{1}$ is bi-colored. If $c_{1} \neq c_{2}$, then one of $v, x_{1}, x_{2}$ and $y, x_{1}, x_{2}$ is bi-colored.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be an infinite set of positive integers, such that there exist four pairwise distinct $a, b, c, d \in S$ with $\operatorname{gcd}(a, b) \neq \operatorname{gcd}(c, d)$. Prove that there exist three pairwise distinct $x, y, z \in S$ such that $\operatorname{gcd}(x, y)=\operatorname{gcd}(y, z) \neq \operatorname{gcd}(z, x)$.
|
There exists $\alpha \in S$ so that $\{\operatorname{gcd}(\alpha, s) \mid s \in S, s \neq \alpha\}$ contains at least two elements. Since $\alpha$ has only finitely many divisors, there is a $d \mid \alpha$ such that the set $B=\{\beta \in$ $S \mid \operatorname{gcd}(\alpha, \beta)=d\}$ is infinite. Pick $\gamma \in S$ so that $\operatorname{gcd}(\alpha, \gamma) \neq d$. Pick $\beta_{1}, \beta_{2} \in B$ so that $\operatorname{gcd}\left(\beta_{1}, \gamma\right)=\operatorname{gcd}\left(\beta_{2}, \gamma\right)=: d^{\prime}$. If $d=d^{\prime}$, then $\operatorname{gcd}\left(\alpha, \beta_{1}\right)=\operatorname{gcd}\left(\gamma, \beta_{1}\right) \neq \operatorname{gcd}(\alpha, \gamma)$. If $d \neq d^{\prime}$, then either $\operatorname{gcd}\left(\alpha, \beta_{1}\right)=\operatorname{gcd}\left(\alpha, \beta_{2}\right)=d$ and $\operatorname{gcd}\left(\beta_{1}, \beta_{2}\right) \neq d$ or $\operatorname{gcd}\left(\gamma, \beta_{1}\right)=\operatorname{gcd}\left(\gamma, \beta_{2}\right)=d^{\prime}$ and $\operatorname{gcd}\left(\beta_{1}, \beta_{2}\right) \neq d^{\prime}$. Comment. The situation can be modelled as a complete graph on the infinite vertex set $S$, where every edge $\{s, t\}$ is colored by $c(s, t):=\operatorname{gcd}(s, t)$. For every vertex the incident edges carry only finitely many different colors, and by the problem statement at least two different colors show up on the edge set. The goal is to show that there exists a bi-colored triangle (a triangle, whose edges carry exactly two different colors). For the proof, consider a vertex $v$ whose incident edges carry at least two different colors. Let $X \subset S$ be an infinite subset so that $c(v, x) \equiv c_{1}$ for all $x \in X$. Let $y \in S$ be a vertex so that $c(v, y) \neq c_{1}$. Let $x_{1}, x_{2} \in X$ be two vertices with $c\left(y, x_{1}\right)=c\left(y, x_{2}\right)=c_{2}$. If $c_{1}=c_{2}$, then the triangle $v, y, x_{1}$ is bi-colored. If $c_{1} \neq c_{2}$, then one of $v, x_{1}, x_{2}$ and $y, x_{1}, x_{2}$ is bi-colored.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b0918e2a-a313-5237-b769-78257de0e044
| 24,151
|
The kingdom of Anisotropy consists of $n$ cities. For every two cities there exists exactly one direct one-way road between them. We say that a path from $X$ to $Y$ is a sequence of roads such that one can move from $X$ to $Y$ along this sequence without returning to an already visited city. A collection of paths is called diverse if no road belongs to two or more paths in the collection. Let $A$ and $B$ be two distinct cities in Anisotropy. Let $N_{A B}$ denote the maximal number of paths in a diverse collection of paths from $A$ to $B$. Similarly, let $N_{B A}$ denote the maximal number of paths in a diverse collection of paths from $B$ to $A$. Prove that the equality $N_{A B}=N_{B A}$ holds if and only if the number of roads going out from $A$ is the same as the number of roads going out from $B$.
|
We recall some graph-theoretical notions. Let $G$ be a finite graph, and let $V$ be the set of its vertices; fix two distinct vertices $s, t \in V$. An $(s, t)$-cut is a partition of $V$ into two parts $V=S \sqcup T$ such that $s \in S$ and $t \in T$. The cut-edges in the cut $(S, T)$ are the edges going from $S$ to $T$, and the size $e(S, T)$ of the cut is the number of cut-edges. We will make use of the following theorem (which is a partial case of the Ford-Fulkerson "min-cut max-flow" theorem). Theorem (Menger). Let $G$ be a directed graph, and let $s$ and $t$ be its distinct vertices. Then the maximal number of edge-disjoint paths from $s$ to $t$ is equal to the minimal size of an $(s, t)$-cut. Back to the problem. Consider a directed graph $G$ whose vertices are the cities, and edges correspond to the roads. Then $N_{A B}$ is the maximal number of edge-disjoint paths from $A$ to $B$ in this graph; the number $N_{B A}$ is interpreted similarly. As in the previous solution, denote by $a$ and $b$ the out-degrees of vertices $A$ and $B$, respectively. To solve the problem, we show that for any $(A, B)$-cut $\left(S_{A}, T_{A}\right)$ in our graph there exists a $(B, A)$-cut $\left(S_{B}, T_{B}\right)$ satisfying $$ e\left(S_{B}, T_{B}\right)=e\left(S_{A}, T_{A}\right)+(b-a) . $$ This yields $$ N_{B A} \leqslant N_{A B}+(b-a) ; \quad \text { similarly, we get } \quad N_{A B} \leqslant N_{B A}+(a-b), $$ whence again $N_{B A}-N_{A B}=b-a$. The construction is simple: we put $S_{B}=S_{A} \cup\{B\} \backslash\{A\}$ and hence $T_{B}=T_{A} \cup\{A\} \backslash\{B\}$. To show that it works, let A and B denote the sets of cut-edges in $\left(S_{A}, T_{A}\right)$ and $\left(S_{B}, T_{B}\right)$, respectively. Let $a_{s}$ and $a_{t}=a-a_{s}$ denote the numbers of edges going from $A$ to $S_{A}$ and $T_{A}$, respectively. Similarly, denote by $b_{s}$ and $b_{t}=b-b_{s}$ the numbers of edges going from $B$ to $S_{B}$ and $T_{B}$, respectively. Notice that any edge incident to none of $A$ and $B$ either belongs to both A and B , or belongs to none of them. Denote the number of such edges belonging to A by $c$. The edges in A which are not yet accounted for split into two categories: those going out from $A$ to $T_{A}$ (including $A \rightarrow B$ if it exists), and those going from $S_{A} \backslash\{A\}$ to $B$ - in other words, going from $S_{B}$ to $B$. The numbers of edges in the two categories are $a_{t}$ and $\left|S_{B}\right|-1-b_{s}$, respectively. Therefore, $$ |\mathrm{A}|=c+a_{t}+\left(\left|S_{B}\right|-b_{s}-1\right) . \quad \text { Similarly, we get } \quad|\mathrm{B}|=c+b_{t}+\left(\left|S_{A}\right|-a_{s}-1\right), $$ and hence $$ |\mathrm{B}|-|\mathrm{A}|=\left(b_{t}+b_{s}\right)-\left(a_{t}+a_{s}\right)=b-a, $$ since $\left|S_{A}\right|=\left|S_{B}\right|$. This finishes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The kingdom of Anisotropy consists of $n$ cities. For every two cities there exists exactly one direct one-way road between them. We say that a path from $X$ to $Y$ is a sequence of roads such that one can move from $X$ to $Y$ along this sequence without returning to an already visited city. A collection of paths is called diverse if no road belongs to two or more paths in the collection. Let $A$ and $B$ be two distinct cities in Anisotropy. Let $N_{A B}$ denote the maximal number of paths in a diverse collection of paths from $A$ to $B$. Similarly, let $N_{B A}$ denote the maximal number of paths in a diverse collection of paths from $B$ to $A$. Prove that the equality $N_{A B}=N_{B A}$ holds if and only if the number of roads going out from $A$ is the same as the number of roads going out from $B$.
|
We recall some graph-theoretical notions. Let $G$ be a finite graph, and let $V$ be the set of its vertices; fix two distinct vertices $s, t \in V$. An $(s, t)$-cut is a partition of $V$ into two parts $V=S \sqcup T$ such that $s \in S$ and $t \in T$. The cut-edges in the cut $(S, T)$ are the edges going from $S$ to $T$, and the size $e(S, T)$ of the cut is the number of cut-edges. We will make use of the following theorem (which is a partial case of the Ford-Fulkerson "min-cut max-flow" theorem). Theorem (Menger). Let $G$ be a directed graph, and let $s$ and $t$ be its distinct vertices. Then the maximal number of edge-disjoint paths from $s$ to $t$ is equal to the minimal size of an $(s, t)$-cut. Back to the problem. Consider a directed graph $G$ whose vertices are the cities, and edges correspond to the roads. Then $N_{A B}$ is the maximal number of edge-disjoint paths from $A$ to $B$ in this graph; the number $N_{B A}$ is interpreted similarly. As in the previous solution, denote by $a$ and $b$ the out-degrees of vertices $A$ and $B$, respectively. To solve the problem, we show that for any $(A, B)$-cut $\left(S_{A}, T_{A}\right)$ in our graph there exists a $(B, A)$-cut $\left(S_{B}, T_{B}\right)$ satisfying $$ e\left(S_{B}, T_{B}\right)=e\left(S_{A}, T_{A}\right)+(b-a) . $$ This yields $$ N_{B A} \leqslant N_{A B}+(b-a) ; \quad \text { similarly, we get } \quad N_{A B} \leqslant N_{B A}+(a-b), $$ whence again $N_{B A}-N_{A B}=b-a$. The construction is simple: we put $S_{B}=S_{A} \cup\{B\} \backslash\{A\}$ and hence $T_{B}=T_{A} \cup\{A\} \backslash\{B\}$. To show that it works, let A and B denote the sets of cut-edges in $\left(S_{A}, T_{A}\right)$ and $\left(S_{B}, T_{B}\right)$, respectively. Let $a_{s}$ and $a_{t}=a-a_{s}$ denote the numbers of edges going from $A$ to $S_{A}$ and $T_{A}$, respectively. Similarly, denote by $b_{s}$ and $b_{t}=b-b_{s}$ the numbers of edges going from $B$ to $S_{B}$ and $T_{B}$, respectively. Notice that any edge incident to none of $A$ and $B$ either belongs to both A and B , or belongs to none of them. Denote the number of such edges belonging to A by $c$. The edges in A which are not yet accounted for split into two categories: those going out from $A$ to $T_{A}$ (including $A \rightarrow B$ if it exists), and those going from $S_{A} \backslash\{A\}$ to $B$ - in other words, going from $S_{B}$ to $B$. The numbers of edges in the two categories are $a_{t}$ and $\left|S_{B}\right|-1-b_{s}$, respectively. Therefore, $$ |\mathrm{A}|=c+a_{t}+\left(\left|S_{B}\right|-b_{s}-1\right) . \quad \text { Similarly, we get } \quad|\mathrm{B}|=c+b_{t}+\left(\left|S_{A}\right|-a_{s}-1\right), $$ and hence $$ |\mathrm{B}|-|\mathrm{A}|=\left(b_{t}+b_{s}\right)-\left(a_{t}+a_{s}\right)=b-a, $$ since $\left|S_{A}\right|=\left|S_{B}\right|$. This finishes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7b346957-4a95-5a74-a325-e4f8cc457152
| 24,160
|
Let $n$ and $k$ be two integers with $n>k \geqslant 1$. There are $2 n+1$ students standing in a circle. Each student $S$ has $2 k$ neighbours - namely, the $k$ students closest to $S$ on the right, and the $k$ students closest to $S$ on the left. Suppose that $n+1$ of the students are girls, and the other $n$ are boys. Prove that there is a girl with at least $k$ girls among her neighbours.
|
We replace the girls by 1's, and the boys by 0 's, getting the numbers $a_{1}, a_{2}, \ldots, a_{2 n+1}$ arranged in a circle. We extend this sequence periodically by letting $a_{2 n+1+k}=a_{k}$ for all $k \in \mathbb{Z}$. We get an infinite periodic sequence $$ \ldots, a_{1}, a_{2}, \ldots, a_{2 n+1}, a_{1}, a_{2}, \ldots, a_{2 n+1}, \ldots $$ Consider the numbers $b_{i}=a_{i}+a_{i-k-1}-1 \in\{-1,0,1\}$ for all $i \in \mathbb{Z}$. We know that $$ b_{m+1}+b_{m+2}+\cdots+b_{m+2 n+1}=1 \quad(m \in \mathbb{Z}) $$ in particular, this yields that there exists some $i_{0}$ with $b_{i_{0}}=1$. Now we want to find an index $i$ such that $$ b_{i}=1 \quad \text { and } \quad b_{i+1}+b_{i+2}+\cdots+b_{i+k} \geqslant 0 $$ This will imply that $a_{i}=1$ and $$ \left(a_{i-k}+a_{i-k+1}+\cdots+a_{i-1}\right)+\left(a_{i+1}+a_{i+2}+\cdots+a_{i+k}\right) \geqslant k $$ as desired. Suppose, to the contrary, that for every index $i$ with $b_{i}=1$ the sum $b_{i+1}+b_{i+2}+\cdots+b_{i+k}$ is negative. We start from some index $i_{0}$ with $b_{i_{0}}=1$ and construct a sequence $i_{0}, i_{1}, i_{2}, \ldots$, where $i_{j}(j>0)$ is the smallest possible index such that $i_{j}>i_{j-1}+k$ and $b_{i_{j}}=1$. We can choose two numbers among $i_{0}, i_{1}, \ldots, i_{2 n+1}$ which are congruent modulo $2 n+1$ (without loss of generality, we may assume that these numbers are $i_{0}$ and $i_{T}$ ). On the one hand, for every $j$ with $0 \leqslant j \leqslant T-1$ we have $$ S_{j}:=b_{i_{j}}+b_{i_{j}+1}+b_{i_{j}+2}+\cdots+b_{i_{j+1}-1} \leqslant b_{i_{j}}+b_{i_{j}+1}+b_{i_{j}+2}+\cdots+b_{i_{j}+k} \leqslant 0 $$ since $b_{i_{j}+k+1}, \ldots, b_{i_{j+1}-1} \leqslant 0$. On the other hand, since $\left(i_{T}-i_{0}\right) \mid(2 n+1)$, from (1) we deduce $$ S_{0}+\cdots+S_{T-1}=\sum_{i=i_{0}}^{i_{T}-1} b_{i}=\frac{i_{T}-i_{0}}{2 n+1}>0 $$ This contradiction finishes the solution. Comment 1. After the problem is reduced to finding an index $i$ satisfying (2), one can finish the solution by applying the (existence part of) following statement. Lemma (Raney). If $\left\langle x_{1}, x_{2}, \ldots, x_{m}\right\rangle$ is any sequence of integers whose sum is +1 , exactly one of the cyclic shifts $\left\langle x_{1}, x_{2}, \ldots, x_{m}\right\rangle,\left\langle x_{2}, \ldots, x_{m}, x_{1}\right\rangle, \ldots,\left\langle x_{m}, x_{1}, \ldots, x_{m-1}\right\rangle$ has all of its partial sums positive. A (possibly wider known) version of this lemma, which also can be used in order to solve the problem, is the following Claim (Gas stations problem). Assume that there are several fuel stations located on a circular route which together contain just enough gas to make one trip around. Then one can make it all the way around, starting at the right station with an empty tank. Both Raney's theorem and the Gas stations problem admit many different (parallel) proofs. Their ideas can be disguised in direct solutions of the problem at hand (as it, in fact, happens in the above solution); such solutions may avoid the introduction of the $b_{i}$. Below, in Comment 2 we present a variant of such solution, while in Comment 3 we present an alternative proof of Raney's theorem. Comment 2. Here is a version of the solution which avoids the use of the $b_{i}$. Suppose the contrary. Introduce the numbers $a_{i}$ as above. Starting from any index $s_{0}$ with $a_{s_{0}}=1$, we construct a sequence $s_{0}, s_{1}, s_{2}, \ldots$ by letting $s_{i}$ to be the smallest index larger than $s_{i-1}+k$ such that $a_{s_{i}}=1$, for $i=1,2, \ldots$. Choose two indices among $s_{1}, \ldots, s_{2 n+1}$ which are congruent modulo $2 n+1$; we assume those two are $s_{0}$ and $s_{T}$, with $s_{T}-s_{0}=t(2 n+1)$. Notice here that $s_{T+1}-s_{T}=s_{1}-s_{0}$. For every $i=0,1,2, \ldots, T$, put $$ L_{i}=s_{i+1}-s_{i} \quad \text { and } \quad S_{i}=a_{s_{i}}+a_{s_{i}+1}+\cdots+a_{s_{i+1}-1} . $$ Now, by the indirect assumption, for every $i=1,2, \ldots, T$, we have $$ a_{s_{i}-k}+a_{s_{i}-k+1}+\cdots+a_{s_{i}+k} \leqslant a_{s_{i}}+(k-1)=k . $$ Recall that $a_{j}=0$ for all $j$ with $s_{i}+k<j<a_{s_{i+1}}$. Therefore, $$ S_{i-1}+S_{i}=\sum_{j=s_{i-1}}^{s_{i}+k} a_{j}=\sum_{j=s_{i-1}}^{s_{i}-k-1} a_{j}+\sum_{j=s_{i}-k}^{s_{i}+k} a_{j} \leqslant\left(s_{i}-s_{i-1}-k\right)+k=L_{i-1} $$ Summing up these equalities over $i=1,2, \ldots, T$ we get $$ 2 t(n+1)=\sum_{i=1}^{T}\left(S_{i-1}+S_{i}\right) \leqslant \sum_{i=1}^{T} L_{i-1}=(2 n+1) t $$ which is a contradiction. Comment 3. Here we present a proof of Raney's lemma different from the one used above. If we plot the partial sums $s_{n}=x_{1}+\cdots+x_{n}$ as a function of $n$, the graph of $s_{n}$ has an average slope of $1 / m$, because $s_{m+n}=s_{n}+1$. 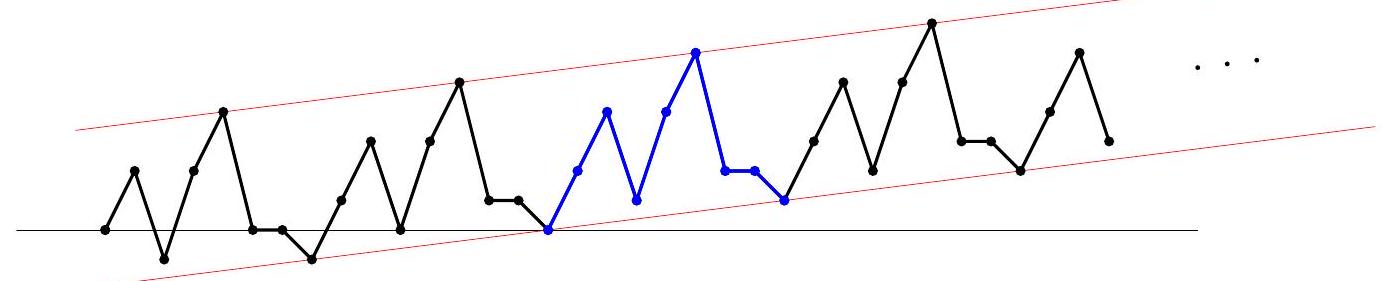 The entire graph can be contained between two lines of slope $1 / m$. In general these bounding lines touch the graph just once in each cycle of $m$ points, since lines of slope $1 / m$ hit points with integer coordinates only once per $m$ units. The unique (in one cycle) lower point of intersection is the only place in the cycle from which all partial sums will be positive. Comment 4. The following example shows that for different values of $k$ the required girl may have different positions: 011001101.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ and $k$ be two integers with $n>k \geqslant 1$. There are $2 n+1$ students standing in a circle. Each student $S$ has $2 k$ neighbours - namely, the $k$ students closest to $S$ on the right, and the $k$ students closest to $S$ on the left. Suppose that $n+1$ of the students are girls, and the other $n$ are boys. Prove that there is a girl with at least $k$ girls among her neighbours.
|
We replace the girls by 1's, and the boys by 0 's, getting the numbers $a_{1}, a_{2}, \ldots, a_{2 n+1}$ arranged in a circle. We extend this sequence periodically by letting $a_{2 n+1+k}=a_{k}$ for all $k \in \mathbb{Z}$. We get an infinite periodic sequence $$ \ldots, a_{1}, a_{2}, \ldots, a_{2 n+1}, a_{1}, a_{2}, \ldots, a_{2 n+1}, \ldots $$ Consider the numbers $b_{i}=a_{i}+a_{i-k-1}-1 \in\{-1,0,1\}$ for all $i \in \mathbb{Z}$. We know that $$ b_{m+1}+b_{m+2}+\cdots+b_{m+2 n+1}=1 \quad(m \in \mathbb{Z}) $$ in particular, this yields that there exists some $i_{0}$ with $b_{i_{0}}=1$. Now we want to find an index $i$ such that $$ b_{i}=1 \quad \text { and } \quad b_{i+1}+b_{i+2}+\cdots+b_{i+k} \geqslant 0 $$ This will imply that $a_{i}=1$ and $$ \left(a_{i-k}+a_{i-k+1}+\cdots+a_{i-1}\right)+\left(a_{i+1}+a_{i+2}+\cdots+a_{i+k}\right) \geqslant k $$ as desired. Suppose, to the contrary, that for every index $i$ with $b_{i}=1$ the sum $b_{i+1}+b_{i+2}+\cdots+b_{i+k}$ is negative. We start from some index $i_{0}$ with $b_{i_{0}}=1$ and construct a sequence $i_{0}, i_{1}, i_{2}, \ldots$, where $i_{j}(j>0)$ is the smallest possible index such that $i_{j}>i_{j-1}+k$ and $b_{i_{j}}=1$. We can choose two numbers among $i_{0}, i_{1}, \ldots, i_{2 n+1}$ which are congruent modulo $2 n+1$ (without loss of generality, we may assume that these numbers are $i_{0}$ and $i_{T}$ ). On the one hand, for every $j$ with $0 \leqslant j \leqslant T-1$ we have $$ S_{j}:=b_{i_{j}}+b_{i_{j}+1}+b_{i_{j}+2}+\cdots+b_{i_{j+1}-1} \leqslant b_{i_{j}}+b_{i_{j}+1}+b_{i_{j}+2}+\cdots+b_{i_{j}+k} \leqslant 0 $$ since $b_{i_{j}+k+1}, \ldots, b_{i_{j+1}-1} \leqslant 0$. On the other hand, since $\left(i_{T}-i_{0}\right) \mid(2 n+1)$, from (1) we deduce $$ S_{0}+\cdots+S_{T-1}=\sum_{i=i_{0}}^{i_{T}-1} b_{i}=\frac{i_{T}-i_{0}}{2 n+1}>0 $$ This contradiction finishes the solution. Comment 1. After the problem is reduced to finding an index $i$ satisfying (2), one can finish the solution by applying the (existence part of) following statement. Lemma (Raney). If $\left\langle x_{1}, x_{2}, \ldots, x_{m}\right\rangle$ is any sequence of integers whose sum is +1 , exactly one of the cyclic shifts $\left\langle x_{1}, x_{2}, \ldots, x_{m}\right\rangle,\left\langle x_{2}, \ldots, x_{m}, x_{1}\right\rangle, \ldots,\left\langle x_{m}, x_{1}, \ldots, x_{m-1}\right\rangle$ has all of its partial sums positive. A (possibly wider known) version of this lemma, which also can be used in order to solve the problem, is the following Claim (Gas stations problem). Assume that there are several fuel stations located on a circular route which together contain just enough gas to make one trip around. Then one can make it all the way around, starting at the right station with an empty tank. Both Raney's theorem and the Gas stations problem admit many different (parallel) proofs. Their ideas can be disguised in direct solutions of the problem at hand (as it, in fact, happens in the above solution); such solutions may avoid the introduction of the $b_{i}$. Below, in Comment 2 we present a variant of such solution, while in Comment 3 we present an alternative proof of Raney's theorem. Comment 2. Here is a version of the solution which avoids the use of the $b_{i}$. Suppose the contrary. Introduce the numbers $a_{i}$ as above. Starting from any index $s_{0}$ with $a_{s_{0}}=1$, we construct a sequence $s_{0}, s_{1}, s_{2}, \ldots$ by letting $s_{i}$ to be the smallest index larger than $s_{i-1}+k$ such that $a_{s_{i}}=1$, for $i=1,2, \ldots$. Choose two indices among $s_{1}, \ldots, s_{2 n+1}$ which are congruent modulo $2 n+1$; we assume those two are $s_{0}$ and $s_{T}$, with $s_{T}-s_{0}=t(2 n+1)$. Notice here that $s_{T+1}-s_{T}=s_{1}-s_{0}$. For every $i=0,1,2, \ldots, T$, put $$ L_{i}=s_{i+1}-s_{i} \quad \text { and } \quad S_{i}=a_{s_{i}}+a_{s_{i}+1}+\cdots+a_{s_{i+1}-1} . $$ Now, by the indirect assumption, for every $i=1,2, \ldots, T$, we have $$ a_{s_{i}-k}+a_{s_{i}-k+1}+\cdots+a_{s_{i}+k} \leqslant a_{s_{i}}+(k-1)=k . $$ Recall that $a_{j}=0$ for all $j$ with $s_{i}+k<j<a_{s_{i+1}}$. Therefore, $$ S_{i-1}+S_{i}=\sum_{j=s_{i-1}}^{s_{i}+k} a_{j}=\sum_{j=s_{i-1}}^{s_{i}-k-1} a_{j}+\sum_{j=s_{i}-k}^{s_{i}+k} a_{j} \leqslant\left(s_{i}-s_{i-1}-k\right)+k=L_{i-1} $$ Summing up these equalities over $i=1,2, \ldots, T$ we get $$ 2 t(n+1)=\sum_{i=1}^{T}\left(S_{i-1}+S_{i}\right) \leqslant \sum_{i=1}^{T} L_{i-1}=(2 n+1) t $$ which is a contradiction. Comment 3. Here we present a proof of Raney's lemma different from the one used above. If we plot the partial sums $s_{n}=x_{1}+\cdots+x_{n}$ as a function of $n$, the graph of $s_{n}$ has an average slope of $1 / m$, because $s_{m+n}=s_{n}+1$.  The entire graph can be contained between two lines of slope $1 / m$. In general these bounding lines touch the graph just once in each cycle of $m$ points, since lines of slope $1 / m$ hit points with integer coordinates only once per $m$ units. The unique (in one cycle) lower point of intersection is the only place in the cycle from which all partial sums will be positive. Comment 4. The following example shows that for different values of $k$ the required girl may have different positions: 011001101.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a8059f7c-3ae8-5c3c-82f0-8a4dc9294697
| 24,163
|
A hunter and an invisible rabbit play a game on an infinite square grid. First the hunter fixes a colouring of the cells with finitely many colours. The rabbit then secretly chooses a cell to start in. Every minute, the rabbit reports the colour of its current cell to the hunter, and then secretly moves to an adjacent cell that it has not visited before (two cells are adjacent if they share a side). The hunter wins if after some finite time either - the rabbit cannot move; or - the hunter can determine the cell in which the rabbit started. Decide whether there exists a winning strategy for the hunter.
|
A central idea is that several colourings $C_{1}, C_{2}, \ldots, C_{k}$ can be merged together into a single product colouring $C_{1} \times C_{2} \times \cdots \times C_{k}$ as follows: the colours in the product colouring are ordered tuples $\left(c_{1}, \ldots, c_{n}\right)$ of colours, where $c_{i}$ is a colour used in $C_{i}$, so that each cell gets a tuple consisting of its colours in the individual colourings $C_{i}$. This way, any information which can be determined from one of the individual colourings can also be determined from the product colouring. Now let the hunter merge the following colourings: - The first two colourings $C_{1}$ and $C_{2}$ allow the tracking of the horizontal and vertical movements of the rabbit. The colouring $C_{1}$ colours the cells according to the residue of their $x$-coordinates modulo 3 , which allows to determine whether the rabbit moves left, moves right, or moves vertically. Similarly, the colouring $C_{2}$ uses the residues of the $y$-coordinates modulo 3, which allows to determine whether the rabbit moves up, moves down, or moves horizontally. - Under the condition that the rabbit's $x$-coordinate is unbounded, colouring $C_{3}$ allows to determine the exact value of the $x$-coordinate: In $C_{3}$, the columns are coloured white and black so that the gaps between neighboring black columns are pairwise distinct. As the rabbit's $x$-coordinate is unbounded, it will eventually visit two black cells in distinct columns. With the help of colouring $C_{1}$ the hunter can catch that moment, and determine the difference of $x$-coordinates of those two black cells, hence deducing the precise column. Symmetrically, under the condition that the rabbit's $y$-coordinate is unbounded, there is a colouring $C_{4}$ that allows the hunter to determine the exact value of the $y$-coordinate. - Finally, under the condition that the sum $x+y$ of the rabbit's coordinates is unbounded, colouring $C_{5}$ allows to determine the exact value of this sum: The diagonal lines $x+y=$ const are coloured black and white, so that the gaps between neighboring black diagonals are pairwise distinct. Unless the rabbit gets stuck, at least two of the three values $x, y$ and $x+y$ must be unbounded as the rabbit keeps moving. Hence the hunter can eventually determine two of these three values; thus he does know all three. Finally the hunter works backwards with help of the colourings $C_{1}$ and $C_{2}$ and computes the starting cell of the rabbit. Comment. There are some variations of the solution above: e.g., the colourings $C_{3}, C_{4}$ and $C_{5}$ can be replaced with different ones. However, such alternatives are more technically involved, and we do not present them here.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A hunter and an invisible rabbit play a game on an infinite square grid. First the hunter fixes a colouring of the cells with finitely many colours. The rabbit then secretly chooses a cell to start in. Every minute, the rabbit reports the colour of its current cell to the hunter, and then secretly moves to an adjacent cell that it has not visited before (two cells are adjacent if they share a side). The hunter wins if after some finite time either - the rabbit cannot move; or - the hunter can determine the cell in which the rabbit started. Decide whether there exists a winning strategy for the hunter.
|
A central idea is that several colourings $C_{1}, C_{2}, \ldots, C_{k}$ can be merged together into a single product colouring $C_{1} \times C_{2} \times \cdots \times C_{k}$ as follows: the colours in the product colouring are ordered tuples $\left(c_{1}, \ldots, c_{n}\right)$ of colours, where $c_{i}$ is a colour used in $C_{i}$, so that each cell gets a tuple consisting of its colours in the individual colourings $C_{i}$. This way, any information which can be determined from one of the individual colourings can also be determined from the product colouring. Now let the hunter merge the following colourings: - The first two colourings $C_{1}$ and $C_{2}$ allow the tracking of the horizontal and vertical movements of the rabbit. The colouring $C_{1}$ colours the cells according to the residue of their $x$-coordinates modulo 3 , which allows to determine whether the rabbit moves left, moves right, or moves vertically. Similarly, the colouring $C_{2}$ uses the residues of the $y$-coordinates modulo 3, which allows to determine whether the rabbit moves up, moves down, or moves horizontally. - Under the condition that the rabbit's $x$-coordinate is unbounded, colouring $C_{3}$ allows to determine the exact value of the $x$-coordinate: In $C_{3}$, the columns are coloured white and black so that the gaps between neighboring black columns are pairwise distinct. As the rabbit's $x$-coordinate is unbounded, it will eventually visit two black cells in distinct columns. With the help of colouring $C_{1}$ the hunter can catch that moment, and determine the difference of $x$-coordinates of those two black cells, hence deducing the precise column. Symmetrically, under the condition that the rabbit's $y$-coordinate is unbounded, there is a colouring $C_{4}$ that allows the hunter to determine the exact value of the $y$-coordinate. - Finally, under the condition that the sum $x+y$ of the rabbit's coordinates is unbounded, colouring $C_{5}$ allows to determine the exact value of this sum: The diagonal lines $x+y=$ const are coloured black and white, so that the gaps between neighboring black diagonals are pairwise distinct. Unless the rabbit gets stuck, at least two of the three values $x, y$ and $x+y$ must be unbounded as the rabbit keeps moving. Hence the hunter can eventually determine two of these three values; thus he does know all three. Finally the hunter works backwards with help of the colourings $C_{1}$ and $C_{2}$ and computes the starting cell of the rabbit. Comment. There are some variations of the solution above: e.g., the colourings $C_{3}, C_{4}$ and $C_{5}$ can be replaced with different ones. However, such alternatives are more technically involved, and we do not present them here.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
78dd9121-b7da-5f45-bfde-3713ea9924b8
| 24,165
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent.
|
Introduce the point $X=A Q \cap C D$; we need to prove that $B, R$ and $X$ are collinear. By means of the circle $(A P R Q)$ we have $$ \angle R Q X=180^{\circ}-\angle A Q R=\angle R P A=\angle R C X $$ (the last equality holds in view of $A B \| C D$ ), which means that the points $C, Q, R$, and $X$ also lie on some circle $\delta$. Using the circles $\delta$ and $\gamma$ we finally obtain $$ \angle X R C=\angle X Q C=180^{\circ}-\angle C Q A=\angle A D C=\angle B A C=180^{\circ}-\angle C R B, $$ that proves the desired collinearity. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent.
|
Introduce the point $X=A Q \cap C D$; we need to prove that $B, R$ and $X$ are collinear. By means of the circle $(A P R Q)$ we have $$ \angle R Q X=180^{\circ}-\angle A Q R=\angle R P A=\angle R C X $$ (the last equality holds in view of $A B \| C D$ ), which means that the points $C, Q, R$, and $X$ also lie on some circle $\delta$. Using the circles $\delta$ and $\gamma$ we finally obtain $$ \angle X R C=\angle X Q C=180^{\circ}-\angle C Q A=\angle A D C=\angle B A C=180^{\circ}-\angle C R B, $$ that proves the desired collinearity. 
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8d04ce75-d0d4-5d0f-853c-ed6e151f58dc
| 24,174
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent.
|
Let $\alpha$ denote the circle ( $A P R Q)$. Since $$ \angle C A P=\angle A C D=\angle A Q D=180^{\circ}-\angle A Q P $$ the line $A C$ is tangent to $\alpha$. Now, let $A D$ meet $\alpha$ again at a point $Y$ (which necessarily lies on the extension of $D A$ beyond $A$ ). Using the circle $\gamma$, along with the fact that $A C$ is tangent to $\alpha$, we have $$ \angle A R Y=\angle C A D=\angle A C B=\angle A R B, $$ so the points $Y, B$, and $R$ are collinear. Applying Pascal's theorem to the hexagon $A A Y R P Q$ (where $A A$ is regarded as the tangent to $\alpha$ at $A$ ), we see that the points $A A \cap R P=C, A Y \cap P Q=D$, and $Y R \cap Q A$ are collinear. Hence the lines $C D, A Q$, and $B R$ are concurrent. Comment 1. Solution 2 consists of two parts: (1) showing that $B R$ and $D A$ meet on $\alpha$; and (2) showing that this yields the desired concurrency. Solution 3 also splits into those parts, but the proofs are different. 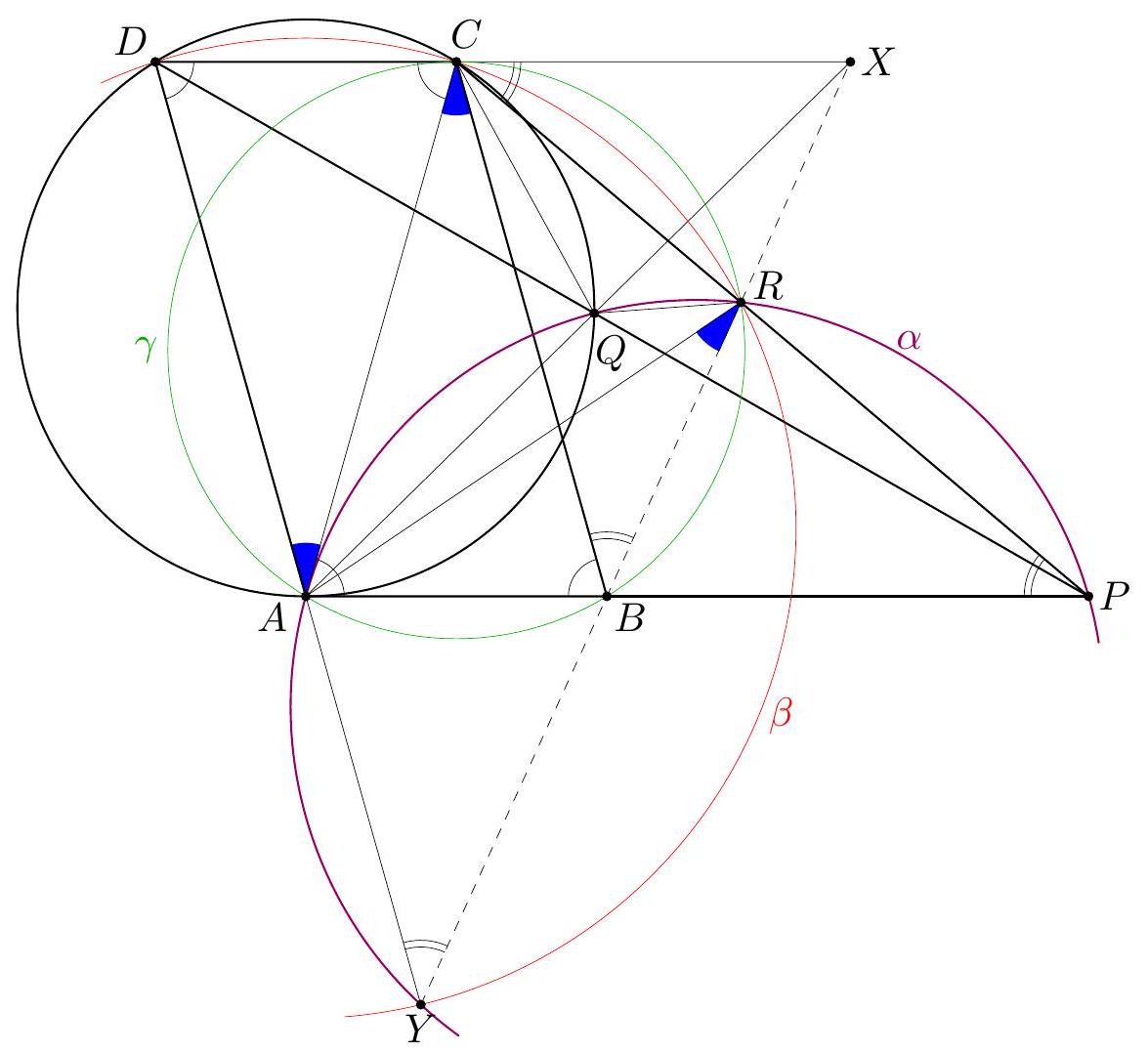
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent.
|
Let $\alpha$ denote the circle ( $A P R Q)$. Since $$ \angle C A P=\angle A C D=\angle A Q D=180^{\circ}-\angle A Q P $$ the line $A C$ is tangent to $\alpha$. Now, let $A D$ meet $\alpha$ again at a point $Y$ (which necessarily lies on the extension of $D A$ beyond $A$ ). Using the circle $\gamma$, along with the fact that $A C$ is tangent to $\alpha$, we have $$ \angle A R Y=\angle C A D=\angle A C B=\angle A R B, $$ so the points $Y, B$, and $R$ are collinear. Applying Pascal's theorem to the hexagon $A A Y R P Q$ (where $A A$ is regarded as the tangent to $\alpha$ at $A$ ), we see that the points $A A \cap R P=C, A Y \cap P Q=D$, and $Y R \cap Q A$ are collinear. Hence the lines $C D, A Q$, and $B R$ are concurrent. Comment 1. Solution 2 consists of two parts: (1) showing that $B R$ and $D A$ meet on $\alpha$; and (2) showing that this yields the desired concurrency. Solution 3 also splits into those parts, but the proofs are different. 
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8d04ce75-d0d4-5d0f-853c-ed6e151f58dc
| 24,174
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent.
|
As in Using the circle $\alpha$ and noticing that $C D$ is tangent to $\gamma$, we obtain $$ \angle R Y A=\angle R P A=\angle R C X=\angle R B C . $$ So $A Y \| B C$, and hence $Y$ lies on $D A$. Now the chain of equalities (1) shows also that $\angle R Y D=\angle R C X$, which implies that the points $C, D, Y$, and $R$ lie on some circle $\beta$. Hence, the lines $C D, A Q$, and $Y B R$ are the pairwise radical axes of the circles $(A Q C D), \alpha$, and $\beta$, so those lines are concurrent. Comment 2. The original problem submission contained an additional assumption that $B P=A B$. The Problem Selection Committee removed this assumption as superfluous.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent.
|
As in Using the circle $\alpha$ and noticing that $C D$ is tangent to $\gamma$, we obtain $$ \angle R Y A=\angle R P A=\angle R C X=\angle R B C . $$ So $A Y \| B C$, and hence $Y$ lies on $D A$. Now the chain of equalities (1) shows also that $\angle R Y D=\angle R C X$, which implies that the points $C, D, Y$, and $R$ lie on some circle $\beta$. Hence, the lines $C D, A Q$, and $Y B R$ are the pairwise radical axes of the circles $(A Q C D), \alpha$, and $\beta$, so those lines are concurrent. Comment 2. The original problem submission contained an additional assumption that $B P=A B$. The Problem Selection Committee removed this assumption as superfluous.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8d04ce75-d0d4-5d0f-853c-ed6e151f58dc
| 24,174
|
Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Prove that the perimeters of the (possibly self-intersecting) quadrilaterals $A D T X$ and $C D Y Z$ are equal.
|
The point $I$ is the intersection of the external bisector of the angle $T C Z$ with the circumcircle $\omega$ of the triangle $T C Z$, so $I$ is the midpoint of the $\operatorname{arc} T C Z$ and $I T=I Z$. Similarly, $I$ is the midpoint of the arc $Y A X$ and $I X=I Y$. Let $O$ be the centre of $\omega$. Then $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively. So $X T=Y Z$. 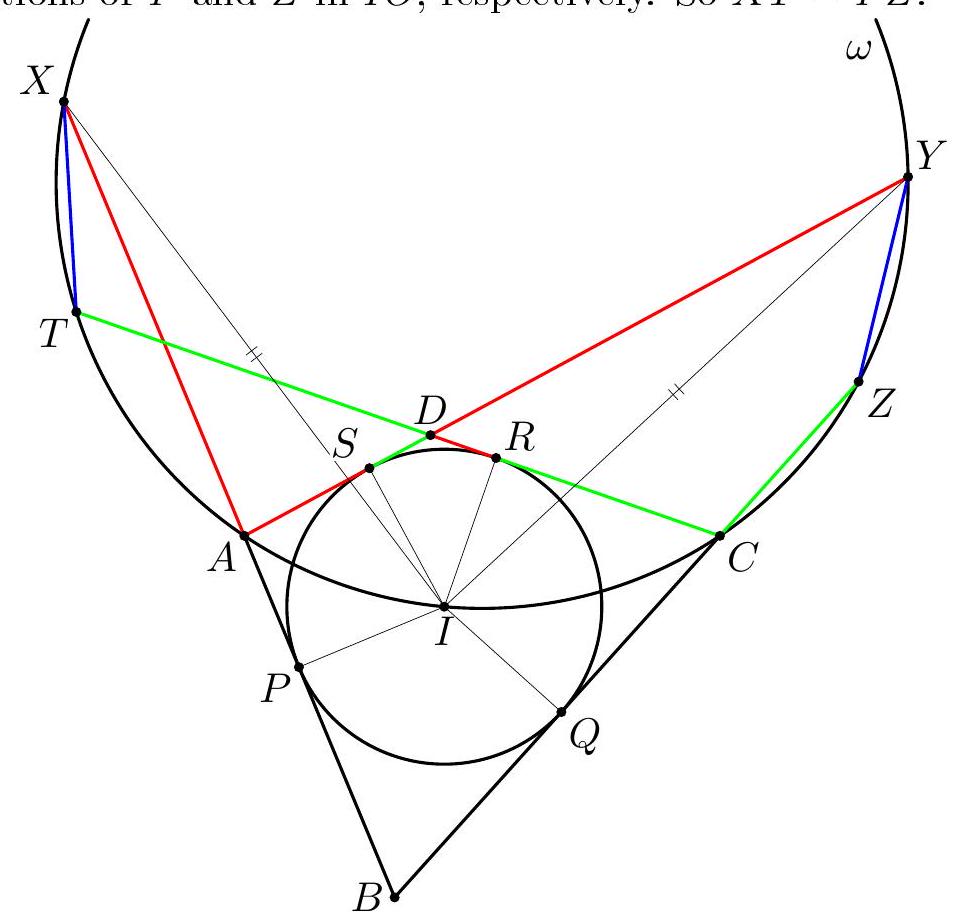 Let the incircle of $A B C D$ touch $A B, B C, C D$, and $D A$ at points $P, Q, R$, and $S$, respectively. The right triangles $I X P$ and $I Y S$ are congruent, since $I P=I S$ and $I X=I Y$. Similarly, the right triangles $I R T$ and $I Q Z$ are congruent. Therefore, $X P=Y S$ and $R T=Q Z$. Denote the perimeters of $A D T X$ and $C D Y Z$ by $P_{A D T X}$ and $P_{C D Y Z}$ respectively. Since $A S=A P, C Q=R C$, and $S D=D R$, we obtain $$ \begin{aligned} P_{A D T X}=X T+X A+A S+ & S D+D T=X T+X P+R T \\ & =Y Z+Y S+Q Z=Y Z+Y D+D R+R C+C Z=P_{C D Y Z} \end{aligned} $$ as required. Comment 1. After proving that $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively, one can finish the solution as follows. Since $X T=Y Z$, the problem statement is equivalent to $$ X A+A D+D T=Y D+D C+C Z $$ Since $A B C D$ is circumscribed, $A B-A D=B C-C D$. Adding this to (1), we come to an equivalent equality $X A+A B+D T=Y D+B C+C Z$, or $$ X B+D T=Y D+B Z . $$ Let $\lambda=\frac{X Z}{A C}=\frac{T Y}{A C}$. Since $X A C Z$ is cyclic, the triangles $Z B X$ and $A B C$ are similar, hence $$ \frac{X B}{B C}=\frac{B Z}{A B}=\frac{X Z}{A C}=\lambda . $$ It follows that $X B=\lambda B C$ and $B Z=\lambda A B$. Likewise, the triangles $T D Y$ and $A D C$ are similar, hence $$ \frac{D T}{A D}=\frac{D Y}{C D}=\frac{T Y}{A C}=\lambda $$ Therefore, (2) rewrites as $\lambda B C+\lambda A D=\lambda C D+\lambda A B$. This is equivalent to $B C+A D=C D+A B$ which is true as $A B C D$ is circumscribed. Comment 2. Here is a more difficult modification of the original problem, found by the PSC. Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Let $U=B C \cap A D$ and $V=B A \cap C D$. Let $I_{U}$ be the incentre of $U Y Z$ and let $J_{V}$ be the $V$-excentre of $V X T$. Then $I_{U} J_{V} \perp B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Prove that the perimeters of the (possibly self-intersecting) quadrilaterals $A D T X$ and $C D Y Z$ are equal.
|
The point $I$ is the intersection of the external bisector of the angle $T C Z$ with the circumcircle $\omega$ of the triangle $T C Z$, so $I$ is the midpoint of the $\operatorname{arc} T C Z$ and $I T=I Z$. Similarly, $I$ is the midpoint of the arc $Y A X$ and $I X=I Y$. Let $O$ be the centre of $\omega$. Then $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively. So $X T=Y Z$.  Let the incircle of $A B C D$ touch $A B, B C, C D$, and $D A$ at points $P, Q, R$, and $S$, respectively. The right triangles $I X P$ and $I Y S$ are congruent, since $I P=I S$ and $I X=I Y$. Similarly, the right triangles $I R T$ and $I Q Z$ are congruent. Therefore, $X P=Y S$ and $R T=Q Z$. Denote the perimeters of $A D T X$ and $C D Y Z$ by $P_{A D T X}$ and $P_{C D Y Z}$ respectively. Since $A S=A P, C Q=R C$, and $S D=D R$, we obtain $$ \begin{aligned} P_{A D T X}=X T+X A+A S+ & S D+D T=X T+X P+R T \\ & =Y Z+Y S+Q Z=Y Z+Y D+D R+R C+C Z=P_{C D Y Z} \end{aligned} $$ as required. Comment 1. After proving that $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively, one can finish the solution as follows. Since $X T=Y Z$, the problem statement is equivalent to $$ X A+A D+D T=Y D+D C+C Z $$ Since $A B C D$ is circumscribed, $A B-A D=B C-C D$. Adding this to (1), we come to an equivalent equality $X A+A B+D T=Y D+B C+C Z$, or $$ X B+D T=Y D+B Z . $$ Let $\lambda=\frac{X Z}{A C}=\frac{T Y}{A C}$. Since $X A C Z$ is cyclic, the triangles $Z B X$ and $A B C$ are similar, hence $$ \frac{X B}{B C}=\frac{B Z}{A B}=\frac{X Z}{A C}=\lambda . $$ It follows that $X B=\lambda B C$ and $B Z=\lambda A B$. Likewise, the triangles $T D Y$ and $A D C$ are similar, hence $$ \frac{D T}{A D}=\frac{D Y}{C D}=\frac{T Y}{A C}=\lambda $$ Therefore, (2) rewrites as $\lambda B C+\lambda A D=\lambda C D+\lambda A B$. This is equivalent to $B C+A D=C D+A B$ which is true as $A B C D$ is circumscribed. Comment 2. Here is a more difficult modification of the original problem, found by the PSC. Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Let $U=B C \cap A D$ and $V=B A \cap C D$. Let $I_{U}$ be the incentre of $U Y Z$ and let $J_{V}$ be the $V$-excentre of $V X T$. Then $I_{U} J_{V} \perp B D$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d245af55-4f94-5ed8-b33c-0da2f89add25
| 24,179
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\Omega$. Let the tangent to $\Omega$ at $D$ intersect the rays $B A$ and $B C$ at points $E$ and $F$, respectively. A point $T$ is chosen inside the triangle $A B C$ so that $T E \| C D$ and $T F \| A D$. Let $K \neq D$ be a point on the segment $D F$ such that $T D=T K$. Prove that the lines $A C, D T$ and $B K$ intersect at one point.
|
Let the segments $T E$ and $T F$ cross $A C$ at $P$ and $Q$, respectively. Since $P E \| C D$ and $E D$ is tangent to the circumcircle of $A B C D$, we have $$ \angle E P A=\angle D C A=\angle E D A, $$ and so the points $A, P, D$, and $E$ lie on some circle $\alpha$. Similarly, the points $C, Q, D$, and $F$ lie on some circle $\gamma$. We now want to prove that the line $D T$ is tangent to both $\alpha$ and $\gamma$ at $D$. Indeed, since $\angle F C D+\angle E A D=180^{\circ}$, the circles $\alpha$ and $\gamma$ are tangent to each other at $D$. To prove that $T$ lies on their common tangent line at $D$ (i.e., on their radical axis), it suffices to check that $T P \cdot T E=T Q \cdot T F$, or that the quadrilateral $P E F Q$ is cyclic. This fact follows from $$ \angle Q F E=\angle A D E=\angle A P E . $$ Since $T D=T K$, we have $\angle T K D=\angle T D K$. Next, as $T D$ and $D E$ are tangent to $\alpha$ and $\Omega$, respectively, we obtain $$ \angle T K D=\angle T D K=\angle E A D=\angle B D E, $$ which implies $T K \| B D$. Next we prove that the five points $T, P, Q, D$, and $K$ lie on some circle $\tau$. Indeed, since $T D$ is tangent to the circle $\alpha$ we have $$ \angle E P D=\angle T D F=\angle T K D, $$ which means that the point $P$ lies on the circle (TDK). Similarly, we have $Q \in(T D K)$. Finally, we prove that $P K \| B C$. Indeed, using the circles $\tau$ and $\gamma$ we conclude that $$ \angle P K D=\angle P Q D=\angle D F C, $$ which means that $P K \| B C$. Triangles $T P K$ and $D C B$ have pairwise parallel sides, which implies the fact that $T D, P C$ and $K B$ are concurrent, as desired. 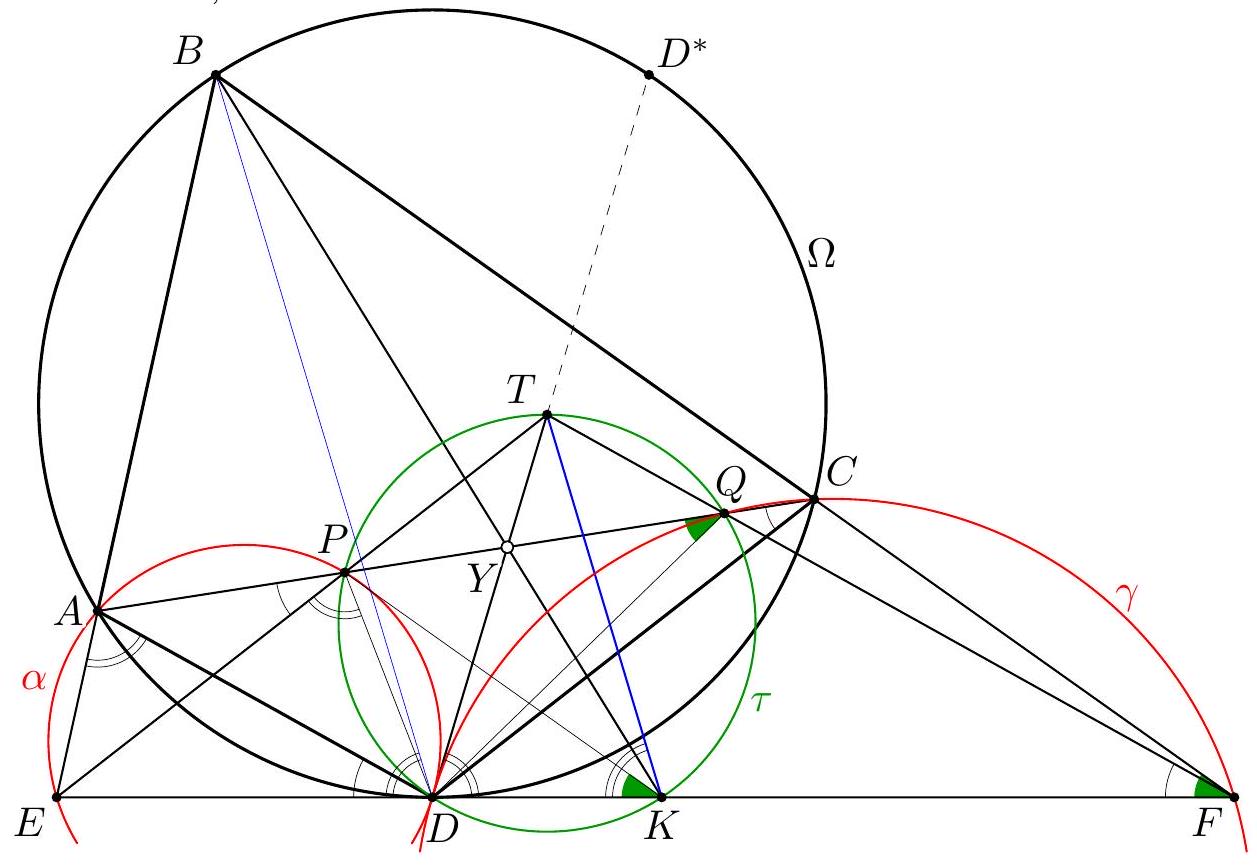 Comment 1. There are several variations of the above solution. E.g., after finding circles $\alpha$ and $\gamma$, one can notice that there exists a homothety $h$ mapping the triangle $T P Q$ to the triangle $D C A$; the centre of that homothety is $Y=A C \cap T D$. Since $$ \angle D P E=\angle D A E=\angle D C B=\angle D Q T, $$ the quadrilateral $T P D Q$ is inscribed in some circle $\tau$. We have $h(\tau)=\Omega$, so the point $D^{*}=h(D)$ lies on $\Omega$. Finally, by $$ \angle D C D^{*}=\angle T P D=\angle B A D, $$ the points $B$ and $D^{*}$ are symmetric with respect to the diameter of $\Omega$ passing through $D$. This yields $D B=D D^{*}$ and $B D^{*} \| E F$, so $h(K)=B$, and $B K$ passes through $Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\Omega$. Let the tangent to $\Omega$ at $D$ intersect the rays $B A$ and $B C$ at points $E$ and $F$, respectively. A point $T$ is chosen inside the triangle $A B C$ so that $T E \| C D$ and $T F \| A D$. Let $K \neq D$ be a point on the segment $D F$ such that $T D=T K$. Prove that the lines $A C, D T$ and $B K$ intersect at one point.
|
Let the segments $T E$ and $T F$ cross $A C$ at $P$ and $Q$, respectively. Since $P E \| C D$ and $E D$ is tangent to the circumcircle of $A B C D$, we have $$ \angle E P A=\angle D C A=\angle E D A, $$ and so the points $A, P, D$, and $E$ lie on some circle $\alpha$. Similarly, the points $C, Q, D$, and $F$ lie on some circle $\gamma$. We now want to prove that the line $D T$ is tangent to both $\alpha$ and $\gamma$ at $D$. Indeed, since $\angle F C D+\angle E A D=180^{\circ}$, the circles $\alpha$ and $\gamma$ are tangent to each other at $D$. To prove that $T$ lies on their common tangent line at $D$ (i.e., on their radical axis), it suffices to check that $T P \cdot T E=T Q \cdot T F$, or that the quadrilateral $P E F Q$ is cyclic. This fact follows from $$ \angle Q F E=\angle A D E=\angle A P E . $$ Since $T D=T K$, we have $\angle T K D=\angle T D K$. Next, as $T D$ and $D E$ are tangent to $\alpha$ and $\Omega$, respectively, we obtain $$ \angle T K D=\angle T D K=\angle E A D=\angle B D E, $$ which implies $T K \| B D$. Next we prove that the five points $T, P, Q, D$, and $K$ lie on some circle $\tau$. Indeed, since $T D$ is tangent to the circle $\alpha$ we have $$ \angle E P D=\angle T D F=\angle T K D, $$ which means that the point $P$ lies on the circle (TDK). Similarly, we have $Q \in(T D K)$. Finally, we prove that $P K \| B C$. Indeed, using the circles $\tau$ and $\gamma$ we conclude that $$ \angle P K D=\angle P Q D=\angle D F C, $$ which means that $P K \| B C$. Triangles $T P K$ and $D C B$ have pairwise parallel sides, which implies the fact that $T D, P C$ and $K B$ are concurrent, as desired.  Comment 1. There are several variations of the above solution. E.g., after finding circles $\alpha$ and $\gamma$, one can notice that there exists a homothety $h$ mapping the triangle $T P Q$ to the triangle $D C A$; the centre of that homothety is $Y=A C \cap T D$. Since $$ \angle D P E=\angle D A E=\angle D C B=\angle D Q T, $$ the quadrilateral $T P D Q$ is inscribed in some circle $\tau$. We have $h(\tau)=\Omega$, so the point $D^{*}=h(D)$ lies on $\Omega$. Finally, by $$ \angle D C D^{*}=\angle T P D=\angle B A D, $$ the points $B$ and $D^{*}$ are symmetric with respect to the diameter of $\Omega$ passing through $D$. This yields $D B=D D^{*}$ and $B D^{*} \| E F$, so $h(K)=B$, and $B K$ passes through $Y$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e5aaeed-78da-52ef-b848-e96334472f3d
| 24,184
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\Omega$. Let the tangent to $\Omega$ at $D$ intersect the rays $B A$ and $B C$ at points $E$ and $F$, respectively. A point $T$ is chosen inside the triangle $A B C$ so that $T E \| C D$ and $T F \| A D$. Let $K \neq D$ be a point on the segment $D F$ such that $T D=T K$. Prove that the lines $A C, D T$ and $B K$ intersect at one point.
|
Consider the spiral similarity $\phi$ centred at $D$ which maps $B$ to $F$. Recall that for any two points $X$ and $Y$, the triangles $D X \phi(X)$ and $D Y \phi(Y)$ are similar. Define $T^{\prime}=\phi(E)$. Then $$ \angle C D F=\angle F B D=\angle \phi(B) B D=\angle \phi(E) E D=\angle T^{\prime} E D, $$ so $C D \| T^{\prime} E$. Using the fact that $D E$ is tangent to $(A B D)$ and then applying $\phi$ we infer $$ \angle A D E=\angle A B D=\angle T^{\prime} F D, $$ so $A D \| T^{\prime} F$; hence $T^{\prime}$ coincides with $T$. Therefore, $$ \angle B D E=\angle F D T=\angle D K T, $$ whence $T K \| B D$. Let $B K \cap T D=X, A C \cap T D=Y$, and $A C \cap T F=Q$. Notice that $T K \| B D$ implies $$ \frac{T X}{X D}=\frac{T K}{B D}=\frac{T D}{B D} $$ So we wish to prove that $\frac{T Y}{Y D}$ is equal to the same ratio. We first show that $\phi(A)=Q$. Indeed, $$ \angle D A \phi(A)=\angle D B F=\angle D A C, $$ and so $\phi(A) \in A C$. Together with $\phi(A) \in \phi(E B)=T F$ this yields $\phi(A)=Q$. It follows that $$ \frac{T Q}{A E}=\frac{T D}{E D} $$  Now, since $T F \| A D$ and $\triangle E A D \sim \triangle E D B$, we have $$ \frac{T Y}{Y D}=\frac{T Q}{A D}=\frac{T Q}{A E} \cdot \frac{A E}{A D}=\frac{T D}{E D} \cdot \frac{E D}{B D}=\frac{T D}{B D} $$ which completes the proof. Comment 2. The point $D$ is the Miquel point for any 4 of the 5 lines $B A, B C, T E, T F$ and $A C$. Essentially, this is proved in both solutions by different methods.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\Omega$. Let the tangent to $\Omega$ at $D$ intersect the rays $B A$ and $B C$ at points $E$ and $F$, respectively. A point $T$ is chosen inside the triangle $A B C$ so that $T E \| C D$ and $T F \| A D$. Let $K \neq D$ be a point on the segment $D F$ such that $T D=T K$. Prove that the lines $A C, D T$ and $B K$ intersect at one point.
|
Consider the spiral similarity $\phi$ centred at $D$ which maps $B$ to $F$. Recall that for any two points $X$ and $Y$, the triangles $D X \phi(X)$ and $D Y \phi(Y)$ are similar. Define $T^{\prime}=\phi(E)$. Then $$ \angle C D F=\angle F B D=\angle \phi(B) B D=\angle \phi(E) E D=\angle T^{\prime} E D, $$ so $C D \| T^{\prime} E$. Using the fact that $D E$ is tangent to $(A B D)$ and then applying $\phi$ we infer $$ \angle A D E=\angle A B D=\angle T^{\prime} F D, $$ so $A D \| T^{\prime} F$; hence $T^{\prime}$ coincides with $T$. Therefore, $$ \angle B D E=\angle F D T=\angle D K T, $$ whence $T K \| B D$. Let $B K \cap T D=X, A C \cap T D=Y$, and $A C \cap T F=Q$. Notice that $T K \| B D$ implies $$ \frac{T X}{X D}=\frac{T K}{B D}=\frac{T D}{B D} $$ So we wish to prove that $\frac{T Y}{Y D}$ is equal to the same ratio. We first show that $\phi(A)=Q$. Indeed, $$ \angle D A \phi(A)=\angle D B F=\angle D A C, $$ and so $\phi(A) \in A C$. Together with $\phi(A) \in \phi(E B)=T F$ this yields $\phi(A)=Q$. It follows that $$ \frac{T Q}{A E}=\frac{T D}{E D} $$  Now, since $T F \| A D$ and $\triangle E A D \sim \triangle E D B$, we have $$ \frac{T Y}{Y D}=\frac{T Q}{A D}=\frac{T Q}{A E} \cdot \frac{A E}{A D}=\frac{T D}{E D} \cdot \frac{E D}{B D}=\frac{T D}{B D} $$ which completes the proof. Comment 2. The point $D$ is the Miquel point for any 4 of the 5 lines $B A, B C, T E, T F$ and $A C$. Essentially, this is proved in both solutions by different methods.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e5aaeed-78da-52ef-b848-e96334472f3d
| 24,184
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$.
|
Let the diagonals $A C$ and $B D$ cross at $H$. Consider the homothety $h$ centred at $H$ and mapping $B$ to $D$. Since $B D_{1} \| D B_{1}$, we have $h\left(D_{1}\right)=B_{1}$. Let the tangents to $\Omega$ at $B$ and $D$ meet $A C$ at $L_{B}$ and $L_{D}$, respectively. We have $$ \angle L_{B} B B_{1}=\angle L_{B} B C+\angle C B B_{1}=\angle B A L_{B}+\angle B_{1} B A=\angle B B_{1} L_{B}, $$ which means that the triangle $L_{B} B B_{1}$ is isosceles, $L_{B} B=L_{B} B_{1}$. The powers of $L_{B}$ with respect to $\Omega$ and $\gamma_{D}$ are $L_{B} B^{2}$ and $L_{B} B_{1}^{2}$, respectively; so they are equal, whence $L_{B}$ lies on the radical axis $T_{D} D$ of those two circles. Similarly, $L_{D}$ lies on the radical axis $T_{B} B$ of $\Omega$ and $\gamma_{B}$. By the sine rule in the triangle $B H L_{B}$, we obtain $$ \frac{H L_{B}}{\sin \angle H B L_{B}}=\frac{B L_{B}}{\sin \angle B H L_{B}}=\frac{B_{1} L_{B}}{\sin \angle B H L_{B}} $$ similarly, $$ \frac{H L_{D}}{\sin \angle H D L_{D}}=\frac{D L_{D}}{\sin \angle D H L_{D}}=\frac{D_{1} L_{D}}{\sin \angle D H L_{D}} $$ Clearly, $\angle B H L_{B}=\angle D H L_{D}$. In the circle $\Omega$, tangent lines $B L_{B}$ and $D L_{D}$ form equal angles with the chord $B D$, so $\sin \angle H B L_{B}=\sin \angle H D L_{D}$ (this equality does not depend on the picture). Thus, dividing (2) by (3) we get $$ \frac{H L_{B}}{H L_{D}}=\frac{B_{1} L_{B}}{D_{1} L_{D}}, \quad \text { and hence } \quad \frac{H L_{B}}{H L_{D}}=\frac{H L_{B}-B_{1} L_{B}}{H L_{D}-D_{1} L_{D}}=\frac{H B_{1}}{H D_{1}} $$ Since $h\left(D_{1}\right)=B_{1}$, the obtained relation yields $h\left(L_{D}\right)=L_{B}$, so $h$ maps the line $L_{D} B$ to $L_{B} D$, and these lines are parallel, as desired.  Comment 2. In the solution above, the key relation $h\left(L_{D}\right)=L_{B}$ was obtained via a short computation in sines. Here we present an alternative, pure synthetical way of establishing that. Let the external bisectors of $\angle A B C$ and $\angle A D C$ cross $A C$ at $B_{2}$ and $D_{2}$, respectively; assume that $\overparen{A B}>\overparen{C B}$. In the right-angled triangle $B B_{1} B_{2}$, the point $L_{B}$ is a point on the hypothenuse such that $L_{B} B_{1}=L_{B} B$, so $L_{B}$ is the midpoint of $B_{1} B_{2}$. Since $D D_{1}$ is the internal angle bisector of $\angle A D C$, we have $$ \angle B D D_{1}=\frac{\angle B D A-\angle C D B}{2}=\frac{\angle B C A-\angle C A B}{2}=\angle B B_{2} D_{1}, $$ so the points $B, B_{2}, D$, and $D_{1}$ lie on some circle $\omega_{B}$. Similarly, $L_{D}$ is the midpoint of $D_{1} D_{2}$, and the points $D, D_{2}, B$, and $B_{1}$ lie on some circle $\omega_{D}$. Now we have $$ \angle B_{2} D B_{1}=\angle B_{2} D B-\angle B_{1} D B=\angle B_{2} D_{1} B-\angle B_{1} D_{2} B=\angle D_{2} B D_{1} . $$ Therefore, the corresponding sides of the triangles $D B_{1} B_{2}$ and $B D_{1} D_{2}$ are parallel, and the triangles are homothetical (in $H$ ). So their corresponding medians $D L_{B}$ and $B L_{D}$ are also parallel. 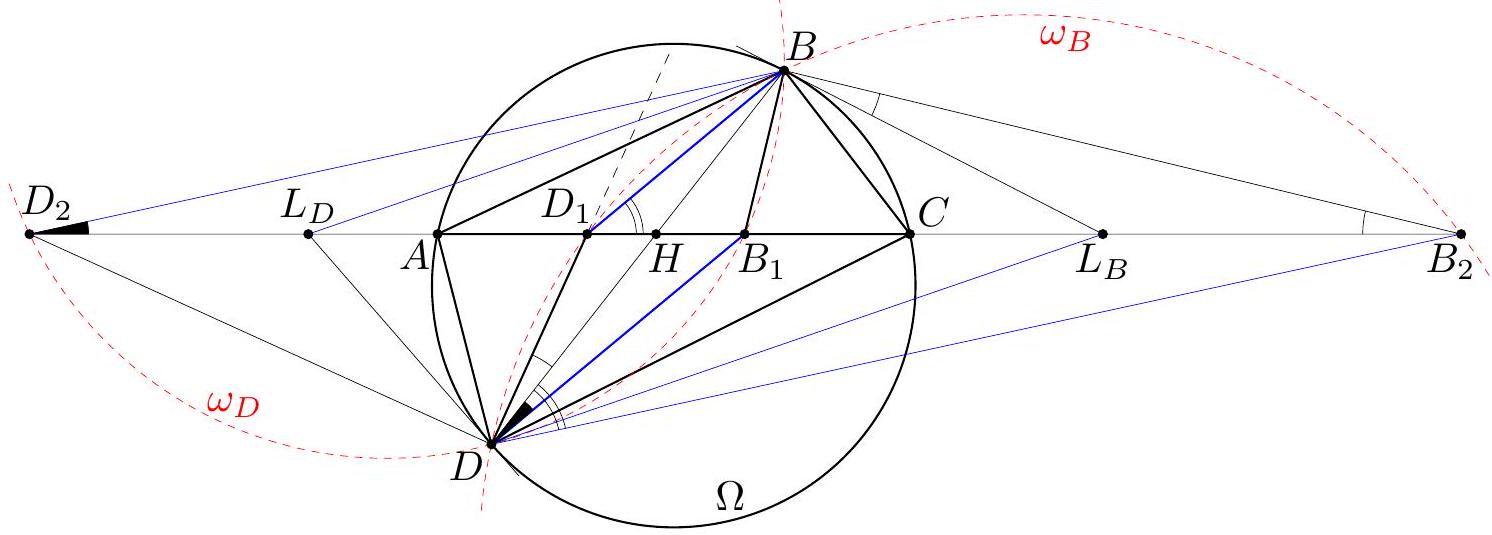 Yet alternatively, after obtaining the circles $\omega_{B}$ and $\omega_{D}$, one may notice that $H$ lies on their radical axis $B D$, whence $H B_{1} \cdot H D_{2}=H D_{1} \cdot H B_{2}$, or $$ \frac{H B_{1}}{H D_{1}}=\frac{H B_{2}}{H D_{1}} . $$ Since $h\left(D_{1}\right)=B_{1}$, this yields $h\left(D_{2}\right)=B_{2}$ and hence $h\left(L_{D}\right)=L_{B}$. Comment 3. Since $h$ preserves the line $A C$ and maps $B \mapsto D$ and $D_{1} \mapsto B_{1}$, we have $h\left(\gamma_{B}\right)=\gamma_{D}$. Therefore, $h\left(O_{B}\right)=O_{D}$; in particular, $H$ also lies on $O_{B} O_{D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$.
|
Let the diagonals $A C$ and $B D$ cross at $H$. Consider the homothety $h$ centred at $H$ and mapping $B$ to $D$. Since $B D_{1} \| D B_{1}$, we have $h\left(D_{1}\right)=B_{1}$. Let the tangents to $\Omega$ at $B$ and $D$ meet $A C$ at $L_{B}$ and $L_{D}$, respectively. We have $$ \angle L_{B} B B_{1}=\angle L_{B} B C+\angle C B B_{1}=\angle B A L_{B}+\angle B_{1} B A=\angle B B_{1} L_{B}, $$ which means that the triangle $L_{B} B B_{1}$ is isosceles, $L_{B} B=L_{B} B_{1}$. The powers of $L_{B}$ with respect to $\Omega$ and $\gamma_{D}$ are $L_{B} B^{2}$ and $L_{B} B_{1}^{2}$, respectively; so they are equal, whence $L_{B}$ lies on the radical axis $T_{D} D$ of those two circles. Similarly, $L_{D}$ lies on the radical axis $T_{B} B$ of $\Omega$ and $\gamma_{B}$. By the sine rule in the triangle $B H L_{B}$, we obtain $$ \frac{H L_{B}}{\sin \angle H B L_{B}}=\frac{B L_{B}}{\sin \angle B H L_{B}}=\frac{B_{1} L_{B}}{\sin \angle B H L_{B}} $$ similarly, $$ \frac{H L_{D}}{\sin \angle H D L_{D}}=\frac{D L_{D}}{\sin \angle D H L_{D}}=\frac{D_{1} L_{D}}{\sin \angle D H L_{D}} $$ Clearly, $\angle B H L_{B}=\angle D H L_{D}$. In the circle $\Omega$, tangent lines $B L_{B}$ and $D L_{D}$ form equal angles with the chord $B D$, so $\sin \angle H B L_{B}=\sin \angle H D L_{D}$ (this equality does not depend on the picture). Thus, dividing (2) by (3) we get $$ \frac{H L_{B}}{H L_{D}}=\frac{B_{1} L_{B}}{D_{1} L_{D}}, \quad \text { and hence } \quad \frac{H L_{B}}{H L_{D}}=\frac{H L_{B}-B_{1} L_{B}}{H L_{D}-D_{1} L_{D}}=\frac{H B_{1}}{H D_{1}} $$ Since $h\left(D_{1}\right)=B_{1}$, the obtained relation yields $h\left(L_{D}\right)=L_{B}$, so $h$ maps the line $L_{D} B$ to $L_{B} D$, and these lines are parallel, as desired.  Comment 2. In the solution above, the key relation $h\left(L_{D}\right)=L_{B}$ was obtained via a short computation in sines. Here we present an alternative, pure synthetical way of establishing that. Let the external bisectors of $\angle A B C$ and $\angle A D C$ cross $A C$ at $B_{2}$ and $D_{2}$, respectively; assume that $\overparen{A B}>\overparen{C B}$. In the right-angled triangle $B B_{1} B_{2}$, the point $L_{B}$ is a point on the hypothenuse such that $L_{B} B_{1}=L_{B} B$, so $L_{B}$ is the midpoint of $B_{1} B_{2}$. Since $D D_{1}$ is the internal angle bisector of $\angle A D C$, we have $$ \angle B D D_{1}=\frac{\angle B D A-\angle C D B}{2}=\frac{\angle B C A-\angle C A B}{2}=\angle B B_{2} D_{1}, $$ so the points $B, B_{2}, D$, and $D_{1}$ lie on some circle $\omega_{B}$. Similarly, $L_{D}$ is the midpoint of $D_{1} D_{2}$, and the points $D, D_{2}, B$, and $B_{1}$ lie on some circle $\omega_{D}$. Now we have $$ \angle B_{2} D B_{1}=\angle B_{2} D B-\angle B_{1} D B=\angle B_{2} D_{1} B-\angle B_{1} D_{2} B=\angle D_{2} B D_{1} . $$ Therefore, the corresponding sides of the triangles $D B_{1} B_{2}$ and $B D_{1} D_{2}$ are parallel, and the triangles are homothetical (in $H$ ). So their corresponding medians $D L_{B}$ and $B L_{D}$ are also parallel.  Yet alternatively, after obtaining the circles $\omega_{B}$ and $\omega_{D}$, one may notice that $H$ lies on their radical axis $B D$, whence $H B_{1} \cdot H D_{2}=H D_{1} \cdot H B_{2}$, or $$ \frac{H B_{1}}{H D_{1}}=\frac{H B_{2}}{H D_{1}} . $$ Since $h\left(D_{1}\right)=B_{1}$, this yields $h\left(D_{2}\right)=B_{2}$ and hence $h\left(L_{D}\right)=L_{B}$. Comment 3. Since $h$ preserves the line $A C$ and maps $B \mapsto D$ and $D_{1} \mapsto B_{1}$, we have $h\left(\gamma_{B}\right)=\gamma_{D}$. Therefore, $h\left(O_{B}\right)=O_{D}$; in particular, $H$ also lies on $O_{B} O_{D}$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5686dd9e-802c-5b66-b5fd-c3ed2189a6c9
| 24,189
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$.
|
Let $B D_{1}$ and $T_{B} D_{1}$ meet $\Omega$ again at $X_{B}$ and $Y_{B}$, respectively. Then $$ \angle B D_{1} C=\angle B T_{B} D_{1}=\angle B T_{B} Y_{B}=\angle B X_{B} Y_{B} $$ which shows that $X_{B} Y_{B} \| A C$. Similarly, let $D B_{1}$ and $T_{D} B_{1}$ meet $\Omega$ again at $X_{D}$ and $Y_{D}$, respectively; then $X_{D} Y_{D} \| A C$. Let $M_{D}$ and $M_{B}$ be the midpoints of the arcs $A B C$ and $A D C$, respectively; then the points $D_{1}$ and $B_{1}$ lie on $D M_{D}$ and $B M_{B}$, respectively. Let $K$ be the midpoint of $A C$ (which lies on $M_{B} M_{D}$ ). Applying Pascal's theorem to $M_{D} D X_{D} X_{B} B M_{B}$, we obtain that the points $D_{1}=M_{D} D \cap X_{B} B, B_{1}=D X_{D} \cap B M_{B}$, and $X_{D} X_{B} \cap M_{B} M_{D}$ are collinear, which means that $X_{B} X_{D}$ passes through $K$. Due to symmetry, the diagonals of an isosceles trapezoid $X_{B} Y_{B} X_{D} Y_{D}$ cross at $K$. 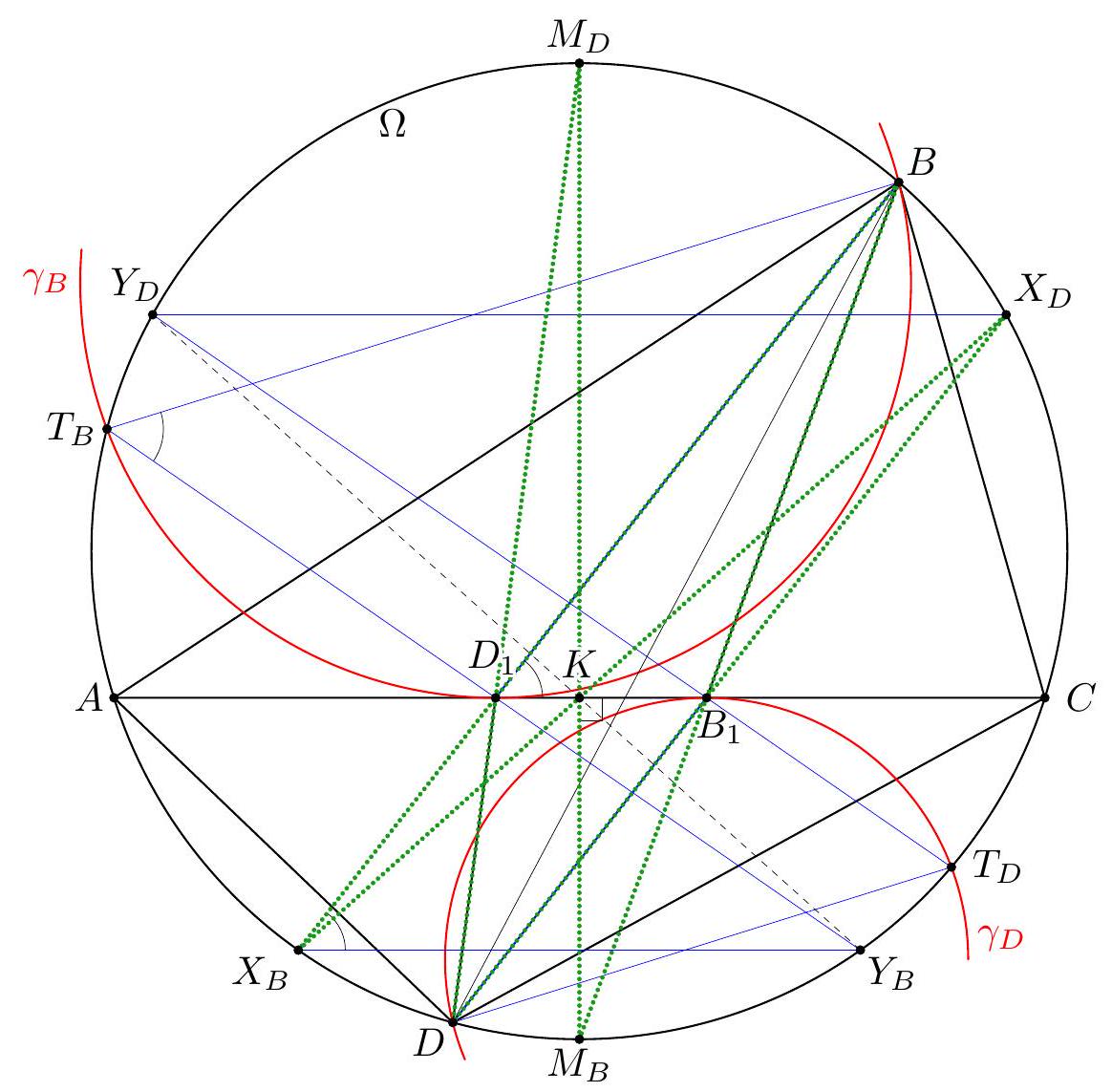 Let $b$ and $d$ denote the distances from the lines $X_{B} Y_{B}$ and $X_{D} Y_{D}$, respectively, to $A C$. Then we get $$ \frac{X_{B} Y_{B}}{X_{D} Y_{D}}=\frac{b}{d}=\frac{D_{1} X_{B}}{B_{1} X_{D}} $$ where the second equation holds in view of $D_{1} X_{B} \| B_{1} X_{D}$. Therefore, the triangles $D_{1} X_{B} Y_{B}$ and $B_{1} X_{D} Y_{D}$ are similar. The triangles $D_{1} T_{B} B$ and $B_{1} T_{D} D$ are similar to them and hence to each other. Since $B D_{1} \| D B_{1}$, these triangles are also homothetical. This yields $B T_{B} \| D T_{D}$, as desired. Comment 4. The original problem proposal asked to prove that the relations $B D_{1} \| D B_{1}$ and $O \in O_{1} O_{2}$ are equivalent. After obtaining $B D_{1} \| D B_{1} \Rightarrow O \in O_{1} O_{2}$, the converse proof is either repeated backwards mutatis mutandis, or can be obtained by the usual procedure of varying some points in the construction. The Problem Selection Committee chose the current version, because it is less technical, yet keeps most of the ideas.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$.
|
Let $B D_{1}$ and $T_{B} D_{1}$ meet $\Omega$ again at $X_{B}$ and $Y_{B}$, respectively. Then $$ \angle B D_{1} C=\angle B T_{B} D_{1}=\angle B T_{B} Y_{B}=\angle B X_{B} Y_{B} $$ which shows that $X_{B} Y_{B} \| A C$. Similarly, let $D B_{1}$ and $T_{D} B_{1}$ meet $\Omega$ again at $X_{D}$ and $Y_{D}$, respectively; then $X_{D} Y_{D} \| A C$. Let $M_{D}$ and $M_{B}$ be the midpoints of the arcs $A B C$ and $A D C$, respectively; then the points $D_{1}$ and $B_{1}$ lie on $D M_{D}$ and $B M_{B}$, respectively. Let $K$ be the midpoint of $A C$ (which lies on $M_{B} M_{D}$ ). Applying Pascal's theorem to $M_{D} D X_{D} X_{B} B M_{B}$, we obtain that the points $D_{1}=M_{D} D \cap X_{B} B, B_{1}=D X_{D} \cap B M_{B}$, and $X_{D} X_{B} \cap M_{B} M_{D}$ are collinear, which means that $X_{B} X_{D}$ passes through $K$. Due to symmetry, the diagonals of an isosceles trapezoid $X_{B} Y_{B} X_{D} Y_{D}$ cross at $K$.  Let $b$ and $d$ denote the distances from the lines $X_{B} Y_{B}$ and $X_{D} Y_{D}$, respectively, to $A C$. Then we get $$ \frac{X_{B} Y_{B}}{X_{D} Y_{D}}=\frac{b}{d}=\frac{D_{1} X_{B}}{B_{1} X_{D}} $$ where the second equation holds in view of $D_{1} X_{B} \| B_{1} X_{D}$. Therefore, the triangles $D_{1} X_{B} Y_{B}$ and $B_{1} X_{D} Y_{D}$ are similar. The triangles $D_{1} T_{B} B$ and $B_{1} T_{D} D$ are similar to them and hence to each other. Since $B D_{1} \| D B_{1}$, these triangles are also homothetical. This yields $B T_{B} \| D T_{D}$, as desired. Comment 4. The original problem proposal asked to prove that the relations $B D_{1} \| D B_{1}$ and $O \in O_{1} O_{2}$ are equivalent. After obtaining $B D_{1} \| D B_{1} \Rightarrow O \in O_{1} O_{2}$, the converse proof is either repeated backwards mutatis mutandis, or can be obtained by the usual procedure of varying some points in the construction. The Problem Selection Committee chose the current version, because it is less technical, yet keeps most of the ideas.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5686dd9e-802c-5b66-b5fd-c3ed2189a6c9
| 24,189
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent.
|
Let $T A$ intersect the circle $(A B C)$ again at $M$. Due to the circles ( $B C E F$ ) and $(A M C B)$, and using the above Claim, we get $T M \cdot T A=T F \cdot T E=T B \cdot T C=T D^{2}$; in particular, the points $A, M, E$, and $F$ are concyclic. Under the inversion with centre $T$ and radius $T D$, the point $M$ maps to $A$, and $B$ maps to $C$, which implies that the circle $(M B D)$ maps to the circle $(A D C)$. Their common point $D$ lies on the circle of the inversion, so the second intersection point $K$ also lies on that circle, which means $T K=T D$. It follows that the point $T$ and the centres of the circles ( $K D E$ ) and $(A D C)$ lie on the perpendicular bisector of $K D$. Since the center of $(A D C)$ is $O_{1}$, it suffices to show now that the points $D, K, E$, and $X$ are concyclic (the center of the corresponding circle will be $O_{2}$ ). The lines $B M, D K$, and $A C$ are the pairwise radical axes of the circles $(A B C M),(A C D K)$ and $(B M D K)$, so they are concurrent at some point $P$. Also, $M$ lies on the circle $(A E F)$, thus $$ \begin{aligned} \Varangle(E X, X B) & =\Varangle(C X, X B)=\Varangle(X C, B C)+\Varangle(B C, B X)=2 \Varangle(A C, C B) \\ & =\Varangle(A C, C B)+\Varangle(E F, F A)=\Varangle(A M, B M)+\Varangle(E M, M A)=\Varangle(E M, B M), \end{aligned} $$ so the points $M, E, X$, and $B$ are concyclic. Therefore, $P E \cdot P X=P M \cdot P B=P K \cdot P D$, so the points $E, K, D$, and $X$ are concyclic, as desired. 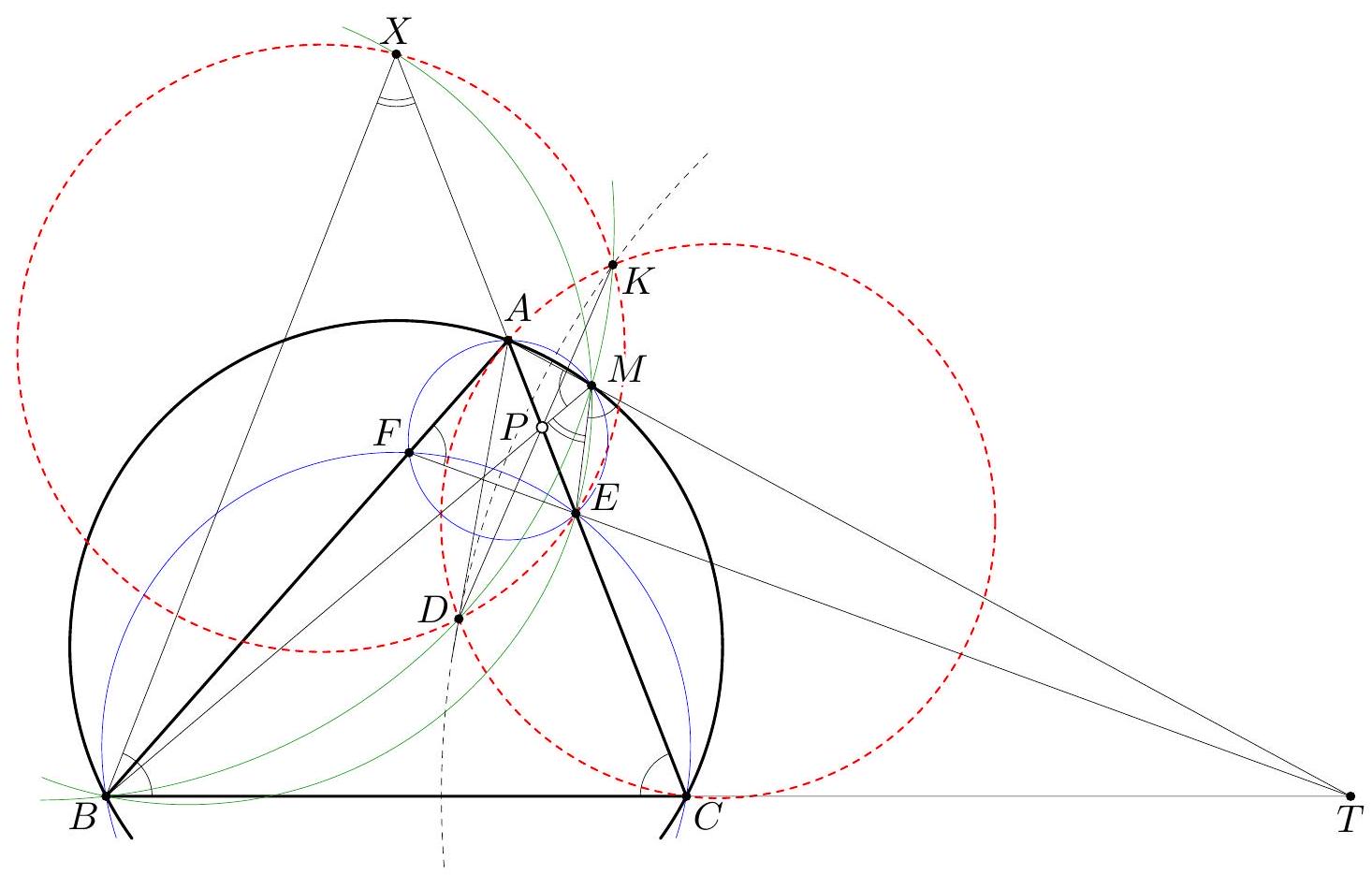 Comment 1. We present here a different solution which uses similar ideas. Perform the inversion $\iota$ with centre $T$ and radius $T D$. It swaps $B$ with $C$ and $E$ with $F$; the point $D$ maps to itself. Let $X^{\prime}=\iota(X)$. Observe that the points $E, F, X$, and $X^{\prime}$ are concyclic, as well as the points $B, C, X$, and $X^{\prime}$. Then $$ \begin{aligned} & \Varangle\left(C X^{\prime}, X^{\prime} F\right)=\Varangle\left(C X^{\prime}, X^{\prime} X\right)+\Varangle\left(X^{\prime} X, X^{\prime} F\right)=\Varangle(C B, B X)+\Varangle(E X, E F) \\ &=\Varangle(X C, C B)+\Varangle(E C, E F)=\Varangle(C A, C B)+\Varangle(B C, B F)=\Varangle(C A, A F), \end{aligned} $$ therefore the points $C, X^{\prime}, A$, and $F$ are concyclic. Let $X^{\prime} F$ intersect $A C$ at $P$, and let $K$ be the second common point of $D P$ and the circle $(A C D)$. Then $$ P K \cdot P D=P A \cdot P C=P X^{\prime} \cdot P F=P E \cdot P X $$ hence, the points $K, X, D$, and $E$ lie on some circle $\omega_{1}$, while the points $K, X^{\prime}, D$, and $F$ lie on some circle $\omega_{2}$. (These circles are distinct since $\angle E X F+\angle E D F<\angle E A F+\angle D C B+\angle D B C<180^{\circ}$ ). The inversion $\iota$ swaps $\omega_{1}$ with $\omega_{2}$ and fixes their common point $D$, so it fixes their second common point $K$. Thus $T D=T K$ and the perpendicular bisector of $D K$ passes through $T$, as well as through the centres of the circles $(C D K A)$ and $(D E K X)$. 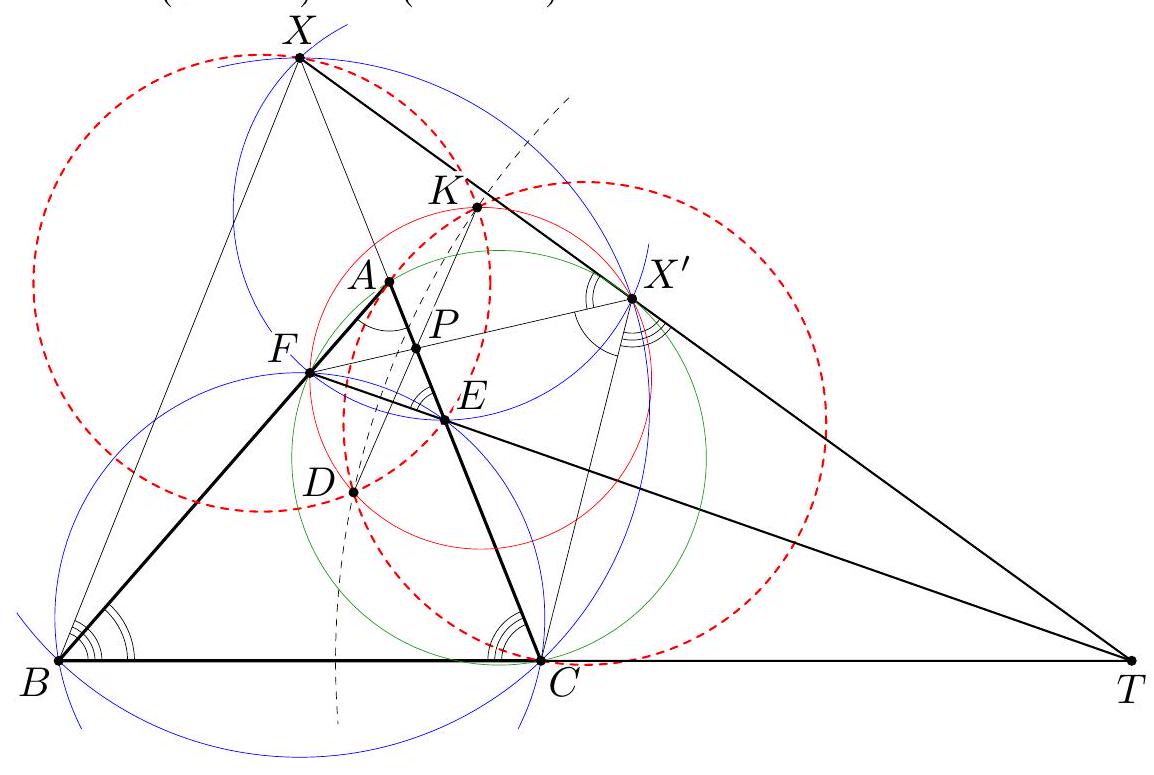
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent.
|
Let $T A$ intersect the circle $(A B C)$ again at $M$. Due to the circles ( $B C E F$ ) and $(A M C B)$, and using the above Claim, we get $T M \cdot T A=T F \cdot T E=T B \cdot T C=T D^{2}$; in particular, the points $A, M, E$, and $F$ are concyclic. Under the inversion with centre $T$ and radius $T D$, the point $M$ maps to $A$, and $B$ maps to $C$, which implies that the circle $(M B D)$ maps to the circle $(A D C)$. Their common point $D$ lies on the circle of the inversion, so the second intersection point $K$ also lies on that circle, which means $T K=T D$. It follows that the point $T$ and the centres of the circles ( $K D E$ ) and $(A D C)$ lie on the perpendicular bisector of $K D$. Since the center of $(A D C)$ is $O_{1}$, it suffices to show now that the points $D, K, E$, and $X$ are concyclic (the center of the corresponding circle will be $O_{2}$ ). The lines $B M, D K$, and $A C$ are the pairwise radical axes of the circles $(A B C M),(A C D K)$ and $(B M D K)$, so they are concurrent at some point $P$. Also, $M$ lies on the circle $(A E F)$, thus $$ \begin{aligned} \Varangle(E X, X B) & =\Varangle(C X, X B)=\Varangle(X C, B C)+\Varangle(B C, B X)=2 \Varangle(A C, C B) \\ & =\Varangle(A C, C B)+\Varangle(E F, F A)=\Varangle(A M, B M)+\Varangle(E M, M A)=\Varangle(E M, B M), \end{aligned} $$ so the points $M, E, X$, and $B$ are concyclic. Therefore, $P E \cdot P X=P M \cdot P B=P K \cdot P D$, so the points $E, K, D$, and $X$ are concyclic, as desired.  Comment 1. We present here a different solution which uses similar ideas. Perform the inversion $\iota$ with centre $T$ and radius $T D$. It swaps $B$ with $C$ and $E$ with $F$; the point $D$ maps to itself. Let $X^{\prime}=\iota(X)$. Observe that the points $E, F, X$, and $X^{\prime}$ are concyclic, as well as the points $B, C, X$, and $X^{\prime}$. Then $$ \begin{aligned} & \Varangle\left(C X^{\prime}, X^{\prime} F\right)=\Varangle\left(C X^{\prime}, X^{\prime} X\right)+\Varangle\left(X^{\prime} X, X^{\prime} F\right)=\Varangle(C B, B X)+\Varangle(E X, E F) \\ &=\Varangle(X C, C B)+\Varangle(E C, E F)=\Varangle(C A, C B)+\Varangle(B C, B F)=\Varangle(C A, A F), \end{aligned} $$ therefore the points $C, X^{\prime}, A$, and $F$ are concyclic. Let $X^{\prime} F$ intersect $A C$ at $P$, and let $K$ be the second common point of $D P$ and the circle $(A C D)$. Then $$ P K \cdot P D=P A \cdot P C=P X^{\prime} \cdot P F=P E \cdot P X $$ hence, the points $K, X, D$, and $E$ lie on some circle $\omega_{1}$, while the points $K, X^{\prime}, D$, and $F$ lie on some circle $\omega_{2}$. (These circles are distinct since $\angle E X F+\angle E D F<\angle E A F+\angle D C B+\angle D B C<180^{\circ}$ ). The inversion $\iota$ swaps $\omega_{1}$ with $\omega_{2}$ and fixes their common point $D$, so it fixes their second common point $K$. Thus $T D=T K$ and the perpendicular bisector of $D K$ passes through $T$, as well as through the centres of the circles $(C D K A)$ and $(D E K X)$. 
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
034ea97d-ab12-5d31-9449-dfdfaaa65f24
| 24,196
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent.
|
We use only the first part of the Common remarks, namely, the facts that the tuples $(C, D, Q, E)$ and $(B, C, E, F)$ are both concyclic. We also introduce the point $T=$ $B C \cap E F$. Let the circle $(C D E)$ meet $B C$ again at $E_{1}$. Since $\angle E_{1} C Q=\angle D C E$, the $\operatorname{arcs} D E$ and $Q E_{1}$ of the circle $(C D Q)$ are equal, so $D Q \| E E_{1}$. Since $B F E C$ is cyclic, the line $A D$ forms equal angles with $B C$ and $E F$, hence so does $E E_{1}$. Therefore, the triangle $E E_{1} T$ is isosceles, $T E=T E_{1}$, and $T$ lies on the common perpendicular bisector of $E E_{1}$ and $D Q$. Let $U$ and $V$ be the centres of circles $(A D E)$ and $(C D Q E)$, respectively. Then $U O_{1}$ is the perpendicular bisector of $A D$. Moreover, the points $U, V$, and $O_{2}$ belong to the perpendicular bisector of $D E$. Since $U O_{1} \| V T$, in order to show that $O_{1} O_{2}$ passes through $T$, it suffices to show that $$ \frac{O_{2} U}{O_{2} V}=\frac{O_{1} U}{T V} $$ Denote angles $A, B$, and $C$ of the triangle $A B C$ by $\alpha, \beta$, and $\gamma$, respectively. Projecting onto $A C$ we obtain $$ \frac{O_{2} U}{O_{2} V}=\frac{(X E-A E) / 2}{(X E+E C) / 2}=\frac{A X}{C X}=\frac{A X}{B X}=\frac{\sin (\gamma-\beta)}{\sin \alpha} $$ The projection of $O_{1} U$ onto $A C$ is $(A C-A E) / 2=C E / 2$; the angle between $O_{1} U$ and $A C$ is $90^{\circ}-\alpha / 2$, so $$ \frac{O_{1} U}{E C}=\frac{1}{2 \sin (\alpha / 2)} $$ Next, we claim that $E, V, C$, and $T$ are concyclic. Indeed, the point $V$ lies on the perpendicular bisector of $C E$, as well as on the internal angle bisector of $\angle C T F$. Therefore, $V$ coincides with the midpoint of the arc $C E$ of the circle (TCE). Now we have $\angle E V C=2 \angle E E_{1} C=180^{\circ}-(\gamma-\beta)$ and $\angle V E T=\angle V E_{1} T=90^{\circ}-\angle E_{1} E C=$ $90^{\circ}-\alpha / 2$. Therefore, $$ \frac{E C}{T V}=\frac{\sin \angle E T C}{\sin \angle V E T}=\frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)} . $$  Recalling (2) and multiplying (3) and (4) we establish (1): $$ \frac{O_{2} U}{O_{2} V}=\frac{\sin (\gamma-\beta)}{\sin \alpha}=\frac{1}{2 \sin (\alpha / 2)} \cdot \frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)}=\frac{O_{1} U}{E C} \cdot \frac{E C}{T V}=\frac{O_{1} U}{T V} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent.
|
We use only the first part of the Common remarks, namely, the facts that the tuples $(C, D, Q, E)$ and $(B, C, E, F)$ are both concyclic. We also introduce the point $T=$ $B C \cap E F$. Let the circle $(C D E)$ meet $B C$ again at $E_{1}$. Since $\angle E_{1} C Q=\angle D C E$, the $\operatorname{arcs} D E$ and $Q E_{1}$ of the circle $(C D Q)$ are equal, so $D Q \| E E_{1}$. Since $B F E C$ is cyclic, the line $A D$ forms equal angles with $B C$ and $E F$, hence so does $E E_{1}$. Therefore, the triangle $E E_{1} T$ is isosceles, $T E=T E_{1}$, and $T$ lies on the common perpendicular bisector of $E E_{1}$ and $D Q$. Let $U$ and $V$ be the centres of circles $(A D E)$ and $(C D Q E)$, respectively. Then $U O_{1}$ is the perpendicular bisector of $A D$. Moreover, the points $U, V$, and $O_{2}$ belong to the perpendicular bisector of $D E$. Since $U O_{1} \| V T$, in order to show that $O_{1} O_{2}$ passes through $T$, it suffices to show that $$ \frac{O_{2} U}{O_{2} V}=\frac{O_{1} U}{T V} $$ Denote angles $A, B$, and $C$ of the triangle $A B C$ by $\alpha, \beta$, and $\gamma$, respectively. Projecting onto $A C$ we obtain $$ \frac{O_{2} U}{O_{2} V}=\frac{(X E-A E) / 2}{(X E+E C) / 2}=\frac{A X}{C X}=\frac{A X}{B X}=\frac{\sin (\gamma-\beta)}{\sin \alpha} $$ The projection of $O_{1} U$ onto $A C$ is $(A C-A E) / 2=C E / 2$; the angle between $O_{1} U$ and $A C$ is $90^{\circ}-\alpha / 2$, so $$ \frac{O_{1} U}{E C}=\frac{1}{2 \sin (\alpha / 2)} $$ Next, we claim that $E, V, C$, and $T$ are concyclic. Indeed, the point $V$ lies on the perpendicular bisector of $C E$, as well as on the internal angle bisector of $\angle C T F$. Therefore, $V$ coincides with the midpoint of the arc $C E$ of the circle (TCE). Now we have $\angle E V C=2 \angle E E_{1} C=180^{\circ}-(\gamma-\beta)$ and $\angle V E T=\angle V E_{1} T=90^{\circ}-\angle E_{1} E C=$ $90^{\circ}-\alpha / 2$. Therefore, $$ \frac{E C}{T V}=\frac{\sin \angle E T C}{\sin \angle V E T}=\frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)} . $$  Recalling (2) and multiplying (3) and (4) we establish (1): $$ \frac{O_{2} U}{O_{2} V}=\frac{\sin (\gamma-\beta)}{\sin \alpha}=\frac{1}{2 \sin (\alpha / 2)} \cdot \frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)}=\frac{O_{1} U}{E C} \cdot \frac{E C}{T V}=\frac{O_{1} U}{T V} $$
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
034ea97d-ab12-5d31-9449-dfdfaaa65f24
| 24,196
|
Let $\omega$ be the circumcircle of a triangle $A B C$, and let $\Omega_{A}$ be its excircle which is tangent to the segment $B C$. Let $X$ and $Y$ be the intersection points of $\omega$ and $\Omega_{A}$. Let $P$ and $Q$ be the projections of $A$ onto the tangent lines to $\Omega_{A}$ at $X$ and $Y$, respectively. The tangent line at $P$ to the circumcircle of the triangle $A P X$ intersects the tangent line at $Q$ to the circumcircle of the triangle $A Q Y$ at a point $R$. Prove that $A R \perp B C$.
|
Let $D$ be the point of tangency of $B C$ and $\Omega_{A}$. Let $D^{\prime}$ be the point such that $D D^{\prime}$ is a diameter of $\Omega_{A}$. Let $R^{\prime}$ be (the unique) point such that $A R^{\prime} \perp B C$ and $R^{\prime} D^{\prime} \| B C$. We shall prove that $R^{\prime}$ coincides with $R$. Let $P X$ intersect $A B$ and $D^{\prime} R^{\prime}$ at $S$ and $T$, respectively. Let $U$ be the ideal common point of the parallel lines $B C$ and $D^{\prime} R^{\prime}$. Note that the (degenerate) hexagon $A S X T U C$ is circumscribed around $\Omega_{A}$, hence by the Brianchon theorem $A T, S U$, and $X C$ concur at a point which we denote by $V$. Then $V S \| B C$. It follows that $\Varangle(S V, V X)=\Varangle(B C, C X)=$ $\Varangle(B A, A X)$, hence $A X S V$ is cyclic. Therefore, $\Varangle(P X, X A)=\Varangle(S V, V A)=\Varangle\left(R^{\prime} T, T A\right)$. Since $\angle A P T=\angle A R^{\prime} T=90^{\circ}$, the quadrilateral $A P R^{\prime} T$ is cyclic. Hence, $$ \Varangle(X A, A P)=90^{\circ}-\Varangle(P X, X A)=90^{\circ}-\Varangle\left(R^{\prime} T, T A\right)=\Varangle\left(T A, A R^{\prime}\right)=\Varangle\left(T P, P R^{\prime}\right) . $$ It follows that $P R^{\prime}$ is tangent to the circle $(A P X)$. Analogous argument shows that $Q R^{\prime}$ is tangent to the circle $(A Q Y)$. Therefore, $R=R^{\prime}$ and $A R \perp B C$.  Comment 1. After showing $\Varangle(P X, X A)=\Varangle\left(R^{\prime} T, T A\right)$ one can finish the solution as follows. There exists a spiral similarity mapping the triangle $A T R^{\prime}$ to the triangle $A X P$. So the triangles $A T X$ and $A R^{\prime} P$ are similar and equioriented. Thus, $\Varangle(T X, X A)=\Varangle\left(R^{\prime} P, P A\right)$, which implies that $P R^{\prime}$ is tangent to the circle ( $A P X$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\omega$ be the circumcircle of a triangle $A B C$, and let $\Omega_{A}$ be its excircle which is tangent to the segment $B C$. Let $X$ and $Y$ be the intersection points of $\omega$ and $\Omega_{A}$. Let $P$ and $Q$ be the projections of $A$ onto the tangent lines to $\Omega_{A}$ at $X$ and $Y$, respectively. The tangent line at $P$ to the circumcircle of the triangle $A P X$ intersects the tangent line at $Q$ to the circumcircle of the triangle $A Q Y$ at a point $R$. Prove that $A R \perp B C$.
|
Let $D$ be the point of tangency of $B C$ and $\Omega_{A}$. Let $D^{\prime}$ be the point such that $D D^{\prime}$ is a diameter of $\Omega_{A}$. Let $R^{\prime}$ be (the unique) point such that $A R^{\prime} \perp B C$ and $R^{\prime} D^{\prime} \| B C$. We shall prove that $R^{\prime}$ coincides with $R$. Let $P X$ intersect $A B$ and $D^{\prime} R^{\prime}$ at $S$ and $T$, respectively. Let $U$ be the ideal common point of the parallel lines $B C$ and $D^{\prime} R^{\prime}$. Note that the (degenerate) hexagon $A S X T U C$ is circumscribed around $\Omega_{A}$, hence by the Brianchon theorem $A T, S U$, and $X C$ concur at a point which we denote by $V$. Then $V S \| B C$. It follows that $\Varangle(S V, V X)=\Varangle(B C, C X)=$ $\Varangle(B A, A X)$, hence $A X S V$ is cyclic. Therefore, $\Varangle(P X, X A)=\Varangle(S V, V A)=\Varangle\left(R^{\prime} T, T A\right)$. Since $\angle A P T=\angle A R^{\prime} T=90^{\circ}$, the quadrilateral $A P R^{\prime} T$ is cyclic. Hence, $$ \Varangle(X A, A P)=90^{\circ}-\Varangle(P X, X A)=90^{\circ}-\Varangle\left(R^{\prime} T, T A\right)=\Varangle\left(T A, A R^{\prime}\right)=\Varangle\left(T P, P R^{\prime}\right) . $$ It follows that $P R^{\prime}$ is tangent to the circle $(A P X)$. Analogous argument shows that $Q R^{\prime}$ is tangent to the circle $(A Q Y)$. Therefore, $R=R^{\prime}$ and $A R \perp B C$.  Comment 1. After showing $\Varangle(P X, X A)=\Varangle\left(R^{\prime} T, T A\right)$ one can finish the solution as follows. There exists a spiral similarity mapping the triangle $A T R^{\prime}$ to the triangle $A X P$. So the triangles $A T X$ and $A R^{\prime} P$ are similar and equioriented. Thus, $\Varangle(T X, X A)=\Varangle\left(R^{\prime} P, P A\right)$, which implies that $P R^{\prime}$ is tangent to the circle ( $A P X$ ).
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0bd30601-3a0f-5524-be06-cc32a84de0bb
| 24,202
|
Let $\omega$ be the circumcircle of a triangle $A B C$, and let $\Omega_{A}$ be its excircle which is tangent to the segment $B C$. Let $X$ and $Y$ be the intersection points of $\omega$ and $\Omega_{A}$. Let $P$ and $Q$ be the projections of $A$ onto the tangent lines to $\Omega_{A}$ at $X$ and $Y$, respectively. The tangent line at $P$ to the circumcircle of the triangle $A P X$ intersects the tangent line at $Q$ to the circumcircle of the triangle $A Q Y$ at a point $R$. Prove that $A R \perp B C$.
|
Let $J$ and $r$ be the center and the radius of $\Omega_{A}$. Denote the diameter of $\omega$ by $d$ and its center by $O$. By Euler's formula, $O J^{2}=(d / 2)^{2}+d r$, so the power of $J$ with respect to $\omega$ equals $d r$. Let $J X$ intersect $\omega$ again at $L$. Then $J L=d$. Let $L K$ be a diameter of $\omega$ and let $M$ be the midpoint of $J K$. Since $J L=L K$, we have $\angle L M K=90^{\circ}$, so $M$ lies on $\omega$. Let $R^{\prime}$ be the point such that $R^{\prime} P$ is tangent to the circle $(A P X)$ and $A R^{\prime} \perp B C$. Note that the line $A R^{\prime}$ is symmetric to the line $A O$ with respect to $A J$.  Lemma. Let $M$ be the midpoint of the side $J K$ in a triangle $A J K$. Let $X$ be a point on the circle $(A M K)$ such that $\angle J X K=90^{\circ}$. Then there exists a point $T$ on the line $K X$ such that the triangles $A K J$ and $A J T$ are similar and equioriented. Proof. Note that $M X=M K$. We construct a parallelogram $A J N K$. Let $T$ be a point on $K X$ such that $\Varangle(N J, J A)=\Varangle(K J, J T)$. Then $$ \Varangle(J N, N A)=\Varangle(K A, A M)=\Varangle(K X, X M)=\Varangle(M K, K X)=\Varangle(J K, K T) . $$ So there exists a spiral similarity with center $J$ mapping the triangle $A J N$ to the triangle $T J K$. Therefore, the triangles $N J K$ and $A J T$ are similar and equioriented. It follows that the triangles $A K J$ and $A J T$ are similar and equioriented.  Back to the problem, we construct a point $T$ as in the lemma. We perform the composition $\phi$ of inversion with centre $A$ and radius $A J$ and reflection in $A J$. It is known that every triangle $A E F$ is similar and equioriented to $A \phi(F) \phi(E)$. So $\phi(K)=T$ and $\phi(T)=K$. Let $P^{*}=\phi(P)$ and $R^{*}=\phi\left(R^{\prime}\right)$. Observe that $\phi(T K)$ is a circle with diameter $A P^{*}$. Let $A A^{\prime}$ be a diameter of $\omega$. Then $P^{*} K \perp A K \perp A^{\prime} K$, so $A^{\prime}$ lies on $P^{*} K$. The triangles $A R^{\prime} P$ and $A P^{*} R^{*}$ are similar and equioriented, hence $\Varangle\left(A A^{\prime}, A^{\prime} P^{*}\right)=\Varangle\left(A A^{\prime}, A^{\prime} K\right)=\Varangle(A X, X P)=\Varangle(A X, X P)=\Varangle\left(A P, P R^{\prime}\right)=\Varangle\left(A R^{*}, R^{*} P^{*}\right)$, so $A, A^{\prime}, R^{*}$, and $P^{*}$ are concyclic. Since $A^{\prime}$ and $R^{*}$ lie on $A O$, we obtain $R^{*}=A^{\prime}$. So $R^{\prime}=\phi\left(A^{\prime}\right)$, and $\phi\left(A^{\prime}\right) P$ is tangent to the circle $(A P X)$. An identical argument shows that $\phi\left(A^{\prime}\right) Q$ is tangent to the circle $(A Q Y)$. Therefore, $R=$ $\phi\left(A^{\prime}\right)$ and $A R \perp B C$. Comment 2. One of the main ideas of Solution 2 is to get rid of the excircle, along with points $B$ and $C$. After doing so we obtain the following fact, which is, essentially, proved in Solution 2. Let $\omega$ be the circumcircle of a triangle $A K_{1} K_{2}$. Let $J$ be a point such that the midpoints of $J K_{1}$ and $J K_{2}$ lie on $\omega$. Points $X$ and $Y$ are chosen on $\omega$ so that $\angle J X K_{1}=\angle J Y K_{2}=90^{\circ}$. Let $P$ and $Q$ be the projections of $A$ onto $X K_{1}$ and $Y K_{2}$, respectively. The tangent line at $P$ to the circumcircle of the triangle $A P X$ intersects the tangent line at $Q$ to the circumcircle of the triangle $A Q Y$ at a point $R$. Then the reflection of the line $A R$ in $A J$ passes through the centre $O$ of $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\omega$ be the circumcircle of a triangle $A B C$, and let $\Omega_{A}$ be its excircle which is tangent to the segment $B C$. Let $X$ and $Y$ be the intersection points of $\omega$ and $\Omega_{A}$. Let $P$ and $Q$ be the projections of $A$ onto the tangent lines to $\Omega_{A}$ at $X$ and $Y$, respectively. The tangent line at $P$ to the circumcircle of the triangle $A P X$ intersects the tangent line at $Q$ to the circumcircle of the triangle $A Q Y$ at a point $R$. Prove that $A R \perp B C$.
|
Let $J$ and $r$ be the center and the radius of $\Omega_{A}$. Denote the diameter of $\omega$ by $d$ and its center by $O$. By Euler's formula, $O J^{2}=(d / 2)^{2}+d r$, so the power of $J$ with respect to $\omega$ equals $d r$. Let $J X$ intersect $\omega$ again at $L$. Then $J L=d$. Let $L K$ be a diameter of $\omega$ and let $M$ be the midpoint of $J K$. Since $J L=L K$, we have $\angle L M K=90^{\circ}$, so $M$ lies on $\omega$. Let $R^{\prime}$ be the point such that $R^{\prime} P$ is tangent to the circle $(A P X)$ and $A R^{\prime} \perp B C$. Note that the line $A R^{\prime}$ is symmetric to the line $A O$ with respect to $A J$.  Lemma. Let $M$ be the midpoint of the side $J K$ in a triangle $A J K$. Let $X$ be a point on the circle $(A M K)$ such that $\angle J X K=90^{\circ}$. Then there exists a point $T$ on the line $K X$ such that the triangles $A K J$ and $A J T$ are similar and equioriented. Proof. Note that $M X=M K$. We construct a parallelogram $A J N K$. Let $T$ be a point on $K X$ such that $\Varangle(N J, J A)=\Varangle(K J, J T)$. Then $$ \Varangle(J N, N A)=\Varangle(K A, A M)=\Varangle(K X, X M)=\Varangle(M K, K X)=\Varangle(J K, K T) . $$ So there exists a spiral similarity with center $J$ mapping the triangle $A J N$ to the triangle $T J K$. Therefore, the triangles $N J K$ and $A J T$ are similar and equioriented. It follows that the triangles $A K J$ and $A J T$ are similar and equioriented.  Back to the problem, we construct a point $T$ as in the lemma. We perform the composition $\phi$ of inversion with centre $A$ and radius $A J$ and reflection in $A J$. It is known that every triangle $A E F$ is similar and equioriented to $A \phi(F) \phi(E)$. So $\phi(K)=T$ and $\phi(T)=K$. Let $P^{*}=\phi(P)$ and $R^{*}=\phi\left(R^{\prime}\right)$. Observe that $\phi(T K)$ is a circle with diameter $A P^{*}$. Let $A A^{\prime}$ be a diameter of $\omega$. Then $P^{*} K \perp A K \perp A^{\prime} K$, so $A^{\prime}$ lies on $P^{*} K$. The triangles $A R^{\prime} P$ and $A P^{*} R^{*}$ are similar and equioriented, hence $\Varangle\left(A A^{\prime}, A^{\prime} P^{*}\right)=\Varangle\left(A A^{\prime}, A^{\prime} K\right)=\Varangle(A X, X P)=\Varangle(A X, X P)=\Varangle\left(A P, P R^{\prime}\right)=\Varangle\left(A R^{*}, R^{*} P^{*}\right)$, so $A, A^{\prime}, R^{*}$, and $P^{*}$ are concyclic. Since $A^{\prime}$ and $R^{*}$ lie on $A O$, we obtain $R^{*}=A^{\prime}$. So $R^{\prime}=\phi\left(A^{\prime}\right)$, and $\phi\left(A^{\prime}\right) P$ is tangent to the circle $(A P X)$. An identical argument shows that $\phi\left(A^{\prime}\right) Q$ is tangent to the circle $(A Q Y)$. Therefore, $R=$ $\phi\left(A^{\prime}\right)$ and $A R \perp B C$. Comment 2. One of the main ideas of Solution 2 is to get rid of the excircle, along with points $B$ and $C$. After doing so we obtain the following fact, which is, essentially, proved in Solution 2. Let $\omega$ be the circumcircle of a triangle $A K_{1} K_{2}$. Let $J$ be a point such that the midpoints of $J K_{1}$ and $J K_{2}$ lie on $\omega$. Points $X$ and $Y$ are chosen on $\omega$ so that $\angle J X K_{1}=\angle J Y K_{2}=90^{\circ}$. Let $P$ and $Q$ be the projections of $A$ onto $X K_{1}$ and $Y K_{2}$, respectively. The tangent line at $P$ to the circumcircle of the triangle $A P X$ intersects the tangent line at $Q$ to the circumcircle of the triangle $A Q Y$ at a point $R$. Then the reflection of the line $A R$ in $A J$ passes through the centre $O$ of $\omega$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0bd30601-3a0f-5524-be06-cc32a84de0bb
| 24,202
|
Let $n \geqslant 100$ be an integer. The numbers $n, n+1, \ldots, 2 n$ are written on $n+1$ cards, one number per card. The cards are shuffled and divided into two piles. Prove that one of the piles contains two cards such that the sum of their numbers is a perfect square.
|
To solve the problem it suffices to find three squares and three cards with numbers $a, b, c$ on them such that pairwise sums $a+b, b+c, a+c$ are equal to the chosen squares. By choosing the three consecutive squares $(2 k-1)^{2},(2 k)^{2},(2 k+1)^{2}$ we arrive at the triple $$ (a, b, c)=\left(2 k^{2}-4 k, \quad 2 k^{2}+1, \quad 2 k^{2}+4 k\right) $$ We need a value for $k$ such that $$ n \leqslant 2 k^{2}-4 k, \quad \text { and } \quad 2 k^{2}+4 k \leqslant 2 n $$ A concrete $k$ is suitable for all $n$ with $$ n \in\left[k^{2}+2 k, 2 k^{2}-4 k+1\right]=: I_{k} $$ For $k \geqslant 9$ the intervals $I_{k}$ and $I_{k+1}$ overlap because $$ (k+1)^{2}+2(k+1) \leqslant 2 k^{2}-4 k+1 $$ Hence $I_{9} \cup I_{10} \cup \ldots=[99, \infty)$, which proves the statement for $n \geqslant 99$. Comment 1. There exist approaches which only work for sufficiently large $n$. One possible approach is to consider three cards with numbers $70 k^{2}, 99 k^{2}, 126 k^{2}$ on them. Then their pairwise sums are perfect squares and so it suffices to find $k$ such that $70 k^{2} \geqslant n$ and $126 k^{2} \leqslant 2 n$ which exists for sufficiently large $n$. Another approach is to prove, arguing by contradiction, that $a$ and $a-2$ are in the same pile provided that $n$ is large enough and $a$ is sufficiently close to $n$. For that purpose, note that every pair of neighbouring numbers in the sequence $a, x^{2}-a, a+(2 x+1), x^{2}+2 x+3-a, a-2$ adds up to a perfect square for any $x$; so by choosing $x=\lfloor\sqrt{2 a}\rfloor+1$ and assuming that $n$ is large enough we conclude that $a$ and $a-2$ are in the same pile for any $a \in[n+2,3 n / 2]$. This gives a contradiction since it is easy to find two numbers from $[n+2,3 n / 2]$ of the same parity which sum to a square. It then remains to separately cover the cases of small $n$ which appears to be quite technical. Comment 2. An alternative formulation for this problem could ask for a proof of the statement for all $n>10^{6}$. An advantage of this formulation is that some solutions, e.g. those mentioned in Comment 1 need not contain a technical part which deals with the cases of small $n$. However, the original formulation seems to be better because the bound it gives for $n$ is almost sharp, see the next comment for details. Comment 3. The statement of the problem is false for $n=98$. As a counterexample, the first pile may contain the even numbers from 98 to 126 , the odd numbers from 129 to 161 , and the even numbers from 162 to 196.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geqslant 100$ be an integer. The numbers $n, n+1, \ldots, 2 n$ are written on $n+1$ cards, one number per card. The cards are shuffled and divided into two piles. Prove that one of the piles contains two cards such that the sum of their numbers is a perfect square.
|
To solve the problem it suffices to find three squares and three cards with numbers $a, b, c$ on them such that pairwise sums $a+b, b+c, a+c$ are equal to the chosen squares. By choosing the three consecutive squares $(2 k-1)^{2},(2 k)^{2},(2 k+1)^{2}$ we arrive at the triple $$ (a, b, c)=\left(2 k^{2}-4 k, \quad 2 k^{2}+1, \quad 2 k^{2}+4 k\right) $$ We need a value for $k$ such that $$ n \leqslant 2 k^{2}-4 k, \quad \text { and } \quad 2 k^{2}+4 k \leqslant 2 n $$ A concrete $k$ is suitable for all $n$ with $$ n \in\left[k^{2}+2 k, 2 k^{2}-4 k+1\right]=: I_{k} $$ For $k \geqslant 9$ the intervals $I_{k}$ and $I_{k+1}$ overlap because $$ (k+1)^{2}+2(k+1) \leqslant 2 k^{2}-4 k+1 $$ Hence $I_{9} \cup I_{10} \cup \ldots=[99, \infty)$, which proves the statement for $n \geqslant 99$. Comment 1. There exist approaches which only work for sufficiently large $n$. One possible approach is to consider three cards with numbers $70 k^{2}, 99 k^{2}, 126 k^{2}$ on them. Then their pairwise sums are perfect squares and so it suffices to find $k$ such that $70 k^{2} \geqslant n$ and $126 k^{2} \leqslant 2 n$ which exists for sufficiently large $n$. Another approach is to prove, arguing by contradiction, that $a$ and $a-2$ are in the same pile provided that $n$ is large enough and $a$ is sufficiently close to $n$. For that purpose, note that every pair of neighbouring numbers in the sequence $a, x^{2}-a, a+(2 x+1), x^{2}+2 x+3-a, a-2$ adds up to a perfect square for any $x$; so by choosing $x=\lfloor\sqrt{2 a}\rfloor+1$ and assuming that $n$ is large enough we conclude that $a$ and $a-2$ are in the same pile for any $a \in[n+2,3 n / 2]$. This gives a contradiction since it is easy to find two numbers from $[n+2,3 n / 2]$ of the same parity which sum to a square. It then remains to separately cover the cases of small $n$ which appears to be quite technical. Comment 2. An alternative formulation for this problem could ask for a proof of the statement for all $n>10^{6}$. An advantage of this formulation is that some solutions, e.g. those mentioned in Comment 1 need not contain a technical part which deals with the cases of small $n$. However, the original formulation seems to be better because the bound it gives for $n$ is almost sharp, see the next comment for details. Comment 3. The statement of the problem is false for $n=98$. As a counterexample, the first pile may contain the even numbers from 98 to 126 , the odd numbers from 129 to 161 , and the even numbers from 162 to 196.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb492231-6bf9-5461-bc69-5b5d4c07c572
| 24,208
|
Prove that there are only finitely many quadruples $(a, b, c, n)$ of positive integers such that $$ n!=a^{n-1}+b^{n-1}+c^{n-1} . $$
|
For fixed $n$ there are clearly finitely many solutions; we will show that there is no solution with $n>100$. So, assume $n>100$. By the AM-GM inequality, $$ \begin{aligned} n! & =2 n(n-1)(n-2)(n-3) \cdot(3 \cdot 4 \cdots(n-4)) \\ & \leqslant 2(n-1)^{4}\left(\frac{3+\cdots+(n-4)}{n-6}\right)^{n-6}=2(n-1)^{4}\left(\frac{n-1}{2}\right)^{n-6}<\left(\frac{n-1}{2}\right)^{n-1} \end{aligned} $$ thus $a, b, c<(n-1) / 2$. For every prime $p$ and integer $m \neq 0$, let $\nu_{p}(m)$ denote the $p$-adic valuation of $m$; that is, the greatest non-negative integer $k$ for which $p^{k}$ divides $m$. Legendre's formula states that $$ \nu_{p}(n!)=\sum_{s=1}^{\infty}\left\lfloor\frac{n}{p^{s}}\right\rfloor $$ and a well-know corollary of this formula is that $$ \nu_{p}(n!)<\sum_{s=1}^{\infty} \frac{n}{p^{s}}=\frac{n}{p-1} $$ If $n$ is odd then $a^{n-1}, b^{n-1}, c^{n-1}$ are squares, and by considering them modulo 4 we conclude that $a, b$ and $c$ must be even. Hence, $2^{n-1} \mid n$ ! but that is impossible for odd $n$ because $\nu_{2}(n!)=\nu_{2}((n-1)!)<n-1$ by $(\bigcirc)$. From now on we assume that $n$ is even. If all three numbers $a+b, b+c, c+a$ are powers of 2 then $a, b, c$ have the same parity. If they all are odd, then $n!=a^{n-1}+b^{n-1}+c^{n-1}$ is also odd which is absurd. If all $a, b, c$ are divisible by 4 , this contradicts $\nu_{2}(n!) \leqslant n-1$. If, say, $a$ is not divisible by 4 , then $2 a=(a+b)+(a+c)-(b+c)$ is not divisible by 8 , and since all $a+b, b+c$, $c+a$ are powers of 2 , we get that one of these sums equals 4 , so two of the numbers of $a, b, c$ are equal to 2. Say, $a=b=2$, then $c=2^{r}-2$ and, since $c \mid n$ !, we must have $c \mid a^{n-1}+b^{n-1}=2^{n}$ implying $r=2$, and so $c=2$, which is impossible because $n!\equiv 0 \not \equiv 3 \cdot 2^{n-1}(\bmod 5)$. So now we assume that the sum of two numbers among $a, b, c$, say $a+b$, is not a power of 2 , so it is divisible by some odd prime $p$. Then $p \leqslant a+b<n$ and so $c^{n-1}=n!-\left(a^{n-1}+b^{n-1}\right)$ is divisible by $p$. If $p$ divides $a$ and $b$, we get $p^{n-1} \mid n$ !, contradicting ( $($ ). Next, using ( $\odot$ ) and the Lifting the Exponent Lemma we get $$ \nu_{p}(1)+\nu_{p}(2)+\cdots+\nu_{p}(n)=\nu_{p}(n!)=\nu_{p}\left(n!-c^{n-1}\right)=\nu_{p}\left(a^{n-1}+b^{n-1}\right)=\nu_{p}(a+b)+\nu_{p}(n-1) $$ In view of $(\diamond)$, no number of $1,2, \ldots, n$ can be divisible by $p$, except $a+b$ and $n-1>a+b$. On the other hand, $p \mid c$ implies that $p<n / 2$ and so there must be at least two such numbers. Hence, there are two multiples of $p$ among $1,2, \ldots, n$, namely $a+b=p$ and $n-1=2 p$. But this is another contradiction because $n-1$ is odd. This final contradiction shows that there is no solution of the equation for $n>100$. Comment 1. The original version of the problem asked to find all solutions to the equation. The solution to that version is not much different but is more technical. Comment 2. To find all solutions we can replace the bound $a, b, c<(n-1) / 2$ for all $n$ with a weaker bound $a, b, c \leqslant n / 2$ only for even $n$, which is a trivial application of AM-GM to the tuple $(2,3, \ldots, n)$. Then we may use the same argument for odd $n$ (it works for $n \geqslant 5$ and does not require any bound on $a, b, c)$, and for even $n$ the same solution works for $n \geqslant 6$ unless we have $a+b=n-1$ and $2 \nu_{p}(n-1)=\nu_{p}(n!)$. This is only possible for $p=3$ and $n=10$ in which case we can consider the original equation modulo 7 to deduce that $7 \mid a b c$ which contradicts the fact that $7^{9}>10$ !. Looking at $n \leqslant 4$ we find four solutions, namely, $$ (a, b, c, n)=(1,1,2,3),(1,2,1,3),(2,1,1,3),(2,2,2,4) $$ Comment 3. For sufficiently large $n$, the inequality $a, b, c<(n-1) / 2$ also follows from Stirling's formula.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there are only finitely many quadruples $(a, b, c, n)$ of positive integers such that $$ n!=a^{n-1}+b^{n-1}+c^{n-1} . $$
|
For fixed $n$ there are clearly finitely many solutions; we will show that there is no solution with $n>100$. So, assume $n>100$. By the AM-GM inequality, $$ \begin{aligned} n! & =2 n(n-1)(n-2)(n-3) \cdot(3 \cdot 4 \cdots(n-4)) \\ & \leqslant 2(n-1)^{4}\left(\frac{3+\cdots+(n-4)}{n-6}\right)^{n-6}=2(n-1)^{4}\left(\frac{n-1}{2}\right)^{n-6}<\left(\frac{n-1}{2}\right)^{n-1} \end{aligned} $$ thus $a, b, c<(n-1) / 2$. For every prime $p$ and integer $m \neq 0$, let $\nu_{p}(m)$ denote the $p$-adic valuation of $m$; that is, the greatest non-negative integer $k$ for which $p^{k}$ divides $m$. Legendre's formula states that $$ \nu_{p}(n!)=\sum_{s=1}^{\infty}\left\lfloor\frac{n}{p^{s}}\right\rfloor $$ and a well-know corollary of this formula is that $$ \nu_{p}(n!)<\sum_{s=1}^{\infty} \frac{n}{p^{s}}=\frac{n}{p-1} $$ If $n$ is odd then $a^{n-1}, b^{n-1}, c^{n-1}$ are squares, and by considering them modulo 4 we conclude that $a, b$ and $c$ must be even. Hence, $2^{n-1} \mid n$ ! but that is impossible for odd $n$ because $\nu_{2}(n!)=\nu_{2}((n-1)!)<n-1$ by $(\bigcirc)$. From now on we assume that $n$ is even. If all three numbers $a+b, b+c, c+a$ are powers of 2 then $a, b, c$ have the same parity. If they all are odd, then $n!=a^{n-1}+b^{n-1}+c^{n-1}$ is also odd which is absurd. If all $a, b, c$ are divisible by 4 , this contradicts $\nu_{2}(n!) \leqslant n-1$. If, say, $a$ is not divisible by 4 , then $2 a=(a+b)+(a+c)-(b+c)$ is not divisible by 8 , and since all $a+b, b+c$, $c+a$ are powers of 2 , we get that one of these sums equals 4 , so two of the numbers of $a, b, c$ are equal to 2. Say, $a=b=2$, then $c=2^{r}-2$ and, since $c \mid n$ !, we must have $c \mid a^{n-1}+b^{n-1}=2^{n}$ implying $r=2$, and so $c=2$, which is impossible because $n!\equiv 0 \not \equiv 3 \cdot 2^{n-1}(\bmod 5)$. So now we assume that the sum of two numbers among $a, b, c$, say $a+b$, is not a power of 2 , so it is divisible by some odd prime $p$. Then $p \leqslant a+b<n$ and so $c^{n-1}=n!-\left(a^{n-1}+b^{n-1}\right)$ is divisible by $p$. If $p$ divides $a$ and $b$, we get $p^{n-1} \mid n$ !, contradicting ( $($ ). Next, using ( $\odot$ ) and the Lifting the Exponent Lemma we get $$ \nu_{p}(1)+\nu_{p}(2)+\cdots+\nu_{p}(n)=\nu_{p}(n!)=\nu_{p}\left(n!-c^{n-1}\right)=\nu_{p}\left(a^{n-1}+b^{n-1}\right)=\nu_{p}(a+b)+\nu_{p}(n-1) $$ In view of $(\diamond)$, no number of $1,2, \ldots, n$ can be divisible by $p$, except $a+b$ and $n-1>a+b$. On the other hand, $p \mid c$ implies that $p<n / 2$ and so there must be at least two such numbers. Hence, there are two multiples of $p$ among $1,2, \ldots, n$, namely $a+b=p$ and $n-1=2 p$. But this is another contradiction because $n-1$ is odd. This final contradiction shows that there is no solution of the equation for $n>100$. Comment 1. The original version of the problem asked to find all solutions to the equation. The solution to that version is not much different but is more technical. Comment 2. To find all solutions we can replace the bound $a, b, c<(n-1) / 2$ for all $n$ with a weaker bound $a, b, c \leqslant n / 2$ only for even $n$, which is a trivial application of AM-GM to the tuple $(2,3, \ldots, n)$. Then we may use the same argument for odd $n$ (it works for $n \geqslant 5$ and does not require any bound on $a, b, c)$, and for even $n$ the same solution works for $n \geqslant 6$ unless we have $a+b=n-1$ and $2 \nu_{p}(n-1)=\nu_{p}(n!)$. This is only possible for $p=3$ and $n=10$ in which case we can consider the original equation modulo 7 to deduce that $7 \mid a b c$ which contradicts the fact that $7^{9}>10$ !. Looking at $n \leqslant 4$ we find four solutions, namely, $$ (a, b, c, n)=(1,1,2,3),(1,2,1,3),(2,1,1,3),(2,2,2,4) $$ Comment 3. For sufficiently large $n$, the inequality $a, b, c<(n-1) / 2$ also follows from Stirling's formula.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e6449900-8e17-5c57-b0a8-26aab1da225b
| 24,217
|
A hunter and an invisible rabbit play a game on an infinite square grid. First the hunter fixes a colouring of the cells with finitely many colours. The rabbit then secretly chooses a cell to start in. Every minute, the rabbit reports the colour of its current cell to the hunter, and then secretly moves to an adjacent cell that it has not visited before (two cells are adjacent if they share a side). The hunter wins if after some finite time either - the rabbit cannot move; or - the hunter can determine the cell in which the rabbit started. Decide whether there exists a winning strategy for the hunter. Answer: Yes, there exists a colouring that yields a winning strategy for the hunter.
|
A central idea is that several colourings $C_{1}, C_{2}, \ldots, C_{k}$ can be merged together into a single product colouring $C_{1} \times C_{2} \times \cdots \times C_{k}$ as follows: the colours in the product colouring are ordered tuples $\left(c_{1}, \ldots, c_{n}\right)$ of colours, where $c_{i}$ is a colour used in $C_{i}$, so that each cell gets a tuple consisting of its colours in the individual colourings $C_{i}$. This way, any information which can be determined from one of the individual colourings can also be determined from the product colouring. Now let the hunter merge the following colourings: - The first two colourings $C_{1}$ and $C_{2}$ allow the tracking of the horizontal and vertical movements of the rabbit. The colouring $C_{1}$ colours the cells according to the residue of their $x$-coordinates modulo 3 , which allows to determine whether the rabbit moves left, moves right, or moves vertically. Similarly, the colouring $C_{2}$ uses the residues of the $y$-coordinates modulo 3, which allows to determine whether the rabbit moves up, moves down, or moves horizontally. - Under the condition that the rabbit's $x$-coordinate is unbounded, colouring $C_{3}$ allows to determine the exact value of the $x$-coordinate: In $C_{3}$, the columns are coloured white and black so that the gaps between neighboring black columns are pairwise distinct. As the rabbit's $x$-coordinate is unbounded, it will eventually visit two black cells in distinct columns. With the help of colouring $C_{1}$ the hunter can catch that moment, and determine the difference of $x$-coordinates of those two black cells, hence deducing the precise column. Symmetrically, under the condition that the rabbit's $y$-coordinate is unbounded, there is a colouring $C_{4}$ that allows the hunter to determine the exact value of the $y$-coordinate. - Finally, under the condition that the sum $x+y$ of the rabbit's coordinates is unbounded, colouring $C_{5}$ allows to determine the exact value of this sum: The diagonal lines $x+y=$ const are coloured black and white, so that the gaps between neighboring black diagonals are pairwise distinct. Unless the rabbit gets stuck, at least two of the three values $x, y$ and $x+y$ must be unbounded as the rabbit keeps moving. Hence the hunter can eventually determine two of these three values; thus he does know all three. Finally the hunter works backwards with help of the colourings $C_{1}$ and $C_{2}$ and computes the starting cell of the rabbit. Comment. There are some variations of the solution above: e.g., the colourings $C_{3}, C_{4}$ and $C_{5}$ can be replaced with different ones. However, such alternatives are more technically involved, and we do not present them here.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A hunter and an invisible rabbit play a game on an infinite square grid. First the hunter fixes a colouring of the cells with finitely many colours. The rabbit then secretly chooses a cell to start in. Every minute, the rabbit reports the colour of its current cell to the hunter, and then secretly moves to an adjacent cell that it has not visited before (two cells are adjacent if they share a side). The hunter wins if after some finite time either - the rabbit cannot move; or - the hunter can determine the cell in which the rabbit started. Decide whether there exists a winning strategy for the hunter. Answer: Yes, there exists a colouring that yields a winning strategy for the hunter.
|
A central idea is that several colourings $C_{1}, C_{2}, \ldots, C_{k}$ can be merged together into a single product colouring $C_{1} \times C_{2} \times \cdots \times C_{k}$ as follows: the colours in the product colouring are ordered tuples $\left(c_{1}, \ldots, c_{n}\right)$ of colours, where $c_{i}$ is a colour used in $C_{i}$, so that each cell gets a tuple consisting of its colours in the individual colourings $C_{i}$. This way, any information which can be determined from one of the individual colourings can also be determined from the product colouring. Now let the hunter merge the following colourings: - The first two colourings $C_{1}$ and $C_{2}$ allow the tracking of the horizontal and vertical movements of the rabbit. The colouring $C_{1}$ colours the cells according to the residue of their $x$-coordinates modulo 3 , which allows to determine whether the rabbit moves left, moves right, or moves vertically. Similarly, the colouring $C_{2}$ uses the residues of the $y$-coordinates modulo 3, which allows to determine whether the rabbit moves up, moves down, or moves horizontally. - Under the condition that the rabbit's $x$-coordinate is unbounded, colouring $C_{3}$ allows to determine the exact value of the $x$-coordinate: In $C_{3}$, the columns are coloured white and black so that the gaps between neighboring black columns are pairwise distinct. As the rabbit's $x$-coordinate is unbounded, it will eventually visit two black cells in distinct columns. With the help of colouring $C_{1}$ the hunter can catch that moment, and determine the difference of $x$-coordinates of those two black cells, hence deducing the precise column. Symmetrically, under the condition that the rabbit's $y$-coordinate is unbounded, there is a colouring $C_{4}$ that allows the hunter to determine the exact value of the $y$-coordinate. - Finally, under the condition that the sum $x+y$ of the rabbit's coordinates is unbounded, colouring $C_{5}$ allows to determine the exact value of this sum: The diagonal lines $x+y=$ const are coloured black and white, so that the gaps between neighboring black diagonals are pairwise distinct. Unless the rabbit gets stuck, at least two of the three values $x, y$ and $x+y$ must be unbounded as the rabbit keeps moving. Hence the hunter can eventually determine two of these three values; thus he does know all three. Finally the hunter works backwards with help of the colourings $C_{1}$ and $C_{2}$ and computes the starting cell of the rabbit. Comment. There are some variations of the solution above: e.g., the colourings $C_{3}, C_{4}$ and $C_{5}$ can be replaced with different ones. However, such alternatives are more technically involved, and we do not present them here.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2ecf232c-cfa7-5942-96ec-82dab8424cc4
| 24,242
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent. Common remarks. The introductory steps presented here are used in all solutions below. Since $A C=B C=A D$, we have $\angle A B C=\angle B A C=\angle A C D=\angle A D C$. Since the quadrilaterals $A P R Q$ and $A Q C D$ are cyclic, we obtain $$ \angle C R A=180^{\circ}-\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A, $$ so the points $A, B, C$, and $R$ lie on some circle $\gamma$.
|
Introduce the point $X=A Q \cap C D$; we need to prove that $B, R$ and $X$ are collinear. By means of the circle $(A P R Q)$ we have $$ \angle R Q X=180^{\circ}-\angle A Q R=\angle R P A=\angle R C X $$ (the last equality holds in view of $A B \| C D$ ), which means that the points $C, Q, R$, and $X$ also lie on some circle $\delta$. Using the circles $\delta$ and $\gamma$ we finally obtain $$ \angle X R C=\angle X Q C=180^{\circ}-\angle C Q A=\angle A D C=\angle B A C=180^{\circ}-\angle C R B, $$ that proves the desired collinearity. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent. Common remarks. The introductory steps presented here are used in all solutions below. Since $A C=B C=A D$, we have $\angle A B C=\angle B A C=\angle A C D=\angle A D C$. Since the quadrilaterals $A P R Q$ and $A Q C D$ are cyclic, we obtain $$ \angle C R A=180^{\circ}-\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A, $$ so the points $A, B, C$, and $R$ lie on some circle $\gamma$.
|
Introduce the point $X=A Q \cap C D$; we need to prove that $B, R$ and $X$ are collinear. By means of the circle $(A P R Q)$ we have $$ \angle R Q X=180^{\circ}-\angle A Q R=\angle R P A=\angle R C X $$ (the last equality holds in view of $A B \| C D$ ), which means that the points $C, Q, R$, and $X$ also lie on some circle $\delta$. Using the circles $\delta$ and $\gamma$ we finally obtain $$ \angle X R C=\angle X Q C=180^{\circ}-\angle C Q A=\angle A D C=\angle B A C=180^{\circ}-\angle C R B, $$ that proves the desired collinearity. 
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c7fc4bf2-0476-5e0b-ae20-875f218cab6c
| 24,251
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent. Common remarks. The introductory steps presented here are used in all solutions below. Since $A C=B C=A D$, we have $\angle A B C=\angle B A C=\angle A C D=\angle A D C$. Since the quadrilaterals $A P R Q$ and $A Q C D$ are cyclic, we obtain $$ \angle C R A=180^{\circ}-\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A, $$ so the points $A, B, C$, and $R$ lie on some circle $\gamma$.
|
Let $\alpha$ denote the circle ( $A P R Q)$. Since $$ \angle C A P=\angle A C D=\angle A Q D=180^{\circ}-\angle A Q P $$ the line $A C$ is tangent to $\alpha$. Now, let $A D$ meet $\alpha$ again at a point $Y$ (which necessarily lies on the extension of $D A$ beyond $A$ ). Using the circle $\gamma$, along with the fact that $A C$ is tangent to $\alpha$, we have $$ \angle A R Y=\angle C A D=\angle A C B=\angle A R B, $$ so the points $Y, B$, and $R$ are collinear. Applying Pascal's theorem to the hexagon $A A Y R P Q$ (where $A A$ is regarded as the tangent to $\alpha$ at $A$ ), we see that the points $A A \cap R P=C, A Y \cap P Q=D$, and $Y R \cap Q A$ are collinear. Hence the lines $C D, A Q$, and $B R$ are concurrent. Comment 1. Solution 2 consists of two parts: (1) showing that $B R$ and $D A$ meet on $\alpha$; and (2) showing that this yields the desired concurrency. Solution 3 also splits into those parts, but the proofs are different. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent. Common remarks. The introductory steps presented here are used in all solutions below. Since $A C=B C=A D$, we have $\angle A B C=\angle B A C=\angle A C D=\angle A D C$. Since the quadrilaterals $A P R Q$ and $A Q C D$ are cyclic, we obtain $$ \angle C R A=180^{\circ}-\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A, $$ so the points $A, B, C$, and $R$ lie on some circle $\gamma$.
|
Let $\alpha$ denote the circle ( $A P R Q)$. Since $$ \angle C A P=\angle A C D=\angle A Q D=180^{\circ}-\angle A Q P $$ the line $A C$ is tangent to $\alpha$. Now, let $A D$ meet $\alpha$ again at a point $Y$ (which necessarily lies on the extension of $D A$ beyond $A$ ). Using the circle $\gamma$, along with the fact that $A C$ is tangent to $\alpha$, we have $$ \angle A R Y=\angle C A D=\angle A C B=\angle A R B, $$ so the points $Y, B$, and $R$ are collinear. Applying Pascal's theorem to the hexagon $A A Y R P Q$ (where $A A$ is regarded as the tangent to $\alpha$ at $A$ ), we see that the points $A A \cap R P=C, A Y \cap P Q=D$, and $Y R \cap Q A$ are collinear. Hence the lines $C D, A Q$, and $B R$ are concurrent. Comment 1. Solution 2 consists of two parts: (1) showing that $B R$ and $D A$ meet on $\alpha$; and (2) showing that this yields the desired concurrency. Solution 3 also splits into those parts, but the proofs are different. 
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c7fc4bf2-0476-5e0b-ae20-875f218cab6c
| 24,251
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent. Common remarks. The introductory steps presented here are used in all solutions below. Since $A C=B C=A D$, we have $\angle A B C=\angle B A C=\angle A C D=\angle A D C$. Since the quadrilaterals $A P R Q$ and $A Q C D$ are cyclic, we obtain $$ \angle C R A=180^{\circ}-\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A, $$ so the points $A, B, C$, and $R$ lie on some circle $\gamma$.
|
As in Using the circle $\alpha$ and noticing that $C D$ is tangent to $\gamma$, we obtain $$ \angle R Y A=\angle R P A=\angle R C X=\angle R B C . $$ So $A Y \| B C$, and hence $Y$ lies on $D A$. Now the chain of equalities (1) shows also that $\angle R Y D=\angle R C X$, which implies that the points $C, D, Y$, and $R$ lie on some circle $\beta$. Hence, the lines $C D, A Q$, and $Y B R$ are the pairwise radical axes of the circles $(A Q C D), \alpha$, and $\beta$, so those lines are concurrent. Comment 2. The original problem submission contained an additional assumption that $B P=A B$. The Problem Selection Committee removed this assumption as superfluous.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram such that $A C=B C$. A point $P$ is chosen on the extension of the segment $A B$ beyond $B$. The circumcircle of the triangle $A C D$ meets the segment $P D$ again at $Q$, and the circumcircle of the triangle $A P Q$ meets the segment $P C$ again at $R$. Prove that the lines $C D, A Q$, and $B R$ are concurrent. Common remarks. The introductory steps presented here are used in all solutions below. Since $A C=B C=A D$, we have $\angle A B C=\angle B A C=\angle A C D=\angle A D C$. Since the quadrilaterals $A P R Q$ and $A Q C D$ are cyclic, we obtain $$ \angle C R A=180^{\circ}-\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A, $$ so the points $A, B, C$, and $R$ lie on some circle $\gamma$.
|
As in Using the circle $\alpha$ and noticing that $C D$ is tangent to $\gamma$, we obtain $$ \angle R Y A=\angle R P A=\angle R C X=\angle R B C . $$ So $A Y \| B C$, and hence $Y$ lies on $D A$. Now the chain of equalities (1) shows also that $\angle R Y D=\angle R C X$, which implies that the points $C, D, Y$, and $R$ lie on some circle $\beta$. Hence, the lines $C D, A Q$, and $Y B R$ are the pairwise radical axes of the circles $(A Q C D), \alpha$, and $\beta$, so those lines are concurrent. Comment 2. The original problem submission contained an additional assumption that $B P=A B$. The Problem Selection Committee removed this assumption as superfluous.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c7fc4bf2-0476-5e0b-ae20-875f218cab6c
| 24,251
|
Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Prove that the perimeters of the (possibly self-intersecting) quadrilaterals $A D T X$ and $C D Y Z$ are equal.
|
The point $I$ is the intersection of the external bisector of the angle $T C Z$ with the circumcircle $\omega$ of the triangle $T C Z$, so $I$ is the midpoint of the $\operatorname{arc} T C Z$ and $I T=I Z$. Similarly, $I$ is the midpoint of the arc $Y A X$ and $I X=I Y$. Let $O$ be the centre of $\omega$. Then $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively. So $X T=Y Z$.  Let the incircle of $A B C D$ touch $A B, B C, C D$, and $D A$ at points $P, Q, R$, and $S$, respectively. The right triangles $I X P$ and $I Y S$ are congruent, since $I P=I S$ and $I X=I Y$. Similarly, the right triangles $I R T$ and $I Q Z$ are congruent. Therefore, $X P=Y S$ and $R T=Q Z$. Denote the perimeters of $A D T X$ and $C D Y Z$ by $P_{A D T X}$ and $P_{C D Y Z}$ respectively. Since $A S=A P, C Q=R C$, and $S D=D R$, we obtain $$ \begin{aligned} P_{A D T X}=X T+X A+A S+ & S D+D T=X T+X P+R T \\ & =Y Z+Y S+Q Z=Y Z+Y D+D R+R C+C Z=P_{C D Y Z} \end{aligned} $$ as required. Comment 1. After proving that $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively, one can finish the solution as follows. Since $X T=Y Z$, the problem statement is equivalent to $$ X A+A D+D T=Y D+D C+C Z $$ Since $A B C D$ is circumscribed, $A B-A D=B C-C D$. Adding this to (1), we come to an equivalent equality $X A+A B+D T=Y D+B C+C Z$, or $$ X B+D T=Y D+B Z . $$ Let $\lambda=\frac{X Z}{A C}=\frac{T Y}{A C}$. Since $X A C Z$ is cyclic, the triangles $Z B X$ and $A B C$ are similar, hence $$ \frac{X B}{B C}=\frac{B Z}{A B}=\frac{X Z}{A C}=\lambda . $$ It follows that $X B=\lambda B C$ and $B Z=\lambda A B$. Likewise, the triangles $T D Y$ and $A D C$ are similar, hence $$ \frac{D T}{A D}=\frac{D Y}{C D}=\frac{T Y}{A C}=\lambda $$ Therefore, (2) rewrites as $\lambda B C+\lambda A D=\lambda C D+\lambda A B$. This is equivalent to $B C+A D=C D+A B$ which is true as $A B C D$ is circumscribed. Comment 2. Here is a more difficult modification of the original problem, found by the PSC. Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Let $U=B C \cap A D$ and $V=B A \cap C D$. Let $I_{U}$ be the incentre of $U Y Z$ and let $J_{V}$ be the $V$-excentre of $V X T$. Then $I_{U} J_{V} \perp B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Prove that the perimeters of the (possibly self-intersecting) quadrilaterals $A D T X$ and $C D Y Z$ are equal.
|
The point $I$ is the intersection of the external bisector of the angle $T C Z$ with the circumcircle $\omega$ of the triangle $T C Z$, so $I$ is the midpoint of the $\operatorname{arc} T C Z$ and $I T=I Z$. Similarly, $I$ is the midpoint of the arc $Y A X$ and $I X=I Y$. Let $O$ be the centre of $\omega$. Then $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively. So $X T=Y Z$.  Let the incircle of $A B C D$ touch $A B, B C, C D$, and $D A$ at points $P, Q, R$, and $S$, respectively. The right triangles $I X P$ and $I Y S$ are congruent, since $I P=I S$ and $I X=I Y$. Similarly, the right triangles $I R T$ and $I Q Z$ are congruent. Therefore, $X P=Y S$ and $R T=Q Z$. Denote the perimeters of $A D T X$ and $C D Y Z$ by $P_{A D T X}$ and $P_{C D Y Z}$ respectively. Since $A S=A P, C Q=R C$, and $S D=D R$, we obtain $$ \begin{aligned} P_{A D T X}=X T+X A+A S+ & S D+D T=X T+X P+R T \\ & =Y Z+Y S+Q Z=Y Z+Y D+D R+R C+C Z=P_{C D Y Z} \end{aligned} $$ as required. Comment 1. After proving that $X$ and $T$ are the reflections of $Y$ and $Z$ in $I O$, respectively, one can finish the solution as follows. Since $X T=Y Z$, the problem statement is equivalent to $$ X A+A D+D T=Y D+D C+C Z $$ Since $A B C D$ is circumscribed, $A B-A D=B C-C D$. Adding this to (1), we come to an equivalent equality $X A+A B+D T=Y D+B C+C Z$, or $$ X B+D T=Y D+B Z . $$ Let $\lambda=\frac{X Z}{A C}=\frac{T Y}{A C}$. Since $X A C Z$ is cyclic, the triangles $Z B X$ and $A B C$ are similar, hence $$ \frac{X B}{B C}=\frac{B Z}{A B}=\frac{X Z}{A C}=\lambda . $$ It follows that $X B=\lambda B C$ and $B Z=\lambda A B$. Likewise, the triangles $T D Y$ and $A D C$ are similar, hence $$ \frac{D T}{A D}=\frac{D Y}{C D}=\frac{T Y}{A C}=\lambda $$ Therefore, (2) rewrites as $\lambda B C+\lambda A D=\lambda C D+\lambda A B$. This is equivalent to $B C+A D=C D+A B$ which is true as $A B C D$ is circumscribed. Comment 2. Here is a more difficult modification of the original problem, found by the PSC. Let $A B C D$ be a convex quadrilateral circumscribed around a circle with centre $I$. Let $\omega$ be the circumcircle of the triangle $A C I$. The extensions of $B A$ and $B C$ beyond $A$ and $C$ meet $\omega$ at $X$ and $Z$, respectively. The extensions of $A D$ and $C D$ beyond $D$ meet $\omega$ at $Y$ and $T$, respectively. Let $U=B C \cap A D$ and $V=B A \cap C D$. Let $I_{U}$ be the incentre of $U Y Z$ and let $J_{V}$ be the $V$-excentre of $V X T$. Then $I_{U} J_{V} \perp B D$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7103088d-2900-554e-a386-f124bf66b12a
| 24,255
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$. Common remarks. We introduce some objects and establish some preliminary facts common for all solutions below. Let $\Omega$ denote the circle $(A B C D)$, and let $\gamma_{B}$ and $\gamma_{D}$ denote the two circles from the problem statement (their centres are $O_{B}$ and $O_{D}$, respectively). Clearly, all three centres $O, O_{B}$, and $O_{D}$ are distinct. Assume, without loss of generality, that $A B>B C$. Suppose that $A D>D C$, and let $H=A C \cap B D$. Then the rays $B B_{1}$ and $D D_{1}$ lie on one side of $B D$, as they contain the midpoints of the arcs $A D C$ and $A B C$, respectively. However, if $B D_{1} \| D B_{1}$, then $B_{1}$ and $D_{1}$ should be separated by $H$. This contradiction shows that $A D<C D$. Let $\gamma_{B}$ and $\gamma_{D}$ meet $\Omega$ again at $T_{B}$ and $T_{D}$, respectively. The common chord $B T_{B}$ of $\Omega$ and $\gamma_{B}$ is perpendicular to their line of centres $O_{B} O$; likewise, $D T_{D} \perp O_{D} O$. Therefore, $O \in O_{B} O_{D} \Longleftrightarrow O_{B} O\left\|O_{D} O \Longleftrightarrow B T_{B}\right\|$ $D T_{D}$, and the problem reduces to showing that  $$ B T_{B} \| D T_{D} $$ Comment 1. It seems that the discussion of the positions of points is necessary for both Solutions below. However, this part automatically follows from the angle chasing in Comment 2.
|
Let the diagonals $A C$ and $B D$ cross at $H$. Consider the homothety $h$ centred at $H$ and mapping $B$ to $D$. Since $B D_{1} \| D B_{1}$, we have $h\left(D_{1}\right)=B_{1}$. Let the tangents to $\Omega$ at $B$ and $D$ meet $A C$ at $L_{B}$ and $L_{D}$, respectively. We have $$ \angle L_{B} B B_{1}=\angle L_{B} B C+\angle C B B_{1}=\angle B A L_{B}+\angle B_{1} B A=\angle B B_{1} L_{B}, $$ which means that the triangle $L_{B} B B_{1}$ is isosceles, $L_{B} B=L_{B} B_{1}$. The powers of $L_{B}$ with respect to $\Omega$ and $\gamma_{D}$ are $L_{B} B^{2}$ and $L_{B} B_{1}^{2}$, respectively; so they are equal, whence $L_{B}$ lies on the radical axis $T_{D} D$ of those two circles. Similarly, $L_{D}$ lies on the radical axis $T_{B} B$ of $\Omega$ and $\gamma_{B}$. By the sine rule in the triangle $B H L_{B}$, we obtain $$ \frac{H L_{B}}{\sin \angle H B L_{B}}=\frac{B L_{B}}{\sin \angle B H L_{B}}=\frac{B_{1} L_{B}}{\sin \angle B H L_{B}} $$ similarly, $$ \frac{H L_{D}}{\sin \angle H D L_{D}}=\frac{D L_{D}}{\sin \angle D H L_{D}}=\frac{D_{1} L_{D}}{\sin \angle D H L_{D}} $$ Clearly, $\angle B H L_{B}=\angle D H L_{D}$. In the circle $\Omega$, tangent lines $B L_{B}$ and $D L_{D}$ form equal angles with the chord $B D$, so $\sin \angle H B L_{B}=\sin \angle H D L_{D}$ (this equality does not depend on the picture). Thus, dividing (2) by (3) we get $$ \frac{H L_{B}}{H L_{D}}=\frac{B_{1} L_{B}}{D_{1} L_{D}}, \quad \text { and hence } \quad \frac{H L_{B}}{H L_{D}}=\frac{H L_{B}-B_{1} L_{B}}{H L_{D}-D_{1} L_{D}}=\frac{H B_{1}}{H D_{1}} $$ Since $h\left(D_{1}\right)=B_{1}$, the obtained relation yields $h\left(L_{D}\right)=L_{B}$, so $h$ maps the line $L_{D} B$ to $L_{B} D$, and these lines are parallel, as desired.  Comment 2. In the solution above, the key relation $h\left(L_{D}\right)=L_{B}$ was obtained via a short computation in sines. Here we present an alternative, pure synthetical way of establishing that. Let the external bisectors of $\angle A B C$ and $\angle A D C$ cross $A C$ at $B_{2}$ and $D_{2}$, respectively; assume that $\overparen{A B}>\overparen{C B}$. In the right-angled triangle $B B_{1} B_{2}$, the point $L_{B}$ is a point on the hypothenuse such that $L_{B} B_{1}=L_{B} B$, so $L_{B}$ is the midpoint of $B_{1} B_{2}$. Since $D D_{1}$ is the internal angle bisector of $\angle A D C$, we have $$ \angle B D D_{1}=\frac{\angle B D A-\angle C D B}{2}=\frac{\angle B C A-\angle C A B}{2}=\angle B B_{2} D_{1}, $$ so the points $B, B_{2}, D$, and $D_{1}$ lie on some circle $\omega_{B}$. Similarly, $L_{D}$ is the midpoint of $D_{1} D_{2}$, and the points $D, D_{2}, B$, and $B_{1}$ lie on some circle $\omega_{D}$. Now we have $$ \angle B_{2} D B_{1}=\angle B_{2} D B-\angle B_{1} D B=\angle B_{2} D_{1} B-\angle B_{1} D_{2} B=\angle D_{2} B D_{1} . $$ Therefore, the corresponding sides of the triangles $D B_{1} B_{2}$ and $B D_{1} D_{2}$ are parallel, and the triangles are homothetical (in $H$ ). So their corresponding medians $D L_{B}$ and $B L_{D}$ are also parallel.  Yet alternatively, after obtaining the circles $\omega_{B}$ and $\omega_{D}$, one may notice that $H$ lies on their radical axis $B D$, whence $H B_{1} \cdot H D_{2}=H D_{1} \cdot H B_{2}$, or $$ \frac{H B_{1}}{H D_{1}}=\frac{H B_{2}}{H D_{1}} . $$ Since $h\left(D_{1}\right)=B_{1}$, this yields $h\left(D_{2}\right)=B_{2}$ and hence $h\left(L_{D}\right)=L_{B}$. Comment 3. Since $h$ preserves the line $A C$ and maps $B \mapsto D$ and $D_{1} \mapsto B_{1}$, we have $h\left(\gamma_{B}\right)=\gamma_{D}$. Therefore, $h\left(O_{B}\right)=O_{D}$; in particular, $H$ also lies on $O_{B} O_{D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$. Common remarks. We introduce some objects and establish some preliminary facts common for all solutions below. Let $\Omega$ denote the circle $(A B C D)$, and let $\gamma_{B}$ and $\gamma_{D}$ denote the two circles from the problem statement (their centres are $O_{B}$ and $O_{D}$, respectively). Clearly, all three centres $O, O_{B}$, and $O_{D}$ are distinct. Assume, without loss of generality, that $A B>B C$. Suppose that $A D>D C$, and let $H=A C \cap B D$. Then the rays $B B_{1}$ and $D D_{1}$ lie on one side of $B D$, as they contain the midpoints of the arcs $A D C$ and $A B C$, respectively. However, if $B D_{1} \| D B_{1}$, then $B_{1}$ and $D_{1}$ should be separated by $H$. This contradiction shows that $A D<C D$. Let $\gamma_{B}$ and $\gamma_{D}$ meet $\Omega$ again at $T_{B}$ and $T_{D}$, respectively. The common chord $B T_{B}$ of $\Omega$ and $\gamma_{B}$ is perpendicular to their line of centres $O_{B} O$; likewise, $D T_{D} \perp O_{D} O$. Therefore, $O \in O_{B} O_{D} \Longleftrightarrow O_{B} O\left\|O_{D} O \Longleftrightarrow B T_{B}\right\|$ $D T_{D}$, and the problem reduces to showing that  $$ B T_{B} \| D T_{D} $$ Comment 1. It seems that the discussion of the positions of points is necessary for both Solutions below. However, this part automatically follows from the angle chasing in Comment 2.
|
Let the diagonals $A C$ and $B D$ cross at $H$. Consider the homothety $h$ centred at $H$ and mapping $B$ to $D$. Since $B D_{1} \| D B_{1}$, we have $h\left(D_{1}\right)=B_{1}$. Let the tangents to $\Omega$ at $B$ and $D$ meet $A C$ at $L_{B}$ and $L_{D}$, respectively. We have $$ \angle L_{B} B B_{1}=\angle L_{B} B C+\angle C B B_{1}=\angle B A L_{B}+\angle B_{1} B A=\angle B B_{1} L_{B}, $$ which means that the triangle $L_{B} B B_{1}$ is isosceles, $L_{B} B=L_{B} B_{1}$. The powers of $L_{B}$ with respect to $\Omega$ and $\gamma_{D}$ are $L_{B} B^{2}$ and $L_{B} B_{1}^{2}$, respectively; so they are equal, whence $L_{B}$ lies on the radical axis $T_{D} D$ of those two circles. Similarly, $L_{D}$ lies on the radical axis $T_{B} B$ of $\Omega$ and $\gamma_{B}$. By the sine rule in the triangle $B H L_{B}$, we obtain $$ \frac{H L_{B}}{\sin \angle H B L_{B}}=\frac{B L_{B}}{\sin \angle B H L_{B}}=\frac{B_{1} L_{B}}{\sin \angle B H L_{B}} $$ similarly, $$ \frac{H L_{D}}{\sin \angle H D L_{D}}=\frac{D L_{D}}{\sin \angle D H L_{D}}=\frac{D_{1} L_{D}}{\sin \angle D H L_{D}} $$ Clearly, $\angle B H L_{B}=\angle D H L_{D}$. In the circle $\Omega$, tangent lines $B L_{B}$ and $D L_{D}$ form equal angles with the chord $B D$, so $\sin \angle H B L_{B}=\sin \angle H D L_{D}$ (this equality does not depend on the picture). Thus, dividing (2) by (3) we get $$ \frac{H L_{B}}{H L_{D}}=\frac{B_{1} L_{B}}{D_{1} L_{D}}, \quad \text { and hence } \quad \frac{H L_{B}}{H L_{D}}=\frac{H L_{B}-B_{1} L_{B}}{H L_{D}-D_{1} L_{D}}=\frac{H B_{1}}{H D_{1}} $$ Since $h\left(D_{1}\right)=B_{1}$, the obtained relation yields $h\left(L_{D}\right)=L_{B}$, so $h$ maps the line $L_{D} B$ to $L_{B} D$, and these lines are parallel, as desired.  Comment 2. In the solution above, the key relation $h\left(L_{D}\right)=L_{B}$ was obtained via a short computation in sines. Here we present an alternative, pure synthetical way of establishing that. Let the external bisectors of $\angle A B C$ and $\angle A D C$ cross $A C$ at $B_{2}$ and $D_{2}$, respectively; assume that $\overparen{A B}>\overparen{C B}$. In the right-angled triangle $B B_{1} B_{2}$, the point $L_{B}$ is a point on the hypothenuse such that $L_{B} B_{1}=L_{B} B$, so $L_{B}$ is the midpoint of $B_{1} B_{2}$. Since $D D_{1}$ is the internal angle bisector of $\angle A D C$, we have $$ \angle B D D_{1}=\frac{\angle B D A-\angle C D B}{2}=\frac{\angle B C A-\angle C A B}{2}=\angle B B_{2} D_{1}, $$ so the points $B, B_{2}, D$, and $D_{1}$ lie on some circle $\omega_{B}$. Similarly, $L_{D}$ is the midpoint of $D_{1} D_{2}$, and the points $D, D_{2}, B$, and $B_{1}$ lie on some circle $\omega_{D}$. Now we have $$ \angle B_{2} D B_{1}=\angle B_{2} D B-\angle B_{1} D B=\angle B_{2} D_{1} B-\angle B_{1} D_{2} B=\angle D_{2} B D_{1} . $$ Therefore, the corresponding sides of the triangles $D B_{1} B_{2}$ and $B D_{1} D_{2}$ are parallel, and the triangles are homothetical (in $H$ ). So their corresponding medians $D L_{B}$ and $B L_{D}$ are also parallel.  Yet alternatively, after obtaining the circles $\omega_{B}$ and $\omega_{D}$, one may notice that $H$ lies on their radical axis $B D$, whence $H B_{1} \cdot H D_{2}=H D_{1} \cdot H B_{2}$, or $$ \frac{H B_{1}}{H D_{1}}=\frac{H B_{2}}{H D_{1}} . $$ Since $h\left(D_{1}\right)=B_{1}$, this yields $h\left(D_{2}\right)=B_{2}$ and hence $h\left(L_{D}\right)=L_{B}$. Comment 3. Since $h$ preserves the line $A C$ and maps $B \mapsto D$ and $D_{1} \mapsto B_{1}$, we have $h\left(\gamma_{B}\right)=\gamma_{D}$. Therefore, $h\left(O_{B}\right)=O_{D}$; in particular, $H$ also lies on $O_{B} O_{D}$.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0869a636-9825-5333-be53-f2580ce6456f
| 24,259
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$. Common remarks. We introduce some objects and establish some preliminary facts common for all solutions below. Let $\Omega$ denote the circle $(A B C D)$, and let $\gamma_{B}$ and $\gamma_{D}$ denote the two circles from the problem statement (their centres are $O_{B}$ and $O_{D}$, respectively). Clearly, all three centres $O, O_{B}$, and $O_{D}$ are distinct. Assume, without loss of generality, that $A B>B C$. Suppose that $A D>D C$, and let $H=A C \cap B D$. Then the rays $B B_{1}$ and $D D_{1}$ lie on one side of $B D$, as they contain the midpoints of the arcs $A D C$ and $A B C$, respectively. However, if $B D_{1} \| D B_{1}$, then $B_{1}$ and $D_{1}$ should be separated by $H$. This contradiction shows that $A D<C D$. Let $\gamma_{B}$ and $\gamma_{D}$ meet $\Omega$ again at $T_{B}$ and $T_{D}$, respectively. The common chord $B T_{B}$ of $\Omega$ and $\gamma_{B}$ is perpendicular to their line of centres $O_{B} O$; likewise, $D T_{D} \perp O_{D} O$. Therefore, $O \in O_{B} O_{D} \Longleftrightarrow O_{B} O\left\|O_{D} O \Longleftrightarrow B T_{B}\right\|$ $D T_{D}$, and the problem reduces to showing that  $$ B T_{B} \| D T_{D} $$ Comment 1. It seems that the discussion of the positions of points is necessary for both Solutions below. However, this part automatically follows from the angle chasing in Comment 2.
|
Let $B D_{1}$ and $T_{B} D_{1}$ meet $\Omega$ again at $X_{B}$ and $Y_{B}$, respectively. Then $$ \angle B D_{1} C=\angle B T_{B} D_{1}=\angle B T_{B} Y_{B}=\angle B X_{B} Y_{B} $$ which shows that $X_{B} Y_{B} \| A C$. Similarly, let $D B_{1}$ and $T_{D} B_{1}$ meet $\Omega$ again at $X_{D}$ and $Y_{D}$, respectively; then $X_{D} Y_{D} \| A C$. Let $M_{D}$ and $M_{B}$ be the midpoints of the arcs $A B C$ and $A D C$, respectively; then the points $D_{1}$ and $B_{1}$ lie on $D M_{D}$ and $B M_{B}$, respectively. Let $K$ be the midpoint of $A C$ (which lies on $M_{B} M_{D}$ ). Applying Pascal's theorem to $M_{D} D X_{D} X_{B} B M_{B}$, we obtain that the points $D_{1}=M_{D} D \cap X_{B} B, B_{1}=D X_{D} \cap B M_{B}$, and $X_{D} X_{B} \cap M_{B} M_{D}$ are collinear, which means that $X_{B} X_{D}$ passes through $K$. Due to symmetry, the diagonals of an isosceles trapezoid $X_{B} Y_{B} X_{D} Y_{D}$ cross at $K$.  Let $b$ and $d$ denote the distances from the lines $X_{B} Y_{B}$ and $X_{D} Y_{D}$, respectively, to $A C$. Then we get $$ \frac{X_{B} Y_{B}}{X_{D} Y_{D}}=\frac{b}{d}=\frac{D_{1} X_{B}}{B_{1} X_{D}} $$ where the second equation holds in view of $D_{1} X_{B} \| B_{1} X_{D}$. Therefore, the triangles $D_{1} X_{B} Y_{B}$ and $B_{1} X_{D} Y_{D}$ are similar. The triangles $D_{1} T_{B} B$ and $B_{1} T_{D} D$ are similar to them and hence to each other. Since $B D_{1} \| D B_{1}$, these triangles are also homothetical. This yields $B T_{B} \| D T_{D}$, as desired. Comment 4. The original problem proposal asked to prove that the relations $B D_{1} \| D B_{1}$ and $O \in O_{1} O_{2}$ are equivalent. After obtaining $B D_{1} \| D B_{1} \Rightarrow O \in O_{1} O_{2}$, the converse proof is either repeated backwards mutatis mutandis, or can be obtained by the usual procedure of varying some points in the construction. The Problem Selection Committee chose the current version, because it is less technical, yet keeps most of the ideas.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose sides have pairwise different lengths. Let $O$ be the circumcentre of $A B C D$. The internal angle bisectors of $\angle A B C$ and $\angle A D C$ meet $A C$ at $B_{1}$ and $D_{1}$, respectively. Let $O_{B}$ be the centre of the circle which passes through $B$ and is tangent to $A C$ at $D_{1}$. Similarly, let $O_{D}$ be the centre of the circle which passes through $D$ and is tangent to $A C$ at $B_{1}$. Assume that $B D_{1} \| D B_{1}$. Prove that $O$ lies on the line $O_{B} O_{D}$. Common remarks. We introduce some objects and establish some preliminary facts common for all solutions below. Let $\Omega$ denote the circle $(A B C D)$, and let $\gamma_{B}$ and $\gamma_{D}$ denote the two circles from the problem statement (their centres are $O_{B}$ and $O_{D}$, respectively). Clearly, all three centres $O, O_{B}$, and $O_{D}$ are distinct. Assume, without loss of generality, that $A B>B C$. Suppose that $A D>D C$, and let $H=A C \cap B D$. Then the rays $B B_{1}$ and $D D_{1}$ lie on one side of $B D$, as they contain the midpoints of the arcs $A D C$ and $A B C$, respectively. However, if $B D_{1} \| D B_{1}$, then $B_{1}$ and $D_{1}$ should be separated by $H$. This contradiction shows that $A D<C D$. Let $\gamma_{B}$ and $\gamma_{D}$ meet $\Omega$ again at $T_{B}$ and $T_{D}$, respectively. The common chord $B T_{B}$ of $\Omega$ and $\gamma_{B}$ is perpendicular to their line of centres $O_{B} O$; likewise, $D T_{D} \perp O_{D} O$. Therefore, $O \in O_{B} O_{D} \Longleftrightarrow O_{B} O\left\|O_{D} O \Longleftrightarrow B T_{B}\right\|$ $D T_{D}$, and the problem reduces to showing that  $$ B T_{B} \| D T_{D} $$ Comment 1. It seems that the discussion of the positions of points is necessary for both Solutions below. However, this part automatically follows from the angle chasing in Comment 2.
|
Let $B D_{1}$ and $T_{B} D_{1}$ meet $\Omega$ again at $X_{B}$ and $Y_{B}$, respectively. Then $$ \angle B D_{1} C=\angle B T_{B} D_{1}=\angle B T_{B} Y_{B}=\angle B X_{B} Y_{B} $$ which shows that $X_{B} Y_{B} \| A C$. Similarly, let $D B_{1}$ and $T_{D} B_{1}$ meet $\Omega$ again at $X_{D}$ and $Y_{D}$, respectively; then $X_{D} Y_{D} \| A C$. Let $M_{D}$ and $M_{B}$ be the midpoints of the arcs $A B C$ and $A D C$, respectively; then the points $D_{1}$ and $B_{1}$ lie on $D M_{D}$ and $B M_{B}$, respectively. Let $K$ be the midpoint of $A C$ (which lies on $M_{B} M_{D}$ ). Applying Pascal's theorem to $M_{D} D X_{D} X_{B} B M_{B}$, we obtain that the points $D_{1}=M_{D} D \cap X_{B} B, B_{1}=D X_{D} \cap B M_{B}$, and $X_{D} X_{B} \cap M_{B} M_{D}$ are collinear, which means that $X_{B} X_{D}$ passes through $K$. Due to symmetry, the diagonals of an isosceles trapezoid $X_{B} Y_{B} X_{D} Y_{D}$ cross at $K$.  Let $b$ and $d$ denote the distances from the lines $X_{B} Y_{B}$ and $X_{D} Y_{D}$, respectively, to $A C$. Then we get $$ \frac{X_{B} Y_{B}}{X_{D} Y_{D}}=\frac{b}{d}=\frac{D_{1} X_{B}}{B_{1} X_{D}} $$ where the second equation holds in view of $D_{1} X_{B} \| B_{1} X_{D}$. Therefore, the triangles $D_{1} X_{B} Y_{B}$ and $B_{1} X_{D} Y_{D}$ are similar. The triangles $D_{1} T_{B} B$ and $B_{1} T_{D} D$ are similar to them and hence to each other. Since $B D_{1} \| D B_{1}$, these triangles are also homothetical. This yields $B T_{B} \| D T_{D}$, as desired. Comment 4. The original problem proposal asked to prove that the relations $B D_{1} \| D B_{1}$ and $O \in O_{1} O_{2}$ are equivalent. After obtaining $B D_{1} \| D B_{1} \Rightarrow O \in O_{1} O_{2}$, the converse proof is either repeated backwards mutatis mutandis, or can be obtained by the usual procedure of varying some points in the construction. The Problem Selection Committee chose the current version, because it is less technical, yet keeps most of the ideas.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0869a636-9825-5333-be53-f2580ce6456f
| 24,259
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent. Common remarks. Let $Q$ be the isogonal conjugate of $D$ with respect to the triangle $A B C$. Since $\angle B A D=\angle D A C$, the point $Q$ lies on $A D$. Then $\angle Q B A=\angle D B C=\angle F D A$, so the points $Q, D, F$, and $B$ are concyclic. Analogously, the points $Q, D, E$, and $C$ are concyclic. Thus $A F \cdot A B=A D \cdot A Q=A E \cdot A C$ and so the points $B, F, E$, and $C$ are also concyclic. 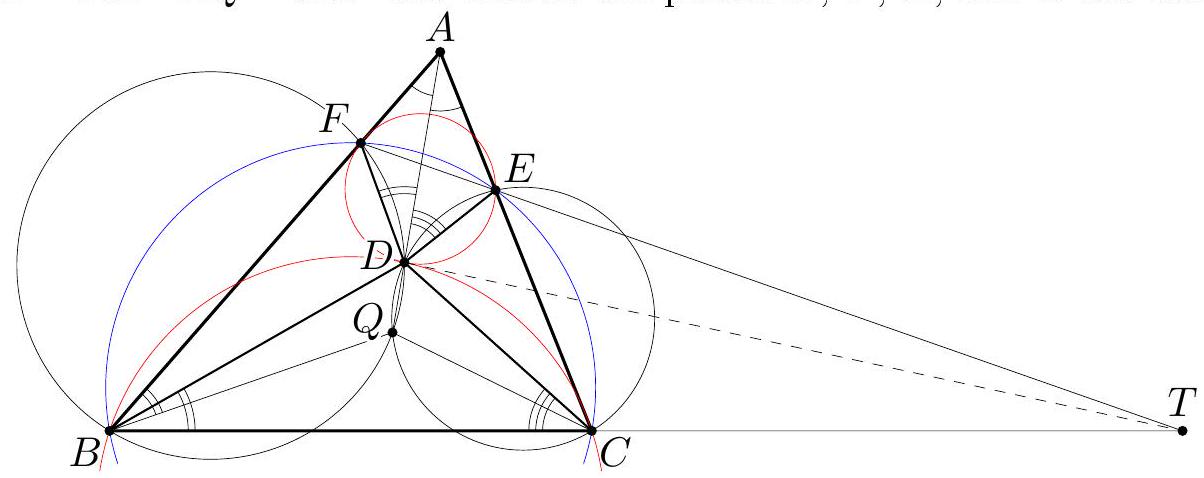 Let $T$ be the intersection of $B C$ and $F E$. Claim. TD $D^{2}=T B \cdot T C=T F \cdot T E$. Proof. We will prove that the circles $(D E F)$ and $(B D C)$ are tangent to each other. Indeed, using the above arguments, we get $$ \begin{aligned} & \angle B D F=\angle A F D-\angle A B D=\left(180^{\circ}-\angle F A D-\angle F D A\right)-(\angle A B C-\angle D B C) \\ = & 180^{\circ}-\angle F A D-\angle A B C=180^{\circ}-\angle D A E-\angle F E A=\angle F E D+\angle A D E=\angle F E D+\angle D C B, \end{aligned} $$ which implies the desired tangency. Since the points $B, C, E$, and $F$ are concyclic, the powers of the point $T$ with respect to the circles $(B D C)$ and $(E D F)$ are equal. So their radical axis, which coincides with the common tangent at $D$, passes through $T$, and hence $T D^{2}=T E \cdot T F=T B \cdot T C$.
|
Let $T A$ intersect the circle $(A B C)$ again at $M$. Due to the circles ( $B C E F$ ) and $(A M C B)$, and using the above Claim, we get $T M \cdot T A=T F \cdot T E=T B \cdot T C=T D^{2}$; in particular, the points $A, M, E$, and $F$ are concyclic. Under the inversion with centre $T$ and radius $T D$, the point $M$ maps to $A$, and $B$ maps to $C$, which implies that the circle $(M B D)$ maps to the circle $(A D C)$. Their common point $D$ lies on the circle of the inversion, so the second intersection point $K$ also lies on that circle, which means $T K=T D$. It follows that the point $T$ and the centres of the circles ( $K D E$ ) and $(A D C)$ lie on the perpendicular bisector of $K D$. Since the center of $(A D C)$ is $O_{1}$, it suffices to show now that the points $D, K, E$, and $X$ are concyclic (the center of the corresponding circle will be $O_{2}$ ). The lines $B M, D K$, and $A C$ are the pairwise radical axes of the circles $(A B C M),(A C D K)$ and $(B M D K)$, so they are concurrent at some point $P$. Also, $M$ lies on the circle $(A E F)$, thus $$ \begin{aligned} \Varangle(E X, X B) & =\Varangle(C X, X B)=\Varangle(X C, B C)+\Varangle(B C, B X)=2 \Varangle(A C, C B) \\ & =\Varangle(A C, C B)+\Varangle(E F, F A)=\Varangle(A M, B M)+\Varangle(E M, M A)=\Varangle(E M, B M), \end{aligned} $$ so the points $M, E, X$, and $B$ are concyclic. Therefore, $P E \cdot P X=P M \cdot P B=P K \cdot P D$, so the points $E, K, D$, and $X$ are concyclic, as desired.  Comment 1. We present here a different solution which uses similar ideas. Perform the inversion $\iota$ with centre $T$ and radius $T D$. It swaps $B$ with $C$ and $E$ with $F$; the point $D$ maps to itself. Let $X^{\prime}=\iota(X)$. Observe that the points $E, F, X$, and $X^{\prime}$ are concyclic, as well as the points $B, C, X$, and $X^{\prime}$. Then $$ \begin{aligned} & \Varangle\left(C X^{\prime}, X^{\prime} F\right)=\Varangle\left(C X^{\prime}, X^{\prime} X\right)+\Varangle\left(X^{\prime} X, X^{\prime} F\right)=\Varangle(C B, B X)+\Varangle(E X, E F) \\ &=\Varangle(X C, C B)+\Varangle(E C, E F)=\Varangle(C A, C B)+\Varangle(B C, B F)=\Varangle(C A, A F), \end{aligned} $$ therefore the points $C, X^{\prime}, A$, and $F$ are concyclic. Let $X^{\prime} F$ intersect $A C$ at $P$, and let $K$ be the second common point of $D P$ and the circle $(A C D)$. Then $$ P K \cdot P D=P A \cdot P C=P X^{\prime} \cdot P F=P E \cdot P X $$ hence, the points $K, X, D$, and $E$ lie on some circle $\omega_{1}$, while the points $K, X^{\prime}, D$, and $F$ lie on some circle $\omega_{2}$. (These circles are distinct since $\angle E X F+\angle E D F<\angle E A F+\angle D C B+\angle D B C<180^{\circ}$ ). The inversion $\iota$ swaps $\omega_{1}$ with $\omega_{2}$ and fixes their common point $D$, so it fixes their second common point $K$. Thus $T D=T K$ and the perpendicular bisector of $D K$ passes through $T$, as well as through the centres of the circles $(C D K A)$ and $(D E K X)$. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent. Common remarks. Let $Q$ be the isogonal conjugate of $D$ with respect to the triangle $A B C$. Since $\angle B A D=\angle D A C$, the point $Q$ lies on $A D$. Then $\angle Q B A=\angle D B C=\angle F D A$, so the points $Q, D, F$, and $B$ are concyclic. Analogously, the points $Q, D, E$, and $C$ are concyclic. Thus $A F \cdot A B=A D \cdot A Q=A E \cdot A C$ and so the points $B, F, E$, and $C$ are also concyclic.  Let $T$ be the intersection of $B C$ and $F E$. Claim. TD $D^{2}=T B \cdot T C=T F \cdot T E$. Proof. We will prove that the circles $(D E F)$ and $(B D C)$ are tangent to each other. Indeed, using the above arguments, we get $$ \begin{aligned} & \angle B D F=\angle A F D-\angle A B D=\left(180^{\circ}-\angle F A D-\angle F D A\right)-(\angle A B C-\angle D B C) \\ = & 180^{\circ}-\angle F A D-\angle A B C=180^{\circ}-\angle D A E-\angle F E A=\angle F E D+\angle A D E=\angle F E D+\angle D C B, \end{aligned} $$ which implies the desired tangency. Since the points $B, C, E$, and $F$ are concyclic, the powers of the point $T$ with respect to the circles $(B D C)$ and $(E D F)$ are equal. So their radical axis, which coincides with the common tangent at $D$, passes through $T$, and hence $T D^{2}=T E \cdot T F=T B \cdot T C$.
|
Let $T A$ intersect the circle $(A B C)$ again at $M$. Due to the circles ( $B C E F$ ) and $(A M C B)$, and using the above Claim, we get $T M \cdot T A=T F \cdot T E=T B \cdot T C=T D^{2}$; in particular, the points $A, M, E$, and $F$ are concyclic. Under the inversion with centre $T$ and radius $T D$, the point $M$ maps to $A$, and $B$ maps to $C$, which implies that the circle $(M B D)$ maps to the circle $(A D C)$. Their common point $D$ lies on the circle of the inversion, so the second intersection point $K$ also lies on that circle, which means $T K=T D$. It follows that the point $T$ and the centres of the circles ( $K D E$ ) and $(A D C)$ lie on the perpendicular bisector of $K D$. Since the center of $(A D C)$ is $O_{1}$, it suffices to show now that the points $D, K, E$, and $X$ are concyclic (the center of the corresponding circle will be $O_{2}$ ). The lines $B M, D K$, and $A C$ are the pairwise radical axes of the circles $(A B C M),(A C D K)$ and $(B M D K)$, so they are concurrent at some point $P$. Also, $M$ lies on the circle $(A E F)$, thus $$ \begin{aligned} \Varangle(E X, X B) & =\Varangle(C X, X B)=\Varangle(X C, B C)+\Varangle(B C, B X)=2 \Varangle(A C, C B) \\ & =\Varangle(A C, C B)+\Varangle(E F, F A)=\Varangle(A M, B M)+\Varangle(E M, M A)=\Varangle(E M, B M), \end{aligned} $$ so the points $M, E, X$, and $B$ are concyclic. Therefore, $P E \cdot P X=P M \cdot P B=P K \cdot P D$, so the points $E, K, D$, and $X$ are concyclic, as desired.  Comment 1. We present here a different solution which uses similar ideas. Perform the inversion $\iota$ with centre $T$ and radius $T D$. It swaps $B$ with $C$ and $E$ with $F$; the point $D$ maps to itself. Let $X^{\prime}=\iota(X)$. Observe that the points $E, F, X$, and $X^{\prime}$ are concyclic, as well as the points $B, C, X$, and $X^{\prime}$. Then $$ \begin{aligned} & \Varangle\left(C X^{\prime}, X^{\prime} F\right)=\Varangle\left(C X^{\prime}, X^{\prime} X\right)+\Varangle\left(X^{\prime} X, X^{\prime} F\right)=\Varangle(C B, B X)+\Varangle(E X, E F) \\ &=\Varangle(X C, C B)+\Varangle(E C, E F)=\Varangle(C A, C B)+\Varangle(B C, B F)=\Varangle(C A, A F), \end{aligned} $$ therefore the points $C, X^{\prime}, A$, and $F$ are concyclic. Let $X^{\prime} F$ intersect $A C$ at $P$, and let $K$ be the second common point of $D P$ and the circle $(A C D)$. Then $$ P K \cdot P D=P A \cdot P C=P X^{\prime} \cdot P F=P E \cdot P X $$ hence, the points $K, X, D$, and $E$ lie on some circle $\omega_{1}$, while the points $K, X^{\prime}, D$, and $F$ lie on some circle $\omega_{2}$. (These circles are distinct since $\angle E X F+\angle E D F<\angle E A F+\angle D C B+\angle D B C<180^{\circ}$ ). The inversion $\iota$ swaps $\omega_{1}$ with $\omega_{2}$ and fixes their common point $D$, so it fixes their second common point $K$. Thus $T D=T K$ and the perpendicular bisector of $D K$ passes through $T$, as well as through the centres of the circles $(C D K A)$ and $(D E K X)$. 
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
58415308-4e7f-503e-b679-616e2edb04da
| 24,265
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent. Common remarks. Let $Q$ be the isogonal conjugate of $D$ with respect to the triangle $A B C$. Since $\angle B A D=\angle D A C$, the point $Q$ lies on $A D$. Then $\angle Q B A=\angle D B C=\angle F D A$, so the points $Q, D, F$, and $B$ are concyclic. Analogously, the points $Q, D, E$, and $C$ are concyclic. Thus $A F \cdot A B=A D \cdot A Q=A E \cdot A C$ and so the points $B, F, E$, and $C$ are also concyclic.  Let $T$ be the intersection of $B C$ and $F E$. Claim. TD $D^{2}=T B \cdot T C=T F \cdot T E$. Proof. We will prove that the circles $(D E F)$ and $(B D C)$ are tangent to each other. Indeed, using the above arguments, we get $$ \begin{aligned} & \angle B D F=\angle A F D-\angle A B D=\left(180^{\circ}-\angle F A D-\angle F D A\right)-(\angle A B C-\angle D B C) \\ = & 180^{\circ}-\angle F A D-\angle A B C=180^{\circ}-\angle D A E-\angle F E A=\angle F E D+\angle A D E=\angle F E D+\angle D C B, \end{aligned} $$ which implies the desired tangency. Since the points $B, C, E$, and $F$ are concyclic, the powers of the point $T$ with respect to the circles $(B D C)$ and $(E D F)$ are equal. So their radical axis, which coincides with the common tangent at $D$, passes through $T$, and hence $T D^{2}=T E \cdot T F=T B \cdot T C$.
|
We use only the first part of the Common remarks, namely, the facts that the tuples $(C, D, Q, E)$ and $(B, C, E, F)$ are both concyclic. We also introduce the point $T=$ $B C \cap E F$. Let the circle $(C D E)$ meet $B C$ again at $E_{1}$. Since $\angle E_{1} C Q=\angle D C E$, the $\operatorname{arcs} D E$ and $Q E_{1}$ of the circle $(C D Q)$ are equal, so $D Q \| E E_{1}$. Since $B F E C$ is cyclic, the line $A D$ forms equal angles with $B C$ and $E F$, hence so does $E E_{1}$. Therefore, the triangle $E E_{1} T$ is isosceles, $T E=T E_{1}$, and $T$ lies on the common perpendicular bisector of $E E_{1}$ and $D Q$. Let $U$ and $V$ be the centres of circles $(A D E)$ and $(C D Q E)$, respectively. Then $U O_{1}$ is the perpendicular bisector of $A D$. Moreover, the points $U, V$, and $O_{2}$ belong to the perpendicular bisector of $D E$. Since $U O_{1} \| V T$, in order to show that $O_{1} O_{2}$ passes through $T$, it suffices to show that $$ \frac{O_{2} U}{O_{2} V}=\frac{O_{1} U}{T V} $$ Denote angles $A, B$, and $C$ of the triangle $A B C$ by $\alpha, \beta$, and $\gamma$, respectively. Projecting onto $A C$ we obtain $$ \frac{O_{2} U}{O_{2} V}=\frac{(X E-A E) / 2}{(X E+E C) / 2}=\frac{A X}{C X}=\frac{A X}{B X}=\frac{\sin (\gamma-\beta)}{\sin \alpha} $$ The projection of $O_{1} U$ onto $A C$ is $(A C-A E) / 2=C E / 2$; the angle between $O_{1} U$ and $A C$ is $90^{\circ}-\alpha / 2$, so $$ \frac{O_{1} U}{E C}=\frac{1}{2 \sin (\alpha / 2)} $$ Next, we claim that $E, V, C$, and $T$ are concyclic. Indeed, the point $V$ lies on the perpendicular bisector of $C E$, as well as on the internal angle bisector of $\angle C T F$. Therefore, $V$ coincides with the midpoint of the arc $C E$ of the circle (TCE). Now we have $\angle E V C=2 \angle E E_{1} C=180^{\circ}-(\gamma-\beta)$ and $\angle V E T=\angle V E_{1} T=90^{\circ}-\angle E_{1} E C=$ $90^{\circ}-\alpha / 2$. Therefore, $$ \frac{E C}{T V}=\frac{\sin \angle E T C}{\sin \angle V E T}=\frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)} . $$  Recalling (2) and multiplying (3) and (4) we establish (1): $$ \frac{O_{2} U}{O_{2} V}=\frac{\sin (\gamma-\beta)}{\sin \alpha}=\frac{1}{2 \sin (\alpha / 2)} \cdot \frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)}=\frac{O_{1} U}{E C} \cdot \frac{E C}{T V}=\frac{O_{1} U}{T V} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $D$ is chosen inside an acute-angled triangle $A B C$ with $A B>A C$ so that $\angle B A D=\angle D A C$. A point $E$ is constructed on the segment $A C$ so that $\angle A D E=\angle D C B$. Similarly, a point $F$ is constructed on the segment $A B$ so that $\angle A D F=\angle D B C$. A point $X$ is chosen on the line $A C$ so that $C X=B X$. Let $O_{1}$ and $O_{2}$ be the circumcentres of the triangles $A D C$ and $D X E$. Prove that the lines $B C, E F$, and $O_{1} O_{2}$ are concurrent. Common remarks. Let $Q$ be the isogonal conjugate of $D$ with respect to the triangle $A B C$. Since $\angle B A D=\angle D A C$, the point $Q$ lies on $A D$. Then $\angle Q B A=\angle D B C=\angle F D A$, so the points $Q, D, F$, and $B$ are concyclic. Analogously, the points $Q, D, E$, and $C$ are concyclic. Thus $A F \cdot A B=A D \cdot A Q=A E \cdot A C$ and so the points $B, F, E$, and $C$ are also concyclic.  Let $T$ be the intersection of $B C$ and $F E$. Claim. TD $D^{2}=T B \cdot T C=T F \cdot T E$. Proof. We will prove that the circles $(D E F)$ and $(B D C)$ are tangent to each other. Indeed, using the above arguments, we get $$ \begin{aligned} & \angle B D F=\angle A F D-\angle A B D=\left(180^{\circ}-\angle F A D-\angle F D A\right)-(\angle A B C-\angle D B C) \\ = & 180^{\circ}-\angle F A D-\angle A B C=180^{\circ}-\angle D A E-\angle F E A=\angle F E D+\angle A D E=\angle F E D+\angle D C B, \end{aligned} $$ which implies the desired tangency. Since the points $B, C, E$, and $F$ are concyclic, the powers of the point $T$ with respect to the circles $(B D C)$ and $(E D F)$ are equal. So their radical axis, which coincides with the common tangent at $D$, passes through $T$, and hence $T D^{2}=T E \cdot T F=T B \cdot T C$.
|
We use only the first part of the Common remarks, namely, the facts that the tuples $(C, D, Q, E)$ and $(B, C, E, F)$ are both concyclic. We also introduce the point $T=$ $B C \cap E F$. Let the circle $(C D E)$ meet $B C$ again at $E_{1}$. Since $\angle E_{1} C Q=\angle D C E$, the $\operatorname{arcs} D E$ and $Q E_{1}$ of the circle $(C D Q)$ are equal, so $D Q \| E E_{1}$. Since $B F E C$ is cyclic, the line $A D$ forms equal angles with $B C$ and $E F$, hence so does $E E_{1}$. Therefore, the triangle $E E_{1} T$ is isosceles, $T E=T E_{1}$, and $T$ lies on the common perpendicular bisector of $E E_{1}$ and $D Q$. Let $U$ and $V$ be the centres of circles $(A D E)$ and $(C D Q E)$, respectively. Then $U O_{1}$ is the perpendicular bisector of $A D$. Moreover, the points $U, V$, and $O_{2}$ belong to the perpendicular bisector of $D E$. Since $U O_{1} \| V T$, in order to show that $O_{1} O_{2}$ passes through $T$, it suffices to show that $$ \frac{O_{2} U}{O_{2} V}=\frac{O_{1} U}{T V} $$ Denote angles $A, B$, and $C$ of the triangle $A B C$ by $\alpha, \beta$, and $\gamma$, respectively. Projecting onto $A C$ we obtain $$ \frac{O_{2} U}{O_{2} V}=\frac{(X E-A E) / 2}{(X E+E C) / 2}=\frac{A X}{C X}=\frac{A X}{B X}=\frac{\sin (\gamma-\beta)}{\sin \alpha} $$ The projection of $O_{1} U$ onto $A C$ is $(A C-A E) / 2=C E / 2$; the angle between $O_{1} U$ and $A C$ is $90^{\circ}-\alpha / 2$, so $$ \frac{O_{1} U}{E C}=\frac{1}{2 \sin (\alpha / 2)} $$ Next, we claim that $E, V, C$, and $T$ are concyclic. Indeed, the point $V$ lies on the perpendicular bisector of $C E$, as well as on the internal angle bisector of $\angle C T F$. Therefore, $V$ coincides with the midpoint of the arc $C E$ of the circle (TCE). Now we have $\angle E V C=2 \angle E E_{1} C=180^{\circ}-(\gamma-\beta)$ and $\angle V E T=\angle V E_{1} T=90^{\circ}-\angle E_{1} E C=$ $90^{\circ}-\alpha / 2$. Therefore, $$ \frac{E C}{T V}=\frac{\sin \angle E T C}{\sin \angle V E T}=\frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)} . $$  Recalling (2) and multiplying (3) and (4) we establish (1): $$ \frac{O_{2} U}{O_{2} V}=\frac{\sin (\gamma-\beta)}{\sin \alpha}=\frac{1}{2 \sin (\alpha / 2)} \cdot \frac{\sin (\gamma-\beta)}{\cos (\alpha / 2)}=\frac{O_{1} U}{E C} \cdot \frac{E C}{T V}=\frac{O_{1} U}{T V} $$
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
58415308-4e7f-503e-b679-616e2edb04da
| 24,265
|
Let $n \geqslant 3$ be an integer, and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers in the interval $[0,1]$. Let $s=x_{1}+x_{2}+\ldots+x_{n}$, and assume that $s \geqslant 3$. Prove that there exist integers $i$ and $j$ with $1 \leqslant i<j \leqslant n$ such that $$ 2^{j-i} x_{i} x_{j}>2^{s-3} $$ (Trinidad and Tobago)
|
Let $1 \leqslant a<b \leqslant n$ be such that $2^{b-a} x_{a} x_{b}$ is maximal. This choice of $a$ and $b$ implies that $x_{a+t} \leqslant 2^{t} x_{a}$ for all $1-a \leqslant t \leqslant b-a-1$, and similarly $x_{b-t} \leqslant 2^{t} x_{b}$ for all $b-n \leqslant t \leqslant b-a+1$. Now, suppose that $x_{a} \in\left(\frac{1}{2^{u+1}}, \frac{1}{2^{u}}\right]$ and $x_{b} \in\left(\frac{1}{2^{v+1}}, \frac{1}{2^{v}}\right]$, and write $x_{a}=2^{-\alpha}, x_{b}=2^{-\beta}$. Then $$ \sum_{i=1}^{a+u-1} x_{i} \leqslant 2^{u} x_{a}\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2^{a+u-1}}\right)<2^{u} x_{a} \leqslant 1 $$ and similarly, $$ \sum_{i=b-v+1}^{n} x_{i} \leqslant 2^{v} x_{b}\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2^{n-b+v}}\right)<2^{v} x_{b} \leqslant 1 $$ In other words, the sum of the $x_{i}$ 's for $i$ outside of the interval $[a+u, b-v]$ is strictly less than 2. Since the total sum is at least 3 , and each term is at most 1 , it follows that this interval must have at least two integers. i.e., $a+u<b-v$. Thus, by bounding the sum of the $x_{i}$ for $i \in[1, a+u] \cup[b-v, n]$ like above, and trivially bounding each $x_{i} \in(a+u, b-v)$ by 1 , we obtain $$ s<2^{u+1} x_{a}+2^{v+1} x_{b}+((b-v)-(a+u)-1)=b-a+\left(2^{u+1-\alpha}+2^{v+1-\beta}-(u+v+1)\right) . $$ Now recall $\alpha \in(u, u+1]$ and $\beta \in(v, v+1]$, so applying Bernoulli's inequality yields $\left.2^{u+1-\alpha}+2^{v+1-\beta}-u-v-1 \leqslant(1+(u+1-\alpha))\right)+(1+(v+1-\beta))-u-v-1=3-\alpha-\beta$. It follows that $s-3<b-a-\alpha-\beta$, and so $$ 2^{s-3}<2^{b-a-\alpha-\beta}=2^{b-a} x_{a} x_{b} . $$ Comment 1. It is not hard to see that the inequality is tight. Suppose that $n=2 k+1$, and we set $x_{k+1}=1, x_{k}=x_{k+2}=\frac{1}{2}+\frac{1}{2^{k}}$, and $x_{k+1-t}=x_{k+1+t}=\frac{1}{2^{t}}$. Then $s=3$ (so the right hand side is 1 ), and $$ \max _{i<j} 2^{j-i} x_{i} x_{j}=2^{2}\left(\frac{1}{2}+\frac{1}{2^{k}}\right)^{2} $$ which can be made arbitrarily close to 1 . Note that $s$ can be made larger by putting in more 1-s in the middle (and this accommodates even $n$ as well). Comment 2. An alternative formulation of the problem is to show that there exists a positive constant $c$ (or find the best such $c$ ) such that $$ \max _{i<j} 2^{j-i} x_{i} x_{j}>c 2^{s} . $$ The above shows that $c=1 / 8$ is the best possible. A somewhat simpler ending to the proof can be given for $c=1 / 32$. End of solution for $c=1 / 32$. As in the original solution, we arrive at $$ s<2^{u+1} x_{a}+2^{v+1} x_{b}+((b-v)-(a+u)-1)=b-a+\left(2^{u+1-\alpha}+2^{v+1-\beta}-(u+v+1)\right) . $$ Now $2^{b-a} x_{a} x_{b} \geqslant 2^{b-a} 2^{-u-1} 2^{-v-1}$, so it is enough to show $s-5<b-a-u-v-2$, or $s<b-a-$ $u-v+3$. The fact that $u+1-\alpha<1$ and $v+1-\beta<1$ implies $2^{u+1-\alpha}+2^{v+1-\beta}<4$, and so $s<b-a+(2+2-u-v-1)=b-a-u-v-3$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 3$ be an integer, and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers in the interval $[0,1]$. Let $s=x_{1}+x_{2}+\ldots+x_{n}$, and assume that $s \geqslant 3$. Prove that there exist integers $i$ and $j$ with $1 \leqslant i<j \leqslant n$ such that $$ 2^{j-i} x_{i} x_{j}>2^{s-3} $$ (Trinidad and Tobago)
|
Let $1 \leqslant a<b \leqslant n$ be such that $2^{b-a} x_{a} x_{b}$ is maximal. This choice of $a$ and $b$ implies that $x_{a+t} \leqslant 2^{t} x_{a}$ for all $1-a \leqslant t \leqslant b-a-1$, and similarly $x_{b-t} \leqslant 2^{t} x_{b}$ for all $b-n \leqslant t \leqslant b-a+1$. Now, suppose that $x_{a} \in\left(\frac{1}{2^{u+1}}, \frac{1}{2^{u}}\right]$ and $x_{b} \in\left(\frac{1}{2^{v+1}}, \frac{1}{2^{v}}\right]$, and write $x_{a}=2^{-\alpha}, x_{b}=2^{-\beta}$. Then $$ \sum_{i=1}^{a+u-1} x_{i} \leqslant 2^{u} x_{a}\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2^{a+u-1}}\right)<2^{u} x_{a} \leqslant 1 $$ and similarly, $$ \sum_{i=b-v+1}^{n} x_{i} \leqslant 2^{v} x_{b}\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2^{n-b+v}}\right)<2^{v} x_{b} \leqslant 1 $$ In other words, the sum of the $x_{i}$ 's for $i$ outside of the interval $[a+u, b-v]$ is strictly less than 2. Since the total sum is at least 3 , and each term is at most 1 , it follows that this interval must have at least two integers. i.e., $a+u<b-v$. Thus, by bounding the sum of the $x_{i}$ for $i \in[1, a+u] \cup[b-v, n]$ like above, and trivially bounding each $x_{i} \in(a+u, b-v)$ by 1 , we obtain $$ s<2^{u+1} x_{a}+2^{v+1} x_{b}+((b-v)-(a+u)-1)=b-a+\left(2^{u+1-\alpha}+2^{v+1-\beta}-(u+v+1)\right) . $$ Now recall $\alpha \in(u, u+1]$ and $\beta \in(v, v+1]$, so applying Bernoulli's inequality yields $\left.2^{u+1-\alpha}+2^{v+1-\beta}-u-v-1 \leqslant(1+(u+1-\alpha))\right)+(1+(v+1-\beta))-u-v-1=3-\alpha-\beta$. It follows that $s-3<b-a-\alpha-\beta$, and so $$ 2^{s-3}<2^{b-a-\alpha-\beta}=2^{b-a} x_{a} x_{b} . $$ Comment 1. It is not hard to see that the inequality is tight. Suppose that $n=2 k+1$, and we set $x_{k+1}=1, x_{k}=x_{k+2}=\frac{1}{2}+\frac{1}{2^{k}}$, and $x_{k+1-t}=x_{k+1+t}=\frac{1}{2^{t}}$. Then $s=3$ (so the right hand side is 1 ), and $$ \max _{i<j} 2^{j-i} x_{i} x_{j}=2^{2}\left(\frac{1}{2}+\frac{1}{2^{k}}\right)^{2} $$ which can be made arbitrarily close to 1 . Note that $s$ can be made larger by putting in more 1-s in the middle (and this accommodates even $n$ as well). Comment 2. An alternative formulation of the problem is to show that there exists a positive constant $c$ (or find the best such $c$ ) such that $$ \max _{i<j} 2^{j-i} x_{i} x_{j}>c 2^{s} . $$ The above shows that $c=1 / 8$ is the best possible. A somewhat simpler ending to the proof can be given for $c=1 / 32$. End of solution for $c=1 / 32$. As in the original solution, we arrive at $$ s<2^{u+1} x_{a}+2^{v+1} x_{b}+((b-v)-(a+u)-1)=b-a+\left(2^{u+1-\alpha}+2^{v+1-\beta}-(u+v+1)\right) . $$ Now $2^{b-a} x_{a} x_{b} \geqslant 2^{b-a} 2^{-u-1} 2^{-v-1}$, so it is enough to show $s-5<b-a-u-v-2$, or $s<b-a-$ $u-v+3$. The fact that $u+1-\alpha<1$ and $v+1-\beta<1$ implies $2^{u+1-\alpha}+2^{v+1-\beta}<4$, and so $s<b-a+(2+2-u-v-1)=b-a-u-v-3$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
93d1a00e-69b6-5797-bdb9-6e9c4448599f
| 24,299
|
For a positive integer $n$ we denote by $s(n)$ the sum of the digits of $n$. Let $P(x)=$ $x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ be a polynomial, where $n \geqslant 2$ and $a_{i}$ is a positive integer for all $0 \leqslant i \leqslant n-1$. Could it be the case that, for all positive integers $k, s(k)$ and $s(P(k))$ have the same parity? (Belarus)
|
With the notation above, we begin by choosing a positive integer $t$ such that $$ 10^{t}>\max \left\{\frac{100^{n-1} a_{n-1}}{\left(10^{\frac{1}{n-1}}-9^{\frac{1}{n-1}}\right)^{n-1}}, \frac{a_{n-1}}{9} 10^{n-1}, \frac{a_{n-1}}{9}\left(10 a_{n-1}\right)^{n-1}, \ldots, \frac{a_{n-1}}{9}\left(10 a_{0}\right)^{n-1}\right\} $$ As a direct consequence of $10^{t}$ being bigger than the first quantity listed in the above set, we get that the interval $$ I=\left[\left(\frac{9}{a_{n-1}} 10^{t}\right)^{\frac{1}{n-1}},\left(\frac{1}{a_{n-1}} 10^{t+1}\right)^{\frac{1}{n-1}}\right) $$ contains at least 100 consecutive positive integers. Let $X$ be a positive integer in $I$ such that $X$ is congruent to $1 \bmod 100$. Since $X \in I$ we have $$ 9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}<10^{t+1} $$ thus the first digit (from the left) of $a_{n-1} X^{n-1}$ must be 9 . Next, we observe that $a_{n-1}\left(10 a_{i}\right)^{n-1}<9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}$, thus $10 a_{i}<X$ for all $i$, which immediately implies that $a_{0}<a_{1} X<\cdots<a_{n} X^{n}$, and the number of digits of this strictly increasing sequence forms a strictly increasing sequence too. In other words, if $i<j$, the number of digits of $a_{i} X^{i}$ is less than the number of digits of $a_{j} X^{j}$. Let $\alpha$ be the number of digits of $a_{n-1} X^{n-1}$, thus $10^{\alpha-1} \leqslant a_{n-1} X^{n-1}<10^{\alpha}$. We are now going to look at $P\left(10^{\alpha} X\right)$ and $P\left(10^{\alpha-1} X\right)$ and prove that the sum of their digits has different parities. This will finish the proof since $s\left(10^{\alpha} X\right)=s\left(10^{\alpha-1} X\right)=s(X)$. We have $P\left(10^{\alpha} X\right)=10^{\alpha n} X^{n}+a_{n-1} 10^{\alpha(n-1)} X^{n-1}+\cdots+a_{0}$, and since $10^{\alpha(i+1)}>10^{\alpha i} a_{n-1} X^{n-1}>$ $10^{\alpha i} a_{i} X^{i}$, the terms $a_{i} 10^{\alpha i} X^{i}$ do not interact when added; in particular, there is no carryover caused by addition. Thus we have $s\left(P\left(10^{\alpha} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)$. We now look at $P\left(10^{\alpha-1} X\right)=10^{(\alpha-1) n} X^{n}+a_{n-1} 10^{(\alpha-1)(n-1)} X^{n-1}+\cdots+a_{0}$. Firstly, if $i<n-1$, then $a_{n-1} X^{n-1}$ has more digits than $a_{i} X^{i}$ and $a_{n-1} X^{n-1} \geqslant 10 a_{i} X^{i}$. It now follows that $10^{(\alpha-1)(i+1)+1}>10^{(\alpha-1) i} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) i+1} a_{i} X^{i}$, thus all terms $10^{(\alpha-1) i} a_{i} X^{i}$ for $0 \leqslant i \leqslant n-1$ come in 'blocks', exactly as in the previous case. Finally, $10^{(\alpha-1) n+1}>10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) n}$, thus $10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1}$ has exactly $(\alpha-1) n+1$ digits, and its first digit is 9 , as established above. On the other hand, $10^{(\alpha-1) n} X^{n}$ has exactly $(\alpha-1) n$ zeros, followed by $01($ as $X$ is $1 \bmod 100)$. Therefore, when we add the terms, the 9 and 1 turn into 0 , the 0 turns into 1 , and nothing else is affected. Putting everything together, we obtain $$ s\left(P\left(10^{\alpha-1} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)-9=s\left(P\left(10^{\alpha} X\right)\right)-9 $$ thus $s\left(P\left(10^{\alpha} X\right)\right)$ and $s\left(P\left(10^{\alpha-1} X\right)\right)$ have different parities, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$ we denote by $s(n)$ the sum of the digits of $n$. Let $P(x)=$ $x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ be a polynomial, where $n \geqslant 2$ and $a_{i}$ is a positive integer for all $0 \leqslant i \leqslant n-1$. Could it be the case that, for all positive integers $k, s(k)$ and $s(P(k))$ have the same parity? (Belarus)
|
With the notation above, we begin by choosing a positive integer $t$ such that $$ 10^{t}>\max \left\{\frac{100^{n-1} a_{n-1}}{\left(10^{\frac{1}{n-1}}-9^{\frac{1}{n-1}}\right)^{n-1}}, \frac{a_{n-1}}{9} 10^{n-1}, \frac{a_{n-1}}{9}\left(10 a_{n-1}\right)^{n-1}, \ldots, \frac{a_{n-1}}{9}\left(10 a_{0}\right)^{n-1}\right\} $$ As a direct consequence of $10^{t}$ being bigger than the first quantity listed in the above set, we get that the interval $$ I=\left[\left(\frac{9}{a_{n-1}} 10^{t}\right)^{\frac{1}{n-1}},\left(\frac{1}{a_{n-1}} 10^{t+1}\right)^{\frac{1}{n-1}}\right) $$ contains at least 100 consecutive positive integers. Let $X$ be a positive integer in $I$ such that $X$ is congruent to $1 \bmod 100$. Since $X \in I$ we have $$ 9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}<10^{t+1} $$ thus the first digit (from the left) of $a_{n-1} X^{n-1}$ must be 9 . Next, we observe that $a_{n-1}\left(10 a_{i}\right)^{n-1}<9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}$, thus $10 a_{i}<X$ for all $i$, which immediately implies that $a_{0}<a_{1} X<\cdots<a_{n} X^{n}$, and the number of digits of this strictly increasing sequence forms a strictly increasing sequence too. In other words, if $i<j$, the number of digits of $a_{i} X^{i}$ is less than the number of digits of $a_{j} X^{j}$. Let $\alpha$ be the number of digits of $a_{n-1} X^{n-1}$, thus $10^{\alpha-1} \leqslant a_{n-1} X^{n-1}<10^{\alpha}$. We are now going to look at $P\left(10^{\alpha} X\right)$ and $P\left(10^{\alpha-1} X\right)$ and prove that the sum of their digits has different parities. This will finish the proof since $s\left(10^{\alpha} X\right)=s\left(10^{\alpha-1} X\right)=s(X)$. We have $P\left(10^{\alpha} X\right)=10^{\alpha n} X^{n}+a_{n-1} 10^{\alpha(n-1)} X^{n-1}+\cdots+a_{0}$, and since $10^{\alpha(i+1)}>10^{\alpha i} a_{n-1} X^{n-1}>$ $10^{\alpha i} a_{i} X^{i}$, the terms $a_{i} 10^{\alpha i} X^{i}$ do not interact when added; in particular, there is no carryover caused by addition. Thus we have $s\left(P\left(10^{\alpha} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)$. We now look at $P\left(10^{\alpha-1} X\right)=10^{(\alpha-1) n} X^{n}+a_{n-1} 10^{(\alpha-1)(n-1)} X^{n-1}+\cdots+a_{0}$. Firstly, if $i<n-1$, then $a_{n-1} X^{n-1}$ has more digits than $a_{i} X^{i}$ and $a_{n-1} X^{n-1} \geqslant 10 a_{i} X^{i}$. It now follows that $10^{(\alpha-1)(i+1)+1}>10^{(\alpha-1) i} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) i+1} a_{i} X^{i}$, thus all terms $10^{(\alpha-1) i} a_{i} X^{i}$ for $0 \leqslant i \leqslant n-1$ come in 'blocks', exactly as in the previous case. Finally, $10^{(\alpha-1) n+1}>10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) n}$, thus $10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1}$ has exactly $(\alpha-1) n+1$ digits, and its first digit is 9 , as established above. On the other hand, $10^{(\alpha-1) n} X^{n}$ has exactly $(\alpha-1) n$ zeros, followed by $01($ as $X$ is $1 \bmod 100)$. Therefore, when we add the terms, the 9 and 1 turn into 0 , the 0 turns into 1 , and nothing else is affected. Putting everything together, we obtain $$ s\left(P\left(10^{\alpha-1} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)-9=s\left(P\left(10^{\alpha} X\right)\right)-9 $$ thus $s\left(P\left(10^{\alpha} X\right)\right)$ and $s\left(P\left(10^{\alpha-1} X\right)\right)$ have different parities, as claimed.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3889b620-936a-5530-bbfc-c75b4a89b52a
| 24,307
|
Let $m, n \geqslant 2$ be integers, let $X$ be a set with $n$ elements, and let $X_{1}, X_{2}, \ldots, X_{m}$ be pairwise distinct non-empty, not necessary disjoint subsets of $X$. A function $f: X \rightarrow$ $\{1,2, \ldots, n+1\}$ is called nice if there exists an index $k$ such that $$ \sum_{x \in X_{k}} f(x)>\sum_{x \in X_{i}} f(x) \text { for all } i \neq k $$ Prove that the number of nice functions is at least $n^{n}$. (Germany)
|
For a subset $Y \subseteq X$, we write $f(Y)$ for $\sum_{y \in Y} f(y)$. Note that a function $f: X \rightarrow$ $\{1, \ldots, n+1\}$ is nice, if and only if $f\left(X_{i}\right)$ is maximized by a unique index $i \in\{1, \ldots, m\}$. We will first investigate the set $\mathcal{F}$ of functions $f: X \rightarrow\{1, \ldots, n\}$; note that $|\mathcal{F}|=n^{n}$. For every function $f \in \mathcal{F}$, define a corresponding function $f^{+}: X \rightarrow\{1,2, \ldots, n+1\}$ in the following way: Pick some set $X_{l}$ that maximizes the value $f\left(X_{l}\right)$. - For all $x \in X_{l}$, define $f^{+}(x)=f(x)+1$. - For all $x \in X \backslash X_{l}$, define $f^{+}(x)=f(x)$. Claim. The resulting function $f^{+}$is nice. Proof. Note that $f^{+}\left(X_{i}\right)=f\left(X_{i}\right)+\left|X_{i} \cap X_{l}\right|$ holds for all $X_{i}$. We show that $f^{+}\left(X_{i}\right)$ is maximized at the unique index $i=l$. Hence consider some arbitrary index $j \neq l$. Then $X_{l} \subset X_{j}$ is impossible, as this would imply $f\left(X_{j}\right)>f\left(X_{l}\right)$ and thereby contradict the choice of set $X_{l}$; this in particular yields $\left|X_{l}\right|>\left|X_{j} \cap X_{l}\right|$. $$ f^{+}\left(X_{l}\right)=f\left(X_{l}\right)+\left|X_{l}\right| \geqslant f\left(X_{j}\right)+\left|X_{l}\right|>f\left(X_{j}\right)+\left|X_{j} \cap X_{l}\right|=f^{+}\left(X_{j}\right) $$ The first inequality follows since $X_{l}$ was chosen to maximize the value $f\left(X_{l}\right)$. The second (strict) inequality follows from $\left|X_{l}\right|>\left|X_{j} \cap X_{l}\right|$ as observed above. This completes the proof of the claim. Next observe that function $f$ can be uniquely reconstructed from $f^{+}$: the claim yields that $f^{+}$has a unique maximizer $X_{l}$, and by decreasing the value of $f^{+}$on $X_{l}$ by 1 , we get we can fully determine the values of $f$. As each of the $n^{n}$ functions $f \in \mathcal{F}$ yields a (unique) corresponding nice function $f^{+}: X \rightarrow\{1,2, \ldots, n+1\}$, the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m, n \geqslant 2$ be integers, let $X$ be a set with $n$ elements, and let $X_{1}, X_{2}, \ldots, X_{m}$ be pairwise distinct non-empty, not necessary disjoint subsets of $X$. A function $f: X \rightarrow$ $\{1,2, \ldots, n+1\}$ is called nice if there exists an index $k$ such that $$ \sum_{x \in X_{k}} f(x)>\sum_{x \in X_{i}} f(x) \text { for all } i \neq k $$ Prove that the number of nice functions is at least $n^{n}$. (Germany)
|
For a subset $Y \subseteq X$, we write $f(Y)$ for $\sum_{y \in Y} f(y)$. Note that a function $f: X \rightarrow$ $\{1, \ldots, n+1\}$ is nice, if and only if $f\left(X_{i}\right)$ is maximized by a unique index $i \in\{1, \ldots, m\}$. We will first investigate the set $\mathcal{F}$ of functions $f: X \rightarrow\{1, \ldots, n\}$; note that $|\mathcal{F}|=n^{n}$. For every function $f \in \mathcal{F}$, define a corresponding function $f^{+}: X \rightarrow\{1,2, \ldots, n+1\}$ in the following way: Pick some set $X_{l}$ that maximizes the value $f\left(X_{l}\right)$. - For all $x \in X_{l}$, define $f^{+}(x)=f(x)+1$. - For all $x \in X \backslash X_{l}$, define $f^{+}(x)=f(x)$. Claim. The resulting function $f^{+}$is nice. Proof. Note that $f^{+}\left(X_{i}\right)=f\left(X_{i}\right)+\left|X_{i} \cap X_{l}\right|$ holds for all $X_{i}$. We show that $f^{+}\left(X_{i}\right)$ is maximized at the unique index $i=l$. Hence consider some arbitrary index $j \neq l$. Then $X_{l} \subset X_{j}$ is impossible, as this would imply $f\left(X_{j}\right)>f\left(X_{l}\right)$ and thereby contradict the choice of set $X_{l}$; this in particular yields $\left|X_{l}\right|>\left|X_{j} \cap X_{l}\right|$. $$ f^{+}\left(X_{l}\right)=f\left(X_{l}\right)+\left|X_{l}\right| \geqslant f\left(X_{j}\right)+\left|X_{l}\right|>f\left(X_{j}\right)+\left|X_{j} \cap X_{l}\right|=f^{+}\left(X_{j}\right) $$ The first inequality follows since $X_{l}$ was chosen to maximize the value $f\left(X_{l}\right)$. The second (strict) inequality follows from $\left|X_{l}\right|>\left|X_{j} \cap X_{l}\right|$ as observed above. This completes the proof of the claim. Next observe that function $f$ can be uniquely reconstructed from $f^{+}$: the claim yields that $f^{+}$has a unique maximizer $X_{l}$, and by decreasing the value of $f^{+}$on $X_{l}$ by 1 , we get we can fully determine the values of $f$. As each of the $n^{n}$ functions $f \in \mathcal{F}$ yields a (unique) corresponding nice function $f^{+}: X \rightarrow\{1,2, \ldots, n+1\}$, the proof is complete.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f80a837e-dda1-5df3-b12b-09d107822a84
| 24,322
|
Let $A B C D E$ be a convex pentagon such that $B C=D E$. Assume there is a point $T$ inside $A B C D E$ with $T B=T D, T C=T E$ and $\angle T B A=\angle A E T$. Let lines $C D$ and $C T$ intersect line $A B$ at points $P$ and $Q$, respectively, and let lines $C D$ and $D T$ intersect line $A E$ at points $R$ and $S$, respectively. Assume that points $P, B, A, Q$ and $R, E, A, S$ respectively, are collinear and occur on their lines in this order. Prove that the points $P, S, Q, R$ are concyclic. (Slovakia)
|
By the conditions we have $B C=D E, C T=E T$ and $T B=T D$, so the triangles $T B C$ and $T D E$ are congruent, in particular $\angle B T C=\angle D T E$. In triangles $T B Q$ and $T E S$ we have $\angle T B Q=\angle S E T$ and $\angle Q T B=180^{\circ}-\angle B T C=180^{\circ}-$ $\angle D T E=\angle E T S$, so these triangles are similar to each other. It follows that $\angle T S E=\angle B Q T$ and $$ \frac{T D}{T Q}=\frac{T B}{T Q}=\frac{T E}{T S}=\frac{T C}{T S} $$ By rearranging this relation we get $T D \cdot T S=T C \cdot T Q$, so $C, D, Q$ and $S$ are concyclic. (Alternatively, we can get $\angle C Q D=\angle C S D$ from the similar triangles $T C S$ and $T D Q$.) Hence, $\angle D C Q=\angle D S Q$. Finally, from the angles of triangle $C Q P$ we get $$ \angle R P Q=\angle R C Q-\angle P Q C=\angle D S Q-\angle D S R=\angle R S Q $$ which proves that $P, Q, R$ and $S$ are concyclic. 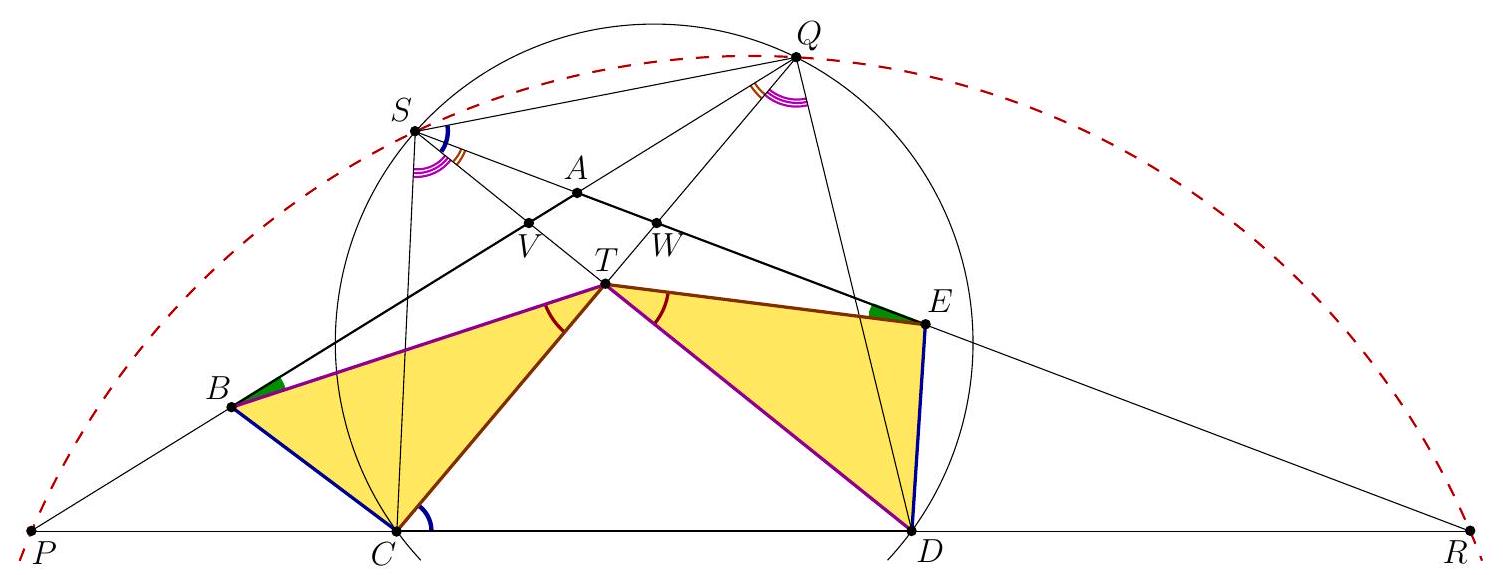
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that $B C=D E$. Assume there is a point $T$ inside $A B C D E$ with $T B=T D, T C=T E$ and $\angle T B A=\angle A E T$. Let lines $C D$ and $C T$ intersect line $A B$ at points $P$ and $Q$, respectively, and let lines $C D$ and $D T$ intersect line $A E$ at points $R$ and $S$, respectively. Assume that points $P, B, A, Q$ and $R, E, A, S$ respectively, are collinear and occur on their lines in this order. Prove that the points $P, S, Q, R$ are concyclic. (Slovakia)
|
By the conditions we have $B C=D E, C T=E T$ and $T B=T D$, so the triangles $T B C$ and $T D E$ are congruent, in particular $\angle B T C=\angle D T E$. In triangles $T B Q$ and $T E S$ we have $\angle T B Q=\angle S E T$ and $\angle Q T B=180^{\circ}-\angle B T C=180^{\circ}-$ $\angle D T E=\angle E T S$, so these triangles are similar to each other. It follows that $\angle T S E=\angle B Q T$ and $$ \frac{T D}{T Q}=\frac{T B}{T Q}=\frac{T E}{T S}=\frac{T C}{T S} $$ By rearranging this relation we get $T D \cdot T S=T C \cdot T Q$, so $C, D, Q$ and $S$ are concyclic. (Alternatively, we can get $\angle C Q D=\angle C S D$ from the similar triangles $T C S$ and $T D Q$.) Hence, $\angle D C Q=\angle D S Q$. Finally, from the angles of triangle $C Q P$ we get $$ \angle R P Q=\angle R C Q-\angle P Q C=\angle D S Q-\angle D S R=\angle R S Q $$ which proves that $P, Q, R$ and $S$ are concyclic. 
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d906533d-1885-56f6-8b1d-646ee15e4cae
| 24,338
|
Let $A B C D E$ be a convex pentagon such that $B C=D E$. Assume there is a point $T$ inside $A B C D E$ with $T B=T D, T C=T E$ and $\angle T B A=\angle A E T$. Let lines $C D$ and $C T$ intersect line $A B$ at points $P$ and $Q$, respectively, and let lines $C D$ and $D T$ intersect line $A E$ at points $R$ and $S$, respectively. Assume that points $P, B, A, Q$ and $R, E, A, S$ respectively, are collinear and occur on their lines in this order. Prove that the points $P, S, Q, R$ are concyclic. (Slovakia)
|
As in the previous solution, we note that triangles $T B C$ and $T D E$ are congruent. Denote the intersection point of $D T$ and $B A$ by $V$, and the intersection point of $C T$ and $E A$ by $W$. From triangles $B C Q$ and $D E S$ we then have $$ \begin{aligned} \angle V S W & =\angle D S E=180^{\circ}-\angle S E D-\angle E D S=180^{\circ}-\angle A E T-\angle T E D-\angle E D T \\ & =180^{\circ}-\angle T B A-\angle T C B-\angle C B T=180^{\circ}-\angle Q C B-\angle C B Q=\angle B Q C=\angle V Q W, \end{aligned} $$ meaning that $V S Q W$ is cyclic, and in particular $\angle W V Q=\angle W S Q$. Since $$ \angle V T B=180^{\circ}-\angle B T C-\angle C T D=180^{\circ}-\angle C T D-\angle D T E=\angle E T W $$ and $\angle T B V=\angle W E T$ by assumption, we have that the triangles $V T B$ and $W T E$ are similar, hence $$ \frac{V T}{W T}=\frac{B T}{E T}=\frac{D T}{C T} $$ Thus $C D \| V W$, and angle chasing yields $$ \angle R P Q=\angle W V Q=\angle W S Q=\angle R S Q $$ concluding the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that $B C=D E$. Assume there is a point $T$ inside $A B C D E$ with $T B=T D, T C=T E$ and $\angle T B A=\angle A E T$. Let lines $C D$ and $C T$ intersect line $A B$ at points $P$ and $Q$, respectively, and let lines $C D$ and $D T$ intersect line $A E$ at points $R$ and $S$, respectively. Assume that points $P, B, A, Q$ and $R, E, A, S$ respectively, are collinear and occur on their lines in this order. Prove that the points $P, S, Q, R$ are concyclic. (Slovakia)
|
As in the previous solution, we note that triangles $T B C$ and $T D E$ are congruent. Denote the intersection point of $D T$ and $B A$ by $V$, and the intersection point of $C T$ and $E A$ by $W$. From triangles $B C Q$ and $D E S$ we then have $$ \begin{aligned} \angle V S W & =\angle D S E=180^{\circ}-\angle S E D-\angle E D S=180^{\circ}-\angle A E T-\angle T E D-\angle E D T \\ & =180^{\circ}-\angle T B A-\angle T C B-\angle C B T=180^{\circ}-\angle Q C B-\angle C B Q=\angle B Q C=\angle V Q W, \end{aligned} $$ meaning that $V S Q W$ is cyclic, and in particular $\angle W V Q=\angle W S Q$. Since $$ \angle V T B=180^{\circ}-\angle B T C-\angle C T D=180^{\circ}-\angle C T D-\angle D T E=\angle E T W $$ and $\angle T B V=\angle W E T$ by assumption, we have that the triangles $V T B$ and $W T E$ are similar, hence $$ \frac{V T}{W T}=\frac{B T}{E T}=\frac{D T}{C T} $$ Thus $C D \| V W$, and angle chasing yields $$ \angle R P Q=\angle W V Q=\angle W S Q=\angle R S Q $$ concluding the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d906533d-1885-56f6-8b1d-646ee15e4cae
| 24,338
|
In the acute-angled triangle $A B C$, the point $F$ is the foot of the altitude from $A$, and $P$ is a point on the segment $A F$. The lines through $P$ parallel to $A C$ and $A B$ meet $B C$ at $D$ and $E$, respectively. Points $X \neq A$ and $Y \neq A$ lie on the circles $A B D$ and $A C E$, respectively, such that $D A=D X$ and $E A=E Y$. Prove that $B, C, X$ and $Y$ are concyclic. (Netherlands)
|
Let $A^{\prime}$ be the intersection of lines $B X$ and $C Y$. By power of a point, it suffices to prove that $A^{\prime} B \cdot A^{\prime} X=A^{\prime} C \cdot A^{\prime} Y$, or, equivalently, that $A^{\prime}$ lies on the radical axis of the circles $A B D X$ and $A C E Y$. From $D A=D X$ it follows that in circle $A B D X$, point $D$ bisects of one of the arcs $A X$. Therefore, depending on the order of points, the line $B C$ is either the internal or external bisector of $\angle A B X$. In both cases, line $B X$ is the reflection of $B A$ in line $B D C$. Analogously, line $C Y$ is the reflection of $C A$ in line $B C$; we can see that $A^{\prime}$ is the reflection of $A$ in line $B C$, so $A, F$ and $A^{\prime}$ are collinear. By $P D \| A C$ and $P E \| A B$ we have $\frac{F D}{F C}=\frac{F P}{F A}=\frac{F E}{F B}$, hence $F D \cdot F B=F E \cdot F C$. So, point $F$ has equal powers with respect to circles $A B D X$ and $A C E Y$. Point $A$, being a common point of the two circles, is another point with equal powers, so the radical axis of circles $A B D X$ and $A C E Y$ is the altitude $A F$ that passes through $A^{\prime}$. 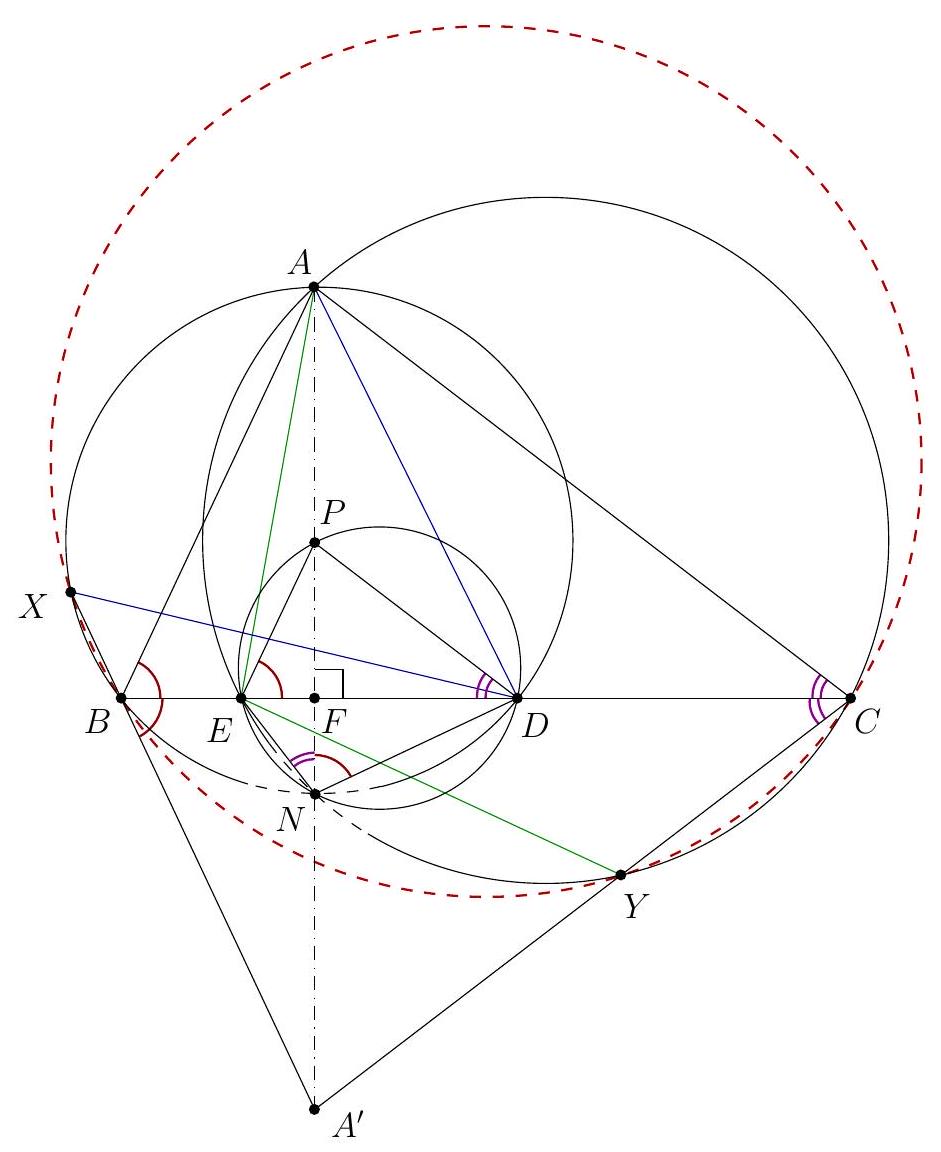
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the acute-angled triangle $A B C$, the point $F$ is the foot of the altitude from $A$, and $P$ is a point on the segment $A F$. The lines through $P$ parallel to $A C$ and $A B$ meet $B C$ at $D$ and $E$, respectively. Points $X \neq A$ and $Y \neq A$ lie on the circles $A B D$ and $A C E$, respectively, such that $D A=D X$ and $E A=E Y$. Prove that $B, C, X$ and $Y$ are concyclic. (Netherlands)
|
Let $A^{\prime}$ be the intersection of lines $B X$ and $C Y$. By power of a point, it suffices to prove that $A^{\prime} B \cdot A^{\prime} X=A^{\prime} C \cdot A^{\prime} Y$, or, equivalently, that $A^{\prime}$ lies on the radical axis of the circles $A B D X$ and $A C E Y$. From $D A=D X$ it follows that in circle $A B D X$, point $D$ bisects of one of the arcs $A X$. Therefore, depending on the order of points, the line $B C$ is either the internal or external bisector of $\angle A B X$. In both cases, line $B X$ is the reflection of $B A$ in line $B D C$. Analogously, line $C Y$ is the reflection of $C A$ in line $B C$; we can see that $A^{\prime}$ is the reflection of $A$ in line $B C$, so $A, F$ and $A^{\prime}$ are collinear. By $P D \| A C$ and $P E \| A B$ we have $\frac{F D}{F C}=\frac{F P}{F A}=\frac{F E}{F B}$, hence $F D \cdot F B=F E \cdot F C$. So, point $F$ has equal powers with respect to circles $A B D X$ and $A C E Y$. Point $A$, being a common point of the two circles, is another point with equal powers, so the radical axis of circles $A B D X$ and $A C E Y$ is the altitude $A F$ that passes through $A^{\prime}$. 
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7e86e206-9283-5d75-99a3-7e698da4f983
| 24,342
|
In the acute-angled triangle $A B C$, the point $F$ is the foot of the altitude from $A$, and $P$ is a point on the segment $A F$. The lines through $P$ parallel to $A C$ and $A B$ meet $B C$ at $D$ and $E$, respectively. Points $X \neq A$ and $Y \neq A$ lie on the circles $A B D$ and $A C E$, respectively, such that $D A=D X$ and $E A=E Y$. Prove that $B, C, X$ and $Y$ are concyclic. (Netherlands)
|
We present another way to prove that line $A P A^{\prime}$ is the radical axis of the circles $A B D$ and $A C E$. It suffices to show that the second intersection point of $A B D$ and $A C E$ lies on $A P$. Define $N$ to be the second intersection of circle $P D E$ and $A P$. From $\angle D N A=\angle D N P=$ $\angle D E P=\angle D B A$ it follows that $N$ lies on circle $A B D$; analogously, we can show that $N$ lies on circle $A C E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the acute-angled triangle $A B C$, the point $F$ is the foot of the altitude from $A$, and $P$ is a point on the segment $A F$. The lines through $P$ parallel to $A C$ and $A B$ meet $B C$ at $D$ and $E$, respectively. Points $X \neq A$ and $Y \neq A$ lie on the circles $A B D$ and $A C E$, respectively, such that $D A=D X$ and $E A=E Y$. Prove that $B, C, X$ and $Y$ are concyclic. (Netherlands)
|
We present another way to prove that line $A P A^{\prime}$ is the radical axis of the circles $A B D$ and $A C E$. It suffices to show that the second intersection point of $A B D$ and $A C E$ lies on $A P$. Define $N$ to be the second intersection of circle $P D E$ and $A P$. From $\angle D N A=\angle D N P=$ $\angle D E P=\angle D B A$ it follows that $N$ lies on circle $A B D$; analogously, we can show that $N$ lies on circle $A C E$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7e86e206-9283-5d75-99a3-7e698da4f983
| 24,342
|
Let $A B C D$ be a cyclic quadrilateral. Assume that the points $Q, A, B, P$ are collinear in this order, in such a way that the line $A C$ is tangent to the circle $A D Q$, and the line $B D$ is tangent to the circle $B C P$. Let $M$ and $N$ be the midpoints of $B C$ and $A D$, respectively. Prove that the following three lines are concurrent: line $C D$, the tangent of circle $A N Q$ at point $A$, and the tangent to circle $B M P$ at point $B$. (Slovakia)
|
We first prove that triangles $A D Q$ and $C D B$ are similar. Since $A B C D$ is cyclic, we have $\angle D A Q=\angle D C B$. By the tangency of $A C$ to the circle $A Q D$ we also have $\angle C B D=\angle C A D=\angle A Q D$. The claimed similarity is proven. Let $R$ be the midpoint of $C D$. Points $N$ and $R$ correspond in the proven similarity, and so $\angle Q N A=\angle B R C$. 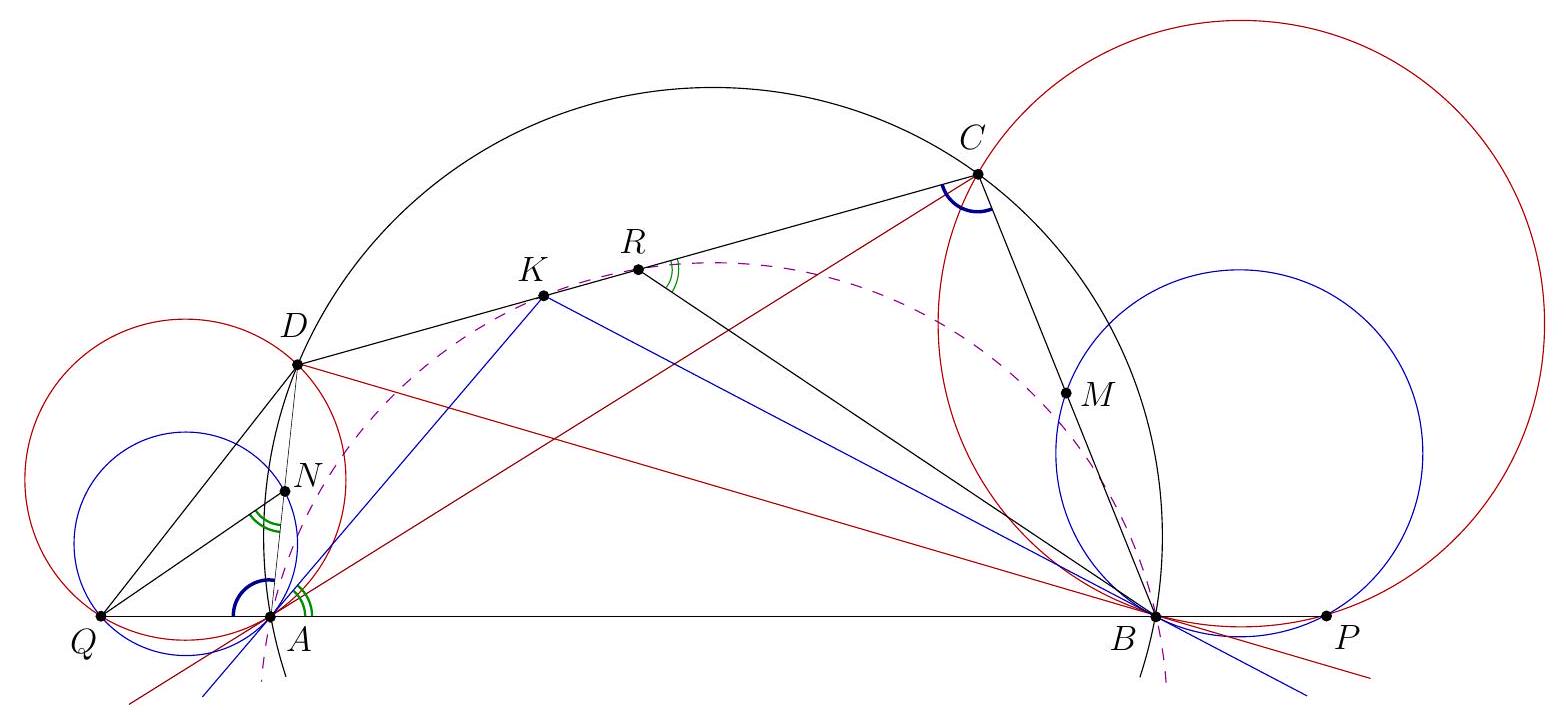 Let $K$ be the second common point of line $C D$ with circle $A B R$ (i.e., if $C D$ intersects circle $A B R$, then $K \neq R$ is the other intersection; otherwise, if $C D$ is tangent to $C D$, then $K=R$ ). In both cases, we have $\angle B A K=\angle B R C=\angle Q N A$; that indicates that $A K$ is tangent to circle $A N Q$. It can be showed analogously that $B K$ is tangent to circle $B M P$. Comment. Note that $M$ and $N$ can be any points on lines $B C$ and $A D$ such that $B M: M C=$ $D N: N A$, as we then simply choose $R$ to be such that $D R: R C$ is that same ratio, and the rest of the proof remains unchanged.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral. Assume that the points $Q, A, B, P$ are collinear in this order, in such a way that the line $A C$ is tangent to the circle $A D Q$, and the line $B D$ is tangent to the circle $B C P$. Let $M$ and $N$ be the midpoints of $B C$ and $A D$, respectively. Prove that the following three lines are concurrent: line $C D$, the tangent of circle $A N Q$ at point $A$, and the tangent to circle $B M P$ at point $B$. (Slovakia)
|
We first prove that triangles $A D Q$ and $C D B$ are similar. Since $A B C D$ is cyclic, we have $\angle D A Q=\angle D C B$. By the tangency of $A C$ to the circle $A Q D$ we also have $\angle C B D=\angle C A D=\angle A Q D$. The claimed similarity is proven. Let $R$ be the midpoint of $C D$. Points $N$ and $R$ correspond in the proven similarity, and so $\angle Q N A=\angle B R C$.  Let $K$ be the second common point of line $C D$ with circle $A B R$ (i.e., if $C D$ intersects circle $A B R$, then $K \neq R$ is the other intersection; otherwise, if $C D$ is tangent to $C D$, then $K=R$ ). In both cases, we have $\angle B A K=\angle B R C=\angle Q N A$; that indicates that $A K$ is tangent to circle $A N Q$. It can be showed analogously that $B K$ is tangent to circle $B M P$. Comment. Note that $M$ and $N$ can be any points on lines $B C$ and $A D$ such that $B M: M C=$ $D N: N A$, as we then simply choose $R$ to be such that $D R: R C$ is that same ratio, and the rest of the proof remains unchanged.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
72991585-f0a9-5544-a427-1c2dd66803d4
| 24,346
|
Let $A B C D$ be a cyclic quadrilateral. Assume that the points $Q, A, B, P$ are collinear in this order, in such a way that the line $A C$ is tangent to the circle $A D Q$, and the line $B D$ is tangent to the circle $B C P$. Let $M$ and $N$ be the midpoints of $B C$ and $A D$, respectively. Prove that the following three lines are concurrent: line $C D$, the tangent of circle $A N Q$ at point $A$, and the tangent to circle $B M P$ at point $B$. (Slovakia)
|
We present a second solution, without using the condition that $A B C D$ is cyclic. Again, $M$ and $N$ can be any points on lines $B C$ and $A D$ such that $B M: M C=D N: N A$. Let $A B$ and $C D$ meet at $T$ (if $A B \| C D$ then $T$ is their common ideal point). Let $C D$ meet the tangent to the circle $A N Q$ at $A$, and the tangent to the circle $B M P$ at $B$ at points $K_{1}$ and $K_{2}$, respectively.  Let $I$ and $J$ be the ideal points of $A D$ and $B C$, respectively. Notice that the pencils $\left(A D, A C, A T, A K_{1}\right)$ and $(Q A, Q D, Q I, Q N)$ of lines are congruent, because $\angle K_{1} A D=\angle A Q N$, $\angle C A D=\angle A Q D$ and $\angle I A T=\angle I Q T$. Hence, $$ \left(D, C ; T, K_{1}\right)=\left(A D, A C ; A T, A K_{1}\right)=(Q A, Q D ; Q I, Q N)=(A, D ; I, N)=\frac{D N}{N A} $$ It can be obtained analogously that $$ \left(D, C ; T, K_{2}\right)=\left(B D, B C ; B T, B K_{2}\right)=(P C, P B ; P J, P M)=(C, B ; I, N)=\frac{B M}{M C} $$ From $B M: M C=D N: D A$ we get $\left(D, C ; T, K_{1}\right)=\left(D, C ; T, K_{2}\right)$ and hence $K_{1}=K_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral. Assume that the points $Q, A, B, P$ are collinear in this order, in such a way that the line $A C$ is tangent to the circle $A D Q$, and the line $B D$ is tangent to the circle $B C P$. Let $M$ and $N$ be the midpoints of $B C$ and $A D$, respectively. Prove that the following three lines are concurrent: line $C D$, the tangent of circle $A N Q$ at point $A$, and the tangent to circle $B M P$ at point $B$. (Slovakia)
|
We present a second solution, without using the condition that $A B C D$ is cyclic. Again, $M$ and $N$ can be any points on lines $B C$ and $A D$ such that $B M: M C=D N: N A$. Let $A B$ and $C D$ meet at $T$ (if $A B \| C D$ then $T$ is their common ideal point). Let $C D$ meet the tangent to the circle $A N Q$ at $A$, and the tangent to the circle $B M P$ at $B$ at points $K_{1}$ and $K_{2}$, respectively.  Let $I$ and $J$ be the ideal points of $A D$ and $B C$, respectively. Notice that the pencils $\left(A D, A C, A T, A K_{1}\right)$ and $(Q A, Q D, Q I, Q N)$ of lines are congruent, because $\angle K_{1} A D=\angle A Q N$, $\angle C A D=\angle A Q D$ and $\angle I A T=\angle I Q T$. Hence, $$ \left(D, C ; T, K_{1}\right)=\left(A D, A C ; A T, A K_{1}\right)=(Q A, Q D ; Q I, Q N)=(A, D ; I, N)=\frac{D N}{N A} $$ It can be obtained analogously that $$ \left(D, C ; T, K_{2}\right)=\left(B D, B C ; B T, B K_{2}\right)=(P C, P B ; P J, P M)=(C, B ; I, N)=\frac{B M}{M C} $$ From $B M: M C=D N: D A$ we get $\left(D, C ; T, K_{1}\right)=\left(D, C ; T, K_{2}\right)$ and hence $K_{1}=K_{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
72991585-f0a9-5544-a427-1c2dd66803d4
| 24,346
|
Let $A B C$ be an acute-angled triangle with $A C>A B$, let $O$ be its circumcentre, and let $D$ be a point on the segment $B C$. The line through $D$ perpendicular to $B C$ intersects the lines $A O, A C$ and $A B$ at $W, X$ and $Y$, respectively. The circumcircles of triangles $A X Y$ and $A B C$ intersect again at $Z \neq A$. Prove that if $O W=O D$, then $D Z$ is tangent to the circle $A X Y$. (United Kingdom)
|
Let $A O$ intersect $B C$ at $E$. As $E D W$ is a right-angled triangle and $O$ is on $W E$, the condition $O W=O D$ means $O$ is the circumcentre of this triangle. So $O D=O E$ which establishes that $D, E$ are reflections in the perpendicular bisector of $B C$. Now observe: $$ 180^{\circ}-\angle D X Z=\angle Z X Y=\angle Z A Y=\angle Z C D $$ which shows $C D X Z$ is cyclic. 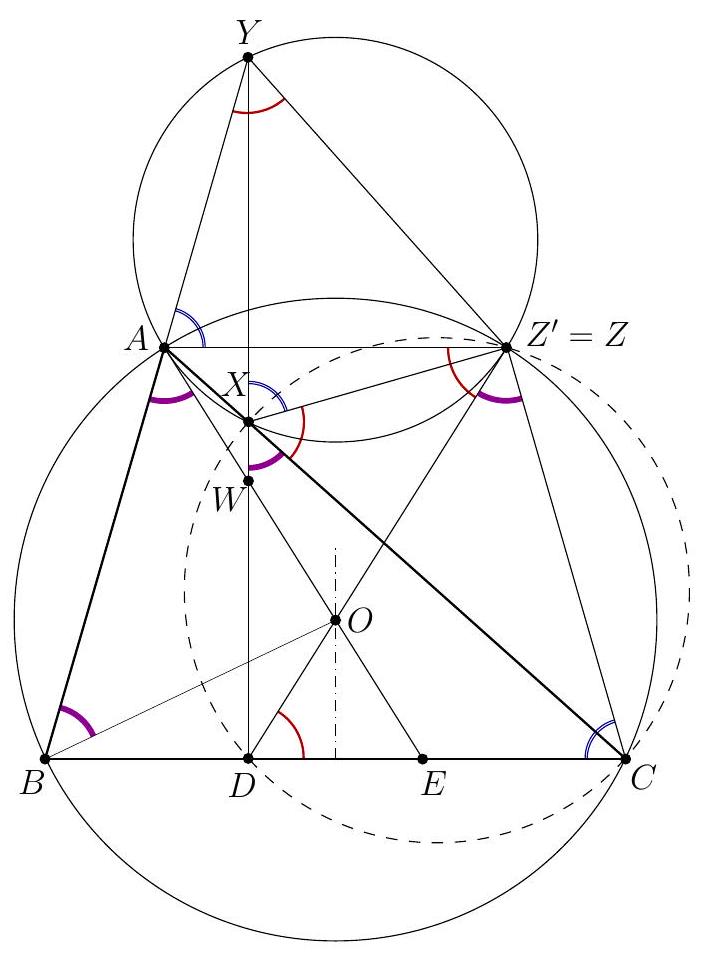 We next show that $A Z \| B C$. To do this, introduce point $Z^{\prime}$ on circle $A B C$ such that $A Z^{\prime} \| B C$. By the previous result, it suffices to prove that $C D X Z^{\prime}$ is cyclic. Notice that triangles $B A E$ and $C Z^{\prime} D$ are reflections in the perpendicular bisector of $B C$. Using this and that $A, O, E$ are collinear: $$ \angle D Z^{\prime} C=\angle B A E=\angle B A O=90^{\circ}-\frac{1}{2} \angle A O B=90^{\circ}-\angle C=\angle D X C, $$ so $D X Z^{\prime} C$ is cyclic, giving $Z \equiv Z^{\prime}$ as desired. Using $A Z \| B C$ and $C D X Z$ cyclic we get: $$ \angle A Z D=\angle C D Z=\angle C X Z=\angle A Y Z, $$ which by the converse of alternate segment theorem shows $D Z$ is tangent to circle $A X Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with $A C>A B$, let $O$ be its circumcentre, and let $D$ be a point on the segment $B C$. The line through $D$ perpendicular to $B C$ intersects the lines $A O, A C$ and $A B$ at $W, X$ and $Y$, respectively. The circumcircles of triangles $A X Y$ and $A B C$ intersect again at $Z \neq A$. Prove that if $O W=O D$, then $D Z$ is tangent to the circle $A X Y$. (United Kingdom)
|
Let $A O$ intersect $B C$ at $E$. As $E D W$ is a right-angled triangle and $O$ is on $W E$, the condition $O W=O D$ means $O$ is the circumcentre of this triangle. So $O D=O E$ which establishes that $D, E$ are reflections in the perpendicular bisector of $B C$. Now observe: $$ 180^{\circ}-\angle D X Z=\angle Z X Y=\angle Z A Y=\angle Z C D $$ which shows $C D X Z$ is cyclic.  We next show that $A Z \| B C$. To do this, introduce point $Z^{\prime}$ on circle $A B C$ such that $A Z^{\prime} \| B C$. By the previous result, it suffices to prove that $C D X Z^{\prime}$ is cyclic. Notice that triangles $B A E$ and $C Z^{\prime} D$ are reflections in the perpendicular bisector of $B C$. Using this and that $A, O, E$ are collinear: $$ \angle D Z^{\prime} C=\angle B A E=\angle B A O=90^{\circ}-\frac{1}{2} \angle A O B=90^{\circ}-\angle C=\angle D X C, $$ so $D X Z^{\prime} C$ is cyclic, giving $Z \equiv Z^{\prime}$ as desired. Using $A Z \| B C$ and $C D X Z$ cyclic we get: $$ \angle A Z D=\angle C D Z=\angle C X Z=\angle A Y Z, $$ which by the converse of alternate segment theorem shows $D Z$ is tangent to circle $A X Y$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3c9a1cbb-ab00-583b-a7fc-07f8b6b9e492
| 24,350
|
Let $A B C$ be an acute-angled triangle with $A C>A B$, let $O$ be its circumcentre, and let $D$ be a point on the segment $B C$. The line through $D$ perpendicular to $B C$ intersects the lines $A O, A C$ and $A B$ at $W, X$ and $Y$, respectively. The circumcircles of triangles $A X Y$ and $A B C$ intersect again at $Z \neq A$. Prove that if $O W=O D$, then $D Z$ is tangent to the circle $A X Y$. (United Kingdom)
|
Notice that point $Z$ is the Miquel-point of lines $A C, B C, B A$ and $D Y$; then $B, D, Z, Y$ and $C, D, X, Y$ are concyclic. Moreover, $Z$ is the centre of the spiral similarity that maps $B C$ to $Y X$. By $B C \perp Y X$, the angle of that similarity is $90^{\circ}$; hence the circles $A B C Z$ and $A X Y Z$ are perpendicular, therefore the radius $O Z$ in circle $A B C Z$ is tangent to circle $A X Y Z$. 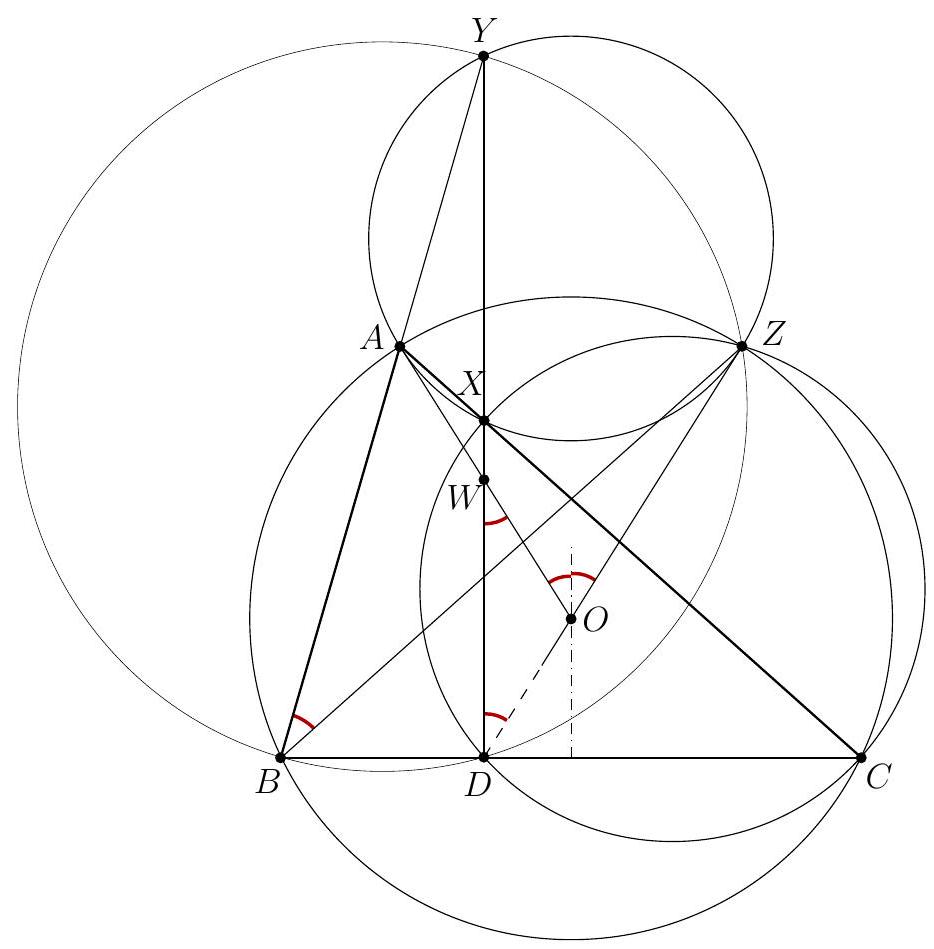 By $O W=O D$, the triangle $O W D$ is isosceles, and $$ \angle Z O A=2 \angle Z B A=2 \angle Z B Y=2 \angle Z D Y=\angle O D W+\angle D W O, $$ so $D$ lies on line $Z O$ that is tangent to circle $A X Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with $A C>A B$, let $O$ be its circumcentre, and let $D$ be a point on the segment $B C$. The line through $D$ perpendicular to $B C$ intersects the lines $A O, A C$ and $A B$ at $W, X$ and $Y$, respectively. The circumcircles of triangles $A X Y$ and $A B C$ intersect again at $Z \neq A$. Prove that if $O W=O D$, then $D Z$ is tangent to the circle $A X Y$. (United Kingdom)
|
Notice that point $Z$ is the Miquel-point of lines $A C, B C, B A$ and $D Y$; then $B, D, Z, Y$ and $C, D, X, Y$ are concyclic. Moreover, $Z$ is the centre of the spiral similarity that maps $B C$ to $Y X$. By $B C \perp Y X$, the angle of that similarity is $90^{\circ}$; hence the circles $A B C Z$ and $A X Y Z$ are perpendicular, therefore the radius $O Z$ in circle $A B C Z$ is tangent to circle $A X Y Z$.  By $O W=O D$, the triangle $O W D$ is isosceles, and $$ \angle Z O A=2 \angle Z B A=2 \angle Z B Y=2 \angle Z D Y=\angle O D W+\angle D W O, $$ so $D$ lies on line $Z O$ that is tangent to circle $A X Y$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3c9a1cbb-ab00-583b-a7fc-07f8b6b9e492
| 24,350
|
Let $A B C$ be a triangle, and let $\ell_{1}$ and $\ell_{2}$ be two parallel lines. For $i=1,2$, let $\ell_{i}$ meet the lines $B C, C A$, and $A B$ at $X_{i}, Y_{i}$, and $Z_{i}$, respectively. Suppose that the line through $X_{i}$ perpendicular to $B C$, the line through $Y_{i}$ perpendicular to $C A$, and finally the line through $Z_{i}$ perpendicular to $A B$, determine a non-degenerate triangle $\Delta_{i}$. Show that the circumcircles of $\Delta_{1}$ and $\Delta_{2}$ are tangent to each other. (Vietnam)
|
Throughout the solutions, $\Varangle(p, q)$ will denote the directed angle between lines $p$ and $q$, taken modulo $180^{\circ}$. Let the vertices of $\Delta_{i}$ be $D_{i}, E_{i}, F_{i}$, such that lines $E_{i} F_{i}, F_{i} D_{i}$ and $D_{i} E_{i}$ are the perpendiculars through $X, Y$ and $Z$, respectively, and denote the circumcircle of $\Delta_{i}$ by $\omega_{i}$. In triangles $D_{1} Y_{1} Z_{1}$ and $D_{2} Y_{2} Z_{2}$ we have $Y_{1} Z_{1} \| Y_{2} Z_{2}$ because they are parts of $\ell_{1}$ and $\ell_{2}$. Moreover, $D_{1} Y_{1} \| D_{2} Y_{2}$ are perpendicular to $A C$ and $D_{1} Z_{1} \| D_{2} Z_{2}$ are perpendicular to $A B$, so the two triangles are homothetic and their homothetic centre is $Y_{1} Y_{2} \cap Z_{1} Z_{2}=A$. Hence, line $D_{1} D_{2}$ passes through $A$. Analogously, line $E_{1} E_{2}$ passes through $B$ and $F_{1} F_{2}$ passes through $C$. 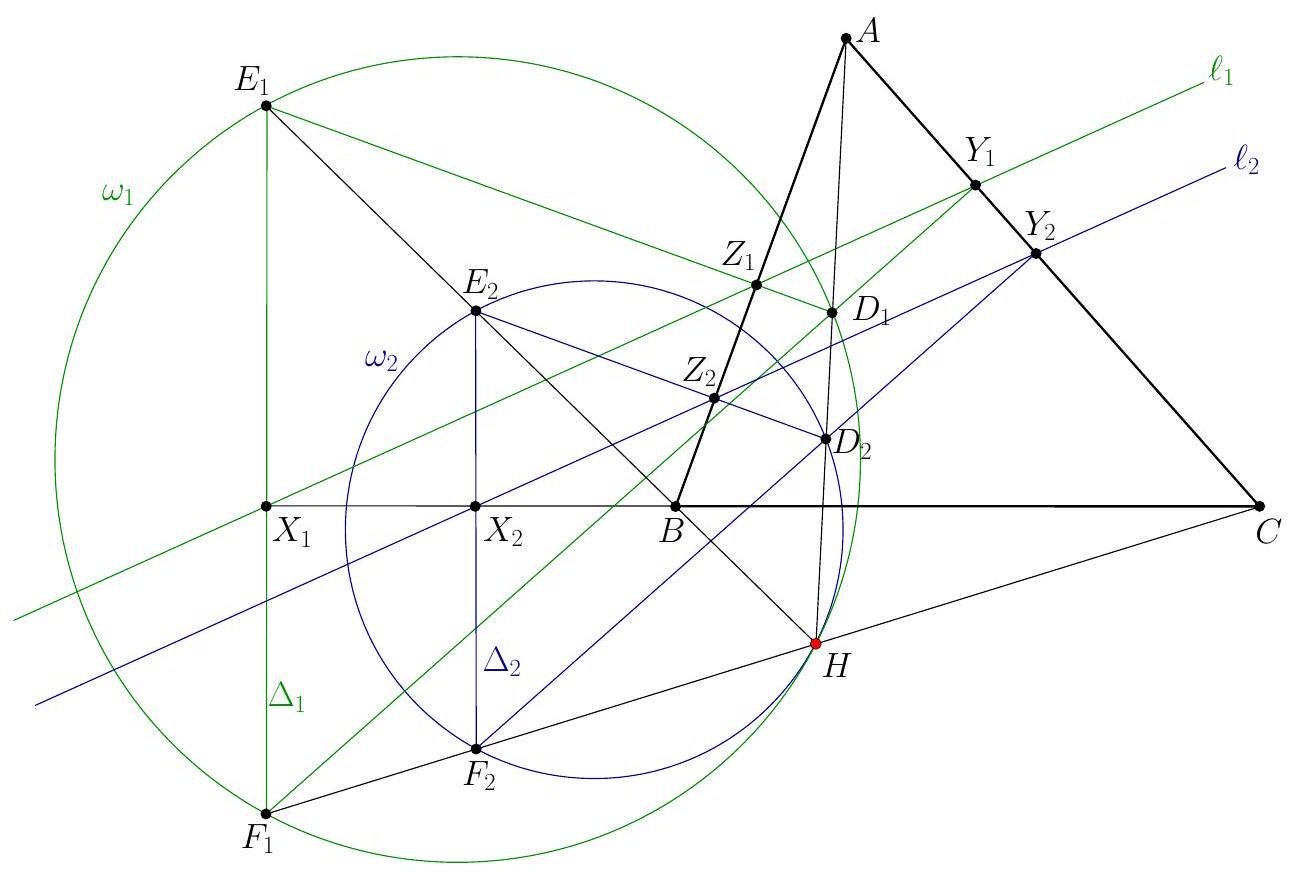 The corresponding sides of $\Delta_{1}$ and $\Delta_{2}$ are parallel, because they are perpendicular to the respective sides of triangle $A B C$. Hence, $\Delta_{1}$ and $\Delta_{2}$ are either homothetic, or they can be translated to each other. Using that $B, X_{2}, Z_{2}$ and $E_{2}$ are concyclic, $C, X_{2}, Y_{2}$ and $F_{2}$ are concyclic, $Z_{2} E_{2} \perp A B$ and $Y_{2}, F_{2} \perp A C$ we can calculate $$ \begin{aligned} \Varangle\left(E_{1} E_{2}, F_{1} F_{2}\right) & =\Varangle\left(E_{1} E_{2}, X_{1} X_{2}\right)+\Varangle\left(X_{1} X_{2}, F_{1} F_{2}\right)=\Varangle\left(B E_{2}, B X_{2}\right)+\Varangle\left(C X_{2}, C F_{2}\right) \\ & =\Varangle\left(Z_{2} E_{2}, Z_{2} X_{2}\right)+\Varangle\left(Y_{2} X_{2}, Y_{2} F_{2}\right)=\Varangle\left(Z_{2} E_{2}, \ell_{2}\right)+\Varangle\left(\ell_{2}, Y_{2} F_{2}\right) \\ & =\Varangle\left(Z_{2} E_{2}, Y_{2} F_{2}\right)=\Varangle(A B, A C) \not \equiv 0, \end{aligned} $$ and conclude that lines $E_{1} E_{2}$ and $F_{1} F_{2}$ are not parallel. Hence, $\Delta_{1}$ and $\Delta_{2}$ are homothetic; the lines $D_{1} D_{2}, E_{1} E_{2}$, and $F_{1} F_{2}$ are concurrent at the homothetic centre of the two triangles. Denote this homothetic centre by $H$. For $i=1,2$, using (1), and that $A, Y_{i}, Z_{i}$ and $D_{i}$ are concyclic, $$ \begin{aligned} \Varangle\left(H E_{i}, H F_{i}\right) & =\Varangle\left(E_{1} E_{2}, F_{1} F_{2}\right)=\Varangle(A B, A C) \\ & =\Varangle\left(A Z_{i}, A Y_{i}\right)=\Varangle\left(D_{i} Z_{i}, D_{i} Y_{i}\right)=\Varangle\left(D_{i} E_{i}, D_{i} F_{i}\right), \end{aligned} $$ so $H$ lies on circle $\omega_{i}$. The same homothety that maps $\Delta_{1}$ to $\Delta_{2}$, sends $\omega_{1}$ to $\omega_{2}$ as well. Point $H$, that is the centre of the homothety, is a common point of the two circles, That finishes proving that $\omega_{1}$ and $\omega_{2}$ are tangent to each other.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, and let $\ell_{1}$ and $\ell_{2}$ be two parallel lines. For $i=1,2$, let $\ell_{i}$ meet the lines $B C, C A$, and $A B$ at $X_{i}, Y_{i}$, and $Z_{i}$, respectively. Suppose that the line through $X_{i}$ perpendicular to $B C$, the line through $Y_{i}$ perpendicular to $C A$, and finally the line through $Z_{i}$ perpendicular to $A B$, determine a non-degenerate triangle $\Delta_{i}$. Show that the circumcircles of $\Delta_{1}$ and $\Delta_{2}$ are tangent to each other. (Vietnam)
|
Throughout the solutions, $\Varangle(p, q)$ will denote the directed angle between lines $p$ and $q$, taken modulo $180^{\circ}$. Let the vertices of $\Delta_{i}$ be $D_{i}, E_{i}, F_{i}$, such that lines $E_{i} F_{i}, F_{i} D_{i}$ and $D_{i} E_{i}$ are the perpendiculars through $X, Y$ and $Z$, respectively, and denote the circumcircle of $\Delta_{i}$ by $\omega_{i}$. In triangles $D_{1} Y_{1} Z_{1}$ and $D_{2} Y_{2} Z_{2}$ we have $Y_{1} Z_{1} \| Y_{2} Z_{2}$ because they are parts of $\ell_{1}$ and $\ell_{2}$. Moreover, $D_{1} Y_{1} \| D_{2} Y_{2}$ are perpendicular to $A C$ and $D_{1} Z_{1} \| D_{2} Z_{2}$ are perpendicular to $A B$, so the two triangles are homothetic and their homothetic centre is $Y_{1} Y_{2} \cap Z_{1} Z_{2}=A$. Hence, line $D_{1} D_{2}$ passes through $A$. Analogously, line $E_{1} E_{2}$ passes through $B$ and $F_{1} F_{2}$ passes through $C$.  The corresponding sides of $\Delta_{1}$ and $\Delta_{2}$ are parallel, because they are perpendicular to the respective sides of triangle $A B C$. Hence, $\Delta_{1}$ and $\Delta_{2}$ are either homothetic, or they can be translated to each other. Using that $B, X_{2}, Z_{2}$ and $E_{2}$ are concyclic, $C, X_{2}, Y_{2}$ and $F_{2}$ are concyclic, $Z_{2} E_{2} \perp A B$ and $Y_{2}, F_{2} \perp A C$ we can calculate $$ \begin{aligned} \Varangle\left(E_{1} E_{2}, F_{1} F_{2}\right) & =\Varangle\left(E_{1} E_{2}, X_{1} X_{2}\right)+\Varangle\left(X_{1} X_{2}, F_{1} F_{2}\right)=\Varangle\left(B E_{2}, B X_{2}\right)+\Varangle\left(C X_{2}, C F_{2}\right) \\ & =\Varangle\left(Z_{2} E_{2}, Z_{2} X_{2}\right)+\Varangle\left(Y_{2} X_{2}, Y_{2} F_{2}\right)=\Varangle\left(Z_{2} E_{2}, \ell_{2}\right)+\Varangle\left(\ell_{2}, Y_{2} F_{2}\right) \\ & =\Varangle\left(Z_{2} E_{2}, Y_{2} F_{2}\right)=\Varangle(A B, A C) \not \equiv 0, \end{aligned} $$ and conclude that lines $E_{1} E_{2}$ and $F_{1} F_{2}$ are not parallel. Hence, $\Delta_{1}$ and $\Delta_{2}$ are homothetic; the lines $D_{1} D_{2}, E_{1} E_{2}$, and $F_{1} F_{2}$ are concurrent at the homothetic centre of the two triangles. Denote this homothetic centre by $H$. For $i=1,2$, using (1), and that $A, Y_{i}, Z_{i}$ and $D_{i}$ are concyclic, $$ \begin{aligned} \Varangle\left(H E_{i}, H F_{i}\right) & =\Varangle\left(E_{1} E_{2}, F_{1} F_{2}\right)=\Varangle(A B, A C) \\ & =\Varangle\left(A Z_{i}, A Y_{i}\right)=\Varangle\left(D_{i} Z_{i}, D_{i} Y_{i}\right)=\Varangle\left(D_{i} E_{i}, D_{i} F_{i}\right), \end{aligned} $$ so $H$ lies on circle $\omega_{i}$. The same homothety that maps $\Delta_{1}$ to $\Delta_{2}$, sends $\omega_{1}$ to $\omega_{2}$ as well. Point $H$, that is the centre of the homothety, is a common point of the two circles, That finishes proving that $\omega_{1}$ and $\omega_{2}$ are tangent to each other.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d7863d3e-504c-5edb-8d0e-467d91760644
| 24,353
|
In an acute-angled triangle $A B C$, point $H$ is the foot of the altitude from $A$. Let $P$ be a moving point such that the bisectors $k$ and $\ell$ of angles $P B C$ and $P C B$, respectively, intersect each other on the line segment $A H$. Let $k$ and $A C$ meet at $E$, let $\ell$ and $A B$ meet at $F$, and let $E F$ and $A H$ meet at $Q$. Prove that, as $P$ varies, the line $P Q$ passes through a fixed point. (Iran)
|
Let the reflections of the line $B C$ with respect to the lines $A B$ and $A C$ intersect at point $K$. We will prove that $P, Q$ and $K$ are collinear, so $K$ is the common point of the varying line $P Q$. Let lines $B E$ and $C F$ intersect at $I$. For every point $O$ and $d>0$, denote by $(O, d)$ the circle centred at $O$ with radius $d$, and define $\omega_{I}=(I, I H)$ and $\omega_{A}=(A, A H)$. Let $\omega_{K}$ and $\omega_{P}$ be the incircle of triangle $K B C$ and the $P$-excircle of triangle $P B C$, respectively. Since $I H \perp B C$ and $A H \perp B C$, the circles $\omega_{A}$ and $\omega_{I}$ are tangent to each other at $H$. So, $H$ is the external homothetic centre of $\omega_{A}$ and $\omega_{I}$. From the complete quadrangle $B C E F$ we have $(A, I ; Q, H)=-1$, therefore $Q$ is the internal homothetic centre of $\omega_{A}$ and $\omega_{I}$. Since $B A$ and $C A$ are the external bisectors of angles $\angle K B C$ and $\angle K C B$, circle $\omega_{A}$ is the $K$-excircle in triangle $B K C$. Hence, $K$ is the external homothetic centre of $\omega_{A}$ and $\omega_{K}$. Also it is clear that $P$ is the external homothetic centre of $\omega_{I}$ and $\omega_{P}$. Let point $T$ be the tangency point of $\omega_{P}$ and $B C$, and let $T^{\prime}$ be the tangency point of $\omega_{K}$ and $B C$. Since $\omega_{I}$ is the incircle and $\omega_{P}$ is the $P$-excircle of $P B C, T C=B H$ and since $\omega_{K}$ is the incircle and $\omega_{A}$ is the $K$-excircle of $K B C, T^{\prime} C=B H$. Therefore $T C=T^{\prime} C$ and $T \equiv T^{\prime}$. It yields that $\omega_{K}$ and $\omega_{P}$ are tangent to each other at $T$. 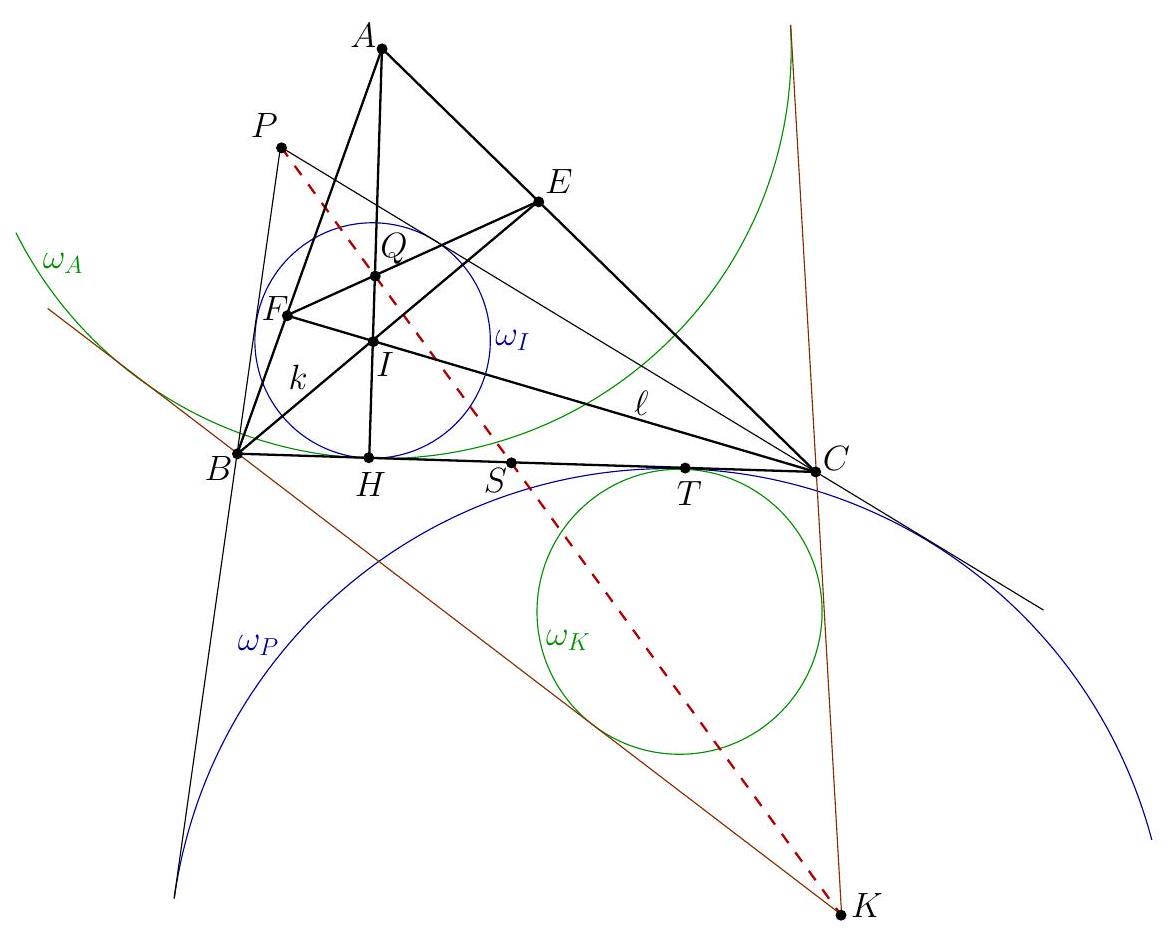 Let point $S$ be the internal homothetic centre of $\omega_{A}$ and $\omega_{P}$, and let $S^{\prime}$ be the internal homothetic centre of $\omega_{I}$ and $\omega_{K}$. It's obvious that $S$ and $S^{\prime}$ lie on $B C$. We claim that $S \equiv S^{\prime}$. To prove our claim, let $r_{A}, r_{I}, r_{P}$, and $r_{K}$ be the radii of $\omega_{A}, \omega_{I}, \omega_{P}$ and $\omega_{k}$, respectively. It is well known that if the sides of a triangle are $a, b, c$, its semiperimeter is $s=(a+b+c) / 2$, and the radii of the incircle and the $a$-excircle are $r$ and $r_{a}$, respectively, then $r \cdot r_{a}=(s-b)(s-c)$. Applying this fact to triangle $P B C$ we get $r_{I} \cdot r_{P}=B H \cdot C H$. The same fact in triangle $K C B$ yields $r_{K} \cdot r_{A}=C T \cdot B T$. Since $B H=C T$ and $B T=C H$, from these two we get $$ \frac{H S}{S T}=\frac{r_{A}}{r_{P}}=\frac{r_{I}}{r_{K}}=\frac{H S^{\prime}}{S^{\prime} T} $$ so $S=S^{\prime}$ indeed. Finally, by applying the generalised Monge's theorem to the circles $\omega_{A}, \omega_{I}$, and $\omega_{K}$ (with two pairs of internal and one pair of external common tangents), we can see that points $Q$, $S$, and $K$ are collinear. Similarly one can show that $Q, S$ and $P$ are collinear, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute-angled triangle $A B C$, point $H$ is the foot of the altitude from $A$. Let $P$ be a moving point such that the bisectors $k$ and $\ell$ of angles $P B C$ and $P C B$, respectively, intersect each other on the line segment $A H$. Let $k$ and $A C$ meet at $E$, let $\ell$ and $A B$ meet at $F$, and let $E F$ and $A H$ meet at $Q$. Prove that, as $P$ varies, the line $P Q$ passes through a fixed point. (Iran)
|
Let the reflections of the line $B C$ with respect to the lines $A B$ and $A C$ intersect at point $K$. We will prove that $P, Q$ and $K$ are collinear, so $K$ is the common point of the varying line $P Q$. Let lines $B E$ and $C F$ intersect at $I$. For every point $O$ and $d>0$, denote by $(O, d)$ the circle centred at $O$ with radius $d$, and define $\omega_{I}=(I, I H)$ and $\omega_{A}=(A, A H)$. Let $\omega_{K}$ and $\omega_{P}$ be the incircle of triangle $K B C$ and the $P$-excircle of triangle $P B C$, respectively. Since $I H \perp B C$ and $A H \perp B C$, the circles $\omega_{A}$ and $\omega_{I}$ are tangent to each other at $H$. So, $H$ is the external homothetic centre of $\omega_{A}$ and $\omega_{I}$. From the complete quadrangle $B C E F$ we have $(A, I ; Q, H)=-1$, therefore $Q$ is the internal homothetic centre of $\omega_{A}$ and $\omega_{I}$. Since $B A$ and $C A$ are the external bisectors of angles $\angle K B C$ and $\angle K C B$, circle $\omega_{A}$ is the $K$-excircle in triangle $B K C$. Hence, $K$ is the external homothetic centre of $\omega_{A}$ and $\omega_{K}$. Also it is clear that $P$ is the external homothetic centre of $\omega_{I}$ and $\omega_{P}$. Let point $T$ be the tangency point of $\omega_{P}$ and $B C$, and let $T^{\prime}$ be the tangency point of $\omega_{K}$ and $B C$. Since $\omega_{I}$ is the incircle and $\omega_{P}$ is the $P$-excircle of $P B C, T C=B H$ and since $\omega_{K}$ is the incircle and $\omega_{A}$ is the $K$-excircle of $K B C, T^{\prime} C=B H$. Therefore $T C=T^{\prime} C$ and $T \equiv T^{\prime}$. It yields that $\omega_{K}$ and $\omega_{P}$ are tangent to each other at $T$.  Let point $S$ be the internal homothetic centre of $\omega_{A}$ and $\omega_{P}$, and let $S^{\prime}$ be the internal homothetic centre of $\omega_{I}$ and $\omega_{K}$. It's obvious that $S$ and $S^{\prime}$ lie on $B C$. We claim that $S \equiv S^{\prime}$. To prove our claim, let $r_{A}, r_{I}, r_{P}$, and $r_{K}$ be the radii of $\omega_{A}, \omega_{I}, \omega_{P}$ and $\omega_{k}$, respectively. It is well known that if the sides of a triangle are $a, b, c$, its semiperimeter is $s=(a+b+c) / 2$, and the radii of the incircle and the $a$-excircle are $r$ and $r_{a}$, respectively, then $r \cdot r_{a}=(s-b)(s-c)$. Applying this fact to triangle $P B C$ we get $r_{I} \cdot r_{P}=B H \cdot C H$. The same fact in triangle $K C B$ yields $r_{K} \cdot r_{A}=C T \cdot B T$. Since $B H=C T$ and $B T=C H$, from these two we get $$ \frac{H S}{S T}=\frac{r_{A}}{r_{P}}=\frac{r_{I}}{r_{K}}=\frac{H S^{\prime}}{S^{\prime} T} $$ so $S=S^{\prime}$ indeed. Finally, by applying the generalised Monge's theorem to the circles $\omega_{A}, \omega_{I}$, and $\omega_{K}$ (with two pairs of internal and one pair of external common tangents), we can see that points $Q$, $S$, and $K$ are collinear. Similarly one can show that $Q, S$ and $P$ are collinear, and the result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e066df6-3a1a-505d-b591-8a23393171eb
| 24,357
|
In an acute-angled triangle $A B C$, point $H$ is the foot of the altitude from $A$. Let $P$ be a moving point such that the bisectors $k$ and $\ell$ of angles $P B C$ and $P C B$, respectively, intersect each other on the line segment $A H$. Let $k$ and $A C$ meet at $E$, let $\ell$ and $A B$ meet at $F$, and let $E F$ and $A H$ meet at $Q$. Prove that, as $P$ varies, the line $P Q$ passes through a fixed point. (Iran)
|
Again, let $B E$ and $C F$ meet at $I$, that is the incentre in triangle $B C P$; then $P I$ is the third angle bisector. From the tangent segments of the incircle we have $B P-C P=$ $B H-C H$; hence, the possible points $P$ lie on a branch of a hyperbola $\mathcal{H}$ with foci $B, C$, and $H$ is a vertex of $\mathcal{H}$. Since $P I$ bisects the angle between the radii $B P$ and $C P$ of the hyperbola, line $P I$ is tangent to $\mathcal{H}$.  Let $K$ be the second intersection of $P Q$ and $\mathcal{H}$, we will show that $A K$ is tangent to $\mathcal{H}$ at $K$; this property determines $K$. Let $G=K I \cap A P$ and $M=P I \cap A K$. From the complete quadrangle $B C E F$ we can see that $(H, Q ; I, A)$ is harmonic, so in the complete quadrangle $A P I K$, point $H$ lies on line $G M$. Consider triangle $A I M$. Its side $A I$ is tangent to $\mathcal{H}$ at $H$, the side $I M$ is tangent to $\mathcal{H}$ at $P$, and $K$ is a common point of the third side $A M$ and the hyperbola such that the lines $A P$, $I K$ and $M H$ are concurrent at the generalised Gergonne-point $G$. It follows that the third side, $A M$ is also tangent to $\mathcal{H}$ at $K$. (Alternatively, in the last step we can apply the converse of Brianchon's theorem to the degenerate hexagon $A H I P M K$. By the theorem there is a conic section $\mathcal{H}^{\prime}$ such that lines $A I, I M$ and $M A$ are tangent to $\mathcal{H}^{\prime}$ at $H, P$ and $K$, respectively. But the three points $H, K$ and $P$, together with the tangents at $H$ and $P$ uniquely determine $\mathcal{H}^{\prime}$, so indeed $\mathcal{H}^{\prime}=\mathcal{H}$.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute-angled triangle $A B C$, point $H$ is the foot of the altitude from $A$. Let $P$ be a moving point such that the bisectors $k$ and $\ell$ of angles $P B C$ and $P C B$, respectively, intersect each other on the line segment $A H$. Let $k$ and $A C$ meet at $E$, let $\ell$ and $A B$ meet at $F$, and let $E F$ and $A H$ meet at $Q$. Prove that, as $P$ varies, the line $P Q$ passes through a fixed point. (Iran)
|
Again, let $B E$ and $C F$ meet at $I$, that is the incentre in triangle $B C P$; then $P I$ is the third angle bisector. From the tangent segments of the incircle we have $B P-C P=$ $B H-C H$; hence, the possible points $P$ lie on a branch of a hyperbola $\mathcal{H}$ with foci $B, C$, and $H$ is a vertex of $\mathcal{H}$. Since $P I$ bisects the angle between the radii $B P$ and $C P$ of the hyperbola, line $P I$ is tangent to $\mathcal{H}$.  Let $K$ be the second intersection of $P Q$ and $\mathcal{H}$, we will show that $A K$ is tangent to $\mathcal{H}$ at $K$; this property determines $K$. Let $G=K I \cap A P$ and $M=P I \cap A K$. From the complete quadrangle $B C E F$ we can see that $(H, Q ; I, A)$ is harmonic, so in the complete quadrangle $A P I K$, point $H$ lies on line $G M$. Consider triangle $A I M$. Its side $A I$ is tangent to $\mathcal{H}$ at $H$, the side $I M$ is tangent to $\mathcal{H}$ at $P$, and $K$ is a common point of the third side $A M$ and the hyperbola such that the lines $A P$, $I K$ and $M H$ are concurrent at the generalised Gergonne-point $G$. It follows that the third side, $A M$ is also tangent to $\mathcal{H}$ at $K$. (Alternatively, in the last step we can apply the converse of Brianchon's theorem to the degenerate hexagon $A H I P M K$. By the theorem there is a conic section $\mathcal{H}^{\prime}$ such that lines $A I, I M$ and $M A$ are tangent to $\mathcal{H}^{\prime}$ at $H, P$ and $K$, respectively. But the three points $H, K$ and $P$, together with the tangents at $H$ and $P$ uniquely determine $\mathcal{H}^{\prime}$, so indeed $\mathcal{H}^{\prime}=\mathcal{H}$.)
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e066df6-3a1a-505d-b591-8a23393171eb
| 24,357
|
Let $A A^{\prime} B C C^{\prime} B^{\prime}$ be a convex cyclic hexagon such that $A C$ is tangent to the incircle of the triangle $A^{\prime} B^{\prime} C^{\prime}$, and $A^{\prime} C^{\prime}$ is tangent to the incircle of the triangle $A B C$. Let the lines $A B$ and $A^{\prime} B^{\prime}$ meet at $X$ and let the lines $B C$ and $B^{\prime} C^{\prime}$ meet at $Y$. Prove that if $X B Y B^{\prime}$ is a convex quadrilateral, then it has an incircle.
|
Denote by $\omega$ and $\omega^{\prime}$ the incircles of $\triangle A B C$ and $\triangle A^{\prime} B^{\prime} C^{\prime}$ and let $I$ and $I^{\prime}$ be the centres of these circles. Let $N$ and $N^{\prime}$ be the second intersections of $B I$ and $B^{\prime} I^{\prime}$ with $\Omega$, the circumcircle of $A^{\prime} B C C^{\prime} B^{\prime} A$, and let $O$ be the centre of $\Omega$. Note that $O N \perp A C, O N^{\prime} \perp A^{\prime} C^{\prime}$ and $O N=O N^{\prime}$ so $N N^{\prime}$ is parallel to the angle bisector $I I^{\prime}$ of $A C$ and $A^{\prime} C^{\prime}$. Thus $I I^{\prime} \| N N^{\prime}$ which is antiparallel to $B B^{\prime}$ with respect to $B I$ and $B^{\prime} I^{\prime}$. Therefore $B, I, I^{\prime}, B^{\prime}$ are concyclic.  Further define $P$ as the intersection of $A C$ and $A^{\prime} C^{\prime}$ and $M$ as the antipode of $N^{\prime}$ in $\Omega$. Consider the circle $\Gamma_{1}$ with centre $N$ and radius $N A=N C$ and the circle $\Gamma_{2}$ with centre $M$ and radius $M A^{\prime}=M C^{\prime}$. Their radical axis passes through $P$ and is perpendicular to $M N \perp N N^{\prime} \| I P$, so $I$ lies on their radical axis. Therefore, since $I$ lies on $\Gamma_{1}$, it must also lie on $\Gamma_{2}$. Thus, if we define $Z$ as the second intersection of $M I$ with $\Omega$, we have that $I$ is the incentre of triangle $Z A^{\prime} C^{\prime}$. (Note that the point $Z$ can also be constructed directly via Poncelet's porism.) Consider the incircle $\omega_{c}$ with centre $I_{c}$ of triangle $C^{\prime} B^{\prime} Z$. Note that $\angle Z I C^{\prime}=90^{\circ}+$ $\frac{1}{2} \angle Z A^{\prime} C^{\prime}=90^{\circ}+\frac{1}{2} \angle Z B^{\prime} C^{\prime}=\angle Z I_{c} C^{\prime}$, so $Z, I, I_{c}, C^{\prime}$ are concyclic. Similarly $B^{\prime}, I^{\prime}, I_{c}, C^{\prime}$ are concyclic. The external centre of dilation from $\omega$ to $\omega_{c}$ is the intersection of $I I_{c}$ and $C^{\prime} Z$ ( $D$ in the picture), that is the radical centre of circles $\Omega, C^{\prime} I_{c} I Z$ and $I I^{\prime} I_{c}$. Similarly, the external centre of dilation from $\omega^{\prime}$ to $\omega_{c}$ is the intersection of $I^{\prime} I_{c}$ and $B^{\prime} C^{\prime}$ ( $D^{\prime}$ in the picture), that is the radical centre of circles $\Omega, B^{\prime} I^{\prime} I_{c} C^{\prime}$ and $I I^{\prime} I_{c}$. Therefore the Monge line of $\omega, \omega^{\prime}$ and $\omega_{c}$ is line $D D^{\prime}$, and the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$ coincide. Hence the external centre $T$ of dilation from $\omega$ to $\omega^{\prime}$ is also on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$.  Now since $B, I, I^{\prime}, B^{\prime}$ are concyclic, the intersection $T^{\prime}$ of $B B^{\prime}$ and $I I^{\prime}$ is on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$. Thus $T^{\prime}=T$ and $T$ lies on line $B B^{\prime}$. Finally, construct a circle $\Omega_{0}$ tangent to $A^{\prime} B^{\prime}, B^{\prime} C^{\prime}, A B$ on the same side of these lines as $\omega^{\prime}$. The centre of dilation from $\omega^{\prime}$ to $\Omega_{0}$ is $B^{\prime}$, so by Monge's theorem the external centre of dilation from $\Omega_{0}$ to $\omega$ must be on the line $T B B^{\prime}$. However, it is on line $A B$, so it must be $B$ and $B C$ must be tangent to $\Omega_{0}$ as desired. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A A^{\prime} B C C^{\prime} B^{\prime}$ be a convex cyclic hexagon such that $A C$ is tangent to the incircle of the triangle $A^{\prime} B^{\prime} C^{\prime}$, and $A^{\prime} C^{\prime}$ is tangent to the incircle of the triangle $A B C$. Let the lines $A B$ and $A^{\prime} B^{\prime}$ meet at $X$ and let the lines $B C$ and $B^{\prime} C^{\prime}$ meet at $Y$. Prove that if $X B Y B^{\prime}$ is a convex quadrilateral, then it has an incircle.
|
Denote by $\omega$ and $\omega^{\prime}$ the incircles of $\triangle A B C$ and $\triangle A^{\prime} B^{\prime} C^{\prime}$ and let $I$ and $I^{\prime}$ be the centres of these circles. Let $N$ and $N^{\prime}$ be the second intersections of $B I$ and $B^{\prime} I^{\prime}$ with $\Omega$, the circumcircle of $A^{\prime} B C C^{\prime} B^{\prime} A$, and let $O$ be the centre of $\Omega$. Note that $O N \perp A C, O N^{\prime} \perp A^{\prime} C^{\prime}$ and $O N=O N^{\prime}$ so $N N^{\prime}$ is parallel to the angle bisector $I I^{\prime}$ of $A C$ and $A^{\prime} C^{\prime}$. Thus $I I^{\prime} \| N N^{\prime}$ which is antiparallel to $B B^{\prime}$ with respect to $B I$ and $B^{\prime} I^{\prime}$. Therefore $B, I, I^{\prime}, B^{\prime}$ are concyclic.  Further define $P$ as the intersection of $A C$ and $A^{\prime} C^{\prime}$ and $M$ as the antipode of $N^{\prime}$ in $\Omega$. Consider the circle $\Gamma_{1}$ with centre $N$ and radius $N A=N C$ and the circle $\Gamma_{2}$ with centre $M$ and radius $M A^{\prime}=M C^{\prime}$. Their radical axis passes through $P$ and is perpendicular to $M N \perp N N^{\prime} \| I P$, so $I$ lies on their radical axis. Therefore, since $I$ lies on $\Gamma_{1}$, it must also lie on $\Gamma_{2}$. Thus, if we define $Z$ as the second intersection of $M I$ with $\Omega$, we have that $I$ is the incentre of triangle $Z A^{\prime} C^{\prime}$. (Note that the point $Z$ can also be constructed directly via Poncelet's porism.) Consider the incircle $\omega_{c}$ with centre $I_{c}$ of triangle $C^{\prime} B^{\prime} Z$. Note that $\angle Z I C^{\prime}=90^{\circ}+$ $\frac{1}{2} \angle Z A^{\prime} C^{\prime}=90^{\circ}+\frac{1}{2} \angle Z B^{\prime} C^{\prime}=\angle Z I_{c} C^{\prime}$, so $Z, I, I_{c}, C^{\prime}$ are concyclic. Similarly $B^{\prime}, I^{\prime}, I_{c}, C^{\prime}$ are concyclic. The external centre of dilation from $\omega$ to $\omega_{c}$ is the intersection of $I I_{c}$ and $C^{\prime} Z$ ( $D$ in the picture), that is the radical centre of circles $\Omega, C^{\prime} I_{c} I Z$ and $I I^{\prime} I_{c}$. Similarly, the external centre of dilation from $\omega^{\prime}$ to $\omega_{c}$ is the intersection of $I^{\prime} I_{c}$ and $B^{\prime} C^{\prime}$ ( $D^{\prime}$ in the picture), that is the radical centre of circles $\Omega, B^{\prime} I^{\prime} I_{c} C^{\prime}$ and $I I^{\prime} I_{c}$. Therefore the Monge line of $\omega, \omega^{\prime}$ and $\omega_{c}$ is line $D D^{\prime}$, and the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$ coincide. Hence the external centre $T$ of dilation from $\omega$ to $\omega^{\prime}$ is also on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$.  Now since $B, I, I^{\prime}, B^{\prime}$ are concyclic, the intersection $T^{\prime}$ of $B B^{\prime}$ and $I I^{\prime}$ is on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$. Thus $T^{\prime}=T$ and $T$ lies on line $B B^{\prime}$. Finally, construct a circle $\Omega_{0}$ tangent to $A^{\prime} B^{\prime}, B^{\prime} C^{\prime}, A B$ on the same side of these lines as $\omega^{\prime}$. The centre of dilation from $\omega^{\prime}$ to $\Omega_{0}$ is $B^{\prime}$, so by Monge's theorem the external centre of dilation from $\Omega_{0}$ to $\omega$ must be on the line $T B B^{\prime}$. However, it is on line $A B$, so it must be $B$ and $B C$ must be tangent to $\Omega_{0}$ as desired. 
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
79438ded-ebe4-50c4-ade7-d245ea9c3dc9
| 24,364
|
For each $1 \leqslant i \leqslant 9$ and $T \in \mathbb{N}$, define $d_{i}(T)$ to be the total number of times the digit $i$ appears when all the multiples of 1829 between 1 and $T$ inclusive are written out in base 10. Show that there are infinitely many $T \in \mathbb{N}$ such that there are precisely two distinct values among $d_{1}(T), d_{2}(T), \ldots, d_{9}(T)$. (United Kingdom)
|
Let $n:=1829$. First, we choose some $k$ such that $n \mid 10^{k}-1$. For instance, any multiple of $\varphi(n)$ would work since $n$ is coprime to 10 . We will show that either $T=10^{k}-1$ or $T=10^{k}-2$ has the desired property, which completes the proof since $k$ can be taken to be arbitrary large. For this it suffices to show that $\#\left\{d_{i}\left(10^{k}-1\right): 1 \leqslant i \leqslant 9\right\} \leqslant 2$. Indeed, if $$ \#\left\{d_{i}\left(10^{k}-1\right): 1 \leqslant i \leqslant 9\right\}=1 $$ then, since $10^{k}-1$ which consists of all nines is a multiple of $n$, we have $$ d_{i}\left(10^{k}-2\right)=d_{i}\left(10^{k}-1\right) \text { for } i \in\{1, \ldots, 8\}, \text { and } d_{9}\left(10^{k}-2\right)<d_{9}\left(10^{k}-1\right) $$ This means that $\#\left\{d_{i}\left(10^{k}-2\right): 1 \leqslant i \leqslant 9\right\}=2$. To prove that $\#\left\{d_{i}\left(10^{k}-1\right)\right\} \leqslant 2$ we need an observation. Let $\overline{a_{k-1} a_{k-2} \ldots a_{0}} \in\left\{1, \ldots, 10^{k}-1\right\}$ be the decimal expansion of an arbitrary number, possibly with leading zeroes. Then $\overline{a_{k-1} a_{k-2} \ldots a_{0}}$ is divisible by $n$ if and only if $\overline{a_{k-2} \ldots a_{0} a_{k-1}}$ is divisible by $n$. Indeed, this follows from the fact that $$ 10 \cdot \overline{a_{k-1} a_{k-2} \ldots a_{0}}-\overline{a_{k-2} \ldots a_{0} a_{k-1}}=\left(10^{k}-1\right) \cdot a_{k-1} $$ is divisible by $n$. This observation shows that the set of multiples of $n$ between 1 and $10^{k}-1$ is invariant under simultaneous cyclic permutation of digits when numbers are written with leading zeroes. Hence, for each $i \in\{1, \ldots, 9\}$ the number $d_{i}\left(10^{k}-1\right)$ is $k$ times larger than the number of $k$ digit numbers which start from the digit $i$ and are divisible by $n$. Since the latter number is either $\left\lfloor 10^{k-1} / n\right\rfloor$ or $1+\left\lfloor 10^{k-1} / n\right\rfloor$, we conclude that $\#\left\{d_{i}\left(10^{k}-1\right)\right\} \leqslant 2$. Comment. More careful analysis shows that $\#\left\{d_{i}\left(10^{k}-1\right): 1 \leqslant i \leqslant 9\right\}=1$ if and only if $n \equiv 1$ $(\bmod 10)$, which is not the case for $n=1829$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each $1 \leqslant i \leqslant 9$ and $T \in \mathbb{N}$, define $d_{i}(T)$ to be the total number of times the digit $i$ appears when all the multiples of 1829 between 1 and $T$ inclusive are written out in base 10. Show that there are infinitely many $T \in \mathbb{N}$ such that there are precisely two distinct values among $d_{1}(T), d_{2}(T), \ldots, d_{9}(T)$. (United Kingdom)
|
Let $n:=1829$. First, we choose some $k$ such that $n \mid 10^{k}-1$. For instance, any multiple of $\varphi(n)$ would work since $n$ is coprime to 10 . We will show that either $T=10^{k}-1$ or $T=10^{k}-2$ has the desired property, which completes the proof since $k$ can be taken to be arbitrary large. For this it suffices to show that $\#\left\{d_{i}\left(10^{k}-1\right): 1 \leqslant i \leqslant 9\right\} \leqslant 2$. Indeed, if $$ \#\left\{d_{i}\left(10^{k}-1\right): 1 \leqslant i \leqslant 9\right\}=1 $$ then, since $10^{k}-1$ which consists of all nines is a multiple of $n$, we have $$ d_{i}\left(10^{k}-2\right)=d_{i}\left(10^{k}-1\right) \text { for } i \in\{1, \ldots, 8\}, \text { and } d_{9}\left(10^{k}-2\right)<d_{9}\left(10^{k}-1\right) $$ This means that $\#\left\{d_{i}\left(10^{k}-2\right): 1 \leqslant i \leqslant 9\right\}=2$. To prove that $\#\left\{d_{i}\left(10^{k}-1\right)\right\} \leqslant 2$ we need an observation. Let $\overline{a_{k-1} a_{k-2} \ldots a_{0}} \in\left\{1, \ldots, 10^{k}-1\right\}$ be the decimal expansion of an arbitrary number, possibly with leading zeroes. Then $\overline{a_{k-1} a_{k-2} \ldots a_{0}}$ is divisible by $n$ if and only if $\overline{a_{k-2} \ldots a_{0} a_{k-1}}$ is divisible by $n$. Indeed, this follows from the fact that $$ 10 \cdot \overline{a_{k-1} a_{k-2} \ldots a_{0}}-\overline{a_{k-2} \ldots a_{0} a_{k-1}}=\left(10^{k}-1\right) \cdot a_{k-1} $$ is divisible by $n$. This observation shows that the set of multiples of $n$ between 1 and $10^{k}-1$ is invariant under simultaneous cyclic permutation of digits when numbers are written with leading zeroes. Hence, for each $i \in\{1, \ldots, 9\}$ the number $d_{i}\left(10^{k}-1\right)$ is $k$ times larger than the number of $k$ digit numbers which start from the digit $i$ and are divisible by $n$. Since the latter number is either $\left\lfloor 10^{k-1} / n\right\rfloor$ or $1+\left\lfloor 10^{k-1} / n\right\rfloor$, we conclude that $\#\left\{d_{i}\left(10^{k}-1\right)\right\} \leqslant 2$. Comment. More careful analysis shows that $\#\left\{d_{i}\left(10^{k}-1\right): 1 \leqslant i \leqslant 9\right\}=1$ if and only if $n \equiv 1$ $(\bmod 10)$, which is not the case for $n=1829$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
72696379-936b-5c3b-92c3-8ffe3acee3b0
| 24,381
|
Let $Q$ be a set of prime numbers, not necessarily finite. For a positive integer $n$ consider its prime factorisation; define $p(n)$ to be the sum of all the exponents and $q(n)$ to be the sum of the exponents corresponding only to primes in $Q$. A positive integer $n$ is called special if $p(n)+p(n+1)$ and $q(n)+q(n+1)$ are both even integers. Prove that there is a constant $c>0$ independent of the set $Q$ such that for any positive integer $N>100$, the number of special integers in $[1, N]$ is at least $c N$. (For example, if $Q=\{3,7\}$, then $p(42)=3, q(42)=2, p(63)=3, q(63)=3, p(2022)=3$, $q(2022)=1$. (Costa Rica)
|
Let us call two positive integers $m, n$ friends if $p(m)+p(n)$ and $q(m)+q(n)$ are both even integers. We start by noting that the pairs $(p(k), q(k))$ modulo 2 can take at most 4 different values; thus, among any five different positive integers there are two which are friends. In addition, both functions $p$ and $q$ satisfy $f(a b)=f(a)+f(b)$ for any $a, b$. Therefore, if $m$ and $n$ are divisible by $d$, then both $p$ and $q$ satisfy the equality $f(m)+f(n)=f(m / d)+$ $f(n / d)+2 f(d)$. This implies that $m, n$ are friends if and only if $m / d, n / d$ are friends. Let us call a set of integers $\left\{n_{1}, n_{2}, \ldots, n_{5}\right\}$ an interesting set if for any indexes $i, j$, the difference $d_{i j}=\left|n_{i}-n_{j}\right|$ divides both $n_{i}$ and $n_{j}$. We claim that if elements of an interesting set are all positive, then we can obtain a special integer. Indeed, if we were able to construct such a set, then there would be a pair of integers $\left\{n_{i}, n_{j}\right\}$ which are friends, according to the first observation. Additionally, the second observation yields that the quotients $n_{i} / d_{i j}, n_{j} / d_{i j}$ form a pair of friends, which happen to be consecutive integers, thus giving a special integer as desired. In order to construct a family of interesting sets, we can start by observing that the set $\{0,6,8,9,12\}$ is an interesting set. Using that $72=2^{3} \cdot 3^{2}$ is the least common multiple of all pairwise differences in this set, we obtain a family of interesting sets by considering $$ \{72 k, 72 k+6,72 k+8,72 k+9,72 k+12\} $$ for any $k \geqslant 1$. If we consider the quotients (of these numbers by the appropriate differences), then we obtain that the set $$ S_{k}=\{6 k, 8 k, 9 k, 12 k, 12 k+1,18 k+2,24 k+2,24 k+3,36 k+3,72 k+8\}, $$ has at least one special integer. In particular, the interval $[1,100 k]$ contains the sets $S_{1}, S_{2}, \ldots, S_{k}$, each of which has a special number. Any special number can be contained in at most ten sets $S_{k}$, from where we conclude that the number of special integers in $[1,100 k]$ is at least $k / 10$. Finally, let $N=100 k+r$, with $k \geqslant 1$ and $0 \leqslant r<100$, so that we have $N<100(k+1) \leqslant$ $200 k$. Then the number of special integers in $[1, N]$ is at least $k / 10>N / 2000$, as we wanted to prove. Comment 1. The statement is also true for $N \geqslant 15$ as at least one of the numbers $7,14,15$ is special. Comment 2. Another approach would be to note that if $p(2 n), p(2 n+1), p(2 n+2)$ all have the same parity then one of the numbers $n, 2 n, 2 n+1$ is special. Indeed, if $q(n)+q(n+1)$ is even then $n$ is special since $p(n)+p(n+1) \equiv p(2 n)+p(2 n+2) \equiv 0(\bmod 2)$. Otherwise, if $q(n)+q(n+1)$ is odd, so is $q(2 n)+q(2 n+2)$ which implies that exactly one of the numbers $2 n, 2 n+1$ is special. Unfortunately, it seems hard to show that the set of such $n$ has positive density: see a recent paper https://arxiv.org/abs/1509.01545 for the proof that all eight patterns of the parities of $p(n), p(n+1), p(n+2)$ appear for a positive proportion of positive integers. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $Q$ be a set of prime numbers, not necessarily finite. For a positive integer $n$ consider its prime factorisation; define $p(n)$ to be the sum of all the exponents and $q(n)$ to be the sum of the exponents corresponding only to primes in $Q$. A positive integer $n$ is called special if $p(n)+p(n+1)$ and $q(n)+q(n+1)$ are both even integers. Prove that there is a constant $c>0$ independent of the set $Q$ such that for any positive integer $N>100$, the number of special integers in $[1, N]$ is at least $c N$. (For example, if $Q=\{3,7\}$, then $p(42)=3, q(42)=2, p(63)=3, q(63)=3, p(2022)=3$, $q(2022)=1$. (Costa Rica)
|
Let us call two positive integers $m, n$ friends if $p(m)+p(n)$ and $q(m)+q(n)$ are both even integers. We start by noting that the pairs $(p(k), q(k))$ modulo 2 can take at most 4 different values; thus, among any five different positive integers there are two which are friends. In addition, both functions $p$ and $q$ satisfy $f(a b)=f(a)+f(b)$ for any $a, b$. Therefore, if $m$ and $n$ are divisible by $d$, then both $p$ and $q$ satisfy the equality $f(m)+f(n)=f(m / d)+$ $f(n / d)+2 f(d)$. This implies that $m, n$ are friends if and only if $m / d, n / d$ are friends. Let us call a set of integers $\left\{n_{1}, n_{2}, \ldots, n_{5}\right\}$ an interesting set if for any indexes $i, j$, the difference $d_{i j}=\left|n_{i}-n_{j}\right|$ divides both $n_{i}$ and $n_{j}$. We claim that if elements of an interesting set are all positive, then we can obtain a special integer. Indeed, if we were able to construct such a set, then there would be a pair of integers $\left\{n_{i}, n_{j}\right\}$ which are friends, according to the first observation. Additionally, the second observation yields that the quotients $n_{i} / d_{i j}, n_{j} / d_{i j}$ form a pair of friends, which happen to be consecutive integers, thus giving a special integer as desired. In order to construct a family of interesting sets, we can start by observing that the set $\{0,6,8,9,12\}$ is an interesting set. Using that $72=2^{3} \cdot 3^{2}$ is the least common multiple of all pairwise differences in this set, we obtain a family of interesting sets by considering $$ \{72 k, 72 k+6,72 k+8,72 k+9,72 k+12\} $$ for any $k \geqslant 1$. If we consider the quotients (of these numbers by the appropriate differences), then we obtain that the set $$ S_{k}=\{6 k, 8 k, 9 k, 12 k, 12 k+1,18 k+2,24 k+2,24 k+3,36 k+3,72 k+8\}, $$ has at least one special integer. In particular, the interval $[1,100 k]$ contains the sets $S_{1}, S_{2}, \ldots, S_{k}$, each of which has a special number. Any special number can be contained in at most ten sets $S_{k}$, from where we conclude that the number of special integers in $[1,100 k]$ is at least $k / 10$. Finally, let $N=100 k+r$, with $k \geqslant 1$ and $0 \leqslant r<100$, so that we have $N<100(k+1) \leqslant$ $200 k$. Then the number of special integers in $[1, N]$ is at least $k / 10>N / 2000$, as we wanted to prove. Comment 1. The statement is also true for $N \geqslant 15$ as at least one of the numbers $7,14,15$ is special. Comment 2. Another approach would be to note that if $p(2 n), p(2 n+1), p(2 n+2)$ all have the same parity then one of the numbers $n, 2 n, 2 n+1$ is special. Indeed, if $q(n)+q(n+1)$ is even then $n$ is special since $p(n)+p(n+1) \equiv p(2 n)+p(2 n+2) \equiv 0(\bmod 2)$. Otherwise, if $q(n)+q(n+1)$ is odd, so is $q(2 n)+q(2 n+2)$ which implies that exactly one of the numbers $2 n, 2 n+1$ is special. Unfortunately, it seems hard to show that the set of such $n$ has positive density: see a recent paper https://arxiv.org/abs/1509.01545 for the proof that all eight patterns of the parities of $p(n), p(n+1), p(n+2)$ appear for a positive proportion of positive integers. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e99e6a20-7be2-5fcc-996e-3cf848c1545f
| 24,384
|
Let $k$ be a positive integer and let $S$ be a finite set of odd prime numbers. Prove that there is at most one way (modulo rotation and reflection) to place the elements of $S$ around a circle such that the product of any two neighbors is of the form $x^{2}+x+k$ for some positive integer $x$. (U.S.A.)
|
Let us allow the value $x=0$ as well; we prove the same statement under this more general constraint. Obviously that implies the statement with the original conditions. Call a pair $\{p, q\}$ of primes with $p \neq q$ special if $p q=x^{2}+x+k$ for some nonnegative integer $x$. The following claim is the key mechanism of the problem: Claim. (a) For every prime $r$, there are at most two primes less than $r$ forming a special pair with $r$. (b) If such $p$ and $q$ exist, then $\{p, q\}$ is itself special. We present two proofs of the claim. Proof 1. We are interested in integers $1 \leqslant x<r$ satsfying $$ x^{2}+x+k \equiv 0 \quad(\bmod r) $$ Since there are at most two residues modulo $r$ that can satisfy that quadratic congruence, there are at most two possible values of $x$. That proves (a). Now suppose there are primes $p, q$ with $p<q<r$ and nonnegative integers $x, y$ such that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ From $p<q<r$ we can see that $0 \leqslant x<y \leqslant r-1$. The numbers $x, y$ are the two solutions of (1); by Vieta's formulas, we should have $x+y \equiv-1(\bmod r)$, so $x+y=r-1$. Letting $K=4 k-1, X=2 x+1$, and $Y=2 y+1$, we obtain $$ \begin{gathered} 4 p r=X^{2}+K \\ 4 q r=Y^{2}+K \end{gathered} $$ with $X+Y=2 r$. Multiplying the two above equations, $$ \begin{aligned} 16 p q r^{2} & =\left(X^{2}+K\right)\left(Y^{2}+K\right) \\ & =(X Y-K)^{2}+K(X+Y)^{2} \\ & =(X Y-K)^{2}+4 K r^{2}, \\ 4 p q & =\left(\frac{X Y-K}{2 r}\right)^{2}+K . \end{aligned} $$ In particular, the number $Z=\frac{X Y-K}{2 r}$ should be an integer, and so $4 p q=Z^{2}+K$. By parity, $Z$ is odd, and thus $$ p q=z^{2}+z+k \quad \text { where } z=\frac{Z-1}{2} $$ so $\{p, q\}$ is special. Proof 2. As before, we suppose that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ Subtracting, we have $$ (x+y+1)(x-y)=r(p-q) . $$ As before, we have $x+y=r-1$, so $x-y=p-q$, and $$ \begin{aligned} & x=\frac{1}{2}(r+p-q-1) \\ & y=\frac{1}{2}(r+q-p-1) \end{aligned} $$ Then, $$ \begin{aligned} k=p r-x^{2}-x & =\frac{1}{4}\left(4 p r-(r+p-q-1)^{2}-2(r+p-q-1)\right) \\ & =\frac{1}{4}\left(4 p r-(r+p-q)^{2}+1\right) \\ & =\frac{1}{4}\left(2 p q+2 p r+2 q r-p^{2}-q^{2}-r^{2}+1\right), \end{aligned} $$ which is symmetric in $p, q, r$, so $$ p q=z^{2}+z+k \quad \text { where } z=\frac{1}{2}(p+q-r-1) $$ and $\{p, q\}$ is special. Now we settle the problem by induction on $|S|$, with $|S| \leqslant 3$ clear. Suppose we have proven it for $|S|=n$ and consider $|S|=n+1$. Let $r$ be the largest prime in $S$; the claim tells us that in any valid cycle of primes: - the neighbors of $r$ are uniquely determined, and - removing $r$ from the cycle results in a smaller valid cycle. It follows that there is at most one valid cycle, completing the inductive step. Comment. The statement is not as inapplicable as it might seem. For example, for $k=41$, the following 385 primes form a valid cycle of primes: 53, 4357, 104173, 65921, 36383, 99527, 193789, 2089123, 1010357, 2465263, 319169, 15559, 3449, 2647, 1951, 152297, 542189, 119773, 91151, 66431, 222137, 1336799, 469069, 45613, 1047941, 656291, 355867, 146669, 874879, 2213327, 305119, 3336209, 1623467, 520963, 794201, 1124833, 28697, 15683, 42557, 6571, 39607, 1238833, 835421, 2653681, 5494387, 9357539, 511223, 1515317, 8868173, 114079681, 59334071, 22324807, 3051889, 5120939, 7722467, 266239, 693809, 3931783, 1322317, 100469, 13913, 74419, 23977, 1361, 62983, 935021, 512657, 1394849, 216259, 45827, 31393, 100787, 1193989, 600979, 209543, 357661, 545141, 19681, 10691, 28867, 165089, 2118023, 6271891, 12626693, 21182429, 1100467, 413089, 772867, 1244423, 1827757, 55889, 1558873, 5110711, 1024427, 601759, 290869, 91757, 951109 , 452033, 136471, 190031, 4423, 9239, 15809, 24133, 115811, 275911, 34211, 877, 6653, 88001, 46261, 317741, $121523,232439,379009,17827,2699,15937,497729,335539,205223,106781,1394413,4140947,8346383,43984757$, 14010721, 21133961, 729451, 4997297, 1908223, 278051, 529747, 40213, 768107, 456821, 1325351, 225961, 1501921, 562763, 75527, 5519, 9337, 14153, 499, 1399, 2753, 14401, 94583, 245107, 35171, 397093, 195907, 2505623, 34680911, 18542791, 7415917, 144797293, 455529251, 86675291, 252704911, 43385123, 109207907, 204884269, 330414209, 14926789, 1300289, 486769, 2723989, 907757, 1458871, 65063, 4561, 124427, 81343, 252887, 2980139, 1496779, 3779057, 519193, 47381, 135283, 268267, 446333, 669481, 22541, 54167, 99439, 158357, 6823, 32497, 1390709, 998029, 670343, 5180017, 13936673, 2123491, 4391941, 407651, 209953, 77249, 867653, 427117, 141079, 9539, 227, 1439 , 18679, 9749, 25453, 3697, 42139, 122327, 712303, 244261, 20873, 52051, 589997, 4310569, 1711069, 291563, 3731527 , 11045429, 129098443, 64620427, 162661963, 22233269, 37295047, 1936969, 5033449, 725537, 1353973, 6964457, 2176871, 97231, 7001, 11351, 55673, 16747, 169003, 1218571, 479957, 2779783, 949609, 4975787, 1577959, 2365007, 3310753, 79349, 23189, 107209, 688907, 252583, 30677, 523, 941, 25981, 205103, 85087, 1011233, 509659, 178259, 950479, 6262847, 2333693, 305497, 3199319, 9148267, 1527563, 466801, 17033, 9967, 323003, 4724099, 14278309, 2576557, 1075021, 6462593, 2266021, 63922471, 209814503, 42117791, 131659867, 270892249, 24845153, 12104557, 3896003, 219491, 135913, 406397, 72269, 191689, 2197697, 1091273, 2727311, 368227, 1911661, 601883, 892657, 28559, 4783, 60497, 31259, 80909, 457697, 153733, 11587, 1481, 26161, 15193, 7187, 2143, 21517, 10079, 207643, 1604381, 657661, 126227, 372313, 2176331, 748337, 64969, 844867, 2507291, 29317943, 14677801, 36952793, 69332267, 111816223, 5052241, 8479717, 441263, 3020431, 1152751, 13179611, 38280013, 6536771, 16319657, 91442699 , 30501409, 49082027, 72061511, 2199433, 167597, 317963, 23869, 2927, 3833, 17327, 110879, 285517, 40543, 4861, 21683, 50527, 565319, 277829, 687917, 3846023, 25542677, 174261149, 66370753, 9565711, 1280791, 91393, 6011, 7283, 31859, 8677, 10193, 43987, 11831, 13591, 127843, 358229, 58067, 15473, 65839, 17477, 74099, 19603, 82847, 21851, 61.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k$ be a positive integer and let $S$ be a finite set of odd prime numbers. Prove that there is at most one way (modulo rotation and reflection) to place the elements of $S$ around a circle such that the product of any two neighbors is of the form $x^{2}+x+k$ for some positive integer $x$. (U.S.A.)
|
Let us allow the value $x=0$ as well; we prove the same statement under this more general constraint. Obviously that implies the statement with the original conditions. Call a pair $\{p, q\}$ of primes with $p \neq q$ special if $p q=x^{2}+x+k$ for some nonnegative integer $x$. The following claim is the key mechanism of the problem: Claim. (a) For every prime $r$, there are at most two primes less than $r$ forming a special pair with $r$. (b) If such $p$ and $q$ exist, then $\{p, q\}$ is itself special. We present two proofs of the claim. Proof 1. We are interested in integers $1 \leqslant x<r$ satsfying $$ x^{2}+x+k \equiv 0 \quad(\bmod r) $$ Since there are at most two residues modulo $r$ that can satisfy that quadratic congruence, there are at most two possible values of $x$. That proves (a). Now suppose there are primes $p, q$ with $p<q<r$ and nonnegative integers $x, y$ such that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ From $p<q<r$ we can see that $0 \leqslant x<y \leqslant r-1$. The numbers $x, y$ are the two solutions of (1); by Vieta's formulas, we should have $x+y \equiv-1(\bmod r)$, so $x+y=r-1$. Letting $K=4 k-1, X=2 x+1$, and $Y=2 y+1$, we obtain $$ \begin{gathered} 4 p r=X^{2}+K \\ 4 q r=Y^{2}+K \end{gathered} $$ with $X+Y=2 r$. Multiplying the two above equations, $$ \begin{aligned} 16 p q r^{2} & =\left(X^{2}+K\right)\left(Y^{2}+K\right) \\ & =(X Y-K)^{2}+K(X+Y)^{2} \\ & =(X Y-K)^{2}+4 K r^{2}, \\ 4 p q & =\left(\frac{X Y-K}{2 r}\right)^{2}+K . \end{aligned} $$ In particular, the number $Z=\frac{X Y-K}{2 r}$ should be an integer, and so $4 p q=Z^{2}+K$. By parity, $Z$ is odd, and thus $$ p q=z^{2}+z+k \quad \text { where } z=\frac{Z-1}{2} $$ so $\{p, q\}$ is special. Proof 2. As before, we suppose that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ Subtracting, we have $$ (x+y+1)(x-y)=r(p-q) . $$ As before, we have $x+y=r-1$, so $x-y=p-q$, and $$ \begin{aligned} & x=\frac{1}{2}(r+p-q-1) \\ & y=\frac{1}{2}(r+q-p-1) \end{aligned} $$ Then, $$ \begin{aligned} k=p r-x^{2}-x & =\frac{1}{4}\left(4 p r-(r+p-q-1)^{2}-2(r+p-q-1)\right) \\ & =\frac{1}{4}\left(4 p r-(r+p-q)^{2}+1\right) \\ & =\frac{1}{4}\left(2 p q+2 p r+2 q r-p^{2}-q^{2}-r^{2}+1\right), \end{aligned} $$ which is symmetric in $p, q, r$, so $$ p q=z^{2}+z+k \quad \text { where } z=\frac{1}{2}(p+q-r-1) $$ and $\{p, q\}$ is special. Now we settle the problem by induction on $|S|$, with $|S| \leqslant 3$ clear. Suppose we have proven it for $|S|=n$ and consider $|S|=n+1$. Let $r$ be the largest prime in $S$; the claim tells us that in any valid cycle of primes: - the neighbors of $r$ are uniquely determined, and - removing $r$ from the cycle results in a smaller valid cycle. It follows that there is at most one valid cycle, completing the inductive step. Comment. The statement is not as inapplicable as it might seem. For example, for $k=41$, the following 385 primes form a valid cycle of primes: 53, 4357, 104173, 65921, 36383, 99527, 193789, 2089123, 1010357, 2465263, 319169, 15559, 3449, 2647, 1951, 152297, 542189, 119773, 91151, 66431, 222137, 1336799, 469069, 45613, 1047941, 656291, 355867, 146669, 874879, 2213327, 305119, 3336209, 1623467, 520963, 794201, 1124833, 28697, 15683, 42557, 6571, 39607, 1238833, 835421, 2653681, 5494387, 9357539, 511223, 1515317, 8868173, 114079681, 59334071, 22324807, 3051889, 5120939, 7722467, 266239, 693809, 3931783, 1322317, 100469, 13913, 74419, 23977, 1361, 62983, 935021, 512657, 1394849, 216259, 45827, 31393, 100787, 1193989, 600979, 209543, 357661, 545141, 19681, 10691, 28867, 165089, 2118023, 6271891, 12626693, 21182429, 1100467, 413089, 772867, 1244423, 1827757, 55889, 1558873, 5110711, 1024427, 601759, 290869, 91757, 951109 , 452033, 136471, 190031, 4423, 9239, 15809, 24133, 115811, 275911, 34211, 877, 6653, 88001, 46261, 317741, $121523,232439,379009,17827,2699,15937,497729,335539,205223,106781,1394413,4140947,8346383,43984757$, 14010721, 21133961, 729451, 4997297, 1908223, 278051, 529747, 40213, 768107, 456821, 1325351, 225961, 1501921, 562763, 75527, 5519, 9337, 14153, 499, 1399, 2753, 14401, 94583, 245107, 35171, 397093, 195907, 2505623, 34680911, 18542791, 7415917, 144797293, 455529251, 86675291, 252704911, 43385123, 109207907, 204884269, 330414209, 14926789, 1300289, 486769, 2723989, 907757, 1458871, 65063, 4561, 124427, 81343, 252887, 2980139, 1496779, 3779057, 519193, 47381, 135283, 268267, 446333, 669481, 22541, 54167, 99439, 158357, 6823, 32497, 1390709, 998029, 670343, 5180017, 13936673, 2123491, 4391941, 407651, 209953, 77249, 867653, 427117, 141079, 9539, 227, 1439 , 18679, 9749, 25453, 3697, 42139, 122327, 712303, 244261, 20873, 52051, 589997, 4310569, 1711069, 291563, 3731527 , 11045429, 129098443, 64620427, 162661963, 22233269, 37295047, 1936969, 5033449, 725537, 1353973, 6964457, 2176871, 97231, 7001, 11351, 55673, 16747, 169003, 1218571, 479957, 2779783, 949609, 4975787, 1577959, 2365007, 3310753, 79349, 23189, 107209, 688907, 252583, 30677, 523, 941, 25981, 205103, 85087, 1011233, 509659, 178259, 950479, 6262847, 2333693, 305497, 3199319, 9148267, 1527563, 466801, 17033, 9967, 323003, 4724099, 14278309, 2576557, 1075021, 6462593, 2266021, 63922471, 209814503, 42117791, 131659867, 270892249, 24845153, 12104557, 3896003, 219491, 135913, 406397, 72269, 191689, 2197697, 1091273, 2727311, 368227, 1911661, 601883, 892657, 28559, 4783, 60497, 31259, 80909, 457697, 153733, 11587, 1481, 26161, 15193, 7187, 2143, 21517, 10079, 207643, 1604381, 657661, 126227, 372313, 2176331, 748337, 64969, 844867, 2507291, 29317943, 14677801, 36952793, 69332267, 111816223, 5052241, 8479717, 441263, 3020431, 1152751, 13179611, 38280013, 6536771, 16319657, 91442699 , 30501409, 49082027, 72061511, 2199433, 167597, 317963, 23869, 2927, 3833, 17327, 110879, 285517, 40543, 4861, 21683, 50527, 565319, 277829, 687917, 3846023, 25542677, 174261149, 66370753, 9565711, 1280791, 91393, 6011, 7283, 31859, 8677, 10193, 43987, 11831, 13591, 127843, 358229, 58067, 15473, 65839, 17477, 74099, 19603, 82847, 21851, 61.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c5c0542b-ea09-5e63-8212-769e1e17c49a
| 24,387
|
For a positive integer $n$ we denote by $s(n)$ the sum of the digits of $n$. Let $P(x)=$ $x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ be a polynomial, where $n \geqslant 2$ and $a_{i}$ is a positive integer for all $0 \leqslant i \leqslant n-1$. Could it be the case that, for all positive integers $k, s(k)$ and $s(P(k))$ have the same parity? (Belarus) Answer: No. For any such polynomial there exists a positive integer $k$ such that $s(k)$ and $s(P(k))$ have different parities.
|
With the notation above, we begin by choosing a positive integer $t$ such that $$ 10^{t}>\max \left\{\frac{100^{n-1} a_{n-1}}{\left(10^{\frac{1}{n-1}}-9^{\frac{1}{n-1}}\right)^{n-1}}, \frac{a_{n-1}}{9} 10^{n-1}, \frac{a_{n-1}}{9}\left(10 a_{n-1}\right)^{n-1}, \ldots, \frac{a_{n-1}}{9}\left(10 a_{0}\right)^{n-1}\right\} $$ As a direct consequence of $10^{t}$ being bigger than the first quantity listed in the above set, we get that the interval $$ I=\left[\left(\frac{9}{a_{n-1}} 10^{t}\right)^{\frac{1}{n-1}},\left(\frac{1}{a_{n-1}} 10^{t+1}\right)^{\frac{1}{n-1}}\right) $$ contains at least 100 consecutive positive integers. Let $X$ be a positive integer in $I$ such that $X$ is congruent to $1 \bmod 100$. Since $X \in I$ we have $$ 9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}<10^{t+1} $$ thus the first digit (from the left) of $a_{n-1} X^{n-1}$ must be 9 . Next, we observe that $a_{n-1}\left(10 a_{i}\right)^{n-1}<9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}$, thus $10 a_{i}<X$ for all $i$, which immediately implies that $a_{0}<a_{1} X<\cdots<a_{n} X^{n}$, and the number of digits of this strictly increasing sequence forms a strictly increasing sequence too. In other words, if $i<j$, the number of digits of $a_{i} X^{i}$ is less than the number of digits of $a_{j} X^{j}$. Let $\alpha$ be the number of digits of $a_{n-1} X^{n-1}$, thus $10^{\alpha-1} \leqslant a_{n-1} X^{n-1}<10^{\alpha}$. We are now going to look at $P\left(10^{\alpha} X\right)$ and $P\left(10^{\alpha-1} X\right)$ and prove that the sum of their digits has different parities. This will finish the proof since $s\left(10^{\alpha} X\right)=s\left(10^{\alpha-1} X\right)=s(X)$. We have $P\left(10^{\alpha} X\right)=10^{\alpha n} X^{n}+a_{n-1} 10^{\alpha(n-1)} X^{n-1}+\cdots+a_{0}$, and since $10^{\alpha(i+1)}>10^{\alpha i} a_{n-1} X^{n-1}>$ $10^{\alpha i} a_{i} X^{i}$, the terms $a_{i} 10^{\alpha i} X^{i}$ do not interact when added; in particular, there is no carryover caused by addition. Thus we have $s\left(P\left(10^{\alpha} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)$. We now look at $P\left(10^{\alpha-1} X\right)=10^{(\alpha-1) n} X^{n}+a_{n-1} 10^{(\alpha-1)(n-1)} X^{n-1}+\cdots+a_{0}$. Firstly, if $i<n-1$, then $a_{n-1} X^{n-1}$ has more digits than $a_{i} X^{i}$ and $a_{n-1} X^{n-1} \geqslant 10 a_{i} X^{i}$. It now follows that $10^{(\alpha-1)(i+1)+1}>10^{(\alpha-1) i} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) i+1} a_{i} X^{i}$, thus all terms $10^{(\alpha-1) i} a_{i} X^{i}$ for $0 \leqslant i \leqslant n-1$ come in 'blocks', exactly as in the previous case. Finally, $10^{(\alpha-1) n+1}>10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) n}$, thus $10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1}$ has exactly $(\alpha-1) n+1$ digits, and its first digit is 9 , as established above. On the other hand, $10^{(\alpha-1) n} X^{n}$ has exactly $(\alpha-1) n$ zeros, followed by $01($ as $X$ is $1 \bmod 100)$. Therefore, when we add the terms, the 9 and 1 turn into 0 , the 0 turns into 1 , and nothing else is affected. Putting everything together, we obtain $$ s\left(P\left(10^{\alpha-1} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)-9=s\left(P\left(10^{\alpha} X\right)\right)-9 $$ thus $s\left(P\left(10^{\alpha} X\right)\right)$ and $s\left(P\left(10^{\alpha-1} X\right)\right)$ have different parities, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$ we denote by $s(n)$ the sum of the digits of $n$. Let $P(x)=$ $x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ be a polynomial, where $n \geqslant 2$ and $a_{i}$ is a positive integer for all $0 \leqslant i \leqslant n-1$. Could it be the case that, for all positive integers $k, s(k)$ and $s(P(k))$ have the same parity? (Belarus) Answer: No. For any such polynomial there exists a positive integer $k$ such that $s(k)$ and $s(P(k))$ have different parities.
|
With the notation above, we begin by choosing a positive integer $t$ such that $$ 10^{t}>\max \left\{\frac{100^{n-1} a_{n-1}}{\left(10^{\frac{1}{n-1}}-9^{\frac{1}{n-1}}\right)^{n-1}}, \frac{a_{n-1}}{9} 10^{n-1}, \frac{a_{n-1}}{9}\left(10 a_{n-1}\right)^{n-1}, \ldots, \frac{a_{n-1}}{9}\left(10 a_{0}\right)^{n-1}\right\} $$ As a direct consequence of $10^{t}$ being bigger than the first quantity listed in the above set, we get that the interval $$ I=\left[\left(\frac{9}{a_{n-1}} 10^{t}\right)^{\frac{1}{n-1}},\left(\frac{1}{a_{n-1}} 10^{t+1}\right)^{\frac{1}{n-1}}\right) $$ contains at least 100 consecutive positive integers. Let $X$ be a positive integer in $I$ such that $X$ is congruent to $1 \bmod 100$. Since $X \in I$ we have $$ 9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}<10^{t+1} $$ thus the first digit (from the left) of $a_{n-1} X^{n-1}$ must be 9 . Next, we observe that $a_{n-1}\left(10 a_{i}\right)^{n-1}<9 \cdot 10^{t} \leqslant a_{n-1} X^{n-1}$, thus $10 a_{i}<X$ for all $i$, which immediately implies that $a_{0}<a_{1} X<\cdots<a_{n} X^{n}$, and the number of digits of this strictly increasing sequence forms a strictly increasing sequence too. In other words, if $i<j$, the number of digits of $a_{i} X^{i}$ is less than the number of digits of $a_{j} X^{j}$. Let $\alpha$ be the number of digits of $a_{n-1} X^{n-1}$, thus $10^{\alpha-1} \leqslant a_{n-1} X^{n-1}<10^{\alpha}$. We are now going to look at $P\left(10^{\alpha} X\right)$ and $P\left(10^{\alpha-1} X\right)$ and prove that the sum of their digits has different parities. This will finish the proof since $s\left(10^{\alpha} X\right)=s\left(10^{\alpha-1} X\right)=s(X)$. We have $P\left(10^{\alpha} X\right)=10^{\alpha n} X^{n}+a_{n-1} 10^{\alpha(n-1)} X^{n-1}+\cdots+a_{0}$, and since $10^{\alpha(i+1)}>10^{\alpha i} a_{n-1} X^{n-1}>$ $10^{\alpha i} a_{i} X^{i}$, the terms $a_{i} 10^{\alpha i} X^{i}$ do not interact when added; in particular, there is no carryover caused by addition. Thus we have $s\left(P\left(10^{\alpha} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)$. We now look at $P\left(10^{\alpha-1} X\right)=10^{(\alpha-1) n} X^{n}+a_{n-1} 10^{(\alpha-1)(n-1)} X^{n-1}+\cdots+a_{0}$. Firstly, if $i<n-1$, then $a_{n-1} X^{n-1}$ has more digits than $a_{i} X^{i}$ and $a_{n-1} X^{n-1} \geqslant 10 a_{i} X^{i}$. It now follows that $10^{(\alpha-1)(i+1)+1}>10^{(\alpha-1) i} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) i+1} a_{i} X^{i}$, thus all terms $10^{(\alpha-1) i} a_{i} X^{i}$ for $0 \leqslant i \leqslant n-1$ come in 'blocks', exactly as in the previous case. Finally, $10^{(\alpha-1) n+1}>10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1} \geqslant 10^{(\alpha-1) n}$, thus $10^{(\alpha-1)(n-1)} a_{n-1} X^{n-1}$ has exactly $(\alpha-1) n+1$ digits, and its first digit is 9 , as established above. On the other hand, $10^{(\alpha-1) n} X^{n}$ has exactly $(\alpha-1) n$ zeros, followed by $01($ as $X$ is $1 \bmod 100)$. Therefore, when we add the terms, the 9 and 1 turn into 0 , the 0 turns into 1 , and nothing else is affected. Putting everything together, we obtain $$ s\left(P\left(10^{\alpha-1} X\right)\right)=s\left(X^{n}\right)+s\left(a_{n-1} X^{n-1}\right)+\cdots+s\left(a_{0}\right)-9=s\left(P\left(10^{\alpha} X\right)\right)-9 $$ thus $s\left(P\left(10^{\alpha} X\right)\right)$ and $s\left(P\left(10^{\alpha-1} X\right)\right)$ have different parities, as claimed.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
929bd952-f883-5010-a996-ce40cb1de0b1
| 24,411
|
Let $A A^{\prime} B C C^{\prime} B^{\prime}$ be a convex cyclic hexagon such that $A C$ is tangent to the incircle of the triangle $A^{\prime} B^{\prime} C^{\prime}$, and $A^{\prime} C^{\prime}$ is tangent to the incircle of the triangle $A B C$. Let the lines $A B$ and $A^{\prime} B^{\prime}$ meet at $X$ and let the lines $B C$ and $B^{\prime} C^{\prime}$ meet at $Y$. Prove that if $X B Y B^{\prime}$ is a convex quadrilateral, then it has an incircle. (Australia)
|
Denote by $\omega$ and $\omega^{\prime}$ the incircles of $\triangle A B C$ and $\triangle A^{\prime} B^{\prime} C^{\prime}$ and let $I$ and $I^{\prime}$ be the centres of these circles. Let $N$ and $N^{\prime}$ be the second intersections of $B I$ and $B^{\prime} I^{\prime}$ with $\Omega$, the circumcircle of $A^{\prime} B C C^{\prime} B^{\prime} A$, and let $O$ be the centre of $\Omega$. Note that $O N \perp A C, O N^{\prime} \perp A^{\prime} C^{\prime}$ and $O N=O N^{\prime}$ so $N N^{\prime}$ is parallel to the angle bisector $I I^{\prime}$ of $A C$ and $A^{\prime} C^{\prime}$. Thus $I I^{\prime} \| N N^{\prime}$ which is antiparallel to $B B^{\prime}$ with respect to $B I$ and $B^{\prime} I^{\prime}$. Therefore $B, I, I^{\prime}, B^{\prime}$ are concyclic.  Further define $P$ as the intersection of $A C$ and $A^{\prime} C^{\prime}$ and $M$ as the antipode of $N^{\prime}$ in $\Omega$. Consider the circle $\Gamma_{1}$ with centre $N$ and radius $N A=N C$ and the circle $\Gamma_{2}$ with centre $M$ and radius $M A^{\prime}=M C^{\prime}$. Their radical axis passes through $P$ and is perpendicular to $M N \perp N N^{\prime} \| I P$, so $I$ lies on their radical axis. Therefore, since $I$ lies on $\Gamma_{1}$, it must also lie on $\Gamma_{2}$. Thus, if we define $Z$ as the second intersection of $M I$ with $\Omega$, we have that $I$ is the incentre of triangle $Z A^{\prime} C^{\prime}$. (Note that the point $Z$ can also be constructed directly via Poncelet's porism.) Consider the incircle $\omega_{c}$ with centre $I_{c}$ of triangle $C^{\prime} B^{\prime} Z$. Note that $\angle Z I C^{\prime}=90^{\circ}+$ $\frac{1}{2} \angle Z A^{\prime} C^{\prime}=90^{\circ}+\frac{1}{2} \angle Z B^{\prime} C^{\prime}=\angle Z I_{c} C^{\prime}$, so $Z, I, I_{c}, C^{\prime}$ are concyclic. Similarly $B^{\prime}, I^{\prime}, I_{c}, C^{\prime}$ are concyclic. The external centre of dilation from $\omega$ to $\omega_{c}$ is the intersection of $I I_{c}$ and $C^{\prime} Z$ ( $D$ in the picture), that is the radical centre of circles $\Omega, C^{\prime} I_{c} I Z$ and $I I^{\prime} I_{c}$. Similarly, the external centre of dilation from $\omega^{\prime}$ to $\omega_{c}$ is the intersection of $I^{\prime} I_{c}$ and $B^{\prime} C^{\prime}$ ( $D^{\prime}$ in the picture), that is the radical centre of circles $\Omega, B^{\prime} I^{\prime} I_{c} C^{\prime}$ and $I I^{\prime} I_{c}$. Therefore the Monge line of $\omega, \omega^{\prime}$ and $\omega_{c}$ is line $D D^{\prime}$, and the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$ coincide. Hence the external centre $T$ of dilation from $\omega$ to $\omega^{\prime}$ is also on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$.  Now since $B, I, I^{\prime}, B^{\prime}$ are concyclic, the intersection $T^{\prime}$ of $B B^{\prime}$ and $I I^{\prime}$ is on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$. Thus $T^{\prime}=T$ and $T$ lies on line $B B^{\prime}$. Finally, construct a circle $\Omega_{0}$ tangent to $A^{\prime} B^{\prime}, B^{\prime} C^{\prime}, A B$ on the same side of these lines as $\omega^{\prime}$. The centre of dilation from $\omega^{\prime}$ to $\Omega_{0}$ is $B^{\prime}$, so by Monge's theorem the external centre of dilation from $\Omega_{0}$ to $\omega$ must be on the line $T B B^{\prime}$. However, it is on line $A B$, so it must be $B$ and $B C$ must be tangent to $\Omega_{0}$ as desired. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A A^{\prime} B C C^{\prime} B^{\prime}$ be a convex cyclic hexagon such that $A C$ is tangent to the incircle of the triangle $A^{\prime} B^{\prime} C^{\prime}$, and $A^{\prime} C^{\prime}$ is tangent to the incircle of the triangle $A B C$. Let the lines $A B$ and $A^{\prime} B^{\prime}$ meet at $X$ and let the lines $B C$ and $B^{\prime} C^{\prime}$ meet at $Y$. Prove that if $X B Y B^{\prime}$ is a convex quadrilateral, then it has an incircle. (Australia)
|
Denote by $\omega$ and $\omega^{\prime}$ the incircles of $\triangle A B C$ and $\triangle A^{\prime} B^{\prime} C^{\prime}$ and let $I$ and $I^{\prime}$ be the centres of these circles. Let $N$ and $N^{\prime}$ be the second intersections of $B I$ and $B^{\prime} I^{\prime}$ with $\Omega$, the circumcircle of $A^{\prime} B C C^{\prime} B^{\prime} A$, and let $O$ be the centre of $\Omega$. Note that $O N \perp A C, O N^{\prime} \perp A^{\prime} C^{\prime}$ and $O N=O N^{\prime}$ so $N N^{\prime}$ is parallel to the angle bisector $I I^{\prime}$ of $A C$ and $A^{\prime} C^{\prime}$. Thus $I I^{\prime} \| N N^{\prime}$ which is antiparallel to $B B^{\prime}$ with respect to $B I$ and $B^{\prime} I^{\prime}$. Therefore $B, I, I^{\prime}, B^{\prime}$ are concyclic.  Further define $P$ as the intersection of $A C$ and $A^{\prime} C^{\prime}$ and $M$ as the antipode of $N^{\prime}$ in $\Omega$. Consider the circle $\Gamma_{1}$ with centre $N$ and radius $N A=N C$ and the circle $\Gamma_{2}$ with centre $M$ and radius $M A^{\prime}=M C^{\prime}$. Their radical axis passes through $P$ and is perpendicular to $M N \perp N N^{\prime} \| I P$, so $I$ lies on their radical axis. Therefore, since $I$ lies on $\Gamma_{1}$, it must also lie on $\Gamma_{2}$. Thus, if we define $Z$ as the second intersection of $M I$ with $\Omega$, we have that $I$ is the incentre of triangle $Z A^{\prime} C^{\prime}$. (Note that the point $Z$ can also be constructed directly via Poncelet's porism.) Consider the incircle $\omega_{c}$ with centre $I_{c}$ of triangle $C^{\prime} B^{\prime} Z$. Note that $\angle Z I C^{\prime}=90^{\circ}+$ $\frac{1}{2} \angle Z A^{\prime} C^{\prime}=90^{\circ}+\frac{1}{2} \angle Z B^{\prime} C^{\prime}=\angle Z I_{c} C^{\prime}$, so $Z, I, I_{c}, C^{\prime}$ are concyclic. Similarly $B^{\prime}, I^{\prime}, I_{c}, C^{\prime}$ are concyclic. The external centre of dilation from $\omega$ to $\omega_{c}$ is the intersection of $I I_{c}$ and $C^{\prime} Z$ ( $D$ in the picture), that is the radical centre of circles $\Omega, C^{\prime} I_{c} I Z$ and $I I^{\prime} I_{c}$. Similarly, the external centre of dilation from $\omega^{\prime}$ to $\omega_{c}$ is the intersection of $I^{\prime} I_{c}$ and $B^{\prime} C^{\prime}$ ( $D^{\prime}$ in the picture), that is the radical centre of circles $\Omega, B^{\prime} I^{\prime} I_{c} C^{\prime}$ and $I I^{\prime} I_{c}$. Therefore the Monge line of $\omega, \omega^{\prime}$ and $\omega_{c}$ is line $D D^{\prime}$, and the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$ coincide. Hence the external centre $T$ of dilation from $\omega$ to $\omega^{\prime}$ is also on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$.  Now since $B, I, I^{\prime}, B^{\prime}$ are concyclic, the intersection $T^{\prime}$ of $B B^{\prime}$ and $I I^{\prime}$ is on the radical axis of $\Omega$ and circle $I I^{\prime} I_{c}$. Thus $T^{\prime}=T$ and $T$ lies on line $B B^{\prime}$. Finally, construct a circle $\Omega_{0}$ tangent to $A^{\prime} B^{\prime}, B^{\prime} C^{\prime}, A B$ on the same side of these lines as $\omega^{\prime}$. The centre of dilation from $\omega^{\prime}$ to $\Omega_{0}$ is $B^{\prime}$, so by Monge's theorem the external centre of dilation from $\Omega_{0}$ to $\omega$ must be on the line $T B B^{\prime}$. However, it is on line $A B$, so it must be $B$ and $B C$ must be tangent to $\Omega_{0}$ as desired. 
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bf0d3a43-230b-55b4-9f25-47fc993b7d01
| 24,441
|
Let $Q$ be a set of prime numbers, not necessarily finite. For a positive integer $n$ consider its prime factorisation; define $p(n)$ to be the sum of all the exponents and $q(n)$ to be the sum of the exponents corresponding only to primes in $Q$. A positive integer $n$ is called special if $p(n)+p(n+1)$ and $q(n)+q(n+1)$ are both even integers. Prove that there is a constant $c>0$ independent of the set $Q$ such that for any positive integer $N>100$, the number of special integers in $[1, N]$ is at least $c N$. (For example, if $Q=\{3,7\}$, then $p(42)=3, q(42)=2, p(63)=3, q(63)=3, p(2022)=3$, $q(2022)=1$.) (Costa Rica)
|
Let us call two positive integers $m, n$ friends if $p(m)+p(n)$ and $q(m)+q(n)$ are both even integers. We start by noting that the pairs $(p(k), q(k))$ modulo 2 can take at most 4 different values; thus, among any five different positive integers there are two which are friends. In addition, both functions $p$ and $q$ satisfy $f(a b)=f(a)+f(b)$ for any $a, b$. Therefore, if $m$ and $n$ are divisible by $d$, then both $p$ and $q$ satisfy the equality $f(m)+f(n)=f(m / d)+$ $f(n / d)+2 f(d)$. This implies that $m, n$ are friends if and only if $m / d, n / d$ are friends. Let us call a set of integers $\left\{n_{1}, n_{2}, \ldots, n_{5}\right\}$ an interesting set if for any indexes $i, j$, the difference $d_{i j}=\left|n_{i}-n_{j}\right|$ divides both $n_{i}$ and $n_{j}$. We claim that if elements of an interesting set are all positive, then we can obtain a special integer. Indeed, if we were able to construct such a set, then there would be a pair of integers $\left\{n_{i}, n_{j}\right\}$ which are friends, according to the first observation. Additionally, the second observation yields that the quotients $n_{i} / d_{i j}, n_{j} / d_{i j}$ form a pair of friends, which happen to be consecutive integers, thus giving a special integer as desired. In order to construct a family of interesting sets, we can start by observing that the set $\{0,6,8,9,12\}$ is an interesting set. Using that $72=2^{3} \cdot 3^{2}$ is the least common multiple of all pairwise differences in this set, we obtain a family of interesting sets by considering $$ \{72 k, 72 k+6,72 k+8,72 k+9,72 k+12\} $$ for any $k \geqslant 1$. If we consider the quotients (of these numbers by the appropriate differences), then we obtain that the set $$ S_{k}=\{6 k, 8 k, 9 k, 12 k, 12 k+1,18 k+2,24 k+2,24 k+3,36 k+3,72 k+8\}, $$ has at least one special integer. In particular, the interval $[1,100 k]$ contains the sets $S_{1}, S_{2}, \ldots, S_{k}$, each of which has a special number. Any special number can be contained in at most ten sets $S_{k}$, from where we conclude that the number of special integers in $[1,100 k]$ is at least $k / 10$. Finally, let $N=100 k+r$, with $k \geqslant 1$ and $0 \leqslant r<100$, so that we have $N<100(k+1) \leqslant$ $200 k$. Then the number of special integers in $[1, N]$ is at least $k / 10>N / 2000$, as we wanted to prove. Comment 1. The statement is also true for $N \geqslant 15$ as at least one of the numbers $7,14,15$ is special. Comment 2. Another approach would be to note that if $p(2 n), p(2 n+1), p(2 n+2)$ all have the same parity then one of the numbers $n, 2 n, 2 n+1$ is special. Indeed, if $q(n)+q(n+1)$ is even then $n$ is special since $p(n)+p(n+1) \equiv p(2 n)+p(2 n+2) \equiv 0(\bmod 2)$. Otherwise, if $q(n)+q(n+1)$ is odd, so is $q(2 n)+q(2 n+2)$ which implies that exactly one of the numbers $2 n, 2 n+1$ is special. Unfortunately, it seems hard to show that the set of such $n$ has positive density: see a recent paper https://arxiv.org/abs/1509.01545 for the proof that all eight patterns of the parities of $p(n), p(n+1), p(n+2)$ appear for a positive proportion of positive integers. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $Q$ be a set of prime numbers, not necessarily finite. For a positive integer $n$ consider its prime factorisation; define $p(n)$ to be the sum of all the exponents and $q(n)$ to be the sum of the exponents corresponding only to primes in $Q$. A positive integer $n$ is called special if $p(n)+p(n+1)$ and $q(n)+q(n+1)$ are both even integers. Prove that there is a constant $c>0$ independent of the set $Q$ such that for any positive integer $N>100$, the number of special integers in $[1, N]$ is at least $c N$. (For example, if $Q=\{3,7\}$, then $p(42)=3, q(42)=2, p(63)=3, q(63)=3, p(2022)=3$, $q(2022)=1$.) (Costa Rica)
|
Let us call two positive integers $m, n$ friends if $p(m)+p(n)$ and $q(m)+q(n)$ are both even integers. We start by noting that the pairs $(p(k), q(k))$ modulo 2 can take at most 4 different values; thus, among any five different positive integers there are two which are friends. In addition, both functions $p$ and $q$ satisfy $f(a b)=f(a)+f(b)$ for any $a, b$. Therefore, if $m$ and $n$ are divisible by $d$, then both $p$ and $q$ satisfy the equality $f(m)+f(n)=f(m / d)+$ $f(n / d)+2 f(d)$. This implies that $m, n$ are friends if and only if $m / d, n / d$ are friends. Let us call a set of integers $\left\{n_{1}, n_{2}, \ldots, n_{5}\right\}$ an interesting set if for any indexes $i, j$, the difference $d_{i j}=\left|n_{i}-n_{j}\right|$ divides both $n_{i}$ and $n_{j}$. We claim that if elements of an interesting set are all positive, then we can obtain a special integer. Indeed, if we were able to construct such a set, then there would be a pair of integers $\left\{n_{i}, n_{j}\right\}$ which are friends, according to the first observation. Additionally, the second observation yields that the quotients $n_{i} / d_{i j}, n_{j} / d_{i j}$ form a pair of friends, which happen to be consecutive integers, thus giving a special integer as desired. In order to construct a family of interesting sets, we can start by observing that the set $\{0,6,8,9,12\}$ is an interesting set. Using that $72=2^{3} \cdot 3^{2}$ is the least common multiple of all pairwise differences in this set, we obtain a family of interesting sets by considering $$ \{72 k, 72 k+6,72 k+8,72 k+9,72 k+12\} $$ for any $k \geqslant 1$. If we consider the quotients (of these numbers by the appropriate differences), then we obtain that the set $$ S_{k}=\{6 k, 8 k, 9 k, 12 k, 12 k+1,18 k+2,24 k+2,24 k+3,36 k+3,72 k+8\}, $$ has at least one special integer. In particular, the interval $[1,100 k]$ contains the sets $S_{1}, S_{2}, \ldots, S_{k}$, each of which has a special number. Any special number can be contained in at most ten sets $S_{k}$, from where we conclude that the number of special integers in $[1,100 k]$ is at least $k / 10$. Finally, let $N=100 k+r$, with $k \geqslant 1$ and $0 \leqslant r<100$, so that we have $N<100(k+1) \leqslant$ $200 k$. Then the number of special integers in $[1, N]$ is at least $k / 10>N / 2000$, as we wanted to prove. Comment 1. The statement is also true for $N \geqslant 15$ as at least one of the numbers $7,14,15$ is special. Comment 2. Another approach would be to note that if $p(2 n), p(2 n+1), p(2 n+2)$ all have the same parity then one of the numbers $n, 2 n, 2 n+1$ is special. Indeed, if $q(n)+q(n+1)$ is even then $n$ is special since $p(n)+p(n+1) \equiv p(2 n)+p(2 n+2) \equiv 0(\bmod 2)$. Otherwise, if $q(n)+q(n+1)$ is odd, so is $q(2 n)+q(2 n+2)$ which implies that exactly one of the numbers $2 n, 2 n+1$ is special. Unfortunately, it seems hard to show that the set of such $n$ has positive density: see a recent paper https://arxiv.org/abs/1509.01545 for the proof that all eight patterns of the parities of $p(n), p(n+1), p(n+2)$ appear for a positive proportion of positive integers. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
de017812-3bfb-5b77-9db3-9487dada8b54
| 24,460
|
Let $k$ be a positive integer and let $S$ be a finite set of odd prime numbers. Prove that there is at most one way (modulo rotation and reflection) to place the elements of $S$ around a circle such that the product of any two neighbors is of the form $x^{2}+x+k$ for some positive integer $x$.
|
Let us allow the value $x=0$ as well; we prove the same statement under this more general constraint. Obviously that implies the statement with the original conditions. Call a pair $\{p, q\}$ of primes with $p \neq q$ special if $p q=x^{2}+x+k$ for some nonnegative integer $x$. The following claim is the key mechanism of the problem: Claim. (a) For every prime $r$, there are at most two primes less than $r$ forming a special pair with $r$. (b) If such $p$ and $q$ exist, then $\{p, q\}$ is itself special. We present two proofs of the claim. Proof 1. We are interested in integers $1 \leqslant x<r$ satsfying $$ x^{2}+x+k \equiv 0 \quad(\bmod r) $$ Since there are at most two residues modulo $r$ that can satisfy that quadratic congruence, there are at most two possible values of $x$. That proves (a). Now suppose there are primes $p, q$ with $p<q<r$ and nonnegative integers $x, y$ such that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ From $p<q<r$ we can see that $0 \leqslant x<y \leqslant r-1$. The numbers $x, y$ are the two solutions of (1); by Vieta's formulas, we should have $x+y \equiv-1(\bmod r)$, so $x+y=r-1$. Letting $K=4 k-1, X=2 x+1$, and $Y=2 y+1$, we obtain $$ \begin{gathered} 4 p r=X^{2}+K \\ 4 q r=Y^{2}+K \end{gathered} $$ with $X+Y=2 r$. Multiplying the two above equations, $$ \begin{aligned} 16 p q r^{2} & =\left(X^{2}+K\right)\left(Y^{2}+K\right) \\ & =(X Y-K)^{2}+K(X+Y)^{2} \\ & =(X Y-K)^{2}+4 K r^{2}, \\ 4 p q & =\left(\frac{X Y-K}{2 r}\right)^{2}+K . \end{aligned} $$ In particular, the number $Z=\frac{X Y-K}{2 r}$ should be an integer, and so $4 p q=Z^{2}+K$. By parity, $Z$ is odd, and thus $$ p q=z^{2}+z+k \quad \text { where } z=\frac{Z-1}{2} $$ so $\{p, q\}$ is special. Proof 2. As before, we suppose that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ Subtracting, we have $$ (x+y+1)(x-y)=r(p-q) . $$ As before, we have $x+y=r-1$, so $x-y=p-q$, and $$ \begin{aligned} & x=\frac{1}{2}(r+p-q-1) \\ & y=\frac{1}{2}(r+q-p-1) \end{aligned} $$ Then, $$ \begin{aligned} k=p r-x^{2}-x & =\frac{1}{4}\left(4 p r-(r+p-q-1)^{2}-2(r+p-q-1)\right) \\ & =\frac{1}{4}\left(4 p r-(r+p-q)^{2}+1\right) \\ & =\frac{1}{4}\left(2 p q+2 p r+2 q r-p^{2}-q^{2}-r^{2}+1\right), \end{aligned} $$ which is symmetric in $p, q, r$, so $$ p q=z^{2}+z+k \quad \text { where } z=\frac{1}{2}(p+q-r-1) $$ and $\{p, q\}$ is special. Now we settle the problem by induction on $|S|$, with $|S| \leqslant 3$ clear. Suppose we have proven it for $|S|=n$ and consider $|S|=n+1$. Let $r$ be the largest prime in $S$; the claim tells us that in any valid cycle of primes: - the neighbors of $r$ are uniquely determined, and - removing $r$ from the cycle results in a smaller valid cycle. It follows that there is at most one valid cycle, completing the inductive step. Comment. The statement is not as inapplicable as it might seem. For example, for $k=41$, the following 385 primes form a valid cycle of primes: 53, 4357, 104173, 65921, 36383, 99527, 193789, 2089123, 1010357, 2465263, 319169, 15559, 3449, 2647, 1951, 152297, 542189, 119773, 91151, 66431, 222137, 1336799, 469069, 45613, 1047941, 656291, 355867, 146669, 874879, 2213327, 305119, 3336209, 1623467, 520963, 794201, 1124833, 28697, 15683, 42557, 6571, 39607, 1238833, 835421, 2653681, 5494387, 9357539, 511223, 1515317, 8868173, 114079681, 59334071, 22324807, 3051889, 5120939, 7722467, 266239, 693809, 3931783, 1322317, 100469, 13913, 74419, 23977, 1361, 62983, 935021, 512657, 1394849, 216259, 45827, 31393, 100787, 1193989, 600979, 209543, 357661, 545141, 19681, 10691, 28867, 165089, 2118023, 6271891, 12626693, 21182429, 1100467, 413089, 772867, 1244423, 1827757, 55889, 1558873, 5110711, 1024427, 601759, 290869, 91757, 951109 , 452033, 136471, 190031, 4423, 9239, 15809, 24133, 115811, 275911, 34211, 877, 6653, 88001, 46261, 317741, $121523,232439,379009,17827,2699,15937,497729,335539,205223,106781,1394413,4140947,8346383,43984757$, 14010721, 21133961, 729451, 4997297, 1908223, 278051, 529747, 40213, 768107, 456821, 1325351, 225961, 1501921, 562763, 75527, 5519, 9337, 14153, 499, 1399, 2753, 14401, 94583, 245107, 35171, 397093, 195907, 2505623, 34680911, 18542791, 7415917, 144797293, 455529251, 86675291, 252704911, 43385123, 109207907, 204884269, 330414209, 14926789, 1300289, 486769, 2723989, 907757, 1458871, 65063, 4561, 124427, 81343, 252887, 2980139, 1496779, 3779057, 519193, 47381, 135283, 268267, 446333, 669481, 22541, 54167, 99439, 158357, 6823, 32497, 1390709, 998029, 670343, 5180017, 13936673, 2123491, 4391941, 407651, 209953, 77249, 867653, 427117, 141079, 9539, 227, 1439 , 18679, 9749, 25453, 3697, 42139, 122327, 712303, 244261, 20873, 52051, 589997, 4310569, 1711069, 291563, 3731527 , 11045429, 129098443, 64620427, 162661963, 22233269, 37295047, 1936969, 5033449, 725537, 1353973, 6964457, 2176871, 97231, 7001, 11351, 55673, 16747, 169003, 1218571, 479957, 2779783, 949609, 4975787, 1577959, 2365007, 3310753, 79349, 23189, 107209, 688907, 252583, 30677, 523, 941, 25981, 205103, 85087, 1011233, 509659, 178259, 950479, 6262847, 2333693, 305497, 3199319, 9148267, 1527563, 466801, 17033, 9967, 323003, 4724099, 14278309, 2576557, 1075021, 6462593, 2266021, 63922471, 209814503, 42117791, 131659867, 270892249, 24845153, 12104557, 3896003, 219491, 135913, 406397, 72269, 191689, 2197697, 1091273, 2727311, 368227, 1911661, 601883, 892657, 28559, 4783, 60497, 31259, 80909, 457697, 153733, 11587, 1481, 26161, 15193, 7187, 2143, 21517, 10079, 207643, 1604381, 657661, 126227, 372313, 2176331, 748337, 64969, 844867, 2507291, 29317943, 14677801, 36952793, 69332267, 111816223, 5052241, 8479717, 441263, 3020431, 1152751, 13179611, 38280013, 6536771, 16319657, 91442699 , 30501409, 49082027, 72061511, 2199433, 167597, 317963, 23869, 2927, 3833, 17327, 110879, 285517, 40543, 4861, 21683, 50527, 565319, 277829, 687917, 3846023, 25542677, 174261149, 66370753, 9565711, 1280791, 91393, 6011, 7283, 31859, 8677, 10193, 43987, 11831, 13591, 127843, 358229, 58067, 15473, 65839, 17477, 74099, 19603, 82847, 21851, 61.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k$ be a positive integer and let $S$ be a finite set of odd prime numbers. Prove that there is at most one way (modulo rotation and reflection) to place the elements of $S$ around a circle such that the product of any two neighbors is of the form $x^{2}+x+k$ for some positive integer $x$.
|
Let us allow the value $x=0$ as well; we prove the same statement under this more general constraint. Obviously that implies the statement with the original conditions. Call a pair $\{p, q\}$ of primes with $p \neq q$ special if $p q=x^{2}+x+k$ for some nonnegative integer $x$. The following claim is the key mechanism of the problem: Claim. (a) For every prime $r$, there are at most two primes less than $r$ forming a special pair with $r$. (b) If such $p$ and $q$ exist, then $\{p, q\}$ is itself special. We present two proofs of the claim. Proof 1. We are interested in integers $1 \leqslant x<r$ satsfying $$ x^{2}+x+k \equiv 0 \quad(\bmod r) $$ Since there are at most two residues modulo $r$ that can satisfy that quadratic congruence, there are at most two possible values of $x$. That proves (a). Now suppose there are primes $p, q$ with $p<q<r$ and nonnegative integers $x, y$ such that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ From $p<q<r$ we can see that $0 \leqslant x<y \leqslant r-1$. The numbers $x, y$ are the two solutions of (1); by Vieta's formulas, we should have $x+y \equiv-1(\bmod r)$, so $x+y=r-1$. Letting $K=4 k-1, X=2 x+1$, and $Y=2 y+1$, we obtain $$ \begin{gathered} 4 p r=X^{2}+K \\ 4 q r=Y^{2}+K \end{gathered} $$ with $X+Y=2 r$. Multiplying the two above equations, $$ \begin{aligned} 16 p q r^{2} & =\left(X^{2}+K\right)\left(Y^{2}+K\right) \\ & =(X Y-K)^{2}+K(X+Y)^{2} \\ & =(X Y-K)^{2}+4 K r^{2}, \\ 4 p q & =\left(\frac{X Y-K}{2 r}\right)^{2}+K . \end{aligned} $$ In particular, the number $Z=\frac{X Y-K}{2 r}$ should be an integer, and so $4 p q=Z^{2}+K$. By parity, $Z$ is odd, and thus $$ p q=z^{2}+z+k \quad \text { where } z=\frac{Z-1}{2} $$ so $\{p, q\}$ is special. Proof 2. As before, we suppose that $$ \begin{aligned} & x^{2}+x+k=p r \\ & y^{2}+y+k=q r . \end{aligned} $$ Subtracting, we have $$ (x+y+1)(x-y)=r(p-q) . $$ As before, we have $x+y=r-1$, so $x-y=p-q$, and $$ \begin{aligned} & x=\frac{1}{2}(r+p-q-1) \\ & y=\frac{1}{2}(r+q-p-1) \end{aligned} $$ Then, $$ \begin{aligned} k=p r-x^{2}-x & =\frac{1}{4}\left(4 p r-(r+p-q-1)^{2}-2(r+p-q-1)\right) \\ & =\frac{1}{4}\left(4 p r-(r+p-q)^{2}+1\right) \\ & =\frac{1}{4}\left(2 p q+2 p r+2 q r-p^{2}-q^{2}-r^{2}+1\right), \end{aligned} $$ which is symmetric in $p, q, r$, so $$ p q=z^{2}+z+k \quad \text { where } z=\frac{1}{2}(p+q-r-1) $$ and $\{p, q\}$ is special. Now we settle the problem by induction on $|S|$, with $|S| \leqslant 3$ clear. Suppose we have proven it for $|S|=n$ and consider $|S|=n+1$. Let $r$ be the largest prime in $S$; the claim tells us that in any valid cycle of primes: - the neighbors of $r$ are uniquely determined, and - removing $r$ from the cycle results in a smaller valid cycle. It follows that there is at most one valid cycle, completing the inductive step. Comment. The statement is not as inapplicable as it might seem. For example, for $k=41$, the following 385 primes form a valid cycle of primes: 53, 4357, 104173, 65921, 36383, 99527, 193789, 2089123, 1010357, 2465263, 319169, 15559, 3449, 2647, 1951, 152297, 542189, 119773, 91151, 66431, 222137, 1336799, 469069, 45613, 1047941, 656291, 355867, 146669, 874879, 2213327, 305119, 3336209, 1623467, 520963, 794201, 1124833, 28697, 15683, 42557, 6571, 39607, 1238833, 835421, 2653681, 5494387, 9357539, 511223, 1515317, 8868173, 114079681, 59334071, 22324807, 3051889, 5120939, 7722467, 266239, 693809, 3931783, 1322317, 100469, 13913, 74419, 23977, 1361, 62983, 935021, 512657, 1394849, 216259, 45827, 31393, 100787, 1193989, 600979, 209543, 357661, 545141, 19681, 10691, 28867, 165089, 2118023, 6271891, 12626693, 21182429, 1100467, 413089, 772867, 1244423, 1827757, 55889, 1558873, 5110711, 1024427, 601759, 290869, 91757, 951109 , 452033, 136471, 190031, 4423, 9239, 15809, 24133, 115811, 275911, 34211, 877, 6653, 88001, 46261, 317741, $121523,232439,379009,17827,2699,15937,497729,335539,205223,106781,1394413,4140947,8346383,43984757$, 14010721, 21133961, 729451, 4997297, 1908223, 278051, 529747, 40213, 768107, 456821, 1325351, 225961, 1501921, 562763, 75527, 5519, 9337, 14153, 499, 1399, 2753, 14401, 94583, 245107, 35171, 397093, 195907, 2505623, 34680911, 18542791, 7415917, 144797293, 455529251, 86675291, 252704911, 43385123, 109207907, 204884269, 330414209, 14926789, 1300289, 486769, 2723989, 907757, 1458871, 65063, 4561, 124427, 81343, 252887, 2980139, 1496779, 3779057, 519193, 47381, 135283, 268267, 446333, 669481, 22541, 54167, 99439, 158357, 6823, 32497, 1390709, 998029, 670343, 5180017, 13936673, 2123491, 4391941, 407651, 209953, 77249, 867653, 427117, 141079, 9539, 227, 1439 , 18679, 9749, 25453, 3697, 42139, 122327, 712303, 244261, 20873, 52051, 589997, 4310569, 1711069, 291563, 3731527 , 11045429, 129098443, 64620427, 162661963, 22233269, 37295047, 1936969, 5033449, 725537, 1353973, 6964457, 2176871, 97231, 7001, 11351, 55673, 16747, 169003, 1218571, 479957, 2779783, 949609, 4975787, 1577959, 2365007, 3310753, 79349, 23189, 107209, 688907, 252583, 30677, 523, 941, 25981, 205103, 85087, 1011233, 509659, 178259, 950479, 6262847, 2333693, 305497, 3199319, 9148267, 1527563, 466801, 17033, 9967, 323003, 4724099, 14278309, 2576557, 1075021, 6462593, 2266021, 63922471, 209814503, 42117791, 131659867, 270892249, 24845153, 12104557, 3896003, 219491, 135913, 406397, 72269, 191689, 2197697, 1091273, 2727311, 368227, 1911661, 601883, 892657, 28559, 4783, 60497, 31259, 80909, 457697, 153733, 11587, 1481, 26161, 15193, 7187, 2143, 21517, 10079, 207643, 1604381, 657661, 126227, 372313, 2176331, 748337, 64969, 844867, 2507291, 29317943, 14677801, 36952793, 69332267, 111816223, 5052241, 8479717, 441263, 3020431, 1152751, 13179611, 38280013, 6536771, 16319657, 91442699 , 30501409, 49082027, 72061511, 2199433, 167597, 317963, 23869, 2927, 3833, 17327, 110879, 285517, 40543, 4861, 21683, 50527, 565319, 277829, 687917, 3846023, 25542677, 174261149, 66370753, 9565711, 1280791, 91393, 6011, 7283, 31859, 8677, 10193, 43987, 11831, 13591, 127843, 358229, 58067, 15473, 65839, 17477, 74099, 19603, 82847, 21851, 61.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
70b3e5d8-ef5c-5dc4-80a6-cf81db614254
| 24,462
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
We introduce the new variables $s:=x+y$ and $t:=x-y$. Equivalently, $x=\frac{s+t}{2}$ and $y=\frac{s-t}{2}$. The inequality becomes $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ for every $s, t \in \mathbb{R}$. We replace $t$ by $-t$ to obtain $$ f(s) f(-t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing the previous two inequalities gives $$ f(s)(f(t)+f(-t)) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This inequality is strict for $s=x_{0}+y_{0}$ and $t=x_{0}-y_{0}$ by assumption. In particular, there exists some $t_{0}=x_{0}-y_{0}$ for which $f\left(t_{0}\right)+f\left(-t_{0}\right) \neq 0$. Since $f(s)\left(f\left(t_{0}\right)+\right.$ $\left.f\left(-t_{0}\right)\right) \geqslant 0$ for every $s \in \mathbb{R}$, we conclude that $f(s)$ must have constant sign.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
We introduce the new variables $s:=x+y$ and $t:=x-y$. Equivalently, $x=\frac{s+t}{2}$ and $y=\frac{s-t}{2}$. The inequality becomes $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ for every $s, t \in \mathbb{R}$. We replace $t$ by $-t$ to obtain $$ f(s) f(-t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing the previous two inequalities gives $$ f(s)(f(t)+f(-t)) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This inequality is strict for $s=x_{0}+y_{0}$ and $t=x_{0}-y_{0}$ by assumption. In particular, there exists some $t_{0}=x_{0}-y_{0}$ for which $f\left(t_{0}\right)+f\left(-t_{0}\right) \neq 0$. Since $f(s)\left(f\left(t_{0}\right)+\right.$ $\left.f\left(-t_{0}\right)\right) \geqslant 0$ for every $s \in \mathbb{R}$, we conclude that $f(s)$ must have constant sign.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
74d52011-fa21-5382-a6cc-cc45ca9abad8
| 607,735
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
We do the same change of variables as in $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ In this solution, we replace $s$ by $-s($ instead of $t$ by $-t)$. This gives $$ f(-s) f(t) \geqslant f\left(\frac{-s+t}{2}\right)^{2}-f\left(\frac{-s-t}{2}\right)^{2} $$ We now go back to the original inequality. Substituting $x=y$ gives $f(2 x) f(0) \geqslant 0$ for every $x \in \mathbb{R}$. If $f(0) \neq 0$, then we conclude that $f$ indeed has constant sign. From now on, we will assume that $$ f(0)=0 . $$ Substituting $x=-y$ gives $f(-x)^{2} \geqslant f(x)^{2}$. By permuting $x$ and $-x$, we conclude that $$ f(-x)^{2}=f(x)^{2} $$ for every $x \in \mathbb{R}$. Using the relation $f(x)^{2}=f(-x)^{2}$, we can rewrite (2) as $$ f(-s) f(t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing this inequality with (1), we obtain $$ (f(s)+f(-s)) f(t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$ and we can conclude as in Solution 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
We do the same change of variables as in $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ In this solution, we replace $s$ by $-s($ instead of $t$ by $-t)$. This gives $$ f(-s) f(t) \geqslant f\left(\frac{-s+t}{2}\right)^{2}-f\left(\frac{-s-t}{2}\right)^{2} $$ We now go back to the original inequality. Substituting $x=y$ gives $f(2 x) f(0) \geqslant 0$ for every $x \in \mathbb{R}$. If $f(0) \neq 0$, then we conclude that $f$ indeed has constant sign. From now on, we will assume that $$ f(0)=0 . $$ Substituting $x=-y$ gives $f(-x)^{2} \geqslant f(x)^{2}$. By permuting $x$ and $-x$, we conclude that $$ f(-x)^{2}=f(x)^{2} $$ for every $x \in \mathbb{R}$. Using the relation $f(x)^{2}=f(-x)^{2}$, we can rewrite (2) as $$ f(-s) f(t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing this inequality with (1), we obtain $$ (f(s)+f(-s)) f(t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$ and we can conclude as in Solution 1 .
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
74d52011-fa21-5382-a6cc-cc45ca9abad8
| 607,735
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
We prove the contrapositive of the problem statement. Assume that there exist $a, b \in \mathbb{R}$ such that $f(a)<0$ and $f(b)>0$. We want to prove that the inequality is actually an equality, i.e. it is never strict. Lemma 1. The function $f$ is odd, i.e. $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$. Proof. We plug in $x=\frac{a+u}{2}$ and $y=\frac{a-u}{2}$ in the original inequality, where $u$ is a free variable. We obtain $$ f(a) f(u) \geqslant f\left(\frac{a+u}{2}\right)^{2}-f\left(\frac{a-u}{2}\right)^{2} . $$ Replacing $u$ with $-u$ and summing the two inequalities as in the previous solutions, we get $$ f(a)(f(u)+f(-u)) \geqslant 0 $$ for every $u \in \mathbb{R}$. Since $f(a)<0$ by assumption, we conclude that $f(u)+f(-u) \leqslant 0$ for every $u \in \mathbb{R}$. We can repeat the above argument with $b$ instead of $a$. Since $f(b)>0$ by assumption, we conclude that $f(u)+f(-u) \geqslant 0$ for every $u \in \mathbb{R}$. This implies that $f(u)+f(-u)=0$ for every $u \in \mathbb{R}$. Now, using that $f$ is odd, we can write the following chain of inequalities $$ \begin{aligned} f(x)^{2}-f(y)^{2} & \leqslant f(x+y) f(x-y) \\ & =-f(y+x) f(y-x) \\ & \leqslant-\left(f(y)^{2}-f(x)^{2}\right) \\ & =f(x)^{2}-f(y)^{2} . \end{aligned} $$ We conclude that every inequality above is actually an inequality, so $$ f(x+y) f(x-y)=f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
We prove the contrapositive of the problem statement. Assume that there exist $a, b \in \mathbb{R}$ such that $f(a)<0$ and $f(b)>0$. We want to prove that the inequality is actually an equality, i.e. it is never strict. Lemma 1. The function $f$ is odd, i.e. $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$. Proof. We plug in $x=\frac{a+u}{2}$ and $y=\frac{a-u}{2}$ in the original inequality, where $u$ is a free variable. We obtain $$ f(a) f(u) \geqslant f\left(\frac{a+u}{2}\right)^{2}-f\left(\frac{a-u}{2}\right)^{2} . $$ Replacing $u$ with $-u$ and summing the two inequalities as in the previous solutions, we get $$ f(a)(f(u)+f(-u)) \geqslant 0 $$ for every $u \in \mathbb{R}$. Since $f(a)<0$ by assumption, we conclude that $f(u)+f(-u) \leqslant 0$ for every $u \in \mathbb{R}$. We can repeat the above argument with $b$ instead of $a$. Since $f(b)>0$ by assumption, we conclude that $f(u)+f(-u) \geqslant 0$ for every $u \in \mathbb{R}$. This implies that $f(u)+f(-u)=0$ for every $u \in \mathbb{R}$. Now, using that $f$ is odd, we can write the following chain of inequalities $$ \begin{aligned} f(x)^{2}-f(y)^{2} & \leqslant f(x+y) f(x-y) \\ & =-f(y+x) f(y-x) \\ & \leqslant-\left(f(y)^{2}-f(x)^{2}\right) \\ & =f(x)^{2}-f(y)^{2} . \end{aligned} $$ We conclude that every inequality above is actually an inequality, so $$ f(x+y) f(x-y)=f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
74d52011-fa21-5382-a6cc-cc45ca9abad8
| 607,735
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
As in In this solution, we construct an argument by multiplying inequalities, rather than adding them as in Solutions 1-3. Lemma 2. $f(b) f(-b)<0$. Proof. Let $x_{1}:=\frac{a+b}{2}$ and $y_{1}:=\frac{a-b}{2}$ so that $a=x_{1}+y_{1}$ and $b=x_{1}-y_{1}$. Plugging in $x=x_{1}$ and $y=y_{1}$, we obtain $$ 0>f(a) f(b)=f\left(x_{1}+y_{1}\right) f\left(x_{1}-y_{1}\right) \geqslant f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2} $$ which implies $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$. Similarly, by plugging in $x=y_{1}$ and $y=x_{1}$, we get $$ f(a) f(-b)=f\left(y_{1}+x_{1}\right) f\left(y_{1}-x_{1}\right) \geqslant f\left(y_{1}\right)^{2}-f\left(x_{1}\right)^{2} . $$ Using $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$, we conclude $f(a) f(-b)>0$. If we multiply the two inequalities $f(a) f(b)<0$ and $f(a) f(-b)>0$, we get $f(a)^{2} f(b) f(-b)<0$ and hence $$ f(b) f(-b)<0 $$ Lemma 3. $f(x) f(-x) \leqslant 0$ for every $x \in \mathbb{R}$. Proof. As in Solution 2, we prove that $f(x)^{2}=f(-x)^{2}$ for every $x \in \mathbb{R}$ and we rewrite the original inequality as $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ We replace $s$ by $-s$ and $t$ by $-t$, and use the relation $f(x)^{2}=f(-x)^{2}$, to get $$ \begin{aligned} f(-s) f(-t) & \geqslant f\left(\frac{-s-t}{2}\right)^{2}-f\left(\frac{-s+t}{2}\right)^{2} \\ & =f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \end{aligned} $$ Up to replacing $t$ by $-t$, we can assume that $f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \geqslant 0$. Multiplying the two previous inequalities leads to $$ f(s) f(-s) f(t) f(-t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This shows that $f(s) f(-s)$ (as a function of $s$ ) has constant sign. Since $f(b) f(-b)<0$, we conclude that $$ f(x) f(-x) \leqslant 0 $$ for every $x \in \mathbb{R}$. Lemma 3, combined with the relation $f(x)^{2}=f(-x)^{2}$, implies $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$, i.e. $f$ is odd. We conclude with the same argument as in Solution 3. Comment. The presence of squares on the right-hand side of the inequality is not crucial as Solution 1 illustrates very well. However, it allows non-constant functions such as $f(x)=|x|$ to satisfy the conditions of the problem statement.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia)
|
As in In this solution, we construct an argument by multiplying inequalities, rather than adding them as in Solutions 1-3. Lemma 2. $f(b) f(-b)<0$. Proof. Let $x_{1}:=\frac{a+b}{2}$ and $y_{1}:=\frac{a-b}{2}$ so that $a=x_{1}+y_{1}$ and $b=x_{1}-y_{1}$. Plugging in $x=x_{1}$ and $y=y_{1}$, we obtain $$ 0>f(a) f(b)=f\left(x_{1}+y_{1}\right) f\left(x_{1}-y_{1}\right) \geqslant f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2} $$ which implies $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$. Similarly, by plugging in $x=y_{1}$ and $y=x_{1}$, we get $$ f(a) f(-b)=f\left(y_{1}+x_{1}\right) f\left(y_{1}-x_{1}\right) \geqslant f\left(y_{1}\right)^{2}-f\left(x_{1}\right)^{2} . $$ Using $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$, we conclude $f(a) f(-b)>0$. If we multiply the two inequalities $f(a) f(b)<0$ and $f(a) f(-b)>0$, we get $f(a)^{2} f(b) f(-b)<0$ and hence $$ f(b) f(-b)<0 $$ Lemma 3. $f(x) f(-x) \leqslant 0$ for every $x \in \mathbb{R}$. Proof. As in Solution 2, we prove that $f(x)^{2}=f(-x)^{2}$ for every $x \in \mathbb{R}$ and we rewrite the original inequality as $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ We replace $s$ by $-s$ and $t$ by $-t$, and use the relation $f(x)^{2}=f(-x)^{2}$, to get $$ \begin{aligned} f(-s) f(-t) & \geqslant f\left(\frac{-s-t}{2}\right)^{2}-f\left(\frac{-s+t}{2}\right)^{2} \\ & =f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \end{aligned} $$ Up to replacing $t$ by $-t$, we can assume that $f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \geqslant 0$. Multiplying the two previous inequalities leads to $$ f(s) f(-s) f(t) f(-t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This shows that $f(s) f(-s)$ (as a function of $s$ ) has constant sign. Since $f(b) f(-b)<0$, we conclude that $$ f(x) f(-x) \leqslant 0 $$ for every $x \in \mathbb{R}$. Lemma 3, combined with the relation $f(x)^{2}=f(-x)^{2}$, implies $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$, i.e. $f$ is odd. We conclude with the same argument as in Solution 3. Comment. The presence of squares on the right-hand side of the inequality is not crucial as Solution 1 illustrates very well. However, it allows non-constant functions such as $f(x)=|x|$ to satisfy the conditions of the problem statement.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
74d52011-fa21-5382-a6cc-cc45ca9abad8
| 607,735
|
Let $\mathbb{R}_{>0}$ be the set of positive real numbers. Determine all functions $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ such that $$ x(f(x)+f(y)) \geqslant(f(f(x))+y) f(y) $$ for every $x, y \in \mathbb{R}_{>0}$. (Belgium)
|
Let $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ be a function that satisfies the inequality of the problem statement. As in $$ f^{n}(y) \geqslant f^{n+2}(y) $$ for every $y \in \mathbb{R}_{>0}$ and every $n \geqslant 0$. Since $f$ takes positive values, this implies that $$ y f(y) \geqslant f(y) f^{2}(y) \geqslant f^{2}(y) f^{3}(y) \geqslant \cdots $$ In other words, $y f(y) \geqslant f^{n}(y) f^{n+1}(y)$ for every $y \in \mathbb{R}_{>0}$ and every $n \geqslant 1$. We replace $x$ by $f^{n}(x)$ in the original inequality and get $$ f^{n}(x)-f^{n+2}(x) \geqslant \frac{y f(y)-f^{n}(x) f^{n+1}(x)}{f(y)} . $$ Using that $x f(x) \geqslant f^{n}(x) f^{n+1}(x)$, we obtain $$ f^{n}(x)-f^{n+2}(x) \geqslant \frac{y f(y)-x f(x)}{f(y)} $$ for every $n \geqslant 0$. The same trick as in Solution 1 gives $$ x>x-f^{2 m}(x)=\sum_{i=0}^{m-1}\left(f^{2 i}(x)-f^{2 i+2}(x)\right) \geqslant m \cdot \frac{y f(y)-x f(x)}{f(y)} $$ for every $x, y \in \mathbb{R}_{>0}$ and every $m \geqslant 1$. Possibly permuting $x$ and $y$, we may assume that $y f(y)-x f(x) \geqslant 0$ then the above inequality implies $x f(x)=y f(y)$. We conclude as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathbb{R}_{>0}$ be the set of positive real numbers. Determine all functions $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ such that $$ x(f(x)+f(y)) \geqslant(f(f(x))+y) f(y) $$ for every $x, y \in \mathbb{R}_{>0}$. (Belgium)
|
Let $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ be a function that satisfies the inequality of the problem statement. As in $$ f^{n}(y) \geqslant f^{n+2}(y) $$ for every $y \in \mathbb{R}_{>0}$ and every $n \geqslant 0$. Since $f$ takes positive values, this implies that $$ y f(y) \geqslant f(y) f^{2}(y) \geqslant f^{2}(y) f^{3}(y) \geqslant \cdots $$ In other words, $y f(y) \geqslant f^{n}(y) f^{n+1}(y)$ for every $y \in \mathbb{R}_{>0}$ and every $n \geqslant 1$. We replace $x$ by $f^{n}(x)$ in the original inequality and get $$ f^{n}(x)-f^{n+2}(x) \geqslant \frac{y f(y)-f^{n}(x) f^{n+1}(x)}{f(y)} . $$ Using that $x f(x) \geqslant f^{n}(x) f^{n+1}(x)$, we obtain $$ f^{n}(x)-f^{n+2}(x) \geqslant \frac{y f(y)-x f(x)}{f(y)} $$ for every $n \geqslant 0$. The same trick as in Solution 1 gives $$ x>x-f^{2 m}(x)=\sum_{i=0}^{m-1}\left(f^{2 i}(x)-f^{2 i+2}(x)\right) \geqslant m \cdot \frac{y f(y)-x f(x)}{f(y)} $$ for every $x, y \in \mathbb{R}_{>0}$ and every $m \geqslant 1$. Possibly permuting $x$ and $y$, we may assume that $y f(y)-x f(x) \geqslant 0$ then the above inequality implies $x f(x)=y f(y)$. We conclude as in Solution 1.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4a5a70b-1c46-5e5a-8e22-961b07abc7d2
| 607,737
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$.
|
The idea is to approximate the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ by the nearest integer with errors $<0.5$. This gives the following sequence $$ 1,1,2,2,2,2,3,3,3,3,3,3,4, \ldots $$ More precisely, for each $k \geqslant 1$, we round $\sqrt{k^{2}-k+1}, \ldots, \sqrt{k^{2}+k}$ to $k$, so that there are $2 k$ copies of $k$. Step 1. We first consider the easier case when $N$ has the form $$ N=m(m+1) . $$ In this case, the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ are approximated by the elements of the multiset $\left\{1_{\times 2}, 2_{\times 4}, 3_{\times 6}, \ldots, m_{\times 2 m}\right\}$. Let $T_{m}$ denote "half of" the multiset, i.e. $$ T_{m}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m}\right\} . $$ We will prove by induction that there exists three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of the elements in the multiset $T_{m}$ such that $u_{k}+v_{k}+w_{k}=2 m+1$ is constant for $k=1,2, \ldots, \frac{m(m+1)}{2}$. When $m=1$, take $1+1+1=3$. When $m=2$, take $(1,2,2)+(2,1,2)+(2,2,1)=(5,5,5)$. Suppose that we have constructed three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of $T_{m-1}$ satisfying $u_{k}+v_{k}+w_{k}=2 m-1$ for every $k=1,2, \ldots, \frac{m(m-1)}{2}$. For $T_{m}$, we note that $$ T_{m}=T_{m-1} \sqcup\left\{m_{\times m}\right\}, $$ and also $$ T_{m}=\left(T_{m-1}+1\right) \sqcup\{1,2, \ldots, m\} . $$ Here $T_{m-1}+1$ means to add 1 to all elements in $T_{m-1}$. We construct the permutations $\left(u_{k}^{\prime}\right)$, $\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1, w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m, v_{k}^{\prime}=r, w_{k}^{\prime}=m+1-r$. It is clear from (1) that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m}$, and that they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime}=2 m+1$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}$. The inductive construction can be visualised by the $3 \times \frac{m(m+1)}{2}$ matrix $$ \left[\begin{array}{cccccc} u_{1} & \ldots & u_{m(m-1) / 2} & m & \ldots & m \\ v_{1}+1 & \ldots & v_{m(m-1) / 2}+1 & 1 & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2}+1 & m & \ldots & 1 \end{array}\right] $$ in which the three rows represent the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right),\left(w_{k}^{\prime}\right)$, and the sum of the three entries of each column is $2 m+1$. Thus, when $N=m^{2}+m$, we can construct permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, N$ such that $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+1+1.5 $$ This gives $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2.5<2023 $$ where we used that $-1<2 m-2 \sqrt{m^{2}+m}<0$ for positive $m$. Step 2. We now proceed to the general case. Let $m$ be such that $$ m(m+1) \leqslant N<(m+1)(m+2) $$ Write $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$ and let $$ L:=\left\lfloor\frac{4}{9} N\right\rfloor . $$ We will make use of the following inequalities below: $$ N>m^{2}, \quad N<(m+2)^{2}, \quad t \leqslant 2 m+1, \quad L+1>4 N / 9, \quad L \leqslant 4 N / 9 . $$ As above, we construct three permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, m(m+1)$ satisfying (2). Now we construct the three required permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$ as follows: For $k=1,2, \ldots, m(m+1)$, if $a_{k} \leqslant L$, take $A_{k}=a_{k}$, and if $a_{k}>L$, take $A_{k}=a_{k}+t$. For $k=m(m+1)+r$ with $r=1,2, \ldots, t$, set $A_{k}=L+r$. Define the permutations $\left(B_{k}\right)$ and $\left(C_{k}\right)$ similarly. Now for $k=1,2, \ldots, m(m+1)$, we show $0 \leqslant \sqrt{A_{k}}-\sqrt{a_{k}} \leqslant 2$. The lower bound is obvious. If $m \leqslant 1$, then $N \leqslant 5$ and hence $\sqrt{A_{k}}-\sqrt{a_{k}} \leqslant \sqrt{5}-\sqrt{1} \leqslant 2$. If $m \geqslant 2$, then $$ \sqrt{A_{k}}-\sqrt{a_{k}}=\frac{A_{k}-a_{k}}{\sqrt{A_{k}}+\sqrt{a_{k}}} \leqslant \frac{t}{2 \sqrt{L+1}} \leqslant \frac{2 m+1}{\frac{4}{3} m} \leqslant 2 . $$ We have similar inequalities for $\left(B_{k}\right)$ and $\left(C_{k}\right)$. Thus $$ 2 \sqrt{N}-4.5<2 m+1-1.5 \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 2 m+1+1.5+6<2 \sqrt{N}+8.5 . $$ For $k=m^{2}+m+1, \ldots, m^{2}+m+t$, we have $$ 2 \sqrt{N}<3 \sqrt{L+1} \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 3 \sqrt{L+t} \leqslant \sqrt{4 N+9 t}<2 \sqrt{N}+8.5 $$ To sum up, we have defined three permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$, such that $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<8.5<2023 $$ holds for every $k=1,2, \ldots, N$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$.
|
The idea is to approximate the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ by the nearest integer with errors $<0.5$. This gives the following sequence $$ 1,1,2,2,2,2,3,3,3,3,3,3,4, \ldots $$ More precisely, for each $k \geqslant 1$, we round $\sqrt{k^{2}-k+1}, \ldots, \sqrt{k^{2}+k}$ to $k$, so that there are $2 k$ copies of $k$. Step 1. We first consider the easier case when $N$ has the form $$ N=m(m+1) . $$ In this case, the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ are approximated by the elements of the multiset $\left\{1_{\times 2}, 2_{\times 4}, 3_{\times 6}, \ldots, m_{\times 2 m}\right\}$. Let $T_{m}$ denote "half of" the multiset, i.e. $$ T_{m}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m}\right\} . $$ We will prove by induction that there exists three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of the elements in the multiset $T_{m}$ such that $u_{k}+v_{k}+w_{k}=2 m+1$ is constant for $k=1,2, \ldots, \frac{m(m+1)}{2}$. When $m=1$, take $1+1+1=3$. When $m=2$, take $(1,2,2)+(2,1,2)+(2,2,1)=(5,5,5)$. Suppose that we have constructed three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of $T_{m-1}$ satisfying $u_{k}+v_{k}+w_{k}=2 m-1$ for every $k=1,2, \ldots, \frac{m(m-1)}{2}$. For $T_{m}$, we note that $$ T_{m}=T_{m-1} \sqcup\left\{m_{\times m}\right\}, $$ and also $$ T_{m}=\left(T_{m-1}+1\right) \sqcup\{1,2, \ldots, m\} . $$ Here $T_{m-1}+1$ means to add 1 to all elements in $T_{m-1}$. We construct the permutations $\left(u_{k}^{\prime}\right)$, $\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1, w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m, v_{k}^{\prime}=r, w_{k}^{\prime}=m+1-r$. It is clear from (1) that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m}$, and that they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime}=2 m+1$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}$. The inductive construction can be visualised by the $3 \times \frac{m(m+1)}{2}$ matrix $$ \left[\begin{array}{cccccc} u_{1} & \ldots & u_{m(m-1) / 2} & m & \ldots & m \\ v_{1}+1 & \ldots & v_{m(m-1) / 2}+1 & 1 & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2}+1 & m & \ldots & 1 \end{array}\right] $$ in which the three rows represent the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right),\left(w_{k}^{\prime}\right)$, and the sum of the three entries of each column is $2 m+1$. Thus, when $N=m^{2}+m$, we can construct permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, N$ such that $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+1+1.5 $$ This gives $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2.5<2023 $$ where we used that $-1<2 m-2 \sqrt{m^{2}+m}<0$ for positive $m$. Step 2. We now proceed to the general case. Let $m$ be such that $$ m(m+1) \leqslant N<(m+1)(m+2) $$ Write $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$ and let $$ L:=\left\lfloor\frac{4}{9} N\right\rfloor . $$ We will make use of the following inequalities below: $$ N>m^{2}, \quad N<(m+2)^{2}, \quad t \leqslant 2 m+1, \quad L+1>4 N / 9, \quad L \leqslant 4 N / 9 . $$ As above, we construct three permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, m(m+1)$ satisfying (2). Now we construct the three required permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$ as follows: For $k=1,2, \ldots, m(m+1)$, if $a_{k} \leqslant L$, take $A_{k}=a_{k}$, and if $a_{k}>L$, take $A_{k}=a_{k}+t$. For $k=m(m+1)+r$ with $r=1,2, \ldots, t$, set $A_{k}=L+r$. Define the permutations $\left(B_{k}\right)$ and $\left(C_{k}\right)$ similarly. Now for $k=1,2, \ldots, m(m+1)$, we show $0 \leqslant \sqrt{A_{k}}-\sqrt{a_{k}} \leqslant 2$. The lower bound is obvious. If $m \leqslant 1$, then $N \leqslant 5$ and hence $\sqrt{A_{k}}-\sqrt{a_{k}} \leqslant \sqrt{5}-\sqrt{1} \leqslant 2$. If $m \geqslant 2$, then $$ \sqrt{A_{k}}-\sqrt{a_{k}}=\frac{A_{k}-a_{k}}{\sqrt{A_{k}}+\sqrt{a_{k}}} \leqslant \frac{t}{2 \sqrt{L+1}} \leqslant \frac{2 m+1}{\frac{4}{3} m} \leqslant 2 . $$ We have similar inequalities for $\left(B_{k}\right)$ and $\left(C_{k}\right)$. Thus $$ 2 \sqrt{N}-4.5<2 m+1-1.5 \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 2 m+1+1.5+6<2 \sqrt{N}+8.5 . $$ For $k=m^{2}+m+1, \ldots, m^{2}+m+t$, we have $$ 2 \sqrt{N}<3 \sqrt{L+1} \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 3 \sqrt{L+t} \leqslant \sqrt{4 N+9 t}<2 \sqrt{N}+8.5 $$ To sum up, we have defined three permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$, such that $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<8.5<2023 $$ holds for every $k=1,2, \ldots, N$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
303e179f-1ec7-5421-b4a8-940a6a0c348b
| 607,740
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$.
|
This is a variation of Let $n$ be an integer satisfying $0 \leqslant n \leqslant m+1$ and define the multiset $T_{m, n}$ by $$ T_{m, n}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m},(m+1)_{\times n}\right\} . $$ In other words, $T_{m, 0}=T_{m}, T_{m, n}=T_{m} \sqcup\left\{(m+1)_{\times n}\right\}$ and $T_{m, m+1}=T_{m+1}$, where $T_{m}$ is the set defined in Solution 1. Claim. There exist three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m, n}$ such that $$ \begin{cases}u_{k}+v_{k}+w_{k}=2 m+1 & (n=0) \\ u_{k}+v_{k}+w_{k} \in\{2 m+1,2 m+2,2 m+3\} & (1 \leqslant n \leqslant m) \\ u_{k}+v_{k}+w_{k}=2 m+3 & (n=m+1)\end{cases} $$ Proof. We proceed by induction on $m$. If $n=0$ or $n=m+1$, the assertion can be proved as in Solution 1. If $1 \leqslant n \leqslant m$, we note that $$ T_{m, n}=T_{m-1, n} \sqcup\left\{m_{\times(m-n)},(m+1)_{\times n}\right\}=\left(T_{m-1, n}+1\right) \sqcup\{1,2, \ldots, m\} . $$ From the hypothesis of induction, it follows that we have three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m-1, n}$ satisfying $u_{k}+v_{k}+w_{k} \in\{2 m-1,2 m, 2 m+1\}$ for every $k$. We construct the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m, n}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}+n$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1$, and $w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+n+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m$ if $1 \leqslant r \leqslant m-n$ while $u_{k}^{\prime}=m+1$ if $m-n+1 \leqslant r \leqslant m, v_{k}^{\prime}=r$, and $w_{k}^{\prime}=m+1-r$. It is clear from the construction that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m, n}$, and they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime} \in\{2 m+1,2 m+2,2 m+3\}$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}+n$. Again, we can visualise the construction using the matrix $$ \left[\begin{array}{ccccccccc} u_{1} & \ldots & u_{m(m-1) / 2+n} & m & \ldots & m & m+1 & \ldots & m+1 \\ v_{1}+1 & \ldots & v_{m(m-1) / 2+n}+1 & 1 & \ldots & \ldots & \ldots & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2+n}+1 & m & \ldots & \ldots & \ldots & \ldots & 1 \end{array}\right] $$ In general, we have $m(m+1) \leqslant N<(m+1)(m+2)$ for some $m \geqslant 0$. Set $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$. Then the approximation of $\{\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}\}$ by the nearest integer with errors $<0.5$ is a multiset $$ \left\{1_{\times 2}, 2_{\times 4}, \ldots, m_{\times 2 m},(m+1)_{\times t}\right\}=T_{m, n_{1}} \sqcup T_{m, n_{2}} $$ with $n_{1}=\lfloor t / 2\rfloor$ and $n_{2}=\lceil t / 2\rceil$. Since $0 \leqslant n_{1} \leqslant n_{2} \leqslant m+1$, by using the Claim we can construct permutations $\left(a_{k}\right)$, $\left(b_{k}\right)$, and $\left(c_{k}\right)$ to satisfy the following inequality: $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5 $$ Since $m<\sqrt{N}<m+2$, it follows that $$ 2 \sqrt{N}-4.5<2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5<2 \sqrt{N}+4.5 $$ and so $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<4.5<2023 $$ 
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$.
|
This is a variation of Let $n$ be an integer satisfying $0 \leqslant n \leqslant m+1$ and define the multiset $T_{m, n}$ by $$ T_{m, n}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m},(m+1)_{\times n}\right\} . $$ In other words, $T_{m, 0}=T_{m}, T_{m, n}=T_{m} \sqcup\left\{(m+1)_{\times n}\right\}$ and $T_{m, m+1}=T_{m+1}$, where $T_{m}$ is the set defined in Solution 1. Claim. There exist three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m, n}$ such that $$ \begin{cases}u_{k}+v_{k}+w_{k}=2 m+1 & (n=0) \\ u_{k}+v_{k}+w_{k} \in\{2 m+1,2 m+2,2 m+3\} & (1 \leqslant n \leqslant m) \\ u_{k}+v_{k}+w_{k}=2 m+3 & (n=m+1)\end{cases} $$ Proof. We proceed by induction on $m$. If $n=0$ or $n=m+1$, the assertion can be proved as in Solution 1. If $1 \leqslant n \leqslant m$, we note that $$ T_{m, n}=T_{m-1, n} \sqcup\left\{m_{\times(m-n)},(m+1)_{\times n}\right\}=\left(T_{m-1, n}+1\right) \sqcup\{1,2, \ldots, m\} . $$ From the hypothesis of induction, it follows that we have three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m-1, n}$ satisfying $u_{k}+v_{k}+w_{k} \in\{2 m-1,2 m, 2 m+1\}$ for every $k$. We construct the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m, n}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}+n$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1$, and $w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+n+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m$ if $1 \leqslant r \leqslant m-n$ while $u_{k}^{\prime}=m+1$ if $m-n+1 \leqslant r \leqslant m, v_{k}^{\prime}=r$, and $w_{k}^{\prime}=m+1-r$. It is clear from the construction that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m, n}$, and they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime} \in\{2 m+1,2 m+2,2 m+3\}$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}+n$. Again, we can visualise the construction using the matrix $$ \left[\begin{array}{ccccccccc} u_{1} & \ldots & u_{m(m-1) / 2+n} & m & \ldots & m & m+1 & \ldots & m+1 \\ v_{1}+1 & \ldots & v_{m(m-1) / 2+n}+1 & 1 & \ldots & \ldots & \ldots & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2+n}+1 & m & \ldots & \ldots & \ldots & \ldots & 1 \end{array}\right] $$ In general, we have $m(m+1) \leqslant N<(m+1)(m+2)$ for some $m \geqslant 0$. Set $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$. Then the approximation of $\{\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}\}$ by the nearest integer with errors $<0.5$ is a multiset $$ \left\{1_{\times 2}, 2_{\times 4}, \ldots, m_{\times 2 m},(m+1)_{\times t}\right\}=T_{m, n_{1}} \sqcup T_{m, n_{2}} $$ with $n_{1}=\lfloor t / 2\rfloor$ and $n_{2}=\lceil t / 2\rceil$. Since $0 \leqslant n_{1} \leqslant n_{2} \leqslant m+1$, by using the Claim we can construct permutations $\left(a_{k}\right)$, $\left(b_{k}\right)$, and $\left(c_{k}\right)$ to satisfy the following inequality: $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5 $$ Since $m<\sqrt{N}<m+2$, it follows that $$ 2 \sqrt{N}-4.5<2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5<2 \sqrt{N}+4.5 $$ and so $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<4.5<2023 $$ 
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
303e179f-1ec7-5421-b4a8-940a6a0c348b
| 607,740
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We define a good parallelogram to be a parallelogram composed of two isosceles right-angled triangles glued together as shown below.  Given any partition into $k$ right-down or right-up paths, we can find a corresponding packing of good parallelograms that leaves an area of $k$ empty. Thus, it suffices to prove that we must leave an area of at least $N$ empty when we pack good parallelograms into an $N \times N$ grid. This is actually equivalent to the original problem since we can uniquely recover the partition into right-down or right-up paths from the corresponding packing of good parallelograms.  We draw one of the diagonals in each cell so that it does not intersect any of the good parallelograms. Now, view these segments as mirrors, and consider a laser entering each of the $4 N$ boundary edges (with starting direction being perpendicular to the edge), bouncing along these mirrors until it exits at some other edge. When a laser passes through a good parallelogram, its direction goes back to the original one after bouncing two times. Thus, if the final direction of a laser is perpendicular to its initial direction, it must pass through at least one empty triangle. Similarly, if the final direction of a laser is opposite to its initial direction, it must pass though at least two empty triangles. Using this, we will estimate the number of empty triangles in the $N \times N$ grid. We associate the starting edge of a laser with the edge it exits at. Then, the boundary edges are divided into $2 N$ pairs. These pairs can be classified into three types: (1) a pair of a vertical and a horizontal boundary edge, (2) a pair of boundary edges from the same side, and (3) a pair of boundary edges from opposite sides. Since the beams do not intersect, we cannot have one type (3) pair from vertical boundary edges and another type (3) pair from horizontal boundary edges. Without loss of generality, we may assume that we have $t$ pairs of type (3) and they are all from vertical boundary edges. Then, out of the remaining boundary edges, there are $2 N$ horizontal boundary edges and $2 N-2 t$ vertical boundary edges. It follows that there must be at least $t$ pairs of type (2) from horizontal boundary edges. We know that a laser corresponding to a pair of type (1) passes through at least one empty triangle, and a laser corresponding to a pair of type (2) passes through at least two empty triangles. Thus, as the beams do not intersect, we have at least $(2 N-2 t)+2 \cdot t=2 N$ empty triangles in the grid, leaving an area of at least $N$ empty as required.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We define a good parallelogram to be a parallelogram composed of two isosceles right-angled triangles glued together as shown below.  Given any partition into $k$ right-down or right-up paths, we can find a corresponding packing of good parallelograms that leaves an area of $k$ empty. Thus, it suffices to prove that we must leave an area of at least $N$ empty when we pack good parallelograms into an $N \times N$ grid. This is actually equivalent to the original problem since we can uniquely recover the partition into right-down or right-up paths from the corresponding packing of good parallelograms.  We draw one of the diagonals in each cell so that it does not intersect any of the good parallelograms. Now, view these segments as mirrors, and consider a laser entering each of the $4 N$ boundary edges (with starting direction being perpendicular to the edge), bouncing along these mirrors until it exits at some other edge. When a laser passes through a good parallelogram, its direction goes back to the original one after bouncing two times. Thus, if the final direction of a laser is perpendicular to its initial direction, it must pass through at least one empty triangle. Similarly, if the final direction of a laser is opposite to its initial direction, it must pass though at least two empty triangles. Using this, we will estimate the number of empty triangles in the $N \times N$ grid. We associate the starting edge of a laser with the edge it exits at. Then, the boundary edges are divided into $2 N$ pairs. These pairs can be classified into three types: (1) a pair of a vertical and a horizontal boundary edge, (2) a pair of boundary edges from the same side, and (3) a pair of boundary edges from opposite sides. Since the beams do not intersect, we cannot have one type (3) pair from vertical boundary edges and another type (3) pair from horizontal boundary edges. Without loss of generality, we may assume that we have $t$ pairs of type (3) and they are all from vertical boundary edges. Then, out of the remaining boundary edges, there are $2 N$ horizontal boundary edges and $2 N-2 t$ vertical boundary edges. It follows that there must be at least $t$ pairs of type (2) from horizontal boundary edges. We know that a laser corresponding to a pair of type (1) passes through at least one empty triangle, and a laser corresponding to a pair of type (2) passes through at least two empty triangles. Thus, as the beams do not intersect, we have at least $(2 N-2 t)+2 \cdot t=2 N$ empty triangles in the grid, leaving an area of at least $N$ empty as required.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fa24c41d-ec9b-56cc-9216-5a5d4a590b19
| 607,746
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We apply an induction on $N$. The base case $N=1$ is trivial. Suppose that the claim holds for $N-1$ and prove it for $N \geqslant 2$. Let us denote the path containing the upper left corner by $P$. If $P$ is right-up, then every cell in $P$ is in the top row or in the leftmost column. By the induction hypothesis, there are at least $N-1$ paths passing through the lower right $(N-1) \times(N-1)$ subgrid. Since $P$ is not amongst them, we have at least $N$ paths. Next, assume that $P$ is right-down. If $P$ contains the lower right corner, then we get an $(N-1) \times(N-1)$ grid by removing $P$ and glueing the remaining two parts together. The main idea is to extend $P$ so that it contains the lower right corner and the above procedure gives a valid partition of an $(N-1) \times(N-1)$ grid.  We inductively construct $Q$, which denotes an extension of $P$ as a right-down path. Initially, $Q=P$. Let $A$ be the last cell of $Q, B$ be the cell below $A$, and $C$ be the cell to the right of $A$ (if they exist). Suppose that $A$ is not the lower right corner, and that (*) both $B$ and $C$ do not belong to the same path as $A$. Then, we can extend $Q$ as follows (in case we have two or more options, we can choose any one of them to extend $Q$ ). 1. If $B$ belongs to a right-down path $R$, then we add the part of $R$, from $B$ to its end, to $Q$. 2. If $C$ belongs to a right-down path $R$, then we add the part of $R$, from $C$ to its end, to $Q$. 3. If $B$ belongs to a right-up path $R$ which ends at $B$, then we add the part of $R$ in the same column as $B$ to $Q$. 4. If $C$ belongs to a right-up path $R$ which starts at $C$, then we add the part of $R$ in the same row as $C$ to $Q$. 5. Otherwise, $B$ and $C$ must belong to the same right-up path $R$. In this case, we add $B$ and the cell to the right of $B$ to $Q$. Note that if $B$ does not exist, then case (4) must hold. If $C$ does not exist, then case (3) must hold. It is easily seen that such an extension also satisfies the hypothesis (*), so we can repeat this construction to get an extension of $P$ containing the lower right corner, denoted by $Q$. We show that this is a desired extension, i.e. the partition of an $(N-1) \times(N-1)$ grid obtained by removing $Q$ and glueing the remaining two parts together consists of right-down or right-up paths. Take a path $R$ in the partition of the $N \times N$ grid intersecting $Q$. If the intersection of $Q$ and $R$ occurs in case (1) or case (2), then there exists a cell $D$ in $R$ such that the intersection of $Q$ and $R$ is the part of $R$ from $D$ to its end, so $R$ remains a right-down path after removal of $Q$. Similarly, if the intersection of $Q$ and $R$ occurs in case (3) or case (4), then $R$ remains a right-up path after removal of $Q$. If the intersection of $Q$ and $R$ occurs in case (5), then this intersection has exactly two adjacent cells. After the removal of these two cells (as we remove $Q), R$ is divided into two parts that are glued into a right-up path. Thus, we may apply the induction hypothesis to the resulting partition of an $(N-1) \times(N-1)$ grid, to find that it must contain at least $N-1$ paths. Since $P$ is contained in $Q$ and is not amongst these paths, the original partition must contain at least $N$ paths.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We apply an induction on $N$. The base case $N=1$ is trivial. Suppose that the claim holds for $N-1$ and prove it for $N \geqslant 2$. Let us denote the path containing the upper left corner by $P$. If $P$ is right-up, then every cell in $P$ is in the top row or in the leftmost column. By the induction hypothesis, there are at least $N-1$ paths passing through the lower right $(N-1) \times(N-1)$ subgrid. Since $P$ is not amongst them, we have at least $N$ paths. Next, assume that $P$ is right-down. If $P$ contains the lower right corner, then we get an $(N-1) \times(N-1)$ grid by removing $P$ and glueing the remaining two parts together. The main idea is to extend $P$ so that it contains the lower right corner and the above procedure gives a valid partition of an $(N-1) \times(N-1)$ grid.  We inductively construct $Q$, which denotes an extension of $P$ as a right-down path. Initially, $Q=P$. Let $A$ be the last cell of $Q, B$ be the cell below $A$, and $C$ be the cell to the right of $A$ (if they exist). Suppose that $A$ is not the lower right corner, and that (*) both $B$ and $C$ do not belong to the same path as $A$. Then, we can extend $Q$ as follows (in case we have two or more options, we can choose any one of them to extend $Q$ ). 1. If $B$ belongs to a right-down path $R$, then we add the part of $R$, from $B$ to its end, to $Q$. 2. If $C$ belongs to a right-down path $R$, then we add the part of $R$, from $C$ to its end, to $Q$. 3. If $B$ belongs to a right-up path $R$ which ends at $B$, then we add the part of $R$ in the same column as $B$ to $Q$. 4. If $C$ belongs to a right-up path $R$ which starts at $C$, then we add the part of $R$ in the same row as $C$ to $Q$. 5. Otherwise, $B$ and $C$ must belong to the same right-up path $R$. In this case, we add $B$ and the cell to the right of $B$ to $Q$. Note that if $B$ does not exist, then case (4) must hold. If $C$ does not exist, then case (3) must hold. It is easily seen that such an extension also satisfies the hypothesis (*), so we can repeat this construction to get an extension of $P$ containing the lower right corner, denoted by $Q$. We show that this is a desired extension, i.e. the partition of an $(N-1) \times(N-1)$ grid obtained by removing $Q$ and glueing the remaining two parts together consists of right-down or right-up paths. Take a path $R$ in the partition of the $N \times N$ grid intersecting $Q$. If the intersection of $Q$ and $R$ occurs in case (1) or case (2), then there exists a cell $D$ in $R$ such that the intersection of $Q$ and $R$ is the part of $R$ from $D$ to its end, so $R$ remains a right-down path after removal of $Q$. Similarly, if the intersection of $Q$ and $R$ occurs in case (3) or case (4), then $R$ remains a right-up path after removal of $Q$. If the intersection of $Q$ and $R$ occurs in case (5), then this intersection has exactly two adjacent cells. After the removal of these two cells (as we remove $Q), R$ is divided into two parts that are glued into a right-up path. Thus, we may apply the induction hypothesis to the resulting partition of an $(N-1) \times(N-1)$ grid, to find that it must contain at least $N-1$ paths. Since $P$ is contained in $Q$ and is not amongst these paths, the original partition must contain at least $N$ paths.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fa24c41d-ec9b-56cc-9216-5a5d4a590b19
| 607,746
|
Let $A B C D$ be a cyclic quadrilateral with $\angle B A D<\angle A D C$. Let $M$ be the midpoint of the arc $C D$ not containing $A$. Suppose there is a point $P$ inside $A B C D$ such that $\angle A D B=$ $\angle C P D$ and $\angle A D P=\angle P C B$. Prove that lines $A D, P M, B C$ are concurrent.
|
Let $X$ and $Y$ be the intersection points of $A M$ and $B M$ with $P D$ and $P C$ respectively. Since $A B C M D$ is cyclic and $C M=M D$, we have $$ \angle X A D=\angle M A D=\angle C B M=\angle C B Y $$ Combining this with $\angle A D X=\angle Y C B$, we get $\angle D X A=\angle B Y C$, and so $\angle P X M=\angle M Y P$. Moreover, $\angle Y P X=\angle C P D=\angle A D B=\angle A M B$. The quadrilateral $M X P Y$ therefore has equal opposite angles and so is a parallelogram.  Let $R$ and $S$ be the intersection points of $A M$ and $B M$ with $B C$ and $A D$ respectively. Due to $A M \| P C$ and $B M \| P D$, we have $\angle A S B=\angle A D P=\angle P C B=\angle A R B$ and so the quadrilateral $A B R S$ is cyclic. We then have $\angle S R B=180^{\circ}-\angle B A S=\angle D C B$ and so $S R \| C D$. In triangles $P C D$ and $M R S$, the corresponding sides are parallel so they are homothetic meaning lines $D S, P M, C R$ concur at the centre of this homothety.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with $\angle B A D<\angle A D C$. Let $M$ be the midpoint of the arc $C D$ not containing $A$. Suppose there is a point $P$ inside $A B C D$ such that $\angle A D B=$ $\angle C P D$ and $\angle A D P=\angle P C B$. Prove that lines $A D, P M, B C$ are concurrent.
|
Let $X$ and $Y$ be the intersection points of $A M$ and $B M$ with $P D$ and $P C$ respectively. Since $A B C M D$ is cyclic and $C M=M D$, we have $$ \angle X A D=\angle M A D=\angle C B M=\angle C B Y $$ Combining this with $\angle A D X=\angle Y C B$, we get $\angle D X A=\angle B Y C$, and so $\angle P X M=\angle M Y P$. Moreover, $\angle Y P X=\angle C P D=\angle A D B=\angle A M B$. The quadrilateral $M X P Y$ therefore has equal opposite angles and so is a parallelogram.  Let $R$ and $S$ be the intersection points of $A M$ and $B M$ with $B C$ and $A D$ respectively. Due to $A M \| P C$ and $B M \| P D$, we have $\angle A S B=\angle A D P=\angle P C B=\angle A R B$ and so the quadrilateral $A B R S$ is cyclic. We then have $\angle S R B=180^{\circ}-\angle B A S=\angle D C B$ and so $S R \| C D$. In triangles $P C D$ and $M R S$, the corresponding sides are parallel so they are homothetic meaning lines $D S, P M, C R$ concur at the centre of this homothety.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8659e4c2-33f4-5e11-82fc-ecd11fb03206
| 607,750
|
Let $A B C D$ be a cyclic quadrilateral with $\angle B A D<\angle A D C$. Let $M$ be the midpoint of the arc $C D$ not containing $A$. Suppose there is a point $P$ inside $A B C D$ such that $\angle A D B=$ $\angle C P D$ and $\angle A D P=\angle P C B$. Prove that lines $A D, P M, B C$ are concurrent.
|
Let $A D$ and $B C$ meet at $T$. Denote by $p_{a}, p_{b}, m_{a}$ and $m_{b}$ the distances between line $T A$ and $P, T B$ and $P, T A$ and $M$ and between $T B$ and $M$ respectively. Our goal is to prove $p_{a}: p_{b}=m_{a}: m_{b}$ which is equivalent to the collinearity of $T, P$ and $M$.  Let $\angle B A C=\angle B D C=\alpha, \angle D B A=\angle D C A=\beta, \angle A D B=\angle A M B=\angle A C B=$ $\angle C P D=\mu, \angle A D P=\angle P C B=\nu$ and $\angle M A D=\angle C A M=\angle M B D=\angle C B M=\chi$. From $\angle A D P=\angle P C B=\nu$ and $\angle M A D=\angle C B M=\chi$ we get $$ \frac{p_{a}}{p_{b}}=\frac{P D \cdot \sin \nu}{P C \cdot \sin \nu}=\frac{P D}{P C} \quad \text { and } \quad \frac{m_{a}}{m_{b}}=\frac{M A \cdot \sin \chi}{M B \cdot \sin \chi}=\frac{M A}{M B} . $$ Hence $p_{a}: p_{b}=m_{a}: m_{b}$ is equivalent to $P D: P C=M A: M B$, and since $\angle C P D=\angle A M B=$ $\mu$, this means we have to show that triangles $P D C$ and $M A B$ are similar. In triangle $P D C$ we have $$ \begin{aligned} & \angle P D C+\angle D C P=180^{\circ}-\angle C P D=180^{\circ}-\mu \\ & \angle P D C-\angle D C P=(\alpha+\mu-\nu)-(\beta+\mu-\nu)=\alpha-\beta . \end{aligned} $$ Similarly, in triangle $M A B$ we have $$ \begin{aligned} & \angle B A M+\angle M B A=180^{\circ}-\angle A M B=180^{\circ}-\mu, \\ & \angle B A M-\angle M B A=(\alpha+\chi)-(\beta+\chi)=\alpha-\beta . \end{aligned} $$ Therefore, $(\angle B A M, \angle M B A)$ and $(\angle P D C, \angle D C P)$ satisfy the same system of linear equations. The common solution is $$ \angle B A M=\angle P D C=\frac{180^{\circ}-\mu+\alpha-\beta}{2} \text { and } \angle M B A=\angle D C P=\frac{180^{\circ}-\mu-\alpha+\beta}{2} . $$ Hence triangles $P D C$ and $M A B$ have equal angles and so are similar. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with $\angle B A D<\angle A D C$. Let $M$ be the midpoint of the arc $C D$ not containing $A$. Suppose there is a point $P$ inside $A B C D$ such that $\angle A D B=$ $\angle C P D$ and $\angle A D P=\angle P C B$. Prove that lines $A D, P M, B C$ are concurrent.
|
Let $A D$ and $B C$ meet at $T$. Denote by $p_{a}, p_{b}, m_{a}$ and $m_{b}$ the distances between line $T A$ and $P, T B$ and $P, T A$ and $M$ and between $T B$ and $M$ respectively. Our goal is to prove $p_{a}: p_{b}=m_{a}: m_{b}$ which is equivalent to the collinearity of $T, P$ and $M$.  Let $\angle B A C=\angle B D C=\alpha, \angle D B A=\angle D C A=\beta, \angle A D B=\angle A M B=\angle A C B=$ $\angle C P D=\mu, \angle A D P=\angle P C B=\nu$ and $\angle M A D=\angle C A M=\angle M B D=\angle C B M=\chi$. From $\angle A D P=\angle P C B=\nu$ and $\angle M A D=\angle C B M=\chi$ we get $$ \frac{p_{a}}{p_{b}}=\frac{P D \cdot \sin \nu}{P C \cdot \sin \nu}=\frac{P D}{P C} \quad \text { and } \quad \frac{m_{a}}{m_{b}}=\frac{M A \cdot \sin \chi}{M B \cdot \sin \chi}=\frac{M A}{M B} . $$ Hence $p_{a}: p_{b}=m_{a}: m_{b}$ is equivalent to $P D: P C=M A: M B$, and since $\angle C P D=\angle A M B=$ $\mu$, this means we have to show that triangles $P D C$ and $M A B$ are similar. In triangle $P D C$ we have $$ \begin{aligned} & \angle P D C+\angle D C P=180^{\circ}-\angle C P D=180^{\circ}-\mu \\ & \angle P D C-\angle D C P=(\alpha+\mu-\nu)-(\beta+\mu-\nu)=\alpha-\beta . \end{aligned} $$ Similarly, in triangle $M A B$ we have $$ \begin{aligned} & \angle B A M+\angle M B A=180^{\circ}-\angle A M B=180^{\circ}-\mu, \\ & \angle B A M-\angle M B A=(\alpha+\chi)-(\beta+\chi)=\alpha-\beta . \end{aligned} $$ Therefore, $(\angle B A M, \angle M B A)$ and $(\angle P D C, \angle D C P)$ satisfy the same system of linear equations. The common solution is $$ \angle B A M=\angle P D C=\frac{180^{\circ}-\mu+\alpha-\beta}{2} \text { and } \angle M B A=\angle D C P=\frac{180^{\circ}-\mu-\alpha+\beta}{2} . $$ Hence triangles $P D C$ and $M A B$ have equal angles and so are similar. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8659e4c2-33f4-5e11-82fc-ecd11fb03206
| 607,750
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear.
|
 We write $\triangle P_{1} P_{2} P_{3} \stackrel{ \pm}{\sim} \triangle Q_{1} Q_{2} Q_{3}$ (resp. $\triangle P_{1} P_{2} P_{3} \approx \triangle Q_{1} Q_{2} Q_{3}$ ) to indicate that two triangles are directly (resp. oppositely) similar. We use directed angles throughout denoted with $\Varangle$. Denote by $A_{b}, A_{c}$ the reflections of $A$ in $B H$ and $C H$ respectively. $B_{c}, B_{a}$ and $C_{a}, C_{b}$ are defined similarly. By definition, $\ell_{a}=B_{c} C_{b}, \ell_{b}=C_{a} A_{c}, \ell_{c}=A_{b} B_{a}$. Let $A_{1}=\ell_{b} \cap \ell_{c}$, $B_{1}=\ell_{c} \cap \ell_{a}, C_{1}=\ell_{a} \cap \ell_{b}$ and let $O_{1}, H_{1}$ be the orthocentre and circumcentre of $\mathcal{T} \equiv \triangle A_{1} B_{1} C_{1}$ respectively. Claim 1. $\triangle A A_{b} A_{c} \approx \triangle A B C$. Proof. Let $P=B H \cap A C, Q=C H \cap A B$, then it is well known that $\triangle A P Q \approx \triangle A B C$. By the dilation with factor 2 centred at $A, \triangle A P Q$ is sent to $\triangle A A_{b} A_{c}$, so we have $\triangle A A_{b} A_{c} \sim \triangle A B C$. Claim 2. $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$ and $A_{1}$ lies on the circumcircle of $\triangle A A_{b} A_{c}$ which is centred at $H$. Proof. Since $B_{a}, C_{a}$ are reflections of $B, C$ in $A H$, we have $\triangle A B_{a} C_{a} \approx \triangle A B C$. Combining this with Claim 1, we have $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$, where $A$ is the centre of this similarity. Therefore, $\Varangle A_{c} A_{1} A_{b}=\Varangle A_{c} A A_{b}$ meaning $A_{1}$ lies on $\odot A A_{b} A_{c}$. By symmetry, $H A_{b}=H A=H A_{c}$, so $H$ is centre of this circle. Claim 3. $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Proof. From Claim 2 we have $$ \Varangle C_{1} A_{1} B_{1}=\Varangle A_{c} A_{1} A_{b} \stackrel{\text { Claim } 2}{=} \npreceq A_{c} A A_{b}=-\Varangle C A B $$ and similarly $\Varangle A_{1} B_{1} C_{1}=-\Varangle A B C, \Varangle B_{1} C_{1} A_{1}=-\Varangle B C A$, which imply $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Denote the ratio of similitude of $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ by $\lambda\left(=\frac{B_{1} C_{1}}{B C}\right)$, then $$ \lambda=\frac{H_{1} A_{1}}{H A}=\frac{H_{1} B_{1}}{H B}=\frac{H_{1} C_{1}}{H C} . $$ Since $H A=H A_{1}$ and similarly $H B=H B_{1}, H C=H C_{1}$ from Claim 2, we get $$ \lambda=\frac{H_{1} A_{1}}{H A_{1}}=\frac{H_{1} B_{1}}{H B_{1}}=\frac{H_{1} C_{1}}{H C_{1}} . $$ Therefore, the circle $A_{1} B_{1} C_{1}$ is the Apollonian circle of the segment $H H_{1}$ with ratio $\lambda$ so the line $H H_{1}$ passes through $O_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear.
|
 We write $\triangle P_{1} P_{2} P_{3} \stackrel{ \pm}{\sim} \triangle Q_{1} Q_{2} Q_{3}$ (resp. $\triangle P_{1} P_{2} P_{3} \approx \triangle Q_{1} Q_{2} Q_{3}$ ) to indicate that two triangles are directly (resp. oppositely) similar. We use directed angles throughout denoted with $\Varangle$. Denote by $A_{b}, A_{c}$ the reflections of $A$ in $B H$ and $C H$ respectively. $B_{c}, B_{a}$ and $C_{a}, C_{b}$ are defined similarly. By definition, $\ell_{a}=B_{c} C_{b}, \ell_{b}=C_{a} A_{c}, \ell_{c}=A_{b} B_{a}$. Let $A_{1}=\ell_{b} \cap \ell_{c}$, $B_{1}=\ell_{c} \cap \ell_{a}, C_{1}=\ell_{a} \cap \ell_{b}$ and let $O_{1}, H_{1}$ be the orthocentre and circumcentre of $\mathcal{T} \equiv \triangle A_{1} B_{1} C_{1}$ respectively. Claim 1. $\triangle A A_{b} A_{c} \approx \triangle A B C$. Proof. Let $P=B H \cap A C, Q=C H \cap A B$, then it is well known that $\triangle A P Q \approx \triangle A B C$. By the dilation with factor 2 centred at $A, \triangle A P Q$ is sent to $\triangle A A_{b} A_{c}$, so we have $\triangle A A_{b} A_{c} \sim \triangle A B C$. Claim 2. $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$ and $A_{1}$ lies on the circumcircle of $\triangle A A_{b} A_{c}$ which is centred at $H$. Proof. Since $B_{a}, C_{a}$ are reflections of $B, C$ in $A H$, we have $\triangle A B_{a} C_{a} \approx \triangle A B C$. Combining this with Claim 1, we have $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$, where $A$ is the centre of this similarity. Therefore, $\Varangle A_{c} A_{1} A_{b}=\Varangle A_{c} A A_{b}$ meaning $A_{1}$ lies on $\odot A A_{b} A_{c}$. By symmetry, $H A_{b}=H A=H A_{c}$, so $H$ is centre of this circle. Claim 3. $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Proof. From Claim 2 we have $$ \Varangle C_{1} A_{1} B_{1}=\Varangle A_{c} A_{1} A_{b} \stackrel{\text { Claim } 2}{=} \npreceq A_{c} A A_{b}=-\Varangle C A B $$ and similarly $\Varangle A_{1} B_{1} C_{1}=-\Varangle A B C, \Varangle B_{1} C_{1} A_{1}=-\Varangle B C A$, which imply $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Denote the ratio of similitude of $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ by $\lambda\left(=\frac{B_{1} C_{1}}{B C}\right)$, then $$ \lambda=\frac{H_{1} A_{1}}{H A}=\frac{H_{1} B_{1}}{H B}=\frac{H_{1} C_{1}}{H C} . $$ Since $H A=H A_{1}$ and similarly $H B=H B_{1}, H C=H C_{1}$ from Claim 2, we get $$ \lambda=\frac{H_{1} A_{1}}{H A_{1}}=\frac{H_{1} B_{1}}{H B_{1}}=\frac{H_{1} C_{1}}{H C_{1}} . $$ Therefore, the circle $A_{1} B_{1} C_{1}$ is the Apollonian circle of the segment $H H_{1}$ with ratio $\lambda$ so the line $H H_{1}$ passes through $O_{1}$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9dea097b-0446-56ec-8785-503f5d9c220e
| 607,754
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear.
|
We use the same notation $A_{b}, A_{c}, B_{c}, B_{a}, C_{a}, C_{b}$ and $A_{1}, B_{1}, C_{1}, O_{1}, H_{1}$ as in Let $O$ be the circumcentre of $\triangle A B C$ and $A_{2}$ be the reflection of $A_{1}$ in $A H$. As $\odot A A_{b} A_{c}$ is centred at $H, A_{2}$ also lies on this circle. By Claim 2, $\Varangle B_{a} A_{1} C_{a}=\Varangle A_{b} A A_{c}=\Varangle B_{a} A C_{a}$, so $A_{1}$ lies on $\odot A B_{a} C_{a}$. Reflecting this in $A H$ gives that $A_{2}$ lies on $\odot A B C$. We now have circles centred at $O$ and $H$ passing through $A$ and $A_{2}$ so these points are symmetric with respect to $O H$. Define $B_{2}$ and $C_{2}$ similarly then $\triangle A B C$ and $\triangle A_{2} B_{2} C_{2}$ are symmetric with respect to $O H$ and also $\odot A B C=\odot A_{2} B_{2} C_{2}$.  Claim 4. $A_{1} A_{2}, B_{1} B_{2}$ and $C_{1} C_{2}$ have an intersection on $\odot A B C$ which we denote by $T$. Proof. Let $T=A_{1} A_{2} \cap B_{1} B_{2}$. Since $A_{1} A_{2} \| B C$ and $B_{1} B_{2} \| A C$, we have $$ \Varangle A_{2} T B_{2}=\Varangle B C A=-\Varangle B_{2} C_{2} A_{2}=\Varangle A_{2} C_{2} B_{2} . $$ So $T$ lies on $\odot A_{2} B_{2} C_{2}=\odot A B C$. Similarly the intersection of $A_{1} A_{2}$ and $C_{1} C_{2}$ lies on $\odot A B C$, so $C_{1} C_{2}$ also passes through $T$. Claim 5. $T$ also lies on $\odot A_{1} B_{1} C_{1}$ and $T$ corresponds to $T$ itself under the similarity $\triangle A_{1} B_{1} C_{1} \approx$ $\triangle A B C$. Proof. We know $\triangle A_{1} B_{1} C_{1} \sim \triangle A B C$ by Claim 3. We also have $$ \Varangle B_{1} T C_{1}=\Varangle B_{2} T C_{2}=\Varangle B_{2} A_{2} C_{2}=-\Varangle B A C \stackrel{\text { Claim } 3}{=} \not B_{1} A_{1} C_{1}, $$ so $T$ lies on $\odot A_{1} B_{1} C_{1}$. The remaining part is concluded by the following angle chase: $$ \Varangle A_{1} B_{1} T=\Varangle A_{1} B_{1} B_{2} \stackrel{B_{1} B_{2} \| A C}{\underline{\|}} \npreceq A_{1} A_{b} A=\Varangle A_{1} A_{2} A=-\Varangle A A_{2} T=-\Varangle A B T . $$ Claim 6. The circumradius of $\triangle A_{1} B_{1} C_{1}$ is equal to $H O$. Proof. Two circles centred at $H$ intersect $\ell_{c}$ at $A_{1}, A_{b}$ and $B_{1}, B_{a}$, so $A_{1} A_{b}$ and $B_{1} B_{a}$ have the same midpoint and thus $A_{1} B_{1}=A_{b} B_{a}$. Consider the spiral symmetry $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$. This takes $H$, the circumcentre of $\triangle A A_{b} A_{c}$, to the circumcentre of $\triangle A B_{a} C_{a}$, denoted by $O_{a}$, which is symmetric to $O$ in $A H$. Hence $\triangle A A_{b} B_{a} \stackrel{ \pm}{\sim} \triangle A H O_{a}$, so $$ \frac{A A_{b}}{B_{a} A_{b}}=\frac{A H}{H O_{a}}=\frac{A H}{H O} \Longrightarrow \frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}} . $$ Also since $\triangle A_{1} O_{1} B_{1} \stackrel{\downarrow}{\sim} \triangle A H A_{b}$ (both of them are $\approx \triangle A O B$ ), we have $$ \frac{A_{1} O_{1}}{A_{1} B_{1}}=\frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}}=\frac{H O}{A_{1} B_{1}} \Longrightarrow A_{1} O_{1}=H O $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear.
|
We use the same notation $A_{b}, A_{c}, B_{c}, B_{a}, C_{a}, C_{b}$ and $A_{1}, B_{1}, C_{1}, O_{1}, H_{1}$ as in Let $O$ be the circumcentre of $\triangle A B C$ and $A_{2}$ be the reflection of $A_{1}$ in $A H$. As $\odot A A_{b} A_{c}$ is centred at $H, A_{2}$ also lies on this circle. By Claim 2, $\Varangle B_{a} A_{1} C_{a}=\Varangle A_{b} A A_{c}=\Varangle B_{a} A C_{a}$, so $A_{1}$ lies on $\odot A B_{a} C_{a}$. Reflecting this in $A H$ gives that $A_{2}$ lies on $\odot A B C$. We now have circles centred at $O$ and $H$ passing through $A$ and $A_{2}$ so these points are symmetric with respect to $O H$. Define $B_{2}$ and $C_{2}$ similarly then $\triangle A B C$ and $\triangle A_{2} B_{2} C_{2}$ are symmetric with respect to $O H$ and also $\odot A B C=\odot A_{2} B_{2} C_{2}$.  Claim 4. $A_{1} A_{2}, B_{1} B_{2}$ and $C_{1} C_{2}$ have an intersection on $\odot A B C$ which we denote by $T$. Proof. Let $T=A_{1} A_{2} \cap B_{1} B_{2}$. Since $A_{1} A_{2} \| B C$ and $B_{1} B_{2} \| A C$, we have $$ \Varangle A_{2} T B_{2}=\Varangle B C A=-\Varangle B_{2} C_{2} A_{2}=\Varangle A_{2} C_{2} B_{2} . $$ So $T$ lies on $\odot A_{2} B_{2} C_{2}=\odot A B C$. Similarly the intersection of $A_{1} A_{2}$ and $C_{1} C_{2}$ lies on $\odot A B C$, so $C_{1} C_{2}$ also passes through $T$. Claim 5. $T$ also lies on $\odot A_{1} B_{1} C_{1}$ and $T$ corresponds to $T$ itself under the similarity $\triangle A_{1} B_{1} C_{1} \approx$ $\triangle A B C$. Proof. We know $\triangle A_{1} B_{1} C_{1} \sim \triangle A B C$ by Claim 3. We also have $$ \Varangle B_{1} T C_{1}=\Varangle B_{2} T C_{2}=\Varangle B_{2} A_{2} C_{2}=-\Varangle B A C \stackrel{\text { Claim } 3}{=} \not B_{1} A_{1} C_{1}, $$ so $T$ lies on $\odot A_{1} B_{1} C_{1}$. The remaining part is concluded by the following angle chase: $$ \Varangle A_{1} B_{1} T=\Varangle A_{1} B_{1} B_{2} \stackrel{B_{1} B_{2} \| A C}{\underline{\|}} \npreceq A_{1} A_{b} A=\Varangle A_{1} A_{2} A=-\Varangle A A_{2} T=-\Varangle A B T . $$ Claim 6. The circumradius of $\triangle A_{1} B_{1} C_{1}$ is equal to $H O$. Proof. Two circles centred at $H$ intersect $\ell_{c}$ at $A_{1}, A_{b}$ and $B_{1}, B_{a}$, so $A_{1} A_{b}$ and $B_{1} B_{a}$ have the same midpoint and thus $A_{1} B_{1}=A_{b} B_{a}$. Consider the spiral symmetry $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$. This takes $H$, the circumcentre of $\triangle A A_{b} A_{c}$, to the circumcentre of $\triangle A B_{a} C_{a}$, denoted by $O_{a}$, which is symmetric to $O$ in $A H$. Hence $\triangle A A_{b} B_{a} \stackrel{ \pm}{\sim} \triangle A H O_{a}$, so $$ \frac{A A_{b}}{B_{a} A_{b}}=\frac{A H}{H O_{a}}=\frac{A H}{H O} \Longrightarrow \frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}} . $$ Also since $\triangle A_{1} O_{1} B_{1} \stackrel{\downarrow}{\sim} \triangle A H A_{b}$ (both of them are $\approx \triangle A O B$ ), we have $$ \frac{A_{1} O_{1}}{A_{1} B_{1}}=\frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}}=\frac{H O}{A_{1} B_{1}} \Longrightarrow A_{1} O_{1}=H O $$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9dea097b-0446-56ec-8785-503f5d9c220e
| 607,754
|
Let $a_{1}<a_{2}<a_{3}<\cdots$ be positive integers such that $a_{k+1}$ divides $2\left(a_{1}+a_{2}+\cdots+a_{k}\right)$ for every $k \geqslant 1$. Suppose that for infinitely many primes $p$, there exists $k$ such that $p$ divides $a_{k}$. Prove that for every positive integer $n$, there exists $k$ such that $n$ divides $a_{k}$. (Netherlands)
|
For every $k \geqslant 2$ define the quotient $b_{k}=2\left(a_{1}+\cdots+a_{k-1}\right) / a_{k}$, which must be a positive integer. We first prove the following properties of the sequence $\left(b_{k}\right)$ : Claim 1. We have $b_{k+1} \leqslant b_{k}+1$ for all $k \geqslant 2$. Proof. By subtracting $b_{k} a_{k}=2\left(a_{1}+\cdots+a_{k-1}\right)$ from $b_{k+1} a_{k+1}=2\left(a_{1}+\cdots+a_{k}\right)$, we find that $b_{k+1} a_{k+1}=b_{k} a_{k}+2 a_{k}=\left(b_{k}+2\right) a_{k}$. From $a_{k}<a_{k+1}$ it follows that $b_{k}+2>b_{k+1}$. Claim 2. The sequence $\left(b_{k}\right)$ is unbounded. Proof. We start by rewriting $b_{k+1} a_{k+1}=\left(b_{k}+2\right) a_{k}$ as $$ \left.a_{k+1}=a_{k} \cdot \frac{b_{k}+2}{b_{k+1}} \Longrightarrow a_{k+1} \right\rvert\, a_{k}\left(b_{k}+2\right) . $$ If the sequence $\left(b_{k}\right)$ were bounded, say by some positive integer $B$, then the prime factors of the terms of the sequence $\left(a_{k}\right)$ could only be primes less than or equal to $B+2$ or those dividing $a_{1}$ or $a_{2}$, which contradicts the property in the statement of the problem. Consider now an arbitrary positive integer $n$. We assume $n>b_{2}$, otherwise we replace $n$ by an arbitrary multiple of $n$ that is bigger than $b_{2}$. By Claim 2 , there exists $k$ such that $b_{k+1} \geqslant n$. Consider the smallest such $k$. From Claim 1, it follows that we must have $b_{k}=n-1$ and $b_{k+1}=n$ (we assumed $n>b_{2}$ to ensure that $k \geqslant 2$ ). We now find that $$ a_{k+1}=a_{k} \cdot \frac{b_{k}+2}{b_{k+1}}=a_{k} \cdot \frac{n+1}{n} . $$ Because $n$ and $n+1$ are coprime, this immediately implies that $a_{k}$ is divisible by $n$. Comment. For $c$ a positive integer, the sequence $a_{k}=c k$ satisfies the conditions of the problem. Another example is $$ a_{1}=1, \quad a_{2}=2, \quad a_{k}=3(k-1) \text { for } k \geqslant 3 . $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<\cdots$ be positive integers such that $a_{k+1}$ divides $2\left(a_{1}+a_{2}+\cdots+a_{k}\right)$ for every $k \geqslant 1$. Suppose that for infinitely many primes $p$, there exists $k$ such that $p$ divides $a_{k}$. Prove that for every positive integer $n$, there exists $k$ such that $n$ divides $a_{k}$. (Netherlands)
|
For every $k \geqslant 2$ define the quotient $b_{k}=2\left(a_{1}+\cdots+a_{k-1}\right) / a_{k}$, which must be a positive integer. We first prove the following properties of the sequence $\left(b_{k}\right)$ : Claim 1. We have $b_{k+1} \leqslant b_{k}+1$ for all $k \geqslant 2$. Proof. By subtracting $b_{k} a_{k}=2\left(a_{1}+\cdots+a_{k-1}\right)$ from $b_{k+1} a_{k+1}=2\left(a_{1}+\cdots+a_{k}\right)$, we find that $b_{k+1} a_{k+1}=b_{k} a_{k}+2 a_{k}=\left(b_{k}+2\right) a_{k}$. From $a_{k}<a_{k+1}$ it follows that $b_{k}+2>b_{k+1}$. Claim 2. The sequence $\left(b_{k}\right)$ is unbounded. Proof. We start by rewriting $b_{k+1} a_{k+1}=\left(b_{k}+2\right) a_{k}$ as $$ \left.a_{k+1}=a_{k} \cdot \frac{b_{k}+2}{b_{k+1}} \Longrightarrow a_{k+1} \right\rvert\, a_{k}\left(b_{k}+2\right) . $$ If the sequence $\left(b_{k}\right)$ were bounded, say by some positive integer $B$, then the prime factors of the terms of the sequence $\left(a_{k}\right)$ could only be primes less than or equal to $B+2$ or those dividing $a_{1}$ or $a_{2}$, which contradicts the property in the statement of the problem. Consider now an arbitrary positive integer $n$. We assume $n>b_{2}$, otherwise we replace $n$ by an arbitrary multiple of $n$ that is bigger than $b_{2}$. By Claim 2 , there exists $k$ such that $b_{k+1} \geqslant n$. Consider the smallest such $k$. From Claim 1, it follows that we must have $b_{k}=n-1$ and $b_{k+1}=n$ (we assumed $n>b_{2}$ to ensure that $k \geqslant 2$ ). We now find that $$ a_{k+1}=a_{k} \cdot \frac{b_{k}+2}{b_{k+1}}=a_{k} \cdot \frac{n+1}{n} . $$ Because $n$ and $n+1$ are coprime, this immediately implies that $a_{k}$ is divisible by $n$. Comment. For $c$ a positive integer, the sequence $a_{k}=c k$ satisfies the conditions of the problem. Another example is $$ a_{1}=1, \quad a_{2}=2, \quad a_{k}=3(k-1) \text { for } k \geqslant 3 . $$
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d9fcab42-576e-5bc6-8e23-3a084b3fdc81
| 607,759
|
A sequence of integers $a_{0}, a_{1}, a_{2}, \ldots$ is called kawaii, if $a_{0}=0, a_{1}=1$, and, for any positive integer $n$, we have $$ \left(a_{n+1}-3 a_{n}+2 a_{n-1}\right)\left(a_{n+1}-4 a_{n}+3 a_{n-1}\right)=0 . $$ An integer is called kawaii if it belongs to a kawaii sequence. Suppose that two consecutive positive integers $m$ and $m+1$ are both kawaii (not necessarily belonging to the same kawaii sequence). Prove that 3 divides $m$, and that $m / 3$ is kawaii. (China)
|
We start by rewriting the condition in the problem as: $$ a_{n+1}=3 a_{n}-2 a_{n-1}, \text { or } a_{n+1}=4 a_{n}-3 a_{n-1} . $$ We have $a_{n+1} \equiv a_{n}$ or $a_{n-1}(\bmod 2)$ and $a_{n+1} \equiv a_{n-1}$ or $a_{n}(\bmod 3)$ for all $n \geqslant 1$. Now, since $a_{0}=0$ and $a_{1}=1$, we have that $a_{n} \equiv 0,1 \bmod 3$ for all $n \geqslant 0$. Since $m$ and $m+1$ are kawaii integers, then necessarily $m \equiv 0 \bmod 3$. We also observe that $a_{2}=3$ or $a_{2}=4$. Moreover, (1) If $a_{2}=3$, then $a_{n} \equiv 1(\bmod 2)$ for all $n \geqslant 1$ since $a_{1} \equiv a_{2} \equiv 1(\bmod 2)$. (2) If $a_{2}=4$, then $a_{n} \equiv 1(\bmod 3)$ for all $n \geqslant 1$ since $a_{1} \equiv a_{2} \equiv 1(\bmod 3)$. Since $m \equiv 0(\bmod 3)$, any kawaii sequence containing $m$ does not satisfy $(2)$, so it must satisfy (1). Hence, $m$ is odd and $m+1$ is even. Take a kawaii sequence $\left(a_{n}\right)$ containing $m+1$. Let $t \geqslant 2$ be such that $a_{t}=m+1$. As $\left(a_{n}\right)$ does not satisfy (1), it must satisfy (2). Then $a_{n} \equiv 1(\bmod 3)$ for all $n \geqslant 1$. We define the sequence $a_{n}^{\prime}=\left(a_{n+1}-1\right) / 3$. This is a kawaii sequence: $a_{0}^{\prime}=0, a_{1}^{\prime}=1$ and for all $n \geqslant 1$, $$ \left(a_{n+1}^{\prime}-3 a_{n}^{\prime}+2 a_{n-1}^{\prime}\right)\left(a_{n+1}^{\prime}-4 a_{n}^{\prime}+3 a_{n-1}^{\prime}\right)=\left(a_{n+2}-3 a_{n+1}+2 a_{n}\right)\left(a_{n+2}-4 a_{n+1}+3 a_{n}\right) / 9=0 . $$ Finally, we notice that the term $a_{t-1}^{\prime}=m / 3$ which implies that $m / 3$ is kawaii.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A sequence of integers $a_{0}, a_{1}, a_{2}, \ldots$ is called kawaii, if $a_{0}=0, a_{1}=1$, and, for any positive integer $n$, we have $$ \left(a_{n+1}-3 a_{n}+2 a_{n-1}\right)\left(a_{n+1}-4 a_{n}+3 a_{n-1}\right)=0 . $$ An integer is called kawaii if it belongs to a kawaii sequence. Suppose that two consecutive positive integers $m$ and $m+1$ are both kawaii (not necessarily belonging to the same kawaii sequence). Prove that 3 divides $m$, and that $m / 3$ is kawaii. (China)
|
We start by rewriting the condition in the problem as: $$ a_{n+1}=3 a_{n}-2 a_{n-1}, \text { or } a_{n+1}=4 a_{n}-3 a_{n-1} . $$ We have $a_{n+1} \equiv a_{n}$ or $a_{n-1}(\bmod 2)$ and $a_{n+1} \equiv a_{n-1}$ or $a_{n}(\bmod 3)$ for all $n \geqslant 1$. Now, since $a_{0}=0$ and $a_{1}=1$, we have that $a_{n} \equiv 0,1 \bmod 3$ for all $n \geqslant 0$. Since $m$ and $m+1$ are kawaii integers, then necessarily $m \equiv 0 \bmod 3$. We also observe that $a_{2}=3$ or $a_{2}=4$. Moreover, (1) If $a_{2}=3$, then $a_{n} \equiv 1(\bmod 2)$ for all $n \geqslant 1$ since $a_{1} \equiv a_{2} \equiv 1(\bmod 2)$. (2) If $a_{2}=4$, then $a_{n} \equiv 1(\bmod 3)$ for all $n \geqslant 1$ since $a_{1} \equiv a_{2} \equiv 1(\bmod 3)$. Since $m \equiv 0(\bmod 3)$, any kawaii sequence containing $m$ does not satisfy $(2)$, so it must satisfy (1). Hence, $m$ is odd and $m+1$ is even. Take a kawaii sequence $\left(a_{n}\right)$ containing $m+1$. Let $t \geqslant 2$ be such that $a_{t}=m+1$. As $\left(a_{n}\right)$ does not satisfy (1), it must satisfy (2). Then $a_{n} \equiv 1(\bmod 3)$ for all $n \geqslant 1$. We define the sequence $a_{n}^{\prime}=\left(a_{n+1}-1\right) / 3$. This is a kawaii sequence: $a_{0}^{\prime}=0, a_{1}^{\prime}=1$ and for all $n \geqslant 1$, $$ \left(a_{n+1}^{\prime}-3 a_{n}^{\prime}+2 a_{n-1}^{\prime}\right)\left(a_{n+1}^{\prime}-4 a_{n}^{\prime}+3 a_{n-1}^{\prime}\right)=\left(a_{n+2}-3 a_{n+1}+2 a_{n}\right)\left(a_{n+2}-4 a_{n+1}+3 a_{n}\right) / 9=0 . $$ Finally, we notice that the term $a_{t-1}^{\prime}=m / 3$ which implies that $m / 3$ is kawaii.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
11044d6b-af7c-5110-bef3-e49b63a73f15
| 607,760
|
A sequence of integers $a_{0}, a_{1}, a_{2}, \ldots$ is called kawaii, if $a_{0}=0, a_{1}=1$, and, for any positive integer $n$, we have $$ \left(a_{n+1}-3 a_{n}+2 a_{n-1}\right)\left(a_{n+1}-4 a_{n}+3 a_{n-1}\right)=0 . $$ An integer is called kawaii if it belongs to a kawaii sequence. Suppose that two consecutive positive integers $m$ and $m+1$ are both kawaii (not necessarily belonging to the same kawaii sequence). Prove that 3 divides $m$, and that $m / 3$ is kawaii. (China)
|
We start by proving the following: Claim 1. We have $a_{n} \equiv 0,1 \bmod 3$ for all $n \geqslant 0$. Proof. We have $a_{n+1}=3 a_{n}-2 a_{n-1}=3\left(a_{n}-a_{n-1}\right)+a_{n-1}$ or $a_{n+1}=4 a_{n}-3 a_{n-1}=3\left(a_{n}-\right.$ $\left.a_{n-1}\right)+a_{n}$, so $a_{n+1} \equiv a_{n}$ or $a_{n-1} \bmod 3$, and since $a_{0}=0$ and $a_{1}=1$ the result follows. Hence if $m$ and $m+1$ are kawaii, then necessarily $m \equiv 0 \bmod 3$. Claim 2. An integer $\geqslant 2$ is kawaii if and only if it can be written as $1+b_{2}+\cdots+b_{n}$ for some $n \geqslant 2$ with $b_{i}=2^{r_{i}} 3^{s_{i}}$ satisfying $r_{i}+s_{i}=i-1$ for $i=2, \ldots, n$ and $b_{i} \mid b_{i+1}$ for all $i=2, \ldots, n-1$. Proof. For a kawaii sequence $\left(a_{n}\right)$, we can write $a_{n+1}=3 a_{n}-2 a_{n-1}=a_{n}+2\left(a_{n}-a_{n-1}\right)$ or $a_{n+1}=4 a_{n}-3 a_{n-1}=a_{n}+3\left(a_{n}-a_{n-1}\right)$, so $a_{n+1}-a_{n}=2\left(a_{n}-a_{n-1}\right)$ or $3\left(a_{n}-a_{n-1}\right)$. Hence, $a_{n}=1+b_{2}+\cdots+b_{n}$ where $b_{2}=2$ or 3 and $b_{i+1}=2 b_{i}$ or $3 b_{i}$. Conversely, given a number that can be written in that way, we consider any sequence given by $a_{0}=0, a_{1}=1$ and $a_{i}=1+b_{2}+\cdots+b_{i}$ for $2 \leqslant i \leqslant n$ and $a_{i}$ given by the kawaii condition for $i \geqslant n+1$. This defines a kawaii sequence containing the given number as $a_{n}$. Let us suppose that $m$ and $m+1$ are kawaii, then they belong to some kawaii sequences and we can write them as in Claim 2 as $m=1+2+\cdots+2^{\ell}+2^{\ell} \cdot 3 \cdot A$ and $m+1=1+2+\cdots+2^{\ell^{\prime}}+2^{\ell^{\prime}} \cdot 3 \cdot A^{\prime}$ where $\ell$ is odd and $\ell^{\prime}$ is even because of modulo 3 reasons. Since $m+1 \equiv m\left(\bmod 2^{\min \left(\ell, \ell^{\prime}\right)}\right)$, we have $\min \left(\ell, \ell^{\prime}\right)=0$, so $\ell^{\prime}=0$. Then $m+1=1+b_{2}+\cdots+b_{j}$ for some $b_{i}$ 's as in Claim 2 with $b_{2}=3$ and $b_{i} \mid b_{i+1}$ : so with $3 \mid b_{i}$ for all $i=2, \ldots, j$. Then $\frac{m}{3}=1+b_{1}^{\prime}+\cdots+b_{j-1}^{\prime}$ with $b_{i}^{\prime}=\frac{b_{i+1}}{3}$ as in Claim 2 and $\frac{m}{3}$ is a kawaii integer.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A sequence of integers $a_{0}, a_{1}, a_{2}, \ldots$ is called kawaii, if $a_{0}=0, a_{1}=1$, and, for any positive integer $n$, we have $$ \left(a_{n+1}-3 a_{n}+2 a_{n-1}\right)\left(a_{n+1}-4 a_{n}+3 a_{n-1}\right)=0 . $$ An integer is called kawaii if it belongs to a kawaii sequence. Suppose that two consecutive positive integers $m$ and $m+1$ are both kawaii (not necessarily belonging to the same kawaii sequence). Prove that 3 divides $m$, and that $m / 3$ is kawaii. (China)
|
We start by proving the following: Claim 1. We have $a_{n} \equiv 0,1 \bmod 3$ for all $n \geqslant 0$. Proof. We have $a_{n+1}=3 a_{n}-2 a_{n-1}=3\left(a_{n}-a_{n-1}\right)+a_{n-1}$ or $a_{n+1}=4 a_{n}-3 a_{n-1}=3\left(a_{n}-\right.$ $\left.a_{n-1}\right)+a_{n}$, so $a_{n+1} \equiv a_{n}$ or $a_{n-1} \bmod 3$, and since $a_{0}=0$ and $a_{1}=1$ the result follows. Hence if $m$ and $m+1$ are kawaii, then necessarily $m \equiv 0 \bmod 3$. Claim 2. An integer $\geqslant 2$ is kawaii if and only if it can be written as $1+b_{2}+\cdots+b_{n}$ for some $n \geqslant 2$ with $b_{i}=2^{r_{i}} 3^{s_{i}}$ satisfying $r_{i}+s_{i}=i-1$ for $i=2, \ldots, n$ and $b_{i} \mid b_{i+1}$ for all $i=2, \ldots, n-1$. Proof. For a kawaii sequence $\left(a_{n}\right)$, we can write $a_{n+1}=3 a_{n}-2 a_{n-1}=a_{n}+2\left(a_{n}-a_{n-1}\right)$ or $a_{n+1}=4 a_{n}-3 a_{n-1}=a_{n}+3\left(a_{n}-a_{n-1}\right)$, so $a_{n+1}-a_{n}=2\left(a_{n}-a_{n-1}\right)$ or $3\left(a_{n}-a_{n-1}\right)$. Hence, $a_{n}=1+b_{2}+\cdots+b_{n}$ where $b_{2}=2$ or 3 and $b_{i+1}=2 b_{i}$ or $3 b_{i}$. Conversely, given a number that can be written in that way, we consider any sequence given by $a_{0}=0, a_{1}=1$ and $a_{i}=1+b_{2}+\cdots+b_{i}$ for $2 \leqslant i \leqslant n$ and $a_{i}$ given by the kawaii condition for $i \geqslant n+1$. This defines a kawaii sequence containing the given number as $a_{n}$. Let us suppose that $m$ and $m+1$ are kawaii, then they belong to some kawaii sequences and we can write them as in Claim 2 as $m=1+2+\cdots+2^{\ell}+2^{\ell} \cdot 3 \cdot A$ and $m+1=1+2+\cdots+2^{\ell^{\prime}}+2^{\ell^{\prime}} \cdot 3 \cdot A^{\prime}$ where $\ell$ is odd and $\ell^{\prime}$ is even because of modulo 3 reasons. Since $m+1 \equiv m\left(\bmod 2^{\min \left(\ell, \ell^{\prime}\right)}\right)$, we have $\min \left(\ell, \ell^{\prime}\right)=0$, so $\ell^{\prime}=0$. Then $m+1=1+b_{2}+\cdots+b_{j}$ for some $b_{i}$ 's as in Claim 2 with $b_{2}=3$ and $b_{i} \mid b_{i+1}$ : so with $3 \mid b_{i}$ for all $i=2, \ldots, j$. Then $\frac{m}{3}=1+b_{1}^{\prime}+\cdots+b_{j-1}^{\prime}$ with $b_{i}^{\prime}=\frac{b_{i+1}}{3}$ as in Claim 2 and $\frac{m}{3}$ is a kawaii integer.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
11044d6b-af7c-5110-bef3-e49b63a73f15
| 607,760
|
A sequence of integers $a_{0}, a_{1}, a_{2}, \ldots$ is called kawaii, if $a_{0}=0, a_{1}=1$, and, for any positive integer $n$, we have $$ \left(a_{n+1}-3 a_{n}+2 a_{n-1}\right)\left(a_{n+1}-4 a_{n}+3 a_{n-1}\right)=0 . $$ An integer is called kawaii if it belongs to a kawaii sequence. Suppose that two consecutive positive integers $m$ and $m+1$ are both kawaii (not necessarily belonging to the same kawaii sequence). Prove that 3 divides $m$, and that $m / 3$ is kawaii. (China)
|
(This solution is just a different combination of the ideas in For $n \geqslant 1$, put $b_{n}=a_{n}-a_{n-1}$. We have $$ a_{t}=a_{0}+\sum_{k=1}^{t}\left(a_{k}-a_{k-1}\right)=\sum_{k=1}^{t} b_{k} . $$ Note that $$ a_{n+1}-3 a_{n}+2 a_{n-1}=b_{n+1}-2 b_{n} \quad \text { and } \quad a_{n+1}-4 a_{n}+3 a_{n-1}=b_{n+1}-3 b_{n} . $$ The conditions on the $b_{i}$ 's for defining a kawaii sequence are $$ b_{1}=a_{1}-a_{0}=1, \quad \text { and } \quad \frac{b_{n+1}}{b_{n}} \in\{2,3\} \quad \text { for } \quad n \geqslant 1 $$ 1. If we have $\frac{b_{n+1}}{b_{n}}=2$ for any $n$ with $1 \leqslant n \leqslant t-1$, then (*) implies that $$ a_{t}=\sum_{k=1}^{t} 2^{k-1}=2^{t}-1 \equiv 0,1(\bmod 3) . $$ 2. If there exists some integer $s$ with $2 \leqslant s \leqslant t-1$ such that $$ \frac{b_{2}}{b_{1}}=\frac{b_{3}}{b_{2}}=\cdots=\frac{b_{s}}{b_{s-1}}=2, \quad \frac{b_{s+1}}{b_{s}}=3 $$ it implies that $3 \mid b_{n}$ for any $n \geqslant s+1$. Similarly to the argument in (1), we obtain $$ a_{t} \equiv \sum_{k=1}^{s} b_{k} \equiv 0,1(\bmod 3) $$ 3. If $\frac{b_{2}}{b_{1}}=b_{2}=3$, we have $3 \mid b_{n}$ for any $n \geqslant 2$, and hence $a_{t} \equiv 1(\bmod 3)$. Combining these, we have proved that $a_{t} \equiv 0,1(\bmod 3)$. We next prove that no positive kawaii integer is divisible by both 2 and 3 . If $b_{2}=2$ for some kawaii sequence, then $2 \mid b_{n}$ and $a_{n} \equiv 1(\bmod 2)$ for all $n \geqslant 2$ in it. If $b_{2}=3$ in some kawaii sequence, then $3 \mid b_{n}$ and $a_{n} \equiv 1(\bmod 3)$ for all $n \geqslant 2$ in it. Now, consider the original problem. Since $m$ and $m+1$ are both kawaii integer, it means $$ m \equiv 0,1(\bmod 3), \quad \text { and } \quad m+1 \equiv 0,1(\bmod 3) $$ and hence we easily obtain $3 \mid m$. Since a kawaii integer $m$ is divisible by $3, m$ must be odd, and hence $m+1$ is even. Take a kawaii sequence $a_{0}, a_{1}, a_{2}, \ldots$ containing $m+1$ as $a_{t}$. The fact that $m+1$ is even implies that $b_{2}=3$ and so $3 \mid b_{n}$ for all $n \geqslant 2$ in this sequence. Set $b_{n}^{\prime}=\frac{b_{n+1}}{3}$ for $n \geqslant 1$. Thus $b_{1}^{\prime}=\frac{b_{2}}{3}=1$, and $\frac{b_{n+1}^{\prime}}{b_{n}^{\prime}}=\frac{b_{n+2}}{b_{n+1}} \in\{2,3\}$ for all $n \geqslant 1$. Define $a_{0}^{\prime}=0$ and $a_{n}^{\prime}=\sum_{k=1}^{n} b_{k}^{\prime}$ for $n \geqslant 1$, then $a_{0}^{\prime}, a_{1}^{\prime}, a_{2}^{\prime}, \ldots$ is a kawaii sequence. Now, $$ a_{t-1}^{\prime}=\sum_{k=1}^{t-1} b_{k}^{\prime}=\frac{1}{3} \sum_{k=2}^{t} b_{k}=\frac{1}{3}\left(-b_{1}+\sum_{k=1}^{t} b_{k}\right)=\frac{1}{3}\left(-1+a_{t}\right)=\frac{m}{3} . $$ This means that $\frac{m}{3}$ is a kawaii integer. Comment. There are infinitely many positive integers $m$ such that $m, m+1, m / 3$ are kawaii. To see this, let $k \geqslant 1$ be a kawaii integer. Then $2 k+1$ and $3 k+1$ are kawaii by Claim 2 in Solution 2, and $3(2 k+1)+1=6 k+4$ and $2(3 k+1)+1=6 k+3$ are also kawaii.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A sequence of integers $a_{0}, a_{1}, a_{2}, \ldots$ is called kawaii, if $a_{0}=0, a_{1}=1$, and, for any positive integer $n$, we have $$ \left(a_{n+1}-3 a_{n}+2 a_{n-1}\right)\left(a_{n+1}-4 a_{n}+3 a_{n-1}\right)=0 . $$ An integer is called kawaii if it belongs to a kawaii sequence. Suppose that two consecutive positive integers $m$ and $m+1$ are both kawaii (not necessarily belonging to the same kawaii sequence). Prove that 3 divides $m$, and that $m / 3$ is kawaii. (China)
|
(This solution is just a different combination of the ideas in For $n \geqslant 1$, put $b_{n}=a_{n}-a_{n-1}$. We have $$ a_{t}=a_{0}+\sum_{k=1}^{t}\left(a_{k}-a_{k-1}\right)=\sum_{k=1}^{t} b_{k} . $$ Note that $$ a_{n+1}-3 a_{n}+2 a_{n-1}=b_{n+1}-2 b_{n} \quad \text { and } \quad a_{n+1}-4 a_{n}+3 a_{n-1}=b_{n+1}-3 b_{n} . $$ The conditions on the $b_{i}$ 's for defining a kawaii sequence are $$ b_{1}=a_{1}-a_{0}=1, \quad \text { and } \quad \frac{b_{n+1}}{b_{n}} \in\{2,3\} \quad \text { for } \quad n \geqslant 1 $$ 1. If we have $\frac{b_{n+1}}{b_{n}}=2$ for any $n$ with $1 \leqslant n \leqslant t-1$, then (*) implies that $$ a_{t}=\sum_{k=1}^{t} 2^{k-1}=2^{t}-1 \equiv 0,1(\bmod 3) . $$ 2. If there exists some integer $s$ with $2 \leqslant s \leqslant t-1$ such that $$ \frac{b_{2}}{b_{1}}=\frac{b_{3}}{b_{2}}=\cdots=\frac{b_{s}}{b_{s-1}}=2, \quad \frac{b_{s+1}}{b_{s}}=3 $$ it implies that $3 \mid b_{n}$ for any $n \geqslant s+1$. Similarly to the argument in (1), we obtain $$ a_{t} \equiv \sum_{k=1}^{s} b_{k} \equiv 0,1(\bmod 3) $$ 3. If $\frac{b_{2}}{b_{1}}=b_{2}=3$, we have $3 \mid b_{n}$ for any $n \geqslant 2$, and hence $a_{t} \equiv 1(\bmod 3)$. Combining these, we have proved that $a_{t} \equiv 0,1(\bmod 3)$. We next prove that no positive kawaii integer is divisible by both 2 and 3 . If $b_{2}=2$ for some kawaii sequence, then $2 \mid b_{n}$ and $a_{n} \equiv 1(\bmod 2)$ for all $n \geqslant 2$ in it. If $b_{2}=3$ in some kawaii sequence, then $3 \mid b_{n}$ and $a_{n} \equiv 1(\bmod 3)$ for all $n \geqslant 2$ in it. Now, consider the original problem. Since $m$ and $m+1$ are both kawaii integer, it means $$ m \equiv 0,1(\bmod 3), \quad \text { and } \quad m+1 \equiv 0,1(\bmod 3) $$ and hence we easily obtain $3 \mid m$. Since a kawaii integer $m$ is divisible by $3, m$ must be odd, and hence $m+1$ is even. Take a kawaii sequence $a_{0}, a_{1}, a_{2}, \ldots$ containing $m+1$ as $a_{t}$. The fact that $m+1$ is even implies that $b_{2}=3$ and so $3 \mid b_{n}$ for all $n \geqslant 2$ in this sequence. Set $b_{n}^{\prime}=\frac{b_{n+1}}{3}$ for $n \geqslant 1$. Thus $b_{1}^{\prime}=\frac{b_{2}}{3}=1$, and $\frac{b_{n+1}^{\prime}}{b_{n}^{\prime}}=\frac{b_{n+2}}{b_{n+1}} \in\{2,3\}$ for all $n \geqslant 1$. Define $a_{0}^{\prime}=0$ and $a_{n}^{\prime}=\sum_{k=1}^{n} b_{k}^{\prime}$ for $n \geqslant 1$, then $a_{0}^{\prime}, a_{1}^{\prime}, a_{2}^{\prime}, \ldots$ is a kawaii sequence. Now, $$ a_{t-1}^{\prime}=\sum_{k=1}^{t-1} b_{k}^{\prime}=\frac{1}{3} \sum_{k=2}^{t} b_{k}=\frac{1}{3}\left(-b_{1}+\sum_{k=1}^{t} b_{k}\right)=\frac{1}{3}\left(-1+a_{t}\right)=\frac{m}{3} . $$ This means that $\frac{m}{3}$ is a kawaii integer. Comment. There are infinitely many positive integers $m$ such that $m, m+1, m / 3$ are kawaii. To see this, let $k \geqslant 1$ be a kawaii integer. Then $2 k+1$ and $3 k+1$ are kawaii by Claim 2 in Solution 2, and $3(2 k+1)+1=6 k+4$ and $2(3 k+1)+1=6 k+3$ are also kawaii.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
11044d6b-af7c-5110-bef3-e49b63a73f15
| 607,760
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
We introduce the new variables $s:=x+y$ and $t:=x-y$. Equivalently, $x=\frac{s+t}{2}$ and $y=\frac{s-t}{2}$. The inequality becomes $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ for every $s, t \in \mathbb{R}$. We replace $t$ by $-t$ to obtain $$ f(s) f(-t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing the previous two inequalities gives $$ f(s)(f(t)+f(-t)) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This inequality is strict for $s=x_{0}+y_{0}$ and $t=x_{0}-y_{0}$ by assumption. In particular, there exists some $t_{0}=x_{0}-y_{0}$ for which $f\left(t_{0}\right)+f\left(-t_{0}\right) \neq 0$. Since $f(s)\left(f\left(t_{0}\right)+\right.$ $\left.f\left(-t_{0}\right)\right) \geqslant 0$ for every $s \in \mathbb{R}$, we conclude that $f(s)$ must have constant sign.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
We introduce the new variables $s:=x+y$ and $t:=x-y$. Equivalently, $x=\frac{s+t}{2}$ and $y=\frac{s-t}{2}$. The inequality becomes $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ for every $s, t \in \mathbb{R}$. We replace $t$ by $-t$ to obtain $$ f(s) f(-t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing the previous two inequalities gives $$ f(s)(f(t)+f(-t)) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This inequality is strict for $s=x_{0}+y_{0}$ and $t=x_{0}-y_{0}$ by assumption. In particular, there exists some $t_{0}=x_{0}-y_{0}$ for which $f\left(t_{0}\right)+f\left(-t_{0}\right) \neq 0$. Since $f(s)\left(f\left(t_{0}\right)+\right.$ $\left.f\left(-t_{0}\right)\right) \geqslant 0$ for every $s \in \mathbb{R}$, we conclude that $f(s)$ must have constant sign.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee1cf4a2-4622-508d-ba8d-eb390f3f34c8
| 607,764
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
We do the same change of variables as in $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ In this solution, we replace $s$ by $-s($ instead of $t$ by $-t)$. This gives $$ f(-s) f(t) \geqslant f\left(\frac{-s+t}{2}\right)^{2}-f\left(\frac{-s-t}{2}\right)^{2} $$ We now go back to the original inequality. Substituting $x=y$ gives $f(2 x) f(0) \geqslant 0$ for every $x \in \mathbb{R}$. If $f(0) \neq 0$, then we conclude that $f$ indeed has constant sign. From now on, we will assume that $$ f(0)=0 . $$ Substituting $x=-y$ gives $f(-x)^{2} \geqslant f(x)^{2}$. By permuting $x$ and $-x$, we conclude that $$ f(-x)^{2}=f(x)^{2} $$ for every $x \in \mathbb{R}$. Using the relation $f(x)^{2}=f(-x)^{2}$, we can rewrite (2) as $$ f(-s) f(t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing this inequality with (1), we obtain $$ (f(s)+f(-s)) f(t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$ and we can conclude as in Solution 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
We do the same change of variables as in $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ In this solution, we replace $s$ by $-s($ instead of $t$ by $-t)$. This gives $$ f(-s) f(t) \geqslant f\left(\frac{-s+t}{2}\right)^{2}-f\left(\frac{-s-t}{2}\right)^{2} $$ We now go back to the original inequality. Substituting $x=y$ gives $f(2 x) f(0) \geqslant 0$ for every $x \in \mathbb{R}$. If $f(0) \neq 0$, then we conclude that $f$ indeed has constant sign. From now on, we will assume that $$ f(0)=0 . $$ Substituting $x=-y$ gives $f(-x)^{2} \geqslant f(x)^{2}$. By permuting $x$ and $-x$, we conclude that $$ f(-x)^{2}=f(x)^{2} $$ for every $x \in \mathbb{R}$. Using the relation $f(x)^{2}=f(-x)^{2}$, we can rewrite (2) as $$ f(-s) f(t) \geqslant f\left(\frac{s-t}{2}\right)^{2}-f\left(\frac{s+t}{2}\right)^{2} $$ Summing this inequality with (1), we obtain $$ (f(s)+f(-s)) f(t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$ and we can conclude as in Solution 1 .
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee1cf4a2-4622-508d-ba8d-eb390f3f34c8
| 607,764
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
We prove the contrapositive of the problem statement. Assume that there exist $a, b \in \mathbb{R}$ such that $f(a)<0$ and $f(b)>0$. We want to prove that the inequality is actually an equality, i.e. it is never strict. Lemma 1. The function $f$ is odd, i.e. $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$. Proof. We plug in $x=\frac{a+u}{2}$ and $y=\frac{a-u}{2}$ in the original inequality, where $u$ is a free variable. We obtain $$ f(a) f(u) \geqslant f\left(\frac{a+u}{2}\right)^{2}-f\left(\frac{a-u}{2}\right)^{2} . $$ Replacing $u$ with $-u$ and summing the two inequalities as in the previous solutions, we get $$ f(a)(f(u)+f(-u)) \geqslant 0 $$ for every $u \in \mathbb{R}$. Since $f(a)<0$ by assumption, we conclude that $f(u)+f(-u) \leqslant 0$ for every $u \in \mathbb{R}$. We can repeat the above argument with $b$ instead of $a$. Since $f(b)>0$ by assumption, we conclude that $f(u)+f(-u) \geqslant 0$ for every $u \in \mathbb{R}$. This implies that $f(u)+f(-u)=0$ for every $u \in \mathbb{R}$. Now, using that $f$ is odd, we can write the following chain of inequalities $$ \begin{aligned} f(x)^{2}-f(y)^{2} & \leqslant f(x+y) f(x-y) \\ & =-f(y+x) f(y-x) \\ & \leqslant-\left(f(y)^{2}-f(x)^{2}\right) \\ & =f(x)^{2}-f(y)^{2} . \end{aligned} $$ We conclude that every inequality above is actually an inequality, so $$ f(x+y) f(x-y)=f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
We prove the contrapositive of the problem statement. Assume that there exist $a, b \in \mathbb{R}$ such that $f(a)<0$ and $f(b)>0$. We want to prove that the inequality is actually an equality, i.e. it is never strict. Lemma 1. The function $f$ is odd, i.e. $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$. Proof. We plug in $x=\frac{a+u}{2}$ and $y=\frac{a-u}{2}$ in the original inequality, where $u$ is a free variable. We obtain $$ f(a) f(u) \geqslant f\left(\frac{a+u}{2}\right)^{2}-f\left(\frac{a-u}{2}\right)^{2} . $$ Replacing $u$ with $-u$ and summing the two inequalities as in the previous solutions, we get $$ f(a)(f(u)+f(-u)) \geqslant 0 $$ for every $u \in \mathbb{R}$. Since $f(a)<0$ by assumption, we conclude that $f(u)+f(-u) \leqslant 0$ for every $u \in \mathbb{R}$. We can repeat the above argument with $b$ instead of $a$. Since $f(b)>0$ by assumption, we conclude that $f(u)+f(-u) \geqslant 0$ for every $u \in \mathbb{R}$. This implies that $f(u)+f(-u)=0$ for every $u \in \mathbb{R}$. Now, using that $f$ is odd, we can write the following chain of inequalities $$ \begin{aligned} f(x)^{2}-f(y)^{2} & \leqslant f(x+y) f(x-y) \\ & =-f(y+x) f(y-x) \\ & \leqslant-\left(f(y)^{2}-f(x)^{2}\right) \\ & =f(x)^{2}-f(y)^{2} . \end{aligned} $$ We conclude that every inequality above is actually an inequality, so $$ f(x+y) f(x-y)=f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee1cf4a2-4622-508d-ba8d-eb390f3f34c8
| 607,764
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
As in In this solution, we construct an argument by multiplying inequalities, rather than adding them as in Solutions 1-3. Lemma 2. $f(b) f(-b)<0$. Proof. Let $x_{1}:=\frac{a+b}{2}$ and $y_{1}:=\frac{a-b}{2}$ so that $a=x_{1}+y_{1}$ and $b=x_{1}-y_{1}$. Plugging in $x=x_{1}$ and $y=y_{1}$, we obtain $$ 0>f(a) f(b)=f\left(x_{1}+y_{1}\right) f\left(x_{1}-y_{1}\right) \geqslant f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2} $$ which implies $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$. Similarly, by plugging in $x=y_{1}$ and $y=x_{1}$, we get $$ f(a) f(-b)=f\left(y_{1}+x_{1}\right) f\left(y_{1}-x_{1}\right) \geqslant f\left(y_{1}\right)^{2}-f\left(x_{1}\right)^{2} . $$ Using $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$, we conclude $f(a) f(-b)>0$. If we multiply the two inequalities $f(a) f(b)<0$ and $f(a) f(-b)>0$, we get $f(a)^{2} f(b) f(-b)<0$ and hence $$ f(b) f(-b)<0 $$ Lemma 3. $f(x) f(-x) \leqslant 0$ for every $x \in \mathbb{R}$. Proof. As in Solution 2, we prove that $f(x)^{2}=f(-x)^{2}$ for every $x \in \mathbb{R}$ and we rewrite the original inequality as $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ We replace $s$ by $-s$ and $t$ by $-t$, and use the relation $f(x)^{2}=f(-x)^{2}$, to get $$ \begin{aligned} f(-s) f(-t) & \geqslant f\left(\frac{-s-t}{2}\right)^{2}-f\left(\frac{-s+t}{2}\right)^{2} \\ & =f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \end{aligned} $$ Up to replacing $t$ by $-t$, we can assume that $f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \geqslant 0$. Multiplying the two previous inequalities leads to $$ f(s) f(-s) f(t) f(-t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This shows that $f(s) f(-s)$ (as a function of $s$ ) has constant sign. Since $f(b) f(-b)<0$, we conclude that $$ f(x) f(-x) \leqslant 0 $$ for every $x \in \mathbb{R}$. Lemma 3, combined with the relation $f(x)^{2}=f(-x)^{2}$, implies $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$, i.e. $f$ is odd. We conclude with the same argument as in Solution 3. Comment. The presence of squares on the right-hand side of the inequality is not crucial as Solution 1 illustrates very well. However, it allows non-constant functions such as $f(x)=|x|$ to satisfy the conditions of the problem statement.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\mathbb{R}$ be the set of real numbers. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that $$ f(x+y) f(x-y) \geqslant f(x)^{2}-f(y)^{2} $$ for every $x, y \in \mathbb{R}$. Assume that the inequality is strict for some $x_{0}, y_{0} \in \mathbb{R}$. Prove that $f(x) \geqslant 0$ for every $x \in \mathbb{R}$ or $f(x) \leqslant 0$ for every $x \in \mathbb{R}$. (Malaysia) Common remarks. We will say that $f$ has constant sign, if $f$ satisfies the conclusion of the problem.
|
As in In this solution, we construct an argument by multiplying inequalities, rather than adding them as in Solutions 1-3. Lemma 2. $f(b) f(-b)<0$. Proof. Let $x_{1}:=\frac{a+b}{2}$ and $y_{1}:=\frac{a-b}{2}$ so that $a=x_{1}+y_{1}$ and $b=x_{1}-y_{1}$. Plugging in $x=x_{1}$ and $y=y_{1}$, we obtain $$ 0>f(a) f(b)=f\left(x_{1}+y_{1}\right) f\left(x_{1}-y_{1}\right) \geqslant f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2} $$ which implies $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$. Similarly, by plugging in $x=y_{1}$ and $y=x_{1}$, we get $$ f(a) f(-b)=f\left(y_{1}+x_{1}\right) f\left(y_{1}-x_{1}\right) \geqslant f\left(y_{1}\right)^{2}-f\left(x_{1}\right)^{2} . $$ Using $f\left(x_{1}\right)^{2}-f\left(y_{1}\right)^{2}<0$, we conclude $f(a) f(-b)>0$. If we multiply the two inequalities $f(a) f(b)<0$ and $f(a) f(-b)>0$, we get $f(a)^{2} f(b) f(-b)<0$ and hence $$ f(b) f(-b)<0 $$ Lemma 3. $f(x) f(-x) \leqslant 0$ for every $x \in \mathbb{R}$. Proof. As in Solution 2, we prove that $f(x)^{2}=f(-x)^{2}$ for every $x \in \mathbb{R}$ and we rewrite the original inequality as $$ f(s) f(t) \geqslant f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} $$ We replace $s$ by $-s$ and $t$ by $-t$, and use the relation $f(x)^{2}=f(-x)^{2}$, to get $$ \begin{aligned} f(-s) f(-t) & \geqslant f\left(\frac{-s-t}{2}\right)^{2}-f\left(\frac{-s+t}{2}\right)^{2} \\ & =f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \end{aligned} $$ Up to replacing $t$ by $-t$, we can assume that $f\left(\frac{s+t}{2}\right)^{2}-f\left(\frac{s-t}{2}\right)^{2} \geqslant 0$. Multiplying the two previous inequalities leads to $$ f(s) f(-s) f(t) f(-t) \geqslant 0 $$ for every $s, t \in \mathbb{R}$. This shows that $f(s) f(-s)$ (as a function of $s$ ) has constant sign. Since $f(b) f(-b)<0$, we conclude that $$ f(x) f(-x) \leqslant 0 $$ for every $x \in \mathbb{R}$. Lemma 3, combined with the relation $f(x)^{2}=f(-x)^{2}$, implies $f(x)+f(-x)=0$ for every $x \in \mathbb{R}$, i.e. $f$ is odd. We conclude with the same argument as in Solution 3. Comment. The presence of squares on the right-hand side of the inequality is not crucial as Solution 1 illustrates very well. However, it allows non-constant functions such as $f(x)=|x|$ to satisfy the conditions of the problem statement.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee1cf4a2-4622-508d-ba8d-eb390f3f34c8
| 607,764
|
Let $k \geqslant 2$ be an integer. Determine all sequences of positive integers $a_{1}, a_{2}, \ldots$ for which there exists a monic polynomial $P$ of degree $k$ with non-negative integer coefficients such that $$ P\left(a_{n}\right)=a_{n+1} a_{n+2} \cdots a_{n+k} $$ for every integer $n \geqslant 1$. (Malaysia) Answer: The sequence $\left(a_{n}\right)$ must be an arithmetic progression consisting of positive integers with common difference $d \geqslant 0$, and $P(x)=(x+d) \cdots(x+k d)$. Common remarks. The following arguments and observations are implicit in the solutions given below. Suppose the sequence $\left(a_{n}\right)$ is an arithmetic progression with common difference $d \geqslant 0$. Then it satisfies the condition with $$ P(x)=(x+d) \cdots(x+k d) $$ This settles one direction. Now suppose $\left(a_{n}\right)$ is a sequence satisfying the condition. We will show that it is a non-decreasing arithmetic progression. Since $P(x)$ has non-negative integer coefficients, it is strictly increasing on the positive real line. In particular, it holds that, for any positive integer $x, y$, $$ P(x)<P(y) \quad \Longleftrightarrow \quad x<y $$ Furthermore, if the sequence $\left(a_{n}\right)$ is eventually constant, then $P(x)=x^{k}$ and the sequence $\left(a_{n}\right)$ is actually constant. Indeed, if $P(x)$ were not the polynomial $x^{k}$, then $P\left(a_{n}\right)=a_{n+1} \cdots a_{n+k}$ cannot be satisfied for $n$ such that $a_{n}=\cdots=a_{n+k}$. By a descending induction, we conclude that $\left(a_{n}\right)$ is constant. Thus we can restrict to the case $\left(a_{n}\right)$ is not eventually constant.
|
We assume that $\left(a_{n}\right)$ is not eventually constant. Step 1. The first goal is to show that the sequence must be increasing, i.e. $a_{n}<a_{n+1}$ for all $n \geqslant 1$. First, by comparing the two equalities $$ \begin{aligned} P\left(a_{n}\right) & =a_{n+1} a_{n+2} \cdots a_{n+k}, \\ P\left(a_{n+1}\right) & =a_{n+2} \cdots a_{n+k} a_{n+k+1}, \end{aligned} $$ we observe that $$ \begin{aligned} & a_{n}<a_{n+1} \Longleftrightarrow P\left(a_{n}\right)<P\left(a_{n+1}\right) \\ & a_{n}>a_{n+1} \Longleftrightarrow \\ & a_{n}=a_{n+1} \Longleftrightarrow a_{n+1}<a_{n+k+1}, \\ & P\left(a_{n}\right)>P\left(a_{n+1}\right) \Longleftrightarrow a_{n+1}>a_{n+k+1}, \\ & \end{aligned}, P\left(a_{n+1}\right) \quad \Longleftrightarrow a_{n+1}=a_{n+k+1} . $$ Claim 1. $\quad a_{n} \leqslant a_{n+1}$ for all $n \geqslant 1$. Proof. Suppose, to the contrary, that $a_{n(0)-1}>a_{n(0)}$ for some $n(0) \geqslant 2$. We will give an infinite sequence of positive integers $n(0)<n(1)<\cdots$ satisfying $$ a_{n(i)-1}>a_{n(i)} \text { and } a_{n(i)}>a_{n(i+1)} . $$ Then $a_{n(0)}, a_{n(1)}, a_{n(2)}, \ldots$ is an infinite decreasing sequence of positive integers, which is absurd. We construct such a sequence inductively. If we have chosen $n(i)$, then we let $n(i+1)$ be the smallest index larger than $n(i)$ such that $a_{n(i)}>a_{n(i+1)}$. Note that such an index always exists and satisfies $n(i)+1 \leqslant n(i+1) \leqslant n(i)+k$ because $a_{n(i)}>a_{n(i)+k}$ by (2). We need to check that $a_{n(i+1)-1}>a_{n(i+1)}$. This is immediate if $n(i+1)=n(i)+1$ by construction. If $n(i+1) \geqslant n(i)+2$, then $a_{n(i+1)-1} \geqslant a_{n(i)}$ by minimality of $n(i+1)$, and so $a_{n(i+1)-1} \geqslant a_{n(i)}>a_{n(i+1)}$. We are now ready to prove that the sequence $a_{n}$ is increasing. Suppose $a_{n}=a_{n+1}$ for some $n \geqslant 1$. Then we also have $a_{n+1}=a_{n+k+1}$ by (3), and since the sequence is non-decreasing we have $a_{n}=a_{n+1}=a_{n+2}=\cdots=a_{n+k+1}$. We repeat the argument for $a_{n+k}=a_{n+k+1}$ and get that the sequence is eventually constant, which contradicts our assumption. Hence $$ a_{n}<a_{n+1} \text { for all } n \geqslant 1 $$ Step 2. The next and final goal is to prove that the sequence $a_{n}$ is an arithmetic progression. Observe that we can make differences of terms appear as follows $$ \begin{aligned} P\left(a_{n}\right) & =a_{n+1} a_{n+2} \cdots a_{n+k} \\ & =\left(a_{n}+\left(a_{n+1}-a_{n}\right)\right)\left(a_{n}+\left(a_{n+2}-a_{n}\right)\right) \cdots\left(a_{n}+\left(a_{n+k}-a_{n}\right)\right) . \end{aligned} $$ We will prove that, for $n$ large enough, the sum $$ \left(a_{n+1}-a_{n}\right)+\left(a_{n+2}-a_{n}\right)+\cdots+\left(a_{n+k}-a_{n}\right) $$ is equal to the coefficient $b$ of the term $x^{k-1}$ in $P$. The argument is based on the following claim. Claim 2. There exists a bound $A$ with the following properties: 1. If $\left(c_{1}, \ldots, c_{k}\right)$ is a $k$-tuple of positive integers with $c_{1}+\cdots+c_{k}>b$, then for every $x \geqslant A$ we have $P(x)<\left(x+c_{1}\right)\left(x+c_{2}\right) \cdots\left(x+c_{k}\right)$. 2. If $\left(c_{1}, \ldots, c_{k}\right)$ is a $k$-tuple of positive integers with $c_{1}+\cdots+c_{k}<b$, then for every $x \geqslant A$ we have $P(x)>\left(x+c_{1}\right)\left(x+c_{2}\right) \cdots\left(x+c_{k}\right)$. Proof. It suffices to show parts 1 and 2 separately, because then we can take the maximum of two bounds. We first show part 1 . For each single $\left(c_{1}, \ldots, c_{k}\right)$ such a bound $A$ exists since $$ P(x)-\left(x+c_{1}\right)\left(x+c_{2}\right) \cdots\left(x+c_{k}\right)=\left(b-\left(c_{1}+\cdots+c_{k}\right)\right) x^{k-1}+(\text { terms of degree } \leqslant k-2) $$ has negative leading coefficient and hence takes negative values for $x$ large enough. Suppose $A$ is a common bound for all tuples $c=\left(c_{1}, \ldots, c_{k}\right)$ satisfying $c_{1}+\cdots+c_{k}=b+1$ (note that there are only finitely many such tuples). Then, for any tuple $c^{\prime}=\left(c_{1}^{\prime}, \ldots, c_{k}^{\prime}\right)$ with $c_{1}^{\prime}+\cdots+c_{k}^{\prime}>b$, there exists a tuple $c=\left(c_{1}, \ldots, c_{k}\right)$ with $c_{1}+\cdots+c_{k}=b+1$ and $c_{i}^{\prime} \geqslant c_{i}$, and then the inequality for $c^{\prime}$ follows from the inequality for $c$. We can show part 2 either in a similar way, or by using that there are only finitely many such tuples. Take $A$ satisfying the assertion of Claim 2, and take $N$ such that $n \geqslant N$ implies $a_{n} \geqslant A$. Then for each $n \geqslant N$, we have $$ \left(a_{n+1}-a_{n}\right)+\cdots+\left(a_{n+k}-a_{n}\right)=b . $$ By taking the difference of this equality and the equality for $n+1$, we obtain $$ a_{n+k+1}-a_{n+1}=k\left(a_{n+1}-a_{n}\right) $$ for every $n \geqslant N$. We conclude using an extremal principle. Let $d=\min \left\{a_{n+1}-a_{n} \mid n \geqslant N\right\}$, and suppose it is attained at some index $n \geqslant N$. Since $$ k d=k\left(a_{n+1}-a_{n}\right)=a_{n+k+1}-a_{n+1}=\sum_{i=1}^{k}\left(a_{n+i+1}-a_{n+i}\right) $$ and each summand is at least $d$, we conclude that $d$ is also attained at $n+1, \ldots, n+k$, and inductively at all $n^{\prime} \geqslant n$. We see that the equation $P(x)=(x+d)(x+2 d) \cdots(x+k d)$ is true for infinitely many values of $x$ (all $a_{n^{\prime}}$ for $n^{\prime} \geqslant n$ ), hence this is an equality of polynomials. Finally we use (backward) induction to show that $a_{n+1}-a_{n}=d$ for every $n \geqslant 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $k \geqslant 2$ be an integer. Determine all sequences of positive integers $a_{1}, a_{2}, \ldots$ for which there exists a monic polynomial $P$ of degree $k$ with non-negative integer coefficients such that $$ P\left(a_{n}\right)=a_{n+1} a_{n+2} \cdots a_{n+k} $$ for every integer $n \geqslant 1$. (Malaysia) Answer: The sequence $\left(a_{n}\right)$ must be an arithmetic progression consisting of positive integers with common difference $d \geqslant 0$, and $P(x)=(x+d) \cdots(x+k d)$. Common remarks. The following arguments and observations are implicit in the solutions given below. Suppose the sequence $\left(a_{n}\right)$ is an arithmetic progression with common difference $d \geqslant 0$. Then it satisfies the condition with $$ P(x)=(x+d) \cdots(x+k d) $$ This settles one direction. Now suppose $\left(a_{n}\right)$ is a sequence satisfying the condition. We will show that it is a non-decreasing arithmetic progression. Since $P(x)$ has non-negative integer coefficients, it is strictly increasing on the positive real line. In particular, it holds that, for any positive integer $x, y$, $$ P(x)<P(y) \quad \Longleftrightarrow \quad x<y $$ Furthermore, if the sequence $\left(a_{n}\right)$ is eventually constant, then $P(x)=x^{k}$ and the sequence $\left(a_{n}\right)$ is actually constant. Indeed, if $P(x)$ were not the polynomial $x^{k}$, then $P\left(a_{n}\right)=a_{n+1} \cdots a_{n+k}$ cannot be satisfied for $n$ such that $a_{n}=\cdots=a_{n+k}$. By a descending induction, we conclude that $\left(a_{n}\right)$ is constant. Thus we can restrict to the case $\left(a_{n}\right)$ is not eventually constant.
|
We assume that $\left(a_{n}\right)$ is not eventually constant. Step 1. The first goal is to show that the sequence must be increasing, i.e. $a_{n}<a_{n+1}$ for all $n \geqslant 1$. First, by comparing the two equalities $$ \begin{aligned} P\left(a_{n}\right) & =a_{n+1} a_{n+2} \cdots a_{n+k}, \\ P\left(a_{n+1}\right) & =a_{n+2} \cdots a_{n+k} a_{n+k+1}, \end{aligned} $$ we observe that $$ \begin{aligned} & a_{n}<a_{n+1} \Longleftrightarrow P\left(a_{n}\right)<P\left(a_{n+1}\right) \\ & a_{n}>a_{n+1} \Longleftrightarrow \\ & a_{n}=a_{n+1} \Longleftrightarrow a_{n+1}<a_{n+k+1}, \\ & P\left(a_{n}\right)>P\left(a_{n+1}\right) \Longleftrightarrow a_{n+1}>a_{n+k+1}, \\ & \end{aligned}, P\left(a_{n+1}\right) \quad \Longleftrightarrow a_{n+1}=a_{n+k+1} . $$ Claim 1. $\quad a_{n} \leqslant a_{n+1}$ for all $n \geqslant 1$. Proof. Suppose, to the contrary, that $a_{n(0)-1}>a_{n(0)}$ for some $n(0) \geqslant 2$. We will give an infinite sequence of positive integers $n(0)<n(1)<\cdots$ satisfying $$ a_{n(i)-1}>a_{n(i)} \text { and } a_{n(i)}>a_{n(i+1)} . $$ Then $a_{n(0)}, a_{n(1)}, a_{n(2)}, \ldots$ is an infinite decreasing sequence of positive integers, which is absurd. We construct such a sequence inductively. If we have chosen $n(i)$, then we let $n(i+1)$ be the smallest index larger than $n(i)$ such that $a_{n(i)}>a_{n(i+1)}$. Note that such an index always exists and satisfies $n(i)+1 \leqslant n(i+1) \leqslant n(i)+k$ because $a_{n(i)}>a_{n(i)+k}$ by (2). We need to check that $a_{n(i+1)-1}>a_{n(i+1)}$. This is immediate if $n(i+1)=n(i)+1$ by construction. If $n(i+1) \geqslant n(i)+2$, then $a_{n(i+1)-1} \geqslant a_{n(i)}$ by minimality of $n(i+1)$, and so $a_{n(i+1)-1} \geqslant a_{n(i)}>a_{n(i+1)}$. We are now ready to prove that the sequence $a_{n}$ is increasing. Suppose $a_{n}=a_{n+1}$ for some $n \geqslant 1$. Then we also have $a_{n+1}=a_{n+k+1}$ by (3), and since the sequence is non-decreasing we have $a_{n}=a_{n+1}=a_{n+2}=\cdots=a_{n+k+1}$. We repeat the argument for $a_{n+k}=a_{n+k+1}$ and get that the sequence is eventually constant, which contradicts our assumption. Hence $$ a_{n}<a_{n+1} \text { for all } n \geqslant 1 $$ Step 2. The next and final goal is to prove that the sequence $a_{n}$ is an arithmetic progression. Observe that we can make differences of terms appear as follows $$ \begin{aligned} P\left(a_{n}\right) & =a_{n+1} a_{n+2} \cdots a_{n+k} \\ & =\left(a_{n}+\left(a_{n+1}-a_{n}\right)\right)\left(a_{n}+\left(a_{n+2}-a_{n}\right)\right) \cdots\left(a_{n}+\left(a_{n+k}-a_{n}\right)\right) . \end{aligned} $$ We will prove that, for $n$ large enough, the sum $$ \left(a_{n+1}-a_{n}\right)+\left(a_{n+2}-a_{n}\right)+\cdots+\left(a_{n+k}-a_{n}\right) $$ is equal to the coefficient $b$ of the term $x^{k-1}$ in $P$. The argument is based on the following claim. Claim 2. There exists a bound $A$ with the following properties: 1. If $\left(c_{1}, \ldots, c_{k}\right)$ is a $k$-tuple of positive integers with $c_{1}+\cdots+c_{k}>b$, then for every $x \geqslant A$ we have $P(x)<\left(x+c_{1}\right)\left(x+c_{2}\right) \cdots\left(x+c_{k}\right)$. 2. If $\left(c_{1}, \ldots, c_{k}\right)$ is a $k$-tuple of positive integers with $c_{1}+\cdots+c_{k}<b$, then for every $x \geqslant A$ we have $P(x)>\left(x+c_{1}\right)\left(x+c_{2}\right) \cdots\left(x+c_{k}\right)$. Proof. It suffices to show parts 1 and 2 separately, because then we can take the maximum of two bounds. We first show part 1 . For each single $\left(c_{1}, \ldots, c_{k}\right)$ such a bound $A$ exists since $$ P(x)-\left(x+c_{1}\right)\left(x+c_{2}\right) \cdots\left(x+c_{k}\right)=\left(b-\left(c_{1}+\cdots+c_{k}\right)\right) x^{k-1}+(\text { terms of degree } \leqslant k-2) $$ has negative leading coefficient and hence takes negative values for $x$ large enough. Suppose $A$ is a common bound for all tuples $c=\left(c_{1}, \ldots, c_{k}\right)$ satisfying $c_{1}+\cdots+c_{k}=b+1$ (note that there are only finitely many such tuples). Then, for any tuple $c^{\prime}=\left(c_{1}^{\prime}, \ldots, c_{k}^{\prime}\right)$ with $c_{1}^{\prime}+\cdots+c_{k}^{\prime}>b$, there exists a tuple $c=\left(c_{1}, \ldots, c_{k}\right)$ with $c_{1}+\cdots+c_{k}=b+1$ and $c_{i}^{\prime} \geqslant c_{i}$, and then the inequality for $c^{\prime}$ follows from the inequality for $c$. We can show part 2 either in a similar way, or by using that there are only finitely many such tuples. Take $A$ satisfying the assertion of Claim 2, and take $N$ such that $n \geqslant N$ implies $a_{n} \geqslant A$. Then for each $n \geqslant N$, we have $$ \left(a_{n+1}-a_{n}\right)+\cdots+\left(a_{n+k}-a_{n}\right)=b . $$ By taking the difference of this equality and the equality for $n+1$, we obtain $$ a_{n+k+1}-a_{n+1}=k\left(a_{n+1}-a_{n}\right) $$ for every $n \geqslant N$. We conclude using an extremal principle. Let $d=\min \left\{a_{n+1}-a_{n} \mid n \geqslant N\right\}$, and suppose it is attained at some index $n \geqslant N$. Since $$ k d=k\left(a_{n+1}-a_{n}\right)=a_{n+k+1}-a_{n+1}=\sum_{i=1}^{k}\left(a_{n+i+1}-a_{n+i}\right) $$ and each summand is at least $d$, we conclude that $d$ is also attained at $n+1, \ldots, n+k$, and inductively at all $n^{\prime} \geqslant n$. We see that the equation $P(x)=(x+d)(x+2 d) \cdots(x+k d)$ is true for infinitely many values of $x$ (all $a_{n^{\prime}}$ for $n^{\prime} \geqslant n$ ), hence this is an equality of polynomials. Finally we use (backward) induction to show that $a_{n+1}-a_{n}=d$ for every $n \geqslant 1$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5c33a9ad-4c9e-5512-84bc-8035568103eb
| 607,767
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.