problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$. (China)
|
The idea is to approximate the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ by the nearest integer with errors $<0.5$. This gives the following sequence $$ 1,1,2,2,2,2,3,3,3,3,3,3,4, \ldots $$ More precisely, for each $k \geqslant 1$, we round $\sqrt{k^{2}-k+1}, \ldots, \sqrt{k^{2}+k}$ to $k$, so that there are $2 k$ copies of $k$. Step 1. We first consider the easier case when $N$ has the form $$ N=m(m+1) . $$ In this case, the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ are approximated by the elements of the multiset $\left\{1_{\times 2}, 2_{\times 4}, 3_{\times 6}, \ldots, m_{\times 2 m}\right\}$. Let $T_{m}$ denote "half of" the multiset, i.e. $$ T_{m}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m}\right\} . $$ We will prove by induction that there exists three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of the elements in the multiset $T_{m}$ such that $u_{k}+v_{k}+w_{k}=2 m+1$ is constant for $k=1,2, \ldots, \frac{m(m+1)}{2}$. When $m=1$, take $1+1+1=3$. When $m=2$, take $(1,2,2)+(2,1,2)+(2,2,1)=(5,5,5)$. Suppose that we have constructed three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of $T_{m-1}$ satisfying $u_{k}+v_{k}+w_{k}=2 m-1$ for every $k=1,2, \ldots, \frac{m(m-1)}{2}$. For $T_{m}$, we note that $$ T_{m}=T_{m-1} \sqcup\left\{m_{\times m}\right\}, $$ and also $$ T_{m}=\left(T_{m-1}+1\right) \sqcup\{1,2, \ldots, m\} . $$ Here $T_{m-1}+1$ means to add 1 to all elements in $T_{m-1}$. We construct the permutations $\left(u_{k}^{\prime}\right)$, $\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1, w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m, v_{k}^{\prime}=r, w_{k}^{\prime}=m+1-r$. It is clear from (1) that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m}$, and that they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime}=2 m+1$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}$. The inductive construction can be visualised by the $3 \times \frac{m(m+1)}{2}$ matrix $$ \left[\begin{array}{cccccc} u_{1} & \ldots & u_{m(m-1) / 2} & m & \ldots & m \\ v_{1}+1 & \ldots & v_{m(m-1) / 2}+1 & 1 & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2}+1 & m & \ldots & 1 \end{array}\right] $$ in which the three rows represent the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right),\left(w_{k}^{\prime}\right)$, and the sum of the three entries of each column is $2 m+1$. Thus, when $N=m^{2}+m$, we can construct permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, N$ such that $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+1+1.5 $$ This gives $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2.5<2023 $$ where we used that $-1<2 m-2 \sqrt{m^{2}+m}<0$ for positive $m$. Step 2. We now proceed to the general case. Let $m$ be such that $$ m(m+1) \leqslant N<(m+1)(m+2) $$ Write $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$ and let $$ L:=\left\lfloor\frac{4}{9} N\right\rfloor . $$ We will make use of the following inequalities below: $$ N>m^{2}, \quad N<(m+2)^{2}, \quad t \leqslant 2 m+1, \quad L+1>4 N / 9, \quad L \leqslant 4 N / 9 . $$ As above, we construct three permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, m(m+1)$ satisfying (2). Now we construct the three required permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$ as follows: For $k=1,2, \ldots, m(m+1)$, if $a_{k} \leqslant L$, take $A_{k}=a_{k}$, and if $a_{k}>L$, take $A_{k}=a_{k}+t$. For $k=m(m+1)+r$ with $r=1,2, \ldots, t$, set $A_{k}=L+r$. Define the permutations $\left(B_{k}\right)$ and $\left(C_{k}\right)$ similarly. Now for $k=1,2, \ldots, m(m+1)$, we show $0 \leqslant \sqrt{A_{k}}-\sqrt{a_{k}} \leqslant 2$. The lower bound is obvious. If $m \leqslant 1$, then $N \leqslant 5$ and hence $\sqrt{A_{k}}-\sqrt{a_{k}} \leqslant \sqrt{5}-\sqrt{1} \leqslant 2$. If $m \geqslant 2$, then $$ \sqrt{A_{k}}-\sqrt{a_{k}}=\frac{A_{k}-a_{k}}{\sqrt{A_{k}}+\sqrt{a_{k}}} \leqslant \frac{t}{2 \sqrt{L+1}} \leqslant \frac{2 m+1}{\frac{4}{3} m} \leqslant 2 . $$ We have similar inequalities for $\left(B_{k}\right)$ and $\left(C_{k}\right)$. Thus $$ 2 \sqrt{N}-4.5<2 m+1-1.5 \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 2 m+1+1.5+6<2 \sqrt{N}+8.5 . $$ For $k=m^{2}+m+1, \ldots, m^{2}+m+t$, we have $$ 2 \sqrt{N}<3 \sqrt{L+1} \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 3 \sqrt{L+t} \leqslant \sqrt{4 N+9 t}<2 \sqrt{N}+8.5 $$ To sum up, we have defined three permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$, such that $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<8.5<2023 $$ holds for every $k=1,2, \ldots, N$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$. (China)
|
The idea is to approximate the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ by the nearest integer with errors $<0.5$. This gives the following sequence $$ 1,1,2,2,2,2,3,3,3,3,3,3,4, \ldots $$ More precisely, for each $k \geqslant 1$, we round $\sqrt{k^{2}-k+1}, \ldots, \sqrt{k^{2}+k}$ to $k$, so that there are $2 k$ copies of $k$. Step 1. We first consider the easier case when $N$ has the form $$ N=m(m+1) . $$ In this case, the numbers $\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}$ are approximated by the elements of the multiset $\left\{1_{\times 2}, 2_{\times 4}, 3_{\times 6}, \ldots, m_{\times 2 m}\right\}$. Let $T_{m}$ denote "half of" the multiset, i.e. $$ T_{m}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m}\right\} . $$ We will prove by induction that there exists three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of the elements in the multiset $T_{m}$ such that $u_{k}+v_{k}+w_{k}=2 m+1$ is constant for $k=1,2, \ldots, \frac{m(m+1)}{2}$. When $m=1$, take $1+1+1=3$. When $m=2$, take $(1,2,2)+(2,1,2)+(2,2,1)=(5,5,5)$. Suppose that we have constructed three permutations $\left(u_{k}\right),\left(v_{k}\right)$, and $\left(w_{k}\right)$ of $T_{m-1}$ satisfying $u_{k}+v_{k}+w_{k}=2 m-1$ for every $k=1,2, \ldots, \frac{m(m-1)}{2}$. For $T_{m}$, we note that $$ T_{m}=T_{m-1} \sqcup\left\{m_{\times m}\right\}, $$ and also $$ T_{m}=\left(T_{m-1}+1\right) \sqcup\{1,2, \ldots, m\} . $$ Here $T_{m-1}+1$ means to add 1 to all elements in $T_{m-1}$. We construct the permutations $\left(u_{k}^{\prime}\right)$, $\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1, w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m, v_{k}^{\prime}=r, w_{k}^{\prime}=m+1-r$. It is clear from (1) that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m}$, and that they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime}=2 m+1$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}$. The inductive construction can be visualised by the $3 \times \frac{m(m+1)}{2}$ matrix $$ \left[\begin{array}{cccccc} u_{1} & \ldots & u_{m(m-1) / 2} & m & \ldots & m \\ v_{1}+1 & \ldots & v_{m(m-1) / 2}+1 & 1 & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2}+1 & m & \ldots & 1 \end{array}\right] $$ in which the three rows represent the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right),\left(w_{k}^{\prime}\right)$, and the sum of the three entries of each column is $2 m+1$. Thus, when $N=m^{2}+m$, we can construct permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, N$ such that $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+1+1.5 $$ This gives $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2.5<2023 $$ where we used that $-1<2 m-2 \sqrt{m^{2}+m}<0$ for positive $m$. Step 2. We now proceed to the general case. Let $m$ be such that $$ m(m+1) \leqslant N<(m+1)(m+2) $$ Write $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$ and let $$ L:=\left\lfloor\frac{4}{9} N\right\rfloor . $$ We will make use of the following inequalities below: $$ N>m^{2}, \quad N<(m+2)^{2}, \quad t \leqslant 2 m+1, \quad L+1>4 N / 9, \quad L \leqslant 4 N / 9 . $$ As above, we construct three permutations $\left(a_{k}\right),\left(b_{k}\right)$, and $\left(c_{k}\right)$ of $1,2, \ldots, m(m+1)$ satisfying (2). Now we construct the three required permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$ as follows: For $k=1,2, \ldots, m(m+1)$, if $a_{k} \leqslant L$, take $A_{k}=a_{k}$, and if $a_{k}>L$, take $A_{k}=a_{k}+t$. For $k=m(m+1)+r$ with $r=1,2, \ldots, t$, set $A_{k}=L+r$. Define the permutations $\left(B_{k}\right)$ and $\left(C_{k}\right)$ similarly. Now for $k=1,2, \ldots, m(m+1)$, we show $0 \leqslant \sqrt{A_{k}}-\sqrt{a_{k}} \leqslant 2$. The lower bound is obvious. If $m \leqslant 1$, then $N \leqslant 5$ and hence $\sqrt{A_{k}}-\sqrt{a_{k}} \leqslant \sqrt{5}-\sqrt{1} \leqslant 2$. If $m \geqslant 2$, then $$ \sqrt{A_{k}}-\sqrt{a_{k}}=\frac{A_{k}-a_{k}}{\sqrt{A_{k}}+\sqrt{a_{k}}} \leqslant \frac{t}{2 \sqrt{L+1}} \leqslant \frac{2 m+1}{\frac{4}{3} m} \leqslant 2 . $$ We have similar inequalities for $\left(B_{k}\right)$ and $\left(C_{k}\right)$. Thus $$ 2 \sqrt{N}-4.5<2 m+1-1.5 \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 2 m+1+1.5+6<2 \sqrt{N}+8.5 . $$ For $k=m^{2}+m+1, \ldots, m^{2}+m+t$, we have $$ 2 \sqrt{N}<3 \sqrt{L+1} \leqslant \sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}} \leqslant 3 \sqrt{L+t} \leqslant \sqrt{4 N+9 t}<2 \sqrt{N}+8.5 $$ To sum up, we have defined three permutations $\left(A_{k}\right),\left(B_{k}\right)$, and $\left(C_{k}\right)$ of $1,2, \ldots, N$, such that $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<8.5<2023 $$ holds for every $k=1,2, \ldots, N$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
94d4c55b-96e6-5b76-9b07-c270fd805215
| 607,768
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$. (China)
|
This is a variation of Let $n$ be an integer satisfying $0 \leqslant n \leqslant m+1$ and define the multiset $T_{m, n}$ by $$ T_{m, n}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m},(m+1)_{\times n}\right\} . $$ In other words, $T_{m, 0}=T_{m}, T_{m, n}=T_{m} \sqcup\left\{(m+1)_{\times n}\right\}$ and $T_{m, m+1}=T_{m+1}$, where $T_{m}$ is the set defined in Solution 1. Claim. There exist three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m, n}$ such that $$ \begin{cases}u_{k}+v_{k}+w_{k}=2 m+1 & (n=0) \\ u_{k}+v_{k}+w_{k} \in\{2 m+1,2 m+2,2 m+3\} & (1 \leqslant n \leqslant m) \\ u_{k}+v_{k}+w_{k}=2 m+3 & (n=m+1)\end{cases} $$ Proof. We proceed by induction on $m$. If $n=0$ or $n=m+1$, the assertion can be proved as in Solution 1. If $1 \leqslant n \leqslant m$, we note that $$ T_{m, n}=T_{m-1, n} \sqcup\left\{m_{\times(m-n)},(m+1)_{\times n}\right\}=\left(T_{m-1, n}+1\right) \sqcup\{1,2, \ldots, m\} . $$ From the hypothesis of induction, it follows that we have three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m-1, n}$ satisfying $u_{k}+v_{k}+w_{k} \in\{2 m-1,2 m, 2 m+1\}$ for every $k$. We construct the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m, n}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}+n$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1$, and $w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+n+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m$ if $1 \leqslant r \leqslant m-n$ while $u_{k}^{\prime}=m+1$ if $m-n+1 \leqslant r \leqslant m, v_{k}^{\prime}=r$, and $w_{k}^{\prime}=m+1-r$. It is clear from the construction that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m, n}$, and they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime} \in\{2 m+1,2 m+2,2 m+3\}$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}+n$. Again, we can visualise the construction using the matrix $$ \left[\begin{array}{ccccccccc} u_{1} & \ldots & u_{m(m-1) / 2+n} & m & \ldots & m & m+1 & \ldots & m+1 \\ v_{1}+1 & \ldots & v_{m(m-1) / 2+n}+1 & 1 & \ldots & \ldots & \ldots & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2+n}+1 & m & \ldots & \ldots & \ldots & \ldots & 1 \end{array}\right] $$ In general, we have $m(m+1) \leqslant N<(m+1)(m+2)$ for some $m \geqslant 0$. Set $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$. Then the approximation of $\{\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}\}$ by the nearest integer with errors $<0.5$ is a multiset $$ \left\{1_{\times 2}, 2_{\times 4}, \ldots, m_{\times 2 m},(m+1)_{\times t}\right\}=T_{m, n_{1}} \sqcup T_{m, n_{2}} $$ with $n_{1}=\lfloor t / 2\rfloor$ and $n_{2}=\lceil t / 2\rceil$. Since $0 \leqslant n_{1} \leqslant n_{2} \leqslant m+1$, by using the Claim we can construct permutations $\left(a_{k}\right)$, $\left(b_{k}\right)$, and $\left(c_{k}\right)$ to satisfy the following inequality: $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5 $$ Since $m<\sqrt{N}<m+2$, it follows that $$ 2 \sqrt{N}-4.5<2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5<2 \sqrt{N}+4.5 $$ and so $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<4.5<2023 $$ 
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer. Prove that there exist three permutations $a_{1}, a_{2}, \ldots, a_{N}$; $b_{1}, b_{2}, \ldots, b_{N}$; and $c_{1}, c_{2}, \ldots, c_{N}$ of $1,2, \ldots, N$ such that $$ \left|\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}-2 \sqrt{N}\right|<2023 $$ for every $k=1,2, \ldots, N$. (China)
|
This is a variation of Let $n$ be an integer satisfying $0 \leqslant n \leqslant m+1$ and define the multiset $T_{m, n}$ by $$ T_{m, n}:=\left\{1_{\times 1}, 2_{\times 2}, 3_{\times 3}, \ldots, m_{\times m},(m+1)_{\times n}\right\} . $$ In other words, $T_{m, 0}=T_{m}, T_{m, n}=T_{m} \sqcup\left\{(m+1)_{\times n}\right\}$ and $T_{m, m+1}=T_{m+1}$, where $T_{m}$ is the set defined in Solution 1. Claim. There exist three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m, n}$ such that $$ \begin{cases}u_{k}+v_{k}+w_{k}=2 m+1 & (n=0) \\ u_{k}+v_{k}+w_{k} \in\{2 m+1,2 m+2,2 m+3\} & (1 \leqslant n \leqslant m) \\ u_{k}+v_{k}+w_{k}=2 m+3 & (n=m+1)\end{cases} $$ Proof. We proceed by induction on $m$. If $n=0$ or $n=m+1$, the assertion can be proved as in Solution 1. If $1 \leqslant n \leqslant m$, we note that $$ T_{m, n}=T_{m-1, n} \sqcup\left\{m_{\times(m-n)},(m+1)_{\times n}\right\}=\left(T_{m-1, n}+1\right) \sqcup\{1,2, \ldots, m\} . $$ From the hypothesis of induction, it follows that we have three permutations $\left(u_{k}\right),\left(v_{k}\right),\left(w_{k}\right)$ of $T_{m-1, n}$ satisfying $u_{k}+v_{k}+w_{k} \in\{2 m-1,2 m, 2 m+1\}$ for every $k$. We construct the permutations $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ of $T_{m, n}$ as follows: - For $k=1,2, \ldots, \frac{m(m-1)}{2}+n$, we set $u_{k}^{\prime}=u_{k}, v_{k}^{\prime}=v_{k}+1$, and $w_{k}^{\prime}=w_{k}+1$. - For $k=\frac{m(m-1)}{2}+n+r$ with $r=1,2, \ldots, m$, we set $u_{k}^{\prime}=m$ if $1 \leqslant r \leqslant m-n$ while $u_{k}^{\prime}=m+1$ if $m-n+1 \leqslant r \leqslant m, v_{k}^{\prime}=r$, and $w_{k}^{\prime}=m+1-r$. It is clear from the construction that $\left(u_{k}^{\prime}\right),\left(v_{k}^{\prime}\right)$, and $\left(w_{k}^{\prime}\right)$ give three permutations of $T_{m, n}$, and they satisfy $u_{k}^{\prime}+v_{k}^{\prime}+w_{k}^{\prime} \in\{2 m+1,2 m+2,2 m+3\}$ for every $k=1,2, \ldots, \frac{m(m+1)}{2}+n$. Again, we can visualise the construction using the matrix $$ \left[\begin{array}{ccccccccc} u_{1} & \ldots & u_{m(m-1) / 2+n} & m & \ldots & m & m+1 & \ldots & m+1 \\ v_{1}+1 & \ldots & v_{m(m-1) / 2+n}+1 & 1 & \ldots & \ldots & \ldots & \ldots & m \\ w_{1}+1 & \ldots & w_{m(m-1) / 2+n}+1 & m & \ldots & \ldots & \ldots & \ldots & 1 \end{array}\right] $$ In general, we have $m(m+1) \leqslant N<(m+1)(m+2)$ for some $m \geqslant 0$. Set $N=m(m+1)+t$ for some $t \in\{0,1, \ldots, 2 m+1\}$. Then the approximation of $\{\sqrt{1}, \sqrt{2}, \ldots, \sqrt{N}\}$ by the nearest integer with errors $<0.5$ is a multiset $$ \left\{1_{\times 2}, 2_{\times 4}, \ldots, m_{\times 2 m},(m+1)_{\times t}\right\}=T_{m, n_{1}} \sqcup T_{m, n_{2}} $$ with $n_{1}=\lfloor t / 2\rfloor$ and $n_{2}=\lceil t / 2\rceil$. Since $0 \leqslant n_{1} \leqslant n_{2} \leqslant m+1$, by using the Claim we can construct permutations $\left(a_{k}\right)$, $\left(b_{k}\right)$, and $\left(c_{k}\right)$ to satisfy the following inequality: $$ 2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5 $$ Since $m<\sqrt{N}<m+2$, it follows that $$ 2 \sqrt{N}-4.5<2 m+1-1.5<\sqrt{a_{k}}+\sqrt{b_{k}}+\sqrt{c_{k}}<2 m+3+1.5<2 \sqrt{N}+4.5 $$ and so $$ \left|\sqrt{A_{k}}+\sqrt{B_{k}}+\sqrt{C_{k}}-2 \sqrt{N}\right|<4.5<2023 $$ 
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
94d4c55b-96e6-5b76-9b07-c270fd805215
| 607,768
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We define a good parallelogram to be a parallelogram composed of two isosceles right-angled triangles glued together as shown below.  Given any partition into $k$ right-down or right-up paths, we can find a corresponding packing of good parallelograms that leaves an area of $k$ empty. Thus, it suffices to prove that we must leave an area of at least $N$ empty when we pack good parallelograms into an $N \times N$ grid. This is actually equivalent to the original problem since we can uniquely recover the partition into right-down or right-up paths from the corresponding packing of good parallelograms.  We draw one of the diagonals in each cell so that it does not intersect any of the good parallelograms. Now, view these segments as mirrors, and consider a laser entering each of the $4 N$ boundary edges (with starting direction being perpendicular to the edge), bouncing along these mirrors until it exits at some other edge. When a laser passes through a good parallelogram, its direction goes back to the original one after bouncing two times. Thus, if the final direction of a laser is perpendicular to its initial direction, it must pass through at least one empty triangle. Similarly, if the final direction of a laser is opposite to its initial direction, it must pass though at least two empty triangles. Using this, we will estimate the number of empty triangles in the $N \times N$ grid. We associate the starting edge of a laser with the edge it exits at. Then, the boundary edges are divided into $2 N$ pairs. These pairs can be classified into three types: (1) a pair of a vertical and a horizontal boundary edge, (2) a pair of boundary edges from the same side, and (3) a pair of boundary edges from opposite sides. Since the beams do not intersect, we cannot have one type (3) pair from vertical boundary edges and another type (3) pair from horizontal boundary edges. Without loss of generality, we may assume that we have $t$ pairs of type (3) and they are all from vertical boundary edges. Then, out of the remaining boundary edges, there are $2 N$ horizontal boundary edges and $2 N-2 t$ vertical boundary edges. It follows that there must be at least $t$ pairs of type (2) from horizontal boundary edges. We know that a laser corresponding to a pair of type (1) passes through at least one empty triangle, and a laser corresponding to a pair of type (2) passes through at least two empty triangles. Thus, as the beams do not intersect, we have at least $(2 N-2 t)+2 \cdot t=2 N$ empty triangles in the grid, leaving an area of at least $N$ empty as required.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We define a good parallelogram to be a parallelogram composed of two isosceles right-angled triangles glued together as shown below.  Given any partition into $k$ right-down or right-up paths, we can find a corresponding packing of good parallelograms that leaves an area of $k$ empty. Thus, it suffices to prove that we must leave an area of at least $N$ empty when we pack good parallelograms into an $N \times N$ grid. This is actually equivalent to the original problem since we can uniquely recover the partition into right-down or right-up paths from the corresponding packing of good parallelograms.  We draw one of the diagonals in each cell so that it does not intersect any of the good parallelograms. Now, view these segments as mirrors, and consider a laser entering each of the $4 N$ boundary edges (with starting direction being perpendicular to the edge), bouncing along these mirrors until it exits at some other edge. When a laser passes through a good parallelogram, its direction goes back to the original one after bouncing two times. Thus, if the final direction of a laser is perpendicular to its initial direction, it must pass through at least one empty triangle. Similarly, if the final direction of a laser is opposite to its initial direction, it must pass though at least two empty triangles. Using this, we will estimate the number of empty triangles in the $N \times N$ grid. We associate the starting edge of a laser with the edge it exits at. Then, the boundary edges are divided into $2 N$ pairs. These pairs can be classified into three types: (1) a pair of a vertical and a horizontal boundary edge, (2) a pair of boundary edges from the same side, and (3) a pair of boundary edges from opposite sides. Since the beams do not intersect, we cannot have one type (3) pair from vertical boundary edges and another type (3) pair from horizontal boundary edges. Without loss of generality, we may assume that we have $t$ pairs of type (3) and they are all from vertical boundary edges. Then, out of the remaining boundary edges, there are $2 N$ horizontal boundary edges and $2 N-2 t$ vertical boundary edges. It follows that there must be at least $t$ pairs of type (2) from horizontal boundary edges. We know that a laser corresponding to a pair of type (1) passes through at least one empty triangle, and a laser corresponding to a pair of type (2) passes through at least two empty triangles. Thus, as the beams do not intersect, we have at least $(2 N-2 t)+2 \cdot t=2 N$ empty triangles in the grid, leaving an area of at least $N$ empty as required.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ffa89abe-caf1-5b81-b52c-f42ac0be717b
| 607,773
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We apply an induction on $N$. The base case $N=1$ is trivial. Suppose that the claim holds for $N-1$ and prove it for $N \geqslant 2$. Let us denote the path containing the upper left corner by $P$. If $P$ is right-up, then every cell in $P$ is in the top row or in the leftmost column. By the induction hypothesis, there are at least $N-1$ paths passing through the lower right $(N-1) \times(N-1)$ subgrid. Since $P$ is not amongst them, we have at least $N$ paths. Next, assume that $P$ is right-down. If $P$ contains the lower right corner, then we get an $(N-1) \times(N-1)$ grid by removing $P$ and glueing the remaining two parts together. The main idea is to extend $P$ so that it contains the lower right corner and the above procedure gives a valid partition of an $(N-1) \times(N-1)$ grid.  We inductively construct $Q$, which denotes an extension of $P$ as a right-down path. Initially, $Q=P$. Let $A$ be the last cell of $Q, B$ be the cell below $A$, and $C$ be the cell to the right of $A$ (if they exist). Suppose that $A$ is not the lower right corner, and that (*) both $B$ and $C$ do not belong to the same path as $A$. Then, we can extend $Q$ as follows (in case we have two or more options, we can choose any one of them to extend $Q$ ). 1. If $B$ belongs to a right-down path $R$, then we add the part of $R$, from $B$ to its end, to $Q$. 2. If $C$ belongs to a right-down path $R$, then we add the part of $R$, from $C$ to its end, to $Q$. 3. If $B$ belongs to a right-up path $R$ which ends at $B$, then we add the part of $R$ in the same column as $B$ to $Q$. 4. If $C$ belongs to a right-up path $R$ which starts at $C$, then we add the part of $R$ in the same row as $C$ to $Q$. 5. Otherwise, $B$ and $C$ must belong to the same right-up path $R$. In this case, we add $B$ and the cell to the right of $B$ to $Q$. Note that if $B$ does not exist, then case (4) must hold. If $C$ does not exist, then case (3) must hold. It is easily seen that such an extension also satisfies the hypothesis (*), so we can repeat this construction to get an extension of $P$ containing the lower right corner, denoted by $Q$. We show that this is a desired extension, i.e. the partition of an $(N-1) \times(N-1)$ grid obtained by removing $Q$ and glueing the remaining two parts together consists of right-down or right-up paths. Take a path $R$ in the partition of the $N \times N$ grid intersecting $Q$. If the intersection of $Q$ and $R$ occurs in case (1) or case (2), then there exists a cell $D$ in $R$ such that the intersection of $Q$ and $R$ is the part of $R$ from $D$ to its end, so $R$ remains a right-down path after removal of $Q$. Similarly, if the intersection of $Q$ and $R$ occurs in case (3) or case (4), then $R$ remains a right-up path after removal of $Q$. If the intersection of $Q$ and $R$ occurs in case (5), then this intersection has exactly two adjacent cells. After the removal of these two cells (as we remove $Q), R$ is divided into two parts that are glued into a right-up path. Thus, we may apply the induction hypothesis to the resulting partition of an $(N-1) \times(N-1)$ grid, to find that it must contain at least $N-1$ paths. Since $P$ is contained in $Q$ and is not amongst these paths, the original partition must contain at least $N$ paths.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $N$ be a positive integer, and consider an $N \times N$ grid. A right-down path is a sequence of grid cells such that each cell is either one cell to the right of or one cell below the previous cell in the sequence. A right-up path is a sequence of grid cells such that each cell is either one cell to the right of or one cell above the previous cell in the sequence. Prove that the cells of the $N \times N$ grid cannot be partitioned into less than $N$ right-down or right-up paths. For example, the following partition of the $5 \times 5$ grid uses 5 paths.  (Canada)
|
We apply an induction on $N$. The base case $N=1$ is trivial. Suppose that the claim holds for $N-1$ and prove it for $N \geqslant 2$. Let us denote the path containing the upper left corner by $P$. If $P$ is right-up, then every cell in $P$ is in the top row or in the leftmost column. By the induction hypothesis, there are at least $N-1$ paths passing through the lower right $(N-1) \times(N-1)$ subgrid. Since $P$ is not amongst them, we have at least $N$ paths. Next, assume that $P$ is right-down. If $P$ contains the lower right corner, then we get an $(N-1) \times(N-1)$ grid by removing $P$ and glueing the remaining two parts together. The main idea is to extend $P$ so that it contains the lower right corner and the above procedure gives a valid partition of an $(N-1) \times(N-1)$ grid.  We inductively construct $Q$, which denotes an extension of $P$ as a right-down path. Initially, $Q=P$. Let $A$ be the last cell of $Q, B$ be the cell below $A$, and $C$ be the cell to the right of $A$ (if they exist). Suppose that $A$ is not the lower right corner, and that (*) both $B$ and $C$ do not belong to the same path as $A$. Then, we can extend $Q$ as follows (in case we have two or more options, we can choose any one of them to extend $Q$ ). 1. If $B$ belongs to a right-down path $R$, then we add the part of $R$, from $B$ to its end, to $Q$. 2. If $C$ belongs to a right-down path $R$, then we add the part of $R$, from $C$ to its end, to $Q$. 3. If $B$ belongs to a right-up path $R$ which ends at $B$, then we add the part of $R$ in the same column as $B$ to $Q$. 4. If $C$ belongs to a right-up path $R$ which starts at $C$, then we add the part of $R$ in the same row as $C$ to $Q$. 5. Otherwise, $B$ and $C$ must belong to the same right-up path $R$. In this case, we add $B$ and the cell to the right of $B$ to $Q$. Note that if $B$ does not exist, then case (4) must hold. If $C$ does not exist, then case (3) must hold. It is easily seen that such an extension also satisfies the hypothesis (*), so we can repeat this construction to get an extension of $P$ containing the lower right corner, denoted by $Q$. We show that this is a desired extension, i.e. the partition of an $(N-1) \times(N-1)$ grid obtained by removing $Q$ and glueing the remaining two parts together consists of right-down or right-up paths. Take a path $R$ in the partition of the $N \times N$ grid intersecting $Q$. If the intersection of $Q$ and $R$ occurs in case (1) or case (2), then there exists a cell $D$ in $R$ such that the intersection of $Q$ and $R$ is the part of $R$ from $D$ to its end, so $R$ remains a right-down path after removal of $Q$. Similarly, if the intersection of $Q$ and $R$ occurs in case (3) or case (4), then $R$ remains a right-up path after removal of $Q$. If the intersection of $Q$ and $R$ occurs in case (5), then this intersection has exactly two adjacent cells. After the removal of these two cells (as we remove $Q), R$ is divided into two parts that are glued into a right-up path. Thus, we may apply the induction hypothesis to the resulting partition of an $(N-1) \times(N-1)$ grid, to find that it must contain at least $N-1$ paths. Since $P$ is contained in $Q$ and is not amongst these paths, the original partition must contain at least $N$ paths.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ffa89abe-caf1-5b81-b52c-f42ac0be717b
| 607,773
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear. (Ukraine)
|
 We write $\triangle P_{1} P_{2} P_{3} \stackrel{ \pm}{\sim} \triangle Q_{1} Q_{2} Q_{3}$ (resp. $\triangle P_{1} P_{2} P_{3} \approx \triangle Q_{1} Q_{2} Q_{3}$ ) to indicate that two triangles are directly (resp. oppositely) similar. We use directed angles throughout denoted with $\Varangle$. Denote by $A_{b}, A_{c}$ the reflections of $A$ in $B H$ and $C H$ respectively. $B_{c}, B_{a}$ and $C_{a}, C_{b}$ are defined similarly. By definition, $\ell_{a}=B_{c} C_{b}, \ell_{b}=C_{a} A_{c}, \ell_{c}=A_{b} B_{a}$. Let $A_{1}=\ell_{b} \cap \ell_{c}$, $B_{1}=\ell_{c} \cap \ell_{a}, C_{1}=\ell_{a} \cap \ell_{b}$ and let $O_{1}, H_{1}$ be the orthocentre and circumcentre of $\mathcal{T} \equiv \triangle A_{1} B_{1} C_{1}$ respectively. Claim 1. $\triangle A A_{b} A_{c} \approx \triangle A B C$. Proof. Let $P=B H \cap A C, Q=C H \cap A B$, then it is well known that $\triangle A P Q \approx \triangle A B C$. By the dilation with factor 2 centred at $A, \triangle A P Q$ is sent to $\triangle A A_{b} A_{c}$, so we have $\triangle A A_{b} A_{c} \sim \triangle A B C$. Claim 2. $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$ and $A_{1}$ lies on the circumcircle of $\triangle A A_{b} A_{c}$ which is centred at $H$. Proof. Since $B_{a}, C_{a}$ are reflections of $B, C$ in $A H$, we have $\triangle A B_{a} C_{a} \approx \triangle A B C$. Combining this with Claim 1, we have $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$, where $A$ is the centre of this similarity. Therefore, $\Varangle A_{c} A_{1} A_{b}=\Varangle A_{c} A A_{b}$ meaning $A_{1}$ lies on $\odot A A_{b} A_{c}$. By symmetry, $H A_{b}=H A=H A_{c}$, so $H$ is centre of this circle. Claim 3. $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Proof. From Claim 2 we have $$ \Varangle C_{1} A_{1} B_{1}=\Varangle A_{c} A_{1} A_{b} \stackrel{\text { Claim } 2}{=} \npreceq A_{c} A A_{b}=-\Varangle C A B $$ and similarly $\Varangle A_{1} B_{1} C_{1}=-\Varangle A B C, \Varangle B_{1} C_{1} A_{1}=-\Varangle B C A$, which imply $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Denote the ratio of similitude of $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ by $\lambda\left(=\frac{B_{1} C_{1}}{B C}\right)$, then $$ \lambda=\frac{H_{1} A_{1}}{H A}=\frac{H_{1} B_{1}}{H B}=\frac{H_{1} C_{1}}{H C} . $$ Since $H A=H A_{1}$ and similarly $H B=H B_{1}, H C=H C_{1}$ from Claim 2, we get $$ \lambda=\frac{H_{1} A_{1}}{H A_{1}}=\frac{H_{1} B_{1}}{H B_{1}}=\frac{H_{1} C_{1}}{H C_{1}} . $$ Therefore, the circle $A_{1} B_{1} C_{1}$ is the Apollonian circle of the segment $H H_{1}$ with ratio $\lambda$ so the line $H H_{1}$ passes through $O_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear. (Ukraine)
|
 We write $\triangle P_{1} P_{2} P_{3} \stackrel{ \pm}{\sim} \triangle Q_{1} Q_{2} Q_{3}$ (resp. $\triangle P_{1} P_{2} P_{3} \approx \triangle Q_{1} Q_{2} Q_{3}$ ) to indicate that two triangles are directly (resp. oppositely) similar. We use directed angles throughout denoted with $\Varangle$. Denote by $A_{b}, A_{c}$ the reflections of $A$ in $B H$ and $C H$ respectively. $B_{c}, B_{a}$ and $C_{a}, C_{b}$ are defined similarly. By definition, $\ell_{a}=B_{c} C_{b}, \ell_{b}=C_{a} A_{c}, \ell_{c}=A_{b} B_{a}$. Let $A_{1}=\ell_{b} \cap \ell_{c}$, $B_{1}=\ell_{c} \cap \ell_{a}, C_{1}=\ell_{a} \cap \ell_{b}$ and let $O_{1}, H_{1}$ be the orthocentre and circumcentre of $\mathcal{T} \equiv \triangle A_{1} B_{1} C_{1}$ respectively. Claim 1. $\triangle A A_{b} A_{c} \approx \triangle A B C$. Proof. Let $P=B H \cap A C, Q=C H \cap A B$, then it is well known that $\triangle A P Q \approx \triangle A B C$. By the dilation with factor 2 centred at $A, \triangle A P Q$ is sent to $\triangle A A_{b} A_{c}$, so we have $\triangle A A_{b} A_{c} \sim \triangle A B C$. Claim 2. $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$ and $A_{1}$ lies on the circumcircle of $\triangle A A_{b} A_{c}$ which is centred at $H$. Proof. Since $B_{a}, C_{a}$ are reflections of $B, C$ in $A H$, we have $\triangle A B_{a} C_{a} \approx \triangle A B C$. Combining this with Claim 1, we have $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$, where $A$ is the centre of this similarity. Therefore, $\Varangle A_{c} A_{1} A_{b}=\Varangle A_{c} A A_{b}$ meaning $A_{1}$ lies on $\odot A A_{b} A_{c}$. By symmetry, $H A_{b}=H A=H A_{c}$, so $H$ is centre of this circle. Claim 3. $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Proof. From Claim 2 we have $$ \Varangle C_{1} A_{1} B_{1}=\Varangle A_{c} A_{1} A_{b} \stackrel{\text { Claim } 2}{=} \npreceq A_{c} A A_{b}=-\Varangle C A B $$ and similarly $\Varangle A_{1} B_{1} C_{1}=-\Varangle A B C, \Varangle B_{1} C_{1} A_{1}=-\Varangle B C A$, which imply $\triangle A_{1} B_{1} C_{1} \approx \triangle A B C$. Denote the ratio of similitude of $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ by $\lambda\left(=\frac{B_{1} C_{1}}{B C}\right)$, then $$ \lambda=\frac{H_{1} A_{1}}{H A}=\frac{H_{1} B_{1}}{H B}=\frac{H_{1} C_{1}}{H C} . $$ Since $H A=H A_{1}$ and similarly $H B=H B_{1}, H C=H C_{1}$ from Claim 2, we get $$ \lambda=\frac{H_{1} A_{1}}{H A_{1}}=\frac{H_{1} B_{1}}{H B_{1}}=\frac{H_{1} C_{1}}{H C_{1}} . $$ Therefore, the circle $A_{1} B_{1} C_{1}$ is the Apollonian circle of the segment $H H_{1}$ with ratio $\lambda$ so the line $H H_{1}$ passes through $O_{1}$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fa80c777-0b7c-52d1-82f3-0261c1f24fbe
| 607,778
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear. (Ukraine)
|
We use the same notation $A_{b}, A_{c}, B_{c}, B_{a}, C_{a}, C_{b}$ and $A_{1}, B_{1}, C_{1}, O_{1}, H_{1}$ as in Let $O$ be the circumcentre of $\triangle A B C$ and $A_{2}$ be the reflection of $A_{1}$ in $A H$. As $\odot A A_{b} A_{c}$ is centred at $H, A_{2}$ also lies on this circle. By Claim 2, $\Varangle B_{a} A_{1} C_{a}=\Varangle A_{b} A A_{c}=\Varangle B_{a} A C_{a}$, so $A_{1}$ lies on $\odot A B_{a} C_{a}$. Reflecting this in $A H$ gives that $A_{2}$ lies on $\odot A B C$. We now have circles centred at $O$ and $H$ passing through $A$ and $A_{2}$ so these points are symmetric with respect to $O H$. Define $B_{2}$ and $C_{2}$ similarly then $\triangle A B C$ and $\triangle A_{2} B_{2} C_{2}$ are symmetric with respect to $O H$ and also $\odot A B C=\odot A_{2} B_{2} C_{2}$. 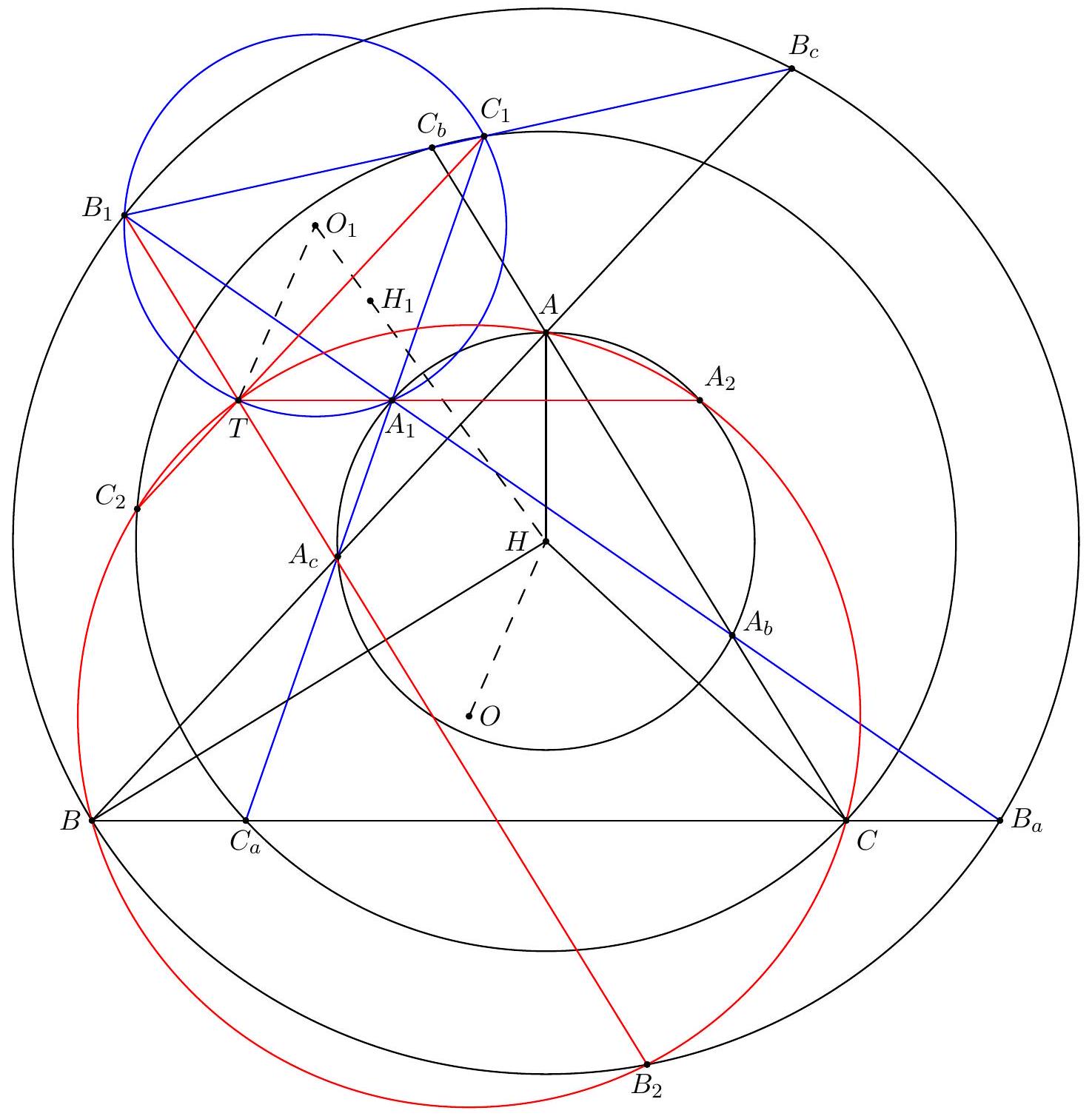 Claim 4. $A_{1} A_{2}, B_{1} B_{2}$ and $C_{1} C_{2}$ have an intersection on $\odot A B C$ which we denote by $T$. Proof. Let $T=A_{1} A_{2} \cap B_{1} B_{2}$. Since $A_{1} A_{2} \| B C$ and $B_{1} B_{2} \| A C$, we have $$ \Varangle A_{2} T B_{2}=\Varangle B C A=-\Varangle B_{2} C_{2} A_{2}=\Varangle A_{2} C_{2} B_{2} . $$ So $T$ lies on $\odot A_{2} B_{2} C_{2}=\odot A B C$. Similarly the intersection of $A_{1} A_{2}$ and $C_{1} C_{2}$ lies on $\odot A B C$, so $C_{1} C_{2}$ also passes through $T$. Claim 5. $T$ also lies on $\odot A_{1} B_{1} C_{1}$ and $T$ corresponds to $T$ itself under the similarity $\triangle A_{1} B_{1} C_{1} \approx$ $\triangle A B C$. Proof. We know $\triangle A_{1} B_{1} C_{1} \sim \triangle A B C$ by Claim 3. We also have $$ \Varangle B_{1} T C_{1}=\Varangle B_{2} T C_{2}=\Varangle B_{2} A_{2} C_{2}=-\Varangle B A C \stackrel{\text { Claim } 3}{=} \not B_{1} A_{1} C_{1}, $$ so $T$ lies on $\odot A_{1} B_{1} C_{1}$. The remaining part is concluded by the following angle chase: $$ \Varangle A_{1} B_{1} T=\Varangle A_{1} B_{1} B_{2} \stackrel{B_{1} B_{2} \| A C}{\underline{\|}} \npreceq A_{1} A_{b} A=\Varangle A_{1} A_{2} A=-\Varangle A A_{2} T=-\Varangle A B T . $$ Claim 6. The circumradius of $\triangle A_{1} B_{1} C_{1}$ is equal to $H O$. Proof. Two circles centred at $H$ intersect $\ell_{c}$ at $A_{1}, A_{b}$ and $B_{1}, B_{a}$, so $A_{1} A_{b}$ and $B_{1} B_{a}$ have the same midpoint and thus $A_{1} B_{1}=A_{b} B_{a}$. Consider the spiral symmetry $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$. This takes $H$, the circumcentre of $\triangle A A_{b} A_{c}$, to the circumcentre of $\triangle A B_{a} C_{a}$, denoted by $O_{a}$, which is symmetric to $O$ in $A H$. Hence $\triangle A A_{b} B_{a} \stackrel{ \pm}{\sim} \triangle A H O_{a}$, so $$ \frac{A A_{b}}{B_{a} A_{b}}=\frac{A H}{H O_{a}}=\frac{A H}{H O} \Longrightarrow \frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}} . $$ Also since $\triangle A_{1} O_{1} B_{1} \stackrel{\downarrow}{\sim} \triangle A H A_{b}$ (both of them are $\approx \triangle A O B$ ), we have $$ \frac{A_{1} O_{1}}{A_{1} B_{1}}=\frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}}=\frac{H O}{A_{1} B_{1}} \Longrightarrow A_{1} O_{1}=H O $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with orthocentre $H$. Let $\ell_{a}$ be the line through the reflection of $B$ with respect to $C H$ and the reflection of $C$ with respect to $B H$. Lines $\ell_{b}$ and $\ell_{c}$ are defined similarly. Suppose lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ determine a triangle $\mathcal{T}$. Prove that the orthocentre of $\mathcal{T}$, the circumcentre of $\mathcal{T}$ and $H$ are collinear. (Ukraine)
|
We use the same notation $A_{b}, A_{c}, B_{c}, B_{a}, C_{a}, C_{b}$ and $A_{1}, B_{1}, C_{1}, O_{1}, H_{1}$ as in Let $O$ be the circumcentre of $\triangle A B C$ and $A_{2}$ be the reflection of $A_{1}$ in $A H$. As $\odot A A_{b} A_{c}$ is centred at $H, A_{2}$ also lies on this circle. By Claim 2, $\Varangle B_{a} A_{1} C_{a}=\Varangle A_{b} A A_{c}=\Varangle B_{a} A C_{a}$, so $A_{1}$ lies on $\odot A B_{a} C_{a}$. Reflecting this in $A H$ gives that $A_{2}$ lies on $\odot A B C$. We now have circles centred at $O$ and $H$ passing through $A$ and $A_{2}$ so these points are symmetric with respect to $O H$. Define $B_{2}$ and $C_{2}$ similarly then $\triangle A B C$ and $\triangle A_{2} B_{2} C_{2}$ are symmetric with respect to $O H$ and also $\odot A B C=\odot A_{2} B_{2} C_{2}$.  Claim 4. $A_{1} A_{2}, B_{1} B_{2}$ and $C_{1} C_{2}$ have an intersection on $\odot A B C$ which we denote by $T$. Proof. Let $T=A_{1} A_{2} \cap B_{1} B_{2}$. Since $A_{1} A_{2} \| B C$ and $B_{1} B_{2} \| A C$, we have $$ \Varangle A_{2} T B_{2}=\Varangle B C A=-\Varangle B_{2} C_{2} A_{2}=\Varangle A_{2} C_{2} B_{2} . $$ So $T$ lies on $\odot A_{2} B_{2} C_{2}=\odot A B C$. Similarly the intersection of $A_{1} A_{2}$ and $C_{1} C_{2}$ lies on $\odot A B C$, so $C_{1} C_{2}$ also passes through $T$. Claim 5. $T$ also lies on $\odot A_{1} B_{1} C_{1}$ and $T$ corresponds to $T$ itself under the similarity $\triangle A_{1} B_{1} C_{1} \approx$ $\triangle A B C$. Proof. We know $\triangle A_{1} B_{1} C_{1} \sim \triangle A B C$ by Claim 3. We also have $$ \Varangle B_{1} T C_{1}=\Varangle B_{2} T C_{2}=\Varangle B_{2} A_{2} C_{2}=-\Varangle B A C \stackrel{\text { Claim } 3}{=} \not B_{1} A_{1} C_{1}, $$ so $T$ lies on $\odot A_{1} B_{1} C_{1}$. The remaining part is concluded by the following angle chase: $$ \Varangle A_{1} B_{1} T=\Varangle A_{1} B_{1} B_{2} \stackrel{B_{1} B_{2} \| A C}{\underline{\|}} \npreceq A_{1} A_{b} A=\Varangle A_{1} A_{2} A=-\Varangle A A_{2} T=-\Varangle A B T . $$ Claim 6. The circumradius of $\triangle A_{1} B_{1} C_{1}$ is equal to $H O$. Proof. Two circles centred at $H$ intersect $\ell_{c}$ at $A_{1}, A_{b}$ and $B_{1}, B_{a}$, so $A_{1} A_{b}$ and $B_{1} B_{a}$ have the same midpoint and thus $A_{1} B_{1}=A_{b} B_{a}$. Consider the spiral symmetry $\triangle A A_{b} A_{c} \stackrel{\downarrow}{\sim} \triangle A B_{a} C_{a}$. This takes $H$, the circumcentre of $\triangle A A_{b} A_{c}$, to the circumcentre of $\triangle A B_{a} C_{a}$, denoted by $O_{a}$, which is symmetric to $O$ in $A H$. Hence $\triangle A A_{b} B_{a} \stackrel{ \pm}{\sim} \triangle A H O_{a}$, so $$ \frac{A A_{b}}{B_{a} A_{b}}=\frac{A H}{H O_{a}}=\frac{A H}{H O} \Longrightarrow \frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}} . $$ Also since $\triangle A_{1} O_{1} B_{1} \stackrel{\downarrow}{\sim} \triangle A H A_{b}$ (both of them are $\approx \triangle A O B$ ), we have $$ \frac{A_{1} O_{1}}{A_{1} B_{1}}=\frac{A H}{A A_{b}}=\frac{H O}{A_{b} B_{a}}=\frac{H O}{A_{1} B_{1}} \Longrightarrow A_{1} O_{1}=H O $$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fa80c777-0b7c-52d1-82f3-0261c1f24fbe
| 607,778
|
Determine all positive, composite integers $n$ that satisfy the following property: if the positive divisors of $n$ are $1=d_{1}<d_{2}<\cdots<d_{k}=n$, then $d_{i}$ divides $d_{i+1}+d_{i+2}$ for every $1 \leqslant i \leqslant k-2$. (Colombia) Answer: $n=p^{r}$ is a prime power for some $r \geqslant 2$.
|
It is easy to see that such an $n=p^{r}$ with $r \geqslant 2$ satisfies the condition as $d_{i}=p^{i-1}$ with $1 \geqslant i \geqslant k=r+1$ and clearly $$ p^{i-1} \mid p^{i}+p^{i+1} $$ Now, let us suppose that there is a positive integer $n$ that satisfies the divisibility condition of the problem and that has two different prime divisors $p$ and $q$. Without lost of generality, we assume $p<q$ and that they are the two smallest prime divisors of $n$. Then there is a positive integer $j$ such that $$ d_{1}=1, d_{2}=p, \ldots, d_{j}=p^{j-1}, d_{j+1}=p^{j}, d_{j+2}=q, $$ and it follows that $$ d_{k-j-1}=\frac{n}{q}, d_{k-j}=\frac{n}{p^{j}}, d_{k-j+1}=\frac{n}{p^{j-1}}, \ldots, d_{k-1}=\frac{n}{p}, d_{k}=n . $$ Thus $$ d_{k-j-1}=\frac{n}{q} \left\lvert\, d_{k-j}+d_{k-j+1}=\frac{n}{p^{j}}+\frac{n}{p^{j-1}}=\frac{n}{p^{j}}(p+1) .\right. $$ This gives $p^{j} \mid q(p+1)$, which is a contradiction since $\operatorname{gcd}(p, p+1)=1$ and $p \neq q$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine all positive, composite integers $n$ that satisfy the following property: if the positive divisors of $n$ are $1=d_{1}<d_{2}<\cdots<d_{k}=n$, then $d_{i}$ divides $d_{i+1}+d_{i+2}$ for every $1 \leqslant i \leqslant k-2$. (Colombia) Answer: $n=p^{r}$ is a prime power for some $r \geqslant 2$.
|
It is easy to see that such an $n=p^{r}$ with $r \geqslant 2$ satisfies the condition as $d_{i}=p^{i-1}$ with $1 \geqslant i \geqslant k=r+1$ and clearly $$ p^{i-1} \mid p^{i}+p^{i+1} $$ Now, let us suppose that there is a positive integer $n$ that satisfies the divisibility condition of the problem and that has two different prime divisors $p$ and $q$. Without lost of generality, we assume $p<q$ and that they are the two smallest prime divisors of $n$. Then there is a positive integer $j$ such that $$ d_{1}=1, d_{2}=p, \ldots, d_{j}=p^{j-1}, d_{j+1}=p^{j}, d_{j+2}=q, $$ and it follows that $$ d_{k-j-1}=\frac{n}{q}, d_{k-j}=\frac{n}{p^{j}}, d_{k-j+1}=\frac{n}{p^{j-1}}, \ldots, d_{k-1}=\frac{n}{p}, d_{k}=n . $$ Thus $$ d_{k-j-1}=\frac{n}{q} \left\lvert\, d_{k-j}+d_{k-j+1}=\frac{n}{p^{j}}+\frac{n}{p^{j-1}}=\frac{n}{p^{j}}(p+1) .\right. $$ This gives $p^{j} \mid q(p+1)$, which is a contradiction since $\operatorname{gcd}(p, p+1)=1$ and $p \neq q$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
10bf348d-545a-5832-bc3e-8f873f8b13af
| 607,779
|
Determine all positive, composite integers $n$ that satisfy the following property: if the positive divisors of $n$ are $1=d_{1}<d_{2}<\cdots<d_{k}=n$, then $d_{i}$ divides $d_{i+1}+d_{i+2}$ for every $1 \leqslant i \leqslant k-2$. (Colombia) Answer: $n=p^{r}$ is a prime power for some $r \geqslant 2$.
|
Since $d_{i} d_{k+1-i}=n$, we have the equivalence: $$ d_{k-i-1}\left|d_{k-i}+d_{k-i+1} \Longleftrightarrow \frac{n}{d_{i+2}}\right| \frac{n}{d_{i+1}}+\frac{n}{d_{i}} . $$ We multiply both sides by $d_{i} d_{i+1} d_{i+2}$ and cancel the $n$ 's to get $$ d_{i} d_{i+1} \mid d_{i} d_{i+2}+d_{i+1} d_{i+2} . $$ Hence, $$ d_{i} \mid d_{i+1} d_{i+2} $$ Moreover, by the condition of the problem, $$ d_{i} \mid d_{i+1}\left(d_{i+1}+d_{i+2}\right)=d_{i+1}^{2}+d_{i+1} d_{i+2} . $$ Combining this with (2) we get that $d_{i} \mid d_{i+1}^{2}$ for all $1 \leqslant i \leqslant k-2$. Let $d_{2}=p$ be the smallest prime divisor of $n$. By induction on $i$ we prove that $p \mid d_{i}$ for all $2 \leqslant i \leqslant k-1$. The base case $d_{2}=p$ is obvious. Let us suppose that $p \mid d_{j}$ for some $2 \leqslant j \leqslant k-2$. Then we have that $$ p\left|d_{j}\right| d_{j+1}^{2} \Longrightarrow p \mid d_{j+1} $$ as $p$ is prime, which completes the induction. This implies that $n$ has to be a prime power, as otherwise there would be another prime $q$ that divides $n$ and we would get that $p \mid q$ which is obviously false. We finally check that the powers of $p$ satisfy the condition in the statement of the problem as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine all positive, composite integers $n$ that satisfy the following property: if the positive divisors of $n$ are $1=d_{1}<d_{2}<\cdots<d_{k}=n$, then $d_{i}$ divides $d_{i+1}+d_{i+2}$ for every $1 \leqslant i \leqslant k-2$. (Colombia) Answer: $n=p^{r}$ is a prime power for some $r \geqslant 2$.
|
Since $d_{i} d_{k+1-i}=n$, we have the equivalence: $$ d_{k-i-1}\left|d_{k-i}+d_{k-i+1} \Longleftrightarrow \frac{n}{d_{i+2}}\right| \frac{n}{d_{i+1}}+\frac{n}{d_{i}} . $$ We multiply both sides by $d_{i} d_{i+1} d_{i+2}$ and cancel the $n$ 's to get $$ d_{i} d_{i+1} \mid d_{i} d_{i+2}+d_{i+1} d_{i+2} . $$ Hence, $$ d_{i} \mid d_{i+1} d_{i+2} $$ Moreover, by the condition of the problem, $$ d_{i} \mid d_{i+1}\left(d_{i+1}+d_{i+2}\right)=d_{i+1}^{2}+d_{i+1} d_{i+2} . $$ Combining this with (2) we get that $d_{i} \mid d_{i+1}^{2}$ for all $1 \leqslant i \leqslant k-2$. Let $d_{2}=p$ be the smallest prime divisor of $n$. By induction on $i$ we prove that $p \mid d_{i}$ for all $2 \leqslant i \leqslant k-1$. The base case $d_{2}=p$ is obvious. Let us suppose that $p \mid d_{j}$ for some $2 \leqslant j \leqslant k-2$. Then we have that $$ p\left|d_{j}\right| d_{j+1}^{2} \Longrightarrow p \mid d_{j+1} $$ as $p$ is prime, which completes the induction. This implies that $n$ has to be a prime power, as otherwise there would be another prime $q$ that divides $n$ and we would get that $p \mid q$ which is obviously false. We finally check that the powers of $p$ satisfy the condition in the statement of the problem as in Solution 1.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
10bf348d-545a-5832-bc3e-8f873f8b13af
| 607,779
|
For positive integers $n$ and $k \geqslant 2$ define $E_{k}(n)$ as the greatest exponent $r$ such that $k^{r}$ divides $n$ !. Prove that there are infinitely many $n$ such that $E_{10}(n)>E_{9}(n)$ and infinitely many $m$ such that $E_{10}(m)<E_{9}(m)$. (Brazil)
|
We let $v_{p}(m)$ denote the $p$-adic valuation of $m$. By Legendre's Formula we know, for $p$ prime, that $v_{p}(n!)=\lfloor n / p\rfloor+\left\lfloor n / p^{2}\right\rfloor+\cdots$. We can see that $E_{9}(n)=\left\lfloor\frac{v_{3}(n!)}{2}\right\rfloor$. Since $v_{5}(n!) \leqslant v_{2}(n!)$ and $E_{10}(n)=\min \left(v_{5}(n!), v_{2}(n!)\right)$, we have $E_{10}(n)=v_{5}(n!)$. Let $l$ be a positive integer. Set $n=5^{2 l-1}$. Then we have $$ E_{10}(n)=v_{5}(n!)=5^{2 l-2}+5^{2 l-3}+\cdots+5+1=\frac{5^{2 l-1}-1}{4}=\frac{n-1}{4} $$ Since $n=5^{2 l-1} \equiv 2(\bmod 3)$, we have $\left\lfloor\frac{n}{3}\right\rfloor=\frac{n-2}{3}$ and it implying $$ v_{3}(n!)=\left\lfloor\frac{n}{3}\right\rfloor+\left\lfloor\frac{n}{3^{2}}\right\rfloor+\left\lfloor\frac{n}{3^{3}}\right\rfloor+\cdots<\frac{n-2}{3}+\frac{n}{3^{2}}+\frac{n}{3^{3}}+\cdots=\frac{n}{2}-\frac{2}{3} . $$ From this we obtain $$ E_{9}(n)=\left\lfloor\frac{v_{3}(n!)}{2}\right\rfloor \leqslant \frac{v_{3}(n!)}{2} \leqslant \frac{n}{4}-\frac{1}{3}<\frac{n}{4}-\frac{1}{4}=E_{10}(n) . $$ In a similar way, we set now $m=3^{4 l-2}$. Then we have $$ v_{3}(m!)=3^{4 l-3}+3^{4 l-4}+\cdots+3+1=\frac{3^{4 l-2}-1}{2}=\frac{m-1}{2} . $$ Note that $m=3^{4 l-2} \equiv 1(\bmod 4)$ and hence $E_{9}(m)=\left\lfloor\frac{v_{3}(m!)}{2}\right\rfloor=\left\lfloor\frac{m-1}{4}\right\rfloor=\frac{m-1}{4}$. We also have $m=3^{4 l-2} \equiv 4(\bmod 5)$ implying $\left\lfloor\frac{m}{5}\right\rfloor=\frac{m-4}{5}$. Therefore we obtain $$ E_{10}(m)=v_{5}(m!)=\left\lfloor\frac{m}{5}\right\rfloor+\left\lfloor\frac{m}{5^{2}}\right\rfloor+\cdots<\frac{m-4}{5}+\frac{m}{5^{2}}+\cdots=\frac{m}{4}-\frac{4}{5}<\frac{m}{4}-\frac{1}{4}=E_{9}(m) $$ We can take infinitely many $n=5^{2 l-1}$ and $m=3^{4 l-2}$ completing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For positive integers $n$ and $k \geqslant 2$ define $E_{k}(n)$ as the greatest exponent $r$ such that $k^{r}$ divides $n$ !. Prove that there are infinitely many $n$ such that $E_{10}(n)>E_{9}(n)$ and infinitely many $m$ such that $E_{10}(m)<E_{9}(m)$. (Brazil)
|
We let $v_{p}(m)$ denote the $p$-adic valuation of $m$. By Legendre's Formula we know, for $p$ prime, that $v_{p}(n!)=\lfloor n / p\rfloor+\left\lfloor n / p^{2}\right\rfloor+\cdots$. We can see that $E_{9}(n)=\left\lfloor\frac{v_{3}(n!)}{2}\right\rfloor$. Since $v_{5}(n!) \leqslant v_{2}(n!)$ and $E_{10}(n)=\min \left(v_{5}(n!), v_{2}(n!)\right)$, we have $E_{10}(n)=v_{5}(n!)$. Let $l$ be a positive integer. Set $n=5^{2 l-1}$. Then we have $$ E_{10}(n)=v_{5}(n!)=5^{2 l-2}+5^{2 l-3}+\cdots+5+1=\frac{5^{2 l-1}-1}{4}=\frac{n-1}{4} $$ Since $n=5^{2 l-1} \equiv 2(\bmod 3)$, we have $\left\lfloor\frac{n}{3}\right\rfloor=\frac{n-2}{3}$ and it implying $$ v_{3}(n!)=\left\lfloor\frac{n}{3}\right\rfloor+\left\lfloor\frac{n}{3^{2}}\right\rfloor+\left\lfloor\frac{n}{3^{3}}\right\rfloor+\cdots<\frac{n-2}{3}+\frac{n}{3^{2}}+\frac{n}{3^{3}}+\cdots=\frac{n}{2}-\frac{2}{3} . $$ From this we obtain $$ E_{9}(n)=\left\lfloor\frac{v_{3}(n!)}{2}\right\rfloor \leqslant \frac{v_{3}(n!)}{2} \leqslant \frac{n}{4}-\frac{1}{3}<\frac{n}{4}-\frac{1}{4}=E_{10}(n) . $$ In a similar way, we set now $m=3^{4 l-2}$. Then we have $$ v_{3}(m!)=3^{4 l-3}+3^{4 l-4}+\cdots+3+1=\frac{3^{4 l-2}-1}{2}=\frac{m-1}{2} . $$ Note that $m=3^{4 l-2} \equiv 1(\bmod 4)$ and hence $E_{9}(m)=\left\lfloor\frac{v_{3}(m!)}{2}\right\rfloor=\left\lfloor\frac{m-1}{4}\right\rfloor=\frac{m-1}{4}$. We also have $m=3^{4 l-2} \equiv 4(\bmod 5)$ implying $\left\lfloor\frac{m}{5}\right\rfloor=\frac{m-4}{5}$. Therefore we obtain $$ E_{10}(m)=v_{5}(m!)=\left\lfloor\frac{m}{5}\right\rfloor+\left\lfloor\frac{m}{5^{2}}\right\rfloor+\cdots<\frac{m-4}{5}+\frac{m}{5^{2}}+\cdots=\frac{m}{4}-\frac{4}{5}<\frac{m}{4}-\frac{1}{4}=E_{9}(m) $$ We can take infinitely many $n=5^{2 l-1}$ and $m=3^{4 l-2}$ completing the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c06bee61-9e98-57f9-97d0-376f913805b2
| 607,781
|
For positive integers $n$ and $k \geqslant 2$ define $E_{k}(n)$ as the greatest exponent $r$ such that $k^{r}$ divides $n$ !. Prove that there are infinitely many $n$ such that $E_{10}(n)>E_{9}(n)$ and infinitely many $m$ such that $E_{10}(m)<E_{9}(m)$. (Brazil)
|
In the setting of First, we take $n=5^{3^{b-1}}$ with $b \geqslant 2$. Because 5 is not a square modulo 3 and $\varphi\left(3^{b}\right)=2 \cdot 3^{b-1}$, we have $n \equiv-1\left(\bmod 3^{b}\right)$. Hence, $$ v_{3}(n!)=\left\lfloor\frac{n}{3}\right\rfloor+\left\lfloor\frac{n}{3^{2}}\right\rfloor+\cdots<\frac{n-2}{3}+\frac{n-8}{9}+\cdots+\frac{n-\left(3^{b}-1\right)}{3^{b}}+\frac{n}{3^{b+1}}+\cdots<\frac{n}{2}-b+\frac{1}{2}, $$ and $E_{10}(n)=\frac{n-1}{4}>\frac{n+1-2 b}{4}>E_{9}(n)$. In the same way, for $m=3^{2 \cdot 5^{b-1}} \equiv-1\left(\bmod 5^{b}\right)$ with $b \geqslant 2$, $E_{10}(m)=\left\lfloor\frac{m}{5}\right\rfloor+\left\lfloor\frac{m}{5^{2}}\right\rfloor+\cdots<\frac{m-4}{5}+\frac{m-24}{25}+\cdots+\frac{m-\left(5^{b}-1\right)}{5^{b}}+\frac{m}{5^{b+1}}+\cdots<\frac{m}{4}-b+\frac{1}{4}$, and $E_{9}(m)=\frac{m-1}{4}>E_{10}(m)$ holds. Comment. From Solution 2 we can see that for any positive real $B$, there exist infinitely many positive integers $m$ and $n$ such that $E_{10}(n)-E_{9}(n)>B$ and $E_{10}(m)-E_{9}(m)<-B$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For positive integers $n$ and $k \geqslant 2$ define $E_{k}(n)$ as the greatest exponent $r$ such that $k^{r}$ divides $n$ !. Prove that there are infinitely many $n$ such that $E_{10}(n)>E_{9}(n)$ and infinitely many $m$ such that $E_{10}(m)<E_{9}(m)$. (Brazil)
|
In the setting of First, we take $n=5^{3^{b-1}}$ with $b \geqslant 2$. Because 5 is not a square modulo 3 and $\varphi\left(3^{b}\right)=2 \cdot 3^{b-1}$, we have $n \equiv-1\left(\bmod 3^{b}\right)$. Hence, $$ v_{3}(n!)=\left\lfloor\frac{n}{3}\right\rfloor+\left\lfloor\frac{n}{3^{2}}\right\rfloor+\cdots<\frac{n-2}{3}+\frac{n-8}{9}+\cdots+\frac{n-\left(3^{b}-1\right)}{3^{b}}+\frac{n}{3^{b+1}}+\cdots<\frac{n}{2}-b+\frac{1}{2}, $$ and $E_{10}(n)=\frac{n-1}{4}>\frac{n+1-2 b}{4}>E_{9}(n)$. In the same way, for $m=3^{2 \cdot 5^{b-1}} \equiv-1\left(\bmod 5^{b}\right)$ with $b \geqslant 2$, $E_{10}(m)=\left\lfloor\frac{m}{5}\right\rfloor+\left\lfloor\frac{m}{5^{2}}\right\rfloor+\cdots<\frac{m-4}{5}+\frac{m-24}{25}+\cdots+\frac{m-\left(5^{b}-1\right)}{5^{b}}+\frac{m}{5^{b+1}}+\cdots<\frac{m}{4}-b+\frac{1}{4}$, and $E_{9}(m)=\frac{m-1}{4}>E_{10}(m)$ holds. Comment. From Solution 2 we can see that for any positive real $B$, there exist infinitely many positive integers $m$ and $n$ such that $E_{10}(n)-E_{9}(n)>B$ and $E_{10}(m)-E_{9}(m)<-B$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c06bee61-9e98-57f9-97d0-376f913805b2
| 607,781
|
5. (ROM) A segment $A B$ is given and on it a point $M$. On the same side of $A B$ squares $A M C D$ and $B M F E$ are constructed. The circumcircles of the two squares, whose centers are $P$ and $Q$, intersect in $M$ and another point $N$. (a) Prove that lines $F A$ and $B C$ intersect at $N$. (b) Prove that all such constructed lines $M N$ pass through the same point $S$, regardless of the selection of $M$. (c) Find the locus of the midpoints of all segments $P Q$, as $M$ varies along the segment $A B$.
|
5. (a) It suffices to prove that $A F \perp B C$, since then for the intersection point $X$ we have $\angle A X C=\angle B X F=90^{\circ}$, implying that $X$ belongs to the circumcircles of both squares and thus that $X=N$. The relation $A F \perp B C$ holds because from $M A=M C, M F=M B$, and $\angle A M C=\angle F M B$ it follows that $\triangle A M F$ is obtained by rotating $\triangle B M C$ by $90^{\circ}$ around $M$. (b) Since $N$ is on the circumcircle of $B M F E$, it follows that $\angle A N M=$ $\angle M N B=45^{\circ}$. Hence $M N$ is the bisector of $\angle A N B$. It follows that $M N$ passes through the midpoint of the $\operatorname{arc} \widehat{A B}$ of the circle with diameter $A B$ (i.e., the circumcircle of $\triangle A B N$ ) not containing $N$. (c) Let us introduce a coordinate system such that $A=(0,0), B=(b, 0)$, and $M=(m, 0)$. Setting in general $W=\left(x_{W}, y_{W}\right)$ for an arbitrary point $W$ and denoting by $R$ the midpoint of $P Q$, we have $y_{R}=\left(y_{P}+\right.$ $\left.y_{Q}\right) / 2=(m+b-m) / 4=b / 4$ and $x_{R}=\left(x_{P}+x_{Q}\right) / 2=(m+m+b) / 4=$ $(2 m+b) / 4$, the parameter $m$ varying from 0 to $b$. Thus the locus of all points $R$ is the closed segment $R_{1} R_{2}$ where $R_{1}=(b / 4, b / 4)$ and $R_{2}=(b / 4,3 b / 4)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. (ROM) A segment $A B$ is given and on it a point $M$. On the same side of $A B$ squares $A M C D$ and $B M F E$ are constructed. The circumcircles of the two squares, whose centers are $P$ and $Q$, intersect in $M$ and another point $N$. (a) Prove that lines $F A$ and $B C$ intersect at $N$. (b) Prove that all such constructed lines $M N$ pass through the same point $S$, regardless of the selection of $M$. (c) Find the locus of the midpoints of all segments $P Q$, as $M$ varies along the segment $A B$.
|
5. (a) It suffices to prove that $A F \perp B C$, since then for the intersection point $X$ we have $\angle A X C=\angle B X F=90^{\circ}$, implying that $X$ belongs to the circumcircles of both squares and thus that $X=N$. The relation $A F \perp B C$ holds because from $M A=M C, M F=M B$, and $\angle A M C=\angle F M B$ it follows that $\triangle A M F$ is obtained by rotating $\triangle B M C$ by $90^{\circ}$ around $M$. (b) Since $N$ is on the circumcircle of $B M F E$, it follows that $\angle A N M=$ $\angle M N B=45^{\circ}$. Hence $M N$ is the bisector of $\angle A N B$. It follows that $M N$ passes through the midpoint of the $\operatorname{arc} \widehat{A B}$ of the circle with diameter $A B$ (i.e., the circumcircle of $\triangle A B N$ ) not containing $N$. (c) Let us introduce a coordinate system such that $A=(0,0), B=(b, 0)$, and $M=(m, 0)$. Setting in general $W=\left(x_{W}, y_{W}\right)$ for an arbitrary point $W$ and denoting by $R$ the midpoint of $P Q$, we have $y_{R}=\left(y_{P}+\right.$ $\left.y_{Q}\right) / 2=(m+b-m) / 4=b / 4$ and $x_{R}=\left(x_{P}+x_{Q}\right) / 2=(m+m+b) / 4=$ $(2 m+b) / 4$, the parameter $m$ varying from 0 to $b$. Thus the locus of all points $R$ is the closed segment $R_{1} R_{2}$ where $R_{1}=(b / 4, b / 4)$ and $R_{2}=(b / 4,3 b / 4)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
67d77e1a-4033-54e9-bf74-cdaf6ab31f0e
| 24,480
|
2. (POL) Let $a, b$, and $c$ be the lengths of a triangle whose area is $S$. Prove that $$ a^{2}+b^{2}+c^{2} \geq 4 S \sqrt{3} $$ In what case does equality hold?
|
2. Using $S=b c \sin \alpha / 2, a^{2}=b^{2}+c^{2}-2 b c \cos \alpha$ and $(\sqrt{3} \sin \alpha+\cos \alpha) / 2=$ $\cos \left(\alpha-60^{\circ}\right)$ we have $$ \begin{gathered} a^{2}+b^{2}+c^{2} \geq 4 S \sqrt{3} \Leftrightarrow b^{2}+c^{2} \geq b c(\sqrt{3} \sin \alpha+\cos \alpha) \Leftrightarrow \\ \Leftrightarrow(b-c)^{2}+2 b c\left(1-\cos \left(\alpha-60^{\circ}\right)\right) \geq 0, \end{gathered} $$ where equality holds if and only if $b=c$ and $\alpha=60^{\circ}$, i.e., if the triangle is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
2. (POL) Let $a, b$, and $c$ be the lengths of a triangle whose area is $S$. Prove that $$ a^{2}+b^{2}+c^{2} \geq 4 S \sqrt{3} $$ In what case does equality hold?
|
2. Using $S=b c \sin \alpha / 2, a^{2}=b^{2}+c^{2}-2 b c \cos \alpha$ and $(\sqrt{3} \sin \alpha+\cos \alpha) / 2=$ $\cos \left(\alpha-60^{\circ}\right)$ we have $$ \begin{gathered} a^{2}+b^{2}+c^{2} \geq 4 S \sqrt{3} \Leftrightarrow b^{2}+c^{2} \geq b c(\sqrt{3} \sin \alpha+\cos \alpha) \Leftrightarrow \\ \Leftrightarrow(b-c)^{2}+2 b c\left(1-\cos \left(\alpha-60^{\circ}\right)\right) \geq 0, \end{gathered} $$ where equality holds if and only if $b=c$ and $\alpha=60^{\circ}$, i.e., if the triangle is equilateral.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8fb04420-1654-5b00-8146-aaccffb4e34d
| 24,509
|
4. (GDR) In the interior of $\triangle P_{1} P_{2} P_{3}$ a point $P$ is given. Let $Q_{1}, Q_{2}$, and $Q_{3}$ respectively be the intersections of $P P_{1}, P P_{2}$, and $P P_{3}$ with the opposing edges of $\triangle P_{1} P_{2} P_{3}$. Prove that among the ratios $P P_{1} / P Q_{1}, P P_{2} / P Q_{2}$, and $P P_{3} / P Q_{3}$ there exists at least one not larger than 2 and at least one not smaller than 2.
|
4. Let $x_{i}=P P_{i} / P Q_{i}$ for $i=1,2,3$. For all $i$ we have $$ \frac{1}{x_{i}+1}=\frac{P Q_{i}}{P_{i} Q_{i}}=\frac{S_{P P_{j} P_{k}}}{S_{P_{1} P_{2} P_{3}}} $$ where the indices $j$ and $k$ are distinct and different from $i$. Hence we have $$ \begin{aligned} f\left(x_{1}, x_{2}, x_{3}\right) & =\frac{1}{x_{1}+1}+\frac{1}{x_{2}+1}+\frac{1}{x_{3}+1} \\ & =\frac{S\left(P P_{2} P_{3}\right)+S\left(P P_{1} P_{3}\right)+S\left(P P_{2} P_{3}\right)}{S\left(P_{1} P_{2} P_{3}\right)}=1 \end{aligned} $$ It follows that $1 /\left(x_{i}+1\right) \geq 1 / 3$ for some $i$ and $1 /\left(x_{j}+1\right) \leq 1 / 3$ for some $j$. Consequently, $x_{i} \leq 2$ and $x_{j} \geq 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
4. (GDR) In the interior of $\triangle P_{1} P_{2} P_{3}$ a point $P$ is given. Let $Q_{1}, Q_{2}$, and $Q_{3}$ respectively be the intersections of $P P_{1}, P P_{2}$, and $P P_{3}$ with the opposing edges of $\triangle P_{1} P_{2} P_{3}$. Prove that among the ratios $P P_{1} / P Q_{1}, P P_{2} / P Q_{2}$, and $P P_{3} / P Q_{3}$ there exists at least one not larger than 2 and at least one not smaller than 2.
|
4. Let $x_{i}=P P_{i} / P Q_{i}$ for $i=1,2,3$. For all $i$ we have $$ \frac{1}{x_{i}+1}=\frac{P Q_{i}}{P_{i} Q_{i}}=\frac{S_{P P_{j} P_{k}}}{S_{P_{1} P_{2} P_{3}}} $$ where the indices $j$ and $k$ are distinct and different from $i$. Hence we have $$ \begin{aligned} f\left(x_{1}, x_{2}, x_{3}\right) & =\frac{1}{x_{1}+1}+\frac{1}{x_{2}+1}+\frac{1}{x_{3}+1} \\ & =\frac{S\left(P P_{2} P_{3}\right)+S\left(P P_{1} P_{3}\right)+S\left(P P_{2} P_{3}\right)}{S\left(P_{1} P_{2} P_{3}\right)}=1 \end{aligned} $$ It follows that $1 /\left(x_{i}+1\right) \geq 1 / 3$ for some $i$ and $1 /\left(x_{j}+1\right) \leq 1 / 3$ for some $j$. Consequently, $x_{i} \leq 2$ and $x_{j} \geq 2$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2b1ac025-ea54-5966-b430-a827e104ab32
| 24,514
|
7. (USS) Prove that a tetrahedron $S A B C$ has five different spheres that touch all six lines determined by its edges if and only if it is regular.
|
7. The spheres are arranged in a similar manner as in the planar case where we have one incircle and three excircles. Here we have one "insphere" and four "exspheres" corresponding to each of the four sides. Each vertex of the tetrahedron effectively has three tangent lines drawn from it to each of the five spheres. Repeatedly using the equality of the three tangent segments from a vertex (in the same vein as for tangent planar quadrilaterals) we obtain $S A+B C=S B+C A=S C+A B$ from the insphere. From the exsphere opposite of $S$ we obtain $S A-B C=S B-C A=S C-A B$, hence $S A=S B=S C$ and $A B=B C=C A$. By symmetry, we also have $A B=A C=A S$. Hence indeed, all the edges of the tetrahedron are equal in length and thus we have shown that the tetrahedron is regular.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. (USS) Prove that a tetrahedron $S A B C$ has five different spheres that touch all six lines determined by its edges if and only if it is regular.
|
7. The spheres are arranged in a similar manner as in the planar case where we have one incircle and three excircles. Here we have one "insphere" and four "exspheres" corresponding to each of the four sides. Each vertex of the tetrahedron effectively has three tangent lines drawn from it to each of the five spheres. Repeatedly using the equality of the three tangent segments from a vertex (in the same vein as for tangent planar quadrilaterals) we obtain $S A+B C=S B+C A=S C+A B$ from the insphere. From the exsphere opposite of $S$ we obtain $S A-B C=S B-C A=S C-A B$, hence $S A=S B=S C$ and $A B=B C=C A$. By symmetry, we also have $A B=A C=A S$. Hence indeed, all the edges of the tetrahedron are equal in length and thus we have shown that the tetrahedron is regular.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
bee9eb0a-c8a6-5d0c-b38f-f7f850b125de
| 24,538
|
3. (HUN) Prove that if all the angles of a convex $n$-gon are equal and the lengths of consecutive edges $a_{1}, \ldots, a_{n}$ satisfy $a_{1} \geq a_{2} \geq \cdots \geq a_{n}$, then $a_{1}=a_{2}=\cdots=a_{n}$. Second Day
|
3. Let $\overrightarrow{O A_{1}}, \overrightarrow{O A_{2}}, \ldots, \overrightarrow{O A_{n}}$ be the vectors corresponding respectively to the edges $a_{1}, a_{2}, \ldots, a_{n}$ of the polygon. By the conditions of the problem, these vectors satisfy $\overrightarrow{O A_{1}}+\cdots+\overrightarrow{O A_{n}}=\overrightarrow{0}, \angle A_{1} O A_{2}=\angle A_{2} O A_{3}=\cdots=$ $\angle A_{n} O A_{1}=2 \pi / n$ and $O A_{1} \geq O A_{2} \geq \cdots \geq O A_{n}$. Our task is to prove that $O A_{1}=\cdots=O A_{n}$. Let $l$ be the line through $O$ perpendicular to $O A_{n}$, and $B_{1}, \ldots, B_{n-1}$ the projections of $A_{1}, \ldots, A_{n-1}$ onto $l$ respectively. By the assumptions, the sum of the $\overrightarrow{O B_{i}}$ 's is $\overrightarrow{0}$. On the other hand, since $O B_{i} \leq O B_{n-i}$ for all $i \leq n / 2$, all the sums $\overrightarrow{O B_{i}}+\overrightarrow{O B_{n-i}}$ lie on the same side of the point $O$. Hence all these sums must be equal to $\overrightarrow{0}$. Consequently, $O A_{i}=O A_{n-i}$, from which the result immediately follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (HUN) Prove that if all the angles of a convex $n$-gon are equal and the lengths of consecutive edges $a_{1}, \ldots, a_{n}$ satisfy $a_{1} \geq a_{2} \geq \cdots \geq a_{n}$, then $a_{1}=a_{2}=\cdots=a_{n}$. Second Day
|
3. Let $\overrightarrow{O A_{1}}, \overrightarrow{O A_{2}}, \ldots, \overrightarrow{O A_{n}}$ be the vectors corresponding respectively to the edges $a_{1}, a_{2}, \ldots, a_{n}$ of the polygon. By the conditions of the problem, these vectors satisfy $\overrightarrow{O A_{1}}+\cdots+\overrightarrow{O A_{n}}=\overrightarrow{0}, \angle A_{1} O A_{2}=\angle A_{2} O A_{3}=\cdots=$ $\angle A_{n} O A_{1}=2 \pi / n$ and $O A_{1} \geq O A_{2} \geq \cdots \geq O A_{n}$. Our task is to prove that $O A_{1}=\cdots=O A_{n}$. Let $l$ be the line through $O$ perpendicular to $O A_{n}$, and $B_{1}, \ldots, B_{n-1}$ the projections of $A_{1}, \ldots, A_{n-1}$ onto $l$ respectively. By the assumptions, the sum of the $\overrightarrow{O B_{i}}$ 's is $\overrightarrow{0}$. On the other hand, since $O B_{i} \leq O B_{n-i}$ for all $i \leq n / 2$, all the sums $\overrightarrow{O B_{i}}+\overrightarrow{O B_{n-i}}$ lie on the same side of the point $O$. Hence all these sums must be equal to $\overrightarrow{0}$. Consequently, $O A_{i}=O A_{n-i}$, from which the result immediately follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8dabbf68-ce2c-5ceb-a499-971a0c04f1d0
| 24,546
|
2. (HUN) Denote by $a, b, c$ the lengths of the sides of a triangle. Prove that $$ a^{2}(b+c-a)+b^{2}(c+a-b)+c^{2}(a+b-c) \leq 3 a b c $$
|
2. By substituting $a=x+y, b=y+z$, and $c=z+x(x, y, z>0)$ the given inequality becomes $$ 6 x y z \leq x^{2} y+x y^{2}+y^{2} z+y z^{2}+z^{2} x+z x^{2}, $$ which follows immediately by the AM-GM inequality applied to $x^{2} y, x y^{2}$, $x^{2} z, x z^{2}, y^{2} z, y z^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
2. (HUN) Denote by $a, b, c$ the lengths of the sides of a triangle. Prove that $$ a^{2}(b+c-a)+b^{2}(c+a-b)+c^{2}(a+b-c) \leq 3 a b c $$
|
2. By substituting $a=x+y, b=y+z$, and $c=z+x(x, y, z>0)$ the given inequality becomes $$ 6 x y z \leq x^{2} y+x y^{2}+y^{2} z+y z^{2}+z^{2} x+z x^{2}, $$ which follows immediately by the AM-GM inequality applied to $x^{2} y, x y^{2}$, $x^{2} z, x z^{2}, y^{2} z, y z^{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
bc2bfce5-c8d9-58c9-90c2-1d2d3355a66b
| 24,559
|
4. (HUN) Each of 17 students talked with every other student. They all talked about three different topics. Each pair of students talked about one topic. Prove that there are three students that talked about the same topic among themselves.
|
4. Let us call the topics $T_{1}, T_{2}, T_{3}$. Consider an arbitrary student $A$. By the pigeonhole principle there is a topic, say $T_{3}$, he discussed with at least 6 other students. If two of these 6 students discussed $T_{3}$, then we are done. Suppose now that the 6 students discussed only $T_{1}$ and $T_{2}$ and choose one of them, say $B$. By the pigeonhole principle he discussed one of the topics, say $T_{2}$, with three of these students. If two of these three students also discussed $T_{2}$, then we are done. Otherwise, all the three students discussed only $T_{1}$, which completes the task.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
4. (HUN) Each of 17 students talked with every other student. They all talked about three different topics. Each pair of students talked about one topic. Prove that there are three students that talked about the same topic among themselves.
|
4. Let us call the topics $T_{1}, T_{2}, T_{3}$. Consider an arbitrary student $A$. By the pigeonhole principle there is a topic, say $T_{3}$, he discussed with at least 6 other students. If two of these 6 students discussed $T_{3}$, then we are done. Suppose now that the 6 students discussed only $T_{1}$ and $T_{2}$ and choose one of them, say $B$. By the pigeonhole principle he discussed one of the topics, say $T_{2}$, with three of these students. If two of these three students also discussed $T_{2}$, then we are done. Otherwise, all the three students discussed only $T_{1}$, which completes the task.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6c504120-855d-530b-bead-d3b3e5672be5
| 24,564
|
2. (POL) Consider the system of equations $$ \left\{\begin{array}{l} a_{11} x_{1}+a_{12} x_{2}+a_{13} x_{3}=0 \\ a_{21} x_{1}+a_{22} x_{2}+a_{23} x_{3}=0 \\ a_{31} x_{1}+a_{32} x_{2}+a_{33} x_{3}=0 \end{array}\right. $$ whose coefficients satisfy the following conditions: (a) $a_{11}, a_{22}, a_{33}$ are positive real numbers; (b) all other coefficients are negative; (c) in each of the equations the sum of the coefficients is positive. Prove that $x_{1}=x_{2}=x_{3}=0$ is the only solution to the system.
|
2. Suppose that $\left(x_{1}, x_{2}, x_{3}\right)$ is a solution. We may assume w.l.o.g. that $\left|x_{1}\right| \geq$ $\left|x_{2}\right| \geq\left|x_{3}\right|$. Suppose that $\left|x_{1}\right|>0$. From the first equation we obtain that $$ 0=\left|x_{1}\right| \cdot\left|a_{11}+a_{12} \frac{x_{2}}{x_{1}}+a_{13} \frac{x_{3}}{x_{1}}\right| \geq\left|x_{1}\right| \cdot\left(a_{11}-\left|a_{12}\right|-\left|a_{13}\right|\right)>0 $$ which is a contradiction. Hence $\left|x_{1}\right|=0$ and consequently $x_{1}=x_{2}=x_{3}=$ 0.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
2. (POL) Consider the system of equations $$ \left\{\begin{array}{l} a_{11} x_{1}+a_{12} x_{2}+a_{13} x_{3}=0 \\ a_{21} x_{1}+a_{22} x_{2}+a_{23} x_{3}=0 \\ a_{31} x_{1}+a_{32} x_{2}+a_{33} x_{3}=0 \end{array}\right. $$ whose coefficients satisfy the following conditions: (a) $a_{11}, a_{22}, a_{33}$ are positive real numbers; (b) all other coefficients are negative; (c) in each of the equations the sum of the coefficients is positive. Prove that $x_{1}=x_{2}=x_{3}=0$ is the only solution to the system.
|
2. Suppose that $\left(x_{1}, x_{2}, x_{3}\right)$ is a solution. We may assume w.l.o.g. that $\left|x_{1}\right| \geq$ $\left|x_{2}\right| \geq\left|x_{3}\right|$. Suppose that $\left|x_{1}\right|>0$. From the first equation we obtain that $$ 0=\left|x_{1}\right| \cdot\left|a_{11}+a_{12} \frac{x_{2}}{x_{1}}+a_{13} \frac{x_{3}}{x_{1}}\right| \geq\left|x_{1}\right| \cdot\left(a_{11}-\left|a_{12}\right|-\left|a_{13}\right|\right)>0 $$ which is a contradiction. Hence $\left|x_{1}\right|=0$ and consequently $x_{1}=x_{2}=x_{3}=$ 0.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cbec98f6-7792-5d0f-a7b0-be38cf2b0126
| 24,575
|
6. (POL) We are given $n \geq 3$ points in the plane. Let $d$ be the maximal distance between two of the given points. Prove that the number of pairs of points whose distance is equal to $d$ is less than or equal to $n$.
|
6. We recall the simple statement that every two diameters of a set must have a common point. Consider any point $B$ that is an endpoint of $k \geq 2$ diameters $B C_{1}, B C_{2}$, $\ldots, B C_{k}$. We may assume w.l.o.g. that all the points $C_{1}, \ldots, C_{k}$ lie on the $\operatorname{arc} C_{1} C_{k}$, whose center is $B$ and measure does not exceed $60^{\circ}$. We observe that for $1<i<k$ any diameter with the endpoint $C_{i}$ has to intersect both the diameters $C_{1} B$ and $C_{l} B$. Hence $C_{i} B$ is the only diameter with an endpoint at $C_{i}$ if $i=2, \ldots, k-1$. In other words, with each point that is an endpoint of $k \geq 2$ we can associate $k-2$ points that are endpoints of exactly one diameter. We now assume that each $A_{i}$ is an endpoint of exactly $k_{i} \geq 0$ diameters, and that $k_{1}, \ldots, k_{s} \geq 2$, while $k_{s+1}, \ldots, k_{n} \leq 1$. The total number $D$ of diameters satisfies the inequality $2 D \leq k_{1}+k_{2}+\cdots+k_{s}+(n-s)$. On the other hand, by the above consideration we have $\left(k_{1}-2\right)+\cdots+\left(k_{s}-2\right) \leq$ $n-s$, i.e., $k_{1}+\cdots+k_{s} \leq n+s$. Hence $2 D \leq(n+s)+(n-s)=2 n$, which proves the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
6. (POL) We are given $n \geq 3$ points in the plane. Let $d$ be the maximal distance between two of the given points. Prove that the number of pairs of points whose distance is equal to $d$ is less than or equal to $n$.
|
6. We recall the simple statement that every two diameters of a set must have a common point. Consider any point $B$ that is an endpoint of $k \geq 2$ diameters $B C_{1}, B C_{2}$, $\ldots, B C_{k}$. We may assume w.l.o.g. that all the points $C_{1}, \ldots, C_{k}$ lie on the $\operatorname{arc} C_{1} C_{k}$, whose center is $B$ and measure does not exceed $60^{\circ}$. We observe that for $1<i<k$ any diameter with the endpoint $C_{i}$ has to intersect both the diameters $C_{1} B$ and $C_{l} B$. Hence $C_{i} B$ is the only diameter with an endpoint at $C_{i}$ if $i=2, \ldots, k-1$. In other words, with each point that is an endpoint of $k \geq 2$ we can associate $k-2$ points that are endpoints of exactly one diameter. We now assume that each $A_{i}$ is an endpoint of exactly $k_{i} \geq 0$ diameters, and that $k_{1}, \ldots, k_{s} \geq 2$, while $k_{s+1}, \ldots, k_{n} \leq 1$. The total number $D$ of diameters satisfies the inequality $2 D \leq k_{1}+k_{2}+\cdots+k_{s}+(n-s)$. On the other hand, by the above consideration we have $\left(k_{1}-2\right)+\cdots+\left(k_{s}-2\right) \leq$ $n-s$, i.e., $k_{1}+\cdots+k_{s} \leq n+s$. Hence $2 D \leq(n+s)+(n-s)=2 n$, which proves the result.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
63049937-310b-558a-b2f4-2aec830ede56
| 24,586
|
2. (HUN) If $a, b$, and $c$ are the sides and $\alpha, \beta$, and $\gamma$ the respective angles of the triangle for which $a+b=\tan \frac{\gamma}{2}(a \tan \alpha+b \tan \beta)$, prove that the triangle is isosceles.
|
2. Angles $\alpha$ and $\beta$ are less than $90^{\circ}$, otherwise if w.l.o.g. $\alpha \geq 90^{\circ}$ we have $\tan (\gamma / 2) \cdot(a \tan \alpha+b \tan \beta)<b \tan (\gamma / 2) \tan \beta \leq b \tan (\gamma / 2) \cot (\gamma / 2)=$ $b<a+b$. Since $a \geq b \Leftrightarrow \tan a \geq \tan b$, Chebyshev's inequality gives $a \tan \alpha+b \tan \beta \geq(a+b)(\tan \alpha+\tan \beta) / 2$. Due to the convexity of the $\tan$ function we also have $(\tan \alpha+\tan \beta) / 2 \geq \tan [(\alpha+\beta) / 2]=\cot (\gamma / 2)$. Hence we have $$ \begin{aligned} \tan \frac{\gamma}{2}(a \tan \alpha+b \tan \beta) & \geq \frac{1}{2} \tan \frac{\gamma}{2}(a+b)(\tan \alpha+\tan \beta) \\ & \geq \tan \frac{\gamma}{2}(a+b) \cot \frac{\gamma}{2}=a+b \end{aligned} $$ The equalities can hold only if $a=b$. Thus the triangle is isosceles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
2. (HUN) If $a, b$, and $c$ are the sides and $\alpha, \beta$, and $\gamma$ the respective angles of the triangle for which $a+b=\tan \frac{\gamma}{2}(a \tan \alpha+b \tan \beta)$, prove that the triangle is isosceles.
|
2. Angles $\alpha$ and $\beta$ are less than $90^{\circ}$, otherwise if w.l.o.g. $\alpha \geq 90^{\circ}$ we have $\tan (\gamma / 2) \cdot(a \tan \alpha+b \tan \beta)<b \tan (\gamma / 2) \tan \beta \leq b \tan (\gamma / 2) \cot (\gamma / 2)=$ $b<a+b$. Since $a \geq b \Leftrightarrow \tan a \geq \tan b$, Chebyshev's inequality gives $a \tan \alpha+b \tan \beta \geq(a+b)(\tan \alpha+\tan \beta) / 2$. Due to the convexity of the $\tan$ function we also have $(\tan \alpha+\tan \beta) / 2 \geq \tan [(\alpha+\beta) / 2]=\cot (\gamma / 2)$. Hence we have $$ \begin{aligned} \tan \frac{\gamma}{2}(a \tan \alpha+b \tan \beta) & \geq \frac{1}{2} \tan \frac{\gamma}{2}(a+b)(\tan \alpha+\tan \beta) \\ & \geq \tan \frac{\gamma}{2}(a+b) \cot \frac{\gamma}{2}=a+b \end{aligned} $$ The equalities can hold only if $a=b$. Thus the triangle is isosceles.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b7e6a15c-a646-5a2f-b544-89d381aa4161
| 24,592
|
3. (BUL) Prove that the sum of distances from the center of the circumsphere of the regular tetrahedron to its four vertices is less than the sum of distances from any other point to the four vertices. Second Day
|
3. Consider a coordinate system in which the points of the regular tetrahedron are placed at $A(-a,-a,-a), B(-a, a, a), C(a,-a, a)$ and $D(a, a$, $-a)$. Then the center of the tetrahedron is at $O(0,0,0)$. For a point $X(x, y, z)$ the sum $X A+X B+X C+X D$ by the QM-AM inequality does not exceed $2 \sqrt{X A^{2}+X B^{2}+X C^{2}+X D^{2}}$. Now, since $X A^{2}=$ $(x+a)^{2}+(y+a)^{2}+(z+a)^{2}$ etc., we easily obtain $$ \begin{aligned} X A^{2}+X B^{2}+X C^{2}+X D^{2} & =4\left(x^{2}+y^{2}+z^{2}\right)+12 a^{2} \\ & \geq 12 a^{2}=O A^{2}+O B^{2}+O C^{2}+O D^{2} \end{aligned} $$ Hence $X A+X B+X C+X D \geq 2 \sqrt{O A^{2}+O B^{2}+O C^{2}+O D^{2}}=O A+$ $O B+O C+O D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (BUL) Prove that the sum of distances from the center of the circumsphere of the regular tetrahedron to its four vertices is less than the sum of distances from any other point to the four vertices. Second Day
|
3. Consider a coordinate system in which the points of the regular tetrahedron are placed at $A(-a,-a,-a), B(-a, a, a), C(a,-a, a)$ and $D(a, a$, $-a)$. Then the center of the tetrahedron is at $O(0,0,0)$. For a point $X(x, y, z)$ the sum $X A+X B+X C+X D$ by the QM-AM inequality does not exceed $2 \sqrt{X A^{2}+X B^{2}+X C^{2}+X D^{2}}$. Now, since $X A^{2}=$ $(x+a)^{2}+(y+a)^{2}+(z+a)^{2}$ etc., we easily obtain $$ \begin{aligned} X A^{2}+X B^{2}+X C^{2}+X D^{2} & =4\left(x^{2}+y^{2}+z^{2}\right)+12 a^{2} \\ & \geq 12 a^{2}=O A^{2}+O B^{2}+O C^{2}+O D^{2} \end{aligned} $$ Hence $X A+X B+X C+X D \geq 2 \sqrt{O A^{2}+O B^{2}+O C^{2}+O D^{2}}=O A+$ $O B+O C+O D$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4fb24d9d-48b7-5449-99ee-f1ce263677f7
| 24,594
|
4. (YUG) Prove the following equality: $$ \frac{1}{\sin 2 x}+\frac{1}{\sin 4 x}+\frac{1}{\sin 8 x}+\cdots+\frac{1}{\sin 2^{n} x}=\cot x-\cot 2^{n} x $$ where $n \in \mathbb{N}$ and $x \notin \pi \mathbb{Z} / 2^{k}$ for every $k \in \mathbb{N}$.
|
4. It suffices to prove $1 / \sin 2^{k} x=\cot 2^{k-1} x-\cot 2^{k} x$ for any integer $k$ and real $x$, i.e., $1 / \sin 2 x=\cot x-\cot 2 x$ for all real $x$. We indeed have $\cot x-\cot 2 x=\cot x-\frac{\cot ^{2} x-1}{2 \cot x}=\frac{\left(\frac{\cos x}{\sin x}\right)^{2}+1}{2 \frac{\cos x}{\sin x}}=\frac{1}{2 \sin x \cos x}=\frac{1}{\sin 2 x}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
4. (YUG) Prove the following equality: $$ \frac{1}{\sin 2 x}+\frac{1}{\sin 4 x}+\frac{1}{\sin 8 x}+\cdots+\frac{1}{\sin 2^{n} x}=\cot x-\cot 2^{n} x $$ where $n \in \mathbb{N}$ and $x \notin \pi \mathbb{Z} / 2^{k}$ for every $k \in \mathbb{N}$.
|
4. It suffices to prove $1 / \sin 2^{k} x=\cot 2^{k-1} x-\cot 2^{k} x$ for any integer $k$ and real $x$, i.e., $1 / \sin 2 x=\cot x-\cot 2 x$ for all real $x$. We indeed have $\cot x-\cot 2 x=\cot x-\frac{\cot ^{2} x-1}{2 \cot x}=\frac{\left(\frac{\cos x}{\sin x}\right)^{2}+1}{2 \frac{\cos x}{\sin x}}=\frac{1}{2 \sin x \cos x}=\frac{1}{\sin 2 x}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6483972f-f758-5e4c-864a-c2bd615dbe2b
| 24,597
|
6. (POL) Let $M, K$, and $L$ be points on $(A B),(B C)$, and $(C A)$, respectively. Prove that the area of at least one of the three triangles $\triangle M A L$, $\triangle K B M$, and $\triangle L C K$ is less than or equal to one-fourth the area of $\triangle A B C$.
|
6. Let $S$ denote the area of $\triangle A B C$. Let $A_{1}, B_{1}, C_{1}$ be the midpoints of $B C, A C, A B$ respectively. We note that $S_{A_{1} B_{1} C}=S_{A_{1} B C_{1}}=S_{A B_{1} C_{1}}=$ $S_{A_{1} B_{1} C_{1}}=S / 4$. Let us assume w.l.o.g. that $M \in\left[A C_{1}\right]$. We then must have $K \in\left[B A_{1}\right]$ and $L \in\left[C B_{1}\right]$. However, we then have $S(K L M)>$ $S\left(K L C_{1}\right)>S\left(K B_{1} C_{1}\right)=S\left(A_{1} B_{1} C_{1}\right)=S / 4$. Hence, by the pigeonhole principle one of the remaining three triangles $\triangle M A L, \triangle K B M$, and $\triangle L C K$ must have an area less than or equal to $S / 4$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
6. (POL) Let $M, K$, and $L$ be points on $(A B),(B C)$, and $(C A)$, respectively. Prove that the area of at least one of the three triangles $\triangle M A L$, $\triangle K B M$, and $\triangle L C K$ is less than or equal to one-fourth the area of $\triangle A B C$.
|
6. Let $S$ denote the area of $\triangle A B C$. Let $A_{1}, B_{1}, C_{1}$ be the midpoints of $B C, A C, A B$ respectively. We note that $S_{A_{1} B_{1} C}=S_{A_{1} B C_{1}}=S_{A B_{1} C_{1}}=$ $S_{A_{1} B_{1} C_{1}}=S / 4$. Let us assume w.l.o.g. that $M \in\left[A C_{1}\right]$. We then must have $K \in\left[B A_{1}\right]$ and $L \in\left[C B_{1}\right]$. However, we then have $S(K L M)>$ $S\left(K L C_{1}\right)>S\left(K B_{1} C_{1}\right)=S\left(A_{1} B_{1} C_{1}\right)=S / 4$. Hence, by the pigeonhole principle one of the remaining three triangles $\triangle M A L, \triangle K B M$, and $\triangle L C K$ must have an area less than or equal to $S / 4$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
de084b00-112e-5921-ad6e-100766369062
| 24,602
|
12. (CZS 6) Given a segment $A B$ of the length 1, define the set $M$ of points in the following way: it contains the two points $A, B$, and also all points obtained from $A, B$ by iterating the following rule: $(*)$ for every pair of points $X, Y$ in $M$, the set $M$ also contains the point $Z$ of the segment $X Y$ for which $Y Z=3 X Z$. (a) Prove that the set $M$ consists of points $X$ from the segment $A B$ for which the distance from the point $A$ is either $$ A X=\frac{3 k}{4^{n}} \quad \text { or } \quad A X=\frac{3 k-2}{4^{n}} $$ where $n, k$ are nonnegative integers. (b) Prove that the point $X_{0}$ for which $A X_{0}=1 / 2=X_{0} B$ does not belong to the set $M$.
|
12. Let us denote by $M_{n}$ the set of points of the segment $A B$ obtained from $A$ and $B$ by not more than $n$ iterations of $(*)$. It can be proved by induction that $$ M_{n}=\left\{X \in A B \left\lvert\, A X=\frac{3 k}{4^{n}}\right. \text { or } \frac{3 k-2}{4^{n}} \text { for some } k \in \mathbb{N}\right\} $$ Thus (a) immediately follows from $M=\bigcup M_{n}$. It also follows that if $a, b \in \mathbb{N}$ and $a / b \in M$, then $3 \mid a(b-a)$. Therefore $1 / 2 \notin M$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
12. (CZS 6) Given a segment $A B$ of the length 1, define the set $M$ of points in the following way: it contains the two points $A, B$, and also all points obtained from $A, B$ by iterating the following rule: $(*)$ for every pair of points $X, Y$ in $M$, the set $M$ also contains the point $Z$ of the segment $X Y$ for which $Y Z=3 X Z$. (a) Prove that the set $M$ consists of points $X$ from the segment $A B$ for which the distance from the point $A$ is either $$ A X=\frac{3 k}{4^{n}} \quad \text { or } \quad A X=\frac{3 k-2}{4^{n}} $$ where $n, k$ are nonnegative integers. (b) Prove that the point $X_{0}$ for which $A X_{0}=1 / 2=X_{0} B$ does not belong to the set $M$.
|
12. Let us denote by $M_{n}$ the set of points of the segment $A B$ obtained from $A$ and $B$ by not more than $n$ iterations of $(*)$. It can be proved by induction that $$ M_{n}=\left\{X \in A B \left\lvert\, A X=\frac{3 k}{4^{n}}\right. \text { or } \frac{3 k-2}{4^{n}} \text { for some } k \in \mathbb{N}\right\} $$ Thus (a) immediately follows from $M=\bigcup M_{n}$. It also follows that if $a, b \in \mathbb{N}$ and $a / b \in M$, then $3 \mid a(b-a)$. Therefore $1 / 2 \notin M$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
66a7d221-4731-503f-b65c-d3081c50e06f
| 24,612
|
15. (GDR 3) Suppose $\tan \alpha=p / q$, where $p$ and $q$ are integers and $q \neq 0$. Prove that the number $\tan \beta$ for which $\tan 2 \beta=\tan 3 \alpha$ is rational only when $p^{2}+q^{2}$ is the square of an integer.
|
15. Given that $\tan \alpha \in \mathbb{Q}$, we have that $\tan \beta$ is rational if and only if $\tan \gamma$ is rational, where $\gamma=\beta-\alpha$ and $2 \gamma=\alpha$. Putting $t=\tan \gamma$ we obtain $\frac{p}{q}=\tan 2 \gamma=\frac{2 t}{1-t^{2}}$, which leads to the quadratic equation $p t^{2}+2 q t-p=0$. This equation has rational solutions if and only if its discriminant $4\left(p^{2}+q^{2}\right)$ is a perfect square, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
15. (GDR 3) Suppose $\tan \alpha=p / q$, where $p$ and $q$ are integers and $q \neq 0$. Prove that the number $\tan \beta$ for which $\tan 2 \beta=\tan 3 \alpha$ is rational only when $p^{2}+q^{2}$ is the square of an integer.
|
15. Given that $\tan \alpha \in \mathbb{Q}$, we have that $\tan \beta$ is rational if and only if $\tan \gamma$ is rational, where $\gamma=\beta-\alpha$ and $2 \gamma=\alpha$. Putting $t=\tan \gamma$ we obtain $\frac{p}{q}=\tan 2 \gamma=\frac{2 t}{1-t^{2}}$, which leads to the quadratic equation $p t^{2}+2 q t-p=0$. This equation has rational solutions if and only if its discriminant $4\left(p^{2}+q^{2}\right)$ is a perfect square, and the result follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e88fc2fc-4fba-50df-9395-9109b2e90027
| 24,619
|
16. (GDR 4) Prove the following statement: If $r_{1}$ and $r_{2}$ are real numbers whose quotient is irrational, then any real number $x$ can be approximated arbitrarily well by numbers of the form $z_{k_{1}, k_{2}}=k_{1} r_{1}+k_{2} r_{2}, k_{1}, k_{2}$ integers; i.e., for every real number $x$ and every positive real number $p$ two integers $k_{1}$ and $k_{2}$ can be found such that $\left|x-\left(k_{1} r_{1}+k_{2} r_{2}\right)\right|<p$.
|
16. First let us notice that all the numbers $z_{m_{1}, m_{2}}=m_{1} r_{1}+m_{2} r_{2}$ ( $m_{1}, m_{2} \in$ $\mathbb{Z})$ are distinct, since $r_{1} / r_{2}$ is irrational. Thus for any $n \in \mathbb{N}$ the interval $\left[-n\left(\left|r_{1}\right|+\left|r_{2}\right|\right), n\left(\left|r_{1}\right|+\left|r_{2}\right|\right)\right]$ contains $(2 n+1)^{2}$ numbers $z_{m_{1}, m_{2}}$, where $\left|m_{1}\right|,\left|m_{2}\right| \leq n$. Therefore some two of these $(2 n+1)^{2}$ numbers, say $z_{m_{1}, m_{2}}, z_{n_{1}, n_{2}}$, differ by at most $\frac{2 n\left(\left|r_{1}\right|+\left|r_{2}\right|\right)}{(2 n+1)^{2}-1}=\frac{\left(\left|r_{1}\right|+\left|r_{2}\right|\right)}{2(n+1)}$. By taking $n$ large enough we can achieve that $$ z_{q_{1}, q_{2}}=\left|z_{m_{1}, m_{2}}-z_{n_{1}, n_{2}}\right| \leq p $$ If now $k$ is the integer such that $k z_{q_{1}, q_{2}} \leq x<(k+1) z_{q_{1}, q_{2}}$, then $z_{k q_{1}, k q_{2}}=$ $k z_{q_{1}, q_{2}}$ differs from $x$ by at most $p$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
16. (GDR 4) Prove the following statement: If $r_{1}$ and $r_{2}$ are real numbers whose quotient is irrational, then any real number $x$ can be approximated arbitrarily well by numbers of the form $z_{k_{1}, k_{2}}=k_{1} r_{1}+k_{2} r_{2}, k_{1}, k_{2}$ integers; i.e., for every real number $x$ and every positive real number $p$ two integers $k_{1}$ and $k_{2}$ can be found such that $\left|x-\left(k_{1} r_{1}+k_{2} r_{2}\right)\right|<p$.
|
16. First let us notice that all the numbers $z_{m_{1}, m_{2}}=m_{1} r_{1}+m_{2} r_{2}$ ( $m_{1}, m_{2} \in$ $\mathbb{Z})$ are distinct, since $r_{1} / r_{2}$ is irrational. Thus for any $n \in \mathbb{N}$ the interval $\left[-n\left(\left|r_{1}\right|+\left|r_{2}\right|\right), n\left(\left|r_{1}\right|+\left|r_{2}\right|\right)\right]$ contains $(2 n+1)^{2}$ numbers $z_{m_{1}, m_{2}}$, where $\left|m_{1}\right|,\left|m_{2}\right| \leq n$. Therefore some two of these $(2 n+1)^{2}$ numbers, say $z_{m_{1}, m_{2}}, z_{n_{1}, n_{2}}$, differ by at most $\frac{2 n\left(\left|r_{1}\right|+\left|r_{2}\right|\right)}{(2 n+1)^{2}-1}=\frac{\left(\left|r_{1}\right|+\left|r_{2}\right|\right)}{2(n+1)}$. By taking $n$ large enough we can achieve that $$ z_{q_{1}, q_{2}}=\left|z_{m_{1}, m_{2}}-z_{n_{1}, n_{2}}\right| \leq p $$ If now $k$ is the integer such that $k z_{q_{1}, q_{2}} \leq x<(k+1) z_{q_{1}, q_{2}}$, then $z_{k q_{1}, k q_{2}}=$ $k z_{q_{1}, q_{2}}$ differs from $x$ by at most $p$, as desired.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e92cceb5-f74b-5189-8721-7ee005972c8a
| 24,622
|
17. (GBR 1) ${ }^{\mathrm{IMO} 3}$ Let $k, m$, and $n$ be positive integers such that $m+k+1$ is a prime number greater than $n+1$. Write $c_{s}$ for $s(s+1)$. Prove that the product $\left(c_{m+1}-c_{k}\right)\left(c_{m+2}-c_{k}\right) \cdots\left(c_{m+n}-c_{k}\right)$ is divisible by the product $c_{1} c_{2} \cdots c_{n}$.
|
17. Using $c_{r}-c_{s}=(r-s)(r+s+1)$ we can easily get $$ \frac{\left(c_{m+1}-c_{k}\right) \cdots\left(c_{m+n}-c_{k}\right)}{c_{1} c_{2} \cdots c_{n}}=\frac{(m-k+n)!}{(m-k)!n!} \cdot \frac{(m+k+n+1)!}{(m+k+1)!(n+1)!} $$ The first factor $\frac{(m-k+n)!}{(m-k)!n!}=\binom{m-k+n}{n}$ is clearly an integer. The second factor is also an integer because by the assumption, $m+k+1$ and ( $m+$ $k)!(n+1)$ ! are coprime, and $(m+k+n+1)$ ! is divisible by both; hence it is also divisible by their product.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
17. (GBR 1) ${ }^{\mathrm{IMO} 3}$ Let $k, m$, and $n$ be positive integers such that $m+k+1$ is a prime number greater than $n+1$. Write $c_{s}$ for $s(s+1)$. Prove that the product $\left(c_{m+1}-c_{k}\right)\left(c_{m+2}-c_{k}\right) \cdots\left(c_{m+n}-c_{k}\right)$ is divisible by the product $c_{1} c_{2} \cdots c_{n}$.
|
17. Using $c_{r}-c_{s}=(r-s)(r+s+1)$ we can easily get $$ \frac{\left(c_{m+1}-c_{k}\right) \cdots\left(c_{m+n}-c_{k}\right)}{c_{1} c_{2} \cdots c_{n}}=\frac{(m-k+n)!}{(m-k)!n!} \cdot \frac{(m+k+n+1)!}{(m+k+1)!(n+1)!} $$ The first factor $\frac{(m-k+n)!}{(m-k)!n!}=\binom{m-k+n}{n}$ is clearly an integer. The second factor is also an integer because by the assumption, $m+k+1$ and ( $m+$ $k)!(n+1)$ ! are coprime, and $(m+k+n+1)$ ! is divisible by both; hence it is also divisible by their product.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
eb086bb1-e809-5223-b06d-dcd654b2f26b
| 24,625
|
18. (GBR 5) If $x$ is a positive rational number, show that $x$ can be uniquely expressed in the form $$ x=a_{1}+\frac{a_{2}}{2!}+\frac{a_{3}}{3!}+\cdots, $$ where $a_{1}, a_{2}, \ldots$ are integers, $0 \leq a_{n} \leq n-1$ for $n>1$, and the series terminates. Show also that $x$ can be expressed as the sum of reciprocals of different integers, each of which is greater than $10^{6}$.
|
18. In the first part, it is sufficient to show that each rational number of the form $m / n!, m, n \in \mathbb{N}$, can be written uniquely in the required form. We prove this by induction on $n$. The statement is trivial for $n=1$. Let us assume it holds for $n-1$, and let there be given a rational number $m / n$ !. Let us take $a_{n} \in\{0, \ldots, n-1\}$ such that $m-a_{n}=n m_{1}$ for some $m_{1} \in \mathbb{N}$. By the inductive hypothesis, there are unique $a_{1} \in \mathbb{N}_{0}, a_{i} \in\{0, \ldots, i-1\}(i=1, \ldots, n-1)$ such that $m_{1} /(n-1)!=\sum_{i=1}^{n-1} a_{i} / i$ !, and then $$ \frac{m}{n!}=\frac{m_{1}}{(n-1)!}+\frac{a_{n}}{n!}=\sum_{i=1}^{n} \frac{a_{i}}{i!} $$ as desired. On the other hand, if $m / n!=\sum_{i=1}^{n} a_{i} / i$ !, multiplying by $n$ ! we see that $m-a_{n}$ must be a multiple of $n$, so the choice of $a_{n}$ was unique and therefore the representation itself. This completes the induction. In particular, since $a_{i} \mid i!$ and $i!/ a_{i}>(i-1)!\geq(i-1)!/ a_{i-1}$, we conclude that each rational $q, 0<q<1$, can be written as the sum of different reciprocals. Now we prove the second part. Let $x>0$ be a rational number. For any integer $m>10^{6}$, let $n>m$ be the greatest integer such that $y=$ $x-\frac{1}{m}-\frac{1}{m+1}-\cdots-\frac{1}{n}>0$. Then $y$ can be written as the sum of reciprocals of different positive integers, which all must be greater than $n$. The result follows immediately.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
18. (GBR 5) If $x$ is a positive rational number, show that $x$ can be uniquely expressed in the form $$ x=a_{1}+\frac{a_{2}}{2!}+\frac{a_{3}}{3!}+\cdots, $$ where $a_{1}, a_{2}, \ldots$ are integers, $0 \leq a_{n} \leq n-1$ for $n>1$, and the series terminates. Show also that $x$ can be expressed as the sum of reciprocals of different integers, each of which is greater than $10^{6}$.
|
18. In the first part, it is sufficient to show that each rational number of the form $m / n!, m, n \in \mathbb{N}$, can be written uniquely in the required form. We prove this by induction on $n$. The statement is trivial for $n=1$. Let us assume it holds for $n-1$, and let there be given a rational number $m / n$ !. Let us take $a_{n} \in\{0, \ldots, n-1\}$ such that $m-a_{n}=n m_{1}$ for some $m_{1} \in \mathbb{N}$. By the inductive hypothesis, there are unique $a_{1} \in \mathbb{N}_{0}, a_{i} \in\{0, \ldots, i-1\}(i=1, \ldots, n-1)$ such that $m_{1} /(n-1)!=\sum_{i=1}^{n-1} a_{i} / i$ !, and then $$ \frac{m}{n!}=\frac{m_{1}}{(n-1)!}+\frac{a_{n}}{n!}=\sum_{i=1}^{n} \frac{a_{i}}{i!} $$ as desired. On the other hand, if $m / n!=\sum_{i=1}^{n} a_{i} / i$ !, multiplying by $n$ ! we see that $m-a_{n}$ must be a multiple of $n$, so the choice of $a_{n}$ was unique and therefore the representation itself. This completes the induction. In particular, since $a_{i} \mid i!$ and $i!/ a_{i}>(i-1)!\geq(i-1)!/ a_{i-1}$, we conclude that each rational $q, 0<q<1$, can be written as the sum of different reciprocals. Now we prove the second part. Let $x>0$ be a rational number. For any integer $m>10^{6}$, let $n>m$ be the greatest integer such that $y=$ $x-\frac{1}{m}-\frac{1}{m+1}-\cdots-\frac{1}{n}>0$. Then $y$ can be written as the sum of reciprocals of different positive integers, which all must be greater than $n$. The result follows immediately.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ff299342-7324-5ce2-ba5e-d82a6ecdfec3
| 24,627
|
22. (HUN 3) The distance between the centers of the circles $k_{1}$ and $k_{2}$ with radii $r$ is equal to $r$. Points $A$ and $B$ are on the circle $k_{1}$, symmetric with respect to the line connecting the centers of the circles. Point $P$ is an arbitrary point on $k_{2}$. Prove that $$ P A^{2}+P B^{2} \geq 2 r^{2} $$ When does equality hold?
|
22. Let $O_{1}$ and $O_{2}$ be the centers of circles $k_{1}$ and $k_{2}$ and let $C$ be the midpoint of the segment $A B$. Using the well-known relation for elements of a triangle, we obtain $$ P A^{2}+P B^{2}=2 P C^{2}+2 C A^{2} \geq 2 O_{1} C^{2}+2 C A^{2}=2 O_{1} A^{2}=2 r^{2} $$ Equality holds if $P$ coincides with $O_{1}$ or if $A$ and $B$ coincide with $O_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
22. (HUN 3) The distance between the centers of the circles $k_{1}$ and $k_{2}$ with radii $r$ is equal to $r$. Points $A$ and $B$ are on the circle $k_{1}$, symmetric with respect to the line connecting the centers of the circles. Point $P$ is an arbitrary point on $k_{2}$. Prove that $$ P A^{2}+P B^{2} \geq 2 r^{2} $$ When does equality hold?
|
22. Let $O_{1}$ and $O_{2}$ be the centers of circles $k_{1}$ and $k_{2}$ and let $C$ be the midpoint of the segment $A B$. Using the well-known relation for elements of a triangle, we obtain $$ P A^{2}+P B^{2}=2 P C^{2}+2 C A^{2} \geq 2 O_{1} C^{2}+2 C A^{2}=2 O_{1} A^{2}=2 r^{2} $$ Equality holds if $P$ coincides with $O_{1}$ or if $A$ and $B$ coincide with $O_{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5827706-2e41-52f6-97c3-9cd7d5ebd82b
| 24,640
|
23. (HUN 4) Prove that for an arbitrary pair of vectors $f$ and $g$ in the plane, the inequality $$ a f^{2}+b f g+c g^{2} \geq 0 $$ holds if and only if the following conditions are fulfilled: $a \geq 0, c \geq 0$, $4 a c \geq b^{2}$.
|
23. Suppose that $a \geq 0, c \geq 0,4 a c \geq b^{2}$. If $a=0$, then $b=0$, and the inequality reduces to the obvious $c g^{2} \geq 0$. Also, if $a>0$, then $$ a f^{2}+b f g+c g^{2}=a\left(f+\frac{b}{2 a} g\right)^{2}+\frac{4 a c-b^{2}}{4 a} g^{2} \geq 0 $$ Suppose now that $a f^{2}+b f g+c g^{2} \geq 0$ holds for an arbitrary pair of vectors $f, g$. Substituting $f$ by $t g(t \in \mathbb{R})$ we get that $\left(a t^{2}+b t+c\right) g^{2} \geq 0$ holds for any real number $t$. Therefore $a \geq 0, c \geq 0,4 a c \geq b^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
23. (HUN 4) Prove that for an arbitrary pair of vectors $f$ and $g$ in the plane, the inequality $$ a f^{2}+b f g+c g^{2} \geq 0 $$ holds if and only if the following conditions are fulfilled: $a \geq 0, c \geq 0$, $4 a c \geq b^{2}$.
|
23. Suppose that $a \geq 0, c \geq 0,4 a c \geq b^{2}$. If $a=0$, then $b=0$, and the inequality reduces to the obvious $c g^{2} \geq 0$. Also, if $a>0$, then $$ a f^{2}+b f g+c g^{2}=a\left(f+\frac{b}{2 a} g\right)^{2}+\frac{4 a c-b^{2}}{4 a} g^{2} \geq 0 $$ Suppose now that $a f^{2}+b f g+c g^{2} \geq 0$ holds for an arbitrary pair of vectors $f, g$. Substituting $f$ by $t g(t \in \mathbb{R})$ we get that $\left(a t^{2}+b t+c\right) g^{2} \geq 0$ holds for any real number $t$. Therefore $a \geq 0, c \geq 0,4 a c \geq b^{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
27d499e4-a989-57ff-bd48-6d3e3e7272e2
| 24,643
|
3. (BUL 3) Prove the trigonometric inequality $\cos x<1-\frac{x^{2}}{2}+\frac{x^{4}}{16}$, where $x \in(0, \pi / 2)$.
|
3. Consider the function $f:[0, \pi / 2] \rightarrow \mathbb{R}$ defined by $f(x)=1-x^{2} / 2+$ $x^{4} / 16-\cos x$. It is easy to calculate that $f^{\prime}(0)=f^{\prime \prime}(0)=f^{\prime \prime \prime}(0)=0$ and $f^{\prime \prime \prime \prime}(x)=$ $3 / 2-\cos x$. Since $f^{\prime \prime \prime \prime}(x)>0, f^{\prime \prime \prime}(x)$ is increasing. Together with $f^{\prime \prime \prime}(0)=0$, this gives $f^{\prime \prime \prime}(x)>0$ for $x>0$; hence $f^{\prime \prime}(x)$ is increasing, etc. Continuing in the same way we easily conclude that $f(x)>0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
3. (BUL 3) Prove the trigonometric inequality $\cos x<1-\frac{x^{2}}{2}+\frac{x^{4}}{16}$, where $x \in(0, \pi / 2)$.
|
3. Consider the function $f:[0, \pi / 2] \rightarrow \mathbb{R}$ defined by $f(x)=1-x^{2} / 2+$ $x^{4} / 16-\cos x$. It is easy to calculate that $f^{\prime}(0)=f^{\prime \prime}(0)=f^{\prime \prime \prime}(0)=0$ and $f^{\prime \prime \prime \prime}(x)=$ $3 / 2-\cos x$. Since $f^{\prime \prime \prime \prime}(x)>0, f^{\prime \prime \prime}(x)$ is increasing. Together with $f^{\prime \prime \prime}(0)=0$, this gives $f^{\prime \prime \prime}(x)>0$ for $x>0$; hence $f^{\prime \prime}(x)$ is increasing, etc. Continuing in the same way we easily conclude that $f(x)>0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e053398d-1082-515c-9ae9-36dc1a541aa8
| 24,662
|
36. (POL 1) Prove that the center of the sphere circumscribed around a tetrahedron $A B C D$ coincides with the center of a sphere inscribed in that tetrahedron if and only if $A B=C D, A C=B D$, and $A D=B C$.
|
36. Suppose that the skew edges of the tetrahedron $A B C D$ are equal. Let $K$, $L, M, P, Q, R$ be the midpoints of edges $A B, A C, A D, C D, D B, B C$ respectively. Segments $K P, L Q, M R$ have the common midpoint $T$. We claim that the lines $K P, L Q$ and $M R$ are axes of symmetry of the tetrahedron $A B C D$. From $L M\|C D\| R Q$ and similarly $L R \| M Q$ and $L M=C D / 2=$ $A B / 2=L R$ it follows that $L M Q R$ is a rhombus and therefore $L Q \perp$ $M R$. We similarly show that $K P$ is perpendicular to $L Q$ and $M R$, and  thus it is perpendicular to the plane $L M Q R$. Since the lines $A B$ and $C D$ are parallel to the plane $L M Q R$, they are perpendicular to $K P$. Hence the points $A$ and $C$ are symmetric to $B$ and $D$ with respect to the line $K P$, which means that $K P$ is an axis of symmetry of the tetrahedron $A B C D$. Similarly, so are the lines $L Q$ and $M R$. The centers of circumscribed and inscribed spheres of tetrahedron $A B C D$ must lie on every axis of symmetry of the tetrahedron, and hence both coincide with $T$. Conversely, suppose that the centers of circumscribed and inscribed spheres of the tetrahedron $A B C D$ coincide with some point $T$. Then the orthogonal projections of $T$ onto the faces $A B C$ and $A B D$ are the circumcenters $O_{1}$ and $O_{2}$ of these two triangles, and moreover, $T O_{1}=T O_{2}$. Pythagoras's theorem gives $A O_{1}=A O_{2}$, which by the law of sines implies $\angle A C B=\angle A D B$. Now it easily follows that the sum of the angles at one vertex of the tetrahedron is equal to $180^{\circ}$. Let $D^{\prime}, D^{\prime \prime}$, and $D^{\prime \prime \prime}$ be the points in the plane $A B C$ lying outside $\triangle A B C$ such that $\triangle D^{\prime} B C \cong \triangle D B C, \triangle D^{\prime \prime} C A \cong \triangle D C A$, and $\triangle D^{\prime \prime \prime} A B \cong \triangle D A B$. The angle $D^{\prime \prime} A D^{\prime \prime \prime}$ is then straight, and hence $A, B, C$ are midpoints of the segments $D^{\prime \prime} D^{\prime \prime \prime}, D^{\prime \prime \prime} D^{\prime}, D^{\prime} D^{\prime \prime}$ respectively. Hence $A D=D^{\prime \prime} D^{\prime \prime \prime} / 2=B C$, and analogously $A B=C D$ and $A C=B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
36. (POL 1) Prove that the center of the sphere circumscribed around a tetrahedron $A B C D$ coincides with the center of a sphere inscribed in that tetrahedron if and only if $A B=C D, A C=B D$, and $A D=B C$.
|
36. Suppose that the skew edges of the tetrahedron $A B C D$ are equal. Let $K$, $L, M, P, Q, R$ be the midpoints of edges $A B, A C, A D, C D, D B, B C$ respectively. Segments $K P, L Q, M R$ have the common midpoint $T$. We claim that the lines $K P, L Q$ and $M R$ are axes of symmetry of the tetrahedron $A B C D$. From $L M\|C D\| R Q$ and similarly $L R \| M Q$ and $L M=C D / 2=$ $A B / 2=L R$ it follows that $L M Q R$ is a rhombus and therefore $L Q \perp$ $M R$. We similarly show that $K P$ is perpendicular to $L Q$ and $M R$, and  thus it is perpendicular to the plane $L M Q R$. Since the lines $A B$ and $C D$ are parallel to the plane $L M Q R$, they are perpendicular to $K P$. Hence the points $A$ and $C$ are symmetric to $B$ and $D$ with respect to the line $K P$, which means that $K P$ is an axis of symmetry of the tetrahedron $A B C D$. Similarly, so are the lines $L Q$ and $M R$. The centers of circumscribed and inscribed spheres of tetrahedron $A B C D$ must lie on every axis of symmetry of the tetrahedron, and hence both coincide with $T$. Conversely, suppose that the centers of circumscribed and inscribed spheres of the tetrahedron $A B C D$ coincide with some point $T$. Then the orthogonal projections of $T$ onto the faces $A B C$ and $A B D$ are the circumcenters $O_{1}$ and $O_{2}$ of these two triangles, and moreover, $T O_{1}=T O_{2}$. Pythagoras's theorem gives $A O_{1}=A O_{2}$, which by the law of sines implies $\angle A C B=\angle A D B$. Now it easily follows that the sum of the angles at one vertex of the tetrahedron is equal to $180^{\circ}$. Let $D^{\prime}, D^{\prime \prime}$, and $D^{\prime \prime \prime}$ be the points in the plane $A B C$ lying outside $\triangle A B C$ such that $\triangle D^{\prime} B C \cong \triangle D B C, \triangle D^{\prime \prime} C A \cong \triangle D C A$, and $\triangle D^{\prime \prime \prime} A B \cong \triangle D A B$. The angle $D^{\prime \prime} A D^{\prime \prime \prime}$ is then straight, and hence $A, B, C$ are midpoints of the segments $D^{\prime \prime} D^{\prime \prime \prime}, D^{\prime \prime \prime} D^{\prime}, D^{\prime} D^{\prime \prime}$ respectively. Hence $A D=D^{\prime \prime} D^{\prime \prime \prime} / 2=B C$, and analogously $A B=C D$ and $A C=B D$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e9201eb-5335-5fb9-97ba-8d81e8f75f67
| 24,681
|
37. (POL 2) Prove that for arbitrary positive numbers the following inequality holds: $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \leq \frac{a^{8}+b^{8}+c^{8}}{a^{3} b^{3} c^{3}} $$
|
37. Using the $\mathrm{A}-\mathrm{G}$ mean inequality we obtain $$ \begin{aligned} & 8 a^{2} b^{3} c^{3} \leq 2 a^{8}+3 b^{8}+3 c^{8} \\ & 8 a^{3} b^{2} c^{3} \leq 3 a^{8}+2 b^{8}+3 c^{8} \\ & 8 a^{3} b^{3} c^{2} \leq 3 a^{8}+3 b^{8}+2 c^{8} \end{aligned} $$ By adding these inequalities and dividing by $3 a^{3} b^{3} c^{3}$ we obtain the desired one.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
37. (POL 2) Prove that for arbitrary positive numbers the following inequality holds: $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \leq \frac{a^{8}+b^{8}+c^{8}}{a^{3} b^{3} c^{3}} $$
|
37. Using the $\mathrm{A}-\mathrm{G}$ mean inequality we obtain $$ \begin{aligned} & 8 a^{2} b^{3} c^{3} \leq 2 a^{8}+3 b^{8}+3 c^{8} \\ & 8 a^{3} b^{2} c^{3} \leq 3 a^{8}+2 b^{8}+3 c^{8} \\ & 8 a^{3} b^{3} c^{2} \leq 3 a^{8}+3 b^{8}+2 c^{8} \end{aligned} $$ By adding these inequalities and dividing by $3 a^{3} b^{3} c^{3}$ we obtain the desired one.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b3745907-4f90-5912-bf56-eb3cb0efa181
| 24,684
|
39. (POL 4) Show that the triangle whose angles satisfy the equality $$ \frac{\sin ^{2} A+\sin ^{2} B+\sin ^{2} C}{\cos ^{2} A+\cos ^{2} B+\cos ^{2} C}=2 $$ is a right-angled triangle.
|
39. Since $\sin ^{2} A+\sin ^{2} B+\sin ^{2} C+\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=3$, the given equality is equivalent to $\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=1$, which by multiplying by 2 is transformed into $$ \begin{aligned} 0 & =\cos 2 A+\cos 2 B+2 \cos ^{2} C=2 \cos (A+B) \cos (A-B)+2 \cos ^{2} C \\ & =2 \cos C(\cos (A-B)-\cos C) \end{aligned} $$ It follows that either $\cos C=0$ or $\cos (A-B)=\cos C$. In both cases the triangle is right-angled.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
39. (POL 4) Show that the triangle whose angles satisfy the equality $$ \frac{\sin ^{2} A+\sin ^{2} B+\sin ^{2} C}{\cos ^{2} A+\cos ^{2} B+\cos ^{2} C}=2 $$ is a right-angled triangle.
|
39. Since $\sin ^{2} A+\sin ^{2} B+\sin ^{2} C+\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=3$, the given equality is equivalent to $\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=1$, which by multiplying by 2 is transformed into $$ \begin{aligned} 0 & =\cos 2 A+\cos 2 B+2 \cos ^{2} C=2 \cos (A+B) \cos (A-B)+2 \cos ^{2} C \\ & =2 \cos C(\cos (A-B)-\cos C) \end{aligned} $$ It follows that either $\cos C=0$ or $\cos (A-B)=\cos C$. In both cases the triangle is right-angled.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
990b02dd-9d90-5c05-9a49-ec4c57a5e7e0
| 24,689
|
4. (BUL 4) Suppose medians $m_{a}$ and $m_{b}$ of a triangle are orthogonal. Prove that: (a) The medians of that triangle correspond to the sides of a right-angled triangle. (b) The inequality $$ 5\left(a^{2}+b^{2}-c^{2}\right) \geq 8 a b $$ is valid, where $a, b$, and $c$ are side lengths of the given triangle.
|
4. (a) Let $A B C D$ be a parallelogram, and $K, L$ the midpoints of segments $B C$ and $C D$ respectively. The sides of $\triangle A K L$ are equal and parallel to the medians of $\triangle A B C$. (b) Using the formulas $4 m_{a}^{2}=2 b^{2}+2 c^{2}-a^{2}$ etc., it is easy to obtain that $m_{a}^{2}+m_{b}^{2}=m_{c}^{2}$ is equivalent to $a^{2}+b^{2}=5 c^{2}$. Then $$ 5\left(a^{2}+b^{2}-c^{2}\right)=4\left(a^{2}+b^{2}\right) \geq 8 a b $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
4. (BUL 4) Suppose medians $m_{a}$ and $m_{b}$ of a triangle are orthogonal. Prove that: (a) The medians of that triangle correspond to the sides of a right-angled triangle. (b) The inequality $$ 5\left(a^{2}+b^{2}-c^{2}\right) \geq 8 a b $$ is valid, where $a, b$, and $c$ are side lengths of the given triangle.
|
4. (a) Let $A B C D$ be a parallelogram, and $K, L$ the midpoints of segments $B C$ and $C D$ respectively. The sides of $\triangle A K L$ are equal and parallel to the medians of $\triangle A B C$. (b) Using the formulas $4 m_{a}^{2}=2 b^{2}+2 c^{2}-a^{2}$ etc., it is easy to obtain that $m_{a}^{2}+m_{b}^{2}=m_{c}^{2}$ is equivalent to $a^{2}+b^{2}=5 c^{2}$. Then $$ 5\left(a^{2}+b^{2}-c^{2}\right)=4\left(a^{2}+b^{2}\right) \geq 8 a b $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4dbdb732-fa12-5a86-bb50-aafc8fad81c3
| 24,692
|
41. (POL 6) A line $l$ is drawn through the intersection point $H$ of the altitudes of an acute-angled triangle. Prove that the symmetric images $l_{a}$, $l_{b}, l_{c}$ of $l$ with respect to sides $B C, C A, A B$ have one point in common, which lies on the circumcircle of $A B C$.
|
41. It is well known that the points $K, L, M$, symmetric to $H$ with respect to $B C, C A, A B$ respectively, lie on the circumcircle $k$ of the triangle $A B C$. For $K$, this follows from an elementary calculation of angles of triangles $H B C$ and noting that $\measuredangle K B C=\measuredangle H B C=\measuredangle K A C$. For other points the proof is analogous. Since the lines $l_{a}, l_{b}$ pass through $K$ and $L$ and $l_{b}$ is obtained from $l_{a}$ by rotation about $C$ for an angle $2 \gamma=\angle L C K$, it follows that the intersection point $P$ of $l_{a}$ and $l_{b}$ is at the circumcircle of $K L C$, that is, $k$. Similarly, $l_{b}$ and $l_{c}$ meet at a point on $k$; hence they must pass through the same point $P$. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
41. (POL 6) A line $l$ is drawn through the intersection point $H$ of the altitudes of an acute-angled triangle. Prove that the symmetric images $l_{a}$, $l_{b}, l_{c}$ of $l$ with respect to sides $B C, C A, A B$ have one point in common, which lies on the circumcircle of $A B C$.
|
41. It is well known that the points $K, L, M$, symmetric to $H$ with respect to $B C, C A, A B$ respectively, lie on the circumcircle $k$ of the triangle $A B C$. For $K$, this follows from an elementary calculation of angles of triangles $H B C$ and noting that $\measuredangle K B C=\measuredangle H B C=\measuredangle K A C$. For other points the proof is analogous. Since the lines $l_{a}, l_{b}$ pass through $K$ and $L$ and $l_{b}$ is obtained from $l_{a}$ by rotation about $C$ for an angle $2 \gamma=\angle L C K$, it follows that the intersection point $P$ of $l_{a}$ and $l_{b}$ is at the circumcircle of $K L C$, that is, $k$. Similarly, $l_{b}$ and $l_{c}$ meet at a point on $k$; hence they must pass through the same point $P$. 
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6fc2763d-bb01-52ec-b67e-6a1cc62f14a2
| 24,698
|
47. (ROM 6) Prove the inequality $x_{1} x_{2} \cdots x_{k}\left(x_{1}^{n-1}+x_{2}^{n-1}+\cdots+x_{k}^{n-1}\right) \leq x_{1}^{n+k-1}+x_{2}^{n+k-1}+\cdots+x_{k}^{n+k-1}$, where $x_{i}>0(i=1,2, \ldots, k), k \in N, n \in N$.
|
47. Using the $\mathrm{A}-\mathrm{G}$ mean inequality we get $$ \begin{gathered} (n+k-1) x_{1}^{n} x_{2} \cdots x_{k} \leq n x_{1}^{n+k-1}+x_{2}^{n+k-1}+\cdots+x_{k}^{n+k-1} \\ (n+k-1) x_{1} x_{2}^{n} \cdots x_{k} \leq x_{1}^{n+k-1}+n x_{2}^{n+k-1}+\cdots+x_{k}^{n+k-1} \\ \cdots \cdots \cdots \\ \cdots \cdots \cdots \\ (n+k-1) x_{1} x_{2} \cdots x_{k}^{n} \leq x_{1}^{n+k-1}+x_{2}^{n+k-1}+\cdots+n x_{k}^{n+k-1} \end{gathered} $$ By adding these inequalities and dividing by $n+k-1$ we obtain the desired one. Remark. This is also an immediate consequence of Muirhead's inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
47. (ROM 6) Prove the inequality $x_{1} x_{2} \cdots x_{k}\left(x_{1}^{n-1}+x_{2}^{n-1}+\cdots+x_{k}^{n-1}\right) \leq x_{1}^{n+k-1}+x_{2}^{n+k-1}+\cdots+x_{k}^{n+k-1}$, where $x_{i}>0(i=1,2, \ldots, k), k \in N, n \in N$.
|
47. Using the $\mathrm{A}-\mathrm{G}$ mean inequality we get $$ \begin{gathered} (n+k-1) x_{1}^{n} x_{2} \cdots x_{k} \leq n x_{1}^{n+k-1}+x_{2}^{n+k-1}+\cdots+x_{k}^{n+k-1} \\ (n+k-1) x_{1} x_{2}^{n} \cdots x_{k} \leq x_{1}^{n+k-1}+n x_{2}^{n+k-1}+\cdots+x_{k}^{n+k-1} \\ \cdots \cdots \cdots \\ \cdots \cdots \cdots \\ (n+k-1) x_{1} x_{2} \cdots x_{k}^{n} \leq x_{1}^{n+k-1}+x_{2}^{n+k-1}+\cdots+n x_{k}^{n+k-1} \end{gathered} $$ By adding these inequalities and dividing by $n+k-1$ we obtain the desired one. Remark. This is also an immediate consequence of Muirhead's inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
79fbb675-834d-5421-b1e6-19f07d2b48e1
| 24,713
|
56. (USS 3) In a group of interpreters each one speaks one or several foreign languages; 24 of them speak Japanese, 24 Malay, 24 Farsi. Prove that it is possible to select a subgroup in which exactly 12 interpreters speak Japanese, exactly 12 speak Malay, and exactly 12 speak Farsi.
|
56. We shall prove by induction on $n$ the following statement: If in some group of interpreters exactly $n$ persons, $n \geq 2$, speak each of the three languages, then it is possible to select a subgroup in which each language is spoken by exactly two persons. The statement of the problem easily follows from this: it suffices to select six such groups. The case $n=2$ is trivial. Let us assume $n \geq 2$, and let $N_{j}, N_{m}, N_{f}, N_{j m}$, $N_{j f}, N_{m f}, N_{j m f}$ be the sets of those interpreters who speak only Japanese, only Malay, only Farsi, only Japanese and Malay, only Japanese and Farsi, only Malay and Farsi, and all the three languages, respectively, and $n_{j}, n_{m}$, $n_{f}, n_{j m}, n_{j f}, n_{m f}, n_{j m f}$ the cardinalities of these sets, respectively. By the condition of the problem, $n_{j}+n_{j m}+n_{j f}+n_{j m f}=n_{m}+n_{j m}+n_{m f}+n_{j m f}=$ $n_{f}+n_{j f}+n_{m f}+n_{j m f}=24$, and consequently $$ n_{j}-n_{m f}=n_{m}-n_{j f}=n_{f}-n_{j m}=c $$ Now if $c<0$, then $n_{j m}, n_{j f}, n_{m f}>0$, and it is enough to select one interpreter from each of the sets $N_{j m}, N_{j f}, N_{m f}$. If $c>0$, then $n_{j}, n_{m}, n_{f}>0$, and it is enough to select one interpreter from each of the sets $N_{j}, N_{m}, N_{f}$ and then use the inductive assumption. Also, if $c=0$, then w.l.o.g. $n_{j}=n_{m f}>0$, and it is enough to select one interpreter from each of the sets $N_{j}, N_{m f}$ and then use the inductive hypothesis. This completes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
56. (USS 3) In a group of interpreters each one speaks one or several foreign languages; 24 of them speak Japanese, 24 Malay, 24 Farsi. Prove that it is possible to select a subgroup in which exactly 12 interpreters speak Japanese, exactly 12 speak Malay, and exactly 12 speak Farsi.
|
56. We shall prove by induction on $n$ the following statement: If in some group of interpreters exactly $n$ persons, $n \geq 2$, speak each of the three languages, then it is possible to select a subgroup in which each language is spoken by exactly two persons. The statement of the problem easily follows from this: it suffices to select six such groups. The case $n=2$ is trivial. Let us assume $n \geq 2$, and let $N_{j}, N_{m}, N_{f}, N_{j m}$, $N_{j f}, N_{m f}, N_{j m f}$ be the sets of those interpreters who speak only Japanese, only Malay, only Farsi, only Japanese and Malay, only Japanese and Farsi, only Malay and Farsi, and all the three languages, respectively, and $n_{j}, n_{m}$, $n_{f}, n_{j m}, n_{j f}, n_{m f}, n_{j m f}$ the cardinalities of these sets, respectively. By the condition of the problem, $n_{j}+n_{j m}+n_{j f}+n_{j m f}=n_{m}+n_{j m}+n_{m f}+n_{j m f}=$ $n_{f}+n_{j f}+n_{m f}+n_{j m f}=24$, and consequently $$ n_{j}-n_{m f}=n_{m}-n_{j f}=n_{f}-n_{j m}=c $$ Now if $c<0$, then $n_{j m}, n_{j f}, n_{m f}>0$, and it is enough to select one interpreter from each of the sets $N_{j m}, N_{j f}, N_{m f}$. If $c>0$, then $n_{j}, n_{m}, n_{f}>0$, and it is enough to select one interpreter from each of the sets $N_{j}, N_{m}, N_{f}$ and then use the inductive assumption. Also, if $c=0$, then w.l.o.g. $n_{j}=n_{m f}>0$, and it is enough to select one interpreter from each of the sets $N_{j}, N_{m f}$ and then use the inductive hypothesis. This completes the induction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2e39f5b0-606a-50f3-96eb-f9f584048753
| 24,740
|
58. (USS 5) A linear binomial $l(z)=A z+B$ with complex coefficients $A$ and $B$ is given. It is known that the maximal value of $|l(z)|$ on the segment $-1 \leq x \leq 1(y=0)$ of the real line in the complex plane $(z=x+i y)$ is equal to $M$. Prove that for every $z$ $$ |l(z)| \leq M \rho, $$ where $\rho$ is the sum of distances from the point $P=z$ to the points $Q_{1}$ : $z=1$ and $Q_{3}: z=-1$.
|
58. The following sequence of equalities and inequalities gives an even stronger estimate than needed. $$ \begin{aligned} |l(z)| & =|A z+B|=\frac{1}{2}|(z+1)(A+B)+(z-1)(A-B)| \\ & =\frac{1}{2}|(z+1) f(1)+(z-1) f(-1)| \\ & \leq \frac{1}{2}(|z+1| \cdot|f(1)|+|z-1| \cdot|f(-1)|) \\ & \leq \frac{1}{2}(|z+1|+|z-1|) M=\frac{1}{2} \rho M . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
58. (USS 5) A linear binomial $l(z)=A z+B$ with complex coefficients $A$ and $B$ is given. It is known that the maximal value of $|l(z)|$ on the segment $-1 \leq x \leq 1(y=0)$ of the real line in the complex plane $(z=x+i y)$ is equal to $M$. Prove that for every $z$ $$ |l(z)| \leq M \rho, $$ where $\rho$ is the sum of distances from the point $P=z$ to the points $Q_{1}$ : $z=1$ and $Q_{3}: z=-1$.
|
58. The following sequence of equalities and inequalities gives an even stronger estimate than needed. $$ \begin{aligned} |l(z)| & =|A z+B|=\frac{1}{2}|(z+1)(A+B)+(z-1)(A-B)| \\ & =\frac{1}{2}|(z+1) f(1)+(z-1) f(-1)| \\ & \leq \frac{1}{2}(|z+1| \cdot|f(1)|+|z-1| \cdot|f(-1)|) \\ & \leq \frac{1}{2}(|z+1|+|z-1|) M=\frac{1}{2} \rho M . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
731c74c9-f50c-5e9e-84a9-525259bb55d1
| 24,746
|
12. (POL 1) If $a$ and $b$ are arbitrary positive real numbers and $m$ an integer, prove that $$ \left(1+\frac{a}{b}\right)^{m}+\left(1+\frac{b}{a}\right)^{m} \geq 2^{m+1} $$
|
12. The given inequality is equivalent to $(a+b)^{m} / b^{m}+(a+b)^{m} / a^{m} \geq 2^{m+1}$, which can be rewritten as $$ \frac{1}{2}\left(\frac{1}{a^{m}}+\frac{1}{b^{m}}\right) \geq\left(\frac{2}{a+b}\right)^{m} $$ Since $f(x)=1 / x^{m}$ is a convex function for every $m \in \mathbb{Z}$, the last inequality immediately follows from Jensen's inequality $(f(a)+f(b)) / 2 \geq$ $f((a+b) / 2)$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
12. (POL 1) If $a$ and $b$ are arbitrary positive real numbers and $m$ an integer, prove that $$ \left(1+\frac{a}{b}\right)^{m}+\left(1+\frac{b}{a}\right)^{m} \geq 2^{m+1} $$
|
12. The given inequality is equivalent to $(a+b)^{m} / b^{m}+(a+b)^{m} / a^{m} \geq 2^{m+1}$, which can be rewritten as $$ \frac{1}{2}\left(\frac{1}{a^{m}}+\frac{1}{b^{m}}\right) \geq\left(\frac{2}{a+b}\right)^{m} $$ Since $f(x)=1 / x^{m}$ is a convex function for every $m \in \mathbb{Z}$, the last inequality immediately follows from Jensen's inequality $(f(a)+f(b)) / 2 \geq$ $f((a+b) / 2)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e9cd467-bf9a-567e-a167-781ad55e49da
| 24,770
|
13. (POL 5) Given two congruent triangles $A_{1} A_{2} A_{3}$ and $B_{1} B_{2} B_{3}\left(A_{i} A_{k}=\right.$ $B_{i} B_{k}$ ), prove that there exists a plane such that the orthogonal projections of these triangles onto it are congruent and equally oriented.
|
13. Translating one of the triangles if necessary, we may assume w.l.o.g. that $B_{1} \equiv A_{1}$. We also assume that $B_{2} \not \equiv A_{2}$ and $B_{3} \not \equiv A_{3}$, since the result is obvious otherwise. There exists a plane $\pi$ through $A_{1}$ that is parallel to both $A_{2} B_{2}$ and $A_{3} B_{3}$. Let $A_{2}^{\prime}, A_{3}^{\prime}, B_{2}^{\prime}, B_{3}^{\prime}$ denote the orthogonal projections of $A_{2}, A_{3}, B_{2}, B_{3}$ onto $\pi$, and let $h_{2}, h_{3}$ denote the distances of $A_{2}, B_{2}$ and of $A_{3}, B_{3}$ from $\pi$. By the Pythagorean theorem, $A_{2}^{\prime} A_{3}^{\prime 2}=A_{2} A_{3}^{2}-\left(h_{2}+h_{3}\right)^{2}=B_{2} B_{3}^{2}-$ $\left(h_{2}+h_{3}\right)^{2}=B_{2}^{\prime}{B_{3}^{\prime}}^{2}$, and similarly $A_{1} A_{2}^{\prime}=A_{1} B_{2}^{\prime}$ and $A_{1} A_{3}^{\prime}=A_{1} B_{3}^{\prime}$; hence $\triangle A_{1} A_{2}^{\prime} A_{3}^{\prime}$ and $\triangle A_{1} B_{2}^{\prime} B_{3}^{\prime}$ are congruent. If these two triangles are equally oriented, then we have finished. Otherwise, they are symmetric with respect to some line $a$ passing through $A_{1}$, and consequently the projections of the triangles $A_{1} A_{2} A_{3}$ and $A_{1} B_{2} B_{3}$ onto the plane through $a$ perpendicular to $\pi$ coincide.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. (POL 5) Given two congruent triangles $A_{1} A_{2} A_{3}$ and $B_{1} B_{2} B_{3}\left(A_{i} A_{k}=\right.$ $B_{i} B_{k}$ ), prove that there exists a plane such that the orthogonal projections of these triangles onto it are congruent and equally oriented.
|
13. Translating one of the triangles if necessary, we may assume w.l.o.g. that $B_{1} \equiv A_{1}$. We also assume that $B_{2} \not \equiv A_{2}$ and $B_{3} \not \equiv A_{3}$, since the result is obvious otherwise. There exists a plane $\pi$ through $A_{1}$ that is parallel to both $A_{2} B_{2}$ and $A_{3} B_{3}$. Let $A_{2}^{\prime}, A_{3}^{\prime}, B_{2}^{\prime}, B_{3}^{\prime}$ denote the orthogonal projections of $A_{2}, A_{3}, B_{2}, B_{3}$ onto $\pi$, and let $h_{2}, h_{3}$ denote the distances of $A_{2}, B_{2}$ and of $A_{3}, B_{3}$ from $\pi$. By the Pythagorean theorem, $A_{2}^{\prime} A_{3}^{\prime 2}=A_{2} A_{3}^{2}-\left(h_{2}+h_{3}\right)^{2}=B_{2} B_{3}^{2}-$ $\left(h_{2}+h_{3}\right)^{2}=B_{2}^{\prime}{B_{3}^{\prime}}^{2}$, and similarly $A_{1} A_{2}^{\prime}=A_{1} B_{2}^{\prime}$ and $A_{1} A_{3}^{\prime}=A_{1} B_{3}^{\prime}$; hence $\triangle A_{1} A_{2}^{\prime} A_{3}^{\prime}$ and $\triangle A_{1} B_{2}^{\prime} B_{3}^{\prime}$ are congruent. If these two triangles are equally oriented, then we have finished. Otherwise, they are symmetric with respect to some line $a$ passing through $A_{1}$, and consequently the projections of the triangles $A_{1} A_{2} A_{3}$ and $A_{1} B_{2} B_{3}$ onto the plane through $a$ perpendicular to $\pi$ coincide.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
74e2c171-5db7-569f-84bc-1c0db6b518de
| 24,772
|
16. (GBR 3) A polynomial $p(x)=a_{0} x^{k}+a_{1} x^{k-1}+\cdots+a_{k}$ with integer coefficients is said to be divisible by an integer $m$ if $p(x)$ is divisible by $m$ for all integers $x$. Prove that if $p(x)$ is divisible by $m$, then $k!a_{0}$ is also divisible by $m$. Also prove that if $a_{0}, k, m$ are nonnegative integers for which $k!a_{0}$ is divisible by $m$, there exists a polynomial $p(x)=a_{0} x^{k}+\cdots+$ $a_{k}$ divisible by $m$.
|
16. We shall prove the result by induction on $k$. It trivially holds for $k=0$. Assume that the statement is true for some $k-1$, and let $p(x)$ be a polynomial of degree $k$. Let us set $p_{1}(x)=p(x+1)-p(x)$. Then $p_{1}(x)$ is a polynomial of degree $k-1$ with leading coefficient $k a_{0}$. Also, $m \mid p_{1}(x)$ for all $x \in \mathbb{Z}$ and hence by the inductive assumption $m \mid(k-1)!\cdot k a_{0}=k!a_{0}$, which completes the induction. On the other hand, for any $a_{0}, k$ and $m \mid k!a_{0}, p(x)=k!a_{0}\binom{x}{k}$ is a polynomial with leading coefficient $a_{0}$ that is divisible by $m$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
16. (GBR 3) A polynomial $p(x)=a_{0} x^{k}+a_{1} x^{k-1}+\cdots+a_{k}$ with integer coefficients is said to be divisible by an integer $m$ if $p(x)$ is divisible by $m$ for all integers $x$. Prove that if $p(x)$ is divisible by $m$, then $k!a_{0}$ is also divisible by $m$. Also prove that if $a_{0}, k, m$ are nonnegative integers for which $k!a_{0}$ is divisible by $m$, there exists a polynomial $p(x)=a_{0} x^{k}+\cdots+$ $a_{k}$ divisible by $m$.
|
16. We shall prove the result by induction on $k$. It trivially holds for $k=0$. Assume that the statement is true for some $k-1$, and let $p(x)$ be a polynomial of degree $k$. Let us set $p_{1}(x)=p(x+1)-p(x)$. Then $p_{1}(x)$ is a polynomial of degree $k-1$ with leading coefficient $k a_{0}$. Also, $m \mid p_{1}(x)$ for all $x \in \mathbb{Z}$ and hence by the inductive assumption $m \mid(k-1)!\cdot k a_{0}=k!a_{0}$, which completes the induction. On the other hand, for any $a_{0}, k$ and $m \mid k!a_{0}, p(x)=k!a_{0}\binom{x}{k}$ is a polynomial with leading coefficient $a_{0}$ that is divisible by $m$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0af30f4b-b77e-588c-a120-e0867bd69489
| 24,781
|
17. (GBR 4) Given a point $O$ and lengths $x, y, z$, prove that there exists an equilateral triangle $A B C$ for which $O A=x, O B=y, O C=z$, if and only if $x+y \geq z, y+z \geq x, z+x \geq y$ (the points $O, A, B, C$ are coplanar).
|
17. Let there be given an equilateral triangle $A B C$ and a point $O$ such that $O A=x, O B=y, O C=z$. Let $X$ be the point in the plane such that $\triangle C X B$ and $\triangle C O A$ are congruent and equally oriented. Then $B X=x$ and the triangle $X O C$ is equilateral, which implies $O X=z$. Thus we have a triangle $O B X$ with $B X=x, B O=y$, and $O X=z$. Conversely, given a triangle $O B X$ with $B X=x, B O=y$ and $O X=z$ it is easy to construct the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
17. (GBR 4) Given a point $O$ and lengths $x, y, z$, prove that there exists an equilateral triangle $A B C$ for which $O A=x, O B=y, O C=z$, if and only if $x+y \geq z, y+z \geq x, z+x \geq y$ (the points $O, A, B, C$ are coplanar).
|
17. Let there be given an equilateral triangle $A B C$ and a point $O$ such that $O A=x, O B=y, O C=z$. Let $X$ be the point in the plane such that $\triangle C X B$ and $\triangle C O A$ are congruent and equally oriented. Then $B X=x$ and the triangle $X O C$ is equilateral, which implies $O X=z$. Thus we have a triangle $O B X$ with $B X=x, B O=y$, and $O X=z$. Conversely, given a triangle $O B X$ with $B X=x, B O=y$ and $O X=z$ it is easy to construct the triangle $A B C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
21b4b762-f754-561b-8e71-6f503e370cac
| 24,784
|
20. (CZS 1) Given $n(n \geq 3)$ points in space such that every three of them form a triangle with one angle greater than or equal to $120^{\circ}$, prove that these points can be denoted by $A_{1}, A_{2}, \ldots, A_{n}$ in such a way that for each $i, j, k, 1 \leq i<j<k \leq n$, angle $A_{i} A_{j} A_{k}$ is greater than or equal to $120^{\circ}$.
|
20. Let us denote the points $A_{1}, A_{2}, \ldots, A_{n}$ in such a manner that $A_{1} A_{n}$ is a diameter of the set of given points, and $A_{1} A_{2} \leq A_{1} A_{3} \leq \cdots \leq A_{1} A_{n}$. Since for each $1<i<n$ it holds that $A_{1} A_{i}<A_{1} A_{n}$, we have $\angle A_{i} A_{1} A_{n}<120^{\circ}$ and hence $\angle A_{i} A_{1} A_{n}<60^{\circ}$ (otherwise, all angles in $\triangle A_{1} A_{i} A_{n}$ are less than $120^{\circ}$ ). It follows that for all $1<i<j \leq n$, $\angle A_{i} A_{1} A_{j}<120^{\circ}$. Consequently, the angle in the triangle $A_{1} A_{i} A_{j}$ that is at least $120^{\circ}$ must be $\angle A_{1} A_{i} A_{j}$. Moreover, for any $1<i<j<k \leq n$ it holds that $\angle A_{i} A_{j} A_{k} \geq \angle A_{1} A_{j} A_{k}-\angle A_{1} A_{j} A_{i}>120^{\circ}-60^{\circ}=60^{\circ}$ (because $\angle A_{1} A_{j} A_{i}<60^{\circ}$ ); hence $\angle A_{i} A_{j} A_{k} \geq 120^{\circ}$. This proves that the denotation is correct. Remark. It is easy to show that the diameter is unique. Hence the denotation is also unique.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
20. (CZS 1) Given $n(n \geq 3)$ points in space such that every three of them form a triangle with one angle greater than or equal to $120^{\circ}$, prove that these points can be denoted by $A_{1}, A_{2}, \ldots, A_{n}$ in such a way that for each $i, j, k, 1 \leq i<j<k \leq n$, angle $A_{i} A_{j} A_{k}$ is greater than or equal to $120^{\circ}$.
|
20. Let us denote the points $A_{1}, A_{2}, \ldots, A_{n}$ in such a manner that $A_{1} A_{n}$ is a diameter of the set of given points, and $A_{1} A_{2} \leq A_{1} A_{3} \leq \cdots \leq A_{1} A_{n}$. Since for each $1<i<n$ it holds that $A_{1} A_{i}<A_{1} A_{n}$, we have $\angle A_{i} A_{1} A_{n}<120^{\circ}$ and hence $\angle A_{i} A_{1} A_{n}<60^{\circ}$ (otherwise, all angles in $\triangle A_{1} A_{i} A_{n}$ are less than $120^{\circ}$ ). It follows that for all $1<i<j \leq n$, $\angle A_{i} A_{1} A_{j}<120^{\circ}$. Consequently, the angle in the triangle $A_{1} A_{i} A_{j}$ that is at least $120^{\circ}$ must be $\angle A_{1} A_{i} A_{j}$. Moreover, for any $1<i<j<k \leq n$ it holds that $\angle A_{i} A_{j} A_{k} \geq \angle A_{1} A_{j} A_{k}-\angle A_{1} A_{j} A_{i}>120^{\circ}-60^{\circ}=60^{\circ}$ (because $\angle A_{1} A_{j} A_{i}<60^{\circ}$ ); hence $\angle A_{i} A_{j} A_{k} \geq 120^{\circ}$. This proves that the denotation is correct. Remark. It is easy to show that the diameter is unique. Hence the denotation is also unique.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
81830774-f743-5f31-87c5-315973f229eb
| 24,795
|
26. (GDR) ${ }^{\text {IMO5 }}$ Let $a>0$ be a real number and $f(x)$ a real function defined on all of $\mathbb{R}$, satisfying for all $x \in \mathbb{R}$, $$ f(x+a)=\frac{1}{2}+\sqrt{f(x)-f(x)^{2}} . $$ (a) Prove that the function $f$ is periodic; i.e., there exists $b>0$ such that for all $x, f(x+b)=f(x)$. (b) Give an example of such a nonconstant function for $a=1$. [^2]
|
26. (a) We shall show that the period of $f$ is $2 a$. From $(f(x+a)-1 / 2)^{2}=$ $f(x)-f(x)^{2}$ we obtain $$ \left(f(x)-f(x)^{2}\right)+\left(f(x+a)-f(x+a)^{2}\right)=\frac{1}{4} $$ Subtracting the above relation for $x+a$ in place of $x$ we get $f(x)-$ $f(x)^{2}=f(x+2 a)-f(x+2 a)^{2}$, which implies $(f(x)-1 / 2)^{2}=$ $(f(x+2 a)-1 / 2)^{2}$. Since $f(x) \geq 1 / 2$ holds for all $x$ by the condition of the problem, we conclude that $f(x+2 a)=f(x)$. (b) The following function, as is directly verified, satisfies the conditions: $$ f(x)=\left\{\begin{array}{cl} 1 / 2 & \text { if } 2 n \leq x<2 n+1, \\ 1 & \text { if } 2 n+1 \leq x<2 n+2, \end{array} \text { for } n=0,1,2, \ldots\right. $$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
26. (GDR) ${ }^{\text {IMO5 }}$ Let $a>0$ be a real number and $f(x)$ a real function defined on all of $\mathbb{R}$, satisfying for all $x \in \mathbb{R}$, $$ f(x+a)=\frac{1}{2}+\sqrt{f(x)-f(x)^{2}} . $$ (a) Prove that the function $f$ is periodic; i.e., there exists $b>0$ such that for all $x, f(x+b)=f(x)$. (b) Give an example of such a nonconstant function for $a=1$. [^2]
|
26. (a) We shall show that the period of $f$ is $2 a$. From $(f(x+a)-1 / 2)^{2}=$ $f(x)-f(x)^{2}$ we obtain $$ \left(f(x)-f(x)^{2}\right)+\left(f(x+a)-f(x+a)^{2}\right)=\frac{1}{4} $$ Subtracting the above relation for $x+a$ in place of $x$ we get $f(x)-$ $f(x)^{2}=f(x+2 a)-f(x+2 a)^{2}$, which implies $(f(x)-1 / 2)^{2}=$ $(f(x+2 a)-1 / 2)^{2}$. Since $f(x) \geq 1 / 2$ holds for all $x$ by the condition of the problem, we conclude that $f(x+2 a)=f(x)$. (b) The following function, as is directly verified, satisfies the conditions: $$ f(x)=\left\{\begin{array}{cl} 1 / 2 & \text { if } 2 n \leq x<2 n+1, \\ 1 & \text { if } 2 n+1 \leq x<2 n+2, \end{array} \text { for } n=0,1,2, \ldots\right. $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d5a0b638-d0e9-5e64-9167-fbd111eae614
| 24,809
|
3. (POL 4) ${ }^{\mathrm{IMO} 4}$ Prove that in any tetrahedron there is a vertex such that the lengths of its sides through that vertex are sides of a triangle.
|
3. A triangle cannot be formed out of three lengths if and only if one of them is larger than the sum of the other two. Let us assume this is the case for all triplets of edges out of each vertex in a tetrahedron $A B C D$. Let w.l.o.g. $A B$ be the largest edge of the tetrahedron. Then $A B \geq A C+A D$ and $A B \geq B C+B D$, from which it follows that $2 A B \geq A C+A D+B C+B D$. This implies that either $A B \geq A C+B C$ or $A B \geq A D+B D$, contradicting the triangle inequality. Hence the three edges coming out of at least one of the vertices $A$ and $B$ form a triangle. Remark. The proof can be generalized to prove that in a polyhedron with only triangular surfaces there is a vertex such that the edges coming out of this vertex form a triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (POL 4) ${ }^{\mathrm{IMO} 4}$ Prove that in any tetrahedron there is a vertex such that the lengths of its sides through that vertex are sides of a triangle.
|
3. A triangle cannot be formed out of three lengths if and only if one of them is larger than the sum of the other two. Let us assume this is the case for all triplets of edges out of each vertex in a tetrahedron $A B C D$. Let w.l.o.g. $A B$ be the largest edge of the tetrahedron. Then $A B \geq A C+A D$ and $A B \geq B C+B D$, from which it follows that $2 A B \geq A C+A D+B C+B D$. This implies that either $A B \geq A C+B C$ or $A B \geq A D+B D$, contradicting the triangle inequality. Hence the three edges coming out of at least one of the vertices $A$ and $B$ form a triangle. Remark. The proof can be generalized to prove that in a polyhedron with only triangular surfaces there is a vertex such that the edges coming out of this vertex form a triangle.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a0dd60d-58b8-5329-b219-9b495b4b8556
| 24,811
|
4. (BUL 2) ${ }^{\mathrm{IMO} 3}$ Let $a, b, c$ be real numbers. Prove that the system of equations $$ \left\{\begin{array}{r} a x_{1}^{2}+b x_{1}+c=x_{2} \\ a x_{2}^{2}+b x_{2}+c=x_{3} \\ \cdots \cdots \cdots \cdots \\ a x_{n-1}^{2}+b x_{n-1}+c=x_{n} \\ a x_{n}^{2}+b x_{n}+c=x_{1} \end{array}\right. $$ has a unique real solution if and only if $(b-1)^{2}-4 a c=0$. Remark. It is assumed that $a \neq 0$.
|
4. We will prove the equivalence in the two directions separately: $(\Rightarrow)$ Suppose $\left\{x_{1}, \ldots, x_{n}\right\}$ is the unique solution of the equation. Since $\left\{x_{n}, x_{1}, x_{2} \ldots, x_{n-1}\right\}$ is also a solution, it follows that $x_{1}=x_{2}=\cdots=$ $x_{n}=x$ and the system of equations reduces to a single equation $a x^{2}+$ $(b-1) x+c=0$. For the solution for $x$ to be unique the discriminant $(b-1)^{2}-4 a c$ of this quadratic equation must be 0 . $(\Leftarrow)$ Assume $(b-1)^{2}-4 a c=0$. Adding up the equations, we get $$ \sum_{i=1}^{n} f\left(x_{i}\right)=0, \quad \text { where } \quad f(x)=a x^{2}+(b-1) x+c $$ But by the assumed condition, $f(x)=a\left(x+\frac{b-1}{2 a}\right)^{2}$. Hence we must have $f\left(x_{i}\right)=0$ for all $i$, and $x_{i}=-\frac{b-1}{2 a}$, which is indeed a solution.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
4. (BUL 2) ${ }^{\mathrm{IMO} 3}$ Let $a, b, c$ be real numbers. Prove that the system of equations $$ \left\{\begin{array}{r} a x_{1}^{2}+b x_{1}+c=x_{2} \\ a x_{2}^{2}+b x_{2}+c=x_{3} \\ \cdots \cdots \cdots \cdots \\ a x_{n-1}^{2}+b x_{n-1}+c=x_{n} \\ a x_{n}^{2}+b x_{n}+c=x_{1} \end{array}\right. $$ has a unique real solution if and only if $(b-1)^{2}-4 a c=0$. Remark. It is assumed that $a \neq 0$.
|
4. We will prove the equivalence in the two directions separately: $(\Rightarrow)$ Suppose $\left\{x_{1}, \ldots, x_{n}\right\}$ is the unique solution of the equation. Since $\left\{x_{n}, x_{1}, x_{2} \ldots, x_{n-1}\right\}$ is also a solution, it follows that $x_{1}=x_{2}=\cdots=$ $x_{n}=x$ and the system of equations reduces to a single equation $a x^{2}+$ $(b-1) x+c=0$. For the solution for $x$ to be unique the discriminant $(b-1)^{2}-4 a c$ of this quadratic equation must be 0 . $(\Leftarrow)$ Assume $(b-1)^{2}-4 a c=0$. Adding up the equations, we get $$ \sum_{i=1}^{n} f\left(x_{i}\right)=0, \quad \text { where } \quad f(x)=a x^{2}+(b-1) x+c $$ But by the assumed condition, $f(x)=a\left(x+\frac{b-1}{2 a}\right)^{2}$. Hence we must have $f\left(x_{i}\right)=0$ for all $i$, and $x_{i}=-\frac{b-1}{2 a}$, which is indeed a solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
beb30744-5c69-5a03-8dbe-c44d5e56ca2e
| 24,814
|
5. (BUL 5) Let $h_{n}$ be the apothem (distance from the center to one of the sides) of a regular $n$-gon $(n \geq 3)$ inscribed in a circle of radius $r$. Prove the inequality $$ (n+1) h_{n+1}-n h_{n}>r . $$ Also prove that if $r$ on the right side is replaced with a greater number, the inequality will not remain true for all $n \geq 3$.
|
5. We have $h_{k}=r \cos (\pi / k)$ for all $k \in \mathbb{N}$. Using $\cos x=1-2 \sin ^{2}(x / 2)$ and $\cos x=2 /\left(1+\tan ^{2}(x / 2)\right)-1$ and $\tan x>x>\sin x$ for all $0<x<\pi / 2$, it suffices to prove $$ \begin{aligned} & (n+1)\left(1-2 \frac{\pi^{2}}{4(n+1)^{2}}\right)-n\left(\frac{2}{1+\pi^{2} /\left(4 n^{2}\right)}-1\right)>1 \\ \Leftrightarrow & 1+2 n\left(1-\frac{1}{1+\pi^{2} /\left(4 n^{2}\right)}\right)-\frac{\pi^{2}}{2(n+1)}>1 \\ \Leftrightarrow & 1+\frac{\pi^{2}}{2}\left(\frac{1}{n+\pi^{2} /(4 n)}-\frac{1}{n+1}\right)>1, \end{aligned} $$ where the last inequality holds because $\pi^{2}<4 n$. It is also apparent that as $n$ tends to infinity the term in parentheses tends to 0 , and hence it is not possible to strengthen the bound. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
5. (BUL 5) Let $h_{n}$ be the apothem (distance from the center to one of the sides) of a regular $n$-gon $(n \geq 3)$ inscribed in a circle of radius $r$. Prove the inequality $$ (n+1) h_{n+1}-n h_{n}>r . $$ Also prove that if $r$ on the right side is replaced with a greater number, the inequality will not remain true for all $n \geq 3$.
|
5. We have $h_{k}=r \cos (\pi / k)$ for all $k \in \mathbb{N}$. Using $\cos x=1-2 \sin ^{2}(x / 2)$ and $\cos x=2 /\left(1+\tan ^{2}(x / 2)\right)-1$ and $\tan x>x>\sin x$ for all $0<x<\pi / 2$, it suffices to prove $$ \begin{aligned} & (n+1)\left(1-2 \frac{\pi^{2}}{4(n+1)^{2}}\right)-n\left(\frac{2}{1+\pi^{2} /\left(4 n^{2}\right)}-1\right)>1 \\ \Leftrightarrow & 1+2 n\left(1-\frac{1}{1+\pi^{2} /\left(4 n^{2}\right)}\right)-\frac{\pi^{2}}{2(n+1)}>1 \\ \Leftrightarrow & 1+\frac{\pi^{2}}{2}\left(\frac{1}{n+\pi^{2} /(4 n)}-\frac{1}{n+1}\right)>1, \end{aligned} $$ where the last inequality holds because $\pi^{2}<4 n$. It is also apparent that as $n$ tends to infinity the term in parentheses tends to 0 , and hence it is not possible to strengthen the bound. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e2eb948-bd51-58de-a837-5371572e41f0
| 24,816
|
6. (HUN 1) If $a_{i}(i=1,2, \ldots, n)$ are distinct non-zero real numbers, prove that the equation $$ \frac{a_{1}}{a_{1}-x}+\frac{a_{2}}{a_{2}-x}+\cdots+\frac{a_{n}}{a_{n}-x}=n $$ has at least $n-1$ real roots.
|
6. We define $f(x)=\frac{a_{1}}{a_{1}-x}+\frac{a_{2}}{a_{2}-x}+\cdots+\frac{a_{n}}{a_{n}-x}$. Let us assume w.l.o.g. $a_{1}<a_{2}<\cdots<a_{n}$. We note that for all $1 \leq i<n$ the function $f$ is continuous in the interval $\left(a_{i}, a_{i+1}\right)$ and satisfies $\lim _{x \rightarrow a_{i}} f(x)=-\infty$ and $\lim _{x \rightarrow a_{i+1}} f(x)=\infty$. Hence the equation $f(x)=n$ will have a real solution in each of the $n-1$ intervals $\left(a_{i}, a_{i+1}\right)$. Remark. In fact, this equation has exactly $n$ solutions, and hence they are all real. Moreover, the solutions are distinct if all $a_{i}$ are of the same sign, since $x=0$ is an evident solution.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
6. (HUN 1) If $a_{i}(i=1,2, \ldots, n)$ are distinct non-zero real numbers, prove that the equation $$ \frac{a_{1}}{a_{1}-x}+\frac{a_{2}}{a_{2}-x}+\cdots+\frac{a_{n}}{a_{n}-x}=n $$ has at least $n-1$ real roots.
|
6. We define $f(x)=\frac{a_{1}}{a_{1}-x}+\frac{a_{2}}{a_{2}-x}+\cdots+\frac{a_{n}}{a_{n}-x}$. Let us assume w.l.o.g. $a_{1}<a_{2}<\cdots<a_{n}$. We note that for all $1 \leq i<n$ the function $f$ is continuous in the interval $\left(a_{i}, a_{i+1}\right)$ and satisfies $\lim _{x \rightarrow a_{i}} f(x)=-\infty$ and $\lim _{x \rightarrow a_{i+1}} f(x)=\infty$. Hence the equation $f(x)=n$ will have a real solution in each of the $n-1$ intervals $\left(a_{i}, a_{i+1}\right)$. Remark. In fact, this equation has exactly $n$ solutions, and hence they are all real. Moreover, the solutions are distinct if all $a_{i}$ are of the same sign, since $x=0$ is an evident solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4cc1e46c-93f9-5aaa-aaea-49f281ddfd44
| 24,819
|
7. (HUN 5) Prove that the product of the radii of three circles exscribed to a given triangle does not exceed $\frac{3 \sqrt{3}}{8}$ times the product of the side lengths of the triangle. When does equality hold?
|
7. Let $r_{a}, r_{b}, r_{c}$ denote the radii of the exscribed circles corresponding to the sides of lengths $a, b, c$ respectively, and $R, p$ and $S$ denote the circumradius, semiperimeter, and area of the given triangle. It is well-known that $r_{a}(p-a)=r_{b}(p-b)=r_{c}(p-c)=S=\sqrt{p(p-a)(p-b)(p-c)}=\frac{a b c}{4 R}$. Hence, the desired inequality $r_{a} r_{b} r_{c} \leq \frac{3 \sqrt{3}}{8} a b c$ reduces to $p \leq \frac{3 \sqrt{3}}{2} R$, which is by the law of sines equivalent to $$ \sin \alpha+\sin \beta+\sin \gamma \leq \frac{3 \sqrt{3}}{2} $$ This inequality immediately follows from Jensen's inequality, since the sine is concave on $[0, \pi]$. Equality holds if and only if the triangle is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. (HUN 5) Prove that the product of the radii of three circles exscribed to a given triangle does not exceed $\frac{3 \sqrt{3}}{8}$ times the product of the side lengths of the triangle. When does equality hold?
|
7. Let $r_{a}, r_{b}, r_{c}$ denote the radii of the exscribed circles corresponding to the sides of lengths $a, b, c$ respectively, and $R, p$ and $S$ denote the circumradius, semiperimeter, and area of the given triangle. It is well-known that $r_{a}(p-a)=r_{b}(p-b)=r_{c}(p-c)=S=\sqrt{p(p-a)(p-b)(p-c)}=\frac{a b c}{4 R}$. Hence, the desired inequality $r_{a} r_{b} r_{c} \leq \frac{3 \sqrt{3}}{8} a b c$ reduces to $p \leq \frac{3 \sqrt{3}}{2} R$, which is by the law of sines equivalent to $$ \sin \alpha+\sin \beta+\sin \gamma \leq \frac{3 \sqrt{3}}{2} $$ This inequality immediately follows from Jensen's inequality, since the sine is concave on $[0, \pi]$. Equality holds if and only if the triangle is equilateral.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
79e40715-76fe-578e-9ce5-484dcc8fbbb6
| 24,822
|
9. (ROM 3) Let $A B C$ be an arbitrary triangle and $M$ a point inside it. Let $d_{a}, d_{b}, d_{c}$ be the distances from $M$ to sides $B C, C A, A B ; a, b, c$ the lengths of the sides respectively, and $S$ the area of the triangle $A B C$. Prove the inequality $$ a b d_{a} d_{b}+b c d_{b} d_{c}+c a d_{c} d_{a} \leq \frac{4 S^{2}}{3} $$ Prove that the left-hand side attains its maximum when $M$ is the centroid of the triangle.
|
9. We note that $S_{a}=a d_{a} / 2, S_{b}=b d_{b} / 2$, and $S_{c}=c d_{c} / 2$ are the areas of the triangles $M B C, M C A$, and $M A B$ respectively. The desired inequality now follows from $$ S_{a} S_{b}+S_{b} S_{c}+S_{c} S_{a} \leq \frac{1}{3}\left(S_{a}+S_{b}+S_{c}\right)^{2}=\frac{S^{2}}{3} $$ Equality holds if and only if $S_{a}=S_{b}=S_{c}$, which is equivalent to $M$ being the centroid of the triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
9. (ROM 3) Let $A B C$ be an arbitrary triangle and $M$ a point inside it. Let $d_{a}, d_{b}, d_{c}$ be the distances from $M$ to sides $B C, C A, A B ; a, b, c$ the lengths of the sides respectively, and $S$ the area of the triangle $A B C$. Prove the inequality $$ a b d_{a} d_{b}+b c d_{b} d_{c}+c a d_{c} d_{a} \leq \frac{4 S^{2}}{3} $$ Prove that the left-hand side attains its maximum when $M$ is the centroid of the triangle.
|
9. We note that $S_{a}=a d_{a} / 2, S_{b}=b d_{b} / 2$, and $S_{c}=c d_{c} / 2$ are the areas of the triangles $M B C, M C A$, and $M A B$ respectively. The desired inequality now follows from $$ S_{a} S_{b}+S_{b} S_{c}+S_{c} S_{a} \leq \frac{1}{3}\left(S_{a}+S_{b}+S_{c}\right)^{2}=\frac{S^{2}}{3} $$ Equality holds if and only if $S_{a}=S_{b}=S_{c}$, which is equivalent to $M$ being the centroid of the triangle.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8cff9ecb-d8a9-56c5-b7c9-0cfeed32a560
| 24,827
|
1. Prove that there exist infinitely many natural numbers $a$ with the following property: the number $z=n^{4}+a$ is not prime for any natural number $n$.
|
1. Set $a=4 m^{4}$, where $m \in \mathbb{N}$ and $m>1$. We then have $z=n^{4}+4 m^{4}=$ $\left(n^{2}+2 m^{2}\right)^{2}-(2 m n)^{2}=\left(n^{2}+2 m^{2}+2 m n\right)\left(n^{2}+2 m^{2}-2 m n\right)$. Since $n^{2}+2 m^{2}-2 m n=(n-m)^{2}+m^{2} \geq m^{2}>1$, it follows that $z$ must be composite. Thus we have found infinitely many $a$ that satisfy the condition of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
1. Prove that there exist infinitely many natural numbers $a$ with the following property: the number $z=n^{4}+a$ is not prime for any natural number $n$.
|
1. Set $a=4 m^{4}$, where $m \in \mathbb{N}$ and $m>1$. We then have $z=n^{4}+4 m^{4}=$ $\left(n^{2}+2 m^{2}\right)^{2}-(2 m n)^{2}=\left(n^{2}+2 m^{2}+2 m n\right)\left(n^{2}+2 m^{2}-2 m n\right)$. Since $n^{2}+2 m^{2}-2 m n=(n-m)^{2}+m^{2} \geq m^{2}>1$, it follows that $z$ must be composite. Thus we have found infinitely many $a$ that satisfy the condition of the problem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
381a903d-9ec4-52b2-b524-d9ddea70c70b
| 24,830
|
2. Let $a_{1}, a_{2}, \ldots, a_{n}$ be real constants and $$ y(x)=\cos \left(a_{1}+x\right)+\frac{\cos \left(a_{2}+x\right)}{2}+\frac{\cos \left(a_{3}+x\right)}{2^{2}}+\cdots+\frac{\cos \left(a_{n}+x\right)}{2^{n-1}} . $$ If $x_{1}, x_{2}$ are real and $y\left(x_{1}\right)=y\left(x_{2}\right)=0$, prove that $x_{1}-x_{2}=m \pi$ for some integer $m$.
|
2. Using $\cos (a+x)=\cos a \cos x-\sin a \sin x$, we obtain $f(x)=A \sin x+$ $B \cos x$ where $A=-\sin a_{1}-\sin a_{2} / 2-\cdots-\sin a_{n} / 2^{n-1}$ and $B=\cos a_{1}+$ $\cos a_{2} / 2+\cdots+\cos a_{n} / 2^{n-1}$. Numbers $A$ and $B$ cannot both be equal to 0 , for otherwise $f$ would be identically equal to 0 , while on the other hand, we have $f\left(-a_{1}\right)=\cos \left(a_{1}-a_{1}\right)+\cos \left(a_{2}-a_{1}\right) / 2+\cdots+\cos \left(a_{n}-a_{1}\right) / 2^{n-1} \geq$ $1-1 / 2-\cdots-1 / 2^{n-1}=1 / 2^{n-1}>0$. Setting $A=C \cos \phi$ and $B=C \sin \phi$, where $C \neq 0$ (such $C$ and $\phi$ always exist), we get $f(x)=C \sin (x+\phi)$. It follows that the zeros of $f$ are of the form $x_{0} \in-\phi+\pi \mathbb{Z}$, from which $f\left(x_{1}\right)=f\left(x_{2}\right) \Rightarrow x_{1}-x_{2}=m \pi$ immediately follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
2. Let $a_{1}, a_{2}, \ldots, a_{n}$ be real constants and $$ y(x)=\cos \left(a_{1}+x\right)+\frac{\cos \left(a_{2}+x\right)}{2}+\frac{\cos \left(a_{3}+x\right)}{2^{2}}+\cdots+\frac{\cos \left(a_{n}+x\right)}{2^{n-1}} . $$ If $x_{1}, x_{2}$ are real and $y\left(x_{1}\right)=y\left(x_{2}\right)=0$, prove that $x_{1}-x_{2}=m \pi$ for some integer $m$.
|
2. Using $\cos (a+x)=\cos a \cos x-\sin a \sin x$, we obtain $f(x)=A \sin x+$ $B \cos x$ where $A=-\sin a_{1}-\sin a_{2} / 2-\cdots-\sin a_{n} / 2^{n-1}$ and $B=\cos a_{1}+$ $\cos a_{2} / 2+\cdots+\cos a_{n} / 2^{n-1}$. Numbers $A$ and $B$ cannot both be equal to 0 , for otherwise $f$ would be identically equal to 0 , while on the other hand, we have $f\left(-a_{1}\right)=\cos \left(a_{1}-a_{1}\right)+\cos \left(a_{2}-a_{1}\right) / 2+\cdots+\cos \left(a_{n}-a_{1}\right) / 2^{n-1} \geq$ $1-1 / 2-\cdots-1 / 2^{n-1}=1 / 2^{n-1}>0$. Setting $A=C \cos \phi$ and $B=C \sin \phi$, where $C \neq 0$ (such $C$ and $\phi$ always exist), we get $f(x)=C \sin (x+\phi)$. It follows that the zeros of $f$ are of the form $x_{0} \in-\phi+\pi \mathbb{Z}$, from which $f\left(x_{1}\right)=f\left(x_{2}\right) \Rightarrow x_{1}-x_{2}=m \pi$ immediately follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cad7f879-4a5f-58c8-8527-e7b92dab7a40
| 24,833
|
4. Let $A B$ be a diameter of a circle $\gamma$. A point $C$ different from $A$ and $B$ is on the circle $\gamma$. Let $D$ be the projection of the point $C$ onto the line $A B$. Consider three other circles $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ with the common tangent $A B: \gamma_{1}$ inscribed in the triangle $A B C$, and $\gamma_{2}$ and $\gamma_{3}$ tangent to both (the segment) $C D$ and $\gamma$. Prove that $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ have two common tangents.
|
4. Let $O$ be the midpoint of $A B$, i.e., the center of $\gamma$. Let $O_{1}, O_{2}$, and $O_{3}$ respectively be the centers of $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ and let $r_{1}, r_{2}, r_{3}$ respectively be the radii of $\gamma_{1}, \gamma_{2}$ and $\gamma_{3}$. Let $C_{1}, C_{2}$, and $C_{3}$ respectively be the points of tangency of $\gamma_{1}, \gamma_{2}$ and $\gamma_{3}$ with $A B$. Let $D_{2}$ and $D_{3}$ respectively be the points of tangency of $\gamma_{2}$ and $\gamma_{3}$ with $C D$. Finally, let $G_{2}$ and $G_{3}$ respectively be the points of tangency of $\gamma_{2}$ and $\gamma_{3}$ with $\gamma$. We have $\mathcal{B}\left(G_{2}, O_{2}, O\right)$, $G_{2} O_{2}=O_{2} D_{2}$, and $G_{2} O=O B$. Hence, $G_{2}, D_{2}, B$ are collinear. Similarly, $G_{3}, D_{3}, A$ are collinear. It follows that $A G_{2} D_{2} D$ and $B G_{3} D_{3} D$ are cyclic, since $\angle A G_{2} D_{2}=\angle D_{2} D A=\angle D_{3} D B=\angle B G_{3} D_{3}=90^{\circ}$. Hence $B C_{2}^{2}=B D_{2} \cdot B G_{2}=B D \cdot B A=B C^{2} \Rightarrow B C_{2}=B C$ and hence $A C_{2}=A B-B C$. Similarly, $A C_{3}=A C$. We thus have $A C_{1}=(A C+A B-B C) / 2=\left(A C_{3}+A C_{2}\right) / 2$. Hence, $C_{1}$ is the midpoint of $C_{2} C_{3}$. We also have $r_{2}+r_{3}=C_{2} C_{3}=A C+B C-A B=2 r_{1}$, from which it follows that $O_{1}, O_{2}, O_{3}$ are collinear. Second solution. We shall prove the statement for arbitrary points $A, B, C$ on $\gamma$. Let us apply the inversion $\psi$ with respect to the circle $\gamma_{1}$. We denote by $\widehat{X}$ the image of an object $X$ under $\psi$. Also, $\psi$ maps lines $B C, C A, A B$ onto circles $\widehat{a}, \widehat{b}, \widehat{c}$, respectively. Circles $\widehat{a}, \widehat{b}, \widehat{c}$ pass through the center $O_{1}$ of $\gamma_{1}$ and have radii equal to the radius of $\widehat{\gamma}$. Let $P, Q, R$ be the centers of $\widehat{a}, \widehat{b}, \widehat{c}$ respectively. The line $C D$ maps onto a circle $k$ through $\widehat{C}$ and $O_{1}$ that is perpendicular to $\widehat{c}$. Therefore its center $K$ lies in the intersection of the tangent $t$ to $\widehat{c}$ and the line $P Q$ (which bisects $\left.\widehat{C} O_{1}\right)$. Let $O$ be a point such that $R O_{1} K O$ is a parallelogram and $\gamma_{2}^{\prime}, \gamma_{3}^{\prime}$ the circles centered at $O$ tangent to $k$. It is easy to see that $\gamma_{2}^{\prime}$ and $\gamma_{3}^{\prime}$ are also tangent to $\widehat{c}$, since $O R$ and $O K$ have lengths equal to the radii of $k$ and $\widehat{c}$. Hence $\gamma_{2}^{\prime}$ and $\gamma_{3}^{\prime}$ are the images of $\gamma_{2}$ and $\gamma_{3}$ under $\psi$. Moreover, since $Q \widehat{A} O K$ and $P \widehat{B} O K$ are parallelograms and $Q, P, K$ are collinear, it follows that $\widehat{A}, \widehat{B}, O$ are also collinear. Hence the centers of $\gamma_{1}, \gamma_{2}, \gamma_{3}$ are collinear, lying on the line $O_{1} O$, and the statement follows. Third solution. Moreover, the statement holds for an arbitrary point $D \in B C$. Let $E, F, G, H$ be the points of tangency of $\gamma_{2}$ with $A B, C D$ and of $\gamma_{3}$ with $A B, C D$, respectively. Let $O_{i}$ be the center of $\gamma_{i}, i=1,2,3$. As is shown in the third solution of (SL93-3), $E F$ and $G H$ meet at $O_{1}$. Hence the problem of proving the collinearity of $O_{1}, O_{2}, O_{3}$ reduces to the following simple problem: Let $D, E, F, G, H$ be points such that $D \in E G, F \in D H$ and $D E=D F, D G=D H$. Let $O_{1}, O_{2}, O_{3}$ be points such that $\angle O_{2} E D=$ $\angle O_{2} F D=90^{\circ}, \angle O_{3} G D=\angle O_{3} H D=90^{\circ}$, and $O_{1}=E F \cap G H$. Then $O_{1}, O_{2}, O_{3}$ are collinear. Let $K_{2}=D O_{2} \cap E F$ and $K_{3}=D O_{3} \cap G H$. Then $O_{2} K_{2} / O_{2} D=$ $D K_{3} / D O_{3}=K_{2} O_{1} / D O_{3}$ and hence by Thales' theorem $O_{1} \in O_{2} O_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
4. Let $A B$ be a diameter of a circle $\gamma$. A point $C$ different from $A$ and $B$ is on the circle $\gamma$. Let $D$ be the projection of the point $C$ onto the line $A B$. Consider three other circles $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ with the common tangent $A B: \gamma_{1}$ inscribed in the triangle $A B C$, and $\gamma_{2}$ and $\gamma_{3}$ tangent to both (the segment) $C D$ and $\gamma$. Prove that $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ have two common tangents.
|
4. Let $O$ be the midpoint of $A B$, i.e., the center of $\gamma$. Let $O_{1}, O_{2}$, and $O_{3}$ respectively be the centers of $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ and let $r_{1}, r_{2}, r_{3}$ respectively be the radii of $\gamma_{1}, \gamma_{2}$ and $\gamma_{3}$. Let $C_{1}, C_{2}$, and $C_{3}$ respectively be the points of tangency of $\gamma_{1}, \gamma_{2}$ and $\gamma_{3}$ with $A B$. Let $D_{2}$ and $D_{3}$ respectively be the points of tangency of $\gamma_{2}$ and $\gamma_{3}$ with $C D$. Finally, let $G_{2}$ and $G_{3}$ respectively be the points of tangency of $\gamma_{2}$ and $\gamma_{3}$ with $\gamma$. We have $\mathcal{B}\left(G_{2}, O_{2}, O\right)$, $G_{2} O_{2}=O_{2} D_{2}$, and $G_{2} O=O B$. Hence, $G_{2}, D_{2}, B$ are collinear. Similarly, $G_{3}, D_{3}, A$ are collinear. It follows that $A G_{2} D_{2} D$ and $B G_{3} D_{3} D$ are cyclic, since $\angle A G_{2} D_{2}=\angle D_{2} D A=\angle D_{3} D B=\angle B G_{3} D_{3}=90^{\circ}$. Hence $B C_{2}^{2}=B D_{2} \cdot B G_{2}=B D \cdot B A=B C^{2} \Rightarrow B C_{2}=B C$ and hence $A C_{2}=A B-B C$. Similarly, $A C_{3}=A C$. We thus have $A C_{1}=(A C+A B-B C) / 2=\left(A C_{3}+A C_{2}\right) / 2$. Hence, $C_{1}$ is the midpoint of $C_{2} C_{3}$. We also have $r_{2}+r_{3}=C_{2} C_{3}=A C+B C-A B=2 r_{1}$, from which it follows that $O_{1}, O_{2}, O_{3}$ are collinear. Second solution. We shall prove the statement for arbitrary points $A, B, C$ on $\gamma$. Let us apply the inversion $\psi$ with respect to the circle $\gamma_{1}$. We denote by $\widehat{X}$ the image of an object $X$ under $\psi$. Also, $\psi$ maps lines $B C, C A, A B$ onto circles $\widehat{a}, \widehat{b}, \widehat{c}$, respectively. Circles $\widehat{a}, \widehat{b}, \widehat{c}$ pass through the center $O_{1}$ of $\gamma_{1}$ and have radii equal to the radius of $\widehat{\gamma}$. Let $P, Q, R$ be the centers of $\widehat{a}, \widehat{b}, \widehat{c}$ respectively. The line $C D$ maps onto a circle $k$ through $\widehat{C}$ and $O_{1}$ that is perpendicular to $\widehat{c}$. Therefore its center $K$ lies in the intersection of the tangent $t$ to $\widehat{c}$ and the line $P Q$ (which bisects $\left.\widehat{C} O_{1}\right)$. Let $O$ be a point such that $R O_{1} K O$ is a parallelogram and $\gamma_{2}^{\prime}, \gamma_{3}^{\prime}$ the circles centered at $O$ tangent to $k$. It is easy to see that $\gamma_{2}^{\prime}$ and $\gamma_{3}^{\prime}$ are also tangent to $\widehat{c}$, since $O R$ and $O K$ have lengths equal to the radii of $k$ and $\widehat{c}$. Hence $\gamma_{2}^{\prime}$ and $\gamma_{3}^{\prime}$ are the images of $\gamma_{2}$ and $\gamma_{3}$ under $\psi$. Moreover, since $Q \widehat{A} O K$ and $P \widehat{B} O K$ are parallelograms and $Q, P, K$ are collinear, it follows that $\widehat{A}, \widehat{B}, O$ are also collinear. Hence the centers of $\gamma_{1}, \gamma_{2}, \gamma_{3}$ are collinear, lying on the line $O_{1} O$, and the statement follows. Third solution. Moreover, the statement holds for an arbitrary point $D \in B C$. Let $E, F, G, H$ be the points of tangency of $\gamma_{2}$ with $A B, C D$ and of $\gamma_{3}$ with $A B, C D$, respectively. Let $O_{i}$ be the center of $\gamma_{i}, i=1,2,3$. As is shown in the third solution of (SL93-3), $E F$ and $G H$ meet at $O_{1}$. Hence the problem of proving the collinearity of $O_{1}, O_{2}, O_{3}$ reduces to the following simple problem: Let $D, E, F, G, H$ be points such that $D \in E G, F \in D H$ and $D E=D F, D G=D H$. Let $O_{1}, O_{2}, O_{3}$ be points such that $\angle O_{2} E D=$ $\angle O_{2} F D=90^{\circ}, \angle O_{3} G D=\angle O_{3} H D=90^{\circ}$, and $O_{1}=E F \cap G H$. Then $O_{1}, O_{2}, O_{3}$ are collinear. Let $K_{2}=D O_{2} \cap E F$ and $K_{3}=D O_{3} \cap G H$. Then $O_{2} K_{2} / O_{2} D=$ $D K_{3} / D O_{3}=K_{2} O_{1} / D O_{3}$ and hence by Thales' theorem $O_{1} \in O_{2} O_{3}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
16c4fb71-936e-5b9f-aedd-fe9383ef99ca
| 24,838
|
5. Given $n$ points in the plane such that no three of them are collinear, prove that one can find at least $\binom{n-3}{2}$ convex quadrilaterals with their vertices at these points.
|
5. We first prove the following lemma. Lemma. If of five points in a plane no three belong to a single line, then there exist four that are the vertices of a convex quadrilateral. Proof. If the convex hull of the five points $A, B, C, D, E$ is a pentagon or a quadrilateral, the statement automatically holds. If the convex hull is a triangle, then w.l.o.g. let $\triangle A B C$ be that triangle and $D, E$ points in its interior. Let the line $D E$ w.l.o.g. intersect $[A B]$ and $[A C]$. Then $B, C, D, E$ form the desired quadrilateral. We now observe each quintuplet of points within the set. There are $\binom{n}{5}$ such quintuplets, and for each of them there is at least one quadruplet of points forming a convex quadrilateral. Each quadruplet, however, will be counted up to $n-4$ times. Hence we have found at least $\frac{1}{n-4}\binom{n}{5}$ quadruplets. Since $\frac{1}{n-4}\binom{n}{5} \geq\binom{ n-3}{2} \Leftrightarrow(n-5)(n-6)(n+8) \geq 0$, which always holds, it follows that we have found at least $\binom{n-3}{2}$ desired quadruplets of points.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
5. Given $n$ points in the plane such that no three of them are collinear, prove that one can find at least $\binom{n-3}{2}$ convex quadrilaterals with their vertices at these points.
|
5. We first prove the following lemma. Lemma. If of five points in a plane no three belong to a single line, then there exist four that are the vertices of a convex quadrilateral. Proof. If the convex hull of the five points $A, B, C, D, E$ is a pentagon or a quadrilateral, the statement automatically holds. If the convex hull is a triangle, then w.l.o.g. let $\triangle A B C$ be that triangle and $D, E$ points in its interior. Let the line $D E$ w.l.o.g. intersect $[A B]$ and $[A C]$. Then $B, C, D, E$ form the desired quadrilateral. We now observe each quintuplet of points within the set. There are $\binom{n}{5}$ such quintuplets, and for each of them there is at least one quadruplet of points forming a convex quadrilateral. Each quadruplet, however, will be counted up to $n-4$ times. Hence we have found at least $\frac{1}{n-4}\binom{n}{5}$ quadruplets. Since $\frac{1}{n-4}\binom{n}{5} \geq\binom{ n-3}{2} \Leftrightarrow(n-5)(n-6)(n+8) \geq 0$, which always holds, it follows that we have found at least $\binom{n-3}{2}$ desired quadruplets of points.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
194df52c-bac1-559b-8c92-055159f824fc
| 24,840
|
6. Under the conditions $x_{1}, x_{2}>0, x_{1} y_{1}>z_{1}^{2}$, and $x_{2} y_{2}>z_{2}^{2}$, prove the inequality $$ \frac{8}{\left(x_{1}+x_{2}\right)\left(y_{1}+y_{2}\right)-\left(z_{1}+z_{2}\right)^{2}} \leq \frac{1}{x_{1} y_{1}-z_{1}^{2}}+\frac{1}{x_{2} y_{2}-z_{2}^{2}} $$
|
6. Define $u_{1}=\sqrt{x_{1} y_{1}}+z_{1}, u_{2}=\sqrt{x_{2} y_{2}}+z_{2}, v_{1}=\sqrt{x_{1} y_{1}}-z_{1}$, and $v_{2}=$ $\sqrt{x_{2} y_{2}}-z_{2}$. By expanding both sides of the equation we can easily verify $\left(x_{1}+x_{2}\right)\left(y_{1}+y_{2}\right)-\left(z_{1}+z_{2}\right)^{2}=\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)+\left(\sqrt{x_{1} y_{2}}-\sqrt{x_{2} y_{1}}\right)^{2} \geq$ $\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)$. Since $x_{i} y_{i}-z_{i}^{2}=u_{i} v_{i}$ for $i=1,2$, it suffices to prove $$ \begin{aligned} & \frac{8}{\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)} \leq \frac{1}{u_{1} v_{1}}+\frac{1}{u_{2} v_{2}} \\ \Leftrightarrow & 8 u_{1} u_{2} v_{1} v_{2} \leq\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)\left(u_{1} v_{1}+u_{2} v_{2}\right) \end{aligned} $$ which trivially follows from the AM-GM inequalities $2 \sqrt{u_{1} u_{2}} \leq u_{1}+u_{2}$, $2 \sqrt{v_{1} v_{2}} \leq v_{1}+v_{2}$ and $2 \sqrt{u_{1} v_{1} u_{2} v_{2}} \leq u_{1} v_{1}+u_{2} v_{2}$. Equality holds if and only if $x_{1} y_{2}=x_{2} y_{1}, u_{1}=u_{2}$ and $v_{1}=v_{2}$, i.e. if and only if $x_{1}=x_{2}, y_{1}=y_{2}$ and $z_{1}=z_{2}$. Second solution. Let us define $f(x, y, z)=1 /\left(x y-z^{2}\right)$. The problem actually states that $$ 2 f\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right) \leq f\left(x_{1}, y_{1}, z_{1}\right)+f\left(x_{2}, y_{2}, z_{2}\right) $$ i.e., that the function $f$ is convex on the set $D=\left\{(x, y, z) \in \mathbb{R}^{2} \mid x y-\right.$ $\left.z^{2}>0\right\}$. It is known that a twice continuously differentiable function $f\left(t_{1}, t_{2}, \ldots, t_{n}\right)$ is convex if and only if its Hessian $\left[f_{i j}^{\prime \prime}\right]_{i, j=1}^{n}$ is positive semidefinite, or equivalently, if its principal minors $D_{k}=\operatorname{det}\left[f_{i j}^{\prime \prime}\right]_{i, j=1}^{k}, k=$ $1,2, \ldots, n$, are nonnegative. In the case of our $f$ this is directly verified: $D_{1}=2 y^{2} /\left(x y-z^{2}\right)^{3}, D_{2}=3 x y+z^{2} /\left(x y-z^{2}\right)^{5}, D_{3}=6 /\left(x y-z^{2}\right)^{6}$ are obviously positive.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
6. Under the conditions $x_{1}, x_{2}>0, x_{1} y_{1}>z_{1}^{2}$, and $x_{2} y_{2}>z_{2}^{2}$, prove the inequality $$ \frac{8}{\left(x_{1}+x_{2}\right)\left(y_{1}+y_{2}\right)-\left(z_{1}+z_{2}\right)^{2}} \leq \frac{1}{x_{1} y_{1}-z_{1}^{2}}+\frac{1}{x_{2} y_{2}-z_{2}^{2}} $$
|
6. Define $u_{1}=\sqrt{x_{1} y_{1}}+z_{1}, u_{2}=\sqrt{x_{2} y_{2}}+z_{2}, v_{1}=\sqrt{x_{1} y_{1}}-z_{1}$, and $v_{2}=$ $\sqrt{x_{2} y_{2}}-z_{2}$. By expanding both sides of the equation we can easily verify $\left(x_{1}+x_{2}\right)\left(y_{1}+y_{2}\right)-\left(z_{1}+z_{2}\right)^{2}=\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)+\left(\sqrt{x_{1} y_{2}}-\sqrt{x_{2} y_{1}}\right)^{2} \geq$ $\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)$. Since $x_{i} y_{i}-z_{i}^{2}=u_{i} v_{i}$ for $i=1,2$, it suffices to prove $$ \begin{aligned} & \frac{8}{\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)} \leq \frac{1}{u_{1} v_{1}}+\frac{1}{u_{2} v_{2}} \\ \Leftrightarrow & 8 u_{1} u_{2} v_{1} v_{2} \leq\left(u_{1}+u_{2}\right)\left(v_{1}+v_{2}\right)\left(u_{1} v_{1}+u_{2} v_{2}\right) \end{aligned} $$ which trivially follows from the AM-GM inequalities $2 \sqrt{u_{1} u_{2}} \leq u_{1}+u_{2}$, $2 \sqrt{v_{1} v_{2}} \leq v_{1}+v_{2}$ and $2 \sqrt{u_{1} v_{1} u_{2} v_{2}} \leq u_{1} v_{1}+u_{2} v_{2}$. Equality holds if and only if $x_{1} y_{2}=x_{2} y_{1}, u_{1}=u_{2}$ and $v_{1}=v_{2}$, i.e. if and only if $x_{1}=x_{2}, y_{1}=y_{2}$ and $z_{1}=z_{2}$. Second solution. Let us define $f(x, y, z)=1 /\left(x y-z^{2}\right)$. The problem actually states that $$ 2 f\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right) \leq f\left(x_{1}, y_{1}, z_{1}\right)+f\left(x_{2}, y_{2}, z_{2}\right) $$ i.e., that the function $f$ is convex on the set $D=\left\{(x, y, z) \in \mathbb{R}^{2} \mid x y-\right.$ $\left.z^{2}>0\right\}$. It is known that a twice continuously differentiable function $f\left(t_{1}, t_{2}, \ldots, t_{n}\right)$ is convex if and only if its Hessian $\left[f_{i j}^{\prime \prime}\right]_{i, j=1}^{n}$ is positive semidefinite, or equivalently, if its principal minors $D_{k}=\operatorname{det}\left[f_{i j}^{\prime \prime}\right]_{i, j=1}^{k}, k=$ $1,2, \ldots, n$, are nonnegative. In the case of our $f$ this is directly verified: $D_{1}=2 y^{2} /\left(x y-z^{2}\right)^{3}, D_{2}=3 x y+z^{2} /\left(x y-z^{2}\right)^{5}, D_{3}=6 /\left(x y-z^{2}\right)^{6}$ are obviously positive.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
10b45882-5d73-508b-bfef-938e3e7a0252
| 24,843
|
10. (SWE 4) ${ }^{\mathrm{IMO} 3}$ Let $1=a_{0} \leq a_{1} \leq a_{2} \leq \cdots \leq a_{n} \leq \cdots$ be a sequence of real numbers. Consider the sequence $b_{1}, b_{2}, \ldots$ defined by: $$ b_{n}=\sum_{k=1}^{n}\left(1-\frac{a_{k-1}}{a_{k}}\right) \frac{1}{\sqrt{a_{k}}} $$ Prove that: (a) For all natural numbers $n, 0 \leq b_{n}<2$. (b) Given an arbitrary $0 \leq b<2$, there is a sequence $a_{0}, a_{1}, \ldots, a_{n}, \ldots$ of the above type such that $b_{n}>b$ is true for infinitely many natural numbers $n$.
|
10. (a) Since $a_{n-1}<a_{n}$, we have $$ \begin{aligned} \left(1-\frac{a_{k-1}}{a_{k}}\right) \frac{1}{\sqrt{a_{k}}} & =\frac{a_{k}-a_{k-1}}{a_{k}^{3 / 2}} \\ & \leq \frac{2\left(\sqrt{a_{k}}-\sqrt{a_{k-1}}\right) \sqrt{a_{k}}}{a_{k} \sqrt{a_{k-1}}}=2\left(\frac{1}{\sqrt{a_{k-1}}}-\frac{1}{\sqrt{a_{k}}}\right) . \end{aligned} $$ Summing up all these inequalities for $k=1,2, \ldots, n$ we obtain $$ b_{n} \leq 2\left(\frac{1}{\sqrt{a_{0}}}-\frac{1}{\sqrt{a_{n}}}\right)<2 $$ (b) Choose a real number $q>1$, and let $a_{k}=q^{k}, k=1,2, \ldots$. Then $\left(1-a_{k-1} / a_{k}\right) / \sqrt{a_{k}}=(1-1 / q) / q^{k / 2}$, and consequently $$ b_{n}=\left(1-\frac{1}{q}\right) \sum_{k=1}^{n} \frac{1}{q^{k / 2}}=\frac{\sqrt{q}+1}{q}\left(1-\frac{1}{q^{n / 2}}\right) . $$ Since $(\sqrt{q}+1) / q$ can be arbitrarily close to 2 , one can set $q$ such that $(\sqrt{q}+1) / q>b$. Then $b_{n} \geq b$ for all sufficiently large $n$. Second solution. (a) Note that $$ b_{n}=\sum_{k=1}^{n}\left(1-\frac{a_{k-1}}{a_{k}}\right) \frac{1}{\sqrt{a_{k}}}=\sum_{k=1}^{n}\left(a_{k}-a_{k-1}\right) \cdot \frac{1}{a_{k}^{3 / 2}} $$ hence $b_{n}$ represents exactly the lower Darboux sum for the function $f(x)=x^{-3 / 2}$ on the interval $\left[a_{0}, a_{n}\right]$. Then $b_{n} \leq \int_{a_{0}}^{a_{n}} x^{-3 / 2} d x<$ $\int_{1}^{+\infty} x^{-3 / 2} d x=2$. (b) For each $b<2$ there exists a number $\alpha>1$ such that $\int_{1}^{\alpha} x^{-3 / 2} d x>$ $b+(2-b) / 2$. Now, by Darboux's theorem, there exists an array $1=$ $a_{0} \leq a_{1} \leq \cdots \leq a_{n}=\alpha$ such that the corresponding Darboux sums are arbitrarily close to the value of the integral. In particular, there is an array $a_{0}, \ldots, a_{n}$ with $b_{n}>b$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
10. (SWE 4) ${ }^{\mathrm{IMO} 3}$ Let $1=a_{0} \leq a_{1} \leq a_{2} \leq \cdots \leq a_{n} \leq \cdots$ be a sequence of real numbers. Consider the sequence $b_{1}, b_{2}, \ldots$ defined by: $$ b_{n}=\sum_{k=1}^{n}\left(1-\frac{a_{k-1}}{a_{k}}\right) \frac{1}{\sqrt{a_{k}}} $$ Prove that: (a) For all natural numbers $n, 0 \leq b_{n}<2$. (b) Given an arbitrary $0 \leq b<2$, there is a sequence $a_{0}, a_{1}, \ldots, a_{n}, \ldots$ of the above type such that $b_{n}>b$ is true for infinitely many natural numbers $n$.
|
10. (a) Since $a_{n-1}<a_{n}$, we have $$ \begin{aligned} \left(1-\frac{a_{k-1}}{a_{k}}\right) \frac{1}{\sqrt{a_{k}}} & =\frac{a_{k}-a_{k-1}}{a_{k}^{3 / 2}} \\ & \leq \frac{2\left(\sqrt{a_{k}}-\sqrt{a_{k-1}}\right) \sqrt{a_{k}}}{a_{k} \sqrt{a_{k-1}}}=2\left(\frac{1}{\sqrt{a_{k-1}}}-\frac{1}{\sqrt{a_{k}}}\right) . \end{aligned} $$ Summing up all these inequalities for $k=1,2, \ldots, n$ we obtain $$ b_{n} \leq 2\left(\frac{1}{\sqrt{a_{0}}}-\frac{1}{\sqrt{a_{n}}}\right)<2 $$ (b) Choose a real number $q>1$, and let $a_{k}=q^{k}, k=1,2, \ldots$. Then $\left(1-a_{k-1} / a_{k}\right) / \sqrt{a_{k}}=(1-1 / q) / q^{k / 2}$, and consequently $$ b_{n}=\left(1-\frac{1}{q}\right) \sum_{k=1}^{n} \frac{1}{q^{k / 2}}=\frac{\sqrt{q}+1}{q}\left(1-\frac{1}{q^{n / 2}}\right) . $$ Since $(\sqrt{q}+1) / q$ can be arbitrarily close to 2 , one can set $q$ such that $(\sqrt{q}+1) / q>b$. Then $b_{n} \geq b$ for all sufficiently large $n$. Second solution. (a) Note that $$ b_{n}=\sum_{k=1}^{n}\left(1-\frac{a_{k-1}}{a_{k}}\right) \frac{1}{\sqrt{a_{k}}}=\sum_{k=1}^{n}\left(a_{k}-a_{k-1}\right) \cdot \frac{1}{a_{k}^{3 / 2}} $$ hence $b_{n}$ represents exactly the lower Darboux sum for the function $f(x)=x^{-3 / 2}$ on the interval $\left[a_{0}, a_{n}\right]$. Then $b_{n} \leq \int_{a_{0}}^{a_{n}} x^{-3 / 2} d x<$ $\int_{1}^{+\infty} x^{-3 / 2} d x=2$. (b) For each $b<2$ there exists a number $\alpha>1$ such that $\int_{1}^{\alpha} x^{-3 / 2} d x>$ $b+(2-b) / 2$. Now, by Darboux's theorem, there exists an array $1=$ $a_{0} \leq a_{1} \leq \cdots \leq a_{n}=\alpha$ such that the corresponding Darboux sums are arbitrarily close to the value of the integral. In particular, there is an array $a_{0}, \ldots, a_{n}$ with $b_{n}>b$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
99383389-c202-5eb7-94e4-1d944299016e
| 24,849
|
2. (ROM 1) ${ }^{\mathrm{IMO} 2}$ Let $a$ and $b$ be the bases of two number systems and let $$ \begin{array}{ll} A_{n}={\overline{x_{1} x_{2} \ldots x_{n}}}^{(a)}, & A_{n+1}={\overline{x_{0} x_{1} x_{2} \ldots x_{n}}}^{(a)}, \\ B_{n}={\overline{x_{1} x_{2} \ldots x_{n}}}^{(b)}, & B_{n+1}={\overline{x_{0} x_{1} x_{2} \ldots x_{n}}}^{(b)}, \end{array} $$ be numbers in the number systems with respective bases $a$ and $b$, so that $x_{0}, x_{1}, x_{2}, \ldots, x_{n}$ denote digits in the number system with base $a$ as well as in the number system with base $b$. Suppose that neither $x_{0}$ nor $x_{1}$ is zero. Prove that $a>b$ if and only if $$ \frac{A_{n}}{A_{n+1}}<\frac{B_{n}}{B_{n+1}} . $$
|
2. Suppose that $a>b$. Consider the polynomial $P(X)=x_{1} X^{n-1}+x_{2} X^{n-2}+$ $\cdots+x_{n-1} X+x_{n}$. We have $A_{n}=P(a), B_{n}=P(b), A_{n+1}=x_{0} a^{n}+$ $P(a)$, and $B_{n+1}=x_{0} b^{n}+P(b)$. Now $A_{n} / A_{n+1}<B_{n} / B_{n+1}$ becomes $P(a) /\left(x_{0} a^{n}+P(a)\right)<P(b) /\left(x_{0} b^{n}+P(b)\right)$, i.e., $$ b^{n} P(a)<a^{n} P(b) $$ Since $a>b$, we have that $a^{i}>b^{i}$ and hence $x_{i} a^{n} b^{n-i} \geq x_{i} b^{n} a^{n-i}$ (also, for $i \geq 1$ the inequality is strict). Summing up all these inequalities for $i=1, \ldots, n$ we get $a^{n} P(b)>b^{n} P(a)$, which completes the proof for $a>b$. On the other hand, for $a<b$ we analogously obtain the opposite inequality $A_{n} / A_{n+1}>B_{n} / B_{n+1}$, while for $a=b$ we have equality. Thus $A_{n} / A_{n+1}<$ $B_{n} / B_{n+1} \Leftrightarrow a>b$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
2. (ROM 1) ${ }^{\mathrm{IMO} 2}$ Let $a$ and $b$ be the bases of two number systems and let $$ \begin{array}{ll} A_{n}={\overline{x_{1} x_{2} \ldots x_{n}}}^{(a)}, & A_{n+1}={\overline{x_{0} x_{1} x_{2} \ldots x_{n}}}^{(a)}, \\ B_{n}={\overline{x_{1} x_{2} \ldots x_{n}}}^{(b)}, & B_{n+1}={\overline{x_{0} x_{1} x_{2} \ldots x_{n}}}^{(b)}, \end{array} $$ be numbers in the number systems with respective bases $a$ and $b$, so that $x_{0}, x_{1}, x_{2}, \ldots, x_{n}$ denote digits in the number system with base $a$ as well as in the number system with base $b$. Suppose that neither $x_{0}$ nor $x_{1}$ is zero. Prove that $a>b$ if and only if $$ \frac{A_{n}}{A_{n+1}}<\frac{B_{n}}{B_{n+1}} . $$
|
2. Suppose that $a>b$. Consider the polynomial $P(X)=x_{1} X^{n-1}+x_{2} X^{n-2}+$ $\cdots+x_{n-1} X+x_{n}$. We have $A_{n}=P(a), B_{n}=P(b), A_{n+1}=x_{0} a^{n}+$ $P(a)$, and $B_{n+1}=x_{0} b^{n}+P(b)$. Now $A_{n} / A_{n+1}<B_{n} / B_{n+1}$ becomes $P(a) /\left(x_{0} a^{n}+P(a)\right)<P(b) /\left(x_{0} b^{n}+P(b)\right)$, i.e., $$ b^{n} P(a)<a^{n} P(b) $$ Since $a>b$, we have that $a^{i}>b^{i}$ and hence $x_{i} a^{n} b^{n-i} \geq x_{i} b^{n} a^{n-i}$ (also, for $i \geq 1$ the inequality is strict). Summing up all these inequalities for $i=1, \ldots, n$ we get $a^{n} P(b)>b^{n} P(a)$, which completes the proof for $a>b$. On the other hand, for $a<b$ we analogously obtain the opposite inequality $A_{n} / A_{n+1}>B_{n} / B_{n+1}$, while for $a=b$ we have equality. Thus $A_{n} / A_{n+1}<$ $B_{n} / B_{n+1} \Leftrightarrow a>b$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
96e39a0c-3dfc-5388-a36c-a1a9ef099cca
| 24,858
|
3. (BUL 6) ${ }^{\mathrm{IMO}}$ In the tetrahedron $S A B C$ the angle $B S C$ is a right angle, and the projection of the vertex $S$ to the plane $A B C$ is the intersection of the altitudes of the triangle $A B C$. Let $z$ be the radius of the inscribed circle of the triangle $A B C$. Prove that $$ S A^{2}+S B^{2}+S C^{2} \geq 18 z^{2} $$
|
3 . We shall use the following lemma Lemma. If an altitude of a tetrahedron passes through the orthocenter of the opposite side, then each of the other altitudes possesses the same property. Proof. Denote the tetrahedron by $S A B C$ and let $a=B C, b=C A$, $c=A B, m=S A, n=S B, p=S C$. It is enough to prove that an altitude passes through the orthocenter of the opposite side if and only if $a^{2}+m^{2}=b^{2}+n^{2}=c^{2}+p^{2}$. Suppose that the foot $S^{\prime}$ of the altitude from $S$ is the orthocenter of $A B C$. Then $S S^{\prime} \perp A B C \Rightarrow S B^{2}-S C^{2}=S^{\prime} B^{2}-S^{\prime} C^{2}$. But from $A S^{\prime} \perp B C$ it follows that $A B^{2}-A C^{2}=S^{\prime} B^{2}-S^{\prime} C^{2}$. From these two equalities it can be concluded that $n^{2}-p^{2}=c^{2}-b^{2}$, or equivalently, $n^{2}+b^{2}=c^{2}+p^{2}$. Analogously, $a^{2}+m^{2}=n^{2}+b^{2}$, so we have proved the first part of the equivalence. Now suppose that $a^{2}+m^{2}=b^{2}+n^{2}=c^{2}+p^{2}$. Defining $S^{\prime}$ as before, we get $n^{2}-p^{2}=S^{\prime} B^{2}-S^{\prime} C^{2}$. From the condition $n^{2}-p^{2}=c^{2}-b^{2}$ $\left(\Leftrightarrow b^{2}+n^{2}=c^{2}+p^{2}\right.$ ) we conclude that $A S^{\prime} \perp B C$. In the same way $C S^{\prime} \perp A B$, which proves that $S^{\prime}$ is the orthocenter of $\triangle A B C$. The lemma is thus proven. Now using the lemma it is easy to see that if one of the angles at $S$ is right, than so are the others. Indeed, suppose that $\angle A S B=\pi / 2$. From the lemma we have that the altitude from $C$ passes through the orthocenter of $\triangle A S B$, which is $S$, so $C S \perp A S B$ and $\angle C S A=\angle C S B=\pi / 2$. Therefore $m^{2}+n^{2}=c^{2}, n^{2}+p^{2}=a^{2}$, and $p^{2}+m^{2}=b^{2}$, so it follows that $m^{2}+n^{2}+p^{2}=\left(a^{2}+b^{2}+c^{2}\right) / 2$. By the inequality between the arithmetic and quadric means, we have that $\left(a^{2}+b^{2}+c^{2}\right) / 2 \geq 2 s^{2} / 3$, where $s$ denotes the semiperimeter of $\triangle A B C$. It remains to be shown that $2 s^{2} / 3 \geq 18 r^{2}$. Since $S_{\triangle A B C}=s r$, this is equivalent to $2 s^{4} / 3 \geq$ $18 S_{A B C}^{2}=18 s(s-a)(s-b)(s-c)$ by Heron's formula. This reduces to $s^{3} \geq 27(s-a)(s-b)(s-c)$, which is an obvious consequence of the AM-GM mean inequality. Remark. In the place of the lemma one could prove that the opposite edges of the tetrahedron are mutually perpendicular and proceed in the same way.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
3. (BUL 6) ${ }^{\mathrm{IMO}}$ In the tetrahedron $S A B C$ the angle $B S C$ is a right angle, and the projection of the vertex $S$ to the plane $A B C$ is the intersection of the altitudes of the triangle $A B C$. Let $z$ be the radius of the inscribed circle of the triangle $A B C$. Prove that $$ S A^{2}+S B^{2}+S C^{2} \geq 18 z^{2} $$
|
3 . We shall use the following lemma Lemma. If an altitude of a tetrahedron passes through the orthocenter of the opposite side, then each of the other altitudes possesses the same property. Proof. Denote the tetrahedron by $S A B C$ and let $a=B C, b=C A$, $c=A B, m=S A, n=S B, p=S C$. It is enough to prove that an altitude passes through the orthocenter of the opposite side if and only if $a^{2}+m^{2}=b^{2}+n^{2}=c^{2}+p^{2}$. Suppose that the foot $S^{\prime}$ of the altitude from $S$ is the orthocenter of $A B C$. Then $S S^{\prime} \perp A B C \Rightarrow S B^{2}-S C^{2}=S^{\prime} B^{2}-S^{\prime} C^{2}$. But from $A S^{\prime} \perp B C$ it follows that $A B^{2}-A C^{2}=S^{\prime} B^{2}-S^{\prime} C^{2}$. From these two equalities it can be concluded that $n^{2}-p^{2}=c^{2}-b^{2}$, or equivalently, $n^{2}+b^{2}=c^{2}+p^{2}$. Analogously, $a^{2}+m^{2}=n^{2}+b^{2}$, so we have proved the first part of the equivalence. Now suppose that $a^{2}+m^{2}=b^{2}+n^{2}=c^{2}+p^{2}$. Defining $S^{\prime}$ as before, we get $n^{2}-p^{2}=S^{\prime} B^{2}-S^{\prime} C^{2}$. From the condition $n^{2}-p^{2}=c^{2}-b^{2}$ $\left(\Leftrightarrow b^{2}+n^{2}=c^{2}+p^{2}\right.$ ) we conclude that $A S^{\prime} \perp B C$. In the same way $C S^{\prime} \perp A B$, which proves that $S^{\prime}$ is the orthocenter of $\triangle A B C$. The lemma is thus proven. Now using the lemma it is easy to see that if one of the angles at $S$ is right, than so are the others. Indeed, suppose that $\angle A S B=\pi / 2$. From the lemma we have that the altitude from $C$ passes through the orthocenter of $\triangle A S B$, which is $S$, so $C S \perp A S B$ and $\angle C S A=\angle C S B=\pi / 2$. Therefore $m^{2}+n^{2}=c^{2}, n^{2}+p^{2}=a^{2}$, and $p^{2}+m^{2}=b^{2}$, so it follows that $m^{2}+n^{2}+p^{2}=\left(a^{2}+b^{2}+c^{2}\right) / 2$. By the inequality between the arithmetic and quadric means, we have that $\left(a^{2}+b^{2}+c^{2}\right) / 2 \geq 2 s^{2} / 3$, where $s$ denotes the semiperimeter of $\triangle A B C$. It remains to be shown that $2 s^{2} / 3 \geq 18 r^{2}$. Since $S_{\triangle A B C}=s r$, this is equivalent to $2 s^{4} / 3 \geq$ $18 S_{A B C}^{2}=18 s(s-a)(s-b)(s-c)$ by Heron's formula. This reduces to $s^{3} \geq 27(s-a)(s-b)(s-c)$, which is an obvious consequence of the AM-GM mean inequality. Remark. In the place of the lemma one could prove that the opposite edges of the tetrahedron are mutually perpendicular and proceed in the same way.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c9142e41-d44b-5cee-a1b7-2f9c92b8c48d
| 24,861
|
5. (CZS 3) Let $M$ be an interior point of the tetrahedron $A B C D$. Prove that $$ \begin{aligned} & \overrightarrow{M A} \operatorname{vol}(M B C D)+\overrightarrow{M B} \operatorname{vol}(M A C D) \\ & \quad+\overrightarrow{M C} \operatorname{vol}(M A B D)+\overrightarrow{M D} \operatorname{vol}(M A B C)=0 \end{aligned} $$ ( $\operatorname{vol}(P Q R S)$ denotes the volume of the tetrahedron $P Q R S)$.
|
5. Denote respectively by $A_{1}, B_{1}, C_{1}$ and $D_{1}$ the points of intersection of the lines $A M, B M, C M$, and $D M$ with the opposite sides of the tetrahedron. Since $\operatorname{vol}(M B C D)=\operatorname{vol}(A B C D) \overrightarrow{M A_{1}} / \overrightarrow{A A_{1}}$, the relation we have to prove is equivalent to $$ \overrightarrow{M A} \cdot \frac{\overrightarrow{M A_{1}}}{\overrightarrow{A A_{1}}}+\overrightarrow{M B} \cdot \frac{\overrightarrow{M B_{1}}}{\overrightarrow{B B_{1}}}+\overrightarrow{M C} \cdot \frac{\overrightarrow{M C_{1}}}{\overrightarrow{C C_{1}}}+\overrightarrow{M D} \cdot \frac{\overrightarrow{M D_{1}}}{\overrightarrow{D D_{1}}}=0 $$ There exist unique real numbers $\alpha, \beta, \gamma$, and $\delta$ such that $\alpha+\beta+\gamma+\delta=1$ and for every point $O$ in space $$ \overrightarrow{O M}=\alpha \overrightarrow{O A}+\beta \overrightarrow{O B}+\gamma \overrightarrow{O C}+\delta \overrightarrow{O D} $$ (This follows easily from $\overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{A M}=\overrightarrow{O A}+k \overrightarrow{A B}+l \overrightarrow{A C}+m \overrightarrow{A D}=$ $\overrightarrow{A B}+k(\overrightarrow{O B}-\overrightarrow{O A})+l(\overrightarrow{O C}-\overrightarrow{O A})+m(\overrightarrow{O D}-\overrightarrow{O A})$ for some $k, l, m \in \mathbb{R}$.) Further, from the condition that $A_{1}$ belongs to the plane $B C D$ we obtain for every $O$ in space the following equality for some $\beta^{\prime}, \gamma^{\prime}, \delta^{\prime}$ : $$ \overrightarrow{O A_{1}}=\beta^{\prime} \overrightarrow{O B}+\gamma^{\prime} \overrightarrow{O C}+\delta^{\prime} \overrightarrow{O D} $$ However, for $\lambda=\overrightarrow{M A_{1}} / \overrightarrow{A A_{1}}, \overrightarrow{O M}=\lambda \overrightarrow{O A}+(1-\lambda) \overrightarrow{O A_{1}}$; hence substituting (2) and (3) in this expression and equating coefficients for $\overrightarrow{O A}$ we obtain $\lambda=\overrightarrow{M A_{1}} / \overrightarrow{A A_{1}}=\alpha$. Analogously, $\beta=\overrightarrow{M B_{1}} / \overrightarrow{B B_{1}}, \gamma=\overrightarrow{M C_{1}} / \overrightarrow{C C_{1}}$, and $\delta=\overrightarrow{M D_{1}} / \overrightarrow{D D_{1}}$; hence (1) follows immediately for $O=M$. Remark. The statement of the problem actually follows from the fact that $M$ is the center of mass of the system with masses $\operatorname{vol}(M B C D)$, $\operatorname{vol}(M A C D), \operatorname{vol}(M A B D), \operatorname{vol}(M A B C)$ at $A, B, C, D$ respectively. Our proof is actually a formal verification of this fact.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. (CZS 3) Let $M$ be an interior point of the tetrahedron $A B C D$. Prove that $$ \begin{aligned} & \overrightarrow{M A} \operatorname{vol}(M B C D)+\overrightarrow{M B} \operatorname{vol}(M A C D) \\ & \quad+\overrightarrow{M C} \operatorname{vol}(M A B D)+\overrightarrow{M D} \operatorname{vol}(M A B C)=0 \end{aligned} $$ ( $\operatorname{vol}(P Q R S)$ denotes the volume of the tetrahedron $P Q R S)$.
|
5. Denote respectively by $A_{1}, B_{1}, C_{1}$ and $D_{1}$ the points of intersection of the lines $A M, B M, C M$, and $D M$ with the opposite sides of the tetrahedron. Since $\operatorname{vol}(M B C D)=\operatorname{vol}(A B C D) \overrightarrow{M A_{1}} / \overrightarrow{A A_{1}}$, the relation we have to prove is equivalent to $$ \overrightarrow{M A} \cdot \frac{\overrightarrow{M A_{1}}}{\overrightarrow{A A_{1}}}+\overrightarrow{M B} \cdot \frac{\overrightarrow{M B_{1}}}{\overrightarrow{B B_{1}}}+\overrightarrow{M C} \cdot \frac{\overrightarrow{M C_{1}}}{\overrightarrow{C C_{1}}}+\overrightarrow{M D} \cdot \frac{\overrightarrow{M D_{1}}}{\overrightarrow{D D_{1}}}=0 $$ There exist unique real numbers $\alpha, \beta, \gamma$, and $\delta$ such that $\alpha+\beta+\gamma+\delta=1$ and for every point $O$ in space $$ \overrightarrow{O M}=\alpha \overrightarrow{O A}+\beta \overrightarrow{O B}+\gamma \overrightarrow{O C}+\delta \overrightarrow{O D} $$ (This follows easily from $\overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{A M}=\overrightarrow{O A}+k \overrightarrow{A B}+l \overrightarrow{A C}+m \overrightarrow{A D}=$ $\overrightarrow{A B}+k(\overrightarrow{O B}-\overrightarrow{O A})+l(\overrightarrow{O C}-\overrightarrow{O A})+m(\overrightarrow{O D}-\overrightarrow{O A})$ for some $k, l, m \in \mathbb{R}$.) Further, from the condition that $A_{1}$ belongs to the plane $B C D$ we obtain for every $O$ in space the following equality for some $\beta^{\prime}, \gamma^{\prime}, \delta^{\prime}$ : $$ \overrightarrow{O A_{1}}=\beta^{\prime} \overrightarrow{O B}+\gamma^{\prime} \overrightarrow{O C}+\delta^{\prime} \overrightarrow{O D} $$ However, for $\lambda=\overrightarrow{M A_{1}} / \overrightarrow{A A_{1}}, \overrightarrow{O M}=\lambda \overrightarrow{O A}+(1-\lambda) \overrightarrow{O A_{1}}$; hence substituting (2) and (3) in this expression and equating coefficients for $\overrightarrow{O A}$ we obtain $\lambda=\overrightarrow{M A_{1}} / \overrightarrow{A A_{1}}=\alpha$. Analogously, $\beta=\overrightarrow{M B_{1}} / \overrightarrow{B B_{1}}, \gamma=\overrightarrow{M C_{1}} / \overrightarrow{C C_{1}}$, and $\delta=\overrightarrow{M D_{1}} / \overrightarrow{D D_{1}}$; hence (1) follows immediately for $O=M$. Remark. The statement of the problem actually follows from the fact that $M$ is the center of mass of the system with masses $\operatorname{vol}(M B C D)$, $\operatorname{vol}(M A C D), \operatorname{vol}(M A B D), \operatorname{vol}(M A B C)$ at $A, B, C, D$ respectively. Our proof is actually a formal verification of this fact.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
78333d7e-5776-5927-a6a2-8c158e9417e1
| 24,866
|
6. (FRA 1) In the triangle $A B C$ let $B^{\prime}$ and $C^{\prime}$ be the midpoints of the sides $A C$ and $A B$ respectively and $H$ the foot of the altitude passing through the vertex $A$. Prove that the circumcircles of the triangles $A B^{\prime} C^{\prime}, B C^{\prime} H$, and $B^{\prime} C H$ have a common point $I$ and that the line $H I$ passes through the midpoint of the segment $B^{\prime} C^{\prime}$.
|
6. Let $F$ be the midpoint of $B^{\prime} C^{\prime}, A^{\prime}$ the midpoint of $B C$, and $I$ the intersection point of the line $H F$ and the circle circumscribed about $\triangle B H C^{\prime}$. Denote by $M$ the intersection point of the line $A A^{\prime}$ with the circumscribed circle about the triangle $A B C$. Triangles $H B^{\prime} C^{\prime}$ and $A B C$ are similar. Since $\angle C^{\prime} I F=\angle A B C=\angle A^{\prime} M C, \angle C^{\prime} F I=\angle A A^{\prime} B=\angle M A^{\prime} C$, $2 C^{\prime} F=C^{\prime} B^{\prime}$, and $2 A^{\prime} C=C B$, it follows that $\triangle C^{\prime} I B^{\prime} \sim \triangle C M B$, hence $\angle F I B^{\prime}=\angle A^{\prime} M B=\angle A C B$. Now one concludes that $I$ belongs to the circumscribed circles of $\triangle A B^{\prime} C^{\prime}$ (since $\left.\angle C^{\prime} I B^{\prime}=180^{\circ}-\angle C^{\prime} A B^{\prime}\right)$ and $\triangle H C B^{\prime}$. Second Solution. We denote the angles of $\triangle A B C$ by $\alpha, \beta, \gamma$. Evidently $\triangle A B C \sim \triangle H C^{\prime} B^{\prime}$. Within $\triangle H C^{\prime} B^{\prime}$ there exists a unique point $I$ such that $\angle H I B^{\prime}=180^{\circ}-\gamma, \angle H I C^{\prime}=180^{\circ}-\beta$, and $\angle C^{\prime} I B^{\prime}=180^{\circ}-\alpha$, and all three circles must contain this point. Let $H I$ and $B^{\prime} C^{\prime}$ intersect in $F$. It remains to show that $F B^{\prime}=F C^{\prime}$. From $\angle H I B^{\prime}+\angle H B^{\prime} F=180^{\circ}$ we obtain $\angle I H B^{\prime}=\angle I B^{\prime} F$. Similarly, $\angle I H C^{\prime}=\angle I C^{\prime} F$. Thus circles around $\triangle I H C^{\prime}$ and $\triangle I H B^{\prime}$ are both tangent to $B^{\prime} C^{\prime}$, giving us $F B^{\prime 2}=$ $F I \cdot F H=F C^{\prime 2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
6. (FRA 1) In the triangle $A B C$ let $B^{\prime}$ and $C^{\prime}$ be the midpoints of the sides $A C$ and $A B$ respectively and $H$ the foot of the altitude passing through the vertex $A$. Prove that the circumcircles of the triangles $A B^{\prime} C^{\prime}, B C^{\prime} H$, and $B^{\prime} C H$ have a common point $I$ and that the line $H I$ passes through the midpoint of the segment $B^{\prime} C^{\prime}$.
|
6. Let $F$ be the midpoint of $B^{\prime} C^{\prime}, A^{\prime}$ the midpoint of $B C$, and $I$ the intersection point of the line $H F$ and the circle circumscribed about $\triangle B H C^{\prime}$. Denote by $M$ the intersection point of the line $A A^{\prime}$ with the circumscribed circle about the triangle $A B C$. Triangles $H B^{\prime} C^{\prime}$ and $A B C$ are similar. Since $\angle C^{\prime} I F=\angle A B C=\angle A^{\prime} M C, \angle C^{\prime} F I=\angle A A^{\prime} B=\angle M A^{\prime} C$, $2 C^{\prime} F=C^{\prime} B^{\prime}$, and $2 A^{\prime} C=C B$, it follows that $\triangle C^{\prime} I B^{\prime} \sim \triangle C M B$, hence $\angle F I B^{\prime}=\angle A^{\prime} M B=\angle A C B$. Now one concludes that $I$ belongs to the circumscribed circles of $\triangle A B^{\prime} C^{\prime}$ (since $\left.\angle C^{\prime} I B^{\prime}=180^{\circ}-\angle C^{\prime} A B^{\prime}\right)$ and $\triangle H C B^{\prime}$. Second Solution. We denote the angles of $\triangle A B C$ by $\alpha, \beta, \gamma$. Evidently $\triangle A B C \sim \triangle H C^{\prime} B^{\prime}$. Within $\triangle H C^{\prime} B^{\prime}$ there exists a unique point $I$ such that $\angle H I B^{\prime}=180^{\circ}-\gamma, \angle H I C^{\prime}=180^{\circ}-\beta$, and $\angle C^{\prime} I B^{\prime}=180^{\circ}-\alpha$, and all three circles must contain this point. Let $H I$ and $B^{\prime} C^{\prime}$ intersect in $F$. It remains to show that $F B^{\prime}=F C^{\prime}$. From $\angle H I B^{\prime}+\angle H B^{\prime} F=180^{\circ}$ we obtain $\angle I H B^{\prime}=\angle I B^{\prime} F$. Similarly, $\angle I H C^{\prime}=\angle I C^{\prime} F$. Thus circles around $\triangle I H C^{\prime}$ and $\triangle I H B^{\prime}$ are both tangent to $B^{\prime} C^{\prime}$, giving us $F B^{\prime 2}=$ $F I \cdot F H=F C^{\prime 2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3171967d-43d7-5af3-8af2-f27ec0af0e1d
| 24,869
|
8. (POL 2) ${ }^{\mathrm{IMO} 1}$ Given a point $M$ on the side $A B$ of the triangle $A B C$, let $r_{1}$ and $r_{2}$ be the radii of the inscribed circles of the triangles $A C M$ and $B C M$ respectively and let $\rho_{1}$ and $\rho_{2}$ be the radii of the excircles of the triangles $A C M$ and $B C M$ at the sides $A M$ and $B M$ respectively. Let $r$ and $\rho$ denote the radii of the inscribed circle and the excircle at the side $A B$ of the triangle $A B C$ respectively. Prove that $$ \frac{r_{1}}{\rho_{1}} \frac{r_{2}}{\rho_{2}}=\frac{r}{\rho} $$
|
8. Let $A C=b, B C=a, A M=x, B M=y, C M=l$. Denote by $I_{1}$ the incenter and by $S_{1}$ the center of the excircle of $\triangle A M C$. Suppose that $P_{1}$ and $Q_{1}$ are feet of perpendiculars from $I_{1}$ and $S_{1}$, respectively, to the line $A C$. Then $\triangle I_{1} C P_{1} \sim \triangle S_{1} C Q_{1}$, hence $r_{1} / \rho_{1}=C P_{1} / C Q_{1}$. We have $C P_{1}=(A C+M C-A M) / 2=(b+l-x) / 2$ and $C Q_{1}=$ $(A C+M C+A M) / 2=(b+l+x) / 2$. Hence $$ \frac{r_{1}}{\rho_{1}}=\frac{b+l-x}{b+l+x} $$ We similarly obtain $$ \frac{r_{2}}{\rho_{2}}=\frac{b+l-y}{b+l+y} \text { and } \frac{r}{\rho}=\frac{a+b-x-y}{a+b+x+y} $$ What we have to prove is now equivalent to $$ \frac{(b+l-x)(a+l-y)}{(b+l+x)(a+l+y)}=\frac{a+b-x-y}{a+b+x+y} $$ Multiplying both sides of (1) by $(a+l+y)(b+l+x)(a+b+x+y)$ we obtain an expression that reduces to $l^{2} x+l^{2} y+x^{2} y+x y^{2}=b^{2} y+a^{2} x$. Dividing both sides by $c=x+y$, we get that (1) is equivalent to $l^{2}=$ $b^{2} y /(x+y)+a^{2} x /(x+y)-x y$, which is exactly Stewart's theorem for $l$. This finally proves the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. (POL 2) ${ }^{\mathrm{IMO} 1}$ Given a point $M$ on the side $A B$ of the triangle $A B C$, let $r_{1}$ and $r_{2}$ be the radii of the inscribed circles of the triangles $A C M$ and $B C M$ respectively and let $\rho_{1}$ and $\rho_{2}$ be the radii of the excircles of the triangles $A C M$ and $B C M$ at the sides $A M$ and $B M$ respectively. Let $r$ and $\rho$ denote the radii of the inscribed circle and the excircle at the side $A B$ of the triangle $A B C$ respectively. Prove that $$ \frac{r_{1}}{\rho_{1}} \frac{r_{2}}{\rho_{2}}=\frac{r}{\rho} $$
|
8. Let $A C=b, B C=a, A M=x, B M=y, C M=l$. Denote by $I_{1}$ the incenter and by $S_{1}$ the center of the excircle of $\triangle A M C$. Suppose that $P_{1}$ and $Q_{1}$ are feet of perpendiculars from $I_{1}$ and $S_{1}$, respectively, to the line $A C$. Then $\triangle I_{1} C P_{1} \sim \triangle S_{1} C Q_{1}$, hence $r_{1} / \rho_{1}=C P_{1} / C Q_{1}$. We have $C P_{1}=(A C+M C-A M) / 2=(b+l-x) / 2$ and $C Q_{1}=$ $(A C+M C+A M) / 2=(b+l+x) / 2$. Hence $$ \frac{r_{1}}{\rho_{1}}=\frac{b+l-x}{b+l+x} $$ We similarly obtain $$ \frac{r_{2}}{\rho_{2}}=\frac{b+l-y}{b+l+y} \text { and } \frac{r}{\rho}=\frac{a+b-x-y}{a+b+x+y} $$ What we have to prove is now equivalent to $$ \frac{(b+l-x)(a+l-y)}{(b+l+x)(a+l+y)}=\frac{a+b-x-y}{a+b+x+y} $$ Multiplying both sides of (1) by $(a+l+y)(b+l+x)(a+b+x+y)$ we obtain an expression that reduces to $l^{2} x+l^{2} y+x^{2} y+x y^{2}=b^{2} y+a^{2} x$. Dividing both sides by $c=x+y$, we get that (1) is equivalent to $l^{2}=$ $b^{2} y /(x+y)+a^{2} x /(x+y)-x y$, which is exactly Stewart's theorem for $l$. This finally proves the desired result.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9baa2f6f-3036-5fb0-97fa-47526399d216
| 24,874
|
9. (GDR 3) Let $u_{1}, u_{2}, \ldots, u_{n}, v_{1}, v_{2}, \ldots, v_{n}$ be real numbers. Prove that $$ 1+\sum_{i=1}^{n}\left(u_{i}+v_{i}\right)^{2} \leq \frac{4}{3}\left(1+\sum_{i=1}^{n} u_{i}^{2}\right)\left(1+\sum_{i=1}^{n} v_{i}^{2}\right) $$ In what case does equality hold?
|
9. Let us set $a=\sqrt{\sum_{i=1}^{n} u_{i}^{2}}$ and $b=\sqrt{\sum_{i=1}^{n} v_{i}^{2}}$. By Minkowski's inequality (for $p=2$ ) we have $\sum_{i=1}^{n}\left(u_{i}+v_{i}\right)^{2} \leq(a+b)^{2}$. Hence the LHS of the desired inequality is not greater than $1+(a+b)^{2}$, while the RHS is equal to $4\left(1+a^{2}\right)\left(1+b^{2}\right) / 3$. Now it is sufficient to prove that $$ 3+3(a+b)^{2} \leq 4\left(1+a^{2}\right)\left(1+b^{2}\right) $$ The last inequality can be reduced to the trivial $0 \leq(a-b)^{2}+(2 a b-1)^{2}$. The equality in the initial inequality holds if and only if $u_{i} / v_{i}=c$ for some $c \in \mathbb{R}$ and $a=b=1 / \sqrt{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
9. (GDR 3) Let $u_{1}, u_{2}, \ldots, u_{n}, v_{1}, v_{2}, \ldots, v_{n}$ be real numbers. Prove that $$ 1+\sum_{i=1}^{n}\left(u_{i}+v_{i}\right)^{2} \leq \frac{4}{3}\left(1+\sum_{i=1}^{n} u_{i}^{2}\right)\left(1+\sum_{i=1}^{n} v_{i}^{2}\right) $$ In what case does equality hold?
|
9. Let us set $a=\sqrt{\sum_{i=1}^{n} u_{i}^{2}}$ and $b=\sqrt{\sum_{i=1}^{n} v_{i}^{2}}$. By Minkowski's inequality (for $p=2$ ) we have $\sum_{i=1}^{n}\left(u_{i}+v_{i}\right)^{2} \leq(a+b)^{2}$. Hence the LHS of the desired inequality is not greater than $1+(a+b)^{2}$, while the RHS is equal to $4\left(1+a^{2}\right)\left(1+b^{2}\right) / 3$. Now it is sufficient to prove that $$ 3+3(a+b)^{2} \leq 4\left(1+a^{2}\right)\left(1+b^{2}\right) $$ The last inequality can be reduced to the trivial $0 \leq(a-b)^{2}+(2 a b-1)^{2}$. The equality in the initial inequality holds if and only if $u_{i} / v_{i}=c$ for some $c \in \mathbb{R}$ and $a=b=1 / \sqrt{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
51adcd28-3570-5e5a-b14e-c441e9fb8cd3
| 24,877
|
1. (BUL 2) Consider a sequence of polynomials $P_{0}(x), P_{1}(x), P_{2}(x), \ldots$, $P_{n}(x), \ldots$, where $P_{0}(x)=2, P_{1}(x)=x$ and for every $n \geq 1$ the following equality holds: $$ P_{n+1}(x)+P_{n-1}(x)=x P_{n}(x) $$ Prove that there exist three real numbers $a, b, c$ such that for all $n \geq 1$, $$ \left(x^{2}-4\right)\left[P_{n}^{2}(x)-4\right]=\left[a P_{n+1}(x)+b P_{n}(x)+c P_{n-1}(x)\right]^{2} $$
|
1. Assuming that $a, b, c$ in (1) exist, let us find what their values should be. Since $P_{2}(x)=x^{2}-2$, equation (1) for $n=1$ becomes $\left(x^{2}-4\right)^{2}=$ $\left[a\left(x^{2}-2\right)+b x+2 c\right]^{2}$. Therefore, there are two possibilities for $(a, b, c)$ : $(1,0,-1)$ and $(-1,0,1)$. In both cases we must prove that $$ \left(x^{2}-4\right)\left[P_{n}(x)^{2}-4\right]=\left[P_{n+1}(x)-P_{n-1}(x)\right]^{2} $$ It suffices to prove (2) for all $x$ in the interval $[-2,2]$. In this interval we can set $x=2 \cos t$ for some real $t$. We prove by induction that $$ P_{n}(x)=2 \cos n t \quad \text { for all } n $$ This is trivial for $n=0,1$. Assume (3) holds for some $n-1$ and $n$. Then $P_{n+1}(x)=4 \cos t \cos n t-2 \cos (n-1) t=2 \cos (n+1) t$ by the additive formula for the cosine. This completes the induction. Now (2) reduces to the obviously correct equality $$ 16 \sin ^{2} t \sin ^{2} n t=(2 \cos (n+1) t-2 \cos (n-1) t)^{2} $$ Second solution. If $x$ is fixed, the linear recurrence relation $P_{n+1}(x)+$ $P_{n-1}(x)=x P_{n}(x)$ can be solved in the standard way. The characteristic polynomial $t^{2}-x t+1$ has zeros $t_{1,2}$ with $t_{1}+t_{2}=x$ and $t_{1} t_{2}=1$; hence, the general $P_{n}(x)$ has the form $a t_{1}^{n}+b t_{2}^{n}$ for some constants $a$, $b$. From $P_{0}=2$ and $P_{1}=x$ we obtain that $$ P_{n}(x)=t_{1}^{n}+t_{2}^{n} . $$ Plugging in these values and using $t_{1} t_{2}=1$ one easily verifies (2).
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
1. (BUL 2) Consider a sequence of polynomials $P_{0}(x), P_{1}(x), P_{2}(x), \ldots$, $P_{n}(x), \ldots$, where $P_{0}(x)=2, P_{1}(x)=x$ and for every $n \geq 1$ the following equality holds: $$ P_{n+1}(x)+P_{n-1}(x)=x P_{n}(x) $$ Prove that there exist three real numbers $a, b, c$ such that for all $n \geq 1$, $$ \left(x^{2}-4\right)\left[P_{n}^{2}(x)-4\right]=\left[a P_{n+1}(x)+b P_{n}(x)+c P_{n-1}(x)\right]^{2} $$
|
1. Assuming that $a, b, c$ in (1) exist, let us find what their values should be. Since $P_{2}(x)=x^{2}-2$, equation (1) for $n=1$ becomes $\left(x^{2}-4\right)^{2}=$ $\left[a\left(x^{2}-2\right)+b x+2 c\right]^{2}$. Therefore, there are two possibilities for $(a, b, c)$ : $(1,0,-1)$ and $(-1,0,1)$. In both cases we must prove that $$ \left(x^{2}-4\right)\left[P_{n}(x)^{2}-4\right]=\left[P_{n+1}(x)-P_{n-1}(x)\right]^{2} $$ It suffices to prove (2) for all $x$ in the interval $[-2,2]$. In this interval we can set $x=2 \cos t$ for some real $t$. We prove by induction that $$ P_{n}(x)=2 \cos n t \quad \text { for all } n $$ This is trivial for $n=0,1$. Assume (3) holds for some $n-1$ and $n$. Then $P_{n+1}(x)=4 \cos t \cos n t-2 \cos (n-1) t=2 \cos (n+1) t$ by the additive formula for the cosine. This completes the induction. Now (2) reduces to the obviously correct equality $$ 16 \sin ^{2} t \sin ^{2} n t=(2 \cos (n+1) t-2 \cos (n-1) t)^{2} $$ Second solution. If $x$ is fixed, the linear recurrence relation $P_{n+1}(x)+$ $P_{n-1}(x)=x P_{n}(x)$ can be solved in the standard way. The characteristic polynomial $t^{2}-x t+1$ has zeros $t_{1,2}$ with $t_{1}+t_{2}=x$ and $t_{1} t_{2}=1$; hence, the general $P_{n}(x)$ has the form $a t_{1}^{n}+b t_{2}^{n}$ for some constants $a$, $b$. From $P_{0}=2$ and $P_{1}=x$ we obtain that $$ P_{n}(x)=t_{1}^{n}+t_{2}^{n} . $$ Plugging in these values and using $t_{1} t_{2}=1$ one easily verifies (2).
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9bee9ff0-e11e-5b3b-a21f-bc2a0f2ee8ef
| 24,880
|
10. (POL 2) ${ }^{\mathrm{IMO} 3}$ Prove that the sequence $2^{n}-3(n>1)$ contains a subsequence of numbers relatively prime in pairs.
|
10. We use induction. Suppose that every two of the numbers $a_{1}=2^{n_{1}}-$ $3, a_{2}=2^{n_{2}}-3, \ldots, a_{k}=2^{n_{k}}-3$, where $2=n_{1}<n_{2}<\cdots<n_{k}$, are coprime. Then one can construct $a_{k+1}=2^{n_{k+1}}-3$ in the following way: Set $s=a_{1} a_{2} \ldots a_{k}$. Among the numbers $2^{0}, 2^{1}, \ldots, 2^{s}$, two give the same residue upon division by $s$, say $s \mid 2^{\alpha}-2^{\beta}$. Since $s$ is odd, it can be assumed w.l.o.g. that $\beta=0$ (this is actually a direct consequence of Euler's theorem). Let $2^{\alpha}-1=q s, q \in \mathbb{N}$. Since $2^{\alpha+2}-3=4 q s+1$ is then coprime to $s$, it is enough to take $n_{k+1}=\alpha+2$. We obviously have $n_{k+1}>n_{k}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
10. (POL 2) ${ }^{\mathrm{IMO} 3}$ Prove that the sequence $2^{n}-3(n>1)$ contains a subsequence of numbers relatively prime in pairs.
|
10. We use induction. Suppose that every two of the numbers $a_{1}=2^{n_{1}}-$ $3, a_{2}=2^{n_{2}}-3, \ldots, a_{k}=2^{n_{k}}-3$, where $2=n_{1}<n_{2}<\cdots<n_{k}$, are coprime. Then one can construct $a_{k+1}=2^{n_{k+1}}-3$ in the following way: Set $s=a_{1} a_{2} \ldots a_{k}$. Among the numbers $2^{0}, 2^{1}, \ldots, 2^{s}$, two give the same residue upon division by $s$, say $s \mid 2^{\alpha}-2^{\beta}$. Since $s$ is odd, it can be assumed w.l.o.g. that $\beta=0$ (this is actually a direct consequence of Euler's theorem). Let $2^{\alpha}-1=q s, q \in \mathbb{N}$. Since $2^{\alpha+2}-3=4 q s+1$ is then coprime to $s$, it is enough to take $n_{k+1}=\alpha+2$. We obviously have $n_{k+1}>n_{k}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ab2ca8b1-3684-5319-a7b6-6c6d47607504
| 24,883
|
11. (POL 3) The matrix $$ \left(\begin{array}{ccc} a_{11} & \ldots & a_{1 n} \\ \vdots & \ldots & \vdots \\ a_{n 1} & \ldots & a_{n n} \end{array}\right) $$ satisfies the inequality $\sum_{j=1}^{n}\left|a_{j 1} x_{1}+\cdots+a_{j n} x_{n}\right| \leq M$ for each choice of numbers $x_{i}$ equal to $\pm 1$. Show that $$ \left|a_{11}+a_{22}+\cdots+a_{n n}\right| \leq M $$
|
11. We use induction. The statement for $n=1$ is trivial. Suppose that it holds for $n=k$ and consider $n=k+1$. From the given condition, we have $$ \begin{gathered} \sum_{j=1}^{k}\left|a_{j, 1} x_{1}+\cdots+a_{j, k} x_{k}+a_{j, k+1}\right| \\ +\left|a_{k+1,1} x_{1}+\cdots+a_{k+1, k} x_{k}+a_{k+1, k+1}\right| \leq M \\ \sum_{j=1}^{k}\left|a_{j, 1} x_{1}+\cdots+a_{j, k} x_{k}-a_{j, k+1}\right| \\ +\left|a_{k+1,1} x_{1}+\cdots+a_{k+1, k} x_{k}-a_{k+1, k+1}\right| \leq M \end{gathered} $$ for each choice of $x_{i}= \pm 1$. Since $|a+b|+|a-b| \geq 2|a|$ for all $a, b$, we obtain $$ \begin{aligned} 2 \sum_{j=1}^{k}\left|a_{j 1} x_{1}+\cdots+a_{j k} x_{k}\right|+2\left|a_{k+1, k+1}\right| & \leq 2 M, \text { that is, } \\ \sum_{j=1}^{k}\left|a_{j 1} x_{1}+\cdots+a_{j k} x_{k}\right| & \leq M-\left|a_{k+1, k+1}\right| \end{aligned} $$ Now by the inductive assumption $\sum_{j=1}^{k}\left|a_{j j}\right| \leq M-\left|a_{k+1, k+1}\right|$, which is equivalent to the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
11. (POL 3) The matrix $$ \left(\begin{array}{ccc} a_{11} & \ldots & a_{1 n} \\ \vdots & \ldots & \vdots \\ a_{n 1} & \ldots & a_{n n} \end{array}\right) $$ satisfies the inequality $\sum_{j=1}^{n}\left|a_{j 1} x_{1}+\cdots+a_{j n} x_{n}\right| \leq M$ for each choice of numbers $x_{i}$ equal to $\pm 1$. Show that $$ \left|a_{11}+a_{22}+\cdots+a_{n n}\right| \leq M $$
|
11. We use induction. The statement for $n=1$ is trivial. Suppose that it holds for $n=k$ and consider $n=k+1$. From the given condition, we have $$ \begin{gathered} \sum_{j=1}^{k}\left|a_{j, 1} x_{1}+\cdots+a_{j, k} x_{k}+a_{j, k+1}\right| \\ +\left|a_{k+1,1} x_{1}+\cdots+a_{k+1, k} x_{k}+a_{k+1, k+1}\right| \leq M \\ \sum_{j=1}^{k}\left|a_{j, 1} x_{1}+\cdots+a_{j, k} x_{k}-a_{j, k+1}\right| \\ +\left|a_{k+1,1} x_{1}+\cdots+a_{k+1, k} x_{k}-a_{k+1, k+1}\right| \leq M \end{gathered} $$ for each choice of $x_{i}= \pm 1$. Since $|a+b|+|a-b| \geq 2|a|$ for all $a, b$, we obtain $$ \begin{aligned} 2 \sum_{j=1}^{k}\left|a_{j 1} x_{1}+\cdots+a_{j k} x_{k}\right|+2\left|a_{k+1, k+1}\right| & \leq 2 M, \text { that is, } \\ \sum_{j=1}^{k}\left|a_{j 1} x_{1}+\cdots+a_{j k} x_{k}\right| & \leq M-\left|a_{k+1, k+1}\right| \end{aligned} $$ Now by the inductive assumption $\sum_{j=1}^{k}\left|a_{j j}\right| \leq M-\left|a_{k+1, k+1}\right|$, which is equivalent to the desired inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8fff0ec9-9c67-5381-8131-0c50c6d8042b
| 24,885
|
12. (POL 6) Two congruent equilateral triangles $A B C$ and $A^{\prime} B^{\prime} C^{\prime}$ in the plane are given. Show that the midpoints of the segments $A A^{\prime}, B B^{\prime}, C C^{\prime}$ either are collinear or form an equilateral triangle.
|
12. Let us start with the case $A=A^{\prime}$. If the triangles $A B C$ and $A^{\prime} B^{\prime} C^{\prime}$ are oppositely oriented, then they are symmetric with respect to some axis, and the statement is true. Suppose that they are equally oriented. There is a rotation around $A$ by $60^{\circ}$ that maps $A B B^{\prime}$ onto $A C C^{\prime}$. This rotation also maps the midpoint $B_{0}$ of $B B^{\prime}$ onto the midpoint $C_{0}$ of $C C^{\prime}$, hence the triangle $A B_{0} C_{0}$ is equilateral. In the general case, when $A \neq A^{\prime}$, let us denote by $T$ the translation that maps $A$ onto $A^{\prime}$. Let $X^{\prime}$ be the image of a point $X$ under the (unique) isometry mapping $A B C$ onto $A^{\prime} B^{\prime} C^{\prime}$, and $X^{\prime \prime}$ the image of $X$ under $T$. Furthermore, let $X_{0}, X_{0}^{\prime}$ be the midpoints of segments $X X^{\prime}, X^{\prime} X^{\prime \prime}$. Then $X_{0}$ is the image of $X_{0}^{\prime}$ under the translation $-(1 / 2) T$. However, since it has already been proven that the triangle $A_{0}^{\prime} B_{0}^{\prime} C_{0}^{\prime}$ is equilateral, its image $A_{0} B_{0} C_{0}$ under $(1 / 2) T$ is also equilateral. The statement of the problem is thus proven.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
12. (POL 6) Two congruent equilateral triangles $A B C$ and $A^{\prime} B^{\prime} C^{\prime}$ in the plane are given. Show that the midpoints of the segments $A A^{\prime}, B B^{\prime}, C C^{\prime}$ either are collinear or form an equilateral triangle.
|
12. Let us start with the case $A=A^{\prime}$. If the triangles $A B C$ and $A^{\prime} B^{\prime} C^{\prime}$ are oppositely oriented, then they are symmetric with respect to some axis, and the statement is true. Suppose that they are equally oriented. There is a rotation around $A$ by $60^{\circ}$ that maps $A B B^{\prime}$ onto $A C C^{\prime}$. This rotation also maps the midpoint $B_{0}$ of $B B^{\prime}$ onto the midpoint $C_{0}$ of $C C^{\prime}$, hence the triangle $A B_{0} C_{0}$ is equilateral. In the general case, when $A \neq A^{\prime}$, let us denote by $T$ the translation that maps $A$ onto $A^{\prime}$. Let $X^{\prime}$ be the image of a point $X$ under the (unique) isometry mapping $A B C$ onto $A^{\prime} B^{\prime} C^{\prime}$, and $X^{\prime \prime}$ the image of $X$ under $T$. Furthermore, let $X_{0}, X_{0}^{\prime}$ be the midpoints of segments $X X^{\prime}, X^{\prime} X^{\prime \prime}$. Then $X_{0}$ is the image of $X_{0}^{\prime}$ under the translation $-(1 / 2) T$. However, since it has already been proven that the triangle $A_{0}^{\prime} B_{0}^{\prime} C_{0}^{\prime}$ is equilateral, its image $A_{0} B_{0} C_{0}$ under $(1 / 2) T$ is also equilateral. The statement of the problem is thus proven.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1aa44403-4162-5035-8c26-c7113ad9447c
| 24,888
|
15. (USS 2) Natural numbers from 1 to 99 (not necessarily distinct) are written on 99 cards. It is given that the sum of the numbers on any subset of cards (including the set of all cards) is not divisible by 100. Show that all the cards contain the same number.
|
15. Assume the opposite. Then one can numerate the cards 1 to 99, with a number $n_{i}$ written on the card $i$, so that $n_{98} \neq n_{99}$. Denote by $x_{i}$ the remainder of $n_{1}+n_{2}+\cdots+n_{i}$ upon division by 100 , for $i=1,2, \ldots, 99$. All $x_{i}$ must be distinct: Indeed, if $x_{i}=x_{j}, i<j$, then $n_{i+1}+\cdots+n_{j}$ is divisible by 100, which is impossible. Also, no $x_{i}$ can be equal to 0 . Thus, the numbers $x_{1}, x_{2}, \ldots, x_{99}$ take exactly the values $1,2, \ldots, 99$ in some order. Let $x$ be the remainder of $n_{1}+n_{2}+\cdots+n_{97}+n_{99}$ upon division by 100 . It is not zero; hence it must be equal to $x_{k}$ for some $k \in\{1,2, \ldots, 99\}$. There are three cases: (i) $x=x_{k}, k \leq 97$. Then $n_{k+1}+n_{k+2}+\cdots+n_{97}+n_{99}$ is divisible by 100, a contradiction; (ii) $x=x_{98}$. Then $n_{98}=n_{99}$, a contradiction; (iii) $x=x_{99}$. Then $n_{98}$ is divisible by 100, a contradiction. Therefore, all the cards contain the same number.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
15. (USS 2) Natural numbers from 1 to 99 (not necessarily distinct) are written on 99 cards. It is given that the sum of the numbers on any subset of cards (including the set of all cards) is not divisible by 100. Show that all the cards contain the same number.
|
15. Assume the opposite. Then one can numerate the cards 1 to 99, with a number $n_{i}$ written on the card $i$, so that $n_{98} \neq n_{99}$. Denote by $x_{i}$ the remainder of $n_{1}+n_{2}+\cdots+n_{i}$ upon division by 100 , for $i=1,2, \ldots, 99$. All $x_{i}$ must be distinct: Indeed, if $x_{i}=x_{j}, i<j$, then $n_{i+1}+\cdots+n_{j}$ is divisible by 100, which is impossible. Also, no $x_{i}$ can be equal to 0 . Thus, the numbers $x_{1}, x_{2}, \ldots, x_{99}$ take exactly the values $1,2, \ldots, 99$ in some order. Let $x$ be the remainder of $n_{1}+n_{2}+\cdots+n_{97}+n_{99}$ upon division by 100 . It is not zero; hence it must be equal to $x_{k}$ for some $k \in\{1,2, \ldots, 99\}$. There are three cases: (i) $x=x_{k}, k \leq 97$. Then $n_{k+1}+n_{k+2}+\cdots+n_{97}+n_{99}$ is divisible by 100, a contradiction; (ii) $x=x_{98}$. Then $n_{98}=n_{99}$, a contradiction; (iii) $x=x_{99}$. Then $n_{98}$ is divisible by 100, a contradiction. Therefore, all the cards contain the same number.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2cd354b-3420-5daa-9da1-09882e85a9cf
| 24,896
|
16. (USS 5) ${ }^{\mathrm{IMO} 2}$ Given a convex polyhedron $P_{1}$ with 9 vertices $A_{1}, \ldots, A_{9}$, let us denote by $P_{2}, P_{3}, \ldots, P_{9}$ the images of $P_{1}$ under the translations mapping the vertex $A_{1}$ to $A_{2}, A_{3}, \ldots, A_{9}$ respectively. Prove that among the polyhedra $P_{1}, \ldots, P_{9}$ at least two have a common interior point.
|
16. Denote by $P^{\prime}$ the polyhedron defined as the image of $P$ under the homothety with center at $A_{1}$ and coefficient of similarity 2 . It is easy to see that all $P_{i}, i=1, \ldots, 9$, are contained in $P^{\prime}$ (indeed, if $M \in P_{k}$, then $\frac{1}{2} \overrightarrow{A_{1} M}=\frac{1}{2}\left(\overrightarrow{A_{1} A_{k}}+\overrightarrow{A_{1} M^{\prime}}\right)$ for some $M^{\prime} \in P$, and the claim follows from the convexity of $P$ ). But the volume of $P^{\prime}$ is exactly 8 times the volume of $P$, while the volumes of $P_{i}$ add up to 9 times that volume. We conclude that not all $P_{i}$ have disjoint interiors.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
16. (USS 5) ${ }^{\mathrm{IMO} 2}$ Given a convex polyhedron $P_{1}$ with 9 vertices $A_{1}, \ldots, A_{9}$, let us denote by $P_{2}, P_{3}, \ldots, P_{9}$ the images of $P_{1}$ under the translations mapping the vertex $A_{1}$ to $A_{2}, A_{3}, \ldots, A_{9}$ respectively. Prove that among the polyhedra $P_{1}, \ldots, P_{9}$ at least two have a common interior point.
|
16. Denote by $P^{\prime}$ the polyhedron defined as the image of $P$ under the homothety with center at $A_{1}$ and coefficient of similarity 2 . It is easy to see that all $P_{i}, i=1, \ldots, 9$, are contained in $P^{\prime}$ (indeed, if $M \in P_{k}$, then $\frac{1}{2} \overrightarrow{A_{1} M}=\frac{1}{2}\left(\overrightarrow{A_{1} A_{k}}+\overrightarrow{A_{1} M^{\prime}}\right)$ for some $M^{\prime} \in P$, and the claim follows from the convexity of $P$ ). But the volume of $P^{\prime}$ is exactly 8 times the volume of $P$, while the volumes of $P_{i}$ add up to 9 times that volume. We conclude that not all $P_{i}$ have disjoint interiors.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a9813380-7f6f-52ea-a4f6-aa55ffc02346
| 24,899
|
17. (YUG 1) Prove the inequality $$ \frac{a_{1}+a_{3}}{a_{1}+a_{2}}+\frac{a_{2}+a_{4}}{a_{2}+a_{3}}+\frac{a_{3}+a_{1}}{a_{3}+a_{4}}+\frac{a_{4}+a_{2}}{a_{4}+a_{1}} \geq 4 $$ where $a_{i}>0, i=1,2,3,4$.
|
17. We use the following obvious consequences of $(a+b)^{2} \geq 4 a b$ : $$ \begin{aligned} & \frac{1}{\left(a_{1}+a_{2}\right)\left(a_{3}+a_{4}\right)} \geq \frac{4}{\left(a_{1}+a_{2}+a_{3}+a_{4}\right)^{2}} \\ & \frac{1}{\left(a_{1}+a_{4}\right)\left(a_{2}+a_{3}\right)} \geq \frac{4}{\left(a_{1}+a_{2}+a_{3}+a_{4}\right)^{2}} \end{aligned} $$ Now we have $$ \begin{aligned} & \frac{a_{1}+a_{3}}{a_{1}+a_{2}}+\frac{a_{2}+a_{4}}{a_{2}+a_{3}}+\frac{a_{3}+a_{1}}{a_{3}+a_{4}}+\frac{a_{4}+a_{2}}{a_{4}+a_{1}} \\ = & \frac{\left(a_{1}+a_{3}\right)\left(a_{1}+a_{2}+a_{3}+a_{4}\right)}{\left(a_{1}+a_{2}\right)\left(a_{3}+a_{4}\right)}+\frac{\left(a_{2}+a_{4}\right)\left(a_{1}+a_{2}+a_{3}+a_{4}\right)}{\left(a_{1}+a_{4}\right)\left(a_{2}+a_{3}\right)} \\ \geq & \frac{4\left(a_{1}+a_{3}\right)}{a_{1}+a_{2}+a_{3}+a_{4}}+\frac{4\left(a_{2}+a_{4}\right)}{a_{1}+a_{2}+a_{3}+a_{4}}=4 . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
17. (YUG 1) Prove the inequality $$ \frac{a_{1}+a_{3}}{a_{1}+a_{2}}+\frac{a_{2}+a_{4}}{a_{2}+a_{3}}+\frac{a_{3}+a_{1}}{a_{3}+a_{4}}+\frac{a_{4}+a_{2}}{a_{4}+a_{1}} \geq 4 $$ where $a_{i}>0, i=1,2,3,4$.
|
17. We use the following obvious consequences of $(a+b)^{2} \geq 4 a b$ : $$ \begin{aligned} & \frac{1}{\left(a_{1}+a_{2}\right)\left(a_{3}+a_{4}\right)} \geq \frac{4}{\left(a_{1}+a_{2}+a_{3}+a_{4}\right)^{2}} \\ & \frac{1}{\left(a_{1}+a_{4}\right)\left(a_{2}+a_{3}\right)} \geq \frac{4}{\left(a_{1}+a_{2}+a_{3}+a_{4}\right)^{2}} \end{aligned} $$ Now we have $$ \begin{aligned} & \frac{a_{1}+a_{3}}{a_{1}+a_{2}}+\frac{a_{2}+a_{4}}{a_{2}+a_{3}}+\frac{a_{3}+a_{1}}{a_{3}+a_{4}}+\frac{a_{4}+a_{2}}{a_{4}+a_{1}} \\ = & \frac{\left(a_{1}+a_{3}\right)\left(a_{1}+a_{2}+a_{3}+a_{4}\right)}{\left(a_{1}+a_{2}\right)\left(a_{3}+a_{4}\right)}+\frac{\left(a_{2}+a_{4}\right)\left(a_{1}+a_{2}+a_{3}+a_{4}\right)}{\left(a_{1}+a_{4}\right)\left(a_{2}+a_{3}\right)} \\ \geq & \frac{4\left(a_{1}+a_{3}\right)}{a_{1}+a_{2}+a_{3}+a_{4}}+\frac{4\left(a_{2}+a_{4}\right)}{a_{1}+a_{2}+a_{3}+a_{4}}=4 . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
79f9f476-2cd0-50ad-9c5b-bd81470b80ad
| 24,902
|
2. (BUL 5) ${ }^{\mathrm{IMO} 5}$ Prove that for every natural number $m \geq 1$ there exists a finite set $S_{m}$ of points in the plane satisfying the following condition: If $A$ is any point in $S_{m}$, then there are exactly $m$ points in $S_{m}$ whose distance to $A$ equals 1.
|
2 . We will construct such a set $S_{m}$ of $2^{m}$ points. Take vectors $u_{1}, \ldots, u_{m}$ in a given plane, such that $\left|u_{i}\right|=1 / 2$ and $0 \neq\left|c_{1} u_{1}+c_{2} u_{2}+\cdots+c_{n} u_{n}\right| \neq 1 / 2$ for any choice of numbers $c_{i}$ equal to 0 or $\pm 1$. Such vectors are easily constructed by induction on $m$ : For $u_{1}, \ldots, u_{m-1}$ fixed, there are only finitely many vector values $u_{m}$ that violate the upper condition, and we may set $u_{m}$ to be any other vector of length $1 / 2$. Let $S_{m}$ be the set of all points $M_{0}+\varepsilon_{1} u_{1}+\varepsilon_{2} u_{2}+\cdots+\varepsilon_{m} u_{m}$, where $M_{0}$ is any fixed point in the plane and $\varepsilon_{i}= \pm 1$ for $i=1, \ldots, m$. Then $S_{m}$ obviously satisfies the condition of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
2. (BUL 5) ${ }^{\mathrm{IMO} 5}$ Prove that for every natural number $m \geq 1$ there exists a finite set $S_{m}$ of points in the plane satisfying the following condition: If $A$ is any point in $S_{m}$, then there are exactly $m$ points in $S_{m}$ whose distance to $A$ equals 1.
|
2 . We will construct such a set $S_{m}$ of $2^{m}$ points. Take vectors $u_{1}, \ldots, u_{m}$ in a given plane, such that $\left|u_{i}\right|=1 / 2$ and $0 \neq\left|c_{1} u_{1}+c_{2} u_{2}+\cdots+c_{n} u_{n}\right| \neq 1 / 2$ for any choice of numbers $c_{i}$ equal to 0 or $\pm 1$. Such vectors are easily constructed by induction on $m$ : For $u_{1}, \ldots, u_{m-1}$ fixed, there are only finitely many vector values $u_{m}$ that violate the upper condition, and we may set $u_{m}$ to be any other vector of length $1 / 2$. Let $S_{m}$ be the set of all points $M_{0}+\varepsilon_{1} u_{1}+\varepsilon_{2} u_{2}+\cdots+\varepsilon_{m} u_{m}$, where $M_{0}$ is any fixed point in the plane and $\varepsilon_{i}= \pm 1$ for $i=1, \ldots, m$. Then $S_{m}$ obviously satisfies the condition of the problem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
dcf8afe5-72b9-5ed6-b4a1-3085ebe2f273
| 24,905
|
5. (HUN 1) ${ }^{\mathrm{IMO}}$ Let $a, b, c, d, e$ be real numbers. Prove that the expression $$ \begin{gathered} (a-b)(a-c)(a-d)(a-e)+(b-a)(b-c)(b-d)(b-e)+(c-a)(c-b)(c-d)(c-e) \\ +(d-a)(d-b)(d-c)(d-e)+(e-a)(e-b)(e-c)(e-d) \end{gathered} $$ is nonnegative.
|
5. Without loss of generality, we may assume that $a \geq b \geq c \geq d \geq e$. Then $a-b=-(b-a) \geq 0, a-c \geq b-c \geq 0, a-d \geq b-d \geq 0$ and $a-e \geq b-e \geq 0$, and hence $$ (a-b)(a-c)(a-d)(a-e)+(b-a)(b-c)(b-d)(b-e) \geq 0 $$ Analogously, $(d-a)(d-b)(d-c)(d-e)+(e-a)(e-b)(e-c)(e-d) \geq 0$. Finally, $(c-a)(c-b)(c-d)(c-e) \geq 0$ as a product of two nonnegative numbers, from which the inequality stated in the problem follows. Remark. The problem in an alternative formulation, accepted for the IMO, asked to prove that the analogous inequality $$ \begin{gathered} \left(a_{1}-a_{2}\right)\left(a_{1}-a_{2}\right) \cdots\left(a_{1}-a_{n}\right)+\left(a_{2}-a_{1}\right)\left(a_{2}-a_{3}\right) \cdots\left(a_{2}-a_{n}\right)+\cdots \\ +\left(a_{n}-a_{1}\right)\left(a_{n}-a_{2}\right) \cdots\left(a_{n}-a_{n-1}\right) \geq 0 \end{gathered} $$ holds for arbitrary real numbers $a_{i}$ if and only if $n=3$ or $n=5$. The case $n=3$ is analogous to $n=5$. For $n=4$, a counterexample is $a_{1}=0, a_{2}=a_{3}=a_{4}=1$, while for $n>5$ one can take $a_{1}=a_{2}=\cdots=$ $a_{n-4}=0, a_{n-3}=a_{n-2}=a_{n-1}=2, a_{n}=1$ as a counterexample.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
5. (HUN 1) ${ }^{\mathrm{IMO}}$ Let $a, b, c, d, e$ be real numbers. Prove that the expression $$ \begin{gathered} (a-b)(a-c)(a-d)(a-e)+(b-a)(b-c)(b-d)(b-e)+(c-a)(c-b)(c-d)(c-e) \\ +(d-a)(d-b)(d-c)(d-e)+(e-a)(e-b)(e-c)(e-d) \end{gathered} $$ is nonnegative.
|
5. Without loss of generality, we may assume that $a \geq b \geq c \geq d \geq e$. Then $a-b=-(b-a) \geq 0, a-c \geq b-c \geq 0, a-d \geq b-d \geq 0$ and $a-e \geq b-e \geq 0$, and hence $$ (a-b)(a-c)(a-d)(a-e)+(b-a)(b-c)(b-d)(b-e) \geq 0 $$ Analogously, $(d-a)(d-b)(d-c)(d-e)+(e-a)(e-b)(e-c)(e-d) \geq 0$. Finally, $(c-a)(c-b)(c-d)(c-e) \geq 0$ as a product of two nonnegative numbers, from which the inequality stated in the problem follows. Remark. The problem in an alternative formulation, accepted for the IMO, asked to prove that the analogous inequality $$ \begin{gathered} \left(a_{1}-a_{2}\right)\left(a_{1}-a_{2}\right) \cdots\left(a_{1}-a_{n}\right)+\left(a_{2}-a_{1}\right)\left(a_{2}-a_{3}\right) \cdots\left(a_{2}-a_{n}\right)+\cdots \\ +\left(a_{n}-a_{1}\right)\left(a_{n}-a_{2}\right) \cdots\left(a_{n}-a_{n-1}\right) \geq 0 \end{gathered} $$ holds for arbitrary real numbers $a_{i}$ if and only if $n=3$ or $n=5$. The case $n=3$ is analogous to $n=5$. For $n=4$, a counterexample is $a_{1}=0, a_{2}=a_{3}=a_{4}=1$, while for $n>5$ one can take $a_{1}=a_{2}=\cdots=$ $a_{n-4}=0, a_{n-3}=a_{n-2}=a_{n-1}=2, a_{n}=1$ as a counterexample.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1dc6d437-bfad-5f30-b0ba-80c1483c5e01
| 24,914
|
9. (POL 1) Let $T_{k}=k-1$ for $k=1,2,3,4$ and $$ T_{2 k-1}=T_{2 k-2}+2^{k-2}, \quad T_{2 k}=T_{2 k-5}+2^{k} \quad(k \geq 3) $$ Show that for all $k$, $$ 1+T_{2 n-1}=\left[\frac{12}{7} 2^{n-1}\right] \quad \text { and } \quad 1+T_{2 n}=\left[\frac{17}{7} 2^{n-1}\right] $$ where $[x]$ denotes the greatest integer not exceeding $x$.
|
9. We use induction. Since $T_{1}=0, T_{2}=1, T_{3}=2, T_{4}=3, T_{5}=5, T_{6}=8$, the statement is true for $n=1,2,3$. Suppose that both formulas from the problem hold for some $n \geq 3$. Then $$ \begin{aligned} & T_{2 n+1}=1+T_{2 n}+2^{n-1}=\left[\frac{17}{7} 2^{n-1}+2^{n-1}\right]=\left[\frac{12}{7} 2^{n}\right] \\ & T_{2 n+2}=1+T_{2 n-3}+2^{n+1}=\left[\frac{12}{7} 2^{n-2}+2^{n+1}\right]=\left[\frac{17}{7} 2^{n}\right] . \end{aligned} $$ Therefore the formulas hold for $n+1$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
9. (POL 1) Let $T_{k}=k-1$ for $k=1,2,3,4$ and $$ T_{2 k-1}=T_{2 k-2}+2^{k-2}, \quad T_{2 k}=T_{2 k-5}+2^{k} \quad(k \geq 3) $$ Show that for all $k$, $$ 1+T_{2 n-1}=\left[\frac{12}{7} 2^{n-1}\right] \quad \text { and } \quad 1+T_{2 n}=\left[\frac{17}{7} 2^{n-1}\right] $$ where $[x]$ denotes the greatest integer not exceeding $x$.
|
9. We use induction. Since $T_{1}=0, T_{2}=1, T_{3}=2, T_{4}=3, T_{5}=5, T_{6}=8$, the statement is true for $n=1,2,3$. Suppose that both formulas from the problem hold for some $n \geq 3$. Then $$ \begin{aligned} & T_{2 n+1}=1+T_{2 n}+2^{n-1}=\left[\frac{17}{7} 2^{n-1}+2^{n-1}\right]=\left[\frac{12}{7} 2^{n}\right] \\ & T_{2 n+2}=1+T_{2 n-3}+2^{n+1}=\left[\frac{12}{7} 2^{n-2}+2^{n+1}\right]=\left[\frac{17}{7} 2^{n}\right] . \end{aligned} $$ Therefore the formulas hold for $n+1$, which completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
79ff53ea-c7d1-58de-ae00-516b3cde9403
| 24,925
|
1. (BUL 7) ${ }^{\mathrm{IMO} 5}$ Let $f$ and $\varphi$ be real functions defined on the set $\mathbb{R}$ satisfying the functional equation $$ f(x+y)+f(x-y)=2 \varphi(y) f(x) $$ for arbitrary real $x, y$ (give examples of such functions). Prove that if $f(x)$ is not identically 0 and $|f(x)| \leq 1$ for all $x$, then $|\varphi(x)| \leq 1$ for all $x$.
|
1. Suppose that $f\left(x_{0}\right) \neq 0$ and for a given $y$ define the sequence $x_{k}$ by the formula $$ x_{k+1}= \begin{cases}x_{k}+y, & \text { if }\left|f\left(x_{k}+y\right)\right| \geq\left|f\left(x_{k}-y\right)\right| \\ x_{k}-y, & \text { otherwise. }\end{cases} $$ It follows from (1) that $\left|f\left(x_{k+1}\right)\right| \geq|\varphi(y)|\left|f\left(x_{k}\right)\right|$; hence by induction, $\left|f\left(x_{k}\right)\right| \geq|\varphi(y)|^{k}\left|f\left(x_{0}\right)\right|$. Since $\left|f\left(x_{k}\right)\right| \leq 1$ for all $k$, we obtain $|\varphi(y)| \leq 1$. Second solution. Let $M=\sup f(x) \leq 1$, and $x_{k}$ any sequence, possibly constant, such that $f\left(x_{k}\right) \rightarrow M, k \rightarrow \infty$. Then for all $k$, $$ |\varphi(y)|=\frac{\left|f\left(x_{k}+y\right)+f\left(x_{k}-y\right)\right|}{2\left|f\left(x_{k}\right)\right|} \leq \frac{2 M}{2\left|f\left(x_{k}\right)\right|} \rightarrow 1, \quad k \rightarrow \infty $$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
1. (BUL 7) ${ }^{\mathrm{IMO} 5}$ Let $f$ and $\varphi$ be real functions defined on the set $\mathbb{R}$ satisfying the functional equation $$ f(x+y)+f(x-y)=2 \varphi(y) f(x) $$ for arbitrary real $x, y$ (give examples of such functions). Prove that if $f(x)$ is not identically 0 and $|f(x)| \leq 1$ for all $x$, then $|\varphi(x)| \leq 1$ for all $x$.
|
1. Suppose that $f\left(x_{0}\right) \neq 0$ and for a given $y$ define the sequence $x_{k}$ by the formula $$ x_{k+1}= \begin{cases}x_{k}+y, & \text { if }\left|f\left(x_{k}+y\right)\right| \geq\left|f\left(x_{k}-y\right)\right| \\ x_{k}-y, & \text { otherwise. }\end{cases} $$ It follows from (1) that $\left|f\left(x_{k+1}\right)\right| \geq|\varphi(y)|\left|f\left(x_{k}\right)\right|$; hence by induction, $\left|f\left(x_{k}\right)\right| \geq|\varphi(y)|^{k}\left|f\left(x_{0}\right)\right|$. Since $\left|f\left(x_{k}\right)\right| \leq 1$ for all $k$, we obtain $|\varphi(y)| \leq 1$. Second solution. Let $M=\sup f(x) \leq 1$, and $x_{k}$ any sequence, possibly constant, such that $f\left(x_{k}\right) \rightarrow M, k \rightarrow \infty$. Then for all $k$, $$ |\varphi(y)|=\frac{\left|f\left(x_{k}+y\right)+f\left(x_{k}-y\right)\right|}{2\left|f\left(x_{k}\right)\right|} \leq \frac{2 M}{2\left|f\left(x_{k}\right)\right|} \rightarrow 1, \quad k \rightarrow \infty $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
435a5343-6a4c-5b6b-8ea6-f408aeb6ae0c
| 24,927
|
10. (NET 3) ${ }^{\text {IMO2 }}$ Prove that for each $n \geq 4$ every cyclic quadrilateral can be decomposed into $n$ cyclic quadrilaterals.
|
10. Consider first a triangle. It can be decomposed into $k=3$ cyclic quadrilaterals by perpendiculars from some interior point of it to the sides; also, it can be decomposed into a cyclic quadrilateral and a triangle, and it follows by induction that this decomposition is possible for every $k$. Since every triangle can be cut into two triangles, the required decomposition is possible for each $n \geq 6$. It remains to treat the cases $n=4$ and $n=5$. $n=4$. If the center $O$ of the circumcircle is inside a cyclic quadrilateral $A B C D$, then the required decomposition is effected by perpendiculars from $O$ to the four sides. Otherwise, let $C$ and $D$ be the vertices of the obtuse angles of the quadrilateral. Draw the perpendiculars at $C$ and $D$ to the lines $B C$ and $A D$ respectively, and choose points $P$ and $Q$ on them such that $P Q \| A B$. Then the required decomposition is effected by $C P, P Q, Q D$ and the perpendiculars from $P$ and $Q$ to $A B$. $n=5$. If $A B C D$ is an isosceles trapezoid with $A B \| C D$ and $A D=B C$, then it is trivially decomposed by lines parallel to $A B$. Otherwise, $A B C D$ can be decomposed into a cyclic quadrilateral and a trapezoid; this trapezoid can be cut into an isosceles trapezoid and a triangle, which can further be cut into three cyclic quadrilaterals and an isosceles trapezoid. Remark. It can be shown that the assertion is not true for $n=2$ and $n=3$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
10. (NET 3) ${ }^{\text {IMO2 }}$ Prove that for each $n \geq 4$ every cyclic quadrilateral can be decomposed into $n$ cyclic quadrilaterals.
|
10. Consider first a triangle. It can be decomposed into $k=3$ cyclic quadrilaterals by perpendiculars from some interior point of it to the sides; also, it can be decomposed into a cyclic quadrilateral and a triangle, and it follows by induction that this decomposition is possible for every $k$. Since every triangle can be cut into two triangles, the required decomposition is possible for each $n \geq 6$. It remains to treat the cases $n=4$ and $n=5$. $n=4$. If the center $O$ of the circumcircle is inside a cyclic quadrilateral $A B C D$, then the required decomposition is effected by perpendiculars from $O$ to the four sides. Otherwise, let $C$ and $D$ be the vertices of the obtuse angles of the quadrilateral. Draw the perpendiculars at $C$ and $D$ to the lines $B C$ and $A D$ respectively, and choose points $P$ and $Q$ on them such that $P Q \| A B$. Then the required decomposition is effected by $C P, P Q, Q D$ and the perpendiculars from $P$ and $Q$ to $A B$. $n=5$. If $A B C D$ is an isosceles trapezoid with $A B \| C D$ and $A D=B C$, then it is trivially decomposed by lines parallel to $A B$. Otherwise, $A B C D$ can be decomposed into a cyclic quadrilateral and a trapezoid; this trapezoid can be cut into an isosceles trapezoid and a triangle, which can further be cut into three cyclic quadrilaterals and an isosceles trapezoid. Remark. It can be shown that the assertion is not true for $n=2$ and $n=3$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
edc40532-7b0a-5d40-bcb7-09cb3656937b
| 24,930
|
11. (NET 6) Consider a sequence of circles $K_{1}, K_{2}, K_{3}, K_{4}, \ldots$ of radii $r_{1}, r_{2}, r_{3}, r_{4}, \ldots$, respectively, situated inside a triangle $A B C$. The circle $K_{1}$ is tangent to $A B$ and $A C ; K_{2}$ is tangent to $K_{1}, B A$, and $B C ; K_{3}$ is tangent to $K_{2}, C A$, and $C B ; K_{4}$ is tangent to $K_{3}, A B$, and $A C$; etc. (a) Prove the relation $$ r_{1} \cot \frac{1}{2} A+2 \sqrt{r_{1} r_{2}}+r_{2} \cot \frac{1}{2} B=r\left(\cot \frac{1}{2} A+\cot \frac{1}{2} B\right), $$ where $r$ is the radius of the incircle of the triangle $A B C$. Deduce the existence of a $t_{1}$ such that $$ r_{1}=r \cot \frac{1}{2} B \cot \frac{1}{2} C \sin ^{2} t_{1} . $$ (b) Prove that the sequence of circles $K_{1}, K_{2}, \ldots$ is periodic.
|
11. Let $\angle A=2 x, \angle B=2 y, \angle C=2 z$. (a) Denote by $M_{i}$ the center of $K_{i}, i=1,2, \ldots$ If $N_{1}, N_{2}$ are the projections of $M_{1}, M_{2}$ onto $A B$, we have $A N_{1}=r_{1} \cot x, N_{2} B=r_{2} \cot y$, and $N_{1} N_{2}=\sqrt{\left(r_{1}+r_{2}\right)^{2}-\left(r_{1}-r_{2}\right)^{2}}=2 \sqrt{r_{1} r_{2}}$. The required relation between $r_{1}, r_{2}$ follows from $A B=A N_{1}+N_{1} N_{2}+N_{2} B$. If this relation is further considered as a quadratic equation in $\sqrt{r_{2}}$, then its discriminant, which equals $$ \Delta=4\left(r(\cot x+\cot y) \cot y-r_{1}(\cot x \cot y-1)\right), $$ must be nonnegative, and therefore $r_{1} \leq r \cot y \cot z$. Then $t_{1}, t_{2}, \ldots$ exist, and we can assume that $t_{i} \in[0, \pi / 2]$. (b) Substituting $r_{1}=r \cot y \cot z \sin ^{2} t_{1}, r_{2}=r \cot z \cot x \sin ^{2} t_{2}$ in the relation of (a) we obtain that $\sin ^{2} t_{1}+\sin ^{2} t_{2}+k^{2}+2 k \sin t_{1} \sin t_{2}=1$, where we set $k=\sqrt{\tan x \tan y}$. It follows that $\left(k+\sin t_{1} \sin t_{2}\right)^{2}=$ $\left(1-\sin ^{2} t_{1}\right)\left(1-\sin ^{2} t_{2}\right)=\cos ^{2} t_{1} \cos ^{2} t_{2}$, and hence $$ \cos \left(t_{1}+t_{2}\right)=\cos t_{1} \cos t_{2}-\sin t_{1} \sin t_{2}=k=\sqrt{\tan x \tan y} $$ which is constant. Writing the analogous relations for each $t_{i}, t_{i+1}$ we conclude that $t_{1}+t_{2}=t_{4}+t_{5}, t_{2}+t_{3}=t_{5}+t_{6}$, and $t_{3}+t_{4}=t_{6}+t_{7}$. It follows that $t_{1}=t_{7}$, i.e., $K_{1}=K_{7}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
11. (NET 6) Consider a sequence of circles $K_{1}, K_{2}, K_{3}, K_{4}, \ldots$ of radii $r_{1}, r_{2}, r_{3}, r_{4}, \ldots$, respectively, situated inside a triangle $A B C$. The circle $K_{1}$ is tangent to $A B$ and $A C ; K_{2}$ is tangent to $K_{1}, B A$, and $B C ; K_{3}$ is tangent to $K_{2}, C A$, and $C B ; K_{4}$ is tangent to $K_{3}, A B$, and $A C$; etc. (a) Prove the relation $$ r_{1} \cot \frac{1}{2} A+2 \sqrt{r_{1} r_{2}}+r_{2} \cot \frac{1}{2} B=r\left(\cot \frac{1}{2} A+\cot \frac{1}{2} B\right), $$ where $r$ is the radius of the incircle of the triangle $A B C$. Deduce the existence of a $t_{1}$ such that $$ r_{1}=r \cot \frac{1}{2} B \cot \frac{1}{2} C \sin ^{2} t_{1} . $$ (b) Prove that the sequence of circles $K_{1}, K_{2}, \ldots$ is periodic.
|
11. Let $\angle A=2 x, \angle B=2 y, \angle C=2 z$. (a) Denote by $M_{i}$ the center of $K_{i}, i=1,2, \ldots$ If $N_{1}, N_{2}$ are the projections of $M_{1}, M_{2}$ onto $A B$, we have $A N_{1}=r_{1} \cot x, N_{2} B=r_{2} \cot y$, and $N_{1} N_{2}=\sqrt{\left(r_{1}+r_{2}\right)^{2}-\left(r_{1}-r_{2}\right)^{2}}=2 \sqrt{r_{1} r_{2}}$. The required relation between $r_{1}, r_{2}$ follows from $A B=A N_{1}+N_{1} N_{2}+N_{2} B$. If this relation is further considered as a quadratic equation in $\sqrt{r_{2}}$, then its discriminant, which equals $$ \Delta=4\left(r(\cot x+\cot y) \cot y-r_{1}(\cot x \cot y-1)\right), $$ must be nonnegative, and therefore $r_{1} \leq r \cot y \cot z$. Then $t_{1}, t_{2}, \ldots$ exist, and we can assume that $t_{i} \in[0, \pi / 2]$. (b) Substituting $r_{1}=r \cot y \cot z \sin ^{2} t_{1}, r_{2}=r \cot z \cot x \sin ^{2} t_{2}$ in the relation of (a) we obtain that $\sin ^{2} t_{1}+\sin ^{2} t_{2}+k^{2}+2 k \sin t_{1} \sin t_{2}=1$, where we set $k=\sqrt{\tan x \tan y}$. It follows that $\left(k+\sin t_{1} \sin t_{2}\right)^{2}=$ $\left(1-\sin ^{2} t_{1}\right)\left(1-\sin ^{2} t_{2}\right)=\cos ^{2} t_{1} \cos ^{2} t_{2}$, and hence $$ \cos \left(t_{1}+t_{2}\right)=\cos t_{1} \cos t_{2}-\sin t_{1} \sin t_{2}=k=\sqrt{\tan x \tan y} $$ which is constant. Writing the analogous relations for each $t_{i}, t_{i+1}$ we conclude that $t_{1}+t_{2}=t_{4}+t_{5}, t_{2}+t_{3}=t_{5}+t_{6}$, and $t_{3}+t_{4}=t_{6}+t_{7}$. It follows that $t_{1}=t_{7}$, i.e., $K_{1}=K_{7}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
71215d8c-1a10-58a3-8f9f-7e48effeaaf1
| 24,933
|
12. (USS 2) ${ }^{\mathrm{IMO} 1} \mathrm{~A}$ set of 10 positive integers is given such that the decimal expansion of each of them has two digits. Prove that there are two disjoint subsets of the set with equal sums of their elements.
|
12. First we observe that it is not essential to require the subsets to be disjoint (if they aren't, one simply excludes their intersection). There are $2^{10}-1=$ 1023 different subsets and at most 990 different sums. By the pigeonhole principle there are two different subsets with equal sums.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. (USS 2) ${ }^{\mathrm{IMO} 1} \mathrm{~A}$ set of 10 positive integers is given such that the decimal expansion of each of them has two digits. Prove that there are two disjoint subsets of the set with equal sums of their elements.
|
12. First we observe that it is not essential to require the subsets to be disjoint (if they aren't, one simply excludes their intersection). There are $2^{10}-1=$ 1023 different subsets and at most 990 different sums. By the pigeonhole principle there are two different subsets with equal sums.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e73c127-6f75-59f2-8e4e-20e44810af7f
| 24,936
|
2. (CZS 1) We are given $3 n$ points $A_{1}, A_{2}, \ldots, A_{3 n}$ in the plane, no three of them collinear. Prove that one can construct $n$ disjoint triangles with vertices at the points $A_{i}$.
|
2. We use induction. For $n=1$ the assertion is obvious. Assume that it is true for a positive integer $n$. Let $A_{1}, A_{2}, \ldots, A_{3 n+3}$ be given $3 n+3$ points, and let w.l.o.g. $A_{1} A_{2} \ldots A_{m}$ be their convex hull. Among all the points $A_{i}$ distinct from $A_{1}, A_{2}$, we choose the one, say $A_{k}$, for which the angle $\angle A_{k} A_{1} A_{2}$ is minimal (this point is uniquely determined, since no three points are collinear). The line $A_{1} A_{k}$ separates the plane into two half-planes, one of which contains $A_{2}$ only, and the other one all the remaining $3 n$ points. By the inductive hypothesis, one can construct $n$ disjoint triangles with vertices in these $3 n$ points. Together with the triangle $A_{1} A_{2} A_{k}$, they form the required system of disjoint triangles.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
2. (CZS 1) We are given $3 n$ points $A_{1}, A_{2}, \ldots, A_{3 n}$ in the plane, no three of them collinear. Prove that one can construct $n$ disjoint triangles with vertices at the points $A_{i}$.
|
2. We use induction. For $n=1$ the assertion is obvious. Assume that it is true for a positive integer $n$. Let $A_{1}, A_{2}, \ldots, A_{3 n+3}$ be given $3 n+3$ points, and let w.l.o.g. $A_{1} A_{2} \ldots A_{m}$ be their convex hull. Among all the points $A_{i}$ distinct from $A_{1}, A_{2}$, we choose the one, say $A_{k}$, for which the angle $\angle A_{k} A_{1} A_{2}$ is minimal (this point is uniquely determined, since no three points are collinear). The line $A_{1} A_{k}$ separates the plane into two half-planes, one of which contains $A_{2}$ only, and the other one all the remaining $3 n$ points. By the inductive hypothesis, one can construct $n$ disjoint triangles with vertices in these $3 n$ points. Together with the triangle $A_{1} A_{2} A_{k}$, they form the required system of disjoint triangles.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d49d3a60-63a0-569e-bf72-6614c1e6a543
| 24,938
|
3. (CZS 4) Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying $x_{1}+x_{2}+\cdots+x_{n}=$ 0 . Let $m$ be the least and $M$ the greatest among them. Prove that $$ x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2} \leq-n m M $$
|
3. We have for each $k=1,2, \ldots, n$ that $m \leq x_{k} \leq M$, which gives $(M-$ $\left.x_{k}\right)\left(m-x_{k}\right) \leq 0$. It follows directly that $$ 0 \geq \sum_{k=1}^{n}\left(M-x_{k}\right)\left(m-x_{k}\right)=n m M-(m+M) \sum_{k=1}^{n} x_{k}+\sum_{k=1}^{n} x_{k}^{2} $$ But $\sum_{k=1}^{n} x_{k}=0$, implying the required inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
3. (CZS 4) Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying $x_{1}+x_{2}+\cdots+x_{n}=$ 0 . Let $m$ be the least and $M$ the greatest among them. Prove that $$ x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2} \leq-n m M $$
|
3. We have for each $k=1,2, \ldots, n$ that $m \leq x_{k} \leq M$, which gives $(M-$ $\left.x_{k}\right)\left(m-x_{k}\right) \leq 0$. It follows directly that $$ 0 \geq \sum_{k=1}^{n}\left(M-x_{k}\right)\left(m-x_{k}\right)=n m M-(m+M) \sum_{k=1}^{n} x_{k}+\sum_{k=1}^{n} x_{k}^{2} $$ But $\sum_{k=1}^{n} x_{k}=0$, implying the required inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
40dbef6c-8d96-56e4-81a6-6376d20ecaf8
| 24,941
|
4. (GDR 1) Let $n_{1}, n_{2}$ be positive integers. Consider in a plane $E$ two disjoint sets of points $M_{1}$ and $M_{2}$ consisting of $2 n_{1}$ and $2 n_{2}$ points, respectively, and such that no three points of the union $M_{1} \cup M_{2}$ are collinear. Prove that there exists a straightline $g$ with the following property: Each of the two half-planes determined by $g$ on $E$ ( $g$ not being included in either) contains exactly half of the points of $M_{1}$ and exactly half of the points of $M_{2}$.
|
4. Choose in $E$ a half-line $s$ beginning at a point $O$. For every $\alpha$ in the interval $\left[0,180^{\circ}\right]$, denote by $s(\alpha)$ the line obtained by rotation of $s$ about $O$ by $\alpha$, and by $g(\alpha)$ the oriented line containing $s(\alpha)$ on which $s(\alpha)$ defines the positive direction. For each $P$ in $M_{i}, i=1,2$, let $P(\alpha)$ be the foot of the perpendicular from $P$ to $g(\alpha)$, and $l_{P}(\alpha)$ the oriented (positive, negative or zero) distance of $P(\alpha)$ from $O$. Then for $i=1,2$ one can arrange the $l_{P}(\alpha)\left(P \in M_{i}\right)$ in ascending order, as $l_{1}(\alpha), l_{2}(\alpha), \ldots, l_{2 n_{i}}(\alpha)$. Call $J_{i}(\alpha)$ the interval $\left[l_{n_{i}}(\alpha), l_{n_{i}+1}(\alpha)\right]$. It is easy to see that any line perpendicular to $g(\alpha)$ and passing through the point with the distance $l$ in the interior of $J_{i}(\alpha)$ from $O$, will divide the set $M_{i}$ into two subsets of equal cardinality. Therefore it remains to show that for some $\alpha$, the interiors of intervals $J_{1}(\alpha)$ and $J_{2}(\alpha)$ have a common point. If this holds for $\alpha=0$, then we have finished. Suppose w.l.o.g. that $J_{1}(0)$ lies on $g(0)$ to the left of $J_{2}(0)$; then $J_{1}\left(180^{\circ}\right)$ lies to the right of $J_{2}\left(180^{\circ}\right)$. Note that $J_{1}$ and $J_{2}$ cannot simultaneously degenerate to a point (otherwise, we would have four collinear points in $M_{1} \cup M_{2}$ ); also, each of them degenerates to a point for only finitely many values of $\alpha$. Since $J_{1}(\alpha)$ and $J_{2}(\alpha)$ move continuously, there exists a subinterval $I$ of $\left[0,180^{\circ}\right]$ on which they are not disjoint. Thus, at some point of $I$, they are both nondegenerate and have a common interior point, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
4. (GDR 1) Let $n_{1}, n_{2}$ be positive integers. Consider in a plane $E$ two disjoint sets of points $M_{1}$ and $M_{2}$ consisting of $2 n_{1}$ and $2 n_{2}$ points, respectively, and such that no three points of the union $M_{1} \cup M_{2}$ are collinear. Prove that there exists a straightline $g$ with the following property: Each of the two half-planes determined by $g$ on $E$ ( $g$ not being included in either) contains exactly half of the points of $M_{1}$ and exactly half of the points of $M_{2}$.
|
4. Choose in $E$ a half-line $s$ beginning at a point $O$. For every $\alpha$ in the interval $\left[0,180^{\circ}\right]$, denote by $s(\alpha)$ the line obtained by rotation of $s$ about $O$ by $\alpha$, and by $g(\alpha)$ the oriented line containing $s(\alpha)$ on which $s(\alpha)$ defines the positive direction. For each $P$ in $M_{i}, i=1,2$, let $P(\alpha)$ be the foot of the perpendicular from $P$ to $g(\alpha)$, and $l_{P}(\alpha)$ the oriented (positive, negative or zero) distance of $P(\alpha)$ from $O$. Then for $i=1,2$ one can arrange the $l_{P}(\alpha)\left(P \in M_{i}\right)$ in ascending order, as $l_{1}(\alpha), l_{2}(\alpha), \ldots, l_{2 n_{i}}(\alpha)$. Call $J_{i}(\alpha)$ the interval $\left[l_{n_{i}}(\alpha), l_{n_{i}+1}(\alpha)\right]$. It is easy to see that any line perpendicular to $g(\alpha)$ and passing through the point with the distance $l$ in the interior of $J_{i}(\alpha)$ from $O$, will divide the set $M_{i}$ into two subsets of equal cardinality. Therefore it remains to show that for some $\alpha$, the interiors of intervals $J_{1}(\alpha)$ and $J_{2}(\alpha)$ have a common point. If this holds for $\alpha=0$, then we have finished. Suppose w.l.o.g. that $J_{1}(0)$ lies on $g(0)$ to the left of $J_{2}(0)$; then $J_{1}\left(180^{\circ}\right)$ lies to the right of $J_{2}\left(180^{\circ}\right)$. Note that $J_{1}$ and $J_{2}$ cannot simultaneously degenerate to a point (otherwise, we would have four collinear points in $M_{1} \cup M_{2}$ ); also, each of them degenerates to a point for only finitely many values of $\alpha$. Since $J_{1}(\alpha)$ and $J_{2}(\alpha)$ move continuously, there exists a subinterval $I$ of $\left[0,180^{\circ}\right]$ on which they are not disjoint. Thus, at some point of $I$, they are both nondegenerate and have a common interior point, as desired.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7e7a000c-3b4b-5bae-9f49-0b9dc5e06ed7
| 24,944
|
5. (GDR 2) Prove the following assertion: The four altitudes of a tetrahedron $A B C D$ intersect in a point if and only if $$ A B^{2}+C D^{2}=B C^{2}+A D^{2}=C A^{2}+B D^{2} $$
|
5. Lemma. If $X, Y, Z, T$ are points in space, then the lines $X Z$ and $Y T$ are perpendicular if and only if $X Y^{2}+Z T^{2}=Y Z^{2}+T X^{2}$. Proof. Consider the plane $\pi$ through $X Z$ parallel to $Y T$. If $Y^{\prime}, T^{\prime}$ are the feet of the perpendiculars to $\pi$ from $Y, T$ respectively, then $$ \begin{aligned} & \\ & X Y^{2}+Z T^{2}=X Y^{\prime 2}+Z T^{\prime 2}+2 Y Y^{\prime 2} \\ & \text { and } \quad Y Z^{2}+T X^{2}=Y^{\prime} Z^{2}+T^{\prime} X^{2}+2 Y Y^{\prime 2} \end{aligned} $$ Since by the Pythagorean theorem $X Y^{\prime 2}+Z T^{\prime 2}=Y^{\prime} Z^{2}+T^{\prime} X^{2}$, i.e., $X Y^{\prime 2}-Y^{\prime} Z^{2}=X T^{\prime 2}-T^{\prime} Z^{2}$, if and only if $Y^{\prime} T^{\prime} \perp X Z$, the statement follows. Assume that the four altitudes intersect in a point $P$. Then we have $D P \perp$ $A B C \Rightarrow D P \perp A B$ and $C P \perp A B D \Rightarrow C P \perp A B$, which implies that $C D P \perp A B$, and $C D \perp A B$. By the lemma, $A C^{2}+B D^{2}=A D^{2}+B C^{2}$. Using the same procedure we obtain the relation $A D^{2}+B C^{2}=A B^{2}+$ $C D^{2}$ 。 Conversely, assume that $A B^{2}+C D^{2}=A C^{2}+B D^{2}=A D^{2}+B C^{2}$. The lemma implies that $A B \perp C D, A C \perp B D, A D \perp B C$. Let $\pi$ be the plane containing $C D$ that is perpendicular to $A B$, and let $h_{D}$ be the altitude from $D$ to $A B C$. Since $\pi \perp A B$, we have $\pi \perp A B C \Rightarrow h_{D} \subset \pi$ and $\pi \perp A B D \Rightarrow h_{C} \subset \pi$. The altitudes $h_{D}$ and $h_{C}$ are not parallel; thus they have an intersection point $P_{C D}$. Analogously, $h_{B} \cap h_{C}=\left\{P_{B C}\right\}$ and $h_{B} \cap h_{D}=\left\{P_{B D}\right\}$, where both these points belong to $\pi$. On the other hand, $h_{B}$ doesn't belong to $\pi$; otherwise, it would be perpendicular to both $A C D$ and $A B \subset \pi$, i.e. $A B \subset A C D$, which is impossible. Hence, $h_{B}$ can have at most one common point with $\pi$, implying $P_{B D}=P_{C D}$. Analogously, $P_{A B}=P_{B D}=P_{C D}=P_{A B C D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. (GDR 2) Prove the following assertion: The four altitudes of a tetrahedron $A B C D$ intersect in a point if and only if $$ A B^{2}+C D^{2}=B C^{2}+A D^{2}=C A^{2}+B D^{2} $$
|
5. Lemma. If $X, Y, Z, T$ are points in space, then the lines $X Z$ and $Y T$ are perpendicular if and only if $X Y^{2}+Z T^{2}=Y Z^{2}+T X^{2}$. Proof. Consider the plane $\pi$ through $X Z$ parallel to $Y T$. If $Y^{\prime}, T^{\prime}$ are the feet of the perpendiculars to $\pi$ from $Y, T$ respectively, then $$ \begin{aligned} & \\ & X Y^{2}+Z T^{2}=X Y^{\prime 2}+Z T^{\prime 2}+2 Y Y^{\prime 2} \\ & \text { and } \quad Y Z^{2}+T X^{2}=Y^{\prime} Z^{2}+T^{\prime} X^{2}+2 Y Y^{\prime 2} \end{aligned} $$ Since by the Pythagorean theorem $X Y^{\prime 2}+Z T^{\prime 2}=Y^{\prime} Z^{2}+T^{\prime} X^{2}$, i.e., $X Y^{\prime 2}-Y^{\prime} Z^{2}=X T^{\prime 2}-T^{\prime} Z^{2}$, if and only if $Y^{\prime} T^{\prime} \perp X Z$, the statement follows. Assume that the four altitudes intersect in a point $P$. Then we have $D P \perp$ $A B C \Rightarrow D P \perp A B$ and $C P \perp A B D \Rightarrow C P \perp A B$, which implies that $C D P \perp A B$, and $C D \perp A B$. By the lemma, $A C^{2}+B D^{2}=A D^{2}+B C^{2}$. Using the same procedure we obtain the relation $A D^{2}+B C^{2}=A B^{2}+$ $C D^{2}$ 。 Conversely, assume that $A B^{2}+C D^{2}=A C^{2}+B D^{2}=A D^{2}+B C^{2}$. The lemma implies that $A B \perp C D, A C \perp B D, A D \perp B C$. Let $\pi$ be the plane containing $C D$ that is perpendicular to $A B$, and let $h_{D}$ be the altitude from $D$ to $A B C$. Since $\pi \perp A B$, we have $\pi \perp A B C \Rightarrow h_{D} \subset \pi$ and $\pi \perp A B D \Rightarrow h_{C} \subset \pi$. The altitudes $h_{D}$ and $h_{C}$ are not parallel; thus they have an intersection point $P_{C D}$. Analogously, $h_{B} \cap h_{C}=\left\{P_{B C}\right\}$ and $h_{B} \cap h_{D}=\left\{P_{B D}\right\}$, where both these points belong to $\pi$. On the other hand, $h_{B}$ doesn't belong to $\pi$; otherwise, it would be perpendicular to both $A C D$ and $A B \subset \pi$, i.e. $A B \subset A C D$, which is impossible. Hence, $h_{B}$ can have at most one common point with $\pi$, implying $P_{B D}=P_{C D}$. Analogously, $P_{A B}=P_{B D}=P_{C D}=P_{A B C D}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b752b592-afd3-57b2-91d9-22c5ba60e04d
| 24,946
|
6. (GDR 3) Show that for any $n \not \equiv 0(\bmod 10)$ there exists a multiple of $n$ not containing the digit 0 in its decimal expansion.
|
6. Let $n=2^{\alpha} 5^{\beta} m$, where $\alpha=0$ or $\beta=0$. These two cases are analogous, and we treat only $\alpha=0, n=5^{\beta} m$. The case $m=1$ is settled by the following lemma. Lemma. For any integer $\beta \geq 1$ there exists a multiple $M_{\beta}$ of $5^{\beta}$ with $\beta$ digits in decimal expansion, all different from 0. Proof. For $\beta=1, M_{1}=5$ works. Assume that the lemma is true for $\beta=k$. There is a positive integer $C_{k} \leq 5$ such that $C_{k} 2^{k}+m_{k} \equiv$ $0(\bmod 5)$, where $5^{k} m_{k}=M_{k}$, i.e. $C_{k} 10^{k}+M_{k} \equiv 0\left(\bmod 5^{k+1}\right)$. Then $M_{k+1}=C_{k} 10^{k}+M_{k}$ satisfies the conditions, and proves the lemma. In the general case, consider, the sequence $1,10^{\beta}, 10^{2 \beta}, \ldots$ It contains two numbers congruent modulo $\left(10^{\beta}-1\right) m$, and therefore for some $k>0$, $10^{k \beta} \equiv 1\left(\bmod \left(10^{\beta}-1\right) m\right)$ (this is in fact a consequence of Fermat's theorem). The number $$ \frac{10^{k \beta}-1}{10^{\beta}-1} M_{\beta}=10^{(k-1) \beta} M_{\beta}+10^{(k-2) \beta} M_{\beta}+\cdots+M_{\beta} $$ is a multiple of $n=5^{\beta} m$ with the required property.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
6. (GDR 3) Show that for any $n \not \equiv 0(\bmod 10)$ there exists a multiple of $n$ not containing the digit 0 in its decimal expansion.
|
6. Let $n=2^{\alpha} 5^{\beta} m$, where $\alpha=0$ or $\beta=0$. These two cases are analogous, and we treat only $\alpha=0, n=5^{\beta} m$. The case $m=1$ is settled by the following lemma. Lemma. For any integer $\beta \geq 1$ there exists a multiple $M_{\beta}$ of $5^{\beta}$ with $\beta$ digits in decimal expansion, all different from 0. Proof. For $\beta=1, M_{1}=5$ works. Assume that the lemma is true for $\beta=k$. There is a positive integer $C_{k} \leq 5$ such that $C_{k} 2^{k}+m_{k} \equiv$ $0(\bmod 5)$, where $5^{k} m_{k}=M_{k}$, i.e. $C_{k} 10^{k}+M_{k} \equiv 0\left(\bmod 5^{k+1}\right)$. Then $M_{k+1}=C_{k} 10^{k}+M_{k}$ satisfies the conditions, and proves the lemma. In the general case, consider, the sequence $1,10^{\beta}, 10^{2 \beta}, \ldots$ It contains two numbers congruent modulo $\left(10^{\beta}-1\right) m$, and therefore for some $k>0$, $10^{k \beta} \equiv 1\left(\bmod \left(10^{\beta}-1\right) m\right)$ (this is in fact a consequence of Fermat's theorem). The number $$ \frac{10^{k \beta}-1}{10^{\beta}-1} M_{\beta}=10^{(k-1) \beta} M_{\beta}+10^{(k-2) \beta} M_{\beta}+\cdots+M_{\beta} $$ is a multiple of $n=5^{\beta} m$ with the required property.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e3cb1c64-1983-5ecc-b85a-36be5fb152b3
| 24,949
|
7. $(\mathbf{G B R} 1)^{\mathrm{IMO} 6}$ (a) A plane $\pi$ passes through the vertex $O$ of the regular tetrahedron $O P Q R$. We define $p, q, r$ to be the signed distances of $P, Q, R$ from $\pi$ measured along a directed normal to $\pi$. Prove that $$ p^{2}+q^{2}+r^{2}+(q-r)^{2}+(r-p)^{2}+(p-q)^{2}=2 a^{2} $$ where $a$ is the length of an edge of a tetrahedron. (b) Given four parallel planes not all of which are coincident, show that a regular tetrahedron exists with a vertex on each plane.
|
7. (i) Consider the circumscribing cube $O Q_{1} P R_{1} O_{1} Q P_{1} R$ (that is, the cube in which the edges of the tetrahedron are small diagonals), of side $b=a \sqrt{2} / 2$. The left-hand side is the sum of squares of the projections of the edges of the tetrahedron onto a perpendicular $l$ to $\pi$. On the other hand, if $l$  forms angles $\varphi_{1}, \varphi_{2}, \varphi_{3}$ with $O O_{1}, O Q_{1}, O R_{1}$ respectively, then the projections of $O P$ and $Q R$ onto $l$ have lengths $b\left(\cos \varphi_{2}+\cos \varphi_{3}\right)$ and $b\left|\cos \varphi_{2}-\cos \varphi_{3}\right|$. Summing up all these expressions, we obtain $$ 4 b^{2}\left(\cos ^{2} \varphi_{1}+\cos ^{2} \varphi_{2}+\cos ^{2} \varphi_{3}\right)=4 b^{2}=2 a^{2} $$ (ii) We construct a required tetrahedron of edge length $a$ given in (i). Take $O$ arbitrarily on $\pi_{0}$, and let $p, q, r$ be the distances of $O$ from $\pi_{1}, \pi_{2}, \pi_{3}$. Since $a>p, q, r,|p-q|$, we can choose $P$ on $\pi_{1}$ anywhere at distance $a$ from $O$, and $Q$ at one of the two points on $\pi_{2}$ at distance $a$ from both $O$ and $P$. Consider the fourth vertex of the tetrahedron: its distance from $\pi_{0}$ will satisfy the equation from (i); i.e., there are two values for this distance; clearly, one of them is $r$, putting $R$ on $\pi_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. $(\mathbf{G B R} 1)^{\mathrm{IMO} 6}$ (a) A plane $\pi$ passes through the vertex $O$ of the regular tetrahedron $O P Q R$. We define $p, q, r$ to be the signed distances of $P, Q, R$ from $\pi$ measured along a directed normal to $\pi$. Prove that $$ p^{2}+q^{2}+r^{2}+(q-r)^{2}+(r-p)^{2}+(p-q)^{2}=2 a^{2} $$ where $a$ is the length of an edge of a tetrahedron. (b) Given four parallel planes not all of which are coincident, show that a regular tetrahedron exists with a vertex on each plane.
|
7. (i) Consider the circumscribing cube $O Q_{1} P R_{1} O_{1} Q P_{1} R$ (that is, the cube in which the edges of the tetrahedron are small diagonals), of side $b=a \sqrt{2} / 2$. The left-hand side is the sum of squares of the projections of the edges of the tetrahedron onto a perpendicular $l$ to $\pi$. On the other hand, if $l$  forms angles $\varphi_{1}, \varphi_{2}, \varphi_{3}$ with $O O_{1}, O Q_{1}, O R_{1}$ respectively, then the projections of $O P$ and $Q R$ onto $l$ have lengths $b\left(\cos \varphi_{2}+\cos \varphi_{3}\right)$ and $b\left|\cos \varphi_{2}-\cos \varphi_{3}\right|$. Summing up all these expressions, we obtain $$ 4 b^{2}\left(\cos ^{2} \varphi_{1}+\cos ^{2} \varphi_{2}+\cos ^{2} \varphi_{3}\right)=4 b^{2}=2 a^{2} $$ (ii) We construct a required tetrahedron of edge length $a$ given in (i). Take $O$ arbitrarily on $\pi_{0}$, and let $p, q, r$ be the distances of $O$ from $\pi_{1}, \pi_{2}, \pi_{3}$. Since $a>p, q, r,|p-q|$, we can choose $P$ on $\pi_{1}$ anywhere at distance $a$ from $O$, and $Q$ at one of the two points on $\pi_{2}$ at distance $a$ from both $O$ and $P$. Consider the fourth vertex of the tetrahedron: its distance from $\pi_{0}$ will satisfy the equation from (i); i.e., there are two values for this distance; clearly, one of them is $r$, putting $R$ on $\pi_{3}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d6ae8fc2-c2b0-5504-b683-37d99038e737
| 24,952
|
8. (GBR 2) ${ }^{\mathrm{IMO} 3}$ Let $m$ and $n$ be nonnegative integers. Prove that $m!n!(m+$ $n)$ ! divides $(2 m)!(2 n)!$.
|
8. Let $f(m, n)=\frac{(2 m)!(2 n)!}{m!n!(m+n)!}$. Then it is directly shown that $$ f(m, n)=4 f(m, n-1)-f(m+1, n-1), $$ and thus $n$ may be successively reduced until one obtains $f(m, n)=$ $\sum_{r} c_{r} f(r, 0)$. Now $f(r, 0)$ is a simple binomial coefficient, and the $c_{r}$ 's are integers. Second solution. For each prime $p$, the greatest exponents of $p$ that divide the numerator $(2 m)!(2 n)$ ! and denominator $m!n!(m+n)$ ! are respectively $$ \sum_{k>0}\left(\left[\frac{2 m}{p^{k}}\right]+\left[\frac{2 n}{p^{k}}\right]\right) \quad \text { and } \quad \sum_{k>0}\left(\left[\frac{m}{p^{k}}\right]+\left[\frac{n}{p^{k}}\right]+\left[\frac{m+n}{p^{k}}\right]\right) $$ hence it suffices to show that the first exponent is not less than the second one for every $p$. This follows from the fact that for each real $x,[2 x]+[2 y] \geq$ $[x]+[y]+[x+y]$, which is straightforward to prove (for example, using $[2 x]=[x]+[x+1 / 2])$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
8. (GBR 2) ${ }^{\mathrm{IMO} 3}$ Let $m$ and $n$ be nonnegative integers. Prove that $m!n!(m+$ $n)$ ! divides $(2 m)!(2 n)!$.
|
8. Let $f(m, n)=\frac{(2 m)!(2 n)!}{m!n!(m+n)!}$. Then it is directly shown that $$ f(m, n)=4 f(m, n-1)-f(m+1, n-1), $$ and thus $n$ may be successively reduced until one obtains $f(m, n)=$ $\sum_{r} c_{r} f(r, 0)$. Now $f(r, 0)$ is a simple binomial coefficient, and the $c_{r}$ 's are integers. Second solution. For each prime $p$, the greatest exponents of $p$ that divide the numerator $(2 m)!(2 n)$ ! and denominator $m!n!(m+n)$ ! are respectively $$ \sum_{k>0}\left(\left[\frac{2 m}{p^{k}}\right]+\left[\frac{2 n}{p^{k}}\right]\right) \quad \text { and } \quad \sum_{k>0}\left(\left[\frac{m}{p^{k}}\right]+\left[\frac{n}{p^{k}}\right]+\left[\frac{m+n}{p^{k}}\right]\right) $$ hence it suffices to show that the first exponent is not less than the second one for every $p$. This follows from the fact that for each real $x,[2 x]+[2 y] \geq$ $[x]+[y]+[x+y]$, which is straightforward to prove (for example, using $[2 x]=[x]+[x+1 / 2])$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
fa5c2763-0029-5690-bdd5-f24ff4b482cc
| 24,954
|
12. (SWE 6) Consider the two square matrices $$ A=\left[\begin{array}{rrrrr} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & -1 & 1 \\ 1 & 1 & -1 & 1 & -1 \end{array}\right] \quad \text { and } \quad B=\left[\begin{array}{rrrrr} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & -1 & -1 \\ 1 & 1 & -1 & 1 & -1 \\ 1 & -1 & -1 & 1 & 1 \\ 1 & -1 & 1 & -1 & 1 \end{array}\right] $$ with entries 1 and -1 . The following operations will be called elementary: (1) Changing signs of all numbers in one row; (2) Changing signs of all numbers in one column; (3) Interchanging two rows (two rows exchange their positions); (4) Interchanging two columns. Prove that the matrix $B$ cannot be obtained from the matrix $A$ using these operations.
|
12. Observe that the absolute values of the determinants of the given matrices are invariant under all the admitted operations. The statement follows from $\operatorname{det} A=16 \neq \operatorname{det} B=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
12. (SWE 6) Consider the two square matrices $$ A=\left[\begin{array}{rrrrr} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & -1 & 1 \\ 1 & 1 & -1 & 1 & -1 \end{array}\right] \quad \text { and } \quad B=\left[\begin{array}{rrrrr} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & -1 & -1 \\ 1 & 1 & -1 & 1 & -1 \\ 1 & -1 & -1 & 1 & 1 \\ 1 & -1 & 1 & -1 & 1 \end{array}\right] $$ with entries 1 and -1 . The following operations will be called elementary: (1) Changing signs of all numbers in one row; (2) Changing signs of all numbers in one column; (3) Interchanging two rows (two rows exchange their positions); (4) Interchanging two columns. Prove that the matrix $B$ cannot be obtained from the matrix $A$ using these operations.
|
12. Observe that the absolute values of the determinants of the given matrices are invariant under all the admitted operations. The statement follows from $\operatorname{det} A=16 \neq \operatorname{det} B=0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b7f7402d-f51a-5d44-a10c-3b9cb94944c5
| 24,967
|
15. (CUB 1) Prove that for all $n \in \mathbb{N}$ the following is true: $$ 2^{n} \prod_{k=1}^{n} \sin \frac{k \pi}{2 n+1}=\sqrt{2 n+1} $$
|
15. If $z=\cos \theta+i \sin \theta$, then $z-z^{-1}=2 i \sin \theta$. Now put $z=\cos \frac{\pi}{2 n+1}+$ $i \sin \frac{\pi}{2 n+1}$. Using de Moivre's formula we transform the required equality into $$ A=\prod_{k=1}^{n}\left(z^{k}-z^{-k}\right)=i^{n} \sqrt{2 n+1} $$ On the other hand, the complex numbers $z^{2 k}(k=-n,-n+1, \ldots, n)$ are the roots of $x^{2 n+1}-1$, and hence $$ \prod_{k=1}^{n}\left(x-z^{2 k}\right)\left(x-z^{-2 k}\right)=\frac{x^{2 n+1}-1}{x-1}=x^{2 n}+\cdots+x+1 $$ Now we go back to proving (1). We have $$ (-1)^{n} z^{n(n+1) / 2} A=\prod_{k=1}^{n}\left(1-z^{2 k}\right) \quad \text { and } \quad z^{-n(n+1) / 2} A=\prod_{k=1}^{n}\left(1-z^{-2 k}\right) $$ Multiplying these two equalities, we obtain $(-1)^{n} A^{2}=\prod_{k=1}^{n}\left(1-z^{2 k}\right)(1-$ $\left.z^{-2 k}\right)=2 n+1$, by (2). Therefore $A= \pm i^{-n} \sqrt{2 n+1}$. This actually implies that the required product is $\pm \sqrt{2 n+1}$, but it must be positive, since all the sines are, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
15. (CUB 1) Prove that for all $n \in \mathbb{N}$ the following is true: $$ 2^{n} \prod_{k=1}^{n} \sin \frac{k \pi}{2 n+1}=\sqrt{2 n+1} $$
|
15. If $z=\cos \theta+i \sin \theta$, then $z-z^{-1}=2 i \sin \theta$. Now put $z=\cos \frac{\pi}{2 n+1}+$ $i \sin \frac{\pi}{2 n+1}$. Using de Moivre's formula we transform the required equality into $$ A=\prod_{k=1}^{n}\left(z^{k}-z^{-k}\right)=i^{n} \sqrt{2 n+1} $$ On the other hand, the complex numbers $z^{2 k}(k=-n,-n+1, \ldots, n)$ are the roots of $x^{2 n+1}-1$, and hence $$ \prod_{k=1}^{n}\left(x-z^{2 k}\right)\left(x-z^{-2 k}\right)=\frac{x^{2 n+1}-1}{x-1}=x^{2 n}+\cdots+x+1 $$ Now we go back to proving (1). We have $$ (-1)^{n} z^{n(n+1) / 2} A=\prod_{k=1}^{n}\left(1-z^{2 k}\right) \quad \text { and } \quad z^{-n(n+1) / 2} A=\prod_{k=1}^{n}\left(1-z^{-2 k}\right) $$ Multiplying these two equalities, we obtain $(-1)^{n} A^{2}=\prod_{k=1}^{n}\left(1-z^{2 k}\right)(1-$ $\left.z^{-2 k}\right)=2 n+1$, by (2). Therefore $A= \pm i^{-n} \sqrt{2 n+1}$. This actually implies that the required product is $\pm \sqrt{2 n+1}$, but it must be positive, since all the sines are, and the result follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8002eb90-4f7f-5cf5-93e9-c976dfe1e9db
| 24,975
|
17. (POL 1) ${ }^{\mathrm{IMO} 5}$ Let $\mathcal{F}$ be a nonempty set of functions $f: \mathbb{R} \rightarrow \mathbb{R}$ of the form $f(x)=a x+b$, where $a$ and $b$ are real numbers and $a \neq 0$. Suppose that $\mathcal{F}$ satisfies the following conditions: (1) If $f, g \in \mathcal{F}$, then $g \circ f \in \mathcal{F}$, where $(g \circ f)(x)=g[f(x)]$. (2) If $f \in \mathcal{F}$ and $f(x)=a x+b$, then the inverse $f^{-1}$ of $f$ belongs to $\mathcal{F}$ $\left(f^{-1}(x)=(x-b) / a\right)$. (3) None of the functions $f(x)=x+c$, for $c \neq 0$, belong to $\mathcal{F}$. Prove that there exists $x_{0} \in \mathbb{R}$ such that $f\left(x_{0}\right)=x_{0}$ for all $f \in \mathcal{F}$.
|
17. Let $f_{1}(x)=a x+b$ and $f_{2}(x)=c x+d$ be two functions from $\mathcal{F}$. We define $g(x)=f_{1} \circ f_{2}(x)=a c x+(a d+b)$ and $h(x)=f_{2} \circ f_{1}(x)=a c x+(b c+d)$. By the condition for $\mathcal{F}$, both $g(x)$ and $h(x)$ belong to $\mathcal{F}$. Moreover, there exists $h^{-1}(x)=\frac{x-(b c+d)}{a c}$, and $$ h^{-1} \circ g(x)=\frac{a c x+(a d+b)-(b c+d)}{a c}=x+\frac{(a d+b)-(b c+d)}{a c} $$ belongs to $\mathcal{F}$. Now it follows that we must have $a d+b=b c+d$ for every $f_{1}, f_{2} \in \mathcal{F}$, which is equivalent to $\frac{b}{a-1}=\frac{d}{c-1}=k$. But these formulas exactly describe the fixed points of $f_{1}$ and $f_{2}: f_{1}(x)=a x+b=x \Rightarrow x=$ $\frac{b}{a-1}$. Hence all the functions in $\mathcal{F}$ fix the point $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
17. (POL 1) ${ }^{\mathrm{IMO} 5}$ Let $\mathcal{F}$ be a nonempty set of functions $f: \mathbb{R} \rightarrow \mathbb{R}$ of the form $f(x)=a x+b$, where $a$ and $b$ are real numbers and $a \neq 0$. Suppose that $\mathcal{F}$ satisfies the following conditions: (1) If $f, g \in \mathcal{F}$, then $g \circ f \in \mathcal{F}$, where $(g \circ f)(x)=g[f(x)]$. (2) If $f \in \mathcal{F}$ and $f(x)=a x+b$, then the inverse $f^{-1}$ of $f$ belongs to $\mathcal{F}$ $\left(f^{-1}(x)=(x-b) / a\right)$. (3) None of the functions $f(x)=x+c$, for $c \neq 0$, belong to $\mathcal{F}$. Prove that there exists $x_{0} \in \mathbb{R}$ such that $f\left(x_{0}\right)=x_{0}$ for all $f \in \mathcal{F}$.
|
17. Let $f_{1}(x)=a x+b$ and $f_{2}(x)=c x+d$ be two functions from $\mathcal{F}$. We define $g(x)=f_{1} \circ f_{2}(x)=a c x+(a d+b)$ and $h(x)=f_{2} \circ f_{1}(x)=a c x+(b c+d)$. By the condition for $\mathcal{F}$, both $g(x)$ and $h(x)$ belong to $\mathcal{F}$. Moreover, there exists $h^{-1}(x)=\frac{x-(b c+d)}{a c}$, and $$ h^{-1} \circ g(x)=\frac{a c x+(a d+b)-(b c+d)}{a c}=x+\frac{(a d+b)-(b c+d)}{a c} $$ belongs to $\mathcal{F}$. Now it follows that we must have $a d+b=b c+d$ for every $f_{1}, f_{2} \in \mathcal{F}$, which is equivalent to $\frac{b}{a-1}=\frac{d}{c-1}=k$. But these formulas exactly describe the fixed points of $f_{1}$ and $f_{2}: f_{1}(x)=a x+b=x \Rightarrow x=$ $\frac{b}{a-1}$. Hence all the functions in $\mathcal{F}$ fix the point $k$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c74b200a-8f79-51b4-a6ed-4805b08b90d1
| 24,980
|
3. (CZS 6) ${ }^{\mathrm{IMO}}$ Prove that the sum of an odd number of unit vectors passing through the same point $O$ and lying in the same half-plane whose border passes through $O$ has length greater than or equal to 1 .
|
3 . We use induction on odd numbers $n$. For $n=1$ there is nothing to prove. Suppose that the result holds for $n-2$ vectors, and let us be given vectors $v_{1}, v_{2}, \ldots, v_{n}$ arranged clockwise. Set $v^{\prime}=v_{2}+v_{3}+\cdots+v_{n-1}, u=v_{1}+v_{n}$, and $v=v_{1}+v_{2}+\cdots+v_{n}=v^{\prime}+u$. By the inductive hypothesis we have $\left|v^{\prime}\right| \geq 1$. Now if the angles between $v^{\prime}$ and the vectors $v_{1}, v_{n}$ are $\alpha$ and $\beta$ respectively, then the angle between $u$ and $v^{\prime}$ is $|\alpha-\beta| / 2 \leq 90^{\circ}$. Hence $\left|v^{\prime}+u\right| \geq\left|v^{\prime}\right| \geq 1$. Second solution. Again by induction, it can be easily shown that all possible values of the sum $v=v_{1}+v_{2}+\cdots+v_{n}$, for $n$ vectors $v_{1}, \ldots, v_{n}$ in the upper half-plane (with $y \geq 0$ ), are those for which $|v| \leq n$ and $|v-k e| \geq 1$ for every integer $k$ for which $n-k$ is odd, where $e$ is the unit vector on the $x$ axis.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (CZS 6) ${ }^{\mathrm{IMO}}$ Prove that the sum of an odd number of unit vectors passing through the same point $O$ and lying in the same half-plane whose border passes through $O$ has length greater than or equal to 1 .
|
3 . We use induction on odd numbers $n$. For $n=1$ there is nothing to prove. Suppose that the result holds for $n-2$ vectors, and let us be given vectors $v_{1}, v_{2}, \ldots, v_{n}$ arranged clockwise. Set $v^{\prime}=v_{2}+v_{3}+\cdots+v_{n-1}, u=v_{1}+v_{n}$, and $v=v_{1}+v_{2}+\cdots+v_{n}=v^{\prime}+u$. By the inductive hypothesis we have $\left|v^{\prime}\right| \geq 1$. Now if the angles between $v^{\prime}$ and the vectors $v_{1}, v_{n}$ are $\alpha$ and $\beta$ respectively, then the angle between $u$ and $v^{\prime}$ is $|\alpha-\beta| / 2 \leq 90^{\circ}$. Hence $\left|v^{\prime}+u\right| \geq\left|v^{\prime}\right| \geq 1$. Second solution. Again by induction, it can be easily shown that all possible values of the sum $v=v_{1}+v_{2}+\cdots+v_{n}$, for $n$ vectors $v_{1}, \ldots, v_{n}$ in the upper half-plane (with $y \geq 0$ ), are those for which $|v| \leq n$ and $|v-k e| \geq 1$ for every integer $k$ for which $n-k$ is odd, where $e$ is the unit vector on the $x$ axis.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
56ddb554-1816-5460-83aa-ea34740b907b
| 24,986
|
6. (POL 2) ${ }^{\mathrm{IMO} 2}$ Does there exist a finite set $M$ of points in space, not all in the same plane, such that for each two points $A, B \in M$ there exist two other points $C, D \in M$ such that lines $A B$ and $C D$ are parallel?
|
6. Yes. Take for $\mathcal{M}$ the set of vertices of a cube $A B C D E F G H$ and two points $I, J$ symmetric to the center $O$ of the cube with respect to the laterals $A B C D$ and $E F G H$. Remark. We prove a stronger result: Given an arbitrary finite set of points $\mathcal{S}$, then there is a finite set $\mathcal{M} \supset \mathcal{S}$ with the described property. Choose a point $A \in \mathcal{S}$ and any point $O$ such that $A O \| B C$ for some two points $B, C \in \mathcal{S}$. Now let $X^{\prime}$ be the point symmetric to $X$ with respect to $\underline{O}$, and $\mathcal{S}^{\prime}=\left\{X, X^{\prime} \mid X \in S\right\}$. Finally, take $\mathcal{M}=\left\{X, \bar{X} \mid X \in S^{\prime}\right\}$, where $\bar{X}$ denotes the point symmetric to $X$ with respect to $A$. This $\mathcal{M}$ has the desired property: If $X, Y \in \mathcal{M}$ and $Y \neq \bar{X}$, then $X Y \| \overline{X Y}$; otherwise, $X \bar{X}$, i.e., $X A$ is parallel to $X^{\prime} A^{\prime}$ if $X \neq A^{\prime}$, or to $B C$ otherwise.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
6. (POL 2) ${ }^{\mathrm{IMO} 2}$ Does there exist a finite set $M$ of points in space, not all in the same plane, such that for each two points $A, B \in M$ there exist two other points $C, D \in M$ such that lines $A B$ and $C D$ are parallel?
|
6. Yes. Take for $\mathcal{M}$ the set of vertices of a cube $A B C D E F G H$ and two points $I, J$ symmetric to the center $O$ of the cube with respect to the laterals $A B C D$ and $E F G H$. Remark. We prove a stronger result: Given an arbitrary finite set of points $\mathcal{S}$, then there is a finite set $\mathcal{M} \supset \mathcal{S}$ with the described property. Choose a point $A \in \mathcal{S}$ and any point $O$ such that $A O \| B C$ for some two points $B, C \in \mathcal{S}$. Now let $X^{\prime}$ be the point symmetric to $X$ with respect to $\underline{O}$, and $\mathcal{S}^{\prime}=\left\{X, X^{\prime} \mid X \in S\right\}$. Finally, take $\mathcal{M}=\left\{X, \bar{X} \mid X \in S^{\prime}\right\}$, where $\bar{X}$ denotes the point symmetric to $X$ with respect to $A$. This $\mathcal{M}$ has the desired property: If $X, Y \in \mathcal{M}$ and $Y \neq \bar{X}$, then $X Y \| \overline{X Y}$; otherwise, $X \bar{X}$, i.e., $X A$ is parallel to $X^{\prime} A^{\prime}$ if $X \neq A^{\prime}$, or to $B C$ otherwise.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f3e2c19a-512d-571f-837d-cc09434efa0d
| 24,993
|
12. II 6 (USS 1) In a certain language words are formed using an alphabet of three letters. Some words of two or more letters are not allowed, and any two such distinct words are of different lengths. Prove that one can form a word of arbitrary length that does not contain any nonallowed word.
|
12. We say that a word is good if it doesn't contain any nonallowed word. Let $a_{n}$ be the number of good words of length $n$. If we prolong any good word of length $n$ by adding one letter to its end (there are $3 a_{n}$ words that can be so obtained), we get either (i) a good word of length $n+1$, or (ii) an $(n+1)$-letter word of the form $X Y$, where $X$ is a good word and $Y$ a nonallowed word. The number of words of type (ii) with word $Y$ of length $k$ is exactly $a_{n+1-k}$; hence the total number of words of kind (ii) doesn't exceed $a_{n-1}+$ $\cdots+a_{1}+a_{0}$ (where $a_{0}=1$ ). Hence $$ a_{n+1} \geq 3 a_{n}-\left(a_{n-1}+\cdots+a_{1}+a_{0}\right), \quad a_{0}=1, a_{1}=3 $$ We prove by induction that $a_{n+1}>2 a_{n}$ for all $n$. For $n=1$ the claim is trivial. If it holds for $i \leq n$, then $a_{i} \leq 2^{i-n} a_{n}$; thus we obtain from (1) $$ a_{n+1}>a_{n}\left(3-\frac{1}{2}-\frac{1}{2^{2}}-\cdots-\frac{1}{2^{n}}\right)>2 a_{n} $$ Therefore $a_{n} \geq 2^{n}$ for all $n$ (moreover, one can show from (1) that $a_{n} \geq$ $(n+2) 2^{n-1}$ ); hence there exist good words of length $n$. Remark. If there are two nonallowed words (instead of one) of each length greater than 1, the statement of the problem need not remain true.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. II 6 (USS 1) In a certain language words are formed using an alphabet of three letters. Some words of two or more letters are not allowed, and any two such distinct words are of different lengths. Prove that one can form a word of arbitrary length that does not contain any nonallowed word.
|
12. We say that a word is good if it doesn't contain any nonallowed word. Let $a_{n}$ be the number of good words of length $n$. If we prolong any good word of length $n$ by adding one letter to its end (there are $3 a_{n}$ words that can be so obtained), we get either (i) a good word of length $n+1$, or (ii) an $(n+1)$-letter word of the form $X Y$, where $X$ is a good word and $Y$ a nonallowed word. The number of words of type (ii) with word $Y$ of length $k$ is exactly $a_{n+1-k}$; hence the total number of words of kind (ii) doesn't exceed $a_{n-1}+$ $\cdots+a_{1}+a_{0}$ (where $a_{0}=1$ ). Hence $$ a_{n+1} \geq 3 a_{n}-\left(a_{n-1}+\cdots+a_{1}+a_{0}\right), \quad a_{0}=1, a_{1}=3 $$ We prove by induction that $a_{n+1}>2 a_{n}$ for all $n$. For $n=1$ the claim is trivial. If it holds for $i \leq n$, then $a_{i} \leq 2^{i-n} a_{n}$; thus we obtain from (1) $$ a_{n+1}>a_{n}\left(3-\frac{1}{2}-\frac{1}{2^{2}}-\cdots-\frac{1}{2^{n}}\right)>2 a_{n} $$ Therefore $a_{n} \geq 2^{n}$ for all $n$ (moreover, one can show from (1) that $a_{n} \geq$ $(n+2) 2^{n-1}$ ); hence there exist good words of length $n$. Remark. If there are two nonallowed words (instead of one) of each length greater than 1, the statement of the problem need not remain true.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
65528e8e-4e7d-5545-b548-290582b2a6fd
| 25,013
|
3. I 3 (SWE 3) ${ }^{\mathrm{IMO}}$ Let $P(x)$ be a polynomial with integer coefficients. If $n(P)$ is the number of (distinct) integers $k$ such that $P^{2}(k)=1$, prove that $$ n(P)-\operatorname{deg}(P) \leq 2 $$ where $\operatorname{deg}(P)$ denotes the degree of the polynomial $P$.
|
3. For $\operatorname{deg}(P) \leq 2$ the statement is obvious, since $n(P) \leq \operatorname{deg}\left(P^{2}\right)=$ $2 \operatorname{deg}(P) \leq \operatorname{deg}(P)+2$ 。 Suppose now that $\operatorname{deg}(P) \geq 3$ and $n(P)>\operatorname{deg}(P)+2$. Then there is at least one integer $b$ for which $P(b)=-1$, and at least one $x$ with $P(x)=1$. We may assume w.l.o.g. that $b=0$ (if necessary, we consider the polynomial $P(x+b)$ instead). If $k_{1}, \ldots, k_{m}$ are all integers for which $P\left(k_{i}\right)=1$, then $P(x)=Q(x)\left(x-k_{1}\right) \cdots\left(x-k_{m}\right)+1$ for some polynomial $Q(x)$ with integer coefficients. Setting $x=0$ we obtain $(-1)^{m} Q(0) k_{1} \cdots k_{m}=1-P(0)=2$. It follows that $k_{1} \cdots k_{m} \mid 2$, and hence $m$ is at most 3 . The same holds for the polynomial $-P(x)$, and thus $P(x)=-1$ also has at most 3 integer solutions. This counts for 6 solutions of $P^{2}(x)=1$ in total, implying the statement for $\operatorname{deg}(P) \geq 4$. It remains to verify the statement for $n=3$. If $\operatorname{deg}(P)=3$ and $n(P)=6$, then it follows from the above consideration that $P(x)$ is either $-\left(x^{2}-\right.$ $1)(x-2)+1$ or $\left(x^{2}-1\right)(x+2)+1$. It is directly checked that $n(P)$ equals only 4 in both cases.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
3. I 3 (SWE 3) ${ }^{\mathrm{IMO}}$ Let $P(x)$ be a polynomial with integer coefficients. If $n(P)$ is the number of (distinct) integers $k$ such that $P^{2}(k)=1$, prove that $$ n(P)-\operatorname{deg}(P) \leq 2 $$ where $\operatorname{deg}(P)$ denotes the degree of the polynomial $P$.
|
3. For $\operatorname{deg}(P) \leq 2$ the statement is obvious, since $n(P) \leq \operatorname{deg}\left(P^{2}\right)=$ $2 \operatorname{deg}(P) \leq \operatorname{deg}(P)+2$ 。 Suppose now that $\operatorname{deg}(P) \geq 3$ and $n(P)>\operatorname{deg}(P)+2$. Then there is at least one integer $b$ for which $P(b)=-1$, and at least one $x$ with $P(x)=1$. We may assume w.l.o.g. that $b=0$ (if necessary, we consider the polynomial $P(x+b)$ instead). If $k_{1}, \ldots, k_{m}$ are all integers for which $P\left(k_{i}\right)=1$, then $P(x)=Q(x)\left(x-k_{1}\right) \cdots\left(x-k_{m}\right)+1$ for some polynomial $Q(x)$ with integer coefficients. Setting $x=0$ we obtain $(-1)^{m} Q(0) k_{1} \cdots k_{m}=1-P(0)=2$. It follows that $k_{1} \cdots k_{m} \mid 2$, and hence $m$ is at most 3 . The same holds for the polynomial $-P(x)$, and thus $P(x)=-1$ also has at most 3 integer solutions. This counts for 6 solutions of $P^{2}(x)=1$ in total, implying the statement for $\operatorname{deg}(P) \geq 4$. It remains to verify the statement for $n=3$. If $\operatorname{deg}(P)=3$ and $n(P)=6$, then it follows from the above consideration that $P(x)$ is either $-\left(x^{2}-\right.$ $1)(x-2)+1$ or $\left(x^{2}-1\right)(x+2)+1$. It is directly checked that $n(P)$ equals only 4 in both cases.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e6650f91-57ec-5dcf-bf24-0444a5aedac3
| 25,019
|
5. I 5 (GBR 3) Let $A_{r}, B_{r}, C_{r}$ be points on the circumference of a given circle $S$. From the triangle $A_{r} B_{r} C_{r}$, called $\triangle_{r}$, the triangle $\triangle_{r+1}$ is obtained by constructing the points $A_{r+1}, B_{r+1}, C_{r+1}$ on $S$ such that $A_{r+1} A_{r}$ is parallel to $B_{r} C_{r}, B_{r+1} B_{r}$ is parallel to $C_{r} A_{r}$, and $C_{r+1} C_{r}$ is parallel to $A_{r} B_{r}$. Each angle of $\triangle_{1}$ is an integer number of degrees and those integers are not multiples of 45 . Prove that at least two of the triangles $\triangle_{1}, \triangle_{2}, \ldots, \triangle_{15}$ are congruent.
|
5. All the angles are assumed to be oriented and measured modulo $180^{\circ}$. Denote by $\alpha_{i}, \beta_{i}, \gamma_{i}$ the angles of triangle $\triangle_{i}$, at $A_{i}, B_{i}, C_{i}$ respectively. Let us determine the angles of $\triangle_{i+1}$. If $D_{i}$ is the intersection of lines $B_{i} B_{i+1}$ and $C_{i} C_{i+1}$, we have $\angle B_{i+1} A_{i+1} C_{i+1}=\angle D_{i} B_{i} C_{i+1}=\angle B_{i} D_{i} C_{i+1}+$ $\angle D_{i} C_{i+1} B_{i}=\angle B_{i} D_{i} C_{i}-\angle B_{i} C_{i+1} C_{i}=-2 \angle B_{i} A_{i} C_{i}$. We conclude that $$ \alpha_{i+1}=-2 \alpha_{i}, \quad \text { and analogously } \quad \beta_{i+1}=-2 \beta_{i}, \quad \gamma_{i+1}=-2 \gamma_{i} $$ Therefore $\alpha_{r+t}=(-2)^{t} \alpha_{r}$. However, since $(-2)^{12} \equiv 1(\bmod 45)$ and consequently $(-2)^{14} \equiv(-2)^{2}(\bmod 180)$, it follows that $\alpha_{15}=\alpha_{3}$, since all values are modulo $180^{\circ}$. Analogously, $\beta_{15}=\beta_{3}$ and $\gamma_{15}=\gamma_{3}$, and moreover, $\triangle_{3}$ and $\triangle_{15}$ are inscribed in the same circle; hence $\triangle_{3} \cong \triangle_{15}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. I 5 (GBR 3) Let $A_{r}, B_{r}, C_{r}$ be points on the circumference of a given circle $S$. From the triangle $A_{r} B_{r} C_{r}$, called $\triangle_{r}$, the triangle $\triangle_{r+1}$ is obtained by constructing the points $A_{r+1}, B_{r+1}, C_{r+1}$ on $S$ such that $A_{r+1} A_{r}$ is parallel to $B_{r} C_{r}, B_{r+1} B_{r}$ is parallel to $C_{r} A_{r}$, and $C_{r+1} C_{r}$ is parallel to $A_{r} B_{r}$. Each angle of $\triangle_{1}$ is an integer number of degrees and those integers are not multiples of 45 . Prove that at least two of the triangles $\triangle_{1}, \triangle_{2}, \ldots, \triangle_{15}$ are congruent.
|
5. All the angles are assumed to be oriented and measured modulo $180^{\circ}$. Denote by $\alpha_{i}, \beta_{i}, \gamma_{i}$ the angles of triangle $\triangle_{i}$, at $A_{i}, B_{i}, C_{i}$ respectively. Let us determine the angles of $\triangle_{i+1}$. If $D_{i}$ is the intersection of lines $B_{i} B_{i+1}$ and $C_{i} C_{i+1}$, we have $\angle B_{i+1} A_{i+1} C_{i+1}=\angle D_{i} B_{i} C_{i+1}=\angle B_{i} D_{i} C_{i+1}+$ $\angle D_{i} C_{i+1} B_{i}=\angle B_{i} D_{i} C_{i}-\angle B_{i} C_{i+1} C_{i}=-2 \angle B_{i} A_{i} C_{i}$. We conclude that $$ \alpha_{i+1}=-2 \alpha_{i}, \quad \text { and analogously } \quad \beta_{i+1}=-2 \beta_{i}, \quad \gamma_{i+1}=-2 \gamma_{i} $$ Therefore $\alpha_{r+t}=(-2)^{t} \alpha_{r}$. However, since $(-2)^{12} \equiv 1(\bmod 45)$ and consequently $(-2)^{14} \equiv(-2)^{2}(\bmod 180)$, it follows that $\alpha_{15}=\alpha_{3}$, since all values are modulo $180^{\circ}$. Analogously, $\beta_{15}=\beta_{3}$ and $\gamma_{15}=\gamma_{3}$, and moreover, $\triangle_{3}$ and $\triangle_{15}$ are inscribed in the same circle; hence $\triangle_{3} \cong \triangle_{15}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
aaca697d-6e6a-5ba1-aa7e-6d475eaa43d1
| 25,025
|
7. II 1 (POL 2) Let $a_{i}, b_{i}$ be coprime positive integers for $i=1,2, \ldots, k$, and $m$ the least common multiple of $b_{1}, \ldots, b_{k}$. Prove that the greatest common divisor of $a_{1} \frac{m}{b_{1}}, \ldots, a_{k} \frac{m}{b_{k}}$ equals the greatest common divisor of $a_{1}, \ldots, a_{k}$.
|
7. Consider an arbitrary prime number $p$. If $p \mid m$, then there exists $b_{i}$ that is divisible by the same power of $p$ as $m$. Then $p$ divides neither $a_{i} \frac{m}{b_{i}}$ nor $a_{i}$, because $\left(a_{i}, b_{i}\right)=1$. If otherwise $p \nmid m$, then $\frac{m}{b_{i}}$ is not divisible by $p$ for any $i$, hence $p$ divides $a_{i}$ and $a_{i} \frac{m}{b_{i}}$ to the same power. Therefore $\left(a_{1}, \ldots, a_{k}\right)$ and $\left(a_{1} \frac{m}{b_{1}}, \ldots, a_{k} \frac{m}{b_{k}}\right)$ have the same factorization; hence they are equal. Second solution. For $k=2$ we easily verify the formula $\left(m \frac{a_{1}}{b_{1}}, m \frac{a_{2}}{b_{2}}\right)=$ $\frac{m}{b_{1} b_{2}}\left(a_{1} b_{2}, a_{2} b_{1}\right)=\frac{1}{b_{1} b_{2}}\left[b_{1}, b_{2}\right]\left(a_{1}, a_{2}\right)\left(b_{1}, b_{2}\right)=\left(a_{1}, a_{2}\right)$, since $\left[b_{1}, b_{2}\right]$. $\left(b_{1}, b_{2}\right)=b_{1} b_{2}$. We proceed by induction: $$ \begin{aligned} \left(a_{1} \frac{m}{b_{1}}, \ldots, a_{k} \frac{m}{b_{k}}, a_{k+1} \frac{m}{b_{k+1}}\right) & =\left(\frac{m}{\left[b_{1}, \ldots, b_{k}\right]}\left(a_{1}, \ldots, a_{k}\right), a_{k+1} \frac{m}{b_{k+1}}\right) \\ & =\left(a_{1}, \ldots, a_{k}, a_{k+1}\right) . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
7. II 1 (POL 2) Let $a_{i}, b_{i}$ be coprime positive integers for $i=1,2, \ldots, k$, and $m$ the least common multiple of $b_{1}, \ldots, b_{k}$. Prove that the greatest common divisor of $a_{1} \frac{m}{b_{1}}, \ldots, a_{k} \frac{m}{b_{k}}$ equals the greatest common divisor of $a_{1}, \ldots, a_{k}$.
|
7. Consider an arbitrary prime number $p$. If $p \mid m$, then there exists $b_{i}$ that is divisible by the same power of $p$ as $m$. Then $p$ divides neither $a_{i} \frac{m}{b_{i}}$ nor $a_{i}$, because $\left(a_{i}, b_{i}\right)=1$. If otherwise $p \nmid m$, then $\frac{m}{b_{i}}$ is not divisible by $p$ for any $i$, hence $p$ divides $a_{i}$ and $a_{i} \frac{m}{b_{i}}$ to the same power. Therefore $\left(a_{1}, \ldots, a_{k}\right)$ and $\left(a_{1} \frac{m}{b_{1}}, \ldots, a_{k} \frac{m}{b_{k}}\right)$ have the same factorization; hence they are equal. Second solution. For $k=2$ we easily verify the formula $\left(m \frac{a_{1}}{b_{1}}, m \frac{a_{2}}{b_{2}}\right)=$ $\frac{m}{b_{1} b_{2}}\left(a_{1} b_{2}, a_{2} b_{1}\right)=\frac{1}{b_{1} b_{2}}\left[b_{1}, b_{2}\right]\left(a_{1}, a_{2}\right)\left(b_{1}, b_{2}\right)=\left(a_{1}, a_{2}\right)$, since $\left[b_{1}, b_{2}\right]$. $\left(b_{1}, b_{2}\right)=b_{1} b_{2}$. We proceed by induction: $$ \begin{aligned} \left(a_{1} \frac{m}{b_{1}}, \ldots, a_{k} \frac{m}{b_{k}}, a_{k+1} \frac{m}{b_{k+1}}\right) & =\left(\frac{m}{\left[b_{1}, \ldots, b_{k}\right]}\left(a_{1}, \ldots, a_{k}\right), a_{k+1} \frac{m}{b_{k+1}}\right) \\ & =\left(a_{1}, \ldots, a_{k}, a_{k+1}\right) . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4be59465-1b34-594f-8749-7c6efd4beb00
| 25,030
|
9. II 3 (CUB 3) Let $x, y, z$ be real numbers each of whose absolute value is different from $1 / \sqrt{3}$ such that $x+y+z=x y z$. Prove that $$ \frac{3 x-x^{3}}{1-3 x^{2}}+\frac{3 y-y^{3}}{1-3 y^{2}}+\frac{3 z-z^{3}}{1-3 z^{2}}=\frac{3 x-x^{3}}{1-3 x^{2}} \cdot \frac{3 y-y^{3}}{1-3 y^{2}} \cdot \frac{3 z-z^{3}}{1-3 z^{2}} $$
|
9. There exist real numbers $a, b, c$ with $\tan a=x, \tan b=y, \tan c=z$. Then using the additive formula for tangents we obtain $$ \tan (a+b+c)=\frac{x+y+z-x y z}{1-x y-x z-y z} $$ We are given that $x y z=x+y+z$. In this case $x y+y z+z x=1$ is impossible; otherwise, $x, y, z$ would be the zeros of a cubic polynomial $t^{3}-\lambda t^{2}+t-\lambda=\left(t^{2}+1\right)(t-\lambda)$ (where $\left.\lambda=x y z\right)$, which has only one real root. It follows that $$ x+y+z=x y z \Longleftrightarrow \tan (a+b+c)=0 . $$ Hence $a+b+c=k \pi$ for some $k \in \mathbb{Z}$. We note that $\frac{3 x-x^{3}}{1-3 x^{2}}$ actually expresses $\tan 3 a$. Since $3 a+3 b+3 c=3 k \pi$, the result follows from (1) for the numbers $\frac{3 x-x^{3}}{1-3 x^{2}}, \frac{3 y-y^{3}}{1-3 y^{2}}, \frac{3 z-z^{3}}{1-3 z^{2}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
9. II 3 (CUB 3) Let $x, y, z$ be real numbers each of whose absolute value is different from $1 / \sqrt{3}$ such that $x+y+z=x y z$. Prove that $$ \frac{3 x-x^{3}}{1-3 x^{2}}+\frac{3 y-y^{3}}{1-3 y^{2}}+\frac{3 z-z^{3}}{1-3 z^{2}}=\frac{3 x-x^{3}}{1-3 x^{2}} \cdot \frac{3 y-y^{3}}{1-3 y^{2}} \cdot \frac{3 z-z^{3}}{1-3 z^{2}} $$
|
9. There exist real numbers $a, b, c$ with $\tan a=x, \tan b=y, \tan c=z$. Then using the additive formula for tangents we obtain $$ \tan (a+b+c)=\frac{x+y+z-x y z}{1-x y-x z-y z} $$ We are given that $x y z=x+y+z$. In this case $x y+y z+z x=1$ is impossible; otherwise, $x, y, z$ would be the zeros of a cubic polynomial $t^{3}-\lambda t^{2}+t-\lambda=\left(t^{2}+1\right)(t-\lambda)$ (where $\left.\lambda=x y z\right)$, which has only one real root. It follows that $$ x+y+z=x y z \Longleftrightarrow \tan (a+b+c)=0 . $$ Hence $a+b+c=k \pi$ for some $k \in \mathbb{Z}$. We note that $\frac{3 x-x^{3}}{1-3 x^{2}}$ actually expresses $\tan 3 a$. Since $3 a+3 b+3 c=3 k \pi$, the result follows from (1) for the numbers $\frac{3 x-x^{3}}{1-3 x^{2}}, \frac{3 y-y^{3}}{1-3 y^{2}}, \frac{3 z-z^{3}}{1-3 z^{2}}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b116ed54-b962-51f7-b740-e323b6578358
| 25,035
|
11. $(\mathbf{G B R})^{\mathrm{IMO} 2}$ Let $a_{1}, a_{2}, a_{3}, \ldots$ be any infinite increasing sequence of positive integers. (For every integer $i>0, a_{i+1}>a_{i}$.) Prove that there are infinitely many $m$ for which positive integers $x, y, h, k$ can be found such that $0<h<k<m$ and $a_{m}=x a_{h}+y a_{k}$.
|
11. Let $\left(a_{k_{i}}\right)$ be the subsequence of $\left(a_{k}\right)$ consisting of all $a_{k}$ 's that give remainder $r$ upon division by $a_{1}$. For every $i>1, a_{k_{i}} \equiv a_{k_{1}}\left(\bmod a_{1}\right)$; hence $a_{k_{i}}=a_{k_{1}}+y a_{1}$ for some integer $y>0$. It follows that for every $r=0,1, \ldots, a_{1}-1$ there is exactly one member of the corresponding $\left(a_{k_{i}}\right)_{i \geq 1}$ that cannot be represented as $x a_{l}+y a_{m}$, and hence at most $a_{1}+1$ members of $\left(a_{k}\right)$ in total are not representable in the given form.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
11. $(\mathbf{G B R})^{\mathrm{IMO} 2}$ Let $a_{1}, a_{2}, a_{3}, \ldots$ be any infinite increasing sequence of positive integers. (For every integer $i>0, a_{i+1}>a_{i}$.) Prove that there are infinitely many $m$ for which positive integers $x, y, h, k$ can be found such that $0<h<k<m$ and $a_{m}=x a_{h}+y a_{k}$.
|
11. Let $\left(a_{k_{i}}\right)$ be the subsequence of $\left(a_{k}\right)$ consisting of all $a_{k}$ 's that give remainder $r$ upon division by $a_{1}$. For every $i>1, a_{k_{i}} \equiv a_{k_{1}}\left(\bmod a_{1}\right)$; hence $a_{k_{i}}=a_{k_{1}}+y a_{1}$ for some integer $y>0$. It follows that for every $r=0,1, \ldots, a_{1}-1$ there is exactly one member of the corresponding $\left(a_{k_{i}}\right)_{i \geq 1}$ that cannot be represented as $x a_{l}+y a_{m}$, and hence at most $a_{1}+1$ members of $\left(a_{k}\right)$ in total are not representable in the given form.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
43f050a2-fd15-58db-a7b5-f55c3f198676
| 25,043
|
12. (GRE) Consider on the first quadrant of the trigonometric circle the $\operatorname{arcs} A M_{1}=x_{1}, A M_{2}=x_{2}, A M_{3}=x_{3}, \ldots, A M_{\nu}=x_{\nu}$, such that $x_{1}<$ $x_{2}<x_{3}<\cdots<x_{\nu}$. Prove that $$ \sum_{i=0}^{\nu-1} \sin 2 x_{i}-\sum_{i=0}^{\nu-1} \sin \left(x_{i}-x_{i+1}\right)<\frac{\pi}{2}+\sum_{i=0}^{\nu-1} \sin \left(x_{i}+x_{i+1}\right) $$
|
12. Since $\sin 2 x_{i}=2 \sin x_{i} \cos x_{i}$ and $\sin \left(x_{i}+x_{i+1}\right)+\sin \left(x_{i}-x_{i+1}\right)=$ $2 \sin x_{i} \cos x_{i+1}$, the inequality from the problem is equivalent to $$ \begin{gathered} \left(\cos x_{1}-\cos x_{2}\right) \sin x_{1}+\left(\cos x_{2}-\cos x_{3}\right) \sin x_{2}+\cdots \\ \cdots+\left(\cos x_{\nu-1}-\cos x_{\nu}\right) \sin x_{\nu-1}<\frac{\pi}{4} \end{gathered} $$ Consider the unit circle with center at $O(0,0)$ and points $M_{i}\left(\cos x_{i}, \sin x_{i}\right)$ on it. Also, choose the points $N_{i}\left(\cos x_{i}, 0\right)$ and $M_{i}^{\prime}\left(\cos x_{i+1}, \sin x_{i}\right)$. It is clear that $\left(\cos x_{i}-\cos x_{i+1}\right) \sin x_{i}$ is equal to the area of the rectangle $M_{i} N_{i} N_{i+1} M_{i}^{\prime}$. Since all these rectangles are disjoint and lie inside the quarter circle in the first quadrant whose area is $\frac{\pi}{4}$, inequality (1) follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
12. (GRE) Consider on the first quadrant of the trigonometric circle the $\operatorname{arcs} A M_{1}=x_{1}, A M_{2}=x_{2}, A M_{3}=x_{3}, \ldots, A M_{\nu}=x_{\nu}$, such that $x_{1}<$ $x_{2}<x_{3}<\cdots<x_{\nu}$. Prove that $$ \sum_{i=0}^{\nu-1} \sin 2 x_{i}-\sum_{i=0}^{\nu-1} \sin \left(x_{i}-x_{i+1}\right)<\frac{\pi}{2}+\sum_{i=0}^{\nu-1} \sin \left(x_{i}+x_{i+1}\right) $$
|
12. Since $\sin 2 x_{i}=2 \sin x_{i} \cos x_{i}$ and $\sin \left(x_{i}+x_{i+1}\right)+\sin \left(x_{i}-x_{i+1}\right)=$ $2 \sin x_{i} \cos x_{i+1}$, the inequality from the problem is equivalent to $$ \begin{gathered} \left(\cos x_{1}-\cos x_{2}\right) \sin x_{1}+\left(\cos x_{2}-\cos x_{3}\right) \sin x_{2}+\cdots \\ \cdots+\left(\cos x_{\nu-1}-\cos x_{\nu}\right) \sin x_{\nu-1}<\frac{\pi}{4} \end{gathered} $$ Consider the unit circle with center at $O(0,0)$ and points $M_{i}\left(\cos x_{i}, \sin x_{i}\right)$ on it. Also, choose the points $N_{i}\left(\cos x_{i}, 0\right)$ and $M_{i}^{\prime}\left(\cos x_{i+1}, \sin x_{i}\right)$. It is clear that $\left(\cos x_{i}-\cos x_{i+1}\right) \sin x_{i}$ is equal to the area of the rectangle $M_{i} N_{i} N_{i+1} M_{i}^{\prime}$. Since all these rectangles are disjoint and lie inside the quarter circle in the first quadrant whose area is $\frac{\pi}{4}$, inequality (1) follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ebcef6be-d88a-52f9-bb72-862392bb9309
| 25,046
|
13. (ROM) Let $A_{0}, A_{1}, \ldots, A_{n}$ be points in a plane such that (i) $A_{0} A_{1} \leq \frac{1}{2} A_{1} A_{2} \leq \cdots \leq \frac{1}{2^{n-1}} A_{n-1} A_{n}$ and (ii) $0<\measuredangle A_{0} A_{1} A_{2}<\measuredangle A_{1} A_{2} A_{3}<\cdots<\measuredangle A_{n-2} A_{n-1} A_{n}<180^{\circ}$, where all these angles have the same orientation. Prove that the segments $A_{k} A_{k+1}, A_{m} A_{m+1}$ do not intersect for each $k$ and $n$ such that $0 \leq k \leq$ $m-2<n-2$.
|
13. Suppose that $A_{k} A_{k+1} \cap A_{m} A_{m+1} \neq \emptyset$ for some $k, m>k+1$. Without loss of generality we may suppose that $k=0, m=n-1$ and that no two segments $A_{k} A_{k+1}$ and $A_{m} A_{m+1}$ intersect for $0 \leq k<m-1<n-1$ except for $k=0, m=n-1$. Also, shortening $A_{0} A_{1}$, we may suppose that $A_{0} \in A_{n-1} A_{n}$. Finally, we may reduce the problem to the case that $A_{0} \ldots A_{n-1}$ is convex: Otherwise, the segment $A_{n-1} A_{n}$ can be prolonged so that it intersects some $A_{k} A_{k+1}, 0<k<n-2$. If $n=3$, then $A_{1} A_{2} \geq 2 A_{0} A_{1}$ implies $A_{0} A_{2}>A_{0} A_{1}$, hence $\angle A_{0} A_{1} A_{2}>$ $\angle A_{1} A_{2} A_{3}$, a contradiction. Let $n=4$. From $A_{3} A_{2}>A_{1} A_{2}$ we conclude that $\angle A_{3} A_{1} A_{2}>\angle A_{1} A_{3} A_{2}$. Using the inequality $\angle A_{0} A_{3} A_{2}>\angle A_{0} A_{1} A_{2}$ we obtain that $\angle A_{0} A_{3} A_{1}>$ $\angle A_{0} A_{1} A_{3}$ implying $A_{0} A_{1}>A_{0} A_{3}$. Now we have $A_{2} A_{3}<A_{3} A_{0}+A_{0} A_{1}+$ $A_{1} A_{2}<2 A_{0} A_{1}+A_{1} A_{2} \leq 2 A_{1} A_{2} \leq A_{2} A_{3}$, which is not possible. Now suppose $n \geq 5$. If $\alpha_{i}$ is the exterior angle at $A_{i}$, then $\alpha_{1}>\cdots>\alpha_{n-1}$; hence $\alpha_{n-1}<\frac{360^{\circ}}{n-1} \leq 90^{\circ}$. Consequently $\angle A_{n-2} A_{n-1} A_{0} \geq 90^{\circ}$ and $A_{0} A_{n-2}>A_{n-1} A_{n-2}$. On the other hand, $A_{0} A_{n-2}<A_{0} A_{1}+A_{1} A_{2}+\cdots+$ $A_{n-3} A_{n-2}<\left(\frac{1}{2^{n-2}}+\frac{1}{2^{n-3}}+\cdots+\frac{1}{2}\right) A_{n-1} A_{n-2}<A_{n-1} A_{n-2}$, which contradicts the previous relation.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. (ROM) Let $A_{0}, A_{1}, \ldots, A_{n}$ be points in a plane such that (i) $A_{0} A_{1} \leq \frac{1}{2} A_{1} A_{2} \leq \cdots \leq \frac{1}{2^{n-1}} A_{n-1} A_{n}$ and (ii) $0<\measuredangle A_{0} A_{1} A_{2}<\measuredangle A_{1} A_{2} A_{3}<\cdots<\measuredangle A_{n-2} A_{n-1} A_{n}<180^{\circ}$, where all these angles have the same orientation. Prove that the segments $A_{k} A_{k+1}, A_{m} A_{m+1}$ do not intersect for each $k$ and $n$ such that $0 \leq k \leq$ $m-2<n-2$.
|
13. Suppose that $A_{k} A_{k+1} \cap A_{m} A_{m+1} \neq \emptyset$ for some $k, m>k+1$. Without loss of generality we may suppose that $k=0, m=n-1$ and that no two segments $A_{k} A_{k+1}$ and $A_{m} A_{m+1}$ intersect for $0 \leq k<m-1<n-1$ except for $k=0, m=n-1$. Also, shortening $A_{0} A_{1}$, we may suppose that $A_{0} \in A_{n-1} A_{n}$. Finally, we may reduce the problem to the case that $A_{0} \ldots A_{n-1}$ is convex: Otherwise, the segment $A_{n-1} A_{n}$ can be prolonged so that it intersects some $A_{k} A_{k+1}, 0<k<n-2$. If $n=3$, then $A_{1} A_{2} \geq 2 A_{0} A_{1}$ implies $A_{0} A_{2}>A_{0} A_{1}$, hence $\angle A_{0} A_{1} A_{2}>$ $\angle A_{1} A_{2} A_{3}$, a contradiction. Let $n=4$. From $A_{3} A_{2}>A_{1} A_{2}$ we conclude that $\angle A_{3} A_{1} A_{2}>\angle A_{1} A_{3} A_{2}$. Using the inequality $\angle A_{0} A_{3} A_{2}>\angle A_{0} A_{1} A_{2}$ we obtain that $\angle A_{0} A_{3} A_{1}>$ $\angle A_{0} A_{1} A_{3}$ implying $A_{0} A_{1}>A_{0} A_{3}$. Now we have $A_{2} A_{3}<A_{3} A_{0}+A_{0} A_{1}+$ $A_{1} A_{2}<2 A_{0} A_{1}+A_{1} A_{2} \leq 2 A_{1} A_{2} \leq A_{2} A_{3}$, which is not possible. Now suppose $n \geq 5$. If $\alpha_{i}$ is the exterior angle at $A_{i}$, then $\alpha_{1}>\cdots>\alpha_{n-1}$; hence $\alpha_{n-1}<\frac{360^{\circ}}{n-1} \leq 90^{\circ}$. Consequently $\angle A_{n-2} A_{n-1} A_{0} \geq 90^{\circ}$ and $A_{0} A_{n-2}>A_{n-1} A_{n-2}$. On the other hand, $A_{0} A_{n-2}<A_{0} A_{1}+A_{1} A_{2}+\cdots+$ $A_{n-3} A_{n-2}<\left(\frac{1}{2^{n-2}}+\frac{1}{2^{n-3}}+\cdots+\frac{1}{2}\right) A_{n-1} A_{n-2}<A_{n-1} A_{n-2}$, which contradicts the previous relation.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
42aa11ca-1850-54f6-9f11-431d9d0cf2d6
| 25,049
|
14. (YUG) Let $x_{0}=5$ and $x_{n+1}=x_{n}+\frac{1}{x_{n}}(n=0,1,2, \ldots)$. Prove that $45<x_{1000}<45,1$.
|
14. We shall prove that for every $n \in \mathbb{N}, \sqrt{2 n+25} \leq x_{n} \leq \sqrt{2 n+25}+0.1$. Note that for $n=1000$ this gives us exactly the desired inequalities. First, notice that the recurrent relation is equivalent to $$ 2 x_{k}\left(x_{k+1}-x_{k}\right)=2 $$ Since $x_{0}<x_{1}<\cdots<x_{k}<\cdots$, from (1) we get $x_{k+1}^{2}-x_{k}^{2}=\left(x_{k+1}+\right.$ $\left.x_{k}\right)\left(x_{k+1}-x_{k}\right)>2$. Adding these up we obtain $x_{n}^{2} \geq x_{0}^{2}+2 n$, which proves the first inequality. On the other hand, $x_{k+1}=x_{k}+\frac{1}{x_{k}} \leq x_{k}+0.2$ (for $x_{k} \geq 5$ ), and one also deduces from (1) that $x_{k+1}^{2}-x_{k}^{2}-0.2\left(x_{k+1}-x_{k}\right)=\left(x_{k+1}+x_{k}-\right.$ $0.2)\left(x_{k+1}-x_{k}\right) \leq 2$. Again, adding these inequalities up, $(k=0, \ldots, n-1)$ yields $$ x_{n}^{2} \leq 2 n+x_{0}^{2}+0.2\left(x_{n}-x_{0}\right)=2 n+24+0.2 x_{n} $$ Solving the corresponding quadratic equation, we obtain $x_{n}<0.1+$ $\sqrt{2 n+24.01}<0.1++\sqrt{2 n+25}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
14. (YUG) Let $x_{0}=5$ and $x_{n+1}=x_{n}+\frac{1}{x_{n}}(n=0,1,2, \ldots)$. Prove that $45<x_{1000}<45,1$.
|
14. We shall prove that for every $n \in \mathbb{N}, \sqrt{2 n+25} \leq x_{n} \leq \sqrt{2 n+25}+0.1$. Note that for $n=1000$ this gives us exactly the desired inequalities. First, notice that the recurrent relation is equivalent to $$ 2 x_{k}\left(x_{k+1}-x_{k}\right)=2 $$ Since $x_{0}<x_{1}<\cdots<x_{k}<\cdots$, from (1) we get $x_{k+1}^{2}-x_{k}^{2}=\left(x_{k+1}+\right.$ $\left.x_{k}\right)\left(x_{k+1}-x_{k}\right)>2$. Adding these up we obtain $x_{n}^{2} \geq x_{0}^{2}+2 n$, which proves the first inequality. On the other hand, $x_{k+1}=x_{k}+\frac{1}{x_{k}} \leq x_{k}+0.2$ (for $x_{k} \geq 5$ ), and one also deduces from (1) that $x_{k+1}^{2}-x_{k}^{2}-0.2\left(x_{k+1}-x_{k}\right)=\left(x_{k+1}+x_{k}-\right.$ $0.2)\left(x_{k+1}-x_{k}\right) \leq 2$. Again, adding these inequalities up, $(k=0, \ldots, n-1)$ yields $$ x_{n}^{2} \leq 2 n+x_{0}^{2}+0.2\left(x_{n}-x_{0}\right)=2 n+24+0.2 x_{n} $$ Solving the corresponding quadratic equation, we obtain $x_{n}<0.1+$ $\sqrt{2 n+24.01}<0.1++\sqrt{2 n+25}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
11231c9b-1998-564e-a1f6-77d9889ea574
| 25,051
|
15. (USS) ${ }^{\mathrm{IMO} 5}$ Is it possible to plot 1975 points on a circle with radius 1 so that the distance between any two of them is a rational number (distances have to be measured by chords)?
|
15. Assume that the center of the circle is at the origin $O(0,0)$, and that the points $A_{1}, A_{2}, \ldots, A_{1975}$ are arranged on the upper half-circle so that $\angle A_{i} O A_{1}=\alpha_{i}\left(\alpha_{1}=0\right)$. The distance $A_{i} A_{j}$ equals $2 \sin \frac{\alpha_{j}-\alpha_{i}}{2}=$ $2 \sin \frac{\alpha_{j}}{2} \cos \frac{\alpha_{i}}{2}-\cos \frac{\alpha_{j}}{2} \sin \frac{\alpha_{i}}{2}$, and it will be rational if all $\sin \frac{\alpha_{k}}{2}, \cos \frac{\alpha_{k}}{2}$ are rational. Finally, observe that there exist infinitely many angles $\alpha$ such that both $\sin \alpha, \cos \alpha$ are rational, and that such $\alpha$ can be arbitrarily small. For example, take $\alpha$ so that $\sin \alpha=\frac{2 t}{t^{2}+1}$ and $\cos \alpha=\frac{t^{2}-1}{t^{2}+1}$ for any $t \in \mathbb{Q}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
15. (USS) ${ }^{\mathrm{IMO} 5}$ Is it possible to plot 1975 points on a circle with radius 1 so that the distance between any two of them is a rational number (distances have to be measured by chords)?
|
15. Assume that the center of the circle is at the origin $O(0,0)$, and that the points $A_{1}, A_{2}, \ldots, A_{1975}$ are arranged on the upper half-circle so that $\angle A_{i} O A_{1}=\alpha_{i}\left(\alpha_{1}=0\right)$. The distance $A_{i} A_{j}$ equals $2 \sin \frac{\alpha_{j}-\alpha_{i}}{2}=$ $2 \sin \frac{\alpha_{j}}{2} \cos \frac{\alpha_{i}}{2}-\cos \frac{\alpha_{j}}{2} \sin \frac{\alpha_{i}}{2}$, and it will be rational if all $\sin \frac{\alpha_{k}}{2}, \cos \frac{\alpha_{k}}{2}$ are rational. Finally, observe that there exist infinitely many angles $\alpha$ such that both $\sin \alpha, \cos \alpha$ are rational, and that such $\alpha$ can be arbitrarily small. For example, take $\alpha$ so that $\sin \alpha=\frac{2 t}{t^{2}+1}$ and $\cos \alpha=\frac{t^{2}-1}{t^{2}+1}$ for any $t \in \mathbb{Q}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0c6b155-6efd-5925-916e-c54dc0534eb3
| 25,054
|
2. (CZS) ${ }^{\mathrm{IMO} 1}$ Let $x_{1} \geq x_{2} \geq \cdots \geq x_{n}$ and $y_{1} \geq y_{2} \geq \cdots \geq y_{n}$ be two $n$-tuples of numbers. Prove that $$ \sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2} \leq \sum_{i=1}^{n}\left(x_{i}-z_{i}\right)^{2} $$ is true when $z_{1}, z_{2}, \ldots, z_{n}$ denote $y_{1}, y_{2}, \ldots, y_{n}$ taken in another order.
|
2. Since there are finitely many arrangements of the $z_{i}$ 's, assume that $z_{1}, \ldots, z_{n}$ is the one for which $\sum_{i=1}^{n}\left(x_{i}-z_{i}\right)^{2}$ is minimal. We claim that in this case $i<j \Rightarrow z_{i} \geq z_{j}$, from which the claim of the problem directly follows. Indeed, otherwise we would have $$ \begin{aligned} \left(x_{i}-z_{j}\right)^{2}+\left(x_{j}-z_{i}\right)^{2}= & \left(x_{i}-z_{i}\right)^{2}+\left(x_{j}-z_{j}\right)^{2} \\ & +2\left(x_{i} z_{i}+x_{j} z_{j}-x_{i} z_{j}-x_{j} z_{i}\right) \\ = & \left(x_{i}-z_{i}\right)^{2}+\left(x_{j}-z_{j}\right)^{2}+2\left(x_{i}-x_{j}\right)\left(z_{i}-z_{j}\right) \\ \leq & \left(x_{i}-z_{i}\right)^{2}+\left(x_{j}-z_{j}\right)^{2} \end{aligned} $$ contradicting the assumption.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
2. (CZS) ${ }^{\mathrm{IMO} 1}$ Let $x_{1} \geq x_{2} \geq \cdots \geq x_{n}$ and $y_{1} \geq y_{2} \geq \cdots \geq y_{n}$ be two $n$-tuples of numbers. Prove that $$ \sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2} \leq \sum_{i=1}^{n}\left(x_{i}-z_{i}\right)^{2} $$ is true when $z_{1}, z_{2}, \ldots, z_{n}$ denote $y_{1}, y_{2}, \ldots, y_{n}$ taken in another order.
|
2. Since there are finitely many arrangements of the $z_{i}$ 's, assume that $z_{1}, \ldots, z_{n}$ is the one for which $\sum_{i=1}^{n}\left(x_{i}-z_{i}\right)^{2}$ is minimal. We claim that in this case $i<j \Rightarrow z_{i} \geq z_{j}$, from which the claim of the problem directly follows. Indeed, otherwise we would have $$ \begin{aligned} \left(x_{i}-z_{j}\right)^{2}+\left(x_{j}-z_{i}\right)^{2}= & \left(x_{i}-z_{i}\right)^{2}+\left(x_{j}-z_{j}\right)^{2} \\ & +2\left(x_{i} z_{i}+x_{j} z_{j}-x_{i} z_{j}-x_{j} z_{i}\right) \\ = & \left(x_{i}-z_{i}\right)^{2}+\left(x_{j}-z_{j}\right)^{2}+2\left(x_{i}-x_{j}\right)\left(z_{i}-z_{j}\right) \\ \leq & \left(x_{i}-z_{i}\right)^{2}+\left(x_{j}-z_{j}\right)^{2} \end{aligned} $$ contradicting the assumption.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4ff135b4-3c04-541a-abc7-c40eb28db586
| 25,057
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.