problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $A B C$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\Theta$. Show that the circumcircle of the triangle $\Theta$ is tangent to $\omega$. (Denmark) Preamble. Let $X=y \cap z, Y=x \cap z, Z=x \cap y$ and let $\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\Delta$ and $\delta$ inscribed into $\Omega$ and $\omega$, respectively. In order to prove that $\Omega$ and $\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\Delta$ to $\delta$ lies on $\omega$ (or $\Omega$ ), or, in other words, to show that $\Delta$ and $\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\omega$ (or $\Omega$ ). We use directed angles throughout all the solutions.
|
Claim 1. The reflections $\ell_{a}, \ell_{b}$ and $\ell_{c}$ of the line $\ell$ in the lines $x, y$, and $z$, respectively, are concurrent at a point $T$ which belongs to $\omega$. 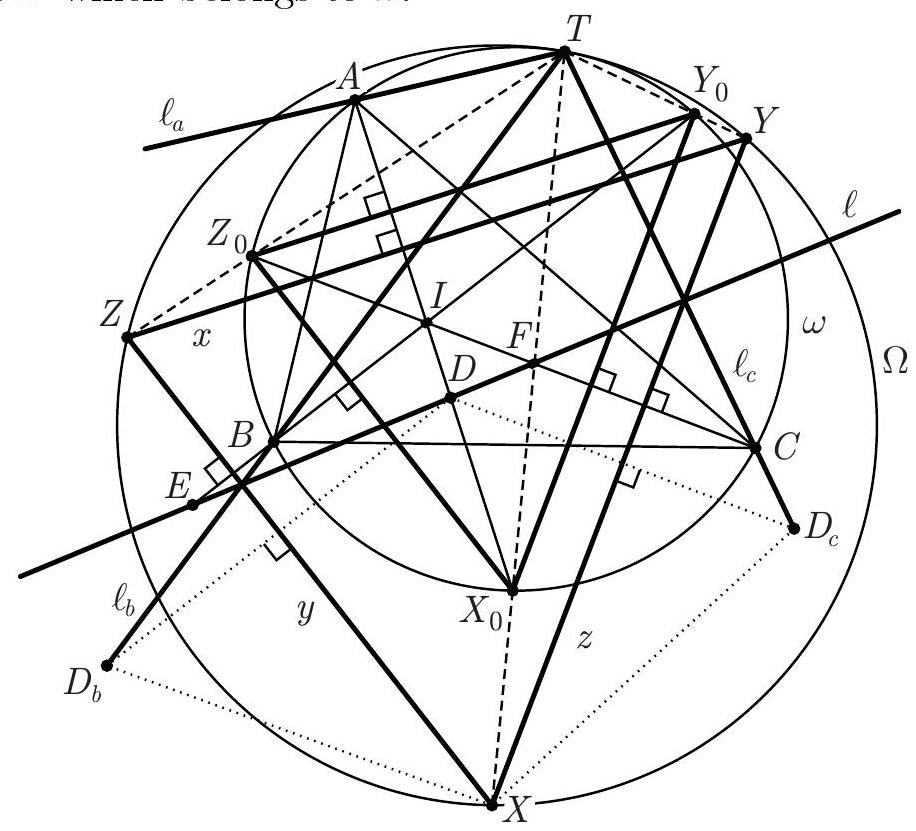 Proof. Notice that $\Varangle\left(\ell_{b}, \ell_{c}\right)=\Varangle\left(\ell_{b}, \ell\right)+\Varangle\left(\ell, \ell_{c}\right)=2 \Varangle(y, \ell)+2 \Varangle(\ell, z)=2 \Varangle(y, z)$. But $y \perp B I$ and $z \perp C I$ implies $\Varangle(y, z)=\Varangle(B I, I C)$, so, since $2 \Varangle(B I, I C)=\Varangle(B A, A C)$, we obtain $$ \Varangle\left(\ell_{b}, \ell_{c}\right)=\Varangle(B A, A C) . $$ Since $A$ is the reflection of $D$ in $x$, $A$ belongs to $\ell_{a}$; similarly, $B$ belongs to $\ell_{b}$. Then (1) shows that the common point $T^{\prime}$ of $\ell_{a}$ and $\ell_{b}$ lies on $\omega$; similarly, the common point $T^{\prime \prime}$ of $\ell_{c}$ and $\ell_{b}$ lies on $\omega$. If $B \notin \ell_{a}$ and $B \notin \ell_{c}$, then $T^{\prime}$ and $T^{\prime \prime}$ are the second point of intersection of $\ell_{b}$ and $\omega$, hence they coincide. Otherwise, if, say, $B \in \ell_{c}$, then $\ell_{c}=B C$, so $\Varangle(B A, A C)=\Varangle\left(\ell_{b}, \ell_{c}\right)=\Varangle\left(\ell_{b}, B C\right)$, which shows that $\ell_{b}$ is tangent at $B$ to $\omega$ and $T^{\prime}=T^{\prime \prime}=B$. So $T^{\prime}$ and $T^{\prime \prime}$ coincide in all the cases, and the conclusion of the claim follows. Now we prove that $X, X_{0}, T$ are collinear. Denote by $D_{b}$ and $D_{c}$ the reflections of the point $D$ in the lines $y$ and $z$, respectively. Then $D_{b}$ lies on $\ell_{b}, D_{c}$ lies on $\ell_{c}$, and $$ \begin{aligned} \Varangle\left(D_{b} X, X D_{c}\right) & =\Varangle\left(D_{b} X, D X\right)+\Varangle\left(D X, X D_{c}\right)=2 \Varangle(y, D X)+2 \Varangle(D X, z)=2 \Varangle(y, z) \\ & =\Varangle(B A, A C)=\Varangle(B T, T C), \end{aligned} $$ hence the quadrilateral $X D_{b} T D_{c}$ is cyclic. Notice also that since $X D_{b}=X D=X D_{c}$, the points $D, D_{b}, D_{c}$ lie on a circle with centre $X$. Using in this circle the diameter $D_{c} D_{c}^{\prime}$ yields $\Varangle\left(D_{b} D_{c}, D_{c} X\right)=90^{\circ}+\Varangle\left(D_{b} D_{c}^{\prime}, D_{c}^{\prime} X\right)=90^{\circ}+\Varangle\left(D_{b} D, D D_{c}\right)$. Therefore, $$ \begin{gathered} \Varangle\left(\ell_{b}, X T\right)=\Varangle\left(D_{b} T, X T\right)=\Varangle\left(D_{b} D_{c}, D_{c} X\right)=90^{\circ}+\Varangle\left(D_{b} D, D D_{c}\right) \\ =90^{\circ}+\Varangle(B I, I C)=\Varangle(B A, A I)=\Varangle\left(B A, A X_{0}\right)=\Varangle\left(B T, T X_{0}\right)=\Varangle\left(\ell_{b}, X_{0} T\right) \end{gathered} $$ so the points $X, X_{0}, T$ are collinear. By a similar argument, $Y, Y_{0}, T$ and $Z, Z_{0}, T$ are collinear. As mentioned in the preamble, the statement of the problem follows. Comment 1. After proving Claim 1 one may proceed in another way. As it was shown, the reflections of $\ell$ in the sidelines of $X Y Z$ are concurrent at $T$. Thus $\ell$ is the Steiner line of $T$ with respect to $\triangle X Y Z$ (that is the line containing the reflections $T_{a}, T_{b}, T_{c}$ of $T$ in the sidelines of $X Y Z$ ). The properties of the Steiner line imply that $T$ lies on $\Omega$, and $\ell$ passes through the orthocentre $H$ of the triangle $X Y Z$. 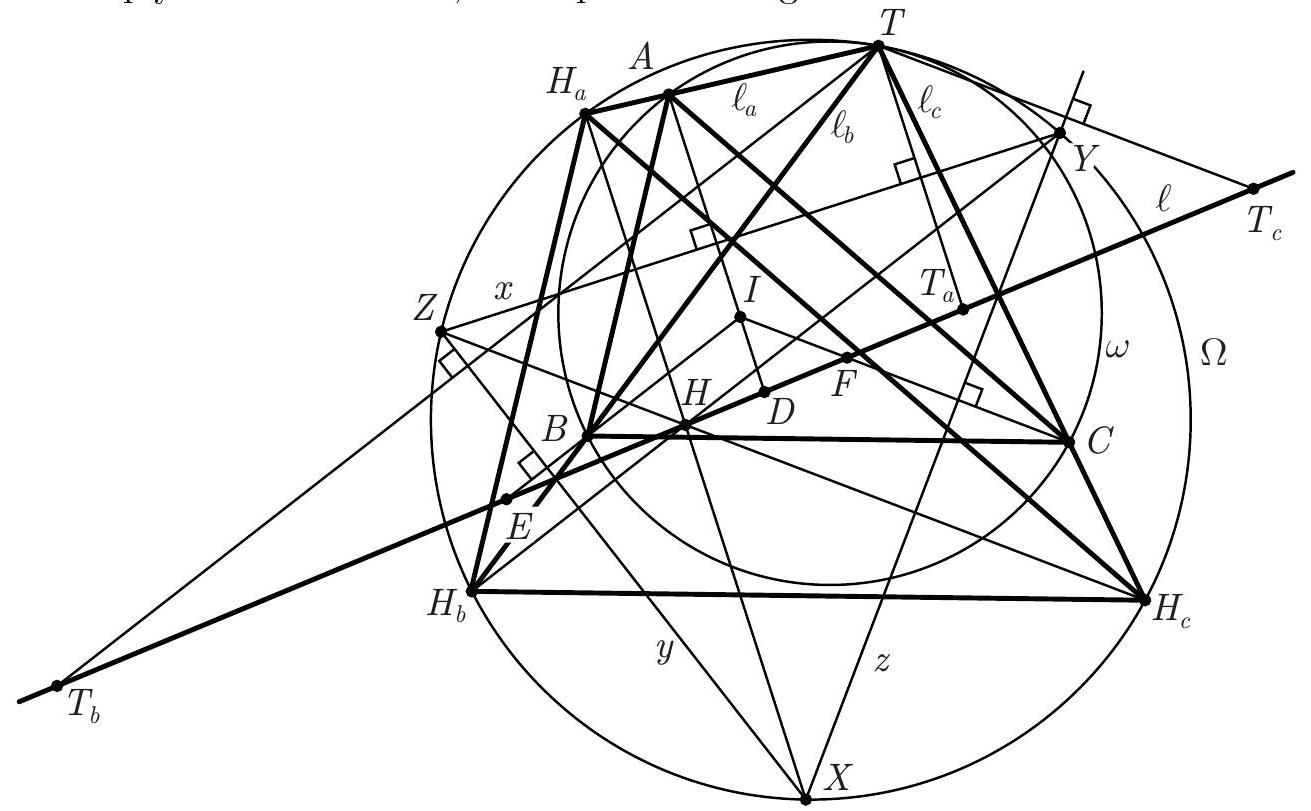 Let $H_{a}, H_{b}$, and $H_{c}$ be the reflections of the point $H$ in the lines $x, y$, and $z$, respectively. Then the triangle $H_{a} H_{b} H_{c}$ is inscribed in $\Omega$ and homothetic to $A B C$ (by an easy angle chasing). Since $H_{a} \in \ell_{a}, H_{b} \in \ell_{b}$, and $H_{c} \in \ell_{c}$, the triangles $H_{a} H_{b} H_{c}$ and $A B C$ form a required pair of triangles $\Delta$ and $\delta$ mentioned in the preamble. Comment 2. The following observation shows how one may guess the description of the tangency point $T$ from Solution 1. Let us fix a direction and move the line $\ell$ parallel to this direction with constant speed. Then the points $D, E$, and $F$ are moving with constant speeds along the lines $A I, B I$, and $C I$, respectively. In this case $x, y$, and $z$ are moving with constant speeds, defining a family of homothetic triangles $X Y Z$ with a common centre of homothety $T$. Notice that the triangle $X_{0} Y_{0} Z_{0}$ belongs to this family (for $\ell$ passing through $I$ ). We may specify the location of $T$ considering the degenerate case when $x, y$, and $z$ are concurrent. In this degenerate case all the lines $x, y, z, \ell, \ell_{a}, \ell_{b}, \ell_{c}$ have a common point. Note that the lines $\ell_{a}, \ell_{b}, \ell_{c}$ remain constant as $\ell$ is moving (keeping its direction). Thus $T$ should be the common point of $\ell_{a}, \ell_{b}$, and $\ell_{c}$, lying on $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\Theta$. Show that the circumcircle of the triangle $\Theta$ is tangent to $\omega$. (Denmark) Preamble. Let $X=y \cap z, Y=x \cap z, Z=x \cap y$ and let $\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\Delta$ and $\delta$ inscribed into $\Omega$ and $\omega$, respectively. In order to prove that $\Omega$ and $\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\Delta$ to $\delta$ lies on $\omega$ (or $\Omega$ ), or, in other words, to show that $\Delta$ and $\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\omega$ (or $\Omega$ ). We use directed angles throughout all the solutions.
|
Claim 1. The reflections $\ell_{a}, \ell_{b}$ and $\ell_{c}$ of the line $\ell$ in the lines $x, y$, and $z$, respectively, are concurrent at a point $T$ which belongs to $\omega$.  Proof. Notice that $\Varangle\left(\ell_{b}, \ell_{c}\right)=\Varangle\left(\ell_{b}, \ell\right)+\Varangle\left(\ell, \ell_{c}\right)=2 \Varangle(y, \ell)+2 \Varangle(\ell, z)=2 \Varangle(y, z)$. But $y \perp B I$ and $z \perp C I$ implies $\Varangle(y, z)=\Varangle(B I, I C)$, so, since $2 \Varangle(B I, I C)=\Varangle(B A, A C)$, we obtain $$ \Varangle\left(\ell_{b}, \ell_{c}\right)=\Varangle(B A, A C) . $$ Since $A$ is the reflection of $D$ in $x$, $A$ belongs to $\ell_{a}$; similarly, $B$ belongs to $\ell_{b}$. Then (1) shows that the common point $T^{\prime}$ of $\ell_{a}$ and $\ell_{b}$ lies on $\omega$; similarly, the common point $T^{\prime \prime}$ of $\ell_{c}$ and $\ell_{b}$ lies on $\omega$. If $B \notin \ell_{a}$ and $B \notin \ell_{c}$, then $T^{\prime}$ and $T^{\prime \prime}$ are the second point of intersection of $\ell_{b}$ and $\omega$, hence they coincide. Otherwise, if, say, $B \in \ell_{c}$, then $\ell_{c}=B C$, so $\Varangle(B A, A C)=\Varangle\left(\ell_{b}, \ell_{c}\right)=\Varangle\left(\ell_{b}, B C\right)$, which shows that $\ell_{b}$ is tangent at $B$ to $\omega$ and $T^{\prime}=T^{\prime \prime}=B$. So $T^{\prime}$ and $T^{\prime \prime}$ coincide in all the cases, and the conclusion of the claim follows. Now we prove that $X, X_{0}, T$ are collinear. Denote by $D_{b}$ and $D_{c}$ the reflections of the point $D$ in the lines $y$ and $z$, respectively. Then $D_{b}$ lies on $\ell_{b}, D_{c}$ lies on $\ell_{c}$, and $$ \begin{aligned} \Varangle\left(D_{b} X, X D_{c}\right) & =\Varangle\left(D_{b} X, D X\right)+\Varangle\left(D X, X D_{c}\right)=2 \Varangle(y, D X)+2 \Varangle(D X, z)=2 \Varangle(y, z) \\ & =\Varangle(B A, A C)=\Varangle(B T, T C), \end{aligned} $$ hence the quadrilateral $X D_{b} T D_{c}$ is cyclic. Notice also that since $X D_{b}=X D=X D_{c}$, the points $D, D_{b}, D_{c}$ lie on a circle with centre $X$. Using in this circle the diameter $D_{c} D_{c}^{\prime}$ yields $\Varangle\left(D_{b} D_{c}, D_{c} X\right)=90^{\circ}+\Varangle\left(D_{b} D_{c}^{\prime}, D_{c}^{\prime} X\right)=90^{\circ}+\Varangle\left(D_{b} D, D D_{c}\right)$. Therefore, $$ \begin{gathered} \Varangle\left(\ell_{b}, X T\right)=\Varangle\left(D_{b} T, X T\right)=\Varangle\left(D_{b} D_{c}, D_{c} X\right)=90^{\circ}+\Varangle\left(D_{b} D, D D_{c}\right) \\ =90^{\circ}+\Varangle(B I, I C)=\Varangle(B A, A I)=\Varangle\left(B A, A X_{0}\right)=\Varangle\left(B T, T X_{0}\right)=\Varangle\left(\ell_{b}, X_{0} T\right) \end{gathered} $$ so the points $X, X_{0}, T$ are collinear. By a similar argument, $Y, Y_{0}, T$ and $Z, Z_{0}, T$ are collinear. As mentioned in the preamble, the statement of the problem follows. Comment 1. After proving Claim 1 one may proceed in another way. As it was shown, the reflections of $\ell$ in the sidelines of $X Y Z$ are concurrent at $T$. Thus $\ell$ is the Steiner line of $T$ with respect to $\triangle X Y Z$ (that is the line containing the reflections $T_{a}, T_{b}, T_{c}$ of $T$ in the sidelines of $X Y Z$ ). The properties of the Steiner line imply that $T$ lies on $\Omega$, and $\ell$ passes through the orthocentre $H$ of the triangle $X Y Z$.  Let $H_{a}, H_{b}$, and $H_{c}$ be the reflections of the point $H$ in the lines $x, y$, and $z$, respectively. Then the triangle $H_{a} H_{b} H_{c}$ is inscribed in $\Omega$ and homothetic to $A B C$ (by an easy angle chasing). Since $H_{a} \in \ell_{a}, H_{b} \in \ell_{b}$, and $H_{c} \in \ell_{c}$, the triangles $H_{a} H_{b} H_{c}$ and $A B C$ form a required pair of triangles $\Delta$ and $\delta$ mentioned in the preamble. Comment 2. The following observation shows how one may guess the description of the tangency point $T$ from Solution 1. Let us fix a direction and move the line $\ell$ parallel to this direction with constant speed. Then the points $D, E$, and $F$ are moving with constant speeds along the lines $A I, B I$, and $C I$, respectively. In this case $x, y$, and $z$ are moving with constant speeds, defining a family of homothetic triangles $X Y Z$ with a common centre of homothety $T$. Notice that the triangle $X_{0} Y_{0} Z_{0}$ belongs to this family (for $\ell$ passing through $I$ ). We may specify the location of $T$ considering the degenerate case when $x, y$, and $z$ are concurrent. In this degenerate case all the lines $x, y, z, \ell, \ell_{a}, \ell_{b}, \ell_{c}$ have a common point. Note that the lines $\ell_{a}, \ell_{b}, \ell_{c}$ remain constant as $\ell$ is moving (keeping its direction). Thus $T$ should be the common point of $\ell_{a}, \ell_{b}$, and $\ell_{c}$, lying on $\omega$.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
191c6ee0-6dcb-52e6-a61e-ee98ff4f8c5f
| 23,672
|
Let $A B C$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\Theta$. Show that the circumcircle of the triangle $\Theta$ is tangent to $\omega$. (Denmark) Preamble. Let $X=y \cap z, Y=x \cap z, Z=x \cap y$ and let $\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\Delta$ and $\delta$ inscribed into $\Omega$ and $\omega$, respectively. In order to prove that $\Omega$ and $\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\Delta$ to $\delta$ lies on $\omega$ (or $\Omega$ ), or, in other words, to show that $\Delta$ and $\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\omega$ (or $\Omega$ ). We use directed angles throughout all the solutions.
|
As mentioned in the preamble, it is sufficient to prove that the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\omega$. Thus, it suffices to prove that $\Varangle\left(T X_{0}, T Y_{0}\right)=$ $\Varangle\left(Z_{0} X_{0}, Z_{0} Y_{0}\right)$, or, equivalently, $\Varangle\left(X X_{0}, Y Y_{0}\right)=\Varangle\left(Z_{0} X_{0}, Z_{0} Y_{0}\right)$. Recall that $Y Z$ and $Y_{0} Z_{0}$ are the perpendicular bisectors of $A D$ and $A I$, respectively. Then, the vector $\vec{x}$ perpendicular to $Y Z$ and shifting the line $Y_{0} Z_{0}$ to $Y Z$ is equal to $\frac{1}{2} \overrightarrow{I D}$. Define the shifting vectors $\vec{y}=\frac{1}{2} \overrightarrow{I E}, \vec{z}=\frac{1}{2} \overrightarrow{I F}$ similarly. Consider now the triangle $U V W$ formed by the perpendiculars to $A I, B I$, and $C I$ through $D, E$, and $F$, respectively (see figure below). This is another triangle whose sides are parallel to the corresponding sides of $X Y Z$. Claim 2. $\overrightarrow{I U}=2 \overrightarrow{X_{0} X}, \overrightarrow{I V}=2 \overrightarrow{Y_{0} Y}, \overrightarrow{I W}=2 \overrightarrow{Z_{0} Z}$. Proof. We prove one of the relations, the other proofs being similar. To prove the equality of two vectors it suffices to project them onto two non-parallel axes and check that their projections are equal. The projection of $\overrightarrow{X_{0} X}$ onto $I B$ equals $\vec{y}$, while the projection of $\overrightarrow{I U}$ onto $I B$ is $\overrightarrow{I E}=2 \vec{y}$. The projections onto the other axis $I C$ are $\vec{z}$ and $\overrightarrow{I F}=2 \vec{z}$. Then $\overrightarrow{I U}=2 \overrightarrow{X_{0} X}$ follows. Notice that the line $\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$; thus $U, V, W$, and $I$ are concyclic. It follows from Claim 2 that $\Varangle\left(X X_{0}, Y Y_{0}\right)=\Varangle(I U, I V)=$ $\Varangle(W U, W V)=\Varangle\left(Z_{0} X_{0}, Z_{0} Y_{0}\right)$, and we are done. 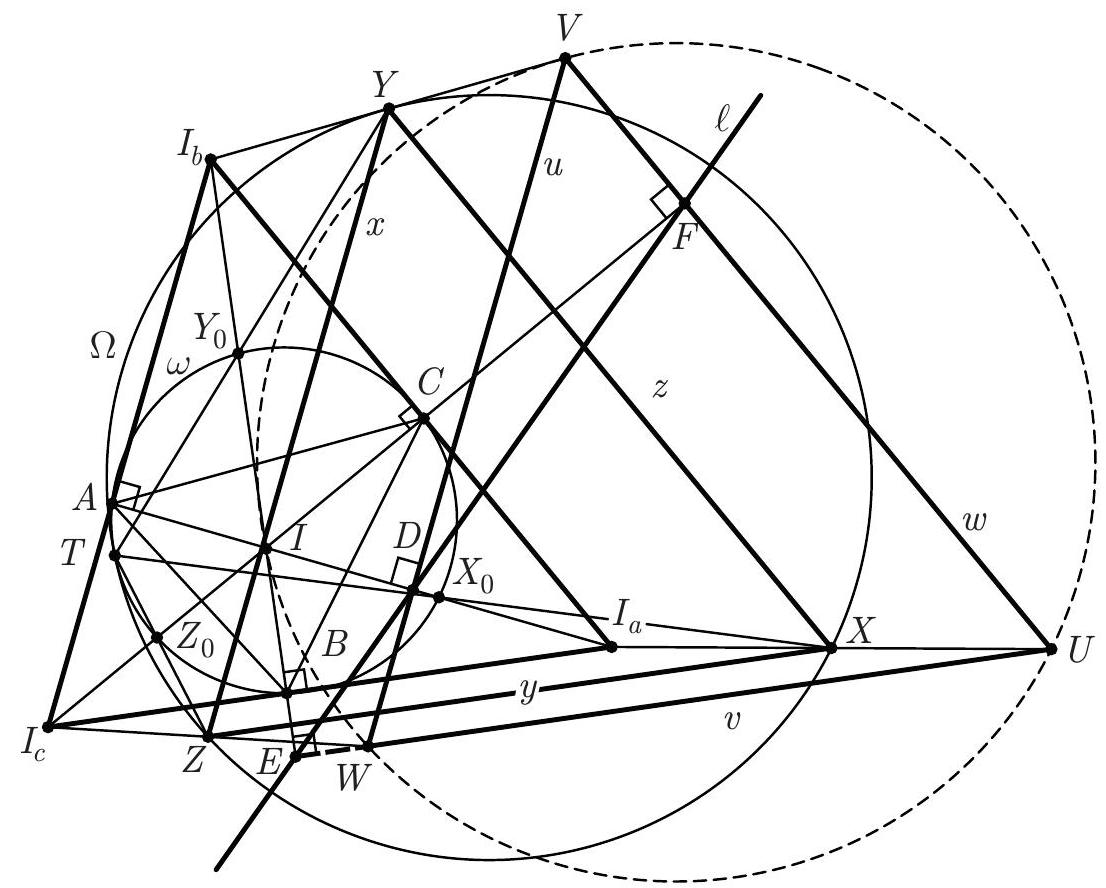
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\Theta$. Show that the circumcircle of the triangle $\Theta$ is tangent to $\omega$. (Denmark) Preamble. Let $X=y \cap z, Y=x \cap z, Z=x \cap y$ and let $\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\Delta$ and $\delta$ inscribed into $\Omega$ and $\omega$, respectively. In order to prove that $\Omega$ and $\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\Delta$ to $\delta$ lies on $\omega$ (or $\Omega$ ), or, in other words, to show that $\Delta$ and $\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\omega$ (or $\Omega$ ). We use directed angles throughout all the solutions.
|
As mentioned in the preamble, it is sufficient to prove that the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\omega$. Thus, it suffices to prove that $\Varangle\left(T X_{0}, T Y_{0}\right)=$ $\Varangle\left(Z_{0} X_{0}, Z_{0} Y_{0}\right)$, or, equivalently, $\Varangle\left(X X_{0}, Y Y_{0}\right)=\Varangle\left(Z_{0} X_{0}, Z_{0} Y_{0}\right)$. Recall that $Y Z$ and $Y_{0} Z_{0}$ are the perpendicular bisectors of $A D$ and $A I$, respectively. Then, the vector $\vec{x}$ perpendicular to $Y Z$ and shifting the line $Y_{0} Z_{0}$ to $Y Z$ is equal to $\frac{1}{2} \overrightarrow{I D}$. Define the shifting vectors $\vec{y}=\frac{1}{2} \overrightarrow{I E}, \vec{z}=\frac{1}{2} \overrightarrow{I F}$ similarly. Consider now the triangle $U V W$ formed by the perpendiculars to $A I, B I$, and $C I$ through $D, E$, and $F$, respectively (see figure below). This is another triangle whose sides are parallel to the corresponding sides of $X Y Z$. Claim 2. $\overrightarrow{I U}=2 \overrightarrow{X_{0} X}, \overrightarrow{I V}=2 \overrightarrow{Y_{0} Y}, \overrightarrow{I W}=2 \overrightarrow{Z_{0} Z}$. Proof. We prove one of the relations, the other proofs being similar. To prove the equality of two vectors it suffices to project them onto two non-parallel axes and check that their projections are equal. The projection of $\overrightarrow{X_{0} X}$ onto $I B$ equals $\vec{y}$, while the projection of $\overrightarrow{I U}$ onto $I B$ is $\overrightarrow{I E}=2 \vec{y}$. The projections onto the other axis $I C$ are $\vec{z}$ and $\overrightarrow{I F}=2 \vec{z}$. Then $\overrightarrow{I U}=2 \overrightarrow{X_{0} X}$ follows. Notice that the line $\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$; thus $U, V, W$, and $I$ are concyclic. It follows from Claim 2 that $\Varangle\left(X X_{0}, Y Y_{0}\right)=\Varangle(I U, I V)=$ $\Varangle(W U, W V)=\Varangle\left(Z_{0} X_{0}, Z_{0} Y_{0}\right)$, and we are done. 
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
191c6ee0-6dcb-52e6-a61e-ee98ff4f8c5f
| 23,672
|
Let $A B C$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\Theta$. Show that the circumcircle of the triangle $\Theta$ is tangent to $\omega$. (Denmark) Preamble. Let $X=y \cap z, Y=x \cap z, Z=x \cap y$ and let $\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\Delta$ and $\delta$ inscribed into $\Omega$ and $\omega$, respectively. In order to prove that $\Omega$ and $\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\Delta$ to $\delta$ lies on $\omega$ (or $\Omega$ ), or, in other words, to show that $\Delta$ and $\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\omega$ (or $\Omega$ ). We use directed angles throughout all the solutions.
|
Let $I_{a}, I_{b}$, and $I_{c}$ be the excentres of triangle $A B C$ corresponding to $A, B$, and $C$, respectively. Also, let $u, v$, and $w$ be the lines through $D, E$, and $F$ which are perpendicular to $A I, B I$, and $C I$, respectively, and let $U V W$ be the triangle determined by these lines, where $u=V W, v=U W$ and $w=U V$ (see figure above). Notice that the line $u$ is the reflection of $I_{b} I_{c}$ in the line $x$, because $u, x$, and $I_{b} I_{c}$ are perpendicular to $A D$ and $x$ is the perpendicular bisector of $A D$. Likewise, $v$ and $I_{a} I_{c}$ are reflections of each other in $y$, while $w$ and $I_{a} I_{b}$ are reflections of each other in $z$. It follows that $X, Y$, and $Z$ are the midpoints of $U I_{a}, V I_{b}$ and $W I_{c}$, respectively, and that the triangles $U V W$, $X Y Z$ and $I_{a} I_{b} I_{c}$ are either translates of each other or homothetic with a common homothety centre. Construct the points $T$ and $S$ such that the quadrilaterals $U V I W, X Y T Z$ and $I_{a} I_{b} S I_{c}$ are homothetic. Then $T$ is the midpoint of $I S$. Moreover, note that $\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$, hence $I$ belongs to the circumcircle of the triangle $U V W$, therefore $T$ belongs to $\Omega$. Consider now the homothety or translation $h_{1}$ that maps $X Y Z T$ to $I_{a} I_{b} I_{c} S$ and the homothety $h_{2}$ with centre $I$ and factor $\frac{1}{2}$. Furthermore, let $h=h_{2} \circ h_{1}$. The transform $h$ can be a homothety or a translation, and $$ h(T)=h_{2}\left(h_{1}(T)\right)=h_{2}(S)=T $$ hence $T$ is a fixed point of $h$. So, $h$ is a homothety with centre $T$. Note that $h_{2}$ maps the excentres $I_{a}, I_{b}, I_{c}$ to $X_{0}, Y_{0}, Z_{0}$ defined in the preamble. Thus the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\Omega$, and this completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $A I, B I$, and $C I$ at points $D, E$, and $F$, respectively, distinct from the points $A, B, C$, and $I$. The perpendicular bisectors $x, y$, and $z$ of the segments $A D, B E$, and $C F$, respectively determine a triangle $\Theta$. Show that the circumcircle of the triangle $\Theta$ is tangent to $\omega$. (Denmark) Preamble. Let $X=y \cap z, Y=x \cap z, Z=x \cap y$ and let $\Omega$ denote the circumcircle of the triangle $X Y Z$. Denote by $X_{0}, Y_{0}$, and $Z_{0}$ the second intersection points of $A I, B I$ and $C I$, respectively, with $\omega$. It is known that $Y_{0} Z_{0}$ is the perpendicular bisector of $A I, Z_{0} X_{0}$ is the perpendicular bisector of $B I$, and $X_{0} Y_{0}$ is the perpendicular bisector of $C I$. In particular, the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$ are homothetic, because their corresponding sides are parallel. The solutions below mostly exploit the following approach. Consider the triangles $X Y Z$ and $X_{0} Y_{0} Z_{0}$, or some other pair of homothetic triangles $\Delta$ and $\delta$ inscribed into $\Omega$ and $\omega$, respectively. In order to prove that $\Omega$ and $\omega$ are tangent, it suffices to show that the centre $T$ of the homothety taking $\Delta$ to $\delta$ lies on $\omega$ (or $\Omega$ ), or, in other words, to show that $\Delta$ and $\delta$ are perspective (i.e., the lines joining corresponding vertices are concurrent), with their perspector lying on $\omega$ (or $\Omega$ ). We use directed angles throughout all the solutions.
|
Let $I_{a}, I_{b}$, and $I_{c}$ be the excentres of triangle $A B C$ corresponding to $A, B$, and $C$, respectively. Also, let $u, v$, and $w$ be the lines through $D, E$, and $F$ which are perpendicular to $A I, B I$, and $C I$, respectively, and let $U V W$ be the triangle determined by these lines, where $u=V W, v=U W$ and $w=U V$ (see figure above). Notice that the line $u$ is the reflection of $I_{b} I_{c}$ in the line $x$, because $u, x$, and $I_{b} I_{c}$ are perpendicular to $A D$ and $x$ is the perpendicular bisector of $A D$. Likewise, $v$ and $I_{a} I_{c}$ are reflections of each other in $y$, while $w$ and $I_{a} I_{b}$ are reflections of each other in $z$. It follows that $X, Y$, and $Z$ are the midpoints of $U I_{a}, V I_{b}$ and $W I_{c}$, respectively, and that the triangles $U V W$, $X Y Z$ and $I_{a} I_{b} I_{c}$ are either translates of each other or homothetic with a common homothety centre. Construct the points $T$ and $S$ such that the quadrilaterals $U V I W, X Y T Z$ and $I_{a} I_{b} S I_{c}$ are homothetic. Then $T$ is the midpoint of $I S$. Moreover, note that $\ell$ is the Simson line of the point $I$ with respect to the triangle $U V W$, hence $I$ belongs to the circumcircle of the triangle $U V W$, therefore $T$ belongs to $\Omega$. Consider now the homothety or translation $h_{1}$ that maps $X Y Z T$ to $I_{a} I_{b} I_{c} S$ and the homothety $h_{2}$ with centre $I$ and factor $\frac{1}{2}$. Furthermore, let $h=h_{2} \circ h_{1}$. The transform $h$ can be a homothety or a translation, and $$ h(T)=h_{2}\left(h_{1}(T)\right)=h_{2}(S)=T $$ hence $T$ is a fixed point of $h$. So, $h$ is a homothety with centre $T$. Note that $h_{2}$ maps the excentres $I_{a}, I_{b}, I_{c}$ to $X_{0}, Y_{0}, Z_{0}$ defined in the preamble. Thus the centre $T$ of the homothety taking $X Y Z$ to $X_{0} Y_{0} Z_{0}$ belongs to $\Omega$, and this completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
191c6ee0-6dcb-52e6-a61e-ee98ff4f8c5f
| 23,672
|
Determine all pairs $(n, k)$ of distinct positive integers such that there exists a positive integer $s$ for which the numbers of divisors of $s n$ and of $s k$ are equal. (Ukraine) Answer: All pairs $(n, k)$ such that $n \nmid k$ and $k \nmid n$.
|
As usual, the number of divisors of a positive integer $n$ is denoted by $d(n)$. If $n=\prod_{i} p_{i}^{\alpha_{i}}$ is the prime factorisation of $n$, then $d(n)=\prod_{i}\left(\alpha_{i}+1\right)$. We start by showing that one cannot find any suitable number $s$ if $k \mid n$ or $n \mid k$ (and $k \neq n$ ). Suppose that $n \mid k$, and choose any positive integer $s$. Then the set of divisors of $s n$ is a proper subset of that of $s k$, hence $d(s n)<d(s k)$. Therefore, the pair $(n, k)$ does not satisfy the problem requirements. The case $k \mid n$ is similar. Now assume that $n \nmid k$ and $k \nmid n$. Let $p_{1}, \ldots, p_{t}$ be all primes dividing $n k$, and consider the prime factorisations $$ n=\prod_{i=1}^{t} p_{i}^{\alpha_{i}} \quad \text { and } \quad k=\prod_{i=1}^{t} p_{i}^{\beta_{i}} $$ It is reasonable to search for the number $s$ having the form $$ s=\prod_{i=1}^{t} p_{i}^{\gamma_{i}} $$ The (nonnegative integer) exponents $\gamma_{i}$ should be chosen so as to satisfy $$ \frac{d(s n)}{d(s k)}=\prod_{i=1}^{t} \frac{\alpha_{i}+\gamma_{i}+1}{\beta_{i}+\gamma_{i}+1}=1 $$ First of all, if $\alpha_{i}=\beta_{i}$ for some $i$, then, regardless of the value of $\gamma_{i}$, the corresponding factor in (1) equals 1 and does not affect the product. So we may assume that there is no such index $i$. For the other factors in (1), the following lemma is useful. Lemma. Let $\alpha>\beta$ be nonnegative integers. Then, for every integer $M \geqslant \beta+1$, there exists a nonnegative integer $\gamma$ such that $$ \frac{\alpha+\gamma+1}{\beta+\gamma+1}=1+\frac{1}{M}=\frac{M+1}{M} . $$ Proof. $$ \frac{\alpha+\gamma+1}{\beta+\gamma+1}=1+\frac{1}{M} \Longleftrightarrow \frac{\alpha-\beta}{\beta+\gamma+1}=\frac{1}{M} \Longleftrightarrow \gamma=M(\alpha-\beta)-(\beta+1) \geqslant 0 . $$ Now we can finish the solution. Without loss of generality, there exists an index $u$ such that $\alpha_{i}>\beta_{i}$ for $i=1,2, \ldots, u$, and $\alpha_{i}<\beta_{i}$ for $i=u+1, \ldots, t$. The conditions $n \nmid k$ and $k \nmid n$ mean that $1 \leqslant u \leqslant t-1$. Choose an integer $X$ greater than all the $\alpha_{i}$ and $\beta_{i}$. By the lemma, we can define the numbers $\gamma_{i}$ so as to satisfy $$ \begin{array}{ll} \frac{\alpha_{i}+\gamma_{i}+1}{\beta_{i}+\gamma_{i}+1}=\frac{u X+i}{u X+i-1} & \text { for } i=1,2, \ldots, u, \text { and } \\ \frac{\beta_{u+i}+\gamma_{u+i}+1}{\alpha_{u+i}+\gamma_{u+i}+1}=\frac{(t-u) X+i}{(t-u) X+i-1} & \text { for } i=1,2, \ldots, t-u . \end{array} $$ Then we will have $$ \frac{d(s n)}{d(s k)}=\prod_{i=1}^{u} \frac{u X+i}{u X+i-1} \cdot \prod_{i=1}^{t-u} \frac{(t-u) X+i-1}{(t-u) X+i}=\frac{u(X+1)}{u X} \cdot \frac{(t-u) X}{(t-u)(X+1)}=1, $$ as required. Comment. The lemma can be used in various ways, in order to provide a suitable value of $s$. In particular, one may apply induction on the number $t$ of prime factors, using identities like $$ \frac{n}{n-1}=\frac{n^{2}}{n^{2}-1} \cdot \frac{n+1}{n} $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine all pairs $(n, k)$ of distinct positive integers such that there exists a positive integer $s$ for which the numbers of divisors of $s n$ and of $s k$ are equal. (Ukraine) Answer: All pairs $(n, k)$ such that $n \nmid k$ and $k \nmid n$.
|
As usual, the number of divisors of a positive integer $n$ is denoted by $d(n)$. If $n=\prod_{i} p_{i}^{\alpha_{i}}$ is the prime factorisation of $n$, then $d(n)=\prod_{i}\left(\alpha_{i}+1\right)$. We start by showing that one cannot find any suitable number $s$ if $k \mid n$ or $n \mid k$ (and $k \neq n$ ). Suppose that $n \mid k$, and choose any positive integer $s$. Then the set of divisors of $s n$ is a proper subset of that of $s k$, hence $d(s n)<d(s k)$. Therefore, the pair $(n, k)$ does not satisfy the problem requirements. The case $k \mid n$ is similar. Now assume that $n \nmid k$ and $k \nmid n$. Let $p_{1}, \ldots, p_{t}$ be all primes dividing $n k$, and consider the prime factorisations $$ n=\prod_{i=1}^{t} p_{i}^{\alpha_{i}} \quad \text { and } \quad k=\prod_{i=1}^{t} p_{i}^{\beta_{i}} $$ It is reasonable to search for the number $s$ having the form $$ s=\prod_{i=1}^{t} p_{i}^{\gamma_{i}} $$ The (nonnegative integer) exponents $\gamma_{i}$ should be chosen so as to satisfy $$ \frac{d(s n)}{d(s k)}=\prod_{i=1}^{t} \frac{\alpha_{i}+\gamma_{i}+1}{\beta_{i}+\gamma_{i}+1}=1 $$ First of all, if $\alpha_{i}=\beta_{i}$ for some $i$, then, regardless of the value of $\gamma_{i}$, the corresponding factor in (1) equals 1 and does not affect the product. So we may assume that there is no such index $i$. For the other factors in (1), the following lemma is useful. Lemma. Let $\alpha>\beta$ be nonnegative integers. Then, for every integer $M \geqslant \beta+1$, there exists a nonnegative integer $\gamma$ such that $$ \frac{\alpha+\gamma+1}{\beta+\gamma+1}=1+\frac{1}{M}=\frac{M+1}{M} . $$ Proof. $$ \frac{\alpha+\gamma+1}{\beta+\gamma+1}=1+\frac{1}{M} \Longleftrightarrow \frac{\alpha-\beta}{\beta+\gamma+1}=\frac{1}{M} \Longleftrightarrow \gamma=M(\alpha-\beta)-(\beta+1) \geqslant 0 . $$ Now we can finish the solution. Without loss of generality, there exists an index $u$ such that $\alpha_{i}>\beta_{i}$ for $i=1,2, \ldots, u$, and $\alpha_{i}<\beta_{i}$ for $i=u+1, \ldots, t$. The conditions $n \nmid k$ and $k \nmid n$ mean that $1 \leqslant u \leqslant t-1$. Choose an integer $X$ greater than all the $\alpha_{i}$ and $\beta_{i}$. By the lemma, we can define the numbers $\gamma_{i}$ so as to satisfy $$ \begin{array}{ll} \frac{\alpha_{i}+\gamma_{i}+1}{\beta_{i}+\gamma_{i}+1}=\frac{u X+i}{u X+i-1} & \text { for } i=1,2, \ldots, u, \text { and } \\ \frac{\beta_{u+i}+\gamma_{u+i}+1}{\alpha_{u+i}+\gamma_{u+i}+1}=\frac{(t-u) X+i}{(t-u) X+i-1} & \text { for } i=1,2, \ldots, t-u . \end{array} $$ Then we will have $$ \frac{d(s n)}{d(s k)}=\prod_{i=1}^{u} \frac{u X+i}{u X+i-1} \cdot \prod_{i=1}^{t-u} \frac{(t-u) X+i-1}{(t-u) X+i}=\frac{u(X+1)}{u X} \cdot \frac{(t-u) X}{(t-u)(X+1)}=1, $$ as required. Comment. The lemma can be used in various ways, in order to provide a suitable value of $s$. In particular, one may apply induction on the number $t$ of prime factors, using identities like $$ \frac{n}{n-1}=\frac{n^{2}}{n^{2}-1} \cdot \frac{n+1}{n} $$
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9040f237-5c97-5091-8fca-1d0b8a83c831
| 23,677
|
Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t . $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia) Answer: No.
|
Arguing indirectly, assume that $x y=a^{2}$ and $z t=c^{2}$ with $a, c>0$. Suppose that the number $x+y=z+t$ is odd. Then $x$ and $y$ have opposite parity, as well as $z$ and $t$. This means that both $x y$ and $z t$ are even, as well as $x y-z t=x+y$; a contradiction. Thus, $x+y$ is even, so the number $s=\frac{x+y}{2}=\frac{z+t}{2}$ is a positive integer. Next, we set $b=\frac{|x-y|}{2}, d=\frac{|z-t|}{2}$. Now the problem conditions yield $$ s^{2}=a^{2}+b^{2}=c^{2}+d^{2} $$ and $$ 2 s=a^{2}-c^{2}=d^{2}-b^{2} $$ (the last equality in (2) follows from (1)). We readily get from (2) that $a, d>0$. In the sequel we will use only the relations (1) and (2), along with the fact that $a, d, s$ are positive integers, while $b$ and $c$ are nonnegative integers, at most one of which may be zero. Since both relations are symmetric with respect to the simultaneous swappings $a \leftrightarrow d$ and $b \leftrightarrow c$, we assume, without loss of generality, that $b \geqslant c$ (and hence $b>0$ ). Therefore, $d^{2}=2 s+b^{2}>c^{2}$, whence $$ d^{2}>\frac{c^{2}+d^{2}}{2}=\frac{s^{2}}{2} $$ On the other hand, since $d^{2}-b^{2}$ is even by (2), the numbers $b$ and $d$ have the same parity, so $0<b \leqslant d-2$. Therefore, $$ 2 s=d^{2}-b^{2} \geqslant d^{2}-(d-2)^{2}=4(d-1), \quad \text { i.e., } \quad d \leqslant \frac{s}{2}+1 $$ Combining (3) and (4) we obtain $$ 2 s^{2}<4 d^{2} \leqslant 4\left(\frac{s}{2}+1\right)^{2}, \quad \text { or } \quad(s-2)^{2}<8 $$ which yields $s \leqslant 4$. Finally, an easy check shows that each number of the form $s^{2}$ with $1 \leqslant s \leqslant 4$ has a unique representation as a sum of two squares, namely $s^{2}=s^{2}+0^{2}$. Thus, (1) along with $a, d>0$ imply $b=c=0$, which is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t . $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia) Answer: No.
|
Arguing indirectly, assume that $x y=a^{2}$ and $z t=c^{2}$ with $a, c>0$. Suppose that the number $x+y=z+t$ is odd. Then $x$ and $y$ have opposite parity, as well as $z$ and $t$. This means that both $x y$ and $z t$ are even, as well as $x y-z t=x+y$; a contradiction. Thus, $x+y$ is even, so the number $s=\frac{x+y}{2}=\frac{z+t}{2}$ is a positive integer. Next, we set $b=\frac{|x-y|}{2}, d=\frac{|z-t|}{2}$. Now the problem conditions yield $$ s^{2}=a^{2}+b^{2}=c^{2}+d^{2} $$ and $$ 2 s=a^{2}-c^{2}=d^{2}-b^{2} $$ (the last equality in (2) follows from (1)). We readily get from (2) that $a, d>0$. In the sequel we will use only the relations (1) and (2), along with the fact that $a, d, s$ are positive integers, while $b$ and $c$ are nonnegative integers, at most one of which may be zero. Since both relations are symmetric with respect to the simultaneous swappings $a \leftrightarrow d$ and $b \leftrightarrow c$, we assume, without loss of generality, that $b \geqslant c$ (and hence $b>0$ ). Therefore, $d^{2}=2 s+b^{2}>c^{2}$, whence $$ d^{2}>\frac{c^{2}+d^{2}}{2}=\frac{s^{2}}{2} $$ On the other hand, since $d^{2}-b^{2}$ is even by (2), the numbers $b$ and $d$ have the same parity, so $0<b \leqslant d-2$. Therefore, $$ 2 s=d^{2}-b^{2} \geqslant d^{2}-(d-2)^{2}=4(d-1), \quad \text { i.e., } \quad d \leqslant \frac{s}{2}+1 $$ Combining (3) and (4) we obtain $$ 2 s^{2}<4 d^{2} \leqslant 4\left(\frac{s}{2}+1\right)^{2}, \quad \text { or } \quad(s-2)^{2}<8 $$ which yields $s \leqslant 4$. Finally, an easy check shows that each number of the form $s^{2}$ with $1 \leqslant s \leqslant 4$ has a unique representation as a sum of two squares, namely $s^{2}=s^{2}+0^{2}$. Thus, (1) along with $a, d>0$ imply $b=c=0$, which is impossible.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd0d9f5b-cc13-59bb-8b39-0543f64fe8fc
| 23,680
|
Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t . $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia) Answer: No.
|
We start with a complete description of all 4-tuples $(x, y, z, t)$ of positive integers satisfying (*). As in the solution above, we notice that the numbers $$ s=\frac{x+y}{2}=\frac{z+t}{2}, \quad p=\frac{x-y}{2}, \quad \text { and } \quad q=\frac{z-t}{2} $$ are integers (we may, and will, assume that $p, q \geqslant 0$ ). We have $$ 2 s=x y-z t=(s+p)(s-p)-(s+q)(s-q)=q^{2}-p^{2} $$ so $p$ and $q$ have the same parity, and $q>p$. Set now $k=\frac{q-p}{2}, \ell=\frac{q+p}{2}$. Then we have $s=\frac{q^{2}-p^{2}}{2}=2 k \ell$ and hence $$ \begin{array}{rlrl} x & =s+p=2 k \ell-k+\ell, & y & =s-p=2 k \ell+k-\ell, \\ z & =s+q=2 k \ell+k+\ell, & t=s-q=2 k \ell-k-\ell . \end{array} $$ Recall here that $\ell \geqslant k>0$ and, moreover, $(k, \ell) \neq(1,1)$, since otherwise $t=0$. Assume now that both $x y$ and $z t$ are squares. Then $x y z t$ is also a square. On the other hand, we have $$ \begin{aligned} x y z t=(2 k \ell-k+\ell) & (2 k \ell+k-\ell)(2 k \ell+k+\ell)(2 k \ell-k-\ell) \\ & =\left(4 k^{2} \ell^{2}-(k-\ell)^{2}\right)\left(4 k^{2} \ell^{2}-(k+\ell)^{2}\right)=\left(4 k^{2} \ell^{2}-k^{2}-\ell^{2}\right)^{2}-4 k^{2} \ell^{2} \end{aligned} $$ Denote $D=4 k^{2} \ell^{2}-k^{2}-\ell^{2}>0$. From (6) we get $D^{2}>x y z t$. On the other hand, $$ \begin{array}{r} (D-1)^{2}=D^{2}-2\left(4 k^{2} \ell^{2}-k^{2}-\ell^{2}\right)+1=\left(D^{2}-4 k^{2} \ell^{2}\right)-\left(2 k^{2}-1\right)\left(2 \ell^{2}-1\right)+2 \\ =x y z t-\left(2 k^{2}-1\right)\left(2 \ell^{2}-1\right)+2<x y z t \end{array} $$ since $\ell \geqslant 2$ and $k \geqslant 1$. Thus $(D-1)^{2}<x y z t<D^{2}$, and $x y z t$ cannot be a perfect square; a contradiction. Comment. The first part of Solution 2 shows that all 4-tuples of positive integers $x \geqslant y, z \geqslant t$ satisfying (*) have the form (5), where $\ell \geqslant k>0$ and $\ell \geqslant 2$. The converse is also true: every pair of positive integers $\ell \geqslant k>0$, except for the pair $k=\ell=1$, generates via (5) a 4-tuple of positive integers satisfying $(*)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Four positive integers $x, y, z$, and $t$ satisfy the relations $$ x y-z t=x+y=z+t . $$ Is it possible that both $x y$ and $z t$ are perfect squares? (Russia) Answer: No.
|
We start with a complete description of all 4-tuples $(x, y, z, t)$ of positive integers satisfying (*). As in the solution above, we notice that the numbers $$ s=\frac{x+y}{2}=\frac{z+t}{2}, \quad p=\frac{x-y}{2}, \quad \text { and } \quad q=\frac{z-t}{2} $$ are integers (we may, and will, assume that $p, q \geqslant 0$ ). We have $$ 2 s=x y-z t=(s+p)(s-p)-(s+q)(s-q)=q^{2}-p^{2} $$ so $p$ and $q$ have the same parity, and $q>p$. Set now $k=\frac{q-p}{2}, \ell=\frac{q+p}{2}$. Then we have $s=\frac{q^{2}-p^{2}}{2}=2 k \ell$ and hence $$ \begin{array}{rlrl} x & =s+p=2 k \ell-k+\ell, & y & =s-p=2 k \ell+k-\ell, \\ z & =s+q=2 k \ell+k+\ell, & t=s-q=2 k \ell-k-\ell . \end{array} $$ Recall here that $\ell \geqslant k>0$ and, moreover, $(k, \ell) \neq(1,1)$, since otherwise $t=0$. Assume now that both $x y$ and $z t$ are squares. Then $x y z t$ is also a square. On the other hand, we have $$ \begin{aligned} x y z t=(2 k \ell-k+\ell) & (2 k \ell+k-\ell)(2 k \ell+k+\ell)(2 k \ell-k-\ell) \\ & =\left(4 k^{2} \ell^{2}-(k-\ell)^{2}\right)\left(4 k^{2} \ell^{2}-(k+\ell)^{2}\right)=\left(4 k^{2} \ell^{2}-k^{2}-\ell^{2}\right)^{2}-4 k^{2} \ell^{2} \end{aligned} $$ Denote $D=4 k^{2} \ell^{2}-k^{2}-\ell^{2}>0$. From (6) we get $D^{2}>x y z t$. On the other hand, $$ \begin{array}{r} (D-1)^{2}=D^{2}-2\left(4 k^{2} \ell^{2}-k^{2}-\ell^{2}\right)+1=\left(D^{2}-4 k^{2} \ell^{2}\right)-\left(2 k^{2}-1\right)\left(2 \ell^{2}-1\right)+2 \\ =x y z t-\left(2 k^{2}-1\right)\left(2 \ell^{2}-1\right)+2<x y z t \end{array} $$ since $\ell \geqslant 2$ and $k \geqslant 1$. Thus $(D-1)^{2}<x y z t<D^{2}$, and $x y z t$ cannot be a perfect square; a contradiction. Comment. The first part of Solution 2 shows that all 4-tuples of positive integers $x \geqslant y, z \geqslant t$ satisfying (*) have the form (5), where $\ell \geqslant k>0$ and $\ell \geqslant 2$. The converse is also true: every pair of positive integers $\ell \geqslant k>0$, except for the pair $k=\ell=1$, generates via (5) a 4-tuple of positive integers satisfying $(*)$.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd0d9f5b-cc13-59bb-8b39-0543f64fe8fc
| 23,680
|
Let $n \geqslant 2018$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ be pairwise distinct positive integers not exceeding $5 n$. Suppose that the sequence $$ \frac{a_{1}}{b_{1}}, \frac{a_{2}}{b_{2}}, \ldots, \frac{a_{n}}{b_{n}} $$ forms an arithmetic progression. Prove that the terms of the sequence are equal. (Thailand)
|
Suppose that (1) is an arithmetic progression with nonzero difference. Let the difference be $\Delta=\frac{c}{d}$, where $d>0$ and $c, d$ are coprime. We will show that too many denominators $b_{i}$ should be divisible by $d$. To this end, for any $1 \leqslant i \leqslant n$ and any prime divisor $p$ of $d$, say that the index $i$ is $p$-wrong, if $v_{p}\left(b_{i}\right)<v_{p}(d)$. $\left(v_{p}(x)\right.$ stands for the exponent of $p$ in the prime factorisation of $x$.) Claim 1. For any prime $p$, all $p$-wrong indices are congruent modulo $p$. In other words, the $p$-wrong indices (if they exist) are included in an arithmetic progression with difference $p$. Proof. Let $\alpha=v_{p}(d)$. For the sake of contradiction, suppose that $i$ and $j$ are $p$-wrong indices (i.e., none of $b_{i}$ and $b_{j}$ is divisible by $\left.p^{\alpha}\right)$ such that $i \not \equiv j(\bmod p)$. Then the least common denominator of $\frac{a_{i}}{b_{i}}$ and $\frac{a_{j}}{b_{j}}$ is not divisible by $p^{\alpha}$. But this is impossible because in their difference, $(i-j) \Delta=\frac{(i-j) c}{d}$, the numerator is coprime to $p$, but $p^{\alpha}$ divides the denominator $d$. Claim 2. $d$ has no prime divisors greater than 5 . Proof. Suppose that $p \geqslant 7$ is a prime divisor of $d$. Among the indices $1,2, \ldots, n$, at most $\left\lceil\frac{n}{p}\right\rceil<\frac{n}{p}+1$ are $p$-wrong, so $p$ divides at least $\frac{p-1}{p} n-1$ of $b_{1}, \ldots, b_{n}$. Since these denominators are distinct, $$ 5 n \geqslant \max \left\{b_{i}: p \mid b_{i}\right\} \geqslant\left(\frac{p-1}{p} n-1\right) p=(p-1)(n-1)-1 \geqslant 6(n-1)-1>5 n, $$ a contradiction. Claim 3. For every $0 \leqslant k \leqslant n-30$, among the denominators $b_{k+1}, b_{k+2}, \ldots, b_{k+30}$, at least $\varphi(30)=8$ are divisible by $d$. Proof. By Claim 1, the 2 -wrong, 3 -wrong and 5 -wrong indices can be covered by three arithmetic progressions with differences 2,3 and 5 . By a simple inclusion-exclusion, $(2-1) \cdot(3-1) \cdot(5-1)=8$ indices are not covered; by Claim 2, we have $d \mid b_{i}$ for every uncovered index $i$. Claim 4. $|\Delta|<\frac{20}{n-2}$ and $d>\frac{n-2}{20}$. Proof. From the sequence (1), remove all fractions with $b_{n}<\frac{n}{2}$, There remain at least $\frac{n}{2}$ fractions, and they cannot exceed $\frac{5 n}{n / 2}=10$. So we have at least $\frac{n}{2}$ elements of the arithmetic progression (1) in the interval $(0,10]$, hence the difference must be below $\frac{10}{n / 2-1}=\frac{20}{n-2}$. The second inequality follows from $\frac{1}{d} \leqslant \frac{|c|}{d}=|\Delta|$. Now we have everything to get the final contradiction. By Claim 3, we have $d \mid b_{i}$ for at least $\left\lfloor\frac{n}{30}\right\rfloor \cdot 8$ indices $i$. By Claim 4 , we have $d \geqslant \frac{n-2}{20}$. Therefore, $$ 5 n \geqslant \max \left\{b_{i}: d \mid b_{i}\right\} \geqslant\left(\left\lfloor\frac{n}{30}\right\rfloor \cdot 8\right) \cdot d>\left(\frac{n}{30}-1\right) \cdot 8 \cdot \frac{n-2}{20}>5 n . $$ Comment 1. It is possible that all terms in (1) are equal, for example with $a_{i}=2 i-1$ and $b_{i}=4 i-2$ we have $\frac{a_{i}}{b_{i}}=\frac{1}{2}$. Comment 2. The bound $5 n$ in the statement is far from sharp; the solution above can be modified to work for $9 n$. For large $n$, the bound $5 n$ can be replaced by $n^{\frac{3}{2}-\varepsilon}$. The activities of the Problem Selection Committee were supported by DEDEMAN LA FANTANA vine la tine
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n \geqslant 2018$ be an integer, and let $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ be pairwise distinct positive integers not exceeding $5 n$. Suppose that the sequence $$ \frac{a_{1}}{b_{1}}, \frac{a_{2}}{b_{2}}, \ldots, \frac{a_{n}}{b_{n}} $$ forms an arithmetic progression. Prove that the terms of the sequence are equal. (Thailand)
|
Suppose that (1) is an arithmetic progression with nonzero difference. Let the difference be $\Delta=\frac{c}{d}$, where $d>0$ and $c, d$ are coprime. We will show that too many denominators $b_{i}$ should be divisible by $d$. To this end, for any $1 \leqslant i \leqslant n$ and any prime divisor $p$ of $d$, say that the index $i$ is $p$-wrong, if $v_{p}\left(b_{i}\right)<v_{p}(d)$. $\left(v_{p}(x)\right.$ stands for the exponent of $p$ in the prime factorisation of $x$.) Claim 1. For any prime $p$, all $p$-wrong indices are congruent modulo $p$. In other words, the $p$-wrong indices (if they exist) are included in an arithmetic progression with difference $p$. Proof. Let $\alpha=v_{p}(d)$. For the sake of contradiction, suppose that $i$ and $j$ are $p$-wrong indices (i.e., none of $b_{i}$ and $b_{j}$ is divisible by $\left.p^{\alpha}\right)$ such that $i \not \equiv j(\bmod p)$. Then the least common denominator of $\frac{a_{i}}{b_{i}}$ and $\frac{a_{j}}{b_{j}}$ is not divisible by $p^{\alpha}$. But this is impossible because in their difference, $(i-j) \Delta=\frac{(i-j) c}{d}$, the numerator is coprime to $p$, but $p^{\alpha}$ divides the denominator $d$. Claim 2. $d$ has no prime divisors greater than 5 . Proof. Suppose that $p \geqslant 7$ is a prime divisor of $d$. Among the indices $1,2, \ldots, n$, at most $\left\lceil\frac{n}{p}\right\rceil<\frac{n}{p}+1$ are $p$-wrong, so $p$ divides at least $\frac{p-1}{p} n-1$ of $b_{1}, \ldots, b_{n}$. Since these denominators are distinct, $$ 5 n \geqslant \max \left\{b_{i}: p \mid b_{i}\right\} \geqslant\left(\frac{p-1}{p} n-1\right) p=(p-1)(n-1)-1 \geqslant 6(n-1)-1>5 n, $$ a contradiction. Claim 3. For every $0 \leqslant k \leqslant n-30$, among the denominators $b_{k+1}, b_{k+2}, \ldots, b_{k+30}$, at least $\varphi(30)=8$ are divisible by $d$. Proof. By Claim 1, the 2 -wrong, 3 -wrong and 5 -wrong indices can be covered by three arithmetic progressions with differences 2,3 and 5 . By a simple inclusion-exclusion, $(2-1) \cdot(3-1) \cdot(5-1)=8$ indices are not covered; by Claim 2, we have $d \mid b_{i}$ for every uncovered index $i$. Claim 4. $|\Delta|<\frac{20}{n-2}$ and $d>\frac{n-2}{20}$. Proof. From the sequence (1), remove all fractions with $b_{n}<\frac{n}{2}$, There remain at least $\frac{n}{2}$ fractions, and they cannot exceed $\frac{5 n}{n / 2}=10$. So we have at least $\frac{n}{2}$ elements of the arithmetic progression (1) in the interval $(0,10]$, hence the difference must be below $\frac{10}{n / 2-1}=\frac{20}{n-2}$. The second inequality follows from $\frac{1}{d} \leqslant \frac{|c|}{d}=|\Delta|$. Now we have everything to get the final contradiction. By Claim 3, we have $d \mid b_{i}$ for at least $\left\lfloor\frac{n}{30}\right\rfloor \cdot 8$ indices $i$. By Claim 4 , we have $d \geqslant \frac{n-2}{20}$. Therefore, $$ 5 n \geqslant \max \left\{b_{i}: d \mid b_{i}\right\} \geqslant\left(\left\lfloor\frac{n}{30}\right\rfloor \cdot 8\right) \cdot d>\left(\frac{n}{30}-1\right) \cdot 8 \cdot \frac{n-2}{20}>5 n . $$ Comment 1. It is possible that all terms in (1) are equal, for example with $a_{i}=2 i-1$ and $b_{i}=4 i-2$ we have $\frac{a_{i}}{b_{i}}=\frac{1}{2}$. Comment 2. The bound $5 n$ in the statement is far from sharp; the solution above can be modified to work for $9 n$. For large $n$, the bound $5 n$ can be replaced by $n^{\frac{3}{2}-\varepsilon}$. The activities of the Problem Selection Committee were supported by DEDEMAN LA FANTANA vine la tine
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
142cd5dd-3a0f-56a5-9322-18045fa09323
| 23,684
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand)
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, and we may assume strict inequality as otherwise $b_{i}=a_{i}$ works. Also, $X$ clearly cannot be empty. If $n \in X$, add $\Delta$ to $a_{n}$, producing a sequence of $c_{i}$ with $\sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i}$, and then scale as described above to make the sum equal to 2 . Otherwise, there is some $k$ with $k \in X$ and $k+1 \in X^{c}$. Let $\delta=a_{k+1}-a_{k}$. - If $\delta>\Delta$, add $\Delta$ to $a_{k}$ and then scale. - If $\delta<\Delta$, then considering $X \cup\{k+1\} \backslash\{k\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. - If $\delta=\Delta$, choose any $j \neq k, k+1$ (possible since $n \geqslant 3$ ), and any $\epsilon$ less than the least of $a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $j \in X$ then add $\Delta-\epsilon$ to $a_{k}$ and $\epsilon$ to $a_{j}$, then scale; otherwise, add $\Delta$ to $a_{k}$ and $\epsilon / 2$ to $a_{k+1}$, and subtract $\epsilon / 2$ from $a_{j}$, then scale.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand)
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, and we may assume strict inequality as otherwise $b_{i}=a_{i}$ works. Also, $X$ clearly cannot be empty. If $n \in X$, add $\Delta$ to $a_{n}$, producing a sequence of $c_{i}$ with $\sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i}$, and then scale as described above to make the sum equal to 2 . Otherwise, there is some $k$ with $k \in X$ and $k+1 \in X^{c}$. Let $\delta=a_{k+1}-a_{k}$. - If $\delta>\Delta$, add $\Delta$ to $a_{k}$ and then scale. - If $\delta<\Delta$, then considering $X \cup\{k+1\} \backslash\{k\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. - If $\delta=\Delta$, choose any $j \neq k, k+1$ (possible since $n \geqslant 3$ ), and any $\epsilon$ less than the least of $a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $j \in X$ then add $\Delta-\epsilon$ to $a_{k}$ and $\epsilon$ to $a_{j}$, then scale; otherwise, add $\Delta$ to $a_{k}$ and $\epsilon / 2$ to $a_{k+1}$, and subtract $\epsilon / 2$ from $a_{j}$, then scale.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e124d444-564b-5d73-b28e-0dff7253c69d
| 23,695
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand)
|
This is similar to Suppose there exists $1 \leqslant j \leqslant n-1$ such that $j \in X$ but $j+1 \in X^{c}$. Then $a_{j+1}-a_{j} \geqslant \Delta$, because otherwise considering $X \cup\{j+1\} \backslash\{j\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. If $a_{j+1}-a_{j}>\Delta$, put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{i}, & \text { otherwise }\end{cases} $$ If $a_{j+1}-a_{j}=\Delta$, choose any $\epsilon$ less than the least of $\Delta / 2, a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $|X| \geqslant 2$, choose $k \in X$ with $k \neq j$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2-\epsilon, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{k}+\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ Otherwise, $\left|X^{c}\right| \geqslant 2$, so choose $k \in X^{c}$ with $k \neq j+1$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2+\epsilon, & \text { if } i=j+1 \\ a_{k}-\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ If there is no $1 \leqslant j \leqslant n$ such that $j \in X$ but $j+1 \in X^{c}$, there must be some $1<k \leqslant n$ such that $X=[k, n]$ (certainly $X$ cannot be empty). We must have $a_{1}>\Delta$, as otherwise considering $X \cup\{1\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. Now put $$ b_{i}= \begin{cases}a_{1}-\Delta / 2, & \text { if } i=1 \\ a_{n}+\Delta / 2, & \text { if } i=n \\ a_{i}, & \text { otherwise }\end{cases} $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand)
|
This is similar to Suppose there exists $1 \leqslant j \leqslant n-1$ such that $j \in X$ but $j+1 \in X^{c}$. Then $a_{j+1}-a_{j} \geqslant \Delta$, because otherwise considering $X \cup\{j+1\} \backslash\{j\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. If $a_{j+1}-a_{j}>\Delta$, put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{i}, & \text { otherwise }\end{cases} $$ If $a_{j+1}-a_{j}=\Delta$, choose any $\epsilon$ less than the least of $\Delta / 2, a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $|X| \geqslant 2$, choose $k \in X$ with $k \neq j$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2-\epsilon, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{k}+\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ Otherwise, $\left|X^{c}\right| \geqslant 2$, so choose $k \in X^{c}$ with $k \neq j+1$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2+\epsilon, & \text { if } i=j+1 \\ a_{k}-\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ If there is no $1 \leqslant j \leqslant n$ such that $j \in X$ but $j+1 \in X^{c}$, there must be some $1<k \leqslant n$ such that $X=[k, n]$ (certainly $X$ cannot be empty). We must have $a_{1}>\Delta$, as otherwise considering $X \cup\{1\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. Now put $$ b_{i}= \begin{cases}a_{1}-\Delta / 2, & \text { if } i=1 \\ a_{n}+\Delta / 2, & \text { if } i=n \\ a_{i}, & \text { otherwise }\end{cases} $$
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e124d444-564b-5d73-b28e-0dff7253c69d
| 23,695
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand)
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, so $\Delta \geqslant 0$. If $\Delta=0$ we can take $b_{i}=a_{i}$, so now assume that $\Delta>0$. Suppose that there is some $k \leqslant n$ such that $|X \cap[k, n]|>\left|X^{c} \cap[k, n]\right|$. If we choose the largest such $k$ then $|X \cap[k, n]|-\left|X^{c} \cap[k, n]\right|=1$. We can now find the required sequence $\left(b_{i}\right)$ by starting with $c_{i}=a_{i}$ for $i<k$ and $c_{i}=a_{i}+\Delta$ for $i \geqslant k$, and then scaling as described above. If no such $k$ exists, we will derive a contradiction. For each $i \in X$ we can choose $i<j_{i} \leqslant n$ in such a way that $j_{i} \in X^{c}$ and all the $j_{i}$ are different. (For instance, note that necessarily $n \in X^{c}$ and now just work downwards; each time an $i \in X$ is considered, let $j_{i}$ be the least element of $X^{c}$ greater than $i$ and not yet used.) Let $Y$ be the (possibly empty) subset of $[1, n]$ consisting of those elements in $X^{c}$ that are also not one of the $j_{i}$. In any case $$ \Delta=\sum_{i \in X}\left(a_{j_{i}}-a_{i}\right)+\sum_{j \in Y} a_{j} $$ where each term in the sums is positive. Since $n \geqslant 3$ the total number of terms above is at least two. Take a least such term and its corresponding index $i$ and consider the set $Z$ which we form from $X$ by removing $i$ and adding $j_{i}$ (if it is a term of the first type) or just by adding $j$ if it is a term of the second type. The corresponding expression of $\Delta$ for $Z$ has the sign of its least term changed, meaning that the sum is still nonnegative but strictly less than $\Delta$, which contradicts $X$ being $\left(a_{i}\right)$-minimising.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand)
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, so $\Delta \geqslant 0$. If $\Delta=0$ we can take $b_{i}=a_{i}$, so now assume that $\Delta>0$. Suppose that there is some $k \leqslant n$ such that $|X \cap[k, n]|>\left|X^{c} \cap[k, n]\right|$. If we choose the largest such $k$ then $|X \cap[k, n]|-\left|X^{c} \cap[k, n]\right|=1$. We can now find the required sequence $\left(b_{i}\right)$ by starting with $c_{i}=a_{i}$ for $i<k$ and $c_{i}=a_{i}+\Delta$ for $i \geqslant k$, and then scaling as described above. If no such $k$ exists, we will derive a contradiction. For each $i \in X$ we can choose $i<j_{i} \leqslant n$ in such a way that $j_{i} \in X^{c}$ and all the $j_{i}$ are different. (For instance, note that necessarily $n \in X^{c}$ and now just work downwards; each time an $i \in X$ is considered, let $j_{i}$ be the least element of $X^{c}$ greater than $i$ and not yet used.) Let $Y$ be the (possibly empty) subset of $[1, n]$ consisting of those elements in $X^{c}$ that are also not one of the $j_{i}$. In any case $$ \Delta=\sum_{i \in X}\left(a_{j_{i}}-a_{i}\right)+\sum_{j \in Y} a_{j} $$ where each term in the sums is positive. Since $n \geqslant 3$ the total number of terms above is at least two. Take a least such term and its corresponding index $i$ and consider the set $Z$ which we form from $X$ by removing $i$ and adding $j_{i}$ (if it is a term of the first type) or just by adding $j$ if it is a term of the second type. The corresponding expression of $\Delta$ for $Z$ has the sign of its least term changed, meaning that the sum is still nonnegative but strictly less than $\Delta$, which contradicts $X$ being $\left(a_{i}\right)$-minimising.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e124d444-564b-5d73-b28e-0dff7253c69d
| 23,695
|
Let $n \geqslant 2$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers such that $$ a_{1}+a_{2}+\cdots+a_{n}=0 $$ Define the set $A$ by $$ A=\left\{(i, j)\left|1 \leqslant i<j \leqslant n,\left|a_{i}-a_{j}\right| \geqslant 1\right\} .\right. $$ Prove that, if $A$ is not empty, then $$ \sum_{(i, j) \in A} a_{i} a_{j}<0 $$ (China)
|
Define sets $B$ and $C$ by $$ \begin{aligned} & B=\left\{(i, j)\left|1 \leqslant i, j \leqslant n,\left|a_{i}-a_{j}\right| \geqslant 1\right\},\right. \\ & C=\left\{(i, j)\left|1 \leqslant i, j \leqslant n,\left|a_{i}-a_{j}\right|<1\right\} .\right. \end{aligned} $$ We have $$ \begin{aligned} \sum_{(i, j) \in A} a_{i} a_{j} & =\frac{1}{2} \sum_{(i, j) \in B} a_{i} a_{j} \\ \sum_{(i, j) \in B} a_{i} a_{j} & =\sum_{1 \leqslant i, j \leqslant n} a_{i} a_{j}-\sum_{(i, j) \notin B} a_{i} a_{j}=0-\sum_{(i, j) \in C} a_{i} a_{j} . \end{aligned} $$ So it suffices to show that if $A$ (and hence $B$ ) are nonempty, then $$ \sum_{(i, j) \in C} a_{i} a_{j}>0 $$ Partition the indices into sets $P, Q, R$, and $S$ such that $$ \begin{aligned} P & =\left\{i \mid a_{i} \leqslant-1\right\} & R & =\left\{i \mid 0<a_{i}<1\right\} \\ Q & =\left\{i \mid-1<a_{i} \leqslant 0\right\} & S & =\left\{i \mid 1 \leqslant a_{i}\right\} . \end{aligned} $$ Then $$ \sum_{(i, j) \in C} a_{i} a_{j} \geqslant \sum_{i \in P \cup S} a_{i}^{2}+\sum_{i, j \in Q \cup R} a_{i} a_{j}=\sum_{i \in P \cup S} a_{i}^{2}+\left(\sum_{i \in Q \cup R} a_{i}\right)^{2} \geqslant 0 . $$ The first inequality holds because all of the positive terms in the RHS are also in the LHS, and all of the negative terms in the LHS are also in the RHS. The first inequality attains equality only if both sides have the same negative terms, which implies $\left|a_{i}-a_{j}\right|<1$ whenever $i, j \in Q \cup R$; the second inequality attains equality only if $P=S=\varnothing$. But then we would have $A=\varnothing$. So $A$ nonempty implies that the inequality holds strictly, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n \geqslant 2$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers such that $$ a_{1}+a_{2}+\cdots+a_{n}=0 $$ Define the set $A$ by $$ A=\left\{(i, j)\left|1 \leqslant i<j \leqslant n,\left|a_{i}-a_{j}\right| \geqslant 1\right\} .\right. $$ Prove that, if $A$ is not empty, then $$ \sum_{(i, j) \in A} a_{i} a_{j}<0 $$ (China)
|
Define sets $B$ and $C$ by $$ \begin{aligned} & B=\left\{(i, j)\left|1 \leqslant i, j \leqslant n,\left|a_{i}-a_{j}\right| \geqslant 1\right\},\right. \\ & C=\left\{(i, j)\left|1 \leqslant i, j \leqslant n,\left|a_{i}-a_{j}\right|<1\right\} .\right. \end{aligned} $$ We have $$ \begin{aligned} \sum_{(i, j) \in A} a_{i} a_{j} & =\frac{1}{2} \sum_{(i, j) \in B} a_{i} a_{j} \\ \sum_{(i, j) \in B} a_{i} a_{j} & =\sum_{1 \leqslant i, j \leqslant n} a_{i} a_{j}-\sum_{(i, j) \notin B} a_{i} a_{j}=0-\sum_{(i, j) \in C} a_{i} a_{j} . \end{aligned} $$ So it suffices to show that if $A$ (and hence $B$ ) are nonempty, then $$ \sum_{(i, j) \in C} a_{i} a_{j}>0 $$ Partition the indices into sets $P, Q, R$, and $S$ such that $$ \begin{aligned} P & =\left\{i \mid a_{i} \leqslant-1\right\} & R & =\left\{i \mid 0<a_{i}<1\right\} \\ Q & =\left\{i \mid-1<a_{i} \leqslant 0\right\} & S & =\left\{i \mid 1 \leqslant a_{i}\right\} . \end{aligned} $$ Then $$ \sum_{(i, j) \in C} a_{i} a_{j} \geqslant \sum_{i \in P \cup S} a_{i}^{2}+\sum_{i, j \in Q \cup R} a_{i} a_{j}=\sum_{i \in P \cup S} a_{i}^{2}+\left(\sum_{i \in Q \cup R} a_{i}\right)^{2} \geqslant 0 . $$ The first inequality holds because all of the positive terms in the RHS are also in the LHS, and all of the negative terms in the LHS are also in the RHS. The first inequality attains equality only if both sides have the same negative terms, which implies $\left|a_{i}-a_{j}\right|<1$ whenever $i, j \in Q \cup R$; the second inequality attains equality only if $P=S=\varnothing$. But then we would have $A=\varnothing$. So $A$ nonempty implies that the inequality holds strictly, as required.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c89402ff-fccc-58b9-93f4-5e6e025d53fd
| 23,702
|
Let $n \geqslant 2$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers such that $$ a_{1}+a_{2}+\cdots+a_{n}=0 $$ Define the set $A$ by $$ A=\left\{(i, j)\left|1 \leqslant i<j \leqslant n,\left|a_{i}-a_{j}\right| \geqslant 1\right\} .\right. $$ Prove that, if $A$ is not empty, then $$ \sum_{(i, j) \in A} a_{i} a_{j}<0 $$ (China)
|
Consider $P, Q, R, S$ as in $$ p=\sum_{i \in P} a_{i}, \quad q=\sum_{i \in Q} a_{i}, \quad r=\sum_{i \in R} a_{i}, \quad s=\sum_{i \in S} a_{i}, $$ and let $$ t_{+}=\sum_{(i, j) \in A, a_{i} a_{j} \geqslant 0} a_{i} a_{j}, \quad t_{-}=\sum_{(i, j) \in A, a_{i} a_{j} \leqslant 0} a_{i} a_{j} . $$ We know that $p+q+r+s=0$, and we need to prove that $t_{+}+t_{-}<0$. Notice that $t_{+} \leqslant p^{2} / 2+p q+r s+s^{2} / 2$ (with equality only if $p=s=0$ ), and $t_{-} \leqslant p r+p s+q s$ (with equality only if there do not exist $i \in Q$ and $j \in R$ with $a_{j}-a_{i}>1$ ). Therefore, $$ t_{+}+t_{-} \leqslant \frac{p^{2}+s^{2}}{2}+p q+r s+p r+p s+q s=\frac{(p+q+r+s)^{2}}{2}-\frac{(q+r)^{2}}{2}=-\frac{(q+r)^{2}}{2} \leqslant 0 $$ If $A$ is not empty and $p=s=0$, then there must exist $i \in Q, j \in R$ with $\left|a_{i}-a_{j}\right|>1$, and hence the earlier equality conditions cannot both occur. Comment. The RHS of the original inequality cannot be replaced with any constant $c<0$ (independent of $n$ ). Indeed, take $$ a_{1}=-\frac{n}{n+2}, a_{2}=\cdots=a_{n-1}=\frac{1}{n+2}, a_{n}=\frac{2}{n+2} . $$ Then $\sum_{(i, j) \in A} a_{i} a_{j}=-\frac{2 n}{(n+2)^{2}}$, which converges to zero as $n \rightarrow \infty$. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n \geqslant 2$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers such that $$ a_{1}+a_{2}+\cdots+a_{n}=0 $$ Define the set $A$ by $$ A=\left\{(i, j)\left|1 \leqslant i<j \leqslant n,\left|a_{i}-a_{j}\right| \geqslant 1\right\} .\right. $$ Prove that, if $A$ is not empty, then $$ \sum_{(i, j) \in A} a_{i} a_{j}<0 $$ (China)
|
Consider $P, Q, R, S$ as in $$ p=\sum_{i \in P} a_{i}, \quad q=\sum_{i \in Q} a_{i}, \quad r=\sum_{i \in R} a_{i}, \quad s=\sum_{i \in S} a_{i}, $$ and let $$ t_{+}=\sum_{(i, j) \in A, a_{i} a_{j} \geqslant 0} a_{i} a_{j}, \quad t_{-}=\sum_{(i, j) \in A, a_{i} a_{j} \leqslant 0} a_{i} a_{j} . $$ We know that $p+q+r+s=0$, and we need to prove that $t_{+}+t_{-}<0$. Notice that $t_{+} \leqslant p^{2} / 2+p q+r s+s^{2} / 2$ (with equality only if $p=s=0$ ), and $t_{-} \leqslant p r+p s+q s$ (with equality only if there do not exist $i \in Q$ and $j \in R$ with $a_{j}-a_{i}>1$ ). Therefore, $$ t_{+}+t_{-} \leqslant \frac{p^{2}+s^{2}}{2}+p q+r s+p r+p s+q s=\frac{(p+q+r+s)^{2}}{2}-\frac{(q+r)^{2}}{2}=-\frac{(q+r)^{2}}{2} \leqslant 0 $$ If $A$ is not empty and $p=s=0$, then there must exist $i \in Q, j \in R$ with $\left|a_{i}-a_{j}\right|>1$, and hence the earlier equality conditions cannot both occur. Comment. The RHS of the original inequality cannot be replaced with any constant $c<0$ (independent of $n$ ). Indeed, take $$ a_{1}=-\frac{n}{n+2}, a_{2}=\cdots=a_{n-1}=\frac{1}{n+2}, a_{n}=\frac{2}{n+2} . $$ Then $\sum_{(i, j) \in A} a_{i} a_{j}=-\frac{2 n}{(n+2)^{2}}$, which converges to zero as $n \rightarrow \infty$. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c89402ff-fccc-58b9-93f4-5e6e025d53fd
| 23,702
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$
|
In the first two steps, we deal with any polynomial $P(x, y, z)$ satisfying $P(x, y, z)=$ $P(x, y, x y-z)$. Call such a polynomial weakly symmetric, and call a polynomial satisfying the full conditions in the problem symmetric. Step 1. We start with the description of weakly symmetric polynomials. We claim that they are exactly the polynomials in $x, y$, and $z(x y-z)$. Clearly, all such polynomials are weakly symmetric. For the converse statement, consider $P_{1}(x, y, z):=P\left(x, y, z+\frac{1}{2} x y\right)$, which satisfies $P_{1}(x, y, z)=P_{1}(x, y,-z)$ and is therefore a polynomial in $x, y$, and $z^{2}$. This means that $P$ is a polynomial in $x, y$, and $\left(z-\frac{1}{2} x y\right)^{2}=-z(x y-z)+\frac{1}{4} x^{2} y^{2}$, and therefore a polynomial in $x, y$, and $z(x y-z)$. Step 2. Suppose that $P$ is weakly symmetric. Consider the monomials in $P(x, y, z)$ of highest total degree. Our aim is to show that in each such monomial $\mu x^{a} y^{b} z^{c}$ we have $a, b \geqslant c$. Consider the expansion $$ P(x, y, z)=\sum_{i, j, k} \mu_{i j k} x^{i} y^{j}(z(x y-z))^{k} $$ The maximal total degree of a summand in (1.1) is $m=\max _{i, j, k: \mu_{i j k} \neq 0}(i+j+3 k)$. Now, for any $i, j, k$ satisfying $i+j+3 k=m$ the summand $\mu_{i, j, k} x^{i} y^{j}(z(x y-z))^{k}$ has leading term of the form $\mu x^{i+k} y^{j+k} z^{k}$. No other nonzero summand in (1.1) may have a term of this form in its expansion, hence this term does not cancel in the whole sum. Therefore, $\operatorname{deg} P=m$, and the leading component of $P$ is exactly $$ \sum_{i+j+3 k=m} \mu_{i, j, k} x^{i+k} y^{j+k} z^{k} $$ and each summand in this sum satisfies the condition claimed above. Step 3. We now prove the problem statement by induction on $m=\operatorname{deg} P$. For $m=0$ the claim is trivial. Consider now a symmetric polynomial $P$ with $\operatorname{deg} P>0$. By Step 2, each of its monomials $\mu x^{a} y^{b} z^{c}$ of the highest total degree satisfies $a, b \geqslant c$. Applying other weak symmetries, we obtain $a, c \geqslant b$ and $b, c \geqslant a$; therefore, $P$ has a unique leading monomial of the form $\mu(x y z)^{c}$. The polynomial $P_{0}(x, y, z)=P(x, y, z)-\mu\left(x y z-x^{2}-y^{2}-z^{2}\right)^{c}$ has smaller total degree. Since $P_{0}$ is symmetric, it is representable as a polynomial function of $x y z-x^{2}-y^{2}-z^{2}$. Then $P$ is also of this form, completing the inductive step. Comment. We could alternatively carry out Step 1 by an induction on $n=\operatorname{deg}_{z} P$, in a manner similar to Step 3. If $n=0$, the statement holds. Assume that $n>0$ and check the leading component of $P$ with respect to $z$ : $$ P(x, y, z)=Q_{n}(x, y) z^{n}+R(x, y, z) $$ where $\operatorname{deg}_{z} R<n$. After the change $z \mapsto x y-z$, the leading component becomes $Q_{n}(x, y)(-z)^{n}$; on the other hand, it should remain the same. Hence $n$ is even. Now consider the polynomial $$ P_{0}(x, y, z)=P(x, y, z)-Q_{n}(x, y) \cdot(z(z-x y))^{n / 2} $$ It is also weakly symmetric, and $\operatorname{deg}_{z} P_{0}<n$. By the inductive hypothesis, it has the form $P_{0}(x, y, z)=$ $S(x, y, z(z-x y))$. Hence the polynomial $$ P(x, y, z)=S(x, y, z(x y-z))+Q_{n}(x, y)(z(z-x y))^{n / 2} $$ also has this form. This completes the inductive step.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$
|
In the first two steps, we deal with any polynomial $P(x, y, z)$ satisfying $P(x, y, z)=$ $P(x, y, x y-z)$. Call such a polynomial weakly symmetric, and call a polynomial satisfying the full conditions in the problem symmetric. Step 1. We start with the description of weakly symmetric polynomials. We claim that they are exactly the polynomials in $x, y$, and $z(x y-z)$. Clearly, all such polynomials are weakly symmetric. For the converse statement, consider $P_{1}(x, y, z):=P\left(x, y, z+\frac{1}{2} x y\right)$, which satisfies $P_{1}(x, y, z)=P_{1}(x, y,-z)$ and is therefore a polynomial in $x, y$, and $z^{2}$. This means that $P$ is a polynomial in $x, y$, and $\left(z-\frac{1}{2} x y\right)^{2}=-z(x y-z)+\frac{1}{4} x^{2} y^{2}$, and therefore a polynomial in $x, y$, and $z(x y-z)$. Step 2. Suppose that $P$ is weakly symmetric. Consider the monomials in $P(x, y, z)$ of highest total degree. Our aim is to show that in each such monomial $\mu x^{a} y^{b} z^{c}$ we have $a, b \geqslant c$. Consider the expansion $$ P(x, y, z)=\sum_{i, j, k} \mu_{i j k} x^{i} y^{j}(z(x y-z))^{k} $$ The maximal total degree of a summand in (1.1) is $m=\max _{i, j, k: \mu_{i j k} \neq 0}(i+j+3 k)$. Now, for any $i, j, k$ satisfying $i+j+3 k=m$ the summand $\mu_{i, j, k} x^{i} y^{j}(z(x y-z))^{k}$ has leading term of the form $\mu x^{i+k} y^{j+k} z^{k}$. No other nonzero summand in (1.1) may have a term of this form in its expansion, hence this term does not cancel in the whole sum. Therefore, $\operatorname{deg} P=m$, and the leading component of $P$ is exactly $$ \sum_{i+j+3 k=m} \mu_{i, j, k} x^{i+k} y^{j+k} z^{k} $$ and each summand in this sum satisfies the condition claimed above. Step 3. We now prove the problem statement by induction on $m=\operatorname{deg} P$. For $m=0$ the claim is trivial. Consider now a symmetric polynomial $P$ with $\operatorname{deg} P>0$. By Step 2, each of its monomials $\mu x^{a} y^{b} z^{c}$ of the highest total degree satisfies $a, b \geqslant c$. Applying other weak symmetries, we obtain $a, c \geqslant b$ and $b, c \geqslant a$; therefore, $P$ has a unique leading monomial of the form $\mu(x y z)^{c}$. The polynomial $P_{0}(x, y, z)=P(x, y, z)-\mu\left(x y z-x^{2}-y^{2}-z^{2}\right)^{c}$ has smaller total degree. Since $P_{0}$ is symmetric, it is representable as a polynomial function of $x y z-x^{2}-y^{2}-z^{2}$. Then $P$ is also of this form, completing the inductive step. Comment. We could alternatively carry out Step 1 by an induction on $n=\operatorname{deg}_{z} P$, in a manner similar to Step 3. If $n=0$, the statement holds. Assume that $n>0$ and check the leading component of $P$ with respect to $z$ : $$ P(x, y, z)=Q_{n}(x, y) z^{n}+R(x, y, z) $$ where $\operatorname{deg}_{z} R<n$. After the change $z \mapsto x y-z$, the leading component becomes $Q_{n}(x, y)(-z)^{n}$; on the other hand, it should remain the same. Hence $n$ is even. Now consider the polynomial $$ P_{0}(x, y, z)=P(x, y, z)-Q_{n}(x, y) \cdot(z(z-x y))^{n / 2} $$ It is also weakly symmetric, and $\operatorname{deg}_{z} P_{0}<n$. By the inductive hypothesis, it has the form $P_{0}(x, y, z)=$ $S(x, y, z(z-x y))$. Hence the polynomial $$ P(x, y, z)=S(x, y, z(x y-z))+Q_{n}(x, y)(z(z-x y))^{n / 2} $$ also has this form. This completes the inductive step.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ac557cc3-f2e6-5bb5-a8e1-1058814cd2b2
| 23,708
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$
|
We will rely on the well-known identity $$ \cos ^{2} u+\cos ^{2} v+\cos ^{2} w-2 \cos u \cos v \cos w-1=0 \quad \text { whenever } u+v+w=0 $$ Claim 1. The polynomial $P(x, y, z)$ is constant on the surface $$ \mathfrak{S}=\{(2 \cos u, 2 \cos v, 2 \cos w): u+v+w=0\} $$ Proof. Notice that for $x=2 \cos u, y=2 \cos v, z=2 \cos w$, the Vieta jumps $x \mapsto y z-x$, $y \mapsto z x-y, z \mapsto x y-z$ in (*) replace $(u, v, w)$ by $(v-w,-v, w),(u, w-u,-w)$ and $(-u, v, u-v)$, respectively. For example, for the first type of jump we have $$ y z-x=4 \cos v \cos w-2 \cos u=2 \cos (v+w)+2 \cos (v-w)-2 \cos u=2 \cos (v-w) . $$ Define $G(u, v, w)=P(2 \cos u, 2 \cos v, 2 \cos w)$. For $u+v+w=0$, the jumps give $$ \begin{aligned} G(u, v, w) & =G(v-w,-v, w)=G(w-v,-v,(v-w)-(-v))=G(-u-2 v,-v, 2 v-w) \\ & =G(u+2 v, v, w-2 v) \end{aligned} $$ By induction, $$ G(u, v, w)=G(u+2 k v, v, w-2 k v) \quad(k \in \mathbb{Z}) $$ Similarly, $$ G(u, v, w)=G(u, v-2 \ell u, w+2 \ell u) \quad(\ell \in \mathbb{Z}) $$ And, of course, we have $$ G(u, v, w)=G(u+2 p \pi, v+2 q \pi, w-2(p+q) \pi) \quad(p, q \in \mathbb{Z}) $$ Take two nonzero real numbers $u, v$ such that $u, v$ and $\pi$ are linearly independent over $\mathbb{Q}$. By combining (2.2-2.4), we can see that $G$ is constant on a dense subset of the plane $u+v+w=0$. By continuity, $G$ is constant on the entire plane and therefore $P$ is constant on $\mathfrak{S}$. Claim 2. The polynomial $T(x, y, z)=x^{2}+y^{2}+z^{2}-x y z-4$ divides $P(x, y, z)-P(2,2,2)$. Proof. By dividing $P$ by $T$ with remainders, there exist some polynomials $R(x, y, z), A(y, z)$ and $B(y, z)$ such that $$ P(x, y, z)-P(2,2,2)=T(x, y, z) \cdot R(x, y, z)+A(y, z) x+B(y, z) $$ On the surface $\mathfrak{S}$ the LHS of (2.5) is zero by Claim 1 (since $(2,2,2) \in \mathfrak{S}$ ) and $T=0$ by (2.1). Hence, $A(y, z) x+B(y, z)$ vanishes on $\mathfrak{S}$. Notice that for every $y=2 \cos v$ and $z=2 \cos w$ with $\frac{\pi}{3}<v, w<\frac{2 \pi}{3}$, there are two distinct values of $x$ such that $(x, y, z) \in \mathfrak{S}$, namely $x_{1}=2 \cos (v+w)$ (which is negative), and $x_{2}=2 \cos (v-w)$ (which is positive). This can happen only if $A(y, z)=B(y, z)=0$. Hence, $A(y, z)=B(y, z)=0$ for $|y|<1,|z|<1$. The polynomials $A$ and $B$ vanish on an open set, so $A$ and $B$ are both the zero polynomial. The quotient $(P(x, y, z)-P(2,2,2)) / T(x, y, z)$ is a polynomial of lower degree than $P$ and it also satisfies (*). The problem statement can now be proven by induction on the degree of $P$. Comment. In the proof of (2.2) and (2.3) we used two consecutive Vieta jumps; in fact from (*) we used only $P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z)$. Solution 3 (using algebraic geometry, just for interest). Let $Q=x^{2}+y^{2}+z^{2}-x y z$ and let $t \in \mathbb{C}$. Checking where $Q-t, \frac{\partial Q}{\partial x}, \frac{\partial Q}{\partial y}$ and $\frac{\partial Q}{\partial z}$ vanish simultaneously, we find that the surface $Q=t$ is smooth except for the cases $t=0$, when the only singular point is $(0,0,0)$, and $t=4$, when the four points $( \pm 2, \pm 2, \pm 2)$ that satisfy $x y z=8$ are the only singular points. The singular points are the fixed points of the group $\Gamma$ of polynomial automorphisms of $\mathbb{C}^{3}$ generated by the three Vieta involutions $$ \iota_{1}:(x, y, z) \mapsto(x, y, x y-z), \quad \iota_{2}:(x, y, z) \mapsto(x, x z-y, z), \quad \iota_{3}:(x, y, z) \mapsto(y z-x, y, z) $$ $\Gamma$ acts on each surface $\mathcal{V}_{t}: Q-t=0$. If $Q-t$ were reducible then the surface $Q=t$ would contain a curve of singular points. Therefore $Q-t$ is irreducible in $\mathbb{C}[x, y, z]$. (One can also prove algebraically that $Q-t$ is irreducible, for example by checking that its discriminant as a quadratic polynomial in $x$ is not a square in $\mathbb{C}[y, z]$, and likewise for the other two variables.) In the following solution we will only use the algebraic surface $\mathcal{V}_{0}$. Let $U$ be the $\Gamma$-orbit of $(3,3,3)$. Consider $\iota_{3} \circ \iota_{2}$, which leaves $z$ invariant. For each fixed value of $z, \iota_{3} \circ \iota_{2}$ acts linearly on $(x, y)$ by the matrix $$ M_{z}:=\left(\begin{array}{cc} z^{2}-1 & -z \\ z & -1 \end{array}\right) $$ The reverse composition $\iota_{2} \circ \iota_{3}$ acts by $M_{z}^{-1}=M_{z}^{\text {adj }}$. Note det $M_{z}=1$ and $\operatorname{tr} M_{z}=z^{2}-2$. When $z$ does not lie in the real interval $[-2,2]$, the eigenvalues of $M_{z}$ do not have absolute value 1 , so every orbit of the group generated by $M_{z}$ on $\mathbb{C}^{2} \backslash\{(0,0)\}$ is unbounded. For example, fixing $z=3$ we find $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right) \in U$ for every $k \in \mathbb{Z}$, where $\left(F_{n}\right)_{n \in \mathbb{Z}}$ is the Fibonacci sequence with $F_{0}=0, F_{1}=1$. Now we may start at any point $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right)$ and iteratively apply $\iota_{1} \circ \iota_{2}$ to generate another infinite sequence of distinct points of $U$, Zariski dense in the hyperbola cut out of $\mathcal{V}_{0}$ by the plane $x-3 F_{2 k+1}=0$. (The plane $x=a$ cuts out an irreducible conic when $a \notin\{-2,0,2\}$.) Thus the Zariski closure $\bar{U}$ of $U$ contains infinitely many distinct algebraic curves in $\mathcal{V}_{0}$. Since $\mathcal{V}_{0}$ is an irreducible surface this implies that $\bar{U}=\mathcal{V}_{0}$. For any polynomial $P$ satisfying (*), we have $P-P(3,3,3)=0$ at each point of $U$. Since $\bar{U}=\mathcal{V}_{0}, P-P(3,3,3)$ vanishes on $\mathcal{V}_{0}$. Then Hilbert's Nullstellensatz and the irreducibility of $Q$ imply that $P-P(3,3,3)$ is divisible by $Q$. Now $(P-P(3,3,3)) / Q$ is a polynomial also satisfying (*), so we may complete the proof by an induction on the total degree, as in the other solutions. Comment. We remark that Solution 2 used a trigonometric parametrisation of a real component of $\mathcal{V}_{4} ;$ in contrast $\mathcal{V}_{0}$ is birationally equivalent to the projective space $\mathbb{P}^{2}$ under the maps $$ (x, y, z) \rightarrow(x: y: z), \quad(a: b: c) \rightarrow\left(\frac{a^{2}+b^{2}+c^{2}}{b c}, \frac{a^{2}+b^{2}+c^{2}}{a c}, \frac{a^{2}+b^{2}+c^{2}}{a b}\right) . $$ The set $U$ in Solution 3 is contained in $\mathbb{Z}^{3}$ so it is nowhere dense in $\mathcal{V}_{0}$ in the classical topology. Comment (background to the problem). A triple $(a, b, c) \in \mathbb{Z}^{3}$ is called a Markov triple if $a^{2}+b^{2}+c^{2}=3 a b c$, and an integer that occurs as a coordinate of some Markov triple is called a Markov number. (The spelling Markoff is also frequent.) Markov triples arose in A. Markov's work in the 1870s on the reduction theory of indefinite binary quadratic forms. For every Markov triple, $(3 a, 3 b, 3 c)$ lies on $Q=0$. It is well known that all nonzero Markov triples can be generated from $(1,1,1)$ by sequences of Vieta involutions, which are the substitutions described in equation (*) in the problem statement. There has been recent work by number theorists about the properties of Markov numbers (see for example Jean Bourgain, Alex Gamburd and Peter Sarnak, Markoff triples and strong approximation, Comptes Rendus Math. 345, no. 2, 131-135 (2016), arXiv:1505.06411). Each Markov number occurs in infinitely many triples, but a famous old open problem is the unicity conjecture, which asserts that each Markov number occurs in only one Markov triple (up to permutations and sign changes) as the largest coordinate in absolute value in that triple. It is a standard fact in the modern literature on Markov numbers that the Markov triples are Zariski dense in the Markov surface. Proving this is the main work of Solution 3. Algebraic geometry is definitely off-syllabus for the IMO, and one still has to work a bit to prove the Zariski density. On the other hand the approaches of Solutions 1 and 2 are elementary and only use tools expected to be known by IMO contestants. Therefore we do not think that the existence of a solution using algebraic geometry necessarily makes this problem unsuitable for the IMO.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$
|
We will rely on the well-known identity $$ \cos ^{2} u+\cos ^{2} v+\cos ^{2} w-2 \cos u \cos v \cos w-1=0 \quad \text { whenever } u+v+w=0 $$ Claim 1. The polynomial $P(x, y, z)$ is constant on the surface $$ \mathfrak{S}=\{(2 \cos u, 2 \cos v, 2 \cos w): u+v+w=0\} $$ Proof. Notice that for $x=2 \cos u, y=2 \cos v, z=2 \cos w$, the Vieta jumps $x \mapsto y z-x$, $y \mapsto z x-y, z \mapsto x y-z$ in (*) replace $(u, v, w)$ by $(v-w,-v, w),(u, w-u,-w)$ and $(-u, v, u-v)$, respectively. For example, for the first type of jump we have $$ y z-x=4 \cos v \cos w-2 \cos u=2 \cos (v+w)+2 \cos (v-w)-2 \cos u=2 \cos (v-w) . $$ Define $G(u, v, w)=P(2 \cos u, 2 \cos v, 2 \cos w)$. For $u+v+w=0$, the jumps give $$ \begin{aligned} G(u, v, w) & =G(v-w,-v, w)=G(w-v,-v,(v-w)-(-v))=G(-u-2 v,-v, 2 v-w) \\ & =G(u+2 v, v, w-2 v) \end{aligned} $$ By induction, $$ G(u, v, w)=G(u+2 k v, v, w-2 k v) \quad(k \in \mathbb{Z}) $$ Similarly, $$ G(u, v, w)=G(u, v-2 \ell u, w+2 \ell u) \quad(\ell \in \mathbb{Z}) $$ And, of course, we have $$ G(u, v, w)=G(u+2 p \pi, v+2 q \pi, w-2(p+q) \pi) \quad(p, q \in \mathbb{Z}) $$ Take two nonzero real numbers $u, v$ such that $u, v$ and $\pi$ are linearly independent over $\mathbb{Q}$. By combining (2.2-2.4), we can see that $G$ is constant on a dense subset of the plane $u+v+w=0$. By continuity, $G$ is constant on the entire plane and therefore $P$ is constant on $\mathfrak{S}$. Claim 2. The polynomial $T(x, y, z)=x^{2}+y^{2}+z^{2}-x y z-4$ divides $P(x, y, z)-P(2,2,2)$. Proof. By dividing $P$ by $T$ with remainders, there exist some polynomials $R(x, y, z), A(y, z)$ and $B(y, z)$ such that $$ P(x, y, z)-P(2,2,2)=T(x, y, z) \cdot R(x, y, z)+A(y, z) x+B(y, z) $$ On the surface $\mathfrak{S}$ the LHS of (2.5) is zero by Claim 1 (since $(2,2,2) \in \mathfrak{S}$ ) and $T=0$ by (2.1). Hence, $A(y, z) x+B(y, z)$ vanishes on $\mathfrak{S}$. Notice that for every $y=2 \cos v$ and $z=2 \cos w$ with $\frac{\pi}{3}<v, w<\frac{2 \pi}{3}$, there are two distinct values of $x$ such that $(x, y, z) \in \mathfrak{S}$, namely $x_{1}=2 \cos (v+w)$ (which is negative), and $x_{2}=2 \cos (v-w)$ (which is positive). This can happen only if $A(y, z)=B(y, z)=0$. Hence, $A(y, z)=B(y, z)=0$ for $|y|<1,|z|<1$. The polynomials $A$ and $B$ vanish on an open set, so $A$ and $B$ are both the zero polynomial. The quotient $(P(x, y, z)-P(2,2,2)) / T(x, y, z)$ is a polynomial of lower degree than $P$ and it also satisfies (*). The problem statement can now be proven by induction on the degree of $P$. Comment. In the proof of (2.2) and (2.3) we used two consecutive Vieta jumps; in fact from (*) we used only $P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z)$. Solution 3 (using algebraic geometry, just for interest). Let $Q=x^{2}+y^{2}+z^{2}-x y z$ and let $t \in \mathbb{C}$. Checking where $Q-t, \frac{\partial Q}{\partial x}, \frac{\partial Q}{\partial y}$ and $\frac{\partial Q}{\partial z}$ vanish simultaneously, we find that the surface $Q=t$ is smooth except for the cases $t=0$, when the only singular point is $(0,0,0)$, and $t=4$, when the four points $( \pm 2, \pm 2, \pm 2)$ that satisfy $x y z=8$ are the only singular points. The singular points are the fixed points of the group $\Gamma$ of polynomial automorphisms of $\mathbb{C}^{3}$ generated by the three Vieta involutions $$ \iota_{1}:(x, y, z) \mapsto(x, y, x y-z), \quad \iota_{2}:(x, y, z) \mapsto(x, x z-y, z), \quad \iota_{3}:(x, y, z) \mapsto(y z-x, y, z) $$ $\Gamma$ acts on each surface $\mathcal{V}_{t}: Q-t=0$. If $Q-t$ were reducible then the surface $Q=t$ would contain a curve of singular points. Therefore $Q-t$ is irreducible in $\mathbb{C}[x, y, z]$. (One can also prove algebraically that $Q-t$ is irreducible, for example by checking that its discriminant as a quadratic polynomial in $x$ is not a square in $\mathbb{C}[y, z]$, and likewise for the other two variables.) In the following solution we will only use the algebraic surface $\mathcal{V}_{0}$. Let $U$ be the $\Gamma$-orbit of $(3,3,3)$. Consider $\iota_{3} \circ \iota_{2}$, which leaves $z$ invariant. For each fixed value of $z, \iota_{3} \circ \iota_{2}$ acts linearly on $(x, y)$ by the matrix $$ M_{z}:=\left(\begin{array}{cc} z^{2}-1 & -z \\ z & -1 \end{array}\right) $$ The reverse composition $\iota_{2} \circ \iota_{3}$ acts by $M_{z}^{-1}=M_{z}^{\text {adj }}$. Note det $M_{z}=1$ and $\operatorname{tr} M_{z}=z^{2}-2$. When $z$ does not lie in the real interval $[-2,2]$, the eigenvalues of $M_{z}$ do not have absolute value 1 , so every orbit of the group generated by $M_{z}$ on $\mathbb{C}^{2} \backslash\{(0,0)\}$ is unbounded. For example, fixing $z=3$ we find $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right) \in U$ for every $k \in \mathbb{Z}$, where $\left(F_{n}\right)_{n \in \mathbb{Z}}$ is the Fibonacci sequence with $F_{0}=0, F_{1}=1$. Now we may start at any point $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right)$ and iteratively apply $\iota_{1} \circ \iota_{2}$ to generate another infinite sequence of distinct points of $U$, Zariski dense in the hyperbola cut out of $\mathcal{V}_{0}$ by the plane $x-3 F_{2 k+1}=0$. (The plane $x=a$ cuts out an irreducible conic when $a \notin\{-2,0,2\}$.) Thus the Zariski closure $\bar{U}$ of $U$ contains infinitely many distinct algebraic curves in $\mathcal{V}_{0}$. Since $\mathcal{V}_{0}$ is an irreducible surface this implies that $\bar{U}=\mathcal{V}_{0}$. For any polynomial $P$ satisfying (*), we have $P-P(3,3,3)=0$ at each point of $U$. Since $\bar{U}=\mathcal{V}_{0}, P-P(3,3,3)$ vanishes on $\mathcal{V}_{0}$. Then Hilbert's Nullstellensatz and the irreducibility of $Q$ imply that $P-P(3,3,3)$ is divisible by $Q$. Now $(P-P(3,3,3)) / Q$ is a polynomial also satisfying (*), so we may complete the proof by an induction on the total degree, as in the other solutions. Comment. We remark that Solution 2 used a trigonometric parametrisation of a real component of $\mathcal{V}_{4} ;$ in contrast $\mathcal{V}_{0}$ is birationally equivalent to the projective space $\mathbb{P}^{2}$ under the maps $$ (x, y, z) \rightarrow(x: y: z), \quad(a: b: c) \rightarrow\left(\frac{a^{2}+b^{2}+c^{2}}{b c}, \frac{a^{2}+b^{2}+c^{2}}{a c}, \frac{a^{2}+b^{2}+c^{2}}{a b}\right) . $$ The set $U$ in Solution 3 is contained in $\mathbb{Z}^{3}$ so it is nowhere dense in $\mathcal{V}_{0}$ in the classical topology. Comment (background to the problem). A triple $(a, b, c) \in \mathbb{Z}^{3}$ is called a Markov triple if $a^{2}+b^{2}+c^{2}=3 a b c$, and an integer that occurs as a coordinate of some Markov triple is called a Markov number. (The spelling Markoff is also frequent.) Markov triples arose in A. Markov's work in the 1870s on the reduction theory of indefinite binary quadratic forms. For every Markov triple, $(3 a, 3 b, 3 c)$ lies on $Q=0$. It is well known that all nonzero Markov triples can be generated from $(1,1,1)$ by sequences of Vieta involutions, which are the substitutions described in equation (*) in the problem statement. There has been recent work by number theorists about the properties of Markov numbers (see for example Jean Bourgain, Alex Gamburd and Peter Sarnak, Markoff triples and strong approximation, Comptes Rendus Math. 345, no. 2, 131-135 (2016), arXiv:1505.06411). Each Markov number occurs in infinitely many triples, but a famous old open problem is the unicity conjecture, which asserts that each Markov number occurs in only one Markov triple (up to permutations and sign changes) as the largest coordinate in absolute value in that triple. It is a standard fact in the modern literature on Markov numbers that the Markov triples are Zariski dense in the Markov surface. Proving this is the main work of Solution 3. Algebraic geometry is definitely off-syllabus for the IMO, and one still has to work a bit to prove the Zariski density. On the other hand the approaches of Solutions 1 and 2 are elementary and only use tools expected to be known by IMO contestants. Therefore we do not think that the existence of a solution using algebraic geometry necessarily makes this problem unsuitable for the IMO.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ac557cc3-f2e6-5bb5-a8e1-1058814cd2b2
| 23,708
|
The infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of (not necessarily different) integers has the following properties: $0 \leqslant a_{i} \leqslant i$ for all integers $i \geqslant 0$, and $$ \binom{k}{a_{0}}+\binom{k}{a_{1}}+\cdots+\binom{k}{a_{k}}=2^{k} $$ for all integers $k \geqslant 0$. Prove that all integers $N \geqslant 0$ occur in the sequence (that is, for all $N \geqslant 0$, there exists $i \geqslant 0$ with $a_{i}=N$ ). ## (Netherlands)
|
We prove by induction on $k$ that every initial segment of the sequence, $a_{0}, a_{1}, \ldots, a_{k}$, consists of the following elements (counted with multiplicity, and not necessarily in order), for some $\ell \geqslant 0$ with $2 \ell \leqslant k+1$ : $$ 0,1, \ldots, \ell-1, \quad 0,1, \ldots, k-\ell $$ For $k=0$ we have $a_{0}=0$, which is of this form. Now suppose that for $k=m$ the elements $a_{0}, a_{1}, \ldots, a_{m}$ are $0,0,1,1,2,2, \ldots, \ell-1, \ell-1, \ell, \ell+1, \ldots, m-\ell-1, m-\ell$ for some $\ell$ with $0 \leqslant 2 \ell \leqslant m+1$. It is given that $$ \binom{m+1}{a_{0}}+\binom{m+1}{a_{1}}+\cdots+\binom{m+1}{a_{m}}+\binom{m+1}{a_{m+1}}=2^{m+1} $$ which becomes $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m-\ell}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ or, using $\binom{m+1}{i}=\binom{m+1}{m+1-i}$, that $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{m+1}+\binom{m+1}{m}+\cdots+\binom{m+1}{\ell+1}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ On the other hand, it is well known that $$ \binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m+1}=2^{m+1} $$ and so, by subtracting, we get $$ \binom{m+1}{a_{m+1}}=\binom{m+1}{\ell} $$ From this, using the fact that the binomial coefficients $\binom{m+1}{i}$ are increasing for $i \leqslant \frac{m+1}{2}$ and decreasing for $i \geqslant \frac{m+1}{2}$, we conclude that either $a_{m+1}=\ell$ or $a_{m+1}=m+1-\ell$. In either case, $a_{0}, a_{1}, \ldots, a_{m+1}$ is again of the claimed form, which concludes the induction. As a result of this description, any integer $N \geqslant 0$ appears as a term of the sequence $a_{i}$ for some $0 \leqslant i \leqslant 2 N$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of (not necessarily different) integers has the following properties: $0 \leqslant a_{i} \leqslant i$ for all integers $i \geqslant 0$, and $$ \binom{k}{a_{0}}+\binom{k}{a_{1}}+\cdots+\binom{k}{a_{k}}=2^{k} $$ for all integers $k \geqslant 0$. Prove that all integers $N \geqslant 0$ occur in the sequence (that is, for all $N \geqslant 0$, there exists $i \geqslant 0$ with $a_{i}=N$ ). ## (Netherlands)
|
We prove by induction on $k$ that every initial segment of the sequence, $a_{0}, a_{1}, \ldots, a_{k}$, consists of the following elements (counted with multiplicity, and not necessarily in order), for some $\ell \geqslant 0$ with $2 \ell \leqslant k+1$ : $$ 0,1, \ldots, \ell-1, \quad 0,1, \ldots, k-\ell $$ For $k=0$ we have $a_{0}=0$, which is of this form. Now suppose that for $k=m$ the elements $a_{0}, a_{1}, \ldots, a_{m}$ are $0,0,1,1,2,2, \ldots, \ell-1, \ell-1, \ell, \ell+1, \ldots, m-\ell-1, m-\ell$ for some $\ell$ with $0 \leqslant 2 \ell \leqslant m+1$. It is given that $$ \binom{m+1}{a_{0}}+\binom{m+1}{a_{1}}+\cdots+\binom{m+1}{a_{m}}+\binom{m+1}{a_{m+1}}=2^{m+1} $$ which becomes $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m-\ell}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ or, using $\binom{m+1}{i}=\binom{m+1}{m+1-i}$, that $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{m+1}+\binom{m+1}{m}+\cdots+\binom{m+1}{\ell+1}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ On the other hand, it is well known that $$ \binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m+1}=2^{m+1} $$ and so, by subtracting, we get $$ \binom{m+1}{a_{m+1}}=\binom{m+1}{\ell} $$ From this, using the fact that the binomial coefficients $\binom{m+1}{i}$ are increasing for $i \leqslant \frac{m+1}{2}$ and decreasing for $i \geqslant \frac{m+1}{2}$, we conclude that either $a_{m+1}=\ell$ or $a_{m+1}=m+1-\ell$. In either case, $a_{0}, a_{1}, \ldots, a_{m+1}$ is again of the claimed form, which concludes the induction. As a result of this description, any integer $N \geqslant 0$ appears as a term of the sequence $a_{i}$ for some $0 \leqslant i \leqslant 2 N$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
814ac8ff-d6c2-5267-954a-91a811562d50
| 23,715
|
You are given a set of $n$ blocks, each weighing at least 1 ; their total weight is $2 n$. Prove that for every real number $r$ with $0 \leqslant r \leqslant 2 n-2$ you can choose a subset of the blocks whose total weight is at least $r$ but at most $r+2$. (Thailand)
|
We prove the following more general statement by induction on $n$. Claim. Suppose that you have $n$ blocks, each of weight at least 1 , and of total weight $s \leqslant 2 n$. Then for every $r$ with $-2 \leqslant r \leqslant s$, you can choose some of the blocks whose total weight is at least $r$ but at most $r+2$. Proof. The base case $n=1$ is trivial. To prove the inductive step, let $x$ be the largest block weight. Clearly, $x \geqslant s / n$, so $s-x \leqslant \frac{n-1}{n} s \leqslant 2(n-1)$. Hence, if we exclude a block of weight $x$, we can apply the inductive hypothesis to show the claim holds (for this smaller set) for any $-2 \leqslant r \leqslant s-x$. Adding the excluded block to each of those combinations, we see that the claim also holds when $x-2 \leqslant r \leqslant s$. So if $x-2 \leqslant s-x$, then we have covered the whole interval $[-2, s]$. But each block weight is at least 1 , so we have $x-2 \leqslant(s-(n-1))-2=s-(2 n-(n-1)) \leqslant s-(s-(n-1)) \leqslant s-x$, as desired. Comment. Instead of inducting on sets of blocks with total weight $s \leqslant 2 n$, we could instead prove the result only for $s=2 n$. We would then need to modify the inductive step to scale up the block weights before applying the induction hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
You are given a set of $n$ blocks, each weighing at least 1 ; their total weight is $2 n$. Prove that for every real number $r$ with $0 \leqslant r \leqslant 2 n-2$ you can choose a subset of the blocks whose total weight is at least $r$ but at most $r+2$. (Thailand)
|
We prove the following more general statement by induction on $n$. Claim. Suppose that you have $n$ blocks, each of weight at least 1 , and of total weight $s \leqslant 2 n$. Then for every $r$ with $-2 \leqslant r \leqslant s$, you can choose some of the blocks whose total weight is at least $r$ but at most $r+2$. Proof. The base case $n=1$ is trivial. To prove the inductive step, let $x$ be the largest block weight. Clearly, $x \geqslant s / n$, so $s-x \leqslant \frac{n-1}{n} s \leqslant 2(n-1)$. Hence, if we exclude a block of weight $x$, we can apply the inductive hypothesis to show the claim holds (for this smaller set) for any $-2 \leqslant r \leqslant s-x$. Adding the excluded block to each of those combinations, we see that the claim also holds when $x-2 \leqslant r \leqslant s$. So if $x-2 \leqslant s-x$, then we have covered the whole interval $[-2, s]$. But each block weight is at least 1 , so we have $x-2 \leqslant(s-(n-1))-2=s-(2 n-(n-1)) \leqslant s-(s-(n-1)) \leqslant s-x$, as desired. Comment. Instead of inducting on sets of blocks with total weight $s \leqslant 2 n$, we could instead prove the result only for $s=2 n$. We would then need to modify the inductive step to scale up the block weights before applying the induction hypothesis.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
26b42b81-9f4b-5228-96fb-50cec98fc285
| 23,718
|
You are given a set of $n$ blocks, each weighing at least 1 ; their total weight is $2 n$. Prove that for every real number $r$ with $0 \leqslant r \leqslant 2 n-2$ you can choose a subset of the blocks whose total weight is at least $r$ but at most $r+2$. (Thailand)
|
Let $x_{1}, \ldots, x_{n}$ be the weights of the blocks in weakly increasing order. Consider the set $S$ of sums of the form $\sum_{j \in J} x_{j}$ for a subset $J \subseteq\{1,2, \ldots, n\}$. We want to prove that the mesh of $S$ - i.e. the largest distance between two adjacent elements - is at most 2. For $0 \leqslant k \leqslant n$, let $S_{k}$ denote the set of sums of the form $\sum_{i \in J} x_{i}$ for a subset $J \subseteq\{1,2, \ldots, k\}$. We will show by induction on $k$ that the mesh of $S_{k}$ is at most 2 . The base case $k=0$ is trivial (as $S_{0}=\{0\}$ ). For $k>0$ we have $$ S_{k}=S_{k-1} \cup\left(x_{k}+S_{k-1}\right) $$ (where $\left(x_{k}+S_{k-1}\right)$ denotes $\left\{x_{k}+s: s \in S_{k-1}\right\}$ ), so it suffices to prove that $x_{k} \leqslant \sum_{j<k} x_{j}+2$. But if this were not the case, we would have $x_{l}>\sum_{j<k} x_{j}+2 \geqslant k+1$ for all $l \geqslant k$, and hence $$ 2 n=\sum_{j=1}^{n} x_{j}>(n+1-k)(k+1)+k-1 $$ This rearranges to $n>k(n+1-k)$, which is false for $1 \leqslant k \leqslant n$, giving the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
You are given a set of $n$ blocks, each weighing at least 1 ; their total weight is $2 n$. Prove that for every real number $r$ with $0 \leqslant r \leqslant 2 n-2$ you can choose a subset of the blocks whose total weight is at least $r$ but at most $r+2$. (Thailand)
|
Let $x_{1}, \ldots, x_{n}$ be the weights of the blocks in weakly increasing order. Consider the set $S$ of sums of the form $\sum_{j \in J} x_{j}$ for a subset $J \subseteq\{1,2, \ldots, n\}$. We want to prove that the mesh of $S$ - i.e. the largest distance between two adjacent elements - is at most 2. For $0 \leqslant k \leqslant n$, let $S_{k}$ denote the set of sums of the form $\sum_{i \in J} x_{i}$ for a subset $J \subseteq\{1,2, \ldots, k\}$. We will show by induction on $k$ that the mesh of $S_{k}$ is at most 2 . The base case $k=0$ is trivial (as $S_{0}=\{0\}$ ). For $k>0$ we have $$ S_{k}=S_{k-1} \cup\left(x_{k}+S_{k-1}\right) $$ (where $\left(x_{k}+S_{k-1}\right)$ denotes $\left\{x_{k}+s: s \in S_{k-1}\right\}$ ), so it suffices to prove that $x_{k} \leqslant \sum_{j<k} x_{j}+2$. But if this were not the case, we would have $x_{l}>\sum_{j<k} x_{j}+2 \geqslant k+1$ for all $l \geqslant k$, and hence $$ 2 n=\sum_{j=1}^{n} x_{j}>(n+1-k)(k+1)+k-1 $$ This rearranges to $n>k(n+1-k)$, which is false for $1 \leqslant k \leqslant n$, giving the desired contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
26b42b81-9f4b-5228-96fb-50cec98fc285
| 23,718
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia)
|
Note that the given graph is connected, since the total degree of any two vertices is at least 2018 and hence they are either adjacent or have at least one neighbour in common. Hence the given graph satisfies the following condition: Every connected component of $G$ with at least three vertices is not complete and has a vertex of odd degree. We will show that if a graph $G$ satisfies condition (1) and has a vertex of degree at least 2 , then there is a refriending on $G$ that preserves condition (1). Since refriendings decrease the total number of edges of $G$, by using a sequence of such refriendings, we must reach a graph $G$ with maximal degree at most 1 , so we are done.  Pick a vertex $A$ of degree at least 2 in a connected component $G^{\prime}$ of $G$. Since no component of $G$ with at least three vertices is complete we may assume that not all of the neighbours of $A$ are adjacent to one another. (For example, pick a maximal complete subgraph $K$ of $G^{\prime}$. Some vertex $A$ of $K$ has a neighbour outside $K$, and this neighbour is not adjacent to every vertex of $K$ by maximality.) Removing $A$ from $G$ splits $G^{\prime}$ into smaller connected components $G_{1}, \ldots, G_{k}$ (possibly with $k=1$ ), to each of which $A$ is connected by at least one edge. We divide into several cases. Case 1: $k \geqslant 2$ and $A$ is connected to some $G_{i}$ by at least two edges. Choose a vertex $B$ of $G_{i}$ adjacent to $A$, and a vertex $C$ in another component $G_{j}$ adjacent to $A$. The vertices $B$ and $C$ are not adjacent, and hence removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. It is easy to see that this preserves the condition, since the refriending does not change the parity of the degrees of vertices. Case 2: $k \geqslant 2$ and $A$ is connected to each $G_{i}$ by exactly one edge. Consider the induced subgraph on any $G_{i}$ and the vertex $A$. The vertex $A$ has degree 1 in this subgraph; since the number of odd-degree vertices of a graph is always even, we see that $G_{i}$ has a vertex of odd degree (in $G$ ). Thus if we let $B$ and $C$ be any distinct neighbours of $A$, then removing edges $A B$ and $A C$ and adding in edge $B C$ preserves the above condition: the refriending creates two new components, and if either of these components has at least three vertices, then it cannot be complete and must contain a vertex of odd degree (since each $G_{i}$ does). Case 3: $k=1$ and $A$ is connected to $G_{1}$ by at least three edges. By assumption, $A$ has two neighbours $B$ and $C$ which are not adjacent to one another. Removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. We are then done as in Case 1. Case 4: $k=1$ and $A$ is connected to $G_{1}$ by exactly two edges. Let $B$ and $C$ be the two neighbours of $A$, which are not adjacent. Removing edges $A B$ and $A C$ and adding in edge $B C$ results in two new components: one consisting of a single vertex; and the other containing a vertex of odd degree. We are done unless this second component would be a complete graph on at least 3 vertices. But in this case, $G_{1}$ would be a complete graph minus the single edge $B C$, and hence has at least 4 vertices since $G^{\prime}$ is not a 4 -cycle. If we let $D$ be a third vertex of $G_{1}$, then removing edges $B A$ and $B D$ and adding in edge $A D$ does not disconnect $G^{\prime}$. We are then done as in Case 1. 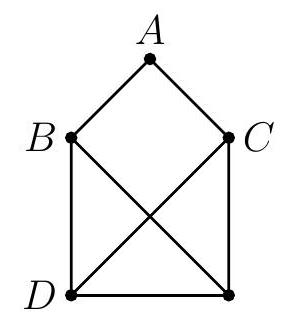 Comment. In fact, condition 1 above precisely characterises those graphs which can be reduced to a graph of maximal degree $\leqslant 1$ by a sequence of refriendings.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia)
|
Note that the given graph is connected, since the total degree of any two vertices is at least 2018 and hence they are either adjacent or have at least one neighbour in common. Hence the given graph satisfies the following condition: Every connected component of $G$ with at least three vertices is not complete and has a vertex of odd degree. We will show that if a graph $G$ satisfies condition (1) and has a vertex of degree at least 2 , then there is a refriending on $G$ that preserves condition (1). Since refriendings decrease the total number of edges of $G$, by using a sequence of such refriendings, we must reach a graph $G$ with maximal degree at most 1 , so we are done.  Pick a vertex $A$ of degree at least 2 in a connected component $G^{\prime}$ of $G$. Since no component of $G$ with at least three vertices is complete we may assume that not all of the neighbours of $A$ are adjacent to one another. (For example, pick a maximal complete subgraph $K$ of $G^{\prime}$. Some vertex $A$ of $K$ has a neighbour outside $K$, and this neighbour is not adjacent to every vertex of $K$ by maximality.) Removing $A$ from $G$ splits $G^{\prime}$ into smaller connected components $G_{1}, \ldots, G_{k}$ (possibly with $k=1$ ), to each of which $A$ is connected by at least one edge. We divide into several cases. Case 1: $k \geqslant 2$ and $A$ is connected to some $G_{i}$ by at least two edges. Choose a vertex $B$ of $G_{i}$ adjacent to $A$, and a vertex $C$ in another component $G_{j}$ adjacent to $A$. The vertices $B$ and $C$ are not adjacent, and hence removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. It is easy to see that this preserves the condition, since the refriending does not change the parity of the degrees of vertices. Case 2: $k \geqslant 2$ and $A$ is connected to each $G_{i}$ by exactly one edge. Consider the induced subgraph on any $G_{i}$ and the vertex $A$. The vertex $A$ has degree 1 in this subgraph; since the number of odd-degree vertices of a graph is always even, we see that $G_{i}$ has a vertex of odd degree (in $G$ ). Thus if we let $B$ and $C$ be any distinct neighbours of $A$, then removing edges $A B$ and $A C$ and adding in edge $B C$ preserves the above condition: the refriending creates two new components, and if either of these components has at least three vertices, then it cannot be complete and must contain a vertex of odd degree (since each $G_{i}$ does). Case 3: $k=1$ and $A$ is connected to $G_{1}$ by at least three edges. By assumption, $A$ has two neighbours $B$ and $C$ which are not adjacent to one another. Removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. We are then done as in Case 1. Case 4: $k=1$ and $A$ is connected to $G_{1}$ by exactly two edges. Let $B$ and $C$ be the two neighbours of $A$, which are not adjacent. Removing edges $A B$ and $A C$ and adding in edge $B C$ results in two new components: one consisting of a single vertex; and the other containing a vertex of odd degree. We are done unless this second component would be a complete graph on at least 3 vertices. But in this case, $G_{1}$ would be a complete graph minus the single edge $B C$, and hence has at least 4 vertices since $G^{\prime}$ is not a 4 -cycle. If we let $D$ be a third vertex of $G_{1}$, then removing edges $B A$ and $B D$ and adding in edge $A D$ does not disconnect $G^{\prime}$. We are then done as in Case 1.  Comment. In fact, condition 1 above precisely characterises those graphs which can be reduced to a graph of maximal degree $\leqslant 1$ by a sequence of refriendings.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
005e6243-ef9d-59ac-8411-1e3f837abe98
| 23,734
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia)
|
As in the previous solution, note that a refriending preserves the property that a graph has a vertex of odd degree and (trivially) the property that it is not complete; note also that our initial graph is connected. We describe an algorithm to reduce our initial graph to a graph of maximal degree at most 1, proceeding in two steps. Step 1: There exists a sequence of refriendings reducing the graph to a tree. Proof. Since the number of edges decreases with each refriending, it suffices to prove the following: as long as the graph contains a cycle, there exists a refriending such that the resulting graph is still connected. We will show that the graph in fact contains a cycle $Z$ and vertices $A, B, C$ such that $A$ and $B$ are adjacent in the cycle $Z, C$ is not in $Z$, and is adjacent to $A$ but not $B$. Removing edges $A B$ and $A C$ and adding in edge $B C$ keeps the graph connected, so we are done. 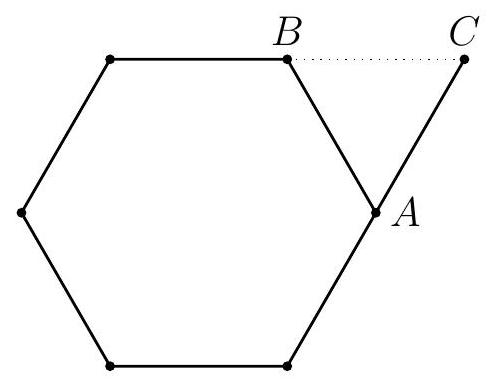 To find this cycle $Z$ and vertices $A, B, C$, we pursue one of two strategies. If the graph contains a triangle, we consider a largest complete subgraph $K$, which thus contains at least three vertices. Since the graph itself is not complete, there is a vertex $C$ not in $K$ connected to a vertex $A$ of $K$. By maximality of $K$, there is a vertex $B$ of $K$ not connected to $C$, and hence we are done by choosing a cycle $Z$ in $K$ through the edge $A B$. 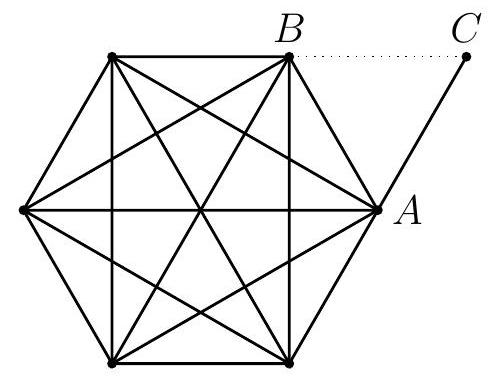 If the graph is triangle-free, we consider instead a smallest cycle $Z$. This cycle cannot be Hamiltonian (i.e. it cannot pass through every vertex of the graph), since otherwise by minimality the graph would then have no other edges, and hence would have even degree at every vertex. We may thus choose a vertex $C$ not in $Z$ adjacent to a vertex $A$ of $Z$. Since the graph is triangle-free, it is not adjacent to any neighbour $B$ of $A$ in $Z$, and we are done. Step 2: Any tree may be reduced to a disjoint union of single edges and vertices by a sequence of refriendings. Proof. The refriending preserves the property of being acyclic. Hence, after applying a sequence of refriendings, we arrive at an acyclic graph in which it is impossible to perform any further refriendings. The maximal degree of any such graph is 1 : if it had a vertex $A$ with two neighbours $B, C$, then $B$ and $C$ would necessarily be nonadjacent since the graph is cycle-free, and so a refriending would be possible. Thus we reach a graph with maximal degree at most 1 as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia)
|
As in the previous solution, note that a refriending preserves the property that a graph has a vertex of odd degree and (trivially) the property that it is not complete; note also that our initial graph is connected. We describe an algorithm to reduce our initial graph to a graph of maximal degree at most 1, proceeding in two steps. Step 1: There exists a sequence of refriendings reducing the graph to a tree. Proof. Since the number of edges decreases with each refriending, it suffices to prove the following: as long as the graph contains a cycle, there exists a refriending such that the resulting graph is still connected. We will show that the graph in fact contains a cycle $Z$ and vertices $A, B, C$ such that $A$ and $B$ are adjacent in the cycle $Z, C$ is not in $Z$, and is adjacent to $A$ but not $B$. Removing edges $A B$ and $A C$ and adding in edge $B C$ keeps the graph connected, so we are done.  To find this cycle $Z$ and vertices $A, B, C$, we pursue one of two strategies. If the graph contains a triangle, we consider a largest complete subgraph $K$, which thus contains at least three vertices. Since the graph itself is not complete, there is a vertex $C$ not in $K$ connected to a vertex $A$ of $K$. By maximality of $K$, there is a vertex $B$ of $K$ not connected to $C$, and hence we are done by choosing a cycle $Z$ in $K$ through the edge $A B$.  If the graph is triangle-free, we consider instead a smallest cycle $Z$. This cycle cannot be Hamiltonian (i.e. it cannot pass through every vertex of the graph), since otherwise by minimality the graph would then have no other edges, and hence would have even degree at every vertex. We may thus choose a vertex $C$ not in $Z$ adjacent to a vertex $A$ of $Z$. Since the graph is triangle-free, it is not adjacent to any neighbour $B$ of $A$ in $Z$, and we are done. Step 2: Any tree may be reduced to a disjoint union of single edges and vertices by a sequence of refriendings. Proof. The refriending preserves the property of being acyclic. Hence, after applying a sequence of refriendings, we arrive at an acyclic graph in which it is impossible to perform any further refriendings. The maximal degree of any such graph is 1 : if it had a vertex $A$ with two neighbours $B, C$, then $B$ and $C$ would necessarily be nonadjacent since the graph is cycle-free, and so a refriending would be possible. Thus we reach a graph with maximal degree at most 1 as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
005e6243-ef9d-59ac-8411-1e3f837abe98
| 23,734
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group.
|
Let $\ell$ be a line separating the points into two groups ( $L$ and $R$ ) with $n$ points in each. Label the points $A_{1}, A_{2}, \ldots, A_{2 n}$ so that $L=\left\{A_{1}, A_{3}, \ldots, A_{2 n-1}\right\}$. We claim that this labelling works. Take a line $s=A_{2 n} A_{1}$. (a) Rotate $s$ around $A_{1}$ until it passes through $A_{2}$; the rotation is performed in a direction such that $s$ is never parallel to $\ell$. (b) Then rotate the new $s$ around $A_{2}$ until it passes through $A_{3}$ in a similar manner. (c) Perform $2 n-2$ more such steps, after which $s$ returns to its initial position. The total (directed) rotation angle $\Theta$ of $s$ is clearly a multiple of $180^{\circ}$. On the other hand, $s$ was never parallel to $\ell$, which is possible only if $\Theta=0$. Now it remains to partition all the $2 n$ angles into those where $s$ is rotated anticlockwise, and the others.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group.
|
Let $\ell$ be a line separating the points into two groups ( $L$ and $R$ ) with $n$ points in each. Label the points $A_{1}, A_{2}, \ldots, A_{2 n}$ so that $L=\left\{A_{1}, A_{3}, \ldots, A_{2 n-1}\right\}$. We claim that this labelling works. Take a line $s=A_{2 n} A_{1}$. (a) Rotate $s$ around $A_{1}$ until it passes through $A_{2}$; the rotation is performed in a direction such that $s$ is never parallel to $\ell$. (b) Then rotate the new $s$ around $A_{2}$ until it passes through $A_{3}$ in a similar manner. (c) Perform $2 n-2$ more such steps, after which $s$ returns to its initial position. The total (directed) rotation angle $\Theta$ of $s$ is clearly a multiple of $180^{\circ}$. On the other hand, $s$ was never parallel to $\ell$, which is possible only if $\Theta=0$. Now it remains to partition all the $2 n$ angles into those where $s$ is rotated anticlockwise, and the others.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8bfa328-e714-53ae-be35-04d0baa8994d
| 23,738
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group.
|
When tracing a cyclic path through the $A_{i}$ in order, with straight line segments between consecutive points, let $\theta_{i}$ be the exterior angle at $A_{i}$, with a sign convention that it is positive if the path turns left and negative if the path turns right. Then $\sum_{i=1}^{2 n} \theta_{i}=360 k^{\circ}$ for some integer $k$. Let $\phi_{i}=\angle A_{i-1} A_{i} A_{i+1}($ indices $\bmod 2 n)$, defined as in the problem; thus $\phi_{i}=180^{\circ}-\left|\theta_{i}\right|$. Let $L$ be the set of $i$ for which the path turns left at $A_{i}$ and let $R$ be the set for which it turns right. Then $S=\sum_{i \in L} \phi_{i}-\sum_{i \in R} \phi_{i}=(180(|L|-|R|)-360 k)^{\circ}$, which is a multiple of $360^{\circ}$ since the number of points is even. We will show that the points can be labelled such that $S=0$, in which case $L$ and $R$ satisfy the required condition of the problem. Note that the value of $S$ is defined for a slightly larger class of configurations: it is OK for two points to coincide, as long as they are not consecutive, and OK for three points to be collinear, as long as $A_{i}, A_{i+1}$ and $A_{i+2}$ do not appear on a line in that order. In what follows it will be convenient, although not strictly necessary, to consider such configurations. Consider how $S$ changes if a single one of the $A_{i}$ is moved along some straight-line path (not passing through any $A_{j}$ and not lying on any line $A_{j} A_{k}$, but possibly crossing such lines). Because $S$ is a multiple of $360^{\circ}$, and the angles change continuously, $S$ can only change when a point moves between $R$ and $L$. Furthermore, if $\phi_{j}=0$ when $A_{j}$ moves between $R$ and $L, S$ is unchanged; it only changes if $\phi_{j}=180^{\circ}$ when $A_{j}$ moves between those sets. For any starting choice of points, we will now construct a new configuration, with labels such that $S=0$, that can be perturbed into the original one without any $\phi_{i}$ passing through $180^{\circ}$, so that $S=0$ for the original configuration with those labels as well. Take some line such that there are $n$ points on each side of that line. The new configuration has $n$ copies of a single point on each side of the line, and a path that alternates between sides of the line; all angles are 0 , so this configuration has $S=0$. Perturbing the points into their original positions, while keeping each point on its side of the line, no angle $\phi_{i}$ can pass through $180^{\circ}$, because no straight line can go from one side of the line to the other and back. So the perturbation process leaves $S=0$. Comment. More complicated variants of this solution are also possible; for example, a path defined using four quadrants of the plane rather than just two half-planes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group.
|
When tracing a cyclic path through the $A_{i}$ in order, with straight line segments between consecutive points, let $\theta_{i}$ be the exterior angle at $A_{i}$, with a sign convention that it is positive if the path turns left and negative if the path turns right. Then $\sum_{i=1}^{2 n} \theta_{i}=360 k^{\circ}$ for some integer $k$. Let $\phi_{i}=\angle A_{i-1} A_{i} A_{i+1}($ indices $\bmod 2 n)$, defined as in the problem; thus $\phi_{i}=180^{\circ}-\left|\theta_{i}\right|$. Let $L$ be the set of $i$ for which the path turns left at $A_{i}$ and let $R$ be the set for which it turns right. Then $S=\sum_{i \in L} \phi_{i}-\sum_{i \in R} \phi_{i}=(180(|L|-|R|)-360 k)^{\circ}$, which is a multiple of $360^{\circ}$ since the number of points is even. We will show that the points can be labelled such that $S=0$, in which case $L$ and $R$ satisfy the required condition of the problem. Note that the value of $S$ is defined for a slightly larger class of configurations: it is OK for two points to coincide, as long as they are not consecutive, and OK for three points to be collinear, as long as $A_{i}, A_{i+1}$ and $A_{i+2}$ do not appear on a line in that order. In what follows it will be convenient, although not strictly necessary, to consider such configurations. Consider how $S$ changes if a single one of the $A_{i}$ is moved along some straight-line path (not passing through any $A_{j}$ and not lying on any line $A_{j} A_{k}$, but possibly crossing such lines). Because $S$ is a multiple of $360^{\circ}$, and the angles change continuously, $S$ can only change when a point moves between $R$ and $L$. Furthermore, if $\phi_{j}=0$ when $A_{j}$ moves between $R$ and $L, S$ is unchanged; it only changes if $\phi_{j}=180^{\circ}$ when $A_{j}$ moves between those sets. For any starting choice of points, we will now construct a new configuration, with labels such that $S=0$, that can be perturbed into the original one without any $\phi_{i}$ passing through $180^{\circ}$, so that $S=0$ for the original configuration with those labels as well. Take some line such that there are $n$ points on each side of that line. The new configuration has $n$ copies of a single point on each side of the line, and a path that alternates between sides of the line; all angles are 0 , so this configuration has $S=0$. Perturbing the points into their original positions, while keeping each point on its side of the line, no angle $\phi_{i}$ can pass through $180^{\circ}$, because no straight line can go from one side of the line to the other and back. So the perturbation process leaves $S=0$. Comment. More complicated variants of this solution are also possible; for example, a path defined using four quadrants of the plane rather than just two half-planes.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8bfa328-e714-53ae-be35-04d0baa8994d
| 23,738
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group.
|
We shall think instead of the problem as asking us to assign a weight $\pm 1$ to each angle, such that the weighted sum of all the angles is zero. Given an ordering $A_{1}, \ldots, A_{2 n}$ of the points, we shall assign weights according to the following recipe: walk in order from point to point, and assign the left turns +1 and the right turns -1 . This is the same weighting as in Solution 3, and as in that solution, the weighted sum is a multiple of $360^{\circ}$. We now aim to show the following: Lemma. Transposing any two consecutive points in the ordering changes the weighted sum by $\pm 360^{\circ}$ or 0 . Knowing that, we can conclude quickly: if the ordering $A_{1}, \ldots, A_{2 n}$ has weighted angle sum $360 k^{\circ}$, then the ordering $A_{2 n}, \ldots, A_{1}$ has weighted angle sum $-360 k^{\circ}$ (since the angles are the same, but left turns and right turns are exchanged). We can reverse the ordering of $A_{1}$, $\ldots, A_{2 n}$ by a sequence of transpositions of consecutive points, and in doing so the weighted angle sum must become zero somewhere along the way. We now prove that lemma: Proof. Transposing two points amounts to taking a section $A_{k} A_{k+1} A_{k+2} A_{k+3}$ as depicted, reversing the central line segment $A_{k+1} A_{k+2}$, and replacing its two neighbours with the dotted lines. 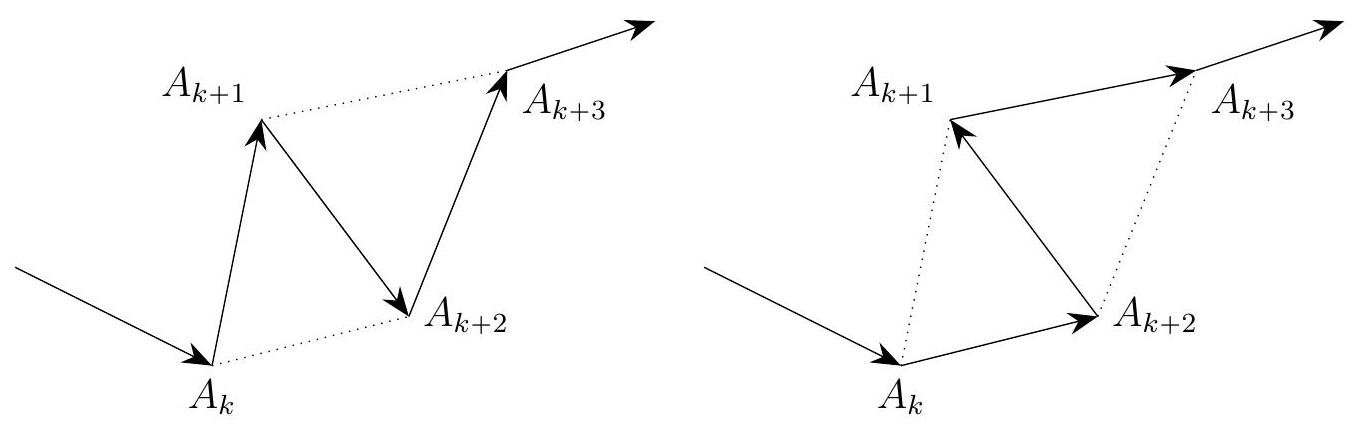 Figure 1: Transposing two consecutive vertices: before (left) and afterwards (right) In each triangle, we alter the sum by $\pm 180^{\circ}$. Indeed, using (anticlockwise) directed angles modulo $360^{\circ}$, we either add or subtract all three angles of each triangle. Hence both triangles together alter the sum by $\pm 180 \pm 180^{\circ}$, which is $\pm 360^{\circ}$ or 0 .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group.
|
We shall think instead of the problem as asking us to assign a weight $\pm 1$ to each angle, such that the weighted sum of all the angles is zero. Given an ordering $A_{1}, \ldots, A_{2 n}$ of the points, we shall assign weights according to the following recipe: walk in order from point to point, and assign the left turns +1 and the right turns -1 . This is the same weighting as in Solution 3, and as in that solution, the weighted sum is a multiple of $360^{\circ}$. We now aim to show the following: Lemma. Transposing any two consecutive points in the ordering changes the weighted sum by $\pm 360^{\circ}$ or 0 . Knowing that, we can conclude quickly: if the ordering $A_{1}, \ldots, A_{2 n}$ has weighted angle sum $360 k^{\circ}$, then the ordering $A_{2 n}, \ldots, A_{1}$ has weighted angle sum $-360 k^{\circ}$ (since the angles are the same, but left turns and right turns are exchanged). We can reverse the ordering of $A_{1}$, $\ldots, A_{2 n}$ by a sequence of transpositions of consecutive points, and in doing so the weighted angle sum must become zero somewhere along the way. We now prove that lemma: Proof. Transposing two points amounts to taking a section $A_{k} A_{k+1} A_{k+2} A_{k+3}$ as depicted, reversing the central line segment $A_{k+1} A_{k+2}$, and replacing its two neighbours with the dotted lines.  Figure 1: Transposing two consecutive vertices: before (left) and afterwards (right) In each triangle, we alter the sum by $\pm 180^{\circ}$. Indeed, using (anticlockwise) directed angles modulo $360^{\circ}$, we either add or subtract all three angles of each triangle. Hence both triangles together alter the sum by $\pm 180 \pm 180^{\circ}$, which is $\pm 360^{\circ}$ or 0 .
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8bfa328-e714-53ae-be35-04d0baa8994d
| 23,738
|
Let $A B C$ be a triangle. Circle $\Gamma$ passes through $A$, meets segments $A B$ and $A C$ again at points $D$ and $E$ respectively, and intersects segment $B C$ at $F$ and $G$ such that $F$ lies between $B$ and $G$. The tangent to circle $B D F$ at $F$ and the tangent to circle $C E G$ at $G$ meet at point $T$. Suppose that points $A$ and $T$ are distinct. Prove that line $A T$ is parallel to $B C$. (Nigeria)
|
Notice that $\angle T F B=\angle F D A$ because $F T$ is tangent to circle $B D F$, and moreover $\angle F D A=\angle C G A$ because quadrilateral $A D F G$ is cyclic. Similarly, $\angle T G B=\angle G E C$ because $G T$ is tangent to circle $C E G$, and $\angle G E C=\angle C F A$. Hence, $$ \angle T F B=\angle C G A \text { and } \quad \angle T G B=\angle C F A $$  Triangles $F G A$ and $G F T$ have a common side $F G$, and by (1) their angles at $F, G$ are the same. So, these triangles are congruent. So, their altitudes starting from $A$ and $T$, respectively, are equal and hence $A T$ is parallel to line $B F G C$. Comment. Alternatively, we can prove first that $T$ lies on $\Gamma$. For example, this can be done by showing that $\angle A F T=\angle A G T$ using (1). Then the statement follows as $\angle T A F=\angle T G F=\angle G F A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Circle $\Gamma$ passes through $A$, meets segments $A B$ and $A C$ again at points $D$ and $E$ respectively, and intersects segment $B C$ at $F$ and $G$ such that $F$ lies between $B$ and $G$. The tangent to circle $B D F$ at $F$ and the tangent to circle $C E G$ at $G$ meet at point $T$. Suppose that points $A$ and $T$ are distinct. Prove that line $A T$ is parallel to $B C$. (Nigeria)
|
Notice that $\angle T F B=\angle F D A$ because $F T$ is tangent to circle $B D F$, and moreover $\angle F D A=\angle C G A$ because quadrilateral $A D F G$ is cyclic. Similarly, $\angle T G B=\angle G E C$ because $G T$ is tangent to circle $C E G$, and $\angle G E C=\angle C F A$. Hence, $$ \angle T F B=\angle C G A \text { and } \quad \angle T G B=\angle C F A $$  Triangles $F G A$ and $G F T$ have a common side $F G$, and by (1) their angles at $F, G$ are the same. So, these triangles are congruent. So, their altitudes starting from $A$ and $T$, respectively, are equal and hence $A T$ is parallel to line $B F G C$. Comment. Alternatively, we can prove first that $T$ lies on $\Gamma$. For example, this can be done by showing that $\angle A F T=\angle A G T$ using (1). Then the statement follows as $\angle T A F=\angle T G F=\angle G F A$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4513a3c6-5660-5088-9dec-2186bb5cc69a
| 23,752
|
Let $A B C$ be an acute-angled triangle and let $D, E$, and $F$ be the feet of altitudes from $A, B$, and $C$ to sides $B C, C A$, and $A B$, respectively. Denote by $\omega_{B}$ and $\omega_{C}$ the incircles of triangles $B D F$ and $C D E$, and let these circles be tangent to segments $D F$ and $D E$ at $M$ and $N$, respectively. Let line $M N$ meet circles $\omega_{B}$ and $\omega_{C}$ again at $P \neq M$ and $Q \neq N$, respectively. Prove that $M P=N Q$. (Vietnam)
|
Denote the centres of $\omega_{B}$ and $\omega_{C}$ by $O_{B}$ and $O_{C}$, let their radii be $r_{B}$ and $r_{C}$, and let $B C$ be tangent to the two circles at $T$ and $U$, respectively.  From the cyclic quadrilaterals $A F D C$ and $A B D E$ we have $$ \angle M D O_{B}=\frac{1}{2} \angle F D B=\frac{1}{2} \angle B A C=\frac{1}{2} \angle C D E=\angle O_{C} D N, $$ so the right-angled triangles $D M O_{B}$ and $D N O_{C}$ are similar. The ratio of similarity between the two triangles is $$ \frac{D N}{D M}=\frac{O_{C} N}{O_{B} M}=\frac{r_{C}}{r_{B}} . $$ Let $\varphi=\angle D M N$ and $\psi=\angle M N D$. The lines $F M$ and $E N$ are tangent to $\omega_{B}$ and $\omega_{C}$, respectively, so $$ \angle M T P=\angle F M P=\angle D M N=\varphi \quad \text { and } \quad \angle Q U N=\angle Q N E=\angle M N D=\psi $$ (It is possible that $P$ or $Q$ coincides with $T$ or $U$, or lie inside triangles $D M T$ or $D U N$, respectively. To reduce case-sensitivity, we may use directed angles or simply ignore angles $M T P$ and $Q U N$.) In the circles $\omega_{B}$ and $\omega_{C}$ the lengths of chords $M P$ and $N Q$ are $$ M P=2 r_{B} \cdot \sin \angle M T P=2 r_{B} \cdot \sin \varphi \quad \text { and } \quad N Q=2 r_{C} \cdot \sin \angle Q U N=2 r_{C} \cdot \sin \psi $$ By applying the sine rule to triangle $D N M$ we get $$ \frac{D N}{D M}=\frac{\sin \angle D M N}{\sin \angle M N D}=\frac{\sin \varphi}{\sin \psi} $$ Finally, putting the above observations together, we get $$ \frac{M P}{N Q}=\frac{2 r_{B} \sin \varphi}{2 r_{C} \sin \psi}=\frac{r_{B}}{r_{C}} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{D M}{D N} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{\sin \psi}{\sin \varphi} \cdot \frac{\sin \varphi}{\sin \psi}=1, $$ so $M P=N Q$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle and let $D, E$, and $F$ be the feet of altitudes from $A, B$, and $C$ to sides $B C, C A$, and $A B$, respectively. Denote by $\omega_{B}$ and $\omega_{C}$ the incircles of triangles $B D F$ and $C D E$, and let these circles be tangent to segments $D F$ and $D E$ at $M$ and $N$, respectively. Let line $M N$ meet circles $\omega_{B}$ and $\omega_{C}$ again at $P \neq M$ and $Q \neq N$, respectively. Prove that $M P=N Q$. (Vietnam)
|
Denote the centres of $\omega_{B}$ and $\omega_{C}$ by $O_{B}$ and $O_{C}$, let their radii be $r_{B}$ and $r_{C}$, and let $B C$ be tangent to the two circles at $T$ and $U$, respectively.  From the cyclic quadrilaterals $A F D C$ and $A B D E$ we have $$ \angle M D O_{B}=\frac{1}{2} \angle F D B=\frac{1}{2} \angle B A C=\frac{1}{2} \angle C D E=\angle O_{C} D N, $$ so the right-angled triangles $D M O_{B}$ and $D N O_{C}$ are similar. The ratio of similarity between the two triangles is $$ \frac{D N}{D M}=\frac{O_{C} N}{O_{B} M}=\frac{r_{C}}{r_{B}} . $$ Let $\varphi=\angle D M N$ and $\psi=\angle M N D$. The lines $F M$ and $E N$ are tangent to $\omega_{B}$ and $\omega_{C}$, respectively, so $$ \angle M T P=\angle F M P=\angle D M N=\varphi \quad \text { and } \quad \angle Q U N=\angle Q N E=\angle M N D=\psi $$ (It is possible that $P$ or $Q$ coincides with $T$ or $U$, or lie inside triangles $D M T$ or $D U N$, respectively. To reduce case-sensitivity, we may use directed angles or simply ignore angles $M T P$ and $Q U N$.) In the circles $\omega_{B}$ and $\omega_{C}$ the lengths of chords $M P$ and $N Q$ are $$ M P=2 r_{B} \cdot \sin \angle M T P=2 r_{B} \cdot \sin \varphi \quad \text { and } \quad N Q=2 r_{C} \cdot \sin \angle Q U N=2 r_{C} \cdot \sin \psi $$ By applying the sine rule to triangle $D N M$ we get $$ \frac{D N}{D M}=\frac{\sin \angle D M N}{\sin \angle M N D}=\frac{\sin \varphi}{\sin \psi} $$ Finally, putting the above observations together, we get $$ \frac{M P}{N Q}=\frac{2 r_{B} \sin \varphi}{2 r_{C} \sin \psi}=\frac{r_{B}}{r_{C}} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{D M}{D N} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{\sin \psi}{\sin \varphi} \cdot \frac{\sin \varphi}{\sin \psi}=1, $$ so $M P=N Q$ as required.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9d8ab3e0-51b5-5536-8d9d-98c6ddd2662a
| 23,755
|
In triangle $A B C$, let $A_{1}$ and $B_{1}$ be two points on sides $B C$ and $A C$, and let $P$ and $Q$ be two points on segments $A A_{1}$ and $B B_{1}$, respectively, so that line $P Q$ is parallel to $A B$. On ray $P B_{1}$, beyond $B_{1}$, let $P_{1}$ be a point so that $\angle P P_{1} C=\angle B A C$. Similarly, on ray $Q A_{1}$, beyond $A_{1}$, let $Q_{1}$ be a point so that $\angle C Q_{1} Q=\angle C B A$. Show that points $P, Q, P_{1}$, and $Q_{1}$ are concyclic. (Ukraine)
|
Throughout the solution we use oriented angles. Let rays $A A_{1}$ and $B B_{1}$ intersect the circumcircle of $\triangle A C B$ at $A_{2}$ and $B_{2}$, respectively. By $$ \angle Q P A_{2}=\angle B A A_{2}=\angle B B_{2} A_{2}=\angle Q B_{2} A_{2} $$ points $P, Q, A_{2}, B_{2}$ are concyclic; denote the circle passing through these points by $\omega$. We shall prove that $P_{1}$ and $Q_{1}$ also lie on $\omega$.  By $$ \angle C A_{2} A_{1}=\angle C A_{2} A=\angle C B A=\angle C Q_{1} Q=\angle C Q_{1} A_{1}, $$ points $C, Q_{1}, A_{2}, A_{1}$ are also concyclic. From that we get $$ \angle Q Q_{1} A_{2}=\angle A_{1} Q_{1} A_{2}=\angle A_{1} C A_{2}=\angle B C A_{2}=\angle B A A_{2}=\angle Q P A_{2} $$ so $Q_{1}$ lies on $\omega$. It follows similarly that $P_{1}$ lies on $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, let $A_{1}$ and $B_{1}$ be two points on sides $B C$ and $A C$, and let $P$ and $Q$ be two points on segments $A A_{1}$ and $B B_{1}$, respectively, so that line $P Q$ is parallel to $A B$. On ray $P B_{1}$, beyond $B_{1}$, let $P_{1}$ be a point so that $\angle P P_{1} C=\angle B A C$. Similarly, on ray $Q A_{1}$, beyond $A_{1}$, let $Q_{1}$ be a point so that $\angle C Q_{1} Q=\angle C B A$. Show that points $P, Q, P_{1}$, and $Q_{1}$ are concyclic. (Ukraine)
|
Throughout the solution we use oriented angles. Let rays $A A_{1}$ and $B B_{1}$ intersect the circumcircle of $\triangle A C B$ at $A_{2}$ and $B_{2}$, respectively. By $$ \angle Q P A_{2}=\angle B A A_{2}=\angle B B_{2} A_{2}=\angle Q B_{2} A_{2} $$ points $P, Q, A_{2}, B_{2}$ are concyclic; denote the circle passing through these points by $\omega$. We shall prove that $P_{1}$ and $Q_{1}$ also lie on $\omega$.  By $$ \angle C A_{2} A_{1}=\angle C A_{2} A=\angle C B A=\angle C Q_{1} Q=\angle C Q_{1} A_{1}, $$ points $C, Q_{1}, A_{2}, A_{1}$ are also concyclic. From that we get $$ \angle Q Q_{1} A_{2}=\angle A_{1} Q_{1} A_{2}=\angle A_{1} C A_{2}=\angle B C A_{2}=\angle B A A_{2}=\angle Q P A_{2} $$ so $Q_{1}$ lies on $\omega$. It follows similarly that $P_{1}$ lies on $\omega$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ead01d78-acc8-5d74-adbc-a9c07781ef40
| 23,757
|
In triangle $A B C$, let $A_{1}$ and $B_{1}$ be two points on sides $B C$ and $A C$, and let $P$ and $Q$ be two points on segments $A A_{1}$ and $B B_{1}$, respectively, so that line $P Q$ is parallel to $A B$. On ray $P B_{1}$, beyond $B_{1}$, let $P_{1}$ be a point so that $\angle P P_{1} C=\angle B A C$. Similarly, on ray $Q A_{1}$, beyond $A_{1}$, let $Q_{1}$ be a point so that $\angle C Q_{1} Q=\angle C B A$. Show that points $P, Q, P_{1}$, and $Q_{1}$ are concyclic. (Ukraine)
|
First consider the case when lines $P P_{1}$ and $Q Q_{1}$ intersect each other at some point $R$. Let line $P Q$ meet the sides $A C$ and $B C$ at $E$ and $F$, respectively. Then $$ \angle P P_{1} C=\angle B A C=\angle P E C $$ so points $C, E, P, P_{1}$ lie on a circle; denote that circle by $\omega_{P}$. It follows analogously that points $C, F, Q, Q_{1}$ lie on another circle; denote it by $\omega_{Q}$. Let $A Q$ and $B P$ intersect at $T$. Applying Pappus' theorem to the lines $A A_{1} P$ and $B B_{1} Q$ provides that points $C=A B_{1} \cap B A_{1}, R=A_{1} Q \cap B_{1} P$ and $T=A Q \cap B P$ are collinear. Let line $R C T$ meet $P Q$ and $A B$ at $S$ and $U$, respectively. From $A B \| P Q$ we obtain $$ \frac{S P}{S Q}=\frac{U B}{U A}=\frac{S F}{S E} $$ so $$ S P \cdot S E=S Q \cdot S F $$  So, point $S$ has equal powers with respect to $\omega_{P}$ and $\omega_{Q}$, hence line $R C S$ is their radical axis; then $R$ also has equal powers to the circles, so $R P \cdot R P_{1}=R Q \cdot R Q_{1}$, proving that points $P, P_{1}, Q, Q_{1}$ are indeed concyclic. Now consider the case when $P P_{1}$ and $Q Q_{1}$ are parallel. Like in the previous case, let $A Q$ and $B P$ intersect at $T$. Applying Pappus' theorem again to the lines $A A_{1} P$ and $B B_{1} Q$, in this limit case it shows that line $C T$ is parallel to $P P_{1}$ and $Q Q_{1}$. Let line $C T$ meet $P Q$ and $A B$ at $S$ and $U$, as before. The same calculation as in the previous case shows that $S P \cdot S E=S Q \cdot S F$, so $S$ lies on the radical axis between $\omega_{P}$ and $\omega_{Q}$. 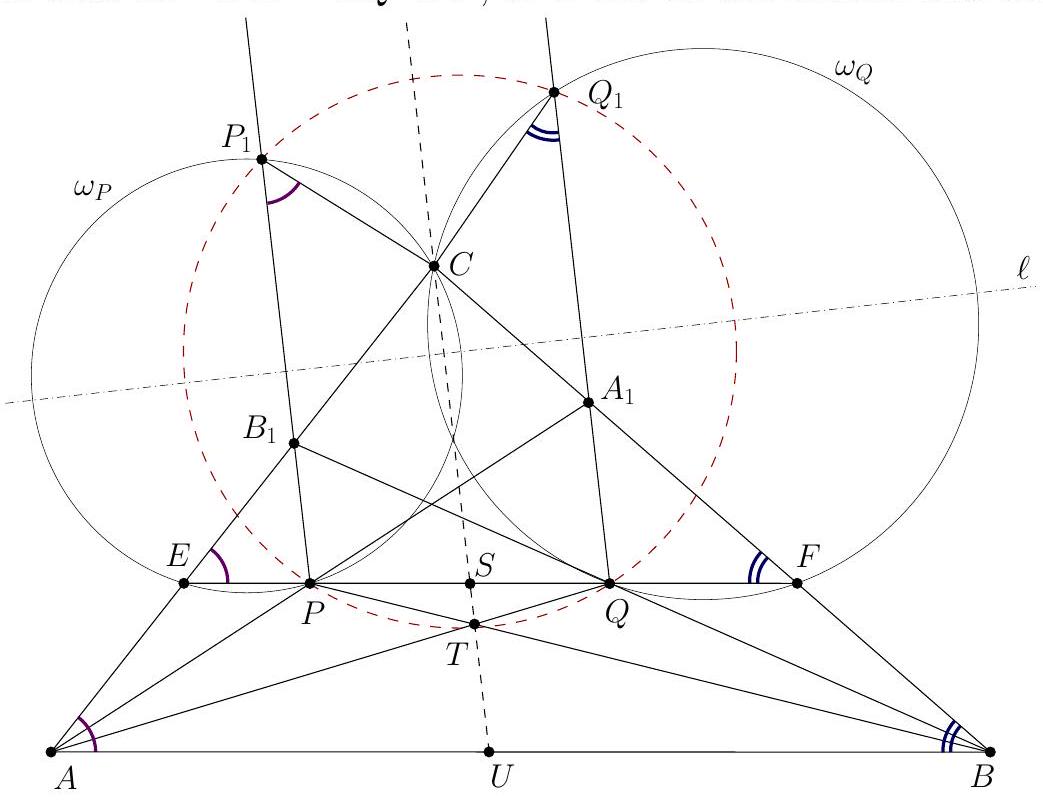 Line $C S T$, that is the radical axis between $\omega_{P}$ and $\omega_{Q}$, is perpendicular to the line $\ell$ of centres of $\omega_{P}$ and $\omega_{Q}$. Hence, the chords $P P_{1}$ and $Q Q_{1}$ are perpendicular to $\ell$. So the quadrilateral $P P_{1} Q_{1} Q$ is an isosceles trapezium with symmetry axis $\ell$, and hence is cyclic. Comment. There are several ways of solving the problem involving Pappus' theorem. For example, one may consider the points $K=P B_{1} \cap B C$ and $L=Q A_{1} \cap A C$. Applying Pappus' theorem to the lines $A A_{1} P$ and $Q B_{1} B$ we get that $K, L$, and $P Q \cap A B$ are collinear, i.e. that $K L \| A B$. Therefore, cyclicity of $P, Q, P_{1}$, and $Q_{1}$ is equivalent to that of $K, L, P_{1}$, and $Q_{1}$. The latter is easy after noticing that $C$ also lies on that circle. Indeed, e.g. $\angle(L K, L C)=\angle(A B, A C)=\angle\left(P_{1} K, P_{1} C\right)$ shows that $K$ lies on circle $K L C$. This approach also has some possible degeneracy, as the points $K$ and $L$ may happen to be ideal.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, let $A_{1}$ and $B_{1}$ be two points on sides $B C$ and $A C$, and let $P$ and $Q$ be two points on segments $A A_{1}$ and $B B_{1}$, respectively, so that line $P Q$ is parallel to $A B$. On ray $P B_{1}$, beyond $B_{1}$, let $P_{1}$ be a point so that $\angle P P_{1} C=\angle B A C$. Similarly, on ray $Q A_{1}$, beyond $A_{1}$, let $Q_{1}$ be a point so that $\angle C Q_{1} Q=\angle C B A$. Show that points $P, Q, P_{1}$, and $Q_{1}$ are concyclic. (Ukraine)
|
First consider the case when lines $P P_{1}$ and $Q Q_{1}$ intersect each other at some point $R$. Let line $P Q$ meet the sides $A C$ and $B C$ at $E$ and $F$, respectively. Then $$ \angle P P_{1} C=\angle B A C=\angle P E C $$ so points $C, E, P, P_{1}$ lie on a circle; denote that circle by $\omega_{P}$. It follows analogously that points $C, F, Q, Q_{1}$ lie on another circle; denote it by $\omega_{Q}$. Let $A Q$ and $B P$ intersect at $T$. Applying Pappus' theorem to the lines $A A_{1} P$ and $B B_{1} Q$ provides that points $C=A B_{1} \cap B A_{1}, R=A_{1} Q \cap B_{1} P$ and $T=A Q \cap B P$ are collinear. Let line $R C T$ meet $P Q$ and $A B$ at $S$ and $U$, respectively. From $A B \| P Q$ we obtain $$ \frac{S P}{S Q}=\frac{U B}{U A}=\frac{S F}{S E} $$ so $$ S P \cdot S E=S Q \cdot S F $$  So, point $S$ has equal powers with respect to $\omega_{P}$ and $\omega_{Q}$, hence line $R C S$ is their radical axis; then $R$ also has equal powers to the circles, so $R P \cdot R P_{1}=R Q \cdot R Q_{1}$, proving that points $P, P_{1}, Q, Q_{1}$ are indeed concyclic. Now consider the case when $P P_{1}$ and $Q Q_{1}$ are parallel. Like in the previous case, let $A Q$ and $B P$ intersect at $T$. Applying Pappus' theorem again to the lines $A A_{1} P$ and $B B_{1} Q$, in this limit case it shows that line $C T$ is parallel to $P P_{1}$ and $Q Q_{1}$. Let line $C T$ meet $P Q$ and $A B$ at $S$ and $U$, as before. The same calculation as in the previous case shows that $S P \cdot S E=S Q \cdot S F$, so $S$ lies on the radical axis between $\omega_{P}$ and $\omega_{Q}$.  Line $C S T$, that is the radical axis between $\omega_{P}$ and $\omega_{Q}$, is perpendicular to the line $\ell$ of centres of $\omega_{P}$ and $\omega_{Q}$. Hence, the chords $P P_{1}$ and $Q Q_{1}$ are perpendicular to $\ell$. So the quadrilateral $P P_{1} Q_{1} Q$ is an isosceles trapezium with symmetry axis $\ell$, and hence is cyclic. Comment. There are several ways of solving the problem involving Pappus' theorem. For example, one may consider the points $K=P B_{1} \cap B C$ and $L=Q A_{1} \cap A C$. Applying Pappus' theorem to the lines $A A_{1} P$ and $Q B_{1} B$ we get that $K, L$, and $P Q \cap A B$ are collinear, i.e. that $K L \| A B$. Therefore, cyclicity of $P, Q, P_{1}$, and $Q_{1}$ is equivalent to that of $K, L, P_{1}$, and $Q_{1}$. The latter is easy after noticing that $C$ also lies on that circle. Indeed, e.g. $\angle(L K, L C)=\angle(A B, A C)=\angle\left(P_{1} K, P_{1} C\right)$ shows that $K$ lies on circle $K L C$. This approach also has some possible degeneracy, as the points $K$ and $L$ may happen to be ideal.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ead01d78-acc8-5d74-adbc-a9c07781ef40
| 23,757
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia)
|
Since $$ \angle A P B+\angle B P C+\angle C P A=2 \pi=(\pi-\angle A C B)+(\pi-\angle B A C)+(\pi-\angle C B A), $$ at least one of the following inequalities holds: $$ \angle A P B \geqslant \pi-\angle A C B, \quad \angle B P C \geqslant \pi-\angle B A C, \quad \angle C P A \geqslant \pi-\angle C B A . $$ Without loss of generality, we assume that $\angle B P C \geqslant \pi-\angle B A C$. We have $\angle B P C>\angle B A C$ because $P$ is inside $\triangle A B C$. So $\angle B P C \geqslant \max (\angle B A C, \pi-\angle B A C)$ and hence $$ \sin \angle B P C \leqslant \sin \angle B A C . $$ Let the rays $A P, B P$, and $C P$ cross the circumcircle $\Omega$ again at $A_{3}, B_{3}$, and $C_{3}$, respectively. We will prove that at least one of the ratios $\frac{P B_{1}}{B_{1} B_{3}}$ and $\frac{P C_{1}}{C_{1} C_{3}}$ is at least 1 , which yields that one of the points $B_{2}$ and $C_{2}$ does not lie strictly inside $\Omega$. Because $A, B, C, B_{3}$ lie on a circle, the triangles $C B_{1} B_{3}$ and $B B_{1} A$ are similar, so $$ \frac{C B_{1}}{B_{1} B_{3}}=\frac{B B_{1}}{B_{1} A} $$ Applying the sine rule we obtain $$ \frac{P B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{C B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{B B_{1}}{B_{1} A}=\frac{\sin \angle A C P}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle P B A} . $$ Similarly, $$ \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin \angle P B A}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle A C P} $$ Multiplying these two equations we get $$ \frac{P B_{1}}{B_{1} B_{3}} \cdot \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin ^{2} \angle B A C}{\sin ^{2} \angle B P C} \geqslant 1 $$ using (*), which yields the desired conclusion. Comment. It also cannot happen that all three points $A_{2}, B_{2}$, and $C_{2}$ lie strictly outside $\Omega$. The same proof works almost literally, starting by assuming without loss of generality that $\angle B P C \leqslant \pi-\angle B A C$ and using $\angle B P C>\angle B A C$ to deduce that $\sin \angle B P C \geqslant \sin \angle B A C$. It is possible for $A_{2}, B_{2}$, and $C_{2}$ all to lie on the circumcircle; from the above solution we may derive that this happens if and only if $P$ is the orthocentre of the triangle $A B C$, (which lies strictly inside $A B C$ if and only if $A B C$ is acute).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia)
|
Since $$ \angle A P B+\angle B P C+\angle C P A=2 \pi=(\pi-\angle A C B)+(\pi-\angle B A C)+(\pi-\angle C B A), $$ at least one of the following inequalities holds: $$ \angle A P B \geqslant \pi-\angle A C B, \quad \angle B P C \geqslant \pi-\angle B A C, \quad \angle C P A \geqslant \pi-\angle C B A . $$ Without loss of generality, we assume that $\angle B P C \geqslant \pi-\angle B A C$. We have $\angle B P C>\angle B A C$ because $P$ is inside $\triangle A B C$. So $\angle B P C \geqslant \max (\angle B A C, \pi-\angle B A C)$ and hence $$ \sin \angle B P C \leqslant \sin \angle B A C . $$ Let the rays $A P, B P$, and $C P$ cross the circumcircle $\Omega$ again at $A_{3}, B_{3}$, and $C_{3}$, respectively. We will prove that at least one of the ratios $\frac{P B_{1}}{B_{1} B_{3}}$ and $\frac{P C_{1}}{C_{1} C_{3}}$ is at least 1 , which yields that one of the points $B_{2}$ and $C_{2}$ does not lie strictly inside $\Omega$. Because $A, B, C, B_{3}$ lie on a circle, the triangles $C B_{1} B_{3}$ and $B B_{1} A$ are similar, so $$ \frac{C B_{1}}{B_{1} B_{3}}=\frac{B B_{1}}{B_{1} A} $$ Applying the sine rule we obtain $$ \frac{P B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{C B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{B B_{1}}{B_{1} A}=\frac{\sin \angle A C P}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle P B A} . $$ Similarly, $$ \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin \angle P B A}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle A C P} $$ Multiplying these two equations we get $$ \frac{P B_{1}}{B_{1} B_{3}} \cdot \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin ^{2} \angle B A C}{\sin ^{2} \angle B P C} \geqslant 1 $$ using (*), which yields the desired conclusion. Comment. It also cannot happen that all three points $A_{2}, B_{2}$, and $C_{2}$ lie strictly outside $\Omega$. The same proof works almost literally, starting by assuming without loss of generality that $\angle B P C \leqslant \pi-\angle B A C$ and using $\angle B P C>\angle B A C$ to deduce that $\sin \angle B P C \geqslant \sin \angle B A C$. It is possible for $A_{2}, B_{2}$, and $C_{2}$ all to lie on the circumcircle; from the above solution we may derive that this happens if and only if $P$ is the orthocentre of the triangle $A B C$, (which lies strictly inside $A B C$ if and only if $A B C$ is acute).
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
98f30154-ff6f-58e5-9e16-52aeae3ea47e
| 23,760
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia)
|
Define points $A_{3}, B_{3}$, and $C_{3}$ as in Observe that $\triangle P B C_{3} \sim \triangle P C B_{3}$. Let $X$ be the point on side $P B_{3}$ that corresponds to point $C_{1}$ on side $P C_{3}$ under this similarity. In other words, $X$ lies on segment $P B_{3}$ and satisfies $P X: X B_{3}=P C_{1}: C_{1} C_{3}$. It follows that $$ \angle X C P=\angle P B C_{1}=\angle B_{3} B A=\angle B_{3} C B_{1} . $$ Hence lines $C X$ and $C B_{1}$ are isogonal conjugates in $\triangle P C B_{3}$. 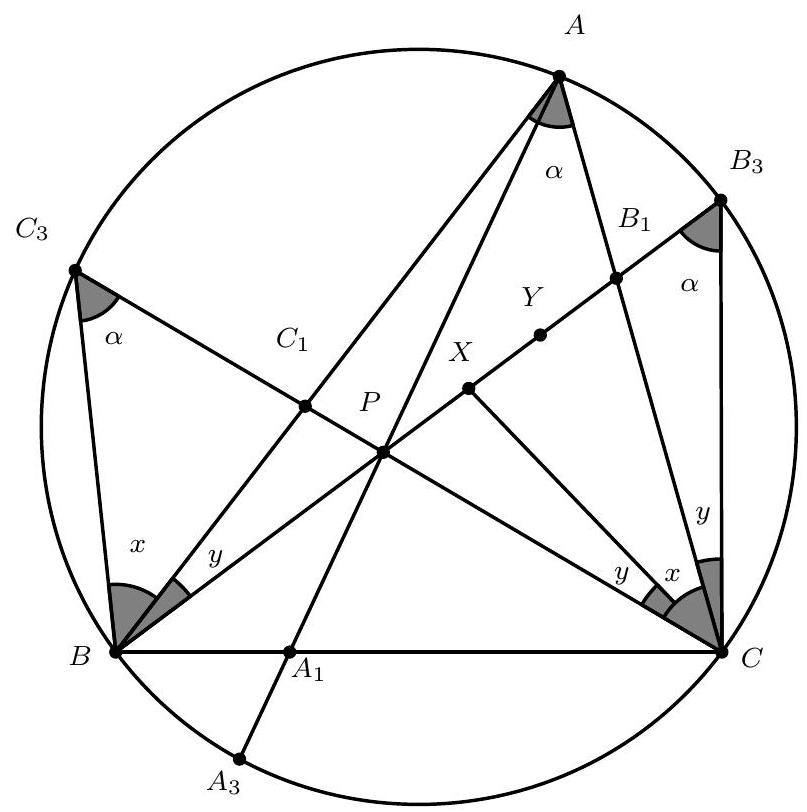 Let $Y$ be the foot of the bisector of $\angle B_{3} C P$ in $\triangle P C B_{3}$. Since $P C_{1}<C_{1} C_{3}$, we have $P X<X B_{3}$. Also, we have $P Y<Y B_{3}$ because $P B_{1}<B_{1} B_{3}$ and $Y$ lies between $X$ and $B_{1}$. By the angle bisector theorem in $\triangle P C B_{3}$, we have $P Y: Y B_{3}=P C: C B_{3}$. So $P C<C B_{3}$ and it follows that $\angle P B_{3} C<\angle C P B_{3}$. Now since $\angle P B_{3} C=\angle B B_{3} C=\angle B A C$, we have $$ \angle B A C<\angle C P B_{3} . $$ Similarly, we have $$ \angle C B A<\angle A P C_{3} \text { and } \angle A C B<\angle B P A_{3}=\angle B_{3} P A . $$ Adding these three inequalities yields $\pi<\pi$, and this contradiction concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia)
|
Define points $A_{3}, B_{3}$, and $C_{3}$ as in Observe that $\triangle P B C_{3} \sim \triangle P C B_{3}$. Let $X$ be the point on side $P B_{3}$ that corresponds to point $C_{1}$ on side $P C_{3}$ under this similarity. In other words, $X$ lies on segment $P B_{3}$ and satisfies $P X: X B_{3}=P C_{1}: C_{1} C_{3}$. It follows that $$ \angle X C P=\angle P B C_{1}=\angle B_{3} B A=\angle B_{3} C B_{1} . $$ Hence lines $C X$ and $C B_{1}$ are isogonal conjugates in $\triangle P C B_{3}$.  Let $Y$ be the foot of the bisector of $\angle B_{3} C P$ in $\triangle P C B_{3}$. Since $P C_{1}<C_{1} C_{3}$, we have $P X<X B_{3}$. Also, we have $P Y<Y B_{3}$ because $P B_{1}<B_{1} B_{3}$ and $Y$ lies between $X$ and $B_{1}$. By the angle bisector theorem in $\triangle P C B_{3}$, we have $P Y: Y B_{3}=P C: C B_{3}$. So $P C<C B_{3}$ and it follows that $\angle P B_{3} C<\angle C P B_{3}$. Now since $\angle P B_{3} C=\angle B B_{3} C=\angle B A C$, we have $$ \angle B A C<\angle C P B_{3} . $$ Similarly, we have $$ \angle C B A<\angle A P C_{3} \text { and } \angle A C B<\angle B P A_{3}=\angle B_{3} P A . $$ Adding these three inequalities yields $\pi<\pi$, and this contradiction concludes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
98f30154-ff6f-58e5-9e16-52aeae3ea47e
| 23,760
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia)
|
Choose coordinates such that the circumcentre of $\triangle A B C$ is at the origin and the circumradius is 1 . Then we may think of $A, B$, and $C$ as vectors in $\mathbb{R}^{2}$ such that $$ |A|^{2}=|B|^{2}=|C|^{2}=1 $$ $P$ may be represented as a convex combination $\alpha A+\beta B+\gamma C$ where $\alpha, \beta, \gamma>0$ and $\alpha+\beta+\gamma=1$. Then $$ A_{1}=\frac{\beta B+\gamma C}{\beta+\gamma}=\frac{1}{1-\alpha} P-\frac{\alpha}{1-\alpha} A, $$ so $$ A_{2}=2 A_{1}-P=\frac{1+\alpha}{1-\alpha} P-\frac{2 \alpha}{1-\alpha} A $$ Hence $$ \left|A_{2}\right|^{2}=\left(\frac{1+\alpha}{1-\alpha}\right)^{2}|P|^{2}+\left(\frac{2 \alpha}{1-\alpha}\right)^{2}|A|^{2}-\frac{4 \alpha(1+\alpha)}{(1-\alpha)^{2}} A \cdot P $$ Using $|A|^{2}=1$ we obtain $$ \frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}=\frac{1+\alpha}{2}|P|^{2}+\frac{2 \alpha^{2}}{1+\alpha}-2 \alpha A \cdot P $$ Likewise $$ \frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}=\frac{1+\beta}{2}|P|^{2}+\frac{2 \beta^{2}}{1+\beta}-2 \beta B \cdot P $$ and $$ \frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2}=\frac{1+\gamma}{2}|P|^{2}+\frac{2 \gamma^{2}}{1+\gamma}-2 \gamma C \cdot P $$ Summing (1), (2) and (3) we obtain on the LHS the positive linear combination $$ \text { LHS }=\frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2} $$ and on the RHS the quantity $$ \left(\frac{1+\alpha}{2}+\frac{1+\beta}{2}+\frac{1+\gamma}{2}\right)|P|^{2}+\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right)-2(\alpha A \cdot P+\beta B \cdot P+\gamma C \cdot P) . $$ The first term is $2|P|^{2}$ and the last term is $-2 P \cdot P$, so $$ \begin{aligned} \text { RHS } & =\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right) \\ & =\frac{3 \alpha-1}{2}+\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{3 \beta-1}{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{3 \gamma-1}{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \\ & =\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \end{aligned} $$ Here we used the fact that $$ \frac{3 \alpha-1}{2}+\frac{3 \beta-1}{2}+\frac{3 \gamma-1}{2}=0 . $$ We have shown that a linear combination of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ with positive coefficients is equal to the sum of the coefficients. Therefore at least one of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ must be at least 1 , as required. Comment. This proof also works when $P$ is any point for which $\alpha, \beta, \gamma>-1, \alpha+\beta+\gamma=1$, and $\alpha, \beta, \gamma \neq 1$. (In any cases where $\alpha=1$ or $\beta=1$ or $\gamma=1$, some points in the construction are not defined.) This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia)
|
Choose coordinates such that the circumcentre of $\triangle A B C$ is at the origin and the circumradius is 1 . Then we may think of $A, B$, and $C$ as vectors in $\mathbb{R}^{2}$ such that $$ |A|^{2}=|B|^{2}=|C|^{2}=1 $$ $P$ may be represented as a convex combination $\alpha A+\beta B+\gamma C$ where $\alpha, \beta, \gamma>0$ and $\alpha+\beta+\gamma=1$. Then $$ A_{1}=\frac{\beta B+\gamma C}{\beta+\gamma}=\frac{1}{1-\alpha} P-\frac{\alpha}{1-\alpha} A, $$ so $$ A_{2}=2 A_{1}-P=\frac{1+\alpha}{1-\alpha} P-\frac{2 \alpha}{1-\alpha} A $$ Hence $$ \left|A_{2}\right|^{2}=\left(\frac{1+\alpha}{1-\alpha}\right)^{2}|P|^{2}+\left(\frac{2 \alpha}{1-\alpha}\right)^{2}|A|^{2}-\frac{4 \alpha(1+\alpha)}{(1-\alpha)^{2}} A \cdot P $$ Using $|A|^{2}=1$ we obtain $$ \frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}=\frac{1+\alpha}{2}|P|^{2}+\frac{2 \alpha^{2}}{1+\alpha}-2 \alpha A \cdot P $$ Likewise $$ \frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}=\frac{1+\beta}{2}|P|^{2}+\frac{2 \beta^{2}}{1+\beta}-2 \beta B \cdot P $$ and $$ \frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2}=\frac{1+\gamma}{2}|P|^{2}+\frac{2 \gamma^{2}}{1+\gamma}-2 \gamma C \cdot P $$ Summing (1), (2) and (3) we obtain on the LHS the positive linear combination $$ \text { LHS }=\frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2} $$ and on the RHS the quantity $$ \left(\frac{1+\alpha}{2}+\frac{1+\beta}{2}+\frac{1+\gamma}{2}\right)|P|^{2}+\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right)-2(\alpha A \cdot P+\beta B \cdot P+\gamma C \cdot P) . $$ The first term is $2|P|^{2}$ and the last term is $-2 P \cdot P$, so $$ \begin{aligned} \text { RHS } & =\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right) \\ & =\frac{3 \alpha-1}{2}+\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{3 \beta-1}{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{3 \gamma-1}{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \\ & =\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \end{aligned} $$ Here we used the fact that $$ \frac{3 \alpha-1}{2}+\frac{3 \beta-1}{2}+\frac{3 \gamma-1}{2}=0 . $$ We have shown that a linear combination of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ with positive coefficients is equal to the sum of the coefficients. Therefore at least one of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ must be at least 1 , as required. Comment. This proof also works when $P$ is any point for which $\alpha, \beta, \gamma>-1, \alpha+\beta+\gamma=1$, and $\alpha, \beta, \gamma \neq 1$. (In any cases where $\alpha=1$ or $\beta=1$ or $\gamma=1$, some points in the construction are not defined.) This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
98f30154-ff6f-58e5-9e16-52aeae3ea47e
| 23,760
|
Let $A B C D E$ be a convex pentagon with $C D=D E$ and $\angle E D C \neq 2 \cdot \angle A D B$. Suppose that a point $P$ is located in the interior of the pentagon such that $A P=A E$ and $B P=B C$. Prove that $P$ lies on the diagonal $C E$ if and only if $\operatorname{area}(B C D)+\operatorname{area}(A D E)=$ $\operatorname{area}(A B D)+\operatorname{area}(A B P)$. (Hungary)
|
Let $P^{\prime}$ be the reflection of $P$ across line $A B$, and let $M$ and $N$ be the midpoints of $P^{\prime} E$ and $P^{\prime} C$ respectively. Convexity ensures that $P^{\prime}$ is distinct from both $E$ and $C$, and hence from both $M$ and $N$. We claim that both the area condition and the collinearity condition in the problem are equivalent to the condition that the (possibly degenerate) right-angled triangles $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar (equivalently, $A P^{\prime} E$ and $B P^{\prime} C$ are directly similar).  For the equivalence with the collinearity condition, let $F$ denote the foot of the perpendicular from $P^{\prime}$ to $A B$, so that $F$ is the midpoint of $P P^{\prime}$. We have that $P$ lies on $C E$ if and only if $F$ lies on $M N$, which occurs if and only if we have the equality $\angle A F M=\angle B F N$ of signed angles modulo $\pi$. By concyclicity of $A P^{\prime} F M$ and $B F P^{\prime} N$, this is equivalent to $\angle A P^{\prime} M=\angle B P^{\prime} N$, which occurs if and only if $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar.  For the other equivalence with the area condition, we have the equality of signed areas $\operatorname{area}(A B D)+\operatorname{area}(A B P)=\operatorname{area}\left(A P^{\prime} B D\right)=\operatorname{area}\left(A P^{\prime} D\right)+\operatorname{area}\left(B D P^{\prime}\right)$. Using the identity $\operatorname{area}(A D E)-\operatorname{area}\left(A P^{\prime} D\right)=\operatorname{area}(A D E)+\operatorname{area}\left(A D P^{\prime}\right)=2$ area $(A D M)$, and similarly for $B$, we find that the area condition is equivalent to the equality $$ \operatorname{area}(D A M)=\operatorname{area}(D B N) . $$ Now note that $A$ and $B$ lie on the perpendicular bisectors of $P^{\prime} E$ and $P^{\prime} C$, respectively. If we write $G$ and $H$ for the feet of the perpendiculars from $D$ to these perpendicular bisectors respectively, then this area condition can be rewritten as $$ M A \cdot G D=N B \cdot H D $$ (In this condition, we interpret all lengths as signed lengths according to suitable conventions: for instance, we orient $P^{\prime} E$ from $P^{\prime}$ to $E$, orient the parallel line $D H$ in the same direction, and orient the perpendicular bisector of $P^{\prime} E$ at an angle $\pi / 2$ clockwise from the oriented segment $P^{\prime} E$ - we adopt the analogous conventions at $B$.)  To relate the signed lengths $G D$ and $H D$ to the triangles $A P^{\prime} M$ and $B P^{\prime} N$, we use the following calculation. Claim. Let $\Gamma$ denote the circle centred on $D$ with both $E$ and $C$ on the circumference, and $h$ the power of $P^{\prime}$ with respect to $\Gamma$. Then we have the equality $$ G D \cdot P^{\prime} M=H D \cdot P^{\prime} N=\frac{1}{4} h \neq 0 . $$ Proof. Firstly, we have $h \neq 0$, since otherwise $P^{\prime}$ would lie on $\Gamma$, and hence the internal angle bisectors of $\angle E D P^{\prime}$ and $\angle P^{\prime} D C$ would pass through $A$ and $B$ respectively. This would violate the angle inequality $\angle E D C \neq 2 \cdot \angle A D B$ given in the question. Next, let $E^{\prime}$ denote the second point of intersection of $P^{\prime} E$ with $\Gamma$, and let $E^{\prime \prime}$ denote the point on $\Gamma$ diametrically opposite $E^{\prime}$, so that $E^{\prime \prime} E$ is perpendicular to $P^{\prime} E$. The point $G$ lies on the perpendicular bisectors of the sides $P^{\prime} E$ and $E E^{\prime \prime}$ of the right-angled triangle $P^{\prime} E E^{\prime \prime}$; it follows that $G$ is the midpoint of $P^{\prime} E^{\prime \prime}$. Since $D$ is the midpoint of $E^{\prime} E^{\prime \prime}$, we have that $G D=\frac{1}{2} P^{\prime} E^{\prime}$. Since $P^{\prime} M=\frac{1}{2} P^{\prime} E$, we have $G D \cdot P^{\prime} M=\frac{1}{4} P^{\prime} E^{\prime} \cdot P^{\prime} E=\frac{1}{4} h$. The other equality $H D \cdot P^{\prime} N$ follows by exactly the same argument.  From this claim, we see that the area condition is equivalent to the equality $$ \left(M A: P^{\prime} M\right)=\left(N B: P^{\prime} N\right) $$ of ratios of signed lengths, which is equivalent to direct similarity of $A P^{\prime} M$ and $B P^{\prime} N$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon with $C D=D E$ and $\angle E D C \neq 2 \cdot \angle A D B$. Suppose that a point $P$ is located in the interior of the pentagon such that $A P=A E$ and $B P=B C$. Prove that $P$ lies on the diagonal $C E$ if and only if $\operatorname{area}(B C D)+\operatorname{area}(A D E)=$ $\operatorname{area}(A B D)+\operatorname{area}(A B P)$. (Hungary)
|
Let $P^{\prime}$ be the reflection of $P$ across line $A B$, and let $M$ and $N$ be the midpoints of $P^{\prime} E$ and $P^{\prime} C$ respectively. Convexity ensures that $P^{\prime}$ is distinct from both $E$ and $C$, and hence from both $M$ and $N$. We claim that both the area condition and the collinearity condition in the problem are equivalent to the condition that the (possibly degenerate) right-angled triangles $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar (equivalently, $A P^{\prime} E$ and $B P^{\prime} C$ are directly similar).  For the equivalence with the collinearity condition, let $F$ denote the foot of the perpendicular from $P^{\prime}$ to $A B$, so that $F$ is the midpoint of $P P^{\prime}$. We have that $P$ lies on $C E$ if and only if $F$ lies on $M N$, which occurs if and only if we have the equality $\angle A F M=\angle B F N$ of signed angles modulo $\pi$. By concyclicity of $A P^{\prime} F M$ and $B F P^{\prime} N$, this is equivalent to $\angle A P^{\prime} M=\angle B P^{\prime} N$, which occurs if and only if $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar.  For the other equivalence with the area condition, we have the equality of signed areas $\operatorname{area}(A B D)+\operatorname{area}(A B P)=\operatorname{area}\left(A P^{\prime} B D\right)=\operatorname{area}\left(A P^{\prime} D\right)+\operatorname{area}\left(B D P^{\prime}\right)$. Using the identity $\operatorname{area}(A D E)-\operatorname{area}\left(A P^{\prime} D\right)=\operatorname{area}(A D E)+\operatorname{area}\left(A D P^{\prime}\right)=2$ area $(A D M)$, and similarly for $B$, we find that the area condition is equivalent to the equality $$ \operatorname{area}(D A M)=\operatorname{area}(D B N) . $$ Now note that $A$ and $B$ lie on the perpendicular bisectors of $P^{\prime} E$ and $P^{\prime} C$, respectively. If we write $G$ and $H$ for the feet of the perpendiculars from $D$ to these perpendicular bisectors respectively, then this area condition can be rewritten as $$ M A \cdot G D=N B \cdot H D $$ (In this condition, we interpret all lengths as signed lengths according to suitable conventions: for instance, we orient $P^{\prime} E$ from $P^{\prime}$ to $E$, orient the parallel line $D H$ in the same direction, and orient the perpendicular bisector of $P^{\prime} E$ at an angle $\pi / 2$ clockwise from the oriented segment $P^{\prime} E$ - we adopt the analogous conventions at $B$.)  To relate the signed lengths $G D$ and $H D$ to the triangles $A P^{\prime} M$ and $B P^{\prime} N$, we use the following calculation. Claim. Let $\Gamma$ denote the circle centred on $D$ with both $E$ and $C$ on the circumference, and $h$ the power of $P^{\prime}$ with respect to $\Gamma$. Then we have the equality $$ G D \cdot P^{\prime} M=H D \cdot P^{\prime} N=\frac{1}{4} h \neq 0 . $$ Proof. Firstly, we have $h \neq 0$, since otherwise $P^{\prime}$ would lie on $\Gamma$, and hence the internal angle bisectors of $\angle E D P^{\prime}$ and $\angle P^{\prime} D C$ would pass through $A$ and $B$ respectively. This would violate the angle inequality $\angle E D C \neq 2 \cdot \angle A D B$ given in the question. Next, let $E^{\prime}$ denote the second point of intersection of $P^{\prime} E$ with $\Gamma$, and let $E^{\prime \prime}$ denote the point on $\Gamma$ diametrically opposite $E^{\prime}$, so that $E^{\prime \prime} E$ is perpendicular to $P^{\prime} E$. The point $G$ lies on the perpendicular bisectors of the sides $P^{\prime} E$ and $E E^{\prime \prime}$ of the right-angled triangle $P^{\prime} E E^{\prime \prime}$; it follows that $G$ is the midpoint of $P^{\prime} E^{\prime \prime}$. Since $D$ is the midpoint of $E^{\prime} E^{\prime \prime}$, we have that $G D=\frac{1}{2} P^{\prime} E^{\prime}$. Since $P^{\prime} M=\frac{1}{2} P^{\prime} E$, we have $G D \cdot P^{\prime} M=\frac{1}{4} P^{\prime} E^{\prime} \cdot P^{\prime} E=\frac{1}{4} h$. The other equality $H D \cdot P^{\prime} N$ follows by exactly the same argument.  From this claim, we see that the area condition is equivalent to the equality $$ \left(M A: P^{\prime} M\right)=\left(N B: P^{\prime} N\right) $$ of ratios of signed lengths, which is equivalent to direct similarity of $A P^{\prime} M$ and $B P^{\prime} N$, as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a078f44b-6bf9-5927-a785-0d0bcfe86124
| 23,766
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Let $N$ and $M$ be the midpoints of the arcs $\widehat{B C}$ of the circumcircle, containing and opposite vertex $A$, respectively. By $\angle F A E=\angle B A C=\angle B N C$, the right-angled kites $A F I E$ and $N B M C$ are similar. Consider the spiral similarity $\varphi$ (dilation in case of $A B=A C$ ) that moves $A F I E$ to $N B M C$. The directed angle in which $\varphi$ changes directions is $\angle(A F, N B)$, same as $\angle(A P, N P)$ and $\angle(A Q, N Q)$; so lines $A P$ and $A Q$ are mapped to lines $N P$ and $N Q$, respectively. Line $E F$ is mapped to $B C$; we can see that the intersection points $P=E F \cap A P$ and $Q=E F \cap A Q$ are mapped to points $B C \cap N P$ and $B C \cap N Q$, respectively. Denote these points by $P^{\prime}$ and $Q^{\prime}$, respectively.  Let $L$ be the midpoint of $B C$. We claim that points $P, Q, D, L$ are concyclic (if $D=L$ then line $B C$ is tangent to circle $P Q D$ ). Let $P Q$ and $B C$ meet at $Z$. By applying Menelaus' theorem to triangle $A B C$ and line $E F Z$, we have $$ \frac{B D}{D C}=\frac{B F}{F A} \cdot \frac{A E}{E C}=-\frac{B Z}{Z C}, $$ so the pairs $B, C$ and $D, Z$ are harmonic. It is well-known that this implies $Z B \cdot Z C=Z D \cdot Z L$. (The inversion with pole $Z$ that swaps $B$ and $C$ sends $Z$ to infinity and $D$ to the midpoint of $B C$, because the cross-ratio is preserved.) Hence, $Z D \cdot Z L=Z B \cdot Z C=Z P \cdot Z Q$ by the power of $Z$ with respect to the circumcircle; this proves our claim. By $\angle M P P^{\prime}=\angle M Q Q^{\prime}=\angle M L P^{\prime}=\angle M L Q^{\prime}=90^{\circ}$, the quadrilaterals $M L P P^{\prime}$ and $M L Q Q^{\prime}$ are cyclic. Then the problem statement follows by $$ \begin{aligned} \angle D P A+\angle A Q D & =360^{\circ}-\angle P A Q-\angle Q D P=360^{\circ}-\angle P N Q-\angle Q L P \\ & =\angle L P N+\angle N Q L=\angle P^{\prime} M L+\angle L M Q^{\prime}=\angle P^{\prime} M Q^{\prime}=\angle P I Q . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Let $N$ and $M$ be the midpoints of the arcs $\widehat{B C}$ of the circumcircle, containing and opposite vertex $A$, respectively. By $\angle F A E=\angle B A C=\angle B N C$, the right-angled kites $A F I E$ and $N B M C$ are similar. Consider the spiral similarity $\varphi$ (dilation in case of $A B=A C$ ) that moves $A F I E$ to $N B M C$. The directed angle in which $\varphi$ changes directions is $\angle(A F, N B)$, same as $\angle(A P, N P)$ and $\angle(A Q, N Q)$; so lines $A P$ and $A Q$ are mapped to lines $N P$ and $N Q$, respectively. Line $E F$ is mapped to $B C$; we can see that the intersection points $P=E F \cap A P$ and $Q=E F \cap A Q$ are mapped to points $B C \cap N P$ and $B C \cap N Q$, respectively. Denote these points by $P^{\prime}$ and $Q^{\prime}$, respectively.  Let $L$ be the midpoint of $B C$. We claim that points $P, Q, D, L$ are concyclic (if $D=L$ then line $B C$ is tangent to circle $P Q D$ ). Let $P Q$ and $B C$ meet at $Z$. By applying Menelaus' theorem to triangle $A B C$ and line $E F Z$, we have $$ \frac{B D}{D C}=\frac{B F}{F A} \cdot \frac{A E}{E C}=-\frac{B Z}{Z C}, $$ so the pairs $B, C$ and $D, Z$ are harmonic. It is well-known that this implies $Z B \cdot Z C=Z D \cdot Z L$. (The inversion with pole $Z$ that swaps $B$ and $C$ sends $Z$ to infinity and $D$ to the midpoint of $B C$, because the cross-ratio is preserved.) Hence, $Z D \cdot Z L=Z B \cdot Z C=Z P \cdot Z Q$ by the power of $Z$ with respect to the circumcircle; this proves our claim. By $\angle M P P^{\prime}=\angle M Q Q^{\prime}=\angle M L P^{\prime}=\angle M L Q^{\prime}=90^{\circ}$, the quadrilaterals $M L P P^{\prime}$ and $M L Q Q^{\prime}$ are cyclic. Then the problem statement follows by $$ \begin{aligned} \angle D P A+\angle A Q D & =360^{\circ}-\angle P A Q-\angle Q D P=360^{\circ}-\angle P N Q-\angle Q L P \\ & =\angle L P N+\angle N Q L=\angle P^{\prime} M L+\angle L M Q^{\prime}=\angle P^{\prime} M Q^{\prime}=\angle P I Q . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d31fa1da-523d-566b-9e09-9c305701f0e1
| 23,770
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Define the point $M$ and the same spiral similarity $\varphi$ as in the previous solution. (The point $N$ is not necessary.) It is well-known that the centre of the spiral similarity that maps $F, E$ to $B, C$ is the Miquel point of the lines $F E, B C, B F$ and $C E$; that is, the second intersection of circles $A B C$ and $A E F$. Denote that point by $S$. By $\varphi(F)=B$ and $\varphi(E)=C$ the triangles $S B F$ and $S C E$ are similar, so we have $$ \frac{S B}{S C}=\frac{B F}{C E}=\frac{B D}{C D} $$ By the converse of the angle bisector theorem, that indicates that line $S D$ bisects $\angle B S C$ and hence passes through $M$. Let $K$ be the intersection point of lines $E F$ and $S I$. Notice that $\varphi$ sends points $S, F, E, I$ to $S, B, C, M$, so $\varphi(K)=\varphi(F E \cap S I)=B C \cap S M=D$. By $\varphi(I)=M$, we have $K D \| I M$.  We claim that triangles $S P I$ and $S D Q$ are similar, and so are triangles $S P D$ and $S I Q$. Let ray $S I$ meet the circumcircle again at $L$. Note that the segment $E F$ is perpendicular to the angle bisector $A M$. Then by $\angle A M L=\angle A S L=\angle A S I=90^{\circ}$, we have $M L \| P Q$. Hence, $\widetilde{P L}=\widetilde{M Q}$ and therefore $\angle P S L=\angle M S Q=\angle D S Q$. By $\angle Q P S=\angle Q M S$, the triangles $S P K$ and $S M Q$ are similar. Finally, $$ \frac{S P}{S I}=\frac{S P}{S K} \cdot \frac{S K}{S I}=\frac{S M}{S Q} \cdot \frac{S D}{S M}=\frac{S D}{S Q} $$ shows that triangles $S P I$ and $S D Q$ are similar. The second part of the claim can be proved analogously. Now the problem statement can be proved by $$ \angle D P A+\angle A Q D=\angle D P S+\angle S Q D=\angle Q I S+\angle S I P=\angle Q I P . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Define the point $M$ and the same spiral similarity $\varphi$ as in the previous solution. (The point $N$ is not necessary.) It is well-known that the centre of the spiral similarity that maps $F, E$ to $B, C$ is the Miquel point of the lines $F E, B C, B F$ and $C E$; that is, the second intersection of circles $A B C$ and $A E F$. Denote that point by $S$. By $\varphi(F)=B$ and $\varphi(E)=C$ the triangles $S B F$ and $S C E$ are similar, so we have $$ \frac{S B}{S C}=\frac{B F}{C E}=\frac{B D}{C D} $$ By the converse of the angle bisector theorem, that indicates that line $S D$ bisects $\angle B S C$ and hence passes through $M$. Let $K$ be the intersection point of lines $E F$ and $S I$. Notice that $\varphi$ sends points $S, F, E, I$ to $S, B, C, M$, so $\varphi(K)=\varphi(F E \cap S I)=B C \cap S M=D$. By $\varphi(I)=M$, we have $K D \| I M$.  We claim that triangles $S P I$ and $S D Q$ are similar, and so are triangles $S P D$ and $S I Q$. Let ray $S I$ meet the circumcircle again at $L$. Note that the segment $E F$ is perpendicular to the angle bisector $A M$. Then by $\angle A M L=\angle A S L=\angle A S I=90^{\circ}$, we have $M L \| P Q$. Hence, $\widetilde{P L}=\widetilde{M Q}$ and therefore $\angle P S L=\angle M S Q=\angle D S Q$. By $\angle Q P S=\angle Q M S$, the triangles $S P K$ and $S M Q$ are similar. Finally, $$ \frac{S P}{S I}=\frac{S P}{S K} \cdot \frac{S K}{S I}=\frac{S M}{S Q} \cdot \frac{S D}{S M}=\frac{S D}{S Q} $$ shows that triangles $S P I$ and $S D Q$ are similar. The second part of the claim can be proved analogously. Now the problem statement can be proved by $$ \angle D P A+\angle A Q D=\angle D P S+\angle S Q D=\angle Q I S+\angle S I P=\angle Q I P . $$
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d31fa1da-523d-566b-9e09-9c305701f0e1
| 23,770
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Denote the circumcircle of triangle $A B C$ by $\Gamma$, and let rays $P D$ and $Q D$ meet $\Gamma$ again at $V$ and $U$, respectively. We will show that $A U \perp I P$ and $A V \perp I Q$. Then the problem statement will follow as $$ \angle D P A+\angle A Q D=\angle V U A+\angle A V U=180^{\circ}-\angle U A V=\angle Q I P . $$ Let $M$ be the midpoint of arc $\widehat{B U V C}$ and let $N$ be the midpoint of arc $\widehat{C A B}$; the lines $A I M$ and $A N$ being the internal and external bisectors of angle $B A C$, respectively, are perpendicular. Let the tangents drawn to $\Gamma$ at $B$ and $C$ meet at $R$; let line $P Q$ meet $A U, A I, A V$ and $B C$ at $X, T, Y$ and $Z$, respectively. As in Solution 1, we observe that the pairs $B, C$ and $D, Z$ are harmonic. Projecting these points from $Q$ onto the circumcircle, we can see that $B, C$ and $U, P$ are also harmonic. Analogously, the pair $V, Q$ is harmonic with $B, C$. Consider the inversion about the circle with centre $R$, passing through $B$ and $C$. Points $B$ and $C$ are fixed points, so this inversion exchanges every point of $\Gamma$ by its harmonic pair with respect to $B, C$. In particular, the inversion maps points $B, C, N, U, V$ to points $B, C, M, P, Q$, respectively. Combine the inversion with projecting $\Gamma$ from $A$ to line $P Q$; the points $B, C, M, P, Q$ are projected to $F, E, T, P, Q$, respectively. 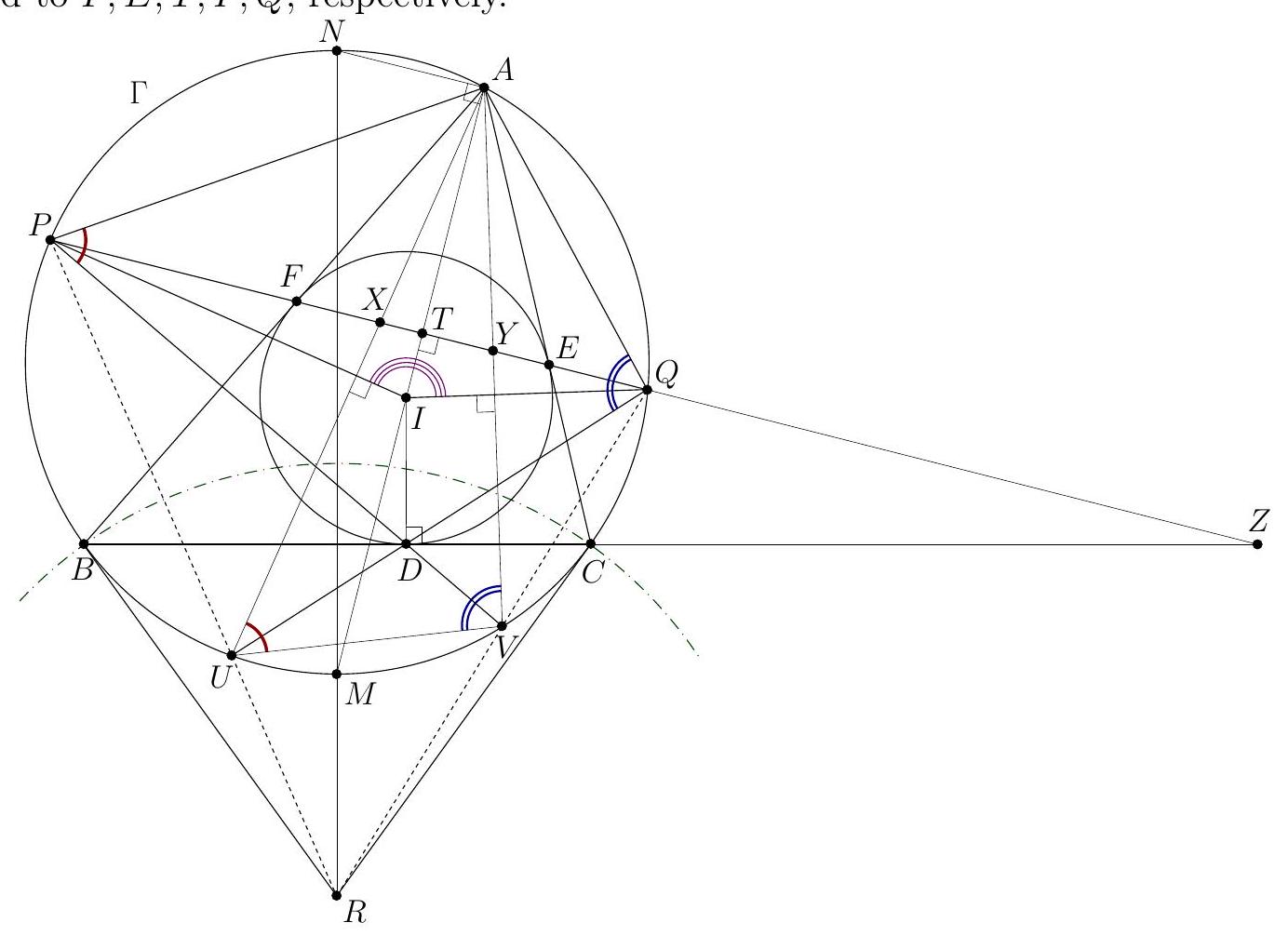 The combination of these two transformations is projective map from the lines $A B, A C$, $A N, A U, A V$ to $I F, I E, I T, I P, I Q$, respectively. On the other hand, we have $A B \perp I F$, $A C \perp I E$ and $A N \perp A T$, so the corresponding lines in these two pencils are perpendicular. This proves $A U \perp I P$ and $A V \perp I Q$, and hence completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Denote the circumcircle of triangle $A B C$ by $\Gamma$, and let rays $P D$ and $Q D$ meet $\Gamma$ again at $V$ and $U$, respectively. We will show that $A U \perp I P$ and $A V \perp I Q$. Then the problem statement will follow as $$ \angle D P A+\angle A Q D=\angle V U A+\angle A V U=180^{\circ}-\angle U A V=\angle Q I P . $$ Let $M$ be the midpoint of arc $\widehat{B U V C}$ and let $N$ be the midpoint of arc $\widehat{C A B}$; the lines $A I M$ and $A N$ being the internal and external bisectors of angle $B A C$, respectively, are perpendicular. Let the tangents drawn to $\Gamma$ at $B$ and $C$ meet at $R$; let line $P Q$ meet $A U, A I, A V$ and $B C$ at $X, T, Y$ and $Z$, respectively. As in Solution 1, we observe that the pairs $B, C$ and $D, Z$ are harmonic. Projecting these points from $Q$ onto the circumcircle, we can see that $B, C$ and $U, P$ are also harmonic. Analogously, the pair $V, Q$ is harmonic with $B, C$. Consider the inversion about the circle with centre $R$, passing through $B$ and $C$. Points $B$ and $C$ are fixed points, so this inversion exchanges every point of $\Gamma$ by its harmonic pair with respect to $B, C$. In particular, the inversion maps points $B, C, N, U, V$ to points $B, C, M, P, Q$, respectively. Combine the inversion with projecting $\Gamma$ from $A$ to line $P Q$; the points $B, C, M, P, Q$ are projected to $F, E, T, P, Q$, respectively.  The combination of these two transformations is projective map from the lines $A B, A C$, $A N, A U, A V$ to $I F, I E, I T, I P, I Q$, respectively. On the other hand, we have $A B \perp I F$, $A C \perp I E$ and $A N \perp A T$, so the corresponding lines in these two pencils are perpendicular. This proves $A U \perp I P$ and $A V \perp I Q$, and hence completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d31fa1da-523d-566b-9e09-9c305701f0e1
| 23,770
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India)
|
Step 1. The external bisector of $\angle B A C$ is the line through $A$ perpendicular to $I A$. Let $D I$ meet this line at $L$ and let $D I$ meet $\omega$ at $K$. Let $N$ be the midpoint of $E F$, which lies on $I A$ and is the pole of line $A L$ with respect to $\omega$. Since $A N \cdot A I=A E^{2}=A R \cdot A P$, the points $R$, $N, I$, and $P$ are concyclic. As $I R=I P$, the line $N I$ is the external bisector of $\angle P N R$, so $P N$ meets $\omega$ again at the point symmetric to $R$ with respect to $A N-i . e$ at $K$. Let $D N$ cross $\omega$ again at $S$. Opposite sides of any quadrilateral inscribed in the circle $\omega$ meet on the polar line of the intersection of the diagonals with respect to $\omega$. Since $L$ lies on the polar line $A L$ of $N$ with respect to $\omega$, the line $P S$ must pass through $L$. Thus it suffices to prove that the points $S, Q$, and $P$ are collinear. 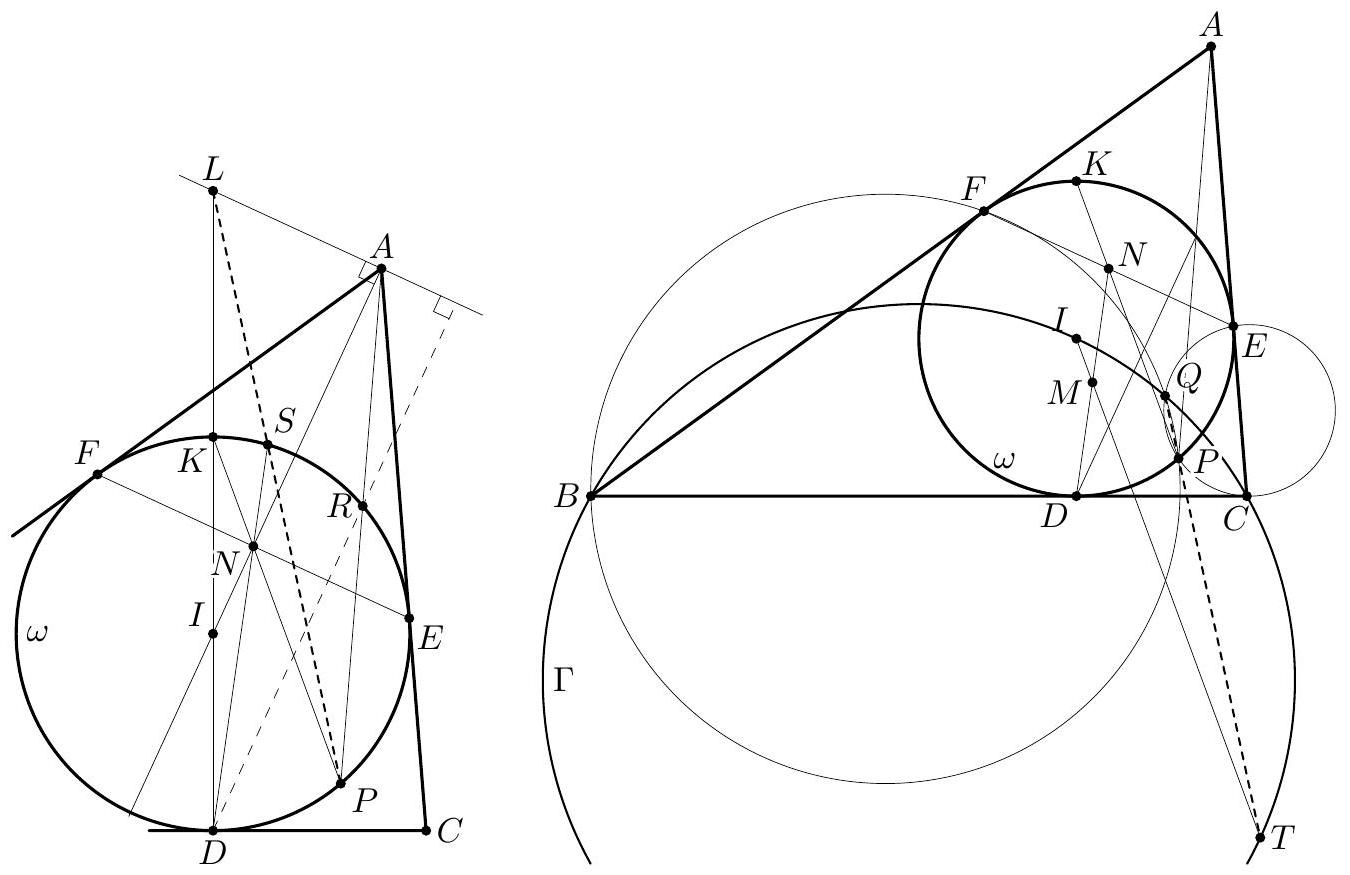 Step 2. Let $\Gamma$ be the circumcircle of $\triangle B I C$. Notice that $$ \begin{aligned} & \angle(B Q, Q C)=\angle(B Q, Q P)+\angle(P Q, Q C)=\angle(B F, F P)+\angle(P E, E C) \\ &=\angle(E F, E P)+\angle(F P, F E)=\angle(F P, E P)=\angle(D F, D E)=\angle(B I, I C) \end{aligned} $$ so $Q$ lies on $\Gamma$. Let $Q P$ meet $\Gamma$ again at $T$. It will now suffice to prove that $S, P$, and $T$ are collinear. Notice that $\angle(B I, I T)=\angle(B Q, Q T)=\angle(B F, F P)=\angle(F K, K P)$. Note $F D \perp F K$ and $F D \perp B I$ so $F K \| B I$ and hence $I T$ is parallel to the line $K N P$. Since $D I=I K$, the line $I T$ crosses $D N$ at its midpoint $M$. Step 3. Let $F^{\prime}$ and $E^{\prime}$ be the midpoints of $D E$ and $D F$, respectively. Since $D E^{\prime} \cdot E^{\prime} F=D E^{\prime 2}=$ $B E^{\prime} \cdot E^{\prime} I$, the point $E^{\prime}$ lies on the radical axis of $\omega$ and $\Gamma$; the same holds for $F^{\prime}$. Therefore, this radical axis is $E^{\prime} F^{\prime}$, and it passes through $M$. Thus $I M \cdot M T=D M \cdot M S$, so $S, I, D$, and $T$ are concyclic. This shows $\angle(D S, S T)=\angle(D I, I T)=\angle(D K, K P)=\angle(D S, S P)$, whence the points $S, P$, and $T$ are collinear, as desired. 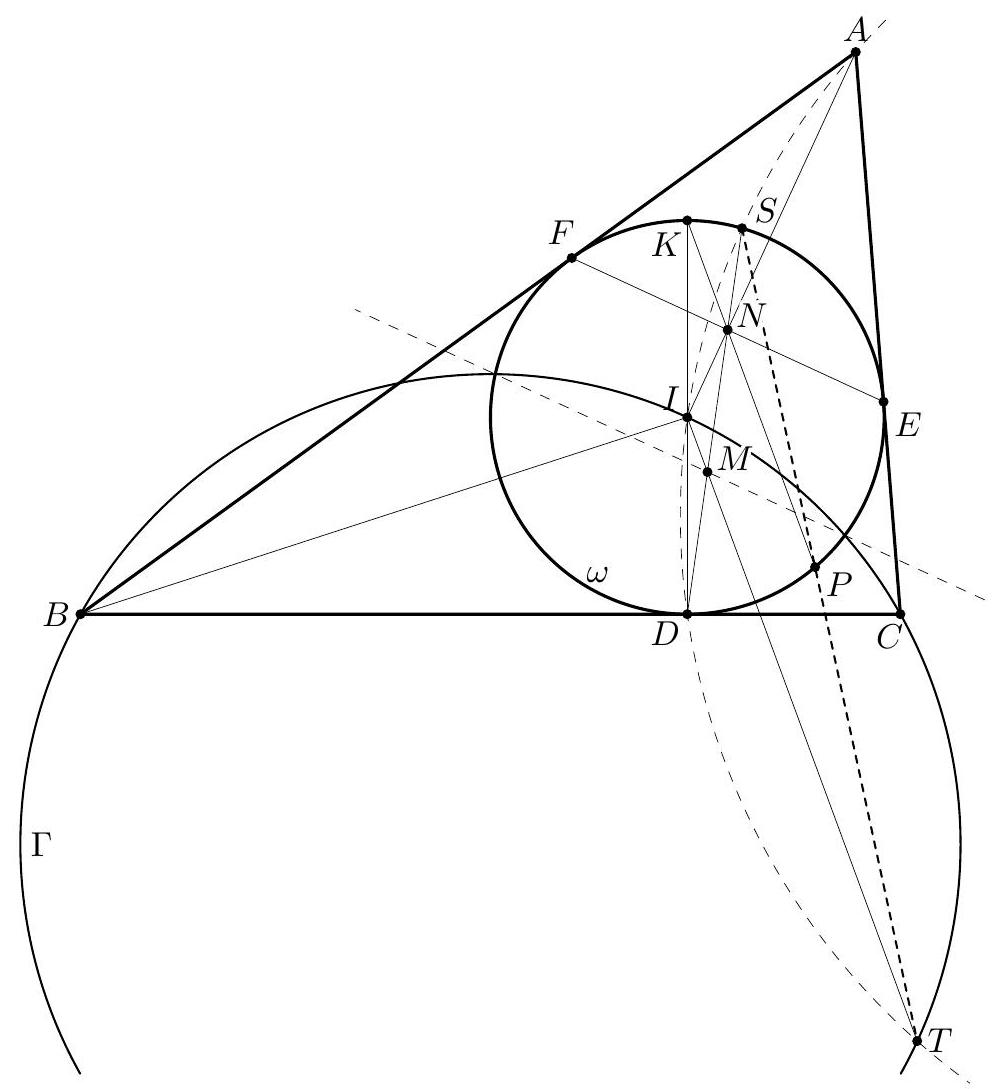 Comment. Here is a longer alternative proof in step 1 that $P, S$, and $L$ are collinear, using a circular inversion instead of the fact that opposite sides of a quadrilateral inscribed in a circle $\omega$ meet on the polar line with respect to $\omega$ of the intersection of the diagonals. Let $G$ be the foot of the altitude from $N$ to the line $D I K L$. Observe that $N, G, K, S$ are concyclic (opposite right angles) so $$ \angle D I P=2 \angle D K P=\angle G K N+\angle D S P=\angle G S N+\angle N S P=\angle G S P, $$ hence $I, G, S, P$ are concyclic. We have $I G \cdot I L=I N \cdot I A=r^{2}$ since $\triangle I G N \sim \triangle I A L$. Inverting the circle $I G S P$ in circle $\omega$, points $P$ and $S$ are fixed and $G$ is taken to $L$ so we find that $P, S$, and $L$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India)
|
Step 1. The external bisector of $\angle B A C$ is the line through $A$ perpendicular to $I A$. Let $D I$ meet this line at $L$ and let $D I$ meet $\omega$ at $K$. Let $N$ be the midpoint of $E F$, which lies on $I A$ and is the pole of line $A L$ with respect to $\omega$. Since $A N \cdot A I=A E^{2}=A R \cdot A P$, the points $R$, $N, I$, and $P$ are concyclic. As $I R=I P$, the line $N I$ is the external bisector of $\angle P N R$, so $P N$ meets $\omega$ again at the point symmetric to $R$ with respect to $A N-i . e$ at $K$. Let $D N$ cross $\omega$ again at $S$. Opposite sides of any quadrilateral inscribed in the circle $\omega$ meet on the polar line of the intersection of the diagonals with respect to $\omega$. Since $L$ lies on the polar line $A L$ of $N$ with respect to $\omega$, the line $P S$ must pass through $L$. Thus it suffices to prove that the points $S, Q$, and $P$ are collinear.  Step 2. Let $\Gamma$ be the circumcircle of $\triangle B I C$. Notice that $$ \begin{aligned} & \angle(B Q, Q C)=\angle(B Q, Q P)+\angle(P Q, Q C)=\angle(B F, F P)+\angle(P E, E C) \\ &=\angle(E F, E P)+\angle(F P, F E)=\angle(F P, E P)=\angle(D F, D E)=\angle(B I, I C) \end{aligned} $$ so $Q$ lies on $\Gamma$. Let $Q P$ meet $\Gamma$ again at $T$. It will now suffice to prove that $S, P$, and $T$ are collinear. Notice that $\angle(B I, I T)=\angle(B Q, Q T)=\angle(B F, F P)=\angle(F K, K P)$. Note $F D \perp F K$ and $F D \perp B I$ so $F K \| B I$ and hence $I T$ is parallel to the line $K N P$. Since $D I=I K$, the line $I T$ crosses $D N$ at its midpoint $M$. Step 3. Let $F^{\prime}$ and $E^{\prime}$ be the midpoints of $D E$ and $D F$, respectively. Since $D E^{\prime} \cdot E^{\prime} F=D E^{\prime 2}=$ $B E^{\prime} \cdot E^{\prime} I$, the point $E^{\prime}$ lies on the radical axis of $\omega$ and $\Gamma$; the same holds for $F^{\prime}$. Therefore, this radical axis is $E^{\prime} F^{\prime}$, and it passes through $M$. Thus $I M \cdot M T=D M \cdot M S$, so $S, I, D$, and $T$ are concyclic. This shows $\angle(D S, S T)=\angle(D I, I T)=\angle(D K, K P)=\angle(D S, S P)$, whence the points $S, P$, and $T$ are collinear, as desired.  Comment. Here is a longer alternative proof in step 1 that $P, S$, and $L$ are collinear, using a circular inversion instead of the fact that opposite sides of a quadrilateral inscribed in a circle $\omega$ meet on the polar line with respect to $\omega$ of the intersection of the diagonals. Let $G$ be the foot of the altitude from $N$ to the line $D I K L$. Observe that $N, G, K, S$ are concyclic (opposite right angles) so $$ \angle D I P=2 \angle D K P=\angle G K N+\angle D S P=\angle G S N+\angle N S P=\angle G S P, $$ hence $I, G, S, P$ are concyclic. We have $I G \cdot I L=I N \cdot I A=r^{2}$ since $\triangle I G N \sim \triangle I A L$. Inverting the circle $I G S P$ in circle $\omega$, points $P$ and $S$ are fixed and $G$ is taken to $L$ so we find that $P, S$, and $L$ are collinear.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
03a06caa-a588-5f2a-8d68-aeb027b308f6
| 23,775
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India)
|
We start as in Step 1. Let $A R$ meet the circumcircle $\Omega$ of $A B C$ again at $X$. The lines $A R$ and $A K$ are isogonal in the angle $B A C$; it is well known that in this case $X$ is the tangency point of $\Omega$ with the $A$-mixtilinear circle. It is also well known that for this point $X$, the line $X I$ crosses $\Omega$ again at the midpoint $M^{\prime}$ of arc $B A C$. Step 2. Denote the circles $B F P$ and $C E P$ by $\Omega_{B}$ and $\Omega_{C}$, respectively. Let $\Omega_{B}$ cross $A R$ and $E F$ again at $U$ and $Y$, respectively. We have $$ \angle(U B, B F)=\angle(U P, P F)=\angle(R P, P F)=\angle(R F, F A) $$ so $U B \| R F$. 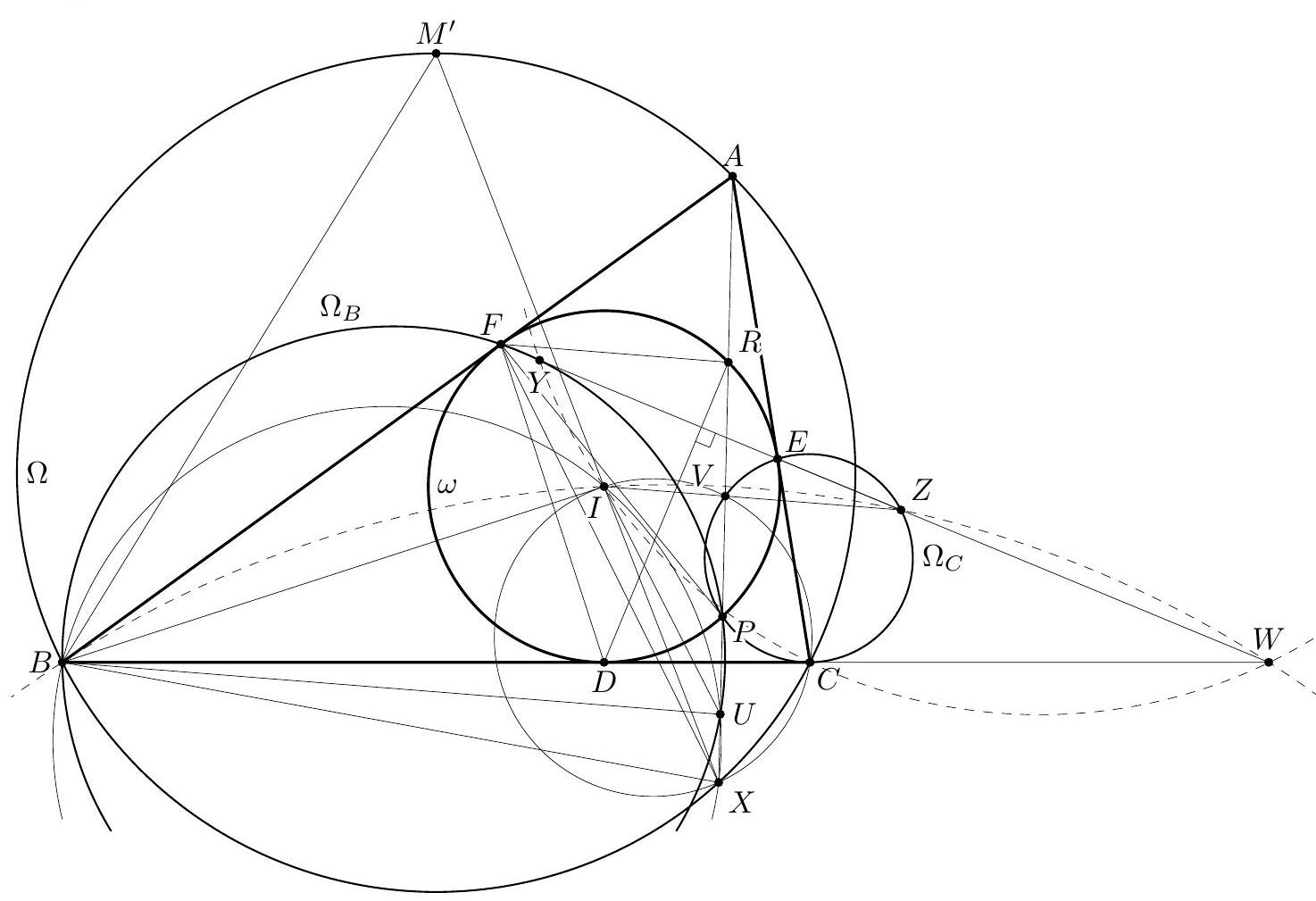 Next, we show that the points $B, I, U$, and $X$ are concyclic. Since $$ \angle(U B, U X)=\angle(R F, R X)=\angle(A F, A R)+\angle(F R, F A)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F) $$ it suffices to prove $\angle(I B, I X)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F)$, or $\angle\left(I B, M^{\prime} B\right)=\angle(D R, D F)$. But both angles equal $\angle(C I, C B)$, as desired. (This is where we used the fact that $M^{\prime}$ is the midpoint of $\operatorname{arc} B A C$ of $\Omega$.) It follows now from circles $B U I X$ and $B P U F Y$ that $$ \begin{aligned} \angle(I U, U B)=\angle(I X, B X)=\angle\left(M^{\prime} X, B X\right)= & \frac{\pi-\angle A}{2} \\ & =\angle(E F, A F)=\angle(Y F, B F)=\angle(Y U, B U) \end{aligned} $$ so the points $Y, U$, and $I$ are collinear. Let $E F$ meet $B C$ at $W$. We have $$ \angle(I Y, Y W)=\angle(U Y, F Y)=\angle(U B, F B)=\angle(R F, A F)=\angle(C I, C W) $$ so the points $W, Y, I$, and $C$ are concyclic. Similarly, if $V$ and $Z$ are the second meeting points of $\Omega_{C}$ with $A R$ and $E F$, we get that the 4-tuples $(C, V, I, X)$ and $(B, I, Z, W)$ are both concyclic. Step 3. Let $Q^{\prime}=C Y \cap B Z$. We will show that $Q^{\prime}=Q$. First of all, we have $$ \begin{aligned} & \angle\left(Q^{\prime} Y, Q^{\prime} B\right)=\angle(C Y, Z B)=\angle(C Y, Z Y)+\angle(Z Y, B Z) \\ & =\angle(C I, I W)+\angle(I W, I B)=\angle(C I, I B)=\frac{\pi-\angle A}{2}=\angle(F Y, F B), \end{aligned} $$ so $Q^{\prime} \in \Omega_{B}$. Similarly, $Q^{\prime} \in \Omega_{C}$. Thus $Q^{\prime} \in \Omega_{B} \cap \Omega_{C}=\{P, Q\}$ and it remains to prove that $Q^{\prime} \neq P$. If we had $Q^{\prime}=P$, we would have $\angle(P Y, P Z)=\angle\left(Q^{\prime} Y, Q^{\prime} Z\right)=\angle(I C, I B)$. This would imply $$ \angle(P Y, Y F)+\angle(E Z, Z P)=\angle(P Y, P Z)=\angle(I C, I B)=\angle(P E, P F), $$ so circles $\Omega_{B}$ and $\Omega_{C}$ would be tangent at $P$. That is excluded in the problem conditions, so $Q^{\prime}=Q$. 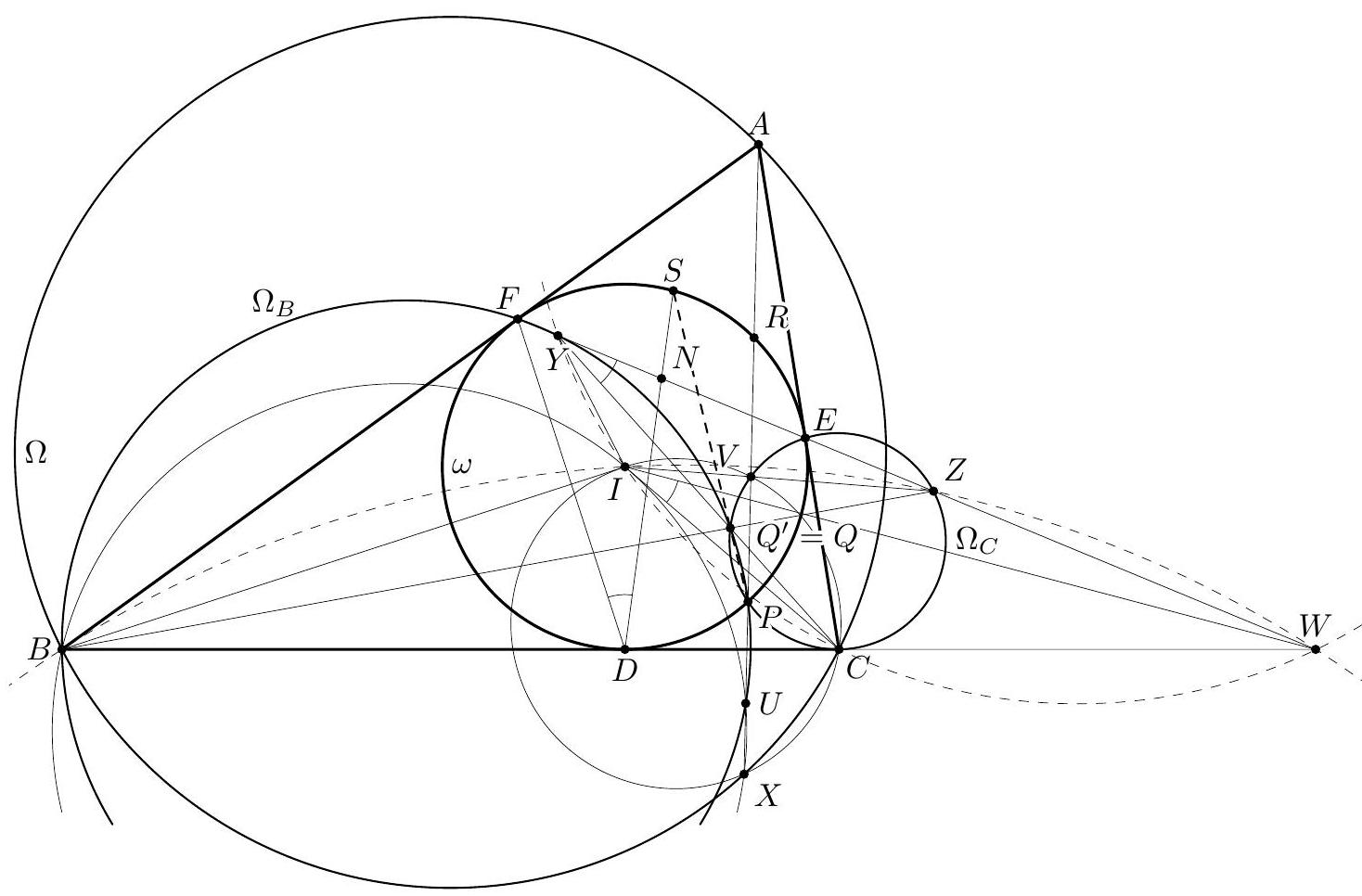 Step 4. Now we are ready to show that $P, Q$, and $S$ are collinear. Notice that $A$ and $D$ are the poles of $E W$ and $D W$ with respect to $\omega$, so $W$ is the pole of $A D$. Hence, $W I \perp A D$. Since $C I \perp D E$, this yields $\angle(I C, W I)=\angle(D E, D A)$. On the other hand, $D A$ is a symmedian in $\triangle D E F$, so $\angle(D E, D A)=\angle(D N, D F)=\angle(D S, D F)$. Therefore, $$ \begin{aligned} \angle(P S, P F)=\angle(D S, D F)=\angle(D E, D A)= & \angle(I C, I W) \\ & =\angle(Y C, Y W)=\angle(Y Q, Y F)=\angle(P Q, P F), \end{aligned} $$ which yields the desired collinearity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India)
|
We start as in Step 1. Let $A R$ meet the circumcircle $\Omega$ of $A B C$ again at $X$. The lines $A R$ and $A K$ are isogonal in the angle $B A C$; it is well known that in this case $X$ is the tangency point of $\Omega$ with the $A$-mixtilinear circle. It is also well known that for this point $X$, the line $X I$ crosses $\Omega$ again at the midpoint $M^{\prime}$ of arc $B A C$. Step 2. Denote the circles $B F P$ and $C E P$ by $\Omega_{B}$ and $\Omega_{C}$, respectively. Let $\Omega_{B}$ cross $A R$ and $E F$ again at $U$ and $Y$, respectively. We have $$ \angle(U B, B F)=\angle(U P, P F)=\angle(R P, P F)=\angle(R F, F A) $$ so $U B \| R F$.  Next, we show that the points $B, I, U$, and $X$ are concyclic. Since $$ \angle(U B, U X)=\angle(R F, R X)=\angle(A F, A R)+\angle(F R, F A)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F) $$ it suffices to prove $\angle(I B, I X)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F)$, or $\angle\left(I B, M^{\prime} B\right)=\angle(D R, D F)$. But both angles equal $\angle(C I, C B)$, as desired. (This is where we used the fact that $M^{\prime}$ is the midpoint of $\operatorname{arc} B A C$ of $\Omega$.) It follows now from circles $B U I X$ and $B P U F Y$ that $$ \begin{aligned} \angle(I U, U B)=\angle(I X, B X)=\angle\left(M^{\prime} X, B X\right)= & \frac{\pi-\angle A}{2} \\ & =\angle(E F, A F)=\angle(Y F, B F)=\angle(Y U, B U) \end{aligned} $$ so the points $Y, U$, and $I$ are collinear. Let $E F$ meet $B C$ at $W$. We have $$ \angle(I Y, Y W)=\angle(U Y, F Y)=\angle(U B, F B)=\angle(R F, A F)=\angle(C I, C W) $$ so the points $W, Y, I$, and $C$ are concyclic. Similarly, if $V$ and $Z$ are the second meeting points of $\Omega_{C}$ with $A R$ and $E F$, we get that the 4-tuples $(C, V, I, X)$ and $(B, I, Z, W)$ are both concyclic. Step 3. Let $Q^{\prime}=C Y \cap B Z$. We will show that $Q^{\prime}=Q$. First of all, we have $$ \begin{aligned} & \angle\left(Q^{\prime} Y, Q^{\prime} B\right)=\angle(C Y, Z B)=\angle(C Y, Z Y)+\angle(Z Y, B Z) \\ & =\angle(C I, I W)+\angle(I W, I B)=\angle(C I, I B)=\frac{\pi-\angle A}{2}=\angle(F Y, F B), \end{aligned} $$ so $Q^{\prime} \in \Omega_{B}$. Similarly, $Q^{\prime} \in \Omega_{C}$. Thus $Q^{\prime} \in \Omega_{B} \cap \Omega_{C}=\{P, Q\}$ and it remains to prove that $Q^{\prime} \neq P$. If we had $Q^{\prime}=P$, we would have $\angle(P Y, P Z)=\angle\left(Q^{\prime} Y, Q^{\prime} Z\right)=\angle(I C, I B)$. This would imply $$ \angle(P Y, Y F)+\angle(E Z, Z P)=\angle(P Y, P Z)=\angle(I C, I B)=\angle(P E, P F), $$ so circles $\Omega_{B}$ and $\Omega_{C}$ would be tangent at $P$. That is excluded in the problem conditions, so $Q^{\prime}=Q$.  Step 4. Now we are ready to show that $P, Q$, and $S$ are collinear. Notice that $A$ and $D$ are the poles of $E W$ and $D W$ with respect to $\omega$, so $W$ is the pole of $A D$. Hence, $W I \perp A D$. Since $C I \perp D E$, this yields $\angle(I C, W I)=\angle(D E, D A)$. On the other hand, $D A$ is a symmedian in $\triangle D E F$, so $\angle(D E, D A)=\angle(D N, D F)=\angle(D S, D F)$. Therefore, $$ \begin{aligned} \angle(P S, P F)=\angle(D S, D F)=\angle(D E, D A)= & \angle(I C, I W) \\ & =\angle(Y C, Y W)=\angle(Y Q, Y F)=\angle(P Q, P F), \end{aligned} $$ which yields the desired collinearity.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
03a06caa-a588-5f2a-8d68-aeb027b308f6
| 23,775
|
Let $\mathcal{L}$ be the set of all lines in the plane and let $f$ be a function that assigns to each line $\ell \in \mathcal{L}$ a point $f(\ell)$ on $\ell$. Suppose that for any point $X$, and for any three lines $\ell_{1}, \ell_{2}, \ell_{3}$ passing through $X$, the points $f\left(\ell_{1}\right), f\left(\ell_{2}\right), f\left(\ell_{3}\right)$ and $X$ lie on a circle. Prove that there is a unique point $P$ such that $f(\ell)=P$ for any line $\ell$ passing through $P$. (Australia)
|
Note that for any distinct points $X, Y$, the circles $g(X)$ and $g(Y)$ meet on $X Y$ at the point $f(X Y) \in g(X) \cap g(Y) \cap(X Y)$. We write $s(X, Y)$ for the second intersection point of circles $g(X)$ and $g(Y)$. Lemma 1. Suppose that $X, Y$ and $Z$ are not collinear, and that $f(X Y) \notin\{X, Y\}$ and similarly for $Y Z$ and $Z X$. Then $s(X, Y)=s(Y, Z)=s(Z, X)$. Proof. The circles $g(X), g(Y)$ and $g(Z)$ through the vertices of triangle $X Y Z$ meet pairwise on the corresponding edges (produced). By Miquel's theorem, the second points of intersection of any two of the circles coincide. (See the diagram for Lemma 5 of Solution 1.) Now pick any line $\ell$ and any six different points $Y_{1}, \ldots, Y_{6}$ on $\ell \backslash\{f(\ell)\}$. Pick a point $X$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$. Reordering the indices if necessary, we may suppose that $Y_{1}, \ldots, Y_{4}$ do not lie on $g(X)$, so that $f\left(X Y_{i}\right) \notin\left\{X, Y_{i}\right\}$ for $1 \leqslant i \leqslant 4$. By applying the above lemma to triangles $X Y_{i} Y_{j}$ for $1 \leqslant i<j \leqslant 4$, we find that the points $s\left(Y_{i}, Y_{j}\right)$ and $s\left(X, Y_{i}\right)$ are all equal, to point $O$ say. Note that either $O$ does not lie on $\ell$, or $O=f(\ell)$, since $O \in g\left(Y_{i}\right)$. Now consider an arbitrary point $X^{\prime}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. As above, we see that there are two indices $1 \leqslant i<j \leqslant 4$ such that $Y_{i}$ and $Y_{j}$ do not lie on $g\left(X^{\prime}\right)$. By applying the above lemma to triangle $X^{\prime} Y_{i} Y_{j}$ we see that $s\left(X^{\prime}, Y_{i}\right)=O$, and in particular $g\left(X^{\prime}\right)$ passes through $O$. We will now show that $f\left(\ell^{\prime}\right)=O$ for all lines $\ell^{\prime}$ through $O$. By the above note, we may assume that $\ell^{\prime} \neq \ell$. Consider a variable point $X^{\prime} \in \ell^{\prime} \backslash\{O\}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. We know that $f\left(\ell^{\prime}\right) \in g\left(X^{\prime}\right) \cap \ell^{\prime}=\left\{X^{\prime}, O\right\}$. Since $X^{\prime}$ was suitably arbitrary, we have $f\left(\ell^{\prime}\right)=O$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\mathcal{L}$ be the set of all lines in the plane and let $f$ be a function that assigns to each line $\ell \in \mathcal{L}$ a point $f(\ell)$ on $\ell$. Suppose that for any point $X$, and for any three lines $\ell_{1}, \ell_{2}, \ell_{3}$ passing through $X$, the points $f\left(\ell_{1}\right), f\left(\ell_{2}\right), f\left(\ell_{3}\right)$ and $X$ lie on a circle. Prove that there is a unique point $P$ such that $f(\ell)=P$ for any line $\ell$ passing through $P$. (Australia)
|
Note that for any distinct points $X, Y$, the circles $g(X)$ and $g(Y)$ meet on $X Y$ at the point $f(X Y) \in g(X) \cap g(Y) \cap(X Y)$. We write $s(X, Y)$ for the second intersection point of circles $g(X)$ and $g(Y)$. Lemma 1. Suppose that $X, Y$ and $Z$ are not collinear, and that $f(X Y) \notin\{X, Y\}$ and similarly for $Y Z$ and $Z X$. Then $s(X, Y)=s(Y, Z)=s(Z, X)$. Proof. The circles $g(X), g(Y)$ and $g(Z)$ through the vertices of triangle $X Y Z$ meet pairwise on the corresponding edges (produced). By Miquel's theorem, the second points of intersection of any two of the circles coincide. (See the diagram for Lemma 5 of Solution 1.) Now pick any line $\ell$ and any six different points $Y_{1}, \ldots, Y_{6}$ on $\ell \backslash\{f(\ell)\}$. Pick a point $X$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$. Reordering the indices if necessary, we may suppose that $Y_{1}, \ldots, Y_{4}$ do not lie on $g(X)$, so that $f\left(X Y_{i}\right) \notin\left\{X, Y_{i}\right\}$ for $1 \leqslant i \leqslant 4$. By applying the above lemma to triangles $X Y_{i} Y_{j}$ for $1 \leqslant i<j \leqslant 4$, we find that the points $s\left(Y_{i}, Y_{j}\right)$ and $s\left(X, Y_{i}\right)$ are all equal, to point $O$ say. Note that either $O$ does not lie on $\ell$, or $O=f(\ell)$, since $O \in g\left(Y_{i}\right)$. Now consider an arbitrary point $X^{\prime}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. As above, we see that there are two indices $1 \leqslant i<j \leqslant 4$ such that $Y_{i}$ and $Y_{j}$ do not lie on $g\left(X^{\prime}\right)$. By applying the above lemma to triangle $X^{\prime} Y_{i} Y_{j}$ we see that $s\left(X^{\prime}, Y_{i}\right)=O$, and in particular $g\left(X^{\prime}\right)$ passes through $O$. We will now show that $f\left(\ell^{\prime}\right)=O$ for all lines $\ell^{\prime}$ through $O$. By the above note, we may assume that $\ell^{\prime} \neq \ell$. Consider a variable point $X^{\prime} \in \ell^{\prime} \backslash\{O\}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. We know that $f\left(\ell^{\prime}\right) \in g\left(X^{\prime}\right) \cap \ell^{\prime}=\left\{X^{\prime}, O\right\}$. Since $X^{\prime}$ was suitably arbitrary, we have $f\left(\ell^{\prime}\right)=O$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5bb95614-4c11-5bd2-9893-d06bc3c94e0e
| 23,779
|
Let $a$ be a positive integer. We say that a positive integer $b$ is $a$-good if $\binom{a n}{b}-1$ is divisible by $a n+1$ for all positive integers $n$ with $a n \geqslant b$. Suppose $b$ is a positive integer such that $b$ is $a$-good, but $b+2$ is not $a$-good. Prove that $b+1$ is prime. (Netherlands)
|
For $p$ a prime and $n$ a nonzero integer, we write $v_{p}(n)$ for the $p$-adic valuation of $n$ : the largest integer $t$ such that $p^{t} \mid n$. We first show that $b$ is $a$-good if and only if $b$ is even, and $p \mid a$ for all primes $p \leqslant b$. To start with, the condition that $a n+1 \left\lvert\,\binom{ a n}{b}-1\right.$ can be rewritten as saying that $$ \frac{a n(a n-1) \cdots(a n-b+1)}{b!} \equiv 1 \quad(\bmod a n+1) $$ Suppose, on the one hand, there is a prime $p \leqslant b$ with $p \nmid a$. Take $t=v_{p}(b!)$. Then there exist positive integers $c$ such that $a c \equiv 1\left(\bmod p^{t+1}\right)$. If we take $c$ big enough, and then take $n=(p-1) c$, then $a n=a(p-1) c \equiv p-1\left(\bmod p^{t+1}\right)$ and $a n \geqslant b$. Since $p \leqslant b$, one of the terms of the numerator an $(a n-1) \cdots(a n-b+1)$ is $a n-p+1$, which is divisible by $p^{t+1}$. Hence the $p$-adic valuation of the numerator is at least $t+1$, but that of the denominator is exactly $t$. This means that $p \left\lvert\,\binom{ a n}{b}\right.$, so $p \nmid\binom{a n}{b}-1$. As $p \mid a n+1$, we get that $a n+1 \nmid\binom{a n}{b}$, so $b$ is not $a$-good. On the other hand, if for all primes $p \leqslant b$ we have $p \mid a$, then every factor of $b$ ! is coprime to $a n+1$, and hence invertible modulo $a n+1$ : hence $b$ ! is also invertible modulo $a n+1$. Then equation (1) reduces to: $$ a n(a n-1) \cdots(a n-b+1) \equiv b!\quad(\bmod a n+1) $$ However, we can rewrite the left-hand side as follows: $$ a n(a n-1) \cdots(a n-b+1) \equiv(-1)(-2) \cdots(-b) \equiv(-1)^{b} b!\quad(\bmod a n+1) $$ Provided that $a n>1$, if $b$ is even we deduce $(-1)^{b} b!\equiv b$ ! as needed. On the other hand, if $b$ is odd, and we take $a n+1>2(b!)$, then we will not have $(-1)^{b} b!\equiv b$ !, so $b$ is not $a$-good. This completes the claim. To conclude from here, suppose that $b$ is $a$-good, but $b+2$ is not. Then $b$ is even, and $p \mid a$ for all primes $p \leqslant b$, but there is a prime $q \leqslant b+2$ for which $q \nmid a$ : so $q=b+1$ or $q=b+2$. We cannot have $q=b+2$, as that is even too, so we have $q=b+1$ : in other words, $b+1$ is prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ be a positive integer. We say that a positive integer $b$ is $a$-good if $\binom{a n}{b}-1$ is divisible by $a n+1$ for all positive integers $n$ with $a n \geqslant b$. Suppose $b$ is a positive integer such that $b$ is $a$-good, but $b+2$ is not $a$-good. Prove that $b+1$ is prime. (Netherlands)
|
For $p$ a prime and $n$ a nonzero integer, we write $v_{p}(n)$ for the $p$-adic valuation of $n$ : the largest integer $t$ such that $p^{t} \mid n$. We first show that $b$ is $a$-good if and only if $b$ is even, and $p \mid a$ for all primes $p \leqslant b$. To start with, the condition that $a n+1 \left\lvert\,\binom{ a n}{b}-1\right.$ can be rewritten as saying that $$ \frac{a n(a n-1) \cdots(a n-b+1)}{b!} \equiv 1 \quad(\bmod a n+1) $$ Suppose, on the one hand, there is a prime $p \leqslant b$ with $p \nmid a$. Take $t=v_{p}(b!)$. Then there exist positive integers $c$ such that $a c \equiv 1\left(\bmod p^{t+1}\right)$. If we take $c$ big enough, and then take $n=(p-1) c$, then $a n=a(p-1) c \equiv p-1\left(\bmod p^{t+1}\right)$ and $a n \geqslant b$. Since $p \leqslant b$, one of the terms of the numerator an $(a n-1) \cdots(a n-b+1)$ is $a n-p+1$, which is divisible by $p^{t+1}$. Hence the $p$-adic valuation of the numerator is at least $t+1$, but that of the denominator is exactly $t$. This means that $p \left\lvert\,\binom{ a n}{b}\right.$, so $p \nmid\binom{a n}{b}-1$. As $p \mid a n+1$, we get that $a n+1 \nmid\binom{a n}{b}$, so $b$ is not $a$-good. On the other hand, if for all primes $p \leqslant b$ we have $p \mid a$, then every factor of $b$ ! is coprime to $a n+1$, and hence invertible modulo $a n+1$ : hence $b$ ! is also invertible modulo $a n+1$. Then equation (1) reduces to: $$ a n(a n-1) \cdots(a n-b+1) \equiv b!\quad(\bmod a n+1) $$ However, we can rewrite the left-hand side as follows: $$ a n(a n-1) \cdots(a n-b+1) \equiv(-1)(-2) \cdots(-b) \equiv(-1)^{b} b!\quad(\bmod a n+1) $$ Provided that $a n>1$, if $b$ is even we deduce $(-1)^{b} b!\equiv b$ ! as needed. On the other hand, if $b$ is odd, and we take $a n+1>2(b!)$, then we will not have $(-1)^{b} b!\equiv b$ !, so $b$ is not $a$-good. This completes the claim. To conclude from here, suppose that $b$ is $a$-good, but $b+2$ is not. Then $b$ is even, and $p \mid a$ for all primes $p \leqslant b$, but there is a prime $q \leqslant b+2$ for which $q \nmid a$ : so $q=b+1$ or $q=b+2$. We cannot have $q=b+2$, as that is even too, so we have $q=b+1$ : in other words, $b+1$ is prime.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
644d3973-999a-50bd-8b39-4ca80095b4e5
| 23,805
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil)
|
First, observe that if $n$ is a positive integer, then $n \in H$ exactly when $$ \left\{\frac{n}{\sqrt{2}}\right\}>1-\frac{1}{\sqrt{2}} . $$ To see why, observe that $n \in H$ if and only if $0<i \sqrt{2}-n<1$ for some $i \in \mathbb{Z}_{>0}$. In other words, $0<i-n / \sqrt{2}<1 / \sqrt{2}$, which is equivalent to (1). Now, write $A=\left\{a_{1}<a_{2}<\cdots<a_{k}\right\}$, where $k=|A|$. Observe that the set of differences is not altered by shifting $A$, so we may assume that $A \subseteq\{0,1, \ldots, n-1\}$ with $a_{1}=0$. From (1), we learn that $\left\{a_{i} / \sqrt{2}\right\}<1-1 / \sqrt{2}$ for each $i>1$ since $a_{i}-a_{1} \notin H$. Furthermore, we must have $\left\{a_{i} / \sqrt{2}\right\}<\left\{a_{j} / \sqrt{2}\right\}$ whenever $i<j$; otherwise, we would have $$ -\left(1-\frac{1}{\sqrt{2}}\right)<\left\{\frac{a_{j}}{\sqrt{2}}\right\}-\left\{\frac{a_{i}}{\sqrt{2}}\right\}<0 . $$ Since $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}=\left\{a_{j} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}+1$, this implies that $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}>1 / \sqrt{2}>$ $1-1 / \sqrt{2}$, contradicting (1). Now, we have a sequence $0=a_{1}<a_{2}<\cdots<a_{k}<n$, with $$ 0=\left\{\frac{a_{1}}{\sqrt{2}}\right\}<\left\{\frac{a_{2}}{\sqrt{2}}\right\}<\cdots<\left\{\frac{a_{k}}{\sqrt{2}}\right\}<1-\frac{1}{\sqrt{2}} . $$ We use the following fact: for any $d \in \mathbb{Z}$, we have $$ \left\{\frac{d}{\sqrt{2}}\right\}>\frac{1}{2 d \sqrt{2}} $$ To see why this is the case, let $h=\lfloor d / \sqrt{2}\rfloor$, so $\{d / \sqrt{2}\}=d / \sqrt{2}-h$. Then $$ \left\{\frac{d}{\sqrt{2}}\right\}\left(\frac{d}{\sqrt{2}}+h\right)=\frac{d^{2}-2 h^{2}}{2} \geqslant \frac{1}{2} $$ since the numerator is a positive integer. Because $d / \sqrt{2}+h<2 d / \sqrt{2}$, inequality (2) follows. Let $d_{i}=a_{i+1}-a_{i}$, for $1 \leqslant i<k$. Then $\left\{a_{i+1} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}=\left\{d_{i} / \sqrt{2}\right\}$, and we have $$ 1-\frac{1}{\sqrt{2}}>\sum_{i}\left\{\frac{d_{i}}{\sqrt{2}}\right\}>\frac{1}{2 \sqrt{2}} \sum_{i} \frac{1}{d_{i}} \geqslant \frac{(k-1)^{2}}{2 \sqrt{2}} \frac{1}{\sum_{i} d_{i}}>\frac{(k-1)^{2}}{2 \sqrt{2}} \cdot \frac{1}{n} . $$ Here, the first inequality holds because $\left\{a_{k} / \sqrt{2}\right\}<1-1 / \sqrt{2}$, the second follows from (2), the third follows from an easy application of the AM-HM inequality (or Cauchy-Schwarz), and the fourth follows from the fact that $\sum_{i} d_{i}=a_{k}<n$. Rearranging this, we obtain $$ \sqrt{2 \sqrt{2}-2} \cdot \sqrt{n}>k-1 $$ which provides the required bound on $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil)
|
First, observe that if $n$ is a positive integer, then $n \in H$ exactly when $$ \left\{\frac{n}{\sqrt{2}}\right\}>1-\frac{1}{\sqrt{2}} . $$ To see why, observe that $n \in H$ if and only if $0<i \sqrt{2}-n<1$ for some $i \in \mathbb{Z}_{>0}$. In other words, $0<i-n / \sqrt{2}<1 / \sqrt{2}$, which is equivalent to (1). Now, write $A=\left\{a_{1}<a_{2}<\cdots<a_{k}\right\}$, where $k=|A|$. Observe that the set of differences is not altered by shifting $A$, so we may assume that $A \subseteq\{0,1, \ldots, n-1\}$ with $a_{1}=0$. From (1), we learn that $\left\{a_{i} / \sqrt{2}\right\}<1-1 / \sqrt{2}$ for each $i>1$ since $a_{i}-a_{1} \notin H$. Furthermore, we must have $\left\{a_{i} / \sqrt{2}\right\}<\left\{a_{j} / \sqrt{2}\right\}$ whenever $i<j$; otherwise, we would have $$ -\left(1-\frac{1}{\sqrt{2}}\right)<\left\{\frac{a_{j}}{\sqrt{2}}\right\}-\left\{\frac{a_{i}}{\sqrt{2}}\right\}<0 . $$ Since $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}=\left\{a_{j} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}+1$, this implies that $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}>1 / \sqrt{2}>$ $1-1 / \sqrt{2}$, contradicting (1). Now, we have a sequence $0=a_{1}<a_{2}<\cdots<a_{k}<n$, with $$ 0=\left\{\frac{a_{1}}{\sqrt{2}}\right\}<\left\{\frac{a_{2}}{\sqrt{2}}\right\}<\cdots<\left\{\frac{a_{k}}{\sqrt{2}}\right\}<1-\frac{1}{\sqrt{2}} . $$ We use the following fact: for any $d \in \mathbb{Z}$, we have $$ \left\{\frac{d}{\sqrt{2}}\right\}>\frac{1}{2 d \sqrt{2}} $$ To see why this is the case, let $h=\lfloor d / \sqrt{2}\rfloor$, so $\{d / \sqrt{2}\}=d / \sqrt{2}-h$. Then $$ \left\{\frac{d}{\sqrt{2}}\right\}\left(\frac{d}{\sqrt{2}}+h\right)=\frac{d^{2}-2 h^{2}}{2} \geqslant \frac{1}{2} $$ since the numerator is a positive integer. Because $d / \sqrt{2}+h<2 d / \sqrt{2}$, inequality (2) follows. Let $d_{i}=a_{i+1}-a_{i}$, for $1 \leqslant i<k$. Then $\left\{a_{i+1} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}=\left\{d_{i} / \sqrt{2}\right\}$, and we have $$ 1-\frac{1}{\sqrt{2}}>\sum_{i}\left\{\frac{d_{i}}{\sqrt{2}}\right\}>\frac{1}{2 \sqrt{2}} \sum_{i} \frac{1}{d_{i}} \geqslant \frac{(k-1)^{2}}{2 \sqrt{2}} \frac{1}{\sum_{i} d_{i}}>\frac{(k-1)^{2}}{2 \sqrt{2}} \cdot \frac{1}{n} . $$ Here, the first inequality holds because $\left\{a_{k} / \sqrt{2}\right\}<1-1 / \sqrt{2}$, the second follows from (2), the third follows from an easy application of the AM-HM inequality (or Cauchy-Schwarz), and the fourth follows from the fact that $\sum_{i} d_{i}=a_{k}<n$. Rearranging this, we obtain $$ \sqrt{2 \sqrt{2}-2} \cdot \sqrt{n}>k-1 $$ which provides the required bound on $k$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
18fd500f-8063-5ced-a70b-8fc3db10c5d3
| 23,809
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil)
|
Again, define $J=\mathbb{Z}_{>0} \backslash H$, so all differences between elements of $A$ are in $J$. We start by making the following observation. Suppose we have a set $B \subseteq\{1,2, \ldots, n\}$ such that all of the differences between elements of $B$ are in $H$. Then $|A| \cdot|B| \leqslant 2 n$. To see why, observe that any two sums of the form $a+b$ with $a \in A, b \in B$ are different; otherwise, we would have $a_{1}+b_{1}=a_{2}+b_{2}$, and so $\left|a_{1}-a_{2}\right|=\left|b_{2}-b_{1}\right|$. However, then the left hand side is in $J$ whereas the right hand side is in $H$. Thus, $\{a+b: a \in A, b \in B\}$ is a set of size $|A| \cdot|B|$ all of whose elements are no greater than $2 n$, yielding the claimed inequality. With this in mind, it suffices to construct a set $B$, all of whose differences are in $H$ and whose size is at least $C^{\prime} \sqrt{n}$ for some constant $C^{\prime}>0$. To do so, we will use well-known facts about the negative Pell equation $X^{2}-2 Y^{2}=-1$; in particular, that there are infinitely many solutions and the values of $X$ are given by the recurrence $X_{1}=1, X_{2}=7$ and $X_{m}=6 X_{m-1}-X_{m-2}$. Therefore, we may choose $X$ to be a solution with $\sqrt{n} / 6<X \leqslant \sqrt{n}$. Now, we claim that we may choose $B=\{X, 2 X, \ldots,\lfloor(1 / 3) \sqrt{n}\rfloor X\}$. Indeed, we have $$ \left(\frac{X}{\sqrt{2}}-Y\right)\left(\frac{X}{\sqrt{2}}+Y\right)=\frac{-1}{2} $$ and so $$ 0>\left(\frac{X}{\sqrt{2}}-Y\right) \geqslant \frac{-3}{\sqrt{2 n}}, $$ from which it follows that $\{X / \sqrt{2}\}>1-(3 / \sqrt{2 n})$. Combined with (1), this shows that all differences between elements of $B$ are in $H$. Comment. Some of the ideas behind Solution 3 may be used to prove that the constant $C=\sqrt{2 \sqrt{2}-2}$ (from Solutions 1 and 2) is optimal, in the sense that there are arbitrarily large values of $n$ and sets $A_{n} \subseteq\{1,2, \ldots, n\}$ of size roughly $C \sqrt{n}$, all of whose differences are contained in $J$. To see why, choose $X$ to come from a sufficiently large solution to the Pell equation $X^{2}-2 Y^{2}=1$, so $\{X / \sqrt{2}\} \approx 1 /(2 X \sqrt{2})$. In particular, $\{X\},\{2 X\}, \ldots,\{[2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor X\}$ are all less than $1-1 / \sqrt{2}$. Thus, by (1) any positive integer of the form $i X$ for $1 \leqslant i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor$ lies in $J$. Set $n \approx 2 X^{2} \sqrt{2}(1-1 / \sqrt{2})$. We now have a set $A=\{i X: i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor\}$ containing roughly $2 X \sqrt{2}(1-1 / \sqrt{2})$ elements less than or equal to $n$ such that all of the differences lie in $J$, and we can see that $|A| \approx C \sqrt{n}$ with $C=\sqrt{2 \sqrt{2}-2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil)
|
Again, define $J=\mathbb{Z}_{>0} \backslash H$, so all differences between elements of $A$ are in $J$. We start by making the following observation. Suppose we have a set $B \subseteq\{1,2, \ldots, n\}$ such that all of the differences between elements of $B$ are in $H$. Then $|A| \cdot|B| \leqslant 2 n$. To see why, observe that any two sums of the form $a+b$ with $a \in A, b \in B$ are different; otherwise, we would have $a_{1}+b_{1}=a_{2}+b_{2}$, and so $\left|a_{1}-a_{2}\right|=\left|b_{2}-b_{1}\right|$. However, then the left hand side is in $J$ whereas the right hand side is in $H$. Thus, $\{a+b: a \in A, b \in B\}$ is a set of size $|A| \cdot|B|$ all of whose elements are no greater than $2 n$, yielding the claimed inequality. With this in mind, it suffices to construct a set $B$, all of whose differences are in $H$ and whose size is at least $C^{\prime} \sqrt{n}$ for some constant $C^{\prime}>0$. To do so, we will use well-known facts about the negative Pell equation $X^{2}-2 Y^{2}=-1$; in particular, that there are infinitely many solutions and the values of $X$ are given by the recurrence $X_{1}=1, X_{2}=7$ and $X_{m}=6 X_{m-1}-X_{m-2}$. Therefore, we may choose $X$ to be a solution with $\sqrt{n} / 6<X \leqslant \sqrt{n}$. Now, we claim that we may choose $B=\{X, 2 X, \ldots,\lfloor(1 / 3) \sqrt{n}\rfloor X\}$. Indeed, we have $$ \left(\frac{X}{\sqrt{2}}-Y\right)\left(\frac{X}{\sqrt{2}}+Y\right)=\frac{-1}{2} $$ and so $$ 0>\left(\frac{X}{\sqrt{2}}-Y\right) \geqslant \frac{-3}{\sqrt{2 n}}, $$ from which it follows that $\{X / \sqrt{2}\}>1-(3 / \sqrt{2 n})$. Combined with (1), this shows that all differences between elements of $B$ are in $H$. Comment. Some of the ideas behind Solution 3 may be used to prove that the constant $C=\sqrt{2 \sqrt{2}-2}$ (from Solutions 1 and 2) is optimal, in the sense that there are arbitrarily large values of $n$ and sets $A_{n} \subseteq\{1,2, \ldots, n\}$ of size roughly $C \sqrt{n}$, all of whose differences are contained in $J$. To see why, choose $X$ to come from a sufficiently large solution to the Pell equation $X^{2}-2 Y^{2}=1$, so $\{X / \sqrt{2}\} \approx 1 /(2 X \sqrt{2})$. In particular, $\{X\},\{2 X\}, \ldots,\{[2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor X\}$ are all less than $1-1 / \sqrt{2}$. Thus, by (1) any positive integer of the form $i X$ for $1 \leqslant i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor$ lies in $J$. Set $n \approx 2 X^{2} \sqrt{2}(1-1 / \sqrt{2})$. We now have a set $A=\{i X: i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor\}$ containing roughly $2 X \sqrt{2}(1-1 / \sqrt{2})$ elements less than or equal to $n$ such that all of the differences lie in $J$, and we can see that $|A| \approx C \sqrt{n}$ with $C=\sqrt{2 \sqrt{2}-2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
18fd500f-8063-5ced-a70b-8fc3db10c5d3
| 23,809
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil)
|
As in Choose $Y$ to be a solution to the Pell-like equation $X^{2}-2 Y^{2}= \pm 1$; such solutions are given by the recurrence $Y_{1}=1, Y_{2}=2$ and $Y_{m}=2 Y_{m-1}+Y_{m-2}$, and so we can choose $Y$ such that $n /(3 \sqrt{2})<Y \leqslant n / \sqrt{2}$. Furthermore, it is known that for such a $Y$ and for $1 \leqslant x<Y$, $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=1$, and $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=1+\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=-1$. Indeed, this is a statement of the fact that $X / Y$ is a best rational approximation to $\sqrt{2}$, from below in the first case and from above in the second. Now, consider the sequence $\{\sqrt{2}\},\{2 \sqrt{2}\}, \ldots,\{(Y-1) \sqrt{2}\}$. The Erdős-Szekeres theorem tells us that this sequence has a monotone subsequence with at least $\sqrt{Y-2}+1>\sqrt{Y}$ elements; if that subsequence is decreasing, we may reflect (using (4) or (5)) to ensure that it is increasing. Call the subsequence $\left\{y_{1} \sqrt{2}\right\},\left\{y_{2} \sqrt{2}\right\}, \ldots,\left\{y_{t} \sqrt{2}\right\}$ for $t>\sqrt{Y}$. Now, set $B=\left\{\left\lfloor y_{i} \sqrt{2}\right\rfloor: 1 \leqslant i \leqslant t\right\}$. We have $\left\lfloor y_{j} \sqrt{2}\right\rfloor-\left\lfloor y_{i} \sqrt{2}\right\rfloor=\left\lfloor\left(y_{j}-y_{i}\right) \sqrt{2}\right\rfloor$ for $i<j$ (because the corresponding inequality for the fractional parts holds by the ordering assumption on the $\left\{y_{i} \sqrt{2}\right\}$ ), which means that all differences between elements of $B$ are indeed in $H$. Since $|B|>\sqrt{Y}>\sqrt{n} / \sqrt{3 \sqrt{2}}$, this is the required set. Comment. Any solution to this problem will need to use the fact that $\sqrt{2}$ cannot be approximated well by rationals, either directly or implicitly (for example, by using facts about solutions to Pelllike equations). If $\sqrt{2}$ were replaced by a value of $\theta$ with very good rational approximations (from below), then an argument along the lines of Solution 3 would give long arithmetic progressions in $\{\lfloor i \theta\rfloor: 0 \leqslant i<n\}$ (with initial term 0 ) for certain values of $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil)
|
As in Choose $Y$ to be a solution to the Pell-like equation $X^{2}-2 Y^{2}= \pm 1$; such solutions are given by the recurrence $Y_{1}=1, Y_{2}=2$ and $Y_{m}=2 Y_{m-1}+Y_{m-2}$, and so we can choose $Y$ such that $n /(3 \sqrt{2})<Y \leqslant n / \sqrt{2}$. Furthermore, it is known that for such a $Y$ and for $1 \leqslant x<Y$, $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=1$, and $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=1+\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=-1$. Indeed, this is a statement of the fact that $X / Y$ is a best rational approximation to $\sqrt{2}$, from below in the first case and from above in the second. Now, consider the sequence $\{\sqrt{2}\},\{2 \sqrt{2}\}, \ldots,\{(Y-1) \sqrt{2}\}$. The Erdős-Szekeres theorem tells us that this sequence has a monotone subsequence with at least $\sqrt{Y-2}+1>\sqrt{Y}$ elements; if that subsequence is decreasing, we may reflect (using (4) or (5)) to ensure that it is increasing. Call the subsequence $\left\{y_{1} \sqrt{2}\right\},\left\{y_{2} \sqrt{2}\right\}, \ldots,\left\{y_{t} \sqrt{2}\right\}$ for $t>\sqrt{Y}$. Now, set $B=\left\{\left\lfloor y_{i} \sqrt{2}\right\rfloor: 1 \leqslant i \leqslant t\right\}$. We have $\left\lfloor y_{j} \sqrt{2}\right\rfloor-\left\lfloor y_{i} \sqrt{2}\right\rfloor=\left\lfloor\left(y_{j}-y_{i}\right) \sqrt{2}\right\rfloor$ for $i<j$ (because the corresponding inequality for the fractional parts holds by the ordering assumption on the $\left\{y_{i} \sqrt{2}\right\}$ ), which means that all differences between elements of $B$ are indeed in $H$. Since $|B|>\sqrt{Y}>\sqrt{n} / \sqrt{3 \sqrt{2}}$, this is the required set. Comment. Any solution to this problem will need to use the fact that $\sqrt{2}$ cannot be approximated well by rationals, either directly or implicitly (for example, by using facts about solutions to Pelllike equations). If $\sqrt{2}$ were replaced by a value of $\theta$ with very good rational approximations (from below), then an argument along the lines of Solution 3 would give long arithmetic progressions in $\{\lfloor i \theta\rfloor: 0 \leqslant i<n\}$ (with initial term 0 ) for certain values of $n$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
18fd500f-8063-5ced-a70b-8fc3db10c5d3
| 23,809
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to $z$.)
|
Arguing indirectly, assume that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=(a+k)^{2}, \quad \text { or } \quad\left\lceil\frac{(2 a)^{2}}{b}\right\rceil=(2 a+k) k $$ Clearly, $k \geqslant 1$. In other words, the equation $$ \left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ has a positive integer solution $(c, k)$, with an even value of $c$. Choose a positive integer solution of (1) with minimal possible value of $k$, without regard to the parity of $c$. From $$ \frac{c^{2}}{b}>\left\lceil\frac{c^{2}}{b}\right\rceil-1=c k+k^{2}-1 \geqslant c k $$ and $$ \frac{(c-k)(c+k)}{b}<\frac{c^{2}}{b} \leqslant\left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ it can be seen that $c>b k>c-k$, so $$ c=k b+r \quad \text { with some } 0<r<k $$ By substituting this in (1) we get $$ \left\lceil\frac{c^{2}}{b}\right\rceil=\left\lceil\frac{(b k+r)^{2}}{b}\right\rceil=k^{2} b+2 k r+\left\lceil\frac{r^{2}}{b}\right\rceil $$ and $$ (c+k) k=(k b+r+k) k=k^{2} b+2 k r+k(k-r) $$ so $$ \left\lceil\frac{r^{2}}{b}\right\rceil=k(k-r) $$ Notice that relation (2) provides another positive integer solution of (1), namely $c^{\prime}=r$ and $k^{\prime}=k-r$, with $c^{\prime}>0$ and $0<k^{\prime}<k$. That contradicts the minimality of $k$, and hence finishes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to $z$.)
|
Arguing indirectly, assume that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=(a+k)^{2}, \quad \text { or } \quad\left\lceil\frac{(2 a)^{2}}{b}\right\rceil=(2 a+k) k $$ Clearly, $k \geqslant 1$. In other words, the equation $$ \left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ has a positive integer solution $(c, k)$, with an even value of $c$. Choose a positive integer solution of (1) with minimal possible value of $k$, without regard to the parity of $c$. From $$ \frac{c^{2}}{b}>\left\lceil\frac{c^{2}}{b}\right\rceil-1=c k+k^{2}-1 \geqslant c k $$ and $$ \frac{(c-k)(c+k)}{b}<\frac{c^{2}}{b} \leqslant\left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ it can be seen that $c>b k>c-k$, so $$ c=k b+r \quad \text { with some } 0<r<k $$ By substituting this in (1) we get $$ \left\lceil\frac{c^{2}}{b}\right\rceil=\left\lceil\frac{(b k+r)^{2}}{b}\right\rceil=k^{2} b+2 k r+\left\lceil\frac{r^{2}}{b}\right\rceil $$ and $$ (c+k) k=(k b+r+k) k=k^{2} b+2 k r+k(k-r) $$ so $$ \left\lceil\frac{r^{2}}{b}\right\rceil=k(k-r) $$ Notice that relation (2) provides another positive integer solution of (1), namely $c^{\prime}=r$ and $k^{\prime}=k-r$, with $c^{\prime}>0$ and $0<k^{\prime}<k$. That contradicts the minimality of $k$, and hence finishes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d376a34c-e06e-517a-bb4f-64e7614602d4
| 23,816
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to $z$.)
|
Suppose that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=c^{2} $$ with some positive integer $c>a$, so $$ \begin{aligned} & c^{2}-1<a^{2}+\frac{4 a^{2}}{b} \leqslant c^{2} \\ & 0 \leqslant c^{2} b-a^{2}(b+4)<b \end{aligned} $$ Let $d=c^{2} b-a^{2}(b+4), x=c+a$ and $y=c-a$; then we have $c=\frac{x+y}{2}$ and $a=\frac{x-y}{2}$, and (3) can be re-written as follows: $$ \begin{aligned} \left(\frac{x+y}{2}\right)^{2} b-\left(\frac{x-y}{2}\right)^{2}(b+4) & =d \\ x^{2}-(b+2) x y+y^{2}+d=0 ; \quad 0 & \leqslant d<b \end{aligned} $$ So, by the indirect assumption, the equation (4) has some positive integer solution $(x, y)$. Fix $b$ and $d$, and take a pair $(x, y)$ of positive integers, satisfying (4), such that $x+y$ is minimal. By the symmetry in (4) we may assume that $x \geqslant y \geqslant 1$. Now we perform a usual "Vieta jump". Consider (4) as a quadratic equation in variable $x$, and let $z$ be its second root. By the Vieta formulas, $$ x+z=(b+2) y, \quad \text { and } \quad z x=y^{2}+d, $$ so $$ z=(b+2) y-x=\frac{y^{2}+d}{x} $$ The first formula shows that $z$ is an integer, and by the second formula $z$ is positive. Hence $(z, y)$ is another positive integer solution of (4). From $$ \begin{aligned} (x-1)(z-1) & =x z-(x+z)+1=\left(y^{2}+d\right)-(b+2) y+1 \\ & <\left(y^{2}+b\right)-(b+2) y+1=(y-1)^{2}-b(y-1) \leqslant(y-1)^{2} \leqslant(x-1)^{2} \end{aligned} $$ we can see that $z<x$ and therefore $z+y<x+y$. But this contradicts the minimality of $x+y$ among the positive integer solutions of (4). The activities of the Problem Selection Committee were supported by Trinity College, Cambridge University of Cambridge
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to $z$.)
|
Suppose that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=c^{2} $$ with some positive integer $c>a$, so $$ \begin{aligned} & c^{2}-1<a^{2}+\frac{4 a^{2}}{b} \leqslant c^{2} \\ & 0 \leqslant c^{2} b-a^{2}(b+4)<b \end{aligned} $$ Let $d=c^{2} b-a^{2}(b+4), x=c+a$ and $y=c-a$; then we have $c=\frac{x+y}{2}$ and $a=\frac{x-y}{2}$, and (3) can be re-written as follows: $$ \begin{aligned} \left(\frac{x+y}{2}\right)^{2} b-\left(\frac{x-y}{2}\right)^{2}(b+4) & =d \\ x^{2}-(b+2) x y+y^{2}+d=0 ; \quad 0 & \leqslant d<b \end{aligned} $$ So, by the indirect assumption, the equation (4) has some positive integer solution $(x, y)$. Fix $b$ and $d$, and take a pair $(x, y)$ of positive integers, satisfying (4), such that $x+y$ is minimal. By the symmetry in (4) we may assume that $x \geqslant y \geqslant 1$. Now we perform a usual "Vieta jump". Consider (4) as a quadratic equation in variable $x$, and let $z$ be its second root. By the Vieta formulas, $$ x+z=(b+2) y, \quad \text { and } \quad z x=y^{2}+d, $$ so $$ z=(b+2) y-x=\frac{y^{2}+d}{x} $$ The first formula shows that $z$ is an integer, and by the second formula $z$ is positive. Hence $(z, y)$ is another positive integer solution of (4). From $$ \begin{aligned} (x-1)(z-1) & =x z-(x+z)+1=\left(y^{2}+d\right)-(b+2) y+1 \\ & <\left(y^{2}+b\right)-(b+2) y+1=(y-1)^{2}-b(y-1) \leqslant(y-1)^{2} \leqslant(x-1)^{2} \end{aligned} $$ we can see that $z<x$ and therefore $z+y<x+y$. But this contradicts the minimality of $x+y$ among the positive integer solutions of (4). The activities of the Problem Selection Committee were supported by Trinity College, Cambridge University of Cambridge
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d376a34c-e06e-517a-bb4f-64e7614602d4
| 23,816
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand) Common remarks. In all solutions, we say an index set $X$ is $\left(a_{i}\right)$-minimising if it has the property in the problem for the given sequence $\left(a_{i}\right)$. Write $X^{c}$ for the complement of $X$, and $[a, b]$ for the interval of integers $k$ such that $a \leqslant k \leqslant b$. Note that $$ \left|1-\sum_{i \in X} a_{i}\right|=\left|1-\sum_{i \in X^{c}} a_{i}\right|, $$ so we may exchange $X$ and $X^{c}$ where convenient. Let $$ \Delta=\sum_{i \in X^{c}} a_{i}-\sum_{i \in X} a_{i} $$ and note that $X$ is $\left(a_{i}\right)$-minimising if and only if it minimises $|\Delta|$, and that $\sum_{i \in X} a_{i}=1$ if and only if $\Delta=0$. In some solutions, a scaling process is used. If we have a strictly increasing sequence of positive real numbers $c_{i}$ (typically obtained by perturbing the $a_{i}$ in some way) such that $$ \sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i} $$ then we may put $b_{i}=2 c_{i} / \sum_{j=1}^{n} c_{j}$. So it suffices to construct such a sequence without needing its sum to be 2 . The solutions below show various possible approaches to the problem. Solutions 1 and 2 perturb a few of the $a_{i}$ to form the $b_{i}$ (with scaling in the case of Solution 1, without scaling in the case of Solution 2). Solutions 3 and 4 look at properties of the index set $X$. Solution 3 then perturbs many of the $a_{i}$ to form the $b_{i}$, together with scaling. Rather than using such perturbations, Solution 4 constructs a sequence $\left(b_{i}\right)$ directly from the set $X$ with the required properties. Solution 4 can be used to give a complete description of sets $X$ that are $\left(a_{i}\right)$-minimising for some $\left(a_{i}\right)$.
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, and we may assume strict inequality as otherwise $b_{i}=a_{i}$ works. Also, $X$ clearly cannot be empty. If $n \in X$, add $\Delta$ to $a_{n}$, producing a sequence of $c_{i}$ with $\sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i}$, and then scale as described above to make the sum equal to 2 . Otherwise, there is some $k$ with $k \in X$ and $k+1 \in X^{c}$. Let $\delta=a_{k+1}-a_{k}$. - If $\delta>\Delta$, add $\Delta$ to $a_{k}$ and then scale. - If $\delta<\Delta$, then considering $X \cup\{k+1\} \backslash\{k\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. - If $\delta=\Delta$, choose any $j \neq k, k+1$ (possible since $n \geqslant 3$ ), and any $\epsilon$ less than the least of $a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $j \in X$ then add $\Delta-\epsilon$ to $a_{k}$ and $\epsilon$ to $a_{j}$, then scale; otherwise, add $\Delta$ to $a_{k}$ and $\epsilon / 2$ to $a_{k+1}$, and subtract $\epsilon / 2$ from $a_{j}$, then scale.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand) Common remarks. In all solutions, we say an index set $X$ is $\left(a_{i}\right)$-minimising if it has the property in the problem for the given sequence $\left(a_{i}\right)$. Write $X^{c}$ for the complement of $X$, and $[a, b]$ for the interval of integers $k$ such that $a \leqslant k \leqslant b$. Note that $$ \left|1-\sum_{i \in X} a_{i}\right|=\left|1-\sum_{i \in X^{c}} a_{i}\right|, $$ so we may exchange $X$ and $X^{c}$ where convenient. Let $$ \Delta=\sum_{i \in X^{c}} a_{i}-\sum_{i \in X} a_{i} $$ and note that $X$ is $\left(a_{i}\right)$-minimising if and only if it minimises $|\Delta|$, and that $\sum_{i \in X} a_{i}=1$ if and only if $\Delta=0$. In some solutions, a scaling process is used. If we have a strictly increasing sequence of positive real numbers $c_{i}$ (typically obtained by perturbing the $a_{i}$ in some way) such that $$ \sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i} $$ then we may put $b_{i}=2 c_{i} / \sum_{j=1}^{n} c_{j}$. So it suffices to construct such a sequence without needing its sum to be 2 . The solutions below show various possible approaches to the problem. Solutions 1 and 2 perturb a few of the $a_{i}$ to form the $b_{i}$ (with scaling in the case of Solution 1, without scaling in the case of Solution 2). Solutions 3 and 4 look at properties of the index set $X$. Solution 3 then perturbs many of the $a_{i}$ to form the $b_{i}$, together with scaling. Rather than using such perturbations, Solution 4 constructs a sequence $\left(b_{i}\right)$ directly from the set $X$ with the required properties. Solution 4 can be used to give a complete description of sets $X$ that are $\left(a_{i}\right)$-minimising for some $\left(a_{i}\right)$.
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, and we may assume strict inequality as otherwise $b_{i}=a_{i}$ works. Also, $X$ clearly cannot be empty. If $n \in X$, add $\Delta$ to $a_{n}$, producing a sequence of $c_{i}$ with $\sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i}$, and then scale as described above to make the sum equal to 2 . Otherwise, there is some $k$ with $k \in X$ and $k+1 \in X^{c}$. Let $\delta=a_{k+1}-a_{k}$. - If $\delta>\Delta$, add $\Delta$ to $a_{k}$ and then scale. - If $\delta<\Delta$, then considering $X \cup\{k+1\} \backslash\{k\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. - If $\delta=\Delta$, choose any $j \neq k, k+1$ (possible since $n \geqslant 3$ ), and any $\epsilon$ less than the least of $a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $j \in X$ then add $\Delta-\epsilon$ to $a_{k}$ and $\epsilon$ to $a_{j}$, then scale; otherwise, add $\Delta$ to $a_{k}$ and $\epsilon / 2$ to $a_{k+1}$, and subtract $\epsilon / 2$ from $a_{j}$, then scale.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2c3a926-6468-5f77-a80c-96544002bd36
| 23,828
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand) Common remarks. In all solutions, we say an index set $X$ is $\left(a_{i}\right)$-minimising if it has the property in the problem for the given sequence $\left(a_{i}\right)$. Write $X^{c}$ for the complement of $X$, and $[a, b]$ for the interval of integers $k$ such that $a \leqslant k \leqslant b$. Note that $$ \left|1-\sum_{i \in X} a_{i}\right|=\left|1-\sum_{i \in X^{c}} a_{i}\right|, $$ so we may exchange $X$ and $X^{c}$ where convenient. Let $$ \Delta=\sum_{i \in X^{c}} a_{i}-\sum_{i \in X} a_{i} $$ and note that $X$ is $\left(a_{i}\right)$-minimising if and only if it minimises $|\Delta|$, and that $\sum_{i \in X} a_{i}=1$ if and only if $\Delta=0$. In some solutions, a scaling process is used. If we have a strictly increasing sequence of positive real numbers $c_{i}$ (typically obtained by perturbing the $a_{i}$ in some way) such that $$ \sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i} $$ then we may put $b_{i}=2 c_{i} / \sum_{j=1}^{n} c_{j}$. So it suffices to construct such a sequence without needing its sum to be 2 . The solutions below show various possible approaches to the problem. Solutions 1 and 2 perturb a few of the $a_{i}$ to form the $b_{i}$ (with scaling in the case of Solution 1, without scaling in the case of Solution 2). Solutions 3 and 4 look at properties of the index set $X$. Solution 3 then perturbs many of the $a_{i}$ to form the $b_{i}$, together with scaling. Rather than using such perturbations, Solution 4 constructs a sequence $\left(b_{i}\right)$ directly from the set $X$ with the required properties. Solution 4 can be used to give a complete description of sets $X$ that are $\left(a_{i}\right)$-minimising for some $\left(a_{i}\right)$.
|
This is similar to Suppose there exists $1 \leqslant j \leqslant n-1$ such that $j \in X$ but $j+1 \in X^{c}$. Then $a_{j+1}-a_{j} \geqslant \Delta$, because otherwise considering $X \cup\{j+1\} \backslash\{j\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. If $a_{j+1}-a_{j}>\Delta$, put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{i}, & \text { otherwise }\end{cases} $$ If $a_{j+1}-a_{j}=\Delta$, choose any $\epsilon$ less than the least of $\Delta / 2, a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $|X| \geqslant 2$, choose $k \in X$ with $k \neq j$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2-\epsilon, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{k}+\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ Otherwise, $\left|X^{c}\right| \geqslant 2$, so choose $k \in X^{c}$ with $k \neq j+1$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2+\epsilon, & \text { if } i=j+1 \\ a_{k}-\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ If there is no $1 \leqslant j \leqslant n$ such that $j \in X$ but $j+1 \in X^{c}$, there must be some $1<k \leqslant n$ such that $X=[k, n]$ (certainly $X$ cannot be empty). We must have $a_{1}>\Delta$, as otherwise considering $X \cup\{1\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. Now put $$ b_{i}= \begin{cases}a_{1}-\Delta / 2, & \text { if } i=1 \\ a_{n}+\Delta / 2, & \text { if } i=n \\ a_{i}, & \text { otherwise }\end{cases} $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand) Common remarks. In all solutions, we say an index set $X$ is $\left(a_{i}\right)$-minimising if it has the property in the problem for the given sequence $\left(a_{i}\right)$. Write $X^{c}$ for the complement of $X$, and $[a, b]$ for the interval of integers $k$ such that $a \leqslant k \leqslant b$. Note that $$ \left|1-\sum_{i \in X} a_{i}\right|=\left|1-\sum_{i \in X^{c}} a_{i}\right|, $$ so we may exchange $X$ and $X^{c}$ where convenient. Let $$ \Delta=\sum_{i \in X^{c}} a_{i}-\sum_{i \in X} a_{i} $$ and note that $X$ is $\left(a_{i}\right)$-minimising if and only if it minimises $|\Delta|$, and that $\sum_{i \in X} a_{i}=1$ if and only if $\Delta=0$. In some solutions, a scaling process is used. If we have a strictly increasing sequence of positive real numbers $c_{i}$ (typically obtained by perturbing the $a_{i}$ in some way) such that $$ \sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i} $$ then we may put $b_{i}=2 c_{i} / \sum_{j=1}^{n} c_{j}$. So it suffices to construct such a sequence without needing its sum to be 2 . The solutions below show various possible approaches to the problem. Solutions 1 and 2 perturb a few of the $a_{i}$ to form the $b_{i}$ (with scaling in the case of Solution 1, without scaling in the case of Solution 2). Solutions 3 and 4 look at properties of the index set $X$. Solution 3 then perturbs many of the $a_{i}$ to form the $b_{i}$, together with scaling. Rather than using such perturbations, Solution 4 constructs a sequence $\left(b_{i}\right)$ directly from the set $X$ with the required properties. Solution 4 can be used to give a complete description of sets $X$ that are $\left(a_{i}\right)$-minimising for some $\left(a_{i}\right)$.
|
This is similar to Suppose there exists $1 \leqslant j \leqslant n-1$ such that $j \in X$ but $j+1 \in X^{c}$. Then $a_{j+1}-a_{j} \geqslant \Delta$, because otherwise considering $X \cup\{j+1\} \backslash\{j\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. If $a_{j+1}-a_{j}>\Delta$, put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{i}, & \text { otherwise }\end{cases} $$ If $a_{j+1}-a_{j}=\Delta$, choose any $\epsilon$ less than the least of $\Delta / 2, a_{1}$ and all the differences $a_{i+1}-a_{i}$. If $|X| \geqslant 2$, choose $k \in X$ with $k \neq j$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2-\epsilon, & \text { if } i=j \\ a_{j+1}-\Delta / 2, & \text { if } i=j+1 \\ a_{k}+\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ Otherwise, $\left|X^{c}\right| \geqslant 2$, so choose $k \in X^{c}$ with $k \neq j+1$, and put $$ b_{i}= \begin{cases}a_{j}+\Delta / 2, & \text { if } i=j \\ a_{j+1}-\Delta / 2+\epsilon, & \text { if } i=j+1 \\ a_{k}-\epsilon, & \text { if } i=k \\ a_{i}, & \text { otherwise }\end{cases} $$ If there is no $1 \leqslant j \leqslant n$ such that $j \in X$ but $j+1 \in X^{c}$, there must be some $1<k \leqslant n$ such that $X=[k, n]$ (certainly $X$ cannot be empty). We must have $a_{1}>\Delta$, as otherwise considering $X \cup\{1\}$ contradicts $X$ being $\left(a_{i}\right)$-minimising. Now put $$ b_{i}= \begin{cases}a_{1}-\Delta / 2, & \text { if } i=1 \\ a_{n}+\Delta / 2, & \text { if } i=n \\ a_{i}, & \text { otherwise }\end{cases} $$
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2c3a926-6468-5f77-a80c-96544002bd36
| 23,828
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand) Common remarks. In all solutions, we say an index set $X$ is $\left(a_{i}\right)$-minimising if it has the property in the problem for the given sequence $\left(a_{i}\right)$. Write $X^{c}$ for the complement of $X$, and $[a, b]$ for the interval of integers $k$ such that $a \leqslant k \leqslant b$. Note that $$ \left|1-\sum_{i \in X} a_{i}\right|=\left|1-\sum_{i \in X^{c}} a_{i}\right|, $$ so we may exchange $X$ and $X^{c}$ where convenient. Let $$ \Delta=\sum_{i \in X^{c}} a_{i}-\sum_{i \in X} a_{i} $$ and note that $X$ is $\left(a_{i}\right)$-minimising if and only if it minimises $|\Delta|$, and that $\sum_{i \in X} a_{i}=1$ if and only if $\Delta=0$. In some solutions, a scaling process is used. If we have a strictly increasing sequence of positive real numbers $c_{i}$ (typically obtained by perturbing the $a_{i}$ in some way) such that $$ \sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i} $$ then we may put $b_{i}=2 c_{i} / \sum_{j=1}^{n} c_{j}$. So it suffices to construct such a sequence without needing its sum to be 2 . The solutions below show various possible approaches to the problem. Solutions 1 and 2 perturb a few of the $a_{i}$ to form the $b_{i}$ (with scaling in the case of Solution 1, without scaling in the case of Solution 2). Solutions 3 and 4 look at properties of the index set $X$. Solution 3 then perturbs many of the $a_{i}$ to form the $b_{i}$, together with scaling. Rather than using such perturbations, Solution 4 constructs a sequence $\left(b_{i}\right)$ directly from the set $X$ with the required properties. Solution 4 can be used to give a complete description of sets $X$ that are $\left(a_{i}\right)$-minimising for some $\left(a_{i}\right)$.
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, so $\Delta \geqslant 0$. If $\Delta=0$ we can take $b_{i}=a_{i}$, so now assume that $\Delta>0$. Suppose that there is some $k \leqslant n$ such that $|X \cap[k, n]|>\left|X^{c} \cap[k, n]\right|$. If we choose the largest such $k$ then $|X \cap[k, n]|-\left|X^{c} \cap[k, n]\right|=1$. We can now find the required sequence $\left(b_{i}\right)$ by starting with $c_{i}=a_{i}$ for $i<k$ and $c_{i}=a_{i}+\Delta$ for $i \geqslant k$, and then scaling as described above. If no such $k$ exists, we will derive a contradiction. For each $i \in X$ we can choose $i<j_{i} \leqslant n$ in such a way that $j_{i} \in X^{c}$ and all the $j_{i}$ are different. (For instance, note that necessarily $n \in X^{c}$ and now just work downwards; each time an $i \in X$ is considered, let $j_{i}$ be the least element of $X^{c}$ greater than $i$ and not yet used.) Let $Y$ be the (possibly empty) subset of $[1, n]$ consisting of those elements in $X^{c}$ that are also not one of the $j_{i}$. In any case $$ \Delta=\sum_{i \in X}\left(a_{j_{i}}-a_{i}\right)+\sum_{j \in Y} a_{j} $$ where each term in the sums is positive. Since $n \geqslant 3$ the total number of terms above is at least two. Take a least such term and its corresponding index $i$ and consider the set $Z$ which we form from $X$ by removing $i$ and adding $j_{i}$ (if it is a term of the first type) or just by adding $j$ if it is a term of the second type. The corresponding expression of $\Delta$ for $Z$ has the sign of its least term changed, meaning that the sum is still nonnegative but strictly less than $\Delta$, which contradicts $X$ being $\left(a_{i}\right)$-minimising.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer and let $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ be a strictly increasing sequence of $n$ positive real numbers with sum equal to 2 . Let $X$ be a subset of $\{1,2, \ldots, n\}$ such that the value of $$ \left|1-\sum_{i \in X} a_{i}\right| $$ is minimised. Prove that there exists a strictly increasing sequence of $n$ positive real numbers $\left(b_{1}, b_{2}, \ldots, b_{n}\right)$ with sum equal to 2 such that $$ \sum_{i \in X} b_{i}=1 $$ (New Zealand) Common remarks. In all solutions, we say an index set $X$ is $\left(a_{i}\right)$-minimising if it has the property in the problem for the given sequence $\left(a_{i}\right)$. Write $X^{c}$ for the complement of $X$, and $[a, b]$ for the interval of integers $k$ such that $a \leqslant k \leqslant b$. Note that $$ \left|1-\sum_{i \in X} a_{i}\right|=\left|1-\sum_{i \in X^{c}} a_{i}\right|, $$ so we may exchange $X$ and $X^{c}$ where convenient. Let $$ \Delta=\sum_{i \in X^{c}} a_{i}-\sum_{i \in X} a_{i} $$ and note that $X$ is $\left(a_{i}\right)$-minimising if and only if it minimises $|\Delta|$, and that $\sum_{i \in X} a_{i}=1$ if and only if $\Delta=0$. In some solutions, a scaling process is used. If we have a strictly increasing sequence of positive real numbers $c_{i}$ (typically obtained by perturbing the $a_{i}$ in some way) such that $$ \sum_{i \in X} c_{i}=\sum_{i \in X^{c}} c_{i} $$ then we may put $b_{i}=2 c_{i} / \sum_{j=1}^{n} c_{j}$. So it suffices to construct such a sequence without needing its sum to be 2 . The solutions below show various possible approaches to the problem. Solutions 1 and 2 perturb a few of the $a_{i}$ to form the $b_{i}$ (with scaling in the case of Solution 1, without scaling in the case of Solution 2). Solutions 3 and 4 look at properties of the index set $X$. Solution 3 then perturbs many of the $a_{i}$ to form the $b_{i}$, together with scaling. Rather than using such perturbations, Solution 4 constructs a sequence $\left(b_{i}\right)$ directly from the set $X$ with the required properties. Solution 4 can be used to give a complete description of sets $X$ that are $\left(a_{i}\right)$-minimising for some $\left(a_{i}\right)$.
|
Without loss of generality, assume $\sum_{i \in X} a_{i} \leqslant 1$, so $\Delta \geqslant 0$. If $\Delta=0$ we can take $b_{i}=a_{i}$, so now assume that $\Delta>0$. Suppose that there is some $k \leqslant n$ such that $|X \cap[k, n]|>\left|X^{c} \cap[k, n]\right|$. If we choose the largest such $k$ then $|X \cap[k, n]|-\left|X^{c} \cap[k, n]\right|=1$. We can now find the required sequence $\left(b_{i}\right)$ by starting with $c_{i}=a_{i}$ for $i<k$ and $c_{i}=a_{i}+\Delta$ for $i \geqslant k$, and then scaling as described above. If no such $k$ exists, we will derive a contradiction. For each $i \in X$ we can choose $i<j_{i} \leqslant n$ in such a way that $j_{i} \in X^{c}$ and all the $j_{i}$ are different. (For instance, note that necessarily $n \in X^{c}$ and now just work downwards; each time an $i \in X$ is considered, let $j_{i}$ be the least element of $X^{c}$ greater than $i$ and not yet used.) Let $Y$ be the (possibly empty) subset of $[1, n]$ consisting of those elements in $X^{c}$ that are also not one of the $j_{i}$. In any case $$ \Delta=\sum_{i \in X}\left(a_{j_{i}}-a_{i}\right)+\sum_{j \in Y} a_{j} $$ where each term in the sums is positive. Since $n \geqslant 3$ the total number of terms above is at least two. Take a least such term and its corresponding index $i$ and consider the set $Z$ which we form from $X$ by removing $i$ and adding $j_{i}$ (if it is a term of the first type) or just by adding $j$ if it is a term of the second type. The corresponding expression of $\Delta$ for $Z$ has the sign of its least term changed, meaning that the sum is still nonnegative but strictly less than $\Delta$, which contradicts $X$ being $\left(a_{i}\right)$-minimising.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2c3a926-6468-5f77-a80c-96544002bd36
| 23,828
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$ (Russia) Common remarks. The polynomial $x^{2}+y^{2}+z^{2}-x y z$ satisfies the condition (*), so every polynomial of the form $F\left(x^{2}+y^{2}+z^{2}-x y z\right)$ does satisfy (*). We will use without comment the fact that two polynomials have the same coefficients if and only if they are equal as functions.
|
In the first two steps, we deal with any polynomial $P(x, y, z)$ satisfying $P(x, y, z)=$ $P(x, y, x y-z)$. Call such a polynomial weakly symmetric, and call a polynomial satisfying the full conditions in the problem symmetric. Step 1. We start with the description of weakly symmetric polynomials. We claim that they are exactly the polynomials in $x, y$, and $z(x y-z)$. Clearly, all such polynomials are weakly symmetric. For the converse statement, consider $P_{1}(x, y, z):=P\left(x, y, z+\frac{1}{2} x y\right)$, which satisfies $P_{1}(x, y, z)=P_{1}(x, y,-z)$ and is therefore a polynomial in $x, y$, and $z^{2}$. This means that $P$ is a polynomial in $x, y$, and $\left(z-\frac{1}{2} x y\right)^{2}=-z(x y-z)+\frac{1}{4} x^{2} y^{2}$, and therefore a polynomial in $x, y$, and $z(x y-z)$. Step 2. Suppose that $P$ is weakly symmetric. Consider the monomials in $P(x, y, z)$ of highest total degree. Our aim is to show that in each such monomial $\mu x^{a} y^{b} z^{c}$ we have $a, b \geqslant c$. Consider the expansion $$ P(x, y, z)=\sum_{i, j, k} \mu_{i j k} x^{i} y^{j}(z(x y-z))^{k} $$ The maximal total degree of a summand in (1.1) is $m=\max _{i, j, k: \mu_{i j k} \neq 0}(i+j+3 k)$. Now, for any $i, j, k$ satisfying $i+j+3 k=m$ the summand $\mu_{i, j, k} x^{i} y^{j}(z(x y-z))^{k}$ has leading term of the form $\mu x^{i+k} y^{j+k} z^{k}$. No other nonzero summand in (1.1) may have a term of this form in its expansion, hence this term does not cancel in the whole sum. Therefore, $\operatorname{deg} P=m$, and the leading component of $P$ is exactly $$ \sum_{i+j+3 k=m} \mu_{i, j, k} x^{i+k} y^{j+k} z^{k} $$ and each summand in this sum satisfies the condition claimed above. Step 3. We now prove the problem statement by induction on $m=\operatorname{deg} P$. For $m=0$ the claim is trivial. Consider now a symmetric polynomial $P$ with $\operatorname{deg} P>0$. By Step 2, each of its monomials $\mu x^{a} y^{b} z^{c}$ of the highest total degree satisfies $a, b \geqslant c$. Applying other weak symmetries, we obtain $a, c \geqslant b$ and $b, c \geqslant a$; therefore, $P$ has a unique leading monomial of the form $\mu(x y z)^{c}$. The polynomial $P_{0}(x, y, z)=P(x, y, z)-\mu\left(x y z-x^{2}-y^{2}-z^{2}\right)^{c}$ has smaller total degree. Since $P_{0}$ is symmetric, it is representable as a polynomial function of $x y z-x^{2}-y^{2}-z^{2}$. Then $P$ is also of this form, completing the inductive step. Comment. We could alternatively carry out Step 1 by an induction on $n=\operatorname{deg}_{z} P$, in a manner similar to Step 3. If $n=0$, the statement holds. Assume that $n>0$ and check the leading component of $P$ with respect to $z$ : $$ P(x, y, z)=Q_{n}(x, y) z^{n}+R(x, y, z) $$ where $\operatorname{deg}_{z} R<n$. After the change $z \mapsto x y-z$, the leading component becomes $Q_{n}(x, y)(-z)^{n}$; on the other hand, it should remain the same. Hence $n$ is even. Now consider the polynomial $$ P_{0}(x, y, z)=P(x, y, z)-Q_{n}(x, y) \cdot(z(z-x y))^{n / 2} $$ It is also weakly symmetric, and $\operatorname{deg}_{z} P_{0}<n$. By the inductive hypothesis, it has the form $P_{0}(x, y, z)=$ $S(x, y, z(z-x y))$. Hence the polynomial $$ P(x, y, z)=S(x, y, z(x y-z))+Q_{n}(x, y)(z(z-x y))^{n / 2} $$ also has this form. This completes the inductive step.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$ (Russia) Common remarks. The polynomial $x^{2}+y^{2}+z^{2}-x y z$ satisfies the condition (*), so every polynomial of the form $F\left(x^{2}+y^{2}+z^{2}-x y z\right)$ does satisfy (*). We will use without comment the fact that two polynomials have the same coefficients if and only if they are equal as functions.
|
In the first two steps, we deal with any polynomial $P(x, y, z)$ satisfying $P(x, y, z)=$ $P(x, y, x y-z)$. Call such a polynomial weakly symmetric, and call a polynomial satisfying the full conditions in the problem symmetric. Step 1. We start with the description of weakly symmetric polynomials. We claim that they are exactly the polynomials in $x, y$, and $z(x y-z)$. Clearly, all such polynomials are weakly symmetric. For the converse statement, consider $P_{1}(x, y, z):=P\left(x, y, z+\frac{1}{2} x y\right)$, which satisfies $P_{1}(x, y, z)=P_{1}(x, y,-z)$ and is therefore a polynomial in $x, y$, and $z^{2}$. This means that $P$ is a polynomial in $x, y$, and $\left(z-\frac{1}{2} x y\right)^{2}=-z(x y-z)+\frac{1}{4} x^{2} y^{2}$, and therefore a polynomial in $x, y$, and $z(x y-z)$. Step 2. Suppose that $P$ is weakly symmetric. Consider the monomials in $P(x, y, z)$ of highest total degree. Our aim is to show that in each such monomial $\mu x^{a} y^{b} z^{c}$ we have $a, b \geqslant c$. Consider the expansion $$ P(x, y, z)=\sum_{i, j, k} \mu_{i j k} x^{i} y^{j}(z(x y-z))^{k} $$ The maximal total degree of a summand in (1.1) is $m=\max _{i, j, k: \mu_{i j k} \neq 0}(i+j+3 k)$. Now, for any $i, j, k$ satisfying $i+j+3 k=m$ the summand $\mu_{i, j, k} x^{i} y^{j}(z(x y-z))^{k}$ has leading term of the form $\mu x^{i+k} y^{j+k} z^{k}$. No other nonzero summand in (1.1) may have a term of this form in its expansion, hence this term does not cancel in the whole sum. Therefore, $\operatorname{deg} P=m$, and the leading component of $P$ is exactly $$ \sum_{i+j+3 k=m} \mu_{i, j, k} x^{i+k} y^{j+k} z^{k} $$ and each summand in this sum satisfies the condition claimed above. Step 3. We now prove the problem statement by induction on $m=\operatorname{deg} P$. For $m=0$ the claim is trivial. Consider now a symmetric polynomial $P$ with $\operatorname{deg} P>0$. By Step 2, each of its monomials $\mu x^{a} y^{b} z^{c}$ of the highest total degree satisfies $a, b \geqslant c$. Applying other weak symmetries, we obtain $a, c \geqslant b$ and $b, c \geqslant a$; therefore, $P$ has a unique leading monomial of the form $\mu(x y z)^{c}$. The polynomial $P_{0}(x, y, z)=P(x, y, z)-\mu\left(x y z-x^{2}-y^{2}-z^{2}\right)^{c}$ has smaller total degree. Since $P_{0}$ is symmetric, it is representable as a polynomial function of $x y z-x^{2}-y^{2}-z^{2}$. Then $P$ is also of this form, completing the inductive step. Comment. We could alternatively carry out Step 1 by an induction on $n=\operatorname{deg}_{z} P$, in a manner similar to Step 3. If $n=0$, the statement holds. Assume that $n>0$ and check the leading component of $P$ with respect to $z$ : $$ P(x, y, z)=Q_{n}(x, y) z^{n}+R(x, y, z) $$ where $\operatorname{deg}_{z} R<n$. After the change $z \mapsto x y-z$, the leading component becomes $Q_{n}(x, y)(-z)^{n}$; on the other hand, it should remain the same. Hence $n$ is even. Now consider the polynomial $$ P_{0}(x, y, z)=P(x, y, z)-Q_{n}(x, y) \cdot(z(z-x y))^{n / 2} $$ It is also weakly symmetric, and $\operatorname{deg}_{z} P_{0}<n$. By the inductive hypothesis, it has the form $P_{0}(x, y, z)=$ $S(x, y, z(z-x y))$. Hence the polynomial $$ P(x, y, z)=S(x, y, z(x y-z))+Q_{n}(x, y)(z(z-x y))^{n / 2} $$ also has this form. This completes the inductive step.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
dbe2b7c2-73c8-58fb-86a3-b280822c6c7b
| 23,836
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$ (Russia) Common remarks. The polynomial $x^{2}+y^{2}+z^{2}-x y z$ satisfies the condition (*), so every polynomial of the form $F\left(x^{2}+y^{2}+z^{2}-x y z\right)$ does satisfy (*). We will use without comment the fact that two polynomials have the same coefficients if and only if they are equal as functions.
|
We will rely on the well-known identity $$ \cos ^{2} u+\cos ^{2} v+\cos ^{2} w-2 \cos u \cos v \cos w-1=0 \quad \text { whenever } u+v+w=0 $$ Claim 1. The polynomial $P(x, y, z)$ is constant on the surface $$ \mathfrak{S}=\{(2 \cos u, 2 \cos v, 2 \cos w): u+v+w=0\} $$ Proof. Notice that for $x=2 \cos u, y=2 \cos v, z=2 \cos w$, the Vieta jumps $x \mapsto y z-x$, $y \mapsto z x-y, z \mapsto x y-z$ in (*) replace $(u, v, w)$ by $(v-w,-v, w),(u, w-u,-w)$ and $(-u, v, u-v)$, respectively. For example, for the first type of jump we have $$ y z-x=4 \cos v \cos w-2 \cos u=2 \cos (v+w)+2 \cos (v-w)-2 \cos u=2 \cos (v-w) . $$ Define $G(u, v, w)=P(2 \cos u, 2 \cos v, 2 \cos w)$. For $u+v+w=0$, the jumps give $$ \begin{aligned} G(u, v, w) & =G(v-w,-v, w)=G(w-v,-v,(v-w)-(-v))=G(-u-2 v,-v, 2 v-w) \\ & =G(u+2 v, v, w-2 v) \end{aligned} $$ By induction, $$ G(u, v, w)=G(u+2 k v, v, w-2 k v) \quad(k \in \mathbb{Z}) $$ Similarly, $$ G(u, v, w)=G(u, v-2 \ell u, w+2 \ell u) \quad(\ell \in \mathbb{Z}) $$ And, of course, we have $$ G(u, v, w)=G(u+2 p \pi, v+2 q \pi, w-2(p+q) \pi) \quad(p, q \in \mathbb{Z}) $$ Take two nonzero real numbers $u, v$ such that $u, v$ and $\pi$ are linearly independent over $\mathbb{Q}$. By combining (2.2-2.4), we can see that $G$ is constant on a dense subset of the plane $u+v+w=0$. By continuity, $G$ is constant on the entire plane and therefore $P$ is constant on $\mathfrak{S}$. Claim 2. The polynomial $T(x, y, z)=x^{2}+y^{2}+z^{2}-x y z-4$ divides $P(x, y, z)-P(2,2,2)$. Proof. By dividing $P$ by $T$ with remainders, there exist some polynomials $R(x, y, z), A(y, z)$ and $B(y, z)$ such that $$ P(x, y, z)-P(2,2,2)=T(x, y, z) \cdot R(x, y, z)+A(y, z) x+B(y, z) $$ On the surface $\mathfrak{S}$ the LHS of (2.5) is zero by Claim 1 (since $(2,2,2) \in \mathfrak{S}$ ) and $T=0$ by (2.1). Hence, $A(y, z) x+B(y, z)$ vanishes on $\mathfrak{S}$. Notice that for every $y=2 \cos v$ and $z=2 \cos w$ with $\frac{\pi}{3}<v, w<\frac{2 \pi}{3}$, there are two distinct values of $x$ such that $(x, y, z) \in \mathfrak{S}$, namely $x_{1}=2 \cos (v+w)$ (which is negative), and $x_{2}=2 \cos (v-w)$ (which is positive). This can happen only if $A(y, z)=B(y, z)=0$. Hence, $A(y, z)=B(y, z)=0$ for $|y|<1,|z|<1$. The polynomials $A$ and $B$ vanish on an open set, so $A$ and $B$ are both the zero polynomial. The quotient $(P(x, y, z)-P(2,2,2)) / T(x, y, z)$ is a polynomial of lower degree than $P$ and it also satisfies (*). The problem statement can now be proven by induction on the degree of $P$. Comment. In the proof of (2.2) and (2.3) we used two consecutive Vieta jumps; in fact from (*) we used only $P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z)$. Solution 3 (using algebraic geometry, just for interest). Let $Q=x^{2}+y^{2}+z^{2}-x y z$ and let $t \in \mathbb{C}$. Checking where $Q-t, \frac{\partial Q}{\partial x}, \frac{\partial Q}{\partial y}$ and $\frac{\partial Q}{\partial z}$ vanish simultaneously, we find that the surface $Q=t$ is smooth except for the cases $t=0$, when the only singular point is $(0,0,0)$, and $t=4$, when the four points $( \pm 2, \pm 2, \pm 2)$ that satisfy $x y z=8$ are the only singular points. The singular points are the fixed points of the group $\Gamma$ of polynomial automorphisms of $\mathbb{C}^{3}$ generated by the three Vieta involutions $$ \iota_{1}:(x, y, z) \mapsto(x, y, x y-z), \quad \iota_{2}:(x, y, z) \mapsto(x, x z-y, z), \quad \iota_{3}:(x, y, z) \mapsto(y z-x, y, z) $$ $\Gamma$ acts on each surface $\mathcal{V}_{t}: Q-t=0$. If $Q-t$ were reducible then the surface $Q=t$ would contain a curve of singular points. Therefore $Q-t$ is irreducible in $\mathbb{C}[x, y, z]$. (One can also prove algebraically that $Q-t$ is irreducible, for example by checking that its discriminant as a quadratic polynomial in $x$ is not a square in $\mathbb{C}[y, z]$, and likewise for the other two variables.) In the following solution we will only use the algebraic surface $\mathcal{V}_{0}$. Let $U$ be the $\Gamma$-orbit of $(3,3,3)$. Consider $\iota_{3} \circ \iota_{2}$, which leaves $z$ invariant. For each fixed value of $z, \iota_{3} \circ \iota_{2}$ acts linearly on $(x, y)$ by the matrix $$ M_{z}:=\left(\begin{array}{cc} z^{2}-1 & -z \\ z & -1 \end{array}\right) $$ The reverse composition $\iota_{2} \circ \iota_{3}$ acts by $M_{z}^{-1}=M_{z}^{\text {adj }}$. Note det $M_{z}=1$ and $\operatorname{tr} M_{z}=z^{2}-2$. When $z$ does not lie in the real interval $[-2,2]$, the eigenvalues of $M_{z}$ do not have absolute value 1 , so every orbit of the group generated by $M_{z}$ on $\mathbb{C}^{2} \backslash\{(0,0)\}$ is unbounded. For example, fixing $z=3$ we find $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right) \in U$ for every $k \in \mathbb{Z}$, where $\left(F_{n}\right)_{n \in \mathbb{Z}}$ is the Fibonacci sequence with $F_{0}=0, F_{1}=1$. Now we may start at any point $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right)$ and iteratively apply $\iota_{1} \circ \iota_{2}$ to generate another infinite sequence of distinct points of $U$, Zariski dense in the hyperbola cut out of $\mathcal{V}_{0}$ by the plane $x-3 F_{2 k+1}=0$. (The plane $x=a$ cuts out an irreducible conic when $a \notin\{-2,0,2\}$.) Thus the Zariski closure $\bar{U}$ of $U$ contains infinitely many distinct algebraic curves in $\mathcal{V}_{0}$. Since $\mathcal{V}_{0}$ is an irreducible surface this implies that $\bar{U}=\mathcal{V}_{0}$. For any polynomial $P$ satisfying (*), we have $P-P(3,3,3)=0$ at each point of $U$. Since $\bar{U}=\mathcal{V}_{0}, P-P(3,3,3)$ vanishes on $\mathcal{V}_{0}$. Then Hilbert's Nullstellensatz and the irreducibility of $Q$ imply that $P-P(3,3,3)$ is divisible by $Q$. Now $(P-P(3,3,3)) / Q$ is a polynomial also satisfying (*), so we may complete the proof by an induction on the total degree, as in the other solutions. Comment. We remark that Solution 2 used a trigonometric parametrisation of a real component of $\mathcal{V}_{4} ;$ in contrast $\mathcal{V}_{0}$ is birationally equivalent to the projective space $\mathbb{P}^{2}$ under the maps $$ (x, y, z) \rightarrow(x: y: z), \quad(a: b: c) \rightarrow\left(\frac{a^{2}+b^{2}+c^{2}}{b c}, \frac{a^{2}+b^{2}+c^{2}}{a c}, \frac{a^{2}+b^{2}+c^{2}}{a b}\right) . $$ The set $U$ in Solution 3 is contained in $\mathbb{Z}^{3}$ so it is nowhere dense in $\mathcal{V}_{0}$ in the classical topology. Comment (background to the problem). A triple $(a, b, c) \in \mathbb{Z}^{3}$ is called a Markov triple if $a^{2}+b^{2}+c^{2}=3 a b c$, and an integer that occurs as a coordinate of some Markov triple is called a Markov number. (The spelling Markoff is also frequent.) Markov triples arose in A. Markov's work in the 1870s on the reduction theory of indefinite binary quadratic forms. For every Markov triple, $(3 a, 3 b, 3 c)$ lies on $Q=0$. It is well known that all nonzero Markov triples can be generated from $(1,1,1)$ by sequences of Vieta involutions, which are the substitutions described in equation (*) in the problem statement. There has been recent work by number theorists about the properties of Markov numbers (see for example Jean Bourgain, Alex Gamburd and Peter Sarnak, Markoff triples and strong approximation, Comptes Rendus Math. 345, no. 2, 131-135 (2016), arXiv:1505.06411). Each Markov number occurs in infinitely many triples, but a famous old open problem is the unicity conjecture, which asserts that each Markov number occurs in only one Markov triple (up to permutations and sign changes) as the largest coordinate in absolute value in that triple. It is a standard fact in the modern literature on Markov numbers that the Markov triples are Zariski dense in the Markov surface. Proving this is the main work of Solution 3. Algebraic geometry is definitely off-syllabus for the IMO, and one still has to work a bit to prove the Zariski density. On the other hand the approaches of Solutions 1 and 2 are elementary and only use tools expected to be known by IMO contestants. Therefore we do not think that the existence of a solution using algebraic geometry necessarily makes this problem unsuitable for the IMO.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial $P(x, y, z)$ in three variables with real coefficients satisfies the identities $$ P(x, y, z)=P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z) . $$ Prove that there exists a polynomial $F(t)$ in one variable such that $$ P(x, y, z)=F\left(x^{2}+y^{2}+z^{2}-x y z\right) . $$ (Russia) Common remarks. The polynomial $x^{2}+y^{2}+z^{2}-x y z$ satisfies the condition (*), so every polynomial of the form $F\left(x^{2}+y^{2}+z^{2}-x y z\right)$ does satisfy (*). We will use without comment the fact that two polynomials have the same coefficients if and only if they are equal as functions.
|
We will rely on the well-known identity $$ \cos ^{2} u+\cos ^{2} v+\cos ^{2} w-2 \cos u \cos v \cos w-1=0 \quad \text { whenever } u+v+w=0 $$ Claim 1. The polynomial $P(x, y, z)$ is constant on the surface $$ \mathfrak{S}=\{(2 \cos u, 2 \cos v, 2 \cos w): u+v+w=0\} $$ Proof. Notice that for $x=2 \cos u, y=2 \cos v, z=2 \cos w$, the Vieta jumps $x \mapsto y z-x$, $y \mapsto z x-y, z \mapsto x y-z$ in (*) replace $(u, v, w)$ by $(v-w,-v, w),(u, w-u,-w)$ and $(-u, v, u-v)$, respectively. For example, for the first type of jump we have $$ y z-x=4 \cos v \cos w-2 \cos u=2 \cos (v+w)+2 \cos (v-w)-2 \cos u=2 \cos (v-w) . $$ Define $G(u, v, w)=P(2 \cos u, 2 \cos v, 2 \cos w)$. For $u+v+w=0$, the jumps give $$ \begin{aligned} G(u, v, w) & =G(v-w,-v, w)=G(w-v,-v,(v-w)-(-v))=G(-u-2 v,-v, 2 v-w) \\ & =G(u+2 v, v, w-2 v) \end{aligned} $$ By induction, $$ G(u, v, w)=G(u+2 k v, v, w-2 k v) \quad(k \in \mathbb{Z}) $$ Similarly, $$ G(u, v, w)=G(u, v-2 \ell u, w+2 \ell u) \quad(\ell \in \mathbb{Z}) $$ And, of course, we have $$ G(u, v, w)=G(u+2 p \pi, v+2 q \pi, w-2(p+q) \pi) \quad(p, q \in \mathbb{Z}) $$ Take two nonzero real numbers $u, v$ such that $u, v$ and $\pi$ are linearly independent over $\mathbb{Q}$. By combining (2.2-2.4), we can see that $G$ is constant on a dense subset of the plane $u+v+w=0$. By continuity, $G$ is constant on the entire plane and therefore $P$ is constant on $\mathfrak{S}$. Claim 2. The polynomial $T(x, y, z)=x^{2}+y^{2}+z^{2}-x y z-4$ divides $P(x, y, z)-P(2,2,2)$. Proof. By dividing $P$ by $T$ with remainders, there exist some polynomials $R(x, y, z), A(y, z)$ and $B(y, z)$ such that $$ P(x, y, z)-P(2,2,2)=T(x, y, z) \cdot R(x, y, z)+A(y, z) x+B(y, z) $$ On the surface $\mathfrak{S}$ the LHS of (2.5) is zero by Claim 1 (since $(2,2,2) \in \mathfrak{S}$ ) and $T=0$ by (2.1). Hence, $A(y, z) x+B(y, z)$ vanishes on $\mathfrak{S}$. Notice that for every $y=2 \cos v$ and $z=2 \cos w$ with $\frac{\pi}{3}<v, w<\frac{2 \pi}{3}$, there are two distinct values of $x$ such that $(x, y, z) \in \mathfrak{S}$, namely $x_{1}=2 \cos (v+w)$ (which is negative), and $x_{2}=2 \cos (v-w)$ (which is positive). This can happen only if $A(y, z)=B(y, z)=0$. Hence, $A(y, z)=B(y, z)=0$ for $|y|<1,|z|<1$. The polynomials $A$ and $B$ vanish on an open set, so $A$ and $B$ are both the zero polynomial. The quotient $(P(x, y, z)-P(2,2,2)) / T(x, y, z)$ is a polynomial of lower degree than $P$ and it also satisfies (*). The problem statement can now be proven by induction on the degree of $P$. Comment. In the proof of (2.2) and (2.3) we used two consecutive Vieta jumps; in fact from (*) we used only $P(x, y, x y-z)=P(x, z x-y, z)=P(y z-x, y, z)$. Solution 3 (using algebraic geometry, just for interest). Let $Q=x^{2}+y^{2}+z^{2}-x y z$ and let $t \in \mathbb{C}$. Checking where $Q-t, \frac{\partial Q}{\partial x}, \frac{\partial Q}{\partial y}$ and $\frac{\partial Q}{\partial z}$ vanish simultaneously, we find that the surface $Q=t$ is smooth except for the cases $t=0$, when the only singular point is $(0,0,0)$, and $t=4$, when the four points $( \pm 2, \pm 2, \pm 2)$ that satisfy $x y z=8$ are the only singular points. The singular points are the fixed points of the group $\Gamma$ of polynomial automorphisms of $\mathbb{C}^{3}$ generated by the three Vieta involutions $$ \iota_{1}:(x, y, z) \mapsto(x, y, x y-z), \quad \iota_{2}:(x, y, z) \mapsto(x, x z-y, z), \quad \iota_{3}:(x, y, z) \mapsto(y z-x, y, z) $$ $\Gamma$ acts on each surface $\mathcal{V}_{t}: Q-t=0$. If $Q-t$ were reducible then the surface $Q=t$ would contain a curve of singular points. Therefore $Q-t$ is irreducible in $\mathbb{C}[x, y, z]$. (One can also prove algebraically that $Q-t$ is irreducible, for example by checking that its discriminant as a quadratic polynomial in $x$ is not a square in $\mathbb{C}[y, z]$, and likewise for the other two variables.) In the following solution we will only use the algebraic surface $\mathcal{V}_{0}$. Let $U$ be the $\Gamma$-orbit of $(3,3,3)$. Consider $\iota_{3} \circ \iota_{2}$, which leaves $z$ invariant. For each fixed value of $z, \iota_{3} \circ \iota_{2}$ acts linearly on $(x, y)$ by the matrix $$ M_{z}:=\left(\begin{array}{cc} z^{2}-1 & -z \\ z & -1 \end{array}\right) $$ The reverse composition $\iota_{2} \circ \iota_{3}$ acts by $M_{z}^{-1}=M_{z}^{\text {adj }}$. Note det $M_{z}=1$ and $\operatorname{tr} M_{z}=z^{2}-2$. When $z$ does not lie in the real interval $[-2,2]$, the eigenvalues of $M_{z}$ do not have absolute value 1 , so every orbit of the group generated by $M_{z}$ on $\mathbb{C}^{2} \backslash\{(0,0)\}$ is unbounded. For example, fixing $z=3$ we find $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right) \in U$ for every $k \in \mathbb{Z}$, where $\left(F_{n}\right)_{n \in \mathbb{Z}}$ is the Fibonacci sequence with $F_{0}=0, F_{1}=1$. Now we may start at any point $\left(3 F_{2 k+1}, 3 F_{2 k-1}, 3\right)$ and iteratively apply $\iota_{1} \circ \iota_{2}$ to generate another infinite sequence of distinct points of $U$, Zariski dense in the hyperbola cut out of $\mathcal{V}_{0}$ by the plane $x-3 F_{2 k+1}=0$. (The plane $x=a$ cuts out an irreducible conic when $a \notin\{-2,0,2\}$.) Thus the Zariski closure $\bar{U}$ of $U$ contains infinitely many distinct algebraic curves in $\mathcal{V}_{0}$. Since $\mathcal{V}_{0}$ is an irreducible surface this implies that $\bar{U}=\mathcal{V}_{0}$. For any polynomial $P$ satisfying (*), we have $P-P(3,3,3)=0$ at each point of $U$. Since $\bar{U}=\mathcal{V}_{0}, P-P(3,3,3)$ vanishes on $\mathcal{V}_{0}$. Then Hilbert's Nullstellensatz and the irreducibility of $Q$ imply that $P-P(3,3,3)$ is divisible by $Q$. Now $(P-P(3,3,3)) / Q$ is a polynomial also satisfying (*), so we may complete the proof by an induction on the total degree, as in the other solutions. Comment. We remark that Solution 2 used a trigonometric parametrisation of a real component of $\mathcal{V}_{4} ;$ in contrast $\mathcal{V}_{0}$ is birationally equivalent to the projective space $\mathbb{P}^{2}$ under the maps $$ (x, y, z) \rightarrow(x: y: z), \quad(a: b: c) \rightarrow\left(\frac{a^{2}+b^{2}+c^{2}}{b c}, \frac{a^{2}+b^{2}+c^{2}}{a c}, \frac{a^{2}+b^{2}+c^{2}}{a b}\right) . $$ The set $U$ in Solution 3 is contained in $\mathbb{Z}^{3}$ so it is nowhere dense in $\mathcal{V}_{0}$ in the classical topology. Comment (background to the problem). A triple $(a, b, c) \in \mathbb{Z}^{3}$ is called a Markov triple if $a^{2}+b^{2}+c^{2}=3 a b c$, and an integer that occurs as a coordinate of some Markov triple is called a Markov number. (The spelling Markoff is also frequent.) Markov triples arose in A. Markov's work in the 1870s on the reduction theory of indefinite binary quadratic forms. For every Markov triple, $(3 a, 3 b, 3 c)$ lies on $Q=0$. It is well known that all nonzero Markov triples can be generated from $(1,1,1)$ by sequences of Vieta involutions, which are the substitutions described in equation (*) in the problem statement. There has been recent work by number theorists about the properties of Markov numbers (see for example Jean Bourgain, Alex Gamburd and Peter Sarnak, Markoff triples and strong approximation, Comptes Rendus Math. 345, no. 2, 131-135 (2016), arXiv:1505.06411). Each Markov number occurs in infinitely many triples, but a famous old open problem is the unicity conjecture, which asserts that each Markov number occurs in only one Markov triple (up to permutations and sign changes) as the largest coordinate in absolute value in that triple. It is a standard fact in the modern literature on Markov numbers that the Markov triples are Zariski dense in the Markov surface. Proving this is the main work of Solution 3. Algebraic geometry is definitely off-syllabus for the IMO, and one still has to work a bit to prove the Zariski density. On the other hand the approaches of Solutions 1 and 2 are elementary and only use tools expected to be known by IMO contestants. Therefore we do not think that the existence of a solution using algebraic geometry necessarily makes this problem unsuitable for the IMO.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
dbe2b7c2-73c8-58fb-86a3-b280822c6c7b
| 23,836
|
The infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of (not necessarily different) integers has the following properties: $0 \leqslant a_{i} \leqslant i$ for all integers $i \geqslant 0$, and $$ \binom{k}{a_{0}}+\binom{k}{a_{1}}+\cdots+\binom{k}{a_{k}}=2^{k} $$ for all integers $k \geqslant 0$. Prove that all integers $N \geqslant 0$ occur in the sequence (that is, for all $N \geqslant 0$, there exists $i \geqslant 0$ with $\left.a_{i}=N\right)$. (Netherlands)
|
We prove by induction on $k$ that every initial segment of the sequence, $a_{0}, a_{1}, \ldots, a_{k}$, consists of the following elements (counted with multiplicity, and not necessarily in order), for some $\ell \geqslant 0$ with $2 \ell \leqslant k+1$ : $$ 0,1, \ldots, \ell-1, \quad 0,1, \ldots, k-\ell $$ For $k=0$ we have $a_{0}=0$, which is of this form. Now suppose that for $k=m$ the elements $a_{0}, a_{1}, \ldots, a_{m}$ are $0,0,1,1,2,2, \ldots, \ell-1, \ell-1, \ell, \ell+1, \ldots, m-\ell-1, m-\ell$ for some $\ell$ with $0 \leqslant 2 \ell \leqslant m+1$. It is given that $$ \binom{m+1}{a_{0}}+\binom{m+1}{a_{1}}+\cdots+\binom{m+1}{a_{m}}+\binom{m+1}{a_{m+1}}=2^{m+1} $$ which becomes $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m-\ell}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ or, using $\binom{m+1}{i}=\binom{m+1}{m+1-i}$, that $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{m+1}+\binom{m+1}{m}+\cdots+\binom{m+1}{\ell+1}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ On the other hand, it is well known that $$ \binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m+1}=2^{m+1} $$ and so, by subtracting, we get $$ \binom{m+1}{a_{m+1}}=\binom{m+1}{\ell} $$ From this, using the fact that the binomial coefficients $\binom{m+1}{i}$ are increasing for $i \leqslant \frac{m+1}{2}$ and decreasing for $i \geqslant \frac{m+1}{2}$, we conclude that either $a_{m+1}=\ell$ or $a_{m+1}=m+1-\ell$. In either case, $a_{0}, a_{1}, \ldots, a_{m+1}$ is again of the claimed form, which concludes the induction. As a result of this description, any integer $N \geqslant 0$ appears as a term of the sequence $a_{i}$ for some $0 \leqslant i \leqslant 2 N$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of (not necessarily different) integers has the following properties: $0 \leqslant a_{i} \leqslant i$ for all integers $i \geqslant 0$, and $$ \binom{k}{a_{0}}+\binom{k}{a_{1}}+\cdots+\binom{k}{a_{k}}=2^{k} $$ for all integers $k \geqslant 0$. Prove that all integers $N \geqslant 0$ occur in the sequence (that is, for all $N \geqslant 0$, there exists $i \geqslant 0$ with $\left.a_{i}=N\right)$. (Netherlands)
|
We prove by induction on $k$ that every initial segment of the sequence, $a_{0}, a_{1}, \ldots, a_{k}$, consists of the following elements (counted with multiplicity, and not necessarily in order), for some $\ell \geqslant 0$ with $2 \ell \leqslant k+1$ : $$ 0,1, \ldots, \ell-1, \quad 0,1, \ldots, k-\ell $$ For $k=0$ we have $a_{0}=0$, which is of this form. Now suppose that for $k=m$ the elements $a_{0}, a_{1}, \ldots, a_{m}$ are $0,0,1,1,2,2, \ldots, \ell-1, \ell-1, \ell, \ell+1, \ldots, m-\ell-1, m-\ell$ for some $\ell$ with $0 \leqslant 2 \ell \leqslant m+1$. It is given that $$ \binom{m+1}{a_{0}}+\binom{m+1}{a_{1}}+\cdots+\binom{m+1}{a_{m}}+\binom{m+1}{a_{m+1}}=2^{m+1} $$ which becomes $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m-\ell}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ or, using $\binom{m+1}{i}=\binom{m+1}{m+1-i}$, that $$ \begin{aligned} \left(\binom{m+1}{0}+\binom{m+1}{1}\right. & \left.+\cdots+\binom{m+1}{\ell-1}\right) \\ & +\left(\binom{m+1}{m+1}+\binom{m+1}{m}+\cdots+\binom{m+1}{\ell+1}\right)+\binom{m+1}{a_{m+1}}=2^{m+1} \end{aligned} $$ On the other hand, it is well known that $$ \binom{m+1}{0}+\binom{m+1}{1}+\cdots+\binom{m+1}{m+1}=2^{m+1} $$ and so, by subtracting, we get $$ \binom{m+1}{a_{m+1}}=\binom{m+1}{\ell} $$ From this, using the fact that the binomial coefficients $\binom{m+1}{i}$ are increasing for $i \leqslant \frac{m+1}{2}$ and decreasing for $i \geqslant \frac{m+1}{2}$, we conclude that either $a_{m+1}=\ell$ or $a_{m+1}=m+1-\ell$. In either case, $a_{0}, a_{1}, \ldots, a_{m+1}$ is again of the claimed form, which concludes the induction. As a result of this description, any integer $N \geqslant 0$ appears as a term of the sequence $a_{i}$ for some $0 \leqslant i \leqslant 2 N$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0993913e-34a6-5199-adeb-87f2c7377125
| 23,843
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia) Common remarks. The problem has an obvious rephrasing in terms of graph theory. One is given a graph $G$ with 2019 vertices, 1010 of which have degree 1009 and 1009 of which have degree 1010. One is allowed to perform operations on $G$ of the following kind: Suppose that vertex $A$ is adjacent to two distinct vertices $B$ and $C$ which are not adjacent to each other. Then one may remove the edges $A B$ and $A C$ from $G$ and add the edge $B C$ into $G$. Call such an operation a refriending. One wants to prove that, via a sequence of such refriendings, one can reach a graph which is a disjoint union of single edges and vertices. All of the solutions presented below will use this reformulation.
|
Note that the given graph is connected, since the total degree of any two vertices is at least 2018 and hence they are either adjacent or have at least one neighbour in common. Hence the given graph satisfies the following condition: Every connected component of $G$ with at least three vertices is not complete and has a vertex of odd degree. We will show that if a graph $G$ satisfies condition (1) and has a vertex of degree at least 2 , then there is a refriending on $G$ that preserves condition (1). Since refriendings decrease the total number of edges of $G$, by using a sequence of such refriendings, we must reach a graph $G$ with maximal degree at most 1 , so we are done.  Pick a vertex $A$ of degree at least 2 in a connected component $G^{\prime}$ of $G$. Since no component of $G$ with at least three vertices is complete we may assume that not all of the neighbours of $A$ are adjacent to one another. (For example, pick a maximal complete subgraph $K$ of $G^{\prime}$. Some vertex $A$ of $K$ has a neighbour outside $K$, and this neighbour is not adjacent to every vertex of $K$ by maximality.) Removing $A$ from $G$ splits $G^{\prime}$ into smaller connected components $G_{1}, \ldots, G_{k}$ (possibly with $k=1$ ), to each of which $A$ is connected by at least one edge. We divide into several cases. Case 1: $k \geqslant 2$ and $A$ is connected to some $G_{i}$ by at least two edges. Choose a vertex $B$ of $G_{i}$ adjacent to $A$, and a vertex $C$ in another component $G_{j}$ adjacent to $A$. The vertices $B$ and $C$ are not adjacent, and hence removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. It is easy to see that this preserves the condition, since the refriending does not change the parity of the degrees of vertices. Case 2: $k \geqslant 2$ and $A$ is connected to each $G_{i}$ by exactly one edge. Consider the induced subgraph on any $G_{i}$ and the vertex $A$. The vertex $A$ has degree 1 in this subgraph; since the number of odd-degree vertices of a graph is always even, we see that $G_{i}$ has a vertex of odd degree (in $G$ ). Thus if we let $B$ and $C$ be any distinct neighbours of $A$, then removing edges $A B$ and $A C$ and adding in edge $B C$ preserves the above condition: the refriending creates two new components, and if either of these components has at least three vertices, then it cannot be complete and must contain a vertex of odd degree (since each $G_{i}$ does). Case 3: $k=1$ and $A$ is connected to $G_{1}$ by at least three edges. By assumption, $A$ has two neighbours $B$ and $C$ which are not adjacent to one another. Removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. We are then done as in Case 1. Case 4: $k=1$ and $A$ is connected to $G_{1}$ by exactly two edges. Let $B$ and $C$ be the two neighbours of $A$, which are not adjacent. Removing edges $A B$ and $A C$ and adding in edge $B C$ results in two new components: one consisting of a single vertex; and the other containing a vertex of odd degree. We are done unless this second component would be a complete graph on at least 3 vertices. But in this case, $G_{1}$ would be a complete graph minus the single edge $B C$, and hence has at least 4 vertices since $G^{\prime}$ is not a 4 -cycle. If we let $D$ be a third vertex of $G_{1}$, then removing edges $B A$ and $B D$ and adding in edge $A D$ does not disconnect $G^{\prime}$. We are then done as in Case 1.  Comment. In fact, condition 1 above precisely characterises those graphs which can be reduced to a graph of maximal degree $\leqslant 1$ by a sequence of refriendings.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia) Common remarks. The problem has an obvious rephrasing in terms of graph theory. One is given a graph $G$ with 2019 vertices, 1010 of which have degree 1009 and 1009 of which have degree 1010. One is allowed to perform operations on $G$ of the following kind: Suppose that vertex $A$ is adjacent to two distinct vertices $B$ and $C$ which are not adjacent to each other. Then one may remove the edges $A B$ and $A C$ from $G$ and add the edge $B C$ into $G$. Call such an operation a refriending. One wants to prove that, via a sequence of such refriendings, one can reach a graph which is a disjoint union of single edges and vertices. All of the solutions presented below will use this reformulation.
|
Note that the given graph is connected, since the total degree of any two vertices is at least 2018 and hence they are either adjacent or have at least one neighbour in common. Hence the given graph satisfies the following condition: Every connected component of $G$ with at least three vertices is not complete and has a vertex of odd degree. We will show that if a graph $G$ satisfies condition (1) and has a vertex of degree at least 2 , then there is a refriending on $G$ that preserves condition (1). Since refriendings decrease the total number of edges of $G$, by using a sequence of such refriendings, we must reach a graph $G$ with maximal degree at most 1 , so we are done.  Pick a vertex $A$ of degree at least 2 in a connected component $G^{\prime}$ of $G$. Since no component of $G$ with at least three vertices is complete we may assume that not all of the neighbours of $A$ are adjacent to one another. (For example, pick a maximal complete subgraph $K$ of $G^{\prime}$. Some vertex $A$ of $K$ has a neighbour outside $K$, and this neighbour is not adjacent to every vertex of $K$ by maximality.) Removing $A$ from $G$ splits $G^{\prime}$ into smaller connected components $G_{1}, \ldots, G_{k}$ (possibly with $k=1$ ), to each of which $A$ is connected by at least one edge. We divide into several cases. Case 1: $k \geqslant 2$ and $A$ is connected to some $G_{i}$ by at least two edges. Choose a vertex $B$ of $G_{i}$ adjacent to $A$, and a vertex $C$ in another component $G_{j}$ adjacent to $A$. The vertices $B$ and $C$ are not adjacent, and hence removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. It is easy to see that this preserves the condition, since the refriending does not change the parity of the degrees of vertices. Case 2: $k \geqslant 2$ and $A$ is connected to each $G_{i}$ by exactly one edge. Consider the induced subgraph on any $G_{i}$ and the vertex $A$. The vertex $A$ has degree 1 in this subgraph; since the number of odd-degree vertices of a graph is always even, we see that $G_{i}$ has a vertex of odd degree (in $G$ ). Thus if we let $B$ and $C$ be any distinct neighbours of $A$, then removing edges $A B$ and $A C$ and adding in edge $B C$ preserves the above condition: the refriending creates two new components, and if either of these components has at least three vertices, then it cannot be complete and must contain a vertex of odd degree (since each $G_{i}$ does). Case 3: $k=1$ and $A$ is connected to $G_{1}$ by at least three edges. By assumption, $A$ has two neighbours $B$ and $C$ which are not adjacent to one another. Removing edges $A B$ and $A C$ and adding in edge $B C$ does not disconnect $G^{\prime}$. We are then done as in Case 1. Case 4: $k=1$ and $A$ is connected to $G_{1}$ by exactly two edges. Let $B$ and $C$ be the two neighbours of $A$, which are not adjacent. Removing edges $A B$ and $A C$ and adding in edge $B C$ results in two new components: one consisting of a single vertex; and the other containing a vertex of odd degree. We are done unless this second component would be a complete graph on at least 3 vertices. But in this case, $G_{1}$ would be a complete graph minus the single edge $B C$, and hence has at least 4 vertices since $G^{\prime}$ is not a 4 -cycle. If we let $D$ be a third vertex of $G_{1}$, then removing edges $B A$ and $B D$ and adding in edge $A D$ does not disconnect $G^{\prime}$. We are then done as in Case 1.  Comment. In fact, condition 1 above precisely characterises those graphs which can be reduced to a graph of maximal degree $\leqslant 1$ by a sequence of refriendings.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4ec6a877-4b94-5c1d-8fa5-e349290ed29b
| 23,855
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia) Common remarks. The problem has an obvious rephrasing in terms of graph theory. One is given a graph $G$ with 2019 vertices, 1010 of which have degree 1009 and 1009 of which have degree 1010. One is allowed to perform operations on $G$ of the following kind: Suppose that vertex $A$ is adjacent to two distinct vertices $B$ and $C$ which are not adjacent to each other. Then one may remove the edges $A B$ and $A C$ from $G$ and add the edge $B C$ into $G$. Call such an operation a refriending. One wants to prove that, via a sequence of such refriendings, one can reach a graph which is a disjoint union of single edges and vertices. All of the solutions presented below will use this reformulation.
|
As in the previous solution, note that a refriending preserves the property that a graph has a vertex of odd degree and (trivially) the property that it is not complete; note also that our initial graph is connected. We describe an algorithm to reduce our initial graph to a graph of maximal degree at most 1, proceeding in two steps. Step 1: There exists a sequence of refriendings reducing the graph to a tree. Proof. Since the number of edges decreases with each refriending, it suffices to prove the following: as long as the graph contains a cycle, there exists a refriending such that the resulting graph is still connected. We will show that the graph in fact contains a cycle $Z$ and vertices $A, B, C$ such that $A$ and $B$ are adjacent in the cycle $Z, C$ is not in $Z$, and is adjacent to $A$ but not $B$. Removing edges $A B$ and $A C$ and adding in edge $B C$ keeps the graph connected, so we are done.  To find this cycle $Z$ and vertices $A, B, C$, we pursue one of two strategies. If the graph contains a triangle, we consider a largest complete subgraph $K$, which thus contains at least three vertices. Since the graph itself is not complete, there is a vertex $C$ not in $K$ connected to a vertex $A$ of $K$. By maximality of $K$, there is a vertex $B$ of $K$ not connected to $C$, and hence we are done by choosing a cycle $Z$ in $K$ through the edge $A B$.  If the graph is triangle-free, we consider instead a smallest cycle $Z$. This cycle cannot be Hamiltonian (i.e. it cannot pass through every vertex of the graph), since otherwise by minimality the graph would then have no other edges, and hence would have even degree at every vertex. We may thus choose a vertex $C$ not in $Z$ adjacent to a vertex $A$ of $Z$. Since the graph is triangle-free, it is not adjacent to any neighbour $B$ of $A$ in $Z$, and we are done. Step 2: Any tree may be reduced to a disjoint union of single edges and vertices by a sequence of refriendings. Proof. The refriending preserves the property of being acyclic. Hence, after applying a sequence of refriendings, we arrive at an acyclic graph in which it is impossible to perform any further refriendings. The maximal degree of any such graph is 1 : if it had a vertex $A$ with two neighbours $B, C$, then $B$ and $C$ would necessarily be nonadjacent since the graph is cycle-free, and so a refriending would be possible. Thus we reach a graph with maximal degree at most 1 as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On a certain social network, there are 2019 users, some pairs of which are friends, where friendship is a symmetric relation. Initially, there are 1010 people with 1009 friends each and 1009 people with 1010 friends each. However, the friendships are rather unstable, so events of the following kind may happen repeatedly, one at a time: Let $A, B$, and $C$ be people such that $A$ is friends with both $B$ and $C$, but $B$ and $C$ are not friends; then $B$ and $C$ become friends, but $A$ is no longer friends with them. Prove that, regardless of the initial friendships, there exists a sequence of such events after which each user is friends with at most one other user. (Croatia) Common remarks. The problem has an obvious rephrasing in terms of graph theory. One is given a graph $G$ with 2019 vertices, 1010 of which have degree 1009 and 1009 of which have degree 1010. One is allowed to perform operations on $G$ of the following kind: Suppose that vertex $A$ is adjacent to two distinct vertices $B$ and $C$ which are not adjacent to each other. Then one may remove the edges $A B$ and $A C$ from $G$ and add the edge $B C$ into $G$. Call such an operation a refriending. One wants to prove that, via a sequence of such refriendings, one can reach a graph which is a disjoint union of single edges and vertices. All of the solutions presented below will use this reformulation.
|
As in the previous solution, note that a refriending preserves the property that a graph has a vertex of odd degree and (trivially) the property that it is not complete; note also that our initial graph is connected. We describe an algorithm to reduce our initial graph to a graph of maximal degree at most 1, proceeding in two steps. Step 1: There exists a sequence of refriendings reducing the graph to a tree. Proof. Since the number of edges decreases with each refriending, it suffices to prove the following: as long as the graph contains a cycle, there exists a refriending such that the resulting graph is still connected. We will show that the graph in fact contains a cycle $Z$ and vertices $A, B, C$ such that $A$ and $B$ are adjacent in the cycle $Z, C$ is not in $Z$, and is adjacent to $A$ but not $B$. Removing edges $A B$ and $A C$ and adding in edge $B C$ keeps the graph connected, so we are done.  To find this cycle $Z$ and vertices $A, B, C$, we pursue one of two strategies. If the graph contains a triangle, we consider a largest complete subgraph $K$, which thus contains at least three vertices. Since the graph itself is not complete, there is a vertex $C$ not in $K$ connected to a vertex $A$ of $K$. By maximality of $K$, there is a vertex $B$ of $K$ not connected to $C$, and hence we are done by choosing a cycle $Z$ in $K$ through the edge $A B$.  If the graph is triangle-free, we consider instead a smallest cycle $Z$. This cycle cannot be Hamiltonian (i.e. it cannot pass through every vertex of the graph), since otherwise by minimality the graph would then have no other edges, and hence would have even degree at every vertex. We may thus choose a vertex $C$ not in $Z$ adjacent to a vertex $A$ of $Z$. Since the graph is triangle-free, it is not adjacent to any neighbour $B$ of $A$ in $Z$, and we are done. Step 2: Any tree may be reduced to a disjoint union of single edges and vertices by a sequence of refriendings. Proof. The refriending preserves the property of being acyclic. Hence, after applying a sequence of refriendings, we arrive at an acyclic graph in which it is impossible to perform any further refriendings. The maximal degree of any such graph is 1 : if it had a vertex $A$ with two neighbours $B, C$, then $B$ and $C$ would necessarily be nonadjacent since the graph is cycle-free, and so a refriending would be possible. Thus we reach a graph with maximal degree at most 1 as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4ec6a877-4b94-5c1d-8fa5-e349290ed29b
| 23,855
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group. Comment. The first three solutions all use the same construction involving a line separating the points into groups of $n$ points each, but give different proofs that this construction works. Although Solution 1 is very short, the Problem Selection Committee does not believe any of the solutions is easy to find and thus rates this as a problem of medium difficulty.
|
Let $\ell$ be a line separating the points into two groups ( $L$ and $R$ ) with $n$ points in each. Label the points $A_{1}, A_{2}, \ldots, A_{2 n}$ so that $L=\left\{A_{1}, A_{3}, \ldots, A_{2 n-1}\right\}$. We claim that this labelling works. Take a line $s=A_{2 n} A_{1}$. (a) Rotate $s$ around $A_{1}$ until it passes through $A_{2}$; the rotation is performed in a direction such that $s$ is never parallel to $\ell$. (b) Then rotate the new $s$ around $A_{2}$ until it passes through $A_{3}$ in a similar manner. (c) Perform $2 n-2$ more such steps, after which $s$ returns to its initial position. The total (directed) rotation angle $\Theta$ of $s$ is clearly a multiple of $180^{\circ}$. On the other hand, $s$ was never parallel to $\ell$, which is possible only if $\Theta=0$. Now it remains to partition all the $2 n$ angles into those where $s$ is rotated anticlockwise, and the others.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group. Comment. The first three solutions all use the same construction involving a line separating the points into groups of $n$ points each, but give different proofs that this construction works. Although Solution 1 is very short, the Problem Selection Committee does not believe any of the solutions is easy to find and thus rates this as a problem of medium difficulty.
|
Let $\ell$ be a line separating the points into two groups ( $L$ and $R$ ) with $n$ points in each. Label the points $A_{1}, A_{2}, \ldots, A_{2 n}$ so that $L=\left\{A_{1}, A_{3}, \ldots, A_{2 n-1}\right\}$. We claim that this labelling works. Take a line $s=A_{2 n} A_{1}$. (a) Rotate $s$ around $A_{1}$ until it passes through $A_{2}$; the rotation is performed in a direction such that $s$ is never parallel to $\ell$. (b) Then rotate the new $s$ around $A_{2}$ until it passes through $A_{3}$ in a similar manner. (c) Perform $2 n-2$ more such steps, after which $s$ returns to its initial position. The total (directed) rotation angle $\Theta$ of $s$ is clearly a multiple of $180^{\circ}$. On the other hand, $s$ was never parallel to $\ell$, which is possible only if $\Theta=0$. Now it remains to partition all the $2 n$ angles into those where $s$ is rotated anticlockwise, and the others.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
505c8a61-7dd8-5520-a005-0192a424acc6
| 23,859
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group. Comment. The first three solutions all use the same construction involving a line separating the points into groups of $n$ points each, but give different proofs that this construction works. Although Solution 1 is very short, the Problem Selection Committee does not believe any of the solutions is easy to find and thus rates this as a problem of medium difficulty.
|
When tracing a cyclic path through the $A_{i}$ in order, with straight line segments between consecutive points, let $\theta_{i}$ be the exterior angle at $A_{i}$, with a sign convention that it is positive if the path turns left and negative if the path turns right. Then $\sum_{i=1}^{2 n} \theta_{i}=360 k^{\circ}$ for some integer $k$. Let $\phi_{i}=\angle A_{i-1} A_{i} A_{i+1}($ indices $\bmod 2 n)$, defined as in the problem; thus $\phi_{i}=180^{\circ}-\left|\theta_{i}\right|$. Let $L$ be the set of $i$ for which the path turns left at $A_{i}$ and let $R$ be the set for which it turns right. Then $S=\sum_{i \in L} \phi_{i}-\sum_{i \in R} \phi_{i}=(180(|L|-|R|)-360 k)^{\circ}$, which is a multiple of $360^{\circ}$ since the number of points is even. We will show that the points can be labelled such that $S=0$, in which case $L$ and $R$ satisfy the required condition of the problem. Note that the value of $S$ is defined for a slightly larger class of configurations: it is OK for two points to coincide, as long as they are not consecutive, and OK for three points to be collinear, as long as $A_{i}, A_{i+1}$ and $A_{i+2}$ do not appear on a line in that order. In what follows it will be convenient, although not strictly necessary, to consider such configurations. Consider how $S$ changes if a single one of the $A_{i}$ is moved along some straight-line path (not passing through any $A_{j}$ and not lying on any line $A_{j} A_{k}$, but possibly crossing such lines). Because $S$ is a multiple of $360^{\circ}$, and the angles change continuously, $S$ can only change when a point moves between $R$ and $L$. Furthermore, if $\phi_{j}=0$ when $A_{j}$ moves between $R$ and $L, S$ is unchanged; it only changes if $\phi_{j}=180^{\circ}$ when $A_{j}$ moves between those sets. For any starting choice of points, we will now construct a new configuration, with labels such that $S=0$, that can be perturbed into the original one without any $\phi_{i}$ passing through $180^{\circ}$, so that $S=0$ for the original configuration with those labels as well. Take some line such that there are $n$ points on each side of that line. The new configuration has $n$ copies of a single point on each side of the line, and a path that alternates between sides of the line; all angles are 0 , so this configuration has $S=0$. Perturbing the points into their original positions, while keeping each point on its side of the line, no angle $\phi_{i}$ can pass through $180^{\circ}$, because no straight line can go from one side of the line to the other and back. So the perturbation process leaves $S=0$. Comment. More complicated variants of this solution are also possible; for example, a path defined using four quadrants of the plane rather than just two half-planes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group. Comment. The first three solutions all use the same construction involving a line separating the points into groups of $n$ points each, but give different proofs that this construction works. Although Solution 1 is very short, the Problem Selection Committee does not believe any of the solutions is easy to find and thus rates this as a problem of medium difficulty.
|
When tracing a cyclic path through the $A_{i}$ in order, with straight line segments between consecutive points, let $\theta_{i}$ be the exterior angle at $A_{i}$, with a sign convention that it is positive if the path turns left and negative if the path turns right. Then $\sum_{i=1}^{2 n} \theta_{i}=360 k^{\circ}$ for some integer $k$. Let $\phi_{i}=\angle A_{i-1} A_{i} A_{i+1}($ indices $\bmod 2 n)$, defined as in the problem; thus $\phi_{i}=180^{\circ}-\left|\theta_{i}\right|$. Let $L$ be the set of $i$ for which the path turns left at $A_{i}$ and let $R$ be the set for which it turns right. Then $S=\sum_{i \in L} \phi_{i}-\sum_{i \in R} \phi_{i}=(180(|L|-|R|)-360 k)^{\circ}$, which is a multiple of $360^{\circ}$ since the number of points is even. We will show that the points can be labelled such that $S=0$, in which case $L$ and $R$ satisfy the required condition of the problem. Note that the value of $S$ is defined for a slightly larger class of configurations: it is OK for two points to coincide, as long as they are not consecutive, and OK for three points to be collinear, as long as $A_{i}, A_{i+1}$ and $A_{i+2}$ do not appear on a line in that order. In what follows it will be convenient, although not strictly necessary, to consider such configurations. Consider how $S$ changes if a single one of the $A_{i}$ is moved along some straight-line path (not passing through any $A_{j}$ and not lying on any line $A_{j} A_{k}$, but possibly crossing such lines). Because $S$ is a multiple of $360^{\circ}$, and the angles change continuously, $S$ can only change when a point moves between $R$ and $L$. Furthermore, if $\phi_{j}=0$ when $A_{j}$ moves between $R$ and $L, S$ is unchanged; it only changes if $\phi_{j}=180^{\circ}$ when $A_{j}$ moves between those sets. For any starting choice of points, we will now construct a new configuration, with labels such that $S=0$, that can be perturbed into the original one without any $\phi_{i}$ passing through $180^{\circ}$, so that $S=0$ for the original configuration with those labels as well. Take some line such that there are $n$ points on each side of that line. The new configuration has $n$ copies of a single point on each side of the line, and a path that alternates between sides of the line; all angles are 0 , so this configuration has $S=0$. Perturbing the points into their original positions, while keeping each point on its side of the line, no angle $\phi_{i}$ can pass through $180^{\circ}$, because no straight line can go from one side of the line to the other and back. So the perturbation process leaves $S=0$. Comment. More complicated variants of this solution are also possible; for example, a path defined using four quadrants of the plane rather than just two half-planes.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
505c8a61-7dd8-5520-a005-0192a424acc6
| 23,859
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group. Comment. The first three solutions all use the same construction involving a line separating the points into groups of $n$ points each, but give different proofs that this construction works. Although Solution 1 is very short, the Problem Selection Committee does not believe any of the solutions is easy to find and thus rates this as a problem of medium difficulty.
|
We shall think instead of the problem as asking us to assign a weight $\pm 1$ to each angle, such that the weighted sum of all the angles is zero. Given an ordering $A_{1}, \ldots, A_{2 n}$ of the points, we shall assign weights according to the following recipe: walk in order from point to point, and assign the left turns +1 and the right turns -1 . This is the same weighting as in Solution 3, and as in that solution, the weighted sum is a multiple of $360^{\circ}$. We now aim to show the following: Lemma. Transposing any two consecutive points in the ordering changes the weighted sum by $\pm 360^{\circ}$ or 0 . Knowing that, we can conclude quickly: if the ordering $A_{1}, \ldots, A_{2 n}$ has weighted angle sum $360 k^{\circ}$, then the ordering $A_{2 n}, \ldots, A_{1}$ has weighted angle sum $-360 k^{\circ}$ (since the angles are the same, but left turns and right turns are exchanged). We can reverse the ordering of $A_{1}$, $\ldots, A_{2 n}$ by a sequence of transpositions of consecutive points, and in doing so the weighted angle sum must become zero somewhere along the way. We now prove that lemma: Proof. Transposing two points amounts to taking a section $A_{k} A_{k+1} A_{k+2} A_{k+3}$ as depicted, reversing the central line segment $A_{k+1} A_{k+2}$, and replacing its two neighbours with the dotted lines.  Figure 1: Transposing two consecutive vertices: before (left) and afterwards (right) In each triangle, we alter the sum by $\pm 180^{\circ}$. Indeed, using (anticlockwise) directed angles modulo $360^{\circ}$, we either add or subtract all three angles of each triangle. Hence both triangles together alter the sum by $\pm 180 \pm 180^{\circ}$, which is $\pm 360^{\circ}$ or 0 .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n>1$ be an integer. Suppose we are given $2 n$ points in a plane such that no three of them are collinear. The points are to be labelled $A_{1}, A_{2}, \ldots, A_{2 n}$ in some order. We then consider the $2 n$ angles $\angle A_{1} A_{2} A_{3}, \angle A_{2} A_{3} A_{4}, \ldots, \angle A_{2 n-2} A_{2 n-1} A_{2 n}, \angle A_{2 n-1} A_{2 n} A_{1}$, $\angle A_{2 n} A_{1} A_{2}$. We measure each angle in the way that gives the smallest positive value (i.e. between $0^{\circ}$ and $180^{\circ}$ ). Prove that there exists an ordering of the given points such that the resulting $2 n$ angles can be separated into two groups with the sum of one group of angles equal to the sum of the other group. Comment. The first three solutions all use the same construction involving a line separating the points into groups of $n$ points each, but give different proofs that this construction works. Although Solution 1 is very short, the Problem Selection Committee does not believe any of the solutions is easy to find and thus rates this as a problem of medium difficulty.
|
We shall think instead of the problem as asking us to assign a weight $\pm 1$ to each angle, such that the weighted sum of all the angles is zero. Given an ordering $A_{1}, \ldots, A_{2 n}$ of the points, we shall assign weights according to the following recipe: walk in order from point to point, and assign the left turns +1 and the right turns -1 . This is the same weighting as in Solution 3, and as in that solution, the weighted sum is a multiple of $360^{\circ}$. We now aim to show the following: Lemma. Transposing any two consecutive points in the ordering changes the weighted sum by $\pm 360^{\circ}$ or 0 . Knowing that, we can conclude quickly: if the ordering $A_{1}, \ldots, A_{2 n}$ has weighted angle sum $360 k^{\circ}$, then the ordering $A_{2 n}, \ldots, A_{1}$ has weighted angle sum $-360 k^{\circ}$ (since the angles are the same, but left turns and right turns are exchanged). We can reverse the ordering of $A_{1}$, $\ldots, A_{2 n}$ by a sequence of transpositions of consecutive points, and in doing so the weighted angle sum must become zero somewhere along the way. We now prove that lemma: Proof. Transposing two points amounts to taking a section $A_{k} A_{k+1} A_{k+2} A_{k+3}$ as depicted, reversing the central line segment $A_{k+1} A_{k+2}$, and replacing its two neighbours with the dotted lines.  Figure 1: Transposing two consecutive vertices: before (left) and afterwards (right) In each triangle, we alter the sum by $\pm 180^{\circ}$. Indeed, using (anticlockwise) directed angles modulo $360^{\circ}$, we either add or subtract all three angles of each triangle. Hence both triangles together alter the sum by $\pm 180 \pm 180^{\circ}$, which is $\pm 360^{\circ}$ or 0 .
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
505c8a61-7dd8-5520-a005-0192a424acc6
| 23,859
|
Let $A B C$ be a triangle. Circle $\Gamma$ passes through $A$, meets segments $A B$ and $A C$ again at points $D$ and $E$ respectively, and intersects segment $B C$ at $F$ and $G$ such that $F$ lies between $B$ and $G$. The tangent to circle $B D F$ at $F$ and the tangent to circle $C E G$ at $G$ meet at point $T$. Suppose that points $A$ and $T$ are distinct. Prove that line $A T$ is parallel to $B C$. (Nigeria)
|
Notice that $\angle T F B=\angle F D A$ because $F T$ is tangent to circle $B D F$, and moreover $\angle F D A=\angle C G A$ because quadrilateral $A D F G$ is cyclic. Similarly, $\angle T G B=\angle G E C$ because $G T$ is tangent to circle $C E G$, and $\angle G E C=\angle C F A$. Hence, $$ \angle T F B=\angle C G A \text { and } \quad \angle T G B=\angle C F A $$  Triangles $F G A$ and $G F T$ have a common side $F G$, and by (1) their angles at $F, G$ are the same. So, these triangles are congruent. So, their altitudes starting from $A$ and $T$, respectively, are equal and hence $A T$ is parallel to line $B F G C$. Comment. Alternatively, we can prove first that $T$ lies on $\Gamma$. For example, this can be done by showing that $\angle A F T=\angle A G T$ using (1). Then the statement follows as $\angle T A F=\angle T G F=\angle G F A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Circle $\Gamma$ passes through $A$, meets segments $A B$ and $A C$ again at points $D$ and $E$ respectively, and intersects segment $B C$ at $F$ and $G$ such that $F$ lies between $B$ and $G$. The tangent to circle $B D F$ at $F$ and the tangent to circle $C E G$ at $G$ meet at point $T$. Suppose that points $A$ and $T$ are distinct. Prove that line $A T$ is parallel to $B C$. (Nigeria)
|
Notice that $\angle T F B=\angle F D A$ because $F T$ is tangent to circle $B D F$, and moreover $\angle F D A=\angle C G A$ because quadrilateral $A D F G$ is cyclic. Similarly, $\angle T G B=\angle G E C$ because $G T$ is tangent to circle $C E G$, and $\angle G E C=\angle C F A$. Hence, $$ \angle T F B=\angle C G A \text { and } \quad \angle T G B=\angle C F A $$  Triangles $F G A$ and $G F T$ have a common side $F G$, and by (1) their angles at $F, G$ are the same. So, these triangles are congruent. So, their altitudes starting from $A$ and $T$, respectively, are equal and hence $A T$ is parallel to line $B F G C$. Comment. Alternatively, we can prove first that $T$ lies on $\Gamma$. For example, this can be done by showing that $\angle A F T=\angle A G T$ using (1). Then the statement follows as $\angle T A F=\angle T G F=\angle G F A$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3f3d20a7-3f67-5c87-8501-a92f49dc72bc
| 23,871
|
Let $A B C$ be an acute-angled triangle and let $D, E$, and $F$ be the feet of altitudes from $A, B$, and $C$ to sides $B C, C A$, and $A B$, respectively. Denote by $\omega_{B}$ and $\omega_{C}$ the incircles of triangles $B D F$ and $C D E$, and let these circles be tangent to segments $D F$ and $D E$ at $M$ and $N$, respectively. Let line $M N$ meet circles $\omega_{B}$ and $\omega_{C}$ again at $P \neq M$ and $Q \neq N$, respectively. Prove that $M P=N Q$. (Vietnam)
|
Denote the centres of $\omega_{B}$ and $\omega_{C}$ by $O_{B}$ and $O_{C}$, let their radii be $r_{B}$ and $r_{C}$, and let $B C$ be tangent to the two circles at $T$ and $U$, respectively.  From the cyclic quadrilaterals $A F D C$ and $A B D E$ we have $$ \angle M D O_{B}=\frac{1}{2} \angle F D B=\frac{1}{2} \angle B A C=\frac{1}{2} \angle C D E=\angle O_{C} D N, $$ so the right-angled triangles $D M O_{B}$ and $D N O_{C}$ are similar. The ratio of similarity between the two triangles is $$ \frac{D N}{D M}=\frac{O_{C} N}{O_{B} M}=\frac{r_{C}}{r_{B}} . $$ Let $\varphi=\angle D M N$ and $\psi=\angle M N D$. The lines $F M$ and $E N$ are tangent to $\omega_{B}$ and $\omega_{C}$, respectively, so $$ \angle M T P=\angle F M P=\angle D M N=\varphi \quad \text { and } \quad \angle Q U N=\angle Q N E=\angle M N D=\psi $$ (It is possible that $P$ or $Q$ coincides with $T$ or $U$, or lie inside triangles $D M T$ or $D U N$, respectively. To reduce case-sensitivity, we may use directed angles or simply ignore angles $M T P$ and $Q U N$.) In the circles $\omega_{B}$ and $\omega_{C}$ the lengths of chords $M P$ and $N Q$ are $$ M P=2 r_{B} \cdot \sin \angle M T P=2 r_{B} \cdot \sin \varphi \quad \text { and } \quad N Q=2 r_{C} \cdot \sin \angle Q U N=2 r_{C} \cdot \sin \psi $$ By applying the sine rule to triangle $D N M$ we get $$ \frac{D N}{D M}=\frac{\sin \angle D M N}{\sin \angle M N D}=\frac{\sin \varphi}{\sin \psi} $$ Finally, putting the above observations together, we get $$ \frac{M P}{N Q}=\frac{2 r_{B} \sin \varphi}{2 r_{C} \sin \psi}=\frac{r_{B}}{r_{C}} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{D M}{D N} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{\sin \psi}{\sin \varphi} \cdot \frac{\sin \varphi}{\sin \psi}=1, $$ so $M P=N Q$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle and let $D, E$, and $F$ be the feet of altitudes from $A, B$, and $C$ to sides $B C, C A$, and $A B$, respectively. Denote by $\omega_{B}$ and $\omega_{C}$ the incircles of triangles $B D F$ and $C D E$, and let these circles be tangent to segments $D F$ and $D E$ at $M$ and $N$, respectively. Let line $M N$ meet circles $\omega_{B}$ and $\omega_{C}$ again at $P \neq M$ and $Q \neq N$, respectively. Prove that $M P=N Q$. (Vietnam)
|
Denote the centres of $\omega_{B}$ and $\omega_{C}$ by $O_{B}$ and $O_{C}$, let their radii be $r_{B}$ and $r_{C}$, and let $B C$ be tangent to the two circles at $T$ and $U$, respectively.  From the cyclic quadrilaterals $A F D C$ and $A B D E$ we have $$ \angle M D O_{B}=\frac{1}{2} \angle F D B=\frac{1}{2} \angle B A C=\frac{1}{2} \angle C D E=\angle O_{C} D N, $$ so the right-angled triangles $D M O_{B}$ and $D N O_{C}$ are similar. The ratio of similarity between the two triangles is $$ \frac{D N}{D M}=\frac{O_{C} N}{O_{B} M}=\frac{r_{C}}{r_{B}} . $$ Let $\varphi=\angle D M N$ and $\psi=\angle M N D$. The lines $F M$ and $E N$ are tangent to $\omega_{B}$ and $\omega_{C}$, respectively, so $$ \angle M T P=\angle F M P=\angle D M N=\varphi \quad \text { and } \quad \angle Q U N=\angle Q N E=\angle M N D=\psi $$ (It is possible that $P$ or $Q$ coincides with $T$ or $U$, or lie inside triangles $D M T$ or $D U N$, respectively. To reduce case-sensitivity, we may use directed angles or simply ignore angles $M T P$ and $Q U N$.) In the circles $\omega_{B}$ and $\omega_{C}$ the lengths of chords $M P$ and $N Q$ are $$ M P=2 r_{B} \cdot \sin \angle M T P=2 r_{B} \cdot \sin \varphi \quad \text { and } \quad N Q=2 r_{C} \cdot \sin \angle Q U N=2 r_{C} \cdot \sin \psi $$ By applying the sine rule to triangle $D N M$ we get $$ \frac{D N}{D M}=\frac{\sin \angle D M N}{\sin \angle M N D}=\frac{\sin \varphi}{\sin \psi} $$ Finally, putting the above observations together, we get $$ \frac{M P}{N Q}=\frac{2 r_{B} \sin \varphi}{2 r_{C} \sin \psi}=\frac{r_{B}}{r_{C}} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{D M}{D N} \cdot \frac{\sin \varphi}{\sin \psi}=\frac{\sin \psi}{\sin \varphi} \cdot \frac{\sin \varphi}{\sin \psi}=1, $$ so $M P=N Q$ as required.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
521563a8-2b34-5d9f-9188-0c9febfbebf1
| 23,873
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia) 
|
Since $$ \angle A P B+\angle B P C+\angle C P A=2 \pi=(\pi-\angle A C B)+(\pi-\angle B A C)+(\pi-\angle C B A), $$ at least one of the following inequalities holds: $$ \angle A P B \geqslant \pi-\angle A C B, \quad \angle B P C \geqslant \pi-\angle B A C, \quad \angle C P A \geqslant \pi-\angle C B A . $$ Without loss of generality, we assume that $\angle B P C \geqslant \pi-\angle B A C$. We have $\angle B P C>\angle B A C$ because $P$ is inside $\triangle A B C$. So $\angle B P C \geqslant \max (\angle B A C, \pi-\angle B A C)$ and hence $$ \sin \angle B P C \leqslant \sin \angle B A C . $$ Let the rays $A P, B P$, and $C P$ cross the circumcircle $\Omega$ again at $A_{3}, B_{3}$, and $C_{3}$, respectively. We will prove that at least one of the ratios $\frac{P B_{1}}{B_{1} B_{3}}$ and $\frac{P C_{1}}{C_{1} C_{3}}$ is at least 1 , which yields that one of the points $B_{2}$ and $C_{2}$ does not lie strictly inside $\Omega$. Because $A, B, C, B_{3}$ lie on a circle, the triangles $C B_{1} B_{3}$ and $B B_{1} A$ are similar, so $$ \frac{C B_{1}}{B_{1} B_{3}}=\frac{B B_{1}}{B_{1} A} $$ Applying the sine rule we obtain $$ \frac{P B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{C B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{B B_{1}}{B_{1} A}=\frac{\sin \angle A C P}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle P B A} . $$ Similarly, $$ \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin \angle P B A}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle A C P} $$ Multiplying these two equations we get $$ \frac{P B_{1}}{B_{1} B_{3}} \cdot \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin ^{2} \angle B A C}{\sin ^{2} \angle B P C} \geqslant 1 $$ using (*), which yields the desired conclusion. Comment. It also cannot happen that all three points $A_{2}, B_{2}$, and $C_{2}$ lie strictly outside $\Omega$. The same proof works almost literally, starting by assuming without loss of generality that $\angle B P C \leqslant \pi-\angle B A C$ and using $\angle B P C>\angle B A C$ to deduce that $\sin \angle B P C \geqslant \sin \angle B A C$. It is possible for $A_{2}, B_{2}$, and $C_{2}$ all to lie on the circumcircle; from the above solution we may derive that this happens if and only if $P$ is the orthocentre of the triangle $A B C$, (which lies strictly inside $A B C$ if and only if $A B C$ is acute).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia) 
|
Since $$ \angle A P B+\angle B P C+\angle C P A=2 \pi=(\pi-\angle A C B)+(\pi-\angle B A C)+(\pi-\angle C B A), $$ at least one of the following inequalities holds: $$ \angle A P B \geqslant \pi-\angle A C B, \quad \angle B P C \geqslant \pi-\angle B A C, \quad \angle C P A \geqslant \pi-\angle C B A . $$ Without loss of generality, we assume that $\angle B P C \geqslant \pi-\angle B A C$. We have $\angle B P C>\angle B A C$ because $P$ is inside $\triangle A B C$. So $\angle B P C \geqslant \max (\angle B A C, \pi-\angle B A C)$ and hence $$ \sin \angle B P C \leqslant \sin \angle B A C . $$ Let the rays $A P, B P$, and $C P$ cross the circumcircle $\Omega$ again at $A_{3}, B_{3}$, and $C_{3}$, respectively. We will prove that at least one of the ratios $\frac{P B_{1}}{B_{1} B_{3}}$ and $\frac{P C_{1}}{C_{1} C_{3}}$ is at least 1 , which yields that one of the points $B_{2}$ and $C_{2}$ does not lie strictly inside $\Omega$. Because $A, B, C, B_{3}$ lie on a circle, the triangles $C B_{1} B_{3}$ and $B B_{1} A$ are similar, so $$ \frac{C B_{1}}{B_{1} B_{3}}=\frac{B B_{1}}{B_{1} A} $$ Applying the sine rule we obtain $$ \frac{P B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{C B_{1}}{B_{1} B_{3}}=\frac{P B_{1}}{C B_{1}} \cdot \frac{B B_{1}}{B_{1} A}=\frac{\sin \angle A C P}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle P B A} . $$ Similarly, $$ \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin \angle P B A}{\sin \angle B P C} \cdot \frac{\sin \angle B A C}{\sin \angle A C P} $$ Multiplying these two equations we get $$ \frac{P B_{1}}{B_{1} B_{3}} \cdot \frac{P C_{1}}{C_{1} C_{3}}=\frac{\sin ^{2} \angle B A C}{\sin ^{2} \angle B P C} \geqslant 1 $$ using (*), which yields the desired conclusion. Comment. It also cannot happen that all three points $A_{2}, B_{2}$, and $C_{2}$ lie strictly outside $\Omega$. The same proof works almost literally, starting by assuming without loss of generality that $\angle B P C \leqslant \pi-\angle B A C$ and using $\angle B P C>\angle B A C$ to deduce that $\sin \angle B P C \geqslant \sin \angle B A C$. It is possible for $A_{2}, B_{2}$, and $C_{2}$ all to lie on the circumcircle; from the above solution we may derive that this happens if and only if $P$ is the orthocentre of the triangle $A B C$, (which lies strictly inside $A B C$ if and only if $A B C$ is acute).
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
640dc937-a8ef-5a11-86d9-5343e5c941ec
| 23,875
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia) 
|
Define points $A_{3}, B_{3}$, and $C_{3}$ as in Observe that $\triangle P B C_{3} \sim \triangle P C B_{3}$. Let $X$ be the point on side $P B_{3}$ that corresponds to point $C_{1}$ on side $P C_{3}$ under this similarity. In other words, $X$ lies on segment $P B_{3}$ and satisfies $P X: X B_{3}=P C_{1}: C_{1} C_{3}$. It follows that $$ \angle X C P=\angle P B C_{1}=\angle B_{3} B A=\angle B_{3} C B_{1} . $$ Hence lines $C X$ and $C B_{1}$ are isogonal conjugates in $\triangle P C B_{3}$.  Let $Y$ be the foot of the bisector of $\angle B_{3} C P$ in $\triangle P C B_{3}$. Since $P C_{1}<C_{1} C_{3}$, we have $P X<X B_{3}$. Also, we have $P Y<Y B_{3}$ because $P B_{1}<B_{1} B_{3}$ and $Y$ lies between $X$ and $B_{1}$. By the angle bisector theorem in $\triangle P C B_{3}$, we have $P Y: Y B_{3}=P C: C B_{3}$. So $P C<C B_{3}$ and it follows that $\angle P B_{3} C<\angle C P B_{3}$. Now since $\angle P B_{3} C=\angle B B_{3} C=\angle B A C$, we have $$ \angle B A C<\angle C P B_{3} . $$ Similarly, we have $$ \angle C B A<\angle A P C_{3} \text { and } \angle A C B<\angle B P A_{3}=\angle B_{3} P A . $$ Adding these three inequalities yields $\pi<\pi$, and this contradiction concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia) 
|
Define points $A_{3}, B_{3}$, and $C_{3}$ as in Observe that $\triangle P B C_{3} \sim \triangle P C B_{3}$. Let $X$ be the point on side $P B_{3}$ that corresponds to point $C_{1}$ on side $P C_{3}$ under this similarity. In other words, $X$ lies on segment $P B_{3}$ and satisfies $P X: X B_{3}=P C_{1}: C_{1} C_{3}$. It follows that $$ \angle X C P=\angle P B C_{1}=\angle B_{3} B A=\angle B_{3} C B_{1} . $$ Hence lines $C X$ and $C B_{1}$ are isogonal conjugates in $\triangle P C B_{3}$.  Let $Y$ be the foot of the bisector of $\angle B_{3} C P$ in $\triangle P C B_{3}$. Since $P C_{1}<C_{1} C_{3}$, we have $P X<X B_{3}$. Also, we have $P Y<Y B_{3}$ because $P B_{1}<B_{1} B_{3}$ and $Y$ lies between $X$ and $B_{1}$. By the angle bisector theorem in $\triangle P C B_{3}$, we have $P Y: Y B_{3}=P C: C B_{3}$. So $P C<C B_{3}$ and it follows that $\angle P B_{3} C<\angle C P B_{3}$. Now since $\angle P B_{3} C=\angle B B_{3} C=\angle B A C$, we have $$ \angle B A C<\angle C P B_{3} . $$ Similarly, we have $$ \angle C B A<\angle A P C_{3} \text { and } \angle A C B<\angle B P A_{3}=\angle B_{3} P A . $$ Adding these three inequalities yields $\pi<\pi$, and this contradiction concludes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
640dc937-a8ef-5a11-86d9-5343e5c941ec
| 23,875
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia) 
|
Choose coordinates such that the circumcentre of $\triangle A B C$ is at the origin and the circumradius is 1 . Then we may think of $A, B$, and $C$ as vectors in $\mathbb{R}^{2}$ such that $$ |A|^{2}=|B|^{2}=|C|^{2}=1 $$ $P$ may be represented as a convex combination $\alpha A+\beta B+\gamma C$ where $\alpha, \beta, \gamma>0$ and $\alpha+\beta+\gamma=1$. Then $$ A_{1}=\frac{\beta B+\gamma C}{\beta+\gamma}=\frac{1}{1-\alpha} P-\frac{\alpha}{1-\alpha} A, $$ so $$ A_{2}=2 A_{1}-P=\frac{1+\alpha}{1-\alpha} P-\frac{2 \alpha}{1-\alpha} A $$ Hence $$ \left|A_{2}\right|^{2}=\left(\frac{1+\alpha}{1-\alpha}\right)^{2}|P|^{2}+\left(\frac{2 \alpha}{1-\alpha}\right)^{2}|A|^{2}-\frac{4 \alpha(1+\alpha)}{(1-\alpha)^{2}} A \cdot P $$ Using $|A|^{2}=1$ we obtain $$ \frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}=\frac{1+\alpha}{2}|P|^{2}+\frac{2 \alpha^{2}}{1+\alpha}-2 \alpha A \cdot P $$ Likewise $$ \frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}=\frac{1+\beta}{2}|P|^{2}+\frac{2 \beta^{2}}{1+\beta}-2 \beta B \cdot P $$ and $$ \frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2}=\frac{1+\gamma}{2}|P|^{2}+\frac{2 \gamma^{2}}{1+\gamma}-2 \gamma C \cdot P $$ Summing (1), (2) and (3) we obtain on the LHS the positive linear combination $$ \text { LHS }=\frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2} $$ and on the RHS the quantity $$ \left(\frac{1+\alpha}{2}+\frac{1+\beta}{2}+\frac{1+\gamma}{2}\right)|P|^{2}+\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right)-2(\alpha A \cdot P+\beta B \cdot P+\gamma C \cdot P) . $$ The first term is $2|P|^{2}$ and the last term is $-2 P \cdot P$, so $$ \begin{aligned} \text { RHS } & =\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right) \\ & =\frac{3 \alpha-1}{2}+\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{3 \beta-1}{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{3 \gamma-1}{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \\ & =\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \end{aligned} $$ Here we used the fact that $$ \frac{3 \alpha-1}{2}+\frac{3 \beta-1}{2}+\frac{3 \gamma-1}{2}=0 . $$ We have shown that a linear combination of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ with positive coefficients is equal to the sum of the coefficients. Therefore at least one of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ must be at least 1 , as required. Comment. This proof also works when $P$ is any point for which $\alpha, \beta, \gamma>-1, \alpha+\beta+\gamma=1$, and $\alpha, \beta, \gamma \neq 1$. (In any cases where $\alpha=1$ or $\beta=1$ or $\gamma=1$, some points in the construction are not defined.) This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside triangle $A B C$. Let $A P$ meet $B C$ at $A_{1}$, let $B P$ meet $C A$ at $B_{1}$, and let $C P$ meet $A B$ at $C_{1}$. Let $A_{2}$ be the point such that $A_{1}$ is the midpoint of $P A_{2}$, let $B_{2}$ be the point such that $B_{1}$ is the midpoint of $P B_{2}$, and let $C_{2}$ be the point such that $C_{1}$ is the midpoint of $P C_{2}$. Prove that points $A_{2}, B_{2}$, and $C_{2}$ cannot all lie strictly inside the circumcircle of triangle $A B C$. (Australia) 
|
Choose coordinates such that the circumcentre of $\triangle A B C$ is at the origin and the circumradius is 1 . Then we may think of $A, B$, and $C$ as vectors in $\mathbb{R}^{2}$ such that $$ |A|^{2}=|B|^{2}=|C|^{2}=1 $$ $P$ may be represented as a convex combination $\alpha A+\beta B+\gamma C$ where $\alpha, \beta, \gamma>0$ and $\alpha+\beta+\gamma=1$. Then $$ A_{1}=\frac{\beta B+\gamma C}{\beta+\gamma}=\frac{1}{1-\alpha} P-\frac{\alpha}{1-\alpha} A, $$ so $$ A_{2}=2 A_{1}-P=\frac{1+\alpha}{1-\alpha} P-\frac{2 \alpha}{1-\alpha} A $$ Hence $$ \left|A_{2}\right|^{2}=\left(\frac{1+\alpha}{1-\alpha}\right)^{2}|P|^{2}+\left(\frac{2 \alpha}{1-\alpha}\right)^{2}|A|^{2}-\frac{4 \alpha(1+\alpha)}{(1-\alpha)^{2}} A \cdot P $$ Using $|A|^{2}=1$ we obtain $$ \frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}=\frac{1+\alpha}{2}|P|^{2}+\frac{2 \alpha^{2}}{1+\alpha}-2 \alpha A \cdot P $$ Likewise $$ \frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}=\frac{1+\beta}{2}|P|^{2}+\frac{2 \beta^{2}}{1+\beta}-2 \beta B \cdot P $$ and $$ \frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2}=\frac{1+\gamma}{2}|P|^{2}+\frac{2 \gamma^{2}}{1+\gamma}-2 \gamma C \cdot P $$ Summing (1), (2) and (3) we obtain on the LHS the positive linear combination $$ \text { LHS }=\frac{(1-\alpha)^{2}}{2(1+\alpha)}\left|A_{2}\right|^{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}\left|B_{2}\right|^{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)}\left|C_{2}\right|^{2} $$ and on the RHS the quantity $$ \left(\frac{1+\alpha}{2}+\frac{1+\beta}{2}+\frac{1+\gamma}{2}\right)|P|^{2}+\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right)-2(\alpha A \cdot P+\beta B \cdot P+\gamma C \cdot P) . $$ The first term is $2|P|^{2}$ and the last term is $-2 P \cdot P$, so $$ \begin{aligned} \text { RHS } & =\left(\frac{2 \alpha^{2}}{1+\alpha}+\frac{2 \beta^{2}}{1+\beta}+\frac{2 \gamma^{2}}{1+\gamma}\right) \\ & =\frac{3 \alpha-1}{2}+\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{3 \beta-1}{2}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{3 \gamma-1}{2}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \\ & =\frac{(1-\alpha)^{2}}{2(1+\alpha)}+\frac{(1-\beta)^{2}}{2(1+\beta)}+\frac{(1-\gamma)^{2}}{2(1+\gamma)} \end{aligned} $$ Here we used the fact that $$ \frac{3 \alpha-1}{2}+\frac{3 \beta-1}{2}+\frac{3 \gamma-1}{2}=0 . $$ We have shown that a linear combination of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ with positive coefficients is equal to the sum of the coefficients. Therefore at least one of $\left|A_{1}\right|^{2},\left|B_{1}\right|^{2}$, and $\left|C_{1}\right|^{2}$ must be at least 1 , as required. Comment. This proof also works when $P$ is any point for which $\alpha, \beta, \gamma>-1, \alpha+\beta+\gamma=1$, and $\alpha, \beta, \gamma \neq 1$. (In any cases where $\alpha=1$ or $\beta=1$ or $\gamma=1$, some points in the construction are not defined.) This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
640dc937-a8ef-5a11-86d9-5343e5c941ec
| 23,875
|
Let $A B C D E$ be a convex pentagon with $C D=D E$ and $\angle E D C \neq 2 \cdot \angle A D B$. Suppose that a point $P$ is located in the interior of the pentagon such that $A P=A E$ and $B P=B C$. Prove that $P$ lies on the diagonal $C E$ if and only if area $(B C D)+\operatorname{area}(A D E)=$ $\operatorname{area}(A B D)+\operatorname{area}(A B P)$. (Hungary)
|
Let $P^{\prime}$ be the reflection of $P$ across line $A B$, and let $M$ and $N$ be the midpoints of $P^{\prime} E$ and $P^{\prime} C$ respectively. Convexity ensures that $P^{\prime}$ is distinct from both $E$ and $C$, and hence from both $M$ and $N$. We claim that both the area condition and the collinearity condition in the problem are equivalent to the condition that the (possibly degenerate) right-angled triangles $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar (equivalently, $A P^{\prime} E$ and $B P^{\prime} C$ are directly similar).  For the equivalence with the collinearity condition, let $F$ denote the foot of the perpendicular from $P^{\prime}$ to $A B$, so that $F$ is the midpoint of $P P^{\prime}$. We have that $P$ lies on $C E$ if and only if $F$ lies on $M N$, which occurs if and only if we have the equality $\angle A F M=\angle B F N$ of signed angles modulo $\pi$. By concyclicity of $A P^{\prime} F M$ and $B F P^{\prime} N$, this is equivalent to $\angle A P^{\prime} M=\angle B P^{\prime} N$, which occurs if and only if $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar.  For the other equivalence with the area condition, we have the equality of signed areas $\operatorname{area}(A B D)+\operatorname{area}(A B P)=\operatorname{area}\left(A P^{\prime} B D\right)=\operatorname{area}\left(A P^{\prime} D\right)+\operatorname{area}\left(B D P^{\prime}\right)$. Using the identity $\operatorname{area}(A D E)-\operatorname{area}\left(A P^{\prime} D\right)=\operatorname{area}(A D E)+\operatorname{area}\left(A D P^{\prime}\right)=2$ area $(A D M)$, and similarly for $B$, we find that the area condition is equivalent to the equality $$ \operatorname{area}(D A M)=\operatorname{area}(D B N) . $$ Now note that $A$ and $B$ lie on the perpendicular bisectors of $P^{\prime} E$ and $P^{\prime} C$, respectively. If we write $G$ and $H$ for the feet of the perpendiculars from $D$ to these perpendicular bisectors respectively, then this area condition can be rewritten as $$ M A \cdot G D=N B \cdot H D $$ (In this condition, we interpret all lengths as signed lengths according to suitable conventions: for instance, we orient $P^{\prime} E$ from $P^{\prime}$ to $E$, orient the parallel line $D H$ in the same direction, and orient the perpendicular bisector of $P^{\prime} E$ at an angle $\pi / 2$ clockwise from the oriented segment $P^{\prime} E$ - we adopt the analogous conventions at $B$.)  To relate the signed lengths $G D$ and $H D$ to the triangles $A P^{\prime} M$ and $B P^{\prime} N$, we use the following calculation. Claim. Let $\Gamma$ denote the circle centred on $D$ with both $E$ and $C$ on the circumference, and $h$ the power of $P^{\prime}$ with respect to $\Gamma$. Then we have the equality $$ G D \cdot P^{\prime} M=H D \cdot P^{\prime} N=\frac{1}{4} h \neq 0 . $$ Proof. Firstly, we have $h \neq 0$, since otherwise $P^{\prime}$ would lie on $\Gamma$, and hence the internal angle bisectors of $\angle E D P^{\prime}$ and $\angle P^{\prime} D C$ would pass through $A$ and $B$ respectively. This would violate the angle inequality $\angle E D C \neq 2 \cdot \angle A D B$ given in the question. Next, let $E^{\prime}$ denote the second point of intersection of $P^{\prime} E$ with $\Gamma$, and let $E^{\prime \prime}$ denote the point on $\Gamma$ diametrically opposite $E^{\prime}$, so that $E^{\prime \prime} E$ is perpendicular to $P^{\prime} E$. The point $G$ lies on the perpendicular bisectors of the sides $P^{\prime} E$ and $E E^{\prime \prime}$ of the right-angled triangle $P^{\prime} E E^{\prime \prime}$; it follows that $G$ is the midpoint of $P^{\prime} E^{\prime \prime}$. Since $D$ is the midpoint of $E^{\prime} E^{\prime \prime}$, we have that $G D=\frac{1}{2} P^{\prime} E^{\prime}$. Since $P^{\prime} M=\frac{1}{2} P^{\prime} E$, we have $G D \cdot P^{\prime} M=\frac{1}{4} P^{\prime} E^{\prime} \cdot P^{\prime} E=\frac{1}{4} h$. The other equality $H D \cdot P^{\prime} N$ follows by exactly the same argument.  From this claim, we see that the area condition is equivalent to the equality $$ \left(M A: P^{\prime} M\right)=\left(N B: P^{\prime} N\right) $$ of ratios of signed lengths, which is equivalent to direct similarity of $A P^{\prime} M$ and $B P^{\prime} N$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon with $C D=D E$ and $\angle E D C \neq 2 \cdot \angle A D B$. Suppose that a point $P$ is located in the interior of the pentagon such that $A P=A E$ and $B P=B C$. Prove that $P$ lies on the diagonal $C E$ if and only if area $(B C D)+\operatorname{area}(A D E)=$ $\operatorname{area}(A B D)+\operatorname{area}(A B P)$. (Hungary)
|
Let $P^{\prime}$ be the reflection of $P$ across line $A B$, and let $M$ and $N$ be the midpoints of $P^{\prime} E$ and $P^{\prime} C$ respectively. Convexity ensures that $P^{\prime}$ is distinct from both $E$ and $C$, and hence from both $M$ and $N$. We claim that both the area condition and the collinearity condition in the problem are equivalent to the condition that the (possibly degenerate) right-angled triangles $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar (equivalently, $A P^{\prime} E$ and $B P^{\prime} C$ are directly similar).  For the equivalence with the collinearity condition, let $F$ denote the foot of the perpendicular from $P^{\prime}$ to $A B$, so that $F$ is the midpoint of $P P^{\prime}$. We have that $P$ lies on $C E$ if and only if $F$ lies on $M N$, which occurs if and only if we have the equality $\angle A F M=\angle B F N$ of signed angles modulo $\pi$. By concyclicity of $A P^{\prime} F M$ and $B F P^{\prime} N$, this is equivalent to $\angle A P^{\prime} M=\angle B P^{\prime} N$, which occurs if and only if $A P^{\prime} M$ and $B P^{\prime} N$ are directly similar.  For the other equivalence with the area condition, we have the equality of signed areas $\operatorname{area}(A B D)+\operatorname{area}(A B P)=\operatorname{area}\left(A P^{\prime} B D\right)=\operatorname{area}\left(A P^{\prime} D\right)+\operatorname{area}\left(B D P^{\prime}\right)$. Using the identity $\operatorname{area}(A D E)-\operatorname{area}\left(A P^{\prime} D\right)=\operatorname{area}(A D E)+\operatorname{area}\left(A D P^{\prime}\right)=2$ area $(A D M)$, and similarly for $B$, we find that the area condition is equivalent to the equality $$ \operatorname{area}(D A M)=\operatorname{area}(D B N) . $$ Now note that $A$ and $B$ lie on the perpendicular bisectors of $P^{\prime} E$ and $P^{\prime} C$, respectively. If we write $G$ and $H$ for the feet of the perpendiculars from $D$ to these perpendicular bisectors respectively, then this area condition can be rewritten as $$ M A \cdot G D=N B \cdot H D $$ (In this condition, we interpret all lengths as signed lengths according to suitable conventions: for instance, we orient $P^{\prime} E$ from $P^{\prime}$ to $E$, orient the parallel line $D H$ in the same direction, and orient the perpendicular bisector of $P^{\prime} E$ at an angle $\pi / 2$ clockwise from the oriented segment $P^{\prime} E$ - we adopt the analogous conventions at $B$.)  To relate the signed lengths $G D$ and $H D$ to the triangles $A P^{\prime} M$ and $B P^{\prime} N$, we use the following calculation. Claim. Let $\Gamma$ denote the circle centred on $D$ with both $E$ and $C$ on the circumference, and $h$ the power of $P^{\prime}$ with respect to $\Gamma$. Then we have the equality $$ G D \cdot P^{\prime} M=H D \cdot P^{\prime} N=\frac{1}{4} h \neq 0 . $$ Proof. Firstly, we have $h \neq 0$, since otherwise $P^{\prime}$ would lie on $\Gamma$, and hence the internal angle bisectors of $\angle E D P^{\prime}$ and $\angle P^{\prime} D C$ would pass through $A$ and $B$ respectively. This would violate the angle inequality $\angle E D C \neq 2 \cdot \angle A D B$ given in the question. Next, let $E^{\prime}$ denote the second point of intersection of $P^{\prime} E$ with $\Gamma$, and let $E^{\prime \prime}$ denote the point on $\Gamma$ diametrically opposite $E^{\prime}$, so that $E^{\prime \prime} E$ is perpendicular to $P^{\prime} E$. The point $G$ lies on the perpendicular bisectors of the sides $P^{\prime} E$ and $E E^{\prime \prime}$ of the right-angled triangle $P^{\prime} E E^{\prime \prime}$; it follows that $G$ is the midpoint of $P^{\prime} E^{\prime \prime}$. Since $D$ is the midpoint of $E^{\prime} E^{\prime \prime}$, we have that $G D=\frac{1}{2} P^{\prime} E^{\prime}$. Since $P^{\prime} M=\frac{1}{2} P^{\prime} E$, we have $G D \cdot P^{\prime} M=\frac{1}{4} P^{\prime} E^{\prime} \cdot P^{\prime} E=\frac{1}{4} h$. The other equality $H D \cdot P^{\prime} N$ follows by exactly the same argument.  From this claim, we see that the area condition is equivalent to the equality $$ \left(M A: P^{\prime} M\right)=\left(N B: P^{\prime} N\right) $$ of ratios of signed lengths, which is equivalent to direct similarity of $A P^{\prime} M$ and $B P^{\prime} N$, as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a4ff220-8089-5716-98a3-59701a5b8378
| 23,880
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Let $N$ and $M$ be the midpoints of the arcs $\widehat{B C}$ of the circumcircle, containing and opposite vertex $A$, respectively. By $\angle F A E=\angle B A C=\angle B N C$, the right-angled kites $A F I E$ and $N B M C$ are similar. Consider the spiral similarity $\varphi$ (dilation in case of $A B=A C$ ) that moves $A F I E$ to $N B M C$. The directed angle in which $\varphi$ changes directions is $\angle(A F, N B)$, same as $\angle(A P, N P)$ and $\angle(A Q, N Q)$; so lines $A P$ and $A Q$ are mapped to lines $N P$ and $N Q$, respectively. Line $E F$ is mapped to $B C$; we can see that the intersection points $P=E F \cap A P$ and $Q=E F \cap A Q$ are mapped to points $B C \cap N P$ and $B C \cap N Q$, respectively. Denote these points by $P^{\prime}$ and $Q^{\prime}$, respectively.  Let $L$ be the midpoint of $B C$. We claim that points $P, Q, D, L$ are concyclic (if $D=L$ then line $B C$ is tangent to circle $P Q D$ ). Let $P Q$ and $B C$ meet at $Z$. By applying Menelaus' theorem to triangle $A B C$ and line $E F Z$, we have $$ \frac{B D}{D C}=\frac{B F}{F A} \cdot \frac{A E}{E C}=-\frac{B Z}{Z C}, $$ so the pairs $B, C$ and $D, Z$ are harmonic. It is well-known that this implies $Z B \cdot Z C=Z D \cdot Z L$. (The inversion with pole $Z$ that swaps $B$ and $C$ sends $Z$ to infinity and $D$ to the midpoint of $B C$, because the cross-ratio is preserved.) Hence, $Z D \cdot Z L=Z B \cdot Z C=Z P \cdot Z Q$ by the power of $Z$ with respect to the circumcircle; this proves our claim. By $\angle M P P^{\prime}=\angle M Q Q^{\prime}=\angle M L P^{\prime}=\angle M L Q^{\prime}=90^{\circ}$, the quadrilaterals $M L P P^{\prime}$ and $M L Q Q^{\prime}$ are cyclic. Then the problem statement follows by $$ \begin{aligned} \angle D P A+\angle A Q D & =360^{\circ}-\angle P A Q-\angle Q D P=360^{\circ}-\angle P N Q-\angle Q L P \\ & =\angle L P N+\angle N Q L=\angle P^{\prime} M L+\angle L M Q^{\prime}=\angle P^{\prime} M Q^{\prime}=\angle P I Q . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Let $N$ and $M$ be the midpoints of the arcs $\widehat{B C}$ of the circumcircle, containing and opposite vertex $A$, respectively. By $\angle F A E=\angle B A C=\angle B N C$, the right-angled kites $A F I E$ and $N B M C$ are similar. Consider the spiral similarity $\varphi$ (dilation in case of $A B=A C$ ) that moves $A F I E$ to $N B M C$. The directed angle in which $\varphi$ changes directions is $\angle(A F, N B)$, same as $\angle(A P, N P)$ and $\angle(A Q, N Q)$; so lines $A P$ and $A Q$ are mapped to lines $N P$ and $N Q$, respectively. Line $E F$ is mapped to $B C$; we can see that the intersection points $P=E F \cap A P$ and $Q=E F \cap A Q$ are mapped to points $B C \cap N P$ and $B C \cap N Q$, respectively. Denote these points by $P^{\prime}$ and $Q^{\prime}$, respectively.  Let $L$ be the midpoint of $B C$. We claim that points $P, Q, D, L$ are concyclic (if $D=L$ then line $B C$ is tangent to circle $P Q D$ ). Let $P Q$ and $B C$ meet at $Z$. By applying Menelaus' theorem to triangle $A B C$ and line $E F Z$, we have $$ \frac{B D}{D C}=\frac{B F}{F A} \cdot \frac{A E}{E C}=-\frac{B Z}{Z C}, $$ so the pairs $B, C$ and $D, Z$ are harmonic. It is well-known that this implies $Z B \cdot Z C=Z D \cdot Z L$. (The inversion with pole $Z$ that swaps $B$ and $C$ sends $Z$ to infinity and $D$ to the midpoint of $B C$, because the cross-ratio is preserved.) Hence, $Z D \cdot Z L=Z B \cdot Z C=Z P \cdot Z Q$ by the power of $Z$ with respect to the circumcircle; this proves our claim. By $\angle M P P^{\prime}=\angle M Q Q^{\prime}=\angle M L P^{\prime}=\angle M L Q^{\prime}=90^{\circ}$, the quadrilaterals $M L P P^{\prime}$ and $M L Q Q^{\prime}$ are cyclic. Then the problem statement follows by $$ \begin{aligned} \angle D P A+\angle A Q D & =360^{\circ}-\angle P A Q-\angle Q D P=360^{\circ}-\angle P N Q-\angle Q L P \\ & =\angle L P N+\angle N Q L=\angle P^{\prime} M L+\angle L M Q^{\prime}=\angle P^{\prime} M Q^{\prime}=\angle P I Q . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3f81144d-aba6-5012-9517-2538043c18d3
| 23,884
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Define the point $M$ and the same spiral similarity $\varphi$ as in the previous solution. (The point $N$ is not necessary.) It is well-known that the centre of the spiral similarity that maps $F, E$ to $B, C$ is the Miquel point of the lines $F E, B C, B F$ and $C E$; that is, the second intersection of circles $A B C$ and $A E F$. Denote that point by $S$. By $\varphi(F)=B$ and $\varphi(E)=C$ the triangles $S B F$ and $S C E$ are similar, so we have $$ \frac{S B}{S C}=\frac{B F}{C E}=\frac{B D}{C D} $$ By the converse of the angle bisector theorem, that indicates that line $S D$ bisects $\angle B S C$ and hence passes through $M$. Let $K$ be the intersection point of lines $E F$ and $S I$. Notice that $\varphi$ sends points $S, F, E, I$ to $S, B, C, M$, so $\varphi(K)=\varphi(F E \cap S I)=B C \cap S M=D$. By $\varphi(I)=M$, we have $K D \| I M$.  We claim that triangles $S P I$ and $S D Q$ are similar, and so are triangles $S P D$ and $S I Q$. Let ray $S I$ meet the circumcircle again at $L$. Note that the segment $E F$ is perpendicular to the angle bisector $A M$. Then by $\angle A M L=\angle A S L=\angle A S I=90^{\circ}$, we have $M L \| P Q$. Hence, $\widetilde{P L}=\widetilde{M Q}$ and therefore $\angle P S L=\angle M S Q=\angle D S Q$. By $\angle Q P S=\angle Q M S$, the triangles $S P K$ and $S M Q$ are similar. Finally, $$ \frac{S P}{S I}=\frac{S P}{S K} \cdot \frac{S K}{S I}=\frac{S M}{S Q} \cdot \frac{S D}{S M}=\frac{S D}{S Q} $$ shows that triangles $S P I$ and $S D Q$ are similar. The second part of the claim can be proved analogously. Now the problem statement can be proved by $$ \angle D P A+\angle A Q D=\angle D P S+\angle S Q D=\angle Q I S+\angle S I P=\angle Q I P . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Define the point $M$ and the same spiral similarity $\varphi$ as in the previous solution. (The point $N$ is not necessary.) It is well-known that the centre of the spiral similarity that maps $F, E$ to $B, C$ is the Miquel point of the lines $F E, B C, B F$ and $C E$; that is, the second intersection of circles $A B C$ and $A E F$. Denote that point by $S$. By $\varphi(F)=B$ and $\varphi(E)=C$ the triangles $S B F$ and $S C E$ are similar, so we have $$ \frac{S B}{S C}=\frac{B F}{C E}=\frac{B D}{C D} $$ By the converse of the angle bisector theorem, that indicates that line $S D$ bisects $\angle B S C$ and hence passes through $M$. Let $K$ be the intersection point of lines $E F$ and $S I$. Notice that $\varphi$ sends points $S, F, E, I$ to $S, B, C, M$, so $\varphi(K)=\varphi(F E \cap S I)=B C \cap S M=D$. By $\varphi(I)=M$, we have $K D \| I M$.  We claim that triangles $S P I$ and $S D Q$ are similar, and so are triangles $S P D$ and $S I Q$. Let ray $S I$ meet the circumcircle again at $L$. Note that the segment $E F$ is perpendicular to the angle bisector $A M$. Then by $\angle A M L=\angle A S L=\angle A S I=90^{\circ}$, we have $M L \| P Q$. Hence, $\widetilde{P L}=\widetilde{M Q}$ and therefore $\angle P S L=\angle M S Q=\angle D S Q$. By $\angle Q P S=\angle Q M S$, the triangles $S P K$ and $S M Q$ are similar. Finally, $$ \frac{S P}{S I}=\frac{S P}{S K} \cdot \frac{S K}{S I}=\frac{S M}{S Q} \cdot \frac{S D}{S M}=\frac{S D}{S Q} $$ shows that triangles $S P I$ and $S D Q$ are similar. The second part of the claim can be proved analogously. Now the problem statement can be proved by $$ \angle D P A+\angle A Q D=\angle D P S+\angle S Q D=\angle Q I S+\angle S I P=\angle Q I P . $$
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3f81144d-aba6-5012-9517-2538043c18d3
| 23,884
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Denote the circumcircle of triangle $A B C$ by $\Gamma$, and let rays $P D$ and $Q D$ meet $\Gamma$ again at $V$ and $U$, respectively. We will show that $A U \perp I P$ and $A V \perp I Q$. Then the problem statement will follow as $$ \angle D P A+\angle A Q D=\angle V U A+\angle A V U=180^{\circ}-\angle U A V=\angle Q I P . $$ Let $M$ be the midpoint of arc $\widehat{B U V C}$ and let $N$ be the midpoint of arc $\widehat{C A B}$; the lines $A I M$ and $A N$ being the internal and external bisectors of angle $B A C$, respectively, are perpendicular. Let the tangents drawn to $\Gamma$ at $B$ and $C$ meet at $R$; let line $P Q$ meet $A U, A I, A V$ and $B C$ at $X, T, Y$ and $Z$, respectively. As in Solution 1, we observe that the pairs $B, C$ and $D, Z$ are harmonic. Projecting these points from $Q$ onto the circumcircle, we can see that $B, C$ and $U, P$ are also harmonic. Analogously, the pair $V, Q$ is harmonic with $B, C$. Consider the inversion about the circle with centre $R$, passing through $B$ and $C$. Points $B$ and $C$ are fixed points, so this inversion exchanges every point of $\Gamma$ by its harmonic pair with respect to $B, C$. In particular, the inversion maps points $B, C, N, U, V$ to points $B, C, M, P, Q$, respectively. Combine the inversion with projecting $\Gamma$ from $A$ to line $P Q$; the points $B, C, M, P, Q$ are projected to $F, E, T, P, Q$, respectively.  The combination of these two transformations is projective map from the lines $A B, A C$, $A N, A U, A V$ to $I F, I E, I T, I P, I Q$, respectively. On the other hand, we have $A B \perp I F$, $A C \perp I E$ and $A N \perp A T$, so the corresponding lines in these two pencils are perpendicular. This proves $A U \perp I P$ and $A V \perp I Q$, and hence completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of acute-angled triangle $A B C$. Let the incircle meet $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let line $E F$ intersect the circumcircle of the triangle at $P$ and $Q$, such that $F$ lies between $E$ and $P$. Prove that $\angle D P A+\angle A Q D=\angle Q I P$. (Slovakia)
|
Denote the circumcircle of triangle $A B C$ by $\Gamma$, and let rays $P D$ and $Q D$ meet $\Gamma$ again at $V$ and $U$, respectively. We will show that $A U \perp I P$ and $A V \perp I Q$. Then the problem statement will follow as $$ \angle D P A+\angle A Q D=\angle V U A+\angle A V U=180^{\circ}-\angle U A V=\angle Q I P . $$ Let $M$ be the midpoint of arc $\widehat{B U V C}$ and let $N$ be the midpoint of arc $\widehat{C A B}$; the lines $A I M$ and $A N$ being the internal and external bisectors of angle $B A C$, respectively, are perpendicular. Let the tangents drawn to $\Gamma$ at $B$ and $C$ meet at $R$; let line $P Q$ meet $A U, A I, A V$ and $B C$ at $X, T, Y$ and $Z$, respectively. As in Solution 1, we observe that the pairs $B, C$ and $D, Z$ are harmonic. Projecting these points from $Q$ onto the circumcircle, we can see that $B, C$ and $U, P$ are also harmonic. Analogously, the pair $V, Q$ is harmonic with $B, C$. Consider the inversion about the circle with centre $R$, passing through $B$ and $C$. Points $B$ and $C$ are fixed points, so this inversion exchanges every point of $\Gamma$ by its harmonic pair with respect to $B, C$. In particular, the inversion maps points $B, C, N, U, V$ to points $B, C, M, P, Q$, respectively. Combine the inversion with projecting $\Gamma$ from $A$ to line $P Q$; the points $B, C, M, P, Q$ are projected to $F, E, T, P, Q$, respectively.  The combination of these two transformations is projective map from the lines $A B, A C$, $A N, A U, A V$ to $I F, I E, I T, I P, I Q$, respectively. On the other hand, we have $A B \perp I F$, $A C \perp I E$ and $A N \perp A T$, so the corresponding lines in these two pencils are perpendicular. This proves $A U \perp I P$ and $A V \perp I Q$, and hence completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3f81144d-aba6-5012-9517-2538043c18d3
| 23,884
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India) Common remarks. Throughout the solution, $\angle(a, b)$ denotes the directed angle between lines $a$ and $b$, measured modulo $\pi$.
|
Step 1. The external bisector of $\angle B A C$ is the line through $A$ perpendicular to $I A$. Let $D I$ meet this line at $L$ and let $D I$ meet $\omega$ at $K$. Let $N$ be the midpoint of $E F$, which lies on $I A$ and is the pole of line $A L$ with respect to $\omega$. Since $A N \cdot A I=A E^{2}=A R \cdot A P$, the points $R$, $N, I$, and $P$ are concyclic. As $I R=I P$, the line $N I$ is the external bisector of $\angle P N R$, so $P N$ meets $\omega$ again at the point symmetric to $R$ with respect to $A N-i . e$ at $K$. Let $D N$ cross $\omega$ again at $S$. Opposite sides of any quadrilateral inscribed in the circle $\omega$ meet on the polar line of the intersection of the diagonals with respect to $\omega$. Since $L$ lies on the polar line $A L$ of $N$ with respect to $\omega$, the line $P S$ must pass through $L$. Thus it suffices to prove that the points $S, Q$, and $P$ are collinear.  Step 2. Let $\Gamma$ be the circumcircle of $\triangle B I C$. Notice that $$ \begin{aligned} & \angle(B Q, Q C)=\angle(B Q, Q P)+\angle(P Q, Q C)=\angle(B F, F P)+\angle(P E, E C) \\ &=\angle(E F, E P)+\angle(F P, F E)=\angle(F P, E P)=\angle(D F, D E)=\angle(B I, I C) \end{aligned} $$ so $Q$ lies on $\Gamma$. Let $Q P$ meet $\Gamma$ again at $T$. It will now suffice to prove that $S, P$, and $T$ are collinear. Notice that $\angle(B I, I T)=\angle(B Q, Q T)=\angle(B F, F P)=\angle(F K, K P)$. Note $F D \perp F K$ and $F D \perp B I$ so $F K \| B I$ and hence $I T$ is parallel to the line $K N P$. Since $D I=I K$, the line $I T$ crosses $D N$ at its midpoint $M$. Step 3. Let $F^{\prime}$ and $E^{\prime}$ be the midpoints of $D E$ and $D F$, respectively. Since $D E^{\prime} \cdot E^{\prime} F=D E^{\prime 2}=$ $B E^{\prime} \cdot E^{\prime} I$, the point $E^{\prime}$ lies on the radical axis of $\omega$ and $\Gamma$; the same holds for $F^{\prime}$. Therefore, this radical axis is $E^{\prime} F^{\prime}$, and it passes through $M$. Thus $I M \cdot M T=D M \cdot M S$, so $S, I, D$, and $T$ are concyclic. This shows $\angle(D S, S T)=\angle(D I, I T)=\angle(D K, K P)=\angle(D S, S P)$, whence the points $S, P$, and $T$ are collinear, as desired.  Comment. Here is a longer alternative proof in step 1 that $P, S$, and $L$ are collinear, using a circular inversion instead of the fact that opposite sides of a quadrilateral inscribed in a circle $\omega$ meet on the polar line with respect to $\omega$ of the intersection of the diagonals. Let $G$ be the foot of the altitude from $N$ to the line $D I K L$. Observe that $N, G, K, S$ are concyclic (opposite right angles) so $$ \angle D I P=2 \angle D K P=\angle G K N+\angle D S P=\angle G S N+\angle N S P=\angle G S P, $$ hence $I, G, S, P$ are concyclic. We have $I G \cdot I L=I N \cdot I A=r^{2}$ since $\triangle I G N \sim \triangle I A L$. Inverting the circle $I G S P$ in circle $\omega$, points $P$ and $S$ are fixed and $G$ is taken to $L$ so we find that $P, S$, and $L$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India) Common remarks. Throughout the solution, $\angle(a, b)$ denotes the directed angle between lines $a$ and $b$, measured modulo $\pi$.
|
Step 1. The external bisector of $\angle B A C$ is the line through $A$ perpendicular to $I A$. Let $D I$ meet this line at $L$ and let $D I$ meet $\omega$ at $K$. Let $N$ be the midpoint of $E F$, which lies on $I A$ and is the pole of line $A L$ with respect to $\omega$. Since $A N \cdot A I=A E^{2}=A R \cdot A P$, the points $R$, $N, I$, and $P$ are concyclic. As $I R=I P$, the line $N I$ is the external bisector of $\angle P N R$, so $P N$ meets $\omega$ again at the point symmetric to $R$ with respect to $A N-i . e$ at $K$. Let $D N$ cross $\omega$ again at $S$. Opposite sides of any quadrilateral inscribed in the circle $\omega$ meet on the polar line of the intersection of the diagonals with respect to $\omega$. Since $L$ lies on the polar line $A L$ of $N$ with respect to $\omega$, the line $P S$ must pass through $L$. Thus it suffices to prove that the points $S, Q$, and $P$ are collinear.  Step 2. Let $\Gamma$ be the circumcircle of $\triangle B I C$. Notice that $$ \begin{aligned} & \angle(B Q, Q C)=\angle(B Q, Q P)+\angle(P Q, Q C)=\angle(B F, F P)+\angle(P E, E C) \\ &=\angle(E F, E P)+\angle(F P, F E)=\angle(F P, E P)=\angle(D F, D E)=\angle(B I, I C) \end{aligned} $$ so $Q$ lies on $\Gamma$. Let $Q P$ meet $\Gamma$ again at $T$. It will now suffice to prove that $S, P$, and $T$ are collinear. Notice that $\angle(B I, I T)=\angle(B Q, Q T)=\angle(B F, F P)=\angle(F K, K P)$. Note $F D \perp F K$ and $F D \perp B I$ so $F K \| B I$ and hence $I T$ is parallel to the line $K N P$. Since $D I=I K$, the line $I T$ crosses $D N$ at its midpoint $M$. Step 3. Let $F^{\prime}$ and $E^{\prime}$ be the midpoints of $D E$ and $D F$, respectively. Since $D E^{\prime} \cdot E^{\prime} F=D E^{\prime 2}=$ $B E^{\prime} \cdot E^{\prime} I$, the point $E^{\prime}$ lies on the radical axis of $\omega$ and $\Gamma$; the same holds for $F^{\prime}$. Therefore, this radical axis is $E^{\prime} F^{\prime}$, and it passes through $M$. Thus $I M \cdot M T=D M \cdot M S$, so $S, I, D$, and $T$ are concyclic. This shows $\angle(D S, S T)=\angle(D I, I T)=\angle(D K, K P)=\angle(D S, S P)$, whence the points $S, P$, and $T$ are collinear, as desired.  Comment. Here is a longer alternative proof in step 1 that $P, S$, and $L$ are collinear, using a circular inversion instead of the fact that opposite sides of a quadrilateral inscribed in a circle $\omega$ meet on the polar line with respect to $\omega$ of the intersection of the diagonals. Let $G$ be the foot of the altitude from $N$ to the line $D I K L$. Observe that $N, G, K, S$ are concyclic (opposite right angles) so $$ \angle D I P=2 \angle D K P=\angle G K N+\angle D S P=\angle G S N+\angle N S P=\angle G S P, $$ hence $I, G, S, P$ are concyclic. We have $I G \cdot I L=I N \cdot I A=r^{2}$ since $\triangle I G N \sim \triangle I A L$. Inverting the circle $I G S P$ in circle $\omega$, points $P$ and $S$ are fixed and $G$ is taken to $L$ so we find that $P, S$, and $L$ are collinear.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4afa6466-ecea-53d2-a8dd-b5f52e6fe016
| 23,888
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India) Common remarks. Throughout the solution, $\angle(a, b)$ denotes the directed angle between lines $a$ and $b$, measured modulo $\pi$.
|
We start as in Step 1. Let $A R$ meet the circumcircle $\Omega$ of $A B C$ again at $X$. The lines $A R$ and $A K$ are isogonal in the angle $B A C$; it is well known that in this case $X$ is the tangency point of $\Omega$ with the $A$-mixtilinear circle. It is also well known that for this point $X$, the line $X I$ crosses $\Omega$ again at the midpoint $M^{\prime}$ of arc $B A C$. Step 2. Denote the circles $B F P$ and $C E P$ by $\Omega_{B}$ and $\Omega_{C}$, respectively. Let $\Omega_{B}$ cross $A R$ and $E F$ again at $U$ and $Y$, respectively. We have $$ \angle(U B, B F)=\angle(U P, P F)=\angle(R P, P F)=\angle(R F, F A) $$ so $U B \| R F$.  Next, we show that the points $B, I, U$, and $X$ are concyclic. Since $$ \angle(U B, U X)=\angle(R F, R X)=\angle(A F, A R)+\angle(F R, F A)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F) $$ it suffices to prove $\angle(I B, I X)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F)$, or $\angle\left(I B, M^{\prime} B\right)=\angle(D R, D F)$. But both angles equal $\angle(C I, C B)$, as desired. (This is where we used the fact that $M^{\prime}$ is the midpoint of $\operatorname{arc} B A C$ of $\Omega$.) It follows now from circles $B U I X$ and $B P U F Y$ that $$ \begin{aligned} \angle(I U, U B)=\angle(I X, B X)=\angle\left(M^{\prime} X, B X\right)= & \frac{\pi-\angle A}{2} \\ & =\angle(E F, A F)=\angle(Y F, B F)=\angle(Y U, B U) \end{aligned} $$ so the points $Y, U$, and $I$ are collinear. Let $E F$ meet $B C$ at $W$. We have $$ \angle(I Y, Y W)=\angle(U Y, F Y)=\angle(U B, F B)=\angle(R F, A F)=\angle(C I, C W) $$ so the points $W, Y, I$, and $C$ are concyclic. Similarly, if $V$ and $Z$ are the second meeting points of $\Omega_{C}$ with $A R$ and $E F$, we get that the 4-tuples $(C, V, I, X)$ and $(B, I, Z, W)$ are both concyclic. Step 3. Let $Q^{\prime}=C Y \cap B Z$. We will show that $Q^{\prime}=Q$. First of all, we have $$ \begin{aligned} & \angle\left(Q^{\prime} Y, Q^{\prime} B\right)=\angle(C Y, Z B)=\angle(C Y, Z Y)+\angle(Z Y, B Z) \\ & =\angle(C I, I W)+\angle(I W, I B)=\angle(C I, I B)=\frac{\pi-\angle A}{2}=\angle(F Y, F B), \end{aligned} $$ so $Q^{\prime} \in \Omega_{B}$. Similarly, $Q^{\prime} \in \Omega_{C}$. Thus $Q^{\prime} \in \Omega_{B} \cap \Omega_{C}=\{P, Q\}$ and it remains to prove that $Q^{\prime} \neq P$. If we had $Q^{\prime}=P$, we would have $\angle(P Y, P Z)=\angle\left(Q^{\prime} Y, Q^{\prime} Z\right)=\angle(I C, I B)$. This would imply $$ \angle(P Y, Y F)+\angle(E Z, Z P)=\angle(P Y, P Z)=\angle(I C, I B)=\angle(P E, P F), $$ so circles $\Omega_{B}$ and $\Omega_{C}$ would be tangent at $P$. That is excluded in the problem conditions, so $Q^{\prime}=Q$.  Step 4. Now we are ready to show that $P, Q$, and $S$ are collinear. Notice that $A$ and $D$ are the poles of $E W$ and $D W$ with respect to $\omega$, so $W$ is the pole of $A D$. Hence, $W I \perp A D$. Since $C I \perp D E$, this yields $\angle(I C, W I)=\angle(D E, D A)$. On the other hand, $D A$ is a symmedian in $\triangle D E F$, so $\angle(D E, D A)=\angle(D N, D F)=\angle(D S, D F)$. Therefore, $$ \begin{aligned} \angle(P S, P F)=\angle(D S, D F)=\angle(D E, D A)= & \angle(I C, I W) \\ & =\angle(Y C, Y W)=\angle(Y Q, Y F)=\angle(P Q, P F), \end{aligned} $$ which yields the desired collinearity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle $\omega$ of acute-angled scalene triangle $A B C$ has centre $I$ and meets sides $B C$, $C A$, and $A B$ at $D, E$, and $F$, respectively. The line through $D$ perpendicular to $E F$ meets $\omega$ again at $R$. Line $A R$ meets $\omega$ again at $P$. The circumcircles of triangles $P C E$ and $P B F$ meet again at $Q \neq P$. Prove that lines $D I$ and $P Q$ meet on the external bisector of angle $B A C$. (India) Common remarks. Throughout the solution, $\angle(a, b)$ denotes the directed angle between lines $a$ and $b$, measured modulo $\pi$.
|
We start as in Step 1. Let $A R$ meet the circumcircle $\Omega$ of $A B C$ again at $X$. The lines $A R$ and $A K$ are isogonal in the angle $B A C$; it is well known that in this case $X$ is the tangency point of $\Omega$ with the $A$-mixtilinear circle. It is also well known that for this point $X$, the line $X I$ crosses $\Omega$ again at the midpoint $M^{\prime}$ of arc $B A C$. Step 2. Denote the circles $B F P$ and $C E P$ by $\Omega_{B}$ and $\Omega_{C}$, respectively. Let $\Omega_{B}$ cross $A R$ and $E F$ again at $U$ and $Y$, respectively. We have $$ \angle(U B, B F)=\angle(U P, P F)=\angle(R P, P F)=\angle(R F, F A) $$ so $U B \| R F$.  Next, we show that the points $B, I, U$, and $X$ are concyclic. Since $$ \angle(U B, U X)=\angle(R F, R X)=\angle(A F, A R)+\angle(F R, F A)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F) $$ it suffices to prove $\angle(I B, I X)=\angle\left(M^{\prime} B, M^{\prime} X\right)+\angle(D R, D F)$, or $\angle\left(I B, M^{\prime} B\right)=\angle(D R, D F)$. But both angles equal $\angle(C I, C B)$, as desired. (This is where we used the fact that $M^{\prime}$ is the midpoint of $\operatorname{arc} B A C$ of $\Omega$.) It follows now from circles $B U I X$ and $B P U F Y$ that $$ \begin{aligned} \angle(I U, U B)=\angle(I X, B X)=\angle\left(M^{\prime} X, B X\right)= & \frac{\pi-\angle A}{2} \\ & =\angle(E F, A F)=\angle(Y F, B F)=\angle(Y U, B U) \end{aligned} $$ so the points $Y, U$, and $I$ are collinear. Let $E F$ meet $B C$ at $W$. We have $$ \angle(I Y, Y W)=\angle(U Y, F Y)=\angle(U B, F B)=\angle(R F, A F)=\angle(C I, C W) $$ so the points $W, Y, I$, and $C$ are concyclic. Similarly, if $V$ and $Z$ are the second meeting points of $\Omega_{C}$ with $A R$ and $E F$, we get that the 4-tuples $(C, V, I, X)$ and $(B, I, Z, W)$ are both concyclic. Step 3. Let $Q^{\prime}=C Y \cap B Z$. We will show that $Q^{\prime}=Q$. First of all, we have $$ \begin{aligned} & \angle\left(Q^{\prime} Y, Q^{\prime} B\right)=\angle(C Y, Z B)=\angle(C Y, Z Y)+\angle(Z Y, B Z) \\ & =\angle(C I, I W)+\angle(I W, I B)=\angle(C I, I B)=\frac{\pi-\angle A}{2}=\angle(F Y, F B), \end{aligned} $$ so $Q^{\prime} \in \Omega_{B}$. Similarly, $Q^{\prime} \in \Omega_{C}$. Thus $Q^{\prime} \in \Omega_{B} \cap \Omega_{C}=\{P, Q\}$ and it remains to prove that $Q^{\prime} \neq P$. If we had $Q^{\prime}=P$, we would have $\angle(P Y, P Z)=\angle\left(Q^{\prime} Y, Q^{\prime} Z\right)=\angle(I C, I B)$. This would imply $$ \angle(P Y, Y F)+\angle(E Z, Z P)=\angle(P Y, P Z)=\angle(I C, I B)=\angle(P E, P F), $$ so circles $\Omega_{B}$ and $\Omega_{C}$ would be tangent at $P$. That is excluded in the problem conditions, so $Q^{\prime}=Q$.  Step 4. Now we are ready to show that $P, Q$, and $S$ are collinear. Notice that $A$ and $D$ are the poles of $E W$ and $D W$ with respect to $\omega$, so $W$ is the pole of $A D$. Hence, $W I \perp A D$. Since $C I \perp D E$, this yields $\angle(I C, W I)=\angle(D E, D A)$. On the other hand, $D A$ is a symmedian in $\triangle D E F$, so $\angle(D E, D A)=\angle(D N, D F)=\angle(D S, D F)$. Therefore, $$ \begin{aligned} \angle(P S, P F)=\angle(D S, D F)=\angle(D E, D A)= & \angle(I C, I W) \\ & =\angle(Y C, Y W)=\angle(Y Q, Y F)=\angle(P Q, P F), \end{aligned} $$ which yields the desired collinearity.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4afa6466-ecea-53d2-a8dd-b5f52e6fe016
| 23,888
|
Let $\mathcal{L}$ be the set of all lines in the plane and let $f$ be a function that assigns to each line $\ell \in \mathcal{L}$ a point $f(\ell)$ on $\ell$. Suppose that for any point $X$, and for any three lines $\ell_{1}, \ell_{2}, \ell_{3}$ passing through $X$, the points $f\left(\ell_{1}\right), f\left(\ell_{2}\right), f\left(\ell_{3}\right)$ and $X$ lie on a circle. Prove that there is a unique point $P$ such that $f(\ell)=P$ for any line $\ell$ passing through $P$. (Australia) Common remarks. The condition on $f$ is equivalent to the following: There is some function $g$ that assigns to each point $X$ a circle $g(X)$ passing through $X$ such that for any line $\ell$ passing through $X$, the point $f(\ell)$ lies on $g(X)$. (The function $g$ may not be uniquely defined for all points, if some points $X$ have at most one value of $f(\ell)$ other than $X$; for such points, an arbitrary choice is made.) If there were two points $P$ and $Q$ with the given property, $f(P Q)$ would have to be both $P$ and $Q$, so there is at most one such point, and it will suffice to show that such a point exists.
|
Note that for any distinct points $X, Y$, the circles $g(X)$ and $g(Y)$ meet on $X Y$ at the point $f(X Y) \in g(X) \cap g(Y) \cap(X Y)$. We write $s(X, Y)$ for the second intersection point of circles $g(X)$ and $g(Y)$. Lemma 1. Suppose that $X, Y$ and $Z$ are not collinear, and that $f(X Y) \notin\{X, Y\}$ and similarly for $Y Z$ and $Z X$. Then $s(X, Y)=s(Y, Z)=s(Z, X)$. Proof. The circles $g(X), g(Y)$ and $g(Z)$ through the vertices of triangle $X Y Z$ meet pairwise on the corresponding edges (produced). By Miquel's theorem, the second points of intersection of any two of the circles coincide. (See the diagram for Lemma 5 of Solution 1.) Now pick any line $\ell$ and any six different points $Y_{1}, \ldots, Y_{6}$ on $\ell \backslash\{f(\ell)\}$. Pick a point $X$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$. Reordering the indices if necessary, we may suppose that $Y_{1}, \ldots, Y_{4}$ do not lie on $g(X)$, so that $f\left(X Y_{i}\right) \notin\left\{X, Y_{i}\right\}$ for $1 \leqslant i \leqslant 4$. By applying the above lemma to triangles $X Y_{i} Y_{j}$ for $1 \leqslant i<j \leqslant 4$, we find that the points $s\left(Y_{i}, Y_{j}\right)$ and $s\left(X, Y_{i}\right)$ are all equal, to point $O$ say. Note that either $O$ does not lie on $\ell$, or $O=f(\ell)$, since $O \in g\left(Y_{i}\right)$. Now consider an arbitrary point $X^{\prime}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. As above, we see that there are two indices $1 \leqslant i<j \leqslant 4$ such that $Y_{i}$ and $Y_{j}$ do not lie on $g\left(X^{\prime}\right)$. By applying the above lemma to triangle $X^{\prime} Y_{i} Y_{j}$ we see that $s\left(X^{\prime}, Y_{i}\right)=O$, and in particular $g\left(X^{\prime}\right)$ passes through $O$. We will now show that $f\left(\ell^{\prime}\right)=O$ for all lines $\ell^{\prime}$ through $O$. By the above note, we may assume that $\ell^{\prime} \neq \ell$. Consider a variable point $X^{\prime} \in \ell^{\prime} \backslash\{O\}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. We know that $f\left(\ell^{\prime}\right) \in g\left(X^{\prime}\right) \cap \ell^{\prime}=\left\{X^{\prime}, O\right\}$. Since $X^{\prime}$ was suitably arbitrary, we have $f\left(\ell^{\prime}\right)=O$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\mathcal{L}$ be the set of all lines in the plane and let $f$ be a function that assigns to each line $\ell \in \mathcal{L}$ a point $f(\ell)$ on $\ell$. Suppose that for any point $X$, and for any three lines $\ell_{1}, \ell_{2}, \ell_{3}$ passing through $X$, the points $f\left(\ell_{1}\right), f\left(\ell_{2}\right), f\left(\ell_{3}\right)$ and $X$ lie on a circle. Prove that there is a unique point $P$ such that $f(\ell)=P$ for any line $\ell$ passing through $P$. (Australia) Common remarks. The condition on $f$ is equivalent to the following: There is some function $g$ that assigns to each point $X$ a circle $g(X)$ passing through $X$ such that for any line $\ell$ passing through $X$, the point $f(\ell)$ lies on $g(X)$. (The function $g$ may not be uniquely defined for all points, if some points $X$ have at most one value of $f(\ell)$ other than $X$; for such points, an arbitrary choice is made.) If there were two points $P$ and $Q$ with the given property, $f(P Q)$ would have to be both $P$ and $Q$, so there is at most one such point, and it will suffice to show that such a point exists.
|
Note that for any distinct points $X, Y$, the circles $g(X)$ and $g(Y)$ meet on $X Y$ at the point $f(X Y) \in g(X) \cap g(Y) \cap(X Y)$. We write $s(X, Y)$ for the second intersection point of circles $g(X)$ and $g(Y)$. Lemma 1. Suppose that $X, Y$ and $Z$ are not collinear, and that $f(X Y) \notin\{X, Y\}$ and similarly for $Y Z$ and $Z X$. Then $s(X, Y)=s(Y, Z)=s(Z, X)$. Proof. The circles $g(X), g(Y)$ and $g(Z)$ through the vertices of triangle $X Y Z$ meet pairwise on the corresponding edges (produced). By Miquel's theorem, the second points of intersection of any two of the circles coincide. (See the diagram for Lemma 5 of Solution 1.) Now pick any line $\ell$ and any six different points $Y_{1}, \ldots, Y_{6}$ on $\ell \backslash\{f(\ell)\}$. Pick a point $X$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$. Reordering the indices if necessary, we may suppose that $Y_{1}, \ldots, Y_{4}$ do not lie on $g(X)$, so that $f\left(X Y_{i}\right) \notin\left\{X, Y_{i}\right\}$ for $1 \leqslant i \leqslant 4$. By applying the above lemma to triangles $X Y_{i} Y_{j}$ for $1 \leqslant i<j \leqslant 4$, we find that the points $s\left(Y_{i}, Y_{j}\right)$ and $s\left(X, Y_{i}\right)$ are all equal, to point $O$ say. Note that either $O$ does not lie on $\ell$, or $O=f(\ell)$, since $O \in g\left(Y_{i}\right)$. Now consider an arbitrary point $X^{\prime}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. As above, we see that there are two indices $1 \leqslant i<j \leqslant 4$ such that $Y_{i}$ and $Y_{j}$ do not lie on $g\left(X^{\prime}\right)$. By applying the above lemma to triangle $X^{\prime} Y_{i} Y_{j}$ we see that $s\left(X^{\prime}, Y_{i}\right)=O$, and in particular $g\left(X^{\prime}\right)$ passes through $O$. We will now show that $f\left(\ell^{\prime}\right)=O$ for all lines $\ell^{\prime}$ through $O$. By the above note, we may assume that $\ell^{\prime} \neq \ell$. Consider a variable point $X^{\prime} \in \ell^{\prime} \backslash\{O\}$ not on $\ell$ or any of the circles $g\left(Y_{i}\right)$ for $1 \leqslant i \leqslant 4$. We know that $f\left(\ell^{\prime}\right) \in g\left(X^{\prime}\right) \cap \ell^{\prime}=\left\{X^{\prime}, O\right\}$. Since $X^{\prime}$ was suitably arbitrary, we have $f\left(\ell^{\prime}\right)=O$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e7f1382c-7015-5f0d-9cd9-e6039b675f13
| 23,892
|
Let $\mathcal{L}$ be the set of all lines in the plane and let $f$ be a function that assigns to each line $\ell \in \mathcal{L}$ a point $f(\ell)$ on $\ell$. Suppose that for any point $X$, and for any three lines $\ell_{1}, \ell_{2}, \ell_{3}$ passing through $X$, the points $f\left(\ell_{1}\right), f\left(\ell_{2}\right), f\left(\ell_{3}\right)$ and $X$ lie on a circle. Prove that there is a unique point $P$ such that $f(\ell)=P$ for any line $\ell$ passing through $P$. (Australia) Common remarks. The condition on $f$ is equivalent to the following: There is some function $g$ that assigns to each point $X$ a circle $g(X)$ passing through $X$ such that for any line $\ell$ passing through $X$, the point $f(\ell)$ lies on $g(X)$. (The function $g$ may not be uniquely defined for all points, if some points $X$ have at most one value of $f(\ell)$ other than $X$; for such points, an arbitrary choice is made.) If there were two points $P$ and $Q$ with the given property, $f(P Q)$ would have to be both $P$ and $Q$, so there is at most one such point, and it will suffice to show that such a point exists.
|
Notice that, for any two different points $X$ and $Y$, the point $f(X Y)$ lies on both $g(X)$ and $g(Y)$, so any two such circles meet in at least one point. We refer to two circles as cutting only in the case where they cross, and so meet at exactly two points, thus excluding the cases where they are tangent or are the same circle. Lemma 1. Suppose there is a point $P$ such that all circles $g(X)$ pass through $P$. Then $P$ has the given property. Proof. Consider some line $\ell$ passing through $P$, and suppose that $f(\ell) \neq P$. Consider some $X \in \ell$ with $X \neq P$ and $X \neq f(\ell)$. Then $g(X)$ passes through all of $P, f(\ell)$ and $X$, but those three points are collinear, a contradiction. Lemma 2. Suppose that, for all $\epsilon>0$, there is a point $P_{\epsilon}$ with $g\left(P_{\epsilon}\right)$ of radius at most $\epsilon$. Then there is a point $P$ with the given property. Proof. Consider a sequence $\epsilon_{i}=2^{-i}$ and corresponding points $P_{\epsilon_{i}}$. Because the two circles $g\left(P_{\epsilon_{i}}\right)$ and $g\left(P_{\epsilon_{j}}\right)$ meet, the distance between $P_{\epsilon_{i}}$ and $P_{\epsilon_{j}}$ is at most $2^{1-i}+2^{1-j}$. As $\sum_{i} \epsilon_{i}$ converges, these points converge to some point $P$. For all $\epsilon>0$, the point $P$ has distance at most $2 \epsilon$ from $P_{\epsilon}$, and all circles $g(X)$ pass through a point with distance at most $2 \epsilon$ from $P_{\epsilon}$, so distance at most $4 \epsilon$ from $P$. A circle that passes distance at most $4 \epsilon$ from $P$ for all $\epsilon>0$ must pass through $P$, so by Lemma 1 the point $P$ has the given property. Lemma 3. Suppose no two of the circles $g(X)$ cut. Then there is a point $P$ with the given property. Proof. Consider a circle $g(X)$ with centre $Y$. The circle $g(Y)$ must meet $g(X)$ without cutting it, so has half the radius of $g(X)$. Repeating this argument, there are circles with arbitrarily small radius and the result follows by Lemma 2. Lemma 4. Suppose there are six different points $A, B_{1}, B_{2}, B_{3}, B_{4}, B_{5}$ such that no three are collinear, no four are concyclic, and all the circles $g\left(B_{i}\right)$ cut pairwise at $A$. Then there is a point $P$ with the given property. Proof. Consider some line $\ell$ through $A$ that does not pass through any of the $B_{i}$ and is not tangent to any of the $g\left(B_{i}\right)$. Fix some direction along that line, and let $X_{\epsilon}$ be the point on $\ell$ that has distance $\epsilon$ from $A$ in that direction. In what follows we consider only those $\epsilon$ for which $X_{\epsilon}$ does not lie on any $g\left(B_{i}\right)$ (this restriction excludes only finitely many possible values of $\epsilon$ ). Consider the circle $g\left(X_{\epsilon}\right)$. Because no four of the $B_{i}$ are concyclic, at most three of them lie on this circle, so at least two of them do not. There must be some sequence of $\epsilon \rightarrow 0$ such that it is the same two of the $B_{i}$ for all $\epsilon$ in that sequence, so now restrict attention to that sequence, and suppose without loss of generality that $B_{1}$ and $B_{2}$ do not lie on $g\left(X_{\epsilon}\right)$ for any $\epsilon$ in that sequence. Then $f\left(X_{\epsilon} B_{1}\right)$ is not $B_{1}$, so must be the other point of intersection of $X_{\epsilon} B_{1}$ with $g\left(B_{1}\right)$, and the same applies with $B_{2}$. Now consider the three points $X_{\epsilon}, f\left(X_{\epsilon} B_{1}\right)$ and $f\left(X_{\epsilon} B_{2}\right)$. As $\epsilon \rightarrow 0$, the angle at $X_{\epsilon}$ tends to $\angle B_{1} A B_{2}$ or $180^{\circ}-\angle B_{1} A B_{2}$, which is not 0 or $180^{\circ}$ because no three of the points were collinear. All three distances between those points are bounded above by constant multiples of $\epsilon$ (in fact, if the triangle is scaled by a factor of $1 / \epsilon$, it tends to a fixed triangle). Thus the circumradius of those three points, which is the radius of $g\left(X_{\epsilon}\right)$, is also bounded above by a constant multiple of $\epsilon$, and so the result follows by Lemma 2 . Lemma 5. Suppose there are two points $A$ and $B$ such that $g(A)$ and $g(B)$ cut. Then there is a point $P$ with the given property. Proof. Suppose that $g(A)$ and $g(B)$ cut at $C$ and $D$. One of those points, without loss of generality $C$, must be $f(A B)$, and so lie on the line $A B$. We now consider two cases, according to whether $D$ also lies on that line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\mathcal{L}$ be the set of all lines in the plane and let $f$ be a function that assigns to each line $\ell \in \mathcal{L}$ a point $f(\ell)$ on $\ell$. Suppose that for any point $X$, and for any three lines $\ell_{1}, \ell_{2}, \ell_{3}$ passing through $X$, the points $f\left(\ell_{1}\right), f\left(\ell_{2}\right), f\left(\ell_{3}\right)$ and $X$ lie on a circle. Prove that there is a unique point $P$ such that $f(\ell)=P$ for any line $\ell$ passing through $P$. (Australia) Common remarks. The condition on $f$ is equivalent to the following: There is some function $g$ that assigns to each point $X$ a circle $g(X)$ passing through $X$ such that for any line $\ell$ passing through $X$, the point $f(\ell)$ lies on $g(X)$. (The function $g$ may not be uniquely defined for all points, if some points $X$ have at most one value of $f(\ell)$ other than $X$; for such points, an arbitrary choice is made.) If there were two points $P$ and $Q$ with the given property, $f(P Q)$ would have to be both $P$ and $Q$, so there is at most one such point, and it will suffice to show that such a point exists.
|
Notice that, for any two different points $X$ and $Y$, the point $f(X Y)$ lies on both $g(X)$ and $g(Y)$, so any two such circles meet in at least one point. We refer to two circles as cutting only in the case where they cross, and so meet at exactly two points, thus excluding the cases where they are tangent or are the same circle. Lemma 1. Suppose there is a point $P$ such that all circles $g(X)$ pass through $P$. Then $P$ has the given property. Proof. Consider some line $\ell$ passing through $P$, and suppose that $f(\ell) \neq P$. Consider some $X \in \ell$ with $X \neq P$ and $X \neq f(\ell)$. Then $g(X)$ passes through all of $P, f(\ell)$ and $X$, but those three points are collinear, a contradiction. Lemma 2. Suppose that, for all $\epsilon>0$, there is a point $P_{\epsilon}$ with $g\left(P_{\epsilon}\right)$ of radius at most $\epsilon$. Then there is a point $P$ with the given property. Proof. Consider a sequence $\epsilon_{i}=2^{-i}$ and corresponding points $P_{\epsilon_{i}}$. Because the two circles $g\left(P_{\epsilon_{i}}\right)$ and $g\left(P_{\epsilon_{j}}\right)$ meet, the distance between $P_{\epsilon_{i}}$ and $P_{\epsilon_{j}}$ is at most $2^{1-i}+2^{1-j}$. As $\sum_{i} \epsilon_{i}$ converges, these points converge to some point $P$. For all $\epsilon>0$, the point $P$ has distance at most $2 \epsilon$ from $P_{\epsilon}$, and all circles $g(X)$ pass through a point with distance at most $2 \epsilon$ from $P_{\epsilon}$, so distance at most $4 \epsilon$ from $P$. A circle that passes distance at most $4 \epsilon$ from $P$ for all $\epsilon>0$ must pass through $P$, so by Lemma 1 the point $P$ has the given property. Lemma 3. Suppose no two of the circles $g(X)$ cut. Then there is a point $P$ with the given property. Proof. Consider a circle $g(X)$ with centre $Y$. The circle $g(Y)$ must meet $g(X)$ without cutting it, so has half the radius of $g(X)$. Repeating this argument, there are circles with arbitrarily small radius and the result follows by Lemma 2. Lemma 4. Suppose there are six different points $A, B_{1}, B_{2}, B_{3}, B_{4}, B_{5}$ such that no three are collinear, no four are concyclic, and all the circles $g\left(B_{i}\right)$ cut pairwise at $A$. Then there is a point $P$ with the given property. Proof. Consider some line $\ell$ through $A$ that does not pass through any of the $B_{i}$ and is not tangent to any of the $g\left(B_{i}\right)$. Fix some direction along that line, and let $X_{\epsilon}$ be the point on $\ell$ that has distance $\epsilon$ from $A$ in that direction. In what follows we consider only those $\epsilon$ for which $X_{\epsilon}$ does not lie on any $g\left(B_{i}\right)$ (this restriction excludes only finitely many possible values of $\epsilon$ ). Consider the circle $g\left(X_{\epsilon}\right)$. Because no four of the $B_{i}$ are concyclic, at most three of them lie on this circle, so at least two of them do not. There must be some sequence of $\epsilon \rightarrow 0$ such that it is the same two of the $B_{i}$ for all $\epsilon$ in that sequence, so now restrict attention to that sequence, and suppose without loss of generality that $B_{1}$ and $B_{2}$ do not lie on $g\left(X_{\epsilon}\right)$ for any $\epsilon$ in that sequence. Then $f\left(X_{\epsilon} B_{1}\right)$ is not $B_{1}$, so must be the other point of intersection of $X_{\epsilon} B_{1}$ with $g\left(B_{1}\right)$, and the same applies with $B_{2}$. Now consider the three points $X_{\epsilon}, f\left(X_{\epsilon} B_{1}\right)$ and $f\left(X_{\epsilon} B_{2}\right)$. As $\epsilon \rightarrow 0$, the angle at $X_{\epsilon}$ tends to $\angle B_{1} A B_{2}$ or $180^{\circ}-\angle B_{1} A B_{2}$, which is not 0 or $180^{\circ}$ because no three of the points were collinear. All three distances between those points are bounded above by constant multiples of $\epsilon$ (in fact, if the triangle is scaled by a factor of $1 / \epsilon$, it tends to a fixed triangle). Thus the circumradius of those three points, which is the radius of $g\left(X_{\epsilon}\right)$, is also bounded above by a constant multiple of $\epsilon$, and so the result follows by Lemma 2 . Lemma 5. Suppose there are two points $A$ and $B$ such that $g(A)$ and $g(B)$ cut. Then there is a point $P$ with the given property. Proof. Suppose that $g(A)$ and $g(B)$ cut at $C$ and $D$. One of those points, without loss of generality $C$, must be $f(A B)$, and so lie on the line $A B$. We now consider two cases, according to whether $D$ also lies on that line.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e7f1382c-7015-5f0d-9cd9-e6039b675f13
| 23,892
|
We say that a set $S$ of integers is rootiful if, for any positive integer $n$ and any $a_{0}, a_{1}, \ldots, a_{n} \in S$, all integer roots of the polynomial $a_{0}+a_{1} x+\cdots+a_{n} x^{n}$ are also in $S$. Find all rootiful sets of integers that contain all numbers of the form $2^{a}-2^{b}$ for positive integers $a$ and $b$. (Czech Republic) Answer: The set $\mathbb{Z}$ of all integers is the only such rootiful set.
|
The set $\mathbb{Z}$ of all integers is clearly rootiful. We shall prove that any rootiful set $S$ containing all the numbers of the form $2^{a}-2^{b}$ for $a, b \in \mathbb{Z}_{>0}$ must be all of $\mathbb{Z}$. First, note that $0=2^{1}-2^{1} \in S$ and $2=2^{2}-2^{1} \in S$. Now, $-1 \in S$, since it is a root of $2 x+2$, and $1 \in S$, since it is a root of $2 x^{2}-x-1$. Also, if $n \in S$ then $-n$ is a root of $x+n$, so it suffices to prove that all positive integers must be in $S$. Now, we claim that any positive integer $n$ has a multiple in $S$. Indeed, suppose that $n=2^{\alpha} \cdot t$ for $\alpha \in \mathbb{Z}_{\geqslant 0}$ and $t$ odd. Then $t \mid 2^{\phi(t)}-1$, so $n \mid 2^{\alpha+\phi(t)+1}-2^{\alpha+1}$. Moreover, $2^{\alpha+\phi(t)+1}-2^{\alpha+1} \in S$, and so $S$ contains a multiple of every positive integer $n$. We will now prove by induction that all positive integers are in $S$. Suppose that $0,1, \ldots, n-$ $1 \in S$; furthermore, let $N$ be a multiple of $n$ in $S$. Consider the base- $n$ expansion of $N$, say $N=a_{k} n^{k}+a_{k-1} n^{k-1}+\cdots+a_{1} n+a_{0}$. Since $0 \leqslant a_{i}<n$ for each $a_{i}$, we have that all the $a_{i}$ are in $S$. Furthermore, $a_{0}=0$ since $N$ is a multiple of $n$. Therefore, $a_{k} n^{k}+a_{k-1} n^{k-1}+\cdots+a_{1} n-N=0$, so $n$ is a root of a polynomial with coefficients in $S$. This tells us that $n \in S$, completing the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
We say that a set $S$ of integers is rootiful if, for any positive integer $n$ and any $a_{0}, a_{1}, \ldots, a_{n} \in S$, all integer roots of the polynomial $a_{0}+a_{1} x+\cdots+a_{n} x^{n}$ are also in $S$. Find all rootiful sets of integers that contain all numbers of the form $2^{a}-2^{b}$ for positive integers $a$ and $b$. (Czech Republic) Answer: The set $\mathbb{Z}$ of all integers is the only such rootiful set.
|
The set $\mathbb{Z}$ of all integers is clearly rootiful. We shall prove that any rootiful set $S$ containing all the numbers of the form $2^{a}-2^{b}$ for $a, b \in \mathbb{Z}_{>0}$ must be all of $\mathbb{Z}$. First, note that $0=2^{1}-2^{1} \in S$ and $2=2^{2}-2^{1} \in S$. Now, $-1 \in S$, since it is a root of $2 x+2$, and $1 \in S$, since it is a root of $2 x^{2}-x-1$. Also, if $n \in S$ then $-n$ is a root of $x+n$, so it suffices to prove that all positive integers must be in $S$. Now, we claim that any positive integer $n$ has a multiple in $S$. Indeed, suppose that $n=2^{\alpha} \cdot t$ for $\alpha \in \mathbb{Z}_{\geqslant 0}$ and $t$ odd. Then $t \mid 2^{\phi(t)}-1$, so $n \mid 2^{\alpha+\phi(t)+1}-2^{\alpha+1}$. Moreover, $2^{\alpha+\phi(t)+1}-2^{\alpha+1} \in S$, and so $S$ contains a multiple of every positive integer $n$. We will now prove by induction that all positive integers are in $S$. Suppose that $0,1, \ldots, n-$ $1 \in S$; furthermore, let $N$ be a multiple of $n$ in $S$. Consider the base- $n$ expansion of $N$, say $N=a_{k} n^{k}+a_{k-1} n^{k-1}+\cdots+a_{1} n+a_{0}$. Since $0 \leqslant a_{i}<n$ for each $a_{i}$, we have that all the $a_{i}$ are in $S$. Furthermore, $a_{0}=0$ since $N$ is a multiple of $n$. Therefore, $a_{k} n^{k}+a_{k-1} n^{k-1}+\cdots+a_{1} n-N=0$, so $n$ is a root of a polynomial with coefficients in $S$. This tells us that $n \in S$, completing the induction.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5391b334-2aef-5bfd-b14e-9e9e8ca45202
| 23,907
|
We say that a set $S$ of integers is rootiful if, for any positive integer $n$ and any $a_{0}, a_{1}, \ldots, a_{n} \in S$, all integer roots of the polynomial $a_{0}+a_{1} x+\cdots+a_{n} x^{n}$ are also in $S$. Find all rootiful sets of integers that contain all numbers of the form $2^{a}-2^{b}$ for positive integers $a$ and $b$. (Czech Republic) Answer: The set $\mathbb{Z}$ of all integers is the only such rootiful set.
|
As in the previous solution, we can prove that 0,1 and -1 must all be in any rootiful set $S$ containing all numbers of the form $2^{a}-2^{b}$ for $a, b \in \mathbb{Z}_{>0}$. We show that, in fact, every integer $k$ with $|k|>2$ can be expressed as a root of a polynomial whose coefficients are of the form $2^{a}-2^{b}$. Observe that it suffices to consider the case where $k$ is positive, as if $k$ is a root of $a_{n} x^{n}+\cdots+a_{1} x+a_{0}=0$, then $-k$ is a root of $(-1)^{n} a_{n} x^{n}+\cdots-$ $a_{1} x+a_{0}=0$. Note that $$ \left(2^{a_{n}}-2^{b_{n}}\right) k^{n}+\cdots+\left(2^{a_{0}}-2^{b_{0}}\right)=0 $$ is equivalent to $$ 2^{a_{n}} k^{n}+\cdots+2^{a_{0}}=2^{b_{n}} k^{n}+\cdots+2^{b_{0}} $$ Hence our aim is to show that two numbers of the form $2^{a_{n}} k^{n}+\cdots+2^{a_{0}}$ are equal, for a fixed value of $n$. We consider such polynomials where every term $2^{a_{i}} k^{i}$ is at most $2 k^{n}$; in other words, where $2 \leqslant 2^{a_{i}} \leqslant 2 k^{n-i}$, or, equivalently, $1 \leqslant a_{i} \leqslant 1+(n-i) \log _{2} k$. Therefore, there must be $1+\left\lfloor(n-i) \log _{2} k\right\rfloor$ possible choices for $a_{i}$ satisfying these constraints. The number of possible polynomials is then $$ \prod_{i=0}^{n}\left(1+\left\lfloor(n-i) \log _{2} k\right\rfloor\right) \geqslant \prod_{i=0}^{n-1}(n-i) \log _{2} k=n!\left(\log _{2} k\right)^{n} $$ where the inequality holds as $1+\lfloor x\rfloor \geqslant x$. As there are $(n+1)$ such terms in the polynomial, each at most $2 k^{n}$, such a polynomial must have value at most $2 k^{n}(n+1)$. However, for large $n$, we have $n!\left(\log _{2} k\right)^{n}>2 k^{n}(n+1)$. Therefore there are more polynomials than possible values, so some two must be equal, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
We say that a set $S$ of integers is rootiful if, for any positive integer $n$ and any $a_{0}, a_{1}, \ldots, a_{n} \in S$, all integer roots of the polynomial $a_{0}+a_{1} x+\cdots+a_{n} x^{n}$ are also in $S$. Find all rootiful sets of integers that contain all numbers of the form $2^{a}-2^{b}$ for positive integers $a$ and $b$. (Czech Republic) Answer: The set $\mathbb{Z}$ of all integers is the only such rootiful set.
|
As in the previous solution, we can prove that 0,1 and -1 must all be in any rootiful set $S$ containing all numbers of the form $2^{a}-2^{b}$ for $a, b \in \mathbb{Z}_{>0}$. We show that, in fact, every integer $k$ with $|k|>2$ can be expressed as a root of a polynomial whose coefficients are of the form $2^{a}-2^{b}$. Observe that it suffices to consider the case where $k$ is positive, as if $k$ is a root of $a_{n} x^{n}+\cdots+a_{1} x+a_{0}=0$, then $-k$ is a root of $(-1)^{n} a_{n} x^{n}+\cdots-$ $a_{1} x+a_{0}=0$. Note that $$ \left(2^{a_{n}}-2^{b_{n}}\right) k^{n}+\cdots+\left(2^{a_{0}}-2^{b_{0}}\right)=0 $$ is equivalent to $$ 2^{a_{n}} k^{n}+\cdots+2^{a_{0}}=2^{b_{n}} k^{n}+\cdots+2^{b_{0}} $$ Hence our aim is to show that two numbers of the form $2^{a_{n}} k^{n}+\cdots+2^{a_{0}}$ are equal, for a fixed value of $n$. We consider such polynomials where every term $2^{a_{i}} k^{i}$ is at most $2 k^{n}$; in other words, where $2 \leqslant 2^{a_{i}} \leqslant 2 k^{n-i}$, or, equivalently, $1 \leqslant a_{i} \leqslant 1+(n-i) \log _{2} k$. Therefore, there must be $1+\left\lfloor(n-i) \log _{2} k\right\rfloor$ possible choices for $a_{i}$ satisfying these constraints. The number of possible polynomials is then $$ \prod_{i=0}^{n}\left(1+\left\lfloor(n-i) \log _{2} k\right\rfloor\right) \geqslant \prod_{i=0}^{n-1}(n-i) \log _{2} k=n!\left(\log _{2} k\right)^{n} $$ where the inequality holds as $1+\lfloor x\rfloor \geqslant x$. As there are $(n+1)$ such terms in the polynomial, each at most $2 k^{n}$, such a polynomial must have value at most $2 k^{n}(n+1)$. However, for large $n$, we have $n!\left(\log _{2} k\right)^{n}>2 k^{n}(n+1)$. Therefore there are more polynomials than possible values, so some two must be equal, as required.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5391b334-2aef-5bfd-b14e-9e9e8ca45202
| 23,907
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil) Common remarks. In all solutions, we will assume that $A$ is a set such that $\{a-b: a, b \in A\}$ is disjoint from $H$, and prove that $|A|<C \sqrt{n}$.
|
First, observe that if $n$ is a positive integer, then $n \in H$ exactly when $$ \left\{\frac{n}{\sqrt{2}}\right\}>1-\frac{1}{\sqrt{2}} . $$ To see why, observe that $n \in H$ if and only if $0<i \sqrt{2}-n<1$ for some $i \in \mathbb{Z}_{>0}$. In other words, $0<i-n / \sqrt{2}<1 / \sqrt{2}$, which is equivalent to (1). Now, write $A=\left\{a_{1}<a_{2}<\cdots<a_{k}\right\}$, where $k=|A|$. Observe that the set of differences is not altered by shifting $A$, so we may assume that $A \subseteq\{0,1, \ldots, n-1\}$ with $a_{1}=0$. From (1), we learn that $\left\{a_{i} / \sqrt{2}\right\}<1-1 / \sqrt{2}$ for each $i>1$ since $a_{i}-a_{1} \notin H$. Furthermore, we must have $\left\{a_{i} / \sqrt{2}\right\}<\left\{a_{j} / \sqrt{2}\right\}$ whenever $i<j$; otherwise, we would have $$ -\left(1-\frac{1}{\sqrt{2}}\right)<\left\{\frac{a_{j}}{\sqrt{2}}\right\}-\left\{\frac{a_{i}}{\sqrt{2}}\right\}<0 . $$ Since $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}=\left\{a_{j} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}+1$, this implies that $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}>1 / \sqrt{2}>$ $1-1 / \sqrt{2}$, contradicting (1). Now, we have a sequence $0=a_{1}<a_{2}<\cdots<a_{k}<n$, with $$ 0=\left\{\frac{a_{1}}{\sqrt{2}}\right\}<\left\{\frac{a_{2}}{\sqrt{2}}\right\}<\cdots<\left\{\frac{a_{k}}{\sqrt{2}}\right\}<1-\frac{1}{\sqrt{2}} . $$ We use the following fact: for any $d \in \mathbb{Z}$, we have $$ \left\{\frac{d}{\sqrt{2}}\right\}>\frac{1}{2 d \sqrt{2}} $$ To see why this is the case, let $h=\lfloor d / \sqrt{2}\rfloor$, so $\{d / \sqrt{2}\}=d / \sqrt{2}-h$. Then $$ \left\{\frac{d}{\sqrt{2}}\right\}\left(\frac{d}{\sqrt{2}}+h\right)=\frac{d^{2}-2 h^{2}}{2} \geqslant \frac{1}{2} $$ since the numerator is a positive integer. Because $d / \sqrt{2}+h<2 d / \sqrt{2}$, inequality (2) follows. Let $d_{i}=a_{i+1}-a_{i}$, for $1 \leqslant i<k$. Then $\left\{a_{i+1} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}=\left\{d_{i} / \sqrt{2}\right\}$, and we have $$ 1-\frac{1}{\sqrt{2}}>\sum_{i}\left\{\frac{d_{i}}{\sqrt{2}}\right\}>\frac{1}{2 \sqrt{2}} \sum_{i} \frac{1}{d_{i}} \geqslant \frac{(k-1)^{2}}{2 \sqrt{2}} \frac{1}{\sum_{i} d_{i}}>\frac{(k-1)^{2}}{2 \sqrt{2}} \cdot \frac{1}{n} . $$ Here, the first inequality holds because $\left\{a_{k} / \sqrt{2}\right\}<1-1 / \sqrt{2}$, the second follows from (2), the third follows from an easy application of the AM-HM inequality (or Cauchy-Schwarz), and the fourth follows from the fact that $\sum_{i} d_{i}=a_{k}<n$. Rearranging this, we obtain $$ \sqrt{2 \sqrt{2}-2} \cdot \sqrt{n}>k-1 $$ which provides the required bound on $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil) Common remarks. In all solutions, we will assume that $A$ is a set such that $\{a-b: a, b \in A\}$ is disjoint from $H$, and prove that $|A|<C \sqrt{n}$.
|
First, observe that if $n$ is a positive integer, then $n \in H$ exactly when $$ \left\{\frac{n}{\sqrt{2}}\right\}>1-\frac{1}{\sqrt{2}} . $$ To see why, observe that $n \in H$ if and only if $0<i \sqrt{2}-n<1$ for some $i \in \mathbb{Z}_{>0}$. In other words, $0<i-n / \sqrt{2}<1 / \sqrt{2}$, which is equivalent to (1). Now, write $A=\left\{a_{1}<a_{2}<\cdots<a_{k}\right\}$, where $k=|A|$. Observe that the set of differences is not altered by shifting $A$, so we may assume that $A \subseteq\{0,1, \ldots, n-1\}$ with $a_{1}=0$. From (1), we learn that $\left\{a_{i} / \sqrt{2}\right\}<1-1 / \sqrt{2}$ for each $i>1$ since $a_{i}-a_{1} \notin H$. Furthermore, we must have $\left\{a_{i} / \sqrt{2}\right\}<\left\{a_{j} / \sqrt{2}\right\}$ whenever $i<j$; otherwise, we would have $$ -\left(1-\frac{1}{\sqrt{2}}\right)<\left\{\frac{a_{j}}{\sqrt{2}}\right\}-\left\{\frac{a_{i}}{\sqrt{2}}\right\}<0 . $$ Since $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}=\left\{a_{j} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}+1$, this implies that $\left\{\left(a_{j}-a_{i}\right) / \sqrt{2}\right\}>1 / \sqrt{2}>$ $1-1 / \sqrt{2}$, contradicting (1). Now, we have a sequence $0=a_{1}<a_{2}<\cdots<a_{k}<n$, with $$ 0=\left\{\frac{a_{1}}{\sqrt{2}}\right\}<\left\{\frac{a_{2}}{\sqrt{2}}\right\}<\cdots<\left\{\frac{a_{k}}{\sqrt{2}}\right\}<1-\frac{1}{\sqrt{2}} . $$ We use the following fact: for any $d \in \mathbb{Z}$, we have $$ \left\{\frac{d}{\sqrt{2}}\right\}>\frac{1}{2 d \sqrt{2}} $$ To see why this is the case, let $h=\lfloor d / \sqrt{2}\rfloor$, so $\{d / \sqrt{2}\}=d / \sqrt{2}-h$. Then $$ \left\{\frac{d}{\sqrt{2}}\right\}\left(\frac{d}{\sqrt{2}}+h\right)=\frac{d^{2}-2 h^{2}}{2} \geqslant \frac{1}{2} $$ since the numerator is a positive integer. Because $d / \sqrt{2}+h<2 d / \sqrt{2}$, inequality (2) follows. Let $d_{i}=a_{i+1}-a_{i}$, for $1 \leqslant i<k$. Then $\left\{a_{i+1} / \sqrt{2}\right\}-\left\{a_{i} / \sqrt{2}\right\}=\left\{d_{i} / \sqrt{2}\right\}$, and we have $$ 1-\frac{1}{\sqrt{2}}>\sum_{i}\left\{\frac{d_{i}}{\sqrt{2}}\right\}>\frac{1}{2 \sqrt{2}} \sum_{i} \frac{1}{d_{i}} \geqslant \frac{(k-1)^{2}}{2 \sqrt{2}} \frac{1}{\sum_{i} d_{i}}>\frac{(k-1)^{2}}{2 \sqrt{2}} \cdot \frac{1}{n} . $$ Here, the first inequality holds because $\left\{a_{k} / \sqrt{2}\right\}<1-1 / \sqrt{2}$, the second follows from (2), the third follows from an easy application of the AM-HM inequality (or Cauchy-Schwarz), and the fourth follows from the fact that $\sum_{i} d_{i}=a_{k}<n$. Rearranging this, we obtain $$ \sqrt{2 \sqrt{2}-2} \cdot \sqrt{n}>k-1 $$ which provides the required bound on $k$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bad4a911-bdaf-5e78-aa7f-6599f1082d58
| 23,916
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil) Common remarks. In all solutions, we will assume that $A$ is a set such that $\{a-b: a, b \in A\}$ is disjoint from $H$, and prove that $|A|<C \sqrt{n}$.
|
Again, define $J=\mathbb{Z}_{>0} \backslash H$, so all differences between elements of $A$ are in $J$. We start by making the following observation. Suppose we have a set $B \subseteq\{1,2, \ldots, n\}$ such that all of the differences between elements of $B$ are in $H$. Then $|A| \cdot|B| \leqslant 2 n$. To see why, observe that any two sums of the form $a+b$ with $a \in A, b \in B$ are different; otherwise, we would have $a_{1}+b_{1}=a_{2}+b_{2}$, and so $\left|a_{1}-a_{2}\right|=\left|b_{2}-b_{1}\right|$. However, then the left hand side is in $J$ whereas the right hand side is in $H$. Thus, $\{a+b: a \in A, b \in B\}$ is a set of size $|A| \cdot|B|$ all of whose elements are no greater than $2 n$, yielding the claimed inequality. With this in mind, it suffices to construct a set $B$, all of whose differences are in $H$ and whose size is at least $C^{\prime} \sqrt{n}$ for some constant $C^{\prime}>0$. To do so, we will use well-known facts about the negative Pell equation $X^{2}-2 Y^{2}=-1$; in particular, that there are infinitely many solutions and the values of $X$ are given by the recurrence $X_{1}=1, X_{2}=7$ and $X_{m}=6 X_{m-1}-X_{m-2}$. Therefore, we may choose $X$ to be a solution with $\sqrt{n} / 6<X \leqslant \sqrt{n}$. Now, we claim that we may choose $B=\{X, 2 X, \ldots,\lfloor(1 / 3) \sqrt{n}\rfloor X\}$. Indeed, we have $$ \left(\frac{X}{\sqrt{2}}-Y\right)\left(\frac{X}{\sqrt{2}}+Y\right)=\frac{-1}{2} $$ and so $$ 0>\left(\frac{X}{\sqrt{2}}-Y\right) \geqslant \frac{-3}{\sqrt{2 n}}, $$ from which it follows that $\{X / \sqrt{2}\}>1-(3 / \sqrt{2 n})$. Combined with (1), this shows that all differences between elements of $B$ are in $H$. Comment. Some of the ideas behind Solution 3 may be used to prove that the constant $C=\sqrt{2 \sqrt{2}-2}$ (from Solutions 1 and 2) is optimal, in the sense that there are arbitrarily large values of $n$ and sets $A_{n} \subseteq\{1,2, \ldots, n\}$ of size roughly $C \sqrt{n}$, all of whose differences are contained in $J$. To see why, choose $X$ to come from a sufficiently large solution to the Pell equation $X^{2}-2 Y^{2}=1$, so $\{X / \sqrt{2}\} \approx 1 /(2 X \sqrt{2})$. In particular, $\{X\},\{2 X\}, \ldots,\{[2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor X\}$ are all less than $1-1 / \sqrt{2}$. Thus, by (1) any positive integer of the form $i X$ for $1 \leqslant i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor$ lies in $J$. Set $n \approx 2 X^{2} \sqrt{2}(1-1 / \sqrt{2})$. We now have a set $A=\{i X: i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor\}$ containing roughly $2 X \sqrt{2}(1-1 / \sqrt{2})$ elements less than or equal to $n$ such that all of the differences lie in $J$, and we can see that $|A| \approx C \sqrt{n}$ with $C=\sqrt{2 \sqrt{2}-2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil) Common remarks. In all solutions, we will assume that $A$ is a set such that $\{a-b: a, b \in A\}$ is disjoint from $H$, and prove that $|A|<C \sqrt{n}$.
|
Again, define $J=\mathbb{Z}_{>0} \backslash H$, so all differences between elements of $A$ are in $J$. We start by making the following observation. Suppose we have a set $B \subseteq\{1,2, \ldots, n\}$ such that all of the differences between elements of $B$ are in $H$. Then $|A| \cdot|B| \leqslant 2 n$. To see why, observe that any two sums of the form $a+b$ with $a \in A, b \in B$ are different; otherwise, we would have $a_{1}+b_{1}=a_{2}+b_{2}$, and so $\left|a_{1}-a_{2}\right|=\left|b_{2}-b_{1}\right|$. However, then the left hand side is in $J$ whereas the right hand side is in $H$. Thus, $\{a+b: a \in A, b \in B\}$ is a set of size $|A| \cdot|B|$ all of whose elements are no greater than $2 n$, yielding the claimed inequality. With this in mind, it suffices to construct a set $B$, all of whose differences are in $H$ and whose size is at least $C^{\prime} \sqrt{n}$ for some constant $C^{\prime}>0$. To do so, we will use well-known facts about the negative Pell equation $X^{2}-2 Y^{2}=-1$; in particular, that there are infinitely many solutions and the values of $X$ are given by the recurrence $X_{1}=1, X_{2}=7$ and $X_{m}=6 X_{m-1}-X_{m-2}$. Therefore, we may choose $X$ to be a solution with $\sqrt{n} / 6<X \leqslant \sqrt{n}$. Now, we claim that we may choose $B=\{X, 2 X, \ldots,\lfloor(1 / 3) \sqrt{n}\rfloor X\}$. Indeed, we have $$ \left(\frac{X}{\sqrt{2}}-Y\right)\left(\frac{X}{\sqrt{2}}+Y\right)=\frac{-1}{2} $$ and so $$ 0>\left(\frac{X}{\sqrt{2}}-Y\right) \geqslant \frac{-3}{\sqrt{2 n}}, $$ from which it follows that $\{X / \sqrt{2}\}>1-(3 / \sqrt{2 n})$. Combined with (1), this shows that all differences between elements of $B$ are in $H$. Comment. Some of the ideas behind Solution 3 may be used to prove that the constant $C=\sqrt{2 \sqrt{2}-2}$ (from Solutions 1 and 2) is optimal, in the sense that there are arbitrarily large values of $n$ and sets $A_{n} \subseteq\{1,2, \ldots, n\}$ of size roughly $C \sqrt{n}$, all of whose differences are contained in $J$. To see why, choose $X$ to come from a sufficiently large solution to the Pell equation $X^{2}-2 Y^{2}=1$, so $\{X / \sqrt{2}\} \approx 1 /(2 X \sqrt{2})$. In particular, $\{X\},\{2 X\}, \ldots,\{[2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor X\}$ are all less than $1-1 / \sqrt{2}$. Thus, by (1) any positive integer of the form $i X$ for $1 \leqslant i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor$ lies in $J$. Set $n \approx 2 X^{2} \sqrt{2}(1-1 / \sqrt{2})$. We now have a set $A=\{i X: i \leqslant\lfloor 2 X \sqrt{2}(1-1 / \sqrt{2})\rfloor\}$ containing roughly $2 X \sqrt{2}(1-1 / \sqrt{2})$ elements less than or equal to $n$ such that all of the differences lie in $J$, and we can see that $|A| \approx C \sqrt{n}$ with $C=\sqrt{2 \sqrt{2}-2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bad4a911-bdaf-5e78-aa7f-6599f1082d58
| 23,916
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil) Common remarks. In all solutions, we will assume that $A$ is a set such that $\{a-b: a, b \in A\}$ is disjoint from $H$, and prove that $|A|<C \sqrt{n}$.
|
As in Choose $Y$ to be a solution to the Pell-like equation $X^{2}-2 Y^{2}= \pm 1$; such solutions are given by the recurrence $Y_{1}=1, Y_{2}=2$ and $Y_{m}=2 Y_{m-1}+Y_{m-2}$, and so we can choose $Y$ such that $n /(3 \sqrt{2})<Y \leqslant n / \sqrt{2}$. Furthermore, it is known that for such a $Y$ and for $1 \leqslant x<Y$, $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=1$, and $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=1+\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=-1$. Indeed, this is a statement of the fact that $X / Y$ is a best rational approximation to $\sqrt{2}$, from below in the first case and from above in the second. Now, consider the sequence $\{\sqrt{2}\},\{2 \sqrt{2}\}, \ldots,\{(Y-1) \sqrt{2}\}$. The Erdős-Szekeres theorem tells us that this sequence has a monotone subsequence with at least $\sqrt{Y-2}+1>\sqrt{Y}$ elements; if that subsequence is decreasing, we may reflect (using (4) or (5)) to ensure that it is increasing. Call the subsequence $\left\{y_{1} \sqrt{2}\right\},\left\{y_{2} \sqrt{2}\right\}, \ldots,\left\{y_{t} \sqrt{2}\right\}$ for $t>\sqrt{Y}$. Now, set $B=\left\{\left\lfloor y_{i} \sqrt{2}\right\rfloor: 1 \leqslant i \leqslant t\right\}$. We have $\left\lfloor y_{j} \sqrt{2}\right\rfloor-\left\lfloor y_{i} \sqrt{2}\right\rfloor=\left\lfloor\left(y_{j}-y_{i}\right) \sqrt{2}\right\rfloor$ for $i<j$ (because the corresponding inequality for the fractional parts holds by the ordering assumption on the $\left\{y_{i} \sqrt{2}\right\}$ ), which means that all differences between elements of $B$ are indeed in $H$. Since $|B|>\sqrt{Y}>\sqrt{n} / \sqrt{3 \sqrt{2}}$, this is the required set. Comment. Any solution to this problem will need to use the fact that $\sqrt{2}$ cannot be approximated well by rationals, either directly or implicitly (for example, by using facts about solutions to Pelllike equations). If $\sqrt{2}$ were replaced by a value of $\theta$ with very good rational approximations (from below), then an argument along the lines of Solution 3 would give long arithmetic progressions in $\{\lfloor i \theta\rfloor: 0 \leqslant i<n\}$ (with initial term 0 ) for certain values of $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $H=\left\{\lfloor i \sqrt{2}\rfloor: i \in \mathbb{Z}_{>0}\right\}=\{1,2,4,5,7, \ldots\}$, and let $n$ be a positive integer. Prove that there exists a constant $C$ such that, if $A \subset\{1,2, \ldots, n\}$ satisfies $|A| \geqslant C \sqrt{n}$, then there exist $a, b \in A$ such that $a-b \in H$. (Brazil) Common remarks. In all solutions, we will assume that $A$ is a set such that $\{a-b: a, b \in A\}$ is disjoint from $H$, and prove that $|A|<C \sqrt{n}$.
|
As in Choose $Y$ to be a solution to the Pell-like equation $X^{2}-2 Y^{2}= \pm 1$; such solutions are given by the recurrence $Y_{1}=1, Y_{2}=2$ and $Y_{m}=2 Y_{m-1}+Y_{m-2}$, and so we can choose $Y$ such that $n /(3 \sqrt{2})<Y \leqslant n / \sqrt{2}$. Furthermore, it is known that for such a $Y$ and for $1 \leqslant x<Y$, $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=1$, and $$ \{x \sqrt{2}\}+\{(Y-x) \sqrt{2}\}=1+\{Y / \sqrt{2}\} $$ if $X^{2}-2 Y^{2}=-1$. Indeed, this is a statement of the fact that $X / Y$ is a best rational approximation to $\sqrt{2}$, from below in the first case and from above in the second. Now, consider the sequence $\{\sqrt{2}\},\{2 \sqrt{2}\}, \ldots,\{(Y-1) \sqrt{2}\}$. The Erdős-Szekeres theorem tells us that this sequence has a monotone subsequence with at least $\sqrt{Y-2}+1>\sqrt{Y}$ elements; if that subsequence is decreasing, we may reflect (using (4) or (5)) to ensure that it is increasing. Call the subsequence $\left\{y_{1} \sqrt{2}\right\},\left\{y_{2} \sqrt{2}\right\}, \ldots,\left\{y_{t} \sqrt{2}\right\}$ for $t>\sqrt{Y}$. Now, set $B=\left\{\left\lfloor y_{i} \sqrt{2}\right\rfloor: 1 \leqslant i \leqslant t\right\}$. We have $\left\lfloor y_{j} \sqrt{2}\right\rfloor-\left\lfloor y_{i} \sqrt{2}\right\rfloor=\left\lfloor\left(y_{j}-y_{i}\right) \sqrt{2}\right\rfloor$ for $i<j$ (because the corresponding inequality for the fractional parts holds by the ordering assumption on the $\left\{y_{i} \sqrt{2}\right\}$ ), which means that all differences between elements of $B$ are indeed in $H$. Since $|B|>\sqrt{Y}>\sqrt{n} / \sqrt{3 \sqrt{2}}$, this is the required set. Comment. Any solution to this problem will need to use the fact that $\sqrt{2}$ cannot be approximated well by rationals, either directly or implicitly (for example, by using facts about solutions to Pelllike equations). If $\sqrt{2}$ were replaced by a value of $\theta$ with very good rational approximations (from below), then an argument along the lines of Solution 3 would give long arithmetic progressions in $\{\lfloor i \theta\rfloor: 0 \leqslant i<n\}$ (with initial term 0 ) for certain values of $n$.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bad4a911-bdaf-5e78-aa7f-6599f1082d58
| 23,916
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to z.) (Russia)
|
Arguing indirectly, assume that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=(a+k)^{2}, \quad \text { or } \quad\left\lceil\frac{(2 a)^{2}}{b}\right\rceil=(2 a+k) k $$ Clearly, $k \geqslant 1$. In other words, the equation $$ \left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ has a positive integer solution $(c, k)$, with an even value of $c$. Choose a positive integer solution of (1) with minimal possible value of $k$, without regard to the parity of $c$. From $$ \frac{c^{2}}{b}>\left\lceil\frac{c^{2}}{b}\right\rceil-1=c k+k^{2}-1 \geqslant c k $$ and $$ \frac{(c-k)(c+k)}{b}<\frac{c^{2}}{b} \leqslant\left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ it can be seen that $c>b k>c-k$, so $$ c=k b+r \quad \text { with some } 0<r<k $$ By substituting this in (1) we get $$ \left\lceil\frac{c^{2}}{b}\right\rceil=\left\lceil\frac{(b k+r)^{2}}{b}\right\rceil=k^{2} b+2 k r+\left\lceil\frac{r^{2}}{b}\right\rceil $$ and $$ (c+k) k=(k b+r+k) k=k^{2} b+2 k r+k(k-r) $$ so $$ \left\lceil\frac{r^{2}}{b}\right\rceil=k(k-r) $$ Notice that relation (2) provides another positive integer solution of (1), namely $c^{\prime}=r$ and $k^{\prime}=k-r$, with $c^{\prime}>0$ and $0<k^{\prime}<k$. That contradicts the minimality of $k$, and hence finishes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to z.) (Russia)
|
Arguing indirectly, assume that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=(a+k)^{2}, \quad \text { or } \quad\left\lceil\frac{(2 a)^{2}}{b}\right\rceil=(2 a+k) k $$ Clearly, $k \geqslant 1$. In other words, the equation $$ \left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ has a positive integer solution $(c, k)$, with an even value of $c$. Choose a positive integer solution of (1) with minimal possible value of $k$, without regard to the parity of $c$. From $$ \frac{c^{2}}{b}>\left\lceil\frac{c^{2}}{b}\right\rceil-1=c k+k^{2}-1 \geqslant c k $$ and $$ \frac{(c-k)(c+k)}{b}<\frac{c^{2}}{b} \leqslant\left\lceil\frac{c^{2}}{b}\right\rceil=(c+k) k $$ it can be seen that $c>b k>c-k$, so $$ c=k b+r \quad \text { with some } 0<r<k $$ By substituting this in (1) we get $$ \left\lceil\frac{c^{2}}{b}\right\rceil=\left\lceil\frac{(b k+r)^{2}}{b}\right\rceil=k^{2} b+2 k r+\left\lceil\frac{r^{2}}{b}\right\rceil $$ and $$ (c+k) k=(k b+r+k) k=k^{2} b+2 k r+k(k-r) $$ so $$ \left\lceil\frac{r^{2}}{b}\right\rceil=k(k-r) $$ Notice that relation (2) provides another positive integer solution of (1), namely $c^{\prime}=r$ and $k^{\prime}=k-r$, with $c^{\prime}>0$ and $0<k^{\prime}<k$. That contradicts the minimality of $k$, and hence finishes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa1cfe4b-ad54-51bf-a4a9-addb57b14fae
| 23,923
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to z.) (Russia)
|
Suppose that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=c^{2} $$ with some positive integer $c>a$, so $$ \begin{aligned} & c^{2}-1<a^{2}+\frac{4 a^{2}}{b} \leqslant c^{2} \\ & 0 \leqslant c^{2} b-a^{2}(b+4)<b \end{aligned} $$ Let $d=c^{2} b-a^{2}(b+4), x=c+a$ and $y=c-a$; then we have $c=\frac{x+y}{2}$ and $a=\frac{x-y}{2}$, and (3) can be re-written as follows: $$ \begin{aligned} \left(\frac{x+y}{2}\right)^{2} b-\left(\frac{x-y}{2}\right)^{2}(b+4) & =d \\ x^{2}-(b+2) x y+y^{2}+d=0 ; \quad 0 & \leqslant d<b \end{aligned} $$ So, by the indirect assumption, the equation (4) has some positive integer solution $(x, y)$. Fix $b$ and $d$, and take a pair $(x, y)$ of positive integers, satisfying (4), such that $x+y$ is minimal. By the symmetry in (4) we may assume that $x \geqslant y \geqslant 1$. Now we perform a usual "Vieta jump". Consider (4) as a quadratic equation in variable $x$, and let $z$ be its second root. By the Vieta formulas, $$ x+z=(b+2) y, \quad \text { and } \quad z x=y^{2}+d, $$ so $$ z=(b+2) y-x=\frac{y^{2}+d}{x} $$ The first formula shows that $z$ is an integer, and by the second formula $z$ is positive. Hence $(z, y)$ is another positive integer solution of (4). From $$ \begin{aligned} (x-1)(z-1) & =x z-(x+z)+1=\left(y^{2}+d\right)-(b+2) y+1 \\ & <\left(y^{2}+b\right)-(b+2) y+1=(y-1)^{2}-b(y-1) \leqslant(y-1)^{2} \leqslant(x-1)^{2} \end{aligned} $$ we can see that $z<x$ and therefore $z+y<x+y$. But this contradicts the minimality of $x+y$ among the positive integer solutions of (4). The activities of the Problem Selection Committee were supported by Trinity College, Cambridge University of Cambridge
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be two positive integers. Prove that the integer $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil $$ is not a square. (Here $\lceil z\rceil$ denotes the least integer greater than or equal to z.) (Russia)
|
Suppose that $$ a^{2}+\left\lceil\frac{4 a^{2}}{b}\right\rceil=c^{2} $$ with some positive integer $c>a$, so $$ \begin{aligned} & c^{2}-1<a^{2}+\frac{4 a^{2}}{b} \leqslant c^{2} \\ & 0 \leqslant c^{2} b-a^{2}(b+4)<b \end{aligned} $$ Let $d=c^{2} b-a^{2}(b+4), x=c+a$ and $y=c-a$; then we have $c=\frac{x+y}{2}$ and $a=\frac{x-y}{2}$, and (3) can be re-written as follows: $$ \begin{aligned} \left(\frac{x+y}{2}\right)^{2} b-\left(\frac{x-y}{2}\right)^{2}(b+4) & =d \\ x^{2}-(b+2) x y+y^{2}+d=0 ; \quad 0 & \leqslant d<b \end{aligned} $$ So, by the indirect assumption, the equation (4) has some positive integer solution $(x, y)$. Fix $b$ and $d$, and take a pair $(x, y)$ of positive integers, satisfying (4), such that $x+y$ is minimal. By the symmetry in (4) we may assume that $x \geqslant y \geqslant 1$. Now we perform a usual "Vieta jump". Consider (4) as a quadratic equation in variable $x$, and let $z$ be its second root. By the Vieta formulas, $$ x+z=(b+2) y, \quad \text { and } \quad z x=y^{2}+d, $$ so $$ z=(b+2) y-x=\frac{y^{2}+d}{x} $$ The first formula shows that $z$ is an integer, and by the second formula $z$ is positive. Hence $(z, y)$ is another positive integer solution of (4). From $$ \begin{aligned} (x-1)(z-1) & =x z-(x+z)+1=\left(y^{2}+d\right)-(b+2) y+1 \\ & <\left(y^{2}+b\right)-(b+2) y+1=(y-1)^{2}-b(y-1) \leqslant(y-1)^{2} \leqslant(x-1)^{2} \end{aligned} $$ we can see that $z<x$ and therefore $z+y<x+y$. But this contradicts the minimality of $x+y$ among the positive integer solutions of (4). The activities of the Problem Selection Committee were supported by Trinity College, Cambridge University of Cambridge
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa1cfe4b-ad54-51bf-a4a9-addb57b14fae
| 23,923
|
Let $a, b, c, d$ be four real numbers such that $a \geqslant b \geqslant c \geqslant d>0$ and $a+b+c+d=1$. Prove that $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<1 $$ (Belgium)
|
The weighted AM-GM inequality with weights $a, b, c, d$ gives $$ a^{a} b^{b} c^{c} d^{d} \leqslant a \cdot a+b \cdot b+c \cdot c+d \cdot d=a^{2}+b^{2}+c^{2}+d^{2} $$ so it suffices to prove that $(a+2 b+3 c+4 d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)<1=(a+b+c+d)^{3}$. This can be done in various ways, for example: $$ \begin{aligned} (a+b+c+d)^{3}> & a^{2}(a+3 b+3 c+3 d)+b^{2}(3 a+b+3 c+3 d) \\ & \quad+c^{2}(3 a+3 b+c+3 d)+d^{2}(3 a+3 b+3 c+d) \\ \geqslant & \left(a^{2}+b^{2}+c^{2}+d^{2}\right) \cdot(a+2 b+3 c+4 d) \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d$ be four real numbers such that $a \geqslant b \geqslant c \geqslant d>0$ and $a+b+c+d=1$. Prove that $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<1 $$ (Belgium)
|
The weighted AM-GM inequality with weights $a, b, c, d$ gives $$ a^{a} b^{b} c^{c} d^{d} \leqslant a \cdot a+b \cdot b+c \cdot c+d \cdot d=a^{2}+b^{2}+c^{2}+d^{2} $$ so it suffices to prove that $(a+2 b+3 c+4 d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)<1=(a+b+c+d)^{3}$. This can be done in various ways, for example: $$ \begin{aligned} (a+b+c+d)^{3}> & a^{2}(a+3 b+3 c+3 d)+b^{2}(3 a+b+3 c+3 d) \\ & \quad+c^{2}(3 a+3 b+c+3 d)+d^{2}(3 a+3 b+3 c+d) \\ \geqslant & \left(a^{2}+b^{2}+c^{2}+d^{2}\right) \cdot(a+2 b+3 c+4 d) \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1b8c7bbb-684b-542a-a1bc-676ff9d11647
| 23,937
|
Let $a, b, c, d$ be four real numbers such that $a \geqslant b \geqslant c \geqslant d>0$ and $a+b+c+d=1$. Prove that $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<1 $$ (Belgium)
|
From $b \geqslant d$ we get $$ a+2 b+3 c+4 d \leqslant a+3 b+3 c+3 d=3-2 a $$ If $a<\frac{1}{2}$, then the statement can be proved by $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d} \leqslant(3-2 a) a^{a} a^{b} a^{c} a^{d}=(3-2 a) a=1-(1-a)(1-2 a)<1 $$ From now on we assume $\frac{1}{2} \leqslant a<1$. By $b, c, d<1-a$ we have $$ b^{b} c^{c} d^{d}<(1-a)^{b} \cdot(1-a)^{c} \cdot(1-a)^{d}=(1-a)^{1-a} . $$ Therefore, $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<(3-2 a) a^{a}(1-a)^{1-a} $$ For $0<x<1$, consider the functions $f(x)=(3-2 x) x^{x}(1-x)^{1-x} \quad$ and $\quad g(x)=\log f(x)=\log (3-2 x)+x \log x+(1-x) \log (1-x) ;$ hereafter, $\log$ denotes the natural logarithm. It is easy to verify that $$ g^{\prime \prime}(x)=-\frac{4}{(3-2 x)^{2}}+\frac{1}{x}+\frac{1}{1-x}=\frac{1+8(1-x)^{2}}{x(1-x)(3-2 x)^{2}}>0 $$ so $g$ is strictly convex on $(0,1)$. By $g\left(\frac{1}{2}\right)=\log 2+2 \cdot \frac{1}{2} \log \frac{1}{2}=0$ and $\lim _{x \rightarrow 1-} g(x)=0$, we have $g(x) \leqslant 0$ (and hence $f(x) \leqslant 1$ ) for all $x \in\left[\frac{1}{2}, 1\right)$, and therefore $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<f(a) \leqslant 1 $$ Comment. For a large number of variables $a_{1} \geqslant a_{2} \geqslant \ldots \geqslant a_{n}>0$ with $\sum_{i} a_{i}=1$, the inequality $$ \left(\sum_{i} i a_{i}\right) \prod_{i} a_{i}^{a_{i}} \leqslant 1 $$ does not necessarily hold. Indeed, let $a_{2}=a_{3}=\ldots=a_{n}=\varepsilon$ and $a_{1}=1-(n-1) \varepsilon$, where $n$ and $\varepsilon \in(0,1 / n)$ will be chosen later. Then $$ \left(\sum_{i} i a_{i}\right) \prod_{i} a_{i}^{a_{i}}=\left(1+\frac{n(n-1)}{2} \varepsilon\right) \varepsilon^{(n-1) \varepsilon}(1-(n-1) \varepsilon)^{1-(n-1) \varepsilon} $$ If $\varepsilon=C / n^{2}$ with an arbitrary fixed $C>0$ and $n \rightarrow \infty$, then the factors $\varepsilon^{(n-1) \varepsilon}=\exp ((n-1) \varepsilon \log \varepsilon)$ and $(1-(n-1) \varepsilon)^{1-(n-1) \varepsilon}$ tend to 1 , so the limit of (1) in this set-up equals $1+C / 2$. This is not simply greater than 1 , but it can be arbitrarily large.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d$ be four real numbers such that $a \geqslant b \geqslant c \geqslant d>0$ and $a+b+c+d=1$. Prove that $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<1 $$ (Belgium)
|
From $b \geqslant d$ we get $$ a+2 b+3 c+4 d \leqslant a+3 b+3 c+3 d=3-2 a $$ If $a<\frac{1}{2}$, then the statement can be proved by $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d} \leqslant(3-2 a) a^{a} a^{b} a^{c} a^{d}=(3-2 a) a=1-(1-a)(1-2 a)<1 $$ From now on we assume $\frac{1}{2} \leqslant a<1$. By $b, c, d<1-a$ we have $$ b^{b} c^{c} d^{d}<(1-a)^{b} \cdot(1-a)^{c} \cdot(1-a)^{d}=(1-a)^{1-a} . $$ Therefore, $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<(3-2 a) a^{a}(1-a)^{1-a} $$ For $0<x<1$, consider the functions $f(x)=(3-2 x) x^{x}(1-x)^{1-x} \quad$ and $\quad g(x)=\log f(x)=\log (3-2 x)+x \log x+(1-x) \log (1-x) ;$ hereafter, $\log$ denotes the natural logarithm. It is easy to verify that $$ g^{\prime \prime}(x)=-\frac{4}{(3-2 x)^{2}}+\frac{1}{x}+\frac{1}{1-x}=\frac{1+8(1-x)^{2}}{x(1-x)(3-2 x)^{2}}>0 $$ so $g$ is strictly convex on $(0,1)$. By $g\left(\frac{1}{2}\right)=\log 2+2 \cdot \frac{1}{2} \log \frac{1}{2}=0$ and $\lim _{x \rightarrow 1-} g(x)=0$, we have $g(x) \leqslant 0$ (and hence $f(x) \leqslant 1$ ) for all $x \in\left[\frac{1}{2}, 1\right)$, and therefore $$ (a+2 b+3 c+4 d) a^{a} b^{b} c^{c} d^{d}<f(a) \leqslant 1 $$ Comment. For a large number of variables $a_{1} \geqslant a_{2} \geqslant \ldots \geqslant a_{n}>0$ with $\sum_{i} a_{i}=1$, the inequality $$ \left(\sum_{i} i a_{i}\right) \prod_{i} a_{i}^{a_{i}} \leqslant 1 $$ does not necessarily hold. Indeed, let $a_{2}=a_{3}=\ldots=a_{n}=\varepsilon$ and $a_{1}=1-(n-1) \varepsilon$, where $n$ and $\varepsilon \in(0,1 / n)$ will be chosen later. Then $$ \left(\sum_{i} i a_{i}\right) \prod_{i} a_{i}^{a_{i}}=\left(1+\frac{n(n-1)}{2} \varepsilon\right) \varepsilon^{(n-1) \varepsilon}(1-(n-1) \varepsilon)^{1-(n-1) \varepsilon} $$ If $\varepsilon=C / n^{2}$ with an arbitrary fixed $C>0$ and $n \rightarrow \infty$, then the factors $\varepsilon^{(n-1) \varepsilon}=\exp ((n-1) \varepsilon \log \varepsilon)$ and $(1-(n-1) \varepsilon)^{1-(n-1) \varepsilon}$ tend to 1 , so the limit of (1) in this set-up equals $1+C / 2$. This is not simply greater than 1 , but it can be arbitrarily large.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1b8c7bbb-684b-542a-a1bc-676ff9d11647
| 23,937
|
A magician intends to perform the following trick. She announces a positive integer $n$, along with $2 n$ real numbers $x_{1}<\ldots<x_{2 n}$, to the audience. A member of the audience then secretly chooses a polynomial $P(x)$ of degree $n$ with real coefficients, computes the $2 n$ values $P\left(x_{1}\right), \ldots, P\left(x_{2 n}\right)$, and writes down these $2 n$ values on the blackboard in non-decreasing order. After that the magician announces the secret polynomial to the audience. Can the magician find a strategy to perform such a trick? (Luxembourg)
|
Let $x_{1}<x_{2}<\ldots<x_{2 n}$ be real numbers chosen by the magician. We will construct two distinct polynomials $P(x)$ and $Q(x)$, each of degree $n$, such that the member of audience will write down the same sequence for both polynomials. This will mean that the magician cannot distinguish $P$ from $Q$. Claim. There exists a polynomial $P(x)$ of degree $n$ such that $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for $i=$ $1,2, \ldots, n$. Proof. We want to find a polynomial $a_{n} x^{n}+\ldots+a_{1} x+a_{0}$ satisfying the following system of equations: $$ \left\{\begin{array}{l} \left(x_{1}^{n}+x_{2}^{n}\right) a_{n}+\left(x_{1}^{n-1}+x_{2}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \left(x_{3}^{n}+x_{4}^{n}\right) a_{n}+\left(x_{3}^{n-1}+x_{4}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \cdots \\ \left(x_{2 n-1}^{n}+x_{2 n}^{n}\right) a_{n}+\left(x_{2 n-1}^{n-1}+x_{2 n}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \end{array}\right. $$ We use the well known fact that a homogeneous system of $n$ linear equations in $n+1$ variables has a nonzero solution. (This fact can be proved using induction on $n$, via elimination of variables.) Applying this fact to the above system, we find a nonzero polynomial $P(x)$ of degree not exceeding $n$ such that its coefficients $a_{0}, \ldots, a_{n}$ satisfy this system. Therefore $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for all $i=1,2, \ldots, n$. Notice that $P$ has a root on each segment $\left[x_{2 i-1}, x_{2 i}\right]$ by the Intermediate Value theorem, so $n$ roots in total. Since $P$ is nonzero, we get $\operatorname{deg} P=n$. Now consider a polynomial $P(x)$ provided by the Claim, and take $Q(x)=-P(x)$. The properties of $P(x)$ yield that $P\left(x_{2 i-1}\right)=Q\left(x_{2 i}\right)$ and $Q\left(x_{2 i-1}\right)=P\left(x_{2 i}\right)$ for all $i=1,2, \ldots, n$. It is also clear that $P \neq-P=Q$ and $\operatorname{deg} Q=\operatorname{deg} P=n$. Comment. It can be shown that for any positive integer $n$ the magician can choose $2 n+1$ distinct real numbers so as to perform such a trick. Moreover, she can perform such a trick with almost all (in a proper sense) $(2 n+1)$-tuples of numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A magician intends to perform the following trick. She announces a positive integer $n$, along with $2 n$ real numbers $x_{1}<\ldots<x_{2 n}$, to the audience. A member of the audience then secretly chooses a polynomial $P(x)$ of degree $n$ with real coefficients, computes the $2 n$ values $P\left(x_{1}\right), \ldots, P\left(x_{2 n}\right)$, and writes down these $2 n$ values on the blackboard in non-decreasing order. After that the magician announces the secret polynomial to the audience. Can the magician find a strategy to perform such a trick? (Luxembourg)
|
Let $x_{1}<x_{2}<\ldots<x_{2 n}$ be real numbers chosen by the magician. We will construct two distinct polynomials $P(x)$ and $Q(x)$, each of degree $n$, such that the member of audience will write down the same sequence for both polynomials. This will mean that the magician cannot distinguish $P$ from $Q$. Claim. There exists a polynomial $P(x)$ of degree $n$ such that $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for $i=$ $1,2, \ldots, n$. Proof. We want to find a polynomial $a_{n} x^{n}+\ldots+a_{1} x+a_{0}$ satisfying the following system of equations: $$ \left\{\begin{array}{l} \left(x_{1}^{n}+x_{2}^{n}\right) a_{n}+\left(x_{1}^{n-1}+x_{2}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \left(x_{3}^{n}+x_{4}^{n}\right) a_{n}+\left(x_{3}^{n-1}+x_{4}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \\ \cdots \\ \left(x_{2 n-1}^{n}+x_{2 n}^{n}\right) a_{n}+\left(x_{2 n-1}^{n-1}+x_{2 n}^{n-1}\right) a_{n-1}+\ldots+2 a_{0}=0 \end{array}\right. $$ We use the well known fact that a homogeneous system of $n$ linear equations in $n+1$ variables has a nonzero solution. (This fact can be proved using induction on $n$, via elimination of variables.) Applying this fact to the above system, we find a nonzero polynomial $P(x)$ of degree not exceeding $n$ such that its coefficients $a_{0}, \ldots, a_{n}$ satisfy this system. Therefore $P\left(x_{2 i-1}\right)+P\left(x_{2 i}\right)=0$ for all $i=1,2, \ldots, n$. Notice that $P$ has a root on each segment $\left[x_{2 i-1}, x_{2 i}\right]$ by the Intermediate Value theorem, so $n$ roots in total. Since $P$ is nonzero, we get $\operatorname{deg} P=n$. Now consider a polynomial $P(x)$ provided by the Claim, and take $Q(x)=-P(x)$. The properties of $P(x)$ yield that $P\left(x_{2 i-1}\right)=Q\left(x_{2 i}\right)$ and $Q\left(x_{2 i-1}\right)=P\left(x_{2 i}\right)$ for all $i=1,2, \ldots, n$. It is also clear that $P \neq-P=Q$ and $\operatorname{deg} Q=\operatorname{deg} P=n$. Comment. It can be shown that for any positive integer $n$ the magician can choose $2 n+1$ distinct real numbers so as to perform such a trick. Moreover, she can perform such a trick with almost all (in a proper sense) $(2 n+1)$-tuples of numbers.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
273d0c10-ea8e-5095-b01a-ac346d904d35
| 23,941
|
Let $n$ and $k$ be positive integers. Prove that for $a_{1}, \ldots, a_{n} \in\left[1,2^{k}\right]$ one has $$ \sum_{i=1}^{n} \frac{a_{i}}{\sqrt{a_{1}^{2}+\ldots+a_{i}^{2}}} \leqslant 4 \sqrt{k n} $$
|
Apply induction on $n$. The base $n \leqslant 16$ is clear: our sum does not exceed $n \leqslant 4 \sqrt{n k}$. For the inductive step from $1, \ldots, n-1$ to $n \geqslant 17$ consider two similar cases. Case 1: $n=2 t$. Let $x_{\ell}=\frac{a_{\ell}}{\sqrt{a_{1}^{2}+\ldots+a_{\ell}^{2}}}$. We have $$ \exp \left(-x_{t+1}^{2}-\ldots-x_{2 t}^{2}\right) \geqslant\left(1-x_{t+1}^{2}\right) \ldots\left(1-x_{2 t}^{2}\right)=\frac{a_{1}^{2}+\ldots+a_{t}^{2}}{a_{1}^{2}+\ldots+a_{2 t}^{2}} \geqslant \frac{1}{1+4^{k}} $$ where we used that the product is telescopic and then an estimate $a_{t+i} \leqslant 2^{k} a_{i}$ for $i=1, \ldots, t$. Therefore, $x_{t+1}^{2}+\ldots+x_{2 t}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$, where log denotes the natural logarithm. This implies $x_{t+1}+\ldots+x_{2 t} \leqslant \sqrt{2 k t}$. Hence, using the inductive hypothesis for $n=t$ we get $$ \sum_{\ell=1}^{2 t} x_{\ell} \leqslant 4 \sqrt{k t}+\sqrt{2 k t} \leqslant 4 \sqrt{2 k t} $$ Case 2: $n=2 t+1$. Analogously, we get $x_{t+2}^{2}+\ldots+x_{2 t+1}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$ and $$ \sum_{\ell=1}^{2 t+1} x_{\ell} \leqslant 4 \sqrt{k(t+1)}+\sqrt{2 k t} \leqslant 4 \sqrt{k(2 t+1)} $$ The last inequality is true for all $t \geqslant 8$ since $$ 4 \sqrt{2 t+1}-\sqrt{2 t} \geqslant 3 \sqrt{2 t}=\sqrt{18 t} \geqslant \sqrt{16 t+16}=4 \sqrt{t+1} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ and $k$ be positive integers. Prove that for $a_{1}, \ldots, a_{n} \in\left[1,2^{k}\right]$ one has $$ \sum_{i=1}^{n} \frac{a_{i}}{\sqrt{a_{1}^{2}+\ldots+a_{i}^{2}}} \leqslant 4 \sqrt{k n} $$
|
Apply induction on $n$. The base $n \leqslant 16$ is clear: our sum does not exceed $n \leqslant 4 \sqrt{n k}$. For the inductive step from $1, \ldots, n-1$ to $n \geqslant 17$ consider two similar cases. Case 1: $n=2 t$. Let $x_{\ell}=\frac{a_{\ell}}{\sqrt{a_{1}^{2}+\ldots+a_{\ell}^{2}}}$. We have $$ \exp \left(-x_{t+1}^{2}-\ldots-x_{2 t}^{2}\right) \geqslant\left(1-x_{t+1}^{2}\right) \ldots\left(1-x_{2 t}^{2}\right)=\frac{a_{1}^{2}+\ldots+a_{t}^{2}}{a_{1}^{2}+\ldots+a_{2 t}^{2}} \geqslant \frac{1}{1+4^{k}} $$ where we used that the product is telescopic and then an estimate $a_{t+i} \leqslant 2^{k} a_{i}$ for $i=1, \ldots, t$. Therefore, $x_{t+1}^{2}+\ldots+x_{2 t}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$, where log denotes the natural logarithm. This implies $x_{t+1}+\ldots+x_{2 t} \leqslant \sqrt{2 k t}$. Hence, using the inductive hypothesis for $n=t$ we get $$ \sum_{\ell=1}^{2 t} x_{\ell} \leqslant 4 \sqrt{k t}+\sqrt{2 k t} \leqslant 4 \sqrt{2 k t} $$ Case 2: $n=2 t+1$. Analogously, we get $x_{t+2}^{2}+\ldots+x_{2 t+1}^{2} \leqslant \log \left(4^{k}+1\right) \leqslant 2 k$ and $$ \sum_{\ell=1}^{2 t+1} x_{\ell} \leqslant 4 \sqrt{k(t+1)}+\sqrt{2 k t} \leqslant 4 \sqrt{k(2 t+1)} $$ The last inequality is true for all $t \geqslant 8$ since $$ 4 \sqrt{2 t+1}-\sqrt{2 t} \geqslant 3 \sqrt{2 t}=\sqrt{18 t} \geqslant \sqrt{16 t+16}=4 \sqrt{t+1} $$
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
47ee4db4-3bc3-5e71-bdba-026d430650f8
| 23,947
|
In a regular 100-gon, 41 vertices are colored black and the remaining 59 vertices are colored white. Prove that there exist 24 convex quadrilaterals $Q_{1}, \ldots, Q_{24}$ whose corners are vertices of the 100 -gon, so that - the quadrilaterals $Q_{1}, \ldots, Q_{24}$ are pairwise disjoint, and - every quadrilateral $Q_{i}$ has three corners of one color and one corner of the other color. (Austria)
|
Call a quadrilateral skew-colored, if it has three corners of one color and one corner of the other color. We will prove the following Claim. If the vertices of a convex $(4 k+1)$-gon $P$ are colored black and white such that each color is used at least $k$ times, then there exist $k$ pairwise disjoint skew-colored quadrilaterals whose vertices are vertices of $P$. (One vertex of $P$ remains unused.) The problem statement follows by removing 3 arbitrary vertices of the 100-gon and applying the Claim to the remaining 97 vertices with $k=24$. Proof of the Claim. We prove by induction. For $k=1$ we have a pentagon with at least one black and at least one white vertex. If the number of black vertices is even then remove a black vertex; otherwise remove a white vertex. In the remaining quadrilateral, there are an odd number of black and an odd number of white vertices, so the quadrilateral is skew-colored. For the induction step, assume $k \geqslant 2$. Let $b$ and $w$ be the numbers of black and white vertices, respectively; then $b, w \geqslant k$ and $b+w=4 k+1$. Without loss of generality we may assume $w \geqslant b$, so $k \leqslant b \leqslant 2 k$ and $2 k+1 \leqslant w \leqslant 3 k+1$. We want to find four consecutive vertices such that three of them are white, the fourth one is black. Denote the vertices by $V_{1}, V_{2}, \ldots, V_{4 k+1}$ in counterclockwise order, such that $V_{4 k+1}$ is black, and consider the following $k$ groups of vertices: $$ \left(V_{1}, V_{2}, V_{3}, V_{4}\right),\left(V_{5}, V_{6}, V_{7}, V_{8}\right), \ldots,\left(V_{4 k-3}, V_{4 k-2}, V_{4 k-1}, V_{4 k}\right) $$ In these groups there are $w$ white and $b-1$ black vertices. Since $w>b-1$, there is a group, $\left(V_{i}, V_{i+1}, V_{i+2}, V_{i+3}\right)$ that contains more white than black vertices. If three are white and one is black in that group, we are done. Otherwise, if $V_{i}, V_{i+1}, V_{i+2}, V_{i+3}$ are all white then let $V_{j}$ be the first black vertex among $V_{i+4}, \ldots, V_{4 k+1}$ (recall that $V_{4 k+1}$ is black); then $V_{j-3}, V_{j-2}$ and $V_{j-1}$ are white and $V_{j}$ is black. Now we have four consecutive vertices $V_{i}, V_{i+1}, V_{i+2}, V_{i+3}$ that form a skew-colored quadrilateral. The remaining vertices form a convex ( $4 k-3$ )-gon; $w-3$ of them are white and $b-1$ are black. Since $b-1 \geqslant k-1$ and $w-3 \geqslant(2 k+1)-3>k-1$, we can apply the Claim with $k-1$. Comment. It is not true that the vertices of the 100 -gon can be split into 25 skew-colored quadrilaterals. A possible counter-example is when the vertices $V_{1}, V_{3}, V_{5}, \ldots, V_{81}$ are black and the other vertices, $V_{2}, V_{4}, \ldots, V_{80}$ and $V_{82}, V_{83}, \ldots, V_{100}$ are white. For having 25 skew-colored quadrilaterals, there should be 8 containing three black vertices. But such a quadrilateral splits the other 96 vertices into four sets in such a way that at least two sets contain odd numbers of vertices and therefore they cannot be grouped into disjoint quadrilaterals. 
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a regular 100-gon, 41 vertices are colored black and the remaining 59 vertices are colored white. Prove that there exist 24 convex quadrilaterals $Q_{1}, \ldots, Q_{24}$ whose corners are vertices of the 100 -gon, so that - the quadrilaterals $Q_{1}, \ldots, Q_{24}$ are pairwise disjoint, and - every quadrilateral $Q_{i}$ has three corners of one color and one corner of the other color. (Austria)
|
Call a quadrilateral skew-colored, if it has three corners of one color and one corner of the other color. We will prove the following Claim. If the vertices of a convex $(4 k+1)$-gon $P$ are colored black and white such that each color is used at least $k$ times, then there exist $k$ pairwise disjoint skew-colored quadrilaterals whose vertices are vertices of $P$. (One vertex of $P$ remains unused.) The problem statement follows by removing 3 arbitrary vertices of the 100-gon and applying the Claim to the remaining 97 vertices with $k=24$. Proof of the Claim. We prove by induction. For $k=1$ we have a pentagon with at least one black and at least one white vertex. If the number of black vertices is even then remove a black vertex; otherwise remove a white vertex. In the remaining quadrilateral, there are an odd number of black and an odd number of white vertices, so the quadrilateral is skew-colored. For the induction step, assume $k \geqslant 2$. Let $b$ and $w$ be the numbers of black and white vertices, respectively; then $b, w \geqslant k$ and $b+w=4 k+1$. Without loss of generality we may assume $w \geqslant b$, so $k \leqslant b \leqslant 2 k$ and $2 k+1 \leqslant w \leqslant 3 k+1$. We want to find four consecutive vertices such that three of them are white, the fourth one is black. Denote the vertices by $V_{1}, V_{2}, \ldots, V_{4 k+1}$ in counterclockwise order, such that $V_{4 k+1}$ is black, and consider the following $k$ groups of vertices: $$ \left(V_{1}, V_{2}, V_{3}, V_{4}\right),\left(V_{5}, V_{6}, V_{7}, V_{8}\right), \ldots,\left(V_{4 k-3}, V_{4 k-2}, V_{4 k-1}, V_{4 k}\right) $$ In these groups there are $w$ white and $b-1$ black vertices. Since $w>b-1$, there is a group, $\left(V_{i}, V_{i+1}, V_{i+2}, V_{i+3}\right)$ that contains more white than black vertices. If three are white and one is black in that group, we are done. Otherwise, if $V_{i}, V_{i+1}, V_{i+2}, V_{i+3}$ are all white then let $V_{j}$ be the first black vertex among $V_{i+4}, \ldots, V_{4 k+1}$ (recall that $V_{4 k+1}$ is black); then $V_{j-3}, V_{j-2}$ and $V_{j-1}$ are white and $V_{j}$ is black. Now we have four consecutive vertices $V_{i}, V_{i+1}, V_{i+2}, V_{i+3}$ that form a skew-colored quadrilateral. The remaining vertices form a convex ( $4 k-3$ )-gon; $w-3$ of them are white and $b-1$ are black. Since $b-1 \geqslant k-1$ and $w-3 \geqslant(2 k+1)-3>k-1$, we can apply the Claim with $k-1$. Comment. It is not true that the vertices of the 100 -gon can be split into 25 skew-colored quadrilaterals. A possible counter-example is when the vertices $V_{1}, V_{3}, V_{5}, \ldots, V_{81}$ are black and the other vertices, $V_{2}, V_{4}, \ldots, V_{80}$ and $V_{82}, V_{83}, \ldots, V_{100}$ are white. For having 25 skew-colored quadrilaterals, there should be 8 containing three black vertices. But such a quadrilateral splits the other 96 vertices into four sets in such a way that at least two sets contain odd numbers of vertices and therefore they cannot be grouped into disjoint quadrilaterals. 
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
038714b1-71ec-5391-b099-2a071b0862ab
| 23,958
|
Let $p$ be an odd prime, and put $N=\frac{1}{4}\left(p^{3}-p\right)-1$. The numbers $1,2, \ldots, N$ are painted arbitrarily in two colors, red and blue. For any positive integer $n \leqslant N$, denote by $r(n)$ the fraction of integers in $\{1,2, \ldots, n\}$ that are red. Prove that there exists a positive integer $a \in\{1,2, \ldots, p-1\}$ such that $r(n) \neq a / p$ for all $n=1,2, \ldots, N$. (Netherlands)
|
Denote by $R(n)$ the number of red numbers in $\{1,2, \ldots, n\}$, i.e., $R(n)=n r(n)$. Similarly, denote by $B(n)$ and $b(n)=B(n) / n$ the number and proportion of blue numbers in $\{1,2, \ldots, n\}$, respectively. Notice that $B(n)+R(n)=n$ and $b(n)+r(n)=1$. Therefore, the statement of the problem does not change after swapping the colors. Arguing indirectly, for every $a \in\{1,2, \ldots, p-1\}$ choose some positive integer $n_{a}$ such that $r\left(n_{a}\right)=a / p$ and, hence, $R\left(n_{a}\right)=a n_{a} / p$. Clearly, $p \mid n_{a}$, so that $n_{a}=p m_{a}$ for some positive integer $m_{a}$, and $R\left(n_{a}\right)=a m_{a}$. Without loss of generality, we assume that $m_{1}<m_{p-1}$, as otherwise one may swap the colors. Notice that $$ m_{a} \leqslant \frac{N}{p}<\frac{p^{2}-1}{4} \quad \text { for all } a=1,2, \ldots, p-1 $$ The solution is based on a repeated application of the following simple observation. Claim. Assume that $m_{a}<m_{b}$ for some $a, b \in\{1,2, \ldots, p-1\}$. Then $$ m_{b} \geqslant \frac{a}{b} m_{a} \quad \text { and } \quad m_{b} \geqslant \frac{p-a}{p-b} m_{a} $$ Proof. The first inequality follows from $b m_{b}=R\left(n_{b}\right) \geqslant R\left(n_{a}\right)=a m_{a}$. The second inequality is obtained by swapping colors . Let $q=(p-1) / 2$. We distinguish two cases. Case 1: All $q$ numbers $m_{1}, m_{2}, \ldots, m_{q}$ are smaller than $m_{p-1}$. Let $m_{a}$ be the maximal number among $m_{1}, m_{2}, \ldots, m_{q}$; then $m_{a} \geqslant q \geqslant a$. Applying the Claim, we get $$ m_{p-1} \geqslant \frac{p-a}{p-(p-1)} m_{a} \geqslant(p-q) q=\frac{p^{2}-1}{4} $$ which contradicts (1). Case 2: There exists $k \leqslant q$ such that $m_{k}>m_{p-1}$. Choose $k$ to be the smallest index satisfying $m_{k}>m_{p-1}$; by our assumptions, we have $1<k \leqslant$ $q<p-1$. Let $m_{a}$ be the maximal number among $m_{1}, m_{2}, \ldots, m_{k-1}$; then $a \leqslant k-1 \leqslant m_{a}<m_{p-1}$. Applying the Claim, we get $$ \begin{aligned} m_{k} \geqslant \frac{p-1}{k} m_{p-1} \geqslant \frac{p-1}{k} & \cdot \frac{p-a}{p-(p-1)} m_{a} \\ & \geqslant \frac{p-1}{k} \cdot(p-k+1)(k-1) \geqslant \frac{k-1}{k} \cdot(p-1)(p-q) \geqslant \frac{1}{2} \cdot \frac{p^{2}-1}{2} \end{aligned} $$ which contradicts (1) again. Comment 1. The argument in Case 2, after a slight modification of estimates at the end, applies as soon as there exists $k<\frac{3(p+1)}{4}$ with $a_{k}<a_{p-1}$. However, this argument does not seem to work if there is no such $k$. Comment 2. If $p$ is small enough, then one can color $\{1,2, \ldots, N+1\}$ so that there exist numbers $m_{1}$, $m_{2}, \ldots, m_{p-1}$ satisfying $r\left(p m_{a}\right)=a / p$. For $p=3,5,7$, one can find colorings providing the following sequences: $$ \left(m_{1}, m_{2}\right)=(1,2), \quad\left(m_{1}, m_{2}, m_{3}, m_{4}\right)=(1,2,3,6), \quad \text { and } \quad\left(m_{1}, \ldots, m_{6}\right)=(1,2,3,4,6,12) $$ respectively. Thus, for small values of $p$, the number $N$ in the problem statement cannot be increased. However, a careful analysis of the estimates shows that this number can be slightly increased for $p \geqslant 11$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $p$ be an odd prime, and put $N=\frac{1}{4}\left(p^{3}-p\right)-1$. The numbers $1,2, \ldots, N$ are painted arbitrarily in two colors, red and blue. For any positive integer $n \leqslant N$, denote by $r(n)$ the fraction of integers in $\{1,2, \ldots, n\}$ that are red. Prove that there exists a positive integer $a \in\{1,2, \ldots, p-1\}$ such that $r(n) \neq a / p$ for all $n=1,2, \ldots, N$. (Netherlands)
|
Denote by $R(n)$ the number of red numbers in $\{1,2, \ldots, n\}$, i.e., $R(n)=n r(n)$. Similarly, denote by $B(n)$ and $b(n)=B(n) / n$ the number and proportion of blue numbers in $\{1,2, \ldots, n\}$, respectively. Notice that $B(n)+R(n)=n$ and $b(n)+r(n)=1$. Therefore, the statement of the problem does not change after swapping the colors. Arguing indirectly, for every $a \in\{1,2, \ldots, p-1\}$ choose some positive integer $n_{a}$ such that $r\left(n_{a}\right)=a / p$ and, hence, $R\left(n_{a}\right)=a n_{a} / p$. Clearly, $p \mid n_{a}$, so that $n_{a}=p m_{a}$ for some positive integer $m_{a}$, and $R\left(n_{a}\right)=a m_{a}$. Without loss of generality, we assume that $m_{1}<m_{p-1}$, as otherwise one may swap the colors. Notice that $$ m_{a} \leqslant \frac{N}{p}<\frac{p^{2}-1}{4} \quad \text { for all } a=1,2, \ldots, p-1 $$ The solution is based on a repeated application of the following simple observation. Claim. Assume that $m_{a}<m_{b}$ for some $a, b \in\{1,2, \ldots, p-1\}$. Then $$ m_{b} \geqslant \frac{a}{b} m_{a} \quad \text { and } \quad m_{b} \geqslant \frac{p-a}{p-b} m_{a} $$ Proof. The first inequality follows from $b m_{b}=R\left(n_{b}\right) \geqslant R\left(n_{a}\right)=a m_{a}$. The second inequality is obtained by swapping colors . Let $q=(p-1) / 2$. We distinguish two cases. Case 1: All $q$ numbers $m_{1}, m_{2}, \ldots, m_{q}$ are smaller than $m_{p-1}$. Let $m_{a}$ be the maximal number among $m_{1}, m_{2}, \ldots, m_{q}$; then $m_{a} \geqslant q \geqslant a$. Applying the Claim, we get $$ m_{p-1} \geqslant \frac{p-a}{p-(p-1)} m_{a} \geqslant(p-q) q=\frac{p^{2}-1}{4} $$ which contradicts (1). Case 2: There exists $k \leqslant q$ such that $m_{k}>m_{p-1}$. Choose $k$ to be the smallest index satisfying $m_{k}>m_{p-1}$; by our assumptions, we have $1<k \leqslant$ $q<p-1$. Let $m_{a}$ be the maximal number among $m_{1}, m_{2}, \ldots, m_{k-1}$; then $a \leqslant k-1 \leqslant m_{a}<m_{p-1}$. Applying the Claim, we get $$ \begin{aligned} m_{k} \geqslant \frac{p-1}{k} m_{p-1} \geqslant \frac{p-1}{k} & \cdot \frac{p-a}{p-(p-1)} m_{a} \\ & \geqslant \frac{p-1}{k} \cdot(p-k+1)(k-1) \geqslant \frac{k-1}{k} \cdot(p-1)(p-q) \geqslant \frac{1}{2} \cdot \frac{p^{2}-1}{2} \end{aligned} $$ which contradicts (1) again. Comment 1. The argument in Case 2, after a slight modification of estimates at the end, applies as soon as there exists $k<\frac{3(p+1)}{4}$ with $a_{k}<a_{p-1}$. However, this argument does not seem to work if there is no such $k$. Comment 2. If $p$ is small enough, then one can color $\{1,2, \ldots, N+1\}$ so that there exist numbers $m_{1}$, $m_{2}, \ldots, m_{p-1}$ satisfying $r\left(p m_{a}\right)=a / p$. For $p=3,5,7$, one can find colorings providing the following sequences: $$ \left(m_{1}, m_{2}\right)=(1,2), \quad\left(m_{1}, m_{2}, m_{3}, m_{4}\right)=(1,2,3,6), \quad \text { and } \quad\left(m_{1}, \ldots, m_{6}\right)=(1,2,3,4,6,12) $$ respectively. Thus, for small values of $p$, the number $N$ in the problem statement cannot be increased. However, a careful analysis of the estimates shows that this number can be slightly increased for $p \geqslant 11$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ed0fcc1a-ba26-5dd5-a635-48cfea031002
| 23,966
|
$4 n$ coins of weights $1,2,3, \ldots, 4 n$ are given. Each coin is colored in one of $n$ colors and there are four coins of each color. Show that all these coins can be partitioned into two sets with the same total weight, such that each set contains two coins of each color. (Hungary)
|
Let us pair the coins with weights summing up to $4 n+1$, resulting in the set $S$ of $2 n$ pairs: $\{1,4 n\},\{2,4 n-1\}, \ldots,\{2 n, 2 n+1\}$. It suffices to partition $S$ into two sets, each consisting of $n$ pairs, such that each set contains two coins of each color. Introduce a multi-graph $G$ (i.e., a graph with loops and multiple edges allowed) on $n$ vertices, so that each vertex corresponds to a color. For each pair of coins from $S$, we add an edge between the vertices corresponding to the colors of those coins. Note that each vertex has degree 4. Also, a desired partition of the coins corresponds to a coloring of the edges of $G$ in two colors, say red and blue, so that each vertex has degree 2 with respect to each color (i.e., each vertex has equal red and blue degrees). To complete the solution, it suffices to provide such a coloring for each component $G^{\prime}$ of $G$. Since all degrees of the vertices are even, in $G^{\prime}$ there exists an Euler circuit $C$ (i.e., a circuit passing through each edge of $G^{\prime}$ exactly once). Note that the number of edges in $C$ is even (it equals twice the number of vertices in $G^{\prime}$ ). Hence all the edges can be colored red and blue so that any two edges adjacent in $C$ have different colors (one may move along $C$ and color the edges one by one alternating red and blue colors). Thus in $G^{\prime}$ each vertex has equal red and blue degrees, as desired. Comment 1. To complete Solution 1, any partition of the edges of $G$ into circuits of even lengths could be used. In the solution above it was done by the reference to the well-known Euler Circuit Lemma: Let $G$ be a connected graph with all its vertices of even degrees. Then there exists a circuit passing through each edge of $G$ exactly once.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$4 n$ coins of weights $1,2,3, \ldots, 4 n$ are given. Each coin is colored in one of $n$ colors and there are four coins of each color. Show that all these coins can be partitioned into two sets with the same total weight, such that each set contains two coins of each color. (Hungary)
|
Let us pair the coins with weights summing up to $4 n+1$, resulting in the set $S$ of $2 n$ pairs: $\{1,4 n\},\{2,4 n-1\}, \ldots,\{2 n, 2 n+1\}$. It suffices to partition $S$ into two sets, each consisting of $n$ pairs, such that each set contains two coins of each color. Introduce a multi-graph $G$ (i.e., a graph with loops and multiple edges allowed) on $n$ vertices, so that each vertex corresponds to a color. For each pair of coins from $S$, we add an edge between the vertices corresponding to the colors of those coins. Note that each vertex has degree 4. Also, a desired partition of the coins corresponds to a coloring of the edges of $G$ in two colors, say red and blue, so that each vertex has degree 2 with respect to each color (i.e., each vertex has equal red and blue degrees). To complete the solution, it suffices to provide such a coloring for each component $G^{\prime}$ of $G$. Since all degrees of the vertices are even, in $G^{\prime}$ there exists an Euler circuit $C$ (i.e., a circuit passing through each edge of $G^{\prime}$ exactly once). Note that the number of edges in $C$ is even (it equals twice the number of vertices in $G^{\prime}$ ). Hence all the edges can be colored red and blue so that any two edges adjacent in $C$ have different colors (one may move along $C$ and color the edges one by one alternating red and blue colors). Thus in $G^{\prime}$ each vertex has equal red and blue degrees, as desired. Comment 1. To complete Solution 1, any partition of the edges of $G$ into circuits of even lengths could be used. In the solution above it was done by the reference to the well-known Euler Circuit Lemma: Let $G$ be a connected graph with all its vertices of even degrees. Then there exists a circuit passing through each edge of $G$ exactly once.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cbd96c77-e1ee-55dc-a6b1-85c4087100fd
| 23,969
|
$4 n$ coins of weights $1,2,3, \ldots, 4 n$ are given. Each coin is colored in one of $n$ colors and there are four coins of each color. Show that all these coins can be partitioned into two sets with the same total weight, such that each set contains two coins of each color. (Hungary)
|
As in Introduce a multi-graph (i.e., a graph with multiple edges allowed) $\Gamma$ whose vertices correspond to coins; thus we have $4 n$ vertices of $n$ colors so that there are four vertices of each color. Connect pairs of vertices $\{1,4 n\},\{2,4 n-1\}, \ldots,\{2 n, 2 n+1\}$ by $2 n$ black edges. Further, for each monochromatic quadruple of vertices $i, j, k, \ell$ we add a pair of grey edges forming a matching, e.g., $(i, j)$ and $(k, \ell)$. In each of $n$ colors of coins we can choose one of three possible matchings; this results in $3^{n}$ ways of constructing grey edges. Let us call each of $3^{n}$ possible graphs $\Gamma$ a cyclic graph. Note that in a cyclic graph $\Gamma$ each vertex has both black and grey degrees equal to 1 . Hence $\Gamma$ is a union of disjoint cycles, and in each cycle black and grey edges alternate (in particular, all cycles have even lengths). It suffices to find a cyclic graph with all its cycle lengths divisible by 4 . Indeed, in this case, for each cycle we start from some vertex, move along the cycle and recolor the black edges either to red or to blue, alternating red and blue colors. Now blue and red edges define the required partition, since for each monochromatic quadruple of vertices the grey edges provide a bijection between the endpoints of red and blue edges. Among all possible cyclic graphs, let us choose graph $\Gamma_{0}$ having the minimal number of components (i.e., cycles). The following claim completes the solution. Claim. In $\Gamma_{0}$, all cycle lengths are divisible by 4. Proof. Assuming the contrary, choose a cycle $C_{1}$ with an odd number of grey edges. For some color $c$ the cycle $C_{1}$ contains exactly one grey edge joining two vertices $i, j$ of color $c$, while the other edge joining two vertices $k, \ell$ of color $c$ lies in another cycle $C_{2}$. Now delete edges $(i, j)$ and $(k, \ell)$ and add edges $(i, k)$ and $(j, \ell)$. By this switch we again obtain a cyclic graph $\Gamma_{0}^{\prime}$ and decrease the number of cycles by 1 . This contradicts the choice of $\Gamma_{0}$. Comment 2. Use of an auxiliary graph and reduction to a new problem in terms of this graph is one of the crucial steps in both solutions presented. In fact, graph $G$ from Solution 1 could be obtained from any graph $\Gamma$ from Solution 2 by merging the vertices of the same color.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$4 n$ coins of weights $1,2,3, \ldots, 4 n$ are given. Each coin is colored in one of $n$ colors and there are four coins of each color. Show that all these coins can be partitioned into two sets with the same total weight, such that each set contains two coins of each color. (Hungary)
|
As in Introduce a multi-graph (i.e., a graph with multiple edges allowed) $\Gamma$ whose vertices correspond to coins; thus we have $4 n$ vertices of $n$ colors so that there are four vertices of each color. Connect pairs of vertices $\{1,4 n\},\{2,4 n-1\}, \ldots,\{2 n, 2 n+1\}$ by $2 n$ black edges. Further, for each monochromatic quadruple of vertices $i, j, k, \ell$ we add a pair of grey edges forming a matching, e.g., $(i, j)$ and $(k, \ell)$. In each of $n$ colors of coins we can choose one of three possible matchings; this results in $3^{n}$ ways of constructing grey edges. Let us call each of $3^{n}$ possible graphs $\Gamma$ a cyclic graph. Note that in a cyclic graph $\Gamma$ each vertex has both black and grey degrees equal to 1 . Hence $\Gamma$ is a union of disjoint cycles, and in each cycle black and grey edges alternate (in particular, all cycles have even lengths). It suffices to find a cyclic graph with all its cycle lengths divisible by 4 . Indeed, in this case, for each cycle we start from some vertex, move along the cycle and recolor the black edges either to red or to blue, alternating red and blue colors. Now blue and red edges define the required partition, since for each monochromatic quadruple of vertices the grey edges provide a bijection between the endpoints of red and blue edges. Among all possible cyclic graphs, let us choose graph $\Gamma_{0}$ having the minimal number of components (i.e., cycles). The following claim completes the solution. Claim. In $\Gamma_{0}$, all cycle lengths are divisible by 4. Proof. Assuming the contrary, choose a cycle $C_{1}$ with an odd number of grey edges. For some color $c$ the cycle $C_{1}$ contains exactly one grey edge joining two vertices $i, j$ of color $c$, while the other edge joining two vertices $k, \ell$ of color $c$ lies in another cycle $C_{2}$. Now delete edges $(i, j)$ and $(k, \ell)$ and add edges $(i, k)$ and $(j, \ell)$. By this switch we again obtain a cyclic graph $\Gamma_{0}^{\prime}$ and decrease the number of cycles by 1 . This contradicts the choice of $\Gamma_{0}$. Comment 2. Use of an auxiliary graph and reduction to a new problem in terms of this graph is one of the crucial steps in both solutions presented. In fact, graph $G$ from Solution 1 could be obtained from any graph $\Gamma$ from Solution 2 by merging the vertices of the same color.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cbd96c77-e1ee-55dc-a6b1-85c4087100fd
| 23,969
|
Consider any rectangular table having finitely many rows and columns, with a real number $a(r, c)$ in the cell in row $r$ and column $c$. A pair $(R, C)$, where $R$ is a set of rows and $C$ a set of columns, is called a saddle pair if the following two conditions are satisfied: (i) For each row $r^{\prime}$, there is $r \in R$ such that $a(r, c) \geqslant a\left(r^{\prime}, c\right)$ for all $c \in C$; (ii) For each column $c^{\prime}$, there is $c \in C$ such that $a(r, c) \leqslant a\left(r, c^{\prime}\right)$ for all $r \in R$. A saddle pair $(R, C)$ is called a minimal pair if for each saddle pair ( $R^{\prime}, C^{\prime}$ ) with $R^{\prime} \subseteq R$ and $C^{\prime} \subseteq C$, we have $R^{\prime}=R$ and $C^{\prime}=C$. Prove that any two minimal pairs contain the same number of rows. (Thailand)
|
We say that a pair $\left(R^{\prime}, C^{\prime}\right)$ of nonempty sets is a subpair of a pair $(R, C)$ if $R^{\prime} \subseteq R$ and $C^{\prime} \subseteq C$. The subpair is proper if at least one of the inclusions is strict. Let $\left(R_{1}, C_{1}\right)$ and $\left(R_{2}, C_{2}\right)$ be two saddle pairs with $\left|R_{1}\right|>\left|R_{2}\right|$. We will find a saddle subpair ( $R^{\prime}, C^{\prime}$ ) of ( $R_{1}, C_{1}$ ) with $\left|R^{\prime}\right| \leqslant\left|R_{2}\right|$; clearly, this implies the desired statement. Step 1: We construct maps $\rho: R_{1} \rightarrow R_{1}$ and $\sigma: C_{1} \rightarrow C_{1}$ such that $\left|\rho\left(R_{1}\right)\right| \leqslant\left|R_{2}\right|$, and $a\left(\rho\left(r_{1}\right), c_{1}\right) \geqslant a\left(r_{1}, \sigma\left(c_{1}\right)\right)$ for all $r_{1} \in R_{1}$ and $c_{1} \in C_{1}$. Since $\left(R_{1}, C_{1}\right)$ is a saddle pair, for each $r_{2} \in R_{2}$ there is $r_{1} \in R_{1}$ such that $a\left(r_{1}, c_{1}\right) \geqslant a\left(r_{2}, c_{1}\right)$ for all $c_{1} \in C_{1}$; denote one such an $r_{1}$ by $\rho_{1}\left(r_{2}\right)$. Similarly, we define four functions $$ \begin{array}{llllll} \rho_{1}: R_{2} \rightarrow R_{1} & \text { such that } & a\left(\rho_{1}\left(r_{2}\right), c_{1}\right) \geqslant a\left(r_{2}, c_{1}\right) & \text { for all } & r_{2} \in R_{2}, & c_{1} \in C_{1} ; \\ \rho_{2}: R_{1} \rightarrow R_{2} & \text { such that } & a\left(\rho_{2}\left(r_{1}\right), c_{2}\right) \geqslant a\left(r_{1}, c_{2}\right) & \text { for all } & r_{1} \in R_{1}, & c_{2} \in C_{2} ; \\ \sigma_{1}: C_{2} \rightarrow C_{1} & \text { such that } & a\left(r_{1}, \sigma_{1}\left(c_{2}\right)\right) \leqslant a\left(r_{1}, c_{2}\right) & \text { for all } & r_{1} \in R_{1}, & c_{2} \in C_{2} ; \\ \sigma_{2}: C_{1} \rightarrow C_{2} & \text { such that } & a\left(r_{2}, \sigma_{2}\left(c_{1}\right)\right) \leqslant a\left(r_{2}, c_{1}\right) & \text { for all } & r_{2} \in R_{2}, & c_{1} \in C_{1} . \end{array} $$ Set now $\rho=\rho_{1} \circ \rho_{2}: R_{1} \rightarrow R_{1}$ and $\sigma=\sigma_{1} \circ \sigma_{2}: C_{1} \rightarrow C_{1}$. We have $$ \left|\rho\left(R_{1}\right)\right|=\left|\rho_{1}\left(\rho_{2}\left(R_{1}\right)\right)\right| \leqslant\left|\rho_{1}\left(R_{2}\right)\right| \leqslant\left|R_{2}\right| . $$ Moreover, for all $r_{1} \in R_{1}$ and $c_{1} \in C_{1}$, we get $$ \begin{aligned} a\left(\rho\left(r_{1}\right), c_{1}\right)=a\left(\rho_{1}\left(\rho_{2}\left(r_{1}\right)\right), c_{1}\right) \geqslant a\left(\rho_{2}\left(r_{1}\right), c_{1}\right) & \geqslant a\left(\rho_{2}\left(r_{1}\right), \sigma_{2}\left(c_{1}\right)\right) \\ & \geqslant a\left(r_{1}, \sigma_{2}\left(c_{1}\right)\right) \geqslant a\left(r_{1}, \sigma_{1}\left(\sigma_{2}\left(c_{1}\right)\right)\right)=a\left(r_{1}, \sigma\left(c_{1}\right)\right) \end{aligned} $$ as desired. Step 2: Given maps $\rho$ and $\sigma$, we construct a proper saddle subpair $\left(R^{\prime}, C^{\prime}\right)$ of $\left(R_{1}, C_{1}\right)$. The properties of $\rho$ and $\sigma$ yield that $$ a\left(\rho^{i}\left(r_{1}\right), c_{1}\right) \geqslant a\left(\rho^{i-1}\left(r_{1}\right), \sigma\left(c_{1}\right)\right) \geqslant \ldots \geqslant a\left(r_{1}, \sigma^{i}\left(c_{1}\right)\right) $$ for each positive integer $i$ and all $r_{1} \in R_{1}, c_{1} \in C_{1}$. Consider the images $R^{i}=\rho^{i}\left(R_{1}\right)$ and $C^{i}=\sigma^{i}\left(C_{1}\right)$. Clearly, $R_{1}=R^{0} \supseteq R^{1} \supseteq R^{2} \supseteq \ldots$ and $C_{1}=C^{0} \supseteq C^{1} \supseteq C^{2} \supseteq \ldots$. Since both chains consist of finite sets, there is an index $n$ such that $R^{n}=R^{n+1}=\ldots$ and $C^{n}=C^{n+1}=\ldots$. Then $\rho^{n}\left(R^{n}\right)=R^{2 n}=R^{n}$, so $\rho^{n}$ restricted to $R^{n}$ is a bijection. Similarly, $\sigma^{n}$ restricted to $C^{n}$ is a bijection from $C^{n}$ to itself. Therefore, there exists a positive integer $k$ such that $\rho^{n k}$ acts identically on $R^{n}$, and $\sigma^{n k}$ acts identically on $C^{n}$. We claim now that $\left(R^{n}, C^{n}\right)$ is a saddle subpair of $\left(R_{1}, C_{1}\right)$, with $\left|R^{n}\right| \leqslant\left|R^{1}\right|=\left|\rho\left(R_{1}\right)\right| \leqslant$ $\left|R_{2}\right|$, which is what we needed. To check that this is a saddle pair, take any row $r^{\prime}$; since $\left(R_{1}, C_{1}\right)$ is a saddle pair, there exists $r_{1} \in R_{1}$ such that $a\left(r_{1}, c_{1}\right) \geqslant a\left(r^{\prime}, c_{1}\right)$ for all $c_{1} \in C_{1}$. Set now $r_{*}=\rho^{n k}\left(r_{1}\right) \in R^{n}$. Then, for each $c \in C^{n}$ we have $c=\sigma^{n k}(c)$ and hence $$ a\left(r_{*}, c\right)=a\left(\rho^{n k}\left(r_{1}\right), c\right) \geqslant a\left(r_{1}, \sigma^{n k}(c)\right)=a\left(r_{1}, c\right) \geqslant a\left(r^{\prime}, c\right) $$ which establishes condition $(i)$. Condition (ii) is checked similarly.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider any rectangular table having finitely many rows and columns, with a real number $a(r, c)$ in the cell in row $r$ and column $c$. A pair $(R, C)$, where $R$ is a set of rows and $C$ a set of columns, is called a saddle pair if the following two conditions are satisfied: (i) For each row $r^{\prime}$, there is $r \in R$ such that $a(r, c) \geqslant a\left(r^{\prime}, c\right)$ for all $c \in C$; (ii) For each column $c^{\prime}$, there is $c \in C$ such that $a(r, c) \leqslant a\left(r, c^{\prime}\right)$ for all $r \in R$. A saddle pair $(R, C)$ is called a minimal pair if for each saddle pair ( $R^{\prime}, C^{\prime}$ ) with $R^{\prime} \subseteq R$ and $C^{\prime} \subseteq C$, we have $R^{\prime}=R$ and $C^{\prime}=C$. Prove that any two minimal pairs contain the same number of rows. (Thailand)
|
We say that a pair $\left(R^{\prime}, C^{\prime}\right)$ of nonempty sets is a subpair of a pair $(R, C)$ if $R^{\prime} \subseteq R$ and $C^{\prime} \subseteq C$. The subpair is proper if at least one of the inclusions is strict. Let $\left(R_{1}, C_{1}\right)$ and $\left(R_{2}, C_{2}\right)$ be two saddle pairs with $\left|R_{1}\right|>\left|R_{2}\right|$. We will find a saddle subpair ( $R^{\prime}, C^{\prime}$ ) of ( $R_{1}, C_{1}$ ) with $\left|R^{\prime}\right| \leqslant\left|R_{2}\right|$; clearly, this implies the desired statement. Step 1: We construct maps $\rho: R_{1} \rightarrow R_{1}$ and $\sigma: C_{1} \rightarrow C_{1}$ such that $\left|\rho\left(R_{1}\right)\right| \leqslant\left|R_{2}\right|$, and $a\left(\rho\left(r_{1}\right), c_{1}\right) \geqslant a\left(r_{1}, \sigma\left(c_{1}\right)\right)$ for all $r_{1} \in R_{1}$ and $c_{1} \in C_{1}$. Since $\left(R_{1}, C_{1}\right)$ is a saddle pair, for each $r_{2} \in R_{2}$ there is $r_{1} \in R_{1}$ such that $a\left(r_{1}, c_{1}\right) \geqslant a\left(r_{2}, c_{1}\right)$ for all $c_{1} \in C_{1}$; denote one such an $r_{1}$ by $\rho_{1}\left(r_{2}\right)$. Similarly, we define four functions $$ \begin{array}{llllll} \rho_{1}: R_{2} \rightarrow R_{1} & \text { such that } & a\left(\rho_{1}\left(r_{2}\right), c_{1}\right) \geqslant a\left(r_{2}, c_{1}\right) & \text { for all } & r_{2} \in R_{2}, & c_{1} \in C_{1} ; \\ \rho_{2}: R_{1} \rightarrow R_{2} & \text { such that } & a\left(\rho_{2}\left(r_{1}\right), c_{2}\right) \geqslant a\left(r_{1}, c_{2}\right) & \text { for all } & r_{1} \in R_{1}, & c_{2} \in C_{2} ; \\ \sigma_{1}: C_{2} \rightarrow C_{1} & \text { such that } & a\left(r_{1}, \sigma_{1}\left(c_{2}\right)\right) \leqslant a\left(r_{1}, c_{2}\right) & \text { for all } & r_{1} \in R_{1}, & c_{2} \in C_{2} ; \\ \sigma_{2}: C_{1} \rightarrow C_{2} & \text { such that } & a\left(r_{2}, \sigma_{2}\left(c_{1}\right)\right) \leqslant a\left(r_{2}, c_{1}\right) & \text { for all } & r_{2} \in R_{2}, & c_{1} \in C_{1} . \end{array} $$ Set now $\rho=\rho_{1} \circ \rho_{2}: R_{1} \rightarrow R_{1}$ and $\sigma=\sigma_{1} \circ \sigma_{2}: C_{1} \rightarrow C_{1}$. We have $$ \left|\rho\left(R_{1}\right)\right|=\left|\rho_{1}\left(\rho_{2}\left(R_{1}\right)\right)\right| \leqslant\left|\rho_{1}\left(R_{2}\right)\right| \leqslant\left|R_{2}\right| . $$ Moreover, for all $r_{1} \in R_{1}$ and $c_{1} \in C_{1}$, we get $$ \begin{aligned} a\left(\rho\left(r_{1}\right), c_{1}\right)=a\left(\rho_{1}\left(\rho_{2}\left(r_{1}\right)\right), c_{1}\right) \geqslant a\left(\rho_{2}\left(r_{1}\right), c_{1}\right) & \geqslant a\left(\rho_{2}\left(r_{1}\right), \sigma_{2}\left(c_{1}\right)\right) \\ & \geqslant a\left(r_{1}, \sigma_{2}\left(c_{1}\right)\right) \geqslant a\left(r_{1}, \sigma_{1}\left(\sigma_{2}\left(c_{1}\right)\right)\right)=a\left(r_{1}, \sigma\left(c_{1}\right)\right) \end{aligned} $$ as desired. Step 2: Given maps $\rho$ and $\sigma$, we construct a proper saddle subpair $\left(R^{\prime}, C^{\prime}\right)$ of $\left(R_{1}, C_{1}\right)$. The properties of $\rho$ and $\sigma$ yield that $$ a\left(\rho^{i}\left(r_{1}\right), c_{1}\right) \geqslant a\left(\rho^{i-1}\left(r_{1}\right), \sigma\left(c_{1}\right)\right) \geqslant \ldots \geqslant a\left(r_{1}, \sigma^{i}\left(c_{1}\right)\right) $$ for each positive integer $i$ and all $r_{1} \in R_{1}, c_{1} \in C_{1}$. Consider the images $R^{i}=\rho^{i}\left(R_{1}\right)$ and $C^{i}=\sigma^{i}\left(C_{1}\right)$. Clearly, $R_{1}=R^{0} \supseteq R^{1} \supseteq R^{2} \supseteq \ldots$ and $C_{1}=C^{0} \supseteq C^{1} \supseteq C^{2} \supseteq \ldots$. Since both chains consist of finite sets, there is an index $n$ such that $R^{n}=R^{n+1}=\ldots$ and $C^{n}=C^{n+1}=\ldots$. Then $\rho^{n}\left(R^{n}\right)=R^{2 n}=R^{n}$, so $\rho^{n}$ restricted to $R^{n}$ is a bijection. Similarly, $\sigma^{n}$ restricted to $C^{n}$ is a bijection from $C^{n}$ to itself. Therefore, there exists a positive integer $k$ such that $\rho^{n k}$ acts identically on $R^{n}$, and $\sigma^{n k}$ acts identically on $C^{n}$. We claim now that $\left(R^{n}, C^{n}\right)$ is a saddle subpair of $\left(R_{1}, C_{1}\right)$, with $\left|R^{n}\right| \leqslant\left|R^{1}\right|=\left|\rho\left(R_{1}\right)\right| \leqslant$ $\left|R_{2}\right|$, which is what we needed. To check that this is a saddle pair, take any row $r^{\prime}$; since $\left(R_{1}, C_{1}\right)$ is a saddle pair, there exists $r_{1} \in R_{1}$ such that $a\left(r_{1}, c_{1}\right) \geqslant a\left(r^{\prime}, c_{1}\right)$ for all $c_{1} \in C_{1}$. Set now $r_{*}=\rho^{n k}\left(r_{1}\right) \in R^{n}$. Then, for each $c \in C^{n}$ we have $c=\sigma^{n k}(c)$ and hence $$ a\left(r_{*}, c\right)=a\left(\rho^{n k}\left(r_{1}\right), c\right) \geqslant a\left(r_{1}, \sigma^{n k}(c)\right)=a\left(r_{1}, c\right) \geqslant a\left(r^{\prime}, c\right) $$ which establishes condition $(i)$. Condition (ii) is checked similarly.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
678bdd5f-ed39-5224-9646-8c4b8fb6038e
| 23,972
|
Let $A B C D$ be a convex quadrilateral. Suppose that $P$ is a point in the interior of $A B C D$ such that $$ \angle P A D: \angle P B A: \angle D P A=1: 2: 3=\angle C B P: \angle B A P: \angle B P C . $$ The internal bisectors of angles $A D P$ and $P C B$ meet at a point $Q$ inside the triangle $A B P$. Prove that $A Q=B Q$. (Poland)
|
Let $\varphi=\angle P A D$ and $\psi=\angle C B P$; then we have $\angle P B A=2 \varphi, \angle D P A=3 \varphi$, $\angle B A P=2 \psi$ and $\angle B P C=3 \psi$. Let $X$ be the point on segment $A D$ with $\angle X P A=\varphi$. Then $$ \angle P X D=\angle P A X+\angle X P A=2 \varphi=\angle D P A-\angle X P A=\angle D P X . $$ It follows that triangle $D P X$ is isosceles with $D X=D P$ and therefore the internal angle bisector of $\angle A D P$ coincides with the perpendicular bisector of $X P$. Similarly, if $Y$ is a point on $B C$ such that $\angle B P Y=\psi$, then the internal angle bisector of $\angle P C B$ coincides with the perpendicular bisector of $P Y$. Hence, we have to prove that the perpendicular bisectors of $X P$, $P Y$, and $A B$ are concurrent.  Notice that $$ \angle A X P=180^{\circ}-\angle P X D=180^{\circ}-2 \varphi=180^{\circ}-\angle P B A . $$ Hence the quadrilateral $A X P B$ is cyclic; in other words, $X$ lies on the circumcircle of triangle $A P B$. Similarly, $Y$ lies on the circumcircle of triangle $A P B$. It follows that the perpendicular bisectors of $X P, P Y$, and $A B$ all pass through the center of circle $(A B Y P X)$. This finishes the proof. Comment. Introduction of points $X$ and $Y$ seems to be the key step in the solution above. Note that the same point $X$ could be introduced in different ways, e.g., as the point on the ray $C P$ beyond $P$ such that $\angle P B X=\varphi$, or as a point where the circle $(A P B)$ meets again $A B$. Different definitions of $X$ could lead to different versions of the further solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral. Suppose that $P$ is a point in the interior of $A B C D$ such that $$ \angle P A D: \angle P B A: \angle D P A=1: 2: 3=\angle C B P: \angle B A P: \angle B P C . $$ The internal bisectors of angles $A D P$ and $P C B$ meet at a point $Q$ inside the triangle $A B P$. Prove that $A Q=B Q$. (Poland)
|
Let $\varphi=\angle P A D$ and $\psi=\angle C B P$; then we have $\angle P B A=2 \varphi, \angle D P A=3 \varphi$, $\angle B A P=2 \psi$ and $\angle B P C=3 \psi$. Let $X$ be the point on segment $A D$ with $\angle X P A=\varphi$. Then $$ \angle P X D=\angle P A X+\angle X P A=2 \varphi=\angle D P A-\angle X P A=\angle D P X . $$ It follows that triangle $D P X$ is isosceles with $D X=D P$ and therefore the internal angle bisector of $\angle A D P$ coincides with the perpendicular bisector of $X P$. Similarly, if $Y$ is a point on $B C$ such that $\angle B P Y=\psi$, then the internal angle bisector of $\angle P C B$ coincides with the perpendicular bisector of $P Y$. Hence, we have to prove that the perpendicular bisectors of $X P$, $P Y$, and $A B$ are concurrent.  Notice that $$ \angle A X P=180^{\circ}-\angle P X D=180^{\circ}-2 \varphi=180^{\circ}-\angle P B A . $$ Hence the quadrilateral $A X P B$ is cyclic; in other words, $X$ lies on the circumcircle of triangle $A P B$. Similarly, $Y$ lies on the circumcircle of triangle $A P B$. It follows that the perpendicular bisectors of $X P, P Y$, and $A B$ all pass through the center of circle $(A B Y P X)$. This finishes the proof. Comment. Introduction of points $X$ and $Y$ seems to be the key step in the solution above. Note that the same point $X$ could be introduced in different ways, e.g., as the point on the ray $C P$ beyond $P$ such that $\angle P B X=\varphi$, or as a point where the circle $(A P B)$ meets again $A B$. Different definitions of $X$ could lead to different versions of the further solution.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c451ede-8480-5029-8bcb-95f5d7648620
| 23,982
|
Let $A B C D$ be a convex quadrilateral. Suppose that $P$ is a point in the interior of $A B C D$ such that $$ \angle P A D: \angle P B A: \angle D P A=1: 2: 3=\angle C B P: \angle B A P: \angle B P C . $$ The internal bisectors of angles $A D P$ and $P C B$ meet at a point $Q$ inside the triangle $A B P$. Prove that $A Q=B Q$. (Poland)
|
We define the angles $\varphi=\angle P A D, \psi=\angle C B P$ and use $\angle P B A=2 \varphi, \angle D P A=$ $3 \varphi, \angle B A P=2 \psi$ and $\angle B P C=3 \psi$ again. Let $O$ be the circumcenter of $\triangle A P B$. Notice that $\angle A D P=180^{\circ}-\angle P A D-\angle D P A=180^{\circ}-4 \varphi$, which, in particular, means that $4 \varphi<180^{\circ}$. Further, $\angle P O A=2 \angle P B A=4 \varphi=180^{\circ}-\angle A D P$, therefore the quadrilateral $A D P O$ is cyclic. By $A O=O P$, it follows that $\angle A D O=\angle O D P$. Thus $D O$ is the internal bisector of $\angle A D P$. Similarly, $C O$ is the internal bisector of $\angle P C B$.  Finally, $O$ lies on the perpendicular bisector of $A B$ as it is the circumcenter of $\triangle A P B$. Therefore the three given lines in the problem statement concur at point $O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral. Suppose that $P$ is a point in the interior of $A B C D$ such that $$ \angle P A D: \angle P B A: \angle D P A=1: 2: 3=\angle C B P: \angle B A P: \angle B P C . $$ The internal bisectors of angles $A D P$ and $P C B$ meet at a point $Q$ inside the triangle $A B P$. Prove that $A Q=B Q$. (Poland)
|
We define the angles $\varphi=\angle P A D, \psi=\angle C B P$ and use $\angle P B A=2 \varphi, \angle D P A=$ $3 \varphi, \angle B A P=2 \psi$ and $\angle B P C=3 \psi$ again. Let $O$ be the circumcenter of $\triangle A P B$. Notice that $\angle A D P=180^{\circ}-\angle P A D-\angle D P A=180^{\circ}-4 \varphi$, which, in particular, means that $4 \varphi<180^{\circ}$. Further, $\angle P O A=2 \angle P B A=4 \varphi=180^{\circ}-\angle A D P$, therefore the quadrilateral $A D P O$ is cyclic. By $A O=O P$, it follows that $\angle A D O=\angle O D P$. Thus $D O$ is the internal bisector of $\angle A D P$. Similarly, $C O$ is the internal bisector of $\angle P C B$.  Finally, $O$ lies on the perpendicular bisector of $A B$ as it is the circumcenter of $\triangle A P B$. Therefore the three given lines in the problem statement concur at point $O$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c451ede-8480-5029-8bcb-95f5d7648620
| 23,982
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Denote by $A^{\prime}$ the reflection of $A$ in $B D$. We will show that that the quadrilaterals $A^{\prime} B K E$ and $A^{\prime} D L F$ are cyclic, and their circumcircles are tangent to each other at point $A^{\prime}$. From the symmetry about line $B C$ we have $\angle B E K=\angle B A K$, while from the symmetry in $B D$ we have $\angle B A K=\angle B A^{\prime} K$. Hence $\angle B E K=\angle B A^{\prime} K$, which implies that the quadrilateral $A^{\prime} B K E$ is cyclic. Similarly, the quadrilateral $A^{\prime} D L F$ is also cyclic.  For showing that circles $A^{\prime} B K E$ and $A^{\prime} D L F$ are tangent it suffices to prove that $$ \angle A^{\prime} K B+\angle A^{\prime} L D=\angle B A^{\prime} D . $$ Indeed, by $A K \perp B C$, $A L \perp C D$, and again the symmetry in $B D$ we have $$ \angle A^{\prime} K B+\angle A^{\prime} L D=180^{\circ}-\angle K A^{\prime} L=180^{\circ}-\angle K A L=\angle B C D=\angle B A D=\angle B A^{\prime} D, $$ as required. Comment 1. The key to the solution above is introducing the point $A^{\prime}$; then the angle calculations can be done in many different ways.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Denote by $A^{\prime}$ the reflection of $A$ in $B D$. We will show that that the quadrilaterals $A^{\prime} B K E$ and $A^{\prime} D L F$ are cyclic, and their circumcircles are tangent to each other at point $A^{\prime}$. From the symmetry about line $B C$ we have $\angle B E K=\angle B A K$, while from the symmetry in $B D$ we have $\angle B A K=\angle B A^{\prime} K$. Hence $\angle B E K=\angle B A^{\prime} K$, which implies that the quadrilateral $A^{\prime} B K E$ is cyclic. Similarly, the quadrilateral $A^{\prime} D L F$ is also cyclic.  For showing that circles $A^{\prime} B K E$ and $A^{\prime} D L F$ are tangent it suffices to prove that $$ \angle A^{\prime} K B+\angle A^{\prime} L D=\angle B A^{\prime} D . $$ Indeed, by $A K \perp B C$, $A L \perp C D$, and again the symmetry in $B D$ we have $$ \angle A^{\prime} K B+\angle A^{\prime} L D=180^{\circ}-\angle K A^{\prime} L=180^{\circ}-\angle K A L=\angle B C D=\angle B A D=\angle B A^{\prime} D, $$ as required. Comment 1. The key to the solution above is introducing the point $A^{\prime}$; then the angle calculations can be done in many different ways.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6f1c89cb-2b7d-5098-9521-655f52d0dbc2
| 23,988
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Note that $\angle K A L=180^{\circ}-\angle B C D$, since $A K$ and $A L$ are perpendicular to $B C$ and $C D$, respectively. Reflect both circles $(B E K)$ and $(D F L)$ in $B D$. Since $\angle K E B=\angle K A B$ and $\angle D F L=\angle D A L$, the images are the circles $(K A B)$ and $(L A D)$, respectively; so they meet at $A$. We need to prove that those two reflections are tangent at $A$. For this purpose, we observe that $$ \angle A K B+\angle A L D=180^{\circ}-\angle K A L=\angle B C D=\angle B A D . $$ Thus, there exists a ray $A P$ inside angle $\angle B A D$ such that $\angle B A P=\angle A K B$ and $\angle D A P=$ $\angle D L A$. Hence the line $A P$ is a common tangent to the circles $(K A B)$ and $(L A D)$, as desired. Comment 2. The statement of the problem remains true for a more general configuration, e.g., if line $B D$ intersect the extension of segment $A E$ instead of the segment itself, etc. The corresponding restrictions in the statement are given to reduce case sensitivity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $\angle A B C>90^{\circ}, \angle C D A>90^{\circ}$, and $\angle D A B=\angle B C D$. Denote by $E$ and $F$ the reflections of $A$ in lines $B C$ and $C D$, respectively. Suppose that the segments $A E$ and $A F$ meet the line $B D$ at $K$ and $L$, respectively. Prove that the circumcircles of triangles $B E K$ and $D F L$ are tangent to each other. (Slovakia)
|
Note that $\angle K A L=180^{\circ}-\angle B C D$, since $A K$ and $A L$ are perpendicular to $B C$ and $C D$, respectively. Reflect both circles $(B E K)$ and $(D F L)$ in $B D$. Since $\angle K E B=\angle K A B$ and $\angle D F L=\angle D A L$, the images are the circles $(K A B)$ and $(L A D)$, respectively; so they meet at $A$. We need to prove that those two reflections are tangent at $A$. For this purpose, we observe that $$ \angle A K B+\angle A L D=180^{\circ}-\angle K A L=\angle B C D=\angle B A D . $$ Thus, there exists a ray $A P$ inside angle $\angle B A D$ such that $\angle B A P=\angle A K B$ and $\angle D A P=$ $\angle D L A$. Hence the line $A P$ is a common tangent to the circles $(K A B)$ and $(L A D)$, as desired. Comment 2. The statement of the problem remains true for a more general configuration, e.g., if line $B D$ intersect the extension of segment $A E$ instead of the segment itself, etc. The corresponding restrictions in the statement are given to reduce case sensitivity.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6f1c89cb-2b7d-5098-9521-655f52d0dbc2
| 23,988
|
In the plane, there are $n \geqslant 6$ pairwise disjoint disks $D_{1}, D_{2}, \ldots, D_{n}$ with radii $R_{1} \geqslant R_{2} \geqslant \ldots \geqslant R_{n}$. For every $i=1,2, \ldots, n$, a point $P_{i}$ is chosen in disk $D_{i}$. Let $O$ be an arbitrary point in the plane. Prove that $$ O P_{1}+O P_{2}+\ldots+O P_{n} \geqslant R_{6}+R_{7}+\ldots+R_{n} $$ (A disk is assumed to contain its boundary.) (Iran)
|
We will make use of the following lemma. Lemma. Let $D_{1}, \ldots, D_{6}$ be disjoint disks in the plane with radii $R_{1}, \ldots, R_{6}$. Let $P_{i}$ be a point in $D_{i}$, and let $O$ be an arbitrary point. Then there exist indices $i$ and $j$ such that $O P_{i} \geqslant R_{j}$. Proof. Let $O_{i}$ be the center of $D_{i}$. Consider six rays $O O_{1}, \ldots, O O_{6}$ (if $O=O_{i}$, then the ray $O O_{i}$ may be assumed to have an arbitrary direction). These rays partition the plane into six angles (one of which may be non-convex) whose measures sum up to $360^{\circ}$; hence one of the angles, say $\angle O_{i} O O_{j}$, has measure at most $60^{\circ}$. Then $O_{i} O_{j}$ cannot be the unique largest side in (possibly degenerate) triangle $O O_{i} O_{j}$, so, without loss of generality, $O O_{i} \geqslant O_{i} O_{j} \geqslant R_{i}+R_{j}$. Therefore, $O P_{i} \geqslant O O_{i}-R_{i} \geqslant\left(R_{i}+R_{j}\right)-R_{i}=R_{j}$, as desired. Now we prove the required inequality by induction on $n \geqslant 5$. The base case $n=5$ is trivial. For the inductive step, apply the Lemma to the six largest disks, in order to find indices $i$ and $j$ such that $1 \leqslant i, j \leqslant 6$ and $O P_{i} \geqslant R_{j} \geqslant R_{6}$. Removing $D_{i}$ from the configuration and applying the inductive hypothesis, we get $$ \sum_{k \neq i} O P_{k} \geqslant \sum_{\ell \geqslant 7} R_{\ell} . $$ Adding up this inequality with $O P_{i} \geqslant R_{6}$ we establish the inductive step. Comment 1. It is irrelevant to the problem whether the disks contain their boundaries or not. This condition is included for clarity reasons only. The problem statement remains true, and the solution works verbatim, if the disks are assumed to have disjoint interiors. Comment 2. There are several variations of the above solution. In particular, while performing the inductive step, one may remove the disk with the largest value of $O P_{i}$ and apply the inductive hypothesis to the remaining disks (the Lemma should still be applied to the six largest disks). Comment 3. While proving the Lemma, one may reduce it to a particular case when the disks are congruent, as follows: Choose the smallest radius $r$ of the disks in the Lemma statement, and then replace, for each $i$, the $i^{\text {th }}$ disk with its homothetic copy, using the homothety centered at $P_{i}$ with ratio $r / R_{i}$. This argument shows that the Lemma is tightly connected to a circle packing problem, see, e.g., https://en.wikipedia.org/wiki/Circle_packing_in_a_circle. The known results on that problem provide versions of the Lemma for different numbers of disks, which lead to different inequalities of the same kind. E.g., for 4 disks the best possible estimate in the Lemma is $O P_{i} \geqslant(\sqrt{2}-1) R_{j}$, while for 13 disks it has the form $O P_{i} \geqslant \sqrt{5} R_{j}$. Arguing as in the above solution, one obtains the inequalities $$ \sum_{i=1}^{n} O P_{i} \geqslant(\sqrt{2}-1) \sum_{j=4}^{n} R_{j} \quad \text { and } \quad \sum_{i=1}^{n} O P_{i} \geqslant \sqrt{5} \sum_{j=13}^{n} R_{j} . $$ However, there are some harder arguments which allow to improve these inequalities, meaning that the $R_{j}$ with large indices may be taken with much greater factors.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
In the plane, there are $n \geqslant 6$ pairwise disjoint disks $D_{1}, D_{2}, \ldots, D_{n}$ with radii $R_{1} \geqslant R_{2} \geqslant \ldots \geqslant R_{n}$. For every $i=1,2, \ldots, n$, a point $P_{i}$ is chosen in disk $D_{i}$. Let $O$ be an arbitrary point in the plane. Prove that $$ O P_{1}+O P_{2}+\ldots+O P_{n} \geqslant R_{6}+R_{7}+\ldots+R_{n} $$ (A disk is assumed to contain its boundary.) (Iran)
|
We will make use of the following lemma. Lemma. Let $D_{1}, \ldots, D_{6}$ be disjoint disks in the plane with radii $R_{1}, \ldots, R_{6}$. Let $P_{i}$ be a point in $D_{i}$, and let $O$ be an arbitrary point. Then there exist indices $i$ and $j$ such that $O P_{i} \geqslant R_{j}$. Proof. Let $O_{i}$ be the center of $D_{i}$. Consider six rays $O O_{1}, \ldots, O O_{6}$ (if $O=O_{i}$, then the ray $O O_{i}$ may be assumed to have an arbitrary direction). These rays partition the plane into six angles (one of which may be non-convex) whose measures sum up to $360^{\circ}$; hence one of the angles, say $\angle O_{i} O O_{j}$, has measure at most $60^{\circ}$. Then $O_{i} O_{j}$ cannot be the unique largest side in (possibly degenerate) triangle $O O_{i} O_{j}$, so, without loss of generality, $O O_{i} \geqslant O_{i} O_{j} \geqslant R_{i}+R_{j}$. Therefore, $O P_{i} \geqslant O O_{i}-R_{i} \geqslant\left(R_{i}+R_{j}\right)-R_{i}=R_{j}$, as desired. Now we prove the required inequality by induction on $n \geqslant 5$. The base case $n=5$ is trivial. For the inductive step, apply the Lemma to the six largest disks, in order to find indices $i$ and $j$ such that $1 \leqslant i, j \leqslant 6$ and $O P_{i} \geqslant R_{j} \geqslant R_{6}$. Removing $D_{i}$ from the configuration and applying the inductive hypothesis, we get $$ \sum_{k \neq i} O P_{k} \geqslant \sum_{\ell \geqslant 7} R_{\ell} . $$ Adding up this inequality with $O P_{i} \geqslant R_{6}$ we establish the inductive step. Comment 1. It is irrelevant to the problem whether the disks contain their boundaries or not. This condition is included for clarity reasons only. The problem statement remains true, and the solution works verbatim, if the disks are assumed to have disjoint interiors. Comment 2. There are several variations of the above solution. In particular, while performing the inductive step, one may remove the disk with the largest value of $O P_{i}$ and apply the inductive hypothesis to the remaining disks (the Lemma should still be applied to the six largest disks). Comment 3. While proving the Lemma, one may reduce it to a particular case when the disks are congruent, as follows: Choose the smallest radius $r$ of the disks in the Lemma statement, and then replace, for each $i$, the $i^{\text {th }}$ disk with its homothetic copy, using the homothety centered at $P_{i}$ with ratio $r / R_{i}$. This argument shows that the Lemma is tightly connected to a circle packing problem, see, e.g., https://en.wikipedia.org/wiki/Circle_packing_in_a_circle. The known results on that problem provide versions of the Lemma for different numbers of disks, which lead to different inequalities of the same kind. E.g., for 4 disks the best possible estimate in the Lemma is $O P_{i} \geqslant(\sqrt{2}-1) R_{j}$, while for 13 disks it has the form $O P_{i} \geqslant \sqrt{5} R_{j}$. Arguing as in the above solution, one obtains the inequalities $$ \sum_{i=1}^{n} O P_{i} \geqslant(\sqrt{2}-1) \sum_{j=4}^{n} R_{j} \quad \text { and } \quad \sum_{i=1}^{n} O P_{i} \geqslant \sqrt{5} \sum_{j=13}^{n} R_{j} . $$ However, there are some harder arguments which allow to improve these inequalities, meaning that the $R_{j}$ with large indices may be taken with much greater factors.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0198f9de-1488-5068-9065-d918115a94b5
| 23,992
|
Let $A B C D$ be a cyclic quadrilateral with no two sides parallel. Let $K, L, M$, and $N$ be points lying on sides $A B, B C, C D$, and $D A$, respectively, such that $K L M N$ is a rhombus with $K L \| A C$ and $L M \| B D$. Let $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$ be the incircles of triangles $A N K$, $B K L, C L M$, and $D M N$, respectively. Prove that the internal common tangents to $\omega_{1}$ and $\omega_{3}$ and the internal common tangents to $\omega_{2}$ and $\omega_{4}$ are concurrent. (Poland)
|
This solution is based on the following general Lemma. Lemma 2. Let $E$ and $F$ be distinct points, and let $\omega_{i}, i=1,2,3,4$, be circles lying in the same halfplane with respect to $E F$. For distinct indices $i, j \in\{1,2,3,4\}$, denote by $O_{i j}^{+}$ (respectively, $O_{i j}^{-}$) the center of homothety with positive (respectively, negative) ratio taking $\omega_{i}$ to $\omega_{j}$. Suppose that $E=O_{12}^{+}=O_{34}^{+}$and $F=O_{23}^{+}=O_{41}^{+}$. Then $O_{13}^{-}=O_{24}^{-}$. Proof. Applying Monge's theorem to triples of circles $\omega_{1}, \omega_{2}, \omega_{4}$ and $\omega_{1}, \omega_{3}, \omega_{4}$, we get that both points $O_{24}^{-}$and $O_{13}^{-}$lie on line $E O_{14}^{-}$. Notice that this line is distinct from $E F$. Similarly we obtain that both points $O_{24}^{-}$and $O_{13}^{-}$lie on $F O_{34}^{-}$. Since the lines $E O_{14}^{-}$and $F O_{34}^{-}$are distinct, both points coincide with the meeting point of those lines.  Turning back to the problem, let $A B$ intersect $C D$ at $E$ and let $B C$ intersect $D A$ at $F$. Assume, without loss of generality, that $B$ lies on segments $A E$ and $C F$. We will show that the points $E$ and $F$, and the circles $\omega_{i}$ satisfy the conditions of Lemma 2 , so the problem statement follows. In the sequel, we use the notation of $O_{i j}^{ \pm}$from the statement of Lemma 2, applied to circles $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$. Using the relations $\triangle E C A \sim \triangle E B D, K N \| B D$, and $M N \| A C$. we get $$ \frac{A N}{N D}=\frac{A N}{A D} \cdot \frac{A D}{N D}=\frac{K N}{B D} \cdot \frac{A C}{N M}=\frac{A C}{B D}=\frac{A E}{E D} $$ Therefore, by the angle bisector theorem, point $N$ lies on the internal angle bisector of $\angle A E D$. We prove similarly that $L$ also lies on that bisector, and that the points $K$ and $M$ lie on the internal angle bisector of $\angle A F B$. Since $K L M N$ is a rhombus, points $K$ and $M$ are symmetric in line $E L N$. Hence, the convex quadrilateral determined by the lines $E K, E M, K L$, and $M L$ is a kite, and therefore it has an incircle $\omega_{0}$. Applying Monge's theorem to $\omega_{0}, \omega_{2}$, and $\omega_{3}$, we get that $O_{23}^{+}$lies on $K M$. On the other hand, $O_{23}^{+}$lies on $B C$, as $B C$ is an external common tangent to $\omega_{2}$ and $\omega_{3}$. It follows that $F=O_{23}^{+}$. Similarly, $E=O_{12}^{+}=O_{34}^{+}$, and $F=O_{41}^{+}$. Comment 3. The reduction to Lemma 2 and the proof of Lemma 2 can be performed with the use of different tools, e.g., by means of Menelaus theorem, by projecting harmonic quadruples, by applying Monge's theorem in some other ways, etc. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with no two sides parallel. Let $K, L, M$, and $N$ be points lying on sides $A B, B C, C D$, and $D A$, respectively, such that $K L M N$ is a rhombus with $K L \| A C$ and $L M \| B D$. Let $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$ be the incircles of triangles $A N K$, $B K L, C L M$, and $D M N$, respectively. Prove that the internal common tangents to $\omega_{1}$ and $\omega_{3}$ and the internal common tangents to $\omega_{2}$ and $\omega_{4}$ are concurrent. (Poland)
|
This solution is based on the following general Lemma. Lemma 2. Let $E$ and $F$ be distinct points, and let $\omega_{i}, i=1,2,3,4$, be circles lying in the same halfplane with respect to $E F$. For distinct indices $i, j \in\{1,2,3,4\}$, denote by $O_{i j}^{+}$ (respectively, $O_{i j}^{-}$) the center of homothety with positive (respectively, negative) ratio taking $\omega_{i}$ to $\omega_{j}$. Suppose that $E=O_{12}^{+}=O_{34}^{+}$and $F=O_{23}^{+}=O_{41}^{+}$. Then $O_{13}^{-}=O_{24}^{-}$. Proof. Applying Monge's theorem to triples of circles $\omega_{1}, \omega_{2}, \omega_{4}$ and $\omega_{1}, \omega_{3}, \omega_{4}$, we get that both points $O_{24}^{-}$and $O_{13}^{-}$lie on line $E O_{14}^{-}$. Notice that this line is distinct from $E F$. Similarly we obtain that both points $O_{24}^{-}$and $O_{13}^{-}$lie on $F O_{34}^{-}$. Since the lines $E O_{14}^{-}$and $F O_{34}^{-}$are distinct, both points coincide with the meeting point of those lines.  Turning back to the problem, let $A B$ intersect $C D$ at $E$ and let $B C$ intersect $D A$ at $F$. Assume, without loss of generality, that $B$ lies on segments $A E$ and $C F$. We will show that the points $E$ and $F$, and the circles $\omega_{i}$ satisfy the conditions of Lemma 2 , so the problem statement follows. In the sequel, we use the notation of $O_{i j}^{ \pm}$from the statement of Lemma 2, applied to circles $\omega_{1}, \omega_{2}, \omega_{3}$, and $\omega_{4}$. Using the relations $\triangle E C A \sim \triangle E B D, K N \| B D$, and $M N \| A C$. we get $$ \frac{A N}{N D}=\frac{A N}{A D} \cdot \frac{A D}{N D}=\frac{K N}{B D} \cdot \frac{A C}{N M}=\frac{A C}{B D}=\frac{A E}{E D} $$ Therefore, by the angle bisector theorem, point $N$ lies on the internal angle bisector of $\angle A E D$. We prove similarly that $L$ also lies on that bisector, and that the points $K$ and $M$ lie on the internal angle bisector of $\angle A F B$. Since $K L M N$ is a rhombus, points $K$ and $M$ are symmetric in line $E L N$. Hence, the convex quadrilateral determined by the lines $E K, E M, K L$, and $M L$ is a kite, and therefore it has an incircle $\omega_{0}$. Applying Monge's theorem to $\omega_{0}, \omega_{2}$, and $\omega_{3}$, we get that $O_{23}^{+}$lies on $K M$. On the other hand, $O_{23}^{+}$lies on $B C$, as $B C$ is an external common tangent to $\omega_{2}$ and $\omega_{3}$. It follows that $F=O_{23}^{+}$. Similarly, $E=O_{12}^{+}=O_{34}^{+}$, and $F=O_{41}^{+}$. Comment 3. The reduction to Lemma 2 and the proof of Lemma 2 can be performed with the use of different tools, e.g., by means of Menelaus theorem, by projecting harmonic quadruples, by applying Monge's theorem in some other ways, etc. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0c8d55c6-b3bd-53f0-a537-51be993daf8d
| 23,995
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other.
|
Let $\Varangle(p, q)$ denote the directed angle between lines $p$ and $q$. The points $B, C, I$, and $I_{A}$ lie on the circle $\Gamma$ with diameter $I I_{A}$. Let $\omega$ and $\Omega$ denote the circles $\left(I_{A} E F\right)$ and $(A I D)$, respectively. Let $T$ be the second intersection point of $\omega$ and $\Gamma$. Then $T$ is the Miquel point of the complete quadrilateral formed by the lines $B C, B I_{A}, C I_{A}$, and $D E F$, so $T$ also lies on circle $(B D E)$ (as well as on circle $(C D F)$ ). We claim that $T$ is a desired tangency point of $\omega$ and $\Omega$. In order to show that $T$ lies on $\Omega$, use cyclic quadrilaterals $B D E T$ and $B I I_{A} T$ to write $$ \Varangle(D T, D A)=\Varangle(D T, D E)=\Varangle(B T, B E)=\Varangle\left(B T, B I_{A}\right)=\Varangle\left(I T, I I_{A}\right)=\Varangle(I T, I A) . $$ 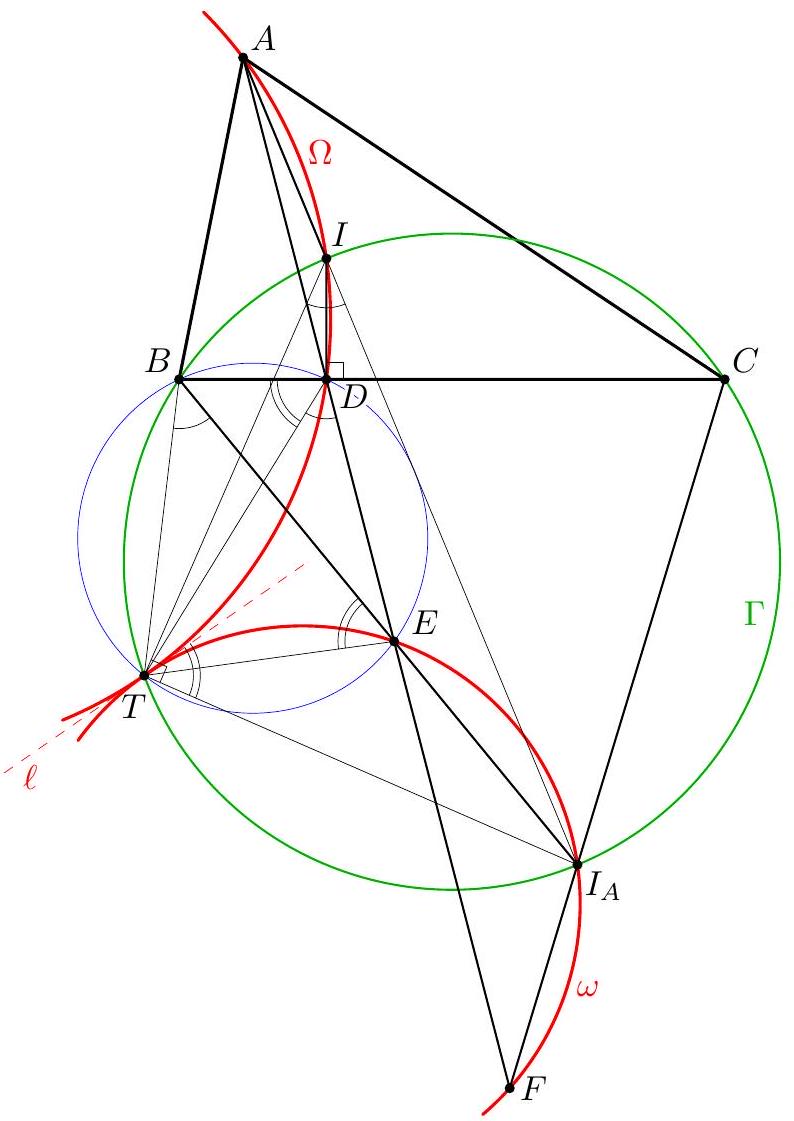 To show that $\omega$ and $\Omega$ are tangent at $T$, let $\ell$ be the tangent to $\omega$ at $T$, so that $\Varangle\left(T I_{A}, \ell\right)=$ $\Varangle\left(E I_{A}, E T\right)$. Using circles $(B D E T)$ and $\left(B I C I_{A}\right)$, we get $$ \Varangle\left(E I_{A}, E T\right)=\Varangle(E B, E T)=\Varangle(D B, D T) . $$ Therefore, $$ \Varangle(T I, \ell)=90^{\circ}+\Varangle\left(T I_{A}, \ell\right)=90^{\circ}+\Varangle(D B, D T)=\Varangle(D I, D T), $$ which shows that $\ell$ is tangent to $\Omega$ at $T$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other.
|
Let $\Varangle(p, q)$ denote the directed angle between lines $p$ and $q$. The points $B, C, I$, and $I_{A}$ lie on the circle $\Gamma$ with diameter $I I_{A}$. Let $\omega$ and $\Omega$ denote the circles $\left(I_{A} E F\right)$ and $(A I D)$, respectively. Let $T$ be the second intersection point of $\omega$ and $\Gamma$. Then $T$ is the Miquel point of the complete quadrilateral formed by the lines $B C, B I_{A}, C I_{A}$, and $D E F$, so $T$ also lies on circle $(B D E)$ (as well as on circle $(C D F)$ ). We claim that $T$ is a desired tangency point of $\omega$ and $\Omega$. In order to show that $T$ lies on $\Omega$, use cyclic quadrilaterals $B D E T$ and $B I I_{A} T$ to write $$ \Varangle(D T, D A)=\Varangle(D T, D E)=\Varangle(B T, B E)=\Varangle\left(B T, B I_{A}\right)=\Varangle\left(I T, I I_{A}\right)=\Varangle(I T, I A) . $$  To show that $\omega$ and $\Omega$ are tangent at $T$, let $\ell$ be the tangent to $\omega$ at $T$, so that $\Varangle\left(T I_{A}, \ell\right)=$ $\Varangle\left(E I_{A}, E T\right)$. Using circles $(B D E T)$ and $\left(B I C I_{A}\right)$, we get $$ \Varangle\left(E I_{A}, E T\right)=\Varangle(E B, E T)=\Varangle(D B, D T) . $$ Therefore, $$ \Varangle(T I, \ell)=90^{\circ}+\Varangle\left(T I_{A}, \ell\right)=90^{\circ}+\Varangle(D B, D T)=\Varangle(D I, D T), $$ which shows that $\ell$ is tangent to $\Omega$ at $T$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a9a2f52c-ba73-5bdd-8081-36f8b6e80382
| 23,999
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other.
|
We use the notation of circles $\Gamma, \omega$, and $\Omega$ as in the previous solution. Let $L$ be the point opposite to $I$ in circle $\Omega$. Then $\angle I A L=\angle I D L=90^{\circ}$, which means that $L$ is the foot of the external bisector of $\angle A$ in triangle $A B C$. Let $L I$ cross $\Gamma$ again at $M$. Let $T$ be the foot of the perpendicular from $I$ onto $I_{A} L$. Then $T$ is the second intersection point of $\Gamma$ and $\Gamma$. We will show that $T$ is the desired tangency point. First, we show that $T$ lies on circle $\omega$. Notice that $$ \Varangle(L T, L M)=\Varangle(A T, A I) \quad \text { and } \quad \Varangle(M T, M L)=\Varangle(M T, M I)=\Varangle\left(I_{A} T, I_{A} I\right), $$ which shows that triangles $T M L$ and $T I_{A} A$ are similar and equioriented. So there exists a rotational homothety $\tau$ mapping $T M L$ to $T I_{A} A$. Since $\Varangle(M L, L D)=\Varangle(A I, A D)$, we get $\tau(B C)=A D$. Next, since $$ \Varangle(M B, M L)=\Varangle(M B, M I)=\Varangle\left(I_{A} B, I_{A} I\right)=\Varangle\left(I_{A} E, I_{A} A\right), $$ we get $\tau(B)=E$. Similarly, $\tau(C)=F$. Since the points $M, B, C$, and $T$ are concyclic, so are their $\tau$-images, which means that $T$ lies on $\omega=\tau(\Gamma)$. 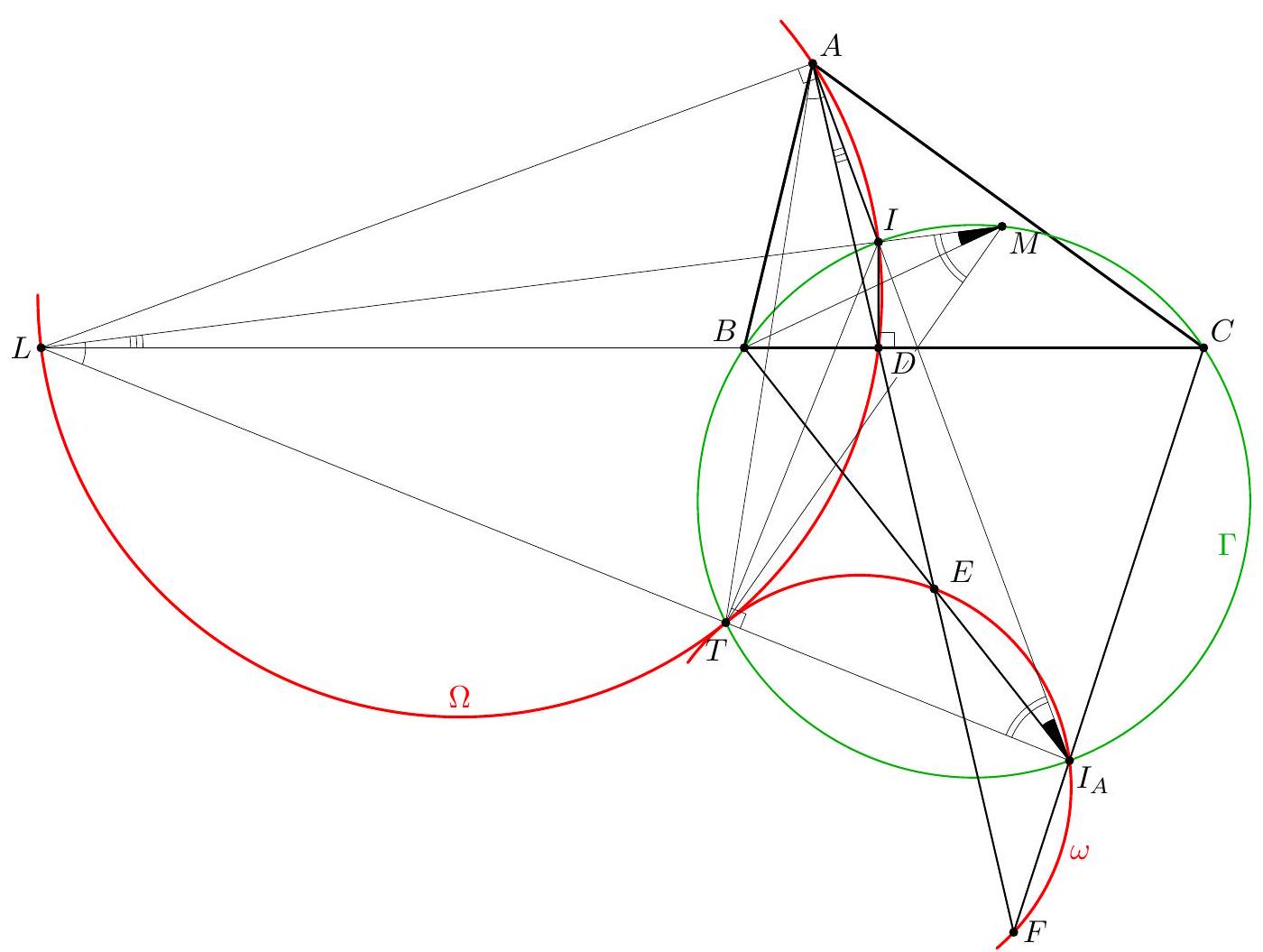 Finally, since $\tau(L)=A$ and $\tau(B)=E$, triangles $A T L$ and $E T B$ are similar so that $$ \Varangle(A T, A L)=\Varangle(E T, E B)=\Varangle\left(E I_{A}, E T\right) . $$ This means that the tangents to $\Omega$ and $\omega$ at $T$ make the same angle with the line $I_{A} T L$, so the circles are indeed tangent at $T$. Comment. In both solutions above, a crucial step is a guess that the desired tangency point lies on $\Gamma$. There are several ways to recognize this helpful property. E.g. one may perform some angle chasing to see that the tangents to $\Omega$ at $L$ and to $\omega$ at $I_{A}$ are parallel (and the circles lie on different sides of the tangents). This yields that, under the assumption that the circles are tangent externally, the tangency point must lie on $I_{A} L$. Since $I L$ is a diameter in $\Omega$, this, in turn, implies that $T$ is the projection of $I$ onto $I_{A} L$. Another way to see the same fact is to perform a homothety centered at $A$ and mapping $I$ to $I_{A}$ (and $D$ to some point $D^{\prime}$ ). The image $\Omega^{\prime}$ of $\Omega$ is tangent to $\omega$ at $I_{A}$, because $\angle B I_{A} A+\angle C I_{A} D^{\prime}=180^{\circ}$. This yields that the tangents to $\Omega$ at $I$ and to $\omega$ at $I_{A}$ are parallel. There are other ways to describe the tangency point. The next solution presents one of them.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of an acute-angled triangle $A B C$ with $A B<A C$. Let the incircle meet $B C$ at $D$. The line $A D$ meets $B I_{A}$ and $C I_{A}$ at $E$ and $F$, respectively. Prove that the circumcircles of triangles $A I D$ and $I_{A} E F$ are tangent to each other.
|
We use the notation of circles $\Gamma, \omega$, and $\Omega$ as in the previous solution. Let $L$ be the point opposite to $I$ in circle $\Omega$. Then $\angle I A L=\angle I D L=90^{\circ}$, which means that $L$ is the foot of the external bisector of $\angle A$ in triangle $A B C$. Let $L I$ cross $\Gamma$ again at $M$. Let $T$ be the foot of the perpendicular from $I$ onto $I_{A} L$. Then $T$ is the second intersection point of $\Gamma$ and $\Gamma$. We will show that $T$ is the desired tangency point. First, we show that $T$ lies on circle $\omega$. Notice that $$ \Varangle(L T, L M)=\Varangle(A T, A I) \quad \text { and } \quad \Varangle(M T, M L)=\Varangle(M T, M I)=\Varangle\left(I_{A} T, I_{A} I\right), $$ which shows that triangles $T M L$ and $T I_{A} A$ are similar and equioriented. So there exists a rotational homothety $\tau$ mapping $T M L$ to $T I_{A} A$. Since $\Varangle(M L, L D)=\Varangle(A I, A D)$, we get $\tau(B C)=A D$. Next, since $$ \Varangle(M B, M L)=\Varangle(M B, M I)=\Varangle\left(I_{A} B, I_{A} I\right)=\Varangle\left(I_{A} E, I_{A} A\right), $$ we get $\tau(B)=E$. Similarly, $\tau(C)=F$. Since the points $M, B, C$, and $T$ are concyclic, so are their $\tau$-images, which means that $T$ lies on $\omega=\tau(\Gamma)$.  Finally, since $\tau(L)=A$ and $\tau(B)=E$, triangles $A T L$ and $E T B$ are similar so that $$ \Varangle(A T, A L)=\Varangle(E T, E B)=\Varangle\left(E I_{A}, E T\right) . $$ This means that the tangents to $\Omega$ and $\omega$ at $T$ make the same angle with the line $I_{A} T L$, so the circles are indeed tangent at $T$. Comment. In both solutions above, a crucial step is a guess that the desired tangency point lies on $\Gamma$. There are several ways to recognize this helpful property. E.g. one may perform some angle chasing to see that the tangents to $\Omega$ at $L$ and to $\omega$ at $I_{A}$ are parallel (and the circles lie on different sides of the tangents). This yields that, under the assumption that the circles are tangent externally, the tangency point must lie on $I_{A} L$. Since $I L$ is a diameter in $\Omega$, this, in turn, implies that $T$ is the projection of $I$ onto $I_{A} L$. Another way to see the same fact is to perform a homothety centered at $A$ and mapping $I$ to $I_{A}$ (and $D$ to some point $D^{\prime}$ ). The image $\Omega^{\prime}$ of $\Omega$ is tangent to $\omega$ at $I_{A}$, because $\angle B I_{A} A+\angle C I_{A} D^{\prime}=180^{\circ}$. This yields that the tangents to $\Omega$ at $I$ and to $\omega$ at $I_{A}$ are parallel. There are other ways to describe the tangency point. The next solution presents one of them.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a9a2f52c-ba73-5bdd-8081-36f8b6e80382
| 23,999
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Let $A I, B I$, and $C I$ meet $\Gamma$ again at $D, E$, and $F$, respectively. Let $\ell$ be the common tangent to $\omega_{B}$ and $\omega_{C}$ at $I$. We always denote by $\Varangle(p, q)$ the directed angle from a line $p$ to a line $q$, taken modulo $180^{\circ}$. Step 1: We show that $Y$ lies on $\Gamma$. Recall that any chord of a circle makes complementary directed angles with the tangents to the circle at its endpoints. Hence, $$ \Varangle(B Y, B I)+\Varangle(C I, C Y)=\Varangle(I B, \ell)+\Varangle(\ell, I C)=\Varangle(I B, I C) . $$ Therefore, $$ \begin{aligned} \Varangle(B Y, B A)+\Varangle(C A, C Y)=\Varangle(B I, B A)+ & \Varangle(B Y, B I)+\Varangle(C I, C Y)+\Varangle(C A, C I) \\ & =\Varangle(B C, B I)+\Varangle(I B, I C)+\Varangle(C I, C B)=0, \end{aligned} $$ which yields $Y \in \Gamma$. 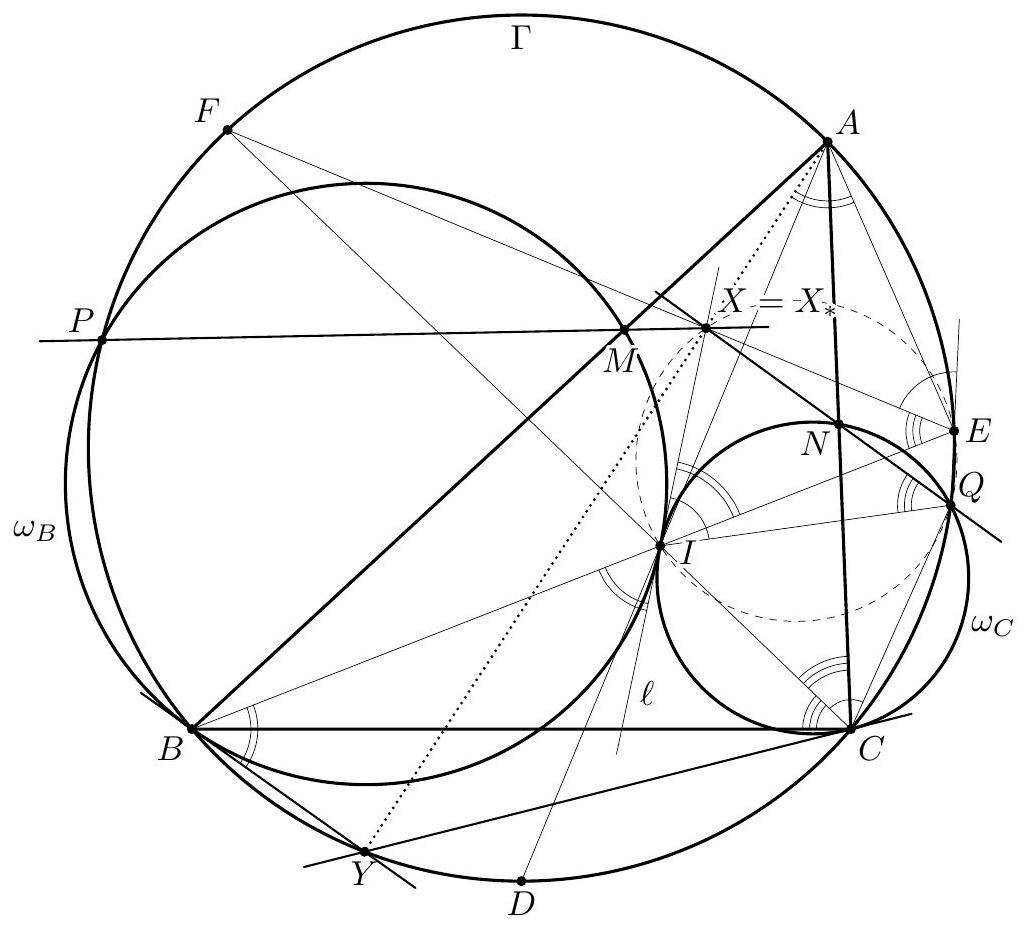 Step 2: We show that $X=\ell \cap E F$. Let $X_{*}=\ell \cap E F$. To prove our claim, it suffices to show that $X_{*}$ lies on both $P M$ and $Q N$; this will yield $X_{*}=X$. Due to symmetry, it suffices to show $X_{*} \in Q N$. Notice that $$ \Varangle\left(I X_{*}, I Q\right)=\Varangle(C I, C Q)=\Varangle(C F, C Q)=\Varangle(E F, E Q)=\Varangle\left(E X_{*}, E Q\right) ; $$ therefore, the points $X_{*}, I, Q$, and $E$ are concyclic (if $Q=E$, then the direction of $E Q$ is supposed to be the direction of a tangent to $\Gamma$ at $Q$; in this case, the equality means that the circle $\left(X_{*} I Q\right)$ is tangent to $\Gamma$ at $\left.Q\right)$. Then we have $$ \Varangle\left(Q X_{*}, Q I\right)=\Varangle\left(E X_{*}, E I\right)=\Varangle(E F, E B)=\Varangle(C A, C F)=\Varangle(C N, C I)=\Varangle(Q N, Q I), $$ which shows that $X_{*} \in Q N$. Step 3: We finally show that $A, X$, and $Y$ are collinear. Recall that $I$ is the orthocenter of triangle $D E F$, and $A$ is symmetric to $I$ with respect to $E F$. Therefore, $$ \Varangle(A X, A E)=\Varangle(I E, I X)=\Varangle(B I, \ell)=\Varangle(B Y, B I)=\Varangle(B Y, B E)=\Varangle(A Y, A E), $$ which yields the desired collinearity. Comment 1. Step 2 in the above solution seems to be crucial. After it has been performed (even without Step 1), there are different ways of finishing the solution. E.g., one may involve the notion of isogonal conjugacy. Let $X_{1}$ and $Y_{1}$ be isogonal conjugates of $X$ and $Y$, respectively, with respect to triangle $A B C$. Since $X A=X I$, triangle $A I X$ is isosceles, and hence the lines $A X$ and $X I$ form equal angles with the internal bisector $A I$ of $\angle B A C$. This means that $A X_{1} \| X I$, or $A X_{1} \| \ell$. On the other hand, the lines $B Y$ and $\ell$ form equal angles with $B I$, so that $B Y_{1} \| \ell$. Similarly, $C Y_{1} \| \ell$. This means that $Y_{1}$ is an ideal point, and $A Y_{1} \| \ell$ as well. Therefore, points $A, X_{1}$, and $Y_{1}$ are collinear, and hence $A, X$, and $Y$ are such.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Let $A I, B I$, and $C I$ meet $\Gamma$ again at $D, E$, and $F$, respectively. Let $\ell$ be the common tangent to $\omega_{B}$ and $\omega_{C}$ at $I$. We always denote by $\Varangle(p, q)$ the directed angle from a line $p$ to a line $q$, taken modulo $180^{\circ}$. Step 1: We show that $Y$ lies on $\Gamma$. Recall that any chord of a circle makes complementary directed angles with the tangents to the circle at its endpoints. Hence, $$ \Varangle(B Y, B I)+\Varangle(C I, C Y)=\Varangle(I B, \ell)+\Varangle(\ell, I C)=\Varangle(I B, I C) . $$ Therefore, $$ \begin{aligned} \Varangle(B Y, B A)+\Varangle(C A, C Y)=\Varangle(B I, B A)+ & \Varangle(B Y, B I)+\Varangle(C I, C Y)+\Varangle(C A, C I) \\ & =\Varangle(B C, B I)+\Varangle(I B, I C)+\Varangle(C I, C B)=0, \end{aligned} $$ which yields $Y \in \Gamma$.  Step 2: We show that $X=\ell \cap E F$. Let $X_{*}=\ell \cap E F$. To prove our claim, it suffices to show that $X_{*}$ lies on both $P M$ and $Q N$; this will yield $X_{*}=X$. Due to symmetry, it suffices to show $X_{*} \in Q N$. Notice that $$ \Varangle\left(I X_{*}, I Q\right)=\Varangle(C I, C Q)=\Varangle(C F, C Q)=\Varangle(E F, E Q)=\Varangle\left(E X_{*}, E Q\right) ; $$ therefore, the points $X_{*}, I, Q$, and $E$ are concyclic (if $Q=E$, then the direction of $E Q$ is supposed to be the direction of a tangent to $\Gamma$ at $Q$; in this case, the equality means that the circle $\left(X_{*} I Q\right)$ is tangent to $\Gamma$ at $\left.Q\right)$. Then we have $$ \Varangle\left(Q X_{*}, Q I\right)=\Varangle\left(E X_{*}, E I\right)=\Varangle(E F, E B)=\Varangle(C A, C F)=\Varangle(C N, C I)=\Varangle(Q N, Q I), $$ which shows that $X_{*} \in Q N$. Step 3: We finally show that $A, X$, and $Y$ are collinear. Recall that $I$ is the orthocenter of triangle $D E F$, and $A$ is symmetric to $I$ with respect to $E F$. Therefore, $$ \Varangle(A X, A E)=\Varangle(I E, I X)=\Varangle(B I, \ell)=\Varangle(B Y, B I)=\Varangle(B Y, B E)=\Varangle(A Y, A E), $$ which yields the desired collinearity. Comment 1. Step 2 in the above solution seems to be crucial. After it has been performed (even without Step 1), there are different ways of finishing the solution. E.g., one may involve the notion of isogonal conjugacy. Let $X_{1}$ and $Y_{1}$ be isogonal conjugates of $X$ and $Y$, respectively, with respect to triangle $A B C$. Since $X A=X I$, triangle $A I X$ is isosceles, and hence the lines $A X$ and $X I$ form equal angles with the internal bisector $A I$ of $\angle B A C$. This means that $A X_{1} \| X I$, or $A X_{1} \| \ell$. On the other hand, the lines $B Y$ and $\ell$ form equal angles with $B I$, so that $B Y_{1} \| \ell$. Similarly, $C Y_{1} \| \ell$. This means that $Y_{1}$ is an ideal point, and $A Y_{1} \| \ell$ as well. Therefore, points $A, X_{1}$, and $Y_{1}$ are collinear, and hence $A, X$, and $Y$ are such.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fbce402b-4d8d-5484-b3d6-05470d9dc6be
| 24,007
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Perform an inversion centered at $I$; the images of the points are denoted by primes, e.g., $A^{\prime}$ is the image of $A$. On the inverted figure, $I$ and $\Gamma^{\prime}$ are the orthocenter and the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$, respectively. The points $P^{\prime}$ and $Q^{\prime}$ lie on $\Gamma^{\prime}$ such that $B^{\prime} P^{\prime} \| C^{\prime} Q^{\prime}$ (since $B^{\prime} P^{\prime}=\omega_{B}^{\prime}$ and $C^{\prime} Q^{\prime}=\omega_{C}^{\prime}$ ). The points $M^{\prime}$ and $N^{\prime}$ are the second intersections of lines $B^{\prime} P^{\prime}$ and $C^{\prime} Q^{\prime}$ with the circumcircles $\gamma_{B}$ and $\gamma_{C}$ of triangles $A^{\prime} I B^{\prime}$ and $A^{\prime} I C^{\prime}$, respectively. Notice here that $\gamma_{C}$ is obtained from $\gamma_{B}$ by the translation at $\overrightarrow{B^{\prime} C^{\prime}}$; the same translation maps line $B^{\prime} P^{\prime}$ to $C^{\prime} Q^{\prime}$, and hence $M^{\prime}$ to $N^{\prime}$. In other words, $B^{\prime} M^{\prime} N^{\prime} C^{\prime}$ is a parallelogram, and $P^{\prime} Q^{\prime}$ partitions it into two isosceles trapezoids. Point $X^{\prime}$ is the second intersection point of circles $\left(I P^{\prime} M^{\prime}\right)$ and $\left(I Q^{\prime} N^{\prime}\right)$ that is - the reflection of $I$ in their line of centers. But the centers lie on the common perpendicular bisector $p$ of $P^{\prime} M^{\prime}$ and $Q^{\prime} N^{\prime}$, so $p$ is that line of centers. Hence, $I X^{\prime} \| B^{\prime} P^{\prime}$, as both lines are perpendicular to $p$. Finally, the point $Y$ satisfies $\Varangle(B Y, B I)=\Varangle(P B, P I)$ and $\Varangle(C Y, C I)=\Varangle(Q C, Q I)$, which yields $\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} I\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)$ and $\Varangle\left(Y^{\prime} C^{\prime}, Y^{\prime} I\right)=\Varangle\left(C^{\prime} Q^{\prime}, C^{\prime} I\right)$. Therefore, $$ \Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} C^{\prime}\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)+\Varangle\left(C^{\prime} I, C^{\prime} Q^{\prime}\right)=\Varangle\left(C^{\prime} I, B^{\prime} I\right)=\Varangle\left(A^{\prime} B^{\prime}, A^{\prime} C^{\prime}\right), $$ which shows that $Y^{\prime} \in \Gamma^{\prime}$. In congruent circles $\Gamma^{\prime}$ and $\gamma_{B}$, the chords $A^{\prime} P^{\prime}$ and $A^{\prime} M^{\prime}$ subtend the same angle $\angle A^{\prime} B^{\prime} P^{\prime}$; therefore, $A^{\prime} P^{\prime}=A^{\prime} M^{\prime}$, and hence $A^{\prime} \in p$. This yields $A^{\prime} X^{\prime}=A^{\prime} I$, and hence $\Varangle\left(I A^{\prime}, I X^{\prime}\right)=$ $\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right)$ 。 Finally, we have $$ \begin{aligned} \Varangle\left(Y^{\prime} I, Y^{\prime} A^{\prime}\right) & =\Varangle\left(Y^{\prime} I, Y^{\prime} B^{\prime}\right)+\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} A^{\prime}\right) \\ & =\Varangle\left(B^{\prime} I, B^{\prime} P^{\prime}\right)+\Varangle\left(I A^{\prime}, I B^{\prime}\right)=\Varangle\left(I A^{\prime}, B^{\prime} P^{\prime}\right)=\Varangle\left(I A^{\prime}, I X^{\prime}\right)=\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right), \end{aligned} $$ which yields that the points $A^{\prime}, X^{\prime}, Y^{\prime}$, and $I$ are concyclic. This means exactly that $A, X$, and $Y$ are collinear.  Comment 2. An inversion at $I$ may also help in establishing Step 2 in Solution 1. Indeed, relation $A^{\prime} X^{\prime}=A^{\prime} I$ yields $X A=X I$, so that $X \in E F$. On the other hand, $I X^{\prime} \| B^{\prime} P^{\prime}$ yields $I X \| \ell$, i.e., $X \in \ell$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ and $I$ be the circumcircle and the incenter of an acute-angled triangle $A B C$. Two circles $\omega_{B}$ and $\omega_{C}$ passing through $B$ and $C$, respectively, are tangent at $I$. Let $\omega_{B}$ meet the shorter arc $A B$ of $\Gamma$ and segment $A B$ again at $P$ and $M$, respectively. Similarly, let $\omega_{C}$ meet the shorter arc $A C$ of $\Gamma$ and segment $A C$ again at $Q$ and $N$, respectively. The rays $P M$ and $Q N$ meet at $X$, and the tangents to $\omega_{B}$ and $\omega_{C}$ at $B$ and $C$, respectively, meet at $Y$. Prove that the points $A, X$, and $Y$ are collinear. (Netherlands)
|
Perform an inversion centered at $I$; the images of the points are denoted by primes, e.g., $A^{\prime}$ is the image of $A$. On the inverted figure, $I$ and $\Gamma^{\prime}$ are the orthocenter and the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$, respectively. The points $P^{\prime}$ and $Q^{\prime}$ lie on $\Gamma^{\prime}$ such that $B^{\prime} P^{\prime} \| C^{\prime} Q^{\prime}$ (since $B^{\prime} P^{\prime}=\omega_{B}^{\prime}$ and $C^{\prime} Q^{\prime}=\omega_{C}^{\prime}$ ). The points $M^{\prime}$ and $N^{\prime}$ are the second intersections of lines $B^{\prime} P^{\prime}$ and $C^{\prime} Q^{\prime}$ with the circumcircles $\gamma_{B}$ and $\gamma_{C}$ of triangles $A^{\prime} I B^{\prime}$ and $A^{\prime} I C^{\prime}$, respectively. Notice here that $\gamma_{C}$ is obtained from $\gamma_{B}$ by the translation at $\overrightarrow{B^{\prime} C^{\prime}}$; the same translation maps line $B^{\prime} P^{\prime}$ to $C^{\prime} Q^{\prime}$, and hence $M^{\prime}$ to $N^{\prime}$. In other words, $B^{\prime} M^{\prime} N^{\prime} C^{\prime}$ is a parallelogram, and $P^{\prime} Q^{\prime}$ partitions it into two isosceles trapezoids. Point $X^{\prime}$ is the second intersection point of circles $\left(I P^{\prime} M^{\prime}\right)$ and $\left(I Q^{\prime} N^{\prime}\right)$ that is - the reflection of $I$ in their line of centers. But the centers lie on the common perpendicular bisector $p$ of $P^{\prime} M^{\prime}$ and $Q^{\prime} N^{\prime}$, so $p$ is that line of centers. Hence, $I X^{\prime} \| B^{\prime} P^{\prime}$, as both lines are perpendicular to $p$. Finally, the point $Y$ satisfies $\Varangle(B Y, B I)=\Varangle(P B, P I)$ and $\Varangle(C Y, C I)=\Varangle(Q C, Q I)$, which yields $\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} I\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)$ and $\Varangle\left(Y^{\prime} C^{\prime}, Y^{\prime} I\right)=\Varangle\left(C^{\prime} Q^{\prime}, C^{\prime} I\right)$. Therefore, $$ \Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} C^{\prime}\right)=\Varangle\left(B^{\prime} P^{\prime}, B^{\prime} I\right)+\Varangle\left(C^{\prime} I, C^{\prime} Q^{\prime}\right)=\Varangle\left(C^{\prime} I, B^{\prime} I\right)=\Varangle\left(A^{\prime} B^{\prime}, A^{\prime} C^{\prime}\right), $$ which shows that $Y^{\prime} \in \Gamma^{\prime}$. In congruent circles $\Gamma^{\prime}$ and $\gamma_{B}$, the chords $A^{\prime} P^{\prime}$ and $A^{\prime} M^{\prime}$ subtend the same angle $\angle A^{\prime} B^{\prime} P^{\prime}$; therefore, $A^{\prime} P^{\prime}=A^{\prime} M^{\prime}$, and hence $A^{\prime} \in p$. This yields $A^{\prime} X^{\prime}=A^{\prime} I$, and hence $\Varangle\left(I A^{\prime}, I X^{\prime}\right)=$ $\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right)$ 。 Finally, we have $$ \begin{aligned} \Varangle\left(Y^{\prime} I, Y^{\prime} A^{\prime}\right) & =\Varangle\left(Y^{\prime} I, Y^{\prime} B^{\prime}\right)+\Varangle\left(Y^{\prime} B^{\prime}, Y^{\prime} A^{\prime}\right) \\ & =\Varangle\left(B^{\prime} I, B^{\prime} P^{\prime}\right)+\Varangle\left(I A^{\prime}, I B^{\prime}\right)=\Varangle\left(I A^{\prime}, B^{\prime} P^{\prime}\right)=\Varangle\left(I A^{\prime}, I X^{\prime}\right)=\Varangle\left(X^{\prime} I, X^{\prime} A^{\prime}\right), \end{aligned} $$ which yields that the points $A^{\prime}, X^{\prime}, Y^{\prime}$, and $I$ are concyclic. This means exactly that $A, X$, and $Y$ are collinear.  Comment 2. An inversion at $I$ may also help in establishing Step 2 in Solution 1. Indeed, relation $A^{\prime} X^{\prime}=A^{\prime} I$ yields $X A=X I$, so that $X \in E F$. On the other hand, $I X^{\prime} \| B^{\prime} P^{\prime}$ yields $I X \| \ell$, i.e., $X \in \ell$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fbce402b-4d8d-5484-b3d6-05470d9dc6be
| 24,007
|
Given a positive integer $k$, show that there exists a prime $p$ such that one can choose distinct integers $a_{1}, a_{2}, \ldots, a_{k+3} \in\{1,2, \ldots, p-1\}$ such that $p$ divides $a_{i} a_{i+1} a_{i+2} a_{i+3}-i$ for all $i=1,2, \ldots, k$. (South Africa)
|
First we choose distinct positive rational numbers $r_{1}, \ldots, r_{k+3}$ such that $$ r_{i} r_{i+1} r_{i+2} r_{i+3}=i \quad \text { for } 1 \leqslant i \leqslant k $$ Let $r_{1}=x, r_{2}=y, r_{3}=z$ be some distinct primes greater than $k$; the remaining terms satisfy $r_{4}=\frac{1}{r_{1} r_{2} r_{3}}$ and $r_{i+4}=\frac{i+1}{i} r_{i}$. It follows that if $r_{i}$ are represented as irreducible fractions, the numerators are divisible by $x$ for $i \equiv 1(\bmod 4)$, by $y$ for $i \equiv 2(\bmod 4)$, by $z$ for $i \equiv 3(\bmod 4)$ and by none for $i \equiv 0(\bmod 4)$. Notice that $r_{i}<r_{i+4}$; thus the sequences $r_{1}<r_{5}<r_{9}<\ldots$, $r_{2}<r_{6}<r_{10}<\ldots, r_{3}<r_{7}<r_{11}<\ldots, r_{4}<r_{8}<r_{12}<\ldots$ are increasing and have no common terms, that is, all $r_{i}$ are distinct. If each $r_{i}$ is represented by an irreducible fraction $\frac{u_{i}}{v_{i}}$, choose a prime $p$ which divides neither $v_{i}, 1 \leqslant i \leqslant k+1$, nor $v_{i} v_{j}\left(r_{i}-r_{j}\right)=v_{j} u_{i}-v_{i} u_{j}$ for $i<j$, and define $a_{i}$ by the congruence $a_{i} v_{i} \equiv u_{i}(\bmod p)$. Since $r_{i} r_{i+1} r_{i+2} r_{i+3}=i$, we have $$ \begin{aligned} i v_{i} v_{i+1} v_{i+2} v_{i+3}=r_{i} v_{i} r_{i+1} v_{i+1} r_{i+2} & v_{i+2} r_{i+3} v_{i+3} \\ & =u_{i} u_{i+1} u_{i+2} u_{i+3} \equiv a_{i} v_{i} a_{i+1} v_{i+1} a_{i+2} v_{i+2} a_{i+3} v_{i+3} \quad(\bmod p) \end{aligned} $$ and therefore $a_{i} a_{i+1} a_{i+2} a_{i+3} \equiv i(\bmod p)$ for $1 \leqslant i \leqslant k$. If $a_{i} \equiv a_{j}(\bmod p)$, then $u_{i} v_{j} \equiv a_{i} v_{i} v_{j} \equiv u_{j} v_{i}(\bmod p)$, a contradiction. Comment. One can explicitly express residues $b_{i} \equiv a_{1} a_{2} \cdot \ldots \cdot a_{i}(\bmod p)$ in terms of $b_{1}, b_{2}, b_{3}$ and $b_{0}=1$ : $$ b_{i+3}=i(i-4)(i-8) \cdot \ldots \cdot(i-4 k+4) b_{r} $$ where $i+3=4 k+r, 0 \leqslant r<4$. Then the numbers $a_{i}$ are found from the congruences $b_{i-1} a_{i} \equiv b_{i}$ $(\bmod p)$, and choosing $p$ so that $a_{i}$ are not congruent modulo $p$ is done in a way very similar to the above solution. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given a positive integer $k$, show that there exists a prime $p$ such that one can choose distinct integers $a_{1}, a_{2}, \ldots, a_{k+3} \in\{1,2, \ldots, p-1\}$ such that $p$ divides $a_{i} a_{i+1} a_{i+2} a_{i+3}-i$ for all $i=1,2, \ldots, k$. (South Africa)
|
First we choose distinct positive rational numbers $r_{1}, \ldots, r_{k+3}$ such that $$ r_{i} r_{i+1} r_{i+2} r_{i+3}=i \quad \text { for } 1 \leqslant i \leqslant k $$ Let $r_{1}=x, r_{2}=y, r_{3}=z$ be some distinct primes greater than $k$; the remaining terms satisfy $r_{4}=\frac{1}{r_{1} r_{2} r_{3}}$ and $r_{i+4}=\frac{i+1}{i} r_{i}$. It follows that if $r_{i}$ are represented as irreducible fractions, the numerators are divisible by $x$ for $i \equiv 1(\bmod 4)$, by $y$ for $i \equiv 2(\bmod 4)$, by $z$ for $i \equiv 3(\bmod 4)$ and by none for $i \equiv 0(\bmod 4)$. Notice that $r_{i}<r_{i+4}$; thus the sequences $r_{1}<r_{5}<r_{9}<\ldots$, $r_{2}<r_{6}<r_{10}<\ldots, r_{3}<r_{7}<r_{11}<\ldots, r_{4}<r_{8}<r_{12}<\ldots$ are increasing and have no common terms, that is, all $r_{i}$ are distinct. If each $r_{i}$ is represented by an irreducible fraction $\frac{u_{i}}{v_{i}}$, choose a prime $p$ which divides neither $v_{i}, 1 \leqslant i \leqslant k+1$, nor $v_{i} v_{j}\left(r_{i}-r_{j}\right)=v_{j} u_{i}-v_{i} u_{j}$ for $i<j$, and define $a_{i}$ by the congruence $a_{i} v_{i} \equiv u_{i}(\bmod p)$. Since $r_{i} r_{i+1} r_{i+2} r_{i+3}=i$, we have $$ \begin{aligned} i v_{i} v_{i+1} v_{i+2} v_{i+3}=r_{i} v_{i} r_{i+1} v_{i+1} r_{i+2} & v_{i+2} r_{i+3} v_{i+3} \\ & =u_{i} u_{i+1} u_{i+2} u_{i+3} \equiv a_{i} v_{i} a_{i+1} v_{i+1} a_{i+2} v_{i+2} a_{i+3} v_{i+3} \quad(\bmod p) \end{aligned} $$ and therefore $a_{i} a_{i+1} a_{i+2} a_{i+3} \equiv i(\bmod p)$ for $1 \leqslant i \leqslant k$. If $a_{i} \equiv a_{j}(\bmod p)$, then $u_{i} v_{j} \equiv a_{i} v_{i} v_{j} \equiv u_{j} v_{i}(\bmod p)$, a contradiction. Comment. One can explicitly express residues $b_{i} \equiv a_{1} a_{2} \cdot \ldots \cdot a_{i}(\bmod p)$ in terms of $b_{1}, b_{2}, b_{3}$ and $b_{0}=1$ : $$ b_{i+3}=i(i-4)(i-8) \cdot \ldots \cdot(i-4 k+4) b_{r} $$ where $i+3=4 k+r, 0 \leqslant r<4$. Then the numbers $a_{i}$ are found from the congruences $b_{i-1} a_{i} \equiv b_{i}$ $(\bmod p)$, and choosing $p$ so that $a_{i}$ are not congruent modulo $p$ is done in a way very similar to the above solution. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
623a7668-e00d-55cd-8312-60872b015f2e
| 24,014
|
For each prime $p$, there is a kingdom of $p$-Landia consisting of $p$ islands numbered $1,2, \ldots, p$. Two distinct islands numbered $n$ and $m$ are connected by a bridge if and only if $p$ divides $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right)$. The bridges may pass over each other, but cannot cross. Prove that for infinitely many $p$ there are two islands in $p$-Landia not connected by a chain of bridges. (Denmark)
|
We prove that for each prime $p>3$ dividing a number of the form $x^{2}-x+1$ with integer $x$ there are two unconnected islands in $p$-Landia. For brevity's sake, when a bridge connects the islands numbered $m$ and $n$, we shall speak simply that it connects $m$ and $n$. A bridge connects $m$ and $n$ if $n \equiv m^{2}+1(\bmod p)$ or $m \equiv n^{2}+1(\bmod p)$. If $m^{2}+1 \equiv n$ $(\bmod p)$, we draw an arrow starting at $m$ on the bridge connecting $m$ and $n$. Clearly only one arrow starts at $m$ if $m^{2}+1 \not \equiv m(\bmod p)$, and no arrows otherwise. The total number of bridges does not exceed the total number of arrows. Suppose $x^{2}-x+1 \equiv 0(\bmod p)$. We may assume that $1 \leqslant x \leqslant p$; then there is no arrow starting at $x$. Since $(1-x)^{2}-(1-x)+1=x^{2}-x+1,(p+1-x)^{2}+1 \equiv(p+1-x)(\bmod p)$, and there is also no arrow starting at $p+1-x$. If $x=p+1-x$, that is, $x=\frac{p+1}{2}$, then $4\left(x^{2}-x+1\right)=p^{2}+3$ and therefore $x^{2}-x+1$ is not divisible by $p$. Thus the islands $x$ and $p+1-x$ are different, and no arrows start at either of them. It follows that the total number of bridges in $p$-Landia does not exceed $p-2$. Let $1,2, \ldots, p$ be the vertices of a graph $G_{p}$, where an edge connects $m$ and $n$ if and only if there is a bridge between $m$ and $n$. The number of vertices of $G_{p}$ is $p$ and the number of edges is less than $p-1$. This means that the graph is not connected, which means that there are two islands not connected by a chain of bridges. It remains to prove that there are infinitely many primes $p$ dividing $x^{2}-x+1$ for some integer $x$. Let $p_{1}, p_{2}, \ldots, p_{k}$ be any finite set of such primes. The number $\left(p_{1} p_{2} \cdot \ldots \cdot p_{k}\right)^{2}-p_{1} p_{2} \cdot \ldots \cdot p_{k}+1$ is greater than 1 and not divisible by any $p_{i}$; therefore it has another prime divisor with the required property.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each prime $p$, there is a kingdom of $p$-Landia consisting of $p$ islands numbered $1,2, \ldots, p$. Two distinct islands numbered $n$ and $m$ are connected by a bridge if and only if $p$ divides $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right)$. The bridges may pass over each other, but cannot cross. Prove that for infinitely many $p$ there are two islands in $p$-Landia not connected by a chain of bridges. (Denmark)
|
We prove that for each prime $p>3$ dividing a number of the form $x^{2}-x+1$ with integer $x$ there are two unconnected islands in $p$-Landia. For brevity's sake, when a bridge connects the islands numbered $m$ and $n$, we shall speak simply that it connects $m$ and $n$. A bridge connects $m$ and $n$ if $n \equiv m^{2}+1(\bmod p)$ or $m \equiv n^{2}+1(\bmod p)$. If $m^{2}+1 \equiv n$ $(\bmod p)$, we draw an arrow starting at $m$ on the bridge connecting $m$ and $n$. Clearly only one arrow starts at $m$ if $m^{2}+1 \not \equiv m(\bmod p)$, and no arrows otherwise. The total number of bridges does not exceed the total number of arrows. Suppose $x^{2}-x+1 \equiv 0(\bmod p)$. We may assume that $1 \leqslant x \leqslant p$; then there is no arrow starting at $x$. Since $(1-x)^{2}-(1-x)+1=x^{2}-x+1,(p+1-x)^{2}+1 \equiv(p+1-x)(\bmod p)$, and there is also no arrow starting at $p+1-x$. If $x=p+1-x$, that is, $x=\frac{p+1}{2}$, then $4\left(x^{2}-x+1\right)=p^{2}+3$ and therefore $x^{2}-x+1$ is not divisible by $p$. Thus the islands $x$ and $p+1-x$ are different, and no arrows start at either of them. It follows that the total number of bridges in $p$-Landia does not exceed $p-2$. Let $1,2, \ldots, p$ be the vertices of a graph $G_{p}$, where an edge connects $m$ and $n$ if and only if there is a bridge between $m$ and $n$. The number of vertices of $G_{p}$ is $p$ and the number of edges is less than $p-1$. This means that the graph is not connected, which means that there are two islands not connected by a chain of bridges. It remains to prove that there are infinitely many primes $p$ dividing $x^{2}-x+1$ for some integer $x$. Let $p_{1}, p_{2}, \ldots, p_{k}$ be any finite set of such primes. The number $\left(p_{1} p_{2} \cdot \ldots \cdot p_{k}\right)^{2}-p_{1} p_{2} \cdot \ldots \cdot p_{k}+1$ is greater than 1 and not divisible by any $p_{i}$; therefore it has another prime divisor with the required property.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6d708399-cd55-58c5-91b6-8146aea69205
| 24,017
|
For each prime $p$, there is a kingdom of $p$-Landia consisting of $p$ islands numbered $1,2, \ldots, p$. Two distinct islands numbered $n$ and $m$ are connected by a bridge if and only if $p$ divides $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right)$. The bridges may pass over each other, but cannot cross. Prove that for infinitely many $p$ there are two islands in $p$-Landia not connected by a chain of bridges. (Denmark)
|
One can show, by using only arithmetical methods, that for infinitely many $p$, the kingdom of $p$-Ladia contains two islands connected to no other island, except for each other. Let arrows between islands have the same meaning as in the previous solution. Suppose that positive $a<p$ satisfies the congruence $x^{2}-x+1 \equiv 0(\bmod p)$. We have seen in the first solution that $b=p+1-a$ satisfies it too, and $b \neq a$ when $p>3$. It follows that $a b \equiv a(1-a) \equiv 1$ $(\bmod p)$. If an arrow goes from $t$ to $a$, then $t$ must satisfy the congruence $t^{2}+1 \equiv a \equiv a^{2}+1$ $(\bmod p)$; the only such $t \neq a$ is $p-a$. Similarly, the only arrow going to $b$ goes from $p-b$. If one of the numbers $p-a$ and $p-b$, say, $p-a$, is not at the end of any arrow, the pair $a, p-a$ is not connected with the rest of the islands. This is true if at least one of the congruences $x^{2}+1 \equiv-a, x^{2}+1 \equiv-b$ has no solutions, that is, either $-a-1$ or $-b-1$ is a quadratic non-residue modulo $p$. Note that $x^{2}-x+1 \equiv x^{2}-(a+b) x+a b \equiv(x-a)(x-b)(\bmod p)$. Substituting $x=-1$ we get $(-1-a)(-1-b) \equiv 3(\bmod p)$. If 3 is a quadratic non-residue modulo $p$, so is one of the numbers $-1-a$ and $-1-b$. Thus it is enough to find infinitely many primes $p>3$ dividing $x^{2}-x+1$ for some integer $x$ and such that 3 is a quadratic non-residue modulo $p$. If $x^{2}-x+1 \equiv 0(\bmod p)$ then $(2 x-1)^{2} \equiv-3(\bmod p)$, that is, -3 is a quadratic residue modulo $p$, so 3 is a quadratic non-residue if and only if -1 is also a non-residue, in other words, $p \equiv-1(\bmod 4)$. Similarly to the first solution, let $p_{1}, \ldots, p_{k}$ be primes congruent to -1 modulo 4 and dividing numbers of the form $x^{2}-x+1$. The number $\left(2 p_{1} \cdot \ldots \cdot p_{k}\right)^{2}-2 p_{1} \cdot \ldots \cdot p_{k}+1$ is not divisible by any $p_{i}$ and is congruent to -1 modulo 4 , therefore, it has some prime divisor $p \equiv-1(\bmod 4)$ which has the required properties.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each prime $p$, there is a kingdom of $p$-Landia consisting of $p$ islands numbered $1,2, \ldots, p$. Two distinct islands numbered $n$ and $m$ are connected by a bridge if and only if $p$ divides $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right)$. The bridges may pass over each other, but cannot cross. Prove that for infinitely many $p$ there are two islands in $p$-Landia not connected by a chain of bridges. (Denmark)
|
One can show, by using only arithmetical methods, that for infinitely many $p$, the kingdom of $p$-Ladia contains two islands connected to no other island, except for each other. Let arrows between islands have the same meaning as in the previous solution. Suppose that positive $a<p$ satisfies the congruence $x^{2}-x+1 \equiv 0(\bmod p)$. We have seen in the first solution that $b=p+1-a$ satisfies it too, and $b \neq a$ when $p>3$. It follows that $a b \equiv a(1-a) \equiv 1$ $(\bmod p)$. If an arrow goes from $t$ to $a$, then $t$ must satisfy the congruence $t^{2}+1 \equiv a \equiv a^{2}+1$ $(\bmod p)$; the only such $t \neq a$ is $p-a$. Similarly, the only arrow going to $b$ goes from $p-b$. If one of the numbers $p-a$ and $p-b$, say, $p-a$, is not at the end of any arrow, the pair $a, p-a$ is not connected with the rest of the islands. This is true if at least one of the congruences $x^{2}+1 \equiv-a, x^{2}+1 \equiv-b$ has no solutions, that is, either $-a-1$ or $-b-1$ is a quadratic non-residue modulo $p$. Note that $x^{2}-x+1 \equiv x^{2}-(a+b) x+a b \equiv(x-a)(x-b)(\bmod p)$. Substituting $x=-1$ we get $(-1-a)(-1-b) \equiv 3(\bmod p)$. If 3 is a quadratic non-residue modulo $p$, so is one of the numbers $-1-a$ and $-1-b$. Thus it is enough to find infinitely many primes $p>3$ dividing $x^{2}-x+1$ for some integer $x$ and such that 3 is a quadratic non-residue modulo $p$. If $x^{2}-x+1 \equiv 0(\bmod p)$ then $(2 x-1)^{2} \equiv-3(\bmod p)$, that is, -3 is a quadratic residue modulo $p$, so 3 is a quadratic non-residue if and only if -1 is also a non-residue, in other words, $p \equiv-1(\bmod 4)$. Similarly to the first solution, let $p_{1}, \ldots, p_{k}$ be primes congruent to -1 modulo 4 and dividing numbers of the form $x^{2}-x+1$. The number $\left(2 p_{1} \cdot \ldots \cdot p_{k}\right)^{2}-2 p_{1} \cdot \ldots \cdot p_{k}+1$ is not divisible by any $p_{i}$ and is congruent to -1 modulo 4 , therefore, it has some prime divisor $p \equiv-1(\bmod 4)$ which has the required properties.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6d708399-cd55-58c5-91b6-8146aea69205
| 24,017
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia)
|
Suppose that $a_{1}, \ldots, a_{n}$ satisfy the required properties. Let $d=\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)$. If $d>1$ then replace the numbers $a_{1}, \ldots, a_{n}$ by $\frac{a_{1}}{d}, \ldots, \frac{a_{n}}{d}$; all arithmetic and all geometric means will be divided by $d$, so we obtain another sequence satisfying the condition. Hence, without loss of generality, we can assume that $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$. We show two numbers, $a_{m}$ and $a_{k}$ such that their arithmetic mean, $\frac{a_{m}+a_{k}}{2}$ is different from the geometric mean of any (nonempty) subsequence of $a_{1} \ldots, a_{n}$. That proves that there cannot exist such a sequence. Choose the index $m \in\{1, \ldots, n\}$ such that $a_{m}=\max \left(a_{1}, \ldots, a_{n}\right)$. Note that $a_{m} \geqslant 2$, because $a_{1}, \ldots, a_{n}$ are not all equal. Let $p$ be a prime divisor of $a_{m}$. Let $k \in\{1, \ldots, n\}$ be an index such that $a_{k}=\max \left\{a_{i}: p \nmid a_{i}\right\}$. Due to $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$, not all $a_{i}$ are divisible by $p$, so such a $k$ exists. Note that $a_{m}>a_{k}$ because $a_{m} \geqslant a_{k}, p \mid a_{m}$ and $p \nmid a_{k}$. Let $b=\frac{a_{m}+a_{k}}{2}$; we will show that $b$ cannot be the geometric mean of any subsequence of $a_{1}, \ldots, a_{n}$. Consider the geometric mean, $g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ of an arbitrary subsequence of $a_{1}, \ldots, a_{n}$. If none of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then they are not greater than $a_{k}$, so $$ g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}} \leqslant a_{k}<\frac{a_{m}+a_{k}}{2}=b $$ and therefore $g \neq b$. Otherwise, if at least one of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then $2 g=2 \sqrt{t} \sqrt{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ is either not an integer or is divisible by $p$, while $2 b=a_{m}+a_{k}$ is an integer not divisible by $p$, so $g \neq b$ again.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia)
|
Suppose that $a_{1}, \ldots, a_{n}$ satisfy the required properties. Let $d=\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)$. If $d>1$ then replace the numbers $a_{1}, \ldots, a_{n}$ by $\frac{a_{1}}{d}, \ldots, \frac{a_{n}}{d}$; all arithmetic and all geometric means will be divided by $d$, so we obtain another sequence satisfying the condition. Hence, without loss of generality, we can assume that $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$. We show two numbers, $a_{m}$ and $a_{k}$ such that their arithmetic mean, $\frac{a_{m}+a_{k}}{2}$ is different from the geometric mean of any (nonempty) subsequence of $a_{1} \ldots, a_{n}$. That proves that there cannot exist such a sequence. Choose the index $m \in\{1, \ldots, n\}$ such that $a_{m}=\max \left(a_{1}, \ldots, a_{n}\right)$. Note that $a_{m} \geqslant 2$, because $a_{1}, \ldots, a_{n}$ are not all equal. Let $p$ be a prime divisor of $a_{m}$. Let $k \in\{1, \ldots, n\}$ be an index such that $a_{k}=\max \left\{a_{i}: p \nmid a_{i}\right\}$. Due to $\operatorname{gcd}\left(a_{1} \ldots, a_{n}\right)=1$, not all $a_{i}$ are divisible by $p$, so such a $k$ exists. Note that $a_{m}>a_{k}$ because $a_{m} \geqslant a_{k}, p \mid a_{m}$ and $p \nmid a_{k}$. Let $b=\frac{a_{m}+a_{k}}{2}$; we will show that $b$ cannot be the geometric mean of any subsequence of $a_{1}, \ldots, a_{n}$. Consider the geometric mean, $g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ of an arbitrary subsequence of $a_{1}, \ldots, a_{n}$. If none of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then they are not greater than $a_{k}$, so $$ g=\sqrt[t]{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}} \leqslant a_{k}<\frac{a_{m}+a_{k}}{2}=b $$ and therefore $g \neq b$. Otherwise, if at least one of $a_{i_{1}}, \ldots, a_{i_{t}}$ is divisible by $p$, then $2 g=2 \sqrt{t} \sqrt{a_{i_{1}} \cdot \ldots \cdot a_{i_{t}}}$ is either not an integer or is divisible by $p$, while $2 b=a_{m}+a_{k}$ is an integer not divisible by $p$, so $g \neq b$ again.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8522d02b-1e10-5eaf-a949-304fc0f8c224
| 24,021
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia)
|
Like in the previous solution, we assume that the numbers $a_{1}, \ldots, a_{n}$ have no common divisor greater than 1 . The arithmetic mean of any two numbers in the sequence is half of an integer; on the other hand, it is a (some integer order) root of an integer. This means each pair's mean is an integer, so all terms in the sequence must be of the same parity; hence they all are odd. Let $d=\min \left\{\operatorname{gcd}\left(a_{i}, a_{j}\right): a_{i} \neq a_{j}\right\}$. By reordering the sequence we can assume that $\operatorname{gcd}\left(a_{1}, a_{2}\right)=d$, the sum $a_{1}+a_{2}$ is maximal among such pairs, and $a_{1}>a_{2}$. We will show that $\frac{a_{1}+a_{2}}{2}$ cannot be the geometric mean of any subsequence of $a_{1} \ldots, a_{n}$. Let $a_{1}=x d$ and $a_{2}=y d$ where $x, y$ are coprime, and suppose that there exist some $b_{1}, \ldots, b_{t} \in\left\{a_{1}, \ldots, a_{n}\right\}$ whose geometric mean is $\frac{a_{1}+a_{2}}{2}$. Let $d_{i}=\operatorname{gcd}\left(a_{1}, b_{i}\right)$ for $i=1,2, \ldots, t$ and let $D=d_{1} d_{2} \cdot \ldots \cdot d_{t}$. Then $$ D=d_{1} d_{2} \cdot \ldots \cdot d_{t} \left\lvert\, b_{1} b_{2} \cdot \ldots \cdot b_{t}=\left(\frac{a_{1}+a_{2}}{2}\right)^{t}=\left(\frac{x+y}{2}\right)^{t} d^{t}\right. $$ We claim that $D \mid d^{t}$. Consider an arbitrary prime divisor $p$ of $D$. Let $\nu_{p}(x)$ denote the exponent of $p$ in the prime factorization of $x$. If $p \left\lvert\, \frac{x+y}{2}\right.$, then $p \nmid x, y$, so $p$ is coprime with $x$; hence, $\nu_{p}\left(d_{i}\right) \leqslant \nu_{p}\left(a_{1}\right)=\nu_{p}(x d)=\nu_{p}(d)$ for every $1 \leqslant i \leqslant t$, therefore $\nu_{p}(D)=\sum_{i} \nu_{p}\left(d_{i}\right) \leqslant$ $t \nu_{p}(d)=\nu_{p}\left(d^{t}\right)$. Otherwise, if $p$ is coprime to $\frac{x+y}{2}$, we have $\nu_{p}(D) \leqslant \nu_{p}\left(d^{t}\right)$ trivially. The claim has been proved. Notice that $d_{i}=\operatorname{gcd}\left(b_{i}, a_{1}\right) \geqslant d$ for $1 \leqslant i \leqslant t$ : if $b_{i} \neq a_{1}$ then this follows from the definition of $d$; otherwise we have $b_{i}=a_{1}$, so $d_{i}=a_{1} \geqslant d$. Hence, $D=d_{1} \cdot \ldots \cdot d_{t} \geqslant d^{t}$, and the claim forces $d_{1}=\ldots=d_{t}=d$. Finally, by $\frac{a_{1}+a_{2}}{2}>a_{2}$ there must be some $b_{k}$ which is greater than $a_{2}$. From $a_{1}>a_{2} \geqslant$ $d=\operatorname{gcd}\left(a_{1}, b_{k}\right)$ it follows that $a_{1} \neq b_{k}$. Now the have a pair $a_{1}, b_{k}$ such that $\operatorname{gcd}\left(a_{1}, b_{k}\right)=d$ but $a_{1}+b_{k}>a_{1}+a_{2}$; that contradicts the choice of $a_{1}$ and $a_{2}$. Comment. The original problem proposal contained a second question asking if there exists a nonconstant sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers such that the geometric mean of every two terms is equal the arithmetic mean of some terms. For $n \geqslant 3$ such a sequence is $(4,1,1, \ldots, 1)$. The case $n=2$ can be done by the trivial estimates $$ \min \left(a_{1}, a_{2}\right)<\sqrt{a_{1} a_{2}}<\frac{a_{1}+a_{2}}{2}<\max \left(a_{1}, a_{2}\right) $$ The Problem Selection Committee found this variant less interesting and suggests using only the first question.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an integer with $n \geqslant 2$. Does there exist a sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers with not all terms being equal such that the arithmetic mean of every two terms is equal to the geometric mean of some (one or more) terms in this sequence? (Estonia)
|
Like in the previous solution, we assume that the numbers $a_{1}, \ldots, a_{n}$ have no common divisor greater than 1 . The arithmetic mean of any two numbers in the sequence is half of an integer; on the other hand, it is a (some integer order) root of an integer. This means each pair's mean is an integer, so all terms in the sequence must be of the same parity; hence they all are odd. Let $d=\min \left\{\operatorname{gcd}\left(a_{i}, a_{j}\right): a_{i} \neq a_{j}\right\}$. By reordering the sequence we can assume that $\operatorname{gcd}\left(a_{1}, a_{2}\right)=d$, the sum $a_{1}+a_{2}$ is maximal among such pairs, and $a_{1}>a_{2}$. We will show that $\frac{a_{1}+a_{2}}{2}$ cannot be the geometric mean of any subsequence of $a_{1} \ldots, a_{n}$. Let $a_{1}=x d$ and $a_{2}=y d$ where $x, y$ are coprime, and suppose that there exist some $b_{1}, \ldots, b_{t} \in\left\{a_{1}, \ldots, a_{n}\right\}$ whose geometric mean is $\frac{a_{1}+a_{2}}{2}$. Let $d_{i}=\operatorname{gcd}\left(a_{1}, b_{i}\right)$ for $i=1,2, \ldots, t$ and let $D=d_{1} d_{2} \cdot \ldots \cdot d_{t}$. Then $$ D=d_{1} d_{2} \cdot \ldots \cdot d_{t} \left\lvert\, b_{1} b_{2} \cdot \ldots \cdot b_{t}=\left(\frac{a_{1}+a_{2}}{2}\right)^{t}=\left(\frac{x+y}{2}\right)^{t} d^{t}\right. $$ We claim that $D \mid d^{t}$. Consider an arbitrary prime divisor $p$ of $D$. Let $\nu_{p}(x)$ denote the exponent of $p$ in the prime factorization of $x$. If $p \left\lvert\, \frac{x+y}{2}\right.$, then $p \nmid x, y$, so $p$ is coprime with $x$; hence, $\nu_{p}\left(d_{i}\right) \leqslant \nu_{p}\left(a_{1}\right)=\nu_{p}(x d)=\nu_{p}(d)$ for every $1 \leqslant i \leqslant t$, therefore $\nu_{p}(D)=\sum_{i} \nu_{p}\left(d_{i}\right) \leqslant$ $t \nu_{p}(d)=\nu_{p}\left(d^{t}\right)$. Otherwise, if $p$ is coprime to $\frac{x+y}{2}$, we have $\nu_{p}(D) \leqslant \nu_{p}\left(d^{t}\right)$ trivially. The claim has been proved. Notice that $d_{i}=\operatorname{gcd}\left(b_{i}, a_{1}\right) \geqslant d$ for $1 \leqslant i \leqslant t$ : if $b_{i} \neq a_{1}$ then this follows from the definition of $d$; otherwise we have $b_{i}=a_{1}$, so $d_{i}=a_{1} \geqslant d$. Hence, $D=d_{1} \cdot \ldots \cdot d_{t} \geqslant d^{t}$, and the claim forces $d_{1}=\ldots=d_{t}=d$. Finally, by $\frac{a_{1}+a_{2}}{2}>a_{2}$ there must be some $b_{k}$ which is greater than $a_{2}$. From $a_{1}>a_{2} \geqslant$ $d=\operatorname{gcd}\left(a_{1}, b_{k}\right)$ it follows that $a_{1} \neq b_{k}$. Now the have a pair $a_{1}, b_{k}$ such that $\operatorname{gcd}\left(a_{1}, b_{k}\right)=d$ but $a_{1}+b_{k}>a_{1}+a_{2}$; that contradicts the choice of $a_{1}$ and $a_{2}$. Comment. The original problem proposal contained a second question asking if there exists a nonconstant sequence $\left(a_{1}, \ldots, a_{n}\right)$ of positive integers such that the geometric mean of every two terms is equal the arithmetic mean of some terms. For $n \geqslant 3$ such a sequence is $(4,1,1, \ldots, 1)$. The case $n=2$ can be done by the trivial estimates $$ \min \left(a_{1}, a_{2}\right)<\sqrt{a_{1} a_{2}}<\frac{a_{1}+a_{2}}{2}<\max \left(a_{1}, a_{2}\right) $$ The Problem Selection Committee found this variant less interesting and suggests using only the first question.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8522d02b-1e10-5eaf-a949-304fc0f8c224
| 24,021
|
For any odd prime $p$ and any integer $n$, let $d_{p}(n) \in\{0,1, \ldots, p-1\}$ denote the remainder when $n$ is divided by $p$. We say that $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ is a $p$-sequence, if $a_{0}$ is a positive integer coprime to $p$, and $a_{n+1}=a_{n}+d_{p}\left(a_{n}\right)$ for $n \geqslant 0$. (a) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{n}>b_{n}$ for infinitely many $n$, and $b_{n}>a_{n}$ for infinitely many $n$ ? (b) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{0}<b_{0}$, but $a_{n}>b_{n}$ for all $n \geqslant 1$ ? (United Kingdom)
|
Fix some odd prime $p$, and let $T$ be the smallest positive integer such that $p \mid 2^{T}-1$; in other words, $T$ is the multiplicative order of 2 modulo $p$. Consider any $p$-sequence $\left(x_{n}\right)=\left(x_{0}, x_{1}, x_{2}, \ldots\right)$. Obviously, $x_{n+1} \equiv 2 x_{n}(\bmod p)$ and therefore $x_{n} \equiv 2^{n} x_{0}(\bmod p)$. This yields $x_{n+T} \equiv x_{n}(\bmod p)$ and therefore $d\left(x_{n+T}\right)=d\left(x_{n}\right)$ for all $n \geqslant 0$. It follows that the sum $d\left(x_{n}\right)+d\left(x_{n+1}\right)+\ldots+d\left(x_{n+T-1}\right)$ does not depend on $n$ and is thus a function of $x_{0}$ (and $p$ ) only; we shall denote this sum by $S_{p}\left(x_{0}\right)$, and extend the function $S_{p}(\cdot)$ to all (not necessarily positive) integers. Therefore, we have $x_{n+k T}=x_{n}+k S_{p}\left(x_{0}\right)$ for all positive integers $n$ and $k$. Clearly, $S_{p}\left(x_{0}\right)=S_{p}\left(2^{t} x_{0}\right)$ for every integer $t \geqslant 0$. In both parts, we use the notation $$ S_{p}^{+}=S_{p}(1)=\sum_{i=0}^{T-1} d_{p}\left(2^{i}\right) \quad \text { and } \quad S_{p}^{-}=S_{p}(-1)=\sum_{i=0}^{T-1} d_{p}\left(p-2^{i}\right) $$ (a) Let $q>3$ be a prime and $p$ a prime divisor of $2^{q}+1$ that is greater than 3 . We will show that $p$ is suitable for part (a). Notice that $9 \nmid 2^{q}+1$, so that such a $p$ exists. Moreover, for any two odd primes $q<r$ we have $\operatorname{gcd}\left(2^{q}+1,2^{r}+1\right)=2^{\operatorname{gcd}(q, r)}+1=3$, thus there exist infinitely many such primes $p$. For the chosen $p$, we have $T=2 q$. Since $2^{q} \equiv-1(\bmod p)$, we have $S_{p}^{+}=S_{p}^{-}$. Now consider the $p$-sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ with $a_{0}=p+1$ and $b_{0}=p-1$; we claim that these sequences satisfy the required conditions. We have $a_{0}>b_{0}$ and $a_{1}=p+2<b_{1}=2 p-2$. It follows then that $$ a_{k \cdot 2 q}=a_{0}+k S_{p}^{+}>b_{0}+k S_{p}^{+}=b_{k \cdot 2 q} \quad \text { and } \quad a_{k \cdot 2 q+1}=a_{1}+k S_{p}^{+}<b_{1}+k S_{p}^{+}=b_{k \cdot 2 q+1} $$ for all $k=0,1, \ldots$, as desired. (b) Let $q$ be an odd prime and $p$ a prime divisor of $2^{q}-1$; thus we have $T=q$. We will show that $p$ is suitable for part (b). Notice that the numbers of the form $2^{q}-1$ are pairwise coprime (since $\operatorname{gcd}\left(2^{q}-1,2^{r}-1\right)=2^{\operatorname{gcd}(q, r)}-1=1$ for any two distinct primes $q$ and $r$ ), thus there exist infinitely many such primes $p$. Notice that $d_{p}(x)+d_{p}(p-x)=p$ for all $x$ with $p \nmid x$, so that the sum $S_{p}^{+}+S_{p}^{-}=p q$ is odd, which yields $S_{p}^{+}=S_{p}(1) \neq S_{p}(-1)=S_{p}^{-}$. Assume that $\left(x_{n}\right)$ and $\left(y_{n}\right)$ are two $p$-sequences with $S_{p}\left(x_{0}\right)>S_{p}\left(y_{0}\right)$ but $x_{0}<y_{0}$. The first condition yields that $$ x_{M q+r}-y_{M q+r}=\left(x_{r}-y_{r}\right)+M\left(S_{p}\left(x_{0}\right)-S_{p}\left(y_{0}\right)\right) \geqslant\left(x_{r}-y_{r}\right)+M $$ for all nonnegative integers $M$ and every $r=0,1, \ldots, q-1$. Thus, we have $x_{n}>y_{n}$ for every $n \geqslant q+q \cdot \max \left\{y_{r}-x_{r}: r=0,1, \ldots, q-1\right\}$. Now, since $x_{0}<y_{0}$, there exists the largest $n_{0}$ with $x_{n_{0}}<y_{n_{0}}$. In this case the $p$-sequences $a_{n}=x_{n-n_{0}}$ and $b_{n}=y_{n-n_{0}}$ possess the desired property (notice here that $x_{n} \neq y_{n}$ for all $n \geqslant 0$, as otherwise we would have $\left.S_{p}\left(x_{0}\right)=S_{p}\left(x_{n}\right)=S_{p}\left(y_{n}\right)=S_{p}\left(y_{0}\right)\right)$. It remains to find $p$-sequences $\left(x_{n}\right)$ and $\left(y_{n}\right)$ satisfying the two conditions. Recall that $S_{p}^{+} \neq S_{p}^{-}$. Now, if $S_{p}^{+}>S_{p}^{-}$, then we can put $x_{0}=1$ and $y_{0}=p-1$. Otherwise, if $S_{p}^{+}<S_{p}^{-}$, then we put $x_{0}=p-1$ and $y_{0}=p+1$. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any odd prime $p$ and any integer $n$, let $d_{p}(n) \in\{0,1, \ldots, p-1\}$ denote the remainder when $n$ is divided by $p$. We say that $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ is a $p$-sequence, if $a_{0}$ is a positive integer coprime to $p$, and $a_{n+1}=a_{n}+d_{p}\left(a_{n}\right)$ for $n \geqslant 0$. (a) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{n}>b_{n}$ for infinitely many $n$, and $b_{n}>a_{n}$ for infinitely many $n$ ? (b) Do there exist infinitely many primes $p$ for which there exist $p$-sequences $\left(a_{0}, a_{1}, a_{2}, \ldots\right)$ and $\left(b_{0}, b_{1}, b_{2}, \ldots\right)$ such that $a_{0}<b_{0}$, but $a_{n}>b_{n}$ for all $n \geqslant 1$ ? (United Kingdom)
|
Fix some odd prime $p$, and let $T$ be the smallest positive integer such that $p \mid 2^{T}-1$; in other words, $T$ is the multiplicative order of 2 modulo $p$. Consider any $p$-sequence $\left(x_{n}\right)=\left(x_{0}, x_{1}, x_{2}, \ldots\right)$. Obviously, $x_{n+1} \equiv 2 x_{n}(\bmod p)$ and therefore $x_{n} \equiv 2^{n} x_{0}(\bmod p)$. This yields $x_{n+T} \equiv x_{n}(\bmod p)$ and therefore $d\left(x_{n+T}\right)=d\left(x_{n}\right)$ for all $n \geqslant 0$. It follows that the sum $d\left(x_{n}\right)+d\left(x_{n+1}\right)+\ldots+d\left(x_{n+T-1}\right)$ does not depend on $n$ and is thus a function of $x_{0}$ (and $p$ ) only; we shall denote this sum by $S_{p}\left(x_{0}\right)$, and extend the function $S_{p}(\cdot)$ to all (not necessarily positive) integers. Therefore, we have $x_{n+k T}=x_{n}+k S_{p}\left(x_{0}\right)$ for all positive integers $n$ and $k$. Clearly, $S_{p}\left(x_{0}\right)=S_{p}\left(2^{t} x_{0}\right)$ for every integer $t \geqslant 0$. In both parts, we use the notation $$ S_{p}^{+}=S_{p}(1)=\sum_{i=0}^{T-1} d_{p}\left(2^{i}\right) \quad \text { and } \quad S_{p}^{-}=S_{p}(-1)=\sum_{i=0}^{T-1} d_{p}\left(p-2^{i}\right) $$ (a) Let $q>3$ be a prime and $p$ a prime divisor of $2^{q}+1$ that is greater than 3 . We will show that $p$ is suitable for part (a). Notice that $9 \nmid 2^{q}+1$, so that such a $p$ exists. Moreover, for any two odd primes $q<r$ we have $\operatorname{gcd}\left(2^{q}+1,2^{r}+1\right)=2^{\operatorname{gcd}(q, r)}+1=3$, thus there exist infinitely many such primes $p$. For the chosen $p$, we have $T=2 q$. Since $2^{q} \equiv-1(\bmod p)$, we have $S_{p}^{+}=S_{p}^{-}$. Now consider the $p$-sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ with $a_{0}=p+1$ and $b_{0}=p-1$; we claim that these sequences satisfy the required conditions. We have $a_{0}>b_{0}$ and $a_{1}=p+2<b_{1}=2 p-2$. It follows then that $$ a_{k \cdot 2 q}=a_{0}+k S_{p}^{+}>b_{0}+k S_{p}^{+}=b_{k \cdot 2 q} \quad \text { and } \quad a_{k \cdot 2 q+1}=a_{1}+k S_{p}^{+}<b_{1}+k S_{p}^{+}=b_{k \cdot 2 q+1} $$ for all $k=0,1, \ldots$, as desired. (b) Let $q$ be an odd prime and $p$ a prime divisor of $2^{q}-1$; thus we have $T=q$. We will show that $p$ is suitable for part (b). Notice that the numbers of the form $2^{q}-1$ are pairwise coprime (since $\operatorname{gcd}\left(2^{q}-1,2^{r}-1\right)=2^{\operatorname{gcd}(q, r)}-1=1$ for any two distinct primes $q$ and $r$ ), thus there exist infinitely many such primes $p$. Notice that $d_{p}(x)+d_{p}(p-x)=p$ for all $x$ with $p \nmid x$, so that the sum $S_{p}^{+}+S_{p}^{-}=p q$ is odd, which yields $S_{p}^{+}=S_{p}(1) \neq S_{p}(-1)=S_{p}^{-}$. Assume that $\left(x_{n}\right)$ and $\left(y_{n}\right)$ are two $p$-sequences with $S_{p}\left(x_{0}\right)>S_{p}\left(y_{0}\right)$ but $x_{0}<y_{0}$. The first condition yields that $$ x_{M q+r}-y_{M q+r}=\left(x_{r}-y_{r}\right)+M\left(S_{p}\left(x_{0}\right)-S_{p}\left(y_{0}\right)\right) \geqslant\left(x_{r}-y_{r}\right)+M $$ for all nonnegative integers $M$ and every $r=0,1, \ldots, q-1$. Thus, we have $x_{n}>y_{n}$ for every $n \geqslant q+q \cdot \max \left\{y_{r}-x_{r}: r=0,1, \ldots, q-1\right\}$. Now, since $x_{0}<y_{0}$, there exists the largest $n_{0}$ with $x_{n_{0}}<y_{n_{0}}$. In this case the $p$-sequences $a_{n}=x_{n-n_{0}}$ and $b_{n}=y_{n-n_{0}}$ possess the desired property (notice here that $x_{n} \neq y_{n}$ for all $n \geqslant 0$, as otherwise we would have $\left.S_{p}\left(x_{0}\right)=S_{p}\left(x_{n}\right)=S_{p}\left(y_{n}\right)=S_{p}\left(y_{0}\right)\right)$. It remains to find $p$-sequences $\left(x_{n}\right)$ and $\left(y_{n}\right)$ satisfying the two conditions. Recall that $S_{p}^{+} \neq S_{p}^{-}$. Now, if $S_{p}^{+}>S_{p}^{-}$, then we can put $x_{0}=1$ and $y_{0}=p-1$. Otherwise, if $S_{p}^{+}<S_{p}^{-}$, then we put $x_{0}=p-1$ and $y_{0}=p+1$. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d3f8731b-51c8-587c-8e29-1eb67c0db32b
| 24,025
|
Determine all functions $f$ defined on the set of all positive integers and taking non-negative integer values, satisfying the three conditions: (i) $f(n) \neq 0$ for at least one $n$; (ii) $f(x y)=f(x)+f(y)$ for every positive integers $x$ and $y$; (iii) there are infinitely many positive integers $n$ such that $f(k)=f(n-k)$ for all $k<n$. (Croatia)
|
We use the notion of a good number from the previous solution. As above, we also denote by $\nu_{p}(n)$ the exponent of a prime $p$ in the prime decomposition of $n$. Say that a positive integer $k$ is big if $f(k)>0$. Let $\mathcal{B}$ be the set of big primes, and let $p_{1}<p_{2}<\ldots$ list the elements of $\mathcal{B}$ (this set might be either finite or infinite). By the problem conditions, we have $$ f(n)=\sum_{i} \nu_{p_{i}}(n) f\left(p_{i}\right) $$ thus, the big numbers are those divisible by at least one big prime. For a positive integer $k$, define its essence $e(k)$ to be the largest product $e$ of (not necessarily different) big primes such that $e \mid k$. In other words, $$ e(n)=\prod_{p_{i} \in \mathcal{B}} p_{i}^{\nu_{p_{i}}(n)} $$ This yields that $k / e(k)$ is not big, so $f(k)=f(e(k))+f(k / e(k))=f(e(k))$. Lemma. Assume that $n$ is a good number. Then $e(k)=e(n-k)$ for all $k<n$. Proof. Arguing indirectly, choose a minimal $k$ for which the claim of the lemma is violated. Clearly, $k$ is big, as otherwise $f(k)=f(n-k)=0$ and hence $e(k)=e(n-k)=1$. There are $t=k / e(k)$ multiples of $e(k)$ in each of the segments $[1, k]$ and $[n-k, n-1]$. On the other hand, there are $t-1$ such multiples on $[1, k-1]$ - and, by minimality of $k$, on $[n-k+1, n-1]$ as well. This yields that $n-k$ is a multiple of $e(k)$. Therefore, $$ f(e(k))=f(k)=f(n-k)=f(e(k))+f\left(\frac{n-k}{e(k)}\right), $$ so the last summand vanishes, hence $\frac{n-k}{e(k)}$ has no big prime divisors, that is, $e(n-k)=e(k)$. This contradicts our choice. Back to the problem, assume that $|\mathcal{B}| \geqslant 2$. Take any good number $n>p_{1} p_{2}$, and let $p_{1}^{\alpha}$ be the largest power of $p_{1}$ smaller than $n$, so that $n \leqslant p_{1}^{\alpha+1}<p_{1}^{\alpha} p_{2}$. By the lemma, $e\left(n-p_{1}^{\alpha}\right)=e\left(p_{1}^{\alpha}\right)=p_{1}^{\alpha}$, which yields $p_{1}^{\alpha} \mid n$. Similarly, $p_{2} \mid n$, so that $n \geqslant p_{1}^{\alpha} p_{2}$. This contradiction shows that $|\mathcal{B}| \leqslant 1$, which by (1) yields that $f$ is listed in the answer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine all functions $f$ defined on the set of all positive integers and taking non-negative integer values, satisfying the three conditions: (i) $f(n) \neq 0$ for at least one $n$; (ii) $f(x y)=f(x)+f(y)$ for every positive integers $x$ and $y$; (iii) there are infinitely many positive integers $n$ such that $f(k)=f(n-k)$ for all $k<n$. (Croatia)
|
We use the notion of a good number from the previous solution. As above, we also denote by $\nu_{p}(n)$ the exponent of a prime $p$ in the prime decomposition of $n$. Say that a positive integer $k$ is big if $f(k)>0$. Let $\mathcal{B}$ be the set of big primes, and let $p_{1}<p_{2}<\ldots$ list the elements of $\mathcal{B}$ (this set might be either finite or infinite). By the problem conditions, we have $$ f(n)=\sum_{i} \nu_{p_{i}}(n) f\left(p_{i}\right) $$ thus, the big numbers are those divisible by at least one big prime. For a positive integer $k$, define its essence $e(k)$ to be the largest product $e$ of (not necessarily different) big primes such that $e \mid k$. In other words, $$ e(n)=\prod_{p_{i} \in \mathcal{B}} p_{i}^{\nu_{p_{i}}(n)} $$ This yields that $k / e(k)$ is not big, so $f(k)=f(e(k))+f(k / e(k))=f(e(k))$. Lemma. Assume that $n$ is a good number. Then $e(k)=e(n-k)$ for all $k<n$. Proof. Arguing indirectly, choose a minimal $k$ for which the claim of the lemma is violated. Clearly, $k$ is big, as otherwise $f(k)=f(n-k)=0$ and hence $e(k)=e(n-k)=1$. There are $t=k / e(k)$ multiples of $e(k)$ in each of the segments $[1, k]$ and $[n-k, n-1]$. On the other hand, there are $t-1$ such multiples on $[1, k-1]$ - and, by minimality of $k$, on $[n-k+1, n-1]$ as well. This yields that $n-k$ is a multiple of $e(k)$. Therefore, $$ f(e(k))=f(k)=f(n-k)=f(e(k))+f\left(\frac{n-k}{e(k)}\right), $$ so the last summand vanishes, hence $\frac{n-k}{e(k)}$ has no big prime divisors, that is, $e(n-k)=e(k)$. This contradicts our choice. Back to the problem, assume that $|\mathcal{B}| \geqslant 2$. Take any good number $n>p_{1} p_{2}$, and let $p_{1}^{\alpha}$ be the largest power of $p_{1}$ smaller than $n$, so that $n \leqslant p_{1}^{\alpha+1}<p_{1}^{\alpha} p_{2}$. By the lemma, $e\left(n-p_{1}^{\alpha}\right)=e\left(p_{1}^{\alpha}\right)=p_{1}^{\alpha}$, which yields $p_{1}^{\alpha} \mid n$. Similarly, $p_{2} \mid n$, so that $n \geqslant p_{1}^{\alpha} p_{2}$. This contradiction shows that $|\mathcal{B}| \leqslant 1$, which by (1) yields that $f$ is listed in the answer.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9fb3d1f3-b4a9-5100-ab76-60467dc699c5
| 24,028
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus)
|
Fix $N>1$, let $p_{1}, \ldots, p_{k}$ be all primes between 1 and $N$ and $p_{k+1}, \ldots, p_{k+s}$ be all primes between $N+1$ and $2 N$. Since for $j \leqslant k+s$ all prime divisors of $p_{j}-1$ do not exceed $N$, we have $$ \prod_{j=1}^{k+s}\left(p_{j}-1\right)=\prod_{i=1}^{k} p_{i}^{c_{i}} $$ with some fixed exponents $c_{1}, \ldots, c_{k}$. Choose a huge prime number $q$ and consider a number $$ n=\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-1} \cdot\left(p_{k+1} \cdot \ldots \cdot p_{k+s}\right) $$ Then $$ \varphi(d(n))=\varphi\left(q^{k} \cdot 2^{s}\right)=q^{k-1}(q-1) 2^{s-1} $$ and $$ d(\varphi(n))=d\left(\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-2} \prod_{i=1}^{k+s}\left(p_{i}-1\right)\right)=d\left(\prod_{i=1}^{k} p_{i}^{q-2+c_{i}}\right)=\prod_{i=1}^{k}\left(q-1+c_{i}\right) $$ so $$ \frac{\varphi(d(n))}{d(\varphi(n))}=\frac{q^{k-1}(q-1) 2^{s-1}}{\prod_{i=1}^{k}\left(q-1+c_{i}\right)}=2^{s-1} \cdot \frac{q-1}{q} \cdot \prod_{i=1}^{k} \frac{q}{q-1+c_{i}} $$ which can be made arbitrarily close to $2^{s-1}$ by choosing $q$ large enough. It remains to show that $s$ can be arbitrarily large, i.e. that there can be arbitrarily many primes between $N$ and $2 N$. This follows, for instance, from the well-known fact that $\sum \frac{1}{p}=\infty$, where the sum is taken over the set $\mathbb{P}$ of prime numbers. Indeed, if, for some constant $\stackrel{p}{C}$, there were always at most $C$ primes between $2^{\ell}$ and $2^{\ell+1}$, we would have $$ \sum_{p \in \mathbb{P}} \frac{1}{p}=\sum_{\ell=0}^{\infty} \sum_{\substack{p \in \mathbb{P} \\ p \in\left[2^{\ell}, 2^{\ell+1}\right)}} \frac{1}{p} \leqslant \sum_{\ell=0}^{\infty} \frac{C}{2^{\ell}}<\infty, $$ which is a contradiction. Comment 1. Here we sketch several alternative elementary self-contained ways to perform the last step of the solution above. In particular, they avoid using divergence of $\sum \frac{1}{p}$. Suppose that for some constant $C$ and for every $k=1,2, \ldots$ there exist at most $C$ prime numbers between $2^{k}$ and $2^{k+1}$. Consider the prime factorization of the factorial $\left(2^{n}\right)!=\prod p^{\alpha_{p}}$. We have $\alpha_{p}=\left\lfloor 2^{n} / p\right\rfloor+\left\lfloor 2^{n} / p^{2}\right\rfloor+\ldots$. Thus, for $p \in\left[2^{k}, 2^{k+1}\right)$, we get $\alpha_{p} \leqslant 2^{n} / 2^{k}+2^{n} / 2^{k+1}+\ldots=2^{n-k+1}$, therefore $p^{\alpha_{p}} \leqslant 2^{(k+1) 2^{n-k+1}}$. Combining this with the bound $(2 m)!\geqslant m(m+1) \cdot \ldots \cdot(2 m-1) \geqslant m^{m}$ for $m=2^{n-1}$ we get $$ 2^{(n-1) \cdot 2^{n-1}} \leqslant\left(2^{n}\right)!\leqslant \prod_{k=1}^{n-1} 2^{C(k+1) 2^{n-k+1}} $$ or $$ \sum_{k=1}^{n-1} C(k+1) 2^{1-k} \geqslant \frac{n-1}{2} $$ that fails for large $n$ since $C(k+1) 2^{1-k}<1 / 3$ for all but finitely many $k$. In fact, a much stronger inequality can be obtained in an elementary way: Note that the formula for $\nu_{p}(n!)$ implies that if $p^{\alpha}$ is the largest power of $p$ dividing $\binom{n}{n / 2}$, then $p^{\alpha} \leqslant n$. By looking at prime factorization of $\binom{n}{n / 2}$ we instantaneously infer that $$ \pi(n) \geqslant \log _{n}\binom{n}{n / 2} \geqslant \frac{\log \left(2^{n} / n\right)}{\log n} \geqslant \frac{n}{2 \log n} . $$ This, in particular, implies that for infinitely many $n$ there are at least $\frac{n}{3 \log n}$ primes between $n$ and $2 n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$, let $d(n)$ be the number of positive divisors of $n$, and let $\varphi(n)$ be the number of positive integers not exceeding $n$ which are coprime to $n$. Does there exist a constant $C$ such that $$ \frac{\varphi(d(n))}{d(\varphi(n))} \leqslant C $$ for all $n \geqslant 1$ ? (Cyprus)
|
Fix $N>1$, let $p_{1}, \ldots, p_{k}$ be all primes between 1 and $N$ and $p_{k+1}, \ldots, p_{k+s}$ be all primes between $N+1$ and $2 N$. Since for $j \leqslant k+s$ all prime divisors of $p_{j}-1$ do not exceed $N$, we have $$ \prod_{j=1}^{k+s}\left(p_{j}-1\right)=\prod_{i=1}^{k} p_{i}^{c_{i}} $$ with some fixed exponents $c_{1}, \ldots, c_{k}$. Choose a huge prime number $q$ and consider a number $$ n=\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-1} \cdot\left(p_{k+1} \cdot \ldots \cdot p_{k+s}\right) $$ Then $$ \varphi(d(n))=\varphi\left(q^{k} \cdot 2^{s}\right)=q^{k-1}(q-1) 2^{s-1} $$ and $$ d(\varphi(n))=d\left(\left(p_{1} \cdot \ldots \cdot p_{k}\right)^{q-2} \prod_{i=1}^{k+s}\left(p_{i}-1\right)\right)=d\left(\prod_{i=1}^{k} p_{i}^{q-2+c_{i}}\right)=\prod_{i=1}^{k}\left(q-1+c_{i}\right) $$ so $$ \frac{\varphi(d(n))}{d(\varphi(n))}=\frac{q^{k-1}(q-1) 2^{s-1}}{\prod_{i=1}^{k}\left(q-1+c_{i}\right)}=2^{s-1} \cdot \frac{q-1}{q} \cdot \prod_{i=1}^{k} \frac{q}{q-1+c_{i}} $$ which can be made arbitrarily close to $2^{s-1}$ by choosing $q$ large enough. It remains to show that $s$ can be arbitrarily large, i.e. that there can be arbitrarily many primes between $N$ and $2 N$. This follows, for instance, from the well-known fact that $\sum \frac{1}{p}=\infty$, where the sum is taken over the set $\mathbb{P}$ of prime numbers. Indeed, if, for some constant $\stackrel{p}{C}$, there were always at most $C$ primes between $2^{\ell}$ and $2^{\ell+1}$, we would have $$ \sum_{p \in \mathbb{P}} \frac{1}{p}=\sum_{\ell=0}^{\infty} \sum_{\substack{p \in \mathbb{P} \\ p \in\left[2^{\ell}, 2^{\ell+1}\right)}} \frac{1}{p} \leqslant \sum_{\ell=0}^{\infty} \frac{C}{2^{\ell}}<\infty, $$ which is a contradiction. Comment 1. Here we sketch several alternative elementary self-contained ways to perform the last step of the solution above. In particular, they avoid using divergence of $\sum \frac{1}{p}$. Suppose that for some constant $C$ and for every $k=1,2, \ldots$ there exist at most $C$ prime numbers between $2^{k}$ and $2^{k+1}$. Consider the prime factorization of the factorial $\left(2^{n}\right)!=\prod p^{\alpha_{p}}$. We have $\alpha_{p}=\left\lfloor 2^{n} / p\right\rfloor+\left\lfloor 2^{n} / p^{2}\right\rfloor+\ldots$. Thus, for $p \in\left[2^{k}, 2^{k+1}\right)$, we get $\alpha_{p} \leqslant 2^{n} / 2^{k}+2^{n} / 2^{k+1}+\ldots=2^{n-k+1}$, therefore $p^{\alpha_{p}} \leqslant 2^{(k+1) 2^{n-k+1}}$. Combining this with the bound $(2 m)!\geqslant m(m+1) \cdot \ldots \cdot(2 m-1) \geqslant m^{m}$ for $m=2^{n-1}$ we get $$ 2^{(n-1) \cdot 2^{n-1}} \leqslant\left(2^{n}\right)!\leqslant \prod_{k=1}^{n-1} 2^{C(k+1) 2^{n-k+1}} $$ or $$ \sum_{k=1}^{n-1} C(k+1) 2^{1-k} \geqslant \frac{n-1}{2} $$ that fails for large $n$ since $C(k+1) 2^{1-k}<1 / 3$ for all but finitely many $k$. In fact, a much stronger inequality can be obtained in an elementary way: Note that the formula for $\nu_{p}(n!)$ implies that if $p^{\alpha}$ is the largest power of $p$ dividing $\binom{n}{n / 2}$, then $p^{\alpha} \leqslant n$. By looking at prime factorization of $\binom{n}{n / 2}$ we instantaneously infer that $$ \pi(n) \geqslant \log _{n}\binom{n}{n / 2} \geqslant \frac{\log \left(2^{n} / n\right)}{\log n} \geqslant \frac{n}{2 \log n} . $$ This, in particular, implies that for infinitely many $n$ there are at least $\frac{n}{3 \log n}$ primes between $n$ and $2 n$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
60fa4bf2-d7a9-5d52-9959-6d718646dc0b
| 24,033
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.