problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
7. (CHN 2) Let $O$ be the center of the circumsphere of a tetrahedron $A B C D$. Let $L, M, N$ be the midpoints of $B C, C A, A B$ respectively, and assume that $A B+B C=A D+C D, B C+C A=B D+A D$, and $C A+A B=$ $C D+B D$. Prove that $\angle L O M=\angle M O N=\angle N O L$.
|
7. The given equations imply $A B=C D, A C=B D, A D=B C$. Let $L_{1}$, $M_{1}, N_{1}$ be the midpoints of $A D, B D, C D$ respectively. Then the above equalities yield $$ \begin{gathered} L_{1} M_{1}=A B / 2=L M \\ L_{1} M_{1}\|A B\| L M \\ L_{1} M=C D / 2=L M_{1} \\ L_{1} M\|C D\| L M_{1} \end{gathered} $$ Thus $L, M, L_{1}, M_{1}$ are coplanar and $L M L_{1} M_{1}$ is a rhombus as well as 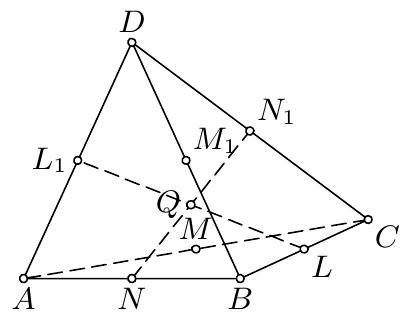 $M N M_{1} N_{1}$ and $L N L_{1} N_{1}$. Then the segments $L L_{1}, M M_{1}, N N_{1}$ have the common midpoint $Q$ and $Q L \perp Q M$, $Q L \perp Q N, Q M \perp Q N$. We also infer that the line $N N_{1}$ is perpendicular to the plane $L M L_{1} M_{1}$ and hence to the line $A B$. Thus $Q A=Q B$, and similarly, $Q B=Q C=Q D$, hence $Q$ is just the center $O$, and $\angle L O M=$ $\angle M O N=\angle N O L=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. (CHN 2) Let $O$ be the center of the circumsphere of a tetrahedron $A B C D$. Let $L, M, N$ be the midpoints of $B C, C A, A B$ respectively, and assume that $A B+B C=A D+C D, B C+C A=B D+A D$, and $C A+A B=$ $C D+B D$. Prove that $\angle L O M=\angle M O N=\angle N O L$.
|
7. The given equations imply $A B=C D, A C=B D, A D=B C$. Let $L_{1}$, $M_{1}, N_{1}$ be the midpoints of $A D, B D, C D$ respectively. Then the above equalities yield $$ \begin{gathered} L_{1} M_{1}=A B / 2=L M \\ L_{1} M_{1}\|A B\| L M \\ L_{1} M=C D / 2=L M_{1} \\ L_{1} M\|C D\| L M_{1} \end{gathered} $$ Thus $L, M, L_{1}, M_{1}$ are coplanar and $L M L_{1} M_{1}$ is a rhombus as well as  $M N M_{1} N_{1}$ and $L N L_{1} N_{1}$. Then the segments $L L_{1}, M M_{1}, N N_{1}$ have the common midpoint $Q$ and $Q L \perp Q M$, $Q L \perp Q N, Q M \perp Q N$. We also infer that the line $N N_{1}$ is perpendicular to the plane $L M L_{1} M_{1}$ and hence to the line $A B$. Thus $Q A=Q B$, and similarly, $Q B=Q C=Q D$, hence $Q$ is just the center $O$, and $\angle L O M=$ $\angle M O N=\angle N O L=90^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6f94ba77-2457-5f51-9b58-edb19a8f1b67
| 24,396
|
8. (NET 1) Let $S$ be a set of $n$ points in the plane. No three points of $S$ are collinear. Prove that there exists a set $P$ containing $2 n-5$ points satisfying the following condition: In the interior of every triangle whose three vertices are elements of $S$ lies a point that is an element of $P$.
|
8. Let $P_{1}\left(x_{1}, y_{1}\right), P_{2}\left(x_{2}, y_{2}\right), \ldots, P_{n}\left(x_{n}, y_{n}\right)$ be the $n$ points of $S$ in the coordinate plane. We may assume $x_{1}<x_{2}<\cdots<x_{n}$ (choosing adequate axes and renumbering the points if necessary). Define $d$ to be half the minimum distance of $P_{i}$ from the line $P_{j} P_{k}$, where $i, j, k$ go through all possible combinations of mutually distinct indices. First we define a set $T$ containing $2 n-4$ points: $$ T=\left\{\left(x_{i}, y_{i}-d\right),\left(x_{i}, y_{i}+d\right) \mid i=2,3, \ldots, n-1\right\} $$ Consider any triangle $P_{k} P_{l} P_{m}$, where $k<l<m$. Its interior contains at least one of the two points $\left(x_{l}, y_{l} \pm d\right)$, so $T$ is a set of $2 n-4$ points with the required property. However, at least one of the points of $T$ is useless. The convex hull of $S$ is a polygon with at least three points in $S$ as vertices. Let $P_{j}$ be a vertex of that hull distinct from $P_{1}$ and $P_{n}$. Clearly one of the points $\left(x_{j}, y_{j} \pm d\right)$ lies outside the convex hull, and thus can be left out. The remaining set of $2 n-5$ points satisfies the conditions.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. (NET 1) Let $S$ be a set of $n$ points in the plane. No three points of $S$ are collinear. Prove that there exists a set $P$ containing $2 n-5$ points satisfying the following condition: In the interior of every triangle whose three vertices are elements of $S$ lies a point that is an element of $P$.
|
8. Let $P_{1}\left(x_{1}, y_{1}\right), P_{2}\left(x_{2}, y_{2}\right), \ldots, P_{n}\left(x_{n}, y_{n}\right)$ be the $n$ points of $S$ in the coordinate plane. We may assume $x_{1}<x_{2}<\cdots<x_{n}$ (choosing adequate axes and renumbering the points if necessary). Define $d$ to be half the minimum distance of $P_{i}$ from the line $P_{j} P_{k}$, where $i, j, k$ go through all possible combinations of mutually distinct indices. First we define a set $T$ containing $2 n-4$ points: $$ T=\left\{\left(x_{i}, y_{i}-d\right),\left(x_{i}, y_{i}+d\right) \mid i=2,3, \ldots, n-1\right\} $$ Consider any triangle $P_{k} P_{l} P_{m}$, where $k<l<m$. Its interior contains at least one of the two points $\left(x_{l}, y_{l} \pm d\right)$, so $T$ is a set of $2 n-4$ points with the required property. However, at least one of the points of $T$ is useless. The convex hull of $S$ is a polygon with at least three points in $S$ as vertices. Let $P_{j}$ be a vertex of that hull distinct from $P_{1}$ and $P_{n}$. Clearly one of the points $\left(x_{j}, y_{j} \pm d\right)$ lies outside the convex hull, and thus can be left out. The remaining set of $2 n-5$ points satisfies the conditions.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
63a1c315-e981-5bb6-b884-466f3cbfe890
| 24,399
|
9. (FRA 3) In the plane we are given a set $E$ of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of $E$, there exist at least 1593 other points of $E$ to which it is joined by a path. Show that there exist six points of $E$ every pair of which are joined by a path. Alternative version. Is it possible to find a set $E$ of 1991 points in the plane and paths joining certain pairs of the points in $E$ such that every point of $E$ is joined with a path to at least 1592 other points of $E$, and in every subset of six points of $E$ there exist at least two points that are not joined?
|
9. Let $A_{1}, A_{2}$ be two points of $E$ which are joined. In $E \backslash\left\{A_{1}, A_{2}\right\}$, there are at most 397 points to which $A_{1}$ is not joined, and at most as much to which $A_{2}$ is not joined. Consequently, there exists a point $A_{3}$ which is joined to both $A_{1}$ and $A_{2}$. There are at most $3 \cdot 397=1191$ points of $E \backslash\left\{A_{1}, A_{2}, A_{3}\right\}$ to which at least one of $A_{1}, A_{2}, A_{3}$ is not joined, hence it is possible to choose a point $A_{4}$ joined to $A_{1}, A_{2}, A_{3}$. Similarly, there exists a point $A_{5}$ which is joined to all $A_{1}, A_{2}, A_{3}, A_{4}$. Finally, among the remaining 1986 points, there are at most $5 \cdot 397=1985$ which are not joined to one of the points $A_{1}, \ldots, A_{5}$. Thus there is at least one point $A_{6}$ joined to all $A_{1}, \ldots, A_{5}$. It is clear that $A_{1}, \ldots, A_{6}$ are pairwise joined. Solution of the alternative version. Let be given 1991 points instead. Number the points from 1 to 1991, and join $i$ and $j$ if and only if $i-j$ is not a multiple of 5 . Then each $i$ is joined to 1592 or 1593 other points, and obviously among any six points there are two which are not joined.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
9. (FRA 3) In the plane we are given a set $E$ of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of $E$, there exist at least 1593 other points of $E$ to which it is joined by a path. Show that there exist six points of $E$ every pair of which are joined by a path. Alternative version. Is it possible to find a set $E$ of 1991 points in the plane and paths joining certain pairs of the points in $E$ such that every point of $E$ is joined with a path to at least 1592 other points of $E$, and in every subset of six points of $E$ there exist at least two points that are not joined?
|
9. Let $A_{1}, A_{2}$ be two points of $E$ which are joined. In $E \backslash\left\{A_{1}, A_{2}\right\}$, there are at most 397 points to which $A_{1}$ is not joined, and at most as much to which $A_{2}$ is not joined. Consequently, there exists a point $A_{3}$ which is joined to both $A_{1}$ and $A_{2}$. There are at most $3 \cdot 397=1191$ points of $E \backslash\left\{A_{1}, A_{2}, A_{3}\right\}$ to which at least one of $A_{1}, A_{2}, A_{3}$ is not joined, hence it is possible to choose a point $A_{4}$ joined to $A_{1}, A_{2}, A_{3}$. Similarly, there exists a point $A_{5}$ which is joined to all $A_{1}, A_{2}, A_{3}, A_{4}$. Finally, among the remaining 1986 points, there are at most $5 \cdot 397=1985$ which are not joined to one of the points $A_{1}, \ldots, A_{5}$. Thus there is at least one point $A_{6}$ joined to all $A_{1}, \ldots, A_{5}$. It is clear that $A_{1}, \ldots, A_{6}$ are pairwise joined. Solution of the alternative version. Let be given 1991 points instead. Number the points from 1 to 1991, and join $i$ and $j$ if and only if $i-j$ is not a multiple of 5 . Then each $i$ is joined to 1592 or 1593 other points, and obviously among any six points there are two which are not joined.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a04451ca-03e7-5179-bbd9-415b39660a12
| 24,401
|
1. (AUS 2) Prove that for any positive integer $m$ there exist an infinite number of pairs of integers $(x, y)$ such that (i) $x$ and $y$ are relatively prime; (ii) $y$ divides $x^{2}+m$; (iii) $x$ divides $y^{2}+m$.
|
1. Assume that a pair $(x, y)$ with $x<y$ satisfies the required conditions. We claim that the pair $\left(y, x_{1}\right)$ also satisfies the conditions, where $x_{1}=\frac{y^{2}+m}{x}$ (note that $x_{1}>y$ is a positive integer). This will imply the desired result, since starting from the pair $(1,1)$ we can obtain arbitrarily many solutions. First, we show that $\operatorname{gcd}\left(x_{1}, y\right)=1$. Suppose to the contrary that $\operatorname{gcd}\left(x_{1}, y\right)$ $=d>1$. Then $d\left|x_{1}\right| y^{2}+m \Rightarrow d \mid m$, which implies $d|y| x^{2}+m \Rightarrow d \mid x$. But this last is impossible, since $\operatorname{gcd}(x, y)=1$. Thus it remains to show that $x_{1} \mid y^{2}+m$ and $y \mid x_{1}^{2}+m$. The former relation is obvious. Since $\operatorname{gcd}(x, y)=1$, the latter is equivalent to $y \mid\left(x x_{1}\right)^{2}+m x^{2}=y^{4}+2 m y^{2}+$ $m^{2}+m x^{2}$, which is true because $y \mid m\left(m+x^{2}\right)$ by the assumption. Hence $\left(y, x_{1}\right)$ indeed satisfies all the required conditions. Remark. The original problem asked to prove the existence of a pair $(x, y)$ of positive integers satisfying the given conditions such that $x+y \leq m+1$. The problem in this formulation is trivial, since the pair $x=y=1$ satisfies the conditions. Moreover, this is sometimes the only solution with $x+y \leq m+1$. For example, for $m=3$ the least nontrivial solution is $\left(x_{0}, y_{0}\right)=(1,4)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
1. (AUS 2) Prove that for any positive integer $m$ there exist an infinite number of pairs of integers $(x, y)$ such that (i) $x$ and $y$ are relatively prime; (ii) $y$ divides $x^{2}+m$; (iii) $x$ divides $y^{2}+m$.
|
1. Assume that a pair $(x, y)$ with $x<y$ satisfies the required conditions. We claim that the pair $\left(y, x_{1}\right)$ also satisfies the conditions, where $x_{1}=\frac{y^{2}+m}{x}$ (note that $x_{1}>y$ is a positive integer). This will imply the desired result, since starting from the pair $(1,1)$ we can obtain arbitrarily many solutions. First, we show that $\operatorname{gcd}\left(x_{1}, y\right)=1$. Suppose to the contrary that $\operatorname{gcd}\left(x_{1}, y\right)$ $=d>1$. Then $d\left|x_{1}\right| y^{2}+m \Rightarrow d \mid m$, which implies $d|y| x^{2}+m \Rightarrow d \mid x$. But this last is impossible, since $\operatorname{gcd}(x, y)=1$. Thus it remains to show that $x_{1} \mid y^{2}+m$ and $y \mid x_{1}^{2}+m$. The former relation is obvious. Since $\operatorname{gcd}(x, y)=1$, the latter is equivalent to $y \mid\left(x x_{1}\right)^{2}+m x^{2}=y^{4}+2 m y^{2}+$ $m^{2}+m x^{2}$, which is true because $y \mid m\left(m+x^{2}\right)$ by the assumption. Hence $\left(y, x_{1}\right)$ indeed satisfies all the required conditions. Remark. The original problem asked to prove the existence of a pair $(x, y)$ of positive integers satisfying the given conditions such that $x+y \leq m+1$. The problem in this formulation is trivial, since the pair $x=y=1$ satisfies the conditions. Moreover, this is sometimes the only solution with $x+y \leq m+1$. For example, for $m=3$ the least nontrivial solution is $\left(x_{0}, y_{0}\right)=(1,4)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6ee818b8-1dde-512b-b68e-ab759b13a9b8
| 24,402
|
10. (ITA 1) ${ }^{\mathrm{IMO5}}$ Let $V$ be a finite subset of Euclidean space consisting of points $(x, y, z)$ with integer coordinates. Let $S_{1}, S_{2}, S_{3}$ be the projections of $V$ onto the $y z, x z, x y$ planes, respectively. Prove that $$ |V|^{2} \leq\left|S_{1}\right|\left|S_{2}\right|\left|S_{3}\right| $$ ( $|X|$ denotes the number of elements of $X$ ).
|
10. Let us set $S(x)=\{(y, z) \mid(x, y, z) \in V\}, S_{y}(x)=\left\{z \mid(x, z) \in S_{y}\right\}$ and $S_{z}(x)=\left\{y \mid(x, y) \in S_{z}\right\}$. Clearly $S(x) \subset S_{x}$ and $S(x) \subset S_{y}(x) \times S_{z}(x)$. It follows that $$ \begin{aligned} |V| & =\sum_{x}|S(x)| \leq \sum_{x} \sqrt{\left|S_{x}\right|\left|S_{y}(x)\right|\left|S_{z}(x)\right|} \\ & =\sqrt{\left|S_{x}\right|} \sum_{x} \sqrt{\left|S_{y}(x)\right|\left|S_{z}(x)\right|} \end{aligned} $$ Using the Cauchy-Schwarz inequality we also get $$ \sum_{x} \sqrt{\left|S_{y}(x)\right|\left|S_{z}(x)\right|} \leq \sqrt{\sum_{x}\left|S_{y}(x)\right|} \sqrt{\sum_{x}\left|S_{z}(x)\right|}=\sqrt{\left|S_{y}\right|\left|S_{z}\right|} $$ Now (1) and (2) together yield $|V| \leq \sqrt{\left|S_{x}\right|\left|S_{y}\right|\left|S_{z}\right|}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
10. (ITA 1) ${ }^{\mathrm{IMO5}}$ Let $V$ be a finite subset of Euclidean space consisting of points $(x, y, z)$ with integer coordinates. Let $S_{1}, S_{2}, S_{3}$ be the projections of $V$ onto the $y z, x z, x y$ planes, respectively. Prove that $$ |V|^{2} \leq\left|S_{1}\right|\left|S_{2}\right|\left|S_{3}\right| $$ ( $|X|$ denotes the number of elements of $X$ ).
|
10. Let us set $S(x)=\{(y, z) \mid(x, y, z) \in V\}, S_{y}(x)=\left\{z \mid(x, z) \in S_{y}\right\}$ and $S_{z}(x)=\left\{y \mid(x, y) \in S_{z}\right\}$. Clearly $S(x) \subset S_{x}$ and $S(x) \subset S_{y}(x) \times S_{z}(x)$. It follows that $$ \begin{aligned} |V| & =\sum_{x}|S(x)| \leq \sum_{x} \sqrt{\left|S_{x}\right|\left|S_{y}(x)\right|\left|S_{z}(x)\right|} \\ & =\sqrt{\left|S_{x}\right|} \sum_{x} \sqrt{\left|S_{y}(x)\right|\left|S_{z}(x)\right|} \end{aligned} $$ Using the Cauchy-Schwarz inequality we also get $$ \sum_{x} \sqrt{\left|S_{y}(x)\right|\left|S_{z}(x)\right|} \leq \sqrt{\sum_{x}\left|S_{y}(x)\right|} \sqrt{\sum_{x}\left|S_{z}(x)\right|}=\sqrt{\left|S_{y}\right|\left|S_{z}\right|} $$ Now (1) and (2) together yield $|V| \leq \sqrt{\left|S_{x}\right|\left|S_{y}\right|\left|S_{z}\right|}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e1e192ee-e9ac-5b7e-aa96-2a1f4be1b91b
| 24,404
|
12. (NET 1) Let $f, g$, and $a$ be polynomials with real coefficients, $f$ and $g$ in one variable and $a$ in two variables. Suppose $$ f(x)-f(y)=a(x, y)(g(x)-g(y)) \quad \text { for all } x, y \in \mathbb{R} $$ Prove that there exists a polynomial $h$ with $f(x)=h(g(x))$ for all $x \in \mathbb{R}$.
|
12. Let us set $\operatorname{deg} f=n$ and $\operatorname{deg} g=m$. We shall prove the result by induction on $n$. If $n<m$, then $\operatorname{deg}_{x}[f(x)-f(y)]<\operatorname{deg}_{x}[g(x)-g(y)]$, which implies that $f(x)-f(y)=0$, i.e., that $f$ is constant. The statement trivially holds. Assume now that $n \geq m$. Transition to $f_{1}(x)=f(x)-f(0)$ and $g_{1}(x)=$ $g(x)-g(0)$ allows us to suppose that $f(0)=g(0)=0$. Then the given condition for $y=0$ gives us $f(x)=f_{1}(x) g(x)$, where $f_{1}(x)=a(x, 0)$ and $\operatorname{deg} f_{1}=n-m$. We now have $$ \begin{aligned} a(x, y)(g(x)-g(y)) & =f(x)-f(y)=f_{1}(x) g(x)-f_{1}(y) g(y) \\ & =\left[f_{1}(x)-f_{1}(y)\right] g(x)+f_{1}(y)[g(x)-g(y)] . \end{aligned} $$ Since $g(x)$ is relatively prime to $g(x)-g(y)$, it follows that $f_{1}(x)-f_{1}(y)=$ $b(x, y)(g(x)-g(y))$ for some polynomial $b(x, y)$. By the induction hypothesis there exists a polynomial $h_{1}$ such that $f_{1}(x)=h_{1}(g(x))$ and consequently $f(x)=g(x) \cdot h_{1}(g(x))=h(g(x))$ for $h(t)=t h_{1}(t)$. Thus the induction is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
12. (NET 1) Let $f, g$, and $a$ be polynomials with real coefficients, $f$ and $g$ in one variable and $a$ in two variables. Suppose $$ f(x)-f(y)=a(x, y)(g(x)-g(y)) \quad \text { for all } x, y \in \mathbb{R} $$ Prove that there exists a polynomial $h$ with $f(x)=h(g(x))$ for all $x \in \mathbb{R}$.
|
12. Let us set $\operatorname{deg} f=n$ and $\operatorname{deg} g=m$. We shall prove the result by induction on $n$. If $n<m$, then $\operatorname{deg}_{x}[f(x)-f(y)]<\operatorname{deg}_{x}[g(x)-g(y)]$, which implies that $f(x)-f(y)=0$, i.e., that $f$ is constant. The statement trivially holds. Assume now that $n \geq m$. Transition to $f_{1}(x)=f(x)-f(0)$ and $g_{1}(x)=$ $g(x)-g(0)$ allows us to suppose that $f(0)=g(0)=0$. Then the given condition for $y=0$ gives us $f(x)=f_{1}(x) g(x)$, where $f_{1}(x)=a(x, 0)$ and $\operatorname{deg} f_{1}=n-m$. We now have $$ \begin{aligned} a(x, y)(g(x)-g(y)) & =f(x)-f(y)=f_{1}(x) g(x)-f_{1}(y) g(y) \\ & =\left[f_{1}(x)-f_{1}(y)\right] g(x)+f_{1}(y)[g(x)-g(y)] . \end{aligned} $$ Since $g(x)$ is relatively prime to $g(x)-g(y)$, it follows that $f_{1}(x)-f_{1}(y)=$ $b(x, y)(g(x)-g(y))$ for some polynomial $b(x, y)$. By the induction hypothesis there exists a polynomial $h_{1}$ such that $f_{1}(x)=h_{1}(g(x))$ and consequently $f(x)=g(x) \cdot h_{1}(g(x))=h(g(x))$ for $h(t)=t h_{1}(t)$. Thus the induction is complete.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c16bd33b-2fe1-5233-a119-25ddaf41ccb1
| 24,409
|
15. (PRK 2) Does there exist a set $M$ with the following properties? (i) The set $M$ consists of 1992 natural numbers. (ii) Every element in $M$ and the sum of any number of elements have the form $m^{k}(m, k \in \mathbb{N}, k \geq 2)$.
|
15. The result follows from the following lemma by taking $n=\frac{1992 \cdot 1993}{2}$ and $M=\{d, 2 d, \ldots, 1992 d\}$. Lemma. For every $n \in \mathbb{N}$ there exists a natural number $d$ such that all the numbers $d, 2 d, \ldots, n d$ are of the form $m^{k}(m, k \in \mathbb{N}, k \geq 2)$. Proof. Let $p_{1}, p_{2}, \ldots, p_{n}$ be distinct prime numbers. We shall find $d$ in the form $d=2^{\alpha_{2}} 3^{\alpha_{3}} \cdots n^{\alpha_{n}}$, where $\alpha_{i} \geq 0$ are integers such that $k d$ is a perfect $p_{k}$ th power. It is sufficient to find $\alpha_{i}, i=2,3, \ldots, n$, such that $\alpha_{i} \equiv 0\left(\bmod p_{j}\right)$ if $i \neq j$ and $\alpha_{i} \equiv-1\left(\bmod p_{j}\right)$ if $i=j$. But the existence of such $\alpha_{i}$ 's is an immediate consequence of the Chinese remainder theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
15. (PRK 2) Does there exist a set $M$ with the following properties? (i) The set $M$ consists of 1992 natural numbers. (ii) Every element in $M$ and the sum of any number of elements have the form $m^{k}(m, k \in \mathbb{N}, k \geq 2)$.
|
15. The result follows from the following lemma by taking $n=\frac{1992 \cdot 1993}{2}$ and $M=\{d, 2 d, \ldots, 1992 d\}$. Lemma. For every $n \in \mathbb{N}$ there exists a natural number $d$ such that all the numbers $d, 2 d, \ldots, n d$ are of the form $m^{k}(m, k \in \mathbb{N}, k \geq 2)$. Proof. Let $p_{1}, p_{2}, \ldots, p_{n}$ be distinct prime numbers. We shall find $d$ in the form $d=2^{\alpha_{2}} 3^{\alpha_{3}} \cdots n^{\alpha_{n}}$, where $\alpha_{i} \geq 0$ are integers such that $k d$ is a perfect $p_{k}$ th power. It is sufficient to find $\alpha_{i}, i=2,3, \ldots, n$, such that $\alpha_{i} \equiv 0\left(\bmod p_{j}\right)$ if $i \neq j$ and $\alpha_{i} \equiv-1\left(\bmod p_{j}\right)$ if $i=j$. But the existence of such $\alpha_{i}$ 's is an immediate consequence of the Chinese remainder theorem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef65ee3c-35fe-5ae0-8e93-8431bfbe9b45
| 24,417
|
16. (KOR 2) Prove that $N=\frac{5^{125}-1}{5^{25}-1}$ is a composite number.
|
16. Observe that $x^{4}+x^{3}+x^{2}+x+1=\left(x^{2}+3 x+1\right)^{2}-5 x(x+1)^{2}$. Thus for $x=5^{25}$ we have $$ \begin{aligned} N & =x^{4}+x^{3}+x^{2}+x+1 \\ & =\left(x^{2}+3 x+1-5^{13}(x+1)\right)\left(x^{2}+3 x+1+5^{13}(x+1)\right)=A \cdot B . \end{aligned} $$ Clearly, both $A$ and $B$ are positive integers greater than 1.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
16. (KOR 2) Prove that $N=\frac{5^{125}-1}{5^{25}-1}$ is a composite number.
|
16. Observe that $x^{4}+x^{3}+x^{2}+x+1=\left(x^{2}+3 x+1\right)^{2}-5 x(x+1)^{2}$. Thus for $x=5^{25}$ we have $$ \begin{aligned} N & =x^{4}+x^{3}+x^{2}+x+1 \\ & =\left(x^{2}+3 x+1-5^{13}(x+1)\right)\left(x^{2}+3 x+1+5^{13}(x+1)\right)=A \cdot B . \end{aligned} $$ Clearly, both $A$ and $B$ are positive integers greater than 1.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6321443a-4258-5ec0-b6a1-0bd8c48c2fa5
| 24,420
|
17. (SWE 1) Let $\alpha(n)$ be the number of digits equal to one in the binary representation of a positive integer $n$. Prove that: (a) the inequality $\alpha\left(n^{2}\right) \leq \frac{1}{2} \alpha(n)(\alpha(n)+1)$ holds; (b) the above inequality is an equality for infinitely many positive integers; (c) there exists a sequence $\left(n_{i}\right)_{1}^{\infty}$ such that $\alpha\left(n_{i}^{2}\right) / \alpha\left(n_{i}\right) \rightarrow 0$ as $i \rightarrow \infty$. Alternative parts: Prove that there exists a sequence $\left(n_{i}\right)_{1}^{\infty}$ such that $\alpha\left(n_{i}^{2}\right) / \alpha\left(n_{i}\right)$ tends to (d) $\infty$; (e) an arbitrary real number $\gamma \in(0,1)$; (f) an arbitrary real number $\gamma \geq 0$.
|
17. (a) Let $n=\sum_{i=1}^{k} 2^{a_{i}}$, so that $\alpha(n)=k$. Then $$ n^{2}=\sum_{i} 2^{2 a_{i}}+\sum_{i<j} 2^{a_{i}+a_{j}+1} $$ has at most $k+\binom{k}{2}=\frac{k(k+1)}{2}$ binary ones. (b) The above inequality is an equality for all numbers $n_{k}=2^{k}$. (c) Put $n_{m}=2^{2^{m}-1}-\sum_{j=1}^{m} 2^{2^{m}-2^{j}}$, where $m>1$. It is easy to see that $\alpha\left(n_{m}\right)=2^{m}-m$. On the other hand, squaring and simplifying yields $n_{m}^{2}=1+\sum_{i<j} 2^{2^{m+1}+1-2^{i}-2^{j}}$. Hence $\alpha\left(n_{m}^{2}\right)=1+\frac{m(m+1)}{2}$ and thus $$ \frac{\alpha\left(n_{m}^{2}\right)}{\alpha\left(n_{m}\right)}=\frac{2+m(m+1)}{2\left(2^{m}-m\right)} \rightarrow 0 \quad \text { as } m \rightarrow \infty $$ Solution to the alternative parts. (1) Let $n=\sum_{i=1}^{n} 2^{2^{i}}$. Then $n^{2}=\sum_{i=1}^{n} 2^{2^{i+1}}+\sum_{i<j} 2^{2^{i}+2^{j}+1}$ has exactly $\frac{k(k+1)}{2}$ binary ones, and therefore $\frac{\alpha\left(n^{2}\right)}{\alpha(n)}=\frac{2 k}{k(k+1)} \rightarrow \infty$. (2) Consider the sequence $n_{i}$ constructed in part (c). Let $\theta>1$ be a constant to be chosen later, and let $N_{i}=2^{m_{i}} n_{i}-1$ where $m_{i}>\alpha\left(n_{i}\right)$ is such that $m_{i} / \alpha\left(n_{i}\right) \rightarrow \theta$ as $i \rightarrow \infty$. Then $\alpha\left(N_{i}\right)=\alpha\left(n_{i}\right)+m_{i}-1$, whereas $N_{i}^{2}=2^{2 m_{i}} n_{i}^{2}-2^{m_{i}+1} n_{i}+1$ and $\alpha\left(N_{i}^{2}\right)=\alpha\left(n_{i}^{2}\right)-\alpha\left(n_{i}\right)+m_{i}$. It follows that $$ \lim _{i \rightarrow \infty} \frac{\alpha\left(N_{i}^{2}\right)}{\alpha\left(N_{i}\right)}=\lim _{i \rightarrow \infty} \frac{\alpha\left(n_{i}^{2}\right)+(\theta-1) \alpha\left(n_{i}\right)}{(1+\theta) \alpha\left(n_{i}\right)}=\frac{\theta-1}{\theta+1} $$ which is equal to $\gamma \in[0,1]$ for $\theta=\frac{1+\gamma}{1-\gamma}$ (for $\gamma=1$ we set $m_{i} / \alpha\left(n_{i}\right) \rightarrow$ $\infty)$. (3) Let be given a sequence $\left(n_{i}\right)_{i=1}^{\infty}$ with $\alpha\left(n_{i}^{2}\right) / \alpha\left(n_{i}\right) \rightarrow \gamma$. Taking $m_{i}>$ $\alpha\left(n_{i}\right)$ and $N_{i}=2^{m_{i}} n_{i}+1$ we easily find that $\alpha\left(N_{i}\right)=\alpha\left(n_{i}\right)+1$ and $\alpha\left(N_{i}^{2}\right)=\alpha\left(n_{i}^{2}\right)+\alpha\left(n_{i}\right)+1$. Hence $\alpha\left(N_{i}^{2}\right) / \alpha\left(N_{i}\right)=\gamma+1$. Continuing this procedure we can construct a sequence $t_{i}$ such that $\alpha\left(t_{i}^{2}\right) / \alpha\left(t_{i}\right)=$ $\gamma+k$ for an arbitrary $k \in \mathbb{N}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
17. (SWE 1) Let $\alpha(n)$ be the number of digits equal to one in the binary representation of a positive integer $n$. Prove that: (a) the inequality $\alpha\left(n^{2}\right) \leq \frac{1}{2} \alpha(n)(\alpha(n)+1)$ holds; (b) the above inequality is an equality for infinitely many positive integers; (c) there exists a sequence $\left(n_{i}\right)_{1}^{\infty}$ such that $\alpha\left(n_{i}^{2}\right) / \alpha\left(n_{i}\right) \rightarrow 0$ as $i \rightarrow \infty$. Alternative parts: Prove that there exists a sequence $\left(n_{i}\right)_{1}^{\infty}$ such that $\alpha\left(n_{i}^{2}\right) / \alpha\left(n_{i}\right)$ tends to (d) $\infty$; (e) an arbitrary real number $\gamma \in(0,1)$; (f) an arbitrary real number $\gamma \geq 0$.
|
17. (a) Let $n=\sum_{i=1}^{k} 2^{a_{i}}$, so that $\alpha(n)=k$. Then $$ n^{2}=\sum_{i} 2^{2 a_{i}}+\sum_{i<j} 2^{a_{i}+a_{j}+1} $$ has at most $k+\binom{k}{2}=\frac{k(k+1)}{2}$ binary ones. (b) The above inequality is an equality for all numbers $n_{k}=2^{k}$. (c) Put $n_{m}=2^{2^{m}-1}-\sum_{j=1}^{m} 2^{2^{m}-2^{j}}$, where $m>1$. It is easy to see that $\alpha\left(n_{m}\right)=2^{m}-m$. On the other hand, squaring and simplifying yields $n_{m}^{2}=1+\sum_{i<j} 2^{2^{m+1}+1-2^{i}-2^{j}}$. Hence $\alpha\left(n_{m}^{2}\right)=1+\frac{m(m+1)}{2}$ and thus $$ \frac{\alpha\left(n_{m}^{2}\right)}{\alpha\left(n_{m}\right)}=\frac{2+m(m+1)}{2\left(2^{m}-m\right)} \rightarrow 0 \quad \text { as } m \rightarrow \infty $$ Solution to the alternative parts. (1) Let $n=\sum_{i=1}^{n} 2^{2^{i}}$. Then $n^{2}=\sum_{i=1}^{n} 2^{2^{i+1}}+\sum_{i<j} 2^{2^{i}+2^{j}+1}$ has exactly $\frac{k(k+1)}{2}$ binary ones, and therefore $\frac{\alpha\left(n^{2}\right)}{\alpha(n)}=\frac{2 k}{k(k+1)} \rightarrow \infty$. (2) Consider the sequence $n_{i}$ constructed in part (c). Let $\theta>1$ be a constant to be chosen later, and let $N_{i}=2^{m_{i}} n_{i}-1$ where $m_{i}>\alpha\left(n_{i}\right)$ is such that $m_{i} / \alpha\left(n_{i}\right) \rightarrow \theta$ as $i \rightarrow \infty$. Then $\alpha\left(N_{i}\right)=\alpha\left(n_{i}\right)+m_{i}-1$, whereas $N_{i}^{2}=2^{2 m_{i}} n_{i}^{2}-2^{m_{i}+1} n_{i}+1$ and $\alpha\left(N_{i}^{2}\right)=\alpha\left(n_{i}^{2}\right)-\alpha\left(n_{i}\right)+m_{i}$. It follows that $$ \lim _{i \rightarrow \infty} \frac{\alpha\left(N_{i}^{2}\right)}{\alpha\left(N_{i}\right)}=\lim _{i \rightarrow \infty} \frac{\alpha\left(n_{i}^{2}\right)+(\theta-1) \alpha\left(n_{i}\right)}{(1+\theta) \alpha\left(n_{i}\right)}=\frac{\theta-1}{\theta+1} $$ which is equal to $\gamma \in[0,1]$ for $\theta=\frac{1+\gamma}{1-\gamma}$ (for $\gamma=1$ we set $m_{i} / \alpha\left(n_{i}\right) \rightarrow$ $\infty)$. (3) Let be given a sequence $\left(n_{i}\right)_{i=1}^{\infty}$ with $\alpha\left(n_{i}^{2}\right) / \alpha\left(n_{i}\right) \rightarrow \gamma$. Taking $m_{i}>$ $\alpha\left(n_{i}\right)$ and $N_{i}=2^{m_{i}} n_{i}+1$ we easily find that $\alpha\left(N_{i}\right)=\alpha\left(n_{i}\right)+1$ and $\alpha\left(N_{i}^{2}\right)=\alpha\left(n_{i}^{2}\right)+\alpha\left(n_{i}\right)+1$. Hence $\alpha\left(N_{i}^{2}\right) / \alpha\left(N_{i}\right)=\gamma+1$. Continuing this procedure we can construct a sequence $t_{i}$ such that $\alpha\left(t_{i}^{2}\right) / \alpha\left(t_{i}\right)=$ $\gamma+k$ for an arbitrary $k \in \mathbb{N}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7f332a53-46b2-5ee1-9c70-749066d0bc22
| 24,423
|
18. (USA 2) Let $[x]$ denote the greatest integer less than or equal to $x$. Pick any $x_{1}$ in $[0,1)$ and define the sequence $x_{1}, x_{2}, x_{3}, \ldots$ by $x_{n+1}=0$ if $x_{n}=0$ and $x_{n+1}=1 / x_{n}-\left[1 / x_{n}\right]$ otherwise. Prove that $$ x_{1}+x_{2}+\cdots+x_{n}<\frac{F_{1}}{F_{2}}+\frac{F_{2}}{F_{3}}+\cdots+\frac{F_{n}}{F_{n+1}} $$ where $F_{1}=F_{2}=1$ and $F_{n+2}=F_{n+1}+F_{n}$ for $n \geq 1$.
|
18. Let us define inductively $f^{1}(x)=f(x)=\frac{1}{x+1}$ and $f^{n}(x)=f\left(f^{n-1}(x)\right)$, and let $g_{n}(x)=x+f(x)+f^{2}(x)+\cdots+f^{n}(x)$. We shall prove first the following statement. Lemma. The function $g_{n}(x)$ is strictly increasing on $[0,1]$, and $g_{n-1}(1)=$ $F_{1} / F_{2}+F_{2} / F_{3}+\cdots+F_{n} / F_{n+1}$. Proof. Since $f(x)-f(y)=\frac{y-x}{(1+x)(1+y)}$ is smaller in absolute value than $x-y$, it follows that $x>y$ implies $f^{2 k}(x)>f^{2 k}(y)$ and $f^{2 k+1}(x)<$ $f^{2 k+1}(y)$, and moreover that for every integer $k \geq 0$, $$ \left[f^{2 k}(x)-f^{2 k}(y)\right]+\left[f^{2 k+1}(x)-f^{2 k+1}(y)\right]>0 $$ Hence if $x>y$, we have $g_{n}(x)-g_{n}(y)=(x-y)+[f(x)-f(y)]+\cdots+$ $\left[f^{n}(x)-f^{n}(y)\right]>0$, which yields the first part of the lemma. The second part follows by simple induction, since $f^{k}(1)=F_{k+1} / F_{k+2}$. If some $x_{i}=0$ and consequently $x_{j}=0$ for all $j \geq i$, then the problem reduces to the problem with $i-1$ instead of $n$. Thus we may assume that all $x_{1}, \ldots, x_{n}$ are different from 0 . If we write $a_{i}=\left[1 / x_{i}\right]$, then $x_{i}=\frac{1}{a_{i}+x_{i+1}}$. Thus we can regard $x_{i}$ as functions of $x_{n}$ depending on $a_{1}, \ldots, a_{n-1}$. Suppose that $x_{n}, a_{n-1}, \ldots, a_{3}, a_{2}$ are fixed. Then $x_{2}, x_{3}, \ldots, x_{n}$ are all fixed, and $x_{1}=\frac{1}{a_{1}+x_{2}}$ is maximal when $a_{1}=1$. Hence the sum $S=$ $x_{1}+x_{2}+\cdots+x_{n}$ is maximized for $a_{1}=1$. We shall show by induction on $i$ that $S$ is maximized for $a_{1}=a_{2}=\cdots=$ $a_{i}=1$. In fact, assuming that the statement holds for $i-1$ and thus $a_{1}=$ $\cdots=a_{i-1}=1$, having $x_{n}, a_{n-1}, \ldots, a_{i+1}$ fixed we have that $x_{n}, \ldots, x_{i+1}$ are also fixed, and that $x_{i-1}=f\left(x_{i}\right), \ldots, x_{1}=f^{i-1}\left(x_{i}\right)$. Hence by the lemma, $S=g_{i-1}\left(x_{i}\right)+x_{i+1}+\cdots+x_{n}$ is maximal when $x_{i}=\frac{1}{a_{i}+x_{i+1}}$ is maximal, that is, for $a_{i}=1$. Thus the induction is complete. It follows that $x_{1}+\cdots+x_{n}$ is maximal when $a_{1}=\cdots=a_{n-1}=1$, so that $x_{1}+\cdots+x_{n}=g_{n-1}\left(x_{1}\right)$. By the lemma, the latter does not exceed $g_{n-1}(1)$. This completes the proof. Remark. The upper bound is the best possible, because it is approached by taking $x_{n}$ close to 1 and inductively (in reverse) defining $x_{i-1}=\frac{1}{1+x_{i}}=$ $\frac{1}{a_{i}+x_{i}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
18. (USA 2) Let $[x]$ denote the greatest integer less than or equal to $x$. Pick any $x_{1}$ in $[0,1)$ and define the sequence $x_{1}, x_{2}, x_{3}, \ldots$ by $x_{n+1}=0$ if $x_{n}=0$ and $x_{n+1}=1 / x_{n}-\left[1 / x_{n}\right]$ otherwise. Prove that $$ x_{1}+x_{2}+\cdots+x_{n}<\frac{F_{1}}{F_{2}}+\frac{F_{2}}{F_{3}}+\cdots+\frac{F_{n}}{F_{n+1}} $$ where $F_{1}=F_{2}=1$ and $F_{n+2}=F_{n+1}+F_{n}$ for $n \geq 1$.
|
18. Let us define inductively $f^{1}(x)=f(x)=\frac{1}{x+1}$ and $f^{n}(x)=f\left(f^{n-1}(x)\right)$, and let $g_{n}(x)=x+f(x)+f^{2}(x)+\cdots+f^{n}(x)$. We shall prove first the following statement. Lemma. The function $g_{n}(x)$ is strictly increasing on $[0,1]$, and $g_{n-1}(1)=$ $F_{1} / F_{2}+F_{2} / F_{3}+\cdots+F_{n} / F_{n+1}$. Proof. Since $f(x)-f(y)=\frac{y-x}{(1+x)(1+y)}$ is smaller in absolute value than $x-y$, it follows that $x>y$ implies $f^{2 k}(x)>f^{2 k}(y)$ and $f^{2 k+1}(x)<$ $f^{2 k+1}(y)$, and moreover that for every integer $k \geq 0$, $$ \left[f^{2 k}(x)-f^{2 k}(y)\right]+\left[f^{2 k+1}(x)-f^{2 k+1}(y)\right]>0 $$ Hence if $x>y$, we have $g_{n}(x)-g_{n}(y)=(x-y)+[f(x)-f(y)]+\cdots+$ $\left[f^{n}(x)-f^{n}(y)\right]>0$, which yields the first part of the lemma. The second part follows by simple induction, since $f^{k}(1)=F_{k+1} / F_{k+2}$. If some $x_{i}=0$ and consequently $x_{j}=0$ for all $j \geq i$, then the problem reduces to the problem with $i-1$ instead of $n$. Thus we may assume that all $x_{1}, \ldots, x_{n}$ are different from 0 . If we write $a_{i}=\left[1 / x_{i}\right]$, then $x_{i}=\frac{1}{a_{i}+x_{i+1}}$. Thus we can regard $x_{i}$ as functions of $x_{n}$ depending on $a_{1}, \ldots, a_{n-1}$. Suppose that $x_{n}, a_{n-1}, \ldots, a_{3}, a_{2}$ are fixed. Then $x_{2}, x_{3}, \ldots, x_{n}$ are all fixed, and $x_{1}=\frac{1}{a_{1}+x_{2}}$ is maximal when $a_{1}=1$. Hence the sum $S=$ $x_{1}+x_{2}+\cdots+x_{n}$ is maximized for $a_{1}=1$. We shall show by induction on $i$ that $S$ is maximized for $a_{1}=a_{2}=\cdots=$ $a_{i}=1$. In fact, assuming that the statement holds for $i-1$ and thus $a_{1}=$ $\cdots=a_{i-1}=1$, having $x_{n}, a_{n-1}, \ldots, a_{i+1}$ fixed we have that $x_{n}, \ldots, x_{i+1}$ are also fixed, and that $x_{i-1}=f\left(x_{i}\right), \ldots, x_{1}=f^{i-1}\left(x_{i}\right)$. Hence by the lemma, $S=g_{i-1}\left(x_{i}\right)+x_{i+1}+\cdots+x_{n}$ is maximal when $x_{i}=\frac{1}{a_{i}+x_{i+1}}$ is maximal, that is, for $a_{i}=1$. Thus the induction is complete. It follows that $x_{1}+\cdots+x_{n}$ is maximal when $a_{1}=\cdots=a_{n-1}=1$, so that $x_{1}+\cdots+x_{n}=g_{n-1}\left(x_{1}\right)$. By the lemma, the latter does not exceed $g_{n-1}(1)$. This completes the proof. Remark. The upper bound is the best possible, because it is approached by taking $x_{n}$ close to 1 and inductively (in reverse) defining $x_{i-1}=\frac{1}{1+x_{i}}=$ $\frac{1}{a_{i}+x_{i}}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9d50c87a-3c88-5bba-adca-c169a2a7b8c8
| 24,426
|
19. (IRE 1) Let $f(x)=x^{8}+4 x^{6}+2 x^{4}+28 x^{2}+1$. Let $p>3$ be a prime and suppose there exists an integer $z$ such that $p$ divides $f(z)$. Prove that there exist integers $z_{1}, z_{2}, \ldots, z_{8}$ such that if $$ g(x)=\left(x-z_{1}\right)\left(x-z_{2}\right) \cdots\left(x-z_{8}\right) $$ then all coefficients of $f(x)-g(x)$ are divisible by $p$.
|
19. Observe that $f(x)=\left(x^{4}+2 x^{2}+3\right)^{2}-8\left(x^{2}-1\right)^{2}=\left[x^{4}+2(1-\sqrt{2}) x^{2}+\right.$ $3+2 \sqrt{2}]\left[x^{4}+2(1+\sqrt{2}) x^{2}+3-2 \sqrt{2}\right]$. Now it is easy to find that the roots of $f$ are $$ x_{1,2,3,4}= \pm i(i \sqrt[4]{2} \pm 1) \quad \text { and } \quad x_{5,6,7,8}= \pm i(\sqrt[4]{2} \pm 1) $$ In other words, $x_{k}=\alpha_{i}+\beta_{j}$, where $\alpha_{i}^{2}=-1$ and $\beta_{j}^{4}=2$. We claim that any root of $f$ can be obtained from any other using rational functions. In fact, we have $$ \begin{aligned} & x^{3}=-\alpha_{i}-3 \beta_{j}+3 \alpha_{i} \beta_{j}^{2}+\beta_{j}^{3} \\ & x^{5}=11 \alpha_{i}+7 \beta_{j}-10 \alpha_{i} \beta_{j}^{2}-10 \beta_{j}^{3} \\ & x^{7}=-71 \alpha_{i}-49 \beta_{j}+35 \alpha_{i} \beta_{j}^{2}+37 \beta_{j}^{3} \end{aligned} $$ from which we easily obtain that $\alpha_{i}=24^{-1}\left(127 x+5 x^{3}+19 x^{5}+5 x^{7}\right), \quad \beta_{j}=24^{-1}\left(151 x+5 x^{3}+19 x^{5}+5 x^{7}\right)$. Since all other values of $\alpha$ and $\beta$ can be obtained as rational functions of $\alpha_{i}$ and $\beta_{j}$, it follows that all the roots $x_{l}$ are rational functions of a particular root $x_{k}$. We now note that if $x_{1}$ is an integer such that $f\left(x_{1}\right)$ is divisible by $p$, then $p>3$ and $x_{1} \in \mathbb{Z}_{p}$ is a root of the polynomial $f$. By the previous consideration, all remaining roots $x_{2}, \ldots, x_{8}$ of $f$ over the field $\mathbb{Z}_{p}$ are rational functions of $x_{1}$, since 24 is invertible in $Z_{p}$. Then $f(x)$ factors as $$ f(x)=\left(x-x_{1}\right)\left(x-x_{2}\right) \cdots\left(x-x_{8}\right), $$ and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
19. (IRE 1) Let $f(x)=x^{8}+4 x^{6}+2 x^{4}+28 x^{2}+1$. Let $p>3$ be a prime and suppose there exists an integer $z$ such that $p$ divides $f(z)$. Prove that there exist integers $z_{1}, z_{2}, \ldots, z_{8}$ such that if $$ g(x)=\left(x-z_{1}\right)\left(x-z_{2}\right) \cdots\left(x-z_{8}\right) $$ then all coefficients of $f(x)-g(x)$ are divisible by $p$.
|
19. Observe that $f(x)=\left(x^{4}+2 x^{2}+3\right)^{2}-8\left(x^{2}-1\right)^{2}=\left[x^{4}+2(1-\sqrt{2}) x^{2}+\right.$ $3+2 \sqrt{2}]\left[x^{4}+2(1+\sqrt{2}) x^{2}+3-2 \sqrt{2}\right]$. Now it is easy to find that the roots of $f$ are $$ x_{1,2,3,4}= \pm i(i \sqrt[4]{2} \pm 1) \quad \text { and } \quad x_{5,6,7,8}= \pm i(\sqrt[4]{2} \pm 1) $$ In other words, $x_{k}=\alpha_{i}+\beta_{j}$, where $\alpha_{i}^{2}=-1$ and $\beta_{j}^{4}=2$. We claim that any root of $f$ can be obtained from any other using rational functions. In fact, we have $$ \begin{aligned} & x^{3}=-\alpha_{i}-3 \beta_{j}+3 \alpha_{i} \beta_{j}^{2}+\beta_{j}^{3} \\ & x^{5}=11 \alpha_{i}+7 \beta_{j}-10 \alpha_{i} \beta_{j}^{2}-10 \beta_{j}^{3} \\ & x^{7}=-71 \alpha_{i}-49 \beta_{j}+35 \alpha_{i} \beta_{j}^{2}+37 \beta_{j}^{3} \end{aligned} $$ from which we easily obtain that $\alpha_{i}=24^{-1}\left(127 x+5 x^{3}+19 x^{5}+5 x^{7}\right), \quad \beta_{j}=24^{-1}\left(151 x+5 x^{3}+19 x^{5}+5 x^{7}\right)$. Since all other values of $\alpha$ and $\beta$ can be obtained as rational functions of $\alpha_{i}$ and $\beta_{j}$, it follows that all the roots $x_{l}$ are rational functions of a particular root $x_{k}$. We now note that if $x_{1}$ is an integer such that $f\left(x_{1}\right)$ is divisible by $p$, then $p>3$ and $x_{1} \in \mathbb{Z}_{p}$ is a root of the polynomial $f$. By the previous consideration, all remaining roots $x_{2}, \ldots, x_{8}$ of $f$ over the field $\mathbb{Z}_{p}$ are rational functions of $x_{1}$, since 24 is invertible in $Z_{p}$. Then $f(x)$ factors as $$ f(x)=\left(x-x_{1}\right)\left(x-x_{2}\right) \cdots\left(x-x_{8}\right), $$ and the result follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
77c2ac62-e8e3-57c3-bf7b-71a16fd1cb6f
| 24,428
|
21. (GBR 2) ${ }^{\mathrm{IMO} 6}$ For each positive integer $n$, denote by $s(n)$ the greatest integer such that for all positive integers $k \leq s(n), n^{2}$ can be expressed as a sum of squares of $k$ positive integers. (a) Prove that $s(n) \leq n^{2}-14$ for all $n \geq 4$. (b) Find a number $n$ such that $s(n)=\overline{n^{2}}-14$. (c) Prove that there exist infinitely many positive integers $n$ such that $s(n)=n^{2}-14$.
|
21. (a) Representing $n^{2}$ as a sum of $n^{2}-13$ squares is equivalent to representing 13 as a sum of numbers of the form $x^{2}-1, x \in \mathbb{N}$, such as $0,3,8,15, \ldots$ But it is easy to check that this is impossible, and hence $s(n) \leq n^{2}-14$. (b) Let us prove that $s(13)=13^{2}-14=155$. Observe that $$ \begin{aligned} 13^{2} & =8^{2}+8^{2}+4^{2}+4^{2}+3^{2} \\ & =8^{2}+8^{2}+4^{2}+4^{2}+2^{2}+2^{2}+1^{2} \\ & =8^{2}+8^{2}+4^{2}+3^{2}+3^{2}+2^{2}+1^{2}+1^{2}+1^{2} \end{aligned} $$ Given any representation of $n^{2}$ as a sum of $m$ squares one of which is even, we can construct a representation as a sum of $m+3$ squares by dividing the odd square into four equal squares. Thus the first equality enables us to construct representations with $5,8,11, \ldots, 155$ squares, the second to construct ones with $7,10,13, \ldots, 154$ squares, and the third with $9,12, \ldots, 153$ squares. It remains only to represent $13^{2}$ as a sum of $k=2,3,4,6$ squares. This can be done as follows: $$ \begin{aligned} 13^{2} & =12^{2}+5^{2}=12^{2}+4^{2}+3^{2} \\ & =11^{2}+4^{2}+4^{2}+4^{2}=12^{2}+3^{2}+2^{2}+2^{2}+2^{2}+2^{2} \end{aligned} $$ (c) We shall prove that whenever $s(n)=n^{2}-14$ for some $n \geq 13$, it also holds that $s(2 n)=(2 n)^{2}-14$. This will imply that $s(n)=n^{2}-14$ for any $n=2^{t} \cdot 13$. If $n^{2}=x_{1}^{2}+\cdots+x_{r}^{2}$, then we have $(2 n)^{2}=\left(2 x_{1}\right)^{2}+\cdots+\left(2 x_{r}\right)^{2}$. Replacing $\left(2 x_{i}\right)^{2}$ with $x_{i}^{2}+x_{i}^{2}+x_{i}^{2}+x_{i}^{2}$ as long as it is possible we can obtain representations of $(2 n)^{2}$ consisting of $r, r+3, \ldots, 4 r$ squares. This gives representations of $(2 n)^{2}$ into $k$ squares for any $k \leq 4 n^{2}-62$. Further, we observe that each number $m \geq 14$ can be written as a sum of $k \geq m$ numbers of the form $x^{2}-1, x \in \mathbb{N}$, which is easy to verify. Therefore if $k \leq 4 n^{2}-14$, it follows that $4 n^{2}-k$ is a sum of $k$ numbers of the form $x^{2}-1$ (since $k \geq 4 n^{2}-k \geq 14$ ), and consequently $4 n^{2}$ is a sum of $k$ squares. Remark. One can find exactly the value of $f(n)$ for each $n$ : $$ f(n)= \begin{cases}1, & \text { if } n \text { has a prime divisor congruent to } 3 \bmod 4 \\ 2, & \text { if } n \text { is of the form } 5 \cdot 2^{k}, k \text { a positive integer; } \\ n^{2}-14, & \text { otherwise. }\end{cases} $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
21. (GBR 2) ${ }^{\mathrm{IMO} 6}$ For each positive integer $n$, denote by $s(n)$ the greatest integer such that for all positive integers $k \leq s(n), n^{2}$ can be expressed as a sum of squares of $k$ positive integers. (a) Prove that $s(n) \leq n^{2}-14$ for all $n \geq 4$. (b) Find a number $n$ such that $s(n)=\overline{n^{2}}-14$. (c) Prove that there exist infinitely many positive integers $n$ such that $s(n)=n^{2}-14$.
|
21. (a) Representing $n^{2}$ as a sum of $n^{2}-13$ squares is equivalent to representing 13 as a sum of numbers of the form $x^{2}-1, x \in \mathbb{N}$, such as $0,3,8,15, \ldots$ But it is easy to check that this is impossible, and hence $s(n) \leq n^{2}-14$. (b) Let us prove that $s(13)=13^{2}-14=155$. Observe that $$ \begin{aligned} 13^{2} & =8^{2}+8^{2}+4^{2}+4^{2}+3^{2} \\ & =8^{2}+8^{2}+4^{2}+4^{2}+2^{2}+2^{2}+1^{2} \\ & =8^{2}+8^{2}+4^{2}+3^{2}+3^{2}+2^{2}+1^{2}+1^{2}+1^{2} \end{aligned} $$ Given any representation of $n^{2}$ as a sum of $m$ squares one of which is even, we can construct a representation as a sum of $m+3$ squares by dividing the odd square into four equal squares. Thus the first equality enables us to construct representations with $5,8,11, \ldots, 155$ squares, the second to construct ones with $7,10,13, \ldots, 154$ squares, and the third with $9,12, \ldots, 153$ squares. It remains only to represent $13^{2}$ as a sum of $k=2,3,4,6$ squares. This can be done as follows: $$ \begin{aligned} 13^{2} & =12^{2}+5^{2}=12^{2}+4^{2}+3^{2} \\ & =11^{2}+4^{2}+4^{2}+4^{2}=12^{2}+3^{2}+2^{2}+2^{2}+2^{2}+2^{2} \end{aligned} $$ (c) We shall prove that whenever $s(n)=n^{2}-14$ for some $n \geq 13$, it also holds that $s(2 n)=(2 n)^{2}-14$. This will imply that $s(n)=n^{2}-14$ for any $n=2^{t} \cdot 13$. If $n^{2}=x_{1}^{2}+\cdots+x_{r}^{2}$, then we have $(2 n)^{2}=\left(2 x_{1}\right)^{2}+\cdots+\left(2 x_{r}\right)^{2}$. Replacing $\left(2 x_{i}\right)^{2}$ with $x_{i}^{2}+x_{i}^{2}+x_{i}^{2}+x_{i}^{2}$ as long as it is possible we can obtain representations of $(2 n)^{2}$ consisting of $r, r+3, \ldots, 4 r$ squares. This gives representations of $(2 n)^{2}$ into $k$ squares for any $k \leq 4 n^{2}-62$. Further, we observe that each number $m \geq 14$ can be written as a sum of $k \geq m$ numbers of the form $x^{2}-1, x \in \mathbb{N}$, which is easy to verify. Therefore if $k \leq 4 n^{2}-14$, it follows that $4 n^{2}-k$ is a sum of $k$ numbers of the form $x^{2}-1$ (since $k \geq 4 n^{2}-k \geq 14$ ), and consequently $4 n^{2}$ is a sum of $k$ squares. Remark. One can find exactly the value of $f(n)$ for each $n$ : $$ f(n)= \begin{cases}1, & \text { if } n \text { has a prime divisor congruent to } 3 \bmod 4 \\ 2, & \text { if } n \text { is of the form } 5 \cdot 2^{k}, k \text { a positive integer; } \\ n^{2}-14, & \text { otherwise. }\end{cases} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
322518c1-97fc-5836-b957-e18e7111ea72
| 24,434
|
3. (CHN 2) The diagonals of a quadrilateral $A B C D$ are perpendicular: $A C \perp B D$. Four squares, $A B E F, B C G H, C D I J, D A K L$, are erected externally on its sides. The intersection points of the pairs of straight lines $C L, D F ; D F, A H ; A H, B J ; B J, C L$ are denoted by $P_{1}, Q_{1}, R_{1}, S_{1}$, respectively, and the intersection points of the pairs of straight lines $A I, B K$; $B K, C E ; C E, D G ; D G, A I$ are denoted by $P_{2}, Q_{2}, R_{2}, S_{2}$, respectively. Prove that $P_{1} Q_{1} R_{1} S_{1} \cong P_{2} Q_{2} R_{2} S_{2}$.
|
3. Consider two squares $A B^{\prime} C D^{\prime}$ and $A^{\prime} B C^{\prime} D$. Since $A C \perp B D$, these two squares are homothetic, which implies that the lines $A A^{\prime}, B B^{\prime}, C C^{\prime}, D D^{\prime}$ are concurrent at a certain point $O$. Since the rotation about $A$ by $90^{\circ}$ takes $\triangle A B K$ into $\triangle A F D$, it follows that $B K \perp D F$. Denote by $T$ the intersection of $B K$ and $D F$. The rotation about some point $X$ by $90^{\circ}$ maps $B K$ into $D F$ if and only if $T X$ bisects an angle between $B K$ and $D F$. Therefore $\angle F T A=$ 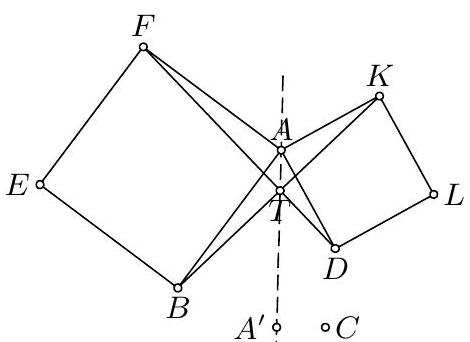 $\angle A T K=45^{\circ}$. Moreover, the quadrilateral $B A^{\prime} D T$ is cyclic, which implies that $\angle B T A^{\prime}=B D A^{\prime}=45^{\circ}$ and consequently that the points $A, T, A^{\prime}$ are collinear. It follows that the point $O$ lies on a bisector of $\angle B T D$ and therefore the rotation $\mathcal{R}$ about $O$ by $90^{\circ}$ takes $B K$ into $D F$. Analogously, $\mathcal{R}$ maps the lines $C E, D G, A I$ into $A H, B J, C L$. Hence the quadrilateral $P_{1} Q_{1} R_{1} S_{1}$ is the image of the quadrilateral $P_{2} Q_{2} R_{2} S_{2}$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (CHN 2) The diagonals of a quadrilateral $A B C D$ are perpendicular: $A C \perp B D$. Four squares, $A B E F, B C G H, C D I J, D A K L$, are erected externally on its sides. The intersection points of the pairs of straight lines $C L, D F ; D F, A H ; A H, B J ; B J, C L$ are denoted by $P_{1}, Q_{1}, R_{1}, S_{1}$, respectively, and the intersection points of the pairs of straight lines $A I, B K$; $B K, C E ; C E, D G ; D G, A I$ are denoted by $P_{2}, Q_{2}, R_{2}, S_{2}$, respectively. Prove that $P_{1} Q_{1} R_{1} S_{1} \cong P_{2} Q_{2} R_{2} S_{2}$.
|
3. Consider two squares $A B^{\prime} C D^{\prime}$ and $A^{\prime} B C^{\prime} D$. Since $A C \perp B D$, these two squares are homothetic, which implies that the lines $A A^{\prime}, B B^{\prime}, C C^{\prime}, D D^{\prime}$ are concurrent at a certain point $O$. Since the rotation about $A$ by $90^{\circ}$ takes $\triangle A B K$ into $\triangle A F D$, it follows that $B K \perp D F$. Denote by $T$ the intersection of $B K$ and $D F$. The rotation about some point $X$ by $90^{\circ}$ maps $B K$ into $D F$ if and only if $T X$ bisects an angle between $B K$ and $D F$. Therefore $\angle F T A=$  $\angle A T K=45^{\circ}$. Moreover, the quadrilateral $B A^{\prime} D T$ is cyclic, which implies that $\angle B T A^{\prime}=B D A^{\prime}=45^{\circ}$ and consequently that the points $A, T, A^{\prime}$ are collinear. It follows that the point $O$ lies on a bisector of $\angle B T D$ and therefore the rotation $\mathcal{R}$ about $O$ by $90^{\circ}$ takes $B K$ into $D F$. Analogously, $\mathcal{R}$ maps the lines $C E, D G, A I$ into $A H, B J, C L$. Hence the quadrilateral $P_{1} Q_{1} R_{1} S_{1}$ is the image of the quadrilateral $P_{2} Q_{2} R_{2} S_{2}$, and the result follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
07efe2f8-7409-5b88-bc6b-bbec4b4aec5d
| 24,437
|
5. (COL 3) Let $A B C D$ be a convex quadrilateral such that $A C=$ $B D$. Equilateral triangles are constructed on the sides of the quadrilateral. Let $O_{1}, O_{2}, O_{3}, O_{4}$ be the centers of the triangles constructed on $A B, B C, C D, D A$ respectively. Show that $O_{1} O_{3}$ is perpendicular to $O_{2} O_{4}$.
|
5. Denote by $K, L, M$, and $N$ the midpoints of the sides $A B, B C, C D$, and $D A$, respectively. The quadrilateral $K L M N$ is a rhombus. We shall prove that $O_{1} O_{3} \| K M$. Similarly, $O_{2} O_{4} \| L N$, and the desired result follows immediately. We have $\overrightarrow{O_{1} O_{3}}=\overrightarrow{K M}+\left(\overrightarrow{O_{1} K}+\overrightarrow{M O_{3}}\right)$. Assume that $A B C D$ is positively oriented. A rotational homothety $\mathcal{R}$ with angle $-90^{\circ}$ and coefficient $1 / \sqrt{3}$ takes the vectors $\overrightarrow{B K}$ and $\overrightarrow{C M}$ into $\overrightarrow{O_{1} K}$ and $\overrightarrow{M O_{3}}$ respectively. Therefore $$ \begin{aligned} \overrightarrow{O_{1} O_{3}} & =\overrightarrow{K M}+\left(\overrightarrow{O_{1} K}+\overrightarrow{M O_{3}}\right)=\overrightarrow{K M}+\mathcal{R}(\overrightarrow{B K}+\overrightarrow{C M}) \\ & =\overrightarrow{K M}+\frac{1}{2} \mathcal{R}(\overrightarrow{B A}+\overrightarrow{C D})=\overrightarrow{K M}+\mathcal{R}(\overrightarrow{L N}) \end{aligned} $$ Since $L N \perp K M$, it follows that $\mathcal{R}(L N)$ is parallel to $K M$ and so is $\mathrm{O}_{1} \mathrm{O}_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. (COL 3) Let $A B C D$ be a convex quadrilateral such that $A C=$ $B D$. Equilateral triangles are constructed on the sides of the quadrilateral. Let $O_{1}, O_{2}, O_{3}, O_{4}$ be the centers of the triangles constructed on $A B, B C, C D, D A$ respectively. Show that $O_{1} O_{3}$ is perpendicular to $O_{2} O_{4}$.
|
5. Denote by $K, L, M$, and $N$ the midpoints of the sides $A B, B C, C D$, and $D A$, respectively. The quadrilateral $K L M N$ is a rhombus. We shall prove that $O_{1} O_{3} \| K M$. Similarly, $O_{2} O_{4} \| L N$, and the desired result follows immediately. We have $\overrightarrow{O_{1} O_{3}}=\overrightarrow{K M}+\left(\overrightarrow{O_{1} K}+\overrightarrow{M O_{3}}\right)$. Assume that $A B C D$ is positively oriented. A rotational homothety $\mathcal{R}$ with angle $-90^{\circ}$ and coefficient $1 / \sqrt{3}$ takes the vectors $\overrightarrow{B K}$ and $\overrightarrow{C M}$ into $\overrightarrow{O_{1} K}$ and $\overrightarrow{M O_{3}}$ respectively. Therefore $$ \begin{aligned} \overrightarrow{O_{1} O_{3}} & =\overrightarrow{K M}+\left(\overrightarrow{O_{1} K}+\overrightarrow{M O_{3}}\right)=\overrightarrow{K M}+\mathcal{R}(\overrightarrow{B K}+\overrightarrow{C M}) \\ & =\overrightarrow{K M}+\frac{1}{2} \mathcal{R}(\overrightarrow{B A}+\overrightarrow{C D})=\overrightarrow{K M}+\mathcal{R}(\overrightarrow{L N}) \end{aligned} $$ Since $L N \perp K M$, it follows that $\mathcal{R}(L N)$ is parallel to $K M$ and so is $\mathrm{O}_{1} \mathrm{O}_{3}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a9fd9eec-cdad-51c2-83c9-e21627111309
| 24,443
|
7. (IND 4) Circles $G, G_{1}, G_{2}$ are three circles related to each other as follows: Circles $G_{1}$ and $G_{2}$ are externally tangent to one another at a point $W$ and both these circles are internally tangent to the circle $G$. Points $A, B, C$ are located on the circle $G$ as follows: Line $B C$ is a direct common tangent to the pair of circles $G_{1}$ and $G_{2}$, and line $W A$ is the transverse common tangent at $W$ to $G_{1}$ and $G_{2}$, with $W$ and $A$ lying on the same side of the line $B C$. Prove that $W$ is the incenter of the triangle $A B C$.
|
7. Let $G_{1}, G_{2}$ touch the chord $B C$ at $P, Q$ and touch the circle $G$ at $R, S$ respectively. Let $D$ be the midpoint of the complementary $\operatorname{arc} B C$ of $G$. The homothety centered at $R$ mapping $G_{1}$ onto $G$ also maps the line $B C$ onto a tangent of $G$ parallel to $B C$. It follows that this line touches $G$ at point $D$, which is therefore the image of $P$ under the homothety. Hence $R, P$, and $D$ are collinear. Since $\angle D B P=\angle D C B=\angle D R B$, it follows that $\triangle D B P \sim \triangle D R B$ and consequently that $D P \cdot D R=D B^{2}$. Similarly, points $S, Q, D$ are collinear and satisfy $D Q \cdot D S=D B^{2}=D P \cdot D R$. Hence $D$ lies on the radical axis of the circles $G_{1}$ and $G_{2}$, i.e., on their common tangent $A W$, which also implies that $A W$ bisects the angle $B A D$. Furthermore, since $D B=D C=D W=\sqrt{D P \cdot D R}$, it follows from the lemma of (SL99-14) that $W$ is the incenter of $\triangle A B C$. Remark. According to the third solution of (SL93-3), both $P W$ and $Q W$ contain the incenter of $\triangle A B C$, and the result is immediate. The problem can also be solved by inversion centered at $W$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. (IND 4) Circles $G, G_{1}, G_{2}$ are three circles related to each other as follows: Circles $G_{1}$ and $G_{2}$ are externally tangent to one another at a point $W$ and both these circles are internally tangent to the circle $G$. Points $A, B, C$ are located on the circle $G$ as follows: Line $B C$ is a direct common tangent to the pair of circles $G_{1}$ and $G_{2}$, and line $W A$ is the transverse common tangent at $W$ to $G_{1}$ and $G_{2}$, with $W$ and $A$ lying on the same side of the line $B C$. Prove that $W$ is the incenter of the triangle $A B C$.
|
7. Let $G_{1}, G_{2}$ touch the chord $B C$ at $P, Q$ and touch the circle $G$ at $R, S$ respectively. Let $D$ be the midpoint of the complementary $\operatorname{arc} B C$ of $G$. The homothety centered at $R$ mapping $G_{1}$ onto $G$ also maps the line $B C$ onto a tangent of $G$ parallel to $B C$. It follows that this line touches $G$ at point $D$, which is therefore the image of $P$ under the homothety. Hence $R, P$, and $D$ are collinear. Since $\angle D B P=\angle D C B=\angle D R B$, it follows that $\triangle D B P \sim \triangle D R B$ and consequently that $D P \cdot D R=D B^{2}$. Similarly, points $S, Q, D$ are collinear and satisfy $D Q \cdot D S=D B^{2}=D P \cdot D R$. Hence $D$ lies on the radical axis of the circles $G_{1}$ and $G_{2}$, i.e., on their common tangent $A W$, which also implies that $A W$ bisects the angle $B A D$. Furthermore, since $D B=D C=D W=\sqrt{D P \cdot D R}$, it follows from the lemma of (SL99-14) that $W$ is the incenter of $\triangle A B C$. Remark. According to the third solution of (SL93-3), both $P W$ and $Q W$ contain the incenter of $\triangle A B C$, and the result is immediate. The problem can also be solved by inversion centered at $W$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3be34b7f-b201-5fd4-9b19-87cd783f8681
| 24,448
|
8. (IND 5) Show that in the plane there exists a convex polygon of 1992 sides satisfying the following conditions: (i) its side lengths are $1,2,3, \ldots, 1992$ in some order; (ii) the polygon is circumscribable about a circle. Alternative formulation. Does there exist a 1992-gon with side lengths $1,2,3, \ldots, 1992$ circumscribed about a circle? Answer the same question for a 1990-gon.
|
8. For simplicity, we shall write $n$ instead of 1992. Lemma. There exists a tangent $n$-gon $A_{1} A_{2} \ldots A_{n}$ with sides $A_{1} A_{2}=a_{1}$, $A_{2} A_{3}=a_{2}, \ldots, A_{n} A_{1}=a_{n}$ if and only if the system $$ x_{1}+x_{2}=a_{1}, x_{2}+x_{3}=a_{2}, \ldots, x_{n}+x_{1}=a_{n} $$ has a solution $\left(x_{1}, \ldots, x_{n}\right)$ in positive reals. Proof. Suppose that such an $n$-gon $A_{1} A_{2} \ldots A_{n}$ exists. Let the side $A_{i} A_{i+1}$ touch the inscribed circle at point $P_{i}$ (where $\left.A_{n+1}=A_{1}\right)$. Then $x_{1}=$ $A_{1} P_{n}=A_{1} P_{1}, x_{2}=A_{2} P_{1}=A_{2} P_{2}, \ldots, x_{n}=A_{n} P_{n-1}=A_{n} P_{n}$ is clearly a positive solution of (1). Now suppose that the system (1) has a positive real solution $\left(x_{1}, \ldots\right.$, $x_{n}$ ). Let us draw a polygonal line $A_{1} A_{2} \ldots A_{n+1}$ touching a circle of radius $r$ at points $P_{1}, P_{2}, \ldots, P_{n}$ respectively such that $A_{1} P_{1}=$ $A_{n+1} P_{n}=x_{1}$ and $A_{i} P_{i}=A_{i} P_{i-1}=x_{i}$ for $i=2, \ldots, n$. Observe that $O A_{1}=O A_{n+1}=\sqrt{x_{1}^{2}+r^{2}}$ and the function $f(r)=\angle A_{1} O A_{2}+$ $\angle A_{2} O A_{3}+\cdots+\angle A_{n} O A_{n+1}=$ $2\left(\arctan \frac{x_{1}}{r}+\cdots+\arctan \frac{x_{n}}{r}\right)$ is continuous. Thus $A_{1} A_{2} \ldots A_{n+1}$ is a closed simple polygonal line if and only if $f(r)=360^{\circ}$. But such an $r$ exists, since $f(r) \rightarrow 0$  when $r \rightarrow \infty$ and $f(r) \rightarrow \infty$ when $r \rightarrow 0$. This proves the second direction of the lemma. For $n=4 k$, the system (1) is solvable in positive reals if $a_{i}=i$ for $i \equiv 1,2$ $(\bmod 4), a_{i}=i+1$ for $i \equiv 3$ and $a_{i}=i-1$ for $i \equiv 0(\bmod 4)$. Indeed, one solution is given by $x_{i}=1 / 2$ for $i \equiv 1, x_{i}=3 / 2$ for $i \equiv 3$ and $x_{i}=i-3 / 2$ for $i \equiv 0,2(\bmod 4)$. Remark. For $n=4 k+2$ there is no such $n$-gon. In fact, solvability of the system (1) implies $a_{1}+a_{3}+\cdots=a_{2}+a_{4}+\cdots$, while in the case $n=4 k+2$ the sum $a_{1}+a_{2}+\cdots+a_{n}$ is odd.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. (IND 5) Show that in the plane there exists a convex polygon of 1992 sides satisfying the following conditions: (i) its side lengths are $1,2,3, \ldots, 1992$ in some order; (ii) the polygon is circumscribable about a circle. Alternative formulation. Does there exist a 1992-gon with side lengths $1,2,3, \ldots, 1992$ circumscribed about a circle? Answer the same question for a 1990-gon.
|
8. For simplicity, we shall write $n$ instead of 1992. Lemma. There exists a tangent $n$-gon $A_{1} A_{2} \ldots A_{n}$ with sides $A_{1} A_{2}=a_{1}$, $A_{2} A_{3}=a_{2}, \ldots, A_{n} A_{1}=a_{n}$ if and only if the system $$ x_{1}+x_{2}=a_{1}, x_{2}+x_{3}=a_{2}, \ldots, x_{n}+x_{1}=a_{n} $$ has a solution $\left(x_{1}, \ldots, x_{n}\right)$ in positive reals. Proof. Suppose that such an $n$-gon $A_{1} A_{2} \ldots A_{n}$ exists. Let the side $A_{i} A_{i+1}$ touch the inscribed circle at point $P_{i}$ (where $\left.A_{n+1}=A_{1}\right)$. Then $x_{1}=$ $A_{1} P_{n}=A_{1} P_{1}, x_{2}=A_{2} P_{1}=A_{2} P_{2}, \ldots, x_{n}=A_{n} P_{n-1}=A_{n} P_{n}$ is clearly a positive solution of (1). Now suppose that the system (1) has a positive real solution $\left(x_{1}, \ldots\right.$, $x_{n}$ ). Let us draw a polygonal line $A_{1} A_{2} \ldots A_{n+1}$ touching a circle of radius $r$ at points $P_{1}, P_{2}, \ldots, P_{n}$ respectively such that $A_{1} P_{1}=$ $A_{n+1} P_{n}=x_{1}$ and $A_{i} P_{i}=A_{i} P_{i-1}=x_{i}$ for $i=2, \ldots, n$. Observe that $O A_{1}=O A_{n+1}=\sqrt{x_{1}^{2}+r^{2}}$ and the function $f(r)=\angle A_{1} O A_{2}+$ $\angle A_{2} O A_{3}+\cdots+\angle A_{n} O A_{n+1}=$ $2\left(\arctan \frac{x_{1}}{r}+\cdots+\arctan \frac{x_{n}}{r}\right)$ is continuous. Thus $A_{1} A_{2} \ldots A_{n+1}$ is a closed simple polygonal line if and only if $f(r)=360^{\circ}$. But such an $r$ exists, since $f(r) \rightarrow 0$  when $r \rightarrow \infty$ and $f(r) \rightarrow \infty$ when $r \rightarrow 0$. This proves the second direction of the lemma. For $n=4 k$, the system (1) is solvable in positive reals if $a_{i}=i$ for $i \equiv 1,2$ $(\bmod 4), a_{i}=i+1$ for $i \equiv 3$ and $a_{i}=i-1$ for $i \equiv 0(\bmod 4)$. Indeed, one solution is given by $x_{i}=1 / 2$ for $i \equiv 1, x_{i}=3 / 2$ for $i \equiv 3$ and $x_{i}=i-3 / 2$ for $i \equiv 0,2(\bmod 4)$. Remark. For $n=4 k+2$ there is no such $n$-gon. In fact, solvability of the system (1) implies $a_{1}+a_{3}+\cdots=a_{2}+a_{4}+\cdots$, while in the case $n=4 k+2$ the sum $a_{1}+a_{2}+\cdots+a_{n}$ is odd.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
516a9a40-daec-5bb6-957c-92702a1fff49
| 24,451
|
9. (IRN 1) Let $f(x)$ be a polynomial with rational coefficients and $\alpha$ be a real number such that $\alpha^{3}-\alpha=f(\alpha)^{3}-f(\alpha)=33^{1992}$. Prove that for each $n \geq 1$, $$ \left(f^{(n)}(\alpha)\right)^{3}-f^{(n)}(\alpha)=33^{1992} $$ where $f^{(n)}(x)=f(f(\ldots f(x)))$, and $n$ is a positive integer.
|
9. Since the equation $x^{3}-x-c=0$ has only one real root for every $c>$ $2 /(3 \sqrt{3}), \alpha$ is the unique real root of $x^{3}-x-33^{1992}=0$. Hence $f^{n}(\alpha)=$ $f(\alpha)=\alpha$. Remark. Consider any irreducible polynomial $g(x)$ in the place of $x^{3}-$ $x-33^{1992}$. The problem amounts to proving that if $\alpha$ and $f(\alpha)$ are roots of $g$, then any $f^{(n)}(\alpha)$ is also a root of $g$. In fact, since $g(f(x))$ vanishes at $x=\alpha$, it must be divisible by the minimal polynomial of $\alpha$, that is, $g(x)$. It follows by induction that $g\left(f^{(n)}(x)\right)$ is divisible by $g(x)$ for all $n \in \mathbb{N}$, and hence $g\left(f^{(n)}(\alpha)\right)=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
9. (IRN 1) Let $f(x)$ be a polynomial with rational coefficients and $\alpha$ be a real number such that $\alpha^{3}-\alpha=f(\alpha)^{3}-f(\alpha)=33^{1992}$. Prove that for each $n \geq 1$, $$ \left(f^{(n)}(\alpha)\right)^{3}-f^{(n)}(\alpha)=33^{1992} $$ where $f^{(n)}(x)=f(f(\ldots f(x)))$, and $n$ is a positive integer.
|
9. Since the equation $x^{3}-x-c=0$ has only one real root for every $c>$ $2 /(3 \sqrt{3}), \alpha$ is the unique real root of $x^{3}-x-33^{1992}=0$. Hence $f^{n}(\alpha)=$ $f(\alpha)=\alpha$. Remark. Consider any irreducible polynomial $g(x)$ in the place of $x^{3}-$ $x-33^{1992}$. The problem amounts to proving that if $\alpha$ and $f(\alpha)$ are roots of $g$, then any $f^{(n)}(\alpha)$ is also a root of $g$. In fact, since $g(f(x))$ vanishes at $x=\alpha$, it must be divisible by the minimal polynomial of $\alpha$, that is, $g(x)$. It follows by induction that $g\left(f^{(n)}(x)\right)$ is divisible by $g(x)$ for all $n \in \mathbb{N}$, and hence $g\left(f^{(n)}(\alpha)\right)=0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7930963a-1bf4-5920-99a2-9d7cc8e5c014
| 24,453
|
1. (BRA 1) Show that there exists a finite set $A \subset \mathbb{R}^{2}$ such that for every $X \in A$ there are points $Y_{1}, Y_{2}, \ldots, Y_{1993}$ in $A$ such that the distance between $X$ and $Y_{i}$ is equal to 1 , for every $i$.
|
1. First we notice that for a rational point $O$ (i.e., with rational coordinates), there exist 1993 rational points in each quadrant of the unit circle centered at $O$. In fact, it suffices to take $$ X=\left\{\left.O+\left( \pm \frac{t^{2}-1}{t^{2}+1}, \pm \frac{2 t}{t^{2}+1}\right) \right\rvert\, t=1,2, \ldots, 1993\right\} $$ Now consider the set $A=\{(i / q, j / q) \mid i, j=0,1, \ldots, 2 q\}$, where $q=$ $\prod_{i=1}^{1993}\left(t^{2}+1\right)$. We claim that $A$ gives a solution for the problem. Indeed, for any $P \in A$ there is a quarter of the unit circle centered at $P$ that is contained in the square $[0,2] \times[0,2]$. As explained above, there are 1993 rational points on this quarter circle, and by definition of $q$ they all belong to $A$. Remark. Substantially the same problem was proposed by Bulgaria for IMO 71: see (SL71-2), where we give another possible construction of a set $A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
1. (BRA 1) Show that there exists a finite set $A \subset \mathbb{R}^{2}$ such that for every $X \in A$ there are points $Y_{1}, Y_{2}, \ldots, Y_{1993}$ in $A$ such that the distance between $X$ and $Y_{i}$ is equal to 1 , for every $i$.
|
1. First we notice that for a rational point $O$ (i.e., with rational coordinates), there exist 1993 rational points in each quadrant of the unit circle centered at $O$. In fact, it suffices to take $$ X=\left\{\left.O+\left( \pm \frac{t^{2}-1}{t^{2}+1}, \pm \frac{2 t}{t^{2}+1}\right) \right\rvert\, t=1,2, \ldots, 1993\right\} $$ Now consider the set $A=\{(i / q, j / q) \mid i, j=0,1, \ldots, 2 q\}$, where $q=$ $\prod_{i=1}^{1993}\left(t^{2}+1\right)$. We claim that $A$ gives a solution for the problem. Indeed, for any $P \in A$ there is a quarter of the unit circle centered at $P$ that is contained in the square $[0,2] \times[0,2]$. As explained above, there are 1993 rational points on this quarter circle, and by definition of $q$ they all belong to $A$. Remark. Substantially the same problem was proposed by Bulgaria for IMO 71: see (SL71-2), where we give another possible construction of a set $A$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2a813521-f780-5802-a503-a63617b96d09
| 24,455
|
10. (IND 5) A natural number $n$ is said to have the property $P$ if whenever $n$ divides $a^{n}-1$ for some integer $a, n^{2}$ also necessarily divides $a^{n}-1$. (a) Show that every prime number has property $P$. (b) Show that there are infinitely many composite numbers $n$ that possess property $P$.
|
10. (a) Let $n=p$ be a prime and let $p \mid a^{p}-1$. By Fermat's theorem $p \mid$ $a^{p-1}-1$, so that $p \mid a^{\operatorname{gcd}(p, p-1)}-1=a-1$, i.e., $a \equiv 1(\bmod p)$. Since then $a^{i} \equiv 1(\bmod p)$, we obtain $p \mid a^{p-1}+\cdots+a+1$ and hence $p^{2} \mid a^{p}-1=(a-1)\left(a^{p-1}+\cdots+a+1\right)$. (b) Let $n=p_{1} \cdots p_{k}$ be a product of distinct primes and let $n \mid a^{n}-1$. Then from $p_{i} \mid a^{n}-1=\left(a^{\left(n / p_{i}\right)}\right)^{p_{i}}-1$ and part (a) we conclude that $p_{i}^{2} \mid a^{n}-1$. Since this is true for all indices $i$, we also have $n^{2} \mid a^{n}-1$; hence $n$ has the property $P$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
10. (IND 5) A natural number $n$ is said to have the property $P$ if whenever $n$ divides $a^{n}-1$ for some integer $a, n^{2}$ also necessarily divides $a^{n}-1$. (a) Show that every prime number has property $P$. (b) Show that there are infinitely many composite numbers $n$ that possess property $P$.
|
10. (a) Let $n=p$ be a prime and let $p \mid a^{p}-1$. By Fermat's theorem $p \mid$ $a^{p-1}-1$, so that $p \mid a^{\operatorname{gcd}(p, p-1)}-1=a-1$, i.e., $a \equiv 1(\bmod p)$. Since then $a^{i} \equiv 1(\bmod p)$, we obtain $p \mid a^{p-1}+\cdots+a+1$ and hence $p^{2} \mid a^{p}-1=(a-1)\left(a^{p-1}+\cdots+a+1\right)$. (b) Let $n=p_{1} \cdots p_{k}$ be a product of distinct primes and let $n \mid a^{n}-1$. Then from $p_{i} \mid a^{n}-1=\left(a^{\left(n / p_{i}\right)}\right)^{p_{i}}-1$ and part (a) we conclude that $p_{i}^{2} \mid a^{n}-1$. Since this is true for all indices $i$, we also have $n^{2} \mid a^{n}-1$; hence $n$ has the property $P$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
22a09f39-d630-57cb-8028-4490b961dc35
| 24,457
|
11. (IRE 1) ${ }^{\mathrm{IMO1}}$ Let $n>1$ be an integer and let $f(x)=x^{n}+5 x^{n-1}+3$. Prove that there do not exist polynomials $g(x), h(x)$, each having integer coefficients and degree at least one, such that $f(x)=g(x) h(x)$.
|
11. Due to the extended Eisenstein criterion, $f$ must have an irreducible factor of degree not less than $n-1$. Since $f$ has no integral zeros, it must be irreducible. Second solution. The proposer's solution was as follows. Suppose that $f(x)=g(x) h(x)$, where $g, h$ are nonconstant polynomials with integer coefficients. Since $|f(0)|=3$, either $|g(0)|=1$ or $|h(0)|=1$. We may assume $|g(0)|=1$ and that $g(x)=\left(x-\alpha_{1}\right) \cdots\left(x-\alpha_{k}\right)$. Then $\left|\alpha_{1} \cdots \alpha_{k}\right|=$ 1. Since $\alpha_{i}^{n-1}\left(\alpha_{i}+5\right)=-3$, taking the product over $i=1,2, \ldots, k$ yields $\left|\left(\alpha_{1}+5\right) \cdots\left(\alpha_{k}+5\right)\right|=|g(-5)|=3^{k}$. But $f(-5)=g(-5) h(-5)=3$, so the only possibility is $\operatorname{deg} g=k=1$. This is impossible, because $f$ has no integral zeros. Remark. Generalizing this solution, it can be shown that if $a, m, n$ are positive integers and $p<a-1$ is a prime, then $F(x)=x^{m}(x-a)^{n}+p$ is irreducible. The details are left to the reader.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
11. (IRE 1) ${ }^{\mathrm{IMO1}}$ Let $n>1$ be an integer and let $f(x)=x^{n}+5 x^{n-1}+3$. Prove that there do not exist polynomials $g(x), h(x)$, each having integer coefficients and degree at least one, such that $f(x)=g(x) h(x)$.
|
11. Due to the extended Eisenstein criterion, $f$ must have an irreducible factor of degree not less than $n-1$. Since $f$ has no integral zeros, it must be irreducible. Second solution. The proposer's solution was as follows. Suppose that $f(x)=g(x) h(x)$, where $g, h$ are nonconstant polynomials with integer coefficients. Since $|f(0)|=3$, either $|g(0)|=1$ or $|h(0)|=1$. We may assume $|g(0)|=1$ and that $g(x)=\left(x-\alpha_{1}\right) \cdots\left(x-\alpha_{k}\right)$. Then $\left|\alpha_{1} \cdots \alpha_{k}\right|=$ 1. Since $\alpha_{i}^{n-1}\left(\alpha_{i}+5\right)=-3$, taking the product over $i=1,2, \ldots, k$ yields $\left|\left(\alpha_{1}+5\right) \cdots\left(\alpha_{k}+5\right)\right|=|g(-5)|=3^{k}$. But $f(-5)=g(-5) h(-5)=3$, so the only possibility is $\operatorname{deg} g=k=1$. This is impossible, because $f$ has no integral zeros. Remark. Generalizing this solution, it can be shown that if $a, m, n$ are positive integers and $p<a-1$ is a prime, then $F(x)=x^{m}(x-a)^{n}+p$ is irreducible. The details are left to the reader.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
53fb5968-2f4b-563a-99e5-6a00e6ffe8de
| 24,458
|
12. (IRE 2) Let $n, k$ be positive integers with $k \leq n$ and let $S$ be a set containing $n$ distinct real numbers. Let $T$ be the set of all real numbers of the form $x_{1}+x_{2}+\cdots+x_{k}$, where $x_{1}, x_{2}, \ldots, x_{k}$ are distinct elements of $S$. Prove that $T$ contains at least $k(n-k)+1$ distinct elements.
|
12. Let $x_{1}<x_{2}<\cdots<x_{n}$ be the elements of $S$. We use induction on $n$. The result is trivial for $k=1$ or $n=k$, so assume that it is true for $n-1$ numbers. Then there exist $m=(k-1)(n-k)+1$ distinct sums of $k-1$ numbers among $x_{2}, \ldots, x_{n}$; call these sums $S_{i}, S_{1}<S_{2}<\cdots<S_{m}$. Then $x_{1}+S_{1}, x_{1}+S_{2}, \ldots, x_{1}+S_{m}$ are distinct sums of $k$ of the numbers $x_{1}, x_{2}, \ldots, x_{n}$. However, the biggest of these sums is $$ x_{1}+S_{m} \leq x_{1}+x_{n-k+2}+x_{n-k+3}+\cdots+x_{n} $$ hence we can find $n-k$ sums that are greater and thus not included here: $x_{2}+x_{n-k+2}+\cdots+x_{n}, x_{3}+x_{n-k+2}+\cdots+x_{n}, \ldots, x_{n-k+1}+x_{n-k+2}+\cdots+x_{n}$. This counts for $k(n-k)+1$ sums in total. Remark. Equality occurs if $S$ is an arithmetic progression.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. (IRE 2) Let $n, k$ be positive integers with $k \leq n$ and let $S$ be a set containing $n$ distinct real numbers. Let $T$ be the set of all real numbers of the form $x_{1}+x_{2}+\cdots+x_{k}$, where $x_{1}, x_{2}, \ldots, x_{k}$ are distinct elements of $S$. Prove that $T$ contains at least $k(n-k)+1$ distinct elements.
|
12. Let $x_{1}<x_{2}<\cdots<x_{n}$ be the elements of $S$. We use induction on $n$. The result is trivial for $k=1$ or $n=k$, so assume that it is true for $n-1$ numbers. Then there exist $m=(k-1)(n-k)+1$ distinct sums of $k-1$ numbers among $x_{2}, \ldots, x_{n}$; call these sums $S_{i}, S_{1}<S_{2}<\cdots<S_{m}$. Then $x_{1}+S_{1}, x_{1}+S_{2}, \ldots, x_{1}+S_{m}$ are distinct sums of $k$ of the numbers $x_{1}, x_{2}, \ldots, x_{n}$. However, the biggest of these sums is $$ x_{1}+S_{m} \leq x_{1}+x_{n-k+2}+x_{n-k+3}+\cdots+x_{n} $$ hence we can find $n-k$ sums that are greater and thus not included here: $x_{2}+x_{n-k+2}+\cdots+x_{n}, x_{3}+x_{n-k+2}+\cdots+x_{n}, \ldots, x_{n-k+1}+x_{n-k+2}+\cdots+x_{n}$. This counts for $k(n-k)+1$ sums in total. Remark. Equality occurs if $S$ is an arithmetic progression.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
293d157e-e212-505e-bbc8-570b22c48a3f
| 24,461
|
13. (IRE 3) Let $S$ be the set of all pairs $(m, n)$ of relatively prime positive integers $m, n$ with $n$ even and $m<n$. For $s=(m, n) \in S$ write $n=2^{k} n_{0}$, where $k, n_{0}$ are positive integers with $n_{0}$ odd and define $f(s)=\left(n_{0}, m+\right.$ $n-n_{0}$ ). Prove that $f$ is a function from $S$ to $S$ and that for each $s=(m, n) \in S$, there exists a positive integer $t \leq \frac{m+n+1}{4}$ such that $f^{t}(s)=s$, where $$ f^{t}(s)=\underbrace{(f \circ f \circ \cdots \circ f)}_{t \text { times }}(s) . $$ If $m+n$ is a prime number that does not divide $2^{k}-1$ for $k=1,2, \ldots, m+$ $n-2$, prove that the smallest value of $t$ that satisfies the above conditions is $\left[\frac{m+n+1}{4}\right]$, where $[x]$ denotes the greatest integer less than or equal to $x$.
|
13. For an odd integer $N>1$, let $S_{N}=\{(m, n) \in S \mid m+n=N\}$. If $f(m, n)=\left(m_{1}, n_{1}\right)$, then $m_{1}+n_{1}=m+n$ with $m_{1}$ odd and $m_{1} \leq \frac{n}{2}<$ $\frac{N}{2}<n_{1}$, so $f$ maps $S_{N}$ to $S_{N}$. Also $f$ is bijective, since if $f(m, n)=$ $\left(m_{1}, n_{1}\right)$, then $n$ is uniquely determined as the even number of the form $2^{k} m_{1}$ that belongs to the interval $\left[\frac{N+1}{2}, N\right]$, and this also determines $m$. Note that $S_{N}$ has at most $\left[\frac{N+1}{4}\right]$ elements, with equality if and only if $N$ is prime. Thus if $(m, n) \in S_{N}$, there exist $s, r$ with $1 \leq s<r \leq\left[\frac{N+5}{4}\right]$ such that $f^{s}(m, n)=f^{r}(m, n)$. Consequently $f^{t}(m, n)=(m, n)$, where $t=r-s, 0<t \leq\left[\frac{N+1}{4}\right]=\left[\frac{m+n+1}{4}\right]$. Suppose that $(m, n) \in S_{N}$ and $t$ is the least positive integer with $f^{t}(m, n)=(m, n)$. We write $(m, n)=\left(m_{0}, n_{0}\right)$ and $f^{i}(m, n)=\left(m_{i}, n_{i}\right)$ for $i=1, \ldots, t$. Then there exist positive integers $a_{i}$ such that $2^{a_{i}} m_{i}=n_{i-1}$, $i=1, \ldots, t$. Since $m_{t}=m_{0}$, multiplying these equalities gives $$ \begin{aligned} 2^{a_{1}+a_{2}+\cdots+a_{t}} m_{0} m_{1} \cdots m_{t-1} & =n_{0} n_{1} \cdots n_{t-1} \\ & \equiv(-1)^{t} m_{0} m_{1} \cdots m_{t-1}(\bmod N) . \end{aligned} $$ It follows that $N \mid 2^{k} \pm 1$ and consequently $N \mid 2^{2 k}-1$, where $k=$ $a_{1}+\cdots+a_{t}$. On the other hand, it also follows that $2^{k}\left|n_{0} n_{1} \cdots n_{t-1}\right|$ $(N-1)(N-3) \cdots(N-2[N / 4])$. But since $$ \frac{(N-1)(N-3) \cdots\left(N-2\left[\frac{N}{4}\right]\right)}{1 \cdot 3 \cdots\left(2\left[\frac{N-2}{4}\right]+1\right)}=\frac{2 \cdot 4 \cdots(N-1)}{1 \cdot 2 \cdots \frac{N-1}{2}}=2^{\frac{N-1}{2}} $$ we conclude that $0<k \leq \frac{N-1}{2}$, where equality holds if and only if $\left\{n_{1}, \ldots, n_{t}\right\}$ is the set of all even integers from $\frac{N+1}{2}$ to $N-1$, and consequently $t=\frac{N+1}{4}$. Now if $N \nmid 2^{h}-1$ for $1 \leq h<N-1$, we must have $2 k=N-1$. Therefore $t=\frac{N+1}{4}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
13. (IRE 3) Let $S$ be the set of all pairs $(m, n)$ of relatively prime positive integers $m, n$ with $n$ even and $m<n$. For $s=(m, n) \in S$ write $n=2^{k} n_{0}$, where $k, n_{0}$ are positive integers with $n_{0}$ odd and define $f(s)=\left(n_{0}, m+\right.$ $n-n_{0}$ ). Prove that $f$ is a function from $S$ to $S$ and that for each $s=(m, n) \in S$, there exists a positive integer $t \leq \frac{m+n+1}{4}$ such that $f^{t}(s)=s$, where $$ f^{t}(s)=\underbrace{(f \circ f \circ \cdots \circ f)}_{t \text { times }}(s) . $$ If $m+n$ is a prime number that does not divide $2^{k}-1$ for $k=1,2, \ldots, m+$ $n-2$, prove that the smallest value of $t$ that satisfies the above conditions is $\left[\frac{m+n+1}{4}\right]$, where $[x]$ denotes the greatest integer less than or equal to $x$.
|
13. For an odd integer $N>1$, let $S_{N}=\{(m, n) \in S \mid m+n=N\}$. If $f(m, n)=\left(m_{1}, n_{1}\right)$, then $m_{1}+n_{1}=m+n$ with $m_{1}$ odd and $m_{1} \leq \frac{n}{2}<$ $\frac{N}{2}<n_{1}$, so $f$ maps $S_{N}$ to $S_{N}$. Also $f$ is bijective, since if $f(m, n)=$ $\left(m_{1}, n_{1}\right)$, then $n$ is uniquely determined as the even number of the form $2^{k} m_{1}$ that belongs to the interval $\left[\frac{N+1}{2}, N\right]$, and this also determines $m$. Note that $S_{N}$ has at most $\left[\frac{N+1}{4}\right]$ elements, with equality if and only if $N$ is prime. Thus if $(m, n) \in S_{N}$, there exist $s, r$ with $1 \leq s<r \leq\left[\frac{N+5}{4}\right]$ such that $f^{s}(m, n)=f^{r}(m, n)$. Consequently $f^{t}(m, n)=(m, n)$, where $t=r-s, 0<t \leq\left[\frac{N+1}{4}\right]=\left[\frac{m+n+1}{4}\right]$. Suppose that $(m, n) \in S_{N}$ and $t$ is the least positive integer with $f^{t}(m, n)=(m, n)$. We write $(m, n)=\left(m_{0}, n_{0}\right)$ and $f^{i}(m, n)=\left(m_{i}, n_{i}\right)$ for $i=1, \ldots, t$. Then there exist positive integers $a_{i}$ such that $2^{a_{i}} m_{i}=n_{i-1}$, $i=1, \ldots, t$. Since $m_{t}=m_{0}$, multiplying these equalities gives $$ \begin{aligned} 2^{a_{1}+a_{2}+\cdots+a_{t}} m_{0} m_{1} \cdots m_{t-1} & =n_{0} n_{1} \cdots n_{t-1} \\ & \equiv(-1)^{t} m_{0} m_{1} \cdots m_{t-1}(\bmod N) . \end{aligned} $$ It follows that $N \mid 2^{k} \pm 1$ and consequently $N \mid 2^{2 k}-1$, where $k=$ $a_{1}+\cdots+a_{t}$. On the other hand, it also follows that $2^{k}\left|n_{0} n_{1} \cdots n_{t-1}\right|$ $(N-1)(N-3) \cdots(N-2[N / 4])$. But since $$ \frac{(N-1)(N-3) \cdots\left(N-2\left[\frac{N}{4}\right]\right)}{1 \cdot 3 \cdots\left(2\left[\frac{N-2}{4}\right]+1\right)}=\frac{2 \cdot 4 \cdots(N-1)}{1 \cdot 2 \cdots \frac{N-1}{2}}=2^{\frac{N-1}{2}} $$ we conclude that $0<k \leq \frac{N-1}{2}$, where equality holds if and only if $\left\{n_{1}, \ldots, n_{t}\right\}$ is the set of all even integers from $\frac{N+1}{2}$ to $N-1$, and consequently $t=\frac{N+1}{4}$. Now if $N \nmid 2^{h}-1$ for $1 \leq h<N-1$, we must have $2 k=N-1$. Therefore $t=\frac{N+1}{4}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
89b61d97-d99c-57f0-a382-30cf17fa0e87
| 24,463
|
14. (ISR 1) The vertices $D, E, F$ of an equilateral triangle lie on the sides $B C, C A, A B$ respectively of a triangle $A B C$. If $a, b, c$ are the respective lengths of these sides, and $S$ the area of $A B C$, prove that $$ D E \geq \frac{2 \sqrt{2} S}{\sqrt{a^{2}+b^{2}+c^{2}+4 \sqrt{3} S}} $$
|
14. Consider any point $T$ inside the triangle $A B C$ or on its boundary. Since $$ \begin{aligned} 2 S & =2\left(S_{A E T F}+S_{B F T D}+S_{C D T E}\right) \\ & \leq A T \cdot E F+B T \cdot F D+C T \cdot D E=(A T+B T+C T) D E \end{aligned} $$ it suffices to find a point $T$ such that $$ (A T+B T+C T)^{2} \geq \frac{a^{2}+b^{2}+c^{2}+4 S \sqrt{3}}{2} . $$ We distinguish two cases: (i) If all angles of $\triangle A B C$ are less than $120^{\circ}$, then the sum $A T+B T+C T$ attains its minimum when $T$ is the Torricelli point, i.e., such that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. In this case, by the cosine theorem we get $$ \begin{aligned} A T^{2}+A T \cdot B T+B T^{2} & =c^{2}, \\ B T^{2}+B T \cdot C T+C T^{2} & =a^{2}, \\ C T^{2}+C T \cdot A T+A T^{2} & =b^{2}, \\ 3(A T \cdot B T+B T \cdot C T+C T \cdot A T) & =4 \sqrt{3}\left(S_{A T B}+S_{B T C}+S_{C T A}\right) \\ & =4 \sqrt{3} S . \end{aligned} $$ Adding these four equalities, we obtain $2(A T+B T+C T)^{2}=a^{2}+$ $b^{2}+c^{2}+4 \sqrt{3} S$. (ii) Let $\angle A C B \geq 120^{\circ}$. We claim that $T=C$ satisfies the requirements. Indeed, $a^{2}+b^{2}+c^{2}+4 \sqrt{3} S=a^{2}+b^{2}+\left(a^{2}+b^{2}-2 a b \cos \angle C\right)+$ $2 \sqrt{3} a b \sin \angle C=2\left(a^{2}+b^{2}\right)+2 a b(\sqrt{3} \sin \angle C-\cos \angle C)=2\left(a^{2}+b^{2}\right)+$ $4 a b \sin \left(\angle C-30^{\circ}\right) \leq 2(a+b)^{2}$, which proves the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
14. (ISR 1) The vertices $D, E, F$ of an equilateral triangle lie on the sides $B C, C A, A B$ respectively of a triangle $A B C$. If $a, b, c$ are the respective lengths of these sides, and $S$ the area of $A B C$, prove that $$ D E \geq \frac{2 \sqrt{2} S}{\sqrt{a^{2}+b^{2}+c^{2}+4 \sqrt{3} S}} $$
|
14. Consider any point $T$ inside the triangle $A B C$ or on its boundary. Since $$ \begin{aligned} 2 S & =2\left(S_{A E T F}+S_{B F T D}+S_{C D T E}\right) \\ & \leq A T \cdot E F+B T \cdot F D+C T \cdot D E=(A T+B T+C T) D E \end{aligned} $$ it suffices to find a point $T$ such that $$ (A T+B T+C T)^{2} \geq \frac{a^{2}+b^{2}+c^{2}+4 S \sqrt{3}}{2} . $$ We distinguish two cases: (i) If all angles of $\triangle A B C$ are less than $120^{\circ}$, then the sum $A T+B T+C T$ attains its minimum when $T$ is the Torricelli point, i.e., such that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. In this case, by the cosine theorem we get $$ \begin{aligned} A T^{2}+A T \cdot B T+B T^{2} & =c^{2}, \\ B T^{2}+B T \cdot C T+C T^{2} & =a^{2}, \\ C T^{2}+C T \cdot A T+A T^{2} & =b^{2}, \\ 3(A T \cdot B T+B T \cdot C T+C T \cdot A T) & =4 \sqrt{3}\left(S_{A T B}+S_{B T C}+S_{C T A}\right) \\ & =4 \sqrt{3} S . \end{aligned} $$ Adding these four equalities, we obtain $2(A T+B T+C T)^{2}=a^{2}+$ $b^{2}+c^{2}+4 \sqrt{3} S$. (ii) Let $\angle A C B \geq 120^{\circ}$. We claim that $T=C$ satisfies the requirements. Indeed, $a^{2}+b^{2}+c^{2}+4 \sqrt{3} S=a^{2}+b^{2}+\left(a^{2}+b^{2}-2 a b \cos \angle C\right)+$ $2 \sqrt{3} a b \sin \angle C=2\left(a^{2}+b^{2}\right)+2 a b(\sqrt{3} \sin \angle C-\cos \angle C)=2\left(a^{2}+b^{2}\right)+$ $4 a b \sin \left(\angle C-30^{\circ}\right) \leq 2(a+b)^{2}$, which proves the desired inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3c1b8a26-d29a-5e0e-8a25-bf900462c0b2
| 24,466
|
15. (MCD 1) ${ }^{\mathrm{IMO} 4}$ For three points $A, B, C$ in the plane we define $m(A B C)$ to be the smallest length of the three altitudes of the triangle $A B C$, where in the case of $A, B, C$ collinear, $m(A B C)=0$. Let $A, B, C$ be given points in the plane. Prove that for any point $X$ in the plane, $$ m(A B C) \leq m(A B X)+m(A X C)+m(X B C) $$
|
15. Denote by $d(P Q R)$ the diameter of a triangle $P Q R$. It is clear that $d(P Q R) \cdot m(P Q R)=2 S_{P Q R}$. So if the point $X$ lies inside the triangle $A B C$ or on its boundary, we have $d(A B X), d(B C X), d(C A X) \leq d(A B C)$, which implies $$ \begin{aligned} m(A B X)+m(B C X)+m(C A X) & =\frac{2 S_{A B X}}{d(A B X)}+\frac{2 S_{B C X}}{d(B C X)}+\frac{2 S_{C A X}}{d(C A X)} \\ & \geq \frac{2 S_{A B X}+2 S_{B C X}+2 S_{C A X}}{d(A B C)} \\ & =\frac{2 S_{A B C}}{d(A B C)}=m(A B C) \end{aligned} $$ If $X$ is outside $\triangle A B C$ but inside the angle $B A C$, consider the point $Y$ of intersection of $A X$ and $B C$. Then $m(A B X)+m(B C X)+m(C A X) \geq$ $m(A B Y)+m(B C Y)+m(C A Y) \geq m(A B C)$. Also, if $X$ is inside the opposite angle of $\angle B A C$ (i.e., $\angle D A E$, where $\mathcal{B}(D, A, B)$ and $\mathcal{B}(E, A, C)$ ), then $m(A B X)+m(B C X)+m(C A X) \geq m(B C X) \geq m(A B C)$. Since these are substantially all possible different positions of point $X$, we have finished the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
15. (MCD 1) ${ }^{\mathrm{IMO} 4}$ For three points $A, B, C$ in the plane we define $m(A B C)$ to be the smallest length of the three altitudes of the triangle $A B C$, where in the case of $A, B, C$ collinear, $m(A B C)=0$. Let $A, B, C$ be given points in the plane. Prove that for any point $X$ in the plane, $$ m(A B C) \leq m(A B X)+m(A X C)+m(X B C) $$
|
15. Denote by $d(P Q R)$ the diameter of a triangle $P Q R$. It is clear that $d(P Q R) \cdot m(P Q R)=2 S_{P Q R}$. So if the point $X$ lies inside the triangle $A B C$ or on its boundary, we have $d(A B X), d(B C X), d(C A X) \leq d(A B C)$, which implies $$ \begin{aligned} m(A B X)+m(B C X)+m(C A X) & =\frac{2 S_{A B X}}{d(A B X)}+\frac{2 S_{B C X}}{d(B C X)}+\frac{2 S_{C A X}}{d(C A X)} \\ & \geq \frac{2 S_{A B X}+2 S_{B C X}+2 S_{C A X}}{d(A B C)} \\ & =\frac{2 S_{A B C}}{d(A B C)}=m(A B C) \end{aligned} $$ If $X$ is outside $\triangle A B C$ but inside the angle $B A C$, consider the point $Y$ of intersection of $A X$ and $B C$. Then $m(A B X)+m(B C X)+m(C A X) \geq$ $m(A B Y)+m(B C Y)+m(C A Y) \geq m(A B C)$. Also, if $X$ is inside the opposite angle of $\angle B A C$ (i.e., $\angle D A E$, where $\mathcal{B}(D, A, B)$ and $\mathcal{B}(E, A, C)$ ), then $m(A B X)+m(B C X)+m(C A X) \geq m(B C X) \geq m(A B C)$. Since these are substantially all possible different positions of point $X$, we have finished the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e6850b7-a38c-5ee0-a3d0-7ff4b4bfe0c8
| 24,468
|
16. (MCD 3) Let $n \in \mathbb{N}, n \geq 2$, and $A_{0}=\left(a_{01}, a_{02}, \ldots, a_{0 n}\right)$ be any $n$-tuple of natural numbers such that $0 \leq a_{0 i} \leq i-1$, for $i=1, \ldots, n$. The $n$-tuples $A_{1}=\left(a_{11}, a_{12}, \ldots, a_{1 n}\right), A_{2}=\left(a_{21}, a_{22}, \ldots, a_{2 n}\right), \ldots$ are defined by $a_{i+1, j}=\operatorname{Card}\left\{a_{i, l} \mid 1 \leq l \leq j-1, a_{i, l} \geq a_{i, j}\right\}, \quad$ for $i \in \mathbb{N}$ and $j=1, \ldots, n$. Prove that there exists $k \in \mathbb{N}$, such that $A_{k+2}=A_{k}$.
|
16. Let $S_{n}=\left\{A=\left(a_{1}, \ldots, a_{n}\right) \mid 0 \leq a_{i}<i\right\}$. For $A=\left(a_{1}, \ldots, a_{n}\right)$, let $A^{\prime}=\left(a_{1}, \ldots, a_{n-1}\right)$, so that we can write $A=\left(A^{\prime}, a_{n}\right)$. The proof of the statement from the problem will be given by induction on $n$. For $n=2$ there are two possibilities for $A_{0}$, so one directly checks that $A_{2}=A_{0}$. Now assume that $n \geq 3$ and that $A_{0}=\left(A_{0}^{\prime}, a_{0 n}\right) \in S_{n}$. It is clear that then any $A_{i}$ is in $S_{n}$ too. By the induction hypothesis there exists $k \in \mathbb{N}$ such that $A_{k}^{\prime}=A_{k+2}^{\prime}=A_{k+4}^{\prime}=\cdots$ and $A_{k+1}^{\prime}=A_{k+3}^{\prime}=\cdots$. Observe that if we increase (decrease) $a_{k n}, a_{k+1, n}$ will decrease (respectively increase), and this will also increase (respectively decrease) $a_{k+2, n}$. Hence $a_{k n}, a_{k+2, n}, a_{k+4, n}, \ldots$ is monotonically increasing or decreasing, and since it is bounded (by 0 and $n-1$ ), it follows that we will eventually have $a_{k+2 i, n}=a_{k+2 i+2, n}=\cdots$. Consequently $A_{k+2 i}=A_{k+2 i+2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
16. (MCD 3) Let $n \in \mathbb{N}, n \geq 2$, and $A_{0}=\left(a_{01}, a_{02}, \ldots, a_{0 n}\right)$ be any $n$-tuple of natural numbers such that $0 \leq a_{0 i} \leq i-1$, for $i=1, \ldots, n$. The $n$-tuples $A_{1}=\left(a_{11}, a_{12}, \ldots, a_{1 n}\right), A_{2}=\left(a_{21}, a_{22}, \ldots, a_{2 n}\right), \ldots$ are defined by $a_{i+1, j}=\operatorname{Card}\left\{a_{i, l} \mid 1 \leq l \leq j-1, a_{i, l} \geq a_{i, j}\right\}, \quad$ for $i \in \mathbb{N}$ and $j=1, \ldots, n$. Prove that there exists $k \in \mathbb{N}$, such that $A_{k+2}=A_{k}$.
|
16. Let $S_{n}=\left\{A=\left(a_{1}, \ldots, a_{n}\right) \mid 0 \leq a_{i}<i\right\}$. For $A=\left(a_{1}, \ldots, a_{n}\right)$, let $A^{\prime}=\left(a_{1}, \ldots, a_{n-1}\right)$, so that we can write $A=\left(A^{\prime}, a_{n}\right)$. The proof of the statement from the problem will be given by induction on $n$. For $n=2$ there are two possibilities for $A_{0}$, so one directly checks that $A_{2}=A_{0}$. Now assume that $n \geq 3$ and that $A_{0}=\left(A_{0}^{\prime}, a_{0 n}\right) \in S_{n}$. It is clear that then any $A_{i}$ is in $S_{n}$ too. By the induction hypothesis there exists $k \in \mathbb{N}$ such that $A_{k}^{\prime}=A_{k+2}^{\prime}=A_{k+4}^{\prime}=\cdots$ and $A_{k+1}^{\prime}=A_{k+3}^{\prime}=\cdots$. Observe that if we increase (decrease) $a_{k n}, a_{k+1, n}$ will decrease (respectively increase), and this will also increase (respectively decrease) $a_{k+2, n}$. Hence $a_{k n}, a_{k+2, n}, a_{k+4, n}, \ldots$ is monotonically increasing or decreasing, and since it is bounded (by 0 and $n-1$ ), it follows that we will eventually have $a_{k+2 i, n}=a_{k+2 i+2, n}=\cdots$. Consequently $A_{k+2 i}=A_{k+2 i+2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0f5658e1-439e-5ba7-9042-35e24cd91138
| 24,472
|
17. (NET 2) ${ }^{\mathrm{IMO} 6}$ Let $n$ be an integer greater than 1 . In a circular arrangement of $n$ lamps $L_{0}, \ldots, L_{n-1}$, each one of that can be either ON or OFF, we start with the situation where all lamps are ON, and then carry out a sequence of steps, $S_{t e p_{0}}, S t e p_{1}, \ldots$. If $L_{j-1}(j$ is taken $\bmod n)$ is ON, then $S_{t e p}^{j}$ changes the status of $L_{j}$ (it goes from ON to OFF or from OFF to ON) but does not change the status of any of the other lamps. If $L_{j-1}$ is OFF, then $S_{t e p}^{j}$ does not change anything at all. Show that: (a) There is a positive integer $M(n)$ such that after $M(n)$ steps all lamps are ON again. (b) If $n$ has the form $2^{k}$, then all lamps are ON after $n^{2}-1$ steps. (c) If $n$ has the form $2^{k}+1$, then all lamps are ON after $n^{2}-n+1$ steps.
|
17. We introduce the rotation operation Rot to the left by one, so that $S_{t e p_{j}}=$ Rot $^{-j} \circ$ Step $_{0} \circ$ Rot $^{j}$. Now writing Step ${ }^{*}={\text { Rot } \circ \text { Step }_{0} \text {, the problem is }}^{-20}$ transformed into the question whether there is an $M(n)$ such that all lamps are $O N$ again after $M(n)$ successive applications of Step*. We operate in the field $\mathbb{Z}_{2}$, representing $O F F$ by 0 and $O N$ by 1 . So if the status of $L_{j}$ at some moment is given by $v_{j} \in \mathbb{Z}_{2}$, the effect of $S t e p_{j}$ is that $v_{j}$ is replaced by $v_{j}+v_{j-1}$. With the $n$-tuple $v_{0}, \ldots, v_{n-1}$ we associate the polynomial $$ P(x)=v_{n-1} x^{n-1}+v_{0} x^{n-2}+v_{1} x^{n-3}+\cdots+v_{n-2} . $$ By means of Step*, this polynomial is transformed into the polynomial $Q(x)$ over $\mathbb{Z}$ of degree less than $n$ that satisfies $Q(x) \equiv x P(x)(\bmod$ $\left.x^{n}+x^{n-1}+1\right)$. From now on, the sign $\equiv$ always stands for congruence with this modulus. (i) It suffices to show the existence of $M(n)$ with $x^{M(n)} \equiv 1$. Because the number of residue classes is finite, there are $r, q, r<q$ such that $x^{q} \equiv x^{r}$, i.e., $x^{r}\left(x^{q-r}-1\right)=0$. One can take $M(n)=q-r$. (Or simply note that there are only finitely many possible configurations; since each operation is bijective, the configuration that reappears first must be $O N, O N, \ldots, O N$.) (ii) We shall prove that if $n=2^{k}$, then $x^{n^{2}-1} \equiv 1$. We have $x^{n^{2}} \equiv$ $\left(x^{n-1}+1\right)^{n} \equiv x^{n^{2}-n}+1$, because all binomial coefficients of order $n=2^{k}$ are even, apart from the first one and the last one. Since also $x^{n^{2}} \equiv x^{n^{2}-1}+x^{n^{2}-n}$, this is what we wanted. (iii) Now if $n=2^{k}+1$, we prove that $x^{n^{2}-n+1} \equiv 1$. We have $x^{n^{2}-1} \equiv$ $\left(x^{n+1}\right)^{n-1} \equiv\left(x+x^{n}\right)^{n-1} \equiv x^{n-1}+x^{n^{2}-n}$ (again by evenness of binomial coefficients of order $n-1=2^{k}$ ). Together with $x^{n^{2}} \equiv x^{n^{2}-1}+$ $x^{n^{2}-n}$, this leads to $x^{n^{2}} \equiv x^{n-1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
17. (NET 2) ${ }^{\mathrm{IMO} 6}$ Let $n$ be an integer greater than 1 . In a circular arrangement of $n$ lamps $L_{0}, \ldots, L_{n-1}$, each one of that can be either ON or OFF, we start with the situation where all lamps are ON, and then carry out a sequence of steps, $S_{t e p_{0}}, S t e p_{1}, \ldots$. If $L_{j-1}(j$ is taken $\bmod n)$ is ON, then $S_{t e p}^{j}$ changes the status of $L_{j}$ (it goes from ON to OFF or from OFF to ON) but does not change the status of any of the other lamps. If $L_{j-1}$ is OFF, then $S_{t e p}^{j}$ does not change anything at all. Show that: (a) There is a positive integer $M(n)$ such that after $M(n)$ steps all lamps are ON again. (b) If $n$ has the form $2^{k}$, then all lamps are ON after $n^{2}-1$ steps. (c) If $n$ has the form $2^{k}+1$, then all lamps are ON after $n^{2}-n+1$ steps.
|
17. We introduce the rotation operation Rot to the left by one, so that $S_{t e p_{j}}=$ Rot $^{-j} \circ$ Step $_{0} \circ$ Rot $^{j}$. Now writing Step ${ }^{*}={\text { Rot } \circ \text { Step }_{0} \text {, the problem is }}^{-20}$ transformed into the question whether there is an $M(n)$ such that all lamps are $O N$ again after $M(n)$ successive applications of Step*. We operate in the field $\mathbb{Z}_{2}$, representing $O F F$ by 0 and $O N$ by 1 . So if the status of $L_{j}$ at some moment is given by $v_{j} \in \mathbb{Z}_{2}$, the effect of $S t e p_{j}$ is that $v_{j}$ is replaced by $v_{j}+v_{j-1}$. With the $n$-tuple $v_{0}, \ldots, v_{n-1}$ we associate the polynomial $$ P(x)=v_{n-1} x^{n-1}+v_{0} x^{n-2}+v_{1} x^{n-3}+\cdots+v_{n-2} . $$ By means of Step*, this polynomial is transformed into the polynomial $Q(x)$ over $\mathbb{Z}$ of degree less than $n$ that satisfies $Q(x) \equiv x P(x)(\bmod$ $\left.x^{n}+x^{n-1}+1\right)$. From now on, the sign $\equiv$ always stands for congruence with this modulus. (i) It suffices to show the existence of $M(n)$ with $x^{M(n)} \equiv 1$. Because the number of residue classes is finite, there are $r, q, r<q$ such that $x^{q} \equiv x^{r}$, i.e., $x^{r}\left(x^{q-r}-1\right)=0$. One can take $M(n)=q-r$. (Or simply note that there are only finitely many possible configurations; since each operation is bijective, the configuration that reappears first must be $O N, O N, \ldots, O N$.) (ii) We shall prove that if $n=2^{k}$, then $x^{n^{2}-1} \equiv 1$. We have $x^{n^{2}} \equiv$ $\left(x^{n-1}+1\right)^{n} \equiv x^{n^{2}-n}+1$, because all binomial coefficients of order $n=2^{k}$ are even, apart from the first one and the last one. Since also $x^{n^{2}} \equiv x^{n^{2}-1}+x^{n^{2}-n}$, this is what we wanted. (iii) Now if $n=2^{k}+1$, we prove that $x^{n^{2}-n+1} \equiv 1$. We have $x^{n^{2}-1} \equiv$ $\left(x^{n+1}\right)^{n-1} \equiv\left(x+x^{n}\right)^{n-1} \equiv x^{n-1}+x^{n^{2}-n}$ (again by evenness of binomial coefficients of order $n-1=2^{k}$ ). Together with $x^{n^{2}} \equiv x^{n^{2}-1}+$ $x^{n^{2}-n}$, this leads to $x^{n^{2}} \equiv x^{n-1}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
253cbf36-f97d-5217-b9cd-ebc98f81de49
| 24,474
|
18. (POL 1) Let $S_{n}$ be the number of sequences $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$, where $a_{i} \in$ $\{0,1\}$, in which no six consecutive blocks are equal. Prove that $S_{n} \rightarrow \infty$ as $n \rightarrow \infty$.
|
18. Let $B_{n}$ be the set of sequences with the stated property $\left(S_{n}=\left|B_{n}\right|\right)$. We shall prove by induction on $n$ that $S_{n} \geq \frac{3}{2} S_{n-1}$ for every $n$. Suppose that for every $i \leq n, S_{i} \geq \frac{3}{2} S_{i-1}$, and consequently $S_{i} \leq$ $\left(\frac{2}{3}\right)^{n-i} S_{n}$. Let us consider the $2 S_{n}$ sequences obtained by putting 0 or 1 at the end of any sequence from $B_{n}$. If some sequence among them does not belong to $B_{n+1}$, then for some $k \geq 1$ it can be obtained by extending some sequence from $B_{n+1-6 k}$ by a sequence of $k$ terms repeated six times. The number of such sequences is $2^{k} S_{n+1-6 k}$. Hence the number of sequences not satisfying our condition is not greater than $$ \sum_{k \geq 1} 2^{k} S_{n+1-6 k} \leq \sum_{k \geq 1} 2^{k}\left(\frac{2}{3}\right)^{6 k-1} S_{n}=\frac{3}{2} S_{n} \frac{2(2 / 3)^{6}}{1-2(2 / 3)^{6}}=\frac{192}{601} S_{n}<\frac{1}{2} S_{n} $$ Therefore $S_{n+1}$ is not smaller than $2 S_{n}-\frac{1}{2} S_{n}=\frac{3}{2} S_{n}$. Thus we have $S_{n} \geq\left(\frac{3}{2}\right)^{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
18. (POL 1) Let $S_{n}$ be the number of sequences $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$, where $a_{i} \in$ $\{0,1\}$, in which no six consecutive blocks are equal. Prove that $S_{n} \rightarrow \infty$ as $n \rightarrow \infty$.
|
18. Let $B_{n}$ be the set of sequences with the stated property $\left(S_{n}=\left|B_{n}\right|\right)$. We shall prove by induction on $n$ that $S_{n} \geq \frac{3}{2} S_{n-1}$ for every $n$. Suppose that for every $i \leq n, S_{i} \geq \frac{3}{2} S_{i-1}$, and consequently $S_{i} \leq$ $\left(\frac{2}{3}\right)^{n-i} S_{n}$. Let us consider the $2 S_{n}$ sequences obtained by putting 0 or 1 at the end of any sequence from $B_{n}$. If some sequence among them does not belong to $B_{n+1}$, then for some $k \geq 1$ it can be obtained by extending some sequence from $B_{n+1-6 k}$ by a sequence of $k$ terms repeated six times. The number of such sequences is $2^{k} S_{n+1-6 k}$. Hence the number of sequences not satisfying our condition is not greater than $$ \sum_{k \geq 1} 2^{k} S_{n+1-6 k} \leq \sum_{k \geq 1} 2^{k}\left(\frac{2}{3}\right)^{6 k-1} S_{n}=\frac{3}{2} S_{n} \frac{2(2 / 3)^{6}}{1-2(2 / 3)^{6}}=\frac{192}{601} S_{n}<\frac{1}{2} S_{n} $$ Therefore $S_{n+1}$ is not smaller than $2 S_{n}-\frac{1}{2} S_{n}=\frac{3}{2} S_{n}$. Thus we have $S_{n} \geq\left(\frac{3}{2}\right)^{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8e917801-b325-5c27-b08e-66eb08c7ae42
| 24,477
|
19. (ROM 2) Let $a, b, n$ be positive integers, $b>1$ and $b^{n}-1 \mid a$. Show that the representation of the number $a$ in the base $b$ contains at least $n$ digits different from zero.
|
19. Let $s$ be the minimum number of nonzero digits that can appear in the $b$ adic representation of any number divisible by $b^{n}-1$. Among all numbers divisible by $b^{n}-1$ and having $s$ nonzero digits in base $b$, we choose the number $A$ with the minimum sum of digits. Let $A=a_{1} b^{n_{1}}+\cdots+a_{s} b^{n_{s}}$, where $0<a_{i} \leq b-1$ and $n_{1}>n_{2}>\cdots>n_{s}$. First, suppose that $n_{i} \equiv n_{j}(\bmod n), i \neq j$. Consider the number $$ B=A-a_{i} b^{n_{i}}-a_{j} b^{n_{j}}+\left(a_{i}+a_{j}\right) b^{n_{j}+k n} $$ with $k$ chosen large enough so that $n_{j}+k n>n_{1}$ : this number is divisible by $b^{n}-1$ as well. But if $a_{i}+a_{j}<b$, then $B$ has $s-1$ digits in base $b$, which is impossible; on the other hand, $a_{i}+a_{j} \geq b$ is also impossible, for otherwise $B$ would have sum of digits less for $b-1$ than that of $A$ (because $B$ would have digits 1 and $a_{i}+a_{j}-b$ in the positions $\left.n_{j}+k n+1, n_{j}+k n\right)$. Therefore $n_{i} \not \equiv n_{j}$ if $i \neq j$. Let $n_{i} \equiv r_{i}$, where $r_{i} \in\{0,1, \ldots, n-1\}$ are distinct. The number $C=$ $a_{1} b^{r_{1}}+\cdots+a_{s} b^{r_{s}}$ also has $s$ digits and is divisible by $b^{n}-1$. But since $C<b^{n}$, the only possibility is $C=b^{n}-1$ which has exactly $n$ digits in base $b$. It follows that $s=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
19. (ROM 2) Let $a, b, n$ be positive integers, $b>1$ and $b^{n}-1 \mid a$. Show that the representation of the number $a$ in the base $b$ contains at least $n$ digits different from zero.
|
19. Let $s$ be the minimum number of nonzero digits that can appear in the $b$ adic representation of any number divisible by $b^{n}-1$. Among all numbers divisible by $b^{n}-1$ and having $s$ nonzero digits in base $b$, we choose the number $A$ with the minimum sum of digits. Let $A=a_{1} b^{n_{1}}+\cdots+a_{s} b^{n_{s}}$, where $0<a_{i} \leq b-1$ and $n_{1}>n_{2}>\cdots>n_{s}$. First, suppose that $n_{i} \equiv n_{j}(\bmod n), i \neq j$. Consider the number $$ B=A-a_{i} b^{n_{i}}-a_{j} b^{n_{j}}+\left(a_{i}+a_{j}\right) b^{n_{j}+k n} $$ with $k$ chosen large enough so that $n_{j}+k n>n_{1}$ : this number is divisible by $b^{n}-1$ as well. But if $a_{i}+a_{j}<b$, then $B$ has $s-1$ digits in base $b$, which is impossible; on the other hand, $a_{i}+a_{j} \geq b$ is also impossible, for otherwise $B$ would have sum of digits less for $b-1$ than that of $A$ (because $B$ would have digits 1 and $a_{i}+a_{j}-b$ in the positions $\left.n_{j}+k n+1, n_{j}+k n\right)$. Therefore $n_{i} \not \equiv n_{j}$ if $i \neq j$. Let $n_{i} \equiv r_{i}$, where $r_{i} \in\{0,1, \ldots, n-1\}$ are distinct. The number $C=$ $a_{1} b^{r_{1}}+\cdots+a_{s} b^{r_{s}}$ also has $s$ digits and is divisible by $b^{n}-1$. But since $C<b^{n}$, the only possibility is $C=b^{n}-1$ which has exactly $n$ digits in base $b$. It follows that $s=n$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c8e7990f-ba4a-5eb9-b82b-c9868ff9c249
| 24,479
|
2. (CAN 2) Let triangle $A B C$ be such that its circumradius $R$ is equal to 1. Let $r$ be the inradius of $A B C$ and let $p$ be the inradius of the orthic triangle $A^{\prime} B^{\prime} C^{\prime}$ of triangle $A B C$. Prove that $p \leq 1-\frac{1}{3}(1+r)^{2}$. Remark. The orthic triangle is the triangle whose vertices are the feet of the altitudes of $A B C$.
|
2. It is well known that $r \leq \frac{1}{2} R$. Therefore $\frac{1}{3}(1+r)^{2} \leq \frac{1}{3}\left(1+\frac{1}{2}\right)^{2}=\frac{3}{4}$. It remains only to show that $p \leq \frac{1}{4}$. We note that $p$ does not exceed one half of the circumradius of $\triangle A^{\prime} B^{\prime} C^{\prime}$. However, by the theorem on the nine-point circle, this circumradius is equal to $\frac{1}{2} R$, and the conclusion follows. Second solution. By a well-known relation we have $\cos A+\cos B+\cos C=$ $1+\frac{r}{R}(=1+r$ when $R=1)$. Next, recalling that the incenter of $\triangle A^{\prime} B^{\prime} C^{\prime}$ is at the orthocenter of $\triangle A B C$, we easily obtain $p=2 \cos A \cos B \cos C$. Cosines of angles of a triangle satisfy the identity $\cos ^{2} A+\cos ^{2} B+\cos ^{2} C+$ $2 \cos A \cos B \cos C=1$ (the proof is straightforward: see (SL81-11)). Thus $$ \begin{aligned} p+\frac{1}{3}(1+r)^{2} & =2 \cos A \cos B \cos C+\frac{1}{3}(\cos A+\cos B+\cos C)^{2} \\ & \leq 2 \cos A \cos B \cos C+\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=1 \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
2. (CAN 2) Let triangle $A B C$ be such that its circumradius $R$ is equal to 1. Let $r$ be the inradius of $A B C$ and let $p$ be the inradius of the orthic triangle $A^{\prime} B^{\prime} C^{\prime}$ of triangle $A B C$. Prove that $p \leq 1-\frac{1}{3}(1+r)^{2}$. Remark. The orthic triangle is the triangle whose vertices are the feet of the altitudes of $A B C$.
|
2. It is well known that $r \leq \frac{1}{2} R$. Therefore $\frac{1}{3}(1+r)^{2} \leq \frac{1}{3}\left(1+\frac{1}{2}\right)^{2}=\frac{3}{4}$. It remains only to show that $p \leq \frac{1}{4}$. We note that $p$ does not exceed one half of the circumradius of $\triangle A^{\prime} B^{\prime} C^{\prime}$. However, by the theorem on the nine-point circle, this circumradius is equal to $\frac{1}{2} R$, and the conclusion follows. Second solution. By a well-known relation we have $\cos A+\cos B+\cos C=$ $1+\frac{r}{R}(=1+r$ when $R=1)$. Next, recalling that the incenter of $\triangle A^{\prime} B^{\prime} C^{\prime}$ is at the orthocenter of $\triangle A B C$, we easily obtain $p=2 \cos A \cos B \cos C$. Cosines of angles of a triangle satisfy the identity $\cos ^{2} A+\cos ^{2} B+\cos ^{2} C+$ $2 \cos A \cos B \cos C=1$ (the proof is straightforward: see (SL81-11)). Thus $$ \begin{aligned} p+\frac{1}{3}(1+r)^{2} & =2 \cos A \cos B \cos C+\frac{1}{3}(\cos A+\cos B+\cos C)^{2} \\ & \leq 2 \cos A \cos B \cos C+\cos ^{2} A+\cos ^{2} B+\cos ^{2} C=1 \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4b8b9453-c2b2-5204-818d-37fd7628a6e3
| 24,482
|
20. (ROM 3) Let $c_{1}, \ldots, c_{n} \in \mathbb{R}(n \geq 2)$ such that $0 \leq \sum_{i=1}^{n} c_{i} \leq n$. Show that we can find integers $k_{1}, \ldots, k_{n}$ such that $\sum_{i=1}^{n} k_{i}=0$ and $$ 1-n \leq c_{i}+n k_{i} \leq n \quad \text { for every } i=1, \ldots, n $$
|
20. For every real $x$ we shall denote by $\lfloor x\rfloor$ and $\lceil x\rceil$ the greatest integer less than or equal to $x$ and the smallest integer greater than or equal to $x$ respectively. The condition $c_{i}+n k_{i} \in[1-n, n]$ is equivalent to $k_{i} \in I_{i}=$ $\left[\frac{1-c_{i}}{n}-1,1-\frac{c_{i}}{n}\right]$. For every $c_{i}$, this interval contains two integers (not necessarily distinct), namely $p_{i}=\left\lceil\frac{1-c_{i}}{n}-1\right\rceil \leq q_{i}=\left\lfloor 1-\frac{c_{i}}{n}\right\rfloor$. In order to show that there exist integers $k_{i} \in I_{i}$ with $\sum_{i=1}^{n} k_{i}=0$, it is sufficient to show that $\sum_{i=1}^{n} p_{i} \leq 0 \leq \sum_{i=1}^{n} q_{i}$. Since $p_{i}<\frac{1-c_{i}}{n}$, we have $$ \sum_{i=1}^{n} p_{i}<1-\sum_{i=1}^{n} \frac{c_{i}}{n} \leq 1 $$ and consequently $\sum_{i=1}^{n} p_{i} \leq 0$ because the $p_{i}$ 's are integers. On the other hand, $q_{i}>-\frac{c_{i}}{n}$ implies $$ \sum_{i=1}^{n} q_{i}>-\sum_{i=1}^{n} \frac{c_{i}}{n} \geq-1 $$ which leads to $\sum_{i=1}^{n} q_{i} \geq 0$. The proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
20. (ROM 3) Let $c_{1}, \ldots, c_{n} \in \mathbb{R}(n \geq 2)$ such that $0 \leq \sum_{i=1}^{n} c_{i} \leq n$. Show that we can find integers $k_{1}, \ldots, k_{n}$ such that $\sum_{i=1}^{n} k_{i}=0$ and $$ 1-n \leq c_{i}+n k_{i} \leq n \quad \text { for every } i=1, \ldots, n $$
|
20. For every real $x$ we shall denote by $\lfloor x\rfloor$ and $\lceil x\rceil$ the greatest integer less than or equal to $x$ and the smallest integer greater than or equal to $x$ respectively. The condition $c_{i}+n k_{i} \in[1-n, n]$ is equivalent to $k_{i} \in I_{i}=$ $\left[\frac{1-c_{i}}{n}-1,1-\frac{c_{i}}{n}\right]$. For every $c_{i}$, this interval contains two integers (not necessarily distinct), namely $p_{i}=\left\lceil\frac{1-c_{i}}{n}-1\right\rceil \leq q_{i}=\left\lfloor 1-\frac{c_{i}}{n}\right\rfloor$. In order to show that there exist integers $k_{i} \in I_{i}$ with $\sum_{i=1}^{n} k_{i}=0$, it is sufficient to show that $\sum_{i=1}^{n} p_{i} \leq 0 \leq \sum_{i=1}^{n} q_{i}$. Since $p_{i}<\frac{1-c_{i}}{n}$, we have $$ \sum_{i=1}^{n} p_{i}<1-\sum_{i=1}^{n} \frac{c_{i}}{n} \leq 1 $$ and consequently $\sum_{i=1}^{n} p_{i} \leq 0$ because the $p_{i}$ 's are integers. On the other hand, $q_{i}>-\frac{c_{i}}{n}$ implies $$ \sum_{i=1}^{n} q_{i}>-\sum_{i=1}^{n} \frac{c_{i}}{n} \geq-1 $$ which leads to $\sum_{i=1}^{n} q_{i} \geq 0$. The proof is complete.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
fa7825ba-a3fb-57cf-b914-942a6b034d91
| 24,484
|
23. (GBR 3) A finite set of (distinct) positive integers is called a " $D S$-set" if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some $D S$-set.
|
23. Let the given numbers be $a_{1}, \ldots, a_{n}$. Put $s=a_{1}+\cdots+a_{n}$ and $m=$ $\operatorname{lcm}\left(a_{1}, \ldots, a_{n}\right)$ and write $m=2^{k} r$ with $k \geq 0$ and $r$ odd. Let the binary expansion of $r$ be $r=2^{k_{0}}+2^{k_{1}}+\cdots+2^{k_{t}}$, with $0=k_{0}<\cdots<k_{t}$. Adjoin to the set $\left\{a_{1}, \ldots, a_{n}\right\}$ the numbers $2^{k_{i}} s, i=1,2, \ldots, t$. The sum of the enlarged set is $r s$. Finally, adjoin $r s, 2 r s, 2^{2} r s, \ldots, 2^{l-1} r s$ for $l=$ $\max \left\{k, k_{t}\right\}$. The resulting set has sum $2^{l} r s$, which is divisible by $m$ and so by each of $a_{j}$, and also by the $2^{i} s$ above and by $r s, 2 r s, \ldots, 2^{l-1} r s$. Therefore this is a $D S$-set. Second solution. We show by induction that there is a $D S$-set containing 1 and $n$. For $n=2,3$, take $\{1,2,3\}$. Assume that $\left\{1, n, b_{1}, \ldots, b_{k}\right\}$ is a $D S$ set. Then $\left\{1, n+1, n, 2(n+1) n, 2(n+1) b_{1}, \ldots, 2(n+1) b_{k}\right\}$ is a $D S$-set too. For given $a_{1}, \ldots, a_{n}$ let $m$ be a sufficiently large common multiple of the $a_{i}$ 's such that $u=m-\left(a_{1}+\cdots+a_{n}\right) \neq a_{i}$ for all $i$. There exist $b_{1}, \ldots, b_{k}$ such that $\left\{1, u, b_{1}, \ldots, b_{k}\right\}$ is a $D S$-set. It is clear that $\left\{a_{1}, \ldots, a_{n}, u, m u, m b_{1}, \ldots, m b_{k}\right\}$ is a $D S$-set containing $a_{1}, \ldots, a_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
23. (GBR 3) A finite set of (distinct) positive integers is called a " $D S$-set" if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some $D S$-set.
|
23. Let the given numbers be $a_{1}, \ldots, a_{n}$. Put $s=a_{1}+\cdots+a_{n}$ and $m=$ $\operatorname{lcm}\left(a_{1}, \ldots, a_{n}\right)$ and write $m=2^{k} r$ with $k \geq 0$ and $r$ odd. Let the binary expansion of $r$ be $r=2^{k_{0}}+2^{k_{1}}+\cdots+2^{k_{t}}$, with $0=k_{0}<\cdots<k_{t}$. Adjoin to the set $\left\{a_{1}, \ldots, a_{n}\right\}$ the numbers $2^{k_{i}} s, i=1,2, \ldots, t$. The sum of the enlarged set is $r s$. Finally, adjoin $r s, 2 r s, 2^{2} r s, \ldots, 2^{l-1} r s$ for $l=$ $\max \left\{k, k_{t}\right\}$. The resulting set has sum $2^{l} r s$, which is divisible by $m$ and so by each of $a_{j}$, and also by the $2^{i} s$ above and by $r s, 2 r s, \ldots, 2^{l-1} r s$. Therefore this is a $D S$-set. Second solution. We show by induction that there is a $D S$-set containing 1 and $n$. For $n=2,3$, take $\{1,2,3\}$. Assume that $\left\{1, n, b_{1}, \ldots, b_{k}\right\}$ is a $D S$ set. Then $\left\{1, n+1, n, 2(n+1) n, 2(n+1) b_{1}, \ldots, 2(n+1) b_{k}\right\}$ is a $D S$-set too. For given $a_{1}, \ldots, a_{n}$ let $m$ be a sufficiently large common multiple of the $a_{i}$ 's such that $u=m-\left(a_{1}+\cdots+a_{n}\right) \neq a_{i}$ for all $i$. There exist $b_{1}, \ldots, b_{k}$ such that $\left\{1, u, b_{1}, \ldots, b_{k}\right\}$ is a $D S$-set. It is clear that $\left\{a_{1}, \ldots, a_{n}, u, m u, m b_{1}, \ldots, m b_{k}\right\}$ is a $D S$-set containing $a_{1}, \ldots, a_{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1529749d-6657-51eb-b797-6be4a713ed58
| 24,494
|
24. (USA 3) Prove that $$ \frac{a}{b+2 c+3 d}+\frac{b}{c+2 d+3 a}+\frac{c}{d+2 a+3 b}+\frac{d}{a+2 b+3 c} \geq \frac{2}{3} $$ for all positive real numbers $a, b, c, d$.
|
24. By the Cauchy-Schwarz inequality, if $x_{1}, x_{2}, \ldots, x_{n}$ and $y_{1}, y_{2}, \ldots, y_{n}$ are positive numbers, then $$ \left(\sum_{i=1}^{n} \frac{x_{i}}{y_{i}}\right)\left(\sum_{i=1}^{n} x_{i} y_{i}\right) \geq\left(\sum_{i=1}^{n} x_{i}\right)^{2} $$ Applying this to the numbers $a, b, c, d$ and $b+2 c+3 d, c+2 d+3 a, d+2 a+$ $3 b, a+2 b+3 c$ (here $n=4$ ), we obtain $$ \begin{gathered} \frac{a}{b+2 c+3 d}+\frac{b}{c+2 d+3 a}+\frac{c}{d+2 a+3 b}+\frac{d}{a+2 b+3 c} \\ \geq \frac{(a+b+c+d)^{2}}{4(a b+a c+a d+b c+b d+c d)} \geq \frac{2}{3} \end{gathered} $$ The last inequality follows, for example, from $(a-b)^{2}+(a-c)^{2}+\cdots+$ $(c-d)^{2} \geq 0$. Equality holds if and only if $a=b=c=d$. Second solution. Putting $A=b+2 c+3 d, B=c+2 d+3 a, C=d+2 a+3 b$, $D=a+2 b+3 c$, our inequality transforms into $$ \begin{aligned} & \frac{-5 A+7 B+C+D}{24 A}+\frac{-5 B+7 C+D+A}{24 B} \\ & +\frac{-5 C+7 D+A+B}{24 C}+\frac{-5 D+7 A+B+C}{24 D} \geq \frac{2}{3} \end{aligned} $$ This follows from the arithmetic-geometric mean inequality, since $\frac{B}{A}+\frac{C}{B}+$ $\frac{D}{C}+\frac{A}{D} \geq 4$, etc.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
24. (USA 3) Prove that $$ \frac{a}{b+2 c+3 d}+\frac{b}{c+2 d+3 a}+\frac{c}{d+2 a+3 b}+\frac{d}{a+2 b+3 c} \geq \frac{2}{3} $$ for all positive real numbers $a, b, c, d$.
|
24. By the Cauchy-Schwarz inequality, if $x_{1}, x_{2}, \ldots, x_{n}$ and $y_{1}, y_{2}, \ldots, y_{n}$ are positive numbers, then $$ \left(\sum_{i=1}^{n} \frac{x_{i}}{y_{i}}\right)\left(\sum_{i=1}^{n} x_{i} y_{i}\right) \geq\left(\sum_{i=1}^{n} x_{i}\right)^{2} $$ Applying this to the numbers $a, b, c, d$ and $b+2 c+3 d, c+2 d+3 a, d+2 a+$ $3 b, a+2 b+3 c$ (here $n=4$ ), we obtain $$ \begin{gathered} \frac{a}{b+2 c+3 d}+\frac{b}{c+2 d+3 a}+\frac{c}{d+2 a+3 b}+\frac{d}{a+2 b+3 c} \\ \geq \frac{(a+b+c+d)^{2}}{4(a b+a c+a d+b c+b d+c d)} \geq \frac{2}{3} \end{gathered} $$ The last inequality follows, for example, from $(a-b)^{2}+(a-c)^{2}+\cdots+$ $(c-d)^{2} \geq 0$. Equality holds if and only if $a=b=c=d$. Second solution. Putting $A=b+2 c+3 d, B=c+2 d+3 a, C=d+2 a+3 b$, $D=a+2 b+3 c$, our inequality transforms into $$ \begin{aligned} & \frac{-5 A+7 B+C+D}{24 A}+\frac{-5 B+7 C+D+A}{24 B} \\ & +\frac{-5 C+7 D+A+B}{24 C}+\frac{-5 D+7 A+B+C}{24 D} \geq \frac{2}{3} \end{aligned} $$ This follows from the arithmetic-geometric mean inequality, since $\frac{B}{A}+\frac{C}{B}+$ $\frac{D}{C}+\frac{A}{D} \geq 4$, etc.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1b4c3179-21b2-555a-8e41-fd6efbde14d6
| 24,496
|
26. (VIE 2) Let $a, b, c, d$ be four nonnegative numbers satisfying $a+b+c+d=$ 1. Prove the inequality $$ a b c+b c d+c d a+d a b \leq \frac{1}{27}+\frac{176}{27} a b c d $$
|
26. Set $$ \begin{aligned} f(a, b, c, d) & =a b c+b c d+c d a+d a b-\frac{176}{27} a b c d \\ & =a b(c+d)+c d\left(a+b-\frac{176}{27} a b\right) . \end{aligned} $$ If $a+b-\frac{176}{a} b \leq 0$, by the arithmetic-geometric inequality we have $f(a, b, c, d) \leq a b(c+d) \leq \frac{1}{27}$. On the other hand, if $a+b-\frac{176}{a} b>0$, the value of $f$ increases if $c, d$ are replaced by $\frac{c+d}{2}, \frac{c+d}{2}$. Consider now the following fourtuplets: $$ \begin{gathered} P_{0}(a, b, c, d), P_{1}\left(a, b, \frac{c+d}{2}, \frac{c+d}{2}\right), P_{2}\left(\frac{a+b}{2}, \frac{a+b}{2}, \frac{c+d}{2}, \frac{c+d}{2}\right), \\ P_{3}\left(\frac{1}{4}, \frac{a+b}{2}, \frac{c+d}{2}, \frac{1}{4}\right), P_{4}\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right) \end{gathered} $$ From the above considerations we deduce that for $i=0,1,2,3$ either $f\left(P_{i}\right) \leq f\left(P_{i+1}\right)$, or directly $f\left(P_{i}\right) \leq 1 / 27$. Since $f\left(P_{4}\right)=1 / 27$, in every case we are led to $$ f(a, b, c, d)=f\left(P_{0}\right) \leq \frac{1}{27} $$ Equality occurs only in the cases $(0,1 / 3,1 / 3,1 / 3)$ (with permutations) and ( $1 / 4,1 / 4,1 / 4,1 / 4)$. Remark. Lagrange multipliers also work. On the boundary of the set one of the numbers $a, b, c, d$ is 0 , and the inequality immediately follows, while for an extremum point in the interior, among $a, b, c, d$ there are at most two distinct values, in which case one easily verifies the inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
26. (VIE 2) Let $a, b, c, d$ be four nonnegative numbers satisfying $a+b+c+d=$ 1. Prove the inequality $$ a b c+b c d+c d a+d a b \leq \frac{1}{27}+\frac{176}{27} a b c d $$
|
26. Set $$ \begin{aligned} f(a, b, c, d) & =a b c+b c d+c d a+d a b-\frac{176}{27} a b c d \\ & =a b(c+d)+c d\left(a+b-\frac{176}{27} a b\right) . \end{aligned} $$ If $a+b-\frac{176}{a} b \leq 0$, by the arithmetic-geometric inequality we have $f(a, b, c, d) \leq a b(c+d) \leq \frac{1}{27}$. On the other hand, if $a+b-\frac{176}{a} b>0$, the value of $f$ increases if $c, d$ are replaced by $\frac{c+d}{2}, \frac{c+d}{2}$. Consider now the following fourtuplets: $$ \begin{gathered} P_{0}(a, b, c, d), P_{1}\left(a, b, \frac{c+d}{2}, \frac{c+d}{2}\right), P_{2}\left(\frac{a+b}{2}, \frac{a+b}{2}, \frac{c+d}{2}, \frac{c+d}{2}\right), \\ P_{3}\left(\frac{1}{4}, \frac{a+b}{2}, \frac{c+d}{2}, \frac{1}{4}\right), P_{4}\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right) \end{gathered} $$ From the above considerations we deduce that for $i=0,1,2,3$ either $f\left(P_{i}\right) \leq f\left(P_{i+1}\right)$, or directly $f\left(P_{i}\right) \leq 1 / 27$. Since $f\left(P_{4}\right)=1 / 27$, in every case we are led to $$ f(a, b, c, d)=f\left(P_{0}\right) \leq \frac{1}{27} $$ Equality occurs only in the cases $(0,1 / 3,1 / 3,1 / 3)$ (with permutations) and ( $1 / 4,1 / 4,1 / 4,1 / 4)$. Remark. Lagrange multipliers also work. On the boundary of the set one of the numbers $a, b, c, d$ is 0 , and the inequality immediately follows, while for an extremum point in the interior, among $a, b, c, d$ there are at most two distinct values, in which case one easily verifies the inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f51b96b3-e91b-50cd-989b-dfbaede94e40
| 24,502
|
3. (SPA 1) Consider the triangle $A B C$, its circumcircle $k$ with center $O$ and radius $R$, and its incircle with center $I$ and radius $r$. Another circle $k_{c}$ is tangent to the sides $C A, C B$ at $D, E$, respectively, and it is internally tangent to $k$. Show that the incenter $I$ is the midpoint of $D E$.
|
3. Let $O_{1}$ and $\rho$ be the center and radius of $k_{c}$. It is clear that $C, I, O_{1}$ are collinear and $C I / C O_{1}=r / \rho$. By Stewart's theorem applied to $\triangle O C O_{1}$, $$ O I^{2}=\frac{r}{\rho} O O_{1}^{2}+\left(1-\frac{r}{\rho}\right) O C^{2}-C I \cdot I O_{1} . $$ Since $O O_{1}=R-\rho, O C=R$ and by Euler's formula $O I^{2}=R^{2}-2 R r$, substituting these values in (1) gives $C I \cdot I O_{1}=r \rho$, or equivalently $C O_{1}$. $I O_{1}=\rho^{2}=D O_{1}^{2}$. Hence the triangles $C O_{1} D$ and $D O_{1} I$ are similar, implying $\angle D I O_{1}=90^{\circ}$. Since $C D=C E$ and the line $C O_{1}$ bisects the segment $D E$, it follows that $I$ is the midpoint of $D E$. Second solution. Under the inversion with center $C$ and power $a b, k_{c}$ is transformed into the excircle of $\widehat{A} \widehat{B} C$ corresponding to $C$. Thus $C D=$ $\frac{a b}{s}$, where $s$ is the common semiperimeter of $\triangle A B C$ and $\triangle \widehat{A} \widehat{B} C$, and consequently the distance from $D$ to $B C$ is $\frac{a b}{s} \sin C=\frac{2 S_{A B C}}{s}=2 r$. The statement follows immediately. Third solution. We shall prove a stronger statement: Let $A B C D$ be a convex quadrilateral inscribed in a circle $k$, and $k^{\prime}$ the circle that is tangent to segments $B O, A O$ at $K, L$ respectively (where $O=B D \cap A C$ ), and internally to $k$ at $M$. Then $K L$ contains the incenters $I, J$ of $\triangle A B C$ and $\triangle A B D$. Let $K^{\prime}, K^{\prime \prime}, L^{\prime}, L^{\prime \prime}, N$ denote the midpoints of arcs $B C, B D, A C, A D, A B$ that don't contain $M ; X^{\prime}, X^{\prime \prime}$ the points on $k$ defined by $X^{\prime} N=N X^{\prime \prime}=$ $K^{\prime} K^{\prime \prime}=L^{\prime} L^{\prime \prime}$ (as oriented arcs); and set $S=A K^{\prime} \cap B L^{\prime \prime}, \bar{M}=N S \cap k$, $\bar{K}=K^{\prime \prime} M \cap B O, \bar{L}=L^{\prime} M \cap A O$. It is clear that $I=A K^{\prime} \cap B L^{\prime}, J=A K^{\prime \prime} \cap B L^{\prime \prime}$. Furthermore, $X^{\prime} \bar{M}$ contains $I$ (to see this, use the fact that for $A, B, C, D, E, F$ on $k$, lines $A D, B E, C F$ are concurrent if and only if $A B \cdot C D \cdot E F=B C \cdot D E \cdot F A$, and then express $A \bar{M} / \bar{M} B$ by applying this rule to $A M B K^{\prime} N L^{\prime \prime}$ and show that $A K^{\prime}, \bar{M} X^{\prime}, B L^{\prime}$ are concurrent). Analogously, $X^{\prime \prime} \bar{M}$ contains $J$. Now the points $B, \bar{K}, I, S, \bar{M}$ lie on a circle $(\angle B \overline{K M}=\angle B I \bar{M}=\angle B S \bar{M})$, and points $A, \bar{L}, J, S, \bar{M}$ do so as well. Lines $I \bar{K}, J \bar{L}$ are parallel to $K^{\prime \prime} L^{\prime}$ (because $\angle \overline{M K} I=\angle \bar{M} B I=$ $\left.\angle \bar{M} K^{\prime \prime} L^{\prime}\right)$. On the other hand, the quadrilateral $A B I J$ is cyclic, and simple calculation with angles shows that $I J$ is also parallel to $K^{\prime \prime} L^{\prime}$. Hence $\bar{K}, I, J, \bar{L}$ are collinear.  Finally, $\bar{K} \equiv K, \bar{L} \equiv L$, and $\bar{M} \equiv M$ because the homothety centered at $M$ that maps $k^{\prime}$ to $k$ sends $K$ to $K^{\prime \prime}$ and $L$ to $L^{\prime}$ (thus $M, K, K^{\prime \prime}$, as well as $M, L, L^{\prime}$, must be collinear). As is seen now, the deciphered picture yields many other interesting properties. Thus, for example, $N, S, M$ are collinear, i.e., $\angle A M S=\angle B M S$. Fourth solution. We give an alternative proof of the more general statement in the third solution. Let $W$ be the foot of the perpendicular from $B$ to $A C$. We define $q=C W, h=B W, t=O L=O K, x=A L$, $\theta=\measuredangle W B O(\theta$ is negative if $\mathcal{B}(O, W, A), \theta=0$ if $W=O)$, and as usual, $a=B C, b=A C, c=A B$. Let $\alpha=\measuredangle K L C$ and $\beta=\measuredangle I L C$ (both angles must be acute). Our goal is to prove $\alpha=\beta$. We note that $90^{\circ}-\theta=2 \alpha$. One easily gets $$ \tan \alpha=\frac{\cos \theta}{1+\sin \theta}, \quad \tan \beta=\frac{\frac{2 S_{A B C}}{a+b+c}}{\frac{b+c-a}{2}-x} $$ Applying Casey's theorem to $A, B, C, k^{\prime}$, we get $A C \cdot B K+A L \cdot B C=$ $A B \cdot C L$, i.e., $b\left(\frac{h}{\cos \theta}-t\right)+x a=c(b-x)$. Using that $t=b-x-q-h \tan \theta$ we get $$ x=\frac{b(b+c-q)-b h\left(\frac{1}{\cos \theta}+\tan \theta\right)}{a+b+c} . $$ Plugging (2) into the second equation of (1) and using $b h=2 S_{A B C}$ and $c^{2}=b^{2}+a^{2}-2 b q$, we obtain $\tan \alpha=\tan \beta$, i.e., $\alpha=\beta$, which completes our proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (SPA 1) Consider the triangle $A B C$, its circumcircle $k$ with center $O$ and radius $R$, and its incircle with center $I$ and radius $r$. Another circle $k_{c}$ is tangent to the sides $C A, C B$ at $D, E$, respectively, and it is internally tangent to $k$. Show that the incenter $I$ is the midpoint of $D E$.
|
3. Let $O_{1}$ and $\rho$ be the center and radius of $k_{c}$. It is clear that $C, I, O_{1}$ are collinear and $C I / C O_{1}=r / \rho$. By Stewart's theorem applied to $\triangle O C O_{1}$, $$ O I^{2}=\frac{r}{\rho} O O_{1}^{2}+\left(1-\frac{r}{\rho}\right) O C^{2}-C I \cdot I O_{1} . $$ Since $O O_{1}=R-\rho, O C=R$ and by Euler's formula $O I^{2}=R^{2}-2 R r$, substituting these values in (1) gives $C I \cdot I O_{1}=r \rho$, or equivalently $C O_{1}$. $I O_{1}=\rho^{2}=D O_{1}^{2}$. Hence the triangles $C O_{1} D$ and $D O_{1} I$ are similar, implying $\angle D I O_{1}=90^{\circ}$. Since $C D=C E$ and the line $C O_{1}$ bisects the segment $D E$, it follows that $I$ is the midpoint of $D E$. Second solution. Under the inversion with center $C$ and power $a b, k_{c}$ is transformed into the excircle of $\widehat{A} \widehat{B} C$ corresponding to $C$. Thus $C D=$ $\frac{a b}{s}$, where $s$ is the common semiperimeter of $\triangle A B C$ and $\triangle \widehat{A} \widehat{B} C$, and consequently the distance from $D$ to $B C$ is $\frac{a b}{s} \sin C=\frac{2 S_{A B C}}{s}=2 r$. The statement follows immediately. Third solution. We shall prove a stronger statement: Let $A B C D$ be a convex quadrilateral inscribed in a circle $k$, and $k^{\prime}$ the circle that is tangent to segments $B O, A O$ at $K, L$ respectively (where $O=B D \cap A C$ ), and internally to $k$ at $M$. Then $K L$ contains the incenters $I, J$ of $\triangle A B C$ and $\triangle A B D$. Let $K^{\prime}, K^{\prime \prime}, L^{\prime}, L^{\prime \prime}, N$ denote the midpoints of arcs $B C, B D, A C, A D, A B$ that don't contain $M ; X^{\prime}, X^{\prime \prime}$ the points on $k$ defined by $X^{\prime} N=N X^{\prime \prime}=$ $K^{\prime} K^{\prime \prime}=L^{\prime} L^{\prime \prime}$ (as oriented arcs); and set $S=A K^{\prime} \cap B L^{\prime \prime}, \bar{M}=N S \cap k$, $\bar{K}=K^{\prime \prime} M \cap B O, \bar{L}=L^{\prime} M \cap A O$. It is clear that $I=A K^{\prime} \cap B L^{\prime}, J=A K^{\prime \prime} \cap B L^{\prime \prime}$. Furthermore, $X^{\prime} \bar{M}$ contains $I$ (to see this, use the fact that for $A, B, C, D, E, F$ on $k$, lines $A D, B E, C F$ are concurrent if and only if $A B \cdot C D \cdot E F=B C \cdot D E \cdot F A$, and then express $A \bar{M} / \bar{M} B$ by applying this rule to $A M B K^{\prime} N L^{\prime \prime}$ and show that $A K^{\prime}, \bar{M} X^{\prime}, B L^{\prime}$ are concurrent). Analogously, $X^{\prime \prime} \bar{M}$ contains $J$. Now the points $B, \bar{K}, I, S, \bar{M}$ lie on a circle $(\angle B \overline{K M}=\angle B I \bar{M}=\angle B S \bar{M})$, and points $A, \bar{L}, J, S, \bar{M}$ do so as well. Lines $I \bar{K}, J \bar{L}$ are parallel to $K^{\prime \prime} L^{\prime}$ (because $\angle \overline{M K} I=\angle \bar{M} B I=$ $\left.\angle \bar{M} K^{\prime \prime} L^{\prime}\right)$. On the other hand, the quadrilateral $A B I J$ is cyclic, and simple calculation with angles shows that $I J$ is also parallel to $K^{\prime \prime} L^{\prime}$. Hence $\bar{K}, I, J, \bar{L}$ are collinear.  Finally, $\bar{K} \equiv K, \bar{L} \equiv L$, and $\bar{M} \equiv M$ because the homothety centered at $M$ that maps $k^{\prime}$ to $k$ sends $K$ to $K^{\prime \prime}$ and $L$ to $L^{\prime}$ (thus $M, K, K^{\prime \prime}$, as well as $M, L, L^{\prime}$, must be collinear). As is seen now, the deciphered picture yields many other interesting properties. Thus, for example, $N, S, M$ are collinear, i.e., $\angle A M S=\angle B M S$. Fourth solution. We give an alternative proof of the more general statement in the third solution. Let $W$ be the foot of the perpendicular from $B$ to $A C$. We define $q=C W, h=B W, t=O L=O K, x=A L$, $\theta=\measuredangle W B O(\theta$ is negative if $\mathcal{B}(O, W, A), \theta=0$ if $W=O)$, and as usual, $a=B C, b=A C, c=A B$. Let $\alpha=\measuredangle K L C$ and $\beta=\measuredangle I L C$ (both angles must be acute). Our goal is to prove $\alpha=\beta$. We note that $90^{\circ}-\theta=2 \alpha$. One easily gets $$ \tan \alpha=\frac{\cos \theta}{1+\sin \theta}, \quad \tan \beta=\frac{\frac{2 S_{A B C}}{a+b+c}}{\frac{b+c-a}{2}-x} $$ Applying Casey's theorem to $A, B, C, k^{\prime}$, we get $A C \cdot B K+A L \cdot B C=$ $A B \cdot C L$, i.e., $b\left(\frac{h}{\cos \theta}-t\right)+x a=c(b-x)$. Using that $t=b-x-q-h \tan \theta$ we get $$ x=\frac{b(b+c-q)-b h\left(\frac{1}{\cos \theta}+\tan \theta\right)}{a+b+c} . $$ Plugging (2) into the second equation of (1) and using $b h=2 S_{A B C}$ and $c^{2}=b^{2}+a^{2}-2 b q$, we obtain $\tan \alpha=\tan \beta$, i.e., $\alpha=\beta$, which completes our proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2ac4292d-f832-5dbf-a43b-2b5ef3c0e0ce
| 24,505
|
6. (GER 1) ${ }^{\mathrm{IMO} 5}$ Let $\mathbb{N}=\{1,2,3, \ldots\}$. Determine whether there exists a strictly increasing function $f: \mathbb{N} \rightarrow \mathbb{N}$ with the following properties: $$ \begin{aligned} f(1) & =2 \\ f(f(n)) & =f(n)+n \quad(n \in \mathbb{N}) \end{aligned} $$
|
6. Notice that for $\alpha=\frac{1+\sqrt{5}}{2}, \alpha^{2} n=\alpha n+n$ for all $n \in \mathbb{N}$. We shall show that $f(n)=\left[\alpha n+\frac{1}{2}\right]$ (the closest integer to $\alpha n$ ) satisfies the requirements. Observe that $f$ is strictly increasing and $f(1)=2$. By the definition of $f$, $|f(n)-\alpha n| \leq \frac{1}{2}$ and $f(f(n))-f(n)-n$ is an integer. On the other hand, $$ \begin{aligned} |f(f(n))-f(n)-n| & =\left|f(f(n))-f(n)-\alpha^{2} n+\alpha n\right| \\ & =\left|f(f(n))-\alpha f(n)+\alpha f(n)-\alpha^{2} n-f(n)+\alpha n\right| \\ & =|(\alpha-1)(f(n)-\alpha n)+(f(f(n))-\alpha f(n))| \\ & \leq(\alpha-1)|f(n)-\alpha n|+|f(f(n))-\alpha f(n)| \\ & \leq \frac{1}{2}(\alpha-1)+\frac{1}{2}=\frac{1}{2} \alpha<1, \end{aligned} $$ which implies that $f(f(n))-f(n)-n=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
6. (GER 1) ${ }^{\mathrm{IMO} 5}$ Let $\mathbb{N}=\{1,2,3, \ldots\}$. Determine whether there exists a strictly increasing function $f: \mathbb{N} \rightarrow \mathbb{N}$ with the following properties: $$ \begin{aligned} f(1) & =2 \\ f(f(n)) & =f(n)+n \quad(n \in \mathbb{N}) \end{aligned} $$
|
6. Notice that for $\alpha=\frac{1+\sqrt{5}}{2}, \alpha^{2} n=\alpha n+n$ for all $n \in \mathbb{N}$. We shall show that $f(n)=\left[\alpha n+\frac{1}{2}\right]$ (the closest integer to $\alpha n$ ) satisfies the requirements. Observe that $f$ is strictly increasing and $f(1)=2$. By the definition of $f$, $|f(n)-\alpha n| \leq \frac{1}{2}$ and $f(f(n))-f(n)-n$ is an integer. On the other hand, $$ \begin{aligned} |f(f(n))-f(n)-n| & =\left|f(f(n))-f(n)-\alpha^{2} n+\alpha n\right| \\ & =\left|f(f(n))-\alpha f(n)+\alpha f(n)-\alpha^{2} n-f(n)+\alpha n\right| \\ & =|(\alpha-1)(f(n)-\alpha n)+(f(f(n))-\alpha f(n))| \\ & \leq(\alpha-1)|f(n)-\alpha n|+|f(f(n))-\alpha f(n)| \\ & \leq \frac{1}{2}(\alpha-1)+\frac{1}{2}=\frac{1}{2} \alpha<1, \end{aligned} $$ which implies that $f(f(n))-f(n)-n=0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a1d6834-ce60-50a2-80d4-9dd9c0ea5f4c
| 24,513
|
7. (GEO 3) Let $a, b, c$ be given integers $a>0, a c-b^{2}=P=P_{1} \cdots P_{m}$ where $P_{1}, \ldots, P_{m}$ are (distinct) prime numbers. Let $M(n)$ denote the number of pairs of integers $(x, y)$ for which $$ a x^{2}+2 b x y+c y^{2}=n $$ Prove that $M(n)$ is finite and $M(n)=M\left(P^{k} \cdot n\right)$ for every integer $k \geq 0$.
|
7. Multiplying by $a$ and $c$ the equation $$ a x^{2}+2 b x y+c y^{2}=P^{k} n $$ gives $(a x+b y)^{2}+P y^{2}=a P^{k} n$ and $(b x+c y)^{2}+P x^{2}=c P^{k} n$. It follows immediately that $M(n)$ is finite; moreover, $(a x+b y)^{2}$ and $(b x+$ $c y)^{2}$ are divisible by $P$, and consequently $a x+b y, b x+c y$ are divisible by $P$ because $P$ is not divisible by a square greater than 1 . Thus there exist integers $X, Y$ such that $b x+c y=P X, a x+b y=-P Y$. Then $x=-b X-c Y$ and $y=a X+b Y$. Introducing these values into (1) and simplifying the expression obtained we get $$ a X^{2}+2 b X Y+c Y^{2}=P^{k-1} n $$ Hence $(x, y) \mapsto(X, Y)$ is a bijective correspondence between integral solutions of (1) and (2), so that $M\left(P^{k} n\right)=M\left(P^{k-1} n\right)=\cdots=M(n)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
7. (GEO 3) Let $a, b, c$ be given integers $a>0, a c-b^{2}=P=P_{1} \cdots P_{m}$ where $P_{1}, \ldots, P_{m}$ are (distinct) prime numbers. Let $M(n)$ denote the number of pairs of integers $(x, y)$ for which $$ a x^{2}+2 b x y+c y^{2}=n $$ Prove that $M(n)$ is finite and $M(n)=M\left(P^{k} \cdot n\right)$ for every integer $k \geq 0$.
|
7. Multiplying by $a$ and $c$ the equation $$ a x^{2}+2 b x y+c y^{2}=P^{k} n $$ gives $(a x+b y)^{2}+P y^{2}=a P^{k} n$ and $(b x+c y)^{2}+P x^{2}=c P^{k} n$. It follows immediately that $M(n)$ is finite; moreover, $(a x+b y)^{2}$ and $(b x+$ $c y)^{2}$ are divisible by $P$, and consequently $a x+b y, b x+c y$ are divisible by $P$ because $P$ is not divisible by a square greater than 1 . Thus there exist integers $X, Y$ such that $b x+c y=P X, a x+b y=-P Y$. Then $x=-b X-c Y$ and $y=a X+b Y$. Introducing these values into (1) and simplifying the expression obtained we get $$ a X^{2}+2 b X Y+c Y^{2}=P^{k-1} n $$ Hence $(x, y) \mapsto(X, Y)$ is a bijective correspondence between integral solutions of (1) and (2), so that $M\left(P^{k} n\right)=M\left(P^{k-1} n\right)=\cdots=M(n)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b23a9844-1f25-5937-bb1a-9435965e4b32
| 24,516
|
9. (IND 4) (a) Show that the set $\mathbb{Q}^{+}$of all positive rational numbers can be partitioned into three disjoint subsets $A, B, C$ satisfying the following conditions: $$ B A=B, \quad B^{2}=C, \quad B C=A, $$ where $H K$ stands for the set $\{h k \mid h \in H, k \in K\}$ for any two subsets $H, K$ of $\mathbb{Q}^{+}$and $H^{2}$ stands for $H H$. (b) Show that all positive rational cubes are in $A$ for such a partition of $\mathbb{Q}^{+}$. (c) Find such a partition $\mathbb{Q}^{+}=A \cup B \cup C$ with the property that for no positive integer $n \leq 34$ are both $n$ and $n+1$ in $A$; that is, $$ \min \{n \in \mathbb{N} \mid n \in A, n+1 \in A\}>34 $$
|
9. We shall first complete the "multiplication table" for the sets $A, B, C$. It is clear that this multiplication is commutative and associative, so that we have the following relations: $$ \begin{aligned} & A C=(A B) B=B B=C \\ & A^{2}=A A=(A B) C=B C=A \\ & C^{2}=C C=B(B C)=B A=B \end{aligned} $$ (a) Now put 1 in $A$ and distribute the primes arbitrarily in $A, B, C$. This distribution uniquely determines the partition of $\mathbb{Q}^{+}$with the stated property. Indeed, if an arbitrary rational number $$ x=p_{1}^{\alpha_{1}} \cdots p_{k}^{\alpha_{k}} q_{1}^{\beta_{1}} \cdots q_{l}^{\beta_{l}} r_{1}^{\gamma_{1}} \cdots r_{m}^{\gamma_{m}} $$ is given, where $p_{i} \in A, q_{i} \in B, r_{i} \in C$ are primes, it is easy to see that $x$ belongs to $A, B$, or $C$ according as $\beta_{1}+\cdots+\beta_{l}+2 \gamma_{1}+\cdots+2 \gamma_{m}$ is congruent to 0,1 , or $2(\bmod 3)$. (b) In every such partition, cubes all belong to $A$. In fact, $A^{3}=A^{2} A=$ $A A=A, B^{3}=B^{2} B=C B=A, C^{3}=C^{2} C=B C=A$. (c) By (b) we have $1,8,27 \in A$. Then $2 \notin A$, and since the problem is symmetric with respect to $B, C$, we can assume $2 \in B$ and consequently $4 \in C$. Also $7 \notin A$, and also $7 \notin B$ (otherwise, $28=4 \cdot 7 \in A$ and $27 \in A$ ), so $7 \in C, 14 \in A, 28 \in B$. Further, we see that $3 \notin A$ (since otherwise $9 \in A$ and $8 \in A$ ). Put 3 in $C$. Then $5 \notin B$ (otherwise $15 \in A$ and $14 \in A$ ), so let $5 \in C$ too. Consequently $6,10 \in A$. Also $13 \notin A$, and $13 \notin C$ because $26 \notin A$, so $13 \in B$. Now it is easy to distribute the remaining primes $11,17,19,23,29,31$ : one possibility is $$ \begin{aligned} & A=\{1,6,8,10,14,19,23,27,29,31,33, \ldots\}, \\ & C=\{3,4,5,7,18,22,24,26,30,32,34, \ldots\} \\ & B=\{2,9,11,12,13,15,16,17,20,21,25,28,35, \ldots\} \end{aligned} $$ Remark. It can be proved that $\min \{n \in \mathbb{N} \mid n \in A, n+1 \in A\} \leq 77$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
9. (IND 4) (a) Show that the set $\mathbb{Q}^{+}$of all positive rational numbers can be partitioned into three disjoint subsets $A, B, C$ satisfying the following conditions: $$ B A=B, \quad B^{2}=C, \quad B C=A, $$ where $H K$ stands for the set $\{h k \mid h \in H, k \in K\}$ for any two subsets $H, K$ of $\mathbb{Q}^{+}$and $H^{2}$ stands for $H H$. (b) Show that all positive rational cubes are in $A$ for such a partition of $\mathbb{Q}^{+}$. (c) Find such a partition $\mathbb{Q}^{+}=A \cup B \cup C$ with the property that for no positive integer $n \leq 34$ are both $n$ and $n+1$ in $A$; that is, $$ \min \{n \in \mathbb{N} \mid n \in A, n+1 \in A\}>34 $$
|
9. We shall first complete the "multiplication table" for the sets $A, B, C$. It is clear that this multiplication is commutative and associative, so that we have the following relations: $$ \begin{aligned} & A C=(A B) B=B B=C \\ & A^{2}=A A=(A B) C=B C=A \\ & C^{2}=C C=B(B C)=B A=B \end{aligned} $$ (a) Now put 1 in $A$ and distribute the primes arbitrarily in $A, B, C$. This distribution uniquely determines the partition of $\mathbb{Q}^{+}$with the stated property. Indeed, if an arbitrary rational number $$ x=p_{1}^{\alpha_{1}} \cdots p_{k}^{\alpha_{k}} q_{1}^{\beta_{1}} \cdots q_{l}^{\beta_{l}} r_{1}^{\gamma_{1}} \cdots r_{m}^{\gamma_{m}} $$ is given, where $p_{i} \in A, q_{i} \in B, r_{i} \in C$ are primes, it is easy to see that $x$ belongs to $A, B$, or $C$ according as $\beta_{1}+\cdots+\beta_{l}+2 \gamma_{1}+\cdots+2 \gamma_{m}$ is congruent to 0,1 , or $2(\bmod 3)$. (b) In every such partition, cubes all belong to $A$. In fact, $A^{3}=A^{2} A=$ $A A=A, B^{3}=B^{2} B=C B=A, C^{3}=C^{2} C=B C=A$. (c) By (b) we have $1,8,27 \in A$. Then $2 \notin A$, and since the problem is symmetric with respect to $B, C$, we can assume $2 \in B$ and consequently $4 \in C$. Also $7 \notin A$, and also $7 \notin B$ (otherwise, $28=4 \cdot 7 \in A$ and $27 \in A$ ), so $7 \in C, 14 \in A, 28 \in B$. Further, we see that $3 \notin A$ (since otherwise $9 \in A$ and $8 \in A$ ). Put 3 in $C$. Then $5 \notin B$ (otherwise $15 \in A$ and $14 \in A$ ), so let $5 \in C$ too. Consequently $6,10 \in A$. Also $13 \notin A$, and $13 \notin C$ because $26 \notin A$, so $13 \in B$. Now it is easy to distribute the remaining primes $11,17,19,23,29,31$ : one possibility is $$ \begin{aligned} & A=\{1,6,8,10,14,19,23,27,29,31,33, \ldots\}, \\ & C=\{3,4,5,7,18,22,24,26,30,32,34, \ldots\} \\ & B=\{2,9,11,12,13,15,16,17,20,21,25,28,35, \ldots\} \end{aligned} $$ Remark. It can be proved that $\min \{n \in \mathbb{N} \mid n \in A, n+1 \in A\} \leq 77$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1f55886a-45a3-56d0-b995-027276efe9a2
| 24,521
|
1. A1 (USA) Let $a_{0}=1994$ and $a_{n+1}=\frac{a_{n}^{2}}{a_{n}+1}$ for each nonnegative integer $n$. Prove that $1994-n$ is the greatest integer less than or equal to $a_{n}$, $0 \leq n \leq 998$.
|
1. Obviously $a_{0}>a_{1}>a_{2}>\cdots$. Since $a_{k}-a_{k+1}=1-\frac{1}{a_{k}+1}$, we have $a_{n}=a_{0}+\left(a_{1}-a_{0}\right)+\cdots+\left(a_{n}-a_{n-1}\right)=1994-n+\frac{1}{a_{0}+1}+\cdots+\frac{1}{a_{n-1}+1}>$ $1994-n$. Also, for $1 \leq n \leq 998$, $$ \frac{1}{a_{0}+1}+\cdots+\frac{1}{a_{n-1}+1}<\frac{n}{a_{n-1}+1}<\frac{998}{a_{997}+1}<1 $$ because as above, $a_{997}>997$. Hence $\left\lfloor a_{n}\right\rfloor=1994-n$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
1. A1 (USA) Let $a_{0}=1994$ and $a_{n+1}=\frac{a_{n}^{2}}{a_{n}+1}$ for each nonnegative integer $n$. Prove that $1994-n$ is the greatest integer less than or equal to $a_{n}$, $0 \leq n \leq 998$.
|
1. Obviously $a_{0}>a_{1}>a_{2}>\cdots$. Since $a_{k}-a_{k+1}=1-\frac{1}{a_{k}+1}$, we have $a_{n}=a_{0}+\left(a_{1}-a_{0}\right)+\cdots+\left(a_{n}-a_{n-1}\right)=1994-n+\frac{1}{a_{0}+1}+\cdots+\frac{1}{a_{n-1}+1}>$ $1994-n$. Also, for $1 \leq n \leq 998$, $$ \frac{1}{a_{0}+1}+\cdots+\frac{1}{a_{n-1}+1}<\frac{n}{a_{n-1}+1}<\frac{998}{a_{997}+1}<1 $$ because as above, $a_{997}>997$. Hence $\left\lfloor a_{n}\right\rfloor=1994-n$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b75a8cea-d7e5-5e78-a476-ebc2faf7ced2
| 24,524
|
10. C5 (SWE) At a round table are 1994 girls, playing a game with a deck of $n$ cards. Initially, one girl holds all the cards. In each turn, if at least one girl holds at least two cards, one of these girls must pass a card to each of her two neighbors. The game ends when and only when each girl is holding at most one card. (a) Prove that if $n \geq 1994$, then the game cannot end. (b) Prove that if $n<1994$, then the game must end.
|
10. (a) The case $n>1994$ is trivial. Suppose that $n=1994$. Label the girls $G_{1}$ to $G_{1994}$, and let $G_{1}$ initially hold all the cards. At any moment give to each card the value $i, i=1, \ldots, 1994$, if $G_{i}$ holds it. Define the characteristic $C$ of a position as the sum of all these values. Initially $C=1994$. In each move, if $G_{i}$ passes cards to $G_{i-1}$ and $G_{i+1}$ (where $G_{0}=G_{1994}$ and $G_{1995}=G_{1}$ ), $C$ changes for $\pm 1994$ or does not change, so that it remains divisible by 1994. But if the game ends, the characteristic of the final position will be $C=1+2+\cdots+1994=$ $997 \cdot 1995$, which is not divisible by 1994. (b) Whenever a card is passed from one girl to another for the first time, let the girls sign their names on it. Thereafter, if one of them passes a card to her neighbor, we shall assume that the passed card is exactly the one signed by both of them. Thus each signed card is stuck between two neighboring girls, so if $n<1994$, there are two neighbors who never exchange cards. Consequently, there is a girl $G$ who played only a finite number of times. If her neighbor plays infinitely often, then after her last move, $G$ will continue to accumulate cards indefinitely, which is impossible. Hence every girl plays finitely many times.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
10. C5 (SWE) At a round table are 1994 girls, playing a game with a deck of $n$ cards. Initially, one girl holds all the cards. In each turn, if at least one girl holds at least two cards, one of these girls must pass a card to each of her two neighbors. The game ends when and only when each girl is holding at most one card. (a) Prove that if $n \geq 1994$, then the game cannot end. (b) Prove that if $n<1994$, then the game must end.
|
10. (a) The case $n>1994$ is trivial. Suppose that $n=1994$. Label the girls $G_{1}$ to $G_{1994}$, and let $G_{1}$ initially hold all the cards. At any moment give to each card the value $i, i=1, \ldots, 1994$, if $G_{i}$ holds it. Define the characteristic $C$ of a position as the sum of all these values. Initially $C=1994$. In each move, if $G_{i}$ passes cards to $G_{i-1}$ and $G_{i+1}$ (where $G_{0}=G_{1994}$ and $G_{1995}=G_{1}$ ), $C$ changes for $\pm 1994$ or does not change, so that it remains divisible by 1994. But if the game ends, the characteristic of the final position will be $C=1+2+\cdots+1994=$ $997 \cdot 1995$, which is not divisible by 1994. (b) Whenever a card is passed from one girl to another for the first time, let the girls sign their names on it. Thereafter, if one of them passes a card to her neighbor, we shall assume that the passed card is exactly the one signed by both of them. Thus each signed card is stuck between two neighboring girls, so if $n<1994$, there are two neighbors who never exchange cards. Consequently, there is a girl $G$ who played only a finite number of times. If her neighbor plays infinitely often, then after her last move, $G$ will continue to accumulate cards indefinitely, which is impossible. Hence every girl plays finitely many times.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9328a757-dd42-51c7-8995-a70942fcd29a
| 24,526
|
12. C7 (BRA) Prove that for any integer $n \geq 2$, there exists a set of $2^{n-1}$ points in the plane such that no 3 lie on a line and no $2 n$ are the vertices of a convex $2 n$-gon.
|
12. Define $S_{n}$ recursively as follows: Let $S_{2}=\{(0,0),(1,1)\}$ and $S_{n+1}=$ $S_{n} \cup T_{n}$, where $T_{n}=\left\{\left(x+2^{n-1}, y+M_{n}\right) \mid(x, y) \in S_{n}\right\}$, with $M_{n}$ chosen large enough so that the entire set $T_{n}$ lies above every line passing through two points of $S_{n}$. By definition, $S_{n}$ has exactly $2^{n-1}$ points and contains no three collinear points. We claim that no $2 n$ points of this set are the vertices of a convex $2 n$-gon. Consider an arbitrary convex polygon $\mathcal{P}$ with vertices in $S_{n}$. Join by a diagonal $d$ the two vertices of $\mathcal{P}$ having the smallest and greatest $x$ coordinates. This diagonal divides $\mathcal{P}$ into two convex polygons $\mathcal{P}_{1}, \mathcal{P}_{2}$, the former lying above $d$. We shall show by induction that both $\mathcal{P}_{1}, \mathcal{P}_{2}$ have at most $n$ vertices. Assume to the contrary that $\mathcal{P}_{1}$ has at least $n+1$ vertices $A_{1}\left(x_{1}, y_{1}\right), \ldots, A_{n+1}\left(x_{n+1}, y_{n+1}\right)$ in $S_{n}$, with $x_{1}<\cdots<x_{n+1}$. It follows that $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}>\cdots>\frac{y_{n+1}-y_{n}}{x_{n+1}-x_{n}}$. By the induction hypothesis, not more than $n-1$ of these vertices belong to $S_{n-1}$ or $T_{n-1}$, so let $A_{k-1}, A_{k} \in S_{n-1}$, $A_{k+1} \in T_{n-1}$. But by the construction of $T_{n-1}, \frac{y_{k+1}-y_{k}}{x_{k+1}-x_{k}}>\frac{y_{k}-y_{k-1}}{x_{k}-x_{k-1}}$, which gives a contradiction. Similarly, $\mathcal{P}_{2}$ has no more than $n$ vertices, and therefore $\mathcal{P}$ itself has at most $2 n-2$ vertices.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. C7 (BRA) Prove that for any integer $n \geq 2$, there exists a set of $2^{n-1}$ points in the plane such that no 3 lie on a line and no $2 n$ are the vertices of a convex $2 n$-gon.
|
12. Define $S_{n}$ recursively as follows: Let $S_{2}=\{(0,0),(1,1)\}$ and $S_{n+1}=$ $S_{n} \cup T_{n}$, where $T_{n}=\left\{\left(x+2^{n-1}, y+M_{n}\right) \mid(x, y) \in S_{n}\right\}$, with $M_{n}$ chosen large enough so that the entire set $T_{n}$ lies above every line passing through two points of $S_{n}$. By definition, $S_{n}$ has exactly $2^{n-1}$ points and contains no three collinear points. We claim that no $2 n$ points of this set are the vertices of a convex $2 n$-gon. Consider an arbitrary convex polygon $\mathcal{P}$ with vertices in $S_{n}$. Join by a diagonal $d$ the two vertices of $\mathcal{P}$ having the smallest and greatest $x$ coordinates. This diagonal divides $\mathcal{P}$ into two convex polygons $\mathcal{P}_{1}, \mathcal{P}_{2}$, the former lying above $d$. We shall show by induction that both $\mathcal{P}_{1}, \mathcal{P}_{2}$ have at most $n$ vertices. Assume to the contrary that $\mathcal{P}_{1}$ has at least $n+1$ vertices $A_{1}\left(x_{1}, y_{1}\right), \ldots, A_{n+1}\left(x_{n+1}, y_{n+1}\right)$ in $S_{n}$, with $x_{1}<\cdots<x_{n+1}$. It follows that $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}>\cdots>\frac{y_{n+1}-y_{n}}{x_{n+1}-x_{n}}$. By the induction hypothesis, not more than $n-1$ of these vertices belong to $S_{n-1}$ or $T_{n-1}$, so let $A_{k-1}, A_{k} \in S_{n-1}$, $A_{k+1} \in T_{n-1}$. But by the construction of $T_{n-1}, \frac{y_{k+1}-y_{k}}{x_{k+1}-x_{k}}>\frac{y_{k}-y_{k-1}}{x_{k}-x_{k-1}}$, which gives a contradiction. Similarly, $\mathcal{P}_{2}$ has no more than $n$ vertices, and therefore $\mathcal{P}$ itself has at most $2 n-2$ vertices.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ec47c5c7-79d4-5b79-9438-d360db2d811c
| 24,531
|
13. G1 (FRA) A semicircle $\Gamma$ is drawn on one side of a straight line $l$. $C$ and $D$ are points on $\Gamma$. The tangents to $\Gamma$ at $C$ and $D$ meet $l$ at $B$ and $A$ respectively, with the center of the semicircle between them. Let $E$ be the point of intersection of $A C$ and $B D$, and $F$ the point on $l$ such that $E F$ is perpendicular to $l$. Prove that $E F$ bisects $\angle C F D$.
|
13. Extend $A D$ and $B C$ to meet at $P$, and let $Q$ be the foot of the perpendicular from $P$ to $A B$. Denote by $O$ the center of $\Gamma$. Since $\triangle P A Q \sim \triangle O A D$ and $\triangle P B Q \sim \triangle O B C$, we obtain $\frac{A Q}{A D}=\frac{P Q}{O D}=\frac{P Q}{O C}=\frac{B Q}{B C}$. Therefore $\frac{A Q}{Q B} \cdot \frac{B C}{C P} \cdot \frac{P D}{D A}=1$, so by the converse Ceva theorem, $A C, B D$, and $P Q$ are concurrent. It follows that $Q \equiv F$. Finally, since the points $O, C, P, D, F$ are concyclic, we have $\angle D F P=\angle D O P=\angle P O C=\angle P F C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. G1 (FRA) A semicircle $\Gamma$ is drawn on one side of a straight line $l$. $C$ and $D$ are points on $\Gamma$. The tangents to $\Gamma$ at $C$ and $D$ meet $l$ at $B$ and $A$ respectively, with the center of the semicircle between them. Let $E$ be the point of intersection of $A C$ and $B D$, and $F$ the point on $l$ such that $E F$ is perpendicular to $l$. Prove that $E F$ bisects $\angle C F D$.
|
13. Extend $A D$ and $B C$ to meet at $P$, and let $Q$ be the foot of the perpendicular from $P$ to $A B$. Denote by $O$ the center of $\Gamma$. Since $\triangle P A Q \sim \triangle O A D$ and $\triangle P B Q \sim \triangle O B C$, we obtain $\frac{A Q}{A D}=\frac{P Q}{O D}=\frac{P Q}{O C}=\frac{B Q}{B C}$. Therefore $\frac{A Q}{Q B} \cdot \frac{B C}{C P} \cdot \frac{P D}{D A}=1$, so by the converse Ceva theorem, $A C, B D$, and $P Q$ are concurrent. It follows that $Q \equiv F$. Finally, since the points $O, C, P, D, F$ are concyclic, we have $\angle D F P=\angle D O P=\angle P O C=\angle P F C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
197f3234-def7-5fe1-9155-ab605bc00539
| 24,534
|
15. G3 (RUS) A circle $\omega$ is tangent to two parallel lines $l_{1}$ and $l_{2}$. A second circle $\omega_{1}$ is tangent to $l_{1}$ at $A$ and to $\omega$ externally at $C$. A third circle $\omega_{2}$ is tangent to $l_{2}$ at $B$, to $\omega$ externally at $D$, and to $\omega_{1}$ externally at $E$. $A D$ intersects $B C$ at $Q$. Prove that $Q$ is the circumcenter of triangle $C D E$.
|
15. We shall prove that $A D$ is a common tangent of $\omega$ and $\omega_{2}$. Denote by $K, L$ the points of tangency of $\omega$ with $l_{1}$ and $l_{2}$ respectively. Let $r, r_{1}, r_{2}$ be the radii of $\omega, \omega_{1}, \omega_{2}$ respectively, and set $K A=x, L B=y$. It will be enough if we show that $x y=2 r^{2}$, since this will imply that $\triangle K L B$ and $\triangle A K O$ are similar, where $O$ is the center of $\omega$, and consequently that $O A \perp K D$ (because $D \in K B$ ). Now if $O_{1}$ is the center of $\omega_{1}$, we have $x^{2}=$ $K A^{2}=O O_{1}^{2}-\left(K O-A O_{1}\right)^{2}=\left(r+r_{1}\right)^{2}-\left(r-r_{1}\right)^{2}=4 r r_{1}$ and analogously $y^{2}=4 r r_{2}$. But we also have $\left(r_{1}+r_{2}\right)^{2}=O_{1} O_{2}^{2}=(x-y)^{2}+\left(2 r-r_{1}-r_{2}\right)^{2}$, so $x^{2}-2 x y+y^{2}=4 r\left(r_{1}+r_{2}-r\right)$, from which we obtain $x y=2 r^{2}$ as claimed. Hence $A D$ is tangent to both $\omega, \omega_{2}$, and similarly $B C$ is tangent to $\omega, \omega_{1}$. It follows that $Q$ lies on the radical axes of pairs of circles $\left(\omega, \omega_{1}\right)$ and $\left(\omega, \omega_{2}\right)$. Therefore $Q$ also lies on the radical axis of $\left(\omega_{1}, \omega_{2}\right)$, i.e., on the common tangent at $E$ of $\omega_{1}$ and $\omega_{2}$. Hence $Q C=Q D=Q E$. Second solution. An inversion with center at $D$ maps $\omega$ and $\omega_{2}$ to parallel lines, $\omega_{1}$ and $l_{2}$ to disjoint equal circles touching $\omega, \omega_{2}$, and $l_{1}$ to a circle externally tangent to $\omega_{1}, l_{2}$, and to $\omega$. It is easy to see that the obtained picture is symmetric (with respect to a diameter of $l_{1}$ ), and that line $A D$ is parallel to the lines $\omega$ and $\omega_{2}$. Going back to the initial picture, this means that $A D$ is a common tangent of $\omega$ and $\omega_{2}$. The end is like that in the first solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
15. G3 (RUS) A circle $\omega$ is tangent to two parallel lines $l_{1}$ and $l_{2}$. A second circle $\omega_{1}$ is tangent to $l_{1}$ at $A$ and to $\omega$ externally at $C$. A third circle $\omega_{2}$ is tangent to $l_{2}$ at $B$, to $\omega$ externally at $D$, and to $\omega_{1}$ externally at $E$. $A D$ intersects $B C$ at $Q$. Prove that $Q$ is the circumcenter of triangle $C D E$.
|
15. We shall prove that $A D$ is a common tangent of $\omega$ and $\omega_{2}$. Denote by $K, L$ the points of tangency of $\omega$ with $l_{1}$ and $l_{2}$ respectively. Let $r, r_{1}, r_{2}$ be the radii of $\omega, \omega_{1}, \omega_{2}$ respectively, and set $K A=x, L B=y$. It will be enough if we show that $x y=2 r^{2}$, since this will imply that $\triangle K L B$ and $\triangle A K O$ are similar, where $O$ is the center of $\omega$, and consequently that $O A \perp K D$ (because $D \in K B$ ). Now if $O_{1}$ is the center of $\omega_{1}$, we have $x^{2}=$ $K A^{2}=O O_{1}^{2}-\left(K O-A O_{1}\right)^{2}=\left(r+r_{1}\right)^{2}-\left(r-r_{1}\right)^{2}=4 r r_{1}$ and analogously $y^{2}=4 r r_{2}$. But we also have $\left(r_{1}+r_{2}\right)^{2}=O_{1} O_{2}^{2}=(x-y)^{2}+\left(2 r-r_{1}-r_{2}\right)^{2}$, so $x^{2}-2 x y+y^{2}=4 r\left(r_{1}+r_{2}-r\right)$, from which we obtain $x y=2 r^{2}$ as claimed. Hence $A D$ is tangent to both $\omega, \omega_{2}$, and similarly $B C$ is tangent to $\omega, \omega_{1}$. It follows that $Q$ lies on the radical axes of pairs of circles $\left(\omega, \omega_{1}\right)$ and $\left(\omega, \omega_{2}\right)$. Therefore $Q$ also lies on the radical axis of $\left(\omega_{1}, \omega_{2}\right)$, i.e., on the common tangent at $E$ of $\omega_{1}$ and $\omega_{2}$. Hence $Q C=Q D=Q E$. Second solution. An inversion with center at $D$ maps $\omega$ and $\omega_{2}$ to parallel lines, $\omega_{1}$ and $l_{2}$ to disjoint equal circles touching $\omega, \omega_{2}$, and $l_{1}$ to a circle externally tangent to $\omega_{1}, l_{2}$, and to $\omega$. It is easy to see that the obtained picture is symmetric (with respect to a diameter of $l_{1}$ ), and that line $A D$ is parallel to the lines $\omega$ and $\omega_{2}$. Going back to the initial picture, this means that $A D$ is a common tangent of $\omega$ and $\omega_{2}$. The end is like that in the first solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
79ab88d2-f547-5bb5-a4d2-99cbc74c4b75
| 24,539
|
[^6]16. G4 (AUS-ARM) ${ }^{\mathrm{IMO} 2} N$ is an arbitrary point on the bisector of $\angle B A C$. $P$ and $O$ are points on the lines $A B$ and $A N$, respectively, such that $\measuredangle A N P=90^{\circ}=\measuredangle A P O . Q$ is an arbitrary point on $N P$, and an arbitrary line through $Q$ meets the lines $A B$ and $A C$ at $E$ and $F$ respectively. Prove that $\measuredangle O Q E=90^{\circ}$ if and only if $Q E=Q F$.
|
16. First, assume that $\angle O Q E=90^{\circ}$. Extend $P N$ to meet $A C$ at $R$. Then $O E P Q$ and $O R F Q$ are cyclic quadrilaterals; hence we have $\angle O E Q=$ $\angle O P Q=\angle O R Q=\angle O F Q$. It follows that $\triangle O E Q \cong \triangle O F Q$ and $Q E=Q F$. Now suppose $Q E=Q F$. Let $S$ be the point symmetric to $A$ with respect to $Q$, so that the quadrilateral $A E S F$ is a parallelogram. Draw the line $E^{\prime} F^{\prime}$ through $Q$ so that $\angle O Q E^{\prime}=90^{\circ}$ and $E^{\prime} \in A B$, $F^{\prime} \in A C$. By the first part $Q E^{\prime}=$  $Q F^{\prime}$; hence $A E^{\prime} S F^{\prime}$ is also a parallelogram. It follows that $E \equiv E^{\prime}, F \equiv F^{\prime}$, and $\angle O Q E=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
[^6]16. G4 (AUS-ARM) ${ }^{\mathrm{IMO} 2} N$ is an arbitrary point on the bisector of $\angle B A C$. $P$ and $O$ are points on the lines $A B$ and $A N$, respectively, such that $\measuredangle A N P=90^{\circ}=\measuredangle A P O . Q$ is an arbitrary point on $N P$, and an arbitrary line through $Q$ meets the lines $A B$ and $A C$ at $E$ and $F$ respectively. Prove that $\measuredangle O Q E=90^{\circ}$ if and only if $Q E=Q F$.
|
16. First, assume that $\angle O Q E=90^{\circ}$. Extend $P N$ to meet $A C$ at $R$. Then $O E P Q$ and $O R F Q$ are cyclic quadrilaterals; hence we have $\angle O E Q=$ $\angle O P Q=\angle O R Q=\angle O F Q$. It follows that $\triangle O E Q \cong \triangle O F Q$ and $Q E=Q F$. Now suppose $Q E=Q F$. Let $S$ be the point symmetric to $A$ with respect to $Q$, so that the quadrilateral $A E S F$ is a parallelogram. Draw the line $E^{\prime} F^{\prime}$ through $Q$ so that $\angle O Q E^{\prime}=90^{\circ}$ and $E^{\prime} \in A B$, $F^{\prime} \in A C$. By the first part $Q E^{\prime}=$  $Q F^{\prime}$; hence $A E^{\prime} S F^{\prime}$ is also a parallelogram. It follows that $E \equiv E^{\prime}, F \equiv F^{\prime}$, and $\angle O Q E=90^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6163831f-a101-5535-bae2-7286e3995dd4
| 24,541
|
17. G5 (CYP) A line $l$ does not meet a circle $\omega$ with center $O . E$ is the point on $l$ such that $O E$ is perpendicular to $l . M$ is any point on $l$ other than $E$. The tangents from $M$ to $\omega$ touch it at $A$ and $B . C$ is the point on $M A$ such that $E C$ is perpendicular to $M A . D$ is the point on $M B$ such that $E D$ is perpendicular to $M B$. The line $C D$ cuts $O E$ at $F$. Prove that the location of $F$ is independent of that of $M$.
|
17. We first prove that $A B$ cuts $O E$ in a fixed point $H$. Note that $\angle O A H=$ $\angle O M A=\angle O E A$ (because $O, A, E, M$ lie on a circle); hence $\triangle O A H \sim$ $\triangle O E A$. This implies $O H \cdot O E=O A^{2}$, i.e., $H$ is fixed. Let the lines $A B$ and $C D$ meet at $K$. Since $E A O B M$ and $E C D M$ are cyclic, we have $\angle E A K=$ $\angle E M B=\angle E C K$, so $E C A K$ is cyclic. Therefore $\angle E K A=90^{\circ}$, hence $E K B D$ is also cyclic and $E K \| O M$. Then $\angle E K F=$ $\angle E B D=\angle E O M=\angle O E K$, from which we deduce that $K F=F E$. However, since $\angle E K H=90^{\circ}$, the  point $F$ is the midpoint of $E H$; hence it is fixed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
17. G5 (CYP) A line $l$ does not meet a circle $\omega$ with center $O . E$ is the point on $l$ such that $O E$ is perpendicular to $l . M$ is any point on $l$ other than $E$. The tangents from $M$ to $\omega$ touch it at $A$ and $B . C$ is the point on $M A$ such that $E C$ is perpendicular to $M A . D$ is the point on $M B$ such that $E D$ is perpendicular to $M B$. The line $C D$ cuts $O E$ at $F$. Prove that the location of $F$ is independent of that of $M$.
|
17. We first prove that $A B$ cuts $O E$ in a fixed point $H$. Note that $\angle O A H=$ $\angle O M A=\angle O E A$ (because $O, A, E, M$ lie on a circle); hence $\triangle O A H \sim$ $\triangle O E A$. This implies $O H \cdot O E=O A^{2}$, i.e., $H$ is fixed. Let the lines $A B$ and $C D$ meet at $K$. Since $E A O B M$ and $E C D M$ are cyclic, we have $\angle E A K=$ $\angle E M B=\angle E C K$, so $E C A K$ is cyclic. Therefore $\angle E K A=90^{\circ}$, hence $E K B D$ is also cyclic and $E K \| O M$. Then $\angle E K F=$ $\angle E B D=\angle E O M=\angle O E K$, from which we deduce that $K F=F E$. However, since $\angle E K H=90^{\circ}$, the  point $F$ is the midpoint of $E H$; hence it is fixed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
166a5fc2-48ed-5824-9923-990c5f9c097c
| 24,544
|
2. A2 (FRA) ${ }^{\mathrm{IMO} 1}$ Let $m$ and $n$ be positive integers. The set $A=\left\{a_{1}, a_{2}, \ldots\right.$, $\left.a_{m}\right\}$ is a subset of $\{1,2, \ldots, n\}$. Whenever $a_{i}+a_{j} \leq n, 1 \leq i \leq j \leq m$, $a_{i}+a_{j}$ also belongs to $A$. Prove that $$ \frac{a_{1}+a_{2}+\cdots+a_{m}}{m} \geq \frac{n+1}{2} . $$
|
2. We may assume that $a_{1}>a_{2}>\cdots>a_{m}$. We claim that for $i=1, \ldots, m$, $a_{i}+a_{m+1-i} \geq n+1$. Indeed, otherwise $a_{i}+a_{m+1-i}, \ldots, a_{i}+a_{m-1}, a_{i}+a_{m}$ are $i$ different elements of $A$ greater than $a_{i}$, which is impossible. Now by adding for $i=1, \ldots, m$ we obtain $2\left(a_{1}+\cdots+a_{m}\right) \geq m(n+1)$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
2. A2 (FRA) ${ }^{\mathrm{IMO} 1}$ Let $m$ and $n$ be positive integers. The set $A=\left\{a_{1}, a_{2}, \ldots\right.$, $\left.a_{m}\right\}$ is a subset of $\{1,2, \ldots, n\}$. Whenever $a_{i}+a_{j} \leq n, 1 \leq i \leq j \leq m$, $a_{i}+a_{j}$ also belongs to $A$. Prove that $$ \frac{a_{1}+a_{2}+\cdots+a_{m}}{m} \geq \frac{n+1}{2} . $$
|
2. We may assume that $a_{1}>a_{2}>\cdots>a_{m}$. We claim that for $i=1, \ldots, m$, $a_{i}+a_{m+1-i} \geq n+1$. Indeed, otherwise $a_{i}+a_{m+1-i}, \ldots, a_{i}+a_{m-1}, a_{i}+a_{m}$ are $i$ different elements of $A$ greater than $a_{i}$, which is impossible. Now by adding for $i=1, \ldots, m$ we obtain $2\left(a_{1}+\cdots+a_{m}\right) \geq m(n+1)$, and the result follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
af700627-3e1e-50ad-858b-a629b72089dd
| 24,553
|
20. N3 (FIN) ${ }^{\text {IMO6 }}$ Find a set $A$ of positive integers such that for any infinite set $P$ of prime numbers, there exist positive integers $m \in A$ and $n \notin A$, both the product of the same number of distinct elements of $P$.
|
20. Let $A$ be the set of all numbers of the form $p_{1} p_{2} \ldots p_{p_{1}}$, where $p_{1}<p_{2}<$ $\cdots<p_{p_{1}}$ are primes. In other words, $A=\{2 \cdot 3,2 \cdot 5, \ldots\} \cup\{3 \cdot 5 \cdot 7,3 \cdot 5 \cdot$ $11, \ldots\} \cup\{5 \cdot 7 \cdot 11 \cdot 13 \cdot 17, \ldots\} \cup \cdots$. This set satisfies the requirements of the problem. Indeed, for any infinite set of primes $P=\left\{q_{1}, q_{2}, \ldots\right\}$ (where $q_{1}<q_{2}<\cdots$ ) we have $$ m=q_{1} q_{2} \cdots q_{q_{1}} \in A \quad \text { and } \quad n=q_{2} q_{3} \cdots q_{q_{1}+1} \notin A $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
20. N3 (FIN) ${ }^{\text {IMO6 }}$ Find a set $A$ of positive integers such that for any infinite set $P$ of prime numbers, there exist positive integers $m \in A$ and $n \notin A$, both the product of the same number of distinct elements of $P$.
|
20. Let $A$ be the set of all numbers of the form $p_{1} p_{2} \ldots p_{p_{1}}$, where $p_{1}<p_{2}<$ $\cdots<p_{p_{1}}$ are primes. In other words, $A=\{2 \cdot 3,2 \cdot 5, \ldots\} \cup\{3 \cdot 5 \cdot 7,3 \cdot 5 \cdot$ $11, \ldots\} \cup\{5 \cdot 7 \cdot 11 \cdot 13 \cdot 17, \ldots\} \cup \cdots$. This set satisfies the requirements of the problem. Indeed, for any infinite set of primes $P=\left\{q_{1}, q_{2}, \ldots\right\}$ (where $q_{1}<q_{2}<\cdots$ ) we have $$ m=q_{1} q_{2} \cdots q_{q_{1}} \in A \quad \text { and } \quad n=q_{2} q_{3} \cdots q_{q_{1}+1} \notin A $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0a0f8ec2-798d-50c5-ae73-c163d6ef8505
| 24,555
|
23. N6 (LAT) Let $x_{1}$ and $x_{2}$ be relatively prime positive integers. For $n \geq 2$, define $x_{n+1}=x_{n} x_{n-1}+1$. (a) Prove that for every $i>1$, there exists $j>i$ such that $x_{i}^{i}$ divides $x_{j}^{j}$. (b) Is it true that $x_{1}$ must divide $x_{j}^{j}$ for some $j>1$ ?
|
23. (a) Let $p$ be a prime divisor of $x_{i}, i>1$, and let $x_{j} \equiv u_{j}(\bmod p)$ where $0 \leq u_{j} \leq p-1$ (particularly $u_{i} \equiv 0$ ). Then $u_{j+1} \equiv u_{j} u_{j-1}+$ $1(\bmod p)$. The number of possible pairs $\left(u_{j}, u_{j+1}\right)$ is finite, so $u_{j}$ is eventually periodic. We claim that for some $d_{p}>0, u_{i+d_{p}}=0$. Indeed, suppose the contrary and let $\left(u_{m}, u_{m+1}, \ldots, u_{m+d-1}\right)$ be the first period for $m \geq i$. Then $m \neq i$. By the assumption $u_{m-1} \not \equiv$ $u_{m+d-1}$, but $u_{m-1} u_{m} \equiv u_{m+1}-1 \equiv u_{m+d+1}-1 \equiv u_{m+d-1} u_{m+d} \equiv$ $u_{m+d-1} u_{m}(\bmod p)$, which is impossible if $p \nmid u_{m}$. Hence there is a $d_{p}$ with $u_{i}=u_{i+d_{p}}=0$ and moreover $u_{i+1}=u_{i+d_{p}+1}=1$, so the sequence $u_{j}$ is periodic with period $d_{p}$ starting from $u_{i}$. Let $m$ be the least common multiple of all $d_{p}$ 's, where $p$ goes through all prime divisors of $x_{i}$. Then the same primes divide every $x_{i+k m}, k=1,2, \ldots$, so for large enough $k$ and $j=i+k m, x_{i}^{i} \mid x_{j}^{j}$. (b) If $i=1$, we cannot deduce that $x_{i+1} \equiv 1(\bmod p)$. The following example shows that the statement from (a) need not be true in this case. Take $x_{1}=22$ and $x_{2}=9$. Then $x_{n}$ is even if and only if $n \equiv 1(\bmod$ 3 ), but modulo 11 the sequence $\left\{x_{n}\right\}$ is $0,9,1,10,0,1,1,2,3,7,0, \ldots$, so $11 \mid x_{n}(n>1)$ if and only if $n \equiv 5(\bmod 6)$. Thus for no $n>1$ can we have $22 \mid x_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
23. N6 (LAT) Let $x_{1}$ and $x_{2}$ be relatively prime positive integers. For $n \geq 2$, define $x_{n+1}=x_{n} x_{n-1}+1$. (a) Prove that for every $i>1$, there exists $j>i$ such that $x_{i}^{i}$ divides $x_{j}^{j}$. (b) Is it true that $x_{1}$ must divide $x_{j}^{j}$ for some $j>1$ ?
|
23. (a) Let $p$ be a prime divisor of $x_{i}, i>1$, and let $x_{j} \equiv u_{j}(\bmod p)$ where $0 \leq u_{j} \leq p-1$ (particularly $u_{i} \equiv 0$ ). Then $u_{j+1} \equiv u_{j} u_{j-1}+$ $1(\bmod p)$. The number of possible pairs $\left(u_{j}, u_{j+1}\right)$ is finite, so $u_{j}$ is eventually periodic. We claim that for some $d_{p}>0, u_{i+d_{p}}=0$. Indeed, suppose the contrary and let $\left(u_{m}, u_{m+1}, \ldots, u_{m+d-1}\right)$ be the first period for $m \geq i$. Then $m \neq i$. By the assumption $u_{m-1} \not \equiv$ $u_{m+d-1}$, but $u_{m-1} u_{m} \equiv u_{m+1}-1 \equiv u_{m+d+1}-1 \equiv u_{m+d-1} u_{m+d} \equiv$ $u_{m+d-1} u_{m}(\bmod p)$, which is impossible if $p \nmid u_{m}$. Hence there is a $d_{p}$ with $u_{i}=u_{i+d_{p}}=0$ and moreover $u_{i+1}=u_{i+d_{p}+1}=1$, so the sequence $u_{j}$ is periodic with period $d_{p}$ starting from $u_{i}$. Let $m$ be the least common multiple of all $d_{p}$ 's, where $p$ goes through all prime divisors of $x_{i}$. Then the same primes divide every $x_{i+k m}, k=1,2, \ldots$, so for large enough $k$ and $j=i+k m, x_{i}^{i} \mid x_{j}^{j}$. (b) If $i=1$, we cannot deduce that $x_{i+1} \equiv 1(\bmod p)$. The following example shows that the statement from (a) need not be true in this case. Take $x_{1}=22$ and $x_{2}=9$. Then $x_{n}$ is even if and only if $n \equiv 1(\bmod$ 3 ), but modulo 11 the sequence $\left\{x_{n}\right\}$ is $0,9,1,10,0,1,1,2,3,7,0, \ldots$, so $11 \mid x_{n}(n>1)$ if and only if $n \equiv 5(\bmod 6)$. Thus for no $n>1$ can we have $22 \mid x_{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a5415524-5a7d-5ca2-bab6-df7592d5a7f7
| 24,563
|
5. A5 (POL) Let $f(x)=\frac{x^{2}+1}{2 x}$ for $x \neq 0$. Define $f^{(0)}(x)=x$ and $f^{(n)}(x)=$ $f\left(f^{(n-1)}(x)\right)$ for all positive integers $n$ and $x \neq 0$. Prove that for all nonnegative integers $n$ and $x \neq-1,0$, or 1 , $$ \frac{f^{(n)}(x)}{f^{(n+1)}(x)}=1+\frac{1}{f\left(\left(\frac{x+1}{x-1}\right)^{2^{n}}\right)} $$
|
5. If $f^{(n)}(x)=\frac{p_{n}(x)}{q_{n}(x)}$ for some positive integer $n$ and polynomials $p_{n}, q_{n}$, then $$ f^{(n+1)}(x)=f\left(\frac{p_{n}(x)}{q_{n}(x)}\right)=\frac{p_{n}(x)^{2}+q_{n}(x)^{2}}{2 p_{n}(x) q_{n}(x)} $$ Note that $f^{(0)}(x)=x / 1$. Thus $f^{(n)}(x)=\frac{p_{n}(x)}{q_{n}(x)}$, where the sequence of polynomials $p_{n}, q_{n}$ is defined recursively by $$ \begin{gathered} p_{0}(x)=x, \quad q_{0}(x)=1, \text { and } \\ p_{n+1}(x)=p_{n}(x)^{2}+q_{n}(x)^{2}, q_{n+1}(x)=2 p_{n}(x) q_{n}(x) . \end{gathered} $$ Furthermore, $p_{0}(x) \pm q_{0}(x)=x \pm 1$ and $p_{n+1}(x) \pm q_{n+1}(x)=p_{n}(x)^{2}+$ $q_{n}(x)^{2} \pm 2 p_{n}(x) q_{n}(x)=\left(p_{n}(x) \pm q_{n}(x)\right)^{2}$, so $p_{n}(x) \pm q_{n}(x)=(x \pm 1)^{2^{n}}$ for all $n$. Hence $$ p_{n}(x)=\frac{(x+1)^{2^{n}}+(x-1)^{2^{n}}}{2} \quad \text { and } \quad q_{n}(x)=\frac{(x+1)^{2^{n}}-(x-1)^{2^{n}}}{2} . $$ Finally, $$ \begin{aligned} \frac{f^{(n)}(x)}{f^{(n+1)}(x)} & =\frac{p_{n}(x) q_{n+1}(x)}{q_{n}(x) p_{n+1}(x)}=\frac{2 p_{n}(x)^{2}}{p_{n+1}(x)}=\frac{\left((x+1)^{2^{n}}+(x-1)^{2^{n}}\right)^{2}}{(x+1)^{2^{n+1}}+(x-1)^{2^{n+1}}} \\ & =1+\frac{2\left(\frac{x+1}{x-1}\right)^{2^{n}}}{1+\left(\frac{x+1}{x-1}\right)^{2^{n+1}}}=1+\frac{1}{f\left(\left(\frac{x+1}{x-1}\right)^{2^{n}}\right)} \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
5. A5 (POL) Let $f(x)=\frac{x^{2}+1}{2 x}$ for $x \neq 0$. Define $f^{(0)}(x)=x$ and $f^{(n)}(x)=$ $f\left(f^{(n-1)}(x)\right)$ for all positive integers $n$ and $x \neq 0$. Prove that for all nonnegative integers $n$ and $x \neq-1,0$, or 1 , $$ \frac{f^{(n)}(x)}{f^{(n+1)}(x)}=1+\frac{1}{f\left(\left(\frac{x+1}{x-1}\right)^{2^{n}}\right)} $$
|
5. If $f^{(n)}(x)=\frac{p_{n}(x)}{q_{n}(x)}$ for some positive integer $n$ and polynomials $p_{n}, q_{n}$, then $$ f^{(n+1)}(x)=f\left(\frac{p_{n}(x)}{q_{n}(x)}\right)=\frac{p_{n}(x)^{2}+q_{n}(x)^{2}}{2 p_{n}(x) q_{n}(x)} $$ Note that $f^{(0)}(x)=x / 1$. Thus $f^{(n)}(x)=\frac{p_{n}(x)}{q_{n}(x)}$, where the sequence of polynomials $p_{n}, q_{n}$ is defined recursively by $$ \begin{gathered} p_{0}(x)=x, \quad q_{0}(x)=1, \text { and } \\ p_{n+1}(x)=p_{n}(x)^{2}+q_{n}(x)^{2}, q_{n+1}(x)=2 p_{n}(x) q_{n}(x) . \end{gathered} $$ Furthermore, $p_{0}(x) \pm q_{0}(x)=x \pm 1$ and $p_{n+1}(x) \pm q_{n+1}(x)=p_{n}(x)^{2}+$ $q_{n}(x)^{2} \pm 2 p_{n}(x) q_{n}(x)=\left(p_{n}(x) \pm q_{n}(x)\right)^{2}$, so $p_{n}(x) \pm q_{n}(x)=(x \pm 1)^{2^{n}}$ for all $n$. Hence $$ p_{n}(x)=\frac{(x+1)^{2^{n}}+(x-1)^{2^{n}}}{2} \quad \text { and } \quad q_{n}(x)=\frac{(x+1)^{2^{n}}-(x-1)^{2^{n}}}{2} . $$ Finally, $$ \begin{aligned} \frac{f^{(n)}(x)}{f^{(n+1)}(x)} & =\frac{p_{n}(x) q_{n+1}(x)}{q_{n}(x) p_{n+1}(x)}=\frac{2 p_{n}(x)^{2}}{p_{n+1}(x)}=\frac{\left((x+1)^{2^{n}}+(x-1)^{2^{n}}\right)^{2}}{(x+1)^{2^{n+1}}+(x-1)^{2^{n+1}}} \\ & =1+\frac{2\left(\frac{x+1}{x-1}\right)^{2^{n}}}{1+\left(\frac{x+1}{x-1}\right)^{2^{n+1}}}=1+\frac{1}{f\left(\left(\frac{x+1}{x-1}\right)^{2^{n}}\right)} \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a6ddbd4f-77b8-597c-b0df-366d7d25bee1
| 24,574
|
7. C2 (COL) In a certain city, age is reckoned in terms of real numbers rather than integers. Every two citizens $x$ and $x^{\prime}$ either know each other or do not know each other. Moreover, if they do not, then there exists a chain of citizens $x=x_{0}, x_{1}, \ldots, x_{n}=x^{\prime}$ for some integer $n \geq 2$ such that $x_{i-1}$ and $x_{i}$ know each other. In a census, all male citizens declare their ages, and there is at least one male citizen. Each female citizen provides only the information that her age is the average of the ages of all the citizens she knows. Prove that this is enough to determine uniquely the ages of all the female citizens.
|
7. Let $a_{1}, a_{2}, \ldots, a_{m}$ be the ages of the male citizens $(m \geq 1)$. We claim that the age of each female citizen can be expressed in the form $c_{1} a_{1}+\cdots+c_{m} a_{m}$ for some constants $c_{i} \geq 0$, and we will prove this by induction on the number $n$ of female citizens. The claim is clear if $n=1$. Suppose it holds for $n$ and consider the case of $n+1$ female citizens. Choose any of them, say $A$ of age $x$ who knows $k$ citizens (at least one male). By the induction hypothesis, the age of each of the other $n$ females is expressible as $c_{1} a_{1}+\cdots+c_{m} a_{m}+c_{0} x$, where $c_{i} \geq 0$ and $c_{0}+c_{1}+\cdots+c_{m}=1$. Consequently, the sum of ages of the $k$ citizens who know $A$ is $k x=b_{1} a_{1}+\cdots+b_{m} a_{m}+b_{0} x$ for some constants $b_{i} \geq 0$ with sum $k$. But $A$ knows at least one male citizen (who does not contribute to the coefficient of $x)$, so $b_{0} \leq k-1$. Hence $x=\frac{b_{1} a_{1}+\cdots+b_{m} a_{m}}{k-b_{0}}$, and the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
7. C2 (COL) In a certain city, age is reckoned in terms of real numbers rather than integers. Every two citizens $x$ and $x^{\prime}$ either know each other or do not know each other. Moreover, if they do not, then there exists a chain of citizens $x=x_{0}, x_{1}, \ldots, x_{n}=x^{\prime}$ for some integer $n \geq 2$ such that $x_{i-1}$ and $x_{i}$ know each other. In a census, all male citizens declare their ages, and there is at least one male citizen. Each female citizen provides only the information that her age is the average of the ages of all the citizens she knows. Prove that this is enough to determine uniquely the ages of all the female citizens.
|
7. Let $a_{1}, a_{2}, \ldots, a_{m}$ be the ages of the male citizens $(m \geq 1)$. We claim that the age of each female citizen can be expressed in the form $c_{1} a_{1}+\cdots+c_{m} a_{m}$ for some constants $c_{i} \geq 0$, and we will prove this by induction on the number $n$ of female citizens. The claim is clear if $n=1$. Suppose it holds for $n$ and consider the case of $n+1$ female citizens. Choose any of them, say $A$ of age $x$ who knows $k$ citizens (at least one male). By the induction hypothesis, the age of each of the other $n$ females is expressible as $c_{1} a_{1}+\cdots+c_{m} a_{m}+c_{0} x$, where $c_{i} \geq 0$ and $c_{0}+c_{1}+\cdots+c_{m}=1$. Consequently, the sum of ages of the $k$ citizens who know $A$ is $k x=b_{1} a_{1}+\cdots+b_{m} a_{m}+b_{0} x$ for some constants $b_{i} \geq 0$ with sum $k$. But $A$ knows at least one male citizen (who does not contribute to the coefficient of $x)$, so $b_{0} \leq k-1$. Hence $x=\frac{b_{1} a_{1}+\cdots+b_{m} a_{m}}{k-b_{0}}$, and the claim follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c2af3787-b5a8-523e-a708-9be7c95830dc
| 24,579
|
8. C3 (MCD) Peter has three accounts in a bank, each with an integral number of dollars. He is only allowed to transfer money from one account to another so that the amount of money in the latter is doubled. (a) Prove that Peter can always transfer all his money into two accounts. (b) Can Peter always transfer all his money into one account?
|
8. (a) Let $a, b, c, a \leq b \leq c$ be the amounts of money in dollars in Peter's first, second, and third account, respectively. If $a=0$, then we are done, so suppose that $a>0$. Let Peter make transfers of money into the first account as follows. Write $b=a q+r$ with $0 \leq r<a$ and let $q=m_{0}+2 m_{1}+\cdots+2^{k} m_{k}$ be the binary representation of $q$ $\left(m_{i} \in\{0,1\}, m_{k}=1\right)$. In the $i$ th transfer, $i=1,2, \ldots, k+1$, if $m_{i}=1$ he transfers money from the second account, while if $m_{i}=0$ he does so from the third. In this way he has transferred exactly $\left(m_{0}+2 m_{1}+\cdots+2^{k} m_{k}\right) a$ dollars from the second account, thus leaving $r$ dollars in it, $r<a$. Repeating this procedure, Peter can diminish the amount of money in the smallest account to zero, as required. (b) If Peter has an odd number of dollars, he clearly cannot transfer his money into one account.
|
proof
|
Yes
|
Yes
|
proof
|
Other
|
8. C3 (MCD) Peter has three accounts in a bank, each with an integral number of dollars. He is only allowed to transfer money from one account to another so that the amount of money in the latter is doubled. (a) Prove that Peter can always transfer all his money into two accounts. (b) Can Peter always transfer all his money into one account?
|
8. (a) Let $a, b, c, a \leq b \leq c$ be the amounts of money in dollars in Peter's first, second, and third account, respectively. If $a=0$, then we are done, so suppose that $a>0$. Let Peter make transfers of money into the first account as follows. Write $b=a q+r$ with $0 \leq r<a$ and let $q=m_{0}+2 m_{1}+\cdots+2^{k} m_{k}$ be the binary representation of $q$ $\left(m_{i} \in\{0,1\}, m_{k}=1\right)$. In the $i$ th transfer, $i=1,2, \ldots, k+1$, if $m_{i}=1$ he transfers money from the second account, while if $m_{i}=0$ he does so from the third. In this way he has transferred exactly $\left(m_{0}+2 m_{1}+\cdots+2^{k} m_{k}\right) a$ dollars from the second account, thus leaving $r$ dollars in it, $r<a$. Repeating this procedure, Peter can diminish the amount of money in the smallest account to zero, as required. (b) If Peter has an odd number of dollars, he clearly cannot transfer his money into one account.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
883ffa2f-7b72-5c54-9744-6f267816945a
| 24,582
|
9. C4 (EST) There are $n+1$ fixed positions in a row, labeled 0 to $n$ in increasing order from right to left. Cards numbered 0 to $n$ are shuffled and dealt, one in each position. The object of the game is to have card $i$ in the $i$ th position for $0 \leq i \leq n$. If this has not been achieved, the following move is executed. Determine the smallest $k$ such that the $k$ th position is occupied by a card $l>k$. Remove this card, slide all cards from the $(k+1)$ st to the $l$ th position one place to the right, and replace the card $l$ in the $l$ th position. (a) Prove that the game lasts at most $2^{n}-1$ moves. (b) Prove that there exists a unique initial configuration for which the game lasts exactly $2^{n}-1$ moves.
|
9. (a) For $i=1, \ldots, n$, let $d_{i}$ be 0 if the card $i$ is in the $i$ th position, and 1 otherwise. Define $b=d_{1}+2 d_{2}+2^{2} d_{3}+\cdots+2^{n-1} d_{n}$, so that $0 \leq b \leq$ $2^{n}-1$, and $b=0$ if and only if the game is over. After each move some digit $d_{l}$ changes from 1 to 0 while $d_{l+1}, d_{l+2}, \ldots$ remain unchanged. Hence $b$ decreases after each move, and consequently the game ends after at most $2^{n}-1$ moves. (b) Suppose the game lasts exactly $2^{n}-1$ moves. Then each move decreases $b$ for exactly one, so playing the game in reverse (starting from the final configuration), every move is uniquely determined. It follows that if the configuration that allows a game lasting $2^{n}-1$ moves exists, it must be unique. Consider the initial configuration $0, n, n-1, \ldots, 2,1$. We prove by induction that the game will last exactly $2^{n}-1$ moves, and that the card 0 will get to the 0 th position only in the last move. This is trivial for $n=1$, so suppose that the claim is true for some $n=m-1 \geq 1$ and consider the case $n=m$. Obviously the card 0 does not move until the card $m$ gets to the 0 -th position. But if we ignore the card 0 and consider the card $m$ to be the card 0 , the induction hypothesis gives that the card $m$ will move to the 0 th position only after $2^{m-1}-1$ moves. After these $2^{m-1}-1$ moves, we come to the configuration $0, m-1, \ldots, 2,1, m$. The next move yields $m, 0, m-1, \ldots, 2,1$, so by the induction hypothesis again we need $2^{m-1}-1$ moves more to finish the game.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
9. C4 (EST) There are $n+1$ fixed positions in a row, labeled 0 to $n$ in increasing order from right to left. Cards numbered 0 to $n$ are shuffled and dealt, one in each position. The object of the game is to have card $i$ in the $i$ th position for $0 \leq i \leq n$. If this has not been achieved, the following move is executed. Determine the smallest $k$ such that the $k$ th position is occupied by a card $l>k$. Remove this card, slide all cards from the $(k+1)$ st to the $l$ th position one place to the right, and replace the card $l$ in the $l$ th position. (a) Prove that the game lasts at most $2^{n}-1$ moves. (b) Prove that there exists a unique initial configuration for which the game lasts exactly $2^{n}-1$ moves.
|
9. (a) For $i=1, \ldots, n$, let $d_{i}$ be 0 if the card $i$ is in the $i$ th position, and 1 otherwise. Define $b=d_{1}+2 d_{2}+2^{2} d_{3}+\cdots+2^{n-1} d_{n}$, so that $0 \leq b \leq$ $2^{n}-1$, and $b=0$ if and only if the game is over. After each move some digit $d_{l}$ changes from 1 to 0 while $d_{l+1}, d_{l+2}, \ldots$ remain unchanged. Hence $b$ decreases after each move, and consequently the game ends after at most $2^{n}-1$ moves. (b) Suppose the game lasts exactly $2^{n}-1$ moves. Then each move decreases $b$ for exactly one, so playing the game in reverse (starting from the final configuration), every move is uniquely determined. It follows that if the configuration that allows a game lasting $2^{n}-1$ moves exists, it must be unique. Consider the initial configuration $0, n, n-1, \ldots, 2,1$. We prove by induction that the game will last exactly $2^{n}-1$ moves, and that the card 0 will get to the 0 th position only in the last move. This is trivial for $n=1$, so suppose that the claim is true for some $n=m-1 \geq 1$ and consider the case $n=m$. Obviously the card 0 does not move until the card $m$ gets to the 0 -th position. But if we ignore the card 0 and consider the card $m$ to be the card 0 , the induction hypothesis gives that the card $m$ will move to the 0 th position only after $2^{m-1}-1$ moves. After these $2^{m-1}-1$ moves, we come to the configuration $0, m-1, \ldots, 2,1, m$. The next move yields $m, 0, m-1, \ldots, 2,1$, so by the induction hypothesis again we need $2^{m-1}-1$ moves more to finish the game.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
411a3b64-8c2b-5cb5-9311-2fcfa5da3e4c
| 24,585
|
1. A1 (RUS) ${ }^{\mathrm{IMO} 2}$ Let $a, b$, and $c$ be positive real numbers such that $a b c=1$. Prove that $$ \frac{1}{a^{3}(b+c)}+\frac{1}{b^{3}(a+c)}+\frac{1}{c^{3}(a+b)} \geq \frac{3}{2} $$
|
1. Let $x=\frac{1}{a}, y=\frac{1}{b}, z=\frac{1}{c}$. Then $x y z=1$ and $$ S=\frac{1}{a^{3}(b+c)}+\frac{1}{b^{3}(c+a)}+\frac{1}{c^{3}(a+b)}=\frac{x^{2}}{y+z}+\frac{y^{2}}{z+x}+\frac{z^{2}}{x+y} $$ We must prove that $S \geq \frac{3}{2}$. From the Cauchy-Schwarz inequality, $$ [(y+z)+(z+x)+(x+y)] \cdot S \geq(x+y+z)^{2} \Rightarrow S \geq \frac{x+y+z}{2} $$ It follows from the A-G mean inequality that $\frac{x+y+z}{2} \geq \frac{3}{2} \sqrt[3]{x y z}=\frac{3}{2}$; hence the proof is complete. Equality holds if and only if $x=y=z=1$, i.e., $a=b=c=1$. Remark. After reducing the problem to $\frac{x^{2}}{y+z}+\frac{y^{2}}{z+x}+\frac{z^{2}}{x+y} \geq \frac{3}{2}$, we can solve the problem using Jensen's inequality applied to the function $g(u, v)=$ $u^{2} / v$. The problem can also be solved using Muirhead's inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
1. A1 (RUS) ${ }^{\mathrm{IMO} 2}$ Let $a, b$, and $c$ be positive real numbers such that $a b c=1$. Prove that $$ \frac{1}{a^{3}(b+c)}+\frac{1}{b^{3}(a+c)}+\frac{1}{c^{3}(a+b)} \geq \frac{3}{2} $$
|
1. Let $x=\frac{1}{a}, y=\frac{1}{b}, z=\frac{1}{c}$. Then $x y z=1$ and $$ S=\frac{1}{a^{3}(b+c)}+\frac{1}{b^{3}(c+a)}+\frac{1}{c^{3}(a+b)}=\frac{x^{2}}{y+z}+\frac{y^{2}}{z+x}+\frac{z^{2}}{x+y} $$ We must prove that $S \geq \frac{3}{2}$. From the Cauchy-Schwarz inequality, $$ [(y+z)+(z+x)+(x+y)] \cdot S \geq(x+y+z)^{2} \Rightarrow S \geq \frac{x+y+z}{2} $$ It follows from the A-G mean inequality that $\frac{x+y+z}{2} \geq \frac{3}{2} \sqrt[3]{x y z}=\frac{3}{2}$; hence the proof is complete. Equality holds if and only if $x=y=z=1$, i.e., $a=b=c=1$. Remark. After reducing the problem to $\frac{x^{2}}{y+z}+\frac{y^{2}}{z+x}+\frac{z^{2}}{x+y} \geq \frac{3}{2}$, we can solve the problem using Jensen's inequality applied to the function $g(u, v)=$ $u^{2} / v$. The problem can also be solved using Muirhead's inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
fe6cac4f-d851-5ab0-96fc-05016190af76
| 24,588
|
10. G4 (UKR) An acute triangle $A B C$ is given. Points $A_{1}$ and $A_{2}$ are taken on the side $B C$ (with $A_{2}$ between $A_{1}$ and $C$ ), $B_{1}$ and $B_{2}$ on the side $A C$ (with $B_{2}$ between $B_{1}$ and $A$ ), and $C_{1}$ and $C_{2}$ on the side $A B$ (with $C_{2}$ between $C_{1}$ and $B$ ) such that $$ \angle A A_{1} A_{2}=\angle A A_{2} A_{1}=\angle B B_{1} B_{2}=\angle B B_{2} B_{1}=\angle C C_{1} C_{2}=\angle C C_{2} C_{1} . $$ The lines $A A_{1}, B B_{1}$, and $C C_{1}$ form a triangle, and the lines $A A_{2}, B B_{2}$, and $C C_{2}$ form a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
|
10. Let the two triangles be $X_{1} Y_{1} Z_{1}, X_{2} Y_{2} Z_{2}$, with $X_{1}=B B_{1} \cap C C_{1}, Y_{1}=$ $C C_{1} \cap A A_{1}, Z_{1}=A A_{1} \cap B B_{1}$, $X_{2}=B B_{2} \cap C C_{2}, Y_{2}=C C_{2} \cap$ $A A_{2}, Z_{2}=A A_{2} \cap B B_{2}$. First, we observe that $\angle A B B_{2}=\angle A C C_{1}$ and $\angle A B B_{1}=\angle A C C_{2}$. Consequently $\angle B Z_{1} A_{1}=\angle B A A_{1}+$ $\angle A B B_{1}=\angle B C C_{2}+\angle C_{2} C A=$ $\angle C$ and similarly $\angle A Z_{2} B_{2}=\angle C$, $\angle A Y_{1} C_{1}=\angle C Y_{2} A_{2}=\angle B$. Also, $\triangle A B B_{2} \sim \triangle A C C_{1}$; hence  $A C_{1} / A C=A B_{2} / A B$. From the sine formula, we obtain $$ \begin{aligned} \frac{A Z_{1}}{\sin \angle A B Z_{1}} & =\frac{A B}{\sin \angle A Z_{1} B}=\frac{A B}{\sin \angle C}=\frac{A C}{\sin \angle B}=\frac{A C}{\sin \angle A Y_{2} C} \\ & =\frac{A Y_{2}}{\sin \angle A C Y_{2}} \Longrightarrow A Z_{1}=A Y_{2} . \end{aligned} $$ Analogously, $B X_{1}=B Z_{2}$ and $C Y_{1}=C X_{2}$. Furthermore, again from the sine formula, $$ \begin{aligned} \frac{A Y_{1}}{\sin \angle A C_{1} Y_{1}} & =\frac{A C_{1}}{\sin \angle A Y_{1} C_{1}}=\frac{A C_{1}}{A C} \frac{A C}{\sin \angle B} \\ & =\frac{A B_{2}}{A B} \frac{A B}{\sin \angle C}=\frac{A B_{2}}{\sin \angle A Z_{2} B_{2}}=\frac{A Z_{2}}{\sin \angle A B_{2} Z_{2}} . \end{aligned} $$ Hence, $A Y_{1}=A Z_{2}$ and, analogously, $B Z_{1}=B X_{2}$ and $C X_{1}=C Y_{2}$. We deduce that $Y_{1} Z_{2} \| B C$ and $Z_{2} X_{1} \| A C$, which gives us $\angle Y_{1} Z_{2} X_{1}=$ $180^{\circ}-\angle C=180^{\circ}-\angle Y_{1} Z_{1} X_{1}$. It follows that $Z_{2}$ lies on the circle circumscribed about $\triangle X_{1} Y_{1} Z_{1}$. Similarly, so do $X_{2}$ and $Y_{2}$. Second solution. Let $H$ be the orthocenter of $\triangle A B C$. Triangles $A H B$, $B H C, C H A, A B C$ have the same circumradius $R$. Additionally, $$ \angle H A A_{i}=\angle H B B_{i}=\angle H C C_{i}=\theta(i=1,2) . $$ Since $\angle H B X_{1}=\angle H C X_{1}=\theta, B C X_{1} H$ is concyclic and therefore $H X_{1}=$ $2 R \sin \theta$. The same holds for $H Y_{1}, H Z_{1}, H X_{2}, H Y_{2}, H Z_{2}$. Hence $X_{i}, Y_{i}, Z_{i}$ $(i=1,2)$ lie on a circle centered at $H$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
10. G4 (UKR) An acute triangle $A B C$ is given. Points $A_{1}$ and $A_{2}$ are taken on the side $B C$ (with $A_{2}$ between $A_{1}$ and $C$ ), $B_{1}$ and $B_{2}$ on the side $A C$ (with $B_{2}$ between $B_{1}$ and $A$ ), and $C_{1}$ and $C_{2}$ on the side $A B$ (with $C_{2}$ between $C_{1}$ and $B$ ) such that $$ \angle A A_{1} A_{2}=\angle A A_{2} A_{1}=\angle B B_{1} B_{2}=\angle B B_{2} B_{1}=\angle C C_{1} C_{2}=\angle C C_{2} C_{1} . $$ The lines $A A_{1}, B B_{1}$, and $C C_{1}$ form a triangle, and the lines $A A_{2}, B B_{2}$, and $C C_{2}$ form a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
|
10. Let the two triangles be $X_{1} Y_{1} Z_{1}, X_{2} Y_{2} Z_{2}$, with $X_{1}=B B_{1} \cap C C_{1}, Y_{1}=$ $C C_{1} \cap A A_{1}, Z_{1}=A A_{1} \cap B B_{1}$, $X_{2}=B B_{2} \cap C C_{2}, Y_{2}=C C_{2} \cap$ $A A_{2}, Z_{2}=A A_{2} \cap B B_{2}$. First, we observe that $\angle A B B_{2}=\angle A C C_{1}$ and $\angle A B B_{1}=\angle A C C_{2}$. Consequently $\angle B Z_{1} A_{1}=\angle B A A_{1}+$ $\angle A B B_{1}=\angle B C C_{2}+\angle C_{2} C A=$ $\angle C$ and similarly $\angle A Z_{2} B_{2}=\angle C$, $\angle A Y_{1} C_{1}=\angle C Y_{2} A_{2}=\angle B$. Also, $\triangle A B B_{2} \sim \triangle A C C_{1}$; hence  $A C_{1} / A C=A B_{2} / A B$. From the sine formula, we obtain $$ \begin{aligned} \frac{A Z_{1}}{\sin \angle A B Z_{1}} & =\frac{A B}{\sin \angle A Z_{1} B}=\frac{A B}{\sin \angle C}=\frac{A C}{\sin \angle B}=\frac{A C}{\sin \angle A Y_{2} C} \\ & =\frac{A Y_{2}}{\sin \angle A C Y_{2}} \Longrightarrow A Z_{1}=A Y_{2} . \end{aligned} $$ Analogously, $B X_{1}=B Z_{2}$ and $C Y_{1}=C X_{2}$. Furthermore, again from the sine formula, $$ \begin{aligned} \frac{A Y_{1}}{\sin \angle A C_{1} Y_{1}} & =\frac{A C_{1}}{\sin \angle A Y_{1} C_{1}}=\frac{A C_{1}}{A C} \frac{A C}{\sin \angle B} \\ & =\frac{A B_{2}}{A B} \frac{A B}{\sin \angle C}=\frac{A B_{2}}{\sin \angle A Z_{2} B_{2}}=\frac{A Z_{2}}{\sin \angle A B_{2} Z_{2}} . \end{aligned} $$ Hence, $A Y_{1}=A Z_{2}$ and, analogously, $B Z_{1}=B X_{2}$ and $C X_{1}=C Y_{2}$. We deduce that $Y_{1} Z_{2} \| B C$ and $Z_{2} X_{1} \| A C$, which gives us $\angle Y_{1} Z_{2} X_{1}=$ $180^{\circ}-\angle C=180^{\circ}-\angle Y_{1} Z_{1} X_{1}$. It follows that $Z_{2}$ lies on the circle circumscribed about $\triangle X_{1} Y_{1} Z_{1}$. Similarly, so do $X_{2}$ and $Y_{2}$. Second solution. Let $H$ be the orthocenter of $\triangle A B C$. Triangles $A H B$, $B H C, C H A, A B C$ have the same circumradius $R$. Additionally, $$ \angle H A A_{i}=\angle H B B_{i}=\angle H C C_{i}=\theta(i=1,2) . $$ Since $\angle H B X_{1}=\angle H C X_{1}=\theta, B C X_{1} H$ is concyclic and therefore $H X_{1}=$ $2 R \sin \theta$. The same holds for $H Y_{1}, H Z_{1}, H X_{2}, H Y_{2}, H Z_{2}$. Hence $X_{i}, Y_{i}, Z_{i}$ $(i=1,2)$ lie on a circle centered at $H$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
29a45435-6682-55f2-9fe2-472f89fe2ad6
| 24,590
|
11. G5 (NZL) ${ }^{\mathrm{IMO} 5}$ Let $A B C D E F$ be a convex hexagon with $A B=B C=$ $C D, D E=E F=F A$, and $\measuredangle B C D=\measuredangle E F A=\pi / 3$ (that is, $60^{\circ}$ ). Let $G$ and $H$ be two points interior to the hexagon such that angles $A G B$ and $D H E$ are both $2 \pi / 3$ (that is, $120^{\circ}$ ). Prove that $A G+G B+G H+D H+$ $H E \geq C F$.
|
11. Triangles $B C D$ and $E F A$ are equilateral, and hence $B E$ is an axis of symmetry of $A B D E$. Let $C^{\prime}, F^{\prime}$ respectively be the points symmetric to $C, F$ with respect to $B E$. The points $G$ and $H$ lie on the circumcircles of $A B C^{\prime}$ and $D E F^{\prime}$ respectively (because, for instance, $\angle A G B=120^{\circ}=$ $\left.180^{\circ}-\angle A C^{\prime} B\right)$; hence from Ptolemy's theorem we have $A G+G B=C^{\prime} G$ and $D H+H E=H F^{\prime}$. Therefore $$ A G+G B+G H+D H+H E=C^{\prime} G+G H+H F^{\prime} \geq C^{\prime} F^{\prime}=C F $$ with equality if and only if $G$ and $H$ both lie on $C^{\prime} F^{\prime}$. Remark. Since by Ptolemy's inequality $A G+G B \geq C^{\prime} G$ and $D H+H E \geq$ $H F^{\prime}$, the result holds without the condition $\angle A G B=\angle D H E=120^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
11. G5 (NZL) ${ }^{\mathrm{IMO} 5}$ Let $A B C D E F$ be a convex hexagon with $A B=B C=$ $C D, D E=E F=F A$, and $\measuredangle B C D=\measuredangle E F A=\pi / 3$ (that is, $60^{\circ}$ ). Let $G$ and $H$ be two points interior to the hexagon such that angles $A G B$ and $D H E$ are both $2 \pi / 3$ (that is, $120^{\circ}$ ). Prove that $A G+G B+G H+D H+$ $H E \geq C F$.
|
11. Triangles $B C D$ and $E F A$ are equilateral, and hence $B E$ is an axis of symmetry of $A B D E$. Let $C^{\prime}, F^{\prime}$ respectively be the points symmetric to $C, F$ with respect to $B E$. The points $G$ and $H$ lie on the circumcircles of $A B C^{\prime}$ and $D E F^{\prime}$ respectively (because, for instance, $\angle A G B=120^{\circ}=$ $\left.180^{\circ}-\angle A C^{\prime} B\right)$; hence from Ptolemy's theorem we have $A G+G B=C^{\prime} G$ and $D H+H E=H F^{\prime}$. Therefore $$ A G+G B+G H+D H+H E=C^{\prime} G+G H+H F^{\prime} \geq C^{\prime} F^{\prime}=C F $$ with equality if and only if $G$ and $H$ both lie on $C^{\prime} F^{\prime}$. Remark. Since by Ptolemy's inequality $A G+G B \geq C^{\prime} G$ and $D H+H E \geq$ $H F^{\prime}$, the result holds without the condition $\angle A G B=\angle D H E=120^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
68426e9e-6d76-533f-9fdc-fb560bb78b3e
| 24,593
|
12. G6 (USA) Let $A_{1} A_{2} A_{3} A_{4}$ be a tetrahedron, $G$ its centroid, and $A_{1}^{\prime}, A_{2}^{\prime}, A_{3}^{\prime}$, and $A_{4}^{\prime}$ the points where the circumsphere of $A_{1} A_{2} A_{3} A_{4}$ intersects $G A_{1}, G A_{2}, G A_{3}$, and $G A_{4}$, respectively. Prove that $$ G A_{1} \cdot G A_{2} \cdot G A_{3} \cdot G A_{4} \leq G A_{1}^{\prime} \cdot G A_{2}^{\prime} \cdot G A_{3}^{\prime} \cdot G A_{4}^{\prime} $$ and $$ \frac{1}{G A_{1}^{\prime}}+\frac{1}{G A_{2}^{\prime}}+\frac{1}{G A_{3}^{\prime}}+\frac{1}{G A_{4}^{\prime}} \leq \frac{1}{G A_{1}}+\frac{1}{G A_{2}}+\frac{1}{G A_{3}}+\frac{1}{G A_{4}} $$
|
12. Let $O$ be the circumcenter and $R$ the circumradius of $\underset{\longrightarrow}{A_{1} A_{2} A_{3} A_{4}}$. We have $O A_{i}^{2}=\left(\overrightarrow{O G}+\left(\overrightarrow{O A_{i}}-\overrightarrow{O G}\right)\right)^{2}=O G^{2}+G A_{i}^{2}+2 \overrightarrow{O G} \cdot \overrightarrow{G A_{i}}$. Summing up these equalities for $i=1,2,3,4$ and using that $\sum_{i=1}^{4} \overrightarrow{G A_{i}}=\overrightarrow{0}$, we obtain $$ \sum_{i=1}^{4} O A_{i}^{2}=4 O G^{2}+\sum_{i=1}^{4} G A_{i}^{2} \Longleftrightarrow \sum_{i=1}^{4} G A_{i}^{2}=4\left(R^{2}-O G^{2}\right) $$ Now we have that the potential of $G$ with respect to the sphere equals $G A_{i} \cdot G A_{i}^{\prime}=R^{2}-O G^{2}$. Plugging in these expressions for $G A_{i}^{\prime}$, we reduce the inequalities we must prove to $$ \begin{aligned} G A_{1} \cdot G A_{2} \cdot G A_{3} \cdot G A_{4} & \leq\left(R^{2}-O G^{2}\right)^{2} \\ \text { and } \quad\left(R^{2}-O G^{2}\right) \sum_{i=1}^{4} \frac{1}{G A_{i}} & \geq \sum_{i=1}^{4} G A_{i} \end{aligned} $$ Inequality (2) immediately follows from (1) and the quadratic-geometric mean inequality for $G A_{i}$. Since from the Cauchy-Schwarz inequality we have $\sum_{i=1}^{4} G A_{i}^{4} \geq \frac{1}{4}\left(\sum_{i=1}^{4} G A_{i}\right)^{2}$ and $\left(\sum_{i=1}^{4} G A_{i}\right)\left(\sum_{i=1}^{4} \frac{1}{G A_{i}}\right) \geq 16$, inequality (3) follows from (1) and from $$ \left(\sum_{i=1}^{4} G A_{i}^{2}\right)\left(\sum_{i=1}^{4} \frac{1}{G A_{i}}\right) \geq \frac{1}{4}\left(\sum_{i=1}^{4} G A_{i}\right)^{2}\left(\sum_{i=1}^{4} \frac{1}{G A_{i}}\right) \geq 4 \sum_{i=1}^{4} G A_{i} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
12. G6 (USA) Let $A_{1} A_{2} A_{3} A_{4}$ be a tetrahedron, $G$ its centroid, and $A_{1}^{\prime}, A_{2}^{\prime}, A_{3}^{\prime}$, and $A_{4}^{\prime}$ the points where the circumsphere of $A_{1} A_{2} A_{3} A_{4}$ intersects $G A_{1}, G A_{2}, G A_{3}$, and $G A_{4}$, respectively. Prove that $$ G A_{1} \cdot G A_{2} \cdot G A_{3} \cdot G A_{4} \leq G A_{1}^{\prime} \cdot G A_{2}^{\prime} \cdot G A_{3}^{\prime} \cdot G A_{4}^{\prime} $$ and $$ \frac{1}{G A_{1}^{\prime}}+\frac{1}{G A_{2}^{\prime}}+\frac{1}{G A_{3}^{\prime}}+\frac{1}{G A_{4}^{\prime}} \leq \frac{1}{G A_{1}}+\frac{1}{G A_{2}}+\frac{1}{G A_{3}}+\frac{1}{G A_{4}} $$
|
12. Let $O$ be the circumcenter and $R$ the circumradius of $\underset{\longrightarrow}{A_{1} A_{2} A_{3} A_{4}}$. We have $O A_{i}^{2}=\left(\overrightarrow{O G}+\left(\overrightarrow{O A_{i}}-\overrightarrow{O G}\right)\right)^{2}=O G^{2}+G A_{i}^{2}+2 \overrightarrow{O G} \cdot \overrightarrow{G A_{i}}$. Summing up these equalities for $i=1,2,3,4$ and using that $\sum_{i=1}^{4} \overrightarrow{G A_{i}}=\overrightarrow{0}$, we obtain $$ \sum_{i=1}^{4} O A_{i}^{2}=4 O G^{2}+\sum_{i=1}^{4} G A_{i}^{2} \Longleftrightarrow \sum_{i=1}^{4} G A_{i}^{2}=4\left(R^{2}-O G^{2}\right) $$ Now we have that the potential of $G$ with respect to the sphere equals $G A_{i} \cdot G A_{i}^{\prime}=R^{2}-O G^{2}$. Plugging in these expressions for $G A_{i}^{\prime}$, we reduce the inequalities we must prove to $$ \begin{aligned} G A_{1} \cdot G A_{2} \cdot G A_{3} \cdot G A_{4} & \leq\left(R^{2}-O G^{2}\right)^{2} \\ \text { and } \quad\left(R^{2}-O G^{2}\right) \sum_{i=1}^{4} \frac{1}{G A_{i}} & \geq \sum_{i=1}^{4} G A_{i} \end{aligned} $$ Inequality (2) immediately follows from (1) and the quadratic-geometric mean inequality for $G A_{i}$. Since from the Cauchy-Schwarz inequality we have $\sum_{i=1}^{4} G A_{i}^{4} \geq \frac{1}{4}\left(\sum_{i=1}^{4} G A_{i}\right)^{2}$ and $\left(\sum_{i=1}^{4} G A_{i}\right)\left(\sum_{i=1}^{4} \frac{1}{G A_{i}}\right) \geq 16$, inequality (3) follows from (1) and from $$ \left(\sum_{i=1}^{4} G A_{i}^{2}\right)\left(\sum_{i=1}^{4} \frac{1}{G A_{i}}\right) \geq \frac{1}{4}\left(\sum_{i=1}^{4} G A_{i}\right)^{2}\left(\sum_{i=1}^{4} \frac{1}{G A_{i}}\right) \geq 4 \sum_{i=1}^{4} G A_{i} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd032b03-8266-570b-9e3b-7446efc95301
| 24,595
|
13. G7 (LAT) $O$ is a point inside a convex quadrilateral $A B C D$ of area $S . K, L, M$, and $N$ are interior points of the sides $A B, B C, C D$, and $D A$ respectively. If $O K B L$ and $O M D N$ are parallelograms, prove that $\sqrt{S} \geq \sqrt{S_{1}}+\sqrt{S_{2}}$, where $S_{1}$ and $S_{2}$ are the areas of $O N A K$ and $O L C M$ respectively.
|
13. If $O$ lies on $A C$, then $A B C D, A K O N$, and $O L C M$ are similar; hence $A C=A O+O C$ implies $\sqrt{S}=\sqrt{S_{1}}+\sqrt{S_{2}}$. Assume that $O$ does not lie on $A C$ and that w.l.o.g. it lies inside triangle $A D C$. Let us denote by $T_{1}, T_{2}$ the areas of parallelograms $K B L O, N O M D$ respectively. Consider a line through $O$ that intersects $A D, D C, C B, B A$ respectively at $X, Y, Z, W$ so that $O W / O X=O Z / O Y$ (such a line exists by a continuity argument: the left side is smaller when $W=X=A$, but greater when $Y=Z=C$ ). The desired inequality is equivalent to $T_{1}+T_{2} \geq 2 \sqrt{S_{1} S_{2}}$. Since triangles $W K O, O L Z, W B Z$ are similar and $W O+O Z=W Z$, we have $\sqrt{S_{W K O}}+\sqrt{S_{O L Z}}=\sqrt{S_{W B Z}}=$ $\sqrt{S_{W K O}+S_{O L Z}+T_{1}}$, which implies $T_{1}=2 \sqrt{S_{W K O} S_{O L Z}}$. Similarly, $T_{2}=2 \sqrt{S_{X N O} S_{O M Y}}$. Since $O W / O Z=O X / O Y$, we have $S_{W K O} / S_{X N O}=S_{O L Z} / S_{O M Y}$.  Therefore we obtain $$ \begin{aligned} T_{1}+T_{2} & =2 \sqrt{S_{W K O} S_{O L Z}}+2 \sqrt{S_{X N O} S_{O M Y}} \\ & =2 \sqrt{\left(S_{W K O}+S_{X N O}\right)\left(S_{O L Z}+S_{O M Y}\right)} \geq 2 \sqrt{S_{1} S_{2}} \end{aligned} $$ Second solution. By an affine transformation of the plane one can transform any nondegenerate quadrilateral into a cyclic one, thereby preserving parallelness and ratios of areas. Thus we may assume w.l.o.g. that $A B C D$ is cyclic. By a well-known formula, the area of a cyclic quadrilateral with sides $a, b, c, d$ and semiperimeter $p$ is given by $$ S=\sqrt{(p-a)(p-b)(p-c)(p-d)} $$ Let us set $A K=a_{1}, K B=b_{1}, B L=a_{2}, L C=b_{2}, C M=a_{3}, M D=b_{3}$, $D N=a_{4}, N A=b_{4}$. Then the sides of quadrilateral $A K O N$ are $a_{i}$, the sides of $C L O M$ are $b_{i}$, and the sides of $A B C D$ are $a_{i}+b_{i}(i=1,2,3,4)$. If $p$ and $q$ are the semiperimeters of $A K O N$ and $C L O M$, and $x_{i}=p-a_{i}$, $y_{i}=q-b_{i}$, then we have $S_{1}=\sqrt{x_{1} x_{2} x_{3} x_{4}}, S_{2}=\sqrt{y_{1} y_{2} y_{3} y_{4}}$, and $S=$ $\sqrt{\left(x_{1}+y_{1}\right)\left(x_{2}+y_{2}\right)\left(x_{3}+y_{3}\right)\left(x_{4}+y_{4}\right)}$. Thus we need to show that $$ \sqrt[4]{x_{1} x_{2} x_{3} x_{4}}+\sqrt[4]{y_{1} y_{2} y_{3} y_{4}} \leq \sqrt[4]{\left(x_{1}+y_{1}\right)\left(x_{2}+y_{2}\right)\left(x_{3}+y_{3}\right)\left(x_{4}+y_{4}\right)} $$ By setting $y_{i}=t_{i} x_{i}$ we reduce this inequality to $1+\sqrt[4]{t_{1} t_{2} t_{3} t_{4}} \leq$ $\sqrt[4]{\left(1+t_{1}\right)\left(1+t_{2}\right)\left(1+t_{3}\right)\left(1+t_{4}\right)}$. One way to prove the last inequality is to apply the simple inequality $$ 1+\sqrt{u v} \leq \sqrt{(1+u)(1+v)} $$ to $\sqrt{t_{1} t_{2}}, \sqrt{t_{3} t_{4}}$ and then to $t_{1}, t_{2}$ and $t_{3}, t_{4}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. G7 (LAT) $O$ is a point inside a convex quadrilateral $A B C D$ of area $S . K, L, M$, and $N$ are interior points of the sides $A B, B C, C D$, and $D A$ respectively. If $O K B L$ and $O M D N$ are parallelograms, prove that $\sqrt{S} \geq \sqrt{S_{1}}+\sqrt{S_{2}}$, where $S_{1}$ and $S_{2}$ are the areas of $O N A K$ and $O L C M$ respectively.
|
13. If $O$ lies on $A C$, then $A B C D, A K O N$, and $O L C M$ are similar; hence $A C=A O+O C$ implies $\sqrt{S}=\sqrt{S_{1}}+\sqrt{S_{2}}$. Assume that $O$ does not lie on $A C$ and that w.l.o.g. it lies inside triangle $A D C$. Let us denote by $T_{1}, T_{2}$ the areas of parallelograms $K B L O, N O M D$ respectively. Consider a line through $O$ that intersects $A D, D C, C B, B A$ respectively at $X, Y, Z, W$ so that $O W / O X=O Z / O Y$ (such a line exists by a continuity argument: the left side is smaller when $W=X=A$, but greater when $Y=Z=C$ ). The desired inequality is equivalent to $T_{1}+T_{2} \geq 2 \sqrt{S_{1} S_{2}}$. Since triangles $W K O, O L Z, W B Z$ are similar and $W O+O Z=W Z$, we have $\sqrt{S_{W K O}}+\sqrt{S_{O L Z}}=\sqrt{S_{W B Z}}=$ $\sqrt{S_{W K O}+S_{O L Z}+T_{1}}$, which implies $T_{1}=2 \sqrt{S_{W K O} S_{O L Z}}$. Similarly, $T_{2}=2 \sqrt{S_{X N O} S_{O M Y}}$. Since $O W / O Z=O X / O Y$, we have $S_{W K O} / S_{X N O}=S_{O L Z} / S_{O M Y}$.  Therefore we obtain $$ \begin{aligned} T_{1}+T_{2} & =2 \sqrt{S_{W K O} S_{O L Z}}+2 \sqrt{S_{X N O} S_{O M Y}} \\ & =2 \sqrt{\left(S_{W K O}+S_{X N O}\right)\left(S_{O L Z}+S_{O M Y}\right)} \geq 2 \sqrt{S_{1} S_{2}} \end{aligned} $$ Second solution. By an affine transformation of the plane one can transform any nondegenerate quadrilateral into a cyclic one, thereby preserving parallelness and ratios of areas. Thus we may assume w.l.o.g. that $A B C D$ is cyclic. By a well-known formula, the area of a cyclic quadrilateral with sides $a, b, c, d$ and semiperimeter $p$ is given by $$ S=\sqrt{(p-a)(p-b)(p-c)(p-d)} $$ Let us set $A K=a_{1}, K B=b_{1}, B L=a_{2}, L C=b_{2}, C M=a_{3}, M D=b_{3}$, $D N=a_{4}, N A=b_{4}$. Then the sides of quadrilateral $A K O N$ are $a_{i}$, the sides of $C L O M$ are $b_{i}$, and the sides of $A B C D$ are $a_{i}+b_{i}(i=1,2,3,4)$. If $p$ and $q$ are the semiperimeters of $A K O N$ and $C L O M$, and $x_{i}=p-a_{i}$, $y_{i}=q-b_{i}$, then we have $S_{1}=\sqrt{x_{1} x_{2} x_{3} x_{4}}, S_{2}=\sqrt{y_{1} y_{2} y_{3} y_{4}}$, and $S=$ $\sqrt{\left(x_{1}+y_{1}\right)\left(x_{2}+y_{2}\right)\left(x_{3}+y_{3}\right)\left(x_{4}+y_{4}\right)}$. Thus we need to show that $$ \sqrt[4]{x_{1} x_{2} x_{3} x_{4}}+\sqrt[4]{y_{1} y_{2} y_{3} y_{4}} \leq \sqrt[4]{\left(x_{1}+y_{1}\right)\left(x_{2}+y_{2}\right)\left(x_{3}+y_{3}\right)\left(x_{4}+y_{4}\right)} $$ By setting $y_{i}=t_{i} x_{i}$ we reduce this inequality to $1+\sqrt[4]{t_{1} t_{2} t_{3} t_{4}} \leq$ $\sqrt[4]{\left(1+t_{1}\right)\left(1+t_{2}\right)\left(1+t_{3}\right)\left(1+t_{4}\right)}$. One way to prove the last inequality is to apply the simple inequality $$ 1+\sqrt{u v} \leq \sqrt{(1+u)(1+v)} $$ to $\sqrt{t_{1} t_{2}}, \sqrt{t_{3} t_{4}}$ and then to $t_{1}, t_{2}$ and $t_{3}, t_{4}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6eb0bccc-5cda-5cf1-a4ac-dcf9249c272f
| 24,598
|
14. G8 (COL) Let $A B C$ be a triangle. A circle passing through $B$ and $C$ intersects the sides $A B$ and $A C$ again at $C^{\prime}$ and $B^{\prime}$, respectively. Prove that $B B^{\prime}, C C^{\prime}$, and $H H^{\prime}$ are concurrent, where $H$ and $H^{\prime}$ are the orthocenters of triangles $A B C$ and $A B^{\prime} C^{\prime}$ respectively.
|
14. Let $B B^{\prime}$ cut $C C^{\prime}$ at $P$. Since $\angle B^{\prime} B C^{\prime}=\angle B^{\prime} C C^{\prime}$, it follows that $\angle P B H=\angle P C H$. Let $D$ and $E$ be points such that $B P C D$ and $H P C E$ are parallelograms (consequently, so is $B H E D$ ). Triangles $B A C$ and $C^{\prime} A B^{\prime}$ are similar, from which we deduce that $\triangle B^{\prime} H^{\prime} C^{\prime}$ and $\triangle B H C$ are similar, as well as $\triangle B^{\prime} P C^{\prime}$ and $\triangle B D C$. Hence $B^{\prime} P C^{\prime} H^{\prime}$ and $B D C H$ are similar, from which we obtain $\angle H^{\prime} P B^{\prime}=\angle H D B$. Now $\angle C D E=\angle P B H=\angle P C H=$ $\angle C H E$ implies that $H C E D$ is a cyclic quadrilateral. Therefore $\angle B P H=\angle D C E=\angle D H E=$ $\angle H D B=\angle H^{\prime} P B^{\prime}$; hence $H H^{\prime}$ also passes through $P$.  Second solution. Observe that $\triangle H B C \sim \triangle H^{\prime} B^{\prime} C^{\prime}, \angle P B H=\angle P C H$ and $\angle P B^{\prime} H^{\prime}=\angle P C^{\prime} H^{\prime}$. By Ceva's theorem in trigonometric form applied to $\triangle B P C$ and the point $H$, we have $\frac{\sin \angle B P H}{\sin \angle H P C}=\frac{\sin \angle H B P}{\sin \angle H B C} \cdot \frac{\sin \angle H C B}{\sin \angle H C P}=\frac{\sin \angle H C B}{\sin \angle H B C}$. Similarly, Ceva's theorem for $\triangle B^{\prime} P C^{\prime}$ and point $H^{\prime}$ yields $\frac{\sin \angle B^{\prime} P H^{\prime}}{\sin \angle H^{\prime} P C^{\prime}}=\frac{\sin \angle H^{\prime} C^{\prime} B^{\prime}}{\sin \angle H^{\prime} B^{\prime} C^{\prime}}$. Thus it follows that $$ \frac{\sin \angle B^{\prime} P H^{\prime}}{\sin \angle H^{\prime} P C^{\prime}}=\frac{\sin \angle B P H}{\sin \angle H P C} $$ which finally implies that $\angle B P H=\angle B^{\prime} P H^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
14. G8 (COL) Let $A B C$ be a triangle. A circle passing through $B$ and $C$ intersects the sides $A B$ and $A C$ again at $C^{\prime}$ and $B^{\prime}$, respectively. Prove that $B B^{\prime}, C C^{\prime}$, and $H H^{\prime}$ are concurrent, where $H$ and $H^{\prime}$ are the orthocenters of triangles $A B C$ and $A B^{\prime} C^{\prime}$ respectively.
|
14. Let $B B^{\prime}$ cut $C C^{\prime}$ at $P$. Since $\angle B^{\prime} B C^{\prime}=\angle B^{\prime} C C^{\prime}$, it follows that $\angle P B H=\angle P C H$. Let $D$ and $E$ be points such that $B P C D$ and $H P C E$ are parallelograms (consequently, so is $B H E D$ ). Triangles $B A C$ and $C^{\prime} A B^{\prime}$ are similar, from which we deduce that $\triangle B^{\prime} H^{\prime} C^{\prime}$ and $\triangle B H C$ are similar, as well as $\triangle B^{\prime} P C^{\prime}$ and $\triangle B D C$. Hence $B^{\prime} P C^{\prime} H^{\prime}$ and $B D C H$ are similar, from which we obtain $\angle H^{\prime} P B^{\prime}=\angle H D B$. Now $\angle C D E=\angle P B H=\angle P C H=$ $\angle C H E$ implies that $H C E D$ is a cyclic quadrilateral. Therefore $\angle B P H=\angle D C E=\angle D H E=$ $\angle H D B=\angle H^{\prime} P B^{\prime}$; hence $H H^{\prime}$ also passes through $P$.  Second solution. Observe that $\triangle H B C \sim \triangle H^{\prime} B^{\prime} C^{\prime}, \angle P B H=\angle P C H$ and $\angle P B^{\prime} H^{\prime}=\angle P C^{\prime} H^{\prime}$. By Ceva's theorem in trigonometric form applied to $\triangle B P C$ and the point $H$, we have $\frac{\sin \angle B P H}{\sin \angle H P C}=\frac{\sin \angle H B P}{\sin \angle H B C} \cdot \frac{\sin \angle H C B}{\sin \angle H C P}=\frac{\sin \angle H C B}{\sin \angle H B C}$. Similarly, Ceva's theorem for $\triangle B^{\prime} P C^{\prime}$ and point $H^{\prime}$ yields $\frac{\sin \angle B^{\prime} P H^{\prime}}{\sin \angle H^{\prime} P C^{\prime}}=\frac{\sin \angle H^{\prime} C^{\prime} B^{\prime}}{\sin \angle H^{\prime} B^{\prime} C^{\prime}}$. Thus it follows that $$ \frac{\sin \angle B^{\prime} P H^{\prime}}{\sin \angle H^{\prime} P C^{\prime}}=\frac{\sin \angle B P H}{\sin \angle H P C} $$ which finally implies that $\angle B P H=\angle B^{\prime} P H^{\prime}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6656b106-1cce-5fae-9cdb-cdac5ce770fc
| 24,601
|
15. N1 (ROM) Let $k$ be a positive integer. Prove that there are infinitely many perfect squares of the form $n 2^{k}-7$, where $n$ is a positive integer.
|
15. We show by induction on $k$ that there exists a positive integer $a_{k}$ for which $a_{k}^{2} \equiv-7\left(\bmod 2^{k}\right)$. The statement of the problem follows, since every $a_{k}+r 2^{k}(r=0,1, \ldots)$ also satisfies this condition. Note that for $k=1,2,3$ one can take $a_{k}=1$. Now suppose that $a_{k}^{2} \equiv-7$ $\left(\bmod 2^{k}\right)$ for some $k>3$. Then either $a_{k}^{2} \equiv-7\left(\bmod 2^{k+1}\right)$ or $a_{k}^{2} \equiv 2^{k}-7$ $\left(\bmod 2^{k+1}\right)$. In the former case, take $a_{k+1}=a_{k}$. In the latter case, set $a_{k+1}=a_{k}+2^{k-1}$. Then $a_{k+1}^{2}=a_{k}^{2}+2^{k} a_{k}+2^{2 k-2} \equiv a_{k}^{2}+2^{k} \equiv-7(\bmod$ $2^{k+1}$ ) because $a_{k}$ is odd.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
15. N1 (ROM) Let $k$ be a positive integer. Prove that there are infinitely many perfect squares of the form $n 2^{k}-7$, where $n$ is a positive integer.
|
15. We show by induction on $k$ that there exists a positive integer $a_{k}$ for which $a_{k}^{2} \equiv-7\left(\bmod 2^{k}\right)$. The statement of the problem follows, since every $a_{k}+r 2^{k}(r=0,1, \ldots)$ also satisfies this condition. Note that for $k=1,2,3$ one can take $a_{k}=1$. Now suppose that $a_{k}^{2} \equiv-7$ $\left(\bmod 2^{k}\right)$ for some $k>3$. Then either $a_{k}^{2} \equiv-7\left(\bmod 2^{k+1}\right)$ or $a_{k}^{2} \equiv 2^{k}-7$ $\left(\bmod 2^{k+1}\right)$. In the former case, take $a_{k+1}=a_{k}$. In the latter case, set $a_{k+1}=a_{k}+2^{k-1}$. Then $a_{k+1}^{2}=a_{k}^{2}+2^{k} a_{k}+2^{2 k-2} \equiv a_{k}^{2}+2^{k} \equiv-7(\bmod$ $2^{k+1}$ ) because $a_{k}$ is odd.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ae52bbcc-aa8b-5aaf-9607-121cbabd433a
| 24,603
|
16. N2 (RUS) Let $\mathbb{Z}$ denote the set of all integers. Prove that for any integers $A$ and $B$, one can find an integer $C$ for which $M_{1}=\left\{x^{2}+A x+B: x \in \mathbb{Z}\right\}$ and $M_{2}=\left\{2 x^{2}+2 x+C: x \in \mathbb{Z}\right\}$ do not intersect.
|
16. If $A$ is odd, then every number in $M_{1}$ is of the form $x(x+A)+B \equiv B$ $(\bmod 2)$, while numbers in $M_{2}$ are congruent to $C$ modulo 2 . Thus it is enough to take $C \equiv B+1(\bmod 2)$. If $A$ is even, then all numbers in $M_{1}$ have the form $\left(X+\frac{A}{2}\right)^{2}+B-\frac{A^{2}}{4}$ and are congruent to $B-\frac{A^{2}}{4}$ or $B-\frac{A^{2}}{4}+1$ modulo 4 , while numbers in $M_{2}$ are congruent to $C$ modulo 4 . So one can choose any $C \equiv B-\frac{A^{2}}{4}+2$ $(\bmod 4)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
16. N2 (RUS) Let $\mathbb{Z}$ denote the set of all integers. Prove that for any integers $A$ and $B$, one can find an integer $C$ for which $M_{1}=\left\{x^{2}+A x+B: x \in \mathbb{Z}\right\}$ and $M_{2}=\left\{2 x^{2}+2 x+C: x \in \mathbb{Z}\right\}$ do not intersect.
|
16. If $A$ is odd, then every number in $M_{1}$ is of the form $x(x+A)+B \equiv B$ $(\bmod 2)$, while numbers in $M_{2}$ are congruent to $C$ modulo 2 . Thus it is enough to take $C \equiv B+1(\bmod 2)$. If $A$ is even, then all numbers in $M_{1}$ have the form $\left(X+\frac{A}{2}\right)^{2}+B-\frac{A^{2}}{4}$ and are congruent to $B-\frac{A^{2}}{4}$ or $B-\frac{A^{2}}{4}+1$ modulo 4 , while numbers in $M_{2}$ are congruent to $C$ modulo 4 . So one can choose any $C \equiv B-\frac{A^{2}}{4}+2$ $(\bmod 4)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef525028-7ae2-54a5-8dd7-4881c7907837
| 24,606
|
2. A2 (SWE) Let $a$ and $b$ be nonnegative integers such that $a b \geq c^{2}$, where $c$ is an integer. Prove that there is a number $n$ and integers $x_{1}, x_{2}, \ldots, x_{n}, y_{1}, y_{2}, \ldots, y_{n}$ such that $$ \sum_{i=1}^{n} x_{i}^{2}=a, \quad \sum_{i=1}^{n} y_{i}^{2}=b, \quad \text { and } \quad \sum_{i=1}^{n} x_{i} y_{i}=c $$
|
2. We may assume $c \geq 0$ (otherwise, we may simply put $-y_{i}$ in the place of $\left.y_{i}\right)$. Also, we may assume $a \geq b$. If $b \geq c$, it is enough to take $n=a+b-c$, $x_{1}=\cdots=x_{a}=1, y_{1}=\cdots=y_{c}=y_{a+1}=\cdots=y_{a+b-c}=1$, and the other $x_{i}$ 's and $y_{i}$ 's equal to 0 , so we need only consider the case $a>c>b$. We proceed to prove the statement of the problem by induction on $a+b$. The case $a+b=1$ is trivial. Assume that the statement is true when $a+b \leq$ $N$, and let $a+b=N+1$. The triple $(a+b-2 c, b, c-b)$ satisfies the condition (since $(a+b-2 c) b-(c-b)^{2}=a b-c^{2}$ ), so by the induction hypothesis there are $n$-tuples $\left(x_{i}\right)_{i=1}^{n}$ and $\left(y_{i}\right)_{i=1}^{n}$ with the wanted property. It is easy to verify that $\left(x_{i}+y_{i}\right)_{i=1}^{n}$ and $\left(y_{i}\right)_{i=1}^{n}$ give a solution for $(a, b, c)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
2. A2 (SWE) Let $a$ and $b$ be nonnegative integers such that $a b \geq c^{2}$, where $c$ is an integer. Prove that there is a number $n$ and integers $x_{1}, x_{2}, \ldots, x_{n}, y_{1}, y_{2}, \ldots, y_{n}$ such that $$ \sum_{i=1}^{n} x_{i}^{2}=a, \quad \sum_{i=1}^{n} y_{i}^{2}=b, \quad \text { and } \quad \sum_{i=1}^{n} x_{i} y_{i}=c $$
|
2. We may assume $c \geq 0$ (otherwise, we may simply put $-y_{i}$ in the place of $\left.y_{i}\right)$. Also, we may assume $a \geq b$. If $b \geq c$, it is enough to take $n=a+b-c$, $x_{1}=\cdots=x_{a}=1, y_{1}=\cdots=y_{c}=y_{a+1}=\cdots=y_{a+b-c}=1$, and the other $x_{i}$ 's and $y_{i}$ 's equal to 0 , so we need only consider the case $a>c>b$. We proceed to prove the statement of the problem by induction on $a+b$. The case $a+b=1$ is trivial. Assume that the statement is true when $a+b \leq$ $N$, and let $a+b=N+1$. The triple $(a+b-2 c, b, c-b)$ satisfies the condition (since $(a+b-2 c) b-(c-b)^{2}=a b-c^{2}$ ), so by the induction hypothesis there are $n$-tuples $\left(x_{i}\right)_{i=1}^{n}$ and $\left(y_{i}\right)_{i=1}^{n}$ with the wanted property. It is easy to verify that $\left(x_{i}+y_{i}\right)_{i=1}^{n}$ and $\left(y_{i}\right)_{i=1}^{n}$ give a solution for $(a, b, c)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d5996d6e-bccf-52e8-9399-b2da4556fba6
| 24,616
|
21. N7 (BLR) Does there exist an integer $n>1$ that satisfies the following condition? The set of positive integers can be partitioned into $n$ nonempty subsets such that an arbitrary sum of $n-1$ integers, one taken from each of any $n-1$ of the subsets, lies in the remaining subset.
|
21. We shall show that there is no such $n$. Certainly, $n=2$ does not work, so suppose $n \geq 3$. Let $a, b$ be distinct elements of $A_{1}$, and $c$ any integer greater than $-a$ and $-b$. We claim that $a+c, b+c$ belong to the same subsets. Suppose to the contrary that $a+c \in A_{1}$ and $b+c \in A_{2}$, and take arbitrary elements $x_{i} \in A_{i}, i=3, \ldots, n$. The number $b+x_{3}+\cdots+x_{n}$ is in $A_{2}$, so that $s=(a+c)+\left(b+x_{3}+\cdots+x_{n}\right)+x_{4}+\cdots+x_{n}$ must be in $A_{3}$. On the other hand, $a+x_{3}+\cdots+x_{n} \in A_{2}$, so $s=\left(a+x_{3}+\cdots+x_{n}\right)+$ $(b+c)+x_{4}+\cdots+x_{n}$ is in $A_{1}$, a contradiction. Similarly, if $a+c \in A_{2}$ and $b+c \in A_{3}$, then $s=a+(b+c)+x_{4}+\cdots+x_{n}$ belongs to $A_{2}$, but also $s=b+(a+c)+x_{4}+\cdots+x_{n} \in A_{3}$, which is impossible. For $i=1, \ldots, n$ choose $x_{i} \in A_{i}$; set $s=x_{1}+\cdots+x_{n}$ and $y_{i}=s-x_{i}$. Then $y_{i} \in A_{i}$. By what has been proved above, $2 x_{i}=x_{i}+x_{i}$ belongs to the same subset as $x_{i}+y_{i}=s$ does. It follows that all numbers $2 x_{i}, i=1, \ldots, n$, are in the same subset. Since we can arbitrarily take $x_{i}$ from each set $A_{i}$, it follows that all even numbers belong to the same set, say $A_{1}$. Similarly, $2 x_{i}+1=\left(x_{i}+1\right)+x_{i}$ is in the subset to which $\left(x_{i}+1\right)+y_{i}=s+1$ belongs for all $i=1, \ldots, n$; hence all odd numbers greater than 1 are in the same subset, say $A_{2}$. By the above considerations, $3-2=1 \in A_{2}$ also. But then nothing remains in $A_{3}, \ldots, A_{n}$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
21. N7 (BLR) Does there exist an integer $n>1$ that satisfies the following condition? The set of positive integers can be partitioned into $n$ nonempty subsets such that an arbitrary sum of $n-1$ integers, one taken from each of any $n-1$ of the subsets, lies in the remaining subset.
|
21. We shall show that there is no such $n$. Certainly, $n=2$ does not work, so suppose $n \geq 3$. Let $a, b$ be distinct elements of $A_{1}$, and $c$ any integer greater than $-a$ and $-b$. We claim that $a+c, b+c$ belong to the same subsets. Suppose to the contrary that $a+c \in A_{1}$ and $b+c \in A_{2}$, and take arbitrary elements $x_{i} \in A_{i}, i=3, \ldots, n$. The number $b+x_{3}+\cdots+x_{n}$ is in $A_{2}$, so that $s=(a+c)+\left(b+x_{3}+\cdots+x_{n}\right)+x_{4}+\cdots+x_{n}$ must be in $A_{3}$. On the other hand, $a+x_{3}+\cdots+x_{n} \in A_{2}$, so $s=\left(a+x_{3}+\cdots+x_{n}\right)+$ $(b+c)+x_{4}+\cdots+x_{n}$ is in $A_{1}$, a contradiction. Similarly, if $a+c \in A_{2}$ and $b+c \in A_{3}$, then $s=a+(b+c)+x_{4}+\cdots+x_{n}$ belongs to $A_{2}$, but also $s=b+(a+c)+x_{4}+\cdots+x_{n} \in A_{3}$, which is impossible. For $i=1, \ldots, n$ choose $x_{i} \in A_{i}$; set $s=x_{1}+\cdots+x_{n}$ and $y_{i}=s-x_{i}$. Then $y_{i} \in A_{i}$. By what has been proved above, $2 x_{i}=x_{i}+x_{i}$ belongs to the same subset as $x_{i}+y_{i}=s$ does. It follows that all numbers $2 x_{i}, i=1, \ldots, n$, are in the same subset. Since we can arbitrarily take $x_{i}$ from each set $A_{i}$, it follows that all even numbers belong to the same set, say $A_{1}$. Similarly, $2 x_{i}+1=\left(x_{i}+1\right)+x_{i}$ is in the subset to which $\left(x_{i}+1\right)+y_{i}=s+1$ belongs for all $i=1, \ldots, n$; hence all odd numbers greater than 1 are in the same subset, say $A_{2}$. By the above considerations, $3-2=1 \in A_{2}$ also. But then nothing remains in $A_{3}, \ldots, A_{n}$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c7a2fab7-3791-5243-8ea3-ac03638ea46e
| 24,621
|
23. S1 (UKR) Does there exist a sequence $F(1), F(2), F(3), \ldots$ of nonnegative integers that simultaneously satisfies the following three conditions? (a) Each of the integers $0,1,2, \ldots$ occurs in the sequence. (b) Each positive integer occurs in the sequence infinitely often. (c) For any $n \geq 2$, $$ F\left(F\left(n^{163}\right)\right)=F(F(n))+F(F(361)) . $$
|
23. By putting $F(1)=0$ and $F(361)=1$, condition (c) becomes $F\left(F\left(n^{163}\right)\right)=$ $F(F(n))$ for $n \geq 2$. For $n=2,3, \ldots, 360$ let $F(n)=n$, and inductively define $F(n)$ for $n \geq 362$ as follows: $$ F(n)= \begin{cases}F(m), & \text { if } n=m^{163}, m \in \mathbb{N} ; \\ \text { the least number not in }\{F(k) \mid k<n\}, & \text { otherwise }\end{cases} $$ Obviously, (a) each nonnegative integer appears in the sequence because there are infinitely many numbers not of the form $m^{163}$, and (b) each positive integer appears infinitely often because $F\left(m^{163}\right)=F(m)$. Since $F\left(n^{163}\right)=F(n),(c)$ also holds. Second solution. Another example of such a sequence is as follows: If $n=$ $p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{k}^{\alpha_{k}}$, is the factorization of $n$ into primes, we put $F(n)=\alpha_{1}+$ $\alpha_{2}+\cdots+\alpha_{k}$ and $F(1)=0$. Conditions (a) and (b) are evidently satisfied for this $F$, while (c) follows from $F\left(F\left(n^{163}\right)\right)=F(163 F(n))=F(F(n))+1$ (because 163 is a prime) and $F(F(361))=F\left(F\left(19^{2}\right)\right)=F(2)=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
23. S1 (UKR) Does there exist a sequence $F(1), F(2), F(3), \ldots$ of nonnegative integers that simultaneously satisfies the following three conditions? (a) Each of the integers $0,1,2, \ldots$ occurs in the sequence. (b) Each positive integer occurs in the sequence infinitely often. (c) For any $n \geq 2$, $$ F\left(F\left(n^{163}\right)\right)=F(F(n))+F(F(361)) . $$
|
23. By putting $F(1)=0$ and $F(361)=1$, condition (c) becomes $F\left(F\left(n^{163}\right)\right)=$ $F(F(n))$ for $n \geq 2$. For $n=2,3, \ldots, 360$ let $F(n)=n$, and inductively define $F(n)$ for $n \geq 362$ as follows: $$ F(n)= \begin{cases}F(m), & \text { if } n=m^{163}, m \in \mathbb{N} ; \\ \text { the least number not in }\{F(k) \mid k<n\}, & \text { otherwise }\end{cases} $$ Obviously, (a) each nonnegative integer appears in the sequence because there are infinitely many numbers not of the form $m^{163}$, and (b) each positive integer appears infinitely often because $F\left(m^{163}\right)=F(m)$. Since $F\left(n^{163}\right)=F(n),(c)$ also holds. Second solution. Another example of such a sequence is as follows: If $n=$ $p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{k}^{\alpha_{k}}$, is the factorization of $n$ into primes, we put $F(n)=\alpha_{1}+$ $\alpha_{2}+\cdots+\alpha_{k}$ and $F(1)=0$. Conditions (a) and (b) are evidently satisfied for this $F$, while (c) follows from $F\left(F\left(n^{163}\right)\right)=F(163 F(n))=F(F(n))+1$ (because 163 is a prime) and $F(F(361))=F\left(F\left(19^{2}\right)\right)=F(2)=1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
fb732421-d563-525e-a4f6-8477fc9cc651
| 24,626
|
26. S4 (NZL) Suppose that $x_{1}, x_{2}, x_{3}, \ldots$ are positive real numbers for which $$ x_{n}^{n}=\sum_{j=0}^{n-1} x_{n}^{j} $$ for $n=1,2,3, \ldots$ Prove that for all $n$, $$ 2-\frac{1}{2^{n-1}} \leq x_{n}<2-\frac{1}{2^{n}} $$
|
26. For $n=1$ the result is trivial, since $x_{1}=1$. Suppose now that $n \geq 2$ and let $f_{n}(x)=x^{n}-\sum_{i=0}^{n-1} x^{i}$. Note that $x_{n}$ is the unique positive real root of $f_{n}$, because $\frac{f_{n}(x)}{x^{n-1}}=x-1-\frac{1}{x}-\cdots-\frac{1}{x^{n-1}}$ is strictly increasing on $\mathbb{R}^{+}$. Consider $g_{n}(x)=(x-1) f_{n}(x)=(x-2) x^{n}+1$. Obviously $g_{n}(x)$ has no positive roots other than 1 and $x_{n}>1$. Observe that $\left(1-\frac{1}{2^{n}}\right)^{n}>$ $1-\frac{n}{2^{n}} \geq \frac{1}{2}$ for $n \geq 2$ (by Bernoulli's inequality). Since then $$ g_{n}\left(2-\frac{1}{2^{n}}\right)=-\frac{1}{2^{n}}\left(2-\frac{1}{2^{n}}\right)^{n}+1=1-\left(1-\frac{1}{2^{n+1}}\right)^{n}>0 $$ and $$ g_{n}\left(2-\frac{1}{2^{n-1}}\right)=-\frac{1}{2^{n-1}}\left(2-\frac{1}{2^{n-1}}\right)^{n}+1=1-2\left(1-\frac{1}{2^{n}}\right)^{n}<0 $$ we conclude that $x_{n}$ is between $2-\frac{1}{2^{n-1}}$ and $2-\frac{1}{2^{n}}$, as required. Remark. Moreover, $\lim _{n \rightarrow \infty} 2^{n}\left(2-x_{n}\right)=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
26. S4 (NZL) Suppose that $x_{1}, x_{2}, x_{3}, \ldots$ are positive real numbers for which $$ x_{n}^{n}=\sum_{j=0}^{n-1} x_{n}^{j} $$ for $n=1,2,3, \ldots$ Prove that for all $n$, $$ 2-\frac{1}{2^{n-1}} \leq x_{n}<2-\frac{1}{2^{n}} $$
|
26. For $n=1$ the result is trivial, since $x_{1}=1$. Suppose now that $n \geq 2$ and let $f_{n}(x)=x^{n}-\sum_{i=0}^{n-1} x^{i}$. Note that $x_{n}$ is the unique positive real root of $f_{n}$, because $\frac{f_{n}(x)}{x^{n-1}}=x-1-\frac{1}{x}-\cdots-\frac{1}{x^{n-1}}$ is strictly increasing on $\mathbb{R}^{+}$. Consider $g_{n}(x)=(x-1) f_{n}(x)=(x-2) x^{n}+1$. Obviously $g_{n}(x)$ has no positive roots other than 1 and $x_{n}>1$. Observe that $\left(1-\frac{1}{2^{n}}\right)^{n}>$ $1-\frac{n}{2^{n}} \geq \frac{1}{2}$ for $n \geq 2$ (by Bernoulli's inequality). Since then $$ g_{n}\left(2-\frac{1}{2^{n}}\right)=-\frac{1}{2^{n}}\left(2-\frac{1}{2^{n}}\right)^{n}+1=1-\left(1-\frac{1}{2^{n+1}}\right)^{n}>0 $$ and $$ g_{n}\left(2-\frac{1}{2^{n-1}}\right)=-\frac{1}{2^{n-1}}\left(2-\frac{1}{2^{n-1}}\right)^{n}+1=1-2\left(1-\frac{1}{2^{n}}\right)^{n}<0 $$ we conclude that $x_{n}$ is between $2-\frac{1}{2^{n-1}}$ and $2-\frac{1}{2^{n}}$, as required. Remark. Moreover, $\lim _{n \rightarrow \infty} 2^{n}\left(2-x_{n}\right)=1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2e3af27e-0758-50d7-a6e8-147b22a16afa
| 24,634
|
27. S5 (FIN) For positive integers $n$, the numbers $f(n)$ are defined inductively as follows: $f(1)=1$, and for every positive integer $n, f(n+1)$ is the greatest integer $m$ such that there is an arithmetic progression of positive integers $a_{1}<a_{2}<\cdots<a_{m}=n$ for which $$ f\left(a_{1}\right)=f\left(a_{2}\right)=\cdots=f\left(a_{m}\right) $$ Prove that there are positive integers $a$ and $b$ such that $f(a n+b)=n+2$ for every positive integer $n$.
|
27. Computing the first few values of $f(n)$, we observe the following pattern: $$ \begin{aligned} f(4 k) & =k, k \geq 3, & f(8) & =3 ; \\ f(4 k+1) & =1, k \geq 4, & f(5) & =f(13)=2 ; \\ f(4 k+2) & =k-3, k \geq 7, & f(2) & =1, f(6)=f(10)=2, \\ & & f(14) & =f(18)=3, f(26)=4 ; \\ f(4 k+3) & =2 . & & \end{aligned} $$ We shall prove these statements simultaneously by induction on $n$, having verified them for $k \leq 7$. (i) Let $n=4 k$. Since $f(3)=f(7)=\cdots=f(4 k-1)=2$, we have $f(4 k) \geq k$. But $f(n) \leq \max _{m<n} f(m)+1 \leq(k-1)+1$, so $f(4 k)=k$. (ii) Let $n=4 k+1, k \geq 7$. Since $f(4 k)=k$ and $f(m)<k$ for $m<4 k$, we deduce that $f(4 k+1)=1$. (iii) Let $n=4 k+2, k \geq 7$. Since $f(17)=f(21)=\cdots=f(4 k+1)=1$, we obtain $f(4 k+2) \geq k-3$. On the other hand, if $f(4 k+1)=f(4 k+1-$ $d)=1$, then $d \geq 8$, and $4 k+1-8(k-3)<0$. So $f(4 k+2)=k-3$. (iv) Let $n=4 k+3, k \geq 7$. We have $f(4 k+2)=k-3$ and $f(m)=k-3$ for exactly one $m<4 k+2$ (namely for $m=4 k-12)$; hence $f(4 k+3)=2$. Therefore, for example, $f(4 n+8)=n+2$ for all $n$; hence we can take $a=4$ and $b=8$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
27. S5 (FIN) For positive integers $n$, the numbers $f(n)$ are defined inductively as follows: $f(1)=1$, and for every positive integer $n, f(n+1)$ is the greatest integer $m$ such that there is an arithmetic progression of positive integers $a_{1}<a_{2}<\cdots<a_{m}=n$ for which $$ f\left(a_{1}\right)=f\left(a_{2}\right)=\cdots=f\left(a_{m}\right) $$ Prove that there are positive integers $a$ and $b$ such that $f(a n+b)=n+2$ for every positive integer $n$.
|
27. Computing the first few values of $f(n)$, we observe the following pattern: $$ \begin{aligned} f(4 k) & =k, k \geq 3, & f(8) & =3 ; \\ f(4 k+1) & =1, k \geq 4, & f(5) & =f(13)=2 ; \\ f(4 k+2) & =k-3, k \geq 7, & f(2) & =1, f(6)=f(10)=2, \\ & & f(14) & =f(18)=3, f(26)=4 ; \\ f(4 k+3) & =2 . & & \end{aligned} $$ We shall prove these statements simultaneously by induction on $n$, having verified them for $k \leq 7$. (i) Let $n=4 k$. Since $f(3)=f(7)=\cdots=f(4 k-1)=2$, we have $f(4 k) \geq k$. But $f(n) \leq \max _{m<n} f(m)+1 \leq(k-1)+1$, so $f(4 k)=k$. (ii) Let $n=4 k+1, k \geq 7$. Since $f(4 k)=k$ and $f(m)<k$ for $m<4 k$, we deduce that $f(4 k+1)=1$. (iii) Let $n=4 k+2, k \geq 7$. Since $f(17)=f(21)=\cdots=f(4 k+1)=1$, we obtain $f(4 k+2) \geq k-3$. On the other hand, if $f(4 k+1)=f(4 k+1-$ $d)=1$, then $d \geq 8$, and $4 k+1-8(k-3)<0$. So $f(4 k+2)=k-3$. (iv) Let $n=4 k+3, k \geq 7$. We have $f(4 k+2)=k-3$ and $f(m)=k-3$ for exactly one $m<4 k+2$ (namely for $m=4 k-12)$; hence $f(4 k+3)=2$. Therefore, for example, $f(4 n+8)=n+2$ for all $n$; hence we can take $a=4$ and $b=8$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5fd71309-33a4-56b1-a161-a394d1dc66fd
| 24,636
|
5. A5 (UKR) Let $\mathbb{R}$ be the set of real numbers. Does there exist a function $f: \mathbb{R} \rightarrow \mathbb{R}$ that simultaneously satisfies the following three conditions? (a) There is a positive number $M$ such that $-M \leq f(x) \leq M$ for all $x$. (b) $f(1)=1$. (c) If $x \neq 0$, then $$ f\left(x+\frac{1}{x^{2}}\right)=f(x)+\left[f\left(\frac{1}{x}\right)\right]^{2} $$
|
5. Suppose that a function $f$ satisfies the condition, and let $c$ be the least upper bound of $\{f(x) \mid x \in \mathbb{R}\}$. We have $c \geq 2$, since $f(2)=f(1+$ $\left.1 / 1^{2}\right)=f(1)+f(1)^{2}=2$. Also, since $c$ is the least upper bound, for each $k=1,2, \ldots$ there is an $x_{k} \in \mathbb{R}$ such that $f\left(x_{k}\right) \geq c-1 / k$. Then $$ c \geq f\left(x_{k}+\frac{1}{x_{k}^{2}}\right) \geq c-\frac{1}{k}+f\left(\frac{1}{x_{k}}\right)^{2} \Longrightarrow f\left(\frac{1}{x_{k}}\right) \geq-\frac{1}{\sqrt{k}} . $$ On the other hand, $$ c \geq f\left(\frac{1}{x_{k}}+x_{k}^{2}\right)=f\left(\frac{1}{x_{k}}\right)+f\left(x_{k}\right)^{2} \geq-\frac{1}{\sqrt{k}}+\left(c-\frac{1}{k}\right)^{2} . $$ It follows that $$ \frac{1}{\sqrt{k}}-\frac{1}{k^{2}} \geq c\left(c-1-\frac{2}{k}\right) $$ which cannot hold for $k$ sufficiently large. Second solution. Assume that $f$ exists and let $n$ be the least integer such that $f(x) \leq \frac{n}{4}$ for all $x$. Since $f(2)=2$, we have $n \geq 8$. Let $f(x)>\frac{n-1}{4}$. Then $f(1 / x)=f\left(x+1 / x^{2}\right)-f(x)<1 / 4$, so $f(1 / x)>-1 / 2$. On the other hand, this implies $\left(\frac{n-1}{4}\right)^{2}<f(x)^{2}=f\left(1 / x+x^{2}\right)-f(1 / x)<\frac{n}{4}+\frac{1}{2}$, which is impossible when $n \geq 8$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
5. A5 (UKR) Let $\mathbb{R}$ be the set of real numbers. Does there exist a function $f: \mathbb{R} \rightarrow \mathbb{R}$ that simultaneously satisfies the following three conditions? (a) There is a positive number $M$ such that $-M \leq f(x) \leq M$ for all $x$. (b) $f(1)=1$. (c) If $x \neq 0$, then $$ f\left(x+\frac{1}{x^{2}}\right)=f(x)+\left[f\left(\frac{1}{x}\right)\right]^{2} $$
|
5. Suppose that a function $f$ satisfies the condition, and let $c$ be the least upper bound of $\{f(x) \mid x \in \mathbb{R}\}$. We have $c \geq 2$, since $f(2)=f(1+$ $\left.1 / 1^{2}\right)=f(1)+f(1)^{2}=2$. Also, since $c$ is the least upper bound, for each $k=1,2, \ldots$ there is an $x_{k} \in \mathbb{R}$ such that $f\left(x_{k}\right) \geq c-1 / k$. Then $$ c \geq f\left(x_{k}+\frac{1}{x_{k}^{2}}\right) \geq c-\frac{1}{k}+f\left(\frac{1}{x_{k}}\right)^{2} \Longrightarrow f\left(\frac{1}{x_{k}}\right) \geq-\frac{1}{\sqrt{k}} . $$ On the other hand, $$ c \geq f\left(\frac{1}{x_{k}}+x_{k}^{2}\right)=f\left(\frac{1}{x_{k}}\right)+f\left(x_{k}\right)^{2} \geq-\frac{1}{\sqrt{k}}+\left(c-\frac{1}{k}\right)^{2} . $$ It follows that $$ \frac{1}{\sqrt{k}}-\frac{1}{k^{2}} \geq c\left(c-1-\frac{2}{k}\right) $$ which cannot hold for $k$ sufficiently large. Second solution. Assume that $f$ exists and let $n$ be the least integer such that $f(x) \leq \frac{n}{4}$ for all $x$. Since $f(2)=2$, we have $n \geq 8$. Let $f(x)>\frac{n-1}{4}$. Then $f(1 / x)=f\left(x+1 / x^{2}\right)-f(x)<1 / 4$, so $f(1 / x)>-1 / 2$. On the other hand, this implies $\left(\frac{n-1}{4}\right)^{2}<f(x)^{2}=f\left(1 / x+x^{2}\right)-f(1 / x)<\frac{n}{4}+\frac{1}{2}$, which is impossible when $n \geq 8$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
49d049ec-7067-55ae-8f5a-fc3824a0cd65
| 24,647
|
6. A6 (JAP) Let $n$ be an integer, $n \geq 3$. Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{i}<x_{i+1}$ for $1 \leq i \leq n-1$. Prove that $$ \frac{n(n-1)}{2} \sum_{i<j} x_{i} x_{j}>\left(\sum_{i=1}^{n-1}(n-i) x_{i}\right)\left(\sum_{j=2}^{n}(j-1) x_{j}\right) . $$
|
6. Let $y_{i}=x_{i+1}+\cdots+x_{n}, Y=\sum_{j=2}^{n}(j-1) x_{j}$, and $z_{i}=\frac{n(n-1)}{2} y_{i}-(n-$ $i) Y$. Then $\frac{n(n-1)}{2} \sum_{i<j} x_{i} x_{j}-\left(\sum_{i=1}^{n-1}(n-i) x_{i}\right) Y=\frac{n(n-1)}{2} \sum_{i=1}^{n-1} x_{i} y_{i}-$ $\sum_{i=1}^{n-1}(n-i) x_{i} Y=\sum_{i=1}^{n-1} x_{i} z_{i}$, so it remains to show that $\sum_{i=1}^{n-1} x_{i} z_{i}>0$. Since $\sum_{i=1}^{n-1} y_{i}=Y$ and $\sum_{i=1}^{n-1}(n-i)=\frac{n(n-1)}{2}$, we have $\sum z_{i}=0$. Note that $Y<\sum_{j=2}^{n}(j-1) x_{n}=\frac{n(n-1)}{2} x_{n}$, and consequently $z_{n-1}=$ $\frac{n(n-1)}{2} x_{n}-Y>0$. Furthermore, we have $$ \frac{z_{i+1}}{n-i-1}-\frac{z_{i}}{n-i}=\frac{n(n-1)}{2}\left(\frac{y_{i+1}}{n-i-1}-\frac{y_{i}}{n-i}\right)>0 $$ which means that $\frac{z_{1}}{n-1}<\frac{z_{2}}{n-2}<\cdots<\frac{z_{n-1}}{1}$. Therefore there is a $k$ for which $z_{1}, \ldots, z_{k} \leq 0$ and $z_{k+1}, \ldots, z_{n-1}>0$. But then $z_{i}\left(x_{i}-x_{k}\right) \geq 0$, i.e., $x_{i} z_{i} \geq x_{k} z_{i}$ for all $i$, so $\sum_{i=1}^{n-1} x_{i} z_{i}>\sum_{i=1}^{n-1} x_{k} z_{i}=0$ as required. Second solution. Set $X=\sum_{j=1}^{n-1}(n-j) x_{j}$ and $Y=\sum_{j=2}^{n}(j-1) x_{j}$. Since $4 X Y=(X+Y)^{2}-(X-Y)^{2}$, the RHS of the inequality becomes $$ X Y=\frac{1}{4}\left[(n-1)^{2}\left(\sum_{i=1}^{n} x_{i}\right)^{2}-\left(\sum_{i=1}^{n}(2 i-1-n) x_{i}\right)^{2}\right] $$ The LHS equals $\frac{1}{4}\left((n-1)^{2}\left(\sum_{i=1}^{n} x_{i}\right)^{2}-(n-1) \sum_{i<j}\left(x_{j}-x_{i}\right)^{2}\right)$. Since $\sum_{i=1}^{n}(2 i-1-n) x_{i}=\sum_{i<j}\left(x_{j}-x_{i}\right)$ also holds, we must prove that $$ \left(\sum_{i<j}\left(x_{j}-x_{i}\right)\right)^{2}>(n-1) \sum_{i<j}\left(x_{j}-x_{i}\right)^{2} $$ Putting $x_{i+1}-x_{i}=d_{i}>0$ (so, $x_{j}-x_{i}=d_{i}+d_{i+1}+\cdots+d_{j-1}$ ) and expanding the obtained expressions, we reduce this inequality to $\sum_{k} k^{2}(n-k)^{2} d_{k}^{2}+2 \sum_{k<l} k l(n-k)(n-l) d_{k} d_{l}>\sum_{k}(n-1) k(n-k) d_{k}^{2}+$ $2 \sum_{k<l}(n-1) k(n-l) d_{k} d_{l}$, which is verified immediately by comparing coefficients. Remark. An inequality significantly stronger than (1) in the second solution has appeared later, as IMO 03-5.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
6. A6 (JAP) Let $n$ be an integer, $n \geq 3$. Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{i}<x_{i+1}$ for $1 \leq i \leq n-1$. Prove that $$ \frac{n(n-1)}{2} \sum_{i<j} x_{i} x_{j}>\left(\sum_{i=1}^{n-1}(n-i) x_{i}\right)\left(\sum_{j=2}^{n}(j-1) x_{j}\right) . $$
|
6. Let $y_{i}=x_{i+1}+\cdots+x_{n}, Y=\sum_{j=2}^{n}(j-1) x_{j}$, and $z_{i}=\frac{n(n-1)}{2} y_{i}-(n-$ $i) Y$. Then $\frac{n(n-1)}{2} \sum_{i<j} x_{i} x_{j}-\left(\sum_{i=1}^{n-1}(n-i) x_{i}\right) Y=\frac{n(n-1)}{2} \sum_{i=1}^{n-1} x_{i} y_{i}-$ $\sum_{i=1}^{n-1}(n-i) x_{i} Y=\sum_{i=1}^{n-1} x_{i} z_{i}$, so it remains to show that $\sum_{i=1}^{n-1} x_{i} z_{i}>0$. Since $\sum_{i=1}^{n-1} y_{i}=Y$ and $\sum_{i=1}^{n-1}(n-i)=\frac{n(n-1)}{2}$, we have $\sum z_{i}=0$. Note that $Y<\sum_{j=2}^{n}(j-1) x_{n}=\frac{n(n-1)}{2} x_{n}$, and consequently $z_{n-1}=$ $\frac{n(n-1)}{2} x_{n}-Y>0$. Furthermore, we have $$ \frac{z_{i+1}}{n-i-1}-\frac{z_{i}}{n-i}=\frac{n(n-1)}{2}\left(\frac{y_{i+1}}{n-i-1}-\frac{y_{i}}{n-i}\right)>0 $$ which means that $\frac{z_{1}}{n-1}<\frac{z_{2}}{n-2}<\cdots<\frac{z_{n-1}}{1}$. Therefore there is a $k$ for which $z_{1}, \ldots, z_{k} \leq 0$ and $z_{k+1}, \ldots, z_{n-1}>0$. But then $z_{i}\left(x_{i}-x_{k}\right) \geq 0$, i.e., $x_{i} z_{i} \geq x_{k} z_{i}$ for all $i$, so $\sum_{i=1}^{n-1} x_{i} z_{i}>\sum_{i=1}^{n-1} x_{k} z_{i}=0$ as required. Second solution. Set $X=\sum_{j=1}^{n-1}(n-j) x_{j}$ and $Y=\sum_{j=2}^{n}(j-1) x_{j}$. Since $4 X Y=(X+Y)^{2}-(X-Y)^{2}$, the RHS of the inequality becomes $$ X Y=\frac{1}{4}\left[(n-1)^{2}\left(\sum_{i=1}^{n} x_{i}\right)^{2}-\left(\sum_{i=1}^{n}(2 i-1-n) x_{i}\right)^{2}\right] $$ The LHS equals $\frac{1}{4}\left((n-1)^{2}\left(\sum_{i=1}^{n} x_{i}\right)^{2}-(n-1) \sum_{i<j}\left(x_{j}-x_{i}\right)^{2}\right)$. Since $\sum_{i=1}^{n}(2 i-1-n) x_{i}=\sum_{i<j}\left(x_{j}-x_{i}\right)$ also holds, we must prove that $$ \left(\sum_{i<j}\left(x_{j}-x_{i}\right)\right)^{2}>(n-1) \sum_{i<j}\left(x_{j}-x_{i}\right)^{2} $$ Putting $x_{i+1}-x_{i}=d_{i}>0$ (so, $x_{j}-x_{i}=d_{i}+d_{i+1}+\cdots+d_{j-1}$ ) and expanding the obtained expressions, we reduce this inequality to $\sum_{k} k^{2}(n-k)^{2} d_{k}^{2}+2 \sum_{k<l} k l(n-k)(n-l) d_{k} d_{l}>\sum_{k}(n-1) k(n-k) d_{k}^{2}+$ $2 \sum_{k<l}(n-1) k(n-l) d_{k} d_{l}$, which is verified immediately by comparing coefficients. Remark. An inequality significantly stronger than (1) in the second solution has appeared later, as IMO 03-5.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1933eca1-e821-556d-8eb1-0f40d4c4157e
| 24,650
|
7. G1 (BUL) ${ }^{\mathrm{IMO} 1}$ Let $A, B, C$, and $D$ be distinct points on a line, in that order. The circles with diameters $A C$ and $B D$ intersect at $X$ and $Y . O$ is an arbitrary point on the line $X Y$ but not on $A D$. $C O$ intersects the circle with diameter $A C$ again at $M$, and $B O$ intersects the other circle again at $N$. Prove that the lines $A M, D N$, and $X Y$ are concurrent.
|
7. The result is trivial if $O$ coincides with $X$ or $Y$, so let us assume it does not. From $O B \cdot O N=O C \cdot O M=O X \cdot O Y$ we deduce that $B C M N$ is a cyclic quadrilateral. Further, if $O$ lies between $X$ and $Y$, then $\angle M A D+$ $\angle M N D=\angle M A D+\angle M N B+\angle B N D=\angle M A D+\angle M C A+\angle A M C=$ $180^{\circ}$. Similarly, we also have $\angle M A D+\angle M N D=180^{\circ}$ if $O$ is not on the segment $X Y$. Therefore $A D N M$ is cyclic. Now let $A M$ and $D N$ intersect at $Z$ and let the line $Z X$ intersect the two circles at $Y_{1}$ and $Y_{2}$. Then $Z X \cdot Z Y_{1}=Z M \cdot Z A=Z N \cdot Z D=Z X \cdot Z Y_{2}$. Hence $Y_{1}=Y_{2}=Y$, implying that $Z$ lies on $X Y$. Second solution. Let $Z_{1}, Z_{2}$ be the points in which $A M, D N$ respectively meet $X Y$, and $P=B C \cap X Y$. Then, from $\triangle O P C \sim \triangle A P Z_{1}$, we have $P Z_{1}=\frac{P A \cdot P C}{P O}=\frac{P X^{2}}{P O}$ and analogously $P Z_{2}=\frac{P X^{2}}{P O}$. Hence, we conclude that $Z_{1} \equiv Z_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. G1 (BUL) ${ }^{\mathrm{IMO} 1}$ Let $A, B, C$, and $D$ be distinct points on a line, in that order. The circles with diameters $A C$ and $B D$ intersect at $X$ and $Y . O$ is an arbitrary point on the line $X Y$ but not on $A D$. $C O$ intersects the circle with diameter $A C$ again at $M$, and $B O$ intersects the other circle again at $N$. Prove that the lines $A M, D N$, and $X Y$ are concurrent.
|
7. The result is trivial if $O$ coincides with $X$ or $Y$, so let us assume it does not. From $O B \cdot O N=O C \cdot O M=O X \cdot O Y$ we deduce that $B C M N$ is a cyclic quadrilateral. Further, if $O$ lies between $X$ and $Y$, then $\angle M A D+$ $\angle M N D=\angle M A D+\angle M N B+\angle B N D=\angle M A D+\angle M C A+\angle A M C=$ $180^{\circ}$. Similarly, we also have $\angle M A D+\angle M N D=180^{\circ}$ if $O$ is not on the segment $X Y$. Therefore $A D N M$ is cyclic. Now let $A M$ and $D N$ intersect at $Z$ and let the line $Z X$ intersect the two circles at $Y_{1}$ and $Y_{2}$. Then $Z X \cdot Z Y_{1}=Z M \cdot Z A=Z N \cdot Z D=Z X \cdot Z Y_{2}$. Hence $Y_{1}=Y_{2}=Y$, implying that $Z$ lies on $X Y$. Second solution. Let $Z_{1}, Z_{2}$ be the points in which $A M, D N$ respectively meet $X Y$, and $P=B C \cap X Y$. Then, from $\triangle O P C \sim \triangle A P Z_{1}$, we have $P Z_{1}=\frac{P A \cdot P C}{P O}=\frac{P X^{2}}{P O}$ and analogously $P Z_{2}=\frac{P X^{2}}{P O}$. Hence, we conclude that $Z_{1} \equiv Z_{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
978f52bf-1016-5a4f-a1ac-4f96915ea790
| 24,652
|
8. G2 (GER) Let $A, B$, and $C$ be noncollinear points. Prove that there is a unique point $X$ in the plane of $A B C$ such that $X A^{2}+X B^{2}+A B^{2}=$ $X B^{2}+X C^{2}+B C^{2}=X C^{2}+X A^{2}+C A^{2}$.
|
8. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points symmetric to $A, B, C$ with respect to the midpoints of $B C, C A, A B$ respectively. From the condition on $X$ we have $X B^{2}-X C^{2}=A C^{2}-A B^{2}=A^{\prime} B^{2}-A^{\prime} C^{2}$, and hence $X$ must lie on the line through $A^{\prime}$ perpendicular to $B C$. Similarly, $X$ lies on the line through $B^{\prime}$ perpendicular to $C A$. It follows that there is a unique position for $X$, namely the orthocenter of $\triangle A^{\prime} B^{\prime} C^{\prime}$. It easily follows that this point $X$ satisfies the original equations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. G2 (GER) Let $A, B$, and $C$ be noncollinear points. Prove that there is a unique point $X$ in the plane of $A B C$ such that $X A^{2}+X B^{2}+A B^{2}=$ $X B^{2}+X C^{2}+B C^{2}=X C^{2}+X A^{2}+C A^{2}$.
|
8. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points symmetric to $A, B, C$ with respect to the midpoints of $B C, C A, A B$ respectively. From the condition on $X$ we have $X B^{2}-X C^{2}=A C^{2}-A B^{2}=A^{\prime} B^{2}-A^{\prime} C^{2}$, and hence $X$ must lie on the line through $A^{\prime}$ perpendicular to $B C$. Similarly, $X$ lies on the line through $B^{\prime}$ perpendicular to $C A$. It follows that there is a unique position for $X$, namely the orthocenter of $\triangle A^{\prime} B^{\prime} C^{\prime}$. It easily follows that this point $X$ satisfies the original equations.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9c8977f1-af1f-58f5-a00c-9d7350dbe400
| 24,655
|
9. G3 (TUR) The incircle of $A B C$ touches $B C, C A$, and $A B$ at $D, E$, and $F$ respectively. $X$ is a point inside $A B C$ such that the incircle of $X B C$ touches $B C$ at $D$ also, and touches $C X$ and $X B$ at $Y$ and $Z$, respectively. Prove that $E F Z Y$ is a cyclic quadrilateral.
|
9. If $E F$ is parallel to $B C, \triangle A B C$ must be isosceles and $E, Y$ are symmetric to $F, Z$ with respect to $A D$, so the result follows. Now suppose that $E F$ meets $B C$ at $P$. By Menelaus's theorem, $\frac{B P}{C P}=\frac{B F}{F A} \cdot \frac{A E}{E C}=\frac{B D}{D C}$ (since $B D=B F, C D=C E, A E=A F)$. It follows that the point $P$ depends only on $D$ and not on $A$. In particular, the same point is obtained as the intersection of $Z Y$ with $B C$. Therefore $P E \cdot P F=P D^{2}=P Y \cdot P Z$, from which it follows that $E F Z Y$ is a cyclic quadrilateral. Second solution. Since $C D=C Y=C E$ and $B D=B Z=B F$, all angles of $E F Z Y$ can be calculated in terms of angles of $A B C$ and $Y Z B C$. In fact, $\angle F E Y=\frac{1}{2}(\angle A+\angle C+\angle B C Y)$ and $\angle F Z Y=\frac{1}{2}\left(180^{\circ}+\angle B+\angle B C Y\right)$, which gives us $\angle F E Y+\angle F Z Y=180^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
9. G3 (TUR) The incircle of $A B C$ touches $B C, C A$, and $A B$ at $D, E$, and $F$ respectively. $X$ is a point inside $A B C$ such that the incircle of $X B C$ touches $B C$ at $D$ also, and touches $C X$ and $X B$ at $Y$ and $Z$, respectively. Prove that $E F Z Y$ is a cyclic quadrilateral.
|
9. If $E F$ is parallel to $B C, \triangle A B C$ must be isosceles and $E, Y$ are symmetric to $F, Z$ with respect to $A D$, so the result follows. Now suppose that $E F$ meets $B C$ at $P$. By Menelaus's theorem, $\frac{B P}{C P}=\frac{B F}{F A} \cdot \frac{A E}{E C}=\frac{B D}{D C}$ (since $B D=B F, C D=C E, A E=A F)$. It follows that the point $P$ depends only on $D$ and not on $A$. In particular, the same point is obtained as the intersection of $Z Y$ with $B C$. Therefore $P E \cdot P F=P D^{2}=P Y \cdot P Z$, from which it follows that $E F Z Y$ is a cyclic quadrilateral. Second solution. Since $C D=C Y=C E$ and $B D=B Z=B F$, all angles of $E F Z Y$ can be calculated in terms of angles of $A B C$ and $Y Z B C$. In fact, $\angle F E Y=\frac{1}{2}(\angle A+\angle C+\angle B C Y)$ and $\angle F Z Y=\frac{1}{2}\left(180^{\circ}+\angle B+\angle B C Y\right)$, which gives us $\angle F E Y+\angle F Z Y=180^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
297192e7-5132-5102-994a-69e85b051689
| 24,658
|
1. A1 (SLO) Let $a, b$, and $c$ be positive real numbers such that $a b c=1$. Prove that $$ \frac{a b}{a^{5}+b^{5}+a b}+\frac{b c}{b^{5}+c^{5}+b c}+\frac{c a}{c^{5}+a^{5}+c a} \leq 1 $$ When does equality hold?
|
1. We have $a^{5}+b^{5}-a^{2} b^{2}(a+b)=\left(a^{3}-b^{3}\right)\left(a^{2}-b^{2}\right) \geq 0$, i.e. $a^{5}+b^{5} \geq$ $a^{2} b^{2}(a+b)$. Hence $$ \frac{a b}{a^{5}+b^{5}+a b} \leq \frac{a b}{a^{2} b^{2}(a+b)+a b}=\frac{a b c^{2}}{a^{2} b^{2} c^{2}(a+b)+a b c^{2}}=\frac{c}{a+b+c} . $$ Now, the left side of the inequality to be proved does not exceed $\frac{c}{a+b+c}+$ $\frac{a}{a+b+c}+\frac{b}{a+b+c}=1$. Equality holds if and only if $a=b=c$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
1. A1 (SLO) Let $a, b$, and $c$ be positive real numbers such that $a b c=1$. Prove that $$ \frac{a b}{a^{5}+b^{5}+a b}+\frac{b c}{b^{5}+c^{5}+b c}+\frac{c a}{c^{5}+a^{5}+c a} \leq 1 $$ When does equality hold?
|
1. We have $a^{5}+b^{5}-a^{2} b^{2}(a+b)=\left(a^{3}-b^{3}\right)\left(a^{2}-b^{2}\right) \geq 0$, i.e. $a^{5}+b^{5} \geq$ $a^{2} b^{2}(a+b)$. Hence $$ \frac{a b}{a^{5}+b^{5}+a b} \leq \frac{a b}{a^{2} b^{2}(a+b)+a b}=\frac{a b c^{2}}{a^{2} b^{2} c^{2}(a+b)+a b c^{2}}=\frac{c}{a+b+c} . $$ Now, the left side of the inequality to be proved does not exceed $\frac{c}{a+b+c}+$ $\frac{a}{a+b+c}+\frac{b}{a+b+c}=1$. Equality holds if and only if $a=b=c$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ff98656-21b7-5527-82a3-a68d18ebf8e6
| 24,661
|
10. G1 (GBR) Let triangle $A B C$ have orthocenter $H$, and let $P$ be a point on its circumcircle, distinct from $A, B, C$. Let $E$ be the foot of the altitude $B H$, let $P A Q B$ and $P A R C$ be parallelograms, and let $A Q$ meet $H R$ in $X$. Prove that $E X$ is parallel to $A P$.
|
10. We first show that $H$ is the common orthocenter of the triangles $A B C$ and $A Q R$. Let $G, G^{\prime}, H^{\prime}$ be respectively the centroid of $\triangle A B C$, the centroid of $\triangle P B C$, and the orthocenter of $\triangle P B C$. Since the triangles $A B C$ and $P B C$ have a common circumcenter, from the properties of the Euler line we get $\overrightarrow{H H^{\prime}}=3 \overrightarrow{G G^{\prime}}=$ $\overrightarrow{A P}$. But $\triangle A Q R$ is exactly the image of $\triangle P B C$ under translation by $\overrightarrow{A P}$; hence the orthocenter of $A Q R$  coincides with H. (Remark: This can be shown by noting that $A H B Q$ is cyclic.) Now we have that $R H \perp A Q$; hence $\angle A X H=90^{\circ}=\angle A E H$. It follows that $A X E H$ is cyclic; hence $$ \angle E X Q=180^{\circ}-\angle A H E=180^{\circ}-\angle B C A=180^{\circ}-\angle B P A=\angle P A Q $$ (as oriented angles). Hence $E X \| A P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
10. G1 (GBR) Let triangle $A B C$ have orthocenter $H$, and let $P$ be a point on its circumcircle, distinct from $A, B, C$. Let $E$ be the foot of the altitude $B H$, let $P A Q B$ and $P A R C$ be parallelograms, and let $A Q$ meet $H R$ in $X$. Prove that $E X$ is parallel to $A P$.
|
10. We first show that $H$ is the common orthocenter of the triangles $A B C$ and $A Q R$. Let $G, G^{\prime}, H^{\prime}$ be respectively the centroid of $\triangle A B C$, the centroid of $\triangle P B C$, and the orthocenter of $\triangle P B C$. Since the triangles $A B C$ and $P B C$ have a common circumcenter, from the properties of the Euler line we get $\overrightarrow{H H^{\prime}}=3 \overrightarrow{G G^{\prime}}=$ $\overrightarrow{A P}$. But $\triangle A Q R$ is exactly the image of $\triangle P B C$ under translation by $\overrightarrow{A P}$; hence the orthocenter of $A Q R$  coincides with H. (Remark: This can be shown by noting that $A H B Q$ is cyclic.) Now we have that $R H \perp A Q$; hence $\angle A X H=90^{\circ}=\angle A E H$. It follows that $A X E H$ is cyclic; hence $$ \angle E X Q=180^{\circ}-\angle A H E=180^{\circ}-\angle B C A=180^{\circ}-\angle B P A=\angle P A Q $$ (as oriented angles). Hence $E X \| A P$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
48a113be-c456-56ee-b420-956f2306b08d
| 24,663
|
11. G2 (CAN) ${ }^{\mathrm{IMO} 2}$ Let $P$ be a point inside $\triangle A B C$ such that $$ \angle A P B-\angle C=\angle A P C-\angle B . $$ Let $D, E$ be the incenters of $\triangle A P B, \triangle A P C$ respectively. Show that $A P, B D$ and $C E$ meet in a point.
|
11. Let $X, Y, Z$ respectively be the feet of the perpendiculars from $P$ to $B C$, $C A, A B$. Examining the cyclic quadrilaterals $A Z P Y, B X P Z, C Y P X$, one can easily see that $\angle X Z Y=\angle A P B-\angle C$ and $X Y=P C \sin \angle C$. The first relation gives that $X Y Z$ is isosceles with $X Y=X Z$, so from the second relation $P B \sin \angle B=P C \sin \angle C$. Hence $A B / P B=A C / P C$. This implies that the bisectors $B D$ and $C D$ of $\angle A B P$ and $\angle A C P$ divide the segment $A P$ in equal ratios; i.e., they concur with $A P$. Second solution. Take that $X, Y, Z$ are the points of intersection of $A P, B P, C P$ with the circumscribed circle of $A B C$ instead. We similarly obtain $X Y=X Z$. If we write $A P \cdot P X=B P \cdot P Y=C P \cdot P Z=k$, from the similarity of $\triangle A P C$ and $\triangle Z P X$ we get $$ \frac{A C}{X Z}=\frac{A P}{P Z}=\frac{A P \cdot C P}{k} $$ i.e., $X Z=\frac{k \cdot A C \cdot B P}{A P \cdot B P \cdot C P}$. It follows again that $A C / A B=P C / P B$. Third solution. Apply an inversion with center at $A$ and radius $r$, and denote by $\bar{Q}$ the image of any point $Q$. Then the given condition becomes $\angle \overline{B C P}=\angle \overline{C B P}$, i.e., $\overline{B P}=\overline{P C}$. But $$ \overline{P B}=\frac{r^{2}}{A P \cdot A B} P B $$ so $A C / A B=P C / P B$. Remark. Moreover, it follows that the locus of $P$ is an arc of the circle of Apollonius through $C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
11. G2 (CAN) ${ }^{\mathrm{IMO} 2}$ Let $P$ be a point inside $\triangle A B C$ such that $$ \angle A P B-\angle C=\angle A P C-\angle B . $$ Let $D, E$ be the incenters of $\triangle A P B, \triangle A P C$ respectively. Show that $A P, B D$ and $C E$ meet in a point.
|
11. Let $X, Y, Z$ respectively be the feet of the perpendiculars from $P$ to $B C$, $C A, A B$. Examining the cyclic quadrilaterals $A Z P Y, B X P Z, C Y P X$, one can easily see that $\angle X Z Y=\angle A P B-\angle C$ and $X Y=P C \sin \angle C$. The first relation gives that $X Y Z$ is isosceles with $X Y=X Z$, so from the second relation $P B \sin \angle B=P C \sin \angle C$. Hence $A B / P B=A C / P C$. This implies that the bisectors $B D$ and $C D$ of $\angle A B P$ and $\angle A C P$ divide the segment $A P$ in equal ratios; i.e., they concur with $A P$. Second solution. Take that $X, Y, Z$ are the points of intersection of $A P, B P, C P$ with the circumscribed circle of $A B C$ instead. We similarly obtain $X Y=X Z$. If we write $A P \cdot P X=B P \cdot P Y=C P \cdot P Z=k$, from the similarity of $\triangle A P C$ and $\triangle Z P X$ we get $$ \frac{A C}{X Z}=\frac{A P}{P Z}=\frac{A P \cdot C P}{k} $$ i.e., $X Z=\frac{k \cdot A C \cdot B P}{A P \cdot B P \cdot C P}$. It follows again that $A C / A B=P C / P B$. Third solution. Apply an inversion with center at $A$ and radius $r$, and denote by $\bar{Q}$ the image of any point $Q$. Then the given condition becomes $\angle \overline{B C P}=\angle \overline{C B P}$, i.e., $\overline{B P}=\overline{P C}$. But $$ \overline{P B}=\frac{r^{2}}{A P \cdot A B} P B $$ so $A C / A B=P C / P B$. Remark. Moreover, it follows that the locus of $P$ is an arc of the circle of Apollonius through $C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
130f69ca-60e0-552c-909c-f71b32ecae6b
| 24,666
|
12. G3 (GBR) Let $A B C$ be an acute-angled triangle with $B C>C A$. Let $O$ be the circumcenter, $H$ its orthocenter, and $F$ the foot of its altitude $C H$. Let the perpendicular to $O F$ at $F$ meet the side $C A$ at $P$. Prove that $\angle F H P=\angle B A C$. Possible second part: What happens if $|B C| \leq|C A|$ (the triangle still being acute-angled)?
|
12. It is easy to see that $P$ lies on the segment $A C$. Let $E$ be the foot of the altitude $B H$ and $Y, Z$ the midpoints of $A C, A B$ respectively. Draw the perpendicular $H R$ to $F P(R \in F P)$. Since $Y$ is the circumcenter of $\triangle F C A$, we have $\angle F Y A=180^{\circ}-2 \angle A$. Also, $O F P Y$ is cyclic; hence $\angle O P F=\angle O Y F=2 \angle A-90^{\circ}$. Next, $\triangle O Z F$ and $\triangle H R F$ are similar, so $O Z / O F=H R / H F$. This leads to $H R \cdot O F=H F \cdot O Z=\frac{1}{2} H F$. $H C=\frac{1}{2} H E \cdot H B=H E \cdot O Y \Longrightarrow$ $H R / H E=O Y / O F$. Moreover, $\angle E H R=\angle F O Y$; hence the triangles $E H R$ and $F O Y$ are similar. Consequently $\angle H P C=\angle H R E=$ $\angle O Y F=2 \angle A-90^{\circ}$, and finally, $\angle F H P=\angle H P C+\angle H C P=\angle A$. 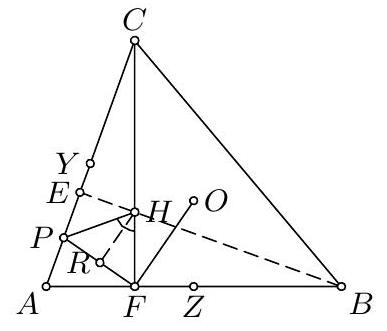 Second solution. As before, $\angle H F Y=90^{\circ}-\angle A$, so it suffices to show that $H P \perp F Y$. The points $O, F, P, Y$ lie on a circle, say $\Omega_{1}$ with center at the midpoint $Q$ of $O P$. Furthermore, the points $F, Y$ lie on the nine-point circle $\Omega$ of $\triangle A B C$ with center at the midpoint $N$ of $O H$. The segment $F Y$ is the common chord of $\Omega_{1}$ and $\Omega$, from which we deduce that $N Q \perp F Y$. However, $N Q \| H P$, and the result follows. Third solution. Let $H^{\prime}$ be the point symmetric to $H$ with respect to $A B$. Then $H^{\prime}$ lies on the circumcircle of $A B C$. Let the line $F P$ meet the circumcircle at $U, V$ and meet $H^{\prime} B$ at $P^{\prime}$. Since $O F \perp U V, F$ is the midpoint of $U V$. By the butterfly theorem, $F$ is also the midpoint of $P P^{\prime}$. Therefore $\triangle H^{\prime} F P^{\prime} \cong F H P$; hence $\angle F H P=\angle F H^{\prime} B=\angle A$. Remark. It is possible to solve the problem using trigonometry. For example, $\frac{F Z}{Z O}=\frac{F K}{K P}=\frac{\sin (A-B)}{\cos C}$, where $K$ is on $C F$ with $P K \perp C F$. Then $\frac{C F}{K P}=\frac{\sin (A-B)}{\cos C}+\tan A$, from which one obtains formulas for $K P$ and $K H$. Finally, we can calculate $\tan \angle F H P=\frac{K P}{K H}=\cdots=\tan A$. Second remark. Here is what happens when $B C \leq C A$. If $\angle A>45^{\circ}$, then $\angle F H P=\angle A$. If $\angle A=45^{\circ}$, the point $P$ escapes to infinity. If $\angle A<45^{\circ}$, the point $P$ appears on the extension of $A C$ over $C$, and $\angle F H P=180^{\circ}-\angle A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
12. G3 (GBR) Let $A B C$ be an acute-angled triangle with $B C>C A$. Let $O$ be the circumcenter, $H$ its orthocenter, and $F$ the foot of its altitude $C H$. Let the perpendicular to $O F$ at $F$ meet the side $C A$ at $P$. Prove that $\angle F H P=\angle B A C$. Possible second part: What happens if $|B C| \leq|C A|$ (the triangle still being acute-angled)?
|
12. It is easy to see that $P$ lies on the segment $A C$. Let $E$ be the foot of the altitude $B H$ and $Y, Z$ the midpoints of $A C, A B$ respectively. Draw the perpendicular $H R$ to $F P(R \in F P)$. Since $Y$ is the circumcenter of $\triangle F C A$, we have $\angle F Y A=180^{\circ}-2 \angle A$. Also, $O F P Y$ is cyclic; hence $\angle O P F=\angle O Y F=2 \angle A-90^{\circ}$. Next, $\triangle O Z F$ and $\triangle H R F$ are similar, so $O Z / O F=H R / H F$. This leads to $H R \cdot O F=H F \cdot O Z=\frac{1}{2} H F$. $H C=\frac{1}{2} H E \cdot H B=H E \cdot O Y \Longrightarrow$ $H R / H E=O Y / O F$. Moreover, $\angle E H R=\angle F O Y$; hence the triangles $E H R$ and $F O Y$ are similar. Consequently $\angle H P C=\angle H R E=$ $\angle O Y F=2 \angle A-90^{\circ}$, and finally, $\angle F H P=\angle H P C+\angle H C P=\angle A$.  Second solution. As before, $\angle H F Y=90^{\circ}-\angle A$, so it suffices to show that $H P \perp F Y$. The points $O, F, P, Y$ lie on a circle, say $\Omega_{1}$ with center at the midpoint $Q$ of $O P$. Furthermore, the points $F, Y$ lie on the nine-point circle $\Omega$ of $\triangle A B C$ with center at the midpoint $N$ of $O H$. The segment $F Y$ is the common chord of $\Omega_{1}$ and $\Omega$, from which we deduce that $N Q \perp F Y$. However, $N Q \| H P$, and the result follows. Third solution. Let $H^{\prime}$ be the point symmetric to $H$ with respect to $A B$. Then $H^{\prime}$ lies on the circumcircle of $A B C$. Let the line $F P$ meet the circumcircle at $U, V$ and meet $H^{\prime} B$ at $P^{\prime}$. Since $O F \perp U V, F$ is the midpoint of $U V$. By the butterfly theorem, $F$ is also the midpoint of $P P^{\prime}$. Therefore $\triangle H^{\prime} F P^{\prime} \cong F H P$; hence $\angle F H P=\angle F H^{\prime} B=\angle A$. Remark. It is possible to solve the problem using trigonometry. For example, $\frac{F Z}{Z O}=\frac{F K}{K P}=\frac{\sin (A-B)}{\cos C}$, where $K$ is on $C F$ with $P K \perp C F$. Then $\frac{C F}{K P}=\frac{\sin (A-B)}{\cos C}+\tan A$, from which one obtains formulas for $K P$ and $K H$. Finally, we can calculate $\tan \angle F H P=\frac{K P}{K H}=\cdots=\tan A$. Second remark. Here is what happens when $B C \leq C A$. If $\angle A>45^{\circ}$, then $\angle F H P=\angle A$. If $\angle A=45^{\circ}$, the point $P$ escapes to infinity. If $\angle A<45^{\circ}$, the point $P$ appears on the extension of $A C$ over $C$, and $\angle F H P=180^{\circ}-\angle A$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
78bfbd6f-ca69-5107-813d-e06a51d57383
| 24,669
|
13. G4 (USA) Let $\triangle A B C$ be an equilateral triangle and let $P$ be a point in its interior. Let the lines $A P, B P, C P$ meet the sides $B C, C A, A B$ in the points $A_{1}, B_{1}, C_{1}$ respectively. Prove that $$ A_{1} B_{1} \cdot B_{1} C_{1} \cdot C_{1} A_{1} \geq A_{1} B \cdot B_{1} C \cdot C_{1} A $$
|
13. By the law of cosines applied to $\triangle C A_{1} B_{1}$, we obtain $$ A_{1} B_{1}^{2}=A_{1} C^{2}+B_{1} C^{2}-A_{1} C \cdot B_{1} C \geq A_{1} C \cdot B_{1} C $$ Analogously, $B_{1} C_{1}^{2} \geq B_{1} A \cdot C_{1} A$ and $C_{1} A_{1}^{2} \geq C_{1} B \cdot A_{1} B$, so that multiplying these inequalities yields $$ A_{1} B_{1}^{2} \cdot B_{1} C_{1}^{2} \cdot C_{1} A_{1}^{2} \geq A_{1} B \cdot A_{1} C \cdot B_{1} A \cdot B_{1} C \cdot C_{1} A \cdot C_{1} B $$ Now, the lines $A A_{1}, B B_{1}, C C_{1}$ concur, so by Ceva's theorem, $A_{1} B \cdot B_{1} C$. $C_{1} A=A B_{1} \cdot B C_{1} \cdot C A_{1}$, which together with (1) gives the desired inequality. Equality holds if and only if $C A_{1}=C B_{1}$, etc.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
13. G4 (USA) Let $\triangle A B C$ be an equilateral triangle and let $P$ be a point in its interior. Let the lines $A P, B P, C P$ meet the sides $B C, C A, A B$ in the points $A_{1}, B_{1}, C_{1}$ respectively. Prove that $$ A_{1} B_{1} \cdot B_{1} C_{1} \cdot C_{1} A_{1} \geq A_{1} B \cdot B_{1} C \cdot C_{1} A $$
|
13. By the law of cosines applied to $\triangle C A_{1} B_{1}$, we obtain $$ A_{1} B_{1}^{2}=A_{1} C^{2}+B_{1} C^{2}-A_{1} C \cdot B_{1} C \geq A_{1} C \cdot B_{1} C $$ Analogously, $B_{1} C_{1}^{2} \geq B_{1} A \cdot C_{1} A$ and $C_{1} A_{1}^{2} \geq C_{1} B \cdot A_{1} B$, so that multiplying these inequalities yields $$ A_{1} B_{1}^{2} \cdot B_{1} C_{1}^{2} \cdot C_{1} A_{1}^{2} \geq A_{1} B \cdot A_{1} C \cdot B_{1} A \cdot B_{1} C \cdot C_{1} A \cdot C_{1} B $$ Now, the lines $A A_{1}, B B_{1}, C C_{1}$ concur, so by Ceva's theorem, $A_{1} B \cdot B_{1} C$. $C_{1} A=A B_{1} \cdot B C_{1} \cdot C A_{1}$, which together with (1) gives the desired inequality. Equality holds if and only if $C A_{1}=C B_{1}$, etc.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
28d60d53-b492-5f4f-9520-748211ce09a7
| 24,671
|
15. G6 (ARM) Let the sides of two rectangles be $\{a, b\}$ and $\{c, d\}$ with $a<c \leq d<b$ and $a b<c d$. Prove that the first rectangle can be placed within the second one if and only if $$ \left(b^{2}-a^{2}\right)^{2} \leq(b d-a c)^{2}+(b c-a d)^{2} $$
|
15. Denote by $A B C D$ and $E F G H$ the two rectangles, where $A B=a, B C=$ $b, E F=c$, and $F G=d$. Obviously, the first rectangle can be placed within the second one with the angle $\alpha$ between $A B$ and $E F$ if and only if $$ a \cos \alpha+b \sin \alpha \leq c, \quad a \sin \alpha+b \cos \alpha \leq d $$ Hence $A B C D$ can be placed within $E F G H$ if and only if there is an $\alpha \in[0, \pi / 2]$ for which (1) holds. The lines $l_{1}(a x+b y=c)$ and $l_{2}(b x+a y=d)$ and the axes $x$ and $y$ bound a region $\mathcal{R}$. By (1), the desired placement of the rectangles is possible if and only if $\mathcal{R}$ contains some point $(\cos \alpha, \sin \alpha)$ of the unit circle centered at the origin $(0,0)$. This in turn holds if and only if the intersection point $L$ of $l_{1}$ and $l_{2}$ lies outside the unit circle. It is easily computed that $L$ has coordinates $\left(\frac{b d-a c}{b^{2}-a^{2}}, \frac{b c-a d}{b^{2}-a^{2}}\right)$. Now $L$ being outside the unit circle is exactly equivalent to the inequality we want to prove. Remark. If equality holds, there is exactly one way of placing. This happens, for example, when $(a, b)=(5,20)$ and $(c, d)=(16,19)$. Second remark. This problem is essentially very similar to (SL89-2).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
15. G6 (ARM) Let the sides of two rectangles be $\{a, b\}$ and $\{c, d\}$ with $a<c \leq d<b$ and $a b<c d$. Prove that the first rectangle can be placed within the second one if and only if $$ \left(b^{2}-a^{2}\right)^{2} \leq(b d-a c)^{2}+(b c-a d)^{2} $$
|
15. Denote by $A B C D$ and $E F G H$ the two rectangles, where $A B=a, B C=$ $b, E F=c$, and $F G=d$. Obviously, the first rectangle can be placed within the second one with the angle $\alpha$ between $A B$ and $E F$ if and only if $$ a \cos \alpha+b \sin \alpha \leq c, \quad a \sin \alpha+b \cos \alpha \leq d $$ Hence $A B C D$ can be placed within $E F G H$ if and only if there is an $\alpha \in[0, \pi / 2]$ for which (1) holds. The lines $l_{1}(a x+b y=c)$ and $l_{2}(b x+a y=d)$ and the axes $x$ and $y$ bound a region $\mathcal{R}$. By (1), the desired placement of the rectangles is possible if and only if $\mathcal{R}$ contains some point $(\cos \alpha, \sin \alpha)$ of the unit circle centered at the origin $(0,0)$. This in turn holds if and only if the intersection point $L$ of $l_{1}$ and $l_{2}$ lies outside the unit circle. It is easily computed that $L$ has coordinates $\left(\frac{b d-a c}{b^{2}-a^{2}}, \frac{b c-a d}{b^{2}-a^{2}}\right)$. Now $L$ being outside the unit circle is exactly equivalent to the inequality we want to prove. Remark. If equality holds, there is exactly one way of placing. This happens, for example, when $(a, b)=(5,20)$ and $(c, d)=(16,19)$. Second remark. This problem is essentially very similar to (SL89-2).
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4a65999a-df8d-52b1-8f61-b99594d0b539
| 24,676
|
16. G7 (GBR) Let $A B C$ be an acute-angled triangle with circumcenter $O$ and circumradius $R$. Let $A O$ meet the circle $B O C$ again in $A^{\prime}$, let $B O$ meet the circle $C O A$ again in $B^{\prime}$, and let $C O$ meet the circle $A O B$ again in $C^{\prime}$. Prove that $$ O A^{\prime} \cdot O B^{\prime} \cdot O C^{\prime} \geq 8 R^{3} $$ When does equality hold?
|
16. Let $A_{1}$ be the point of intersection of $O A^{\prime}$ and $B C$; similarly define $B_{1}$ and $C_{1}$. From the similarity of triangles $O B A_{1}$ and $O A^{\prime} B$ we obtain $O A_{1}$. $O A^{\prime}=R^{2}$. Now it is enough to show that $8 O A_{1} \cdot O B^{\prime} \cdot O C^{\prime} \leq R^{3}$. Thus we must prove that $$ \lambda \mu \nu \leq \frac{1}{8}, \quad \text { where } \quad \frac{O A_{1}}{O A}=\lambda, \quad \frac{O B_{1}}{O B}=\mu, \quad \frac{O C_{1}}{O C}=\nu $$ On the other hand, we have $$ \frac{\lambda}{1+\lambda}+\frac{\mu}{1+\mu}+\frac{\nu}{1+\nu}=\frac{S_{O B C}}{S_{A B C}}+\frac{S_{A O C}}{S_{A B C}}+\frac{S_{A B O}}{S_{A B C}}=1 . $$ Simplifying this relation, we get $$ 1=\lambda \mu+\mu \nu+\nu \lambda+2 \lambda \mu \nu \geq 3(\lambda \mu \nu)^{2 / 3}+2 \lambda \mu \nu $$ which cannot hold if $\lambda \mu \nu>\frac{1}{8}$. Hence $\lambda \mu \nu \leq \frac{1}{8}$, with equality if and only if $\lambda=\mu=\nu=\frac{1}{2}$. This implies that $O$ is the centroid of $A B C$, and consequently, that the triangle is equilateral. Second solution. In the official solution, the inequality to be proved is transformed into $$ \cos (A-B) \cos (B-C) \cos (C-A) \geq 8 \cos A \cos B \cos C $$ Since $\frac{\cos (B-C)}{\cos A}=-\frac{\cos (B-C)}{\cos (B+C)}=\frac{\tan B \tan C+1}{\tan B \tan C-1}$, the last inequality becomes $(x y+1)(y z+1)(z x+1) \geq 8(x y-1)(y z-1)(z x-1)$, where we write $x, y, z$ for $\tan A, \tan B, \tan C$. Using the relation $x+y+z=x y z$, we can reduce this inequality to $$ (2 x+y+z)(x+2 y+z)(x+y+2 z) \geq 8(x+y)(y+z)(z+x) $$ This follows from the AM-GM inequality: $2 x+y+z=(x+y)+(x+z) \geq$ $2 \sqrt{(x+y)(x+z)}$, etc.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
16. G7 (GBR) Let $A B C$ be an acute-angled triangle with circumcenter $O$ and circumradius $R$. Let $A O$ meet the circle $B O C$ again in $A^{\prime}$, let $B O$ meet the circle $C O A$ again in $B^{\prime}$, and let $C O$ meet the circle $A O B$ again in $C^{\prime}$. Prove that $$ O A^{\prime} \cdot O B^{\prime} \cdot O C^{\prime} \geq 8 R^{3} $$ When does equality hold?
|
16. Let $A_{1}$ be the point of intersection of $O A^{\prime}$ and $B C$; similarly define $B_{1}$ and $C_{1}$. From the similarity of triangles $O B A_{1}$ and $O A^{\prime} B$ we obtain $O A_{1}$. $O A^{\prime}=R^{2}$. Now it is enough to show that $8 O A_{1} \cdot O B^{\prime} \cdot O C^{\prime} \leq R^{3}$. Thus we must prove that $$ \lambda \mu \nu \leq \frac{1}{8}, \quad \text { where } \quad \frac{O A_{1}}{O A}=\lambda, \quad \frac{O B_{1}}{O B}=\mu, \quad \frac{O C_{1}}{O C}=\nu $$ On the other hand, we have $$ \frac{\lambda}{1+\lambda}+\frac{\mu}{1+\mu}+\frac{\nu}{1+\nu}=\frac{S_{O B C}}{S_{A B C}}+\frac{S_{A O C}}{S_{A B C}}+\frac{S_{A B O}}{S_{A B C}}=1 . $$ Simplifying this relation, we get $$ 1=\lambda \mu+\mu \nu+\nu \lambda+2 \lambda \mu \nu \geq 3(\lambda \mu \nu)^{2 / 3}+2 \lambda \mu \nu $$ which cannot hold if $\lambda \mu \nu>\frac{1}{8}$. Hence $\lambda \mu \nu \leq \frac{1}{8}$, with equality if and only if $\lambda=\mu=\nu=\frac{1}{2}$. This implies that $O$ is the centroid of $A B C$, and consequently, that the triangle is equilateral. Second solution. In the official solution, the inequality to be proved is transformed into $$ \cos (A-B) \cos (B-C) \cos (C-A) \geq 8 \cos A \cos B \cos C $$ Since $\frac{\cos (B-C)}{\cos A}=-\frac{\cos (B-C)}{\cos (B+C)}=\frac{\tan B \tan C+1}{\tan B \tan C-1}$, the last inequality becomes $(x y+1)(y z+1)(z x+1) \geq 8(x y-1)(y z-1)(z x-1)$, where we write $x, y, z$ for $\tan A, \tan B, \tan C$. Using the relation $x+y+z=x y z$, we can reduce this inequality to $$ (2 x+y+z)(x+2 y+z)(x+y+2 z) \geq 8(x+y)(y+z)(z+x) $$ This follows from the AM-GM inequality: $2 x+y+z=(x+y)+(x+z) \geq$ $2 \sqrt{(x+y)(x+z)}$, etc.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
42d71a55-497e-57dd-ade3-d6fb70e5c2fc
| 24,679
|
17. G8 (RUS) Let $A B C D$ be a convex quadrilateral, and let $R_{A}, R_{B}, R_{C}$, and $R_{D}$ denote the circumradii of the triangles $D A B, A B C, B C D$, and $C D A$ respectively. Prove that $R_{A}+R_{C}>R_{B}+R_{D}$ if and only if $$ \angle A+\angle C>\angle B+\angle D . $$
|
17. Let the diagonals $A C$ and $B D$ meet in $X$. Either $\angle A X B$ or $\angle A X D$ is geater than or equal to $90^{\circ}$, so we assume w.l.o.g. that $\angle A X B \geq 90^{\circ}$. Let $\alpha, \beta, \alpha^{\prime}, \beta^{\prime}$ denote $\angle C A B, \angle A B D, \angle B D C, \angle D C A$. These angles are all acute and satisfy $\alpha+\beta=\alpha^{\prime}+\beta^{\prime}$. Furthermore, $$ R_{A}=\frac{A D}{2 \sin \beta}, \quad R_{B}=\frac{B C}{2 \sin \alpha}, \quad R_{C}=\frac{B C}{2 \sin \alpha^{\prime}}, \quad R_{D}=\frac{A D}{2 \sin \beta^{\prime}} $$ Let $\angle B+\angle D=180^{\circ}$. Then $A, B, C, D$ are concyclic and trivially $R_{A}+$ $R_{C}=R_{B}+R_{D}$. Let $\angle B+\angle D>180^{\circ}$. Then $D$ lies within the circumcircle of $A B C$, which implies that $\beta>\beta^{\prime}$. Similarly $\alpha<\alpha^{\prime}$, so we obtain $R_{A}<R_{D}$ and $R_{C}<R_{B}$. Thus $R_{A}+R_{C}<R_{B}+R_{D}$. Let $\angle B+\angle D<180^{\circ}$. As in the previous case, we deduce that $R_{A}>R_{D}$ and $R_{C}>R_{B}$, so $R_{A}+R_{C}>R_{B}+R_{D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
17. G8 (RUS) Let $A B C D$ be a convex quadrilateral, and let $R_{A}, R_{B}, R_{C}$, and $R_{D}$ denote the circumradii of the triangles $D A B, A B C, B C D$, and $C D A$ respectively. Prove that $R_{A}+R_{C}>R_{B}+R_{D}$ if and only if $$ \angle A+\angle C>\angle B+\angle D . $$
|
17. Let the diagonals $A C$ and $B D$ meet in $X$. Either $\angle A X B$ or $\angle A X D$ is geater than or equal to $90^{\circ}$, so we assume w.l.o.g. that $\angle A X B \geq 90^{\circ}$. Let $\alpha, \beta, \alpha^{\prime}, \beta^{\prime}$ denote $\angle C A B, \angle A B D, \angle B D C, \angle D C A$. These angles are all acute and satisfy $\alpha+\beta=\alpha^{\prime}+\beta^{\prime}$. Furthermore, $$ R_{A}=\frac{A D}{2 \sin \beta}, \quad R_{B}=\frac{B C}{2 \sin \alpha}, \quad R_{C}=\frac{B C}{2 \sin \alpha^{\prime}}, \quad R_{D}=\frac{A D}{2 \sin \beta^{\prime}} $$ Let $\angle B+\angle D=180^{\circ}$. Then $A, B, C, D$ are concyclic and trivially $R_{A}+$ $R_{C}=R_{B}+R_{D}$. Let $\angle B+\angle D>180^{\circ}$. Then $D$ lies within the circumcircle of $A B C$, which implies that $\beta>\beta^{\prime}$. Similarly $\alpha<\alpha^{\prime}$, so we obtain $R_{A}<R_{D}$ and $R_{C}<R_{B}$. Thus $R_{A}+R_{C}<R_{B}+R_{D}$. Let $\angle B+\angle D<180^{\circ}$. As in the previous case, we deduce that $R_{A}>R_{D}$ and $R_{C}>R_{B}$, so $R_{A}+R_{C}>R_{B}+R_{D}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e52615d2-b782-5d9a-bed0-aef881cabc0a
| 24,682
|
18. G9 (UKR) In the plane are given a point $O$ and a polygon $\mathcal{F}$ (not necessarily convex). Let $P$ denote the perimeter of $\mathcal{F}, D$ the sum of the distances from $O$ to the vertices of $\mathcal{F}$, and $H$ the sum of the distances from $O$ to the lines containing the sides of $\mathcal{F}$. Prove that $$ D^{2}-H^{2} \geq \frac{P^{2}}{4} $$
|
18. We first prove the result in the simplest case. Given a 2 -gon $A B A$ and a point $O$, let $a, b, c, h$ denote $O A, O B, A B$, and the distance of $O$ from $A B$. Then $D=a+b, P=2 c$, and $H=2 h$, so we should show that $$ (a+b)^{2} \geq 4 h^{2}+c^{2} $$ Indeed, let $l$ be the line through $O$ parallel to $A B$, and $D$ the point symmetric to $B$ with respect to $l$. Then $(a+b)^{2}=(O A+O B)^{2}=(O A+$ $O D)^{2} \geq A D^{2}=c^{2}+4 h^{2}$. Now we pass to the general case. Let $A_{1} A_{2} \ldots A_{n}$ be the polygon $\mathcal{F}$ and denote by $d_{i}, p_{i}$, and $h_{i}$ respectively $O A_{i}, A_{i} A_{i+1}$, and the distance of $O$ from $A_{i} A_{i+1}$ (where $A_{n+1}=A_{1}$ ). By the case proved above, we have for each $i, d_{i}+d_{i+1} \geq \sqrt{4 h_{i}^{2}+p_{i}^{2}}$. Summing these inequalities for $i=1, \ldots, n$ and squaring, we obtain $$ 4 D^{2} \geq\left(\sum_{i=1}^{n} \sqrt{4 h_{i}^{2}+p_{i}^{2}}\right)^{2} $$ It remains only to prove that $\sum_{i=1}^{n} \sqrt{4 h_{i}^{2}+p_{i}^{2}} \geq \sqrt{\sum_{i=1}^{n}\left(4 h_{i}^{2}+p_{i}^{2}\right)}=$ $\sqrt{4 H^{2}+D^{2}}$. But this follows immediately from the Minkowski inequality. Equality holds if and only if it holds in (1) and in the Minkowski inequality, i.e., if and only if $d_{1}=\cdots=d_{n}$ and $h_{1} / p_{1}=\cdots=h_{n} / p_{n}$. This means that $\mathcal{F}$ is inscribed in a circle with center at $O$ and $p_{1}=\cdots=p_{n}$, so $\mathcal{F}$ is a regular polygon and $O$ its center.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
18. G9 (UKR) In the plane are given a point $O$ and a polygon $\mathcal{F}$ (not necessarily convex). Let $P$ denote the perimeter of $\mathcal{F}, D$ the sum of the distances from $O$ to the vertices of $\mathcal{F}$, and $H$ the sum of the distances from $O$ to the lines containing the sides of $\mathcal{F}$. Prove that $$ D^{2}-H^{2} \geq \frac{P^{2}}{4} $$
|
18. We first prove the result in the simplest case. Given a 2 -gon $A B A$ and a point $O$, let $a, b, c, h$ denote $O A, O B, A B$, and the distance of $O$ from $A B$. Then $D=a+b, P=2 c$, and $H=2 h$, so we should show that $$ (a+b)^{2} \geq 4 h^{2}+c^{2} $$ Indeed, let $l$ be the line through $O$ parallel to $A B$, and $D$ the point symmetric to $B$ with respect to $l$. Then $(a+b)^{2}=(O A+O B)^{2}=(O A+$ $O D)^{2} \geq A D^{2}=c^{2}+4 h^{2}$. Now we pass to the general case. Let $A_{1} A_{2} \ldots A_{n}$ be the polygon $\mathcal{F}$ and denote by $d_{i}, p_{i}$, and $h_{i}$ respectively $O A_{i}, A_{i} A_{i+1}$, and the distance of $O$ from $A_{i} A_{i+1}$ (where $A_{n+1}=A_{1}$ ). By the case proved above, we have for each $i, d_{i}+d_{i+1} \geq \sqrt{4 h_{i}^{2}+p_{i}^{2}}$. Summing these inequalities for $i=1, \ldots, n$ and squaring, we obtain $$ 4 D^{2} \geq\left(\sum_{i=1}^{n} \sqrt{4 h_{i}^{2}+p_{i}^{2}}\right)^{2} $$ It remains only to prove that $\sum_{i=1}^{n} \sqrt{4 h_{i}^{2}+p_{i}^{2}} \geq \sqrt{\sum_{i=1}^{n}\left(4 h_{i}^{2}+p_{i}^{2}\right)}=$ $\sqrt{4 H^{2}+D^{2}}$. But this follows immediately from the Minkowski inequality. Equality holds if and only if it holds in (1) and in the Minkowski inequality, i.e., if and only if $d_{1}=\cdots=d_{n}$ and $h_{1} / p_{1}=\cdots=h_{n} / p_{n}$. This means that $\mathcal{F}$ is inscribed in a circle with center at $O$ and $p_{1}=\cdots=p_{n}$, so $\mathcal{F}$ is a regular polygon and $O$ its center.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
fc70fd4b-6f90-548e-8a30-ff9dd95679b9
| 24,685
|
2. A2 (IRE) Let $a_{1} \geq a_{2} \geq \cdots \geq a_{n}$ be real numbers such that $$ a_{1}^{k}+a_{2}^{k}+\cdots+a_{n}^{k} \geq 0 $$ for all integers $k>0$. Let $p=\max \left\{\left|a_{1}\right|, \ldots,\left|a_{n}\right|\right\}$. Prove that $p=a_{1}$ and that $$ \left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right) \leq x^{n}-a_{1}^{n} $$ for all $x>a_{1}$.
|
2. Clearly $a_{1}>0$, and if $p \neq a_{1}$, we must have $a_{n}<0,\left|a_{n}\right|>\left|a_{1}\right|$, and $p=-a_{n}$. But then for sufficiently large odd $k,-a_{n}^{k}=\left|a_{n}\right|^{k}>(n-1)\left|a_{1}\right|^{k}$, so that $a_{1}^{k}+\cdots+a_{n}^{k} \leq(n-1)\left|a_{1}\right|^{k}-\left|a_{n}\right|^{k}<0$, a contradiction. Hence $p=a_{1}$. Now let $x>a_{1}$. From $a_{1}+\cdots+a_{n} \geq 0$ we deduce $\sum_{j=2}^{n}\left(x-a_{j}\right) \leq$ $(n-1)\left(x+\frac{a_{1}}{n-1}\right)$, so by the AM-GM inequality, $$ \left(x-a_{2}\right) \cdots\left(x-a_{n}\right) \leq\left(x+\frac{a_{1}}{n-1}\right)^{n-1} \leq x^{n-1}+x^{n-2} a_{1}+\cdots+a_{1}^{n-1} $$ The last inequality holds because $\binom{n-1}{r} \leq(n-1)^{r}$ for all $r \geq 0$. Multiplying (1) by $\left(x-a_{1}\right)$ yields the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
2. A2 (IRE) Let $a_{1} \geq a_{2} \geq \cdots \geq a_{n}$ be real numbers such that $$ a_{1}^{k}+a_{2}^{k}+\cdots+a_{n}^{k} \geq 0 $$ for all integers $k>0$. Let $p=\max \left\{\left|a_{1}\right|, \ldots,\left|a_{n}\right|\right\}$. Prove that $p=a_{1}$ and that $$ \left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right) \leq x^{n}-a_{1}^{n} $$ for all $x>a_{1}$.
|
2. Clearly $a_{1}>0$, and if $p \neq a_{1}$, we must have $a_{n}<0,\left|a_{n}\right|>\left|a_{1}\right|$, and $p=-a_{n}$. But then for sufficiently large odd $k,-a_{n}^{k}=\left|a_{n}\right|^{k}>(n-1)\left|a_{1}\right|^{k}$, so that $a_{1}^{k}+\cdots+a_{n}^{k} \leq(n-1)\left|a_{1}\right|^{k}-\left|a_{n}\right|^{k}<0$, a contradiction. Hence $p=a_{1}$. Now let $x>a_{1}$. From $a_{1}+\cdots+a_{n} \geq 0$ we deduce $\sum_{j=2}^{n}\left(x-a_{j}\right) \leq$ $(n-1)\left(x+\frac{a_{1}}{n-1}\right)$, so by the AM-GM inequality, $$ \left(x-a_{2}\right) \cdots\left(x-a_{n}\right) \leq\left(x+\frac{a_{1}}{n-1}\right)^{n-1} \leq x^{n-1}+x^{n-2} a_{1}+\cdots+a_{1}^{n-1} $$ The last inequality holds because $\binom{n-1}{r} \leq(n-1)^{r}$ for all $r \geq 0$. Multiplying (1) by $\left(x-a_{1}\right)$ yields the desired inequality.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a1afad0b-199d-5117-8907-6699c83491fc
| 24,690
|
24. C1 (FIN) ${ }^{\mathrm{IMO} 1}$ We are given a positive integer $r$ and a rectangular board $A B C D$ with dimensions $|A B|=20,|B C|=12$. The rectangle is divided into a grid of $20 \times 12$ unit squares. The following moves are permitted on the board: One can move from one square to another only if the distance between the centers of the two squares is $\sqrt{r}$. The task is to find a sequence of moves leading from the square corresponding to vertex $A$ to the square corresponding to vertex $B$. (a) Show that the task cannot be done if $r$ is divisible by 2 or 3 . (b) Prove that the task is possible when $r=73$. (c) Is there a solution when $r=97$ ?
|
24. We shall work on the array of lattice points defined by $\mathcal{A}=\left\{(x, y) \in \mathbb{Z}^{2} \mid\right.$ $0 \leq x \leq 19,0 \leq y \leq 11\}$. Our task is to move from $(0,0)$ to $(19,0)$ via the points of $\mathcal{A}$ so that each move has the form $(x, y) \rightarrow(x+a, y+b)$, where $a, b \in \mathbb{Z}$ and $a^{2}+b^{2}=r$. (a) If $r$ is even, then $a+b$ is even whenever $a^{2}+b^{2}=r(a, b \in \mathbb{Z})$. Thus the parity of $x+y$ does not change after each move, so we cannot reach $(19,0)$ from $(0,0)$. If $3 \mid r$, then both $a$ and $b$ are divisible by 3 , so if a point $(x, y)$ can be reached from $(0,0)$, we must have $3 \mid x$. Since $3 \nmid 19$, we cannot get to $(19,0)$. (b) We have $r=73=8^{2}+3^{2}$, so each move is either $(x, y) \rightarrow(x \pm 8, y \pm 3)$ or $(x, y) \rightarrow(x \pm 3, y \pm 8)$. One possible solution is shown in Fig. 1. (c) We have $97=9^{2}+4^{2}$. Let us partition $\mathcal{A}$ as $\mathcal{B} \cup \mathcal{C}$, where $\mathcal{B}=$ $\{(x, y) \in \mathcal{A} \mid 4 \leq y \leq 7\}$. It is easily seen that moves of the type $(x, y) \rightarrow(x \pm 9, y \pm 4)$ always take us from the set $\mathcal{B}$ to $\mathcal{C}$ and vice versa, while the moves $(x, y) \rightarrow(x \pm 4, y \pm 9)$ always take us from $\mathcal{C}$ to $\mathcal{C}$. Furthermore, each move of the type $(x, y) \rightarrow(x \pm 9, y \pm 4)$ changes the parity of $x$, so to get from $(0,0)$ to $(19,0)$ we must have an odd number of such moves. On the other hand, with an odd number of such moves, starting from $\mathcal{C}$ we can end up only in $\mathcal{B}$, although the point $(19,0)$ is not in $\mathcal{B}$. Hence, the answer is no. Remark. Part (c) can also be solved by examining all cells that can be reached from $(0,0)$. All these cells are marked in Fig. 2.  Fig. 1  Fig. 2
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
24. C1 (FIN) ${ }^{\mathrm{IMO} 1}$ We are given a positive integer $r$ and a rectangular board $A B C D$ with dimensions $|A B|=20,|B C|=12$. The rectangle is divided into a grid of $20 \times 12$ unit squares. The following moves are permitted on the board: One can move from one square to another only if the distance between the centers of the two squares is $\sqrt{r}$. The task is to find a sequence of moves leading from the square corresponding to vertex $A$ to the square corresponding to vertex $B$. (a) Show that the task cannot be done if $r$ is divisible by 2 or 3 . (b) Prove that the task is possible when $r=73$. (c) Is there a solution when $r=97$ ?
|
24. We shall work on the array of lattice points defined by $\mathcal{A}=\left\{(x, y) \in \mathbb{Z}^{2} \mid\right.$ $0 \leq x \leq 19,0 \leq y \leq 11\}$. Our task is to move from $(0,0)$ to $(19,0)$ via the points of $\mathcal{A}$ so that each move has the form $(x, y) \rightarrow(x+a, y+b)$, where $a, b \in \mathbb{Z}$ and $a^{2}+b^{2}=r$. (a) If $r$ is even, then $a+b$ is even whenever $a^{2}+b^{2}=r(a, b \in \mathbb{Z})$. Thus the parity of $x+y$ does not change after each move, so we cannot reach $(19,0)$ from $(0,0)$. If $3 \mid r$, then both $a$ and $b$ are divisible by 3 , so if a point $(x, y)$ can be reached from $(0,0)$, we must have $3 \mid x$. Since $3 \nmid 19$, we cannot get to $(19,0)$. (b) We have $r=73=8^{2}+3^{2}$, so each move is either $(x, y) \rightarrow(x \pm 8, y \pm 3)$ or $(x, y) \rightarrow(x \pm 3, y \pm 8)$. One possible solution is shown in Fig. 1. (c) We have $97=9^{2}+4^{2}$. Let us partition $\mathcal{A}$ as $\mathcal{B} \cup \mathcal{C}$, where $\mathcal{B}=$ $\{(x, y) \in \mathcal{A} \mid 4 \leq y \leq 7\}$. It is easily seen that moves of the type $(x, y) \rightarrow(x \pm 9, y \pm 4)$ always take us from the set $\mathcal{B}$ to $\mathcal{C}$ and vice versa, while the moves $(x, y) \rightarrow(x \pm 4, y \pm 9)$ always take us from $\mathcal{C}$ to $\mathcal{C}$. Furthermore, each move of the type $(x, y) \rightarrow(x \pm 9, y \pm 4)$ changes the parity of $x$, so to get from $(0,0)$ to $(19,0)$ we must have an odd number of such moves. On the other hand, with an odd number of such moves, starting from $\mathcal{C}$ we can end up only in $\mathcal{B}$, although the point $(19,0)$ is not in $\mathcal{B}$. Hence, the answer is no. Remark. Part (c) can also be solved by examining all cells that can be reached from $(0,0)$. All these cells are marked in Fig. 2.  Fig. 1  Fig. 2
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
96c4004d-ab7f-5072-b840-d647e1de2784
| 24,704
|
27. C4 (FIN) Determine whether or not there exist two disjoint infinite sets $\mathcal{A}$ and $\mathcal{B}$ of points in the plane satisfying the following conditions: (i) No three points in $\mathcal{A} \cup \mathcal{B}$ are collinear, and the distance between any two points in $\mathcal{A} \cup \mathcal{B}$ is at least 1. (ii) There is a point of $\mathcal{A}$ in any triangle whose vertices are in $\mathcal{B}$, and there is a point of $\mathcal{B}$ in any triangle whose vertices are in $\mathcal{A}$.
|
27. Suppose that such sets of points $\mathcal{A}, \mathcal{B}$ exist. First, we observe that there exist five points $A, B, C, D, E$ in $\mathcal{A}$ such that their convex hull does not contain any other point of $\mathcal{A}$. Indeed, take any point $A \in \mathcal{A}$. Since any two points of $\mathcal{A}$ are at distance at least 1 , the number of points $X \in \mathcal{A}$ with $X A \leq r$ is finite for every $r>0$. Thus it is enough to choose four points $B, C, D, E$ of $\mathcal{A}$ that are closest to $A$. Now consider the convex hull $\mathcal{C}$ of $A, B, C, D, E$. Suppose that $\mathcal{C}$ is a pentagon, say $A B C D E$. Then each of the disjoint triangles $A B C, A C D, A D E$ contains a point of $\mathcal{B}$. Denote these points by $P, Q, R$. Then $\triangle P Q R$ contains some point $F \in \mathcal{A}$, so $F$ is inside $A B C D E$, a contradiction. Suppose that $\mathcal{C}$ is a quadrilateral, say $A B C D$, with $E$ lying within $A B C D$. Then the triangles $A B E, B C E, C D E, D A E$ contain some points $P, Q, R, S$ of $\mathcal{B}$ that form two disjoint triangles. It follows that there are two points of $\mathcal{A}$ inside $A B C D$, which is a contradiction. Finally, suppose that $\mathcal{C}$ is a triangle with two points of $\mathcal{A}$ inside. Then $\mathcal{C}$ is the union of five disjoint triangles with vertices in $\mathcal{A}$, so there are at least five points of $\mathcal{B}$ inside $\mathcal{C}$. These five points make at least three disjoint triangles containing three points of $\mathcal{A}$. This is again a contradiction. It follows that no such sets $\mathcal{A}, \mathcal{B}$ exist.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
27. C4 (FIN) Determine whether or not there exist two disjoint infinite sets $\mathcal{A}$ and $\mathcal{B}$ of points in the plane satisfying the following conditions: (i) No three points in $\mathcal{A} \cup \mathcal{B}$ are collinear, and the distance between any two points in $\mathcal{A} \cup \mathcal{B}$ is at least 1. (ii) There is a point of $\mathcal{A}$ in any triangle whose vertices are in $\mathcal{B}$, and there is a point of $\mathcal{B}$ in any triangle whose vertices are in $\mathcal{A}$.
|
27. Suppose that such sets of points $\mathcal{A}, \mathcal{B}$ exist. First, we observe that there exist five points $A, B, C, D, E$ in $\mathcal{A}$ such that their convex hull does not contain any other point of $\mathcal{A}$. Indeed, take any point $A \in \mathcal{A}$. Since any two points of $\mathcal{A}$ are at distance at least 1 , the number of points $X \in \mathcal{A}$ with $X A \leq r$ is finite for every $r>0$. Thus it is enough to choose four points $B, C, D, E$ of $\mathcal{A}$ that are closest to $A$. Now consider the convex hull $\mathcal{C}$ of $A, B, C, D, E$. Suppose that $\mathcal{C}$ is a pentagon, say $A B C D E$. Then each of the disjoint triangles $A B C, A C D, A D E$ contains a point of $\mathcal{B}$. Denote these points by $P, Q, R$. Then $\triangle P Q R$ contains some point $F \in \mathcal{A}$, so $F$ is inside $A B C D E$, a contradiction. Suppose that $\mathcal{C}$ is a quadrilateral, say $A B C D$, with $E$ lying within $A B C D$. Then the triangles $A B E, B C E, C D E, D A E$ contain some points $P, Q, R, S$ of $\mathcal{B}$ that form two disjoint triangles. It follows that there are two points of $\mathcal{A}$ inside $A B C D$, which is a contradiction. Finally, suppose that $\mathcal{C}$ is a triangle with two points of $\mathcal{A}$ inside. Then $\mathcal{C}$ is the union of five disjoint triangles with vertices in $\mathcal{A}$, so there are at least five points of $\mathcal{B}$ inside $\mathcal{C}$. These five points make at least three disjoint triangles containing three points of $\mathcal{A}$. This is again a contradiction. It follows that no such sets $\mathcal{A}, \mathcal{B}$ exist.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
691d923e-666f-56e8-abe4-908181b593e1
| 24,711
|
28. C5 (FRA) ${ }^{\mathrm{IMO} 6}$ Let $p, q, n$ be three positive integers with $p+q<n$. Let $\left(x_{0}, x_{1}, \ldots, x_{n}\right)$ be an $(n+1)$-tuple of integers satisfying the following conditions: (i) $x_{0}=x_{n}=0$. (ii) For each $i$ with $1 \leq i \leq n$, either $x_{i}-x_{i-1}=p$ or $x_{i}-x_{i-1}=-q$. Show that there exists a pair $(i, j)$ of distinct indices with $(i, j) \neq(0, n)$ such that $x_{i}=x_{j}$.
|
28. Note that w.l.o.g., we can assume that $p$ and $q$ are coprime. Indeed, otherwise it suffices to consider the problem in which all $x_{i}$ 's and $p, q$ are divided by $\operatorname{gcd}(p, q)$. Let $k, l$ be the number of indices $i$ with $x_{i+1}-x_{i}=p$ and the number of those $i$ with $x_{i+1}-x_{i}=-q(0 \leq i<n)$. From $x_{0}=x_{n}=0$ we get $k p=l q$, so for some integer $t>1, k=q t, l=p t$, and $n=(p+q) t$. Consider the sequence $y_{i}=x_{i+p+q}-x_{i}, i=0, \ldots, n-p-q$. We claim that at least one of the $y_{i}$ 's equals zero. We begin by noting that each $y_{i}$ is of the form $u p-v q$, where $u+v=p+q$; therefore $y_{i}=(u+v) p-$ $v(p+q)=(p-v)(p+q)$ is always divisible by $p+q$. Moreover, $y_{i+1}-y_{i}=$ $\left(x_{i+p+q+1}-x_{i+p+q}\right)-\left(x_{i+1}-x_{i}\right)$ is 0 or $\pm(p+q)$. We conclude that if no $y_{i}$ is 0 then all $y_{i}$ 's are of the same sign. But this is in contradiction with the relation $y_{0}+y_{p+q}+\cdots+y_{n-p-q}=x_{n}-x_{0}=0$. Consequently some $y_{i}$ is zero, as claimed. Second solution. As before we assume $(p, q)=1$. Let us define a sequence of points $A_{i}\left(y_{i}, z_{i}\right)(i=0,1, \ldots, n)$ in $\mathbb{N}_{0}^{2}$ inductively as follows. Set $A_{0}=$ $(0,0)$ and define $\left(y_{i+1}, z_{i+1}\right)$ as $\left(y_{i}, z_{i}+1\right)$ if $x_{i+1}=x_{i}+p$ and $\left(y_{i}+1, z_{i}\right)$ otherwise. The points $A_{i}$ form a trajectory $L$ in $\mathbb{N}_{0}^{2}$ continuously moving upwards and rightwards by steps of length 1 . Clearly, $x_{i}=p z_{i}-q y_{i}$ for all $i$. Since $x_{n}=0$, it follows that $\left(z_{n}, y_{n}\right)=(k q, k p), k \in \mathbb{N}$. Since $y_{n}+z_{n}=n>p+q$, it follows that $k>1$. We observe that $x_{i}=x_{j}$ if and only if $A_{i} A_{j} \| A_{0} A_{n}$. We shall show that such $i, j$ with $i<j$ and $(i, j) \neq(0, n)$ must exist. If $L$ meets $A_{0} A_{n}$ in an interior point, then our statement trivially holds. From now on we assume the opposite. Let $P_{i j}$ be the rectangle with sides parallel to the coordinate axes and with vertices at $(i p, j q)$ and $((i+$ 1) $p,(j+1) q)$. Let $L_{i j}$ be the part of the trajectory $L$ lying inside $P_{i j}$. We may assume w.l.o.g. that the endpoints of $L_{00}$ lie on the vertical sides of $P_{00}$. Then there obviously exists $d \in\{1, \ldots, k-1\}$ such that the endpoints of $L_{d d}$ lie on the horizontal sides of $P_{d d}$. Consider the translate $L_{d d}^{\prime}$ of $L_{d d}$ for the vector $-d(p, q)$. The endpoints of $L_{d d}^{\prime}$ lie on the vertical sides of $P_{00}$. Hence $L_{00}$ and $L_{d d}^{\prime}$ have some point $X \neq A_{0}$ in common. The translate $Y$ of point $X$ for the vector $d(p, q)$ belongs to $L$ and satisfies $X Y \| A_{0} A_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
28. C5 (FRA) ${ }^{\mathrm{IMO} 6}$ Let $p, q, n$ be three positive integers with $p+q<n$. Let $\left(x_{0}, x_{1}, \ldots, x_{n}\right)$ be an $(n+1)$-tuple of integers satisfying the following conditions: (i) $x_{0}=x_{n}=0$. (ii) For each $i$ with $1 \leq i \leq n$, either $x_{i}-x_{i-1}=p$ or $x_{i}-x_{i-1}=-q$. Show that there exists a pair $(i, j)$ of distinct indices with $(i, j) \neq(0, n)$ such that $x_{i}=x_{j}$.
|
28. Note that w.l.o.g., we can assume that $p$ and $q$ are coprime. Indeed, otherwise it suffices to consider the problem in which all $x_{i}$ 's and $p, q$ are divided by $\operatorname{gcd}(p, q)$. Let $k, l$ be the number of indices $i$ with $x_{i+1}-x_{i}=p$ and the number of those $i$ with $x_{i+1}-x_{i}=-q(0 \leq i<n)$. From $x_{0}=x_{n}=0$ we get $k p=l q$, so for some integer $t>1, k=q t, l=p t$, and $n=(p+q) t$. Consider the sequence $y_{i}=x_{i+p+q}-x_{i}, i=0, \ldots, n-p-q$. We claim that at least one of the $y_{i}$ 's equals zero. We begin by noting that each $y_{i}$ is of the form $u p-v q$, where $u+v=p+q$; therefore $y_{i}=(u+v) p-$ $v(p+q)=(p-v)(p+q)$ is always divisible by $p+q$. Moreover, $y_{i+1}-y_{i}=$ $\left(x_{i+p+q+1}-x_{i+p+q}\right)-\left(x_{i+1}-x_{i}\right)$ is 0 or $\pm(p+q)$. We conclude that if no $y_{i}$ is 0 then all $y_{i}$ 's are of the same sign. But this is in contradiction with the relation $y_{0}+y_{p+q}+\cdots+y_{n-p-q}=x_{n}-x_{0}=0$. Consequently some $y_{i}$ is zero, as claimed. Second solution. As before we assume $(p, q)=1$. Let us define a sequence of points $A_{i}\left(y_{i}, z_{i}\right)(i=0,1, \ldots, n)$ in $\mathbb{N}_{0}^{2}$ inductively as follows. Set $A_{0}=$ $(0,0)$ and define $\left(y_{i+1}, z_{i+1}\right)$ as $\left(y_{i}, z_{i}+1\right)$ if $x_{i+1}=x_{i}+p$ and $\left(y_{i}+1, z_{i}\right)$ otherwise. The points $A_{i}$ form a trajectory $L$ in $\mathbb{N}_{0}^{2}$ continuously moving upwards and rightwards by steps of length 1 . Clearly, $x_{i}=p z_{i}-q y_{i}$ for all $i$. Since $x_{n}=0$, it follows that $\left(z_{n}, y_{n}\right)=(k q, k p), k \in \mathbb{N}$. Since $y_{n}+z_{n}=n>p+q$, it follows that $k>1$. We observe that $x_{i}=x_{j}$ if and only if $A_{i} A_{j} \| A_{0} A_{n}$. We shall show that such $i, j$ with $i<j$ and $(i, j) \neq(0, n)$ must exist. If $L$ meets $A_{0} A_{n}$ in an interior point, then our statement trivially holds. From now on we assume the opposite. Let $P_{i j}$ be the rectangle with sides parallel to the coordinate axes and with vertices at $(i p, j q)$ and $((i+$ 1) $p,(j+1) q)$. Let $L_{i j}$ be the part of the trajectory $L$ lying inside $P_{i j}$. We may assume w.l.o.g. that the endpoints of $L_{00}$ lie on the vertical sides of $P_{00}$. Then there obviously exists $d \in\{1, \ldots, k-1\}$ such that the endpoints of $L_{d d}$ lie on the horizontal sides of $P_{d d}$. Consider the translate $L_{d d}^{\prime}$ of $L_{d d}$ for the vector $-d(p, q)$. The endpoints of $L_{d d}^{\prime}$ lie on the vertical sides of $P_{00}$. Hence $L_{00}$ and $L_{d d}^{\prime}$ have some point $X \neq A_{0}$ in common. The translate $Y$ of point $X$ for the vector $d(p, q)$ belongs to $L$ and satisfies $X Y \| A_{0} A_{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9476532d-a436-51f5-89bb-30b9f603cd0d
| 24,714
|
29. C6 (CAN) A finite number of beans are placed on an infinite row of squares. A sequence of moves is performed as follows: At each stage a square containing more than one bean is chosen. Two beans are taken from this square; one of them is placed on the square immediately to the left, and the other is placed on the square immediately to the right of the chosen square. The sequence terminates if at some point there is at most one bean on each square. Given some initial configuration, show that any legal sequence of moves will terminate after the same number of steps and with the same final configuration.
|
29. Let the squares be indexed serially by the integers: ..., $-1,0,1,2, \ldots$. When a bean is moved from $i$ to $i+1$ or from $i+1$ to $i$ for the first time, we may assign the index $i$ to it. Thereafter, whenever some bean is moved in the opposite direction, we shall assume that it is exactly the one marked by $i$, and so on. Thus, each pair of neighboring squares has a bean stuck between it, and since the number of beans is finite, there are only finitely pairs of neighboring squares, and thus finitely many squares on which moves are made. Thus we may assume w.l.o.g. that all moves occur between 0 and $l \in \mathbb{N}$ and that all beans exist at all times within $[0, l]$. Defining $b_{i}$ to be the number of beans in the $i$ th cell $(i \in \mathbb{Z})$ and $b$ the total number of beans, we define the semi-invariant $S=\sum_{i \in \mathbb{Z}} i^{2} b_{i}$. Since all moves occur above 0 , the semi-invariant $S$ increases by 2 with each move, and since we always have $S<b \cdot l^{2}$, it follows that the number of moves must be finite. We now prove the uniqueness of the final configuration and the number of moves for some initial configuration $\left\{b_{i}\right\}$. Let $x_{i} \geq 0$ be the number of moves made in the $i$ th cell $(i \in \mathbb{Z})$ during the game. Since the game is finite, only finitely many of $x_{i}$ 's are nonzero. Also, the number of beans in cell $i$, denoted as $e_{i}$, at the end is $$ (\forall i \in \mathbb{Z}) e_{i}=b_{i}+x_{i-1}+x_{i+1}-2 x_{i} \in\{0,1\} $$ Thus it is enough to show that given $b_{i} \geq 0$, the sequence $\left\{x_{i}\right\}_{i \in \mathbb{Z}}$ of nonnegative integers satisfying (1) is unique. Suppose the assertion is false, i.e., that there exists at least one sequence $b_{i} \geq 0$ for which there exist distinct sequences $\left\{x_{i}\right\}$ and $\left\{x_{i}^{\prime}\right\}$ satisfying (1). We may choose such a $\left\{b_{i}\right\}$ for which $\min \left\{\sum_{i \in \mathbb{Z}} x_{i}, \sum_{i \in \mathbb{Z}} x_{i}^{\prime}\right\}$ is minimal (since $\sum_{i \in \mathbb{Z}} x_{i}$ is always finite). We choose any index $j$ such that $b_{j}>1$. Such an index $j$ exists, since otherwise the game is over. Then one must make at least one move in the $j$ th cell, which implies that $x_{j}, x_{j}^{\prime} \geq 1$. However, then the sequences $\left\{x_{i}\right\}$ and $\left\{x_{i}^{\prime}\right\}$ with $x_{j}$ and $x_{j}^{\prime}$ decreased by 1 also satisfy (1) for a sequence $\left\{b_{i}\right\}$ where $b_{j-1}, b_{j}, b_{j+1}$ is replaced with $b_{j-1}+1, b_{j}-2, b_{j+1}+1$. This contradicts the assumption of minimal $\min \left\{\sum_{i \in \mathbb{Z}} x_{i}, \sum_{i \in \mathbb{Z}} x_{i}^{\prime}\right\}$ for the initial $\left\{b_{i}\right\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
29. C6 (CAN) A finite number of beans are placed on an infinite row of squares. A sequence of moves is performed as follows: At each stage a square containing more than one bean is chosen. Two beans are taken from this square; one of them is placed on the square immediately to the left, and the other is placed on the square immediately to the right of the chosen square. The sequence terminates if at some point there is at most one bean on each square. Given some initial configuration, show that any legal sequence of moves will terminate after the same number of steps and with the same final configuration.
|
29. Let the squares be indexed serially by the integers: ..., $-1,0,1,2, \ldots$. When a bean is moved from $i$ to $i+1$ or from $i+1$ to $i$ for the first time, we may assign the index $i$ to it. Thereafter, whenever some bean is moved in the opposite direction, we shall assume that it is exactly the one marked by $i$, and so on. Thus, each pair of neighboring squares has a bean stuck between it, and since the number of beans is finite, there are only finitely pairs of neighboring squares, and thus finitely many squares on which moves are made. Thus we may assume w.l.o.g. that all moves occur between 0 and $l \in \mathbb{N}$ and that all beans exist at all times within $[0, l]$. Defining $b_{i}$ to be the number of beans in the $i$ th cell $(i \in \mathbb{Z})$ and $b$ the total number of beans, we define the semi-invariant $S=\sum_{i \in \mathbb{Z}} i^{2} b_{i}$. Since all moves occur above 0 , the semi-invariant $S$ increases by 2 with each move, and since we always have $S<b \cdot l^{2}$, it follows that the number of moves must be finite. We now prove the uniqueness of the final configuration and the number of moves for some initial configuration $\left\{b_{i}\right\}$. Let $x_{i} \geq 0$ be the number of moves made in the $i$ th cell $(i \in \mathbb{Z})$ during the game. Since the game is finite, only finitely many of $x_{i}$ 's are nonzero. Also, the number of beans in cell $i$, denoted as $e_{i}$, at the end is $$ (\forall i \in \mathbb{Z}) e_{i}=b_{i}+x_{i-1}+x_{i+1}-2 x_{i} \in\{0,1\} $$ Thus it is enough to show that given $b_{i} \geq 0$, the sequence $\left\{x_{i}\right\}_{i \in \mathbb{Z}}$ of nonnegative integers satisfying (1) is unique. Suppose the assertion is false, i.e., that there exists at least one sequence $b_{i} \geq 0$ for which there exist distinct sequences $\left\{x_{i}\right\}$ and $\left\{x_{i}^{\prime}\right\}$ satisfying (1). We may choose such a $\left\{b_{i}\right\}$ for which $\min \left\{\sum_{i \in \mathbb{Z}} x_{i}, \sum_{i \in \mathbb{Z}} x_{i}^{\prime}\right\}$ is minimal (since $\sum_{i \in \mathbb{Z}} x_{i}$ is always finite). We choose any index $j$ such that $b_{j}>1$. Such an index $j$ exists, since otherwise the game is over. Then one must make at least one move in the $j$ th cell, which implies that $x_{j}, x_{j}^{\prime} \geq 1$. However, then the sequences $\left\{x_{i}\right\}$ and $\left\{x_{i}^{\prime}\right\}$ with $x_{j}$ and $x_{j}^{\prime}$ decreased by 1 also satisfy (1) for a sequence $\left\{b_{i}\right\}$ where $b_{j-1}, b_{j}, b_{j+1}$ is replaced with $b_{j-1}+1, b_{j}-2, b_{j+1}+1$. This contradicts the assumption of minimal $\min \left\{\sum_{i \in \mathbb{Z}} x_{i}, \sum_{i \in \mathbb{Z}} x_{i}^{\prime}\right\}$ for the initial $\left\{b_{i}\right\}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
857ae9c0-97e4-5e3c-945d-617466019059
| 24,717
|
3. A3 (GRE) Let $a>2$ be given, and define recursively $$ a_{0}=1, \quad a_{1}=a, \quad a_{n+1}=\left(\frac{a_{n}^{2}}{a_{n-1}^{2}}-2\right) a_{n} $$ Show that for all $k \in \mathbb{N}$, we have $$ \frac{1}{a_{0}}+\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{k}}<\frac{1}{2}\left(2+a-\sqrt{a^{2}-4}\right) . $$
|
3. Since $a_{1}>2$, it can be written as $a_{1}=b+b^{-1}$ for some $b>0$. Furthermore, $a_{1}^{2}-2=b^{2}+b^{-2}$ and hence $a_{2}=\left(b^{2}+b^{-2}\right)\left(b+b^{-1}\right)$. We prove that $$ a_{n}=\left(b+b^{-1}\right)\left(b^{2}+b^{-2}\right)\left(b^{4}+b^{-4}\right) \cdots\left(b^{2^{n-1}}+b^{-2^{n-1}}\right) $$ by induction. Indeed, $\frac{a_{n+1}}{a_{n}}=\left(\frac{a_{n}}{a_{n-1}}\right)^{2}-2=\left(b^{2^{n-1}}+b^{-2^{n-1}}\right)^{2}-2=$ $b^{2^{n}}+b^{-2^{n}}$. Now we have $$ \begin{aligned} \sum_{i=1}^{n} \frac{1}{a_{i}}= & 1+\frac{b}{b^{2}+1}+\frac{b^{3}}{\left(b^{2}+1\right)\left(b^{4}+1\right)}+\cdots \\ & \cdots+\frac{b^{2^{n}-1}}{\left(b^{2}+1\right)\left(b^{4}+1\right) \ldots\left(b^{2}+1\right)} \end{aligned} $$ Note that $\frac{1}{2}\left(a+2-\sqrt{a^{2}-4}\right)=1+\frac{1}{b}$; hence we must prove that the right side in (1) is less than $\frac{1}{b}$. This follows from the fact that $$ \begin{aligned} & \frac{b^{2^{k}}}{\left(b^{2}+1\right)\left(b^{4}+1\right) \cdots\left(b^{2^{k}}+1\right)} \\ & \quad=\frac{1}{\left(b^{2}+1\right)\left(b^{4}+1\right) \cdots\left(b^{2^{k-1}}+1\right)}-\frac{1}{\left(b^{2}+1\right)\left(b^{4}+1\right) \cdots\left(b^{2^{k}}+1\right)} \end{aligned} $$ hence the right side in (1) equals $\frac{1}{b}\left(1-\frac{1}{\left(b^{2}+1\right)\left(b^{4}+1\right) \ldots\left(b^{2^{n}}+1\right)}\right)$, and this is clearly less than $1 / b$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
3. A3 (GRE) Let $a>2$ be given, and define recursively $$ a_{0}=1, \quad a_{1}=a, \quad a_{n+1}=\left(\frac{a_{n}^{2}}{a_{n-1}^{2}}-2\right) a_{n} $$ Show that for all $k \in \mathbb{N}$, we have $$ \frac{1}{a_{0}}+\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{k}}<\frac{1}{2}\left(2+a-\sqrt{a^{2}-4}\right) . $$
|
3. Since $a_{1}>2$, it can be written as $a_{1}=b+b^{-1}$ for some $b>0$. Furthermore, $a_{1}^{2}-2=b^{2}+b^{-2}$ and hence $a_{2}=\left(b^{2}+b^{-2}\right)\left(b+b^{-1}\right)$. We prove that $$ a_{n}=\left(b+b^{-1}\right)\left(b^{2}+b^{-2}\right)\left(b^{4}+b^{-4}\right) \cdots\left(b^{2^{n-1}}+b^{-2^{n-1}}\right) $$ by induction. Indeed, $\frac{a_{n+1}}{a_{n}}=\left(\frac{a_{n}}{a_{n-1}}\right)^{2}-2=\left(b^{2^{n-1}}+b^{-2^{n-1}}\right)^{2}-2=$ $b^{2^{n}}+b^{-2^{n}}$. Now we have $$ \begin{aligned} \sum_{i=1}^{n} \frac{1}{a_{i}}= & 1+\frac{b}{b^{2}+1}+\frac{b^{3}}{\left(b^{2}+1\right)\left(b^{4}+1\right)}+\cdots \\ & \cdots+\frac{b^{2^{n}-1}}{\left(b^{2}+1\right)\left(b^{4}+1\right) \ldots\left(b^{2}+1\right)} \end{aligned} $$ Note that $\frac{1}{2}\left(a+2-\sqrt{a^{2}-4}\right)=1+\frac{1}{b}$; hence we must prove that the right side in (1) is less than $\frac{1}{b}$. This follows from the fact that $$ \begin{aligned} & \frac{b^{2^{k}}}{\left(b^{2}+1\right)\left(b^{4}+1\right) \cdots\left(b^{2^{k}}+1\right)} \\ & \quad=\frac{1}{\left(b^{2}+1\right)\left(b^{4}+1\right) \cdots\left(b^{2^{k-1}}+1\right)}-\frac{1}{\left(b^{2}+1\right)\left(b^{4}+1\right) \cdots\left(b^{2^{k}}+1\right)} \end{aligned} $$ hence the right side in (1) equals $\frac{1}{b}\left(1-\frac{1}{\left(b^{2}+1\right)\left(b^{4}+1\right) \ldots\left(b^{2^{n}}+1\right)}\right)$, and this is clearly less than $1 / b$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c873014f-6983-5d6f-8efe-0c4227bc30d3
| 24,719
|
30. C7 (IRE) Let $U$ be a finite set and let $f, g$ be bijective functions from $U$ onto itself. Let $S=\{w \in U: f(f(w))=g(g(w))\}, \quad T=\{w \in U: f(g(w))=g(f(w))\}$, and suppose that $U=S \cup T$. Prove that for $w \in U, f(w) \in S$ if and only if $g(w) \in S$.
|
30. For convenience, we shall write $f^{2}, f g, \ldots$ for the functions $f \circ f, f \circ g, \ldots$ We need two lemmas. Lemma 1. If $f(x) \in S$ and $g(x) \in T$, then $x \in S \cap T$. Proof. The given condition means that $f^{3}(x)=g^{2} f(x)$ and $g f g(x)=$ $f g^{2}(x)$. Since $x \in S \cup T=U$, we have two cases: $x \in S$. Then $f^{2}(x)=g^{2}(x)$, which also implies $f^{3}(x)=f g^{2}(x)$. Therefore $g f g(x)=f g^{2}(x)=f^{3}(x)=g^{2} f(x)$, and since $g$ is a bijection, we obtain $f g(x)=g f(x)$, i.e., $x \in T$. $x \in T$. Then $f g(x)=g f(x)$, so $g^{2} f(x)=g f g(x)$. It follows that $f^{3}(x)=g^{2} f(x)=g f g(x)=f g^{2}(x)$, and since $f$ is a bijection, we obtain $x \in S$. Hence $x \in S \cap T$ in both cases. Similarly, $f(x) \in T$ and $g(x) \in S$ again imply $x \in S \cap T$. Lemma 2. $f(S \cap T)=g(S \cap T)=S \cap T$. Proof. By symmetry, it is enough to prove $f(S \cap T)=S \cap T$, or in other words that $f^{-1}(S \cap T)=S \cap T$. Since $S \cap T$ is finite, this is equivalent to $f(S \cap T) \subseteq S \cap T$. Let $f(x) \in S \cap T$. Then if $g(x) \in S$ (since $f(x) \in T$ ), Lemma 1 gives $x \in S \cap T$; similarly, if $g(x) \in T$, then by Lemma $1, x \in S \cap T$. Now we return to the problem. Assume that $f(x) \in S$. If $g(x) \notin S$, then $g(x) \in T$, so from Lemma 1 we deduce that $x \in S \cap T$. Then Lemma 2 claims that $g(x) \in S \cap T$ too, a contradiction. Analogously, from $g(x) \in S$ we are led to $f(x) \in S$. This finishes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
30. C7 (IRE) Let $U$ be a finite set and let $f, g$ be bijective functions from $U$ onto itself. Let $S=\{w \in U: f(f(w))=g(g(w))\}, \quad T=\{w \in U: f(g(w))=g(f(w))\}$, and suppose that $U=S \cup T$. Prove that for $w \in U, f(w) \in S$ if and only if $g(w) \in S$.
|
30. For convenience, we shall write $f^{2}, f g, \ldots$ for the functions $f \circ f, f \circ g, \ldots$ We need two lemmas. Lemma 1. If $f(x) \in S$ and $g(x) \in T$, then $x \in S \cap T$. Proof. The given condition means that $f^{3}(x)=g^{2} f(x)$ and $g f g(x)=$ $f g^{2}(x)$. Since $x \in S \cup T=U$, we have two cases: $x \in S$. Then $f^{2}(x)=g^{2}(x)$, which also implies $f^{3}(x)=f g^{2}(x)$. Therefore $g f g(x)=f g^{2}(x)=f^{3}(x)=g^{2} f(x)$, and since $g$ is a bijection, we obtain $f g(x)=g f(x)$, i.e., $x \in T$. $x \in T$. Then $f g(x)=g f(x)$, so $g^{2} f(x)=g f g(x)$. It follows that $f^{3}(x)=g^{2} f(x)=g f g(x)=f g^{2}(x)$, and since $f$ is a bijection, we obtain $x \in S$. Hence $x \in S \cap T$ in both cases. Similarly, $f(x) \in T$ and $g(x) \in S$ again imply $x \in S \cap T$. Lemma 2. $f(S \cap T)=g(S \cap T)=S \cap T$. Proof. By symmetry, it is enough to prove $f(S \cap T)=S \cap T$, or in other words that $f^{-1}(S \cap T)=S \cap T$. Since $S \cap T$ is finite, this is equivalent to $f(S \cap T) \subseteq S \cap T$. Let $f(x) \in S \cap T$. Then if $g(x) \in S$ (since $f(x) \in T$ ), Lemma 1 gives $x \in S \cap T$; similarly, if $g(x) \in T$, then by Lemma $1, x \in S \cap T$. Now we return to the problem. Assume that $f(x) \in S$. If $g(x) \notin S$, then $g(x) \in T$, so from Lemma 1 we deduce that $x \in S \cap T$. Then Lemma 2 claims that $g(x) \in S \cap T$ too, a contradiction. Analogously, from $g(x) \in S$ we are led to $f(x) \in S$. This finishes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a17b1084-61fc-59a2-9d0e-97ded75bee6c
| 24,722
|
7. A7 (ARM) Let $f$ be a function from the set of real numbers $\mathbb{R}$ into itself such that for all $x \in \mathbb{R}$, we have $|f(x)| \leq 1$ and $$ f\left(x+\frac{13}{42}\right)+f(x)=f\left(x+\frac{1}{6}\right)+f\left(x+\frac{1}{7}\right) . $$ Prove that $f$ is a periodic function (that is, there exists a nonzero real number $c$ such that $f(x+c)=f(x)$ for all $x \in \mathbb{R})$.
|
7. We are given that $f(x+a+b)-f(x+a)=f(x+b)-f(x)$, where $a=1 / 6$ and $b=1 / 7$. Summing up these equations for $x, x+b, \ldots, x+6 b$ we obtain $f(x+a+1)-f(x+a)=f(x+1)-f(x)$. Summing up the new equations for $x, x+a, \ldots, x+5 a$ we obtain that $$ f(x+2)-f(x+1)=f(x+1)-f(x) . $$ It follows by induction that $f(x+n)-f(x)=n[f(x+1)-f(x)]$. If $f(x+1) \neq f(x)$, then $f(x+n)-f(x)$ will exceed in absolute value an arbitrarily large number for a sufficiently large $n$, contradicting the assumption that $f$ is bounded. Hence $f(x+1)=f(x)$ for all $x$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
7. A7 (ARM) Let $f$ be a function from the set of real numbers $\mathbb{R}$ into itself such that for all $x \in \mathbb{R}$, we have $|f(x)| \leq 1$ and $$ f\left(x+\frac{13}{42}\right)+f(x)=f\left(x+\frac{1}{6}\right)+f\left(x+\frac{1}{7}\right) . $$ Prove that $f$ is a periodic function (that is, there exists a nonzero real number $c$ such that $f(x+c)=f(x)$ for all $x \in \mathbb{R})$.
|
7. We are given that $f(x+a+b)-f(x+a)=f(x+b)-f(x)$, where $a=1 / 6$ and $b=1 / 7$. Summing up these equations for $x, x+b, \ldots, x+6 b$ we obtain $f(x+a+1)-f(x+a)=f(x+1)-f(x)$. Summing up the new equations for $x, x+a, \ldots, x+5 a$ we obtain that $$ f(x+2)-f(x+1)=f(x+1)-f(x) . $$ It follows by induction that $f(x+n)-f(x)=n[f(x+1)-f(x)]$. If $f(x+1) \neq f(x)$, then $f(x+n)-f(x)$ will exceed in absolute value an arbitrarily large number for a sufficiently large $n$, contradicting the assumption that $f$ is bounded. Hence $f(x+1)=f(x)$ for all $x$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d4744189-a1c3-51fa-8a3a-d0ce7ebdc5a5
| 24,733
|
8. A8 (ROM) ${ }^{\mathrm{IMO} 3}$ Let $\mathbb{N}_{0}$ denote the set of nonnegative integers. Find all functions $f$ from $\mathbb{N}_{0}$ into itself such that $$ f(m+f(n))=f(f(m))+f(n), \quad \forall m, n \in \mathbb{N}_{0} $$
|
8. Putting $m=n=0$ we obtain $f(0)=0$ and consequently $f(f(n))=f(n)$ for all $n$. Thus the given functional equation is equivalent to $$ f(m+f(n))=f(m)+f(n), \quad f(0)=0 $$ Clearly one solution is $(\forall x) f(x)=0$. Suppose $f$ is not the zero function. We observe that $f$ has nonzero fixed points (for example, any $f(n)$ is a fixed point). Let $a$ be the smallest nonzero fixed point of $f$. By induction, each $k a(k \in \mathbb{N})$ is a fixed point too. We claim that all fixed points of $f$ are of this form. Indeed, suppose that $b=k a+i$ is a fixed point, where $i<a$. Then $$ b=f(b)=f(k a+i)=f(i+f(k a))=f(i)+f(k a)=f(i)+k a $$ hence $f(i)=i$. Hence $i=0$. Since the set of values of $f$ is a set of its fixed points, it follows that for $i=0,1, \ldots, a-1, f(i)=a n_{i}$ for some integers $n_{i} \geq 0$ with $n_{0}=0$. Let $n=k a+i$ be any positive integer, $0 \leq i<a$. As before, the functional equation gives us $$ f(n)=f(k a+i)=f(i)+k a=\left(n_{i}+k\right) a $$ Besides the zero function, this is the general solution of the given functional equation. To verify this, we plug in $m=k a+i, n=l a+j$ and obtain $$ \begin{aligned} f(m+f(n)) & =f(k a+i+f(l a+j))=f\left(\left(k+l+n_{j}\right) a+i\right) \\ & =\left(k+l+n_{j}+n_{i}\right) a=f(m)+f(n) . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
8. A8 (ROM) ${ }^{\mathrm{IMO} 3}$ Let $\mathbb{N}_{0}$ denote the set of nonnegative integers. Find all functions $f$ from $\mathbb{N}_{0}$ into itself such that $$ f(m+f(n))=f(f(m))+f(n), \quad \forall m, n \in \mathbb{N}_{0} $$
|
8. Putting $m=n=0$ we obtain $f(0)=0$ and consequently $f(f(n))=f(n)$ for all $n$. Thus the given functional equation is equivalent to $$ f(m+f(n))=f(m)+f(n), \quad f(0)=0 $$ Clearly one solution is $(\forall x) f(x)=0$. Suppose $f$ is not the zero function. We observe that $f$ has nonzero fixed points (for example, any $f(n)$ is a fixed point). Let $a$ be the smallest nonzero fixed point of $f$. By induction, each $k a(k \in \mathbb{N})$ is a fixed point too. We claim that all fixed points of $f$ are of this form. Indeed, suppose that $b=k a+i$ is a fixed point, where $i<a$. Then $$ b=f(b)=f(k a+i)=f(i+f(k a))=f(i)+f(k a)=f(i)+k a $$ hence $f(i)=i$. Hence $i=0$. Since the set of values of $f$ is a set of its fixed points, it follows that for $i=0,1, \ldots, a-1, f(i)=a n_{i}$ for some integers $n_{i} \geq 0$ with $n_{0}=0$. Let $n=k a+i$ be any positive integer, $0 \leq i<a$. As before, the functional equation gives us $$ f(n)=f(k a+i)=f(i)+k a=\left(n_{i}+k\right) a $$ Besides the zero function, this is the general solution of the given functional equation. To verify this, we plug in $m=k a+i, n=l a+j$ and obtain $$ \begin{aligned} f(m+f(n)) & =f(k a+i+f(l a+j))=f\left(\left(k+l+n_{j}\right) a+i\right) \\ & =\left(k+l+n_{j}+n_{i}\right) a=f(m)+f(n) . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e03d8b85-844c-5db0-8310-a426a4a51434
| 24,736
|
11. (NET) Let $P(x)$ be a polynomial with real coefficients such that $P(x)>$ 0 for all $x \geq 0$. Prove that there exists a positive integer $n$ such that $(1+x)^{n} P(x)$ is a polynomial with nonnegative coefficients.
|
11. All real roots of $P(x)$ (if any) are negative: say $-a_{1},-a_{2}, \ldots,-a_{k}$. Then $P(x)$ can be factored as $$ P(x)=C\left(x+a_{1}\right) \cdots\left(x+a_{k}\right)\left(x^{2}-b_{1} x+c_{1}\right) \cdots\left(x^{2}-b_{m} x+c_{m}\right) $$ where $x^{2}-b_{i} x+c_{i}$ are quadratic polynomials without real roots. Since the product of polynomials with positive coefficients is again a polynomial with positive coefficients, it will be sufficient to prove the result for each of the factors in (1). The case of $x+a_{j}$ is trivial. It remains only to prove the claim for every polynomial $x^{2}-b x+c$ with $b^{2}<4 c$. From the binomial formula, we have for any $n \in \mathbb{N}$, $$ (1+x)^{n}\left(x^{2}-b x+c\right)=\sum_{i=0}^{n+2}\left[\binom{n}{i-2}-b\binom{n}{i-1}+c\binom{n}{i}\right] x^{i}=\sum_{i=0}^{n+2} C_{i} x^{i} $$ where $$ C_{i}=\frac{n!\left((b+c+1) i^{2}-((b+2 c) n+(2 b+3 c+1)) i+c\left(n^{2}+3 n+2\right)\right) x^{i}}{i!(n-i+2)!} $$ The coefficients $C_{i}$ of $x^{i}$ appear in the form of a quadratic polynomial in $i$ depending on $n$. We claim that for large enough $n$ this polynomial has negative discriminant, and is thus positive for every $i$. Indeed, this discriminant equals $D=((b+2 c) n+(2 b+3 c+1))^{2}-4(b+c+1) c\left(n^{2}+\right.$ $3 n+2)=\left(b^{2}-4 c\right) n^{2}-2 U n+V$, where $U=2 b^{2}+b c+b-4 c$ and $V=(2 b+c+1)^{2}-4 c$, and since $b^{2}-4 c<0$, for large $n$ it clearly holds that $D<0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
11. (NET) Let $P(x)$ be a polynomial with real coefficients such that $P(x)>$ 0 for all $x \geq 0$. Prove that there exists a positive integer $n$ such that $(1+x)^{n} P(x)$ is a polynomial with nonnegative coefficients.
|
11. All real roots of $P(x)$ (if any) are negative: say $-a_{1},-a_{2}, \ldots,-a_{k}$. Then $P(x)$ can be factored as $$ P(x)=C\left(x+a_{1}\right) \cdots\left(x+a_{k}\right)\left(x^{2}-b_{1} x+c_{1}\right) \cdots\left(x^{2}-b_{m} x+c_{m}\right) $$ where $x^{2}-b_{i} x+c_{i}$ are quadratic polynomials without real roots. Since the product of polynomials with positive coefficients is again a polynomial with positive coefficients, it will be sufficient to prove the result for each of the factors in (1). The case of $x+a_{j}$ is trivial. It remains only to prove the claim for every polynomial $x^{2}-b x+c$ with $b^{2}<4 c$. From the binomial formula, we have for any $n \in \mathbb{N}$, $$ (1+x)^{n}\left(x^{2}-b x+c\right)=\sum_{i=0}^{n+2}\left[\binom{n}{i-2}-b\binom{n}{i-1}+c\binom{n}{i}\right] x^{i}=\sum_{i=0}^{n+2} C_{i} x^{i} $$ where $$ C_{i}=\frac{n!\left((b+c+1) i^{2}-((b+2 c) n+(2 b+3 c+1)) i+c\left(n^{2}+3 n+2\right)\right) x^{i}}{i!(n-i+2)!} $$ The coefficients $C_{i}$ of $x^{i}$ appear in the form of a quadratic polynomial in $i$ depending on $n$. We claim that for large enough $n$ this polynomial has negative discriminant, and is thus positive for every $i$. Indeed, this discriminant equals $D=((b+2 c) n+(2 b+3 c+1))^{2}-4(b+c+1) c\left(n^{2}+\right.$ $3 n+2)=\left(b^{2}-4 c\right) n^{2}-2 U n+V$, where $U=2 b^{2}+b c+b-4 c$ and $V=(2 b+c+1)^{2}-4 c$, and since $b^{2}-4 c<0$, for large $n$ it clearly holds that $D<0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6fd1b6cb-2913-57be-b51d-9f89f5546d09
| 24,747
|
12. (ITA) Let $p$ be a prime number and let $f(x)$ be a polynomial of degree $d$ with integer coefficients such that: (i) $f(0)=0, f(1)=1$; (ii) for every positive integer $n$, the remainder of the division of $f(n)$ by $p$ is either 0 or 1. Prove that $d \geq p-1$.
|
12. Lemma. For any polynomial $P$ of degree at most $n$, the following equality holds: $$ \sum_{i=0}^{n+1}(-1)^{i}\binom{n+1}{i} P(i)=0 $$ Proof. See (SL81-13). Suppose to the contrary that the degree of $f$ is at most $p-2$. Then it follows from the lemma that $$ 0=\sum_{i=0}^{p-1}(-1)^{i}\binom{p-1}{i} f(i) \equiv \sum_{i=0}^{p-1} f(i)(\bmod p) $$ since $\binom{p-1}{i}=\frac{(p-1)(p-2) \cdots(p-i)}{i!} \equiv(-1)^{i}(\bmod p)$. But this is clearly impossible if $f(i)$ equals 0 or 1 modulo $p$ and $f(0)=0, f(1)=1$. Remark. In proving the essential relation $\sum_{i=0}^{p-1} f(i) \equiv 0(\bmod p)$, it is clearly enough to show that $S_{k}=1^{k}+2^{k}+\cdots+(p-1)^{k}$ is divisible by $p$ for every $k \leq p-2$. This can be shown in two other ways. (1) By induction. Assume that $S_{0} \equiv \cdots \equiv S_{k-1}(\bmod p)$. By the binomial formula we have $$ 0 \equiv \sum_{n=0}^{p-1}\left[(n+1)^{k+1}-n^{k+1}\right] \equiv(k+1) S_{k}+\sum_{i=0}^{k-1}\binom{k+1}{i} S_{i}(\bmod p), $$ and the inductive step follows. (2) Using the primitive root $g$ modulo $p$. Then $$ S_{k} \equiv 1+g^{k}+\cdots+g^{k(p-2)}=\frac{g^{k(p-1)}-1}{g^{k}-1} \equiv 0(\bmod p) . $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
12. (ITA) Let $p$ be a prime number and let $f(x)$ be a polynomial of degree $d$ with integer coefficients such that: (i) $f(0)=0, f(1)=1$; (ii) for every positive integer $n$, the remainder of the division of $f(n)$ by $p$ is either 0 or 1. Prove that $d \geq p-1$.
|
12. Lemma. For any polynomial $P$ of degree at most $n$, the following equality holds: $$ \sum_{i=0}^{n+1}(-1)^{i}\binom{n+1}{i} P(i)=0 $$ Proof. See (SL81-13). Suppose to the contrary that the degree of $f$ is at most $p-2$. Then it follows from the lemma that $$ 0=\sum_{i=0}^{p-1}(-1)^{i}\binom{p-1}{i} f(i) \equiv \sum_{i=0}^{p-1} f(i)(\bmod p) $$ since $\binom{p-1}{i}=\frac{(p-1)(p-2) \cdots(p-i)}{i!} \equiv(-1)^{i}(\bmod p)$. But this is clearly impossible if $f(i)$ equals 0 or 1 modulo $p$ and $f(0)=0, f(1)=1$. Remark. In proving the essential relation $\sum_{i=0}^{p-1} f(i) \equiv 0(\bmod p)$, it is clearly enough to show that $S_{k}=1^{k}+2^{k}+\cdots+(p-1)^{k}$ is divisible by $p$ for every $k \leq p-2$. This can be shown in two other ways. (1) By induction. Assume that $S_{0} \equiv \cdots \equiv S_{k-1}(\bmod p)$. By the binomial formula we have $$ 0 \equiv \sum_{n=0}^{p-1}\left[(n+1)^{k+1}-n^{k+1}\right] \equiv(k+1) S_{k}+\sum_{i=0}^{k-1}\binom{k+1}{i} S_{i}(\bmod p), $$ and the inductive step follows. (2) Using the primitive root $g$ modulo $p$. Then $$ S_{k} \equiv 1+g^{k}+\cdots+g^{k(p-2)}=\frac{g^{k(p-1)}-1}{g^{k}-1} \equiv 0(\bmod p) . $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c94bbbf5-84e8-5d6b-80f7-a62d5c8e771a
| 24,750
|
13. (IND) In town $A$, there are $n$ girls and $n$ boys, and each girl knows each boy. In town $B$, there are $n$ girls $g_{1}, g_{2}, \ldots, g_{n}$ and $2 n-1$ boys $b_{1}, b_{2}, \ldots$, $b_{2 n-1}$. The girl $g_{i}, i=1,2, \ldots, n$, knows the boys $b_{1}, b_{2}, \ldots, b_{2 i-1}$, and no others. For all $r=1,2, \ldots, n$, denote by $A(r), B(r)$ the number of different ways in which $r$ girls from town $A$, respectively town $B$, can dance with $r$ boys from their own town, forming $r$ pairs, each girl with a boy she knows. Prove that $A(r)=B(r)$ for each $r=1,2, \ldots, n$.
|
13. Denote $A(r)$ and $B(r)$ by $A(n, r)$ and $B(n, r)$ respectively. The numbers $A(n, r)$ can be found directly: one can choose $r$ girls and $r$ boys in $\binom{n}{r}^{2}$ ways, and pair them in $r$ ! ways. Hence $$ A(n, r)=\binom{n}{r}^{2} \cdot r!=\frac{n!^{2}}{(n-r)!^{2} r!} $$ Now we establish a recurrence relation between the $B(n, r)$ 's. Let $n \geq 2$ and $2 \leq r \leq n$. There are two cases for a desired selection of $r$ pairs of girls and boys: (i) One of the girls dancing is $g_{n}$. Then the other $r-1$ girls can choose their partners in $B(n-1, r-1)$ ways and $g_{n}$ can choose any of the remaining $2 n-r$ boys. Thus, the total number of choices in this case is $(2 n-r) B(n-1, r-1)$. (ii) $g_{n}$ is not dancing. Then there are exactly $B(n-1, r)$ possible choices. Therefore, for every $n \geq 2$ it holds that $$ B(n, r)=(2 n-r) B(n-1, r-1)+B(n-1, r) \quad \text { for } r=2, \ldots, n $$ Here we assume that $B(n, r)=0$ for $r>n$, while $B(n, 1)=1+3+\cdots+$ $(2 n-1)=n^{2}$ 。 It is directly verified that the numbers $A(n, r)$ satisfy the same initial conditions and recurrence relations, from which it follows that $A(n, r)=$ $B(n, r)$ for all $n$ and $r \leq n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
13. (IND) In town $A$, there are $n$ girls and $n$ boys, and each girl knows each boy. In town $B$, there are $n$ girls $g_{1}, g_{2}, \ldots, g_{n}$ and $2 n-1$ boys $b_{1}, b_{2}, \ldots$, $b_{2 n-1}$. The girl $g_{i}, i=1,2, \ldots, n$, knows the boys $b_{1}, b_{2}, \ldots, b_{2 i-1}$, and no others. For all $r=1,2, \ldots, n$, denote by $A(r), B(r)$ the number of different ways in which $r$ girls from town $A$, respectively town $B$, can dance with $r$ boys from their own town, forming $r$ pairs, each girl with a boy she knows. Prove that $A(r)=B(r)$ for each $r=1,2, \ldots, n$.
|
13. Denote $A(r)$ and $B(r)$ by $A(n, r)$ and $B(n, r)$ respectively. The numbers $A(n, r)$ can be found directly: one can choose $r$ girls and $r$ boys in $\binom{n}{r}^{2}$ ways, and pair them in $r$ ! ways. Hence $$ A(n, r)=\binom{n}{r}^{2} \cdot r!=\frac{n!^{2}}{(n-r)!^{2} r!} $$ Now we establish a recurrence relation between the $B(n, r)$ 's. Let $n \geq 2$ and $2 \leq r \leq n$. There are two cases for a desired selection of $r$ pairs of girls and boys: (i) One of the girls dancing is $g_{n}$. Then the other $r-1$ girls can choose their partners in $B(n-1, r-1)$ ways and $g_{n}$ can choose any of the remaining $2 n-r$ boys. Thus, the total number of choices in this case is $(2 n-r) B(n-1, r-1)$. (ii) $g_{n}$ is not dancing. Then there are exactly $B(n-1, r)$ possible choices. Therefore, for every $n \geq 2$ it holds that $$ B(n, r)=(2 n-r) B(n-1, r-1)+B(n-1, r) \quad \text { for } r=2, \ldots, n $$ Here we assume that $B(n, r)=0$ for $r>n$, while $B(n, 1)=1+3+\cdots+$ $(2 n-1)=n^{2}$ 。 It is directly verified that the numbers $A(n, r)$ satisfy the same initial conditions and recurrence relations, from which it follows that $A(n, r)=$ $B(n, r)$ for all $n$ and $r \leq n$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5c5bd624-19c2-526d-b6f9-f8c81b3074af
| 24,752
|
14. (IND) Let $b, m, n$ be positive integers such that $b>1$ and $m \neq n$. Prove that if $b^{m}-1$ and $b^{n}-1$ have the same prime divisors, then $b+1$ is a power of 2 .
|
14. We use the following nonstandard notation: ( $1^{\circ}$ ) for $x, y \in \mathbb{N}, x \sim y$ means that $x$ and $y$ have the same prime divisors; $\left(2^{\circ}\right)$ for a prime $p$ and integers $r \geq 0$ and $x>0, p^{r} \| x$ means that $x$ is divisible by $p^{r}$, but not by $p^{r+1}$. First, $b^{m}-1 \sim b^{n}-1$ is obviously equivalent to $b^{m}-1 \sim \operatorname{gcd}\left(b^{m}-1, b^{n}-\right.$ $1)=b^{d}-1$, where $d=\operatorname{gcd}(m, n)$. Setting $b^{d}=a$ and $m=k d$, we reduce the condition of the problem to $a^{k}-1 \sim a-1$. We are going to show that this implies that $a+1$ is a power of 2 . This will imply that $d$ is odd (for even $d$, $a+1=b^{d}+1$ cannot be divisible by 4 , and consequently $b+1$, as a divisor of $a+1$, is also a power of 2 . But before that, we need the following important lemma (Theorem 2.126). Lemma. Let $a, k$ be positive integers and $p$ an odd prime. If $\alpha \geq 1$ and $\beta \geq 0$ are such that $p^{\alpha} \| a-1$ and $p^{\beta} \| k$, then $p^{\alpha+\beta} \| a^{k}-1$. Proof. We use induction on $\beta$. If $\beta=0$, then $\frac{a^{k}-1}{a-1}=a^{k-1}+\cdots+a+1 \equiv k$ $(\bmod p)($ because $a \equiv 1$ ), and it is not divisible by $p$. Suppose that the lemma is true for some $\beta \geq 0$, and let $k=p^{\beta+1} t$ where $p \nmid t$. By the induction hypothesis, $a^{k / p}=a^{p^{\beta} t}=m p^{\alpha+\beta}+1$ for some $m$ not divisible by $p$. Furthermore, $$ a^{k}-1=\left(m p^{\alpha+\beta}+1\right)^{p}-1=\left(m p^{\alpha+\beta}\right)^{p}+\cdots+\binom{p}{2}\left(m p^{\alpha+\beta}\right)^{2}+m p^{\alpha+\beta+1} $$ Since $p \left\lvert\,\binom{ p}{2}=\frac{p(p-1)}{2}\right.$, all summands except for the last one are divisible by $p^{\alpha+\beta+2}$. Hence $p^{\alpha+\beta+1} \| a^{k}-1$, completing the induction. Now let $a^{k}-1 \sim a-1$ for some $a, k>1$. Suppose that $p$ is an odd prime divisor of $k$, with $p^{\beta} \| k$. Then putting $X=a^{p^{\beta}-1}+\cdots+a+1$ we also have $(a-1) X=a^{p^{\beta}}-1 \sim a-1$; hence each prime divisor $q$ of $X$ must also divide $a-1$. But then $a^{i} \equiv 1(\bmod q)$ for each $i \in \mathbb{N}_{0}$, which gives us $X \equiv p^{\beta}(\bmod q)$. Therefore $q \mid p^{\beta}$, i.e., $q=p$; hence $X$ is a power of $p$. On the other hand, since $p \mid a-1$, we put $p^{\alpha} \| a-1$. From the lemma we obtain $p^{\alpha+\beta} \| a^{p^{\beta}}-1$, and deduce that $p^{\beta} \| X$. But $X$ has no prime divisors other than $p$, so we must have $X=p^{\beta}$. This is clearly impossible, because $X>p^{\beta}$ for $a>1$. Thus our assumption that $k$ has an odd prime divisor leads to a contradiction: in other words, $k$ must be a power of 2 . Now $a^{k}-1 \sim a-1$ implies $a-1 \sim a^{2}-1=(a-1)(a+1)$, and thus every prime divisor $q$ of $a+1$ must also divide $a-1$. Consequently $q=2$, so it follows that $a+1$ is a power of 2 . As we explained above, this gives that $b+1$ is also a power of 2 . Remark. In fact, one can continue and show that $k$ must be equal to 2 . It is not possible for $a^{4}-1 \sim a^{2}-1$ to hold. Similarly, we must have $d=1$. Therefore all possible triples $(b, m, n)$ with $m>n$ are $\left(2^{s}-1,2,1\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
14. (IND) Let $b, m, n$ be positive integers such that $b>1$ and $m \neq n$. Prove that if $b^{m}-1$ and $b^{n}-1$ have the same prime divisors, then $b+1$ is a power of 2 .
|
14. We use the following nonstandard notation: ( $1^{\circ}$ ) for $x, y \in \mathbb{N}, x \sim y$ means that $x$ and $y$ have the same prime divisors; $\left(2^{\circ}\right)$ for a prime $p$ and integers $r \geq 0$ and $x>0, p^{r} \| x$ means that $x$ is divisible by $p^{r}$, but not by $p^{r+1}$. First, $b^{m}-1 \sim b^{n}-1$ is obviously equivalent to $b^{m}-1 \sim \operatorname{gcd}\left(b^{m}-1, b^{n}-\right.$ $1)=b^{d}-1$, where $d=\operatorname{gcd}(m, n)$. Setting $b^{d}=a$ and $m=k d$, we reduce the condition of the problem to $a^{k}-1 \sim a-1$. We are going to show that this implies that $a+1$ is a power of 2 . This will imply that $d$ is odd (for even $d$, $a+1=b^{d}+1$ cannot be divisible by 4 , and consequently $b+1$, as a divisor of $a+1$, is also a power of 2 . But before that, we need the following important lemma (Theorem 2.126). Lemma. Let $a, k$ be positive integers and $p$ an odd prime. If $\alpha \geq 1$ and $\beta \geq 0$ are such that $p^{\alpha} \| a-1$ and $p^{\beta} \| k$, then $p^{\alpha+\beta} \| a^{k}-1$. Proof. We use induction on $\beta$. If $\beta=0$, then $\frac{a^{k}-1}{a-1}=a^{k-1}+\cdots+a+1 \equiv k$ $(\bmod p)($ because $a \equiv 1$ ), and it is not divisible by $p$. Suppose that the lemma is true for some $\beta \geq 0$, and let $k=p^{\beta+1} t$ where $p \nmid t$. By the induction hypothesis, $a^{k / p}=a^{p^{\beta} t}=m p^{\alpha+\beta}+1$ for some $m$ not divisible by $p$. Furthermore, $$ a^{k}-1=\left(m p^{\alpha+\beta}+1\right)^{p}-1=\left(m p^{\alpha+\beta}\right)^{p}+\cdots+\binom{p}{2}\left(m p^{\alpha+\beta}\right)^{2}+m p^{\alpha+\beta+1} $$ Since $p \left\lvert\,\binom{ p}{2}=\frac{p(p-1)}{2}\right.$, all summands except for the last one are divisible by $p^{\alpha+\beta+2}$. Hence $p^{\alpha+\beta+1} \| a^{k}-1$, completing the induction. Now let $a^{k}-1 \sim a-1$ for some $a, k>1$. Suppose that $p$ is an odd prime divisor of $k$, with $p^{\beta} \| k$. Then putting $X=a^{p^{\beta}-1}+\cdots+a+1$ we also have $(a-1) X=a^{p^{\beta}}-1 \sim a-1$; hence each prime divisor $q$ of $X$ must also divide $a-1$. But then $a^{i} \equiv 1(\bmod q)$ for each $i \in \mathbb{N}_{0}$, which gives us $X \equiv p^{\beta}(\bmod q)$. Therefore $q \mid p^{\beta}$, i.e., $q=p$; hence $X$ is a power of $p$. On the other hand, since $p \mid a-1$, we put $p^{\alpha} \| a-1$. From the lemma we obtain $p^{\alpha+\beta} \| a^{p^{\beta}}-1$, and deduce that $p^{\beta} \| X$. But $X$ has no prime divisors other than $p$, so we must have $X=p^{\beta}$. This is clearly impossible, because $X>p^{\beta}$ for $a>1$. Thus our assumption that $k$ has an odd prime divisor leads to a contradiction: in other words, $k$ must be a power of 2 . Now $a^{k}-1 \sim a-1$ implies $a-1 \sim a^{2}-1=(a-1)(a+1)$, and thus every prime divisor $q$ of $a+1$ must also divide $a-1$. Consequently $q=2$, so it follows that $a+1$ is a power of 2 . As we explained above, this gives that $b+1$ is also a power of 2 . Remark. In fact, one can continue and show that $k$ must be equal to 2 . It is not possible for $a^{4}-1 \sim a^{2}-1$ to hold. Similarly, we must have $d=1$. Therefore all possible triples $(b, m, n)$ with $m>n$ are $\left(2^{s}-1,2,1\right)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
df017481-922e-5ba3-836c-e9407b76f6db
| 24,755
|
15. (RUS) An infinite arithmetic progression whose terms are positive integers contains the square of an integer and the cube of an integer. Show that it contains the sixth power of an integer.
|
15. Let $a+b t, t=0,1,2, \ldots$, be a given arithmetic progression that contains a square and a cube $(a, b>0)$. We use induction on the progression step $b$ to prove that the progression contains a sixth power. (i) $b=1$ : this case is trivial. (ii) $b=p^{m}$ for some prime $p$ and $m>0$. The case $p^{m} \mid a$ trivially reduces to the previous case, so let us have $p^{m} \nmid a$. Suppose that $\operatorname{gcd}(a, p)=1$. If $x, y$ are integers such that $x^{2} \equiv y^{3} \equiv a$ (here all the congruences will be $\bmod p^{m}$ ), then $x^{6} \equiv a^{3}$ and $y^{6} \equiv a^{2}$. Consider an integer $y_{1}$ such that $y y_{1} \equiv 1$. It satisfies $a^{2}\left(x y_{1}\right)^{6} \equiv$ $x^{6} y^{6} y_{1}^{6} \equiv x^{6} \equiv a^{3}$, and consequently $\left(x y_{1}\right)^{6} \equiv a$. Hence a sixth power exists in the progression. If $\operatorname{gcd}(a, p)>1$, we can write $a=p^{k} c$, where $k<m$ and $p \nmid c$. Since the arithmetic progression $x_{t}=a+b t=p^{k}\left(c+p^{m-k} t\right)$ contains a square, $k$ must be even; similarly, it contains a cube, so $3 \mid k$. It follows that $6 \mid k$. The progression $c+p^{m-k} t$ thus also contains a square and a cube; hence by the previous case it contains a sixth power and thus $x_{t}$ does also. (iii) $b$ is not a power of a prime, and thus can be expressed as $b=b_{1} b_{2}$, where $b_{1}, b_{2}>1$ and $\operatorname{gcd}\left(b_{1}, b_{2}\right)=1$. It is given that progressions $a+b_{1} t$ and $a+b_{2} t$ both contain a square and a cube, and therefore by the inductive hypothesis they both contain sixth powers: say $z_{1}^{6}$ and $z_{2}^{6}$, respectively. By the Chinese remainder theorem, there exists $z \in \mathbb{N}$ such that $z \equiv z_{1}\left(\bmod b_{1}\right)$ and $z \equiv z_{2}\left(\bmod b_{2}\right)$. But then $z^{6}$ belongs to both of the progressions $a+b_{1} t$ and $a+b_{2} t$. Hence $z^{6}$ is a member of the progression $a+b t$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
15. (RUS) An infinite arithmetic progression whose terms are positive integers contains the square of an integer and the cube of an integer. Show that it contains the sixth power of an integer.
|
15. Let $a+b t, t=0,1,2, \ldots$, be a given arithmetic progression that contains a square and a cube $(a, b>0)$. We use induction on the progression step $b$ to prove that the progression contains a sixth power. (i) $b=1$ : this case is trivial. (ii) $b=p^{m}$ for some prime $p$ and $m>0$. The case $p^{m} \mid a$ trivially reduces to the previous case, so let us have $p^{m} \nmid a$. Suppose that $\operatorname{gcd}(a, p)=1$. If $x, y$ are integers such that $x^{2} \equiv y^{3} \equiv a$ (here all the congruences will be $\bmod p^{m}$ ), then $x^{6} \equiv a^{3}$ and $y^{6} \equiv a^{2}$. Consider an integer $y_{1}$ such that $y y_{1} \equiv 1$. It satisfies $a^{2}\left(x y_{1}\right)^{6} \equiv$ $x^{6} y^{6} y_{1}^{6} \equiv x^{6} \equiv a^{3}$, and consequently $\left(x y_{1}\right)^{6} \equiv a$. Hence a sixth power exists in the progression. If $\operatorname{gcd}(a, p)>1$, we can write $a=p^{k} c$, where $k<m$ and $p \nmid c$. Since the arithmetic progression $x_{t}=a+b t=p^{k}\left(c+p^{m-k} t\right)$ contains a square, $k$ must be even; similarly, it contains a cube, so $3 \mid k$. It follows that $6 \mid k$. The progression $c+p^{m-k} t$ thus also contains a square and a cube; hence by the previous case it contains a sixth power and thus $x_{t}$ does also. (iii) $b$ is not a power of a prime, and thus can be expressed as $b=b_{1} b_{2}$, where $b_{1}, b_{2}>1$ and $\operatorname{gcd}\left(b_{1}, b_{2}\right)=1$. It is given that progressions $a+b_{1} t$ and $a+b_{2} t$ both contain a square and a cube, and therefore by the inductive hypothesis they both contain sixth powers: say $z_{1}^{6}$ and $z_{2}^{6}$, respectively. By the Chinese remainder theorem, there exists $z \in \mathbb{N}$ such that $z \equiv z_{1}\left(\bmod b_{1}\right)$ and $z \equiv z_{2}\left(\bmod b_{2}\right)$. But then $z^{6}$ belongs to both of the progressions $a+b_{1} t$ and $a+b_{2} t$. Hence $z^{6}$ is a member of the progression $a+b t$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c0322346-a3a1-50de-bd89-8837eed7a690
| 24,757
|
16. (BLR) In an acute-angled triangle $A B C$, let $A D, B E$ be altitudes and $A P, B Q$ internal bisectors. Denote by $I$ and $O$ the incenter and the circumcenter of the triangle, respectively. Prove that the points $D, E$, and $I$ are collinear if and only if the points $P, Q$, and $O$ are collinear.
|
16. Let $d_{a}(X), d_{b}(X), d_{c}(X)$ denote the distances of a point $X$ interior to $\triangle A B C$ from the lines $B C, C A, A B$ respectively. We claim that $X \in P Q$ if and only if $d_{a}(X)+d_{b}(X)=d_{c}(X)$. Indeed, if $X \in P Q$ and $P X=$ $k P Q$ then $d_{a}(X)=k d_{a}(Q), d_{b}(X)=(1-k) d_{b}(P)$, and $d_{c}(X)=(1-$ $k) d_{c}(P)+k d_{c}(Q)$, and simple substitution yields $d_{a}(X)+d_{b}(X)=d_{c}(X)$. The converse follows easily. In particular, $O \in P Q$ if and only if $d_{a}(O)+$ $d_{b}(O)=d_{c}(O)$, i.e., $\cos \alpha+\cos \beta=\cos \gamma$. We shall now show that $I \in D E$ if and only if $A E+B D=D E$. Let $K$ be the point on the segment $D E$ such that $A E=E K$. Then $\angle E K A=$ $\frac{1}{2} \angle D E C=\frac{1}{2} \angle C B A=\angle I B A$; hence the points $A, B, I, K$ are concyclic. The point $I$ lies on $D E$ if and only if $\angle B K D=\angle B A I=\frac{1}{2} \angle B A C=$ $\frac{1}{2} \angle C D E=\angle D B K$, which is equivalent to $K D=B D$, i.e., to $A E+B D=$ $D E$. But since $A E=A B \cos \alpha, B D=A B \cos \beta$, and $D E=A B \cos \gamma$, we have that $I \in D E \Leftrightarrow \cos \alpha+\cos \beta=\cos \gamma$. The conditions for $O \in P Q$ and $I \in D E$ are thus equivalent. Second solution. We know that three points $X, Y, Z$ are collinear if and only if for some $\lambda, \mu \in \mathbb{R}$ with sum 1 , we have $\lambda \overrightarrow{C X}+\mu \overrightarrow{C Y}=\overrightarrow{C Z}$. Specially, if $\overrightarrow{C X}=p \overrightarrow{C A}$ and $\overrightarrow{C Y}=q \overrightarrow{C B}$ for some $p, q$, and $\overrightarrow{C Z}=k \overrightarrow{C A}+$ $l \overrightarrow{C B}$, then $Z$ lies on $X Y$ if and only if $k q+l p=p q$. Using known relations in a triangle we directly obtain $$ \begin{array}{rlrl} \overrightarrow{C P} & =\frac{\sin \beta}{\sin \beta+\sin \gamma} \overrightarrow{C B}, & \overrightarrow{C Q}=\frac{\sin \alpha}{\sin \alpha+\sin \gamma} \overrightarrow{C A} \\ \overrightarrow{C O} & =\frac{\sin 2 \alpha \cdot \overrightarrow{C A}+\sin 2 \beta \cdot \overrightarrow{C B}}{\sin 2 \alpha+\sin 2 \beta+\sin 2 \gamma} ; & \overrightarrow{C D}=\frac{\tan \beta}{\tan \beta+\tan \gamma} \overrightarrow{C B} \\ \overrightarrow{C E} & =\frac{\tan \beta}{\tan \beta+\tan \gamma} \overrightarrow{C A}, & \overrightarrow{C I} & =\frac{\sin \alpha \cdot \overrightarrow{C A}+\sin \beta \cdot \overrightarrow{C B}}{\sin \alpha+\sin \beta+\sin \gamma} \end{array} $$ Now by the above considerations we get that the conditions (1) $P, Q, O$ are collinear and (2) $D, E, I$ are collinear are both equivalent to $\cos \alpha+\cos \beta=$ $\cos \gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
16. (BLR) In an acute-angled triangle $A B C$, let $A D, B E$ be altitudes and $A P, B Q$ internal bisectors. Denote by $I$ and $O$ the incenter and the circumcenter of the triangle, respectively. Prove that the points $D, E$, and $I$ are collinear if and only if the points $P, Q$, and $O$ are collinear.
|
16. Let $d_{a}(X), d_{b}(X), d_{c}(X)$ denote the distances of a point $X$ interior to $\triangle A B C$ from the lines $B C, C A, A B$ respectively. We claim that $X \in P Q$ if and only if $d_{a}(X)+d_{b}(X)=d_{c}(X)$. Indeed, if $X \in P Q$ and $P X=$ $k P Q$ then $d_{a}(X)=k d_{a}(Q), d_{b}(X)=(1-k) d_{b}(P)$, and $d_{c}(X)=(1-$ $k) d_{c}(P)+k d_{c}(Q)$, and simple substitution yields $d_{a}(X)+d_{b}(X)=d_{c}(X)$. The converse follows easily. In particular, $O \in P Q$ if and only if $d_{a}(O)+$ $d_{b}(O)=d_{c}(O)$, i.e., $\cos \alpha+\cos \beta=\cos \gamma$. We shall now show that $I \in D E$ if and only if $A E+B D=D E$. Let $K$ be the point on the segment $D E$ such that $A E=E K$. Then $\angle E K A=$ $\frac{1}{2} \angle D E C=\frac{1}{2} \angle C B A=\angle I B A$; hence the points $A, B, I, K$ are concyclic. The point $I$ lies on $D E$ if and only if $\angle B K D=\angle B A I=\frac{1}{2} \angle B A C=$ $\frac{1}{2} \angle C D E=\angle D B K$, which is equivalent to $K D=B D$, i.e., to $A E+B D=$ $D E$. But since $A E=A B \cos \alpha, B D=A B \cos \beta$, and $D E=A B \cos \gamma$, we have that $I \in D E \Leftrightarrow \cos \alpha+\cos \beta=\cos \gamma$. The conditions for $O \in P Q$ and $I \in D E$ are thus equivalent. Second solution. We know that three points $X, Y, Z$ are collinear if and only if for some $\lambda, \mu \in \mathbb{R}$ with sum 1 , we have $\lambda \overrightarrow{C X}+\mu \overrightarrow{C Y}=\overrightarrow{C Z}$. Specially, if $\overrightarrow{C X}=p \overrightarrow{C A}$ and $\overrightarrow{C Y}=q \overrightarrow{C B}$ for some $p, q$, and $\overrightarrow{C Z}=k \overrightarrow{C A}+$ $l \overrightarrow{C B}$, then $Z$ lies on $X Y$ if and only if $k q+l p=p q$. Using known relations in a triangle we directly obtain $$ \begin{array}{rlrl} \overrightarrow{C P} & =\frac{\sin \beta}{\sin \beta+\sin \gamma} \overrightarrow{C B}, & \overrightarrow{C Q}=\frac{\sin \alpha}{\sin \alpha+\sin \gamma} \overrightarrow{C A} \\ \overrightarrow{C O} & =\frac{\sin 2 \alpha \cdot \overrightarrow{C A}+\sin 2 \beta \cdot \overrightarrow{C B}}{\sin 2 \alpha+\sin 2 \beta+\sin 2 \gamma} ; & \overrightarrow{C D}=\frac{\tan \beta}{\tan \beta+\tan \gamma} \overrightarrow{C B} \\ \overrightarrow{C E} & =\frac{\tan \beta}{\tan \beta+\tan \gamma} \overrightarrow{C A}, & \overrightarrow{C I} & =\frac{\sin \alpha \cdot \overrightarrow{C A}+\sin \beta \cdot \overrightarrow{C B}}{\sin \alpha+\sin \beta+\sin \gamma} \end{array} $$ Now by the above considerations we get that the conditions (1) $P, Q, O$ are collinear and (2) $D, E, I$ are collinear are both equivalent to $\cos \alpha+\cos \beta=$ $\cos \gamma$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ec471414-e14c-5d19-b97d-f4c6d7751d83
| 24,760
|
18. (GBR) The altitudes through the vertices $A, B, C$ of an acute-angled triangle $A B C$ meet the opposite sides at $D, E, F$, respectively. The line through $D$ parallel to $E F$ meets the lines $A C$ and $A B$ at $Q$ and $R$, respectively. The line $E F$ meets $B C$ at $P$. Prove that the circumcircle of the triangle $P Q R$ passes through the midpoint of $B C$.
|
18. By symmetry, assume that $A B>A C$. The point $D$ lies between $M$ and $P$ as well as between $Q$ and $R$, and if we show that $D M \cdot D P=D Q \cdot D R$, it will imply that $M, P, Q, R$ lie on a circle. Since the triangles $A B C, A E F, A Q R$ are similar, the points $B, C, Q, R$ lie on a circle. Hence $D B \cdot D C=D Q \cdot D R$, and it remains to prove that $$ D B \cdot D C=D M \cdot D P $$ However, the points $B, C, E, F$ are concyclic, but so are the points $E, F, D, M$ (they lie on the nine-point circle), and we obtain $P B \cdot P C=$ $P E \cdot P F=P D \cdot P M$. Set $P B=x$ and $P C=y$. We have $P M=\frac{x+y}{2}$ and hence $P D=\frac{2 x y}{x+y}$. It follows that $D B=P B-P D=\frac{x(x-y)}{x+y}$, $D C=\frac{y(x-y)}{x+y}$, and $D M=\frac{(x-y)^{2}}{2(x+y)}$, from which we immediately obtain $D B \cdot D C=D M \cdot D P=\frac{x y(x-y)^{2}}{(x+y)^{2}}$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
18. (GBR) The altitudes through the vertices $A, B, C$ of an acute-angled triangle $A B C$ meet the opposite sides at $D, E, F$, respectively. The line through $D$ parallel to $E F$ meets the lines $A C$ and $A B$ at $Q$ and $R$, respectively. The line $E F$ meets $B C$ at $P$. Prove that the circumcircle of the triangle $P Q R$ passes through the midpoint of $B C$.
|
18. By symmetry, assume that $A B>A C$. The point $D$ lies between $M$ and $P$ as well as between $Q$ and $R$, and if we show that $D M \cdot D P=D Q \cdot D R$, it will imply that $M, P, Q, R$ lie on a circle. Since the triangles $A B C, A E F, A Q R$ are similar, the points $B, C, Q, R$ lie on a circle. Hence $D B \cdot D C=D Q \cdot D R$, and it remains to prove that $$ D B \cdot D C=D M \cdot D P $$ However, the points $B, C, E, F$ are concyclic, but so are the points $E, F, D, M$ (they lie on the nine-point circle), and we obtain $P B \cdot P C=$ $P E \cdot P F=P D \cdot P M$. Set $P B=x$ and $P C=y$. We have $P M=\frac{x+y}{2}$ and hence $P D=\frac{2 x y}{x+y}$. It follows that $D B=P B-P D=\frac{x(x-y)}{x+y}$, $D C=\frac{y(x-y)}{x+y}$, and $D M=\frac{(x-y)^{2}}{2(x+y)}$, from which we immediately obtain $D B \cdot D C=D M \cdot D P=\frac{x y(x-y)^{2}}{(x+y)^{2}}$, as needed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f12624d2-84f6-56ca-ac9f-35b35b4cc1fc
| 24,765
|
19. (IRE) Let $a_{1} \geq \cdots \geq a_{n} \geq a_{n+1}=0$ be a sequence of real numbers. Prove that $$ \sqrt{\sum_{k=1}^{n} a_{k}} \leq \sum_{k=1}^{n} \sqrt{k}\left(\sqrt{a_{k}}-\sqrt{a_{k+1}}\right) $$
|
19. Using that $a_{n+1}=0$ we can transform the desired inequality into $$ \begin{aligned} & \sqrt{a_{1}+}+a_{2}+\cdots+a_{n+1} \\ & \quad \leq \sqrt{1} \sqrt{a_{1}}+(\sqrt{2}-\sqrt{1}) \sqrt{a_{2}}+\cdots+(\sqrt{n+1}-\sqrt{n}) \sqrt{a_{n+1}} \end{aligned} $$ We shall prove by induction on $n$ that (1) holds for any $a_{1} \geq a_{2} \geq \cdots \geq$ $a_{n+1} \geq 0$, i.e., not only when $a_{n+1}=0$. For $n=0$ the inequality is obvious. For the inductive step from $n-1$ to $n$, where $n \geq 1$, we need to prove the inequality $$ \sqrt{a_{1}+\cdots+a_{n+1}}-\sqrt{a_{1}+\cdots+a_{n}} \leq(\sqrt{n+1}-\sqrt{n}) \sqrt{a_{n+1}} $$ Putting $S=a_{1}+a_{2}+\cdots+a_{n}$, this simplifies to $\sqrt{S+a_{n+1}}-\sqrt{S} \leq$ $\sqrt{n a_{n+1}+a_{n+1}}-\sqrt{n a_{n+1}}$. For $a_{n+1}=0$ the inequality is obvious. For $a_{n+1}>0$ we have that the function $f(x)=\sqrt{x+a_{n+1}}-\sqrt{x}=$ $\frac{a_{n+1}}{\sqrt{x+a_{n+1}}+\sqrt{x}}$ is strictly decreasing on $\mathbb{R}^{+}$; hence (2) will follow if we show that $S \geq n a_{n+1}$. However, this last is true because $a_{1}, \ldots, a_{n} \geq a_{n+1}$. Equality holds if and only if $a_{1}=a_{2}=\cdots=a_{k}$ and $a_{k+1}=\cdots=a_{n+1}=$ 0 for some $k$. Second solution. Setting $b_{k}=\sqrt{a_{k}}-\sqrt{a_{k+1}}$ for $k=1, \ldots, n$ we have $a_{i}=\left(b_{i}+\cdots+b_{n}\right)^{2}$, so the desired inequality after squaring becomes $$ \sum_{k=1}^{n} k b_{k}^{2}+2 \sum_{1 \leq k<l \leq n} k b_{k} b_{l} \leq \sum_{k=1}^{n} k b_{k}^{2}+2 \sum_{1 \leq k<l \leq n} \sqrt{k l} b_{k} b_{l}, $$ which clearly holds.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
19. (IRE) Let $a_{1} \geq \cdots \geq a_{n} \geq a_{n+1}=0$ be a sequence of real numbers. Prove that $$ \sqrt{\sum_{k=1}^{n} a_{k}} \leq \sum_{k=1}^{n} \sqrt{k}\left(\sqrt{a_{k}}-\sqrt{a_{k+1}}\right) $$
|
19. Using that $a_{n+1}=0$ we can transform the desired inequality into $$ \begin{aligned} & \sqrt{a_{1}+}+a_{2}+\cdots+a_{n+1} \\ & \quad \leq \sqrt{1} \sqrt{a_{1}}+(\sqrt{2}-\sqrt{1}) \sqrt{a_{2}}+\cdots+(\sqrt{n+1}-\sqrt{n}) \sqrt{a_{n+1}} \end{aligned} $$ We shall prove by induction on $n$ that (1) holds for any $a_{1} \geq a_{2} \geq \cdots \geq$ $a_{n+1} \geq 0$, i.e., not only when $a_{n+1}=0$. For $n=0$ the inequality is obvious. For the inductive step from $n-1$ to $n$, where $n \geq 1$, we need to prove the inequality $$ \sqrt{a_{1}+\cdots+a_{n+1}}-\sqrt{a_{1}+\cdots+a_{n}} \leq(\sqrt{n+1}-\sqrt{n}) \sqrt{a_{n+1}} $$ Putting $S=a_{1}+a_{2}+\cdots+a_{n}$, this simplifies to $\sqrt{S+a_{n+1}}-\sqrt{S} \leq$ $\sqrt{n a_{n+1}+a_{n+1}}-\sqrt{n a_{n+1}}$. For $a_{n+1}=0$ the inequality is obvious. For $a_{n+1}>0$ we have that the function $f(x)=\sqrt{x+a_{n+1}}-\sqrt{x}=$ $\frac{a_{n+1}}{\sqrt{x+a_{n+1}}+\sqrt{x}}$ is strictly decreasing on $\mathbb{R}^{+}$; hence (2) will follow if we show that $S \geq n a_{n+1}$. However, this last is true because $a_{1}, \ldots, a_{n} \geq a_{n+1}$. Equality holds if and only if $a_{1}=a_{2}=\cdots=a_{k}$ and $a_{k+1}=\cdots=a_{n+1}=$ 0 for some $k$. Second solution. Setting $b_{k}=\sqrt{a_{k}}-\sqrt{a_{k+1}}$ for $k=1, \ldots, n$ we have $a_{i}=\left(b_{i}+\cdots+b_{n}\right)^{2}$, so the desired inequality after squaring becomes $$ \sum_{k=1}^{n} k b_{k}^{2}+2 \sum_{1 \leq k<l \leq n} k b_{k} b_{l} \leq \sum_{k=1}^{n} k b_{k}^{2}+2 \sum_{1 \leq k<l \leq n} \sqrt{k l} b_{k} b_{l}, $$ which clearly holds.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6f557291-8915-541d-a1d8-4cd2024559bb
| 24,768
|
2. (CAN) Let $R_{1}, R_{2}, \ldots$ be the family of finite sequences of positive integers defined by the following rules: $R_{1}=(1)$, and if $R_{n-1}=\left(x_{1}, \ldots, x_{s}\right)$, then $$ R_{n}=\left(1,2, \ldots, x_{1}, 1,2, \ldots, x_{2}, \ldots, 1,2, \ldots, x_{s}, n\right) $$ For example, $R_{2}=(1,2), R_{3}=(1,1,2,3), R_{4}=(1,1,1,2,1,2,3,4)$. Prove that if $n>1$, then the $k$ th term from the left in $R_{n}$ is equal to 1 if and only if the $k$ th term from the right in $R_{n}$ is different from 1.
|
2. For any sequence $X=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ let us define $$ \bar{X}=\left(1,2, \ldots, x_{1}, 1,2, \ldots, x_{2}, \ldots, 1,2, \ldots, x_{n}\right) $$ Also, for any two sequences $A, B$ we denote their concatenation by $A B$. It clearly holds that $\overline{A B}=\bar{A} \bar{B}$. The sequences $R_{1}, R_{2}, \ldots$ are given by $R_{1}=(1)$ and $R_{n}=\overline{R_{n-1}}(n)$ for $n>1$. We consider the family of sequences $Q_{n i}$ for $n, i \in \mathbb{N}, i \leq n$, defined as follows: $Q_{n 1}=(1), \quad Q_{n n}=(n), \quad$ and $\quad Q_{n i}=Q_{n-1, i-1} Q_{n-1, i} \quad$ if $1<i<n$. These sequences form a Pascal-like triangle, as shown in the picture below: | $Q_{1 i}:$ | | 1 | | | | | | | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | $Q_{2 i}$ : | | | | 1 | | 2 | | | | $Q_{3 i}$ : | | | 1 | | 12 | | 3 | | | $Q_{4 i}$ : | | 1 | | 112 | | 123 | | 4 | | $Q_{5 i}$ : | 1 | | 1112 | | 2123 | | 1234 | | We claim that $R_{n}$ is in fact exactly $Q_{n 1} Q_{n 2} \ldots Q_{n n}$. Before proving this, we observe that $Q_{n i}=\overline{Q_{n-1, i}}$. This follows by induction, because $Q_{n i}=$ $Q_{n-1, i-1} Q_{n-1, i}=\overline{Q_{n-2, i-1}} \overline{Q_{n-2, i}}=\overline{Q_{n-1, i}}$ for $n \geq 3, i \geq 2$ (the cases $i=1$ and $n=1,2$ are trivial). Now $R_{1}=Q_{11}$ and $$ R_{n}=\overline{R_{n-1}}(n)=\overline{Q_{n-1,1} \ldots Q_{n-1, n-1}}(n)=Q_{n, 1} \ldots Q_{n, n-1} Q_{n, n} $$ for $n \geq 2$, which justifies our claim by induction. Now we know enough about the sequence $R_{n}$ to return to the question of the problem. We use induction on $n$ once again. The result is obvious for $n=1$ and $n=2$. Given any $n \geq 3$, consider the $k$ th elements of $R_{n}$ from the left, say $u$, and from the right, say $v$. Assume that $u$ is a member of $Q_{n j}$, and consequently that $v$ is a member of $Q_{n, n+1-j}$. Then $u$ and $v$ come from symmetric positions of $R_{n-1}$ (either from $Q_{n-1, j}, Q_{n-1, n-j}$, or from $\left.Q_{n-1, j-1}, Q_{n-1, n+1-j}\right)$, and by the inductive hypothesis exactly one of them is 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
2. (CAN) Let $R_{1}, R_{2}, \ldots$ be the family of finite sequences of positive integers defined by the following rules: $R_{1}=(1)$, and if $R_{n-1}=\left(x_{1}, \ldots, x_{s}\right)$, then $$ R_{n}=\left(1,2, \ldots, x_{1}, 1,2, \ldots, x_{2}, \ldots, 1,2, \ldots, x_{s}, n\right) $$ For example, $R_{2}=(1,2), R_{3}=(1,1,2,3), R_{4}=(1,1,1,2,1,2,3,4)$. Prove that if $n>1$, then the $k$ th term from the left in $R_{n}$ is equal to 1 if and only if the $k$ th term from the right in $R_{n}$ is different from 1.
|
2. For any sequence $X=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ let us define $$ \bar{X}=\left(1,2, \ldots, x_{1}, 1,2, \ldots, x_{2}, \ldots, 1,2, \ldots, x_{n}\right) $$ Also, for any two sequences $A, B$ we denote their concatenation by $A B$. It clearly holds that $\overline{A B}=\bar{A} \bar{B}$. The sequences $R_{1}, R_{2}, \ldots$ are given by $R_{1}=(1)$ and $R_{n}=\overline{R_{n-1}}(n)$ for $n>1$. We consider the family of sequences $Q_{n i}$ for $n, i \in \mathbb{N}, i \leq n$, defined as follows: $Q_{n 1}=(1), \quad Q_{n n}=(n), \quad$ and $\quad Q_{n i}=Q_{n-1, i-1} Q_{n-1, i} \quad$ if $1<i<n$. These sequences form a Pascal-like triangle, as shown in the picture below: | $Q_{1 i}:$ | | 1 | | | | | | | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | $Q_{2 i}$ : | | | | 1 | | 2 | | | | $Q_{3 i}$ : | | | 1 | | 12 | | 3 | | | $Q_{4 i}$ : | | 1 | | 112 | | 123 | | 4 | | $Q_{5 i}$ : | 1 | | 1112 | | 2123 | | 1234 | | We claim that $R_{n}$ is in fact exactly $Q_{n 1} Q_{n 2} \ldots Q_{n n}$. Before proving this, we observe that $Q_{n i}=\overline{Q_{n-1, i}}$. This follows by induction, because $Q_{n i}=$ $Q_{n-1, i-1} Q_{n-1, i}=\overline{Q_{n-2, i-1}} \overline{Q_{n-2, i}}=\overline{Q_{n-1, i}}$ for $n \geq 3, i \geq 2$ (the cases $i=1$ and $n=1,2$ are trivial). Now $R_{1}=Q_{11}$ and $$ R_{n}=\overline{R_{n-1}}(n)=\overline{Q_{n-1,1} \ldots Q_{n-1, n-1}}(n)=Q_{n, 1} \ldots Q_{n, n-1} Q_{n, n} $$ for $n \geq 2$, which justifies our claim by induction. Now we know enough about the sequence $R_{n}$ to return to the question of the problem. We use induction on $n$ once again. The result is obvious for $n=1$ and $n=2$. Given any $n \geq 3$, consider the $k$ th elements of $R_{n}$ from the left, say $u$, and from the right, say $v$. Assume that $u$ is a member of $Q_{n j}$, and consequently that $v$ is a member of $Q_{n, n+1-j}$. Then $u$ and $v$ come from symmetric positions of $R_{n-1}$ (either from $Q_{n-1, j}, Q_{n-1, n-j}$, or from $\left.Q_{n-1, j-1}, Q_{n-1, n+1-j}\right)$, and by the inductive hypothesis exactly one of them is 1 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
172ac2b7-f771-54a7-b47e-95f52d3c9ebc
| 24,771
|
20. (IRE) Let $D$ be an internal point on the side $B C$ of a triangle $A B C$. The line $A D$ meets the circumcircle of $A B C$ again at $X$. Let $P$ and $Q$ be the feet of the perpendiculars from $X$ to $A B$ and $A C$, respectively, and let $\gamma$ be the circle with diameter $X D$. Prove that the line $P Q$ is tangent to $\gamma$ if and only if $A B=A C$.
|
20. To avoid dividing into cases regarding the position of the point $X$, we use oriented angles. Let $R$ be the foot of the perpendicular from $X$ to $B C$. It is well known that the points $P, Q, R$ lie on the corresponding Simson line. This line is a tangent to $\gamma$ (i.e., the circle $X D R$ ) if and only if $\angle P R D=\angle R X D$. We have $$ \begin{aligned} \angle P R D & =\angle P X B=90^{\circ}-\angle X B A=90^{\circ}-\angle X B C+\angle A B C \\ & =90^{\circ}-\angle D A C+\angle A B C \end{aligned} $$ and $$ \angle R X D=90^{\circ}-\angle A D B=90^{\circ}+\angle B C A-\angle D A C $$ hence $\angle P R D=\angle R X D$ if and only if $\angle A B C=\angle B C A$, i.e, $A B=A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
20. (IRE) Let $D$ be an internal point on the side $B C$ of a triangle $A B C$. The line $A D$ meets the circumcircle of $A B C$ again at $X$. Let $P$ and $Q$ be the feet of the perpendiculars from $X$ to $A B$ and $A C$, respectively, and let $\gamma$ be the circle with diameter $X D$. Prove that the line $P Q$ is tangent to $\gamma$ if and only if $A B=A C$.
|
20. To avoid dividing into cases regarding the position of the point $X$, we use oriented angles. Let $R$ be the foot of the perpendicular from $X$ to $B C$. It is well known that the points $P, Q, R$ lie on the corresponding Simson line. This line is a tangent to $\gamma$ (i.e., the circle $X D R$ ) if and only if $\angle P R D=\angle R X D$. We have $$ \begin{aligned} \angle P R D & =\angle P X B=90^{\circ}-\angle X B A=90^{\circ}-\angle X B C+\angle A B C \\ & =90^{\circ}-\angle D A C+\angle A B C \end{aligned} $$ and $$ \angle R X D=90^{\circ}-\angle A D B=90^{\circ}+\angle B C A-\angle D A C $$ hence $\angle P R D=\angle R X D$ if and only if $\angle A B C=\angle B C A$, i.e, $A B=A C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4a7cc4f7-6543-5ea8-b800-7ac88d3a67fd
| 24,774
|
21. (RUS) ${ }^{\mathrm{IMO} 3}$ Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying the conditions $$ \left|x_{1}+x_{2}+\cdots+x_{n}\right|=1 \quad \text { and } \quad\left|x_{i}\right| \leq \frac{n+1}{2} \quad \text { for } \quad i=1,2, \ldots, n $$ Show that there exists a permutation $y_{1}, \ldots, y_{n}$ of the sequence $x_{1}, \ldots, x_{n}$ such that $$ \left|y_{1}+2 y_{2}+\cdots+n y_{n}\right| \leq \frac{n+1}{2} $$
|
21. For any permutation $\pi=\left(y_{1}, y_{2}, \ldots, y_{n}\right)$ of $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$, denote by $S(\pi)$ the sum $y_{1}+2 y_{2}+\cdots+n y_{n}$. Suppose, contrary to the claim, that $|S(\pi)|>\frac{n+1}{2}$ for any $\pi$. Further, we note that if $\pi^{\prime}$ is obtained from $\pi$ by interchanging two neighboring elements, say $y_{k}$ and $y_{k+1}$, then $S(\pi)$ and $S\left(\pi^{\prime}\right)$ differ by $\left|y_{k}+y_{k+1}\right| \leq n+1$, and consequently they must be of the same sign. Now consider the identity permutation $\pi_{0}=\left(x_{1}, \ldots, x_{n}\right)$ and the reverse permutation $\overline{\pi_{0}}=\left(x_{n}, \ldots, x_{1}\right)$. There is a sequence of permutations $\pi_{0}, \pi_{1}, \ldots, \pi_{m}=\overline{\pi_{0}}$ such that for each $i, \pi_{i+1}$ is obtained from $\pi_{i}$ by interchanging two neighboring elements. Indeed, by successive interchanges we can put $x_{n}$ in the first place, then $x_{n-1}$ in the second place, etc. Hence all $S\left(\pi_{0}\right), \ldots, S\left(\pi_{m}\right)$ are of the same sign. However, since $\left|S\left(\pi_{0}\right)+S\left(\pi_{m}\right)\right|=(n+1)\left|x_{1}+\cdots+x_{n}\right|=n+1$, this implies that one of $S\left(\pi_{0}\right)$ and $S\left(\overline{\pi_{0}}\right)$ is smaller than $\frac{n+1}{2}$ in absolute value, contradicting the initial assumption.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
21. (RUS) ${ }^{\mathrm{IMO} 3}$ Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying the conditions $$ \left|x_{1}+x_{2}+\cdots+x_{n}\right|=1 \quad \text { and } \quad\left|x_{i}\right| \leq \frac{n+1}{2} \quad \text { for } \quad i=1,2, \ldots, n $$ Show that there exists a permutation $y_{1}, \ldots, y_{n}$ of the sequence $x_{1}, \ldots, x_{n}$ such that $$ \left|y_{1}+2 y_{2}+\cdots+n y_{n}\right| \leq \frac{n+1}{2} $$
|
21. For any permutation $\pi=\left(y_{1}, y_{2}, \ldots, y_{n}\right)$ of $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$, denote by $S(\pi)$ the sum $y_{1}+2 y_{2}+\cdots+n y_{n}$. Suppose, contrary to the claim, that $|S(\pi)|>\frac{n+1}{2}$ for any $\pi$. Further, we note that if $\pi^{\prime}$ is obtained from $\pi$ by interchanging two neighboring elements, say $y_{k}$ and $y_{k+1}$, then $S(\pi)$ and $S\left(\pi^{\prime}\right)$ differ by $\left|y_{k}+y_{k+1}\right| \leq n+1$, and consequently they must be of the same sign. Now consider the identity permutation $\pi_{0}=\left(x_{1}, \ldots, x_{n}\right)$ and the reverse permutation $\overline{\pi_{0}}=\left(x_{n}, \ldots, x_{1}\right)$. There is a sequence of permutations $\pi_{0}, \pi_{1}, \ldots, \pi_{m}=\overline{\pi_{0}}$ such that for each $i, \pi_{i+1}$ is obtained from $\pi_{i}$ by interchanging two neighboring elements. Indeed, by successive interchanges we can put $x_{n}$ in the first place, then $x_{n-1}$ in the second place, etc. Hence all $S\left(\pi_{0}\right), \ldots, S\left(\pi_{m}\right)$ are of the same sign. However, since $\left|S\left(\pi_{0}\right)+S\left(\pi_{m}\right)\right|=(n+1)\left|x_{1}+\cdots+x_{n}\right|=n+1$, this implies that one of $S\left(\pi_{0}\right)$ and $S\left(\overline{\pi_{0}}\right)$ is smaller than $\frac{n+1}{2}$ in absolute value, contradicting the initial assumption.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
87b66c6f-518d-5275-8cdb-2e237a258b9e
| 24,777
|
22. (UKR) (a) Do there exist functions $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ f(g(x))=x^{2} \quad \text { and } \quad g(f(x))=x^{3} \quad \text { for all } x \in \mathbb{R} ? $$ (b) Do there exist functions $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ f(g(x))=x^{2} \quad \text { and } \quad g(f(x))=x^{4} \quad \text { for all } x \in \mathbb{R} ? $$
|
22. (a) Suppose that $f$ and $g$ are such functions. From $g(f(x))=x^{3}$ we have $f\left(x_{1}\right) \neq f\left(x_{2}\right)$ whenever $x_{1} \neq x_{2}$. In particular, $f(-1), f(0)$, and $f(1)$ are three distinct numbers. However, since $f(x)^{2}=f(g(f(x)))=$ $f\left(x^{3}\right)$, each of the numbers $f(-1), f(0), f(1)$ is equal to its square, and so must be either 0 or 1 . This contradiction shows that no such $f, g$ exist. (b) The answer is yes. We begin with constructing functions $F, G:(1, \infty)$ $\rightarrow(1, \infty)$ with the property $F(G(x))=x^{2}$ and $G(F(x))=x^{4}$ for $x>$ 1. Define the functions $\varphi, \psi$ by $F\left(2^{2^{t}}\right)=2^{2^{\varphi(t)}}$ and $G\left(2^{2^{t}}\right)=2^{2^{\psi(t)}}$. These functions determine $F$ and $G$ on the entire interval $(1, \infty)$, and satisfy $\varphi(\psi(t))=t+1$ and $\psi(\varphi(t))=t+2$. It is easy to find examples of $\varphi$ and $\psi$ : for example, $\varphi(t)=\frac{1}{2} t+1, \psi(t)=2 t$. Thus we also arrive at an example for $F, G$ : $$ F(x)=2^{2^{\frac{1}{2} \log _{2} \log _{2} x+1}}=2^{2 \sqrt{\log _{2} x}}, \quad G(x)=2^{2^{2 \log _{2} \log _{2} x}}=2^{\log _{2}^{2} x} $$ It remains only to extend these functions to the whole of $\mathbb{R}$. This can be done as follows: $$ \widetilde{f}(x)= \begin{cases}F(x) & \text { for } x>1 \\ 1 / F(1 / x) & \text { for } 0<x<1, \widetilde{g}(x)=\left\{\begin{array} { c l } { G ( x ) } & { \text { for } x > 1 } \\ { x } & { \text { for } x \in \{ 0 , 1 \} ; } \end{array} \left\{\begin{array}{cl} 1 / G(1 / x) & \text { for } 0<x<1 \\ x & \text { for } x \in\{0,1\} \end{array}\right.\right.\end{cases} $$ and then $\quad f(x)=\widetilde{f}(|x|), \quad g(x)=\widetilde{g}(|x|) \quad$ for $x \in \mathbb{R}$. It is directly verified that these functions have the required property.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
22. (UKR) (a) Do there exist functions $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ f(g(x))=x^{2} \quad \text { and } \quad g(f(x))=x^{3} \quad \text { for all } x \in \mathbb{R} ? $$ (b) Do there exist functions $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ f(g(x))=x^{2} \quad \text { and } \quad g(f(x))=x^{4} \quad \text { for all } x \in \mathbb{R} ? $$
|
22. (a) Suppose that $f$ and $g$ are such functions. From $g(f(x))=x^{3}$ we have $f\left(x_{1}\right) \neq f\left(x_{2}\right)$ whenever $x_{1} \neq x_{2}$. In particular, $f(-1), f(0)$, and $f(1)$ are three distinct numbers. However, since $f(x)^{2}=f(g(f(x)))=$ $f\left(x^{3}\right)$, each of the numbers $f(-1), f(0), f(1)$ is equal to its square, and so must be either 0 or 1 . This contradiction shows that no such $f, g$ exist. (b) The answer is yes. We begin with constructing functions $F, G:(1, \infty)$ $\rightarrow(1, \infty)$ with the property $F(G(x))=x^{2}$ and $G(F(x))=x^{4}$ for $x>$ 1. Define the functions $\varphi, \psi$ by $F\left(2^{2^{t}}\right)=2^{2^{\varphi(t)}}$ and $G\left(2^{2^{t}}\right)=2^{2^{\psi(t)}}$. These functions determine $F$ and $G$ on the entire interval $(1, \infty)$, and satisfy $\varphi(\psi(t))=t+1$ and $\psi(\varphi(t))=t+2$. It is easy to find examples of $\varphi$ and $\psi$ : for example, $\varphi(t)=\frac{1}{2} t+1, \psi(t)=2 t$. Thus we also arrive at an example for $F, G$ : $$ F(x)=2^{2^{\frac{1}{2} \log _{2} \log _{2} x+1}}=2^{2 \sqrt{\log _{2} x}}, \quad G(x)=2^{2^{2 \log _{2} \log _{2} x}}=2^{\log _{2}^{2} x} $$ It remains only to extend these functions to the whole of $\mathbb{R}$. This can be done as follows: $$ \widetilde{f}(x)= \begin{cases}F(x) & \text { for } x>1 \\ 1 / F(1 / x) & \text { for } 0<x<1, \widetilde{g}(x)=\left\{\begin{array} { c l } { G ( x ) } & { \text { for } x > 1 } \\ { x } & { \text { for } x \in \{ 0 , 1 \} ; } \end{array} \left\{\begin{array}{cl} 1 / G(1 / x) & \text { for } 0<x<1 \\ x & \text { for } x \in\{0,1\} \end{array}\right.\right.\end{cases} $$ and then $\quad f(x)=\widetilde{f}(|x|), \quad g(x)=\widetilde{g}(|x|) \quad$ for $x \in \mathbb{R}$. It is directly verified that these functions have the required property.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d75be264-71d8-54ea-8df4-b42d1ee61f7b
| 24,780
|
23. (GBR) Let $A B C D$ be a convex quadrilateral and $O$ the intersection of its diagonals $A C$ and $B D$. If $$ O A \sin \angle A+O C \sin \angle C=O B \sin \angle B+O D \sin \angle D, $$ prove that $A B C D$ is cyclic.
|
23. Let $K, L, M$, and $N$ be the projections of $O$ onto the lines $A B, B C, C D$, and $D A$, and let $\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}, \beta_{1}, \beta_{2}, \beta_{3}, \beta_{4}$ denote the angles $O A B$, $O B C, O C D, O D A, O A D, O B A, O C B, O D C$, respectively. We start with the following observation: Since $N K$ is a chord of the circle with diameter $O A$, we have $O A \sin \angle A=N K=O N \cos \alpha_{1}+O K \cos \beta_{1}$ (because $\angle O N K=\alpha_{1}$ and $\angle O K N=\beta_{1}$ ). Analogous equalities also hold: $O B \sin \angle B=K L=O K \cos \alpha_{2}+O L \cos \beta_{2}, O C \sin \angle C=L M=$ $O L \cos \alpha_{3}+O M \cos \beta_{3}$ and $O D \sin \angle D=M N=O M \cos \alpha_{4}+O N \cos \beta_{4}$. Now the condition in the problem can be restated as $N K+L M=K L+$ $M N$ (i.e., $K L M N$ is circumscribed), i.e., $$ \begin{aligned} O K\left(\cos \beta_{1}-\cos \alpha_{2}\right)+O L\left(\cos \alpha_{3}-\cos \beta_{2}\right) \\ +O M\left(\cos \beta_{3}-\cos \alpha_{4}\right)+O N\left(\cos \alpha_{1}-\cos \beta_{4}\right)=0 \end{aligned} $$ To prove that $A B C D$ is cyclic, it suffices to show that $\alpha_{1}=\beta_{4}$. Assume the contrary, and let w.l.o.g. $\alpha_{1}>\beta_{4}$. Then point $A$ lies inside the circle $B C D$, which is further equivalent to $\beta_{1}>\alpha_{2}$. On the other hand, from $\alpha_{1}+\beta_{2}=\alpha_{3}+\beta_{4}$ we deduce $\alpha_{3}>\beta_{2}$, and similarly $\beta_{3}>\alpha_{4}$. Therefore, since the cosine is strictly decreasing on $(0, \pi)$, the left side of (1) is strictly negative, yielding a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
23. (GBR) Let $A B C D$ be a convex quadrilateral and $O$ the intersection of its diagonals $A C$ and $B D$. If $$ O A \sin \angle A+O C \sin \angle C=O B \sin \angle B+O D \sin \angle D, $$ prove that $A B C D$ is cyclic.
|
23. Let $K, L, M$, and $N$ be the projections of $O$ onto the lines $A B, B C, C D$, and $D A$, and let $\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}, \beta_{1}, \beta_{2}, \beta_{3}, \beta_{4}$ denote the angles $O A B$, $O B C, O C D, O D A, O A D, O B A, O C B, O D C$, respectively. We start with the following observation: Since $N K$ is a chord of the circle with diameter $O A$, we have $O A \sin \angle A=N K=O N \cos \alpha_{1}+O K \cos \beta_{1}$ (because $\angle O N K=\alpha_{1}$ and $\angle O K N=\beta_{1}$ ). Analogous equalities also hold: $O B \sin \angle B=K L=O K \cos \alpha_{2}+O L \cos \beta_{2}, O C \sin \angle C=L M=$ $O L \cos \alpha_{3}+O M \cos \beta_{3}$ and $O D \sin \angle D=M N=O M \cos \alpha_{4}+O N \cos \beta_{4}$. Now the condition in the problem can be restated as $N K+L M=K L+$ $M N$ (i.e., $K L M N$ is circumscribed), i.e., $$ \begin{aligned} O K\left(\cos \beta_{1}-\cos \alpha_{2}\right)+O L\left(\cos \alpha_{3}-\cos \beta_{2}\right) \\ +O M\left(\cos \beta_{3}-\cos \alpha_{4}\right)+O N\left(\cos \alpha_{1}-\cos \beta_{4}\right)=0 \end{aligned} $$ To prove that $A B C D$ is cyclic, it suffices to show that $\alpha_{1}=\beta_{4}$. Assume the contrary, and let w.l.o.g. $\alpha_{1}>\beta_{4}$. Then point $A$ lies inside the circle $B C D$, which is further equivalent to $\beta_{1}>\alpha_{2}$. On the other hand, from $\alpha_{1}+\beta_{2}=\alpha_{3}+\beta_{4}$ we deduce $\alpha_{3}>\beta_{2}$, and similarly $\beta_{3}>\alpha_{4}$. Therefore, since the cosine is strictly decreasing on $(0, \pi)$, the left side of (1) is strictly negative, yielding a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
71d0b7c8-2f1d-5362-8966-021721700d6f
| 24,783
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.